ТРЕХМЕРНЫЕ ЗАДАЧИ
МАТЕМАТИЧЕСКОЙ
ТЕОРИИ УПРУГОСТИ
И ТЕРМОУПРУГОСТИ
КЛАССИЧЕСКАЯ
И МИКРОПОЛЯРНАЯ ТЕОРИЯ.
СТАТИКА, ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ,
ДИНАМИКА.
ОСНОВЫ И МЕТОДЫ РЕШЕНИЯ
ВТОРОЕ, ПЕРЕРАБОТАННОЕ
И ДОПОЛНЕННОЕ ИЗДАНИЕ
Под общей редакцией
В.Д.КУПРАДЗЕ
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1976

531
Т66
УДК 531
АВТОР Ы:
К У П Р А Д 3 Е В. Д., Г Е Г Е Л И А Т. Г.,
БАШЕЛЕЙШВИЛИ М. О., БУРЧУЛАДЗЕ Т. В.
Трехмерные задачи математической теории упруго-
упругости и термоупругости, монография, под общей редак-
редакцией В. Д. Купрадзе
Книга посвящена подробному анализу математиче-
математических основ теории упругости. На современном уровне
математической строгости впервые с одинаковой полнотой
рассмотрены трехмерные задачи статики, гармонических
колебаний и общей динамики линейной теории упругости,
термоупругости и моментной упругости. Методом много-
многомерных сингулярных интегральных уравнений и син-
сингулярных потенциалов, развитым в книге, исследованы
общие вопросы теории и получены представления решений
в рядах и квадратурах, допускающие эффективную реа-
реализацию на ЭВМ.
Рис. 2, библиография 540 назв.
®Главная редакция
.?_ _-	физико-математической литературы
@2W6 ^u-ZO	издательства «Наука», 1976
с изменениями и дополнениями

ОГЛАВЛЕНИЕ
Предисловие	 9
Глава I
ОСНОВНЫЕ ПОНЯТИЯ И АКСИОМАТИЗАЦИЯ
§ 1. Напряжения 	 11
1. Внутренние и внешние силы (И). 2. Массовые и поверхностные силы. Массовый мо-
момент A2). 3. Силовые и моментные напряжения A2).
§ 2. Комлоненты напряжений 	 14
1. Компоненты тензоров «силового и моментного напряжения A4). 2. Выражение вектора
силового напряжения через компоненты (тензора) силового * напряжения ;( 14). 3. Выраже-
Выражение вектора моментного напряжения через компоненты (тензора) моментного напряже-
напряжения A5).
§ 3. Смещения и вращения 	 15
1. Вектор смещения A5). 2. Вектор вращения A6).
§ 4. Основные уравнения в компонентах напряжения	 17
1. Уравнения движения в классической теории A7). 2. Уравнения движения в моментной
теории A9).
§ 5. Закон Гука в классической теории	 21
1. Компоненты (тензора) деформации B1). 2. Формулировка закона Гука B2). 3. Изо-
Изотропная среда B3). 4. Трансверсально-изотропная среда B4).
§ 6. Энергия деформации в классической теории	 25
1. Закон сохранения энергии B5). 2. Удельная энергия деформации B7).
§ 7. Энергия деформации и закон Гука в моментной теории	 29
1. Закон сохранения энергии B9). 2. Удельная энергия деформации C2). 3. Закон
Гука C3). 4. Изотропная среда (с центром симметрии) C3).
§ 8. Термоупругость. Закон Дюамеля—Неймана	 35
1. Деформация с изменением температуры C5). 2. Закон сохранения энергии C5).
3. Закон Дюамеля — Неймана C6). 4. Изотропная среда C7).
§ 9. Уравнение теплопроводности	 38
§ 10. Упругие стационарные колебания	 39
1. Классическая теория упругости C9). 2. Моментная теория упругости D0). 3. Тео-
Теория термоупругости D0).
§ 11. Аксиоматизация теории	 41
1. Классическая теория упругости D2). 2. Моментная теория упругости D4). 3. Тео-
Теория термоупругости D6).
§ 12. Матричная запись основных уравнений	 48
1. Классическая теория упругости D9). 2. Моментная теория упругости D9). 3. Тео-
Теория термоупругости E0).
§ 13. Оператор напряжения	 50
1. Классическая теория E1). 2. Моментная теория E1). 3. Термоупругость E2).
§ 14. Постановка основных задач	 53
1. Классическая теория E4). 2. Моментная теория E6). 3. Теория термоупругости
E7). 4. Задачи для неоднородных сред E8).
§ 15. Некоторые дополнения и библиографические справки	 59
1. О дифференциальных операторах теории упругости E9). 2. О некоторых простран-
пространствах функций и поверхностях класса Л, (а) F1). 3. Библиографические справки F4).
Глава II
ОСНОВНЫЕ СИНГУЛЯРНЫЕ РЕШЕНИЯ
§ 1. Фундаментальные решения уравнений классической теории упругости
1. Уравнение статики. Матрица Кельвина F5). 2. Уравнение колебания. Матрица Куп-
радзе(бб). 3. Основные свойства матрицы Купрадзе F8).
§ 2. Фундаментальные решения уравнений моментной теории упругости
1. Уравнение колебаний G0). 2. Уравнение статики G2).
1*
65
70

4	ОГЛАВЛЕНИЕ
§ 3. Фундаментальные решения уравнений термоупругости	'. . 73
1. Уравнение колебаний G3). 2. Союзное уравнение G5). 3. Уравнение статики G5).
§ 4. Сингулярные решения уравнений классической теории упругости ....... 75
1. Уравнение статики G5). 2. Уравнение колебаний G7).
§ 5. Сингулярные решения уравнений моментной теории упругости	 78
1. Уравнение колебаний G8). 2. Уравнение статики G9).
§ 6. Сингулярные решения уравнений термоупругости	 80
1. Уравнение колебаний (80). 2. Уравнение статики (82).
§ 7. Различные замечания и библиографические справки	 83
Задачи .	 84
Глава III
ТЕОРЕМЫ ЕДИНСТВЕННОСТИ
§ 1. Задачи статики в классической теории	 . 85
1. Формулы Грина (85). 2. Решение вспомогательного уравнения (87). 3. Основная
лемма (87). 4. Теоремы единственности (88). 5. Уравнение А (дх) и — рт2м = 0 (90).
6. Неоднородная среда (91).
§ 2. Задачи установившихся упругих колебаний	 91
I. Общее представление регулярйых в D+ решений (91). 2. Разложение регулярных ре-
решений (93). 3. Условие излучения в теории упругости (94). 4. Представление решения
уравнения колебаний в области D~~ (97). 5. Теоремы единственности для внешних задач
(99). 6. Теоремы единственности для "неоднородных сред A02)
§ 3. Задачи установившихся термоупругих колебаний	 103
1. Разложение регулярного решения уравнения термоупругости A03). 2. Формулы
Грина A04). 3. Условие термоупругого излучения A05). 4. Теоремы единственности
для внешних задач A06). 5. Теоремы единственности в задачах термоупругих псевдоколе-
псевдоколебаний A07).
§ 4. Задачи статики в моментной теории	 108
1. Формулы Грина A08). 2. Решение вспомогательного уравнения (НО). 3. Теоремы
единственности в задачах статики A10).
§ 5. Задачи установившихся моментно-упругих колебаний	 111
1. Разложение регулярного решения уравнения М (дх, а) ^ = 0A11). 2. Условие излу-
излучения A14). 3. Вспомогательные оценки A14). 4. Теоремы единственности A16).
§ 6. Теоремы единственности в задачах динамики	 117
1. Энергетические тождества A17). 2. Теоремы единственности A19).
§ 7. Некоторые справки и библиографические справки	 120
Задачи	 122
Глава IV
СИНГУЛЯРНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
§ 1. Вводные замечания. Специальные классы функций и их свойства	 123
1. О сингулярных интегралах и интегральных уравнениях A23). 2. Функции класса G и
Z A25). 3. Сингулярное ядро и сингулярный интеграл A27).
§ 2. Интеграл с ядром со слабой особенностью	 . 131
1. Элементарные свойства A31). 2. О производных интегралов с ядром, обладающим сла-
слабой особенностью A33).
§ 3. Сингулярные интегралы	 136
1. Сингулярные интегралы в классах функций С0» 3. Теорема Жиро A36). 2. Сингулярные
интегралы в классах функций Cs» a A39). 3. Интегралы с ядром специальной конструк-
конструкции A44). 4. Сингулярные интегралы на многообразиях A46). 5. Сингулярные опера-
операторы в пространствах L . Теорема Кальдерона и Зигмунда A52).
§ 4. Формула перестановки порядка интегрирования в повторных сингулярных инте-
интегралах. Композиция сингулярных ядер	 156
1. Общая формула перестановки порядка интегрирования в повторных сингулярных
интегралах A56). 2. Пример A57).
§ 5. Регуляризация сингулярных операторов	 161
1. Метод Жиро A61). 2. Метод Михлина A63). 3. Регуляризация сингулярных опера-
операторов, распространенных на замкнутых поверхностях A65).
§ 6. Основные теоремы	 170
1. Теоремы Нетера A70). и2. Свойства дифференцируемости решений сингулярных инте-
интегральных уравнений. Теоремы вложения A72).

ОГЛАВЛЕНИЕ
§ 7. Сингулярная резольвента. Свойства и применения	 178
1. Преобразование ядра A79). 2. Отображение локального оператора на круг A80).
3. Отображение на бесконечную плоскость A81). 4. Локальная регуляризация A82).
5. Оператор глобальной регуляризации A86). 6. Функциональные уравнения резоль-
резольвенты. Первая теорема Фредгольма A-87). 7. Вторая теорема Фредгольма A90). 8. Биор-
Биортонормирование фундаментальных решений союзных систем A93). 9. Третья теорема
Фредгольма A95).
§ 8. Заключительные замечания	 197
Задачи	 199
Глава V
ТЕОРИЯ ПОТЕНЦИАЛА
§ 1. Некоторые вспомогательные операторы, формулы и теоремы	 200
1. Определение Ш+ (у, 6) и Ш" {у, 6) B00). 2. Определение операторов Q)h, Jf., и -—.
Связь между ними B00). 3. Теорема Стокса и ее применения B03). 4. Формула пред-
представления решения на S B07).
§ 2. Граничные свойства для поверхностных интегралов типа потенциала ..... 210
§ 3. Потенциалы простого и двойного слоя. Угловые граничные значения	 215
§ 4. Потенциал двойного слоя с плотностью класса С0* ^ (S)	•. 217
§ 5. Граничные свойства первых производных потенциала простого слоя	 221
§ 6. Производные потенциалов простого и двойного слоя с дифференцируемой плот-
плотностью 	 224
§ 7. О дифференциальных свойствах потенциалов теории упругости	 226
§ 8. Теоремы типа Ляпунова—Таубера в теории упругости	 227
1.	Теоремы Ляпунова—Таубера для гармонического потенциала двойного слоя B27).
2.	Теоремы типа Ляпунова—Таубера в теории упругости B28). 3. Одна вспомогательная
теорема B30).
§ 9. Граничные свойства потенциалов третьей и четвертой задач	 233
1.	Граничные условия третьей и четвертой задач. Приведение к эквивалентному виду B33).
2.	Потенциалы третьей и четвертой задач и их свойства B35). 3. Теоремы -типа Ляпунова—
Таубера для потенциалов третьей и четвертой задач B37). 4. Формулы Сомилиана для
третьей и четвертой граничных задач B39).
§ 10. Объемные потенциалы	 239
1. Определения. Элементарные свойства B39). 2. Вычисление производных второго по*
рядка B40). 3. Теорема о распространении функций B43). 4. Объемные потенциалы
с дифференцируемыми плотностями B45). 5. Характер интеграла типа объемного потен-
потенциала вблизи бесконечно удаленной точки B45).
§ 11. Библиографические справки	 248
Задачи	 248
Глава VI
ГРАНИЧНЫЕ ЗАДАЧИ УПРУГОГО РАВНОВЕСИЯ (СТАТИКА)
§ 1. Граничные задачи для неоднородных уравнений	 250
§ 2. Интегральные уравнения граничных задач	'	 251
§ 3. Теоремы Фредгольма и теоремы вложения	 254
§ 4. Теоремы о характеристических числах	 259
§ 5. Существование решений граничных задач	 261
1. Задачи A)+и (II)- B61). 2. Задачи (Ц)+ и (I)- B62). 3. Другой способ доказательства
теорем существования для задач (I)- и (П)+ B68). 4. Задачи (Ш)+ и (IV)" B70). 5. За-
Задачи (III)-и (IV)+ B71). 6. Задачи (VI)+ и (VI)- B72). 7. Задача (V)+B72).
§ 6. Вопросы корректности	 275
1. Постановка вопроса B75). 2. Первая основная задача статики B77). 3. Вторая основ-
основная задача статики B78).
§ 7. Библиографические справки	 279
Задачи	 280
Глава VII
ГРАНИЧНЫЕ ЗАДАЧИ УСТАНОВИВШИХСЯ УПРУГИХ КОЛЕБАНИЙ
§ 1. Внутренние задачи	 281
1. Приведение к интегральным уравнениям B81). 2. Тензоры Грина B83). 3. Формулы
представлений B86). 4. Однородные внутренние задачи. Спектр собственных частот B87).

ОГЛАВЛЕНИЕ
§ 2. Основные теоремы теории колебаний	 290
1. Первая теорема Ляпунова—Таубера в теории упругости B90). 2. Свойства собствен-
собственных частот и собственных функций B93). 3. Теоремы о простоте полюсов резольвенты B97).
4. Исследование внутренних задач. Условия разрешимости в резонансном случае C02).
§ 3. Внешние задачи	 306
со со
1. Разрешимость для произвольных частот колебания; задачи A)~, (II)" C06). 2. Другие
задачи C08).
§ 4. Некоторые замечания и библиографические справки	 310
Задачи	 311
Глава VIII
СМЕШАННЫЕ ЗАДАЧИ ДИНАМИКИ
§ 1. Первая основная задача	 313
1. Условия для данных задачи. Основная теорема C13). 2. Приведение к специальному
случаю C15). 3. Усредняющее ядро. Свойства средней функции C16). 4. Доказательство
существования а (х, i) C19). 5. Преобразование Лапласа. Приведение к эллиптической
задаче C21). 6. Единственность, существование, представление и дифференциальные
свойства Ъ9 (х, х) C21). 7. Гладкость и0 (х, х) относительно х С П_ C22). 8. Асимпто-
Асимптотические по т оценки для и0 (х, х) C23). 9. Некоторые^ простейшие неравенства C25).
10. Асимптотические по т оценки первых производных ° C27). 11. Асимптотические
по х оценки вторых производных "° **' Т) C29). 12. Некоторые свойства преобразования
ох-ох.
Лапласа C30). ЛЗ. Доказательство существования и0 (дс, t) и и (*, t) C31). 14. Вычисле-
Вычисление и (х, t) и завершение доказательства основной теоремы C33).
§ 2. Вторая основная задача	 334
1. Постановка я условия для данных задачи. Основная теорема C34). 2. Преобразование
Лапласа. Решение эллиптической задачи C35). 3. Гладкость и0 (х, х) относительно х ?
? П^ C36). 4. Асимптотические по х оценки для и0 (х, х) и производных C37). 5. До-
Доказательство существования и вычисление решения второй основной задачи C39).
§ 3. Внешние задачи	 340
1. Постановка задач C40). 2. Основная лемма C41). 3. Исследование первой внешней
задачи C42).
§ 4. Заключительные замечания. Библиографические справки	 342
Задачи	 345
Глава IX
МОМЕНТНАЯ ТЕОРИЯ УПРУГОСТИ
§ 1. Введение	 347
1. Основные уравнения C47). 2. Оператор напряжения C47). 3. Основные задачи C47).
4. Формулы Сомилиана C49). 5. Потенциалы C50). 6. Теорема Ляпунова — Таубера C51).
§ 2. Исследование задач статики	 351
1. Сведение граничных задач к интегральным уравнениям C51). 2. Исследование инте-
интегральных уравнений C52). 3. Теоремы существования для задач A)+ и (II)- C55).
4. Теоремы существования для задач (Н)+ и (I)- C56). 5. Теоремы существования для
задач (Ш)+ и (IV)- C59). 6. Теоремы существования для задач (III)— и (IV)+ C60).
§ 3. Задачи колебания	 360
1. Сведение задач к интегральным уравнениям C60). 2. Исследование интегральных
уравнений C61). 3. Тензоры Грина C61). 4. Внутренние задачи C64). 5. Внешние за-
задачи C65).
§ 4. Задачи динамики	 365
1. Постановка и приведение к специальному виду C65). 2. Преобразование Лапласа.
Решение эллиптической задачи. Аналитичность решения C66). 3. Асимптотические по г
оценки ^в (*, X) и ее производных. Решение динамической задачи C67).
§ 5. Заключительные замечания и библиографические справки	 370
Задачи	 371

ОГЛАВЛЕНИЕ	7
Глава X
ТЕОРИЯ ТЕРМОУПРУГОСТИ
§ 1. Введение	 373
§ 2. Установившиеся термоупругие колебания	 374
1.	Союзная система. Свойства фундаментальных решений. Тождества Грина C74).
2.	Общее представление регулярных решений однородного уравнения C78). 3. Основ-
Основные свойства термоэластопотенциалов C80). 4. Основные граничные задачи. Приведение
к интегральным уравнениям C84). 5. Теоремы Фредгольма C85). 6. Внутренние задачи.
Спектр собственных частот. Теоремы единственности C86). 7. Изучение интегральных
уравнений внешних задач C88). 8. Применения в теории внешних задач. Доказательство
теорем существования C92).
§ 3. Задачи статики и псевдоколебаний	 401
1. Задачи статики D01). 2. Псевдоколебания D01).
§ 4. Динамические задачи термоупругости	 405
1. Первая задача. Постановка и приведение к специальному виду D05). 2. Преобразова-
Преобразование Лапласа. Решение эллиптической задачи D07). 3^ Гладкость й9 (х, х) относительно
If П D08). 4. Асимптотические по т оценки для Uj^^ix, х) [и ее производных D09).
5. Асимптотические оценки по т для сН^) ^х. х) D10). 6. Оценки относительно х производ-
производ№)(х, х). Некоторые вспомогательные ^неравенства D14). 7. Завершение
решения динамической задачи D17).
§ 5. Дополнительные замечания. Библиографические справки	 41в
Задачи	 420
Глава XI
ГРАНИЧНЫЕ ЗАДАЧИ ДЛЯ СРЕД,
ОГРАНИЧЕННЫХ НЕСКОЛЬКИМИ ПОВЕРХНОСТЯМИ
§ 1. Основные граничные задачи упругого равновесия	 422
1. Постановка граничных задач и теоремы единственности D22). 2. Решение граничных
задач (I) ± D24). 3. Решение граничных задач (II) ±, (III) i D26). 4. Тензоры Грина для
областей, ограниченных несколькими замкнутыми поверхностями D28).
§ 2. Смешанные задачи статики 	 430
1. Теоремы существования для смешанных статических задач (IV) i D30). 2. Решение
смешанной задачи (V)+ D33). 3. Теоремы существования для статических смешанных
задач (VI)+, (VII)+, (V)- D35).
§ 3. Граничные задачи колебания	 437
1. Однородные внутренние задачи колебания. Спектр собственных частот D37). 2. Внеш-
@ (О (О
ние задачи колебания (I)"", (II)"", (III)"". Приведение к интегральным уравнениям.	Основ-
уравнениям.	Основой со
ные теоремы D39). 3. Теоремы существования для внешних задач колебания A)~,	(И)""#
со	со	со
(III)- D41). 4. Внешние смешанные граничные задачи колебания (IV)-, (V)-	D44).
§ 4. Заключительные замечания	 447
Задачи	 448
Глава XII
ГРАНИЧНО-КОНТАКТНЫЕ ЗАДАЧИ ДЛЯ НЕОДНОРОДНЫХ СРЕД
1.	Основные гранично-контактные задачи	 449
2.	Интегральные уравнения главной контактной задачи	 451
3.	Решение гранично-контактных задач статики	 457
4.	Решение гранично-контактных задач для уравнения установившихся колебаний 465
5.	Функциональные уравнения гранично-контактных задач	 475
1. Первая задача статики A)+ D75). 2. Вторая задача статики (П)+ D80). 3. Смешан-
Смешанная гранично-контактная задача статики D81). 4. Гранично-контактные задачи колеба-
колебания D82). 5. Теоремы эквивалентности D84). 6. Гипотеза Коши. Изучение статических
задач. Обобщенные решения D89). 7. Изучение динамических задач. Спектр собственных
частот. Обобщенные решения D93). 8. Доказательство теорем существования в общем
случае D96). 9. Задачи для неограниченной области D98).
f 6. Заключительные замечания	 498

8	ОГЛАВЛЕНИЕ
Глава XIII
РЕШЕНИЯ В ОБОБЩЕННЫХ РЯДАХ ФУРЬЕ
§ 1. Первая и вторая основные задачи теории упругости (статика)	 501
1. Теорема о полноте для задачи A)+E01). 2. Первый способ (задача I) E02). 3. Второй
способ (задача I) E05). Л. Третий способ (задача I) E06). 5. Теорема о полноте для за-
задачи (И)+ E08). 6. Первый способ ^(задачи (И)+ и (II)-) E10). 7. Второй способ (за-
(задача II) E12). 8. Третий способ (задача II) E13).
§ 2. Другие задачи (статика)	 514
1. Задачи III и IV E14). 2. Задача (VI) E16). 3. Смешанные задачи [E18).
§ 3. Гранично-контактные задачи статики и колебания 	, . 521
1. Гранично-контактные задачи статики E21). 2. Задачи колебания E27).
§ 4. Граничные задачи термоупругости		528
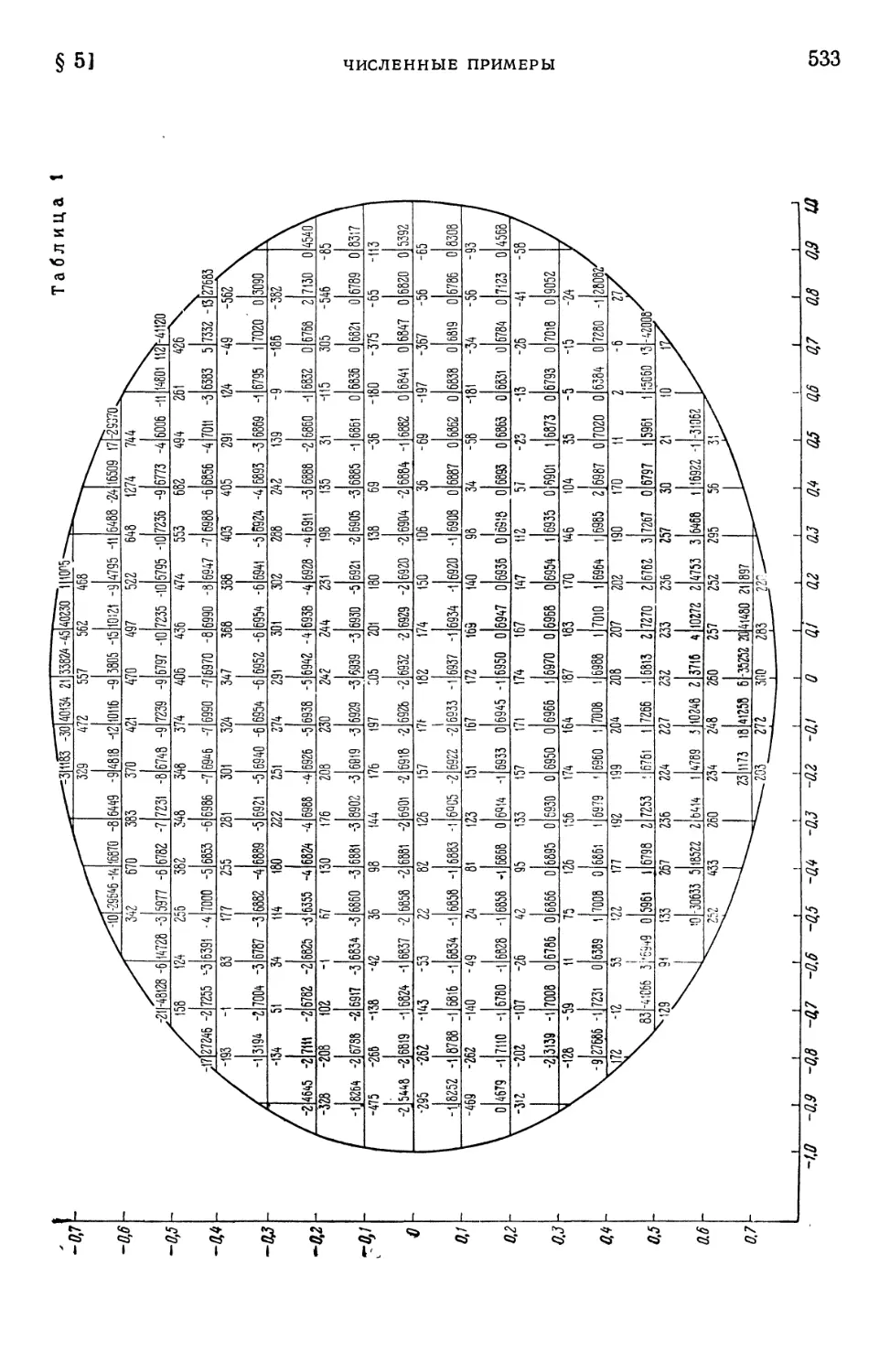
§ 5. Численные примеры		532
§ 6. Способ последовательных приближений		538
1. Задачи для однородных сред E38). 2. Гранично-контактные задачи E42).
§ 7. Заключительные замечания и библиографические справки	 544
Задачи . , . ,	 545
Глава XIV
РЕШЕНИЯ В РЯДАХ И КВАДРАТУРАХ
§ 1. Эффективное решение основных граничных задач классической теории упругости
для сферы и сферической полости в неограниченной среде	 546
1. Задача A)± E46). 2. Задача (И)± E53). 3. Задача (Ш)± E57). 4. Задача (IV)± E61).
§ 2. Граничные и некоторые другие задачи для трансверсально-изотропного упругого
полупространства и бесконечного слоя	 563
1. Вспомогательные формулы E63). 2. Граничные задачи и теоремы единственности для
полупространства E67). 3. Решение задачи A)+для полупространства E70). 4. Решение за-
задачи (II)+ для полупространства E74). 5. Решение задачи (III)+ для полупространства E78).
6. Задача о действии жесткого штампа на упругое полупространство неродственные за-
задачи E81). 7. Эффективное решение задачи о жестком штампе для некоторых конкретных
случаев E83). 8. Эффективное решение задачи о трещине для некоторых конкретных слу-
случаев E87). 9. Решение задачи (Н)+ для бесконечного слоя E90).
§ 3. Применение некоторых новых представлений гармонических функций и прин-
принципа симметрии для эффективного решения задач теории упругости ....... 595
1. Некоторые гармонические функции, связанные с упругими смещениями E95). 2. Про-
Продолжение решений E96). 3. Эффективное решение некоторых трехмерных граничных за-
задач E97).
§ 4. Задачи термоупругости в бесконечных областях, ограниченных системой плоско-
плоскостей	 599
1. Постановка задач для полупространства F00). 2. Фундаментальные решения и фор-
формулы представлений для системы D.3), D.4) F03). 3. Решение задач А и В для системы
D.11). Теоремы единственности F06). 4. Решение задач V и VI для полупространства F08).
5.	Теоремы о принципе симметрии для системы D.11) F09). 6. Решение некоторых гра-
граничных задач для системы D.11) в четверти пространства F10). 7. Решения задач Дирихле,
Неймана и смешанной для метагармонического уравнения в четверти пространства F13).
8. Решение задач Дирихле, Неймана и смешанной для неоднородного метагармонического
уравнения в четверти пространства F15). 9. Решение задач V, VI и смешанной в четверти
пространства для уравнений термоупругости F17). 10. Решение граничных задач для си-
системы D.11) в прямоугольном трехграннике (восьмая часть ^пространства) F18). 11. Реше-
Решение задач V, VI и смешанных для уравнений термоупругости в области D+ F22).
§ 5. (Продолжение). Применение интеграла Фурье	 623
1. Представления решений уравнений термоупругости F23). 2. Решение задачи I для
полупространства F25). 3. Решение задачи II для полупространства ,F27). 4. Другие
задачи F30). 5. Теоремы о принципе симметрии для уравнений термоупругости F32).
6.	Граничные задачи для четверти пространства F34). 7. Граничные задачи для бесконеч-
бесконечного прямоугольного трехгранника F36).
Задачи . ,	.-• в «¦,.**»••«« г » и *•©»*•	637
Литература		638
Основные обозначения	#		659
Предметный указатель		661

ПРЕДИСЛОВИЕ
В лучших книгах по теории упругости изложение теории трехмерных
граничных задач до сих пор ограничивается рассмотрением лишь тел спе-
специальной конфигурации (полупространство, сфера, некоторые другие слу-
случаи тел вращения и т. д.); при этом наибольшее внимание уделяется вопро-
вопросам статики, значительно меньше вопросам колебаний и еще меньше —
вопросам общей динамики. Это обстоятельство не случайно; в нем находит
отражение исторический ход развития теории упругости, которая в течение
всего предшествующего периода была занята главным образом изучением
тел частных профилей и интересовалась прежде всего проблемами статиче-
статического равновесия.
Было бы неверно приписывать такое положение одной лишь важности
указанных задач для целей технической теории упругости; истинная при-
причина состоит в том, что методы классической теории упругости были недо-
недостаточны для построения строгой и достаточно полной общей теории трех-
трехмерных граничных задач.
В противоположность трехмерным задачам, теория плоской задачи,
разрабатываемая главным образом методами классического анализа (теория
аналитических функций, теория интегральных уравнений Фредгольма и,
позднее, теория одномерных сингулярных интегральных уравнений), полу-
получила широкое развитие и нашла совершенное выражение в классическом
труде Н. И. Мусхелишвили «Некоторые основные задачи математической
теории упругости», первое издание которого вышло в 1933 году.
Положение существенно изменилось в настоящее время. Теперь теорию
трехмерных задач можно построить различными средствами; укажем две
из подобных возможностей. С одной стороны, — это современная теория
обобщенных решений дифференциальных уравнений (методы гильбертовых
пространств, вариационные методы), с другой, — теория многомерных син-
сингулярных потенциалов и сингулярных интегральных уравнений.
Первое направление, основанное на идеях современного функциональ-
функционального анализа, незнакохмых классической механике, отличается большой
общностью, охватывая случай переменных коэффициентов и граничных
многообразий общего вида, но благодаря именно этой общности служит
прежде всего для доказательства теорем существования неклассических
решений, требуя при переходе к классическим решениям дополнительных,
иногда существенных, ограничений.
Современное изложение этих вопросов достаточно подробно дается
в статьях G. F i с h e r a, «Existence Theorems in Elasticity», и «Boundary
Value Problems of Elasticity with Unilateral Constraints», Handbuch der
Physik, VIa/2, Springer Verlag, 1972 иС. Dafermos, «On the Existence
and Asymptotic Stability of Solutions to the Equations of Therinoelasticity>.
Arch. Rat. Mech. Anal. 29, 4, 1968.
Второе направление, которое опирается на активно развивающуюся
в последнее время теорию сингулярных интегралов и интегральных уравне-
уравнений, представляет прямое развитие господствующих в классической меха-
механике идей теории потенциала и фредгольмовых уравнений и, уступая

10	ПРЕДИСЛОВИЕ
первому направлению в общности, позволяет подробно исследовать наиболее
важные для теории и приложения случаи, сохраняя при этом ту степень
наглядности и эффективности, которые характерны для методов классиче-
классической механики сплошных сред.
Предлагаемая книга — продукт второго направления. В ней, на совре-
современном уровне математической строгости, впервые с одинаковой в принципе
полнотой, изложена общая теория трехмерных граничных задач статики,
колебаний и общей динамики для линейных уравнений с постоянными и
кусочно-постоянными коэффициентами классической теории упругости,
термоупругости и моментной теории упругости.
Общим вопросам (теоремы существования и единственности, анализ
дифференциальных свойств решений, непрерывная зависимость от данных
задачи и др.) в книге отводится значительное место, но большое внимание
уделяется также вопросам фактического конструирования решений в таком
виде, который должен позволить их численную реализацию при весьма
общих условиях.
С этой целью решения представляются в виде обобщенных рядов Фурье,
которые не требуют для своего построения знания собственных функций
и собственных чисел каких-либо вспомогательных граничных задач; в некото-
некоторых частных случаях найдены новые представления решений в квадратурах.
Нам кажется, что приведенные в книге простые конструкции решений
и представления с помощью явных обратимых операторов несложных струк-
структур, вместе с подробным анализом гладкости решений, при современном
состоянии средств вычислительной техники могут служить основой для
составления удобных алгоритмов численных расчетов и для оценок прибли-
приближений.
Книга является переработанным и дополненным изданием монографии
тех же авторов, вышедшей в 1968 году в издании Тбилисского универси-
университета; она была благожелательно принята читателем и тираж быстро разо-
разошелся; первое издание было удостоено Государственной премии Грузин-
Грузинской ССР 1971 года.
Второе издание подверглось значительным изменениям и дополнениям.
Стремясь сделать книгу доступной для широкого круга читателей, авторы
перестроили изложение, заново написали почти все главы, упростили ряд
локазательств, устранили замеченные опечатки и ошибки.
Для пользования книгой необходимо иметь в виду,' что главы разбиты
на параграфы, параграфы — на пункты и нумерация формул в каждом
параграфе своя, сквозная; номер формулы обозначается двумя числами,
поставленными в скобках, например, E.9) обозначает девятую формулу
в пятом параграфе; при ссылках на формулы, кроме номера формулы, ука-
указывается номер главы, например, (VIII, 3.6) обозначает шестую формулу
в третьем параграфе восьмой главы. При ссылках на формулу внутри дан-
данной главы указание на номер главы опускается.
Подобным же образом, но без скобок, обозначается номер теоремы,
леммы, определения и замечания; например, теорема V, 2.10 обозначает
теорему десятую во втором параграфе пятой главы. При ссылках внутри
данной главы указание на номер главы не делается. Все главы, кроме
первой, сопровождаются задачами; некоторые из них могут служить
предметом самостоятельных работ исследовательского значения.
Список литературы включает названия, которыми авторы располагали
при работе над книгой; он не является полным, не претендует на безупреч-
безупречность библиографического отбора и не содержит указаний на работы, опу-
опубликованные позднее 1972 года.
Тбилиси, 1972 р.	Авторы

ГЛАВА 1
ОСНОВНЫЕ ПОНЯТИЯ И АКСИОМАТИЗАЦИЯ
Первая глава носит вводный характер. Здесь приведены основные поня-
понятия классической теории упругости, термоупругости и моментной теории
упругости. Рассуждения, поясняющие физические основы этих теорий,
приведенные в основном в §§ 1—10, не имеют своей целью обосновать с пози-
позиции физики основы теории упругости. Они не полны и не претендуют на
современность изложения. Цель этих рассуждений — перекинуть мост
между теорией упругости как разделом механики и математической теорией
упругости и этим облегчить чтение книги механикам, которые еще не при-
привыкли к аксиоматическому построению теории упругости, а также помочь
математикам, изучавшим математическую теорию упругости, придать неко-
некоторым терминам (напряжения, смещения, изотропия и т. д.), формально
выступающим в аксиоматической теории, определенный физический смысл.
Читатели, не нуждающиеся в этих пояснениях, могут пропустить §§ 1—10,
а интересующиеся физическими основами могут ознакомиться с литературой,
указанной в § 15.
В первой главе сформулированы основные предположения классиче-
классической теории упругости, термоупругости и моментной теории упругости сна-
сначала в терминах механики, а затем проведена аксиоматизация этих теорий.
Классическую теорию упругости, теорию термоупругости и моментную
теорию упругости объединим общим названием — теория упругости.
В физических основах теории упругости лежит допущение о примени-
применимости для некоторых сред, называемых упругими, теории деформаций,
напряжений и закона Гука (закона связи между напряжениями и деформа-
деформациями). Различное понимание теории деформаций, напряжений и закона
Гука порождает различные теории. Так, построена классическая теория
упругости для изотропных и анизотропных сред, теория термоупругости,
моментная теория упругости и др.
§ 1. Напряжения
1. Внутренние и внешние силы. Если в рассматриваемой среде отсут-
отсутствуют внешние воздействия и среда не деформирована, то все ее части нахо-
находятся в механическом равновесии друг с другом. Если же каким-либо воз-
воздействием среда выведена из этого естественного состояния, т. е. деформи-
деформирована, то первоначальное равновесное расположение молекул меняется,
части уже не находятся в механическом равновесии друг с другом. При таком
деформированном состоянии в среде возникают силы, которые стремятся
вернуть тело к естественному состоянию.
Внутренние силы, вызванные изменением расположений молекул,
характеризуются молекулярными силами и обладают незначительными ра-
радиусами действия по сравнению с расстояниями, рассматриваемыми в теории

12	основные понятия и аксиоматизация	[рл# i
упругости. Поэтому принято считать, что внутренние силы, действующие
на какую-нибудь часть среды со стороны остального тела, действуют
только через границу этой части.
Силы, действующие из окружающей среды, называются внешними си-
силами и делятся на массовые и поверхностные силы.
2. Массовые и поверхностные силы. Массовый момент. Если рассматри-
рассматриваемая среда соприкасается с воздействующей на нее внешней средой, то
на поверхности соприкосновения возникают «силы близкого действия», на-
называемые поверхностными, такой же природы, как и описанные выше.
Очевидно, что не всякое внешнее воздействие на рассматриваемую среду
можно представить поверхностными силами. Силы тяготения являются при-
примером такого воздействия. В теории упругости, кроме поверхностных сил,
вводят массовые силы. Предполагают, что воздействие этих сил на элемен-
элементарную частицу среды статически эквивалентно силе, приложенной к центру
масс частицы, и паре сил. Эти силы и моменты пар предполагаются пропор-
пропорциональными массам частиц, на которые они действуют. Их называют мас-
массовыми силами и массовыми моментами.
Рассмотрим частицу с массой Am. Пусть центр масс частицы находится
в точке х. Как было отмечено, воздействие сил, зависящих от масс, можно
представить в виде силы, приложенной в центре масс, и пары сил. Обозна-
Обозначим вектор этой силы через ЗГ (Am), а момент пары — через *§ (Am). Пред-
Предположим, что существуют пределы
Дт->0 Ьт
которые зависят только от точки х и, в динамическом случае, от времени t
Обозначим эти пределы через ЗГ (х, f) и $ (х, t) соответственно, и понятия
массовая сила и массовый момент будем употреблять для этих векторов.
Из принятого предположения вытекает, что действие сил, зависящих
от масс, на частицу AD с массой Am можно представить в виде массовой
силы ЗГ (х, t) Am и массового момента 9 (х, t) Am с точностью до беско-
бесконечно малых по сравнению с Am. Эти векторы можно представить и так:
ЗГ (х, t) р (х) mes (AD), 9 (х, t) р (x) mes (AD),
где р — плотность среды, a mes (AD) — объем, занятый частицей AD.
Плотность среды определяется как предел отношения Am/mes (AD),
когда mes (AD) стремится к нулю таким образом, чтобы AD всегда содер-
содержала точку х.
В классической теории упругости, в отличие от моментной теории,
не учитывают влияния массовых моментов, предполагая, что они равны
нулю (9 (х, t) = 0).
3. Силовые и моментные напряжения. Для характеристики внутренних
сил в теории упругости вводя! понятие напряжения. Возьмем точку внутри
рассматриваемой среды и мысленно проведем через эту точку малую поверх-
поверхность. Обозначим выбранную точку и поверхность через х и AS соответ-
соответственно. Внутренние силы, вызванные действием части среды, находящейся
по одну сторону от поверхности AS, на другую, можно представить в виде
сил, приложенных в точках поверхности AS.
Направления этих сил зависят от выбранной части. Воздействия друг
на друга частей среды, находящихся по разные стороны от поверхности AS,
характеризуются равными по величине, но противоположно направленными

Л Ц	НАПРЯЖЕНИЯ	13
силами. Чтобы определить, о каких воздействиях идет речь, поступим сле-
следующим образом: проведем в точке х нормаль к поверхности AS, выберем
на ней определенное положительное направление и будем рассматривать
действие той части среды на другую, которая находится с положительной
стороны нормали.
Предполагается, что действие указанных сил, приложенных к AS, ста-
статически эквивалентно действию силы и пары. Обозначим вектор силы
через 7\ а момент пары через М, и рассмотрим отношения
7/mes(AS), M/mes(AS).
Предполагается также, что пределы этих отношений, когда площадь поверх-
поверхности AS—mes (AS) стремится к нулю, существуют. Эти пределы зависят
от выбранной точки х и от нормали п. Выбором противоположного направ-
направления на п изменяется знак пределов. Выбирая другую нормаль, т. е.
рассматривая другую поверхность, проходящую в точке х, получим иную
картину, вызванную воздействием уже других частей среды. В соответствии
с этим изменяются Т и М и, следовательно, пределы приведенных отноше-
отношений. Вместе с тем предполагается, что эти пределы не зависят от формы
поверхности AS. Точнее, пределы не изменяются, если их вычислить для
другой поверхности, проходящей через ту же точку х, с той же нормалью п.
Отметим также, что если рассматривается динамическая картина дефор-
деформации, то приведенные пределы будут зависеть и от времени. Введем обо-
обозначения
= lim —-Г	цс») = Hm M
mes (AS) > ** ~ ilX11 mes (AS)
В силу сказанного выше, т<п> и \i(n\ кроме направления п, зависят также
от точки х и времени t.
т(п) (х, t) называется вектором силового напряжения, а ^х(/г> (х, t) —
вектором моментного напряжения в точке х по направлению п в момент
времени t.
Заметим, для устранения недоразумений, что векторы т<л> и |х<л> вообще
не направлены по п.
В классической теории упругости предполагают, что \к{п) = 0. В момент-
ной же теории упругости такое предположение не делается. Ввиду того,
что в классической теории нет моментных напряжений, вместо термина
«силовое напряжение» будем употреблять просто «напряжение».
Мы уже встретились с двумя основными различиями между классиче-
классической и моментной теорией упругости. В моментной теории, в отличие от клас-
классической, вводятся в рассмотрение массовые моменты и моментные напря-
напряжения. Отсюда и название этой теории *).
Определение напряжений (силового — в классической теории и сило-
силового и моментного — в моментной теории) в каждой точке по любому направ-
направлению, в каждый момент времени из рассматриваемого промежутка, является
одной из основных задач теории упругости.
г) В литературе встречаются различные названия для моментной теории упругости.
Называют ее асимметричной теорией упругости, теорией Коссера, теорией упругости с враща-
вращательными воздействиями |частиц,!теорией упругости микрополярных сред, микрополярной
теорией упругости, нелокальной теорией упругости, теорией упругости среды второго
класса и т. д.
Отметим, что рассматривались различные представления модели сплошной среды, учи-
учитывающие моментные напряжения и оправдывающие приведенные названия. Подробнее об
этом будет сказано в главе IX, посвященной моментной теории.

14
ОСНОВНЫЕ ПОНЯТИЯ И АКСИОМАТИЗАЦИЯ
[Рл. I
Из принятого предположения вытекает, что поверхностные силы (сило-
(силовые и моментные напряжения), действующие на малую поверхность AS
с нормалью /г, статически эквивалентны силе т*я> mes (Д5) и моменту
\iW mes (AS) с точностью до бесконечно малых высшего порядка по отно-
отношению к mes (AS).
§ 2. Компоненты напряжений
1.	Компоненты тензоров г) силового и моментного напряжения. В каж-
каждой точке среды можно провести бесконечно много различных направлений
и, следовательно, для представления полной картины напряжений в точке
приходится знать напряжения (силовые — в классической, и силовые и
моментные — в моментной теории упругости) по всем этим направлениям.
Однако если известны напряжения в точке по трем взаимно перпенди-
перпендикулярным направлениям, то можно вычислить, с некоторой точностью,
напряжения в этой точке по любому направлению.
Возьмем прямоугольную и прямолинейную систему координат ХгХ2Х3.
Обозначим напряжения т<я> и \i{n), когда п совпадает с направлением оси Xi%
через т<1) и \i{iK а координаты этих век-
торов в системе ХгХ2Х3—через Тц,т/2>
тгз и М-д» Мч*2> Мчз соответственно.
Рассмотрим матрицу || T{f (х, /)[зхз-
Ниже мы покажем, что вектор силового
напряжения xw (х, f) по любому напра-
направлению п (в точке х в момент времени t)
выразится с помощью элементов матрицы
IIх// (•*' ^I1* Элементы этой матрицы назы-
^ ваются компонентами силового напряже-
1 ния. Легко доказать, что эти девять скат
лярных величин образуют тензор второго
ранга, который называют тензором сило-
силового напряжения. Таким образом, компо-
компоненты силового напряжения суть компо-
компоненты тензора напряжения.
Совершенно аналогично определяются компоненты моментного напря-
напряжения и тензор моментного напряжения.
2.	Выражение вектора силового напряжения через компоненты (тен-
(тензора) силового напряжения. Пусть х — произвольная точка рассматривае-
рассматриваемой среды, а п = (п1у п2, п3) — произвольный единичный вектор, направ-
направление которого не совпадает с направлением координатных осей и не про-
противоположно им. Проведем через точку х три плоскости, параллельные
координатным плоскостям, и рассмотрим малый тетраэдр, образованный
этими плоскостями и плоскостью, нормальной к п, проведенной на близком
расстоянии от точки х. Обозначим через AS ту грань тетраэдра, которая
нормальна к п (рис. 1).
Из условий равновесия следует равенство нулю суммы главного век-
вектора внешних сил и главного вектора инерционных сил.
При вычислении главного вектора внешних сил, действующих на тетра-
тетраэдр, следует учесть силовые напряжения, действующие на грани этого
тетраэдра, и главный вектор массовых сил, действующих на массу тэтраэдра.
*) В этой книге мы не пользуемся тензорным исчислением. Слово «тензор» у нас употреб-
употребляется в качестве термина (точнее, в качестве составной части терминов «тензор силового
напряжения», «тензор моментного напряжения», «тензор деформации» и т. д.) для обозначе-
обозначения некоторых величин. Эти величины действительно образуют тензоры, что дает право на сво-
свободное употребление термина «тензор».
Рис. К

Л 31	СМЕЩЕНИЯ И ВРАЩЕНИЯ	1 5
Вычислим силовые напряжения, действующие на грани тетраэдра.
Площадь грани тетраэдра, перпендикулярной к осиОХг, равна |дг| mes (AS)
и, следовательно, силовое напряжение, действующее на тетраэдр через эту
грань со етороны внешней по отношению к тетраэдру части среды, равно
%i?) (x, t) nt mes (AS) с точностью до малой высшего порядка по сравнению
с mes (AS) (см. § 1, п. 3). Силовое напряжение, действующее через грань AS,
равно т<Л> (х, t) mes (AS).
Главный вектор массовых и инерционных сил, действующих на тетра-
тетраэдр, пропорционален массе тетраэдра, и, следовательно, его объему, т. е.
является величиной бесконечно малой высшего порядка по сравнению
с mes (AS). Сумму всех этих векторов, представляющую главный вектор
внешних сил, следует приравнять нулю. Разделив полученное равенство на
mes (AS) и перейдя к пределу, при mes (AS) —¦ 0, получим векторное
соотношение
з
которое .в компонентах примет вид
тГ (*,*) = ? ru(x9t)nu /=1,2,3.	B.1)
Если направление п совпадает с направлением какой-нибудь коорди-
координатной оси или противоположно ему, то справедливость формул B.1) оче-
очевидна. Формулы B.1) дают искомые представления силового напряжения
по любому направлению в точке через компоненты тензора силового напря-
напряжения в той же точке. Эти соотношения были найдены Коши. Они справед-
справедливы как в классической, так и в моментной теории упругости.
3. Выражение вектора моментного напряжения через компоненты (тен-
(тензора) моментного напряжения. Вычислим главные моменты внешних и инер-
инерционных сил, действующих на тетраэдр и их сумму приравняем нулю. Рас-
Рассуждением, аналогичным приведенному в предыдущем пункте, получаем
векторное соотношение
з
которое в компонентах запишется так:
з
№ (х, t) = 2 V4i (x, t) щ (/ = 1,2, 3).	B.2)
Получены соотношения между моментным напряжением по любому
направлению в точке и моментными напряжениями по трем взаимно перпен-
перпендикулярным направлениям в той же точке.
Заметим, что в классической теории упругости \\а и \х\п) предпола-
предполагаются равными нулю и поэтому соотношения B.2) не рассматриваются.
§ 3. Смещения и вращения
1. Вектор смещения. Предположим, что в начальный момент времени t0
среда находится в состоянии покоя — она не деформирована и к ней не^при-
ложены силы. Подвергнем ее деформированию. Для математического описа-
описания деформированного состояния введем неподвижную прямоугольную
систему осей координат ОХ±Х2Х3. Пусть среда в момент времени tQ зани-
занимает область D с границей S, а в момент времени t — область Dt с гра-
границей S'.

|б	OCHOBHbTF ПОНЯТИЯ И АКСИОМАТИЗАЦИЯ	[Гл J
Рассмотрим какую-нибудь точку х = (хх> х2, х3) среды, находящейся
в покое (х (Е D = D [} S). При деформации среды точка х меняет положе-
положение, т. е. подвергается смещению. Обозначим ее положение в момент вре-
времени t через х* = (х{> х{, лф.
Разность г) хг — х называется вектором смещения или просто смещением,
точнее, значением вектора смещения в точке х в момент t, и обозначается
через и (х, f), а его компоненты в выбранной системе — через иг (х, t),
и2 (х, *), и3 (х, О-
Таким образом, каждой точке х недеформированного состояния среды
(х 6 D) в любой момент t из рассматриваемого промежутка времени [t0, ?xl,
т. е. каждой паре (х, t) из множества D X [t0, ^1, ставится в соответствие
вектор смещения и (ху f) = хг — х.
2. Вектор вращения. Вектором смещения и (х, f) каждой точки х рас-
рассматриваемой сплошной среды в любой момент времени t вполне опреде-
определяется картина деформации. Но материальную среду естественно предста-
представить не как сплошную, представляющую множество математических точек
трехмерного евклидова пространства, а как совокупность материальных
частиц. Таким представлением мы уже пользовались выше, при введении
напряжений и при выводе основных для теории упругости соотношений
между напряжениями в точке. Тогда элементарный объем среды мы рас-
рассматривали как твердое (жесткое) тело и применяли к нему законы статики.
Рассматривая среду с самого начала в виде совокупности математиче-
математических точек, заполняющих некоторую область, мы встретились бы с серьез-
серьезными затруднениями, например, уже при выводе основных соотношений,
на которых основывается теория упругости. По-видимому, когда прихо-
приходится пользоваться закономерностями физики, необходимо представлять
среду в виде совокупности материальных частиц.
С другой стороны, рассмотрение среды как сплошной необходимо, если
мы желаем применить методы математического анализа. Эти две концепции
обычно согласуются следующим образом: сначала среду рассматривают
как совокупность материальных частиц, выводят необходимые соотношения,
вытекающие из такого представления, а потом, реализуя идеализацию, т. е.
представляя среду как сплошную, применяют аппарат математического
анализа.
Если среду с самого начала представим как сплошную, то картина дефор-
деформации вполне определится вектором смещения. Если же представим ее как
совокупность материальных частиц, картина несколько изменится.
Рассмотрим произвольную частицу среды. Пусть центр тяжести этой
частицы находится в точке х в состоянии покоя. Введем новую систему
прямоугольных и прямолинейных осей координат с началом в точке х,
жестко закрепленную с рассматриваемой частицей. Оси ноеой системы напра-
направим параллельно соответствующим осям неподвижной системы.
Частицу будем представлять как твердое (жесткое) тело. Тогда ее дви-
движение определяется шестью скалярными величинами, например, смеще-
смещением точки х (которое определяется тремя координатами вектора смещения
относительно неподвижной системы) и вращением частицы вокруг центра
тяжести (которое также определяется тремя скалярными величинами —
углами поворота подвижной системы относительно осей координат непо-
неподвижной системы, например, углами Эйлера).
1) Точка и соответствующий радиус-вектор обозначаются одним и тем же символом.
Таким образом, под х* — х понимается вектор, началом которого является точка х, а концом —
точка хг. Следовательно, ** — х = (х\ — xlt х\ — х2, х\ — х3).

ОСНОВНЫЕ УРАВНЕНИЯ В КОМПОНЕНТАХ НАПРЯЖЕНИЯ	17
Среда при деформации в момент времени t займет новое положение
относительно неподвижной системы. Точка х займет положение х*. х1 — х =
= и (х, t) определяет вектор смещения точки х. Новое положение займет
и подвижная система относительно неподвижной. Она поворачивается.
Обозначим углы поворота через с^ (я, f)> cd2 (x> t) и са3 (*, 0- (Вектор
ю (*, t) = (ayг (х, f), оо2 (х, f), oK (х, t)) будем называть вектором внутрен-
внутреннего вращения или просто внутренним вращением точки х в момент вре-
времени t.
Если теперь представим среду как сплошную, то движение каждой
ее точки будет характеризоваться не тремя скалярными величинами (ком-
(компонентами вектора смещения), а шестью (компонентами вектора смещения
и вектора внутреннего вращения).
Такое рассмотрение принято в моментной теории упругости. В класси-
классической теории упругости вектор внутреннего вращения не рассматривают
как независимый от смещения, а связывают с ним (см. Love [II, Мусхе-
лишвили [11, Ландау, Лифшиц [11, Филоненко-Бородич [11 и др.) фор-
формулой *)
з
С0г. = -7>-(rot U)t = —
Таким образом, каждая точка среды в моментной теории упругости
обладает шестью степенями свободы, а в классической теории упругости —
тремя степенями свободы.
§ 4. Основные уравнения в компонентах напряжения
1. Уравнения движения в классической теории. Выделим из среды про-
произвольную часть и обозначим область, занимаемую этой частью, через Q,
а ее границу — через Г. Напишем условие равновесия выделенной части.
Для этого надо просуммировать внешние силы, действующие на нее, и при-
приравнять сумму инерционным силам с обратным знаком. Аналогично сле-
следует поступить и с моментами.
При подсчете сил в предположениях классической теории упругости
следует учесть:
1) Напряжения. В каждой точке у поверхности Г в момент времени t
) р	у р	р
действует напряжение %м (у, f), где п — нормаль к поверхности Г в точке у,
внешняя по отношению к Q. Сумма этих сил выражается интегралом
еде dY — элемент площади поверхности Г.
2) Массовые силы. В каждой точке х области (или части) Q в момент
времени t действует массовая сила вГ (х, t). Сумма этих сил выражается
интегралом
где dx — элемент объема, р — плотность среды, которую, если не оговорено
обратное, будем считать не зависящей от положения точки х и от времени t.
х) Хотя тензорным исчислением мы не пользуемся, все-таки употребляем, и очень часто,
единичный тензор — символ Кронекера 6ty и так называемый s-тензор—символ Леви-Чивита
Ъщ. Ьц = 0, если i ф /, и 8ц = 1, ъць = 1 или е^ = —1, в зависимости от того, образуют ли
i, /, k четное или нечетное число перестановок чисел 1, 2, 3; г^к = 0, если по крайней мере два
из трех индексов i, /, k равны.
2 В. Д. Купрадзе

18	основные понятия и аксиоматизация
3) Инерционные силы. Если и (х, f) — смещение точки х, то ускорение
этой точки в момент времени t равно д2и (х, t)/dt2, а силы инерции, при-
приложенные к элементу объема dx, равны
Р
Сумма этих сил дается интегралом
д2и (х,
Q
Из условий равновесия (равенство нулю суммы главного вектора актив-
активных сил и главного вектора инерционных сил.) следует равенство
J т<»> (у, t)dr + \ pF (x, t)dx = \p ^ t] dx.	D.1)
Г	Q	Q
Аналогичный подсчет моментов и условие равновесия (равенство нулю
суммы главного момента активных сил и главного момента инерционных
сил) дают формулу
[у X %™(yJ)dT + Jp* x3T(x,t) dx=\px x дЩ^' ° dx. D.2)
Г	Q	Q
Знак «X» между векторами означает их векторное умножение.
Векторное равенство D.1) с учетом формул B.1) примет вид
з
J ^faggj	J	J	ОТ
Г 1=1	Q	Q
и в силу формулы Гаусса—Остроградского перепишется так:
Отсюда в силу произвольности Q следует равенство
0. (/=1,2,3),	D.3)
справедливое в любой точке рассматриваемой среды и в любой момент
времени.
Подвергнем аналогичному преобразованию равенство D.2). С учетом B.1)
оно принимает вид
Q It к
Применяя формулу Гаусса—Остроградского, получим
С U к
Q hk

* 4]	ОСНОВНЫЕ УРАВНЕНИЯ В КОМПОНЕНТАХ НАПРЯЖЕНИЯ	19
Первый член в левой части обращается в нуль в силу D.3) и, следовательно.
2
U к
Отсюда окончательно получаем
Равенство D.4) показывает, что компоненты напряжения (в классиче-
классической теории) образуют симметричную матрицу (т. е. тензор напряжений
симметричен) и, следовательно, независимыми из девяти скалярных вели-
величин %ц (х, 0 остаются шесть, которые связаны между собой тремя соотно-
шениями D.3).
Соотношения D.3) носят название основных уравнений движения (дина-
(динамики) классической теории упругости в компонентах напряжения.
Если известны компоненты напряжения хц и компоненты смещения ut
в каждой точке рассматриваемой среды и в любой момент времени, то в клас-
классической теории упругости вполне определено деформированное и напря-
напряженное состояние среды. Нахождение этих девяти скалярных величин и
является основной задачей классической теории упругости. Напоминаем, что
они связаны пока только тремя соотношениями D.3).
Предположим, что внешние силы не зависят от времени. Тогда есте-
естественно считать смещения и напряжения независимыми от времени и урав-
уравнения D.3) принимают вид
2*^L + p5r.(x) = ().	D.5,
i
Уравнения D.5) называют уравнениями равновесия.
2. Уравнения движения в моментной теории. Рассмотрим произволь-
произвольную часть среды и напишем условия равновесия этой части.
Подсчет сил в предположениях моментной теории производится совер-
совершенно таким же образом, как в классической теории и приводит к соотно-
соотношению D.3).
При подсчете моментов, кроме моментов сил, надо учесть самостоятель-
самостоятельные моменты пар. Остановимся на этом более подробно.
Обозначим выделенную часть через Q, а границу — через Г. При под-
подсчете моментов, действующих на эту часть, следует учесть:
1)	момент силовых напряжений:
J У X т<*> (у, t) dY\
г
2)	м о м е н т н ы е напряжения:
г
3) момент массовых сил:
J р* х Т (х9 0 dx\
Q
4)маабовые моменты:
2*

20	основные понятия и аксиоматизация	грл# j
5) моменты инерционных сил:
— J Р*
х
д*и (х,
6) «с п и н о в ы й» момент, соответствующий внутренним враще-
вращениям
, t)
где ? — специальная динамическая характеристика *) (см. Аэро, Кувшин-
ский [1]—[3], Пальмов [11, Nowacki [41 [и др.).
Из условий равновесия следует равенство
j [У X т<»> (у, t) + ц(»> (у, Щ dY + J [px X Т (х, t) + р^ (х, t)] dx =
Преобразуем эту формулу, /-я компонента первого слагаемого левой
части, с учетом B.1), B.2) и формулы Гаусса—Остроградского, примет вид
J 2
J S [S (
[ 2
В силу этого предыдущая формула перепишется так:
J2
Из этого соотношения, в силу произвольности Q, применяя формулу D.3),
которая, как уже было отмечено выше, справедлива и в моментной теории,
получим
1д^1 S	./) = ^^2^.	D-6)
Уравнения D.3) и D.6) представляют собой основные уравнения движе-
движения моментной теории упругости в компонентах напряжения.
Основными уравнениями равновесия моментной теории в компонентах
напряжения будут D.5) и
2	°- D-7)
х) Здесь ради простоты за элементарный объем принят шар с равномерно распределенными
массами (симметричный волчок). В случае несимметричного волчка 9 заменяется тензором
момента инерции.

? 5]	ЗАКОН ГУКА В КЛАССИЧЕСКОЙ ТЕОРИИ	2J
Отметим, что уравнение D.6) в классической теории заменяется уравне-
уравнением D.4), выражающим симметричность тензора напряжений. В моментной
теории тензоры напряжений асимметричны (отсюда и встречающееся в лите-
литературе название — асимметричная теория).
§ 5. Закон Гука в классической теории
1. Компоненты (тензора) деформации. Все сказанное до сих пор отно-
относится к любой сплошной среде, для которой применимы основные законы
механики и имеет смысл понятие напряжения. В теории упругости рас-
рассматриваются упругие среды. Свойства упругости среды выражаются спе-
специальной зависимостью (которая носит название закона Гука) между напря-
напряжениями и деформациями, точнее, между величинами, характеризующими
напряженное и деформированное состояние среды.
Напряженное состояние, как уже отмечалось, характеризуется ком-
компонентами напряжения %ц (см. § 2).
Введем теперь величины, характеризующие деформированное состоя-
состояние. Под деформацией понимается такое изменение положения точек среды,
при котором меняются взаимные расстояния между точками. Очевидно,
не всякое изменение положения точек среды вызвано деформацией. При жест-
жестком перемещении среды, (жесткое поступательное перемещение и жесткий
поворот) меняются положения точек среды — точки смещаются, но взаим-
взаимные расстояния между ними не изменяются и, следовательно, среда не дефор-
деформируется.
Возьмем произвольную точку х = (хЛу х2, х3) недеформированной среды
(в момент времени t0) и рассмотрим малую окрестность этой точки. Рас-
Рассмотрим произвольную точку выделенной окрестности; обозначим ее через
х + ?. Вычислим изменение малого вектора ? = (?19 |2, ?3) при деформации.
Здесь х является началом этого вектора, а х + | — его концом. Точка х
в момент времени t займет положение х + и (х, t)f а точка х -f | — поло-
положение х + ? + и (х + 2> t). Таким образом, изменение вектора |, которое
обозначим через Д| (#, t) или просто через Д?, вычисляется по формуле
Д?(х, t) = u(x + Z, t) — u(x9t).
Применяя формулу Тейлора и отбрасывая в виду малости вектора g члены
более высокого, чем |?|, порядка малости, получим
JUt ул> ч g.	E.1)
^ш^шт	UXi	*' '
/
Рассмотрим представление
дщ __ 1 / дщ . дщ \ , 1 / ^м; 5w/ \
dXj	2 \ dXj ' dxi J 2 \ 5x/ dxt ) "
Величины ~	~- образуют антисимметричную матрицу. Они суть ком-
OXj	OXi
поненты вектора вихря и и характеризуют малый поворот рассматриваемой
части среды как целого. Если введем обозначения
0Л (*,/) = 4- (rot и (х, t))k = 4- V дщ^ ° гкт	E,2)
ТО
19—2-л-	<м>

22	основные понятия и аксиоматизация	[Гл# i
Назовем О = (ftl9 02, Ф3) вектором жесткого вращения, а #!, 02, Oj — ком~
понентами вектора жесткого вращения. Не следует смешивать вектор жест-
жесткого вращения Ф с вектором внутреннего вращения со, рассмотренным нами
в моментной теории (см. § 3).
Величины
образуют симметричную матрицу. Их называют компонентами (тензора)
деформации (в точке х в момент t).
В этих обозначениях формула E.1) примет вид
откуда следует, что деформацию вблизи каждой точки можно рассматри-
рассматривать как линейную и однородную функцию координат.
Деформированное состояние характеризуется изменениями расстояний
между точками. Следовательно, деформированное состояние в любой точке х
может быть охарактеризовано изменениями длин (или квадрата длин) всех
малых векторов вида |.
Будем рассматривать малые смещения. Вектор смещения и его произ-
производные по декартовым координатам будем считать настолько малыми, что
произведениями этих величин можно пренебречь. Вычислим | g + Д| |2 — | ? |2.
Из формулы E.1) получим
^-	E-6)
Точно так же выражается квадрат длины векторного приращения |Д||а:
EJ)
Из формул E.6) и E.7) видно, что изменение расстояний между точками
и, следовательно, деформированное состояние, характеризуется исключи-
исключительно компонентами деформации.
Если компоненты деформации равны нулю: eti (x, t) = 0, то малая
окрестность точки х находится в таком же состоянии, что и в момент вре-
времени ?0 (т. е. в недеформированном состоянии). Можно сказать, что состоя-
состояние этой окрестности в момент времени t может отличаться от состояния
ее в момент времени t0 только лишь жестким смещением. Если же вц (х, t) = О
для всякой точки х рассматриваемой среды, то приведенное заключение
справедливо для всей среды.
Очевидно, справедливо и обратное утверждение: если в какой-нибудь
окрестности точки х расстояние между любыми двумя точками не меняется
(т. е. расстояния в моменты времени t0 и t совпадают), то компоненты дефор-
деформации равны нулю: e?J- (x, t) = 0.
2. Формулировка закона Гука. Из сказанного в предыдущем пункте
ясно, что должна существовать зависимость между компонентами напря-
напряжений и соответствующими им компонентами деформации. Закон Гука

5]	закон гука в классической теории	23
предполагает самую простую, линейную зависимость между этими величи-
величинами. Этот закон математически записывается так:
гц(х, *)= Ъст{х, t)eik(x, t),	E.8)
где с^цг (х, t) — некоторые числа, которые носят название упругих постоян-
постоянных. Они постоянны в том смысле, что не зависят от компонент деформации
и, следовательно, от компонент напряжения.
В этой книге мы будем предполагать (не напоминая об этом каждый раз),
что упругие постоянные не зависят от времени. Кроме того, будем рассма-
рассматривать случай специальной, но весьма важной зависимости этих постоян-
постоянных от положения точки х.
Если упругие постоянные не зависят от положения точки в среде, то
среду называют однородной (в смысле упругих свойств, но не в смысле рас-
распределения масс, с которым она явно не связана). Если же упругие постоян-
постоянные меняются от точки к точке, то среда [называется неоднородной.
Из симметричности матриц ||тг/|| и \eti\ следует
сцш = cijki = cjiik — саы-	E.9)
Ввиду этого число различных упругих постоянных от восьмидесяти одного
сводится к тридцати шести. Ниже мы покажем, что эти постоянные, кроме
E.9), удовлетворяют еще условию
E.10)
в силу которого указанное число уменьшается до двадцати одного.
Закон Гука предполагает также, что компоненты деформаций выра-
выражаются (линейно и однозначно) через компоненты напряжений, т. е. си-
система E.8) однозначно разрешима относительно компонент деформаций
eif= T&CtfikTik.	E.8')
?, k
Формулы E.8) и E.8') содержат предположение об упругости рассматри-
рассматриваемой среды; под упругостью понимается свойство среды восстанавливать
свою форму после прекращения действия на нее сил. Точнее, упругость —
это такое состояние сплошной среды, при котором между напряжениями и
деформациями существует взаимно однозначная зависимость, причем нуле-
нулевым напряжениям отвечают нулевые деформации.
Упругие постоянные определяются экспериментально. О методах опре-
определения упругих постоянных можно найти обстоятельные сведения в рабо-
работах, указанных в § 15 (см. 15.18), где приведены также таблицы численных
значений упругих постоянных для многих материалов.
3. Изотропная среда. Компоненты деформаций и напряжений и по-
постоянные, связанные законом Гука, зависят от ориентации осей координат.
Если упругие постоянные среды ciflk не зависят от ориентации осей коорди-
координат, или, как иногда говорят, упругие свойства среды одинаковы во всех
направлениях у то ©реду называют изотропной. Если среда не является изо-
изотропной, ее называют анизотропной.
Число различных упругих постоянных в изотропной среде сводится
к двум. Это нетрудно показать (см., например, Love [I I, Sneddon, Berry [11,
Филоненко-Бородич [11, Лехницкий [II), воспользовавшись формулой
E.8) и свойствами компонент деформаций и напряжений. Получаются
соотношения:
= h&ifiik + f* (&ifijk + б^бу,).	E.11)

24	основные понятия и аксиоматизация	(рл# i
Подставляя E.11) в E.8), имеем
Т|/ (*,/) = Я6„ S ^ (*,*) + 2|x^7 (х, /).	E.12)
Постоянные X и \i носят название постоянных Ламе. Они, вообще, зави-
зависят от положения точки. Мы будем рассматривать в основном однородные
(в смысле упругих свойств) среды и, если обратное не будет оговорено, будем
предполагать, что А, и \л не зависят от положения точки х.
Формула E.12) выражает закон Гука для изотропной среды. Иногда
(см., например, Мусхелишвили [1]) вводят обозначение
в(*. *)= 2 ***(*, *)	E.13)
k
и закон Гука записывают в виде
tu (x9 t) = UUS (*, t) + 2^ец (х9 t),	E.14)
или, используя формулы E.4), в виде
(*^L iaga)	E.15)
где и = (Их, н2, и3) — вектор смещения.
В закон Гука мы включили также предположение о разрешимости
системы E.14) относительно компонент деформации для любых значений
компонент напряжений. Это условие, как легко видеть, сводится к условиям
(х=^0, ЗА, + 2ц=?0,	E.16)
при выполнении которых из E.14) получаем
e{J(x, Q^-j-^fr, 0t	S^(**)	E14')
Иногда вводят в рассмотрение другие упругие постоянные: модуль
упругости Е (который называют также модулем Юнга), коэффициент Пуас-
Пуассона а, модуль всестороннего сжатия k, пуассоново число т. Эти числа свя-
связаны с постоянными Ламе следующими соотношениями:
) f
4. Трансверсально-изотропная среда. Трансверсально-изотропной назы-
называют (см. Love [11) упругую среду, если имеется ось такая, что в любой
плоскости, перпендикулярной к этой оси, упругие свойства среды одинаковы
по всем направлениям; иначе говоря, все плоскости, перпендикулярные
указанной оси, являются плоскостями изотропии.
Предположим, что декартова система координат выбрана таким обра-
зом, чтобы ось Х3 была направлена перпендикулярно к плоскости изотропии.
Тогда упругие постоянные не будут меняться при вращении этой системы
вокруг оси Xs. Таким образом, среда обладает трансверсальной изотропией
тогда и только тогда, когда существует такая система Х^^Х^ декартовых
координат, при вращении котврой вокруг оси Х3, т. е. при преобразовании
вида
Х{ = Х\ COS ф + *2 Sin ф, ;С2 = Х2СО8ф	Л^Пф, Хз = Хз	E.18)
упругие постоянные не меняются. Здесь ф — произвольный угол.

Л б]	ЭНЕРГИЯ ДЕФОРМАЦИИ В КЛАССИЧЕСКОЙ ТЕОРИИ	25
В этом случае число различных упругих постоянных (см. Love [11,
Лехницкий [11, Sneddon, Berry [11 и др.) равно пяти и закон Гука при-
принимает вид
ти = сге1г + с2е22 + с3е33,
Т22 = ^2^11 ~Г ^1^22 ~Г
Т23 =
Т13 =
Tf9 	 7" (
E.19;
Мы не будем останавливаться более подробно на изучении трансвер-
сально-изотропных сред. К этому вопросу мы вернемся в конце книги.
Отметим здесь только следующее. Соотношения E.19), как алгебраическая
система уравнений для компонент деформации, должны быть разрешимы
относительно этих компонент для любых Хц. Это условие налагает некоторые
ограничения на постоянные
Численные значения постоянных для многих сред вычислены экспери-
экспериментально (см. Huntington [II, Лехницкий [11).
Вместо термина «трансверсально-изотропная среда» употребляют также
термин «гексагональная система», так как в этом случае среда обладает
гексагональной упругой симметрией.
§ 6. Энергия деформации в классической теории
1. Закон сохранения энергии. Пусть упругая среда [в момент вре-
времени t0 находится в естественном состоянии и занимает в системе Х1Х2Х3
область D с границей S. Рассмотрим состояние среды в момент времени
t (t > to)9 когда она внешними воздействиями выведена из состояния покоя
и находится в деформированном состоянии.
Вычислим работу, произведенную силами, вызвавшими деформации
от момента t0 до t. Такими силами в классической теории упругости являются
внешние напряжения и массовые силы. В этой теории не учитываются влия-
влияния тепловых источников и предполагается, что процесс деформации проте-
протекает настолько медленно, что в каждый момент времени в теле устанавли-
устанавливается термодинамическое равновесие, причем процесс протекает изотер-
изотермически.
Обозначим через Ж (t) работу, производимую внешними напряжениями
и массовыми силами в промежутке времени (t0, t), а через &31 (t) — эту же
работу в промежутке времени (t, t + df). Вычислим сначала d0? (t).
Точка среды, занимающая в состоянии покоя положение х, в момент
времени t займет положение х + и (х, f), а в момент времени t + dt — поло-
положение х + и (х, t + dt). Следовательно, смещение точки х за промежуток
времени dt будет и (х, t + dt) — и (х, t)> которое с точностью до бесконечно
малых высшего порядка но отношению к dt можно представить в виде
dt
Выделим малую часть поверхности S вокруг точки у ? S и обозначим ее
через dS. Внешние напряжения, действующие на площадку dS, можно

26	основные понятия и аксиоматизация	[Гл. I
представить (см. п. 3, § 1) в виде т(л> (#, t) dS, где п = (пг, п2, п3) — орт
внешней нормали поверхности «S в точке у. Таким образом, работа внешних
напряжений, действующих на площадку dS в промежутке времени (/, t + df),
будет равна
а вся работа, производимая внешними напряжениями, выразится интегралом
S	i
Аналогично вычисляется работа, совершаемая массовыми силами SF
за промежуток (t, t + df):
D	i
Следовательно (см. B.1)),
S i.j	D i
Отсюда, применяя формулу Гаусса—Остроградского, получим
D t9j
С помощью формулы D.3) и обозначения
первый интеграл в правой части формулы F.1) примет вид dE(k) (t)/dt.
?(k> (t) есть кинетическая энергия среды в момент времени t. Кинетическая
энергия частицы с массой dm = р dx в момент времени t равна -^ pv2 (x, t) dx,
где v (%, t) — скорость частицы в момент времени t, т. е. v (x, t) =
= ди (ху t)ldt. Сумма всех этих величин и есть кинетическая энергия среды.
Из F.2) следует, что кинетическая энергия не зависит от деформиро-
деформированного состояния в данный момент времени.
Изучим теперь второе слагаемое в правой части формулы F.1). Преоб*
разуем выражение ' * ' dt. Очевидно, с точностью до бесконечно малых
высшего порядка по отношению к dt это выражение можно представить
в виде
дЩ (*, 0 dt _ but (x, t + dt) __ дщ (x, t) = d дщ (x, t) ^
dxf dt	dxj	dxj	dXf *
Таким образом,
где elf—компоненты деформации (см. E.4)).

А 6]	ЭНЕРГИЯ ДЕФОРМАЦИИ В КЛАССИЧЕСКОЙ ТЕОРИИ	27
Из F.1), F.2), F.4) следует
d®, = dEik) + J ^ тн deu dx-	F-5)
D t,/
Предположим теперь, что рассматриваемая среда изотропная, с упру-
упругими постоянными Ламе X и |х. Введем функцию
Е (*, t) = А ( ? е« (х, О)' + Ц S */* (х, *).	F.6)
Она представляет собой квадратичную форму относительно компонент
деформации, и в силу закона Гука (см. E.14))
дЕ	дЕ V4 дец	а -
Из F.5) и F.7) следует, что
d® = dE{k) + dE{p\	F.8)
где
()@ \(х, f)dx,	F.9)
Интегрируя F.8) от t0 до t и принимая во внимание, что ?(к) (^0) =
?^> (f) 0, получим
F.10)
(t) представляет потенциальную энергию деформации тела в момент
времени t. Она, в отличие от кинетической энергии ?(k> (f), существенно
зависит от деформированного состояния и представляет собой работу, кото-
которую должны совершить внешние напряжения и массовые силы, чтобы вызвать
данное деформированное состояние.
Формула F.10) выражает закон сохранения энергии: работа всех сил,
вызвавших деформированное состояние, численно равна сумме кинетиче-
кинетической энергии среды и потенциальной энергии деформации.
Формула F.10) справедлива и для анизотропной среды. Рассмотрим
произвольную (не обязательно изотропную) упругую среду и введем в рас-
рассмотрение функцию
Я (*,. 0 = у . S стеи (х, t) еы (х, /),	F.6')
где СцЫ — упругие постоянные, определенные законом Гука (см. E.8)).
В силу формул E.10), E.8) и предположения, что СцЫ не зависят от вре-
времени, получим
дЕ	VI			дЕ __ VI дец	/(* 7П
"Ш~ ~~ LJ °^ывы ~ Т/" "W ~" Zj Т/г ~дГ'	( * '
k,l	' i, j
Отсюда, если введем функцию F.9), в которой Е (х, t) определена на
основании F.6'), получим формулу F.10).
2. Удельная энергия деформации. Из F.9) видно, что? (х, t) представ-
представляет собой потенциальную энергию, рассчитанную на единицу объема
(в точке х в момент времени t). Ее называют удельной энергией деформации
{классической теории).
Таким образом, удельная энергия деформации для произвольной ани-
анизотропной среды выражается формулой F.6'), а для изотропной среды —

28	основные понятия и аксиоматизация	[Гл. I
формулой F.6). Применяя формулы E.19), из F.6') можно вычислить удель-
удельную энергию деформации для трансверсально-изотропных сред и для дру-
других частных случаев анизотропии.
Выражение для удельной энергии деформации было получено приме-
применением закона Гука и пока не обоснованного предположения E.10). Однако
оно может быть получено и без применения закона Гука и предположе-
предположения E.10).
Временно отвлечемся от того, что мы знаем об удельной энергии дефор-
деформации и обозначим через Е (ху t) работу деформирования или, что то же
самое, потенциальную энергию деформации, рассчитанную на единицу
объема в точке х в момент L Это надо понимать в том смысле, что рас-
рассматривается среда, находящаяся в состоянии покоя в момент времени /Ot
и берется малая часть dD с центром тяжести в точке х. Вычисляется потен-
потенциальная энергия деформации этой части в момент t. Предел отношения
энергии к mes (dD), когда mes (dD) стремится к нулю, и есть Е (х, t).
Напомним, что кинетическая энергия не используется при вычислении
работы, производимой деформацией.
Будем называть Е удельной энергией деформации; изменение Е в про-
промежутке времени (t, t + dt) обозначим через dE. Из F.5) следует, что
dE (х, t) = 2 **/ (х, t) deu (x9 t).	F.11)
Величины ец вполне характеризуют деформированное состояние среды*
и потенциальная энергия, зависящая также исключительно от деформиро-
деформированного состояния, должна являться функцией этих величин. По этой при-
причине вместо Е (х, t) и Е будем писать иногда Е (etj) (x, t) и Е (еИ) соответ-
соответственно.
Разложим Е (ец) по степеням ец вблизи состояния покоя (ец = 0) в
отбросим члены выше второго порядка относительно ец (рассматриваются
малые деформации). Будем иметь
Е (еИ) = Со + 2 сиеа + ^ . ? {с,/*Л/*«,	F.12)
где с0, Сцу cijkl — постоянные или, точнее, величины, не зависящие от ком-
компонент деформации и, следовательно, от компонент напряжений, но, вообще
говоря, зависящие от положения точки в среде.
Ввиду того, что тензор деформации симметричен ец = eib произведе-
произведение е^-е^ не меняется при перестановке индексов в каждой из пар (/, /) и (k, /).
Кроме того, это произведение не меняется и при перестановке самих этих
пар. Поэтому без ограничения общности можно считать, что коэффициенты Сц
и djki удовлетворяют этим же условиям, т. е.
Сц = Сц, СцЫ = СпЫ = СШк = Ст.	F.13)
Из соотношения F.11) следует, что
щг=х"-	<6Л4>
Таким образом, частная производная функции Е по какой-либо из ком-
компонент деформации есть одноименная компонента напряжения.
Производную Е по компонентам деформации можно вычислить, исполь-
используя выражение F.12). Будем иметь
дЕ	. у*
-Щ7 = СИ + jbfijkfiki-

Л 7|	ЭНЕРГИЯ ДЕФОРМАЦИИ И ЗАКОН ГУКА В МОМЕНТНОЙ ТЕОРИИ	29
Следовательно,
Заметим, что в разложении F.12) с0 = О, так как из условия ец = О
следует равенство Е = 0 (в начальный момент t = t0 среда находится в неде-
формированном состоянии). Кроме того, если отсутствуют деформации,
то отсутствуют и напряжения, т. е., если все e{j = 0, то и все т^ = 0. В силу
этого из предыдущей формулы заключаем, что Сц = 0.
Следовательно,
1 ^ " - "	F.15)
= 4 2
и для компонент напряжения получим
*//= 2 *'/***•	F.16)
Соотношения F.16), устанавливающие связь между компонентами напря-
напряжений и деформаций, выражают закон Гука для любой упругой среды в рам-
рамках классической теории: деформации среды пропорциональны приложенным
напряжениям, точнее, деформации суть линейные комбинации напряжений.
Следует отметить, что упругие постоянные cifkl удовлетворяют условиям
E.10)* (см. F.13)), которые выше были приняты как предположения.
Приведенные рассуждения можно рассматривать как физические сооб-
соображения, обосновывающие закон Гука.
Из F.15) и F.16) можно получить другие представления удельной
энергии деформации, например,
Е = Щхцеф	F.17)
откуда
Можно показать, что постоянные cijkl образуют тензор четвертого
порядка.
Из физического смысла следует, что удельная энергия деформации пред-
представляет собой положительно определенную квадратичную форму шести
независимых величин ец. Это условие налагает на упругие постоянные неко-
некоторые ограничения. В случае изотропной среды эти ограничения сводятся
к следующему:
IX > 0, 3^ + 2(x>0.	F.19)
Хотя экспериментально показано (см. по этому поводу Мусхелиш-
вили [13, Ландау, Лифшиц [1], Love [II, Grammel [11, Huntington [1]
и др.), что X > 0, |л > 0, однако мы подчиним эти постоянные более слабым
ограничением F.19).
Отметим, что из F.19) следует E.16).
§ 7. Энергия деформации и закон Гука в моментной теории
1. Закон сохранения энергии. Пусть в начальный момент t = t0
среда находится в недеформированном состоянии. Рассмотрим последую-
последующее деформированное состояние в момент времени t и вычислим работу
внешних воздействий, вызвавших его. Такими воздействиями в моментной

30	основные понятия и аксиоматизация	грл# |
теории являются внешние силовые и моментные напряжения и массовые
силы и моменты.
Появление моментных напряжений и массовых моментов было связано
с появлением внутренних вращений. Поэтому естественно предположить,
что указанные моменты совершают работу только на внутренних враще-
вращениях, а силовые напряжения и массовые силы — только на смещениях.
Обозначим через 52 (t) работу, производимую всеми указанными силами
и моментами за промежуток времени (t0, t), а через dffl, (t) — работу, совер-
совершенную за промежуток (t, t + dt). Вычислим d@t (t). Работа, произво-
производимая силовыми напряжениями и массовыми силами, была вычислена
в § 6 (правая часть равенства F.1)). Вычислим работу, производимую
моментными напряжениями. Рассмотрим точку среды, которая в состоянии
покоя (в момент времени t0) занимает положение х. В моментной теории
упругости (см. § 3) каждая точка х обладает шестью степенями свободы
и ее состояние в момент времени t характеризуется вектором смещения
и (х, t) и вектором внутреннего вращения со (х, t). Приращение вектора вра-
вращения за промежуток времени (t, t -f- dt) обозначим через dco (х, t):
d(x>(x, t) = (dco^x, t), d(o2(x, t), d@3(x, /)) = co(x, t-\-dt) — (d(x, t).
Это приращение, с точностью до бесконечно малых высшего порядка па
сравнению с dt, представится в виде
да) (х, 0
dt
dt.
Работа, производимая внешними моментными напряжениями, действующими
на площадке dS за промежуток времени (/, t + dt), равна
где п — единичная нормаль поверхности S в точке у, внешняя по отноше-
отношению к области D, занимаемой средой, а у — точка, находящаяся в центре
тяжести площадки dS.
Применяя формулу B.2), легко вычислить работу, производимую внеш-
внешними моментными напряжениями, действующими на 5 за промежуток
(t, t + dt). Будем иметь
S	,l
или, после применения формулы Гаусса—Остроградского,
f dt
J
2
Работа, производимая массовыми моментами, действующими на D
за промежуток времени (tf t + dt), равна
2
D	i
Следовательно, для мощности ddlldt имеем

Л 7|	ЭНЕРГИЯ ДЕФОРМАЦИИ И ЗАКОН ГУКА В МОМЕНТНОЙ ТЕОРИИ	31
Преобразуем первый интеграл в правой части G.1) с помощью D.3),
а третий интеграл — с помощью D.6). Получим
Введем обозначение:
^J2[(^ilJ(^|^J]	G.2)
2
D i
Тогда
dt	dt
b t. /
Воспользовавшись формулой F.3) и формулами
*°ffi° Л = со, (х, * + Л) — со, (х, 0 = Ad* (x, О,
i(x% t) ,,	 dtoj (x, t + dt) __ d(Oj(x, t) __ - fleat- (*, Q
справедливыми с точностью до бесконечно малых высшего порядка по отног
шению к dt, подынтегральному выражению можно придать следующий вид;
S (у* it + (i,, d(o/t-) J dx9	G.4)
где
Величинам u?i можно придать более удобный вид (см. E.3), E.4)),
% = «/, + S e*/i (**—<*>*),	G.6)
где eft — компоненты деформации в классической теории, а ^ — компо-
компоненты жесткого вращения (см. § 5, п. 1).
Назовем величины ufi компонентами деформации в моментной теории,
а со,, — компонентами кручения—изгиба.
Из G.3) и G.4) следует, что
где
D i9 j
?(k) (f) есть кинетическая энергия среды. Она не зависит от состояния
деформации в рассматриваемый момент времени t. Следовательно, dEik> есть
приращение кинетической энергии за промежуток времени (tt t + dt).
d?(p> зависит только от состояния деформации. В самом деле, если
среда из естественного состояния покоя выведена любым деформированием

32	основные понятия и аксиоматизация	[Гл. I
(в смысле моментной теории) и потом (в момент времени t) перешла в новое
со стояние покоя, то ?<k> (t) = 0, и, следовательно, &$, = dE^K Таким
образом, d?(p> есть работа деформации за промежуток (t, t + dt) или
d?(p) = ?(р) (t + dt) — ?(p> (t)9 где ?<р> (?) есть работа, которую должны
совершить внешние воздействия (силовые и моментные напряжения,
массовые силы и моменты), чтобы вызвать деформированное состояние,
соответствующее моменту времени t.
Таким образом, формулой G.7) выражен закон сохранения энергии:
мощность равна сумме скоростей изменения кинетической и потенциальной
энергии.
2. Удельная энергия деформации. Теперь легко получить выражение
для удельной энергии деформации в моментной теории. Обозначим ее через
Е (х, t) и определим как работу деформирования или, что то же самое,
как потенциальную энергию деформации, рассчитанную на единицу объема
в точке х в момент времени / (см. § 6, п. 2).
Пусть dE (x, t) — приращение Е за промежуток времени (t, t + dt);
тогда из G.8) получим
dE = 2 (т/7 dua + V>n da»)*	G.9)
Разложим Е по степеням ulf и (oif вблизи состояния покоя {иц = 0, ю17 = 0)
и отбросим в разложении члены, содержащие иц и оо?/ в степенях выше вто-
второй (рассматриваются малые деформации). Будем иметь
Е = Со + ^CijUij + S C\fuii + 4- Ц CijikUijUik +
S C<d(d +	S ciU®	GЛ0)
Изучим разложение G.10). Так как при и(/=0 и cot/==0 величина Едолжна
равняться нулю, с0 = 0.
Из G.9) имеем
Х	!*	G11)
Частные производные от ?" по ^^ и со?/- можно вычислить и из представле-
представления G.10). Вычисляя из G.10) эти производные и учитывая G.11), получим
Vu = <%i j-iS clfiktoik + 4- S cUfyG)^ + -^- S c'ikifUik*	G.12')
z fe,/	^ г. k	z i9k
Если отсутствуют деформации, т. е. если иц = со/; = 0, то должны отсут-
отсутствовать и напряжения, т. е. должны выполняться равенства xif = (х?/ = 0.
Учитывая эти условия, из G.12) и G.12') получим сц = Cq = 0.
Таким образом, удельная энергия деформации (см. G.10)) примет вид
Е — у S (CijikUifulk-\- c'ijik(Oij(oik +c"ijikuij(oik).	G.13)
Рассмотрим среду, обладающую центром симметрии. Такая среда обла-
обладает свойством инвариантности упругих постоянных при замене направле-
направлений осей координат на противоположные. Легко видеть, что при такой

Л 7]	ЭНЕРГИЯ ДЕФОРМАЦИИ И ЗАКОН ГУКА В МОМЕНТНОЙ ТЕОРИИ	33
замене координат величины uti не меняются, а величины сог/- меняют знак
на противоположный.
В дальнейшем, не оговаривая этого, всегда будем считать, что среда
обладает центром симметрии. Заменяя направление осей координат на
противоположное, из G.13) получаем cifki = 0 и, окончательно,
Е=Т S (CijlkUijUik + C'ijik<dij(i)ik)*	G.13')
Z i, /, hk
3. Закон Гука. Так как произведения ици1к и со^со^ не меняются при
перестановке пар индексов (/, /) и (I, k), без ограничения общности можно
считать, что
= c'tktf.	G.14)
Теперь соотношения G.12) и G.12') примут вид
Tt-/= ^CijikUik, 11ц = ^c'ijik(oik.	GЛ5)
Равенства G.15) выражают закон Гука в моментной теории.
Отметим, что соотношения G.15) должны быть разрешимыми относи-
относительно компонент деформации и^и компонент кручения—изгиба cot/-. Это усло-
условие налагает на упругие постоянные ctj-lk и Cqik определенные ограничения.
Подробнее об этом для изотропной среды будет сказано в следующем пункте.
Упругие постоянные определяются из эксперимента. В этом направ-
направлении в моментной теории пока еще мало что известно.
4. Изотропная среда (с центром симметрии). Если среда изотропная,
то обычными приемами можно показать (см. Аэро, Кувшинский [2], Паль-
мов [1], Nowacki [81), что закон Гука G.15) принимает вид
% = Х8а ? "kk + О* — а) и// + 0* + а) иф	G.16)
k
»U = 8б<7 S <*kk + (» + Р) *>U + iP — P) ®/|.	GЛ6')
Здесь а, р, о, 8, X, ц — упругие постоянные.
Таким образом, изотропная среда с центром симметрии характери-
характеризуется шестью упругими постоянными.
Выясним теперь, каким условиям должны удовлетворять упругие по-
постоянные, чтобы соотношения G.16) и G.16') были разрешимы относительно
иц и o)t7.
Складывая хш из G.16) получим
Если ЗА, + 2\х ф 0, то отсюда можно найти ?и«. Подставляя значение
в выражение для тш получим
Если а ф 0 и [л ф 0, то а^ можно найти из выражения для тг/. Окончательно
получаем соотношения
3 В. Д. Купрадве

34
основные понятия и аксиоматизация
Р) И-// ~ (° —
и, аналогично,
справедливые при
Удельная энергия деформации в этом случае примет вид
2Е = X 2 и«И// + (М- + «) S. "//«// + (fx —а) ?
" /	/	f
. G.18)
+• (у + Р)
+ (» —Р)
G-19>
Таким образом, Е представляет собой квадратичную форму восемнадцати
величин иц и cot/. Из физического смысла Е следует, что эта форма должна
быть положительно определенной (Е есть работа, затраченная силовыми и
моментными напряжениями и массовыми силами и массовыми моментами
для перехода среды в данное деформированное состояние из состояния покоя,
рассчитанная на единицу объема). Это условие налагает на упругие постоян-
постоянные некоторые ограничения.
Перенумеруем величины utj и со/у в удобной для нас форме:
Тогда выражение для 2Е запишется в виде
2Е = (К + 2ц) g? + 2^,62 + 2Xg,b + (Я + 2jx) g
+ (8 + 2») it + 2eg4?5 + 28g4g6 + (8 + 2o) Й + 2еЬ6б + (e + 2o) |62
+ 2 (у — a) g16gi7 + (u + P) g?e + 2 (» —
+ (ii + a) fl7 + (y + P) g?8.
Необходимое и достаточное условие положительной определенности
этой формы заключается в положительности всех главных миноров матрицы
ГГ1
НОГ!
on-

§8]
ТЕРМОУПРУГОСТЬ. ЗАКОН ДЮАМЕЛЯ—НЕЙМАНА
35
здесь
I =
Х + 2\х
X
X
X
X
Н =
111 =
\i — a
0
0
— a 0
+ a О
0	u +
0	о —
0
О
о —
IV = V =
+ a 0	fx — a 0
0	u + p 0	о — р
-^-a 0	jx+a 0
0	d —p 0	t)+ p
Условие положительности главных миноров сводится к следующему:
[л>0, ЗЯ + 2ц,>0, а>0, и>0, 3s + 2u>0, р>0. G.20)
Таким образом, условия G.20) являются необходимыми и достаточными
условиями положительной определенности квадратичной формы G.19).
Условия G.20) мы будем считать всегда выполненными. Заметим, что
из G.20) следует G.18).
Применяя формулы G.5), G.6), закону Гука (см. G.16), G.16')) можно
придать более удобный вид:
§ 8. Термоупругость. Закон Дюамеля—Неймана
1.	Деформация с изменением температуры. В предыдущих рассуждениях
не учитывалась температура среды. Рассуждения велись так, будто темпе-
температура одна и та же во всех ее точках и не меняется при деформации. В дей-
действительности же деформация среды сопровождается изменением темпера-
температуры и, наоборот: изменение температуры среды сопровождается ее дефор-
деформацией, вызванной тепловыми расширениями. Если, например, действие
каких-нибудь тепловых источников изменяет температуру среды, даже при
отсутствии внешних напряжений и массовых сил, происходит деформация.
Будем считать, что в момент времени t0 среда находится в состоянии
покоя и температура равна То, а в момент t, под воздействием массовых и
поверхностных сил и тепловых источников, перешла в деформированное
состояние с температурой Т. Т — абсолютная температура. Она зависит
от положения точки и от времени.
Если мы хотим более полно охарактеризовать деформированное состоя-
состояние среды, то надо учесть и те изменения в деформированном состоянии,
которые возникли в результате изменения температуры 6 = Т — То.
2.	Закон сохранения энергии. Обозначим через s?(t) работу деформа-
деформации, т. е. работу, производимую внешними воздействиями для достижения
данного деформированного состояния среды в момент времени t. Тогда зФ (t)
будет работой внутренних сил напряжений за промежуток времени (t0, f).
Пусть ds4- (f) — работа деформации за промежуток (t, t + dt)9 а Q (t)
и dQ (t) — теплота, поглощенная средой за промежуток (/0, t) и (tt t + dl).
соответственно.

36	ОСНОВНЫЕ ПОНЯТИЯ И АКСИОМАТИЗАЦИЯ	грл \
Закон сохранения энергии (первый принцип термодинамики) можно
записать в виде;
d& = ds4> + dQ,	(8.1)
где <% @ — внутренняя энергия среды в момент времени t, a d<S прира-
приращение внутренней энергии & в интервале (t, t + dt).
Примем те же предположения относительно точности вычислений, что
и в классической теории упругости.
Работа деформации (см. F.5)) вычисляется по формуле
=\ >, TUdeudx
и, следовательно,
= f
D
deu dx
He вводя новых обозначений, предположим, что все величины, рас-
рассматриваемые в этом пункте, рассчитаны на единицу объема. Тогда фор-
формула (8.2) запишется в виде
dS = S rif deu + dQ.	(8.3)
Величину dQ с помощью второго принципа термодинамики можно пред-
представить в виде
dQ = Td?*,	(8.4)
где ?? — энтропия среды, рассчитанная на единицу объема.
Таким образом
dS = S xu deu + T d&>.	(8.5)
Если введем свободную энергию (рассчитанную на единицу объема), опреде-
определяемую равенством
то из (8.5) получим
dE = S т17 deti—&>dT.	(8.6)
t, /
3. Закон Дюамеля—Неймана. Применим теперь прием из п. 2 § 6.Роль
удельной энергии деформации здесь выполняет Е — свободная энергия,
рассчитанная на единицу объема. Очевидно, что если пренебречь температур-
температурными влияниями, то свободная энергия ?, введенная в этом параграфе,
совпадает с величиной ? из § 6.
Здесь состояние среды описывается механическими характеристиками вц
(компоненты деформации) и тепловой характеристикой Т (абсолютная тем-
температура). В соответствии с этим свободную энергию Е будем считать функ-
функцией этих величин.
Ниже всегда будем предполагать, что изменение температуры 0 мало
по сравнению с Го. Разложим Е в окрестности естественного состояния
покоя (вц = 0, 0 = 0). Будем иметь
Е (еф 0) = с0 + eft + S спец + ± Г S omeaekl + 2 ? сцеф + с2021.
hi	Liii*kti	iti	J
(8,7)

§ 3]	ТЕРМОУПРУГОСТЬ. ЗАКОН ДЮАМЕЛЯ-НЕЙМАНА	37
Остальные члены в разложении отброшены в силу малости etj и G. с0 =
= Е (О, 0), и так как при etj = 0 и 0 = 0 среда находится в естественном
состоянии покоя, заключаем, что с0 = 0.
Очевидно,
и из (8.6) следует
Из (8.8) и (8.7) следуют равенства
0)==0( Cf/e|Let(/.	(8.9)
В последнем соотношении величины дЕ/де^ и xt/- вычислены для естествен-
ного состояния покоя. Поэтому %ц = 0, и, следовательно, ct/- = 0.
В силу симметричности тензора е(]- произведение Вцвм не меняется при
перестановке индексов i и /, k и /. Это произведение не меняется также при
перестановке пар (i, /) и (&, /). Поэтому без ограничения общности можно
считать, что коэффициенты в (8.7) Сц и СцЫ удовлетворяют условиям
CU = C/ *» CUkl == Cjikl = Cijlk = %f/'	(8-1 0)
Вычислим частную производную по ец от ? из (8.7) и из (8.8), и сравним их.
Получим равенства
**/ =2 ci!kleki + dfi.	(8.11)
Полученные соотношения, устанавливающие линейную зависимость между
компонентами деформации, температурой и компонентами напряжения,
носят название закона Дюамеля—Неймана, Очевидно, если пренебречь
влиянием температуры, закон Дюамеля—Неймана обратится в закон Гука
классической теории для произвольной анизотропной среды.
4. Изотропная среда. Если среда изотропна, то (ср. с F.6) и с E.12))
выражение для свободной энергии запишется в виде (см., например, No-
wacki [1]—[6], Коваленко [II)
а закон Дюамеля—Неймана в виде
)	(8.12)
Здесь Я и \i — постоянные Ламе, а у и m определяются формулами
? = B|х + ЗХ) а, /я = — cJT0,
где а — коэффициент линейного теплового расширения, а се — удельная
теплоемкость при постоянной деформации е = \еИ\ (см. Nowacki [1]—[6],
Melan, Parkus [13, Лебедев [11).
Соотношение (8.12), в тех же предположениях относительно упругих
постоянных, что и в классической теории (см. E.16)), можно разрешить
относительно компонент деформации. Получим (ср. с E.14'))
ут

38	основные понятия и аксиоматизация	[Гл. I
Если в выражение (8.12) внесем выражения компонент деформации через
компоненты смещения, то будем иметь
, t)-yQ(x, <)) + !*( **?;° + дЩЦ\ °). (8Л2')
§ 9. Уравнение теплопроводности
Когда температура в различных точках среды различна, происходит
естественный перенос тепла, называемый теплопроводностью, от мест с высо-
высокой температурой к местам с более низкой температурой. Перенос тепла
в среде имеет атомно-молекулярный характер и происходит без макроскопи-
макроскопических движений.
Предположим, что рассматриваемая среда однородная и изотропная,
и, кроме того, справедливы предположения о малости приращения G =
= Т — То и скорости изменения температуры. Предположим выполненными
также условия, при которых применим закон Дюамеля—Неймана.
Уравнение теплопроводности запишется (см. Carslaw [I], Carslaw,
Jaeger [1], Nowacki [3]) в виде:
1 "~W — k
где Т — абсолютная температура среды, §Р — энтропия, рассчитанная на
единицу объема, q — количество тепла, производимое в единице объема
за единицу времени, k — коэффициент теплопроводности.
Выразим энтропию через основные механические и тепловые характе-
характеристики среды — компоненты деформации и температуру. Согласно Biot [1 ]
это соотношение имеет вид
~~ «+-?-.	(9.2)
где ^eit — объемное расширение, у — коэффициент, определенный в п. 4 §8;
i
б — удельная теплоемкость единицы объема.
Подставив (9.2) в (9.1), получим
Пользуясь равенством Т = То + 9 и малостью 0, предыдущее уравнение
можно записать в виде
2C29 1 ае VI два	1 п	,q оч
i	l	i
где к = klb называется коэффициентом температуропроводности;
Уравнение (9.3) представляет собой уравнение теплопроводности. В ком-
компонентах смещения оно запишется в следующем виде:
где Д — оператор Лапласа.

С
УПРУГИЕ СТАЦИОНАРНЫЕ КОЛЕБАНИЯ
39
Постоянные и, т], у определяются экспериментально (см. литературу
в § 15). Будем предполагать, что они удовлетворяют неравенствам .
YAl>0, x>0.	(9.5)
Условие (9.5) выполняется для всех физических сред (см. Carslaw [11, Лан-
Ландау, Лифшиц [21).
§ 10. Упругие стационарные колебания
В дальнейшем всегда, если не оговаривается обратное, будем считать,
что рассматриваемые упругие среды изотропны и однородны по отношению
к упругим свойствам и обладают центром симметрии в моментной теории.
Кроме того, постоянные, участвующие в рассматриваемых ниже формулах,
предположим не зависящими от времени.
1. Классическая теория упругости. В этой теории основные уравнения
движения даются формулами D.3). Компоненты напряжений связаны с ком-
компонентами деформаций и смещений законом Гука E.12) или E.15).
Пусть внешние воздействия (массовые и поверхностные силы) суть
периодические функции времени. Примем для определенности, что функ-
функция #", участвующая в уравнениях движения D.3), имеет вид
ЗГ(х, t) = Sr^ (x)cosco/-f <F<2> (x)sinco/,	A0.1)
где со, называемая частотой колебания, — некоторое действительное число,
и что аналогично представимы внешние напряжения. Тогда естественно
предположить, что компоненты смещений и, следовательно, деформаций и
напряжений, будут зависеть от времени таким же образом, т. е.
42)
щ (х, /) = u\l) (х) cos со/ + *42) (х) sin со/,
еЬ1 (х, /) = е{ц (х) cos со/ + $? (х) sin со/,
nf (jc, /) = т1/} (jc) cos со/ + tif (x) sin со/.
Подставляя A0.1) и A0.2) в D.3) и E.15), получаем
>	1 о
/ 	 1, Zr,
A0.2)
A0.3)
A0.3')
Введем комплексные величины
т*/ (х) = tIV (x) + h(k)> (x),	A0.4)
где/ — мнимая единица; тогда A0.3) и A0.3') можно записать в виде
„ (х) =
A0.6)
Уравнения A0.5) и A0.6) представляют собой основные соотношения ста-
стационарных колебаний классической теории упругости.

40	основные понятия и аксиоматизация	грл i
2. Моментная теория упругости. Уравнения движения в моментной тео-
теории даются формулами D.3) и D.6). Компоненты силовых и моментных
напряжений связаны с компонентами деформации и кручения—изгиба,
а также с компонентами смещения и вращения законом Гука G.16), G.16')
или G.21), G.2Г).
Предположим, что внешние воздействия (массовые силы и массовые
моменты, внешние силовые и моментные напряжения) — периодические
функции времени, а именно, массовая сила У в D.3) представлена в виде
A0.1), а массовый момент в D.6) —в виде
9(х, t) = 9{l) (x)cosco/ + ^B> (x)sin©f.	A0.7)
Будем считать, что аналогично представимы и внешние напряжения.
Тогда естественно предположить, что компоненты смещения и враще-
вращения и, следовательно, компоненты деформации и кручения—изгиба, а также
компоненты силовых и моментных напряжений, зависят от времени анало-
аналогично, т. е.
щ (х, /) = u\l) (x) cos со/ + и(*2) (х) sin ©/,
со, (х9 /) = ©J1} (x) cos cot + ©*2) (х) sin ©/,
iHj (x, /) = и\У (х) cos со/ + *4/} (х) sin со/,
щ} (X, /) = ©^ (X) COS О)/ + ©(f2) (X) Sin СО/,
%ц (х, /) = т^ (х) cos ©/ + T^f (x) sin со/,
jai7 (x, /) = jxW (x) cos ©/ + [42) (х) sin со/.
Подставив A0.1), A0.7) и A0.8) в D.3), D.6), G.21) и G.2Г), получим
совершенно так же, как в предыдущем пункте уравнение A0.5), следующее
соотношение:
A0.8)
2 % + 2 WiKx) + pS, (дс) + /со2©/ (дс) = 0	A0.9)
i	i\ k
и уравнения G.21), G.2Г), в которых
щ (х) = и{,1) (х) + mf} (х), (oj (х) = ©(/> (х) + Ц2)
У, (х) = <Г<-!) (х) + i^2) (х), У, (х) = ф" (х) + »(/2) (х),	(ШЛО)
%kj (Х) = TiV (х) + п$ (x)f |*л/ (x) = |xiV W ^
3. Теория термоупругости. Состояние среды здесь определяется уравне-
уравнением D.3) и уравнением теплопроводности (9.3) или (9.4). Величины, уча-
участвующие в этих соотношениях, связаны законом Дюамеля—Неймана
(8.12), (8.12').
Предположим, что внешние воздействия (массовые силы, внешние напря-
напряжения и тепловые источники) периодически зависят от времени. Массовые
силы определяются соотношением A0.1). Аналогично представляются внеш-
внешние напряжения и источник тепла в (9.3):
Q (х, /) = QA) (x) cos со/ + QB) (x) sin со/.	A0.11)
Тогда естественно предположить справедливость представлений A0.2) и
6 (х, /) = б*1) (х) cos со/ + 6B) (х) sin ©/.	A0.12)
В принятых предположениях справедливы соотношения A0.5), тепловое
уравнение
Л0 + — Э + кот] div и = — — Q,	A0.13)

§ Ц]	АКСИОМАТИЗАЦИЯ ТЕОРИИ	41
и соотношение Дюамеля—Неймана (8.12'). В этих формулах
6 (х) = 6A) (х) + Ю<2> (х)9 Q (х) = QO> (х) + *Q<2> (х)	A0.14)
и приняты обозначения A0.4).
§ 11. Аксиоматизация теории
Ниже применяются следующие обозначения: R — множество действи-
действительных чисел; Z — множество комплексных чисел; %Г = [t0, tx\ =
= \t (E R\ t0 ^ t ^ /x}; ?3 — трехмерное евклидово пространство; х =
= (xlf x2, x8) = (**), у = (i/x, t/2, f/g) = (yt), . . . —точки пространства ?3;
D — область из Es с кусочно-гладкой границей S; D = D [} S.
Заданием упругой среды с математической точки зрения можно назы-
называть задание области, занимаемой средой в некоторый момент времени t0
и постоянных величин: плотности р и постоянных Ламе А, и [А в классической
теории упругости; постоянных р, X, \i, а, ^, 8, о, р — в моментной теории
упругости; р, К9 р,, у, х, г) — в термоупругости. В связи с этим, среду и
область, занимаемую средой, будем обозначать одной и той же буквой D.
Если необходимо подчеркнуть, что среда D характеризуется постоянными
р, Я, |i (рассматривается классическая теория), то для ее обозначения будем
употреблять запись D (р, К, \i). Аналогичный смысл имеют записи D (р, 1, |а,
а, <!/, 6, о, Р), D (р, Я,, [I, y, и> г]). Эти постоянные должны удовлетворять
некоторым соотношениям вида G.20).
Основной целью теории является определение состояния упругой среды,
т. е. определение компонент вектора смещения, компонент деформации и
напряжения — в классической теории упругости; этих же величин и тем-
температуры — в теории термоупругости; компонент вектора смещения и вра-
вращения, компонент деформации и кручения—изгиба, компонент силового и
моментного напряжений — в моментной теории упругости; все эти величины
являются действительными функциями, зависящими от положения точки
в среде и от момента времени из сегмента 0~. Иными словами, все эти вели-
величины — действительные функции, областью определения которых служит
множество D X <7~.
Высказывание «ср есть действительная функция, определенная на мно-
множестве «5^» заменим краткой записью ср: s& —* R\ теперь очевиден смысл
записи ф : зФ —> Z — «ср есть комплекснозначная функция, определенная
на множестве s&».
Таким образом, и( : D X Т —> /?, хИ : D X Т -— /?, Э : D X Т —^ R
и т. д., где иь %ц и 0 — компоненты смещений, напряжений и приращение
температуры соответственно, участвующие, например, в формулах (8.12)
или (9.4); ut : D —> Z, т<7 : D —»Z, где и( и %ц определены соотношениями
A0.4).
Для построения математической теории упругости необходимо ограни-
ограничить рассматриваемые функции некоторыми требованиями гладкости. При-
Приведенные выше выводы основных соотношений (уравнения движения, закон
Гука и т. д.) справедливы только при соблюдении некоторых условий глад-
гладкости рассматриваемых функций. До сих пор на эти функции не накладыва-
накладывались какие-либо ограничения. Рассуждения носили формальный характер
или, как иногда говорят, требовалось все, что было нужно для справедли-
справедливости применяемых выкладок. Цель такого рассмотрения, как отмечалось
выше, — выработать некоторые соображения, которые позволят сформули-
сформулировать аксиоматическую теорию вопроса. Именно этим займемся в настоя-
настоящем параграфе.

42	основные понятия и аксиоматизация	[Гл I
Введем некоторые классы функций, необходимые в дальнейшем; напри-
например, классы функций, определенные на различных множествах евклидова
пространства произвольного измерения. Пусть ср — функция, определенная
в области Q m-мерного евклидова пространства Ет.
11.1.	Определение, ф принадлежит классу С0 (Q), если <р непре-
непрерывна в Q; ф принадлежит классу Ck (Q), где k — целое положительное
число, если в каждой точке х области Q существуют все частные производ-
производные функции ф по декартовым координатам точки х до порядка k включи-
включительно, и эти производные непрерывны в Q.
Если ф принадлежит классу Ck (Q), k — произвольное неотрицательное
целое число, то будем писать, что ф ? Ck (Q).
11.2.	Определе ни е. Функция ф непрерывно продолжима в точке
у ? dQ из Q, где через dQ обозначена граница множества Q, если суще-
существует конечный предел
lim ф (х).
Пусть 2 — произвольное подмножество границы dQ.
11.3.	Определение, ф 6 Ck (Q U 2), если ф ? Ck (Q) и, кроме
того, ф и все ее производные по декартовым координатам до порядка k вклю-
включительно, непрерывно продолжимы в каждой точке множества 2.
Таким образом, например, Ф 6 Ck (Q) означает, что ф ? Ck (Q) и ф и
все ее производные до порядка k включительно непрерывно продолжимы
в каждой точке границы Q.
Легко доказывается следующее предложение:
11.4.	Теорема. Если ф ? С0 (Q), то функция tp, определенная на
множестве Я равенствами г|) (у) = ф (у), если у ? Q; г|э (у) = lim ф (х),
если у 6 dQ, непрерывна на множестве Q.
11.5.	Определение. Если ф — вектор или матрица, определен-
определенная в Q, то ф g Ck (Q) [ф 6 Ck (п)] означает, что каждая ее компонента
принадлежит классу Ck (Q) [Ck (QK.
1. Классическая теория упругости. Введем следующие определения
или аксиомы:
11.6.	Упругая среда есть область D трехмерного евклидова простран-
пространства и набор чисел р, к и [л, удовлетворяющих условиям:
р>0, jx>0, 3X + 2jx>0;	A1.1)
р называется плотностью среды, а X и \х — постоянными Ламе.
11.7. Упруго-динамическое состояние среды D (р, X, \i) в промежутке
времени <7~ = [^0, ^3, соответствующее массовой силе &~, есть пара [а, %\3
удовлетворяющая условиям:
n
A1.2)
/
л с j* i / dtif , dtif \	/i i o\
= Ми UIVU-\-\i i-^	1- - ' \ 9	(ll.o)
где У = (STlf &~2, ^3) и и = (их, w2» w3) — действительные векторы, ат =
= 11 Tt/ |зхз — действительная матрица, (?Г\ : D X <Т —> /?, и{: D X &~ —» R,

§ 11]	АКСИОМАТИЗАЦИЯ ТЕОРИИ	43
%ц : D X дг —* У?); г/ называется вектором смещения, а и, — компонентой
(вектора) смещения; т — тензором напряжения, а т(/—компонентой (тен-
(тензора) напряжения.
Соотношение A1.2) называется уравнением упруго-динамического со-
состояния, а соотношение A1.3) —законом Гука.
На языке предыдущих параграфов содержание определений A1.6)
и A1.7) можно изложить так. Рассматривается изотропная и однородная
(по отношению к упругим свойствам) среда с постоянными Ламе X и (ы. Плот-
Плотность масс этой среды, обозначаемая через р, предполагается постоянной.
Предполагается также положительная определенность удельной энергии
деформации (см. F.19)). Компоненты напряжений считаются непрерывно
дифференцируемыми как по декартовым координатам точки среды, так и
по времени, а компоненты смещений — дважды непрерывно дифференци-
дифференцируемыми по тем же переменным (предположение I из 11.7). Предполагаются
также применимыми уравнения движения D.3) (предположение II из 11.7)
и закон Гука E.15) (предположение III из 11.7).
Подставляя A1.3) в A1.2), получим соотношение
\i Аи{ -f- (X -}- |л) -х— div и -
которое называется уравнением динамики (классической теории) или, точнее,
уравнением упруго-динамического состояния среды D (р, X, (х), соответ-
соответствующего массовой силе #", в компонентах смещения. Это соотношение
можно записать в векторной форме:
<П-4>
здесь
Au = (Ault Au2, Аи3), Ащ-.
Y \dxj ' dx2 ' dx3 )
11.8. Упруго-статическое состояние среды D (p, Я,, ja), соответствующее
массовой силе @~\ есть пара [и, т1, удовлетворяющая условиям:
A1.5)
A1.6)
где^Г = (^"lf ^2, ^3) им = (их, «2» ^з) —действительные векторы, а т =
= IITt/ Цзхз — действительная матрица C~{ : D —» /?, и{ : D —> /?, xf/ : D —> /?);
и — вектор смещения, т — тензор напряжения. Соотношение A1.5) назы-
называется уравнением упруго-статического состояния, а A1.6) — законом Гука.
Подставляя A1.6) в A1.5), получим уравнение статики (классической
теории) или, точнее, уравнение упруго-статического! состояния среды
D (р, Х9 pt), соответствующего массовой силе ff~ в компонентах смещения
|лЛи + (А, + ц) grad divw + p5r = Q.	A1,7)

44
основные понятия и аксиоматизация
[Гл. I
Определения 11.6 и 11.8 означают, что рассматривается ситуация, описанная
в 11.6 и 11.7, с той разницей, что внешние воздействия, а также смещения
и напряжения, не меняются во всем рассматриваемом промежутке времени.
11.9. Упруго-колебательное состояние среды D (р, A,, jli), соответствую-
соответствующее массовой силе &~9 есть пара [и, т1, удовлетворяющая условиям:
A1.8)
III) т,у = Utj divu + ii(^- + ^L
1.9)
где $Г = ({Г19
II Ц
и м = (ulf и 2
1 2 з)	(
= II Ti/ Цзхз — комплексная матрица
й
и3) — комплексные векторы, ат =
: D —> Z, иь : D —> Z, тг7 : D —» Z);
й
II /	7
© — произвольное действительное число, называемое частотой колебания.
Определения 11.6 и 11.9 представляют собой аксиоматическое изложение
основ стационарных колебаний, рассмотренных в § 10.
Соотношение A1.8) называется уравнением упруго-колебательного
состояния, а A1.9) — законом Гука.
Подставляя A1.9) в A1.8), получаем уравнение колебания или, точнее,,
уравнение упруго-колебательного состояния среды D (р, X, \х) в компонен-
компонентах смещения, соответствующего массовой силе $Г и частоте колебания со:
+ (X + v)grad div" + P°>2и + P@~ = °-	(ИЛ0)
2. Моментная теория упругости, В этой теории:
11.10. Упругая среда есть область D трехмерного евклидова пространства
и набор чисел р, X, fx, a, <^, s, u, P, удовлетворяющих условиям:
Р>0, |i>0, ЗХ + 2^>0, ^ГЕ>0, а>0, е>0, 3
A1.11)
11.11. Упруго-динамическое состояние среды D (р, 9t, fx, а, ^7, г, и, |3)
в промежутке времени ^= [?0, ^1, соответствующее массовой силе^ и мас-
массовому моменту ^, есть четверка [и, со, т, ц|, удовлетворяющая условиям:
I) w,
П
A1.12)
III) xa =
-g- + (I* ~ «) -g- ~
A1.13)
где
= (ff-ly &-it &-3), 9 = (^XJ »„ S?s), u = («i, u,, и3), и = (шlr
(o2, co3) — действительные векторы, a т = ||тг/ Цзхз и ц = | ц.г/ Цзхз — дей-
действительные матрицы, определенные на множестве D х 3" Ф~и 9lt ut, (at>

Л Hj	АКСИОМАТИЗАЦИЯ ТЕОРИИ	45
Tij9 \iij : D x &~ —* /?); и = (u() называется вектором смещения, со = (cot) —
вектором вращения, т = || х^ || — тензором силового напряжения, а \х =
= I V^i II — тензором моментного напряжения.
Соотношения A1.12) и A1.12') называются уравнениями упруго-динами-
упруго-динамического состояния, а A1.13) и A1.13') — законом Гука.
Приведенные аксиомы определяют однородную и изотропную среду
с центром симметрии и ее динамическое состояние с точки зрения моментной
теории (ср. с D.3), D.6), G.21), G.21')).
Подставляя A1.13) и A1.13') в A1.12) и A1.12'), получаем уравнение
динамики (моментной теории) или уравнение упруго-динамического состоя-
состояния среды D (р, к, (д>, а, </, 8, о, р) в компонентах смещения и вращения,
соответствующих массовой силе 5*" и массовому моменту <S\
(fx + а) Аи + (к + [г — а) grad div> + 2аrot со + рЗГ = р-0-, A1.14)
(и+ Р) Асо + (е + и — Р) grad divco + 2аrot и — 4асо + р^ = ? ~. A1.14')
11.12. Упруго-статическое состояние среды D (p, k, ja, а, ^/, 8, и, Р),
соответствующее массовой силе ^ и массовому моменту ^, есть четверка
[и, и), т, [д>], удовлетворяющая условиям:
I) и, соб C2(D) П &ф); т, (хб С1^);
A1.15)
III) ти-«>„ 2^ + (^ + «)^- + (р-а)^
где ^ = (iFt), ^ = (^г), а = (иь), со = (сог) — действительные векторы,
а яг = || %ц ||зхз, ^ = II ^i/ Цзхз — действительные матрицы (&ь $ь иь со,,
%ц, \хч : D —> R), Соотношения A1.15) и A1.15') называются уравнениями
упруго-статического состояния, а A1.16) и A1.16') — законом Гука. и = (и(),
со = (сог), т = || %ц || и ц = |] [iij || называются соответственно вектором сме-
смещения, вектором вращения, тензором силового напряжения и тензором
моментного напряжения.
Подставляя A1.16) и A1.16') в A1.15) и A1.15'), получаем уравнение
статики или уравнение упруго-статического состояния среды D (р, Я, \ху а,
^, е, о, Р), соответствующего массовой силе SF и массовому моменту (S\
(|х + а) Аи + (к + (л — а) grad div а + 2а rot со + р#~ = 0, A1.17)
Р) А® + (е + и —Р)grad divco + 2аrot а — 4асо + р^ = 0. A1.17')
Упруго-статическое состояние получается фактически из упруго-дина-
упруго-динамического состояния, если предположим, что массовая сила и массовый мо-
момент, а также смещения, вращения и напряжения (силовые и моментные) не
зависят от времени в рассматриваемом промежутке.

46	ОСНОВНЫЕ ПОНЯТИЯ И АКСИОМАТИЗАЦИЯ	[РЛ- |
11.13. У пру го-колебательное состояние среды D (р, Я, ц, а, <?, е, о, P),
соответствующее массовой силе $Г и массовому моменту %, есть четверка
[и, со, т, ц], удовлетворяющая условиям:
I) и, со 6 С2 (D) П С1 (D); т, [х 6 С1 (D);
A1.18)
И) 2
а*,-
= 0;	A1.18')
A1.19)
где 5^" == (#";)> ^ = (^), ^ == (и{)9 со = (cot) — комплексные векторы,
а т = II т*7 Цзхз, [А = ipif Цзхз — комплексные матрицы (ЗГiy 9i9 ut, (oi9
%fj, jjif/ : D —» Z); a — произвольное действительное число, называемое
частотой колебания.
Соотношения A1.18) и A1.18') называются уравнениями упруго-колеба-
упруго-колебательного состояния, а A1.19), A1.19') — законом Гука.
Подставляя A1.19), A1.19') в A1.18) и A1.18'), получаем уравнение
колебания или уравнение упруго-колебательного состояния среды D (р, Я,
[I, a, ^7, 8, и, Р), соответствующего массовой силе &~, массовому моменту *3
и частоте колебания а:
(\к + а) Аи + (^ + \х — a) grad div и + 2а rot со + ра2и + р^" = 0, A1.20)
(D + р) Асо + (е + о — Р) grad divco + 2аrot и — 4асо + ^со + р^ = 0. A1.20')
Аксиомы 11.10 и 11.13 определяют ситуацию, описанную в п. 2, § 10.
3. Теория термоупругости. В этой теории:
11.14. Термоупругая среда есть область D трехмерного евклидова про-
пространства и набор чисел р, X, \i> у, г], к, удовлетворяющих условиям
Р>0, (i>0, ЗЛ + 2^>0, 7/T,>0f x>0.	A1.21)
11.15. Термоупруго-динамическое состояние среды D (р, X, \х, у, т], х)
в промежутке времени <Э~ = [^0, ^iL соответствующее массовой силе ф*
и тепловому источнику Q, есть тройка [и, т, 9], удовлетворяющая следую-
следующим условиям:
A1.22)
А0—TW-^*™« + -^Q = b	(И-22')
(^ g)	A1.22")

К Ц]	АКСИОМАТИЗАЦИЯ ТЕОРИИ	47
где Q и 0 — действительные скалярные функции, & ='(&mi) и и = (а,) —
действительные векторные функции, а х = || xty ||зхз — действительная матрич-
матричная функция, определенные на множестве
Назовем 0 температурой среды, а = (щ) — вектором смещения, т =
= || %ц || — тензором напряжения.
Соотношения A1.22) и A1.22') называются уравнениями термоупруго-
динамического состояния, а A1.22") — законом Дюамеля—Неймана.
Подставляя A1.22") в A1.22), получим
[I Аи -f- (A,-f- (i) grad diva — ygradO-f- piF= р-^тг»	A1.23)
Соотношения A1.23) и A1.22') представляют уравнение динамики (тео-
(теории термоупругости) или уравнение термоупруго-динамического состояния
среды D (р, Я, fi, у, xi, и)» соответствующего массовой силе @~ и тепловому
источнику Q.
11.16. 4Тер моу пру го-статическое состояние среды D (р, Я, jx, у, т|, х),
соответствующее массовой силе 2Г и тепловому источнику Q, есть тройка
[и, т, 01, удовлетворяющая условиям:
A1.24)
A1.24')
A1.25)
где Q и 0 — действительные скалярные функции, #" = {З7j) и и = (ut) —
действительные векторные функции, ат — || тг/ Цзхз — действительная матрич-
матричная функция (yi9 Q, ui9 %ij, 0 : D —* /?).
Подставляя A1.25) в A1.24), получаем
ц Аи + (А, + ^i) grad div и — у grad 0 + p#~ = 0.	A1.26)
Соотношения A1.26) и A1.24') называются уравнением статики (теории
термоупругости) или уравнением термоупруго-статического состояния среды
D (р, X, \х, у, т), х) в компонентах смещения, соответствующего массовой
силе SF и тепловому источнику Q.
11.17. Термоупруго-колебательное состояние среды D (р, Я, jx, y9 т], х),
соответствующее массовой силе ST и тепловому источнику Q есть тройкг
[w, т, 0], удовлетворяющая условиям:
A1.27)
п>
4-Q = 0.	A1.27')
A1.28)

48	основные понятия и аксиоматизация	[Гл. I
где Q и 6 — комплексные скалярные функции, SF = (@~д и и = (и{) —
комплексные векторные функции, а т = || хц ||3хз — комплексная матричная
функция (&*i9 Q, ui9 т/;-, 9 : D —* Z); со — произвольное действительное
число, называемое частотой колебания, и — вектор смещения, |т?/||— тен-
тензор напряжения, 9— температура.
Соотношения A1.27) и A1.27') называются уравнением термоупруго-коле-
термоупруго-колебательного состояния, а A1.28) — законом Дюамеля—Неймана.
Подставляя A1.28) в A1.27), получаем
li Аи + (Я + [л) grad div и — ygrad 9 + рсо2и + р^ = 0.	A1.29)
Соотношения A1.29) и A1.27') называются уравнением колебания или,
точнее, уравнением (в компонентах смещения) термоупруго-колебательного
состояния среды D (р, к9 \i, у, tj, x), соответствующего массовой силе У9
тепловому источнику Q и частоте колебания со.
§ 12. Матричная запись основных уравнений
Для краткости удобно пользоваться матричной записью основных урав-
уравнений. С этой целью примем следующие соглашения. Всякий /э-мерный век-
вектор v = (vu . . ., vp) будем рассматривать как одностолбцевую матрицу
Ivf II
Произведение матрицы а = [| atj ||mXp размера т хр на матрицу Ъ =
— II btj \\pxn размера р хп определяется как матрица с = || cif \\mxn размера
т хп, где
Ctf = 2a«A/-	A2.1)
к
В частности, произведение матрицы размера т хр на р-мерный вектор
будет m-мерным вектором
av =
A2.2)
В дальнейшем потребуется ввести матричные дифференциальные опера-
операторы. Матричный дифференциальный оператор является матрицей, элементы
которой суть дифференциальные операторы. Если aik — дифференциальный
оператор, a bki — функция, на которую можно воздействовать оператором
aiky то под aikbkj будем понимать функцию, полученную воздействием диффе-
дифференциального оператора aik на функцию Ъщ.
Таким образом, если а = || aik \\тХр — матричный дифференциальный
оператор, а Ъ = \ Ъц \р^п — матричная функция, то ab будет матричной
функцией с — | Сц \\тжп, где функции Сц определены формулой A2.1).
Bj частности, если а = || пц ||тХр — матричный дифференциальный оператор,
a v = (vl9 . . ., vp) — векторная функция, то av будет векторной функцией,
определенной из A2.2).
Если а = || а,ц \пър — матричная функция, а Ъ = || Ъц \р^п — матричный
дифференциальный оператор, то аЪ будет матричным дифференциальным
оператором с = || ci} \\mxn, где Сц определены формулой A2.1) и aik в A2.1)
представляют, фактически, коэффициенты дифференциальных операторов blk.

Л 12]	МАТРИЧНАЯ ЗАПИСЬ ОСНОВНЫХ УРАВНЕНИЙ	49
Уточнения и обобщения приведенных определений последуют ниже,
в ходе рассуждений.
1. Классическая теория упругости. Введем матричный дифференциаль-
дифференциальный оператор
Л(д*) = |Л,,(д,)||зхз,
где
Тогда уравнение (см. A1.4)) упруго-динамического состояния среды
D (р, Я, fi), соответствующего массовой силе & = (@~i), в компонентах сме-
смещения или уравнение динамики запишется следующим образом:
р-Ц-,	A2.3)
а уравнение статики (см. A1.7)) — в виде
А(дх)и +р&~ = 0.	A2.4)
Уравнение упруго-колебательного состояния (см. A1.10)) среды D (р, X, \х),
соответствующего массовой силе ST = (ЗГt) и частоте колебаний о, или урав-
уравнение колебания, примет вид
А (дх) и + рсо2и + рТ = 0.	A2.5)
В формуле A2.3) предполагается (см. A1.7)), что &~f: D х 0~ —* /?,
щ : D х Т —+ Rf и, кроме того, и ? С2 (D х Т) [\ С1 Щ х Т). В формуле
A2.4) предполагается (см. 11.8) 9~t : D -» /?, щ : D -¦ /? и а 6 С2 (?>) П
П С1 (D), a в формуле A2.5) — Sri, : D —> Z, щ : D -* Z и w 6 С2 (D) f|
П С1 (D) (см. 11.9).
Удобно также ввести оператор Л {дХУ со) = || Л^- (дх, со) ||3хз,
Л,7 (ах, со) = Аа (дх) + б,/Рсо2 = 8if (|хД + рсо2) + (X + ^) ^-. A2.6)
Тогда уравнение A2.5) примет вид
Л,у(^,со)а + р^ = 0.	A2.5')
2. Моментная теория упругости. Введем матричный дифференциальный
оператор
М = М(дх) = \\Ма(дхЦ6х6	A2.7)
и представим его в виде
где
> = I Mi/} (дх) Цзхз (k = 1, 2, 3, 4),
(dj = (|i + a) OijA + (A, -|- \x — a) ¦
Mff (dx) = M[?} (dj = — 2a
4 В. Д. Купрадзе
A2.8)

50	основные понятия и аксиоматизация	мрл i
Тогда уравнение упруго-динамического состояния (см. A1.14), A1.14')) среды
D (р, A,, fx, а, е/, е, и, Р), соответствующего массовой силе &~ = E^-) и мас-
массовому моменту ^ = (j§t) в компонентах смещения, или уравнение динамики,
запишется в виде
r^%	A2.9)
где % = (Ui) п Ж = (Ж() — шестикомпонентные векторы, причем %ь = ut
при i = 1, 2, 3 и % = со^з при г = 4, 5, 6; Ж{ = ^ при * = 1, 2, 3 и
^ = ^_3 при i = 4, 5, 6; г — диагональная матрица размера 6 хб:
г = II гц Цехе, причем Гц = 0 при i ф /, ги = р при i = 1, 2, 3 и ти = ^/ при
1 = 4, 5, 6.
^ и Ж иногда будем записывать в виде % = (а, со), Ж = (З2",^).
Уравнение статики (см. A1.17), A1.17')) той же среды запишется в виде
0,	A2.10)
а уравнение колебания (с частотой колебания а) — в виде
2ги = 0.	A2.11)
В формуле A2.9) (см. A1.11)) % : D х Г — /?, ^г:О х Т -> /?;
в формуле A2.10) (см. A1.12)) % : D — /?, 5»?: D — /?, а в формуле A2.11)
(см. A1.13)) ?^,: : D —» Z, 5^f : D —> Z и а — произвольное действительное
число.
Если введем обозначение М (дХУ о) = || М^- (дх, а) ||бХб,
Мг7 (ал, а) = Mt7 (dx) + 8ца2гф
то A2.11) примет вид
0.	A2.1 Г)
3. Теория термоупругости. Введем матричный дифференциальный опе-
оператор
В (дх, со) = || Ви(дх,п) !|4Х4,	A2.12)
где ?fe/ (Зх, со) = Akj (дХ9 со) при / = 1, 2, 3; 5Л4 (дХ9 со) = —у ^ при
fe - 1, 2, 3; В4/ (д„ со) = /сот] ^-, при / = 1, 2, 3; ?44 (д„ со) = А + -^-.
Тогда уравнение термоупруго-колебательного состояния (см. A1.27'),
A1.29)) среды D (р, к, \iy у, г\, х), соответствующего массовой силе ЯГ ==
= (^",), тепловому источнику Q и частоте колебаний со в компонентах смеще-
смещения, или уравнение колебания, запишется в виде
<o)U + 3№ = 0,	A2.13)
где U = (Ui) и Ж — (Жг) — четырехкомпонентные векторы, причем U\ =
= щ при / = 1, 2, 3; с74 = 9, Жь = р$Г( при / = 1, 2, 3 и <2^4 = ^- Q.
При со = 0 A2.13) обращается в уравнение статики (теории термоупру-
термоупругости).
§ 13. Оператор напряжения
1. Классическая теория. Рассмотрим упругую среду D (p, A,, fx). Пусть
х = (х19 х2у х3) — точка среды, а п (х) = (п1 (х), п2 (х)9 п3 (х)) — произ-
произвольный единичный вектор. Для вычисления напряжения в точке х по на-
направлению п (х) в момент времени / была получена формула B.1). Подставив

* 13]	ОПЕРАТОР НАПРЯЖЕНИЯ	51
в B.1) выражения компонент напряжений через компоненты смещений (за-
(закон Гука), получим
что можно записать и так:
T(»)(jc,0 = ^(x)divtt(^/) + 2^^^ + |i[n(x)Xrota(x,/)]f A3.1)
причем
_J_
an (x) ~ Z
i
Введем матричный дифференциальный оператор
T(dXfn(xj)^\\Tif(dx,n(x))l
где
Ти(дХ9 п(х)) = Ut (х)-щ + ,шу (x)-J- + |*в?У з^..	A3.2)
Тогда
т^ = Т(дХУп(х))щ	A3.3)
71 E^, п (х)) будем называть оператором напряжения (классической теории
упругости).
Мы встретимся также с оператором напряжения более общего вида;
X
обозначим его через Т (дх, п)9 назовем оператором обобщенного напряжения
и определим формулой
K I
A3.4)
Очевидно, Т = Т9 т. е. оператор напряжения получается из оператора обоб-
обобщенного напряжения, если положим и = [г.
Оператор Т при % = \л (X + |i) (X + Sjj,) обозначим через Л9 и назовем
оператором псевдонапряжения.
X
Иногда применяют векторную форму записи для выражений Ти и Jfu;
-+- 2(ы) dw . (Я, + |
]. A3.6)
2. Моментная теория. Рассмотрим упругую среду D (р, Я, |ы, а, ^/, е,
о, р). Силовое напряжение %in) (x, 0 и моментное напряжение \х(п) (х, t)
в точке х по направлению я (х) в момент времени / вычисляются по формулам

52	основные понятия и аксиоматизация	грл> I
B.1) и B.2), которые в силу закона Гука (см. G.21), G.2Г)) принимают вид
2	A3.7)
]	A3.7')
Введем матричный дифференциальный оператор
Г = Г (dx, n (x)) -1| Tt, (dx, n
где Г(й) (дх, п (х)) = || 71*' (дх, п (х))||зхз,
ТУ (дх, п (х)) = Ял, (^) -J- + (ц — a) nj (х) -^ + (ц + а) бG -
Т{ц (дх, п (х)) = — 2а S гит (х), Т{$ (дх, п(х)) = О,
A3.9)
дх,
Tfl (д„ n (x)) = em (x) -±- + (u—p) Л/ (x) -|- + (u + p) S
тогда
т<") (x, t) = Г") (а„ я (х)) и + ГB1 (а„ я (х)) со,	A3.10)
A3.11)
(/=1,2,3),	A3.12)
^n)(x, t) = [Т (дХУ п (х)) #],+з (/ = 1, 2, 3).	A3.13)
Здесь ^ = (Ui) — шестикомпонентный вектор, причем % = щ при i = 1,
2, 3 и Йс = ®«_8 ПРИ i = 4» 5» 6-
Т будем называть оператором напряжения (моментной теории уп-
упругости).
3. Термоупругость. Рассмотрим термоупругую среду D (р, А,, \ху у,
т), х). Напряжение среды в точке х в момент времени ? вычисляется по фор-
формуле B.1). Применяя закон Дюамеля—Неймана (см. (8.12')), получим
т<«>(%, t) = T(dx, n(x))u(x) — yn(x)Q9	A3.14)
где Т — оператор напряжений классической теории, и — вектор смещения,
а 0 — температура.
Рассмотрим матричный дифференциальный оператор
Р(дх, п(х)) = \\Ра(дх, n(x))hx4,	A3.15)
определенный формулой
Ри(дх,п(х)) = ТИ(дх, п(х)), при U / = 1, 2, 3, 1	16
Pt, (дх, п (х)) = — уп{ (х),	при i = 1, 2, 3. /	1 "
Тогда соотношение A3.14) примет вид
H*)(x9t) = P(dx,n(x))U,	A3.17)
где U = (Ui)<— четырехкомпонентный вектор, причем Ut = щ при i = 1,
2, 3 и (/4 = 8.

Л 14]	ПОСТАНОВКА ОСНОВНЫХ ЗАДАЧ	53
§ 14. Постановка основных задач
Как уже отмечалось выше, основной задачей теории упругости является
определение упругого (динамического, статического или колебательного)
состояния среды в классической и моментной теории упругости и термоупру-
термоупругого (динамического, статического или колебательного) состояния — в тео-
теории термоупругости.
Если, например, известно упруго-динамическое состояние среды
D (р, A,, \i), соответствующее массовой силе !F9 т. ё. (см. п. 1, § 11), если
известны вектор смещения и = (ut) и тензор напряжения т = || тц |, опреде-
определенные в § 11, то можно вычислить деформации по формулам E.4) и тем самым
определить деформированное и напряженное состояние среды. Но для опре-
определения упруго-динамического состояния, соответствующего массовой силе
&~> т. е. для определения пары [и, т] на множестве D х ^~, достаточно знать
смещение и на этом множестве. Тогда компоненты напряжений определяются
из A1.3). Аналогично обстоит дело и при рассмотрении других состояний.
Все сказанное справедливо, когда речь идет об одном-единственном,
каким-либо образом определенном состоянии. Но состояние среды, напри-
например, упруго-динамическое, соответствующее массовой силе #~, не опреде-
определяется единственным образом.
В §§ 1—10 было рассмотрено деформированное состояние среды, созда-
создаваемое внешними воздействиями. В классической теории упругости под внеш-
внешним воздействием понимаются массовые силы и внешние напряжения, кото-
которые задаются независимо друг от друга; в моментной теории внешними воз-
воздействиями считаются, кроме массовых сил и моментов, внешние силовые
и моментные напряжения, и для определения единственно возможного дефор-
деформированного состояния необходимо задать все эти величины.
Кроме того, при выводе основных соотношений мы исходим из опреде-
определенного первоначального состояния. Предполагалось, хотя легко освобо-
освободиться от этого ограничения, что в начальный момент среда находится в со-
состоянии покоя. Если бы мы исходили из*другого начального состояния, то по-
получили бы другую картину деформированного состояния. Таким образом,
для единственности упругого состояния необходимо задавать и начальное
состояние.
Формулируя аксиомы упругих (термоупругих) состояний, мы не при»
нимаем во внимание внешние поверхностные воздействия, испытываемые
изучаемой средой через свою границу. Мы не учитываем также механиче-
механического состояния среды до интересующего нас момента времени, хотя от этого
явно зависит ее динамическое состояние. Поэтому, естественно, упругие
состояния, описываемые введенными аксиомами, определены неоднозначно.
Этому соответствует тот факт, что общие решения дифференциальных уравне-
уравнений упругих состояний содержат произвольные функции.
Между тем, в реальных условиях всякое упругое (термоупругое) состоя-
состояние реализуется вполне однозначно или обладает физически допустимой
многозначностью. Реализуемые в действительности упругие состояния суть те
частные (конкретные) состояния, которые отбираются из всей совокупности
упругих состояний, описываемых аксиомами, по дополнительному требова-
требованию, состоящему в удовлетворении определенных граничных и начальных
условий.
Кроме этого, выбранное состояние должно обладать свойством непрерыв-
непрерывной зависимости от граничных и начальных данных (см. гл. VI, § 6). Дело
в том, что эти данные берутся из наблюдений с помощью тех или иных изме-
измерений и поэтому всегда отличаются от точных значений. Следовательно,
конкретное состояние, которое найдено с помощью указанных приближенных
данных, будет иметь практическую ценность, если оно «в той же мере»

54	основные понятия и аксиоматизация	грл i
отличается от истинного состояния, в какой «мере» данные отличаются от
своих точных значений. Это свойство называется свойством непрерывной
зависимости от данных задачи.
Таким образом, если доказано существование и единственность состоя-
состояния, удовлетворяющего аксиомам, граничным и начальным условиям, и не-
непрерывно зависящего от данных задачи, то можно надеяться, что построено
математическое описание физически реализуемого упругого состояния. Поста-
Поставленная так задача называется корректной х).
После этого имеет смысл поставить весьма важную задачу о фактическом
Конструировании этого состояния в том или ином смысле; например, получе-
получение его приближенного числового значения с помощью практически осущест-
осуществимых вычислений (например, на базе ЭВМ).
Доказательству существования, единственности, непрерывной зависи-
зависимости от данных и фактическому конструированию упругого (термоупругого)
состояния посвящается настоящая книга.
14.1.Определение. Функцию ф, определенную в области D, будем
называть регулярной, если ф (Е С2 (D) и ф ? С1 (D).
Таким образом, регулярная функция в области D имеет в этой области
непрерывные вторые производные, а сама функция и все первые производные
непрерывно продолжимы в каждой граничной точке области D.
Матрицу (вектор) назовем регулярной, если все ее элементы (компоненты)
регулярны.
В дальнейшем мы исследуем упругие и термоупругие состояния как
ограниченных, так и неограниченных сред. Более того, при исследовании
задач определения упругого (термсчупругого) состояния среды D часто при-
приходится вводить в рассмотрение вспомогательную задачу для среды, допол-
дополняющей D до всего пространства. В связи с этим, удобно ввести следующие
обозначения: конечную область, ограниченную кусочно-гладкой поверх-
поверхностью S, будем обозначать через D+, а дополнение множества D+ = D+|J5
до всего пространства обозначим через D". Таким образом,
Орт нормали поверхности S в точке х (х? 5), внешней по отношению к D+,
обозначим через п (х). Через п будет обозначен этот орт в точке у ? S. Таким
образом, п = п (у).
14.2.	Определение. Функцию ф, определенную в области D,
будем называть финитной в этой области, если замыкание множества тех то-
точек х б D, где ф (х) ф О, лежит в D [\х 6 D | ф (х) Ф 0| с D ].
14.3.	Определение. Если функция ф, определенная в D+ (D~),
непрерывно продолжима в точке у ? S, то через ф+ (у) или |ф (у)\+ [ф~ (у)
или {ф (у)}~] будем обозначать предел
= lim ф(х) [ф-(у) = {ф(у)Г = lim
1. Классическая теория. В классической теории упругости ставится
три основных типа задач определения упругого состояния: динамические,
статические и колебательные. Эти типы задач в корне отличаются друг от
друга и требуют различных подходов к их исследованию.
1) В задачах математической физики нередко встречаются некорректно поставленные
задачи. (Интерес к таким задачам возрос в последние годы (см. Тихонов [1 ], Лаврентьев [1,2]
и др.)- С некорректно поставленными задачами приходится иметь дело и в этой книге. Отметим,
что при исследовании этих задач существенно применяются решения некоторых специально
построенных корректных задач.

5 141	постановка основных задач	55
Каждый из трех типов содержит шесть основных задач.
Первая основная задача динамики: найти упруго-
динамическое состояние [и, т] среды D+ (р, A,, \i) [D~ (p, X, \i) ] в проме-
промежутке времени W~ = [t0, tx ], соответствующее массовой силе Ф", по гранич-
граничному условию
v\y,t)eSxr:u+(y,t) = f(y,t) [u-(y,t) = f(y9t)]	A4.1)
.и по начальным условиям
д% Ц	A4.2)
Здесь SF = (&~()9 f = (ft)9 ф = (ф?) и if = (грЛ) — заданные векторы
Для краткости будем обозначать эту задачу через A)+ [(I)" 3 и называть
ее первой внутренней [внешней ] задачей динамики.
Вторая основная задача динамики формулируется
совершенно так же, как первая; заменяется только граничное условие A4.1)
следующим:
V(y, 06 SxT : \Т(ду, n)u(y))+ = f(y, t)[\T(dy, n) u(y)\-= f(yy /)]. A4.3)
Обозначим эту задачу через (Н)+ [(II)" ] и назовем ее второй внутренней
[внешней ] задачей динамики.
Третья и четвертая основные задачи отличаются от
предыдущих граничными условиями.
В третьей внутренней и внешнейJ) задаче (за-
(задача (Ш±)
V (У* t)?SxT: \u(y, t) n}± = g(y, t)9	A4.4)
\Т(дю п)и(у, t) — n[nT(dy, n)u(y, t)]\± = h(y91).	A4.4')
Вчетвертой внутренней и внешней	(задача (IV)±) задаче
\f(y,t)eSx Т\
\	A4.5)
).	A4.5')
Здесь g — скалярная, a h = (ht) — векторная функция g : S х &~ —* R,
h(: S хТ -> /?.
Граничными условиями отличаются от остальных пятая и шестая задачи
(задачи (У)± и (VI)±).
Пятую задачу будем называть также основной смешанной задачей. В этом
случае граница среды представлена в виде объединения четырех непересекаю-
4
щихся множеств2) 5 = []Sk и на Sk задается граничное условие /г-й задачи.
fei
1)	Если в предложении участвуют двойной знак =? или ^,то это предложение следует
понимать как сокращенную запись двух предложений: одно — когда (в этом предложении
двойной знак заменяется верхним знаком, и второе — когда нижним.
2)	Не исключается случай, когда одно или два из этих множеств—пустое множество.
Если, например, S2 = S2 = S4 == 0, то 5 = Sj и пятая задача сводится к первой.

56	ОСНОВНЫЕ ПОНЯТИЯ И АКСИОМАТИЗАЦИЯ	грл \
В качестве граничного условия шестой задачи примем усло-
условия вида V (У, t)e S х 2Г:
\Т(ду, п)и(у, t) + o(y9 t)u(y,'t)}+ = f(y9 t), 1	б
[\Т(ду, n)u(y9 t) — a(y9 t)u(y9 t)}- = f(y, t)]9 J
где a = | oi} ||зхз — вещественная непрерывная матрица, заданная на S х Т>
все главные миноры которой положительны. Во всех этих задачах началь-
начальные условия одинаковы и означают задание в начальный момент времени
t = t0 смещения среды и скорости изменения смещений.
В первой задаче на границе заданы смещения, во второй — внешние
напряжения. В третьей задаче на границе задаются нормальная составляю-
составляющая смещения и касательные составляющие внешних напряжений, в четвер-
четвертой, наоборот, на границе задаются нормальная составляющая напряжения
и касательные составляющие смещения. В пятой задаче граница среды раз-
разделена на четыре части, на одной части задаются смещения, на другой — нап-
напряжения, на третьей — нормальная составляющая смещения и касательные
составляющие напряжения, на четвертой — нормальная составляющая
напряжения и касательные составляющие смещения. Наконец, в шестой
задаче на границе задается специальная комбинация смещений и напряжений.
Можно привести много практических задач, когда реализуются ситуации,
описываемые приведенными задачами.
Можно доказать (это следует из приведенных ниже рассуждений), что
поставленные выше задачи эквивалентны следующим задачам:
Первая основная внутренняя [внешняя] задача динамики A)+ [A)~ ]:
найти регулярное решение уравнений динамики A2.3) или A1.4) по гранич-
граничному условию A4.1) и по начальным условиям A4.2).
Аналогично формулируется вторая (П)±, третья (II 1)±, четвертая (IV)*,
пятая (V)± и шестая (VI)± граничные задачи динамики.
Основные задачи статики и колебания формулируются так же, но без
начальных условий. Например, первая задача статики (задача ,A)*) форму-
формулируется так: найти упруго-статическое состояние [и, т] среды D+ (р, X, |л),
соответствующее массовой силе ^, по граничному условию
здесь ИГ = (@~i) и / = (fi) — заданные векторы: ft : S —> R, SF{ : D± —* /?.
Эта задача эквивалентна следующей: найти регулярное решение уравнения
статики A2.4) или A1.7) по граничному условию A4.1).
Приведенные выше задачи при отсутствии массовых сил {$Г = 0), с ну-
нулевыми граничными и начальными условиями в задачах динамики и с нуле-
нулевыми граничными условиями в задачах статики и колебания, будем называть
однородными задачами. Принятую нами нумерацию сохраним и для однород-
однородных задач, снабдив соответствующий номер нижним индексом 0. Например,
(П)о*~ будет обозначать вторую (на границе равны нулю напряжения) внут-
внутреннюю однородную задачу.
Аналогично, для задач установившихся колебаний с частотой со будем
пользоваться той же нумерацией, но с буквой со над номером', например,
(IV)o будет обозначать четвертую внутреннюю однородную задачу колебания.
2. Моментная теория. В моментной теории, так же как и в классиче-
классической, ставятся задачи трех основных типов: динамики, статики и колебания.
В каждом из них шестнадцать задач1), соответствующих рассмотренным выше
х) Подробнее об этих задачах будет сказано в главе IX.

л 14]	постановка основных задач	57
первым четырем задачам классической теории. Эти задачи формулируются*
как в классической теории. Приведем формулировку четырех типичных задач,
которые будут подробно исследованы в этой книге.
Задачи динамики. Найти упруго-динамическое состояние
[и9 со, т, \х] среды D± (р, Я, [а, а„ <^, 8, и, Р) в промежутке времени
&~ = [t0, ti\9 соответствующее массовой силе ST и массовому моменту 2? по
начальным условиям ух ? D±:
и (х, tQ) = ф (х), со (х, t0) = h (x), |
J
и по граничным условиям у (у, t) ? S х &~:
и±(у, t) = f(y, t), co±(t/, t) — g(y9 t)	A4.8)
в случае первой задачи (задача (I)*1);
{ТМ (ду> п) и (у, t) + Г<2> фу, п) со (у9
A4.9)
в случае второй задачи (задача (П)±);
и±(у, t) = f(y, t), j7lD) (ду9 п)(о(у, t)\± = g(y, t)	A4.10)
в случае третьей задачи (задача
= f(y9 t)9 \ТЫ(ду9 n)u(y,t) + TW(dy9 n)a(y9 t)\± = g(y9 t)
в случае четвертой задачи (задача (IV)±).
В этих задачах 9~ = (Tt)9 <3 = (9t)9 f = (ft), g = (gt)9 Ф = (ф,),
Л = (h()9 гр = (%), x = (Xi) — трехкомпонентные векторы: iFl9 S, : D± x
Х^-Л; Л, ft: S xf- /?; Ф„ Я,, tf<f x<: D± — R.
Таким образом, задачи динамики заключаются в отыскании упругого
динамического состояния среды в некотором промежутке времени, если изве-
известны: массовые силы и моменты, смещения и вращения и скорости их измене-
изменения в начальный момент времени и, кроме того, заданы на границе смещения
и вращения — в первой задаче, силовые и моментные напряжения — во
второй задаче, смещения и моментные напряжения — в третьей задаче и вра-
вращения и силовые напряжения — в четвертой задаче.
Эти задачи эквивалентны следующим:
Найти регулярное решение % = (а, со) уравнения динамики A2.9) по на-
начальным условиям A4.7), и по одному из условий A4.8)—A4.11).
Аналогично ставятся задачи статики и колебания. Например, в первой
вадаче статики (задача A)*) ищется упруго-статическое состояние, если на
границе S заданы смещения и вращения.
3. Теория термоупругости. Здесь задачи также делятся на три основ-
основных типа, хотя задачи статики, как это будет разъяснено в главе X, не пред*
ставляют самостоятельного интереса.
Приведем формулировку некоторых задач термоупругого колебания.
Найти термоупруго-колебательное состояние [и, т, 0] среды D± (р, Х9,
й» Y» ТЬ х)> соответствующее массовой силе ЗГ и тепловому источнику Q по
граничным условиям:
u± = f9 Q± = g	A4.9'>
со
в случае первой задачи (задача (II*1);
\P(de,n)U\± = f, {§Y=g	A4.10')

58
ОСНОВНЫЕ ПОНЯТИЯ И АКСИОМАТИЗАЦИЯ
[Гл. I
в случае второй задачи (задача (И)*);
, ( (дв\±
A4.110
¦в случае третьей задачи (задача
\Р(ду, n)U\± = f, 8± = g	. A4.12)
(О
в случае четвертой задачи (задача (IV)±).
Эти задачи можно привести к следующим, эквивалентным задачам.
Найти регулярное решение U = (и, 9) уравнения A2.13) по граничному
условию A4.9') — для первой задачи, A4.10') — для второй задачи, A4.1 Г) —
для третьей задачи, A4.12) — для четвертой
задачи.
4. Задачи для неоднородных сред. В этой
книге в основном рассматриваются однород-
однородные (в смысле упругих свойств) среды. Рас-
Рассмотрение неоднородных сред связано с
серьезными осложнениями. Эти осложнения
примерно такого характера, как при переходе
от уравнений с постоянными коэффициентами
к уравнениям , с переменными коэффициен-
коэффициентами. Но трудности изучения задач для
неоднородных сред этим не исчерпываются.
В задачах механики важно получить не
только то, «что получается», а необходимо
также всем основным понятиям и условиям,
встречающимся в исследовании (условия раз-
разрешимости, единственности, эллиптичности
и т. д.), придать определенный механический
смысл. Это связано с дополнительными
серьезными трудностями. Именно эти причины вынудили нас отказаться от
рассмотрения общей теории неоднородных, а также анизотропных сред.
Вместе с тем, как мы увидим в главе XII, посвященной гранично-контакт-
гранично-контактным задачам, можно исследовать один специальный, но весьма важный для
практики случай неоднородности. Пусть Sk — замкнутая поверхность,
a Df — конечная часть пространства Е3, ограниченная этой поверхностью
(k = 1,2, 3). Предположим, что Dt cz Df, Df a Df, и введем обозначения
Dx = Df\Dt D2 = Df\Df, D = D, (J D2.
Пусть однородная изотропная среда с постоянными Ламе Xf и \ij занимает
область Df; j = 1,2. Таким образом, область D занята неоднородной средой,
состоящей из кусков, занимающих области Dt и D2. S2 — поверхность раз-
раздела этих кусков, aSj и53 представляют собой «обыкновенные» границы рас-
рассматриваемого неоднородного тела (рис. 2).
Мы будем рассматривать граничные задачи, когда на поверхностях S1 и
S3 задаются любые из указанных выше граничных условий, а на S2 заданы
условия контакта, выражающие заданный скачок смещений и напряжений
при переходе через точки поверхности S2. В частности, особый интерес с ме-
механической точки зрения представляет тот случай, когда эти скачки равны
нулю, т. е. когда смещения и напряжения остаются непрерывными. Таким
образом, задачи статики классической теории будут формулироваться так:
Рис. 2.

Л 15]	НЕКОТОРЫЕ ДОПОЛНЕНИЯ И БИБЛИОГРАФИЧЕСКИЕ УКАЗАНИЯ	59
Найти регулярное решение уравнений A4.8) в D, удовлетворяющее кон-
контактному условию \/у ? S2:
limu(x) — \\ти(х) = /(*/), A4.13)
Dt =э х -> у <=S2 D2=ix -* у &S2
lim Т(д„п)и(х)— lim Г(дх, п)и(х) = <р(у) A4.14)
и одному из приведенных выше граничных условий на поверхностях Sx и S2.
Эти задачи, в зависимости от вида граничных условий на 5Х и 52, будем назы-
называть ( и соответственно обозначать) первой, второй, третьей, четвертой, пятой
и шестой задачами.
/ и ф в A4.13) и A4.14) — заданные векторы на S2. Если на Sj и S2 заданы
различные условия из числа упомянутых выше, будем иметь смешанные
задачи.
Выделим особо тот случай, когда 5j «стягивается» в точку, а 53 «расши-
«расширяется» до бесконечности, точнее, когда неоднородная среда занимает все
пространство Е3 и состоит из двух однородных частей, одна из которых зани-
занимает область Df, а другая — область D~ = E^\(Df [) S2). В таком случае
граничное условие на 5j отсутствует ввиду отсутствия самой Sx; граничное
условие на SB заменяется условием на бесконечности, а условия контакта на
S2 сохраняются в прежнем виде. Эту задачу будем называть главной контакт-
контактной задачей.
Мы рассмотрели случай, когда исследуемая упругая среда составлена из
двух различных упругих кусков («двухкомпонентное» тело). Нетрудно видеть,
что аналогичные гранично-контактные задачи могут быть поставлены и для
«многокомпонентных» упругих сред (см. гл. XIII, § 3).
§ 15. Некоторые дополнения и библиографические справки
I. О дифференциальных операторах теории упругости. Основные задачи
теории упругости были сформулированы в предыдущем параграфе, как задачи
теории дифференциальных уравнений в частных производных.
Естественно выяснить место, занимаемое этими задачами в общей теории
дифференциальных уравнений.
Выясним, какому типу уравнений, например, по классификации Петров-
Петровского (см. 15.17), относятся основные уравнения, точнее, .системы уравнений
теории упругости.
Уравнения статики и колебания классической теории (системы A2.4)
и A2.5)), моментной теории (системы A2.10) и A2.11)) и теории термоупру-
термоупругости (система A2.13)) суть уравнения эллиптического типа.
В этом легко убедиться, вычислив определитель характеристической
матрицы; например, для уравнений статики (и колебания) моментной теории
упругости, характеристическая матрица имеет вид
где
x(I)=«xiviu хD)=Шзхз, б-(ь, ъ, а
х!7 = 0» + «) S*/!2 + (Я + |*—а) Ып til = (о + Р) 8*,? + (е
det X (I) = (I* + аJ (Я. + 2|i) (о + РJ (е + 2и) | g |12,
и, следовательно, det % (?) ф 0, если | =/= 0 (см. G.20)).

60	основные понятия и аксиоматизация	[Рл# I
Сложнее обстоит дело с уравнениями динамики. Они не принадлежат,
строго говоря, ни к одному из типов по классификации Петровского.
Например, характеристическое уравнение для уравнения динамики класси-
классической теории имеет вид
Следовательно, два овала (см. Петровский [11) из этой поверхности совпадают,
и поэтому уравнение динамики классической теории можно рассматривать
лишь как предельный случай гиперболических систем.
Для уравнений динамики моментной теории появляются две пары совпа-
совпадающих овалов, а уравнения динамики термоупругости не принадлежат ни
к одному из классических типов.
Отметим, что согласно современной классификации (см. Bers, John,
Schechter) уравнения статики A2.4), A2.10) относятся к строго эллиптическим
системам, а уравнения колебания A2.5) и A2.11) — суть эллиптические
системы.
Операторы А (дх), А (дх, со), М (дх) и М (дХ9 со) самосопряженные,
а В (дХ9 со) не является самосопряженным. Построим оператор В* (дХ9 ©)»
сопряженный с В (дХ9 со).
В* (дХ9 со) определяется равенством
[В (дх, со) U) °Vdx = JU • [В* (дх, со)V] dx,
D
справедливым для любых финитных четырехкомпонентных векторов
U = (Ui), V = (Vt) в области D из класса С2 (D).
Здесь знак «°» между векторами означает скалярное произведение, т. е.
Ф«/, где ф = (фг) и / = (f'i) — /п-мерные векторы, определяется равенством
Ф°/==2фЛ« Чтобы избежать недоразумений, отметим, что в книге часто
i
применяется произведение векторов, например, ф* и /, обозначаемое симво-
символом ф/ (без каких-либо знаков между ними), определяемое равенством ф/ =
= /ф = S/t-фь очевидно, при действительных / и ф ф°/ = ф/.
Легко проверить равенства
4
D k, /==1
= [ ^ V*Bli (dx, ©) Vfdx =\U B* (dx, o) V dx9
Dk,j=l	D
где
B*kj (дх, со) = Bkf (ax, со), Blf (дх, со) = 7 ^-,
B*k4(dx, со) = im-g^, B44 (дх, со) = A —^-; k> j = lf 2, 3.
Для наших целей удобно пользоваться не сопряженной матрицей
а матрицей В\ которую будем называть союзной и определять так:
В (дх, со) = 1 B'kj (дх, со)||4Х4,
Bkj (дх, со) = Bkj (дХУ со), В4/ (дх, со) = у -^-,
Bk4 (дх, со) = — шц -^—, 544 {дХ9 со) = А + -^-.

Я J51	НЕКОТОРЫЕ ДОПОЛНЕНИЯ И БИБЛИОГРАФИЧЕСКИЕ УКАЗАНИЯ	61
2. О некоторых пространствах функций и поверхностях класса JIk (a).
Для того чтобы поставленные выше задачи теории упругости имели регуляр-
регулярные решения, необходимо подчинить краевые условия (граничные данные
в задачах статики и колебания и граничные и начальные условия в задачах
динамики) некоторым ограничениям, иными словами, выбирать их из опре-
определенных классов функций. Иногда требуется иметь решение с гладкостью
более высокого порядка, чем регулярность. В этих случаях следует выбирать
данные из классов достаточно гладких функций.
Для выяснения некоторых вопросов, например, о корректности задач,
удобно в рассматриваемых классах функций вводить метрику — расстояние
между элементами (функциями) или норму элемента. Таким образом, вво-
вводятся в рассмотрение различные нормированные пространства функций.
При исследовании задач, поставленных в предыдущем параграфе, в этой
книге применяется в основном метод сингулярных интегральных уравнений.
Вопросы существования решения задач и установления свойств гладкости
решений приводятся к соответствующим вопросам для сингулярных интег-
интегральных уравнений, распространенных по поверхностям, являющимся гра-
границами рассматриваемых упругих сред. Кроме того, решения задач будут
выражаться интегралами типа потенциала, распространенными в основном
по этим поверхностям.
Свойства решений сингулярных интегральных уравнений, а также интег-
интегралов типа потенциала, существенно зависят от свойств поверхностей.
Приведем в этом пункте определения основных пространств функций
и классов поверхностей, с которыми будем иметь дело в дальнейшем.
Предложение «ср принадлежит классу С0* а (D)» (записывается символом
<р ? С°\а (D)) означает при ограниченной области D, что для любых х и х' из D
выполняется неравенство
где с — положительное постоянное число, выбранное для ф и не зависящее
от х и х' из D, 0 < а ^ 1 и
Если жеО — неограниченная область, то запись ср ? С°>а (D) означает,
что указанное выше неравенство выполняется для любых хих'изО, подчи-
подчиненных ограничению | х — х' | ^ 1.
Очевидно, если <p?C°'a(D), a > 0, то ср равномерно непрерывна
в области D.
15.1.	Определение. фбС0'0 (D), если <р равномерно непрерывна
в области D.	___
Таким образом, С0- ° (D) = С0 (D), где С0 (D) — класс функций, опре-
определенный в предыдущем параграфе.
Приведем следующее простое предложение.
15.2.	Теорема. Если ф ? С0- a (D), a > 0, то функция ф непрерывно
продолжима в каждой точке поверхности S, и функция г|э, определенная на D
равенствами я|) (jc) = ф(*)> если х 6 D, и гр (у) = lim ф (х)9 если у 6 S, удов-
D
летворяет неравенству
I ^ (х) — ц(х')
для любых х, х'ёО.
15.3.	Определение. ф? Ckia (D), где k — произвольное целое
положительное число, иО^а^ 1, если ф имеет все производные по декар-

62	ОСНОВНЫЕ ПОНЯТИЯ И АКСИОМАТИЗАЦИЯ	[Рл# J
товым координатам до порядка к включительно, эти производные равномерно
непрерывны в области D и все производные порядка k принадлежат классу
С0- а (D).	_
Очевидно, Ск*° (D) = Ск (D), Заметим также, что в литературе
иногда класс Ск>а (D) обозначается через Ск*а (D).
Совершенно аналогично определяются классы Ск (D) и Ск*а (D) и в том
случае, когда DczEm, где т — произвольное натуральное число.
15.3'. Определение. Пространство Ск (D) есть линейное норми-
нормированное пространство, элементами которого служат элементы множества
Ck (D)\ сумма элементов и произведение элемента на число определяется
формулой
(Ф + <р') (х) = ф (х) + <р' (х), (сф) (х) = сер (х),
а норма элемента — формулой
|(D, /г) ==	7 ,	SUp
X €= D
Суммирование совершается по всевозможным целым неотрицательным pl9 p%
и р3» ГДе Р = Pi + Р2 + Рз-
15.3".Определ ение. Пространство Ck*a (D) есть линейное норми-
нормированное пространство с элементами из множества Cfe- a (D) с нормой
а) = ||Ф||иэ, *)+ max sup
[x — x'
Пространство С0-а (D) называют пространством Гёльдера (см. Мусхе-
лишвили [21) и иногда обозначают через На.
15.4. О п р е д е л_е ние. Матрица ф == || ф/; ||тХр принадлежит классу
Сй (D) [Cfe- a (D), C^ (D) ], если ф|/ 6 Ск (D) [Ф„ 6 Cfe*« (D), Ф/:/ Cfr (D)!
для любых i = 1, . . ., т и / = 1, . . ., р.
Пусть п = (пг, п2, п3) — произвольный ненулевой вектор, б — произ-
произвольное положительное число, а х с Е3. Обозначим через Ц (х, п, 6) круг-
круглый цилиндр в ?3, имеющий высоту 26, осью которого служит я, центром сим-
симметрии — точка х и радиус основания равен 6.
Через Ш (х, 6) обозначим шар с центром в точке х и радиуса б. Следова-
Следовательно,
ZZ7(x, 6) = \y?Es\\x — y\<6\.
Границу этого шара обозначим через С (х> б), следовательно,
С(х, 6) =
15.5. Определение. Поверхность S принадлежит классу Лк (а),
где k — произвольное натуральное число, и О^а^ 1, если существует
такое положительное число dt что каждой точке z? S можно поставить в со-
i	i
ответствие некоторую ортонормальную систему векторов v (г) = iyx (г),
i	i
V2 B)> Va (z))> i — 1» 2, 3, таким образом, чтобы часть S, заключенная внутри
з
цилиндра Ц (г, v (г), d), которую обозначим через S (г, d), не имела общих
точек с основаниями этого цилиндра и допускала представление вида

Л J5]	НЕКОТОРЫЕ ДОПОЛНЕНИЯ И БИБЛИОГРАФИЧЕСКИЕ УКАЗАНИЯ	63
в системе (z), где (г) — система координат в Е3 с началом в точке 2, соответ-
1	2 -	3
ствующая базису v (г), v B), v B); glf ?2, |3 — координаты точки лс ? S
в этой системе и при этом
7*€С*.«(т(г, d)),
Здесь т B, d) — проекция S (г, d) на плоскость g3 = 0. Плоскость
|3 == 0 в дальнейшем обозначим через т (г); % (г) — касательная плоскость
з
поверхности S в точке 2, a v B) — нормаль к этой поверхности в точке 2.
Поверхность класса Лх @) называют гладкой поверхностью, поверхность
класса Лх (оь), а > 0 —поверхностью Ляпунова и поверхность Л2 @) — по-
поверхностью с непрерывной кривизной.
Нетрудно показать, что JIk (а)аЛк ф), если а > р, и Лк (а)^с: Лп (Р),
если /г > п и а, р — любые числа.
Если S 6 Лк @) для любого натурального k, то будем писать S 6 «#<»
и назовем поверхность S бесконечно-дифференцируемой.
Нам нужно будет также рассмотреть поверхности с краем. Пусть 5 —
двумерное, связное, ограниченное многообразие с краем (вообще не компакт-
компактное). Такую поверхность S мы будем называть разомкнутой поверхностью.
Включение S 6 Лк (а) определяется так же, как в определении 15.5, но все
условия определения, указанные в 15.5, должны выполняться для точек мно-
множества 5, где S — замыкание множества S в пространстве Е3.
По определению, поверхность S кусочно-гладкая класса Лк (а), если 5
можно разбить на конечное число частей простыми гладкими кривыми так,
чтобы каждая из этих частей принадлежала классу Лк (а).
Таким образом, поверхность 5 будет кусочно-гладкой поверхностью*
если ее можно разделить на конечное число гладких частей гладкими про-
простыми линиями.
Поверхность куба, а также поверхность круглого конечного цилиндра,
очевидно, замкнутые кусочно-гладкие поверхности. Более того, эти поверх-
поверхности принадлежат классу Лж кусочно.
15.6.	Определение. Пусть S ? Лг @). f — функция, определен-
определенная на 5; х 6 S B, d), a glf ?а, |3 — координаты точки х в системе (z). Опре-
Определим на т B, d) функцию fz следующим образом: f2 (|ь |2) = / (х).
По определению, f?Ck'$(S), если для всякой точки zfSy
h e Ck> » (т B, d)). / = || f4 \пхр е Ck> » (S), если fif 6 Ck- * E) для всякого
i = 1, . . ., m\ / = 1, . . ., p.
В множестве Ck* 3 E) можно ввести сумму элементов и произведение
элемента на число; тогда Ck*|3 (S) обратится в линейное множество. В этом
множестве можно ввести понятие нормы. Она вводится так же, как при опре-
определении пространства Ck>a (D), но вместо производных по декартовым коор-
координатам берутся производные в смысле определения V. 1.1—V.1.3 или
V.1.12.
Полученное таким образом пространство обозначается тем же символом
Ck'$ (S), а норма элемента / в этом пространстве — через ||/||(S, *,р).
Справедлива следующая
15.7.	Теорема. Если функция f, определенная на S, класса Лх @),
удовлетворяет для любых ху у 6 S неравенству
где с = const > 0, а = const, 0 < а < 1, то f 6 С0»а E).

64	OCHOBHbTF ПОНЯТИЯ И АКСИОМАТИЗАЦИЯ
Поверхность S разделяет две области в Е3. Одна из них ограничена, дру-
другая неограничена. Обозначим эти области соответственно через D+ и D".
Таким образом, Е3 = D+ U 5 (J D'.
Пусть п (у) = (п1 (у), п2 (у), п3 (у)) — орт нормали поверхности S
в точке у, внешней по отношению к области D+.
Доказывается следующая теорема (см. Гюнтер [11).
15.8.	Теорема. Если S ? JIk (a), k ^ 1, то п 6 Ck~l* а (S).
3. Библиографические справки.
15.9.	Достаточно подробный обзор результатов, полученных в класси-
классической теории упругости до 1927 года, приводится в книге Love [11.
Некоторые из последующих результатов, полученных до 1958 года,
вошли в обзор Goodier, Hodge [11. Ценные литературные указания содер-
содержатся в книгах: Sokolnikoff [1J, Grioli [11, Solomon [11, Лурье [21, Teodo-
rescu [5], Kecs, Teodorescu [11.
Обзор работ советских ученых дается в статьях: Шапиро- [11, Шер-
ман [3], Купрадзе [9, 13], Мусхелишвили, Черный [1].
15.10.	Обзор результатов по моментной теории упругости имеется
в книгах: Grioli [11, Nowacki [21, в работах Koiter [43, Пальмов [13 и др.
15.11.	Обзор результатов по термоупругости содержится в книгах:
Love [13, Лебедев [1], Timoshenco, Goodier [1], Melan, Parkus [11, No-
Nowacki [1, 31 и др., а также в обзорной статье Шачнев [11.
15.12.	Физические основы классической теории упругости рассматри-
рассматриваются в книгах: Love [11, Папкович [11, Green, Zerna [11, Kittel [11,
Седов [1, 21, Ландау, Лифшиц [11 и др.
15.13.	Физические основы моментной теории рассматриваются в рабо-
работах: Voigt [I], Cosserat E., Cosserat F. [1], Аэро, Кувшинский [1, 2, 31,
Пальмов [II, Nowacki [81 и др. Ом. также библиографию к главе IX.
15.14.	С физическими основами теории термоупругости можно позна-
познакомиться в книгах: Nowacki [1, 31, Ландау, Лифшиц [13 и др.
15.15.	В этой книге не рассматривается плоская задача теории упру-
упругости; с ней читатель может познакомиться в книге Мусхелишвили [11.
Обзор литературы по плоской задаче см. также Мусхелишвили [1, 33,
Векуа И., Мусхелишвили [13 и др.
15.16.	Задачи колебания упругих сред изучались многими авторами.
Обзор старых работ по этим вопросам — см. в книге Love [13 и некоторые
последующие — в обзоре Goodier, Hodge [1]. Граничные задачи стационар-
стационарных колебаний изучались в работах: Love [I], Weyl [1], Купрадзе [8, 133;
в них содержатся необходимые литературные указания.
По динамическим задачам классической теории упругости см. Франк,
Мизес [11, гл. 12 (написана С. Л. Соболевым) и библиографию к восьмой
главе настоящей книги.
15.17.	Теории общих систем уравнений в частных производных и об-
общим дифференциальным операторам в частных производных посвящены
многочисленные работы. Отметим следующие (в основном обзорные): Пет-
Петровский [1, 31, Гельфанд, Петровский, Шилов [11, Вишик, Мышкис, Олей-
ник [11, Бицадзе [13, Hormander [11, Agmon, Douglis, Nirenberg [11, Ed-
Edwards [11.
15.18.	Большое число работ посвящено определению упругих постоян-
постоянных. Обстоятельные сведения по этому вопросу содержатся в работах: Born,
Huang fl], Grammel 111, Kittel [11, Huntington [11, Timoshenko, Woinow-
ski-Krieger 111.

ГЛАВА II
ОСНОВНЫЕ СИНГУЛЯРНЫЕ РЕШЕНИЯ
Из первой главы читатель знает, что предстоит рассмотреть большое
число граничных, гранично-контактных и других задач для широкого класса
систем линейных уравнений в частных производных второго порядка. Для
решения этих задач мы применяем методы потенциалов и теории интеграль-
интегральных уравнений.
Потенциалы строятся, как обычно, с помощью фундаментальных или
других сингулярных решений соответствующих дифференциальных урав-
уравнений.
Несмотря на то, что рассматриваемые дифференциальные уравнения
принадлежат различным каноническим типам, а некоторые не принадлежат
ни одному из классических типов, во всех случаях основную роль будут
играть фундаментальные и другие сингулярные решения уравнений эллипти-
эллиптического типа; характерной особенностью таких решений является наличие
точечной сингулярности вида | х р1, где | л: | = У^х\ + х\ + х\, и простой
механический смысл: в классической теории упругости, в момёнтной теории
и в термоупругости они выражают соответственно смещения, смещения и вра-
вращения, смещения и температуру в бесконечной среде, возникающие под воз-
воздействием сосредоточенных в начале координат единичных сил, сил и момен-
моментов, сил и источников тепла, соответственно.
В этой главе будут построены явные выражения указанных решений
и исследованы основные свойства.
§ 1. Фундаментальные решения уравнений
классической теории упругости
1. Уравнение статики. Матрица Кельвина. Пусть изотропная упругая
среда заполняет пространство ?3ив точке х — О действует сосредоточенная
сила величиной в две единицы, направленная по оси х*, / = 1, 2, 3; тогда
смещение точки х = (х19 х2, х3), П (х) = (Г1; (х)> Г2/ (х), Г3/ (х))9 вызван-
вызванное указанной силой, вычисляется (см. Love [1 ], гл. VIII) по формуле
rkf(x)=X'8kj\x\-1 + [i'xkxj\x\-b k, / = 1, 2, 3,	A.1)
где
(К + 2|г)Г\ |х' = (X + И) [4я[г (X + 2ц)Г A.2)
и X и ja — постоянные Ламе.
Для нас важен не только физический смысл векторов П (х), но и то, что
они представляют решения уравнения статики (I, 12.4) при отсутствии объем-
объемных сил, в каждой точке пространства Е3, кроме начала координат. В этом
можно убедиться непосредственным вычислением.
5 В. Д. Купрадзе

66	ОСНОВНЫЕ СИНГУЛЯРНЫЕ РЕШЕНИЯ	[Рл Ц
В самом деле, если A.1) перепишем в виде
6fc,	д2\ х\
2л{^ I х |	uXfeOXj
и заметим, что
А	*	Г\	All	?
для k-YL компоненты вектора А (дх) П (х) получим
S Аы (дх) Ги (х) = fiA (к^птг — ^' -Щт-) + (Я- + |х) 4- div П (х) = 0.
Введем матрицу
Г (х) = || ГЛ, (х) Цзхз =«Г1 (х)9 ГЧх)у Г3 (х) ||	A.4)
и назовем ее матрицей фундаментальных решений Кельвина (см. Love [1],
гл. VIII).
Матрица Г (х) симметричная и каждый столбец ее, а также строка, удов-
удовлетворяют уравнению статики при отсутствии объемных сил, в произвольной
точке х 6 ?з> кроме начала координат. Таким образом х),
А(дх)Г(х) = 0, хфО.	A.5)
2. Уравнение колебания. Матрица Купрадзе. Матрица фундаментальных
решений однородного уравнения колебания A, 12.5')
А(дх, со)и = 0	A.6)
имеет вид
Г(*. со) = ||Г*,(х, со) Цзхз,
Г*/ (X, со) - 2j V6^a^ + Pt-dx^dxj)	\Г\
1 = 1
где i — мнимая единица, kx n k2 — неотрицательные числа, определенные
равенствами
k\ = pco2(?t + 2ЦГ1. k\ = pcoV,	A.8)
щ = б2/ Bя[х)~1, fr = (—lI (гярсо2)-1.	A.9)
Пусть П (х, со) = (Г1; (ху со), Г2/ (х, со), Г3/ (х, со)), / = 1, 2, 3.
Вектор Г1 (х, со) удовлетворяет A.6), Агра / = 1, 2, 3, в каждой точке
пространства ?3> кроме начала координат.
В самом деле, учитывая формулы
. д , , 2\ Т- /	ч	О '	^2	еХР (^1 1Х1)
,._,.'	1	d exp (ik,\ х I)
divr/(*, «) =^71+2^^7-ui'
для fe-й компоненты вектора А (дХ9 со) П (х, со), получаем
з
S Аы (дх, со) Г// (х, со) = fx (A + kl) Yki (х, со) + (X + ц) -^— div Г; (х, со) = 0.
1) В формуле A.5) 0 в правой части обозначает матрицу размера 3X3 с нулевыми эле-
элементами.

§ 1J ФУНДАМЕНТАЛЬНЫЕ РЕШЕНИЯ КЛАССИЧЕСКОЙ ТЕОРИИ УПРУГОСТИ	57
Г (х, со) будем называть матрицей Купрадзе. Каждый столбец этой матрицы^
а также каждая строка, являются решением уравнений A.6) при х =ф= 0.
Приведем один простой способ построения указанной матрицы. Перво-
Первоначальный ее вывод приведен в работе Купрадзе [7].
Вычисляя в определителе det А (дх, со) алгебраическое дополнение эле-
элемента Aki (дх, со), получим
T^^B^} + kl)' (U0)
Подставляя в A.6) вместо и матрицу
f(dx, со)||зхзФ,	A.11)
где ф — скалярная функция, и учитывая, что
3	3
S Аи Фх> <*>) s?u (дх, со) ф = S Аы (дХ9 со) st>n {дх, со) ф =
= 6fc/det Л (а„ со) Ф = 8kf\i2 (X + 2[х) (Д + ki) (Д + kl)\
для определения функции ф получим уравнение
Так как все элементы матрицы \si>ki (дх, со)|| содержат множитель
(А + Щ ф, достаточно найти функцию
которая удовлетворяет уравнению
Мы ищем такое конкретное решение последнего уравнения, у которого
частные производные второго порядка имеют изолированную особенность
вида | х I; если такое решение существует, оно должно удовлетворять усло-
условиям
Г1
я|х\Г
Отсюда
Можно проверить, что функция яр удовлетворяет указанным выше ус-
условиям.
Учитывая A.10) и подставляя найденное значение (Д -f- ki) ф =
= 1jli2(X + 2jut) ]~x if? в A.11), получим матрицу и (х, со), которая совпадает
с матрицей Купрадзе.
При определении функции i|) мы подразумевали, что &? ф kl: t& — kl =
= (X + fi) pco2 [\x (X + 2ix)T~l. Отсюда в силу (I, 5.16) условие kl = $
эквивалентно условию со = 0. Этот случай был рассмотрен выше. Но, если
допустим формально, что &2 —> k\ = k , то соответствующее частное решение
можно получить из выражения if путем предельного перехода; при этом
<ф = exp (ik | х

68	ОСНОВНЫЕ СИНГУЛЯРНЫЕ РЕШЕНИЯ	грл JJ
3. Основные свойства матрицы Купрадзе. В пункте 2 мы уже доказали
одно основное свойство матрицы Г (х, со), которое заключается в следующем:
1.1.	Теорема. Каждый столбец и каждая строка матрицы Г (х, со)
являются решением уравнения A.6) во всех точках х ? ?3» кроме начала ко-
координат.
1.2.	Т е о р е м а. При любом х 6 E3f—со < со < оо, справедлива оценка
|Гл/(х, (o)\^c(Kii)\x\-\ К /=1, 2, 3,
где с (Я, р>) — положительное число, зависящее только от A,, fj>.
Доказательство. Учитывая формулу
exp (tfe; 1 * |) exp(ifr|*|) Fц (tog |*| — 1) , *^*у f 3A —
Fц
\
из A.7) имеем
AЛ2)
Применяя теорему о среднем значении, получаем оценку
|A — i*,-|x|)exp(ifti|x|)— l|^*?|jc|2f /=1, 2,	A.13)
в силу которой из A.12) следует соотношение
I TkJ (х, со) | ^ FХ
Формула A.7) теряет смысл при в) = 0.
Обозначим
, со) = Г (*, со) — Г (л:),	A.14)
где Г (х) — матрица Кельвина A.4).
1.3. Теорема. Для всех х ? Е3у — оо < со < оо, справедлива оценка
где с (X, \i) — положительное число.
Учитывая A.12), A.1) и A.14), имеем
2
VL Г exp(te.|*|)l
, со) = ^jKja, ^Ui^	Pl
?R?L '
• +3	Uli	Jj.0-15)
Применяя теорему о среднем значении, имеем
\(l—ikt\x\)exp(iki\x\)—l	?-й|*|а|^|А,|3|*|%	A.16)
и из A.15) непосредственно следует
^	]	A-17)

Я I]	ФУНДАМЕНТАЛЬНЫЕ РЕШЕНИЯ КЛАССИЧЕСКОЙ ТЕОРИИ УПРУГОСТИ	gg
1.4. Теорема. Для х ? ^з\ч{°}
В самом деле, из A.17) при со—>0 имеем Г^- (х, со) —¦ 0.
1.5. Теорема. Для всех х 6 Е39 — оо < со < оо, справедлива оценка
j (*, <*>)
t и р=1, 2, 3,
с (Я, fi) — положительное число.
Из A.15) следует
(х, со)
Г
у I
— Р/
3A—^/I«|)e
— I
щх.
2 - (A? | x |3
3A- «, | х |) exp («, I x |)	 ** | x |2 - (A? | x
\х\3
— <ft, | x |) exp (tfe, | x |) —
I a: I2
1	Q	Т
3 A — ikt | х |) exp (ikt \x\)	~ k] \ х |2 — ik3t \ x f
— 3	^-р	^	J. A.18)
Учитывая A.13), A.16), а также оценки
| exp (ikt \х\) — 1 — iki | х | ^ U\ \ x |2,
из A.18) получим
dtkj (x, со)
Из теоремы 1.5 следует
1.6. Теорема. Для х
hm
dxv
• "^7 f ^ '
т^—,
dxD
, /, р = 1, 2, 3.
A.19)
A.20)
Аналогично доказывается также следующая
1.7. Теорема. Вторые производные элементов матрицы Г (х, со)
по декартовым координатам точки х имеют в окрестности начала изолиро-
изолированную особенность вида \ х I.

70	ОСНОВНЫЕ СИНГУЛЯРНЫЕ РЕШЕНИЯ	грл J|
§ 2. Фундаментальные решения уравнений
моментной теории упругости
1. Уравнение колебаний. Однородное уравнение установившихся коле-
колебаний моментной теории упругости (см. (I, 12.11)) имеет вид
M(dxt a)U = 09	B.1)
где
М(д„ c) = \Mki{dx, o)\^ = \MMZ MM2\	B.2)
причем
1 = 6Л/ (|i + а) (Д + о?) + (X + (х — а) /
з
о=1
Aftf = б», (о + Р) (А + oi) + (е + » — Р)
2 per2 2 ^сг2 — 4а
?^ (и, со) — шестикомпонентный вектор, а — частота колебаний, ekjp —
9	9?
символ Леви-Чивита; G\ ^ 0, а 02 может принимать любое действительное
значение.
Обозначим алгебраическое дополнение элемента Mkf(dx, a) (fe, / = 1.6I)
в определителе det M E^, а), через Jlkj (dXJ а). После элементарных, хотя
и громоздких вычислений, для элементов Jtki (дх, о) матрицы
получим
A)
^/ =(Хо
х
2аа0 х» в и ч/	2 4)
X (А + *?> (А + ^) (А + ^) (А
4а2
+ а) (и
х) Символ /= 1,6 означает: /. = 1, 2, . . ., 6.

С 2]	ФУНДАМЕНТАЛЬНЫЕ РЕШЕНИЯ МОМЕНТНОЙ ТЕОРИИ УПРУГОСТИ	71
где
1 — 4а	/Г| г
з и &1 удовлетворяют условиям
4а2
B.6)
Легко заметить, что Ж (дх, а), (как и М (дХУ о)) является самосопряженным
оператором, т. е. Ж (dXJ a) = [Ж (—дх, о)]', где штрих означает операцию
транспонирования (строк-столбцов).
Подставляя в B.1) вместо % матрицу
%=\Ж(дк, о)]' Ф = Г ,, "Г Ф.	B.7,
где ф — искомая скалярная функция, получим
det М (дх, а) ф = а0 (А + k\) (А + й?) (Д + Щ* (Д + &IJ Ф == 0.
В B.7) каждый элемент содержит множитель а0 (А + Щ (А + fei) Ф,
поэтому достаточно найти именно функцию "ф = а% (Д + Щ) (А + fel) Ф-
Очевидно, для ее определения имеем уравнение
(А + k\) (A + kl) (А + Щ) (А + k\) -ф = 0.
Для того чтобы матрица решений B.7) оказалась фундаментальной, мы
должны найти такое решение последнего уравнения, частные производные
шестого порядка которого имеют особенности лишь вида | х \~х. Такое реше-
решение, если оно существует, должно удовлетворять условиям
(Д + *?+,) (А + k\+2) (A + k2l+s) ц = Bп \х\Г1 exp (ikt \х\), I = ТГ1,
«5 = /Cj,	^26 = «2»	^7 == ^3*
Рассматривая эти соотношения как систему уравнений относительно
if, Ая|), ДАг|) и ДДАгр найдем
4
Ф = S At Bя | jc I) ехр № | х |),	B.8)
где
Л, = (&?+1 _ к*) (%+2 - k*)-1 (k2M - k*)-K	B.9)
Соотношение B.8) позволяет легко проверить, что г|? удовлетворяет всем
поставленным выше условиям.
Выражение_для -ф (см. B.8)) мы получили в предположении, что постоян-
постоянные Ы\ (I = 1,4) отличны друг от друга. В нашем случае, принимая <J/o2 —
— 4a > 0, из B.5) и B.6) получаем kl > 0, / = ITT, Если <^a2 — 4a < 0,
то, учитьфчя значения kl и k\
о а2	~2 I J* I	4(Х'2
2йз. 4= а, + а2+
и формулу B.5), будем иметь ^ > 0, ki > 0, й| < 0 и Ы\ < 0.

72
ОСНОВНЫЕ СИНГУЛЯРНЫЕ РЕШЕНИЯ
[Гл. II
Случаи, когда некоторые из k\ равны друг другу, нужно рассмотреть
отдельно, путем предельного перехода в выражении для tf.
В дальнейшем необходимо, чтобы kl =/= kl. Это неравенство, как легко
видеть из выражений для kl и М, всегда выполняется. Кроме того, мы пред-
предполагаем <^а2 — 4а =f= 0.
Принимая во внимание, что (А + kl) (A + kl) ср = а^1у? и учитывая
значение г|), из B.7), если учесть еще B.3) и B.4), получим матрицу фундамен-
фундаментальных решений U (х, а), которую обозначим через Ч? (х, а). Таким
образом,
ш1х О> =
(ж. а)
(х, а)|зхз, /=Т74,
4 3
1=1 р=
¦-4а) ' k)
1=1
B.10)
2.1. Теорема. Каждый столбец матрицы W (х, а), рассматриваемый
как вектор, удовлетворяет системе B.1) во всех точках пространства E3f
кроме начала координат.
Справедливость этой теоремы очевидна из приведенных выше рассужде-
рассуждений. Можно ее получить также из B.10) непосредственным вычислением.
Доказанные в п. 3 § 1 теоремы относительно матрицы Купрадзе, с неко-
некоторыми изменениями остаются в силе и для матрицы W (х, о). Доказательство
предоставляется читателю.
2. Уравнение статики. В этом случае а = 0 и из B.5) и B.6) следует
4а
Ш=-
4ац
BЛ1)
Введем обозначения
4а \V.
J
(ц + а)
B.12)

§ 3]	ФУНДАМЕНТАЛЬНЫЕ РЕШЕНИЯ УРАВНЕНИЙ ТЕРМОУПРУГОСТИ	73-
Учитывая B.11) и B.12), из B.10), в результате элементарных вычисле-
вычислений, для матрицы фундаментальных решений статики моментной теории
упругости получаем следующее выражение:
хрш
*	"	ехр(
1*1 Ц(
1 а2 Г (Х+ц)|*| , Р + и exp(-ojx|)-l 1
2n\idxkdxj\. 2(А,+ 2ц) ~ 4ц	|х|	J'
д 1 — exp (—а4 | х \
°/лр Ш~р	\х~\
0^1
1 a2 гехр(-о3|х|)~ехр(—а4 | л: |) exp (—а4 | дс |) ~ 1
8я ддслдху L	«U|	|il*l
1
-I
B.13).
2.2. Теорема. Матрица^ (х) удовлетворяет однородному уравнению
статики моментной теории упругости в каждой точке пространства Е3,
кроме начала координат.
Из вида B.13) легко заключить, что в окрестности | х | = оо имеем
1 (х) = О (| х Г1), ?$ (х) = W$ (х) = О (| х Г2), |
с) = и {\ х | )у /г, / = 1, z, о.	j
Из сравнения B.10) и B.13) замечаем, что сингулярные части матриц
(я, а) и W (х) одинаковы и определяются формулами
1 ,
I * П
4я Г*' (ц + а) (X + 2ц) I * П (ц + а) (X + 2ц)
-Р V/
§ 3. Фундаментальные решения уравнений термоупругости
1. Уравнение колебаний. Для уравнения термоупругости (I, 12.13) —
B(dx,w)U=0,	C.1)
где U — четырехкомпонентный вектор, имеем
det В (дх, ®) = ц2 (К + 2|i) (А + Х$ (А + Ц) (А + ^)8	C.2)
и
Т + T+2JT + *»• Л1Л2 — — fti, лз=—,
Здесь постоянная fef определена из A.8).

74
ОСНОВНЫЕ СИНГУЛЯРНЫЕ РЕШЕНИЯ
[Гл. II
Алгебраическое дополнение элемента Bkj (дх, со) в детерминанте
det В (дх, со), которое обозначим через 3Skl (дх, со), равно
, со) = (х2 (Я + 2ц) A — 6*4) A — б/4) (-^ (А + Я,?) (Д + *!) (Д + А|) —
4-
—8^w,
	 6*4) тг— (Д ¦
С/Л,
+ ц* (Я + 2ц) б*46,4 (Д + ft!) (А + ЦТ; к, / = 1, 4. C.4)
Подставляя в C.1) вместо (У матрицу
|;ф,	C.5)
где ф — скалярная функция, а штрих означает операцию транспонирования
получим
4
S 5«(^, <о)&ц(дх, a>)(p = 8kidetB(dx, со)ф =
= |Л2 (X + 2\i) 8kf (A + Я?) (Д + Я|) (Д + ^зJ Ф = 0, k, / = 1, 4,
и для функции яр = [х2 (X + 2fx) (Д + XI) ф имеем уравнение
(Д + М)(Д + М)(Д + М)ф = О.
Из тех же соображений, что и выше, функцию гр (х) выбираем в виде
з
exp (iXj | х |)
—о	о	о	о	*
\&		 1^1 (\	.^__ \ ^ 1 I V I
/-4—I "™~~ // \ /-I—2 ~~~" If I '
где ^4 = Хи Х5 = Х2, и, помня, что $щ (дху со) содержит множитель (Д + XI),
после внесения значения гр (х) в C.5), получим матрицу фундаментальных
решений уравнения C.1):
Ф(*. СО) = [| Ф^ (ЛГ, @
4Х4,
C.6)
где
9 со)=
1
!, C.7)
2я (X, 4- 2м-) (Л| — X2)
S Р; = <
2* аз-л*
C.8)

? 4]	СИНГУЛЯРНЫЕ РЕШЕНИЯ КЛАССИЧЕСКОЙ ТЕОРИИ УПРУГОСТИ	75
Легко проверить, что каждый вектор-столбец в фундаментальной матрице
Ф (х, со) имеет единственную особенность в точке х = 0, и притом порядка не
более | х I. Кроме того, из C.6) непосредственным вычислением доказывается
3.1. Теорема. Каждый столбец матрицы Ф (х, со) удовлетворяет
системе C.1) всюду в пространстве Е3, кроме начала координат.
Заметим, что матрица Ф (х, со) несимметрична и ее строки, рассматри-
рассматриваемые как векторы, не удовлетворяют уравнению C.1).
Матрицу Ф (х, со) мы получили в предположении Х\ Ф А|. Случай
Х{ = AJ следует рассмотреть отдельно, примейяя предельный переход в C.6)
(см. задачу 5).
2. Союзное уравнение. Обозначим через Ф* (лс, со) = || Ф?/ (jc, со) ||4Х4
матрицу, полученную из матрицы Ф (х, со) перестановкой строк и столбцов
и заменой х на —х; будем иметь
= Ф/л(—х, со), ft, / = 171.	C.9)
Прямым вычислением доказывается
3.2. Теорема. Каждый столбец матрицы Ф* (х, со), рассматривае-
рассматриваемый как вектор, удовлетворяет союзному уравнению В* (дХу со) и = О
(Blj (дху со) = B,k (—дх, со)) во всех точках пространства Е3, кроме начала
координат.
3. Уравнение статики. Из матриц Ф (я, <») и Ф* (х, со) при со —» О
получаем
ф (х) = || <Dfc/ (х) ||4Х4, Ф* (х) = || Oli (х) ||4Х4,	C.10)
где
Щ] (х) - A —М A — 0/4) ГЛ/ (х) + 4jx(^ + 2fX) |7| +-2JT Г71Э
а ГЛ/ (а:) определяется формулой A.1).
Легко проверяются следующие теоремы:
3.3.	Теорема. Матрицы Ф (х) и Ф* (х) соответственно удовлетво-
удовлетворяют однородному уравнению статики (см. A, 11.24) и AЭ 11.24')) и союзному
уравнению для всех х 6 ?3\{0}-
3.4.	Теорема. Элементы матриц Ф (х> со) — Ф (х) и Ф* {х, со) —
— Ф* (х) в точке х = 0 ограничены, а первые производные имеют изолирован-
изолированные особенности вида \ х |~г.
(В
3.5.	Теорема. Вторые производные элементов Ф^ (х, со) =
== Фл/ (х, со) — Ф*7 (х), Ф^/ (х, со) = ф;, (х, со) — Ф1/ (х) (ft, / = 1, 2, 3),
Ф44 (х, со) = Ф44 (х, со) в окрестности точки х = 0 имеют особенность вида
О	9
|х р1, а вторые производные элементов ФЛ4 и Ф4/ (&, / = 1,2, 3) — ограни-
ограничены.
§ 4. Сингулярные решения уравнений
классической теории упругости
1. Уравнение статики. С помощью фундаментальных решений можно
образовать новые сингулярные решения тех же уравнений, играющие боль-
большую роль в теории граничных задач.
Введем матрицу
Т (дХ9 п (х)) Г (х) = [|(Т (дх> п (х)) Г (x))kJ ||зхз,	D.1)

76	ОСНОВНЫЕ СИНГУЛЯРНЫЕ РЕШЕНИЯ	[Рл Ц
где Т (дх, п (х)) и Г (х) — матрицы, определенные выражениями (I, 13.2)
и A.4) соответственно, а п (х) — произвольный единичный вектор. Спра-
Справедлива
4.1. Теорема. Каждый столбец матрицы
\Т(дю п(у))Т(у—х)Г = \Т(дХ9 п(х))Г(х — у)]*
относительно точки х удовлетворяет однородному уравнению статики
А(дх)и = 0	D.2)
всюду в Е3, кроме точки х = у.
В самом деле,
з
\Т{ду> п (у)) Г (у—x)]'kf'— ? Тц(дУ9 п {у))Тш{у—х)
i=i
и
{А (дх) [Т {ду> п (у)) Г (у — x)Y)kf = S Ар (дх) Ти (д„ п (у)) Г1р (у — х)=
3	3
= S ТцФд* п (У)) 2 Akp(dx)Ylp{y — x) = 0,
i=i	р=1
так как Г (х — у) симметрична и удовлетворяет уравнению D.2) всюду в Е3$
кроме точки у (см. 1.15).
Рассмотрим теперь матрицу
Т (дх, п (х))Г (х) = 1 \Т (дХ9 п (х)) Г {x)kl ||зкз,	D.3)
где Т — матрица, определенная из (I, 13.4).
Совершенно так же, как 4.1, доказывается
4.2. Теорема. Столбцы матрицы
—х)]
{дру п(у))Г(у
удовлетворяют уравнению D.2) для всех х 6
4.3. Теорема. Для всякой точки х 6 Е3 справедлива, оценка
т (дх, п (х)) Г (x))hi | < с (К р., н)\х Г2,	D.4)
где с (%, р>, х) не зависит от х.
Справедливость этого утверждения следует из равенства
= [(хр' — рХ') 6ki — 3 (ix + х) р' ^ 2 щ (х) i^
/=!
где W и у* — постоянные, определенные из A.2).

* 4]	СИНГУЛЯРНЫЕ РЕШЕНИЯ КЛАССИЧЕСКОЙ ТЕОРИИ УПРУГОбТИ	77
Воспользовавшись тождеством
3	3
ж ^ f%, (X) Xj	ж 1	X iXj
S ~1^г = 2 Xw(d" я (X))TZ?>	D)-
где
Лы(дху п (х)) = щ (х)-^- — nk{x)-^> *, / = 1 э 2, 3,	D.7)
можно D.5) переписать в виде
6 3
о
2
Этим представлением мы воспользуемся впоследствии (см. V, § 4).
В § I главы V будут подробно рассмотрены также свойства матрицы
Л (дх, п (х)) = || Mki (дху п (х))Цвхз.	D.9)
к
Матрица Т (дх, п (х)) Г {х) при к = рр' (X') обращается в матрицу
J? (дх9 п (х)) Г (х) согласно (I, 13.6). Таким образом,
з
6.. ^--1 п, (х) х,
(Jf{dx, п {х))Г(х))ц-	^ 2j -Т7|И +
;=1
2. Уравнение колебаний. Рассмотрим матрицу
Т (дХ9 п (х)) Г (х, со) = 1 (г (дх$ п (х)) Г (х, ©)jft/ Цзхз,	DЛ1)
где Г (х, ю) — матрица Купрадзе.
Нетрудно проверить равенство .
3
(т (дх> п (х)) Г (х, co))ki = -?} V щ (х) ^г
1x1
exp (ikf \x\)	н
2 3
д3
р=1
где рр определяется из A.9),
Учитывая тождество

78	основные сингулярные решения	[Гл#
где Жщ (дх, п (х)) определена из D.7), можно D.12) переписать в виде
(дХ9 п (х)) Г (х, ©))л/ = -? ^ щ (х) ^ еХр(|^|Х|) +
1=\
2я
* ежр№|х|)	a exp №|«|I
d*j	|х|	' v 7 dxk \x\ J '
+ (и +1) 2 •*« (д« я W) гч (х- ю)- DЛЗ>
Ввиду симметричности матрицы Г (х, ю) и перестановочности операто-
операторе
ров Акр (дх, <о) и Тп (ду9 п (у)), совершенно так же, как теорема 4.1, дока-
доказывается
4.4. Теорема. Матрица
[т (дуу п (у)) Г(у — х, со)] - || [т {дуу п (у)) Г (у—х9 ю)]*/|зхз. D.14)
удовлетворяет уравнен ию
А(дх, ©)и(х) = 0	D.15)
в каждой точке х б |^}
Перепишем D.12) в следующем виде:
(Т (дх> п (х)) Г (х, со)),,- = (т (дХ9 п (х)) Г (х))ц + (г (д» п (х)) Г (дс, со)),,, D.16)
где (Т (дх, п (х)) Г (х, со)),7 и Г (х, со) определяются из D.5) и A.14). Из
D.16) на основании теоремы 1.6 следует
4.5. Теорема. Для всех х 6 2?
lim Т (дХ9 п (х)) Г (*, со) = Т (дХ9 п (х)) Г (х)
и в окрестности нуля справедлива оценка
| (т (дХ9 п (х)) Г (х, <о))л/1 < const | х |-2.
§ 5. Сингулярные решения уравнений
моментной теории упругости
1. Уравнение колебаний. Прилагая оператор Т (дг, п (х)) (см. I, 13.8)
к фундаментальной матрице решений уравнений моментной теории (см.
B.10)), получим
T(dx,n(x))W(x,o) = ^
(TWY
где
, , Л VI a/ exp (t*.'I*I)

л 5]
сингулярные решения моментной теории упругости
79
= 2ц
х, п (х)) ?р,} (х, а)
0=1
1=1 р,
2
4 з
1
1л
„ я
, а)
ex
и i	1 о Ч
E.2)
1=1
Для матрицы
\Т (ду, п (у)) У(у-х9 о)]' = || [Т (дУ9 п (у)) W (у—х, a)]i, ||6X6 E.3>
справедлива
5.1. Теорема. Каждый столбец матрицы E.3) удовлетворяет урав-
уравнению B.1) для всех х ? Е3\\у].
Доказательство аналогично доказательству теоремы 4.1.
2. Уравнение статики. При а —¦ 0 элементы матрицы E.1) упрощаются
и принимают вид
= 2ц
кр (дх, п (х)) ЧДО (х) +
1 г г \ д м ат 1 . 1 «
д г
= 2ц
Г
s: l
t 1
J'
х, п (x))
0=1
з
1
1 — exp (— q4 | л: |
	T
p ^
#i Гг^ Ч>"D) ^^ О- "Ь^ д exP (—g3 I x 1) ,
dn (x)
\ exp
)
E.4).

80	основные сингулярные решения	[рл ц
Имеет место
5.2. Теорема. Каждый столбец матрицы
[Т{д9, п (у)) W (у—х)Г = ЦТ(д99 п(у)) W (у — x)U/|bx6	E.5)
удовлетворяет однородному уравнению статики моментной теории для всех
хеЕ3\\у\.
Учитывая, что для матрицы
справедливы теоремы, аналогичные теоремам § 1, заключаем, что сингуляр-
сингулярные части матриц Т (дд9 п (у)) ? (у — х, а) и Т (ду, п (*/))? (у — х) совпа-
совпадают и имеют вид
[Т(дв, п (у)) Ч (у-х, o)ftV ЖШ I^TTJ-
IT (дУ9 п (у)) V (y—x, a)W = 0A),
[T(dy,n(y))W(y—х,а)Щ> = 0A),	> E-6)
IT (dyi n (y)) W(y—x, a)]lky =
l Г »i
2я Ltf + w) (s-f2i>)
3
v(s-+-o —p)
JD=1
где О обозначает ограниченную при х —* у величину. Этим представлением
мы воспользуемся в дальнейшем (см. гл. IX).
§ 6. Сингулярные решения уравнений термоупругости
1. Уравнение колебаний. Введем матрицы
# (дх, п (х), со) = || Фkf (дХ9 п (х), со) ||4Х4,	F.1)
U (дх, п (х), со) = || Uki (дх, п (х), со) ||4Х4,	F.2)
Q (дх, п (х)) = || Qkf (дХ9 п (х)) ||4Х4,	F.3)
где
&\i (дх, п (x)t со) = A — 8k4) A — б/4)| бь/ix '. / ч 4- Xnk (х) •=—\- риг* (х) ^-1 —
V	t/#* \л/	с/л.	с/л. /
\	1	к/
— icoTN/4 A — 8ki) nk (x) — 6M6/4, F.4)

51
СИНГУЛЯРНЫЕ РЕШЕНИЯ УРАВНЕНИЙ ТЕРМОУПРУГОСТИ
81
я (х), (о) = A — 8ki) A — б/4)
пй (х) ?.
nk (х) + 6
-, F.5)
= A— бм)A— б/4)
F.6)
и вычислим произведение матриц ^, ^ и Q на матрицу Ф* (х, оо), определен-
определенную выражением C.9).
Имеем
& (дх, п (х), со) Ф* (х, со) = || (& {dXf n (x)t со) Ф* (х, со))/г/||4х4, F.7)
п (х), со) Ф* (х, со)),у = 2 1A — 6^) A — б/4) -^8/г/ а^Г +
3	2	1
^^/ (дх, п (х)) — 2\iat V JCkp (dXf п (х)) д^дх + р со2% (х) щ -^ —
— tmfij* A — 6*4) Р/ - Р«Л1* (х) + 2^ 2 JTfep (dx> /г (х)) ^ -
— У&н A — б/4) Р/ -^ —
, F.8)
(дХ9 П (X), СО) Ф* (X, СО) = || (А (дХ9 П (X), СО) Ф* (X, ©))Л/ |4Х4,
F.9)
_б,4)A— б/4) L?
L
(х)) — 2ца/
х, п (х))
А _
(х) + 2fi
(д
Г з
	б/4) Р/ V !
1р=\
9 п (х)) J-
J
6 В. Д. Купрадзе

82	основные сингулярные решения	[рл j]
Q (дх, П (X)) Ф* (X, СО) = || (Q FХ, П (X)) Ф* (X, (й)к, |4Х4,	F.11)
(Q (дх, п (х)) Ф* (х, ©))*/ = A - б*4) Ф*ц (х, со) +
3
Составим матрицы
[# (д„, /г (у), со) Ф*0/—х, со)]' = |[# (д„, /I (у), со) Ф*(*/ — а:, со)]^у ||4ж4,	F.13)
У), со) Ф* (y — xt со)]' = |j[^(^, n (у), со) Ф'(у — х, co)]kf\\4x4>	F.14)
a,, п (у)) Ф\у — ху со)]' =|[Q (dyt n (у)) Ф*(у — х, (ojhihxb	F.15)
и докажем теорему:
6.1. Теорема. Каждый столбец матриц [& (ду9 п (у), со) Ф* {у —
-	х, со) Г, № (ду, п {у)у со) Ф* {у — х, со) Г и [Q (ду9 п (у)) Ф* (у -
—	х, со) Г, рассматриваемый как вектор, удовлетворяет уравнению C.1) # лю-
любой точке х? Е3\{у\.
Действительно,
(В (дХ9 со) \& {дуу п(у)\ (о)Ф*(у — х, ю)]')л/ =
4
= 2 Вм (дх, со) [# (^, /г (у), со) Ф* (у — х% ©)]'„ =
4
= S в*< (а^ ©) # ip (ду> п (У)> <»)ф*р1 (У — х> ©) =
4	4
= S ^ * (^, я (у).») 2 Дм (а„ ю) ф,р (х—у,(о)=о.
р=1	I	1=1
Здесь мы воспользовались равенствами (см. теорему 3.1 и C.9))
4
5	5*1 (а*> «) ф*р (х — г/, ю) = 0; i,p=l,4,
г=1
Фр/ (У — *, ю) = Фгр (х —г/, со).
Совершенно аналогично доказывается теорема и для матриц
[&(ду,п(у),<о)Ф*(у — х,<л)]г и №(д„,п(у))Ф*(у —*.©)]'.
2. Уравнение статики. Из формул F.7), F.9) и F.11), переходя к пре-
пределу при ю —¦ 0, получим
Ф (дх, П (X)) Ф* (X) = || (Ф (дх, П (X)) Ф* (X))kl ||4Х4,	F.16)
6	(дх, П (X)) Ф* (X) = || (Й (дх, П (X) Ф* (*))*/|4Х4,	F.17)
Q (дх, П (X)) Ф* (X) = || (Q (Зл Л (ДГ)) Ф* (JC))*/ ||4Х4,' F.18)
где
(Ф (д„ п (х)) Ф* (x))ki = A - 8М) A — б/4) (Т (дх, п (х)) Г (*))*/ +
"•" 4я(ХЧ2ц) dx	2я |*|' * ' '

с у]
РАЗЛИЧНЫЕ ЗАМЕЧАНИЯ И БИБЛИОГРАФИЧЕСКИЕ СПРАВКИ
(A (dXf п (х)) ф* (*))„• = A — s,4) A - б/4) (г (дх, п (х))	г (x))kj -
4л (А, 4- 2ц) ал (*) дху "*"	2я ал (х) | х Г
(Q (а„ п (х)) Ф* (x))k, = A — б,4) ф;7 (х) —
ЛЛ1-^) a aijci .	6fe46M a i
2|ы) дп(х) дх. ~^~ 2я дп(х) \х\*
(Т (дх, п (х)) Г (x))ki (к, j = 1, 2, 3) получается из D.8), если к = \i. Соста-
Составим; как и выше, матрицы
\& (ду, п (у)) Ф* (у — х)] = ||\Ф (ду, п(у))Ф* (y — x)hihxb С6-22)
[& (ду, п (у)) Ф* (у — х)] = || \й (ду, п (у)) Ф* (y — x)]kf ||4x4, F.23)
[Q (ду, П (у)) Ф* (у — X)] = || [Q (в,, П (У)) Ф* (У — *)Ь/||4Х4,	F.24)
и докажем теорему
6.2. Теорема. Каждый столбец матриц [&(др п (у))Ф* (у — х)]\
Ш (ду, п (у)) Ф* {у — х) У и [Q(dy, n (у)) Ф* (у — х) ]', рассматриваемый
как вектор, удовлетворяет однородному уравнению статики (см. (I, 11.24)
и (I, 11.24')) для всех х? Es\{y\.
Эта теорема получается из теоремы 6.1 при со = 0.
§ 7. Различные замечания и библиографические справки
В современной теории дифференциальных уравнений фундаментальные
решения рассматриваются как линейные непрерывные функционалы, опре-
определенные на некотором множестве основных функций и удовлетворяющие
неоднородному дифференциальному уравнению с правой частью, равной
функции Дирака. Такая точка зрения позволяет применить к рассматривае-
рассматриваемому уравнению преобразование Фурье и привести построение преобразова-
преобразования Фурье от фундаментального решения к алгебраической задаче (к реше-
решению системы алгебраических уравнений), которая в случае дифференциаль-
дифференциальных операторов с постоянными коэффициентами разрешима всегда (см.
Hormander [1]); после этого обратное преобразование Фурье восстанавли-
восстанавливает искомое фундаментальное решение.
Конечно, построенные выше фундаментальные решения могли быть
получены таким путем.
Не пользуясь, однако, в нашем изложении теорией и аппаратом обобщен-
обобщенных функций, мы избрали другой, более элементарный путь, который
к тому же в интересующих нас случаях приводит к цели быстрее, минуя
вычисления, связанные с обратным преобразованием Фурье.
Фундаментальные и другие сингулярные решения выражены в явном
виде и в элементарных функциях; этот факт имеет нем*аловажное значение.
Если бы мы ограничили свою задачу построением теории разрешимости
задач, поставленных в главе I, можно было обойтись одними теоремами
о существовании фундаментальных решений и об их основных свойствах.
Но наряду с теорией разрешимости важной задачей является разработка
методов вычисления решений; для достижения этой цели явные и элементар-
элементарные выражения основных сингулярных решений служат существенным
инструментом: эти решения весьма просто порождают полные совокуп-
совокупности частных решений, которые позволяют выразить явно приближенные
значения искомых решений различных задач (см. гл. XIII); вместе с тем,,

34	основные сингулярные решения	[рл# ц
явные выражения основных сингулярных решений придают методу потен-
потенциалов и сингулярных интегральных уравнений особую наглядность.
Создание теории сингулярных интегральных уравнений с ядром типа
Коши, принявшей к настоящему времени в некотором смысле завершенный
вид, в основном в работах тбилисской школы, активно способствовало раз-
развитию метода потенциалов и интегральных уравнений в теории плоских
задач математической физики. По этим вопросам читатель может найти исчер-
исчерпывающие сведения в монографиях: Бицадзе [1, 2], Векуа И. [1J, Векуа Н.
[1], Гахов [11, Купрадзе [7, 9, 13], Лурье [1, 2], Михлин [1], Мусхе-
лишвили [1, 3], Хведелидзе [1].
С другой стороны, развитие теории многомерных сингулярных интеграль-
интегральных уравнений сыграло исключительную роль для перенесения методов
фундаментальных решений в теорию пространственных задач и для значи-
значительного расширения рамок исследования.
Сингулярные решения систематически применялись в работах В. Д. Ку-
Купрадзе в теории граничных задач установившихся упругих и электромагнит-
электромагнитных колебаний (Купрадзе [7, 8, 13 J).
Явные выражения фундаментальных решений уравнений моментной
теории упругости и термоупругости получены другим путем в работах:
Nowacki [1,3, 81, Купрадзе и Бурчуладзе [31, Доманьский, Пискорек
til и др.
Матрица сингулярных решений D.10) встречается в работах: Lauri-
cella [1], Weyl [1], Шерман [13, Купрадзе [73, Башелейшвили [11, мат-
матрица D.1) — в работах Купрадзе [8, 13], Гегелиа [6, 131, Башелейшвили [31,
Бурчуладзе [11 и др.
Полезные сведения о фундаментальных решениях сообщаются в книгах:
John [11, Miranda [11, Bers, John, Schechter [11, Hormander [11 и др.
Особо следует отметить две знаменитые старые работы: Fredholm [13
и Levi [11.
ЗАДАЧИ
1.	Для матрицы Ч? (х, а) (см. B.10)) доказать теоремы, аналогичные теоремам'1.2—1.6.
2.	Найти фундаментальную матрицу для уравнения B.1) в том случае, когда о/о2—4а= 0.
3.	Применением преобразования Фурье найти матрицу ^? (х, о) (NowacKi [8]).
4.	Применением преобразования Фурье найти фундаментальную матрицу для уравне-
уравнения C.1).
5.	Найти фундаментальную матрицу для уравнения C.1) в том случае, когда Щ = Щ =
-.5-,.+,.
6.	Построить сингулярную матрицу E.1) для уравнения B.1), когда о/а2 — 4а = 0.
7.	Построить сингулярные матрицы F.7), F.9) и F.11) для уравнения C.1), когда
8.	Из фундаментального решения уравнения динамики изотропного упругого тела
(см. Love [1], гл. XIII, формула C6)) в том случае, когда %(х)=етх, получить матрицу
Купрадзе (см. A.7)) (Чичинадзе [1]).

ГЛАВА ТТТ
ТЕОРЕМЫ ЕДИНСТВЕННОСТИ
В этой главе доказаны теоремы единственности для основных граничрых
и начально-граничных задач классической теории упругости, микрополяр-
микрополярной упругости и термоупругости. Рассматриваются задачи для внутренних
и внешних (бесконечных) областей в случае статики, гармонических колеба-
колебаний и общей динамики.
Доказательства основываются на применении классического принципа
энергии и его обобщении.
§ 1. Задачи статики в классической теории
1. Формулы Грина. Если / = (flt /2, . . ., fm) и <р = (фх, q>2, . . ., <pm) —
вещественные или комплексные векторы, то произведение /хр = ср/ будет
т
обозначать билинейную форму /ф — 2 fk4>k-
_k=\	_
1.1. Теорема. Если и ? С1 (D+) П С2 (D+), v 6 С1 (D+) и А (дх)и
абсолютно интегрируемо в D+, a S ? Лг (а), а ^ 0, то
\ [vA(dx)u + E(v, u)]dx=\v+\T(dy9 n)u\+d,S.	A.1)
D+	S
Здесь А (дх) и Т (dyi n) — операторы, определенные в I, § 12, п. 1 и
I, § 13, п. 1, а
Доказательство. Легко проверяется тождество
з/з
где (см. (I, 5.15))
В условиях теоремы интеграл по D+ от левой части A.3) существует.
С другой стороны, при этих условиях к интегралу J 2li 5F \ 2j vptpq(u)) dx
D+ q	p
применима формула Гаусса—Остроградского (см. Kellog [1]); поэтому
\[vA {дх) и + Е (v, и)] dx = j J ^ ( 2 vpxpq (и) \ пУ dyS

86	ТЕОРЕМЫ ЕДИНСТВЕННОСТИ	[Гл> JJJ
Но (см. (I, 2.1) и (I, 13.3))
и теорема доказана.
Здесь и в дальнейшем за положительное направление нормали на S
оринято направление, внешнее по отношению к области D+.
1.2. Замечание. Доказательство применимости формулы Гаусса—
Остроградского в условиях теоремы 1.1 носит неэлементарный характер
{см. Kellog [1]).
Доказательство упрощается, если условие S ? Л1 (а) заменить на
S 6 Л2 @). В этом случае, построив вписанные параллельные поверхности
и применив для них формулу A.1), очевидным предельным переходом полу-
получаем доказательство теоремы (см. Соболев [2], Смирнов [2]). Наконец, если
требование интегрируемости Л (dx) unoD+ заменим требованием и? С2 (D+),
оставив без изменения другие условия теоремы, или даже несколько ослабив
требование, налагаемое на S, доказательство еще более упрощается. В таком
виде оно приводится в большинстве книг по анализу и теории потенциала
(см., например, Михлин [81, Miranda [1]).
Выражение для Е (v, и) A.2) перепишем в следующем виде:
РФЯ
JLI \1 / dVp	dl)q \ / дпр	dtLq \	y-i *v
' 3 ZmA \ dxp dxq ) \ dxp dxq J ' v • /
P * Я
Очевидно,
?(t>, u) = E(u, v).	A.5)
В частности, если p= Ъ (черта сверху указывает на комплексно-сопряжен-
комплексно-сопряженную величину), то
РФЯ	Р, Я
Если и — действительный вектор и является вектором упругого смещения,
то Е (и, и) совпадает с удельной энергией деформации, введенной в I, § 6,
пп. 1 и 2. Пусть и есть регулярное действительное решение в области D+
уравнения статики А (дх) и (х) = 0 (тогда, очевидно, Аи абсолютно инте-
интегрируемо в D+) и v = и; тогда A.1) примет вид
\Е(и, u)dx= f u+\Tu\+dS.	A.7)
d*	s
Формулы A.1) и A.7) будем называть формулами Грина в области D+.
Для бесконечной области D~ справедлива
1.3. Теорема. Если S G Лх (а), а ^ 0 и и является регулярным
действительным решением уравнения А (дх) и = 0 в области D", удовлетво-
удовлетворяющим в окрестности \х \ = оо условию
/	/1\	1 и,	1 О Q	/1 Q\
то
\Е(и, u)dx = —\tr\Tu\-dS.	A.9)

г ji	ЗАДАЧИ СТАТИКИ В КЛАССИЧЕСКОЙ ТЕОРИИ	87
Для доказательства применим формулу Грина A.7) к конечной области
DR = D~ П Ш (О, R), где R > О — достаточно большое число; согласно
принятому условию относительно положительной нормали на S теперь
положительная нормаль к границе DR — внутренняя; поэтому получаем
f E(u, u)dx=— \w\Tu\-dS— J uTudS.	A.10)
DR	S	C(O.R)
В силу A.8) интеграл, распространенный на С (О, /?), при R —> оо стре-
стремится к нулю. Поэтому предел правой, а следовательно, и предел левой
части существуют и равны друг другу. Теорема доказана.
1.4.	Замечание. Формулы A.7) и A.9) остаются в силе, когда S
есть объединение конечного числа замкнутых, ограниченны*, непересека-
непересекающихся кусочно-гладких поверхностей Sk9 k = 1, . . ., m, класса Лг (а).
1.5.	Замечание. Если введем обобщенную билинейную форму
? / х V4 / dvp дир , /л ,	ч dvp
где x — произвольное действительное число, то формулы A.1), A.7), A.9)
к	к
остаются справедливыми при замене Е (у, и) и Т (дуу п) на Е (v, и) и Т (dv, n)
соответственно.
2. Решение вспомогательного уравнения. Для исследования единствен-
единственности решения задач статики необходимо построить все действительные реше-
решения уравнения Е (а, и) = 0 из класса С2 (Ев). Это уравнение в силу A.6)
эквивалентно системе уравнений
«. ^ + $ = 0. Р + Я. т?-"ё- = 0. Р, .= 1,2,3. A.11)
Общее решение системы A.11), и, следовательно, уравнения Е (и, и) = 0,
как нетрудно убедиться, имеет вид
и(х)=[ахх]-+-Ь,	A.12)
где а и Ь — произвольные действительные постоянные трехкомпонентные
векторы.
Очевидно, вектор жесткого смещения A.12) удовлетворяет равенствам
ухеЕ3:А(дх)и(х) = 0, Т(дху п(х))и(х) = 0.
Легко проверяется также, что если вектор жесткого смещения A.12)
удовлетворяет условию A.8), то он тождественно равен нулю.
3. Основная лемма. Регулярное решение и однородных задач (I)*,
(И)*, ...» (VII*1, в случае бесконечной области, удовлетворяющее условию
A.8), есть решение уравнения Е (и, и) = 0 класса С2.
Покажем сначала, что во всех однородных задачах, кроме (VII*1, произ-
произведение иТи на граничной поверхности S обращается в нуль, а в задаче
* равняется — иои = —^ovqupuq. Для задач A)*, A1)*, (Vl^ — это
Р Q
Р, Q
)* (V)±
очевидно. Для задач (III)*, (IV)*, (V)±—вытекает из тождеств
иТи = и\Ти — п (Ти)п\ + ип (Ти)п = (и — пип) Ти + ип (Ти)п.
Обращаясь теперь к формулам A.7) и A.9) и учитывая неотрицательность
и непрерывность формы Е {и, и), получаем Е (и, и) = 0 и лемма доказана.

88	теоремы единственности	[рл in
4. Теоремы единственности. Имеют место следующие теоремы:
1.6.	Теорема. Задачи (I)+, (IV)+, (VI)+ допускают не более одного
регулярного решения,
1.7.	Теорема. Любые два регулярных решения задачи (П)+ могут
отличаться лишь аддитивным вектором жесткого смещения A.12).
1.8.	Теорема. Задача AП)+ допускает не более одного регулярного
решения, если S не является поверхностью вращения] если S — поверхность
вращения, отличная от сферы, любые два регулярных решения могут отли-
отличаться аддитивным вектором вида
и(х) = со[ах(х — х°I	A.13)
где с0 — произвольное действительное число, а — орт оси вращения, х° =
= (л^, х\, х%) — произвольная точка на оси вращения; если S — сфера с цен-
центром в точке *°, то два регулярных решения могут отличаться лишь векто-
вектором вида
u(x)=^ck[8kx(x — x%	A.14)
k
где bk =F1?, б2?, 63k), ck — произвольные действительные числа.
1.9.	Теорема. Задача (V)+ допускает не более одного регулярного
решения, если выполнено по крайней мере одно из следующих условий:
1) mes Sx ф О, 2) mes S4 Ф 0, 3) mes Sx = mes S4 = 0 и S не является
поверхностью вращения. Если mes Sx = mes S4 = 0 и S есть поверхность
вращения, то имеет место ситуация, описанная в теореме A.8).
1.10.	Теорема. Задачи (I)", (П)~, . . ., (VI)", допускают не более
одного регулярного решения, удовлетворяющего условию A.8).
Доказательство 1.6—1.10. Пусть и' и и" — произвольные регу-
регулярные решения какой-либо из указанных выше задач, в случае бесконечной
области удовлетворяющие условию A.8). Тогда разность и = и' — и" есть
регулярное решение соответствующих однородных задач и согласно основ-
основной лемме представляется в виде A.12).
В случае бесконечной области и (х) удовлетворяет условию A.8) и
согласно п. 2, и = 0 в области ?>"". Это доказывает теорему 1.10.
Для задачи A)+ имеем и+ = 0, следовательно, а = b = 0 и ух ? D+: u = Q.
Для задачи (IVL" имеем (и — пип)+ = 0, {Tu)t = 0; из первого условия
следует а = b == 0 и отсюда V* 6 D+: и = 0.
Для задачи (VI)+ имеем \Ти -\- сш}+ = 0; так как Ти = 0 и а — поло-
положительно определенная матрица, то и+ = 0 и ух ? D+: и = 0. Это дока-
доказывает теорему 1.6.
Теорема 1.7 непосредственно вытекает из основной леммы.
Докажем теперь теорему 1.8. Так как решение имеет вид A.12), по-
постоянные векторы а и b должны быть выбраны так, чтобы выполнялись гра-
граничные условия третьей задачи
Ы+ = 0, {Т(ду, п)и\+ — п{(Т(ду, п)и)п\+ = 0.
Второе из этих условий выполняется для произвольных а и b (см. п. 2).
Следовательно, а и b должны быть подчинены условию
VyeS:n(y)([axy\ + b) = 0.	A.15)
Пусть условие A.15) выполнено и векторы а и b одновременно не равны
нулю; тогда а Ф 0, так как в противном случае из A.15) следует п (у) b = 0,
что может иметь место лишь в том случае, если 5 есть плоскость или цилиндр,
простирающийся в бесконечность. Исключая этот случай как не соответ-
соответствующий рассматриваемому, представим вектор b в виде суммы b = с + d,

§ 1]	ЗАДАЧИ СТАТИКИ В КЛАССИЧЕСКОЙ ТЕОРИИ	gg
где с — параллелен, ad — перпендикулярен к вектору а. Тогда найдется
вектор х° = (х°1У х%9 *§), такой, что d = —[а X х°]. Поэтому всякое решение
однородной задачи (Ш)+ представится в виде
х°)] + с9	A.16)
где векторы а и с удовлетворяют условию
)] + с) = 0.	A.17)
Введем ортогональную систему координат (|) с началом в точке х* и
с направлением оси |2 вдоль вектора а; ?а и 13 выбираются в перпендикуляр-
перпендикулярной плоскости произвольно. Тогда условие A.17) принимает вид
е(у)п(у)=09	A.18)
где е (у) = (\с\, — \a\(\Zi |ah2), Tjlf т]2, ц3 — координаты точки у в новой
системе.
Если Ф (тIэ т]2, т]3) = 0 есть уравнение поверхности 5 в системе (?),
то из условия A.18) вытекает равенство
\ю\ дФ	дФ . дФ л	.л 1Л.
Если с Ф 0, то из A.19) получим
Ф (%, Л2. %) =
.где F — произвольная дифференцируемая функция. Но это могло иметь
место в том случае, если бы 5 была бесконечным цилиндром. Отсюда следует
с = 0, и тогда из A.19) получаем
Ф(т)ь 42, Лз) = F(T|b тй + тй) = О;	A.20>
но это значит, что S есть поверхность вращения с осью вращения |1в Исклю-
Исключая и этот случай, получаем а = Ь = 0 и первое утверждение теоремы до-
доказано.
Рассмотрим теперь тот случай, когда S есть поверхность вращения.
В этом случае всякое решение однородной задачи (Ш)+ дается формулой
и(х)=[ах (х — х0)),	A.21)
где х° — точка, лежащая на оси вращения. Легко проверить, что и (х)у
заданный равенством A.21), действительно есть решение однородной за-
задачи (Ш)+.
Заметим еще, что если S — поверхность вращения, отличная от сферы
и и (х) = [ах(х — х°) ], v (х) = [Ьх(х — х°) ] — два решения, то v = сои,
где с0 — действительное число. Этим доказано второе утверждение теоремы.
Отсюда следует и третье утверждение и, следовательно, теорема доказана.
Наконец, теорема 1.9 непосредственно следует из предыдущих.
Естественно поставить вопрос, насколько необходимы те ограничения,
которые выше были приняты для получения теорем единственности. Не будем
здесь обсуждать, можно ли отказаться от требования регулярности; сделаем
лишь одно замечание относительно поведения на бесконечности, которое
показывает, что принятые выше условия «близки» к необходимым. Выше

90	ТЕОРЕМЫ ЕДИНСТВЕННОСТИ	[рл JJJ
было доказано, что задача (I)" имеет единственное решение, удовлетворяющее
условию A.8). Изменим эти условия «слегка», заменив их следующими:
*, /=1,2,3,	A.22)
где несколько ослаблено первое и усилено второе из условий A.8). При этом
теорема единственности нарушается. Пусть 5 есть сфера радиуса R, с цен-
центром в начале. Легко убедиться, что вектор и = (ии и29 ив), где
1 9 о п ооч
удовлетворяет условиям A.22), есть регулярное в D~ решение и обращается
в нуль на S, не будучи тождественным нулем.
5. Уравнение А (дх) и — рт2» = 0. Почти без всяких изменений при-
приведенные выше доказательства теорем единственности остаются в силе
для уравнения
ди — рх2и = Ъ,	A.24)
где т = а + /©, а > 0, р > 0 — плотность среды; это уравнение встречается
в качестве важного вспомогательного средства в задачах динамики (см.
гл. VIII). В отличие от уравнения статики, решение уравнения A.24), вообще
говоря, есть комплексный вектор и это обстоятельство должно быть учтено
при применении техники доказательства, используемого выше.
Ограничимся рассмотрением задач (I) и (II), которые встречаются
в задачах динамики.
1.11. Теорема. Задачи A)+ и (И)+ для уравнения A.24) допускают
не более одного регулярного решения.
Для доказательства, очевидно, достаточно показать, что соответству-
соответствующие однородные задачи имеют лишь тривиальные решения. Пусть и — ре-
решение однородной задачи и и — комплексно-сопряженный вектор. Тогда
из A.1) будем иметь
рт2 J \u\2dx+ J E(u, u)dx=0.
^Отделяя вещественную и мнимую части и учитывая вещественность
Е(и, и) (см. A.6)), получим
9(о2 — (о2) j \u\2dx+ J Е(п, u)dx=0, 2ipaco I \u\2dx = 0;
D+	D+	D+
отсюда для a > 0 и произвольного со ? ( —о°, °°) имеем и (х) = 0, л: ? D+.
1.12. Теорема. Задачи (I)" н (II)" <9ля уравнения A.24) допускают
не более одного регулярного решения, удовлетворяющего условию A.8).
Пусть ы# и w"—два различных решения. К разности и = и1 —и/'
в области DR = D~ [\ Ш (О, /?) применим формулу A.1), полагая v = и;
получим
и)] dx=— J uTu dS.
C(O,R)

Л 2]	ЗАДАЧИ УСТАНОВИВШИХСЯ УПРУГИХ КОЛЕБАНИЯ	91
Перейдя к пределу при R —* оо, в силу A.8) получим
, u)]dx = 0;
отсюда, как и выше, следует ух ? D~: и = 0.
6. Неоднородная среда. Для гранично-контактных задач статики в не-
неоднородных средах (см. I, § 14, п. 4) справедливы следующие теоремы:
1.13.	Теорема. Первая и четвертая задачи для неоднородной среды
в области D = Dx [} D2 допускают не более одного регулярного решения.
1.14.	Теорема. Два регулярных решения второй задачи для неод-
неоднородного тела в области D могут отличаться лишь вектором жесткого
смещения.
1.15.	Теорема. Задача (Ш)+, когда среда не есть тело вращения,
в области D+ допускает не более одного регулярного решения', когда же среда
есть тело вращения, отличное от шарового кольца, решение определяется
с точностью до аддитивного вектора вида A.13). Если среда есть шаровое
кольцо, то решение определено с точностью до аддитивного вектора вида
A.14).
Пусть теперь 53 (см. I, § 14, п. 4) расширяется до бесконечности; тогда
D2=E3\Dt, и мы имеем задачи для бесконечной неоднородной области с ка-
каверной. Для таких задач верна
1.16.	Теорема. Задачи (I)", (II)", (III)", (IV)" допускают не более
одного решения, удовлетворяющего условию A.8).
Наконец, для главной контактной задачи (см. I, § 14, п. 4), т. е. когда
бесконечная неоднородная среда состоит из внешней бесконечной области
и внутренней области без каверны, справедлива та же теорема 1.16.
Доказательство этих теорем основано на двукратном применении формул
Грина A.1) соответственно в областях Dx и D2, с учетом гранично-контакт-
гранично-контактных условий.
Аналогично исследуются задачи со смешанными краевыми условиями.
В этом случае теоремы единственности сохраняются без изменений, если
хотя бы на одной из границ, внутренней или внешней, заданы смещения.
Некоторые изменения потребуются в случае, когда на границе смещения не
задаются.
§ 2. Задачи установившихся упругих колебаний
1. Общее представление регулярных в D+ решений. Пусть и и v —
регулярные в D+ векторы и А (дх) и, А (дх) v — абсолютно интегрируемы
в D+. Тогда из A.1) и A.5) непосредственно следует
[vA(dx, со)и — иА(дх, «>)v\dx= J \vT(dy, n)u — uT(dy, n)v\*dyS. B.1)
o	s
В области D+\UI (z, e), где z ? D+ и & — достаточно малое положительное
число, применим тождество B.1), в котором примем v (х) = Г' (х — г, 0),
где Г'' (jc — г, со) есть /-й столбец матрицы фундаментальных решений (см.
II» § 1) уравнения колебаний
А (дх, со) и = \1 Да + (К + [I) grad div и + рсо2а = 0.	B.2)

92	теоремы единственности	[Гл jjj
Принимая во внимание равенства (см. Купрадзе и др. [1])
lim j Г7(х— 2, со) А (дх, co)udx = J Г7 (х — 2, со)Л(д*, &)udx9
lim J Tf (У — г, (д)Т(ду, n)u{y)dyS^^
8-*° С B, 8)
lim [ и(у)Т (дю n)Tf (y—z, со) dyS = 2W/ (z),
S-*° C(l 8)
получим
2&y (z) = — Г7 (х — 2, со) Л (дх, со) м (х) йдс +
— и+ (у) Т (dQ, п) Г7 {у — 2, со)] dJS. B.3)
Если, в частности, и — регулярное в D+ решение неоднородного уравнения
А (дХ9 со) и + Ф = 0, где Ф б С E+)9 то из B.3) будем иметь
J Р{х —
-\и+ (у) [Т {дю п) Г7" {у — 2, со)] dySy B.4)
или, в матричной записи,
2и(*)= J Г(х —2, ш)Ф(х)Л+ [Г(у — 2, со){Г(^, n)^(r/)}+dvS —
- J {T (ду9 п) T(y — z, со) Г а+ (у) dyS\ B.5)
и, наконец, если Ф (х) = 0, то
2w(z) = j Г (у — z, со) {Т (д„п) u(y)}+d,S —
-\\Т{ду% n)T(y—z, со)}'и+ (y)dgS. B.6)
S
Таким образом, доказана
2.1.	Теорема. Регулярное в D+ решение неоднородного уравнения
колебаний представляется выражением B.5) и решение однородного урав-
уравнения — выражением B.6).
2.2.	Замечание. Очевидно, если г ? D", в левой части равенства
B.6) будем иметь нуль и, следовательно, справедливо равенство
8(z)u(z)= \г(у — 2, <о)\Т(ду, n)u(y)\+dyS —
- \ \Т(ду, п) Г (у —г, со)Г и+ (у) d?% 2 D+ U О", B.7)
где
( 2, 2 6 D+9

§ 2]	ЗАДАЧИ УСТАНОВИВШИХСЯ УПРУГИХ КОЛЕБАНИЙ	93
2.3. Замечание. Если в равенстве ( 2.7) перейдем к пределу при
(о —¦ 0, то получим формулу общих представлений для регулярных в Ь+
решений уравнения статики:
8 (г) и (z) = J Г(y—z) \Т(ду, п)и (у)\+ dvS —
(дуу n)r(y — z)Yu+(y)d,S% zeD+[)D~. B.9)
— \\Т
2.4.	Теорема. Регулярное решение однородного уравнения B.2)
имеет непрерывные частные производные любого порядка в произвольной
точке, не принадлежащей S.
Доказательство в том случае, когда z ? D+ следует из B.6), а в случае
z 6 D' из той же формулы, написанной для области D~ [\ Ш (О, R), где
R > О достаточно большое, так, чтобы S с Ш (О, R) и г 6 Ш (О, #).
2. Разложение регулярных решений. Имеет место следующая
2.5.	Теорема. Регулярное решение и = (ии и2, и3) однородного урав-
уравнения колебаний B.2) представляется в виде суммы
u = u(t» + uisK	B.10)
где и{р) и w(s) — регулярные векторы, удовлетворяющие условиям
(A + ^)w^)==0, rota<p> = 0,	B.11)
(А + k§) u^ = 0, div a<s> = 0,	B,12)
причем
Доказательство. Пусть и — дважды дифференцируемая функ-
функция в некоторой области D а Е3 и
1
B.13)
Тогда w<p> + m(s) = и. Пусть и есть регулярное решение уравнения колеба-
колебаний B.2). Теорема будет доказана, если покажем, что
= 0,	B.14)
=0,	B.15)
(A-t-??)diva=0.	B.16)
Согласно теореме 2.4 к уравнению B.2) можно применить операцию
div; тогда, учитывая тождество div grad = А, получим (А + k\) div и = 0.
Аналогично, операция rot с учетом тождества rot grad = 0, приводит к урав-
уравнению (А + Щ rot и = 0.
Наконец, применив к обеим частям уравнения B.2) оператор (А + k\)
и учитывая B.16), которое уже доказано, получим B.14). Итак, регулярное
в D решение уравнения колебаний B.2) представляется в виде суммы без-
безвихревого (потенциального) и соленоидального векторов, которые в D удо-
удовлетворяют уравнению Гельмгольца
(Д + ?2)о=0,	B.17)
для k = kt и k = k2 соответственно.

94	теоремы единственности	[рл# л]
3. Условие излучения в теории упругости. Введем
2.6. Определение. Регулярное в D" решение и = (ut, и2, и3)
однородного уравнения колебаний B.2) удовлетворяет условию излучения,
если для и(р) и a<s>, заданных равенствами B.13), выполняются условия
Нти<*>(*)=0,	B.18)
Hm R \^-^--ik^P) (x)] = 0,	B.19)
lima*5* (x) = 0,	B.20)
Шл R [ ди1Ц(х) — iW* (*)] = 0,	B.21)
где R — длина радиус-вектора точки х = (хг, х2, х3); производная по R есть
частная производная по сферической координате R точки х, или, что то же
самое, производная по направлению радиус-вектора, и стремление к пределу
равномерное относительно х,
2.7. Теорема. Если регулярное решение и уравнения колебаний B.2)
удовлетворяет условию излучения, то
dxk ~—dR dxk
duis) (x) _ du{s)(x) dR
dxk ~ dR -dx^+U(R ^ k-l>2>6-	B-26)
Доказательство. Вектор, w(p> (x), определенный формулой
B.13), есть решение уравнения Гельмгольца B.17) при k = kx и удовлетво-
удовлетворяет условию излучения Зоммерфельда B.18), B.19) (см. Sommerfeld [11
и Купрадзе [7]). Поэтому, вне сферы С (О, р), содержащей внутри поверх-
поверхность 5, uip) можно представить формулой Грина
1 Г / eikllx~y* duSp) (a)	& Jk^x—y] \
u(pUx)=-r- \ [-.	;	r-^	u^p) (if)-^	1	г- ]d,S. B.24)
v ; 4л J V | x — у | dp	w dp | x — у | / « v ;
C(O, p)
Действительно, опишем вокруг точки х сферу радиусом г, настолько
большим, чтобы С (О, р) а Ш (х, г) и в области Ш(х, г)\Ш (О, р) представим
и^р) с помощью формулы Грина
1 Г / eikt^x~y} duSp) (у)	d eik^x~y* \
^'"я J 1 \х — у\ dp	U '^ dp \x — yl) u '
C(O,p)
С (х, г)
Интеграл по С (х, г) перепишем в виде
431 J \ Г \~д?	l 1UP ) + UP (У) Г2 } (
С(х,г)
Этот интеграл при г —> оо стремится к нулю ,на основании условия излучения
B.18), B.19), и окончательно имеем B.24).
Дифференцируя B.24), получаем
duSp) (х) _ 1 Г dvjr.y) dr
С(О,р)

§ 2]	задачи установившихся упругих колебаний	95
где мы обозначили г = | х — у | и v (г, у) = —	—^ —и<р>(у)———.
Но
— — dv _l V* д° ( дг д^ \
так как точка # находится на С (О, р), где р — конечно.
Следовательно, B.25) можно переписать в виде
С<О,р)
если учесть очевидные равенства -^~- = О G?"), -д~ = О (^R"), и B.22)
доказано. Совершенно аналогично доказывается B.23).
С помощью равенств
из B.24) получаем
= О (R-1),	B.26)
),	B.27)
и, аналогично,
(jc) = О (i?),	B.28)
— f^s> (х) = О (/?-•).	B.29)
Сформулируем полученный результат.
2.8.	Теорема. Для регулярного в D~ решения однородного урав-
уравнения колебаний B.2), удовлетворяющего условию излучения B.18)—B.21),
имеют место асимптотические равенства B.26)—B.29).
2.9.	Теорема. Если и = uip) + u(s) — регулярное в D~ решение урав-
уравнения B.2), удовлетворяющее условию излучения B.26)—B.29), то
Т (дх, п (х)) иУ» (х) — ikx (к + 2(г) им (х) = О (R~2)9	B.30)
Т(дх, п(х))и^ (х) — ik2ixu^s) (x) = O(R~2).	B.31)
Доказательство. Пусть х лежит на сфере С (О, R) и Ro — орт
радиус-вектора х.
Учитывая условия rot и^р) = 0 и div u{s) = 0 и используя соотноше-
соотношения B.22), B.23), B.26)—B.29), получим
B.32)
),	B.33)
ikx (RQuW) = О (R~\	B.34)
rota<s> — ik2[R0xuW] = O(R-2).	B.35)

96	ТЕОРЕМЫ ЕДИНСТВЕННОСТИ	[Гл. III
Действительно, из того, что div u{s) = О и из оценки B.23) имеем
k
Аналогично, из условия rot u{p) = 0 и оценки B.22) следует
B.37)
Умножим скалярно вектор Ro на (—^	ik2uisn и используем оценки
B.36), B.29); тогда получим B.32).
Умножим векторно Ro на (-^	ikiuSpA и используем B.37) и B.27);
тогда получим B.33).
/ди{р)	\
Наконец, скалярное умножение векторов Ro и 1-^	ikxuSp)u в силу,
B.22), дает B.34)
= div "(Р) —ikl
Векторное умножение Ro на (-^	^2w(s)j, в силу B.23), дает B.35)
— (к2№0 X */<*>] =
Согласно формуле (I, 13.1), в силу B.11) и B.12), имеем
Ти^ (х) = 2fx i^- + №o div u<p\	B.38)
(x) = 2fx-^ + (х [/?о X rot и<*>|.	B.39)
Учитывая B.34) и B.27), получим
TuW (х) = 1]xikxuS^
Используя формулу
Ro (RouM) = и,™ + [Ro X [Ro X иЩ\9
вытекающую из векторного тождества
\а х [Ь х с]] = ft (ас) — с (аЬ),	B АО)
и принимая во внимание B.33), будем иметь
ТиМ (х) — ikx (К + 2ц) ^(/?) (х) = О (R~2).
Таким же путем из B.39), учитывая B.29) и B.35), получим
Ти^ (х) = 2ixik2u^ (х) + A [^о х [Ro x ^(s) |] tfea + 0 (iT2).
Применяя B.40) и учитывая B.32), получим
7VS> (х) — *7e2fxw<s> (jc) = О (R~2),
и теорема доказана.

* 2]	ЗАДАЧИ УСТАНОВИВШИХСЯ УПРУГИХ КОЛЕБАНИЙ	97
2.10. Теорема. Для потенциальной и соленоидальной составляю-
составляющих регулярного решения уравнения колебаний B.2), удовлетворяющего
условию излучения, имеют место оценки
= О (R~3).	B.41)
Доказательство. Из B.32), B.33) и B.26), B.28) следует
х [Ro X и<">]] + и<*>(#0и(8)) = O(R~3).
Применяя здесь формулу двойного векторного произведения B.40), получим
(<><>) = О (R~3).
Аналогично, из оценки
X [Ro X и^рЦ] -f- a(p) (Rou(s)) = 0 (R~3)
следует (u(p)u(s)) = 0 (R~3), и теорема доказана.
Заметим теперь, что условия, аналогичные B.26)—B.31), имеют место для
каждого столбца матриц Г<"> (х — у, со) и Г(8> (х — у, со), где Т(р) и Г<5>
обозначают потенциальную и соленоидальную части матрицы фундамен-
фундаментальных решений Г (л: — у, со) соответственно.
Действительно, из равенств B.13) могут быть получены соотношения
У* ) •	2зт рсо2 || dxk dx,- \х — у | |зхз'
B.42)
ГE'(х — у, о>) = -^-1
и отсюда прямым вычислением — оценки
Г1р)(х-у, ^^^-^^Цх^-Цзхз^^ + О^-2),	B.43)
|^pi + 0(^),	B.44)
— y, ю) = О(?-•),	B.45)
; —г/, со) —tfe2(j-r(s'(x —г/, со) = О(^-2),	B.46)
[7?в X Г(р) (х — у, со)] = О (/Г2),	B.47)
(/?0Г(8) (х — у, со)) = О (Я~2).	B.48)
Из B.32) и B.33). на основании B.43) и B.44) получаем
3),	B.49)
3).	B.50)
Отметим, что в формулах B.47)—B.50) под произведением (скалярным или
векторным) вектора на матрицу понимается соответствующее произведение
на вектор-столбец матрицы.
4. Представление решения уравнения колебаний в области D~. Оценки,
полученные в предыдущем пункте, позволяют найти представление регуляр-
регулярных в ?)~ решений, удовлетворяющих условию излучения B.26)—B.29).
7 В. Д. Купрадзе

gg	теоремы единственности	[рл jjj
Пусть и = (и1э м2, и3) — такое решение. Применив формулу B.6), в области
Ш (О, R) П D' будем иметь
(z — y,(o)\T(dy,n)u(y)\-dyS +
+ J \Т (ду, п) Г (у —2, <u)\'u-{y)dyS+ J Г (г —у, со) Т (ды% п)и(у)
S	C(O,R)
- J {T{dyjn)T{y — z^)Yu{y)dyS. B.51)
C(O,R)
Представим и (у) и Г (х — у, со) в виде
и (у) = и{р) (у) + a(s)(f/), Г (г — у, со) = Г(р) (г —у, со) + r(s)(z — t/, со)
и внесем в B.51). Интеграл по С (О, R) перепишем в следующем виде:
J {Г(г — у, со)Га — [Т(ду,п)Г(у — z,<u)Yu\djS =
С (О, R)
= [ {Г(р) (г-у, оо) [Г«(р) — ikx (Я + 2ц) ы(р)] +
С (О, Л)
+ r(s)B-t/, e) [Tuis) —ik&u™] -
— и{р) [TTlp)(y—г, со) — ^1(Х, + 2ц)Г(р)B — у, ©)] —
_«(s)[rr<s)(y—г, (о) — ik2nTis)(y—z, ю)] +Г<Р) [Tu{s) —ik2lnu(s)] +
-uis)[TT(p)(y — г, со) — ^(Я + 2|*)Г<Р)@—z, о)]+
+ 1-[^(Я + 2ц) — &#] [ы(р)Г(8)(г—у, ©) — M(s)r(p)(z — t/,
Принимая во внимание оценки B.30), B.31), B.43)—B.46), ( 2.49), B.50)
и переходя к пределу в B.51) при R —» оо, найдем, что интеграл по С (О, R)
обращается в нуль. Поэтому
Ъх (z) = - j Г(г — у, со) [Ти (у)Г d? + )' [Г (^, n)Y(y — z, со)]' м" (у) d,S. B.52)
Этому представлению можно придать вид (см. замечание 2.2)
б (z) и B) = - j Г (г — у, со) [Ти (у)Г djS +
+ j [T (d^, и) Г (у — г, со)]' «Г (у) d,JS, B.53)
S
который объемлет случай г 6 ?>+ U О".
2.11.	Следствие. Регулярное во всем пространстве Е3 решение
однородного уравнения колебаний, удовлетворяющее условию излучения,
есть тождественный нуль.
В указанных условиях в формуле B.6) за S можно принять сферу
С (х9 R). Переходя к пределу при R —> оо и принимая во внимание условия
на бесконечности, получаем и = 0.
2.12.	Следствие. Регулярное в D+ U D" решение однородного
уравнения колебаний, удовлетворяющее условию излучения и контактному
условию вдоль S
и+ = *Г, \Т (д„ п) и (х/)}+ = {Г (ду, п) и (уч-
(учесть тождественный нуль.

я 2]	ЗАДАЧИ УСТАНОВИВШИХСЯ УПРУГИХ КОЛЕБАНИЙ	99
Доказательство следует из формулы B.6), написанной для точки z ? D+,
и формулы B.53), написанной для точки z ? D+. Составив разность и учи-
учитывая направление нормалей, в силу контактных условий получим и (z) = О,
z€D+.
Рассуждение незначительно изменяется в том случае, когда г ? D~\
вывод остается в силе и в этом случае.
Сделаем еще одно замечание, имеющее значение для физического ис-
истолкования полученных оценок. Пусть точка х лежит на сфере С (О, R).
Согласно B.26) и^р\х) убывает на бесконечности как О (i?), а ее касатель-
касательная составляющая, равная [Ro X и^р) (#)], согласно B.33) убывает при
этом как О (#~2).
Для соленоидального вектора a(s> (х), который согласно B.28) убывает
как О (i?), наоборот, нормальная составляющая, в соответствии с B.32),
убывает как О (R~2). Это показывает, что на далеких расстояниях и^р) (х)
направлен перпендикулярно к фронту распространения волны, a u^s) (x)
лежит в касательной к фронту плоскости, т. е. первый выражает продольные
колебания, а второй — поперечные. Аналогично можно истолковать все
другие оценки; например, соотношения B.41) показывают, что и^ и u{s)
асимптотически почти перпендикулярны и т. д.
5. Теоремы единственности для внешних задач. Докажем теорему.
2.13. Теорема. Регулярное в D~ решение однородного уравнения ко-
колебаний А (дх, со) и = 0, удовлетворяющее условию излучения и на границе S
одному из однородных условий:
1) \и\- = 0, 2) \Ти\- = 0, 3) \ип\- = 0, \Ти — п(пТи)\- = 0,
4) \и — л(/ш)}- = 0, \пТи\~=:0, 5) {и}- = 0 на Sl9 {Tu\~ = 0 на S2,
|ия}- = 0, \Ти — п(пТи)}~ = 0 на S3, \u — n(nu)\- = 09 (пТи)" = О на 54,
где 5 = 5Х U 52 U S3 U S4, 6) \Ти + ои}- = 0, где а = аг + ш2, а2 < 0,
есть тождественный нуль.
Доказательство. Применим формулу B.1) к решению и и ком-
комплексно-сопряженному вектору и в области Ш (О, R) fl D~. Объемные инте-
интегралы обратятся в нуль и в задачах I, И, III, IV, V исчезнут также интегралы
на S вследствие граничных условий, а в задаче VI будем иметь
\иТи—ПТиУA^ = 21 \o2(y)\u(y)\2dyS.	B.54)
Преобразуем интеграл по С (О, R) следующим образом:
[ {uTu — uTu)dyS=* I {u{p)[Tu(p) + ik1(X-\-2ii)l{p)] +
€@,R)	C(O,R)
+ u{p) [ТЪ{8) + ik2liZ{s)] + u{s) [Tu{p) + ikx (X + 2ц) и{р)] +
uis)
Tu{s) — ik2iiuis)] — Z{s) [TuiP) — ikx (X + 2p) uip)] -
Z{s)[Tu{s)—ik2liu{s)]} dljS — 2ikl(k + 2VL) f [u^
C(O R)
-2ik2li J U(s) |2d^ — 2i [k2ix + k±(X + 2|i)] J Re (u{p)~uis}) dyS.
C{O,R)	C(O,R)
C(O, R)
J
C(O,R)
7*

100	ТЕОРЕМЫ ЕДИНСТВЕННОСТИ	[Рл Ц{
Перейдя к пределу при R —> оо и используя формулы B.30), B.31),
B.41), вместе с условием излучения, получим в задачах I, II, III, IV, V
2ikx (к + 2\л) lim J | и<"> |2 dyS + 2ik2[i lim f | u^ \2dyS = 0,
*•*« C(O,R)	#-»oo C(OtR)
а в задаче VI
( \u(p)fdyS+2ik2ii lim [ |a<s>|2^ —
О, R)	Я-»со С (О, R)
С (
и, следовательно, во всех случаях имеем
lim J \u(p)\2dS = 0, lim J |a(s)|2rfS = 0.	B.55)
#-»°° С (O R)	i?->0° @(OR)
J	J
С (O, R)	i?->0° @(O,R)
Доказательство теоремы заканчивается с помощью леммы, которую
мы назовем основной и здесь докажем.
2.14. Основная лемма. Регулярное в D~~ решение уравнения
Аи + k2u = 0, k2 > 0, удовлетворяющее условию излучения и условию
lim J
-*00 с (о,
lim J \u(x)\2dj(S = Q,	B.56)
есть тождественный нуль.
Пусть г, Ф, ф — сферические координаты точки х с началом в D+. Из ре-
регулярности и условия излучения для и (г, #, ф) следует, что ее ряд Фурье
по полной системе сферических функций должен иметь вид
оо п
и (г, #, ф) = 2 2 ТТ Я"+1/2 (kr) **" (C0S *) ^")cos тф + 6^"'sln тф)' B>57)
где #i_(&r) —функция Ганкеля первого рода с индексом га + — (см.
Ватсон [1 ] и Гобсон [11). В самом деле, записав ряд Фурье в обычной форме
оо п
и (г, #, ф) = ? S Pn (cos #) (а^ (г) cos тф + р?} (г) sin тф) B.57')
а=0 т=0
и допустив, что условиям:, которым удовлетворяет сумма ряда, удовлетво-
удовлетворяют все слагаемые в отдельности, приходим к ряду B.57). Это можно также
показать вполне строго, и это будет сделано ниже; теперь же продолжим
доказательство леммы.
Из полноты и свойств ортогональности сферических функций вытекает,
согласно теореме Парсеваля,
2л Л	со п
| ги (г, *, ф) f sin ft d$ йф = J) ^ Я а« )УГ' H*Un (kr) Г +
/2=0 m=0
B,58)
а из условия B.56) следует
S S {\a
n=0 m=Q

с 2]	ЗАДАЧИ УСТАНОВИВШИХСЯ УПРУГИХ КОЛЕБАНИЙ	JQ1
и для каждого фиксированного п
lim a™ V~r H%/2 (kr) = 0, lim b%] V? H%/2{kr) = О,	B.59)
r->co	r-»oo
С другой стороны, из асимптотической формулы
Hr—	B-60)
ясно, что B.59) может иметь место лишь при пт} = 6^} = 0, и основная
лемма доказана.
Можно показать (см. Векуа И. [11 и Rellich [1]), что лемма остается
в силе и в следующей формулировке: регулярное в D~ решение уравнения
Аи + k2u = 0, k2 > 0, удовлетворяющее условию B.56), есть тождествен-
тождественный нуль.
Основная лемма и указанное выше ее доказательство встречаются
впервые в краткой заметке В. Д. Купрадзе [1 ]; в этой заметке нет доказа-
доказательства того, что B.57) действительно есть ряд Фурье для и (х), это было
показано позже рядом авторов (см. Freudenthal [1 ], Векуа И. [1 ], Купрадзе
[4], Смирнов [2]). Приведем одно из доказательств.
В области D" П Ш_ (О, R), при достаточно большом R, применим фор-
формулу Грина к решению и (г, #, ср) и регулярным в D~ решениям
v™ (г, #, ф) = -U НЩШ (kr) Р™ (cos О) cos тФ,
V г
(г, ф, Ф) = -±r H(nlll/2 (kr) P™ (cos #) sin mq>.	B.61)
V г
Будем иметь
о= Пой» 4*
С {О, R)
— и (R, #, ф) ^щ- dS. B.62)
Из B,60) легко находим, что для больших R
Поэтому в силу условия излучения при /? —> оо из B.62) получаем
j
так как при этом сумма и первое слагаемое в B.62) не изменяются, имеем
1
С (O*R)

102	ТЕОРЕМЫ ЕДИНСТВЕННОСТИ	[Рл
Внеся сюда значения Vm] из B.61), получаем
B.63)
где
2л л
О О
(я __ f 2, m = О\
коэффициент Фурье ряда B.57').
чеви
Но из B.63) очевидно, что a?° (R) = a^0 "+^2_ , и, аналогично,
и идентичность рядов B.57) и B.57') доказана.
Из обращения и (х) в нуль в окрестности ) х\ = оо,*по свойству аналитич-
аналитичности, с помощью аналитического продолжения нахоДим и (х) = 0, ух g D~.
Теперь доказательство теоремы 2.13 получается из оценок B.55), кото-
которые согласно основной лемме дают
6. Теоремы единственности для неоднородных сред. Пусть неоднородная
среда составлена из двух тел, граничащих вдоль замкнутой поверхности S2
(см. I, § 14, п. 4), причем внешняя среда простирается в бесконечность, а вну-
внутренняя (заключенная внутри конечной области, ограниченной поверх-
поверхностью S2) содержит каверну с границей St. Назовем так составленное тело
D = Dx U D2.
2.15. Теорема. Решения однородных гранично-контактных задач
для области D, с граничным условием на Su совпадающим с одним из указан-
указанных выше шести однородных условий, удовлетворяющие условию излученияг
есть тождественный нуль.
Рассмотрим, для примера, первую задачу.
В области между 5Х и 52, с одной стороны, и в области Ш (О, R) fl D2,
при R — достаточно большом, с другой, применим формулу B.1) к векторам и
и и. Составляя сумму, принимая во внимание направления нормалей и одно-
однородные контактные условия на 52, вместе с условием на Sl9 после перехода
к пределу при R —* сю, так же, как в п. 5, найдем и (х) = 0, х 6 D2. Отсюда
в силу условий на S2 находим
u+(z) = 0, [Til)(dZin(z))u(z)]+ = 01 z?S2.
Представив и (х) в области между 5Х и 52, т. е. в области Dly формулой
Сомилиана B.6), будем иметь
u(x) = j \ril)(x — y,<»)T{l)u(y)dyS, xeDv	B.64)
Рассматривая интеграл B.64) как решение первой однородной внешней
задачи в области вне Sb на основании теоремы 2.13 можем записать:
s.
следовательно, согласно B.64) имеем w (х) = 0, л* 6 Dl9 и теорема доказана.
Для других задач доказательство аналогичное.

К 3]	ЗАДАЧИ УСТАНОВИВШИХСЯ ТЕРМОУПРУГИХ КОЛЕБАНИЙ	JQ3
§ 3. Задачи установившихся термоупругих колебаний
1. Разложение регулярного решения уравнения термоупругости. Пусть
U — (и, м4), где и = (их> иг, и3) — вектор упругого смещения, а «4 — тем-
температура,— есть регулярное решение однородного уравнения установив-
установившихся термоупругих колебаний. Это уравнение, как мы видели в I, § 12,
п. 3, имеет следующий вид:
А (дх) и—у grad а4 + рсо2 и = О,
Да4 + — и4 -)- /сот) div и = 0.
3.1. Теорема. Регулярное решение уравнения C.1) допускает в об-
области регулярности представление
U = (ц, и4) = (и{1) + ^B), ^4)»	C.2)
г5^ w = wA) + wB) w
(Д + Х\) (А + Л|) и{1) = 0, rot а(|) = 0,	C.3)
а постоянные А|, Я|, Я| определяются из равенств
2л 2 Ш рСО2
рСО2 f
Так же как в § 2, п. 1 можно показать, что регулярное решение урав-
уравнения C.1) в области регулярности бесконечно дифференцируемо.
Из C.1) имеем
и _	+ И gra(j jjy w _j—У_^ gra(j M
pco2 to	pco2
pco2 to	pco2	pea2
Пусть
) = - ¦—Iй- grad div u. + -^r grad u4,	C.7)
I
тогда
rotwA) = 0, divaB) = 0.	C.9)
Из C.8), учитывая значение AJ, получаем
(Д + Xl) u{2) = 0.	C.10)
Из формулы C.9) имеем
(X + 2[л) ДиA) + рсоУ ° — у grad ы4 = 0,	C.11)
(Я + 2^i) Д div u(l) + pco2 div аA) — v Аа4 = 0.	C.12)
Если значение
—-^Авд—^-и.	C.13)

104	ТЕОРЕМЫ ЕДИНСТВЕННОСТИ	грл
из уравнения (ЗЛ) внесем в C.12), то получим
>|)а4 = 0.	C.14)
Из C.13) и C.14) будем иметь
(Д + Я?)(Д + Л1)<ИуиA)=0.	C.15)
С другой стороны, выполнив операцию (А + Я?) (Д + Ц) над h<*>,
определенной формулой C.7), и учитывая C.15) и C.14), получим оконча-
окончательно
(Д + А,?) (Д + Я22) и{1) = 0.	C.16)
Формулы C.9), C.10), C.14), C.16) доказывают теорему.
3.2. Теорема. Регулярное решение уравнения C.1) допускает в об-
области регулярности представление вида
C.17)
где
Vil) = (i>A\ vj, V{2) = (v™, vd, УC) = (t;<3\ 0),	C.18)
0,	C.19)
rot v{l) = 0, rot v{2) = 0, div v{3) = 0.	C.20)
Доказательство. Пусть
В силу C.16) отсюда следует
(Д + Л2)уA)=0, (Д + Я|)оB>=0	C.22)
и, кроме того,
причем и4 есть решение скалярного уравнения того же вида, которому
удовлетворяет вектор ыA); поэтому, по аналогии,
и4 = О} + ^4,	C.23)
где
к2 — кх	л,,— л2	^324)
(Д + Я2) о4 = 0,	(Д + А|) v4 = 0.
Теперь ясно, что если примем v{3) = wB), все утверждения теоремы
будут соблюдены в силу C.22), C.23), C.21), C.24), C.9).
Этот результат можно получить непосредственно из общего представле-
представления регулярного решения уравнения термоупругих установившихся колеба-
колебаний (см. X, § 2, п. 2), так как матрица фундаментальных решений системы
C.1) (см. II, § 3) сама удовлетворяет условию теоремы 3.2. •
2. Формулы Грина. Пусть U = (и, и4) — регулярный четырехмерный
вектор, решение уравнения C,1) и U=(u, u&) — комплексно-сопряженный
вектор.

§ 3]	ЗАДАЧИ УСТАНОВИВШИХСЯ ТЕРМОУПРУГИХ КОЛЕБАНИЙ	ДО5
Очевидно, что
А (дх) и — 7 6га(* ^4 4- Р«2и = 0, ]
Дп4—^ы4_шЛ(Цуп = 0 J	<3'25)
Имеем
3
и grad  = 2"^" &&*> ~ и* div "•
Пользуясь тождеством (см. A.1))
[иА(дх)и + Е(и, u)]dx = \u+\Tu\+dS
= \u+\Tu\+
S
и применяя теорему Гаусса—Остроградского, получим
j [и (А (дх) и — у grad u4) -+- Е (и, и) — уи4 div и] dx =
= \и+\Ти — упиЛ+ dS. C.26)
Внесем значение Ди4 из C.25) в тождество
I (и4 Да4 + grad и4 grad a4) dx = \ щ -~- dS;
тогда будем иметь
— у ^u4dlvudx = ^j- ^u^dx+ ^ J grad щ grad щ dx —
Сравнивая C.26) и C.27), получаем
, C.28)
где PU = Ти — yntit (см. I, § 13, п. 3).
Перейдя к комплексно-сопряженному выражению в C.28), составив
разность и приняв во внимание, что Е (и, и) = Е (и, и), будем иметь
f I grad а412 dx = f [uPU + -X-u^ — uPU + -Д-а4 ^) dS. C.29)
3
icot]
3. Условие термоупругого излучения. Теоремы единственности во внеш-
внешних задачах термоупругих колебаний могут быть доказаны при наложении
на решения некоторых условий на бесконечности, аналогичных (но не иден-
идентичных) условиям, которые были в § 2, п. 3 введены для решения уравнения
упругих колебаний.
Величины А|, Ц — решения уравнения C.6) при у Ф 0, являются (см.
гл. X, § 3, п. 2), комплексными числами. Выберем значения Хг и &а таким

106	ТЕОРЕМЫ ЕДИНСТВЕННОСТИ	грл (JJ
образом, чтобы обеспечить положительность их мнимой части, т. е. будем
считать
I1 = *i + $i, Я2 = а2 + Ф2, Pi>0, P2>0.	C.30)
3.3. Определение. Регулярное в D~ решение однородного уравне-
уравнения термоупругих колебаний C.1) удовлетворяет условию излучения, если
для иA>, иB>, и4> заданных равенствами C.7), C.8), выполняются условия
= 0(R-'), k= 1,2,3,
где R — длина радиус-вектора точки х, производная по R — производная
по направлению радиус-вектора и стремление к пределу — равномерное
относительно направления R.
Согласно теореме 2.9 условие для иB) можно переписать в следующем
виде (см. § 2, п. 3):
Ти{2) — ш 1/"р|шB) = о (R~l).	C.32)
Заметим, что из явных выражений матрицы фундаментальных решений
уравнения термоупругости (см. гл. II), на основании теоремы 3.2 без труда
усматривается, что условия C.31) (и даже более сильные) удовлетворяются
каждым вектор-столбцом указанной матрицы.
В главе X (§ 2, п. 2) будут построены формулы общих представлений
регулярных решений в области D+ и D~ уравнения термоупругости; в случае
бесконечной области D~ существенную роль будут играть условия термоупру-
термоупругого излучения, подобно тому как это имело место при получении общих
представлений регулярных решений уравнения упругих колебаний (см. § 2).
4. Теоремы единственности для внешних задач.
3.4. Теорема. Регулярное в D~ решение однородного уравнения тер-
термоупругих колебаний C.1), удовлетворяющее условию термоупругого излуче-
излучения и одному из следующих граничных условий на S:
= 0, 2)
3) \и\~ = 0, [^-} = 0, 4)
есть тождественный нуль.
Доказательство. В области Ш (О, R) П D~ для достаточно боль-
большого R применим тождество C.29); учитывая условие на бесконечности
C.31), C.32), можем писать
i
111 (О, .
+
J
С (О, R)

§ 3] ЗАДАЧИ УСТАНОВИВШИХСЯ ТЕРМОУПРУГИХ КОЛЕБАНИЙ \QJ
Приняв во внимание граничные условия, указанные в теореме, будем иметь
для всех задач
J
C(O,R)
C(O,R)
Так как ТаB) + ш V^ppt w<2> = о (i?"), после перехода к пределу при
R —» со, получим
R^C(OtR)
откуда
lim
J \um?dyS + -l- J|grada4|2d* = 0,
f |wB)|2d^S = 0, \\gradutfdx = O.	C.33)
Первое из равенств C.33), вместе с уравнением (А + Ц) мB) = О,
согласно основной лемме 2.14 дает иB) = 0. Второе из равенств C.33) пока-
показывает, что щ = const. Но из поведения на бесконечности эта постоянная
равна нулю, и, следовательно, и4 = 0» x?D~. Наконец, из C.7), C.13)
следует и^ = Оив результате U = (иA) + аB>, и4) = 0. Теорема доказана.
3.5. Замечание. Мы рассмотрели теоремы единственности для внеш-
внешних задач установившихся термоупругих (и упругих) колебаний. Для
внутренних задач колебаний, вообще говоря, теоремы единственности не
имеют места и нарушаются за счет появления частот собственных коле-
колебаний. Этого вопроса мы коснемся в главах VII, IX, X.
5. Теоремы единственности в задачах термоупругих псевдоколебаний.
Применяемая выше техника доказательства теорем единственности в об-
области D~ остается в силе не только в D", но и в D+, если вместо уравнения
установившихся колебаний рассматривается следующее уравнение:
А (дх) и — у grad а4 — рт2а = 0,
C.34)
где т = а + ш, а > 0. Это уравнение играет важную вспомогательную
роль при изучении динамических задач термоупругости. Поэтому остано-
остановимся на нужных в главе X теоремах единственности.
3.6. Теорема. Первая, вторая, третья и четвертая граничные за-
задачи для однородного уравнения C.34) допускают в области D+ не более одного
регулярного решения.
Пусть U = (и, иА) — решение одной из названных однородных задач
и U = (и, м4) комплексно-сопряженный вектор. Тогда, аналогично формуле
C.28), устанавливается тождество
±»'i?}dS- <3-35>

108	ТЕОРЕМЫ ЕДИНСТВЕННОСТИ	^ря JJJ
Благодаря однородности граничных условий интегралы по 5 во всех
случаях равны нулю. Отделяя вещественную и мнимую части в C.35) и поль-
пользуясь свойством Е (и, и) A.6), получим
J |р (а2_со2) | и Р + Е {и, и) + JL | а4|2 + i -JL- | grad а4 |2} dx =. 0, C.36)
J {2расо | и |2 + -2- -pJL-1 grad u412} d* = 0. C.37)
D+
Если о) = 0, то из C.36) получаем U = (и, a4) = 0 в D+\ если же со =f= 0,
то из C.37) и = 0, а а4 = const, и из C.34) U = (а, а4) = 0 в D+. Это же дока-
доказательство остается в силе для задач в области D~, если решения удовлетво-
удовлетворяют асимптотическим условиям
1,2, k= 1,2,3,
1,2,3.
C.38)
Можно легко убедиться, что фундаментальные решения уравнения
C.34) удовлетворяют на бесконечности более сильным, чем C.38), условиям
(см. гл. X, § 2, п. 2).
Можно получить ряд интересных теорем единственности о термоупругих
установившихся колебаниях неоднородных сред того же характера, как
в случае упругих колебаний (см. § 2, п. 6). Доказательство предоставляем
читателю.
§ 4. Задачи статики в моментной теории
1. Формулы Грина. Пусть % = (и, со) и %' = (и\ со') — шестикомпо-
нентные векторы и и = (и19 и2, и3), со = (со1у со2, со3), и' = (и\у щ, а^)>
со' =t (cox, cog, cog) определены в замкнутой области Z)+. Предположим, что
граница S области D_+ принадлежит классу Л1 (а), а ^ 0, %? С2 (D+) f|
П С1 (D+), ^' G C1(D+) и М (дх) % абсолютно интегрируемо в области
D+.M(dx) — оператор, определенный из (I, 12.7) и (I, 12.8).
В принятых допущениях, аналогично теореме 1.1, доказывается тож-
тождество Грина
x= j \<U'T<U\+dS9	DЛ)
где Т — оператор моментного напряжения (I, 13.8),
+

§41
ЗАДАЧИ СТАТИКИ В МОМЕНТНОЙ ТЕОРИИ
109
3s
Zj дх( dxj ' " Zl I dxf
dcok
^
д(д,-
Zj
dxf
Справедливость этого тождества есть следствие теоремы Гаусса—Остро-
Гаусса—Остроградского и легко проверяемого тождества
<U'M (дх) <U + E (<U\ %L) = div R%
где Rf =
+
), a xt/ и \xif определяются из (I, 11.13)
и (I, 11.13') соответственно.
Заметим, что в формуле D.1) % и %' можно считать как действительными,
так и комплексными векторами. Если, например, %' = %у то D.2) примет вид
Zj dxk '
i, i
dxf
Z
dxk
О/	2_~ VI
ч з и Zj
dcok
dxk
D.3)
Если % — действительный вектор, то Е (%у %) совпадает с удельной
энергией деформации (см. (I, 7.19)), при условии, что ui} и со0 определены
из (I, 7.5) в (I, 7.19).
Мы будем пользоваться формулой D.1) в том частном случае, когда %
является регулярным в области D+ решением уравнения М (дх) % = 0;
(в этом случае, очевидно, М% абсолютно интегрируемо в D+), %' = % и
S 6 Лг (а).
В этих предположениях D.1) принимает вид
IS.	D.4)
D+
Формулы D.1) и D.4) будем называть формулами Грина.
Построим формулу Грина для области D". Предположим, что S ?
? Лг (а), а ^> 0, % есть регулярное решение уравнения М% = 0в области
D~ и %' = %. Пусть, кроме того, в окрестности | х \ = оо соблюдаются условия
щ(х) = О(\х\-1)9	е>, = о(\хП9 /=1,2,3,
_ Л л у 1-14
W
—
Тогда
J
= - \%- \TU\~dS.
D.5)
D.6)
Для доказательства применим формулу Грина D.1) в области D^ = D~(]
П Я/ {О, R), где Л — достаточно большое положительное число. Условия

НО	ТЕОРЕМЫ ЕДИНСТВЕННОСТИ	[Рл JJ]
применимости этой формулы в DR выполнены (М% — абсолютно интегри-
интегрируемо в DR для любого R). Имеем
j E(U, U)dx = - J Vr \TUYdS — J 4T%dS:	D.7)
DR	S	С (О* R)
В силу D.5) интеграл, распространенный по С (О, R), стремится к нулю,
когда R —> оо. Пределы правой и, следовательно, левой части существуют
и равны друг другу. Теорема доказана.
2. Решение вспомогательного уравнения. Найдем все действительные
решения уравнения Е (%% %) = 0 класса С2 (Е3). В силу D.3) рассматривае-
рассматриваемое уравнение эквивалентно следующей системе уравнений:
и* — п дщ л- dui 2 к V dUk — п
dXj ' dxi 3
отсюда
Общее решение этой системы в указанном классе и, следовательно
общее решение уравнения Е (^, %) = 0, дается формулой
М = (и,<о), и = [ахх] + Ь, со = а,	D.8)
где а и b — произвольные действительные постоянные трехкомпонентные
векторы.
3. Теоремы единственности в задачах статики. Докажем следующие
теоремы:
4.1.	Теорема. Задачи A)+ и (Ш)+ имеют не более одного решения.
4.2.	Теорема. Любые два решения задачи (П)+ могут отличаться
аддитивным вектором жесткого смещения (жесткий поворот и жесткое
поступательное перемещение), т. е. выражением вида D.8).
4.3.	Теорема. Любые два решения задачи (IV)+ могут отличаться
жестким поступательным перемещением, т. е. выражением вида % = (и, со),
где и = b и со = 0, b — произвольный постоянный вектор.
4.4.	Теорема. Задачи A)~, (П)~, (Ш)~, (IV)" допускают не более
одного решения, удовлетворяющего условиям D.5).
Доказательство теорем 4.1—4.4. Пусть %' к%"— произволь-
произвольные решения любой из перечисленных выше задач и удовлетворяют усло-
условиям D.5) в случае внешних задач.
Тогда % = %'—%" будет решением соответствующей однородной
задачи, т. е. будет регулярным вектором, удовлетворяющим уравнению
М% = 0 и во внешних задачах — условиям D.5). Кроме того, во всех слу-
случаях
\% (У) Т фю п) % (у)\± = и± (у) {7W (д„ п) и {у) + ГB) {ду, п) со (у)}± +

§5]
ЗАДАЧИ УСТАНОВИВШИХСЯ МОМЕНТНО-УПРУГИХ КОЛЕБАНИЙ
111
Применяя к % формулу Грина (D.1) или D.6)), получим соотношение
Е (%, %) = 0. Следовательно, % представится формулой D.8). Если %
соответствует задаче A)+, то должно выполняться условие %+ = 0, т. е.
и+ = 0 и со+ =0. Это условие в силу D.8) дает % = 0 в D+. Для задачи (Ш)+
должны выполняться условия и+ = 0 и (ТD>со)+ = 0. Отсюда в силу D.8)
следует % = 0 в области D+. Теорема 4.1 доказана.
Для доказательства теоремы 4.2 достаточно заметить, что %у определен-
определенное формулой D.8), является решением однородной задачи (П)+. Это прямо
следует из соотношений
= Ot T(dXfn(x))U(x) = 0,
где % — вектор вида D.8), которые легко проверить.
В случае задачи (IV)+ должны выполняться условия со+ = 0 и (
+ ГB)со)+ = 0. Отсюда в силу D.8) заключаем а = 0. Теорема 4.3 доказана.
Доказательство теоремы 4.4 следует непосредственно из D.5) и D.8).
§ 5. Задачи установившихся моментно-упругих колебаний
1. Разложение регулярного решения уравнения М (дх, а) % = 0.
Сначала докажем теорему.
5.1.	Теорема. Если % = (и, со) ? С2 (D) и удовлетворяет в D урав-
уравнению М (дХ9 о) % = 0, то % е О (D).
Доказательство аналогично доказательству теоремы 2.4 и опирается на
представление регулярного решения уравнения М (дх, о) % = 0 формулой
Сомилиана, подобной представлению B.6) и выводимой так же, как эта
последняя.
5.2.	Теорема. Если % = (и, со) ? С4 (D) и М (дх, о) % = 0, то
(/=1,2,3), и=
/==1
где
-*!) (A + *?) (A + *» w'
©B) =
i« (A ^ m (A +fe|) w>
E.1)
ы удовлетворяют следующим условиям:
(Д + /г2)ы<1) = 0, rotM<1> = 0; (Д+ *l)©A) = 0,	rotco<1) = 0;
(Д + kl) u<2> = 0, divM<2> = 0; (Д +/fe|) ю<2> = 0,	div to*2) = 0;
0, divu<3> = 0; (Д+ yfe2)©C> = 0,	div©<3> = 0,
E.2;

112	ТЕОРЕМЫ ЕДИНСТВЕННОСТИ	[Гл# |Ц
при
^7a2_4a	4a2
+ ат и 4- jj т (ц + а) (Р + и) э
1,2
• «4 —
pa2 ©7 a2 — 4a
1 ц + a p 4- и "
E.3)
Доказательство. Сначала покажем справедливость равенства
з
ы= S и(/)- Имеем
— k\) (A + fef) (A + Ш + (k\ — kl) (A + fejf) (A -f kl) J a =
Аналогично доказывается равенство со = 2 со(^. Заметим, что для
1
доказательства равенств и = $j a(^ и со = 2 w171 мы не пользовались
формулами E.2), E.3); следовательно, для произвольных векторов и и со
класса С4 (О)-разложения a = XI ^(/), fi> = S ^^^ справедливы для любых
*i, ^2, *з, М, удовлетворяющих условию kf Ф k), при i ф /, /, / = 1, 2, 3, 4.
Однако для регулярного решения уравнения М (дх, о) % = 0 это ограниче-
ние для постоянных &!, / = 1, 2, 3, 4 отпадает.
Действительно, можно проверить, что м</>, со^>, / == 1, 2, 3, определен-
определенные из формул E.1)—E.3), могут быть записаны в следующем виде:
=	p-grad diva,	соП) =	grad divco,
Р) (^я2 — af) (А + fe§) rot (о	B) _
/7() = _
2aaf (^ — ^J)
/7C) — (d + P) (fe? - gf) (A + fe|) rot Q)	C) __ qi + q)(fef-- aj) (A+ fe|) rot и
~	2aaf(^^)	» '	-	2aai(*8*|)
и при этом согласно E.3) kl Ф kl и
a = M(i> + ^B) + ^C), о) = со^> + соB) 4-
Покажем теперь справедливость равенств E.2). Очевидно, для и и со
имеем
(fx ~f- a) At^ + (Я + |ы — a) grad div и + 2a rot со + Р<*2^ = О,	E.4Х)
(и + Р) Асо 4 (е + и — р) grad div со 4 2<* rot и 4 (<^<72 — 4а) со = 0. E.4^)

? 5]
ЗАДАЧИ УСТАНОВИВШИХСЯ МОМЕНТНО-УПРУГИХ КОЛЕБАНИЙ
Рассматривая операцию rot от обеих частей равенства E.4Х), вследствие
тождества rot grad = 0, получим
А + irrV)rot« + jr^rrot rot • =
Аналогично из E.42)
rot «+^hrot rot«- °-
Снова рассматривая операцию rot от обеих частей равенств E.5!) и E.52),
и пользуясь тождеством rot rot rot = —Arot, получим
0,	E.6х)
Внеся сюда значения rot rot и и rot rot со из E.52) и E.5!), получим
Wa>+ , ^У ^ft, Arotco =
два тождественных равенства для rot и и rot <o.
Перепишем, например, первое в следующем виде:
— 4a .	4a2	\ A , pa2 Vo* — 4a
в силу E.3) его можно записать еще в виде
(А + Щ (А + k\) rot и = 0,	E.70
и аналогично
(А + ?§) (А + k\) rot co = 0.	E.7,)
Эти равенства будут играть вспомогательную роль при доказательстве
равенства E.2).
С помощью тождества grad div = А + rot rot придадим E.4Х) следу-
следующий вид:
(X + 2[л) Да + (к -f- fi—а) rot rot а + 2а rot <a + р<т2а = 0;
отсюда
(Д + *?) а = - *•++-" rot rot и - -j|L. rot с,	EД)
и аналогично из E.42)
8+°~Р	^tH.	E.82)
Рассматривая операцию расходимости от этих равенств и учитывая то-
тождество div rot = 0, будем иметь
= 0,	E.90
= 0#	E.92)
8 В. Д. Кудрадзе

ТЕОРЕМЫ ЕДИНСТВЕННОСТИ	грд Ш
Из E.9i) следует, что div мB> = div иC) = 0, а из E.92) — div
= div co<3> = 0. Из E.7X) следует равенство rot Ф"> = 0, а из E.72) — ра-
равенство rot CD*1* = 0.
Для завершения доказательства остается показать, что
(Д + k\) (Д + Щ (Д + ki) и = 0,	E.100
(Д + Щ (Д + Щ (Д + Щ со = 0.	E.102)
Первое получается из E.8х) с помощью операции (Д + Щ (Д + /ф,
если при этом учесть E.7х) и E.72). Аналогично, из E.82), E.7Х), E.72)
получается и второе равенство E.102). Теорема доказана.
2. Условие излучения. Пусть % (и, со) ? СB> (D~) и удовлетворяет
уравнению М (дХУ о) % = 0 в области D".
5.3. Определение. % удовлетворяет условию излучения, если
в окрестности \ х \ = оо
) = оA), /=1,2,3,
(x) = о
= 0
где u,W и со('> — векторы, определенные в теореме 5.2.
Повторив рассуждения, которые применялись для доказательства
теоремы 2.8, получим следующую теорему:
5.4. Теорема. Если % (и, со) есть регулярное в D~ решение уравнения
М (дХ9 о) % = О и удовлетворяет условию излучения, то
UU) (х) = О (R-1),	©</) (х) = О (R'1), /=1,2, 3; )
	 Г\ ( ТУ—2\
E.11)
E.12)
3. Вспомогательные оценки. Докажем лемму.
5.5. Лемма» Регулярное в D~ решение уравнения М (дху о) % = О,
удовлетворяющее условию излучения, в окрестности \ х \ = оо удовлетворяет
условиям
E.13)
EЛ4,)
E.142)
(пЩх) ы<3) (х)) -f (»-+- Р) (ш<2>(х) ©<3) (х)) = О (| х р3), E.15)

* 5|	ЗАДАЧИ УСТАНОВИВШИХСЯ МОМЕНТНО-УПРУГИХ КОЛЕБАНИЙ	Ц5
еде
-A)	« ра2	дB)	 с ра2	*C) 	о рст2
„„_„_.	„„_„„_. м_м-^. ^i6)
?
0=1,2,3; </=l,. ..,6.
= 6W (8 + 2u) fta, Л^2; = 6W (u + P) *4, Л^ = (t)
p = 4,5,6; ^7= 1,. ..,6.
Доказательство этой леммы получается повторением рассуждений,
которыми мы пользовались при доказательстве теорем 2.7, 2.8, 2.9, 2.10;
несколько новой является оценка E.15). Приведем ее доказательство.
Учитывая тождество
2а rot co<3> (x) = (м- + a) (k\ — а\) и<3> (*),
которое нетрудно проверить, например, исходя из двух видов для и^(х)
и соC>(лг), которые мы выше получили, и воспользовавшись асимптотическим
равенством
#0 х со<3> (х) = _ JL rot cot3) (х) + 0 (/Г2),
которое следует из -^	/fts<o<3> = О (Л), в результате векторного
умножения на орт Ro радиус-вектора R, получим
1J^ ^^	). E.17)
Умножим это равенство векторно на а<2) (*) и применим формулу B.40);
тогда будем иметь
х) (tfo"<2) W) = 25Гз [(» + Р) А1—
— (<^ff2 — 4а)] (и<2> (ж) X
Но #0ыB) (х) = О (/?) и, следовательно,
= 2^-з [(и + Р) Щ - (Jo* — 4а)] («B) (х) х 5W(J)) + О (Я
E.18)
Аналогично получается равенство
Ro (со<2> (х) ^Щс)) = ^ [(ц + а) ^ — ра2] E«5)(х) X и<2> (х)) + О (Я). E.19)
Из E.18) и E.19) следует
^	(л;)) +(о + Р)(©B)(*) «C) (л:))] = ¦
X (о<3> (х)) 4- О (Я-3). E.20)

Цб	ТЕОРЕМЫ ЕДИНСТВЕННОСТИ	[Гл. Ш
Но, как нетрудно убедиться,
g	— {Jtf — 4a)] + ^±1 [(I* + <*>)% — рст21 = 0,
и из E.20) вытекает E.15).
4. Теоремы единственности. Докажем теперь основную теорему этого
параграфа.
5.6. Теорема. Регулярные и удовлетворяющие условиям излучения
решения однородных задач A)~, (И)", (Ш)~, (IV)" для установившихся момент-
но-упругих колебаний тождественно равны нулю.
Доказательство. Пусть р — положительное число, выбранное
таким образом, чтобы D+ а Ш (О, р), а % — регулярное решение одной из
указанных выше задач, которое удовлетворяет условию излучения. Оче-
Очевидно, что % также будет решением соответствующей однородной задачи,
удовлетворяющим условиям E.11) и E.12)^_в которых kf заменены на —k}.
Рассмотрим % и % в области Ш (О, p)\D+ и запишем две формулы Грина:
одну для % и % и другую для % и % и составим их разность. Объемные ин-
интегралы исчезнут и будем иметь
J [%- (TUT—U- (TUr) ds = J тти—Ити) ds.
= J тти—
С(О.р)
В случае задачи A)~: %~ ¦= %~ =0; в случае задачи (П)~: (Т%)~ =
= (Т%)~ = 0 и, следовательно, интеграл в левой части предыдущего.равен-
предыдущего.равенства в обоих случаях обратится в нуль. Этот интеграл обращается в нуль
и в случае задач (III)" и (IV)".
В самом деле,
В задаче (Ш)~: и~ =п~ = 0и (ТD)ю)~ = (ГD)ю)~= 0, а в задаче (IV)~J
©- = ©- = 0 и (ТA)и + ТB)соГ = (Т^п + Г<2)«)- = 0. Таким образом,
во всех случаях
J (UT%—UT%)dS = 0.	E.21)
С(О. р)
Преобразуем подынтегральное выражение:
Далее,
где Л<*> определяются из E.16). Отсюда в сияу E.13) и E.11) следует ра-
равенство

Л gi	ТЕОРЕМЫ ЕДИНСТВЕННОСТИ В ЗАДАЧАХ ДИНАМИКИ	Ц7
следовательно,
Ъ	+ (p~3).	E.22)
/'k
Учитывая E.14Х) и E.142), из E.22) получаем
Ш%— UTU = 2/ Re (S fyHAWWh + %B>А<3>%<3> + %C)А<2>%B>\ +0 (р).
Но
Re(??<2>4<3>%<3> +1?C)Л<2>%<2>) = Re
и поэтому
Отсюда в силу E.15) получим
(е + 2о) Аг21 ©(» |2 + (о + р) *з I «C> |2] + О (р-З).
Подставляя полученную оценку в E.21), и приняв во внимание (I, 7.20)
и E.3), будем иметь
lim f \u<k>\2dS = 0, lim f |cG<*>|2dS = 0, k= 1,2,3;
p->oo J	p->oo J
6 (СЬ р)	С @, p)
и, наконец, согласно основной лемме 2.14 получаем доказательство теоремы.
§ 6. Теоремы единственности в задачах динамики
1. Энергетические тождества. В этом параграфе доказываются теоремы
единственности для внутренних и внешних задач динамики классической
упругости, термоупругости и моментной упругости.
Доказательство опирается на энергетические соображения, связанные
с законом сохранения энергии, приведенные в I, §§ 6—8.
Преобразуем формулы Грина A.1), C.26) и D.1), в которых теперь
будем считать соответственно и9 U = (и, а4) и % = (и9 со) действительными
и зависящими, кроме точки х9 еще от времени t.
Пусть в A.1) и (ху t) есть решение однородного динамического уравне-
уравнения упругости, соответствующего A, 11.4), a v = -^-. В силу очевидных
тождеств
JL

118
ТЕОРЕМЫ ЕДИНСТВЕННОСТИ
(Гл. III
A.1) переписывается в следующем виде
D+
F.D
или
где
J W
?(/г) = [ -|- ~ dx — кинетическая и ?<"> = -i- f Е (и, и) dx —
+
D+
D+
потенциальная энергия движения.
Подобным же образом поступаем в отношении тождества D.1). Пусть
% = {и, со) есть решение однородного динамического уравнения моментной
теории, соответствующего (I, 11.14), (I, 11.14').
Положим % = -fir и воспользуемся тождествами
ди д<
JlJl
2 dt
dt
2 d/ а | аса
| "о"~я7
Т dt I ~дГ •
тогда D.1) примет вид
р I ди
Y\~
D+
Y\~dt
д(д
2 , 1
dx
= J {^Y
9 F.2)
= J Щ~У ! TUV dS,
или
где
|)
Для получения уравнения энергии термоупругости будем исходить из
интегрального тождества
J \v(Au —
D+
iv, и) — yu^divv] dx= j \v\+\PU}+dS,
S
F.3)
в котором v = (vl9 v2, v3) и U = (а, м4) — произвольные регулярные век-
векторы. Это тождество выводится совершенно аналогично C.26). Пусть U =
= (и, а4) есть решение однородного динамического уравнения термоупру-
термоупругости, соответствующего (I, 11.23), (I, 11.22), a v = -^-.
В силу тождеств
ди |2

С g]	ТЕОРЕМЫ ЕДИНСТВЕННОСТИ В ЗАДАЧАХ ДИНАМИКИ	Ц9
<6.3) примет следующий вид:
— 11-|- \-?г\ -\-Е(и, u)\dx — у Г Ui-^rdivu dx = |{"gjr} \PU\+dS. F.4)
d+	d+	s
Преобразуем интеграл —у \ и4-^- div и dx; так как Д^4 = ^--§^ +
D+
, то
"|rW D+	' D+
2y]x J d* l 4l ' t]
D+	D+	S
Подставив в F.4), приходим к искомой энергетической формуле
D+	D+
В левой части этого равенства, кроме производных по времени кинети-
кинетической и потенциальной энергии, присутствуют еще производная функции
тепловой энергии ~- | | иА\2 dx и функция диссипации — j | grad a4 |2 dx
D+	D+
(см. Nowacki [8]).
6.1.	Замечание. Формулы F.1), F.2), F.5) остаются в силе в об-
области D", если решение удовлетворяет условиям, достаточным для обращения
в нуль при R —* со поверхностных интегралов по С (О, R).
2. Теоремы единственности. Теперь нетрудно показать, что однородные
задачи, т. е. задачи с нулевыми начальными данными и нулевыми граничными
значениями для искомой функции, при отсутствии объемных сил имеют только
тривиальное решение.
Для конечной области имеют место следующие теоремы:
6.2.	Теорема. Единственным регулярным решением однородных
динамических задач I, II, III, IV, V классической упругости является тож-
тождественный нуль.
Действительно, во всех задачах правая часть формулы F.1) обращается
в нуль и, следовательно,
а так как в начальный момент эта постоянная равна нулю, она остается
нулем для всех значений t и -J~ = О, Е (и, и) == 0; отсюда, очевидно,
и = 0.
6.3. Теорема. Единственным регулярным решением основных одно-
однородных задач динамических уравнений термоупругости является тождествен-
тождественный нуль.

120	ТЕОРЕМЫ ЕДИНСТВЕННОСТИ	Ц*л JJ]
Действительно, для всех основных задач термоупругости правая часть
формулы F.5) обращается в нуль; поэтому
и, следовательно, интеграл
Я
уменьшается со временем либо остается постоянным и равным нулю. Но так
как подынтегральное выражение неотрицательно и равно нулю в начальный'
момент, должно равняться нулю каждое из слагаемых; отсюда следует
и = 0, а4 = 0.
6.4. Теорема. Единственным регулярным решением однородных
задач динамики моментной упругости I, II, III, IV является тождествен-
тождественный нуль.
Как нетрудно видеть, во всех случаях правая часть формулы F.2)
обращается в нуль и, следовательно,
: = const.
Так как в начальный момент эта постоянная равна нулю, она не изменится
ди
со временем и
_
dt
= 0, ^- =0, ?(%, %) = 0; отсюда % = (и,со) = 0.
6.5. Замечание. Если выполнены условия, указанные в замеча-
замечании 6.1, то теоремы 6.3—6.5 остаются в силе и в бесконечной области D~*
§ 7. Некоторые справки и библиографические справки
Теоремы единственности играют особо важную роль для математического
изучения задач физики и механики: без исследования единственности (или
неединственности) решения математической задачи нельзя утверждать, что
полученное решение действительно описывает исследуемое физическое
состояние. Кроме того, мы увидим, что интересующие нас задачи классической
теории упругости, микрополярной упругости и термоупругости приводят -
к определенным системам линейных сингулярных интегральных уравнений
и для этих систем остается в силе классическая теория интегральных урав-
уравнений Фредгольма второго рода. Благодаря этому, из теорем единственности
мы получим также теоремы существования.
Условия, при которых реализуются доказанные выше теоремы един-
единственности, являются достаточными, но не необходимыми, хотя, вообще
говоря, близки к последним (см. пример в п. 4). Важно то, что во всех слу-
случаях принятые достаточные условия выполняются для решений в тех клас-
классах, в которых они строятся.
Разыскание необходимых условий представляет известный интерес,
однако является трудной задачей, требующей точного учета многих факторов,
от которых зависит решение задачи. Важные результаты, полученные
в последнее время по этим вопросам, можно найти в книге Кнопса и Пейна
(Knops, Payne [11).
Существует несколько методов доказательства теорем единственности
теории упругости. Важнейшими следует признать доказательства, основан-
основанные на принципе энергии, и доказательства, полученные с помощью прин-
принципа аналитического продолжения. Мы пользуемся первым методом. Второй

§ 7]	НЕКОТОРЫЕ СПРАВКИ И БИБЛИОГРАФИЧЕСКИЕ УКАЗАНИЯ	121
метод, с помощью которого пока удалось доказать теоремы единственности
только для статических задач, основан на теоремах Дафина (Duffin [I])
об аналитическом продолжении регулярных решений уравнения А (дх) и = ®
через плоскую часть границы и их можно найти в указанной выше книге
Knops, Payne [13.
Теоремы об аналитическом продолжении решений несколько более
общих уравнений (уравнения колебаний, уравнения термоупругости),
независимо от Дафина, и другим путем, были получены сначала Обола-
швили (см. XIV, § 3) и затем Купрадзе и Бурчуладзе (см. XIV, §§ 4, 5).
Теоремы единственности статики и динамики для многих задач класси-
классической теории упругости были доказаны в работах Неймана (Neumann [1J),
Кирхгофа (Kirchhoff [1]), Е.иФ. Коссера (E.Cosserat,F.Cosserat [1]), Альманзи
(Almansi [11). Новейшие результаты, показывающие, что в ряде случаев можно
«смягчить» классические признаки и указать условия, необходимые и доста-
достаточные, содержатся в книге Knops, Payne [13. К сожалению, в этой книге
совершенно не затрагиваются важные вопросы единственности для уравне-
уравнений колебаний упругости, микрополярной упругости и термоупругости;
в нашем изложении этим вопросам уделяется значительное место. Соответ-
Соответствующие результаты принадлежат авторам, а также Напетваридзе [61
и Чичинадзе [13.
В истории теорем единственности для задач колебаний большую роль
сыграл так называемый «принцип излучения» или «условие излучения»,
сформулированное Зоммерфельдом в 1912 году э работах об уравнениях
Гельмгольца (см. Sommerfeld [11).
Доказательство принципа излучения для уравнения Гельмгольца было
указано в 1933 году В. Д. Купрадзе [11. Позже условие излучения и теоремы
единственности для названного уравнения стали предметом работ многих
авторов (Magnus [13, Freudenthal [11, Векуа И. [1, 31, Rellich [11, Аваза-
швили [13, Мецхваришвили [13 и др.), а для задач теории упругости усло-
условия излучения рассматривались в работах Купрадзе [31 и Бакаляева [11.
При этом в работах Векуа И. [11 и Rellich [11 единственность устанавли-
устанавливается в более общих условиях, чем условия Зоммерфельда.
В этих работах рассматриваются граничные задачи в бесконечных
областях, граница которых лежит целиком в конечной части пространства.
Теоремы единственности для бесконечных областей с границей, простира-
простирающейся в бесконечность, оказались труднее, и для таких областей до сих
пор получены лишь частные результаты. Приведем здесь три теоремы такого
рода для полупространства х3 ^ 0 из книги Knops, Payne [13.
7.1. Теорема. Пусть uil)(x) и иB)(х)—два регулярных в полу-
пространстве х3 ^ 0 решения уравнений статики А (дх) и = 0, принима-
принимающие на граничной плоскости х3 = 0 равные значения. Если выполнены условия
А	. О	А	. 1	/А	/Т 1 \
Т+^Т и т^ + ~> И*0	G-1)
lim | х Г | и*11 (х) — и?' (х) | = 0, 1=1,2,3,	G,2)
то
и^(х) = и<2Цх), x?D (D = \х\хг^0\).
При этом условие G.1) является необходимым,
7.2. Теорема. Если Ти{1Цх) и Tui2)(x) (m. е. два различных поля
напряжений) имеют равные значения на границе х3 = 0 и выполнены условия
I	G,3)
lim |тае(*)| = 0, а,р=1,2 г

122	теоремы единственности	[Гл. Ш
и условия
то
ТФ> (х) = 7V2> (х), x?D; D =
при этом у смещения определяются с точностью до жесткого движения тела;
условие G.4) является необходимым.
7.3. Теорема. Если на граничной плоскости х3 = 0 выполнены условия
]	M	]= 0, 1=1,2
условия
К'ДО-и^-О; [тзз(ыи)(у))-Тзз(ыB)(У))]=0, » = 1,2
а «а бесконечности условие
lim | л: Г11 aj" (х) — *42> (х) | = О,
и, кроме того,
то в полупространстве х3 ^ 0 поле напряжений Т (и^1)(х) — иB)(х))
тождественно равно нулю, а смещения отличаются друг от друга лишь
жестким движением; условие G.5) является необходимым.
Очевидно, теорема 7.3 относится соответственно к задачам III и IV.
ЗАДАЧИ
1.	Доказать теорему единственности для динамической задачи теории упругости с гра-
граничными условием Ти + а (у) и (задача VI), где а (у) — заданная на S матрица класса
Гель дер а.
Указание: см. теорему 6.2.
к
2.	Исследовать единственность решения основных задач с обобщенной энергией Е (v, и)
к
и обобщенным напряжением Т (ду, п) и.
Указание: см. замечание 1.5.
3.	Доказать теоремы единственности для неоднородной области с конечным числом
включений, когда на граничных поверхностях задаются различные граничные условия (сме-
(смешанная задача). Рассмотреть случаи статики и установившихся колебаний.
Указание: см. § 1, п. 6.
4.	Исследовать единственность решения основных гранично-контактных задач для урав-
уравнения установившихся термоупругих колебаний.
5.	Доказать теоремы единственности для основных гранично-контактных задач уравне-
уравнения установившихся колебаний моментной теории упругости.
6.	Исследовать единственность решения граничных задач установившихся термоупру-
термоупругих колебаний, с одним из следующих краевых условий: 1) заданы PU\ —^—{- h (у) и4>
2) заданы и и -~^- + h (у) щ, 3) заданы PU + g (у) U, -^- + /ш4, 4) заданы PU + е (у) -^-,
а4, где h (у) — скалярная функция, g (у) — матрица 3X3, и е (у) — трехкомпонентный вектор.
7.	Доказать теоремы единственности в неоднородной области D = Dt[]D2 (см. § 1 п. 6)
для различных динамических задач.
8.	Сформулировать задачи, аналогичные задачам III и IV классической теории (см. I,
§ 14 п. 1) для уравнения термоупругих колебаний, и доказать теоремы единственности.
9.	Сформулировать задачи, аналогичные задачам III и IV классической теории
(см. I, § 14 п. 1) для уравнения установившихся колебаний моментной упругости, и доказать
для них теоремы единственности.
10.	Распространить результаты предыдущих задач на задачи с обобщенной энергией и
обобщенным напряжением.

ГЛАВА IV
СИНГУЛЯРНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЬНЫЕ
УРАВНЕНИЯ
В последующих главах будут широко использоваться сингулярные
интегралы, распространенные по поверхностям, представляющим границу
упругой среды, а также по областям трехмерного пространства, занятого
самой средой. Существенно будет применяться также теория интегральных
уравнений, содержащих эти интегралы.
Настоящая глава посвящается этим вопросам. Здесь исследуются основ-
основные свойства сингулярных операторов в различных функциональных про-
пространствах; приводятся (без подробных доказательств) теоремы типа теорем
Фредгольма и Нетера и устанавливаются свойства дифференцируемости ре-
решений сингулярных интегральных уравнений; получены теоремы вложения
и т. д.
В § 7 развита теория сингулярной резольвенты и заново доказаны
теоремы Фредгольма для интегральных уравнений первой и второй гранич-
граничных задач классической теории упругости.
§ 1. Вводные замечания. Специальные классы
функций и их свойства
1. О сингулярных интегралах и интегральных уравнениях. Укажем
в этом параграфе некоторые из тех сингулярных интегралов и интегральных
уравнений, которые встречаются при исследовании основных задач, постав-
поставленных в первой главе.
Пусть 5 — замкнутая гладкая поверхность, ограничивающая конеч-
конечную область D+. D~ = E3\D+.
В главе III было доказано, что любое регулярное решение уравнения
А(дх)и + &~ = 0	A.1)
дается формулой
2и(х) = \т(г — х)Р(г)Aг+1т(у—х)\Т{ду,п)и{у)\+dJS—
D+	S
\	. A.2)
Здесь А — матричный дифференциальный оператор, определенный фор-
формулой (I, 12.1); Г — матрица Кельвина (см. гл. II); Т — оператор напряже-
напряжения (см. (I, 13.2)); п — орт нормали поверхности S в точке у, внешней по
отношению к D+.

124	СИНГУЛЯРНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ	(Гл# IV
Из A.2) заключаем, что
^\т(г—x)T{z)dz	A.3)
2 /За-
/Заявляется решением уравнения A.1).
Таким образом, если уравнение A.1) имеет регулярное решение, то F,
определенная формулой A.3), является частным решением этого уравнения.
Но мы априори не знаем, существует или нет регулярное решение уравне-
уравнения A.1) и, следовательно, нельзя утверждать, что F, определенная из A-.3),
представляет решение уравнения A.1).
Нахождение частного решения уравнения A.1) важно, так как подста-
подстановкой и = v + F решение этого уравнения приводится к решению более
простого, однородного уравнения А (дх) v = 0.
Таким образом, нужно доказать, что F из A.3) является решением урав-
уравнения A.1); для этого необходимо вычислить вторые производные от F по
декартовым координатам точки х. Решение этой задачи в свою очередь тре-
требует исследования интеграла
A.4)
D+
z — x\-Hzm — xm)(zr — xr)(zk — xk)(zf — x,) — 3[6kf(zm —
r — Xr) + 6/m (Zk — Xk) (Zr — Xr) + 6/r (Zk — Xk) (Zm — Xm) +
brk(zm—xm)(zi — xf)] I z — x Г6 +
z_x|-з(&mA. + 8rk8mi)\; A.5)
й/ и \i' — постоянные, определенные из (II, 1.2).
Из A.5) видно, что ядро интеграла A.4) допускает оценку О (| z — х |"8).
Следовательно, этот интеграл не существует в обычном несобственном смысле.
Ниже будет показано существование этого интеграла в смысле главного зна-
значения. Таким образом, поставленная задача приводит к изучению сингуляр-
сингулярного интеграла A.4).
Заметим, что второе и третье слагаемые в правой части формулы A.2)
принадлежат классу С00 (?>+). Поэтому характер гладкости решения урав-
уравнения A.1) определяется, по существу, характером гладкости интеграла
A.3), и, таким образом, сводится к исследованию свойства дифференцируе-
мости сингулярного интеграла A.5).
Если речь идет не об уравнении A.1), а об уравнении колебания
А(дХ9 (о)н + #~ = 0,	A.6)
то задача нахождения одного частного решения этого уравнения приводит
к изучению сингулярного интеграла
J
где Г (х, со) — матрица Купрадзе.
Ядро интеграла A.7) допускает оценку О (| z — х |~*3), и при изучении
уравнений A.6) мы приходим к сингулярным интегралам.
Заметим, что совершенно так же обстоит дело при нахождении частных
решений неоднородных уравнений моментной теории упругости и термо-
термоупругости.

§ I)	СПЕЦИАЛЬНЫЕ КЛАССЫ ФУНКЦИЙ И ИХ СВОЙСТВА	125
Пусть первая внутренняя задача классической теории упругости имеет
решение и. Тогда и представляется в виде A.2), где вместо и+ следует подста-
подставить f. Таким образом, третье слагаемое в правой части формулы A.2) при-
примет вид
w (х) = 117- (дд, п) Г (y—x)\'f(y) dyS.	A.8)
При вычислении граничных значений функции и, представленной
формулой A.2), приходится вычислять граничные значения интеграла
w (х), в выражение которого входит значение интеграла A.8) в граничной
точке z? S. Но ядро интеграла A.8) обладает (см. гл. II) особенностью
вида \у— х |~2. Следовательно, интеграл A.8) не существует в обычном
несобственном смысле, если х ? S.
Ниже будет показано, что при некоторых условиях, наложенных на
5 и /, интеграл A.8) существует в смысле главного значения при х 6 S.
Не приводя здесь все сингулярные интегралы, с которыми будем иметь
дело в последующих главах, заметим, что речь будет идти о сингулярных
интегралах, распространенных на области D+ и D~ и сингулярных интегра-
интегралах, распространенных по поверхности 5, а также об интегральных урав-
уравнениях, содержащих эти интегралы. Нужно будет установить свойства
дифференцируемости указанных интегралов и решений сингулярных инте-
интегральных уравнений, показать справедливость для этих уравнений общих
теорем типа теорем Фредгольма и Нетера.
Изучению этих вопросов посвящена настоящая глава.
2. Функции класса О и Z. Введем некоторые специальные классы функ-
функций, которые встретятся в дальнейшем в качестве ядер сингулярных ин-
интегралов.
Пусть А и В — ограниченные множества из ?3> а k (x, у) — функция,
определенная относительно х на А и относительно у на В. Точнее, функция k
определена на произведении А х В, кроме, быть может, диагонали этого
произведения.
1.1. Определение. Функция k принадлежит классу G (т), 0 ^
< т < +оо на Л хВ, если k непрерывна на Л хВ, кроме, быть может,
точек типа х = у, и существует положительная постоянная с такая, что
V (х9 у)е А х В
\k
1.2. Определение. Функция k принадлежит классу Gx (m, а),
О < а ^ 1, если k ? G (т) и для всех х\ хп ^ А и у ? В справедлива
оценка
\k(x\y) — k(*", у)| ^с|х' — х"|*[р„(*', х")]-т-«,
где с = const, a
у — х'\, \у—х"\\>
Функция k принадлежит классу G2 (т, Р), 0 <iP ^ 1, если &? G (т) и для
всех х?А и у\ yf'^B справедлива оценка
|k(х, у') — k(х, у")\^с\у' — у"р[рх(*/', /)Г
Функция k принадлежит классу G (т, а, Р), если k?Gt (m, а) и
G2(m, P).
Отметим некоторые свойства функций этих классов.
1.3. Теорема. Если k? Gt (m, a) [G3 (m, P), G (m, a, p) 1 на A X B,
SlA и SiES, rno fc?Gi (я*, a) [G2 (m, p), G (m, a, P)l на Аг X Bv

126	СИНГУЛЯРНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ	(Гл. IV
1.4.	Теорема. Если k^Gx (m, а) Ю2 (т9 р) 1 на А х В и расстояние
между множествами А и В — положительное число, то ke С°*а (А)
ike c°'*(B)i
1.5.	Теорема. Если т' > /п, а' <з а, р' <; р, то
Gr (m, а) с Gx(m', а'), G2(m, Р) с G2(m', P'), G(m, а, р) с G(m', а\ р').
1.6.	Теорема. ?слм «а АхВ
К е Gx (ть ах) [G2 (тъ рх), G (тъ аъ рх)],
*2 € Gx{m2> a2)[G2(m2, p2), G(m2, a2, р2)],
то на Ах В,
kx±k2e G1 (т, a) [G2(т, р), G (т, а, Р)],
где
a = min)a1, a2}, p = min {Plf p2), m — max \тъ т2\,
а
k^k^Gx^ + m^ a)[G2(m1 + m29 P), G^ + zr^, a, P)].
1.7.	Определение. Пусть к (х, у) =|| fe?/ (x, (/) ||рх^. Тогда
keGt(m, а) [G2(m, P), G (m, а, р)] на Л X В, если fet,6Gi(/n, a)
[G2 (m, p), G (/n, a, P)] на A x B; i = 1, . . ., p\ j = 1, . . ., q.
1.8.	Теорема. Производные т-го порядка, т > 0, до декартовым
координатам точки х матрицы k (х, у) = Г (х — у) [Г (х — у, ca), W (х — у),
W (х — у, а), Ф (х, со), Ф (я, со)] (см. гл. II) принадлежат классу G (т+ 1,1,1)
на D X D, где D — произвольная конечная область из Е3.
1.9.	Теорема. Если S6 Лх (а), то матрица fe, определенная равенст-
равенством k (х, у) = [Т (дд, п)Т (у — х) П IT (ду, п)Т (у — х, со) Г, [Т (ду, п) X
xW(y -J)l', IT (ду, п)Ч (у — х, а)]', [Р (ду, п)Ф(у - х, со) Г,
[R (дуу п) Ф (у — х, со) Г} (см. гл. II), принадлежит классу G B, 1, а) на
S X S.
1.9'. Теорема. Если S6«tfi (a), то матрица k (х, у) = Г (д., я) х
X Г (у - х) - Г (дх, v)T(y- х) [Т(ду, п)Ч?(у-х)-Т (дху v) W {у-
— х) ] принадлежит классу G B — а, а, а) на S X S. Здесь п — орт нор-
нормали поверхности S в точке у, а v — в точке х.
Доказательства этих предложений читатель может найти в работах
Giraud [Пи Гегелиа [3], [101, [12].
Пусть D — некоторая область из Е3 и k —функция, определенная на
произведении D X Е3.
1.10.	Определение. fe62(m, s, а) в области D, где s — целое
неотрицательное число, т > 0, 0 <а < 1, если выполнены следующие
условия:
1)	для всякого *?D, ye E3\\0\, t > 0:
k(x, ty) = t-^k(x,y);
2)	k (x, у) и все ее производные по декартовым координатам точки у,
как функции от х% принадлежат классу Cs*a (D) при любом #?С@, 1).
Матрица k = || kif ||рх<? принадлежит классу Z (m, s, а), если kue
е Z (m, s, а) при i = 1, . . ., р\ j == 1, . . ., q.
1.11.	Теорема. Матрицы Г и V (определенные в гл. II) принадле-
принадлежат классу Z A, оо, 1) в любой области DczE3, а производные порядка s
этих матриц по декартовым координатам точки у принадлежат классу
Z (s + 1, оо, 1) в D. Если k (х, у) = ! ср., (х) Тн{ц) ||зхз, где <рц? О* (D),
то ke Z A, s, a).

§ 1]	СПЕЦИАЛЬНЫЕ КЛАССЫ ФУНКЦИЙ И ИХ СВОЙСТВА	127
Заметим, что матрицы Г (х, со), W (х9 о) и Ф (#, со), а также их производ-
производные, не принадлежат классу Z. Эти матрицы не удовлетворяют первому
условию определения 1.10.
1.12. Теорема. Если k?Z (m, 0, а) в области D, то о (jc, у) =
= k (х9 х — #), принадлежит классу Gx (m, а) на D X D.
В самом деле,
о(х, у) =	k(х, Х~~У ),
<х—у)|х —УГ6С(О, 1),
при х, y?D.
Далее,
- Г '	l—L\.b(x' х'~
~у
Отсюда, учитывая неравенства
- II*' —у| —К —у|1
'-у|т
|
—у д^ —у
- \х'-хГ\
* Ру(х',Х»)>
получим требуемую оценку.
1.13. Замечание* Классы G и Z могут быть введены и для функций,
определенных на подмножествах евклидова пространства любого измерения.
Соответствующие поправки в определениях очевидны.
3. Сингулярное ядро и сингулярный интеграл. Пусть D — ограничен-
ограниченная область из ?3э a k — функция, принадлежащая классу G C) на D X D.
Тогда интеграл
'k(x,y)dy	A.9)
не существует вообще в обычном несобственном смысле, т. е. не существует
предел
lim j k(x9y)dy,	A.10)
8->0 D\oQ (x)
не зависящий от формы ае (х), где ае (х) — произвольная область диаметра 8,
содержащая точку х.
Рассмотрим один простой пример. Пусть
Ь (У 11\ =?= (y	11 \ Iy —— 11 \ I Y ——— It I""	(\ I I \
Очевидно, keGC) на E3 X E3.

128	СИНГУЛЯРНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ	[Гл. IV
Введем сферические координаты
У\ = xi + r sin # cos ф, г = | х — t/1,
#2 = *2 + г sin # sin ф, 0 ^ # ^ я,
Уз = *з + г cos О,	0 < ф < 2я,
dy = r2 sin
и вычислим интеграл
AЛ2)
Ш (х,6)\ве(х)
где б и 8 — произвольные положительные числа, причем е < б; ае
область из Е3, содержащая точку х и ограниченная поверхностями
1)	г = а1е, О	00^
2)	г = аг8,
3)	А-==а38,	^
4)	/• = а4е, я <: ф ^ 2я, — ^ О ^ я;
alf а2, а3, а4 — произвольные положительные числа, не превосходящие
единицу.
Имеем
J (*2 — У*)(хз — Уз)\х — y\'*dy = \ In
3
Пусть теперь л; — произвольная точка области D. Возьмем б настолько
малым, чтобы Ш (х, S)cfl, Тогда
(х2 — У2)(х3 — у3)\х — у
e (х)
= J (х2 — у2)(х3 — Уз)\х —
D\UI(x,6)
Из этого равенства видно, что предел A.10), когда k определено из
A.11), зависит от произвольных постоянных al9 a2, a3 и а4, т. е. от формы
области а8 (х). Таким образом, интеграл A.9) не существует ни в одной точке
области D в обычном несобственном смысле.
Если в приведенных рассуждениях примем ах = а2 = а3 = а4> т« в,
если а8 (х) = ZZ/ (а:, е), то
Следовательно, интеграл A.9) для fe, определенного равенством A.11),
существует в смысле главного значения в каждой точке области D и вычис-
вычисляется по формуле
J (*2 — Уг)(х3—у3)\х — y\'bdy= \ (х2 — у2)(х3 — у3)\х — у\-Ыу,
D	D\UIixf6)
где б выбрана таким образом, чтобе Ш (х, 8)<?D.

§ IJ	СПЕЦИАЛЬНЫЕ КЛАССЫ ФУНКЦИЙ И ИХ СВОЙСТВА	129
1.14. Теорема. Если tF^C0-a (D), 0 < а <: 1, то существует
в смысле главного значения интеграл
в каждой точке области D и вычисляется с помощью обычных несобственных
интегралов по формуле
'	D\IlI(x,6)
где k (x, у) = Г (х — у) [Г (х — у, to), W (x — у), ? (х — у, о), Ф (х — у, а) ].
Доказательство этой теоремы содержится в работе Гегелиа [2].
Интеграл, определенный в смысле главного значения, будем называть син-
сингулярным интегралом. Если k?G C) на D XD и интеграл A.9) не сущест-
существует в обычном несобственном смысле Римана, но является равномерно
сходящимся сингулярным интегралом в области D, то k будем называть
сингулярным ядром. Если же fe? G (/га), где 0 < т < 3, то k будем называть
ядром со слабой особенностью.
Таким образом, fe, определенное равенством A.11), — сингулярное
ядро. Сингулярным ядром является также
°(х,у)— dXidXf ,
где k — любая матрица, участвующая в 1.14.
Пусть kt Z C, s, а) в области D, s ^> 0, а ^ 0. Тогда
D	\Z
s-»0
\Ш (x9 6)	Ш (х9 Ь)\Ш (х, е)
Переходя к сферическим координатам, для второго слагаемого в правой
части предыдущего равенства получим
6
limlnT \k(x> ТГ^т)^
Здесь dyS — элемент площади сферы С (х, 1); б > 0 выбрано таким
образом, чтобы Ш(х, 8) с D, а 0 < 8 < 8.
Для существования указанного предела необходимо и достаточно, чтобы
С(х*
Таким образом, мы доказали следующее предложение:
1.15. Теорема. Функция k класса Z C, .s, а) является сингулярным
ядром тогда и только тогда, когда выполнено условие A.13). При выполнении
этого условия
— y)dy= J
О\Ш(х9
г б)
еде 6 — произвольное положительное число, подчиненное условию Ш (х, б) с
Если задана функция k класса Z C, s, а), то теорема 1.15 дает простой
способ для проверки, является или нет k сингулярным ядром. При этом часто
оказывается полезной следующая теорема:
9 В. Д. Купралзе

130	СИНГУЛЯРНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ	[ГлЛУ
1.16.	Теорема. Если k? Z B, 1, а) в области D, а > 0, то
—щ— (/=1,2,3),
сингулярные ядра класса Z C, 0, а).
Доказательство этой теоремы легко следует из теоремы Эйлера об одно-
однородных функциях (см., например, Фихтенгольц [13, стр. 454). ,
Из теоремы 1.16 непосредственно следует, например, теорема 1.14.
1.17.	Теорема. Если k^Z C, 0, 0) в области D, а > 0, фб С0- а (D)
и выполнено условие A.13) в каждой точке x?D, то существует в каждой
точке х ?D сингулярный интеграл
\
D
Доказательство легко следует из 1.15 и из равенства
xtx — y)y {у)dy = q>(х) lim j k(x, x — y)dy +
6^° ?>\ЯМ*.6)
, 6)
Рассмотрим теперь произвольную функцию k класса G C) на А X В.
Пусть х ? Л П В. Введем сферические координаты точки у с полюсом в точке х
(см. A.12)). Предположим, что существует предел
\im\x — y\3k(x, y) = f{x, О, ф).
г->0
Здесь, при вычислении предела, #ифне меняются. Иными словами, рассмат-
рассматривается луч, идущий от точки х и проходящий через у и допускается су-
существование предела, когда у —> х^ по этому лучу.
Введем обозначения:
6° (*,!/) = /(*, #,Ф)| У Г,
k (х, у) — ?° (*, y) = h (x, у).
Если k? G C, а, Р), 0 < а < 1, 0 < |3 <з 1, то можно утверждать, что
h?G C — р, а, р), a k^Z C, 0, а).
Таким образом, k представляется в виде
k{x,y) = k»(x,x — y) + h(x9y).	A.14)
где k°eZ C, 0, а) и h?G C — р, а, р), 0 < а, р < 1. Следовательно, k
будет сингулярным ядром, если k° удовлетворяет условию A.13).
Мы будем иметь дело в основном с ядрами, представимыми в виде A.14).
Покажем, например, что имеет место
1.18. Теорема. Матрицы
— у, ср) д*Ф(х — у, со) д2? (х — у, а)
— сингулярные матрицы, представимые в виде A.14).
В самом деле, Г (х, со) представится в виде (см. гл. II)
0(х, о)),	A.15)
где Г (х) — матрица Кельвина, а Г° (х, со) обладает всеми производными
по декартовым координатам точки х в ?3\|0}> причем производные второго
порядка имеют изолированную особенность вида | х \~1.
Аналогичные представления справедливы и для Y и Ф.

§ 2]	ИНТЕГРАЛ С ЯДРОМ СО СЛАБОЙ ОСОБЕННОСТЬЮ	131
1.19. Замечание. Сингулярный интеграл и сингулярное ядро могут
быть определены, с очевидными изменениями в формулировках, и для мно-
множеств евклидова пространства любого измерения т. Для наших целей пред-
представляют интерес т = 3 и т = 2.
§ 2. Интеграл с ядром со слабой особенностью
1. Элементарные свойства. Отметим некоторые свойства интегралов
с ядром, обладающим слабой особенностью.
Пусть А и В — ограниченные области из Ет, a k — функция, определен-
определенная на Л х В.
2.1. Теорема. Если k?G (г) на А X В, где т > г, и ф — суммируемая
функция на В, то интеграл
/С(ф)(*)= \k(x,y)<p(y)dy	B.1)
существует почти для всех х^А, и является суммируемым на А.
Доказательство следует из существования интеграла
\k(x,y)\dx
А
и из теоремы Фубини (см., например, Смирнов [3], § 68).
2.2. Теорема. Если k?G (г) на А X В, О < г < /я,
р > тП^г , то К (ф) (х) существует для всех х?А и К (ф)?С° (Л).
Доказательство. Пусть условия теоремы выполнены. Тогда
.0, б-» 0,
равномерно относительно *?Л. Это предложение непосредственно следует
из неравенства
J \k{x, y)y{y)\dy^\\ \k{x, y)\P' dyV/P' \ \
где рг = р (р — I).
Теперь легко оценить интегралы
Л= 1 \k(x*,y)<p(y)\dy9 J2= J \k(x",y)cp(y)\dy,
Ш(х'< 6)ПВ	Ш{х\Ь)[\В
где *', х"?А | х1 — х" | < 6/2. Кроме того,
В\Ш (
J
В\Ш (х, 6)
когда | х' — л:" | —> 0, и из неравенства
следует доказательство теоремы 2.2.
2.3. Теорема. Если k?G (г) на А х В, г < т и ф??р (В), р > \у
то К (Ф)е^ (Л), где q = р B - -^-).

132	СИНГУЛЯРНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ	[Гл. IV
Доказательство. Очевидно,
Я	2т—г	\ т	т—г	р—1
I t? I v 1 ]\ I "^ I гп I и\ \Р i Р Bт—г) I гг) A f\ \2т—f \ ь ( y t/\ I P
I rv уЛ> у У I \	I м' у УI Г I	I т VC//I	I *^ V > с// I
Применив к правой части неравенство Гёльдера с показателями
р Bт — г)	р Bт — г)	р
т '	т — г ' р— 1*
получим
а	2т—г	\ т
I k (х, у) \-ЦГ | Ф (у) \р dy \р v™-')
Следовательно,
С	F9m-r	p т-г Г» Л	2СТ-Г
)\К(<р)(х)\ т йх^сРЫР т )dx)\k(x,y)\ m \q>(y)\Pdy =
А	А В
А В
р im—r) Г	Г*	2т
)
r) Г	Г*
)\4iy)\*dy)\k(x,
......... У)\т dx,
В	А
где св — положительная постоянная, зависящая только от р, а
Теперь в силу неравенства
г Bт — г)<Ст2,
имеем
Г	2т—г	2т—г
)\К{ч>){х)( т dx^cPl<tC~-	B.2)
А
Из B.2) следует доказательство теоремы.
2.4. Теорема. Если k?G (г) на А X В, г < т, то оператор /С,
определенный равенством B.1), переводит пространство Lp (В) (р > 1)
в LQ (A), q = рB—— \и является линейным ограниченным оператором.
Из 2.3 имеем
где
Отсюда и следует доказательство теоремы 2.4.
2.5. Теорема. Если k?G (г) на А X В, г < т, р > ™_ , то опе-
оператор К переводит пространство Lo (В) в Loo (А) и является линейным
ограниченным оператором.
Доказательство следует из неравенства Гёльдера.

§ 2]	ИНТЕГРАЛ С ЯДРОМ СО СЛАБОЙ ОСОБЕННОСТЬЮ	133
2.6. Теорема. Если k^Gi (г, а) на А X В, О < г < тЛ а > О,
ф? Ьр (В), J4 <р < +со, то К (ф), определенный формулой B.1), при-
т — г
надлежит классу С0»7 (Л), где
{{т — г) р — т \
а> —р—г
Если фб Ln (В), то К (ф)€ С°<у (Л), где у = rnin {m — г, а}.
Доказательство. Пусть х\ х"^.А, h=\ х' — х" \.
Тогда
/С(ф)(х') — /С(ф)(х")= S Л.
/г=1
где
/1== f k(x', y)y(y)dy, /2 = — j k(x\ y)(p(y)dyt
Ш{г2Н)(]В	Ul(x\2h)()B
№ (*', У) — * (^, У)] Ф (У) dy.
B\U1 (x'92h)
Оценим эти интегралы. Очевидно, что
Ш (
X
J \x' — y\-">'dyY
',-2Л)ПВ	J
где p = [{m — r) p — m\ p г.
Аналогично оцениваются У2 и У3- Теорема доказана.
2. О производных интегралов с ядром, обладающим слабой особен-
особенностью. Докажем следующую теорему.
2.7. Теорема. Если k?G (г) на А X В, г < т — 1, ^- 6 G (г + 1)
яа Л X Б и фб С0 (В), то в каждой точке х? А, существует производная ~^-
ОХ;
Доказательство. Обозначим через /б функцию, определенную на
[О, +оо), следующим образом: /б (t) = 0, если t? [0, б]; I6(t) == 1, если
f? [26, + со), I6(t) имеет производные любого порядка на @, +со) к
О « /б @ < 1 на @, +оо).
Рассмотрим функцию k^, определенную на Л X В равенством
и интеграл
Очевидно, существует производная ^ в каждой точке #6 А и

134	СИНГУЛЯРНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ	[Гл. IV
Легко усмотреть, что при б —> О выражения
\К6(Ч>)(х) —
(X)
стремятся к нулю равномерно относительно х?А. Отсюда (см., например,
Фихтенгольц [2 ]) следует доказательство теоремы.
Если в 2.7 г > т — 1, то формула B.3) не имеет места. Для исследова-
исследования этих случаев нам понадобится одно вспомогательное предложение.
Пусть || аы (х) \\mxm — матрица, определенная в Ету все главные миноры
которой положительны. Кроме того, aki и их частные производные по xf
непрерывны в Ет (k, i = 1, . . ., m, 1 < / <: т).
Обозначим через N (х, б) эллипсоид, определенный как множество тех
точек у?Ет, для которых
т
2 аы (х) (xk — yk) (x, — yt) < б2,
k, i = \
через v (x, б) — его границу, а чераз Nf (х, б) — ортогональную проекцию
множества N (х, б) на гиперплоскость Xj = 0. Здесь б — произвольное поло-
положительное число. Границу v (x, б) можно разделить на две части таким обра-
образом, чтобы уравнение каждой из этих частей записывалось в виде
B.4)
где yd) = (у19 . . ., У;_1У 0, у}+1у . . ., ут)? N}. (x9 б).
Рассмотрим некоторую точку у = (у19 . . ., ут) из v (х, б) и точку
лежащую на v (x + Ax/t б) с координатами
Уах,- = (#i, • • ., У/-1, У/ + Д#/, J//+1, • • ., Ут),
где
Дху = @, ..., О, Дх/, 0, ...,
(на /-м месте стоит число Дх7). у6 (х, уи)) обладает производными по xf9 и
lim Ml = ^б(^ Уи)) =1+0 (б).	B.5)
Если ач = const, i, j = 1, . . ., m, то roax y; = 1.
2.8. Теорема. Пусть k? G (г) на A X B> -^; 6 G (rr) на A X B,
где г и r' — произвольные действительные числа; х?А и N (х, б)^В для не-
некоторого б > 0. Тогда существует Уб^*' у*. Она непрерывна на Nt (xy б) и
справедливо равенство
д	с и	,	г dk (x, у) .
B\N (х, б)	B\N (x, б)
- J k{xty)^JLdyi,	B.6)
v(x, б)
где
dyi = cos (n (у), xf)dyv(x, 6),
^ (y) — °Pm нормали многообразия v (x, б) в точке y? v (x, б), внешней по
отношению N (x, 6), a d^/v (x, б) — элемент площади поверхности v (х, б)
в точке у.

§ 2]	ИНТЕГРАЛ С ЯДРОМ СО СЛАБОЙ ОСОБЕННОСТЬЮ	135
Доказательство. Имеем
-g|- J k(x, y)dy= lim -д^- J [k(x-\-Axf9 y) — k(x, y)]dy —
1 B\N (x, 6)	\Xj->Q	1 B\N (Xi 6)
— lim --г—	Г	k(x-\- Axit r\)dr\~\-
1	MM (x, Axff 6)
'	"B) («• **/• 6)
где
BT\N(x + te,, 8)),
„ 8))\(B\N(x, 6)).
Далее,
Л1™л-Щ ... i	k(x+&x,.y)dy-
(xf Ax.t 6)
= lim -E- J
"" J	dxf
N. (x, 6)
где
Аналогично вычисляется предел интеграла, распространенного на
ЛД2) (х9 Ад:/, б). Если примем во внимание, что dy^!) = dyi, когда интегри-
интегрирование совершается на части v (х, б), являющейся границей N^v, и dy^ =
= —dyi9 когда интегрирование совершается по остальной части, то из пре-
предыдущих формул непосредственно следует 2.8.
Докажем теперь теорему (см. Михлин [II).
2.9. Теорема. Если ke Z (т — 1, 1, 0) в области D, ср? С0*06 (Z?),
0 < а <« 1, то существуют все частные производные первого порядка по де-
декартовым координатам точки х в области D интеграла
. x—y)q>(y)dy,
°Xf о
— ф(х) \ k(х, х — у)(у; — х-)d9S; /=1	 т.	B.7)
С (х. 1)
Доказательство. Пусть *6 D и Ш (х9 б) 6 D. Тогда в силу 2.8
имеем
JL Г k(x9 x — y)y{y)dy= Г дк{Хдх.~~~У)У
D\UI (х9 #)	D\W (x, 6)
k(x, x — У) \1 __ \ cP(y)dgC(x% 6).
,6)	У

136	СИНГУЛЯРНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ	[Гл, IV
Если #6 С (х, б), то
k(x, x—y) =
|Х	 ?/1
dyC(x9 8) = 8«*-ЫуС(х, 1
Следовательно,
J
С (x. 6)
= J k(x, x —
С (*, 1)
= ф (x) \ k (x, x—y) {yj — xj) dyC (x, 1).
C(x,l)
Далее,
dk(xt x — и) л t. / \	д * ,	ч
=дк(х9 х — у)	щ-к(х, х — у),
где ду& (х, х — у) — производная функции k (х, х — у) по Xj, вычисленная
по первому аргументу, т. е. значение производной —я 2' при z = х — у,
djk (х, х — у)^ Z (т — 1, 0, 0) и, следовательно, является ядром со слабой
особенностью, а ^— k (x, x — у) в силу A.16) удовлетворяет условию
A.13) и является сингулярным. Теорема доказана.
§ 3. Сингулярные интегралы
1. Сингулярные интегралы в классах функций С0' Р. Теорема Жиро.
Пусть D — конечная область из Ет (т > 2), ограниченная замкнутой
поверхностью S, aS0 — Другая замкнутая т — 1-мерная поверхность, ле-
лежащая в D (SodD) и ограничивающая область DoczD. Обозначим через р
расстояние между множествами S и 50. Очевидно, р > 0.
3.1. Теорема (Жиро). Если fe? Z (m, 0, а) в области D, 0 < а < 1
и ф6С°- Р (D), где 0 < р < а, то К (фNС0' е (Do), где
(*, x — y)q>{y)dy	C.1)
и интеграл в C.1) определен в смысле главного значения.
Доказательство. Выше было доказано, что К (ф) (х) сущест-
существует для всех х €?>о- Если хб?>о> то /С (ф) (х) можно представить в виде
К (Ф) (х) = Кг (Ф) (х) + /Ся (Ф) (я),	C.2)
где
/Ci(<p)(x)= J*(x, х—
D f
= q>(x) J fe(x, x—y)dy>

§ 31	сингулярные интегралы	137
Рассмотрим сначала Кг (ф). Пусть х', x"(zDOt г = \х' —х"\ <-|-«
Имеем
Кг (Ф) (*') — Кг (Ф) <**) = Jj h (*', *Г).	C.4)
где
Jt(x\ х?)= \ [k{x\ x' — y)—k{x\ x" — y)][q>(y)—q>(x")]dy +
D\UI(x',p)
— Ф (X*)]	\	k (X', X' — у) dy,
D\I?I(x', p)
J
— ( й (х", х" — у) [ф (у)
Ш (*', 2г)
J	k{x',x' —
\Ш (» 2)
J
Ш (х', р)\Ш (ж», 2г)
У4(х', х") =	f	[fe(дс', х' — у) — /г(хГ, х" — г/)][Ф(у) — <р(д*)]dy.
Ш(л:',р)\Ш(ж',2г)
Оценим эти интегралы. Имеем (см. 1.12)
\}г(х', x")\^c\x'—x"Y- J	1р„(х', х")
D\U1 (X'.p)
Отсюда | Л (л/, л") | <: с \ х' — х" |Э,
|Л(^. x*)l^c J \y — x'^dy + c \ \у
Ш (*',2г)	Ш (х', 2г)
^с [ [у—x'\*-mdy =c\x' — х*|Э,
Ш (ж', 2г)
|/а(л/, Л 1 = 0,
J	[р,(х', х")\-"-«\у—х"рdy.
)\Ш('2)
Если у? Ш (х'г р)\Ш (х', 2г), то 2р9 (д:', л;") > | д:' — у | и
\*Г — у\^2\х'—у\.
Поэтому
|/4(л:', ^)|<с|^'— х"|а	J	\x' — y\V-m-*dy^с\х' — х"\К
Ш (Xе9 р)\Ш {х'9 2г)
Подставляя эти оценки в C.4), получим
I Кг (Ф) {х') — Кг (Ф) (*") I *S с | х'— х" \К	C.5)

138	СИНГУЛЯРНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ	[Гл. IV
Оценим теперь разность /С2 (ф) (х') — /С2 (ф) (хя). Имеем
К, (Ф) (х') — К2 (Ф) (Xя) = Л (х', х") + J, (х', х"),
где
/i(*'. х") = [ф(л:') — фЮ1 \k{x', x' — y)dy,
J2(x', дг") = ф(х") J [?(*', x'—y)—k{x", x" — y)]dy.
D
Jt (x', x") = [ф (x') — ф (*")]	J	* (X', X' — */) dy.
D\Ul(x', p)
Поэтому
|Л(^, x")\^:c\x' — x"\\
J2 (x', x") = ф (дГ) Г f k (*', x' — y)dy—
[	= ф
D\m\x"9 p)	J
где
I3(x\ Л==
D\IlT(x'
Ш (*% о
Ш (х\ о
гегралы:
р+\х'—х |
¦ J
1
?Р)
)\Ш
1
D\h
k(x
Д.
:', х' —
k(x",
, р)
IP, (л
Q 1 Х' 	 J
y) — k(xf\ x" — y)]dy9
x" — y)dy>
x"—y)dy.
Аналогично получается оценка | /3 (x\ x") \ <j с | x' — x" p.
Подставляя эти оценки в C.6) и принимая во внимание, что ф ограни-
ограничена на 5, получим
| К2 (Ф) (^') — К2 (Ф) (Л | ^ с | х' — х" р.	C.7)
Из C.7), C.5) и C.2) следует доказательство теоремы 3.1.Совершенно так же
доказываются несколько более общие теоремы.
3.2. Теорема. Если fe? Z (m, 0, а) в области Do, 0 < а <г 19
Ф е С0' ° (D) и «ф 6 С0* а (Do X D), где 0 < р < а, то интеграл
ф(х, у)^(х, x—y)q>(y)dy
принадлежит классу С0*® (Do).
Если, в частности, -ф (х, у) == ^x (x)'ty2 (у), то в теореме 3.2 требование
-фбС0'" можно заменить требованием г[?6 С°*р.

§ 3]	СИНГУЛЯРНЫЕ ИНТЕГРАЛЫ	139
Отметим одно следствие указанных теорем, когда k не зависит от х.
Этим следствием мы будем часто пользоваться в дальнейшем.
3.3. Теорема. Пусть k — функция, определенная на ?тч\|0[
и имеющая в этом множестве все производные любого порядка. Предположим,
кроме того, что k (ty) = t~mk (у) для всех у? Ет> t > 0 и
J
С (О, 1)
Если гре С°'а (Do), q>eC°'a(D), DoczD, то интеграл
/С.(Ф)(*)=
принадлежит классу C°'a(D0).
3.4. Теорема. Пусть (см. 1.14)
k(x, y) = k°(x, x — y) — h(x, у),
где k°?Z (т, О, а) в области Do, 0<а < 1, h?G (т — а, а, а) на Do X D
и Ф6 С0-* (D) 0 < р < а. Тогда интеграл
/С(Ф)(*)= jk(x, y)y{y)dy	C.8)
принадлежит классу С°* (o)
Справедлива и более общая теорема (см. Giraud [1], Гегелиа [10], [12]).
3.5. Теорема. Если k?G (/я, а, а) на Do XD, 0 <а< 1, фб C°-P(D),
€ < р < а и k является сингулярным ядром, то К (ф), определенная фор-
мулой C.8), принадлежит классу C°'p(D0).
2. Сингулярные интегралы в классах функций С*- а. Пусть D — конеч-
конечная область из Ету ограниченная кусочно-гладкой поверхностью S, a So —
также кусочно-гладкая поверхность, лежащая в области D и ограничиваю-
ограничивающая область Do. Таким образом, DoaD.
Рассмотрим сингулярное ядро k класса Z (m, s, а) в области Do. Тогда
J k(x9 x — y)dyS = Q,	C.9)
С (х, 1)
и сингулярный интеграл C.1) существует вВ„ при некоторых ограниче-
ограничениях, наложенных на ф.
Пусть т = 2; рассмотрим функцию & ( х, .х ~~ у,), определенную на
Do X С @, 1). Разложим эту функцию в ряд Фурье:
( ттт) - S [G-{Х)У*Ш
/г=1
2
/г=1
Здесь
(jTjJ	(^Slnn*; aoo =
в силу C.9).

140	СИНГУЛЯРНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ	[Гл. IV
Теперь, при некоторых ограничениях, наложенных на k и <р, интеграл
C.1) можно записать в виде
п, j
Аналогично можно поступить в случае произвольного т. В самом деле,
разложим k (xf *~ у Л по т-мерным сферическим функциям
где Ynj есть /-я сферическая функция порядка /г. Подставляя C.11) в C.1),
получим ряд вида (ЗЛО).
Функции Ynf> определенные на С @, 1), продолжим на Ет\{ 0 \ сле-
следующим образом:
Очевидно, что Уя/, определенная таким образом на	?т\.{0|, удовлетворяет
условиям
Ущ Фс) = t-mYa, (х), при любом t > 0 и	х6 ?»,\{0};) 3 12)
, 1)).	|
Теперь интеграл (ЗЛО) можно переписать в виде
Рассмотрим функцию У, определенную на?ш\{0}и удовлетворяющую
условиям C.12). Предположим, кроме того, что
С @, 1)
и изучим сингулярный.интеграл
о
J Y(x)dxS = 0,
C.14)
Полученные результаты можно распространить на ряд C.13) или, что
то же самое, на интеграл C.1).
Рассмотрим интеграл несколько более общего вида, чем C.14).
(x — y)H(x, y)dy,	C.15)
где Н — функция, определенная на Do x D.
3.6. Теорема. Если Н, -^-, ~ принадлежат классу С°*а (Do x D)9
0 < а, то в области D 0 существует -^~, t/ ояа принадлежит классу С0'fi (/? 0)>
где р — произвольное число из интервала @, а).

§ 3]	сингулярные интегралы	141
Доказательст во. Пусть *6 Do и б > 0 выбрано так, чтобы
Ш (х, 8)aD. Тогда в силу теоремы 2.8 справедлива формула
JL j Y(x — y)H(x, y)dy = J ±:[Y(x — y)H(x9 y)]dy-
1 D\m {x, 6)	d\ui {xf б) '
— j Y(x—y)H(x, y)dyi,
С (x, 6)
где dyf = n, (y) dyC (x, б), п (у) = (пг (у), . . ., nm (у)) — орт нормали
сферы С (х, 6) в точке у, внешней по отношению Ш (х, б).
Следовательно,
±- \ Y(x-y)H(x, y)dy= J Y{x-y)dHlx'y)dy-
1 D\lll (x, 6)	п\Ш {x, 6)
_ J dY%~y) V (x, y)dy— J Y(x — y)H (x, y) dyf.
D\IU (x, 5)	7	С (x, 6)
С помощью формулы Гаусса—Остр о граде ко го второй интеграл в правой
части можно преобразовать следующим образом:
_ J «^„„.„4,- J у *-»«%**,-
D\UI {x9 6)	О\Ш (х, б)
^JY(x — y)H(x9y)dyi+ J Y(x—y)H(x, у)dyK
S	С (х, б)
где dyj при у 6 S определяется формулой dyj = Лу (у) dyS, /iy (у) =
== (ni (У)» • • •» пт (У)) — орт нормали поверхности S в точке у. Таким об-
образом,
J Y (x — y) H (x, y)dy — — | Y (x — у) Н (x, y) dyf ¦
fj\m (xt 6)	S
D\III (x9 6)
Переходя в этой формуле к пределу, когда б —* 0, в силу 3.2 получим
J Y(x — y)H(x, y)dyi. C.16)
Теперь из теоремы 3.2 следует справедливость теоремы 3.6.
Заметим, что в приведенных выше формулах под Н (х, у) при у? S по-
понимается предел lim H (х9 г), т. е. Я+ (х, у).
D=>z->y(=S
Из (ЗЛ6) и из теоремы 3.1 следует
3.7. Теорема. Если Н (х, у) = Нг (х)-Н2 (у) и Нъ ^ принад-
дН	k
лежат классу С0'а (Do)9 а Н2, -*ф принадлежат классу С0*а (D), 0 < а < 1,
/по существует в области Do ^- и принадлежит классу С0*а (Do).

142	СИНГУЛЯРНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ	[Гл. IV
Пусть jl9 . . ., /s — последовательность целых чисел, заключенных
между 1 и т A <: jk < m, k = 1, 2, . . ., s). Введем обозначения
[Я (х, y)]W = -?~[Н (х, у)]*-" + -?-№ (х,
k = 1, ..., s; [H(x, y)]W = Я (х, у).	(ЗЛ7)
Если Я (л:, у) = ф (л:), то
Методом математической индукции можно доказать, что
а*Д(х, у) , дкН(х, у)	дкН(х,у)
+	+	+
,	.	dkH(x, у)	dkH(x, у)	.
dx,Y ¦ -^ikjyik дУпдУ12дх1Удх1к-
, .... 	дН(х,„)	, .._ ¦
дУ\дх1---дх1дУ1 '
х, у) , . . а*я (х, у)
¦	^Я(х, t/)	¦ #> # . аЖл:, у)
^ • • • dyidxidy; " ' дхдУ• •'дУ
Введем следующий термин: HW удовлетворяет какому-нибудь условию,
если все производные, входящие в его выражение, удовлетворяют этому
условию. Теперь очевиден, например, смысл записи
С0- «(Do х D).
3.8. Теорема. Если функции Н, ЯШ, . . ., #fs1 принадлежат классу
С°а (Do X D), то существуют частные производные
dxh ' • • • ' дхи..-дхи
в области Do, которые принадлежат классу С0- & (Do), где О < Р < а. Кроме
того,
У— = Г К (дс — у) [Я (дс, у)][« Лг/ —
*±1 Г» ,ft_f+i
Ду, Ду.	 (К (х—у) [Я (х, у)]''-21) dt/7'-^.	C.18)
Доказательство легко следует из предыдущей теоремы.
3.9.	Следствие. Если Не С5' а (Do X D), 0 < а <? 1, то Y, опре-
определенная из C.15), принадлежит классу Cs' ^ ф0), где 0 < р < а.
3.10.	Сл едств и е. Если Н (х, у) = Ях (д:)-Я2 (^), НгеО>а (?H),
Я26 Cs*а (D), 0 < а < 1, то Y, определенная формулой C.15), принадлежит
классу Oa(D0).

§ 3]	сингулярные интегралы	143
3.11. Следствие. Если
дф	ds(p
ф"^7
принадлежат классу С°*а (D), 0 <а < 1, то существуют частные производ-
производные
dSx?
a*,, • ' • -
где *F — функция, определенная формулой C.14). Эти производные принад-
принадлежат классу С°'а (Do) и
3.12.	Следствие. Если q>6 Cs* а (?>), 0 <а < 1, то W, определен-
определенная из C.14), принадлежит классу О а (Do)-
3.13.	Замечание. Приведенные предложения 3.6—3.12 справед-
справедливы и в том случае, когда область интегрирования D неограничена (см. Ге-
гелиа [2]) или D = Ет (этот случай содержит предыдущий), но тогда на Н
и ф надо наложить некоторые ограничения на бесконечности.
Справедлива следующая
3.14.	Теорема. Если
ф'
дхГ • * * *» дх, . . . дх.
принадлежат классу Lp (Em)f\COi(X (D), то
. . . дх.
принадлежат классу C°'a (Do), еде
X(x)=
(интеграл определен в смысле главного значения). Кроме того, при k < s,
дх
1 =[у(х~у) А
Н ¦ ¦ ¦ dx'k J	ду>г
Е
dy.	C.20)
Доказательство этой теоремы содержится в работе Гегелиа [2].
3.15. Теорема. Если k — сингулярное ядро класса Z (га, s, а) в об-
ласти Do, s — целое неотрицательное число, а — произвольное действитель-
действительное неотрицательное число, не превосходящее единицу, ц>^С$* 0 (D),0 <p < а,
то интеграл C.1) принадлежит классу CSi & (Do).
Доказательство этой теоремы можно получить методом, указанным
в начале этого параграфа, или несколько изменив рассуждения в доказа-
доказательстве теоремы 3.1.
Совершенно так же получается и более общая теорема.

144	СИНГУЛЯРНЫР ИНТЕГРАЛЫ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ	[Гл. IV
3.16. Теорема. Если k — сингулярное ядро класса Z (m> s, а) в об-
ш Do, 0 < s, 0 <а <¦ 1, Н принадлежит классу О* а (Do X D), то
иляпный интегпал
k(x, x — y)H(x, у) dy	C.21)
ласти Do.
сингулярный интеграл
принадлежит классу О 3(D0) для произвольного |3? @, а).
3. Интегралы с ядром специальной конструкции. Рассмотрим интеграл
J [а(х) — а (у)] k (х, х — у) <р (у) dy,	C.22)
D
где а — функция, определенная в D.
Справедлива следующая
3.17. Теорема. Если k — сингулярное ядро класса Z (m, s, а) в об-
области ?>0, 0 < s, 0 < а < 1, аб Cs* ^ (?>), фб Cr- ^ (D), 0 < |3 < а, то инте-
интеграл C.22) принадлежит классу Cr+l'$ (Do) для любого г = 0, 1, . . ., s — 1.
Доказательство этой теоремы основывается на следующих леммах.
Пусть х, y(zDy х Ф у9 a lxg — вектор у — х.
Введем обозначение
а (у) —а (х)	да (х) х
\У*\	д1 '	У*	C.23)
О,	х=у.
3.18. Теорема. Если а? С1^ (D), 0 < р < 1, то со 6 С0- '* (D X D).
В самом деле, справедлива формула
1
\У
— а (х) __ Г да (х + t (у — х)) ,, _ VI щ — xt f
из которой, при х Ф у, получим
m	1
1=1	О
Очевидно, со (х, у) —> 0, когда у —* х. Кроме того,
®(*. /) —со (л;, г/") =
У\—*1 С[ da(x + t(y'-x)) il(f
J L~ ^
'-x| J L
О
Г y't — xt y"j-
где у' = (f/t'), у" = {y"i) —точки области D. Из этой формулы следует
оценка:

§ 3]	СИНГУЛЯРНЫЕ ИНТЕГРАЛЫ	145
Отсюда, рассматривая отдельно два случая, \у" — х\ ^ | у' — х | и
\ у" — х | > | у' — х\9 получаем оценку
ю(х, у') — со(х, /) = 0(|у' —/р).
Покажем теперь, что со (*', у) — о) (л:", г/) = О (| л:' — *" |Р).
Пусть | х' — у | < 2 | *' — х" |; тогда \ х" — г/1 <з 3 |х' — х" | и из
C.24) получим оценки:
\ у) = О(\х' — y\Z) = O(\x' —
Если | х' — у | > 2 | х' — х" |, то | х" — у \ > \ х' — х" |, и будем иметь
где
. /." ^ — f \da{x"+t{y-x»)) да (х«) 1 „
ал* ,у)—] [	Wi	^—J аи
о
Очевидно,
а*(*', У) — а«(**, У) = О (|а:'
следовательно,
Предложение 3.18 доказано.
3.19. Теорема. Если а? Сь |J) (D), то функция
определенная на D х Ет, является сингулярным ядром класса Z (m, О, Р).
Доказательство этой теоремы элементарно. Заметим только, что
® (*> У) = — ®(*» —^/)» откуда следует равенство
J
С(х, 1)
Рассуждением, аналогичным примененному при доказательстве пред-
предложения 3.6 из C.22) и C.21), можно получить (см. Гегелиа [10 3) доказа-
доказательство теоремы 3.13.
Справедлива и более общая
3.20. Теорема. Если k — сингулярное ядро класса Z (m, s, а) в об-
пасти Do, s > 0, 0<а<1, а? Cs- а (Do X D), фб Сг^ (D), E < а, то
, у) — а(х, x)]k(x, x — y)q>{y)dy	C.25)
принадлежит классу С7' р (Do) йля любого г = 0, 1, ..., s — 1.
10 В. Д. Купрадзе

146	СИНГУЛЯРНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ	[Гл. IV
3.21.	Определение. Пусть k (х> у)—функция, определенная для всех
пар точек (х, у), где x?D0 и y?D, кроме, быть может, пар вида (х, х)> и не-
непрерывна на указанном множестве. Предположим, кроме того, что она обла-
обладает следующим свойством: для любой функции ф класса Cr> p (D) интеграл
]k(x9 y)q>{y)dy
D
принадлежит классу Сг+г>& (Do) при любом г = О, 1, . . ., s— 1. Такую
функцию k мы будем называть ядром класса R (s, Р) на Do X D.
Из теоремы 3.20 следует, например, что, если k?Z (m, s, а) в Do, и
аеО а (Do X D), то
п(х, у) = [а(х, у) — а(х, x)]k(x, x — у)
принадлежит классу R (s, р) на Do X D при любом |3 < а.
4. Сингулярные интегралы на многообразиях. Как было отмечено выше,
при исследовании граничных задач, поставленных в главе I, встречаются
сингулярные интегралы, распространенные на двумерных многообразиях,
лежащих в Е3. Изучим эти интегралы.
Пусть S — замкнутая гладкая поверхность, ограничивающая конеч-
конечную область D+. Обозначим через п (х), где хб S, орт нормали поверхности S
в точке х, внешней по отношению к D+. Пусть d — положительное число, вы-
выбранное для этой поверхности, в определении 1,15.5. В 1,15.5 через S (г, d)
была обозначена часть S, заключенная внутри цилиндра Ц (г, v3 (z), d).
Рассмотрим множество
\S(z, d/4)\zeS].
Это множество покрывает S и в силу компактности множества S из этого по-
покрытия можно выбрать конечное покрытие S. Пусть это есть множество
U(S) = {s(z, d/4) , . . ., S (I d/4)}.	C.26)
Рассмотрим функцию ky принадлежащую классу G B) на S X 5. Таким
образом, k непрерывна в каждой точке (х, у), где х? S, y? S, х Ф у и
k(x, y) = O(\x — y\-*).
Назовем k сингулярным ядром, если интеграл
J k(x, y)dyS
S\S(x, 8)
стремится к конечному пределу, когда е —> 0, равномерно относительно х? S.
Из этого определения легко получается следующее предложение:
3.22.	Если k — сингулярное ядро класса G B) на S X S и cpg C°'a (S),
0 < а, то в каждой точке х 6 S существует сингулярный интеграл
К (Ф) (х)= \k (х, у) Ф (у) dyS = Urn f k (*, у) ф (у) dyS. C.27)
S	e^° S\SU, e)
Справедлива следующая теорема (ср. с теоремой 3.5):
3.23. Теорема (Жиро). Если 8^Лг (a), k — сингулярное ядро
класса G B, а, а) на S X S, фб С0» р (S), 0 < |3 < а < \,jno сингулярный
интеграл C.27) принадлежит классу С0' р (S).
Доказательство. Пусть условия теоремы выполнены. Покажем,
что для любых х' и х" из S

§ 3]	сингулярные интегралы	147
Очевидно, не нарушая общности, можно считать, что | *'¦—х*\ <-т-.
Пусть #'6 S ( z, -^-Л для некоторого z? S. Тогда х"? S (z, -^-V Имеем
где
/х (х) = J k (х, */) ф (у) d^S, /2 (х) = \ k (х, у)
SB, rf)	S\SB, d)
/2 (*') — ^2 (*") оценивается элементарно, так как расстояние от точек х'
и х" до множества интегрирования 5\S (г, d) — не меньше d/4.
Рассмотрим теперь /, (л:). Введем новую систему декартовых коорди-
координат — систему (г) (см. определение 1,15.5). Координаты точек х и у в си-
системе (z) обозначим соответственно через %lf |2, |3 и Ль Лг» Лз- Пусть т (z) —
касательная плоскость поверхности S в точке г; т (г, d) — проекция точек
множества S (г, d) на плоскость т (z), параллельная п (г); ? = (?lf |2, 0),
т| = (Tjlf Tj2, 0). Очевидно, т (г, d) — круг плоскости т (г) с центром в точке г
и радиуса d; ?, ц?т (z).
Отметим следующее простое предложение:
3.24. Если S6«/7r(a), г — произвольное натуральное число, то 02?
б С'*« (х (г, d))9 где
Теперь для 1г имеем
где ф (т]) = ф (у) при y?S (z9 d), k (|, n) = fe (x, у) при х, y?S (z, d),
dyS = в2 (t|) dt], dr] = dr]1dr]2.
Легко показать, что k (|, г)) принадлежит классу G B, a, a) на т 'z, d) X
X т (z, d), и требуемая оценка для /х следует из теорем 3.24, 3.5 и из нера-
неравенства
— т||,	C.30)
где с — некоторая постоянная.
3.25. Теорема. Если S^JIt (a), 0 < а <з 1 и k — одна из матриц,
являющаяся сингулярным решением, построенным в главе II, то k принад-
принадлежит классу G B, а, а) на S X S.
Доказательство. Рассмотрим сначала матрицу k (x, у) =
= Т (дх, п (х)) Г (х — у). Имеем
6	(xH)(xy)
X
=1
где
Д
1 2

fx (X + 2ц) 2 (А, + 2ц)
3 (
4я
¦].
J_ Г (А + Зц)х	Л + Ц 1
Сз 2д L 2ц(Х + 2ц) 2(А+2ц) J*
10*

148	СИНГУЛЯРНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ [Гл. IV
Очевидно, | kki (х, у)\ < с \ х — у | и, следовательно, fe? G B).
Покажем теперь, что \k(x'9 y)—k(x", у) \ < с \ х' — х"\а [ру (х', х")
для любых х'9 х", y?S. Рассмотрим слагаемое
u)= nk {x) {Xj ~ т)
У)	7=J[—
Имеем
y)	______
y)-	______
Учитывая неравенство (см. 1,15.8)
| nk (x') — nk {х) | ^ с | х — х |а,
легко получить требуемую оценку. Аналогично оцениваются и другие сла-
слагаемые.
Докажем теперь, что k (х, у) = Т (дх, п (х)) Г (х — у) является сингу-
сингулярным ядром, т. е. существует предел интеграла
J k(xiy)df/S9
S\S (x, 6)
когда б —> О, равномерно относительно x?S.
Легко показать справедливость неравенства
з
i=i
в силу которого остается показать существование предела интеграла
f	Alfe (*) (XI -~ Щ) — Щ (X) (Xk — Ук) А О
S\S (Xi 6)
когда 8-^0, равномерно относительно #? S. Для этого в свою очередь до-
достаточно показать, что интеграл
f	nk (х) (xi — yi) — щ (х) (xk — yk) d?	,3 22)
SB, d)\S(x, б)
стремится к конечному пределу равномерно относительно x?S(z,-^j,
когда б —> 0.
Пусть х, у? S (г, d). Рассмотрим систему (г). Формулы преобразования
координат будут иметь вид
3	3
au(z)lh yt = zt + 5j ^УB)Л/*	C.33)
Таким образом,
Xi — У( = S a?/ (z) E/ — Л/) = «a (z) (ii — %) + art B) (Ь — Л2) +
+ a »B) [V. Ei, У — Тг (%, Л,)] = [aa (z) + a,3 (г) а?г(а|^2)] (Ь — %) +

К 3]	СИНГУЛЯРНЫЕ ИНТЕГРАЛЫ	149
где (?х, ?2, 0) — точка, лежащая на отрезке, соединяющем точки (?ь Ёг, 0)
и (ТЬ. Лг. 0)- Отсюда
Х{ — У1 = Рд B, X) (Ь — %) + Р/2 (Z, X) (Ь — Т)г) + ^iz (*, У),
где
Ри B, х) = аа (г) + оя (г) ^(a|'S2) ,
) х) = аг2 B) + а„ (z)
Следовательно,
2
2
Xj — Vi _ /=1
а: — г/ |з	"Г | дс — ^ |9 •	У0-0*'
где hiz (х, у)\х — йГ36 G B — а).
Совершенно так же можно показать, что
I* — У\-6 = \ У ^/B,^)(Ь — Л|)F/ — Л/I~~ + ^«(^У), C.35)
где feo6 G C — a), a af/ — некоторые функции, удовлетворяющие условию,
что квадратичная форма a^Utf — положительно определенная.
Таким образом,
2
J U~!/|3^	J
(d)	M
4-
J fv , w« wt Л'
* d) /j a*/ (*> *) Ut — rjf) A/ — Л/)
U /=l	J
+ j h(xyy)dyS, C.36)
где ftgG B — а). Из этой формулы непосредственно следует требуемая рав-
равномерная сходимость интеграла C.32).
Теорема доказана для k (х, у) = Т (дх, п (х)) Г (х — у).
Аналогично доказывается теорема для матриц [Т (дд, п) Г (х — у) 1\
Т (дю п) Г (х — у, со), Т (дху п (х)) Т (х — у) и других.
Теперь из теорем 3.23 и 3.25 следует
3.26.	Теорема. Если Sk:JI1 (a), 0 < a <: 1, k есть любая из мат-
матриц, перечисленных в теореме 3.25, а фб С0-C (S), 0 < C < а, то сингуляр-
сингулярный интеграл C.27) существует в каждой точке х? S и является функцией
класса С0- & (S).
3.27.	Замечание. При доказательстве сходимости интеграла C.32)
приходится доказывать существование предела
Ит | &°E> S-

150	СИНГУЛЯРНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ	[Гл. IV
где % (|, б) есть ортогональная проекция множества S (х, б) на плоскость
т (г), х (g, б) не является кругом, но легко показать (см. Гегелиа [10]), что
lim [ #>(?,? —т|)А|=Нт f k°(l, l— ц) йц.
Здесь fe° (g, | — т]) есть ядро первого интеграла, стоящего в правой ча-
части равенства C.36).
Применяя представления вида C.34)—C.36) и предыдущие теоремы
этого параграфа, можно обобщить теорему 3.26.
3.28. Теорема. Если S^JIS (а), где s — произвольное неотрицатель-
неотрицательное целое число, а а6 @, 13; k есть любая из матриц, являющаяся сингуляр-
сингулярным решением, построенным в главе II, ср? С5' |3E), 0 < |3 < а, то сингу-
сингулярный интеграл C.27) принадлежит классу О P (S) и \\К (<p)||(s# s,,3) ^
||||
||P||(, .P)
Заметим, что теоремы 3.24—3.28 с очевидными изменениями в форму-
формулировках сохраняют силу (см. Гегелиа [12]) и для разомкнутой поверхности.
3.29.	Замечание. Из доказательства теоремы 3.25 видно, что k
принадлежит классу G B, а, а) и, кроме того, для любого г6 S на т (г, d) X
X т (г, d) справедливо представление
К F, Л) = "г & I — Л) + vz (Е, т|),	C.37)
где w2G Z B, 0, а) на т (z, d), a yz6 G B — а, а, а). Здесь &2 (g, tj) = fe (д:, t/),
при х, у ? S (z, d).
*
3.30.	Определение. fe6GB,a,a), если fee G B, а, а), и допускает
представление C.37).
В дальнейшем нам понадобятся в основном функции класса G B, а, а).
При изучении сингулярных интегралов с ядром из класса G B, а, а)
часто применяется следующий прием. Пусть требуется установить определен-
определенное свойство интеграла C.27) для точек, лежащих на S (z, б), где z6 S и
б < d. Тогда естественно представить К (ф) в виде суммы
К (Ф) (х) = J А (х, у) Ф (у) rf^S + J ? (х, у) Ф (у) dfi. C.38)
S(z, rf)	S\S(z,d)
Второе слагаемое в правой части легко изучается, так как при х? S (z, б)
оно не содержит сингулярности. Для изучения первого слагаемого проще
всего (а иногда необходимо) перейти на плоскость % (z), с помощью замены
переменных. Таким образом, будем иметь
J k(x,y)q>(y)dyS= j ftz(S,Ti)e2(Ti)<p(Ti)*|-	C.39)
S(z, d)	x{Zid)
Формула C.39) пока имеет формальный характер. Для установления
этого равенства сначала следует определить сингулярный интеграл, стоящий
в правой части, и потом показать справедливость равенства C.39). Это можно
сделать следующим образом:
По определению,
J k (x, у) ф (у) dy = lim f k (x, у) <р (у) dyS =
S(z,d)	s^0S(d)\S()
2l, e)
где т2 (I, e) — ортогональная проекция множества S (x, e) на плоскость х (z).

* 3]	сингулярные интегралы	151
Если теперь интеграл, стоящий в правой части равенства C.39), опре-
определим формулой
J К g, ц) в2 (TJ) Ф (г\) dx\ = lim J kz gf r\) в2(yi) Ф (tj) dt|, C.40)
X B, uf)	8">° XB, rf)\Tz (|, 8)
то уже приведенное рассуждение доказывает равенство C.39).
Заметим, что сингулярный интеграл, стоящий в левой части равенства
C.40)^распространен на часть евклидова пространства. На таких множествах
сингулярный интеграл мы определили не формулой C.40), а равенством
J kz g, г)) в2 (т|) ф (л) di\ = lim J kz g, т|) 62 (т|) Ф (т|) dr). C.41)
x(z,d)	8">0 т B, d)\lU (I, e)
Здесь символ J снабжен значком * для того, чтобы подчеркнуть, что
речь идет об определении сингулярного интеграла в смысле главного зна-
значения.
Таким образом, мы получили два определения сингулярного интеграла.
Определение формулой C.40) возникло из совершенно естественного опреде-
определения сингулярного интеграла, распространенного на многообразиях, а
определение формулой C.41) — вполне естественное для интегралов, рас-
распространенных на областях евклидова пространства.
Установим связь между этими интегралами. Это необходимо, если мы
хотим перенести результаты, полученные для интегралов, распространенных
на областях, на интегралы, распространенные на многообразиях.
Введем на плоскости т (х) полярные координаты с началом в точке х.
Пусть хг — точка границы множества S (х, е), а 5е — ^е проекция на плос-
плоскость т (х). Пусть полярные координаты точки |8 есть 8 и Ф. Обозначим
угол между прямой, проходящей через точки х и ?8 и плоскостью т (г), сим-
символом a g, #). Легко показать, что
cos a g, О) = —,	^	^—^-,
{«з (В + (ni (I)cos * + п2 (D sin #J}1/2
где п (х) — орт внешней нормали, а пг (?), п2 (I) и пг (|) — координаты
вектора п (х) в системе (г).
Заметим, что если S^JI1(a)9 то cos a g9 d) удовлетворяет условию
С°-а (т (г, d)), равномерно относительно #? [0, 2я1.
Теперь легко написать уравнение границы множества т2 g, 8) в указан-
указанной полярной системе. Имеем
r = ecosag, О).
С помощью этой формулы легко установить требуемую связь.
3.31. Теорема. Если S? Лх (a), k — сингулярное ядро класса
G B, а, а) и фб C°-a(S), mo существуют интегралы C.40) а C.41) в каждой
точке х? S (z9 d), и справедливо равенство
G
J ^(?,т]H2(г1)Ф(г]^т1 = -0г(Юсог©Ф<
tB# -
1, C.42)

152	СИНГУЛЯРНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ	[Гл. IV
где
<*г (I) = \»2 A> #) In cos а (|, ft) <sM>,	C.43)
a uz — функция, определенная из C.37).
Подробное доказательство этой теоремы читатель может найти в работах
Михлина [11 и Гегелиа [103.
5. Сингулярные операторы в пространствах Lp. Теорема Кальдерона
и Зигмунда. Рассмотрим сначала сингулярные операторы в пространствах
Lp (Ет), р > 1. Если фб Lp (Em)9 то
\<p(x)\rdx\l/P.
А. Кальдерон и А. Зигмунд (см. Calderon, Zygmund [1]) доказали сле-
следующую теорему о сингулярных операторах.
3.32. Теорема. Если k — сингулярное ядро класса Z (т, 0, а) на Ет9 и
J \k(x9x — у)\р' dyS^c, —г Н	= 1, р>1	C.44)
для любого х? Ет9 то сингулярный интеграл
К (ф) (х) = I k(x9 х — yL>{y)dy
является линейным ограниченным оператором, переводящим Lp (Em) в себя.
Таким образом, если ф? Lp (Em)9 то, в условиях теоремы C.32), сущест-
существует К (ф) (х) почти для всех х?Ет9 К (фN Lp (Em) и
C.45)
где с не зависит от ф.
Нам понадобятся свойства сингулярных операторов в пространствах
Lp (S), где 5 — замкнутая поверхность Ляпунова в Е3 (точнее, поверхность
класса Лг (а)). Введем сначала пространство Lp (S).
Рассмотрим покрытие C.26) поверхности S и обозначим, ради простоты,
через S/ множество 5 (z, d). Пусть Ег (х)у . . ., Ек (х) — функции, определен-
определенные на S и удовлетворяющие следующим условиям:
1)	?,eC°'a(S);
2)	Et(x)^0, xeS;
3)	f Et(x) = \9 xeS:
4)	[хе8\Е,(х)ф0] =SfaS(z, d/2).
Предположим, кроме того, что если S,nSf Ф 0, то найдется такой ин-
индекс /, что SiflSjCiSi.
3.33. Определение. Систему функций \Et\, удовлетворяющую
условиям 1)—4), будем называть разложением единицы на 5.
Легко доказать существование разложения единицы. Более того, си-
система {?,-} может быть построена эффективно. Справедливо и более общее
предложение (см. Гегелиа [lOJ).

§ 3]	сингулярные интегралы	153
3.34. Теорема. Если S^Jln (а), то существует на S разложение
единицы \Е(\9 где каждая функция Е, принадлежит классу О-а(«$).
Пусть ф — функция, определенная на 5. Тогда ??-<р равно нулю вне S,.
Определим на т, функцию ?,ф равенством
где %t = т (z, d).
3.35. Определение. Определим интеграл от ф на 5 равенством
J Ф (х) d*S = ? J Е. (I) Ф
а норму в пространстве Lp (S) — равенством
/р
i
Здесь через в,: обозначена в2 (см. C.28)) при z = z.
3.36. Теорема. Если S^J11 (а), &—сингулярное ядро класса G B, а, а)
на S X S, q>? Lp E), р > 1, то сингулярный интеграл C.27) существует
почти для всех х? S и
с не зависит от ф.
Доказательство. Имеем
к
is
is
где \Ei\ — разложение единицы (см. 3.33). Очевидно, что
j Е, (х) | К (Ф) (х) \pdxS = \ Et (x) | К (ф) (х) |р dxSt
S	с*
где Sf — носитель функции Е^
Кроме того,
К (ф) (х) = J] J k (х, у) Е, (у) Ф (у) dyS.
Отсюда, в силу неравенства Гёльдера,
j Е, (х)\К (ф) (х) |" dxS ^ с ^ J Et (х) | Ю (Ф) (дс) |" dxS,
где
= J * (x, у) ?,- (у) Ф (г/) dyS = J fe (х, у) Я/ (у) Ф
S	о*

154	СИНГУЛЯРНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ	[Гл. IV
Если х(Е Sj, то
Ю (ер) (х) ={«/(§, т)) Е, (»]) ф (л) в,- (л) dr) + J и,- A, т)) ?,• (rj) Ф (т]) 6, (rtf А),
/
где My и у;- обозначают и2 и v7 при z—z.
Требуемая оценка для первого интеграла получится из теоремы Каль-
дерона и Зигмунда, а для второго интеграла соответствующая оценка полу-
получается элементарно, так как v}^G B —а, а, а).
Заметим, что теорема 3.36 справедлива и для разомкнутой поверхности S.
Нам понадобится несколько более общее пространство, нежели опреде-
определенное выше пространство Lp (S). Приведем определение этого пространства.
Рассмотрим множества всех векторов вида
ф = (ф1, . . . ,фт),
где ф,- — определенная на 5 комплекснозначная функция класса Lp (S),
р > 1, i = 1, . . ., т. Пусть
Ф (х) • -ф (х) = ? ф,
|) (х) = (Хф +
где г|) = (я]?!, . . ., t|)m), а 1 и т — комплексные числа.
Введем норму
Обозначим через L{vm) (S) полученное таким образом линейное норми-
нормированное пространство.
Легко показать, что всякий линейный функционал F над пространством
Lpm) (S) представится в виде
F(9) =
где -ф = (г^!, . . ., -фт) — некоторый элемент пространства L)?* E), где
Рассмотрим линейный сингулярный оператор вида
Л (ф) (х) = а (х) ф (х) + | Р (х, г/) ф (у) dyS,	C.46)
где а (х) = || aif (х) ||тХт — матрица, определенная на «S, а р (х, у) =
= II Р*/ (^» У) llmxm — матрица сингулярных ядер класса G B, а, а), а > 0.
Интеграл, участвующий в C.46), определен в смысле главного значения.
В силу теоремы 3.36 Л является линейным ограниченным оператором, пере-
переводящим Lpm) (S) в себя.
Найдем оператор Л, сопряженный с оператором Л. По определению, Л
есть линейный ограниченный оператор, переводящий L(D^) (S) в себя, такой,
что
J А (ф) (х) о Ф (х) dxS = J ф (х) о Л (ф) (х)
при любых фб L^m) (S) и фе U71* E).

§ 3]	сингулярные интегралы	155
Имеем,
h(x)oa
\dxS J
где а* и P* — матрицы, полученные соответственно из а и р, путем транспо-
транспонирования и заменой элементов на комплексно-сопряженные.
Можно показать (см. об этом более подробно в следующем параграфе),
что в предыдущей формуле можно переставить порядок интегрирования.
Тогда получим
J Г
<p(x)dxS.
Отсюда следует, что
А (Н>) (х) = а* (х) ф (*) + J P* (у, х) ф (у) dyS.	C.47)
Очевидно, приведенное рассуждение не изменится, если под Lpm) (S)
будем подразумевать пространство вещественных векторов (над полем ве-
вещественных чисел) с нормой, определенной той же формулой.
Рассмотрим сингулярный оператор /С, определенный формулой C.27).
Докажем одно предложение, которым часто будем пользоваться впослед-
впоследствии.
3.37. Теорема. Если S — поверхность Ляпунова, &? G B) на
S X S и оператор /С, определенный из C.27), является ограниченным опера-
оператором из Lp (S) в Lp (S), р > U то оператор Ка является вполне непрерыв-
непрерывным из LL, (S) в Lt E), где
Ка (Ф) (х) = J [a (x) — а (у)] k (х, у) Ф (у) dyS	C.48)
<и а — произвольная непрерывная функция на S.
Доказательство. Очевидно, Ка является ограниченным опера-
оператором из Lv (S) в Lp (S). В самом деле,
где | а | ^ АЛ
Докажем теперь, что Ка является вполне непрерывным из Lp (S) в Lp (S).
Предположим сначала, что а^С0Л (S); тогда очевидно, что Ка является
вполне непрерывным из Lp (S) в Lp (S). Пусть \ап\ — последовательность
функции, сходящаяся равномерно к а, и ап?С°>1 (S) при п = 1, 2, . . ..
Тогда, очевидно, || Кпп -— Ка \\ —* 0 при п —» оо и, следовательно, Ки является
вполне непрерывным оператором из Lp (S) в Lp (S).
В доказательстве были использованы две простые теоремы. Первая за-
заключается в следующем. Если S — поверхность Ляпунова и К 6 G (г) на S X 5,
где г < 2, то оператор К, определенный равенством C.27), является вполне
непрерывным из LP (S) в Lp (S). Вторая теорема такова. Если КЛя — вполже
непрерывный оператор из Lp (S) в Lp (S) при п = 1, 2, % . ., и | Кап — Ка I —+
—*• 0, когда п —> оо, то Ка— также вполне непрерывный из Lp (S) в Lp (S).

156	СИНГУЛЯРНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ	[Гл. IV
Доказательство этих теорем можно найти, например, в книгах: Люстер-
ник, Соболев [11 или Канторович, Акилов [11.
Из теорем 3.36 и 3.37 следует
3.38. Теорема. Если S? Лг (а), а > 0, k — сингулярное ядро
класса G B, а, а), а6 С E), то оператор C.48) является вполне непрерывным
из Lt (S) в Lp (S).
§ 4. Формула перестановки порядка интегрирования
в повторных сингулярных интегралах.
Композиция сингулярных ядер
!. Общая формула перестановки порядка интегрирования в повторных
сингулярных интегралах. Справедлива следующая
4.1. Теорема. Если Sg Лг (а), и и v — сингулярные ядра класса
G B, р, у) на S X 5, ф6 С0-6 E X 5 X 5), а, р, у, б > 0, то для любогохt S
\и(х, y)dys\v(y9 z)y(x, у, z)dzS = — O(x)y(xf x, x) +
+ | d? | и (xt у) v (y9 z) ф (х9 у, z) dyS, D.1)
где
f f	f	f
ф (#) = d-,S I w (jc, y) v (y9 z) dyS — \ и (xt y) d^S I v (y, z) dzS.
с ' <?	5	s
Доказательство этой теоремы ведется по следующей схеме, указанной
Жиро. Имеем
(*)= J u(x,y)djS\v(y9 г)ц>(х,у,
= j и (х, у) duS J v (у, z) [ф (jc, y,z) — q> (x, у, y)\ d,S +
+ ju(x9 y)lq>(x, у, у)— <p(x, x, x)]dyS ^v(y, z)dzS +
+ Ф (x, x, x) j и (x, y)djs\v (y9 z)
(x) = J dzS J и(x, y)v(y, z) ф(x, y9 z)dyS =
= j d2S J a U, y) v (y9 z) fф (x9 y9 z) — ф {x9 y9 y))
?\{x> y)Vf(x9 y, y) — y(x9x9 x)]v(y9
+ Ф(x9 x, x) I dzS J и(хч y)v(y9 z)dgS.
Очевидно, что v (r/, z) [ф (x9 y9 z) — ф (jc, y9 у)} и и (х9 у) [ф (х, ^, у) —
— Ф (x, ^, x)l принадлежат классу G B — т|, tj, ц), где т] = min {a, p, у, S|.
Теперь D.1) следует из того факта, что можно переставить порядок интегри-

§ 4]	ФОРМУЛА ПЕРЕСТАНОВКИ ПОРЯДКА ИНТЕГРИРОВАНИЯ	157
рования в повторных интегралах, один из которых регулярный, а другой —
сингулярный.
Можно доказать и следующее предложение:
4.2. Если S^JI1(a)i и {х, у) и v (х9 у) — сингулярные ядра класса
G B, р, у) (у, р > 0) и фб Lv (S) (р > 1), то почти для всех х? S справед-
справедливо равенство
+ J Ф (г) dJS | и (х, у) v(у, z) dyS. D.2)
Доказательство. Множество функций класса С0»6 (S) (б > 0)
всюду плотно в Lp (S), Поэтому можно подобрать такую последовательность
{ф„|, которая сходится к ф по норме пространства Lp (S) и почти для всех
#? S. Кроме того, ф„? С0' 6 E) при п = 1, 2, . . .. По доказанному, формула
D.1) справедлива для фп (п = 1, 2, . . .). Теперь доказательство получится
предельным переходом в равенстве D.2), написанном для ср„.
Можно получить для Ф более удобное выражение, а именно,
J u(xiy)v(y,z)dyS.	D.3,
J
d) S(x,
Заметим, что эти теоремы справедливы, если 56 Ет. В этом случае они
несколько обобщают результат Трикоми (Tricomi [1, 2 3 и Михлин [1]).
Теоремы 4.1 и 4.2 справедливы также, если S есть m-мерное ляпуновское
многообразие.
2. Пример. Рассмотрим теперь один достаточно общий пример ядер и
и о, и вычислим функцию Ф, соответствующую их композиции.
Пусть
3
и (х, у) = [h (х, у)]'3 S и, (х, у) (xf — уь),
3
v(x, у) = [h (х, у)Т3 S vt (х9 у) (xt — у()9
D.4)
где
3
ft2 (х, у) = 2 Ki (x> У) (х* — Уд (Xf — yi)y
uh vh h(j (t, / = 1, 2, 3) — заданные на S X S функции класса С°-а, S —
замкнутая поверхность класса Л1 (a), x = (х,:), у = (yt). Кроме того, все
главные миноры матрицы || hif Цзхз положительны на S X S.
Пусть z?S и рассмотрим локальную систему координат B),
Преобразуя функции
и<1> (х, у) = [h" (х, у)]-3 2 «il) (х) (xt - yt),
, у)}'3 i v^(x, y)(Xi-yt),
l
hll) (x, y) = 1/ t
Г I. /=1
ap (x) = m (x, x), v(tl > (x) == o/ (x, x), lift (x) = /i?/ (x, x),

158	СИНГУЛЯРНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
[Гл. IV
с псшощью C.33) получим
«<*> (х, у) = [ЯA) (х, у)]'3 2 и',1'(г, ж) (Ь
1=1
Р<»> (х, у) = [ft(i> (х, y)]~s ? ^' (z, х) it
-%),
где
, *) = S u(>1)(x)aif(z)t v\l) (z9 x) =
i
— r\t)(t, —
Можно доказать, что для любых х и у из S B, d) справедливо неравенство
2
— Ч<) F/ — Л/)Е** IЕ — Ч|2,	D.5)
где
2, л-) =
? = A1; ?U, 0), ti = (%, Ц2, 0),
„ х | о РУг Къ) и(^) t<? y\ _J_
а |g = ^2 (?) — уравнение части S B, d) в системе B).
Пусть точки х и г/ лежат на S B, d) и пусть
F	4. /=1
г, х) =
z, x),
«,/-1.2).
Рассмотрим функции
ui2)(x, y)=
, у)]
определенные на S (г, d) x S B, d).
Теперь легко показать, что
2
ф B) = — lim \ di) \ V ^:2) B, 2) 6
, х
Г B, rf) T(z,k) i
«<а> (г.
, ?a *^ fe 8) 6l6/]3 2 it 5a
D.6)
3/2 3

§ 4]	ФОРМУЛА ПЕРЕСТАНОВКИ ПОРЯДКА ИНТЕГРИРОВАНИЯ	159
где Т (г, X) — множество тех точек ц (г\и ц2) гиперплоскости т B), для ко-
которых
2
Введем новые координаты на плоскости % (г). Пусть
Ь = 2*</(*)?/>	D.8)
где 1^, 12 — координаты точки | = (|lf E2) в новом базисе, a at/. B) выбраны
таким образом, чтобы выполнялось равенство
i ^(г,г)Ы,= Ъ?.	D.9)
i, /=1	1=1
Выбор постоянных а.ц (г) указанным условием возможен в силу D.5).
Теперь Очевидно, что
2	2
2 М/Ч*. z)fo — Л*)A/ — Л/)= S (Si —Л*J.	D.10)
где %, Лз — координаты точки х\ = (т|1э г\2) в новом базисе.
Легко вычислить якобиан преобразования D.8). Будем иметь
^ (?l. Ei) D Ы > П2) ]/"det I hf) B, г) | '	' ^
В самом деле,
PEvy =det 11^BI1.	D.12)
Далее,
^ г, г) Ь?, = i S t ^ (г, 2) ( Д а« B) Й ) (|; а;/ B) й) =
2/2
2/2
S ( S
и в силу D.9)
2
где 6fe/ — символ Кронекера. Из этого равенства следует, что
?f	D.13)
где значок * при || aif || означает операцию транспонирования матрицы, а
Е — единичная матрица. Следовательно,
Отсюда в силу D.12) следует D.11).
Очевидно, также, что
[	D.14)
где
«?} (z) = 2 и™ B, г) аы (г), «48) B) = 2 № (z, z) aki B).

160	СИНГУЛЯРНЫ? ИНТЕГРАЛЫ V ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ (Гл. IV
Областью Т (г, к) будет множество тех точек (tjJ), для которых
Обозначим эту сферу через Cv
Из D.7)—D.14) следует, что
2
X
Введем обозначения
Легко усмотреть, что Jif (X) = 0, если i ф / и Уа (Я,) = Jи (%) (i, / = 1, 2).
Следовательно,
ф(г) == ^ . '; ' / lim Ju (X),	D.15)
Предел функции J1X (к), когда А, —^ 0, вычислен у Жиро (см. Giraud
[1], стр. 321):
lim Ju (X) = я^ [ 2П D") ],	DЛ6)
где Г (/) — гамма-функция Эйлера.
Докажем теперь, что
?u<3)(z)t,<.3>(z)= S Я»,(г)«Р>(г,г)ор(г,2),	D.17)
где Hif (z) есть отношение алгебраического дополнения элемента hq* (г)
в детерминанте det | hffl B, г)|| к самому детерминанту.
В самом деле,
S «13>(г)«13) (г) = S
l
2	2
= S *42) B, z) ^2) B, z) 2 afei B) a« B).
fe. /==1	i=i
Теперь для доказательства D.17) достаточно показать, что
Но это равенство легко получается из D.13).
В силу D.15)—D.17) окончательно получаем

§ 5]	регуляризация сингулярных операторов	161
Заметим, что приведенное рассуждение не изменится, если S есть т-
мерное многообразие в Ет+1, а в выражении для и и v (см. D.4)) число 3
заменено на т, а 2 — на т — 1.
В заключение этого параграфа сделаем следующее замечание. Теорема 4.1
остается справедливой, если ф = (ф1э . . ., ф„), и = | Ф ||^ /=1, v = [ v1* ||? /==ь
где и**, v*l и Ц){ (i, j = 1, . . ., га) удовлетворяют тем же условиям, что и н,
v и ф в теореме 4.1. В этом случае под uv и скр понимаются обычные произве-
произведения матрицы на матрицу и матрицы на вектор. Ф = ||Ф*/1 вычисляется
формулой D.3).
Подробное доказательство приведенных формул, а также их обобщения
имеются в работе Гегелиа [7].
§ 5. Регуляризация сингулярных операторов
1. Метод Жиро. Пусть S — замкнутая поверхность Ляпунова
°а (S), a k — сингулярное ядро класса G* B, а, а) на S X S (см.
определение 3.30). Рассмотрим оператор
К (ф) (х) = а (х) Ф (х) + J k (xt у) Ф (у) dyS,
и поставим следующую задачу: найти оператор
К' (ф) (х) = а' (х) ф (х) + J к9 (х, у) ф (у) d?,
удовлетворяющий условию
К' (К (ф)) (х) = а (х) Ф (х) + J h (x, у) Ф (у) d^S,
где а Ф 0 на S, /i? G (г) на 5 X 5, а г < 2.
Оператор К', удовлетворяющий этим условиям, называют регуляриза-
тором оператора К.
Из формулы перестановки ясно, что если ядро k' — регулярное, то опе-
оператор К' не будет регуляризатором. Следовательно, к! должно быть сингу-
сингулярным ядром. Кроме того, при решении поставленной задачи нам придется
исследовать композицию К'К и применить формулу перестановки порядка ин-
интегрирования в повторных сингулярных интегралах, полученную в преды-
предыдущем параграфе. Для проведения указанного рассуждения необходимо,
чтобы а' и kr удовлетворяли некоторым условиям гладкости. Потребуем,
чтобы а' е С0'а (S), afe'eG* B, а, а) на S X S.
Именно так ставит задачу регуляризации Ж- Жиро (см. Giraud [1]).
Применяя формулу перестановки для композиции операторов К и К\
получим
К' (К (Ф)) (х) = \а' (х) а (х) + Ф (х)] <р (х) +
+ J Г а'(*)*(*, *) + *'(*, г)а(г)+\#(х, y)k(y, z) djs\ cp(z)d2S9 E.1)
где ф — функция, полученная из формулы D.1), если положим в этой фор-
формуле v и и соответственно k и kr и изменим знак полученнбго. выражения.
11 В. Д. Купрадзе

162	СИНГУЛЯРНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ [Гл. IV
Из E.1) видно, что поставленная задача регуляризации будет решена,
если о! и k' выбраны так, чтобы
а'(х)а(х) + Ф(х)фО, xQS,	E.2)
a'(x)k(x9 z)+k'(x, z)a{z) + \k'{x,y)k{y> z)dyS = O(\x — z\r) на S X S,
E.3)
где г < 2.
Заметим, что в одномерном случае, т. е. когда 5 — кривая на комплекс-
комплексной плоскости, х, у, z — точки этой плоскости, dyS = dyr а
k (x9 y) = b (х) [л (у — х)]-1 + h (х, у),
где h — регулярное ядро, задача регуляризации решается элементарно
(см. Мусхелишвили [2 3). В самом деле, пусть
тогда условие E.2) примет вид
а
[a'(x)b(x) + b'
где г < 1. В этом случае
а'(х)а(х) + Ь'(х)Ь(х)фО9 x?S, 1
[a'(x)b(x) + b'(x)a(x)][n(z — х)Г1 = О(\х — z|-'), j	( * '
f
J
и поэтому
j
k' (х, у)k(у, z)duS = \k' (х, у)h(y,z)dyS = O(\x — 2r|-0. E.5)
Условие E.4) эквивалентно условию а' (х) b (х) + Ь' (х) а (х) = 0.
Если потребуем, чтобы
а2(х) — Ь2(х)ф0, xeS,	E.6)
то можно брать, например, а' = а и Ь' == —Ь.
Таким образом, в одномерном случае, если выполнено условие E.6),
регуляризатором оператора К является К\ при а' = а и Ь' = —Ь.
В двумерном случае задача регуляризации оказывается гораздо сложнее.
В этом случае, вообще, не выполняется условие E.5) и это затрудняет реше-
решение поставленной задачи. Кроме того, дополнительные трудности вызывает
и то обстоятельство, что не всегда удается выразить Ф в явном виде.
Перейдем к изучению нашей основной двумерной задачи. Очевидно,
а' и k' зависят от а и сингулярной части ядра k и не зависят от его регуляр-
регулярной части.
Пусть \Si) и \Si) —два покрытия поверхности S типа П (S)
(см. C.26)). Предположим, что замыкание множества SI содержится в
St (S'iCzSi). Введем обозначения. Пусть при z = z
a, F) = a, F), в, (g) = вг (|), ©,© = ©,(©,
Щ (|, Л) = U2 (I, T]), V{ (|, T|) = Vz (I, T|), k{ (|, T]) = kz (g, Г)),
?	f E.7)
Ut (Ф) (I) = [at (I) — St (l) со, ©] Ф (I) + J в, (g) a, (g, § — tj) Ф (n) dt|f
где ©2, Лг, 1/г, и2 и в2 определены из C.28), C.37) и C.43).

§ 5]	регуляризация сингулярных операторов	163
Ut (ф) (?) определен для | ? *ь где т, — ортогональная проекция мно-
i
жества St на плоскость т (г).
Пусть нам удалось построить функцию а\ на т,- и сингулярное ядро щ
на %i х Т; таким образом, чтобы при |, ??<•:
a! (I) [сц (l) — @c (I) со, (?)] + Ф* (?) ^ 0,	E.8)
О(Ц — СГГХ E.9)
t
где Tj — ортогональная проекция множества SI на плоскость т (z), г < 2,
ф* — функция, участвующая в формуле перестановки порядка интегри-
интегрирования в случае ядер в; (?) ut (?, ? — т]) и wt- (g, g — т|) при сингулярных
интегралах, определенных формулой C.41).
Теперь легко доказать, что оператор К' является регуляризатором опе-
оператора К, если положим
k' (х, у) = 2 j^U*) и* (^ У) [©*'
Здесь \Et (х)\ — разбиение единицы, а\ (х) = a;- (g), a)'L(x) = со/ (g),
?,- (х) = ?;• (I), М/ {х, у) = и? (|, | — т|) при х, у с Sif a cot- — функция,
определенная так же, как со,, но для &;-.
В этом методе не указываются условия, при выполнении которых можно
построить регуляризатор. Иначе говоря, не выясняется, при каких пред-
предположениях относительно а и k можно строить а[ и и[ по условиям E.8) и
E.9). Ж. Жиро (см. Giraud [1]) строит такие функции для оператора /С,
когда ядро есть функция вида D.4). Для матричных сингулярных операторов,
встречающихся в первой и второй основных задачах теории упругости, такие
функции (матрицы) построил В. Д. Купрадзе (см. об этом подробнее в § 7).
От указанного недостатка свободен метод регуляризации С. Г. Михлина.
Этот метод применим для интегралов, распространенных на Ет при любом
т > 0. Нам необходим случай т = 2; поэтому рассмотрим задачу регуля-
регуляризации сингулярных интегралов, распространенных на Е2.
2. Метод Михлина. В этом параграфе изучим вопрос регуляризации
сингулярных интегралов, распространенных на двумерном евклидовом про-
пространстве ?2. Предположим, что и — сингулярное ядро класса Z B, 0, а),
а > 0 на Е2, а? С0- а (?2), и рассмотрим оператор
и(х, х — у) <р (у) dy + В (<р) (х),	E.10)
где В — вполне непрерывный оператор из Lp (Е2) в Lp (?2)» /? > 1. Инте-
Интеграл определен в смысле главного значения
j и(х9 х — у) 4(y)dy = Mm J и(х9 х—y)q>(y)dy.	E.11>
Ег	е->° Ег\Ш (х, 8)
Поставим следующую задачу регуляризации. Найти оператор
А' (Ф) (х) = а' (х)<р(*) + J W (х, x — y)<p(y)dy-\-B'
Е%

J64	СИНГУЛЯРНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ	[Гл. IV
(где функции а', и' и оператор В1 удовлетворяют тем же условиям, которым
удовлетворяли а, и и В соответственно) по условию
где Во — вполне непрерывный оператор из Lh (?2) в Lp (?2).
Приступая к решению этой задачи, рассмотрим функцию
определенную на ?2 X С (О, 1), которую назовем характеристикой опера-
оператора А. Здесь Ф — аргумент точки х~у —д < ф^: я.
Разложим характеристику в ряд Фурье
X (*,*)= S а*(*)***.	E.13)
fl=	ОО
Очевидно, а0 = а (см. A.13)). Рассмотрим функцию
<*(*,«) = 2 fl«W6/n*,	E.14)
П=—СХ>
где
2T	при п=^ ° и а*° = а° = а>	E.15)
и назовем ее символом оператора А.
Понятие символа, введенное С. Г. Михлиным (см. Михлин [13), как мы
убедимся ниже, играет весьма важную роль в теории сингулярных инте-
интегральных операторов.
Предположим, что на Е2 X С @, 1)
т1|а(*,Ф)|>0,	E.16)
и рассмотрим функцию а' (х, д) = [а (х, О)]. Разложим а' в ряд Фурье
и составим функцию
S
Х'(х,Ъ)= S an(x)ein*>	E.17)
где ап = — .', а , при пФ О ао = ао = а .
Пусть
ы''(я, х — у) = \х — у\~2[% (х, Щ — а! (х)].	E.18)
Легко доказать, что и' — сингулярное ядро класса Z B, 0, а) на Е2
и а' ? С0' а (?2) (см. об этом более подробно в § 6).
Рассмотрим стереографическую проекцию Е2 на единичную сферу.
Пусть стереографическая проекция точки x(z E2 есть точка I указанной сферы.
Теперь, каждой функции ?, определенной на ?2, можно поставить в соот-
соответствие функцию Wc, определенную на сфере формулой Тс (I) = W (х).
5.1. Теорема (Михлин). Если выполняется условие E.16) и ос (?, #)
непрерывна относительно I на сфере, равномерно по Ф ? (—я, я), то оператор
А', в котором а' и и' определены равенствами E.17) и E.18), для любого вполне
непрерывного В' является регуляризатором оператора А в простран-
пространстве Lp (?2).

§ 5]	регуляризация сингулярных операторов	165
Доказательство этой теоремы основывается на теореме о композиции
сингулярных интегралов (см. Михлин [1]), которая гласит, что композиция
сингулярных интегралов соответствует произведение их символов. Теперь,
так как символы операторов А и А' взаимно обратны, их композиции соот-
соответствует символ, тождественно равный единице. Но оператор, обладающий
этим свойством, имеет вид ср + Во (ф), где Во— вполне непрерывный опе-
оператор.
Рассмотрим операторы
Аи (Ф) (х) = ац (х) ф (х) + ] uif (х, х — у) <р (у) dy + Вц (<р) (х), E.19)
я?
где ?, /== 1, . . ., т\ aif€ С0* а {Е2)\ uij — сингулярное ядро класса Z B, 0, а),
а > 0, Bi} — вполне непрерывный оператор из Lp (Е2) в Lp (Е2), р > I.
Пусть
А = || Ац \\mxm, Я = || пц Hmxrn, " = || Щ\ ||mXm, В = || В/у ||mXm,
Л (Ф) (х) = а (х) ф (х) + J а (х, x — y)y(y)dy + B (Ф) (х)
и а (х, #) = |at/ (х, #) llmxm, где аг/. (х, О) — символ оператора Aif.
Совершенно так же, как 5.1, доказывается следующая теорема (см. Ми-
Михлин [1]).
5.2. Теорема. Если
inf|det(i(x, #)|>0,
ас (?, Ф) непрерывно относительно I равномерно по О, то существует сингу-
сингулярный оператор А*', обладающий теми же свойствами, что и Af и компози-
композиция А1 А, в пространстве L(pm) (E2) представится в виде
где Е = || &i} ||тХт, В — вполне непрерывный оператор из Ь(от) (Е2) в Ьрт)
3. Регуляризация сингулярных операторов, распространенных на замк-
замкнутых поверхностях. Пусть S — замкнутая поверхность Ляпунова (ком-
(компактное многообразие), а?С°* а (S)f k—сингулярное ядро класса G* B, a, a)f
а > 0. Рассмотрим сингулярный оператор, определенный в п. 1, и поставим
следующую задачу регуляризации.
Найти сингулярный оператор К' таким образом, чтобы
где В о — вполне непрерывный оператор из Lp (S) в Lp E), р > 1.
Приведем решение этой задачи сначала только схематически. Здесь нам
приходится повторять рассуждения Ж. Жиро (см. п. 1) в несколько изменен-
измененной форме. Примем в этом параграфе без изменения все обозначения из п. 1.
Продолжим al9 ®i и со^ на всем пространстве Е2 (Е2 = % (z)), & ut —
на Е2 X Е2 таким образом, чтобы оператор Uif определенный формулой
*
Ut (ф) (I) = [а, (|) + ®, (I) Щ (I)] Ф (|) + J в, (Н) и, (I, I — п) ф (Ц) di\, E.21,
Е%
допускал регуляризатор вида
U\ (Ф) © = at © Ф (I) + j щ E, ? — -л) Ф (ri) d%
\ (Ф) © = at © Ф (I) + j щ E, ? — -л) Ф

]56
СИНГУЛЯРНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ	[ГЛ# IV
т. е. оператор
U\ (ф) (I) = а\ (I) [ас (I) + в, (?) со; (?)] Ф (|
J
"t: F, I — Л)
,- (л) со, (ti)]} Ф (tj) dr\ =
где В/ — вполне непрерывный оператор из Lp (?) в Lp (Е2), р > 1.
Рассмотрим разбиение единицы на 5 — \Е(\ (см. определение C.33)).
Определим Et на xt- равенством Et (|) = ?"?- (jc), а на т (z)\rf- — равенством
?, (Е) = 0.
Пусть
а' (х) = -S [fli W + col (х)] Et (х),	E.22)
*' (^ У) = S [©Г1 (У) 1/?7^УЖЫ *; (х, у)},
E.23)
Докажем, что оператор /С" из п. 1, в котором а' и &' определены из E.22)
и E.23), является регуляризатором оператора /С.
В самом деле, композицию К'К можно представить в виде
где
В (ф) (х) = J] J[aJ (х) + соI (х)] J
S
^ (а:, у) = ai (g, ? — л)	при	(х, у) 6 S; X St\
к] (х, у) = 0	при	(х, у) 6 (S? X S)\(S, X S^
coj (x) = coj F)	при	x^Sf, (Df(x) = 0 при
e,w = e,;(S)	при	xes,, e,(x) = o ii
; (х, уN
Г1
х) — УЩу)) k (х, у)
, г)VEt{y)El(z)<p(г)d,S + [a,(x)
; (x)] j о, (х, у) КЩуУф (У) ^ + J и (х, у) 2^U dfi J*
71 (Ф) (х) =
s
X
»? W] ?t (x) a (x) Ф (x) + [a; (x)
dy5 + I VEt(x)Et(y) в (у) kt (x, у) а (у) Ф (у) dyS +
+ J УЩх) k'i (x, у) 6Г' (y) dyS\k (y, z) ?Ei{y)Ei(z) Ф (z) dyS j
г/) = и,- (g, I — ц), vt (x, y) = vt (l, ц) при (x, y) € S(- x S,;
u,(x, y) = o,(x,y) = 0 при (
v, = vz при z = z.

§ 5]	Регуляризация сингулярных операторов	167
Нетрудно установить, что В (ср) — вполне непрерывный оператор из
Lp (S) в Lp (S). Это непосредственно следует из теоремы 3.38.
Покажем, что Т (ф) представим в виде q> + В° (ф), где В0 — вполне
непрерывный оператор из Lp (S) в Lp (S).
В самом деле,
т (ф) (х) = 2
+ 2 { / ^ ^ Iе' <*!') VT^tf) - e, (go
X и, (IS |< — лО + \V~EM) — УТЛГ)] [а, (тH +
+»« (ло ©< (noi «*«'. e—ло) Ф| (ло rfn'+
где ф,- (r]f) = ф (у), если т]1'6 т* и ф^ (т|0 = 0, если г]1'^ т (г)\тг; if есть орто-
ортогональная проекция точки у на плоскость т (г). Аналогичный смысл имеют
обозначения ц>( (?*), (ot- (|*) и т. д. В интегралах вместо -Б2 можно писать
i	t
т (г), т. е. касательную плоскость поверхности S в точке г.
Из этого равенства (см. теоремы 3.37, 3.38) следует требуемое представ-
представление оператора Т.
Укажем теперь достаточные условия, при выполнении которых приве-
приведенные выше схематические рассуждения можно считать обоснованными.
Пусть S ?Лг (а), а > 0 и х? S. Обозначим через tx единичный касатель-
касательный вектор поверхности S в точке х, а через Тх (S) — множество всех таких
векторов. Объединение множеств Тх (S) при х? S .обозначим через Т (S).
Таким образом, Т (S) = [} TX(S).
В Т (S) известным образом вводится топология, и оно становится косым
произведением. Базисным пространством этого произведения служит S,
а слоем — Тх (S).
В дальнейшем нам придется иметь дело с функциями вида Q (x, tx),
определенными для всякого x?S и tx?T (S).
Пусть
где h (tx) — непрерывная функция, отображающая Т (S) в 5, с помощью
которой каждому tx^T (S) поставлена в соответствие начальная точка х.
Скажем, что Q (x, tx) обладает определенным свойством на Т (S), если этим
свойством обладает Q* (tx) на Т (S).
Рассмотрим оператор К, определенный в п. 1, где а? С0- а E) и k — син-
сингулярное ядро класса G* B, а, а). Таким образом, k допускает представление
вида C.37). При | = z (координаты точки z — в системе (г), очевидно, —
О, 0, 0). Имеем
(	) = hi "г (г, У.
где единичный вектор т)| tjI* с началом в точке z обозначен через tz.

168	СИНГУЛЯРНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ [Гл, IV
Назовем характеристикой оператора К функцию
,tz) = a{z) + uz(zjz),	E.24)
определенную на S X Т E).
Зафиксируем точку z на 5, и на плоскости т (z) введем полярные коор-
координаты с началом в точке z. Обозначим через # полярный угол, соответствую-
соответствующий вектору tz, $6 (—я, я]. Тогда % (z, tz) можно рассматривать как функ-
функцию Ф, определенную на (—я, я]. Разложим эту функцию в ряд Фурье
%(z,tz) = S an(z)e^9	E.25)
где в силу сингулярности k, а0 = а.
Введем другую функцию, определенную на S X Т (S) равенством
o(z,tz)= S an(z)ein\	E.26)
n(z)ein\
П=—СХ>
где а*п определен из E.15). Назовем a (z, tz) символом оператора К.
Легко показать, что в ограничениях, наложенных на К (К6 G* B, а, а)),
ряды E.25) и E.26) сходятся абсолютно и % и а — непрерывные функции
на Т E).
5.3.	Определение. Назовем К оператором нормального типа,
если
inf \o(z,tj\>0.
T(S)
Докажем теперь теорему, из которой легко следует решение поставлен-
поставленной задачи регуляризации.
5.4.	Теорема. Если S — замкнутая поверхность Ляпунова, k —
сингулярное ядро класса G* B, а, а), а? С°«а E) и оператор К—нормального
типа, то оператор Ut (см. E.7)) можно продолжить на т (zt) таким образом,
чтобы оператор, полученный продолжением, удовлетворял условиям теоремы
Михлина (см. 5.1).
Доказательство. Покажем сначала, что оператор U\ можно про-
продолжить так, чтобы его символ at (g, t%) удовлетворял условию
inf|a,(E,*5)|>0.	E.27)
Пусть б — произвольное положительное число, не превосходящее d/2.
Рассмотрим множество | S (z, 6) | z? S\, и выберем из этого множества ко-
конечное покрытие поверхности S.
Пусть \S (z, б)} —такое покрытие. Введем обозначения
Si = S[z, б), Ti==T\z1 б), ut = ult.m.
г
i
ii— круг в касательной плоскости х (z).
i	I
Продолжим at (?) из %t на т (z) следующим образом. Пусть ?€ т (z)\t?.
Обозначим через | точку из тм являющуюся зеркальным отражением точки ?
относительно границы т,. Определим at (?) формулой at (?) = at (Q. Анало-
Аналогично продолжим функции Oj, (и{ и ut.
Например,
(^ )h Г,	E-28)
где g — точка, являющаяся зеркальным отражением точки Z относительно
i	i
границы %i9 а ц — произвольная точка плоскости т (z), не совпадающая с z.

§ 51	регуляризация сингулярных операторов	169
Легко показать, что вг(?) и cot (?) принадлежат классу С°*а и, кроме
того, О, (go =1иш/ (go = 0, если ?' = г.
Предположим, что функции, участвующие в формуле E.21), продолжены
указанным выше способом. Характеристикой %t (?, Ф) = %( (g, ^ этого
оператора будет
Ъ F. '*) = а* О + в, (|) щ © + 0, (|) щ (gf **).
Следовательно, x* (?> ^) = % (г, fA при g = г и поэтому аг (g, /у =
= о lzy U\ при | = 2. Теперь в силу непрерывности а,- и а и нормальности
оператора К можно выбрать положительное число б таким образом, чтобы
б < d/2 и
для любого /. Но
inf |cr;(g, t?\ = inf |а<(§,
Первая часть теоремы доказана. Легко доказывается и вторая часть
теоремы.
Из этой теоремы непосредственно следует основная теорема о регуля-
регуляризации.
5.5. Теорема. Если S 6 Лг (а), а > 0, adC0-a (S), k — сингуляр-
сингулярное ядро класса G* B, а, а) и оператор К, определенный в п. 1, — нормаль-
нормального типа, то поставленная выше задача регуляризации разрешима в про-
пространстве Lp (S) для любого р > 1.
Пусть теперь а = || ац ||mxm, k = || kif ||mXm, где ачеС°- а (S), k4 — син-
сингулярное ядро класса G* B, а, а) на S X S; ?, / == 1, . . ., /п. Обозначим через
5^у и oi} характеристику и символ оператора
и (Ф) W = аи (х) ф (х) + j fe,y (x,
s
соответственно.
Рассмотрим оператор
К (Ф) (х) = а (X) Ф (х) + J & (х, у) ф (г/) d^S,	E.29)
где ф = (ф1э . . ., фт). Характеристикой и символом этого оператора на-
назовем матрицы х = II %ц \\ткт и о = || Оц \тхт соответственно.
5.6. Теорема. Если S^,JI1 (а), а > 0, а?С°>а (S), кц — сингуляр-
сингулярное ядро класса G* B, а, а) и
inf|det(j|>0,	E.30)
то оператор E.29) допускает регуляризацию в пространстве L{Dm) (S), для
любого р > 1.
Доказательство этой теоремы не отличается от доказательства тео-
теоремы 5.5.
Оператор E.29) называют оператором нормального типа, если выпол-
выполняется условие E.30).

170	СИНГУЛЯРНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ	[Гл. IV
§ 6. Основные теоремы
1. Теоремы Нетера. Пусть К— сингулярный оператор, определенный
из E.29). Из теоремы 5.6 следуют некоторые теоремы, которые понадобятся
в дальнейшем.
Ниже будем считать, не упоминая об этом каждый раз, что оператор К
удовлетворяет условиям теоремы 5.6. Таким образом, будем считать, что
5 — поверхность Ляпунова, а?С°*а (S), &? G* B, а, а) и является сингуляр-
сингулярным, а оператор К — нормального типа.
Справедливы следующие теоремы.
6.1.	Теорема. Уравнения К (ф) = 0 и К* (ф) = 0 имеют конечное
число линейно независимых решений в пространстве Lpm) (S) для любого
р > 1, т. е. подпространства Lffi (S) и L{p% (S) пространства Lpm) (S),
являющиеся пространствами нулей операторов К и К* соответственно,
имеют конечную размерность.
Обозначим число линейно независимых векторов из Lpm) (S), удовлет-
удовлетворяющих уравнению К (ф) = 0, через v, а число линейно независимых реше-
решений сопряженного уравнения /С* (ф) = 0 — через v*. Таким образом,
v = dim Ь{$ (S), v* = dim l}?h E), р'1 + р' = 1.
6.2.	Определение. Число к = v — v* называется индексом опе-
оператора К и обозначается через ind /С.
6.3.	Теорема. Оператор К нормально разрешим, т. е. для разреши-
разрешимости уравнения К (ф) = f в пространстве Lpm) (S), где /? Lpm) (S), необ-
необходимо и достаточно, чтобы
4 где {ty*} — полная система линейно независимых решений уравнения К* (Ф) =
= 0 (в пространстве l}^ (S)), а
6.4.	Теорема, ind К = —ind К\ где К' — регуляризатор опера-
оператора К.
6.5.	Следствие. Индекс оператора К не зависит от его вполне не-
непрерывной части, т. е.
ind К = ind (К + В),
где В — вполне непрерывный оператор из Lpm) (S) в Lpm) (S).
Рассмотрим оператор
К% (Ф) (х) = а (х) Ф (х) + X J k (х, у) ф (у) dД
где X — комплексное число, а 5, a, k и ф — те же самые, что и выше.
6.6.	Теорема. Пусть Х1 и Х2 — две точки комплексной плоскости,
L — непрерывная кривая этой плоскости, соединяющая точки Хг и Х2- ^сли
Ki —оператор нормального типа для любого X?L, то
ind Kxt = ind Кк.
6.7.	Следствие. Если L—непрерывная кривая комплексной плоско-
плоскости, соединяющая начало координат с точкой Хо и оператор К—нормального
типа для любого Х?Ь, то

§ 6]	ОСНОВНЫЕ ТЕОРЕМЫ	171
6.8. Следствие. Если К — нормального типа и символ а — косо-
симметричная матрица, то ind К = 0.
Приведем краткие доказательства этих теорем. Более общие теоремы,
а также подробные доказательства, имеются в книге Михлина [1 ].
Докажем теорему 6.1. Пусть К — нормального типа, тогда и К* — нор-
нормального типа. Это следует из вида /С*, полученного в §3 (см. C.47)). Оче-
Очевидно,
= |deta*|>8>0.
Далее, в силу теоремы 5.6 существует регуляризатор К' оператора К,
т. е. К1 (К (ф)) = Ф + В (ф), где В — вполне непрерывный оператор из
L{pm) (S) в Lpm) (S). Отсюда следует, что всякое решение уравнения К (ф) =
= 0 является решением уравнения ф + В (ф) = 0. Но это уравнение имеет
конечное число линейно независимых решений. Теорема для К доказана.
Приведенное доказательство годится и для/С*, так как и К* является опера-
оператором нормального типа.
Заметим, что в силу доказанной теоремы v и v* — (конечные) целые
числа, и их разность, вполне определенная, также целое число.
Доказательство теоремы 6.3 ничем не отличается от доказательства соот-
соответствующей теоремы в случае одномерных интегралов, приведенной в книге
Мусхелишвили [2] (стр. 210—223).
Докажем теорему 6.4. Пусть К — оператор нормального типа. Тогда
существует регуляризатор К (см. теорему 5.6). Таким образом, К'К — опе-
оператор типа Фредгольма. Отсюда следует, что уравнения
= О и (/С'/С)*(Ф) = О
имеют одинаковое число линейно независимых решений. Обозначим это число
через [г. Пусть число линейно независимых решений уравнения К' (ф) = 0
и /С'*(ф) = 0, соответственно, v' и v'*. Обозначим линейно независимые реше-
-ия уравнения К (ф) = 0 через q>lf ..., фу, а уравнения К' (ф) = 0 — через
{, . . ., ф;,'. Тогда, если К' (К (ф)) = 0, то
ния
Ф1
V
К (Ф) =]S с/ф).	F.1)
где Cj — некоторые постоянные. В силу предыдущей теоремы для разреши-
разрешимости уравнения F.1) необходимо и достаточно, чтобы
= 0; t = l,...,vf	F.2)
У с, f ф'.
Ы\ S
где |ф/}? — полная система линейно независимых решений уравнения
/(* (ф) = 0. Пусть г — ранг матрицы | тъ? ||, где ты — интеграл, участвующий
в F.2).
Если рассмотрим F.2) как систему относительно cf-9 то убедимся, что
v' — г постоянных остаются произвольными. Теперь легко подсчитать
число линейно независимых решений уравнения К' (К (ф)) = 0. Имеем
ц = V + V' — Г.
Кроме того, (К'К)* = К*К'* и, следовательно, /С* является регуляриза-
тором оператора/С'*. Повторяя приведенное выше рассуждение для этих опе-
операторов, долечим \х = v*+ v*' —г. Отсюда v — v* = —(v' —v'*). Теорема
6.4 доказаны-
Докажем теперь теорему 6.5. Пусть К — оператор нормального типа,
тогда существует его регуляризатор К', но К' является регуляризатором и

172	СИНГУЛЯРНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ	[Гл. IV
для К + В. Это следует из того, что К'В — вполне непрерывна, как компо-
композиция ограниченного и вполне непрерывного оператора. Следовательно, из
6.4 получаем
ind К = — ind К и ind (К + В) = — ind /С.
Из приведенного рассуждения получаем следующее предложение.
Если К — нормального типа и Л — произвольный линейный ограничен-
ограниченный оператор из Lpm) (S) в Lpm) (S), удовлетворяющий неравенству 1Л||^
^Itf'IT1. то
ind (K + A) = ind К.
Теперь из этого предложения получается доказательство теоремы 6.6.
В самом деле, пусть Хо?_ L: тогда в силу нормальности К, можно найти такую
окрестность А^о точки Хо на комплексной плоскости, что при Х? Д^
Теперь из предыдущего предположения следует, что
ind Кк = ind Кх при А, € Дя,0.
Рассмотрим множество ]Aa,,U.? l- Выберем из этого множества конеч-
конечное покрытие L. Теперь очевидно окончание доказательства теоремы 6.6.
Из 6.6 следует, что в условиях 6.7
ind Кх0 = ind /Со.
Но /С© (ф) = аф, и в силу нормальности Ко det а Ф 0. Поэтому Ко (ф) ==¦
= 0 имеет только тривиальное решение ф = 0. Тривиальное решение имеет
также уравнение /Со (ф) = 0. Следовательно, ind /Со = 0 6.7 доказана.
Аналогично доказывается следствие 6.8.
2. Свойства дифференцируемости решений сингулярных интегральных
уравнений. Теоремы вложения. Рассмотрим интегральное уравнение
где К — оператор, определенный равенством E.29).
В этом параграфе доказывается, что если аи f удовлетворяют некоторым
условиям гладкости, a k — сингулярное, достаточно гладкое ядро, то вся-
всякое решение ф уравнения К (ф) = f класса Ь(рт) (S) удовлетворяет соответ-
соответствующим условиям гладкости.
Такое предложение легко получается, если оператор К обратим.
6.9.	Определение. Оператор К принадлежит классу G* B, а, а),
если S^Jl1(a), a^COa(S) и k — сингулярное ядро класса G* B, а, а).
6.10.	Теорема. Если S^JI1 (а), К — обратимый оператор класса
G* B, а, а) на S X S в пространстве Lpm) (S), р > 1, 1 ^ а > 0, и обрат-
обратный оператор К также принадлежит классу G* B, а, а), то всякое решение
класса Lpm) (S) уравнения К (q>) = /, еде f? С0' 3 (S), 0 < р < а, принадле-
принадлежит классу С0- ® (S).
Доказательство этой теоремы следует из теоремы Жиро (см. теорему
3.23), и из равенства ф = К'1 (/).
Заметим, что предложение «если ф? Lpm) (S), то ф? COt r' (S)» понимается
следующим образом: ф класса Lpm) (S) эквивалентна, в смысле Lpm) (S)f
некоторой функции ф', которая принадлежит классу С0»|3 (S).

§ 6]	ОСНОВНЫЕ ТЕОРЕМЫ	173
Рассмотрим интегральный оператор Бицадзе,
/С(Ф) (х) = ±\в (х, у) Ф (у) d?,
где
B = \bij\^XA\ bij = bji, i, /=1,2,3,4, 632 = &4i, 642 = &13, ^43 = ^21»
bi2 (*, У) = [л3 {у) (У2 — х2) — п2 (у) (уз — х3)] \х — у |,
*ia (*. У) = [% (У) (й> — *а) — "з (У) (Л — *i)] I * — у Г3,
Ьи (х, у) = \п2 (у) (yt — хг) — пх (у) (у2 — х2)] \х — у |,
Для оператора К справедливо равенство К = К'1 (см. Бицадзе [21,
а также Гегелиа [101) и из 6.10 следует
6.11.	Т ео р ем а. Если Se^x(a)9 feC°>$ E), Р<а<1, а К —
интегральный оператор Бицадзе (см. Бицадзе [2 ]), то всякое решение урав-
уравнения К (ф) = f класса L{pm) (S), р > 1, принадлежит классу С0' ** (S).
В общем случае, т. е. когда не предполагается обратимость оператора /(,
дело обстоит сложнее, но нужные нам свойства решений все же можно полу-
получить с помощью результатов предыдущего параграфа. Роль обратного опе-
оператора в этих рассуждениях будет играть регуляризатор, обладающий
некоторым «хорошим» свойством. Очевидно, если К' — регуляризатор опе-
оператора К, то регуляризатором этого оператора является также К' + В,
где В — произвольный вполне непрерывный оператор. Решение интересую-
интересующей нас задачи зависит фактически от возможности выбора достаточно глад-
гладкого оператора В, или, точнее, от возможности выбора достаточно гладкого
регуляризатора.
6.12.	Теорема. Если Sg Лг (а), К — оператор класса G* B, а, а)
на S и является оператором нормального типа, a f^C0^ (S), 0 < р <а ^
^ 1, то всякое решение уравнения К (ф) = / класса L{pm) (S), р > 1, при-
принадлежит классу С0» Р (S).
Доказательство этой теоремы основывается на следующем соображении.
Допустим, что существует регуляризатор К' класса G* B, а, а) оператора К
в пространстве Lpm) (S), и
К' (К (Ф)) (х) = ф (х) + J h (х, у) Ф (у) dyS,	F.3,
где h?GB—а, а, а) на S X S. Тогда теорема 6.12 является простым
следствием теорем 2.3, 2.5, 2.6, 3.23. В самом деле, всякое решение ф уравне-
уравнения К (ф) = /, очевидно, является решением уравнения
Ф (х) + J h (х9 у) Ф (у) dyS = К* (/) (х),	F.4)
правая часть которого в силу теоремы 3.23 принадлежит классу С0» ** (S).
Теперь из 2.3 следует, что если (p^Lpm)(S) и удовлетворяет F.4), то
Фе 4т) E), где
Применяя опять теорему 2.3, заключаем, что ФЕ^Г> (S)» где

174	СИНГУЛЯРНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ	[Гл. IV
Повторяя это рассуждение п раз, заключаем, что ф? L\m) (S), где
Так как qn —» оо, когда п —> оо, то из теоремы 2.5 заключаем, что ф ?
? L^) (S), а теперь из 2.6 следует, что ср? С0' 3 E). Таким образом, теорема
6.12 доказана.
Теперь покажем, что в условиях теоремы 6.12 можно подобрать регуля-
ризатор К' таким образом, чтобы К'К допускала представление вида F.3).
Доказательство приводим для т = 1. Доказательство в общем случае
фактически не отличается от случая т = 1.
Заметим, что если выполнены условия теоремы 6.12, то будут выпол-
выполнены и условия теоремы 5.5. Поэтому рассуждения, приведенные в п. 3 § 5,
справедливы. Покажем, что регуляризатор /С', построенный в п. 3 § 5,
удовлетворяет требуемым условиям, т. е. К' принадлежит классу G* B, а, а)
и К' К представима б виде F.3).
Рассмотрим оператор Ui9 определенный формулой E.21), в которой аь
©г-, (Ьь и ядро и( продолжены способом, примененным при доказательстве
теоремы 5.4.
Легко усмотреть, что характеристика этого оператора
X (?, О) = х (Е, h) = а( (?) + в, © щ (I) + в, (?) и? (|, О),
и все его производные по О непрерывны на т (z) х С, где С = [0, 2я I. Более
i
того, эти производные и сама функция % (?, #) принадлежат классу С0* а (т (г))
по переменному |, равномерно относительно #6 С.
Покажем, что символ оператора Ui9 который обозначим через ot (|, О),
и все его производные по $ непрерывны на т (z) x С. Кроме того, эти функ-
i
ции принадлежат классу С0» а (х (г)) по переменному |, равномерно относи-
относительно $ ? С.
Пусть
) = а, (I) + в, (I) со/: (|) + в, (I) S К © cos м# +13„ (Е) sin n.0), F.5)
где
2л	2я
а„ (Е) = -^ J щ (Е, *) cos n# d*f ря (S) = 4" J а^ (l> d) sin
J
о	о
Интегрированием по частям легко получить оценки
I Рп (Г)—р„ (Г) I < csn- * | г—г |«,
где s — произвольное натуральное число, a cs — постоянная, не завися-
зависящая от п.
Символ оператора Ut выражается формулой
а, (I, д) = а, (I) + в, (I) (о,- (I) + 2яв, A) § (а„ (?) cos nO + рл © sin n#) п^. F.6)
1
Теперь в силу хорошо известной связи между порядком убывания коэф-
коэффициентов Фурье и свойством дифференцируемое™ самой функции (см. Бари

§ 6]	ОСНОВНЫЕ ТЕОРЕМЫ	175
[11, Lorentz [11 или Зигмунд [11, [21), заключаем, что al (g, d) обладает
требуемыми свойствами. Этими же свойствами обладает и [а< (|, О)]'1, так
как
inf |a,(g,*)|>0.
|et B), tf€=0
Отсюда в силу тех же теорем заключаем, что характеристика %1 (?, О)
i
регуляризатора К' удовлетворяет условию С°>a (т, (г)), равномерно относи-
относительно #? С
Изучим теперь композицию К'К. Легко заметить, что
принадлежит классу G \2	~, -|-, -^Л. Это следует из того факта, что Et
(UE( — разложение единицы на 5) принадлежит классу С°'аE). Кроме
того,
УЕй(х)Ей{у)щ(х9 yNGB, 1L9
VEi(x)E1{y)vi(x9 y)eoB — a>iL,
Здесь речь идет о регуляризаторе, построенном в предыдущем параграфе,
и все обозначения, принятые в п. 3 § 5, сохранены.
Применим формулу перестановки порядка интегрирования для инте-
интегралов в выражении В (ф). Можно показать (см. подробно об этом Гегелиа
[12]), что
)= I B(xf
где В — ядро класса G [2— -^-, qp qp) на S X S.
Изучим теперь оператор Г. Для этого достаточно изучить выражение
Et (I)
[at (I) + St (I) co,
+ \ Ut (I, I — Ц) йц \ 6,; (T|) И, (Tl, Л — О Ф<
+ f (a; AN,A) a,(g, I—ti) + t»,(S,6 — лЦа
). F.7)
К оставшейся части оператора Т можно применить рассуждения, при-
приведенные выше для В.

176	СИНГУЛЯРНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ	[Гл. IV
Композицию Щ Ui (ф) можно представить в виде
U\ (Ut (Ф)) © = Ф| © + В? (ф) ©,	F,8)
где
— вполне непрерывный оператор. Для наших целей достаточно показать,
i	i
что ядро Bi?G B — а, а, а) на т (г, d) х т B, d).
Докажем, что это действительно так. С этой целью найдем явное выра-
выражение для Bt.
В выражение оператора В{ входит интеграл
( щ (g, \ — л) [а, (п) — а, (|) + в, (л) o>t- (т|) — 8, (g) ©f (g)] Ф (r\)dr]f
ядро которого обладает требуемым свойством.
Кроме указанного интеграла, вполне непрерывную часть может дать
только повторный интеграл в формуле F.7)
*	*
/ (Ф) (I) = J u't (|, I—ti) dr\ \ в, ft) щ (Л, TJ — С) ф (Q dg.
х©	хО
Применяя здесь формулу перестановки порядка интегрирования, будем
иметь
*	*
/ (ф) (I) = — ф (S) Ф| © + | ф (О * J «I (Б, S—ч) @<- (ч) "<• (ч, ч—
х©	xQ
Представим внутренний интеграл в следующем виде:
J и'{A,1—Ч)в?(ч)и,(л
х©
где
i)
Т, (I, С) = j щ (I, | — т]) [в, (т,) ад (л, л — 0 — ©/ © Ш (t Ч — О] <*Ч-
х©
Докажем, что со, — чисто сингулярное ядро, аТ, — регулярное. Пусть
это так. Тогда
-Ф©Ф*©+ J
х©
вместе со слагаемым
*
a'i (I) [at (I) + в, (I) о>{ ©J ф (|) + J {a; © в, (g) m a, 4—4) +
x©
+ «', (g, g—4) [a* © + ©t © ®«©ll Ф (Ч) dr\

* gi	ОСНОВНЫЕ ТЕОРЕМЫ	177
даст тождественный оператор, а
J ?,(!, Qq>(QdZ
войдет как слагаемое в выражение оператора Bt.
Докажем, что со,- — чисто сингулярное ядро. Очевидно,
щ (?, I — S) = в,- (?) J и\ (|, т) ис A, g—С—т) Л,
и требуемое представление для юг вытекает из легко проверяемого равенства
щA, x)ut(l,t(l — О — T)dT = rm J Ui{l,x)ui{l,l—С
Остается изучить Y.-. Для наших целей достаточно показать, что Ч?\- при-
i	i
надлежит классу G B — y> 7> У) на т B» ^) х т B> ^)» г^е V — произвольное
число из интервала @, а). Доказательство этого факта требует довольно гро-
громоздких вычислений, выполненных в работах Гегелиа [121, [131.
Подводя итог приведенным рассуждениям, можно утверждать, что тео-
теорема 6.12 справедлива, если C <а/4. Полученное неестественное ограниче-
ограничение р < а/4 вызвано тем, что функции Еь (х), участвующие в разложении еди-
единицы на 5, принадлежат классу С°*а (S). Тогда для V^t (x) можно утвер-
утверждать только, что (см. Мусхелишвили [2]) она принадлежит классу C°»a/4(S).
Отсюда в свою очередь следуют условия вида
- ±, f ,-)
на S X S, являющиеся причиной указанного ограничения.
Теорема 6.12 будет полностью доказана, если докажем, что всякое
решение класса L{vm) (S) уравнения /Сф = f, при выполнении условий тео-
теоремы, будет принадлежать классу С0-C (S (г, d/З)) для любого z^S.
Пусть z — произвольная точка поверхности 5. Рассмотрим такое ко-
конечное покрытие USt поверхности S, в состав которого входит S (z, d/2) =\
= Sx. Выбираем теперь разложение единицы UEt таким образом, чтобы оно
удовлетворяло всем требованиям и, кроме того, Е{ (х) = 1 при x?S (z,
d/З). Теперь очевидно, что, например, функции
принадлежат классу G B — а, а, а) на S (г, d/З) Х 5 (г, dfS).
Теорема 6.12 доказана.
Доказанные выше теоремы могут быть обобщены. Из теоремы 3.28 и из
формулы обращения Бицадзе (см. Бицадзе [21, а также Гегелиа [10]) непо-
непосредственно следует теорема, обобщающая 6.11.
6.13.	Теорема. Если S^JIr+1 (a), 0 < а <з 1, /6 Cr> 3(S), а К —
интегральный оператор Бицадзе, то всякое решение уравнения К (ф) = f
класса Ll>4) (S), p > 1, принадлежит классу Сг* а (S), |3 <a.
Рассмотрим теперь общий сингулярный оператор, определенный фор-
формулой E.29).
6.14.	Предположим, что S?Jlr(a), 0 <a <? 1, agCr»sE) и /?
€Cr^ (S), где 0 < р <a, k — сингулярное ядро класса G* B, а, а). Пусть,
кроме того, ядро k по первому аргументу принадлежит классу Cr*ua (S (г, б))
равномерно относительно второго на S\S (z, 26) при любом б ? @, d/2);
12 В. Д. Купрадзе

178	СИНГУЛЯРНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ	[рл# JY
uz?Z B, г, а) и vze R (г, а) (см. C.37)), A.10) и C.21)) на т (г, d) для любого
6.15. Теорема. Если выполняются условия 6.14 и К — оператор
нормального типа, то всякое решение уравнения К (ф) = / класса Lpm) (S),
р > 1, принадлежит классу Cr- P (S). ?с./ш, я/?бШ? того, /С — обратим, то
Доказательство этой теоремы проводится по той же схеме, что и теоремы
6.12. Оператор К'> построенный в п. 3 § 5, и в этом случае обладает нужными
свойствами, но при доказательствах надо воспользоваться теоремами из
п. 2 § 3.
6.16.	Предположим, что S?JIr(a), 0 <<х <Л; а?С° (S) flC-3 ($о)>
/6 Lp E)ПСГ' Р (So), р > 1, Р<а, k — сингулярное ядро на S X S класса
G* B, а, а); ядро k по первому аргументу принадлежит классу Сг» а (So),
ыг? 2 B, г, а) и uz6 R (г, а) на т (z, d) для любого zg 50, So = S (z0, б).
6.17.	Теорема. Если оператор К — нормального типа и выполняются
условия 6.16, то всякое решение уравнения К (<р) = f класса Lpm) (S) принад-
принадлежит классу С* Р E (z0, б')), где б' — произвольное число из интерва-
интервала @, б).
§ 7. Сингулярная резольвента. Свойства и применения
Теоремы, полученные в § 6 для нормальных операторов с сингулярными
ядрами общего вида из класса G B, а, а), в применении к конкретным опера-
операторам теории упругости, могут быть дополнены и уточнены. Можно, напри-
например, получить явное (приближенное) выражение регуляризующего оператора,
перейти от теорем Нетера к теоремам Фредгольма, детально исследовать
роль параметра, получить аналитическое представление решения сингуляр-
сингулярного интегрального уравнения, доказать свойства ортогональности и биорто-
биортогональности решений. Эти результаты можно получить также из изложен-
изложенной выше общей теории, но для этих целей полезно ввести понятие син-
сингулярной резольвенты, как решения некоторых функциональных урав-
уравнений, изучение которых, подобно классической теории, приводит к основ-
основным теоремам Фредгольма.
Эти вопросы рассматриваются в настоящем параграфе (более подробно
см. Giraud [1, 2] и Купрадзе [131).
Как было показано (см. теорему 3.25, замечание 3.29 и определение 3.30),
ядра сингулярных операторов теории упругости являются сингулярными
ядрами (в смысле теоремы 1.15) и принадлежат классу G B, а, а).
Для конкретности мы остановимся на изучении ядра
k (xt y) = T (дх, п (х)) Т(х — у),	G.1)
и, без умаления общности, можем ограничиться рассмотрением оператора
К (Ф) (х) = Ф (х) — х J k (х, у) Ф (у) dfi,	G.2)
являющегося типичным для рассматриваемых в книге задач (к — параметр).

§7]
СИНГУЛЯРНАЯ РЕЗОЛЬВЕНТА. СВОЙСТВА И ПРИМЕНЕНИЯ
179
1. Преобразование ядра. Главная (сингулярная) часть k (x, у) дается
матрицей (см. C.31))
и (х, х — у) = || uki (х, х — у) Цзхз,
G.3)
G.4)
}(х,х — у) = -х——^\nk(x)r^—^r — ni(x)^=^T{y
2л
Пусть z ? 5 — произвольная точка на 5 и (z) — местная система коор-
координат с началом в z. Пусть 8 < d и х, у ? S (z, e)czS B, d). Согласно C.34)
можно записать
я*/ (х* х — у)= . * |2 X
X
(z- x) (h - ^i) - «/ W S P« <г- *) E/ - Л,)
O(\x — у Г2). G.5)
Здесь (J-j, |2, |3) и (Л1» Л2» Лз) — координаты точек х и у в местной системе B);
пусть еще | = EХ, |2, 0), т] = (Ли.'Пг» 0)-
Очевидно,
тт^т = sin *.	G-6>
и для малых 8
оеA), |а/3(г)
где символ о8 A) обозначает величину, стремящуюся к нулю вместе с е.
Теперь G.5) перепишется в виде
№ — <*ki(z)nf (x)\cos
(*) nk(x) — a,
O(|jc — y\a~2), G.7)
Введем обозначения
At B, *) = a2/ (г) /гх (л:) — au (z) n2 (x), '
B?- (г, x) = a3/ (z)nx (x)—au(z)n3(x),
Ct (г, x) = аы (z) n2 (x) — a2/ B) n3 (x)
G.8)
0	Аг cos О + A2 sin О Bx cos * + 52 sin О
gf *) = /| — >4i cos A — Л2 sin 0 0	d cos * + C8sin
Bxcosfl — i52sin'& — Cjcosd —C2sin* 0
G.9)
Тогда для и (х, х — у), при х, y?S B, e), будем иметь
G.10)
12*

СИНГУЛЯРНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ	[Гл# IV
2. Отображение локального оператора на круг. Пусть б < е, S (z, 8) с:
(г, е). Рассмотрим локальный оператор
x?S(z9e)9	G.11)
S B, 6)
и отобразим его на круг Ш (г, б), лежащий в касательной плоскости т (z).
Пусть при ортогональном проектировании
Ф (х) = Ф2 F), й (х, у) Ф ((/) dS = k2 (|, л) Ф. (Л) ©2 (Л) dri,
где
Для достаточно малого б имеем, по определению,
\
)\
\
2. 6)	e/-*°SB, 6)\S(X. 8')
= Hm f
8'^°Ш( б)\
8')
где if/ (z, б) — проекция S (г, б), а тг (g, s') — ортогональная проекция
S (х, е') на т (г).
Выше (см. п. 4 § 3) было показано, что границей множества т2 (g, s')
является кривая
г = 8' cos a (?,#),	G.13)
где
cos ос Сё Ф) =
{4
п (х) — орт внешней нормали в точке х? S (г, б), а дх (?), /г2 (|),
координаты вектора п (х) в системе (г). Очевидно,
lim	f	kz (|, Ti) ф2 (л)в2 (л) dn = Hm	f	kz (g, тО Ф2 (т|)вгСп)
в'->0д/( б)\х2E, 8')	е'^0Ш( Ь)\Ш(Ь ')
J
Первый интеграл справа существует в смысле главного значения, второй
вычисляется следующим образом (см. п. 4 § 3):
lim	J	*2(Ь.т0
•'"^ШЧ* е')\тг<?, в')
8'
f
е'-»0
Й'-4.О J
О г
где
, A) = - J [& F, 0) + o8 A)] In cos a (i,«) d*.	G-14)

г yi	СИНГУЛЯРНАЯ РЕЗОЛЬВЕНТА. СВОЙСТВА И ПРИМЕНЕНИЯ	181
Теперь ясно, что искомое отображение локального оператора К2 (ф) (х)
на круг Ш (z, б) имеет следующий вид:
[Е — хе,©а>г(?)]Ф,E) — * J
Я/B, б)
G.15)
где сингулярный интеграл понимается в смысле главного значения, а
В (ф) — вполне непрерывный оператор.
3. Отображение на бесконечную плоскость. Распространим опера-
оператор G.15) на плоскость Е2 с помощью преобразования
u1 = -7=Bl==, и2= г 6Еа =.	G.16)
При таком преобразовании круг с центром в точке g, радиуса у> переходит
в замкнутую область тг (и, у), ограниченную алгебраической кривой четвер-
четвертого порядка
г =	у	+ О (v2),	G.17)
1Л4 cos* #-j-2? sindcosdjCsin2#	"
где
л — (б2 + и\ + и\) [(б2 + и»* + ufu|] '
(б- 4- и? 4- «D2 [(б2 4- и2J 4- "i«2l
B6Ч«1Т^	(?Л8)
(б2 4- «f 4- «D3 [(б2 + "!J
и w = (и1у м2), © = (v 1, о2) — точки, соответствующие точкам ? (|lf |a),
Рассматривая отношение первых квадратичных форм преобразуемых
областей, находим
1:ш |М—О|» _ 	1		,71Q
?? | g _ г] |2 ~ л cos2 О 4- 25 sin ^ cos # + С sin2 # *	^ #1*'
Поэтому
f foF» ^) +°еО) |
J —и —л I2
Я/B, 6)
f
(
J	|U —0|
?2\т2(а, v)
\ A cos2 # + 2В cos ¦» sin § + С sinafl + °eA) j dy. G-*9 )
(«, о) + 5, (l) = g2 (i, *) + о8 A), ег (о) = ег (г)),

J82	СИНГУЛЯРНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ	[рл jy
Но
lim | Qdv=\\m J Qdv+lim	[	Qdv, G.21)
v-*° ?a\T2(tt' Y)	V-*0 Е2\Ш(и< y)	V^° Ш (и,- Y)\tz(«* Y)
здесь Q—подынтегральная функция в формуле G.19').
Первый интеграл справа существует в смысле главного значения, вто-
второй вычисляется следующим образом:
lim	J	Qdv =
V-*0 ш (и, \)\xz(u, Y)
2я
= lim\ I—-—	f-— z v z v Фг v x
О г
X (	¦	1- Oo (I)\ dv =
\ A (v) cos2 ф + 25 (u) sin ^ cos 0 + С (v) sin2 Ф	v /
== — Рг (u) ®z (u) Zz iu) Фг (u)j	G.22)
где
о
x U	!
(и) cos2ф -}- 25 sin ф cos ^ -j- С sin2 О •
Теперь ясно, что искомое отображение оператора G.15) на плоскость Ег
имеет вид
[Е — х92 (и) (ш2 (и) + ^2 (а) р2 (а))] фг (и) —
(и, 0)+оеA)]8г@)ЕЛ0) .,
-;¦
где интеграл имеет смысл главного значения, а В (ф) (и) — вполне непрерыв-
непрерывный оператор.
Таким образом, для регуляризации локального оператора G.11) доста-
достаточно выполнить регуляризацию оператора G.24).
4. Локальная регуляризация. Характеристика оператора G.24) (см. п. 2
§ 5) равна
Рг(и))] —*{
^ + Ое A))} G.25)

? 73	СИНГУЛЯРНАЯ РЕЗОЛЬВЕНТА. СВОЙСТВА И ПРИМЕНЕНИЯ	183
На основании G.13), G.14), G.12), G.18), G.20), G.23) можно убедиться,
что
lim К («) + ?г (и) рг (и)] = 0, limЭг(v)b(v)=l, lim о,A) = 0,
е-» 0	е-»0	е-»-0
lim (A cos2ft + 2В sin ft cos ft + С sin2ft) = 1,
8->0
Следовательно, выбирая 8 > 0 достаточно малым, можно характеристику
X (и, ft) сделать сколь угодно близкой матрице
?—xg2(g, ft),	G.26)
т. е. символ (см. п. 2, § 5), соответствующий характеристике Е — щг (g, ft),
будет сколь угодно мало отличаться от символа оператора G.24).
Теперь заметим, что, как было показано в п. 2 § 5, по заданной характе-
характеристике находится соответствующий символ; а именно, в случае одного опе-
оператора, из коэффициентов Фурье характеристики символ (точнее, его коэф-
коэффициенты Фурье) получается по формуле E.14); отсюда ясно, что и наоборот,
имея символ оператора, по формуле E.13) восстанавливаем характеристику
и, следовательно, оператор с точностью до аддитивного вполне непрерывного
оператора.
В случае матричного оператора вида А = || Aif\\, заданного формулой
E.20), символом называется матрица, составленная из символов aif (g, ft)
операторов Aif, т. е. a (g, ft) = || oi} (g, ft) ||. Поэтому, когда задана характе-
характеристика оператора А, символ a (g, ft) строится как указано выше, а из сим-
символа, наоборот, может быть восстановлен оператор Л. Согласно теореме 5.2,
если inf| det a (g, ft) |> 0, существует символ а (?, ft) = || at] (?, ft)|| регуля-
ризующего оператора А', такой, что
откуда
det a k,
где а*/ (|, ft) — алгебраическое дополнение элемента of{ (I, ft) в определи-
определителе det а (|, ft). Из сказанного ясно, что для построения регуляризующего
локального оператора необходимо показать, что det о (g, ft) Ф 0, и затем
по формуле G.27) восстановить один из таких операторов.
Выписывая символ, соответствующий характеристике Е — xg2 (g, ft),
где матрица gz (g, ft) задана формулой G.9), и пользуясь с этой целью фор-
формулами E.14), получим для элементов матрицы a (g, ft):
а„Й,О)=1, i= 1,2,3,
*12& *)= — 2пШ[А1(г, |)cosft + Л2(z, g)sinft],
<Ъ(?. 0) = —аи(|, ft),
^1з F, ft) = — 2яЫ [Вх B, g) cos ft + B2 (z, I) sin ft],
<ЪЙ, ^) = -ст13(?, ft),
в» F. *) = — 2mx/[Cx(z, ?)cosft + C2(z, i) sm ft],

184	СИНГУЛЯРНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ	[Гл# ]"У
Отсюда находим
det а (?, Ф) = 1 — 4я2х2/2 (Я?2 + jx?2 + v?2),
где
М*> 8 = ^B, I) cos # + Л2(г, ?)sind,
2B:, |)sln*t
vM(z, 0 = Cx(z
Из свойств поверхности Ляпунова следует
причем
limco^z, |) = 0, k=l, 2, 3.
e->0
Выражая направляющие косинусы at]- (z) через углы Эйлера, найдем
Поэтому
det а (?, #) = 1 — 4я2х2/2 A + v (г, g)),
где
Таким образом, выбрав 8 достаточно малым, можно добиться, чтобы корни
уравнения
1 _ 4я2х2/2 A + v (z, I)) = 0,	G.29)
равные
были сколь угодно близки к значениям
Итак, для значений^, отличных от корней уравнения G.29), которые
расположены сколь угодно близко от точек G.30), может быть построен
символ а (|, #) регуляризующего оператора А1 по формуле G.27) и затем
восстановлен регуляризующий оператор. Таким путем получим
Л'
= а & х) Ф F) + х J -j^%$- Ф (Ч) rfri + Б (Ф) ©, G.31)

§ 7]	СИНГУЛЯРНАЯ РЕЗОЛЬВЕНТА. СВОЙСТВА И ПРИМЕНЕНИЯ	185
где
аи (g, х) = 4- {1 — 2я2х? [С? (z, Q + С\ (г, g)]},
2fc(?, х) = -^-{1—2л2х? [B\{z, Ъ) + В\{гу g)]},
азз (I, х) = -i- {1 — 2я2х? [Л2 (г, g) + At (г, g)]},
5i2 = аа = X (BlCl + В2С2)' ^13 = ^3i == — "|- (^A + Л2С2),
и ftz (g, 0) — однозначно определенная матрица, которая также находится
явно (см. Купрадзе [13]).
Найдем еще значения х, для которых det a (g, x) = 0. Пользуясь ма-
малостью 8, достаточно найти корни уравнения det о! (г, х) = 0. Это уравнение
имеет следующий вид:
( + sin2 d + sin4 О) +AB + sin2*) —1 =0.
Решая его, находим
т 1 г	A + sing.O) ± У\ +2 sin* ft —3 sin4#
Ai—1) А2,з—	2 sin4 Ь	'
Все три корня вещественны и положительны. Вещественность A2t3
следует из неравенства 1 + 2 sin2 Ф > 3 sin4 О, а положительность — из
неравенства 1 + sin2 # > j/^1 + 2 sin2 Ф — 3 sin4 #. Кроме того, из нера-
неравенства
±]/"l +2 sin2 О — 3sin4# ^2 sin4О
вытекает, что минимальные абсолютные значения корней Д2 и Д3 не меньше
единицы, максимальные же значения достигаются при # = Ои равны беско-
бесконечности. Соответствующие корням ?Д1>2,3 значения х равны
На комплексной плоскости х, вдоль вещественной оси, проведем разрезы
(± -q-t» ± °°)» и назовем плоскость с разрезами ГГ. Точки xlt2, x3l4, >^5,6t
а также точки х = =±= у- плоскости П' не принадлежат.
Теперь можно составить на плоскости П' оператор
А" (Ф) (g) = {a (g, х)}-1 Л' (Ф) G) = ф © +
+ ^ J («Г1 тт=^р- ф (ч) dr> + ^ ^ х^"х в (ф) ©•
который вместе с оператором Л' является локальным регуляризатором. Из
определения символа ясно, что символ оператора А'\ назовем его o/f (g, #),
равен

СИНГУЛЯРНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ
Составляя композицию А" А (ср) (?), учитывая, что символ композиции
равен произведению символов компонент и, согласно формуле перестановки
D.1), равен Е + х2Ф (?, к), где Ф (?, к) определяется из формулы D.3), и
принимая во внимание, что по условию
получим
? +х2 Ф (?,*)== {а (|,х)Г.	G.32)
Ввиду того, что на плоскости IT
detla&x)}-1^ О,
будем иметь
det(? + x2(D(l, x))=f 0, xell',	G.32')
Очевидно, преобразования, обратные тем, которые привели к оператору
А"', порождают оператор, заданный на 5 (z, 6), и регуляризующий оператор
G.11). Обозначим этот оператор следующим образом:
Нг (Ф) (х) = ф (х) + х J hz (х, у) ф {у) dyS,	G.33)
S B, 6)
где ft2 (х, у)—сингулярное ядро (Купрадзе [13]).
5. Оператор глобальной регуляризации. Пусть Ski k= I, 2, . . ., п, есть
область на 5, состоящая из точек х, отстоящих от точки zk на расстоянии
\х—г*|<6, F<d). Выбрав п достаточно большим,* можно добиться, чтобы S =
п
= U Sk и любая точка #? S была внутренней по крайней мере для одной
из областей Sk и SkczS (z*, d). Построим для каждой из областей Sk
локальный регуляризатор с ядром h^(x, у). На множестве SX^ матрицу
hzk (*> У) определим так, чтобы как функция х — она была ограничена,
а как функция у — удовлетворяла условию Гёльдера.
Пусть
F,(x) = [62 — \zk — x\*]\ xeSkt
Fk(x) = 09 xeS\Sk.	G.34)
Очевидно, Fk (x), k = 1, . . ., я, непрерывна и непрерывно дифферен-
дифференцируема для всех х? S. Так как любая х? S является внутренней точкой по
крайней мере одной из Sk, k = 1, . . ., м, то
t
Положим
Ш = -^f-> A: = 1, 2, .... п.	G.34')
Очевидно,
S/*W=1.	G-35)
Введем матрицу
h{x,y)=t lk(x)h2k{x,y),	G.36)
которая определена на всей поверхности S. Покажем, что именно она будет

* 7]	СИНГУЛЯРНАЯ РЕЗОЛЬВЕНТА. СВОЙСТВА И ПРИМЕНЕНИЯ	187
служить ядром глобального регуляризатора для оператора К (ф) (х) =
= ф (х)— х f k (х, у) ф (у) dyS.
В самом деле, если х? Si9 то из G.34), G.34') в силу G.35) имеем
если же x^StflSj, то hj (х, у) = hj (х, у), и G.36) запишем в виде
h (х, у) = ^S h (*) [h2k (х9 у)—fizi (jc, у)} + /у (*, у), .
откуда в силу G.34), G.34') снова имеем
h (х, у) = hzi (x9 у),
и наше утверждение доказано.
6. Функциональные уравнения резольвенты. Первая теорема Фред-
гол ьм а. Рассмотрим сингулярное интегральное уравнение с оператором G.2)
К (ф) (х) = Ф (х) — х J k (jc, у) Ф (у) dyS = f (x)	G.37)
s
и запишем его в следующем виде:
(Е — х/Со)Ф = /,	G.38)
где ? — единичный оператор, а
/Соф =
s
Пусть
s
есть регуляризатор уравнения G.37). Запишем регуляризатор в виде
Н(Ф) = (? + иЯ0)ф,	G-39)
где
#0Ф = J ft (х, у; х) ф (у) dg St
s
Предполагается х^П'. Во всех задачах теории упругости это условие
выполнено; более того, в этих задачах х = 1 или х = —1, и в принятых нами
предположениях относительно К и (х,
исключенные значения х (см. G.3Г)) отличны от±1.
Рассмотрим композицию НК (ф) (х). Согласно свойствам регуляризатора
получим интегральное уравнение Фредгольма второго рода
[Е + х2Ф (х, х)] Ф (х) + х J F (х, у; х) <р (у) dy S = X (х),	G,40)
где
F(x% у; x) = ft(x, у; х) —*(х, у) —х Jft(x, g; x)?(?, у)^5, G.41)
s
-X (х) = / W + к j Л (х, г/; к) j (У) dyS.	G.41')

Jgg	СИНГУЛЯРНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ	[Гл# JV
Пусть х? П' и отлично от полюсов резольвенты уравнения Фредгольма
G.40). Решение его представим в виде
Ф (х) = [Е + х2Ф (х, х)]/ (х) + х J #! (*, у; к) / (у) d^S,	G.42)
s
где резольвента Фредгольма Nt (х, у; х) равна
Л^1(х,г/;х)=[? + х2Ф(х, х)]-*А(х, у;к) + О(\х— */|«-2), а>0. G.43)
В силу теоремы 3.26 срб С°-а (S), когда /6 С0-« E) и 5с=Л, (а). Мы еще
не можем утверждать, что G.42) есть решение исходного уравнения G.37).
Выразим решение уравнения G.37) в виде
Ф (х) « ф(*) — х J К (*, у; — х) ф (у) rf^S,	G.44)
где ft' (д:? г/; —х) есть матрица, полученная из матрицы h (x, у; —х) переста-
перестановкой строк-столбцов. Подставляя это решение в G.37) и используя теорему
о перестановке сингулярных интегралов, будем иметь
\Е — х*ЧГ (х; х)]$(х) — х J jft'(*, У\ — х) + *(дс, у) —
— х J*(x, Qft'(?, у; — n)dls\^{y)dyS = f(x)> G.44')
где согласно D.3)
Ч(х\ x) = lim [( ( kx(xy I)ft'(Б, у; — xJ^sld^S,	G.45)
е->о i \s d* e)	J
где
ki(x, Q = u(x, x — l) = —ki(x, I).
Покажем, что
V(x; к) = — Ф(х, х).	G.46)
Из G.45) имеем
f h(l, y;
s ixJ 8)
= — lim \dgS [ ft(*. g; —
+ lim J d? \ [h (x, I; — x) ^(g, r/) —
— h (g, y; — x) ^ (x, g)I4gS = — Ф (x, - x).
Отсюда вследствие симметричности матрицы сГ1 (х, к) и в силу G.32) полу-
получаем G.46). Теперь покажем, что ядро уравнения G.44') фредгольмово;
для этого перепишем это ядро в виде
у; —x) + kx(x, у) —к \kx{x, g)ft'(g, у; —X)dlS + O(\x — y\*-\
G.47)

iR 7j	СИНГУЛЯРНАЯ РЕЗОЛЬВЕНТА. СВОЙСТВА И ПРИМЕНЕНИЯ	189
и сравним с ядром G.41), в котором х заменим на —х, и ядро перепишем
в виде
F(x, у\ — х) = Л(х, у; — х)— kx{xy у) + к \h(x, ?; — х) X
X kx (|, у) dtS + О (| х — у |«-2). G.48)
Учитывая свойство кососимметричности G.45) и G.3), а также вид ядра
h (x, |; х), которые позволяют показать, что
замечаем: главные части ядер G.47) и G.48) получены друг из друга транс-
транспозицией строк-столбцов, и так как G.48) — фредгольмово по условию, та-
таким будет и ядро G.47). Этим доказано, что уравнение G.44') является урав-
уравнением Фредгольма второго рода
г' (х, у; — х) + k (x, у) —
— х k(x, ?)ft'(g, У> —K)diS\ty(y)dl/S = f(x).	G.49)
s	J
Пусть х отлично от полюсов резольвенты этого уравнения; тогда его ре-
решение выразится в виде
ф (х) = [Е + х2Ф (х, х)]-1 / (х) + х J R (х, у; х) [Е + х2Ф (у, к)]'1 f {у) dyS,
G.50)
где R (х, у; х) — резольвента Фредгольма.
Внося это значение -ф (х) в G.44) и вновь пользуясь формулой переста-
перестановки сингулярных интегралов, получаем
<р (х) = [Е + х2Ф (х, х)]-1 / (х) — х J К (х, у; — х) (Е + х2Ф (у, х)) +
S
или, обозначив
ЛМ*. У; к) = —К{х, у; —к)[Е + *?Ф(у, х)]-1 +О(|х — у|«-2), G.51)
будем иметь окончательно
J	. G.52)
x J
Таким образом, показано, что сингулярное уравнение G.37) имеет реше-
решение в классе Гёльдера и, следовательно, оно (решение) должно совпадать
с найденным выше решением G.42) уравнения Фредгольма G.40).
Подставим значение q> (x) из G.52) в уравнение G.37) и примем во вни-
внимание равенство G.46); тогда будем иметь
N%(x9 у; K) — k{x, у)[Е + к2Ф(у, х)] —
— х j
у; K)dlS = 0. G,53)

190	СИНГУЛЯРНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ	[Гл# IV
Если в равенстве G.42) вместо f (x) подставим равное ему выражение
Ф (*) — х \ k (х9 у) ф (у) dgS,
s
то, на основании формулы перестановки, получим
ЛМ*. У> х) —[? + х2Ф(х, к)]-1***, у)— х J Nx(x9 Е; x)A(g, y)dsS. G.54)
Таким образом:
а)	если уравнение G.37) имеет решение в классе С°*а (S), то для х?ГГ
и отличных от полюсов некоторой мероморфной функции, это решение пред-
представится формулой G.42);
б)	для х ? ГГ и отличных от точек некоторого дискретного множества,
уравнение G.37) действительно имеет решение в классе C°*a(S); оно един-
единственно и представимо формулой G.52).
Следовательно, для х ? ГГ и отличных от точек некоторого дискретного
множества, решение существует, единственно, принадлежит классу С0'а (S)
и представляется двумя формулами, G.42) и G.52).
Отсюда ввиду произвольности f (x) находим
Nx{xyy\ и) = N2(x, у; к)
тождественно относительно дс, у и для указанных выше значений х. В силу
мероморфности Nx и N2 из этого следует совпадение полюсов этих функций.
Обозначим
N = NX = N2
и тогда G.53) и G.54) примут вид
N(x, у; n) — k(x, у)[Е + к2Ф(у, х)р — х J*(x, ?)#(?, у; x)^S = 0, G.55)
, у; х)— [? + х2Ф(#, х)Г^(х, у) —х J^(x, g; x)A(|f r/)^S = O. G.56)
Мы получили теорему, аналогичную первой теореме Фредгольма: существует
сингулярная резольвента N (х, у; х), мероморфная функция параметра
хE1Г, удовлетворяющая функциональным уравнениям G.55) а G.56) и такая,
что для к ^П' и отличных от полюсов N (х, у; х), уравнение G.37) имеет
решение, единственное и представимое формулой
= f? + х2Ф (х, х)]-1 / (х) + х J # (х, ?; х) / (?) d^S.	G.57)
7. Вторая теорема Фредгольма. Пусть х = х0 есть полюс резольвенты и
р	оо
, у; х)= S fl(a)U, у)(х —xo)-a+ S ^@) (х, у)(х — х0У5. G.58)
0
Покажем, что матрицы В<а) — непрерывные функции, а матрицы
в точке х = у имеют полюс второго порядка.

§7]
СИНГУЛЯРНАЯ РЕЗОЛЬВЕНТА. СВОЙСТВА И ПРИМЕНЕНИЯ
191
Рассмотрим уравнение
(? — (— %
где
G.59)
(х) = Ptf>y = f Pi4) (x, у; х) ф (у) й?,
{oO)q= \P (x, у;
У, х)=
, у;
Р@)(х, у; х) = Р(х, у; х);
Р(х, у; х) = [? + х2Ф(х, х)Г^(х, у; х),
Х(х) = [Е + х2Ф (х, х)]-1^^);
G.60)
Решение уравнения G.40) представляется в виде
ч
ц)(х) = ty(x)-\- 2 (—к)п F(on~l) ty (л:),	G.61)
где я|; есть решение уравнения G.59). Действительно, внеся G.61) в G.40)
и учитывая G.59), G.60), убеждаемся в справедливости сказанного.
Выразив *ф (х) через X (х) и учитывая G.60), найдем
,*/;*) +
Если t7 > 1 выбран так, чтобы FW(x, у; х) был непрерывным (что всегда
возможно), то Р (х, у\ х) будет непрерывной функцией х я у и мероморфной
функцией х?П'. Сравнивая это выражение с G.57), найдем
у; х) = [? + х2Ф(д;, х)]/!^, у; х) + Р(х9 у; к).
Первое слагаемое справа — голоморфная функция переменной х в пло-
плоскости П/ второе, как уже сказано, — мероморфная функция переменной х.
Поэтому в разложении, N (х, у; х) в ряд Лорана, отрицательные степени
(х — х0) могут войти только от второго слагаемого и, следовательно,
В{а)(х, у) — непрерывные функции х и у вместе с Р (х, у; к).
Положительные степени (х— х0) возникают от первого слагаемого и,
следовательно, Ат(х, у) имеют сингулярность матрицы h(x9y\ x) в точке
х = у, что нужно было показать.
Внесем разложение G.58) в G.55) и G.56), и сравним коэффициенты
при степенях (х — хо)~р, (х — хо)х-р; получим
= 09	G.62)
— щ J
_ J
(x, y) — x0 J k (x9 l) В"» (g, y) d^
= 0,
= 09 G.63)
G.64)
=0. G.65)

192	сингулярные интегралы и интегральные уравнения	[Гл. IV
Равенство G.64), в котором у будем рассматривать как параметр, есть
однородное уравнение, соответствующее уравнению G.37) для к = и0,
Ф (х) — х0 J k (х, I) Ф © d6S = 0.	G.66)
Следовательно, согласно G.64) уравнение G.66) удовлетворяется ка-
каждым из трех вектор-столбцов, составляющих матрицу ВМ (х, у). Назовем
эти векторы-столбцы Bip) (jc, у), k = 1, 2, 3. Так как ?<*» (ху у) отлична от
k
тождественного нуля, то хотя бы один из В^рК k = 1, 2, 3 не есть тождест-
тождественный нуль. Но уравнение G.66), как приводимое к уравнению Фред-
гольма, допускает лишь конечное число линейно независимых решений
Ф*1) (х), фB)(х), . . ., ф(г> (х) и его произвольное решение, в частности,
k
В{р) (х, у) для любого у, представляется в виде
В{р) (х, у) = S U (У) Ф7 (х),	G.67)
где $>{ (у) — определенные непрерывные функции (скаляры).
Уравнение G.62) перепишем следующим образом:
Вру (х, y) — K0Jk'&, у)В(рУ(х, g)deS = O, k=l9 2, 3; G.68)
k
где В(рУ (х, у) — транспонированная матрица В{р) (х, у) и В^р)' (х, у) —
k-я вектор-строка в матрице В^р) (х, у). Считая х за параметр, видим, что
G.68) есть союзное уравнение по отношению к G.66)
G.69)
Ф (У) — *о J k' A> У) Ф (I) dtS = 0.
Пусть ty<l) (у), . . ., t|)<r*) (у) — линейно независимые решения уравне-
уравнения G.69); конечность г^ вытекает из тех же соображений, что и конечность г.
Поэтому,
В{рУ (х, y)=%^i(x)ipf(y)i	G.70)
где (pi (x) — определенные непрерывные скалярные функции.
Проектируя G.67) на ось xs, s = 1,2, 3, будем иметь
Blp)(x, */)=? UL
k	s
но, по определению, Ыр) (х, у) = В[ру (х, у) и, следовательно,
В{рУ (х, у)=Ъ <р1(х)Ф(У),
1=1
где ipi == (\j){, ij)|, ij)|), / = 1 ... г. Подставив эти значения в G.68) и bog-
пользовавшись линейной независимостью ф.{ (х), получим
) о J(E, У) ^©^ 0, /=1,..., г.
Отсюда ясно, что
G.71)
Проектируя G.70) на ось хл, fe = 1, 2, 3, будем иметь
ipy
Bipy(xt у)=

СИНГУЛЯРНАЯ РЕЗОЛЬВЕНТА. СВОЙСТВА И ПРИМЕНЕНИЯ	193
В (x, y)=Zj tyk (у) Ф7 (x),	G.72)
где <p' (x) есть r^ линейно независимых векторов
фУ (X) = (ф{, ф2, фз)> / = 1, . . ., Г*.
Подставив G.72) в уравнение G.66), и учитывая линейную независимость
функции i|?? (г/), найдем
ф'(х) — Kojk (х, ?) фу (I) d*S = О, / = 1, ..., гШ9
следовательно, г > г#, и, окончательно, из G.71), г = г^. Этим доказана вто-
вторая теорема Фредгольма для сингулярного уравнения G.37).
8. Биортонормирование фундаментальных решений союзных систем.
Из функциональных уравнений резольвенты вытекает следующее уравнение:
у; v)dY]S = v^\N(xi у; k) — N{x, у; v)
х)#(х, у; v),	G.73)
в котором х и v — параметры. Это функциональное уравнение аналогично
известному из классической теории интегральных уравнений функциональ-
функциональному уравнению Гурса—Хейвуда (см. Goursat [11, Heywood, Frechet [1]).
Для одного сингулярного уравнения оно получено Жиро (см. Giraud [1]),
для уравнений теории упругости его вывод приводится в книге Купрад-
зе [13].
Обозначим
N (х9 у\ х) = у (х, у\ х) + А (а:, у; х),	G.74)
где
Р	CD
у(х, у; х)= Л Б(а)(х, у) (к—хо)"а, А(х, у; х) =
Пусть х — х0 = и, v — х0 = v.
Внеся эти выражения в G.73) и сравнивая коэффициенты слагаемых,
содержащих переменные иио отрицательных степенях, получим
(х-
—v) JY(x, л; x)y(t], ^ v)dTls = v(x, у; х) — y(*, у; v). G.75)
В результате сравнения членов с положительными степенями перемен-
переменных и и v, находим
, л; х)Л(т|, у; v)dnS = (x —v)-1^^ y;x) — Л(х, у; v)]
+ vA(x, у; v)O((/, v)[? + v2O(r/, v)] +
к% у; v);	G.76)
при сравнении членов с неотрицательными степенями переменной и, находим
J А (х, т); х) у (л, у; v) dnS = хФ (х, к) [Е + х2Ф (xf x)] у (х9 у; v), G.77)
13 В. Д. Купрадзе

194	СИНГУЛЯРНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ	(рл# fV
и, наконец, сравнение остальных членов дает
у(х, г); х)Л(г), у; v)dr)S = y(x, у; v)vO(y, v)[? + v2(P(y, v)]. G.78)
;¦
Из G.76) следует, что А (х, у\ к) есть резольвента ядра А (х, у; 0). В са-
самом деле, полагая в G.76) v = 0, видим, что это соотношение обращается
в G.56), т. е. в уравнение резольвенты. При к = 0 из G.56) имеем
# (*, у; 0) = k (x, у), или
* {х, У) = У (х> У\ 0) + А (х, у; 0).	G.79)
Далее, полагая в G.77) х = 0 и в G.78) v = 0, получим
\А(х9 л; 0)y(Л, У; v)dY]S=\y(xi у; к)А(г\, у; 0)^ = 0; G.80)
отсюда для х = 0, v = 0 имеем
\А{х, л; 0O(г), у; 0)d^S=\y(x9 ц; О)Л(т], у; 0)^5 = 0. G.81)
До сих пор предполагалось, что р (порядок полюса) — призвольное
натуральное число. В случае р — 1 имеет место
7.1. Теорема. Если {q/ (x)}rk=i, {tyk {х))гк==\ есть полная система
линейно независимых решений союзных однородных сингулярных интеграль-
интегральных уравнений и к = х0 есть простой полюс резольвенты, то всегда можно
считать выполненными условия
^ [^	G.82)
Доказательство. Для р = 1 имеем
B(i){Xy у) = —щУ{х, у; 0),	G.83)
и согласно G.64) можем писать у(х, у\ 0) — х0 J k(x, Qy(l, y\ 0)dsS = 0.
Внесем сюда значение k (x, у) из G.79), и используем свойство орто-
ортогональности G.81); тогда получим
у(х, у; 0) — щ \у{х, g; 0O(|, у; 0)^S = 0.	G.84)
Подставив сюда значение 7 (х, у\ 0) из G.83), будем иметь
или, в проекциях
3
&V У) + S J 5SA) (х, |) В^(|, у) d%S = 0.	G.85)
Но согласно G-67)
Поэтому после внесения этого выражения в G.85) и сравнения коэффициен-
коэффициентов при линейно независимых элементах, получаем G.82).

я 7]	СИНГУЛЯРНАЯ РЕЗОЛЬВЕНТА. СВОЙСТВА И ПРИМЕНЕНИЯ	195
Эти равенства выражают свойство биортонормируемости фундаменталь-
фундаментальных решений союзных систем, соответствующих простому полюсу резоль-
резольвенты.
9. Третья теорема Фредгольма. Пусть х = х0 есть полюс резольвенты.
Справедлива следующая
7.2. Теорема. Необходимым и достаточным условием разрешимости
неоднородного сингулярного уравнения G.37) служит соблюдение условий
J г|>' (х) f(x)dS = O, / = 1,2	 г,	G.86)
где [tyf (x)Yf=\ — полная система линейно независимых решений союзной
однородной системы уравнений G.69).
Доказательство. Необходимость получается из G.37) умноже-
умножением на г|)'" (х) и интегрированием по 5.
Достаточность доказывается следующим образом.
Пусть со (х) и а (х) — решения уравнений
у; 0)(*(y)dyS = f(x),	G.87)
о(х) — х0\а (х9 у\ 0) о (у) dyS = / (*);	G.88)
s
тогда
= со (х) + a(x) — f (х)	G.89)
удовлетворяет уравнению G.37). Действительно, согласно G.79) уравнение
G.37) принимает вид
Ф (*) — *о J {V (*> У* °) + А <*• У* °I Ф (У) dyS = f (*)'•	^7-9°)
подставив сюда G.89) и приняв во внимание G.87) и G.88), получаем
J у (х, ущ 0) [а (у) — f {у)) dJS + | А (х, у; 0) [со (у) — f (у)} dyS = 0. G.91)
Заменим в G.87) и G.88) х на у и у на |; умножим первое на
А (х, у\ 0) d^S и второе на у (х, #; 0) d^S слева и интегрируем по 5. Выполнив
допустимые здесь перестановки интегралов и приняв во внимание формулы
ортогональности, найдем, что ср (х) действительно удовлетворяет уравнению
G.37).Таким образом, задача сводится к решению уравнений G.87) и G.88).
Уравнение G.88) есть уравнение с сингулярным ядром А (х% у\ 0), и его ре-
резольвентой, согласно G.76), является А (х, у\ х); поэтому х=х0 не является
характеристическим числом для уравнения G.88), и его решение находится
по первой теореме Фредгольма, уже доказанной выше.
Что же касается решения со (х), то оно может быть построено лишь в том
случае, если f (x) удовлетворяет некоторым дополнительным условиям. Это
следует из того, что уравнение G.87) есть уравнение Фредгольма с непрерыв-
непрерывным ядром у (х, у; 0), и из соотношения G.75) видно, что его резольвентой
служит у (х, у\ х). Следовательно, х = х0, как полюс резольвенты, есть ха-
характеристическое число уравнения G.87) и по третьей теореме Фредгольма
для разрешимости этого уравнения достаточно выполнения условий
\	= Q, i=l, 2,..., /,	G.92)
13*

196	СИНГУЛЯРНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ	[Гл. IV
где {hl {y))\=\ — полная система линейно независимых решений союзного
однородного уравнения
h (у) — х0 J у' (g, у; 0) h (?) rfgS = 0.	G.93)
Покажем, что / = г и система [h1 (у)}\=\ совпадает с полной системой
фундаментальных решений уравнения G.69), союзного с G.37).
Для этого обратимся к уравнению G.62) и используя G.79), перепишем
его в виде
у\ 0) + АF, у\
Из формулы ортогональности
которая выводится так же, как формулы G.81), следует
BiP) (*, у) — щ\ В{р) (х, В 7 A, у; 0) dfi = 0
s
или
В{рУ(х, у)—щ1у'& у; 0)В{РУ (х, 6)dgS=-
и в проекциях
В{р)'(х, у) —Но|тF. У\ 0)В(рУ(х,
Но согласно G.70)
где {ф7 (y)}i — полная система линейно независимых решений союзного
G.37) уравнения G.69). Таким образом, эта система является решением урав-
уравнения G.93) и, следовательно, / > г.
С другой стороны, уравнение G.93) имеет столько же линейно незави-
независимых решений, сколько имеется таких решений у однородного уравнения,
соответствующего уравнению G.87). Если бы это число было больше г, то
тогда, вследствие того, что однородное уравнение, соответствующее уравне-
уравнению G.88), имеет лишь тривиальное решение, исходное однородное уравне-
уравнение G.66) имело бы больше, чем г, линейно независимых решений, что не
верно и, следовательно, / = г. Отсюда ясно, что достаточные для разреши-
разрешимости G.87) условия имеют вид
J
г;
и, следовательно, они же являются условиями, достаточными для разреши-
разрешимости сингулярного интегрального уравнения G.37).

я g]	ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ	\QJ
§ 8. Заключительные замечания
Теория одномерных сингулярных интегральных уравнений разработана
почти с такой же полнотой, как теория интегральных уравнений Фредгольма.
Она изложена в книге Мусхелишвили [2], где имеются также подробные би-
библиографические справки по этим вопросам.
Многомерным называют сингулярное интегральное уравнение, если раз-
размерность т множества интегрирования не меньше двух (т > 2).
Размерность множества интегрирования в теории Фредгольма не играет
существенной роли, в то время как для сингулярных уравнений она весьма
существенна. Выше были отмечены некоторые причины этого обстоятельства.
Существует единственное одномерное сингулярное ядро — ядро Коши.
Все остальные одномерные сингулярные ядра сводятся к этому ядру. Су-
Существуют различные классы двумерных и, тем более, многомерных сингуляр-
сингулярных ядер. Указанное обстоятельство значительно осложняет изучение мно-
многомерного случая по сравнению с одномерным.
Изучение сингулярных интегралов с ядром Коши и уравнений с такими
интегралами можно связать с хорошо разработанной теорией функций ком-
комплексного переменного. В многомерных случаях аналогичные связи не
эффективны.
Теорию одномерных сингулярных интегральных уравнений можно по-
построить с помощью формулы перестановки порядка интегрирования, не при-
применяя теорию функций комплексного переменного. Формулы перестановки
многомерных интегралов гораздо сложнее, и, кроме того, ядро, полученное
после перестановки
со (х, z) = J и (х; у) v (y9 z) dyS
(см. D.1), для ф (х, у, г) — ц)(Ху г)), в отличие от одномерного случая, не всегда
регулярно, в чем легко убедиться. Это обстоятельство вызывает сущест-
существенные затруднения при решении задачи регуляризации. Кроме того, отсюда
видно, что, вообще, итерированное ядро не лучше итерируемых, и метод
итерации здесь не применим. Трудность заключается и в том, что не всегда
удается получить для Ф (см. D.1), D.3)) удобное выражение.
Важной задачей теории сингулярных интегральных уравнений является
нахождение индекса уравнения (см. определение 6.2). Это—задача топологии.
Рассмотрим одномерный сингулярный интегральный оператор
К (Ф) (t) = A(t) Ф (t) + -Ш- J -^г Л + h (Ф) (/), *
где А = || Ац ||mXm, В = || В(;\\тхт, ф = (фъ . . ., фт), a h — вполне не-
непрерывный оператор. Оператор К называют оператором нормального типа,
если
det (А (/) + В (*)) ф 0, det (A (t) — В (t)) ФО, t?S.
С помощью функции det [(А + В)~1 (А — В)] естественным образом опре-
определяется отображение множества S на единичную окружность с центром
в начале координат. Степень этого отображения и есть индекс оператора /С.
Это предложение есть теорема Нетера—Мусхелишвили. Она допускает обоб-
обобщение и на многомерный случай.
Рассмотрим, ради простоты, оператор /(, определенный формулой E.29).
Обозначим через tx единичный касательный вектор поверхности S в точке х,
а через Тх (S) — множество всех таких векторов. Пусть
T(S)= [}TX(S)\
в Т (S) известным образом вводится топология, и оно становится трехмерным

198	СИНГУЛЯРНЫЕ ИНТЕГРАЛЫ И ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ	грл jy
ориентируемым многообразием — пространством касательных векторов. Сим-
Символ оператора К, точнее, о (h (tx), tx), определенный в п. 3 § 5, определяет
отображение пространства касательных векторов на пространство неособен-
неособенных матриц размерности га х т. Неособенных потому, что рассматриваются
операторы нормального типа, т. е. det а Ф 0. Пространство неособенных
матриц размерности га х т, естественно, отображается на Bга — 1)-мерную
единичную сферу. Таким образом, с помощью символа определяется отобра-
отображение пространства Т (S) на Bга — 1)-мерную сферу. Степень этого отобра-
отображения и есть индекс оператора /С.
Эта весьма важная теорема, полученная применением современных
средств топологии, доказана в различных предположениях рядом авторов.
См. по этому поводу работы: Михлин [1],Вольперт [1 ], Atiyah, Singer [13,
Seeley [1], Bojarski [1], Берикашвили [1] и др.
В одномерном случае имеется простая формула для вычисления индекса
(см. Мусхелишвили [2] или Векуа Н. [1]):
x = J- Гдп, det (А-8I
2я L ё det (Л + В) Js9
где символ [ Is означает приращение выражения, заключенного в скобках,
при обходе S один раз в положительном направлении.
В многомерном случае такой простой формулы пока не существует.
Индексы операторов, которые встретятся нам в этой книге, вычисляются
с помощью теорем 6.6—6.8. Эти теоремы имеются в работах: Giraud [2],
Михлин [1], Вольперт [1] и др.
Рассмотрение операторов, не обладающих свойством нормальности, ока-
оказывается весьма трудной задачей. По этим вопросам интересующемуся чи-
читателю советуем обратиться к работе Бицадзе [2].
Интерес к теории многомерных сингулярных интегральных уравнений
вызван не только задачами теории упругости. Эта теория находит многочис-
многочисленные применения в задачах гидроаэромеханики, теории крыла самолета,
теоретической физики, геофизики и др. Кроме того, она имеет и самостоя-
самостоятельное теоретическое значение, связывая многие разделы современной
математики.
Следует отметить, что во многих случаях задачи математической физики
можно привести к уравнениям Фредгольма, но гораздо естественнее они
приводятся к сингулярным интегральным уравнениям, исследование ко-
которых проще, чем исследование соответствующих уравнений Фредгольма.
Некоторые задачи с помощью сингулярных интегральных уравнений ре-
решаются в явном виде — в квадратурах. В некоторых случаях задачи мате-
математической физики приводятся к уравнениям Фредгольма, но полное иссле-
исследование этих уравнений не удается (см., например, Weyl [2 3 и замечания
в Шерман [3] и др.). Вместе с этим упомянутые задачи могут быть исследо-
исследованы достаточно просто и строго с помощью сингулярных интегральных
уравнений.
Первые работы по многомерным сингулярным интегральным уравне-
уравнениям принадлежат Трикоми и Жиро (см. Tricomi [1, 2], Giraud [I ]). Эти ра-
работы были упомянуты выше.
Жиро изучил эту теорию для ядер вида D.4) и применил к исследова-
исследованию граничных задач общего линейного эллиптического уравнения в част-
частных производных второго порядка.
Для общих ядер рассуждения Жиро не обоснованы и требуют уточнения.
Обобщениям и уточнениям исследования Жиро посвящены работы Геге-
лиа [3, 7, 9, 123. В частности, задача регуляризации у Жиро для ядер вида
D.4) решается методом, указанным в п. 1 § 5, совершенно строго, но в общем
случае этот метод не проходит и требует изменений, приведенных в п. 2 § 5.

задачи	199
Это сделано в работе Гегелиа [9]. Метод регуляризации, указанный в п. 2
§ 5, опирается на теорему Михлина о регуляризации сингулярных опера-
операторов, распространенных по всему евклидову пространству.
Михлин ввел понятие символа, который сыграл важную роль в этой
теории. Все основные теоремы, в частности, теорема об индексе, формули-
формулируются в терминах символа. С помощью символа вводится понятие нормаль-
нормальности оператора и доказывается, что всякий такой оператор допускает ре-
регуляризацию.
Для операторов классической теории упругости, термоупругости и мо-
ментиой упругости оказалось возможным построить теорию регуляризации
и доказать основные теоремы Фредгольма более элементарно, на базе иссле-
исследования так называемых функциональных уравнений резольвенты; такое
исследование было начато в работе Giraud [1, 2], продолжено и дополнено
в книге Купрадзе [13]; эти результаты изложены в § 7 настоящей главы.
В применениях важно знать, имеют ли рассматриваемые уравнения глад-
гладкие (дифференцируемые до определенного порядка) решения. Эти вопросы
подробно исследованы в работах Гегелиа [2, 6, 10, 11, 13] и Капанадзе
[1, 2, 3].
Двумерные сингулярные интегральные операторы встречаются в теории
обобщенных аналитических функций, принадлежащей И. Н. Векуа (см.
Векуа [2]). Эти операторы исследованы в работах Векуа И. [2] и Ман-
джавидзе [1 ] и др.
Особо следует отметить цикл работ Кальдерона и Зигмунда (см. Cal-
deron, Zygmund [1 ]—[4]), где сингулярные операторы исследуются в весьма
общих предположениях. Именно эти работы и работы Михлина вызвали
в последнее время бурное развитие этой теории и связанных с ней вопросов.
Читатель, интересующийся новыми результатами по указанным воп-
вопросам, может ознакомиться с работами Бицадзе [1 ] и сборниками: Псев-
Псевдодифференциальные операторы, Москва, 1967; Singular Integrals, Pro-
Proceedings of symposia in pure Mathematics; vol. 10, AMS Providence, 1968,
а также с литературой, цитированной в этих изданиях.
В рамках этой книги невозможно изложить теорию многомерных син-
сингулярных интегральных уравнений более подробно и указать все направле-
направления ее развития. При изложении мы имели в виду применения этой теории
в задачах упругости, термоупругости и моментной упругости, но и эта скром-
скромная задача потребовала рассмотрения почти всех основных вопросов общей
теории. Надеемся, что теория, изложенная выше, найдет дальнейшее при-
применение и в других задачах математической физики.
ЗАДАЧИ
1.	Изучить сингулярные интегральные уравнения, распространенные на многообра-
многообразиях с краями, и получить формулы вычисления индекса для таких интегральных операторов.
2.	Справедливы ли теоремы Фредгольма для сингулярных уравнений смешанных задач
(см. п. 7 § 5, гл. VI) классической теории упругости?
3.	Исследовать задачу 2 для моментной теории упругости.
4.	Развить теорию резольвенты и с ее помощью доказать теоремы Фредгольма для урав-
уравнений третьей и четвертой статических (колебательных) задач классической теории.
5.	Развить теорию резольвенты и с ее помощью доказать справедливость теоремы. Фред-
Фредгольма для уравнений всех шестнадцати основных задач (см. гл. IX) моментной теории упру-
упругости.
6.	Распространить теорию сингулярных интегралов и интегральных уравнений, изло-
изложенную в §§ 1—6, на случай неограниченного многообразия.
7.	Исследовать сингулярные интегральные уравнения контактных задач (см. гл.
хп, § 6).
8.	С помощью теории резольвенты установить свойства дифференцируемости решений
сингулярных интегральных уравнений и доказать теоремы вложения.
9.	Решить в явном виде сингулярные интегральные уравнения моментной теории упру-
упругости, соответствующие статистическим задачам в случае шара (см. Натрошвили
еории упр]
[1, 2, 6]).

ГЛАВА V
ТЕОРИЯ ПОТЕНЦИАЛА
В этой главе будут исследованы граничные свойства потенциалов, пред-
представляющих решения граничных и гранично-контактных задач теории упру-
упругости, в частности граничные свойства производных указанных потенциалов
произвольного порядка.
§ 1. Некоторые вспомогательные операторы,
формулы и теоремы
1. Определение Ш+ (у, б) и Ш~ (у, 6). Пусть 5—замкнутая или разом-
разомкнутая поверхность класса Лх (а), у — точка поверхности, п = (nlf n2t n3) —
орт положительной нормали поверхности 5 в точке у и d — положительная
постоянная, участвующая в определении класса Л1 (а). Рассмотрим шар
Ш (у, б), где б — положительное число. Если у не лежит на границе поверх-
поверхности 5 (граничной точки не существует, если 5 замкнута) и б — достаточно
малое число, то Ш (у> б) поверхностью S разделится на две части. Часть
Ш (у, б), находящуюся со стороны положительной нормали п, обозначим
через Ш~ {у, б), а Ш (у, б) \ (Ш~ (у, б) [} S) обозначим через Ш+ (у, б).
Если S — замкнутая поверхность, ограничивающая область D+, то
в силу принятого раньше соглашения, положительной считается внешняя
нормаль. Таким образом, в этом случае
Ш+ (у, б) = Ш (у, б) П D\ ЯГ (у, 8) = Ш (у, б) n D-f
где D~ = E3\(D+ U S).
Назовем Ш+ (у, б) внутренней б-окрестностью точки у относительно S
(независимо от того, 5 замкнута или нет), а Ш~ (у, б) — внешней б-окрест-
ностью точки у относительно 5. Иногда, если это не вызывает недоразуме-
недоразумения, вместо «внутренняя б-окрестность точки у относительно S» будем го-
говорить «внутренняя б-окрестность точки у», или, еще короче, «внутренняя
окрестность точки у».
2. Определение операторов 2Dk, Mkj и dS . Связь между ними.
Пусть / — функция, определенная в Ш+ (у, б) [Ш~(у, б)] и принадлежащая
классу С1 (Ш+ (у, б)) [С1 (Ш~ (у, б))]. Тогда существует предел
df(y)\+ _	v	df(x) r(df(y)\- „	lim
д ) - "	d ' [\ д ) -n-iy*>*
dxk

К I]	ВСПОМОГАТЕЛЬНЫЕ ОПЕРАТОРЫ, ФОРМУЛЫ И ТЕОРЕМЫ	201
Введем обозначения (см. Гюнтер [11)
где
Ш\+ = lim
^
aV(«r «)—4г-Я*^-. *-1.2.3.
Символом S)k (дИ, п) f~ {у) обозначим выражение
3>ь1д n)f-(u)~ (дПу) \~ nJ дПу)\~	П2>
где
V дп (у) ) я/- {у9 6) э х^у jU k dxk
Пусть ф — функция, определенная на S; предположим, что существует
в Д/+ (у, б) функция /, принадлежащая классу С1 (Ш+ (у, б)) и удовлетворяю-
удовлетворяющая условию
Ф(У) = Г(У).
Тогда, по определению,
2>k О*, п) Ф {у) = фк (дд9 п) Г (у), k = 1, 2, 3,	A.3)
где й>* (<Э9, /г) /+ (у) определен из A.1).
Если существует в Ш~ (у, б) функция f, принадлежащая С1 (Ш~ (у, 6))
и удовлетворяющая условию
то тем же символом SDk (dyj n) ф (у) обозначим ?Dk (dg, п) /" (у).
Таким образом, по определению,
= ®k(dy, п)Г(у).	A.4)
Кроме операторов 3)k, мы будем применять некоторые другие операторы,
представляющие определенные комбинации операторов ?Dk (ду9 п).
Пусть /+ (у) и f~ {у) — определенные выше функции; введем обозначения:
у,
(^)(^)- *./-1.2,3.
где (см. (II, 4.7) и A.2))
*Ы Фв, я) = я, -^	nk -щ- = д,^ (а„ п) — nk3>, (dg, п). A.6)

202
ТЕОРИЯ ПОТЕНЦИАЛА
[Гл. V
Аналогично положим
или
, я) Ф (У) = Jlki ФУ, n)f+(y)
„ п)Г(у),
A.7)
A.8)
где в A.7) ф (у) — функция, определенная на 5 и удовлетворяющая усло-
условию ф (у) = Г (У), a feC1 (Ш+ (у, б)).
Аналогично определяется смысл равенства A.8).
Из A.6) следует
з
ФкФр п)<р(у)= S п,Жк1(ди, n)q>(y).	A.9)
Теперь, придавая в A.6) k и / значения 1, 2 и 3, выпишем следующие опе-
операторы:
д	д	б
ш П) =
Г13 (ду, п) =
Легко заметить, что операторы
ds,
A.10)
^—рг
удовлетворяют условиям
= 0.
Из определения операторов 3bk (ду, п), Mkj (ду, п) и
3	3
A.11)
вытекает
A.12)
n), *,/=!. 2, 3,
где 8j;7r — символ Леви-Чивита.
Рассмотрим антисимметричный матричный оператор
(дК, п(х)) =
х. я(х))||зхз,
A.13)
Мщ (дх, п (х)) определен из A.6), п (х) — произвольный единичный вектор,
х — произвольная точка в Е3. Если и — регулярный вектор, то выраже-
выражение Л (дх, п (х)) и имеет смысл при любом х? Е3 и, как нетрудно проверить,
ди
(дх,
дп
п (х) div и-\-[п (х) х rot и].
A.14)
Учитывая A.12), последнее выражение в проекциях можно переписать
в виде
n(x))u)k
A.15)

§ J]	ВСПОМОГАТЕЛЬНЫЕ ОПЕРАТОРЫ, ФОРМУЛЫ И ТЕОРЕМЫ	203
и на основании A.14) обобщенному вектору напряжения (см. A.13.5)) можно
придать вид
Т(дх, п(х))и=~Т (дХ9 п(х))и + (х + fx)Ж(дх, п(х))и, A.16)
где
71 (дХ9 п{х)) и = (к + 2fi) n(x) div и —р[п(х) х rota].	A.17)
Справедлива следующая (см. Гюнтер [1], стр. 24—26).
1.1. Теорема. Если S — поверхность Ляпунова и ф? С1 E), то
для любого yd S существует функция f указанного выше {см. A.1) и A.3)) вида,
определенная неединственным образом; 2Dk (дуу п) ф (у) и Жщ (ду, п) ф (у)
(k, j = 1, 2, 3) не зависят от выбора f и
Фи (ду, п) Ф 6 С (S), Mkj (дуу л) ф 6 С (S).
3. Теорема Стокса и ее применения. Пусть ф и гр принадлежат классу
С1 (S). Тогда для любого у 6 5 справедливы формулы
, п)у(у), J
Выпишем известные из дифференциальной геометрии формулы
(см. Гюнтер [1])
= 2Di(dy, n)nk=
= cos (Qyfe) cos (LpXy) t cos (Q^fe) cos (C^/)
h	AЛУ)
где /?! и iR2 — радиусы кривизны главных сечений, имеющих на поверх-
поверхности 5 направления Lx и L2.
Для средней кривизны из A.19) следует
К {у) = S Д>/ (ду, п) щ = -±- + -i-.	A -20)
1.2. Т е о р е м а (Стоке). ?слы S — поверхность Ляпунова (замкну-
(замкнутая или разомкнутая) и <р? С1 E), то
*-
где L — контур поверхности 5. Если поверхность замкнутая, то правая
часть обращается в нуль.
Доказательство теоремы можно найти, например, в книге Гюнтер [1].
Учитывая A.12), теорему Стокса для замкнутой поверхности класса Лх (а)
можно записать в следующем виде:
= 0, k, / = 1, 2, 3.	A.21)
На основании A.9), A.18), A.21) для замкнутой поверхности Б^Л2 @)
можно получить равенство
\
Dtidy, nL>(y)dS = lniK(yL>(y)dSi *=1, 2, 3.	A.22)
Докажем следующие теоремы:

204	теория потенциала	[рл у
1.3. Теорема. Если и и v принадлежат классу С1 (S) и S — замкну-
замкнутая поверхность Ляпунова, то
\[иЛ(ду9 n)v — vM(dy, n)u]dS = J ? Лп{д99 n)(upt)dS = 6. A.23)
Действительно,
иЛ(ду, n)v — vJ[(dy, n)u= ? \щЛн(дф n)vf — и{Мч(ду, n)uf] =
3	3
= S [Ur?fi(dg, п)и{ + и,Лп(ду, п)и/\= S Лп(ду, n)(ufv{)
и теорема 1.3 следует из теоремы Стокса.
1.4. Теорема. Если и^С1 (S) и S — замкнутая поверхность Ля-
Ляпунова, то
у, п)[щ{у)Тш{у — x)]dyS = 0, k=\, 2, 3, xEE39 A.24)
где rjk(y — х) определяется формулой (II, 1,1); когда x?S, интеграл по-
нимается в смысле главного значения.
Доказательство. Когда точка х не лежит на S, т. е. когда xgD+
или x?D~, функция и, (у) Tjk(y — х) удовлетворяет условиям теоремы
Стокса и справедливость формулы A.24) вытекает из предыдущей теоремы.
Пусть теперь х — точка поверхности S. Поместим в ней начало местной
системы координат (х)9 введенную в главе I, § 15. Формулы преобразования
имеют вид
где ть, ti2, % — координаты точки у в системе (х). Кроме того,
3	3
S aki (х) аа (х) = 2 aik (х) at, (x) = бЛ/,
4 = 1	1 = 1
3	3
S	?а(х) а/3(х), ak2(x)= S
5 /а (дс) а/2 (х), аЛз W =nk(x)9 k = 1, 2, 3.
Из A.25), учитывая A.26), получаем
з
Л* = S <*;* (*) (У/ — ^/).	A-27)
i
з
п,(у)= Sa/ftW/it(ti).	A.28)
Обозначим через Z(f боковую поверхность области Ц (х9 п (x)t8){]D+,
где Ц (х, п (х), б) — круглый цилиндр, определенный в главе I (см. I, п. 2
§ 15). Таким образом, U,t— цилиндрическая поверхность, которая целиком
находится внутри области D+. Выберем б так, чтобы 26 < d, где d — постоян-
постоянная, участвующая в определении поверхности Ляпунова. К основанию ци-
цилиндра Ц (х, п (х), б) в D+ прикрепим полушар с центром в точке @, 0, —6),
радиусом б. Поверхность пол у шара обозначим через С$".

§ 1]
ВСПОМОГАТЕЛЬНЫЕ ОПЕРАТОРЫ, ФОРМУЛЫ И ТЕОРЕМЫ
205
Пусть L (б)—контур разомкнутой поверхности S\5 (х, б), где 5 (х, б) —
кусок поверхности 5, вырезанный из 5 цилиндром Ц (х, п (л:), б).
Применяя к разомкнутой поверхности 5\S (х, б) теорему Стокса, на осно-
основании A.12) видим, что для завершения доказательства теоремы в случае
х? S достаточно доказать, что
lim J
6-»0LF
— x)dyl = 0, k=l, 2, 3,
/, 1=1
Следовательно, справедливость равенства A.24) будет установлена, если
будет доказано, что
lim J ui(y)Tik(y — x)dyl = 0, i, /, k% /=l, 2, 3,
A.29)
Так как L (б) является контуром и для разомкнутой поверхности
tt, то имеем
Lib)
—х)йу1 = J
LF)
J
Займемся сначала вычислением интегралов
J	ds,(y)	"A k, 1, l-l, 2, 3.
Но на U,t
На основании A.26) и A.28) имеем
dTjk (У — х)	_ yj	dTfk (л)
где
ir Sfk , . ,q,r=\
б COS ф,	ТJ = б Sin ф,
п2 (л) = — sin ф,
ar/
/fc
¦ = (82pcoscp — 6lpsin<
Т)а — t,
A.32)
A.33)
где Ф (Tilf тJ) — уравнение куска S (х, 6) в системе (х).

206
ТЕОРИЯ ПОТЕНЦИАЛА
[Гл. V
Принимая во внимание A.31)—A.33), после элементарных вычисле-
вычислений, получим
(</)
2/2
¦<	2я
р=1	0
А/6,-,
4- ^2 (ф) F 4- V б2 4- ^2 (Ф))
Г с/, г=1
F^cos ф + $2а sin ф) (б1г cos ф + К sin ф) X
slnq>)
/б2 4- 'Ф2 F -
62 t (ф) (бг<у COS ф 4- 62g Sin ф)
(ф)
. A.34)
В точках Сб" имеем
цг = б cos ф sin 6, т]2 = 6 sin ф sin 0, % = — б + в cos 9,
/гг (т]) = — cos ф sin 6, д2 (т]) = — sin ф sin В, пц (у\) = — cos 9,
зх, d^S = б2 sin 9 <29 йф, |т)| ==26sln~,.
= б {^- [sin 9 (в1р sin
cos
5- [cos 9 (81Рcos Ф + б2^ sin Ф) — 8Вр sin 9] Гм} d9 dVf A.35)
t
• (!*36)
Учитывая A-34) и A.36) и пользуясь свойством поверхности Ляпунова
A.37)
получим
Г дГ,к(у-х) d с
<С1б«->0, при б —0,
Итак, мы доказали
г
(у)
1, 2, 3,
A.38)
A.39)

§ I]	ВСПОМОГАТЕЛЬНЫЕ ОПЕРАТОРЫ, ФОРМУЛЫ И ТЕОРЕМЫ	207
Оценим интегралы по L (б) в правой части A.30). Так как и^С1 (S),
имеем
\Щ{У) — Щ(х)\<А\у — х\9 * = 1, 2, 3,
кроме того,
|Г,*(у — x)\<j^T{> *, /=1,2,3.
В силу последних формул
J [ui(y) — ul(x))rik(y-x)dyl ^c J Л' = 2яс6—0, приб —0, A.40)
LF)	L*<<»
где Z/ (б) — окружность радиуса б (проекция L (б) на касательную пло-
плоскость).
Учитывая теперь A.38) и A.40) из A.30) получим A.29) и теорема 1.4
доказана полностью.
Формулу A.24) можно переписать в виде
J \[Лфт п)Г(у — х)]'и{у)-Г(у — х)Ж(ду, n)u(y)\dyS = 0, x?EB, A.41)
где
з
\Ж(дуу п)Г(у — х)П,= 2 *пФу
A.42)
Так как A.41) имеет место для любых А/ и [г', подставляя в это соотношение
^' = 1, ц/ = 0, получим
J [Ж (ди, п) lvSrr и (у) + jJ— Ж (ду, п) и {у)] dyS = 0, х 6 ?„ A.43)
S
где Е — единичная матрица.
С помощью рассуждений, аналогичных тем, которые применялись при
доказательстве теоремы 1.4, легко доказать и следующую теорему:
1.5. Теорема. Если и^С1 (S) и Б^Лг (а), 0 < а ^ 1, то
т п)Г(у — х, &)]'и{у) — Г(у — х9 <й)Мфу, п)и(у)\ dyS=0, х? Ев,
A.44)
еде Г (у — х, со) — матрица Купрадзе (см. (II, 1.7)), а
у, п)Г(у — x9a>)yki = -(K + v.')JIkt{dy9 п) ^^~х^ +
3 2
vv
0= 1 /=1
4. Формула представления решения при лг(Е S. В главе 111 мы получили
формулы общих представлений решения уравнений классической теории
упругости, термоупругости и моментной упругости, когда точка х ле-
лежит в D+ или D~. Здесь получим эти представления для л:? S, ограничиваясь
для простоты классическим случаем.

208
ТЕОРИЯ ПОТЕНЦИАЛА
[Гл. V
1.6. Теорема. Если 5 6 Лг (а), 0 < а «^ 1 и и является регулярным
решением уравнения A1,4.2), то
— х)Т(ду, п)и(у)—[т(дд, п)Г(у — х)\ и
, x e S,
A.45)
где Г (у — л:) — матрица Кельвина, Т (ду9 п) и (у) — обобщенный вектор
напряжения (I, 13, 5),
7Xk)
[Т(ду, я)Г(у-х)Гц--^Д)|у_!.
а интеграл понимается в смысле главного значения.
Доказательство опирается на результаты предыдущего пункта. Пусть
x?S. Рассмотрим местную систему координат (х). Применим формулу Со-
милиана A11/2.9) к области, которая ограничена замкнутой поверхностью
[5\S (x, S)] U U,t\jCt- Так как точка х находится вне рассматриваемой
области, то имеем
| {г {у — х) Т (д„ п)и(у) — [т (<59, п)Г(у-х)] и (у)} d,S =
{Т(у — х)Т(д99 п)иц) — [т(ду9 п)Г{у —
t
A.47)
Очевидно, при б —¦ О
J r(y — x)T(dg,n)u{y)dyS
и в силу A.37)
J T{y—x)T{dgin)u{y)dyS <c0 J
]."пГГ = 4яс1'
—1/5)—О,
- 2ясоб In (V2 + 1) [У\ + (|J + |] - О
Таким образом,
lim J Г {у—х) Т (дд, п)и(у) dvS = 0.	A.48)
Для вычисления второго интеграла в A.47) рассмотрим тождество
, п)Г(у—х)\ u(y)d?= J [Тф„, п)Г(у—х)\ \и{у) —
J [т(д„ п)Г(у~xjJrfeSaW. A.49)
? t

§11
ВСПОМОГАТЕЛЬНЫЕ ОПЕРАТОРЫ. ФОРМУЛЫ И ТЕОРЕМЫ
209
Первый интеграл в правой части оценивается так же, как выше, и в пре-
пределе равен нулю. Повторяя рассуждения предыдущего пункта, получим
Jim J
t
JL-
где Е — единичная матрица.
Учитывая A.25), A.26) и A.28), будем иметь
з
2 п* (Л)
дп(у) \у — х\
и используя A.33) и A.35), найдем
|2я
——T
\у — х\
Отсюда вытекает, в частности, известная формула
' = — lim (
L.^—
(y) \y — x\
^4-Ti—
дп(у)\у —
<2ксв5«.
. A.50)
Итак, мы получили
lim J [Т(ду, n)Y(y—x)]duS = E.
e*44
Перейдя к пределу при б —> 0 в A.49), и учитывая предыдущие формулы,
будем иметь
lim
J [т(д„ п)Г(у — х)] u{y)dyS = u(x).
+
A.51)
Наконец, приняв во внимание A.48) и A.51), получаем доказательство
теоремы 1.6.
Учитывая A11,2.9) и A.45), можем написать
т(ду, п)и{у)У — [Т{ди, п)Т(у — *)]'(и
Г 2,
о, xeD-.
Совершенно аналогично доказывается формула
A.52)
A.53)
A.54)
где t] (х) = 0 при x?D+, r\ (х) = 1 при *6 S и т\ (х) = 2, при x?D~.
И В. Д. Купрадзе

210	ТЕОРИЯ ПОТЕНЦИАЛА	[Рл у
Формулы A.52) и A.54) остаются справедливыми для уравнений уста-
установившихся колебаний классической теории упругости, термоупругости и
для моментной теории, если вместо Г (х — у) рассматривается соответствую-
соответствующая фундаментальная матрица.
§ 2. Граничные свойства для поверхностных интегралов
типа потенциала
Пусть 5 — замкнутая или разомкнутая гладкая поверхность в ?3»
z — точка поверхности, a v — орт положительной нормали к поверхности S
в точке 2.
Рассмотрим круглый конус с вершиной в точке г, осью вращения ко-
которого служит прямая, проходящая по v. Предположим, что плоский угол
при вершине этого конуса а < л. Введем следующие обозначения: через
К (z, а) обозначим часть Е3, заключенную внутри указанного конуса,
Q+(z, а, 6) = /С (z, а)ПЯГ(г, б),
Q'(z9 а, 6) = /C(z, а)ПДГ(г, 6).
м
). I
где Ш+ (z, б) [Ш (z, б)] внутренняя (внешняя) б-окрестность точки г от-
относительно S (см. § 1, п. 1).
Пусть G (S) — некоторая окрестность поверхности 5, т. е. область из Е3,
содержащая 5. Предположим, что F — функция, определенная в G (S)\S.
2.1. Определение. Угловым граничным значением функции F
в точке zg «S изнутри (извне) назовем предел
lim	F(x) f lim	F(x)]9
,6)э^г	IQ- (z,a, &) =э x->z	J
Q+ B, a, 6)
если он существует для любого а из интервала @, я), и не зависит от а.
Угловое граничное значение в точке z?S изнутри (извне) обозначается
через F+ (z) или \F (z)}+, [F~ (z) или \F (г)}-].
Очевидно, если F непрерывно продолжима в точке г? 5 изнутри (извне),
то существует угловое граничное значение этой функции в точке z изнутри
(извне). Обратное предложение не верно, в чем можно убедиться на примере.
Предположим, что функция k удовлетворяет следующим условиям:
1)	k^Gx B, у) на D+xS [D~xS] для некоторого у > 0 (см. определе-
определение IV, 1.2);
2)	существует угловое граничное значение F+ (z) [F~ (z)] интеграла
F(x)= J>(*. y)duS.
s
где z? 5;
3)	существует сингулярный интеграл
F(z)=\k(z, y)dyS
s
в смысле главного значения (см. гл. IV, § 1, п. 3).
2.2. Теорема. Если S — гладкая поверхность, соблюдены условия
1) —3), фб L (S) и z является точкой Лебега для ср, то для любого а 6 @, я)
\im
{\k(x, y)<p(y)dyS— f k(z, y)<p(y)dvS\=\F+(z) —
№	3\8(г.г)	I
S\S U.4

5 2]	ГРАНИЧНЫЕ СВОЙСТВА ДЛЯ ПОВЕРХНОСТНЫХ ИНТЕГРАЛОВ	211
еде
e==|x_z| и xeQ+(z, a, 8){xeQ-(z, а9 &)}.
Доказательство. Пусть условия теоремы 2.2 выполнены. Из 2)
и 3) следует, что если
\х — 2| = е, jc6Q+B, a, 8)[xeQ'(z9 а, б)],
то
hml\k(x, y)dyS- f k(z, y)dys) = F+(z) — F(z),
**0
б(х, y)dyS— f k(z, y)dyS] = F- (z) — F (z)].
S\S(..e,	J	J
Следовательно, для доказательства теоремы достаточно показать, что
lim/B, х, е) = О,
где
(г, х, в)=\к(х9 y)f(y)dyS— J k(zy y)f(y)dyS,
S	S\S(Z,8)
, a, 6)[jc6Q"B, a, 6)].
Так как z является точкой Лебега для ф и / = ф (у) — <р B), /? L (S), то
Нт ¦—¦ [ \f{y)\dyS = O.	B.2)
р —ь О	•*
Не нарушая общности, можно считать, что / — неотрицательная функ-
функция на S. Представим f B, х, 8) в виде суммы
з
/B, Ху 8)= S /* B, X, 8, Г]),
где
/i(z, х, 8, г])= f [k(x, y) — k(zy y)]f(y)dS9
S\S (z, -Л)
/2B, x, 8, т|)= J [k(xy y) — k(zy y)]f(y)dS%
S(Zi ti)\SB, eV
/3B, x, e, rO= I k(xy y)f(y)dS.
S B. 8)
Покажем сначала, что
\\mfl(zy xy 8, г]) = 0.
Из условия 1) следует:
14*

212	ТЕОРИЯ ПОТЕНЦИАЛА	fj-jj#
Если 2е < т), т. е. 2 | z — х \ < ц, то ввиду того, что \у — г\ > г\,
B, х, е, т))|^Ctl8v j/{у)d^O,	B.3)
при 8 —> 0 (сл — некоторая постоянная, зависящая от г\).
Рассмотрим теперь /2 (z, х, 8, т]). Имеем
S B, t|)\S (z, e) IP^2'
Но, если y? S (z, л)\5 B, s), x? Q+ (z, a, 6), | z — x\ = e и числа ef
т], б выбраны достаточно малыми, то
\x — y\^\z — y\s'm$,	B.4)
где 2р = я — а.
Следовательно,
Рассмотрим касательную плоскость к поверхности 5 в точке z и обозна-
обозначим ее через т (z). Пусть т (г, г]), т (г, е)и(/' — ортогональные проекции на
т (г) множеств 5 (г, т]), 5 (z, e) и точки у соответственно.
Тогда для f2 имеем
тB, n)\x(z, e) |2 У '
где са — некоторая постоянная, зависящая от а, 02 — функция, определен-
определенная из (IV,3.28), а /0 (у') = / (у). Очевидно, при у' ? т (z, т])
где с = const и, следовательно,
\Гш(г. х, г, г$\^сагУ J	¦ У* .
tB Л)\ТB 8) '	^
, 8)
Переходя к полярным координатам в плоскости т (z), с полюсом 2, по-
получим
8	О
где г = \z — t/% а Ф — полярный угол точки у'.
Пусть
р 2л
j
Очевидно,

{ч 2]	ГРАНИЧНЫЕ СВОЙСТВА ДЛЯ ПОВЕРХНОСТНЫХ ИНТЕГРАЛОВ	21&
Поэтому в силу теоремы Фубини (см. Смирнов [3]), ф абсолютно не-
непрерывна на @, г\) и почти для всех г? @, ц)
2 я
Таким образом,
л	f	л
|/2B, X, 8, T])l^ca8V V Ф 2-1уГ ==Са&У\\ ^-И + B + ?)
Из B.2) следует, что
lim^- = 0.	B.5)
В силу этого
f2(z9 х, е, л) —0, когда е-*0.	B.6)
Остается оценить f3 (z, x, 8, г\). Если
•^€Q+B, a, б), [#6Q~(z, a, б)], y^S(z9 e), |z — x| = s,
то
Отсюда для f3 получаем оценку:
S B. 8)
В силу B.2)
Iimf9(z9 х, е, т])->0.
Теперь в силу B.6) и B.3) получаем доказательство теоремы.
Совершенно аналогично доказывается несколько более общая
2.3. Теорема. Если S — гладкая поверхность, k удовлетворяет
условию 1), существует предел
\im[\k{x, y)d9S— f k(zt y)dyS\,	B.7)
p x? Q+ (z, a, 6) [x? Q" B, a, 6)], | z—x\ =8, qp? L (S) м 2 является
точкой Лебега для ф, /по
lim j Jfe (х, у) Ф (у) d^ — J ? (г, у) Ф (у) d,SJ = Фа (г) Ф (г),
S\S(z9e)
где л: 6 Q+ B, а, б) [*6 Q" (zf а, б) ], | г — х \ = е, Фа (г) — лр^л B.7).
Теоремы 2.2 и 2.3 остаются справедливыми, если k == || kit,\i м т — мат-
матрица, а ф = (<рь ф2, . . ., фт) — вектор.

214	ТЕОРИЯ ПОТЕНЦИАЛА	[Рл# у
С помощью теорем, доказанных в этом параграфе, можно вычислить
угловые граничные значения интегралов типа потенциала. Рассмотрим один
достаточно общий пример. Пусть
k(x, у)=\\Ьи(х, у)||зхз,	B.8)
где
з
j A fin	B0(yi — xi)(yc — x{)
• II у — *1	\у — *13
Л 0, В 0 — произвольные постоянные.
Составим функцию типа потенциала
К (ф) (х) = ? (х, г/) ф (у) dyS,	B.10)
где ф = (ф1э ф2, ф3) — плотность.
Вычислим угловые граничные значения интеграла К (ф) с помощью
теоремы 2.2. Для этого необходимо найти угловые граничные значения
интеграла
B.10')
и его значение в точке х? S.
Учитывая A.39), получим
i, /=1,2, 3, х?Е3.	B.11)
Кроме этого,
— 2л, *es,
0, хб^'
В силу B.11) и B.12) имеем теорему:
2.4. Теорема. ?а/ш S — замкнутая поверхность Ляпунова, ограни-
ограничивающая конечную область D+, и F — функция, определенная из B.10'), то
-?, хб5,	B.13)
0, хе D",
г5в ? — единичная матрица.
2.5, Теорема. ?Ъш 5 — поверхность Ляпунова (замкнутая или
разомкнутая) и ф? Lp (S), р > 1, то существуют угловые граничные значе-
значения интеграла B.10) почти всюду на S и вычисляются по формулам
К± (Ф) (z) = ± Ф (г) + J k (г, у) Ф (у) dS,	B.14)
где интеграл в правой части понимается в смысле главного значения.
Доказательство. Заметим, что k удовлетворяет условиям тео-
теоремы 2.2. В самом деле, так как 5б«/7х (а) при а > 0, легко показать, что

* gi	ПОТЕНЦИАЛЫ ПРОСТОГО И ДВОЙНОГО СЛОЯ	215
на DxS k^G-L B, а), где D — произвольная конечная область из Е3. Кроме
того, существует интеграл F (х) в смысле главного значения во всех точ-
точках х? S, не являющихся граничными точками поверхности. Доказательство
аналогично IV, 3.25.
Предположим, что S — замкнута, тогда в силу теоремы 2.4, F непре-
непрерывно продолжима на S, как из D+, так и из D". Следовательно, существуют
ее угловые граничные значения во всех точках поверхности S,
Если примем во внимание определение сингулярного интеграла и то,
что почти все точки поверхности 5 являются точками Лебега для ф, из тео-
теоремы 2.2 непосредственно следует 2.5 в случае замкнутой поверхности 5.
Пусть теперь S — разомкнута. Дополним S до замкнутой поверхности
поверхностью 50. Пусть D+ — конечная область, ограниченная поверх-
поверхностью SU*S0. Мы предполагаем, что положительной нормалью на S(JSO
является нормаль, направленная из D+. Продолжим ср из S на SLJS0 форму-
формулой ф (у) = О, если у? 50.
Применяя уже доказанную часть теоремы, получим формулу B.14) и
для разомкнутой поверхности S.
§ 3. Потенциалы простого и двойного слоя.
Угловые граничные значения
При исследовании граничных задач, поставленных в первой главе,
большую роль играют интегралы вида
V. (Ф) (x) = \v (х — у) Ф (у) dySf	C.1)
.5?
где v (х) = Г (х) — матрица Кельвина (см. A1,1.4)), или v (х) = Г (х, со) —
матрица Купрадзе (см. (П. 1.7)), или v (х) = W (х, а) — матрица фундамен-
фундаментальных решений моментной теории упругости (см. A1,2.10)), или же v (x) =
= Ф (х, со) — матрица фундаментальных решений уравнения A1,3.1) (см.
A1,3.6)). v — называется ядром, а ф — плотностью интеграла; ф — вектор,
определенный на 5. Если v (х) = Г (х) или v (х) = Г (х, со), то ф — трех-
трехмерный вектор ф = (фь ф2, ф3); если v (х) = Ф (х, со), то ф — четырех-
четырехмерный вектор ф = (фх, ф2, ф3, Ф4); если же v (х) = ? (х, а), то ф —
шестимерный вектор.
Интегралы C.1) в теории упругости играют такую же роль, какую играет
потенциал простого слоя в теории граничных задач гармонических функций
(см., например, Гюнтер [1]) или обобщенные потенциалы (см., например,
Miranda [1]) простого слоя в теории граничных задач эллиптических урав-
уравнений в частных производных второго порядка. Интеграл C.1), кроме того,
как в этом убедимся впоследствии, обладает граничными свойствами, анало-
аналогичными граничным свойствам потенциала простого слоя. В связи с этим,
интеграл C.1) назовем потенциалом простого слоя.
Нам нужно будет, кроме того, изучить интегралы вида
C.2)
где w (х — у) = [Т (ду9 п) Г (у — л:) Г — матрица сингулярных решений
уравнений статики (см. теорему 11,4.1) или w (х — у) = [Т (дуу п)х
X Г (у — х, со)]'—матрица сингулярных решений уравнений колебания (см.
теорему 11,4.4), или w (х — у) = [Т (дуу п) W (у — х> о)]' —матрица сингу-
сингулярных решений уравнений колебания моментной теории упругости (см. тео-
теорему 11,5.1), или же w (х — у) = \& (ду, п, со) Ф* (у — ху со)]', w (х — у) =
= \к (ду9 /г, со) Ф* (у — х, со)Г, w(x — y)=[Q (дуу п) Ф* (у - х, со)]' -

216	ТЕОРИЯ ПОТЕНЦИАЛА	[Рл# у
матрицы сингулярных решений уравнений колебания термоупругости (см,
к
теорема 11,6.1). Можно рассмотреть случай, когда w (х — у) = [Т (ду, п) х
X Г (у — x)Y, w(x — y)= IT (ду, п)Т (у — х, со)]' и др.
Интеграл C.2) будем называть потенциалом двойного слоя. Вычислим
угловые граничные значения этого потенциала. Рассмотрим сначала слу-
чай, когда w (х — у) = [Т (ду, п) Г (у — х)У (см. A.46)).
Докажем теорему.
3.1. Теорема. Если S — поверхность Ляпунова (замкнутая или
разомкнутая) и ф? LD (S), р > 1, то почти всюду на S существуют угловые
X
граничные значения интеграла C.2), где w (х — у) = [Т (ду, п) Г (у — х)\\
и вычисляются по формулам
Г(у-г)] <p(y)dyS;	C.3)
п)
интеграл в C.3) понимается в смысле главного значения.
Доказательство. Положим в B.9)
Ао = уХ — (i|i'f BQ = ji' (x + \i);	C.4)
тогда
k(x, У) = [т(ду9 п)Т{у —
и из теоремы 2.5 следует 3.1.
Нетрудно доказать и более общую теорему.
3.2. Теорема. Если S — поверхность Ляпунова (замкнутая или ра-
X
зомкнутая), срб Lp E), р > 1, w (х — у) = [Т (дуу п) Г (у — х, со)]', или
w(x — y)= [Т (ду, л) Т (у — xt о)]', или W(x — y)= [<? (дуу пу со) х
X Ф* (у — х, со)Г, то почти всюду на S существуют угловые граничные
значения W (ср) (г) и *
W± (Ф) (г) = + Ф (г) + f w (г — у) Ф (у) djS,	C.5)
s
где интеграл в правой части понимается в смысле главного значения.
X
Пусть w (х — у) = [Т (ду, п) Г (у — х, со)]'. Легко заметить, что
[^(ду, п)Т(у—х, со)] =[т(ду, п)Т(у-х)} +[т(ду, п)Т(у — х,ь)] ,
где второе слагаемое в правой части допускает оценку (см. теорему 11,1.5)
\[т(ду, п)Т(у — х, со)] |<с.	C.6)
Пользуясь C.6), легко установим существование угловых граничных
значений вектора
Wo (ф)(*) = J [^(ду. п)Т(у — х, со)] <p{y)djS	C.7)
почти во всех точках z поверхности S и
— г, со)] <p{y)djS.	C.8)

§ 4]	ПОТЕНЦИАЛ ДВОЙНОГО СЛОЯ С ПЛОТНОСТЬЮ КЛАССА C°»3(S)	- 217
Теперь доказательство теоремы при w (х —у) = it (д&, п) Г (у— х% со)]'
следует из теоремы 3.1 и из представления
|[
—хч со)]
Т(ду,п)Г(у
= \[т(ду, п)Т(у — х)} Ф(у)dyS + J \т (ду, п)Г(У — *, со)] Ф(у)dyS.
Аналогично рассматривается случай, когда w (х — у) = [Т (ду, п) х
X Т (у — х, о) У или w (х — у) = \&(ди, п, со) Ф* (у — х, со) ]' и другие.
§ 4. Потенциал двойного слоя с плотностью класса C°^(S)
В предыдущем параграфе мы изучили потенциал двойного слоя C.2)
с плотностью из класса Lp E). Рассмотрим теперь этот потенциал, когда
Фб С0' уE), где 0 < C ^ 1. Изучим сначала случай, когда w (х — у) =
= [Т (ду, п) Г (у — х)У9 т. е. интеграл
W (Ф) (х) =\{Т (ди, п) Г (у-х)У Ф (у) dyS.	D.1)
Пусть 5 — замкнутая поверхность Ляпунова; тогда (ввиду того, что
9?C°'6(S)) из теоремы 3.1 следует существование угловых граничных зна-
значений интеграла D.1) почти для всех г? S, и
W± (Ф) (г) = ч= Ф (г) + W (Ф) (г),	D.2)
где W (ф) (z) — значение интеграла D.1) в точке z?S, определенное
в смысле главного значения.
В этом параграфе мы докажем, что в указанных предположениях фор-
формула D.2) справедлива во всех точках z поверхности 5. Кроме того, W (ф)
непрерывно продолжима на S как из D+, так и из D~ и, следовательно,
в формуле D.2) под W+ (ф) (z) и W~ (ф) (z) можно подразумевать не только
угловые граничные значения интеграла D.1), но и его граничные значения,
определенные равенствами (г? S)
= lim W(q>)(x), W~(q>)(z)= lim
Докажем теорему, частным случаем которой является формулированное
выше предложение.
4.1. Теорема. Если S — замкнутая поверхность класса Лх (а),
О < а ^ 1, ограничивающая конечную область D+ и 0 < р < а, ф? С0* Р E),
то функция W( (ф), определенная в D+ равенством
принадлежит классу С0*!3 (D+). Более того х),
II ^ (ф) !(/>+, о, Э) ^ с IIФ 1E, о, 3).
где с — положительная постоянная, не зависящая от ф.
Доказательство. Пусть х', х" принадлежат D+; б = | х' — х" |.
Не нарушая общности, можно считать 66 < df где d — постоянная, участву-
участвующая в определении класса Лг (а).
1) См. в главе 1 определения 15.3, 15.3', 15.3*.

218
теория потенциала
[Гл. у
Рассмотрим отдельно три возможных случая:
2)
3) p(x',S) = \x' — z'
или
", S) = |x" — г"|<26;
S) = |x" — z" | ^ 26, |*'_2'|<-i.
В случае 1) имеем
Wt (Ф) (х') — IF, (ф) (х") = W (Ф) (х') - Г (Ф) (а:") =
= J \[Т(д„, п)Т(у- *')]' -[Т(а„ n)T(g — x")]'\ ф(i/)djS.
Отсюда в силу теоремы IV,! .9 имеем
'f~^' |Ф(у
Рассмотрим случай 2). Пусть р (х\ S) = \х' — г' | < 26, z'? 5. Имеем
Wt (ф) (x')—Wt (Ф) {х") \^\Wt (Ф) {х1)— Wt (Ф) (г') | + | Wt (Ф) {z') — Wt (q
Очевидно,
^^ (ф) (*') — ^^ (ф) (z') = HF (Ф) (х') + ф B') — IF (ф) {г') =
-Ф(г')
= J [Г(а„ я)Г (у—д:')]'Ф(У)^— j [Г (а„, п)Г(у — г')]'
= J [T фи, п)Т(у — х')}' [Ф(у) — Ф(z')Jd^S —
— J [Г (а„ я) Г {у — г')]' [Ф (у) — Ф (z'
+ Г j [Т (ду, п) Г (у— х')]' dvS — j [Т (ду, п) Г (у— г')]' djS\ Ф (г') + Ф (zr) =
av, п)Г(у—х'))'-[Т(ду, n)T(y~z')]'\[ci>(y)
Здесь применены формулы
| [Т (ду, п)Т{у — х')]' й? = - 2?,
J [Т {ди, п)Т(у — г')]' d,S = - ?,
полученные в § 2 (см. B.13)). Следовательно
D-4)

§ 41	ПОТЕНЦИАЛ ДВОЙНОГО СЛОЯ С ПЛОТНОСТЬЮ КЛАССА С°* В (S)	219
где
у, п)Г(у — *')]' — г
/2 = J [Г (д„ /г) Г ((/ — г')]' [Ф (У) - Ф B'
/з = J [^ (av, п)Г(у — х')]' [ф (у) — ф (г')]
S ('6
/4= J {[Г(а„, п)Г(у—х')Г — \Т(ду9 ri
SB',d/2)\S B% 6)
Оценим /х. Так же как в случае 1), имеем
Ш^с\х'-х"\ J \^(y) — 4>(zi)\dl/S^c\
S\S (z\ d/2)
Отсюда
l/il^l*' — дГ|Э.	D.5)
Оценим /2. Имеем
XB', 6)
Следовательно,
|/2|^c|*'-x"P-	D.6)
Аналогично получается оценка
\7э\^с\х'-х"\К	D.7)
Оценим /4- Имеем
ей
J |2'_^||^_ yf\9y{z\
2)S(\6)
б
Отсюда
D.8)
Складывая неравенства D.5)—D.8), получим
| W, (Ф) (*') - W, (Ф) (/) | <; с | *' - хГ \\
Оценим теперь
Имеем
| W, Ш B') — W, (ф) (ХГ) |< | ^, (ф) B') - И?, (ф) B") | + | W, (ф) (Z*) -
где
Разность
оценивается совершенно так же, как

220	теория потенциала	[Гл. V
а для первого слагаемого в правой части предыдущего неравенства получим
Wt (Ф) (z') — Wt (Ф) (z") = - Ф (*') + W (Ф) (г') + Ф (z") - W (Ф) (гГ).
Следовательно,
| Г, (Ф) (г') - Wt (Ф) (/') | ^ с | z' - Г | + | W (Ф) (z') -
В силу теоремы !V,3,26 имеем
\W(<p)(z') —
и, следовательно,
Складывая полученные неравенства, имеем
| H7, (ф) (х') — Wt (Ф) (х") К с | х' — х» |В.	D.9)
Это рассуждение не изменится, если
p(x\S) = | лг" — г"|<26, Ь = \х'—х'\.
Исследуем теперь случай 3). Очевидно,
') — W, (Ф) (х") = J {[Г (д„ л) Г (у — х')Г -
— [Т (ду, п)Г(у — хГ)]' \ [Ф (у) — Ф (z')]
где
/2= j
S (*'. d/2)
Если y€S\S(z', d/2), то
поэтому
и, следовательно,
В силу этого неравенства,
s
Если i/6 S (z', d/2), то | у — 2' | ==s 2 | у — х' | ^ 4 | у — х" |, откуда полу-
получаем оценку
Первая часть теоремы доказана. Теперь легко завершить все доказа-
доказательство.
Рассмотрим потенциал двойного слоя
(x — y)q>(y)dyS,	D.10)
где w (х — у) = IT (дд, п)Т (у — х) V, или w (х — у) = [Т (dg, n) x
X Г (у — х, со)Г, или w (х — у) = [Г (д,, и) ^ (у — х, а)]' и т. д.

Л 5) ГРАНИЧНЫЕ СВОЙСТВА ПРОИЗВОДНЫХ ПОТЕНЦИАЛА ПРОСТОГО СЛОЯ	221
Из 4.1 легко следует справедливость следующей теоремы:
4.2. Теорема. Если S — замкнутая поверхность класса Лг (а),
О < а ^ 1, ограничивающая конечную область D+ и ср? С0' Р (S), 0 < р < а,
то функция Wt (ф), определенная равенством D.3), принадлежит классу
С0-» (D*) и
|| Wi (ф) ||(D+, 0, 3) < С 1 ф ||(S, 0, 3).
Рассмотрим теперь потенциал двойного слоя D.10) в области D" =
= E3\(D+(}S).
Функция (матрица) \|э, по определению, принадлежит классу C°*a(D~)9
если грб СР-аф~[\Ш @, г)) для любого г > 0.
Пусть
Совершенно аналогично теоремам 4.1 и 4.2 доказывается
4.3.	Теорема. Если S — замкнутая поверхность класса Лг (а),
0 < а ^ 1, ограничивающая бесконечную область D" и ф? С0» P(S), 0 < Р <
<а, то функция We (ф) принадлежит классу C°*$(D~) и
II We (ф) ||(D-, 0. 3) ^ С I Ф II(S. 0, 3)*
Незначительно модифицируя приведенные рассуждения, можно дока-
доказать несколько более общую теорему.
4.4.	Теорема. Если S — поверхность класса Лг (а), 0 < а ^ 1
{замкнутая или разомкнутая), ф? Lv (S) и ф? С0* ° (So), 0 < р < а, где
So — часть S, ограниченная гладкой кривой, то потенциал двойного слоя
D.10) непрерывно продолжим в каждой внутренней точке поверхности So
и граничные значения вычисляются по формулам D.2). Кроме того, существует
такая внутренняя (внешняя) окрестность поверхности Sl9 что в этой окрест-
окрестности W (ф) принадлежит классу С0' ®.
Здесь Sj — произвольная часть 50, не содержащая точек границы So.
§ 5. Граничные свойства первых производных
потенциала простого слоя
Исследуем граничные свойства первых производных (по декартовым
координатам) потенциала простого слоя
(х) = j Г(х — у)ц>(у) dyS,	E.1)
где фб Lp (S), р > 1, а Г (jc — у) — матрица Кельвина.
Из E.1) для x6S, имеем
где (см. (II. 1.3))
dxt	Wi	( +V>)°* dyi \y_

222	теория потенциала	[Гл. V
Приняв во внимание A.2), можем писать
=A—(х- + ю V, а. л,-^ + ,-г>, ft.
+ ю V ? Tj^ »Ч ? () • E.3)
Учитывая формулу
dyidyk
получим
д (д*\у — х\\ 	 с, д	)	nk (yi —
)	дп \у — х\	\
	 с,
ik	dyi Ял I v — x I
Если учесть формулу A1,4.6), то предыдущее равенство перепишется
в виде
-У Л (д п)№
\-2ni2>k(dy,n)-r-lr.
Следовательно, E.3) принимает вид
Рассмотрим потенциал
где
ф|/* (У) = л* I— (V + м»') Sfe, + 2^i'n^fi/] фу (у);
очевидно,
Рассмотрим теперь потенциал, соответствующий второму слагаемому
в E.4) справа:
Щ (%) (X) = j Ф, (у) 2>i (дуу п) {у^

§ 5] ГРАНИЧНЫЕ СВОЙСТВА ПРОИЗВОДНЫХ ПОТЕНЦИАЛА ПРОСТОГО СЛОЯ	223
Учитывая A.9), имеем
3
Щ (ф/) (х) = J ^ Ф|/ (У) *и (ду, п) * dyS,	E.6)
s i\
s i=\
где
Ф// (У) = Л/Ф/ (У).
Принимая во внимание B.11) и теорему 2.5, находим
\vt (Ф/)(*Л± = J 2>, (д„ /г) |у^г| Ф/ (у)dyS.	E.7)
Аналогичные рассуждения применяются и для установления граничных
свойств интегралов типа потенциалов, соответствующих остальным слагае-
слагаемым в выражении E.4), E.2). Учитывая это обстоятельство и приняв во вни-
внимание E.5) и E.7), приходим к следующей теореме:
5.1. Теорема. Если S — поверхность Ляпунова (замкнутая или ра-
разомкнутая), ф? Lp (S), р > 1, то существуют почти для всех z? S угловые
граничные значения первых производных (по декартовым координатам) по-
потенциала простого слоя — E.1), и вычисляются по формулам
= ± 2п [(V + Ю ФА (г)-2^4 (V9)J v4 + d-^jp, E.8)
где v = (vb v2, v3) — орт положительной нормали поверхности S в точке 2,
а под
dzi
понимается значение интеграла E.2) при х = г? S, определенное в смысле
главного значения.
Учитывая E.8) и тождество
k=l
dVk (q>) (x)
т (дг, v)V (фХг)}* = ± ф(г) + Т (дг, v)V(q>)(z).	E.9)
получаем
Исследуем граничные свойства первых производных потенциала про-
простого слоя с плотностью ф из класса С0* рE).
В § 4 были изучены граничные свойства потенциала двойного слоя
с плотностью из класса С°> $ E); при этом мы опирались на теоремы 3.1 и
IV,3.26. Совершенно так же исследуются граничные свойства производных
первого порядка потенциала простого слоя с помощью теорем 5.1 и IV,3.26.
Справедлива следующая
5.2. Теорема. Если S — замкнутая поверхность класса Лг (а),
О <а ^ 1, ограничивающая конечную область D+ (D~ = E3\(D+[}S))9
ф? С0- P(S), 0 < Р < а, то первые производные по декартовым координатам
потенциала простого слоя E.1) принадлежат классу С0*13 (D+) (C°-f3 (D~)).
Эти производные непрерывно продолжимы на S, как из D+, так и из D~;
в каждой точке z?S имеет место равенство E.8) и
I V (Ф) И(Г>±, 1. 0) ^С I Ф 1E,0,3).

224	теория потенциала	[Рл# v
Исходя из этой теоремы, можно исследовать граничные свойства век-
х
тора Т (дх, v) V (ф) (х) при ф? С0* |3 (S) и получить формулу E.9).
Наконец, используя теорему 5.2, можно показать, что производные пер-
первого порядка (потенциала простого слоя) по направлениям, лежащим в ка-
касательной плоскости, непрерывны, когда точка х пересекает границу.
§ 6. Производные потенциалов простого и двойного слоя
с дифференцируемой плотностью
Сначала докажем теорему.
6.1. Теорема. Если ф? С1*р (S) и S — замкнутая поверхность клас-
класса Л\ (а), 0 < р < а ^ 1, то потенциал двойного слоя
й(Ч>)=1[т(дУ9п)Т(у — х)\ Ф(у)dyS	FЛ)
можно представить в виде
^(Ф^-^Г^Ф) — -^v(Jlq)) + (K+ii)V(jr<p),	F.2)
еде w (ф) и v (ф) — гармонические потенциалы двойного и простого слоя
F'3)
F-4)
а V (ф) — потенциал простого слоя (см. C.1)).
Доказательство. Представим F.1) (см. A.16)) в виде
где
= ] {[~Т(ду>п)Т(у — х)] +{*+v.)[J[(dy9n)r{y—x)]'}<v(y)dip9 F.5)
(Э„ n)T(y-x)\kf = -±- Ffe/ 4-т^Ьг + •*" ^ n)IF^r) • F-6)
^	IFr
а [^# (ду, п)Т (у — х)У определяется из A.42).
На основании A.41) и A.43), из F.5) вытекает доказательство теоремы.
Согласно F.2) для вычисления производных потенциала F.1) достаточно
знать производные гармонических потенциалов F.3) и F.4) и потенциала
простого слоя. Таким образом, для исследования производных первого по-
х
рядка от W (ф) нужно показать существование производных первого по-
порядка гармонического потенциала двойного слоя, так как при сделанных
ограничениях производные других потенциалов (т. е. потенциалов простого
слоя), как мы видели, существуют. Производные первого порядка гармо-
гармонического потенциала двойного слоя хорошо изучены (см., например,
Когп [41, или Гюнтер [1]). Здесь мы представим соответствующие резуль-
результаты в удобной для нас форме.
Учитывая тождество
дх i дп | у — ;

Л g]	ПРОИЗВОДНЫЕ ПОТЕНЦИАЛОВ ПРОСТОГО И ДВОЙНОГО СЛОЯ	225
и применяя A.21) при х? S, получим
3
ду (Жду)	(п оч
Таким образом, справедлива
6.2. Теорема. Если y(zCl\f(S) u S— замкнутая поверхность
к
класса Лг (а), 0 < Р <а ^ 1, то потенциал двойного слоя — W (ср) при-
принадлежит классу С1- Р (D+) и С1* Р (D~).
В § 5 мы изучили граничные свойства первых производных потенциала
простого слоя. Имея в виду вычисление производных второго порядка этого
потенциала, докажем теорему
6.3. Теорема. Если ф? С1* & (S) и S — замкнутая поверхность
класса Л2(а), О < р <а ^ 1, то производные первого порядка потенциала
простого слоя C.1) представляются в виде
д-Ш- = w (ф<0) + v (ф«>) + у (Х«>),	F.9)
где w, v и V — введенные выше потенциалы, а <р(*> = (ф1г, ф2?, ф31),
= (Фи, fe> f3J) " Х(о= (tin %2» 1ы) — векторы:
ы (У) = Л? [2|*
>1 Фу> п) щ (У) - К (у) щщ (у) +
(пФ) К (у) — 2 ^/ (^, л) Ф/ (У) + Лк1 {ду, п
= К
1ш {У) = К |] 0/ Ф,, л) Ф/ (у) — (пФ) /С (у) + -#^ (^, п) (пФ), F.10)
) — средняя кривизна (см. A.20)) поверхности S в точке у.
Доказательство. Будем исходить из E.2), где ядро интеграла
определяется из E.4). Учитывая легко выводимые равенства
у! l
J Ф< (УJ)t (ду9 п) {y^xl d,S = v(ntK(У)Ф/(У) — SDt (ду, п)Ф/(у)),
s
- (п/Ф/) К (у)] dyS + (Я' + \l')v\ 6ki [(п/Ф/) К (У) — ®f (дуу п) Ф/ (у)] \,
J %-nfnfS>k (dyi п) |у.1.х| dvs = °f nininkK(у)Ф/(у) — ?>*(а^, п)
^	¦	3
'|п/Ф/ ^Жп(д„, п) (d^-=-fl)d,S = J V Ты(у-х)Жц
S	l \	S 1 1
S 1 = 1
из E.2) и E.4) получаем F.9), и теорема 6.3 доказана.
15 В. Д. Купрадзе

226	теория потенциала	[рл у
В дальнейшем нужна еще одна формула для производных первого по-
порядка гармонического потенциала двойного слоя. Пусть ф? С2» 0 (S) и S —
замкнутая поверхность класса Л2(а), 0 <а^ 1; тогда, учитывая A.2),
A.22) и F.8), в результате элементарных вычислений, находим для x^S
^—^- = w(^)i^)-\'v\K(yK)i^—S ^jJliw].	F.11)
Совершенно аналогично, для производных первого порядка гармониче-
гармонического потенциала простого слоя получаем
— w (д,«р) + v [&м — щК {у) Ф (у)], хе S.	F.12)
§ 7. О дифференциальных свойствах потенциалов
теории упругости
Результаты предыдущих параграфов дают возможность вычислить и ис-
исследовать производные любого порядка от потенциалов теории упругости
в замкнутых областях, ограниченных поверхностью интегрирования.
Предположим, что 5 — замкнутая поверхность, ограничивающая ко-
конечную область D+, a D" = E3\(D+\JS).
7.1. Теорема. Если SeJIM (а), ф? О » (S), 0 < р < а «^ 1, 0^
«^ I ^ k -\- 1, то потенциал двойного слоя
где k — произвольное, целое, неотрицательное число. Более того9
7.2. Теорема. Если S? Jlk+1 (а) и фб С- & (S), 0 < р < а < 1,
0 ^ / ^ k9 то потенциал простого слоя
V (фN
Докажем эти теоремы. Теорему 7.1 при й = 0 и / = 0 мы
доказали в § 4, а при & = 0и/=1 — в §6 (см. теорему 6.2). При k = 1
интерес представляет случай / = 2. В этом случае, принимая во внимание
F.2), F.8), F.9), F.11) и F.12), получаем
G.1)
М

§8]
ТЕОРЕМЫ ТИПА ЛЯПУНОВА—ТАУБЕРА В ТЕОРИИ УПРУГОСТИ
227
где проекции векторов ф('> э яр<^> и %<*> имеют вид
+ (х + v) nt [2ц'л, (пЖ (ду9 п) Ф) — (V + ц') (Ж (ду9 п) Ф (г/)),],
13
К (у) 2>t (ду9 п) Фд (у) — V S>i (дд9 п) Мц (ду9 п) ф* (у) +
/-1
—^(д99 п)(Ж(д
у9 n)<p(y))k\
у, л) (Ж (ду> п) Ф(у)),—
-п?К(у) (Ж (ду9 п) Ф (y))k + в« [к(у)(пЖц>) —
- ? Я>1 (дуу п) (Ж (ду9 п) Ф (у))]
/=1	J
+ 2 (ц + *) I*'
S
— @)k (диУ п) [п,
G.2)
При наших ограничениях ф<*> е С1- 3 (S),
С0- р E) и х@ 6 С0- Р (S);
к
поэтому существуют частные производные второго порядка потенциала W (ф)
и вычисляются из G.1). В этом случае W (ф)? С2' 3 (D+) и W (фN С2» Р (D").
Ясно, как следует продолжить рассуждение для доказательства теоремы 7.1
при произвольном k @ ^ / ^ k + 1).
Теорему 7.2 при fe = 0 и / = 0 мы доказали в § 5. При k = 1 и / = О
доказательство очевидно. При k = 1 и / = 1 доказательство вытекает из
F.9) и F.11). Аналогично доказывается теорема 7.2 при произвольном
k @ < I ^ k).
В доказательствах теорем 7.1 и 7.2 ядрами потенциалов были матрицы
X
Г (дг — у) и [Т (ду9 п) Г (у — х)У. Но теоремы справедливы и легко доказы-
доказываются и в том случае, когда ядрами служат сингулярные решения уравне-
уравнения моментной теории упругости и термоупругости.
§ 8. Теоремы типа Ляпунова—Таубера
в теории упругости
1. Теоремы Ляпунова—Таубера для гармонического потенциала двои-»
ного слоя. В теории гармонического потенциала известны теоремы о свой-
ствах нормальных производных (или производных первого порядка) потен-
потенциала двойного слоя, имеющие важные применения в теории граничных за-
задач. Эти теоремы формулируются следующим образом (см., например, Гюн»
тер [1]):
15*

228	теория потенциала	[рл# у
8.1. Теорема. Если выполнено одно из следующих условий:
1°. Ф — непрерывна на S и 9 < А \ z — у \ (8 — угол между нормалями
к поверхности в точках г и у), или
2°. | Ф (у) — Ф (г) | < В | г — у |, 6 < А \ z — у |а, 0 < а ^ 1 и если
потенциал двойного слоя F.3) обладает одной из производных
dw \-
j
/ dw \+
\ dv ) '
обладает и другой, и имеет место равенство
dw \ + / dw \ —
)
8.2.	Теорема. ?сла 5 — замкнутая поверхность класса Лг (а) и
Ф(Е С1» Р (S), 0 <р <а< 1, то потенциал двойного слоя имеет производ-
производные первого порядка, принадлежащие классам С0» Р (D+) а С°>f5 (D~) w выпол-
выполняется равенство
/_дау
\ dv
2. Теоремы типа Ляпунова—Таубера в теории упругости. Теоремы,
аналогичные приведенным выше, справедливы и для потенциалов двойного
слоя теории упругости. Некоторым видоизменением и обобщением тео-
теоремы 8.1 является следующая теорема для потенциала двойного слоя в теории
упругости:
8.3.	Теорема. Если существует один из пределов (TW)+ или (TW)~9
принадлежащий классу С0' Р, регулярного соответственно в D+ и D~ потен-
циала двойного слоя, то существует и другой и при этом имеет место
равенство
Эту теорему, имеющую полезные применения, будем называть теоремой
Ляпунова—Таубера в теории упругости. Доказательство теоремы 8.3 тре-
требует применения теории многомерных сингулярных интегральных уравне-
уравнений и теории граничных задач; доказательство будет приведено в главе VII.
8.4. Теорема. Если S — замкнутая поверхность класса Лг(а) и
ф? С1' Р (S), 0 < р < а ^ 1, то потенциал двойного слоя W (ф) (см. J6.1))
имеет производные первого порядка, принадлежащие классам С0» & (D+) и
С0» 0 (D~) и выполняется равенство
[т (дг, v) W (ф)] + —\т {dz, v) W (ф)] ~ = 2 (х - у) Л (дг, v) Ф (г), (8.1)
где ус и у — произвольные действительные числа, а Ж — матрица, опре-
определенная из A.13).
Доказательство. В §6 для W (ф), в условиях теоремы 8.1,
мы получили представление
\y-x\
[	J], (8.2)
где Е — единичная матрица.

? gj	ТЕОРЕМЫ ТИПА ЛЯПУНОВА —ТАУБЕРА В ТЕОРИИ УПРУГОСТИ	229
к.
Из теоремы 6.2 следует, что первые производные W (ф) принадлежат
классам С0- » (D+) и С0' е BГ).
Итак, для доказательства теоремы 8.4 остается вычислить оператор
Г (д*, v) от W (ф), исследовать его граничные свойства и получить (8.1).
Из (8.2) имеем
T{dxt v) #(Ф) =4г J Р
s L
где
+ JT (дх, v) [{х + 11)Г(у-х)~-2^уЕ_х1]Я(ду, /i)<p(iW, (8.3)
Л	!	= VV.J	!		(84)
dv \u — x\ Aj l dxi \u — xl '	v • '
Для дальнейшего упрощения (8.3) заметим, что
3
dvdn \y-r-xl	?j dsk (x) dsk (y) \y — x\9
где
3	3
a V о л, a "a	V о г, д ла\
osk (x) ?j 1*к l dxj dsk (y)	^J lin l dyj * v * '
— символ Леви-Чивита; кроме того,
dv
= 2я{л' (к + ji) (у + |л).	(8.8)

230	ТЕОРИЯ ПОТЕНЦИАЛА	[Рл# у
Используя A.21) и (8.5), при x^S, после элементарных вычислений
получаем
f d2	1
1 §rad^ -W \y-x\ ф (У) ^S = J &ad* \y-x\ Ж (а*" П) ф (У) d«^'
(8.9)
На основании (8.7) и (8.9), после ряда преобразований, (8.3) принимает
вид (x?S)
1
3
д
L^M\y\k(y) L
+ (-3. _ в) Mki (dxt v) T7^77] | M (dy, n) Ф Ц d^. (8.10)
Перейдем в (8.10) к пределу при х —* z? S; пользуясь рассуждением,
приведенным в § 5, получим
(д2, v) W (ф)}1 = ± (х — 7) Я (д„ v) Ф (г) +
{ 3
4- —А ' V ^	1	^ ,
"•" 2я J y 2-ь dskw \y-*\ dsk(y)
S \ k=l
Из последней формулы легко следует формула (8.1) и, тем самым, дока-
доказательство теоремы 8.4.
3. Одна вспомогательная теорема. В дальнейшем полезно иметь другой
(эквивалентный) вид формулы (8.11). Предварительно докажем теорему.

§8]
ТЕОРЕМЫ ТИПА ЛЯПУНОВА-ТАУБЕРА В ТЕОРИИ УПРУГОСТИ
231
8.5. Теорема. Если S — замкнутая поверхность класса Лг (а) и
С1 (S), то имеют место равенства
S ft—
I, /, ?=1, 2, 3; 26
(8.12)
При доказательстве этой теоремы мы будем существенно пользоваться
рассуждениями и результатами из пунктов 3 и 4, § 1.
Так как доказательства формул, входящих в (8il2), ничем не отличаются
друг от друга, мы докажем только одну из них.
Применяя теорему Стокса (теорема 1.2) и учитывая представление
.6)
у-г! д\у-г\ д
= J
J
L (б)
д (д\у-г\д\у-г\ д
для доказательства справедливости второй из формул (8.12) достаточно по-
показать* что
< — z\ д\У — *\ А 1 >=/.,_ Л	/о 1 оч
lim J [ф/(у) — Ф/(г)]-
г?. I ^f
Принимая во внимание A.25) и A.26),
д	1
E) и S6 Лг (а), имеем
^/г	дуг dv |г/ — г|
Таким образом, формула (8.13) доказана.
(8.15)

232	теория потенциала	[рл# у
Учитывая A.25), A.26), A,33),-A.35) и (8.15), после длинных, но неслож-
несложных вычислений, получим
г д \d\y-z\ д\у — г\ д 1
J dsiW \
t
ду	ду, dv \y^
^	J {63F2pcos9—6lpsin9)F1Gcos(p + 82Gsin(p) X
р, ?, /-=1	О
X (б1г cos ф + К sin ф) •$ (ф) + б2 (82р cos ф — 81р sin ф) [б3г F1Gcos ф + 62<7sin ф) +
+ bag Фи c°s Ф + б2г sin ф)] я|р2 (ф) + S (82р cos ф — б1р sin ф) х
_ JL
х бзА^3 (фI [S2 + ^2 (ф)Г 2 ^ф. (8.16)
Второй и третий члены в правой части стремятся к нулю при б —> О,
так как | гр2 (ф) | < с0б4 и | гр3 (ф) | < С!б6. Итак, остается показать, что и
первый член при б —> 0 стремится к нулю.
Если учесть (I, 15.1), A,15.2) и A.33), то имеем
2	2
ф(ф) = Ф(ть, %)= S [а/*(вЛ1.в1ь)-в/*@,0)]т1/Л»+ S ajk@, 0)mk,
(8.17)
где
Подставляя (8.17) в (8.16) и учитывая, что
2я
J (82р cos ф—81р sin ф) (б1<7 cos ф + б2<7 sin ф) (б1л cos ф + б2г sin ф) (Ао cos2 ф +
+ 2В0 sin ф cos ф -J- Co sin2 ф) dq> = О,
где Л о, 50, Со — произвольные постоянные, заметим, что подынтегральное
выражение можно переписать следующим образом:
(б2р cos ф — б1р sin ф) (б1<7 cos ф -f 82q sin ф) (б1г cos ф + б2г sin ф) X
б*
Отсюда, поскольку
— <*/* @, 0I<сб« и г|
заключаем, что первый интеграл в правой части в (8.16), при б—>0, стре-
стремится к нулю, как ба. Итак, формула (8.14) и вместе с нею теорема 8.5 до-
доказаны.

§ 9] ГРАНИЧНЫЕ СВОЙСТВА ПОТЕНЦИАЛОВ ТРЕТЬЕЙ И ЧЕТВЕРТОЙ ЗАДАЧ	233
Из (8.12) очевидно (см. Гюнтер [11), что функции
(8.18)
k=l
5
существуют и принадлежат классу С0* & (S), 0 < C ^ 1. Этим существенно
воспользуемся в дальнейшем.
На основании теоремы 8.5 формула (8.11), после очевидных преобразова-
преобразований, перепишется следующим образом:
{Т(дг, v
2л
f
J
з
д
^ Zj dsk(z)\y — z\ dsk(y)
Zj
, /i) Ф(у) + (х + у-В) V
зв
Г
Lfe/
'-*|« J	\У — г\
3	3
п/ (г* - »*) S (г/ - h) vi vft (*/ - »/) S (г; - »*)rt/
	f^fVli	+ 3V	f^ETF	+ 3(B-x)x
X
(8.19)
Компоненты матриц, входящих в эту формулу, представляют линейные
комбинации членов, стоящих под интегралами в (8.18) и поэтому интегралы
от этих выражений принадлежат классу С0* & (S) @ < |3 ^ 1).
§ 9. Граничные свойства потенциалов
третьей и четвертой задач
1. Граничные условия третьей и четвертой задач. Приведение к эквива-
эквивалентному виду. Граничные условия третьей и четвертой задач имеют сле-
следующий вид (см. A,14.4), A,14.4'), A,14.5) и A,14.5'))
в третьей задаче
\Т(дг, v)u — v(vT(d2, v)u)\± = ff {av}± = /4,	(9.1)
в четвертой задаче
\u — vuv\± = f9 \(vT(d2t v)u)}± = U,	(9.2)
где f (flt /a, /3) и /4 заданы на 5, v (vx, v2, v3) — орт внешней нормали 5
в точке z.

234	теория потенциала	[Гл# у
Представляется целесообразным несколько преобразовать условия
(9.1) и (9.2).
Учитывая A,13.5), для х = \х первое условие из (9.1) можно переписать
в виде
*L_v(v|j-)] +(i[vrotaj}± — /;	(9.3)
на основании тождества
dv ~
имеем
подставляя это значение в (9.3), получим
(9.4)
Условия (9.1) и (9.4) эквивалентны, если поверхность S имеет непрерыв-
непрерывную кривизну в каждой точке (т. е. если S? Л2 @)) и, кроме того, /46 С1 (S).
Условия (9.4) запишем в матричном виде. Для этого введем матрицу
Н{рХ9 v) = \\Hki(dXf v)|l4X3,	(9.5)
где
[± ^	^e^v,, (9.6)
где SDk (дх, v) есть оператор, определенный из A.2); теперь (9.4) можно
записать в виде
\Н(д„ v)u\± = F(z), z6 5,	(9.7)
где F = (Flf F29 F3, F*) и
Fk = -fk + 2^Фк (дг, v) /4, k = 1, 2, 3, F4 = U.	(9.8)
Для видоизменения граничных условий четвертой задачи заметим, что
(vT (дг, v) и) = 2pi (v -^) + X div и.	(9.9)
Принимая во внимание равенство
= -S Ж/(а„ v)f, — K(z)\uv}± + \d\vu\±,
где К (z) — средняя кривизна поверхности 5 в точке г (см. A.20)), и учи-
учитывая (9.9), граничные условия четвертой задачи можно записать в следую-
следующем виде:
= /, {(Я + 2(л) div и — 2jx/C (z) uv\± = /4 + 2ц t Д)у (д„ v)/,.
(9.10)

9] ГРАНИЧНЫЕ СВОЙСТВА ПОТЕНЦИАЛОВ ТРЕТЬЕЙ И ЧЕТВЕРТОЙ ЗАДАЧ 235
Если S? JI2 @) и /6 С1 (S), то (9.2) и (9.10) эквивалентны.
Введем матрицу
R(dx, v) = \Rk,(dn v)||4x3,	(9.11)
где
* [(X + 2|*) JL — 2^/С B) vy] ; (9.12)
тогда (9.10) примет вид
\R(dz, v)u\± = F(z), zeS,	(9.13)
где F = (Flf F2, F3, F4) и
^ = /*, *=lf2f3f /74 = f4 + 2fi|^(a2,v)f/.	(9.14)
2. Потенциалы третьей и четвертой задач и их свойства. Потенциалами,
которые выражают решения третьей и четвертой граничных задач (см. (9.7)
и (9.13)), являются
и (Ф) (*) = J [R (д„ п) Г {у — х)У <р (у) d^S,	(9.15)
v (ф) (х) = ! [Я (ау, я) Г (у — х)]' ф (у) dyS,	(9.16)
где ф = (ф2, ф2, ф3, ф4) и гр = (гр!, \|J, г|K, ty4) — четырехкомпонентные век-
векторы, Удовлетворяющие условиям
?	S = 0f	(9.17)
k =Л	k
S — замкнутая поверхность класса Л2 (а), 0 < а ^ 1,
-х)]' (9Л8)
/-A-6,,)^_^F,^,-^-4-«.т^-п^Ь
«(у —хJ>, (д„ я) л, + б,4 S «,Г«(у—дс); (9.19)
J	t=l
/С (у) — средняя кривизна поверхности 5 в точке у.
Граничные свойства самих потенциалов и (ф) и v (if) для наших
целей несущественны, хотя, как легко видеть, они получаются непосредст-
непосредственно из (9.15) и (9.16), так как слагаемые, входящие в эти потенциалы,
представляют комбинацию потенциалов типа простого слоя и гармонического
потенциала двойного слоя, граничные свойства которых были изучены в
предыдущих параграфах.

236	ТЕОРИЯ ПОТЕНЦИАЛА	[Рд# у
Исследуем граничные свойства векторов
Я (дх, v) и (Ф) (х) = J Я (д„ v) [Я (д„ л) Г (у—х)]' ф (у) dyS, (9 20)
#(д* v)p(f)W = J R (дх, v) [Н(д„ n)T(y — x)]'^(y)duS, (9.21)
S
где Н (дх, v) и R (дх, v) — матричные операторы, определенные из (9.5)
и (9.11), v — орт нормали в точке z? S, а
\Н(дх, v) [R (д„ п)Т(у—х)}'}w =
-5Г (я/л*—6W) ^ 17^
V ВД—х) — п, Уп,Г„&-
2^rt^T?iT-2tA 2
6M A — 6/4) ^ F/7 — щщ) v(
i 91 =1
L
2 y"~x)\: (9-22)
',, п)Г(у — x)]f \k] = A — 8Ы) A — б/4) -r-- [vk (vn) — nk] X
д	l i 1 / с ,	, о i
^
-к.g^-17=17«/(a- »)«,+

с 9] ГРАНИЧНЫЕ СВОЙСТВА ПОТЕНЦИАЛОВ ТРЕТЬЕЙ И ЧЕТВЕРТОЙ ЗАДАЧ	237
п)пМ~
где й>л (дг, v) Vj (k9 j = 1, 2, 3) заданы из A.19).
Учитывая (9.17), (9.22), (9.23) и принимая во внимание граничные свой-
свойства потенциала простого слоя, гармонического потенциала двойного слоя,
производных первого порядка гармонического потенциала простого слоя,
получаем теорему:
9.1. Теорема. Если S? Л2 (а) и фб С0- * E), г|>6 С°><5 E), 0 < р <
<а ^ 1, то для любого z? S существуют \Н (d2, v) и (ф) (г)}± и {R (дг,
v) v (г|)) (z)\±, принадлежат классу Са» $(S) и имеют место равенства
д„ v)[R(dg, n)T(y—z)Y4>(y)duSy
\R(dzt v)v(q)(z)\±= ± ip(z) + \R(d29 v)[H(dy, n)T(y—z)Y^(y)dyS1
еде интегралы в правой части понимаются в смысле главных значений.
3. Теоремы типа Ляпунова—Таубера для потенциалов третьей и четвер-
четвертой задач. Для исследования третьей и четвертой граничных задач полезны
теоремы:
9.2. Теорема. Если S? Л2 (а) и фб C°^(S)9 0 < р < а ^ 1, то
{R (д2, v) и (ф) z)\+ и \R (дг, v) и (ф) (z)\~ существуют, принадлежат
классу С0»!j (S) и
{R (dzy v) и (Ф) (z)l+ = \R (дг, v) и
9.3. Теорема. Если S6 Л2 (а), (г^, гр2, яр3)€ С1' ^ (S), г[Lе С°-р (S),
О < р < а < 1, то \Н (д2, v) и (^) (г)[+ и {Я (d2f v) v (г|)) (г)Г
ствуют, принадлежат классу С0*i3 (S) и имеют место равенства
\Н(д„ v)v(q)(z)\+=\H(dZ9 v)v(^)(z)\~.
Доказательство. Сначала докажем теорему 9.2. Если х? S,
из (9.15) получаем
R @„ v) и (ф) (х) = J R (дх, v) [R (ду, п)Т(у — х)У Ф (у) ^S, (9.24)
где
v)[R(d,9
[з
Г*/ (У — х) — щ S
1
—х)
J
(. 1=1

238	теория потенциала	|РЛ>
— х)— t щ
S v^r,!^—*) — ?
3	I
— 2lxK(z)K(y) S v^ra^ — x) L fe, /=1,4.(9.25)
f, ^=i	J
Принимая во внимание граничные свойства потенциалов простого слоя,
гармонических потенциалов простого и двойного слоев, из (9.24), учиты-
учитывая (9.25), заключаем, что существуют \R(dZ9 v)u(cp)(z)\+ и \R(dz, v) и (ср)(г)Г
и равны друг другу.
Таким образом, теорема 9.2 доказана.
Перейдем к доказательству теоремы 9.3. Прежде всего вычислим
Н (дх, v) v (ty) (х). Из (9.16) после громоздких, но элементарных преобра-
преобразований (см. задачу 4), получим
2 ^
S I	/=1
(9.26)
где А — матрица с элементами
[
3	1
- ж TF^I ®k (дг' v) V/ + 4nii 2 ^{дг' v) v<a>/ (^э л) Л|Г|1 (у ~ х)
—х)\
2
з
/4 ^ "^<Г«(У—«). *, /=Х4. (9.27)

§ 10]	ОБЪЕМНЫЕ ПОТЕНЦИАЛЫ	239**
В силу теоремы Стокса (см. теорема 1.2), имеем
s /«1
S
и формула (9.26) принимает вид
I	/=sb1
(9.28)
Учитывая свойства потенциалов, входящих в (9.28), убеждаемся в су-
существовании \Н (дг, v) v (if>) (z)}+ и {Я (dZ9 v) у (i?>) (z)}~ и в их равенстве
друг другу.
Теорема 9.3. доказана.
4. Формулы Сомилиана для третьей и четвертой граничных задач.
В заключение приведем некоторые формулы, играющие важную роль при
исследовании третьей и четвертой граничных задач,
6{х)и(х)=\\[Н(ду9 п)Г(у — x)]'(R{dyf n)u)+ —
— х)]'(Н(ду9 n)u)+\dyS, (9.29)
r\(x)u(x)=l\[R(dy, п)Г(у—х)]'(Н(ду9 п)и)~ —
s
— x)]'(R(dy, n)u)-\dyS9 (9.30)
где 6 (#) и т) (х) определяются из A.53) и A.54).
Доказательство этих представлений получается из формул Сомилиана,
(см. A.52) и A.54)) обычным путем, если учесть определение операторов Rn H.
Формулы (9.29) и (9.30) остаются справедливыми и для уравнения уста-
установившихся колебаний классической теории упругости, если вместо Г (у — х)
рассматривается матрица Купрадзе.
§ 10. Объемные потенциалы
1. Определения. Элементарные свойства. Объемным потенциалом
будем называть интеграл вида
*(Ф)(*) = j * {х — У) ф (У) dy,	A0.1).
D
где D — некоторая область из ?3» а 2й — одна из матриц фундаментальных
решений, построенных во второй главе.
Таким образом:
1)	2k (х) = Г (#), где Г (х) — матрица Кельвина (см. п. 1, § 1, гл. И),
или
2)	2k (х) = Г (х, со), где Г (х, со) — матрица Купрадзе (см. п. 2, § 1,
гл. II), или

240	теория потенциала	[Гл# v
3)	2k (х) = W (х), где W (х) — матрица фундаментальных решений урав-
уравнений статики моментной теории упругости (см. п. 2, § 2, гл. II), или
4)	2k (х) = ? (х, о), где W (х, а) — матрица фундаментальных решений
уравнений колебания моментной теории упругости (см. п. 1, § 2, гл. И), или
5)	2k (х) = Ф (х, со), где Ф (х, со) — матрица фундаментальных решений
уравнений установившихся термоупругих колебаний (см. п. 1, § 3, гл. II).
Плотность ф = (ф.) —трехмерный вектор в случаях 1) и 2), шестиком-
понентный вектор — в случаях 3) и 4) и четырехкомпонентный вектор —
в случае 5). ф*— вообще комплекснозначная функция (ф, : D —* Z).
Мы будем интересоваться в основном теми случаями, когда D — огра-
ограниченная область с кусочно-гладкой границей S или D — бесконечная
область, являющаяся дополнением до всего пространства замкнутой ограни-
ограниченной области с кусочно-гладкой границей S. В первом случае вместо D
будем писать D+, а во втором —D".
Начнем с изучения интеграла
К (Ф) (х) = I k (х — у) Ф (у) dy.	A0.2)
D+
Из результатов главы IV § 4 непосредственно следует
ЮЛ. Теорема. Если Фб ^i (D+), то К (ф) (х) существует почти
для всех х^ЕУ* и К (<р)? Ьг (D+); /С(ф) (х) существует в каждой точке x?,D~
<D- = E3\D+) и К (Ф)е(> (?Г).
Если ф^ Ьр (D+) и 2р > 3, то К (q>)g С0' »* (D+), где ix — произвольное
число, удовлетворяющее условиям p\i < 2р — 3, \х < 1.
Для наших целей необходимо указать условия, при выполнении которых
К (ф), определенная из A0.2), является регулярной функцией в области D+.
10.2. Теорема. Если ф — ограниченная интегрируемая функция
в области D+ (т. е. ф??«> Ф+))> то К (ф), определенная формулой A0.2),
принадлежит классу С1' »* (D), где D+ — произвольная область из Е3, a \i —
произвольное число из промежутка @, 1); кроме того,
= J
m=1, 2, 3.	A0.3)
Доказательство следует из результатов главы IV, § 2 и из теоремы IV, 1.8.
Из этой теоремы вытекает следующая
10.3.	Теорема. Если ф? L^ (D+) и S? Л1 (а) @ < а ^ 1), то
К (ср) принадлежит классу СЬаE) (точнее, сужение отображения К (у)
на множестве S принадлежит классу С1* а (S)).
2. Вычисление производных второго порядка. Докажем следующее
предложение.
10.4.	Теорема. Если ф? С0- а (D+), 0 < а < 1, то К (ф), опреде-
определенная из A0.2), принадлежит классу С2- а (Q), где Q — произвольная область
из Е3, замыкание которой лежит в D+ (?2czD+) и
II К (ф) ||(Q, г. а) ^ С || ф ||(D+. 0, а).
Доказательство. Рассмотрим случай, когда 2& — матрица
Кельвина (случай 1). Покажем, что в этом случае, при выполнении условий
теоремы, в каждой точке xgD+
J r(x-
J	1
j, m=l, 2, 3,	A0.4)

? JO]	ОБЪЕМНЫЕ ПОТЕНЦИАЛЫ	241
где у (i, т) = || ykj (/, т) Цзхз — матрица, элементы которой определены ра-
равенством
yki (i, /n)= 4
8tp — символ Кронекера, \л' и %'— постоянные, определенные из A1,1.2).
Интеграл в правой части равенства A0.4), который понимается в смысле
главного значения, существует в силу теоремы IV,L14,
Докажем справедливость равенства A0.4). В силу теоремы IV,2.9
— ( I —-г— (У* — х,;)^]фD A0.6)
\c (x, о	'
Вычислим интеграл, стоящий в правой части равенства A0.6), заклю-
заключенный в скобках. Имеем
Г drkf(x — y)	Л,	Л .	Л ._
	_	(х. — у л dtjb = — i
C(x,\)
где
Jii= \ (Xi—yd{Xj —
С (x,1)
Jklmt = \ (Xi — Уд (Xi — yj) (Xk — Ук) (Xm ~ У
С (x, 1)
Введя сферические координаты (см. (IV, 1.12))
у{ = х{ + rF1/sin@<cos9 + 62/:sin'0>sin9-(-63,cos'e<), i = l, 2, 3, A0.7)
легко вычислить Jif и «/^/т/. Получим
Ju = J dy J [бх/бх,- sin2 * cos2 ф + б«ба/ sin2 О sin2 <p +
+ б3?б3/ cos2 'О* + (б1гб2/ + баД/) sin2 ft sin ф cos ф +
+ (в«в8/ + б8 Ay) sin * cos f) cos Ф -f Ff A/ + 88 A/) X
X sin * cos * sin ф] sin ^ dft	y- So,
-Jg- (S
+ 263163/63^63^ + 61 ААабв/п + 6i/63/63Aj6lm + бз^бх/б^б
+ бз^б^б^б^ + 61/62/б1Лб8т + бх А/баА/n + бг.бх/б^б
Следовательно,
J
С (х. 1)
16 В. Д. Купрадзе

242	теория потенциала	[рл# у
Таким образом, формула A0.4) справедлива.
Из формулы A0.4) и из теоремы IV,3.1 следует доказательство теоремы
при 2k (х) = Г (х).
Аналогично доказывается теорема и в других случаях.
Пусть D (дх) обозначает один из матричных дифференциальных опера-
операторов, введенных в первой главе.
Таким образом: 1) D (дх) = А (дх), или 2) D (дх) = А (дх, со), или 3)
D (дх) = М (дх), или 4) D (дх) = М (дх, а), или 5) D (дх) = В (дХУ со).
10.5. Теорема. Если ф^ С0- а (D+), а > 0, то К (ф), определенная
из A0.2), представляет регулярное решение уравнения
<p = 0,	A0.8)
где 2k в A0.2) есть матрица фундаментальных решений уравнения D (дх) и =
= 0, построенная во второй главе.
Регулярность К (ф) была уже показана выше. Покажем справедливость
равенства A0.8). Рассмотрим случай 1), т. е. будем считать D = А и 2k = Т.
Имеем
\А(дх)К},= ^^
m=l	m=\
J
D+ /=1
3
3	\	( 3
D+ /1 Xi	t	il
J
m= 1
3
Г (x —
Интегральный член в правой части исчезает. Кроме того,
3	3
IV (У. /) Ф (x)]t = ^ y<* а. /) Ф* (*) = 4* [ -7Г - 3 (х + If) ]
m= 1	m, /г=1
Учитывая эти формулы и A1,1.2), получим
.3	3
т=1
Отсюда следует A0.8).
Теорема 10.5 доказана при D = А. Аналогично доказывается и для дру-
других случаев.
Можно доказать и более общее предложение.

« JO]	ОБЪЕМНЫЕ ПОТЕНЦИАЛЫ	243
10.6.	Теорема. Если q>^Lp (D+), р > 1, то почти для всех x?D+9
существуют вторые производные интеграла A0.2). Эти производные при-
принадлежат классу Lp (D+) и почти для всех x?D+ выполняется равенство A0.8).
Доказательство следует из теоремы 10.5.
Приведем здесь же непосредственное следствие доказанных выше теорем.
10.6'. Теорема. Если ф^ Loo (D+), то К (ф) — определенная из
A0.2), принадлежит классу С1* а (D+), существуют ее вторые производные
по декартовым координатам, которые принадлежат классу Lp (D+) для лю-
любого р > 1 и почти для всех x?D+ выполняется равенство A0.8).
Аналогично изучается интеграл
/С(Ф)(*)= J k(x — y)<p(y)dy.	A0.9)
D~
В этом случае надо наложить на ф некоторые дополнительные ограниче-
ограничения в окрестности бесконечно удаленной точки. Если ф (*) = 0 для вся-
всякого х в некоторой окрестности бесконечно удаленной точки, то изучение
интеграла A0.9) не отличается от изучения интеграла A0.2).
3. Теорема о распространении функций. В дальнейшем (см. гл. VIII—X)
используется следующее предложение о распространении функций с сохра-
сохранением свойств гладкости.
10.7.	Теорема. Пусть Q и D —области Е3, причем Q с D и граница
dQ области Q принадлежит классу Лг (а), где г — неотрицательное целое
число, а af [0, 1 ]. Если f — функция, определенная на Q (/ : Q —> /?) и
принадлежит классу Сг- а (Q), то существует функция ф, определенная на
D (ф: D —> R) такая, что ф? Cr> a (D) и yx^Q: у (х) = f (x).
Докажем сначала два вспомогательных предложения.
10.8.	Пусть I = (аг, Ьг\ а2, Ь2\ 0, b), I* = (alf bx\ a2, b2, —b, b),
где b, alf а2, bl9 h2 — действительные числа и f?Cr>a (I). Тогда существует
функция ф, определенная на /* и удовлетворяющая условиям: ф(=-Cr«a (/*)
и у x?l: ф (х) = f(x).
В самом деле. Определим г + 1 чисел А,ь Х2, . . ., Хг+1 из линейной
системы уравнений
=l, k = 09 1,2
г.
Эта система однозначно разрешима, так как ее определителем является
определитель Вандермонда.
Распространим / по непрерывности до замыкания множества / и построим
функцию ф на /* следующим образом: yx^I: (p(x) = f(x) и	1*\1
г+1
<р (*)=]!>]
Легко показать, что построенная функция ф осуществляет продолжение,
указанное в 10.8.
Предположим, что /fCr»a(Q).
10.8'. Пусть v#G дп существует окрестность Vy такая, что можно
построить функцию ц>у, определенную на Vy (ф^: Vy —> R) и удовлетворяю*
щую условиям: цу? &•а (Vy) и yx?Vy[)Q : уи (х) = f (x). Тогда суще-
существует функция ф, определенная на Е3 (ф: Е3 —* R), такая, что ф? Cr*a (E2)
и	Q () /()
16*

244	теория потенциала	грл у
Пусть условия предложения 10.8' выполнены, тогда уу? Й существует
шар Ш (у, by) (Sv > 0), такой, что можно построить функцию ф^: Ш (у9
8у) —* /?, обладающую свойством:
у)) и
Если у? Qy то справедливость этого предложения очевидна. Если же y^dQ,
то оно вытекает из условия предложения 10.8'.
Пусть Q — ограниченная область. Тогда из множества [ill (у, -у-)»
«/^QJ можно подобрать конечное число окрестностей Ш1 = Ш (у19
— 6^ \ .,. ., Шк = Ш (yk, убу V объединение которых покрывает й. Тогда
очевидно, Q покрывается также множествами
U Ши U Ш"и
где Ш\ = Ш (yi9 4-8*,), ОП = Ш (yif б,.).
Пусть ф,-: Е3 —> /?, определенная следующим образом: у{ (х) = фу. (х),
если х^Ш\ = Ш (yh 8у.); у{ (х) = / (л:), если х? &\Ш'1 и ф,- (л:) = 0, если
x?E3\(?i\jan)\ очевидно, <pt (х) = f(x), если x^D.
Построим функцию ht: Е3 —» /?, удовлетворяющую следующим усло-
условиям:
he 6 С00 (?3), Vx € Д7,: /i, (х) = 0, Vx 6 Е3\Ш'с: Ы (х)=1.
Введем функции
Нг=1— К H2 = hx{\—h2), ...f Hh = hl...hh_1{\—hk).
Очевидно, Н^С00 (Es) и Ht (х) = 0, если х^Ш} и f >/ или х^Е3\ОП.
Кроме того, #х (х) + • • • + Н{(х) = 1 — ht (х). . . /г, (х) = 1, если х ? Ш}.
Очевидно, Ф/Я/g СГ' а (?3) и Ф*Я, = 0, если д:^ E3\UI'i. Следовательно,
функция ф, определенная на Е3 равенством
k
ф = S ф«#?э
удовлетворяет условиям 10.8'. В самом деле, ф^Сг»а(?8)- Если х? Q, то
Ф« (х) = / (х) для любого i = 1, . . ., k, и поэтому
Докажем теорему 10.7. Пусть у — произвольная точка границы dQ.
Рассмотрим локальную систему координат (у) (см. определение 1.15.5).
Уравнение границы dQ вблизи точки у напишется в виде ?3 = У у (?ъ ?2)»
где уу?Сг>а (т (у, d)). Кроме того, для всех точек | = (Ej, |2, |3) множе-
множества Q^, которое является пересечением цилиндра (см. 1.15.5) с областью Q,
будет выполняться одно из двух неравенств: либо ?3 ^ Чу (li> ?2) либо
?з < 7^ (ii» ^2)- Предположим, что |3 > Y?, (ii. ^2)-
Переход от первоначальной системы к системе (у) осуществляется орто-
ортогональным преобразованием х = /(?, где К — матрица преобразования.
Вместо Еъ ?2> ?з введем новые координаты ?{, ??» ?з формулами
Si = ?1 • S2 = ?2, |з = Ь — Чу (Si , S2).
Тогда

Л JO]	ОБЪЕМНЫЕ ПОТЕНЦИАЛЫ	245
Пусть f* (?ь 12, ?3) = f (*S), а /** (Г) = Г (Si, S2, SS) + 7, (Si, S2).
Очевидно, /*? Сг' а и /**? Сг' а (Q^). В силу 10.8 /** можно продолжить с со-
сохранением класса из Qy на Q*y, где
У, d) и — d<^<d}.
Обозначим эту функцию через ср**.
Таким образом, ф**^Сла в окрестности точки у и ср** (?') = /** (?'),
если |' g Qr
Построим функции
Ф* (g) = Ф** (|ь |2, ?з — т, (Si, S2)), Ф (*) = Ф* (/С1*).
Очевидно, ф* (|) и, следовательно, ф (х) принадлежит классу Cr» a в окрест-
окрестности точки у; кроме того, ф* (х) = f (x), если х? Qy. Теперь доказатель-
доказательство теоремы следует из теоремы 10.8'.
4. Объемные потенциалы с дифференцируемыми плотностями. Приве-
Приведем одно применение теоремы, доказанной в предыдущем пункте.
Пусть ff? Cr> a (D+), S ? Лр (а) (р = г, р = г + 1_или р = г + 2) и
D — ограниченная область из ?3, содержащая в себе D+. Здесь г — целое
неотрицательное число, а а? @, 1).
Продолжим /у из D+ в D с сохранением класса согласно теореме 10.7.
Обозначим полученную функцию через ф7- и рассмотрим объемный потен-
потенциал A0.1).
Из следствия IV.3.11 и формулы A0.4) следует
10.9. Теорема. Если f? Cra (D+) и S^JIP (а), то К (ф), определен-
определенная из A0.1), принадлежит классу С7- a(D+) и
Кроме того, сужение функции К (ф) на S принадлежит классу Ср> а (S) и
Очевидно, К (ф), определенная из A0.1), будет частным решением урав-
уравнения D (дх) и + f = 0 в области D+, когда 2k — матрица фундаменталь-
фундаментальных решений этого уравнения.
5. Характер интеграла типа объемного потенциала вблизи бесконечно
удаленной точки. Пусть D — ограниченное или неограниченное измеримое
множество из m-мерного евклидова пространства Ет. Рассмотрим интеграл
типа объемного потенциала
V(<p)(x)= \u(x — y)q>(y)dy;	A0.10)
\
D
здесь х = (хи . . ., хт), у = (#х, . . ., ут) — точки из Ет\ <р = (ф1э . . ., щ)%
(Pi : D —+ Z к является измеримой и ограниченной на D. Кроме того, в окрест-
окрестности | X | = оо
и = II иц 11'хл, ui}- Ет —> Z. и/у является непрерывной функцией на Ет \{О\.
В окрестности х = 0:
а в окрестности | х | = оо

'246	ТЕОРИЯ ПОТЕНЦИАЛА	[рл у
В этих предположениях существуют такие положительные постоянные р
и ср, что
Д/@, р):
y p):	\ир
>:	|Ф<(*)|^сР, A0.12)
V*6 [?т\Я/ @, р)] ПD:	| Ф/ (х) | <ср\х\-н. A0.1-2')
10.10. Теорема. Если выполнены перечисленные выше условия (см.
A0.11)—A0.12')), то интеграл A0.10) существует в каждой точке х^Ет и
V*е Ет\Ш @, 2р): | V, (ф) W | < с \х \~\
где положительная постоянная с зависит только от р, m, ft0, felf /i.
Доказательство. Предположим, что | jc | > 2р. Представим
5
множество D в виде объединения D = 1ФЬ где
tp), D2 = Dfl [Ш(х, if-)\ZZ/(x,p)], D3 = Dn^@, p),
|x|)\{zZ/(x,i|J-) иЯ/@,р)|1, D5 =
Представим У (ф) в виде
где
/(Л)
Vw(V)(x)= )u(x—t
и оценим V^*> (ф) (ft = 1, . . ., 5).
Пусть y?D-i\ тогда | х — у \ < р и из A0.11) получаем
Кроме того, если y^Dly то | # | >|'#| — р. Следовательно, | у | > р и из
A0.12') следует оценка
Таким образом,
Если y^Du то | t/1 > | х |/2, поэтому
Ср.т,л,Лв.иГ*.	A0.14)
Оценим VB> (ф). Имеем при y^D2i что р < | х — у\. Следовательно, из
A0.11')
\Щ,(х — У)\^ср\х — y\-h\
Кроме того, если у g D2, то | у \ >| х |/2, следовательно, |г/| >р и из A0.12*)
следует оценка
\

* JO]	ОБЪЕМНЫЕ ПОТЕНЦИАЛЫ	247
Теперь для VB) получаем
Vf > (Ф) (х) ^ ср j | х — у Г "Ч У Г* rfy.
Отсюда
\х\
».».*,М • (Ю.15)
Р
Если y?Ds, то р < | х — у |, следовательно,
и I У I < Р> поэтому
Кроме того, если у f D3, то \х — */|>|х| — I */1 > I * I — PJ отсюда
\х — у\ >\х |/2. Поэтому
Если y^D^, то р < | х — у\\ следовательно,
| иц (х — у) | ^ ср | х — у |~~ *•
Кроме того, | у | > р и поэтому
IФ* (у) I ^ со IУI"" •
Таким образом,
Vi4)(<p)M=ssc0 \\x — y\-h'\y
Если у ?¦ D4, то | х — у \ > | х |/2. Поэтому
|У(-4)(ш)(х) I ^c h Ax\~~^ f r~~hrm~x d
Пусть y?Db. Тогда p <\x — y\\ отсюда
I tin (x — y)\ ^ c01 x — у Г*1.
Кроме того, ) у | > 2| х |; следовательно, | у \ > р и из A0.12') следует оценка:
Таким образом,
Г"
j\x — уГн"
^D*;. \x — y\ > \у\ — |дг|; отсюда |*—#|>|#|—	|
Следовательно,
оо
|V!5)(9)(x)|<c0.m^ J ^-^^"^dr^cp.^fe^jjcl^1. A0.18)
2 ) х |
Из A0.14)—A0.18) следует доказательство теоремы.

248	теория потенциала
10.11. Теорема. Если выполнены условия A0.11)—A0.12'), где 0 <
< h < т, 0 < hx < m, h > т — hl9 то
V х 6 Ет\Ш @, 2р): | V, (<р) (х) | ^ с \ х \~а,
где а = min {/i, hly hx + /i — m\.
Доказательство этой теоремы получается точно так же, как в случае
теоремы 10.10.
§11. Библиографические справки
Теории потенциала посвящены многочисленные работы. Отметим неко-
некоторые: Когп [4], Levi [1], Schmidt [1], Lichtenschtein [1], Kellog 11],
Giraud [1,3, 4], Friedrichs [1], Fichera [1,2, 3], Ляпунов [1], Гюнтер [1].
В этих работах в основном изучаются регулярные потенциалы. Регу-
Регулярными называются потенциалы, ядра которых суммируемы и в том случае,
когда точка, являющаяся параметром, принадлежит множеству интегри-
интегрирования.
Значительно меньше работ посвящено сингулярным потенциалам. Потен-
Потенциалы теории упругости, как мы убедились, сингулярные. Достаточно полно
изучены лишь одномерные сингулярные потенциалы. Эти результаты содер-
содержатся в работах Векуа Н. [1], Голузина [1], Магнарадзе [1], Мусхели-
швили [1, 2], Привалова [1], Fichera [1, 2, 31 и др.
Многомерные сингулярные потенциалы изучаются в работах: Бицадзе
[2], Гегелиа 11, 5, 10], Купрадзе [4, 9, 10], Miranda [I], Calderon, Zyg-
mund [3], Giraud [1], Magenes [1].
В. Д. Купрадзе (см. Купрадзе [4,9]) изучил эластопотенциалы простого
и двойного слоя и получил формулы C.5) и E.9), когда плотность принадле-
принадлежит классу С0*13 (S). В работах Гегелиа [1, 5, 6, 8, 10] исследованы эти по-
потенциалы, когда плотность принадлежит классу Lp (S), р > 1 или классам
С"- & (S). В этих же работах изучены дифференциальные свойства потенциа-
потенциалов в замкнутых областях.
Теоремы 2.2 и 2.3 получены в работе Гегелиа [5]; в ней же доказаны
теоремы более общие, чем приведенные в § 2.
Теоремы 2.2 и 2.3 справедливы для потенциалов, представленных инте-
интегралами Лебега—Стилтьеса; такое обобщение имеется в работе Джане-
Джанелидзе [1].
Результаты §§ 4 и 5 содержатся в работах Гегелиа [6, 8, 10] и подробно
приведены в предыдущем издании этой книги (см. Купрадзе и др. [1 ]).
Результаты §§ 6 и 7 приводятся в работах Гегелиа [6, 8, 10], но без
подробных доказательств; доказательство и различные обобщения имеются
в работах Давитадзе [1, 2] и в предыдущем издании книги (см. Купрадзе
и др. [1]).
Теоремы Ляпунова—Таубера для потенциалов теории упругости и дру-
другие аналогичные теоремы доказаны в работах Купрадзе [4, 9] и Башелей-
швили, Гегелиа [2].
Содержание параграфов 1, 5, 6, 7, 8, 9 или вовсе не излагалось в преды-
предыдущем издании книги (см. Купрадзе и др. [1 ]) или приводилось с другими
доказательствами. Приведенное здесь изложение см. Башелейшвили [16, 18].
ЗАДАЧИ
1. Показать, что для S ? Л2 @)
з
где К (у) — средняя кривизна в точке у.

§ И]	БИБЛИОГРАФИЧЕСКИЕ СПРАВКИ	249
2. Показать, что
3	3
(л rot и) = 2 gj 2
3.	Сформулировать и доказать теорему 8.1 для потенциала двойного слоя F.1).
4.	Применяя оператор Ж, доказать, что
д*	[	д д 1	д д	1 i
>	—«I 'длдг* 1# —*l nkdvdzf \у — г\ +
д2	1	а2	1
*1
Г \у-2\ ==dsJ(y)dsk(z) пГ1
5. Показать, что если S ? Л2 @), то
з
t, 1=1
и для сферы радиуса а
a2 a2 =j_
а
6. Показать, что для сферы радиуса а:
Ж"	^	gn
k=\ k
где grt — сферическая функция п-то порядка:
б)	a*MMgn = л (л + 1) gn
где gnj — проекция вектора gn на ось xf-.
7. Показать, что
а)	grad div^ (pn+2gn) = 2p*gn + 2p^ (аж, л (*
4- p2 grad div^ (pngn);
б)	grad div^ (pngn) = np«^n -f Bn — 1) x div^ (p»gn) + (л — 1) Ж (дх, п (х)) (pngn) _
- р2Ж (дх, n (x)) Ж (дх> n (x)) (pngn)y
где х = (*i, x2, x3).
8. Показать, что главный вектор и главный момент от потенциала двойного слоя
(см. F.1)), при 5 ? Лл (а) и ф^ С1. 3 E), 0 < Р <J а ^ 1, вычисляются по формуле
J [Т (dz, v) W (ф)}± dz5 = 0, J [2 х {Г (d2, v) W (Ф)}±] dS =
3	S
= (± 1 — 1) (х — ц) J [ф B) х vj dzS.

Г Л А В A VT
ГРАНИЧНЫЕ ЗАДАЧИ УПРУГОГО РАВНОВЕСИЯ
(СТАТИКА)
В этой главе изучаются шесть основных задач статики, поставленные
8 главе I, § 14. Задачи статики, в известном смысле, являются модельными
для других задач; поэтому в этой главе на примере статических задач под-
подробно будут рассмотрены такие вопросы, как доказательство фредгольмовости
основных сингулярных операторов, различные теоремы вложения, вопросы
корректности и др., имеющие общее значение и применяемые и в других
главах.
§ 1. Граничные задачи для неоднородных уравнений
Пусть S — замкнутая поверхность, ограничивающая конечную об-
область D+ из Е3. Рассмотрим первую внутреннюю основную граничную задачу
статики классической теории упругости — задача (I):
Найти регулярное решение (см. 1,14.1) уравнения
A(dx)v+<p(x) = Ot	A.1)
по граничному условию
v+(z) = O(z\ z?S,
где Ф = (Ф1э Ф2, Ф3) — заданный на 5 вектор, ф = (q>lf ср2, ср3) — объем-
объемная сила, заданная в области D+, а А (дх) — матричный дифференциальный
оператор, определенный в A,12.4).
Если ф?С°'а (D+), а > О, то в силу теоремы V,10.5, К (Ф), опреде-
определенный из (V, 10.2) есть регулярное решение уравнения A.1). Пусть v —
регулярное решение задачи A)+. Рассмотрим вектор
u = v — К(Ф).	A.2)
Очевидно, и является регулярным решением уравнения
A(dx)u = 0,	A.3)
удовлетворяющим граничному условию
и+(г) = ФB)—/c+M(z), *es*
Таким образом, задача A)+ для неоднородного уравнения A.1) при-
приведена к задаче для соответствующего однородного уравнения A.3)
Найти регулярное в области D+ решение уравнения A.3) по граничному
условию
if и /г> ^з) — заданный на 5 вектор.

§ 2]	ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ ГРАНИЧНЫХ ЗАДАЧ	251
Эту задачу будем обозначать символом A)+ ив дальнейшем под A)+
будем подразумевать именно ее.
Заметим, что из теоремы V,10.2 вытекает
1.1. Теорема. Если Sg Лг (а), ф? С'-1 (D+), Ф ? Сг- а (S), г — про-
произвольное натуральное число, 0 < а <: 1, то /, определенный равенством
принадлежит классу Cr> a (S).
Аналогично можно поступить относительно первой внешней граничной
задачи (задача (I)") для области D". В этом случае К (ф) (х), определенный
из (V,10.9), представляет частное решение в D", если ф в окрестности беско-
бесконечно удаленной точки удовлетворяет некоторым дополнительным усло-
условиям (см. V, п. 2, § 10).
Ясно, что аналогично можно поступить и в других случаях (внутренних
и внешних задач, поставленных в гл. I, § 14); поэтому в дальнейшем, если
обратное не оговаривается особо, будем рассматривать только однородные
уравнения.
Таким образом, все граничные задачи первой главы для неоднородных
уравнений приводятся к соответствующим задачам для однородных уравне-
уравнений с помощью объемных потенциалов, свойства которых изучены
8 главе V, § 10.
§ 2. Интегральные уравнения граничных задач
В этой и последующих главах мы будем иногда пользоваться новыми
обозначениями, а именно, V (ф) (х) = V (х\ ф) = V (х), W (ф) (*)= W (х\ ф) =
= W (х) и т. д.
Предположим, S — замкнутая поверхность класса Л, (а), ограничиваю-
ограничивающая конечную (бесконечную) область D+ (D~) из Es, занятую упругой одно-
однородной изотропной средой с постоянными Ламе 1 и ц. Пусть /^С°«^ E),
где 0 < р <а < 1.
ч Решение первой внутренней (внешней) граничной задачи — A)+ ((I)")
ищем в виде потенциала двойного слоя
W(x; <p)=\[T(dy,n)T(y — x)]'q>(y)dySt	B.1)
s
где ф — искомый вектор из класса С0» ^ (S),
^ ]• B-2)
Учитывая граничные свойства потенциала B.1) (см. V,4.2) и граничное
условие задач (II*1, для определения неизвестного вектора ф получим син-
сингулярное интегральное уравнение
Это уравнение будем обозначать символом (I)^ а соответствующее ему
однородное уравнение — (I)?. Относительно двойного знака ^= см. сноску
на стр. 55.

252	граничные задачи упругого равновесия	[Гл. VI
Интеграл, входящий в уравнение A)±, сингулярный в силу теоремы
IV,3.25 и понимается в смысле главного значения.
Если решение первой внутренней (внешней) граничной задачи будем
искать в виде потенциала
U (х; Ф) = J [N (ду, п)Г(у — х)]' Ф (у) dJS9	B.3)
s
где ф — искомый вектор класса С0 (S), а
in ф„ п) г (у- т, -^Khr+ibt-*''(a"n) im ~ T-'VXk)'
l
то, учитывая граничные свойства потенциала B.3) и граничное условие пер-
первой задачи, для определения ф получим интегральное уравнение
=Р Ф (г) + J [N (ду9 п) Г (у — г)Г Ф (у) duS = / (г).	B.4)
Легко заметить, что уравнение B.4) есть интегральное уравнение Фред-
гольма второго рода. Здесь / — заданный вектор класса С0 (S), a S, как
и выше, замкнутая поверхность класса Лл (а).
Решение второй внутренней (внешней) граничной задачи (И)+ ((II)")
будем искать в виде потенциала простого слоя
V (х; я|>) = J Г (х — у) г|) (у) dvS,	B.5)
где г|) (у) — искомый вектор из класса С0- C (S), Sg Лл (а), 0 < Р < а < 1,
а Г (х — у) — матрица Кельвина (см. A1,1.4)).
Учитывая граничные свойства операции Т от потенциала B.5) (см.
(V,5.9)) и граничное условие задачи (II)+((II)~), для вектора а|) получим
интегральное уравнение
± гр (z) 4* \Т (d2t v) Г (z — у) я|) (у) dyS = f (г),
где
>< V* v)k-
Однородное уравнение, соответствующее уравнению (И)*, обозначим
символом (П)о1.
Интеграл, входящий в уравнение (И)*—сингулярный в силу тео-
теоремы IV,3.25 и понимается в смысле главного значения.
Решение третьей внутренней внешней) граничной задачи — (Ш)+
((Ш)~) ищем в виде
и(х\ ф)= J [R{dyt n)T{y — x)]f^(y)dySi	B.7)
где ф = (ф*, ф2, ф3, ф4) — искомый четырехкомпонентный вектор из клас-
класса С0- * (S), 5 ? Л2 (а), 0 < р < а < 1, а матрица [R (ду, п) Т (у — x)Y
определяется из (V,9.18).

Л 2]	ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ ГРАНИЧНЫХ ЗАДАЧ	253
_ Вектор и {х\ ф) действительно является решением уравнения A.3) при
x^S. Для доказательства достаточно показать, что каждый столбец мат-
матрицы [R (ду, п) Г (у— х)]\ рассматриваемый как вектор, является реше-
решением уравнения A.3) при х ф у. Последнее доказывается так же, как в тео-
теореме 11,4.1.
Заметим, что потенциал B.7) не изменяется, если вместо ф внесем век-
вектор яр, равный
з
Ф* = Ф* — я* S Я/Ф/> ?=1,2,3, % = ф4,	B.8)
/1
т. е.
J [/? (ду, п)Т(у — х)У яр (у) d^S = \[R (ду, п)Г(у — х)]' <р (у) dyS.
s	s
Но яр, определенный из B.8), удовлетворяет условию
з
S = 0.
Подчиним вектор ф в B.7) этому условию и в дальнейшем будем счи-
считать, что
3
/г=1
Учитывая теорему V,9.1 и граничное условие задачи (III)* ((Ш)~)
(см. (V,9.7)), для определения вектора ф получим сингулярное интегральное
уравнение
=Р Ф (г) + J H (дг, v) [R (ду, п) Г 0/ — г)Г Ф (У) dyS = F (г),	(Ш)±
где ядро определяется из (V,9.22), интеграл понимается в смысле главного
значения, F (Fl9 F2i F3, F4) — заданный четырехкомпонентный вектор и
F4eOHS), Fkec°**(S)9 k= 1,2, з.
Приняв во внимание тождества (см. (V,9.6) и (V,9.8))
Sv^ca,, v) = o, /=1,2,3, Ьл = о,
будем иметь следующую теорему:
2.1. Теорема. Бся/со решение ф = (ф1э ф2, ф3, ф4) уравнения (Ш)±
з
удовлетворяет условию $j д^ф^ (г/) = 0, у? S.
k=\
Решение четвертой внутренней (внешней) граничной задачи —(IV)+ ((IV)")
ищем в виде
v(x; я|))= J
B.9)
где яр = (ярх, яр2, tp3, tyd — неизвестный четырехкомпонентный вектор
класса С0' <5 E), S^JI2 (а), 0 < р < а < 1, матрица [Н (ду, п) Y (у — х)У
определена из (V, 9.19).
Так же как в случае третьей задачи, можно считать, что вектор tp удо-
3
влетворяет условию 2 nk^>k (у) =. О, y^S.

254	граничные задачи упругого равновесия	[Рл# VI
Учитывая теорему V,9.1 и граничное условие задачи (IV)+ ((IV)~) (см.
(V, 9.13)), для определения вектора i|5 получим сингулярное интегральное
уравнение
[	(IV)±
где ядро уравнения определяется из (V,9.23), интеграл понимается в смысле
главного значения, F (Fl9 F2, FH9 F4)— заданный вектор и Fk^ С1* ° (S),
к = 1, 2, 3, FAeC°^(S).
Совершенно так же, как и выше, учитывая тождества (см. (V,9.12) и
(V.9.14)),
? vtRki (д* v) = 0, /=1,2,3, S v*F* - О,
получим доказательство теоремы.
2.2. Теорема. Всякое решение я|) = (\|)lf г|J, я|K, г|>4) уравнения (IV)*
з
удовлетворяет условию 2 г|5л (у) nk = 0, yf S.
k=\
К рассмотрению задачи (V)+ мы обратимся позже (см. § 5, п. 7).
Решение задачи (VI)+ (см. гл. I, § 14) ищем в виде B.5); для определения
вектора г|р в случае внутренней задачи получим интегральное уравнение
ф(г) + J [Т(дЖ9 v)T(z — y) + a(z)Г (г — у)}ф(у)d^ = / (г), (VI)±
s
а для внешней задачи — уравнение
о
Интегралы, входящие в полученные интегральные уравнения (кроме
B.4)), как отмечалось выше, — сингулярные, и понимаются в смысле глав-
главного значения. Таким образом, получены сингулярные интегральные уравне-
уравнения, распространенные на поверхностях, ограничивающих упругую среду.
Несмотря на это, как будет показано ниже, для этих уравнений справедливы
теоремы Фредгольма. Кроме того, в силу (IV,3.46) и (IV,3.47), операторы,
порожденные левыми частями уравнений A)+ и (II)", (I)" и (П)+, рассмотрен-
рассмотренные соответственно в пространствах L{p\S) и L{p (S), р > 1, \1р + \1р' =
= 1, — взаимно сопряженные, и операторы, порожденные левыми частями
уравнений (Ш)+ и (IV)", (III)" и (IV)+, рассматриваемые соответственно в про-
пространствах Lp4) (S) и L^ (S),— сопряженные по отношению друг к другу.
§ 3. Теоремы Фредгольма и теоремы вложения
Для сингулярных интегральных уравнений, которые получены в пре-
предыдущем параграфе, мы уже доказали основные теоремы Фредгольма в гла-
главе IV, § 7, пп. 6, 7, 9. Здесь будет указан другой способ исследования этих
уравнений.
3.1. Теорема. Каждый из операторов, порожденный левыми ча-
частями (II*1, (И)*, (HiI*1, (IV)^ и (VI)^, принадлежит нормальному типу.
Доказательство. Оператор, порожденный левой частью урав-
уравнения A)+, обозначим через К+. Аналогичный смысл имеют обозначения /С
2 3 4 6
/С*, /С*, /С*, Я*.

К 3]	ТЕОРЕМЫ ФРЕДГОЛЬМА И ТЕОРЕМЫ ВЛОЖЕНИЯ	255
Вычислим символические матрицы этих операторов (см. определение
IV,5.3 и формулу (IV,5.26)). Рассмотрим оператор
h (ф) = — ф (г) + J [Т (ду9 п) Г (у—г)]' Ф (у) dyS.
В главе IV, п. 3, § 5, был указан прием вычисления символа. Для этого
следует представить ядро в виде (IV,3.27) и вычислить характеристику
(см. (IV,5.26) и (IV,5.29)). Требуемое представление ядра фактически было
получено при доказательстве теоремы IV,3.25 (см. замечание IV,3.29).
Предположим, Sg ^\ (а)> ос > 0. Если (/? S и г? S, то
з
S
-z\«, ?=1,2,3,
и согласно B.2) и A1,4.6) имеем
[Т(ди, п)Г(у — г)]'к1 = uki(y, z) + ц (К' — \x')Mki (дг, v), ' ., C.1>
где
«*/(!/. 2N С2B —а, а).
Рассмотрим локальную систему координат — (г) (см. определение
1, 15.5). Формулы преобразования имеют вид
з
Ук^гк+^ак1(г)х\1%	C.2)
где t\l9 т]2, тK — координаты точки у в системе (г).
Пользуясь преобразованием C.2), так же как в главе IV, §§ 3 и 4, можж>
преобразовать Лк] (дг9 v) | у — г\~\ при этом найдем, что для y(-S (г, d)
справедливо представление
з
¦**/ (^ v) | у — z Г1 = g	*
где 8,-^ — символ Леви-Чивита, г] = (т^, г]2, 0).
Учитывая C.1) и C.3), для характеристики оператора К* получим вы-
выражение
где
XU B. 9) = - 6,ft> %+ki (z, в) = ц (V - и') S в,„ («г2 cos 0 + «„ sin 0) =
cosG = т]г ИГ1, sin 9 = % | т) |-' —Ж0^я.
Теперь по формуле (IV,5.26) (см. (IV.5.29)) вычисляется символ опе-
оператора /С+:
o+(z,Q)=\o+ki(z, 0)|зх3,	C.5)

256
ГРАНИЧНЫЕ ЗАДАЧИ УПРУГОГО РАВНОВЕСИЯ
[Гл. VI
где
= i, 2, з.
1
Для детерминанта det a+ (г, 0) имеем
det а+ B, в) = - 1 + i BлK [ - %+ (г, G) J& (г, Э) ^ (г, 0) +
+ хГ2(г, 6) хГз(*. 0) 5Сгз (г. в)] + «я2 {[ij, (z, в)]' + [i[3 (г, в)]
Учитывая C.4) и (V,L26), находим
det a+ (z, 0) = — 1 + 4я2 [|г (V — ц')]2 = — 1 + ^2 (X +
1
Это доказывает, что оператор К+ — нормального типа.
Оператор
fa (z,
0. C.6)
i
является сопряженным для оператора /С+ (см. (IV,3 46), (IV,3.47)) и (см. до-
доказательство теоремы IV,6.1)
det a" B, 9) = det а+ (z, 9) = — 1 + jn2 (Я + 2|ыГ2.
1
Аналогично вычисляется символ оператора К". Имеем
det а" (г, 9) = 1 — ^г2 (А, + 2p,)-2,
2	1
и, так как оператор К+ — сопряженный для оператора /С", то
det a+ (z, 9) = det а" (г, 9) = 1 — fx2 (X + 2ц)~2.
2	1	2
Таким образом, оператор /С", а также /С" и /С — нормального типа.
з
Рассмотрим оператор К*- Символ этого оператора согласно теореме 2.1
и (V,9.22) получаем в виде
о+ (г, 9) =
— 1 0 0 Фг (z, 9)
0—1 0 Ф2 (г, 0)
0 о	— 1 Ф8B, 9)
0 0 0—1
где
Фк (z, 9) = i2n К (z) (ak2 sin 9 — akl cos 9) +
+ S (a/;2sin9 — aa cos
i
,fe=l, 2, 3.

Л 3]	ТЕОРЕМЫ ФРЕДГОЛЬМА И ТЕОРЕМЫ ВЛОЖЕНИЯ	257
Следовательно,
det a+(z, 0) = 1
з
и оператор К* — нормального типа.
4	3
Оператор /С"", сопряженный для оператора /С+, — также оператор нор-
нормального типа.
3	4
Аналогично рассматриваются операторы К" и /С+.
6 6	2 2
Оператор К+ (К") отличается от К+ (К~) вполне непрерывным слагае-
слагаемым и поэтому является оператором нормального типа.
1	2	6
3.2. Теорема. Операторы К*, /С* и /С*— фредгольмовы в простран-
пространстве L{p\S), а операторы /С* и К±— в пространстве Lp*] (S) для любого р > I.
Доказательство. Так как каждый из этих операторов — нор-
нормального типа, то для них справедливы теоремы IV, 6.1, IV, 6.3 и следствие
IV, 6.5. Следовательно, остается доказать, что их индексы в указанных про-
пространствах равны нулю. Для доказательства воспользуемся след-
следствием IV, 6.7.
Рассмотрим оператор
^v (ф) (г) = — ф (г) + 7 J [Т (ду, п) Г (у—г)]' ф (у) dyS,
где у — комплексный параметр. Очевидно, что
det av B,0) =
i	i	i
где Оу (г, 0) — символ оператора К у Таким образом, det av (z, 0) обращается
в нуль только в двух точках,
2) и Tf = -,i
и из следствия IV, 6.7 вытекает, что оператор Ку — фредгольмов при у = I
в пространстве Lp3) (S), т. е. К+ — фредгольмов в пространстве ЬРЪ) (S).
Аналогично доказывается теорема и для других операторов. Докажем
з
ее для /(+.
Рассмотрим оператор
Kv (Ф) (г) = — ф (z) + у I H (дх, v) [R (ду, п) Г (у — г)Г Ф (У)
3	3	3
Очевидно, Кг = К+* Обозначим символ этого оператора через ау (г, 0).
Имеем
det av(z, 0)= 1 Ф О,
з
и, следовательно, из IV, 6.7 следует фредгольмовость оператора Ку при
у= 1.
Из IV, п. 2 § 6, следуют необходимые в дальнейшем теоремы вложения,
3.3. Теорема. Если S^JIr+1(a) и f?Cr>* E), 0<р<а<1,
г — произвольное целое неотрицательное число, то всякое решение
класса ЬРЪ) (S) уравнений (I)*, (II)*, (VI)* принадлежит классу С'* (S).
17 В, Д. Куярадзе

258	граничные задачи упругого равновесия	[Гл# yi
3.4.	Теорема. Если S<E«/7r+2 (а) и f? Cr- e (S), 0 < р < а < 1, то
всякое решение класса Lp4) (S) уравнений (Ш)±, (IV)* принадлежит
классу Cr- P(S).
Доказательство 3.3 и 3.4 следует из теоремы IV, 6.15.
Доказанная в 3.2 фредгольмовость рассматриваемых операторов в про-
пространстве суммируемых функций недостаточна при исследовании класси-
классических задач, поставленных в главе I, § 15. В самом деле, если, например,
Ф есть решение уравнения A)+ класса Lp3) (S), то потенциал W (х\ ф) не будет
непрерывно продолжимым на S и, следовательно, не может представлять ре-
решения задачи A)+. Теоремы, необходимые для исследования классических
задач, могут быть получены из 3.3 и 3.4.
3.5.	Определение. Пусть М и N — линейные операторы, пере-
водящие Сг* $ (S) в себя. Будем говорить, что для уравнений М (ф) = / и
N (ф) = / справедливы теоремы Фредгольма в пространстве Cr* ** (S), если
1)	уравнения
М (ф) = 0 и N (ф) = О
имеют конечное и одинаковое число линейно независимых решений в простран-
пространстве О 3 (S);
2)	для разрешимости уравнения
в пространстве С- ® (S) необходимо и достаточно выполнение условий
где фA>, ф<2>, . . ., ф<п> — полная система линейно независимых решений
уравнения N (ф) = 0 в пространстве Cr* p (S), а (/-Ф(Аг)) — скалярное произ-
произведение векторов f и ф(/г);
3) для разрешимости уравнения
n(v)=и fecr-*(S)
в пространстве Cr» p(S) необходимо и достаточно выполнение условий
f.tf*>)dS = O; ft=l, л,
где a()A), a|)B), . . ., ip(/I) — полная система линейно независимых решений
уравнения М (\р) = 0 в пространстве Сг> &(S).
3.6.	Теорема. Если S ? «Яг+1 (а) и fe Cr* $ (S), 0 < р < а < 1,
г — произвольное целое неотрицательное число, то для уравнений A)+ и (И)",
(I)" и (П)+ справедливы теоремы Фредгольма в пространстве Cr> $ (S).
3.7.	Теорема. Если 5еЛг+2 (а) и f€Cr-*(S), 0 < Р < а <: 1,
г — произвольное целое неотрицательное число, то для уравнений (Ш)+ и
(IV)-, (III)" и (IV)+ справедливы теоремы Фредгольма в пространстве Cr* $ (S).
Доказательство. Пусть S?JIr+1 (а) и / 6 Cr- ^ E). Рассмотрим
1	2
уравнения A)+ и (II)". Операторы /С+ и /С" — взаимно сопряженные в со-
сопряженных пространствах Lp3) (S) и L$,3) (S), где р — произвольное действи-
действительное число больше единицы и г/р -\- \/р' = I.
Из 3.2 следует, что
1) уравнение A)о~ имеет конечное число (обозначим это число через п)
линейно независимых решений — фA), . . ., ф(л) в пространстве Lp3) (S);

* 4]	теоремы о характеристических числах	259
столько же линейно независимых решений я|)A), . . ,, я|)(л) имеет уравне
ние (II)"" в пространстве L{p (S);
2) для разрешимости уравнения (IL" в пространстве Lp3) (S) необходимо
и достаточно выполнение условий
3) для разрешимости уравнения (II) в пространстве L{p E) необхо-
необходимо и достаточно выполнение условий
= 0, k =ТГп.
В силу теоремы 3.3 г|)<*>еСг- & (S) и ф(*>бСг' е (S); * = 1, п, для лю-
любого Р < а. Отсюда следует, что A)+ и (II)" удовлетворяют условиям 1), 2) и
3) определения 3.5.
Теорема 3.6 доказана для уравнений A)+ и (II)".
Аналогично доказывается теорема 3.6 для уравнений A)~ и (И)+ и тео-
теорема 3.7.
Укажем еще раз, что в главе IV, § 7 применимость теорем Фредгольма
к уравнениям A)*, (И)*, (VI)* была показана непосредственно (минуя тео*
ремы вложения); это же можно сделать и для уравнения (IIII1 h(IV)±.
§ 4. Теоремы о характеристических числах
В этом параграфе будет доказано несколько теорем о характеристических
числах уравнений (I )± и (И)*. Эти теоремы обобщают для классической
теории упругости известные теоремы о характеристических числах инте-
интегральных уравнений граничных задач Дирихле и Неймана.
Из граничных свойств потенциалов двойного и простого слоя следуют
равенства:
I [(- 1 + X)W+(z) + A + X)W-(z)) = Ф(z) + X \[T(dyyn)Y{y—z)]'y{y)dyStD.1)
Х){Т(д2, v)V(z)}-} =
D.2)
I	+ \
где Я, и X — взаимно сопряженные комплексные числа, a W и V определены
соответственно из B.1) и B.5).
4.1. Теорема. Все характеристические числа ядра Т (дг> v) Г (г — у)
вещественны.
Допустим противоположное и пусть X — а — ib, где а и Ь — вещественны
и Ъ отлично от нуля, есть характеристическое число ядра Т (д2, v) Г (z — у),
т. е.
ф (z) + X J Т (д„ v) Г B — y)ip (y)dyS = 0.	D.3)
В этом случае X = а + ib будет характеристическим числом ядра
[Т(ди,п)Г(у-г)]',т. е.
Ф (г) + * J [Г (д„ я) Г (у — г)]' <р (у) d^ = 0.	D.4)
17»

260	ГРАНИЧНЫЕ ЗАДАЧИ УПРУГОГО РАВНОВЕСИЯ	[Гл VI
Для данного значения параметра Я уравнение D.3) будет иметь решение
^(z) = %(z) + %(z),	D.5)
не равное тождественно нулю. Построим соответствующий потенциал по
формуле B.5). Имеем V = Vt + iV2. Учитывая D.3) и D.2), получаем
(U + 2а + 1) [Т (дг9 v)V(z)r + (М— 1 — 2ib) [Т (дг, v) V(г)]' = 0, D.6)
откуда следует, что
(АЗЕ + 2а + 1) (TVxy + (АЛ — 1) (TVJ- + 2& GVt)" = 0,	D.7)
(АЛ + 2а + 1) GV2)+ + (М — 1) GV2)~ — 2Ь GVJ- = 0.	D.8)
Умножим эти равенства соответственно на (V2)+ = (V2)~ и (Fx)+ = (Vx)",
составим разность и проинтегрируем по S; тогда, принимая во внимание
формулу (III, 2.1), как в D+, так и в D~, получаем
2Ь | [(^Г GVJ- + (V2T (TV2n dS = 0.	D.9)
Отсюда, так как по предположению Ъ Ф 0, находим
J J- (TVJT + <УР (TVJ-] dS = 0.	D.10)
Учитывая, что Vx (x) и V2 (x) являются регулярными решениями урав-
уравнения А (дх) и = 0 в D" и используя (III, 1.9), получим
J E (V^) dx = 0, \E (V29 V2) dx = 0.
D"
Но в таком случае, вследствие положительности квадратичной формы
Е (V, V), а также по свойствам потенциала B.5), получим
Vi(*) = 0, V2(x) = 0, x
Кроме того, учитывая формулу
(TVky — (TVky = 2фЛ (z), k = 1, 2; z 6 Sf
получаем
Это противоречие доказывает, что Ь = 0 и, следовательно, % — а яв-
является действительной величиной.
4.2. Теорема. Характеристические числа ядер Т (d2, v) Г (г — у)
и [Т (дду п)Т (у — z)Y no абсолютному значению не меньше единицы.
В самом деле, ввиду того, что Ь = 0, из D.6) получаем
f (У1Г Wi)- dS - \ (УгГ (TVtr dS	J E (Vi9 Vt) dx + J E (Vb Vt) dx
л Л i	S	D+	D-
I (Vty (TVtr dS+\
Js	Js
dS+\ (Vt)+ (TVi)+ dS	\e (Vit Vjdx-
Отсюда имеем \а\ > 1 и теорема доказана.
4.3. Теорема. Характеристические числа ядра Т (дг, v) Г (г — у)
являются простыми полюсами резольвенты.

* 5]	СУЩЕСТВОВАНИЕ РЕШЕНИЙ ГРАНИЧНЫХ ЗАДАЧ	261
Допустим противоположное, и пусть, например К = —к0 есть полюс
второго порядка; тогда согласно (IV, 7.64) и (IV, 7.65), будем иметь
= 0,	D.11)
= -J-BB)(z,y). D.12)
Рассмотрим у как параметр. Обозначим
B{k2) (z> у) = г|I (z), в[1) (z, у) = ih (z),
где fe принимает одно из значений 1, 2, 3, и построим потенциалы B.5) с плот-
плотностями, равными гр! (z) и г|;2 (z). Эти потенциалы будут удовлетворять ус-
условиям
tltxHrn^^-lllrvrlkr+wr 1 DЛЗ)
которые вытекают из представления D.2) и уравнения D.11) (первое) и из
D.2) и D.12) (второе).
Умножим первое равенство D.13) на —V 2> второе на Vl9 сложим и про-
проинтегрируем по 5; получим
\E<yX9Vddx— \E(V1,V1)dx = 0;	D.14)
если же первое равенство D.13) умножим на Vx и проинтегрируем по S, то
получим
(l-j-^о) | -?* (Vx, Vx) rfjc -f- A—x0) I E (Уъ Vt) dx = 0.	D.15)
D+	D-
Равенства D.14) и D.15) совместны только в том случае, если
J E (Vlt VJ dx= \Е (Уг, Vt) dx = 0,
D+	D~
откуда следует, что V1 (х) = 0, x?D+ [} D и, следовательно, \рг (z) = 0;
это противоречит предположению о том, что порядок полюса выше единицы.
Теорема доказана.
§ 5. Существование решений граничных задач
1. Задачи A)+ и (П)~. Предположим, S^JI1(a) и докажем, что уравне-
уравнения A)о~ и (И)(Г имеют лишь тривиальные решения в пространстве С0'13 E)
для любого р.
Допустим противоположное и пусть уравнение (П)о~ имеет нетривиаль-
нетривиальное решение г|)(=С°'& (S). Рассмотрим потенциал простого слоя
V(x; y) =
Очевидно,
1)	A(dx)V(x; tj)) = O, xeD
2)	\T(dX9v)VB;jp)f = 09 zeS, V(x;
3)V(x;ip) = O(\xn и	= 0(\х
в окрестности бесконечно удаленной точки.

262	ГРАНИЧНЫЕ ЗАДАЧИ УПРУГОГО РАВНОВЕСИЯ	[Рл Щ
Следовательно, из теоремы III, 1.10 заключаем, что V (х; г|)) == 0 при
'. Но
и в силу теоремы III, 1.6 V (х; я|э) = 0 при x?D+.
Учитывая формулу
\Т(дг, v)V(z', Щ+— {Т (дг, v)V(г; г|))Г = 2г|)(г),
получим г|^ (е) = 0, z?S.
Таким образом, уравнение (Н)<Г имеет только тривиальное решение
в пространстве С0* Р (S); но тогда из теоремы 3.6 следует, что только три-
тривиальное решение имеет и уравнение A)^ в пространстве С0' & (S).
5.L Теорема. Если S6«#i (а) и /? С0» & (S), /по задача (II)" ижеетл
единственное регулярное решение, удовлетворяющее условию (III, 1.8). Кроме
того, это решение дается в виде потенциала простого слоя V (х; \р), где
ty — решение уравнения (II)".
Доказательство. В условиях теоремы уравнение (II)" имеет
единственное решение^ в пространстве С0' P(S). Рассмотрим потенциал V(x;ty).
Очевидно, он представляет регулярное решение задачи (II)" в области D~,
удовлетворяющее условию (III, 1.8). .
Таким образом, существование решения доказано. Единственность была
доказана в главе III, п. 4, § 1.
Выше мы получили, что при S^t/I1 (а) и /6 С0» & (S), 0 < Р <<х < 1,
уравнение A)+ имеет решение ср в классе С0» & (S). Но потенциал W (х; ф)
при фбС°* & (S) не является, вообще говоря, регулярным вектором в D+ и,
таким образом, нельзя утверждать, что он дает решение задачи (I)".
5.2.	Теорема. Если S?JI2 (а) и /6 С1' |3 E), то задача A)+ имеет
решение и притом единственное. Это решение дается потенциалом двой-
двойного слоя W (х\ ф), где ф — решение уравнения A)+.
Доказательство. Из теоремы 3.6 следует, что уравнение A)+
имеет единственное решение ф класса С1- ^ E). В этом случае потенциал двой-
двойного слоя W (х\ ф) представляет регулярное решение задачи A)+ (см. тео-
теорему V, 7.1; впрочем, для этого достаточно, чтобы S ?Лг (а) ). Существование
решения доказано. Единственность следует из теоремы III, 1.6.
Из теоремы 3.6 получить утверждение теоремы 5.2 при менее жестких
условиях относительно S нельзя. Несмотря на это, так же как в случае
задачи Дирихле (см. Гюнтер [1]), можно доказать теорему.
5.3.	Теорема. Если S^JJi (а) и f?Cl>® (S), то существует един-
единственное регулярное решение задачи A)+.
Доказательство приведем несколько ниже.
Используя теоремы 3.6, 5.1, 5.2, 5.3 и V, 7.1, V,7.2, можно заключить
следующее:
5.4.	Теорема. Если S 6Лм (а) и /6 С- е (S) @ < I ^ k + 1), ре-
решение (регулярное при I ^ 1) задачи A)+ существует и принадлежит
классу С1**' (D+) @ < Р'<Р).
5.5.	Теорема. Если S 6 Лм (а) и f? С1- & (S) @ ^ / ^ ft), то ре-
решение задачи (II)" существует, принадлежит классу С/+1< $' (D~) и дается
потенциалом простого слоя V (х\ я|)), где 0 < Р' < р.
2. Задачи (П)+ и A)~. Докажем сначала, что при 8?ЛХ (а) уравне-
уравнения (II)oi~a A)сГ имеют по шести линейно независимых решений, и они состав-
составляют полные системы решений.

с 51	СУЩЕСТВОВАНИЕ РЕШЕНИЙ ГРАНИЧНЫХ ЗАДАЧ	263
Вычислим значение потенциала двойного слоя W (х; ф) при q> = ф</> t
/ = ТГб, где
Ф}%) = в|/ + (Мб/-взА,)У1 +
+ (бзЛ,— MeM + ^iA/-68А/), '=1.2,3. E.1)
Учитывая тождества
, п) Г (у — х)]3* (у2 — х2) — [Т (дуу п)Т(у—x)Jk (уз — х3) =
^ I У —
[7@^ п)Т(у—х)]и(и — *з) — [Т(ду, п)Т(у — x)]3k(у, — хг) =
[Т(ди, п)Т(у—x)]ik{yt — xJ — lT{ду, п)Т(у—x)]lk(y2 — х,) =
где оператор ds . ., fe = 1, 2, 3 определен из (V, 1.10), будем иметь
Wk (х; Ф</>) = J [Г (а„ л) Г (у — х)]1к d,S + хг |б6/ [ [Т (ду, п)Т(у — х)]и dyS —
-	б8/ J [Т{ду, п)Т(у-х)]«dyS) + х21б4/ f [Г(ду, п)Г(у—x)]3kdyS —
-	8bi f [T (д„ п) Г (y-x)Ju dyS] + х3 J6B/j [Т (д„ я) Г (у — x)]u dyS—
- б4/ J [Г (ду, я) Г (у—х)]№ dyS\ + (Я,' - (О X
X
4т
(г/)
Принимая во внимание (V, 2.13) и тождество (см. доказательство фор-
формулы (V, 1.41))
имеем
Г(х;фС/>) = —б(х)ф</)(х), JC6?3,	E.2)
где б (#) определен из (V, 1.53).
Из E.2) при х = 2 6S, получим
J	=0, / =ТД	E.3)
Таким образом, мы доказали, что уравнению AM" удовлетворяют "шесть
линейно независимых векторов

264	ГРАНИЧНЫЕ ЗАДАЧИ УПРУГОГО РАВНОВЕСИЯ	[Гл# yj
Покажем теперь, что эта совокупность образует полную систему решений.
Рассмотрим союзное уравнение (П)о~. Очевидно, оно имеет по крайней мере
шесть линейно независимых решений *ф</> (г); / = 1, 6.
Пусть -фG) (г) есть решение, линейно независимое от предыдущих реше-
решений; тогда
где Cj (/ = 1,6) — произвольные постоянные, также является решением
уравнения (П)о~. Составим потенциалы простого слоя
F(*;f) и V(x;
Как решения однородных задач (П)о\ они представляют некоторые век-
векторы жестких смещений и, следовательно,
V (x; ^) = V (x\ ^<7>) — 2j CjV (x; ty</>) = A + [© x xj,	E.4)
где A (Aly A2, Л3), со = (®l9 co2, co3) — произвольные постоянные векторы,
a x = (xl9 x2i x3). Подберем постоянные cl9 c2f • . ., c6 так, чтобы удовлетво-
удовлетворить условиям
rotV(x;^» ^ —n f	^5'5)
Мы считаем, что начало координат находится в области D*.
Условия E.5) перепишем в виде
Si с, ^Т {у) фЩ) dS = J Г {у) $т (у) dS, |
Sc/1 м(У)Ф(/)(У)dS=\M(у)фЮ(у)dS, j
е/Л^ — символ Леви-Чивита.
Докажем, что детерминант системы E.6) не равен нулю. Допустим про-
противоположное, пусть детерминант системы E.6) равен нулю. Тогда найдутся
постоянные с\9 cl, . ¦ ., cl, которые одновременно не равняются нулю и
удовлетворяют условиям
Введем обозначение:
потенциал простого слоя V (х9 г|)*) удовлетворяет условиям
V(x; if) = Л* -}- [со* х х], хе D+,
еде Л* и со* — произвольные постоянные векторы,
V @; ф*) = 0, roty (*; ф*) |,=о = 0.

§ 5]	СУЩЕСТВОВАНИЕ РЕШЕНИЙ ГРАНИЧНЫХ ЗАДАЧ	265
Отсюда получаем
F(jc;t|)*) = O, xeD+.
Потенциал простого слоя непрерывно «переходит через границу» i>,
принадлежит классу С1* 0 (D~) и на бесконечности удовлетворяет условиям
dV(P	\~% &= 1,2,3.
Применяя теорему III, 1.10, получим
У(х;<ф*) = 0, x
Итак,
Но последнее равенство в силу E.8) невозможно ввиду линейной неза-
независимости векторов г|;^>, я|)<2>, . . ., г|)F). Таким образом, доказано, что де-
детерминант системы E.6) отличен от нуля.
Подставим в E.4) определенные из E.6) постоянные с/: (/= 1, 6); тогда,
на основании E.5) получим
У(*;ф) = 0, xeD*.
Отсюда, так же как и выше, получим
q(z) = ^G) (г) — § с^Щг) = 0, г 6 S,
или
Это противоречие доказывает наше утверждение относительно пол-
полноты aj)<» (z); отсюда следует полнота и системы ф('')(г).
Обратимся к исследованию задачи (П)+ и соответствующего интеграль-
интегрального уравнения
фB)+ f T(dZ9v)T(z — y)y(y)dyS = f(z).	(ИГ
s
По третьей теореме Фредгольма необходимое и достаточное условие
разрешимости уравнения (П)+ имеет вид
= 0, /=1,6,	E.9)
где ф(^ задаются формулой E.1). Подставляя ф('*> в E.9), получаем
з
» = 0, J У. ^ijkyifi (У)dS = 0; &= 1,2,3.	E.10)
условия выражают равенство нулю главного вектора и главного момента
внешних усилий. Необходимость условий E.10) вытекает также из формул
A11,2.1).
Таким образом, имеет место
5.6. Теорема. Если S^JIX (а) и /? С0* & (S), задача (П)+ разрешима
при выполнении условий E.10). Решение представляется потенциалом

266	граничные задачи упругого равновесия	[Гл. VI
простого слоя и определено с точностью до аддитивного вектора жесткого
смещения.
Учитывая теоремы 3.6, 5.6 и V, 7.2, совершенно так же, как и выше, по-
получаем следующий результат:
5.7. Теорема. Если S?Jlk+i (а) и f?Cl*J (S) @ < / ^ k), то ре-
решение задачи (П)+ принадлежит классу Cl+l> 3' (D+) (О < р' < Р).
Для исследования разрешимости задачи A)~, вместо уравнения A)~
рассмотрим следующее уравнение:
Ф (z) + J [Т(ду,п)Т(у — г)]' Ф (У)dyS = F(z),	E.11)
где
F(z) = f(z)— ?
fe
Так как ф(й) и i|)<*> —союзные системы линейно независимых решений,
соответствующих простому полюсу резольвенты (см. теорему 4.3), их можно
считать биортонормированными (см. теорему IV, 7.1). Тогда уравнение
<5.11) разрешимо. Пусть ф есть его решение.
Представим ф(/е) (г) в виде линейной комбинации векторов
= ^ с) \ T(z-
тогда, как нетрудно убедиться, решение задачи A)~ будет иметь вид
6	6
и(х; ц>)= \lT(d99 п)Г(у—х)]' cp(y)dyS+% с, 2 с? f Г (х — yWJ)(y)dyS.
S	k=l	,=1 S
E.12)
Таким образом, доказана
5.8.	Теорема. Если S<E«#2 (а) и f?O** (S), 0 < р <а^ 1, то
задача (I)" имеет регулярное решение и оно представляется в виде E.12).
Полученное решение единственно, несмотря на то, что однородное урав-
уравнение A)о имеет нетривиальные решения. Это вытекает из того, что потен-
потенциалы двойного слоя W (х\ ф(Л))> как регулярные решения задачи A)~,
равны нулю при х 6 D~.
Имеет место
5.9.	Теорема. Если S6«^i (а) и f? С1*|5 (S), то существует един-
единственное регулярное решение задачи A)~, удовлетворяющее на бесконечности
условиям
и = О(\хП, ^ = О(|хГ), Л-1,2,3.
Доказательства теорем 5.9 и 5.3 получаются одновременно.
Рассмотрим потенциал двойного слоя W (x; f). В условиях теорем 5.3
и 5.9, учитывая теорему V, 7.1, имеем W (х; /) ? С1- е' в D+ и в ?Г @ < Р' <
< Р). Таким образом, принимая во внимание теорему V, 7.1 заключаем, что
(TWy = (TW)" и принадлежит классу С0- iV(S). Следовательно, W (x\ f)
в ?)+ и в D~ представляется потенциалом простого слоя. Потенциал простого

§ 5]	СУЩЕСТВОВАНИЕ РЕШЕНИЙ ГРАНИЧНЫХ ЗАДАЧ	267
слоя, совпадающий с W (х; f) в D+, обозначим через Vl9 а тот, который сов-
совпадает с W (х; /) в D", — через V2. Тогда потенциал простого слоя
V = -L{V2-VX)	E.13)
решает одновременно задачи (I)" и A)+.
Действительно, значение на S потенциала Vx равно \W (г; f)}+, а потен-
потенциала V2 равно [W (г; /)}"". Поэтому значение потенциала V на S опреде-
определяется равенством
v_{W(z; f)}~ - {W (г; f)}+ _.
2	*
это доказывает наше утверждение.
Для доказательства теорем 5.3 и 5.9 остается убедиться в том, что Vx
и V 2 принадлежат С1' р/ bD+ ив D~.
Так как V2 является решением задачи (II)",
\T(d»v)Vt(z)\- = T(dt9 v)W(z;f),
где Т (d2, v) W?C°-$(S) и S^JIl(aI то плотность потенциала V2 при-
принадлежит классу С0'fi (S), а 1/2 принадлежит классу С1* р', как bD+, так и bD"".
Докажем, что и V\ принадлежит классу С0^' вО+и вО". Действительно,
l/j является решением задачи (П)+
\T(d29v)V1(z)\+ = T(d29 v)W(z;f).
Пусть V\ — такое решение этой задачи, для которого удовлетворяются
условия
Ki@) = 0f votxV[(x)\x^ = Q.	E.14)
Из теоремы 5.6 следует, что V\ принадлежит классу С1* р/ как в D+,
так и в D~. Кроме того, V\ определен единственным образом в силу E.14).
Далее, очевидно, что
б
где <p(k) (ф^}, ф^Л), ФCЛ)) определены из E.1), a ck — пока произвольные по-
постоянные.
Представим теперь ф(/г) (х) в виде следующей линейной комбинации:
6
ф<*> (х) = ^ c\k) \ г(х — у)V/} (у)d,s, jc
где C/fe) — определенные постоянные.
Учитывая, что Vx (x) = W (х\ /), jc?D+, имеем
б
где
(q, Ci, с3) = В7 @; /), .2 (с4, с5, с6) = rot Г (х;
Так как Jfin 6С°^ (S), / = 1, 6, то V (х\ ф</>) € С1^, как в D+, так
J
и в D", / = 1, 6. Таким образом, Уг?С1*&' и теорема доказана полностью.
Используя теоремы 3.6, 5.8, 5.9 и V, 7.1, имеем теорему
5.10. Теорема. Если S 6 c/7fe+1 (а) и /• ? С- MS) @ < / ^ к + 1),
то решение (регулярное при 1^1) задачи (I)" существует и принадлежит
классу CL*V (D~) @ < |3' < р).

268	ГРАНИЧНЫЕ ЗАДАЧИ УПРУГОГО РАВНОВЕСИЯ	[Гл# VI
3. Другой способ доказательства теорем существования для задач (I)"
и (Н)+. В предыдущем пункте мы убедились, что задача (I)" всегда разре-
разрешима и решение представляется в виде E.12). В этом случае, кроме решения
уравнения (I)", нужно найти также все решения однородного уравнения (II)<f.
Естественно попытаться привести задачу (I)" к интегральному уравнению,
не имеющему собственных вектор-функций. Такое уравнение, кроме того,
удобнее и для численного решения.
Вместо уравнения (П)+ рассмотрим уравнение
я|> (г) + \Т{д„ v) Г (г — у)${у) dyS	±- Т (дг9 v) Г (z)a—
- -{- Т (д„ v) М (г) Ь = f (z), E.15)
где М (z) — матрица, определенная из E.7), SG«/?i (а), /€ С0'|5 E), 0<
<Р <а< 1,
a=\T{y)y{y)dS\ b=\M(у)ф(у)dS.	E.16)
S	S
Покажем, что если уравнение E.15) имеет решение, то необходимо
а=09 6 = 0,	E.17)
если только соблюдены условия равенства нулю главного вектора и главного
момента внешних усилий.
Учитывая E.2) при х == г 6 S и вытекающие из E.2) при x?D+ формулы
J IT (ду, п) Г (у)]' фс/> (у) dS = — 2Ф</> @) = - 2 (81/f б2/, б3/),
J [Т (ду, п)М (у)]' Ф</> (у) dS = —2 rot Ф< /> (х) U=o = — 4 (б4/, б5/, ббу),
а также легко проверяемое тождество
Т (дг, v)T(z — y)ip (у) Ф(/> (г) = [Т (д2, v) Г (г — r/)J' ф<'> (г) ф (у),
из E.15) получаем
fii/fli + б2/«2 + б3/а3 + 64,*! + 65/fe2 + 6вА = J (/' Ф(/)) d<S>
или
J	l	E.18)
где ^/ — вектор
У = {УиУ*> Уз)-
Если главный вектор и главный момент равны нулю, то из E.18) следует
а = 0 и 6 = 0, что и требовалось доказать.
Таким образом, при соблюдении условий равенства нулю главного век-
вектора и главного момента внешних усилий, всякое решение уравнения E.15)
является в то же время решением уравнения (И)+.
Докажем теперь, что уравнение E.15) всегда разрешимо.

Л 5]	СУЩЕСТВОВАНИЕ РЕШЕНИЙ ГРАНИЧНЫХ ЗАДАЧ	269
Рассмотрим для этого однородное уравнение, получаемое из E.15)
при / = 0, и покажем, что оно не имеет отличных от нуля решений. Пусть
t|j* (г) — какое-либо решение этого однородного уравнения. Так как / = О,
то, очевидно, для г|)* (г) выполнены условия E.17). В этом случае полученное
однородное уравнение соответствует граничному условию
Отсюда, применяя теорему III, 1.7, получим
V(x; гр*) = А + [со х xl xeD+f
где Л и (о — произвольные постоянные векторы, а х = (х19 х2, х3). При-
Принимая во внимание, что а* = 6* = 0, получаем А = со = 0, и из предыду-
предыдущей формулы будем иметь
откуда
ф* (г) = 0.
Итак, однородное уравнение, соответствующее уравнению E.15), не
имеет решений, отличных от нулевого.
Следовательно, уравнение E.15) имеет единственное решение ф. Под-
Подставив это значение в E.15), получим решение задачи (П)+, если только со-
соблюдены условия равенства нулю главного вектора и главного момента
внешних усилий.
Решение задачи A)~ ищем в виде
= \
\	J6, E.19)
где
у = J IT (дд9 п) Г (у)]' Ф (у) d^S9 8=1 [Т (ду, п) М (у)]' Ф (у) dJS\
тогда, для определения ф, получаем интегральное уравнение
Ф(г)+ j \Т(ду9п)Т{у— z)]'cp(y)dyS — ±Т(г)у — -f M{zN=f{z). E.20)
Выше мы доказали, что союзное однородное уравнение в простран-
пространстве С0' & (S) имеет только нулевое решение. Отсюда следует, что уравне-
уравнение E.20) всегда разрешимо. Чтобы полученное таким образом решение было
регулярным в D", нужно потребовать f^C1^ (S), S 6 Л2 (а), 0 < Р < а <: 1.
Итак, доказана
5.11. Теорема. Если Sgt/72(a) и f?C1*® (S), mo задача (Г)" имеет
единственное регулярное решение^ представимое в виде E.19) и удовлетворяю-
удовлетворяющее на бесконечности условию (III, 1.8).
Замечание. Выше мы изучали задачи A)+ и (П)+, применяя син-
сингулярные интегральные уравнения. Задачи A)+ и (I)" можно исследовать,
также применяя интегральные уравнения Фредгольма. В этом случае для
задачи A)+ всегда разрешимое интегральное уравнение Фредгольма имеет
вид B.4), а в случае задачи (I)", если решение ищем в виде
U (*; ф) = J 1Щду, п)Т(у — х)]' Ф(у)dyS—±-Y (x)а,
где
i= \[N(dy9n)T(y)Yv
..j,

270	граничные задачи упругого равновесия	[Гл# VI
для определения q> получаем разрешимое всегда интегральное уравнение
Фредгольма
[ lN(dy, п)Г(у— z)Y Ф {у) dyS—^T{z)a = f(z). E.20')
Доказательство разрешимости полученных интегральных уравнений осу-
осуществляется применением оператора N (см. (I, 13.6) ). Таким путем полу-
получаются другие доказательства теорем 5.2, 5.8, 5.3 и 5.9.
4. Задачи (Ш)+ и (IV)~. Рассмотрим интегральное уравнение (III)jJ"*
Докажем, что если S?JI2 (а) не является поверхностью вращения, то урав-
уравнение (Ш)о~ имеет только тривиальное решение. Допустим, что уравне-
уравнение (Ш)о^ имеет отличное от нуля решение, которое обозначим через ф* (г) =
= (ф*, ф*, фз, фЭ- Так как S^JI2 (а), то из (П1)о\ учитывая теорему 3.7
и используя теорему 4 § 21 из второй главы монографии Гюнтера (см.
Гюнтер [1]), получаем щ? CUa (S) иф^ С0' а (S), k = 1, 2, 3. В этом
случае легко докажем, что смещения и напряжения, соответствующие по-
потенциалу B.7), являются непрерывными векторами вплоть до границы S.
Применяя теорему III, 1.8, получаем и (х\ ф*) = 0, #? D+, если S не
является поверхностью вращения. Отсюда имеем (R (dZ9 v) и (z; ф*))+ = О,
г? S. Принимая во внимание V,9.2 и учитывая III, 1.10, получим и(х\ ф*)=
= 0, х 6 D". Но
0 = (Я (dz, v)u(z\ Ф*)Г — (Я ф„ v) и (z; Ф*)Г = 2Ф* (г).
Итак, уравнение (Ш)о~ имеет только нулевое решение, если S не есть по-
поверхность вращения. Таким образом, имеем
5.12. Теорема. Если S е Л2 (а), /4е С1- * (S), /fee С°-МЯ fe =
= 1, 2, 3, 0 <р <а<1 w S «е является поверхностью вращения, то за-
задача AН)+ имеет единственное регулярное решение, которое дается фор-
формулой B.7).
Рассмотрим теперь случай, когда S является сферой. В этом случае
вместо уравнения (Ш)+, будем исходить из уравнения
где
) + \ Н (дг, v)[R{dy,n)T {у — z)Y 4>(y)dyS-^-H (d29v)M(z)A =
E.21)
А = J \R (dgy п) М (у)]' ф (у) dS (Л4 = 0 в силу теоремы 2.1),
М (у) определено из E.7).
Для сферы из E.21) получаем
з
* - 1. 2, 3.	E.22)
= [ S
5 ь/=1
Уравнение E.21) разрешимо всегда, если 5 есть сфера. В самом деле,
пусть / (z) = 0; из E.22) имеем А = 0; в этом случае согласно теореме
III, 1.8
и(х; ф) = [сох^], *6D+.
Учитывая, что rot и (х\ ф) |x=o = 2со = Л =0, получаем и (х; ц>) =
= 0, х? D+. Отсюда следует ф (z) = 0.

Л 5]	СУЩЕСТВОВАНИЕ РЕШЕНИЙ ГРАНИЧНЫХ ЗАДАЧ	271
Когда S является поверхностью вращения, отЛичной от сферы, можно
считать, что ось вращения совпадает с какой-либо из координатных осей,
в частности, с осью хг\ в этом случае в E.21) надо считать Л2 = А3 = 0.
При этом разрешимость уравнения E.21) доказывается совершенно анало-
аналогично предыдущему.
Итак, если S — поверхность вращения, отличная от сферы, для суще-
существования регулярного решения в условиях теоремы 5.12 требуется ра-
равенство нулю главного момента относительно оси вращения; в этом случае
смещения не определяются однозначно внутри D+ и допустимо жесткое
вращение тела, как целого, вокруг оси вращения; если же границей яв-
является сфера, то для существования решения задачи (Ш)+, требуется ра-
равенство нулю главного момента внешних усилий; в этом случае допустимо
жесткое вращение вокруг центра.
Решение задачи (IV)" ищем в виде
v(x; ф) = f \Н (ду, п) Г (у—х)]' ty(y) dJS—-~- М (х) В,	E.23)
где
В = J [Я (ду9 п) М (у)]' г|) (у) dSf (В4 = 0 в силу теоремы 2.2);
для определения гр имеем уравнение
E.24)
Это уравнение разрешимо всегда, так как союзное однородное уравнение
имеет лишь тривиальное решение. В случае поверхности, которая не яв-
является поверхностью вращения, в E.24) следует считать В = 0. Таким обра-
образом, справедлива
5.13. Теорема. Если Se Л2 (а) и fk? С1- f3'E), * = 1, 2, 3,
/46 С°-Р (S), 0 < Р <а ^ 1, то задача (IV)" имеет единственное регуляр-
регулярное решение, которое имеет вид E.23). В том случае, когда S не является
поверхностью вращения, В = 0.
5. Задачи (III)" и (IV)+. Для задач (III)" и (IV)+ мы получили интег-
интегральные уравнения
+ [ Я(дг, v)[R (д99п)Т(у — г))' Ф(у)dyS = /(г),	(III)-
Доказывается, что интегральные уравнения (III)"и (IV)+ имеют един-
единственные р'ешения. Рассмотрим, например, (III)". Допустим, что (III)o~
имеет ненулевое решение ф* (г); тогда, так как S ^ Л2 (а), будем иметь
Ф4 6 С1' * E) и ф** е С0' 3 (S), k = 1, 2, 3, 0 < р < а ^ 1. В этом случае
смещения и напряжения непрерывны вплоть до границы S и удовлетворяют
на бесконечности условию (III, 1.8). Применяя теорему III, 1.10, получаем
и(х; ф*) = 0, x?D-.

272	гранитные задачи упругого равновесия	[Гл# VI
Принимая во внимание теорему V, 9*2, и применяя III, 1.6, получаем
и (х\ ф*) = 0, х 6 D+. Но тогда
0 = (Я (д„ v)u(z; Ф*)Г — (Я (дг, v) и (г; Ф*))+ = 2Ф* (г).
Итак, справедлива
5.14.	Теорема. Если 5 ? Л2 (a)9fke С0--3 E), А = 1, 2, 3, f4 €
€ С1-!5 E), 0 < р <а <; 1, то задача (III)" имеет единственное регулярное
решение, которое дается формулой B.7).
5.15.	Т ео р ем а. Если 5?Л2(а), ^^«'(S), ft = 1, 2, 3 и
/4 6 С0- $ E), 0 < р < a ^ 1, то задача (IV)+ имеет единственное регуляр-
регулярное решение, которое дается формулой B.9).
6. Задачи (VI)+h (VI)"~, Однородное уравнение (VI)o~ допускает только
тривиальное решение. Пусть это не так и тф* (z) есть некоторое нетривиаль-
нетривиальное решение. Применяя теорему III, 1.6, получим V (х; -ф*) = 0, jc? ^+-
Отсюда, по непрерывности (V (г; я|}*))~ = 0, применяя теорему III, 1.10,
получим V (х; i|>*) = 0, х е D". Так как (Т (д„ v) V (z; <ty*))+— (Т (дг,
v) V (z; г)?*))" = 2if)* (г), то г|э* (z) = 0. Полученное противоречие доказывает
наше утверждение. Заметим, что уравнение, союзное с уравнением (VI)+,
Ф (z) + f \[Т (ду, п) Г (у —г)]' + о' (у) Г (у — г)\ Ф (у) dyS = F (г),
s
решает задачу A)~, если решение задачи (I)" будем искать в виде
и(*;ф)= f \1Т(дд,п)Т(у—хI' + о'(у)Г(у — x)\q>(y)dyS.
s
Аналогичные рассуждения применяются для уравнения (VI)if, и, на
основании теоремы III, 1.10, доказывается, что уравнение (VI)" имеет лишь
тривиальное решение. Заметим, что в этом случае нормаль направлена
из D~ в D+. Если нормаль направлена из D+ в D", то для доказательства
разрешимости задачи (VI)" достаточно, чтобы форма
з
k,j=l
была отрицательно определенной. Заметим, что союзное уравнение (VI)"
решает задачу A)+.
Таким образом, доказана
5.16. Теорема. Если S € Лг (а) и F 6 С0* з (S), 0 < р < a < 1,
mo задачи (VI)+ и (VI)" имеют единственные регулярные решения, которые
представляются потенциалом s простого слоя.
7. Задача (V)+. Пусть 5 — замкнутая поверхность класса Л2 @), огра-
ограничивающая область D+, Sx — некоторая связная часть 5 и 52 = 5X5!.
Замкнутую кривую у на S, общую границу Бг и 52 отнесем к 52, считая St
открытым и S2 замкнутым множеством.
Ищется решение уравнения A.3), непрерывное в D+\y, имеющее непре-
непрерывные первые две производные в Ь+, допускающее применение формул
(III, 2.9) (решение класса В) и удовлетворяющее смешанным граничным
условиям
= 0, zeSlt	E.25)
zeS*	E.26)
где / — вектор класса С0» & E), 0 < р ^ 1.

§ 5]	СУЩЕСТВОВАНИЕ РЕШЕНИЙ ГРАНИЧНЫХ ЗАДАЧ	273
Ниже будет доказана
5.17. Теорема. Если существует вектор /*, определенный на
S? Л2 @), принадлежащий классу С0* & E), совпадающий на S2c вектором f,
и такой, что
3
( fk dS = 0, f У stfkytfi dS = Ot k = 1, 2, 3,	E.27)
то смешанная задача (V)+ имеет решение^ классе В.
Очевидно, теорему 5.17 можно формулировать в терминах механики
следующим образом: если силы класса С°> &(S2), действующие на тело в точ-
точках S2, можно непрерывно дополнить силами из того же класса, приложен-
приложенными к точкам поверхности Sx так, чтобы полная система сил была стати-
статически эквивалентной нулю, то задача (V)+ имеет решение в классе В. '
К поверхности Sr «пристроим» (с соблюдением необходимой гладкости)
поверхность S3 так, чтобы она, кроме точек 7, нигде не встречалась с S2
и чтобы объединение S1[j S3 образовало замкнутую поверхность, огра-
ограничивающую конечную область Dl9 содержащую Z)+. Пусть D2 = D1\L>+
и G (х, у) есть тензор Грина задачи A)+ для области Dx =D+U D2
(см. VII, п. 2, § 1). Сначала допустим, что задача (V)+ в классе В имеет реше-
решение. Применяя к нему, совместно с тензором G (х, у), в котором точку х будем
считать фиксированной в D2, а точку у — пробегающей D+, тождество
J \[Т(ду, n)G(x, y)]fu(y) — G(x, у)Т(ду, п)и\ dyS = 0, xeD2,
и учитывая E.25) и E.26), будем иметь
([Т (ду, п) G (х, у)]' и {у) dyS =\G{x,y)f {у) d,S, x e D2. E.28)
Считая точку х принадлежащей области D2, мы можем рассматривать
равенство E.28) как некоторое функциональное уравнение относительно
и (у). При этом покажем, что если уравнение E.28) имеет решение и (у) =
= w* (у), у 6 52, то вектор и (х), определенный в D+ равенством
и(х) = J [Т(ду, n)G(x, y)]'u* (у) dyS-\G{x, y)f(y)dyS, x?D\ E.29)
будет решением задачи (V)+ в классе В.
Чтобы в этом убедиться, очевидно, достаточно проверить лишь выпол-
выполнение граничных условий E.25) и E.26). Первое из этих условий выполнено
благодаря тому, что G (х, у) и [Т (ду, п) G (x, y)Y равномерно, относительно
у ? S2, стремятся к нулю, когда точка х стремится к точке z ? Sx. Чтобы
показать выполнение условия E.26), заметим, что из E.28) вытекает
D JlTZ^ST{dx9 V) J G (X' У) f {У) dyS =
= Mm Т (дх, v) | [Т (<3V, n) G (x, y)Y и* (у) d^S.
Левая часть этого равенства, по свойствам потенциала простого слоя, су-
существует и принадлежит классу С0'!3 (S2), но тогда, по свойству потенциала
двойного слоя (см. V, 8.3),
lim T (дх, v) [ \T (dUi n) G(х, у)]' и* (у) dyS ==
= lim T(dx,x)\[T(dg,n)G{x,y)]'u*(y)dJS. E.30)
О+э«»гб5	?	?
18 В. Д Купрадзе

274	граничные задачи упругого равновесия	[ГЛф yi
Произведя операцию Т (дХ9 v) над равенствами E.28) и E.29), и учиты-
учитывая кроме соотношения E.30), еще свойства разрыва на границе Т (дх, v)-
операции от потенциала простого слоя, получим {Т (dz, v)u (z)}+ = f (г),
ze s2.
Таким образом, решение задачи (VL сводится к вопросу о разрешимости
функционального уравнения E.28).
Известна следующая теорема Фикера (см. Fichera [31).
5.18. Теорема. Если существуют вектор /, определенный и непре-
непрерывный на S?J12 @), и три вектора ср(А;> (л:), k = 1, 2, 3, определенных
и непрерывных в D+ и имеющих непрерывные первые производные в D+, и при
этом выполнены условия
3)	J
s
4)	J[zt.(<p<*).v) — zk(yW-v)]d2 = 0, i, k= 1,2,3,
где 2 — регулярная замкнутая поверхность, ограничивающая любую под-
подобласть в замкнутой области D+9 v — нормаль в точке z к поверхности S
и cp(fc).v — скалярное произведение, то функциональное уравнение E.28)
имеет решение.
Мы покажем, что если выполнены условия теоремы 5.17, то выполнены и
условия теоремы 5.18, следовательно, разрешимо уравнение E.28); отсюда же,
как показано выше, следует существование решения задачи (V)+ в классе В.
Итак, пусть выполнены условия теоремы 5.17. Будем решать задачу
(П)+ с граничным заданием
(Т(dz, v) V(г; У)У = f (г), z?S.	E.31)
Эта задача исследована выше (см. пункт 2). Пусть %ik (V) — компоненты
тензора напряжения, соответствующего потенциалу простого слоя V (х; Ч?),
т. е. решению задачи (П)+; тогда
D? + ^), i.k- 1,2,3.
В силу теоремы 5.6 xlk (V)eC0-V (D+), i, k = 1, 2, 3 (G < p' < p)
и имеют непрерывные первые производные в ?>+. Кроме того, для z?S,
L т« (V) (z) v* = ^ (z), i=l,2,3;	E.32)
для ?D+
и, если т<1> (F) = (та, тг2, тг8), то
ШутЮ(У) = 0,	E.33)
div (х,т<*) — хк«*>) = л:?Л* EJ V—xkAi (дх) V = 0,	E.34)
откуда для произвольной замкнутой поверхности 2 из D+ имеем
0.	E.35)

к g]	вопросы корректности	275
Но условия E.32)—E.35) совпадают с условиями теоремы 5.18, если
будем считать
ц>(кЦх) = х^(х), хе&+, k=l, 2, 3.
Таким образом, показано, что из условий теоремы 5.17 вытекают усло-
условия теоремы 5.18, и, следовательно, вывод этой теоремы о существовании
решения функционального уравнения E.28). Этим теорема 5.17 доказана
полностью.
§ 6. Вопросы корректности
1. Постановка вопроса. В третьей главе были доказаны теоремы един-
единственности решения основных задач (задачи статики, колебания и динамики)
теории упругости, а в настоящей главе были исследованы и вопросы суще-
существования решений задач статики. Вопросам существования решений задач
колебания и динамики будут посвящены следующие главы.
В этих задачах требуется определение упругого состояния (статиче-
(статического, колебательного или динамического), соответствующего данной мас-
массовой силе по краевым условиям (граничные условия в задачах статики и
колебания и гранично-начальные условия в задачах динамики). Но эти
данные (массовая сила и краевые условия) в технических задачах опреде-
определяются с помощью измерения и содержат некоторую погрешность. В связи
с этим с некоторой погрешностью определяется и упругое состояние.
Из сказанного ясно, что особый интерес для практики представляет
случай, когда малому изменению данных соответствует малое изменение
соответствующего состояния.
Таким образом, кроме доказательства теорем единственности и суще-
существования решений задач, необходимо еще изучение вопроса о непрерывной
зависимости решения от данных. Эти три свойства (единственность, су-
существование и непрерывная зависимость от данных) принято называть
корректностью задачи.
Определение упругого состояния, как это было показано в главе I,
эквивалентно нахождению решения определенного дифференциального урав-
уравнения (система основных уравнений в компонентах смещения), принадлежа-
принадлежащего некоторому классу функций.
Как правило, за этот класс принимается множество регулярных функ-
функций, определенных в области D (занимаемой средой) — в задачах статики
и колебания и в области D х @, оо)—в задачах динамики. Обозначим этот
класс функций через Сг.
Для существования решения указанного класса приходится подчинить
данные некоторым ограничениям-. Например, в задачах статики граничные
данные выбирались из класса Cl>a (S) или С°-а (S) (S — граница среды);
из того же класса выбираются данные в задачах колебаний, а в задачах
динамики к этому требованию добавляется еще требование существования
производных по t до определенного порядка.
Обозначим класс функций, из которых выбираются граничные данные
через С2.
В задачах статики массовую силу мы выбирали из класса C°»a(D).
В задачах колебания (гл. VII) достаточны те же требования, что и в задачах
статики, а в задачах динамики (гл. VIII) приходится выбирать массовую
силу из более узкого класса.
Обозначим через С3 класс функций, из которого выбирается массовая
сила (свободный член уравнения), а через С4 — класс функций начальных
данных.
18*

276	ГРАНИЧНЫЕ ЗАДАЧИ УПРУГОГО РАВНОВЕСИЯ	[Рл# VI
Иногда полезно, кроме классических (регулярных) решений основных
задач теории упругости, вводить в рассмотрение обобщенные решения.
Тогда значительно расширяется класс функций Сг и соответственно классы С2,
С3 и С4. Например, за С2 в задачах статики и колебания можно принять
класс функций, представимых в виде определенных интегралов типа потен-
потенциала с плотностями из класса Lp (S). Тогда за С2 можно принять Lp E),
а за С3 — Lp (D).
Теперь основные задачи теории упругости можно формулировать сле-
следующим образом:
Найти решение и класса Сх основного уравнения по граничным данным f
из класса С2 и массовой силе Ж из класса С3 (в задачах статики и колеба-
колебания) и по начальным данным ф из класса С4 (в задачах динамики).
Поставленная задача будет корректна, если для любого /?С2, Ж^С3
и ер ? С4 существует единственное решение и основного уравнения из класса С1
и, если решение и непрерывно зависит от данных, т. е. «малым изменениям» /,
Ж и ф соответствует «малое изменение» а.
В приведенной формулировке необходимо уточнить смысл понятия
«изменение» /, Ж , Ф и и, С этой целью в множествах функций Съ С2, С3
и С4 вводят метрику — расстояние между элементами. Целесообразно
в каждом множестве ввести свою метрику. Обозначим их соответственно
через рх, р2, р3 и р4.
Пусть данным /A)бС2, Ж{1) ? С3, ФANС4 соответствует решение
иМ ?С1У а данным /<2> gC2, Ж™ 6 С3 и ф<2> 6 С4 —решение и™ еСх. Тогда
можно говорить о непрерывной зависимости от данных, например, в следу-
следующем смысле: пусть для любых /A> е С2, /B>GC2, Ж{1\ Ж^еС3 и *1*
ФB) ? С4 справедлива оценка
Тогда, очевидно, если /A> близка к /<2) в смысле метрики пространства С2,
Ж{1) к Ж{2) в смысле С3 и фA> к фB) —в смысле С4, то решение и^\ соответ-
соответствующее данным /A), Ж{Х), фA) будет близко к решению аB), соответству-
соответствующему данным /B), Ж{2), фB), в смысле метрики пространства Сг.
Вместо этой простой зависимости можно требовать выполнения оценки
где Ф — положительная функция своих аргументов, и
Вводя в множествах Сг, С2, С3 и С4 метрику по-разному, получаем различ-
различное понимание непрерывной зависимости. Может оказаться, что решение
непрерывно зависит от данных в некотором смысле, но не зависит непре-
непрерывно при другом определении этого понятия.
Множества функций С\, С2, С3 и С4 в задачах теории упругости — ли-
линейные множества. В этих множествах можно ввести норму элемента и обра-
обратить их в линейные нормированные пространства. Тогда метрика вводится
естественным образом (если норма элемента f^C2 обозначена символом ||/||2,
то метрика р2 в этом пространстве определяется равенством р2 (/A), fi2)) =
= || /A> —/B) |1г и с ее помощью определится понятие непрерывной зави-
зависимости.
Отметим, что задача о непрерывной зависимости решения от данных
имеет смысл, если заранее доказаны теоремы единственности и существова-
существования решения, точнее, если доказано, что для любых /6С2, Ж ?С3 и ф6^4
поставленная задача имеет решение из класса Clf и оно единственно.

к gj	вопросы корректности	277
Как будет показано ниже, полученные представления решений задач
теории упругости в виде определенных (как правило, интегральных) агре-
агрегатов, а также полученные оценки решений сингулярных интегральных
уравнений (гл. IV) и потенциалов (гл. V) дадут возможность сравнительно
легко установить непрерывную зависимость решений от данных и этим
решить вопрос о корректности поставленных задач.
6.1.	Замечание. В основные уравнения движения входят упругие
постоянные, которые, так же как и данные, получаются из опыта и опре-
определены с некоторой погрешностью. Можно было в задаче о корректности
включить и непрерывную зависимость решений от этих постоянных. Мы
советуем читателю задуматься над этим вопросом. Он интересен и решается
легко.
2. Первая основная задача статики. Исследуем вопрос о корректности
первой внутренней задачи (задача A)+) статики для однородного уравне-
уравнения А (дх) и = 0.
6.2.	Определение. Первая внутренняя задача A)+ (для урав-
уравнения А (дх) и = 0) (т, ос)-корректна (га — произвольное натуральное число,
а ас @, 1)), если: 1) для любого /gCm>a (S) она разрешима, 2) решение
единственно и 3) || и ||(jD+t m% a) ^c \\ f \\{s, m, a> (см. I, 15, 3").
6.3.	Теорема. Если S?JI2 (а), то первая внутренняя задача A, а)-
корректна.
Доказательство. Мы уже знаем (см. теорему VI, 5.2), что
\/f?Cha(S) первая внутренняя задача имеет единственное решение,
которое представляется в виде потенциала двойного слоя
и(х)=\[Т (д„ п)Т(у — х)У ср (у) dyS,
где ф — решение интегрального уравнения A)+ (см. § 2 гл. VI).
В условиях теоремы решение ф интегрального уравнения A)+ (см. IV,
6.15") принадлежит классу Cl'a(S) и справедлива оценка
II ф ||(S. I,a)^c||/||(S, l.a)-
В силу теоремы V, 7.1
Из этих оценок следует доказательство теоремы.
6.4.	Замечание. С помощью теоремы 5.3 можно доказать A, а)-
корректность первой основной задачи и при условии S ? ЛЛ (а).
6.5.	Теорема. Если S^JIm+1(a)t mo первая внутренняя задача
(т, а)-корректна.
Доказательство следует из теорем IV, 6.15" и V, 7.1.
Аналогично исследуется вопрос о корректности первой внешней задачи.
Рассмотрим теперь первую внутреннюю задачу (задача A)+) для неодно-
неоднородного уравнения А (дх) и = Ж*
6.6.	Определение. Первая внутренняя задача A)+ для урав-
уравнения А (дх) и = Ж (m, a, а)-корректна, если: 1) A)+ разрешима для лю-
любого fee™*" (S) и Ж 6 Cm-!'a (D+); 2) решение единственно и 3) || и ||(d+. m, a)<
^ c\f \\(S, т, а) + С || Ж ||(?И-, m_i, а).
Здесь и — решение задачи A)+, соответствующее массовой силе Ж
т — произвольное натуральное число.
6.7.	Теорема. Если S?Jlm+\ (a), то первая внутренняя задача
(m, a, а)-корре.ктна.

278	граничные задачи упругого равновесия	[рл# у]
Доказательство теоремы единственности и существования уже было
приведено выше. Там же было показано, что решение этой задачи представ-
представляется в виде •
и(х)= J [Т(ду, п)Г(у — х)]'у(у) dyS + -^ Jr(x — zK@i0)(z)dz, F.1)
ot
где Do" — произвольная область, содержащая D+, а Ж@) — распростране-
распространение Ж из D+bD$, согласно теоремам V, 7.1, V, 10.4. ср—решение интеграль-
интегрального уравнения
— <р(г)+ \[T(dy,n)T(y — z)Yq>(y)dlS = f(z) — -^- \r(z — x)Ze°(x)dx.
S	+
F.2)
Из теоремы IV, 6.15 следует оценка:
||<P||(S, m, a) ^C||/||(S, m, a) 4~ C\\^\\(D+, m—\, a)*
Отсюда в силу теоремы V. 10.4 получается искомая оценка.
3. Вторая основная задача статики. Совершенно аналогично можно
определить (т, а)-корректность второй основной задачи, но тогда эта за-
задача не будет корректной ни при каких условиях, наложенных на S.
В этом случае не существует решения задачи (П)+ для любого / ? С1» а (S).
Для некоторых f(zCl*a(S) задача имеет бесконечное число решений и не
имеет смысла постановка вопроса о непрерывной зависимости от данных.
Введем подпространство С™«а (S) пространства С71»а (S) следующим
образом:
Qm, a E) — это множество тех векторов из Cm- a (S), которые удовле-
удовлетворяют условиям E.10). Норму элемента из Cf» a (S) определим той же
формулой, что и в Cw'а (S).
Тогда для любого /GCf'a(S) вторая задача разрешима (см. теорему
5.6), но не единственным образом.
Если несколько изменим постановку задачи, то можно добиться и един-
единственности ее решения.
Поставим вторую внутреннюю задачу (задача (П)+) следующим образом:
Найти регулярное решение уравнения А (дх) и = Ж> по граничному
условию (Т (ду, п) и)+ = / и по заданному значению и и rot и в некоторой
точке области D+: и {х°) = a, rot и (х°) = b (x° 6 ?>+)-
Поставленная таким образом задача однозначно разрешима для любого
(S)
Теперь, так же как в случае первой задачи, можно исследовать вопрос
о непрерывной зависимости решения от данных для второй задачи.
Можно было поставить вторую задачу иначе: искать не решение и урав-
уравнения А (дх) и = Ж , а Ти, т. е. вместо смещений искать напряжения.
Тогда для любого /6Cf»a(S) эта задача единственно разрешима, и легко
исследуется непрерывная зависимость решения Ти от данных.
Аналогично исследуется корректность остальных задач статики, а также
задач колебания и динамики.
Нетрудно распространить эти рассуждения для определения коррект-
корректности задач термоупругости и моментной упругости и указать соответству-
соответствующие оценки.

Л 7]	БИБЛИОГРАФИЧЕСКИЕ СПРАВКИ	279
§ 7. Библиографические справки
Для доказательства теорем существования решений граничных задач
упругого равновесия (статика) мы применили аппарат теории многомерных
сингулярных интегральных уравнений и сингулярных потенциалов. При этом,
как мы видели, оказалось необходимым значительное расширение схем
исследования, применяемых в граничных задачах теории гармонических
функций.
Вопросы существования решений граничных задач статики классиче-
классической теории упругости рассматривались и раньше. Фредгольм, Лауричелла,
Марколонго, Коря (см. Fredholm [23, Lauricella [I, 2], Marcolongo [1],
Korn [1, 2]) исследовали первую основную задачу статики. Корн, Боджо,
Вейль (см. Korn [3], Bogio [1], Weyl [1]) рассмотрели также вторую основную
задачу. Эти исследования нельзя считать завершенными. В некоторых из ука-
указанных работ вторая граничная задача приводится к уравнениям Фред-
гольма, но эти уравнения не эквивалентны исследуемой задаче: их ядра весьма
сложны и исследование уравнений не удается. В некоторых же работах игно-
игнорируется сингулярность полученных интегральных уравнений и обращаются
с ними, как с уравнениями Фредгольма (см. Bogio [1], а также позднюю
работу Kinoshita, Mura [1]).
Из более поздних работ следует отметить работы Lichtenstein [1], Шер-
ман [2], Fichera [1]. Первые две относятся к первой задаче, в работе же
Fichera [1] граничные задачи исследуются методом, отличным от метода
интегральных уравнений.
В работах Купрадзе [13, 8, 14] первая и вторая основные задачи впер-
впервые были изучены методом сингулярных интегральных уравнений. Изло-
Изложение этих вопросов, приведенное в §§ 2—5 (пп. 1, 2 и 6), имеется
в работах Купрадзе [8, 13, 16, 14], Гегелиа [8], а также Михлина [11.
Особо следует отметить позднюю работу Купрадзе (см. Купрадзе [18]),
где применением результатов Фикера (см. Fichera [4]) исследуется пятая
задача статики классической теории упругости (см. § 5, п. 7).
Задачи A)+ и A1)+ для областей, ограниченных несколькими замкнутыми
поверхностями, изучены в работах Башелейшвили [3, 11] и Бурчу-
ладзе [11]. Методом, указанным в этой главе, исследованы задачи A)+
и (П)+ для одного частного случая анизотропных тел в работе Кахниа-
швили [1].
Задача AП)+ впервые была поставлена и решена Адамаром (см. На-
damard [1]) для случая упругого круга и шара. В одном частном случае
задача (IV)+ приведена к интегральному уравнению Фредгольма второго
рода в работе Вейля (см. Weyl [1]).
Задачи (II I)* и (IV)* изучены в работе Башелейшвили, Гегелиа [2]
(подробное изложение полученных в этой работе результатов имеется также
в книге Купрадзе и др. [1 ]), а при обобщенной постановке (применением
оператора Т (dZf v)) — в работах Амашукели [1, 2] и Амашукели, Баше-
Башелейшвили, Гегелиа [13 (см. также работы Башелейшвили [5, 9, 11, 12]
и Квиникадзе [1, 2, 3, 4]).
Приведенное в этой главе изложение теории задач (III)* и (IV)*, а также
другой способ доказательства теорем существования для задач A)~ и (Н)+
(§ 5, п. 3) см. Башелейшвили [16, 3].
Задачи (II1, (И)*, (Ш)* и (IV)* для случая упругой сферы эффективно
решены в работах Натрошвили [1, 21 (см. гл. XIV, § 1). Решения этих же
задач внутри и вне m-мерного (т > 2) шара представлены квадратурами
в работе Башелейшвили [171.

280	граничные задачи упругого равновесия	[Гл yi
В заключении отметим, что в формулировке граничных задач статики
(задачи (I)*, (П)±,. . .) мы требовали от искомого вектора регулярность
и теоремы существования были доказаны при определенных условиях глад-
гладкости граничной поверхности и других данных задачи. Если эти условия
не выполняются, то в указанной классической постановке решения могут
не существовать. Тогда полезны общие постановки граничных задач, в ко-
которых ищутся не регулярные, а так называемые слабые или обобщенные
решения. Ценность обобщенных решений заключается в том, что во-первых
доказывается их единственность, и, что особенно важно, при повышении
гладкости данных *?до ^классических требований, они часто обращаются
в классические решения.
ЗАДАЧИ
1.	Доказать, что решение уравнения (П)^\ удовлетворяющее условиям Г if> dS = 0,
[" [г/Х'фЗ dS = 0, есть тождественный нуль.
2.	Доказать, что решение однородного уравнения соответствующего B.4) в области D"
есть тождественный нуль, если S? Л2 (а) и
a) j
s
или
б)
S
3.	Из формул (III, 2.9) показать, что вектор ср = (р^\ где ф^ определен из E.1), удов-
удовлетворяет уравнению (I)jj~ (см. Купрадзе и др. [1 ]).
4.	Доказать, что интегральные уравнения Фредгольма B.4) для области D+ и E.20')
имеют единственные решения при «S? «#2 (а)> /€ ?*' ^ ($)* 0 <5 Р <J ct ^ 1.
5.	Доказать теоремы 5.3 и 5.9 применением потенциала двойного слоя (см. (V, 6.1)) при
к = jlijli' (А/).
6.	Показать, что тензор Грина задачи A)+, составленный регулярным потенциалом
двойного слоя (см. задачу 5), удовлетворяет условию
у х 6 ?>+: f IG (*, у) Г2 dy < А = const.
0+
7.	Исследовать существование решения задачи (V)*.
Указание. Применить соображения и теоремы, используемые в § 5, п. 7.
к
8.	Применением обобщенного оператора Т (dz> v) исследовать граничные задачи
I)* и (IV)* (См. Амашукели [2], Башелейшвили [1, 16], Квиникадзе 11]).

ГЛАВА VII
ГРАНИЧНЫЕ ЗАДАЧИ УСТАНОВИВШИХСЯ
УПРУГИХ КОЛЕБАНИЙ
СО	00	СО	СО	00
В этой главе изучаются задачи колебания A)±, (П)±, (Ш)±, (IV)* и (VI)±,
поставленные в главе I, § 14, п. 1, для того случая, когда исследуе-
исследуемая область, занятая упругой средой, ограничена одной замкнутой по-
поверхностью S класса Лг (а), а >0. Конечную (внутреннюю) область, огра-
ограниченную поверхностью S, обозначим, как выше, через D+, а бесконечную
(внешнюю) — через D'. При этом предполагается, что граничные данные,
а также правые части уравнений, принадлежат классу С1'ав областях их
задания.
§ 1. Внутренние задачи
1. Приведение к интегральным уравнениям. Мы будем (если обратное
не оговаривается) считать дифференциальные уравнения (I, 12.5) однород-
однородными. Этого всегда можно достигнуть (см. VI, § 1) с помощью частного
решения вида
~"(х — у9
где Ж — правая часть уравнения.
00	00
Начнем с рассмотрения задач A)± и (П)±. Будем искать их решения
соответственно в следующем виде:
\Т{дт n)Y(y—x, <u)Yv{y)djSt и (х) = \г{х—у, <o)q>{y)dyS,
где ф и г|) — неизвестные векторы класса С0» ® (S), р > 0.
В силу свойств потенциалов (см. V, §§ 3—5) и граничных условий для
со	со
эадач A)± и (II)- (см. I, § 14, п. 1), будем иметь
=Р ФB) + j IT(д„ п)Т(у — z, со)]' Ф(у)dyS = /(z),
± г|> (z) + | {Г (аг, v) Г (г — у, ©)] г|) (у) d^S = f (z).	(fi)±
Верхний знак соответствует внутренним задачам, нижний — внешним.
Полученные интегральные уравнения, в которых интегралы понимаются
в смысле главного значения, относятся к тому типу сингулярных уравнений,
теория которых изложена в главе четвертой. Точнее, они отличаются соответ-

282	ГРАНИЧНЫЕ ЗАДАЧИ УСТАНОВИВШИХСЯ УПРУГИХ КОЛЕБАНИЙ [рл
ственно от уравнений A)± и (П)±, рассмотренных в главе VI, §3, вполне
непрерывными слагаемыми. Поэтому (см. VI, 3.2) операторы, порожденные
<0	СО	г
левыми частями уравнений A)± и (П)±, суть операторы нормального типа
со	со
и, кроме того, для уравнений A)±и (П)± справедливы теоремы Фредгольма,
СО	©
Рассмотрим задачи (Ш)± и (IV)±. Будем искать их решения соответ-
соответственно в виде
и (х) = J [R (дд, п)Т(у — х, со)]' Ф (у) d?9
и (х) = J \Н ф„ п) Г(у—х, со)]'
где R и Я — операторы, определенные формулами (V, 9.5) и (V, 9.11), ср и
гр — искомые четырехкомпонентные векторы.
Доказывается, что для всяких суммируемых ср и i|), векторы, определен-
определенные предыдущими равенствами, удовлетворяют однородным уравнениям
колебания (см. 1, § 13, п. 1)
А(дх,(о)и(х) = 0
в каждой точке x?E3\S.
Это вытекает из следующих легко проверяемых равенств:
А(дху <о)[#(<5„ п)Т(у — х, со)]' = 0, А(дх, со)|Я(^, п)Т(у—х, со)]'= 0,
если х Ф у. Здесь через 0 обозначены матрицы размеров 3 х4, все элементы
которых равны нулю.
Если воспользуемся записью граничных условий задач (Ш)± и (
принятой в главе V, § 9, и рассуждениями и обозначениями этого пара-
параграфа, для определения искомых векторов ф и i|) получим уравнения
± Ф (г) + [ Н (dzy v) [R {ду, п) Г (у — г, со)]' ф (у) dyS = / (г), (Ш)±
s
=Р tj) (г) + J /? (д2У v) [Я фу, п)Т(у — г% со)]' ф (у) dyS = f(Z). (IV)±
Верхний знак соответствует внутренним задачам, а нижний — внешним.
Эти уравнения отличаются от уравнений AП)±и (IV)±, рассмотренных
в главе VI, только вполне непрерывными слагаемыми, поэтому (см. VI, 3.2)
операторы, порожденные левыми частями, суть операторы нормального
типа и, кроме того, для этих уравнений справедливы теоремы Фредгольма.
Совершенно аналогично к интегральным уравнениям приводятся за-
6)	СО
дачи (VI)+ и (VI)". Будем искать решения этих задач в виде
и(х) = J Г(х — у9 со)ф(у)djS.
s
Для определения искомого вектора i|) получаем уравнения
— уу (o)]^(y)d,? = f(z)y (Vl)±
которые отличаются от сингулярных уравнений, например, главы VI, лишь
вполне непрерывными аддитивными операторами.

К 1]	ВНУТРЕННИЕ ЗАДАЧИ	283
2. Тензоры Грина. Для изучения внутренних задач колебания необхо-
необходимо иметь решения некоторых специальных внутренних задач статики,
которые называются тензорами Грина. Эти тензоры, кроме того, встре-
встречаются и в других задачах (см., например, гл. XI, XII, XIII); здесь мы зай-
займемся их построением.
Первым тензором Грина, или тензором Грина первой основной задачи
статики, называется матрица G(i> (x> у) размера 3x3, зависящая от двух
точек х и у и удовлетворяющая следующим условиям:
1)	для x?D+ и не совпадающей с у, G(d (х, у) удовлетворяет уравне-
уравнению статики
A(dx)G{l)(x, y) = 0;
2)	для граничной точки z?S и y^S
3) в области D+ матрица G(i> (#, у) представляется в виде
О<1) (*, y) = T(x — y) — vii)(x, у),
где 0(D (х, у) — регулярное всюду в D+ решение уравнения
А(дх)и = О.
Ясно, что построение первого тензора Грина приводится к решению
первой основной задачи статики для D+ с неоднородным граничным усло-
условием. Согласно теореме VI, 5.2 эта задача разрешима. Тем самым суще-
существование первого тензора Грина доказано.
Четвертым тензором Грина, или тензором Грина четвертой задачи ста-
статики, называется матрица GD> (х, у) размера 3 хЗ, которая удовлетворяет
указанным выше условиям 1), 3) и условию
2) [R C2, v) GD) B, у)Т = 0, г е S, yiS.
Из теоремы VI, 5.15 следует существование тензора Грина G^ (x, у).
Пусть S не является поверхностью вращения; тогда тензор Грина
третьей граничной задачи можно определить как матрицу GC) (*, у) раз-
размера 3 хЗ, которая удовлетворяет условиям 1), 3) и условию
2) [Н (dz, v) GC) (г, у)]+ = 0, z 6 S, у Z S.
Существование третьего тензора Грина в рассматриваемом случае
следует из теоремы VI, 5.12.
Если ищется тензор Грина шестой задачи GF> (x, у) в области D+, то
условие 2) следует заменить условием
2) [Т(д2, v)GF)(z, y)f + o(z)Gl6)(zt y) = 0,
и существование этого тензора также вытекает из теоремы VI, 5.16.
Сложнее обстоит дело с доказательством существования второго тен-
тензора Грина или тензора Грина второй основной задачи статики в области D+.
Этот тензор нельзя определить, вообще говоря, аналогично первому
тензору, из однородного условия второй граничной задачи, так как в этом
случае пришлось бы для построения t;B> (x> у) решать вторую задачу для
области D+ со следующим граничным условием:
IT (dz, v) оB) B, у)Т = Т (dZ9 v) Г (z — у), г е 5, у е D\

284	ГРАНИЧНЫЕ ЗАДАЧИ УСТАНОВИВШИХСЯ УПРУГИХ КОЛЕБАНИЙ
Но согласно теореме VI, 5.6 такая задача не всегда разрешима. Поэтому
второй тензор Грина, в отличие от первого, определим следующим образом:
1)	для x?D+ и отличных от у9 GB) (x9 у) есть решение уравнения
A(dx)G{2) (х9 у)= ^ X (х) * X (У)>
где X М * X (у) есть матрица {% (х) %1(у)9 х (х) ъ(У)> X (х) ХзШ>
(k)	((k)	(k)	(k) \
a X {x) = VXi (x), X2W» XsWJ» k=\9..., 6, есть совокупность векторов, полу-
полученных ортонормированием в D+ полной совокупности линейно независимой
системы векторов жесткого смещения;
2)	GB) удовлетворяет граничному условию
\Т (dZ9 v) GB) (z, y)]+ = 0, ze S, yeD+;
3)	GB) в области D+ представляется в виде
GB) (х9 у) = П (х, у) — 0B) (х9 у)9
где П (х, у) есть матрица
((!)	B)	C)	\
с, у), П(^, у)9П(х9 у)] = —Г(х — у) —
1 л ik)	(r)	r r (Aj)	(г)
+ T 2 х <*) ¦ х ДО J 1 х ©r<S—ч) x (л) « *ь (l.i)
fe , г=1	D+ D+
A)	B) C)
а 0B) *= @B), 0B), VB)) — регулярная матрица в D+, удовлетворяющая
уравнению
A(dx)vB)(x9 y) = 09 x?D+.
Нетрудно проверить, что при х Ф у
б (k) (k)
А(дх)П(х, у)= ^ %№* х(У);
это есть следствие того, что
^4 C,) х (х) = О, А (дх) )J(x — t)x{l)dt = -2% (х),
(О
Чтобы найти 0B) (х9 у) i = 1,2, 3, т. е. чтобы найти матрицу оB) (л:, у),
очевидно, надо решить следующую граничную задачу:
(О
А (дх) оB) (х9 у) = 0, х9 у 6 ?>+,
(О	<*>
[Т(а2, v) оB) (г, у)]+= Г(а2, v)Ei (г, у)9 zeS (I= 1, 2, 3).
Согласно теореме VI, 5.6, для разрешимости этой задачи необходимо
и достаточно, чтобы
г(д2, v)ri (г, y)){x(z) d2S =
О (Ы, 2,...,6; t = l, 2, 3). A.2)

§ 1]	ВНУТРЕННИЕ ЗАДАЧИ	285
Покажем, что эти условия действительно выполняются в силу выбора
матрицы П (х, у).
Имея в виду определение произведения а * Ь и учитывая равенства
Т (дх> п) % (х) = О, & = 1, 2, . . ., 6, из выражения для П (х, у) получаем
@	(О
Тф„ v)U(z, У)=±-Т(дж, v)T(z — y) —
6
- 4- 2 т (д* v> Jг (z—э V и) х! (у) rfg. A -з)
fe=l	D+
На основании A.3) перепишем условия A.2) в следующем виде:
((т {д„ v) (Г (г — у)) х* (z) dzS —
— 2 J J l7^' v)rB~E) X F))x B)X^(f/LSdi=-0 (r=l,2, ..., 6). A.4)
k=l D+ S
Легко проверить, что
/	(k) \ (r)	(r) (k)
[T(dzt v)T(z — l)% ©J X (г) = {Т(д„ v)T(z — l)Y X (z) X (g).
Поэтому второе слагаемое в левой части A.4) равно
- ЭГ (Х B) d2S J (x © х! (у) dt	A.5)
1	(
^=1
Из формулы общего представления регулярных решений имеем
ЗС(х)= — 4" J [T1^, л)Г(у —х)Г X (У)^Л ^6D+» &==1» 2»--.6, A.6)
.и A.5) принимает следующий вид:
(г) (k)	(k)
2 с [Г) К*)
J % E) x
и, так как совокупность { х J i ортонормирована в D+, предыдущий интеграл
(г)
равен х* (У)- Внеся этот результат в A.4) и учитывая A.6), получаем тож-
тождество. Тем самым показано, что условия A.2) действительно выполняются.
(О
Полученные таким образом векторы аB) (х, у), i = 1, 2, 3, очевидно,
определены с точностью до шести аддитивных векторов жестких смещений.
Поэтому можно нормировать оB) (х, у) так, чтобы соблюдались условия
(О	(*)
Щ2)(х, у) х (x)dx = 09 1= 1,2,3; &=1,2,...,6.
С другой стороны, непосредственно проверяется равенство
J П(^> У) X W^ = 0, i=l, 2, 3; ft=l, 2,..., 6.
D+

286	ГРАНИЧНЫЕ ЗАДАЧИ УСТАНОВИВШИХСЯ УПРУГИХ КОЛЕБАНИЙ [рл#
Чтобы в этом убедиться, достаточно воспользоваться свойством умно-
умножения
а*Ь = \аЬъ ab2> ab3],
где а, Ь, с — произвольные векторы. В силу сказанного будем иметь
г (О	(k)
J GB)(x, у) % (x)dx = 0, i=l, 2, 3; k=l, 2,...,6.	A.7)
D+
Этот вывод второго тензора Грина принадлежит Г. Вейлю [1]. Мы
привели его с некоторыми изменениями и уточнениями.
Совершенно аналогично определяется третий тензор Грина, когда
упругая среда ограничена поверхностью вращения (см. Амашукели [4]).
Тензоры Грина, существование которых мы доказали, обладают свой-
свойством симметрии, а именно:
G(x9 y) = G'(y9x).	A.8)
Это доказывается, как обычно, применением формулы Грина, а в случае
второго тензора^дополнительным использованием условий нормировки A.7).
3. Формулы представлений. Как мы убедились в предыдущем параграфе,
тензоры Грина обладают всеми свойствами фундаментальных решений, ко-
которые были использованы при выводе формул общих представлений регуляр-
регулярных решений (см. (III, 2.5) и (III, 2.6)). Поэтому справедливы также сле-
следующие представления регулярного вектора:
2u{x)= Jg(i,(x, у)(Т{ду, ri)u(y)YdyS—][T{dy, n)GA) (t/, x)]'u+(#) rf«,S—
- J+ GU) (x, y) A idy) и (у) dy; A.9)
2u(x) = | GB) (At, г/) (Т (ду, п)и(y))+ dyS—^T(dy, n) GB) (у, х)]' и*(у) dyS +
6
+ J и (у) 2 (x (у) * (x (x) dy — J GB) (x, у) Л (ay) a (t/) dy. A.10)
Появление дополнительного члена в A.10) связано со свойством 1)
второго тензора Грина GB> (х, у).
Справедливы аналогичные представления с помощью тензоров Грина
GC), GD) и GF). Если и — регулярный вектор, то справедливо, например,
представление
= JgF)(x, у){Т(дУ9 n)u(y))+dyS—\[T(dyt n)Gi6)(y, x)]'u+(y)dyS-
\
— f GF)(xf y)A(dy)u(y)dy. A.11)
Пусть и — решение первой основной задачи статики. Воспользуемся
представлением A.9); в силу свойства симметрии A.8) и свойства 2) первого
тензора Грина будем иметь
2и(х) = - J [Т (дУ9 п) GA) (у, х)Х f (у) dyS.	A.12)

§ и	внутренние задачи	287
На основании этих же соображений решение второй основной задачи
представляется с помощью A.10) в следующем виде:
2u(x)= JGl2)(x,y)f(y)dyS+ ("(</)? %(y)*X(x)dy.	A.12')
Если имеется в виду нормированное решение
= 0, 4=1,2,... ,6,	A.13)
то представление примет вид
\	A.14)
Аналогичные представления справедливы для решения третьей, четвер-
четвертой и шестой граничных задач. Если, например, и есть решение шестой гра-
граничной задачи, то, пользуясь представлением A.11), равенством A.8) и
свойством 2) для G{6) (*> у), а именно:
[Т (ду9 п) GF)Q/, x)Y = — GF)(x, у) а (у),
получим
2и(х)= \G{&)(x,y)f{y)dyS.	A.15)
Из A.12), A.14), A.15) следует справедливость предельных равенств
lim\lT(dy,n)G{l)(y, x)]'f(y)dyS = — 2f{z), x?D\ zeS; A.16)
lim [Т(дхг>v)GB)(x, y)f(y)dyS = 2f(z)>	A.17)
lim (T(dxt v) + a(z)) f GF) (x, y)f (y) dyS = 2f{z).	A.18)
*->*	s
1.1. Замечание. Мы рассмотрели внутренние статические задачи.
Что касается внешних статических задач, то в этом случае существование
тензоров Грина вытекает непосредственно из теорем существования для
вадач (I)", (II)", (III)"» (IV)", (VI)", доказанных в главе VI. При этом еле-
дует иметь в виду, что во второй задаче % (х)=0 и П (*, у) совпадает с^ Г(*—у).
1. 2. Замечание. Вместо второго статического тензора Грина
при изучении второй основной граничной задачи колебания можно восполь-
воспользоваться вторым (динамическим) тензором Грина для уравнения А (дх,
со) и = 0, где со == ш0, со0 > 0. Построение такого тензора проще, так как
не требует дополнительных рассмотрений, которые были привлечены выше
для получения статического тензора. Это связано с тем, что для уравнения
A (dxt too0) и = 0 вторая граничная задача разрешима всегда.
4. Однородные внутренние задачи. Спектр собственных частот. Имея
тензоры Грина для внутренних задач статики, построенные в предыдущих
пунктах, мы можем теперь вернуться к задачам колебания. Покажем, что

288 граничные задачи установившихся упругих колебаний ц*л. VII
(О	со
решения однородных задач колебания A)о и (П)о можно выразить в виде
решения интегрального уравнения
2и(х) — со2 \G(x9y)u(y)dy = 0, x?D\	A.19)
D+
где под G (лс, у) подразумевается G(i) (x, у) или GB> (а:, у) соответственно.
Для этого докажем взаимную эквивалентность однородных задач A)о,
со
(Н)о и соответствующих интегральных уравнений A.19). Из A.9), в котором
первое слагаемое обращается в нуль в силу свойства первого тензора-Грина
и свойства A.8), а второе — в силу граничного условия, получаем
2и (х) = — \G(i) (х, у) А (ду) и (у) dy = co2 J G(n (x> у) и (у) dy.
D+	D+
Переходя ко второй задаче, сначала покажем, что решение однородной
задачи колебания для любого со, отличного от нуля, удовлетворяет усло-
условиям
\u(y)%(y)dy = 0, 6= 1,2,.,,,6.	A-20)
В самом деле, из формулы Грина
D+
= J (v (у) Т (дд, п) и {у)—и (у) Т (ду§ п) v (у)) dJS,
в которую подставим v = % (у), k = 1, 2, . . ., 6, а и (у) будем считать на-
названным выше решением, получим
= 0, 6=1,2,..., 6.
Теперь, обращаясь к формуле A.10), заметим, что уничтожаются первые
три слагаемых; первое — в силу граничного условия, второе — в силу
свойства 2) тензора G<2) (x, у) и третье — в силу A.20); следовательно,
имеем
2и (х) = со2 | GB) (х, у) и (у) dy.	A.21)
Докажем теперь обратное предложение: всякое регулярное решение
уравнения A.19) есть решение соответствующей задачи A)о или (П)о. Для
первой задачи это следует из формулы Пуассона (см. V, 10.5) и граничных
свойств тензора G(i) (x, у); что касается второй задачи, то граничное условие
выполняется в силу свойства G2 (x, у).
Покажем, что и удовлетворяет также уравнению
А(дх,(о)и(х) = 0.
Из A.21), с помощью формулы Пуассона
2А (дх) и = — 2(о2и + со2 | А фх) GB) (x, у) и (у) dy,

ВНУТРЕННИЕ ЗАДАЧИ	289
имеем
2А (дх> со) и (х) = со2 \А (дх) GB) (x, у) и (у) dy.
Но, по определению,
А (дх) GB) (x, y)= S X (*) * % (#)•
Воспользуемся свойством умножения
(a*b)c = {a1(bc), a2(bc), as(bc)) = a(bc),
тогда получим
Но
Ш2 б <*)	Г (Л)
Л (дх, со) а (л) = -^ Д X (*) J 1 (У) и {У) dy.
I
D+
так как всякое решение уравнения
к, у) и (у) dy
в силу A.7) удовлетворяет этому условию.
Уравнение A.19) есть однородное уравнение Фредгольма с симметричным
ядром класса L2. Согласно теореме Гильберта—Шмидта отсюда следует
существование дискретного спектра действительных собственных чисел
или собственных значений параметра со2 для которых интегральные урав-
уравнения A.19) имеют отличные от нуля решения. Эти числа называются соб-
собственными частотами соответствующих однородных задач.
Легко показать, что собственные частоты первой задачи строго поло-
положительны, а для второй задачи — неотрицательны. При этом со = 0 яв-
является собственным числом, которому соответствуют шесть линейно неза-
независимых решений (см. гл. VI, § 5, п. 2). Итак, справедливы следующие
теоремы:
со
1.3. Теорема. Внутренняя однородная задача колебания A)о имеет
дискретный спектр собственных частот, являющихся характеристическими
числами интегрального уравнения
— а>г \G{l)(xty)u(y)dy = 0.
D+
Эти частоты строго положительны.
(О
1.4. Т е о р е м а. Внутренняя однородная задача колебания (Н)о
имеет дискретный спектр действительных собственных частот, являющихся
характеристическими числами интегрального уравнения
2и (х) — со2 | GB) (х, у) и {у) dy = 0.
Эти числа неотрицательны, причем со = 0 есть собственное число
шестого ранга и соответствующие собственные векторы суть векторы
жесткого перемещения.
19 В. Д. Купрадае

290	ГРАНИЧНЫЕ ЗАДАЧИ УСТАНОВИВШИХСЯ УПРУГИХ КОЛЕБАНИЙ
Аналогично исследуются задачи AП)<Г, (IV)o и (VI)o . Рассмотрим,
<*> ,
например, задачу (VI)o. Покажем, что всякое регулярное решение этой
задачи является решением интегрального уравнения A.19), в котором
G (х, у) = GF) (х, у).
В A.11) первые два слагаемых в сумме обращаются в нуль ввиду гра-
ничного условия задачи (VI)o и свойства 2) тензора G{Q) (x, у). Следова-
Следовательно,
2ц (х) — со2 j GF) {х9 у) и (у) dy = 0.
D+
Легко доказать и обратное предложение: всякое регулярное решение
этого уравнения есть решение задачи (VI)o • Это следует из формулы Пуас-
Пуассона (см. V, 10.5).
§ 2. Основные теоремы теории колебаний
1. Первая теорема Ляпунова—Таубера в теории упругости. В теории
гармонического потенциала известны две теоремы о свойствах нормальных
производных потенциала двойного слоя, имеющие важные применения
в теории граничных задач; это так называемые первая и вторая теоремы
Ляпунова—Таубера. Аналогичные теоремы имеют место для потенциалов
двойного слоя в теории упругости. Одна из этих теорем (вторая) непосред-
непосредственно следует из результатов гл. V, § 8, п. 2.
Здесь будет доказана (см. Купрадзе [13], Доманьский [1]) следующая
(первая) теорема:
2.1. Теорема. Если существует один из пределов (TW)+ или (TW)~,
принадлежащий классу С°> а (S), регулярного соответственно в D+ и D~ по-
потенциала двойного слоя W {х\ ф), то существует и другой; при этом имеет
место равенство
(Т (dz, n) W (г; Ф))+ = (Т (dz, n) W (г; <р))-.
Эту теорему будем называть теоремой (первой) Ляпу-
Ляпунова — Таубера в теории упругости.
Согласно теореме II, 1.7, доказательство можно вести без ограничения
общности для случая со = 0.
Пусть, для определенности, существует предел (TW)~.
Построим в D+ потенциал простого слоя
по граничному условию
GV)+ = (TWy.	B.1)
Для неизвестной плотности гр согласно формулам (V, 5.9)	получаем
(д„ v)T(z — y)<p (у) d? = (Г (д29 v) W (z; q>))-.	B.2)
Для разрешимости этого уравнения (см. (VI, 5.10)) необходимо и доста-
достаточно соблюдение условий
0, k=\, ...,6,	B.3)

* 2]	ОСНОВНЫЕ ТЕОРЕМЫ ТЕОРИИ КОЛЕБАНИЙ	291
(fe)
где % (z), k = 1, . . ., 6 — полная система линейно независимых решений
союзного однородного уравнения
X (г) + J (Т (ду, п)Г(у — z))f % (у) dyS = 0.	B.4)
Однородное уравнение, соответствующее B.2), имеет также шесть ли-
нейно независимых решений ib (z)9 k= 1, 2, . . ., 6, и потенциалы простых
слоев с плотностями, равными i|)(z), как решения второй внутренней одно-
однородной статической задачи, представят векторы жестких смещений; легко
(k)
показать, что они линейно независимы и, следовательно, х можно выразить
в виде линейных комбинаций потенциалов V (х\ \f>).
Поэтому условия B.3) можно переписать еще в следующем виде:
\	Q9 *=1	6.	B.5)
s
Согласно V, 3.1 имеем
W (г; Ф) = Ф (z) + J (T (ди, п)Т(у — z))' <p (у) duS.
Рассматривая это равенство как интегральное уравнение относительно ф
при заданном W~ и применяя третью теорему Фредгольма, будем иметь
f (/г)
)JS = 04 k=l ,..., 6.	B.6)
(k)
Так как V (х; •ф) и W {х\ ф) — регулярные в D~ решения уравнений
упругости, то в D" справедлива формула Грина
О = j [v(х-, (ф) А(дх)W(х; ф) — W(х; Ф) А(дх)V(х; ?)] dx =
D-
= J [v~ {у; %]) \Т (дууп) W (у; Ф)Г — W- {у- Ф) [т (дууп) V (у; ^)] } dyS.	B J)
Согласно V, 5.1 имеем
\T(dy,n)V\y\ у)] =[Т(ду, n)V[y; y)\ — 2 ф(у), *=1	6.	B.8)
Но, в данном случае
поэтому из B.8)
Г ( W\Y (ft)
\T(dt,n)V\y,Kf)\ =-2^(y), k=\	6
и, следовательно, ввиду B.6) из B.7) получаем
)v[y; y)\T(dy,n)W(y:q>)]-dyS = 09 Л = 1	6,
что и следовало доказать.
19*

292	ГРАНИЧНЫЕ ЗАДАЧИ УСТАНОВИВШИХСЯ УПРУГИХ КОЛЕБАНИЙ ffn Щ]
Таким образом, доказано существование потенциала простого слоя,
удовлетворяющего граничному условию B.1).
Рассмотрим вектор
= W(x\ ф) — V(x; q)=\y	y
\	, B.9)
Имеем
и согласно B.1) будем иметь
B.10)
Ввиду того, что и есть регулярное в D~ решение уравнений упругости,
его можно выразить с помощью формулы общих представлений, именно:
2и(х) = J {[Т(ду, п)Т(у — х)У и(у) —
— T(x — y)[T(dfpn)u(y)]-\dySi xeD~. B.П)
Составляя разность B.11) и B.9) и учитывая B.10), будем иметь
J \Т{ду, п)Т(у — х)У [и-(у) — Ф(у)]dyS = 0, х6 ?Г.
Перейдя здесь к пределу, приближаясь к граничной точке извне, по-
получим
[и-B)_
+ j [Г фт п)Т{у — г)]' [иг (у) — Ф(у)] dgS = 0, гб 5.
Это однородное интегральное уравнение B.4) и его общее решение
имеет вид
?ck%(y)9 yes.
Поэтому
ck%(z\ zeS.	B.12)
Пусть теперь точка x(zD+\ тогда, очевидно,
0 = j {[Г (ду, п)Т(у — х)У и-(у) — Т(х — у)[Т (ду, п) и {у)]
s
и на основании B.10) и B.12) можем записать
2jCk\[T{dyfn)T(y — x)]'x(y)dyS = 0, xeD\ B.13)

? 2]	ОСНОВНЫЕ ТЕОРЕМЫ ТЕОРИИ КОЛЕБАНИЙ	293
Из формулы общего представления регулярного в D+ решения легко
заключить, что
(/г)	Г	(k)
2X(х) = j [T (д„ п)Т(у—x)Y %{y)dJS% x? D\
следовательно, B.13) принимает вид
W(x;y) — V(x; i|>) + 2 ? cft x(*)= 0, xeD*;
НО
[Tidy, п)х(у)\ =о, yest
и, следовательно,
{TWY = GV)+,
и так как
(ТУГ =
получаем окончательно
(TWY ==
2. Свойства собственных частот и собственных функций. В этом пункте
будет доказано несколько общих теорем, которые лежат в основе теории
граничных задач колебания, как внутренних, так и внешних.
2.2. Теорема. Необходимым и достаточным условием для того,
чтобы уравнение
\	(l)~ B.14)
имело нетривиальное решение, является равенство параметра со2 одной
со
из собственных частот задачи (П)о . Если со2 есть v-кратная собственная
частота для этой задачи, то интегральное уравнение B.14) имеет v ли-
линейно независимых решений и они совпадают с граничными значениями соб-
ственных функций задачи (П)о .
Необходимость. Пусть уравнение B.14) имеет нетривиальное
решение; покажем, что в этом случае со2 есть собственная частота задачи (
Допустим, что это не так, т. е. со2 отлично от собственных частот задачи
0)
(И)о и тем не менее уравнение B.14) имеет нетривиальное решение. Тогда
союзное уравнение
Ф(г)+ J 1Т(д29 v)T(z — y, со)]ф(у)^5 = 0, (И);	B.15)
также допускает нетривиальное решение ср. Рассмотрим потенциал простого
слоя
V(x;<p), xeD+.
Очевидно, этот потенциал есть решение однородной внутренней задачи
о". Но ввиду тоге
частот этой задачи,
(Н)о • Но ввиду того, что, по предположению, со2 отлично от собственных
B.16)

294	ГРАНИЧНЫЕ ЗАДАЧИ УСТАНОВИВШИХСЯ УПРУГИХ КОЛЕБАНИЙ ^рл j
Отсюда по непрерывности потенциала простого слоя и в силу поведе-
поведения на бесконечности по теореме единственности первой внешней задачи
колебания (см. III, 2.13), имеем
V(x; ф) = 0, x6D".	B.17)
Из B.16) и B.17) следует ф (у) = 0, yd S, что противоречит сделанному
допущению.
Достаточность. Пусть со2 есть v-кратная частота задачи A1K*
и и, к = 1, . . ., v — соответствующие линейно независимые собственные
(k)
векторы (решения). Покажем, что граничные значения и+, к = 1, . . ., v
линейно независимы. Пусть это неверно и
Рассмотрим вектор
Тогда А (дх, со) и = 0, и+ = 0, (ТиУ = 0; отсюда на основании формулы
общих представлений регулярных решений имеем и (х) = 0, a:?D+, что
(к)
противоречит линейной независимости и, k = 1, . . ., v.
(/г)
Так как u, k = 1, . . ., v есть решения интегрального уравнения A.19),
со ,
как собственные векторы задачи (И)о , их первые производные по коорди-
координатам в замкнутой области D+ принадлежат классу С°-а. Поэтому из фор-
формулы общих представлений будем иметь
Перейдя в этом равенстве к пределу при х —¦ z, x?D+, z?S, получим
<*) f (fe)
+)) Td)T	)Y+)dS = O4 265, ft=l	v.-
Таким образом, интегральное уравнение B.14) имеет по крайней мере v
(/г)
линейно независимых решений и+ (у)> к = 1, . . ., v.
Покажем, что других линейно независимых решений оно не имеет.
Допустим обратное, и пусть число решений |я этого уравнения больше v,
( К )
jn >v. Тогда союзное уравнение B.15) также имеет \i решений ф, к =
= 1. . . .» |х.
Образуем потенциалы простых слоев
у(;с;(ф), fe=l,...f[i.
Очевидно, они линейно независимы, вместе с системой ф, к = 1, . . ., |Л,
со
и являются решениями задачи (П)о\ которая, однако, допускает только v
линейно независимых * решений, и, следовательно, \х = v.
Теорема 2.2 доказана полностью.

? 2] ОСНОВНЫЕ ТЕОРЕМЫ ТЕОРИИ КОЛЕБАНИЙ	295
2.3. Теорема. Необходимым и достаточным условием для	того,
чтобы уравнение
^	B.18)
имело нетривиальное решение, является равенство параметра со2 одной
со
из собственных частот задачи A)о . Если со2 есть v-кратная собственная
частота этой задачи, то интегральное уравнение B.18) имеет v линейно
независимых решений и они совпадают с граничными значениями Т-операции
со
над решениями задачи A)о .
Необходимость. Поступая так же, как выше, допустим, что со2
не есть собственная частота задачи A)о~, но уравнение B.18) допускает не-
нетривиальное решение ф. Образуем потенциал простого слоя V (х; ф).
со
Этот потенциал решает однородную задачу (П)о~, удовлетворяет на беско-
бесконечности условию излучения и по теореме единственности (см. III, 2.13)
есть тождественный нуль в D~. По непрерывности V (х; ф) является решением
со
и задачи A)о , но со2, по предположению, отлично от собственных частот
этой задачи, и поэтому V (х; ф) = 0, x?D+. Отсюда, очевидно, ф = 0, что
противоречит предположению. Необходимость доказана.
Достаточность. Пусть со2 есть v-кратная собственная частота
со	(Л)
задачи A)о иг/, & = 1, . . ., v — соответствующие линейно независимые
СО	(*)
собственные векторы задачи A)о~. Так как и есть решения интегрального
уравнения A.19), их первые производные принадлежат классу C°'a(S)
и, следовательно, применима формула общих представлений, которая в силу
граничного условия и+ = О будет иметь следующий вид:
(k)	c	Г	(k) 1+
2 и (х) = J Г (х — у, со) [Т (ду, п) и (у)\ dyS, x?D\	B.19)
Воздействуем Г-оператором на обе части этого равенства и перейдем
к пределу из D+; тогда получим
- [т (дг, п (z)) (u\z)}+ + J [T (dz, n (z)) T(z — y, со)] [т\дУ9 п)и\у)]+dyS = 0, zQS.
S
Таким образом, показано, что уравнение B.18) имеет по крайней мере
v линейно независимых решений [Т (д2, п (z)) и (z) ]+.
Линейная независимость последних показывается так же, как и выше.
Покажем, что уравнение B.18) других линейно независимых решений
не имеет. Это можно показать, например, следующим образом. Пусть ф
есть произвольное решение. Потенциал простого слоя V (х; ф), как решение
со
второй однородной внешней задачи (П)о~, удовлетворяющее на бесконечности
условиям излучения, равен в D~ нулю. По непрерывности, в области D+
этот потенциал простого слоя представит регулярное решение первой одно-
со
родной задачи A)о > поэтому
где ck — постоянные.
<*>.

296	ГРАНИЧНЫЕ ЗАДАЧИ УСТАНОВИВШИХСЯ УПРУГИХ КОЛЕБАНИЙ {рл VII
В силу этого
[Т (дг% п (г)) V (z; Ф)]+-[Т {дг, п (г)) V {г; <р)Г = 2Ф (z) = ? ch\ T (dZ9 n (г)) и (г)\ ,
(А)
следовательно, совокупность [Т (дг, п (г)) и (z)I+, k = 1, . . ., v составляет
полную систему линейно независимых решений уравнения B.18), что и
следовало показать. Этим теорема 2.3 доказана полностью.
(д	СО	(О
Аналогичные теоремы справедливы для уравнений (III)o~, (IV)oT, (VI)о".
со
Рассмотрим, например, уравнение (VI)cT- Справедлива следующая
2.4. Теорема. Необходимым и достаточным условием для того,
чтобы уравнение
J [T(d2i n{z))T(z — y, со) +
B.20)
имело нетривиальное решение, является равенство параметра со2 одной
Ш -4-
из собственных частот задачи A)о • ?"^^^ ш2 есть v-кратная собственная
частота этой задачи, то интегральное уравнение B.20) имеет v линейно
независимых решений и они совпадают с граничными значениями Т-опера-
со
ции над решениями задачи A)о .
Доказательство необходимости совпадает с аналогичным местом при
доказательстве необходимости в теореме 2.3. В самом деле, различие состоит
со
лишь в том, что уравнению B.20) соответствует задача (VI)о", подобно тому
со
как уравнению B.18) соответствует задача (П)о~. Но обе эти однородные
внешние задачи допускают лишь нулевые решения в D".
Что касается доказательства достаточности, то и оно аналогично дока-
доказательству достаточности в теореме 2.3, ибо, как очевидно из B.19),
J Г (г — у, <о)[т(ду, n)u(y)]+djS = 0,
s
и, следовательно, уравнение B.20) совпадает с уравнением B.18).
2.5. Теорема. Необходимым и достаточным условием нетривиаль-
нетривиальной разрешимости уравнения
-\\[Т(ду,п)Т(у — *,©)]' +Г (г — у, ©) а (у) \у (у) dyS = 0 B.21)
является равенство параметра со2 одной из собственных частот задачи (VI)о-
со
Если со2 есть v-кратная собственная частота (VI)о", то уравнение B.21)
имеет v линейно независимых решений и они совпадают с граничными зна-
чениями решений задачи ()
Необходимость. Пусть уравнение B.21) имеет нетривиальное
со
решение. Покажем, что о2 есть собственная частота задачи (VI)о". Допустим,
со
что это не так, т. е. со2 отлично от собственных частот задачи (VI)jJ, и тем

§ 2]	OCHOBHblF ТЕОРЕМЫ ТЕОРИИ КОЛЕБАНИЙ	297
не менее уравнение B.21) имеет нетривиальное решение. Тогда союзное
уравнение
<p(z)+J[r(d2, п(г))Т(г — у, а) + о (г) Г (у — г, со)] ц> (у) dyS = О, (VI); B.22)
также имеет нетривиальное решение ср.
Образуем потенциал простого слоя V (х; ф). Этот потенциал представит
со
регулярное в D+ решение задачи (VI)o и, следовательно, V {х\ ср) = 0, так
как, по предположению, со2 отлична от собственных частот.
Повторив теперь не раз примененное рассуждение для плотности по-
потенциала простого слоя, получим ф = 0. Это противоречит допущению и
доказывает необходимость.
Достаточность. Пусть со2 есть v-кратная собственная частота
со	(k)
задачи (VI)o , и а, & = 1, . . ., v — соответствующие собственные векторы.
Очевидно, они линейно независимы. Из формулы общих представлений,
на основании граничного условия
[Т(дЖ9п(г))и(г)\ +o(z)u+(z)=0,
имеем
2и(х) = - J \[Т(ду, п)Т(у — х, со)]' +Г(у — дс, со)а(у)\ u
s
Перейдя здесь к пределу из D+ при х —* г, z?S, получим
(Л)	г	(Ь)
и+(г) + ) \1Т(д99 п)Т(у — г, со)]' +Т(у — г, ю)а((/I a
Так же как выше, показывается, что других решений уравнение B.21)
не имеет, и теорема 2.5 доказана полностью.
3. Теоремы о простоте полюсов резольвенты. В § 4 главы VI было
доказано, что характеристические числа сингулярных интегральных урав-
уравнений основных задач (первой и второй) статики являются простыми по-
полюсами резольвент.
Здесь будут доказаны две аналогичные теоремы для задач колебания.
Рассмотрим этот вопрос относительно первых двух основных задач (см.
задачу 3 в конце настоящей главы).
со
2.6. Теорема. Если со2 есть собственная частота задачи A)о или
(П)о, то соответствующее интегральное уравнение находится на характе-
характеристическом числе и это число есть простой полюс резольвенты.
Доказательство. Первая часть теоремы вытекает из теоремы 2.2
и 2.3. Для доказательства утверждения теоремы относительно полюса ре-
резольвенты допустим обратное, т. е. будем считать, что характеристическое
со
число, например, интегрального уравнения задачи (П)о ,
Ф (z) + J [T {дг, v) Г (г — у, со)] Ф (у) dyS = 0, г 6 5,	B.23)

298	ГРАНИЧНЫЕ ЗАДАЧИ УСТАНОВИВШИХСЯ УПРУГИХ КОЛЕБАНИЙ (рл VII
есть полюс га-го порядка, где т > 1. Тогда, так же как в главе IV, § 7,
будем иметь, для коэффициентов главной части разложения резольвенты
в окрестности полюса, равенства
В{т) (г, у)+\[Т (д„ v) Г (г — g, co)J В(пг) (|, у) d? = 0,	B.24)
J
, v)T{z—t, <u))B{m-l)(t, y)dlS = B{m) B, у) B.25)
и при этом B(m> (z, */) не есть тождественный нуль; напомним, что в этих
уравнениях у играет роль параметра.
Из B.25) согласно третьей теореме Фредгольма имеем
j
B(m) B, у)%(г) dJS, k = 1 ,..., v,	B.26)
(k)
где г|?, k = 1, . . ., v есть полная система решений союзного уравнения
у B) + j [T (dv, п) Г (у —г, со)]' ф (у) d,5 = 0.	B.27)
По теореме 2.2 эти решения совпадают с граничными значениями по-
(k)	С	(k)
тенциалов простых слоев V (х\ ф) = J Г (х — у9 со) ф (у) dQS, k = 1,
2, . . ., v, плотности которых образуют полную систему решений данного
уравнения B.23).
Покажем, что граничные значения комплексно-сопряженных потен-
потенциалов простых слоев
V\x\ Ф / J г (х — У> ®)Ф(У)dyS
также образуют полную систему решений уравнения B.27). Ясно, что V (х;
ф) удовлетворяет уравнению А (дх, со) и = 0, так как вместе с Г(* — у, со)
и комплексно-сопряженная с нею матрица Г (х — у, со) является матрицей
фундаментальных решений того же уравнения. Поэтому по формуле общего
представления решений можем писать
V B; фО = J {т{г — у9 со)[т(дУ9 n)V {у; ф')] —
J
-[Т(д,,п)Т(у — 2,
Но так как (TV)* = 0, (TV)" = 0, предыдущая формула принимает вид
что и следовало показать. Из этого следует, что условия разрешимости
B.26) могут быть еще записаны в следующем виде:
= 0,	B.28)

§2]
ОСНОВНЫЕ ТЕОРЕМЫ ТЕОРИИ КОЛЕБАНИЙ
299
Пусть в качестве вектора В{т) (z, у) выбрано некоторое решение урав-
уравнения B.23), например, ф, q ^ v; тогда B.28) принимает вид
J фр(г; ф)^25 = 0.	B.29)
s
Легко проверить, что
/ Ы\ (?) (?) / (q)\	\—{ (?)\ W!
V\z\ ФУ ф — yV\z\ ф/=2Пт[^и; Ф j Ф Г	B.30)
В области 111@, R)(]D~, где R — произвольное конечное положи-
тельное число, применим формулу Грина к векторам V (х; ф), V (х; ~ф).
Тогда будем иметь
\V\z\ <p)lTV\z\ Ф )\ —V\z; v)[TV\z\ ф ) J }d2S = 0.
S\JC (O, R)
На основании граничных условий получаем
[TV [г; ц>)\ =-2Ф(г),
yes,
TV\z; ср)\ =— 2ф(г),
и предыдущее равенство принимает вид
s
- J Ю
С (О./?)
и вследствие B.29), B.30), B.31) окончательно будем иметь
J [V\z; ф) TV — V\z\ ф ) TV\ d,S = —4Пт J
С (О,/?)	S
B.31)
B.32)
С другой стороны, выражение, стоящее слева в последнем равенстве,
на основании условий излучения (см. III, п. 4, § 2) может быть преобразо-
преобразовано следующим образом:
j [V, (TV,) — Vq (TV,)] dS= J [(Vqp) + V(QS)) (TV{ap) + 7V
(O.R)	C(OfR)
<S)) -
j
G(O.R)
- (V[p)
J
O
[-/со
(P) + 7V<S))] ^ J
C(O,R)
is) + о (R-1)] — (V[p) + Vqs)) [m
+ ico V^VQS) + о (R-1)]} dS, -B.33)
где для краткости введены обозначения
- ш
V{qp\ Vq*] — потенциальная и соленоидальная составляющие вектора Vq%
аналогично Vpp\ Vqs).

300	ГРАНИЧНЫЕ ЗАДАЧИ УСТАНОВИВШИХСЯ УПРУГИХ КОЛЕБАНИЙ ffjj VII
Перейдя к пределу при R —¦оо в B.32) и использовав оценки, вытека-
вытекающие из условия излучения, получим
lim J | V(QP) |2dS + 2/co Vv> lim I | V{QS) |2 dS = 0.
t R)	R+coc (JOf R)
Отсюда
C(O.R)	R^coC(OiR)
и по основной лемме (см. Ill, 2.14)
Vq = V[x; ф) = 0, xeD~, q=l,...,v.
Отсюда согласно B.31)
(?)
<p(z) = O, z?S, q=l,...,v.
Это противоречит первоначальному допущению и, следовательно, т = 1.
Теорема доказана.
2.7. Замечание. Приведенное выше доказательство теоремы 2.6
остается, по существу, без изменений для уравнения AK":
\
S
2.8. Теорема. Если S?JI2(a) и со2 есть собственная частота
задачи A)о , то ш2 является характеристическим числом интегрального
уравнения
j [Г (<Э2, /гB)) Г (г — у, со) + a (z) T(z — y, со)) <р (у) d^ = 0 B.34)
и это число есть простой полюс резольвенты.
Первая часть утверждения вытекает из теоремы 2.4. Для доказательства
второй части утверждения теоремы допустим обратное, т. е. будем считать,
что характеристическое число уравнения B.34) есть полюс m-го порядка,
где т > 1. Будем иметь, как и выше,
^ n(z))Y(z — g, со) -\-g(z)T(z — ?, со)] В{т) (g, у) d%S = О,
(m—1)	г
— В (z, y)-\- [T(dz, n(z))T{z — |, со) + cr (z) Г (г — g, co)]x
где 5<m) (г, г/), по предположению, не есть тождественный нуль. По третьей
теореме Фредгольма можем писать
с , .	(*)
|fi( m)(z. У) г|) B)^ = 0, fe=l,...,v,	B.35)
(k)
где г|) , k = 1, . . ., v есть полная система решений союзного интегрального
уравнения
- ф (z) + J {[Т (дуу п) Г (у — 2, со)]' + Г (г — f/, со) а (у) Ц> (у) d^5 = 0. B.36)
s

§ 2]	ОСНОВНЫЕ ТЕОРЕМЫ ТЕОРИИ КОЛЕБАНИЙ	301
1«)
Очевидно, решению <ф (г) этого уравнения соответствует вектор
(k)	i (k)\ i (k)\
u(x) = W[x; q>) + V[x;oyL	B.37)
(k)	(k)	(k)
где W (x\ г|э) есть потенциал двойного слоя с плотностью if, a F (х; ai|)) —
(*)
потенциал простого слоя с плотностью агр, который совпадает с одним из
о)
собственных векторов задачи A)о •
(Я)
Согласно теореме 2.4 граничные значения Г-операции над вектором а,
«7)
[Tur, q = 1, . . ., v, образуют полную систему решений интегрального
уравнения B.34). Поэтому условия разрешимости B.35) будут иметь вид
)[Ти\ гр dS = 0, Л = 1	v,
где согласно сказанному fi(m) B, у) = [fu (z)]+; в частности,
[т{и) (^dS = 0,	B.38)
где q — некоторое фиксированное число, q ^ v.
(k)
Здесь мы предполагаем существование [TW (г; г|?)]+; для того чтобы
(k)	(k)
это имело место, достаточно считать \|?6C1*a(S). Но так как of), & = 1, . . ., v
(k)
есть решение однородного уравнения B.36), то при 5?Л2 (а) \р действи-
действительно принадлежит указанному классу (см. IV, 6.15).
(?)	»
Вместе с а, решением задачи A)о , очевидно, будет также и комплексно-
iS)
сопряженный вектор и, и равенство B.38) эквивалентно равенству
,Т и J i|)dS = 0.	B.39)
s
Имеем тождество
(D)\+{q) (о) / (q) \+	Г/ (?)\+(<7)"|
Ти) $—y\Tu)=2iIm[\Tu) -ф J •	B.40)
(<7) (?)
В области Я/ (О, /?) П^~ применим формулу Грина к векторам и и и.
Будем иметь
J U W и / — и-\Т и) \dS = 0.	B.41)
На основании граничных условий имеем
U У = 2 ф, U / = 2 ф.
B.42)
Пользуясь формулами «скачков» для потенциалов двойного и простого
слоя и теоремой 2.1, можно показать справедливость равенства
\Т и) +ои+ = [Ти) +О1Г.	B.43)

302	ГРАНИЧНЫЕ ЗАДАЧИ УСТАНОВИВШИХСЯ УПРУГИХ КОЛЕБАНИЙ ^Л. у|]
Отсюда в силу того, что и+ = и* = 0, имеем
/ (<7)\-	/ (<?)\ +	(?)	/ G)\-	/ (<7)\ + _<?)
\Т и) =\Т и) —аи', \Т и ) = \Ти ) —аи'.
B.44)
Теперь, на основании B.40), B.42) и B.44), формула B.41) примет
следующий вид:
С (О. R)
J [иЛти) -иЛТ и) \dS +
О. R)
С	Г/ (?0\+(<7)"|	С	(io) iQ) \
-f j 4Пт [ V Т и ) г|; J dS + J 2Пт \ и~ о и~ ) dS = 0.
Согласно условиям ортогональности B.39) окончательно будем иметь
J [иЛТи) —и'КТи) \dS-\-2ilm) \й'аи') dS = 0. B.45)
С (О, R)	S
Преобразуем интеграл по С (О, R) согласно B.33), обозначив потенциаль-
(^7)	Я)	(?)
ную и соленоидальную составляющие и через и{р) и a(s), и тогда будем иметь
J [и~ \Т и ) — и-\Т и ) J dS =
С (О, R)
= — 2/со
J luH'dS— 2шУ]л J
u(s)\ dS.
С (О. И)	С (О, R)
Таким образом, формула B.45) принимает вид
2
J a(p) d5 — 2i(oVix ) \ u
(О. R)	С {O,R)
J	Vi ) \ {s) dS + 2i lm) \ иГои') dS =
С (О. R)
Потребуем теперь от матрицы а соблюдение интегрального условия
Im
j [I (у) а (у) I (у)) dS ^ 0,	B.46)
где Е (у) — произвольная интегрируемая функция 1); тогда будем иметь
I (?) |2
J	/?-»OO J
(О. R)	G (O,
lim
R-+CQ J	J
С (О. R)	G (O, R)
откуда, как и выше, следует
и из формул B.42) получаем г|) = 0, что противоречит первоначальному
допущению и, следовательно, m = 1. Теорема 2.8 доказана полностью.
4. Исследование внутренних задач. Условия разрешимости в резонанс-
резонансном случае. Общие теоремы, доказанные в предыдущих параграфах, позво-
позволяют построить полную теорию разрешимости соответствующих внутренних
и внешних задач.
В этом пункте будут рассмотрены неоднородные внутренние задачи.
') Очевидно, это условие вытекает из условия (см. гл. III, § 2, п. 5), которым мы поль-
пользовались при доказательстве теоремы единственности для шестой внешней задачи в D~.

К 2]	ОСНОВНЫЕ ТЕОРЕМЫ ТЕОРИИ КОЛЕБАНИЙ	303
Первая задача. Найти в D+ регулярное решение и (х) уравнения
А(д„со)и(х) = —Ж(х),
удовлетворяющее на S граничному условию и+ (у) = f (у), где
Ищем решение в виде
и(х)= J [Т(ду9 п)Г(у — х, со)]'ф(у) dyS + \ J Г(л: —у, со)Ж(y)dy.
S	+
J
D+
B.47)
Тогда, как мы уже знаем, интегральное уравнение для ср (х) будет иметь
следующий вид:
-Ч>(г)+1[Т(ду,п)Г(у — 2, co)]fq)(y)dyS=f(z)	~ J Г (г — у, со) Ж (у) dy.
S	D+
B.48)
Согласно теореме 2.3 некоторое, не более чем счетное, дискретное мно-
множество значений со2 является для этого уравнения характеристическим.
Для всех других значений со2, очевидно, задача разрешима непосредственно
и решение имеет вид B.47).
Переходим к исследованию того случая, когда со2 является характери-
характеристическим.
Согласно теореме 2.3 эти значения являются вместе с тем собственными
частотами однородной задачи A)о и условия разрешимости уравнения B.48)
имеют следующий вид:
J /(*) ф (z)d2S	L ) j г (г — у, <oK«(y)dyU (z)d2S = 0, B.49)
где \f>, k = 1, . . ., v есть полная система решений союзного однородного
уравнения
-№) + \Т{дЖ9п(г))Г(г — у, со) ty{y) d^S = 0.
s
(AM
Но та же теорема 2.3 утверждает, что г|э совпадают с граничными
значениями Г-операции над собственными векторами — решениями первой
однородной задачи и, k = 1, . . ., v. Поэтому условия B.49) записы-
записываются следующим образом:
J / (TuYdS - -i- J { J Г (z — у, со) Ж (у) dy\ (Tu (z)Y d^ = 0. B.50)
S	S
Преобразуем эти условия. Имеем
Т J I J+ Г {z — y^] Ж (y) dy\ №
{4" j Г B — У, оз) {Tu (z)Y dA Ж (у) dy:
но из формулы общих представлений регулярных решений, согласно с гра-
ничным условием (и (z)Y = 0, имеем
2 и (у) = ] Г(г — yyco)[Tu(z)j d2S, y?D*.

304	ГРАНИЧНЫЕ ЗАДАЧИ УСТАНОВИВШИХСЯ УПРУГИХ КОЛЕБАНИЙ
Внеся это значение в B.50), имеем окончательно
\f\Tu) dS— \3№{y)u(y)dy=-0f 6-l,..Mv.	B.51)
В частности, если положим Ж = 0 (что можно сделать без ограничения
общности (см. гл. VI, § 1), условия B.51) примут вид
/ (У) \Т (дду п) и (у)) d? = 0,	B.52)
а если считать / = 0, то эти условия напишутся в виде
г	Ш
\3№{y)u (y)dy = O, k=* l,...,v.	B.53)
D+
Условия B.52) и B.53) допускают очевидную механическую интерпре-
интерпретацию.
Условия B.52) показывают, что при рассмотрении первой внутренней
неоднородной задачи граничные значения вектора смещений могут иметь
критическую (т. е. характеристическую) частоту колебания, если только
этот вектор ортогонален вектору напряжения на границе, возникающего
в теле при собственных колебаниях с той же собственной частотой.
Аналогично, условия B.53) показывают, что внешние силы могут иметь
критическую частоту колебания, если только они (силы) ортогональны
смещениям, возникающим в теле при собственных колебаниях с указанной
собственной частотой.
Иначе говоря, можно не опасаться наступления явлений резонанса,
несмотря на совпадение частот собственных и вынужденных колебаний,
если только гарантировано выполнение указанных выше условий ортого-
ортогональности.
Вторая задача. Найти в D+ регулярное решение и (х) уравнения
удовлетворяющее граничному условию
(T(d9,n)u(y)r =
Решение этой задачи ищем в виде
и(х)=]Г(х — у, (d)^(y)dl/S + ~Y j
S	D+
Для плотности получим интегральное уравнение
"¦ 4- JT &*>v) г (г—^
D+
Согласно теореме 2.2, если со2 отлично от собственной частоты однород-
однороден
ной задачи (П)о, то интегральное уравнение B.54) разрешимо для произ-
произвольной правой части. Если же со2, наоборот, есть собственная частота
указанной задачи, то уравнение B.54) разрешимо только при условии
\f{y) Ф [y)djS—±- j j )J{dZ9n(z))T(z — yM3»{y) dy\ Ф
(?=l,...,v),	B.55)

я 2]	ОСНОВНЫЕ ТЕОРЕМЫ ТЕОРИИ КОЛЕБАНИЙ	305
где ф, k = 1, . . ., v есть полная система решений союзного однородного
уравнения
Ф(z) + j [Т(ду, п)Т{у — г, со)]' ф(у)dyS = 0.
S
Но по той же теореме ф совпадают с граничными значениями собствен-
ных векторов—решений однородной задачи (П)о, v, k — 1, . . ., v. Поэтому
условия B.55) примут вид
]f(y) v + (y)dyS	Ljl }T(dz,n(z))r(z — y9a>KVQf)dy\ v + (z)dzS=0
(k=l,...,v),	B.56)
или, как и выше, на основании формулы общего представления и граничных
условий (Tv)+ = 0 на 5, окончательно будем иметь
(*о	г (*>
\Ж(у) v (y)dy = 0, k=l,...,v.	B.57)
D+
D+
Мы получили необходимые и достаточные условия разрешимости второй
основной внутренней неоднородной задачи, в том случае, когда со2 является
собственной частотой соответствующей однородной задачи. Само собой
понятно, что решение не будет единственным.
СО	(О	СО
Аналогично исследуются задачи (III)+, (IV)+ и (VI)+. Рассмотрим,
со
например, задачу (VI)+.
Шестая задача. Определим в D+ регулярное решение уравнения
по граничному условию на S:
Разыскивая решение в виде
\
S	D+
получим интегральное уравнение
ф(*)+ j[T(dz,n(z))r(z — г/, со) + а (г) Г (г—y
s
= !(У)	^ \[Т (dZ9 n (z)) + ст (z)] Г(г — у,<оKв(у) dy. B.58)
D+
Согласно теореме B.5), если со2 отлично от собственных частот соответ-
ствующей однородной задачи (VI)o , то уравнение B.58) однозначно разре-
разрешимо для произвольной правой части.
Пусть теперь со2 есть одна из собственных частот задачи (VI)o. Условия
разрешимости будут иметь вид
\f{z)<p{z)dS	i-J J )JT(d2, п
(A=l,..,,v),	B.59)
20 В. Д. Купрадзе

306	ГРАНИЧНЫЕ ЗАДАЧИ УСТАНОВИВШИХСЯ УПРУГИХ КОЛЕБАНИЙ
(k)
где ф , k = 1, . . ., v есть полная система линейно независимых решений
союзного однородного уравнения
Ф(г)+ ^[(Т(ду,п)Г(у — г,со))' + Г(г — у,со)о (y)]cp(y)d!/S = O.
s
(k)
Но по теореме 2.5 ф совпадают с граничными значениями решений
0)	(k)
однородной задачи (VI)о w9 k — 1, . . ., v, и условия разрешимости при-
приобретают вид
}f(z)w + (z) dS	i-J i \[T (д„ п (г))+о(г)]Г(г—у, с*)Щу) dy\ [ w (г)) d2S = 0.
Преобразуя их, как и выше, по формуле общих представлений, полу-
получим на основании граничного условия
(k)
2ewdy = 0, k=l,...9v, •	B.60)
D+
Мы получили необходимые и достаточные условия разрешимости не-
неоднородной задачи, когда о2 есть собственная частота соответствующей
однородной задачи. Решение задачи неоднозначно.
§ 3. Внешние задачи
(О	СО
1. Разрешимость для произвольных частот колебания. Задачи (I)", (II)".
Общие теоремы, доказанные в § 2, позволяют доказать разрешимость рас-
рассмотренных выше задач для произвольного значения частоты колебания
в случае бесконечной области (внешние задачи). В этом состоит принципиаль-
принципиальное отличие внешних задач колебания от внутренних и это существенное
свойство внешних задач есть следствие условия излучения, которое исклю-
исключает собственные колебания бесконечной области.
ю
3.1. Теорема. Задача (I)" имеет и притом единственное решение
для произвольного вектора f?Cl>a (S) и при любом значении параметра со2.
Решение выражается потенциалом двойного слоя, если со2 отлично от
О) ,
собственных частот однородной внутренней задачи (П)о, и выражается
линейной комбинацией потенциала двойного слоя с потенциалом простого
О)
слоя, если со2 есть одна из собственных частот задачи (П)о .
Доказательство. Пусть сначала со2 не есть собственная ча-
стота задачи (П)о; тогда согласно теореме 2.2, однородное уравнение, соот-
ветствующее задаче AH , имеет лишь тривиальное решение и, следовательно,
в этом случае справедливость теоремы показана.
©
Пусть теперь со2, наоборот, есть собственная частота задачи (П)о .
В этом случае согласно теореме 2.2 необходимые и достаточные условия
разрешимости имеют вид

§ 3]	ВНЕШНИЕ ЗАДАЧИ	307
где / (у) — граничное значение искомого решения, а {ф (y)}k=i — полная
система решений союзного однородного уравнения
Ф (*) + J \Т Ф„ п (г)) Г (г — у, со)] Ф (у) dyS = 0.
S
Введем вектор
v	(/г)
% A )
где t|) (у), & = 1, . . ., v — полная система решений однородного уравне-
ния задачи AH
^{z)+\[T{dy>n)Y{y — z,<*)]'^{y)dyS = O.	C.1)
S
В силу теоремы 2.6 и согласно гл. IV, п. 8, § 7, можем считать, что си-
стемы векторов {ф (y))k=\ и { ф (t/)}^=i — биортонормированы. Поэтому
б	A
р {ф y))	{ ф ()}
достаточно выбрать постоянные Ak в виде
чтобы иметь
Это условие обеспечивает разрешимость уравнения
ф B) + J [Г (аг л) Г (у — г, со)]' ф {у) dyS = F (г),
s
Пусть -ф (г) есть его некоторое решение. Построим потенциал двойного
слоя W (х\ я|)) и рассмотрим вектор
и (х) = W (х; ф) — S ^^ U (Ф*).
k=l
<fe) v	(fe
где каждый из векторов {ф*}?=1 есть линейная комбинация векторов {ф!
составленная так, чтобы
[V\z\<pJ\ = фB), &=l,...,v.
Это всегда можно сделать в силу теоремы 2.2 и, следовательно, и (х)
00
действительно есть решение задачи A)~. Теорема 3.1 доказана.
Важно отметить, что полученное решение единственное, несмотря на
то, что интегральное уравнение C.1) имеет ненулевые решения; это — след-
следствие того, что потенциалы двойного слоя с указанными плотностями равны
нулю в D" согласно теореме единственности.
СО
3.2. Теорема. Задача (II)" имеет и притом единственное решение
для произвольного вектора f ? С0» а (S) и при любом значении параметра со2.
Решение выражается потенциалом простого слоя, если со2 отлично
со
от собственных частот однородной внутренней задачи A)о , и выражается
20*

308	ПРАНИЧНЫЕ ЗАДАЧИ УСТАНОВИВШИХСЯ УПРУГИХ КОЛЕБАНИЙ [рл# yj|
линейной комбинацией потенциала простого слоя с потенциалом двойного
со
слоя, если со2 есть одна из собственных частот задачи A)о .
Доказательство. Первая часть теоремы доказывается так же,
как выше, на основании теоремы 2.3.
СО
Пусть со2 есть собственная частота задачи (I)J".
В силу теоремы 2.3 необходимые и достаточные условия разрешимости
имеют вид
где/ — граничное значение вектора Ти, a \ty(y)\l=i— полная система
решений союзного уравнения
- я|)(г) + J [Т (дуу п)Г(у — z, <о)]'ф (у) dyS = 0.
s
Введем вектор
(k)
где Ak — постоянные, a |q> (y)}k=i — полная система решений однородного
со
уравнения задачи A1)<Г,
<> v	{k) v
Так же, как выше, системы { ср \k=u \ "ф U=i можно считать биортонор-
П	б	A
{ р \	ф U
мированными. Поэтому, выбирая постоянные Ak в виде
убеждаемся, что интегральное уравнение
- Ф {г) + J [Т {д2> п (г)) ГB — у, а))] Ф (у) dyS = F (z)
s
разрешимо. Пусть ф (у) есть его некоторое решение. Построим потенциал
простого слоя V (х\ ф) и рассмотрим вектор
и (х) = V (х; Ф) — ^ Л,Г U; г|;J,	C.2)
fe=i
где каждый из векторов {tjxj^i есть линейная комоинация векторов {i|)U=i,
составленная так, чтобы
что можно всегда сделать на основании теоремы 2.3. Таким образом, на
основании теоремы 2.1 заключаем, что и (х), определенная формулой C.2),
есть решение нашей задачи. Однозначность полученного решения показы-
показывается так же, как выше.
со	о)	о)
2. Другие задачи. Аналогично исследуются задачи (III)", (IV)" и (VI)";
@
например, для задачи (VI)" имеем следующую теорему:

3]	ВНЕШНИЕ ЗАДАЧИ	309
to
3.3. Теорема. Задача (VI)" имеет и притом единственное решение
для произвольного вектора /?С°'а (S) и при любом значении параметра со2.
Если со2 отлично от собственных частот однородной внутренней за-
О)
дачи A)о , то решение выражается потенциалом простого слоя. Если же шй
совпадает с любой из собственных частот задачи A)о , то решение выражается
в виде комбинации потенциала простого слоя и смешанного потенциала,
составленного из двойного и простого слоя.
Доказательство. Первая часть теоремы, касающаяся того
случая, когда со2 не есть собственная частота, доказывается так же, как
выше.
Приведем доказательство в том случае, когда со2 есть одна из собственных
°° 4-
частот задачи A)о .
В силу теоремы 2.4 необходимые и достаточные условия разрешимости
имеют вид
где / — граничное значение вектора (Г и + аи) на S, а {г|) }k=\ — полная
система линейно независимых решений союзного уравнения
— z, со)]' + Г(г/ — zt<*)o(y)}ty(y)dyS = 0. C.3)
S
Введем вектор
V	(k)
где Ak — постоянные, а { ф }?=i — полная система решений однородного
со
уравнения задачи (VI)o"
- Ф (z) + J [Т (дг, п (z)) T(z — yt со) + о (z) Г (z — у, со)] <р (у) dyS = 0.
Согласно теореме IV, 7.1, так же, как выше, можно считать системы векто-
(k)	(k)
ров { ф \k=\ и | «ф }l=i биортонормированными. Поэтому, выбирая постоян-
постоянные Ak в виде
s
легко убеждаемся, что интегральное уравнение
29 п(г))Г(г—y,(*) + G(z)r(z—у, (о)]<р(у) dt/S = F(z)
s
разрешимо. Пусть ф (у) есть его некоторое решение. Построим потенциал
простого слоя V {х\ ф) и рассмотрим вектор
v	Г / (fe)\	/	(k)\l
u(x) = V (х; Ф) - 2 Ak k U ¦ J + У U с ф J J,	C.4)
где векторы {г|)„. (y)\l=i есть линейная комбинация векторов \ty(y)\l^u
составленная так, чтобы
\T{dx.nB))[W {z\%) + v{z;a%)\} = Ф (г).	C.5)

310	ГРАНИЧНЫЕ ЗАДАЧИ УСТАНОВИВШИХСЯ УПРУГИХ КОЛЕБАНИЙ [рл#
Это можно сделать согласно теореме 2.4. Покажем, что и (х)> определенная
0)
формулой C.4), есть решение задачи (VI)", Для этого, очевидно, достаточно
проверить выполнение граничного условия. Имеем
¦ C.6)
С другой стороны, нетрудно проверить справедливость равенства
{(T + c)[lF(z;?)+^^
C.7)
Но согласно уравнению C.3),
/ {Ь)\	(	(k)\
W+ [z; ipJ + V+[z\a%) = 09 k=l9.. .,v;	C.8)
следовательно, на основании C.5), C.7) и C.8) равенство C.6) принимает вид
v	( Г / (/г)\	/	(/г)\1Н
(Tu)-(z) + ou-(z) = F(z)-% Ak{T [W{z;^) + V{z;o^)\\ =
V	(k)
= F(z)— 2 Ak<p(z) = f(z).
Этим теорема 3.3 доказана полностью. Однозначность полученного
решения устанавливается так же, как и раньше.
3.4. Замечание. Тот факт, что внешние задачи оказались разре-
разрешимыми в потенциалах для всех значений параметра со2, указывает на воз-
возможность априорной конструкции решения в таком виде, который приводит
к интегральным уравнениям, разрешимым по первой теореме Фредгольма.
Однако в общем случае разыскание подобных искусственных конструкций
затруднительно, и, как мы видели, в этом нет никакой необходимости.
Достаточно каждый раз пользоваться потенциалами либо простого, либо
двойного слоя и хотя при этом приходим, вообще говоря, к необходимости
обращаться к третьей теореме Фредгольма, но интегральные уравнения
сами указывают тот набор функций, которые обеспечивают разрешимость.
В том случае, когда полюс является простым, как в рассмотренных выше
задачах, такими функциями служат совокупности фундаментальных решений
данного и союзного уравнения, а в случае полюса высшего порядка — со-
совокупность так называемых главных функций этих же уравнений (см. по
этому вопросу Купрадзе [6], [13]).
§ 4. Некоторые замечания и библиографические справки
Задачи колебания стали предметом систематического изучения позже
задач равновесия.
Самой значительной работой классического периода, посвященной
этим вопросам, является статья Вейля 1915 г. об асимптотическом законе
распределения частот собственных колебаний трехмерного упругого тела
произвольной формы (см. Н. Weyl [1]). Собственные колебания характери-
характеризуются тем, что вектор смещения и (х) зависит от времени по закону ?lGV,
k = 1, 2, . . ., где постоянные со^ служат частотами собственных колебаний.

—) J'
? 4]	НЕКОТОРЫЕ ЗАМЕЧАНИЯ И БИБЛИОГРАФИЧЕСКИЕ СПРАВКИ	311
Вейль доказал, что число собственных колебаний с частотами, меньшими
некоторого числа соо, при возрастании соо стремится к пределу
где v — объем тела и А,, |х — постоянные Ляме. Этот результат Вейля,
который получил важные применения в теории излучения (см. Debye [1]),
был затем уточнен и распространен на собственные функции в ряде работ
(см. в связи с этим Pleijel [1] и Бурчуладзе [1]).
Цикл работ по теории колебаний упругих тел принадлежит В. Д. Куп-
радзе; в них построена общая теория первой и второй основных задач для
внешней (бесконечной) среды на базе принципа излучения, распространен-
распространенного для упругих колебаний (см. Купрадзе [6, 13]).
Еще раньше аналогичная теория внешних задач метагармонического
уравнения и системы уравнений Максвелла была изучена в работах Куп-
Купрадзе [2, 4] и И. Векуа [1].
Распространение теорем о свойствах собственных функций и собствен-
собственных частот для задач (III) и (IV) дается в работе Амашукели [3, 41.
ЗАДАЧИ
1.	Построить тензор Грина для задачи (III), в области, ограниченной поверхностью
вращения, в частности, сферой.
2.	Методом § 2 доказать теорему Ляпунова — Таубера для потенциалов двойного
слоя задач (III) и (IV).
3.	Исследовать полюсы резольвенты интегральных уравнений третьей и четвертой задач.
4.	Вывести условия разрешимости задач (III) и (IV) в резонансном случае.
5.	Решить внешние задачи колебания методом главы X (см. X, § 2, п. 8).
6.	Исследовать смешанную задачу (задача (V)) для оператора А (дх, со).
7.	Изучить граничные задачи для оператора А (дх, со), когда на границе заданы сме-
смешанные условия типа ut, и2, [Т (ду, п) и]3 и др. аналогичные.

ГЛАВА VIII
СМЕШАННЫЕ ЗАДАЧИ ДИНАМИКИ
Задачи, в которых, кроме граничных условий, удовлетворяются и
начальные условия, называются начально-граничными, смешанными или
динамическими задачами. В отличие от задач об установившихся колеба-
колебаниях, в собственно динамических задачах изучается распространение коле-
колебаний.
В простейшем и наиболее важном для приложения случае линейной
теории однородных изотропных упругих тел задача сводится к разысканию
интегралов вырожденной гиперболической системы дифференциальных урав-
уравнений теории упругости или системы уравнений термоупругости, которая не
относится к классическим каноническим типам, удовлетворяющих в неко-
некоторой области D х [0, сю) заданным начальным и граничным условиям
(I, §§ 14 и 15).
При изучении этих задач возникают новые математические трудности,
которые соответствуют усложнению физической картины динамического
состояния по сравнению со статическим состоянием или с установившимися
колебаниями.
В бесконечной однородной изотропной упругой среде возможны два
типа распространяющихся фронтов упругих колебаний — продольные и
поперечные.
В ограниченных телах, имеющих отражающие границы, число пере-
перемещающихся фронтов растет вместе со временем, и напряженное состояние
тела есть результат наложения совокупности падающих и отраженных волн;
в некоторых случаях (в области взаимодействия разнородных сред) возни-
возникают также так называемые поверхностные и обменные волны.
Математический аппарат для описания этой физической картины едва
ли может быть достаточно простым; и в самом деле, трехмерные задачи ди-
динамики в общем виде до сих пор мало исследованы по сравнению с другими
задачами теории упругости, по крайней мере теми методами, которыми по-
последние изучены достаточно хорошо.
Наиболее известные из имеющихся результатов относятся к изучению
бесконечного пространства с начальными условиями (задача Коши), крае-
краевых задач для полупространства и некоторых специальных областей, до-
допускающих разделение переменных.
Если, однако, потребовать от поверхности и других данных задачи
повышенную степень гладкости по сравнению с той, которая требуется
в задачах статики и установившихся колебаний, то при некоторых условиях
согласования данных оказывается возможным не только доказать теоремы
существования, но и получить сравнительно простые аналитические пред-
представления решения.
В этой главе нас будут интересовать классические решения задач теории
упругости с граничными и начальными условиями; эти решения входят

§ 1]	ПЕРВАЯ ОСНОВНАЯ ЗАДАЧА	313
в класс функции С {D х [0, оо)[ ПС2 \D х [0, сю)} или С1 {D х
Х[0, оо)}ПС2 \D х [0, оо)}.
Гладкость решения гиперболического уравнения «не превышает» глад-
гладкости данных задачи; было бы естественно эти последние выбирать из класса
C2\D х [0, со)}. Но, оставаясь в рамках элементарной теории эласто-
потенциалов, мы требуем от данных задачи выполнения более жестких
условий, позволяющих сохранить обычную степень эффективности, харак-
характерную для классической механики.
Следует заметить, что эти требования, существенные с математической
точки зрения, не являются столь же существенными с точки зрения при-
приложений. Так, например, поверхности, применяемые в технике и допуска-
допускающие хотя бы однократное дифференцирование, практически почти всегда
имеют несколько следующих производных. Исключение составляют поверх-
поверхности с углами и ребрами; но и для таких поверхностей полученные решения
могут служить приближенными решениями, если считать углы и ребра
соответствующим образом сглаженными.
Независимо от сказанного, проблема расширения класса данных за-
задачи, при которых еще существуют корректные классические решения,
является важной математической задачей. Здесь этих вопросов касаться
не будем.
§ 1. Первая основная задача
1. Условия для данных задачи. Основная теорема. В цилиндре D+ x
X [0, оо) ищется регулярный вектор и (х, t) в классе С (D+ X [0, оо)) f|
П С2 (D+ X [0, оо)), удовлетворяющий следующим условиям:
А фх) и (х, f) — р *ffi ° = F (х, 0,	A.1)
(А (дх) = |х А + (Я + |х) grad div),
lim и (х, t) = cp<°> (x), Hm ди{*'/] = <р<1> (х),	A,2)
*0	*0 ог
dt
lim u{x9t) = f(y,f)9	A.3)
где F (x, 0, x e D\ t > 0, q><°> (x), «p^ (x), x 6 D5, f (y, t)9 у ? S9 t > 0 -
заданные вектор-функции.
Пусть
Г. Существуют непрерывные производные вида
rF(*, 0
3е. Для t > 0, f (-, t) € С2- P(S), P 5> 0; для у € S, f (9, •) € C7 [0, oo);
4°. Функция ?з = |3 (|1э |2)> выражающая локальное уравнение поверх-
поверхности S, принадлежит классу С7, т. е. S 6 Л1 @)х).
х) В несколько иной постановке это требование можно значительно смягчить (см.
Рухадзе Р. [1]).

314 СМЕШАННЫЕ ЗАДАЧИ ДИНАМИКИ	[рл V111
Потребуем еще, чтобы для х 6 D+, у 6 S функции F (x,	t) и f (у, t)
и их указанные производные для больших значений t, были	по модулю
ограничены выражением с exp (o0t), где с — положительная и	о0 — неот-
неотрицательная постоянные.
Для существования классического решения, очевидно,	необходимо
выполнение согласования S
Ф@) (У) = f (у, 0), ф<1> (у) = ^§^- • •	A.4)
Если бы искомое решение имело столько непрерывных вплоть до гра-
границы производных по t, сколько их имеется у граничной функции /, то
условий согласования A.4) было бы недостаточно и к ним следовало бы
добавить дополнительные условия вида
^	S. m = 2, 3, 4, 5,	A.5)
где
Ч>М(х) = А(дх)^-*Цх)-([ am^l^° ) .	A.6)
В самом деле, дифференцируя последовательно по t уравнение A.1),
подставив t = 0 и использовав начальные данные, найдем
=Ф(т)(^ т = 2, 3, 4, 5,	A.6')
t=Q
откуда и следуют условия согласования A.5I).
Механический смысл этих условий «согласования высшего порядка»
состоит в том, что они оказываются необходимыми для существования реше-
решения, допускающего столько же производных по ty сколько ях имеется у гра-
граничной функции f {у, t).
Условия A.5), вместе с условиями A.4), которые, как мы видели, необ-
необходимы для существования решения с повышенной гладкостью, позволяют
доказать существование решения, которое безусловно удовлетворяет тре-
требованиям классического решения, хотя нельзя утверждать того же относи-
относительно существования производных высших порядков по /. Но этого и не
требуется для классического решения.
Мы докажем следующую теорему:
1.1. Теорема. Если данные задачи принадлежат указанным выше
классам и, кроме того, удовлетворяют условиям согласования A.4) и A.5),
то существует классическое решение первой основной задачи динамики; это
решение единственно и может быть представлено интегралом Лапласа
a+ico
1 е*й(х' x)dx>
О—too
еде
Здесь принято р = 1.

? 1]	ПЕРВАЯ ОСНОВНАЯ ЗАДАЧА	315
ряд равномерно сходится, Qk (х) и ф^> (х, х) выражаются в квадратурах
с помощью данных задачи,
т == а-(-ш, а = const, tf :^> аб J> а0.
2. Приведение к специальному случаю. Здесь мы покажем, что функ-
функции ср(т) (л;), т = 2, 3, 4, 5, определенные равенством A.6), и условия
согласования A-4), A.5) позволяют, без ограничения общности, привести
краевую задачу, поставленную в п. 1, к аналогичной задаче, но с нулевыми
начальными данными, специальной правой частью уравнения и специальным
граничным значением на S.
Это достигается введением некоторой вектор-функции о (ху f), которая
определяется следующим образом: для х ? Еъ, t ^ 0, а (х, t) пять раз
непрерывно дифференцируема по t, удовлетворяет условиям
=?т)(х), гп = О, 1,2,3,4, 5; x?D+	A.7)
и для больших значений t обращается в нуль.
Такая функция была применена в теории задачи Коши С. Л. Соболе-
Соболевым. Впоследствии эта же функция была использована в работах по сме-
смешанным задачам гиперболических уравнений О. А. Ладыженской.
Существование о (jc, t) будет доказано в следующем пункте. Здесь это
примем без доказательства. Пусть
ио(х, f) = u{x, f) — a(x9 f),	A.8)
где и (х, t) — решение исходной задачи. Тогда в силу A.1)—A.3) и A.7),
«0 (х, t) будет решением новой задачи, а именно:
А (дх) щ (х, t) - d"uft; t] = Fo (x, 0,	A.9)
limuo(x9 0 = 0, \\тдщ(*; t] =0y	A.10)
lim uo(x,t) = fo(y, t)	A.11)
где
/>•(*, t) = F(x, t) — A(dx)o(x, t)+d2o(dxt; °,	A.12)
t) — o{y, 0,	A.13)
и из A.12), A.13) в силу определения cp(m> (л:) будем иметь на основании A,7)
и A.5)
m = 0, 1, 2, 3;	A.14)
=0' ^^5, m = 0, I, ...9S.	A.15)
t=o
Таким образом, и0 (х, t) есть решение краевой задачи, аналогичной
исходной, и притом с нулевыми начальными данными, с правой частью урав-
уравнения, удовлетворяющей условиям A.14), и с граничным значением, для
которого выполнены условия A.15). К этой новой задаче мы пришли без
ограничения общности в постановке исходной задачи (см. ниже, п. 4).

316	СМЕШАННЫЕ ЗАДАЧИ ДИНАМИКИ	[Гл. VIII
3. Усредняющее ядро. Свойства средней функции. Пусть t фиксировано
и отлично от нуля и х, ? — произвольные точки в Я3- Рассмотрим неотри-
неотрицательную функцию со( Т ) непрерывную и непрерывно дифференци-
дифференцируемую произвольное число раз, равную нулю для \х — ?\^ t н \х — ?| <
<4-«.
Примером подобных функций, которые называются усредняющими
ядрами, может служить функция
CO I
\ г /
О,
где г = | х — С1.
Пусть D* — произвольная конечная область с границей S*, такая,
что D+ cz D*; пусть [л (jc) —пять раз непрерывно дифференцируемая функ-
функция, определенная в D*; рассмотрим интеграл
называемый средним для функции \i (x).
Среднее для |х (х) обладает следующими свойствами:
а) для t ?> 0 — бесконечно дифференцируемо по х;
б)
- ?.а|1}-
(U61
a$\ ohtXtki — определенные числа, не зависящие от |х (дс).
Свойство а) есть следствие определения усредняющего ядра. Для дока-
доказательства свойства б) нормируем функцию со так, чтобы I ?^-1 dr==r —.
о
Введя сферические координаты с началом в точке х, для достаточно
малых t можем записать
? 2 л л,
\ О О
поэтому
J J J2.co(-^

§ J]	ПЕРВАЯ ОСНОВНАЯ ЗАДАЧА	317
Выделив точку х сферой малого радиуса б, имеем
р(х9 f)= J ••• + J —+И*).
Первое слагаемое справа, при t —* 0, стремится к нулю; второе можно
сделать сколь угодно малым, выбирая б достаточно малой; отсюда следует
свойство б).
Чтобы доказать свойство в), рассмотрим производную 5' для малых
значений t\ имеем
Ф (*» 0	[ f /*\ 1 f ( г \ л> If /у\ 1 ^ / г
-Hr^^-li-J «*«)-7Гш (—)^==- —J И?O?м(т
D*
ji:4(J:j
D* i=l	t=l D*
-4 SI тБ-(т) ^^<«-т S J •'<o-(T)T
1 D*	l D*
SБ() S J
1=1 D*	t=l D*
/•=1 S*
3
i=l D*	D*
Первое слагаемое справа, для достаточно малых t> обращается в нуль,
I х —— Т I
так как при этом ¦—у^- J> 1. Очевидно, равно нулю и третье слагаемое;
следовательно,
D*
Имеем
где
1=1
к HIk — шаровой слой с центром в х 6 ?>+, радиусом — < и /, лежащий для
малых значений h D*.

318	СМЕШАННЫЕ ЗАДАЧИ ДИНАМИКИ	[Рл# \Щ|
Применив теорему о среднем, получим
3	t 2n n
t=l	t/2 О О
3
где
= — J со (т) dx.
Далее, с помощью подстановки xi — ?* = ^хо имеем
где Шх — шаровой слой с центром в х и радиусами V2 и 1. Перейдя в (*)
к пределу при t —¦ 0, в виду ограниченности Xi~~"^ и непрерывности » ,
1 г '	^?/
получим
Для доказательства свойства г) следует повторить предыдущие рассуж-
дения в отношении п' —-. Покажем это для второй производной.
Для малых значений t имеем
i=l D*	i=l D*
t=l D*	t=l
D*
__LV f ^
/1 ?>*
t=l O*
te /«=1 D*
о
i у

§ 1]
ПЕРВАЯ ОСНОВНАЯ ЗАДАЧА
319
~ '2 Zj J <*,<?
/1 ?*
Применяя теперь теорему о среднем, как это было сделано выше, получим
з
lim
где а{Д U / = 1, 2, 3 — определенные числа.
4. Доказательство существования а (х, t). Пусть
A.17)
где
2j
= 0,1	5,
а (х(А;) (jc), ^ = 0, 1, . . ., 5 — произвольные дифференцируемые вектор-
функции, которые определим так, чтобы выполнялись равенства A.7). Пока-
Покажем, что это действительно можно сделать.
Согласно свойству б) средней функции, очевидно,
lim а (л:, t) = lim [д, <°> (*, t) = ^ (x), xeD+,
t->Q	t-*Q
и, полагая \i@) (x) = ср@) (а:), будем иметь
Выписав, далее, выражения для ¦—-, . . ., ^, замечаем, что
г
-t-
i '
51
A.18)
и т. д. Нетрудно проверить, что все слагаемые в этих выражениях, содержа-
содержащие множитель tky k t> 0, при t —> 0 стремятся к нулю.

320
СМЕШАННЫЕ ЗАДАЧИ ДИНАМИКИ
\Щ1
Поэтому, перейдя к пределу в A.18) при t —> 0, получим
3
и, полагая
Далее,
|*A)(х) = фA)(«) —
' бУдем иметь
полагая
будем иметь
Далее
A.18')
полагая
i, j;
.3)	)
ЦкЬ dXidx,dxk
B)
будем иметь
СТГк
, A.18")
Продолжая эти вычисления, мы удовлетворим условиям A.7), если
вектор-функции \iik) (x), k = 2, 3, 4, 5, определим из равенств A.18),
A.18') и др., последовательно.

g 1]	ПЕРВАЯ ОСНОВНАЯ ЗАДАЧА	321
Это, очевидно, требует, чтобы векторы ф@) (х), фA) (х), F (х, t) и их
производные, через которые выражаются все q>(m) (х) и их производные,
были заданы в области D*, где определяются \i{k) (х), k = О, 1, . . ., 5.
Таким образом, необходимо продолжить вектор-функции ср@) (х), срA) (х),
F (х, t) в область D* с сохранением дифференциальных свойств. Именно
для этого мы потребовали от локального уравнения поверхности 5 принад-
принадлежность классу С7 (см. гл. V, п. 3, § 10). Если ф@>, фA), F заданы в расши-
расширенной (произвольной) области D*, необходимость такого ограничения
для S отпадает.
Легко видеть, что вектор о (х, /), определенный формулой A.17), на
основании свойств средних функций, удовлетворяет всем требованиям,
приписанным ему в п. 2.
5. Преобразование Лапласа. Приведение к эллиптической задаче. Пусть
х = а + ш — комплексная переменная, рассматриваемая в полуплоско-
полуплоскости а ^> аб > а0; эту полуплоскость будем обозначать через По0.
Ввиду ограничений, наложенных на Fo (х, t) и /0 (у, t), в полуплоско-
полуплоскости Пао существуют преобразования (Лапласа)
оо	оо
J e-*F0 (х, t) dt = Fo (x, т), j e-% (у, t) dt = f0 (у, т).	A.19)
Рассмотрим граничную задачу эллиптического типа
А (дх) о,, (х, т) — т2а0 (х, х) = Ро (х, т), х 6 D
lim ii0 (х, т) = f0 (у, т), у? S,
Э
A.20)
которая может быть получена из задачи A.9)—A.11) формальным приме-
применением преобразования Лапласа
и* (*, г) = J е-* щ (х, 0 dt.	A.21)
о
На основании A.14) и A.15), интегрируя по частям равенства A.19),
получаем
0
У» 0
)
о
отсюда вытекают равномерные относительно х Е О+, г/G S оценки
1^о(^т)|^р^, IfoO^l^jlp	A.24)
которые в дальнейшем играют важную роль.
6. Единственность, существование, представление и дифференциальные
свойства й0 (х, т). Согласно VII, 1.3, задача A.20) для т 6 Пст# имеет и при-
21 В. Д. Купрадзе

322	СМЕШАННЫЕ ЗАДАЧИ ДИНАМИКИ	|рл \Ц\}
том единственное решение. Это решение представляется в виде суммы потен-
потенциалов двойного слоя и объемных масс
где
,т) = Г(*;Ф) — U(x\ 4"^о)э
W(х; Ф) = J [Т[ду, п)Т(х — у, ix))' Ф(у)d,S,
Г (х — у, ix) — матрица фундаментальных решений оператора А (дх) —
— т2?, а плотность ф потенциала двойного слоя W (х\ ф) есть решение
сингулярного интегрального уравнения
которое в полуплоскости П0о разрешимо по первой теореме Фредгольма
(см. VII, § 2 п. 4).
Решение и0 (х, т), определенное формулой (*), является классическим.
Это — следствие того, что правая часть интегрального уравнения согласно
теореме V, 10.3, принадлежит, в наших предположениях, классу С1»13 (S),
и гладкость решения интегрального уравнения определяется теоре-
теоремой IV, 6.15.
С другой стороны, известно, что гладкость потенциала двойного слоя
и объемных масс не меньше гладкости плотностей этих потенциалов, если
только S — достаточно гладкая поверхность (см. V, 7.1 и V, 10.3).
Отсюда следует, что при сделанных в п. 1 § 1 предположениях относи-
относительно данных задачи, и0 (х, х) есть классическое решение задачи A.20).
7. Гладкость и0 (х, т) относительно т ? П0о. Представим и0 (х, х)
в виде суммы решений двух задач,
А (дх) и<2> (х, т) — х2«<2 > (х, т) = Fo (х, х) + т2а<1) (х, т), х 6 1У, )
A-26)
Эти задачи исследованы в гл. VI, VII. Решение задачи A.25) может быть
представлено интегралом (см. (VII, 1.12))
иA> (х, т) = - -1- j [Т фю п) G' (х, у)]% (у, т) dJS,	A.27)
s
а задача A.26) эквивалентна интегральному уравнению Фредгольма второго
рода (см. VII, § 1, п. 4)
4j G(x9 y)l$\y,	\
?>+	D+
A.28)

с 1]	ПЕРВАЯ ОСНОВНАЯ ЗАДАЧА	323
где G (х, у) — тензор Грина статического оператора А (дх) = (лА +
¦ + (^ + И*) grad div с граничным условием первой основной задачи для
области D+.
Особенность тензора Грина в замкнутой области определяется особен-
особенностью его главной части; для х, у 6 D имеют место оценки (см. Бурчуладзе,
Рухадзе [1])
Этими оценками существенно воспользуемся ниже (см. пп. 8—11)*
Так как f0 (у, т) — аналитическая функция параметра т в полуплоско-
полуплоскости Пао по определению, такова же, согласно A.27), и вектор-функция
и{о} (ху х) для т ? Пао. Аналитичность вектор-функции ио2) (х> х) как функ-
функции т ? Пао вытекает из следующего рассуждения: уравнение A.28) в полу-
полуплоскости Пао разрешимо для произвольной правой части, так как однород-
однородное уравнение, как эквивалентное однородной задаче, соответствующей A.26),
имеет лишь тривиальное решение (см. VII, 1.3). Выразив решение уравне-
уравнения A.28) по формуле Фредгольма и замечая, что резольвента и правая часть
суть аналитические функции параметра т в полуплоскости Пао, заключаем,
что и ио2) есть аналитическая функция т ? Пао.
Наконец, из сказанного следует, что и0 (х, х) = uol) -f- uo2) есть анали-
аналитическая функция т для х ? D+ и т g Пао.
8. Асимптотические по т оценки для а0 (х, т). Как мы уже знаем,
и, (х, т) = и^ (х, т) + й<2) (х, т).	A.29)
Найдем оценки для и{01) (х, т). Как решение задачи A.25), йо1) (х, х)
может быть представлено интегралом
(х, x)=\[N(ду9 п)Г(х — у)]'Ф@)djS,
где Л^ (дд, п) — оператор псевдонапряжения, введенный в главе I, п. 1
§ 13, ф — решение интегрального уравнения Фредгольма
= fQ(zy т), z?S. A.28')
Вследствие того, что | N (ду, п) Г (г — у)\ <	^, а > 0, будем иметь
/^
для резольвенты \ R (у, z)\ <	^^9 и так как уравнение A.28') разре-
\у —z I
шимо однозначно, на основании A.24) для решения получим оценку
отсюда для Wo} (х, х) следует равномерно относительно х 6 D+
21*

324	СМЕШАННЫЕ ЗАДАЧИ ДИНАМИКИ	^рл ЩЦ
Обратимся теперь к оценке для ио2) (jc, т). Пусть Я = Fo + т?й§\
Из уравнения A.28), применяя неравенство Коши—Буняковского, получим
k*)l^4-lTl4[J \G{x,y)\*dyVh ["J |
-f Г j \G(x, y)fdy\h Г J \H(y,
Отсюда на основании A.24), A.30) и согласно свойству тензора Грина
J \G\2 dy <: С следует равномерно относительно х ? D+, т 6 Па#,
>!+?ь-	(Ь31)
Оценим интеграл
J
D+
ао2)
Из тождества Грина (см. (III, 2.1)) для ао2) (х, т) и комплексно-сопря-
комплексно-сопряженного иЪ2) (дс, т), на основании A.26) имеем
(Т2 _^2) J | „~B) (у> т) ,2 dy = _ J 2B) (у, т) Н {уу r)dy+\ и») (у, т) Я (у, т) dg;
+	+
D+	D+	D+
отсюда нетрудно получить неравенство
D*	D+
("J |«<2)|2df/ll/' Г J \H(y, T)\*dyV\ A.32)
Пусть б — фиксированная постоянная, удовлетворяющая неравен-
неравенству 0 < б < въ; рассмотрим в отдельности случаи 1) | со | ^ б и 2) | со | < б.
В первом случае из A.32) следует
|"J | й<«> (х, х) |» rfxlV" ^ 25TO Г J |Я(*' x^
но согласно A.24) и A.30)
Г} \Н{х,х)\ЫхУ/г^^,	A.34)
и из A.33) в силу A.34) получаем
FJ \й?Цх,т)\*Aху*^1§р, тбП0о.	A.35)
Рассмотрим теперь случай 2) | со |< б. Из тождества Грина (см. (III, 1.1))
имеем
J [5<2) (X, Т) А (дх) Ы<2) (X, Х) + Е (Ы<2), ЦB))] ^ = J Ы<2> (У, т) Г (Зр, П) «<2> (I/, TjdjS,
S
f [ы<2) (т2й<2) + Я) 4- Е («о2). «о2)I dx = 0,

§ 1]
ПЕРВАЯ ОСНОВНАЯ ЗАДАЧА
325
или
J г@2 _ 0,2) | ?B) р + 2/асо | йB) |
D+
|2 + 2B) Я
dx = 0. A.36)
Билинейная форма Е (и, v) определена в главе III формулой (III, 1.4).
Легко проверить, что (см. (III, 1.6))
Поэтому из A.36) следует
(о* _ (о2) j | и<2> |2 dx < — Re } u<2> (х, т) Н (х, т)
и так как а2 — со2 Е> 0, неравенство Коши—Буняковского дает
и, наконец, согласно A.34)
j
A.37)
Учитывая^оиенки A.35) и A.37), из A.31) получаем равномерную отно-
относительно x?D+ для т ^ Пао оценку
A.38)
Теперь на основании A.30) из A.29) имеем
которая справедлива для т g Пав, равномерно по л: G D+.
9. Некоторые простейшие неравенства. Для дальнейшего необходимо
иметь асимптотические по т оценки первых двух производных по*;
для и0 (х, т) в любой строго собственной подобласти D', с границей 5',
г (S, S') > 0. Установим сначала некоторые простейшие вспомогательные
неравенства.
1°. Полагая х 6 D', дифференцируя выражение для aoU (jc, t) из п. 8
по xt, i = 1, 2, 3 и приняв во внимание указанные там же оценки, будем
иметь
с
J \Х-У12~а'
С
A.39)
где а > 0 — произвольное число, а у* 6 S. Совершенно аналогично полу-
получается оценка
A*39?)

326:
СМЕШАННЫЕ ЗАДАЧИ ДИНАМИКИ
[Гл. VIII
2°. Пусть
ф {Ху t) =* J G (х, у) [Ро (у, т) + ч2и{01) (у, т)] dy,
Тогда
D+
Отсюда на основании A.24), A.30) получаем
Ф (jc, т)
T7F' ЛС
3°. Представим Ф (х, т) в виде
Ф(х, т) = «
о., /=1, 2, 3.	A.40)
где
[
G(xt
«, ^),
(х, т) = т2| G(x, у)
(*)
D+
Пусть х ?D'\ в силу равенства G (х, у) = Г (^ — у) — g (xf у) можем
писать
t— —— J
D+
) T)cos(ft, xt)djS+ J Г(х~у) a/7°Jyy; T) dy-\ -jjjL Fody.
S
Далее,
D+
D+
j
D+
j
D+
Отсюда следует:
', t, /=1, 2, 3.
A.41)
Чтобы получить оценку A.41) для ФB) (х, т), представим его в виде
(%, т),	(*¦)
где
ФBЛ>(Х,Т)=1
Так как х ? D'9 для ФB« 2) можем писать
^ с
, ФB'2)(х, т) = — т
D+
Представим Ф<2> !)(л:, т) в виде
, Т),
A.41')
(***)

§11
ПЕРВАЯ ОСНОВНАЯ ЗАДАЧА
327
где
фB.1Л) =Т2
D+\D"	D"
a Dn zd D' —замкнутая область, ограниченная поверхностью S", причем
расстояния г (S", S) > О, г (S\ S') > 0. Следовательно, для х 6 D' будем
иметь
- 1.D I c
A.41")
Далее,
OTB.i.2)
dxt
г"%
[
I)"
а2фB,1,2)
2 f аГ -A)
т I^ Uo cos
2 Г дТ дйЬ1)
/	\ * о , 2 Г дТ дйЬ1
{n' Xi) dyS +T J -*ч~й
Отсюда в силу A.39) получаем
(МП
Наконец, из (*), (**),(***), A.41), A.4Г), A.4Г')» A.4Г) имеем оконча-
окончательно
|а2Ф(д:, т)
I-
Сп, /,/=1,2,3.	A.42)
4°. В принятых здесь обозначениях A.28) имеет вид
' (х, т) = — — ти G (х, у)
—±-Ф{х, т),
+; A.43)
j
D+
отсюда
0+
дФ
dxt
dx,
и согласно A.37) и 1.40) получаем
A.44)
дао
10. Асимптотические по т оценки первых производных -jj—г» Из ра-
равенства
= J [JV (д„ л) Г (х — у)]' Ф {у, х) dyS,
для
', имеем
дзц
С ;	1 о о
' |т |7 > * 	 I, ^, О,
A.45)

328
СМЕШАННЫЕ ЗАДАЧИ ДИНАМИКИ
[Гл. VIII
Из A.43)
дх(
и согласно A.40)
10
1 2 f <Ю
1 дФ(х, т)
A.46)
l
Для оценки интеграла
разобьем его на слагаемые
D+
где
Имеем
D,
, = D+\Di , а > 0.
2)(**,t)|CJ
D,
здесь я* — некоторая точка из Dx.
Согласно A.38) отсюда получаем
A.47)
Далее, на основании A.37)
D2	LD+
Объединяя с предыдущим это неравенство, находим
' '
2
Выбирая а так, чтобы 2 — За ^ 0, т. е. а <: -г-, согласно A.46) будем иметь
:, т)
с
и, наконец, из A.45) и A.48)
ди0 (х, т)
1о„ »^-§-,	A.48)
4-, i=l,2,3. A.49)

§ п
ПЕРВАЯ ОСНОВНАЯ ЗАДАЧА
329
П. Асимптотические по т оценки вторых производных *t .*г
Считая x?D\ из A.39') имеем
Р {х, т)
i, / = 1, 2, 3,
A.50)
а из A.43) получаем
uhz\y, x)dy—^
J
D+
=_ 2.	 \	Г f (х —
2 J a^ u ^
O+
дх;дх;	2 j dXi dtji
5+
Отсюда на основании A.38) и A.42) можем писать
D+
_дГ_
dXf
P^-, x^D'.	A.51)
Для оценки интеграла
dy9
представим его в виде суммы е7 = е/i + ^72» где
dy,
= D+\D1( p>0.
Тогда будем иметь
дй<2> (/.
с i
dyt	|J U — i
|т|
2+а
, A.52)
и на основании A.44)
naif
1 ^f
Объединяя A.52) и A.53), получаем
l , i
dy^ | т ,2 (i-p) - A.53)

330	СМЕШАННЫЕ ЗАДАЧИ ДИНАМИКИ	грл VIII
2	4
Полагая а = -g-, Р = -д-, будем иметь
Подставив в A.51), имеем
а2и<2> <*,
С
,1+i/». XZ°'	С1'53')
и, наконец, объединяя A.50) и A.53'), получаем
, х)
114-1/9
., xeD', те По., *, /=1, 2, 3. A,54)
12. Некоторые свойства преобразования Лапласа. Пусть рассматри-
рассматривается преобразование Лапласа, зависящее от параметра, в котором v (jc, t)
и v (x, r) соответственно оригинал и изображение
v (х, т)= ^e-rtv(x, t)dt.
Известны следующие свойства преобразования Лапласа, зависящего от
параметра:
Iе. Если для х 6 D+ и % 6 ПОе функция v (x, х) удовлетворяет следую-
следующим условиям:
а)	аналитически зависит от т;
аз
б)	| | v (х, о + ш) | dco — сходится равномерно относительно х е D+;
в)	lim v х, т) = 0 равномерно относительно х G D+9 то у л:, т) — яв-
IX Кос
ляется изображением и оригинал определяется интегралом
где а — произвольное действительное число, большее а0.
2°. В классе непрерывных функций оригинал определяется по задан-
заданному изображению единственным образом всюду, за исключением, быть
может, точки / = 0.
3°. В любой точке t, где v (л:, t) дифференцируема по t, справедливо
обращение A.55).
Применим эти свойства преобразования Лапласа для обращения инте-
интегралов A.19). На основании A.12), A.13) и ввиду дифференцируемости
по t функции о (х9 t), из A.19) согласно свойству 3° вытекает
Fo(x, 0 = ^- J ext~F0(x, x)dx,	A.56)
o
ext ~fo to* *) ^	(i.56')
J
О— too
<T-f- ioo
— ioo

§ 1]	ПЕРВАЯ ОСНОВНАЯ ЗАДАЧА	331
13. Доказательство существования и0 (х, t) и и (х, t). Рассмотрим ин-
интегральное уравнение
со
J e~xt и0 (jc, t) dt = й0 (x, x),	A.57)
о
где и0 (х, х) есть решение граничной задачи A.20).
Вектор и0 (л:, х) — решение задачи A.20), как было установлено выше,
удовлетворяет условиям, которые необходимы для применения свойств Г
и 2° преобразования Лапласа из предыдущего пункта. Поэтому решение
интегрального уравнения A.57) в классе непрерывных функций существует,
единственно и имеет вид
(j-f-too
G—loo
При этом интеграл не зависит от значения а из области Пао.
Покажем, что вектор и0 (х, t), определенный равенством A.58), есть
классическое решение задачи A.9) — A.11).
Проверим сначала выполнение уравнения A.9). Для этого вычислим
значение выражения
А(дх)и0(х, t) — d2u°(*' °, xeD'.
Подставляя здесь вместо и0 (х, f) его значение из A.58), учитывая при
этом оценки A.38), A.49), A.54), позволяющие внести оператор (А (дх) — -^Л
под знак несобственного интеграла, и, приняв во внимание A.56), будем
иметь
a -f-ioo
А(дх)и0{х, t)~ дЧ»? ° =гНГ j ext[A(dx)u0(x, x)-x2u0(x, x)]dT =
j
О— /оо
CT-h-ioo
= Ш \ eXtpo(x> *)dT; = F0(x, f)
Чтобы проверить выполнение граничного условия A.11), нужно в A.58)
перейти под знаком интеграла к пределу при х —> у, где у — произвольная
фиксированная точка на 5. Для законности такого предельного перехода
достаточно выполнение условий:
а)	существование предела подынтегральной функции;
б)	достижение этого предела равномерно относительно х в любом конеч-
конечном промежутке изменения т;
в)	существование несобственного интеграла от предельной функции;
г)	равномерная относительно х сходимость несобственного интеграла
в окрестности точки у.
В данном случае эти условия выполнены. Условие а) есть следствие того,
что и0 (х, т) есть решение граничной задачи A.20). Условие б) есть следствие
равномерной непрерывности и0 (ху т) относительно обеих переменных в конеч-
конечном цилиндре D+ X {x?Z|Rex = a, |Imx| < N\, где N — произвольное
конечное положительное число. Условия в) и г) вытекают из оценок A.24)
и A.38).

332	СМЕШАННЫЕ ЗАДАЧИ ДИНАМИКИ	ffjj \/ЦТ
Выполнив переход к пределу под знаком интеграла и воспользовавшись
равенством A.56'), получим
ОГ-Моо
Нт ц0 (х, t) = -^ f extf0 (у, х) dx = /0 (у, t), у 6 S.
Для проверки выполнения начальных условий рассмотрим интеграл
где у есть замкнутый контур, лежащий в полуплоскости Пао, соста-
составленный из отрезка [а — iN, а + iN] и полуокружности опирающейся на
указанный отрезок как на диаметр. При t = О этот интеграл равен нулю
по теореме Коши. Переходя к пределу при N —* оо и применяя, вместе
с оценкой A.38), рассуждение, приведенное выше относительно предельного
перехода, теперь по t, под знаком несобственного интеграла, найдем
0= lim и»(х, 0) = \\muQ(x, t).
Точно так же проверяется выполнение второго начального условия,
если аналогичное рассуждение применим к производной
G+ too
О—too
в которой полагается t = 0. В самом деле, и теперь аналитическая функция,
стоящая под интегралом, при N —* оо в точках полуокружности обращается
в нуль достаточно быстро. Для законности же дифференцирования по t
под знаком сходящегося интеграла достаточно соблюдение следующих
условий:
а)	существование производной по t подынтегральной функции, равно-
равномерно относительно т в любом конечном интервале изменения т;
б)	равномерная сходимость несобственного интеграла от производной
по t относительно параметров х и t.
Нетрудно проверить, что эти условия в нашем случае выполнены;
для этого достаточно воспользоваться неравенством A.38) и видом подынте-
подынтегральной функции.
Наконец, из A.58) находим для а ^ аб 5> а0:
сю
5Г J
Согласно неравенству A.38) интеграл в правой части равномерно огра-
ограничен по х 6 D* и, следовательно, и0 (х, f) имеет конечный порядок роста
по / и | щ (х, 0l< Ce°ot. Аналогично, согласно неравенствам A.49) и A.54)
показывается, что из A.58) следуют
ди0
дх,
= 1, 2, 3. A.59)
Таким образом, вектор и0 (х, t), определенный формулой A.58), удо-
удовлетворяет всем условиям задачи A.9), A.10), A.11) и является ее единствен-
единственным классическим (в силу п. 6) решением. Поэтому согласно A.8) существует

Л 1] ПЕРВАЯ ОСНОВНАЯ ЗАДАЧА	333
единственное классическое решение первой основной	краевой задачи дина-
динамики A.1), A.2), A.3) и имеет вид
9 f).	A.60)
14. Вычисление и (х, t) и завершение доказательства основной теоремы.
В полуплоскости х ? ПОв несобственный интеграл
оэ
и (х, т) = J е-^и (х, t) dt	A.61)
о
сходится (см. конец предыдущего параграфа). Так как и (х, t) дифферен-
дифференцируема по t9 согласно свойству 3° преобразования Лапласа (см. п. 12),
будем иметь
CJ-Иоо
а— too
Умножив A.1) на e~~xt и интегрируя, находим
Je~xt [А(дх)и(х, t) — ^]dt = P(х, т),	A.63)
где
F(x, t)=J e-^F(x, t)dt.
о
Но согласно A.60)
А(дх)и(х, t) = A(dx)u0(x, t) + A(dx)o(x, f)\
в силу неравенств A.59) и вследствие того, что А (дх) а (х, t) для боль
ших значений t равно нулю, имеем
| А (дх) и (х, t) | ^ Сеа°\ xeD\	A.64)
Поэтому, выполняя в A.63) интегрирование по частям, получаем
А(дх)и(х, х)— х2й(х, х) = Р(х, х) — тф@)(л;) — фA) (л:).	A.65)
В A.61) можно перейти к пределу при х —¦ y?S под знаком интеграла и
оо	оэ
lim и (х, х) = [ е-« lim и (х, t)dt=\ e~xt f (yy t) dt = f (у, т). A.66)
x-*y	5	x->y	$
Таким образом, мы установили, что и (jc, т), стоящая под интегралом
в A.62), есть решение граничной задачи
А(дх)й(х, х) — х2и(х, т) = Ф(х, т), xeD\
A.67)
lim и (х, х) = f(y, т), у е S,
х-* у	)
где
ф (х, х) = Р (х, т) — тФ@) (х) — ФA) (х).
В главе XIII будет показано, что решение задачи A.67) выражается
рядом
й(х, т)= S Qk(x)<p<k)(x, т),	A.68)

334	СМЕШАННЫЕ ЗАДАЧИ ДИНАМИКИ	1рл VIII
где
у, %)djS9
= /(у, т)	L | Г(у — г, пт)Ф(г, т)&,
о+
Г (а: — z, it) — матрица фундаментальных решений оператора А (дк) — т2?,
Г (x^k) — г, it), & = 1, 2, . . ., г? S — значения Г (х — г, гг) в точках к{к\
которые произвольно фиксируются вне замкнутой области D+; ф(/г) (у, т) —
определенная линейная комбинация векторов
/>_0f /т), r^>(JC</> —у, it), Г<3>(л</)— у, <т), / = 1, 2, ...,
Ряд A.68) равномерно сходится во всякой замкнутой области, лежащей
внутри D+.
Внеся A.68) в A.62) и приняв во внимание результат, установленный
в предыдущем пункте, мы приходим к основной теореме, сформулирован-
сформулированной в п. 1.
Очевидно, вектор
uN(x>t)==-4uTl J ^'О*(т)Ф<*)(х, т)Л,	A.69)
fe = l o — iao
где N — конечно, дает приближенное решение первой основной динамиче-
динамической задачи.
§ 2. Вторая основная задача
1. Постановка и условия для данных задачи. Основная теорема. В ци-
цилиндре D+ х [0, оо) ищется регулярный вектор в классе С1 (D+ X
X [0, оо)) П С2 (D+ X [0, оо)), решение уравнения
А(дх)и(х, f)—*Z^JL=F(x,f)9	B.1)
удовлетворяющий начальным условиям
c,*) = q>0(x), lim ди(*'() =<рЫ(х)	B.2)
tй at
dt
и граничному условию
UmT(dx,n(y))u(x,t) = f{ytt), yeS, }
(ди	\	B.3)
Ти = и, -н	1- Ал di v и + и, \п X rot а]).
Заданные вектор-функции Z7 (х, ?), ф@)(*), фA) (х) и поверхность S
удовлетворяют тем же условиям, что и в п. 1 § 1, а граничная вектор-функ-
вектор-функция / (у, 0 такова, что для t > 0, относительно у
f(y,t)e&>t(S),
и для у/у 6 «S, относительно t,
f(y,t)e С7 [О,

2]	вторая основная задача	335
Полная система условий согласования теперь имеет вид
;
где ф(т) (у) определены по формуле A.6) и непрерывно дифференцируемы
по у до порядка G — т). Имеет место
2.1. Теорема. Если данные задачи принадлежат указанным клас-
классам и, кроме того, выполнены условия согласования B.4), то существует клас-
классическое решение второй основной задачи динамики; это решение единственно
и представляется интегралом Лапласа
G-f-iOO
O—ica
где о > Go > стЛ — произвольная постоянная, ряд
равномерно сходится, Hk (т) ^(A:) (x, т) выражаются в квадратурах с по-
помощью заданных функций, т = а + too.
Так же как выше, доказательство теоремы опирается на редукцию исход-
ной задачи к некоторой специальной задаче того же вида, как первоначаль-
первоначальная, но со специальными данными. Эта редукция и здесь достигается с по-
помощью вектор-функции а (х, t), введенной в п. 2 § 1 в данном случае с по-
помощью условий B.4). При этом приведенная задача относительно и0 (х, t),
uo(x,t) = u(x,t) — a(x,t),	B.5)
имеет вид
A(dx)u0(x,t)— д2щ^ ° =FQ(x, t), xeD\0^t<oo,	B.6)
duo{*;t} =0,	B.7)
m
lim Tuo(x, t) = fQ (y, t), yeS,	B.8)
x->y
где
Напомним, что Fь (х, t) и fo(y, t) удовлетворяют условиям A.14) и
A.15); кроме того, указанная редукция не предполагает какого-либо огра-
ограничения общности в постановке исходной задачи.
2. Преобразование Лапласа. Решение эллиптической задачи. Рассмотрим
граничную задачу эллиптического типа
А{дх)й0(х,х)— x2uo(x,r) = Fo(x,T)t xeD+9	B.10)
Vim Тщ(х, T) = f0G/,T), y6S,	BЛ1)
которая может быть получена из задачи B.6) — B.8) формальным примене-
применением преобразования Лапласа
оо
\	B.12)

336
СМЕШАННЫЕ ЗАДАЧИ ДИНАМИКИ
ГГл. VIII
Здесь Ро (х, т) и /0 (у, т) обозначают преобразования Лапласа соот-
соответственно функций Fo (х, f) и /0 (у, f), заданных равенствами B.S); Fo (x, т)
и fo (У* п) удовлетворяют неравенствам A.24).
В главах III и VII было показано, что задача B.10), B.11) для т?Пао
имеет единственное решение; оно может быть представлено в виде суммы по-
потенциалов
где
М*,т) = У(х;ЧО — U{x\ 4"
V(x; ф) = j T(x — у, п
B.13)
U (*; ~Г ^°) = 4" 1Г {х~у>
>т) dy>
D+
B.14)
и гр — плотность потенциала простого слоя V (х; гр) — есть решение син-
сингулярного интегрального уравнения
(У) + J Т(ду, п)Т(у— г, *т)
= fo.{y, т) + TV (у; -f
B.15)
которое в полуплоскости т ? ПСТо разрешимо по первой теореме Фредгольма.
Полученное решение есть классическое; это показывается так же, как
соответствующее предложение в п. 6 § 1.
3. Гладкость и0 (лг, т) относительно т? Пао. Пусть а0 — произвольное
положительное число. Представим и0 (я, т) в виде суммы решений двух
задач
А (дх) и{01) (х, т) —
= 0,
х е
B.16)
9 т) = 0,
B.17)
Пусть G (ху у; —а§) есть тензор Грина оператора А (дх) — $1Е для
второй задачи в области D+\ существование этого тензора очевидно (см.
гл. VII, § 1) и, кроме того, для х, y(zD+ будем иметь (см. § 1, п. 7)
dG
\х-у\»
B.18)
Задачи B.16), B.17) изучены в главе VII. Решение задачи B.16) может
быть представлено интегралом
Г/A
Uq
"= 4" J
у; ~
B.19)

к 2]	вторая основная задача	337
а задача B.17) эквивалентна интегральному уравнению Фредгольма вто-
второго рода:
Й2)(*, т) + 4 (*2 -52) fG (*• ^ - 58I™ (у>
j (Xf y- _ a^) [Fo -f (Г — ao) uh}] dy. B.20)
Покажем это; пусть и{02) (х, т) — решение задачи B.17). Запишем его
формулой общего представления с помощью тензора Грина
(х, т) = ) G (х, у: - ol) {Ти^У dyS -
- \[Т (ду, п) G]' Ы2)Г dyS- \ [GA W — {AG)' йП dy.
Первые два слагаемых справа обращаются в нуль согласно граничному
условию и в силу свойства тензора Грина; поэтому, на основании B.17) и
вследствие того, что AG = OoG, будем иметь
, х) = - (т2 -hi) [ G (*, у; - 5§) ~иР (У, х) dy -
D+
- f
Обратное предположение очевидно, и наше утверждение доказано»
С другой стороны, известно, что однородная задача, соответствующая B.17),
имеет лишь тривиальное решение для т ? ПСТо, поэтому однородное интеграль-
интегральное уравнение, соответствующее B.20), не имеет отличных от нуля решений
и, следовательно, неоднородное уравнение B.20) разрешимо при т?Пао
для произвольной правой части.
Теперь мы можем доказать, что и0 (х> т) есть аналитическая функция
параметра т в полуплоскости ПСТв. В самом деле, ввиду того, что f0 (yy т)
по определению есть аналитическая функция т в ПСТв, согласно B.19) анали-
аналитической функцией т является и uol) (x, х) в замкнутой области х? D+.
Выразив, далее, и{о2) (х, т), с помощью резольвенты Фредгольма, как
решение уравнения B.20) и замечая, что в полуплоскости П0в, как правая
часть уравнения, так и резольвента суть аналитические функции т для
x?D+, заключаем, что и{02) (х, т) аналитически зависит от т при
^(:Па(), x?D+, следовательно, и0 (х, т) = и{01) (х, т) + и{02) (jc, т) есть ана-
аналитическая функция т в полуплоскости Пав для х ? D+.
4. Асимптотические по т оценки для й0 (х9 т) и производных. Оценим
в отдельности каждое слагаемое в правой части равенства
и0 (х, т) = и(о1) (х, т) + и$>2) (х, т).	B.21)
Для и(ог) (х, т) непосредственно из B.19), на основании A.24) и B.18),
получаем
|25l)(*.*)|^-f^-, *е^+, тбПао#	B.22)
Для uq2) (x, т) необходимые оценки получаются из рассмотрения инте-
интегрального уравнения B.20), аналогично тому, как соответствующие оценки
22 В. Д. Купрадзе

338	СМЕШАННЫЕ ЗАДАЧИ ДИНАМИКИ	[fjj VIII
в п. 8 § 1 были получены из интегрального уравнения A.28). Обратим вни-
внимание на то, что ядра уравнений A.28) и B.20) зависят одинаково от пара-
параметра т, а правые части определяются соответственно выражениями
Р0(х, т) + х2^1} (х, х) и Fo (х, х) + (т2 — 5g) и{01) (х, х).
Благодаря этому, как нетрудно в том убедиться, производя вычисления,
преобразования и выводы пп. 8 и 9 § 1 остаются в силе и, совершенно так же
как в случае первой задачи, и в данном случае приходим к неравенствам
I «о(x, т) | ^ -fiv , хе D+, т€ Пао,	B.23)
дио(х, т)
dxi
| X B+2/3 »
^о (*,
B.24)
аналогичным неравенствам A.38), A.49), A.54).
Эти неравенства позволили в п. 13 § 1 показать существование функции
ио (х* t)9 удовлетворяющей всем необходимым условиям первой задачи.
В случае второй задачи неравенства B.23), B.24) оказываются недостаточ-
недостаточными для проверки граничного условия, хотя для проверки остальных усло-
условий они вполне достаточны. Чтобы выяснить, как следует дополнить нера-
неравенства B.23), B.24), заметим, что проверка граничного условия требует:
а) внесения оператора Г (дХ9 п) под знак несобственного интеграла A.62)
для x?D' и б) переход к пределу под знаком интеграла при х —* zfS.
Законность операции а) очевидна; она вытекает из оценки B.24). Для
законности операции б) было бы достаточно, например, выполнение нера-
неравенства
ф	B.25)
равномерно относительно х в окрестности точки z на S.
Для Т (дХ9 п) uq2) (х, х) это неравенство вытекает из оценки A.48),
которая сохраняет силу и в данном случае. Остается показать справедли-
справедливость неравенства B.25; для Т (дх, п) и{01) (х, х). Чтобы это сделать, заметим,
что
К (У, т) = ] е-« Д, (У, t)dt = ±] е-™ Щ^> dt=-L }Г\У, г),
о	о
где
]-* д'%{»'() dt.	B.26)
0
С другой стороны, из B.19) следует на основании B.26)
Т (дх, п) иЪх> (х, т) | < -^ J | Т (дх, п)а\\ ^V1> (у, т) -
-/Г (г, т) | dvS + '^"l^
и отсюда вытекает оценка
» f \T(dx,n)G\\~tivl)(y,r)-
' S (Z; 6)
где S B; 6) = S П Ш (z; 6), б — фиксированное число.

к 2]	вторая основная задача	339
Здесь для перехода к B.27) от предыдущего неравенства, мы восполь-
воспользовались очевидными неравенствами
! Wl) (*, т)| < С, j Г (дх, п) G (х, у; — S§) dyS
s
J \Т(дх,пH\\}Г>(У,х)-1Г1} (z,x)\dyS <C.
S\S (z; 6)
Далее, из B.26) имеем
?o(VI) (У, x)-%VI) (z, x) = ] e~xt [/0(V1) iy, 0 -/iVI) (г, 01 dt, B.28)
0
где
f(Vl) . Л ^6/o (j/, t)
/о (У, *) =	jfi	•
Ho
\tiVl) (y, t) — ^VI) (г, 0l <М(г, *)|y —z|.	B.29)
и Л (z, t) = О (exp aot)\ это следует из того, что A (z, /) выражается через
производные по у в окрестности z от функции /oIV) (#, 0» которые (произ-
(производные), по условию, имеют по t рост порядка меньшего или равного а0.
Внося B.29) в B.28), получаем
\ПУП(у.т)-}Г»{г.х)\<С\у-г\.
Учитывая это неравенство, из B.27) находим
СтЛ^-Дг,	B.30)
равномерно относительно х в окрестности точки z?S. Таким образом, не-
неравенство B.25) доказано и законность операции б) обоснована.
5. Доказательство существования и вычисление решения второй основ-
основной задачи. Пусть и0 (х, т)— решение эллиптической задачи B.10), B.11).
Рассмотрим вектор-функцию
o-f-fco
± J	х, x)dx,	B.31)
(J—too
где а — произвольное действительное положительное число, удовлетворяю-
удовлетворяющее условию (^ > оо > ст0.
Вполне аналогично тому, как это было сделано в п. 13 § 1, можно по-
показать, что B.31) удовлетворяет уравнению B.6) и начальным условиям
B.7). Покажем, что удовлетворяется и граничное условие B.8). Действи-
Действительно, полагая x?D\ из B.31) на основании B.24) можем записать
a-fioo
Т (д„ п) щ {х, /) = -Jjp J е«Ти0 (х, т) dx.	B.32)
О—too
Для перехода к пределу под знаком интеграла при х —¦ z?S достаточно
выполнения условий а)—г), указанных в п. 13 § 1. Первые три здесь выпол-
выполняются по тем же соображениям, как и в п. 13 § 1, условие же г) обеспечи-
обеспечивается неравенством B.25).
Совершая предельный переход по х в B.32) и учитывая A.19), получаем
lim Т (дх, п) uQ {х, t) = /0 [у, t), у 6 S.
22*

340	СМЕШАННЫЕ ЗАДАЧИ ДИНАМИКИ	грл VIII
Этим заканчивается доказательство существования и единственности
и0 (х, t) — классического решения приведенной задачи; переход к теореме
существования решения задачи B,1)—B.3) осуществляется так же, как
в случае первой задачи.
Можно показать (см. п. 11 § 1), что найденное и (х, t) имеет вид
м(х, ;)=_!_ ) e«u(x,x)dT,
o—ico
где и (х, х) есть решение эллиптической задачи
А (дх) и (х, т) — хги (х, х) = Ф (х, т), хе D+,
ПтТ(дх, п(у))й{х, т) =\e-«f(y, t)dt, yeS,
где
ф (х, х) = F{x, х) — тФ<°) (х) — ФA) (х).
В главе XIII будет показано, что решение последней задачи выражается
рядом
и {х, х) = S Hk (x) ф(*> (х, «),	B.34)
k=i
где
\
, т) = ?(«/, т)	^- J
D+
(y9 т) — определенные линейные комбинации векторов
/)—2, it), 7ТC>(х^> —2, tx), /= 1,2, ...,ft.
Ряд B.34) сходится равномерно в D'.
Внеся B.34) в B.33), получим доказательство основной теоремы для
второй задачи.
Замечание относительно приближенного решения, сделанное в конце
п. 11 § 1, остается в силе и в этом случае.
§ 3. Внешние задачи
1. Постановка задач. Внешними задачами будем называть задачи ди-
динамики для неограниченных сред, границами которых служат конечные
замкнутые поверхности Ляпунова. Обозначим такую область через D",
а ее границу — через S. Изучается задача об отыскании регулярной трех-
компонентной вектор-функции и = (ult и2, и3) в цилиндре D" X [0, оо),
которая для всякого x?D~ и <6@, оо) удовлетворяет уравнению A.1),
начальным условиям A.2), граничному условию
\/yeSy te[09oo):u-(y,t)=f(y9t)	C.1)
в случае первой задачи и
)	C.2)

л 3]	ВНЕШНИЕ ЗАДАЧИ	341
в случае второй задачи и условию
при | а: | = оо. Здесь символ О зависит от t.
Эти задачи не имеют более одного решения (см. гл. III, § 6).
Исследуем ради простоты только первую задачу. Вторая задача иссле-
исследуется так же, как в § 2, учитывая коррективы, сделанные ниже для первой
внешней задачи.
Предположим, что требования п. 1 § 1 выполнены (условия 1°—4°,
A.4) и A.5)) и, кроме того, вблизи | х \ = оо функции F (x, f), ф@) (х), ф<!> (х)
и их производные, которые участвуют в определении функции а (х, t)y удов-
удовлетворяют условиям, необходимым для сходимости несобственных интегра-
интегралов в выражении для о (х, t).
Докажем следующую теорему:
3.1.	Теорема. В приведенных условиях первая внешняя задача одно-
однозначно разрешима.
В доказательстве будет указан также алгоритм построения решения.
Заметим, что поставленные задачи приемом, указанным в п. 2—4 § 1,
сводятся к соответствующим задачам с нулевыми начальными данными.
Таким образом, достаточно исследовать задачу при ср@) = срA> = 0.
С целью сохранения обозначений предыдущих параграфов, обозначим
через /0, FQ соответственно граничную функцию и правую часть уравнения
движения после указанного преобразования задачи.
Отметим, что /0 и Fo принадлежат к тем же классам, которым принад-
принадлежали f и F и удовлетворяют тем же условиям роста относительно времени
и затухания на бесконечности относительно точки.
Условие согласования для f0 и Fo примет вид A.14) и A.15).
2. Основная лемма. Дальнейшие рассуждения основываются на сле-
следующем предложении:
3.2.	Лемма. Если для некоторого (Jo > о0 существует вектор-функ-
вектор-функция и0 = (и01, и02, а03), где uoi: D~ X Па(; —> Z, которая удовлетворяет
условиям:
1)	v x(:D~: и0 (х, т) — аналитическая функция в Пао;
2)	V(*, tND- x Пао:
I Щ(х, т) |
1+8 '
для некоторых положительных С и г (р^Рх + Рг + Рз^ 1» 2);
3)	и 0 регулярная функция в D~ и v (*> ^)€^" X Пао удовлетворяет
уравнению A.20);
4)	V @, т) 6 5 X Пао:
^о (У. ^) = /о (У, т);
5)	а0 удовлетворяет условию: при |х|—>оо
то ио(х, 0> определенная формулой A.58), дает решение поставленной
задачи.
Доказательство этой леммы элементарно, но доказательство существо-
существования функции а0, которая удовлетворяет перечисленным условиям, пред-
представляет значительные трудности. Эти трудности преодолеваются так же,

342	СМЕШАННЫЕ ЗАДАЧИ ДИНАМИКИ	грл \}\Ц
как в соответствующей внутренней задаче. Отметим некоторую специфику
внешних задач, которая вызвана неограниченностью области, занимаемой
средой, и условием 5).
3. Исследование первой внешней задачи. Из результатов главы VII
ясно, что существует единственная функция и0, удовлетворяющая условиям
3)—5). Таким образом, надо проверить, что функция, построенная с учетом
условий 3)—5), удовлетворяет также условиям 1) и 2).
Для доказательства аналитичности и0 относительно т поступаем так же,
как в п. 7 § 1, но вместо тензора Грина оператора А (дх) применим тензор
Грина оператора А (дх) — а§?, где Е = || бг/ ||3хз, а а0 — некоторое неот-
неотрицательное число.
Тензор G (ху у; а0), построенный таким образом, и его производные
при х = у будут удовлетворять условиям п. 7 § 1, а характер G (х, у; о0)
в окрестности бесконечно удаленной точки полностью определяется харак-
характером фундаментального решения Г (х — у; а0) уравнения А (дх) и —
— olu = 0.
В последующих рассуждениях при доказательстве аналитичности
иЬ (х, т) надо воспользоваться корректностью задачи или соответствую-
соответствующего интегрального уравнения.
Заметим, что интегральный оператор A.28) заменится оператором
и(о2)
, х) + -?- j G (х, у; Ъо) и{о2) (у, т) dy,
который является вполне непрерывным в пространстве L2(D~).
Кроме того, оценка для Ро из A.24) заменится оценкой
где С (х) — неотрицательная функция, интегрируемая с квадратом
в области D".
Учитывая указанные изменения, приемами пп. 8—11 § 1 можно пока-
показать справедливость оценок 2) из основной леммы.
§ 4. Заключительные замечания.
Библиографические справки
В § 1 были указаны некоторые новые обстоятельства физического ха-
характера, которые отличают динамические (смешанные) задачи от задач рав-
равновесия и установившихся колебаний. Теперь мы можем отметить некоторые
другие отличительные моменты.
Рассматривая теоремы существования статики или стационарных коле-
колебаний, мы убедились, что условия, задаваемые в постановке задач, вместе
с тем или иным предположением об их гладкости были достаточны для дока-
доказательства существования классических решений.
В смешанных задачах динамики мы встречаемся с другой ситуацией.
В постановке этих задач, кроме уравнения состояния, задаются граничные
и начальные данные, которые предполагаются согласованными естествен-
естественным образом; однако, как мы видели, этого, вообще говоря, недостаточно
для доказательства теоремы существования; следует добавить, на первый
взгляд неожиданное, предположение о существовании некоторых количе-

Л 4]	ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ. БИБЛИОГРАФИЧЕСКИЕ СПРАВКИ	343
ственных связей между данными задачи, выражаемых равенствами A.5),
а именно:
(dm-2F(yyt)
Чтобы оценить роль этих условий, проследим главные этапы доказа-
доказательства в обратном порядке. Доказательство основного факта о том, что
выражения A.58), A.60) представляют искомое решение, существенно опи-
опирается на оценки A.38), A.49), A.54); эти оценки получены как результат
оценок A.24) и, наконец, эти последние, — прямое следствие предполо-
предположений A.4), A.10), A.14) и A.15). Но откуда возникли последние три не-
несамоочевидных предположения? Чтобы ответить на этот вопрос, необходимо
вспомнить, что A.10), A.14), A.15) получены в результате наличия равенств
A.6'), т. е.
ат-2
дт~2 F (х, t)
—2
частным случаем которых являются равенства A.5).
Но равенства A.6') и, следовательно, равенства A.5) выражают свой-
свойства гипотетического решения исходной задачи, которое допускает непрерыв-
непрерывные вплоть до границы производные порядка т. Назовем такое решение су-
суперклассическим; при т = 1 оно совпадает с классическим решением.
Таким образом условия A.6') (а значит, и условия A.5)) являются необ-
необходимыми для существования супер классического решения и вполне вероятно,
что они окажутся условиями, достаточными для существования классиче-
классического решения.
Это предположение привело нас к условиям A.6') и вытекающим из них
свойствам A.10), A.14), A.15). Дальнейшее состоит в проверке сделан-
сделанного предположения и, как мы уже знаем, приводит к уточнению значения га
и доказательству существования классического решения.
Сказанное полностью сохраняет силу для смешанных динамических
задач моментной теории упругости и термоупругости.
Обширной главой математической физики, в которой смешанные задачи
динамики находят важные применения, является теория дифракции упругих,
электромагнитных, акустических и др. волн.
С точки зрения приложений, и главным образом по соображениям отно-
относительной простоты математической теории, наибольший интерес представ-
представляют задачи дифракции в таких областях, которые простираются в беско-
бесконечность и имеют границы частного вида: пространство со щелью, полупро-
полупространство, четверть пространства, внешность сферы, внешность цилиндра
и др. Поэтому большая часть имеющихся в литературе работ по смешанным
динамическим задачам отнЬсятся именно к такого рода областям. Многие
из этих задач решаются в квадратурах. Обзор важнейших работ этого рода
можно найти в книге авторского коллектива В. М. Бабич, М. Б. Капилевич,
С. Г. Михлин и др. в серии СМБ, посвященной линейным дифференциаль-
дифференциальным уравнениям математической физики (Москва, 1964, гл. IX).
Исторически, первой большой работой такого характера следует счи-
считать исследования Вольтерра, посвященные задаче Коши для уравнений
теории упругости (см. Volterra [1]). Основную роль в этой работе играют
специальные решения уравнений теории упругости, представляющие сме-
смещения бесконечного пространства под воздействием сосредоточенной в точке
х° (х°, х°, xl) силы, равной 6B), где б (t) — функция времени Дирака;
они были найдены Стоксом.

344	СМЕШАННЫЕ ЗАДАЧИ ДИНАМИКИ	ррл VIII
Если сила действует в направлении оси xk, k = 1,2, 3, то соответствую-
соответствующие смещения Ты (х —х°, f), k, i = 1, 2, 3, имеют значения
г	г	( 1, А > 0;
где г = | * — х° |, 7а = t — —, уъ = < — —; е (Л) = j 0> fc < Q. /Л — коор-
координатные орты и Г (х — х°, ^) = || Yki (x — х°, t) || есть симметричная матри-
матрица фундаментальных решений динамических уравнений теории упругости.
С помощью этой матрицы решение задачи Коши для бесконечного простран-
пространства выражается формулой Вольтерра
, ?)=__ f г (л:0 — х) ф@) (л:) dx + | Г(л:0~л;,
j J Г(а:0 — x,to^
0 г <аа0—t)
, t)dx dt.
Следующим важным этапом в развитии этих* исследований явилась ра-
работа Лэмба (см. Lamb [1])по решению задачи Коши для полуцростран-
ства хъ > 0, когда на границе полупространства х3 = 0 действует верти-
вертикальный или горизонтальный сосредоточенный импульс; в первом случае
граничные условия имеют вид
T33 = ^diva + 2fx -g~~= —6(
а во втором
Чз = 0» х13 = х23 = — б (хх) б (х
Лэмб решал эти задачи методом Фурье; его результаты послужили началом
большого числа работ этого характера, в которых задачи и метод Лэмба
обобщались в различных направлениях (см. Нарышкина [11, Петрашень
Ш и др.).
На базе фундаментальных решений Г (х — х°, t), вообще говоря, можно
построить теорию потенциала для динамических уравнений теории упру-
упругости, подобно тому как это сделано для уравнений статики и установив-
установившихся колебаний. В этом направлении заслуживают внимания работы
Мюнтца (см. Мюнтц [1]) и Бабича (см. Бабич [1]); другие попытки этого
рода оказались не особенно успешными.
Следующий крупный шаг был сделан С. Л. Соболевым (см. Франк и
Мизес [1], гл. 12), который, пользуясь методом комплексных волн (см.
Смирнов, Соболев [1 ]) и развитием метода характеристик, получил в замкну-
замкнутом виде решение задачи Коши для полупространства, когда на границе за-
заданы условия первой или второй основных задач теории упругости.
В. И. Смирнову принадлежит решение смешанной задачи для шара
в случае волнового уравнения методом функционально-инвариантных ре-
решений (см. Смирнов [2]). Важные результаты содержатся в работах: Лады-
Ладыженская [11, Петрашень [11, Бабич [11, Боровиков [1] и др.

ЗАДАЧИ	345
Значительно меньше работ имеется в литературе по смешанным задачам
теории упругости относительно тел с конечной границей произвольной формы;
по-видимому, одной из первых работ этого рода являются работы Купрадзе,
Бурчуладзе [6]—[81, Гегелиа [19], Магнарадзе [5] — [7].
ЗАДАЧИ
1.	Решить вторую основную задачу динамики при заданном на границе векторе обобщен
к
ного напряжения Т (ду, п) «.
2.	Решить задачи динамики с граничными условиями задач (III), (IV) и (VI)
(см. I, § 14).
3.	Решить задачу динамики при заданных граничных значениях первых двух состав-
составляющих вектора смещения и третьей составляющей вектора напряжения.
4.	Найти в замкнутом виде решение динамической задачи для двугранника х2^ О,
хз^ О» — °° <С xi < оо и трехгранника хх^ 0, х2^ О, х3^» О, если на одной из граней
заданы: а) вектор смещения, или б) вектор напряжения, или в) касательные напряжения и
нормальное смещение, или г) нормальное напряжение и касательные смещения, а на других
гранях заданы условия типа либо в) либо г).
5.	Найти в замкнутом виде решение динамической задачи для двугранника (трехгран-
(трехгранника) с углом, равным я/2« (п^ О — целое число), если на гранях заданы: а) касательные
напряжения и нормальное смещение, или б) нормальное напряжение и касательные смеще-
смещения, или в) на одной из граней заданы условия типа а) и на других — условия типа б).
Указание к задачам 4 и 5. Выразить в квадратурах решения указанных
задач для уравнений установившихся псевдоколебаний методом главы XIV, § 3; исследовать
асимптотический характер в зависимости от параметра т и затем применить способ решения,
указанный в настоящей главе.

ГЛАВА IX
МОМЕНТНАЯ ТЕОРИЯ УПРУГОСТИ
Некоторые вопросы моментной теории упругости уже были рассмотрены
в предыдущих главах. В первой главе выведены основные уравнения движе-
движения в компонентах напряжения (см. (I, 4.3), (I, 4.6)), закон Гука (см. (I, 7.16),
(I. 7.16') или (I, 7.21), A, 7.21')), выражения для энергии деформации (см.
(I, 7.19)) и вытекающие из положительности этих выражений условия для
упругих коэффициентов (I, 7.20).
В первой же главе (I, § 11, п. 2) дается аксиоматическое построение
моментной теории упругости; приводятся уравнения динамического ((I,
11.14), (I, 11.14')), статического (A, 11.17), A, 11.17')) и колебательного
((I, 11.20), (I, 11.20')) состояния в компонентах смещения и вращения; даны
матричные записи уравнений (см. 1, § 12, п. 2); введен оператор напряжения
(см. 1, § 13, п. 2); указаны некоторые основные математические задачи (см.
1, § 14, п. 2) теории.
Во второй главе (II, § 2, § 5) построены сингулярные и фундаменталь-
фундаментальные решения.
В третьей главе доказываются теоремы единственности решений основ-
основных задач динамики (III, § 6), статики (III, § 4) и колебания (III, § 5);
вводятся условия излучения (определение III, 5.3).
В этой главе исследуются некоторые математические задачи моментной
теории упругости; доказываются теоремы существования классических ре-
решений; устанавливается гладкость решений в зависимости от гладкости
граничных и начальных данных, массовых сил и массовых моментов, а также
от гладкости границы среды; даются формулы представления решений в виде
интегралов типа потенциала; изучаются обобщенные решения, исследуется
вопрос о корректности поставленных задач.
Мы увидим, что методы исследования, примененные в других разделах
нашей книги при решении этих вопросов для задач классической теории
упругости, позволяют решить их с той же полнотой и для моментной теории.
Это обстоятельство имеет принципиальное значение: доказательство
корректности математических задач, формулируемых исходя из гипотез,
лежащих в основе моментной теории, может указывать на законность этих
гипотез, все еще встречающих критическое отношение у некоторой части
исследователей.
Мы не будем здесь обсуждать вопрос о практической ценности момент-
моментной теории, сравнивать ее выводы с результатами классической теории,
останавливаться на методах вычисления упругих постоянных и т. д.
Читатель, интересующийся этими вопросами, может обратиться к ли-
литературе, указанной в § 5, где он найдет, между прочим, и ряд противоре-
противоречивых утверждений.

§ 1]	ВВЕДЕНИЕ	347
§ 1. Введение
В первом параграфе приводятся сведения, необходимые для дальней-
дальнейшего. Здесь собраны и последовательно изложены результаты предыдущих
глав, относящиеся к моментной теории упругости.
1. Основные уравнения. В дальнейшем удобно пользоваться матричной
записью основных уравнений в компонентах смещения и вращения. Основ-
Основные уравнения (см. § 12, гл. I) динамики, статики и колебания пишутся
соответственно в виде
г^-9	A.1)
0,	A.2)
М (дх) <Ы + рЖ + о2гШ = 0.	A.3)
Здесь М — матрица размера 6x6, определенная из (I, 12.7'), и (I, 12.8),
% и Ж — шестикомпонентные векторы.
Первые три компоненты вектора % образуют вектор смещения и =
= (и19 и2, и3), а четвертая, пятая и шестая компоненты образуют вектор
вращения со = (со^ со2, со3). Первые три компоненты вектора Ж образуют
массовую силу У = (Ф9 У2> &~з), последние три — массовый момент 9 —
= (919 9» 99).
В связи с этим % к Ж иногда будем записывать в виде % = (и, со) и
Ж = (*F, ^). р — плотность среды, а — частота колебания, г = || тц ||6х6,
где тц = 0 для i =f= j и ги = р, при i = 1, 2, 3 и ru = J, при i = 4, 5, 6,
3 — динамическая характеристика среды (см. I, § 4, п. 2).
2. Оператор напряжения. Напряжение в точке х по направлению п (х),
где п (х) — произвольный единичный вектор, в моментной теории есть (см.
I, § 13, п. 2) вектор Т (дх, п (х)) % (х), где Т — матричный дифференциаль-
дифференциальный оператор размера 6x6, определенный из (Г, 13.8) и (I, 13.9), а^= (и, со).
Первые три компоненты этого вектора образуют вектор силового напряже-
напряжения х(п {х)) (xt t) в точке х по направлению п (х) (см. (I, 13.10)), соответствую-
соответствующий вектору смещения и и вектору вращения со; последние три компоненты
вектора Т (дху п (х)) % (х) образуют вектор моментного напряжения
^(п (х)) (д^ fj в Точке х по направлению п (х), соответствующий тому же век-
вектору смещения и и вектору вращения со (см. (I, 13.11)).
Таким образом,
xf{x)) (х, t) = [Т (д„ п (х)) %L (*)]/ =
= [Т{1) (д„ п(х))и(х) + ГB) (д„ п(х)) со (jc)]7, A.4)
(/=1,2,3). A.5)
3. Основные задачи. Рассматривается упругая среда, занимающая огра-
ограниченную область трехмерного евклидова пространства Е3, границей кото-
которой служит связная поверхность Ляпунова. Эта область обозначается че-
через D+, а ее граница через S. Рассматривается также среда, занимающая
бесконечную область D~ = E3\D+. Сформулируем сначала внутренние за-
задачи статики, т. е. задачи статики для области D+.
Найти шестикомпонентный вектор % = (а, со), и = (и19 и2, и3), со =
= (g>i> ®2» ^a) класса С1 (D+) fl С2 (D+)9 удовлетворяющий в области D4"
уравнению A.2) и одному из следующих граничных условий:
A.6)

348	моментная теория упругости	[рл# IX
—	первая внутренняя основная задача или задача A)+;
VyeS: [T(dyin)<U(y)]+ = f(y)	A.7)
—	вторая внутренняя основная задача или задача (И)+;
VJ/6S: 1Н(ду,п)<Щу)Г = ?(У)	(I-8)
—	третья внутренняя основная задача или задача AП)+;
У/yeS: [R(dy9n)<U(y)r = f(y)	A.9)
—	четвертая внутренняя основная задача или задача (IV)+.
Здесь / = (/], • • ., /6) — шестикомпонентный вектор, определенный
на S (ft: S —* R). Этот вектор удобно записать в виде / ~ (fA), /B))» гДе
/A) = (fu /2> /з). fB) = (/4, /5, /e); H и Я —матричные дифференциальные
операторы
Н(дх,п(х)) =
R(dxyn(x)) =
Е
о
о
о
ТB) (дх> п (х))
Е
AЛ0)
A.11)
7<2>, Л4> — определены из (I, 13.9); ? - || Ец ||зхз, ?*/ = 6„; через О
обозначена матрица размера 3x3, все элементы которой — нули.
Очевидно, первые три компоненты вектора Н (дху п (х)) % (х) образуют
вектор смещения и (х), а последние три — вектор моментного напряжения
в точке х по направлению п (х), с обратным знаком, т. е. —\xin (x)) (х), соот-
соответствующий вектору вращения со (% = (и, со)).
Первые три компоненты вектора R (дху п (х)) % (х) образуют вектор
силового напряжения, т. е. т<п <*>> (х), а последние три — вектор вращения
со (х). Таким образом, во внутренних основных задачах требуется нахождение
решения % = (и, со) уравнения A.2) класса С1 (D+) fl С2 (D+), при задан-
заданных на границе S: смещениях и вращениях — в первой задаче, силовых и
моментных напряжениях — во второй задаче, смещениях и моментных на-
напряжениях — в третьей задаче, силовых напряжениях и вращениях —
в четвертой задаче.
Внешние задачи ставятся аналогично внутренним. Следует только везде
заменить верхний индекс «+» на «—» и потребовать от решения % = (иу со)
выполнения следующих условий (см. (III, 4.5)) на бесконечности:
dUj (X)
Подобно классической теории и здесь можно ввести граничные условия,
аналогичные условиям третьей, четвертой, пятой и шестой задач классиче-
классической теории и тогда возникает большая серия новых задач моментной теории.
Мы рассмотрим здесь указанные выше четыре задачи, а некоторые другие
отнесем к задачам в конце главы.
Задачи колебания ставятся аналогично задачам статики.
Найти_шестикомпонентный вектор % = (Ui) в области D+ (ЭД,: D+—>Z)
класса С1 (D+) f| С2 (D+), являющийся решением уравнения A.3) в области
D+ и удовлетворяющий граничному условию A.6) — первая внутренняя
о
задача (задача A)+), или граничному условию A.7) — вторая внутренняя
о
задача (задача (П)+), или граничному условию (L8) — третья внутренняя

1]	ВВЕДЕНИЕ	349
задача (задача (Ш)+), или граничному условию A.9) — четвертая внутрен-
о
няя задача (задача (IV)+).
Аналогично формулируются внешние задачи. Надо дополнительно по-
потребовать от решения удовлетворения условию излучения (см. определение
III, 5.3).
В задачах динамики ищется решение^ = {%ь) уравнения A.1) в области
D+ X Т, где Т = Uo, tx\, Ut ' D+ X ST — /?, принадлежащее классу
С1 (D+ х ?Г) П С2 (D+ X ?Г), удовлетворяющее, кроме граничных усло-
условий, указанных выше, еще начальным условиям	D^
= ср<°> (х),	A.13)
-фA)(х).	A.14)
4. Формулы Сомилиана. Так же как в классической теории, доказывается
справедливость следующих теорем:
Пусть D —конечная область, ограниченная поверхностями Sl9 S2, . . .
.. ., Smj где S, — компактное многообразие Ляпунова (принадлежит
классу Лх (а), а > 0); кроме того, S, П ^/ = 0» * =^= /» U / = h 2, . . ., m.
1.1. Теорема. ?сла ^ = (Ui)\ принадлежит классу С1 (D) П С2 (D),
то у* б ^3*
= - j W(x — z) [M (dz)<U(z)] dz+\ xY(x — y) [T(dy> n)<U{y)} d^S —
D	S
- \ [T(dy, n)W(y — x)Y *U{y)dyS.	A.15)
Здесь б (х) = 2, если #?D; б (х) = 0, если x? E3\D и б (х) = 1, если л;? S;
S = US,: V^/65:
<U(y)= lim <U(z)9 T(dy, n)<U(y)= lim T (dz1 n)M(z),
D э 2->(/	Оэ2->г/
? — матрица фундаментальных решений уравнений статики моментной тео-
теории упругости. Последний интеграл в правой части формулы A.15), когда
x(^S, следует понимать в смысле главного значения.
Формулу A.15) будем называть формулой Сомилиана. Этой формуле
можно придать другой, более удобный для исследования третьей и четвер-
четвертой задач, вид.
1.2. Теорема. Если Ч^С1 (D) П С2 (D), то у*€ ?3:
D
+ j [H {dy, n)W(y — x)}' R (д„, п) % (у) duS —
— J [R(du, n)W(y-x))' H {dy> n)%{y)d?.	A.16)
1.3. Теорема. Пусть %?С1 (D) П С2 (D) (%: D — Z). Тогда
справедливы формулы, полученные из A.15) и A.16) заменой Ч (•) на Ч (•, а)
и М (дх) на М (дх, а).

350	моментная теория упругости	[рл# IX
5. Потенциалы. Рассмотрим некоторые интегралы типа потенциала.
1.4. Теорема. Если S — кусочно-гладкая поверхность и ф? /- (S)
(Ф — суммируема на S), то интегралы
(x — y)y(y)dySt	A.17)
= \\Т(ди, n)Y(y—x)]'4>(y)d!)S,	A.18)
= J [Н(ду, n)W(y — x)]'q>(y)dyS,	A.19)
J
52(Ф)(х) == \\R (ду, n)W(y — x)Y ф (у) dyS	A.20)
удовлетворяют уравнению A.2) в каждой точке x?Es\S и принадлежат
классу С°° (E3\S).
Если S — граница конечной области D+ и D~ = ?3\(D+ (J S), то из
результатов гл. V следует справедливость следующих теорем:
1.5. Теорема. Если S^JIk(a) и <р?С1>ь (S), 0 < / < ft, k —
произвольное натуральное число, 0 < C <а < 1, то Т (^), определенный
формулой A.17), принадлежит классам С1+1* & (D+) w C/+1- » (D~), u V z? S:
[5Г(аг^)У(Ф)г)]±=±фB) + Т(а,^)Г(ф)B).	A.21)
Здесь, как и выше,
[Т (dz, v) Г (Ф) (г)]+ = lim T (d« v) F (Ф) (х),
Э
v — орт нормали поверхности S в точке г. Аналогично определяется
[Т(дг, v)F (Ф)(г))-.
1.6.	Теорема. Если S?Jlk (а), ф ? С1» & (S), 0 < / < ft, ft — д/?о
извольное целое положительное число, 0 < (J <а < 1, mo F (ф), определен-
определенный формулой A.18), принадлежит классам С1* е (D+)9 Cli 3 (D"), а \fz ? S:
[Ж (Ф) (г)]± =ТФB) + Г (Ф) (г).	A.22)
1.7.	Теорема. Если S 6 Л* (а), <р 6 О Э (S), 0</<ft, 0<p^<
< а <: 1, то #<«> (ф) а а»<2) (ф) принадлежат классам С^ е (D+), C^* ^ (D~),
а ^B) (ф) а ^?A) (ф) принадлежит классам C/+1* p (D±) а v 2€ S:
[/? (d2, v) 5» (Ф) (г)]* = ± <р (z) + Я (dZf v) 5^ (q>) (г),	A.23)
[Я (аг, v) Ж (Ф) (z)]* = ч= Ф (z) + Я (Зг, v) Я (ф) (г).	A.24)
Здесь через й?A) обозначен трехкомпонентный вектор, образуемый пер-
первыми тремя компонентами вектора 91, а через i%B)— вектор, образуемый
последними тремя компонентами вектора i%. Аналогичный смысл имеют
обозначения Ж^ и 26™.
1.8. Теорема. Если S^JIr (а), а > Ом ф? MS), то формулы A.21)—
A.24) справедливы почти для всех z?S (почти для всех z^Sсуществуют син-
сингулярные интегралы, участвующие в этих формулах).
Рассмотрим теперь отображения, определенные интегралами A.17)—
A.20), в которых W (г) заменяется на Ч? B, а), где Ч? (г, а) — матрица
фундаментальных решений уравнений колебаний (см. (II, 2.10)).
Полученные таким образом отображения обозначим соответственно
через Т^\ Ж^\ Ш\ ШК

« 2J	ИССЛЕДОВАНИЕ ЗАДАЧ СТАТИКИ	351
1.9. Теорема. Теоремы 1.5—1.8 остаются верными, если в их фор-
формулировках вместо Т\ W, Ж и 91 будем предполагать соответственно faK
6. Теорема Ляпунова—Таубера. Приведем одно предложение, аналог
которого для гармонических потенциалов носит название теоремы Ляпу-
Ляпунова—Таубера.
1.10. Теорема. Если S ? Л2 @), ср ? С0 (S), существует один иэ
пределов [Н (дг, v) % (z)]+ или [Н (дг, v) % (z)]~, где
U(x)=\ [H (ду, n)W(y — x)Y Ф (У) dyS,
s
то существует и другой, и
[Н {д„ v) % (г)]+ = [Я (дг, v) U {г)Г.	A.23')
Доказательство. Справедливо представление
u, n)V(y-z)]' =
, г),
где ГD) и Wq определены соответственно из (I, 13.9) и (II, 2.15); Q — матрица
со слабой особенностью класса G A, 1,1).
В силу этого представления для доказательства теоремы 1.10, достаточно
показать справедливость равенства
[ГD) {дж, v)v(z)}+ = [ТD)(дг, v)v(z)Y,	A.24')
если известно существование одного из пределов, участвующих в теореме
1.10 или, что то же самое, если известно существование одного из пределов,
участвующих в равенствах A.24').
Здесь
v(x)=\ [Т{4\ду, n)%{y — x)]\{
где фB) — вектор, образуемый последними тремя компонентами вектора ср.
Доказательство последнего предложения следует из теоремы Ляпунова —
Таубера для потенциалов классической теории упругости (см. V, § 8).
§ 2. Исследование задач статики
1. Сведение граничных задач к интегральным уравнениям. Исследуем
граничные задачи статики для однородного уравнения
Решение первой внутренней и внешней задачи будем искать в виде по-
потенциала
U(x) = W (Ф) (х) = J \Т {ди, п)Ч?(у — х)\ Ф (у) dyS,	B.1)
второй внутренней и внешней задачи — в виде
B.2)
J
s
третьей внутренней и внешней задачи — в виде
U (х) = & (Ф) (х) = J [R (ду9 n)W(y — х)]' Ф (у) dySy	B.3)

352	моментная теория упругости	(рл |х
четвертой внутренней и внешней задачи — в виде
%{х) = Ж (г|;) (х) = J [Я (д„ п) W (у — х)\ ф (у) dfi.	B.4)
Здесь ф и г|) — шестикомпонентные векторы, которые следует определить
так, чтобы потенциалы давали решения соответствующих задач. Легко
проверить, что если ср — суммируемый вектор на S, то векторы
Т (ф), W (ф), 52 (ф), Ж (ф) удовлетворяют уравнению М (dj % = О, как
в области D+, так и в области D", и условиям A.12) на бесконечности.
Если учесть граничные свойства потенциалов и граничные условия задач,
получим сингулярные интегральные уравнения для первой внутренней и
внешней задачи
[Т(ду, n)W{y — z))'q>(y)dvS=:i(z);	(I)
для второй внутренней и внешней задачи
для третьей внутренней и внешней задачи
+ Ф (г) + | Я (<Эг, v) [R (д,, л) Т (j/ — г)]' <р (у) dJS = f (г);	A11I
для четвертой внутренней и внешней задачи
± Ф (г) + J R (дг, v) \H (dg, n)W(y — z)\ ц> (у) d,S = / (z).	(IV)*
Соответствующие однородные интегральные уравнения (f = 0) обозначим
теми же символами, снабжая их нижним индексом нуль.
1
2. Исследование интегральных уравнений. Обозначим через Ж+ опера-
оператор, порожденный левой частью уравнения A)+. Аналогичный смысл имеют
обозначения Ж~, Х±, Ж* и Ж±.
2.1. Теорема. Операторы Ж+ и Ж', Ж~ и Ж+, Ж+ и Ж~, Ж~ и Ж\
рассмотренные в сопряженных пространствах L^6) (S) и Lp (S), где
— -|	г = 19 — взаимно сопряженные.
1	2	1	2
Для операторов Ж+ и Ж~ч Ж" и Ж+ это утверждение очевидно, а для
3	4 3	4
операторов Ж+ и Ж~, Ж~ и Ж* следует из тождества
{R(дж, v)[Я(dg, nL(z — у)]'у = Я(dy, n)[R(дгУ vL>(y — г)]%
которое легко проверяется.
Используя оценки
3
Е {ъ—
1=1
=L2, 3, B.5)
справедливые для любых г, y?S ?JIi(a) (п ~ п (у), v = п (г)), можно
убедиться в справедливости следующего представления:
[Т {ду, п) W (у — г)Г = Р B, z — у) + Л {у, г),	B.6)

§2]
ИССЛЕДОВАНИЕ ЗАДАЧ СТАТИКИ
353
где Р (z, г — у) и Рх (уу г) — матрицы размера 6x6, PX^G2 B —а, а)
(см. определение IV, 1.2), a
(i)
где аг и а4 — постоянные, определенные равенствами
jn2 — а\х — аХ	о2 — Ро — ре
1 2л (м- +а)(к + 2\i)' 4 2я (и -f- P) (в 4- 2о) #
Введем локальную систему координат (г) (см. (IV, 3.33))
B.7)
B.8)
B.9)
где т]!, т]2, Лз — координаты точки у в системе (г). Через у' обозначим орто-
ортогональную проекцию точки у на касательную плоскость т (г) (см. определе-
определение I, 15.5). Координатами точки у' в системе (г) будут ц1У ц29 0. Введем
полярную систему координат в плоскости т (г)
г)! = pcos 6, г]2 = р sin 0,
1
Обозначим характеристику (см. (IV,5.24), (IV,5.25)) оператора Ж* через
+. Будем иметь
%&? =—\» #=l,Z,o, /72=1,4.
Xi2m) = —X2im) = am [v2 (an (z) cos 0 + ai2 (z)sin 0) — vx (a2i (г) cos 0 + a22 B) sin 0)],
Xi3l) = — ХзГ = am [v3 (an B)cos 0 + aX2B) sin 0) — vi (a3i B) cos 0 + a32 B) sin 0)],
1	1
X231 = — Хз2г) = am [v3 (a21 B) cos 0 -f a22 B) sin 0) — v2 (a3i B) cos 0 + a32 B) sin 0)J.
1	1
Вычисляя символ (см. (IV,5.26)) a+ B, 0) оператора «3f+, получим
О
\ ' '	U	V 7	/ ||^<^4u	II	^
где
a<4>B, 6)
k Ф /; A,/=1,2,3; m
1
Учитывая специальный вид матрицы a+ B, 0), получим
det a+ B, 0) = det о*1) (г, 0)*det a<4)B, 0).
23 В. Д. Купрадзе

354	моментная теория упругости	[рл# IX
Аналогично классическому случаю, легко найти
det ii> (г, 9) = (x^jr - ^J-1, det i«>(*. 6) =
Из условий A,7.20) заключаем, что
и
1
Следовательно, \/z?S и v^6 Ю, 2я): det a+ (г, 6) ф 0, и оператор
Ж+ — нормального типа.
1	1
Учитывая представление B.6), для символа а" получим а" (z, 0) =
i_	i_ I		 i_
= Иа^1|бхб, где opq = ojq\ р 4= ц\ Р, q = 1,6; okk = 1, k= 1,6. Поэтому
det or" = det a+ =f= 0,
l
и, следовательно, оператор J^~ — нормального типа.
3	3
Вычислим символы операторов Ж+ и Ж . Справедливо представление
Н (dz, v) [R (ду, п) W(y — z)Y = Q(y, z — у) + Qx (у, z),
где Qx (*/, г) и Q (у, 2 — у) — матрицы размера 6x6, Qx ? G2 B — а, а),a
, II QA)
QD) I
где Qfl = P\)\ QKki = PKk}\ P\l! и РГ/ определены из B.7) и B.8). Q$ —
вполне определенные функции, явный вид которых нет необходимости вы-
выписывать.
з
Вычисляя символ оператора Ж+9 получим
° "	B.10)
и - : ^D) "
гДе Й1/ = к/, к/ = о{)\ fe, / = 1, 2, 3.
Из B.10) вытекает, что
det or+ (z, 0) = det a+ (z, 0) Ф 0.
з
Аналогично вычисляется символ оператора Ж"
3	3
Таким образом, операторы $?+ и Ж" — нормального типа. Так как опе-
3	4 3	4
раторы Ж* и Ж~, Ж~ и Ж+ взаимно сопряженные, отсюда следует нормаль-
4	4
ность операторов Ж+ и Ж~.
12	3	4
Покажем, что индексы операторов Ж±, Ж±9 Ж± и Ж± равны нулю
в пространстве Lp6) (S).

§ 2]	исследование задач статики	355
Рассмотрим оператор
Ж1 (Ф)(г) = - Ф(г) + у J [Тфу, п)Ч?(у — г)]' Ф(у)dgS9
где у — комплексный параметр. Тогда
i
где ау — символ оператора Жу.
Из условия A,7.20) при y€ Ю, 11, следует, что
det<rv B,6)^0.
Тогда (см. IV,6.7)
ind Ж\ (ф) = 0,
при у = 1.
Точно так же можно показать равенство нулю индексов для других
операторов.
Таким образом, справедлива следующая
12	3	4
2.2.	Теорема. Операторы Ж±у Ж±, Ж± и Ж* — фредгольмовы
в пространстве L?6) (S).
Аналогично классическому случаю (см. VI, § 3) доказывается
2.3.	Теорема. Если S 6 Лг+1 (а) и /6 Сг> $, 0<р<а<1, г —
произвольное неотрицательное число, то всякое решение класса Lp6) (S)
уравнения A)±, (И)±, (Ш)± и (IV)± принадлежит классу Cr> 3 (S).
2.4.	Теорема. Если S 6 Лг+1 (а) и f? Cr» a (S), то 5ля уравнений
A)±, (И)*, (П1)±, (IV)± справедливы теоремы Фредгольма в пространстве
С- 6 (S).
3. Теоремы существования для задач A)+ и (П)~. Докажем теорему
2.5.	Теорема. Если S ?Лг (а), то однородные уравнения A)о~ и
5" имеют только тривиальные решения в классе (?'® (S), ($? @. 1)-
В самом деле, пусть уравнение (П)о"
имеет нетривиальное решение i|)°6C°*p(S). Рассмотрим потенциал
U0 (х) - J У (х — у) ^ (у) d^S.	B.11)
Учитывая свойства матрицы W (х — у)у и то, что г|)° является решением
однородного интегрального уравнения (Н)о~, будем иметь
1) М фх) U0 (х) = 0, при х 6 D+ U D~\
3) в окрестности бесконечно удаленной точки
«?(*) = О (|*Г1), ^(х) = о(\хГ1),	B.12)
(Я0- (и?, °, «з, со?, о§, ей); t, /=1,2, 3).

356	моментная теория упругости	[рл IX
Из теоремы 111,4.4 следует, что %Q (х) = 0 при x?D"\ Тогда (см.
теорему 1.5)
Отсюда в силу теоремы 111,4.1 %° (х) = 0 при x?D+, поэтому
Принимая во внимание граничное свойство потенциала B.11), получим
2^(z) = \Т(д„ v)и°(г)}+— \Т(д„ v)и°(г)} = 0.	B.14)
Полученное противоречие показывает, что уравнение (П)<Г имеет
только тривиальное решение класса С1- р (S). В силу теоремы 2.4 тривиаль-
тривиальное решение класса С1' 0 (S) имеет и уравнение A)о~. Теорема доказана.
2.6. Теорема. Если S 6 Лг+1 (a), f ? Сг- ^ (S) @ < р < а < 1), то
задачи A)+ а (II)" имеют решения для любого f. Они единственны и предста-
вимы в виде B.1) а B.2) соответственно.
Кроме того, в условиях теоремы эти решения принадлежат классу
Сг' Р (D+) и С^1- Р (D") соответственно.
Доказательство следует из теорем 2.5, 1.6 и 1.5.
4. Теоремы существования для задач (И)+ и A)~. Пусть S ? Лг (а).
Рассмотрим однородные уравнения
Ф (z) + J
Э„ v) Y B — y)Y Ф (У) d^S = 0.
2.7. Теорема. Векторы
==A, 0, 0, 0, 0, 0),	<рD> (z) = @f -г3, г,, 1, 0, 0),
= @,1,0,0,0,0),	Ф<5>(*) = B3,0,-2^0,1,0), BЛ5)
фC) (г) = @, 0, 1, 0, 0, 0),	ф<«> B) = (— 22, 2Х, 0, 0, 0, 1)
образуют полную систему линейно независимых решений уравнений A)о"
в классе С0' а (S).
Доказательство. Сначала докажем, что каждый из векторов
ф(/) (/ = 1,6) удовлетворяет уравнению A)<Г.
В самом деле, формулой B.15) вектор ф(^ определен не только на S,
но и во всем пространстве, и, следовательно, в области D+.
Кроме того, этот вектор представляет решение задачи (П)о^ (см. 111,4.2).
Поэтому из формулы A.15) получим
2Ф(/)(х) = - \[T(dy,n)W(y—x)Y&n(y)dJS, / = !7б.
Переходя к пределу при D+9*—* z?:S и учитывая A.22), легко убе-
убедимся в справедливости утверждения.
Далее аналогично классическому случаю доказывается, что множество
векторов ф*1*, . . ., ф<6) образует полную систему линейно независимых
решений уравнения A)^".

* 2]	ИССЛЕДОВАНИЕ ЗАДАЧ СТАТИКИ	357
Исследуем задачу (Н)+:
Выпишем необходимое и достаточное условие разрешимости	этого
уравнения. По третьей теореме Фредгольма имеем
O, ?=17б,	B.16)
где ц>{к) (у) определены из B.15), и подставляя их в B.16) получаем следую-
следующие условия:
j = O- 6=1,2,3;	B.17)
2 вад^^Н dt,S = 0, k= 1, 2, 3,	B.18)
{ |/
которые выражают равенство нулю главного вектора и главного момента
внешних усилий.
2.8. Теорема. Если Se«#r+1(a), /€C^P(S), 0<C<a<l,
г > 1 и удовлетворяются условия B.17), B.18), то задача (П)+ имеет реше-
решение, представимое в виде потенциала B.2), где гр — решение класса Cr> *> (S)
интегрального уравнения (П)+. Кроме того, это решение принадлежит
классу С+1- Р (D+).
Исследуем задачу (I)". Если решение этой задачи будем искать в виде
потенциала B.1) с неизвестной плотностью ср, то для определения ф получим
интегральное уравнение (I)". Для разрешимости этого уравнения, как было
показано выше, необходимо и достаточно выполнение условий
J / (У)
J / (У) Ф (У) dyS = О, / = Т7б,	B.19)
гдег|)A), . . ., \|){б) —система линейно независимых решений уравнений (П)о".
Таким образом, если S?JIr+1 (a), f?Cr* 3 (S), 0 < E < a <: 1 и вы-
выполнены условия B.19), то задача (I)" имеет решение, представимое в виде
потенциала B.1), где ф — решение интегрального уравнения (I)" в классе
&- Р (S).
Потенциал B.1) удовлетворяет более жестким ограничениям на беско-
бесконечности, чем условия A.12). А именно, первые три компоненты Ж (ф) (х)
имеют порядок О (\ х |), а последние три — О (| х |). Первые три компо-
компоненты производной —д	имеют порядок О (\ х |~3), а последние три —
О (| х Г).
Указанным обстоятельством обусловлено то, что задача (I)"" не для вся-
всякого / имеет решение, представимое в виде B.1).
Ниже мы докажем, что задача (I)" всегда разрешима (при определенных
условиях гладкости f и S).
Будем искать решение (I)" не в виде B.1), а в виде
= \[Т (дууп)Ч?(у — х)]' <p{y)dyS+ \4(x — y)q(y)dyS> B.2O>
где ф и г|) — искомые шестикомпонентные векторы класса Cr» p (S). Предпо-
Предположим, что S?Jlr+1(a) @ <р <a <: 1).

358	моментная теория упругости	[рл# IX
Очевидно, %, определенное из B.20), удовлетворяет уравнению М (дх) %=
= 0. Кроме того, если ф и гр из класса Cr- 3 (S), то % ? Cr* P (D~) и удовлет-
удовлетворяет условиям A.12).
Граничное условие для определения искомых ф и -ф дает
Ф B) + ( [Т C,, п) Т (у — г)У Ф (у) d^S = / (г) — ГW (г —у) ф (у) d^. B.21)
5	s
Условие разрешимости этого уравнения пишется в виде
Яf (г) — ( W (z — у) ф (у) d»SI ф</> B) d2S = 0, / = ТГбГ B.22)
S	J
где t|)A), . . ., t|)F> — множество линейно независимых решений уравне-
уравнений (П)о~.
Покажем, что г|) можно подобрать таким образом, чтобы было выпол-
выполнено условие B.22) для любого f.
В самом деле, B.22) перепишется в виде
Л/= [ / (z) ф</> B) d^S = l/f YB — #)г|>(#)
Отсюда
г—f/)]'
== J / J
Так как VP(z — y)]' = W(y — z)9 то
B.23)
и, следовательно, условие разрешимости B.22) принимает вид B.23), где
Г (ф<'>) (у)= f T
Но У (ф(/)) принадлежит классу Сг+г» а (D+) (см. теорему 2.8) (г > 1),
т. е. является регулярной в области D+ и (см. теорему 1.5)
IT (ду, п) Г (ф</>) ((/)]+ = г|)</) (у) + J [Г (дуу п) Т (у — z
Так как г|)(/) является решением уравнения (П)о", правая часть предыдущего
равенства обращается в нуль.
Таким образом, Т Сф(/)) является решением задачи (Н)о".
Напишем формулу Сомилиана A.15) для Т (ф(/))- Будем иметь
2Т (ф</>) (х) = - J [Г (<Э9, n) ^F (у — х)]'
Переходя к пределу, когда D+Э*—¦ z(zS, получим
2Т (ф</>) (г) = Г (ф</>) B) - J IT C^ я) Т (у — 2)]' У (ф(/>)
т. е. Т (V;)) является решением уравнения A)о~.

к 2]	исследование задач статики	359
Если к этому добавить, что из линейной независимости ty(/> следует ли-
линейная независимость Т Сф(/))» то легко показать возможность выбора \|)
из условий B.23).
2.9.	Теорема/ Если Se«#r+1 (a), f?Cr> & (S), 0< р <а< 1, г> 1,
то задача A)~ однозначно разрешима. Решение представляется в виде B.20),
где г|) определяется из B.23), а ср из уравнения B.21). Это решение при-
принадлежит классу Сг- & (D~).
5. Теоремы существования для задач (Н1)+ и (IV)".
2.10.	Теорема. Однородные уравнения
—Ф (z) + J Я (д„ v) [R (ду9 п) ? (у —г)]' Ф (у) dyS = 0, A11)+
-ф (z) + J /? (дг, v) [Я (д„, /г) Y (t/ — г)]' ф (г) d,S = 0	(IV)-
имеют только тривиальные решения в пространстве С1* а (S) (предпола-
(предполагается, что S^Jl^ (а)).
Доказательство. Покажем, что уравнение (IV)o~ имеет только
тривиальное решение. Допустим обратное; пусть уравнение (IV)o~ имеет
нетривиальное решение ф^С1' ^ (S).
Составим потенциал
U»(x) = j [H (ду, п) ? (у — х)У Фо (у) d,S.	B.24)
Очевидно, он удовлетворяет уравнению М(дх)%°=^0 и условиям на
бесконечности A.12). Учитывая граничное свойство этого потенциала, по-
получаем
\Я{д„ v)^(z)J- = O.
Таким образом, %° есть решение задачи (IV)o~. По теореме 111,4.4 получим
\fxeD~: ^о(х) = О.
Тогда vz€ S:
[Н (д„ v) У? (г)Г = 0.
Но вектор %Q представим в виде B.24) и из теоремы Ляпунова—Таубера
заключаем, что
[Я (дж, v) U° B)]+ = [Я (дж, v) %* (z)}- = 0.
Таким образом, %Q является решением задачи (III)f. Поэтому
Следовательно, %° (х), определенная по формуле B.24), тождественно равна
нулю, как в D+, так и в D~.
Из формулы A.23) получаем
2Ф° (z) = [R (д29 v) U0 (г)]+ — [R (д29 v) <№° (г)]~ = 0.
Полученное противоречие доказывает, что уравнение (IV)o~ имеет только
тривиальное решение. Тогда только тривиальное решение имеет и союзное
уравнение (П1)о~.
2.11. Т е о р е м а. Если Serfr+1{a), f?Cr*V(S), 0<р<а<1,
г > 1, то задачи (Ш)+ и (IV)" разрешимы. Решение задачи (Ш)+ представимо
в виде B.3), где ф — решение интегрального уравнения (Ш)+ класса С' 8 (S).
Решение задачи (IV)" представимо в виде B.4), где гр — решение интеграль-
интегрального уравнения (IV)" класса Cr* $ (S).
Эти решения принадлежат классам Cr» <° (D+) и Cr» -: (D") соответственно.

360	моментная теория упругости	[рл# IX
6, Теоремы существования для задач (Ш)~ и (fV)+. Рассмотрим одно-
однородное уравнение
Ф (z) + J Н (д„ v) [R (Э„ п) ? (у — z)]r Ф (у) d^ = 0.	(Ш)~
Докажем теорему
2.12. Теорема. Система векторов
фО> (х) = A,0, 0, 0, 0, 0), фB) (х) = @, 1, 0, 0, 0, 0),
фC) (х) = @, 0, 1,0, 0, Q)	B.25)
образует полную систему линейно независимых решений уравнений j(III)o".
Доказательство. Легко доказать, что эти векторы линейно
независимы и удовлетворяют уравнению AИ)<Г. В самом деле, если учесть,
что
R Фт п) ф<'> = 0, Н(д1п л)ф(/) = ф(/) (/ = 1,2,3),
то из формулы Сомилиана (см. A.16)) следует
2ф(/> (х) = - J [R (дх, п {х)) Ч? (x — y)Y Ф(/) (у) dyS.
Вычисляя от обеих частей этого равенства операцию Н (дх, v) и пере-
переходя в полученном равенстве к пределу при D+ Э х —* 2 6 S, из A.24) полу-
получим желаемый результат.
Аналогично классическому случаю доказывается, что множество век-
векторов B.25) образует полную систему линейно независимых решений урав-
уравнений (Ш)оГ.
С помощью теорем 2.2—2.4 и 2.12 задачи (Ш)~ и (IV)+ исследуются со-
совершенно так же, как задачи (И)+ и A)~.
§ 3. Задачи колебания
1. Сведение задач к интегральным уравнениям. Исследуем задачи,
поставленные в п. 5, § 1 для однородного уравнения
M(dx)U + o2rU = 0.	C.1)
Предположим, что граница области — S .принадлежит классу Лг (а),
а >0.
Будем искать решение первой внутренней и внешней задачи (см. п. 5, § 1)
в виде
F><«> (Ф) (х) = \[Т (д„ п) У (у—х, а)]' Ф (у) dyS,	C.1')
(Ф) (х) = \
(г, а) — матрица фундаментальных решений уравнений C.1), построен-
построенная во второй главе A1,2.10), а ф — искомый шестикомпонентный вектор—
ш = (фх, . ., фв), ф^: S — Z.
Из теоремы 11,5.1 непосредственно следует, что если ф суммируема на S,
то 2р(со (ф) удовлетворяет уравнению C.1), как в области D+, так и в области
D". Кроме того, 2Р<<*) (ф) удовлетворяет условиям излучения (см. п. 2, § 5,
гл. III).
о
Граничное условие задачи A)± в силу теоремы 1.9 дает почти для всех
=Р Ф (z) + | [Т (ду, п)Ч(у — г, а)}' ср (у) dyS = / B).	A)±

g 3]	ЗАДАЧИ КОЛЕБАНИЯ	361
Будем искать решение второй основной внутренней и внешней задачи
о
(задача (И)±) в виде
Г (*) (х) = | W (х — уу а) $(у) d?y	C.2)
где ур — шестикомпонентный суммируемый вектор на S.
а
В силу теоремы 1.9 граничное условие задачи (П)± даст
± ф (г) + | [Т (д29 v) ? (г — у, а)] ф (у) dyS = / (z).	(H)±
Если решение третьей внутренней и внешней задачи ищем (задача
в виде
<%(*) (ф) (х) = ([R (ду9 п) 4{у — ху а)]' Ф (у) d&	C.3)
s
то получим уравнения
+ Ф (z) + J H (dZ9 v) IR (ду, п)Ч(у — г, о)]' Ф (у) d,S = /(«). (IН)±
о
Для четвертой внутренней и внешней задачи (задача (IV)±) получается
±ф (г) + J R (д29 v) [Я (^, п) W(y — z, о)]' ф (у) d^S = / B), (IV)±
если искать решение этой задачи в виде
Ж^ (ф) (х) = J [Я (ду9 п) Ч (у — х, о)]' ф (у) dJS.	C.4)
2. Исследование интегральных уравнений. Все интегральные уравне-
о о
ния A)+—(IV) — сингулярные. Это следует из того факта, что ядра этих
уравнений отличаются от ядер соответствующих уравнений статики адди-
аддитивным ядром со слабой особенностью (см. § 5, гл. II).
Из результатов главы.IV следует справедливость следующих теорем:
3.1. Теорема. Если S6^r+i(a)» feCr>V(S), 0<P<a<l,
о о о	а
г > 1, то любое суммируемое решение уравнений A)±, (П)*, (HI)*,
принадлежит классу Сг* ^ (S).
a ,	о
3.2.	Теорема. Уравнения A)+, . . ., (IV) — фредгольмовы в про-
пространствах Lp (S) и Cr* $ (S).
3. Тензоры Грина. Введем специальные матрицы, называемые тензо-
тензорами Грина. Эти матрицы существенно применяются для исследования за-
задач колебания.
3.3.	Определение. Первым тензором Грина моментной теории
упругости назовем матрицу G(i) размера 6x6, определенную на D+XD+
и для любого y?D+ удовлетворяющую следующим условиям:
1)	yx?D+ матрица G(d (xt у) представима в виде
GA) (х, y) = V(x — y) — V{l) (x, у),	C.5)
где V(D — регулярная функция относительно первого аргумента в области
D+ и
M(dx)V{l)(x,y) = 0;	C.6)
2)	\fzeS:
$	C.7)

362	моментная теория упругости	[рл IX
Здесь *Р — матрица фундаментальных решений уравнений статики мо
ментной теории (см. § 2, гл. II).
Докажем существование тензора G(i). Для этого достаточно показать
существование такой регулярной матрицы V(i) в области D+ (во всех этих
рассуждениях второй аргумент у произвольно зафиксирован в области D+),
которая является решением уравнения C.6) и удовлетворяет граничному
условию
S 1/	W	)
Таким образом, /-й столбец матрицы V(d является решением задачи
<1)+, где f(z) =4i(z-y).
В предыдущем параграфе было доказано существование решения этой
задачи (если S?JIr (а), то V (z — jy), рассматриваемая как функция точки
z на 5, принадлежит классу Cr- a (S)).
Таким образом, существование первого тензора Грина G(d доказано.
Совершенно так же, как в классическом случае, доказывается
3.4.	Теорема, у (х, y)?D+xD+:
G(i, (x,0) = [G<n (y,x)]'.	C.8)
Кроме того, G(i> как по первому, так и по второму аргументу в D+, а также
по обоим аргументам в D+xD+> суммируема с квадратом.
Было бы естественно определить второй тензор Грина аналогично пер-
первому — заменить лишь в определении условие 2) следующим:
\T(dZtv)Gi2) (z,y)r = 0.
Но тогда для определения 1/B) пришлось бы решать вторую задачу с гра-
граничным условием
\Т (дЖ9 v) VB) (z, у)Г = Т (дг, v) V (г —у).
Согласно результатам предыдущего параграфа (теорема 2.8), такая за-
задача не всегда разрешима.
Чтобы обойти указанное затруднение, введем следующее определение.
Если ф = (фх, . . ., фт) и \f> = (ip!, . . ., -фя), то через ф *гр будем
обозначать матрицу
Ф*Ф = 1|ф*Ф/1?, *,/=!. - • мб.
Задача (II)cf", как это было доказано в § 2, имеет шесть линейно незави-
независимых решений, которые даются формулой B.25). Обозначим через %A)> . . .
. . ., хF) совокупность векторов, полученных из B.25) ортонормированием
в области D+. Таким образом, хA)» • • •> %<6) есть полная система линейно
независимых и ортонормированных решений (в области D+) задачи (Н)о^.
3.5.	Определение. Вторым тензором Грина моментной теории
будем называть матрицу GB> размера 6x6, определенную на D+XD*
UGB))kj- D+XD+*—* Z] и для любого фиксированного y(z.D+ удовлетво-
удовлетворяющую следующим условиям:
1) yx?D+ матрица GB) (x, у) представима в виде
GB) (х, y) = U (х, у) — Vm (xt у),	C.9)
где
в
П (х, У) = -^хР(х — у)	\- ^ %<k> (х) * | W (у — l) Х<*> (g) dl—
k=\	D+
21
fe=l D+
6
"T 2 tk) W * %{П {У) J J
D+ D+

§ 3]	ЗАДАЧИ КОЛЕБАНИЯ	363
() — регулярная матрица относительно первого аргумента в области D*
размера 6x6 и
M(dx)VB)(x,y) = 0;	C.10)
2) vzGS:
T(d2,v)G{2)(z,y) = 0.	C.11)
Легко проверяется, что yx?D+ и х ф у:
М (дх) GB) (х, у) = f tk) (*> * Xlk) (</)•	C.12)
fe=l
Теперь для определения VB) имеем задачу:
1)	VB) — регулярное решение уравнения (ЗЛО) относительно первого
аргумента;
2)	vz€ S: [Т (д2, v) УB) (г, у)]* = Т (дг9 v) П (г, у).
Таким образом, /-й столбец матрицы VB) является решением задачи
(Н)+, где f есть /-й столбец матрицы Г (<Э2, v) П (г, у).
Легко проверить, что f удовлетворяет условию разрешимости этой за-
задачи и этим самым существование второго тензора Грина доказано.
Аналогично строятся третий и четвертый тензоры Грина.
3.6. Определение. Третьим тензором Грина назовем матрицу GC>
размера 3x3, определенную на D+XD+, и для любого у из D+ удовлетворяю-
удовлетворяющую следующим условиям:
1) \/x?D+ : GC) (x, у) представима в виде
х, y) = W (x — y) — V{Z) (x, y\
где VC) является регулярным решением уравнения
M(dx)Vi3) (x,y) = 0
в области D+\
2) Н (дх, v) GC) (x, у) непрерывно продолжима в каждой точке z?S и
Существование такой матрицы следует из теоремы 2.11.
Обозначим через /iA), /iB) и /iC) линейно независимые ортонормирован-
ные решения задачи (IV)<j!~.
3.7. Определение. Четвертым тензором Грина будем называть
матрицу GD) размера 6x6, которая для любого x^D+ и y?D+ представима
в виде
0D) (х9 y) = J (х, y) — V{4) (x, у),	C.13)
где
з
J (х, у) = -±-У(х — у)—±- ^ hik) W * J W (^ — Э h(k) © d% —
k=\	D+
—г 2 J? (x~y) hU) (l) dl *h(k) {y)+
fel D+
2
fe=l D+
3
-f 2 Wfc) {x) * wr> (y) I I hW (l) Y ^ — л)
fel	+D+
D+D+
— регулярная матрица относительно первого аргумента в области D+ и

364	моментная теория упругости	[Гл. IX
Кроме того, будем предполагать, что \fz?S:
z,y) = 0.	C.14)
3.8.	Замечание. Теорема 3.4 остается верной, если в ее формули-
формулировке G(D заменим на GB) или GC>, или GD>.
° 4- ° 4-
4. Внутренние задачи. Исследуем теперь задачи (I)o—(IV)o •
а
3.9.	Теорема. Задача A)о эквивалентна интегральному уравнению
Щ(х)—о* j GA) (x, у) г% (У) dy = 0	C.15)
а
в том смысле, что если задача A)о имеет регулярное решение %, то оно удов-
удовлетворяет уравнению C.15) и, наоборот, если интегральное уравнение C.15)
а
имеет регулярное решение %, то оно дает решение задачи A)<Г.
Аналогичные теоремы справедливы и для, остальных задач (П)о\ AП)о
а
и (IV)o с единственным различием, что в C.15) вместо G(d будут фигуриро-
фигурировать GB), GC> и GD> соответственно.
Напомним, что г = || rif [|бхб, где Гц = бг/р, если i = 1, 3, / = 1, 6, и
Гц = b^f, если t == 4, 6, / = 1, 6, р и f — неотрицательные постоянные.
Уравнение C.15) можно переписать в виде
Г (х) — a2 J Ж {х, у) Г {у) dy = 0,	C.15')
D+
где Т (х) = х •% (х), X(x,y) = -lj-7t GU) (х, у) х, х = [ хг/ ||бХб, х/у =
885 ву"К1р» если t = ТТЗ, / = Т7б, и xt7 = 6цУУ, если f = 476", / = 1,6.
Уравнение C.15') в силу теоремы 3.4 и замечания 3.8 является инте-
интегральным уравнением с симметрическим ядром.
3.10.	Теорема. Интегральное уравнение C.15) имеет счетное мно-
множество собственных значений и все они положительны.
Такая же теорема справедлива для интегрального уравнения, соответ-
о
ствующего задаче (IH)d.
а	а
Интегральные уравнения, соответствующие задачам (И)о и (IV)o , имеют
счетное число собственных значений и все они неотрицательные.
Из теорем 3.9 и ЗЛО следует
3.11.	Теорема. Все рассматриваемые внутренние задачи имеют
счетное множество положительных собственных частот; о = 0 является
для второй внутренней задачи шестикратной собственной частотой, а для
четвертой внутренней задачи — трехкратной собственной частотой.
Аналогично теореме VI 1,6.2 доказывается
а
3.12.	Теорема. Задача A)о нетривиально разрешима тогда и только
тогда, когда нетривиально разрешимо уравнение (П)о . Размерность простран-
пространен _
ства нулей оператора, порожденного левой частью уравнения (П)о , и крат-
кратность собственной частоты а2 задачи (l)t совпадают. Кроме того, решениями
о
уравнения A1)^ являются граничные значения Т-операции над решением за-
G ,
дачи A)о •
Аналогичные теоремы справедливы и для остальных задач.

§ 4]	задачи динамики	365
5. Внешние задачи. Исследование внешних задач основывается на при-
приведенных выше теоремах и проводится совершенно так же, как в классиче-
классической теории (см. гл. VII, § 3).
3.13.	Теорем a.EcAuSe<Hr+i (a),/6Cr«>& (S), г>1,0<р<а<1,
а	о	а	а
то задача A)~, [(П)~, (III)", (IV)"" 3 (однозначно) разрешима для любого о
и решение принадлежит классу Cr* p (D~).
3.14.	Замечание. Можно указать представления решений этих
задач в виде интегралов типа потенциала и уточнить классы, к которым они
принадлежат.
§ 4. Задачи динамики
Метод решения смешанных задач динамики классической теории упру-
упругости, изложенный в главе VIII, можно распространить для решения основ-
основных смешанных задач динамики моментной теории упругости.
Здесь это будет показано на примере первой внутренней задачи.
1. Постановка и приведение к специальному виду. В бесконечном ци-
цилиндре D+ х Т (Т = [0, оо)) ищется регулярный вектор % = (ц, со) из
условий:
^	D.1)
-: Hm U (xy t) = <р<°> (*), lim Щ^- = фо> (*),	D.2)
V(y,t)eSx$~: lim U(x,t) = f (у, t),	D.3)
D+ э х~>у
тлеЖ(х, О, *6О+, ^>0; <рМ(х),<рМ(х), x?D"+;f (у, 0, yeS, t > 0 - за-
заданные шестикомпонентные вектор-функции. От этих функций и от поверх-
поверхности S потребуем те же условия гладкости, как в первой динамической за-
задаче классической теории (см. гл. VIII, § 2, п. 1).
Как и в главе VIII, ищем классическое решение, принадлежащее, по
определению, классу С1 (ZT Х^~)П С2 {D+ X Т).
Для существования такого решения необходимо выполнение «естествен-
«естественных условий согласования»
Ф@)(*/) = f О/, 0), <pU> (у) = ZUJL4. t==o.	D.4)
Исходя из тех же соображений, как в случае классической теории, по-
потребуем еще соблюдения «условий согласования высших порядков»
<P(m)G/)=(-
_, yeSy m = 2, 3, ..., 7,	D.5)
где
ф(ш) (X) = r-1 М фх)
Г1 — матрица, обратная матрице г.
Совершенно так же, как в главе VIII, § 2, пп. 2, 3, 4, можно показать,
что задачу |D.1)—D.3)[, без ограничения общности, можно привести к ана-
аналогичной задаче с нулевыми начальными данными, специальной правой
частью уравнения и специальным граничным значением на S. Решение

366	моментная теория упругости	[рл jx
«приведенной» задачи (назовем его %0 (х, t)) связано с решением исходной
задачи равенством
<Ц0 (*, t) = % (д, t) — 2 (x, t\	D.6)
где 2 (x, t) — шестикомпонентная вектор-функция, которая строится вполне
аналогично классическому случаю (см. гл. VIII, § 2, пп. 3, 4). Для
%Q (jt, t) имеем задачу
^ 3«0,	D.7)
^^ = 0,	D.8)
Vti,t)eSx T: lim Mo (xt t) = f0 (y, t),	D.9)
D+
где
= —П о(Х. —	(- (X, —Г	„	.	D1())
Из D.10) в силу определения ф(т) (х) и 2 (х, f) согласно D.4), D.5)
следует
= 0, т = 0, 1	б; (Ш =0, т = 0, 1	7. D.11)
2. Преобразование Лапласа. Решение эллиптической задачи. Аналитич-
Аналитичность решения. Пусть т = т1 -{- ix2, тх > xi > т0, где т0 > 0 — показатель
экспоненциального роста по времени t первоначальных данных задачи и их
допустимых производных, зависящих от времени (см. гл. VIII, § 2). Тогда
в полуплоскости тх > Ti > т0, которую обозначим Пт#> существуют инте-
интегралы
, т) = j е-* 3%0 (*, t) dt, /о (у, т)
00
и являются аналитическими функциями параметра т.
Рассмотрим граничную задачу эллиптического типа:
ух 6 D+: М (дх) Uo (х9 т) — т2г^0 (х, т) = ^ (х, т),
>fyeS:	lim ^0 (х, т) = /0 (у, т),
х->у
DЛЗ)
которая получается из задачи {D.7)—D.9)} формальным применением преоб-
преобразования Лапласа
Интегрируя по частям равенства D.12), на основании D.11) получаем
равномерные оценки
l*o(x,T)|<j^p l/oG/^l^-p^p x?D\ yeS, теПт#. D.14)
скости
4.1. Теорема. Эллиптическая граничная задача D.13) в полупло-
пи т ? ПТо не может иметь более одного регулярного решения.

5 4]	задачи динамики	367
Доказательство этой теоремы единственности непосредственно следует
из формулы Грина A11,4.1), совершенно так же, как в классической теории
(см. теорему 111,1.11).
Для доказательства существования %0 (х, т) представим его в виде
суммы
, т) = %{о1) (х9 т) + UP (х, х),	D.15)
где Цо1) (х, х) — решение задачи
IS: Hm&0(x,x) = f0(y,x), J	DЛ6)
а $о2) (х, х) — решение задачи
Ни«?><*, т) = 0.	<4Л7)
х->у
Задача D.16) исследована в пп. 1, 2, § 2, где показывается, в частности,
что в наших предположениях %о1) (х, х) является классическим решением.
Можно показать (см. гл. VIII, § 2, п. 7), что (Q$) (x, х) представляется инте-
интегралом
U{ol) (х, х) = — -L J [Т (ду, n)G\X) (х, у)\ fo(y, т) d^S,	D.18)
где G(i) (х, у) — тензор Грина статического оператора М (дх) с граничным
условием первой основной задачи для области D+ (см. § 3, п. 3).
Используя свойства тензора Грина G(i> (x, у) и формулу Пуассона,
можно показать, что задача D.17) эквивалентна интегральному уравнению
Фредгольма второго рода
4 J G<n (*. У) г&о2) (У, т) dy =
=	Хт\ Gm (х, у) \Жо(у, т) + т2г^'> (у, т)] dy. D.19)
D+
Из теоремы единственности 4.1 следует, что соответствующее однород-
однородное уравнение в полуплоскости ПТо имеет лишь тривиальное решение и
следовательно, D.19) однозначно разрешимо для х?ПХо. Легко показать
также, что в принятых предположениях это решение является классическим.
Так как f0 (у, х), */?S, по определению, является аналитической функ-
функцией т?ПТо, то из представления D.18) следует аналитичность Ц{01) (х, х),
Аналитичность Щ2) (х, х) как функции х ? Пт§ вытекает из однозначной
разрешимости и аналитичности правой части уравнения D.19) (см. гл. VIII,
§ 2, п. 7). Итак, %0 = $/,о1) + Ц{02) является классическим решением задачи
D.13), x?D+ и аналитической функцией х?ПТв.
3. Асимптотические по х оценки %$ (х, т) и ее производных. Решение
динамической задачи.
Как было показано,
#о {х, х) = <ffl>1 > (х, х) + Ш2) (х, х).	D.20)

368	моментная теория упругости	[рл# IX
Сначала найдем оценку для %о1) (х> т). Для этого целесообразно вместо
представления D.18) воспользоваться таким интегральным представлением
^о1* С** t), которое приводит для плотности потенциала не к сингулярному
интегральному уравнению, а к уравнению со слабой особенностью.
По аналогии с классической теорией (см. гл. I, § 13, п. 1), введем опе-
оператор псевдонапряжения моментной теории (см. гл. I, § 13, п. 1).
Пусть
1Nil) (дх> п (х)), МB) (дх, п(х))\\
где
(dx,n(x)) = \N^ixz,
(дх, п (х)) = (А + Ц — а) щ (х) -^ + (х — а) (п, ~ — Щ
3
N?> (дх, п (х)) = 2а S e,/tn,, М/' C,, п (дс)) = О,
S=l
^ (дх, п (х)) = (е + о — Р) п^ + (к" — р) ^- ^- — щ ^
(е + 2о) Р + (^ + Р)
Вычисления показывают, что
nL?(y-x)]'\^ix^f_6, б>0.	D.22)
Заметим также, что для потенциала двойного слоя
справедливы те же формулы «скачков», которые имеют место для обычного
потенциала двойного слоя моментной теории (см. теорему 1.6).
%q1) (x, т) будем теперь искать в виде \fx, y?S:
т
#J*> (х, т) - \[N (дУ9 п) Т (у — х)) Ф (у) dyS + ^ А/&к) (х — у,)9 D.23)
где ф — неизвестный вектор, Л; — постоянные, которые определятся ниже,
Wik), I < k < 6, k-и вектор-столбец матрицы Y, y^D* — пока произ-
произвольно зафиксированные точки, т > 0 — натуральное число.
Согласно D.22) для ф (у) получим интегральное уравнение Фредгольма
со слабой особенностью
-Ф B) + J [N {dyi n) W {у —г)]' ф (у) dJS =
-/о B, Т) —

л 4]
задачи динамики
369
Пусть {ip(t)}?Li — полная система линейно независимых решений союз-
союзного однородного уравнения (отсюда очевиден выбор т в D.23)).
Необходимое и достаточное условие разрешимости D.24) имеет вид
2
— yf)?i)(z)d2S=
= J
z, т)
(z)
D.25)
Можно показать (см. Купрадзе [8], Бурчуладзе [1]), что существуют
точки #,??>", j=\, 2, . . ., га, такие, что хотя бы для одного k== 1, 2, . . ., 6,
детерминант алгебраической системы D.25) отличен от нуля и, следова-
следовательно, Af однозначно определяются из D.25).
Пусть R (z, у) — резольвента уравнения D.24). Согласно D.22)
| R (г, у)
2_6
. Следовательно, для решения D.24) получаем оценку
— y,)\ +
Отсюда в силу D.25) и DЛ4) получаем равномерную оценку
1( )l ^
что в свою очередь согласно D.22) и D.23) дает
D.27)
Оценка для <$o2) (*> t) получается из уравнения D.19) совершенно так
же, как в классической теории (см. гл. VIII, § 2, п. 8). Повторяя те же вы-
выкладки, будем иметь
2)|^	\	D.28)
D.29)
Наконец, D.27) и D.21) согласно D.20) дают
которая выполняется для т?ПТв, равномерно по x(fD+.
Оценки для первых и вторых производных Цо (х, т) по хь I == 1, 2, 3
получаются повторением тех рассуждений, которые были применены в клас-
классическом случае (см. гл. VIII, § 4, п. 6); при этом будем иметь
дй0 (х, т)
дх.
дШ„ (х, т)
дх. дх.
т~>
x?D\ теПТо, D czD+.
В силу оценок D.29), D.30) вектор
2ш J
Xt—too
удовлетворяет всем условиям «приведенной задачи» (см. п. 1).
24 В. Д. К.упрадзе
D.30)

370	моментная теория упругости	[рЛв IX
Это показывается совершенно так же, как в главе VIII, § 2, пп. 13, 14.
Наконец, исключение вектора 2 (х, t) совершается так же, как в главе
VIII, § 2, п. 14.
Этим завершается доказательство существования классического реше-
решения первой внутренней задачи динамики моментной теории. Другие задачи
исследуются аналогично (см. гл. VIII, § 3). Подробное изложение задач ди-
динамики имеется в работах Напетваридзе О. И.
§ 5. Заключительные замечания и библиографические
справки
В первой главе были сформулированы предположения, на которых
построена теория упругости. Напомним, что в основе теории лежит пред-
предположение о равенстве нулю моментов сил, действующих на частицы.
Такая идеализированная модель хорошо описывает упругое состояние
многих материалов. Значения напряжений, возникающих при деформации
большинства реальных упругих тел, с удовлетворительной точностью сов-
совпадают со значениями напряжений, вычисленных с помощью идеализиро-
идеализированной модели в предположениях классической теории. Эти предположения
подтверждаются также многочисленными экспериментами, проводимыми
в течение многих лет.
Однако в некоторых, особенно крупнозернистых, материалах при боль-
больших градиентах напряжений были обнаружены значительные отклонения
реальной картины от идеализированной в предположениях классической
теории.
Кроме того, классическая теория упругости не позволяет удовлетво-
удовлетворительно описать распространение коротких акустических волн в кристал-
кристаллах, высоких полимерах и других материалах.
Эти и другие аналогичные соображения послужили причиной поисков
более усовершенствованных моделей сплошной среды.
Первые попытки такого рода приписываются Фойгту (см. Voigt [1]).
Фойгт предположил, что взаимодействие двух соприкасающихся частей
среды сводится не только к главному вектору, но и к главному моменту.
Таким путем, фактически, наряду с силовым напряжением было введено и
моментное напряжение (см. § 1 гл. I).
Это предположение нашло систематическое развитие у Коссера (см.
Е. Cosserat, F. Cosserat [I ]). Они исходят из представления о дискретной
структуре среды, представляя ее как совокупность идеально жестких малых
частей, которые в идеализированной модели рассматриваются как точки.
Таким образом, вводится «сплошная» среда, каждая точка которой обладает
шестью степенями свободы.
Эти работы долго оставались незамеченными; играли свою роль и труд-
трудности, связанные с физическим обоснованием подобной теории, и сложность
математического аппарата, который требовался для ее исследования.
В последнее время, когда по известным причинам сильно возрос инте-
интерес ко всяким уточнениям в науке, внимание ученых привлекли и указанные
выше предположения.
Так возникло новое направление в теории сплошной среды — моментная
теория упругости в смысле, принятом в первой главе, а также в некоторых
других пониманиях (со стесненным вращением, среда высших классов,
сильно нелокальные теории и т. д.).
За последние двадцать лет по этим вопросам опубликованы сотни
работ. Работы Аэро, Кувшинский [1, 2], Grioli [1J, Tiersten [1], Mindlin 11],

ЗАДАЧИ	37)
Koiter [41, Nowacki [8], Пальмов 11J, Teodoresku [3, 4], Кунин [1] и дру-
другие послужили бурному развитию теории.
Много работ посвящено обоснованию моментной теории упругости;
исследуются физические основы, строятся различные модели с микрострук-
микроструктурой, выводятся уравнения движения, условия совместности функций
напряжения, формулы для энергии деформации и др., исходя из различных
принципов механики. Приводятся сравнения классической и моментной
теорий.
Обсуждается вопрос об эффекте моментных напряжений. Рассматри-
Рассматривается прохождение упругих волн в среде с микроструктурой и т. д.
Некоторые работы посвящаются представлению решения основных урав-
уравнений в виде, подобном представлению Папковича—Нейбера,или посредством
нескольких гармонических, аналитических и других функций.
Во многих работах решаются конкретные задачи моментной теории
(задача Сен-Венана, осесимметричная задача, задача о сосредоточенном мо-
моменте, задача Ламе, задачи о кручении и изгибе бруса, изгибе плит, задачи
для сферы и полупространства, задачи о концентрации напряжений и др.)-
Многие работы посвящены также плоским задачам.
С литературой по этим вопросам можно ознакомиться в книгах No-
Nowacki [81, Teodoresku [3, 4].
Общим математическим вопросам (теоремы единственности и существо-
существования решений основных граничных задач, свойства гладкости решений,
корректность задач, представление решений в виде интегралов типа потен-
потенциала, фундаментальные решения и др.) посвящено много работ. Отметим
некоторые из них: Nowacki [8], Башелейшвили [15], Iesan [1, 2], Teodo-
rescu [3, 4], Напетваридзе [5, 6], Чичинадзе [1, 3], Оболашвили [3], Баше-
Башелейшвили, Гегелиа, Маисаиа [1].
ЗАДАЧИ
Исследовать задачи 1—14.
Найти решение U— (и, со) уравнения A.2) в области ?>*, принадлежащее классу
С1 (?>-) П С2 (D^) и, в случае внешних задач, удовлетворяющее условию A.12), по гранич-
граничному условию:
1. Задача (V)±:
(ду, п)и(у)+Т<2) (дуу п) со (у) -п[ТA) (ду, п)и(у)+ТB) (ду$ п)<п(у)]а}± =
2.	Задача (VI)±:
V	У в s • I" @I? = f (У)> 1ГD) @у* п) со (у)]± = g (у),
\Т<1) (д9, п)и(у)+Т<2) (ду, п)(о(у)-п[Т{1) (ду, п)и(у) + 7*2> (ду, п) со (у)]п}± = h {у)
3.	Задача (VII)*:
V	У € 5 •• {" (У) — п [и (у)\п)± = / (*/), @ (у)]± = g (у),
{[ГA) (ду, п) и (у) + ГB) (д„, п) со (у)]п\± = h (у).
4.	Задача (VIII)±:
VyeS:{u(y)-n[u (y)]n}± = f(y)y [ГD) (dy,n)a>(y)]±=g(y)t
{[ГA) (ду, п) и (у) 4- ГB) (ду, п) со (у)]п\± = h (у),
24*

372	моментная теория упругости	[рЛв
5. Задача
[u(y)]±=g(y)>
|ГD) {ди% п) и{у)-п [ГD) (ду> п) to Q,)]n\± = h (y).
6. Задача
yt n) (*(у)-п [ГD> (а„, я) со
7. Задача (Xl)*:
dy, n)a>(y))n}±=h(y).
8. Задача (XIII1:
S/yeS:\(n(y)-n[a>(y)]n}±=f(y)y [T{1) (ду, п) и {у)+Т™ (dyt n) со
9. Задача (XIIII*1;
{Г<4> (dyy n) (o(y)~n [ГD> (dy, n) со (у)]я}± = /i (j,);
p, n) u (y) + rB) (ay,
10 Задача (XIV)±:
|TA) (dy, n) a (t/) + TB) (dyy n) (o(y)-n [Г<г> (ду, п) и (у) + T^ (ду, п) со (у)]я\± = ф {у).
11.	Задача (XV) ±
V У€ 5 : {и{у)-п[и(у)]п}± = f (у), )[ГA) (ау, я) « + ГB) ^, п) }±
[со (у)]± = /I (t/), {ГD) (ду, /г) (о(у)-п [ГD) (dyf я) со (у)] п}± =
12.	Задача (XVI)±:
:|«((/)-M[a^)]rt}± = /(r/), [ГA)(ау> п)и(у)^Т{2) (ду> n)
{со (у) - п [со (*/)Ы± = /г (у), \ТD) (ду, п) со (у)]± =
13.	На границе 5 задана линейная комбинация граничных условий, взаимно сопряжен-
сопряженных задач. Задачи типа шестой классической задачи (см. п. 1 § I, 14).
16
14.	Граница 5 представлена в виде объединения S = (J^fe» гДе «St- p| S/ = 0, i ф j и
на Sk задано граничное условие k-й задачи (^=1, ..., XVI).
15.	Поставить и исследовать задачи колебания, соответствующие поставленным выше
задачам статики (V)——(XVIK=.
16.	Исследовать смешанные задачи колебания, соответствующие задачам 13 и 14.
17.	Исследовать задачи динамики (III)——(XVI)—.
18.	Вывести другие формулы Сомилиана, удобные для исследования задач (V)—
и (XVI)=t.
19.	Исследовать внешние динамические задачи моментной теории.
20.	Исследовать гранично-контактные задачи моментной теории.

ГЛАВА X
ТЕОРИЯ ТЕРМОУПРУГОСТИ
В этой главе сначала подробно изучаются задачи установившихся термо-
термоупругих колебаний и затем на этой основе, подобно тому, как это делается
в главе VIII, строится теория общединамических задач; доказывается суще-
существование классического решения и указывается способ его построения.
§ 1. Введение
Уравнения и задачи термоупругости являются дальнейшим уточнением
соотношений и задач классической теории упругости; если моментная теория
упругости, основы и методы которой были изложены в главах I и IX, пред-
представляет математическую теорию, которая вследствие гипотез, положенных
в ее основу, нуждается в экспериментальной проверке и подтверждении, тео-
теория термоупругости вышла из этой стадии развития и концепция напряжен-
напряженного состояния, как результат взаимодействия полей деформации и темпера-
температуры, [составляющая сущность термоупругости, приводит к выводам, хо-
хорошо согласующимся с наблюдаемыми фактами.
Основные уравнения и типичные задачи теории термоупругости были
приведены в главе I (см. гл. I, §§8,9, И—14).
Вопрос сводится к изучению задач с граничными и начальными условиями
для уравнения движения «термоупругой» среды, которое имеет вид
д2и
liAu-\-(X-\- (ы) grad diva — 7 grad 0 + р5г = Р-77г>
A.1)
Такое изучение стало возможным сравнительно недавно, хотя история
термоупругости как научной дисциплины восходит к истокам классической
теории упругости. Трудности задач динамической термоупругости в извест-
известной мере связаны с тем, что система уравнений A.1) не принадлежит ни од-
одному из основных типов уравнений математической физики (см. гл. I, § 15,
п. 1), и построению ее теории предшествовали обширные исследования по
теории граничных задач эллиптических дифференциальных уравнений в ча-
частных производных.
Сначала мы исследуем подробно один частный, но важный случай тер-
термоупругого состояния, которое возникает, когда внешние усилия и источ-
источники зависят от времени по синусоидальному закону (которое в первой главе
было названо установившимися термоупругими колебаниями). Уравнения
этого состояния задаются (см. I, § 11, п. 3) в виде
\х Аи + (X + М-> grad div и — у grad 0 + P^2w + р&~ = О,
Д8 + —6 + fa>T,divtt + — Q = 0.

374	теория термоупругости
Значение установившихся термоупругих колебаний состоит не только
в важной самостоятельной роли этого встречающегося в технике физического
состояния, но также в том, что их изучение, как будет показано ниже (см. § 4),
открывает путь к изучению динамических задач общего вида.
Простейшим случаем уравнения A.1) является тот, который соответ-
соответствует состоянию, не зависящему от времени; это — так называемое термо-
термоупруго-статическое состояние, уравнение которого имеет вид (см. I, § 11,
п. 3)
|iAa + (А, -\- [*>) grad div и — 7 grad ^ + Р^~ — О,
Система уравнений A.1), вместе с соответствующими начальными и гра-
граничными условиями, составляет предмет изучения связной или сопряженной
теории термоупругости.
В течение продолжительного времени изучалась другая, упрощенная
теория, известная под названием раздельной, температурно-напряженной,
квазистатической и т. д., смысл которой состоит в различных дополни-
дополнительных допущениях, хотя и не всегда достаточно мотивированных, но поз-
позволяющих упростить исследуемую проблему.
Наиболее распространенными из таких допущений являются пренебре-
д Л.	д2и
жение членом r)-rr-a\vu или членом р-ш или и тем и другим, и некоторые
другие. Эти допущения позволяют разделить, полностью или частично, си-
систему уравнений A.1) на уравнения упругости и- уравнение теплопровод-
теплопроводности и приводят "к рассмотрению сначала чисто тепловой задачи, а затем
задачи упругости, в которой решение тепловой задачи участвует как задан-
заданная величина. При таком подходе системы A.1) и A.3) полностью^ разделя-
разделяются, если только связь не сохраняется специальным характером гранич-
граничных условий (см. задачу 3 в конце главы).
Мы не будем пользоваться ни одним из указанных упрощений и зай-
займемся построением общей теории, сначала для системы A.2), а затем и для
системы A.1).
§ 2. Установившиеся термоупругие колебания
1. Союзная система. Свойства фундаментальных решений. Тождества
Грина. Система уравнений A.2) в матричной форме записывается в следующем
виде (см. I, § 12, п. 3):
В(дХ9 со)<У(х) + <^(х) = 0,	B.1)
где
U = (U,) = (и, иА), а4 = 6, Ж = {ЖЬ\ 3№( = р0-? 1=1,2,3; 3№t*=^QP
В(дх, (u) = \\Bki(dxt (о) ||4х4,
Bkf (дХ9 со) = Akj (дх, со), Вы (dXf со) = — у —,
84/(д„ ю) = нот1-^ К /=1,2, 3 и Вы{д^ со) = Д + -?-.

г 2]	УСТАНОВИВШИЕСЯ ТЕРМОУПРУГИЕ КОЛЕБАНИЯ	375
Эта система — эллиптическая. Ее характеристическая матрица имеет вид
^
о	о	0	1
и для произвольного действительного | = (?х, |2> §з)> удовлетворяющего
3
условию 2 ^ = *• имеем
2
Матрицу В*(дх, со) = || B*ki (дХУ со) ||4Х4, где B*kf(dx, со) = B/fe (— д*, со),
/, k= 1, 2, 3, 4, будем называть союзным оператором (см. гл. II, § 3, п. 2).
Легко убедиться, что оператор В* (дх, со) может быть получен из опе-
оператора В (дх, со) простой заменой у на Шц и наоборот. Эту операцию (т. е.
замену у на шт] и наоборот) мы будем ниже обозначать знаком ~ (тильда)
над символом оператора; в данном случае операция * совпадает с операцией ~
и вместо В*(дХ9 со) можно писать В (дх, со). Это обстоятельство позволяет
достигнуть однсобразия в обозначениях и в том случае, когда указанное сов-
совпадение операции * и ~ не имеет места.
В векторной форме однородная союзная система запишется в виде
уравнений
[I Аи + (к -}- \л) grad div и — тц grad щ + рой/ = 0,)
B-2)
где
(и, пА) = и =
В главе II, §3, п. 1 построены фундаментальные решения однородного
уравнения В (дХ9 со) U (х) = 0. Введем некоторые новые обозначения:
ф(*. со)=||ФA\ ФB>, ФC>, O<4>i = ||Oft/|kx4,
ФD»(х,ш) = (Ф'Ч«рП; ф(й)-Ык), ч4*\ фП а-1,2,з.4.
Непосредственной проверкой можно убедиться, что в окрестности точки
х = 0
Ф^> (х, со) = О A), Ф14) (х, со) = О A), А = 1, 2, 3,	B.3)
и
Ф'(У — *, со) = Ф*(а: — ^ ю) = Ф(х —у, со),	B.3')
где Ф (х — у, со) = Ф* (^ — г/, со) (см. гл. И, § 3, п. 2) — матрица фунда-
фундаментальных решений союзной однородной системы B.2). Согласно теоре-
теоремам II, 3.4 и II, 3.5 имеем
Ф (jc, со) — Ф (х) = const + О(\х |),
О(|хГ), i, / = 1,2, 3; й=1,2, 3, 4, ^ BА)

376	теория термоупругости	[рл> х
где Ф (х) — фундаментальная матрица решений однородной системы, соот-
соответствующей A.3).
Докажем здесь несколько важных тождеств Грина. Пусть U = (и, а4)
и U = (и, щ) — регулярные в D+ векторы и BU, BU — абсолютно интегри-
интегрируемы в D+; тогда
J \UB{dX9 (оH —
e J{{up0-uPU)+ (u^-uJ^ydS, B.5)
где
PU = Tu — упиА9 PU= Tu — 1(дцпи4	B.6)
и PU есть вектор (термоупругого) напряжения, введенный в главе I,
§ 13, п. 3.
Рассмотрим разность
UB{dx, со)й—иВ(дх, co)U.
Очевидно,
UBU — UBU = и(Аи — шг\ grad a4 + Р«2а) +
-^-uA-\-yd\vu\ —и(Аи — у grad и4 + р(о2и) —
^4 + -~-^4 + i(or\dlvuj = (uAu — uAu) +
+ D Да4—a4 Да4) + 7 (a4 div u-\- и grad a4) — tcor] (u grad a4 + a4 div a).
Ho
= 2 a^"(a4"^ ~ " grad >
w4 div и = ^ -^ (ы4^) — a grad a4;
k
следовательно,
UBU — UBU = (а Ла — a Ли) + (и 4 A w4 — a4 А ы4
+т 2 "(^ ~ M 2 i
Интегрируя по D+ и используя формулу Гаусса—Остроградского, получим
\(UBU-UBU)dx= \UuTu— иТи)+ (a4
+ У 2 ^4^Л — '«г] ^ ^4^^]4" ^S = J l и (Ти — iwxyiuj —
k	k	'	S ^
„,4—i,^)}+^. B.7)

§ 2]
УСТАНОВИВШИЕСЯ ТЕРМОУПРУГИЕ КОЛЕБАНИЯ
377
Введем (см. гл. II, § 6, п. 1) матричный дифференциальный оператор
размера 4X4
Х9 п, y) =
x, n,
— V'h
ооо
B.8)
где символ Т обозначает матрицу Т (дх, п) = || Tki (дх, п) Цзхз, Т — опе-
оператор напряжения классической теории (см. I, § 13). Если U = (и, и4), то,
цно,
B.9)
рр
очевидно,
*U ^ (Ти-упщ, %¦) еее (PU, -?¦
Матрицу, полученную из матрицы B.8) заменой у на шт], обозначим
U (дх, п, со); тогда тождество B.7) примет следующий вид:
f (UBU — UBU)dx= [(U&U — U&UydyS.	B.10)
Если U = (и, и4) и О = (и, и±)9 в частности, регулярные решения соот-
соответственно уравнений В (дх, со) U = 0 и В (дх, со) С/ = 0, то из B.10) имеем
dS = 0.	B.11)
Это равенство остается в силе и для области D", если U и U удовлетво-
удовлетворяют условиям (термоупругого) излучения (III, § 3, п. 3).
Важно при этом заметить, что указанные условия для U и О идентичны,
так как переход от оператора В (дх, со) к оператору В (дх, со) осуществляется
заменой у на шг\ и наоборот, а эта операция не меняет параметров XI и Х|.
Применим формулу B.11) к конечной области D"fl^/(O, p) и покажем,
что при р —» со интеграл по С (О, р) стремится к нулю.
Имеем
Q (О, р)
= \ [и(Ти — гс
С (О )
= J (uTu
С (О. р)
С (О, р)
G (O. P)
= J
и,
f \u{2)(Tu{2)
С @,9)
следовательно,
с
(О, Р)
- /со]
— и<2> GV2> —
B.12)

378	теория термоупругости	[рл# х
Отметим некоторые другие полезные тождества Грина, основанные на
тождестве
— UMU = uPU + щ -ф	uPU — щ-^-
1 4 дп	4 дп
= QUSPU —
(см. ниже формулу B.25)). Это показывает, что во всех тождествах Грина
поверхностный интеграл
J (*/?# — USlU)±dS
можно заменить на интеграл
и таким образом получить новые тождества.
Наконец, выпишем еще одну формулу Грина, которая уже доказана
в главе III, § 3, п. 2 и будет ниже часто встречаться:
Л \\muufdx=[\ZPU ^^-u-^—uPU + -J~u^-]+ dS;
B.13)
здесь U = (и, и4) есть регулярное решение однородного уравнения термо-
термоупругости, соответствующего B.1), a U = (и, а4) — комплексно-сопряжен-
комплексно-сопряженный с U вектор.
2. Общее представление регулярных решений однородного уравнения.
Пусть x?D+ и Ш (х, г) cD+. В области D+\LU (x, г) применим формулу
B.10) к регулярному вектору U — (u, м4) и вектору Ф<к)(у — х9 со) =
), k = 1, 2, 3, 4. Так как
В\(дд9 со)Ф<*>(*/—*, со) = 0,
то в силу B.3) и B,9) будем иметь
j	—х9 <o)B(dff9 co)U(y)dy =
D+\m (x, e)
— I [итФ^Цу—x, со) — ф(*)(у — jc,
= j
5
J
C(jCf 8)
tt (x) I
С U
С U, 8)
|L	. B.14)
С (х* е)

? 2]	УСТАНОВИВШИЕСЯ ТЕРМОУПРУГИЕ КОЛЕБАНИЯ	379
Пользуясь свойствами фундаментальных решений (см. II, § 3, п. 1),
можно показать
д д*\х-у\	%щ	д	1
2я X -f- 2jli dn dz/; д*/&	2я (X -f- 2ja.) dz/? | x — у \
""*" ~2л~ d*/* | a:— t/1	' 2л ~3д~ U — f/| "i"
Gy 4> X- = 0 (I x — у Г1), i, fe = 1, 2, 3.
Кроме того, согласно формулам
С (X, 8)
С д 1 4	Г E 1
J ': <fy/j \х — у | v ~" 3 iki	J а/г | x — i .
С (X, 8)	С U, 8)
получим
о •	bib	 193
lim | (T<f>^),dtlS=l 0,	i + k, i, k=\, 2, 3,
0,	fe = 4, t=l, 2, 3,
j. \ - T/i j o , U,	A5= 1, л, u,
-oc(iE, *П " 12, fe = 4.
Внеся эти значения в B.14), будем иметь для k = 1, 2, 3, 4
2М*) = ф(^Ч^/ — ^t &)'{&№)* dJS — (U(y))+& (дп, п) Ф^(у — х9 со) d.S —
s	s
— [ ф(Ь)(у — х, (о)В(ду, (o)U(y)dy, B.15)
или, в векторной форме,
2U (х)= \ Ф' (у — ху со
— | [& (dv, п)Ф(г/ — х, со)]' (fjydJS— \ Ф'(у — х, со) BUdy. B.16)
Если, в частности,
В(ду, со) г/ (у) = 0, г/е?>+,
то B.16) дает общее представление регулярных решений однородного урав-
уравнения термоупругости B.1°) х) в виде
2G (х) = J Ф'@ —х, со)(Ж/)+^— } Й(с\, п)Ф(у—х, со)]' [U (y)]+ d^S,
B.17)
L) Имеется в виду однородное уравнение, соответствующее уравнению B.1). В дальней-
дальнейшем подобные обозначения специально не оговариваются.

380
ТЕОРИЯ ТЕРМОУПРУГОСТИ
[Гл. X
или, согласно B.3'),
2V (х) = J Ф(х — */, со)(<Ш)+ dgS—\[k(дуу п)Ф'(х — у, о)]'[U(y)]+
x?D\ B.18)
или
2U(x)=\O(x— у, (o){MU)+dyS—l[k(dyi п)Ф(у—х, со)]' [U (y)]+duS,
xeD+. B.19)
Когда х ?D~, формулы B.18), B.19) принимают вид
[ Ф (х — у, со) (Ж/У dJS — j f <%Ф' (х — у, со)]' [U (у)]+ d^S = 0 B.20)
ф (*_ j,t
= 0. B.21)
Само собой очевидно, что подобные же представления могут быть со-
составлены для регулярных решений союзного уравнения B.2).
Общее представление, аналогичное B.18), B.19), имеет место и в обла-
области D", если вектор U (х), кроме условия регулярности, удовлетворяет
условию термоупругого излучения (см. III, §3, п. 3). Доказательство этого
предложения не отличается от того, которое приводилось в главе III, §2,
п. 4, при выводе формулы общих представлений в IT для регулярных реше-
решений уравнения классической теории, удовлетворяющих условию упругого
излучения.
3. Основные свойства термоэластопотенциалов. Введем потенциалы
простого слоя
V(x; ф)= J Ф(х —
у,
двойного слоя
W(x;
уу п)Ф'(х—у9
и объемных масс
U(x: x)= J Ф(х — У, <*)%{y)dy;
B.22)
B.23)
B.24)
здесь ф, г|), % — четырехмерные векторы.
Кроме указанных, мы будем пользоваться также следующими потен-
потенциалами (смешанного типа). Пусть 0* (дх, п (х), у) и Q (дХ9 п (х)) (см. II,
§6, п. 1) матричные операторы размера 4x4:
п(х),
Q(dx, rc(x)) =
0 0 0 — 1
0 0 0 -?-
an

« 2]	УСТАНОВИВШИЕСЯ ТЕРМОУПРУГИЕ КОЛЕБАНИЯ	381
где Е — единичная матрица размера 3x3. Очевидно, ^(/ и QU, когда U =
= (м, а4) — четырехмерный вектор, есть четырехмерные векторы/ равные
соответственно
9U = (PU, -и4) = (Ти-упи49 -и,)9 QU = (а, -Jl) . B.25)
Переход от !Р к ^ происходит, как в случае 5?, заменой у на шт). Вводим по-
потенциалы
\ ф)= J [# (ду9 п)Ф'{х — у9 ©)Г Ф(у)^	B.26)
9, п) Ф' (х — у, со)]' г|> (у) d^S.	B.27)
Ниже будет показано, что с помощью указанных пяти потенциалов
можно построить общую теорию для граничных задач основных типов, ко-
которые сформулированы в I, § 14, п. 3.
Сначала установим некоторые свойства потенциалов V, W, Z, й, U.
Прежде всего, первые четыре удовлетворяют однородному уравнению
B.1°) для jc^S, a U (х; %) есть решение уравнения Пуассона
В (дХ9 со) U (х; х) = -2% (х)9 х 6 D\
Первое утверждение вытекает из результатов главы II. Можно восполь-
воспользоваться и простым правилом, которое облегчает получение этих результатов.
По свойству транспозиции произведения матриц
\Яфу9 п)Ф'(х — у9 (о))'Ц(у) = Ф(х — у9 ы)&{дЦ9п)Щу)9
где по условию дифференциальный оператор Ж действует по точке у на ма-
матрицу Ф (х — у, со), стоящую слева, как это ясно из смысла операции. Дей-
Действуя, далее, оператором В (дХ9 со) при х([5, и используя свойство ассоциа-
ассоциативности произведения матриц, получим
В(дХ9 со) W[х\ г])) = 0, x?S.
Ясно, что сказанное справедливо и для потенциалов Z (х; ф)ий (х\ гр),
В (дХ9 со) Z (х; ф) = О, В (дХ9 со) Q (х; г|>) = 0, х 6 S.
Действуя оператором В (дХ9 со) над тождеством B.16), учитывая, что
потенциалы простого и двойного слоя есть решения, и обозначив В (дХ9 со) X
X U (х) = х (х), приходим для U (х; %) к уравнению [Пуассона.
Этот результат был доказан для % (х) ? С0' a(D+) в главе V, § 10. Перей-
Перейдем к установлению граничных свойств потенциалов.
Поведение потенциала двойного слоя
9 п)Ф'{х — у9 (o)]fyp(y)dyS
при стремлении точки х из D+ или D" к точке z(ES, когда плотность
<ф?С°- a(S), совпадает с поведением статического термоупругого потенциала
двойного слоя с той же плотностью
= J

382
теория термоупругости
[рл#
при указанном предельном переходе; здесь ^° обозначает оператор 31 при
(о = 0. Это вытекает из тождества
W (х; ф) =
(х;
[W (х; ф)—
(х;
и из непрерывности выражения, стоящего в квадратных скобках в правой
части, что в свою очередь есть следствие формул [B.4).
Пусть а = || akj- ||4Х4, Ь = || bkj |4Х4 и ср = (ф1э . . ., ф4). Рассмотрим
вектор аЬц) и найдем его k-ю составляющую (abq>)k\ будем иметь:
Ф/ = ?
очевидно, справедливо равенство
(аЬ'У ф = ba'tp =
Вычислим А-ю составляющую вектора
B.28), будем иметь
(x—у) ЦO
у)
B.28)
Применяя
!=1, 2, 3,
= f
S
2
1, /=1
B.29)
или, согласно B.9),
7k, A>= 1,2,3,
; ¦) = 4r J
B.30)
где Wh i = 1, 2, 3, 4 — непрерывные функции. Из B.29) и B.30) видно,
что термоупругий статический потенциал двойного слоя ведет себя около
границы S частично как упругий статический потенциал двойного слоя и
частично как гармонический потенциал двойного слоя, точнее, первое от-
относится к первым трем составляющим, второе — к [четвертому составляю-
составляющему.
Приняв во внимание сказанное, будем иметь
\lk(dyf п)Ф'(г — у, (o)]f^(y)dySy	B.31)
W~B; у) = ф(z) + J \к (ду, п)Ф' (г— г/, со)]' я|)(у) dyS.	B.32)
Из этих формул, аналогично тому, как это делается в случае потенциала
простого слоя в классической теории (см. гл. V, § 5), получаем
\Я (<Э2, v) V (г; Ф)Г = ф B) + j 31 {д„ v) Ф (z — у, со) Ф (у) dyS, B.33)
, v) V (г; ф)Г = -Ф (z) + J i% (дг> v) Ф (г — у, со)
B.34)

Л 2]	УСТАНОВИВШИЕСЯ ТЕРМОУПРУГИЕ КОЛЕБАНИЯ	383
Чтобы исследовать поведение около границы потенциала Z (х\ ф), вы-
выпишем формулы B.29) для данного случая и примем во внимание определе-
определение оператора Q (дх, п (х))\ тогда получим
[Q(dz, v)Z{z; ф)]+ = -ф(*)+ jQ(d2, v)[?(d,, п)Ф'(г — у9 со)]'^
B.35)
[Q(d29 v)Z(z; ф)Г = фB)+J.Q(a2f v)[!P(dy, п)Ф'(г — у, со)]'
B.36)
Повторив предыдущие рассуждения для потенциала ?2 (х; г|)), получим
, v) Q (z; t|>)]+ = ф (г) + j 5* (д„ v) [Q (д,, /г) Ф' (г — у, со)]' г|> (^) d,S, B.37)
[^ (<Э2, v) Q (г; ф)Г = — Ф (г) + I ^ (д„ v) [Q (д,, я) Ф' (z — у, со)]'
B.38)
Для термоупругих потенциалов двойного слоя W (х; г|)), Z (х\ ф),
Q (л:; ф) справедливы также теоремы, аналогичные теореме VII, 2.1 (теорема
Ляпунова—Таубера). Покажем это, например, для потенциала Z (х; ф).
2.1. Теорема. Если существует один из пределов [fPZ (z; ф) ]+ или
Z (г\ ф)]"" и принадлежит классу С0* а (S), то существует и другой и
Пусть Z{ (х\ ф), i == 1, 2, 3, 4 — составляющие вектора Z (я; ф) и
г (л:; ф) — вектор с составляющими Zl9 Z2, Z3. Так как
(^Z(x; ф))л = (^Z), = (Tz(jc; Ф))л — 7^Z4(x; ф), fe= 1, 2, 3,
@>Z(x; ф)L = —Z4(x; ф),
доказательство теоремы сводится к доказательству равенств
(Гг (х; ф))? = (Тг (х\ ц>Ш, /г = 1, 2, 3, (Z4 (х; ф))+ = (Z4 (x, ф)Г. B.39)
Для составляющих Zk (х\ ф), k = 1,2, 3, 4, согласно B.28) будем иметь
4
— У, <о)Ф,U/)<*A ft=l,2f3, 4.
2*(х;ф)=[ 2 &цФы{х — У, <о)Ф,U/)<*A ft=l,2f3, 4.
Приняв во внимание определение оператора Ф (дуу п) и свойство сим-
симичности Фк, = Ф1к> k, i = 1,2, 3, можем писать для k = 1, 2, 3, 4
з
метричности
з
х; Ф) - j 2 ^ /*ф« (* — *• ©
3	3
= J S Г/'Ф^Ф/ (У) d*S — t>CflT1 J 2 И/Ф
S ». ;=1	S /=1

384	теория термоупругости	[Гл# х
Это выражение преобразуем следующим образом:
з
z* (*; ф) = J 2 т,&№ (х—у) Ф/ (у) dys +
S t, /=1
3
+ J 2 г/* [ф« (*—#> <°)—ф«* (*—у)] Ф/ (у) <&—
S i, /=1
- icor, | I g п/Ф/. (у) + -^- Ф4 (У) I Ф*4 (х — У, ©) dyS, k = 1, 2, 3, 4, B.40)
где <D(fe (л: — г/), t, k = 1, 2, 3 — элементы матрицы фундаментальных ре-
решений статического уравнения A.3°). Согласно B.4) разность (см. теорему II,
3.5)
J-д?д^[Ф^х—у' (°) — ф^(х—у)]ср1(у)с1в8, 1 = 1, 2, 3; k=l, % 3, 4;
m, n= 1, 2, 3,
есть непрерывный вектор, и ввиду B.3) непрерывен интеграл
\ ^	k= 1,2,3.
Поэтому в равенстве B.40) справа непрерывны (вместе с Г-операцией)
последние два интегральных слагаемых; первое же слагаемое справа для
k = 1, 2, 3 не что иное, как составляющая статического потенциала двой-
двойного слоя классической теории, для которого доказываемая теорема спра-
справедлива (см. VII, 2.1).
Наконец, необходимо еще заметить, что при k = 4 в силу B.3) непре-
непрерывна составляющая Z4 (x; ф). Следовательно, справедливость B.39) оче-
очевидна и теорема 2.1 доказана.
4. Основные граничные задачи. Приведение к интегральным уравнениям.
Постановка основных задач термоупругости была дана в главе I, § 13, п. 3.
Первая задача приводится к нахождению четырехкомпонентного век-
вектора U = (и, и4), являющегося соответственно в D+ или D" регулярным
решением уравнения
В(дх, ю) 1/"(х) +30 (*)=* 0	B.41)
(удовлетворяющим в D~ условию термоупругого излучения) по граничным
условиям:
и± = /, и% = f
4.
Во второй задаче граничные условия имеют вид
в третьей
и в четвертой

§ 2]	установившиеся термоупругие колебания	385
Здесь <2^ = (9819 5^2, <5^з> <^4). / = (/i» /а» /з) — заданные векторы,
f4 — заданный скаляр. Удобно еще ввести четырехкомпонентный вектор
F = (Fl9F99FZ9FJ = (f9fJ.
Решение первой задачи будем искать в виде
U
второй задачи — в виде
U
третьей задачи — в виде
U{x)
четвертой задачи — в виде
где ф, г|), X, (х — искомые четырехкомпонентные векторы из класса С0' a(S).
Тогда согласно свойствам потенциалов уравнение B.41) будет удовлет-
удовлетворено автоматически, а граничные условия в силу формул B.31)—B.38)
дадут для вектор-функции ф, i|), X, \x следующие интегральные уравнения:
1 [ Ф (z — у, й>) Ж (у) dy, B.42)
D±
y | ^ Ф» v) Ф (г — у, со) Ж (у) dy, B.43)
D±
J \Q(dt9 v)[$> (ду9 п)Ф' (z — y, a>)]'}
= F (г) — 1 J Q Eг, v) Ф (г — у, со) 5g (у) dy, B.44)
D±
VL{z)+j\P(dt9v)[Q(dy9n)<l>'(z — y9 a)]'} [i(y)dvS =
— y9 co)Ze(y)dy. B.45)
5. Теоремы Фредгольма. Системы интегральных уравнений, получен-
полученные выше, являются сингулярными системами, аналогичными сингулярным
системам граничных задач классической теории упругости.
Доказательство законности теорем и альтернативы Фредгольма для
сингулярных уравнений граничных задач термоупругости, по существу,
получается повторением рассуждений, которые для этой же цели были ис-
использованы в главе IV, § 7 для оператора G.2).
25 В. Д. Куирадзе

386	теория термоупругости	[рл# х
Для конкретности остановимся на исследовании уравнения B.42). Пере-
Перепишем систему B.42) в проекциях
з
*fc (*) + X J 2 Т1* (дУ> "> Ф*< (Z — У) % (У) dyS + Wk (фь 1р2, -фз, %) = Ffc,
k= 1,2,3, B.46)
s
B.47)
4
при >c = 1 и F'k = Fk — -^ \ ^j ^kffii dy будет подразумеваться пер-
где р	k
4
вая внешняя задача, а при х = —1 и /^ = —F* + у [ V ^kt^i dy —
первая внутренняя задача.
Wk (tyi, • • •> 'Фй)» ^ = 1, 2, 3, 4 — вполне непрерывные [операторы, за-
зависящие от г^х, . . ., г|;4; при этом в первых трех уравнениях B.46) *ф1э г|;2,
•фз войдут в качестве плотностей сингулярных интегралов, аналогичных
интегралам, которые рассматривались в главе IV, § 7, а в четвертом урав-
уравнении B.47) не вполне непрерывным является лишь внеинтегральный еди-
единичный оператор. Поэтому детерминант символической матрицы системы
B.46), B.47) совпадает с детерминантом символической матрицы, рассма-
рассматриваемой в главе IV, § 7, п. 4 и выводы, которые сделаны там, остаются
в силе и в данном случае. Таким образом, доказана
2.2. Теорема. Для интегральных уравнений B.42)—B.45) спра-
справедливы теоремы и альтернатива Фредгольма.
6. Внутренние задачи. Спектр собственных частот. Теоремы единствен-
единственности. В главе III, § 3, п. 4 было доказано, что основные внешние задачи
термоупругости, при выполнении условий термоупругого излучения на бес-
бесконечности, допускают единственные решения для любых значений пара-
параметра со2. Для внутренних задач это не так, и можно указать дискретное мно-
множество значений со2, для которых теорема единственности нарушается.
Первая основная однородная задача (u\s = О,
щ\э = 0). Из формулы B.13) для области D+, на основании граничных усло-
условий, следует
j
откуда «4 = const и, по граничному условию, «4 (х) = 0,
Из равенства (III, 3.13) и (III, 3.8) теперь имеем divwA) = div t/ = 0,
а из (III, 3.7) вытекает и^1)(х) = 0, x?D+. Поэтому согласно (III, 3.2),
и (х) = аB)(х); но и&Цх), согласно (III, 3.10), удовлетворяет условиям
(А + А|) и{2) (х) = 0, uB) \s = 0, div и{2) (х) = 0, х 6 D+. B.48)
Отсюда заключаем, что для всех со2, отличных от собственных чисел
задачи B.48) (частная задача Дирихле для уравнения Гельмгольца), и^2)(х) =
= 0 и, следовательно,
дп
Вторая основная однородная задача (PU\S = 0,
= 0У Из той же формулы B.13) согласно граничным условиям щ = С,

* 2|	УСТАНОВИВШИЕСЯ ТЕРМОУПРУГИЕ КОЛЕБАНИЯ	387
а из (III, 3.13), div и^Цх) .= Сг. Поэтому (III, 3.7) дает и<1Цх) = 0 и, сле-
следовательно, Сх = О, и снова из (III, 3.13), С = О, т. е. «4 = 0.
С другой стороны,
= Tu — yntit = 2ix^- +\i[nx rot a] = 2ц-^-+ |г [я X rotu<2>l.
Поэтому для ui2)(x) имеем следующую однородную краевую задачу:
Отсюда вытекает для всех со2, отличных от собственных частот задачи
B.49), иB){х) = 0 и, следовательно, для указанных значений со2
2.3.	Замечание. Из рассмотрения второй задачи следует, что
собственные числа задачи B.49) есть подмножество множества собственных
частот второй однородной задачи теории упругости (Н)о :
А (дх, со) а = 0, Tu\s = 0.	B.50)
Третья основная однородная задача (w|s = 0,
-р =0j. Из B.13) имеем согласно граничным условиям щ = С; из
(III, 3.13), div u^= d; из (III, 3.7) и^ = 0, из (III, 3.13) С = 0, и = и™
и для иB) (х) получаем граничную задачу B.48); следовательно, собственные
частоты третьей задачи те же, что и для первой граничной задачи.
Четвертая основная однородная задача (PU\s =¦¦=
= 0, u^\s = 0). Повторив рассуждения, приведенные выше, находим: соб-
собственные частоты четвертой задачи совпадают с частотами второй задачи.
2.4.	Замечание. Как мы видели, во всех внутренних однородных
задачах щ = 0, поэтому U = (и, 0) и и является решением одной из следую-
следующих граничных задач теории упругости:
А (дх, со) и = 0, и \s = 0 или Ти \s = 0.
Это решение, кроме того, удовлетворяет дополнительному условию:
div и (х) = 0, х ? D+.
Итак, множество собственных частот (и собственных векторов) любой
из внутренних однородных задач термоупругости включается в множество
собственных частот (и собственных векторов) первой или второй однородной
внутренней задачи теории упругости. Собственные частоты задач тер-
термоупругости совпадают с теми собственными частотами соответствующих
задач теории упругости, которым отвечают смещения, удовлетворяющие
условию div и = 0.
2.5.	Замечание. Из § 2, п. 1 следует, что между решениями си-
систем В (дх, со) U = 0 и В (дх, со) 0 = 0, т. е. между векторами U (и, и4)
и 0 (и, щ), существует связь, а именно, и = и, и4 — -^и4.
Поэтому рассуждения, которые применялись при доказательстве теорем
единственности для внутренних и внешних задач системы В (дх, со) U = 0,
и которые опираются на равенство щ = 0, остаются в силе и для задач со-
сопряженной системы
В (дХ9 со) 0 = 0.
25*

388	теория термоупругости	грл х
7. Изучение интегральных уравнений внешних задач. Для доказатель-
доказательства теорем существования решений внешних задач термоупругости пред-
предварительно изучим подробнее интегральные уравнения этих задач.
Это изучение основано на некоторых общих теоремах, подобных тем,
которые в главе VII были использованы при исследовании внешних задач
теории упругости.
2.6. Теорема. Необходимым и достаточным условием для того,
чтобы уравнение
= 0	B.51)
имело нетривиальное решение, является равенство параметра со2 одной из
собственных частот второй однородной внутренней основной задачи термо-
упругости (И)о . Если со2 есть v-кратная собственная частота этой задачи,
то интегральное уравнение B.51) имеет v линейно независимых решений и они
^совпадают с граничными значениями собственных вектор-функций задачи (И)о •
Необходимость. Пусть уравнение B.51) имеет нетривиальное
решение; покажем, что в этом случае со2 есть собственная частота задачи
(II)cf. Допустим, что это не так. Тогда союзное уравнение
,, п (z)) Ф (z — у, со) ф (у) dyS = 0
допускает нетривиальное решение ф. Потенциал простого слоя
V (*; ф) = J Ф (* — у, со) ф (у) dyS,
s
очевидно, есть решение второй однородной внутренней граничной задачи
для сопряженного уравнения В (дх, со) V = 0, т. е.
В(дк, (?>)V (х\ ф) = 0, jc? D+, \3l(dz, n(z)) V\* = 0.
Из замечания 2.5 известно, что 1/4 (х\ ф) = 0; 1/4 = -^- У4, где V есть
решение задачи
В(дх, со)V = 0, х ~ D\ \&(дг, п(z))V]+ = 0,	(ll)t
и поэтому
V (х; (p) = V (x).
со ,
Так как со2 отлично от собственных частот задачи (П)о , то V (х) = 0,
+, или
Но тогда по непрерывности потенциала простого слоя V (х; ф) и по тео-
теореме единственности для первой внешней задачи III, 3.4, ф (у) = 0. Это
противоречит допущению и тем самым необходимость доказана.
Достаточность. Пусть со2 есть v-кратная собственная частота
задачи (П)^" и ?/<*>(*) = (u<k\x), 0), k = 1, 2, . . ., v, — соответствующие
линейно независимые собственные векторы; легко убедиться, что их гранич-
граничные значения lUik)(z)V, k = 1, 2, . . ., v, также линейно независимы
,{см. теор. VII, 2.2).

УСТАНОВИВШИЕСЯ ТЕРМОУПРУГИЕ КОЛЕБАНИЯ	389
(о
Согласно замечанию 2.4 собственные векторы задачи (П)о входят в мно-
множество собственных решений второй внутренней однородной задачи теории
упругости, которые являются решениями интегрального уравнения (VII,
1.19) и поэтому принадлежат классу Cl'a(D+).
Применяя формулу общих представлений B.18) для U(k)(x), будем иметь
в силу граничных условий \М (дг, п (z)) Uih)]+ = О,
2U{k){x) = - J ийC„п)Ф'(х — i/, со)]' [U{k)(y)]+dyS9 x?D\
Перейдя здесь к пределу при х —* z?S, получим
г — y,a>)}[U(k)(y)]+duS = 0, zeS.
Это и есть интегральное уравнение B.51). Повторив рассуждения, при-
приведенные при доказательстве !теоремы VI 1,2.2, найдем без труда, что
[U{k)(z)]+, k = 1, 2, . . ., v, составляют полную систему решений уравне-
уравнения B.51).
Теорема 2.6 доказана.
2.7.	Теорема. Необходимым и достаточным условием для того»
чтобы уравнение
- Ф (г) + J & (<Э2, п (г)) Ф (г — у, со) <р (у) dyS = 0	B.52)
имело нетривиальное решение, является равенство параметра со2 одной из
собственных частот первой внутренней однородной основной задачи термо-
упругости A)о • Если со2 есть v-кратная собственная частота этой задачи^
то интегральное уравнение B.52) имеет v линейно независимых решений и они
совпадают с граничными значениями Si-операции над решениями задачи A)о •
Необходимость доказывается повторением рассуждений, примененных
при доказательстве необходимости в теореме VII, 2.3, с учетом теоремы един-
единственности термоупругости.
Достаточность также получается из рассуждений, использованных при
доказательстве достаточности в той же теореме VII, 2.3, если при этом вос-
воспользоваться формулой общих представлений B.18).
2.8.	Теорема. Необходимым и достаточным условием для тогог
чтобы уравнение
Х{2) + J q фг9 п {z)) [# {ду9 П) Ф' (г — у, со)]' % {у) dyS = 0	B.53)
имело нетривиальное решение, является равенство параметра со2 одной из
собственных частот второй внутренней однородной задачи термоупруго-
термоупругости (U)t.
Если со2 есть собственная частота кратности v для этой задачи, то
интегральное уравнение B.53) имеет v линейно независимых решений и они
совпадают с граничными значениями собственных вектор-функций задачи A1)о .
Необходимость. Пусть уравнение B.53) имеет нетривиальное
решение А, (г). Покажем, что в этом случае со2 будет собственной частотой
задачи (Н)о.

390	теория термоупругости	[рл# х
Пусть это не так. Рассмотрим потенциал U (х) = Z (х; X). По теореме
единственности для третьей внешней задачи III, 3.4 будем иметь
Z(x;X) = 0, x?D-.
На основании теоремы 2.1 можем записать
\9> (ду, п) Z(у; Я)]+ = [0> (ду, п) Z(у; Х)]~.
Таким образом, потенциал Z (х; X) с плотностью X (у) решает граничную
задачу
Поэтому в силу теоремы единственности для четвертой внутренней од-
однородной задачи будем иметь Z4 (х; X) = 0. Отсюда (—4 ^; М = 0 и,
следовательно, Z (х; X) есть в D" решение задачи (П)о . Но по предположению
<д2 отлично от собственной частоты этой задачи, поэтому
Z(x;?L) = O, x?D\
Отсюда следует, что X (у) = 0, а это противоречит предположению и
необходимость доказана.
Сделаем теперь следующее замечание. Пусть X (у) — некоторое решение
однородного уравнения B.53). Тогда Z (х; X) = 0, x?D". Но этот же по-
потенциал есть решение четвертой внутренней граничной задачи; следовательно,
четвертая составляющая Z4 (x; X) в D+ по теореме единственности есть то-
тождественный нуль. Таким образом,
Z4(x;X) = 0, xeD+[)D-.
Нетрудно проверить, что
Z4(x; Я) = J [&х{ду,п)Ф{4у (х — у, ю)МУ)+
где, напомним,
Но, по определению оператора Q и строению матрицы Ф (х — у, о),
имеем
[QZ(y; X)T — [QZ{y\ Х)у = — 2Х{у\ yeS.
С другой стороны, (QZ (х; Я)L = -^ , xgD+. Поэтому Я4 (у) = 0, y?S.
Обращение в нуль четвертой составляющей решения интегрального
уравнения позволяет заметить, что система B.53) есть система из трех урав-
уравнений относительно Xlf X2f X3 и имеет следующий вид:
з
К{г)+\ S &k<b(ty B — y,<*)h(y)djS = 0, t = l,2,3. B.54)
Достаточность. Пусть со2 есть v-кратная Собственная частота
(О
задачи (П)о и Uw(x) = (а(^(х), 0), /г==1, . . ., v—соответствующие соб-
собственные вектор-решения. Из формулы общих представлений регулярных
решений будем иметь
2Uik)(x) = - \[Щдд, /г)Ф' (х — у,©)]' [?/(

§ 2]	УСТАНОВИВШИЕСЯ ТЕРМОУПРУГИЕ КОЛЕБАНИЯ	391
Учитывая, что U{k)(x) = 0, перейдем здесь к пределу при х —»
тогда, ввиду того, что
Stt (ду, п) = 0>; (дуу п), / = 1,2,3,
для [U{k){z)Y получаем интегральное уравнение B.54); других решений
это уравнение иметь не может, и, следовательно, теорема 2.8 доказана пол-
полностью.
2.9. Теорема. Необходимым и достаточным условием для того,
чтобы уравнение
— ц (г) + J 3> (дг9 п (z)) [Q (ду, п) Ф' (г — у, со)]' (х (у) dyS = 0 B.55)
имело нетривиальное решение, является равенство параметра со2 одной из
собственных частот первой внутренней однородной граничной задачи термо-
упругости A)о . Если со2 есть v-кратная собственная частота этой задачи,
то уравнение B.55) имеет v линейно независимых решений и они совпадают
с М-операцией над собственными решениями задачи ()
Необходимость. Пусть уравнение B.55) имеет нетривиальное
решение. Покажем, что со2 при этом необходимо совпадает с одной из соб-
со
ственных частот задачи A)о . Допустим, что это неверно. Рассмотрим потен-
потенциал
U (х) = Q (x; ii).
По теореме единственности для четвертой внешней задачи имеем
Q(x; |ы) = 0, x6D".
Принимая во внимание определение оператора Q и пользуясь теоремой
Ляпунова—Таубера для гармонического потенциала двойного слоя, получим
Таким образом, потенциал Q (x; fx) решает задачу
В(дх, co)Q = 0, x?D+, [Q (ду9 n) Q]+ = 0.
Поэтому в силу теоремы единственности третьей внутренней однородной
задачи будем иметь Q4 (x; \i) = 0 и, следовательно, Q (x; \i) есть в D+ pe-
шение задачи AK". Но, по предположению, со2 отлично от собственной ча-
частоты этой задачи и поэтому Q (а:; |л) = 0, x?D+. Тогда и \i (у) = 0, что про-
противоречит допущению, и необходимость доказана.
Сделаем здесь следующее замечание. Пусть \i — некоторое решение
уравнения B.55). Тогда, как мы видели, Q (x\ jut) = 0, x(zD~. Этот же по-
со
тенциал в D+ есть решение задачи A)о\ поэтому Q4 (x; \i) = 0,
С другой стороны,
и, так как (!?Q)~ = 0 и по определению
будем иметь
Поэтому система уравнений B.55) обратится в систему из трех уравне-
уравнений относительно \il9 |x2, fx3,
3
- М*) + f 2 Г* (d*« n B))ф<°' B — У, ю) (х& (у) d^S = 0, 1 = 1,2,3. B.55')

392	теория термоупругости	[ГЛф X
со
Достаточность. Пусть со2 есть собственная частота задачи A)о
и ?/<*> = (а(Аг), 0), k=l, . . ., v — соответствующие собственные векторы.
К ним применима формула общих представлений и если еще примем во вни-
внимание граничное условие первой задачи, то будем иметь
2и{к)(х)=\ф(х — у, co
s
Но так как <%(J{k)= (Tu{k\ 0), то предыдущее равенство принимает вид
Взяв оператор Т (дх, п) от последнего вектора и перейдя к пределу при
х—>z?S, получим интегральное уравнение B.55'), что и следовало пока-
показать. Теорема 2.9 доказана.
8. Применение в теории внешних задач. Доказательство теорем суще-
существования. Результаты предыдущего пункта позволяют доказать разреши-
разрешимость внешних задач термоупругости для любых значений частоты коле-
колебаний.
Первая задача. Согласно теореме 2.6 интегральное уравнение
со
задачи A)о~ имеет характеристическое число только в том случае, когда со2
ю
совпадает с собственной частотой однородной задачи (II)?*. Следовательно,
нам предстоит исследовать вопрос о разрешимости уравнения B.42) именно
в этом случае.
Так как все регулярные решения уравнения термоупругости B.41), удов-
удовлетворяющие условию термоупругого излучения, представляются линейной
комбинацией потенциалов простого и двойного слоя с объемным потенциалом
со
(с финитной плотностью), естественно искать решение задачи (I)" в виде
U(x) = W(x; ф) + V(x; g) + U (x; 1 Ж),	B.56)
где if) и g неизвестные (искомые) векторы. Граничное условие первой задачи
согласно свойствам термоэластопотенциалов приводит для я|э к интегральному
уравнению
* (г) + J [* {ду, п) Ф' (г — у, со)]'
s
\ \	—V(z\g). B.57)
D"
Как было сказано (см. теорему 2.6), однородное уравнение, соответ-
соответствующее B.57), имеет v линейно независимых решений {грсл>}%=1; будем счи-
считать их ортонормированными.
Условия разрешимости уравнения B.57) имеют следующий вид:
Ak, *=l,2,...,v,	B.58)
где {ф(/г)'(z)}2Ui — линейно независимые решения союзного однородного
уравнения
Ф (z) + I St (дг, п (г)) Ф' (у — z, со) Ф (у) duS = 0	B.59)

§ 2]	"УСТАНОВИВШИЕСЯ ТЕРМОУПРУГИЕ КОЛЕБАНИЯ	393
[
Уравнения B.58) переписываются в виде
\V(z;g)cp^)(z)dS= \\ф(г — у, (о) g (у) d^) (z) d2S
f rj
f j	y	..v.
Потенциал простого слоя
J Ф( z,
V(x; ф<*>) = J Ф(х —
плотностью которого служит решение союзного однородного уравнения
B.59), очевидно является решением задачи
В (дх, со) V = 0, х 6 D\ (&Vy = 0
и поэтому (см. §2, п. 6), по теореме единственности для внутренних задач,
1/4 (х, ф(Л)) = 0, *?D+;ho это означает (см. замечание 2.5), что задача (H)rf
со
совпадает с задачей (П)^. Таким образом, условия разрешимости B.58) могут
быть еще записаны в виде
Ak, fe=l,2,,,.,v.	B.60)
Согласно теореме 2.6 V (г; y(k)) = \\>(k\ и условия разрешимости прини-
принимают вид
Теперь остается произвольный до сих пор вектор g (г) 6 С0» a(S) выбрать
равным
v
2	B-61)
и тогда, вследствие предположенной ортонормированности системы
{ф(/г!B)}1=1, условия B.60) будут выполнены и разрешимость уравнения B.57)
доказана.
Мы получили следующую теорему:
2.10. Теорема. Решение первой внешней задачи термоупругости
существует, единственно и представляется суммой B.56), в которой ур(у)
есть решение интегрального уравнения B.57), разрешимого для произвольной
правой части, когда вектор g (г) выбран согласно B.61). Если со2 не есть сов-
со ,
ственное число задачи (П)о , то g = 0.
Вторая задача. Пусть со2 совпадает с одной из собственных
® -+-
частот задачи (I)J и имеет кратность v. Решение ищем в виде суммы
B.62)

394	теория термоупругости	[рЛф х
где V (х\ ф) — потенциал простого слоя с неизвестной плотностью ф, W (х) —
некоторое регулярное решение уравнения В (дх, со) W (х) = О, х ? D", удо-
удовлетворяющее условию термоупругого излучения и U (х\ -к~<™\ —п0"
тенциал объемных масс с плотностью -о-^-
Граничные условия второй задачи, воспроизводимые оператором
31 (<Эг, п (г)) для вектора ф приводят к интегральному уравнению
— Ф (z)+j & (dz> n (z)) Ф (z — у, со) Ф (у) dyS J
S
= F (z) — 1 \& (дг9 п (г)) ф(г — у,(о)Ж (у) dy — {&№ (г))'. B.62')
Как было показано (см. теорему 2.7), соответствующее однородное урав-
уравнение имеет v линейно независимых решений {q>(k\z)}k=u которые мы можем
считать ортонормированными.
Условие разрешимости уравнения B.62')
Bk9 &=l,2,...,v,	B.63)
где {-фСЛ)Bг)}^=1 — полная система решений однородного союзного уравне-
уравнения и
\(z)	|
может быть записано в виде
J \9Ш (z)T [W (г; *<*>)Г^ = 2Bk9 k = 1, 2,..., v,
где
W{x; ф<*>) = J [Я (ду, п)Ф' (z — y, со)]' фк)(У) dJS.
Действительно, так как ty{k){y) удовлетворяют уравнению
-<|>(г) + J [Я{ду, п)Ф(у—z, со)Гг|)(у)dyS = 0,
которое в силу B.3') имеет вид
— ф(г)+ J [Я(ду9 n)O'(z — y, (o)]'my)d!/S = 0,
s
О)
то потенциалы двойного слоя W (x; \f>(/j>) решают задачу (l)t- Поэтому (см.
замечание 2.5) f 4 = 0 и, следовательно, W (x; tyik)) есть решение задачи
A)о . Очевидно, [W (г; 1|з<*>)]~ = 2^k)(z) и условия разрешимости B.63) при-
принимают вид
\dS = 2Bk, k=\929...,v.	B.64)

? 2]	УСТАНОВИВШИЕСЯ ТЕРМОУПРУГИЕ КОЛЕБАНИЯ	395
Для векторов W (х) и W(x;^k)), как регулярных решений уравнений
В (дх, со) W (х) = 0 и BW = О соответственно, удовлетворяющих условию
термоупругого излучения, справедлива в D" формула B.12) и поэтому
J \[9№{г)Г [W(z; ф<*>)]- — фШ(z\
Из теоремы Ляпунова—Таубера для ^потенциала W (x\ ty{k)) имеем
и, следовательно, условия разрешимости B.64) приобретают вид
j [Ш (г; ф<*))]+ [IF (г)]" rfS = 2Bk9 k = 1, 2 ,..., v.	B.65)
j
@
Так как W (x; tyik)) есть решение задачи (I)^~, 1F4 = O и IF (*; o|)^>) ока-
зывается также решением задачи A)о , справедливо соотношение
Поэтому условия разрешимости B.65) записываются в виде
dS = 2Bk, k= 1, 2,..., v;
J
и, наконец, на основании теоремы 2.7 эти условия принимают следующий
вид:
\q>^(z){W(z)]-dS = 2Bk, k=l,...,v.	B.66)
Остается, произвольный до сих пор, потенциал W (х) "выбрать как реше-
решение граничной задачи
1=1
которая на основании теоремы 2.10 разрешима. Вследствие ортонормиро-
ванности J9(fe)B)}^=i условия B.66) выполняются автоматически и разре-
разрешимость уравнения B.62) доказана. Тем самым доказана разрешимость за-
@
дачи (II)".
Решение единственно, несмотря на существование нетривиальных ре-
решений однородного интегрального уравнения, так как потенциал простого
слоя, составленный с помощью этих решений, как плотностей, по теореме
единственности есть тождественный нуль. Таким образом, доказана сле-
следующая
2.11. Теорема. Решение второй основной задачи термоупругости
для внешней среды D~ существует, единственно и представляется суммой
B.62), в которой ф {у) есть решение интегрального уравнения B.62'), раз-
разрешимого, если выполнены условия B.63); эти последние выполнены, если по-
потенциал W (х) есть решение граничной задачи B.67), которая разрешима.
(О
Если со2 не есть собственное число задачи A)о , то W (х) = 0, jt?D~.
Третья задача. В силу теоремы 2.8 требуется особое исследова-
вне только в том случае, когда со2 есть собственная частота задачи (П)о~
кратности v.

396	теория термоупругости	[рл# х
Допустив это, ищем решение в виде
U(x) = Z(х; X) + Q(а:) + U (х\ 1 т),	B.68)
где Z (х: X) и (/ fx; y^j — термоэластопотенциалы, определенные фор-
формулами B.26), B.24), a Q (х) — некоторое регулярное решение уравнения
В (дгч со) Q (х) = 0, x?D~, удовлетворяющее термоупругому излучению.
со
Граничные условия задачи (III)", воспроизводимые оператором Q (дх, п)>
дают для неизвестной плотности X (у) интегральное уравнение
X(z) + J Q (dz, n(z)) \Ф (ду9 п)Ф' (z — y, со)]' X(у)dyS =
= F (z) — 1 J Q (дг, п (z)) Ф{2 — у,<*)Ж (у) dy — [QQ (z)]~. B.69)
D~
По теореме 2.8 соответствующее однородное интегральное уравнение
имеет v линейно независимых решений {A,(fe)(z)}JUi, которые будем считать
ортонормированными.
Поэтому условия разрешимости уравнения B.69) имеют вид
B.70)
где {jx(Aj)(z)}aUi есть полная система линейно независимых решений союз-
союзного однородного уравнения
+ \\Q (ду, п)\& (д2, /г(г))Ф' {у —г, со)]'}' [г (у)d? = 0 B.71)
s
1 f Л/аг, п(г))Ф(г — у,
si	d~
Преобразуем ядро уравнения B.71); имеем
Ф (д„ п) Ф' (у — г, со) Q' (ду9 п)=Ф (дг, п (г)) [Q (ду, п)Ф(у — 2, co)]f.
Рассмотрим потенциал
Q (х; (х(Л)) = J [Q (ду9 п) Ф(у — х, со)]' [г*
Очевидно, он решает задачу
В (дХ9 со) Й (х\ \i<k>) = 0, л:6 ?>+,
поэтому по теореме единственности Q4 = 0, jc6^D+ и, следовательно, для
и Q(x; [л<л>) есть одновременно решение задачи
Кроме того, {Фй)+ — (#Q)" = 2\i^k) и условия разрешимости B.70) прини-
принимают вид
J [Q (дг, п (z)) Q (г)Г [#Й (г, (i<*>)r dS = — 2Ck, k=lt. M|v. B.72)
Покажем, что B.72) может быть переписано в виде
^*0r^ = -2CA, *=l,2,...fv.	B.73)

fi 2]	УСТАНОВИВШИЕСЯ ТЕРМОУПРУГИЕ КОЛЕБАНИЯ	397
В самом деле, по определению, имеем
3
Потребуем от произвольной (пока) вектор-функции Q (х) удовлетво-
удовлетворение условия
тогда условия B.72) принимают вид
dS = — 2Ck, &=l,2,...,v.	B.75)
С другой стороны, имеем равенство
) 2
так как
и, следовательно, B.73) доказано. Остается убедиться в справедливости до-
допущения B.75').
Как было показано выше, Q4 (л;; ^(/г)) = 0, x?D+f следовательно (-д~) =
= 0; с другой стороны, согласно B.28) будем иметь
4
Q4 (г, ,!*>) = j 2 Q.. @ , Я) Ф.4(у —х,
S i /1
заметим, что по определению (см. B.25))
Qfi(dy,n) = 09 i + u t,/== 1,2,3, Q«(^,n)=lt /=1,2,3,
следовательно,
= J ^ ФD (у-х, со) |i«*> (t/) rf/ + J ^ Ф44(г<*> (у) dS.
Напомним, что согласно B.3)
, -±-Фи(у — x9(o) = O(\y — x\-1), i = 1,2,3,
и, кроме того,
Таким образом, Q4 (x\ \iik)) есть линейная комбинация потенциалов про-
простого слоя и нормальной производной гармонического потенциала двойного
слоя.

398	теория термоупругости	[рл# х
Применяя к этому последнему теорему Ляпунова—Таубера, будем
иметь
Применив формулу Грина B.12) к Q (х) и Q (х; \i{k))9 получим
f Q- (г) (ЖГ dS = f (Ж (г))" Q" (г; ^х(/г)) rf5,
s	s
и условия B.73) переписываются в виде
(г)Г Я' (г; ji<fe>) dS = — 2СЛ, fe = 1, 2 ,..., v.	B.76)
J
-^j =0, B.76) примет вид
dS = —2СЛ, Л= 1, 2f..., v.	B.77)
J
По теореме Ляпунова—Таубера
[Q E2, п{г))й{г\ ji(*>)]+ = [Q(az, /г(г)) Q>;
и B.77) приобретает следующий вид:
J [«Q(z)r[QQ(z;[iW)]+dS = — 2Ck9 k= 1, 2 ,..., v.	B.78)
Но ввиду того, что Q4 = 0, x(zD+ и, следовательно, (QQ)+ = й+; применяя
теорему 2.8, будем иметь Q+ = Xik) (z) и условия разрешимости B.78) при-
принимают окончательно следующий вид:
= — 2Ck, k= 1, 2,.,., v.	B.79)
Потенциал Я (х) ищем в виде решения задачи
Д(О ге5, B.80)
которая согласно теореме 2.11 разрешима. Поскольку в граничных данных
Ц1)= 0 (см. п. 7), сделанное выше допущение B.74) выполняется автомати-
автоматически. Разрешимость уравнения B.69) и вместе с ним разрешимость задачи
(О
(III)" доказаны. Решение единственно, так как потенциал Z (x\ K(k)) с плот-
плотностью №k> есть тождественный нуль.
Таким образом, получена следующая |
2.12. Теорема. Решение третьей задачи термоупругости в области
D~ существует, единственно и представимо в виде B.68), где X (у) —решение
интегрального уравнения B.69), а потенциал Q (х) есть решение задачи B.80),
которая разрешима. Если со2 отлично от собственной частоты задачи
то Я (х) = 0.
Четвертая задача. Пусть со2 есть собственная частота задачи
A)о. Решение задачи (IV) ищем в виде
t/(*) = О (*; у)+ Z (*) + ?/(*;-! 5»),	B.81)

§ 2]	УСТАНОВИВШИЕСЯ ТЕРМОУПРУГИЕ КОЛЕБАНИЯ	399
где \i (у) — неизвестная плотность потенциала Q (x\ fi), a \Z (x) — произ-
произвольный регулярный вектор, удовлетворяющий уравнению В (дх, со) Z (х) =
= 0, x?D~ и условию термоупругого излучения.
Граничные условия четвертой задачи, воспроизводимые оператором
& (д2, п (г)), для jli (у) дают интегральное уравнение
- р (г) + J ^ (d2, n (г)) [Q C,, п) Ф' (г — г/, со)]' fi
= /7B) — Y J &{д„п{г))Ф(г — у,а)Ж{у)Aу-@>г(г)Г. B.82)
J
D"
Согласно теореме 2.9 условия разрешимости этого уравнения имеют вид
=1,2	v,	B.83)
где {X(/j)}iUi — полная система линейно независимых решений союзного
уравнения
1 \0>(ду, n)\Q(d2, п{г))Ф'(у — г, со)УУK(y)dyS = 0 B.84)
S ID'	J
Полную систему решений однородного уравнения, соответствующего
B.82), обозначим через {fx(fe)(z)}]Ui и будем считать ортонормированной.
Преобразуем ядро союзного уравнения B.84). Имеем
Q(d21 п{г))Ф'{у — г9 со) &' (ду, n)=Q(dz, п(г))[& (ду9 п)Ф(у — 2,со)]'.
Рассмотрим потенциал
Z (х; X{k)) = j [^ (Эу> /г) Ф (у—х, со)]' Я(Л) (у) dJS.
Этот потенциал решает задачу
В (дх, со) Z = 0, a: G O+, (QZ)+ = О,
и, по теореме единственности, Z4 = 0 в D+; следовательно, Z (л:; Я(Л)) одно-
временно есть решение задачи A)о. Кроме того, имеем (QZ) —(QZ) =
= —2№k) (z) и условия разрешимости B.83) принимают вид
iS = 2Dk, fe= 1Э 2,	, v.	B.85)
Покажем, что B.85) можно привести к равенству
dS = 2Dk, A=l,2,...,v.	B.86)
Действительно,
если только удовлетворяется условие
Z; = 0.	B.87)

400	теория термоупругости	[Гл. X
С другой стороны,
wzy B)- =
если только
Zr = 0.	B.88)
При этом, очевидно, эквивалентность B.85) и B.86) будет доказана.
Покажем справедливость B.88). Как было показано, Z4 (х) = 0, х с D+,
следовательно, Zt = 0. С другой стороны, согласно формуле B.28)
= J
/ — х,
Заметим теперь, что согласно B.3) для / = 1, 2, 3 Фи (у — х, со) —
ограничены, а их первые производные (см. (III, 3.6)) допускают особенность
вида \х — у]'1 и Ф^ также имеет сингулярность типа \х — у \~1. Далее,
на основании определения оператора & (ду, /г), 9>it при iy / = 1, 2, 3 содер-
содержит операцию однократного дифференцирования по геометрической коор-
координате, а 9>4, и ^\4 для i = 1, 2, 3, 4, вовсе не содержат операторов диффе-
дифференцирования. Следовательно, Z4 (x; А,<*>) есть потенциал типа простого
слоя, и поэтому 0 = Zt = ZJ".
Таким образом, условие B.88) выполнено.
Из B.86) на основании тождества Грина (см. B.12)) получаем
J 2Г (г) \kZ (г; l(k))]~ dS = 2Dk9 Ы1.2	 v;	B.89)
согласно предположению B.87) перепишем B.89) в виде
J Z~ (г) \Ф Z (z; %{k))]- dS = 2Db ft = 1, 2, ..., v.	B.90)
Далее, применяя теорему Ляпунова—Таубера (^Z)+ = (^Z)" и прини-
принимая во внимание, что Z4 = 0 в D+ и, следовательно, (^Z)+ = (J?Z)+ =
= E?Z)+, замечаем, что B.90) переписывается в виде
J Z~ (г) (i%Z)+dS = 2Dk9 k = 1, 2, .. ., v,	B.91)
и, наконец, на основании теоремы 2.9,
= ixik)(z), k=U 2, ..., v,
и окончательно, условия разрешимости принимают вид
(г) fxw (z) dS = 2Db ft = 1, 2, ..., v.
Потенциал Z (л:) находится как решение задачи
В (дх> со) Z (х) = 0, * е Я", Z~ (г) = S 2D,iI( ° B).	B.92)
il
Согласно теореме 2.10 эта задача разрешима и, так как \ь[1){г) = 0
(см. п. 7), условие B.87) выполняется автоматически. Следовательно, раз-

§ 3j	ЗАДАЧИ СТАТИКИ И ПСЕВДОКОЛЕБАНИЙ	401
решимость уравнения B.82) и вместе с ним — задачи (IV)"*, — доказана.
Решение единственно. Итак, доказана
2.13. Теорема. Решение четвертой задачи термоупругости в обла-
области D", существует, единственно и представляется в виде суммы B.81),
где \х (у) есть решение интегрального уравнения B.82), разрешимого, если
потенциал Z (х) выбран как решение задачи B.92), которая разрешима.
Если со2 не есть собственное число задачи (I)o"\ то Z (х) = 0.
§ 3. Задачи статики и псевдоколебаний
Два частных случая уравнения B.1) заслуживают особого внимания;
это случай, когда со = 0 и случай, когда со = it, где т = Re т + ilrn т,
Rex >0.
В первом случае уравнения A.2) принимают вид
\xAu-\- (А,-|- (x)grad divu-—7§гас' U4 + p^" = 0, ^
1 _	(ЗЛ)
4 I x W.	>
и представляют систему дифференциальных уравнений эластотермостатики;
во втором случае уравнения B.1) обращаются в систему уравнений
(хАа + (^ + [*>) grad diva — Ygradu4—рт2и = — (
—^4 — r]Tdiva = — — Q,
которую мы в главе III условно назвали уравнением термоупругих псевдоко-
псевдоколебаний.
1. Задачи статики. Во всех рассматриваемых граничных задачах в слу-
случае уравнения C.1), задача определения их есть независимая (от и) задача
^^
Поэтому найденное значение щ (х), будучи внесено в уравнение
\хАи (х) + (^ + t*>) grad div и (х) = у grad щ (х) — р&~ (х),
приводит к задачам теории упругости относительно и (х):
А (дх) и(х) = у grad щ (х) — р&~ (х), x?D+ (D"),
u+(z) = / (z) (и- (z) = / (z)) или (Tu (z))+ = / (z) ((Tu (z)Y = f (z)).
Однако если в граничных условиях значения и и и± связаны более слож-
сложным образом, чем в основных задачах, например, если вместо щ на границе
задается значение энтропии (см. гл. I, §§ 8, 9), указанное выше полное раз-
разделение не имеет места и задачу следует рассматривать как связную.
Рассмотрение этого случая предоставляется читателю (см. задачу № 3).
2. Псевдоколебания. Как отмечалось в главе III, § 3, п. 5, этот случай
представляет интерес, как существенный элемент динамической теории (см.
следующий параграф).
Для уравнения C.2) и основных граничных задач в D+ и D" в главе III,
§ 3, п. 5, были доказаны теоремы единственности, согласно которым вну-
26 В. Д. Купрадае

402f	теория термоупругости	[рл# х
тренние и внешние однородные задачи имеют лишь тривиальные решения
при Re т >>0.
Теперь мы имеем возможность доказать для этих задач и теоремы су-
существования. .
Для этого сначала установим некоторые свойства параметров Xk, k =
= 1, 2, 3, как функции комплексного параметра т = а + ш, а > 0; этими
свойствами мы будем пользоваться не только здесь.
Перепишем уравнения (III, 3.6), определяющие %ky в следующем виде:
рт'	куц
C.3)
Параметр е играет важную роль; его значения заключаются в интервале
@, 1) и для большинства реальных тел значительно меньше единицы (см.
Nowacki [1, 3]). В том случае, когда 8 = 0, реализуется разделение полей
деформации и температуры, т. е. имеем раздельную теорию и из C.3) следует
м	> ^T+2ir» Лз	•
Сложнее обстоит дело при 8 >>0.
Мы покажем, что существует определенное неотрицательное значение
параметра а, назовем его ое > 0, такое, что при 8 > 0 в полуплоскости
а Е>а8 коэффициенты Xkt k = 1, 2, 3 имеют следующие свойства:
а)	К =сс*+'*Ръ ^=1,2, З.и pfe >0, k = 1, 2, 3;
б)	^ = Xk (т), А == 1, 2, 3 — аналитические функции и для больших
значений | т |, Xk (т) = О (| т |), k = 1, 2, 3.
Для i3 эти свойства очевидны. Покажем их справедливость для %i
и А,2. Для этого заметим, что Х\ и А! либо оба комплексные, либо оба отри-
отрицательные вещественные числа. Для того чтобы в этом убедиться, рассмо-
рассмотрим два случая: 1) со = 0 и 2) <о Ф 0. В случае 1) формулы C.3) прини-
принимают вид
[	g]	^	C.4)
Отсюда ясно, что М и А,! отличны от нуля; кроме того, составив дискри-
дискриминант соответствующего квадратного уравнения, находим
?_ i\ | и I Р°2 I2 л Р°2 _
2 .2 Г q I p(j2 ^ 8О -
V2 .2 Г q
и, следовательно, №,^2 — действительные. Из C.4) очевидно, что A,jf, A^
имеют один и тот же знак, и так как согласно C.4) сумма (Ц + ^1) — отри-
отрицательна, заключаем
Х? = — d\ Xi = —b\ a>0,
C.5)
т. е. в этом случае А| и А| — отрицательные вещественные величины.
Перейдем к рассмотрению случая 2).
Пусть

&3J	ЗАДАЧИ СТАТИКИ И ПСЕВДОКОЛЕБАНИЙ	4US
тогда C.3) принимает вид
Покажем, что 2lf z2 — комплексные числа. Из C.6) следует справедли-
справедливость сказанного по крайней мере для одной из zk, k = 1, 2. Пусть zx =»
= а + ф, Р + 0 и г2 = б, где б действительно и не равно нулю, как этого
требует C.6). Внеся значения zk, k = 1, 2 в C.6), получим
pro
x (к 4- 2м.) '
*~ V х +^ + 2^j'
Р = -Х^7-	C.7)
На этом основании в результате элементарных преобразований будем
иметь
t	11
и, следовательно, 8 = 0, что противоречит допущению.
Из C.5) ясно, что Х\ и А| лишь в том случае могут быть положительными
вещественными, если zx = а2т, z2 = 62т, где а2, Ь2 —действительны. По-
Покажем, что г1э 22 в рассматриваемой полуплоскости не принимают такие зна-
значения.
Сначала заметим, что равенства zx = а2т, z2 = Ъ2% не могут иметь места
одновременно; действительно, в противном случае из C.6) имели бы а < 0.
Остается показать, что указанное равенство не имеет места и для одной из
zkf k = 1, 2. Из. C.6) имеем
Г ("~^1 + rf2jr) ~ х(Я + 2|*)Г
C.8)
и, следовательно, zl9 z2 — аналитические функции параметра т в полупло-
полуплоскости, из которой исключены корни уравнения
1±1 _1- _?Е_ V _ 4 Рт — о-	П сп
но, как легко видеть, эти корни равны
^ш=^^-[^—е)±21У1].	(ЗЛО)
Обозначим
^--ЧйГ-О-8):	C.11)
тогда можно утверждать, что zl9 22, как аналитические функции параметра т
в полуплоскости a j> а8, не могут здесь совпадать с выражением вида я2т,
которое не является аналитической функцией т.
Из предыдущего ясно также, что в полуплоскости Re т ?> ае, 2? =? 22
и, следовательно,
Свойство а) доказано полностью.
26*

404	теория термоупругости	(Гл>
Для доказательства свойства б) заметим, что из C.3) имеем
± К 1^Г" + Я + 2|* J ~ x(X + 2|i)J*
C.12)
Следовательно, Ях, Х2 — аналитические функции т в полуплоскости, из
которой исключены точки, удовлетворяющие равенствам
т /п + р , р^ 1 , i/ri+p i рт I2 4рт 1 = о
2 U *	* 4- 2(ы J ± V [ к ^ Я, + 2ц J	х (Я, + 2ji) J
Первое из этих равенств предполагает неравенство Re т < ае, второе же
приводит к равенству т = 0, и, следовательно, аналитичность Xl9 А,2
в полуплоскости Re т >> сг8 доказана.
Наконец, из C.12) очевидно, что
V2 = O(|t|), A,ft2 = 0(|x|2)	C.13)
и свойство б) доказано полностью.
Продолжим теперь доказательство теорем существования для задач
псевдоколебаний. Матрица фундаментальных решений однородного уравне-
уравнения C.2°) получается из матрицы решений однородного уравнения B. Г)
подстановкой со = ix\ эти решения содержат выражения exp (iXk \ х — у\),
k — 1, 2, 3 и в силу доказанного выше свойства а), в полуплоскости Re т >
^>ае, для эластопотенциалов, в которых выражаются решения граничных
задач, будут на бесконечности удовлетворены условия затухания более
сильные, чем те, которые в главе III, § 3, п. 3 были использованы для дока-
доказательства теорем единственности. Отсюда следуют интересующие нас
теоремы единственности.
Далее, очевидно, интегральные уравнения граничных задач и теперь
будут сингулярными, но с главными частями, совпадающими с главными
частями соответствующих интегральных уравнений для уравнения B.1).
Это следствие того, что главные части в обоих случаях получаются добавле-
добавлением и вычитанием соответствующим образом выбранного выражения для
решения статической задачи; но эти последние в рассматриваемых случаях
идентичны. Поэтому интегральные уравнения, разрешающие граничные за-
задачи, относятся к типу, для которого теоремы и альтернатива Фредгольма
справедливы.
Но однородные интегральные уравнения, соответствующие рассматри-
рассматриваемым неоднородным, при Re т >> <*е согласно теоремам единственности
имеют лишь нулевые решения и, следовательно, неоднородные интегральные
уравнения при Re т >> ог разрешимы для произвольных значений правых
частей.
Таким образом, имеем теорему
3.1. Теорема. Если Re т > ае, задачи A)±, (Н)±, (IH)±, (IV)±
для уравнения C.2) разрешимы. Решения единственны и представляются
с таком виде:
н
для задачи (I)*
4)	C.14)

4]	ДИНАМИЧЕСКИЕ ЗАДАЧИ ТЕРМОУПРУГОСТИ	405
для задачи (П)±
( \)	C.15)
it
для задачи (III)*
U{x) = Z {x; X) + (У (х; -^- 3»),	C.16)
для задачи (IV)±
(ЗЛ7>
где г|), ф, X, jut — решения соответствующих сингулярных интегральных
уравнений.
§ 4. Динамические задачи термоупругости
Метод решения смешанных задач динамики классической теории упру-
упругости, изложенный в главе VIII, распространяется на решения основных
смешанных задач динамической термоупругости. Здесь покажем это подробно
на примере первой задачи, а относительно других приведем краткие поясне-
пояснения и необходимые библиографические указания.
I. Первая задача. Постановка и приведение к специальному виду.
В цилиндре D+ X [0, оо) ищется регулярный вектор U = (иъ и2, и3, и±) =
= {и, и4) из условий
А (дх) и (х9 f) — у grad ц4 (х, t) — р "
t)	L^0 ^di t) LQ	) j
lim a (jc, 0 = Ф(°) (x), lim du{x' f) = ф<г> (х),	D.2)
lim a4 (x, 0 = cpi0) (jc),	D.3)
lim и(х, t) = f(y, 0,	D.4)
S
D+
lim a4(x, t) = U(y> t)9	D.5>
где
T(x, t), Q{x, t), xfD+, t^09 ф@)(х), ФA)(х), Ф40) (x), xeD+,
/A/, 0, /4(^ t), yfS,t^O
— заданные функции. На вопросе о гладкости данных, по существу совпадаю-
совпадающих с теми, которые были приняты в главе VIII, здесь не будем останавли-
останавливаться и уточнения, необходимые в теории термоупругости, сделаем по ходу
изложения.
Как и в классической теории упругости, ищем классическое решение
задачи, входящее, по определению, в класс С (D+x [0,oo)) (]C2(D+ X [0, оо)).

406
ТЕОРИЯ ТЕРМОУПРУГОСТИ
[Гл. X
Для существования такого решения, очевидно, необходимо выполнение
^естественных условий согласования»
ф@) (</) = /(</> о),
)> yes. D.6)
Исходя из тех же соображений, как в случае упругости, потребуем
еще соблюдение условий согласования высших порядков
Ф4
у, 0
, tn = 2, 3, ..., 7,
)
D.7)
где
- хт) div
(«ш-
t=0
D.8)
Эти условия получаются последовательным дифференцированием по ? урав-
уравнения D.1) и подстановкой при t = 0 начальных данных. Таким образом,
будем предполагать, что искомое решение удовлетворяет условиям
дти (х, t)
dt
(ху t)
dtm
»0, 1, .... 7
О, 1, ..., 6,
D.9)
где ф(т>(л;) и ф^т)(х) дифференцируемы соответственно до порядка G — т)
"И F — т) включительно.
Совершенно так же, как в главе VIII, §2, пп. 2—4, можно показать, что
доставленную задачу без ограничения общности можно привести к анало-
аналогичной задаче с нулевыми начальными данными, специальной правой частью
уравнения и специальным граничным значением на S. Решение «приведен-
«приведенной» задачи, назовем его UQ (x, t) = (uOi u04), связано с решением исходной
равенством
U0(x, t) = U(x, t) —
D.10)
где 2 (х, t) = (ст, а4) — четырехкомпонентная вектор-функция Соболева
(см. гл. VIII, § 1, п. 2). Тогда для Uo (x, t) будем иметь
А(дх)щ{х,
x, t) —
д2и
f
= ho(x, t),
limU0(x, 0 = 0, lim
=0,
lim U0{x, t) = F0(y9 0,
D.11)

§ 41
ДИНАМИЧЕСКИЕ ЗАДАЧИ ТЕРМОУПРУГОСТИ
407
где
Ж$ = (h0, /i04), Fo = (/0, /04),
ho(x, t) = h(x, t) — A(dx)o(x,
9 t) = h,{xyt) — Да4(х,
D.12)
и из D.12) в силу определения ф(т>(л:), cpjm)(*)> согласно D.6), D.7), D.9) и
определения вектор-функции 2 (х, t), будем иметь
M</> 0 = /(</, t) — o{y, t), fot(y, t) = U(yti) — Ot(y, t)9
. 0
:, t)
dt"
(m-f-2) __
= 0t m = 0, . •., 5,
, о
/=0
=l, ..., 5,
fo (.V, 0
= 0, m = 0, 1, ..., 7;
(У,
dtm
= 0, m = 0, 1,
D.13)
2. Преобразование Лапласа. Решение эллиптической задачи. Пусть
х = а -[- Ш — комплексная переменная в полуплоскости П^, а > сто >> <х0,
где
ао = тах{а8, а},
а — показатель экспоненциального роста по времени первоначальных дан-
данных задачи и их требуемых производных, зависящих от времени (см. гл. VIII,
§2, п. 1), а а8 определяется из C.11).
Тогда существуют интегралы
Ж0(х, T)=\e—t3%0(x,t)dt, F0(y, т) = J e~4F0(y, t)dt.	D.14)
о	о
Рассмотрим граничную задачу эллиптического типа
А (дх) й0 (х, т) — у grad й0/к (х, т) — рт2и0(х, т) = /г0 (х, т),
ДиО4(л:, т)	иОФ(х9 т) — r]Tdiva0 = /гО4(л;, т),л: 6 D+; l /a i^
х, т) = Fo (у, т), y^S,
которая получается из задачи D.11) формальным применением преобразова-
преобразования Лапласа
с, 0 Л.
D.16)

408
ТЕОРИЯ ТЕРМОУПРУГОСТИ
[Гл. X
Интегрированием по частям из равенств D.14) в силу D.13) получаем
О
D.17)
dt6
t = о
1 1с-г, д1К(*>
Т7 J е	ж?
, 1 Г т,
+ Л
' Т8
';¦"
D.18)
и, следовательно, имеем равномерные по x?D+, у 6 S, оценки
С
|т|9
|Т|8
D.19)
D.20)
В § 3, п. 2 мы уже указывали, что задача D.15) имеет, и притом един-
единственное, регулярное решение в D+ и это решение представляется в виде
C.14). Найденное решение является классическим. Это есть следствие того,
что правая часть интегрального уравнения для г|) (у) принадлежит классу
С2«0 E). Последнее обстоятельство нетрудно проверить, выписав явное выра-
выражение правой части уравнения, согласно теореме V, 10.3 (см. гл. VIII, § 1, п. 6).
3. Гладкость 1/0(Х, %) относительно т? П0о. Представим Оо в виде суммы
Оо (х, т) =
где йоХ) есть решение задачи
A(dx)ui>l)(x, т) = 0, xe
Аи$ (х, т) = 0, х 6
a Uq2) есть решение задачи
Л {дх) и{о] — 7 grad и$
т) + О{о2) (х, т),

(у, т)}+ = /р
= /г0 + Р^2 ^о!)
) = /гО4+ 4" ^ +rjTdiv
D.21)
D.22)
D.23)
D.24)
Эти задачи имеют единственные решения. Решение задач D.22), D.23)
может быть представлено в виде
2Й}
'(*, т) =	1т\[Т{ду, n)G(y, x)]'J0{y, x)dyS,
s
>(x,T)=_4-f wx,i
v '	2 J dn
D.25)

§4]
ДИНАМИЧЕСКИЕ ЗАДАЧИ ТЕРМОУПРУГОСТИ
409
где G (ху у) и g (x, у) — тензор и функция Грина соответственно для опера-
операторов А (дх) и А, с граничными условиями Дирихле в D+, а задача D.24)
эквивалентна решению интегро-дифференциального уравнения:
и{о2)
и(о2)
^-j G(x, у) grad и$ dy =
D+
+ -^ J G (х,- у)
D+
=	lT J G(x, у) [ho + рт2^1' + vgrad ый>] dy,
D*
^ + ir J S (x, У) uloV dy + lg- J g(x, y) div W dy =
0+	0+
=	g- J ^(x, y) [/io4 + -^
D.26)
/о (У> T)» /04 (^/» T) — аналитические функции параметра т в полуплоскости
ПСТв; поэтому, согласно представлению D.25), аналитическими функциями т
будут и ио1] U, т) и «oV (ху т). Чтобы показать, аналитичность Uq2) (ху т)
как функции т, преобразуем D.26); оно приводится к интегральному урав-
уравнению Фредгольма второго рода. Действительно,
\G(x,
D+
D+ i=l
dy, k=l, 2, 3;
D+
O+
— J
D+
, y)ii{02)dy.
Подставив эти значения в D.26), убеждаемся в справедливости сказанного.
Полученное уравнение в полуплоскости Пав разрешимо для произволь-
произвольной правой части, так как соответствующее однородное уравнение, как эк-
Бивалентное однородной задаче A)о , имеет лишь тривиальное решение.
Выразив решение уравнения D.26) по первой теореме Фредгольма, и
заметив, что как резольвента, так и правая часть — аналитические функ-
функции т в полуплоскости Пае, приходим к выводу об аналитичности решения,
т.е. Оо2)(хут), как функции т.
Наконец, из изложенного следует аналитичность UQ = Uq1) + f/o2), как
функции параметра т в полуплоскости Пао.
4. Асимптотические по т оценки для (f(l)(x, т) и ее производных.
Как решение задачи D.22), D.23), Оо1) может быть представлено в виде
«i1} {x, r) = J [N (ду, п)Т(х — у)\ 'Ф (у) dyS,
s
Ж-|^г
D.27)

410
ТЕОРИЯ ТЕРМОУПРУГОСТИ
[Гл. X
где N (ду, п) — оператор псевдонапряжения, введенный в главе I, § 13, п. 1
и Ф. Ф4 — решения интегральных уравнений Фредгольма
- Ф (z) + \[N (ди, п) Г (г — у)]' ф (у) d? = }0 B) т),
ч
— Ф4(г) + -2J- J-5J- |г_^у| Ф4(У)<*„5 = fot(г, т).
D.28)
Отсюда для решений ср B, х) и ср4 (г, т) имеем
с	с
| ф B, Т) I ^ Г~~ПГ » I Ф4B» х) I ^ , ,8 ¦
и для Uq1) (х, т), равномерно относительно х
справедливы оценки
п...
D.29)
Для дальнейшего необходимо иметь асимптотические по т оценки для
первых двух производных по х,_ вектор-функции Оо1 , в любой строго вну-
внутренней подобласти D'czD+.
Пусть x?D'; из D.27) получим
дхь
'—f/l3
С С	dS
|Т|9 J |д;_у|2-8и_
-, D.30)
где 8 > 0 произвольное положительное число, а у* — точка на S.
Таким же образом согласно D.27) получаем
D.31)
Повторив аналогичные рассмотрения для вторых производных, получим
D.32)
5. Асимптотические оценки по т для Uc,2)(x, т). Введем для правых
частей D.26) обозначения
2 (х, т) = — -L j G (х, у) [ho (у, х) + Р-С2й^1) (у, т) -f 7 grad ufi»] dy;
D+
D.33)
и оценим модули ^и 1 относительно т, используя установленные выше
оценки
D.34)

? 4]
ДИНАМИЧЕСКИЕ ЗАДАЧИ ТЕРМОУПРУГОСТИ
411
Пользуясь свойствами G (х, у) и g (х, у) (тензора Грина оператора А (дх)
и функции Грина оператора Д для задач Дирихле) из формулы Гаусса—
Остроградского будем иметь
J G(х, у) grad и® {у, х) dy = - J
D+
Ь+ k \ i
(у, т) dy, D.34')
O+
у, т) dy = — j ub
D+
D.34")
где ek9 k = 1, 2, 3 — координатные орты.
Поэтому на основании D.34) можем записать
I Г	"*
= ~2~ J I И °"
D-
¦iJ
Г
D.35)
Обращаясь теперь к D.26) и применяя неравенство Коши—Буняковского,
будем иметь на основании D.35)
D.36)
(х, г) | < С | т | j J | йй> |2 dyV/2 + С | т| j J | div
Таким образом, для того, чтобы получить необходимую оценку для
0о2) (х, т), достаточно иметь оценки интегралов
\ grad
D+
Для векторов f/o и (/J выпишем формулу Грина (III, 3.26)
| \й(о2) [А(дх)и{о2) —
dx
D+
1 grad

412	теория термоупругости	[рл х
Учитывая дифференциальные уравнения, которым удовлетворяют 0q2>
и Uq2) и граничные условия, можем записать
{рт* | й@2) Р + Е D2), йР) — уй$ div^2»} dx
D+
— J ("о2) [Ло(х, т) + рт2^ + 7grad й$]} dx, D.37)
+
D+
f
	I w 04 I
0+ v *
D+
Вычисляя из D.38) интеграл — 7 I 11$ div uq2 dx и подставив в D.37),
получим
Г	^B^ i2 • f г~» ~Г2^ <ч'B)\ * V Г ^{2^ i2
ОТ^ I ill о	^^ -р I h (по 9 U о ) "X Н	I Ш 04 "Я "
J	J Л3* J
И+	D+ D+
_)—L_ f 1 gra(j ^2) 12 dx = — f jao2) [Яо + рт2аоП + 7 grad uoV]] dx —
6*	D+
+
Преобразуем в правой части D.39) слагаемые
J 42) grad ий> dx, J йй> div й{01) dx.
J	J
СУ*	D+
Имеем
j	{
D+	D+ ^ ft
D+ ^ ft	ft
= — f div м^ый' dx,
J 4(div«JV j{ У] ^- (J^V)- V Щ
D+	D+ ^ k	k
D+	D+ ^ k	k
A	u{V(ol) dx.
Поэтому для правой части D.39), которую назовем q (т), на основании D.34)
будем иметь
j +	|grad^>|dxI/2. D.40)

41
ДИНАМИЧЕСКИЕ ЗАДАЧИ ТЕРМОУПРУГОСТИ
413
Введем следующие обозначения:
0+
с2 (т) = j | grad й$ |2 dx, d2 (т) = j | div u&2) |2 dx.
0+	D+
Формула D.39) принимает вид
рт^ (т) + -Х- Ь2 (т) + -L- с2 (т) + d2 (т) = 9 (т),
D.41)
D.4Г)
где
D*
для комплексно-сопряженного тождества D.4 Г) будем иметь
рт2а2 (т) + -Х- Ь2 (т) + -JL с2 (т) + d2 (т) = ^ (т).	D.42)
Умножив первое на х, второе на т и составив сумму, получим
р (тт2 + тт2) а2 (т) + -^ (т + т) б2 (т) + Я- с2 (т) + (т + т) d? (т) = т<7 (т) + xq (т).
Учитывая положительность коэффициентов при всех слагаемых слева
и очевидное равенство (см. III, § 1, п. 1)
* где W ^ О,
получим, согласно D.40),
с Vf а
[TF
^ С {^ а (т) + ply 6 (т) + ^ с (т) + ^ d (т)},
D.43)
Эти неравенства можно переписать в виде
D.44)
где введено обозначение
Из D.44) получаем
= а(т) + 6 (т)
' VI

414
ТЕОРИЯ ТЕРМОУПРУГОСТИ
(Гл. X
и, складывая эти неравенства, будем иметь
т. е. I (т) <; -_. Подставив это неравенство в D.44), будем иметь оконча-
окончательно
На основании D,45) и D.36) теперь имеем
D.45)
D.46)
6. Оценки относительно т производных по х,: от 01Р(х^ т). Некоторые
вспомогательные неравенства. Оценим производные от выражений, стоящих
в правой части D.26) в любой строго внутренней подобласти Dr с границей S\
такой, что x?D'czD+; r (S, S') > 0. Пусть D"c=D+ — замкнутая область,
ограниченная поверхностьюS", такая, чтоD'aD" и г (S, S") >0,г (S', S")>
> 0. Имеем для
, т) = - -L j G(х, t/) {Ао(у, т) +
+
+ 7 grad
-Ь
D+\D"
	F J G(*' ^ grad ^} ^ =
D.47)
Для с?!, согласно D.34) и ввиду дифференцируемости тензора Грина при
", xeD'9 получаем
дЗх
С
¦ i, /=1,2,3;
D.48)
Представим G в виде
G(х, у) = Г (х— у) — v(л:, у),
где Г (л: — у) — фундаментальное решение уравнений теории упругости
и v (х, у) — регулярная часть матрицы Грина; тогда
= ,72 + Л
D.49)
для <?'„ имеем
\дх~дх~
-±-1 v(x,
Т7, i,/=1,2, 3,
а для
~ Т J 1 ^~
У) щ
1

§4]
ДИНАМИЧЕСКИЕ ЗАДАЧИ ТЕРМОУПРУГОСТИ
415
Дифференцируя последнее равенство еще раз, согласно D.30), D.34) будем
иметь
дх/дх/
rjr7 * i, / = 1, 2, 3;
D.50)
Обратимся теперь к оценке<?8. Сначала преобразуем33 по формуле D.34')
-I- 1
Для Зъ имеем непосредственно
D" [ k
^s, i,/= 1,2,3;
D.51)
a <?3 преобразуем следующим образом:
ds
—И221
и04
Дифференцируя JQ, дважды, будем иметь на основании D.34)
(->	.	too. -. /- TSf
D.52)
Кроме этого, имеем
д"ш ==	к~ j G grad y u$ dy =
	j-JreradSa>.
77
^l у grad мй} dr/ = ^321 + 0/322,
и на основании D.34), D.31) будем иметь
С
, i, 7 =1,2,3;
D.53)
С/с/
Преобразуем производную -^^ , i = 1, 2, 3;
t( 2 } dyt s т и 2 J
S"
—L J ГА grad
O"
Отсюда
О У -/^ У • 9 I fly- °
dS
y гаг о А -A) .
2 J

416
ТЕОРИЯ ТЕРМОУПРУГОСТИ
[Гл. X
и, следовательно, согласно оценкам D.31), D.32),
- ? / /	 1 о о
D.54)
Объединяя оценки D.48)—D.54), получим окончательно для первых
и вторых производных
11	\\
*,/ = 1,2,3;
D.55)
Совершенно аналогично на основании D.34) будем иметь для первых
и вторых производных по х{ от I (ху т)
а2/
^-ГПб> l» i — *» Z» °>»
D.56)
Оценим первые производные:
(х, т)
(*¦
, t= 1,2,3: х
dxi	dxt
Определим g rad UoV (x, т) из второго равенства D.26) и подставим ре-
результат в первое из этих равенств; после простых преобразований получим
aJ2)(*,T) = — ?f J G(x, у)ик2){у, x)dy + -g- J /e(x,z)oj4)(z,T)d2 +
+ ^ J /C(x, z)div^2)(z, T)dz + -b J G(x,y)gradZ(y, т)^+^(х, т) =
D+
= П (x, x) + Г2 (x, t) + Y3 (x, т)
где
K(x, z)= J G(x,
, z)dy.
x, т), D.57)
D.58)
В силу свойств G (х, у) и g (у, г), применяя известные теоремы о компо-
композиции ядер (см. Miranda [1]), имеем
К /д- 2) = О (\п I х	z I)		О Л х	^ I) j = 12 3	D 59)
Оценим первые производные по xt от У^ (х, т), й = 1, . . ., 4. На
основании D.46), так же как в случае динамических задач классической
теории упругости (см. гл. VIII, § 2, пп. 10, 11), получаем
-§-' «= 1, 2, 3,
D.60)
Для К2 (*> т) согласно D.59) и D.46) находим непосредственно
д?2 (х, т)
D.61)
Аналогично оценивается -^-; в силу D.59) и D.45) имеем
D.62)

§ 4]
ДИНАМИЧЕСКИЕ ЗАДАЧИ ТЕРМОУПРУГОСТИ
417
Оценку для производной —А?* %) получаем на основании D.35) и D.56)
совершенно так же, как для интеграла J3 (*» т) (см. D.51), D.54)), повторяя
те же выкладки
*xt |^- |x |6'
Таким образом, учитывая D.55), D.60)—D.63) из D.57) ролучаем окон-
окончательно
г
|т
, t=l,2,3, а>0,
Аналогично, на основании D.26), D.35), D.46), для
Эх,
.3+а
D.64)
будем иметь
D.65)
Итак, согласно D.64), D.65) имеем равномерную оценку для
дх(
i = 1, 2, 3 в любой строго внутренней подобласти основной области D+.
Для получения оценок вторых производных от О{02) (х, т) по х,, в обла-
области D", представим векторОо2) (х, х) с помощью формулы общих представле-
представлений (см. B.16))
(х) = J Ф (х — t/, /т)
— J [U (ду, п) &(у — х, ix)] (U@2) (у, т))+ d,JS— J Ф (х — у, h) f {у, т) dy,
S
D.66)
где
Пусть х65'; тогда в силу D.46), D.64), D.65), D.34), D.30), D.31)
и ввиду того, что
дкф(х — г/, iT)
\x-y\W
из D.66) получаем окончательно
х, т)
, а>0,
f, i, /=1,2,3.
D.67)
D.68)
7. Завершение решения динамической задачи. Объединив оценки D.29),
D.31), D.32), D.46), D.64), D.65) и D.68), будем иметь на основании D.21)
I#о(х, т)| ^ ,^|Д ,	х 6 Т)\	D.69)
t=t,2, 3, а>0, xgD',	D.70)
c, т)
(¦*, Т)
, <,/=!, 2,3, а>0,
D.71)
В. Д. Купрадзе

418	теория термоуиругости	[Гл X
причем оценки равномерные относительно х в соответствующих областях.
В силу этих оценок вектор
а-Н'оо
и»(х>Ъ = Ш J *х(йо(х,т)с1т,	D.72)
а—too
удовлетворяет всем условиям приведенной задачи (см. 4.11). Это показы-
показывается совершенно так же, как было сделано в главе VIII, в § 2, п. 13для
решения динамической задачи классической теории.
Далее, из формулы D.10) находится вектор U (x, f) — решение перво-
первоначальной задачи (см. D.1)—D.5)). Так же, как в главе VIII, § 2, пп. 13, 14,
исключается вектор 2 (x, t) путем приведения к неоднородной эллипти-
эллиптической задаче D.15) с правой частью, равной вектору
(*, т)-рт<р@)(х) — РфA)(*) — 7§гас1фГ(х), Й4—^ cpiO)(*) —
Эта задача решается явно (см. гл. XIII) в обобщенных рядах Фурье.
Выше была рассмотрена первая задача. В детальном исследовании Кахни-
ашвили [4] рассмотрены все основные задачи термоупругости и построена
их полная теория (см. Кахниашвили [4, 53).
§ 5. Дополнительные замечания.
Библиографические справки
Система дифференциальных уравнений термоупругости A.1) состоит из
уравнения движения упругой среды, принадлежащего гиперболическому
(вырожденному) типу и из уравнения теплопроводности, относящегося
к параболическому типу. Эта система, как уже отмечалось (см. I, § 15,
п. 1), не входит в известные канонические классы уравнений математичес-
математической физики.
Несмотря на это, как мы видели, для системы A.1) и системы уравнений
термоупругих колебаний A.2) оказываются корректными соответственно
начально-граничные (смешанные) и граничные задачи, так же как это имеет
место для системы дифференциальных уравнений теории упругости.
Вместе с тем,- уравнения термоупругости обнаруживают принципиально
новые черты по сравнению с уравнениями теории упругости.
Прежде всего это относится к вопросу о существовании частот собствен-
собственных колебаний ограниченного тела. С точки зрения уравнений теории упру-
упругости, для таких тел существует дискретное (счетное) множество собственных
частот (см. гл. VII, теоремы 1.3 и 1.4). С точки зрения уравнений термоупру-
термоупругости, вообще говоря, вопрос остается открытым; во всяком случае, можно
указать класс задач, когда собственные частоты отсутствуют.
Мы видели (см. § 2, п. 6), что множество собственных частот любой из
внутренних однородных задач термоупругости входит в множество собствен-
собственных частот первой или второй внутренней задачи теории упругости, и совпа-
совпадает с теми собственными частотами последних, которым соответствуют сме-
смещения, удовлетворяющие условию div и = 0. Отсюда следует, что собствен-
собственными частотами термоупругих задач могут быть только собственные числа
следующих задач (см. B.48) и B.49)):
(А + Лз) иB) (х) = 0, div u{2) (х) = 0, х 6 D\
D.73)

« 5]	ДОПОЛНИТЕЛЬНЫЕ ЗАМЕЧАНИЯ. БИБЛИОГРАФИЧЕСКИЕ СПРАВКИ	419
ИЛИ
(Д + II) иB\х) = 0, d iv u<2> (х) = 0,
=0.	D.74)
Мы покажем сейчас на примере (см. Dafermos [1]), что существуют
случаи, когда решения задачи D.73) суть только тождественные нули.
Пусть D есть область n-мерного пространства Еп> для которой ска-
скалярная краевая задача на собственные значения
До + А&> = 0: 0|5 = О	D.75)
допускает лишь простые характеристические числа. Покажем, что для этой
области единственным решением задачи D.73) является и{2) = 0. Так как
ранг характеристического числа задачи D.75) равен единице, решение задачи
D.73) имеет вид ui2) = cv, где с есть /г-мерный постоянный вектор, a v —
собственная функция задачи D.75). Пусть ct =f= 0, i = 1, . . ., ky k ^ n
и ck+1 = . , . = cn = 0. Из условия div u{2) = 0 следует
D.76)
где f (yl9 . . ., Уп-i) — произвольная дифференцируемая функция, опре-
определенная в области
{(Ух. .... </«-i)*. </,= -§-- ^. i=h...9k—U
Hi = xi+1, i=k, > . ., n—h x?D} .
Пусть x — произвольная точка в области D. На граничной поверхности S
найдется по крайней мере одна такая точка х\ что
С i	Ck	ci	ck
поэтому из D.76), согласно D.73) и D.75) будем иметь
V (Хг, . . . , Хп) = V (ХЬ . . . , Хп) = 0
и наше утверждение доказано.
Отсюда ясно, что в данном случае задачи термоупругости, которые при-
приводят к задаче D.73) (см. § 2, п. 6), в области D не имеют собственных частот,
и внутренние неоднородные задачи разрешимы для произвольных граничных
значений из допустимого класса.
Предоставляем читателю построить пример, который позволит сделать
аналогичный вывод для задач термоупругости, приводимых к задаче D,74)
(см. § 2, п. 6).
Нетрудно указать пример, когда при наличии кратного характеристи-
характеристического числа у задачи D.75), задача D.73) имеет нетривиальное решение.
Пусть, например, D есть круг единичного радиуса на плоскости, с центром
в начале координат. В этом случае краевая задача D.75), если за Х| принят
один из корней функции Бесселя первого рода, скажем, первого порядка,
27*

420	теория термоупругости	[Гл# х
будет иметь два линейно независимых регулярных решения, в полярных
координатах (| х | = г, <р),
Л (Цг) cos ф,
а векторной задаче D.73) удовлетворяет вектор
Ы<2»(г,ф) = (и<2>,«<р2') = @(У
Второе обстоятельство, которое качественно отличает термоупругую
трактовку от чисто упругой, обнаруживается при рассмотрении внешних
задач.
В термоупругих задачах фаза, соответствующая продольным колеба-
колебаниям, расщепляется на две фазы, которые с возрастанием расстояния убывают
по экспоненциальному закону и лишь поперечные колебания сохраняют
характер медленно затухающих упругих поперечных колебаний. Этому
соответствует тот факт, что условия термоупругого излучения содержат одно
условие типа условия Зоммерфельда, в то время как в условиях упругого
излучения их два.
В статье Dafermos [11 доказывается, что решение уравнения термо-
термоупругости с однородными начально-граничными условиями при t —> оо
почти всюду стремится к нулю. Это находится в согласии с рассмотренным
выше свойством установившихся термоупругих колебаний.
Вопросам термоупругости в последние годы посвящается большое число
работ. В известной книге В. Новацкого (см. Nowacki [3]), представляющей
первую попытку изложить современную теорию термоупругости в виде
самостоятельной монографии, и в приложении к русскому переводу этой
книги, написанном В. А. Шачневым, дана хорошо подобранная, богатая
библиография. См. также Jentsch [II.
Однако, если иметь в виду собственно теорию граничных и начально-
граничных задач теории термоупругости, нужно сказать, что до сих пор
в литературе по большей части встречались лишь отдельные и частные
исследования, посвященные этим вопросам. Одна из немногих работ, с боль-
большой общностью трактующая вопросы существования решений смешанных
(начально-граничных) задач термоупругости, — цитированная выше работа
Dafermos [11. К сожалению, эта работа до сих пор, насколько известно нам,
не опубликована в полном виде и из краткого изложения не всегда удается
составить полное представление о результатах и, особенно, о подробно-
подробностях доказательств. Метод, применяемый в этой работе, есть метод обобщен-
обобщенных решений в гильбертовых пространствах и, как указывает автор, при-
примыкает к методу Вишика [21. Что же касается теорем существования
для установившихся колебаний, то здесь прежде всего следует назвать
работы Ignaczak, Nowacki [I, 21, которые оказали влияние на характер
результатов, изложенных в §§ 2 и 3.
По поводу содержания насгоящей главы см. Купрадзе, Бурчуладзе [31
и Кахниашвили [4], [51.
ЗАДАЧИ
1. Получить общее представление регулярных решений уравнения В (дх, ю) U = 0
с помощью потенциалов Z (x; W) и Q (jc; 1?).
Указание. Воспользоваться тождеством. f (UBU — UBU) dx = I (QU &U —
CO	CO
2. Исследовать задачу (IV)" путем сведения к задаче (III)"*
Указание. См. задачу 1.

задачи	42L
3.	Исследовать решение уравнения A.3) с заданными на границе значениями а) энтра-
пии и напряжения и б) энтропии и смещения.
4.	Получить решения внешних задач установившихся термоупругих колебаний методом
главы VII.
5.	Исследовать кратность полюсов резольвенты в задачах термоупругости и доказать
соотношения биортогональности.
6.	Решить динамические задачи термоупругости типа III и IV (см. гл. I, § 14, п. 1).
7.	Сформулировать и решить динамическую задачу термоупругости с заданными на гра-
границе значениями: а) нормального смещения и касательных напряжений или б) нормаль-
нормального напряжения и касательных смещений, сохранив обычные условия для температуры или
для потока тепла.
8.	Сформулировать и решить динамическую задачу термоупругости при заданных на гра-
границе значениях для первых двух составляющих смещения и третьей составляющей напряже-
напряжения при обычных условиях для температуры и потока тепла.
9.	Построить в замкнутом виде решения всех тех динамических задач термоупругости,
для которых решения соответствующих задач установившихся термоупругих колебаний
(и псевдоколебаний) выражаются в квадратурах методами главы XIV, §§ 4 и 5.
Указание Исследовать зависимость от параметра т решений промежуточных
задач, которые выражены в квадратурах, и затем применить способ решения динамической
задачи, описанный в настоящей главе.

ГЛАВА XI
ГРАНИЧНЫЕ ЗАДАЧИ ДЛЯ СРЕД,
ОГРАНИЧЕННЫХ НЕСКОЛЬКИМИ
ПОВЕРХНОСТЯМИ
В этой главе рассмотрены различные основные и смешанные граничные
задачи статики и-гармонических колебаний классической теории упругости
для конечных и бесконечных областей, ограниченных несколькими замкну-
замкнутыми поверхностями. Построены соответствующие тензоры Грина и доказаны
теоремы существования и единственности решений указанных задач.
§ 1. Основные граничные задачи упругого равновесия
1. Постановка граничных задач и теоремы единственности. До сих пор
предполагалось, что упругая среда ограничена одной поверхностью S (S —
связное, компактное многообразие). В этой главе будут исследованы стати-
статические и колебательные граничные задачи теории упругости (основные и
смешанные), когда упругая изотропная среда ограничена несколькими
замкнутыми двумерными поверхностями Skt k = О, 1, . . ., т; Sk —связ-
—связное, компактное, ограниченное многообразие Ляпунова, причем S^flS, — 0,
k, j = О, 1, . . ., m; k Ф /'.
Пусть Е3, как и выше, трехмерное евклидово пространство, DkaE3 —
конечная область, ограниченная поверхностью Sk, k = О, 1, . . . , m,
причем So охватывает все остальные поверхности, а эти последние не охва-
охватывают друг друга;
		mm
Dk = Dk[)Sk, S= U Sk9 D+ = D0\ U Dkf
т. e. D+ конечная связная область, с границей S. Мы рассмотрим также внеш-
внешние задачи, подразумевая при этом тот случай, когда So «расширяется»
до бесконечности, и такую неограниченную область будем обозначать D~;
следовательно, O~=?3\U Dk —бесконечная (неограниченная) связная
т
область, с границей S' = U Sk. Пусть, далее, а (у) == а' (у) есть комплексно-
/e=i
значная матрица класса С°'а.
В этой главе будут исследованы следующие основные и смешанные
граничные задачи:
Для конечной области (внутренние задачи). Определить в области D*
регулярный вектор и {х), который является решением системы А (дх, со) и +

К J j	ОСНОВНЫЕ ГРАНИЧНЫЕ ЗАДАЧИ УПРУГОГО РАВНОВЕСИЯ	423
+ $& {%) — 0, удовлетворяющим одному из следующих, граничных условий
(на S):
1)	«+ (#) = / (у) — задача A)+,
2)	[Т(ду,п)и}+ =¦/ (У) — задача <11)+,
3)
(Л
Re а (у) е С0- a(S) есть положительно определенная матрица — задача AП)+,
4)	u+(y) = f^(yl y?Sk, k = O,l,...,r, 0<r<m,
\Т()Г + {)+() РЦ) yeSk, k = r+l	m,
a
Re о (у) с C°- a(Sk) неотрицательно определенная матрица — задача (IV)+,
5)
0)
а (у) е С0- a(Sk) неотрицательно определенная матрица — задача (V)+,
6)	[Tu(y)r-\-o(y)u+{y) = fib>(y), yeSk, k = O,l,...,r,
\Tu (y)]+ = /(*¦) (у), у G Sk, k = r + 1, . . ., m,
a (y) e C°- a(Sk) положительно определенная матрица—задача (VI)+,
7)	[Ти (у)Г = /<ft> (у), yeSk, k = O,\,...,r,
) f^() yeSk, k = r+\	, m,
@
Re a (y)(zC°>a(Sk) положительно определенная матрица —задана (VII)+1).
Здесь Ж (х)е.С°'а(?>+), / (у), fik) {у), k = 0, 1, . . ., т — заданные
векторы; относительно гладкости последних будет сказано отдельно при
исследовании граничных задач. Нормаль на S, внешняя по отношению
к облгхти D+.
Для бесконечной области D~ (внешние задачи). Определить в области D~
регулярный вектор и (х)> который является решением системы А (дх, со) и +
+ Ш (х) = 0, удовлетворяющим на бесконечности условию упругого излу-
излучения и одному из граничных условий на S':
8)	и~ (у) = f (у) — задача A)~,
9)	[Ти (у)Г = f(y) — задача (П)",
10)
Re о (у) ~ С0- a(S') положительно определенная матрица, если со = 0, и
Irn a (у) С: С0* a(S') неотрицательно определенная матрица, если ш Ф 0»
03
задача (III)',
11)	tr(y) = f(*4y)9 yeSk9 fe=l,2, ...,r, l^r<m>
\T()r + ()-(y) = f^(y), Л = г+ 1, . . . , m,
') Как выяснится ниже, выбор основных потенциалов при исследовании граничных
задач существенно будет зависеть от того, какое граничное условие задано на поверхности *S0.

424	ГРАНИЧНЫЕ ЗАДАЧИ ДЛЯ СРЕД. ОГРАНИЧЕННЫХ ПОВЕРХНОСТЯМИ [рл XI
Re о (у) ? С0- *(Sk) неотрицательно определенная матрица, если со = 0, и
Лти (у) —неотрицательно определенная матрица, если со =? О, —за-
—задача (IV)-,
12)
Re а (у)с С0' a(Sk) положительно определенная матрица, при со = 0, и
Im а (#) ? С0- a(Sk) — неотрицательно определенная матрица, при со Ф О, —
а)
задача (V)".	_
Здесь 5^ ? С0' а (D~)—заданный финитный вектор; нормаль на S' =
m
= U ^д, — внешняя по отношению к области D~.
i
При со = 0 имеем соответствующие статические задачи A)^, (III*1 и т. д.
Как и выше, однородные задачи будем обозначать соответственно через
, (H)? и т. д.
Согласно формулам (III, 1.7), (III, 1.9), совершенно так же, как
в главе III, получаются доказательства следующих теорем единственности:
1.1. Теорема. Однородные статические задачи A)?, A1)о~, (Ш)?»
~, (V)?, (У1)о*\ QJ\\)t имеют лишь тривиальные решения, а задача (\Y)t до-
k
k
пускает шесть линейно независимых решений \%\k=i — векторов жестких
смещений.
(О	(й
1.2. Теорема. Однородные внешние задачи колебания A)о~, (П)о\
(D	@	6)
(Ш)о", (IV)n", (V)o~ допускают только тривиальные решения.
00 4- ^ -4-	Ш 4-
Для внутренних задач колебания A)о , (Що , • • ., (VII)o теоремы един-
единственности не имеют места и доказывается существование дискретных спек-
спектров частот собственных колебаний.
Заметим также, что полученные в этой главе интегральные уравнения,
как и выше, — сингулярные; интегралы понимаются в смысле главного
значения. Но легко установить, как это будет ясно из дальнейшего, что они
принадлежат тому типу сингулярных интегральных уравнений, теория
которых изложена в главе IV (ср. гл. VI, VII); различие — лишь в
присутствии вполне непрерывных слагаемых и, следовательно, при иссле-
исследовании этих уравнений мы вправе пользоваться теорией Фредгольма.
Перейдем теперь к исследованию поставленных граничных задач
и подробно рассмотрим типичные; при этом задачи статики и колебания
будут рассмотрены отдельно.
2. Решение граничных задач (I)*. Решение задачи A)+будем искать
в виде
и(х) = llT(dytn)V(x—y)Y4>(y)dyS —
S
4 \	A.1)
D+
где ф 6 С0' a(S) — неизвестный вектор.

§ 1J	ОСНОВНЫЕ ГРАНИЧНЫЕ ЗАДАЧИ УПРУГОГО РАВНОВЕСИЯ	425
Согласно граничному условию для <р (у) получаем сингулярное интег-
интегральное уравнение
= /(z)-4" J T(z — yKfg(y)dy. A.2)
D+
Соответствующая однородная система имеет только тривиальное
решение.
Действительно, допустим противоположное. Тогда однородная союзная
система
\	r(y-z)\ty(y)d^ = O, z?S A.3)
имеет нетривиальное решение г|) (г).
Рассмотрим потенциал простого слоя
x?Dk9 6=1,2, .. . , m.
На основании свойств V (х; г|э) и из системы A.3) заключаем, что
V (х; г|>) — регулярное решение однородной задачи
lim[T(dX9 n(z)) — E]V(x; г|>) = 0, г? Sk9 k=l,2,...t m,
х-±г
где Е — единичная матрица размера 3x3.
Если учесть, что нормаль на Sk, k = 1, . . ., /п, внешняя для области D"\
является внутренней для Dki k = 1, . . ., m, и, что V (х; г|>) g С1- a(DkI
то согласно теореме единственности III, 1.6, становится очевидным, что
указанная однородная задача имеет только тривиальное решение, и, следо-
следовательно,
1/(х;г|)) = 0, xeDk9 6=1,2, ...,m.	A.4)
Легко заметить, что V (х; г|)) — регулярное решение и следующей одно-
однородной задачи (в неограниченной области):
A(dx)V = 0, xeE3\D0>
lim [Т (дХ9 п (г)) — Е] V (х; Ц) = 0, z e So,
V(x) = O(\x\-1), TV = 0(\x\-2), при |х| — оо.
Следовательно, согласно теореме 1.2, учитывая направление нормали,
получаем
V	0	E\D	A.5)
Наконец, ввиду непрерывности V (х; if), заключаем, что
Поэтому, так как УбС1-а(?>+), в силу теоремы 1.1 имеем
A.6)

426	ГРАНИЧНЫЕ ЗАДАЧИ ДЛЯ СРЕД, ОГРАНИЧЕННЫХ ПОВЕРХНОСТЯМИ
Из (.1.4)—A.6), как обычно, получаем
что противоречит допущению.
Итак, справедлива
1.3, Теорема. Задача A)+, при f ? С1- a(S), Ж 6 С0' a (Z)+)
однозначно разрешима и решение представимо формулой A.1), в которой
плотность ф есть решение системы A.2), разрешимой для произвольной
правой части.	¦*..,.
Рассмотрим теперь первую внешнюю граничную задачу A)~ и будем
искать решение в виде
и (х) = J [Г (ду, п) Г (х — у)]' Ф (у) dyS —
-)Т(х — у)ч{у)й? ±-\T(x — y)Z${y)dy. A.7)
Для вектора cp?C°-a(S) получим систему интегральных уравнений
(принимая во внимание направление нормали на S'):
A.8)
Система A.8) разрешима для произвольной правой части. Пусть это не так
и гр (у) — нетривиальное решение соответствующей однородной союзной
системы уравнений
Рассмотрим потенциал простого слоя
V(x; г|>) = | Г {Х—у)у(у) duS, x?Dk, k = 1, ..., m.
Нетрудно видеть, что I/ (x; г|)) — регулярное решение задачи
A(dx)V = 0, xeDki fe=lf2, ..., m,
iimfT1^, nB))— "?lV(jt; г|;) = 0, e6Sfe, *=1,...., /n.
Следовательно, согласно известной теореме единственности
|	/?=!,..., m.
Отсюда, как и выше, приходим к противоречию, г|; (г) = 0, z?S'.
Таким образом, справедлива следующая
1.4. Теорема. Задача (I)" >гры / е С1- a(S') a <5^ g C°-a (D")
однозначно разрешима и решение представляется формулой A.7), в которой
плотность у (у) есть решение системы A.8), разрешимой для произвольной
правой части.
3. Решение граничных задач (И)*, (Ш)*. Представим решение за-
задачи (П)+ в виде
J	±^T{x — yK№{y)dy.	A.9)

§ И	ОСНОВНЫЕ ГРАНИЧНЫЕ ЗАДАЧИ УПРУГОГО РАВНОВЕСИЯ	427
Для вектора яр ? С0» a{S), согласно граничному условию, получаем
систему сингулярных интегральных уравнений
i|) (г) + J T (dz, v) Г B — у) -ф (у) d^S =
s
D+
Докажем, что соответствующая однородная система имеет шесть линейно
независимых решений.
Действительно, рассмотрим однородную союзную систему уравнений
= 0.	A.11)
Этой системе удовлетворяют линейно независимые векторы жестких сме-
k
щений х (х), k = 1, 2, . . ., 6.
Действительно, согласно формуле общих представлений (III, 2.9L
которая справедлива и в этом случае, имеем
k	1 Г	k
Перейдя здесь к пределу, когда х —> z?*S, получаем уравнение A.11).
Следовательно,1^. 11) имеет по крайней мере шесть линейно независимых
k
решений % (у), k = 1,2, . . ., 6. Так же, как в главе VI, легко доказывается,
что A.11) других решений не имеет.
Итак, для разрешимости A.10), необходимо и достаточно выполнения
соотношений
A.12)
Но, как легко проверить,
Т j J Т (°» У) Г (г — у) 5»
+
j J
S ?>+
D+
D+
Следовательно, соотношения A.12) принимают вид
O, fe=l,...,6,	A.13)
что выражает равенство нулю главного вектора и главного момента внешних
(поверхностных и объемных) сил.
Из формулы Грина (III, 1.1) непосредственно следует, что A.13) является
и необходимым условием разрешимости задачи (П)+. Таким образом, спра-
справедлива
1.5. Теорем а. Для разрешимости граничной задачи (П)+ необхо-
необходимо и достаточно выполнение условий A.13); при соблюдении этих условий
решение представляется формулой A.9).

428 ГРАНИЧНЫЕ ЗАДАЧИ ДЛЯ СРЕД, ОГРАНИЧЕННЫХ ПОВЕРХНОСТЯМИ
Решение неоднозначно и определяется с точностью до аддитивного
произвольного вектора жесткого смещения.
Решение задачи (II)"" ищем в виде
и(х)=\т(х—y)q(y)dyS + ~jr(x — y)M(y)dy.	A.14)
S'	D-
Для плотности гр (у) получаем интегральное уравнение
= f (г) --- $ Т(дг, v)T(z — y)Sf6{y)dy. A.15)
S'	D~
Ha основании теорем единственности 1.1 и 1.2 легко показать, что
уравнение A.15) разрешимо для произвольной правой части и, следовательно,
имеет место
1.6.	Теорема. Граничная задача (II)" однозначно разрешима и
решение дается формулой A.14), где г|э — единственное решение интеграль-
интегрального уравнения A.15).
В силу теорем единственности 1.1 и 1.2 исследование граничных задач
(Ш)± дополнительных трудностей не содержит, и, повторив приведенные
выше рассуждения, убеждаемся в справедливости следующих теорем:
1.7.	Теорема. Граничная задача (Ш)+ однозначно разрешима а
решение выражается формулой
где t|? — единственное решение интегрального уравнения
D+
1.8. Теорема. Граничная задача (III)" однозначно разрешима и
решение выражается формулой
и(х) = J Т(х—у)^(у) dyS + 4" \V(x
S'	D-
где г); — единственное решение интегрального уравнения
у (z) -Ь j [Т (дгУ v) + ст (г)] Г (z — у) г|> (у) d^S
о-
4. Тензоры Грина для областей, ограниченных несколькими замкнутыми
поверхностями. Тензоры Грина мы уже применяли при изучении внутрен-
внутренних задач колебания (см. гл. VII).
Пусть G(i)(a:, x°; D+)— тензор Грина первой задачи статики для области D+
с полюсом в точке x°?D+; определяется этот тензор совершенно так же,
как в главе VII, а существование его следует из теоремы 1.3*

Л |]	ОСНОВНЫЕ ГРАНИЧНЫЕ ЗАДАЧИ УПРУГОГО РАВНОВЕСИЯ	429
Основные свойства G(i)(jt, x°; D+) доказываются совершенно так же,
как в главе VII; напомним некоторые из этих свойств:
a)	A(dx)JG{l)(x9y;D+)F(y)dy = — 2F{x)9
где
б)	lim J [Т {ду, п) 0('„ (х, у; D+))' f (у) dyS = - 2f (г),
x->z s
где
в)	1}™Т(дх> П (Z)) i GA) {X* y; D+) *ly)dyS =
Т (dz, v) G(d B, #; Z)+) ф (у) d^5, x 6 D+\D, г б S,
lim Г (dXf n (z)) f
s
= — 4>(z)+\T(dz,v)Gii)(z,y;D+)q>(y)dyS,
s
где DczD* — произвольная область с границей S ? «/7Х (а); при этом S(]S =
5= 0; ф (t/) ^ С0- a(S), нормаль на S — внутренняя по отношению к области D,
г) интеграл J G(d (jc, у; D+) ф (t/) d^S изменяется непрерывно при
переходе точки х через поверхность S.
Пусть GC) (х, х°; D+) — тензор Грина третьей статической задачи (Ш)+
для области D+. Определяется этот тензор совершенно так же, как в главе VII,
а существование следует из теоремы 1.7.
Так же, как выше, легко доказываются следующие свойства этого
тензора:
а) A(dx) J GC) (х, у\ D+) F (у) dy = — 2F (х), х ? D,
D
, F(y)eO>-«(D);
б)	Пт[Т(дх, n(z)) + a(z)]\GC)(x, у; D+)
в)	hmT(dx,n{z))[Gi3)(x,y;D+L>{y)dyS =
х+г	|
— «p (z) + j T (дг, v) G<3) (z, t/; Z)+) q> (y) dyS, x 6 ^\5, z € S,
lim 7* E,, n (z)) f GC) (x, y\ D+) ф (у)d^S =
= — ф(г) + \т(дг, v)GC)(z, y;D+)q>(y)dyS, x?D, гб5;
s
r) интеграл J GC) (x, y; D+) ф (у) dyS непрерывен при переходе точки х
через S.

430	ГРАНИЧНЫЕ ЗАДАЧИ ДЛЯ СРЕД, ОГРАНИЧЕННЫХ ПОВЕРХНОСТЯМИ [рл XI
Для исследования вопроса о спектре внутренних задач колебания
необходим также тензор Грина второй статической задачи (П)+*- Его нельзя
строить аналогично предыдущим, так как задача (П)+ не всегда разрешима,
¦^о для наших целей достаточно построить тензор Грина второй задачи
(О
колебания (П)+ для области D+ при со = ш0, где соо > 0 — произвольное
фиксированное число. Построение такого тензора не представляет никаких
трудностей, так как для уравнения А (дХ9 ш0) и = 0 вторая граничная
задача разрешима всегда, что в свою очередь является следствием того, что
однородная задача (П)о , <^о > 0> допускает только тривиальное решение.
Обозначим этот тензор через GB> (х> х°; D+, ico0).
До сих пор речь шла о внутренних задачах. Что касается внешних
статических задач (I)", (И)", (III)", то в этом случае существование соот-
соответствующих тензоров Грина вытекает непосредственно из теорем существо-
существования 1.4, 1.6 и 1.8. Обозначим эти тензоры через G(t) (x, x°; D~)y i = 1,
2, 3 Ясно, что в области D~ они также облс*дают всеми указанными выше
свойствами.
§ 2. Смешанные задачи статики
1. Теоремы существования для смешанных статических задач (!V)±.
г
Пусть D(r) = D0\\jDk9 a Gn, (#, у; D(r)) есть тензор Грина первой за-
ы
дачи A)+ для области D<r>, r<Cm.
Ищем решение смешанной задачи (IV)+ в виде
J [Т (ду, п) GA) U у, D<r))Y fik) (y)d«S
D+
где ф (у) ? C°- a (Sfe), & = r-f~l,...,m — неизвестный вектор.
На основании свойств а) и б) тензора Gci> (дс, f/; D(r)) все условия за-
задачи (IV)+ автоматически удовлетворяются, кроме граничного условия на
поверхностях Sfef & = г + 1, . . ., т. Для удовлетворения этих последних,
согласно свойствам в) и г), относительно ср (у) получаем систему интегральных
уравнений
ф(г) + 2 J fr (d» v) + стBI °(»>B> У; D(r)^ Ф(У)d^5 = ^(г)' B-2)
гб5й, fe = r+ I	m,
где
F (z) = f<*> B) + i- [Г (d* v) + a (z)J X
- f
265ft, & = r+l, .,,, m.

J2]	СМЕШАННЫЕ ЗАДАЧИ СТАТИКИ	431
Ясно, что если feC°<a(S), где / (г) = /<*>(*), z?Sk, k = 0, . . ., m,
что мы и предполагаем, то
F(z)eC°-«( О Sk).
\k=r+i !
С другой стороны, на основании определения тензора Грина, при
гуе и sk
l
имеем
\Т (дгу v) + a B)] G(d B, у; D<">) = Г (d2, v) Г (г — у) + /? (г, у);
здесь /? B, ^) — регулярная матрица; поэтому B.2) представляет систему
сингулярных интегральных уравнений, которая изучена в главе IV. Таким
образом, можно утверждать, что для нее справедливы альтернатива и теоремы
Фредгольма.
Покажем, что B.2) однозначно разрешимо. Действительно, пусть ф (у) —
нетривиальное решение соответствующей однородной системы; рассмотрим
потенциал
очевидно v (x) — регулярное решение однородной задачи
A(dx)v = 0,
= U, Z t *bfe, « = Г -\- 1, . » ., /72.
Следовательно, согласно теореме единственности 1.1,
u(x) = 0, xeD*.	B.3)
Отсюда в силу свойства г)
A(dr)v = 0, x?Dk9 k — r-{-l,...,m,
limi>(x) = 0, z?Sk, k — r-\-l,...fm9
т. e.
v(x) = 0, x?Dk, k = r+l,...,m.	B.4)
Из B.3) и B.4), как обычно, получаем
~zSk9 k = r-{- 1, ..., т.
Таким образом, справедлива следующая
2.1.	Теорема. Статическая смешанная задача (IV)+ однозначно
разрешима и решение представляется формулой B.1), где плотность ф (у)
есть решение интегрального уравнения B.2), которое разрешимо для про-
произвольной правой части.
2.2.	Замечание. Если в частности, г = /п, то
= D0\ U #*
i

432 ГРАНИЧНЫЕ ЗАДАЧИ ДЛЯ СРЕД, ОГРАНИЧЕННЫХ ПОВЕРХНОСТЯМИ [Гл X!
и формула B.1) примет вид
т
и (х)«- - -i- 2 J fТ (а«" я> G<») (*. К *>+)]* f(ft) (У) 4? 4-
2
4=0 s
k
-f 4" J G(i)(x, у; D+) dV («/) rff/, B.5)
и мы получаем представление решения граничной задачи A)+ в области D+
с помощью тензора Грина G(i) (x, у; D+).
2.3.	Замечание. Ясно, что теорема 2.1 верна и в том случае, когда
а (г) = 0, z?Sky k = r + 1, • . ., m.
2.4.	Замечание. Согласно теореме 2.1 мы можем теперь построить
тензор Грина задачи (IV)+ G<4> (x, у; D+) и доказать для него основные свой-
свойства, аналогичные свойствам а), б), в), г). Легко убедиться в том, что при
этом решение и (х) задачи (IV)+ представляется формулой
и (х) = - -~
т 2 JGD> (x> y; D+) fl k) {y) duS
1 f
"+¦ "о" I GD)(x, у; D+K@(y)dy, x?D+ B.6)
Рассмотрим теперь внешнюю смешанную задачу (IV)". Пусть
D^ = Ез\ U Dk и G(d (^, у; D«})
— тензор Грина первой задачи (I)" для бесконечной области D«). Решение
задачи (IV)" будем искать в виде
и(х) = - \ 2 J [Т (ду, п) Gii, (х, у; D?>)]' f(Л)
fe=r-hl S,
Напомним, что здесь нормаль на U Sfe — внешняя по отношению к обла-
?ТИ D".
Так же как выше, для определения неизвестного вектора q> 6 С0- a(Sk)t
k = r -f- I, . . ., m, получим систему сингулярных интегральных уравнений
= F B), B,8)
где F g C°*a(iSft), ^ = г + 1, . . ., m — известный вектор.

Л 2]	СМЕШАННЫЕ ЗАДАЧИ СТАТИКИ	433
На основании теорем единственности 1.1 и 1.2 и в силу свойств тензора
Грина G(i)(x, у; DiT}), так же как для внутренней задачи, легко устанавли-
устанавливается разрешимость B.8) для произвольной правой части.
Таким образом, имеет место
2.5.	Теорема. Статическая внешняя смешанная задача (IV)" од-
однозначно разрешима и решение выражается формулой B.7), в которой
плотность ф представляет единственное решение интегрального урав-
уравнения B.8).
2.6.	Замечание. Если, в частности, г — m, to DiT = D~ и фор-
формула B.7) принимает вид
= -±^\ [T(dy,n)GlX)(x, у; D-)]' fk) (y)dyS +
*?D~, B.9)
и мы получаем представление решения задачи (I)" с помощью тензора Грина
0A, (дс, у; ?Г).
2.7.	Замечание. Очевидно, теорема 2.5 верна и в том случае,
когда
(t(z)eeO, z?Sk, k = r-{- 1, ..., т.
2.8.	Замечание. Так же как выше, в соответствии с 2.5, можно
построить тензор Грина задачи (IV)" — GD)(x, у; D~), и решение (этой задачи)
выразится формулой
4- ^
и (х) = - 4- ^ J [Т (ду, п) Gw (х, у; D-)]' f k) (у) duS +
m
т S JGD) (x> y; D"} f(k) {y) dyS~
k=r+lSk
-^\G{A){x,y\D-)M{y)dy\ xeD'. B.10)
2. Решение смешанной задачи (V)+. Пусть 5m+16«/?i (a) —произволь-
—произвольная замкнутая поверхность, охватывающая все поверхности Sk, k =
=^0,1, . . ., m; Dm+1 — конечная область, ограниченная поверхностью Sm+1;
m
= Dm+i\ U Dk; G(i)(x, у; D^) — тензор Грина первой задачи A)+
k+l
для области Dm\.\.
Решение задачи (V)+ представим в виде
B.11)
D+
В. Д. Купрадзе

'434	ГРАНИЧНЫЕ ЗАДАЧИ ДЛЯ СРЕД, ОГРАНИЧЕННЫХ ПОВЕРХНОСТЯМИ [Гл. XI
Для определения вектора <р (г/) 6 С0- a(Sk), k = 0, ...,/¦, получаем
систему интегральных уравнений
B.12)
U Sk,
легко выписывается
где F(z)?C°'al U Sk\—заданный вектор, который
в явном виде.
Покажем, что система B.12) разрешима по первой теореме Фредгольма.
Действительно, пусть ф — некоторое решение соответствующей однород-
однородной системы, построим потенциал
Имеем г)
A(dx)v (x) = 0,
v+(z) = 0, ze U
k
Следовательно, в силу теоремы 1.1 v (x) = 0, x?D+. Отсюда, учитывая
непрерывность потенциала v (x) и некоторые свойства тензора Грина, заклю-
заключаем, что v (х) есть также регулярное решение однородных задач
A(dx)v(x) = 09 x?Dk, limt>(x) = 0f
дс->г
A(dx)v(x) = 0, xe?»m5
Поэтому согласно теореме 1.1
v(x) = 09 xeDk, k=\,2, ..., n xeDm+1\D0.
Таким образом,
v(x) = 0, xeDm+1.
Отсюда
() О eS k = 0, 1, ..., r,
что и доказывает наше утверждение. Таким образом, справедлива
2.9. Теорема. Смешанная задача (V)+ однозначно разрешима, и
решение выражается формулой B.11); плотность потенциала ср (у) опре-
определяется однозначно из уравнения B.12).
г) Предполагается, что г <; /я.

* 2]	СМЕШАННЫЕ ЗАДАЧИ СТАТИКИ	435
Пусть теперь г = т, о (г) = 0, иначе говоря, пусть на всех поверх-
поверхностях Sk,k = 0, 1, . . ., т заданы значения напряжения Ти. Имеем Dw+i =
= DllZli = Dm+u и формула B.11) примет вид
m
= 2 J
4 I Ga)(x9 y; Dm+1)^(y)dy9 x?D\ B.13)
D+
где ф (#) — решение интегрального уравнения
= F>(z)	~ J Т(дг, v)G(d(z, y; Dm+iJg(y)dy. B.14)
D+
Можно показать, что соответствующая однородная система имеет шесть
линейно независимых решений и для разрешимости B.14) необходимо и
достаточно выполнение следующих условий:
m
k=0Sh
(О
;(y)dr/ = O, t=l, 2, ..,, 6.	B.15)
Таким образом, при соблюдении условий B.15) формула B.13) дает
решение граничной задачи (П)+ для области D+ с помощью тензора Грина
G(\)(x9 у; Dm+1), где Dm+1czE3 — произвольная конечная область, ограни-
ограниченная одной поверхностью Sm+1.
2.10. Замечание. Согласно теореме 2.9 можно построить тензор
Грина GE> (x, у; D+) смешанной задачи (V)+, и решение этой задачи предста-
представится в виде
г
ttW = T 2 J GE) (X> y
/72
—Г 2
4" J
D+
3. Теоремы существования для статических смешанных задач (VI)+,
(VII)+, (V)~. Эти задачи изучаются аналогично, согласно уже указанной
схеме, с использованием тензора Грина третьей задачи GC>(x, у; D)> и при
этом область D для каждой задачи подбирается специальным образом.
Поэтому, не приводя подробного исследования, сформулируем теоремы
существования.
28*

436	ГРАНИЧНЫЕ ЗАДАЧИ ДЛЯ СРЕД, ОГРАНИЧЕННЫХ ПОВЕРХНОСТЯМИ
2.11. Теорема. Граничная задача (VI)+ однозначно разрешима а
решение дается формулой
:, у; ?><'>)
Г
"Г 2 J G<3>(*. У> D^)fW(y)duS+-L JgC)(x, у D^Je(y)dy, B.17)
r _	I m	\
где D(r) = Do \ U Dk, ф ? C0' a |J Sfe) — решение интегрального уравнения
которое разрешимо для произвольной правой части.
2.12. Теорема. Граничная задача (VII)+ однозначно разрешима
и решение имеет вид
J G<3>(x' у' D"+l) ф
m
+"f 2 JGC) ^y; D^x) /(/г) (y) dyS + тJ
B.18)
^Vi = Dm+i\ U Sfe» ФсС°'а( U Sfe ) — решение интегрального урав-
нения
9B)+ 2 1 Пдг, v)GC) (г, у; D^+i)Ч>(У)dyS = /<fe)(г) —
fe=osft
	g- Г C„ v)
J G(8, B, у;
D+
которое разрешимо для произвольной правой части.

* 3]	ГРАНИЧНЫЕ ЗАДАЧИ КОЛЕБАНИЯ	437
2.13. Теорема. Смешанная внешняя гранщная задача (V)" одно-
однозначно разрешима и решение дается формулой
т	'
и(х) = ? I G(a,U у\ ^)фО/)^ + 4-S J GC3>U jr.
+ -f J GC)(x' ^; D
где D{^ = Ея\ [} Dk> cp ? С0' a( U 5^ I — единственное решение интеграль-
fe=l	\fe=r-hl /
«ого уравнения
m
Ф B) + 2 J Г 0»' V> G<3> B' У' D-') Ф
J
Sk
f Г(<Э2, v)J2 f
o-	j
2.14. Замечание. На основании теорем существования 2.11 и 2.12
можно построить тензоры Грина смешанных задач (VI)+ и (VII)+; обозначив
их соответственно через GF)(x, y\ D+) и G{7)(x> у; D+), представим реиюние
задачи (VI)+ в виде
т
"(*)*-Т- 2 J G<6> (л' У; ?>+)/(й)(У)^5+ -i- J G(e, (x, у; D+KV{y)dy,
fe==OSfe	О+
B.20)
и задачи (VII)+ в виде
(у)d95 + -i- J
k	D+
B.21)
§ 3. Граничные задачи колебания
1. Однородные внутренние задачи колебания. Спектр собственных ча-
частот. В предыдущих параграфах были построены тензоры Грина для вну-
внутренних задач: G{k)(x, у; D+), k = 1, 3, . . ., 7, и GB)(x, у; D+, ш0).
Применяя, как обычно, формулу Грина, и учитывая свойства этих
тензоров, а также равенство а (г) = a' (z), можно доказать свойство симме-
симметрии
G(x, у; D+) = G'(y, x; D+).	C.1)
Как мы видели, тензоры Грина обладают всеми свойствами фундамен-
фундаментальных решений, которые были использованы при выводе формул пред-

438	ГРАНИЧНЫЕ ЗАДАЧИ ДЛЯ СРЕД, ОГРАНИЧЕННЫХ ПОВЕРХНОСТЯМИ [рл XI
ставлений регулярных векторов. Поэтому легко установить, что для регу-
регулярного в D+ вектора и (х) справедливы представления
2и(х) = J Gik) (х, у; D+) [Та (у)]+ dyS~-
-\[T(du,n)Gm(x, y; D+)]' и*
— J Glk)(x, у; D+)A(dy)udy, C.2)
D+
где
m
x?D\ S= U S,, k=\, 3	7,
7=0
2u(x) = J GB) (x, y, D\ 1щ) [Tu (y))+ dyS —
s
_ J [T {dy, n) g;2)\xt y\ D+, ico0)]' u+{y)dyS —
JB> (x, y\ D\ i®o)A(dy, i(oo)u(y)dy, xeD\ C.3)
Исходя из формул C.2) и C.3), учитывая граничные свойства тензоров
Грина, так же как в главе VII, устанавливается, что решения и (х) однород-
ных внутренних задач колебания A)о , (Ш)о , . . ., (VII)o удовлетворяют
соответственно однородным интегральным уравнениям
— ^ J Gih)(x, у; D+)u(y)dy = 09 x?D\ k=\f 3, .... 7, C,4)
+
J
D+
а решение задачи (П)о~—уравнению
u(x)	g-i- J GB) (x, y; D\ tcoo) и (у) dy = O, x? D\	C.5)
D+
Верно и обратное утверждение: всякое регулярное решение интеграль-
интегральных уравнений C.4), C.5) является и решением соответствующих однородных
внутренних задач. Это непосредственно следует из формул C.4) и C.5) на
основании формулы Пуассона и граничных свойств тензоров Грина.
Уравнения C.4) и C.5) есть однородные интегральные уравнения Фред-
гольма с симметричными ядрами из L2 (D+); следовательно, согласно извест-
известной теореме Гильберта—Шмидта существует дискретный спектр действитель-
действительных собственных частот соответствующих однородных внутренних задач
колебания.
На основании формулы Грина легко установить также, что все собствен-
собственные частоты неотрицательны; точнее, собственные частоты всех задач строго
(О
положительны, кроме задачи (П)о > и cd = 0 является собственной частотой
шестого ранга для последней.
Наконец, заметим следующее: можно утверждать, что если со2 отлично
от собственных частот рассматриваемой задачи, то соответствующая неодно-
неоднородная внутренняя задача колебания однозначно разрешима для произволь-
произвольных граничных данных; если же со2 совпадает с одной из собственных частот

Л 3]	ГРАНИЧНЫЕ ЗАДАЧИ КОЛЕБАНИЯ	439
этой задачи, то для разрешимости неоднородной задачи на граничные данные
накладывается конечное число условий (это число равно рангу собственной
частоты) ортогональности, которые можно выразить с помощью собственных
векторов рассматриваемой задачи, соответствующих данной собственной
частоте.
Заметим, что здесь также можно доказать основные теоремы теории
колебания, подобно тому как это было сделано в главе VII, и на их основе
явно выписать условия разрешимости всех рассматриваемых внутренних
задач колебания в резонансном случае (см. гл. VII, § 2, п. 4).
О)	u)	ft)
2. Внешние задачи колебания A)~, (П)~, (П1)~. Приведение к инте-
интегральным уравнениям. Основные теоремы. Будем искать решения задач
СО	(О	(О
(I)", (II)", (III)" соответственно в следующем виде:
и (х) = J [Т (дуу п)Т(х — у, со)]' Ф (у) d^S + -1- J Г (х — у; со) Ж (у) dy, C.6)
и(х)= |Г(х— у, co)^(t/)^S + 4- J Г(х—#; (oJ%(y)dy,	C.7)
S'	D-
u{x)=j Г(х — у, @)li(y)dvS + -L J T(x — y, «>)Ze(y)dy,	C.8)
5?'	D-
где ф, i|), (x — неизвестные векторы класса С0' a(S')
m	m
S'= U Sk, xeD- = E9\ U Dk;
k=l	k=l
нормаль на S' — внешняя по отношению к области D".
В силу свойств потенциалов и граничных условий для интересующих
здесь нас задач, получаем интегральные уравнения
- Ф(z) + J [T (ду, n)T(z — y9 со)]' Ф {у)dyS = {F (z),	C.9)
f	B)
<|>(z)+J Т(д„ v)Y(z — yy со)ф(у)^5= F (z),	C.10)
S'
VL(z)+ \[T (дЖ9 v) + а (г)] Г (z — у, со) ц {у) dyS = f (z),	C.11)
S'
(г) =f(z)	i- J Г (z — у, со) Ж (у) dy,	C.9')
D~
	L J Т(д„ v)T(z — y, (o)9«(y)dy9	C.10')
—4- J [7(аг, г) + аB)]Г(г — y9 <oKV(y)dy. (ЗЛУ)
где
(i)
D-
Относительно решения соответствующих однородных интегральных
уравнений, подобно тому как это было сделано в главе VII, § 2, пп. 2, 3,
можно доказать несколько общих теорем, которые лежат в основе исследова-
исследования рассматриваемых задач колебания.

440	ГРАНИЧНЫЕ ЗАДАЧИ ДЛЯ СРЕД, ОГРАНИЧЕННЫХ ПОВЕРХНОСТЯМИ |рл< XI
Предварительно сделаем несколько общих замечаний.
т
Пусть D1 = U Dk, и рассмотрим внутреннюю однородную задачу
А{дх, co)a = 0, x?D\
\imu(x)= О, г 6 S',
которую будем обозначать через Io~(D').
/	©,
Пусть и (х), x?Df — нетривиальное решение задачи IJ" (?>,),
= 1, . . ., т\ тогда векторы и'(х), x?D'9 определенные формулой
W. *€*>/. ^	(ЗЛ2)
О, xe
будут нетривиальными решениями задачи Ijjf" (Dr).
i 2	!> k
Из C.12) следует, что если \(Ojk}kL\ и \и (х)\~=и x^Df — собствен-
собственные частоты и собственные вектор-функции задачи 1о~ (?>,), / = 1, . . ., т,
существование которых было доказано в главе VII, то собственными часто-
частотами и собственными функциями задачи Io~ (D') будут
{<o?*}*U, {'"'(*)}Г==1, 1 = U 2, ..„ т9 хеЕГ,	C.13)
где
'u(x),xeD,9	(ЗЛ4)
Таким образом, существуют дискретный спектр собственных частот и
со
соответствующие собственные вектор-функции задачи Io (D')> которые
выражаются формулами C.13) и C.14).
Ясно, что сказанное остается в силе (с соответствующими изменениями)
и для задач (П)^ (?>') и (Ш)^ (D').
Наконец, пусть и (х), xkzD' —регулярное решение уравнения А (дх,
о) и = 0. Справедлива следующая формула представлений (см. гл. III):
— у, (о)[Т(ду,	^
+ J [Т(ду9 п)Т(х—у, (D)]'u+(y)dyS, x?D\	C.15)
Принимая во внимание эти замечания и повторяя дословно рассуждения
главы VII, § 2, пп. 2, 3, убеждаемся в справедливости следующих теорем:
3.1. Теорема. Необходимым и достаточным условием того, чтобы
уравнение
[	C.16)

jj 3]	ГРАНИЧНЫЕ ЗАДАЧИ КОЛЕБАНИЯ	441
имело нетривиальное решение, является равенство параметра со2 одной из
со
собственных частот задачи \\o(Dr). Если со2 есть v-кратная собственная
частота этой задачи, то C.16) имеет v линейно независимых решений,
и они совпадают с граничными значениями собственных вектор-функций
СО
задачи ltf(D').
3.2.	Теорема. Необходимым и достаточным условием того, чтобы
уравнение
^г9 п{г))Г(г — у, со)ф(у)dyS = 0, z?S'	C.17)
имело нетривиальное решение, является равенство параметра со2 одной из
со
собственных частот задачи lo (D'). Если со2 есть v-кратная собственная
частота этой задачи, то интегральное уравнение C.17) имеет v линейно
независимых решений и они совпадают с граничными значениями Т-операции
со
над решениями задачи lo (D').
3.3.	Теорема. Необходимым и достаточным условием того, чтобы
уравнение
J	C.18)
S'
имело нетривиальное решение, является равенство параметра со2 одной из
со
собственных частот задачи lo (D'). Если со2 есть v-кратная собственная
частота этой задачи, то интегральное уравнение C.18) имеет v линейно
независимых решений, и они совпадают с граничными значениями Т-операции
над решениями задачи lo(D').
3.4. Теорема. Необходимым и достаточным условием нетривиальной
разрешимости интегрального уравнения
— z, (o)e{y)}X(y)dyS = 0,
C.19)
со
является равенство параметра со2 одной из собственных частот задачи 11 Io (D').
Если со2 есть v-кратная собственная частота этой задачи, то уравнение
C.19) имеет v линейно независимых решений, и они совпадают с граничными
О)
значениями решений задачи Шо (D').
со
3.5. Теорема. Если со2 есть собственная частота задачи Io (D'),
то со2 является характеристическим числом для однородных интегральных
уравнений C.17) и C.18), и это число есть простой полюс резольвенты. Если
со
же со2 есть собственная частота задачи По (D'), то и для уравнения C.16)
оно является характеристическим числом, и это число есть простой полюс
соответствующей резольвенты.
(О	(О
3. Теоремы существования для внешних задач колебания (I)", (II)",
со
(Ш)~. Результаты предыдущего параграфа позволяют так же, как
со
в главе VII, § 3, доказать разрешимость внешних задач колебаний (I)"*,
со	со
(П)~, (III)" для произвольного значения частоты колебания со2.

442 граничные задачи для сред, ограниченных поверхностями [Гл. XI
а)
Начнем с задачи (I)" и будем искать решение в виде
и (х) = W (х; Ф) + U (х; -L Ж) + V(х; g)9	C.20)
где Ф € Cl-a(S'), g € С0* a(S') — неизвестные векторы, W (х; ф) = J IT (ду> п) X
хГ {х —у у со) Г ф (у) dyS — потенциал двойного слоя, V (х; g) = j Г (х —
— У* <°) ё (У) duS — потенциал простого слоя, U (х; Ж) = I Г(д:—г/,со)х
X Ж> (у) dy — объемный потенциал.
Для неизвестного вектора ф (у) получаем интегральное уравнение C.9)
с правой частью
A)
F(z) — V(z; g), zeS'.
(О
Если со2 не есть собственная частота задачи По (?>'), то согласно тео-
теореме ЗЛ это интегральное уравнение разрешимо (для произвольной правой
части) и, следовательно, можем считать g (у) = 0, и задача решена.
со	k
Пусть теперь со2 есть собственная частота задачи Но" (D') и {г|з (г)\1=\ —
полная система решений соответствующего союзного уравнения
~4>{z)+llT(d» n(z))T(z — y9 (D)]^(y)dyS = 0, z65', C.21)
а {ф (z)}k=i — полная система решений исходного однородного интеграль-
интегрального уравнения C.16). В силу теоремы 3.5 можно считать системы векторов
k	к
\ц> (z)\k=i и {г|) (z)}J5Li биортонормированными на S'.
Условия разрешимости интегрального уравнения C.9) имеют вид
I V (z; g) ф (z) dS = J F (z) y>(z)dS, к = 1, ..., v.	C.22)
С другой стороны, заметим, что векторы
V\x; f), k= 1, ..., v,
(д
образуют полную систему решений задачи По (D') для данного значения
к
параметра со*. Следовательно, согласно теореме 3.1 \V (z; \t>ML=b 2^5', есть
полная система решений однородного интегрального уравнения C.16)з
таким образом, будем иметь
h 	 1 О	X>
^	К 	 if ?9 • • •> Vf
т. e.
к	/ к \
фB:) = 1/\2; tyjj, fe=l, .<.., v,	C.23)
где

Л 3]	ГРАНИЧНЫЕ ЗАДАЧИ КОЛЕБАНИЯ	443
Выбираем теперь вектор g B) в виде
?//¦•(*).	C-24)
где Af- — произвольные постоянные. Из C.22) согласно C.23) будем иметь
A)	/г
(z)dS,
j Л, [ i(z)i(z)dS = J {F{z)\p{
/=1 S'	S'
i	i
и, ввиду биортонормированности {cpJJLi и {г|)}У=ь отсюда получаем
| A)	/г
А* = ], f (z)*(*)d5> fe= 1, 2, ..., v.	C.25)
Итак, справедлива
(О
3.6. Теорема. Задача A)~ имеет, и притом единственное, решение
для произвольного значения параметра со2, которое представляется форму-
формулой C.20).
со
Если со2 отлично от собственных частот задачи Но (С),/no g(z) = 0,
а плотность ф (у) — единственное решение интегрального уравнения C.9).
?Ъш а/се со2 есть собственная частота задачи По (?>'), ^^ g (z) определяется
формулами C.24) и C.25), а ф (у) есть решение интегрального уравнения C.9)
A)
с правой частью F (z) — V B; g)> которое разрешимо согласно третьей теореме
Фредгольма
0)	СО
На доказательстве теорем существования для задач (Н)~ и AП)~ не
останавливаемся, так как оно аналогично доказательству соответствующих
теорем главы VII.
Итак, можно утверждать, что имеют место следующие теоремы:
со
3.7. Теорема. Задача (II)" имеет, и притом единственное, решение
для произвольного значения параметра со2; это решение представляется форму-
формулой
если со2 отлично от собственных частот задачи Ц {D'), то g (z) =0, и плот-
плотность г|? B)—единственное решение интегрального уравнения (ЗЛ0);если же со2
О)
есть собственная частота задачи Io (D')> то g (z) определяется формулой
где
{ B)}J=i — полная система решений союзного с C.10) интегрального уравне-
уравнения, a ty (z) — решение интегрального уравнения C.10) с правой частью
B)
F (z)—[TW B; g)] , которое разрешимо по третьей теореме Фредгольма.

444	ГРАНИЧНЫЕ ЗАДАЧИ ДЛЯ СРЕД, ОГРАНИЧЕННЫХ ПОВЕРХНОСТЯМИ [рл# XI
3.8. Теорема. Задача (III) имеет, ипритом единственное, решение
для произвольного значения параметра со2, которое представляется формулой
u(x) = V{х; ц) + U (дс; 4"
если со2 отлично от собственных частот задачи 1© (?>')> то g (z) = 0, и плот-
плотность \1 (у) — единственное решение интегрального уравнения C.11);если же со2
со
есть собственная частота задачи 1о (?>')> то g (z) определяется формулой
?(*)=? с Д(г),
где
C)
F
= L Cfi Я (г), С,= J F (z) Цг) dS,
i=l	S'
X (z){7=1 — полная система решений союзного с C.11) интегрального уравне-
уравне)	311)
ния, а \х (z) —решение интегрального уравнения C.11) с правой частью
F (z) — {[7 (дг9 п (z)) +.о (z)] [W (г; g) + V (г, ag)]}-9
которое разрешимо по третьей теореме Фредгольма.
СО	(О
4. Внешние смешанные граничные задачи колебания (IV)", (V)".
Согласно теоремам 3.6 и 3.7 можно построить тензоры Грина для внешних
со	со
задач колебания (I)" и (Н)~; обозначим их соответственно через G(d (x, у;
D", со) и GB) (x, у; D", со). Легко доказать для этих тензоров свойства а),
со	to
б), в), г) (см. § 1, п. 4). Применим их для решения задач (IV)" и (V)
Пусть DiT} = ?3\ U Вц и G(i)(jc, у; ?>A\ со) —тензор Грина первой
со
внешней задачи колебания (I) для области
со
Решение задачи (IV)" будем искать в виде
и (х) =
+ f G(d (x, y\ D(«\ ш) а {у) g (у) dyS\ —
+ -§¦ tGA) (x> ^; ^ ш) ^(y) rfy; *€?r> C#26)
где ф, g* — неизвестные векторы класса С°- a(S').

3]	ГРАНИЧНЫЕ ЗАДАЧИ КОЛЕБАНИЯ	445
Нетрудно заметить, что все условия задачи (IV)" удовлетворены, кроме
граничных условий на Skt k = r + 1, . . ., m, которые в свою очередь
порождают интегральное уравнение (относительно ф (у))
т
Ф (*) + 2 \[Т (дг, п (z)) + a (z)} GA) (г, у; D?\ cd) ф (у
D)
= F (z)— {\Т (д2У п (г)) + а(г)] [WG{1) (г, g) + VG(l) (г; ag)]}'f C.27)
где
D)	1
F (z) = /с*) (г) + 4"
BI J [Г (д„, n) Go, (г, у; D?, со)]' /(ft) (.t/) dvS-
— ~\[Т (дг, п (г)) + а (z)l G(I) (г, у; Г%\ со) ^ (у) dy,
г 6
6-
k = r + 1,. • • , m,
m
(z; g)= 2 J [Г (ду, n) G;,, (г, у; D(^>, co)]> {y) dttS,
(z; ag) =
= 2 J
Заметим, что для однородного интегрального уравнения, соответствую-
соответствующего C.27), имеет место теорема 3.3 с тем отличием, что в этой теореме за-
со	со ,	,	m
дачу it (D') следует заменить задачей Io"(D (r)), где D {r) = (J Dfe. Дока-
зательство этого утверждения мы опускаем. После этого, так же как и выше,
почти непосредственно получается следующая
со
3.9. Теорема. Задача (IV)" имеет, и притом единственное, решение
и (а:), которое представляется формулой C.26); если со2отлично от собственных
со
частот задачи Io~(D (О), то g (z) = 0, и плотность <р (z) есть единственное
решение интегрального уравнения C.27); если же со2 есть собственная частота
0)
задачи it (D (г)), то g (z) определяется формулой
V f
g (г) = S
где
% & = 2 d' '* (z))

446	ГРАНИЧНЫЕ ЗАДАЧИ ДЛЯ СРЕД, ОГРАНИЧЕННЫХ ПОВЕРХНОСТЯМИ [рл XT
jij) (z)}/=i — полная система решений союзного с C.27) интегрального урав-
уравнения, а ф (г) — решение интегрального уравнения C.27), которое разрешимо
по третьей теореме Фредгольма.
со
Наконец, рассмотрим задачу (V)". Решение ищем в виде
и (*) = ? f GB) (х, у; D'J'K со) Ф (у) dyS +
г j
+ 2
2 ПТ Фу> n> G<2> (*• #;
х, у; D'co(r), о))
+ -f j GB) (^ У; D'~(r)> ©) 3» (У) dy, *6 D", C.28)
где ф, g^C°*a—неизвестные векторы,
m
Djr) = ?3\ U О,.
Для ф (у) имеем интегральное уравнение
г
Ф (г) + 2 J lr (а" n (z» + ст (г>1 G<2) (г, у; D'Jr), ©) Ф (у) dw5 =
ft=lSfc
E)
= F (г)-[\Т (дг, п (z))+a{z)][Wam (г; g) + VGB) (г; а^)]}-, C.29)
где
/(ft)B)
^
л B))
а (г)] j GB) (г, у; Z)L(r>, со) /(
	1- } \Т (д„ п (г)) + ст (г)! GB) (г, у; D'JrK to)
=l, 2, .... r;
ag) =

я 4]	заключительные замечания	447
Так же как выше, доказывается
со
ЗЛО. Теорема. Задача (V)" имеет, и притом единственное, решение
и (х), которое представляется формулой C.28); если со2 отлично от собствен-
них частот задачи Ijj~ (D (r))» где D {г = [} Dk, то g (z) = 0 и плотность ф (z)
есть единственное решение интегрального уравнения C.29); если же со2 есть
со
собственная частота задачи Iq~(D (r)), to g (z) определяется формулой
где
дф (z),
jij) (z)}7=i —полная система решений союзного с C.29) интегрального уравне-
уравнения, а ф (z) — решение интегрального уравнения C.29), которое разрешимо
по третьей теореме Фредгольма.
§ 4. Заключительные замечания
Для однородных упругих тел, ограниченных несколькими непересекаю-
непересекающимися замкнутыми поверхностями, вообще говоря, можно рассматривать
граничные задачи трех типов:
а)	когда на всей границе упругого тела задаются одни и те же граничные
условия (задачи I, II, III);
б)	когда на каждой отдельной поверхности границы упругого тела
выполняется один и тот же тип граничных условий, но эти условия различны
на различных поверхностях (задачи IV, V, VI, VII);
в)	когда на одной части отдельной поверхности границы выполняется
одно граничное условие, а на других ее частях другие.
В этой главе были исследованы задачи с граничными условиями вида а)
и б); при этом существенно была использована теория многомерных сингу-
сингулярных интегральных уравнений на замкнутых многообразиях, изложенная
в главе IV. Наиболее общие результаты в этом направлении получены в
работах Бурчуладзе [5, 7, 9, 12, 14]. Эти же задачи еще раньше изучались в
работах: Купрадзе [13, 5], Шерман [2, 3], Башелейшвили [71, Перлин
[1], Купрадзе, Бурчуладзе [1] и др.
Относительно граничных задач типа в) отметим следующее. Эти задачи,
без всяких затруднений, можно свести к сингулярным интегральным урав-
уравнениям, распространенным на открытых многообразиях (на многообразиях
с краями). Общая теория подобных уравнений до настоящего времени не
разработана с такой полнотой, чтобы было возможно применить ее в задачах
механики. Читатель, который интересуется этими вопросами, может обра-
обратиться к сборникам, цитированным в главе IV, § 8, а также к работе Вишик,
Эскин [1L
Особо следует отметить работу Fichera [41, посвященную трехмерным
задачам статики изотропного упругого тела. В этой работе автор не поль-
пользуется теорией сингулярных интегральных уравнений, развивает метод
Пиконе и исследует общие смешанные граничные задачи.
Решение трехмерной смешанной граничной задачи статики см. Куп-
Купрадзе [18] (см. гл. VI, § 5, п. 7).

448 граничные задачи для сред, ограниченных поверхностями [рл XI
ЗАДАЧИ
(Относительно обозначений см. § 1, п. 1.)
1.	Решить задачу статики классической теории упругости для конечной или бесконечной
области, когда на S&, k = 0, 1, . . ., т, т^>0, задаются: (пи), Ти— п (пТи) или (пТи),
и — п (пи).
2.	Решить задачу статики классической теории упругости, когда на границе заданы:
на Sk, к = 0, 1, . . ., г, (пи), Ти — п (пТи);
на Sk, k = r 4- 1, . . ., m, (пТи), и — п (пи).
3.	Решить смешанную задачу статики классической теории упругости, когда на гра-
границе заданы:
на Ski	/г== 0,	1,
на Sk,	k = гг +	1,
на Sk,	k = г2 +	1,
на 5^,,	/г = г3 +	1,
4.	Решить задачи 1, 2, 3 классической теории упругости для уравнения колебаний
А (дх, со) w = 0.
5.	Исследовать задачи типа 1, 2, 3, 8, 9, 10 § 1 п. 1 для уравнения связной теории
термоупругости В (дх, со) U = 0.
6.	Исследовать задачу типа 5, б, 7, 11, 12 § 1 п. 1 для уравнения связной теории
термоупругости.
7.	Поставить и исследовать задачу типа задачи 2 для уравнения теории термоупругости.
8.	Поставить и исследоввть задачу типа 3 для уравнения теории термоупругости.
9.	Поставить и исследовать задачу типа 2 для уравнения моментной теории упругости
М {дх, о) U = 0.
10.	Поставить и исследовать задачу типа 3 для уравнения моментной теории упругости.
* *ъ
, m,
и;
Ти;
(пи),
(пТи)
Ти-
, и ¦
¦ п (пТи);
— п (пи).

ГЛАВА XII
ГРАНИЧНО-КОНТАКТНЫЕ ЗАДАЧИ
ДЛЯ НЕОДНОРОДНЫХ СРЕД
В этой главе доказываются основные теоремы существования решений
гранично-контактных задач общего вида для неоднородных упругих сред.
Неоднородная среда, в принятом нами понимании, — это упругое тело,
содержащее конечное число включений, часть из которых сами представляют
упругие среды, каждая со своими постоянными Ламе,а другая часть является
пустотелой. Неоднородные тела подобной «зернисто-пористой» структуры
в основном исчерпывают характер неоднородностей, встречающихся в боль-
большинстве приложений.
Изучение гранично-контактных задач для подобных сред, естественно,
связано с новыми математическими осложнениями и в общей постановке эти
задачи в литературе мало ^исследованы; исключение составляют некоторые
частные задачи (задачи о штампе и др.), которым посвящено довольно много
отдельных исследований.
§ 1. Основные гранично-контактные задачи
В главе I, § 14, п. 4 поставлены основные гранично-контактные задачи
для неоднородных упругих тел.
Пусть конечная область Do ограничена гладкими замкнутыми поверх-
поверхностями 50, Sl9 . . ., Sm, из которых So охватывает все остальные, S2, . . ., Sm
не имеют общих точек и друг друга не охватывают. Конечную область, огра-
ничейную поверхностью Sk (k = 1, . . ., m), назовем Dk, D+ = (J Dk
k=\
Этой геометрической картине приводятся в соответствие физические
задачи, если Dk, k = 0, 1, 2, . . . , г, заполнены однородными изотроп-
изотропными упругими средами с постоянными Xk, [ik, а остальные Dk9 k = г +1,...
. . ., т — пустотелые включения, и если при этом такое составное тело
подвержено действию внешних усилий.
Неоднородная среда описанного вида имеет границы двух родов: границы
в обычном смысле, на которых заданы граничные условия одного из видов,
перечисленных в главе I, § 14, и границы, вдоль которых соприкасаются
смежные разнородные упругие среды — границы контактов. На границах
контактов будем предполагать заданными скачки смещений и напряжений.
у,
Ниже нам придется рассматривать операторы А (дХ7 со), Т (дх, v), Т (дх, v)
и др. в различных упругих средах. Введем для них обозначения
Л<*> (дх, щ), Tw(dx, v), Т(дх, v), k = 0, 1,.... г,
29 В. Д. Купрадзе

450	гранично-контактные задачи для неоднородных сред [Гл. XII
где
= У<Л,- А + (А* + М a^aZ + ^й/'
= 2н* ^ + V div + ц* lv х rot],
(Я* + ^ — **) v, ^-
i',/= 1,2,3,
\/ {дХ9 v) = S ^ -^
к*, — произвольные постоянные (k = 0, 1, . . ., г).
Мы будем рассматривать также задачи для неоднородной бесконечной
т
среды. В этом случае поверхность 50 отсутствует и Do¦= D~ = ?3\ U ^^J ПРИ
этом области Dk (k = 0, 1, . . ., г), как и выше, заполнены однородными
изотропными упругими средами с постоянными Xk9 \ik, а остальные Dk (k =
= г + 1, . . ., т) — пустотелые включения.
Приведем математическую формулировку задач.
Задачи для конечной области. Определить в областях Dk, k = 0, г,
регулярный вектор и, удовлетворяющий:
а) в Dk9 k = 0, г, уравнениям
б) на Sk, k == 1, 2, . . ., г, контактным условиям
(а)- —(и)+ = Р>,
дг, v) w }~ — {Г^> (<Э2, v) u}+ =
, т	\
в) на 50 U ( [) SJ одному из граничных условий:
1)	и = 1	—задача (I),
2)	Г<°> C2> v)u = f	— задача (II),
3)	tf<°> (a2, v)^==9 —задача (III),
4)	/?<°> E2, v) м = Ф — задача (IV),
5)	Т<°> (дг, v) и — ои = /— задача (VI).
Здесь <^(*>, & = 0, . . ., г — заданные векторы в областях Dk\flk)
U
Указанные граничные условия можно задавать на разных поверхностях
различно; этому соответствуют различные смешанные задачи.
Если поверхность 50 отсутствует, т. е. Do представляет бесконечную
среду, граничные условия на So заменяются условиями на бесконечности
(они различны в случае статики и установившихся колебаний); сформули-
сформулированная таким образом задача названа в главе I, § 14 (пункт 4) главной
контактной задачей.

2]	ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ ГЛАВНОЙ КОНТАКТНОЙ ЗАДАЧИ	451
Задачи для бесконечной области. Определить в областях D~ =
т		и
Е3 \ U Dk и Dki k = 1, r, регулярный вектор и, удовлетворяющий:
а) в D" уравнению
б) в D^,, k = 1, . . ., г — уравнениям
в) на Sb fe = 1, . . ., г, — контактным условиям
(и)" —(и)+ = Р>,
(дг, v) мр— (Г^) (аг, v) ^}+ =
г)	на U Sk одному из граничных условий:
k=r+\
1)	u = f	—задача (I);
2)	Т<°> (Зг, v)u = f	—задача (II);
3)	Н^ (dz,v) и = у	—задача (III);
4)	/?<°> ((Э2, v) a = ф	— задача (IV);
5)	Т<°> (а2, v)u — ou=f— задача (VI);
д)	на бесконечности условию излучения (см. III, 2.6).
Положительной нормалью будем считать на Sk, k=l, m, внешнюю
относительно Dk нормаль, а на So — внутреннюю относительно Do.
Постановки задач статики и колебания, как видим, формально не разли-
различаются; исследование их, однако, требует отдельного рассмотрения.
1.1.	Замечание. Для теоретической геофизики интересна внешняя
задача в том случае, когда г = т. Эта задача, которая в I, § 14, п. 4 названа
главной контактной, допускает значительное упрощение (см. ниже, замеча-
замечания 5.4 и 5.12).
1.2.	Замечание. Приведенные гранично-контактные задачи можно
обобщить в различных направлениях; можно, например, считать, что вклю-
включения сами содержат упругие, из другого материала, и пустотелые включе-
включения и т. д.
§ 2. Интегральные уравнения главной
контактной задачи
В главной контактной задаче r = m=l, D0 = ?13\D1 и она форму-
формулируется следующим образом (см. I, § 14, п. 4). Найти в областях Dx и Do
регулярные векторы и{1) и а@), удовлетворяющие уравнениям
Л<'>(д„<ог)и<'>(х) = 0, x?Dn r = 0, 1,
на 5j контактным условиям
{«<1>(г)}+-{и<°>B)Г=/2(гЦ
{ТЫ (дг, v) «П> B)}+—1Г«» (дг, v) ц<0) (z)\-=fa{z), J	BЛ>
и на бесконечности —условию излучения; здесь
/гбС'-Ч5!). Ue&'-'iSj, 5хбЛ2(а), 0<р<а<1.
29*

452
гранично-контактные задачи для неоднородных сред [рл# XII
Предварительно приведем одну вспомогательную формулу. Пусть
#(*)=] \тфу, п) Г {у — х)] Ф (у) dS,
или
где ф — вектор класса С1'
B.2)
(а), к —произвольная постоянная,
х
Г (у — х) — матрица Кельвина (см. (II, 1.4)), [Т (ду, п) Г (у — х)У выра-
выражение, определенное из (II, 4.5), п = п (у) — орт нормали.
В главе V, § 8, п. 2 для Т (дх, v) W (х) мы получили выражение, содер-
содержащее первые производные вектора ф. В дальнейшем необходимо также иметь
выражение, не содержащее производных ф.
Применяя к (V, 8.10) теорему Стокса (см. теорема V, 1.2), при x^S
получим
Т (дх, v)W(x)=It (дху v) [т {ду, п) Г (у — х)} Ф (у) dS,	B.3)
где
2п {т (a,, v) [т (дуу п) Г (у
х)] }kf =
'—У\
~f) S Жы {дх'v)
у'п)
г, /=i
B.4)
Теперь мы можем приступить к построению интегрального уравнения
главной контактной задачи. Ее решение будем искать в виде
= J {[Г(^, п)П") (у—х, в),)]' aogs(y) +
Si
+ П°> (t/ — х, «о) Ро ?s (У)} dS, х е Do,
= J {[Г(<?„ я) П») 0/—дс, юх)] «i^(t/) +
Si
+ Г*1» (у — х,со^р^з(У)}dS, xeDly
B.5)
где ал, Рг и х, (г = 0, 1) произвольные постоянные, которые будут опреде-
определены ниже, g2 (у) и g-3 (у) искомые векторы, g2€Ci;e(S1L ^зб^0^ (S^
8^Л2(а),0 <р <а^ 1; Г<^>(г/ — х, ©,) и [Т (ду, п) Г") (у — дс, ©

« 2]
ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ ГЛАВНОЙ КОНТАКТНОЙ ЗАДАЧИ
453
матрицы (II, 1.7) и (II, 4.13), в которых принято А, = Хп \i = [д>г, х = хг,
0) = С0г,
p
\y — x\
|
ni дГк	\y — x\	J
з
, + %r) 2 Мц (ду, п) ГЙ' (у—x, (or),
i=i
a\r) = 62i Bя ц.Г1, рг = (-1I
B.6)
рг и сог — плотность и частота колебаний области Dn г — 0, 1.
В силу граничных свойств потенциалов, входящих в B.5), будем иметь
Т {ду, п) Пг> {у — z, со,)] аг
St r=0
Второе условие из B.1) целесообразно переписать в несколько ином
(эквивалентном) виде.
Учитывая тождества (см. (V, 1.6))
Т (дх, v) им (х) = Т^ (дх, v) а<х> (х) + (y1 — Vil)J[ (дХ9 у) и™ (х),
Yo
Т (dXi v) uS^ (х) = Т^ (дх, v) uS^ (х) -\- (у0 — fx0) ^ (дх, v) ^^ (^)>
где у0 и 7i — произвольные постоянные, и применяя теорему V, 1.1, имеем
{г{дг. v) u^ (z)f — {т(diy v) u^ (z)} =\T^ (дг, v)
дг> v) [(Yi —
5г> v)
Пусть
Tl —fx1 = 7o_fxo;	B.8)
тогда правая часть предыдущего выражения известна на Si, а именно,
{т (dzt v) и^ (г)}+ - {т {д2, v) и<о) (г)}" = F3 (г),	B.9)
где
= /3
(z), F2 (z) = /2 B).	B.10)

454	гранично-контактные задачи для неоднородных сред [рл XII
Замечая, что
Т(ду9 п) Г<"> (у — х9 ®г) = Т(дуу п) П'> (у—
(у—х, сог), B.11)
где значение f (ду, п) Г<г> (у —х) определяется из (II, 4.5) при к = хг,
B.12)
— х9 ог) —Г<'> (У — х),
и учитывая (V, 8.10), из B.5) получим
s,
(=1
-*1 ДIу — ¦»
— ¦»П а 1
д" п) g2 {у)\а'
+ 2яГ (дх, v) [ Г (ду, п) Г(^ (у — х, (or) ] argi (y)J dS +
Si
Т (д„ v) П') (у—х, ©г) рг^з (У) dS,
где
I
i
B.13)
B.14)
+ (Мт + ?г) S •<**/ (^»v)г*/ (у—^со^)'
Br = Bfxr)"x (Yr + \ir) (nr + |ыг) br,
br = (Xr + Цг) (Xr + г^г,), r = 0, 1.
Перейдя в B.13) к пределу при х —^ z^St и принимая во внимание, что
в силу теоремы II, 1.7 Г (d2, v) [Т (дуу п) Т^г) (у — г, сог)]' имеет сингуляр-
сингулярность вида _., на основании теорем V, 8.5 и V, 8.9, получаем
{Т {дг, v)
' - {т (д21 v) и<°> (г)} = ф, + р0^ gs (г) +
№i — Vi) ai + (хо — То) a0] ^ (^. v) ^2 (^) +
л 1	f	3

? 2]	ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ ГЛАВНОЙ КОНТАКТНОЙ ЗАДАЧИ	455
	г|
+ 2лТ (дг, v) [ Г (dv, n) f<') (г/—г, ©r)J g2 (t/) \a,dS +
г, v) Г<г» (у — г, eor) g3 (f/) dS. B.15)
J S
Определим теперь входящие в B.7) и B.15) произвольные постоянные а0,
ai» Ро> Pi» хо» xi> 7о и Vi- Постоянные yQ и Yi удовлетворяют условию B.8).
Подчиним 7о> Yi дополнительно условию
= 0;
тогда
Чтобы избавиться от производных g2 в B.15), достаточно положить
B.17)
Чтобы иметь интегральное уравнение второго рода, достаточно в B.7)
и B.15) коэффициенты внеинтегральных слагаемых подчинить условиям
ао + а1=—1, ро + В1=1.	B.18)
В качестве второго условия для Ро и рх, учитывая некоторые соображе-
соображения простоты, примем
—PoN + Pi(*i = O.	B.19)
Принимая во внимание значения Вг и уп из B.17)—B.19) получим
i.ioM,t	р	(—l)r f ^

456	ГРАНИЧНО-КОНТАКТНЫЕ ЗАДАЧИ ДЛЯ НЕОДНОРОДНЫХ СРЕД (рл
В дальнейшем мы всегда будем предполагать, что постоянные аг, (Зг,
уг и хг (г = 0, 1) имеют значения B.16) и B.20).
уг
Оператор Т (дг, v), для уг, заданного значением B.16), обозначим через
L(r) (дг, v), а оператор Т (dz, v), для хг, заданного формулой B.20), —
через К{п (дг, v).
Учитывая последние обозначения и принимая во внимание B.1), B.9)
и B.10), из B.7) и B.15) получаем сингулярные интегральные уравнения для
главной контактной задачи
g2 (г) + j [А (г, у) g2 (у) + В (г, у) g3 (у)} dS = F2 (г),
J
1С (г, у) g2 (у) + О (г, у) g3 (у)) dS = FB (г),
B.21)
где
F3 (z) = {L(D E2, v)
, v)
а члены матриц А (у, г), Б (у, z), С (г, у) и D (у, z) имеют значения
г и) — — б
г, у)— 2я|ол
!__J_ _L
1=1
l fig —
(fa - Ho) (Vi-
(г/ —
B.22)

§ 3]
Сц(г,
РЕШЕНИИ ГРАНИЧНО-КОНТАКТНЫХ ЗАДАЧ СТАТИКИ
У*—У/
457
« (Но + HiJ FiHi + 6оНо) I У — г I3 я (Hi + Но)
[»/ (h ~ Ук) ~ Ч С*/ - У,)] S Bг - »«)v/
iHo v
2
х
=
2
r=0
„ v)
г=1
Hi — M'O + HiHo (ai — flp) ЬЧ
(Но + HiJ
1
I {/ - г I3
—2,
r=0
B.22)
Доказательство справедливости теорем Фредгольма для уравнений B.21),
а также исследование разрешимости будет дано в следующем параграфе.
о
При сог = 0, г = 0, 1, Т{п (у — г, соГ) = 0 и выражения для Akj B, у),
Bkj B> y)> Cki (z, у) и Dkj (г, у) значительно упрощаются.
§ 3. Решение гранично-контактных задач статики
В этом параграфе рассмотрим вторую гранично-контактную задачу
статики для конечной неоднородной среды; другие задачи рассматриваются
аналогично.
Граничные и контактные условия в рассматриваемом случае имеют вид
(дг9 v)
°> (дг9 v)
dZi v)
So,
C.1)
где L(r) (<Э2, v) (r = 0, 1) получены из f (дг, v), для уг определенных из B.16),
Flt F2 и F3 —заданные векторы, F^C0**^), F2eCl'*{SJ, F3?C°> *(SJ
(а), 5хеЛ2(а), 0 <P <a< 1.

458
ГРАНИЧНО-КОНТАКТНЫЕ ЗАДАЧИ ДЛЯ НЕОДНОРОДНЫХ СРЕД (рл XII
Начало координат поместим в области Do, а положительным направле-
направлением нормали на поверхностях 5Х и So будем считать направление внешней
нормали по отношению Dx и Do соответственно.
Решение задачи C.1) будем искать в виде
— [/С<°> (dV9 п) Г<°> {у — х)У g2 (у) \ ро dS9 х б Do,
А,
— [Ю1) (дю п) П1) (у — x)Y g2 (у)} р!
C.2)
где рг (г = 0, 1) определены из B.20), gl (у), g2 (у) и gs (у) — искомые
векторы, значения матриц Г(г) (у — х) и [К{г) (ду9 п) Г(г) (у — х) Г полу-
получаются соответственно из (II, 1.4) и (II, 4.3), полагая X = %п |х = \х,г и
г_0 1
Учитывая B.4) и B.13), получаем из C.2)
(дХ9 v) и<°> (jc) =
v) Г^°> (у— х) ft {у) dS +
+ j i^@) Фх, v) Г») (у—х) gs (у)—
(д„ v) [/С<°> (а^ п) Г<°> (у—х)Г g2 (у)} Р„ dS, х€ А,,
v) и<о) (д) = f L<°> (а„ v) Г<°> («/ — х) ft (у) dS +
+
_L
2л
Z
„ v) Г<°- {у — х) gs {у) —
!
ds, (x) I j/ - x I
1 у — jc П d	1_
^, \ dv \y —
х\
^- в0) мщ (dx,
-L
C.3)

§ 3]
РЕШЕНИЕ ГРАНИЧНО-КОНТАКТНЫХ ЗАДАЧ СТАТИКИ
459
(дх, v) u<i> (x) = | I Ld) (a,, v) IW (if — x) g3 {y) -
,	lIm
2я Г1
Im V
2я Г1 Zj 5s, (х) | у - х | ds, (у)
r — jc I
C.3)
где значения матриц Tin (дх, v) Г(г) (у — х) и L<r) (дх, v) Г<л) (г/ — х) полу-
получаются соответственно из (II, 4.1) и (II, 4.3) при X = Хп ц = (хг, х == иЛ,
Y = 7r, к, и 7г заданы формулами B.16) и B.20), а выражение для
Т10) (дх, v) 1К{0) (ду, п) Г<°> (у — х)У получается из B.4) при X = Ji0,
И1 = Н-о. V = М-о. и = 5<о-
Учитывая C.1) и свойства потенциалов, входящих в C.2) и C.3), на
основании теоремы V, 8.5, после элементарных преобразований получаем
ft (z) +
j Gu
B,
(г) + J Gn B, у) ft
J1
+ J[G12B, y)g2(y) +
+ O13B, y)er3(y)]dS = F1B), 2 6 So,
+ J [G%i(z, y)gi(y) +
•f G23 B, y) g3 (y)] dS = F, B), 2 6 Slf
. y)gi(M)dS+ j [G32B, y)^2(y) +
+ 0,3B, y)^s(f/)]rfs = F3B), zeslt
C.4)
где
G12 B, y) = - Г<°> (a,, v) [/C<°>
Gn(z, #)== — П°>(у—2), G22B, |/) =
—2),
n) Г <°> (y — z)]'po,
(y — z)p0.
, у), G23 B, у) =
, у),
Ga B, г/) = — L<°> (az> v) Г«°> (у—г), G32 B, у) = С (г, у), G33 B, у) = D (г, г/),
значения А (г, г/), В (г, у), С (г, у) a D (г, г/) получаются из B.22) при <ог= 0,
г = 0, 1.
Некоторые члены в C.4) имеют сингулярность вида | г — у\~2', из резуль-
результатов IV, § 3, п. 4 следует, что эти члены сингулярные (см. определение сингу-
сингулярного интеграла — IV, § 3, п. 4). Остальные слагаемые уравнения C.4)
имеют сингулярности вида |г — у\~2+6, а > 0.

460	ГРАНИЧНО-КОНТАКТНЫЕ ЗАДАЧИ ДЛЯ НЕОДНОРОДНЫХ СРЕД [Гл. XII
Покажем, что сингулярные интегральные уравнения C.4) нормально
разрешимы и для них справедливы теоремы Фредгольма.
Перепишем C.4) в следующем виде:
8г (*) + | lGn (*. У)а (*)а (У) Si (У) + G12 (г, у) a {z) р (у) g2 (у) +
+ 6\3 (г, у) a (z) р (у) g3 (у)] dS = Фг (z),
g2 (г) + [ \Gn (г, у) р B) а (у) gl (у) + G22 (г, у) р (г) Р (у) g2 (у) +
s
+ G23 B, у) р B) Р (Jf) g3 (у)] dS = Ф2 B),
?з (Z) + J №и (г, у) Р B) а (t/) ft (г/) + GS2 (г, у) Р B) р (у) g2 (у) +
S
где
1, zeS0,	/0,
П ,C<J	PB)= , _, «j
0, гб^,	I 1, 26-Ьх,
Из C.5) видно, что gt (z) = 0, когда zQ St> и gk (z) = 0, когда г™ 50,
й = 2, 3.
Совершенно так же, как в VI, § 3, можно вычислить символический
определитель системы C.5); имеем
det Ф (г, 6) = [ 1 — a20a4 (г)] [ 1 — р2р4 (г)] [ 1 — ?2Р4 (г)],	C.7)
где
О" = Ут (К + 2^гГх» г =*0, 1, р = (
^7 = iM-f — М-о + (ai — a0) м^о] (И-i + M";
отсюда
det(D(z, 0)=l_ag = bo(l
detO(z, в) = A— р2)A— ^
С другой стороны,
4- аг) \
+ A + a0 + 6J jij (|хх + |ло)
Таким образом,
deta>(*, e) = (i— р2)A— ^2)>о, zest.
Отсюда, в силу IV, 5.6, следует нормальная разрешимость системы C.5).
Далее, так же как в VI, § 3, можно показать справедливость теорем
Фредгольма для системы C.5).

§ 3]	РЕШЕНИЕ ГРАНИЧНО-КОНТАКТНЫХ ЗАДАЧ СТАТИКИ	461
Вместо системы C.4) рассмотрим систему
А (г) + J Gu (г, у) gl (у) dS + J [Glt B, у) gi (у) + Gu (г, у).?8 G/)l <*S -
s,	s,
-1 Г«» (d,, v) Г<°> B) A — | T<°> (d2, v) M<°> B) M = Ft (г), z 6 50>
g* (г) + J Gn B, y) gl (y) dS + J EG22 B, y) g2 (y) + Gw (z, y) g3 (y)] dS +
?s (г) + j G81 (г, y) ft (t/) dS + J [Gv (z, y) g2 (y) + G33 (г, у) gs {y)\ dS +
+1 L«» (йг, v) Г<°> B) A + I L<°> (a« v) M<o) (Z) M = F8 B), 2 6 Slf
где
Л = и<»> (x) | ,=o, ^ = rot
B) = rot, Г<°> B — x) U=o = {2nii0)-1 2j Чп -щ -|7|- >
a l
C.9)
м@) (х) определен из C.2), &kfl — символ Леви-Чивита.
Система C.8) отличается от C.4) вполне непрерывными слагаемыми.
Поэтому для нее также имеют место теоремы Фредгольма.
Покажем, что если система C.8) имеет регулярное решение, то необ-
необходимо
Л = 0, М = 0,	(ЗЛО)
если только выполняются условия
{Pi(y)dS + lf.3(y)dS = O,
с	Г S1	(ЗЛ1)
являющиеся условиями равенства нулю главного вектора и главного момента
внешних усилий, действующих на границу области Do. В условии C.11)
в силу B.10)
h B) = Fb (г) + (ft — Yi) Л (dz1 v) F2 (z) =
= \T<1) (дг, v)u^ (z)}+— {Г<°> (дж9 v)u<V (г)]'. C.12)
В самом деле, учитывая вычисления главы VI, § 5, п. 2 и принимая
во внимание, что главный вектор и главный момент Г-операции от потен-

462	ГРАНИЧНО-КОНТАКТНЫЕ ЗАДАЧИ ДЛЯ НЕОДНОРОДНЫХ СРЕД [рл XII
циала (VI, 2.1) на любой замкнутой поверхности класса Лг (а) (а >0) равен
нулю, на основании формулы (V, 1.41), получим из C.8)
— 2CО J J fу х g3 (у)} dS + (|х0 — хо) J [у X Ж (дуу п) g2 (у)] dSj + М =
\
Sa
2р0 \\\yxg»Ш dS + (fx0 — О I 1УXЖ {ду, п)g2 (у)) dS\ =
[s,	s,	\
C.13)
Отсюда
Л= J/7i(y)rfS+ J/3Q/№ М=- \[yxFi{y)]dS+ \[yxfs(y)\dS.
s0	s,	sn	s.
Таким образом, доказано, что если соблюдены условия C.11), из C.13)
вытекает Л = М = 0, т. е. при условии равенства нулю главного вектора
и главного момента внешних усилий, действующих на границу области Do,
всякое решение glt g2, g3 системы C.8) есть,в то же время решение исходной
системы C.4).
Покажем теперь, что система C.8) разрешима. Рассмотрим для этого
однородную систему, получаемую из C.8) при Ft (z) = F2 (z) = F3 (z) = 0,
и докажем, что она не имеет отличных от нуля решений. Пусть gl5 g2
и g3 — какое-либо решение этой (однородной) системы. Так как Рх =
= F2 = F3 = 0, то из C.12), очевидно, /3 = 0 и для gx, g2 и g3 выполнены
условия C.10). В этом случае однородная система соответствует гранично-
контактной задаче со следующими условиями:
C.14)
IJ силу теорем IV, 6.12 и IV, 6.15 для решения glf g2» §з системы C.4)
пол\м ем^п1 С0- '(So^^eC1' ^S^HggeC0' P(S!). Отсюда, так как80еЛг (а)
и S j Л 2 (а) (а > 0), заключаем, что смещения и@) (х) и и{1) (х), и напряжения
Г@^ (дхч v) и@) (х) и ТA) (дХУ v) u^1} (x) непрерывны вплоть до соответствую-
соответствующих границ. Принимая во внимание C.14) и применяя теорему III, 1.14,
получаем
) = [Л<°> X х\ + В@), х е О0,
где Л@), ЛA), В<0) и ВA) —произвольные постоянные векторы.
Теперь, учитывая C.10), на основании C.9) будем иметь
2Л<°> = М = 0, В@) = Л = 0,
и
C.15)

Я 3]
РЕШЕНИЕ ГРАНИЧНО-КОНТАКТНЫХ ЗАДАЧ СТАТИКИ
463
Так как из второго условия C.14) следует
то, применяя теорему III, 1.6 в области Dlt получим
u(D(x)=0, хбА-
C.16)
Вектор ы@) (х) непрерывен при переходе точки х через поверхность So,
поэтому
принимая также во внимание, что выражение
{7<°>(дг, v)«<o)(z)}- = — 2gl(z), zeS0,	C.17)
существует и принадлежит классу С0- e(S0), на основании теоремы единствен-
единственности в области D2 = E:i\(Dl\jD0), получаем
иЮ)(х) = 0, xeD2.	C.18)
Отсюда на основании C.17) следует
ft(z) = 0, г€5о.	C.19)
Сопоставление формул C.2), C.15), C.16), C.18) и C.19) дает
= J
—x)g3{y) — [/C<J> (^, я)П1» (y-x)]'g2 (у)} pt dS=
Рассмотрим теперь векторы
«<°>(х) = J \r^(y —
j
5,
Из C.20) и C.21) имеем
{и<°> (г)}+ = 2p0gr2 (г), {/С<°> (д„ v
= 2p0g3(z).
откуда в силу B.20) получаем
= o.
Но справедливы тождества
{ди, п)и<
f
J
B3\D
j
S,
r
C.21)
C>22)
C.24)

464	ГРАНИЧНО-КОНТАКТНЫЕ ЗАДАЧИ ДЛЯ НЕОДНОРОДНЫХ СРЕД [рл# XII
где
(х)J +
з
[2b, (ЬЛ + Ьо^о)] 2j \ "gj- + ^Г ) +
р, =1
3
{г) ди(г) \2
?)
Формулы C.24) получаются совершенно так же, как (III, 1.7) и (III, 1.9).
Учитывая C.23), из C.24) получаем
Отсюда, принимая во внимание условия на бесконечности, получаем
Ъ - }	C.25)
Из C.22) и C.25) следует
g2 (z) = О,
Итак, система C.8) разрешима единственным образом. Если главный
вектор и главный момент внешних усилий, действующих на границу областиД0,
равны нулю, вторая гранично-контактная задача (см. C.1)) разрешима и
решение представляется формулой C.2) с точностью до аддитивного жесткого
смещения.
Исследование других гранично-контактных задач протекает совершенно
аналогично.
При исследовании первой, третьей и четвертой задач предполагается
S0?JI2 (а) (а > 0), а в шестой задаче —80^Лг (а).
Напишем теперь союзную с C.8) однородную систему. Нетрудно убе-
убедиться, что ее получим, если решение следующей гранично-контактной задачи
будем искать в виде
F«»(x)= J[7-(»>(^, n)T^(y—x)]'h1(y)dS— \{Г<°Ну — x)h%(y) +
+ [L<») фу, п) Г<°) (y — x)]'hs (y)\ dS — 1 n*> (x) a — | M(») (jc) p, jc € Я3\Ди
^ — x)\'hz{y)\dS, x?DQ,
= Jin»^—

§ 4]	РЕШЕНИЕ ЗАДАЧ ДЛЯ УРАВНЕНИЙ УСТАНОВИВШИХСЯ КОЛЕБАНИЙ	465
где
а = а<°> (*) |*=о, Р = rot а<°> (х) |
, n) П°>(*/ —*)]' h1(y)dS— J {Г<°> (у — хIц(у) +
,, n) П°> (y — x)]
Начало координат находится в области Dx.
Полученная таким образом однородная система имеет только нулевое
решение и, следовательно, неоднородная система имеет единственное реше-
решение, если Sj€Jl2 (а), а > 0, / = 0, 1.
Итак, попутно мы решили следующую задачу, союзную второй гра-
гранично-контактной задаче: найти в областях Do и E3\D0(Ez\D0 =
регулярные векторы V@) (x) и Vil) (x), удовлетворяющие:
1)	в E3\D0 уравнению
2)	в Do уравнению
3) на Si контактным условиям
2, v)
4) на So условию
где фх B), ф2 B) и ф3 (г) — заданные векторы, ФхбС0' P(SX), ФзбС1
ФзбС1- ^Si), а 5,6 Л2 (а), / - 0, 1, 0<р <а< 1.
Другие гранично-контактные задачи статики для неоднородной бес-
бесконечной упругой среды исследуются аналогичным образом.
§ 4. Решение гранично-контактных задач
для уравнений установившихся колебаний
Для уравнений установившихся колебаний гранично-контактные задачи
сформулированы в § 1. Здесь мы рассмотрим следующую задачу: определить
в областях Do и D2 регулярные векторы u(Q) (x) и аA) (л:), удовлетворяющие
условиям
А@)(дх, со0)и@)(*) = 0, xeD0y АA)(дх,щ)и{1)(х) = 0, *е?>2, D.1)
\ui0)(z)}+— {u{
{L@) (д„ v) гг@) (z)}+ — {LA) C,, v) t/A) (г)}~ = F3 B), 2 6 SOf
D.2)
где Fly F2 и F3 —заданные векторы, /^е С0-» (SJ, /^абС1'Р (So), F3€
eC°-P(S0), S06^2(a), 8геЛ2(а), 0 <р <а<1.
Легко заметить, что эта задача эквивалентна аналогичной задаче для
бесконечной неоднородной среды, сформулированной в § 1.
30 В. Д. Купрадзе

466	ГРАНИЧНО-КОНТАКТНЫЕ ЗАДАЧИ ДЛЯ НЕОДНОРОДНЫХ СРЕД [ГЛ. XII
Решение будем искать в виде
и@) (х) = J Г(в)(у—х, wo)gl(y)dS + [ {[Кт(ду, п)Г@)(у—х, «„)
— T{0)(y—x,(o0)g3(y))$0dS,
gt(y) -
eD0, D.3)
ЫA)(*) = J
a)
ff, n)Ta)(y—x,
) — TA)(y —x,
где рг (г = 0,1) задаются из B.20), gt (у), g2 (у) и g3 (у) — искомые векторы,
значения элементов матриц Г<г) (у — х, сог) и К(г) 0У, п) Г<г) (у — х, сог)
получаются из B.6), для хг определенных из B.20).
Из D.3) получаем
Tw(dx, v)u{0)(x)= J Tm (дх, v)Tw(y—x, «>0)g1(y)dS +
+ j {Tw (dx, v) [Ki0) фу, п) Г@) (y—x, щ)}' g2 (y) —
s»
— Г@) (д„ v) Г@) (y — x, a») g3 (y)) p0 dS, xe Do,
L@) (dx, v) «@) (x) = f L@) (a,, v) Г@) (y — x, coo) A (y) dS +
s},	\ D.4)
+ J {L@) (a,, v) [Kl0) (ду, п) Г@) (y — x, ©о)]' g2 (y) -
-	L<0) C,, v) Г@> (у — x, щ) g3 (y)\ p0 dS, xeD0,
LA) (a,, v) uA) (x) = [ {LA) (d,, v) [A:A) (ду, п) ГA) (y—x, ©O] 'ft («/) —
s.
-	LA) (д„ v) Га) (y — x, щ) g3 (y)} p! dS, x e D,,
где элементы матриц Г(г) C^, v) Г<г> (г/ — х, <ог) и L(r) (а^, v) Г<г) (^ — д:, ter)
(г == 0,1) получаются из B.14), если уг = (д.г и ^г = (—1)г (^0 — ^1) Mv X
X (ц.о + ^i)» а
(^о + (J-o)
exp (ik!?1 \u — x
X
°l kdV dX;
х
exp (»M0> | у - х |) - ехр (tfe<0) I У -

Я 4]	РЕШЕНИЕ ЗАДАЧ ДЛЯ УРАВНЕНИЙ УСТАНОВИВШИХСЯ КОЛЕБАНИЙ	467
v) [K{r)(dyy n)Tlr)(y — x9<or)Y)kf=*Bn) MfxA/
д ехР I
\xr) (fx0
«.	-
* ^
dn dxk	\y — x |
exp (*&{r) 11
dxk
X
| r/ — jc I	r dv dxf	\y — a: |
X
IУ — x I	Pr©?ftr (I1
#2 ^2 Г ехр (^|r) | у — x |) — exp ('^ I г/ — л: |)
dv дп дхь dXj j	\y — x \
X
\y-x\
yr и пг определены из B.16) и B.20).
Из краевых условий задачи для определения gl9 g29 g3 получаем систему
уравнений:
— §"i (z) + j Gn (г, у) ft ((/) dS + J [G12 B, у) ft (у) +
S\	So
J Ga B» У) ft (У) d5 + j lG22 B» У) ft (У) +
S,
— gs (г) + j Gn (z, y) ft (г/) d5 + ([G32 (г, у) g2 (у) -f
s,	s,,
D.6)
где
Gn (z, y) = T@) (дг, v)r<0) (y — z, co0),
Gu B, y) = T@) (aa v) [Ki0) (ду, п) Г<0) (г/ — г, cO]' p0>
, v)T(O)(y — z,
2, г/) = Г@)(г/—г, со0).
<0)
G3i (г, г/) = L<0) Eг, v) Г@) (y—z, щ), G22 (г, у) = А {г, у),
Gw(z,y) = B(z,y),
G32 B, У) = С (г, у), Gsa B, у) = D (z, у),
J
а члены матриц А (г, у), В (г, #), С (г, j/)hD (г, #) определены из B.22).
Перепишем D.6) в виде
D.7)
is
(У)dS =
= 1,2,3, s = 50
D.8)
30*

468
ГРАНИЧНО-КОНТАКТНЫЕ ЗАДАЧИ ДЛЯ НЕОДНОРОДНЫХ СРЕД [рл#
где
*«
-Iй
lit
D.9)
Из системы D.8), очевидно, gx (z) = 0, когда 2?S0, ngk (z) = 0, когда
zesu k -2,3.
Для D.8) справедливы теоремы Фредгольма; в самом деле, D.8) отли-
отличается от системы, исследованной в предыдущем параграфе, лишь вполне
непрерывными слагаемыми.
Выпишем союзную с D.8) однородную систему
O, z^S, k= 1,2,3. D.10)
Ее получим, если решается гранично-контактная задача
Ро {Ki0) (dz, v) V@) (z)} —pj. {Кщ (dz, v) VA) B)}+ = 0,
— Ро {У@> (z)}" + Pi {УA) (z)}+ = 0, 26 «So,
и решение разыскивается в виде
Vw(x) = J [7<0)(д„ п)Г@)(у-х, «Й0)]'А1(У)^ +
+ J {Г@)(г/—х, «о) ft, (у) + [L@) (а„ п)Г<0) СУ — JC, <во)]4
D.11)
Эту однородную гранично-контактную задачу в дальнейшем будем
называть задачей 1@>.
Справедлива следующая
4.1. Теорема. Необходимым и достаточным условием существования
нетривиального решения однородной системы интегральных уравнений, соот-
соответствующей системе D.6), является существование нетривиального ре-
решения однородной задачи 1@> для частот колебаний coo, cof.
Необходимость. Пусть задача 1@) для частот coo, coi имеет
только тривиальное решение. Покажем, что в этом случае однородная система,
соответствующая D.6), имеет лишь тривиальное решение. Допустим противо-
противоположное. Тогда, по второй теореме Фредгольма, союзная однородная си-
система, соответствующая задаче 1@), имеет нетривиальные решения; обозна-
обозначим их через
h{p) (Mf\ №\ h[l\

Л 4]	РЕШЕНИЕ ЗАДАЧ ДЛЯ УРАВНЕНИЙ УСТАНОВИВШИХСЯ КОЛЕБАНИЙ	469
и составим потенциалы
V@)(x; h(p)) = J [Ti0)(dy, n)rlO)(y-x,«>o)]'h[p)(y)dS +
+ f {Г@) (y-x, coo)hip) (y) + [L@) (ду, п)Г@) (у-х, coo)]' h{3p) (y)} dS,
=j \Yll)(y-x,
y, n)TA)(y—x,
dS, x? Do.
D.12)
Очевидно, V{0) (x; /i(p>) и V{1) (x; /г(р)) будут решениями задачи 1<°» и
по условию должны быть тождественными нулями, т. е.
V{0) (x; h{p)) = 0, xe
Но тогда, построив векторы
j
s,
1Г@) (y—x,
, Vll) (x; hlP)) = 0,
)(у-.х, too)]'h\p)(у)dS +
[L@) (д„ п)Г@) (y-x, «*)
D.13)
; Л<">) = j {ГA) (у-х, щ) hip) (y) +
dy, n)TA)(y — x,
Ш
D.14)
будем иметь
[W@) (г; кПГ = - 2MP) (г), {L@) (dft v) U7@) (z;
{ГA) (г; А<">)Г = 2^p) (z), {LA> (a,, v) ГA) (г;
+ = 2ft?p)(z),
), гб50.
D.15)
Мы выше заметили, что для уравнений D.8) и D.10) справедливы теоремы
Фредгольма. Поэтому из D.10), учитывая, что Sj?Jl2 (а) (/ = 0,1) и исполь-
используя теорему VI, 3.6, получаем, в частности, h[p)?Cl>$ (Si), 0 <р<а^1.
Применяя теорему V, 8.4, из D.13) и D.14) будем иметь
= 0, ze>*i.	D.16)
и W{1) (x\ №р)) решают следующую гра-
Следовательно, Ww (x;
нично-контактную задачу:
Aw(dx,a>1)WA)(x;hlP)) = 0, x
2)	[Wi0) (z; /i(p))}+ + [W(l) (z; h(p))
{L@)(dz,v)Wl0)(z; ^
3)	{Ti0)(dz,
= 0,
D.17)

470	ГРАНИЧНО-КОНТАКТНЫЕ ЗАДАЧИ ДЛЯ НЕОДНОРОДНЫХ СРЕД [рл
Совершенно так же, как в главе III, доказывается, что эта задача имеет
единственное решение. Таким образом,
W{0) (*; h(p)) = 0, хе A,, Wil) (x; h{p)) = 0, хе D%.
На основании последних формул, из D.15) следует ftf/> = ft(p) = 0,
и D.14) принимает вид
= \[Ti0)(dytn)Ti0\y-x, coQ)\'h[p\y)dSt xtDo.
Si
Этот вектор есть регулярное вне St решение уравнения Л@> (dXf соо) x
X Wi0) (*; й(р)) = 0, удовлетворяет на Sx условию D.16) и на бесконеч-
бесконечности условию излучения; по теореме единственности (см. теорема III, 2.13)
такое решение есть нуль в области D0U D2- Итак,
Wi0) (x; hiP)) = 0, xeD0[)D2.
Учитывая также формулу D.13), получим
[Wi0){z; h{p))r—{Vi0)(z; h{p))}+ = 2hip)(z) = 0, zgSb
Следовательно,
это противоречие доказывает необходимость условия.
Достаточность. Допустим, что задача 1<°> для частот о? и of
имеет т линейно независимых решений У@) (х\ h^) и Vil) (х; А(^>), р =
= 1, т. Покажем, что совокупность векторов
где
{/Сс0) (аж, v)И0* (z; h{p))}l C0 = (ii (щ + \ю)'\ Л= 1,2,3,
есть система линейно независимых решений однородной системы, соответ-
соответствующей системе D.6).
Докажем сначала линейную независимость системы {g{p) (z)}?. До-
Допустим противоположное. Пусть.
g(i)(z)=
0=1
где 1 ^ i ^ т, а штрих при символе .^1 означает, что при суммировании
опускается слагаемое, соответствующее р = i. Тогда вектор
0=1
будет удовлетворять условиям
Из этих условий вытекает
Й(О)(х) = О, x?
что противоречит линейной независимости Vi0) (x; /i(p»).

§ 4]	РЕШЕНИЕ ЗАДАЧ ДЛЯ УРАВНЕНИЙ УСТАНОВИВШИХСЯ КОЛЕБАНИЙ	471
Покажем теперь, что векторы g<p) (z) (р = 1, т) являются решениями
однородной системы, соответствующей D.6).
Выписав формулу (III, 2.6) для области Dl9 для матрицы
Г@)(# —х9 со0) и вектора V[0) (x; h{p)) получаем
( 2V@)(x; /г(р)), x?Dl9
I р ^у — х, соо) Т (рц* я) * \У> h I === {а	"~ гТ (^* ^)
5	10,	х ^ /у1.
Формула (III, 2.53) для области D2 с оператором К{0) (ду, п) дает
f [lKi0)(dvt п)Г{0)(у — х9 щ)У [V@)(y\ h{p))}~ —
si
>V{0) (r- hip)) ran
Из D.19) и D.20) имеем
0) (y-x, <o0)[T^ (dy, n)Vw (y; A<">)]+ dS
0. D.21)
Применяя формулу (III, 2.6) для Г*1) {у — х, сох) и V{1) (x; Л^)) в обла-
области ?>iU Do, получаем
J {Tw(y-x, щ) [Ka\dv, n)V^(y; Л'">I + _
- [Ка)(ду, п)Га)(у -х, со,)} [У111 (у; h(p))}+} dS =
( 2Vil) (x; h{p)), хеДиО,,
1	0,	xeD2.
Учитывая граничные условия гранично-контактной задачи 1<°>, из
последней формулы получаем
\у-х, щ)\ [vW\hlP))r}fildS = 0, xeD2. D.22)
Вычислим предел Т@> (<Э2, v)-onepauHH над D.21) при х—>z?Su со-
составим разность предельных значений D.21) и D.22) и разность предельных
значений L(r) (d2, v) (г = 0,1) операции от этих же выражений при х —*
—>гс50; тогда получим однородную систему, соответствующую системе
D.6); отсюда заключаем, что \g(p) (z)}f действительно является решением
однородной системы, соответствующей системе D.6).
Остается показать, что упомянутая однородная система других линейно
независимых решений не имеет. Допустим противоположное. Пусть назван-
названная однородная система имеет i > m линейно независимых решений. Тогда
союзная система D.10) будет иметь i линейно независимых решений

472
ГРАНИЧНО-КОНТАКТНЫЕ ЗАДАЧИ ДЛЯ НЕОДНОРОДНЫХ СРЕД [рл< XII
Составим потенциалы D.11) с этими плотностями; они, очевидно, дают
решение задачи 1@>. Но так как для соо и cof эта задача имеет лишь т линейно
независимых решений, то должно быть
Q{r) (х; hip)) = Vir) (x; hlP)) — 2 ckpVir) (x; hlk)) = О,
fe=l
= m+ 1 ,...,*; /- = 0, 1,
Построим вектор
Hir) (х; hw) = W(r) (x; h{p)) — 2 ckpW(r) (x;
где \F(r) (x; Л**)) определяются формулой D.14).
Очевидно, векторы Я@) {х\ h^) и Я^Х) (х\ h^) будут решениями задачи
D.17) и поэтому равны нулю. Таким образом, #(г> (х; Ыр)) = 0.
Отсюда, повторяя приведенные выше рассуждения, получаем
это противоречит линейной независимости векторов |й(р)}, р = 1, i.
Итак, доказано, что однородная система, соответствующая D.6), имеет
т линейно независимых решений.
4.2. Теорема. Вторая гранично-контактная задача установив-
установившихся колебаний имеет единственное решение.
Рассмотрим отдельно два случая.
1)	Когда для частот соо и (а1 задача 1@) имеет только тривиальное реше-
решение, тогда однородная система, соответствующая системе D.6), тоже имеет
только тривиальное решение и неоднородная система разрешима. Потен-
Потенциалы, определенные зависимостями D.3), дают решение задачи.
2)	Когда для частот соо и (йг задача 1@) имеет т линейно независимых
решений, тогда решение второй гранично-контактной задачи будем искать
в виде
m
1=1
где w<°> (x) и u^l) (x) определены из D.3), a
(х; А<'>) = f [T<0) (ду, п)Г@) (y-x, «„)]' h[l> (y) dS +
s
4°Ef) + [Li0)(dy, n)Tm(y — x, щ)]'№>(y)} dS,
f
s,
x,
J {Tw(y —
(г. Л<») =-4 J
d
0,
-x, «0 tf
+ [LA)(ду, п) ГA) (у — х,
dS, x€ D2,
D.23)
где

4]	РЕШЕНИЕ ЗАДАЧ ДЛЯ УРАВНЕНИЙ УСТАНОВИВШИХСЯ КОЛЕБАНИЙ	473
суть фундаментальные решения системы D.10), а постоянные Ащ опреде-
определяются равенствами
i
D.24)
и Фу (z), / = 1, 2, 3, определены формулами D.9).
Для определения векторов gl9 g2, g3 получим систему интегральных
уравнений D.8); в ее правой части будет стоять вектор с девятью составляю-
составляющими, которые последовательно совпадают с составляющими следующих
векторов:
L(Z)-S
m
! (Z) — S
„ v)
S
(z;
- [tf* (г;
{[L@>(a2,v)/?<0)(z;A('))]+-
D.25)
Принимая во внимание D.11) и D.23), получаем
{д„ v)/?«»(z; /t<'">)]+ = [Т<°) Eг, v)#<°>(z; Л<0)]-=>
= I?1'0» (ада v) У<°> (г; /г<'))]+, г 6 Sx; D.26)
кроме того,
(г;
(г; /г((>)]-,
D.27)
где У@) (а:; Л<*>) и FA) (л; /i<'>) представляют решения гранично-контакт-
гранично-контактной задачи 1@).
Учитывая равенство
И'Цдг, v) = K^(dz, v) + {yr — xr)J[(dz, v), л = 0, 1,
и используя условия задачи 1@>, получим из D.27)
; h")]+-[R" (z;
(г;
	2 (i*^-2— 1)hi'» (z) + P5
Если введем обозначения
-eJ'> (z), .
. D.28)
D.29)

474	гранично-контактные задачи для неоднородных сред [рл XII
то, учитывая D.26) и D.28), в правой части вместо D.25) будем иметь
1=1
Ф2 B)—
i=l
m
ФзB)— ЕЛA)^з°
— 0
(г) а3 B),
U
где аг (г), а2 (г) = а3 (г) определены формулами D.9); векторы g{i) (г) =
^ \ё\() (z) ai (г)> §21) (z) a2 (z)» ё"з° (z) аз (г)} являются фундаментальными
решениями однородной системы, соответствующей -D.8).
Условие разрешимости неоднородной системы D.8) примет вид
D.30)
Покажем, что
Составим потенциалы
И°Чх; Л@) = J [Ti0)(dy, n)Tw(y-x, щ)]'
J
{у) dS +
So
— дс,
dS,
где ftp, /4'\ ^зг> —фундаментальные решения однородной системы D.10).
Очевидно, V@)' (x; Ы1)) и F'1" (х; Л<1)') будут решениями гранично-
контактной задачи
А<°Цд„ <o0
B;
B;
Согласно теореме единственности получаем
^@) (*•, /i<0) = 0, хб ?>2. vA) (х; л@) = 0,
отсюда с учетом D.31) будем иметь
и

К 5]	ФУНКЦИОНАЛЬНЫЕ УРАВНЕНИЯ ГРАНИЧНО-КОНТАКТНЫХ ЗАДАЧ	475
где Vil) (х\ /г@) определен в D2 второй формулой D.31) и является регуляр-
регулярным решением уравнений А^1) (дХ9 о)х) Vil) (х: Ы^) = 0 в области D2,
удовлетворяющим на бесконечности условию излучения. В силу (III, 2.1)
для векторов Vil) (x\ /i(t)) и Vil) (x\ /t</>) имеем
(г; hU))}~-
— \V{l)(z; hU))]- [LA) (д„ v)V{l)(z; /г@)]~} dS = 0. D.32)
Так как характеристические числа рассматриваемой системы являются
простыми полюсами резольвенты (см. Рухадзе Ж. [1 ]), то системы фунда-
фундаментальных векторов g№- (z) и h(}'] (z) можно считать биортонормированными,
l> 1=1*	D.33)
0, i Ф j.
Принимая во внимание D.32) и D.33), убеждаемся, что условие разреши-
разрешимости D.30) выполнено в силу определения постоянных ЛA) (см. D.24)).
Этим доказательство теоремы 4.2 завершается.
Аналогично исследуются другие гранично-контактные задачи устано-
установившихся колебаний.
§ 5. Функциональные уравнения гранично-контактных задач
В этом параграфе излагается другой подход к решению гранично-кон-
гранично-контактных задач, основанный на некоторой функциональной трактовке тож-
тождеств Грина; конструктивное применение этих тождеств в различных ситуа-
ситуациях приводит вместо интегрального уравнения для плотности потенциала
к эквивалентному функциональному уравнению непосредственно для иско-
искомого решения.
Таким путем доказываются общие теоремы существования и в ряде
важных с физической точки зрения частных случаев удается проще полу-
получить окончательный результат.
1. Первая задача статики A)+. Пусть D^n обозначает область (см § 1, п. 1)
и G(?) (x, y\ D(r)) есть тензор Грина первой статической задачи для области
D(r) с постоянными Ламе ^0, \i0. Существование этого тензора было доказано
в главе XI.
Предположим сначала, что гранично-контактная задача A)+ допускает
регулярное решение и (у). Пусть x?Dk, к = 1, 2, . . ., г. К вектору и(у)
и вектору G(i{ {у, х\ D(r)), i = 1, 2, 3, применим в Dk, k=l, 2, . . ., г,
с оператором А{к) (дц) формулу Грина
j [щу)А*\дуN\\\{у, х; D")-G$](y, x; &
Dk\W (x, e)
j {(у)Т^(ду, n)G$\(y, x
8)
- G{?! (j,, x; D") {Tw\dy, n) и (</))+} dyS. E.1)

476	ГРАНИЧНО-КОНТАКТНЫЕ ЗАДАЧИ ДЛЯ НЕОДНОРОДНЫХ СРЕД [рл# XII
Так как, по допущению, решение существует, то
Кроме того, нетрудно убедиться, что
A{k) {ду)Мг1 (у. *; Я(г)) = -^ grad div j}$) (у, К &'>),
где
8)
J
Dk\lll (xt 8)
Очевидно,
Hm J a
«-»°C< 8)
J
*, 8)
= a(x)lim J
Элементарные вычисления показывают, что
\L (Хо + 2il0) ii0 ц0 J °ч +
|у —дс| д\у — х\\ д	1
dy,	<fy; j а/г (?/) | г/ — л: I
1 Г
Н" L
2|х0) ц0J
cos
-hvk-	E-3)
Поэтому равенство E.1) принимает следующий вид:
-^ J и to) g^d div G|?l (y, x; D(r)) dy +
(dy, n) G|S| (у, л:; D«'>)-G{?| [T(ft)«(y)]+} d,5. E.4)
t=l, 2, 3; k=l, 2, ..., r, E.6)
где

5] функциональные уравнения гранично-контактных задач 477
В равенстве E.4) перейдем к пределу при е—»0; руководствуясь тем, что
Dk\?
lim I а (у) grad div G{?{ (у, х; D{r)) dy
в->° Dk\?Il (x, 8)
j
существует в смысле главного значения, получим
j а (у) grad div G}?} (у, x; Dir))dy
D
< (х) = -^f j «(У) grad div <?{?{ dy + J G|
+ J {4(?! [T^u]+-u+(y) [t^G®}} dyS. E.8)
Оставляя точку х в области Dk, применим формулу Грина в области D,,
j ф k, j = 1, 2, . . ., г, с оператором Аи> (ду) к векторам G(iJ(y, л:; D(r)) и
и (у); тогда получим
Di
(у, х; &г)) dy + ^ 6\°г\Ж1 >\у) dy +
+ \ [<ЗЭД (Г(/»«)+- «+ (у) (г('' G[?!)] d,S. E.9)
Складывая E.8) и E.9) для всех значений /, / ф k, получим
г
2
= ^ 77 J"{y) grad dlv ^(<?'(y> x; D(r)) dy+2
6=1
J {G}?|(rwa)+-u+(y).(TwG|S|)} dA jcgDb Л = 1	г. E.10)
С другой стороны, при фиксированной в Dk точке х справедливо соотношение
J {U-(y)T<0>G((?!-.Gffi [Twu}-}d,S+ J GfiHy, x; D<'>)ЯГ%)dy = 0.
D
m
US
fe=0
E.11)
Сложив равенства E.10) и E.11) и приняв во внимание контактные
условия на поверхностях Sk9 k = 1, . . ., г, и граничные условия на поверх-
поверхностях So и Sk, k = r + 1, . . ., m, получим
(х) = 2 -? J "(y)graddivG|?l (г/, х;
0=1
P=l Sp
Dkt &=1, ..., r; t = 1, 2, 3,	E.12)
y, n) = T{p) (dy, n) — T@) (dy, n),	^.13)

478	гранично-контактные задачи для неоднородных сред [рл# XI!
Hl (*) = - 2 J G«\F(P) (У) dvS + 2 J Г(Ч(?! /<Р) Of)
р-1 Sn	0 = 1 Sc
2 J 7'<0>GJ8/a,)d^+2jG}?|5r'"
S+ J G}?J5»@)(y)^. E.14)
До сих пор точка х была зафиксирована в Dkf k = 1, . .., г; теперь
поместим ее в области Do; тогда вместо формулы E.10), тем же путем,
получим
0 - 2 Т J uWP*AdlvG№ dy+%1 6\°г\^ (у)
P~l ° Dp
Выразим w (x) в Do с помощью формулы общего представления, напра-
направив положительную нормаль внутрь Do; будем иметь
2щ (х) = J [Г0) Ь\Ци-(у) — Gj?! (Г«" «ГJ
k=0
xeD0: t = l, 2, 3. E.16)
Складывая равенства E.15) и E.16) и принимая во внимание гранич-
граничные и контактные условия, а также граничные свойства тензора Грина,
получим
2иь (х) = J] —о J и (У) grad div Mil аУ —
° Dv
E.17)
где Ht (x) определяется в области Do формулой E.14).
Формулы E.12) и E.17) запишем в векторной форме. Для этого введем
матрицу
grad div Л = | grad div ЛA), grad div ЛB), grad div ЛC)|,
где А есть матрица

§ 5]	ФУНКЦИОНАЛЬНЫЕ УРАВНЕНИЯ ГРАНИЧНО-КОНТАКТНЫХ ЗАДАЧ	479
Тогда E.12) и E.17) запишутся в следующем виде:
г
в (ж)«(х) = 2 iJ- J terad div G(i) & x; D(r> )Yu W dy —
0=1	DD
-пухи	EЛ8)
где
lk9 x?Dk, k=lt . . ., г,
2%|o.	EЛ9)
Таким образом, доказана
5.1.	Теорема. Регулярное решение задачи A)+ есть решение функ-
функционального уравнения E.18).
5.2.	Замечание. Из вида уравнения E.18) ясно, что если значе-
значение и (х) найдено в Dk> k = 1, . . •, г, то значение в Do находится непосред-
непосредственно из E.18) согласно E.19).
5.3.	Замечание. Приведение к функциональным уравнениям за-
задачи (VI)+ формально выполняется согласно этой же схеме, так как тензор
Грина этой задачи — G[e\ (х, y\ D(r)) на поверхностях Sk, k = 1, . . , г,
обладает теми же свойствами, что и GjiJ (х, у, D(r)), а на поверхностях So
и Sk> k = r + 1, . . ., m, имеет свойства, вытекающие из самой гранич-
граничной задачи. На этом основании можно утверждать, что функциональным
уравнением задачи (VI)+ будет то же уравнение E.18), в котором тензор
G(i) U> У> D(n) следует заменить тензором G\q\ (x, y\ D(r)) и Н (х) считать
равным
(*) = 2 f J [71"» (дв, п) G<°>] 7(р) (У) dvS - J (G@) {у, х; D^yF^ (у) dyS +
p=i [sB	s0
[G\°6](y, x; Din)}'W»(y)dy)+ J G\§(y, x; №)Ж> (y)dy—
-jj Щ&. x; &r))Yf(y)duS+ 2 J [G(°)(t/, x; D^'f^d^. E.20)
Uo	D=r+lSp
5.4. Замечание. В частном случае, когда отсутствуют пустотелые
включения, г = т и D(r) обращается в Do — конечную область с грани-
границей So, тензоры G(ij и Gje} обращаются в тензоры Gjij (x, у; Do) и
GF) (^, ^/; ^о)« Если, кроме того, So расширяется до бесконечности, тен-
тензоры G[i\ и GF), как нетрудно убедиться, обращаются в Г@) (х—у), т. е.
в матрицу фундаментальных решений с постоянными Ламе Хо, fx0, и функ-
функциональные уравнения E.18), E.19) принимают вид
=2 iS" J[grad div r@> (x~y)r a {y) dy~
H(Jt), x€Dft, fe=l,..., m; E.21)

480
ГРАНИЧНО-КОНТАКТНЫЕ ЗАДАЧИ ДЛЯ НЕОДНОРОДНЫХ СРЕД [рл# XII
2и (х) = J] -^ J [grad div Г<°> (х — у)]'и (у) dy —
°
Dp
P=IS,
г@) С -
, * 6
E.22)
где
/*(*) = 2
J
J П°)(х — yKV<°){y)dg.
Как отмечалось выше, этот случай представляет особый интерес для
теоретической геофизики.
2. Вторая задача статики (П)+. Для приведения этой задачи к функ-
функциональным уравнениям, предположим сначала, что она допускает регуляр-
регулярное решение и (х) и G&] (х, у; D(r)) есть статический тензор Грина задачи
(И)+ для области D(r) с постоянными А,о и \х0. Мы знаем из главы VII, что
такой тензор существует в случае области, ограниченной одной замкнутой
поверхностью. Не представляет, однако, труда показать, что этот вывод
остается в силе и в том случае, когда область ограничена несколькими по-
поверхностями. Итак, будем предполагать, что G§\ (x, у; D(r)) удовлетворяет
условиям главы VII и уравнению той же главы.
Пусть x?Dk> k = 1, 2, . . ., г; применяя к вектору дЦ] (у, х\ D{r))
и предполагаемому решению и (у) формулу Грина в области Dk с операто-
оператором A(k) (ду), получим формулу E.1), в которой Gjij (у, х\ D(r)) заменен
на 0$ (у, х; D<").
Так как
-^ grad div Д<°) +^
равенство E.1) принимает вид
S
J и (у) grad div G<°> (*/, *; DM) dy +
Dk\LLl(x9e)
77
+ J G$](x, у;
Dk\m (Xf 8)
r)) ^(y) dy
= f {ы+
a,, n)

S 5|	ФУНКЦИОНАЛЬНЫЕ УРАВНЕНИЯ ГРАНИЧНО-КОНТАКТНЫХ ЗАДАЧ	481
Вследствие того, что характер сингулярности G^] (у, х\ DKf)) тот же,
что и у G(i) (уу х\ D(r)), дальнейшие преобразования совпадают с теми, кото-
которые применялись выше, и с учетом граничных условий на So и Sk, k =
= 1, . . ., m, приводят к зависимостям
г
8 (х) и (х) = ? -jj- J [grad div G<°> (у, x; D^)]' и (у) dy —
1 ° D
0=1
- 2 I [74")(ду, п)G<°>(у, х; DO)]'иг(у)dyS + H(x)+Jj ai%W» E.23)
/o=l 5~j	/==1
где
0=1
, x; D^)]'3ieM(y)dy)+ JG^>(x, y;
/, дг, О('))]7(у)^ + 2 1 [G$@, ^ Д(г))]70/)<*А E.24)
и uj — постоянные, причем
JW. / = 1, ..., 6.	E.25)
Так как вторая задача решается с точностью до аддитивного жесткого
смещения, эти слагаемые в уравнении E.23) можно отбросить.
Таким образом, доказана
5.5.	Теорема. Регулярное решение задачи (П)+ есть решение функ-
функционального уравнения E.23), определенное с точностью до произвольного
аддитивного вектора жесткого смещения.
5.6.	Замечание. Из вида E.23) ясно, что если значение и (х)
известно в Dk> k = 1, .- ., г, значение в Do находится непосредственно
из E.23).
5.7.	Замечани е. Если г = m, ToD(r) = Do и тензор G$) {x, у; D(r))
обращается в тензор G&) (х, у; Do).
5-8. Замечание. Используя тензоры Грина задач (П1)+ и (IV)+
для области D(r), можно получить аналогичные функциональные уравнения
для гранично-контактных задач (III) и (IV).
3. Смешанная гранично-контактная задача статики. До сих пор мы
предполагали заданными на границах So к Sk, k = r + 1, . . ., т, одни
и те же величины, а именно, либо смещения, либо напряжения, либо их
комбинации. Можно рассмотреть более общий случай, когда на различных
граничных поверхностях задаются различные величины; тогда будем иметь
смешанные гранично-контактные задачи и для этих задач также могут быть
составлены функциональные уравнения тем же путем. Формально это де-
делается во всех случаях одним и тем же способом; для конкретности мы огра-
31 В. Д. Купрадзе

482	ГРАНИЧНО-КОНТАКТНЫЕ ЗАДАЧИ ДЛЯ НЕОДНОРОДНЫХ СРЕД [рл ХЦ
ничимся выводом функциональных уравнений в том случае, когда гранич-
граничные условия имеют, например, следующий вид:
2)	u(y) = f(y), y?Sk, k = r+l, ..., rx
3)	(
где а (у) — неотрицательно определенная матрица; что касается контактных
условий на поверхностях Sk, k = 1, . . ., г, и дифференциальных уравне-
уравнений в Do и Dk9 k = 1, . . ., г, то они, разумеется, остаются без изменения.
Пусть Gcm (x9 y\ Din) есть тензор Грина для области D{r) с указанными
граничными условиями 1)—3) и с постоянными Ламе Хо, fi0. Такой тензор
был построен в главе XI. Он имеет на Skf k = 1, . . ., г, те же граничные
свойства, что и все другие встречавшиеся выше тензоры; поэтому, повторяя
рассуждения, аналогичные уже неоднократно приведенным, получим
г
8(х)и(х)= 2 -j-J- J [graddivG(°M>(#, x; D^)yu{y)dy-
°
_	xe I) Dk, E.26)
p=i
где
H(x)=X\\ \T@)Gi°J(y, x;
p==i
- J
+ J
D
J [GfJ (у, х; йЮ)\'Ж» (у)dy\
dp	.	)
, х; E*r>)]'f(M)dvS
l
l S
S lr| 2 )[?J(y, x; Din)]'f(y)dS.
p=r+l Sp	P=rt+l Sp
E.27)
Таким образом, доказана
5.9. Теорема. Регулярное решение рассматриваемой смешанной гра-
гранично-контактной задачи есть решение функционального уравнения E.26).
4. Гранично-контактные задачи колебания. Способ, которым гранично-
контактные задачи статики были приведены к функциональным уравнениям,
распространяется и на уравнение колебания. Это связано с тем, что, как
было показано в предыдущей главе, тензоры Грина для интересующих нас
граничных условий и для областей, ограниченных несколькими поверхно-
поверхностями, существуют для уравнения колебания при любых значениях пара-
параметра со2, за исключением некоторого дискретного множества, являющегося
совокупностью частот собственных колебаний. Поэтому в дальнейшем бу-
будем считать со2 отличным от собственной частоты рассматриваемой за-
т
дачи для области D(r) = (J Dk с постоянными Ламе %0, [i0. После этого
остается применить к тензору Грина рассматриваемой задачи и регулярному

Л 5]	ФУНКЦИОНАЛЬНЫЕ УРАВНЕНИЯ ГРАНИЧНО-КОНТАКТНЫХ ЗАДАЧ	483
решению задачи, существование которого пока предполагается, формулы
Грина точно так, как это делалось выше в статических задачах. Тогда каж-
каждый раз будем получать равенство E.1). В отличие от статических задач,
теперь в этом равенстве следут писать
)и(у) = —(о*и(уУ— Ж^(у\ y?Dkt k=l, . . ., г,
, x; D<'>; co) = -^ graddivG<°> — со2-K*-G<0> (#, х;
где G@> (у, х\ D^\ ю) есть указанный выше динамический тензор Грина.
Повторив затем те же преобразования, что в статическом случае, без вся-
всяких изменений, получим искомые функциональные уравнения.
Таким образом, справедлива
(О	О)	(О	(О
5.10. Теорема. Регулярные решения задач (I)+, (II)+, (HI)+, (IV)+f
(VI)+ и смешанных задач есть решения функциональных уравнений
у; DC); ©) и (y)dy-\-
¦^S- J [grad div G<°> ]'u (y) dy —
J+tf(x),x€D0U (^5^,E.28)
ft-1	r	E'29)
К 	 1, . . ., Г,
где под G@) (x, y\ D(r>; со) понимается динамический тензор Грина Соот-
Соответствующей граничной задаче для области D<r> с постоянными Хо, jx0,
а вектор Н (Н19 Я2, Я3) определен, например, в первой задаче формулой
E.14), во второй — формулой E.24), в шестой — формулой E.20) и в сме-
смешанной задаче, рассмотренной в п. 3, формулой E.27), причем каждый раз
в качестве тензора Грина берется соответствующий тензор G{0)(x, у; ?)(г>; <о).
5.11.	Замечание. Из E.28), E.29) следует, что, зная и {х) в Dk,
k = 1, . . ., г, значение и (х) в Do получается непосредственно из E.28).
5.12.	Замечание. Если г = т и So — расширяется до бесконеч-
бесконечности, то тензор G<°> (x, y\ D(r>; со) превращается в матрицу фундаменталь-
фундаментальных решений колебания Г@) (х — у\ со) с постоянными %0, \х0 и функцио-
функциональное уравнение E.28) принимает следующий вид:
2( jlf) J—у; co)u(y)dy
p=l	°
2 S
P=l ° Dp
~S~ flgrad div r<0) (x -
r
-2 Jl^(p)(^, п)Г<°)(х — у; a>)ra-(y)^ + «(x)t E.30)
31*

484	гранично-контактные задачи для неоднородных сред [рл XII
где
m
—у; co)Yf(P)(y)dyS— [г<°> (* — */; <x>)F(p) (у) djS +
sp
J r<°>(* — */; ©K»<P)(y)^)+ Jr<°> (* — //;
5. Теоремы эквивалентности. Для получения функциональных урав-
уравнений гранично-контактных задач мы делали предположения о существо-
существовании регулярных решений этих задач. Однако нашей конечной целью
является доказательство именно теорем существования для указанных за-
задач и функциональные уравнения служат лишь средством для достижения
этой цели. Таким образом, возникает задача доказать, во-первых, сущест-
существование решений полученных функциональных уравнений в классе
С1 (D) П С2 (D) и, во-вторых, показать, что эти решения являются вместе
с тем решениями соответствующих гранично-контактных задач. Сначала
займемся второй проблемой и назовем ее задачей эквивалентности.
Мы остановимся подробно на исследовании этого вопроса на примере
задачи A)+, как на типичном случае, и некоторые особенности, которые
характерны для других задач, укажем отдельно.
Итак, пусть уравнение E.28), где G@) = G\i], имеет решение и в классе
С1 (D) ПС2 (D), где D = D+U Do.
со
Покажем, что и (х) удовлетворяет всем условиям задачи A)+ (см. п. 1, § 1).
Пусть x?D0. Применяя оператор Л@) (дх, со) к обеим частям равенства
E.28), причем оператор вносится под знаки интегралов, и учитывая равен-
равенства
А{0)(дх, <b)G{?{(jc, у; D('\ о>) = 0, А@) (дх, со) [graddivG}?J]' -О,
А{0)(дх, о» [f*"'(dr n)G|?j]' = O,
а также формулу Пуассона, получим
), xeD0.	E.31)
Пусть теперь x?Dk, k = 1, . . ., г\ применив в Dk формулу Грина
с оператором A(k) (ду) к векторам и (у) и GJ?) (у, х\ D(r); со), i = 1, 2, 3,
получим формулу E.1). Эту формулу, далее, преобразуем так же, как
в § 5, п. 1, имея, однако, в виду, что теперь нельзя воспользоваться равен-
равенством
(ду) и(у) = — ^и {у) — 3»i*> {у);
поэтому получим
iА (х) = ^ J и {у) grad div G<o| dy — со* -jii. J и (у) Gj?> (x, у; D<'>; со) dy —
° Dk	° Dk
- J G(uH(/° (dy)u{y)dy+ J {g(o> [ Л*)м]+ —a+(y) [t<*)G}?) Jld^S. E.32)

К 5]	ФУНКЦИОНАЛЬНЫЕ УРАВНЕНИЯ ГРАНИЧНО-КОНТАКТНЫХ ЗАДАЧ	4g5
Оставляя точку х в области Dk и применяя формулу Грина в области D,,
j Ф k, j — 1, . . ., г, с оператором Л<» (ду), к векторам и (у) и
G[i\ (у, х; Dlr); со), будем иметь
r — u+(y) [T</)G(J)]}rf S. E.33)
Из E.32) и E.33) получаем
i Mdd ^S?! ^l 2 ? j
2 7Г	2 ?
0=1 ° Dp	o=l ° D.
Sv
, k=U . . ., n i=U 2, 3.	E.34)
Далее, при фиксированной в Dk точке х на основании E.31) можем
писать
J {[ ^<0) G\°]]'u-(y) - G<J) [Т<°> и (у)]'} duS + j G{?i (х, у; D^) ¦«) 5»(О q,) dy = о.
/г=0
Комбинируя это равенство с E.28), получим
2
г	m
+ 2 jG{?)[r<o)a]-rfvS- 2 J [T^G\o)yf{y)dS- j
P=l Sp	p=r+l Sp	So
— |G<iJ(*. У' Dln> в>K®{0) (у) dy + H (x), x<EDk, ft=l, 2	r

486	ГРАНИЧНО-КОНТАКТНЫЕ ЗАДАЧИ ДЛЯ НЕОДНОРОДНЫХ СРЕД [рл
и, наконец, комбинируя полученное равенство с E.34), переписав его в век-
векторной форме, будем иметь
г
2 \G\V)(X> У> Dir)'> ®)АМ(ду, <*)u{y)dy-Yi [
Р=1 Ор	р=1 Sp
г	г
- [ты и (у)\- \ dys + 2 J гт<о> am' (и- - и+) dys-%\ (т°&у f (у) d&s +
\ S	lS
J
So
2 J	y%
р=\ Sp	p=lSp
, y; D<o; ©)a»(O)(y)dy_Я(х) = 0, ^6^,, ^ = 1, ..., r. E.35)
Принимая во внимание значение Н (х), определяемое формулой E.14)
и переписанное предварительно в векторной форме, будем иметь
, ®)u{y)dy—
F@) Gm]' V — u+>> duS
P=lSp
r	r
+ 2
P=l Sp
- 2 J Go) (^ y; D(r); ®
1 D
Sp	P=l
Сейчас мы докажем, что равенство E.36) выполняется и в том случае,
когда x^D0. В самом деле, пусть x?D0; применим формулу Грина в Dkf
4= 1, . . ., г, с оператором A{k) (ду) к и (у) п G(i| (у, х; D{r); со); получим
T7 J [graddivG{O}]'a(y)^—c^S "^ J
- 2 I G((iiA(p) (<v«(у) ^ + S J
P=l Dp	p=l Sp
= 0. E.37)
С другой стороны, формула общих представлений дает
2ы(х)= J
т
+ G|?) (x, t/; D('); со) 5g@> (y) dy, x € Z)o.

Л 5]	ФУНКЦИОНАЛЬНЫЕ УРАВНЕНИЯ ГРАНИЧНО-КОНТАКТНЫХ ЗАДАЧ	487
Комбинируя это равенство с E.28), для хбА) получаем
г	т
1	° D	\
0)
Dp	р=\	Dp
-2
l
H(x)~ I [T^G\<}r\'f(y)dgS - 2 J
So	p=r+lS
и, наконец, комбинируя последнее равенство с E.37), получим E.36) при
D0, что и следовало показать.
Обозначим выражение, стоящее в E.36) слева, через Ми (х); будем иметь
0, xe(i Dk.	E.38)
Вычислив разности
(Ми)" — (Ми)+, (Г<0> Ми)' — (Г<°> Ми)+,
получим
k=l, 2, ..., г. E.39)
Поэтому E.38) принимает следующий вид:
j
G|O)(x, у; DO; со)[Л<*>(^, со) и (у) + 3g«» (у)] dy = 0
Отсюда с помощью формулы Пуассона получаем
AM (дх, со) и (х) = — Ж» (х\ xeDp, р = 1, 2, .. ., г. E.40)
Обращаясь к E.28) и учитывая свойства тензора Грина GjSj (x, y\ D(r); ю),
находим
Формулы E.31), E.39)—E.41) доказывают следующую теорему:
5.13. Теорема. Решение функционального уравнения E.28) класса
С2 (D) П С1 (D) в случае G@) = Gj?}, есть регулярное решение задачи A)+.
Приведенное доказательство теоремы эквивалентности сохраняется
без изменения для статической задачи A)+, так как и в этом случае суще-
существует (статический) тензор Грина G\\] (x, у; Dir)).
Далее, как уже было отмечено в начале настоящего параграфа, дока-
доказательство сохраняется для всех гранично-контактных задач, динамических
и статических, формально без всякого изменения, за исключением второй
статической задачи; в этом случае, вследствие того, что со = 0 является
частотой собственных колебаний для области D(r), заполненной однород-
однородной средой, доказательство теоремы экивалентности требует незначительной
модификации.

488	ГРАНИЧНО-КОНТАКТНЫЕ ЗАДАЧИ ДЛЯ НЕОДНОРОДНЫХ СРЕД [рл XII
Итак, пусть функциональное уравнение E.23) имеет в классе
С2 (D) П С1 (D) решение и. Как мы видели выше, при доказательстве
теоремы 5.13, решающим пунктом, на котором основывается все доказатель-
доказательство, служит утверждение о том, что в области Do, и (х), есть решение урав-
уравнения
А<°> (дх) и (х) = — Ж^ (х), х 6 А>.	E.42)
Поэтому и в данном случае следует прежде всего показать именно это.
Пусть x?D0. Действуем оператором А@) (дх) на обе части равенства E.23)
и примем во внимание, что (см. стр. 284)
б
AW(dx)G$\(x,y;Dir))= 2 %(х)* х(у),
Л@) (дх) [grad divG{2°! (У,х; ?>(г))]' = [S grad divffi(y) * xWJ = О,
S
E.43)
тогда будем иметь
2Л<°> (дх) и (х) = Л(°> (дх) Н (х), х б Do.	E.44)
Вычисляя значение Л@) (дх) Н (х) по формуле E.24) (для чего следует
использовать равенства E.43) и формулу Пуассона), получим
6	Г	г	г
%(х) — Ь J х(у)/7(р)(у)^5+ Zj J x
m
с k	с k	V f
+ J %(У)№[) (H)dy— J l{y)f{y)dyS— Zj J
Подставляя в E.32), находим
(д,) и (х) + 5»№) (х) = -f S X W 2 — 1 X (У) Рш (У) dyS +
+ j i (У) №Р\у) dyj + J[ х (У) ^@> (У) dy - ] X (У) / (У) dyS -
m	\
- S J %(y)f{y)dyS\

§ 5]	ФУНКЦИОНАЛЬНЫЕ УРАВНЕНИЯ ГРАНИЧНО-КОНТАКТНЫХ ЗАДАЧ	489
Таким образом, для того, чтобы выполнялось равенство E.42), необхо-
необходимо и достаточно соблюдение условий
г
S [- J X (У)Р{р) (У)dS+\ % {у)Ш»\у)dy] + J х(уK*со> (у) dy-
Р=1 [ Sp	Dp	J Do
-J %(y)f(y)dS- S J X(y)f{y)dS = O, ?=1,2,...,6. E.45)
So	P=r-f 1 Sp
Потребуем от данных задачи выполнения условий E.45).
Дальнейшие рассуждения, как уже отмечалось, дословно совпадают
с теми, которые применялись при доказательстве теоремы 5.13 и мы прихо-
приходим к следующей теореме:
5.14.	Теорема. Если выполнены условия E.45), то решение функцио-
функционального уравнения E.23) класса С2 (D) П С1 (D) есть регулярное решение
второй гранично-контактной статической задачи (П)+.
5.15.	Замечание. Сделаем относительно условий E.45) несколько
замечаний. Если отсутствуют включения, т. е. г = 0, то будем иметь вторую
(обычную) задачу для однородного тела, ограниченного несколькими поверх-
поверхностями, и условия E.45) обращаются в следующие:
i
т
к
X(y)^i0)(y)dy— Ь J X(y)f(y)dS = O, ?=1,2, . . . , 6, E.46)
о=0
т. е. в обычные необходимые и достаточные условия разрешимости.
Если г > 0, но F(p) (у) = 0, р = 1, 2, . • ., г, т. е. напряжения не испы-
испытывают разрывов вдоль контактных границ и во включениях отсутствуют
объемные силы, Ж{Г)) = 0, р = 1, 2, . . ., г, то условия E.45) прини-
принимают следующий вид:
т
j %(y)W°>(y)dy~l%{y)f{y)dS- 2 1
Do	So	o=r-\-l
~l%{y)f{y)dS- 2 1 X(y)f{y)dS = O, Ы	6,
So	o=r-\-l SD
E.47)
т. е., по существу, сохраняют характер предыдущих.
Если г = т и отсутствует So, то условия E.45) имеют вид
т
S Г—I
Г—I X (У)FlP) (У) dy + J % (У) Ж" (у) dy] +
+ IxU/)^(O)O/)^ = O, fc=l,2	6. E.48)
D-
Наконец, если в последнем случае Ж(р) = 0, и 5^<0) = 0, будем иметь
= O, k = 1, 2, . . . , 6.	E.49)
6. Гипотеза Коши. Изучение статических задач. Обобщенные решения.
Для большинства упругих материалов отношения -у- отличаются друг от

490	ГРАНИЧНО-КОНТАКТНЫЕ ЗАДАЧИ ДЛЯ НЕОДНОРОДНЫХ СРЕД (рл
друга незначительно. В свое время даже была принята гипотеза Коши
о равенстве коэффициентов Пуассона
E.50)
всех упругих тел.
Здесь будет рассмотрен этот случай, который имеет самостоятельное
практическое значение и важен также в теоретическом отношении, так как
исследование общего случая, как мы увидим, приводится к нему (см. п. 8).
В условиях гипотезы Коши уравнения, полученные выше, упрощаются.
В самом деле, теперь
Л<*> (дх) = JJ*. Л<°> (дх), Г<*> (дХ9 п) = В* Г«» {дХ9 а)9
Т^Цдг% п) = TW —7<°> = fAfe""fA° Г(°>.
v х ;	м-о
Поэтому функциональные уравнения задач (Г)+, . . ., (VI)+ принимают
следующий вид:
6 (х)и{х) = со2 ^ A — -g") J G<0) (х, у; D<o; со) и {у) dy —
где
2, xeD0,
и Я (х) в каждой задаче имеет свое (заданное) значение.
Для статических задач уравнение E.51) упрощается еще более и имеет
вид
S (х) и (х) = - ^ fcbL J [7«» (dg, n) GO) (у, х; Dw )Г «Г (у) d^S + Н (х),
Г
хе U О*.	E.52)
Согласно теоремам из III, § 1, п. 6, однородные гранично-контактные
статические задачи, кроме второй, допускают лишь нулевые решения, вто-
вторая же задача имеет ненулевое решение, являющееся жестким смещением.
На этом основании, в соответствии с теоремами эквивалентности, можно
утверждать, что однородные функциональные уравнения, соответствующие
уравнению E.52) для всех задач, кроме второй, имеют лишь тривиальные
решения»

§ 5]	ФУНКЦИОНАЛЬНЫЕ УРАВНЕНИЯ ГРАНИЧНО-КОНТАКТНЫХ ЗАДАЧ	491
Можно показать, что функциональные уравнения второй задачи E.52)
тоже допускают только нулевое решение. Допустим противное, пусть uQ
есть решение уравнения
8(х)ио(х)+ S^T1 j[T(O)Gll\]'uo(y)dyS = O, x^D*. E.53)
По теореме эквивалентности, ввиду того, что выполнено E.45), и0 (х)
будет решением второй однородной гранично-контактной задачи и, следова-
следовательно, по теореме единственности и0 (х) есть % (л:), где % (л:) — вектор же-
жесткого смещения. Представим это решение в виде
б
k
где х (*)» & = U • • «> 6, будем считать выбранными так, чтобы выполня-
г
лись условия ортонормировки в U Dkf что всегда можно сделать без огра-
«ичения общности.
Подставив в E.53) ио(х) = %(х), умножив скалярно fca %(x) и про-
г
интегрировав по области U Dh9 получим
г
¦k=0
Up —f
J Л f X (x) [Г@) (Э„ n) G® (у, x; DM)]' % (y) dyS=0; E.53')
как нетрудно проверить (см. (VII, 1.8)),
X W [Г@) (а„, п) G$ (у, х; D<'>)]' %(y) = {7 E„ /г)
кроме этого, согласно (VII, 1.7) имеем
J G{%' (х, у) х(х) rf х= J Gg}' (х, у) х (х) rfx = 0, k = ТТб,
следовательно, из E.53') получаем %(х) = 0*
Для дальнейшего существенно от функциональных уравнений перейти
к эквивалентным интегральным уравнениям. Это можно сделать путем пре-
предельного перехода в E.52) из Do к граничной точке на S^. Пользуясь форму-
формулами «скачков» для потенциала двойного слоя, из E.52) получим
и B) + ^ ?т^7 J ^@> (ду ")G<0) Of. * Dir) )У ""
й=1, 2, ..., г.	E.54)
Напомним, что в зависимости от выбора G@> и Н имеем все рассматри-
рассматриваемые задачи. Докажем следующую теорему:
5.16. Теорема. Всякому решению и~ (z) интегрального уравнения
E.54) соответствует определенное решение функционального уравнения

492	гранично-контактные задачи для неоднородных сред [рл XII
E.52) и и" (г) есть предельное на Sk, k = 1, 2, , . ., г, значение из Do этого
решения уравнения E.52).
Доказательство. Пусть и~ (z) есть решение интегрального
уравнения E.54). Построим вектор v (x), определенный равенством
6 (х) v (х) = — > ™-™ [Т<°> (д0, п) G<°> (t/, х; D<r>)]' ь
E 55)
тогда, на основании E.54) и согласно свойствам потенциала двойного слоя,
г
получаем it (z) = w" (г). Поэтому, а (х) = г/ (х), х? [} Dk, и мы убеж-
убеждаемся в равносильности интегрального уравнения E.55) и функционального
уравнения E.52).
5.17. Теорем а. Однородное интегральное уравнение, соответствую-
соответствующее уравнению- E.54), допускает лишь тривиальное решение.
Доказательство. Пусть Uq~(z) есть нетривиальное решение
однородного интегрального уравнения; согласно теореме 5.16 вектор
б (х)щ(*) = — ? !^=^ J [Г<°> {ду, n)G(O) (t/, x;
х? U D*
будет решением однородного функционального уравнения, соответст-
соответствующего уравнению E.52). Но, согласно теоремам эквивалентности и
единственности, это уравнение имеет только нулевое решение и, следо-
следовательно,
n) G@> {у'
откуда щ (г) = 0; теорема доказана.
Ядро интегрального уравнения E.54) в рассматриваемых задачах
имеет вид
где w (у, г) допускает слабую особенность. Поэтому эти уравнения отно-
относятся к классу сингулярных уравнений, для которых справедлива теория
Фредгольма при значениях параметра интегрального уравнения, принадле-
принадлежащих плоскости IT (см. гл. IV, § 7, п. 4). В данном случае IT есть комплекс-
комплексная плоскость с разрезами вдоль отрезков вещественной оси ( ^ тг~т> :t °°) >
где/0 = -т——^—. Параметрами, стоящими перед сингулярными интегра-
/l0 -f- Z\X0
лами в E.54), являются каждый раз множители ^/?~~*х° , k = 1, 2, . . ., г,
[1/ -j- [i0
которые по модулю меньше единицы, и следовательно, к этим уравнениям
применима теория Фредгольма.

§ 5]	ФУНКЦИОНАЛЬНЫЕ УРАВНЕНИЯ ГРАНИЧНО-КОНТАКТНЫХ ЗАДАЧ	493
Это позволяет на основании теоремы E.17) высказать следующее
утверждение:
5.18. Теорема. Неоднородное интегральное уравнение E.54) разре-
разрешимо для произвольной правой части.
Теперь мы можем сделать выводы. Если решение интегрального урав-
нения E.54) принадлежит классу С1» а I U Sk , то по теореме 5.16 решение
\k=i )
функционального уравнения E.52) существует и принадлежит классу
С*ф)[\ С1 (О).
Но в таком случае, по теореме эквивалентности, существует решение
соответствующей гранично-контактной задачи в указанном классе. Такие
решения задачи будем называть классическими.
Легко указать достаточные условия для существования классического
г
решения. Для этого достаточно, например, чтобы U Sk?JI2 (а), Н (г) ? Сх'а;
k=i
для того, чтобы обеспечить последнее условие, достаточно от данных задачи
потребовать соответствующую гладкость.
Если решение интегрального уравнения E.54) не обладает гладкостью,
необходимой для того, чтобы соответствующее решение функционального
уравнения принадлежало классу C2(D)fl С1 (D), то данная гранично-
контактная задача не имеет решения в классическом смысле.
В этом случае решение функционального уравнения будет обобщенным
решением задачи. Ясно, что, повышая гладкость данных, можно обобщенное
решение превратить в классическое.
7. Изучение динамических задач. Спектр собственных частот. Обобщен-
Обобщенные решения. Продолжая считать принятой гипотезу Коши, покажем, что
все однородные гранично-контактные задачи колебания в случае конечной
г
области U Dk имеют дискретный спектр действительных частот СОбСТВеН-
ных колебаний.
Для этого нам придется предварительно рассмотреть некоторые вспомо-
вспомогательные математические задачи, которые представляют не что иное, как
СО	СО	СО	СО	(О
задачи A)+, (П)+, (Ш)+, (IV)+, (VI)+, в специальном случае, когда параметр
<о = iv, где v есть произвольное положительное число. Прежде всего пока-
0 4-	Ю 4-
жем, что однородные вспомогательные задачи A)о , . . ., (VI)o не могут
иметь решений, отличных от нуля.
В самом деле, пусть и0 (х) есть произвольное решение некоторой из них.
К вектору и0 (х) и комплексно-сопряженному с ним вектору и0 (х) применим
формулу Грина
и0(х) А (дх)щ(х) dx=lu0(у) Т{дуу п)п0 (у)dS—\E(щ, и0)dx,
Г	S	D
где Е (и0, и0) — положительно определенная форма, определенная форму-
формулой (III, 1.6).
При этом указанную операцию в каждой из областей DkJ k = 0, 2 . . .
. . ., г, выполним с помощью операторов
г.

494	гранично-контактные задачи для неоднородных сред [Гл#
Учитывая равенства
р = и, 1, . . . , г,
контактные условия на Sk, k = 1, 2, . . ., г,
нулевые граничные условия на So и Sfc, ft = г + 1, . . ., т, а также на-
направления нормалей, после сложения полученных тождеств Грина будем
иметь
v2 J
J
U Dfe
откуда
a0W = 0, x? U Dkf
fe=0
что мы и утверждали.
С другой стороны, мы знаем, что вспомогательные задачи эквивалентны
функциональным уравнениям E-28), в которых вместо G@) (x, у; D(r>; со)
теперь надо писать G@>^ (х, у; D(r>; tv).
Поэтому однородные уравнения E.28), соответствующие уравнениям
E-28), допускают только тривиальные решения и, следовательно, неодно-
неоднородные уравнения разрешимы для произвольных правых частей, как это
было показано в предыдущем параграфе, путем перехода к эквивалентным
интегральным уравнениям.
Таким образом, все неоднородные вспомогательные задачи разрешимы.
Введем вспомогательный тензор Грина Н (х, у; iv), определенный
следующим образом:
хфу;
2)	AW(dX9iv)H(x9y;iv) = 0, x?Dk, &=l,...,r, x + y\
3)	Я" (z, y\ iv) = H+ B, y; iv), !T<*> Я (z, y; iv)]+ =
= [TWH(z9y;iv)}-9 zeSk, k=l9...9r9 хфу;
4)	на So и Sk, k = r + 1, . , ., m, выполняются граничные условия
00	CO	CD
одной из задач AH, (П)о, . . ., (VIH;
5)	H(x,y;iv) = TM(x—y;iv) — **Цх9у)9 x?Dh9 k = 0, 1, . . . , г,
где vW (х, у) — матрица регулярных решений уравнения Л<*> C^., iv) v{k) =
= 0, Г(/е) (х — у; /v) — матрица Купрадзе с постоянными Xk, \ik и пара-
параметром tv.
Из сказанного ясно, что построение тензора Я (jc, у; iv) сводится
к решению неоднородных вспомогательных задач, которые, как было пока-
показано, разрешимы. Таким образом, существование тензора Я (л:, у; iv) для
всех рассматриваемых задач доказано.
С помощью формулы Грина, как это делается, по существу, в простей-
простейшем случае функции Грина, можно показать, что
H(xiy;iv) = H'(y,x;iv).	E.56)

6 5]	ФУНКЦИОНАЛЬНЫЕ УРАВНЕНИЯ ГРАНИЧНО-КОНТАКТНЫХ ЗАДАЧ	495
Рассмотрим интегральное уравнение
H{x,y;iv)u(y)dy.	E.57)
Простой проверкой устанавливается, что его регулярные решения
удовлетворяют условиям:
2)	АЫ{дХ9(о)и(х) = 09 xeDk, А5=1,2	г;
3)	и+ = «г, (Г<*>и)+ = (Г<°> и)-;
4)	на So и Sk, k = r + 1, . . ., m, выполняются граничные условия
одной из однородных задач A)о, • • ., (VI )о > в зависимости от выбора
Н (ху у; /v). Без труда проверяется также обратное утверждение: регу-
регулярный вектор, удовлетворяющий перечисленным условиям, есть решение
интегрального уравнения E.57).
В силу свойств симметрии E.56), на основании теоремы Гильберта—
Шмидта, можно утверждать существование дискретного спектра действи-
действительных характеристических чисел уравнения E.57) и, следовательно, су-
существование дискретного спектра собственных частот однородных задач
О)	(О	Г
AM", . . ., (VI)o" в области U Dk.
Теперь мы можем перейти к изучению неоднородных задач A)+, . . .
О)
. . ., (VI)+, предположив, что со2 отлично от собственной частоты однород-
однородной задачи, соответствующей изучаемой.
Составив интегральное уравнение, получающееся из E.51) предельным
переходом из Dky k = 1, 2, . . ., г, получим
l
J|Т@) {д<"п) G<0> {y'z: D(r); <D)r""
p
^	, fe= 1, ... , r. E.58)
2 erSr	l^^
P=l °	Dp
Учитывая то, что со2 отлично от собственной частоты, подобно тому, как
это было сделано при доказательстве теорем 5.16—5.18, докажем теорему.
5.19. Теорема. Однородное интегральное уравнение, соответствую-
соответствующее уравнению E.58), допускает лишь тривиальное решение; неоднородное
уравнение E.58) разрешимо для произвольной правой части и его решению
соответствует определенное решение функционального уравнения E.51),
для которого решение интегрального уравнения служит предельным на Sk
значением.
Ясно, что и в данном случае из этой теоремы можно сделать те выводы,
которые в предыдущем параграфе были сделаны из теоремы 5.18. В частности
если решение интегрального уравнения E.58) не обладает такой степенью
гладкости, которая необходима для принадлежности решения функцио-
функционального уравнения E.51) классу С2 {D){\ С1 (D)y то рассматриваемая гра-
гранично-контактная задача не имеет решения в классическом смысле
и в этом случае решение функционального уравнения может быть принято
за обобщенное решение задачи.

496	ГРАНИЧНО-КОНТАКТЫБ1Е ЗАДАЧИ ДЛЯ НЕОДНОРОДНЫХ СРЕД [Гл. XII
8. Доказательство теорем существования в общем случае. В предыду-
предыдущих параграфах теорема существования решений гранично-контактных за-
задач была доказана при соблюдении гипотезы Коши, т. е. при допущении
неизменности коэффициента Пуассона для всех упругих тел. Теперь мы
отказываемся от этой гипотезы и, считая коэффициенты Пуассона различ-
различных тел произвольными, но достаточно близкими друг к другу, покажем,
что из предыдущего получается доказательство теорем существования для
всех гранично-контактных задач и в этом случае.
Предварительно преобразуем функциональное уравнение E.28), вос-
воспользовавшись тождествами
f <*) (дх, п) = -J- [((i* — щ) Т<°> (д,, л) + mkn (х) div), k = 1, 2, . . . , г,
г
и считая х? U Dk; в результате будем иметь
fei
H^2 t(l~f0) J
l	D
- i 2(fA* ~ ^o) i[r<o) g(o) r u"(j/) ^s+s S" i[grad div g<0) r u {y) dy~
° l	Sp	D=l ° Dp
r
~ i S m* Jfn (y) dlv G@) ]/ a"(y) d»s+я (x); E-59)
0 1 S
2
напомним, что здесь под G<°> и Я (х) понимаются выражения, соответствую-
соответствующие рассматриваемой задаче.
Ввиду того, что по предположению, mk, k = 1, 2, . . ., г — малые по
абсолютной величине числа, представим их в виде произведения mk =
= e-/ife, k = 1, 2, . . ., г, где 8 — малое действительное число, и решение
функционального уравнения E.59) ищем .в виде ряда по степеням 8
и(х)= ?е'а<'*> (*), х? [} Dkt	E.60)
;=о	k=i
где uW — неизвестные векторы. Предположим сначала, что ряд E.60)
сходится равномерно и сумма ряда, так же как векторы u(i\ принадле-
принадлежат классу Са\ U Ък |.
U=i /
Внеся ряд E.60) в равенство E.59) и сравнив коэффициенты при рав-
равных степенях е, получим
г
2 JS* и«> (х) = - J- ^ (»k — Vo) f l^°>0@) у [ttco
2
0=1	p
t = 0,1,2,...,	E.61)

? 5]	ФУНКЦИОНАЛЬНЫЕ УРАВНЕНИЯ ГРАНИЧНО-КОНТАКТНЫХ ЗАДАЧ	497
где
Q@)
г
(х) = 2 — J tgrad div G<°> ]' u< '-1
°
- -к- 2 n4[n (y) div G<0) Y [ua~
1 S
1 = 1,2,...	E.62)
Таким образом, мы пришли к рекуррентной последовательности задач,
рассмотренных в предыдущих параграфах (в случае гипотезы Коши).
В самом деле, система E.61) имеет тот же вид, что и система E.51), если
будет показано, что свободный член принадлежит О I U DfeJ; но это следует
из равенства
) = V Лё. [ [grad divG<°> ]f [ц<*> (у) —
(У)Г
: [} Dk)= max {|а^> (х)| + Л<'>}, * = 0, 1,...,
в справедливости которого нетрудно убедиться.
Далее, введем обозначение
где ЛA) — коэффициент Гёльдера для и^ в (J D^, и пусть р есть пока-
fe==i
затель Гёльдера для и@>. Очевидно, значения этих постоянных зависят
от данных задачи. Можно показать, что
Ml «<•>; U
W; [} Dk\ t = l,2,...t
fe=i /
где h — конечная постоянная, зависящая от р и (J Dk (см. Купрадзе [131,
Гогниашвили [И, Ж. Рухадзе [И).
Поэтому ряд
мажорирует ряд E.60) и, следовательно, последний абсолютно и равномерно
сходится для значений е, удовлетворяющих неравенству
|e|<ft-4	E.63)
32 В. Д. Купрадзе

498	ГРАНИЧНО-КОНТАКТНЫЕ ЗАДАЧИ ДЛЯ НЕОДНОРОДНЫХ СРЕД [рл#
Если ряд E.60) определяет вектор и (х) класса С2 (D)OC1 (D), то, под-
подставив его в E.28), найдем единственное решение задачи в классическом
смысле. Если же сумма ряда E.60) не принадлежит указанному классу, то,
оставаясь решением функционального уравнения E.28), и (х) не будет реше-
решением задачи в обычном смысле; в этом случае мы будем его считать обобщен-
обобщенным решением задачи.
9. Задачи для неограниченной области. До сих пор рассматривались
задачи для конечной области. Если So расширяется до бесконечности, то Do
т
обращается в ?3\ U &ь ее мы обозначим через D~. Гранично-контактные
условия на поверхностях SkJ k = 1, . . ., г, остаются прежние и граничные
условия на Sk, k — г + 1, . . ., га, также выбираются из уже известных
в той или иной комбинации. Область D(r), тензор Грина которой играет
существенную роль в предыдущем изложении, теперь обращается в беско-
т
нечную область ?>« = ?3\ U &k- Как мы уже знаем, в неограниченной
области к требованию регулярности нужно еще добавить требование удовлет-
удовлетворения условию излучения на бесконечности, чтобы обеспечить единствен-
единственность решения. При этом все однородные задачи допускают лишь тривиаль-
тривиальные решения.
В главе XI было показано, что для всех рассматриваемых граничных
задач (колебаний и равновесия) существуют тензоры Грина в области D»*
с постоянными Ляме Хо и Цо. Учитывая это обстоятельство, мы сможем
повторить рассуждения, которые применялись при рассмотрении задач в ог-
ограниченных областях и, таким образом, построить функциональные урав-
уравнения, аналогичные уравнениям E.28), в которых G@) (х, y\ DiT; со) обозна-
обозначает тензор Грина соответствующей задачи для неограниченной области.
В частности, когда г = га, т. е. когда нет пустотелых включений, вместо
G@) (х, у; D'iT; со) в функциональных уравнениях будет участвовать матрица
фундаментальных решений уравнения колебаний с постоянными Ляме Хо, ц0.
Из сказанного нетрудно заключить, что доказательства теорем существо-
существования, которые применялись в случае задач для ограниченных областей,
остаются в силе и теперь, и дают теоремы существования во всех случаях
для любого значения параметра со2.
В частности, вторая статическая задача для неограниченной области,
в отличие от той же задачи для конечной области, разрешима для произволь-
произвольных данных.
§ 6. Заключительные замечания
По теоремам существования для гранично-контактных задач теории
упругости в кусочно-однородных телах имеется немного работ. Одним из
первых, методом теории потенциалов и интегральных уравнений, исследо-
исследовал эти вопросы В. Д. Купрадзе (см. Купрадзе [131), который еще раньше
теми же методами изучал аналогичные вопросы для электромагнитных волн.
Дальнейшее развитие эти исследования по теории упругости нашли
в работах Башелейшвили, Гегелиа [11, Купрадзе, Бурчуладзе [31, Ру-
хадзе Ж. [1—53 и по термоупругости Jentsch [1], [9], [3].
Недавно эти же вопросы методами гильбертовых пространств, рассмот-
рассмотрел Фикера (см. Fichera [73).
В § 5 в пп. 1—9 теоремы существования были доказаны в условиях
гипотезы Коши. Распространение на общий случай приводит к условию
E.63).

§ 6]	ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ	499
Хотя в физическом смысле это условие не представляет существен-
существенного ограничения, проверка его связана с большими трудностями.
Этого можно было избежать, если бы теория Фредгольма была доказана,
например, для функционального уравнения E.28) или для соответствующего
интегрального уравнения. Это уравнение представляет собой нагруженное
сингулярное интегральное уравнение, причем присутствует интеграл по
объему (многообразие с краем) и интеграл по замкнутой поверхности ука-
указанного объема.
Поэтому представляет значительный интерес распространение теории
Фредгольма на такие уравнения.
Возможность такого распространения вероятна, на что указывает и тот
факт, что доказательство теорем существования, изложенное в §§ 2—4, не
требует никаких ограничений от постоянных Пуассона.
Из других задач, связанных с методами, изложенными здесь, представ-
представляют большой интерес гранично-контактные динамические задачи класси-
классической теории упругости, термоупругости и моментной теории упругости
для составных кусочно-однородных тел.

ГЛАВА XIII
РЕШЕНИЯ В ОБОБЩЕННЫХ РЯДАХ ФУРЬЕ
После того как произведен подробный математический анализ общих
вопросов теории граничных задач, следует выразить решения в таком виде,
который позволил бы применить их в практических расчетах. Одним из рас-
распространенных средств для достижения такой цели служит приближение
искомой функции с помощью некоторой совокупности других функций,
свойства которых хорошо изучены и которые достаточно просты. Эта идея
лежит, в частности, в основе метода Фурье. В этой главе мы изложим одно
видоизменение этого метода, основанное на той же идее, но как расчетный
способ, обладающее большей эффективностью, чем обычный метод Фурье.
Если исключить небольшое числе частных случаев, когда классический
метод Фурье вполне эффективен как расчетный метод, значение его в этом
смысле следует признать ограниченным. Применение метода Фурье для ре-
решения граничных задач предполагает разложение искомой функции по эле-
элементам базисной системы функции, которые в общем случае сами являются
решениями не менее сложных граничных задач и численная реализация ме-
метода возможна лишь при условии знания собственных функций и собственных
чисел этих задач.
Видоизменение, которое будет описано ниже, и которое назовем мето-
методом обобщенных рядов Фурье, свободно от этих черт неэффективности и
позволяет, непосредственно из данных задачи, конструировать необходимую
базисную систему и коэффициенты разложения.
Благодаря этому решения, получаемые обобщенным методом Фурье,
используются и для построения приближенных численных решений. Важно
заметить, что для нового метода характерна такая общность, которая позво-
позволяет применять его для решения разнообразных задач, в том числе и тех,
которые пока не поддаются решению другими методами (см. Купрадзе и др.
{11, стр. 472); при этом достигается хорошая точность, подтверждаемая
сравнением приближенных значений, даваемых этим методом, с точными
решениями, которые известны заранее.
Значение подобных сравнений, разумеется, относительно, и полное ре-
решение вопроса о достоинствах нового метода как расчетного, может быть
получено только установлением точных формул для оценок приближения.
Такими формулами мы еще не располагаем, и в настоящее время об обобщен-
обобщенном методе Фурье в этом смысле можно сказать лишь то, что известно вообще
о представлении решений граничных задач рядами по полным системам
функций, ортонормированных в некоторых функциональных пространствах.
Эти вопросы требуют дальнейшего изучения и могут привести к важным
дополнениям метода.
Применения для решения различных задач имеют стандартный харак-
характер и мы остановимся лишь на некоторых типичных задачах, ограничив-
ограничившись краткими указаниями относительно других.

§ Jj ПЕРВАЯ И ВТОРАЯ ОСНОВНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ (СТАТИКА) 501
§ 1. Первая и вторая основные задачи
теории упругости (статика)
1. Теорема о полноте для задачи A)+. Пусть D+ есть область, ограни-
ограниченная поверхностью S и S? Лг (a); D" — дополнение D+[} S_jxo ?3- Пусть
и (х) есть ([произвольный регулярный вектор класса С1 (?>+) f] С2 (D+).
Согласно (III, 2.5) можем записать
б(х)и(х)= [Т(х — у) [Т(ду9 п)и(у)]+ dyS — J [Т(ду9 п)Т(х — у)]' и+ (у)duS -
— y)A(dy)u(y)dy, A.1)
J
где
0, x?D~.
Допустим, что и (х) есть регулярное решение первой внутренней задачи
статики A)+. Тогда A.1) принимает следующий вид:
=1т(х — y)cp(y)dyS — F(x)9 xeD\	A.2)
F(x), xeD~,	A.3)
где
) = 1Т(ду9п)и(у)}+,
A.4)
Пусть S' есть произвольная гладкая замкнутая поверхность, охваты-
охватывающая S и не имеющая с ней общих точек. Конечную область, ограничен-
ограниченную поверхностью S', обозначим D'. Пусть {x*}?Li — счетная совокуп-
совокупность точек на S', распределенная всюду плотно.
1.1. Теорема. Счетная совокупность векторов {T(t) {xk — y))t=\>
i = 1, 2, 3, — линейно независима и полна в пространстве L2 (S).
Доказательство, а) Линейная независимость.
Пусть
3 N
где cik — постоянные, N — произвольное натуральное число.
Рассмотрим вектор
v(x)= S S cikT(i) (xk—x)t хе D\
Очевидно, этот вектор есть регулярное решение задачи для D+:
A(dx)v(x) = 0, v+(y) = O, yeS,
и по теореме единственности III, 1.6 равен нулю в D+. Вследствие аналитич-
ности в /У, отсюда следует v (х) = 0, x?D\ или, в проекциях,
3 N
S 2 СиГц(# — х) = 09 /=1,2,3; xeD'.

502	РЕШЕНИЯ В ОБОБЩЕННЫХ РЯДАХ ФУРЬЕ	[рл XIII
Приближая переменную точку х из D' к произвольно выбранной на S'
точке xk° из множества {xfe}?Li тремя разными путями так, чтобы обраща-
обращались в нуль соответственно '* л~~~х , i = 1, 2, 3, заметим, что в матрице
OXi
jp (xk,, — х} согласно (II, 1.3) одно слагаемое в каждой проекции, а именно
ClkoTll (Xk° — X), C2k0T22 (Xk« — Х\ Сз
неограниченно возрастает по модулю, в то время как другие слагаемые
остаются при этом ограниченными. Это возможно лишь при условии cikb = О,
i = 1, 2, 3; ввиду произвольности точки xko на S' это доказывает линейную
независимость совокупности
б) Полнота. Пусть А,(#)? ^2 (S) есть произвольный вектор. Так
как L2 (S) — полное гильбертово пространство, необходимое и достаточное
условие полноты совокупности A.5) состоит в том, чтобы из условий орто-
ортогональности
= 0, 1 = 1,2,3; 6=1,2,...	A.6)
вытекало почти всюду на 5 равенство X (у) = 0.
Рассмотрим потенциал
V(x;l)=\T(x—y)X{y)dyS.
Согласно условию A.6) и выбору точек хк ? S' будем иметь
В области E3\D' потенциал V {х;Х) представляет регулярное решение
однородной задачи
А (дх) V (х; X) = 0, х 6 E3\D\ V (х; I) \s- = 0,
и по теореме единственности V (х\ Я) = 0, x?Es\D'.
Отсюда вследствие аналитичности в D~ имеем V (х\ К) = 0, х 6 D~y и,
следовательно, [Т (дуу п) V]' = 0. Но последнее условие согласно свой-
свойствам потенциала простого слоя равносильно интегральному уравнению на S,
b(z)—\T(dz,v)T(z—y)X(y)dyS =
и по теоремам вложения главы IV, § 6, п. 2 всякое решение его, класса L2(S),
есть элемент класса С0'а (S). Ввиду непрерывности потенциала простого
слоя с плотностью из класса С0» а (S) отсюда получаем
и по теореме единственности III, 1.6, окончательно будем иметь V (х; X) = 0,
x?D+. Поэтому К (у) = 0; это доказывает полноту совокупности A.5) и
теорема 1.1 доказана полностью.
2. Первый способ (задача I). Перенумеруем элементы совокупности A.5)
следующим образом:
\
- у), ?=1,
A.7)

Л 1] ПЕРВАЯ И ВТОРАЯ ОСНОВНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ (СТАТИКА) 503
где lk = k—3 |--ir-| и f^J — обозначает наибольшую целую часть
числа k.
Вместо совокупности A.7) введем новую, эквивалентную совокупность
п—г
(У) = ^A) (У\ <»{п) (У) = ^(п) (У) - S Сял
fei
где коэффициенты cnk определяются условиями ортогональности
тогда
I i[^n* (у) g>*;) (у) dS — сп: I I (oiM (у) |2 dS = 0.
s	s
Ввиду линейной независимости векторов г|э<Л> (у), вектор со^> (у) отли-
отличен от тождественного нуля; поэтому
J ${п) (у) в>и) (У) <Я
cni = —.	, /= 1, 2,...,я— 1; n=lf2,.#.
J \v"Hy)\*dS
5
Наконец, пусть
Очевидно, бесконечная система
{q><ft>(*)}?-ь у€5	A.8)
полна в Lt (S) и ортонормирована на 5. Очевидно также, что
Фй)(г/)=2аьГ'A/). 6=1,2,...,	A.9)
где aks — известные коэффициенты ортонормирования.
Содержание первого способа состоит в следующем: неизвестный вектор
Ф (у) представляется рядом Фурье по элементам системы A.8), т. е.
со
Ф@)~ S ®т?тЧУ),	A-10)
где
|, m=l,2f...	AЛ1)
есть коэффициенты Фурье, которые определяются функциональным уравне-
уравнением A.3).
Действительно, поскольку A.3) имеет место для всех x?D~, можем
писать
|	F(x% /=1,2,..,	A.12)

504	РЕШЕНИЯ В ОБОБЩЕННЫХ РЯДАХ ФУРЬЕ	[Гл. XIII
Перепишем A.12) в виде
3
dS = F(x% *=l,2f...	AЛЗ)
где /* есть орт координатной оси Oxky k = 1, 2, 3.
Пусть т — произвольное натуральное число и s = I™% 1- Найдем
значение коэффициента Фш. Умножим A.13) скалярно на вектор
и просуммируем по f от 1 до s, имея в виду, что можно считать, по опреде-
определению,
<**.* = 0 при &>/п;
тогда получим
S ^3(^i)+^)(^-i/)9(y)dS= У Лт1>(Л	A.14)
i
Из A.7) очевидно, что
Г(к)(х1-у) = ^ц-1)+к{у), *= 1,2,3; /-1,2,...
Поэтому A.14) принимает вид
ffS iam93ii^)^ii-l)+\y)}^(y)dS=^AmiF(xi). A.15)
J U=l i=l	J	г==1
S
Но легко убедиться, что
и на основании A.9), A.11) имеем из A.15)
= t AmiF (x%	A.16)
:1
где m=l, 2, ... и s = \ l I. Таким образом, коэффициенты Фурье
найдены.
Рассмотрим вектор
N
~	'	xeD+, A.17)
где N — произвольное натуральное число; покажем, что он представляет
приближение к точному решению в смысле равномерной сходимости при
N —> сю в произвольной замкнутой области, лежащей внутри D+. Для этого
составим разность
(N	\
ФЫ — Zj фк<Р(к)(У)
Gi	J

§ 11 ПЕРВАЯ И ВТОРАЯ ОСНОВНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ (СТАТИКА) 505
и оценим ее модуль по формуле Коши—Буняковского
Г(<)(ж-у)[ф(у)-
2
•=1
2
(=1 S
- g Ф*Ф(*> (If) j I djS <4
3
Г«> (х-
g { j
X
/г=1
Вследствие того, что интеграл
X
2	Н/2
равномерно ограничен в D#, где D^cz D+, и так как ввиду полноты системы*
A.8)
I	N
lim [ ф(у) —2 Ф*Ф(ЛH
имеем
Заметим, что uN (x) есть регулярное в D+ решение уравнений статики
А (дх) и = 0 для любого N.
1.2. Замечание. Мы рассмотрели внутреннюю задачу. Все ска-
сказанное сохраняет силу для внешней задачи (I)". Но вместо A.2) теперь бу-
будем иметь
2и(х) = [Т(х —
где
= 1Т(ду, n)u(y)]~9
Кроме того, и это существенно, вспомогательная поверхность S' теперь
должна быть выбрана строго внутри D4" и счетная совокупность точек {**}j!Li
взята на этой поверхности. При этих условиях доказательство теоремы, ана-
аналогичной теореме 1.1, не представляет особого труда.
Опираясь на эту теорему, можно построить решение подобно тому как
это было сделано для задачи A)+.
3. Второй способ (задача I). Пусть и(х) есть решение задачи A)+;
тогда

506	РЕШЕНИЯ В ОБОБЩЕННЫХ РЯДАХ ФУРЬЕ	[Рл# XIII
будет решением задачи
A(dx)v(x) = 0, x?D+; v+(z) = ?2(z)t zeS,	A.19)
где
T(z — yJ№{y)dy.	A.20)
D+
Согласно (VII, 1.12), решение последней задачи представляется фор-
формулой
= — \ [T(dyj n)G(i, (у, x)YQ(y)dyS, хе&9	A.21)
где G(i)(x, у) есть тензор Грина.
Так как Q (y)?L2 (S), в силу теоремы 1.1 можем писать
Й (у) ~ S
k
Рассмотрим вектор
V? (х) = S Й*Ф<*> W = S Q* S a^(s) (х) = S S
fe=l	fe=l s=l	fe=l s=l
A.22)
и покажем, что он является приближенным (в смысле равномерной сходи-
сходимости) решением задачи A)+.
Прежде всего из вида вектора vN(x) ясно, что он решает граничную
задачу
Но решение этой задачи согласно A.21) представляется формулой
(у, х)}'
B
На этом основании, составив разность | v (х) — vN (x) \ и применив
неравенство Коши—Буняковского, так же как выше, найдем
v(x) = lima^ (л:);
N->co
наконец, из A.18) имеем
u(x) = limv»(x) + ± \T(x—yJe(y)dy, x?D\
Это и есть искомое решение.
Ясно, что описанный способ применяется, с очевидными изменениями,
и для решения задачи (I)".
4. Третий способ (задача I). В функциональном уравнении A.3) заме-
заменим интеграл по S суммой по какой-либо формуле механических квадратур;
при этом получим
Ъ ANkY{x — ykL>{yk) = F(x), xeD',	A.23)

R l] ПЕРВАЯ И ВТОРАЯ ОСНОВНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ (СТАТИКА) 507
где Аи — заданные числа и ук, k = 1, 2, . . ., N9 — определенные для
данной квадратурной формулы точки на S; так как равенство A.23) спра-
справедливо для любого jcgZ>", переменной х придадим Af произвольных зна-
значений из D":
х'б?Г, i=l,2,...,tf;
тогда A.23) обратится в систему алгебраических, линейных относительно
tp (yk), уравнений
2
или, в проекциях,
S ? A%TiM(xi—tfLm(llk) = Fi{xt)% f =1,2	ЛГ; /=1,2,3.A.24)
fes=l m=l
Это — система 3N уравнений с 3N неизвестными
Ч>т(УкЪ m= 1,2,3; k= 1, 2 ,..., N.
Найдя отсюда неизвестные и подставив их в A.2), где интеграл заменен
суммой по той же формуле механических квадратур, получим для прибли-
приближенного решения выражение
2uN(x)= S ANkT{x — /)Ф(/) — F(x\ x?D\	A.25)
В вычислительном смысле этот способ проще предыдущих, но здесь
не исследован вопрос о сходимости процесса.
1.3. Замечание. При использовании первых двух способов мы
применяли полную ортонормированную систему векторов; можно, однако,
воспользоваться и первоначально заданной неортогональной системой A.7).
В самом деле, определим постоянные bk из условия
IN	II
Ф (У)— S М>(/0 Щ =min	A.26)
k=i	IIl2 (S)
при фиксированном N. Отсюда обычным путем получаем
N
/г=1
или, согласно A.7),
/г=1 S	S
С другой стороны, из A.12) имеем
= Fm(xk)> m= 1, 2, 3; k =
Следовательно, коэффициенты bfe должны быть найдены из системы
уравнений
2 [	и	A.27)
t [f±2]\
которая, по известным свойствам линейно независимых векторов, однозначно
разрешима.

508	решения в обобщенных рядах фурьв	[ГЛв XIII
Заметим, что, как мы видели, обобщенный полином
N
2
61
где ф(/г) (у) определены из A.9) и составляют ортонормированную систему,
а Фк — коэффициенты Фурье вектора ср (у) по этой системе, — удовлетворяет
условию A.26). Но в L2 (S), как строго нормированном пространстве, суще-
существует единственный обобщенный полином наилучшего приближения;
поэтому
S ф*ф(*> (</)=? M>(fe)G/)= S
fe=l	/г=1	fe=l
и, следовательно,
N
6S= S flikgO*. s=l, 2	JV.
/e=i
Иногда при рассмотрении первой задачи интересуются лишь граничным
значением напряжений; тогда полезно воспользоваться указанным выше
приемом, который дает почти всюду значение ф (у) = Ти (у), y^S, непо-
непосредственно, без решения задачи. Этим же приемом можно воспользо-
воспользоваться и для решения первой задачи. Найдя постоянные ck из условия
II	? * II
/ (У) — S^Vt (У)\ = т*п> гДе / есть граничное значение и, и заметив,
что согласно A.2 Г) имеем
N	N
и» (х) ее V 4 (х) = - ^ J (Щ (у, х)У V
1	S	1
можем писать
1^
1
где и (х) — решение задачи. Отсюда с помощью неравенства Коши—Буня-
ковского получаем
V х 6 D^ciD+: Hm uN (x) = u (*)-.
N-*co
5. Теорема о полноте для задачи (Н)+. Согласно формуле A.1) для
задачи (И)+ имеем
?D+; A.28)
\yj	A.29)
где теперь
= \T(x—y)f(y)dyS- ^T(x—yKV{y)dy. A.30)
Вместо теоремы 1.1 здесь используется
1.4. Теорема. Счетная совокупность векторов
{T(dy,n)T(i)(xk — yh x'(if)}*U, '=1,2,3; / = 1	6,

Я ]] ПЕРВАЯ И ВТОРАЯ ОСНОВНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ (СТАТИКА) 509
где ху — ортонормированные на S векторы жесткого смещения, линейно
независима и полна в L2 (S). Здесь (г^}Г==1 6 S' — произвольная, счетная,
всюду плотная на S' совокупность точек, S' cz D".
Доказательство, а) Линейная независимость.
Пусть
S S сшт(дд, п)г("(**—у) + ? са(у) = о, yes,
i=\ k—l	k=\
где cikJ ck — постоянные и N — произвольное натуральное число.
Рассмотрим вектор
Он удовлетворяет условиям
Отсюда по теореме о необходимых и достаточных условиях разрешимости
эадачи (П)+ имеем
6
jii	= -c<t / = l,2 ,..„6.
Поэтому (Tv)+ — 0, и, следовательно,
v(x) = S S @(/ ) S
l fe
где af — определенные постоянные. Очевидно, теперь можно повторить рас-
рассуждения, которые применялись при доказательстве теоремы 1.1, и так же
как там, приходим к выводу, что все cik = 0, cf = 0.
Этим линейная независимость доказана.
б) П о л н о т а. Пусть X (у) ? L2 (S) есть произвольный вектор и пусть
Т {ду, п)Г^(х* -У)Ь(У)<1у$ = <>> t = l,2,3; Л—=1,2,... A.31)
Рассмотрим потенциал двойного слоя
W(x; Я)= J [Т(дУ9 n)T(x—y)YX(y)d!/S.
В силу A.31) и так как точки xk всюду плотно покрывают поверхность S',
имеем W (х; X) = 0, **€«?'• Отсюда jto теореме единственности для задачи
(II)" получаем W (x;^,) = 0, x?Es\D' и, также как выше (см. доказатель-
доказательство полноты в теореме 1.1), будем иметь
Отсюда [Т {ду9 п) W (у; Х)\" = 0 и по теореме VII, 2.1

510	РЕШЕНИЯ В ОБОБЩЕННЫХ РЯДАХ ФУРЬЕ	[Гл#
Согласно теореме единственности для задачи (П)+ получаем
Составляя разность W~—W+ и принимая во внимание значения W (х9
в D+ и в D", получаем
Но согласно A.32)
б
jiS = -ip?, /=1.2,..„6,
и окончательно, К (у) = 0. Полнота, и тем самым теорема 1.4, доказаны.
Перенумеруем элементы совокупности {Т (дд9 п) Г(о (xk—*/)|Г=и
I = 1, 2, 3, следующим образом:
/ Г*±Е1 \
Ъ{к)(у) = Т(д,9п)ТЫ\х1 6 -у), fe=l,2f...
и ортонормируем систему {tyik) (y)}k=i; получим {у{к) (у)}Г=ь где
к
S (s)U/)> ft=l, 2„..	A.33)
s=l
и &?S — известные коэффициенты ортонормирования. Покажем, что, при-
присоединив к совокупности A.33) полную совокупность векторов жестких
смещений {% (у)}/=!, ортонормированных на S, получим полную ортогональ-
ортогональную систему. Очевидно, для этого достаточно показать, что
(	= 0, fe=l,2,w,,; /= 1. 2	6.
s
Но это вытекает из формулы общего представления, написанного для
вектора % (х), так как хк ? D" и
0, i= 1,2,3; / = 1, 2,..., 6; k= 1. 2 f...
6. Первый способ (задачи (Н)+ и (Л)"). Представим неизвестный век-
вектор ф (у) рядом Фурье
где
<Dm = | ^m)(y)(p(y)dSJ m= 1, 2,mmm9	A.34)
j= 1. 2	6.	A.35)
Коэффициенты Фт, т = 1, 2, . . ., определяются из функционального
уравнения A.29), а Ф_Л, & = 1, 2, . . ., 6, остаются неопределенными.

Я I] ПЕРВАЯ И ВТОРАЯ ОСНОВНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ (СТАТИКА) 51I
Читателю нетрудно убедиться, что, повторив рассуждения, приведенные
при выводе формул A.12)—A.16), теперь получим
Фт=ЪВшР(х'),	A.36)
1=1
где
Bmi = Ьт%з^/1 + Ьт%Ы_ХР + bmt3lЛ s = р±? ] , т = 1, 2,.,,
Рассмотрим вектор
S
S -^ (У)) d,S +1F (х), A.37)
*=i	/
где N — произвольное натуральное число. Тогда, так же как выше, найдем
u(x) = limuN(x)9 xeD*>	A.38)
N
где uN (x) задается формулой A.37), которая согласно формуле общего
представления для вектора жесткого смещения, запишется еще в следующем
виде:
N
, п)Г(х — у)}' ^ Ф*Ф<*> (y)dyS + ^
S	fe=l	k=l
Отсюда следует, что найденное приближенное решение определяется
с точностью до аддитивного жесткого смещения. Задавая дополнительные
условия, обеспечивающие единственность решения задачи, приближенное
решение определим однозначно. Например, считая заданными дополнительно
условия ортогональности
= 0, /5=1,2,,,., 6,
будем иметь Ф_к = 0, и приближенное решение uN (x) определяется одно-
однозначно.
Мы рассмотрели задачу (П)+. Конечно, при этом предполагалось, что
задача имеет решение; без такого предположения мы не могли пользоваться
функциональными уравнениями A.28), A.29). Но предположение существо-
существования решения, как мы знаем из главы VI, накладывает на данные задачи
определенные условия типа ортогональности.
В задаче (II)" таких условий, как известно, нет; она разрешима всегда.
В связи с этим теперь полной системой будет
)Z=u t = 1,2,3; yeS,
где xk ? S' и S' расположена строго внутри D+. Других особенностей по
сравнению с внутренней задачей здесь не имеется; приближенное решение
строится так же как выше, и определяется однозначно.

512	РЕШЕНИЯ В ОБОБЩЕННЫХ РЯДАХ ФУРЬЕ	[Гл# XIII
7, Второй способ (задача II). Пусть и есть решение задачи (П)+, тогда
v(x) = u(x) — ± JT(x — yK»Uf)dy	A.39)
D+
будет решением следующей задачи:
А (дх) v(х) = 0, х 6 D+; \T (dB, v) v(z)\+ = Q (г),	A.40)
где
Q(г) = /(*)-! |(Т(аг,г)Г(г — y)K№(y)dy.
D+
Ввиду того, что Q (г) ?L2(S), на основании теоремы 1.4 можем за-
записать
со	6	b
?2B)= Xj "Ь^ф^ ' (Z) —|- ^J u2
fe=l	/г—1
где
й=1, 2М>.,
Q_^= \x(z)Q(z)dSy &=1,2,,..,6.
Покажем, что
Q.k=\f(z)%(z)dS—i
j
Так как
— y)Y%(z)d2S,
5
будем иметь
Q-* = J / (г) X (z) rfS + | 5» (y) % (y) rfy.	A.42)
Но условие, необходимое и достаточное для существования решения,
дает
\
\f(z)%(z)dS+ \3%(y)%(y)dy = 0, 6=1,2,. «.,6,	A.43)
5	D+
и поскольку существование решения предполагается априори, условие
A.43) выполнено и, следовательно,
Q_fe = 0, ? = 1,2, . ...6.
Построим вектор
N k	/ rs-4-21	\
V (х) = S S Qik6*sr(le) U1 3 J — х j,	A.44)
fel l
s=l
и покажем, что этот вектор равномерно стремится к точному решению за-
задачи (Н)+ при N —> оо.

К ] J ПЕРВАЯ И ВТОРАЯ ОСНОВНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ (СТАТИКА) 513
Из вида vN (x) ясно, что он удовлетворяет условиям
N
А (дх) -> (х) = О, х6 ?>+; {^ (ду% п) vN (у)\+ = Jj Q*cp<*> (у), yGS.
л/
Очевидно, вектор 2 ^^Ф(/е) (^/) удовлетворяет условиям разрешимости.
Согласно (VII, 1.12') точное решение задачи имеет следующий вид;
6 к
2v (х) = J GB) (х, у) Q (у) dyS + ? ад (*),
где
Jk
v{y)%{y)dy,
и аналогично,
Л/	6
' (а:) = J GB) (х, у) 5] ^ф(Л>) (У) ^5 + ^] bk% (x), х6 />+^
где
Пусть ck = bk — ak; рассмотрим выражение
6 ft	Г	N
— v* (x) + 1 2 с, х (х) = j j GB) (*, ») Q (У) — 2
fe=l	S	L	fe=i
и оценив его модуль при помощи неравенства Коши—Буняковского, полу-
получим
1 ? *
v(x) = lim vN (x)	2~ 2jCk% (x)>
и, наконец, из A.39) имеем
Внешняя задача, которая разрешима всегда, решается вполне анало-
аналогично.
8. Третий способ (задача II). Заменив в функциональном уравне-
уравнении A.29) интеграл по S суммой согласно какой-либо формуле механических
квадратур, получим
|t AiN) [T (dyk, n (yk)) Г (*-/)]' Ф (/) = F (х), х 6 D',
где значение различных символов то же самое, что и в формуле A.23).
Далее, поступая так же, как выше, при пользовании третьим способом,
придем к системе из 3N линейных алгебраических уравнений относительно
неизвестных
S ? ЛГГтГ/т(х'-/)Фт(^)=Л(х0, / = l,2f3;*=l,2,...,tf.A.45)
fe=l OT=1
33 В. Д. Купрадзе

514	РЕШЕНИЯ В ОБОБЩЕННЫХ РЯДАХ ФУРЬЕ	[Рл XIII
Разрешимость этой системы обусловлена теоремой существования ре-
решения задачи (Н)+.
Найдя отсюда неизвестные ц подставив их в соотношение A.28), кото-
которое предварительно представляется суммой по той же формуле квадратур,
будем иметь для приближенного решения следующее выражение:
2м" (х) = - g ЛГ [Т (dyk, п (/)) Г (х—у*)}' Ф (ук) + F (х), х 6 D+.
Однозначность решения можно обеспечить условиями нормировки
(VII, 1.13).
§ 2. Другие задачи (статика)
1. Задачи III и IV. Граничные условия третьей внутренней задачи (Ш)+
(см. гл. I, § 14, п. 1) имеют следующий вид:
)
[Т (дгу п (г)) и (г)Г — п (z) [Т &, п (z)) и (z))+n = f (z), j
гДе [•••]/! обозначает здесь проекцию на направление нормали вектора, стоя-
стоящего в скобках, f4 (z) — заданная на S функция и f (z) — заданный на S
вектор.
Таким образом, на S задаются нормальная составляющая вектора сме-
смещений и касательные составляющие вектора напряжений.
Введем матрицу (см. (V, 9.5)) размера 4X3
Н (дх, п {z)) = || Hki (дх, п (z)) ||4хз,	B.2)
определенную в главе V, § 9.
Согласно теореме III, 1.8, если «S отлично от поверхности вращения
(здесь мы примем это предположение), задача (Ш)+ имеет единственное ре-
регулярное в D+ решение в условиях, указанных в главе V, § 9. Для этого
решения, очевидно, справедливо представление A.1), которое существенно
используется для построения приближенных решений. Однако в данном
случае его следует предварительно преобразовать.
Введем матричный оператор размера 4X3, определенный формулой
(V, 9.11), (V, 9.12):
R (dXJ n (z)) = || Rkl (дх, п (z)) ||4хз.	B.3)
В силу определения Н и R равенство A.1) примет вид
6 (х) щ (х) = —[R (д„, п) Г( ° (у — х) [Н (дю п) и (y)f dyS +
+ \Н(д„ n)T(i\y — x)[R(dy9 n)u(y)fdyS— $TU)(x—y)A(dg)u(y)dy,
i= 1,2,3,	B.4)
или, в векторном виде,
6 {х) и(х) = - j IR (ду, п) Г {у — х)У \Н и (у)Г dt? +
+ j \H (dg, п)Т(у — x)Y [R и (у)Г d^S— | Г (х — у) А (д„) и (у) dy, B.5)
который совпадает с (V, 9.28) с точностью до слагаемого объемного по-
потенциала.

с 21	ДРУГИЕ ЗАДАЧИ (СТАТИКА)	515
Принимая во внимание данные задачи, из B.5) имеем
2и(х) = j [Я{ду, п)Т(у — х)У Ф{у)dyS — F(х), x6D\
J [Н(ду9 п)Т(у — х)}' Ф(у)dyS = F(х), х6?Г,
где
и
= [ \R (ду, п)Т(у — х)}' g {у) dyS — [ Г (х — у)Ж (у) dy.
S	D+
2.1. Теорема. Счетная совокупность векторов
[Н(ду9 n)Y{i) {хк - y)}t=u
линейно независима и полна в пространстве L2 (S).
Доказательство, а) Линейная независимость.
Пусть
S S с1кн {ду, п) ги) (/ - у) = о, у е s,	B.6)
i fei
где с^ — постоянные и N — произвольное натуральное число. Рассмотрим
вектор
V(x)=?S cikT(t)(xk-x).
Этот вектор решает такую задачу
A{dx)V{x) = 0, x?D\ (ЯУ)+ = 0,	B.7)
и V = 0 по теореме единственности III, 1.8. Дальнейшее совпадает с тем,
что в подобной ситуации встречалось выше неоднократно, и на этом доказа-
доказательство первой части теоремы заканчивается.
б) Полнота. Пусть X (у) ? L2 (S) — произвольный вектор и имеют
место условия ортогональности
0, i = 1,2,3; ?=1,2,,.. B.8)
Рассмотрим потенциал
WH (х; X) = J [Я E,, /г) Г (х — г/)Г А, (у) djS.
Ввиду условий B.8) и выбора точек x^gS', будем иметь
По теореме единственности III, 1.10 отсюда следует, что WH (x; X) =0,
x?E3\D', и по аналитичности WH(x\ К) = 0, х^О". Поэтому
,, л) Гя (*;*,)]- = 0
и, принимая во внимание граничные свойства оператора R {дм п (г)), по-
получаем на S почти всюду
|, п{г))[Н(ду9 n)T(z — y)Y
33*

516	РЕШЕНИЯ В ОБОБЩЕННЫХ РЯДАХ ФУРЬЕ	[Рл# XIII
Решение этого уравнения класса L2 (S), согласно теоремам вложения
IV, § 6, п. 2 принадлежит классу С°« а («S), и согласно теореме, аналогичной
теореме Ляпунова—Таубера, VII, 2.1, которую нетрудно доказать и в данном
случае, будем иметь
А (дх) WH (*; к) = О, х f D+, (HWHy = 0.
и по теореме единственности III, 1.8 WH(x\ X) = 0, x?D+. Наконец, из
равенства (RWH)+ — (RWH)~ = 2Х (z) имеем X (z) = 0, z? S, и полнота до-
доказана. Тем самым доказана полностью теорема 2.1.
Дальнейшие рассуждения совпадают (с очевидными изменениями)
с теми, которые в соответствующем месте применялись при рассмотрении
задачи (П)+, например, первым способом, и приближенное выражение для
решения будет иметь вид, аналогичный A.37).
Читатель легко найдет также решение задачи AП)+ с помощью второго
и третьего способов, на которых мы останавливаться не будем.
2.2.	Замечание. В том случае, когда «S — поверхность тела вра-
вращения, следует воспользоваться теоремой III, 1.8 и (с очевидными измене-
изменениями) повторить рассуждения, использованные при рассмотрении задачи
(Н)+, для которой решение также существует только при выполнении до-
дополнительных условий.
2.3.	Замечание. Приближенное решение задачи (III)" для про-
произвольного S строится аналогично.
2.4.	Замечание. Приближенные решения задач (IV)+ и (IV)" по-
получаются аналогично и (с очевидными изменениями) для произвольного S
и произвольных граничных данных из соответствующих классов (см. гл. VI).
2. Задачи VI. Граничные условия задачи VI имеют следующий вид:
В главе VI доказана теорема существования решения этой задачи
в классе С1 (D+) f|C2 (D+), и формула представлений A.1) в данном случае
запишется следующим образом:
2и (х) = - j \1Т (ду, п) Г (х—у)]' + о (У) Г (х—у)} <р (у) dfi + F (*), х 6 D\
s
где
ф(У) = и+0
F(x)=\T(x—y)f[y)dfi+ J Г{х —
S	D+
2.5. Теорема. Счетная совокупность векторов
[Т(ду, л)Г<'> (х* — у) + о(у)ГМ (xk — y))^u i= 1,2,3,
линейно независима и полна в L2 (S).
Доказательство, а) Линейная независимость.
Пусть
?

с 2]	ДРУГИЕ ЗАДАЧИ (СТАТИКА)	517
где cik — постоянные и N — произвольное натуральное число. Рассмотрим
вектор
1=1 fe =i
который является решением граничной задачи
и по теореме единственности III, 1.6 равен тождественному нулю. В дальней-
дальнейшем рассуждения повторяются и мы не будем их воспроизводить.
б) Полнота. Пусть X (у) 6 L2 (S) — произвольный вектор, удов-
удовлетворяющий условиям
= 04 i= 1,2,3; 6=1,2,... B.9)
s
Покажем, что почти всюду на S X (у) = 0.
Рассмотрим смешанный потенциал U (х; X) = W (х; X) + V (х; оХ).
В силу B.9) и вследствие характера распределения точек xk на S'
имеем U (х\ X) = 0, х ? S' и поэтому согласно теореме единственности для
внешней задачи (I)" имеем U (х\ X) = 0, *:? E3\JD'. Отсюда по свойству ана-
аналитичности U (х\ X) = 0, jc?D~,h так же как выше, согласно теоремам вло-
вложения главы IV, § 6, п. 2,Х? С°-а (S). С другой стороны, легко прове-
проверяется равенство
\\Т(д„ n(z)) + o(z)]U(z; X)\+=\\T(dz, n(z)) + o(z)]U(г; A,)}-, z ? S.
и так как [(Т + о) UY =0, то вектор U (х; X) решает граничную задачу
\(T+ o)U}+= 0,
и по теореме единственности III, 1.6 для задачи VI получаем U (х; А,) = 0,
x?D+ и, наконец, по свойству потенциалов X (у) = 0. Полнота, и тем самым
теорема, доказаны.
Перенумеруем систему векторов \{Т + о) Г(о (хк — у)]"=и * = 1, 2, 3,
следующим образом:
Ч'(А;) (у) = \Т (dv, n) -f- о (у)] Г(/&)\х 3 —у), 6=1,2,...
Дальнейшие рассуждения совпадают с теми, которые в этой ситуации
применялись в задаче A)+, и приближенное решение строится аналогично,
всеми тремя способами. Решение, полученное, например, вторым способом,
имеет вид:
а(х) = lim vw(х) + ±-\Г{х—уK«(у)dy, x6 D\
где
ГИ-2-|
а коэффициенты Qk и aks определяются (с очевидными изменениями) так же,
как в формулах A.9) и A.22).
2.6. Замечание. Решение внешней (VI)"" задачи не отличается от
решения внутренней.

518	РЕШЕНИЯ В ОБОБЩЕННЫХ РЯДАХ ФУРЬЕ	[Рл XIII
3. Смешанные задачи. В этом параграфе мы будем иметь дело с обла-
областями, ограниченными несколькими поверхностями и все обозначения бу-
будут те же, что в главе XI. Покажем способ построения приближенного ре-
решения более подробно для одной из типичных смешанных задач; читателю
будет нетрудно самостоятельно перенести этот способ на другие задачи.
Рассмотрим следующую задачу. Найти в области D+ регулярный вектор
и (х) — решение системы уравнений
удовлетворяющее граничным условиям
6 = 0, 1	г,
где 0 <: г < т, а (z) — неотрицательно определенная матрица класса
С°>а (S), и будем искать его приближенное решение, например, вторым
способом.
Пусть Dk — область, расположенная строго внутри Dky k= I,..,
„ . ., m, Do — область, включающая Do, S'k — граница D&, k = 0, 1,...
m
. . ., m, S' = U S'k9 r (S, S') >0, \xk}k=i — всюду плотное на S' счетное
/г=0
множество точек.
Введем матрицу
М(х — y)=\M^t M<2>,
определенную следующим образом:
— у), у eU
k=0
М{х—у)= •
о(у)]Г(х — у), ye U S*. хб^з-
m
2.7. Теорема. Совокупность векторов
xk~y)]^u 1=1,2,3, y
линейно независима и полна в пространстве L2 (S).
Доказательство первой части теоремы предоставляется чи-
читателю; оно получается так же, как в предыдущих случаях, на основании
теоремы единственности рассматриваемой задачи.
Наметим здесь путь доказательства полноты. Пусть X (у)? L2 (S) —
произвольный вектор, удовлетворяющий условиям ортогональности
(	(yS = 09 1=1,2,3; ?=1,2,.,.	B.11)
s
Рассмотрим потенциал
S J r(* — y)°(y)bWjS. B.12)

? 2]	ДРУГИЕ ЗАДАЧИ (СТАТИКА)	519
Согласно B.11) и вследствие плотности всюду на S' точек xk, будем иметь
U (х; X) = 0, x?S'.
Отсюда по теореме единственности для первой основной задачи получаем
По свойству аналитичности фигурирующих здесь потенциалов из пре-
предыдущего вытекает, что
U(x;X) = 09 xe U Dk U (Е9\р0).	B.13)
fe=i
Переходя к пределу в B.13), когда х —> z, где 2 6 (J SA, и в равенстве
г
TU fx; А,) = 0, когда х —¦ 2, г? |J Sk9 получим для X (у) на S сингулярное
интегральное уравнение; по теореме вложения из главы IV, § 6, п. 2 реше-
решение этого уравнения класса L2(S) вкладывается в класс Cl'a(S)y причем
Se://2(a).
На этом основании теперь можно утверждать, что U (х; X) есть решение
задачи
t/+(z;A,) = O, z?Sk, fe = 0, 1,...,/-; {(T + a)U(z; к)\+ = 0,
z€Sfe, fe= r+ 1,. .., m,
и в силу теоремы единственности XI, 1.1 для смешанной задачи имеем
?/(х;Я) = 0, x?D+.	B.14)
Наконец, из B.13) и B.14) следует Л, (у) = 0 и полнота доказана.
Введем обозначение
, ^=1,2,...,	B.15)
где 4= & — 3 j--§—]• Пусть {ф(/г)(у)}^=1 есть система, полученная из B.15)
ортонормированием на S
Ф(А|(»)=|4/*(/)(!/) yeS, ft=l,2,...,	B.16)
где dki i — коэффициенты ортонормирования. Нетрудно заметить, что
Г/±?1
13 J —
'(#)==
и s,,
J J — у),
B.17)
ye и
Пусть и (х) — точное решение задачи, существование которого доказано
в главе XI. Введем обозначение
B.18)

520	РЕШЕНИЯ В ОБОБЩЕННЫХ РЯДАХ ФУРЬЕ	(рл XIII
где v (х) есть решение следующей задачи:
A(dx)v(x) = Q9 x?D\
ztSk, k = r + 1,..., m,
причем
pl\	z?Sk9 k = 09l,...9r,
D+
k = r-\- 1,..., m.
Пусть
Q(z) = Q<*>(z), zeSk, fe = 0f 1, . . . f m.
Представим Q (у) рядом Фурье по системе {ф^
2f
Qk<p{k) (у), у € S, &k == J Ф(Л) (у) ^ (^/) ^S.
Введем векторы:
N k	/ ¦ /+2
Q(^) (y) = ? Олф(*) (у), yeS.	B.20)
Согласно формуле (XI, 2.6) для v (x) можем записать
г
1 \i г
^ iavJ J
m
+ 4~ У f gm(x> y;D+)Q(y)duS. B.21)
где GM (x, y; Z)+) — тензор Грина рассматриваемой смешанной задачи для
области D+. С другой стороны, очевидно, что v{N) (x) есть решение следую-
следующей граничной задачи:
fe = 0,l	r,
гб5й, * = r + 1,. . ., m,
и по той же формуле (XI, 2.6) будем иметь
- ±- J] \[Т (дв, п) G'm (х, у; D*)Y Q(«) (у) dvS
} 2 jG(xy;D+)G<*'>(j,)dS	B.22)

Я 3]	ГРАНИЧНО-КОНТАКТНЫЕ ЗАДАЧИ СТАТИКИ И КОЛЕБАНИЯ	521
Из B.18), B.21) и B.22) заключаем, что равномерно имеет место равен-
равенство
где
U^] — x) + -L J T(x—
k=l /=1	D+
2.8.	Замечание. Читатель легко построит приближенное реше-
решение этой задачи первым и третьим способом по аналогии, используя резуль-
результаты настоящего параграфа.
2.9.	Замечание. Задачи I—IV и VI, для которых приближенные
решения строились выше для того случая, когда область D ограничена един-
единственной поверхностью S, могут быть решены по схеме § 2, п. 3 и в том слу-
случае, когда рассматриваемая область ограничена несколькими поверхностями.
§ 3. Гранично-контактные задачи статики и колебания
1. Гранично-контактные задачи статики. Способы приближенного ре-
решения, описанные в предыдущих параграфах, распространяются для гра-
гранично-контактных задач в неоднородных средах. Рассмотрим несколько
типичных примеров (см. гл. I, § 14, п. 4).
а) В, главе XII было показано существование регулярного решения
главной гранично-контактной задачи. Рассмотрим случай статики и выпи-
выпишем формулы представлений для регулярного решения с учетом контактных
условий на S; предполагая массовые силы равными нулю, будем иметь
2и(х) = j Г<х> (X — y)(TWu)+d9S— J [ТЫ (ду9 п)Г<1> {x — y)]'u+{y)dyS,
xeD\	C.1)
0= JlWfx — y)(T^u)+dyS — \\ТЫ (dyt n)T<l>{x—y)Yu+(y)dyS,
xeD~,	C.2)
C.3)
0== |[Г<2>(д^,/г)Г<2>(* — y)]'u+(y)dyS— \r™(x — y)(TW u)+dyS — F(x)t
C.4)
где F (x) — заданный вектор. Очевидно, найдя векторы и* (у), (Т{1^и)+ из
системы C.2), C.4), будем иметь и полное решение задачи.
Пусть Sx и S2 — произвольные замкнутые поверхности, первая из ко-
которых принадлежит области D+, вторая охватывает поверхность S, так что
r(Sl9S)>09 r(S2tS)>0.
Конечные области, ограниченные поверхностями Sx и S2, обозначим соот-
соответственно через D1 и D2. Пусть на Sx и S2 выбраны произвольные всюду
плотно расположенные счетные множества точек {jcfijJ^Li и {*B)}?=i соот-
соответственно.

522	РЕШЕНИЯ В ОБОБЩЕННЫХ РЯДАХ ФУРЬЕ	[Гл XIII
Введем матрицу размера 6x6, записанную в виде блочной матрицы
>; У) =
, C.5)
и векторы
Ф (У) = (Фь • • ., Фе) = (и+, (Т™и)+); Ф = (О, О, О, F19 F2t F9) = @; F).
Тогда C.2), C.4), считая внихх? {*?2>К когда xg?>~, x? {xfi)}, когда Arg
запишутся в виде векторного уравнения
J #'
= 1, 2, ...	C.6)
Матрица, транспонированная по отношению к матрице Н (jcfi>, ^2); f/)>
будет иметь следующий вид:
н (xKlu, 4>; у) = (^A) «2„ у), яB) (*?2), у), яC) (*&,, у).
ЯD) «»,, У), ЯE) D„ У), ЯF) (JC*1)f У)\. C.7)
Рассмотрим счетную совокупность векторов
{#(/)(^ </)}?=ъ /=1.2	6,	C.8)
где, как уже было отмечено, при / = 1, 2, 3, хк = л:?2>, а при / = 4, 5, 6,
х = хA).
3.1. Теорема. Система C.8) линейно независима и полна в L2 (S).
Доказательство. Линейная независимость.
Пусть
S S с/л//(/)(«?2>, ») + t S с/*я(/)Di), у) = о, Уе s, C.9)
где не все cjk равны нулю.
Введем векторы
vA> (jc) = S S с,* ГA) ft* - х), У<2> (*) = S S с,* ГB) (*?„ - х).
/=lfc=xl	f=4fe=l
Рассматривая проекции, нетрудно заметить, что из C.9) следует
)+ + (T( V2))~ = 0, (уA))+ + (уB))~ = 0,
и вследствие того, что v(l) (x) и yB^(x) — регулярные решения уравнений
упругости соответственно, bD+ и D", на основании теоремы III, 2.15, бу-
будем иметь
Далее, рассуждая так же как выше в подобной ситуации, найдем что
все cJk равны нулю. Это противоречие доказывает первую часть теоремы.
Полнота. Пусть 1 (у) — произвольный шестимерный вектор из
L2 (S) и имеют место равенства
\	= 0> /=!,..., 6; ?=1,2,...	C.10)

Л 3]	ГРАНИЧНО-КОНТАКТНЫЕ ЗАДАЧИ СТАТИКИ И КОЛЕБАНИЯ	523
Рассмотрим векторы
VU> (х;Х)=\ [Т^(ду, п)Г^(х — у)]' а(у) duS -
1/<2> (х; Х)=\ [Г<2> (ду, п) Г<2> (х — у)]а (у) dyS — { Г<2> (х — у) р (у) de S,
где а (у) = (klt %2, К3) и Р((/) = (к^ Хь, Л,„). Согласно C.10) имеем
УA) (*&);*) = 0, И2)D,;Я,) = 0,
и ввиду непрерывности получаем
Так как V(l)(x; X) и 1/^2)(л:; X) — регулярные решения уравнений статики для
x^S и удовлетворяют на бесконечности условиям теоремы единственности,
из предыдущего получаем
1/U)(х; А,) = 0, хеЕ3\В2, 1Л2>(х;Я) = 0, xeDv
Отсюда путем аналитического продолжения находим
y C.11)
— y))'a(y)dyS— \r^(x—y)$(y)dyS = O, xgD+ C.12)
т. е. а, р есть решение системы однородных функциональных уравнений,
соответствующих системе C.2), C.4). По теореме вложения всякое ре-
решение этой системы класса L2(S) включается в класс С1* a(S). В этом можно
убедиться, перейдя в C.11), C.12) от функциональных уравнений к инте-
интегральным.
С другой стороны, из той же теоремы единственности III, 2.15 следует,
что решение однородной системы C.2), C.4) класса С1- a(S) есть нуль Ha(j) =
^ Р (У) = 0> т- е- ^ (У) = 0; и тем самым полнота доказана.
Введем обозначение
и введем ортонормированную на S систему векторов
<p(s)G/)=I) L
где ZSf k — коэффициенты ортонормирования. Представим вектор ср ря-
рядом Фурье по системе {y{k) }
=, s фтф(т)(у).	(злз)
т=1
где
S
— коэффициенты Фурье. Их можно определить из C.6), для чего перепишем
ее в следующем виде:
^5 = Ф (д*^). *=1,2		C.14)

524
РЕШЕНИЯ В ОБОБЩЕННЫХ РЯДАХ ФУРЬЕ
[Гл. XIII
где (*, k = 1, . . ., 6 — координатные орты в шестимерном векторном про-
пространстве.
В самом деле, найдем, например, Фт, где га — произвольное натураль-
натуральное число. Для этого умножим первое равенство C.14) (т. е. равенство, соот-
соответствующее значению k = 1) на вектор
второе — на вектор
и т. д., ,
s-e равенство —
Imimi1* При S =
tn% /71—2 I m% tit-
ТПл Г71—3 | *Г71» J7
771» 771—4 I 771» /71-
/ t*1 1 /
на вектор
m-j-5
m
/+/„/ +
m + 3
эи . 6 ,
-/Wtini4, при s =
i ^4 i / /Ь_
6
m+ 1
/71
1рИ S = -g-
Складывая полученные равенства, будем иметь
a)), m=l,2,
Пусть
4" J Я' (x' x;
- 4- Ф (x),
C.15)
Очевидно, для точного решения задачи имеем
f -(Ui{x), Ut{x), U
и{х)-\ (Ut (x),
Ub (x), U6 (x)), x € D~,
и соответственно для
l	(U[N)(x),UbN)(x),UiN)(x)), л^х. .
Оценивая разность и (х) — M(iV)(^) по неравенству Коши—Буняков-
ского, получаем и (х) = lim u{N)(x)t причем стремление к пределу равно-
N•+00
мерное для всех лс, лежащих строго внутри D+ и D".
б) Бесконечная область с постоянными Хо, (л0, несущая т упругих вклю-
включений из различных материалов, не имеющих общих точек. Напомним обо-
обозначения (см. гл. XII, § 1): Еъ — полное трехмерное пространство, Dk — об-

§ 3]	ГРАНИЧНО-КОНТАКТНЫЕ ЗАДАЧИ СТАТИКИ И КОЛЕБАНИЯ	525
ласть &-го включения; k = 1, . . ., т\ Sk — граница k-vo включения,
т
D* = (J Dkf D~ = E3\D+; положительная нормаль направлена из Dk вовне.
Ищется регулярный вектор, удовлетворяющий условиям
V х е Dk:	Л<*> (дх) и = \ik Аи + (А,л + \ik) graddiva = Ф* (*), k = 1,..., m\
: a-(y) — u+ (y) = P(t/), (Г°а)~ — (Tfea)+ = F*(y\ k = 1, ..., m.
Величины, стоящие справа, заданы; знаки -+• и — обозначают предельные
значения на границе из Dk и из D~ соответственно. Формулы общих предста-
представлений, если принять во внимание условия контактов вдоль Sk, ?=1, . . .д
дадут
V хе D,: 2и(х) = J Г^ {х-у)(Т*и)~ dyS-\ {T*Tk {у — х))' и~ {у) dyS + Tk(x),
sk	sk
C.16)
j {TkYk (y - x))' и- (у) dyS
V x 6 ?S\S*: 0 = j Г* (x — y) (T°u)~ dyS — j {TkYk (y - x))' и- (у) dyS +
), C.17)
j=1, ..., m,
= - J Г°(х — f
m
и st
i=l
C.18)
m	m
и st	и st
t=l	i=l
wx<E U Df: 0 =
= — J T*(x—y)(T*u)-djS+ J
m	m
.u^i	.uxs<
C.19)
^"m+i (*) = J Г0 {x — у) Ф° [у) dy.
Введем в рассмотрение матрицы
[У — х))', —Г* (х—у)\\зхб', y^Sk, yx?E3; k— 1,..., т;
0;	У с S,-, j =h k; j = 1, .,., m;
, y) = || (TT° (y — x))', —Г0 (x—у) Цзхб; у 6 ? 51, v * 6 Я„

526	РЕШЕНИЯ В ОБОБЩЕННЫХ РЯДАХ ФУРЬЕ	[рл XIII
и шестикомпонентный вектор
тогда C.17) и C.19) примут вид
V х 6 E3\Dk: j Mik) (х> у) Я (у) dyS = 3~k (x); k = 1, ..., m; C.20)
U 5*
V*€ .О D*: J M@)(x, r/)X(y)d,S=>-;72+1(x).	C.21)
Подставим в C.20) % = х°е50 и в C.21) x = x)eSl9 x = X/GS2, . . ., x =
= xf 6Sm,/= 1,2, . . ., где So есть замкнутая поверхность, охватываю-
охватывающая D+, a §!, 52, . . . ., Sm — поверхности, вписанные соответственно
в Dl9 D2, . . ., Dm. Тогда будем иметь
J M{k) {х% у) Х(у) dyS = Гк (дф, Л = 1, .,., т;
), у) А. (У) d^ =
m
j M@) K, y) X (г/) dvS = &-m+l «) (/ = 1,2,...).
Слева в этих равенствах стоят векторы, компонентами которых служат ска-
лярные ( в смысле L2 U Si\ I произведения X (у) на векторы из счетного мно-
жества
ye U Sh p = l, 2,3; /=1, 2, ...,	C.22)
а справа стоят заданные величины. Перенумеруем элементы множества C.22)
так, чтобы каждому элементу отнести определенный номер из натурального
ряда, и обозначим полученное множество через (ф(п)(^))й=ь Доказывается,
(т
и s
множество.
Определим постоянные ап, п = 1, . . ., N, где W произвольно фикси-
фиксировано, из условия минимума среднеквадратичной нормы
IN	II
^ (У)— 5j апЧ>{п) (Ум	= min-
П=1	Ц,

К 3]	ГРАНИЧНО-КОНТАКТНЫЕ ЗАДАЧИ СТАТИКИ И КОЛЕБАНИЯ	527
Это приводит для ап к разрешимой системе линейных уравнений
TV
2 а„(<р(п>, <р<*>) = (Л.
2
N
Доказывается, что в L2:X(y) = lim 2 апф(") (у). Внесем в C.16) и C.18)
Af->oo д=1
вместо X (у) значение 2 #пФ(я)(У) и результат обозначим uN (х). Доказы-
вается, что для произвольного положительного г > О найдется такое No (s),
что для N > No, во всякой строго внутренней точке x?D+\JD~t будем иметь
| uN (х) — и (х) \ < 8, где и (х) есть точное решение.
с) Конечное упругое тело с границей So и постоянными ХОу \хОу несущее
т упругих включений из различных материалов. Решение этой задачи полу-
получится из решения предыдущей, если в последнем Г° (х — у) заменим тен-
тензором Грина G0 (х9 у) для области Do с границей So; например, в первой за-
задаче этот тензор, как легко видеть, имеет следующий вид:
(цР)(х, y) = T°ip)(x — у)— § ?пр)(х)у{п)(у) (р=1, 2, 3), х, yeD0,
где (ф(Л) (у)\? есть совокупность, полученная ортонормированием множе-
множества {Г?„(*? — У))Т-и P=U 2, 3 и f(np)(x)= Jr?p,(z —х)Ф<«>(г)^, еле-
довательно, приближенное значение и°(ху у) задано явно, и остальное
сводится к предыдущему. Очевидно, C.16), C.17) останутся без изменений,
а C.18) и C.19) примут следующий вид:
\/х е Dr г 2и (х) = — J G0 (х — у) (Т°иГ dJS + J (T°G° (у, х))' и"
m	m
U si	U si
1=1	i=l
+ J (T^ (y, x))' f (y) d,jS—srm+1 {х)г
0==- J G°(x—y){T°u)-dyS+ \ (ТЮ»{у, x))'u-(y)dl/S +
So
2. Задачи колебания. Перенесение методов приближенного решения,
которые выше применялись к задачам статики, на задачи теории колебания
не требует никаких принципиальных дополнений. Достаточно вместо ма-
матрицы Кельвина теперь рассматривать матрицу Купрадзе Г (х — у, со)
(см. гл.II) и иметь в виду, что параметр со2 должен быть отличен от частот
собственных колебаний исследуемой задачи. В главе VII было показано,
что в этом случае имеют место основные теоремы существования и един-
единственности, вместе с формулами представлений регулярного решения; но
этого, как мы видели, достаточно для применения описанных способов при-
приближенного решения. Что касается внешних задач, то в этом случае, как
было показано в главе VII, теоремы существования и единственности, при
условии излучения, имеют место для любых значений параметра со2 и, сле-
следовательно, приближенные методы всегда применимы.

528	РЕШЕНИЯ В ОБОБЩЕННЫХ РЯДАХ ФУРЬЕ	грл XII1
Следует, однако, иметь в виду, что приходится пользоваться теоремами
единственности для вспомогательных граничных задач в областях, которые
возникают в связи с введением вспомогательной поверхности S' (см. § 1, п. 1),
поэтому нужно позаботиться о том, чтобы заданное значение со2 не совпадало
также с собственными числами этой вспомогательной задачи. Это условие,
однако, без ограничения общности, всегда можно считать выполненным,
так как поверхность S' произвольна.
Более подробно на приближенном решении задач колебания мы оста-
останавливаться не будем, предоставляя читателю самостоятельно рассмотреть
эти задачи.
§ 4. Граничные задачи термоупругости
Если иметь в виду общий случай граничных задач связной теории термо-
термоупругости, то, очевидно, сохранится аналогия с задачами колебания, и то,
что было сказано в предыдущем параграфе относительно частот колебания со2,
остается в силе и здесь.
В остальном применение описанных приближенных способов реализуется
в задачах термоупругости без каких-либо существенных изменений. Однако
применяемые в этом случае матрицы сингулярных решений имеют размер-
размерность 4x4, и для того, чтобы подчеркнуть некоторые особенности, связанные
с этим обстоятельством, мы подробно рассмотрим одну из основных гранич-
граничных задач. Другие задачи читатель без труда разберет самостоятельно.
Пусть, например, ищется приближенное решение второй, внутренней
основной задачи.
Согласно главе X эта задача состоит в построении регулярного в D+
решения уравнения
В(дх,
удовлетворяющего на S условиям (PU)+ = f, \-^~) = f& или, сокращенно,
y = g, где U = (и, иД, PU = Ти- упи±, g = (flf /2, f8f /4) и В (дХ9 со)
есть матричный дифференциальный оператор (I, 12.12).
Согласно формуле общего представления регулярного вектора (X, 2.19)—
(X, 2.20), имеем
б(х)U(x)=j<D(x—y, а))(ЯU(y))+ dyS —
s
п)Ф'(х—у, <b)\'U
Ф(х—У, а)В(ду9 <o)U{y)dy.	D.1)
— J
D+
Пусть теперь U (х) есть решение второй основной задачи термоупругости.
Как было показано в главе X, эта задача всегда разрешима, если только ю
отлично от собственных чисел задачи (X, 2.49). Предполагая это условие
выполненным, формулу D.1) можем переписать в следующем виде:
2V (х) = - J \к (ду, п)Ф(у — х, со)]' Ф (у) d,S + F (x), x?D\ D.2)
J \к (дуу п)Ф(у — х, со)]' Ф {у) dvS = F (x), х 6 D-,	D.3)

к 4]	граничные задачи термоупругости	529
где
D.4)
и
F(x)=\ Ф(х—у, <»)g(y)dyS + J Ф(х—у,
S	D+
Докажем теорему
4.1. Теорема, Счетная совокупность векторов
{&(ду, п)Ф{1)(у—х\ <d)}2U, t=l, 2, 3, 4 —
линейно независима и полна в L2 (S).
Доказательство, а) Линейная независимость.
Пусть
S S сшШ{дд, п)Ф<О(у_х*, о)) = 0, yeS,	D.5)
где cfft — постоянные и N — произвольное натуральное число. Рассмотрим
вектор
4 JV	_
V(x)= S S с«Ф^')(х—xk, со) jceS'.
1=1 ^=1
Согласно с D.5) этот вектор есть регулярное в D+ решение задачи
В(дх, co)V(x) = 0, xeD\ (&V)+ = 0,
и так как спектр собственных частот однородной задачи (И)о^ совпадает со
спектром задачи (Н)о~ (см. замечание X, 2.5), а со2, согласно принятому ус-
условию, отлично от последних, то V (х) = 0, x?D+; отсюда по свойству ана-
аналитичности будем иметь V (х) = О, *?D', и далее, повторяя обычные рас-
рассуждения, приходим к выводу, что все cik — 0. Линейная независимость
доказана.
б) Полнота. Пусть X (у) есть произвольный четырехмерный век-
вектор из L2 (S), удовлетворяющий условиям
= 09 t = l, 2, 3, 4; k=l, 2, ..,D.5')
Введем потенциал
W (х; А,) = J [Я (ду, п) Ф(у—х9 со)]' X (у) dyS =
y, п)Ф'{х—у, <d)]'X(y)dyS.
В силу D.5') и ввиду плотности расположения точек xk на S' будем иметь
W(x; X) = 0, x?S'.
На бесконечности потенциал W удовлетворяет условиям термоупру-
термоупругого излучения и является регулярным решением уравнения В (дх> со) W ==
s= 0. Поэтому, согласно теореме единственности для первой основной внеш-
внешней задачи (см гл. III)
W(x; X) = 0,
Отсюда по аналитичности
34 В. Д. Купрадзе

530	РЕШЕНИЯ В ОБОБЩЕННЫХ РЯДАХ ФУРЬБ	[рл XIII
и, следовательно,
Перейдя к пределу извне, когда х —* z? «S, получим для А, (у) сингулярное
интегральное уравнение. Решение этого уравнения класса L2 (S) согласно
теоремам IV, § 6, п. 2, включается в класс G- a(S). Поэтому, применяя
к W (х\ X) теорему Ляпунова—Таубера (см. VII, 2.1), получим
и ввиду того, что со2 отлична от собственной частоты второй однородной за-
задачи, имеем W (х; %) = 0, x?D+ и, наконец, из граничных свойств потен-
потенциала W (х; К)9 X (у) = 0 и полнота, а тем самым и теорема, доказаны.
Перенумеруем элементы совокупности {&Ф{1)(у — xk, co)}?L=i, i = 1, 2,
3, 4 следующим образом:
со), z4-ft_4[i=i]f fe=l, 2, ...
D.6)
и систему {i|r (#)}?=i ортонормируем на S по Шмидту; получим
=1, cp{k\y) = S hk9Sq>{s) (у), k=l, 2, ...	D.7)
где hk% s — коэффициенты ортонормирования.
Очевидно, полна и комплексно-сопряженная совокупность
:•	D.70
Неизвестный вектор q> (у) представим рядом Фурье по системе D.7')
где
фт = I ф(/») (у) ф (у) dyS, т = 1, 2, .. #
Эти коэффициенты вычисляются из функционального уравнения D.3),
В самом деле, из D.3) можно записать, в частности,
J \Яфт п)Ф(у—х\ (x>)]'cp
или еще,
4
\[к(дд, п)Ф<*>(у—хК (о)]Ф(у)} jk dJS = F(**), f=l, 2	 D.8)
где /*, & = 1, 2, 3, 4 — координатные орты четырехмерного векторного про-
пространства.
Пусть т — произвольное натуральное число и s = Г^—] .
Умножим D.8) скалярно на вектор
Cmi = V ^.g/1 + ftmt 4,_2/2 + hm% 4,.i

§ 4]	граничные задачи термоупругости	531
и просуммируем по i от 1 до s, имея в виду, что, по определению, можно по-
положить
hm, k = °э при
тогда получим
4 s
S k=l t=l	1=1
D.9)
Из D.6) имеем
Поэтому D.9) принимает следующий вид:
4 s	s
" :miF(x% D.10)
Но нетрудно проверить равенство
4 s
fel i
и на основании D.7) имеем из D.10)
где
1=1, 2, .„; s=[ m^3 ]>
Таким образом, коэффициенты Фурье найдены.
Построим вектор
) = __^j Ш(ду,п)Ф(у—х, со)]' ^
j	у
S
если f/ (х) есть точное решение задачи, то, применяя неравенство Коши—Бу*
няковского, получим, как обычно
U (х) = lim UW (л:), х 6 5# cz D+
для всех д:, расположенных строго внутри D+. Стремление к пределу в Ь^
равномерное.
(j(N) есть искомое приближенное решение рассматриваемой задачи.
4.2. Замечание. Применение второго и третьего способа очевидно.
Другие задачи термоупругости решаются аналогично, с очевидными изме-
изменениями.
34*

532	РЕШЕНИЯ В ОБОБЩЕННЫХ РЯДАХ ФУРЬЕ	[рл
§ 5. Численные примеры
Для иллюстрации практической эффективности описанных способов
приближенного решения рассмотрим несколько численных примеров.
Найдем гармоническую в области D, ограниченной эллипсом
хг = cos /, х2 = 0,75 sin /,
функцию, принимающую на границе 5 значения
Очевидно, точное решение задачи задается функцией
и (xv хг) = arctg х*~~2 , х (xv л:2) 6 D.
Х1 	 *
Приближенные значения решения, найденные первым и вторым спосо-
способом в узлах сетки (внутри эллипса) с шагом h = 0,1 при вспомогательном
контуре S' (конфокальном эллипсе)
#! = 1,1 cos т, х2 = 0,85 sin т,
для N = 24, приводятся в таблице 1: в каждой точке (узле сетки) верхнее
левое число, умноженное на 10~6, равно погрешности первого способа, и
правое верхнее число, умноженное на 10~6, соответствует погрешности вто-
второго способа; для сравнения был также применен метод сеток (метод конеч-
конечных разностей); соответствующая погрешность выражается нижним числом,
умноженным на 10~6.
Мы видим, что степень приближения во всех случаях высокая, особенно
для первого способа; в этом случае погрешность почти нигде не превышает
миллионных долей.
Для иллюстрации третьего способа рассмотрим несколько примеров.
I. Ищется решение функционального урав-
уравнения
2я
S
где S — окружность единичного радиуса, D+ — соответствующий круг,
•ф — угол между нормалью в точке y^S и направлением ху.
Точное решение есть ф = 1; это — единственное регулярное решение.
Применяя формулу прямоугольников, разобьем интервал @,2я) на N рав-
равных частей точками ук\ при этом
2я
где а, = i-j-p / = 1, . . м N. Пусть *л, & = 1, * • ., N лежат на концен-
концентрической окружности радиуса р @ <р < 1), на отрезках Oyk. Нетрудно
заметить, что

§5]
ЧИСЛЕННЫЕ ПРИМЕРЫ
533
еэ —
а го oj
.11
I

534	РЕШЕНИЯ В ОБОБЩЕННЫХ РЯДАХ ФУРЬЕ	^Л. XIII
где а) = -—-, tyik — угол между нормалью в точке y^S и направле-
направлением хку1.
Решая системы, порождаемые E.1), находим:
a)	при р = 0,95,	N = 40,	<р (у1) = ... = ф (у^) = ф = 0,87,
b)	при р = 0,9,	N = 40,	ф = 0,91,
c)	при р = 0,1,	ЛГ = 40,	ф= 1,00002,
d)	при р = 0,01,	// = 40,	ф= 1,000005
II. Ищется решение задачи Дирихле для эл-
эллипса
хг = cos /, х2 = 0,5 sin /,
при граничных условиях на S:
и (хи х2) \s = f(x) = 0,5 (*? + xl).
Точным решением задачи, как легко проверить, является функция
и(хи х2) = 0,2 + 0,3(х21 — х$).
Имеем
^l^	l	*> E.2)
Согласно третьему способу функциональное уравнение E.3) заменяется
системой линейных алгебраических уравненийх). Используем формулу Гаусса
с 16 ординатами в интервале (—1.1).
Положение точки у на S в уравнении E.3) определяется параметром t9
О < t <: 2я.
Введя новую переменную t = A + а) я, уравнению E.3) прида-
придадим вид
1
J ф (a) In У [cos A + а)п — х1]2 + [0,5 sin A + а) п — х2]2 da =
-1
1
=-4- J /и \4гarcts 0>соГГ7^21 «+<*»da- E-4)
x) Замечание к корректуре, S. Christiansen («On Kupradzes Funkfional Equations for
Plane Harmonic Problems», Z. angew. Math» Mech.f 1975, 55, № 4) показал, что при реше-
решении третьим способом плоской задачи Дирихле необходимо иметь в виду: если внешний
радиус отображения области D+ меньше единицы, существует (единственная) кривая 5Х
такая, что уравнение E.3) при / = 0 для x?Si допускает нетривиальное решение. Если
за вспомогательную кривую выбрана эта критическая кривая, то для избавления от неже-
нежелательного решения нужно присоединить к уравнению E.3) условие равенства нулю
интеграла по 5 от <р; этому условию, очевидно, удовлетворяет корректное решение, но
не удовлетворяет решение «паразитическое».

§ 51	ЧИСЛЕННЫЕ ПРИМЕРЫ
Точки xk фиксируем на конфокальном эллипсе St
хг = аг cos т, х2 = Ьг sin т,
так, чтобы значения узлов Гаусса, соответствующие этим точкам, совпа-
совпадали с узлами ук на основном эллипсе. Учитывая далее, что
cos i|) , с d > „ 0,5 sin t — Ь-i sin x ,
J7=Vr ^ = St arctS cosf-a.cosx da =
0,5 — 0,5a, cos t cos т — б, sin ^ sin т ,
	 i,-yp 	da<
из E.4) после применения формулы квадратур Гаусса будем иметь
16
Л116) ф (at) In {[cos A + a,) n — ax cos A + a>]2 +
16
| 2 A™ [cos2 A + at) n + 0,25 sin2 A + a,) n] X
X . . 1 t..2 [0,5 — 0,
— 61sin(l +a,)^sin(l +а;)я],	E.5)
1*де Л(*16)— коэффициенты используемой квадратурной формулы.
Благодаря специальному выбору точек хк имеем
н, как нетрудно видеть,
Ф 0/0 = Ф (У17~0, * = 1э 2	16.	E.6)
Поэтому можно ограничиться -рассмотрением 'системы из восьми урав-
вений.
Рассмотрим несколько случаев выбора вспомогательного контура:
а) при ах = 2, Ьг = 1 решение системы E.5) дается таблицей
ф (yi) = 20,0201504,	ф (у2) = — 12,7255234,
Ф(у3) = 3,33231100,	ф (у4) = -1,01333008,
= 0,40868940,	ф (у*) = 0,070016210,
у?) = 0,05396402,	Ф (у8) = —0,13162008.
Значения ф (у9), . . ., ф (у16) находятся из формулы E.6). Подставив
найденные значения ф (у1) в формулу E.2), предварительно заменив инте-
интеграл той же формулой квадратур Гаусса, будем иметь
16
и(х) = -1- ^ А?6) [cos2 (I -f a,) я + 0,25 sin2 A + at) я] X
X -j—l—Tr2 [0,5 — 0,5;^ cos A + at) я — x2 sin A + a,) n\ +
\x — у I
16
Ai ф(а^1п|х — у |.	(*)•/)

536
РЕШЕНИЯ В ОБОБЩЕННЫХ РЯДАХ ФУРЬЕ
[Гл. XIII
Ниже приводится таблица, в которой для четырех различных точек
внутри эллипса указаны приближенные значения и (х), вычисленные по
формуле E.7), и точные значения; кроме того, указываются модули откло-
отклонений приближенного решения.
X
0,01; 0
0,1; 0
0,5; 0
0,9; 0
и(х)
0,199930
0,199247
0,283090
0,405242
U (X)
0,20003
0,20300
0,27500
0,44200
| и{х)—и (х) |
0,00010
0,00371
0,00809
0,03675
б) при at = 5, bx = 3, решением системы E.5) является
ф (у1) = — 0,1428199, ф (у2) = —0,3384742,
I = — 0,0327377,
1 = 0,1189288,
ф (у») = 0,03063215,
( = — 0,0282381,
Ф (у6) = 0,1418435,
Ф (у8) = — 0,1243106.
Внеся эти значения в E.5), найдем приближенные значения и (х).
В следующей таблице для семи различных точек внутри эллипса даются
полученные приближенные значения решения и (х), точные значения и от-
отклонения:
X
0,01; 0
0,1; 0
0,5; 0
0,9; 0
0,2; —0,2
0; 0,3
0,8; 0,1
~U(X)
0,19993
0,20290
0,27486
0,44282
0,20010
0,17257
0,38860
U (X)
0,20003
0,20300
0,27500
0,44300
0,20000
0,17300
0,38900
| U (X)—U (X) |
0,00010
0,00010
0,00014
0,00017
0,00010
0,00043
0,00039
III. В качестве третьего примера рассмотрим
решение первой основной задачи статики для
упругого круга. Пусть радиус круга равен единице и для гранич-
граничных значений смещений имеем
 (У) = h (у) = — 1 + 4#
U2 (у) = f2(y) = 2 — 2y\
или, в полярных координатах,
иг A, О) = /х (-&) = 1 + 2 cos 20 + 3 sin 20,
2у1У2,
Пусть А, = 2, [I = 1. Точным решением задачи, как легко проверить,
будет вектор и (х) с компонентами на декартовых координатных осях
их {х) = 2,8 + 0,24 — 3,8x1 + 6jti*2,
п2 (х) = 3,4 — 3,44 — 1,4*1 + 2ххх2.

§ 5]
численные примеры
537
Представим и (х) при помощи формулы Грина
	JL \[Т(ду, n)T(x — y)Yf(y)dyS>
n)T(x—y)Yf{y)dJS.
E.8)
E.9)
где
УП -\t21
причем
Вычисляя интеграл
г (*; /) == -^ J it (ду, п) г (ж—у)]' / {у) dyS, х е D-,
S
найдем (л: = (р, ^0))
w {г. гч	Г BА, + Зм>) cos 2О0 + C^ + 5|ы) sin 2d0 ¦
o)]
А— Г (A>+ti)cos2O0-f-^sta2O0 ,
. П — — [	2ра(^ + 2|л)	^
и функциональное уравнение E.9) запишется в следующем виде:
2а
f 1Гц(х—y)
2я
[ 1Г21 (х — у) ф1 (у) + Г22 {х — у) ф2 (у)} dO = я^2 (х;
E.10)

538
РЕШЕНИЯ В ОБОБЩЕННЫХ РЯДАХ ФУРЬЕ
[Гл. XIII
Для приближенного решения этой системы применим формулу квадра-
квадратур Гаусса с 12 ординатами; вспомогательные точки xk = (pkJ до/О» k =
= 1, . . ., 12, зафиксируем на концентрической окружности радиуса, рав-
равного 6, так, чтобы точка хк лежала на радиусе, проходящем через точку yk.
Решая полученную систему из 24 линейных уравнений, находим
ф1 (у1) = —3,2898639, ф2 (у1) = 0,3048392,
ф1 (у2) = —4,8003739, ф2 (у2) = —0,1237495, .
ф1 (i/З) = _4,7148752, ф2 (у3) = —0,7438623,
ф1 (^) = 0,0943634, ф2 (у4) = —0,7585132,
ф1 (у5) = 5,1369463, ф2 (уь) = 0,3207615,
ф1 (г/в) = i f 1388360, ф2 (у6) = 0,8489420,
ф1 (у*) = —5,0928226, ф2 (у7) = —0,2840868,
ф1 (у8) ==—1,3594572,
ф1 (у9) = 4,6837652,
ф1(уЮ) = 4,0164068,
ср1(у11) = 0,1862522,
ф1 (у12) = —2,2725934,
I = —0,8604027,
ф2(у9) = 0,0759234,
ф2(уЮ) = 0,8436435,
ф2(уп) = 0,7829098,
ф2 (у12) = 0,4897975.
Остается подставить эти значения ф^0» t = 1, 2; / = 1, . . ., 12,
в E.8), которую предварительно следует заменить при помощи той же фор-
формулы квадратур (Гаусса) с 12 ординатами, и тогда для приближенного ре-
решения будем иметь выражение
12
E.11)
i=i
где Л^ — коэффициенты квадратурной формулы.
Ниже приводятся значения, вычисленные по формуле E.11) для соста-
составляющих по осям координат:
Составляющие
по осям
й(*)
Точка
0? 0,1
0; о,1
0,5; 0.5
0,5; 0.5
0,5; 0
0,5; 0
Приближенное
решение
и (х)
2,763
3,385
3,450
2,730
2,851
2,549
Точное решение
и(х)
2,762
3,386
3,400
2,700
2,850
2,550
Отклонение
\Ъ (х) — и(х)|
0,001
0,001
0,050
0,030
0,001
0,001
§ 6. Способ последовательных приближений
1. Задачи для однородных сред. В этом параграфе будет показано, что
интегральные уравнения основных статических задач упругости решаются
некоторой модификацией метода последовательных приближений, основан-
основанной на общих теоремах из глав IV и VI. Для первых двух основных задач
это было недавно показано Фам Тхи Лаем (см. Pham The Lai HI).

R g]	СПОСОБ ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ	539
Рассмотрим сначала первую основную внутреннюю задачу; ее инте-
интегральное уравнение (см. гл. VI) имеет вид
Ф(г) — х \[Т(дд, n)T(y—z)]'<t(y)djS = F(Z),	F.1)
где х = L Относительно резольвенты уравнения F.1) в главе VI была до-
доказана
6.1. Теорема, а) характеристические числа вещественны, Ь) в ин-
интервале (—1.1) характеристических чисел нет, с) х == 1 не есть характери-
характеристическое число, а х = —1 есть характеристическое число шестого ранга,
d) полюсы резольвенты — простые.
Вследствие того, что значение х = —1 является характеристическим,
решение уравнения F.1) при х = 1 нельзя выразить классическим рядом
Неймана. В связи с этим рассмотрим уравнение
Ф<*)—2=7" J
s
где v.' — комплексный параметр; очевидно, при и' = 1 уравнение F.2) об-
обращается в уравнение F.1) для я = 1.
Формально, решение уравнения F.2) может быть записано в виде
ф(г)=Ё(«?ФF)(г). 2 65,	F.3)
6=0
где
F.4)
s
J [T(d9, п)Г(у~z)]'4>^-
Пусть K(z, у) = \Т(д„ п)Т(г—у)]',
/СФ = Г17-ф„ п)Т(у—z)Y ф
согласно теоремам IV, 3.23 и IV, 3.25,
/СфбС°««E), если <p?C°<<*(S),
и
Пусть
/С'Ф = | К"(х, уL>(y)d!/S, р = 1, 2, ..., ЯЧ*. у) — tf (х, г/).
Из F.4) получаем
или

540	РЕШЕНИЯ В ОБОБЩЕННЫХ РЯДАХ ФУРЬЕ	[Рл XIII
и ряд F.3) принимает следующий вид:
№ + K\k F (г).	F.5)
Таким образом, дело сводится к доказательству абсолютной и равномерной
сходимости ряда F.5) при х' = 1. Для этого заметим, что когда х' описы-
описывает окружность у' единичного радиуса с центром в начале координат, то
параметр
х =
2-х'
описывает в своей плоскости окружность у с диаметром, совпадающим с отрез-
отрезком вещественной оси	^-, 1 .
Согласно теореме 6.1 вектор ф (z), решение уравнения F.1), есть голо-
голоморфная функция параметра х в области, содержащей внутри себя окруж-
окружность у. Следовательно, это решение, рассматриваемое как функция х',
будет голоморфным в некоторой области, содержащей внутри себя окруж-
окружность у'. Отсюда ясно, что ряд F.5) при х' = 1 сходится абсолютно и рав-
равномерно.
Итак, решение уравнения F.1) при х = 1 представляется абсолютно
и равномерно сходящимся рядом
k=0
Перейдем к рассмотрению второй внутренней
основной задачи. Соответствующее интегральное уравнение со-
согласно VI, §2, имеет вид
Ф (г) + х f T (дг, п (г)) T(z — y)q> {у) d,S = F (z),	F.6)
при х = 1, где F (г) — заданный вектор.
Условия, необходимые и достаточные для разрешимости задачи, согласно
VI, 5.6, имеют вид
j x(z)F (z) dS = 0, / = 1, 2, ..., 6,	F.7)
где {% B)}/e=,i — полная система векторов жесткого смещения. Относительно
резольвенты уравнения F.6) (см. гл. VI) справедлива теорема 6.1.
Фам Тхи Лаю принадлежит также предложение:
Если ф е С?'а (S), где
С°/аF0=={ф:фбСо'аE); Ji(*Mz)dS = 0, /=1, 2, ..., б!
и если
„ п(г))\т(г — 0)ф(у)^"Г —0, 265,	F.8)
mo ф =! 0.

§ 5]	способ последовательных приближений	541
В самом деле, из условия F.8) вытекает
Ф (г) + j T (д29 n(z)) Т{г — у)ц> (у) dgS = О, z 6 S.	F.9)
Уравнение, союзное с уравнением F.9), как известно из главы VI, имеет
в качестве полной системы собственных решений совокупность шести ли-
i
нейно независимых векторов жесткого смещения %(z), i = 1, . . ., 6; сле-
следовательно, полная система собственных решений уравнения F.9) также
состоит из шести векторов. Так как, согласно теореме 6.1, полюсы резольвент
этих уравнений простые, соответствующие им фундаментальные решения
(см. гл. IV) биортонормируются, и мы можем считать биортонормирование
выполненным.
Пусть ф0 (z) есть некоторое решение уравнения F.9) из класса С% a(S);
тогда
6
Фо(г)= 21 W>*>(z),
где {фо*1 (z)}!^! — линейно независимые собственные решения однородного
/
уравнения F.9). Умножая на % (z), / == 1, . . ., 6 и интегрируя по S, вслед-
вследствие биортонормированности и принадлежности ф0 классу Cxa(S)9 будем
иметь а, = 0, и предложение Фам Тхи Лая доказано.
Ищем формальное решение уравнения F.6) в виде ряда
Ф(г)= J/V*^).	F.10)
Тогда
фA) (z) = _ j T (дг,п) T(z — y) Ф(О) (
F.11)
ф(*)(Z) = - j T(дг, n)T(z — y)q><*-*>{у)dyS.
Пусть
?Ф = J Г (дг, п (г)) Г (z — у) <р (у) dyS.
Покажем, что если ф 6 Сх' аE), то LфGC% a(S). Согласно граничным свой-
свойствам потенциала простого слоя
п) \ T(z — y)q>(y)dysVr — ф(г).
s	J
Но первое слагаемое справа принадлежит классу (?{ a(S), так как выра-
выражает граничное значение напряжения, соответствующего полю смещений
j Г (х — у) ф (у) dyS, которое существует по условию задачи, короче го-
говоря, как граничное значение решения второй внутренней задачи. Второе же
слагаемое принадлежит классу C§a(S) по предположению* Отсюда, вслед-
вследствие того, что F (z)?Cfya (S), из F.11) следует

542	РЕШЕНИЯ В ОБОБЩЕННЫХ РЯДАХ ФУРЬЕ	[Рл# XIII
и если ряд F.10) равномерно сходится, то и сумма его
cpB)€Cox'a(S).
Но, по доказанному выше, в классе С^ a(S) однородное уравнение F.9)
допускает только нулевое решение и, следовательно, в этом классе решение
неоднородного уравнения голоморфно при | х | ^ 1, в частности, при х = 1.
Таким образом, ряд F.10) равномерно и абсолютно сходится при х = 1
и можно писать
для единственного в классе С?' a(S) решения. Общее решение уравнения F.6)
класса С°- a(S) будет иметь следующий вид:
2 «<Pj*> (г),
1
2
k =1
где {<роЛ)}|=»1— полная система решений однородного уравнения класса
C°*a(S). Чтобы сделать это доказательство вполне строгим, следует на S
и F наложить некоторые условия гладкости, которые позволяют перейти
от представления F.10) к F.11).
К этому же выводу можно прийти из следующего рассуждения. Запи-
Запишем решение уравнения F.6) в виде
(z, у; K)F(y)dyS9
где R (z, д; к) — сингулярная резольвента. Вследствие того, что к = 1
есть простой полюс, справедливы соотношения (см. гл. IV)
zf y\ х),
Ф(г)= F(z) — ^-.?ibk{z)\x{y)F{y)duS — x J А (г, у; y)F(y)dyS,
k=l	S	S
где A (z, g; x) — голоморфная относительно х матрица.
Согласно условию разрешимости F.7) первый интеграл справа исчезает и
l(z, у;
или для решения при х = lf
<p(z) = F(z) — ] A(z, у; l)F(y)dyS.
Дальнейшее очевидно.
6.2. Замечание. Этот способ применим и к задачам III, IV, VI
для произвольного S?JI2 (а) (для III и IV в том случае, когда S не есть по-
поверхность вращения), но мы не будем входить в соответствующие подроб-
подробности.
2. Гранично-контактные задачи.
а) Главная гранично-контактная задача (см# I, § 14, п. 4). Пусть рас-
рассматривается случай единственного включения D* с поверхностью S и вы-

§ g]	СПОСОБ ПОСЛЕДОВАТЕЛЬНЫХ ПРИБЛИЖЕНИЙ	543
полнена гипотеза Коши. Тогда из (XII, 5.52) и (XII, 5.54) будем иметь
интегральное уравнение
к J tr<°> (ду, п)Г<°> (*/—*)]' и~(у)dyS = F(г),	F.12)
где
и F (г) — заданный вектор. Согласно теореме 6.1 и ввиду того, что
11*1+1*0
для решения уравнения F.12) можно применить обычный метод последова-
последовательных приближений, предполагая достаточную гладкость правой части
и поверхности S. Решение будет иметь вид
и- (г) = S
где
= J Kk (Zf y) F {y) dyS
и Kk (z, у) есть k-e итерированное ядро для уравнения F.12).
б) Другие гранично-контактные задачи. Теорема, аналогичная теореме
6.1, может быть получена и для других задач.
Для задачи VI, например, она доказана Купрадзе [13, 171, и так как
интегральные уравнения теперь имеют вид
> 2; D0)]'u-(y)dl/S = F(z), F.13)
где под G@) (r/, z\ Do) подразумевается тензор Грина соответствующей задачи
для области ?H, с постоянными Ламе 2lo> Ш» & F (z) — соответственным об-
образом заданный вектор, то решение может быть построено в виде ряда
Неймана
2(?r?r)	FЛ4)
k=0
где
и Kk (z, у) есть k-e итерированное ядро уравнения F.13).
Простой подстановкой F.14) в функциональные уравнения типа C.3)
для соответствующих задач получаем значения искомого решения всюду
в D0\S.
6.3. Замечание. Вопрос о применении последовательных при-
приближений для решения второй задачи остается открытым. Вероятно, таким
путем можно построить решения и некоторых новых задач, например, сме-
смешанных, некоторых внешних и др. Рассмотрение этих вопросов предостав-
предоставляется читателю.

544	РЕШЕНИЯ В ОБОБЩЕННЫХ РЯДАХ ФУРЬЕ	[Рл XIII
§ 7. Заключительные замечания и библиографические справки
Первые два способа, описанные в § 1, п. 2, являются способом построе-
построения точных решений — без использования интегральных уравнений, если
заранее известно существование решения задачи в соответствующем классе
функций.
Мы видели, что для систем уравнений теории упругости и термоупру-
термоупругости существуют системы частных решений, полные в L2, и что решение
каждой граничной задачи класса L2 для названных уравнений, если они
существуют, представляется рядом Фурье относительно систем упомянутых
частных решений. Существенным при этом является тот факт, что для вы-
вычисления коэффициентов Фурье требуется лишь ортонормирование исполь-
используемых частных решений, и что эти последние непосредственно порождаются
любым фундаментальным решением задачи и выражаются в элементарных
функциях вместе с ними.
Таким образом, для того, чтобы выразить решение любой из рассмо-
рассмотренных выше граничных задач рядом Фурье с известными коэффициен-
коэффициентами, достаточно иметь теорему существования и явные выражения фун-
фундаментального решения дифференциального уравнения задачи.
Приближенные решения, полученные выше, являются суммами первых N
членов этих рядов Фурье и при N —¦> со равномерно стремятся к точным|ре-
шениям.
Обычно принято считать, что метод Фурье, связанный с разделением пе-
переменных, допускает эффективную реализацию только для некоторых кон-
конкретных областей. На самом деле, как мы видели, при достаточно общих
предположениях относительно области и других данных задачи, решение
всегда выражается в виде ряда Фурье, с явно задаваемыми коэффициентами.
В связи с этим, этот метод мы назвали методом обобщенных рядов Фурье.
В действительности, в идейном отношении он близок к так .называемому
методу уравнений Фишера—Рисса, получившему широкое развитие, приме-
применительно к уравнениям эллиптического типа, в работах современных италь-
итальянских математиков (Пиконе, Америо, Фикера и др.)> (см. Miranda [11).
Основное отличие нашего метода от метода уравнений Фишера—Рисса со-
состоит в том, что в первом содержится общий процесс построения необходимой
полной совокупности частных решений, играющей здесь главную роль (см.
Купрадзе [171).
Заметим, что обсуждаемый метод при некотором развитии может быть
применен и для получения теорем существования. Именно таким путем
получено в известной работе Fichera [4l доказательство теорем существова-
существования для основных задач (в том числе и для общей смешанной задачи) эла-
стостатики.
Методом обобщенных рядов Фурье теорема существования для задачи
об акустической дифракции доказана в работе Пааташвили [31.
Первое изложение метода обобщенных рядов Фурье было дано в совме-
совместных работах Купрадзе и Алексидзе [11, [21 и более подробно в книге Куп-
Купрадзе [131.
В дальнейшем метод был распространен для решения некоторых клас-
классов смешанных задач эллиптического типа (Бурчуладзе [61, [101, [111),
для решения гранично-контактных задач в неоднородных средах (Рухадзе Ж.
[11), для бигармонических задач (Шефер [2!) и др.
С другой стороны, было показано распространение метода на параболи-
параболические уравнения (Купрадзе [151, Напетваридзе [21, [31, [41, Доманьский,
Пискорек, Роек [11), на системы уравнений гидродинамики; на системы
уравнений Максвелла для общей задачи дифракции в неоднородных средах
(Купрадзе [171), на граничные задачи электродинамики (Полищук [11) и др.

задачи	545
Общим для всех работ является основная теорема о полноте в L2 (S)
совокупности счетного, бесконечного множества частных решений, порождае-
порождаемых выбранным фундаментальным решением.
Применение последовательных приближений для решения первой и
второй основных задач, основанное на теоремах глав IV, VI, дано Фам Тхи
Лаем (см. Pham The Lai HI).
ЗАДАЧИ
1.	Рассмотреть смешанные задачи с граничными условиями, отличными от рассмотрен-
рассмотренных в § 2, п. 3.
2.	Рассмотреть гранично-контактные задачи, отличные от задачи § 3, п. 1.
3.	Рассмотреть смешанные гранично-контактные задачи.
4.	Решить задачи I, III и IV для уравнений термоупругости.
5.	Решить смешанные задачи моментной теории упругости.
6.	Решить задачу, аналогичную главной гранично-контактной для термоупругости.
7.	Решить ту же задачу (см. задачу 6) для моментной теории упругости.
8.	Построить приближенные решения различных трехмерных задач способами, указан-
указанными в § 1, пп. 2, 3, 4.
9.	Доказать сходимость приближения в третьем способе (см. § I, п. 4), и дать оценки
10.	Дать оценки погрешностей для приближенного процесса первого и второго способа
(см. § 1, пп. 2, 3).
35 В. Д. Купрадзе

ГЛАВА XIV
РЕШЕНИЯ В РЯДАХ И КВАДРАТУРАХ
В этой главе указываются некоторые новые случаи эффективного по-
построения решений граничных задач упругости и термоупругости для кон-
конкретных конечных и бесконечных областей.
§ 1. Эффективное решение основных граничных задач
классической теории упругости для сферы
и сферической полости в неограниченной среде
1. Задача A)±. Задача A)+ для сферы ставится следующим образом
(см. I, § 14): найти в области Ш (О, R) регулярное решение и уравнений
A.1)
по граничному условию
A.2)
где S = С (О, R) — сферическая поверхность радиуса R, f — заданный
на S вектор.
Решение ищем в виде потенциала
и(х)=\[Т(ду, п)Т(х—y)]'g{y)dySf xeUI(O9R)9	A.3)
где g — искомый вектор,
y, n)
= T
!. 2.3.
Переходя в A.3) к пределу, когда х—* z?S и учитывая A.2), для опре-
определения g получим сингулярное интегральное уравнение
{	A.5)

ЗАДАЧИ ДЛЯ СФЕРЫ И СФЕРИЧЕСКОЙ ПОЛОСТИ
547
Будем полагать временно, что f^C2*a(S)f О <<х ^ 1. Ниже это требова-
требование будет ослаблено. Тогда и g^C2fCC(S) (см. VI, 3.3).
В силу равенств
(г,- - у,) (г„ - yk)
8kl
д*\г-у\
(п и v — орты нормалей в точках у и г соответственно), уравнение A.5) при-
принимает вид
Введем сферические координаты:
дс1 = рсо$ф081п60, у1 == /? cos ф sin 0,	гх =/? cos ф0 sin 90,
х2 = р sin ф0 sin 90, у2 = R sin ф sin Э,	г2 = /? sin ф0 sin 90,
jcs = р cos Эо,	Уз = /? cos 6,	г3 = /? cos 0O,
Пусть
A.9)
= f(%f Фо)= Zl fm(%> Фо)»
СЮ
» Фо)= Zj gm(%% Фо)'
m=Q
(gmu Sm2t ётз) — сферические вектор-функ
fm (%> Фо) S fm (Z) = ^±^ J Pm (COS у) f (у) dyS,
s
F0, ф0) = gm (Z) = 2^,A f Pm (COS Y) gr (y) dyS,
где fm =¦• (fmu fm2, fm3) и g
ции порядка т:
A.10)
Pm (I) — полином Лежандра m-го порядка, у — угол между радиус-векто*
3
рами Ох и Оу, cos 7 = ^^ ? **?*•
Известно, что (см. Смирнов [31)
1	i
(Ml)
Отсюда с помощью рекуррентного соотношения
(т + 1) Ят+1 (|) — Bт + 1) ЕРт A) + m/Vj (g) = 0,
35*

548
РЕШЕНИЯ В РЯДАХ И КВАДРАТУРАХ
^ XJV
ПОЛЕЧИМ
т=0
Х
Лег^о доказывается, что если z?S, то
c»s2 (г)
= -4- [slnToctge0^--cos?01|-],
где -г- (fe = 1, 2, 3) определяются из (V, 1.10);
2)
_, о о
—i,t, о,
ч а2 - ' Г g2 I
A.13)
(см. задачу 5, гл. V);
3) оператор ^- (k = 1, 2, 3) не изменяет порядок сферической функции;
4)
(U4)
На основании A.9)—A.11) очевидна справедливость тождеств
Рассмотрим теперь вектор

Я J'i	ЗАДАЧИ ДЛЯ СФЕРЫ И СФЕРИЧЕСКОЙ ПОЛОСТИ	549
По формуле A.12)
00
*<*>- 2 Bm+l)Bm + Z)R^ gad (Hy [p^g, (»)] -
от=О
rn=O
Элементарные вычисления дают
grad div [pm+2gm (г)] = 2pmgm (z) + 2pJ? (д„ v) \p™gm (г)] +
+ 4xdiv [pngn B)] + p2grad div [pmgm(z)\,
p2 grad div [pmgm B)] = mpmgm B) + Bm— 1) xdiv [pmgm B)] -f
+ (m — 1) pM (д„ v) tp»gm (г)] — ргМ (д„ v) J? (d,, v) lp*gm (г)].
Используя эти последние тождества в A.17), будем иметь
^ W — ?j [ Bm + 1) Bm + 3) /?m»l	Dm2 — 1) p*Rm-3 J P 8mKz) "T
0
] Р# ^' v)
~
Dm*-
00
дует
m=0
По непрерывности вектора V в Ев, из полученного разложения еле-
+RJC (д„ v) gm (z) + 2R*M (дг, v) Л (дг, v) gm (г)]. A.18)
Исходя из формул A.15), A.16) и A.18), уравнение A.8) можно пере-
переписать следующим образом:
т=0

550	РЕШЕНИЯ В РЯДАХ И КВАДРАТУРАХ
Используя тождество
— RJ({d2y v)gm(z) +
3
и принимая во внимание ортогональность и полноту сферических функций,
из предыдущего равенства получим
z, v) gm (г) + R*ym [v gradj ? ^g- = fm (г), A.20)
где
n — 2(m+l) , 4bm(m+l)
^m— 2m+1 ^ D
R __ 2(g +^)	8bm{mt 1)
2m+1 ^ Dma— l)Bm
8bm{m-t- 1)
2m + 1	Dma — 1) Bm 4- 3) • Ym Dm2 — I) Bm + 3) *
Воздействуем оператором -г— на fe-ую проекцию A.20) и просуммируем
по k (k = 1, 2, 3); учитывая A.13) и A.14), найдем
г/ B)	9т -f- I V dtmi B)
(г)	2(m + 2) Zj as,-(г) #
Теперь из A.20) следует
amgm (z) + Rfimdi (дг, v) gm (z) = г|;т (г),	A.22)
где
Снова, действуя оператором «^ (дг, v) на равенство A.22) и применяя
A.19), будем иметь
(ат — рт) Ж (дг, v) gm (г) = J? {дг, v) ^ (г) — (/* + 1) Р^т (г) -
Подставляя найденное выражение ^# (d2f v) gm(z) в A.22) и учитывая
тождество
2^f} i	j^g
получим
l«OT («m — ft») — m (m -f 1) fa] gm (г) = (am — pj /m B) — Щ>тЛ (дг, v) fm (г)
•> т=0,оо. A.23)
.	 ^°/ V*/
/=1

ЗАДАЧИ ДЛЯ СФЕРЫ И СФЕРИЧЕСКОЙ ПОЛОСТИ
551
Разложим в ряд потенциал A.3).
Заметив, что
_?, 1	= (А	М Г *W
дп\х—у\ \дп R)\\x —
У\Л
f J
— р ># (д v)
	2
\x~ y\ Z R dxf[x-y\>
для A.3) будем иметь
jj-graddiv l\x-
Отсюда получаем
•w—
w=0
2
т=0
X graddiv t(-8-)"«.«] -
2j
m=0
x
Заменим здесь gmB) значением из A.23). После некоторых преобразо-
преобразований получим искомое решение задачи A)+ в виде ряда
_
m=0
— А,— 2р]
X
Xgraddiv[(-|-)mfmB)]
Приняв во внимание A.10) и легко доказываемые равенства
A.24)
1
R
2т+1 / р \т
)
m=2
/ р \т /C0SV)_ f Г
0
1 3p^COS7
A.251

552	РЕШЕНИЯ В РЯДАХ И КВАДРАТУРАХ	[рл#
будем иметь окончательно
и(х)= J K + (x, y)f(y)dyS, хеш (О, R),	A.26)
где
К + (х ) = \\к±(х
[A.27)
dt
о
?2~2i?p^cosY + pVK/2 /?	#а J/1-H*
В теории упругости A.26) представляет аналог известной формулы Пуас-
Пуассона для сферы (см. Натрошвили [11).
Доказывается, что A.26) является единственным решением задачи (I)*
в классе С (Ш (О, #)) П С2 (Ш (О, #)), при f6 С E).
Из A.26) получается также формула среднего значения
Л
о
Аналогично решается и задача (I)"", но здесь приведем другой способ
ее решения. Ищем решение задачи (I)" в виде потенциала
a(x)=J{|tf(dff n)T(x—у))' +
s
,Я), A.28)
где g — искомый вектор, Г (дс — у) — матрица Кельвина (см. (II, 1.4)),
\N(dg, n)Y(x—y)Xki =
!. 2,3.
Переходя в A.28) к пределу при х—»z^S и используя A.6), получаем
интегральное уравнение
Требуя снова достаточную гладкость от функций f ng, тем же путем, как
и выше, найдем
ы) Bт + 1) , /Ч
Разложим A.28) в ряд и внесем вместо gm (г) его выражение через fm (г).
В результате получим
!—/?а) У

« ;1 J	ЗАДАЧИ ДЛЯ СФЕРЫ И СФЕРИЧЕСКОЙ ПОЛОСТИ	553
Полученный ряд и есть искомое решение задачи A)~.
При помощи формул A.25) это решение можно переписать в виде
A)
К	)f)d& Е\Ш@ R),	A.29)
где
A)	lid)	||
К (х, y) = \Kjf(x, у)\\3х3>
v *' J (p2-
0
аир определены из A.27).
Легко доказывается, что при/?C(S) вектор, определенный из A.29)»
представляет единственное решение задачи A)~ в классе
, R))nC2(E3\UI(O, R)).
Если f&Clta(S)f то найденные решения — регулярные функции.
2. Задача (Н)^ Задача (П)+для сферы ставится следующим обра-
8ом (см. гл. I, § 14): найти в области Ш (О, R) регулярное решение и
уравнений статики A.1) по граничному условию
\Т(дг, v)и(*)}+ =/="(*). 265,	A.31)
где F — заданный достаточно гладкий на S вектор, Т (дг, v) — оператор
напряжения (I, 13.2).
Решение задачи (П)+ ищем в виде
u(x)=lr(x—y)g(y)dyS, xeiII(O,R),	A.32)
где Г (дг — у) — матрица Кельвина, g" — искомый вектор.
Обычным путем, для g получим интегральное уравнение (см. гл. VI, §2)
A.33)
где
аЛк1{д., vj-fj^i]' *. /-1. 2, 3, A.34)
о, Ъ, JCkj (дг, v) — определены из A.4). В силу тождеств A.6) и A.7), иа
A.4) и A.34) имеем
\Т(д„, п)Т(г — у)]' = [Т(дг, v)V(z — y)], г,

554	решения в рядах и квадратурах	|ГЛ# XIV
Это соотношение дает возможность сразу написать разложение по сфе-
сферическим функциям для уравнения A.33):
_	Jvgrad2
от=0
Отсюда следует
з
&тёт (*) + Щ>тД Фг* v) 5m (^) + /?27m [v g^^dj V W^ = FOT B), A.35)
где 6m = am + 2, amy pm и vm определены из A.21).
Уравнение A.35) решается так же, как A.20); при этом
|6т (бт — рт) — т (т + 1) рт ] gm {г) = (бт — $т) Fm (z) — Щ>тЛ (д„ v) Fm B) —
~ ^ ^ - t-m S\ 1) У, '	S
При m = 0, A.36) обращается в равенство
"О;-. A.36)
A.37).
а при m = 1, бх — Pi — 2yi = 0, и, следовательно, для существования ре-
решения необходимо
Эти условия выражают равенство нулю главного вектора и главного мо-
момента внешних усилий.
Умножим A.36) на (-jr) и найдем rot от обеих частей
Bm + 1) [(Я. + 2ц) Bт - 1) - 2 Q, + ц) (т + 1)] Г	. .. / рт г- ,Л"| ,
~ 2{(>,+ 2|i)Bm-l)-2(X+(i)«(m+l)] [ ё	\ Rm т()) J "
. A.38)
Из A.37) и A.38) очевидно, g0 и rot (-jrgi (^)) остаются произвольными
постоянными векторами (в силу чего в решении появляется произвольное
жесткое смещение).

§ 1]	ЗАДАЧИ ДЛЯ СФЕРЫ И СФЕРИЧЕСКОЙ ПОЛОСТИ	555
Применяя A.11) и A.12), из A.32) получаем
X grad div ?
I m=0
m—\
2m + 3 \R
(г)
Подставляя здесь вместо gm (z) выражение из A.36) и используя тождества
^-)m gm (г)] = grad (х [(^у gm (
получим
Л«„3) [xiot (g>«B))] +<Ч^-Р2) grad div [(-$
ptgrad div [(|-)m Fm(z)] } + С + (xCd)], A.39)
2

556
РЕШЕНИЯ В РЯДАХ И КВАДРАТУРАХ
(Гл. XIV
где
—А,)т — Л, —
[г т
лC) = —
\кт [2 (A, -f И-) т2 — 2fxm + А, + 2ц] '
2\xm(m — 1) *
/? (A, + \i)
AЛ0)
2ц [2 (А, + Ц) /тг2—2|ыт + А, + 2ц]'
	R BтХ + А, + 2М>)
2цт (w — 1) [2 (X Н- ц) т2 — 2fi/n + А, 4- 2ц] '
С, СA) — произвольные постоянные векторы; знак 2 означает, что сумми-
суммирование для Ат] и А(т начинается с т = 2.
Учитывая A.25) в A.39) и A.40), находим интегральные выражения для
векторов смещения и напряжения
B)
+
где
хеш (О, R),
B)	B)
A.41)
A.42)
Зр? cos у
R*
!*•
ах = оо + tDx =
= (R2 — 2Rptcos у + p2*2K'2.
A.43)
Формула A.41) представляет аналог формулы Неймана для гармониче-
гармонических функций (см. Натрошвили [11).
Легко доказывается, что A.41) является единственным (с точностью до
слагаемого вектора жесткого смещения) решением задачи (П)+ при F? С (S).
Совершенно аналогично решается задача (II)" и решение имеет вид
Г B)
u(x)=)K-(x9y)F(y)dyS9
A.44)
A.45)

Я' Ц	ЗАДАЧИ ДЛЯ СФЕРЫ И СФЕРИЧЕСКОЙ ПОЛОСТИ	557
где
B)_
К (х,у)
dp ^3j + р\ dxtdx/ dXidXj
дх, у* dp
i,/= 1,2,3,
J Q*(rt l at, t — 1, A
I|
+ 6Х.Ц + Зц* N
(p*-RW)dt 1
	J' 2 =
Q. (^ = ( 2 _
A.46)
12 + 6X\X
3. Задача (III)±. Задачу (III)+ формулируем следующим образом
(см. I, § 14): найти в области Ш (О, R) регулярное решение уравнений A.1)
по граничному условию
\Т(дг, v)u — v
где F4 и F = (Fl9 F2, Fs) — заданные на S величины.
Решение будем искать в виде '
и (х) = J K+ (х, у) \Т (дд, п) и (у)]+ dyS + [xCW I + С,
2)
где матрица К+(х, у) определена из A.43), а С и СA> —произвольные посто-
постоянные векторы.
В силу тождества
[Т (ду9 п) и (у)]+ = {Т (ду, п) и(у) — п (Т(ду, п) и {у) п)}+ + nq {у),
где q (у) = (Г (дд9 п) ип)+$ можно и (х) придать вид
u(x) = RW(x) + RW(x)>	A.48)
где
/?(i) (х) = J Я+ (х9 у) F (у) dyS9 #<2> (х) = J /C+ (х, у) nq (у) dyS.
S	S
Обозначив
ф B) = F4 (z) — (vi?d> B))+
из условия A,47), для определения q получим уравнение
(v#<2> (з))+ — -ф B) — (Cv).	A.49)
Разложим^ A.49) по сферическим функциям.

558	решения в рядах и квадратурах	[Гл# XIV
Предварительно займемся разложением (vR{2) (г))+.
Принимая во внимание A.39), имеем
B) (х) = ? ' № A (X) + Л <f X diV h (X) + А™
/?B) (х) = ? ' № Am (X) + Л <f X diV hm (X) + А™ [X FOt hm (x)] +
m=l
+ А$ (Я2 — р2) grad div hm (x) + AkV grad div /tm (x)},	A.50)
где A{m (i — 1, 2, . . ., 5) определены из A.42),
J (-^-)m Pm(cosy)nq(y)dgS.
s
Используя рекуррентные формулы
(m + 1.) Pm+1 (I) — Bm + 1) gPm (?) + mPm-1 A) = 0,
mtPm (I) + A — I2) ^m (S) = тРт„х (l)s
легко доказать равенства
^i (f
где
Отсюда находим
w=2
m = 2, со.
00
Теперь, предполагая, что гр(г)= S 'Фт (^) и учитывая ортогональность
т=0
и полноту совокупности сферических функций, из A.49) заключаем:
(заметим, что (vC) = 7 —ъ*— сферическая функция первого порядка).
к1
к=1
Используем A.51), A.52) и тождества
USr]- "•54)
[ж rot hm (x)] = — (m + 1) hm (*) + grad (xhn (x))

? I ]	ЗАДАЧИ ДЛЯ СФЕРЫ И СФЕРИЧЕСКОЙ ПОЛОСТИ	559
для преобразования равенства A.50):
х
+ S
2
m=2
w= 1
g LVX
Отметим, что вектор С, входящий в выражение <7i(z), не может остаться
произвольным. В самом деле, равенство нулю главного вектора внешних
усилий дает
S
Подставляя в A.55) вместо qm(z) значения из A.53), получим
RB)(x) =
4ji#3 ?}	dm
S
X grad ( (^- )m Pm (cos у) ф (у) dyS +
m=2
где
dm = 2 (A. + 2ц) m2 + A.m—2ц,
^B) = ^B) —(VC).
Отсюда, используя A.25), можно писать
X f Ф6(Д:, y)^{y)dJS + ^grad [ЗЯ, + 4ц — 2цр?] J Ф,(х,

560	РЕШЕНИЯ В РЯДАХ И КВАДРАТУРАХ	[Гл. 'XIV
где
Pi.2 —	TW+W)	f IP* I О 1. ' — A, A
Q @ = (/?»— 2Rpt cos 7 + p2^2K/2.
A.56)
Учитывая A.48), и выполнив некоторые преобразования, будем иметь
и(х) = J /(*(*, y)fiy)djS + [xCA)], х€Я/(О, /?),	A.57)
где СA) — произвольный вектор, / = (Flf F2, F3f \p)f
C)	II C)
~(l-S/4)[K+if (x
i==1'2, 3, /=1,2,3,4,
B,)
K+ {x, у) и Ф5 определены из A.43) и A.56).
В силу теоремы единственности решения задачи (Н1)+ для шара, вектор
смещения определяется с точностью до слагаемого вектора жесткого враще-
вращения. Этим и объясняется присутствие произвольного вектора [л:СA)] в фор-
формуле A.57). Аналогично решается и задача (III)"". Решение имеет вид
C)
K

], xeE9\UI(O9R),
s
где
JB)
K-(x,y)F(y)S;
s
C)	II C)
K) \iq
i = 1,2,3, / = 1,2,3, 4,

Ц	ЗАДАЧИ ДЛЯ СФЕРЫ И СФЕРИЧЕСКОЙ ПОЛОСТИ	§61
ф*5(х, у) = .	2 J Г^-q*77)	Б" I л+^+ц, *"•
о
определена из A.46).
4. Задача (IV)±. Задачу (IV)+ формулируем следующим образом (см.
(V,9.10)): найти в области Ш (О, i?) регулярное решение уравнений A.1) по
граничному условию
\u — v(uv)\+=F9	A.58)
= JF4,	A.59)
где F = (Fl9 F2, F3) и F4 — заданные на S величины*
Решение задачи (IV)+ будем искать в виде
A)
Очевидно,
[м (у)]+ =\и(у) — п (пи) \+ + ng (у),
где g (у) = (пи)+. В силу A.58) можно записать
К+ )F ) dS ЯB) ) j К
+ (х, у)F (у) dyS, ЯB) (х) = j К+ (х, у) ng (у) dyS,
g (у) является искомой функцией.
Из условия A.59) для определения g получим уравнение
Используя A.24), A.25), A.51) и A.52), легко показать, что
m=0	m=0
(X)- R
gm B) =
36 В. Д. Купрадзе
l '60)
^	H(z),	A.61)
где
A.62)

562
РЕШЕНИЯ В РЯДАХ И КВАДРАТУРАХ
[Рл# XIV
Пусть Щг)= 2 Hm(z)- Тогда из A.61), учитывая A.62), находим
т=0
i, m==0, oo. A.63)
При помощи тождеств A.51), A.52) и A.54), ЯB) (#) перепишется следую-
следующим образом:
Заменим здесь gm (z) ее значением из A.63). После несложных преобразова-
преобразований будем иметь
$у Н
2 ±М
т=0
где
dt
— X -f- 2ц -f-
28JI5
™ ""	4 (Я 4- 2ц)
Подставляя это выражение в A.60), получаем
f D)
а (#) = J К+ (>
S
A.64)
A.65)
где
f=(Fv F2, Fs, H), K+(x,
1.2, а, 4.
K
ti (x, д) и Фв (х, д) определены из A.27) и A.64).

Л 2]	ЗАДАЧИ ДЛЯ ТРАНСВЕРСАЛЬНО-ИЗОТРОПНОГО ПОЛУПРОСТРАНСТВА	563
Аналогично решается задача (IV)" и решение дается формулой
г D)
u(x)=\K-(x,y)f(y)dyS, xeEs\LU(O,R),	A.66)
где
f = (Л,/7,,/7,, Я*). F = (Fi> F2> fb) =\u — v(vo)}-, F4 = (T (d« v)u v)-,
#* = F4-{(X + 2fA)div Я<3) B) - $ (vtf<3> (г))}",
s
D)	11D)
K) \K
II
9 */)||3x4,
2 дх
•=1,2,3, /=1,2,3,4,
(J L Q*(t) p J
Лз = [— (ЗЯ + 10|x) + i l/23^ + 68^4-28fx2] [4
К и (*» i/) — определена из A.30).
§ 2. Граничные и некоторые другие задачи
для трансверсально-изотропного упругого полупространства
и бесконечного слоя
1. Вспомогательные формулы. В этом параграфе мы будем иметь дело
с однородными уравнениями статики трансверсально-изотропного упругого
тела. Закон Гука для этого случая был приведен в главе I, § 5, п. 4.
Основные однородные уравнения статики трансверсально-изотропного
упругого тела в компонентах вектора смещения можно записать в виде
(см. Love [11 или Лехницкий [1, 21):
д2и-. . ,	ч
B.1)
где сХ1, cS3, с13, с44, с66 ~~ упругие постоянные из закона Гука х), и19 а2
и и3 — компоненты вектора смещения.
~ = 0,
д2их , д2и2 , д2и2 , d2ti2 , ( , v д2иъ п
х) Здесь, в отличие от главы 1, § 5, п. 4, для коэффициентов Гука используются другие
обозначения, совпадающие с распространенными обозначениями.
36*

564
РЕШЕНИЯ В РЯДАХ И КВАДРАТУРАХ
[Гл. XIV
Если
Си = см = \>» с33 = си = А, + 2м„ с13 = Х9	B.2)
то система B.1) обращается в систему уравнений статики изотропной
упругой среды.
Фундаментальная матрица для системы B.1) имеет вид (см. Kroner [11,
Башелейшвили [31, Купрадзе и др. [13):
fel
а*
дх\
дхгдх2 '
дх2 ' ™дх2дх3
^ дхгдх3
B.3)
где
Ф* = (^з — Уз) In (rk + x3 — y3) — rk,
rk = Vak [{хг — yif + (x2 — у2)Ц + (x3 — уг)\ B.4)
а коэффициенты имеют значения
2пси
2псисыак (а2 — а3)
\ («2 — «я)
«* = ¦
(а2 —
. S т*-о,
B.5)
—1
6hf — символ Кронекера, ах = С44С66 , а а2 и а3 — корни квадратного урав-
уравнения
а2 + [(Ci3 + C44J—cuc3q—C44] a + C33C44 = 0.	B.6)
Если имеет место B.2), то Т(х — д) обратится в матрицу Кельвина
(см. (II, 1.4)).
Введем оператор обобщенного напряжения следующим образом:
v)ibK3,	B.7)
где
c66v2 ^- + C44V3 ^,
12
> v) = aovx -^- -f
> /л )— v — -4-av —
? /3 v) —с v —4-с v —4- с v —
С7ЛГ-|	ОХа	ОХо
' 23
Ч Л	^ I ft	^
B.8)

Л 2]	ЗАДАЧИ ДЛЯ ТРАНСВЕРСАЛЬНО-ИЗОТРОПНОГО ПОЛУПРОСТРАНСТВА	565
где а0, Ро» 7о и
ные условиям
— произвольные действительные постоянные, подчинен-
подчинен= Сц — с6
Если, в частности, а0 = с1г — 2с66, у0 = с66, р0 = с13, б0 = сш то
оператор обобщенного напряжения переходит в оператор напряжения.
Для вектора обобщенного напряжения, действующего на площадку, про-
проходящую через точку х, с нормалью v == (vx, v2, v3), будем иметь на основа-
основании B.7) и B.8)
где
Ж"
du2
a
° HZ
(P(dX9v)u)k=%
и	 1 о Я
К	 1 , Z, О,
, 	 duf
ох9
^оо 	 О&п "гГ! '
Ж"
B.10)
T32 — C44
T31 — C44
тзз —
дх2
Если нормаль совпадает с осью x3t из Bfc10) получаем
а для вектора напряжения —
(Т (дх, v) и), = т23 = с44 (^ + |^) ,
дх2 '
B.11)
B.12)
Совершенно так же, как в V, § 1, п. 3, получим общее представление ре-
регулярных решений уравнения B.1) в виде
B.13)
6(х)и(х)= J {[& (ду9 п)Г(у-х))' \и(у)\+ —
где б (х) — выражение, определенное из (V, 1.53), п — внутренняя нормаль

566	РЕШЕНИЯ В РЯДАХ И КВАДРАТУРАХ	[рл ? IV
в точке д,
[Р(ду, п)Т(у — х)У = \ 2 A\V I ,	B.14)
IU=i II зхз
~ак^+уо) шм(д^)+{c«a>+8w)d
(С66
"if J
№ = - (c44Y, + 606ft) ^ J- + (С66 + vo) *
( , k= 1, 2, 3 определены из (V, 1.10).
vsk \У)
Пусть в B.13) x?D+, S — граница области х3 ^ 0, У~х\ + xi + xl ^
^ R. Очевидно, S = «S1US2, где S± — область х\ + х$ ^ i?2, a S? — по-
поверхность полусферы У х{ + xi + xi = /?, с центром в начале и радиусом R.
Предположим, что вектор и на бесконечности удовлетворяет условиям
и(у) = О (/?-«)f ?P EV, n) u(y) =
где a > 0.
Устремляя /? к бесконечности и учитывая оценки
Т(х — у) = О (Я), 9 {оу, п)Т(у —
в силу которых
lim
будем иметь из B.13)
со
2и(х) = J J ([9 (дд, п)Т(у—х)]' \и(у)}+ —
—со
— Г (у — x)\&{dvi n)u(y)\*)dytdy^ x?D\ B.15)
где D+ — полупространство \х (хи х2, хв) б^з» *з > ®\\ вектор 3> (ду, п) и
определен формулами B.11), а
х)Г = —I S«l'/i »	BЛ6)
IU=i II зхз

2]
задачи для трансверсально-изотропного полупространства 567
где
= «if' =
-**) So
«if' =
П32 ' =
33 }
¦—
I ft
причем
— У,?)
l '
Оператор 0> (дт n) при p0 = c13 и 80 = c44 обозначим через Т (дуу п),
а для
И О0—
ЧЯ 4-
R
ро=
через iV (dyi п). Очевидно, формула B.15) остается в силе и для операто-
операторов Т (дуу п) и N (ди, п).
2. Граничные задачи и теоремы единственности для полупространства.
Рассмотрим для полупространства D+ следующие граничные задачи: найти
в D+ регулярное решение и уравнений B.1), удовлетворяющее на 5 од-
одному из граничных условий:
2)
3)
4)
Заданные на границе векторы должны иметь определенную гладкость
на S и определенный порядок обращения в нуль на бесконечности. К этим
условиям мы вернемся ниже.
Кроме указанных задач, будут рассмотрены также некоторые смешан-
смешанные задачи.
Однородные задачи будем обозначать (как и раньше) символами (I)+
)+ (IV)+

568
РЕШЕНИЯ В РЯДАХ И КВАДРАТУРАХ
[Гл. XIV
Покажем, что задачи (I)+, (II)+, (III)+, (IV)+ имеют только нулевые ре-
решения.
Рассмотрим задачу A)+. Используя B.15), когда $опуй определены из
B.18), получим
со
2и (х) = - j J Г (х—у) \N (д„ п) и\+ dyx dy2.
—со
Вычисляя N (дх> v) и (х), переходя к пределу, когда х (xlt x2, х3) —•
—* 2 (г19 г29 0) 6 S, получим
00
\N(dz,
Легко убедиться, что N (дг9 v) Г (г — у) = 0 и, следовательно,
(dz,v) и\+ = 0.
Итак, если \и (z)\* = 0, то {TV (<52, v) u[+ = 0 и из B.15) следует
Рассмотрим теперь задачу A1)^". Из B.15) имеем
Перейдя к пределу, при х lxlf х2, хв) —> z (zx, z2, 0) G S, получим
00
22) + J J 1 ^ (av, л) Г (j/ — г))' Ф (г/15 г/2) dyx dy2 = 0,
где
¦2) = \и\
о	о
0
0
lAfsjL Bi — Уд
Г си р»
Г — ^г
причем
ая)
• Р =lzi — Уг) -r[z2 — Уъ) •
Полученное сингулярное интегральное уравнение для определения ср за-
запишем в проекциях:
Ч 1/ Сза f f
	оо
!. ZJ+2JJ- J/ -^ J J	pi	dyx
u,
B.19)

§ 2] задачи для трансверсально-изотропного полупространства 569
Значения фх и ф2 из первого и второго уравнения подставим в третье,
получим
oo	-I
1 J -Sr1 4>з (Tx. т2) dTl dx2 dyx dy, = 0,
—oo	J
где
В силу формулы композиции сингулярных интегралов (см. гл. IV, § 4,
пп. I, 2)
00
_L
Фз (gj>

l Г f
лГ J J
уравнение для определения ср3 принимает вид
Отсюда, если
имеем
Фз (Zi> ^2) = 0.
Подставляя это значение <р3 в B.19), получим
Ф1 (Zi, г2) = Ф2 BХ, г2) = О,
Таким образом,
Итак, если \0> (dZ9 v) и\+=0 и 6^= ± l/^, то {и (z)}+ =0 и из
B.15) заключаем и (х) = 0, x?D+.
В случае изотропного упругого тела, из условия 8= =? 1/ — получаем

570
РЕШЕНИЯ В РЯДАХ И КВАДРАТУРАХ
[Гл. XIV
Совершенно аналогично доказывается, что задачи (Ш)+ и (IV)+ имеют
единственные регулярные решения при любых значениях параметра б0
(см. Купрадзе и др. [11).
3. Решение задачи A)+ для полупространства. Решение задачи A)+ для
полупространства будем искать в виде
со
и(х) = j J [N(др п)Т{у — х)]'g(ylt у2) dyxdyv
B.20)
где g = (glt g2, gs) — искомый вектор, а матрица [N (ду, п) Г (у — x)V —
определяется из B.16), в котором для |J0 и б0 следует подставить значения
из B.18), и выражается так:
\N{du, п)Г(у — х))' =
2л / I
где
Ek =
дх^дх.
дхл дх2 дхя
, Fk =
дхг д
г д 1
д {
д j
н JL±
к дхп гь
— Va9) '
"ak (\k
B.21)
~ ,/—4 [/ 77»
Фк и г^ определяются из B.17).
Принимая во внимание равенства
a 1
л;3 rk
= afe _
e
— У if
Л	'
al(*2—»г)* aJt(*2 —
[2.22)

§ 2] задачи для трансверсально-изотропного полупространства 571
легко показать, что если х (хг> х2, xs)?D+f то
00
J J дхг rk
—со	—с»
оо
[B.23)
JJ дх*дх* JJ ах>дх*
—оо	~оэ
оо
Я О 1
2л
ak
В самом деле, делая замену переменных
B.24)
имеем, например,
оо 2л
о о
2л
Аналогично доказывается справедливость остальных равенств B.23).
Переходя к пределу в B.20), и учитывая, что [W (дуу п) Г {у — г) Г == О,
получаем g (гх, г2) = / (zlf г2), где / — граничное значение вектора смеще-
смещения при х3 = 0 и /t Cla(S). Подставляя полученное значение вектора
g (г19 г2) в B.20), будем иметь
00
и (х) = J J IN {ди, п) Г (у — x)Y f (у19 у2) dyt dy2.
От заданного вектора / потребуем выполнение условий
\tk\<AR, R = Vzt + zi^l,
^	R>1* k=l> 2> 3'
B.25)
B.26)
где A > 0 — постоянная, а fk — проекция вектора / на ось xk.
Можно показать, что в этих ограничениях вектор и (х), определенный из
B.25), является единственным регулярным решением задачи A)+, удовлетво-
удовлетворяющим на бесконечности условиям
и(х) = 0 (| х h»), 9 (д„ v) u(x) = 0(\x |- A+a>).
В случае изотропного упругого тела, ядро в B.25) имеет вад
— 0 —
^/ — 0 - б/з) У/1
где
= (х, — ^)«+ (х9 — f/,

572	решения в рядах и квадратурах	[рл XIV
Пусть теперь вектор / (г1у г2) абсолютно интегрируем на всей плоскости,
т. е. существует преобразование Фурье
f(Pl P2) = "У j f fa, x2) ехр [i (Pi*! + p2x2)] dxy dx2,	B.27)
—oo
и обращение
00
i, x3) = -±- J J F (Pl, p2) exp [— i (plXl + рЛ)] dPl dp2.	B.28)
Подставим это значение / (xl9 x2) в B.25) и вычислим интегралы
00
J J "ЩЦ 7 ехр'"
—oo
JJ a^exP|-'to + »)]^^- k, j, 1=1, 2, 3.
— 00
Пусть
=lf 2'
Учитывая B.24), имеем
Пусть
Зг = ехр 1— i (ргхг + р
теперь
оо 2я
Г* Г*
% i
+ Pl	B.29)
Тогда предыдущая' формула примет вид
3t = exp [- I {PlXl
и, так как
оо
ехр |— ipR cos (ф — ф)] = о70 (pi?) + 2 2 (— On<?^ (pi?) cos /г (ф — ф), B.30)
получаем
3, = 2пехр [-1(PlXl +
Принимая во внимание, что
00
= y==. a>0,

? 2] ЗАДАЧИ ДЛЯ ТРАНСВЕРСАЛЬНО-ИЗОТРОПНОГО ПОЛУПРОСТРАНСТВА
и, используя формулу обращения Фурье—Бесселя, получаем
00
Г &о (Р#) 9 dp = exp (— aR)
J Y
?73
Применяя эту формулу, будем иметь
+ Pi
/=1,2,3, B.31)
откуда
~Ш \ J ачГ"Г ехр |—
00	'
+ pi] X
X
±—-2
. B.32)
Используя тождества
*3
/=1, 2, 3,
где
Р/ =
Л2,
из B.31) находим
оо
] с С <^3Ф/
— I 1	.—ехо I	t
Ы J J дхьдХ{дхп к!
2зх
а,
. B.33)
Принимая во внимание B.28), B.32) и B.33), решению задачи A)+ можно
придать вид
)] ^ (Pi, Pa) ^Pi dp2» B.34)
—ST j} 2 1 *»|ezp (- -^ V^
-оо 1=1	Ч Г '
X ехр [—
где
<4

574	РЕШЕНИЯ В РЯДАХ И КВАДРАТУРАХ	[рл XIV
Из B.34) для изотропного упругого тела получаем
оо
и(х) = ~|J|iVfe/||3x3exp (— XsVpi +pi)exp[—i(pixi + р2х2)] F(pu p2)dpidp2,
где
—ОО
'	12 	 yV2l	Г
Я'/И |а' определены из (II, 1.2).
Из B.25) для компонентов вектора напряжения получаем
Т(дх, v)u = (Ti3, т23, таз) = —2^-
где
1 i
	1- С44
r (fe) ==
31
г (k) = ( —1)^ C4
32	(V
) _ (—if cu (с1Лак + c18) Vak F2fe -f-
13 (кгп^ +
Отсюда легко получаются значения компонентов вектора напряжения
в случае изотропного упругого тела.
Из B.34) непосредственным вычислением получается значение вектора
напряжения, как для трансверсально-изотропного, так и изотропного упру-
упругого тела.
4. Решение задачи (Н)+ для полупространства. Рассмотрим случай,
когда на границе упругого полупространства задано значение вектора напря-
напряжения Т (дх, v) и = (т13, т23, т33), определенного формулой B.12). Решение

« 2] задачи для трансверсально-изотропного полупространства 575
ищем в виде
00
и (х) = J J М.(хг, х2,
— 00
где h {уъ у2) — искомый вектор, а
М (х; у) =
s; yl9 у2) h (ylf у2) dyx dy2,	B.35)
Akak
д2Фь
их.
Ф^ и rk определены из B.17), ak9 pfe, yk и б^ даны формулой B.5); Ak и Bk —
пока произвольные действительные постоянные.
Из B.35) для вектора напряжения находим
00	d
Т (дХ9 v) и = J j ^ I Tif (х; у) || А (уь W) dyx dy2,	B.36)
-00 ^=1
где
(—1 )fe (с33 + clsak)
2яси(в8 —а3,
Ttf' - A^ [P* ^ ^ + («» + W ^5%-] '
Подберем произвольные постоянные Лй и Bfe так, чтобы удовлетворялись
условия
оэ
J J
dy2
—оо fe=l
fe=l
где ? — единичная матрица.
Учитывая B.22), B.23) и значения Т$9 из B*37) для определения Ак и
Bk получим уравнения
%	:
/2——A,

576	РЕШЕНИЯ В РЯДАХ И КВАДРАТУРАХ	(Рл# XIV
откуда
R
J' **~
Имея в виду B.37), и перейдя к пределу при х (xl9 х2, xs)—* z (zlf г2, 0),
из B.36) будем иметь
2l, *2) = f(Zlf Z2),
где / (г1э г2) — заданное значение вектора напряжения, / ? С0- a(S).
Подставляя найденное значение вектора ft (zl5 г2) в B.35), получим
и (х) =	5^- f f У | Ац* {х; у) ||/ (г/i, у2) dyx dy%,
—00 k—1
где
дх, '
rk ' * дх\ У '
Л23 ='
Здесь коэффициенты имеют следующие значения:
1 о" ^13 /
' _ (—l)fe (cuak + c]3)
(-D* V^u (cr] ^ + Cl3) (82ft
(С11сзз — 4
„- _ (—l)fe 1^5^(cnak + ci3) F2fe + 83k)	__ . „ q
(cnc33 — 40 (i^a2 — коз)
Если теперь найденное значение вектора h (zl9 z2) подставим в B.36),
то для вектора напряжения получим
оо 3
Т (дх, v) и (х) = - -±- \ J 2 | Btf |/ (уи уг) dyx dy2,	B.39)
—оо k=l
где
Ззг^пл I/ -^i._^_^_f	^з-=а^.__^_з

я 2] задачи для трансверсально-изотропного полупространства 577
а коэффициенты имеют значения
. * , (—i)fe F
В случае изотропного упругого тела B.38) и B.39) принимают соответ-
соответственно следующий вид:
где
с»
" W = ~г7Г J J
2ц
д2г
2fx
jLt) r
у^ dyi
2 (X + ц)
dx3dxf '
-, ft,/=1,2,
г,
где
Я*/ =
Г (dx, v) и (х) = зг J JIIВ*/ (**•
— 00
i — A — 6/3)

, /г, /—i, z, o.
Пусть теперь для вектора / справедливы формулы B.27) и B.28). Прини-
Принимая во мнимание B.31) и формулы
exp [—i (рм + p2j/2)] dyx
PkPj exp
(—-^VpI + pI]
exp [—
, k,j=\,2,
, k = 1, 2,
из B.38) получим
-w—sr
- B.40)
—00 1=1
№*)]F (ft.
2. B.41)
37 В. Д. Купрадзе

578	решения в рядах и квадратурах	[рл# XIV
где
п =- yv + ^Гь^Г' с12 =с21
ru)_ Р/ 'аУ^4
U22 —	77= "Г „2 i ~2 >
32 =
a aj, PJ, vi, S'z и г\ определены выше.
Совершенно аналогично, подставляя значение f (xl9 x2) из B.28) в B.39)
и учитывая B.32) и B.33), получим
00 3
„ v) и (х) = 4г J J SI D$ 1 ехр (~ ~v
—со /==1
X ехр I— i (PiXx + р2^2)] F (px> p2) dpx rfp2, B.42)
где
> *./=!. 2,
u = у — D31 =
Для изотропного упругого тела B.41) и B.42) несколько упрощаются.
Как и в п. 3, и здесь можно доказать, что при f ? С0»a (S) и
\fk\<A9 R=
1М<
вектор w (#), определенный из B.38), является единственным решением за-
задачи (П)+, удовлетворяющим на бесконечности условиям
и{х) = О(\х |-а), Т (дх, v)u{x) = 0(\x |-<1-н*>).
5. Решение задачи (Ш)+ для полупространства. В случае оператора
Т (dXi v) граничные условия задачи (III)* можно записать так:
{Т(дг, v) «W- - си (^ + -|j-)_ uii ^ - /, Bl, га),
{ЫзB)}+ = /8B1, 2а).
Решение ищем в виде
оо 3
" <*) = Я S I L<«' ^ (^ь %) dyi dm,	B.43)
fc=i

* 2]	ЗАДАЧИ ДЛЯ ТРАНСВЕРСАЛЬНО-ИЗОТРОПНОГО ПОЛУПРОСТРАНСТВА
579
гДе g (Ун У г) — искомый вектор,
А {—
Ли Лл (Л = 1, 2, 3) — пока произвольные действительные постоянные;
аь (Зь yk я bk — известные коэффициенты; rk и Фк — функции, определен-
определенные формулами B.17).
Из B.43) получаем
с» 3
(хм, т23, «а) = J J 2 | М\Р (х; у) | g (yu y2) dyi dy2,	B.44)
J J 2
—00 k=l
где
Элементы М\*} (х; у) (i, / = 1, 2, 3) зависят от координат точек х (хъ х2, х3)
и У (Уъ Уъ> 0)- Подберем произвольные постоянные А я Ak (&=1, 2, 3) так,
чтобы выполнялись условия
3
^t^ Л/f^^ B z * и и \ 	П i i — 10*^
3 oo	3 oo
2И
fe=l —00
Некоторые из последних условий удовлетворяются автоматически в силу
свойств коэффициентов ak и yk, и для определения А и Ak (k = 1, 2, 3)
остаются следующие условия:
3
A {yk + 8k) — О V A Sfe — 1
J7*

580	решения в рядах и квадратурах	[рл# XIV
откуда
д =	j д __	g|j (сзз + ci3ak) F2fe + Safe)	?=1 2 3
В силу последних формул, и в результате перехода в B.44) к пределу при
х (хъ х2> х3) -* z (г19 г2, 0), получаем
g(*l» Z2) = f{Zl> Z2),
где / — вектор с компонентами fl9 /2 и /3; fk 6 С0* а (S), Л = 1, 2, /3 6 С1*а (S);
кроме того,
\fh\<A,	k=l9 2, |/8|<Л/?, /? = l/zFb3^1f
I^K-ртГ. *=1. 2, |/,|<^-. Я>1.
Внеся найденное значение g (гг> г2) в B.43) и учитывая значения коэф-
коэффициентов А и Ak (k ~ I, 2, 3), получаем
оо 3
причем
Здесь коэффициенты имеют следующие значения:
k	з
/I =	j	, 2л Ль = и,
*
n _ (— ^
Uk =	г-г
Сц {а2 — ав)
Совершенно аналогично, если найденное значение вектора g подставим
в B.44) и вычислим т83, то для вектора напряжения получим
со 3
T(dx, v)u{x) = -± JJ 2||G(^|/(r/b y2)dyidy2,	B.46)
—СО k=l
где

я 2] задачи для трансверсально-изотропного полупространства 581
(—• l)fe (с33 + ci3ak)

3
cn (a2 — a8
.	 \\k (г г r^ \ n (f\
^11 (^2 	 ^3/	^11 (^2 	^3/
h	 1 О Q
/v —— X , Zj у kJ •
Допустим теперь, что для заданного вектора / (хъ х2) справедливы соот-
соотношения B.27) и B.28). Используя формулы B.31), B.32) и B.40), можно
B.45) переписать в виде
rr ^Ц	ехр 1--р±
и{х) = ^- Улнтl V
JJ 4-Г1'
—с» 1=1
ехр I— i (рххг + р2л;2)] х
p2, B.47)
где
Л, /=1, 2, Я# = -?-
Подобным образом, принимая во внимание формулы B.32) и B.33), для
компонентов вектора напряжения из соотношения B.46) получим
Т(дх,
47=«, A/ -
B.48)
При наших условиях относительно вектора / можно показать, что вектор
и (х), определенный из B.45), является единственным регулярным решением
задачи (Ш)+.
Аналогично решается четвертая граничная задача (задача (IV)+) для по-
полупространства (см. Купрадзе и др. [1]).
6. Задача о действии жесткого штампа на упругое полупространство
и родственные задачи. Рассмотрим упругое полупространство х3 > 0.
Допустим, что на некоторую часть S плоскости хг = 0 давит абсолютно жест-
жесткое тело, прижимаемое к границе силой, параллельной оси х3 (при этом пред-
предполагается, что трение между границей S и штампом отсутствует), а осталь-
остальная часть Sx плоскости х3 = 0 свободна от действия внешних сил. Требуется
определить поле напряжений и смещений в полупространстве, а также уста-

582	решения в рядах и квадратурах	[рл XIV
новить зависимость между силой, действующей на штамп, и его перемеще-
перемещением.
Эта задача известна в литературе под названием задачи о давлении
штампа.
Математическая постановка задачи о давлении жесткого штампа на
трансверсально-изотропное полупространство приводит к -следующей гра-
граничной задаче: найти решение уравнений B.1) в полупространстве х3 > О,
при следующих граничных условиях:
для	х3 = 0 и г(гх, z2)eSx, (т13)+= (т23)+= (т33)+= О,	1
B.49)
для х3 = О и z fa, z2) € S, (т13)+ = (т23)+ == 0, (ц3)+ = Ф (zj, z2), J
где (т13)+, (т23)+, (т33)+ обозначают (как и выше) граничные значения компо-
компонент вектора напряжения; Ф (гх, z2) — заданная функция, которая представ-
представляется в виде
i, z2) == azx + bz2 + с —
причем azx + bz2 + с выражает жесткое перемещение штампа, a z3 =
*= Ф Bi> гг) есть уравнение той части поверхности штампа, по которой он
соприкасается с полупространством. Постоянные а, 6, с при решении задачи
остаются неизвестными; после ее решения, однако, их можно определить из
условий равновесия штампа. В самом деле, пусть сила ^, прижимающая
штамп, действует вдоль оси х3. Тогда
j (T33)+dzx dz2 = ^, J zx (i33ydz1 dz2 = J z2 (T3d)+dz1dz2 = 0.
Представим решение задачи (П)+ (см. B.38)) в виде
3	3
S k=l
Так как согласно B.49)/х =/2=0, когда у (уъ у2, O)^U
а /3 (уи у2)=0 при у (уъ у2, 0) ^ 5Х, из последней формулы, после перехода
к пределу при х (хг, х2, х3) —> z (z1? z2, 0) 6 S, получим
J_ СцЧКдя + Кда) Г Г	8(Уъ
— (Т)
B.50)
В частности, для изотропного упругого тела, ввиду того, что а2 = а3 = 1
и справедливы формулы B.2), имеем
где ? и 0 модуль Юнга и коэффициент Пуассона.
Таким образом, для определения усилий под штампом получено интег-
интегральное уравнение первого рода B.50). В том случае, когда это уравнение
решается явно (в общем случае, применяя результаты Zaremba [1 ], можно
доказать только существование решения), смещения и напряжения внутри
полупространства вычисляются по формулам B.38) и B.39).

§2]
ЗАДАЧИ ДЛЯ ТРАНСВЕРСАЛЬНО-ИЗОТРОПНОГО ПОЛУПРОСТРАНСТВА
583
Рассмотрим еще один подход к задаче о давлении штампа. Принимая во
внимание B.49), и пользуясь B.28) и B.41) для определения h = F3 (ръ р2),
получаем пару интегральных уравнений
+ V"<h) Г Г
-с1з) JJ
h(Pi, р2) ехр [— i {рггг
г(гх, z2, 0)e
h (ръ р2) ехр [— i (przt
dp2 = 0,
9 г2),
г2,
B.51)
Сделанные выше общие замечания относительно задачи о давлении жест-
жесткого штампа на упругое полупространство остаются в силе и для следующих
смешанных граничных задач: найти решение уравнений B.1) в полупростран-
полупространстве х3 > 0, при следующих условиях:
для х3 = 0 на	5Х	(«з)+ = /зB1, г*)*
(Ti3)+ = /!iB1,	z2),	(т23)+ = /2 Blf г2),
для х3 = 0 на	S	(т13)+ = fx Blf 22),
+ = /2B1,	г2),	(т33)+ = ^з (^1» г2),
B.52)
где f 1э /2, fs и F3 — заданные функции, обладающие необходимыми свойст-
свойствами гладкости (эту задачу часто называют задачей о трещине);
2)	для	х3 = 0	на Sx (т13)+ = /1, (т23)+ = /2, (х33)+ = /3,
для	х3 = 0	на S (иху = Т7!, (а2)+ = F2, (т33)+ = Fg;
3)	для	*3 = 0	на 5г
для	д:3 = 0	на S
На бесконечности смещения и напряжения равны нулю.
В 1), 2) и 3) условия на S и на S1 можно поменять местами.
7. Эффективное решение задачи о жестком штампе для некоторых кон-
конкретных случаев. В этом пункте будут применены уравнения, полученные
в предыдущем пункте.
Для определения усилий под штампом в п. 6 было получено интегральное
уравнение
1
где
» —— С-\ о
B.53)
Уравнение B.50') внешне совпадает с известным уравнением для изо-
изотропного упругого тела. Когда W (zlf г2) = Ч? (р), где р = ]/' г| + г\ и S есть
круг, оно (в изотропном случае) решено И. Я. Штаерманом (см. Штаерман [11)
и А.И.Лурье (см. Лурье [1]). В общем случае задача о жестком штампе,
когда S есть изотропный круг, решена Л. А. Галиным (см. Галин 111). Ре-
Решение Галина можно использовать и в нашем (анизотропном) случае. Таким
образом, когда S есть круг, задача о жестком штампе для уравнений B.1)
решается в замкнутом виде (в квадратурах).

584
решения в рядах и квадратурах
[Рл
Укажем другой метод решения задачи о жестком штампе, когда 5' есть
круг радиуса а. Допустим, как и выше что штампом служит жесткое тело
вращения. Тогда, сделав замену переменных
Zx = р cos г|), г2 = р sin -ф,
рг = R cos ф, p2 = R sin q>,
заметим, что функции h (plt р2) и W (zl9 z2) (см. B.53)), участвующие в B.51),
зависят только от R и р, т. е.
Уравнения B.51) на основании B.30) принимают вид
00
jlx(R)Jo(pR)RdR = 0, p>a,
B.54)
Эти уравнения являются частным случаем более общих уравнений
B.55)
в которых A (R) — неизвестная функция, / (р) и g (p) — известные функции»
а — заданная константа, Jv — функция Бесселя v-ro порядка.
При —2 <5 а <5 0, v > max (	а, —1	2L V решение уравне-
уравнений B.55), когда g (р) и / (р) интегрируемые функции, имеет вид (см. Коре-
Коренев [1J, стр. 126)
а
о—а/2 п1—а/2 f»
ГЦ+а/2) J
(xR) G2
914-а/2п1—а/2
Г(Д/2)
J
где
,(*)=-а?J/(p)p1+v(*a—P2)a/2 dP> <Ш= J
•	х
В нашем случае g(p) = 0,/(р) = W (p), v = 0, а = —1, и учитывая, что

л 2] задачи для трансверсально-изотропного полупространства 585
из последней формулы получаем решение уравнений B.54)
B.56)
Подставляя найденное значение Fs (ръ р2) в B.41) и B.42), и приняв во
внимание, что F г (рг, р2) = F2 {ръ Ръ) == 0» получаем явные значения для
компонент вектора смещения и напряжения.
Рассмотрим теперь один частный случай. Пусть (ив)+ = Ф (гъ z2) = е,
г (г19 г2, 0) 6 5, 8—постоянная. Эта задача имеет применение в строительной
механике, в частности, в теории прочности фундаментов. Для изотропного
упругого тела задача рассмотрена в книге Ф. Франка и Ф. Мизеса (Frank,
Mises [11, стр. 290—295) и в монографии И. Снеддона (см. Sneddon [1],
стр. 513—517).
Учитывая зависимость B.53), в нашем случае будем иметь
Т(р)=-
спсзз — ci3
г— . 1г—\ в = 80,
B.57)
где е0 — новая постоянная. Подставляя значение Ч? (р) в B.56), получаем
Р .	v 2е0 sin а Vр\ -f p\
Внесем полученное значение F3 (plf p2) в зависимость B.41), и примем,
во внимание, что F1{p1, p2) = F2(ply p2) =0; тогда для компонент век-
вектора смещения, после вычисления элементарных интегралов на основании,
B.30) получим
-^f J
где р = Vxi + x%, 6J и г} — коэффициенты, входящие в B.38).
Пользуясь формулами (см. Градштейн и Рыжик II ], стр. 777)
00
(ехр (— ах) Jo фх) sin сх — = arcsin
Rea>|Im6|,

586
РЕШЕНИЯ В РЯДАХ И КВАДРАТУРАХ
[Гл. XIV
и приняв еще во внимание B.57), из предыдущих формул получаем
3 , „ьг
„ pi
cu(a2-a3)
A-
*=2
(а2 — а3)
k=2
4
( — аз)
к)
-arcsin-
2а2
, fe=l, 2, 3.
B.59)
Применяя последнюю формулу, можем вычислить компоненты вектора
смещения в любой точке упругого полупространства. В частности, если
учесть, что при хд = О
О, с< р,
B.60)
то из B.59) получим для компонентов вектора смещения внутри и вне штампа
значения
с„с33— см)(г -I/", P2\ %
(J ^^^I U-,
2oe
-, 9>а;
8,
-^¦arcsin~-, pE>a,
Используя формулы
- arcsin
4
I 2aMft — a2 + pa + -?-
= 1,2.

2]	ЗАДАЧИ ДЛЯ ТРАНСВЕРСАЛЬНО-ИЗОТРОПНОГО ПОЛУПРОСТРАНСТВА	587
A-Ад у а*
xl
дх° ~ ,-/	4
x2
2a2Ak — a2 + p2 + —
д . 2a aV~Ak
-г—- arcsin —_	-—			=	—-
из B.59) для компонентов вектора напряжения получаем
2ае
- «з) ^2aMfc - a2 + р^ + -±
- О + р2+%
-а2 + р2+--^
з	t	.
2аг
тзз = —
п
~ си (а,
- a3) \2a*Ak - a2 + p2 + ^
Используя последнюю формулу и соотношения B.60), находим, что т13
и т23 внутри и вне штампа при х3 = 0, как и следовало ожидать, равны нулю,
а т33 при jc3 = 0 и a < p равен нулю и
2е
Too J111
К«8) Va* - р-
В случае изотропного полупространства имеем
Это совпадает с формулой И. Снеддона (см. Снеддон [1 ], стр. 514, фор-
формула A0.53)).
Совершенно аналогично можно исследовать другой, не менее важный
частный случай, когда (ив)+ = Ф (х19 х2) = Ъ + & A — -||Л, где 6, 8 и a —
постоянные, а р2 = х\ + х^.
Заметим, наконец, что когда S является кругом радиуса а, применением
парных интегральных уравнений можно решить задачу о жестком штампе
в общем случае, т. е. когда Ф (zlf г2) не удовлетворяет условию Ф (г1э г2) =
= Ф (р), а является произвольной функцией, удовлетворяющей общим
условиям гладкости.
8, Эффективное решение задачи о трещине для некоторых конкрет-
конкретных случаев. Задача о трещине была сформулирована в конце п. 6 (см.
B.52)); без ограничения общности граничные условия можно привести

588	решения в рядах и квадратурах	[рл XIV
к следующим:
для хн = 0 и г (*!, г2, 0) ? Sl9 (щ)+ = О, (т13)+ = О, (т23)+ = О,
для хг = О и г (г1э z2, 0) 6 S, (т23)+ = О, (т13)+ = О,
Ы+ = -^B1, Z2).
B.61)
Эти граничные условия и формулы B.47) и B.48) дают для нормальных
компонент вектора смещения и напряжения
оо 3
и* = 4гЯ У v -; vr'K: :iif/ eXP i — -^ ) х
/г=2
X exp I— i (рххг + р2л;2)] Fs (ply p2) dpx dp2,
со 3
1	ХМ--1) (сисзз — С1з) У Ч D / x9R \ „
j ^^z —— i i i уг ——————^——^—^^—^^— ^^ exo (¦"-"" — j ^^
—со /г=2
X exp [— i {рххх + p2x2)] F3 (plf p2) dpx dp2,
B.62)
где
F3 (jpv p2) = — I J (a3)+ exp [/ (pxxx + Рг^)] ^xi ^*2» ^ = I/Pi + P% B.63)
s
Из B.62), используя B.61), для определения F3 (pl9 p2) получаем
1
2л;
-^ J J exp 1— i (px2! + р2г2)] F3 (px, p2) dpxdp2 = 0,	z (zx, z2, 0) 6 S^
—oo
CO
J J R exp I— i (p^x + p2z2)] F3 (PlJ p2) dpx dp2=&0 (г1э z2), z {zl9 z2, 0) 6 5,
—со
где
С11С33 "~
LUUS3 '
Совершенно так же, как в п. 7, предыдущие уравнения перепишутся
в виде
00
¦gj- JJ exp I— iptf cos (ф — г|))] F3 (R, <f>)RdRd<(> = 0,
-^ J J exp [— ipR cos (ф — ф)] Fs (/?, <p) RidRd^=^Q (p, tf), p ^ a.
Пусть функции Fb (Ry ф) и ^ 0 (p, -ф) зависят только от R и р, и
тогда уравнения для определения F3 (#» ф) примут вид
J #g (/?) Jo (P^) dR = 0>o(p), p < a.
Последние уравнения являются частным случаем уравнений B.55) при а = 1.

Л 2]	ЗАДАЧИ ДЛЯ ТРАНСВЕРСАЛЬНО-ИЗОТРОПНОГО ПОЛУПРОСТРАНСТВА	589
При v > —	ос и а > О решение уравнений B.55) имеет вид (см. Коре-
Коренев [13, стр. 124)
А (*) =
a
где
(xR)G,(x)dx.
В нашем случае g (p) =*= 0, / (p) = ^0(p). a = 1, v = 0, A {R) = g (#)f
и из последней формулы, учитывая обозначение для ^0 (г1э г2), после не-
несложных вычислений получаем
Подставив найденное значение Fs (/?!, р2) в B.47) и B.48), находим зна-
значения компонент вектора смещения и напряжения в явном виде.
Рассмотрим один пример. Пусть давление <Р (г19 z2) постоянно и S есть
круг радиуса а, т. е. &(zl9 z2) =&> 0. Подставляя это значение в предыду-
предыдущую формулу, получаем
Р	v 2&*0 сг1 {V^^l + l^%) / sin aR	cos aR \
n спсзз — ci3 ^	'
Подставив полученное значение F3 (plf /72) в B.62), для нормальной состав-
составляющей вектора смещения получим
ия =	г-2- —	—
^- arcsin	2fl / .	+ а A -
где Л^ определяется формулой B.59).
Используя B.60), из последней формулы при х3 = 0 и р ^ а, как и сле-
следовало ожидать, получаем (н8)+ = 0, а при хъ = 0 и р < а
(цзГ = w= ifW^ + ^У^.	B.64)
С11С33 "" С13
Если ш = е при р = 0, то
и выражение B.64) можно переписать в виде
4+'4-1.

590	решения в рядах и квадратурах	[рл XIV
Отсюда следует, что под действием внутреннего давления, если давление
постоянно, трещина расширяется и принимает эллипсоидальную форму.
Аналогичный результат имеет место и для изотропного упругого тела (см.
Sneddon [13, стр. 546—547).
Совершенно аналогично из B.62) можно вычислить нормальную компо-
компоненту вектора напряжения. Имеем
ГА
V lrk
V'1
2a2Ak -а24-р2+ —
ak
Отсюда, при х8 = 0 и р < fl, как и следовало ожидать, (т33Г = —«
а при р > а
(ТззГ = &1 ( «_ _
arcsin —).
Так же как в п. 7, здесь можно рассмотреть общий случай, когда функция
^о (р> 'Ф) является произвольной, a S есть круг радиуса а.
Результаты пп. 7 и 8 легко обобщаются для смешанных задач, указанных
в конце п. 6.
9. Решение задачи (П)+ для бесконечного слоя. Рассмотрим задачу
о равновесии трансверсально-изотропного упругого слоя, ограниченного
двумя параллельными плоскостями.
Речь идет о нахождении решений уравнений B.1) для области 0 <5 х3 <3
<3 Л, при заданных граничных условиях на плоскостях х3 = 0 и xs = h>
ограничивающих слой, и при некоторых условиях на бесконечности.
Мы будем рассматривать случай задания напряжений на гранях слоя
при х3 = 0 \T(dztv)u(z)\+ = f(z1, z2),
при xB = R \Т(д2, v)u(z)\+ = F(zl9 z2),
где / и F — заданные векторы. Искомые напряжения (и смещения) должны
обращаться в нуль на бесконечности: характер их убывания может быть раз-
различным и зависит от задания нагрузок на плоскостях, ограничивающих слой.
Ищем решение задачи (П)+ в виде
—оо 1=1
00 _3 _	/ (h—y
~оо 1=1
X exp [— i (p^, + p2*2)] h (pv p2) dpxupv B.66)

§ 2] задачи для трансверсально-изотропного полупространства 591
где g(pu р2) и h (рь р2) — искомые векторы, R = У pi + pi С$ (к, /,.
/=1,2,3) имеют те же значения,- что и в B.41), а
Из B.66) для вектора напряжения имеем
со 3
X exp I— i (pix! + P2X2)] g (рь Pi) dpi dp2 + -^ 11 ^ II ^iV II X
-00 г=1
X exp J- (/t~g)J?] exp [-1 (Plxx + p2x2)] ft (p1( p2) dPl dp2, B.67)
где
(=1
B.68).
Учитывая граничные условия B.65), из B.67) для определения искомых
векторов имеем
Ё-JWi-
—00
со 3
+ —fft1
^ 2я J J Zj
Я 2
р2г2)] g (ft,
_«\«p|-
! = f(Z1, Z2),
00 3
00
2~ J J exP I—i (Pizi + P2Z2)] h (pi, /7Я) dpxdp2 = ^B!, г2);.
отсюда, используя преобразование Фурье, получим
g (Л. Р,)+
2
2 |^i'/ lexp (— -?!Ц ^ (Л. Ps) = ^(Л. Ра).
B.69)

592
РЕШЕНИЯ В РЯДАХ И КВАДРАТУРАХ
[Гл. XIV
Г (Pi. P2) = 4г J J / (zl9 za) exp [t (pa + p2z2)] dzx dz2,
—00
00
F* (Pi» P2) = -2~ JIF (zi> Z2) exp [i (pa + p222)] dzj. dz2.
—00
Перепишем B.69) в виде
«i2	—«_
«22	— а2з|А(Рг, P2) = f*(Pi>
B.70)
3	3
2	3
I^«2«3«i3
1 g" (pl9 p2) + /г (Pi, p2) = Z7* (ft,
B.69')
где
-^-). ». /-I. 2,
B.71)
Определяя из второго векторного уравнения B.69') вектор h и подстав-
подставляя в первое, получим
ц Аи* ^1з
21 ^22 ^23 g" (Pi, P2) =
— Va2a3a13 —]/~a2a3a23 a3
»pJ, B.72)
где
-U—
(z./o;

Л 2]	ЗАДАЧИ ДЛЯ ТРАНСВЕРСАЛЬНО-ИЗОТРОПНОГО ПОЛУПРОСТРАНСТВА	593
Совершенно аналогично, из B.69') для вектора h получаем
Ло
А12
д
Л22
' ^32
— ^23
^33
i, p2) = /7*(Pi» P2) —
аи
^12	3
I *	Z о Хо	г	л о л о	i$«
,ft). B.74)
Обозначим алгебраическое дополнение элемента Akj в детерминанте
| Akj || через s4>kj (k, j = 1, 2, 3). После элементарных вычислений, получим
B.75)
Совершенно так же для детерминанта Д = | Akf \
+ А зз*^зз получаем
+
Решая уравнение B.72), будем иметь
в12
^ I X
X
Г (л, Р2)—
, B.77)
38 В. Д. Купрадзе

594
где
РЕШЕНИЯ В РЯДАХ И КВАДРАТУРАХ
PkPj
[Гл. XIV
2hR
DR2
Va2a3
hR
Boo =
1 — В
D '
B.78)
Из B.74) имеем
Л (Pi, Pi) =
^22 "^^23
alt
(Pi, Pi)-I
«22	«23 /*(Pl. P2)
B.79)
Подставляя полученные значения векторов g я h соответственно в B.66)
и B.67), получим выражения смещений и напряжений в точках бесконеч-
бесконечного слоя.
Остается исследовать сходимость полученных интегралов.
Напишем условия равновесия бесконечного слоя, т. е. условия равен-
равенства нулю главного вектора и главного момента внешних усилий. Учитывая
B.65), для этих условий будем иметь
со	со
J j fk (*i, z.) dZl dz2 = j \Fk (Zl) z2) dzx dz2,
—CO	—CO
CO
J J zk [fa (Zl, z2) — F3 (Zl, 22)] dzx dz2 = 0,
k = 1, 2, 3,
6=1,2,
— Z^hiZ,, 22) — Fx(Zl, 22)]}dZld22 = 0.
С учетом зависимостей B.70), последние условия перепишутся в виде
/»@, 0) = ^@, 0),	*= 1,2,3,"
. =0
=о
B-80)
дрг др2 / р1=р2 =о *
Применяя B.77), B.79) и B.80), заметим, что интегралы, входящие в фор-
формулы B.66) и B.67), сходятся.
Таким образом эффективное решение задачи (И)+для бесконечного слоя
завершено. Аналогично можно получить решения задач A)+, (II 1)+ и других
смешанных задач (в связи с § 2 см. Башелейшвили 1141), Купрадзе и др. [1].

§ 3] применение новых представлений гармонических функций 595
§ 3. Применение некоторых новых представлений
гармонических функций и принципа симметрии
для эффективного решения задач теории упругости
1. Некоторые гармонические функции, связанные с упругими смеще-
смещениями. В плоской теории упругости существует тесная связь между реше-
решениями граничных задач (первой и второй) и теорией аналитических функций
комплексной переменной. Эта связь основана на известных представлениях
Колосова—Мусхелишвили (см. Мусхелишвили [1]) для составляющих сме-
смещений и напряжений, с помощью двух пар аналитических функций; эти пред-
представления имеют следующий вид:
2\х (щ -f- ш2) — ХФ (z) — Z(P' (г) —q
x22 — ix12 = Ф (z) + Ф (z) + гФ' (z) + W B),
6 = 2 (X, + ц) div м = xu + т22 = 4 Re Ф (г) = 4 Re cp' (г),
C.1)
Отсюда вытекают равенства
Re 1хф (г) - *р'(г)
rot u]Xl,
Im fxrp (г) + гф7 (г) + «ф (г)] = 2jia9 + (^ + р) х2 div ^,
Re [2Ф (г) + гФ' (г) + V (г)	L ^
т22
Im
= ^22 + № + ц) хч 3j- div м,
W (z)] = т12 + тх2тГ = т12 + (Я + ji) x2 ~ div и.
C.2)
Они показывают, что выражения, стоящие в правых частях (равенств
C.2)), являются гармоническими функциями. Исходя из этого, естественно
предположить (см. Оболашвили [1]), что трехмерные аналоги указанных
комбинаций компонент смещений и напряжений
Ф\ (*i, х2, х3) = 2\шг -f y-^- \x rot u\Xt,
Ф3(хг х29 х3) =2
Pi (%, х2, xs) = т13 +
F2 (Xli х2, х3) = т2
x3^~ div
div
g~- div
C.3)
38*

596	РЕШЕНИЯ В РЯДАХ И КВАДРАТУРАХ	[рл XIV
также являются функциями гармоническими. Действительно, как показы-
показывают прямые вычисления, эти комбинации оказываются решениями уравне-
уравнения Лапласа, при отсутствии объемных сил, и удовлетворяют уравнению
Пуассона, если объемные силы присутствуют.
Представления C.3) позволяют получить решения некоторых задач
(например, задачи для бесконечного пространства с круговой щелью или со
щелью вдоль полуплоскости) в квадратурах.
2. Продолжение решений. Исходя из представлений Колосова—Мусхе-
лишвили, можно сделать заключение о свойствах продолжимости смещений и
напряжений через плоскую часть границы. Рассматривая пока плоский слу-
случай, заметим, что если граница области D содержит часть прямой х2 = О,
ai ^ xi ^ а2 и на эт°й части т12 = 0 и и2 = О, то, как нетрудно вывести из
представлений C.1) и C.2), будем иметь
Im [ф (хг) — хгц>' (хг) — Ц (Xi)] = 0, Im [х<р (хг) + *i<p' (*i) + ф (*i)l = 0,
<h ^ хг < а2.
Отсюда следует, что голоморфные функции cp(z) — 2q>'(z) — i|)(z) и хф(г) +
+ гф'(г) + ty (г) можно продолжить аналитически через прямую х2 = О
в область D*, представляющую зеркальное отражение области D относительно
прямой х2 = 0.
С помощью этих продолжений определяются продолжения напряжений
и смещений.
Исходя из этих свойств решений плоской задачи, перенеся их по аналогии
на пространственные задачи и распространив для уравнений движения,
Е. Оболашвили доказала следующие лемму и теоремы:
3.1. Лемма. Если вектор и = (иг (х), и2 (х), иъ (х)) удовлетворяет
уравнению А (дХУ со)и(х) = 0 в области D, то вектор и@) = (и[°)(х)$ и^()
иЦ»(х)), где
(х) = (а\ — а\ — al) иг (х*) + 2ага2щ (х*) + 2ага3и3 (х*),
(х) = 2aia2ux (x*) + (al — а\ — а|) и2 (х*) + 2а2а3а3 (х*),
(х) = 2аЛих (х*) + 2а2а3и2 (х*) + (а* — а\ — а?) щ (х*),
есть решение того же уравнения в области D*, где D* — зеркальное отобра-
оюение области D относительно плоскости агхг + а2х2 + ^zxz + аА = 0,
з
^ а? = 1ах* — точка, соответствующая точке х при указанном ото-
i=\
бражении.
Справедливость леммы следует из равенств
х] = х{_ 2at {аххх + а2х2 -f а3х3 + а4), f = 1, 2, 3;
div и<°> (х) = — div и (х*), Д (дх) = Д (дх*).
3.2. Теорема. ?сла граница упругого тела D содержит часть пло-
плоскости агхг + а2х2 + а3х3 + а4 = 0 (обозначаемую далее через S) и вектор
и = (иъ и2, иг) в области D есть регулярное решение уравнения А (дх, со) и =
= 0, а на S обращаются в нуль касательные составляющие вектора смещения
и — п (и-п) и нормальная составляющая напряжения (Ти-п) (п — единичная
нормаль к 5), то вектор и (х) непрерывно продолжается через S и вектор
U = (U1$ U2, ?/3), где
| и = (иг(х), u2(x), us(x)), О
является регулярным решением того же уравнения в области D [}S [)D*.

* 3] применение новых представлений гармонических функций 597
3.3. Теорема. Если в условиях теоремы 3.2 граничные на S условия
заменены условиями обращения в нуль нормальной составляющей смещения
(и-п) и касательных составляющих напряжения Ти—п (пТи), то вектор
и (х) непрерывно продолжается через плоскость S и вектор U = (Uly U2, U3),
где
и = (иг(х), и2(х)у и3{х)), x?D;
x 6 D*9
является регулярным решением уравнения А (дх, со) U = О в области D (J S\J
U D*.
Эти теоремы представляют в теории упругости аналог известного прин-
принципа симметрии Римана—Шварца и доказательство их основано на принципе
симметрии для уравнения Гельмгольца; (см. Оболашвили *) [1, 2 3; см.
также Купрадзе, Бурчуладзе [5] и [6]).
3. Эффективное решение .некоторых трехмерных граничных задач.
С помощью функций C.3), теорем 3.2 и 3.3 для полупространства в случае
изотропного упругого тела эффективно решается некоторый класс смешанных
граничных задач (кроме граничных задач (I) и (II)), из которых мы рассмотрим
здесь следующие:
а)	Найти решение уравнений статики изотропного упругого тела в бес-
бесконечном пространстве с круговой щелью, когда на обеих сторонах щели
задается вектор смещения;
б)	найти решение уравнений статики изотропного упругого тела в двух-
граннике х2^0, х3 ^ 0, —оо << хг << оо, или з трехграннике хг ^ 0, х2 ^> О,
х3 ^ 0, когда на одной из граней заданы: 1) вектор смещения или 2) вектор
напряжения, или 3) касательные напряжения и нормальное смещение или
4) нормальное напряжение и касательные смещения, или 5) вне полукруга
х\ + х\ ^> а2, х2 ^ 0 в случае двухгранника, и вне четверти круга х\ +
•\- х\ ^ а2, хг ^> 0, х2^0в случае трехгранника, задан вектор смещения,
а внутри — касательные напряжения и нормальное смещение; на других
гранях заданы условия 3) и 4). Задача б) с граничными условиями 1)—4) ре-
решается и для уравнения колебания
А(дх, со)и = 0;
в)	найти решение уравнений колебания А (дХУ со) и = 0 в двухграннике
или в трехграннике с раствором п/2п (п ^ 0 — целое число), когда на гранях
заданы: 1) касательные напряжения и нормальное смещение, или 2) нормаль-
нормальное напряжение и касательные смещения, или 3) на одной грани заданы усло-
условия 1), а на остальных гранях — условия 2).
Решение задачи а). Считая объемные силы отсутствующими,
в силу C.3) замечаем, что функция Ф3 (хъ х2, х3)— гармоническая в беско-
бесконечном пространстве с щелью х\ + х\ ^ а2, — будет удовлетворять условию
[Ф8 (*г. *2> 0)]± = 2ц [us (xlt x2, 0)]± = f± (xl9 х2), при х\ + х\ < а2, (*)
где верхний и нижний знаки берутся соответственно при х3 —* +0 и х3 —¦ —0.
1) После выхода первого издания настоящей книги авторам стало известно о работе
Duff in R. [1], в которой доказаны теоремы о продолжении решений уравнения Л (дх) и=0у
при условии обращения в нуль на S: а) вектора смещения, Ь) вектора напряжения, с) каса-
касательных составляющих напряжения и нормальной составляющей смещения, d) касательных
составляющих смещения и нормальной составляющей напряжения. Метод доказательства —
отличный от указанного выше; упомянутые результаты относятся к статическим задачам и
нашли интересные применения в доказательстве теорем единственности в задачах для полу-
полупространства (см. гл. III, § 7). В работе Duffin [1] граничные задачи не рассматриваются.
Существуют и другие теоремы продолжения в теории упругости, см. об этом Bramble [1, 2].

598	решения в рядах и квадратурах	(рл х IV
Рассмотрим две регулярные, гармонические в бесконечном простран-
пространстве с щелью х\ + х\ ^ а2, функции
*, *3) =	9
O/v v Y\ Ф3 (*i, *2, *8) — Ф3 (%, х2, — х3)
Ы (Xi> л2, Лз; =	2	•
В силу значения [Ф3 (хъ х2, 0) |± они удовлетворяют граничным усло-
условиям
Й+(^, х2, 0) = —Q-(^, Xa, O) = ^=il = F(jc1, a:2), xf
Гармоническая функция <ф, равная / (jcr, x2) на верхней и нижней сторо-
сторонах кругового диска и исчезающая на бесконечности, представляется форму-
формулой Гобсона (см. Галин fll, Hobson IIJ)
*i> *2> *з) = Д> J ^("af-farctgM)/(#!, y2)dy1dy29
s
где S — круг х\ + х\ ^ а2,
x\ — x\
Функция -ф (xl9 x2, x8), являясь четной функцией относительно хп и
имеющая непрерывные вторые производные в бесконечном пространстве
с круговой щелью, очевидно, удовлетворяет условию
-гт—- =0, при xi-\-xi>d\
1/Л3 Х3=\)
ф (xv х2, 0) = / (х19 х2), при х\ + А ^ а2.
Отсюда следует, что достаточно построить г|) (х1у х2, л;3) в полупро-
полупространстве хъ > 0, при заданных граничных условиях. Такая гармоническая
функция строится формулой Кочина (см. Галин [11). Наоборот, с помощью
принципа Римана—Шварца, последняя задача приводится к задаче Гобсона.
Таким образом, из решения Кочина можно получить решение Гобсона, и
наоборот.
Функция Q (хъ х2, xs), являясь нечетной функцией относительно х39
в силу (*) удовлетворяет условию
0, при х(-{-1
?(х19 х2), при х2-\-х\
Очевидно, функция Q (xlf x2, хь) представляется интегралом
*"v	Хо Г F {tit и )
ее [%i9 х2, Хз) = -^— I 	1	dyi dy2»
s
Таким образом, функция Ф3 (хъ х2, х9) = я|? + Q найдена.
Теперь с помощью выражения
—г1- + -ir1- ¦+ -л^-)	> х\ + Х2 ^ а2,

§ 4]	ЗАДАЧИ ТЕРМОУПРУГОСТИ В БЕСКОНЕЧНЫХ ОБЛАСТЯХ	599
определяется значение (div u)Xs==±o. Подставляя это значение div и в основ-
основные уравнения статики, для определения иг, и2У и3 приходим к задаче, уже
решенной выше.
Когда на обеих сторонах круговой щели заданы значения вектора напря-
напряжений, эта задача, при помощи функции Треффтца, была решена С. Г. Мих-
линым (см. Михлин [7]).
Решение задачи б). Пусть на грани х2 = 0, х3 ^ 0 имеем гра-
граничные условия
Т12 = Т23 = Щ = 0.	(а)
а на грани х3 = 0, х2 ^ 0
ИХ = fl (Хц Х2), U2 = /2 (Хц Х2), п3 = /8 (*1, Х2).	(Ь)
Рассмотрим функции
U\C^i» x2i x3)y U2{Xi, х2У x3), и 3\х-±, x2, x3) =
f r/i(Xx, X2, X3), U2(Xu X2, X3), и3(Хг, X2> X3), ПрИ X2^0, X3>0,
1 ^i(^i» — x2 , x3), -»-w2(^i» — X2» ^з)» м3(х1э — х2, дс8), при х2^0, x3^0.
(c)
В силу теоремы 3.2 они определяют вектор, являющийся решением
основных уравнений статики в полупространстве х3 ^ 0. Из граничных ус-
условий (Ь) следует:
- х2),
Из требования совместимости условий (а) и (Ь) следует /2 (jcx, 0) = 0.
Таким образом, U = (U ъ U2, U3) является решением задачи A)+ в случае
полупространства, выражаемым в квадратурах. В силу (с) его значения
в двухграннике х2 ^ 0, х3 ^> 0, —оо << хх <С оо дает искомые величины
Ui \Xi, Х2, Х3), U2 \Х-±, Х2, Х3), п3 \Х-±1 X2i Х3).
Если вместо условий (а) заданы неоднородные граничные условия
Ti2 U,=o = г|I (хи х3), т23 |х,=о = г|52 (^i, х3), и2 (х19 0, х3) = г|K (х1У х3), х3 ^ 0,
то эти условия легко приводятся к однородным.
Решения задачи б) с другими граничными условиями и задачи в) с по-
помощью теорем C.2) и C.3) также приводятся к решению соответствующей
задачи для полупространства, которое строится явно (см. Оболашвили [2]).
§ 4. Задачи термоупругости в бесконечных областях,
ограниченных системой плоскостей
Задачи связаной теории термоупругости являются динамическими зада-
задачами. Общая теория динамических задач, включающая доказательство основ-
основных теорем существования и единственности, как мы видели в предыдущих
главах, построена в предположении фиксирования границы рассматриваемых
областей в конечной части пространства. Если граница или ее некоторые ча-
части простираются в бесконечность, граничные и начально-граничные задачи

600	РЕШЕНИЯ В РЯДАХ И КВАДРАТУРАХ	ff^ XIV
теории упругости в общем случае мало изучены, и до сих пор достигнутые
в этом смысле успехи ограничиваются частными результатами г).
Эти результаты имеют более общий характер в том случае, когда граница
бесконечной области составлена из некоторых систем плоскостей или систем
прямолинейных отрезков (в плоском случае); сюда относятся задачи для полу-
полупространства и полуплоскости, задачи для некоторых других долей простран-
пространства и плоскости, задачи для двугранных и трехгранных углов и другие.
Для многих задач такого рода, допустив существование решения в неко-
некотором, достаточно широком классе функций, можно найти явное выражение
предполагаемого решения и непосредственной подстановкой проверить его.
При положительном результате проверки найденное решение является одним
из возможных в данном классе.
Эта «неопределенность» исчезнет, если доказаны соответствующие тео-
теоремы единственности. Теоремы единственности, вероятно, могут быть полу-
получены из принципа симметрии (см. § 4, п. 5 и § 5, п. 5) подобно тому как они
доказаны для статических задач теории упругости (см. Duffin [1] и п. 2).
Число задач термоупругости, для которых оказалось возможным полу-
получить такие результаты, достаточно велико. Мы ограничимся здесь рассмотре-
рассмотрением некоторых из этих задач. Пусть на границе области заданы: I — сме-
смещения и температура, II — напряжения и поток тепла, III — смещения и
поток тепла, IV — напряжения и температура, V — касательные составляю-
составляющие смещения, нормальная составляющая напряжения и линейная комбина-
комбинация температуры с объемным расширением (энтропия), VI — нормальная
составляющая смещения, касательные составляющие напряжения и линейная
комбинация потока тепла с нормальной производной объемного расширения
(поток энтропии), VII — касательные составляющие смещения, нормальная
составляющая напряжения и поток тепла, VIII — нормальная составляющая
смещения, касательные составляющие напряжения и температура, IX — ус-
условия задачи V относительно смещений и напряжений и линейная комбинация
потока тепла с температурой, X — условия задачи VI относительно напряже-
напряжения и смещения и линейная комбинация потока тепла с температурой.
Явные решения этих задач получаются применением принципа симмет-
симметрии, распространенного для термоупругости (см. предыдущий параграф),
либо с помощью интегралов Фурье, в комбинации с принципом симметрии.
Мы начнем с рассмотрения задач V и VI, которые ближе примыкают к об-
общим методам, изученным раньше.
1. Постановка задач для полупространства. Пусть Е3 — трехмерное
евклидово пространство х\хъ х21 х3), Охгх2х3—ортогональная, прямоли-
прямолинейная, левая система координат. В полупространстве х3 ^> 0 ищется регу-
регулярное решение и (ии и2, и3), иА — уравнений термоупругости
\х Аи -J- (Л + (л) graddiv и + (о2и — y.gjrad и4 = 0,	D.1)
Да4 + — и4 + mi] div и = 0,	D.2)
удовлетворяющее на граничной плоскости х3 = 0 одному из условий:
Задача V. Заданы касательные составляющие вектора смещений,
нормальная составляющая вектора напряжений и произвольная линейная
комбинация температуры и объемного расширения.
х) Замечание к корректуре. В этом направлении в последние годы получены зна-
значительные результаты (см. И. И. В о р о в и ч, В. М. Александров, В. А. Б а-
б е ш к о, Неклассические задачи теории упругости. «Наука», Москва, 1974).

§ 4]	ЗАДАЧИ ТЕРМОУПРУГОСТИ В БЕСКОНЕЧНЫХ ОБЛАСТЯХ	501
Задача VI. Заданы нормальная составляющая вектора смещений,
касательные составляющие вектора напряжений и произвольная линейная
комбинация потока тепла с нормальной производной объемного расширения.
Граничные условия запишутся в следующем виде:
Задача V:
иг = фх (*!, х2),	щ = ф2 (%, л;2),
%*(и) = Фз(*1> х2), aa4 + bdivw = 94(x1, х2).
Задача VI:
us = q>1(xl9 х2),	T13(a) = a|J(x1, х2),
т23 (и) = я|?з (*i> х2), -^ (аи4 + Ъ div и) = ф4 (^, х2),
где фг- (xlf *2), tfo (xlf x2), i = 1, . . ., 4 — заданные на х3 = 0 функции,
а к b — постоянные.
Из условий задачи V можно найти значения и4 и div и на плоскости
*3 = 0, а из условий задачи VI — значения -^- и ^— (div и) на той же пло-
скости.
Действительно, в случае задачи V имеем
A,div и + 2|х -^ — v^4 = Фз (%» *2)>
где ф5 (хъ х2) — заданная на х3 = 0 функция. Присоединив сюда условие
аиА + b div и — ф4 (хъ х2) и считая а (X + 2(х) + 67 + 0, находим -^ и и4;
следовательно, div и = ф6 (jclf дс2), а4 = ф7 (х1э х2), где ф6, ф7 — заданные
функции.
В частности, при а = 1, b = 0 имеем задачу V с заданной температурой
на границе; при а = 0, b = 1—ту же задачу с заданной на границе дилатацией
и при а = -|-, b = у — задачу V с заданным значением энтропии, где с —
удельная теплоемкость при постоянной деформации, 0О — начальная темпе-
температура.
Обратимся к условиям задачи VI. Имеем
dxj
НО
з=:о м- \Y2 h дхг J9 дх3 \х,=о м- VY r^2 /
п — (^. ^L E5fL а"з Дид ^i \,
следовательно, на плоскости х3 = 0 известны касательные составляющие
вектора rot ы.
Переписав уравнение D.1) в виде
(К + 2jli)graddiva — |ыrot rot и + co2a — у grad и4 = 0
и проектируя его на ось х3, получим
^-div"—i* [dr (rot ")г —4"(rot u)ll+ c°2 ~v S"= 0>

602	РЕШЕНИЯ В РЯДАХ И КВАДРАТУРАХ	[Рл XIV
и в пределе, для х3 = 0,
Таким образом, на граничной плоскости х3 = 0 заданы соотношения
(Я + 2|i) ?- (div а) — v gj- = ^ (*, х2),
Ь ^ (div и) + a gj- = ф4 (хх, *,);
отсюда, при условии а (X + 2|i) + 67 Ф 0» получаем
5~- = % (*i> *2)> g^- (div и) = i|>7 (X!, а:2),
где г|?0> ф7 — известные функции.
В частном случае при а = 1, Ь = 0 имеем задачу VI с заданным на пло-
плоскости х3 = 0 значением потока тепла, при а = 0, 6=1 — ту же задачу
с заданным на х3 = 0 значением —— (div и) и при а = -|-, b = у — за-
дачу VI с заданным значением потока энтропии.
С другой стороны, из D.1) и D.2) очевидно, что вектор (div uy а4) удов-
удовлетворяет в области хъ > 0 системе уравнений
[(к -f- 2|х) Д + со2] div и — у Ди4 = 0,	D.3)
?<DT|div и + ( Д + -^-) и, = 0.	D.4)
Отсюда следует, что задачи V и VI приводятся соответственно к решению
вспомогательных граничных задач для системы D.3), D.4) с граничными дан-
данными при х3 = 0:
Задача А.
и4 = h (*i, *2)> div u = f2 (*!, х2).
Задача В.
|~- = h (xi, xt), g^- (div и) = /2 (xx, x2),
гДг /i» /2 — заданные функции.
Достаточно показать, что 1) задачи А и В (однозначно) разрешимы,
2) решения этих задач выражаются в квадратурах и 3) с помощью этих реше-
решений, решения исходных задач V и VI строятся в квадратурах.
Справедливость утверждения 3) показывается легко. Пусть имеется ре-
решение задачи А. Проектируя D.1) на оси хх и х2, для определения иг и и2
приходим к граничным задачам Дирихле для уравнения Гельмгольца
Дг^ + -^ut = Fi (*i> *2, х*)' Ui 1*з==0 =	) i 12	45^
где
(	^4-diva + i"& ^=1'2,	D.6)
заданные функции.

§4)
ЗАДАЧИ ТЕРМОУПРУГОСТИ В БЕСКОНЕЧНЫХ ОБЛАСТЯХ
603
Проекция же D.1) на ось х3 приводит для определения и3 к граничной
задаче Неймана для уравнений Гельмгольца
Аи3 + ^г и3 =
29 х3),
=diva
где fbu F3 — заданные функции и
* 3 (¦*!» -^2» Хз) ==
D.7)
D.8)
Задачи D.5) и D.7) решаются в квадратурах (см. п. 4).
Пусть теперь имеется решение задачи В для системы D.3), D.4).
Проекция уравнения D.1) на ось х3 приводит к граничной задаче Дирихле
для определения и3 (хг, х2, х3)
*2),	D.9)
где /%,(*!, х2, л:3) = — ^alT	7 g^
функции.
С другой стороны, из граничных условий задачи VI следует
ди2
— заданные
D.10)
где г|M, i]N — заданные функции.
Поэтому, проектируя D.1) на оси хг и х2, для определения их и w2 при-
приходим к задачам Неймана для уравнения Гельмгольца; решения этих задач,
как уже сказано, выражаются в квадратурах; они определяют составляю-
составляющие их и и2.
2. Фундаментальные решения и формулы представлений для системы
D.3), D.4). Введем вектор
и систему D.3), D.4) запишем в виде
где
f co)=
D.11)
Для детерминанта матрицы 3?(дх, со) имеем
где
2ц) *
D.12)

604
РЕШЕНИЯ В РЯДАХ И КВАДРАТУРАХ
[Рл XIV
где
Введем в рассмотрение векторы
V(D (t,(l)
= ( А + -^
= [(X + 2ц) A -f со2] ф,
D.13)
D.13')
а ф — произвольная (скалярная) функция.
Для того, чтобы векторы D.13) были решениями системы D.11), оче-
очевидно, достаточно подчинить ф условию
(А + М)(А + Я22)Ф = 0;	D.14)
отсюда
где г (х, у) = \х — у\. Подставив это значение q> в D.13') и выполнив эле-
элементарные вычисления, находим
ехр(а?)
ехр(а2г)
(а2г) 1
„A) — toTl /exp(tV) exp ((Я^г) \
°« — %\-Ц \ ~г	г )'
г,B) _ У ( ^exp(atr) ^exp(tV) \
^ — XT — Л| \	?	7	/'
Матрицу
каждый столбец которой есть решение системы D.11), назовем фундаменталь-
фундаментальной; она имеет следующий вид:
Ф(х—у; со, у) =
где для краткости выражения exp (i^r) обозначены через
Введем «сопряженный» оператор
|(Х + 2|ы) А 4- со2 /сот] ||
\
D.16)
k = 1, 2.
-уА
1) Предполагается А,? =^= А,|; обратное приводит к равенству е =
воречит физической гипотезе 0 < 8 <^ I, {см. NowacKi [1, 3]).
= 1, что проти-

§ 4]	ЗАДАЧИ ТЕРМОУПРУГОСТИ В БЕСКОНЕЧНЫХ ОБЛАСТЯХ	605
и рассмотрим тождество
t?i — tfxAt;2) + (v2Av2 —
Для области D+ с границей S имеем
J \vSti— vSfv] dv = § [(% + 2ц) (^ g-1 — Vl
D+	S
J
Введем операторы (матрицы)
, д	с
0	Ж 1	|| -*-5Г
D.18')
тогда DЛ8) запишется в виде равенства
—v2v) dx = J (JiVt; — у//Ь) dS.	D.19)
j
D+	S
Фундаментальная матрица Ф (х— y\ cd, 7), соответствующая оператору
3?(дх, со), строится так же, как была построена матрица Ф. Легко при этом
обнаружить, что
Ф' (х—у\ со, 7) = Ф (х—у\ со, 7);	D.20)
здесь штрих обозначает переход к транспонированной матрице.
Малым шаром Ш (х, е) радиуса 8 с поверхностью С (х, г) исключим
х ? D+ и в области D+\ Ш(х, г) применим формулу D.19) к регулярному век-
вектору v (vl9 v2) и вектору
_*; ©, у) = (Ф1к, Ф2к), Л=1,2;
тогда, вследствие того, что
& (ду9 со) Ф^) (у — х; со, 7) = 0, Ф<*> {у — х; со, 7) = О (| х — у Г1),
получим
j ф^(у — *;со, y)gv(y)dy= \ [ф(*> (у — х; со, 7) Nv{y) —
D+\UJ (X, Е)	S
— v(у) М><*> (у—х; ш, vM^fS —о(х) J М><*> (у — х\ со, v)d^ + О(е);
С { )
С (*, 8)
6=1,2. D.21)
Учитывая равенство
Г д 1
I "з—i	г duS = 4я
j an \x — y\ y
С (Х9 8 )
и определения Л^ (дт у) и Ф (у — х\ со, у)9 будем иметь
j У\/Ф (г/ — л:; со, 7) d^ = 4я (X + 2|г) ? + О (е),	D.22)
С (Х9 8)
где ?— единичная матрица размера 2x2.

606	РЕШЕНИЯ В РЯДАХ И КВАДРАТУРАХ	[ГЛф XW
Переписав D.21) в матричной форме, приняв во внимание D.20) и D.22)
и перейдя к пределу приъ --> 0, получим
4л;(к + 2ja) v (х) = }Ф{х — у; со, 7) Nv(у) dyS—
— J[M>(*— */;со, y)Yv(y)duS— J <X>{x — y;co,y)&v(y)dy. D.23)
Введем потенциалы
^ (х; Ф) = J Ф (х—у; со, 7) Ф (У) dyS,
s
W (л:; г|)) = J |Л^EП, у)Ф (х — у\ со, у)\' ty(y) d^S.
Обычным способом показывается справедливость предельных равенств
(NV (г; Ф))± = ± 2я (Я + 2(х) Ф (г) + NV (г; ф),	}	D-24)
B) _|- ft^ (z; <ф), г е S.
В задачах, которые нас интересуют, поверхность S совпадает с бесконеч-
бесконечной плоскостью или с ее частью. В связи с этим, необходимо исследовать воп-
вопрос о сходимости интегралов по таким областям. При этом существенную
роль будет играть тот факт, что параметры Хг и Х2, которые удовлетворяют ус-
условиям D.12) и при у Ф 0 являются комплексными, допускают два равно-
равноправных знака (см. X, § 3) и мы можем без ограничения общности остано-
остановиться на одном из них.
Выберем знак таким образом, чтобы решения убывали на бесконечности
как е~а I х ', где а > 0.
При этих условиях в потенциалах простого и двойного слоя достаточно
считать плотности функциями, ограниченными на бесконечности.
3. Решение задач А и В для системы D.11). Теоремы единственности.
Задача А. В полупространстве х3 ^ 0 ищется регулярное решение
уравнений
удовлетворяющее на границе х3 = 0 условию v (z) = f (z), где / = (flf f2)
заданный, ограниченный на бесконечности вектор.
Представим решение потенциалом двойного слоя
v(x) = W(х; хр)= II \N {дп{у)9 у)Ф(х —у; а>9 y)\f
согласно D.24), для плотности я|) (у) будем иметь
00
JJ {N(dn{y), у)Ф(г — у; и, y)
и так как на плоскости х9 = О
{N(dn(y), у)Ф(г—у; со, у)\' =0,	D.25)

§ 4]	ЗАДАЧИ ТЕРМОУПРУГОСТИ В БЕСКОНЕЧНЫХ ОБЛАСТЯХ	507
находим 'Ф (г) == — o,^o ч и, следовательно,
y2. D.26)
ЗадачаВ. В области хг ^ 0 ищется регулярное решение уравнения
D.11), удовлетворяющее условию -^- = f (z), где f (z)— заданный
вектор, ограниченный на бесконечности.
Решение ищем в виде потенциала простого слоя
00
v (х) = V (х\ ф) = J J Ф (х — у; со, 7) ф (У) dy± dy2,
—оо
и тогда, в силу D.24), для плотности ср (у) будем иметь
оо
2л {X + 2[л) ф (г) + j J W (дп B)) у) Ф (г — у; со, у) Ф (у) dyx dy2 =
и так как на плоскости х3 — О
iV EЯ B), у) Ф (г — г/; со, 7) = 0,	D.27)
находим ф (z) = -^—,л , о ч и, следовательно,
ZJl (A -f- Z\l)
J i Ф {х ~ у; w> 7) F {y) dyi dy*	D-28)
— оо
Найденные решения единственны. Чтобы убедиться в этом, достаточно
показать, что соответствующие однородные задачи имеют лишь тривиальные
решения.
Пусть v@)(x) есть решение однородной задачи А. Представив его по фор-
формуле D.23), будем иметь
оо
4я (I + 2ц) и@) (х) = | J Ф (х — у; со, у) N »«» (у) dyx dyz.	D.29)
—оо
Отсюда по формулам D.24)
00
2я (X + 2ц) AW°>(z) = J j W (да (г), Y) Ф (г — У, ®.
и в силу D.27) Nv^0)(z) = 0. Внеся это значение i\fa<°> (у) в D.29), получаем
о<°> (х) = 0.
Пусть теперь с;<°)(л:) есть решение однородной задачи В. Очевидно, что
при этом Nvi0)(z) = 0. В этом случае формула D.23) дает
оо
4я (X + 2ц) 1><°> (х) = — J J {iV (ая ,„„ v) Ф (ж—У! ©. ?)>' "@) (У) dyx dy2. D.30)

608	РЕШЕНИЯ В РЯДАХ И КВАДРАТУРАХ	[ГЛ. XIV
Перейдя к пределу при х —» г, будем иметь
00
2я (Я + 2ц) у<о> (г) = — J J {Я (д„ „„ у) Ф B — г/; со, Т)}' о«» (у) ^ dy2,
—оо
и в силу D.25) для всех хв = О имеем у@) (z) = 0. Учитывая это в D.30),
получаем а@) (х) = 0.
4. Решение задач V и VI для полупространства. После получения реше-
решения задач А и В для системы D.11), процедура, указанная в конце п. 1, поз-
позволяет найти явные решения задач V и VI для полупространства.
Как было показано, для этого достаточно иметь решения следующих
задач Дирихле и Неймана для полупространства:
и на границе хъ = 0 задано либо ф = /, либо -^ = f.
Решение первой из этих задач (задача Дирихле) дается формулой
^з > О
D.31)
^з > О
а решение второй (задача Неймана) выражается формулой
ГГГ
-JrJ J J Gmix.z)Fit)dz.
«a > 0
D.32)
где
' 2)
exp [ T7= | x — z |)	exp ^L \ x* — '<
x = (^, л:2, x3), x = (a:x, x2, —x3)
и F и / удовлетворяют условиям, достаточным для сходимости рассматривае-
рассматриваемых несобственных интегралов.
Внеся в D.31) вместо F (z) значения Ft B), 1=1,2, из D.6) и значения
/ (У) = ф?» f = It 2, из D.5), найдем значения их (х) и и2 (х).
Для получения значения иъ (х) вносим в D.32) значение F (z) = F3 (z)
из D.8) и значение / (у) = /3 из D.7). При этом следует иметь в виду, что
(div а, гг4), присутствующие в выражении правых частей и граничных зна-
значениях, равны div и = olf а4 = у2 и вектор a (olf v2) определен форму-
формулой D.26).
Таким образом, решение задачи V получено в квадратурах.
Для решения задачи VI поступаем следующим образом: внеся в D.31)
вместо F (г) значение F3 (z) из D.10) и значение/ (у) из D.9), получаем значе-

Л 4]	ЗАДАЧИ ТЕРМОУПРУГОСТИ В БЕСКОНЕЧНЫХ ОБЛАСТЯХ	609
ние и3 (х) в произвольной точке х = (х19 х2> х3) полупространства х3 > 0.
Далее, подставляя в D.32) вместо F (г) значение F{ (z), i = 1, 2, из D.6) и
значение f (у) из DЛ0), находим иг (х) и и2 (х). При этом
и вектор v {vl9 v2) определяется формулой D.28).
5. Теоремы о принципе симметрии для системы D.11). Докажем для
системы D.11) две теоремы, аналогичные теореме (принципу)'симметрии для
метагармонической (гармонической) функции. Пусть а — плоская часть гра-
границы основной области D задается уравнением аххг + а2х2 + а3х3 + а4 = 0
и х* есть зеркальное отображение в этой плоскости точки х9 принадлежащей D;
предполагается, что D лежит по одну сторону а. Тогда по известным форму-
формулам имеем
2at-
Xi =Xi
а{ + a\ 4- a\	' l — l> Z> 6*
Кроме того, по свойству инвариантности оператора Лапласа относительно
рассматриваемого преобразования, будем иметь
Д (дх) и = А (дх*) и.
Теорема 4.1. Если вектор v (x) есть регулярное в D решение си-
системы D.11) и на плоской части границы о обращается в нуль, то вектор
есть регулярное в области D (J a U D* решение системы D.11).
Теорема 4.2. Если вектор v (x) есть регулярное вб решение системы
D.11) и на плоской части границы а обращается в нуль его нормальная произ-
производная, то вектор
V(x) = {
v{x), хбД
v(x% x?D*
есть регулярное в области D [} а U D* решение системы D.11).
Для доказательства теоремы 4.1, очевидно, достаточно показать, что:
а) в области D* V(x) есть регулярное решение системы D.11); Ь) нормальная
производная V (х) непрерывно продолжается через а; с) V (х) удовлетворяет
системе D.11) в точках а. Утверждение пункта а) следует из того, что в системе
D.11) участвует лишь оператор Лапласа, который, как отмечено, инвариан-
инвариантен при зеркальном отображении; справедливость утверждения Ь) показы-
показывается непосредственным вычислением.
Что касается пункта с), то он доказывается следующим образом:
Пусть St U а есть полная граница области D. Применим формулу D.23)
при х ? D к вектору V (х):
— J \МФ(х—у; со, y)}fV+(y)dyS. D.33)
StUo
Выпишем ту же формулу в случае, когда х ? D*,
0= J Ф(х—у; со, y)(NV)+dyS— j \М{х — у; со, у)}'V+G/KS. D.34)
•Si U о	S,Uo
39 В. Д. Купрадзе

610	РЕШЕНИЯ В РЯДАХ И КВАДРАТУРАХ	[Рл# XIV
Повторим эту процедуру относительно области D*:
4я (Я + 2jx) У (х) = — J Ф (х—у; со, у) (NV)
\ U
J
s\ U
+ j {ЛГФ(х —у;а>, y)\fV~(y)d&S> xeD\ D.35)
SiUa
0 = — J Ofr—y;®,y)(NV)-dl? +
S\ U a
+ J \№{x — y;«>9y)V]r(y)djS9 x?D; D.36)
si U a
здесь S* — зеркальное отражение Sv
Из формул D.33)—D.36), приняв во внимание непрерывность V и -^- на
а, получим
J {#Ф(х — у; со, y)\'V(y)dyS, xeD[)o[)D\
что и доказывает пункт с) и, следовательно, теорему 4.1.
Аналогично доказывается теорема 4.2.
6. Решение некоторых граничных задач для системы D.11) в четверти
пространства. В области —оо <3 хх <; оо, 0 ^ х2 <j ©о, 0 ^ л:3 <Э °о ищется
регулярное решение системы D.11), удовлетворяющее на гранях-границах
одному из следующих граничных условий:
A.	*8 = 0, 0 < х% < оо: v = f(D (%, jc2); л;2 = 0, 0 ^ л:8<оо: у = /B) (хх> ^3);
B.	а:3 = 0, 0 < х2 < оо: -~- = f(D (^, х2); х2 = 0, 0 < *3<оо: -^- = fB) (хг, х3);
С. д:8 = 0» 0 < д:3 < оо: о » /d) (^, х2); х2 = 0, 0	^
Решение задачи А представим в виде суммы
v(x) = v<l> (x) + v^ (Х\	D.37)
где v<l) (х) и оB) (х) — регулярные решения уравнений D.11), причем v{l)(x) =
= /<1> (хъ х2) на грани хъ = 0, 0 ^ х2 < оо и t><x> (х) = 0 на грани х2 = 0,
0 ^ х9 <3 сх> и, наоборот, иB) (х) == /B) (х19 х3) на грани х2 = 0, 0 ^ х3 < сх>
и у<2^ (х) = 0 на грани xs = 0, 0 ^ х2 <С оо.
При этих условиях, очевидно, сумма v{l) (x) + v{2) (x) есть решение
задачи А. Так как на грани х2 = 0, 0 ^ х3 < со, vil) (x) = 0, к вектору
рA) (л:), как решению системы D.11), можно применить принцип симметрии,
доказанный в п. 5. Это дает для х3 ^ 0
- оо<-х.<0. ^"(^-^ ^'
Следовательно, Va) (x) удовлетворяет граничным условиям на х9 = Оз
<оо, -оо<х1<оо;

§4]
ЗАДАЧИ ТЕРМОУПРУГОСТИ В БЕСКОНЕЧНЫХ ОБЛАСТЯХ	611
Таким образом, для нахождения 1/A> (х) имеем граничную задачу А
в полупространстве х3 ^ 0, рассмотренную в п. 3, решение которой дается
формулой D.26) и в данном случае имеет следующий вид:
— lN(dn{y)9 У) Ф(х —у*; со, т)П/A) (Уъ y*)dy» D.38)
где j/* = {у19 — j/a, 0), у = (у19 у29 0).
Обращаясь к построению vi2) (x)9 замечаем, что вследствие граничного
условия vB) (х) = 0 при хъ = 0, 0 ^ х2 <С сю, принцип симметрии приме-
применяется относительно плоскости х3 = 0; в результате получим
Очевидно, что 1/B) (х) удовлетворяет граничным условиям на х2 = 0:
Таким образом, для нахождения V™ (х) пришли к той же задаче А из п. 3
и решение ее имеет вид
-{-СО	-[-00
-оо	О
— [N (дп (^*), у) Ф (х — у*; со, у)]'} /B) (ух, у3) dy3, D.39)
где у* = (у1у 0, — уд), У = ({/i, 0, Уз)-
Нетрудно видеть, что сумма
v (х) = VM (х) +1/B) (х),	D.39')
когда х принадлежит области —оо <3 хг <3 оо, 0 ^ х2 <! оо, 0 ^ х3 <3 сю,
есть искомое решение задачи А настоящего пункта. Кроме того, из теоремы
единственности для задачи А п. 3 следует единственность найденного решения.
Задача В. Решение снова ищем в виде суммы
= v^ (х) | tA2) (х)
где v{l) (х) и v{2) (х) — регулярные решения системы D.11), причем Ы!> (х)
удовлетворяет граничным условиям
(х) _\!{1ЧхъЧ), *з = 0> 0^х2<оо, _оо<л;1<оо,
а для v{Z)(x) выполняются следующие граничные условия:
dvi2) (х) _ | /B) (-^1» *з).. ^2 = 0, 0 ^ х3 < оо, — оо < хг < оо,
дп	[0,	х3 = 0, 0^а:2<<оо, —oo^Xj^oo.
Введем вектор V{l)(x)\ согласно свойству симметрии по теореме 4.2 п. 5
имеем
Т/A) /х)
{Х)-' 	-	0, -оо<х2<0, -oo<xx<oo,
39*

612	РЕШЕНИЯ В РЯДАХ И КВАДРАТУРАХ	[рл XIV
Следовательно, для Vil) (х) заданы
dVA) (х) \ /A) (xi> Х2)'< Х9 = О,	0<х2<оо, — oo<^< оо,
дп	I /A) (*ъ — Х2)\ *8 = 0, — оо < ха < 0, — оо < хг < со, %
и задача приведена к граничной задаче В п. 3 для полупространства х3 ^ О,
решение которой дается формулой D.28); после некоторых преобразований
это решение принимает следующий вид:
-f-oo	-f-°°
Vil) W = 2я(Х + 2Ю J dyi I №(X — y< «>• Т) + Ф(^ — У*! «>. T)] X
I	(А. Ч- 2ц) /i»> (У1, у2) — v^11 (»i, »a) Ц .
X	fA) l и u\	\ У*'
II	'2 \!>U У2)	II
У = {У1, Уз, °). У* = {.Уи — Уа, 0)-
Для построения t)B) (x) введем вектор
ОО < Хх < ОО,
который, как нетрудно видеть, удовлетворяет граничным условиям
dV{2)(x) _ f f{2) (xi» хз); ^2 = °» 0^х3<оо, — oo<x1<oo,
^	~~ { /B) (х^ _ Х8); ^2 = 0, — СО < Хъ < 0, — ОО < Хг < ОО.
Следовательно, и в данном случае вопрос сведен к решению задачи В
из п. 3 для полупространства х2 ^ 0. Это решение дается формулой D.28),
которая после упрощения принимает вид
+ОО	+00
v) J d& J №(* — У> ю' V) + ф(^ — У*> ©• 7I X
Х
где у = (й, 0, уз)» У* = (Ух» 0» — Уз)-
Ясно, что сумма о (х) == УA) (х) + Vl2) (x) представляет искомое ре-
решение нашей задачи при —оо < хг <С оо, 0 ^ х2 << оо, 0 ^ х3 <С оо.
Единственность найденного решения вытекает из единственности ре-
решения задачи В п. 3.
Задача С. Представим решение в виде
(x) есть регулярное решение D.11) с граничными условиями
х3 = 0, 0^*2<оо, — оо<хх<оо: 0<i> (х) = Р> {хг, х
dvA)
<	о<Х<оо:	0
а рB) (л:) — решение той же системы с граничными условиями
х2 = 0, 0 < х3 < оо, — оо < хг < оо:
<оо, — oo<jc1<oo:

я 4]	ЗАДАЧИ ТЕРМОУПРУГОСТИ В БЕСКОНЕЧНЫХ ОБЛАСТЯХ	513
Пусть
(х)\ х3 ^ 0, 0 ^ х2 < со, — сю < хг < оо,
0,	0 ^ Х2 < СО, — ОО < *! < ОО,
X = \X\i Х21 — Х$).
Для определения 1/A) (х), согласно принципу симметрии (теорема 4.2t
п. 5), имеем задачу В (п. 3) при х3^ 0, а для определения V{2)(x) (теорема 4.1,
п. 5) — задачу А (п. 3) при х2 ^ 0.
Граничные условия для VA) (x) и VB) (x) имеют соответственно следую-
следующий вид:
	СО<^ X!<. CO,
— со <[ хг <С со;
= 0,	0^Х3<^со, —оо^Хх^со»
дп ~" I — /B) (^i, — Х3), х2 = 0, — со <: Хъ ^ 0, — со << Хх << со.
Решение первой дается формулой D.26) и имеет в данном случае вид
7
— у*; со, v)]'l ^A) (yi*yJdy2,	D.42)
# = (Л» Л. 0), у* = (г/х, — у2, 0),
а решение второй *— выражается формулой D.28), имеющей здесь следую-
следующий вид:
1 d^' f 1Ф(*—# °>. Y) —Ф(*—0*;<».Y)] x
Таким образом, решение задачи С выразится суммой
D.43')
при —оо << хг <3 со, 0 ^ л:2 <С со, 0 ^ л:3 < со.
Найденное решение единственно, так как единственны решения задач А
и В из п. 3.
7. Решения задач Дирихле, Неймана и смешанной для метагармониче-
ского уравнения в четверти пространства. Решения указанных задач можно
получить как частный случай из результатов предыдущего параграфа.
Для этого достаточно положить вD.11O = 0и и2 = 0. Тогда т] = С7 = 0
и система D.11) обращается в скалярное уравнение Гельмгольца
^.	D.44)

614
РЕШЕНИЯ В РЯДАХ И КВАДРАТУРАХ
[Гл. XIV
Решение задачи А (задачи Дирихле). Так как q> =
= иг, и2 = 0, граничные условия задачи А п. 6 принимают вид
оо: ф = f\1} (xt, x2), fal) (хг, х2) = О,
х, = О, О ^ дг3 < оо: Ф = /}2> (Xl, х3), № С«х. х») = 0.
Далее, согласно D.12)
1	А- + 2(л ' 2 х
Поэтому матрица Ф (х— у\ со, 7) согласно D.16) принимает вид
\г х У,	о
— у;а>, 0) = Ф(д; — у; со, 0) =
0
а2 \ х—у i
D.45)
D.46)
D.47)
и матрица N (дп, у) согласно D.18') обращается в матрицу
% д
д
дп
D.48)
Согласно указанному, будем иметь
Ф (х) = Vl (х) = v[l\x) + v{2\x),
и согласно D.39')
1 = 0,
D.49)
Но согласно D.38) и D.47), D.48), D.45)
U,/ ч	1 +Ь Т
'W= -г^Г J d^ J
дп(у*) \х
, I r-ti* П ...
¦ _у«| J П (Уи У г) dy»
где у = (#15 г/2, 0), у* = (г/1( —г/2, 0), а согласно D.39) и D.45), D.47),
D.48)
Г" Г
—оо	О
*-»*
где у = (t/x, 0, у8)э »*= (»i, 0, —уд).
Следовательно, имеем окончательно
-f-oo -f-oo
с) eiK I л:—г* I
х—г I
— оо
-f-00	-f0
где г = Bl, г2> 0), г* - (zu — г„ 0), С = (Si. 0, W.
Ь, 0, —

ft 4j	ЗАДАЧИ ТЕРМОУПРУГОСТИ В БЕСКОНЕЧНЫХ ОБЛАСТЯХ	615
Решение задачи В (задача Неймана). Так же как
выше, в соответствии с п. 6, граничные условия принимают вид
D.51)
Поступая далее совершенно аналогично, согласно D.40), D.41), D.51),
D.47), получаем
I Г° С° Г еа' ' *
*~г •
-f-oo -{-оо
i J d^ J |Л1=СГ + T7=4T-J /P ^. U^. D-52)
0
где
г = (^, г2, 0), г* = B!, — г2, 0), С = (&, 0, у,	С* = (Si, 0, — &)•
Решение задачи С (смешанная	задача). Гранич-
Граничные условия имеют вид
: ф = У1 = /Г)(х1,д:2),	$Х) (хг, х2) = 0, 1
. —==— = ;! (х1э х3),	/2 (xi, х3) = и, j
и далее, согласно D.53), D.47), D.48), D.42), D.43), имеем
+	J
1 Г а Г
—оо О
-{-со -f-oo
+ -as- f rfb f [C'Tl' - C'^l'i ^ (Ь. Ы dl3, D.54)
—оо О
где
Формулы D.50), D.52), D.54) другим путем были получены в работе
Оболашвили [2L
8. Решение задач Дирихле, Неймана и смешанной для неоднородного
метагармонического уравнения в четверти пространства. Здесь решаются
задачи А, В и С из п. 7 для неоднородного уравнения
D.55)
Именно к таким задачам, как мы увидим в следующем параграфе, при-
приводятся решения задач V и VI для системы уравнений термоупругости D.1),
D.2) в указанной области.
Сначала построим функцию Грина для задачи А. Это можно сделать
в квадратурах. В самом деле, пусть
eiK I х-у |

616	РЕШЕНИЯ В РЯДАХ И КВАДРАТУРАХ	[Рл# XIV
есть функция Грина задачи А, п. 7. Тогда для определения gA (x, у) имеем
задачу Дирихле для однородного метагармонического уравнения с гранич-
граничными условиями:
о: gA(x, y) = f[l) (%, х2) = €\х — у\ '
y) = f{(xu *,) = -?-!—_.
Эта задача решается формулой D.50), в которой следует положить
Функция Грина для задачи А построена, и решение неоднородной за-
задачи А для уравнения D.55) выражается формулой
-\-CD
f
= Ф(х) — -^ J df/x J | GA{x,y)F(y)dy3dy2,	D.56)
—со	О О
где ф (х) определяется из D.50). Для сходимости тройного интеграла D.56)
достаточно потребовать определенный характер убывания F (у) на беско-
бесконечности.
Функция Грина задачи В, п. 7 имеет вид
Л т ч	е*К\х-у\
где gB (x, у) находится из формулы D.52), в которой следует положить
A)	д еа*! г~~у'	fB)	д еа*] 1~у'
| 2 —
и решение неоднородной задачи В для уравнения D.55) представится в виде
-f-oo 4"°° +°°
= Ф(х) — ^ J rift J dt/2 I GB(x,y)F(y)dys,	D.57)
0	0
где ф (л:) определена формулой D.52).
Наконец, функция Грина для задачи С, п. 7, имеющая вид
eat i х—у |
строится с помощью формулы D.54), в которой следует положить
B)
Решение неоднородной задачи С для уравнения D.55) представляется
формулой
-|-00	-f-CD	-{-СО
ф(х) = ф(х)—^ J dt/, J dt/2 J GQ{x,y)F(y)dy3,	D.58)
—oo 0	0
в которой ф (х) определена из формулы D.54).

§ 4J	ЗАДАЧИ ТЕРМОУПРУГОСТИ В БЕСКОНЕЧНЫХ ОБЛАСТЯХ	617
Замечание. Нетрудно убедиться, что квадратуры в формулах D.50),
D.52), D.54), которые дают соответственно gA (х, у), gB (x, у) и gQ (x, у)у
вычисляются до конца и, таким образом, функции Грина могут быть запи-
записаны в явном виде.
9. Решение задач V, VI и смешанной в четверти пространства для
уравнений термоупругости. Результаты предыдущих параграфов позволяют
выписать в квадратурах решения следующих задач для уравнений термо-
термоупругости.
Задача V(b четверти пространства). На обеих гранях заданы каса-
касательные составляющие вектора смещения, нормальная составляющая напря-
напряжения и температура, т. е.
х2 = 0, 0 ^ х3 <5 оо, — оо <4 хг <3 со: и1У и39 т22, а4.
Задача VI (в четверти пространства). На обеих гранях заданы
нормальная составляющая вектора смещения, касательные составляющие
напряжений и потока тепла, т. е.
х3 = 0, 0 ^ х2 <3 оо, — оо <3 хг <? оо: и3, т13, т23, ^-;
т12, т23, -?.
ах2
Смешанная задача. На одной грани заданы условия задачи V,
а на второй — условия задачи VI, т. е.
0 0	г, и2, т33, и4;
2	3	2, т12, т23, -gj.
Решение задачи V(b четверти пространства). Как мы уже
знаем (см. п. 1), граничные условия этой задачи позволяют найти на гранях
значения div и и и4; но вектор v = (div и, а4), как решение системы D.11)
по указанным граничным данным в четверти пространства, определяется
формулой D.39').
Далее, из D.1), D.2) имеем
D.59)
|ы дхг
где, как уже сказано, правая часть — известная функция. Кроме урав-
уравнения D.59), для иг (х) известны граничные значения на обеих гранях, т. е.
имеем задачу Дирихле в четверти пространства для неоднородного мета-
гармонического уравнения D.59), решение которой дается формулой D.56).
Для составляющей и2 (х) имеем уравнение
Аи2 -\	и2 =	=!-J— -5— div и + -1- -ir^	D.60)
и граничные условия: на грани х3 = 0, 0 ^ х2 <2 оо, —со < хх < оо
известны значения и2, а на грани х2 = 0, 0 ^ х3 <3 со, —со <i a:j <5 со —-
значения -^-, т. е. нормальной производной, которая находится из задан-
ного выражения х22 (х). Таким образом, получена задача С (смешанная
задача) для неоднородного метагармонического уравнения D.60). Решение
этой задачи дается формулой D.58).

618	РЕШЕНИЯ В РЯДАХ И КВАДРАТУРАХ	[Гл# XIV
Для составляющей и3 (х) имеем уравнение
Аи* -\	щ =	:rj-- -—diva -4- — -г1-	D.61)
и граничные условия: на грани х3 = О, 0 ^ х2 <: оо заданы значения -т~_,
которая находится из выражения для т33 (х), а на грани х2 = О, 0 ^ xs <J оо
известны значения самой и3 (х). Приходим снова к задаче С для неоднород-
неоднородного метагармонического уравнения D.61). Решение дается формулой D.58),
в которой в данном случае следует поменять местами переменные х2 и х3.
Решение задачи VI (в четверти пространства). Граничные
условия этой задачи позволяют (см. п. 1) найти на гранях значения нор-
нормальной производной div и и нормальной производной температуры и4.
Значения div и и и4 находятся в четверти пространства решением задачи В
из п. 6.
Для составляющей их (х) имеем уравнение D.59) и граничные условия:
на грани х3 = 0, 0 ^ х2 <3 оо задана нормальная производная -т-Ч кото-
ох3
рая находится из выражения х13 (х), а на грани х2 = 0, 0 ^ х3 <3 со задана
нормальная производная -^-, определяемая из выражения х12 (х). Таким
образом, мы пришли к задаче Неймана для уравнения D.59), решение ко-
которой дается формулой D.57).
Легко видеть, что для определения и2 (х) и и3 (х) приходим к смешан-
смешанным задачам (задача С) для неоднородного метагармонического уравнения,
решение которых дается формулой D.58).
Решение смешанной задачи. Граничные условия этой
задачи, очевидно, позволяют на грани х3 = 0, 0 ^ х2 <5 со найти div и
и ц4* з на грани х2 = 0, 0 <: х3 < со — значения нормальных производ-
производных div и и м4; следовательно, для определения div и и а4 имеем задачу С
для системы D.11) в четверти пространства, решение которой дается фор-
формулой D.43').
Для построения ut (x), i = 1, 2, 3, имеем
=!=-i--3—diva + — --*-
1 ' (U	|Ll	dXi	' \X dX{
а для граничных условий, как нетрудно усмотреть из вида граничных дан-
данных, имеем: для их (х) услоьия смешанной задачи, для и2 (х) условия задачи
Дирихле и для и3 (х) — условия задачи Неймана. Решения этих задач
даются формулами D.58), D.56) и D.57) соответственно.
10. Решение граничных задач для системы D.11) в прямоугольном трех-
трехграннике (восьмая часть пространства). Условимся называть грань 0^хх<3
<С со, 0 ^ х2<<оо, х3 = 0 :Sly грань хг = 0, 0 ^ х2 <: со, 0 ^jc3 <3 co:S2
и грань 0 ^ хх < со, х2 = 0, 0 ^ х3 << оо : S3 и область, ограниченную
плоскостями Slf S2, S3,—через D+. В области D+ищется регулярное реше-
решение системы D.11), удовлетворяющее одному из следующих граничных
условий;
A.	xeSi. v = !<»(%, х2), xeS2: v = fW(x2ix3),
В.	xeSi: -*L = fiD(Xl,xjt xeS2: -*L

? 4]
С.
D.
ЗАДАЧИ ТЕРМОУПРУГОСТИ В БЕСКОНЕЧНЫХ ОБЛАСТЯХ
dv
519
dxs
¦ = fM (хх, JC2),
v = /<3> (jcx, л:3);
v ==/B) (х2, Хз),
Г- ах — / №» ^з;»
Решение задачи А. Представим решение в виде суммы
v (х) = v™ {x) + 0B) (х),	D.62)
где уA) (х) и аB) (x) — решения уравнения D.11), удовлетворяющие гранич-
граничным условиям
х е Sx: v^ = /d) (Xl,^2), x 6 S2: tK1) =0,	x? S3: v^ =
очевидно, при этом D.62) будет искомым решением задачи А. Вследствие
нулевых значений на грани х ? S2 применяем принцип симметрии отно-
относительно S2; тогда для V{1) (x) будем иметь
yd) (Х*), ^ <3 0, х2 ^ 0, х3 ^ 0, х* = (— х1? х,, *3);
следовательно, для VA> (x) имеем граничные условия:
(
— /<3) (— xlt x3), — оо < xt «S 0, хй = 0,
(х) =
Таким образом, для нахождения VA) (x) получили граничную задачу
Дирихле для четверти пространства (х2^0) П (х9^§). Решение этой задачи
было получено в п. 6 и дано формулой D.39'). Для построения уB) (^'вслед-
(^'вследствие нулевых значений на плоскости S3 применим принцип симметрии от-
относительно этой плоскости, тогда будем иметь
f с (х), хг2*0,	х2^0, xs^0,
0 ^ хг < оо,
0,
0, х* =
х2,
Следовательно, для Vi2)(x) имеем граничные условия
О,
(x) =
0,
), х2<0у х3 = 0,
хг = 0, *2<0,
0.
Для построения VB'(x) снова получили задачу Дирихле в области
(х1^0) П (^3^=0) Для системы D.11). Эта задача, как указано выше,
решена в квадратурах в п. 6.
Рассмотрим сумму
v (x) = VM (х) -|- У<2> (х);	D.63)
для х ? {хг ^ 0} П !^2 Зэ 0} П {-«з Зг 0} находим искомое решение.
Единственность найденного решения очевидна.

620
РЕШЕНИЯ В РЯДАХ И КВАДРАТУРАХ
[Гл. XIV
Решение задачи В. Решение ищем в виде суммы
v (х) = iK1) (x) + v™ (х),	D.64)
где t)A) (x)f t>B) (л:)— решения системы D.11), удовлетворяющие граничным
условиям
= /B)(л:2, х3),
Очевидно, при этом D.64) будет искомым решением задачи В. Ввиду
того, что на S2,
тогда получим
р
^—
0, применяем свойство симметрии относительно S2>
^ (х*\ хг < 0, х2 ^ 0, х3 ^0, х* = (— хъ х2,
и, следовательно, для Vil) (x) имеем граничные условия:
0.
дп
о, х2 = 0,
Итак, для построения V{l)(x) приходим к граничной задаче Неймана
в четверти пространства \х2 ^ 0} fl \хз ^ 0}. Решение этой задачи также
получено в п. 6.
Совершенно аналогично, вследствие нулевых значений нормальных
производных на плоскости S3, применяя свойство симметрии относительно
этой плоскости, будем иметь
V^\x) = |	* ~*^ ~~~" » . —- >
и, следовательно, для граничных условий V{2) (x) получаем равенства
,	х kz *^i»
дп ' =\	0,	Xi<0, x2<0, х3==0,
!)(—Ж2, JC3), Хг = 0, Х2<0, Х3=2=0.
(х)
Построение УB> (х) также требует решения задачи Неймана в четверти
пространства, решенной в п. 6.
Рассматривая сумму
v (х) = VW (х) + V& (х)	D.65)
для х ? D+, убеждаемся в том, что искомое решение построено.

Л 4]
ЗАДАЧИ ТЕРМОУПРУГОСТИ В БЕСКОНЕЧНЫХ ОБЛАСТЯХ
Q2J
Решение задачи С. Решение опять ищется в виде суммы двух
решений системы D.11) иA) (х) и а<2> (х), удовлетворяющих граничным ус-
условиям
дп
= 0,
с,), х е 52: »<*> = 0,	х € 53: сA) = Р
По свойству симметрии вводим вектор
У") IX) = I
0) Хз
очевидно, УA) (х) есть решение D.11), удовлетворяющее условиям
/A) (*и х2), х 6 Si,
yd) (x) =
и для его построения имеем смешанную задачу для D.11) в четверти про-
пространства \х2 ^> 0\ П {*з ^ 0}. Эта задача была решена в п. 6 и решение
дано формулой D.43').
Для построения аB) (л:) по свойству симметрии относительно плоскости
53 введем вектор
(х)
-{ 1
0,
0,
он удовлетворяет системе D.11) в области \х1^0\ П
ным условиям
U$	Х\ ^^ U, Л
X — (Xi, Х2, X3)J
. ^ 0} и гранич-
Поэтому построение VB) (л:) требует решения смешанной задачи С в четвер-
четверти пространства \хг^> 0} fl \х3^ 0}. Эта задача была решена в п. 6 и реше-
решение дано формулой D.43') с очевидными изменениями расположения осей.
Решение задачи Д. Разыскивая решение в виде суммы v{l) (x)
и vB) (х), согласно принципу симметрии вводим векторы УA) (х) и Vi2) (x),
определенные формулами
0, х2 ^ 0,
\
; 0,
0,
0, х* =
0, х* = (-
х3).
Тогда, как нетрудно заметить по аналогии с предыдущими случаями, для
построения Vil) (х) придется решить задачу Неймана в области \хг^ 0\ f|
П{х2:^0[, а для построения УB) (х)— решить смешанную задачу в обла-
области |х2^> 0\ П |х3^0|. Сумма V(l) (x) и V{2" (x), взятая в области D+, очеви-
очевидно, даст единственное решение искомой задачи.

622	РЕШЕНИЯ В РЯДАХ И КВАДРАТУРАХ	(Рл XIV
11. Решение задач V, VI и смешанных для уравнений термоупругости
в области /?+. Здесь мы решаем следующие четыре задачи для уравнений
термоупругости в бесконечной области, ограниченной прямоугольным
триэдром (Slf S2, S3).
Задача V. На всех гранях заданы касательные составляющие сме-
смещения, нормальная составляющая напряжения и температура, т. е.
x?.&±i ы>1, 11%, т33, ?/4;
X vl *^2 • ^2' ^3» ^11» ^4»
X \2 »^3 * ^1» ^3» *^22' ^4*
Задача VI. На всех гранях заданы нормальная составляющая сме-
смещения, касательные составляющие напряжения и поток тепла, т. е.
X С ^1 • ^3» ^13» ^23» ~~дх—'
X 6 ^2 • ^1» ^12» Т13» ~§^ »
•^ С «^3 • ^2» ^23» ^21» "~qZ—*
Смешанная задача. На двух гранях заданы условия задачи V,
а на третьей грани — условия задачи VI, т. е.
с S •	дц4
дх%
Смешанная задача. На двух гранях заданы условия задачи VI,
а на третьей грани — условия задачи V, т. е.
х ? 6Х: а3, т13, т2
•^ G ^2 • Uly T12> T13» ~^J >
x6S3: «f a3, т22, ы4.
Чтобы получить решения этих задач, мы поступаем так же, как в п. 9:
сначала из решений граничных задач для системы D.11) были получены ре-
решения соответствующих граничных задач в четверти пространства для
метагармонического уравнения (однородного и неоднородного); затем ин-
интересующие нас задачи термоупругости были приведены к задачам для мета-
гармонических функций. Следовательно, теперь необходимо из решений,
полученных для задач А, В, С, D в п. 10, вывести решения соответствующих
задач для метагармонического уравнения в бесконечном триэдре; мы уже
знаем из пп. 7 и 8, что это можно сделать, полагая в решениях системы D.11)
7 = 0, я2 = 0. Дальнейшее есть повторение рассуждений п. 9 с той лишь
разницей, что теперь вследствие наличия третьей грани принцип симметрии
будет использован относительно всех (трех) граней.
Мы рассмотрели модельные задачи. Можно получить решения в квад-
квадратурах ряда других, не менее важных задач, получающихся путем ком-
комбинаций предыдущих, а также задач для полупространства, для бесконеч-
бесконечного слоя, полуслоя и т. д. и различных углов с граничными условиями
основных задач термоупругости. Некоторые из этих задач рассмотрены
в § 5.

§ 5]	(ПРОДОЛЖЕНИЕ). ПРИМЕНЕНИЕ ИНТЕГРАЛА ФУРЬЕ	623
§ 5 (продолжение). Применение интеграла Фурье
1. Представления решений уравнений термоупругости. Как известно
(см. III, § 3, п. 1), решение уравнений термоупругости
U = (и;и4) = (ил, и2, и3, и4),
- (к -f- |ы) grad div и + ^u —
E.1)
Аи4 Н—— и4 + icori di v и = О
можно представить в виде
(У = (а<1) +иB); и4),
где
(А + *,?) (А + А|) иA) = 0, rotnA)=0,	E.2)
(А + A,f) (Д + Я|) и4 = 0,	E.3>
(Д + А,з)мB)=0, divnB) = 0	E.4)
и %\9 %29 ^з определяются формулами
1 x'A-f-2jn Л, —j— 2jlx хЛ/ + 2|ы	v ;
Введем векторы v(l), уB) и скаляры ох, у2:
t>! = (Д -)- я|) и^ y2 = (A + ^i)w4.	E.8)
Очевидно, что
-=0, fe=l,2,	E.9)
= 0, fe=l,2.	E.10)
Внесем в E.1) и = ыA) + ы<2> и заменим ы'х> и «4 по формулам E.9),
E.10); тогда получим
L Л 	М
Д <Ъ ~
+ ,2\а
Л§ — Л,
В силу условий
E.11)

624	РЕШЕНИЯ В РЯДАХ И КВАДРАТУРАХ	[Гл# XIV
соотношения E.11) примут следующий вид:
t>23=0> EЛ2)
— -ц .	1 Гм-—
E.13)
Уравнение E.12) удовлетворим, полагая
^	<5Л4)
Покажем, что при этом удовлетворяется и уравнение E.13). Рассма-
Рассматривая группу слагаемых, зависящих от iH1), vlf ввиду зависимостей E.14),
E.15), E.10), E.5) будем иметь
—	Кг	ш*_х!(Х + 2|i) J
'ч f.-Л ___ Ql 2 (\ I Qn \	/^ 2 ___ 12\ Fr.i2 __ Q( 2 /Qk I Оц \ 1 I v 1 I On	I	*
Ш	/Ъ| ^Л ^~ ZifAtf.	\*^2 ~~~ 1/ I """" **1 V" "~T~ ^'H'/J L *" Л» *Т~ «{Л	J
Аналогично предыдущему, получаем
Так как из E.14), E.15) следует rot о<*> =0, k = 1, 2, то будем
иметь также
O.	E.16)
Из сказанного вытекает
5.1. Лемма. Если v{k\ vk, k = 1, 2 связаны соотношениями E.14),
E.15) и удовлетворяют уравнениям
(А 4-4)^ = 0, (Д + А*К = 0,
то
a wB) удовлетворяет уравнениям
(Д + ^)ЫB)=0,
есть решение уравнений термоупругости E.1).

Л 5]	(ПРОДОЛЖЕНИЕ). .ПРИМЕНЕНИЕ ИНТЕГРАЛА ФУРЬЕ	525
2. Решение задачи I для полупространства. На плоскости xz = О за-
заданы условия
От заданных функций здесь и всюду ниже будем требовать представи-
представимость интегралами Фурье, т. е. будем считать, что
i,x2) = JL J J /4 &, g2) е-1 (i.x.-K.«.) d& dg,, k = 1,..., 4, E.17)
—	00
где, согласно формулам обращения,
сю
Mli. Ь) = ^ j I Ф* (*i. *•) «' <S«*«-«.*.) d* dx2, k = 1	4. E.18)
—	со
Ищем решение уравнений E.1) в виде
вГ Я ' а* «!•
E.19)
где а^), а<2>, аC) — неизвестные векторы, а а4 и а5—неизвестные
скаляры; положим
^+^-*а J в-<
= JL | j «C) fo,
Тогда на основании формул E.9) можно считать, что
[E.20)
y'I»(x)=1L (Я22-Я?) \\ а*1' (Ь, Ь) e-*«V *&* е-' (Ь
—оо
а из E.10) имеем таким же образом
оо
vx(х) = -%г (Ч — М) | J a4 &, g.) ^'
—00
оь(х)=- 2^(^ — ^ J J a8 A1( |2) е-
—00
40 В. Д. Купрадзе
E.21)

626
РЕШЕНИЯ В РЯДАХ И КВАДРАТУРАХ
[Гл. XIV
Легко проверить, что о(Л> (х) и vk (x), k = 1, 2, удовлетворяют соот-
соответствующим уравнениям Гельмгольца для произвольных значений плот-
плотностей а*1*, а<2>, а4, аб. Проверим это, например, для а*1* (х)\ имеем
Поэтому для того, чтобы (/ = (а^> + иB); а4) = (а; а4) было решением
уравнений E.1), согласно лемме 5.1 достаточно удовлетворить усло-
условиям E.14), E.15) и а<2> (|х, |2) выбрать таким образом, чтобы
diva<2> (jc) = O.
Добавив сюда еще условия на границе х3 = О,
2)» * = 1 f 2, 3, 4,
E.22)
E.23)
будем иметь полную систему условий для определения неизвестных
а<2), аC), а4, аБ. Записывая условия E.14), E.15), E.22), E.23) и прини-
принимая во внимание E.17), получаем
¦ а4 = О,
~l r ш2 —Я?(Я+2ц)
Л'
2)
а{
{2>
= /ь
«з11 + <42) + «з3) = /з,	а4 + а5 = /4-
Простым преобразованием эту систему можно привести к виду
E.24)
E.25)
где
—M, *= 1.2,3,

г gi	(ПРОДОЛЖЕНИЕ). ПРИМЕНЕНИЕ ИНТЕГРАЛА ФУРЬЕ	627
Детерминант полученной системы равен
Так как ^ =? 0, необходимо исследовать уравнение
С0г©2
Ш2 iyt — %1 Vt — Xl — 0 — со! (]/"/ — Х| Vt — Ц —0 = 0, E.26)
где t = а + а.
Очевидно, нас интересуют неотрицательные вещественные корни этого
уравнения. На основании некоторых общих соображений физического ха-
характера, изложенных ниже, следует ожидать отсутствия подобных корней
для произвольного значения параметра у\ мы ограничимся строгим доказа-
доказательством этого свойства для случая малых значений у, как наиболее важ-
важного для приложений.
Рассмотрим функцию
д(/,у) = со2(Vt—ц Vt—ц —t)—coi {yr^kiyt—ц —t)
и покажем, что при 7 = 0 она не имеет действительных корней.
Полагая в E.26) у = 0, получаем
Vt — Ч yt — Xl — t = 0,	E.27)
так как согласно E.5) теперь %\= ^?2 ' ^2 = ~^Г и Ш1 = "» co2=f0.
Возведя в квадрат E.27), получим
Следовательно, единственным вещественным корнем уравнения E.27)
может быть
который, однако, как показывает проверка, ему не удовлетворяет. Отсюда
по непрерывности Д (/, у) относительно у вытекает справедливость нашего
утверждения. Тем самым разрешимость системы E.24) в рассматриваемом
случае доказана и решение найдено в виде E.19).
3. Решение задачи II для полупространства. Граничные условия на-
х3 = 0 имеют следующий вид:
Если решение этой задачи мы снова будем искать в виде E.19), то, по-
поступая так же, как в предыдущем параграфе, для определения о^1), а<2>,
аC), а4, а5 получаем систему уравнений, аналогичную E.24), в которой
изменятся лишь последние четыре уравнения. Это связано с тем, что пер-
первые семь уравнений системы E.24), выражающие условия E.14), E.15)
и E.22), очевидно, остаются в силе во всех задачах в неизменном виде и
меняются лишь последние четыре уравнения, соответствующие гранич-
граничным условиям. В данном случае эти уравнения (последние четыре из
40*

628
РЕШЕНИЯ В РЯДАХ И КВАДРАТУРАХ
[Гл. XIV
системы E.24)), как нетрудно убедиться, имеют следующий вид:
I г*(Щ _1_ l/t2 I ?2	-Г2,**1) I l/t2 I ?2
-f-аз ^ -f- г si -hS2 — Mai +^ci+§2
af>)
+ Й-^аГ + Vtl + U-tiaP] + Y(«4 + og = -/„
Присоединив к ним первые семь уравнений из E.24) и выполнив необ-
необходимые преобразования, относительно a<3> (|lf g2) и a4 (li> ^2) получим
систему из двух уравнений:
(«2Г2 —
(к + 2ц) rxr
где
E.28)
Детерминант системы E.28) равен
¦ {[2 (Й + Й) — А|] -~ [(Й + й) (^2Г2 —
+ (Я, + 2(Л) Г\Г2 (СО1Г2	С02/*1) + COlO>2 (Г2 —' П)] 	4(Л
Так как „т, =f 0, необходимо исследовать уравнение
= B/—
М @2
@2	СО]
2ц) yt — я,?
СО3СО2I 1
-X
co2)
— $yt — А| = 0, E.29)
где / =

К 5]	(ПРОДОЛЖЕНИЕ). ПРИМЕНЕНИЕ ИНТЕГРАЛА ФУРЬЕ	629
Для малых значений параметра у это уравнение допускает один веще-
вещественный корень. Это вытекает из того, что при 7 = 0 уравнение E.29)
обращается в классическое уравнение Рэлея (см. Купрадзе, Соболев [1]):
#(/) = Bt — klJ — 4*]Л— ^"[Л — А| = 0.	E.30)
Это уравнение имеет лишь один вещественный корень и при этом не
выше первого порядка. В самом деле, рассматривая знаки функции R (t)
при t = AJ и при больших значениях t = Г2, замечаем:
= 2 (ti — Xl) T2 + Xi + O (T~4) < 0.
Отсюда следует существование по крайней мере одного действитель-
действительного корня в интервале (А|, оо). Другие два корня *), если они действительны,
не могут лежать в том же интервале. Это следует из того, что производ-
производная /?' (t) для t > Ц сохраняет постоянный отрицательный знак. В самом
деле,
так как
что и доказывает наше утверждение. Из сказанного, кроме того, вытекает,
что корень из интервала (Л|, оо) не является корнем выше первого порядка.
Покажем, что в интервале [0, AJ] действительные корни лежать не
могут. Допустив противоположное, будем иметь для точек интервала [Х\, А,2> ]
B/ _ ID2 — 4ti yT^YV - *з| = 0,
и это противоречие доказывает сказанное. Для точек интервала @, Х\)
имеем
XIJ
Bt - XIJ + и у\Г^Щ УТГЛЦ=о,
что также показывает отсутствие действительных корней в интервале @, Х\).
Этим наше утверждение относительно уравнения E.30) доказано полностью.
Очевидно, что по непрерывности A (f, у) как функции у эта же картина
поведения корней сохранится и для уравнения E.29) при малых значениях
параметра у. Однако некоторые соображения физического характера ука-
указывают на то, что это свойство сохранится для произвольных конечных зна-
значений 7- В самом деле, как известно, вещественному корню уравнения E.30)
соответствует на сейсмограммах так называемая поверхностная волна Рэлея
и только она, как для малых, так и для сильных землетрясений, если речь
идет о колебании упругого полупространства, граничащего с пустотой.
Для уравнений термоупругости, которые лучше чем уравнения упругости
1) Освободившись от иррациональностей, легко увидеть, что уравнение E.30) не может
иметь более трех корней.

630	РЕШЕНИЯ В РЯДАХ И КВАДРАТУРАХ	[Гл XIV
описывают закономерности распространения колебаний, не может суще-
существовать новых действительных корней, ибо в противном случае им должны
на сейсмограммах соответствовать новые пики, которые, как мы указали
выше, никогда не наблюдаются, если упругое полупространство граничит
с пустотой, и появляются впервые лишь при условии, когда пустота заме-
заменяется жидкой или упругой средой (см. Купрадзе, Соболев [1]).
Конечно, эти соображения носят лишь эвристический характер и не
служат строгим доказательством отсутствия у уравнения E.29) в интер-
интервале @, оо) более, чем одного действительного корня. Строгое доказатель-
доказательство этого предложения должно быть получено, например, методом изуче-
изучения многозначной функции A (t, у) на соответствующей римановой поверх-
поверхности, как для одного случая это сделано в работе Купрадзе, Соболев [11.
Как было показано выше, для малых значений у существует единствен-
единственный действительный корень и его порядок не превышает единицы. Это об-
обстоятельство важно, как обеспечивающее существование интегралов E.19)
в смысле главных значений. Этим исчерпывается исследование второй
задачи.
4. Другие задачи. После того как первые две задачи были исследованы
подробно, мы не будем останавливаться столь же подробно на остальных
задачах, так как с точки зрения наличия полярности в ядрах интегра-
интегралов E.19) они вполне аналогичны первой либо второй задаче. Как было
уже сказано, при отыскании решения в виде E.19) для каждой задачи при-
придется иметь дело с системой одиннадцати уравнений с одиннадцатью неиз-
неизвестными типа E.24), в которых меняются (от задачи к задаче) лишь послед-
последние четыре уравнения. Поэтому для каждой задачи достаточно выписать
именно эти уравнения, соответствующие граничным условиям. Мы так
и поступим.
3 а д а ч а III. На плоскости х3 = 0 заданы
«1 (*i, *а) = Ф1 (*ъ Ч), ti2 = ф2, и3 == ф3, -?¦?¦ = Ф4-
Эти граничные условия приводят к системе
A)	B) , C) г	A) , B) • _C) г
1 + oti = fi, а2 •+¦ а2 + о&2 = /2»
+ 43) = /з,	па* + г2а5 = - fb
которая вместе с первыми семью уравнениями из E.24) сводится к следующей:
J (со2г2 —
где справа, здесь и всюду ниже, f( обозначают известные выражения, зави-
зависящие только от граничных данных, а со,, г( определены в п. 2.
Детерминант этой системы равен (с точностью постоянного множи-
множителя +0)
А (*, У) = -~ (со2г2 — сол) t + (о)! — со2) /у8.

г gi	(ПРОДОЛЖЕНИЕ). ПРИМЕНЕНИЕ ИНТЕГРАЛА ФУРЬВ	531
Для у = О имеем
Д (/, 0) = co2S @,
где
S(t) = t — Yt — ^Vt~X^°
совпадает с детерминантом из первой задачи (см. п. 2).
Задача IV. Граничные условия на х3 = 0, t3i = Ф1 (xl9 x2)t т82 =
^ Фг» тзз = Фз» и* == Ф4» приводят к системе
1 г
	1,
и '2'
1 Гл /^П) | ^B) I ^C)\ . :<г /^,A) | ^,B) I „C)\1 ,
Л [^Ь1 \Щ -J- Ctj -f- CCj у ~f- 1%2 \ОС2 "т~ ^2 -р ^2 /J г
+ (Я + 2(х) ha^1) + г2о42} + г3^3)] + у (а4 + а5) = — /3,
которая, так же как выше, приводится к системе из двух уравнений:
Bt	Я3) ОС3 +	^ (^1^2	<O2ri) »4 = fu
co2 — со,) + (Я + 2fx) (co,r| — со2г])] a4 = /i.
Детерминант этой системы равен
A (t, у) = B/ — *D [Я (со2 — соО * + (Я + 2fi) (щг22 — ©аг?)] — 4fxr^ (со^ — со2п)
и при 7 = 0
где /? @ — функция Рэлея (см. п. 3).
Задачи V и VI. Эти задачи были решены другим методом в § 4.
Здесь они решаются в интегралах Фурье.
Граничные условия пятой задачи
^ = Фх (*ъ *а)> ^2 = Ф2> *зз = Фз, Щ = ф4
приводят к системе
> + а{2' + а{3>) + /Ь (aj« + af> + c43))] +
+ у (а4 + as) = f3,
=/2, «4 + «5 = А,
которая редуцируется, как и выше, к системе
(со2 — со,) + (X + 2ц) (щг\ — cosr2)] «4 = ft,
«з3) + -^ [/ (<oi — со2)] а4 = /г.
Детерминант этой системы
А (*, v) — (Я + 2|i) гз (о, — со2) / + (К + 2ц) г3 (ca2r2—ю,г|) =

632	РЕШЕНИЯ В РЯДАХ И КВАДРАТУРАХ	[рл XIV
для вещественных t в нуль обращается лишь в точке t = AJ, порождая
полярность порядка 1/2. Таким образом, пятая задача решена в квадра-
квадратурах для произвольного у.
Граничные условия шестой задачи
*31 = <Pl (*Ъ Х2), *32 = Ф2, «3 = Фз> -gj1 = Ф4
приводят к системе
ih D° + ^ + <43)) + riai(I) + rrf» + r3a{3>	1-
+ <43))
=/3, r,a4 + ^«s = — h
и, далее, к системе из двух уравнений
Bt - Л!) с43) + -2L- trx (о, — <о2) <n = f\,
ГТ
= /г-
Детерминант Д (^, v) равен
д (t> У) = B/ — А|) (о)! — со2) п — 2/ri (coi — со2) = — l2^ (щ — со2),
который, очевидно, для вещественных значений t в нуль не обращается.
Таким образом, и данная задача решается в квадратурах для произволь-
произвольного у (относительно задач VII, VIII, IX, X — см. Бурчуладзе [16]).
5. Теоремы о принципе симметрии для уравнений термоупругости.
В § 4 было показано, как с помощью некоторого свойства симметрии реше-
решений уравнений термоупругости строятся решения в квадратурах для гра-
граничных задач V и VI в другранных и трехгранных углах. Для того чтобы
построить решения других задач в квадратурах в этих областях, необ-
необходимо сформулировать общий принцип симметрии для уравнений E.1).
Этому посвящен настоящий пункт. Имеет место следующая
5.2. Лемма. Если U (х) = (и (х)\ а4 (х)) = (иг (х)9 и2 (#), и3 (х),
и& (х)) есть регулярное решение уравнений E.1) в области х ? D и D* есть
зеркальное отображение D через плоскую часть границы а,
k=
то вектор U* (x) = (и* (х)\ и\ (х)) = (и*х(х), и\ (х), и\ (х), и\ (х)) с компонентами
и] (х) = 4" [(я? — а\ — аз) иг (х*) -}- 2ага2и2 (х*) -f 2ахагиъ <
E.31)
и2 (х) = -д \1а\а2щ (**). + («1—а? — al) Щ (х*) + 2а2аъиъ (х)\,
ul (х) = -г- [2а\а2иг (х*) -{- 2а2аз^2 (^*) + (^з — ^i — ^2) "з (**)]»
«4 (л:) = — и4 (х*)у
г) Предполагается, что D лежит по одну сторону от плоскости а.

§ 5J	(ПРОДОЛЖЕНИЕ). ПРИМЕНЕНИЕ ИНТЕГРАЛА ФУРЬВ	533
где х* есть зеркальное отображение точки х через а, т. е.
х\ = xt — -~L (aixi + а2х2 + а&ъ + а4),
3
1= 1,2,3, Л= S а|,
fe=i
является регулярным решением системы E.1) в области х ? D*.
Доказательство леммы основывается на легко проверяемых равенствах:
Д (дж) = Д (d**), div и* (х) = — div и (х*).
Проверим утверждение леммы, например, для первого уравнения си-
системы E.1). Имеем для х ? D*
*= -j- |iA (дх.) [(a] — at — at) щ (хт) + 2axa2u2 (x*) + 2aia3w3 (**)] —
^	-^№-<?- ai) ux (x) +
(**)] ^
-= 4" (a? — a2 — °з) Г|лД (a,.)"i (Л +
{р 1
— у ди*д{р 1 + -^ Г (хА (а,*) a2 (jc*) + (X + ^) ^- div и (х*) +
дх*3 —~^ > ¦ ~<"~ ' ' дх1
Далее имеем
А (дх) и\ (х) + -^- и\ (х) + tori div и* (jc) =
= _ [ Д (ах.) ^4 (л:*) + -^Г  (х*) + '©Л div и (**)] = 0.
Лемма доказана.
5.3. Теорема. ?сла вектор U (х) = (а (х); а4 (х)) есть регулярное
eD решение уравнений E.1) а яа плоской части границы а обращаются в нуль
касательная составляющая вектора смещения, нормальная составляющая
напряжения и температура, т. е.
) = 0, (PU-n) = 0, а4 = 0,
где п = (л1э п2, /г3) — орт нормали, то вектор V (х) = (о1э а2, у3,
есть регулярное в области D (J a U D* решение системы уравнений E.1).

634	РЕШЕНИЯ В РЯДАХ И КВАДРАТУРАХ	[рл XIV
5.4. Теорема. Если вектор U (х) = (и (х); щ (х)) есть регулярное
eD решение уравнений E.1) и на плоской части границы о обращаются в нуль
нормальная составляющая вектора смещения, касательная составляющая
напряжения и поток тепла, т. е.
то вектор V (х) = (vl9 v2, v3, t>4)
lU(x)*
\
есть регулярное в D [} о [} D* решение системы уравнений E.1).
Мы докажем эти теоремы способом, которым аналогичные теоремы были
доказаны в § 4, п. 5. С этой целью введем четыре пятимерных вектора
HV = (и — п(и-п), (PU-ri), ы4),
PU — n(P(J.n), — (и.п), -
— п{и*п), (PU-ti), м4),
E.32)
где
U = (и; м4), PU = Tu —
Ти = 2\л-^г-\-%пАхчи + \х [nrotu].
Простыми тождественными преобразованиями можно показать, что
при этом формула общих представлений регулярных решений уравнения
термоупругости (см. X, § 2, п. 2) принимает следующий вид:
= J [ЯФ'{х — у, (*)]'FU{y)dsS— \ [Рф'(х—у, со)]' HU(y)dJS. E.33)
Далее, как в условиях теоремы 5.3, так и в условиях теоремы 5.4, имеют
место равенства
lim HV(x)= lim HV(x), lim FV (x)= lim FV(x)9
96	^?	9€	Э?
(V (x) определен в теоремах 5.3 и 5.4), которые проверяются непосред-
непосредственно с помощью формул E.31) и определения векторов HU и FU.
Применяя теперь формулу E.33) и повторив рассуждения § 4, п. 5,
получим доказательство обеих теорем.
6. Граничные задачи для четверти пространства. Пусть D есть четверть
пространства —оо <3 х2 <3 оо, 0 ^ хх <3 оо, 0 ^ х3 <С оо. Ищется регу-
регулярное в D решение системы E.1), удовлетворяющее на грани St: —со <
<3 х2 <5 оо, 0 ^ хг <3 со, х3 = 0, одному из условий первой, второй, тре-
третьей, четвертой, пятой и шестой задач, а на грани S: —со <3 х2 < со, хг = 0,
0 ^ х3 <со — условиям задачи пятой либо задачи шестой.
Прежде всего покажем, что условия на грани S всегда можно привести
к нулевым. В самом деле, продолжая данные на S на плоскость —оо < х2 <

§ 5]	(ПРОДОЛЖЕНИЕ). ПРИМЕНЕНИЕ ИНТЕГРАЛА ФУРЬЕ	635
< оо, хг = 0, —оо <* х3 ^ 0 нулями, будем иметь в полупространстве
хг ^ О граничные задачи V или VI для уравнений термоупругости. Решения
этих задач в квадратурах известны. Вычитая их из искомых решений, бу-
будем иметь для разности на Sj вполне определенные граничные данные,
а на S — нулевые.
Пусть на S обращаются в нуль касательная составляющая смещения,
нормальная составляющая напряжения и температура, т. е.
Тогда согласно теореме 5.3 вектор V (х) = (vl9 v2, v3, v±)
f U (x), хЕД
\U*(x), x?D* (D*:— co<^^0, — oo<x2<oo,
где U* (x) определяется формулами E.31), и есть в области х3 > 0 регу-
регулярное решение E.1). При этом, поскольку уравнение плоскости S есть
хг = 0, имеем
l	0 л1
г* —г	E'34)
3	3'
и, следовательно согласно E.31) будем иметь
щ (х) = их {х)% и2 (х) = — и2 (**), и3 (х) = — и3 (**)>
E.35)
где
х = (дгх, х2, х3), х = (—Xi, х2, ^з).
Пусть на грани St заданы условия задачи I:
vx = u. (хъ х2, 0) = ф! (хъ х2)у v2 = u2 = ф2,
V* = «з = Фз> У4 = 1/4 = ф4, (ДГЬ Х2) 6 Sle
Тогда согласно E.34), E.35) на S* (—оо < х2 <3 оо, —со < atj ^ 0, х8 = 0)
будем иметь:
vi {хи х2, 0) = щ (хи ль, 0) = щ (х*) = а, (—хь ^2, 0) = ф, (—хи х2),
v2 = u2 = — u2(—xu x2j 0) = — ф2(— хи х2),
v3 = u3 = — u3(—xu х2, 0) = —<рз(—*ь х2),
v4 = u4 = —u4(—хи х2, 0) = —ф4(— хи х2\ (хи х2)€SJ.
Таким образом, для построения V (х) получили первую задачу в полу-
полупространстве xs ^ 0 для системы E.1). Эта задача решена в п. 2. Значе-
Значение V (х) в области х ? D есть искомое решение исходной задачи.
Переходим к случаю, когда на S2 заданы условия задачи II:
т32 И = х32 (а) = fx (jjjjL + -^-) = ф2 (хъ х
Чз (У) = тзз (У) = Ь div « + 2^i -^ — y«4 =

636	РЕШЕНИЯ В РЯДАХ И КВАДРАТУРАХ	[Гл. XIV
Тогда согласно E.34) и E.35) будем иметь на S*:
= 42 (U*) = — ^ (-|^- + |~") = — ф2 (— ХЪ Х2),
Тзз(Ю = *зз (U*) = Л div и + 2\i-^-—yt? = — т33 (?/) = — q>3(— хи х2\
ди*д	диА
Следовательно, для вектора У (х) получена вторая задача в полупро-
полупространстве xz ^ 0. Эта задача решена в п. 3, и значение V (х) в области х ? D
есть решение исходной задачи.
Случаи, когда на Sj заданы граничные условия задач III, IV, V, VI,
VII, VIII, не требуют отдельного рассмотрения, так как эти граничные ус-
условия продолжаются в области D* на S* аналогично условиям первой или
второй задач, рассмотренных выше.
Мы рассмотрели тот случай, когда на грани S были заданы условия
пятой задачи. Если же на указанной грани обращаются в нуль нормаль-
нормальная составляющая смещения, касательная составляющая напряжения и
поток тепла (условия шестой задачи), то согласно теореме 5.4 для вектора
V (х) снова придем к граничным задачам в полупространстве с усло-
условиями первой, второй, третьей, четвертой, пятой, шестой, седьмой или
восьмой задач. Все эти задачи решены в пп. 2, 3, 4 и решения интересую-
интересующих нас задач в четверти пространства получаются из значений V (х)
при х ? D.
7. Граничные задачи для бесконечного прямоугольного трехгранника.
Пусть D есть восьмая часть пространства 0 ^ хг < оо, 0 ^ х2 <2 °°> 0 ^
^ х3 < оо.
Три грани области D обозначим следующим образом:
S: 0 ^ хг << со, х2 = 0,	0
S2: х1 = 0,
Здесь могут быть решены в квадратурах следующие задачи: на грани Sx
заданы условия одной из восьми изученных выше задач, на грани S и S2
(либо на обеих) — условия задачи пятой, либо условия задачи шестой или
на одной из граней— первые и на второй— последние условия. Все эти
задачи решаются, по существу, совершенно одинаково. Поэтому мы рас-
рассмотрим одну из них.
Пусть, например, на S заданы условия задачи V, а на S2— условия
задачи VI. Прежде всего приведем к нулю данные на S. С этой целью про-
продолжим граничные данные на S (четверть плоскости) на всю плоскость х2 == О
нулями. Решив пятую задачу для полупространства х2 ^ 0, составим раз-
разность искомого и найденного только что решения. Очевидно, эта разность
будет удовлетворять на S однородным граничным условиям пятой задачи,
на S2 неоднородным (заданным) условиям шестой задачи и на Sx вполне
определенным (также заданным) условиям одной из восьми основных задач.

ЗАДАЧИ	637
Пользуясь теоремой 5.3, построим вектор V (х)> который в двуграннике 0 <;
^ xi < со, —оо << х2 < оо, 0 ^ х3 < ею будет решением уравнений E.1),
удовлетворяющим на грани 0 ^ хг << сю, —сю <1 х2 ^ 0, лг3 = 0 тем же
условиям, что и на Sl9 а на грани Xj = 0,—сю < х2 ^ 0, 0 ^ х3 < сю ус-
условиям шестой задачи. Эта задача решена в предыдущем пункте и зна-
значение этого решения в D будет искомым для исходной задачи (в связи
с § 4, 5 см. Купрадзе, Бурчуладзе [5], [6]).
ЗАДАЧИ
1.	Решить задачу A)+ способом, которым решена задача A)~.
2.	Решить задачи A)^ (П)^1, (Ш)-^ и (IV)^ для m-мерного шара (см. Башелейшвили
[17]).
3.	Решить задачи (III)— и (IV)—, применяя интегральные уравнения (VI, 5.21), (VI, 5.24),
(III)" и (IV)+.
4.	Решить сингулярное интегральное уравнение
Kg = g(z) + X J JC(dZt v.) [z? g(y)dS = /(г),
s
где S — сферическая поверхность, / — заданный на S вектор. Напишите глобальный регуля-
ризатор для оператора /С.
5.	Доказать, что задача (I)— для сферы имеет единственное решение в классе
С2 (D+) П С(Б+), [С2 (D-) ПС (Б-)), где D+= Ш (О, R).
6.	Найти явные выражения тензоров Грина задач A)+, (П)+, (П1)+ и (IV)+ для шара
и трансверсально-изотропного полупространства.
7.	Решить задачу о слое конечной толщины, ограниченном двумя параллельными пло-
плоскостями, с заданием на гранях различных условий типа десяти основных, указанных в § 4.
8.	Решить задачу о полуслое, ограниченном двумя параллельными плоскостями и их
ортогональным пересечением третьей плоскостью, при задании на указанном пересечении
граничных условий пятой либо шестой задачи, а на параллельных гранях — условий типа
одной из десяти основных.
9.	Решить задачу для двугранного угла с раствором я/2т, где т> 0 — целое число,
с различными граничными данными на гранях.
10.	Решить задачу для трехгранных углов с раствором я/2т, где т^> 0 — целое, с раз-
различными (соответственно выбранными) условиями на боковых гранях.
11.	Решить различные гранично-контактные задачи для пространства, составленного
из двух полупространств, с различными упругими и термическими коэффициентами.
12.	Рассмотреть названные задачи для уравнений моментной теории.
13.	Рассмотреть решение граничных задач для бесконечных областей одного из указан-
указанных выше видов, содержащих различные конечные каверны или включения.
14.	Найти эффективное выражение (в квадратурах) решения уравнений статики класси-
классической теории упругости для полушара, удовлетворяющего на полусфере одному из условий
задач A)+, (П)+, (Ш)+, (IV)+, а на круге условиям задач (Ш)+ или (IV)+.

ЛИТЕРАТУРА
РУССКИЙ АЛФАВИТ
Абрамян Д. Л., Александров А. Я.
A] Осесимметрические задачи теории упругости. Труды Второго Всесоюзного съезда
по теоретической и прикладной механике. Механика твердого тела, вып. 3. «Наука»,
Москва A966), 7—38.
Авазашвили Д. 3.
[1] Пространственная задача дифракции для электромагнитных колебаний. Сообщ.
АН Грузинской ССР 14 A953), 321—328.
|2] Об одной задаче дифракции акустической волны для многосвязных и слоистых об-
областей. Третий Всесоюзный симпозиум по дифракции волн, Тбилиси, 1964. Рефе-
Рефераты докладов. «Наука», Москва, 1964, 52—54.
Авазашвили Д. 3., Купрадзе В. Д.
[1] Теорема единственности в теории распространения электромагнитных гармониче-
гармонических колебаний в неоднородном трехмерном пространстве. Сообщ. АН Грузинской
ССР 1, № 1 A940), 35—41.
Алексидзе М. А., Арвеладзе Н. М., Лекишвили Н. Л.э Пер та я К. В.
[1] О решении граничных задач с помощью неортогональных рядов. Сообщ. АН Гру-
Грузинской ССР 49 A968), 281—286.
Амашукели Т. М.
[1] Об основных граничных задачах для трансверсально-изотропных упругих сред.
Труды Грузинского политехи, ин-та, № 4 A16) A967), 3—16.
12] Некоторые обобщенные пространственные смешанные задачи теории упругости.
Труды Грузинского политехи, ин-та, № 7 A19) A967), 3—14.
13] Третья и четвертая граничные задачи колебания теории упругости. Труды XV на-
научно-технической конференции Грузинского политехи, ин-та, вып. 2 A972), 21—29.
[4] Тензоры Грина для третьей и четвертой задач теории упругости. Труды Ин-та прикл.
матем. Тбилисского ун-та 3 A972), 17—28.
E] Свойства гладкости решений неоднородных задач теории упругости. Труды Грузин-
Грузинского политехи, ин-та, № 6 A62) A973), 29—32.
Амашукели Т. М., Башелейшвили М. О., Гегелиа Т. Г.
[1] О некоторых пространственных задачах теории упругости. Третий Всесоюзный
съезд по теоретической и прикладной механике, Москва, 1968. Аннотации докла-
докладов. «Наука», Москва, 1968, стр. 20.
Амбарцумян С. А.
[1] Теория анизотропных пластин. Прочность, устойчивость и колебания. «Наука»,
Москва, 1967.
Амензаде Ю. А.
[1] Изгиб призматического бруса, ослабленного круговой полостью. Изв. АН Армян-
Армянской ССР 10, № 3 A957), 47—63.
[2] Местные напряжения при кручении призматического бруса квадратного сечения
с круглыми несоосными отверстиями. Изв. АН СССР, ОТН, механ. и машиностр.,
№ 5 A959), 143—148.
А р ж а н ы х И. С.
[1] Интегральные уравнения основных задач теории поля и теории упругости. Изд-во
АН Узбекской ССР, Ташкент, 1954.
Арутюнян Н.Х., Абрамян Б. Л.
[1] Кручение упругих тел. Физматгиз, Москва, 1963.
Арутюнян Н. X., Мхитарян СМ.
[1] Контактные задачи для тел с упругими креплениями. XIII Международный кон-
конгресс по теоретической и прикладной механике, Москва, 1972. Аннотации докла-
докладов. «Наука», Москва, 1972.

ЛИТЕРАТУРА
639
А э р о Э. Л., Кувшинский Е, В.
[1] Основные уравнения теории упругости сред с вращательным взаимодействием частиц.
Физика твердого тела 2, № 7 A960), 1399—1409.
[2] Континуальная теория асимметрической упругости. Равновееие изотропного тела.
Физика твердого тела 6. № 9 A964), 2689—2699.
Бабич В. М.
[1] Фундаментальные решения динамических уравнений теории упругости для неод-
неоднородной среды. ПММ 25, № 1 A961), 38—45.
Бабич В. М., Капилевич М. Б., М и х л и н С. Г., Натансон Г. И..
Риз П. М., Слободецкий Л. Н., Смирнов М. М.
[1] Линейные уравнения математической физики. СМБ. «Наука», Москва, 1964.
Бакаляев А. С.
[1] Теорема единственности в стационарных краевых задачах теории упругости
ДАН СССР 1 A936), 51—54.
Бари Н. К.
[1] Тригонометрические ряды. Физматгиз, Москва, 1961.
Башелейшвили М. О.
[1] Граничные задачи колебания упругого тела. Кандидатская диссертация, Тбилисский
гос. ун-т, Тбилиси, 1953.
[2] Решение первой основной задачи статики ортотропного упругого тела для много-
многосвязных областей. Сообщ. АН Грузинской ССР 16, № 8 A955), 577—582.
[3] О фундаментальных решениях дифференциальных уравнений анизотропного упру-
упругого тела. Сообщ. АН Грузинской ССР 19, № 4 A957), 393—400.
[4] Аналог формулы Пуассона в теории упругости. Труды Вычислительного центра АН
Грузинской ССР 1 A960), 97—101.
[5] Эффективное решение некоторых основных граничных задач статики ортотропного
упругого тела методом интегральных уравнений. Труды Вычислительного центра
АН Грузинской ССР 2 A962), 99—121.
[6] Эффективное решение основных задач статики анизотропного упругого тела для
сплошного эллипса и для бесконечной плоскости с эллиптическим отверстием. Труды
Тбилисского матем. ин-та АН Грузинской ССР 28 A962), 3—20.
[7] Решение основных пространственных граничных задач изотропного упругого тела,
ограниченного несколькими поверхностями. Труды Вычислительного центра
АН Грузинской ССР 4 A963), 131—139.
[8] Решение плоских граничных задач статики анизотропного упругого тела. Труды
Вычислительного центра АН Грузинской ССР 3 A963), 93—139.
[9| Аналог формулы Дини в теории упругости. Труды Вычислительного центра
АН Грузинской ССР 4 A964), 121—129.
[10] Об одном способе исследования некоторых плоских граничных задач анизотроп-
анизотропного упругого тела для многосвязных областей. Труды Вычислительного центра
АН Грузинской ССР 4 A963), 141—166.
[11] Об одном способе решения третьей и четвертой граничных задач статики анизо-
анизотропного упругого тела. Сообщ. АН Грузинской ССР 34, № 2 A964), 283—290.
[12J О решении основных плоских граничных задач кусочно-неоднородных анизотропных
упругих сред методом интегральных уравнений Фредгольма. Труды Грузинского
политехи, ин-та, № 2 A00) A965), 3—11.
[13] Об основных плоских граничных задачах для неоднородных анизотропных упру-
упругих тел. Труды Тбилисского гос. ун-та 117 A966), 279—293.
[14] Решение основных граничных задач статики для ортотропного упругого полупро-
полупространства. Труды Тбилисского гос. ун-та 129 A968), 47—55.
[15] Решение плоских граничных задач статики моментной теории упругости. Сообщ.
АН Грузинской ССР 56, № 1 A969), 41—44.
[16J Об одном обобщении теоремы типа Ляпунова—Таубера в теории упругости. Сообщ.
АН Грузинской ССР 61, № 3 A971), 553—556.
[17] Эффективное решение основных задач теории упругости внутри и вне д-мерного
шара. Сообщ. АН Грузинской ССР 63, № 3 A971), 553—556.
[18] Об одном варианте решения третьей и четвертой трехмерных граничных задач
статики изотропного упругого тела. Аннотации докладов семин. Ин-та прикл.
матем. Тбилисского ун-та 7 A973), 59—73.
Башелейшвили М. О., Бурчуладзе Т. В., Гегелиа Т. Г.
[1] О некоторых граничных задачах теории упругости. Второй Всесоюзный съезд по
теоретической и прикладной механике, Москва, 1964. Аннотации докладов. «Наука».
Москва, 1964, стр. 30.
Башелейшвили М. О., Гегелиа Т. Г.
[1] Об основных пространственных граничных задачах для составных изотропных упру-
упругих сред ДАН СССР 160, № 1 (]965), 50—53.
[2] Исследование третьей и четвертой трехмерных граничных задач статики изотроп-
изотропного упругого тела. Труды Ин-та прикл. матем. Тбилисского ун-та 3 A972), 29—67.

640	ЛИТЕРАТУРА
Башелейшвили М. О., Гегелиа Т. Г., Маисаиа О. И.
[1] Некоторые граничные задачи моментной теории упругости. Аннотации докл. семин.
Ин-та прикл. матем. Тбилисского ун-та 2 A970), 43—47.
Белоносов СМ.
[1] Основные плоские статические задачи теории упругости для односвязных и дву-
связных областей. Изд-во Сиб. отд. АН СССР, Новосибирск, 1962.
Берикашвили Н. А.
[1] Об индексе сингулярных интегральных операторов, распространенных на двумер-
двумерных многообразиях. Сообщ. АН Грузинской ССР 34 A964), 257—264.
Бицадзе А. В.
[1] Уравнения смешанного типа. Изд-во АН СССР, Москва, 1959.
[2] Краевые задачи для эллиптических уравнений второго порядка. «Наука», Москва,
1966.
Боровиков В. А.
[1 О двумерной задаче дифракции на многоугольнике. ДАН СССР 144, № 4 A962),
743—746.
Бурчуладзе Т. В.
II] К теории граничных задач колебания упругого тела. Труды Тбилисского ун-та 64
A957), 215-240.
[2] О некоторых граничных задачах для анизотропных упругих тел. Труды Тбилис
ского матем. ин-та АН Грузинской ССР 27 A960), 293—332.
[3] Применение сингулярных интегральных уравнений для решения некоторых гра-
граничных задач. Труды Тбилисского матем. ин-та АН Грузинской ССР 28 A962),
21—40.
[4] Тензоры Грина и их некоторые применения. Труды Грузинского политехи, ин-та,
№ 8 (93) A963), 87—119.
[5] О некоторых смешанных задачах для многосвязных областей. Труды Тбилисского
ун-та 110 A965), 79—88.
|6] О приближенном решении граничных задач для одного класса эллиптических систем.
Дифференциальные уравнения 1, № 9 A965), 1231 —1245.
|7] Об одном способе решения некоторых граничных задач для многосвязных обла-
областей. Сообщ. АН Грузинской ССР 41, № 1 A966), 11 — 18.
|8] Смешанные граничные задачи в многосвязной области. Международный конгресс
математиков (ICM), Москва, 1966. Прикладная математика и математическая физика
(тезисы). «Наука», М., 1966, стр. 30.
19] Смешанные граничные задачи для одного класса эллиптических систем в много-
многосвязных областях. Труды Тбилисского матем. ин-та АН Грузинской ССР 32 A967).
29—53.
i 10] Об одном способе приближенного решения граничных задач. Труды Тбилисского
матем. ин-та АН Грузинской ССР 32 A967), 54—93.
|11] Приближенные решения граничных задач со смешанными краевыми условиями.
Труды Тбилисского матем. ин-та АН Грузинской ССР 35, № 2 A969), 5—31.
|12] Граничные задачи теории упругости для многосвязных областей. Труды Тбилис-
Тбилисского ун-та 129 A968), 57—78.
[13] О некоторых пространственных граничных задачах теории упругости со смешан-
смешанными краевыми условиями. Третий Всесоюзный съезд по теоретической и приклад-
прикладной механике, Москва, 1968. Аннотации докладов. «Наука», Москва, 1968, 54—55.
[14] О некоторых пространственных задачах теории упругости со смешанными крае-
краевыми условиями. Труды Грузинского политехи, ин-та, № 5 A33) A969), 140—150.
[15] Двумерные граничные задачи термоупругости. Труды Тбилисского Матем. ин-та
АН Грузинской ССР 39 A971), 5—22.
[16] Эффективные решения некоторых граничных задач термоупругости. Труды Грузин-
Грузинского политехи, ин-та, № 7 A971), 93—107.
[17] Граничные задачи термоупругости со смешанными краевыми условиями. Труды
Тбилисского матем. ин-та АН Грузинской ССР 44 A974), 10—29.
Бурчуладзе Т. В., Рухадзе Р. В.
11] О тензорах Грина в теории упругости. Дифференциальные уравнения 10, № 6 A974).
Вайнберг Д. В., Синявский А. Л.
fl] Приближенный расчет оболочек с вырезами методами теории потенциала. Проблемы
механики сплошной среды. Изд-во АН СССР, Москва, 1961.
В е к у а И. Н.
[1] О метагармонических функциях. Труды Тбилисского матем. ин-та АН Грузинской
ССР 12 A943), 105—174.
[2] Новые методы решения эллиптических уравнений. Гостехиздат, Москва, 1948.
[3] О доказательстве некоторых теорем единственности, встречающихся в теории уста-
установившихся колебаний. ДАН СССР 80, № 3 A951), 341—343.
14J Обобщенные аналитические функции. Физматгиз, Москва, 1959.

ЛИТЕРАТУРА	641
[5] Теория тонких пологих оболочек переменной толщины. Изд-во «Мецниереба», Тбилиси,
1965.
[6] О методах построения и интегрирования уравнений равновесия теории тонких обо-
оболочек. XIII Международный конгресс по теоретической и прикл. механике. Москва,
1972. Аннотации докладов. «Наука», Москва, 1972.
Веку а И. Н., Мусхелишвили Н. И.
[1] Методы аналитических функций в теории упругости. Труды Всесоюзного съезда
по теоретической и прикладной механике. I960 (обзорные доклады). Изд-во АН СССР,
Москва, 1962, 310—338.
В е к у а Н. П.
[1] Системы сингулярных интегральных уравнений и некоторые граничные задачи.
2-е изд., Физматгиз, Москва, 1970.
Вишик М. И., Ладыженская О. А.
[1] Краевые задачи для уравнений в частных производных и некоторых классов опе-
операторных уравнений. УМН 11, № 6 G2) 1956, 41—97.
Вишик М. И., Мышкис А. Д., Олейник О. А.
[1 ] Дифференциальные уравнения с частными производными. Математика в СССР за сорок
лет 1 (обзорные статьи). Физматгиз, Москва, 1959, 563—646.
Вишик М. И., Э с к и н Г. И.
[1] Уравнения в свертках переменного порядка. Труды Московского матем. о-ва 16
A967), 25—51.
Вольперт А. И.
[1] Эллиптические системы на сфере и двумерные сингулярные интегральные уравне-
уравнения. Матем. сб. 59 A01) (дополнительный) A962), 195—214.
Ворович И. И., Прокопов В. К.
П] Некоторые вопросы трехмерной теории упругости. Третий Всесоюзный съезд по
теоретической и прикладной механике, Москва, 1968. Аннотации докладов. «Наука»,
Москва, 1968, стр. 81.
Галеркин Б. Г.
[1J К вопросу об исследовании напряжений и деформаций в упругом изотропном теле.
ДАН СССР, сер. А, № 14 A930), 353—358.
Галин Л. А.
[1] Контактные задачи теории упругости. Гостехиздат, Москва—Ленинград, 1953.
Г а х о в Ф. Д.
[1] Краевые задачи. 2-е изд., Физматгиз, Москва, 1963.
Гегелиа Т. Г.
A ] Граничные свойства обобщенных пространственных потенциалов. Труды Тбилисского
гос. ун-та 56 A955), 185—206.
|2] Об одном обобщении теоремы Жиро. Сообщ. АН Грузинской ССР 16, № 9 A955),
657—664.
|3] Основная лемма И. И. Привалова для пространственных потенциалов. Сообщ.
АН Грузинской ССР 18, № 3 A957), 257—264.
D] О свойствах некоторых классов непрерывных функций при трансформации Гильберта
в ?«. Сообщ. АН Грузинской ССР 19, № 3 A957), 257—261.
[5] Об ограниченности сингулярных операторов. Сообщ. АН Грузинской ССР 20, № 5
A958), 517—523.
[6] О поведении обобщенного потенциала вблизи границы множества интегрирования.
Труды Тбилисского матем. ин-та АН Грузинской ССР 26 A959), 189—193.
17] Дифференциальные свойства некоторых интегральных преобразований. Труды Тби-
Тбилисского матем. ин-та АН Грузинской ССР 26 A959), 195—225.
[8] О композиции сингулярных ядер. ДАН СССР 135, № 4 A960), 767—770.
[9] О свойствах многомерных сингулярных интегралов в пространстве Lp (S, р). ДАН
СССР 139, № 2 A962), 279—282.
[10] О граничных значениях функции типа потенциала. Труды Вычислительного центра
АН Грузинской ССР 2 A961), 285—313.
[11] Свойства дифференцируемости решений поверхностных сингулярных интегральных
уравнений. Труды Грузинского политехи, ин-та, № 1 (81) A962), 69—77.
[12] О формуле перестановки порядка интегрирования в повторных сингулярных инте-
интегралах. Труды Тбилисского матем. ин-та АН Грузинской ССР 28 A962), 41—52.
113J О некоторых основных пространственных граничных задачах теории упругости.
Труды Тбилисского матем. ин-та АН Грузинской ССР 28 A962), 53—72.
[14| О регуляризации сингулярных интегральных операторов. Труды Тбилисского матем.
ин-та АН Грузинской ССР 29 A963), 229—237.
fl5| Некоторые вопросы теории многомерных сингулярных интегральных уравнений,
теории потенциала и их приложений в теории упругости. Докторская диссертация.
Тбилисский матем. ин-т АН Грузинской ССР, Тбилиси, 1963.
[16] Об одной формуле обращения А. Бицадзе. Труды Вычислительного центра АН Гру-
Грузинской ССР 3 A963), 81—87.
Va41 В. Д. Купоалзе

642	ЛИТЕРАТУРА
[17] Об одном свойстве решений сингулярных интегральных уравнений. Труды Тбилис-
Тбилисского гос. ун-та 110 A965), 43—56.
[18] Некоторые специальные классы функций и их свойства. Труды Тбилисского матем.
ин-та АН Грузинской ССР, 32. Сб. работ по уравнениям математической физики 1
A967). 94—139.
A9] О трехмерных граничных задачах теории упругости для неограниченных областей.
Симпозиум по механике сплошной среды и родственным проблемам анализа. Тбилиси,
1971. Аннотации докладов. Изд-во АН Грузинской ССР, Тбилиси, 1971.
120] О дифференциальных свойствах решений многомерных сингулярных интегральных
уравнений. Международный конгресс математиков (ICM), Москва, 1966. Дифферен-
Дифференциальные уравнения с частными производными (тезисы). «Наука», Москва, 1966,
25—26.
Гегелиа Т. Г., Маисаиа О. И.
[1] Аксиоматическая теория упругих состояний. Вторая научная сессия Ин-та прикл.
матем. Тбилисского ун-та. Тбилиси, 1970. Тезисы докладов. Изд-во Тбилисского
ун-та, Тбилиси, 1970, стр. 12.
Гегелиа Т. Г., Чичинадзе Р. К.
[1] Исследование некоторых граничных задач среды Коссера. Аннотации докл. семин.
Ин-та прикл. матем. Тбилисского ун-та 9 A974), стр. 21—27.
Гельфанд И. М., Петровский И. Г., Шилов Г. Е.
[1] Теория систем дифференциальных уравнений с частными производными. Труды
III Всесоюзного математического съезда, 3, Изд-во АН СССР, Москва, 1958, 65—72.
ГиоргашвилиЛ. Г.
[1] Гранично-контактные задачи статики моментной теории упругости для кусочно-
неоднородных изотропных сред. Аннотации докл. семин. Ин-та прикл. матем. Тбилис-
Тбилисского ун-та 7 A973), 33—44.
[2] Об одной задаче дифракции. Труды Ин-та прикл. матем. Тбилисского ун-та 3 A972),
73—85.
[3] Об одном варианте гранично-контактных задач для составных изотропных сред
статики моментной теории упругости. Аннотации докл. семин. Ин-та прикл. матем.
Тбилисского ун-та 8 A973), 53—63.
Гогниашвили 3. М.
[1] О существовании решения одной основной граничной задачи для неоднородной
упругой среды. Труды Грузинского политехи, ин-та, № 1 (81) A962), 79—84.
Голузин Г. М.
[1] Геометрическая теория функций комплексного переменного. Гостехиздат, Москва—
Ленинград, 1952.
Горгидзе А. Я.
[1] Растяжение и кручение составных брусьев, близких к призматическим. Сообш. АН
Грузинской ССР 8, № 9—10 A947), 605—612.
|2] Кручение растянутого призматического бруса, составленного из различных мате-
материалов. Сообщ. АН Грузинской ССР 9, № 3 A948), 161—165.
[3] Изгиб парой сил растянутого призматического бруса, составленного из различных
материалов. Сообщ. АН Грузинской ССР 9, № 9—10 A948), 539—545.
[4] Растяжение и изгиб парой сил естественно закрученных брусьев. Сообщ. АН Гру-
Грузинской ССР 13, №2 A952), 73—80.
Градштейн И. С, Рыжик И. М.
[1] Таблицы интегралов, сумм, рядов и произведений. Физматгиз, Москва, 1963.
Гродский Г. Д.
[1] Интегрирование общих уравнений равновесия изотропного упругого тела при по-
помощи ньютоновых потенциалов и гармонических функций. Изв. АН СССР, Отд.
матем. и естеств. наук, № 4 A935), 588—614.
Г ю н т е р Н. М.
[1] Теория потенциала и ее применение к основным задачам математической физики.
Гостехиздат, Москва, 1953.
Давитадзе Дж. Б.
[1] Поведение потенциалов теории упругости в замкнутых областях. Труды Тбилис-
Тбилисского политехи, ин-та, № 5 A25) A968), 3—14.
[2] О регуляризаторе одной системы сингулярных интегральных уравнений. Труды
Батумского пед. ин-та 12 A965), 259—269.
Данилюк И. И.
[1] Лекции по краевым задачам для аналитических функций и сингулярным интеграль-
интегральным уравнениям. Изд-во Новосибирского ун-та, Новосибирск, 1964.
Джавахишвили Г. И.
[1] О представлении общих решений уравнений трансверсально-изотропных упругих
сред. Труды Ин-та прикл. матем. Тбилисского ун-та 3 A972), 95—100.
Джанелидзе Г. Ю.
[1] Задача Альманзи. Труды Ленинградского политехи, ин-та. Динамика и прочность
машин, Кя 210 A960), 25—38.

ЛИТЕРАТУРА	643
Джанелидзе О. П.
[1] Об основной лемме И. И. Привалова. Труды Тбилисского математ. ин-та АН Гру-
Грузинской ССР 29 A964), 239—244.
Д и н н и к А. Н.
[11 Продольный изгиб. Кручение. Изд-во АН СССР, Москва, 1955.
Доманьский 3.
[1] Свойства оператора напряжений потенциала двойного слоя статической теории
упругости. Arch. Mech. stosow. 20, 3 A968), 347—354.
Доманьский 3., Пискорек А., Роек 3.
[1] О применении метода Фишера—Рисса—Купрадзе для решения первой задачи Фурье-
Rocz. Pol. Tow. Mat., Ser. 1, Prace Mat. 16 A972), 137—147.
Жуковский Н. Е.
[11 Теоретическая механика. Гостехиздат, Москва, 1950.
Забрей ко П. П., Кошелев А. И., Красносельский М. А., Мих-
л и н С. Г., Р а к о в щ и к Л. С, С т е ц е н к о В. Я.
11] Интегральные уравнения. СМБ. «Наука», Москва, 1968.
Зазашвили Ш. П.
[1] Некоторые граничные задачи плоской теории термоупругости. Аннотации докл.
семин. Ин-та прикл. матем. Тбилисского ун-та 5 A971), 13—17.
Зерагия П. К.
[1] Об одной граничной задаче для уравнения Апц = 0. Труды Груз, политехи, ин-та,
№ 25 A952), 33—44.
Ильин В. А.
[1] О фундаментальных системах функции оператора Лапласа в произвольной области
и об асимптотической оценке фундаментальных чисел. ДАН СССР 177, № 1 A967),
25—28.
[2] О разрешимости смешанных задач для гиперболического и параболического уравне-
уравнений. УМН 15, № 2 (92) A960), 97—154.
Ильюшин А. А., Победря Б. Е.
[1] Основы математической теории термовязко-у пру гости. «Наука», Москва, 1970.
Каландия А. И.
[1] Об одной плоской задаче несимметричной упругости. Труды Тбилисского матем.
ин-та АН Грузинской ССР 35 A969), 45—51.
Каландия А. И., Ж г е н т и В. С.
[1] О плоских задачах моментной теории упругости. Труды Тбилисского матем. ин-та
АН Грузинской ССР 33 A967), 57—75.
Канторович Л. В.
|1] Функциональный анализ и прикладная математика. УМН 3, № 6B8) A948). 89—185.
Канторович Л. В., А к и л о в Г. П.
[1] Функциональный анализ в нормированных пространствах. Физматгиз, Москва, 1959.
КапанадзеР. В.
[1] О пространствах, инвариантных относительно сингулярного интегрального преоб-
преобразования. Труды Тбилисского матем. ин-та АН Грузинской ССР 32 A967),
164—171.
[2J О некоторых свойствах сингулярных операторов в нормированных пространствах.
Труды Тбилисского ун-та 129 A968), 17—26.
[3] Приближение непрерывных функций сферическими полиномами. Сообщ. АН Гру-
Грузинской ССР 45, № 1 A967), 21—26.
Капшивый А. А., Положий Г. Н., Чемерис В. С.
[1] О методе р-аналитических функций в осесимметричной теории упругости. Третий
Всесоюзный съезд по теоретической и прикладной механике. Москва, 1968. Аннота-
Аннотации докладов. «Наука», Москва, 1968, 150—151.
Кахниашвили Н. С.
[1] Об одном случае элементарного представления фундаментальных решений диффе-
дифференциальных уравнений анизотропного упругого тела. Труды Тбилисского ун-та
64 A957), 123—126.
[2] Исследование плоских задач теории упругости методом теории потенциалов. Труды
Тбилисского гос. ун-та 50 A953), 23—59.
[3] Исследование плоских задач теории упругости методом теории потенциалов для
многосвязных областей. Труды Тбилисского ун-та 56 A955), 173—183.
[4] Некоторые оценки в теории термоупругости. Сообщ. АН Грузинской ССР 65, № 3
A972), 547—550.
[5] К доказательству теорем существования для основных динамических задач термо-
термоупругости. Сообщ. АН Грузинской ССР 66, № 3 A972), 549—552.
Квиникадзе Г. П.
[1] Третья и четвертая граничные задачи плоской теории упругости для установив-
установившихся колебаний изотропных тел. Сообщ. АН Грузинской ССР 32, № 3 A963),
535—542.

644	ЛИТЕРАТУРА
[2] Смешанные задачи плоской теории установившихся колебаний изотропного упругого
тела. Кандидатская диссертация, Тбилисский матем. ин-т АН Грузинской ССР,
Тбилиси, 1964.
[3] О существовании решений некоторых плоских граничных задач теории упругости
установившихся колебаний изотропного упругого тела. Труды Тбилисского ун-та
117 A966), 295—331.
|4] О существовании спектра собственных частот для обобщенных смешанных задач
теории упругости в случае многосвязных областей. Труды Тбилисского ун-та 129
A968), 79—111.
[5] Решение некоторых граничных задач изгиба пластинки. Труды Ин-та прикл. матем.
Тбилисского ун-та 3 A972), 115—126.
Коваленко А. Д.
[1] Основы термоупругости. Изд-во «Наукова думка», Киев, 1970.
Коренев Б. Г.
[1] Введение в теорию бесселевых функций. «Наука», Москва, 1971.
Короткина М. Р.
[1] О моментных напряжениях в дискретных системах. В сб. «Упругость и неупругость».
Вып. 1, Изд-во Московского ун-та, Москва, 1971.
К о ч и н Н. Е.
[1] Влияние шага решетки на ее гидродинамические характеристики. Прикладная
математика и механика, 5, вып. 2, 1941, 165—192.
Крачковский С. Н., Диканский А. С.
[1] Фредгольмовы операторы и их обобщения. В сб. «Итоги науки», Математический
анализ 1968. ВИНИТИ, Москва, 1969, 39—73.
Кувшинский Е. В., Аэро Э. Л.
[1] Континуальная теория асимметрической упругости. Учет «внутреннего» вращения.
Физика твердого тела 5, № 9 A963), 2591—2598.
К у н и н И. А.
[1 ] Теория упругой среды с микроструктурой. В сб. «Прочность и пластичность». «Наука»,
Москва, 1971, 65—70.
Купрадзе В. Д.
[1] О принципе излучения А. Зоммерфельда. ДАН СССР, № 2 A934), 1—7.
[2] Метод интегральных уравнений в теории дифракции. Матем. сб. 41, № 4 A935),
562—581.
[3] Теоремы единственности в краевых задачах теории упругости. Труды Тбилисского
ун-та 2 A936), 256—272.
[4] Zur Frage der Ausbreitung elektromagnetischer Wellen in einem inhomogenen ebenen
Medium. Сотр. Math. 6 A939), 228—233.
[5] К решению задачи Дирихле для многосвязной области. Сообщ. Грузинского фи-
филиала АН СССР 1, № 8 A940), 569—571.
[6] Некоторые новые теоремы об уравнении колебания и их применения в граничных
задачах. Труды Тбилисского ун-та 26 (А) A945), 1—И.
[7] Граничные задачи теории колебаний и интегральные уравнения. Гостехиздат, Москва,
1950.
(8] Граничные задачи теории установившихся колебаний. УМН 8, № 3 E5) A953), 21—74.
[9] Randwertaufgaben der Schwingungsteorie und Integralgleichungen. Berlin, 1956.
[10] Граничные задачи теории упругости для кусочно-неоднородных тел. Сообш. АН
Грузинской ССР 22, № 2—3 A959), 129—136.
Ill] К теории граничных задач для неоднородных упругих тел. Сообщ. АН Грузинской
ССР 22, № 4 A959), 401—408.
[12] О краевых задачах теории упругости для кусочно-неоднородных тел. Сообщ. АН
Грузинской ССР 22, № 5 A959), 521—528.
[13] Методы потенциала в теории упругости. Физматгиз, Москва, 1963 (англ. перевод
этой книги: Potential Methods in the Theory of Elasticity. Jerusalem, 1965).
[14] Dynamical Problems in Elasticity. Progress in Solid Mechanics 3, Amsterdam,
1963.
[15] Об одном методе приближенного решения предельных задач математической физики.
Ж- вычисл. матем. и матем. физики 4, № 6 A964), 1118.
[16] Metody teorii potencjalu w teorii sprezystosci. Warszawa, 1966.
[17] О приближенном решении задач математической физики. УМН 22, № 2 A967),
59-107.
[18] К решению трехмерной смешанной граничной задачи теории упругости. Сб. «Меха-
«Механика сплошной среды и родственные проблемы анализа», посвященный 80-летию
акад. Н. И. Мусхелишвили. «Наука», Москва, 1972.
Купрадзе В. Д., Алексидзе М. А.
[1] Об одном приближенном методе решения граничных задач. Сообщ. АН Грузинской
ССР 30, № 5 A963), 529—536.
[2] Метод функциональных уравнений для приближенного решения некоторых гра-
граничных задач. Ж. вычисл. матем. и матем. физики 4, № 4 A964), 683—715.

ЛИТЕРАТУРА	545
Купрадзе В. Д., Башелейшвили М. О.
[1] Новые интегральные уравнения анизотропной теории упругости. Сообш. АН Гру-
Грузинской ССР 15, № 6 A954), 407—414.
[2] Новые интегральные уравнения анизотропной теории упругости и их примене-
применения при решении граничных задач. Сообш. АН Грузинской ССР 15, № 7 A954).
495—502.
Купрадзе В. Д., Бурчуладзе Т. В.
[1] Общая смешанная граничных задача теории упругости и теории потенциала. Сообш.
АН Грузинской ССР 32, № 1 A963), 27—34.
B] Общая .смешанная граничная задача теории упругости и теории потенциала. Второй
Всесоюзный съезд по теоретической и прикладной механике. Москва, 1964. Аннота-
Аннотации докладов. «Наука», Москва, 1964, стр. 43.
C] Граничные задачи термоупругости. Дифференциальные уравнения 5, № 1 A969).
3—43.
[4] Некоторые граничные задачи термоупругости, решаемые в квадратурах 1. Диффе-
Дифференциальные уравнения 5, № 10 A969), 1735—1761.
[5] Некоторые граничные задачи термоупругости, решаемые в квадратурах II. Диффе-
Дифференциальные уравнения 5, № 11 A969), 1923—1939.
[61 Решение динамических задач теории упругости. Аннотации докл. семин. Ин-та
прикл. матем. Тбилисского ун-та 3 A970), 66—77.
[7] Доказательство существования и вычисление решений основных смешанных задач
динамики трехмерного упругого тела произвольной формы. Труды Тбилисского матем.
ин-та АН Грузинской ССР 39 A971), 23—42.
[8] On dynamic problem? of the theory of elasticity. Trends in elasticity and thermoe-
lasticity (Witold Nowacki, Anniversary Volume). Wolters-Woordhoff Publishing.,
1971, 137—149.
Купрадзе В. Д., Бурчуладзе Т. В., Г е г е л и а Т. Г.
[1] Основные начально-краевые задачи теории упругости. XIII Международный кон-
конгресс по теоретической и прикладной механике, Москва, 1972. Аннотации докладов.
«Наука», Москва, 1972.
Купрадзе В. Д., Гегелиа Т. Г.„ Башелейшвили М. О., Бурчу-
Бурчуладзе Т. В.
A| Трехмерные задачи математической теории упругости. Изд-во Тбилисского ун-та,
Тбилиси, 1968.
Купрадзе В. Д., Соболев С. Л.
[1] К вопросу о распространении упругих волн на границе двух сред с различными
упругими свойствами. Труды Сейсмолог, ин-та АН СССР, № 10 A930).
Лаврентьев М. М.
[1] О некоторых некорректных задачах математической физики. Изд-во Сибирского
отд. АН СССР, Новосибирск, 1962.
[2] О постановке некоторых некорректных задач математической физики. В сб. «Неко-
«Некоторые вопросы вычислительной и прикладной математики». «Наука», Сибирское отд.
АН СССР, Новосибирск, 1966, 258—276.
Ладыженская О. А.
[1] Смешанная задача для гиперболического уравнения. Гостехиздат, Москва, 1953,
Ландау Л. Д., Л и ф ш и ц Е. М.
[1] Теория упругости. «Наука», Москва, 1965.
[2] Статистическая физика. Изд. 2-е, «Наука», Москва, 1964.
Лейбензон Л. С.
[1] Вариационные методы решения задач теории упругости. Гостехиздат, Москва, 1943.
[2] Курс теории упругости. Гостехиздат, Москва, 1947.
Лебедев Н. Н.
[1] Температурные напряжения в теории упругости. ОНТИ, Москва, 1937.
Лехницкий С. Г.
[1] Теория упругости анизотропного тела. Гостехиздат, Москва, 1950.
[2] Анизотропные пластинки. Гостехиздат, Москва, 1947.
[3] Кручение анизотропных и неоднородных стержней. Физматгиз, Москва, 1971.
Лопатинский Я. Б.
[1] Фундаментальная система решений системы линейных дифференциальных уравне-
уравнений эллиптического типа. ДАН СССР 71, № 3 A950), 433—436.
[2] Нормальные фундаментальные решения системы линейных дифференциальных урав-
уравнений эллиптического типа. ДАН СССР 78, № 5 A951), 865—867.
Лурье А. И.
[1] Пространственные задачи теории упругости. Гостехиздат, Москва, 1955.
[2] Теория упругости. Физматгиз, Москва, 1970.
Люстёрник Л. А., Соболев В. И.
[1] Элементы функционального анализа. Изд. 2-е, Физматгиз, Москва, 1965.
Ляпунов А. М.
у но
1] Ра
[1] Работы по теории потенциала. Гостехиздат, Москва—Ленинград, 1949.

646	ЛИТЕРАТУРА
МагнарадзеЛ. Г.
[1] 06 одном обобщении теоремы И. И. Привалова и его применении к некоторым
линейным граничным задачам теории функций и к сингулярным интегральным урав-
уравнениям. ДАН СССР 68, № 4 A949)^ 657—660.
[2] Некоторые граничные задачи математической физики для поверхностей с угловыми
линиями. Труды Тбилисского матем. ин-та 7 A940), 25—46.
[3] Об общих представлениях регулярных решений некоторых нестационарных урав-
уравнений в пространствах Банаха. Труды Международного симпозиума в Тбилиси,
1963. «Наука», Москва, 2 A965), 323—330.
14] Об одном классе нестационарных уравнений в банаховом пространстве на диффе-
дифференцируемом многообразии. Аннотации докл. семин. Ин-та прикл. матем. Тбилис-
Тбилисского ун-та, № 2 A969), 53—63.
15] Об общих представлениях некоторых классов решений линейных нестационарных
дифференциальных уравнений с частными производными и horom методе решения
задач Коши—Дирихле и аналогичных. Труды Ин-та прикл. матем. Тбилисского
ун-та 2 A969), 71—92.
[6] Об общих представлениях решений линейных дифференциальных уравнений не-
нестационарных и неоднородных полей с помощью гармонических и аналитических
функций. Аннотации докладов семин. Ин-та прикл. матем. Тбилисского ун-та, № 3
A970), 49—57.
[7] О новых формулах, аналогичных формулам Г. В Колосова, Н. И. Мусхелишвили,
И. Н. Векуа и др. для некоторых основных неоднородных, изотропных стационар-
стационарных и нестационарных физических полей. Симпозиум по механике сплошной среды
и родственным проблемам анализа. Тбилиси, 1971. Аннотации докладов. Изд-во АН
Грузинской ССР. Тбилиси, 1971.
'8] К решению граничных задач для некоторых слабо неоднородных упругих тел.
Аннотации докладов семин. Ин-та прикл. матем. Тбилисского ун-та, № 8 A973).
47—52.
Маисаиа О. И., Чичинадзе Р. К.
[1] Некоторые граничные задачи моментной теории упругих колебаний. Аннотации
докладов семин. Ин-та прикл. матем. Тбилисского ун-та № 2 A970). 49—52
МайзельВ. М. .
[1] Температурная задача теории упругости. Изд-во АН Украинской ССР, Киев. 1951.
Манджавидзе Г. Ф.
[1] Граничная задача линейного сопряжения со смещениями и ее связь с теорией обоб-
обобщенных аналитических функций. Труды Тбилисского матем. ин-та АН Грузинской
ССР 33 A967), 82—92.
|2] Граничные задачи линейного сопряжения и некоторые их приложения. Докторская
диссертация. Тбилисский ун-т, Тбилиси, 1970.
Мецхваришвили Я. Г.
[1] О некоторых свойствах регулярных решений колебательного уравнения. Труды
Тбилисского ун-та (А), № 26 A945), 13—22.
Мецховришвили Ш. С.
[1] Задачи безмоментного напряженного состояния горообразной оболочки. Труды
Тбилисского матем. ин-та АН Грузинской ССР 24 A957), 179—193.
М и х л и н С. Г.
1] Решение одной трехмерной задачи теории упругости. ПММ 10, № 2A946), 301—304.
2 Интегральные уравнения и их приложения. Гостехиздат, Москва, 1949.
3^ Прямые методы в математической физике. Гостехиздат, Москва—Ленинград, 1950.
4	Проблема минимума квадратичного функционала. Гостехиздат, Москва, 1952.
5	Лекции по линейным интегральным уравнениям. Физматгиз, Москва, 1959.
6	Многомерные сингулярные интегралы и интегральные уравнения. Физматгиз, Москва,
1962.
[7] Численная реализация вариационных методов. Физматгиз, Москва, 1966.
f8] Курс математической физики. Физматгиз, Москва. 1968.
М и х л и н С. Г., С м о л и ц к и й X. М.
fl] Приближенные методы решения дифференциальных и интегральных уравнений.
СМБ, «Наука», Москва, 1965.
Мусхелишвили Н. И,
|1] Некоторые основные задачи математической теории упругости. Изд. 5-е, Физматгиз,
Москва, 1966.
|2] Сингулярные интегральные уравнения. Изд. 3-е, «Наука», Москва, 1968.
[3] Приложения теории функций комплексного переменного в теории упругости. В сб.
«Приложения теории функций в механике сплошной среды». Труды Международ-
Международного симпозиума в Тбилиси, 1963. «Наука», Москва. 1965, 32—55.
Мусхелишвили Н. И., Черный Г. Г.
[1] Развитие механики в СССР за 50 лет. Третий Всесоюзный съезд по теоретической
. и прикладной механике. Москва, «Наука», Москва, 1968.

ЛИТЕРАТУРА
М ю н т ц Г. М.
[1] Интегральные уравнения. Гостехиздат, Москва, 1934.
Напетваридзе О. И.
[1] Об основной контактной граничной задаче теории теплопроводности. Сообщ. АН
Грузинской ССР 33, № 2 A964), 271—278.
[2] О приближенном решении третьей краевой задачи теории теплопроводности. Сообщ.
АН Грузинской ССР 35, № 2 A964), 271—276.
[3] О существовании решения контактной граничной задачи теории теплопроводности.
Сообщ. АН Грузинской ССР 37, № 2 A965), 259—262.
[4] О приближенном- решении задачи Коши—Неймана для уравнения теплопроводности.
Труды Тбилисского ун-та ПО A965), 109—114.
[5] Потенциалы моментной теории упругости. Труды Тбилисского матем. ин-та АН
Грузинской ССР 39 A971), 75—92.
[6] О граничных задачах моментной теории упругости. Аннотации докладов семии.
Ин-та прикл. матем. Тбилисского ун-та, № 5 A971), 53—67.
Нарышкина Е. А.
[1] О колебаниях твердого упругого полупространства, граничащего вдоль плоскости
с упругой сжимаемой жидкостью. Труды Сейсмолог, ин-та АН СССР, № 21 A933).
[2] Колебания полупространства при любых начальных условиях. Труды Сейсмолог.
ин-та АН СССР, № 45 A934).
Натансон И. П.
[1] Конструктивная теория функций. Гостехиздат, Москва, 1949.
[2] Теория функций вещественной переменной. Гостехиздат, Москва, 1957.
Н а т р о ш в и л и Д. Г.
[1] Эффективное решение основных граничных задач статики для однородного шара.
Труды Ин-та прикл. матем. Тбилисского ун-та 3 A972), 127—140.
[2] Эффективное решение третьей и четвертой граничных задач теории упругости для
сферы. Сообщ. АН Грузинской ССР 67, № 3 A972), 557—560.
[3J Некоторые основные и смешанные задачи для полушара. Аннотации докладов
семин. Ин-та прикл. матем. Тбилисского ун-та, № 8 A973), 9—17.
[4] Главная контактная задача для сферы. Аннотации докладов семин. Ин-та прикл.
матем. Тбилисского ун-та, № 8 A973), 19—22.
Никольский Е. Н.
[1] Алгоритм Шварца в задаче теории упругости о напряжениях. ДАН СССР 135,
№ 3 A960), 549—552.
Никольский СМ.
[1] Приближение функции многих переменных и теоремы вложения. «Наука», Москва,
1969.
Новожилов В. В.
[1] Теория упругости. Судпромгиз, Ленинград, 1958.
Оболашвили Е. И.
[1] Эффективное решение некоторых пространственных задач теории упругости. Rev.
Roumaine Math. Pures Appi. 11, № 8 A966), 965—972.
[2] Решение некоторых граничных задач теории упругости и теории оболочек. Док-
Докторская диссертация. Тбилисский матем. ин-т АН Грузинской ССР, Тбилиси, 1966.
[3] Некоторые граничные задачи моментной теории упругости. Труды Тбилисского матем.
ин-та АН Грузинской ССР 39 A971), 49—50.
Пааташвили Л. А.
[1] О приближенном решении некоторых задач математической физики. Кандидатская
диссертация. Тбилисский матем. ин-т АН Грузинской ССР, Тбилиси, 1965.
[2] Приближенное решение основной граничной задачи электродинамики. Сообщ. АН
Грузинской ССР 39, № 3 A965), 543—550.
[3] Доказательство существования и приближенное решение основной задачи акусти-
акустической дифракции. Труды Тбилисского ун-та 117 A966), 265—278.
Пальмов В. А.
[1] Основные уравнения теории несимметричной упругости. ПММ 28, № 3A964),
401—408.
Папкович П. Ф.
[1] Выражение общего интеграла основных уравнений теории упругости через гармо-
гармонические функции. Изв. АН СССР, сер. матем. и естествен, наук, № 10 A932),
1425—1435.
[2] Теория упругости. Оборонгиз, Москва, 1939.
! р л и н
[1] Об
Об одном методе решения основных пространственных задач теории потенциала
и теории упругости для областей, ограниченных двумя замкнутыми поверхностями.
Инженер ый журнал 4, № 1 A964), 79—89.
Петрашень Г. И.
[1 ] Динамические задачи теории упругости. Учен, записки Ленинградского ун-та 1, № 149,
вып. 24, сер. матем. A951), 1—75.

648	ЛИТЕРАТУРА
Петровский И. Г.
[1] О некоторых проблемах теории уравнений с частными производными. УМН 1,
№ 3—4 A3—14) A946), 44—70.
[2] К теории уравнений с частными производными. Юбилейный сб., посвященный трид-
тридцатилетию Великой Октябрьской социалистической революции. I. Изд-во АН СССР,
Москва—Ленинград, 1947, 214—230.
[3] Лекции по теории интегральных уравнений. Гостехиздат, Москва—Ленинград, 1948.
[4] Лекции об уравнениях с частными производными. Изд. 3-е, Физматгиз Москва,
1961.
Полищук И. М.
[1] Об одном методе решения граничной задачи электродинамики. Радиотехника и
электроника 11, № 10A966), 1753—1758.
Положий Г. М.
J1J К вопросу о (р, ^-аналитических функциях комплексного переменного и их при-
применениях. Rev. Roumaine Math. Pures Appl. 2 A957), 331—361.
Положий Г. М., .4 е м е р и с В. С.
[1] Об интегральных уравнениях осесимметричной теории упругости. Исследования
по современным проблемам теории функций комплексного переменного (сб. статей).
Физматгиз, Москва, 1961, 399—412.
Попов Г. Я., Ростовцев Н. А.
[1] Контактные (смешанные) задачи теории упругости. Труды Второго Всесоюзного
съезда по теоретической и прикладной механике. Вып. 3. «Наука», Москва, 1966,
235—252.
Привалов И. И.
[1] Граничные свойства аналитических функций. Изд. 2-е, Гостехиздат, Москва-
Ленинград, 1950.
Расулов М. Л.
[1] Метод контурного интеграла. «Наука», Москва, 1966.
Рухадзе А. К.
[1] К задаче изгиба упругих брусьев, составленных из различных материалов. Сообш.
АН Грузинской ССР 1, № 2 A940), 107—114.
[2] Вторичные эффекты в задаче изгиба парой бруса, составленного из различных мате-
материалов. Сообщ. АН Грузинской ССР 4, № 2A943), 115—122.
C] Задача изгиба парой естественно закрученных призматических брусьев, составленных
° из различных упругих материалов. Сообш. АН Грузинской ССР 13, № 5 A952).
265—272.
|4| Задача изгиба парой сил стержня, составленного из различных упругих материалов.
Сообщ. АН Грузинской ССР 14, № 9 A953), 525—532.
Рухадзе Ж. А.
fl] Граничные задачи теории упругости для кусочно-неоднородных изотропных сред.
Кандидатская диссертация. Тбилисский матем. ин-т АН Грузинской ССР, Тбилиси,
1965.
1,2] О краевых задачах теории упругости для кусочно-неоднородных ортотропных тел.
Сообщ. АН Грузинской ССР 30, № 1 A963), 11 — 18.
|3] Решение краевых задач теории упругости для кусочно-неоднородных сред методом
обобщенных рядов Фурье. Труды Грузинского политехи, ин-та 4 (97) A964),
11 — 19.
[4] Теорема существования для краевых задач теории упругости кусочно-неоднородных
ортотропных тел. Сообщ. АН Грузинской ССР 30, № 6 A963), 713—720.
[5] О краевых задачах колебания плоского бесконечного неоднородного упругого изо-
изотропного тела. Сообщ. АН Грузинской ССР 35, № 3A964), 531—538.
[6] Основные гранично-контактные задачи теории термоупругих колебаний. Сообщ. АН
Грузинской ССР 56, № 2 A969), 285—288.
[7] Эффективное решение задач термоупругих колебаний для некоторых плоских об-
областей. Труды Грузинского политехи, ин-та, № 5 A33) A969), 164—171.
Рухадзе Р. В.
flj О разрешимости первой основной смешанной задачи динамики трехмерного упругого
тела. Сообщ. АН Грузинской ССР 73, № 2 A974), 289—292.
Савин Г. Н.
[1] Концентрация напряжений около отверстий. Гостехиздат, Москва—Ленинград, 195L
[2] Распределение напряжений около отверстий. Изд-во «Наукова думка», Киев, 1968.
[3] Основные задачи плоской моментной теории упругости. В сб. «Концентрация на-
напряжений», № 2. Изд-во «Наукова думка». Киев, 1968. 145—166.
Саркисян В. С.
[1] Некоторые задачи теории упругости анизотропного тела. Изд-во Ереванского ун-та,
Ереван, 1970.
СванадзеК. Н.
[1] Некоторые вопросы моментной теории упругости для случая установившихся коле-
колебаний. Труды Кутаисского пед. ин-та. 32 A969), 299—306.

ЛИТЕРАТУРА	649
[2] G решении основных плоских граничных задач установившихся колебаний с учетом
моментных напряжений. Сообщ. АН Грузинской ССР 62, № 2 A971), 285—288.
С е д о в Л. И.
[1] Введение в механику сплошной среды. Физматгиз, Москва, 1962.
[2] Механика сплошной среды, чч. I—IV. Изд-во Московского ун-та, Москва, 1968.
Слободянский М. Г.
[1] Общие формы решений уравнений упругости для односвязных и многосвязных об-
областей, выраженные через гармонические функции. ПММ 18 A954), 55—74.
Смирнов В. И.
[1] Курс высшей математики, том П. Изд. 10-е, Гостехиздат, Москва, 1950.
[2] Курс высшей математики, том IV. Изд. 2-е, Гостехиздат, Москва, 1951.
[3] Курс высшей математики, том V. Физматгиз, Москва, 1959.
Смирнов В. И., Соболев С. Л.
[1] О применении нового метода к изучению упругих колебаний в пространстве при
наличии осевой симметрии. Труды Сейсмолог, ин-та АН СССР, № 26 A933).
Соболев С. Л.
[1] Некоторые применения функционального анализа в математической физике. Изд-во
Ленинградского ун-та, Ленинград, 1950.
[2] Уравнения математической физики. Гостехиздат, Москва, 1954.
Сретенский Л. Н.
[1] Теория ньютоновского потенциала. Гостехиздат, Москва, 1946.
Тихонов А. Н.
[1] О решении некорректно поставленных задач и методе регуляризации. ДАН СССР
151, № 3 A963), 501—504.
Тихонов А. Н., Самарский А. А.
[1] Уравнения математической физики. Физматгиз, Москва, 1966.
У ф л я н д Я. С.
fl) Интегральные преобразования в задачах теории упругости. Изд-во АН СССР,
Москва—Ленинград, 1963.
Урушадзе Г. И.
[1] О микроскопических моментах в поликристаллических веществах. Аннотации док-
докладов семин. Ин-та прикл. матем. Тбилисского ун-та, № 4 A971), 45—49.
12] О поверхностных волнах в твердых телах. Аннотации докладов семин. Ин-та прикл.
матем. Тбилисского ун-та, № 6A972), 37—41.
Филоненко-Бородич М. М.
[1] Теория упругости. Гостехиздат, Москва, 1947.
Фихтенгольц Г. М.
[1] Курс дифференциального и интегрального исчисления, т. I. Гостехиздат, Москва—
Ленинград, 1947.
[2] Курс дифференциального и интегрального исчисления, т. П. Гостехиздат, Москва-
Ленинград, 1948.
[3] Курс дифференциального и интегрального исчисления, т. III. Гостехиздат, Москва—
Ленинград, 1949.
Халилов 3. И.
[1] Приближение решений краевых задач для общих эллиптических систем. Труды
Ин-та физ. и матем. АН Азербайджанской ССР 6 A953), 88—96.
ХатиашвилиГ. М.
[1] Задачи Альманзи—Митчелла для однородного анизотропного цилиндрического тела.
Труды Вычислительного центра АН Грузинской ССР 3 A962), 141—160.
|2] Задачи Альманзи для составного анизотропного цилиндрического тела. Труды Вычи-
Вычислительного центра АН Грузинской ССР 4 A963), 29—70.
[3] Некоторые пространственные задачи для анизотропных цилиндрических тел. Труды
Тбилисского матем. ин-та АН Грузинской ССР 32 A967), 148—163.
Хведелидзе Б. В.
fl) Линейные разрывные граничные задачи теории функций, сингулярные интегральные
уравнения и некоторые их приложения. Труды Тбилисского матем. ин-та АН Гру-
Грузинской ССР 23 A956), 3—158.
Цандеков М. И.
|1] Основные граничные задачи теории установившихся колебаний упругого изотроп-
изотропного тела для областей с угловыми особенностями. Труды Тбилисского гос. ун-та
56A955), 207—230.
Ч и ч и н а д з е Р. К.
[1] Теоремы единственности упруго-динамического состояния моментной теории. Анно-
Аннотации докладов семин. Ин-та прикл. матем. Тбилисского ун-та, № 5 A971), 47—52.
12] О матрицах фундаментальных решений уравнений динамики и колебаний в теории
упругости. Труды Ин-та прикл. матем. Тбилисского ун-та 3 A972), 183—186.
[3] Исследование третьей и четвертой трехмерных граничных задач статики моментной
теории упругости. Аннотации докладов семин. Ин-та прикл. матем. Тбилисского
ун-та, № 7 A973), 5—11.
42 В. Д. Купрадзе

650	ЛИТЕРАТУРА
Шапиро Г. С.
[I] Пространственные задачи теории упругости. Механика в СССР за тридцать лет.
Гостехиздат, Москва—Ленинград, 1950, 165—191.
Шаташвили С. X.
[1] Об одной смешанной пространственной задаче теории установившихся упругих ко-
колебаний. Труды Грузинского политехи, ин-та, № 1, F2), A959), 33—44.
[2] Изучение одной пространственной смешанной задачи теории установившихся коле-
колебаний. Труды Грузинского политехи, ин-та, № 3A15) A967), 23—32.
Ш а ч н е в В. А.
[1] О новых результатах в теории сопряженной термоупругости. В книге В. Н о в а а-
к и й. Динамические задачи термоупругости. «Мир», Москва, 1970, 237—250.
Шереметьев М. П.
[1] Пластинки с подкрепленным краем. Изд-во Львовского ун-та, Львов, 1960.
Ш е р м а н Д. И.
[l] Пространственная статическая задача теории упругости с заданными смещениями
на границе. ПММ 7, № 5 A943), 341—360.
[2] Об одной задаче кручения. ДАН СССР 63, № 5 A948), 499—502.
[3] Основные плоские и контактные (смешанные) задачи статической теории упругости.
Механика в СССР за тридцать лет. Гостехиздат, Москва—Ленинград, 1950, 192—
225.
Ш е ф е р Г.
[1] О приближенном решении основной бигармонической задачи. Сообш. АН Грузин
ской ССР 35, № 3 A965), 527—534.
[2] О приближенном решении бигармонической задачи для пространственной области.
Сообщ. АН Грузинской ССР 40, № 1 A965), 31—37.
Ш т а е р м а н И. Я.
[1] Контактные задачи теории упругости. Гостехиздат, Москва—Ленинград, 1949.
Я н е н к о Н. Н.
[1] Метод дробных шагов решения многомерных задач математической физики. «Наука»,
Новосибирск, 1967.
ЛАТИНСКИЙ АЛФАВИТ
Agmon S., Douglis A., Nirenberg L.
[1J Estimates near the boundary for solutions of elliptic partial differential equations
satisfying general boundary conditions I. Comm. Pure Appl. Math. 12, № 4 A959),
623—727 (русский перевод: Агмон С, Дуглис А., Ниренберг Л.
Оценки решений эллиптических уравнений вблизи границы, ИЛ, Москва, 1962).
12] Estimates near the boundary for solutions of elliptic partial differential equations
satisfying general boundary conditions II. Comm. Pure Appl. Math. 17, № 1 A964),
35-92.
Almansi E.
[1] Un teorema sulle deformazioni elastiche dei solidi isotropi. Atti Accad. Naz. Lincei
Rend. Cl. Sci. Fis. Mat. Natur., s. 5 16 A907), 865—867.
Atiyah M. R, Singer I. M.
[1] The index of elliptic operators on compact manifolds. Bull. Amer. Math. Soc. 69,
№ 3 A963), 422—433.
Becke.rt H.
fl| Ober die klassischen Randwertaufgaben in der Theorie der Warmespannungen in stu-
ckweise stetigen, anisotropen Korpern unter Kopplungsbedingungen. Z. Angew. Math.
Mech. 52A972), 111 — 122.
Bers L.
[1] Theory of psevdoanalitic functions. Lecture notes, New York Univ., New York 1953.
B) Mathematical aspects of subsonic and transonic gas dynamics. Surveys in Applied
Math., Ill, Inst ©f Math. Sci. New York Univ., New York, 1958 (русский перевод:
Б е р с Л., Математические вопросы дозвуковой и околозвуковой газовой дина-
динамики. ИЛ, Москва, 1961).
Bers L., John F., Schechter M.
[1] Partial differentia] equations. Interscience Pubi., New York—London—Sydney, 1964
(русский перевод: Б е р с Л., Джон Ф., Шех тер М., Уравнения с част-
частными производными. «Мир». Москва, 1966).
В i о t M. А.
|1] Thermoeiasticity and irreversible thermodynamics. J. Appl. Phy*. 27, № 3A956)
240—253.
Bogsio T.
[1] Nuova risolutione di un problema ioundamentale della teoria dell elasticita. Attl
della Reale Accad. dei Lincei 16, № 2 A907), 248—255.

ЛИТЕРАТУРА	651
В о j a r s к i В.
[1] On the index problem for systems of singular integral equations. Bull. Acad. Polon.
Sci. Ser. Sci. Math. Astronom. Phys. 11 A963), 653—655.
В о ley В. А.
[1] A method for the construction of fundamental solutions in elasticity theory. J. Math.
Phys. 36, № 3 A957), 261—268.
В о 1 ey В. А., Т о 1 i n s 1. S.
[1] Transient coupled thermoelastic boundary value problems in the half-space. J. Appl.
Mech. Trans. ASME 29 A962) (русский перевод: Боли Б. А., Т о л и н з И. С.,
Неустановившиеся граничные задачи взаимосвязанной теории термоупругости для
полупространства. Прикладная механика 29, № 4A962), 37—47).
Born M., Huang К.
[1] Dynamical theory of cristal lattices. Clarendon Press, Oxford, 1954 (русский перевод:
Борн М., Кунь X., Дийамическая теория кристаллических решеток. ИЛ,
Москва, 1958).
Boussinesq J.
[1] Applications des potentiales a Petude de l'equilibre et du mouvements des solides
elastiques. Paris, 1885.
Bramble J. H.
[1] Continuation of solutions of the equations of elasticity. Proc. London. Math. Soc,
Ser. 3, 10 A960), 335—353.
[2] Continuation of solutions of the equations of elasticity across a spherical boundary.
J. Math. Anal. Appl. 2 A961), 72—85.
BrowderF. E.
[1] Regularity properties at the boundary of solutions of elliptic boundary value pro-
problems. Bull. Amer. Math. Soc. 62, № 5A956), p. 381.
[2] On the regularity properties of solutions of elliptic differential equations. Comm.
Pure Appl. Math. 9 A956), 351—361.
Calderon A.
[1] Singular integrals. Bull. Amer. Math. Soc. 72A966), 426—465.
Calderon A., Weiss M., Zygmund A.
[1] On the existence of singular integrals. Proc. Symp. Pure Math. 10 A967), 56—73.
Calderon A., Zygmund A.
[1] On the singular integrals. Amer. J. Math. 78, № 2A956), 289—309.
[2] Singular integral operators and differential equations. Amer. J. Math. 79, № 4 A957),
901—921.
[3] On the existence of certain singular integrals. Acta Math. 88, № 1—2 A952), 85—139.
[4] Local properties of solutions of elliptic partial differential equations. Studia Math. 20,
№ 2 A961), 171—225.
Сатрапа to S.
[1] Sui problemi al contorno per sistemi di equazioni differentiali lineari del tipo dell'ela-
sticita. Ann. Scuola Norm. Sup., Pisa 13, № 3 A959), 275—302.
[2] Proprieta di taluni spazi di Banach connessi con la teoria dell'elasticita. Ann. Scuola
Norm. Sup., Pisa 16, № 2 A962), 121 — 149.
С а г s I a w H. S.
[1] Introduction to the mathematical theory of the conduction of heat in solids. New
York, Dover Publications. 1945 (русский перевод: К а р с л о у X. С, Теория теп-
теплопроводности. Гостехиздат, Москва, 1947).
С а г s I a w H. S., J a e g e г J. С.
[1] The conduction of heat in solids. Oxford, 1947 (русский перевод со 2-го изд.:
Г. К а р с л о у и Д. Е г е р, Теплопроводность твердых тел. Физматгиз, Москва.
1964).
Cosserat E., Cosserat F.
[1] Sur les equations de la theorie de I'elasticite. С R. Acad. Sci., Paris 126A898),
1129—1132.
f2] Theorie des corps deformables. Herman, Paris, 1909.
Chadwick P.
[1] Thermoelasticity. The dynamical theory. Progress of solid mechanics. Amsterdam,
1960
Daiermos CM.
[1] On the existence and the asymptotic stability of solutions of the equations of linear
thermoelasticity. Arch. Rational Mech. Anal. 29, JMb 4A968), 241—271.
D e b у е P.
[1] Zur Theorie der spezifishen Warmen. Ann. d. Physic IV, Folge 39 A912), 789—83У.
Denbigh K- G.
[1] The thermodynamics of the steady state. London—New York, 1951 (русский пере-
перевод: Д е н б и г К., Термодинамика стационарных необратимых процессов. ИЛ,
Москва, 1954).
42*

652	ЛИТЕРАТУРА
Doetsch G.
[1] Einfuhrung in Theorie und Anwendung der Laplace—Transformation. Birkhauser Verb,
Basel—Stuttgart, 1958.
Douglis A., Nirenberg L.
[1] Interior estimates for elliptic system of partial differential equations. Comm. Pure
Appl. Math., 8, № 4 A955), 503—538.
Duff in R. J.
[1] Annalitic continuation in elasticity. J. Rational Mech. Anal. 5, № 6 A956), 939—950.
Duvaut G., Lions J. L.
[1] Les inequations en mecanique et en physique. Paris, 1972.
Edwards R. E.
fl] Functional analysis. Holt, Rinehart and Winston, New York—Chicago—San Francis-
Francisco—Toronto—London, 1965 (русский перевод: Эдварде Р., Функциональный
анализ. «Мир», Москва, 1969).
Е г i с k s e n J. L.
[1] Nonexistence theorems in linearized elastostatics. J. Differential Equations 1, № 4
A965), 446—451.
Eubanks R. A., Sternberg E.
[1] On the completeness of the Boussinesq—Papkovich functions. J. Rational Mech.
Anal. 5, № 5 A956), 735—746 (русский перевод: Юбенкс P. A., G т е р н б е р г Э.,
О полноте функций напряжений Буссинеска—Папковича. Механика, сб. перев. 6 D6)
A957), 99—109).
F i с h e r a G.
[1] Theoremi di completezza sulla frontiera di un dominio per taluni sistemi di funzioni.
Ann. Mat. Рига Appl. 27 A948), 1—28.
[2] Una introduzione a la teoria delle equazioni integrali singulari. Rend. Mat. e Appl.
17, № 1—2 A958), 82—191.
[3] Applicazione della teoria del potenziale di superficie ad alcuni problem! di anaiisi
funczionale lineare. J. Mat. Battaglini 78 A949), 71—80.
[4] Sull' esistenza e sul calcolo delle soluzioni dei problemi al contorno, relativi а1Г equi-
librio di un corpo elastico. Ann. Scuola Norm. Sup., Pisa 4, s. 3. № 1—2 A950),
35—99.
[5] Sul problema elastostatico di Signorini con ambigue condizioni al contorno. Rend.
Accad. Naz. Lincei, s. 8 34 A963), 138—142.
[6] Linear elliptic differential systems and eigenvalue problems. Lecture notes in mathe-
mathematics. 8. Springer—Verlag, Berlin—Heidelberg—New York, 1965.
[7] Existence theorems in elasticity. Handb. d. Physik, Bd. VI/2, № 3, Springer—Verlag,
Heidelberg, 1973.
Frank Ph., M i s e s R.
[1] Die Differential und Integralgleichungen, Bd. II. Braunschweig, 1935 (русский пере-
перевод: Франк Ф., Мизес Р., Дифференциальные и интегральные уравнения
математической физики, ОНТИ, Москва, 1937).
Fredholm 1.
[1J Sur l'integrale fondamentale d'une equation differentielle elliptique ч coefficients
constants. Rend. Circ. Math. Palermo 25 A908).
[2] Solution d'un probleme fondamental de la theorie de 1'elasticite. Ark. Mat. Astronom.
Fys. 2, № 28 A906), 3—8.
Freudenthal H.
fl] Uber ein Beugungsproblem aus der elektromagnetischen Lichttheorie. Compositio
Math. 6 A938), 221—227.
Freudenthal A.M., Geiringer H.
[1] The mathematical theories of the inelastic Continuum. Handbuch der Physik, vol. VII,
Elasticity and Plasticity. Springer—Verlag, 1958.
F r i e d r i с h s K- O.
[1] A theorem of Lichtenstein. Duke Math. J. 14A947), 67—82.
[2] On the boundary value problems of the theory of elasticity and Korn's inequality.
Ann. of Math. 48A947), 441—471.
[3] On the differentiability of solutions of linear elliptic differential equations. Comm.
Pure Appl. Math. 6, № 3 A953), 299—326.
Friedman A.
[lj Partial differential equations of parabolic type. Inc. Englewood Cliffs, Prentice—Hall,
1964 (русский перевод: Фридман А., Уравнения с частными производными
параболического типа. «Мир», Москва, 1968).
Fung Y. С.
[1] Foundation of Solid Mechanics. Prentice—Hall, New York, 1965.
G i г a u d G.
[1] Equations a integrates principaies Etude suivie d'une application. Ann. Sci. Ecole
Norm. Sup. 51 A934), 251—372.

ЛИТЕРАТУРА	653
[2] Equations et systemes d'equations ou figurent des valeurs principales d'integrales.
C. R. Akad. Sci., Paris 204 A937), 628—630.
[3] Sur differentes questions relatives aux equations du type elliptique. Ann. Sci. Ecole
Norm. Sup. 47 A930), 197—266.
G г a m m e 1 R.
[1] Mechanik der elastischen Korper. Handbuch der Physik, Bd. VI. Springer—Verlag,
Berlin, 1928.
Greco D.
[1] Nuove formole integrali di maggiorazione per le soluzioni di un equazione lineare
di tipo ellipttico ed applicazioni alia teoria del potenziale. Ricerche Mat. 5 A956),
126—149.
Green A. E., Z e r n a W.
[1] Theoretical elasticity. Clarendon Press, Oxford, 1954.
G r i о 1 i G.
[1] Mathematical theory of elastic equilibrium. Springer—Verlag, Berlin—Gottingen—
Heidelberg, 1962.
B] Problemi d'integrazione integrale del problema fondamentale dell'elastostatica. Simpo-
sio internaz. Applic. analisi fis. Mat.. Gagliari—Sassari, 1964, Roma, 1965,
67—77.
Go b e r t J.
fl] Une inegalite fondamentale de la theorie de Telasticite. Bull. Soc. Roy. Sci, Liege,
3_4 A962), 182—191.
Goodier J. N., Hodge P. G.
Ц] Elasticity and plasticity. Surv. Appl. Math., John Wiley and Sons inc., New York,
Chapman and Hall Ltd., London, 1958 (русский перевод: Гудьер Дж. Н.,
X о д ж Ф. Г. Упругость и пластичность. ИЛ, Москва, 1960).
Goursa t E.
[1] Cours d'analyse mathematique, t. III. Gauthier—Villars, Paris, 1911 (русский пере-
перевод с пятого французского издания: Г у р с а Э., Курс математического анализа
т. III. ГТТИ, Москва—Ленинград, 1934).
Groot S. R., d e
[1] Thermodynamics of irreversible processes. North Holland publishing company, Amster-
Amsterdam. Interscience publishers Inc., New York, 1952 (русский перевод: Гроот С. Р.,
Термодинамика необратимых процессов. Гостехиздат, Москва, 1956).
Groot S. R. de, M a z u r P.
[1] Non-equilibrium thermodynamics. North Holland publishing company, Amsterdam,
1962 (русский перевод: Гроот СР., Мазур П., Неравновесная термодина-
термодинамика. «Мир», Москва, 1964).
Hadamard J.
[1] Sur 1 equilibre des plaaues elastiques circullaires libres ou appuyees et celui de la
sphere isotrope. Ann. Ecole Norm. Sup., ser. 3 6, 18 A901), 313—342.
Hamming R. W.
[1] Numerical methods for scientists and engineers. McGraw-Hill, New York—San Fran-
Francisco—Toronto—London, 1962 (русский перевод: X e м м и н г Р. В., Численные
методы. «Мир», Москва, 1968).
Hayes M.
[1] On the displacement boundary value problems in linear elastostatics. Quart. J. Mech.
Apll. Math. 19, № 2 A966), 151—155.
HetnarskiR. B.
[1] Coupled thermoelastic problem for the half-space. Bull. Acad. Polon. Sci., Ser. Sci.
Tech. 12, № 1 A964), 49—57.
Heywood H. В., Frechet M.
[1] L'equation de Fredholm et ses applications a la Physique mathematique. Hermann,
Paris, 1912.
Hobson E. W.
[1] The theory of spherical and ellipsoidal harmonics. Cambridge Univ. Press, Cambridge,
1931 (русский перевод: Г об сон Е. В., Теория сферических и эллипсоидаль-
эллипсоидальных функций. ИЛ, Москва, 1952).
HormanderL.
[1J On the theory of general partial differential operators. Acta math. 94 A955), 161—
248 (русский перевод: Хёрмандер Л., К теории общих дифференциальных
операторов в частных производных. ИЛ, Москва, 1959).
[2] Linear partial differential operators. Springer—Verlag, Berlin—Gottingen—Heidel-
Berlin—Gottingen—Heidelberg, 1963 (русский перевод: Хёрмандер Л., Линейные дифференциальные
операторы с частными производными. «Мир», Москва, 1965).
Huntington H. В.
A] The elastic constants of cristals. Solid state physics 7 A958), 213—242 (русский пере-
перевод: Хантингтон Г., Упругие постоянные кристаллов. Успехи физ. наук 74,
вып. 2—3 A961), 303—335).

654	ЛИТЕРАТУРА
1 esan D.
fl] Existence theorems in the theory of micropolar elasticity. Internat. J. Engrg. Sci. 8,
№ 9A970), 777—791.
[2] Existence theorems in micropolar elastostatics. Internat J. Engrg. Sci. 9, № 1 A971),
59—78.
Jgnaczak J., Nowacki W.
[1] Osobliwe rownania calkowe termosprezystosci. Rozpr. In. Syn., 4, № 13 A965), 655—
670.
12] Singular integral equations of thermoelasticity. Internat. J. Engrg. Sci. 5, № 1 A966),
53—68.
Jentsch L.
[1] Zur Thermoelastostatik stuckweise homogener Kdrper. Arch. Rational Mech. Anal. 24,
№ 2 A967), 141—172.
[2] Die elastostatischen Greenschen Tensoren fur den Halbraum mit Anwendungen auf
Warmespannungsprobleme. ZAMM 48A968), Heft 2, 177—126.-
[3] Ober Warmespannungen in Korpern mit stuckweise konstanten Lameschen Elastizi-
tatsmoduln. Schriftenreihe fur Mat. Mech. Deutsch. Akad. d. Wiss., Heft 14, Ber-
Berlin, 1972.
John F.
[1] Plane waves and spherical means applied to partial differential equations. Interscience
Publishers Inc., New York. Interscience Publishers Ltd., London, 1955 (русский
перевод: Й о н Ф., Плоские волны и сферические средние. ИЛ, Москва, 1958).
Kecs W., Teodorescu P.P.
[1] Aplicatii ale teoriei distributiilor in mecanicS. Ed. Ac. RS Romania, Bucure§ti, 1970.
К e 1 1 о g O. D.
[1] Foundations of potential theory. Springer—Verlag, Berlin, 1929.
Kinoshita N., Mura T.
[1] On boundary value problem of elasticity. Res. Rept. Fac. Engrg. Meiji. Univ., № 8
A956), 56—82.
К i г с h h о f f G.
fl] Vorlesungen uber mathematische Physik, Bd. 1—4. Aufl. Leipzig, 1897 (русский
перевод: Кирхгоф Г. Р., Механика. Лекции по математической физике. Изд-во
АН СССР, Москва, 1962).
К i t t e 1 С h.
[1] Introduction to solid state physics. McGraw-Hill, New York—Willey—London, 1956
(русский перевод: Киттель Ч., Введение в физику твердого тела. Физматгиз,
Москва, 1963).
Knops R. J.
[1] Uniqueness for the whole space in classical elasticity. J. London Math. Soc. 39, № 4
A964), 708—712.
Knops R/J., Payne L. E.
[1] Uniqueness theorems in linear elasticity. Springer tracts in natural philosopy, vol. 19,
Springer—Verlag, Berlin—Heidelberg—New York, 1971.
Koiter W. T.
[1] Approximate solutions of Wiener—Hopf type integral equations with applications.
I.	General theory. Proc. Koninkl. Nederh Akad. Wetensch. B57, № 5 A954), 558—564.
[2] Approximate solution of Wiener—Hopf type integral equations with applications.
II.	Proc. Koninkl. Nederl. Akad. Wetensch. A58, № 2 A955), 257—258.
[3] General theorems for elastic-plastic solids. Progress in solid mechanics, vol. 1, North
Holland publishing company, Amsterdam, 1960 (русский перевод: К о й т е р В. Т.,
Общие теоремы теории упруго-пластических сред. ИЛ, Москва, 1961).
[4] Couple-stresses in the theory of elasticity. Proc. Koninkl. Nederl. Akad. Wetensch.
B67, № 1 A964), 17—44 (русский перевод: К ой тер В. Т., Моментные напря-
напряжения в теории упругости. Механика, сб. перев., 3(91) A965), 89—112).
К о m р i s V.
[1] Losung singularer Integralgleichungen der Elastizitatstheorie im Falle unstetig vor-
gegebener Spannungen auf dem Rande. Zeitschrift Ang. Math. Mech. 50 A970), 131 —
133.
К о г п А.
[1] Sur les equations de l'elasticite. Ann. Sci. Ecole Norm. Sup., ser. 3 24 A907), 9—75.
[2] Solution generate du probleme d'equilibre dans la theorie de l'elasticite dans le cas
ou les efforts sont donnees a la surface. Ann. Fac. Sci. Univ. Toulouse, 2-me ser. 10
(J908), 165—269.
13] Ober die Losung des Grundproblems der Elastizitatstheorie. Math. Ann. 75 A914),
497549
[4] Lehrbuch der Potentialtheorie, Bd. 1, II. Berlin, 1899.
Kroner E.
11] Das Fundamentalintegral der anisotropen elastischen Differentialgleichungen. Z. Piiy-
sik 136 № 4 A953), 402—410.

ЛИТЕРАТУРА	655
Lamb H.
Г11 On the propagation of tremors over the surface of elastic solid. Phil. Trans. Roy.
Soc London, ser. A, 203, № 1 A904).
Lame G.
[1] Lemons sur les coordonnees curvilignes et leurs divers applications. Paris, 1859.
[2] Suirintegrazione delle equazioni deirequilibrio dei corpi elastici isotropi. Rend. R.
Accad. Lincei, ser. 5, 15 A906), 426—432.
La urice lla G.
[1] Alcune applicazioni della teoria delle equazioni funzionali alia Fisica—Mathematica.
11 Nuovo Cimento, s. 5, 13A907), 104—118, 155—174, 237—262, 501—518.
12] Lemons sur la theorie mathematique de l'elasticite des corps solides. Paris, 1852.
\3) Sur {'integration de 1'equation relative a l'equilibre des plaques elastiques encastrees.
Acta Math. 32 A909), 201—256.
Le vi E. E.
|1] Sulle equazione lineari totalmente ellittiche alle derivate parziali. Rend. Circ. Mat.
Palermo 24 A907), 275—317 (русский перевод: Л е в и Е. Е., О линейных эллипти-
эллиптических уравнениях в частных производных. УМН, вып. 8 A940), 249—292).
Lichtenstein L.
il] Neuere Entwicklung der Theorie partieller Differentiai-gleichungen zweiter Ordnung
vom elliptischen Typus. Encyclopadie der Math. Wissensch. 2, № 32, Leipzig A923—
1927), 1279—1340.
|2] Ober die erste Randwertaufgabe der Elastizitatstheorie. Math. Z. 20 A924), 21—28.
Lions J. L.> Ma genes E.
Ill Problemes aux limites non homogenes et applications, vol. 1. Dunod, Paris, 1968 (рус-
(русский перевод: Лионе Ж. Л., Мадженес Э., Неоднородные граничные
задачи и их приложения. «Мир», Москва, 1971).
Lorentz G. G.
il J Fourier— Koeffizienten und Funktionenklassen. Math. Z. 51 A948), 135—149.
Love A. E. H.
[1] A treatise on the mathematical theory of elasticity. 4-th edit., Cambridge Univers.
Press, 1959 (русский перевод: Л я в А., Математическая теория упругости. ОНТИ,
Москва—Ленинград, 1935).
Magenes E.
П) Sulla teoriea del potenziale. Rend. Sem. Mat. Univ. Padova, 24 A955), 510—522.
Magenes E., Stampacchia G.
flj 1 problemi al contorno per le equazione differenziali di tipo ellittico. Ann. Sci. Norm.
Sup., Pisa, Ser. 3 123 A958), 247—357.
Marcolongo R.
[1] Teoria matematica dell equilibrio dei corpe elastici. Milan, 1904.
M a u г i n K.
[1] Metody przestrzeni Hilberta. Polska Akademia Nauk, Monografie Matematycene, 36,
Warszawa, 1959 (русский перевод: Морен К., Методы гильбертова пространства,
«Мир», Москва, 1965).
М е 1 a n E., Parkus H.
[1J Warmespannungen infolge stationarer Tempera turf elder. Springer—Verlag, Wien, 1953
(русский перевод: М е л а н Е., П а р к у с Г., Термоупругие напряжения.
Физматгиз, Москва, 1958).
Milne-Thomson L. М.
[1] Plane elastic systems. Springer—Verlag, Berlin—Gottingen—Heidelberg, 1960.
[2] Antiplane elastic systems. Springer—Verlag, Berlin, 1962.
M i n d 1 i n R. D.
|1J influence of couple-stresses on stress concentrations. Experimental Mechanics 3 A963),
1—7 (русский перевод: Мин длин Р. Д., Влияние моментных напряжений
на концентрап'ю напряжений. Механика, сб. перев., 4 (86) A964), 115—160).
Mindlin R. D., 1 listen H. F.
A) Effects of couple-stresses in linear elasticity. Arch. Rational Mech. Anal., 11, № 5
A962), 415—448 (русский перевод: Миндлин Р. Д. Тирстен Г. Ф., Эф-
Эффекты моментных напряжений в линейной теории упругости. Механика, сб. перев.,
4 (86) A964), 80—115).
Miranda С.
[1] Equazioni alle Derivate Parziali di Tipo Ellipttico. Springer—Verlag, Berlin—Got-
Berlin—Gottingen—Heidelberg, 1955 (русский перевод: Миранда К., Уравнения с част-
частными производными эллиптического типа. ИЛ, Москва, 1957).
Morrey C.B.
[1] Second order elliptic systems of differential equations. Contributions to the theory
of partial differential equations. Ann. of Math. Studies, № 33 A954), 101—159.
[2] Elliptic differential equations with Holder continuous coefficients. Ann. Math. Soc.
Notices 5 A958), p. 466.

656	ЛИТЕРАТУРА
Neuber H.
[1] Ein neuer Ansatz zur Losung raumlicher Probleme der Elastizitatstheorie. Z. Angew.
Math. Mech. 14 A934), 203—212.
[2] Kerbspannungslehre. Springer—Verlag, Berlin, 1958.
Neumann F.
[1] Vorlesungen iiber die Theorie der Elasticity t der festen Korper und des Lichtathers.
Teubner, Leipzig, 1885.
Nirenberg L.
[1] On elliptic partial differential equations. Ann. Scuola Norm. Sup., Pisa 13, № 2
A959), 115—162.
N о w а с к i W.
[1] On some problems of thermoelasticity. Problems of continuum mechanics. Philadel-
Philadelphia, 1961.
[2] Thermoelasticity. Pergamon Press, Oxford, 1962.
[3] Dynamiczne zagadnienia termosprezystosci. PWN Warszawa, 1966 (русский сокра-
сокращенный перевод: Новадкий В., Динамические задачи термоупругости. «Мир»,
Москва, 1970).
[4] Couple-stresses in the theory of thermoelasticity, 1. Bull. Acad. Polon. Sci., Ser. Sci.
Techn. 14, № 2 A966), 129—138.
[5] Couple-stresses in the theory of thermoelasticity, II. Bull. Acad. Polon. Sci., Ser.
Sci. Techn. 14, № 3 A966), 263—272.
[6] Couple-stresses in the theory of thermoelasticity, III. Bull. Acad. Polon. Sci., Ser.
Sci. Techn. 14, № 8 A966), 801—809.
[7] Моментные напряжения в термоупругости. Прикл. механика 3, № 1 A967), 3—17.
[8] Teoria niesymetryczney spr§zystosci. PWN, Warszawa, 1971.
Palais R. S.
[1] Seminar on the Atiyah—Singer index theorem. Princeton Univ. Press, Princeton—
New Jersey, 1965 (русский перевод: Пале Р., Семинар по теореме Атьи—Зин-
Атьи—Зингера об индексе. «Мир», Москва, 1970).
Р а г k u s H.
[1] Instationare Warmespannungen. Springer—Verlag, Wien, 1959 (русский перевод:
П а р к у с Г., Неустановившиеся температурные напряжения. Физматгиз, Москва,
1963).
[2] Methods of solution of thermoelastic boundary value problems. Proc. Third Sym.
on Naval Struct. Mechanics, Pergamon Press, New York, 1963.
Payne L. E., Wienberger H. F.
[1] On Korn's inequality. Arch. Rational Mech. Anal. 8, № 2 A961), 89—98.
Pearson С. Е.
[1] Theoretical Elasticity. Harvard Univ. Press., Cambridge—Massachusetts, 1959.
Pham The Lai
[1] Potentiels elastiques, tenseurs de Green et de Neumann. Mechanique 6, № 2 A967),
211—242.
P 1 e i j e 1 A.
[1] Proprietes asymptotiques des fonktions et valeurs propres de certains problemes de vib-
vibrations. Ark. Mat. Astr. Fys. 27A, 13 A940), 1—100.
P r a g e r W.
[1] Einfuhrung in die Kontinuummechanik. Birkhauser Verlag, Basel—Stuttgart, 1961
(русский перевод: П р а г е р В., Введение в механику сплошных сред. ИЛ,
Москва, 1963).
R е 1 1 i с h F.
[1] Uber das asymptotische Verhalten der Losungen von Аи -j- Xu ~ 0 in unendlichen
Gebieten. Jber. Deutsch. Math. Verein, 53 A943), 57—65.
[2] Das Eigenwertproblem von Am -f- Xu = 0 in Halbrohren. Studies Essayer prs. to R.
Courant, 1948, 329—344.
R i e d e г G.
[1J Iterationsverfahren und Operatorgleichungen in der Elastizitatstheorie. Abh. Braun-
Braunschweig. Wiss. Gesell. 14 A962), s. 109.
B] Mechanische Deutung und Klassifizierung einiger Integralverfahren der ebenen Eiasti-
zitatstheorie. Bull. Acad. Polon. Sci., Ser. Sci. Techn. 16A968), 101 — 114.
R u d i n W.
[1] Principles of mathematical analysis. McGraw-Hill, New York—Toronto—London,
1953 (русский перевод: Р у д и н У., Основы математического анализа. «Мир»,
Москва, 1966).
Schmidt E.
[1] Betnerkung zur Potenzialtheorie. Mathematische Abhandlungen Hermann Amandus
Schwarz zu seinem funfzigjarigen Doktorjubilaum. Berlin, 1914.
See ley R. T.
[1] The index of elliptic systems of singular integral operators. J. Math. Anal. Appl.
7A963), 289—309.

ЛИТЕРАТУРА	657
Ser г i n J. В.
[1] Existence theorems for some hydrodinamical free boundary problems. J. Rational
Mech. Anal. 1 A952), 1—48.
Sneddon 1. N.
[1] Fourier transforms. McGraw-Hill, New York—Toronto—London 1951 (русский пере-
перевод: И. С н е д д о н, Преобразования Фурье. Москва, ИЛ, 1955).
[2] Elements of partial differential equations. McGraw-Hill, New York, 1956.
[3] Dual equations in elasticity. Applications of the theory of functions in continuum
mechanics. Proceedings of the international symposium held in Tbilisi, 1963, Moscow,
1965, 76—94.
Sneddon I. N.. Berry D. S.
[1] The classical theory of elasticity. Springer—Verlag, Berlin—Gottingen—Heidelberg,
1958 (русский перевод: И. Н. Снеддон и Д. С. Б е р р и, Классическая
теория упругости. Физматгиз, Москва, 1961).
Sneddon I. N., Lowengrub
[1] Crack problems in the classical theory of elasticity. New York—Sydney—Toronto, 1969.
Sokolnikoffl. S.
[1] Mathematical theory of elasticity. McGraw-Hill, New York—London, 1946. Second
edition, McGraw-Hill, New York—Toronto—London, 1956.
Solomon L.
[1] Elasticite lineaire. Masson, Paris, 1968.
Sommerfeid A.
[1] Die Greensche Funktion der Schwingungleichung. Jber. Deutsch. Math. Verein. 21
A912), 309—353.
S о u t h w e 1 1 R. V.
[1] An introduction to the theory of elasticity. Clarendon Press, Oxford, 1936 (русский
перевод: Саусвелл Р., Введение в теорию упругости, ИЛ, Москва, 1948).
Stein Е, М.
[1] Singular integrals and differentiability properties of functions. Princeton Univ. Press,
Princeton—New Jersey, 1970 (русский перевод: Стейн И. М., Сингулярные
интегралы и дифференциальные свойства функций. «Мир», Москва, 1973).
Stone М. Н.
A] Linear transformations in Hilbert space and their applications to analysis. Amer.
Math. Soc. Colloquium Pub., vol. 15, New York, 1932.
S z e f e r G.
[1] On the solution of certain system of dual integral equations and its application in
the theory of elasticity. Bull. Acad. Polon. Sci., Ser. Sci. Techn. 13, Nb 2 A965),
79—87.
Teodorescu P. P.
[1] Sur le probleme du demi-quart d'espace elastique soumis a Faction d'une charge tan-
gentialle. Rev. Roumaine Sci. Techn., Ser. Mec. Appl. 10, № 1 A965), 81 — 108.
[2] Sur le calcul du quart d'espace elastique. Rev. Roumaine Sci. Techn., Ser. Mec. Appl.
11, № 5 A966), 1141—1172.
[3] Probleme spatiale in teoria elasticitatii. Edit. Academiei, Bucuresti, 1970.
[4] Dinamica corpurilor liniar elastice. Edit. Academiei, Bucuresti, 1972.
Timoshenko S. P., Goodier J. N.
[1] Theory of elasticity. McGraw-Hill, Second Edit., New York, 1951.
Timoshenko S. P., Woino wsky - Krieger S.
[1] Theory of plates and shells. McGraw-Hill, Second Edit. New York—Toronto—Lon-
York—Toronto—London, 1959 (русский перевод: Тимошенко С. П., Войновский-К ри-
риге р С, Пластинки и оболочки. «Наука», Москва, 1966).
Tomson W.
[1J Dynamical problems regarding elastic spheroidal shells and spheroids of incompres-
incompressible liquid. Mathematical and Phys. papers, vol. 3, Cambridge, 1892.
T r e f f t z E.
[1] Mechanik der elastischen Korper. Handbuch der Physik, VI, Springer—Verlag, Berlin,
1928 (русский перевод: Треффц Е. — Математическая теория упругости. ГТТИ,
Москва, 1934).
Tricomi F. G.
[1] Formula d'inversione dell' ordine di due integrazioni doppie «con asterisco». Rend.
Accad. Naz. Lincei 3, ser. 6a № 9 A926), 535—539.
[2] Equazioni integrali contenenti il valor principale di un integrale doppio. Math. Z.
27 A928), 87—133.
TruesdellC.
[1] The mechanical foundations of elasticity and fluid dynamics. J. Rational Mechan.
Anal. 1 A952), 125—300; 2 A953), 595—616.
Turteltaub M. J., Sternberg E.
[1] Elastostatic uniqueness in the half space. Arch. Rational Mech. Anal. 24, № 3 A967),
233—242.

558	литература
Vo i g t W.
[1] Theoretische Studien fiber die Elasticity tsverhalnisse der Kristalle. Abh. der Konigl.
Ges. Wiss., Gottingen. 34 A887).
[2] Lehrbuch der Kristailphysik. Berlin, 1928.
V о 1 t e г г а V.
[1] Sulle equazioni integro-differenziali della teoria dell' elasticity. Rend. Accad. Naz
Lincei, s. V, 18 A909).
[2] Drei Vorlesungen fiber neuere Fortschritte der Mathematischen Physik, gehalten im
September 1909 an der Clark—University. Leipzig—Berlin, 1914.
W asow W. R., Forsythe G. E.
П! Finite-difference methods for partial differential equations- John Wiley and Sons,
Inc., New York—London, 1960 (русский перевод: В а з о в В. Р., Форсайт ЖЕ.,
Разностные методы дифференциальных уравнений в частных производных. ИЛ.
Москва, 1963).
Was h i г <u К.
[1| Variational methods in elasticity and plasticity. Pergamon Press, Oxford» 1968.
W a t s о n G. N.
[1] Theory of Bessel functions. Cambridge, 1944 (русский перевод: Ватсон Г. Н.,
Теория бесселевых функций. ЙЛ, Москва, 1949).
Webster A. G.
[1] The dynamics of particles and rigid elastic and fluid bodies. B. G. Teubner, Leipzig,
1904 (русский перевод: Вебстер А. Г., Механика материальных точек, упругих
и жидких тел. ГТТИ, Москва—Ленинград, 1933).
Weiner J. Н.
[1] A uniqueness theorems for the coupled thermoelastic problems. Quart. Appl. Math.
15, № 1 A957), 102—105.
Weyl H.
|1] Das asymptotische Verteilungsgesetze der Eigenschwingungen eines beliebig gestal-
teten elastischen Korpers. Rend. Circ. Mat. Palermo 39 A915), 1—49.
12] Kapazitat von Strahlungsfeldern. Math, Z. 55, № 2 A952), 187—198.
Zorsk i H.
[1] Singular solutions tor thermoelastic media. Bull. Acad. Polon. Sci., Ser. Sci. Techn.
6, № 6A958), 331—339.
Zaremba S.
[1] Sur un probleme mixte relatif a Pequation de Laplace. Bulletin de TAcademie des
sci. de Cracovie, Cl. des sci. math, et natur., ser. A A910), (русский перевод:
Заремба С, Об одной смешанной задаче, относящейся к уравнению Лапласа.
УМН 1, № 34 A946). 125—146).
Zygmund A.
[1] Trigonometric Series, v. I. Cambridge, Univers. Press, 1959 (русский перевод: Зиг-
Зигмунд А., Тригонометрические ряды, т. 1. «Мир», М., 1965).
[2J Trigonometric series, v. II. Cambridge, Univers. Press, 1959 (русский перевод' Зиг-
Зигмунд А., Тригонометрические ряды, т. II, «Мир», Москва, 1965).
[3J lntegrales singulieres. Universite de Secretariat rnathematique d'Orsay, 1965.

ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
A U В — объединение множеств А и В
А (] В — пересечение множеств А и В
А\В — разность множеств А и В
А — замыкание множества А
дА — граница множества А
0 — пустое множество
х? А — х — элемент множества А
х (J А —л: не является элементом множества А
А а В — А является подмножеством мно-
множества В
A CfZ В — А не является подмножеством мно-
множества В
{а ? А | Р (а)} —множество тех элементов из А,
для которых истинно высказывание Р (а)
А X В = {(а, Ь), а? А к b ? В} — декартово
произведение множеств А и В
у — квантор всеобщности (ух. . .читается
гак: «для всякого х. . .»)
3 — квантор существования (з* - . .читается
гак: «существует х. . .»)
R — множество действительных чисел
Z — множество комплексных чисел
Ет — m-мерное евклидово пространство
х== (хг, , . ., хт), у = (у1у . . ., ут), г =
= (zx, ., гт) — точки пространства Ет
гл.
— норма элемента х
\х\ = у х\ -+-
в пространстве Ет
D+ — ограниченная область трехмерного ев-
евклидова пространства Е3
D~ = E3\D+ — дополнение замыкания D+
до всего пространства
5 = dD+ = dD- — граница области D+ (D~)
Ш {х, 6) = {у^Е% \\х — у \ < б} — открытый
шар в пространстве Ен с центром в точке х
и радиуса б
С (х, б) = \у?Е.л 11 х — у | = 6} — граница
шара Ш (х, 6}
Ц (*, п, б) — круглый открытый цилиндр
в Е3, имеющий высоту 26, осью которого
служит п = {пх, п2, п3), центром сим-
симметрии — точка х и радиус основания
которого равен б
S (х, б) = S П U (*. л. б) ПРИ ^65, п —
нормаль поверхности S в точке л:
(' ^) = min {\yf — л: | |"|}
р (jc, A) — расстояние от точ-
точки х до множества А
6t-y — символ Кронекера
&ijk — символ Леви-Чивита х)
X, \i — постоянные Ламе
Я, fx, a, e, v, p — упругие по-
постоянные микрополяр-
микрополярной (моментной)изотроп-
(моментной)изотропной однородной среды
и» Л» V — термоупругие по-
постоянные
J — специальная динамиче-
динамическая характеристика ми-
микрополярной среды
р — плотность среды
и = (иъ u2, u3) — вектор сме-
смещения
со = (со1, GJ, со3) — вектор-
вращения
9 — разность температуры
U = (UltU2t U3,U,) = (uy 6)
U = (Ult . . ., U6) = (и, со)
xitl) {x, t) — вектор силового
напряжения в точке х
по направлению п = (пъ
п2, п3) в момент времени t
|ы(«) (х, t) — вектор мОхМент-
ного напряжения в точ-
точке х по направлению п =
= (п1, п2, п3) в момент
времени t
&~(х, f) — массовая сила
$? (х, t) — массовый момент
Q(x, t) — тепловой источник
ец — компоненты деформа-
деформации в классической упру-
упругости и термоупругости
иц — компоненты деформа-
деформации в моментной упруго-
упругости
cujy — компоненты круче-
кручения — изгиба в момент-
моментной упругости
%ij — компоненты силового
напряжения в классиче-
классической и моментной упру-
упругости
3
5
4
3
3
8
12
12
I 1
п.
2
1
2
1
3
2
1) Справа указывается глава, параграф и пункт, рде впервые вводится обоваачение.

660
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
\iij — компоненты моментно-
го напряжения
B) — локальная система
координат
с (г) — касательная плоскость
поверхности в точке z
п (z) — орт внешней нормали
поверхности в точке г
1
15
f 15
т (z, d) —	I
P™ — функция Лежандра III
H\)i) — функция Ганкеля III
rW=irf/W|3x3 ~ м^-
рица фундаментальных
решений Кельвина	II
Г (х, со) = || Гч (*, со) |зх3 -
матрица фундаменталь-
фундаментальных решений Купрадзе II
рица фундаментальных
решений уравнения ста-
статики в моментной упру-
упругости	II
матрица фундаменталь-
фундаментальных решений уравнений
колебаний в моментной
упругости	II 2
Ф(х, «В)=|Ф (ж,ш)|4х4-
матриц? фундаменталь-
фундаментальных решений уравнения
колебаний в термоупру-
термоупругости	II 3
^iky (х> У) — тензор Грина VII 1
&-й задачи
Ф+ (у) ~ {ф (#)}"*" — гранич-
граничное значение функции ф
из D+ в точке y?dD+ I 14
Ф" (у) = {ф(у)}~ — граничное
значение функции ф из
D- в точке y?dD~	I 14
Ck (Q) — множество fe-раз не-
непрерывно дифференци-
дифференцируемых функций в об-
области Q
С* (Q)-
Gt (my a) —
G2 (m, p) -
G (m, a, P) —
G* (m, a, p) —
Z (m, 5, a) —
Lp (Q) -
L(pm) E) -
Я E, P) -
1
I
I
I
IV
IV
IV
IV
IV
IV
IV
IV
IV
15
15
15
2
2
2
2
2
5
5
11
И
15
15
1
3
1
3
3
3
15
О
о
2
2
2
2
2
2
4
2
5
5
3
2
4 (дх) — основной дифферен-
дифференциальный оператор в
классической упругости
А (дх, (д) — дифференциаль-
дифференциальный оператор колебания
в классической упругости
В (дХУ со) — дифференциаль-
дифференциальный оператор колебания
в термоупругости
М (дх) — основной диффе-
дифференциальный оператор в
моментной упругости
М {дХу а) — дифференциаль-
дифференциальный оператор колебания
в моментной упругости
оператор напряжения в
классической упругости
^) 11^/(^)!|х
оператор обобщенного
напряжения в классиче-
классической упругости
u
оператор псевдонапря-
псевдонапряжения в классической
упругости
оператор напряжения
в моментной упругости
оператор напряжения в
термоупругости
<Р (дх, /I, (О) —
01 (дх, п, со) —
Q (дх. п) —
# (д*. «> Y) —
п, у) —
Т 15
12
12
12
12
12
13
) 13
I 13
13
И
I)
II
X
X
з- v
б— 1Х
	 v
<3
.•«— 1л
Д — оператор Лапласа
±яуп,±—
дп ?j дх{
ГфОИЗВОД-
ная
п =
по направлению
)
. п) —
\
V
V
13
6
6
6
2
2
9
I
13
3
\
1
1
1
1
1
3
1
3
2
2

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Анизотропная среда 23
Асимметричная теория упругости
Бицадзе оператор 173
13
вектор внутреннего вращения 17? 22
<— жесткого вращения 22
—	моментного напряжения 13
—	силового напряжения 13
**!¦ смещения 16
Внешние задачи колебания 306
Внутреннее вращение 17
Внутренние задачи колебаний 281
Вольтерра формула 344
Гексагональная система 25
Гельмгольца уравнение 93. 121
Гёльдерй неравенство 132
—	пространство 62
Гильберта — Шмидта георема 289
Гобсона формула 59b
Гранично-контактные задачи 449, 475, 490, 521
*	, существование решения 472
6	, теоремы эквивалентности 484
Грина тензор 273, 283, 323, 361
	 динамический 287
построение 283
	 построение гъз
	, свойство симметрии 286
	, существование 283
•	, — для внешних статических задач
*— тождество 108
—	формул» 85, 104, '09
Гука закон 21
	для изотропной ереды 24
Дб ух компонентное тело 59
Деформация 21
•—, (забота 32
—	с изменением температуры 35
	, работа 36
«»-, удельная энергия 32
Дирихле задача 386, 613
Дюамеля — Неймана закон 36, 37
	для изотропной среди 37
287
перемещение среды 21
—	, вектор жесткого вращения 22
Жиро метод реруляризаиии сингулярных опе-
операторов 161
*— теорема 136
•» формула 156
Задача о давлении штампа 582
*— о трещине 587
Задачи внешние 340
**— —, разрешимость 341
1— гранично-контактные 449, 475, 490, 521
	, существование решения 472
.	., теоремы эквивалентности 484
•— динамические 312
—-- начально-граничные 312
•— "мешанные 312
•- статические внешние 287
Задачи статические внутренние 287
-— установившихся моментно-упругих колеба-
колебаний 111
.	, теоремы единственности 116
,	, условие излучения 114
Закон Гука 21
*	в моментной теории 33
•	для изотропной средв1 37
л	G центром симметрии 33, 35
ш	трансверсально изотропной <зреды 25
—	Дюамеля — Неймана 36, 37
	для изотропной среды 37
—	сохранения энергии 27
Зоммерфельда удоовие излучения 94* 121
Изотропная среда 23
Индекс еингулярного оператора 170
Интеграл сингулярный 124, 129
	многомерный 197
	 на многообразиях 146
	 одномерный 197
— средний для функции 316
—* с ядром специальной конструкции 144
Кальдерона и Зигмунда теорема 152
Кельвина матрица 65
Классическая теория упругости 12, 17
	, внутренние задачи динамики 55, 56
	, главная контактная задача 59
	, задачи статики 58, 85
	, — установившихся упругих колебаний 91
	,	f предвтавление регулярных ре-
решений 91, 92
_	,	. разложение регулярных реше-
решений 93
	, однородные задачи 56
	, оператор напряжения 51
	, _ обобщенного напряжения 51
	, — псевдонапряжения 51
>	, основная смешанная задача 55
	. основные задачи 19, 54, 55
*	, сингулярные решения уравнений 75, 83
	. теорема Ляпунова — Таубера 227
	, упругая среда 42
	,	, упруго-динамическое еоетояние 42»
44, 49
	,	9 упруро-колебательнве состояние 44,
49
	. уравнение колебаний 77
	, — етатики 65, 75
	, формулы Грина 85, 104
	. __ Сомилиана 239, 349
фундаментальные решения уравнений 65#
83
62
Классы поверхностей 61»
—	функций 54, 61, 63
Колебания стационарные 39
Колосова—Мусхелишвили представления 595
Компоненты кручения — изгиба 31
—	силового напряжения 14
Контактные условия 58, 59, 450
Корректность задачи 275, 277
Коссера теория 13
Коши—Буняковскоро неравенство 324
Коэффициент температуропроводности 38
Критическая частота колебаний внешних сил 304
Купрадзе матрица 66, 72

662
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Ламе постоянные 24
Лапласа интеграл 335
— преобразование 321, ¦ 407
	, зависящее от параметра 330
	,	, свойства 330
Лебега точка 210, 211, 215
Леви-Чивита символ 17
Ляпунова поверхность 63
Матрица Купрадзе 66, 72
—	фундаментальных решений Кельвина 65
Метод обобщенных рядов Фурье 500, 544
Микрополярная теория упругости 13
Михлина метод регуляризации 163, 164
Модели сплошной среды 370
Модуль всестороннего сжатия 24
—	упругости 24
—	Юнга 24
Момент инерционных сил 20
—	массовый 12
—	спиновый 20
Моментная теория упругости 12, 346
	, внешние задачи 348
	, граничные условия 348
	f задачи статики 108
_,	f	, теоремы единственности 110
	, компоненты деформации 31
	, оператор напряжения 52, 347
	, основные задачи 347, 348
	, — уравнения 347
	,	движения 19
	1	равновесия 20
	, тензоры Грина 361
—	•	, теорема Ляпунова — Таубера 351
	, теоремы существования 359, 360
	f	f упруго-динамическое состояние 44,
50
	,	, упруго-колебательное состояние 46
	,	, упруго-статическое состояние 45
—	, уравнения динамики 60
	, — колебаний 70, 78
	т — статики 72, 79
	, формулы Грина 108, 109
	, — Сомилиана 349
Напряжение моментное 15
—	силовое 14, 15
Кеймана задача 613. 615
—	формула 556
Нелокальная теория упругости 13
Неоднородная среда 23, 449, 521
•	, гранично-контактные задачи 449, 475, 490,
521
	,	, классическое решение 493
¦	,	, существование решения 472
	,	, теоремы эквивалентности 484
	, задачи для бесконечной области 450
	,	конечной неоднородной среды 457
	,	неограниченной области 498
	,	, граничные услоеия 498
Неравенство Коши—буняковского 324
Нетера—Мусхелишвили теорема 197
Нетера теорема 170
Объемный потенциал 239
Однородная среда 23
Оператор Бицадзе 173
—	напряжения в классической теории 5J
	 моментной теории 52
—	обобщенного напряжения 51
—	псевдонапряжения 51
Парсеваля теорема 100
Плотность среды 12
Поверхность гладкая 63
—	кусочно-гладкая 63
—Ляпунова 63
—	разомкнутая 63
—	'с непрерывной кривизной 63
Потенциал двойного слоя 216, 380
—	объемный 239» 380
—	простого слоя 215, 380
—	регулярный 248
—	сингулярный 248
	многомерный 248
Представления Колосова—Мусхелишвили 595
*-* с помощью тензоров Грина 286
Преобразование Лапласа 321, 470
	, зависящее от параметр?. 330
	,	, свойства 330
Приближенное решение задач колебания 521—528
	статики 501—521
	термоупругости 528—531
	, численные примеры 532
Принцип излучения 1?!
—	симметрии Римана — Шварца 597
Пространство Гёльдера 62
—	линейное нормированное 62
Псевдоколебания 401
Пуассона коэффициент 24
—	формула 552
Работа внешних напряжений 26
—	деформации 32
—	массовых сил 26
Разложение единицы 152, 153
Регуляризатор оператора 161
Регуляризация сингулярных операторор 161
	, двумерный случай 162
	, метод Жиро 161
	, — Михлина 163
	, одномерный случай 1б>
Резольвента сингулярная 178
Римана — Шварца принцип симметрии 59/
Силы близкого действия 21
—	внешние 12
—	внутренние 12
—	инерционные 18
—	массовые 12, 17
—	поверхностные 12
Символ сингулярного оператор? 164, 199
Сингулярная матрица 130
Сингулярное ядро 129, 146
Сингулярные интегралы 124. 129
	, методы изучения 150
	, определения 151
Смещение 16
Снеддона формула 587
Сомилиана формула 239
Союзная матрица 60
Спектр собственных частот 287. 386
Среда анизотропная 23
—	изотропная 23
—	неоднородная 23, 449
—	однородная 23
—	сплошная 16
	, модели 370
—	с центром симметрии 32
—	трансверсально-изотропная 24
—	упругая 42, 44
Стационарные колебания 39
Стокса теорема 203
Гензор 14
—	деформации 22
—	Грина 273
—	моментного напряжения 14
—	напряжений симметричный 19
Теорема Гильберта — Шмидта 289
—	Жиро 136
—	Кальдерона и Зигмунда 152
—	Ляпунова—Таубера 227
	в теории упругости 228
—	Нетерэ 170
—	Нетера —Мусхелишвили 197
—	о распространении функций 243
—	Стокса 203
—	существования для задачи об акуетической
дифракции 544
—	Фикера 274
—	Фредгольма 190
¦— Фубини 131
—	Эйлера 130
Теория Коссера 13
—	многомерных сингулярных интегральных урав-
уравнений 84
—	потенциала 248
—	сингулярных интегральных уравнений с яд-
ядром Коши 84
—	термоупругости 40, 373
	, внешние задачи 420
	, граничные задачи 528
	, задачи динамики 60
	. — для неоднородных сред 58

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
663
Теория термоупругости, задачи установившихся
термоупругих колебаний 103
	1	1 представления регулярных реше-
решений 103, 104
	 квазистатическая 374
	, общая теория граничных задач 381
¦	, основные граничные задачи 384
	, — задачи 57
	, — однородные задачи 386, 387
	, потенциалы двойного слоя 380
	, _ объемных масс 380
	, — простого слоя 380
—•-, представление регулярных решений одно-
однородного уравнения 378
	. — решений уравнений термоупругости 623
	, преобразование Лапласа 407
	, псевдоколебания 401
	 раздельная 374
	, разрешимость внешних задач 392
	, — внутренних неоднородных задач 419
	 связная 374
*	, система дифференциальных уравнений тер-
термоупругости 418
	сопряженная 374
	, состояние среды термоупруго-динамиче-
термоупруго-динамическое 46
¦— —,	термоупруго-колебательное 47, 50
	, союзная система 375
	, существование нетривиального решения
задач 388, 391
	, — частот собственных колебаний ограни-
ограниченного тела 418
	температурно-напряженная 374
	, теоремы о принципе симметрии 632
	, термоупругая среда 46
	, термоэластопотенциалы 380
	, тождества Грина 376
1	¦ уравнение колебаний 73, 80
	, — союзное 75
	, — статики 75, 82
	>, — термоупругих эластопотенциалов 40)
	, эллиптическая задача 407
—	упругости асимметричная 13
	 классическая 12, 13 15, 17
	 микрополярная 13
	микрополярных сред 13
—	— 1\юментная 12, 15, 346
	 нелокальная 13
—	— с вращательными воздействиями частиц 13
—*— среды второго класса 13
Угловое граничное значение функции п то
извне 210
	 изнутри 210
Упругие постоянные 23
Уравнение Гурса—Хейвуда 193
—	термоупругих эластопотенциалов 401
—	энергии термоупругости 118
Уравнения движения в моментной теории
—	равновесия 19
Условие излучения 94, 121
—	равновесия выделенной части среды 17
—	термоупругого излучения 105
Условия контакта 58
Усредняющее ядро 31 i
Фикера теорема 274
Формула Вольтерра 344
—	Гобсона 598
Формулы представлений 286
—	Сомилиана 239, 34S
Фредгольма резольвента 188, 189
Фредгольмовость операторов П57
Фубини теорема 131
Функция регулярная 54
—	финитная 54
Фурье метод 500, 544
	обобщенных рядов 500, 544
Характеристика сингулярного оператора 164
19
Эйлера теорема 130
Эластопотенциал 248
Эллиптическая задача 335
Энергия деформации потенциальная
—	— удельная 27, 29
—, закон сохранения 27
—	среды кинетическая 26
—	частицу кинетическая 26
27
K)HF8 МОДУЛЬ 24
Ядре сингулярное 129.
— усредняющее 316
146

Виктор Дмитриевич Купрадае*
Тенгиз Георгиевич Гегелиа,
Михаил Онуфриевич Вашслейшвила,-
Тенгиз Владимирович Бурчуладзе
ТРЕХМЕРНЫЕ ЗАДАЧИ
МАТЕМАТИЧЕСКОЙ ТЕОРИИ УПРУГОСТИ
И ТЕРМОУПРУГОСТИ
nob общей редакцией В. Д. Купрадэе
М, 1976 р.. 664 стр. с илл.
Редакторы: В. Л. Добровольский* В. И Розальская
Техн. редактор Н. В. Кошелева, Корректор J1. Н Боровина
Сдано набор 10/IV 1975 г Подписано к печати 30/1 1976 г.
Бумага тип. № 3 70X 108Vie- физ. печ, л. 41,5. Условн. печ. л. 58,К
Уч.-изд. л. 58,53. Тираж 4000 экз	Т-01877 Ценя книги 4 р. 42 к.
Заказ N9 353
Издательство «Наука»
Главная редакция физико-математической литературы
117071, Москва, В-71, Ленинский проспект» 15
Ленинградская типография № 6 Союзполиграфпрома
при Государственном комитете Совета Министров СССР
по делам издательств, полиграфии и книжной торговли
193144 Лрчингоад. ^.-144, ул. Моисеенко. 10.
Отпечатано с матриц в 1-й типографии из-ствея «Наука», Ленин-
Ленинград, В-34, 9-я линия, д. 12.