Автор: Пухначев Ю.В.
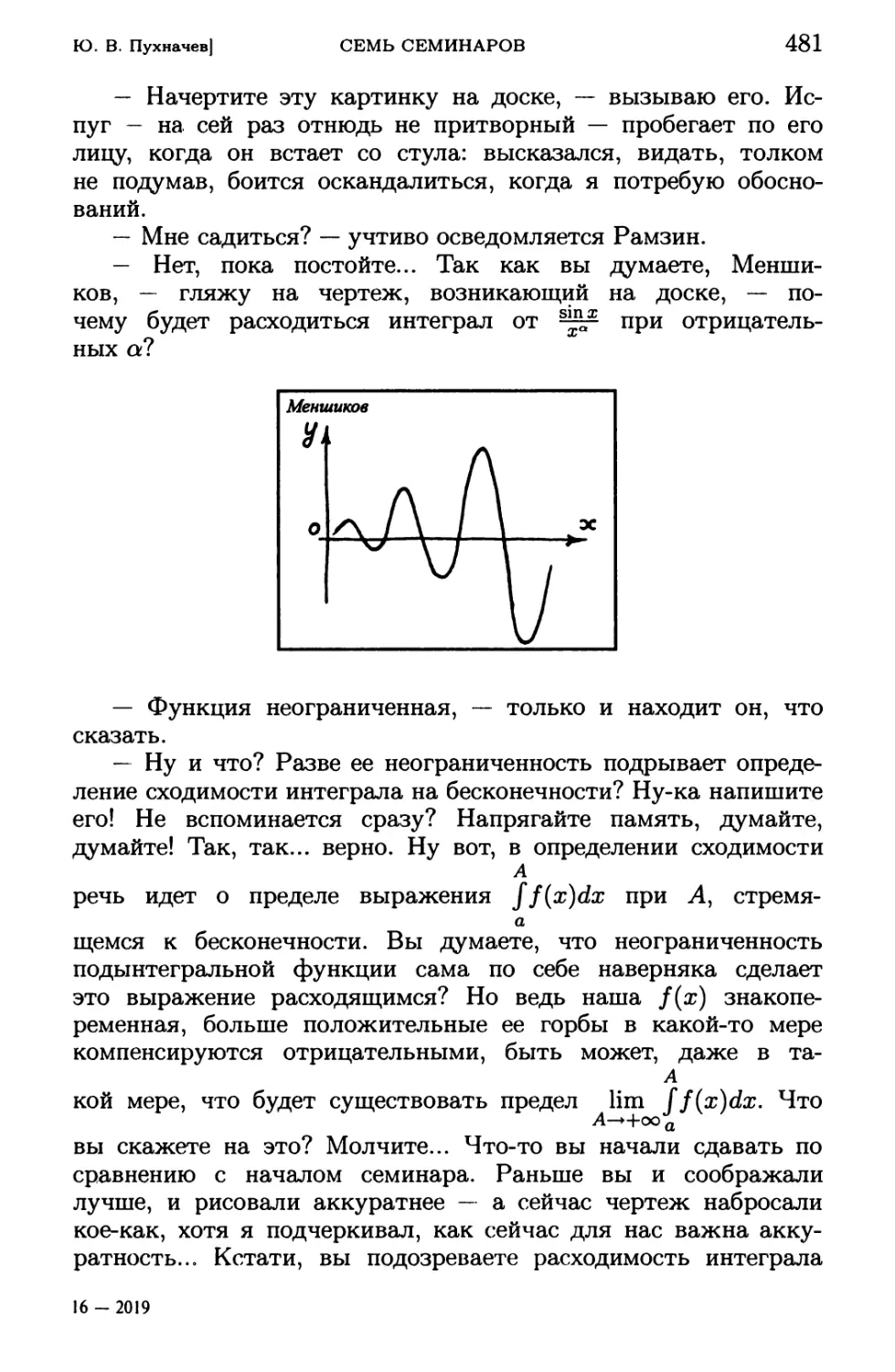
Теги: анализ математический анализ функциональный анализ математика
ISBN: 5-89155-137-3
Год: 2005
Текст
Ю. В. ПУХНАЧЕВ
СЕМЬ СЕМИНАРОВ
ПО МАТЕМАТИЧЕСКОМУ
АНАЛИЗУ
Москва
Физматкнига
2005
1.1.К 22.161
ИНН
УДК Ч7(075.Н)
I' ( II С II ИИ1 1.1
illwlJlt-Mllli // I It'll,НИ,
•nun h(ip|M4 пойдет VAMJl.Jl Кудрявцев,
Ah.XJU'MUh A A ( \l\UipChUU
IIKK ИУХИЛЧЙВ К). В. Семь семинаров по математическому анализу. — М.:
Фи-шаиснша, 2005. — 592 с. ISBN 5-89155-137-3
Изложение материала в книге ведется на примере решения конкретных задач. При
этом не только объясняется, как их решать, но и разбираются типичные ошибки и
заблуждения студентов при их решении. Эта особенность позволяет особо рекомендовать
книгу как учебное пособие для изучающих основы математического анализа. Книга
также может стать методическим пособием для преподавателей вузов естественно-научного
профиля, ведущих практические занятия по математическому анализу в студенческих
группах. В ней предлагается ряд методических приемов, которые помогут воспитывать
современного специалиста — хорошо образованного, инициативного, изобретательного,
способного работать в команде, готового браться за решение самых сложных задач и
успешно их решающего. Хотя предметом книги является математика, это не мешает
переносить предлагаемые методические приемы на преподавание других наук.
Для студентов и преподавателей вузов естественно-научного профиля.
ПУХНА ЧЁВ Юрий Васильевич
СЕМЬ СЕМИНАРОВ ПО МАТЕМАТИЧЕСКОМУ АНАЛИЗУ
Верстка М. В. Селяткин
Подписано в печать 30.10.2005. Формат 60x90/16
Печать офсетная. Усл. печ. л. 37. Уч.-изд. л. 39,3
Тираж 1000 экз. Заказ 2019
Издательство «Физматкнига»
141700, г. Долгопрудный Московской области, Институтский пер., 66
Тел./факс: (095) 408-76-81, 409-93-28
E-mail: publishers@mail.mipt.ru
Интернет-магазин литературы по фундаментальным и прикладным наукам
www.fizmatkniga.ru
Отпечатано в ППП «Типография «Наука» АИЦ «Наука» РАН
121099, Москва, Г-99, Шубинский пер., 6
ISBN 5-89155-137-3
© Пухначёв Ю. В., 2005
Оглавление
Предисловие 4
Глава 1. Последовательности 15
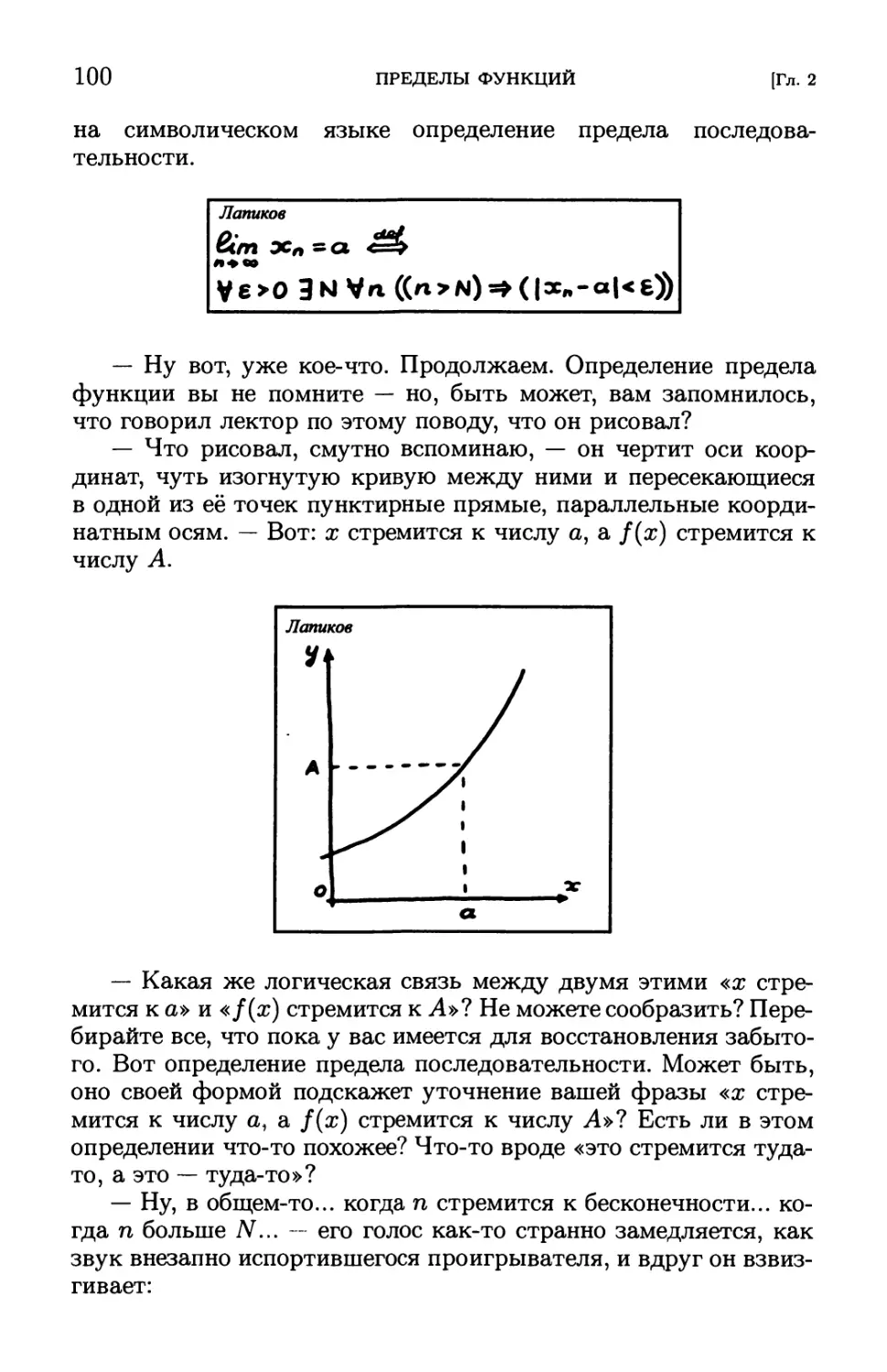
Глава 2. Пределы функций 99
Глава 3. Дифференцирование функций 180
Глава 4. Формула Тейлора 272
Глава 5. Интегрирование функций 342
Глава 6. Несобственные интегралы 431
Глава 7. Числовые ряды 514
Приложение 577
ПРЕДИСЛОВИЕ
На протяжении многих лет я вел практические занятия по
математическому анализу в Московском физико-техническом
институте. Эту книгу я адресую прежде всего своим коллегам — всем
тем, кто преподает или собирается преподавать высшую
математику в вузе. Вместе с тем она может оказаться интересной и
полезной преподавателям других дисциплин и студентам,
которые готовят себя к научной деятельности в самых различных
направлениях. Потому что главной темой этой книги является
не математика.
Одной из важнейших целей преподавательской работы я
считаю формирование у студентов психологических основ будущего
профессионального мастерства. (Если брать проблему во всей ее
полноте, то следовало бы говорить о духовном воспитании
студентов, но это задача гораздо более сложная, и я лишь упомяну
ее, не обсуждая.)
Для достижения заявленной мною цели недостаточно
совершенствовать лишь изложение учебного материала. На мой
взгляд, она достигается главным образом благодаря
пробуждению и развитию духовной энергии, которую в большей или
меньшей мере носит в себе каждый (подчеркиваю: каждый)
студент.
Мне всегда было интересно следить за тем, как по ходу
решения задачи, поставленной перед студентами, у них возникают
плодотворные идеи, а затем постепенно прокладывается путь к
верному ответу. И я старался вести занятия так, чтобы
активизировать этот процесс и как бы выставлять его напоказ — тогда
и мне было удобнее наблюдать и изучать его, да и студентам,
думал я, нелишне видеть и понимать, как действует механизм
математического мышления.
На своих занятиях я никогда не пытался внушать
студентам, будто мой авторитет заведомо обеспечен званием
преподавателя — во всяком случае считал недопустимой для себя позу
ПРЕДИСЛОВИЕ
5
мудреца, вещающего с высокой трибуны беспрекословные
истины непосвященным. Я рассматривал студентов как своих
равноправных собеседников, как свободных творцов. Давая им задачу
по новому, только что начатому разделу учебной программы, я
иногда предлагал им попытаться решить ее без моих
наставлений и подсказок, самостоятельно изобретая нужные для этого
методы и понятия. Раз за разом я убеждался, что студентам это
удается чаще, чем я предполагал, а решения порой бывали
такими, что мне хотелось взять на вооружение свежую мысль —
взять у тех, кого я сам должен вооружать знаниями.
Как-то раз, когда такой прием привел к особенно яркому
результату, мне вспомнилась легенда про французского
математика Жана Понселе. Будучи офицером наполеоновской армии,
он попал в русский плен и в глубоком тылу, в Саратове,
маялся от безделья и решил заняться геометрией, но не мог найти
нужной литературы — и тогда он задумал восстановить по
памяти школьный учебник геометрии, чтобы дальше заниматься по
нему, и восстановил-таки, а когда вернулся во Францию и
сравнил с учебником подлинным, обнаружил, что воссоздал совсем
не такую геометрию, какую учил в школе, — это была
проективная геометрия. Испытание памяти обернулось рождением новой
науки.
Где гарантия, что кто-то из сидящих в вузовской аудитории
молодых людей не новый Понселе? или новый Лобачевский? А
если таковой гарантии нет, то почему бы не дать им хоть
чуточную возможность заявить о своей способности к великим
свершениям? И еще вопрос: за что мы, преподаватели, вправе
порицать своих студентов в их рассуждениях? За ошибки? Но этому
вопросу по-библейски можно противопоставить другой: что есть
истина? Или за то, что они решают поставленную задачу не так,
как хотелось бы нам? не так, как принято? Но, помнится, и
Лобачевского упрекали в чем-то подобном. Что же утверждало его в
сознании своей правоты? Отсутствие внутренних противоречий
в его логических построениях.
Внутреннее противоречие — вот, пожалуй, единственное, что
может заслуживать упрека в рассуждениях студента. Если же
противоречий нет — пусть он свободно развивает свою мысль, и
мы обязаны помочь ему в этом. Появилось противоречие — мы
обязаны помочь в его исправлении, выпрямить студенту пути
до конечного результата, помочь в становлении — ну, пусть не
нового Лобачевского, но нового таланта во всяком случае.
Всякая бессмыслица при попытке выразить ее связными словами
()
ПРЕДИСЛОВИЕ
рассыпается сама собой, — говорил Джонатан Свифт. Не
рассыпается — значит не бессмыслица. Всякая такая мысль должна
быть доведена до окончательной формулировки, а там — время
ей судья. Я убеждал студентов, что такой программой действий
следует руководствоваться всегда — и когда решаешь
простенькую задачу в аудитории, и когда берешься за очередную научную
работу, и когда планируешь дальнейшую жизнь.
Перед собой же я ставил такую программу, рисовал
такой идеальный образ преподавателя, ведущего практические
занятия в форме беседы со студентами: он дает
выговориться каждому, кто взял слово, доброжелательно выслушивает
любое предложение или суждение, даже самое неуверенное
и сырое, создает в аудитории такую атмосферу, в которой
студент может высказать любую идею, не боясь, что она
окажется безрезультатной, не сомневаясь, что каждый его
успех, пусть незначительный, заслужит похвалу; когда
удачные высказывания студентов, поддержанные направляющими
репликами преподавателя, становятся затравками
плодотворных дискуссий о том или ином понятии, теореме, задаче
из учебного курса; когда окончательные формулировки его
положений зачастую даются самими студентами, а не
преподавателем, и опять-таки не по его приговору, а по общему
размышлению выясняется ошибочность или
бесперспективность неудачных идей; когда один раздел курса за другим
полностью воссоздается в ходе таких дискуссий, искусно
руководимых преподавателем, непринужденных и обстоятельных
одновременно.
И только в двух случаях я обрывал своих собеседников, два
слова были запретными в аудитории, где я вел занятия. Одно
из них — можно. Если кто-то, получив задачу, спрашивал
меня, можно ли решать ее таким-то способом, я отвечал ему, что
хозяин задачи — он сам и потому волен применить любой из
известных ему способов. Самостоятельность — вот лучшая почва
для выращивания тех плодов просвещения, о которых я говорю.
А другое запретное слово — первый. В студенческой группе не
должно быть и речи, не должно быть и мысли о том, кто самый
лучший. Первое место — лишь одно, и кто не занял его, будет
чувствовать себя уязвленным. Первое место может занять кто-
то один, свое место — каждый. Найти свое место в работе над
конкретной задачей, в группе, в жизни — вот главное.
Я старался вовлечь в общую дискуссию каждого студента
сообразно с его способностями. Один предлагает хорошие идеи (хо-
ПРЕДИСЛОВИЕ
7
тя не всегда умеет их реализовать), другой силен в практической
реализации идей (хотя бы и не своих), третий сноровисто
вычисляет, четвертый зорко подмечает огрехи в чужих рассуждениях
и вычислениях — и каждый имеет шанс достичь собственного
успеха на своем пути.
Я стремился разглядеть в каждом студенте его сильную
черту, которая обеспечит ему достойное место в общей работе.
Никогда я не сомневался в том, что это достижимо. При первой
же встрече со студенческой группой, с которой мне
предстояло заниматься, вслушиваясь в речь одного, другого, третьего,
я неизменно убеждался: какие они все разные! Мне хотелось,
чтобы они почувствовали, как это ценно. Бывало, во время той
же первой встречи со своими будущими учениками я спрашивал
кого-нибудь из них: скажите, сколько людей сейчас живет на
Земле? Несколько миллиардов, — отвечал он, не понимая, к
чему я клоню. Тогда я спрашивал его вновь: а вы не лишний? Ведь
несколько миллиардов людей на Земле уже есть — зачем же еще
вы? И успокаивал его, растерянного: нет на Земле двух
абсолютно одинаковых людей — так что нечего бояться, что кто-то
продублирует вашу судьбу и будет претендовать на точно то же, что
и вы, место под солнцем. Среди бесконечно разнообразных, все
более многочисленных задач, встающих перед человечеством,
будет что выбрать и вам. Надо только понастойчивее искать свою
задачу — и найти ее. Надо только понять себя, распознать свои
способности, свои личностные особенности и сообразно с ними
найти свое место в жизни. Надо, чтобы обязательно состоялась
эта решающая для всякой человеческой судьбы встреча:
человек нашел предмет своего призвания — актуальное дело нашло
своего хозяина.
Я пытался ежеминутно видеть каждого своего студента на
фоне его большого будущего, где его ждет какая-то очень
важная задача. Как преподаватель, я считал себя обязанным помочь
ему найти ее. По меньшей мере — вывести его на путь, ведущий
к ней. По крайней мере — внушить ему, что такая задача
существует и, быть может, не одна. Он же, напротив, единственен для
нее в том смысле, что лучше него ее никто не решит. И потому
он существует на этой Земле, и потому он обязан существовать,
обязан получить от жизни то, что ему предначертано, — и труд,
и успехи, и неудачи, и награду.
Я убеждал в этом своих студентов словами Александра
Твардовского: «Вся суть в одном-единственном завете: то, что скажу,
до времени тая, я это знаю лучше всех на свете — живых и мерт-
м
ПГКДИСМОИИК
пых пин*» iu.mi.ko я. ( Ikh'ih'I'i» то слоно никому другому я нико-
I дп (м.1 ни ш что пс мог передоверить. Даже Льву Толстому —
тми, 1я. 11с скажет пусть себе он бог. А я лишь смертный. За
снос и ответе, я об одном при жизни хлопочу: о том, что знаю
лучше исех на свете, сказать хочу. И так, как я хочу.»
Скачать хочу... Но прежде надобно научиться говорить. И я
читал своим студентам другие строки того же поэта: «В деле
своем без излишней тревоги мы затвердили с давнишней поры
то, что горшки обжигают не боги. Ну, а не боги, так — дуй до
горы. Только, по той продвигаясь дороге, нам бы вдобавок
усвоить пора: верно, горшки обжигают не боги, но обжигают их —
мастера!»
Научиться мастерству — вот ближайшая цель, которая
ставится перед студентами в учебной аудитории, когда они решают
одну задачу за другой. Но посвящать эти упражнения лишь
выработке технических навыков в решении конкретных задач
значило бы использовать учебное время далеко не на полную
мощность, а может быть и впустую: ведь вполне возможно, что в
будущей практической деятельности некоторым студентам
придется решать задачи, совсем не похожие на те, что задавались
им в учебных аудиториях. Однако и в этом случае очень многое
могут дать, если преподаватель осознает их значение, побочные
психологические воздействия учебных упражнений. Стоит лишь
вселить в студента ощущение успеха от каждой решенной задачи
— и одна маленькая удача за другой, добытая упорством и
изобретательностью, понемногу выработает в нем нечто, что
впоследствии позволит ему решить любую задачу: не только
профессиональные знания и навыки, но и такие важные качества, как
уверенность в своих силах, увлеченность, инициативность,
самостоятельность, организованность, настойчивость, привычка
доводить до конца начатое дело, верность избранному пути,
творческая устойчивость...
Как-то раз, встретив одного из бывших своих студентов,
я спросил его: «Можете ли вы одной фразой выразить самое
главное из того, что вам дал физтех?» Он подумал
несколько секунд и отчеканил: «Неразрешимых задач не бывает.»
В этих словах отозвалось нечто более фундаментальное, чем
образование, — и я был доволен таким ответом, хотя он не
имел никакого отношения ни к специфике физтеха, ни к науке,
которую я преподавал. Но ведь мы были не на экзамене! Да
и что с того, если мой давнишний студент когда-то чего-то
не усвоил на моих семинарах? С таким настроем, который
ПРЕДИСЛОВИЕ
9
звучал в его словах, он теперь самостоятельно и успешно изучит
любую науку.
Знания и мастерство бесплодны, если не подкреплены волей
и характером. И я стремился развить и укрепить эти
оплодотворяющие начала в каждом своем студенте. Он перейдет на
следующий курс — психологический тренинг поможет ему в
дальнейшем преодолевать боязнь неудач, спады активности,
трудности общения. Он закончит вуз — психологическая закалка
поможет ему верно оценить перспективы своей профессиональной
деятельности, найти оптимальную для себя позицию в спектре
специальностей и в сфере человеческих взаимоотношений,
повысит шансы на получение работы, на более быстрое и уверенное
освоение основной профессии и смежных занятий.
Как важны надежные психологические тылы в наше
неспокойное время! И как часто мы забываем об их значении! Когда
крупинка одаренности наращивается в душе молодого
человека уверенностью в своих силах, потом увлеченностью,
самостоятельностью, то с каждой новой добавкой уже приобретенные
черты погружаются в душевные глубины, перестают осознаваться
— зрелый специалист вряд ли отдает себе отчет в них.
Подобная неосознаваемость способна породить ложное мнение, будто
мастерство можно воспитать само по себе, сразу. Думающий так
подобен голодному мужику из известной басни, который поедал
каравай за караваем, но все не мог избавиться от голода, а
потом, съевши маленькую булочку, вдруг почувствовал себя сытым
и в сердцах воскликнул: «Надо было с булочки и начинать!»
Профессиональные знания и навыки — это лишь верхушка айсберга;
подводная, скрытая от поверхностного взгляда его часть — это
психологические основы мастерства.
Задача преподавателя, если описывать ее в том же образном
ключе, состоит в воспроизведении айсбергов. Если
ограничиться при этом лишь надводной частью, успеха не будет, как не
будет его, если таким же образом воспроизвести лишь
верхушку реального айсберга: опущенная на воду, она почти целиком
уйдет в глубину, а на виду останется лишь куцый кусочек. Вот
символ несостоятельности тех, кто в преподавании математики
видит только преподавание и только математику, кто
вдалбливает в головы студентов готовые решения задач из учебников,
кто требует точно следовать своим установкам, кто равнодушен
к мыслям, чувствам, личности студента.
Неверно думать, что, забывая о психологии, такой
преподаватель ничего не дает своим студентам в плане психологического
10
ПРЕДИСЛОВИЕ
развития. Дает — и притом нечто очень вредное, культивируя в
них бациллу исполнительства. Это качество и составляет
подводную часть тех карликовых айсбергов, которые плодит
преподаватель, видящий свою задачу лишь в передаче студентам
профессиональных знаний и навыков. Такие айсберги нередко тонут: на
памяти любого, кто работал со студентами, есть отличники,
которые, окончив вуз с блестящими оценками, не смогли проявить
себя и затерялись в серых буднях. Чего не хватало им в
жизни? Умелые и исполнительные, они, вероятно, думали, что
автоматически станут большими учеными, стоит лишь досконально
выполнить учебную программу вуза. А вышло нечто
противоположное. Да и могло ли получиться иначе у того, кто
добровольно распластал свою неповторимую живую одаренность под
бумажным листком с мертвыми буквами стереотипного учебного
плана?
А ведь мечталось, наверное, что она станет сияющей
вершиной могучей горы. Знать бы только, что основания таких гор
складываются из материала отнюдь не школярского, а
духовного, которого нет в вузовских программах и учебниках.
Но там и быть его не может. Программы, планы, занятия,
задания — это всего лишь инструменты, которые помогут студенту,
если он сумеет ими воспользоваться, в реализации его
собственной жизненной программы. Он должен составить ее сам, если
мечтает о большом будущем, а не ждать в готовом виде от нас,
преподавателей, хотя мы можем, конечно, поучаствовать в ее
составлении — что-то подсказать, что-то посоветовать. Главным
фактором при ее выполнении должна стать опять-таки
собственная духовная энергия студента, а не наши указания и советы. В
наших силах, разумеется, сильнее разжечь в нем эту энергию
или, хотя это труднее, изменить ее направленность. Мы даже
можем попытаться что-то изменить в нем самом, чтобы он
лучше соответствовал своей жизненной роли. Но если мы желаем
удачи своим студентам, то сами взаимно должны быть
изменчивыми и приспосабливать преподавание к каждому из них в
соответствии с его жизненным предназначением, чтобы те знания
и навыки, все те интеллектуальные и психологические средства,
которые получит наш ученик, наилучшим образом служили ему
в дальнейшем.
Что до меня, то мне было просто неинтересно преподавать
математику вообще, скучновато-неизменную из года в год,
уныло-стандартную для всех и каждого. Зафиксированная в
учебных планах, она представлялась мне лишь скелетной ос-
ПРЕДИСЛОВИЕ
11
новой для гибкой разработки стольких ее вариантов, сколько
студентов было в группе, с которой мне предстояло
заниматься, — для каждого свой вариант сообразно с его натурой: вот
этому умнице, генератору идей, пожалуй, нужна математика с
акцентом на понятия и концепции, этому умельцу — на методы
и алгоритмы, этому критику — на доказательства и логику...
Мое преподавание было некой равнодействующей всех этих
мысленных составляющих. Естественным образом оно и получалось
таким в ходе занятий-бесед, в которые каждый из собеседников
вносит свой вклад. Вместе с тем воссоздаваемая в таких беседах
математика, на мой взгляд, располагает к тому, чтобы каждый
студент воспринимал ее по-своему, усваивал в форме, наиболее
приспособленной к его натуре и потому наиболее
эффективной — в ближайшее время, для выполнения учебных заданий, и
в будущем, для достижения жизненных целей.
Не следует опасаться, будто такое «акцентированное»
преподавание вырастит из студентов однобоких, ограниченных
специалистов, владеющих математикой лишь в узких пределах своих
пристрастий. От этого убережет дискуссионная манера, в
которой ведутся занятия. Тот, кто по ходу общей дискуссии
выступил в своем амплуа, должен внимательно следить за
последующими выступлениями, хорошо понимать их, чтобы не упустить
нить рассуждения и иметь возможность выступить вновь. Так не
только обеспечивается полнота образования, но и
вырабатывается наиболее результативный стиль работы в коллективе, очень
полезный будущим специалистам, — ведь наверняка никому из
них не придется работать в одиночку. А коллективный труд
наиболее успешен тогда, когда каждый член коллектива понимает
общую задачу, выполняет ту часть работы, которая наиболее ему
удается, представляет, чем занят каждый из его коллег, и умеет
с ними сотрудничать.
И если в описании моего метода преподавания кому-то
почудится проповедь индивидуализма, я возражу: нет, напротив,
мой метод нацелен как раз на воспитание духа коллективного
труда, на наибольшую эффективность такого труда — но
отвергает конформистский «коллективизм» как не лучший способ ее
достижения и утверждает в качестве стимула гарантированную
каждому возможность занять в коллективе свое достойное место
адекватно своим способностям и стремлениям, возможность
наиболее полно и своеобразно раскрыть себя, достичь наибольшего
личного успеха. Плохо, конечно, если стремление к нему вредит
общей работе. Хорошо, если способствует. Тогда ради наивысшей
12
ПРЕДИСЛОВИЕ
ее эффективности остается оптимально сложить, не подавляя,
усилия всех участников общего дела.
Это, как правило, достижимо даже при их резком
изначальном несходстве. Само по себе оно не вредно. Надобно лишь
умно расставить всех по участкам общего фронта работ и толково
наставить. Вспоминается мудрая притча Григория Сковороды:
«Колесо часовой машины спросило у Другаго: «Скажи мне, для
чего ты качаешься не по нашей склонности, но в противную
сторону?» «Мене, — отвечало Другое, — так сделал мой Майстер,
и сим вам не только не мешаю, но еще воспомоществую к тому,
дабы наши часы ходили по рассуждению солнечного круга.» По
разным природным склонностям и путь жития разный. Однак
всем один конец — честность, мир и любовь.»
Я охотно обсуждал со студентами свои взгляды на процесс
обучения, на роль психологического фактора, духовного начала
в этом процессе и в будущей деятельности специалиста.
Однажды, когда мы разговаривали об этом, я рассказал два сходных
меж собою случая из жизни двух ученых. Один из этих людей —
Альбрехт Галлер. Плодовитый поэт, естествоиспытатель,
энциклопедист, он жил в 18-м веке и полагал, что овладел всеми
знаниями своего времени. Как-то летом он скакал верхом на лошади;
лошадь споткнулась, Галлер упал с нее и, ударившись о землю,
потерял сознание. Очнувшись, он заволновался, не отшибло ли
ему память. Достал из походной сумки карандаш, бумагу и
написал список всех рек мира, впадающих непосредственно в моря
и океаны. Вернувшись домой, сверился со справочником и
успокоился — в списке не было пропусков.
Второй случай произошел уже в наше время и был гораздо
трагичнее. В начале 1962 года на обледенелом шоссе Москва-
Дубна столкнулись грузовик и легковая автомашина. В машине
находился знаменитый физик Лев Ландау. Роковой удар
пришелся как раз по нему. В состоянии клинической смерти его
доставили в больницу. Врачи совершили невозможное: через
полтора месяца после катастрофы он пришел в себя, через три к
нему вернулся дар речи. И одной из первых фраз, которую он
произнес без запинок и без ошибок, желая доказать, что он —
прежний Ландау, что не утратил себя, было... нет, не
описание какого-то замысловатого явления природы, не
формулировка сложного физического закона — то было его любимое
изречение Ленина: «Никто не повинен в том, если он родился рабом;
но раб, который не только чуждается стремлений к своей
свободе, но оправдывает и прикрашивает свое рабство, есть вызы-
ПРЕДИСЛОВИЕ
13
вающий законное чувство негодования, презрения и омерзения
холуй и хам».
По сравнению с этим фактом происшествие с Галлером
кажется просто анекдотом. И не потому, что там дело шло дашь о
кратковременной потере сознания, а здесь — о жизни и смерти.
Нет, в сравнении этих двух случаев становится ясным, насколько
духовное начало для ученого важнее, существеннее,
фундаментальнее, нежели эрудиция и мастерство. Мысль об этом должна
стать для нас, преподавателей, основополагающей в нашей
работе, если мы прочим своим студентам большое будущее. Или мы
надеемся, что они приходят в вуз уже духовно зрелыми людьми?
а если чего-то и недостает, то образуется вскоре? само собой? Нет,
конечно, это не так. Формирование психологических основ
уверенного мастерства — дело, длящееся годами, требующее
особого внимания и специфических усилий преподавателя (тем более,
если он желает повлиять и на духовное развитие студента).
Вот этот важный, если не важнейший, аспект преподавания
и является главной темой моей книги. Форму изложения этой
темы можно определить как стенограмму практических занятий
по анализу, как запись дискуссий, где каждый студент, собеседуя
с друзьями и с преподавателем, создает для себя свою
собственную математику. Из боязни затянуть изложение я не стал
передавать речь студентов со всеми свойственными реальной речи
заминками и повторами, и это несколько приукрасило моих
героев: самые сильные выглядят чересчур уж одаренными, самые
слабые — слишком отзывчивыми на педагогические воздействия
(буквально за несколько занятий, прямо на глазах они
подтягиваются почти до уровня сильнейших). В подобной идеализации,
если она чувствуется в книге, «повинна» глубокая вера автора
в способности студентов, которые должен раскрыть, пробудить
и развить преподаватель, и в успех работы преподавателя, если
он отдает делу всю свою энергию и душу.
Содержание книги соответствует начальному этапу
традиционного курса математического анализа, но отражает его отнюдь
не так систематически, как в учебниках — ведь у этой книги
другие цели. Ее главы лишь условно можно назвать семинарами —
каждая охватывает тематику нескольких занятий.
Условен и состав студенческой группы, выступающей в
книге: эти персонажи носят собирательный характер — каждый из
них, по замыслу автора и на основании его педагогического
опыта, олицетворяет один из типов поведения студентов на
практических занятиях в вузе.
14
ПРЕДИСЛОНИН
Собирательным можно считать и образ преподавателя,
авторское «я», от лица которого ведется изложение. Дело в том,
что педагогическими навыками я в значительной мере обязан
своим коллегам по кафедре высшей математики МФТИ. В
первую очередь я хотел бы назвать Льва Дмитриевича
Кудрявцева, руководившего кафедрой в 1954-89 годах. Многое дал
он по части преподавательского искусства каждому из тех, кто
тогда преподавал математику на физтехе. Он помогал мне
советами на всем протяжении работы над этой книгой. Разработке
отдельных ее положений так или иначе, в ходе деловых
разговоров и приятельских бесед способствовали Л. А. Беклемишева,
Д. В. Беклемишев, А. А. Болибрух, И. А. Бочек, А. В. Бу-
линский, П. Б. Гусятников, А. Д. Кутасов, А. А. Мальцев,
А. Ю. Петрович, Т. С. Пиголкина, В. Р. Почуев, С. С. Рышков,
А. П. Савин, А. Н. Тулайков, В. А. Ходаков, В. И. Чехлов,
М. И. Шабунин, Г. Н. Яковлев, Т. X. Яковлева... упомянуть всех
не представляется возможным. Творческая и по-человечески
приятная атмосфера кафедры служила питательной средой при
возникновении этой книги. Всем своим коллегам по физтеху я
выражаю за это глубокую, искреннюю благодарность.
Я благодарен также И. А. Худо л ей и М. В. Селяткину,
которые готовили рукопись этой книги к печати.
Глава 1
ПОСЛЕДОВАТЕЛЬНОСТИ
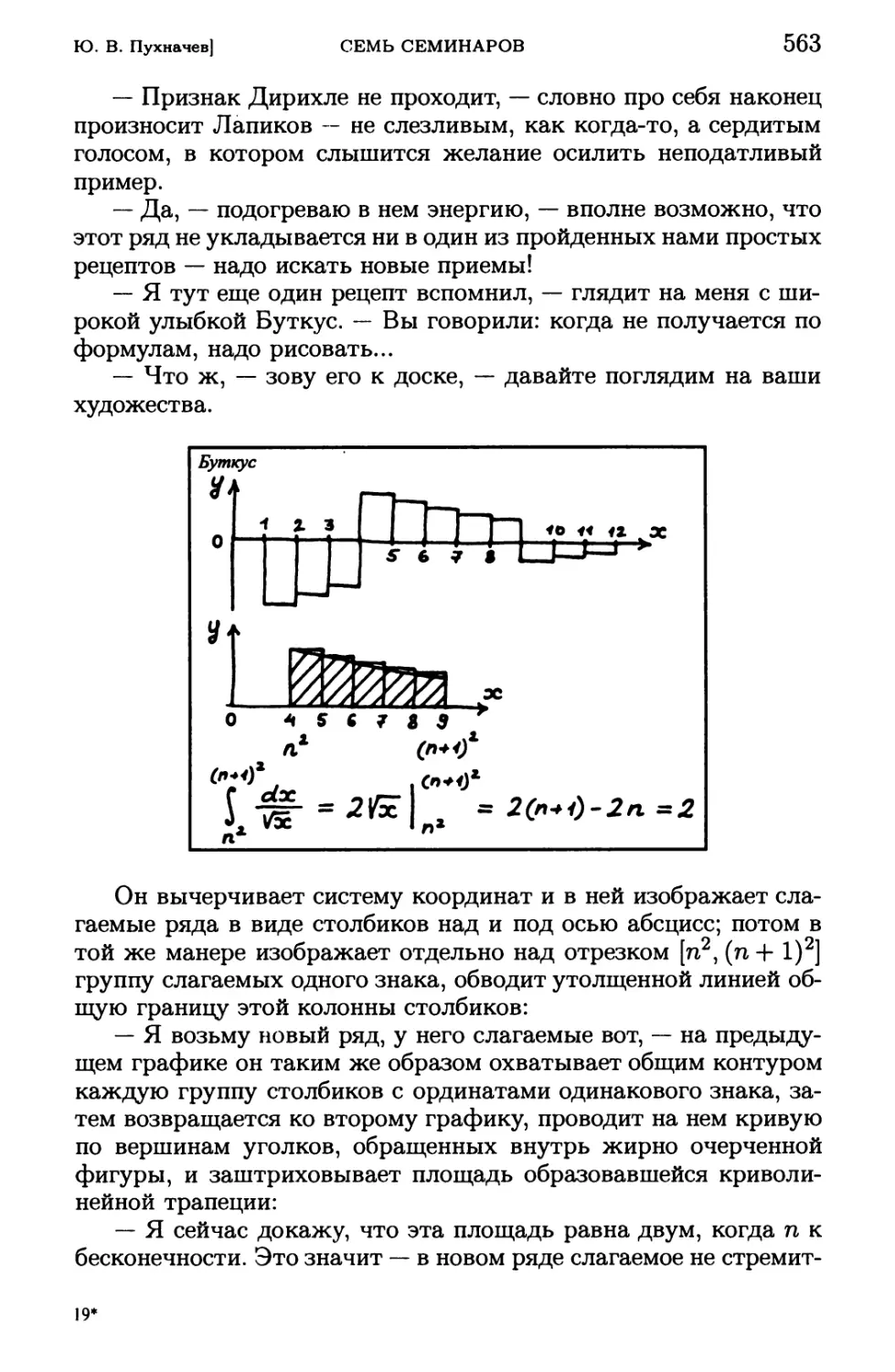
— Здравствуйте, ребята ! Я буду вести в вашей группе
практические занятия по математическому анализу. Моя фамилия —
Пухначев, имя и отчество — Юрий Васильевич.
По-школьному стремительно они вскочили и
остолбенело вытянулись при моем появлении в аудитории, а после
моего кивка: «Садитесь...», — опустились на свои места
неторопливо и вразнобой, иные в нарочито небрежных
позах, словно в утверждение статуса своей студенческой
вольности.
— Теперь, ребята, я хотел бы услышать ваши фамилии и
имена. И еще пусть каждый скажет, откуда он приехал.
Во всю ширь просторной аудитории тремя поперечными
рядами выстроились сомкнутые столы. Опрашиваю слева направо
сидящих за ними.
Сутеев Игорь (Пермь). Рамзин Сергей (Киев). Лапиков
Егор (Рязань). Миклашевский Павел (Москва). Горт Александр
(Львов).
Кочин Дмитрий (Новосибирск). Стрельцов Юрий (Москва).
Староста группы Кулагин Андрей (Севастополь). Синица
Людмила (Ярославль). Аргунова Галина (Кострома). Мухин Евгений
(Владимир).
Костюк Виталий (Харьков). Гарин Михаил (Нижний
Тагил). Меншиков Николай (Ростов-на-Дону). Чюмин Семен
(Весьегонск). Сынчиков Владимир (Усть-Пинега). Буткус Ли-
нас (Шяуляй).
— Итак, как я уже сказал, мы с вами будем заниматься
математикой.
— Высшей математикой! — поправляет меня Лапиков, так
и сияющий белками восторженно распахнутых глаз, румянцем
пухленьких щек.
16
ПОСЛЕДОВАТЕЛЬНОСТИ
|Гл. 1
— Высшей, если угодно. Кстати, где, по вашему мнению,
грань, отделяющая элементарную математику от высшей? Без
какого понятия не определить ни производной, ни интеграла,
сведения о которых в школьном курсе именуются элементами
высшей математики? Вы затрудняетесь ответить? Я подскажу
вам: без понятия предельного перехода. Мы познакомимся
сегодня с его простейшей разновидностью, занимаясь числовыми
последовательностями. А для этого мы прежде всего должны
определить понятие числовой последовательности. Пусть каждому
натуральному числу — единице, двойке, тройке, а короче говоря
— произвольному, обозначаемому буквой п, поставлено в
соответствие некоторое вещественное число. Чтобы не забывать об
установленном соответствии, обозначим эти числа ai,ei2, ...an —
то есть перенумеруем их. Множество таких чисел назовем
числовой последовательностью ап. Все поняли это определение? Судя
по вашему молчанию, все. Тогда попробуйте построить какие-
нибудь последовательности.
— Два, четыре, восемь, шестнадцать и так далее. Каждому
натуральному числу п ставится в соответствие число 2П, — с
уверенной дикторской четкостью произносит щеголеватый Рамзин.
— Хорошо, — киваю ему и записываю его пример на доске.
— А можно, — озорно прищуривается Миклашевский, —
поставить в соответствие каждому натуральному числу само это
число.
— Пример, подкупающий своей простотой, — заношу на доску
и это предложение.
Пауза — и звонкий голос Синицы:
— Можно еще взять обратные величины к числам
натурального ряда.
— Давайте возьмем. Теперь нам уже вполне хватит примеров
для дальнейшего разговора. Посмотрим на два последних и
попытаемся выяснить: в чем у этих последовательностей сходство
и в чем различие?
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
17
— Сходство в том, что это последовательности, —
нерешительно подает голос Чюмин.
— И в обеих — только положительные числа, — добавляет
Лапиков.
— Обе они какие-то ... ну ... неуклонные, что ли, — стараясь
чем-то подкрепить нечеткость своих слов, Мухин отстукивает
ребром ладони по краю стола, ведя ее сначала вправо, затем
влево.
— Ну да, монотонные, — нервозно-торопливо поддакивает
Горт, и вслед за ним еще несколько голосов повторяют: «конечно,
разумеется, обе они монотонные».
— Так вы знакомы с понятием монотонности? — стараюсь
убедиться в этом по их взглядам. — Как же определяется
монотонная последовательность?
— Монотонность — это возрастание или убывание, — голос
Костюка звучен и тверд.
— Вы заменили одно слово другими. Я же жду от вас
определения. Как, например, определить монотонно возрастающую
последовательность?
— У нее каждый член больше предыдущего, — басит грузный
Меншиков.
— Но, очевидно, — подхватываю его мысль, — в таком
сравнении могут участвовать не только два соседних, но и два
произвольных члена последовательности, — пишу на доске ат < ап, —
лишь бы ...
Я обрываю фразу выжидающей паузой, и Горт тотчас
продолжает:
— Лишь бы выполнялось т < п.
Записываю это неравенство слева от прежнего, окружаю оба
скобками.
— Здесь еще не хватает какой-то детали, которая указывала
бы логическую связь между обоими неравенствами.
— Знака следования, — предлагает Костюк, и я соединяю
неравенства стрелочкой: (га < п) => (ат < ап).
— Осталось оговорить, что же это за га и п.
— Очевидно, любые, — беспечно бросает Миклашевский.
— Верно. Это слово я хотел бы записать особым символом,
но не знаю будет ли он понятен вам.
Миклашевский чертит в воздухе уголок вершиной вниз и
перечеркивает его по горизонтали.
— Вот-вот. Значит, вам в школе рассказывали про
кванторы?
18
ПОСЛЕДОВАТЕЛЬНОСТИ
[Гл. 1
— Рассказывали! — громким радостным хором отвечает
аудитория. Кажется, в этом хоре участвуют все. Но такое
впечатление может оказаться обманчивым, как обманчив вечерний вид
освещенных окон многоэтажного дома: на первый взгляд, свет
горит чуть ли не в каждом окне — но, если пересчитать
неосвещенные, выяснится, что их больше половины... Быть может,
столь же превратное впечатление создают и выкрики всезнаек,
громкие, но не такие уж многочисленные?
— Тише, ребята, тише! Так я не услышу тех, кому не
рассказывали об этом. Давайте договоримся сразу, что на подобные
вопросы вы будете отвечать так, как это принято у подрывников.
Когда они заложат заряды, то старший спрашивает: «Готовы
ли?» И все молчат. А кто не готов, кричит: «Я не готов!»
Старший ждет некоторое время, вновь справляется о готовности, и
только тогда, когда ответом будет полное молчание, он
заключает, что теперь уж готовы все. Спрашиваю еще раз: рассказывали
вам в школе про кванторы или нет?
— У нас в школе не рассказывали, — еле слышно произносит
Аргунова.
— И у меня ... у нас тоже, — присоединяется к ней Кочин.
На вид он гораздо старше остальных, школа у него явно
далеко позади, и школьные знания, видимо, сильно подзабылись.
— Тогда сделаем краткое отступление в область логической
символики. Мы будем применять следующие символы,
заменяющие часто употребляемые термины — шесть логических
связок: ] (не), Д (и), V (или), => (следует), О (эквивалентно),
def
«<=> (эквивалентно по определению) и два квантора: V (любой),
3 (существует). Просьба к тем, кто видит эти значки впервые:
запишите их, постарайтесь запомнить, а по ходу наших занятий
они окончательно закрепятся у вас в памяти. Так как же,
Стрельцов, — наугад выхватываю одного из хора кричавших
«рассказывали!» — мы запишем определение того факта, что
некоторая последовательность монотонно возрастает? Прошу
вас к доске.
Без запинки, хотя несколько медлительно выписывает он все,
что требовалось от него. Есть какое-то тонкое сходство между со-
бранностью его аккуратного до элегантности облика и тем, как
Ю. В. Иухначев|
СЕМЬ СЕМИНАРОВ
19
соразмерно и компактно располагает он на доске
каллиграфически стройные символы.
— Этому определению, — оборачивается он ко мне,
закончив, — удовлетворяют первая и вторая из наших
последовательностей. Показать?
— Покажите. Все правильно. А если нам встретится такая,
например, последовательность: 1, 1, 2, 2, 3, 3 и так далее? Как
мы ее назовем?
— Мы назовем ее монотонно неубывающей и в ее
определении вместо знака строгого неравенства поставим знак
нестрогого: ат < ап. Легко видеть, что всякая возрастающая
последовательность является также неубывающей.
Прошу его выписать определения монотонно убывающей
и монотонно невозрастающей последовательности, подвести под
них последовательность ^ и, поблагодарив, отправляю его на
место.
— Итак, ребята, все три последовательности, которые вы
предложили, оказались монотонными. Чего доброго, вы еще
подумаете, что таковы все последовательности вообще. Может
быть, кто-то придумает пример немонотонной
последовательности?
— Минус один, один, минус один, один, а в общем виде
(—1)п, — гипнотически глядя на меня немигающим взглядом,
медленно и четко говорит Сутеев.
— Очень хорошо, — записываю на доске его пример. —
Вы чем то удивлены, Чюмин? — ловлю изумленный, комично
утрированный очками взгляд рыжеватого паренька с заднего
ряда.
— А разве такие последовательности бывают? — запинаясь,
спрашивает он.
— Не понимаю, что вас так смутило? — удивляюсь на этот
раз я.
20
послкдовлтюлыюсти
[Гл. 1
— Разве числа, которые мы ставим в соответствие
натуральному ряду, могут повторяться?
— А почему бы и нет? В определении последовательности на
этот счет нет никакого запрета. Бывают даже такие
последовательности, все члены которых одинаковы — их называют
стационарными. Учли? Тогда, — обращаюсь уже ко всем, — продолжим
сравнение натурального ряда с последовательностью величин,
обратных к его числам. На сей раз выясним, чем они
отличаются друг от друга. Попробуем-ка спросить об этом одного из тех,
кто не рвется отвечать, — например, Кулагина.
— Одна последовательность возрастает, другая убывает.
— Об этом уже говорилось.
— У одной есть границы — я имею в виду ^, а натуральный
ряд не ограничен.
В вырезе отложного воротничка ковбойки, плотно
обтягивающей его коренастую фигуру, проглядывает тельняшка, внося
в его неброскую внешность черточку бравой солидности, вполне
приличествующую званию старосты.
— Очень хорошо. Чем же, ребята, ограничена сверху
последовательность ^?
— Единицей! — отвечают они дружным хором.
— Верно, все ее члены меньше или равны единице. А чем она
ограничена снизу?
— Нулем! — звучит столь же слаженный хор.
— Есть предложение, — неторопливо говорит Рамзин,
выждав небольшую паузу, — выразить ее ограниченность с
помощью одного числа: все члены последовательности по модулю
меньше или равны единицы.
— Тоже верно. Не будет ошибки, если мы скажем, что все ее
члены по модулю меньше или равны двум или трем... Вообще,
когда речь идет о некоторой ограниченной последовательности
ап, часто не так важно, какое именно положительное число М
ограничивает ее члены по абсолютной величине (пишу на доске
\о>п\ < М). Важно, что это число существует и годится в
ограничители для члена последовательности с любым номером п, —
последнюю фразу я говорю нарочито медленно, громко и
четко. — Вы слышите, Аргунова: опять те же ключевые слова —
«существует», «любой». Может быть попытаетесь, заменяя их
символами, написать определение ограниченности?
— Ой, нет, лучше я в другой раз, — лепечет она и вся как-то
сжимается, словно пытаясь зарыться в складки своего глухого
темного платья, воздушно висящего на ее худощавой фигурке.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
21
— Ладно, принуждать не будем, поищем смельчаков на
мужской половине. Не попробуете ли, Кочин?
Узколицый, сухощавый, невысокий, в недорогом, но
опрятном костюме, он идет к доске, чуть склонив голову, словно в
сомнении, шагом неспешным, но решительным, ставя ногу на
каблук (должно быть, только что из армии); пишет не быстро, с
задержками, но в конце концов без ошибки переводит сказанное
мною на язык символов.
— Очень хорошо, садитесь. Вы неплохо осваиваетесь с
этими новыми значками. Обратите внимание на порядок
кванторов, ребята, — поясняю написанное Кочиным. — Если мы его
изменим, получится утверждение о том, что для каждого члена
последовательности найдется превосходящее его по модулю
действительное число — утверждение довольно пустое, поскольку
его можно высказать по отношению к любой
последовательности. Как видите, даже этот незамысловатый пример убеждает
нас быть внимательными к порядку разноименных кванторов.
Одноименные, если они стоят рядом, переставлять можно, это
ошибки не привнесет. Подведем итог сделанному нами: мы
определили ограниченность последовательности. Покажем, что
этому определению удовлетворяет наша последовательность ^.
Действительно, 3 М = 1 > ОУ п (\ап\ = £ < 1). Для любителей
наглядности я проиллюстрирую это утверждение на числовой оси.
Обратимся теперь к натуральному ряду. Как мы уже
отмечали, он представляет собою неограниченную последовательность.
Что это значит? Кто хотел бы выразить этот факт с помощью
логических символов? Горт? Пожалуйста, к доске.
— Неверно, что существует такое М, — начинает он еще на
ходу и размашисто пишет на доске определение ограниченности
с пририсованным слева уголком отрицания.
— В принципе правильно. Но в математике не принято
давать негативные определения, то есть начинающиеся со слов
22
ПОСЛЕДОВАТЕЛЬНОСТИ
[Гл. 1
«неверно, что». Как же избавиться от нежелательного
начала?
— Очень просто! — Костюк словно ждал этого вопроса. —
Неверно, что существует какое-то ограничение М — это значит,
что для любого М неверно, что для любого п удовлетворяется
неравенство \ап\ < М.
Пишу этот вывод на символическом языке под строчкой,
написанной Гортом, и продолжаю:
— Вдумаемся в написанное мной: неверно, что неравенство
выполняется для любого п — это значит, что существует п, для
которого оно не выполняется. То есть для любого М существует
п такое, что неверно \ап\ < М. (Записываю ниже и этот вывод).
Но отрицать это неравенство — значит утверждать неравенство
\ап\ > М. Так ведь? Напишите это, Саша. Всем понятно
рассуждение, которое было проведено?
Обвожу взглядом аудиторию. Заглядываю в тетради
сидящих на первом ряду. У Лапикова подробно и аккуратно
переписано все, что писалось на доске. У Миклашевского — чистые
страницы.
— Миклашевский, не слишком ли вы надеетесь на свою
память? И не берут ли в этом с вас пример другие? — положив
мел, пускаюсь в путь между столами. — Я очень советую вам,
ребята, по возможности полнее записывать в свои тетради то,
что говорится в аудитории и пишется на доске: короткая
сиюминутная заметка стоит воза воспоминаний. И на лекциях
рекомендую поступать точно так же — аккуратно вести конспекты.
Еще прошу приносить эти конспекты с собой на семинары —
пригодится. На семинарах, если кто-то не понял чего-либо из
сказанного или написанного на доске, пусть поднимает руку. Об
этом, ребята, давайте договоримся твердо и навсегда: если кому-
то из вас покажется неясной любая мелочь, которая
встретится вам на протяжении семестра, — обязательно дайте мне об
этом знать. Не стыдитесь своей непонятливости! Математика,
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
23
как вы знаете, — наука дедуктивная, то есть логически
выводящая одни положения из других. И если какое-то из
предшествующих положений осталось непонятным для вас, вы не
сумеете должным образом уяснить последующие, так что ваши
знания окажутся подобными дому, построенному на песке. Так
всем ли было понятно сказанное до сих пор? Молчите. Что ж,
молчание — знак согласия. Продолжаем. Садитесь, Горт. Итак,
мы получили определение неограниченности. А заодно
познакомились с полезным приемом, который позволяет строить
отрицания утверждений, содержащих кванторы. (Жестом прохожу
сверху вниз по трем последним строчкам символов,
содержащих кванторы.) Он прост: знак отрицания перепрыгивает через
кванторы слева направо, меняя их один на другой, пока не
доберется до соотношения из символов, оговоренных кванторами:
это соотношение следует заменить на противоположное.
Опробуем теперь в деле полученное нами определение
неограниченности. Посмотрим, удовлетворяет ли ему натуральный ряд, в
неограниченности которого мы уверены. Кто провел бы такую
проверку?
Чтобы не терять достигнутого темпа, хорошо бы и на этот
раз вызвать кого-то из тех, кто заявлял о своем знакомстве с
кванторами.
— Может быть, Синица? Давайте, ради наглядности
снова будем иллюстрировать свои утверждения на числовой
оси.
Не без изящества, свойственного всему ее миловидному
облику (короткая прическа, белый отложной воротничок, узорчатая
кофточка), аккуратно рисует она ровную прямую с
разметочными штришками 0, 1, 2, 3...
— Какое бы положительное число М мы ни взяли, — на
числовую ось ложится высокая и тонкая засечка, — найдется член
нашей последовательности, больший по абсолютной величине, —
правее засечки М появляется жирная точка. — А в этом и
состоит неограниченность.
— Верно, садитесь. Но вот что любопытно в поведении нашей
последовательности: найдя ее член правее произвольного
положительного М, мы видим ... что, ребята?
I ПОСЛЕДОВАТЕЛЬНОСТИ [Гл. 1
П отигт слышится нестройный, но уверенный хор, в
котором я различаю голоса Миклашевского, Стрельцова, Рамзина,
Косгкжа:
Что и все следующие члены лежат правее М; что они
больше М по модулю.
Да, сильная, видать, группа. Но не буду торопиться с
окончательным суждением. Пока что высказывались самые бойкие,
желающие себя показать. Как проявят себя другие? Кто знает!
Подождем...
— В том, что вы говорите, выражается нечто большее,чем
просто неограниченность — не правда ли, ребята? Вы
чувствуете, вероятно, что на примере натурального ряда мы вскрыли
интересное математическое понятие, которому стоило бы дать
свое определение. Попробуем это сделать. Кто начнет? Хотите
вы, Миклашевский? Пожалуйста.
Он словно вспархивает над столом — кудрявый, во
франтоватом пиджачке из искусственной кожи — и, подлетев к доске:
— Для любого М > О найдется такое п, что для любого п
большего... Нет, надо тому п дать какое-то особое обозначение —
по что ли...
— Возьмите N, — подсказываю я.
— Ну или N, — покладисто кивает он. — Тогда сначала: для
любого М > О найдется такое N, что для любого п, большего N,
член ап будет по модулю больше М.
— Неплохо. Запишите это на доске в символической форме.
Верно; но не кажется ли вам, что выражение Vn > N стоило бы
расщепить? Как вы его понимаете?
— Для любого п, удовлетворяющего неравенству п> N...
— Так и пишите: Уп(п > N)... А дальше?
Не дожидаясь новых вопросов, он сообразительно ставит
вслед за скобками стрелочку логического следования и далее —
неравенство \ап\ > М.
— Хорошо, садитесь. Запишите это определение, ребята.
Последовательности, удовлетворяющие ему, называются
бесконечно большими или стремящимися к бесконечности. Итак,
натуральный ряд не только неограничен, но и стремится к
бесконечности. В нем объединились эти два свойства. Возможно, вы спро-
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
25
сите: а вдруг оба свойства сопутствуют друг другу всегда? Быть
может, любая бесконечно большая последовательность неогра-
ничена и наоборот — любая неограниченная последовательность
стремится к бесконечности? Исследуем эти два вопроса по
порядку. Итак, если последовательность бесконечно большая, то
можно ли утверждать, что она неограничена?
Шарю взглядом по молчащей аудитории:
— Кого бы вызвать к доске? Может быть, кого-то из тех,
кто до сих пор не подавал голоса? Может быть, вас, Сынчиков?
Прошу!
Проходит, наверное, не меньше минуты, пока он снимает
очки и укладывает их в очечник, пока выбирается из-за стола и
добредает до доски — весь какой-то блеклый, понурый.
— Для начала, — советую я, — стоит вновь выписать
определения неограниченности и стремления к бесконечнсти.
Ни малейшим движением не отзывается он на мой совет.
— Пишите же!
Он начинает: ЗМ ... останавливается, после минутного
раздумья исправляет: VM — и медленно, правда, теперь уже без сбоев
пишет определение неограниченности. Строчкой ниже пытается
выписать определение бесконечно большой последовательности:
вырисовывает VM , стирает квантор всеобщности, долго думает,
заменяет его квантором существования, потом стирает и его, но
уже не пишет ничего взамен, уставившись взглядом в пол.
— Забыли? Можете взять свою тетрадь.
Наконец оба определения красуются на доске.
— Предположим, — подталкиваю Сынчикова к
продолжению, — что для некоторой последовательности ап справедливо
второе высказывание. Давайте посмотрим, следует ли из него
первое.
Ни движения, ни звука с его стороны.
— Ну, рассуждайте же! Пусть последовательность ап
стремится к бесконечности. Возьмем произвольное положительное
М... Продолжайте!
Те же неподвижность и молчание.
— Может быть, вам удобнее начать с конца? Какое
неравенство должно выполняться в утверждении, которое вы хотите
доказать?
Не сразу, а выждав чуть не полминуты, он протягивает руку
к неравенству \ап\ > М в определении неограниченности.
— Найдутся ли такие ап в последовательности, если она
удовлетворяет определению стремления к бесконечности? Посмот-
26
ПОСЛЕДОВАТЕЛЬНОСТИ
[Гл. 1
рите на это определение внимательно: есть ли там такое
неравенство?
— Есть, — наконец произносит он глухим, еле слышным
голосом.
— И при каких п оно выполняется? Отвечайте же, не молчите!
— При п, больших N.
— А откуда берется это N? Прочтите-ка сначала определение
того, что последовательность стремится к бесконечности.
Монотонно и медленно, словно говорящая машина, он
выговаривает:
— Для любого М , большего нуля, найдется такое N...
— Читаете вы верно. Чтобы лучше это понять, попробуйте
каким-нибудь наглядным способом представить себе, что
выражают эти определения, — например, с помощью числовой оси.
Нарисуйте ее! Ну вот: представьте себе, что мы взяли какое-то
большое положительное число М — отметьте его на оси!
Хорошо. Наша последовательность по условию стремится к
бесконечности. Вот определение этого факта. Как же, если поглядеть
на него, ведут себя члены последовательности по отношению к
числу Ml
— Они ... больше его, если ...
Собрав все свое терпение, жду продолжения фразы.
— Если п больше N.
— Отлично! Рисуйте на числовой оси члены с номерами,
большими N. Какие это номера? Назовите хотя бы несколько!
- N + I ... N +2 ...
— Рисуйте их, рисуйте же! Картина, кажется, уже ясна: она
выражает тот факт, что наша последовательность стремится к
бесконечности. Перейдем теперь к определению
неограниченности. «Для любого М , большего нуля», — начинается оно. Если
опять обратиться к числовой оси, то что мы должны там
нарисовать, Сынчиков? Вы опять замерли?
- Вот... число М, — скованно указывает он на прежнюю
засечку.
— Ну, хорошо. Читайте дальше определение
неограниченности.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
27
— Существует п такое .... что \ап\ > М.
— На чертеже, который вы нарисовали, есть такое ап1
— Вот, — указывает он тем же жестом на а#+1-
— Ну, конечно! Так какой после всего сказанного назовем
мы нашу последовательность ап — ограниченной или
неограниченной?
— Неограниченной.
— Верно. А теперь давайте окончательно и аккуратно
покажем, что из утверждения о том,что некоторая
последовательность ап стремится к бесконечности, следует утверждение
о том, что эта последовательность неограничена. Ради
пущей четкости повторим второе утверждение. Начинайте, Сын-
чиков!
— Для любого М больше нуля, — говорит он, и в наступившей
паузе я повторяю нарочито пространно, чтобы перевести
логический код, буквально воспроизводимый Сынчиковым, на более
доходчивый, более усвояемый язык:
— Вот мы взяли произвольное положительное М...
— Существует п...
Снова пауза, и снова я веду «вторым голосом»:
— И должно найтись такое п, что ...
— Что \ап\ > М.
— Как же искать это п?
На числовой оси, которую мы с ним рисовали за
рассуждением о бесконечном возрастании последовательности ап, он снова
указывает кружок с пометкой а^+ь
— Вы хотите сказать, что это п определяется из
условия...
Оборвав фразу, жду от Сынчикова окончания. Заканчивать
однако приходится самому:
— Из условия стремления последовательности к
бесконечности. Не так ли?
-Так.
Я вновь приписываю знак равенства к буковке п в
определении неограниченности и передаю мел Сынчикову. Поняв мою
безмолвную просьбу, он пририсовывает за знаком равенства
N + 1.
— Теперь, — говорю, подбавив в свой тон повелительную
интонацию, — напишите вновь и перескажите словами
утверждение о неограниченности последовательности ап.
— Для любого М больше нуля... найдется п, равное N + 1,
такое...
28
ПОСЛЕДОВАТЕЛЬНОСТИ
[Гл. 1
— Найдется, — перебиваю его, — п, равное N + 1, где N
определяется... откуда оно определяется, Сынчиков? Из какого
условия?
— Где N определяется из условия... из того, что
последовательность стремится к бесконечности...
Он останавливается, несколько сбитый с толку моим
вмешательством, и после глубокой паузы продолжает:
— Найдется п, равное N + 1, где N ... из того, что стремится
к бесконечности... п, равное N + 1, такое, что \ап\ > М.
— А это и есть неограниченность, — резюмирую подчеркнуто
отчетливо и замедленно (только бы не выказать своей
поспешностью, как раздосадовала меня столь тягомотная задержка на
таком пустяковом вопросе! В конце концов, я сам только что
декларировал перед ребятами, что всякая неясность, возникшая у
любого из них, должна быть разобрана до конца!) — Итак,
Сынчиков доказал, что неограниченность последовательности
следует из того, что последовательность стремится к бесконечности.
Вам-то самому теперь это понятно, Сынчиков?
Он впервые поднимает на меня взгляд и с неожиданной, хотя
и еле ощутимой в его шелестящем голосе твердостью отвечает:
— Дома я все это обязательно выучу.
— Будем надеяться. Садитесь. Посмотрим теперь, ребята,
следует ли из неограниченности стремление к бесконечности.
— Нет, — уверенно заявляет Лапиков. — Существуют
последовательности, которые неограничены, но не стремятся к
бесконечности.
— Например?
— Например, (—2)п.
— Вы думаете, что эта последовательность не стремится к
бесконечности? — удивленно смотрю на него, и вдруг мне
становится понятным, откуда возникло его заблуждение; вина в этом
моя: я переоценил способность к обобщениям у своих
подопечных — в дальнейшем следует быть предупредительнее к их
недогадливости, а сейчас надо поскорее устранить недоразумение.
— А ну-ка к доске, Лапиков! Нарисуйте числовую ось и на
ней — как вы представляете себе стремление к бесконечности.
Давайте, я буду диктовать соответствующее определение, а вы —
сопровождать мои слова отметками на числовой оси. Итак, для
любого положительного М (он ставит засечку справа от нуля)
найдется такой номер N, что для любого п, большего N, будет
выполняться неравенство \ап\ > М. Что же вы отмечаете
члены последовательности лишь справа от засечки М? Ведь чис-
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
29
ла, большие некоторого положительного М по абсолютной
величине, — не только те, что больше М, но и те ...
— Но и те, что меньше минус М, я все понял, —
наклоняет он свою гладко стриженную голову в покорно-благодарном
движении.
— Вы слишком прочно связали свое представление о
стремлении к бесконечности с конкретным чертежом, на котором мы
демонстрировали бесконечное возрастание конкретной
последовательности — натурального ряда. Признаюсь, ребята, здесь
есть и моя вина: я не предостерег вас заранее от подобной
привязанности. Однако нет худа без добра: теперь вы ясно видите,
как она вредна, и, надеюсь, усвоите на будущее: в конкретных
иллюстрациях всегда есть много несущественного, лишнего по
сравнению с иллюстрируемой ими абстрактной истиной, и это
лишнее, несущественное не должно прилипать к сути. Но это
еще не вся польза, которую можно извлечь из заблуждения
Лапикова. Оно позволит нам расширить нашу терминологию.
Если для любого положительного числа можно указать номер,
начиная с которого все члены последовательности будут больше
этого числа, иными словами, будут лежать справа от него на
числовой оси — говорят, что последовательность стремится к
плюс бесконечности. Именно так ведет себя последовательность
ап = п — посмотрите еще раз на наш чертеж. Таков же
характер стремления к бесконечности и у последовательности
ап = 2п (поясняю это на числовой оси). По аналогии можно
определить и стремление к минус бесконечности. Теперь
становится ясным, в чем заключалось заблуждение Лапикова: он
представлял себе стремление к бесконечности односторонне —
как стремление к плюс бесконечности. А последовательность
ап = (—2)п действительно не стремится к плюс бесконечности,
это Лапиков подметил верно. Кстати, Егор, вы смогли бы это
доказать?
— Боюсь, что нет.
Признаться, боюсь и я. Еще больше боюсь, что его попытка
доказательства окажется такой же мучительной, как наш
недавний разговор с Сынчиковым. И тогда замрет поступательный ход
беседы, которая так удачно начала складываться. Да, поспешил
я с высокой оценкой этой группы. Выслушав сильнейших, теперь
надо прислушаться к слабейшим, определить средний уровень
моих собеседников и выбрать оптимальный темп дискуссии, в
которой мог бы поучаствовать каждый студент. Что ж,
продолжу разговор с Лапиковым.
30
ПОСЛЕДОВАТЕЛЬНОСТИ
[Гл. 1
— Не можете, так не можете. Будем надеяться, что сможете
позднее, когда узнаете побольше подходящих
последовательностей, когда понаблюдаете, как с ними работают другие. А сейчас
я хотел бы выяснить, как вы представляете себе минус
бесконечность. Сможете ли вы сформулировать определение того факта,
что некоторая последовательность стремится к минус
бесконечности? Рискнете?
Авось, рассуждение по аналогии у него получится.
— Рискну, — отвечает он, помолчав секунду-другую, и тянет
мел к моему последнему чертежу, где я предусмотрительно
засек на числовой оси не только положительное М, но и
отрицательное — М.
— Это когда для любого отрицательного числа можно найти
номер... такой номер, что все следующие члены
последовательности будут левее этого числа.
— Правильно. Теперь...
Но он не дает мне продолжить:
— А последовательность ап = (—2)п и к минус бесконечности
не будет стремиться!
— Тоже верно. Молодец. Итак, ребята, последовательность
ап = (—2)п, как выясняется, не стремится ни к плюс, ни к
минус бесконечности. Правда, сам изобретатель столь интересной
последовательности еще не доказал этого, оставил на потом.
Однако, что касается стремления к бесконечности, не разделяемой
знаками плюс и минус, то оно у нашей последовательности
налицо. Это ясно уже из такой детали: в неравенстве, которым
заканчивается определение стремления к бесконечности, члены
последовательности берутся по абсолютной величине. Из членов
вашей последовательности, Лапиков, при этом получается 2n, a
это уже разбиравшийся нами пример стремления к
бесконечности. Вы хорошо это поняли? Да? Скоро я проверю это, садитесь.
Проводив его взглядом до места, обращаюсь к остальным:
— Скажите откровенно, ребята: не кажутся ли вам чересчур
затянутыми подобные разговоры у доски? Если да, то
наберитесь терпения — такие ситуации будут возникать на каждом
семинаре. Прошу вас отнестись к этому с пониманием: я должен
добиваться, чтобы каждый из вас хорошо усвоил основные
положения курса. Каждый, а не только те, кто все схватывает с
полуслова. Кстати, скорость усвоения знаний еще не
определяет уровень владения ими. При любой скорости, если не снижать
ее и не забывать уже усвоенное, даже тугодум способен достичь
вполне приличного уровня и добиться своих успехов. Уверен-
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
31
ность в этом подкрепляется еще и тем, что медлительные слоны
чаще добиваются успехов в науке, чем бойкие мотыльки. Так
что не отчаивайтесь, ребята, если чего-то не поняли сразу,
никогда не стыдитесь своего непонимания и незнания, стремитесь
к доске не только тогда, когда вы все понимаете — нет, скорее
тогда, когда вы чего-то не понимаете. Я постараюсь вам помочь.
А чтобы самые понятливые во время наших разговоров у
доски не томились от безделья, я буду давать им факультативные
задачи. Но даже и без таких задач им будет чем заняться —
своими репликами, советами, возражениями пусть помогают
тому, кто у доски старается разобраться в чем-то недопонятом,
и одновременно тем самым пусть помогают мне находить
самые убедительные доводы для разъяснения трудных мест. Все
мы коллеги, участники общих дискуссий, где ваши знания
складываются как результат совместного поиска. В этих дискуссиях
ценны и удачные выступления, которые доставляют нам новые
знания, и неудачные, возражая которым, мы оттачиваем знания
уже полученные. Двинемся же дальше по этому пути.
Продолжим поиск последовательностей, которые не ограничены, но к
бесконечности не стремятся.
— Сейчас, сейчас, сейчас, — торопливо бормочет Мухин и
что-то чертит рукою в воздухе.
— Не лучше ли нарисовать на доске? Прошу!
Он порывисто встает из-за стола, гремя стулом; космы его
кудлатой шевелюры, кажется, никогда не знавались с расческой,
клапаны огромных карманов фланелевой куртки топорщатся в
разные стороны... Сделав несколько шагов, он вдруг
останавливается:
— Я уже и без доски могу: один, ноль, два, ноль, три, ноль,
четыре, ноль — вот такая последовательность.
И вопросительно смотрит на меня. Я записываю на доске
названные им числа.
— Любопытная последовательность — правда, ребята? —
приглашаю аудиторию к обсуждению. — Давайте проверим,
действительно ли она неограничена и действительно ли не
стремится к бесконечности, как полагает Мухин?
— То, что она неограничена, это ясно, — продолжает сам
автор примера. — Это просто сразу видно: вот взяли какое-то
М — положительное, разумеется — взяли какое-то
положительное М, а потом — пойдем по последовательности, по ненулевым
членам — один, два, три, четыре и так дальше — когда -нибудь
обязательно найдем такой член, который больше М.
32
ПОСЛЕДОВАТЕЛЬНОСТИ
[Гл. 1
— Большее, чем М, число найдется, а следующее уже будет
меньше; значит, к бесконечности не стремится, —
непринужденно и ни к кому не обращаясь произносит Меншиков. Одетый в
синий спортивный костюм, он широко развалился на стуле;
кажется, будто он пришел на семинар отдохнуть после тяжелой
тренировки.
— Очень интересное умозаключение! — неподдельно
изумляюсь его словам. — Уже не считаете ли вы, Меншиков, что
к бесконечности могут стремиться лишь монотонные
последовательности? Только что ведь мы рассматривали
последовательность (—2)п: немонотонна, а к бесконечности стремится
исправно. А ну, ребята, придумаем специально для Меншикова
еще один пример бесконечно большой, но не монотонной
последовательности — скажем, исключительно с положительными
членами.
Тишина. И лукавый голосок Синицы:
— Два, один, четыре, три, шесть, пять...
— Отлично! А почему эта последовательность стремится к
бесконечности? Объявляю конкурс: кто даст лучший ответ на
мой вопрос?
— Потому что она и по четным членам стремится к
бесконечности, и по нечетным тоже, — высказывает свое мнение
Чюмин.
— Потому что найдется такое N, после которого все члены
будут больше любого наперед заданного М, — рассудительно
произносит Костюк.
— Потому что она удовлетворяет определению стремления к
бесконечности, — тотчас вслед заявляет Горт.
— Победил Горт. Он уточнил верную идею Костюка
ссылкой на определение, а в математике это вернейший путь
разрешения любых каверзных вопросов, любых сомнений и
недоразумений — в будущем мы еще не раз убедимся в этом, —
подвожу итоги конкурса. — Так пусть же Горт и отстаивает
свое утверждение. Поскольку определение бесконечно большой
последовательности начинается с того, что берется
произвольное положительное число М, то я вправе взять М = 3,5. Далее
в определении говорится: существует N такое, что для любых
п > N выполняется неравенство \ап\ > М. Какое же N вы
возьмете, Горт, для М = 3,5?
— Сейчас... N = 4. — Он поясняет свой ответ графиком.
— А если М = 4,5?
— Минуточку... Опять-таки N = 4.
Ю. В. Пухначев] СЕМЬ СЕМИНАРОВ 33
— А если М = 5?
- Тогда... N = 6.
— Надеюсь, ребята, теперь все видят, сколь непроста здесь
зависимость N от М. Это не то, что в натуральном ряду:
нашел число, большее заданного М, и будь уверен, что все
последующие числа также будут больше М. Но ведь определение
стремления к бесконечности вовсе и не требует столь же
целеустремленного поведения от всех бесконечно больших
последовательностей. Оно требует только то, о чем в нем говорится:
для любого положительного М должен найтись такой номер ЛГ,
чтобы все члены последовательности с большими номерами
превосходили М по модулю. С последовательностью Синицы дело
обстоит именно так, и, стало быть, она стремится к
бесконечности. Садитесь, Горт. Вернемся теперь к последовательности
Мухина, к вопросу о том, стремится ли к бесконечности она.
— Не стремится, потому что не удовлетворяет определению
стремления к бесконечности, — отчетливо и мерно
произносит Сутеев своим странным, каким-то механическим
голосом.
— Подход хорош, — киваю ему, жестом приглашая его к
доске, — но формулировка ответа не совсем удачна: ведь мы уже
условились избегать негативных утверждений. Лучше сказать,
что последовательность Мухина удовлетворяет определению
последовательности, не стремящейся к бесконечности. Кстати, есть
ли у нас такое определение? Нет? Тогда, Сутеев, давайте
построим его — благо, теперь мы уже знаем как это делается. Ради уве-
34
ПОСЛЕДОВАТЕЛЬНОСТИ
[Гл. 1
ренности выпишем сначала определение бесконечно большой
последовательности... так, так, хорошо... а ниже напишем
определение противоположного свойства... Существует М, для любого
АГ, хорошо... Как ловко у вас это получается! Осталось написать
отрицание того факта, что для любого п выполняется
логическое следование ((n > N) =*► (\ап\ > М)). Вы затрудняетесь это
сделать, Сутеев? Ребята, кто поможет?
— Написать не «для любого п», а «существует п», и
стрелочку перечеркнуть — это будет означать «не следует», — советует
Миклашевский.
— Извините, перечеркнутой стрелочки нет среди принятых
нами логических символов. Давайте не выходить за пределы
их списка, постараемся скомбинировать отрицание следования
только из них.
Долгая пауза. Внимательно оглядываю сосредоточенно
нахмуренные физиономии ребят, безуспешно пытающихся
выполнить мое задание, и останавливаюсь взглядом на спокойном лице
Гарина с чуть приметной улыбкой на нем, так контрастирующей
со всеобщей насупленностью.
— Вы уже придумали, как выйти из положения?
— Да вроде бы, — слегка пожимает он плечами. — Отрицать,
что для любого п выполняется какое-то следование — это все
равно, что утверждать: существует п, при котором предпосылка
выполнена и в то же время не выполняется следствие. В нашем
случае это будет выглядеть так: Зп((п > N) А (\ап\ < М)).
Гарин
ал te cmfi&juu-mcsL к &есмон£Дмаспш,:
3M>0 VN 3*t (C^>N)A(|aA|6M))
— Абсолютно верно! И в дальнейшем, ребята, когда вам
придется отрицать высказывание вида А => В, пишите А А -^В. Но
вернемся к нашим рассуждениям. Определение, построенное
Сутеевым, начинается со слов «найдется М». Как же искать это М?
Чем оно определяется?
Растерянная тишина наступает за моим вопросом. «Как это
чем? — некоторое время спустя недоуменно переспрашивает
Горт. — Оно существует — и все!» «Может быть, даже не
одно,» — в тон ему добавляет Костюк. «Главное, что
существует,» — поддакивает Рамзин. Наконец слово берет Стрельцов:
— По-моему, М определяется характером
последовательности, ее строением что ли ...
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
35
— В этом соображении что-то есть. Не разовьете ли его у
доски, Стрельцов, применительно к последовательности Мухина?
— Я его и сам не до конца понимаю, — без особой охоты
берет он мел, сменив у доски Сутеева. — Но попробую, ладно.
Существует М... А зачем нам нужно это М? Чтобы
выполнялось последнее неравенство \ап\ < М, чтобы нашелся такой член
последовательности, который удовлетворит этому неравенству...
то-есть, нашелся подходящий номер п... нашелся за любым
номером N. сколь угодно большим... Этот член последовательности
ап — очевидно, нуль, один из этих нулей, которых бесконечно
много... вот они, на четных местах... Тогда пусть М будет
равно... ну, допустим, единице... тогда |0| < 1... все четко!... а этот
номер п — просто какой-нибудь четный номер и все... Как это
теперь у нас будет? Существует М = 1 такое, что для любого
N существует такое п, большее N... большее N и четное...
взять 2N1... а что, очень даже годится... существует такое
п = 2N > N, что \ап\ = |a2w| = |0| < 1 = М. Вроде бы все
получилось, — и он ровной строчкой тянет символическую
запись своего рассуждения.
— Воистину, ребята, — гляжу на него, довольный, — кто ясно
мыслит, ясно излагает — даже тогда, когда мысль только
зарождается: в такие моменты вы можете наблюдать, как она
развивается, можете поучиться умению ее развивать. Какой же вывод
сделаем мы из рассмотренного примера, Стрельцов?
— Из неограниченности последовательности, — продолжает
он все тем же ровным тоном, — еще не следует, что она стремится
к бесконечности: существуют неограниченные
последовательности, не стремящиеся к бесконечности.
— Именно такова последовательность Мухина. Но, я
думаю, — продолжаю, отослав на место Стрельцова, — она
подскажет нам не один лишь этот вывод. Вглядимся в нее
внимательнее, ребята: что еще характерного замечаете вы в
ней?
— Такое впечатление, — отзывается Кочин, — будто здесь две
последовательности. Первая — это натуральный ряд: один, два,
три и так далее, а другая вся из нулей, то есть она ... стабильная
что ли?
— Стационарная, — поправляю его. — Вам не откажешь в
наблюдательности, Кочин. Я хотел бы отметить характерную
деталь вашего открытия. Выбирая числа из последовательности
Мухина, вы называли их в том же порядке, в каком они
располагаются в содержащей их последовательности. В этом — важ-
36
ПОСЛЕДОВАТЕЛЬНОСТИ
[Гл. 1
ная черта понятия, с которым мы сейчас познакомимся. Если из
элементов некоторой последовательности ап набирается новая и
при этом сохраняется порядок следования элементов, то новая
последовательность называется подпоследовательностью
исходной и обозначается аПк. Индекс к здесь служит для
перечисления членов подпоследовательности, а все остальное указывает
на ту последовательность, из которой они извлечены. Итак,
натуральный ряд есть подпоследовательность последовательности
Мухина. Тот и другой ряд чисел я напишу отдельно, один под
другим. Внимательно посмотрите на обе последовательности,
ребята. Припомните их характерные черты, поразмышляйте, не
находятся ли эти черты в какой-то логической связи, и, быть
может, нам посчастливится сформулировать какую-либо теорему.
Думаем!
— Я уже придумал! — вскидывает руку Горт. — Если дана...
— Стоп, стоп! — обрываю его. — Придумали теорему,
попытайтесь ее доказать, доказали — проанализируйте
доказательство в надежде обнаружить какие-то новые интересные ее
аспекты, выполнили до конца мое очередное задание — вернитесь
к предыдущим: быть может, вы и поймете и решите их лучше,
чем прежде. Но не мешайте своей торопливостью думать
другим. Когда я начну спрашивать — тогда и тяните руку.
Выдерживаю паузу в несколько минут.
— Ну как, ребята? Кто придумал какую-нибудь теорему?
Поднимите руки! Ого, какие мы сообразительные! Горт,
Мухин, Рамзин, Кулагин, Чюмин, Синица ... Вот ей и давайте и
предоставим слово — будем джентльменами.
— Из любой неограниченной последовательности можно
выбрать подпоследовательность, стремящуюся к бесконечности.
— Очень хорошо! Все остальные имели в виду ту же самую
теорему? Да? А кто ее доказал?
Руки поднимают Горт, Мухин, Рамзин.
— Нет, ребята, — жестом отказываю им, — вам сегодня я
давал слово уже не раз. А вот, как я заметил, еще хотел выступить
Чюмин, который у доски еще не бывал — его-то я и вызову.
Он начинает уверенно и продуманно:
— Если некоторая последовательность ап неограничена, то
для нее справедливо утверждение: V М > 03 п (\ап\ > М). Ну
вот, взяли какое-то положительное М, и для него нашли ап,
которое удовлетворяет неравенству. Обозначим его аП1. Возьмем
еще одно число М, большее |аП1|, и для него подберем такой
член ап, который больше него по модулю. Обозначим его аП2 ...
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
37
— Минуточку, минуточку! Начали вы очень четко, а теперь
четкость, понемногу теряете. Следите за нею! Когда вы
приглашены к доске, вы говорите не для себя и не для меня, а для всех
сидящих перед вами, помните об этом! Как я вижу, на место М
в определение неограниченности вы будете подставлять разные
числа — так и обозначайте их по-разному: М\, М2, Мз... Давайте
снова — с определения неограниченности.
— Хорошо. Берем в этом определении произвольное
положительное М\. Для него находим в нашей последовательности член
аПл, который по модулю больше этого Mi. Потом берем число
М2 > \a»ni\- Для него находим больший его по модулю член аП2
и так далее.
— Что ж, построение весьма понятное. В итоге возникает
подпоследовательность аПк. Будет ли она стремиться к
бесконечности? Вы это доказали?
Чюмин растерянно смотрит на меня:
— Вы знаете, я об этом забыл...
Общий хохот покрывает его слова. Он, видимо, уже заслужил
в группе репутацию чудака. Это чувствуется по направленным
на него снисходительным взглядам — у кого-то с долей
сочувствия, у Рамзина — с оттенком надменного презрения.
— Забыл! — улыбаюсь и я. — Забыл о самом главном, ради
чего мы раскладывали весь наш пасьянс! Но хватит
смеяться, ребята, — я пока что не могу поручиться, что никто из
вас не может оказаться в столь же анекдотической ситуации.
Давайте-ка все вместе спасать положение. Садитесь, Чюмин.
Прежде всего разберемся в том, что сделано. Может быть
алгоритм Чюмина не так уж плох и из любой неограниченной
последовательности будет выбирать только бесконечно
возрастающие подпоследовательности? Или же можно представить
себе такую неограниченную последовательность, из которой при
неудачном применении только что описанного алгоритма будет
выбрана отнюдь не бесконечно возрастающая
подпоследовательность?
Проходит минута, другая... По лицам ребят вижу, что
искомое так и не найдено. И вновь нечто контрастирующее со
всеобщим недоуменно-безнадежным настроением чудится мне в
непроницаемом лице молчальника Гарина.
— Вам что-то удалось найти?
— Да вроде бы.
— Поделитесь, не утаивайте.
— Если взять такую последовательность: 1, ^, 2, §, 3, §,...
38
ПОСЛЕДОВАТЕЛЬНОСТИ
[Гл. 1
— Очень интересная последовательность! Напишите-ка ее на
доске.
— Ну чего там писать? И так все понятно.
— Боже, какой ленивец! Я, если угодно, приказываю: идите!
Откликнувшись понимающей улыбкой на мою шутливо-
утрированную начальственность, он вперевалку шагает к доске.
Грубошерстный пиджак округляет и без того полную его
фигуру, подчеркивая свойственный всей его натуре оттенок флегмы
и добродушия.
— Вот, значит, такая последовательность 1,^,2,|,3,|,... Чю-
мин предлагает взять для начала произвольное положительное
Mi, — так я возьму не очень большое, меньшее \ и для него
подберу как раз эту ^. Условие ведь у нас какое? Чтобы выбрать
член последовательности, больший М\. Я это условие соблюдаю.
Потом надо взять число М2, больше только что выбранного
члена последовательности, то есть больше \. Я возьму такое М2,
чтобы оно в то же время было меньше |. Для этого числа М2
надо выбрать из последовательности член, больший этого М2 по
модулю. Выберу |. Потом возьму число Мз, большее |, но
меньшее |, и для него выберу из последовательности |. Получается
подпоследовательность 5»§»f»5 и так ^алее- Она ограничена,
потому что все ее члены не превосходят единицы. Значит, она не
может стремиться к бесконечности. Мы ведь уже доказали
теорему: если последовательность стремится к бесконечности, значит
неограничена. А тогда — если ограничена, то к бесконечности не
стремится.
— Очень хороший пример и хорошее рассуждение. Теперь
ясно видно, что алгоритм Чюмина может и не выполнить своего
назначения. Спасибо, Гарин, садитесь. Продолжим, ребята,
разработку искомого алгоритма — безотказного.
Продолжительное молчание только однажды нарушается
негромким голосом Меншикова — он указывает взглядом на
запись алгоритма Чюмина:
— Может быть, заменить условие Мь+\ > \аПк\ на другое:
Мк+1 >\аПк\ + 1?
Протоколирую это предложение на доске. Молчание
продолжается. Выждав с минуту, прерываю его сам:
— Все вы, ребята, слышали: современная наука носит
коллективный характер, научные результаты сегодня
достигаются трудом больших исследовательских коллективов. Будем на
уровне современной науки — будем учиться работать коллектив-
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
39
но. Когда идет обсуждение какой-либо задачи и кто-то высказал
свое суждение — пусть остальные постараются разглядеть
рациональное зерно в этой реплике, попытаются скомбинировать
новое соображение с ранее высказанными и на этой основе внести
свой вклад в развитие общего рассуждения. Мне кажется, что
хороший повод для тренировки в подобном сотрудничестве дает
последнее предложение Меншикова: в нем, если присмотреться
можно увидеть...
— Да-да! — перебивает меня Горт; он устремляется к доске,
додумывая свое рассуждение на ходу:
— Если взять натуральный ряд... да, если взять целые
числа, начиная с единицы; взять сначала единицу и потом число
Mi > 1, а для него уже подобрать член последовательности из
условия |аП1| > Mi, потом возьмем M<i > 2 и найдем аП2, по
модулю большее М2 — ну и так далее.
Переведя дух, он продолжает спокойнее:
— Очевидно, если какая-то последовательность
положительных величин bk стремится к плюс бесконечности, то и
последовательность больших величин с& тоже бесконечно возрастает.
— Эту теорему еще надо доказать! — прерывает его Костюк.
— Да это даже и не теорема, так — лемма, —
отмахивается Горт и глядит на меня. — Если нужно, я ее, конечно,
докажу. Нужно? Да? Потом? Хорошо. У нас все получается по этой
лемме: \аПк\ > Mk > fc, и поскольку последовательность
натуральных чисел к стремится к плюс бесконечности, то туда
же стремится подпоследовательность |anJ, а
подпоследовательность аПк просто бесконечно большая.
— Что ж, — пристально рассматриваю все написанное и
нарисованное им на доске, — я думаю, мы признаем ваше
рассуждение совершенно строгим, если вы докажете лемму, на которую
опираетесь.
Тишину, в которой Горт начинает свои выкладки,
нарушает резкий скрипучий голос — это Буткус впервые решился
выступить:
— Есть еще идея. Можно?
— Слушаем вас.
— Что, если построить подпоследовательность...
Он неуклюже поднимается со стула, не очень ладно
скроенный, угловатый в движениях; приглашение пройти к доске не
принимает:
— Я не знаю, как формулами, я словами. Первый элемент
подпоследовательности надо взять первый элемент последова-
40
ПОСЛЕДОВАТЕЛЬНОСТИ
[Гл. 1
тельности. Потом смотреть второй элемент: если меньше
первого по модулю, выбросить, если больше — писать в
подпоследовательность. Смотреть третий элемент последовательности: если
по модулю больше первого и больше второго — писать в
подпоследовательность, если нет — выбросить. И дальше так же
смотреть: если какой-то элемент последовательности по модулю
больше всех, до него которые, элементов, то писать его в
подпоследовательность; когда он не такой, не писать.
Господи, какой он косноязычный! И, как на грех, не может
выразить свое предложение формулами. Не дай бог, если эту
неловкость в русском языке, в языке формул ребята припишут
туманности мыслей — я уже жалею, что внушал им недавно:
кто ясно мыслит, ясно излагает. Тем более, что идея Буткуса,
если вдуматься в нее, совершенно верна. Надо срочно поддержать
парня!
— Заманчивое построение! И вполне четкое, несмотря на то,
что описано без единой формулы. Но будет ли построенная
подпоследовательность стремиться к бесконечности? Вы доказали
это, Буткус?
— Не доказал! — сокрушается он. — Я старался, и не доказал.
— Ничего страшного. Семинар наш еще не кончился: может
быть, мы еще познакомимся с чем-то таким, что подскажет нам
простое доказательство. Так что, ребята, давайте в дальнейшем
относительно каждого нового положения, которое мы изучим,
будем интересоваться: что из пройденного ранее оно помогает
прояснить или углубить? В свою очередь, пройденное ранее
время от времени будем просматривать с вопросом: что там
осталось неясного или недоказанного? Что допускает новую
трактовку или предлагает интересную проблему? Между прочим, —
оглядываюсь на доску, где Горт заканчивает свои выкладки, —
Саша только что выполнил работу именно такого рода: доказал
лемму, которую мы раньше приняли на веру. Давайте посмотрим
его доказательство. Так, так... Сотрите свои выкладки с доски
и можете садиться, Саша, — у вас все правильно. Согласны, ре-
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
41
бята? А помните, как мы обнаружили, что натуральный ряд не
просто неограничен, но еще и стремится к бесконечности? Это
наблюдение содержит свою проблему: какое свойство
последовательности в сочетании с ее неограниченностью гарантирует ее
стремление к бесконечности?
— Монотонность! — слышатся несколько голосов.
— Хороший ответ. Судя по быстрое и единодушию, с которым
вы его дали, упражнения в теории не прошли для вас даром. Я
думаю, что даже те, кто совсем недавно затруднялся в
теоретических рассуждениях, смогли бы теперь доказать теорему, к
которой мы пришли: любая неограниченная и монотонная
последовательность стремится к бесконечности. Может быть,
попробуете вы, Лапиков?
Поднявшись со стула, он тотчас опускает голову:
— Боюсь, что не сумею...
В беленькой рубашечке, пестреньком джемпере
заботливой маминой вязки, он похож на школьника, который просит
прощения.
— Опять это ваше паническое присловье, Егор! Прежде чем
капитулировать, вы могли бы сами проверить, сумеете или не
сумеете. Вы не знаете, как это сделать? Я только что советовал
всем время от времени просматривать пройденное и искать, что
там осталось неясного или недоказанного. Один такой должок у
нас образовался по вашей милости. Вы в свое время правильно
догадались, что последовательность ап = (—2)п не стремится к
плюс бесконечности. Но доказательства не дали. Не попытаетесь
ли доказать сейчас? Если вам это удастся, значит, можно
надеяться на большее, можно браться за следующие, более трудные
задачи. К доске, Егор! Вам наверняка понадобится отрицание
утверждения о том, что некоторая последовательность ап
стремится к плюс бесконечности. Как строить отрицание любого
утверждения, записанного в символическом виде, помните?
— Поменять в этом утверждении все кванторы на другие.
— Давайте еще раз покажем всем, как происходит такой
переход от некоего исходного утверждения к его отрицанию. Итак,
напишите определение последовательности, стремящейся к плюс
бесконечности.
Он начинает: VM>03JVVn-n опускает мел.
— А ведь определение, которого я от вас жду, совсем
недавно приводил Горт... — Под мою диктовку он пишет
завершающие скобки ((n > N) => (ап > М)), потом быстро меняет
кванторы.
42
ПОСЛЕДОВАТЕЛЬНОСТИ
[Гл. 1
— Хорошо, хорошо, — одобряю его действия. — Ваша боязнь
проходит, правда? Или она снова возвращается, когда вы
остановились перед заключительным высказыванием, которое теперь
надо изменить на противоположное? Забыли, как строить
отрицание следования? Я напомню: отрицать, что А влечет В —
значит утверждать, что выполняется посылка А и не выполняется
следствие В. В нашем случае это выглядит...
Еще на дождавшись, пока я договорю, он пишет: ((n > N)
и (ап < М)).
Лапиков
ум>
Зм>
0 3N Vn
0 VNf 3n
((n>
((«>
N)*
•N)u
(a„
(ar
^>M))
,«M))|
— Да, — смотрю на доску, — пишете вы быстро, и теперь
боюсь уже я: молсет быть, вы сконструировали это отрицание
чисто формально, по стандартному рецепту? Понимаете ли вы,
что написали? Давайте разбираться. Вот начало: ЭМ > 0. Каким
мы возьмем это М? Задумались? Покажите на числовой оси, как
ложатся на нее члены последовательности ап = (—2)п. Хорошо.
Теперь снова к строчке символов, над которой мы размышляем.
Где работает искомое М?
— Вот, в неравенстве ап < М.
— Какие же ап будут удовлетворять этому неравенству?
— Отрицательные, наверное. Тут подошло бы даже М,
равное нулю.
— Но М, как гласит начало нашего отрицания, должно быть
больше нуля.
— Тогда... Ну пусть хотя бы единица. Все ясно — существует
М = 1 такое, что для любого N найдется п... любое нечетное,
что п > N и ап = (-2)п < 0 < 1.
— Отлично! Зачем же было хныкать? Вы справились с этой
задачей и явно способны решить более трудную. Беремся за
теорему: любая неограниченная и монотонная последовательность
стремится к бесконечности. Впрочем, возвращайтесь обратно и
работайте за столом. А к доске я вызову...
Пробежав взглядом по аудитории, останавливаю его на Чю-
мине.
— Вызову вас. Сможете сделать то, о чем я прошу?
Конечно, смогу! Вы только скажите, как.
И, заметив, что все вот-вот взорвутся смехом, быстро
поправляется:
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
43
— Я хотел сказать: посоветуйте, с чего начать.
— Охотно — и мой совет будет относиться к решению
любой задачи. Сначала четко сформулируйте для себя, что у вас
имеется для ее решения и в чем должен состоять результат. В
нашем случае, когда задача заключается в доказательстве
теоремы, следует написать, что дано и что требуется доказать.
Пожалуйста, к доске. Как, например, на символическом языке
выражается тот факт, что некоторая последовательность ап неогра-
ничена?
Он пишет VnVm-и останавливается.
— Не помню...
— Не помните?! А ведь мы говорили об этом совсем недавно!
Давайте договоримся с вами раз и навсегда: определения
основных математических понятий — неограниченности, стремления
к бесконечности и тому подобное — вы будете знать назубок.
Дома вызубрите сегодня же те из них, с которыми мы
познакомились на этом занятии. И так делайте всякий раз. То же
самое я советовал бы вам по поводу лекций: выслушали утром
лекцию — вечером просмотрите все, что записали на ней,
затвердите все данные лектором определения, формулировки теорем,
разберите доказательство каждой теоремы, а если что
непонятно — обязательно выясните у товарищей или спросите у меня
на ближайшем семинаре. Договорились? Да? Ну, тогда
продолжайте работать, Чюмин... Что вы делаете? Вы стираете то, что
написали? Погодите: может быть, еще пригодится, когда будете
писать определение монотонности.
Он оборачивается ко мне, словно не расслышав моих слов,
снова смотрит на доску и, расплываясь в конфузливой улыбке, —
снова на меня:
— Я ведь и начал писать определение монотонности.
Выписывает его до конца, до неравенства ат < ап,
приговаривая «пусть ап неубывающая», и без остановки строчкой ниже
пишет определение неограниченности.
— Да вы все помните! Вас только нужно подталкивать
время от времени! А ну — теперь определение бесконечно большой
последовательности.
Хотя и медленнее, но появляется и оно — еще одной строчкой
ниже, с приписанным слева через двоеточие словом «доказать».
Спрашиваю:
— Я могу советовать дальше? Сравните то, что дано, с тем
что требуется доказать. Даже не вдумываясь в смысл этих
строчек, легко заметить некоторый разнобой символов. А посколь-
44
ПОСЛЕДОВАТЕЛЬНОСТИ
[Гл. I
ку символы мы вправе применять какие угодно, давайте
попробуем сгладить этот разнобой. Скажем, последняя строчка — я
ориентируюсь на нее, потому что к ней направлены все наши
рассуждения — начинается с комбинации V М > О 3 N, а
предпоследняя — с комбинации V М > 0 3 п, почти такой же, за
исключением второй буквы. Не стоит ли заменить эту букву на
N, чтобы усилить сходство с последней строкой? Заменить,
разумеется, на протяжении всей строки. Сравниваем последнюю
строчку с первой. Какая замена напрашивается?
— т на N.
— Отлично! Мы с вами понимаем друг друга! Перепишите все
строки заново с учетом предложенных исправлений. А теперь
сравните неравенства, которыми заканчиваются исправленные
строки.
— Да, — смущенный, он смешно выпячивает нижнюю губу, —
все доказано. Из первых двух строк следует третья. Для любого
М находим N такое, что |алг > М|, и тогда для любого п > N
будет выполняться ап> ам > М.
— О, нет! Чтобы сделать такой вывод, надо уладить еще
одно различие в этих строчках, на которое вы закрыли глаза.
Ну-ка поглядите внимательно: в первой фигурируют
элементы последовательности an, а далее — их абсолютные
величины. Или вы все еще полагаете, будто наши
рассуждения относятся лишь к положительным числам? Если бы
последовательность ап состояла из положительных
элементов, тогда, конечно, никакого различия бы не было — тогда
\а>п\ = &п- Но разве можно ожидать это от произвольной
монотонно неубывающей и неограниченной последовательно-
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
45
сти? В ней вполне могут содержаться отрицательные числа.
Думаю, что вы и сами сможете привести соответствующий
пример. Вы поняли, что это должна быть за
последовательность? Среди ее членов должны быть отрицательные
числа, она должна монотонно возрастать и при том возрастать
неограниченно.
— Отрицательные числа, возрастать... ага! Вот такая,
например, последовательность: минус два, минус один, ноль, один, два,
три ... А ведь дальше все члены будут положительными!
— В этой последовательности — да. Но будет ли это точно
так же с любой неограниченной и монотонно неубывающей
последовательностью?
— Да... кажется, будет...
— Вы смогли бы это доказать? Молчите... Тогда следующий
совет: если не удается решить задачу в той формулировке, в
которой вы ее получили, попробуйте поискать для нее
другую, эквивалентную формулировку. Вы подозреваете, что
любая неограниченная и монотонно неубывающая
последовательность содержит, начиная с некоторого номера, лишь
положительные члены? Вы хотите доказать, что это
должно быть так? Ваше утверждение равносильно следующему:
это не может быть не так. Предположите, что это не так, и
покажите, что из допущенного предложения вытекает нечто
невозможное — например, несовместимое с исходными данными.
Иными словами, проведите доказательство от противного. Итак,
допускаем, что все члены нашей последовательности
неположительны. Вы могли бы еще в какой-либо форме выразить это
допущение?
— В виде неравенства, наверное: ап < 0.
— А это неравенство — что говорит оно о
последовательности ап?
— Что она ограничена сверху.
— Точно! По-моему, уже наклевывается определенное
противоречие с одним из исходных положений. С каким,
догадываетесь?
— С тем, что последовательность неограничена.
— Но отрицание неограниченности — это ограниченность,
притом полная, с обеих сторон, а мы пока лишь имеем
ограниченность сверху. А как насчет ограниченности снизу?
Затрудняетесь с ответом? Что ж, напомню вам средство, которое уже не
раз нам помогало. Когда ни слова, ни формулы ничего не
подсказывают, попробуйте перейти на язык графиков. Начертите чис-
46 ПОСЛЕДОВАТЕЛЬНОСТИ [Гл. 1
ловую ось и на ней попробуйте изобразить вашу
последовательность.
С первых же отметок на оси его осеняет:
— Последовательность-то неубывающая и, значит,
ограничена снизу своим первым членом!
— Конечно! Напишите-ка это в виде неравенства! Так ...
ап > а\. И для каких п это справедливо? Для всех? Да? Так
отметьте это соответствующим квантором! Ну вот, верно:
Vrc(an > a\) Но в определении ограниченности, как вы знаете,
должны фигурировать абсолютные величины членов
последовательности.... О, я вижу, вы хорошо усвоили суть модульных
неравенств! — хвалю быстроту, с которой он, бегло глянув на
числовую ось, ловко орудуя тряпкой и мелом, придает своему
неравенству вид Vn(|an| < |ai|).
Положив тряпку, он с некоторой важностью в голосе, еще
недавно таком неуверенном, произносит:
— А это и есть ограниченность.
— И противоречие с исходным условием неограниченности.
Это противоречие доказывает, что любая неограниченная и
монотонно неубывающая последовательность, начиная с какого-то
номера, состоит лишь из положительных членов. Для них,
опираясь на предыдущее, мы уже можем утверждать, что их
неограниченность и монотонное неубывание влекут стремление к
бесконечности. Теорема доказана. Согласитесь, — смотрю на
Лапикова, — что она оказалась совсем не трудной, как вы боялись
вначале: чтобы Чюмин ее доказал, от меня потребовалось лишь
несколько подсказок. И обратите внимание, ребята, — все мои
подсказки были однотипны: замените эту букву другой, для
этого утверждения найдите другую форму выражения, другое
толкование. Учтите этот прием на будущее и, если по ходу решения
какой-то задачи окажетесь в тупике, поварьируйте элементы ее
условия и уже построенных вами умозаключений, подчиняя
такие вариации цели всей работы: тогда возможно, сбоку от
тупикового пути откроется перспективный. Принимаете мой совет?
Садитесь на место, Чюмин. А теперь, — говорю, обращаясь ко
всей аудитории, — я сделаю небольшую паузу, а вы ребята,
постарайтесь догадаться, зачем я ее сделал.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
47
Буткус не дает мне договорить:
— Я доказал, что она стремится к бесконечности!
— «Она», — улыбаюсь ему, — это, очевидно, построенная вами
подпоследовательность. Вы верно поняли, ради чего я устроил
паузу: чтобы закончить ваше незавершенное рассуждение.
Повторите его... Действительно, с помощью теоремы, которую
только что доказал Чюмин, нетрудно сделать решающий шаг, перед
которым вы остановились. Прошу вас.
— Моя подпоследовательность аПк неограничена, — с жаром
продолжает он, топая к доске. — Если бы она была ограниче-
на, то и наша последовательность ап была бы ограничена, --
несколькими перекошенными строчками символов он
подкрепляет этот вывод. — А это не может быть, это противоречит
условию.
— Подпоследовательность аПк еще и монотонно неубывает, —
азартно, в тон ему, перехватываю у него слово, — потому что
аПк = max{ai,a2, ...anfc}, а с расширением числового множества
его максимум не может уменьшиться.
— А отсюда следует, что аПк стремится к бесконечности, —
ставит он последнюю точку.
— Отлично, садитесь.
И вновь к аудитории:
— Мне сейчас, ребята пришла в голову любопытная
диаграмма — посмотрите. Пусть поле доски изображает множество всех
последовательностей. Разобьем его на две части, — провожу на
доске вертикальную черту. — Пусть слева будут
неограниченные последовательности, справа — ограниченные. Теперь я хо-
48
ПОСЛЕДОВАТЕЛЬНОСТИ
[Гл. 1
чу очертить область бесконечно возрастающих
последовательностей. Где мне ее поместить?
— Слева, — говорит, как припечатывает, Костюк, и многие
соглашаются с ним.
— Почему?
— Потому что всякая бесконечно возрастающая
последовательность неограничена, — раньше других отвечает Синица. И я
рисую прямоугольник со скругленными углами слева от
вертикальной прямой.
— А куда поместить монотонные неограниченные
последовательности?
— В прямоугольник! — мигом откликается Мухин, и еще
несколько голосов эхом подхватывают:
— В эту рамку! Внутрь прямоугольника!
— Почему?
— А потому, — не теряя солидности среди общего порыва,
произносит Рамзин, — что любая монотонная неограниченная
последовательность бесконечно возрастает, мы это доказали.
— Хорошо ... Ну, а теперь через вертикаль, отделяющую
на диаграмме неограниченные последовательности от
ограниченных, шагнем к новой теме. Однако прежде, ребята, я
хотел бы выяснить: все ли было вам понятно до сих пор? Как,
Мухин?
— Кажется, все ...
— А вы что скажете, Аргунова?
— Я в этих... в кванторах с трудом разбираюсь.
— Если с трудом, то рано или поздно разберетесь. А вы, Ко-
чин, уже освоились с ними?
— Честно говоря, еще нет. Но привыкну, наверное, — и тогда
уж пойму.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
49
— Прекрасный ответ! И вы, вероятно, знаете, что для
выработки такой привычки требуется немногое, всего три вещи —
работа, работа и работа. Так ведь, Аргунова? Впрочем, назовите
фразы с кванторами, которые вам особенно трудно было понять.
— Ну, например... отрицание того, что последовательность
стремится к бесконечности.
— Вот это? — пишу на доске строчку символов.
— Ага. Прочтите его, пожалуйста.
Читаю медленно, внятно:
— Существует М, большее нуля, такое что для любого сколь
угодно большого номера N найдется номер п такой, что п
больше N и тем не менее ап по абсолютной величине меньше или
равно М.
— Написано «для любого ЛГ», а вы читаете «для любого сколь
угодно большого» ...
— И вы не понимаете, почему я так его называю, это N?
— Что оно какое-то большое, понимаю, а когда начинаю
разбираться, опять ничего не понимаю.
— Давайте попробуем разобраться вместе. Вдумаемся
сначала, как появляются слова «сколь угодно большое» в определении
бесконечно большой последовательности — найдите его в своей
тетрадке, а я запишу его с ваших слов на доске. Для любого М,
большего нуля, найдется такое ЛГ, что для любого п из п > N
следует \ап\ > М. Все верно. Теперь найдите отрицание этого
определения и тоже продиктуйте мне. Хорошо. Смотрим на
первое утверждение, где говорится, что некоторая
последовательность ап стремится к бесконечности. Вот мы взяли произвольное
положительное М и нашли член последовательности, начиная с
которого все последующие члены по абсолютной величине будут
превосходить это число М. Но ведь определение требует, чтобы
так оно было с любым М. Поэтому для уверенности испытаем в
той же роли еще одно число. Каким же его взять — больше или
меньше прежнего? Конечно, больше! Меньшее брать не имеет
смысла — его превзойдут все те же члены, которые
превосходили прежнее М. Вот так — вы чувствуете? — и приплетается к
слову «любое» слово «большое». На двух опробованных М мы,
конечно, не успокоимся, поскольку определение говорит о
любом М; мы будем брать все новые, все большие числа — и на-
50
ПОСЛЕДОВАТЕЛЬНОСТИ
[Гл. 1
зовем последовательность бесконечно большой лишь тогда, если
для сколь угодно большого М отыщется — пусть среди очень
далеких номеров — такое iV, что для последующих членов
неравенство \ап\ > М не нарушится уже ни разу. Вы заметили, как
естественно прозвучали в моем рассуждении слова «сколь
угодно большое»? Но если последовательность не стремится к
бесконечности — переведите взгляд на определение этого факта! —
то мы ничего не добьемся наращиванием N: за любым сколь
угодно большим N, обязательно попадется такой номер п, при
котором неравенство нарушится. Вновь, как вы заметили, слова
«сколь угодно большое» прозвучали естественно и закономерно,
обусловленные смыслом рассуждения. Теперь вам понятно,
Аргунова, откуда они берутся?
-Да.
— Запомнили то, что я говорил? Да? Теперь, когда снова
будете разбираться в этих определениях, вдумайтесь в них
так же, как мы это делали сейчас, — и недоразумения
исчезнут.
— Впрочем, призыв к вдумчивости имеет отношение ко всем
здесь сидящим, — обвожу взглядом аудиторию после короткой
паузы. — С этим пожеланием я и хочу перейти к новой теме.
Вспомним последовательность, которую в самом начале
семинара называла Синица: 1, 5» 5' 1' • • • > п> •*• ^ак мы Уже выяснили>
эта последовательность ограничена и сверху и снизу. И вот что
любопытно: когда я спросил, каким именно числом она
ограничена сверху, вы в один голос ответили «единицей», хотя на
роль ограничителя здесь годится и двойка, и тройка, и любое
большее число. А когда я поинтересовался, каким числом эта
последовательность ограничена снизу, вы также единодушно
заявили «нулем», хотя и на сей раз можно было назвать другое —
любое неположительное число. Вы сразу почувствовали особое
положение единицы и нуля среди всех чисел, которыми можно
ограничить нашу последовательность сверху и снизу. Это
действительно так: единица служит для нашей последовательности
точной верхней гранью, нуль — точной нижней гранью. О
точных гранях, вероятно уже говорилось на лекциях — не так ли,
Стрельцов?
— Говорилось, — подтверждает он. — Лектор доказал, что
всякое ограниченное снизу числовое множество имеет точную
нижнюю грань, а ограниченное сверху — точную верхнюю.
— Подозреваю, что доказательство этой теоремы и все, что
связано с понятиями точных граней, было не очень легким для
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
51
понимания. Может быть, стоит повторить здесь то, что говорил
лектор?
— Стоит, стоит, — звучат голоса.
— Что было вам особенно непонятно, Миклашевский? —
обращаюсь к одному из просящих.
— Я, — розовеет он, — я вообще не был на той лекции.
— Ну что мне с вами делать? Надеюсь, пример
последовательности ^ позволил вам составить хоть какое-то
представление о точных гранях. Как вы думаете, что такое точная верхняя
грань? Сформулируйте это применительно к некоторой
ограниченной последовательности ап.
— Точная верхняя? — морщит он лоб.
— Эта наименьшая из всех верхних граней для ап. — тихо
подсказывает Стрельцов.
— Справедливо, — киваю ему. — Обозначение для нее такое:
М = sup{an}. А точная нижняя?
— Наибольшая из всех нижних, — сообразительно отвечает
Миклашевский.
— Тоже справедливо. Обозначение: т = inf {an}. А как вы
выразили бы на символическом языке определение того факта, что
некоторое число М является точной верхней гранью
последовательности an, а число т — ее точной нижней гранью? Впрочем,
эту задачу я хотел бы поставить перед всеми
присутствующими, учитывая, что многие хотели бы обновить в своей памяти
информацию о точных гранях. Пусть каждый, не заглядывая
в конспект лекции, попробует написать у себя в тетради одно
из двух заказанных мною определений — кому какое нравится.
— А они ведь по-существу одинаковые, эти оба
определения, — замечает Кулагин.
— Верно. Но тот, кто их не помнит или не знает, — тот
станет вырабатывать их заново, опираясь на конкретные примеры,
которые удастся придумать, скажем, на последовательность ^
— а ведь она по-разному ведет себя близ своей точной нижней
и своей точной верхней грани. Примеры и представления
одних окажутся плодотворнее для выработки определения точной
верхней грани, у других дело лучше пойдет с нижней.
Окончательные же формулировки мы получим, сравнивая между собой
все наши достижения, — негромко говорю, разгуливая между
столами, заглядывая в тетради, где уже выстраиваются цепочки
символов. Повернув обратно, вызываю к доске одного за другим
Меншикова, Синицу, Буткуса, Чюмина, Горта, Кулагина — тех,
на чьих результатах надеюсь устроить содержательное обсужде-
52 ПОСЛЕДОВАТЕЛЬНОСТИ [Гл. 1
ние понятия точной верхней грани: определять точную нижнюю
почему-то не стал никто.
Рамзин иронично глядит на доску:
— У Чюмина наблюдается, мягко говоря, нечто странное.
— В самом деле, Чюмин, — присоединяюсь к
справедливому замечанию, — в том, что вы написали, трудно разобраться.
Прежде всего, зачем вы берете абсолютную величину an? Ведь
тогда согласно вашему определению одна и та же точная верхняя
грань должна быть, например, у последовательностей ^ и — ^,
поскольку абсолютные величины их членов совпадают. Между
тем, точные верхние грани у них неодинаковы — смотрите, я
поясню это на числовой оси.
— Да, — соглашается он, — скобки вокруг ап нужно убрать.
— Уберем и давайте посмотрим, что у нас получилось.
Он, по-видимому, не может без странностей. Что ж,
постараюсь найти им полезное применение. Разбор модульных
неравенств пригодится нам в недалеком будущем, когда речь пойдет
о пределах последовательностей.
Ю, В. Пухначев)
СЕМЬ СЕМИНАРОВ
53
— Итак, неравенство \ап — М\ < е. Можно ли записать его
в каком-то ином виде? Хорошее упражнение для вас, Лапиков.
— Сейчас попробую, — отзывается он, приняв
сосредоточенную мину. — Наверное, —е<ап — М<е?
— Совершенно верно. И еще вариант: М — е < ап < М+е.
Теперь смотрите, Чюмин: нужно ли вам второе из этих неравенств?
Очевидно, нет, поскольку, как подметили многие, все члены ап
не превосходят М, а стало быть, все они меньше М + е.
Достаточно оставить М — е < ап. Кстати, это совпадает с последним
неравенством Горта.
— А в принципе и со вторым неравенством Кулагина, и с
неравенством Синицы тоже, — подмечает Мухин.
— Верно. Посмотрим, ребята, остальные строчки — все ли
вам понятно в них? Вот, скажем, первое из высказываний,
написанных на доске: вы его понимаете, Сынчиков?
При звуке своей фамилии он мгновенно вскидывает глаза на
доску, ни на миллиметр ни изменив при этом своей скрюченной
позы, не шелохнувшись ни единым мускулом. После
нескольких секунд мертвенной неподвижности читает медленно и
тихо:
— Для любого п... ап меньше или равно М.
— Прочли точно. А как понимаете?
— Для любого п ап меньше или равно М, — тем же тоном
слово в слово повторяет он.
Да, с ним я, видно, намучаюсь...
— Не могли бы вы это выразить как-то иначе, другими
словами?
Он молчит в своем каменном оцепенении.
— Не попробуете ли? — обращаюсь к Аргуновой.
— Наверное... все ап не превышают М?
— Ну да. И поэтому М представляет собою одну из верхних
граней последовательности ап. Кстати, кто написал это
высказывание?
— Я, — признается Меншиков. — Но это еще не все, чем
определяется точная верхняя грань, я понимаю.
— Не отыщите ли недостающее в других строчках? Что
означает, например, вторая?
— Что, если взять любое число, меньшее М, то найдется член
последовательности, его превышающий.
— Между прочим, — близоруко щурится на доску
Миклашевский, — концовка второй строчки 3 п (ап > К) — это по
существу отрицание первой.
54
ПОСЛЕДОВАТЕЛЬНОСТИ
[Гл. 1
— По существу да. Вторая строчка, таким образом,
утверждает, что любое число, меньшее М, уже не является верхней
гранью для последовательности ап, то есть М есть наименьшая
из верхних граней последовательности. Стало быть, две первые
строки в совокупности исчерпывающе выражают наше
представление о точной верхней грани.
Я отмечаю первую строчку цифрой 1, вторую — цифрой 2 и
вписываю между ними букву «и».
— Смотрите, у нас получилось в принципе то же самое,
что у Кулагина. Чтобы не загромождать доску повторениями,
сотрем лишние строки. Сотрем и исправленную запись Чюмина,
поскольку она повторяет часть написанного Гортом. Теперь
о том, что написал Буткус. Он, по всей видимости,
полагает, что среди членов последовательности обязательно должен
быть такой, который совпадает с точной верхней гранью. Так,
Буткус?
— Так, — кивает он.
— В подобных случаях говорят, что последовательность
достигает своей точной верхней грани. Такова наша «модельная»
последовательность ^: ее точная верхняя грань — единица, и
среди ее членов есть это число. Но подобное случается отнюдь не со
всеми последовательностями. Возьмите, например ту, о которой
мы уже говорили с Чюминым: -™. Какова у нее точная верхняя
грань, Буткус?
— Нуль.
— Но среди членов этой последовательности все ненулевые,
то есть она своей точной верхней грани не достигает. Итак, если
говорить в общем, среди членов последовательности могут
содержаться такие, что равны ее точной верхней грани, а могут и
не содержаться. И обе возможности полностью укладываются в
утверждение V п (ап < М), уже встречавшееся на доске. С
учетом такого уточнения ваша запись, Буткус, не дает ничего нового
и должна быть стерта. Остаются определения Горта и
Кулагина. Очевидно, они эквивалентны друг другу и отличаются лишь
формой выражения. Какой же из этих двух вариантов, —
спросите вы, — я порекомендую вам? Пользуйтесь любым, кому
какой покажется удобнее. О вкусах не спорят. Хотя, впрочем, было
бы интересно знать, какие у кого из вас вкусы. Кочин, к доске!
Попробуем определить, что значит, что некоторое число М не
является точной верхней гранью некоторой последовательности
ап. Как вы понимаете, я прошу вас построить отрицание
только что выработанного нами определения точной верхней грани.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
55
Каким же из двух вариантов этого определения — Горта или
Кулагина — вы воспользуетесь в своих построениях?
Он медлит с ответом и внимательно смотрит на доску.
— Вариантом Кулагина, пожалуй. Он как-то понятнее.
— Хорошо. Действуйте.
— Число М является точной верхней гранью
последовательности ап — это значит, что оно удовлетворяет и первому и
второму условию, — подчеркивает он для верности мелом написанные
Кулагиным строчки. — Число М не является точной верхней
гранью последовательности ап... это значит... это значит, что
оно не удовлетворяет или первому или второму условию. Да,
или первому или второму, — повторяет он, нажимая на слово
«или».
Его голос постепенно становится все свободнее и увереннее:
— Пусть не выполнено первое условие... отрицание — значит,
меняем квантор... то есть 3 п (ап > М). Ну да, значит, М вообще
не является верхней гранью для ап.
— Не разберете ли этот случай на примере? — предлагаю
ему. — Возьмите последовательность ап = ^ и число М = \.
Он пишет подсказанное мною на доске и умолкает,
сосредоточенно глядя то на одно, то на другое равенство.
Пытаюсь ему помочь:
— Последовательность можно написать в развернутом виде:
п — 1 I I I
Он следует моему совету и, не роняя достоинства поспешным
ответом, продолжает секунду спустя:
— Все понятно: существует элемент, который больше одной
второй.
— А если это выразить с помощью кванторов?
Он пишет 3 п и останавливается в нерешительности. Жду с
надеждой, что он справится с заминокй сам. Справился: на доске
появляется Зп = 1 (а\ = 1 > ^).
— Хорошо, продолжайте.
— Теперь, если не выполнено второе условие... Опять
отрицание...
В молчаливой сосредоточенности он безошибочно
проводит и обращение кванторов, и замену неравенства: 3 М' < М
V п (ап < М'). Дождавшись, когда он кончит, спрашиваю:
— Не находите ли вы что-то знакомое в выражении
V п(ап< М')?
— Для любого п... Опять как в определении верхней грани?
Нет, подождите... А впрочем — действительно...
56 ПОСЛЕДОВАТЕЛЬНОСТИ [Гл. 1
Не запутается ли он? Кажется, эта проблема для него
сложновата. Подсказываю:
— По всей видимости, число М' тоже является верхней
гранью для последовательности ап. Но оно меньше числа М.
Значит...
Оборвав фразу, предоставляю Кочину ее продолжение. Он не
заставляет себя ждать:
— Значит, М — это верхняя грань для ап, но не точная.
И сообразительно переходит к примеру:
— Если взять ту же последовательность ^ и М = 2, то тут...
сейчас... М' = § < 2 и все ап = £ < |.
Довольный успехом, он позволяет себе порассуждать:
— Взяли любое число, меньшее единицы, — допустим,
половину — оно не удовлетворяет первому пункту; взяли большее
единицы, допустим, двойку, — не удовлетворяет второму пункту.
Значит, точная грань — единица.
— Вы полностью правы. Спасибо, Кочин, садитесь. Ну вот,
ребята, о понятии точной верхней грани мы поговорили
довольно. Примемся теперь за точную нижнюю. Кто даст ее
определение? А ну-ка, Миклашевский, попробуйте! Все верно, садитесь.
Пользуясь этим определением, убедимся, ребята, в том, что
точная нижняя грань хорошо знакомой нам последовательности ^
равна, как уже говорилось, нулю. В самом деле, во-первых, все
дроби вида ^ неотрицательны, во-вторых, какое бы
положительное е мы ни взяли, найдется п такое, что ^ < е. Однако про
Ю. В. Пухначев) СЕМЬ СЕМИНАРОВ 57
нашу последовательность можно сказать большее: если какой-то
ее член оказался меньше е, то...
Я отворачиваюсь от доски к аудитории и тут же мой взгляд
сталкивается с цепким взглядом Сутеева — он перехватывает
начатую мною фразу:
— То меньше е будут и все следующие члены
последовательности.
— Вы ловите мою мысль на лету. Сутеев. Выразите ее на
доске в символическом виде.
Молча выходит он к доске, неестественно прямой в своей
похожей на китель черной куртке, молча пишет строчку символов.
— Скажите, Сутеев, а почему последовательность так ведет
себя близ нуля?
— Потому что нуль — ее предел, — отвечает он,
поддержанный еще несколькими голосами.
— Очень хорошо. Я вижу, ребята, что вы еще со школы
знакомы с понятием предела. Но сейчас я попрошу вас забыть на
несколько минут свои знания о нем. Вообразим, что мы
впервые формулируем это понятие. Не считайте подобную имитацию
открытия пустым занятием и вообще — не жалейте о времени,
когда мы с вами изобретаем понятия и придумываем теоремы,
которые можно найти в любом справочнике. Конечно, мне было
бы и быстрей и проще продиктовать вам рецепты из
справочников и показать, как они употребляются на практике. Но ведь вы
учитесь не затем, чтобы лишь применять в типовых ситуациях
стандартные рецепты. Вы — будущие исследователи. И потому я
хотел бы обучать вас в обстановке, максимально приближенной к
исследовательской работе. Быть может, в будущем, вам
посчастливится выдвинуть какое-нибудь новое научное понятие. Тогда,
возможно, вы вспомните нашу игру в первооткрывателей, и вам
окажутся полезными мои советы, сказанные по ее ходу.
Прежде всего я вновь хотел бы предостеречь вас от привязанности
к конкретным примерам, в обличий которых вам всегда будет
являться любая новая математическая сущность. Вы должны
будете различить, что в каждом из этих примеров отражает
лежащую в его основе суть, а что — лишь своеобразие данного
конкретного примера. Вот, скажем, наша последовательность ^:
58
ПОСЛЕДОВАТЕЛЬНОСТИ
[Гл. 1
какие мы отметим в ней черты, которыми вовсе не должна, на
наш взгляд, обладать каждая последовательность, стремящаяся
к некоторому пределу? Какие ее признаки сочтем
несущественными, чтобы на основании родства по другим, существенным
признакам можно было бы подвести под понятие предела
другие последовательности?
— Монотонность! — моментально откликаются Синица,
Кулагин, Костюк.
— Верно. Кто приведет пример немонотонной
последовательности, стремящейся, к некоторому пределу?
— Например, ^ ' , — с благородной расстановкой отвечает
Рамзин. — Ее предел — тоже нуль.
— Но, стремясь к нему, она располагается своими
элементами по обе стороны от нуля. Стало быть, Сутеев, написанное
вами нуждается в уточнении... О, вы вновь понимаете меня с
полуслова: действительно, £-рамки должны быть
двусторонними: —е < ап < е
— Можно еще написать так: \ап\ < £, — предлагает Чюмин.
Разбор его неудачной формулы для точной верхней грани
явно пошел ему на пользу!
— Верно. И еще одно обобщение напрашивается. Какое,
ребята? Как вы думаете? Молчите? Ну-ка посмотрите еще раз, к
какому пределу стремятся обе наши последовательности?
— Ну, конечно! — восклицает Стрельцов. — Не все же
последовательности обязаны стремиться к нулю!
— Но если последовательность стремится к произвольному
числу А, какое это внесет уточнение в определение предела?
Наверное, вы и на сей раз будете на высоте, Сутеев? Все
правильно. Садитесь на место. Вот, ребята, мы с вами и воссоздали
определение того факта, что число А есть предел
последовательности ап.
И приписываю к написанному: А = lim an <=>.
п—>оо
— В нашей символической формулировке теперь есть все
необходимое. Но спросим себя еще раз: не подмешалось ли к
вашему представлению о пределе что-нибудь лишнее, что-нибудь
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
59
специфическое лишь для той последовательности, на примере
которой мы реконструировали наше определение, — для
последовательности ^? Скажем, всем ли ясно, что фигурирующий в
этом определении номер N — это вовсе не тот номер, за которым
последовательность впервые приблизилась к своему пределу на
расстояние, меньшее el
— Конечно! — отвечает за всех Горт. — Ведь
последовательность ап может быть и не монотонной: приблизилась к пределу,
отошла, снова приблизилась...
— Но для каждого конкретного е обязательно найдется такой
номер N, за которым она уже не отойдет от А дальше, чем на
£, — завершает Костюк картину, набросанную Гортом.
Уже не первый раз я наблюдаю, как ответы Горта и Костюка
следуют друг за другом: речь одного словно тянет за язык
другого, неточная или незаконченная мысль одного исправляется
или завершается другим. Мне нравится следить за этим
своеобразным соперничеством; сравнивая обоих, я при всей внешней
их непохожести уже научился видеть в них сходные черты
облика: непритязательность скромной одежды, беспокойную остроту
взгляда в минуты напряженного раздумья...
— Вы оба правы, — киваю Горту и Костюку. — В
определение не следует вносить ничего чуждого. Но то, что
органично с ним связано, стоит держать в памяти неразрывно с ним.
Помните, — обращаюсь к Аргуновой, — мы говорили об этом по
поводу бесконечно больших последовательностей? «Для любого
М», — стояло в их определении, а мы читали: «для любого сколь
угодно большого М». А здесь? Написано «для любого £», — а
читается?
— Для любого £... сколь угодно малого, да? — пробует
прочесть она.
— Совершенно верно! Ведь речь идет о приближении членов
последовательности к ее пределу, а величина е служит здесь
мерой близости. Далее: очевидно, чем меньше будет е, тем...
Гляжу на нее в надежде, что она продолжит, и, не
дождавшись, продолжаю сам:
— Тем, вообще говоря, больше будет число ЛГ, стоящее в
определении предела вслед за е. Для каждого е — свое N. Потому
и читается: найдется N, зависящее от е\ нередко даже и
пишется: N(e). И, наконец, последнее: я советовал вам, ребята,
запоминать всякое определение во всех возможных его вариантах.
В определении предела последовательности, как мы уже знаем,
варианты допускает заключительное неравенство: можно писать
60
ПОСЛЕДОВАТЕЛЬНОСТИ
[Гл. 1
либо \ап - А\ < е, либо А — е < ап < А + е. Как вы полагаете,
какая из двух форм удобнее?
— Без модульных скобок вообще-то работать проще, —
откликается Миклашевский.
— За одним, пожалуй, исключением. Догадываетесь, что я
имею в виду? Нет? А вспомните: дав определение нового
понятия, мы, как правило, тут же определяли противоположное. Так
было, когда мы говорили об ограниченности, о монотонном
возрастании. Ну-ка идите к доске, выразите на языке символов тот
факт, что некоторое число В не является пределом
последовательности ап. Так,так... Осталось написать отрицание
завершающего неравенства.
— Здесь, конечно, удобнее модуль: \ап — В\ > е.
— Согласен с вами, садитесь. Теперь два новых термина,
ребята. Последовательность, имеющая предел, называется
сходящейся; последовательность, не имеющая предела, —
расходящейся. И, наконец, небольшое упражнение: как выразить на языке
символов, что последовательность ап сходится?
— Надо приписать перед определением предела квантор
существования, точнее, выражение ЗА, — заключает после
короткого обсуждения Синица.
— Верно. Я рад, что уже многие из вас очень бойко
обращаются с кванторами и прочей математической символикой. Это
хорошо, но только при одном условии: если за символами вы
ясно видите суть выражаемых ими понятий. В этом я хотел бы
убедиться. Давайте, ребята, вчитаемся еще раз в символическую
запись определения предела, вдумаемся в его смысл и
попытаемся как можно короче и проще пересказать словами его суть.
Для затравки рисую на доске числовую ось и на ней —
штришок с отметкой А.
— Я вижу, это готов сделать Стрельцов. Пожалуйста.
— Начиная с какого-то номера N...
— Замрите! - перебиваю его возгласом детской игры, и он
застывает, держа над столом чуть согнутые ладони. —
Поглядите, ребята, на Стрельцова: он явно забыл упомянуть в начале
своего заявления какую-то важную деталь.
Ю В. Пухначев)
СЕМЬ СЕМИНАРОВ
61
— Ну да, конечно, — понимающе улыбается он. — Надо
начать иначе. Возьмем какое-то е (словно срисовывая его жест,
я ставлю на числовой оси по сторонам от штришка А засечки-
скобки А — е и А + е ) и тогда, начиная с какого-то номера iV, все
члены последовательности будут находиться внутри интервала
(А-е,А + е).
— А вне интервала?
— От силы первые N членов, быть может, только некоторые
из них.
— Очень хорошо. Мне кажется, ребята, такое представление
о пределе, несмотря на его простоту, очень плодотворно и
подскажет нам не одну теорему о сходящихся последовательностях.
Давайте продолжим нашу игру в первооткрывателей. Впрочем,
чтобы не изобретать велосипеды, сначала повторим теоремы,
которые доказывал вам лектор. Не вспомните ли хотя бы одну из
них, Меншиков?
— Если последовательность сходится, то она имеет предел.
— Выражения «сходиться» и «иметь предел» — синонимы.
То, что вы сказали, не теорема, а просто тавтологическая фраза.
Вспомните что-нибудь еще!
— Если последовательность сходится, то она ограничена.
— Верно. Что еще? Вы на лекции-то ходите?
— Конечно! — оскорбленно гудит он.
— И конспект ведете? А после лекций читаете его?
— Не всегда, — рокочет он поглуше.
— Так что же, больше вы нам ничего не скажете? Или
лектор доказал одну только теорему об ограниченности сходящейся
последовательности?
— Что-то еще было, это точно, только никак не
вспоминается, — оправдывается Меншиков.
— Будем надеяться, что вспомнится к случаю. А может быть,
нам удастся придумать такие теоремы, о которых лектор и не
упоминал? Вы должны идти дальше своих учителей! Не
потренироваться ли в этом сейчас?
Проходит несколько минут, и в настоявшейся тишине
особенно звучно раздается резкий голос Буткуса:
— Есть!
62
ПОСЛЕДОВАТЕЛЬНОСТИ
[Гл. 1
— Что? — оборачиваюсь к нему.
— Что-то, — вышагивает он к доске под улыбки ребят.
— Пусть последовательность ап сходится к числу А. И мы
изменяли... мы изменили какие-то первые члены у нее. Она все
равно будет сходиться к числу А — вот теорема.
— Вы придумали как ее доказать?
— Я придумал, как ее доказать: сначала взять определение,
где А — предел последовательности ап. Для любого е найдется
N. Для какого-то е это N меньше, чем номера членов, которые
изменили. Тогда для этого е взять другое iV, больше всех
номеров членов, которые изменили. Для всех других е оставить
старое N.
— Суть верна, и доказательство довольно четкое, садитесь, —
утвердительно киваю ему, не вдаваясь в редактирование его
грамматических неряшливостей и тем самым призывая ребят
не обращать на них придирчивого внимания, — Кто придумает
еще какую-нибудь теорему?
— Если последовательность сходится, — вскоре поднимает
руку Мухин, — то ее первый член равен ее точной верхней
грани.
— Вас, — не соглашаюсь с ним, — как когда-то Лапикова,
попутала привязанность к конкретным примерам, Мухин. Ваше
утверждение, очевидно, подсказано последовательностью ^. А
если взять — ^?
п
— Вернее: если последовательность сходится, то ее первый
член равен либо точной верхней, либо точной нижней грани, —
молниеносно поправляется он.
— Опять неверно: возьмите последовательность а\ = О,
^2 = 0, аз = 0, а дальше ап = '~"п' .
— Тогда так: один из первых ее членов равен либо точной
верхней, либо точной нижней грани, — столь же
незамедлительно парирует он.
— Один из первых членов? Скажите уж просто: один из
членов.
— Сходящаяся последовательность достигает либо своей
точной верхней, либо своей точной нижней грани, — срывает Рамзин
успех окончательной формулировки.
— Вот это верно! Очень жаль, Мухин, что вы, автор
хорошей идеи, проворонили приоритет в ее четком выражении. Даю
вам возможность взять реванш. Попытайтесь доказать теорему,
предложенную Рамзиным. К доске, Мухин! А вы, ребята,
внимательно следите за его доказательством.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
63
Он начинает с того, что повторяет мой чертеж: числовая ось
и на ней — прямая засечка между двумя изогнутыми.
Удивительно, как он рисует: старательная рука напряжена, мел уперт
в линолеум доски так, что та едва не продавливается, — а
получается все вкривь и вкось. И речь его — как спутанный клубок:
— Вот, значит, произвольное е (еще раз очерчивает
изогнутые засечки) — нет, сначала это А (корявая буква появилась над
прямой засечкой) — к которому сходится наша
последовательность ап — вот оно, это А — берем произвольное е — тогда,
начиная с какого-то номера, все члены последовательности будут
вот тут, внутри, от А — е до А + е (эти отметки появились у
изогнутых засечек) — начиная с какого-то номера N — в интервале
(А — е, А + е) — все остальные, все предыдущие вне
интервала (краем глаза замечаю, как вскинулись при этих словах Горт,
Рамзин... но я останавливаю их незаметным для Мухина жестом)
— нет, не все! — вернее, может быть, что не все — просто какие-
то, у которых номер меньше — они будут вне интервала. Если
все они справа (на числовой оси появляется несколько кружков,
монотонно приближающихся справа к отметке А+е ) — то берем
самый большой — это будет точная верхняя грань для ап — если
они все справа. Если слева (еще несколько кружков монотонно
тянутся слева к отметке А — е) — то наименьший возьмем — это
будет точная нижняя грань. А если и справа и слева — тогда ап
достигает обеих граней.
— Ну-ну ... Никто не заметил ошибки в этом доказательстве,
ребята? Неужели никто?
Для Горта мои вопросы прозвучали как тяжкий упрек в
невнимательности: нахмурившись, он пристально смотрит на
доску:
— Ошибка есть, — тянет он не очень уверенно несколько
секунд спустя. И оживляясь:
— Да, конечно! Если взять ап = ^, которая стремится к нулю,
а в качестве е взять двойку ...
— Ну-ка, — оборачиваюсь к Мухину, — поищите члены
последовательности 1 за пределами интервала (—2, +2).
— А зачем он берет такое большое el — Мухин словно просит
у меня защиты от коварных происков Горта.
— Разве он не имеет на это права? Можно брать произвольное
е — так разрешили вы сами.
— Тогда, конечно, не произвольное! Сейчас, сейчас! Вот,
лучше так — выбрать какой-то член аПо — какой-то такой член,
который не совпадает с А, — и взять е меньше, чем \аПо — А\.
64
ПОСЛЕДОВАТЕЛЬНОСТИ
[Гл. 1
— А если такое аПо не найдется?
Он растерянно смотрит на меня, будто онемев.
— Как быть тогда, ребята? — передаю свой вопрос
аудитории. К моему удивлению, сразу на него не отвечает никто. Пока
длится раздумье, прохаживаюсь между столами, заглядываю в
тетради. Сынчиков рисует новый чертежик, где точно на засечку
А посажен единственный кружок с отметкой ап. Догадался? Но
вызывать его не рискую: слишком утомительно для остальных
было бы повторять с ним игру в молчанку.
— Что ж вы молчите, Мухин? — возвращаюсь к своему
столу. — Неужели не догадываетесь, что тогда все члены
последовательности совпадают с числом А? Тогда оно будет как
точной верхней, так и точной нижней гранью
последовательности. Садитесь! Не сообразить такого пустяка! И вы, ребята,
что-то тоже не на высоте! Боюсь, что вас утомили теоретические
рассуждения. Перейдем-ка к примерам.
— Вы будете давать нам последовательности, а мы будем
искать их пределы? — наивно смотрит на меня Лапиков.
— Будете искать пределы тех последовательностей, которые
сходятся. Или вы считаете, что все последовательности —
сходящиеся? Может быть, ребята, кто-то приведет специально для
Лапикова пример расходящейся последовательности? Не
попробуете ли, Миша? — обращаюсь к Гарину.
— Допустим, ап = (—1)п.
— Почему эта последовательность не сходится?
— Потому что, — как подарок, преподносит Чюмин, — у нее
два предела: плюс единица и минус единица.
— Очень интересное заявление! Тут необходим толковый
комментарий...
— Последовательность не может иметь двух пределов! —
вскрикивает, не давая мне договорить, Меншиков — Это
доказывал лектор!
— Вот оно! — улыбаюсь ему. — Важные теоремы, как и
хорошие анекдоты, вспоминаются к случаю. Что ж, если вы глубоко
усвоили прочитанное на лекции, вы сумеете доказать, что минус
единица не является пределом последовательности (—1)п.
Прощу вас к доске.
С показным неудовольствием от того, что его поднимают с
насиженного места, он тяжело поднимается со стула, к доске
идет нога за ногу, мел поднимает, словно гирю:
— Окружим минус единицу г-окрестностью с полушириной
^-тр-... ну, то есть ~'2~ ' = 1. Если бы минус единица была
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
65
пределом последовательности (—1)п, то все ее члены, начиная с
какого-то номера N, лежали бы в указанной окрестности. А
если бы пределом нашей последовательности была плюс единица...
— Стоп, стоп! Я вижу, вы воспроизводите доказательство
теоремы о том, что последовательность не может иметь двух
пределов. А ведь я просил вас о другом: доказать, что минус
единица не является пределом последовательности (—1)п. Задача
сходная, но иная. Надо как-то перенести на нее знакомые вам
рассуждения и приемы.
Глаза его, медленно повернувшиеся в мою сторону,
постепенно яснеют, словно он просыпается от крепкого сна.
— Повторите, — прошу его, — что вы хотите доказать.
— Что минус единица не является пределом... Ах, да!
И, не дожидаясь моих советов, пишет на доске отрицание
определения предела:
— Существует £...
Вяло смотрит на свой чертеж и вопросительно — опять на
меня:
— Все-таки я возьму это е равным единице.
— Берите его равным чему угодно, рассуждайте как вам
угодно — лишь бы ваше доказательство было верным, строгим.
— Возьму, значит, равным единице, — облегченно
продолжает он. — Тогда последнее неравенство будет: |(—1)п — (—1)| > 1.
Он замолкает.
— Дальше, дальше! — нажимаю на него. — Для любого N
должно найтись большее его п, при котором это неравенство
удовлетворится.
— Ну, правильно, — говорит на это Меншиков.
— «Правильно»! Он меня похвалил! Это я должен был бы
вас похвалить за такое продолжение, если бы оно пришло вам в
голову! Так какое п здесь лучше взять?
— Какое? Гм... какое п взять... Четкое какое-то...
Например, п = 2N. Ну, разумеется: |(-1)27V + 1| = |1 + 1| > 1... да.
Все.
— Благодарю вас! — отвешиваю ему насмешливый поклон. —
Садитесь: с этой задачей, действительно, все. Но ведь в ней,
ребята, была и определенная сверхзадача: научиться переносить
решения одних проблем на другие, похожие. Я хотел бы убедиться,
что вы научились этому. Попытайтесь сформулировать какую-
нибудь теорему, которая доказывалась бы примерно по той же
схеме, которую мы только что использовали. Молчите? Я дам
нам небольшую подсказку — выражу суть этой схемы чертежом.
66
ПОСЛЕДОВАТЕЛЬНОСТИ
[Гл. 1
Опять ничего стоящего не приходит в голову? Придется уж мне
самому, — подпускаю шутливую интонацию, —
продемонстрировать перед вами выдающиеся образцы творческого мышления.
Пусть А — предел некоторой последовательности, В — число
меньшее, чем А.
— Они будут больше А — £, а £ можно такое взять, что А — е
больше В — значит, ап > В — начиная с какого-то номера, —
подхватывает Мухин.
— Истинно так! И окончательная формулировка теоремы
такова: пусть А — предел некоторой последовательности, В —
число меньшее, чем А; тогда, начиная с некоторого номера, члены
последовательности будут превышать В. Иногда эта теорема
будет нам встречаться в таком варианте: если последовательность
стремится к положительному пределу, то начиная с какого-то
номера все ее члены положительны. Такое утверждение
пригодится нам при решении примеров. Сейчас мы перейдем к ним:
будем смотреть различные последовательности и для тех из них,
которые сходятся, станем искать пределы. Предвижу, что в
отдельных случаях вам без особых выкладок удастся угадывать
пределы сходящихся последовательностей. Но исповедуемая
нами математическая строгость, конечно, не удовольствуется
догадкой. Быть безукоризненно строгим — значит показать, что
найденный ответ удовлетворяет определению предела, то есть —
вспомните это определение! — для любого е найти N такое, что
для членов ап с большими номерами будет выполняться
неравенство \ап — А\ < £, — короче, определить зависимость N(e).
Потренируемся-ка в этом на примере двух-трех
последовательностей попроще. Возьмем для начала ап = ^.
— Ну, тут-то все тривиально, нечего и делать! —
пренебрежительно бросает Миклашевский.
— А коли так — делайте! — приглашаю его к доске.
— Если ^ < £, то п > i. Очевидно, N = К
— Вы извините меня за придирчивость, но ведь N —
натуральное, целое число, а ^ может оказаться и дробным.
— Хорошо, возьмем от него целую часть: N = [^]. Если
*>[jLTOs< щ <£
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
67
— Что-то не верится в справедливость последнего
неравенства. Ведь из него следует, что ^ < [^], то есть, что число меньше
своей целой части.
— Надо взять iV = [i] + 1, — заботливо советует Стрельцов.
— Пожалуйста, — не возражает Миклашевский. — Если
п > Ш + L T0 i < [Хррт < т = е.
— Рассмотрим в том же плане, — не отпускаю его, — еще две
последовательности: ^ и -£г, где s > 0,р > 1.
— Обе к нулю, — предсказывает он, еще не начиная писать
доказательство своего пророчества.
Вглядываюсь в выражение для N(e), бегло выведенное им
для последовательности ^ далее: N = [-4=] + 1.
— Написали, не сославшись на условие s > 0. Разве оно тут
лишнее?
Подумав, он отвечает верно:
— Это условие нужно для того, чтобы неравенство ^ < е
сохранило знак после извлечения корня.
— А где, по-вашему, сработает условие р > 1?
Он отрывает мел от доски, опасаясь, что второпях где-то
ошибется:
— Тут сложнее... Если -^- < £... Взять логарифм... Нет, не
сразу, нужно так: ~ < рп. Тогда при малом е в обеих частях
неравенства будут числа больше единицы... Значит, после
логарифмирования неравенство сохранит знак! Ну вот: N(e) = [^t] + 1.
Разбирательство с моими претензиями к решению столь
простых примеров утомило его:
— И так мы будем поступать с каждой последовательностью?
Каждый раз выводить и доказывать формулу для N(e)?
— Не нравится? Впрочем, я подозреваю, что подобная
перспектива покажется мрачной любому. Избежать ее
позволяют так называемые теоремы о сходимости, доказанные вам
на лекции. Кто мог бы их перечислить? Хотите вы, Рамзин?
Пожалуйста.
Явно польщенный таким доверием, он соглашается не без
важности, к доске выходит не спеша; Миклашевский тихо
удаляется, не ожидая моего разрешения.
— Только прошу вас, Рамзин, — почетче.
— Хорошо. Есть такая, например, теорема: если
последовательность монотонно возрастает и ограничена сверху, то она
сходится. Аналогично, последовательность сходится, если она моно-
68
ПОСЛЕДОВАТЕЛЬНОСТИ
[Гл. 1
тонно убывает и ограничена снизу. Еще вводилось понятие
фундаментальной последовательности, то есть такой, которая
удовлетворяет критерию Коши: V е > 03iVVnVp((n > N) =Ф
=Ф (|ап+р — ап\ < е)). Если последовательность фундаментальна,
то она сходится. И наоборот: если последовательность сходится,
то она удовлетворяет критерию Коши. Еще была «теорема о двух
милиционерах»: если три последовательности связаны
неравенством ап < Ьп < Сп и крайние сходятся к одному пределу, то
средняя сходится тоже и притом к тому же пределу. Имеют
место также теоремы о сумме, произведении и частном сходящихся
последовательностей ап и Ьп: предел их суммы равен сумме их
пределов, предел произведения — произведению пределов,
предел частного — частному пределов.
— Если предел последовательности, которая в знаменателе,
не равен нулю, — с видом прозорливца предупреждает Менши-
ков.
— Верно, — оглядываюсь в его сторону. — Садитесь, Рамзин,
спасибо. Чтобы получше утвердить в вашей памяти, ребята, этот
довольно громоздкий свод теорем, я хотел бы вновь
обратиться к диаграмме, которую мы не так давно рисовали. В правой
ее половине мы размещали ограниченные последовательности, в
лево — неограниченные. Среди них мы выделяли те, что
стремятся к бесконечности. Давайте подумаем; как расположить на
такой диаграмме сходящиеся последовательности?
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
69
— Справа! Если последовательность сходится, то она
ограничена! — слышится несколько голосов. Уловив среди них звонкий
голос Синицы, приглашаю ее к доске:
— Рисуйте. Вы очерчиваете лишь часть ограниченных
последовательностей. Это значит, видимо, что не все они —
сходящиеся.
— Конечно: (—1)п ограничена, но расходится.
— И еще я вижу, что вы рисуете свой овал симметрично
области бесконечно возрастающих последовательностей. Это очень
правильно. Сходящиеся последовательности во многом подобны
стремящимся к бесконечности. Возможно, кого-то из вас, ребята,
удивит такое уподобление. Чтобы оправдать его, вернее всего
обратиться к высшим инстанциям в математических сомнениях —
к определениям. Найдите в своих тетрадях определение
сходимости к некоторому конечному пределу и определение стремления
к бесконечности, сравните оба — сходство налицо. Оно
проявляется во многом. Например, мы говорим: из всякой
неограниченной последовательности можно выбрать бесконечно
возрастающую подпоследовательность ...
— А из любой ограниченной последовательности, — смекает
Синица, куда я клоню, — можно выбрать сходящуюся
подпоследовательность.
— Теорема Больцано-Вейерштрасса, — вставляет Буткус.
— Верно, — на миг оборачиваюсь к нему. И вновь Синице:
— Монотонная и неограниченная последовательность
бесконечно возрастает...
— Монотонная и ограниченная сходится, — завершает она
сравнение, довольная своей догадливостью.
— Укажите это на диаграмме. Некрасиво получается: область
монотонных последовательностей оказалась разорванной.
— Сейчас я подправлю...
70
ПОСЛЕДОВАТЕЛЬНОСТИ
[Гл. L
— Отлично! Сходящиеся и бесконечно возрастающие
последовательности сблизились еще больше, словно заявляя о своем
тайном родстве. Садитесь, Люда, спасибо. Вы можете
улыбнуться, ребята, той тщательности, с которой мы вырисовывали эту
диаграмму. Но ведь вы, надеюсь, понимаете, чего я добиваюсь
этим рисованием: того, чтобы в вашей памяти разнообразные
математические факты складывались в стройную систему.
Подчеркивать их взаимосвязи с помощью внешних приемов —
диаграмм и графиков, терминов и символов — отнюдь не лишне.
Вот, скажем, интервал (А — е, А + е) в рассуждениях о
сходимости называют ^-окрестностью точки А и обозначают ее
символом U(А, е). Сходным образом совокупность чисел,
превосходящих по модулю некоторое положительное М, называют М-
окрестностью бесконечности и обозначают £/(оо, M). Тот, кто по
сходству терминов попытается поглубже выяснить родство
стоящих за ними понятий, возможно, обнаружит: если от чисел,
лежащих в некоторой окрестности бесконечности, взять
обратные величины, то все они лягут в некоторую окрестность нуля.
От такого построения недалеко до вывода: если
последовательность ап стремится к бесконечности, то последовательность ^-
стремится к нулю. А уж отсюда можно извлечь важное
практическое соображение. Разговор о нем я опять начну с
терминологии. Последовательности, стремящиеся к нулю, отличаются
особым наименованием: они называются бесконечно малыми. Это
слово вы увидите, взяв какой-либо старинный учебник по
математическому анализу, скажем, Валле-Пуссена или Билибина:
«Анализ бесконечно малых», — написано на обложках этих книг.
Понятие, упоминавшееся в названии науки, очевидно, играет в
ней немалую роль. И действительно, проследив за выкладками
опытного математика, вы заметите: он часто вводит бесконечно
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
71
малые величины в вычисления, связанные с предельным
переходом. Например, уже известным нам приемом из бесконечно
большой последовательности ап образует бесконечно малую дробь ^-.
Если же последовательность ап стремится к конечному пределу
Л, математик делает замену ап = А + ап, где ап бесконечно
мала. Возможность такой замены нетрудно подтвердить, вспомнив
определение сходимости с неравенством \ап — А\ < е в конце:
отсюда ясно, что разность ап — А бесконечно мала. Выгоды от
подобной замены предвидеть легко. Скажем, вам дано
произведение последовательностей ап и Ьп, стремящихся к числам А и
В соответственно. Несложные преобразования показывают, что
произведение апЬп представимо в виде А В плюс бесконечно
малая последовательность, то есть стремится к АВ. Кто пояснит
мне, какие теоремы о бесконечно малых последовательностях
использовал я в своих выкладках? И кто вспомнит, не заглядывая
в лекции, весь перечень теорем о бесконечно малых?
С забавной синхронностью вскидывают руки Горт и Костюк.
— Пожалуйста, Виталий, — выбираю второго.
— Произведение бесконечно малой величины на постоянную
бесконечно мало. Произведение или сумма конечного количества
72
ПОСЛЕДОВАТЕЛЬНОСТИ
[Гл. 1
бесконечно малых величин тоже бесконечно мала. Вы
использовали эти теоремы. Первую можно сформулировать в более
общем виде: произведение бесконечно малой величины на
ограниченную бесконечно мало.
— Спасибо, садитесь. Все теоремы, которые выписаны на
доске, я просил бы вас, ребята, знать назубок. Они — основные
наши инструменты в поисках пределов сходящихся
последовательностей. Среди них могут оказаться довольно сложные. Но
вполне вероятно, что ту или иную сложную последовательность
нам удастся ограничить с обеих сторон простыми,
стремящимися к одному пределу, — взгляните на теорему под номером
три! — и отсюда будет следовать, что наша сложная
последовательность стремится к тому же пределу. Или, быть может, мы
сумеем разложить какую-то замысловатую последовательность
на сумму последовательностей совсем элементарных —
взгляните на теорему под номером четыре! — и опять ответ получится
незамедлительно. При этом, замечу, в роли простых,
элементарных последовательностей, как правило, будут выступать
последовательности jpr, где s > О, и ~г, где р > 1 (вариант: gn, где
\q\ < 1). Миклашевский уже показал нам, как подводить их под
определение предела. Теоремы о сходимости также опираются в
своих доказательствах на это определение, поэтому полученные
с их помощью выводы можно считать вполне строгими. Вот вам,
Миклашевский, и ответ на ваш вопрос о том, всегда ли мы будем
выводить зависимость N(e), доказывая сходимость той или иной
последовательности. А теперь — примеры. Я буду давать вам их
тройками.
Пишу на доске: ап = ^^; ап = (J2")?+i+3"+*; an =
= у/п+ 1 - у/п.
— Решайте.
Брожу между столами, заглядываю в тетради. Сынчиков
замер над первым примером. «Может быть, попробуете как-то
преобразовать эту дробь?» — подсказываю ему и иду дальше.
Аргунова, быстро сделав первый пример, приводит второй к виду
(--)n+i
о/ ?2чп ,о — и останавливается. Что мешает ей сделать послед-
ний решающий шаг? Для Кочина непреодолимым
препятствием оказывается третий пример: он преобразует
последовательность в произведение y/n(J\ + ^ — 1), но один из сомножителей
бесконечно убывает, другой — бесконечно возрастает... Когда я
предлагаю ему свою помощь, отказывается. Что ж, вера в свои
Ю. В. Пухначев|
СЕМЬ СЕМИНАРОВ
73
силы — черта полезная. Пусть выпутывается сам. Иду дальше,
стараясь понять ход мыслей каждого. Жду, пока выбравшие
верный путь пройдут его до конца, а выбравшие неверный —
убедятся в его бесперспективности. Потом по одному вызываю к
доске тех, чьи решения — верные или неверные — кажутся мне
поучительными.
Сутеев демонстрирует решение первого примера.
— Ответ правильный, — комментирую написанное им, — но
к решению можно придраться. Вы сразу пишите lim ^^ =
= lim ? з7, а ведь выражение, стоящее что в левой, что в пра-
вой части равенства, бессмысленно, покуда не доказано, что та и
другая последовательность, к которой вы приписали символ
предела lim, сходится. Стирайте... да нет, не все! Достаточно стереть
символ предела — и тогда останутся преобразования
последовательности самой по себе, никаких нареканий не вызывающие. К
итоговому выражению уже применимы теоремы о сумме
сходящихся последовательностей, их произведении и частном.
Увлекшись, провожу все рассуждение сам:
— Действительно, рассмотрим, что произошло с нашей
дробью после того, как мы разделили ее числитель и знаменатель
на п2. Сначала поглядим, что получилось в числителе. Два
слагаемых. Первое — это хорошо знакомая нам последовательность
^, стремящаяся к нулю. А второе слагаемое — это квадрат той
же последовательности, то есть ее произведение на себя. Значит,
к нему применима теорема о произведении сходящихся
последовательностей: lim \ = lim ^ • lim £ = 0-0 = 0. Итак, в
71—►ОО71 71—►ОО71 71—ЮО71
числителе налицо сумма двух сходящихся и притом
бесконечно малых последовательностей. По теореме о пределе суммы
заключаем: предел числителя равен нулю. Теперь перейдем к
знаменателю. Первое его слагаемое, единицу, можно
рассматривать как стационарную и, стало быть, сходящуюся
последовательность. Ее предел — единица. Второе слагаемое — это
произведение стационарной последовательности, двойки, на
последовательность ^. Я не стану разлагать дробь ^ на множители,
74
ПОСЛЕДОВАТЕЛЬНОСТИ
[Гл. 1
чтобы каждый исследовать отдельно, — сошлюсь на только что
полученный вывод о ее стремлении к нулю. Снова используем
теорему о произведении двух сходящихся последовательностей:
Пт А = lim 2- lim Л- = 2-0 = 0. Итак, в знаменателе мы имеем
га—юо71 га—>оо га—юо71
сумму двух сходящмхся последовательностей. Предел первой —
единица, второй — нуль. По теореме о пределе суммы получаем,
что предел знаменателя — единица. И поскольку он не равен
нулю, ко всей дроби можно применить теорему о пределе частного
двух последовательностей: берем предел числителя, нуль, делим
на предел знаменателя, единицу, и получаем искомый ответ: при
п, стремящемся к бесконечности, предел дроби ^^ равен нулю.
Я правильно истолковал написанное вами, Сутеев? Садитесь.
Смотрю на кислую физиономию Миклашевского:
— Конечно, такие выкладки могут показаться чрезмерно
подробными, но зато благодаря им решение примера становится
обоснованным до последней мелочи. Впрочем, оно не утратит
обоснованности, если какие-то логические переходы мы заменим
ссылками на ранее полученные результаты. Кстати, к этому
приему прибегнул и я, когда при рассмотрении знаменателя не стал
исследовать последовательность ^, а просто напомнил, что с
ней мы уже разбирались при рассмотрении числителя. Я мог бы
поступить еще радикальнее: после деления числителя и
знаменателя исходной дроби на п2 указать на возникшие выражения
^ и ^-, а затем сказать, что это уже хорошо изученные нами
бесконечно малые последовательности вида ^, где s > 0.
Оставалось бы еще разобрать выражение ^, показать, что оно тоже
бесконечно мало, — и тогда тотчас последовал бы неоспоримый
вывод: предельный переход дает в числителе сумму двух нулей,
то есть нуль, в знаменателе — сумму единицы и нуля, то есть
единицу, так что предел дроби равен нулю.
Лицо Миклашевского, как барометр, показывает, что
пасмурная перспектива нудной работы сменяется ясными видами на
быстрый успех. Продолжаю:
— Собственно, своим рассуждением я выложил вам, ребята,
весь арсенал методов, при помощи которых нам удастся решить
и эти, и следующие примеры. Я даю вам в формульном виде
какую-то последовательность, и прошу исследовать ее на
сходимость, а вы так или этак преобразуете ее формулу,
припоминаете подходящие теоремы или ранее решенные примеры и из всего
этого выстраиваете путь к ответу, то есть выясняете, сходится
последовательность или расходится. Если сходится, то вывод о
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
75
ее сходимости, как правило, будет получаться вместе с ее
пределом.
Миклашевскому уже не терпится показать на доске свое
решение второго примера.
— И здесь знакомая последовательность, — с ловкостью
фокусника он получает в числителе и знаменателе степень (—|)п, —
Дальше все тривиально: предел этой степени — нуль, предел всей
дроби — одна треть.
Ну, герой! С усмешкой отправляю его на место. Окликаю
Аргунову, завязшую в решении этого примера:
— Понятно?
— Понятно...
Костюк приравнивает третью последовательность к дроби
у/п+1+у/п'
— В знаменателе — сумма бесконечно больших величин.
Числитель — постоянен. Значит, вся дробь бесконечно мала, то есть
стремится к нулю.
— Верно, садитесь. Кто по-другому доказал бесконечную
малость этой дроби?
Кулагин дает оценку:
— Дробь меньше такой: тгк* А она стремится к нулю как ^7,
где s = \ > 0.
— Вы исходите из оценки > 3 г < гЛ=. Тогда вопрос:
верно ли, что из бесконечной малости некоторой величины следует
бесконечная малость меньшей величины? Я в этом сомневаюсь.
Вот неравенство: — п < ^. Но из него не следует, что —п
стремится к нулю!
Озадаченный моим возражением, Кулагин чуть нагибает
голову, не сводя с меня упрямых глаз, думает несколько секунд —
и взрывчато:
— Но ведь наша-то дробь , * г положительна!
— Ну-ка припишите к своей прежней оценке неравенство,
которое выражает ваше последнее утверждение! Что получилось?
— Получилось, что можно применить теорему о двух
милиционерах — я ее и имел в виду!
76
ПОСЛЕДОВАТЕЛЬНОСТИ
[Гл. 1
— Об этом надо было сказать вслух и заранее. Теперь все
получается строго. Запомните ребята: эти милиционеры работают
только на пару! Если вы хотите доказать сходимость
последовательности с помощью оценок — делайте их обязательно с двух
сторон! Теперь еще три примера: ап = 3;;ап = ^-;ап = ^-. По-
прежнему полагаем s > 0,р > 1.
Снова иду между столами. Даже не вчитываясь в то, что
пишут ребята, интересно понаблюдать, как они пишут. Авторучка
в руке у Горта так и летает над тетрадной страницей, покрывая
ее узором формул, где по сторонам от основной цепочки
выкладок стремительно возникают всяческие примечания, пояснения,
проверочные вычисления... Мухин продуктивен не менее, только
его «продуктивность» — иного свойства: напишет строчку — и
тут же ее зачеркнет, напишет новую — опять зачеркнет... Буткус
пишет редко, но, чувствуется, метко.
— Можно вас на минуту? — зовет меня Кочин. С
готовностью спешу к нему. Я уже давно раздумывал над тем, как
лучше предлагать ему свою помощь. Положение у него
двусмысленное. С одной стороны, ему, переростку, работается труднее, чем
остальным, сразу пересевшим со школьной скамьи на вузовскую
и сохранившим школьные знания во всей свежести. С другой
стороны, ему, старшему, неловко обнаруживать свои пробелы перед
младшими. Нет, никакого комплекса неполноценности в нем не
заметно, он уже почувствовал, что новое усваивается им
неплохо, а забывшееся старое удается наверстывать. Но тем не менее
ему не хочется задавать во всеуслышание вопросы, выдающие
его слабости. Лучше восстановить забытое и вернуть упущенное
в тихой беседе с преподавателем у себя за столом. Хорошо, что он
сам догадался подзывать меня в трудные моменты. А слишком
часто дергать меня он не станет — парень он, видно,
самостоятельный и гордый.
— Какие проблемы, Дима? — подсаживаюсь к нему.
— Забыл, что означает п\.
—- Это произведение всех целых чисел от единицы до п.
— Спасибо, буду помнить.
Иду дальше. Сынчиков по каким-то неисповедимым
причинам начинает с последнего примера и пишет: ^ = int\\\n- Этот
проблеск мысли не должен угаснуть безрезультатно! Гадаю,
что появится вслед за этим равенством и, ничего не
дождавшись, шепчу, склонившись над Сынчиковым, чтобы не мешать
другим:
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
77
— А почему бы не написать так: ^- = т^ш • £? Что
представляет собой первый сомножитель в правой части равенства?
И приписываю под левой частью ап. Под сомножителем, на
который я указал, он пишет ап-\.
— Думайте дальше: ап получается из ап-\ умножением на
число 2. Что можно сказать про это число, если учесть, что п
стремится к бесконечности?
Он молчит, не сводя глаз с написанного мною равенства.
Подсказываю ему начало ответа:
— При всех п, больших р, это число...
— Меньше единицы, — заканчивает он.
— Итак, начиная с какого-то номера N, большего р, элемент
ап получается из ап-\ умножением на число, меньшее единицы.
Значит, как ведет себя, начиная с такого номера,
последовательность ап?
— Убывает.
— Последовательность убывает... не упоминается ли
убывание последовательности в какой-либо теореме о сходимости?
Откройте-ка их список, просмотрите его.
— Если убывает и ограничена снизу, то сходится.
— Отлично! Наша последовательность убывает. Но
ограничена ли она снизу? Думайте, думайте!
— Ограничена нулем.
— И отсюда следует, что она...
— Имеет предел.
В своем уютном углу он соображает явно лучше, чем у доски,
на виду у всей группы!
— Чему же равен этот предел? Смотрите, вот вы написали:
&п — а>п-1 • п- Стоящая в левой части переменная величина ап
имеет предел. Стоящая в правой части an_i тоже имеет и
притом, очевидно, тот же. Мы еще не знаем чему он равен, но уже
доказали, что он существует. Обозначим его А. И величина ^
тоже имеет предел — правда? Какой же?
— Нуль.
— Видите, ко всем участникам этого равенства применима
операция предельного перехода. И если ее применить, учитывая,
что предел произведения сходящихся последовательностей равен
произведению их пределов, — каким станет равенство? Верно,
А = А • 0. Так чему отсюда равно А?
— Нулю.
Чюмин внимательно слушает наш разговор и вдруг пишет
у себя в тетради вслед за условием первого примера: ■^2L- =
78
ПОСЛЕДОВАТЕЛЬНОСТИ
[Гл. 1
= ^(^zr). Похоже, что дело пойдет! Иду к сидящим в первом
ряду.
Наклоняюсь к Рамзину, который покрывает безуспешными
выкладками уже вторую страницу своей тетради:
— Над чем вы бьетесь?
— Хочу доказать, что последовательность ап = -^- убывает.
Снизу она ограничена, потому что положительна; если докажу,
что убывает, будет ясно, что сходится. Получается пока только
вот что: ап+\ = ^ап + -^т. Если бы только доказать, что она
сходится! Тогда перейдем к пределу — обозначим его А —и сразу
получается А = ^ — а отсюда А = 0: ведь р ф I.
— Ну-ка напишите на доске свое равенство для an+i и ап.
Верное равенство, ребята, не правда ли? А вот такое, Рамзин,
тоже верно: 6 = 5 + 1? Тоже, не возражаете. Но наряду с ним
верны еще и такие: 6 = 4 + 2 = 3 + 3. Понимаете о чем я толкую?
Нет? Вспомните, когда мы обсуждали приемы решения
математических задач, я не раз вам говорил: один и тот же
математический объект можно порою записать в различных формах.
Это справедливо и для соотношения между an+i и ап — правда,
Чюмин?
Почувствовав в моем вопросе приглашение к выступлению,
он говорит:
— Надо разделить an+i на ап.
Рамзин, оторопев то ли от простоты разумной идеи, то ли от
неожиданности, что ему подает руку помощи столь никчемный,
на его взгляд, человек, несколько секунд глядит на Чюмина,
потом безмолвно и как-то замедленно пишет то, что ему
подсказали...
— Черт возьми, все верно! — произносит он раздраженно. —
Начиная с номера [zzy], последовательность убывает. Дальше
все ясно.
И, бросив мел, идет на место, не слыша моих просьб
написать решение подробно, — начатые им выкладки дописываю
я сам.
— Очень удачный подход, спасибо, — с улыбкой смотрю на
Чюмина.
— А ведь так же можно решить и третий пример! — сияет
Синица.
— Ну, наконец-то! — улыбаюсь я. — А то мне уж казалось, что
для вас впустую прошел мой совет: найдя удачный прием для
решения одной задачи, подумать, где он мог бы пригодиться еще,
в каких похожих задачах. Между прочим, я ради этого и даю
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
79
вам примеры тройками, чтоб недалеко было искать новые
приложения удачных уловок, которые придут вам в голову. Скажем,
в примерах нынешней тройки однотипным способом выясняется
монотонность последовательностей. Но это еще не все. Обратите
внимание: как только мы обнаруживаем монотонность и
ограниченность наших последовательностей, нам тут же приходит
на ум теорема, где из сочетания этих свойств вытекает
сходимость. Тем самым о себе заявляет важный принцип,
чрезвычайно помогающий при решении задач: по какому-либо одному или
нескольким элементам условия или уже построенных
умозаключений вспомнить встречавшиеся ранее логические конструкции,
где те же элементы участвуют в тех же сочетаниях. Другие
элементы этих конструкций могут подсказать вам, как развивать
дальнейшие рассуждения.
Выкладки, которые в продолжение моего монолога
воспроизводит на доске Синица, мало отличаются от тех, что я провел
вместе с Сынчиковым. Обязательно использую это, чтобы
поддержать его!
— Посмотрите, ребята, на решение Синицы. Таким же
способом этот пример решили Горт, Стрельцов, Костюк, Гарин, Сын-
чиков...
Услышав свою фамилию в ряду таких светил, Сынчиков чуть
заметно улыбается, не поднимая глаз.
Он улыбается! Ей-богу, дело пойдет!
— Ну, а второй пример? Кто его решил? Никто? Странно!
Ведь его можно решить так же, как первый. Но давайте вернемся
к нему потом, если останется время. Кто желает, пусть
попробует решить его самостоятельно, как факультативный. А сейчас —
очередная тройка примеров: ап = 0)(р > 1);ап = у/п.
Третий же пример я задам особым, так называемым рекуррентным
способом, когда очередной член последовательности выражается
через предыдущие, чаще — через непосредственно
предшествующий ему. Вот он, третий пример: an+i = ^(ап + -^-),ао > О, х > 0.
— У первой последовательности предел единица? —
некоторое время спустя, плутовато улыбаясь, спрашивает Кулагин.
— Похоже. Это только ваша догадка?
— Да я тут взял и посчитал на калькуляторе несколько
первых членов для р = 2 — вижу, что они приближаются к
единице.
— Очень здравый подход, когда речь идет только о
выдвижении гипотезы. Но доказали ли вы ее?
— Нет, не доказал...
80
ПОСЛЕДОВАТЕЛЬНОСТИ
[Гл. 1
— А это разве не очевидно? — удивляется Миклашевский. —
Ведь tfp — это все равно, что р*; показатель степени стремится
к нулю — значит, степень стремится к единице.
— Как, ребята? — обращаюсь к аудитории. — Согласимся мы
с таким рассуждением? Нет ли в нем логических пробелов?
Судя по вашему молчанию, их нелегко заметить. Тогда я
почетче напишу то, что сказал Миклашевский: limp^ = р*^»71. Что
п—юо
вы скажете теперь, ребята? Утверждалось ли в наших теоремах
о сходимости нечто подобное? Нет. Стало быть, Миклашевский,
ваше рассуждение необосновано. Не скажу, что написанное мною
равенство неверно; вы можете доказать его дома, если желаете...
— Хорошо, — отрывисто отвечает он. — Докажу.
— Но тогда уж докажите совершенно строго!
— Я тут вспомнил, — просится к доске с новой идеей Ко-
стюк, — еще одну теорему, которую давал лектор: если
последовательность сходится, то сходится и любая ее
подпоследовательность и притом к тому же пределу.
— И что вам эта теорема здесь дает? — переключаюсь на
него.
— Прежде всего, я вижу, что последовательность р*
убывает с ростом п: лектор еще раньше доказал, что степень числа,
большего единицы, тем меньше, чем меньше показатель.
Снизу эта последовательность ограничена единицей. Значит,
предел у нее есть. Тот же предел будет иметь
подпоследовательность ее членов с четными номерами. Обозначим его А. Далее:
А = lim р" = lim р^ = lim ур* = \f~A\ А = у/А. Отсюда А = 1.
— Ребята, — оборачиваюсь к аудитории, — ну уж теперь-то,
в столь четких рассуждениях вы не можете не заметить ошибку.
— Ошибка примерно та же, что у Миклашевского, —
откликается Горт. — Неявно используется равенство lim ур* =
п—>оо v
= 4/ lim pn . А оно необосновано.
V п—>оо
— Странно, Костюк, — укоризненно качаю головой, — что вы
сами не ощутили свой грубый просчет. Садитесь. Подумаем еще
немного над этим примером, ребята.
И через несколько минут:
— У кого-нибудь есть решение? Нет? Я чувствую, друзья, что
вы страдаете распространенным недостатком студентов:
начинаете применять полезные советы преподавателя не по
собственному разумению, а только после того, как преподаватель укажет
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
81
вам, где их можно применить. Ну-ка полистайте свои тетради
и отыщите тот прием, который был бы очень полезен в нашем
примере.
Не найдут — так хотя бы повторят материал семинара.
— Не нашли? Плохо, очень плохо. А ведь я подчеркивал, что
этот прием очень часто оказывается полезным при работе со
сходящимися последовательностями. Про нашу последовательность
tfp мы предполагаем, что она сходится к единице. Значит,
целесообразна замена tfp = 1 + ап.
— А чем второе отличается от первого? — недоумевает
Рамзин.
— Тем, что ап бесконечно мала.
— Но ведь это надо еще доказать!
— Совершенно верно. Однако, если это действительно так,
доказать ее стремление к нулю, возможно, будет легче, чем
стремление исходной последовательности к единице, потому что
введение бесконечно малых величин, как правило, облегчает
выкладки — я в свое время показывал и подчеркивал это.
— Возвести обе части равенства tfp = 1 + ап в n-ную
степень? — мечтательно вопрошает Меншиков.
— А почему бы и нет? — приглашаю его к доске.
— Можно теперь разложить по биному: 1 + пап...
— А дальше писать лень? — с усмешкой спрашиваю его.
— По правде сказать, да, — вторит он моей шутливой
интонации.
— Так не пишите.
— Но ведь равенство нарушится!? — удивляется он уже
всерьез.
— Да, разумеется, — оно превратится в неравенство. Кстати,
какого знака?
— Сейчас... ап, очевидно, положительна, поскольку
положительная степень числа, большего единицы, тоже больше
единицы. Весь хвост бинома будет положительным. Получается
р > 1 + пап. Ну и что?
— Да то, что все уже сделано! — возбужденно вырывается
к доске Горт, — получается 0 < ап < ^-, по теореме о двух
милиционерах ап стремится в нулю.
— Видите, Меншиков, не зря говорят: лень — двигатель
прогресса. Лени у вас хоть отбавляй, надо только научиться
пользоваться ее запасами. Садитесь оба. Все поняли решение этой
задачи? — спрашиваю у аудитории. — Давайте пройдемся еще разок
по его основным этапам. Ответ, так быстро и верно угаданный,
82
ПОСЛЕДОВАТЕЛЬНОСТИ
[Гл. 1
поначалу казался недосягаемым. Первый сдвиг произошел,
когда мы представили корень tfp суммой двух слагаемых, одним
из которых был предполагаемый предел. Затем последовало
возведение в n-ную степень. Выражение (1 + ап)п напомнило нам
о биноме Ньютона — и дело пошло. А теперь давайте
рассмотрим проделанное нами с обобщающей точки зрения. И тогда мы
увидим за своими действиями два общих, два очень важных
приема, которые уже не раз выручали нас. Первый прием
заключается в том, чтобы каждый элемент условия задачи представлять
во всех возможных вариантах. Разложение tfp на два
слагаемых, возведение полученного равенства в n-ную степень — так
применяли мы этот прием. Когда же при взгляде на выражение
(1 + ап)п мы вспомнили про бином Ньютона, то в этом нашел
свое применение второй прием: мысленно беря элементы условия
по отдельности или в различных комбинациях дополнять их до
структур, которые уже встречались в прежних рассуждениях и
в которых те же элементы находятся в тех же отношениях, что
и в формулировке задачи. Если дополняющие элементы играют
в этих структурах роль предпосылок, ищите такие элементы в
условии задачи, углубляя тем самым ее анализ. Напомню, что
это слово в буквальном переводе означает «разложение,
расчленение» — оно внушает нам, что условия задачи должно
разлагаться на возможно более мелкие части. Если же дополняющие
элементы в привлеченных к рассуждению структурах играют
роль следствий, вводите их в развитие своего рассуждения.
Обогатив тем самым набор используемых элементов, продолжайте
таким же образом варьировать и достраивать их до тех пор,
пока не удастся выстроить путь от исходных данных задачи к ее
решению. Если выстраиваемый путь ведет вас в тупик,
возвратитесь к условию и посмотрите, насколько полно использовали
вы его элементы в своих построениях и насколько отвечали эти
построения тому, что требуется в задаче. И вновь начинайте
поиск решения — ищите новые варианты элементов условия, новые
способы их преобразования, новые сочетания элементов, взятых
в тех или иных вариантах, новые возможности достроить такие
сочетания... Быть может, то, что я говорю, выглядит слишком
схематично, но по ходу решения дальнейших примеров
изложенное мною еще не раз получит конкретное выражение. Так что
вернемся к нашим примерам. На очереди у/п. По виду очень
напоминает tfp. Видимо, здесь пригодна та же идея, что была
применена нами в предыдущем примере — попытайтесь
перенести ее на новый пример!
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
83
— Здесь она мало что дает, — несколько минут спустя
жалуется Лапиков. — Выходит, что у/п ограничен — и все.
— Покажите свои выкладки на доске.
— Я делаю замену у/п = 1 + /?п, потом получаю п > 1+
+ п/?п, потом ~р > /Зп > 0. Последовательность ^^ стремится
к единице, а не к нулю.
— И теорема о двух милиционерах не применима. Кстати, вы
не знаете, почему она так называется?
— Для нее есть сравнение: если два милиционера идут в
одно отделение, то и пьяный, которого они ведут с боков, будет
там же, как бы он ни шатался, — сообщает он под улыбки
ребят.
— В одно отделение! А ваши милиционеры направляются в
разные. Сложный оказался пример, да? Но ведь, Лапиков, я
просил перенести на него идею решения предыдущего, а не
скопировать ее! А вы повторили схему решения до мелочей.
— Надо взять еще один член в разложении бинома, — не
поднимая головы, произносит Гарин.
— И решать квадратное неравенство? — с сомнением
отзывается Рамзин.
Лапиков между тем дополняет прежнюю оценку: п > 1+
+ п(Зп+П2 Рп- И в наступившей паузе отчетливо слышен
робкий голос Аргуновой:
— Может быть, убрать второе слагаемое?
Это сказала Аргунова? Дело пойдет!
— Очень верное соображение! — отвечаю ей. — Реализуйте
его, Лапиков. Оставить в разложении бинома Ньютона два
первых слагаемых, как хотели вы, или три первых, как казалось
Рамзину, — это лишь некоторые из возможных вариантов
превращения равенства п = (1 + /Зп)п в неравенство. А ведь я
советую вам рассматривать все варианты возможных
преобразований, чтобы отыскать лучший. И Аргунова нашла его, так что
главная заслуга в решении примера принадлежит ей. Ну вот,
теперь милиционеры идут к одной цели. Получается, что /Зп стре-
84
ПОСЛЕДОВАТЕЛЬНОСТИ
[Гл. 1
мится к нулю, стало быть, lim у/п = 1. Решаем третий пример.
71—ЮО
Поскольку его форма нова для вас, я дам на него побольше
времени.
Брожу между столами. Проходя мимо стола, за которым
сидит Гарин, издали замечаю по символике выкладок, что он
занимается не тем примером, над которым думают все. Но
приготовленный было мною совет не отвлекаться сменяется, как только
я вглядываюсь в его тетрадь, совсем иным возгласом:
— Ребята, оставим на минуту наш пример. Я хочу, чтобы все
посмотрели то, что придумал Гарин. Речь идет о нерешенной
нами задаче с последовательностью ап = ~. Покажите свое
решение, Миша.
Смущаясь и отнекиваясь, он выходит, наконец, к доске:
— Ну, значит, *£, где р > 1, s > 0. Раз р больше единицы,
обозначим его р = 1 + а, где а > 0. Преобразуем —• = (^г~)п.
Воспользуемся решением предыдущего примера: lim у/п = 1.
П—КХ)
Можно доказать, что также и lim \/п? = 1, — если надо, я это
п—>оо
потом сделаю. А раз так, то, начиная с какого-то номера по бу-
дет y/tf < 1 + § и, значит, 0 < ^ = ($f)n < (Щ)п. Тут в
основании степени число, меньшее единицы, значит вся степень
стремится к нулю. Окончательно: при s > 0 и р > 1 lim *£ = 0.
п—►ооР
— Оригинально! — восторженно рокочет Меншиков.
— Просто блестяще! — соглашаюсь я. — Но для полного
блеска стоило бы доказать, что lim у/п? = 1, если s > 0.
П—КХ)
— Ну, значит, пусть нам дано какое-то такое s. Если оно
целое, то представим у/п? в виде у/п -... • у/п. Тут в произведе-
" v '
s раз
нии корней каждый сомножитель стремится к единице, значит,
и всё произведение тоже. Если s не целое, то возьмем
наименьшее превосходящее его целое число к и напишем неравенство
1 < (tfn)s < (</п)к = у/п •... • у/п. Корень >/п^ у нас теперь за-
к раз
жат между единицей и величиной, которая стремится к единице.
Отсюда по теореме о двух милиционерах lim y/r^ = 1.
п—>оо
— Красивое решение — правда, ребята? Нет, вы только
посмотрите — какое красивое! И сколько в нем таких черт, с
которыми обычно связывается представление о творчестве!
Неожиданность исходной идеи: а что, если представить данное выра-
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
85
жение в виде единой степени? Известная доля риска, скрытая
в таком замысле: удастся ли поставить получившуюся сложную
конструкцию на фундамент известных нам теорем о
сходимости? Счастливо припомнившийся результат когда-то решенной
задачи, умелое его сопряжение с задачей нынешней, изящество
и четкость окончательного выражения идеи... Нет, честное слово,
в этих выкладках есть многое, что пишут поэты о
возникновении стихотворных строк: «туман их появленья, их нарастание в
тревожной тишине, без плана, вспышками идущее сцепленье...»
И в то же время за выкладками Гарина отчетливо видны строгие
и простые приемы решения недавно пройденных нами задач на
последовательности. В этом, пожалуй, самое поучительное, что
можно извлечь из удачи Гарина: накапливай и совершенствуй
свои знания и навыки — и счастье творчества тебя не минует!
Очень хорошо, Миша. Садитесь. Спасибо за прекрасное решение.
С выражением бесстрастного спокойствия на лице, ничуть
не расцвеченном радостью успеха, он идет к себе,
провожаемый взглядами ребят, и я выдерживаю торжественное молчание
в продолжение этого триумфального шествия. Затем спокойно,
неторопливо :
— Итак, получается lim ^ = О, где s > О, р > 1. Запомните
этот предел, ребята. Он еще часто будет встречаться вам. Иногда
мы будем упоминать его в такой форме: любая
последовательность рп с основанием, большим единицы, возрастает быстрее,
чем любая последовательность п3 с показателем, большим
нуля. Кто желает, тот пусть подставит в формулу такого предела
вместо п произвольную последовательность Ьп, стремящуюся к
плюс бесконечности, и дома докажет, что lim Ц£- = 0. А теперь
п—юо Р
вернемся к очередному примеру.
Тишина. И с минуту спустя — голос Горта, непривычно
негромкий, обращенный к своим раздумьям:
— И убывать она может, и возрастать...
— Вы о чем, Саша?
— Да я об этой рекуррентной последовательности. Никак не
пойму: монотонная она? Или нет? Составил отношение an+i к
ап: получилось ^(1 + 4-). Если ап меньше у/х, отношение полу-
чается больше единицы, значит, ап+\ больше an,
последовательность возрастает. Если ап больше у/х, отношение меньше
единицы, последовательность убывает. А вот станет ли она когда-
нибудь меньше у/х или останется больше у/х — совершенно
непонятно.
86
ПОСЛЕДОВАТЕЛЬНОСТИ
[Гл. 1
— Последовательность не может стать меньше у/х, — по
обыкновению твердо заявляет Сутеев, глядя прямо перед собой
чуть опущенными глазами.
— Почему? Поясните.
— Каждый член последовательности выражается
полусуммой положительных величин, произведение которых равно
постоянной величине х. А в школе доказывалось, что такая
полусумма не меньше у/х. Среднее арифметическое больше или равно
среднего геометрического.
— Вот, Саша, ответ на ваш вопрос. И, как мне кажется,
решение всего примера. Правда ведь? — перевожу взгляд на Ко-
чина.
Он тотчас встает, как по команде, и, выйдя к доске,
повторяет, что последовательность убывает, а снизу ограничена числом
у/х (отмечаю похвалой его внимательность и память),
следовательно, имеет предел (хвалю его за краткость и четкость
рассуждения — его, считаю, следует поощрять за каждую малую
удачу), затем переходит к пределу в рекуррентной формуле и
находит его значение: у/х.
Наблюдая за его вычислениями из глубины аудитории,
приговариваю:
— Некоторые — не будем уж называть фамилии! — пытались
решить этот пример, вводя бесконечно малые величины, и
запутались, несмотря на все ухищрения.
— Но ведь вы сами говорили, — выдает себя Лапиков, — что
это универсальный принцип! И потом — раньше в этой тройке
все примеры были такие!
— А вы и рады работать по шаблону! Есть принцип
поуниверсальнее — не превращать в догму ни один из принципов. Вы
закончили, Кочин? Садитесь.
И тут, когда Кочин идет на место, а я поворачиваюсь к доске,
чтобы написать новое задание, Чюмин вдруг произносит:
— Что-то не было задачек на критерий Коши...
Эк, дернуло его! Из примеров, закрепляющих основные
теоремы, у меня, действительно, остались лишь примеры на кри-
Ю. В Пухначев]
СЕМЬ СЕМИНАРОВ
87
терий Коши — а после заявления Чюмина все будут знать как
их решать. Но ничего — я и их сумею подать так, что над ними
придется попотеть.
— Запишите новое задание, ребята. Надо исследовать эти три
последовательности на сходимость и расходимость: ап = 1 + ^+
4-i 4- 4-i-n — sini , sin2 , . sinn _ i , 1 , 1 , , I
— Тут только по критерию Коши и делать! — бросает
Миклашевский, глядя, как быстро разделывается с первым примером
Синица, вызванная к доске.
— Но и азбучных истин при этом не следовало бы забывать! —
замечаю, заглядывая в его тетрадь. — Идите-ка к доске,
покажите, как вы решили второй пример — ваша ошибка очень уж
поучительна. Интересно, как это вам удалось одним махом
избавиться от синусов?
— Но ведь синус — величина ограниченная!
— Вы знаете точное выражение этого факта?
— Конечно: | sinn| < 1 для любого п, значит, \Щрр-\ < ^г.
— Но в ваших выкладках что-то не видно, чтобы каждое
слагаемое вида Щр" оценивалось по абсолютной величине: вы
оцениваете их скопом.
Он хмурится, недовольный столь пустяковой, на его взгляд,
придиркой, а я между тем продолжаю:
88
ПОСЛЕДОВАТЕЛЬНОСТИ
[Гл. 1
— На формулу | sinn| < 1 можно опираться смело — это
было еще в школе. Но подобную формулу для нескольких
синусов, хотя бы для двух, типа | sinm + sinn| < 2, вам доказывали
вряд ли.
— А разве это неверно? Разве можно подобрать такие тип,
чтобы неравенство не выполнялось?
— Нельзя, согласен с вами. Но поймите, в математике мы
черпаем свои выводы не из моря правдоподобных
предположений, а из довольно узкого колодца несомненных утверждений. И
в этом колодце есть, между прочим, формула очень полезного
неравенства, которую вы без труда докажете и которую я очень
советовал бы вам запомнить. Вот она: модуль суммы нескольких
величин меньше суммы их модулей или равен ей.
— Ну, тогда все хорошо! — мигом повеселев, он хватается за
тряпку, чтобы вставить в цепь неравенств недостающее звено. —
Избавляемся по этой формуле от синусов, а дальше все, как в
предыдущем примере. Последовательность фундаментальная и,
значит, сходится. А предел надо находить?
— Нет, речь здесь идет лишь о факте сходимости. Садитесь.
Решаем теперь третий пример.
Впервые им приходится иметь дело с расходящейся
последовательностью. Десяток предыдущих примеров, где основной
целью был поиск пределов и сходимость принималась как
должное, видимо, заставил ребят напрочь забыть о том, что такое
расходимость. По инерции, да и по внешнему сходству с
предыдущими последовательностями, они и очередную считают
сходящейся. Бродя между столами и заглядывая в тетради, я вижу,
что все до единого стараются доказать недоказуемое, подогнать
злополучную последовательность под критерий Коши.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
89
— Что это вы написали? N = [|]? — шепотом, чтобы
преждевременно не подавать слишком легкой подсказки остальным,
спрашиваю Стрельцова. — Но ведь по формуле критерия Коши
N зависит только от е.
— Оййй ! — уязвленно морщится он. — Действительно! Надо
постараться избавиться от р.
Постарайтесь, постарайтесь...
— N должно зависеть только от е, я знаю, — опережая мои
вопросы, оправдывается по поводу той же формулы Кочин,
когда я подхожу к нему как бы невзначай. — Я сейчас пытаюсь
получить другую оценку, без р.
Попытайтесь, попытайтесь...
Измученные бесплодными попытками добиться
невозможного, они уже не могут сдерживать в себе разочарование.
— Везде р, везде это р\ — тихо стонет Горт.
— Нужно р убрать! — гулким шепотом убеждает Гарин Ко-
стюка.
Попотейте, дорогие, попотейте! Это лучше отучит вас от
инерции мышления, чем любые увещевания.
Я возвращаюсь к столу, и, усаживаясь, замечаю, как
удовлетворенно выпрямляется, оторвавшись от своей тетради, Буткус.
Нашел-таки философский камень? Или понял наконец истинный
смысл задачи?
Подходя к нему, издали вижу в его тетради символическую
запись отрицания фундаментальности.
Можно давать отбой:
— Вы все, ребята, пытались доказать сходимость третьей из
последних последовательностей, а между тем она ... расходится.
Буткус, к доске!
— Зачем же так... жестоко?! — поднимает на меня
трагедийный взор Синица.
— Как вы догадались, что последовательность расходится? —
спрашиваю Буткуса, когда он уже стоит у доски и докладывает
о своей находке.
— Мне показалось: если взять первые десять слагаемых, то
сумма будет такая же, что если взять сто потом.
— Десять? Сто?! Зачем так много? — стремительно
подхватывает Рамзин. — Надо взять сначала одну вторую,
потом следующие два слагаемых и заменить каждое меньшим,
одной четвертью; сразу видно, что они в сумме
превышают одну вторую; сумма следующих четырех ее превышает
тоже, если сделать такую же замену... Таким образом, после-
90
ПОСЛЕДОВАТЕЛЬНОСТИ
[Гл. 1
довательность бесконечно возрастает, следовательно,
расходится.
— Да и по критерию Коши все просто получается, по
условию нефундаментальности, — торопится изложить свою точку
зрения Горт. — Надо взять е = ^, в сумме ^- + ... + ^-
заменить все слагаемые наименьшим, оценить всю сумму снизу
дробью ^-, потом р положить равным п, получится |ап+р — ап\ > ^,
стало быть, последовательность расходится.
— Хорошо вы мыслите, ребята, когда известно, в каком
направлении мыслить! Но ведь поиск направления — это тоже
ваша задача. Умение решать ее не менее важно, чем умение
хорошо вычислять, чем эрудиция, логика. Все эти интеллектуальные
факторы необходимы исследователю, но не менее важен для него
волевой фактор — исследовательский характер. Выбрать тему
научной работы, цель ближайшего исследования, не изменить ей
несмотря на временные трудности и неверие окружающих, если в
ней твердо уверены вы сами, и отказаться от нее, если вы поняли
ее нереальность, — это должно быть у вас непременно. Утратив
способность ко всему этому, вы еще можете остаться научными
работниками, выполняя чьи-то задания, но вряд ли уже будете
работниками творческими, готовыми к большим, ярким делам.
Впрочем, я тут же хотел бы предостеречь вас от
распространенного заблуждения романтических мечтателей о великом научном
будущем — от несклонности браться за будничные, невзрачные
на первый взгляд задачи. Дело в том, что в повседневном
потоке таких задач обычно и всплывают замечательные проблемы,
на которых вы могли бы во всю мощь проявить свое дарование.
Поэтому я желаю вам быть одинаково сильными на обоих
флангах исследовательского диапазона — и в блестящих
нестандартных идеях, и в здравом подходе к простым задачам. Последнее,
кстати, частенько будет выручать вас при отсутствии
блестящих идей: иногда решение весьма сложных на первый взгляд
проблем удается сконструировать на основе стандартных
методов. И начинать решение любой задачи я советовал бы вам не с
молитвы о ниспослании гениальной догадки, а с четкой записи
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
91
условий, их внимательного анализа... Но давайте займемся этим
не на словах, а на практике. Прежде всего я прошу вас еще раз
внимательно проследить все наши рассуждения о
последовательности ап = 1 + ^ + з + ... + ^. Запомните ее определение и наш
вывод: эта последовательность расходится. К ней мы еще не раз
вернемся, когда станем проходить теорию числовых рядов — там
она именуется гармоническим рядом. На лекциях
рассматривалась еще одна знаменитая последовательность: (1 + ^)п, и лектор
доказывал, что она ограничена сверху и с ростом п монотонно
возрастает. Отсюда тотчас следовал вывод, что она сходится. Ее
предел обозначается через е. Это число играет очень важную
роль в математике. В частности, оно служит основанием
натуральных логарифмов. Ввиду важности числа е нам стоило бы
порешать задачи, связанные с ним. Вот одна из них. Пусть дана
последовательность qn, стремящаяся к плюс бесконечности. Из
нее образуем новую последовательность ап = (1 + ^-)Чп- Как вы
думаете, будет ли сходиться последовательность ап и, если будет,
то к какому пределу?
— Будет! К числу е! — мнение аудитории единодушно.
— Докажите.
Через несколько минут тишины — голос Лапикова:
— Скажите, а числа qn, вообще говоря, не целые?
— Нет.
— Жаль.
Еще через несколько минут он же:
— Скажите, а последовательность qn не монотонна?
— Вообще говоря, нет.
— Жаль.
Иду между столами. В тетрадях ребят — пусто! Если по
поводу предыдущего примера каждый с первой же минуты писал
свои соображения, пусть фантастические, то на этот раз — ни
строки! Еще минута, другая — и интерес к задаче полностью
угаснет у них... воскресишь ли его тогда? Нужно немедленно
начать разговор — с любой, пусть самой завалящей идейки,
которую выдаст кто-нибудь из ребят. Слежу за ними во все глаза.
— Аргунова, вы что-то написали? Покажите всем на доске!
— Нет, что вы, это я не думая написала!
— Мало ли что! Иногда и бессмыслица подсказывает
глубокие соображения. Леонардо да Винчи не зря советовал ученикам
искать сюжеты картин, всматриваясь в пятна сырости на стенах.
Идите к доске, не смущайтесь. Так, (1 + ттт)'9т1'> хорошо. Что
будем делать с этим выражением, ребята? Как свяжем его с тем,
92
ПОСЛЕДОВАТЕЛЬНОСТИ
[Гл. 1
что нам дано, с последовательностью (1 + j-)qnt Прежде всего
послушаем, что скажет на этот счет сама Аргунова.
— С одной стороны, [qn] меньше <7П, показатель степени в
первом выражении меньше, чем во втором. А основание— больше...
— Надо все делать последовательно: оценить qn, потом
основание 1 + ;г-, потом всю степень, — решительно заявляет Костюк.
— Вам и карты в руки! — приглашаю его к доске. —
Садитесь, Аргунова. Спасибо за то, что сдвинули дело с мертвой
точки. Теперь в каждом новом соображении мы должны настойчиво
искать возможность прицепить к нему какую-нибудь теорему о
сходимости. Вот, скажем, Костюк написал: [qn] < qn.He
вспоминаются ли вам, ребята, какие-то теоремы о сходимости, где
фигурировали бы неравенства?
— Теорема о двух милиционерах, — поясняет свои планы
Костюк.
— Верно. Но с вашим единственным неравенством мы,
кажется, недосчитаемся одного из этих милиционеров.
— Сейчас я обеспечу вам обоих — пожалуйста: [qn] < qn <
< [Яп] + 1 — незамедлительно реагирует он. Затем подробно и
последовательно сводит исходную задачу к вопросу о сходимости
последовательности (1 + т^т)^'-
- А тут уже все очевидно! — спешит поставить последнюю
точку Миклашевский. — У нас получилась подпоследователь-
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
93
ность последовательности (1 + ^)п, и стремится она к тому же
пределу.
— И не очевидно вовсе! — осаживает Миклашевского Ко-
чин. — Сказано ведь: qn не монотонная, значит, и [qn] не
монотонная тоже.
— Слушайте, ребята! Слушайте! — поддерживаю его. — Ну-ка
Кочин, повторите еще раз то, что вы сказали.
Слегка смутившись от того, что он внезапно стал центром
внимания, Кочин развивает свою мысль:
— Я что хочу сказать? В этой вот последовательности — я про
(1 + -)п — число п возрастает монотонно, по закону натурального
ряда. И любая подпоследовательность натурального ряда тоже
будет монотонной, это так, пусть. Но [qn] — разве она обязана
быть монотонной? А если она не монотонная — значит, это не
подпоследовательность натурального ряда.
— Очень проницательное возражение! — утвердительно
киваю ему. — Мы уже рассматривали однажды целочисленную
немонотонную последовательность: 2, 1,4,3,6,5... Как же вы,
Миклашевский, упустили из виду такой вариант? Сколько раз
напоминать вам о строгости? Надеюсь, ребята, — обвожу
взглядом аудиторию, — теперь все понимают, что сходимость
последовательности (1+ттт) ' ПРИ всей ее очевидности еще нуждается в
доказательстве. Будем искать его все вместе — садитесь, Костюк.
— Может быть, [qn] надо тоже как-то ограничить, какими-то
неравенствами? Заключить в какие-то рамки? — подает мысль
Горт.
94
ПОСЛЕДОВАТЕЛЬНОСТИ
[Гл. 1
— А толку? — бурчит Меншиков. — Ограничивали qn, и все
впустую.
— А теперь по-другому ограничим, — не сдается Горт, —
монотонными последовательностями. Вот так, скажем, ведет себя
[gn], — набрасывает он, приглашенный к доске, график
последовательности, — а я хочу ограничить ее такими вот монотонными
ступеньками: рп < [qn] < гп.
— А ведь верно! — чует смысл Кулагин. —
Последовательность гп можно сразу построить: rn = max{[^i], ...[<Zn]}-
— А рп = min{[qi]...[qn]}, — мгновенно добавляет Мухин.
— Минимум? — вскидывает брови Горт. — Но ведь с ростом
п он не будет возрастать! А нам нужно, чтобы рп монотонно
возрастала.
— Согласны? — спрашиваю Мухина. — Построение
последовательности рп — не такое уж простое дело, ребята. Его надо
хорошенько обдумать.
Снова длительное, беспросветное молчание. Чувствую, что
на этот раз спасать положение придется мне самому.
— Представьте, ребята, что вы входите в телефонную будку,
а телефон не работает. Что делать?
— Стукнуть по нему! — отвечает смешливый хор.
— А если в будку с испорченным телефоном входит мастер,
что делает он?
— Тоже стучит! — веселится хор.
— И если аппарат не работает даже после этих
профессиональных ударов, то мастер...
— Вешает бумагу «аппарат не работает» и уходит! —
хихикает Синица.
— Но допустим, что мастер попался дотошный. Он будет
докапываться до первопричин поломки и разберет аппарат до
винтиков. С такого мастера нам бы и следовало взять пример.
И если у нас не ладится рассуждение, нужно разобрать его до
определений тех понятий, которые фигурируют в этом
рассуждении. Скажем, в задаче, над которой мы сейчас бьемся, речь
идет о последовательности [qn]. Она, как и последовательность
qn, очевидно, стремится к плюс бесконечности. Что это значит?
Напишите на доске, Мухин. Так, так... В конце написанного
вами определения стоит неравенство [qn] > М. Не напоминает ли
это вам какое-то неравенство с [qn], которое мы уже однажды
писали?
— Стойте, стойте, стойте! — заклинает он меня, замерев. И
вдруг кидается к графику, нарисованному Гортом, молча про-
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
95
черчивает рукой на доске этакую лесенку, подпирающую
россыпь точек снизу, и начинает торопливо излагать:
— Возьмем М\ = 1 и найдем номер N\} — такой номер ,
после которого все [qn] больше единицы — это можно сделать,
потому что [qn] стремится к плюс бесконечности — потом возьмем
M<i = 2 и найдем номер N<i — такой номер, за которым все [qn]
больше двойки — потом будем брать Мз = 3, М± = 4 и так
далее — номера для них будут N$,N4 — и эти рп, которые нам
нужны, будем брать как раз на ступеньках...
Покуда он рисует члены последовательности рп, бдительный
Гарин тихонько замечает:
— Среди номеров N могут быть и совпадающие. Вон, судя по
графику, N2 = N3 = N4...
— Вы понимаете возражение Гарина? — оборачиваюсь к
Мухину. — Опишите строго построение последовательности рп.
Но Мухину это не под силу, да и сам Гарин не решается на
это.
— Ладно, — даю ребятам поблажку, — попробуйте дома
вывести формулу зависимости р от п. Ее отсутствие нам не мешает -
мы отчетливо представляем себе, как строится
последовательность рп и можем обсуждать ее свойства.
— Последовательность рп монотонно не убывает, но в ней
могут отсутствовать некоторые натуральные числа, — рассуждает
Горт.
96
ПОСЛЕДОВАТЕЛЬНОСТИ
[Гл. 1
— То есть рп, с точностью до повторения ее членов, будет
подпоследовательностью натурального ряда, — окончательно
уточняет Костюк.
— Совершенно верно, — одобряю эти соображения, — Ну, вот,
последовательность [qn] заключена в рамки рп < [qn] < rn. Что
дальше, Мухин?
— Надо подумать, — его энтузиазм окончательно иссяк.
— Думаем вместе, ребята! Садитесь Мухин.
— Но уж теперь-то все очевидно! — тянет
Миклашевский в негодующей истоме. — Все числа в последнем
неравенстве целые. Раз (1 + ^)п монотонная, то можно написать
(1 + -^)Рп < (1 + ттт)^п' < (1 + ?г)Гт1* Если из последовательности
рп выкинуть повторяющиеся члены, получится
подпоследовательность натурального ряда. И с гп то же самое сделаем —
и тоже получится подпоследовательность натурального ряда.
Значит, lim (1 + ^-)Рп = lim (1 + ;МГп = е. И по теореме о двух
п-+оо Рп п—юо Тп
милиционерах lim (1 + т^т)^п' = е. А отсюда по доказанному
раньше lim (1 + ~)9п = е.
п—юо Чп
— Да, после этих ваших рассуждений, действительно, все
очевидно. Мы решили задачу до конца — и по ходу ее решения
убедились, как помогает при выяснении запутанных вопросов
обращение к определениям. Всегда имейте это в виду, ребята! Прошу
вас, запишите в свои тетради без логических пробелов решение
последней задачи. Вы что-то хотите сказать, Горт?
— Да, — вновь устремляется он к доске, — я придумал, как
совсем коротко доказать, что та степень с целой частью qn
стремится к е. Исходим из определения числа е: lim (1 + ^)п = е;
то есть V е > О 3 Nx(e) V п > Nx (е - е < (1 + £)п < е + е).
Потом — определение того, что [qn] стремится к бесконечности:
V Л/'i З N2(N\) Vn>^2 ([qn] > N\). И сводим оба высказывания
в одно: V е > О 3 N2 (Ще)) \fn>N2 (e-e < (1 + щ)Ы < е+е).
Все.
Он кладет мел и круто поворачивает в обратный путь. Не
чувствуя в нем желания разбавлять словами красивое трехстро-
чие из символов, начертанное им на доске, растолковываю его
ребятам сам. Резюмирую:
— С таким доказательством решение задачи о пределе
выражения (1 + ^-)Яп становится совсем отчетливым. Но
напоминаю: мы решали ее в предположении о том, что qn стремится
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
97
к плюс бесконечности. Дома решите ее с последовательностью
<7П, стремящейся к минус бесконечности, а затем докажите, что
lim (1 + ^-)Чп = е при qn, стремящейся к бесконечности вообще.
— Вы обещали давать примеры тройками, — напоминает
Лапиков.
— Ну, если обещал, придется подыскать что-то еще. Один
момент... Пусть даны две последовательности: сходящаяся ап и
расходящаяся Ьп. Что можно сказать про их сумму Сп?
— Что она расходится, — уверенно отвечает несколько
человек и среди них — Мухин.
— Почему? — не теряю веры в то, что ему сегодня
посчастливится дать строгое решение хотя бы одного примера.
— Потому что ап с ростом п все ближе к своему пределу, а
Ьп все растет.
— Откуда вы взяли, что она возрастающая?
— Но ведь она расходится!
— Ах, ребята! — с сожалением качаю головой. — И вас я
чувствую, не миновало распространенное заблуждение: «если
последовательность расходится, то она неограничена или даже
стремится к бесконечности». Разве среди расходящихся
последовательностей нет ограниченных?
— Ну, конечно, есть — выручает заблудших друзей
Стрельцов. — Хотя бы такая: (—1)п.
— Здесь опять надо исходить из определений, иначе
запутаемся, — категорически заявляет Рамзин. — Можно я попробую
решить эту задачу?
— Попробуйте.
Он пишет на доске определение сходимости ап,
расходимости Ьп и, отчеркнув их горизонтальной прямой, — подлежащее
доказательству определение расходимости Сп.
— С последнего и следует начинать, — убежденно говорит
он. — Существует £, — голос его уже заметно потерял в
уверенности. — Гм... существует £...
— Заминка? — осторожно осведомляюсь я. — Нет, не
подумайте, что я вас тороплю. Но все-таки интересно: сколько
времени взяли бы вы для полного доказательства?
98
ПОСЛЕДОВАТЕЛЬНОСТИ
[Гл. 1
— Минут двадцать! — решительно отвечает он.
— А сколько запросили бы вы, Кочин?
— Часа, я думаю, мне хватило бы. Ну, может быть, двух...
— Какие все у нас оптимисты! — покачивает головой Менши-
ков. — Я бы эту задачу взял на дом.
— А можно я кое-что на доске подправлю? — с хитрецой
спрашивает Кулагин.
— Разве Рамзин где-то ошибся? — недоумеваю я.
— Нет, я в вашей записи хочу кое-что подправить.
— В моей?! Подправьте, если вам так хочется.
Он стирает черточку в знаке равенства, превращая его в
минус, и, оглянувшись на мою понимающую усмешку, заменяет
плюс на знак равенства.
— Сами ведь говорили: рассматривать все варианты условия.
Если бы сп была сходящейся, то сходилась бы и 6П, как разность
двух сходящихся последовательностей, а это противоречит
условию. Следовательно, сп расходится.
Звучный возглас удивления, восхищения, и даже зависти,
которым встречает это решение аудитория, рассыпается
подтрунивающим по собственному же адресу смешком: проглядеть такой
простой, такой верный ход!
И я присоединяюсь улыбкой сожаления к этому самоунижи-
тельному смешку:
— Признаться, я думал, что такое решение придет в голову
многим из вас. «Правда — хорошо, а счастье — лучше», — гласит
известная поговорка. А по отношению к занятиям математикой
я сказал бы так: знать ее правила необходимо, но и смекалка
никогда не помешает. Наш сегодняшний семинар окончен. На
следующем будем разбирать новую тему: «Пределы функций».
Глава 2
ПРЕДЕЛЫ ФУНКЦИЙ
— Ребята, вам на лекциях уже рассказывали про пределы
функций?
— Рассказывали! — круто мотнул вихрастой головой
Лапиков.
— В таком случае, — смотрю в его доверчивые глаза, —
быть может, вы напомните нам основные положения этой
темы?
— Что — прямо так? Сразу? — растерянно мямлит он. —
Тогда разрешите, я сейчас посмотрю это быстренько по
конспекту...
— По конспекту? — напускаю на себя сердитое удивление. —
А как же наш уговор? Мы с вами договаривались, что после
каждого занятия — лекции или семинара — вы будете
повторять и накрепко заучивать все то, что узнали и записали. А вы,
как я вижу, наш уговор не соблюдаете, пройденное не
заучиваете...
— Почему не заучиваю? Я заучиваю, — оправдывается он, —
Просто сейчас...
— «Просто сейчас забыл то, о чем вы спрашиваете», —
заканчиваю за него. — Что ж, такое может случиться со
всяким, в любой момент, быть может, в такой, когда под
рукой нет ни конспекта, ни справочника. Для таких
случаев очень пригождается искусство вспоминать забытое.
Давайте сейчас и потренируемся в этом искусстве.
Постарайтесь вспомнить, где вам раньше встречалось понятие
предела — а там попробуем действовать по аналогии. К доске,
Егор!
— У нас был предел последовательности, про него я все
помню, — с наивной уверенностью берет он мел и пишет
4*
100 ПРЕДЕЛЫ ФУНКЦИЙ [Гл. 2
на символическом языке определение предела
последовательности.
— Ну вот, уже кое-что. Продолжаем. Определение предела
функции вы не помните — но, быть может, вам запомнилось,
что говорил лектор по этому поводу, что он рисовал?
— Что рисовал, смутно вспоминаю, — он чертит оси
координат, чуть изогнутую кривую между ними и пересекающиеся
в одной из её точек пунктирные прямые, параллельные
координатным осям. — Вот: х стремится к числу a, a f(x) стремится к
числу А.
— Какая же логическая связь между двумя этими «х
стремится к а» и «f(x) стремится к А»? Не можете сообразить?
Перебирайте все, что пока у вас имеется для восстановления
забытого. Вот определение предела последовательности. Может быть,
оно своей формой подскажет уточнение вашей фразы «х
стремится к числу a, a f(x) стремится к числу А»? Есть ли в этом
определении что-то похожее? Что-то вроде «это стремится туда-
то, а это — туда-то»?
— Ну, в общем-то... когда п стремится к бесконечности...
когда п больше N... — его голос как-то странно замедляется, как
звук внезапно испортившегося проигрывателя, и вдруг он
взвизгивает:
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
101
— Ой, кажется вспомнил! В конце должно стоять
\f(x) — А\ < £, а в самом начале е; в середине \х — а\ < 5,
значит перед ним 8... а потом для любого х... вспомнил!
И, сдерживаясь опасением ошибки, он медленно пишет
символическую формулировку определения предела функции:
V в 3 8 V х ((\х - а\ < 8) =► (\f(x) - А\ < в)).
— Почти верно. Можно еще указать, что е больше нуля и 8
тоже, но есть недоговорка поважнее. Кто заметил, какая?
— х не равно а, — звучат голоса — звучат не очень уверенно:
наверное, среди ребят есть и такие, кто не вспомнил при моем
вопросе, что в определении предела должно стоять условие х ф а,
или не понимает, зачем оно должно там стоять.
— Смысл этого условия, ребята, помогут понять примеры
функций, вероятно, упоминавшихся на лекциях. Вот функция
sgnx. Возведем ее в квадрат и нарисуем соответствующий гра-
фик. Очевидно, получившаяся функция стремится к единице,
когда ее аргумент стремится к нулю. С определением предела
такое представление согласуется вполне: разность \f(x) —1|
всюду в окрестности нуля равна нулю и, стало быть, меньше
произвольно малого е. Всюду, за исключением самого нуля — здесь
разность \f(x) — 1| = |/(0) — 1| равна единице. Вдумаемся: чему
учит нас этот пример? Умению отделять друг от друга две
вещи: значение функции в некоторой точке и предел функции при
стремлении аргумента к этой точке. Кстати, на прошлом
семинаре я говорил вам, как важно умение расщеплять математическое
рассуждение на возможно мелкие детали, умение отделять эти
102
ПРЕДЕЛЫ ФУНКЦИЙ
[Гл. 2
детали друг от друга. Но если мы хотим сформулировать
понятие предела функции в некоторой точке независимо от значения
функции в этой точке, мы должны в самом определении предела
специально оговорить, что не станем рассматривать неравенство
\f(x) — А\ < е при предельном значении х, иными словами, что
значение аргумента х должно не совпадать с его предельным
значением. Это можно указать, например, так: 0 < \х — а\ < 6 —
ведь если \х—а\ строго больше нуля, то это значит, что х не равен
а. Возвращаясь к графику функции, который рисовал Лапиков,
я бы даже предположил, что эта функция может быть вовсе не
определенной в точке а. В таком случае на графике я обозначил
бы это с помощью двух стрелочек. Что стоило бы еще добавить
в определение предела функции?
Дотошный Горт подмечает любую недоговорку:
— Надо добавить, что х принадлежит области определения
/(х), какому-то интервалу, причем обязательно интервалу, не
отрезку, — ведь у нас точка а окружается двусторонней
окрестностью, которая должна целиком лежать в области определения
/(#), а это можно всегда сделать только в случае интервала.
Почему целиком? Потому что если окрестность выходит за пределы
интервала и мы возьмем в ней х, не принадлежащий
интервалу, — мы ведь говорим «любой х из окрестности» — а потом
подставим в неравенство \f(x) — А\ < £, оно потеряет смысл.
— Разумно. Ну вот, определение восстановлено во всех
деталях. А теперь, Лапиков, начертите на доске, где-нибудь сбоку,
прямоугольник с шириной вдвое большей, чем длина только что
написанной вами строчки символов, и с такой высотой, чтобы в
нем поместился десяток таких строчек. Разделите этот прямо-
уголник вертикальной линией пополам. И еще раз пополам —
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
103
горизонтальной. Эта таблица, когда мы ее заполним, позволит
нам упорядочить разнообразные определения, относящиеся к
понятию предела функции. То определение предела, которое вы
вывели, напишите в левом верхнем квадранте таблицы сверху.
Начните так: lim/(x) = А <==> а дальше пишите выведенное ва-
х—>а
ми определение. Хорошо. На прошлом семинаре я подчеркивал,
что по ходу математического рассуждения очень помогает
способность представлять каждую его деталь во всех возможных
ее вариантах. Давайте-ка мимоходом испытаем в себе эту
способность. Какую форму, Лапиков, может принять неравенство
\f(x) — А\ < в? Верно, А — в < f(x) < А + е. Отсюда, между
прочим, видно, что функция, имеющая предел в какой-то точке,
ограничена в некоторой окрестности этой точки — заметьте это в
своих тетрадях, ребята! — на момент оборачиваюсь к аудитории.
И вновь Лапикову:
— Если вы действительно прорабатывали и заучивали
пройденное на прошлом семинаре, то помните, как мы тогда
познакомились еще с одним способом прочтения последнего
неравенства — когда оно выполнено, то говорят, что величина f(x) лежит
в ^-окрестности числа А; обозначают это так: f(x) Е U(A, е).
А как вы переписали бы подобным образом неравенство
0 < \х — а\ < 81 Так, так, все та же буква U... только,
чтобы показать, что х не может совпадать с центральной точкой
окрестности, над буквой U ставят точку: х G U(a,8). При этом
х может лежать и справа от а, и слева — это не имеет никакого
значения, лишь бы только х не совпадал с а, вот главное.
Замечу, что определение, которое вы вспомнили, называется
определением предела функции на языке окрестностей. Вы
восстановили его по аналогии с определением предела
последовательности. Садитесь, Лапиков. И если в будущем при решении
задач вам станет отказывать память, попробуйте действовать
104
ПРЕДЕЛЫ ФУНКЦИЙ
[Гл. 2
так же — по аналогии: вспоминайте что-нибудь аналогичное
забытому, по аналогии пристраивайте к восстановленному
недостающее...
— Аналогия может и подвести, — голосом оракула замечает
Стрельцов.
— Может, не спорю. И потому возникающее по аналогии
целое надо постоянно контролировать своим пониманием существа
дела, приложением к конкретным примерам. Сейчас мы с кем-
нибудь, например, с Сутеевым, так и поступим — испытаем
определение, которое вспомнил Лапиков, на графике, который он
нарисовал. График ведь вполне согласуется с нашим пониманием
предела функции? В этом никто не сомневается? Начинайте
читать определение предела, Сутеев, и сверяйте его с графиком, да
не спешите.
— Для любого £, — отчетливо читает он, тут же откладывает
отрезочек е по обе стороны от отметки А на вертикальной оси
и тянет пунктирные линии от засечек к графику функции, —
найдется такое 5, — он откладывает скобочки по обе стороны
от а, восстанавливает из них пунктирные вертикали, — что
если взять произвольный х, лежащий в 5-окрестности а, но не
совпадающий с а, — пунктирная вертикаль тянется из точки х
вверх и, встретив график функции, поворачивает к
вертикальной оси, — то величина f(x) будет лежать в ^-окрестности числа
А, — пунктир вонзился в вертикальную ось между засечками
А — в и А + е.
— Хорошо, садитесь. По ходу своих рассуждений мы
предположили, что наша функция f(x) в точке а не определена вовсе.
Такое бывает — например, дробь ^^ не определена при х, рав-
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
105
ном нулю: ведь при нулевом знаменателе она не имеет смысла.
Ну, а если бы функция f(x) была определена в точке а? Какие
варианты следовало бы здесь различать?
— Значение функции в точке а либо равно, либо не равно
ее пределу в этой точке, — схватывает направление моей мысли
Миклашевский.
— И если равно...
— То функция называется непрерывной в этой точке.
— Верно. Напишите-ка на доске определение
непрерывности — где-нибудь рядом с нашей таблицей.
С небрежной легкостью начинает он копировать написанное
Лапиковым.
— Только заменить А на /(a)...
— Не только! — возражаю резким тоном, который должен
напомнить Миклашевскому мои прошлые выговоры ему за
нестрогость.
Мел в его руке замирает на миг ...
Сообразил:
— Ну, конечно, тут есть еще одна мелочь, — бросает он,
выдерживая прежнюю небрежную интонацию. И,
продолжая строчить все так же свободно, верно пишет неравенство
для х:
— Очевидно, в этом случае х может совпадать с а.
— Точно! — подкрепляю его мнение. — Совпадение х с а
сейчас уже не вызовет недоразумений: если х = а, то \f(x) — f(a)\ =
= 0 < е. Учтите это, ребята! Отметьте в своих тетрадях! Итак,
мы сформулировали определение непрерывности функции f(x)
в некоторой точке а из ее области определения. Если функция
непрерывна в каждой точке некоторого интервала...
— То она называется непрерывной на этом интервале, —
бойко заканчивает Миклашевский.
— Верно. Кстати, каждая из элементарных функций
непрерывна на всей области своего существования. Ну что ж, садитесь,
Миклашевский. Теперь, ребята, неплохо было бы
проиллюстрировать конкретными примерами разобранные нами определения.
Кто хотел бы пойти к доске? Вы, Рамзин?
106
ПРЕДЕЛЫ ФУНКЦИЙ
[Гл. 2
Он усваивает теорию лучше многих других, гордится своими
знаниями, боится ударить лицом в грязь и потому будет
действовать со вдумчивой осторожностью — а для начала это очень
кстати.
— К доске, Рамзин. Возьмем функцию у/х. Если х стремится
к некоторому ненулевому числу а, то к чему стремится у/х?
-К у/Б.
— То есть к своему значению в этой точке. Как
догадались?
— Функция у/х непрерывна, как всякая элементарная
функция.
— Догадались вы верно, а теперь докажите строго, что у/х
действительно стремится к у/а при х, стремящемся к а, — иными
словами, покажите, что она удовлетворяет определению
непрерывности. Я даю вам е, попробуйте найти такое 5, чтобы при
\х — а\ < 6 выполнялось \у/х — у/а\ < е.
— То есть при а — 5 < х < а + S выполнялось бы у/а — е <
< у/х < у/а + £, — он хорошо усвоил мой совет стараться
представить каждую деталь во всех возможных вариантах и выбрать
наиболее подходящий; умолкнув, тщательно рисует график и,
отложив отрезок е по обе стороны от отметки у/а на
вертикальной оси, внимательно разглядывает нарисованное.
— Смею надеяться, что е меньше у/а? Большее ведь брать не
имеет смысла.
Его не проведешь! Киваю в знак согласия. Он возводит в
квадрат неравенство для у/х, преобразует его к виду а — (2ву/а—
-в2) <х<а + (2ву/а + в2).
— Ограничения для х в определении предела функции
выглядят так: а — 6 < х < а + S. Значит, разумно взять либо
S = 2ву/а — е2, либо 5 = 2еу/а + е2. Чтобы не рисковать, возьмем
меньшее: 6 = 2в\/а — е2.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
107
— Но 8 должно быть величиной положительной, —
нетерпеливо напоминает Горт.
— Извините, — подчеркнуто учтиво оборачивается к нему
Рамзин, — я предположил, что е < у/а, значит е2 < ву/а и
потому 2еу/а — е2 > 0. Итак, — возвращается он к своим выкладкам,
— будем брать х в пределах: а — 2ву/а+е2 < х < а + 2ву/а — е2. Из
первого неравенства извлекается квадратный корень: у/а — е <
\[х, а из второго... второе можно усилить: х < а + 2ву/а — е2 <
< а + 2ву/а + е2, отсюда получаем у/х < у/а + е. Полагаю, что
все сделано, — не без довольства докладывает он мне. — Вы
мне даете £, я вычисляю 8 = 2ву/а — е2 и доказываю: как только
а—8 < х < а+8, то выполняется неравенство у/а—е < х < у/а+е.
— Неплохо, садитесь. Теперь, ребята, еще немного теории.
Если продолжать нынешний семинар по аналогии с предыдущим,
когда речь шла о последовательностях, то вслед за определением
предела функции следовало бы написать ...
— Его отрицание, — заканчивает за меня Костюк.
— Ну-ка напишите, — приглашаю Кочина. — Вы поняли мою
просьбу? Напишите определение того, что число А не является
пределом функции f(x) в точке а, — и начинаю в правом верхнем
углу таблицы: \imf(x) ф А <=>.
х—*а
Решительно выйдя к доске, он несколько секунд водит по ней
взглядом, но останавливается, к моему удивлению, не на
определении предела, а на графике у = sgn2x.
— Разрыв — это когда х близок к какой-то точке... к какой-
то... (решительный его порыв, похоже, не очень-то подкреплен
сообразительностью) ну, скажем, к нулю, а значения функции в
жив этой точке различаются на какую-то величину... какую-то
не малую... ну, то есть... как бы это сказать...
— Постойте, Кочин, — перебиваю его, — разве вы не помните,
как на прошлом семинаре мы разбирали правило, по которому
строятся отрицания для высказываний, содержащих кванторы?
И указываю на определение предела в левой верхней клетке
таблицы.
Помогло:
— Ну да: все кванторы — на обратные...
— Пишите отрицание в правой верхней клетке таблицы,
продолжайте строчку, которую начал я. Хорошо, хорошо...
Кванторы вы поменяли верно. Поглядите еще раз на определение
предела. Что будем делать с заключительным выражением в
скобках? Помните, как это делается? Нет? Тогда запомните, повто-
108
ПРЕДЕЛЫ ФУНКЦИЙ
[Гл. 2
ряю еще раз: отрицанием следования А =^ В служит
высказывание ЛД-»В. Смысл его в том, что одновременно
выполнена посылка Л и не выполнено следствие В. Ну вот,
отрицание проведено вами до конца и без ошибок (он написал «и»
вместо символа Д, но я пропускаю это мимо глаз — пусть
пишет, как ему понятнее). Прочтите про себя написанное вами
высказывание и растолкуйте вслух своими словами, что оно
означает.
— То, что х стремится к a... a f(x) не стремится к А.
— Я все-таки попросил бы от вас более подробного
истолкования. В написанном вами отрицании есть точная мера
этого «нестремления». Видите, в конце: \f(x) — А\ > е. И это
самое е стоит в самом начале отрицания: Зе. Раз оно стоит в
самом начале, то оно не зависит ни от чего последующего — ни
от выбора х, ни от ширины той 5-окрестности, где подбирается
х... Оно зависит лишь от характера конкретной функции,
которая в точке а не стремится к числу А. Давайте же возьмем
какую-нибудь конкретную функцию... ну, скажем, у = sgn2x,
которая вам так понравилась, и на ее примере разберем
построенное вами отрицание. В какой точке мы станем ее исследовать,
Кочин?
— В нуле.
— В нуле... Аргумент х стремится к нулю, а функция не
стремится... к чему она не стремится, Кочин? — указываю на точку
в начале координат.
— Не стремится к нулю, — отвечает Кочин, не отрывая
взгляда от мела в моей руке.
— Вот и покажите, что написанное вами высказывание
справедливо для функции у = sgn2x при а = 0 и А = 0. Перепишите
его с такой заменой. И снова попытайтесь прочесть своими
словами. Если угодно — теми же самыми, с которых вы когда-то
начинали: «Значения функции около интересующей нас точки
отличаются от значения функции в самой этой точке больше,
чем на какую-то определенную величину», — так, кажется, вы
говорили? На какую же величину могут различаться значения
функции sgn2x близ нуля и в самом нуле?
К). В. Пухначев]
СЕМЬ СЕМИНАРОВ
109
— На единицу! — быстро следует уверенный ответ: Кочин,
видимо, ухватил суть дела.
— Это различие, — добиваюсь предельной ясности, —
выражено, очевидно, вот этой скобкой: \f(x) — 0|. А нужное нам в
должно быть не больше этой величины. Какое же возьмем е?
— Половину, — смотрит он на меня благодарным взглядом.
— По-моему, вы все понимаете, — жестом отсылаю его к
записям на доске. — Читайте же, читайте то, что вы
написали.
— Существует е = ^ такое, что какую бы мы ни взяли
5-окрестность нуля, в ней найдется х такой, что \х — 0| < 8 и
\f(x) — 0| > \; тут х ненулевой — тогда |/(х) — 0| = |1 — 0| > \.
И пояснения на чертеже четко следуют за его четкими
словами.
— Прекрасно, садитесь. Итак, ребята, мы построили
отрицание того факта, что некоторая функция f(x) при х, стремящемся
к некоторому значению а, стремится к некоторому числу А. Мы
продемонстрировали также, что функция sgn2x при х,
стремящемся к нулю, не стремится к нулю. Если учесть, что нуль —
это значение функции sgn2x в начале координат, то наш
последний вывод приобретает еще одно толкование: рассмотренная
нами функция при х, стремящемся к нулю, не стремится к своему
значению в этой точке. То есть...
Выжидающей паузой предлагаю ребятам продолжить.
Тотчас Миклашевский:
— То есть она не непрерывна в нуле.
— Не непрерывна, — продолжаю, — или, как еще говорят,
разрывна. Кстати, Миклашевский, напомните нам, как вы
совсем недавно формулировали понятие непрерывности.
— Если значение функции в некоторой точке а равно ее
пределу в этой точке, то функция там непрерывна.
— А как вы понимаете, что функция разрывна в точке а?
— Наверное, так, что предел функции в точке а не совпадает
со значением функции в этой точке, если оно существует.
— Разве? Вы предполагаете, что функция обязана иметь
предел в точке а? Этого может и не быть, и потому мы не
можем говорить о пределе функции как о чем-то само собой
разумеющемся. Позвольте-ка, я задам вам один посторонний
вопрос: скажите, можно ли провести через вершину
четырехугольника прямую так, чтобы она рассекла его на три
треугольника?
— На три? — он морщит лоб. — Вряд ли.
110
ПРЕДЕЛЫ ФУНКЦИЙ
[Гл. 2
— Тем не менее это возможно, если четырехугольник не
выпуклый — смотрите!
— Если не выпуклый, то конечно! Это тривиально! —
спохватывается он.
— А разве все четырехугольники выпуклые? Нет ведь — и
точно так же не все функции, определенные в некоторой точке,
имеют в ней предел. Но вернемся к делу. Так как же выразить
тот факт, что некоторая функция f(x) не непрерывна в
некоторой точке а? Если вам это трудно сделать сразу, Миклашевский,
давайте предварительно хорошенько вспомним еще раз: что
значит, что функция непрерывна в точке а?
Неудача заставила его собраться:
— Это значит, что функция определена в этой точке, имеет
в ней конечный предел и этот предел совпадает со значением
функции в этой точке, — размеренно диктует он.
— Правильно. Ну, а теперь: что значит, что функция не
непрерывна — или, как говорят, разрывна — в точке а?
— Это значит, — он взвешивает слова, — что функция в этой
точке либо не определена, либо определена, но не имеет
конечного предела в этой точке или имеет, но он не совпадает со
значением функции в этой точке.
— Правильно. Еще один контрольный вопрос — на
внимательность и сообразительность: какие из перечисленных вами
вариантов мы иллюстрировали примерами?
— Минуту... Функция, сейчас была которая, sgn2x это,
наверное, самый последний вариант: предел есть, но не совпадает со
значением в предельной точке, в нуле то есть. Не имеет
предела... кажется, не было... да, по-моему, такого варианта не было.
Не определена... тоже вроде не было!
— Этот-то как раз был: я говорил, что дробь ^^ не
определена в нуле. А насчет функции, которая вообще не имеет предела в
какой-то точке, вы правы, — такого варианта не было. Здесь надо
придумать какой-то конкретный пример. Думаем все. Садитесь,
Миклашевский.
Синица листает свой аккуратный конспект:
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
111
— А вот на лекциях была такая функция: sin ^. Про нее,
кажется, лектор и говорил: не имеет предела в нуле.
— Лектор доказал это?
— Нет, он просил нас доказать это самостоятельно.
— Что ж, давайте сейчас и докажем. Надо бы нарисовать
на доске график этой функции. Кто у нас сегодня отличался по
этой части? Вы, Сутеев, не правда ли? Прошу вас к доске.
Четкий рисунок возникает на ней. Я отмечаю абсциссы
самых удаленных от начала координат нулей и экстремумов: ±- и
7Г
— Теперь, Сутеев, докажите, что эта функция действительно
не стремится ни к какому пределу при х, стремящемся к нулю.
Он тяжело смотрит на меня и молчит.
— Что же вы?
—Я не могу,—говорит он тем же твердым голосом,каким
подкупал меня раньше, давая безупречные ответы на мои вопросы.
Нездоров, что ли? Я теряюсь в подобных ситуациях —
наверное, потому, что встречаюсь с ними крайне редко и оттого
не успел выработать соответствующую реакцию на них.
Обычно студенты отзывчивы на мои наводящие слова, советы,
просьбы; некоторые не просто исполняют их, а идут дальше, находя
в них что-то, побуждающее к поиску. Мне очень хотелось бы,
чтобы у таких искателей в свою очередь возникали бы
соображения, которые вовлекали бы всех остальных в общую работу.
И тогда в идеале знания, которые я должен преподносить им
в готовом виде, воссоздавались бы ими самими в процессе
коллективного самостоятельного творчества. Да, самостоятельного
и свободного. Принудительное преподавание — решительно не
для меня.
— Что ж, садитесь, если не можете...
112
ПРЕДЕЛЫ ФУНКЦИЙ
[Гл. 2
— А почему мы, — врезается в неловкую тишину сверлящий
голос Буткуса, — написали только одно определение предела?
На лекции давали два! Одно на языке окрестностей, а другое...
— Стоп! — прерываю его. — А другое, Чюмин?
— На русском языке, наверное?
— На языке последовательностей! — не терпится Горту дать
верный ответ.
— Правильно, — киваю ему. Потом вновь Буткусу:
— Давайте напишем на доске это определение в левой
нижней клетке нашей таблицы. Снова начинаем: lim/(x) = А «<=>...
х—>а
Продолжайте, Линас. Написали верно. А теперь в правой ниж-
ней клетке таблицы опишите на языке последовательностей, что
f(x) не стремится к А при х, стремящемся к а. Все хорошо — и то,
что вы написали, Линас, и то, что у вас сработала реакция,
которая должна стать для всех нас естественной: когда не удается
применить некоторое теоретическое положение, мы перебираем
все его варианты, все равносильные ему положения и пытаемся
применить их. Правда, мне кажется, Линас, что ни одно из
написанных нами отрицаний не выражает то, что нам нужно: оба
означают, что функция не стремится к некоторому числу А. Мы
же хотим доказать, что наша функция не стремится ни к какому
числу вообще ...
Не говоря ни слова, Буткус снова берется за мел, снизу от
обоих отрицаний повторяет их с той разницей, что на месте
выражения lim/(x) ф А ^=> ставит V А.
х—>а
— О, верно! Но эти строчки отрицают уже не определения
предела функции, а нечто другое. Что же?
Все так же молча снизу от обоих определений
предела функции он переписывает их, заменяя выражение
lim/(x) = А Ф=> на ЗА.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
113
— Очень хорошо, Буткус, садитесь. Вернемся теперь,
ребята, к функции sin^, докажем, что она не имеет предела при х,
стремящемся к нулю. Жду хороших идей на этот счет.
В ожидании хороших идей проходит минута, другая ...
— Что, никак не удается применить к нашей функции ни
одно из этих отрицаний? — с этими словами я подхожу к доске,
рисую в конце каждой из четырех строк, написанных Буткусом,
стрелки эквивалентности и повторяю их ниже, с левого края
следующих строк. — Помнится, когда мы говорили о
последовательностях, то сразу вслед за утверждением о сходимости называли
еще что-то эквивалентное ему...
— Критерий Коши! — вырывается у Меншикова, и вот уже
по моему пригласительному жесту он выходит к доске,
притворно удрученный, что выдал себя. Вставая из-за стола, он успел
заглянуть в тетрадь Гарина, где, по-видимому, увидел все
нужное ему, и потому держится уверенно — вслед за нарисованными
мною обоюдоострыми стрелками пишет формулировки критерия
Коши и его отрицания.
— Какие же удобства, — спрашиваю его, — обещает нам
критерий Коши?
Томный его взор, побродив туда-сюда вдоль частокола
символов, вяло склоняется в мою сторону: «А бог его знает», —
написано в нем.
— Не видите? Кто поможет, ребята? — обернувшись к
аудитории, останавливаю взгляд на Кулагине.
— Там, — кивает он на определение предела функции и на
его отрицание, — везде стоит А, а там, — переводит он глаза на
критерий Коши и его отрицание, — никакого А нет, там проще.
114
ПРЕДЕЛЫ ФУНКЦИЙ
[Гл. 2
Если бы мы по-старому доказывали, что предела нет, — для
любого А существует е и так далее, — то как будто мы для каждого
А должны были бы это проверить и потом сказать, что предела
нет вообще, а если по критерию Коши, то без всякого А, только
значения функции смотрим и все.
— Верное понимание, — поддерживаю эту мысль. — А
поскольку излишеств лучше избегать, чтобы они не повлекли за
собою перегрузок в работе и нежелательного переутомления, —
вновь обращаюсь к Меншикову, — то для функций, не
имеющих в некоторой точке никакого предела, лучше использовать
не прежние наши определения этого факта, а... что, Меншиков?
— Отрицание критерия Коши.
— Совершенно верно. Вот и примените его к функции sin ^.
— Существует е... Тут е можно взять любое меньшее двух...
Для любого 6 найдутся х' и х"... вот эти например, — на кончиках
волн, сверху и снизу... Разность — два, значит, больше е.
— Набросок рассуждения вы дали неплохой, теперь
распишите его на символическом языке в окончательном виде.
Существует £, равное... каким вы его возьмете?
— Да любым, лишь бы меньше двух...
— Ну, например?
— Я же сказал — любое ...
— Конкретно, Меншиков!
— Ну, единица...
Да, парень с ленцой — и немалой! Не знаю, сумею ли
выбить ее из него, но по крайней мере постараюсь, чтобы каждую
поставленную перед ним задачу он решал до конца.
Не отпускаю его прежде, чем он выписывает до единого
знака отрицание критерия Коши применительно к функции sin j в
нуле.
— Как видите, наша функция в нуле не удовлетворяет
критерию Коши, следовательно, не имеет в этой точке конечного
предела, а далее отсюда следует, что функция sin ^ в нуле разрывна.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
115
Ну, что ж, с примерами разрывных функций мы с вами, ребята,
повозились немало, а между тем эти примеры — не из самых
сложных. Каждая из разобранных нами функций имела разрыв
лишь в одной единственной точке. Математика знает функции и
подиковинней — например, такие, которые имеют разрыв в
каждой точке области своего существования. Не придумаете ли хотя
бы одну из них?
Непосредственный Мухин тотчас тянет руку:
— Лектор нам давал одну красивую функцию...
И поводит в воздухе пальцами, словно пианист, который
бегло перебирает сначала черные, а потом белые клавиши.
— Такую функцию...
— Может быть, ее лучше нарисовать? — приглашаю его к
доске.
Он чертит систему координат, ведет горизонтальный
точечный пунктир на некоторой высоте над осью абсцисс, затем
отстукивает еще одну такую же россыпь точек на самой оси:
— При рациональных х функция равна единице, при
иррациональных — нулю, функция Дирихле она называется.
Приписываю рядом два равенства, выражающих
определение функции Дирихле.
- Сумеете доказать, что она всюду разрывна?
- Возьмем сначала какую-то рациональную точку... Тут
опять, наверное, лучше по отрицанию критерия Коши?
— Попробуйте, воля ваша.
— Если окрестность — сколь угодно узкая окрестность этой
рациональной точки — то там можно найти — всегда можно
найти еще одну рациональную и одну иррациональную — разность
значений функции единица — по модулю, конечно, единица — а
е надо взять, например, одну вторую...
116
ПРЕДЕЛЫ ФУНКЦИЙ
[Гл. 2
Поддерживая стандарт строгости, заявленный мною в
разговоре с Меншиковым, заставляю Мухина выстроить свои
соображения ровной цепью логических символов до
окончательного вывода: в любой точке функция Дирихле
разрывна.
— Садитесь, Мухин. Теперь, ребята, еще одно задание:
придумать функцию, которая разрывна всюду за исключением одной
точки.
Задумались... Помочь, что ли? Вряд ли стоит тратить много
времени на столь частный вопрос:
— Видимо, здесь опять удобно использовать функцию
Дирихле. Как-то перекроить ее...
И, подняв руку ладонью вперед, свожу пальцы так, словно
сжимаю поводья. Навстречу моему жесту энергично
поднимается Костюк:
— Я бы взял такую функцию: х2, умноженный на функцию
Дирихле.
У доски он несколько медлит, график предложенной им
функции возникает не сразу, но, как только он возник,
Костюк начинает плести вокруг начала координат сетку
прямоугольников:
— Тут снова по критерию Коши: для любого е надо брать
окрестность нуля с шириной у/ё вправо и влево, тогда все
точки графика не выйдут за прямоугольник. Значит, функция
стремится к нулю, когда х стремится к нулю. А в
ненулевых точках — разрыв, доказывается так же, как Мухин
доказывал.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
117
— Все верно, садитесь. Вспомним теперь, ребята: когда на
прошлом семинаре речь шла о последовательностях, то мы
разбирали не только такие случаи, когда последовательность
стремится к какому-то конечному пределу, но и такие, когда она
стремится... к чему, Стрельцов?
— К бесконечности.
— Напишете что-нибудь аналогичное для функций?
— Написать-то напишу, только...
— Что «только»?
— Много писать придется. Ведь х тоже может стремиться
к бесконечности. Много вариантов получается. Такой,
например: аргумент стремится к конечному значению, а функция к
бесконечности. Или такой: аргумент стремится к бесконечности,
а функция к конечному значению. Или такой случай, когда и
аргумент и функция стремятся к бесконечности... Опять же к
бесконечности можно стремиться по-разному — можно к плюс
бесконечности, можно к минус...
— Это вы все правильно говорите. Самое время вспомнить о
том, что математика — наука экономная, она умеет подводить
массу частных случаев под один закон, под одно понятие. Кто
попробует это сделать?
Молчание.
— Ну-ка, переберем все термины, которые употребили на
прошлом занятии, посмотрим, не применимы ли какие-то из них
одновременно и к конечной точке, и к бесконечности.
Молчание. И голос Миклашевского:
— Окрестность бесконечности!
— Мне кажется, вы все поняли. Все и напишите на доске.
Ведь теперь-то писать придется немного.
Он переписывает определение предела функции на языке
окрестностей:
— Если речь идет про ^-окрестность определенной точки
а, то выражение «х попадает в U(а, 6)» надо понимать так:
О < \х — а\ < 6. Если же речь идет про 5-окрестность
бесконечности, то мы напишем [/(оо,5) и попадание в эту окрестность
будем понимать как неравенство |х| > 5.
— А если речь идет про ^-окрестность... ну, скажем, минус
бесконечности?
— Тогда пишем неравенство х < — 8\ я считаю S
положительным, как обычно.
— Хорошо. Тогда напишите на символическом языке: при х,
стремящемся к бесконечности, f(x) стремится к минус бесконеч-
118
ПРЕДЕЛЫ ФУНКЦИЙ
[Гл. 2
ности. Сначала напишите с символом окрестности, потом — с
неравенствами. Верно, садитесь на место.
Оборачиваюсь к аудитории:
— Все понятно? Тогда нарисуем график некоторой функции,
удовлетворяющей такому условию. Пусть это сделает кто-то из
тех, кто сегодня еще ни разу не выходил к доске — например,
Сынчиков.
Может быть, сегодня он выступит лучше, чем в прошлый раз?
Его реакцию на мой вызов не назовешь обнадеживающей:
опять нужно дожидаться, пока он снимет очки и уложит их в
очечник, пока выберется из-за стола... К доске он выходит, не
отрывая глаз от пола.
— Вы представляете себе такую функцию? — осторожно
осведомляюсь для начала. — Нет? Тогда прочтите то, что написал
Миклашевский... Прочли верно. Теперь читайте медленнее,
символ за символом, и изображайте прочитанное на чертеже.
Начинайте! Для любого г... Да рисуйте, рисуйте!
— Я не знаю, что рисовать, — еле слышно выговаривает он.
— Сначала хотя бы оси координат, а потом — то, что
первым стоит в определении нашей функции. Говорится про е —
отмечайте е.
Коротким штришком он ставит отметку на вертикальной оси,
над началом координат.
— Но рисуйте со смыслом, с учетом того, что говорится про
е в определении. Где оно там фигурирует?
— Вот, — указывает он на неравенство f(x) < —£.
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
119
Может быть, по виду неравенства он догадается сам, как
исправиться? Без моей подсказки? Слава богу, догадался: ставит
на вертикальной оси отметку —£ ниже начала координат. И еще
радость: он сам покрывает штриховкой ^-окрестность минус
бесконечности на вертикальной оси. Но на следующем шагу вновь
спотыкается. Надо указать (^-окрестность бесконечности на
горизонтальной оси. Словно во сне, он пишет — 6 < х < й, пытается
рисовать, видит, что неравенство неверное, стирает его и пишет
-6 > х > S.
С изумлением гляжу на это странное выражение:
— Но ведь у вас получается, что отрицательная величина — 6
больше положительной 6\
— По модулю, по модулю, — позванивают тихие подсказки.
Он стирает только что написанное неравенство и пишет
\х\ > 6. Следующий шаг снова делает сам — правильно
указывает на оси абсцисс ^-окрестность бесконечности. Но двинуться
дальше опять не может.
— Насколько я понял ваш рисунок, — подстегиваю его
словом и жестикуляцией над графиком, — точки графика, лежащие
ниже —е, лежат дальше от вертикальной оси, чем на расстоянии
6. Иными словами, они лежат... в какой области? Очертите её.
Очерчивает верно.
— А если я задам е побольше? — отчеркиваю штрих на
вертикальной оси ниже прежнего. Засечками, более удаленными
от начала координат, он отчеркивает на оси абсцисс новую
120
ПРЕДЕЛЫ ФУНКЦИЙ
[Гл. 2
^-окрестность бесконечности и верно обрисовывает область
координатной плоскости, где должны лежать соответствующие
точки будущего графика.
— А если взять е еще больше? Продолжайте рисовать! Все в
принципе верно. Не намекает ли вам это на ход графика,
который мы хотим построить?
Неровная, но в общем правильная загогулина возникает на
доске.
— Какую знакомую вам кривую это вам напоминает?
Он молчит, а тишина аудитории так и сочится истомленным
шепотом: «парабола, парабола».
Что мне делать с ним? Темп, нормальный для всех
остальных, ему явно не под силу. Он, видимо, не может продвигаться в
своих рассуждениях столь же широкими шагами. Я готов
пройти с ним тот же путь шажками помельче, но, делая это у доски,
где мои действия воспринимаются, как пример для подражания,
я тормозил бы мысль ребят, способных на большее. А на своем
месте он соображает лучше, чем на виду у всей аудитории, — я
уже заметил это на прошлом семинаре. Мягко, без всякой
интонации порицания говорю:
— Сядьте, пожалуйста, на место, Сынчиков, и попробуйте
самостоятельно довести этот пример до конца — напишите
формулу функции, которая здесь подходит — ребята верно советуют
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
121
вам взять параболу ветвями вниз, — и покажите, что она
удовлетворяет определению, которое мы написали.
И вновь ко всей аудитории, в прежнем энергичном темпе:
— Говоря о последовательностях, мы употребляли понятие
ограниченности. Приложимо ли оно к функциям? Как,
Лапиков?
— Конечно! Синус, например, — функция ограниченная: для
любых х он меньше единицы.
— Для любого х функция sinx по абсолютной величине не
превосходит единицы, — даю уточненный вариант его ответа. —
А если говорить не о синусе, а о произвольной ограниченной
функции /(х)? — перевожу взгляд на Рамзина. — Как будет
выглядеть условие ее ограниченности?
— Существует положительное М такое, что для любого х из
области определения f(x) выполняется |/(х)| < М, — копирует
он мой обстоятельный тон.
— Верно. Часто, впрочем, говорят об ограниченности
функции не на всей области ее определения, а на отдельных участках.
Говорят, например, об ограниченности функции в окрестности
какой-либо точки а, или, как тогда кратко выражаются, в точке
а. Попробуем разобраться, что понимается под этим
выражением: функция f(x) ограничена в точке а. Костюк, вы, кажется,
имеете свое мнение на этот счет?
— Я думаю, это надо понимать так: для любого
положительного S существует положительное М такое, что для любого х
из ^-окрестности точки а выполняется неравенство |/(х)| < М.
— А я думаю, — звонко выпаливает Синица, — что надо
сказать по-другому: существует положительное S такое и существу-
ет положительное М такое, что для любого х из ^-окрестности
точки а выполняется |/(х)| < М.
— Как вы думаете, Аргунова, кто прав?
— Да вроде бы Виталик прав, — тихо шелестит её голос, — и
Люда тоже, — добавляет она под общий смешок.
— Может быть, поставим вопрос на голосование? —
предлагаю я шутливым тоном, поддерживая улыбки на лицах ребят.
— Давайте, как на настоящих выборах, предоставим слово до-
122
ПРЕДЕЛЫ ФУНКЦИЙ
[Гл. 2
веренным лицам обеих гипотез. Синица, к доске! Агитируйте за
свою гипотезу!
— А она сама за себя агитирует.
— Но все-таки проиллюстрируйте её на каком-нибудь
примере. Возьмите функцию, которая в каких-то точках ограничена,
как мы это интуитивно себе представляем, а в каких-то не
ограничена — например, f(x) = tgx.
— Ну, пусть tgx. В нуле она ограничена, — ведь правда? То
есть, как я говорю, существует некоторая окрестность нуля,
например, с размером ^, и существует ограничение на значения
тангенса в этой окрестности — это, очевидно, единица: для
любого х, не превосходящего по модулю f, tgx меньше 1.
— Отлично. Теперь слово вам, Костюк.
— С моей гипотезой все в порядке тоже! Хотите, чтоб я
рассмотрел ограниченность тангенса в нуле? Пожалуйста. Какую
бы окрестность нуля я ни брал, я всегда буду находить ограни-
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
123
чение на тангенс для всех иксов из этой окрестности, — и он
рисует около нуля сближающиеся скобочки.
— Погоди, погоди! — одергивает его неусыпно бдительный
Горт. — Ты что же их сужаешь?
— А зачем мне их расширять? Я стягиваю их к точке!
Ограниченность же в точке исследуется!
— Да это жульничество просто! — кипятится Горт. — Ты же
говоришь: «любая окрестность»! Любая — значит, и сколь угодно
узкая, и сколь угодно широкая. А ты все подтасовываешь под
сколь угодно узкую! Вот жулик!
— Стоп, стоп! — урезониваю его. — Предвыборная компания
не допускает оскорблений. Переходим к голосованию. Кто за
гипотезу Синицы? Десять голосов. Кто за гипотезу Костюка? Пять
голосов. Кто воздержался? Двое.
— Чудно как-то, — бормочет Миклашевский. — В
математике—и голосование.
— Действительно, чуднб, — киваю ему. — Но что вы
предложите взамен, чтобы выбрать между двумя определениями? Это
ведь не теорема, которую можно либо доказать, либо
опровергнуть противоречащим примером. В выборе определений мы
совершенно вольны. Как же выбрать лучшее? А, Миклашевский?
— Надо посмотреть, какое больше соответствует делу,
положению вещей... ну, как это еще сказать...
— Чьими глазами посмотреть? Где этот непогрешимый
арбитр? Его нет среди нас, и потому приходится полагаться на
общественное мнение. А оно, как видите, разделилось.
— Я придумал! — вскакивает Горт. — Надо испытать
следствия из определений! И если какое-то будет абсурдным, нам
всем покажется абсурдным, надо такое определение отвергнуть!
— Разумный подход! Как говорил какой-то литературный
герой, чтобы лучше понять связь между душой и телом, хорошо
бы выяснить, в чем сходство между душегрейкой и телогрейкой.
Я вижу, вы хотите выйти к доске, Горт?
— Да! Я напишу по всем правилам логики — логику ведь
еще никто не отменял? — отрицание ограниченности функции в
точке.
— Ограниченности по Костюку?
— Да, конечно! — бросает он, не отрываясь от доски и не
замечая улыбок в аудитории по поводу его горячечного
энтузиазма. — Напишу отрицание и покажу, что оно просто не
выдерживает критики. Вот это отрицание: существует 6 такое, что для
любого М найдется х такое, что |/(х)| > М. Теперь я, используя
124
ПРЕДЕЛЫ ФУНКЦИЙ
[Гл. 2
это выражение, исследую на неограниченность все тот же
тангенс во все том же нуле и у меня получается, что тангенс в нуле
удовлетворяет условию неограниченности: существует 5,
например, равное ^, такое, что для любого М найдется х — найдется,
конечно, около точек ±^ — такой, что \х — 0| < \ и | tgx| > М.
Получается, что тангенс в нуле неограничен. Это же очевидный
абсурд! Значит, надо принять определение ограниченности не по
Костюку, а по Синице! Тогда все будет на месте. В нуле
тангенс ограничен, Люда это показала, а в точке |, например, —
неограничен. Можно построить отрицание ограниченности....
— Ограниченности по Синице?
— Да, разумеется! Построить отрицание ограниченности
тангенса в точке ^ и показать, что тут все будет верно. Вот это
отрицание: для любого 6 и для любого М найдется такой х из
5-окрестности точки ^, что |tgx| > М. — Он быстро черкает
необходимые отметки на графике. — Я даже могу не пояснять.
— Что ж, убедили. Принимаем то определение
ограниченности в точке, которое дала Синица. Напишите его поаккуратнее,
Горт, а ниже напишите определение неограниченности в точке.
Вы поменяли местами символы 6 и М...
— Они стоят под одноименными кванторами, а в таком случае
перестановка допускается.
— Хорошо, садитесь.
Все-таки, по-моему, никакой особой разницы у этих
определений нет, мое тоже можно было бы взять, — негромко ворчит
Костюк.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
125
— Как вы помните, ребята, — продолжаю, словно не слыша
этой реплики, — на прошлом семинаре мы, говоря о
последовательностях, довольно подробно исследовали логические
взаимосвязи между понятиями неограниченности и стремления к
бесконечности. Можно предвидеть, что определение
неограниченности функции в некоторой точке будет напоминать определение
того факта, что при стремлении аргумента к некоторой точке
функция стремится к бесконечности. Кстати, кто воспроизвел
бы нам это определение? Кто еще не выходил к доске?
— Чюмин, — услужливо оповещает Рамзин, явно предвкушая
злорадное удовольствие от ляпсусов чудаковатого однокашника.
— Что ж, пусть это сделает Чюмин.
Я тоже уверен, что он что-нибудь напутает, но это нам сейчас
даже на пользу: разбираясь в его нелепицах, лучше освоим
верную формулировку. Ну, так и есть — он пишет 3 е > 0V 6 > О
Эх(0<|х-а|<*)(|/(х)|>е).
— Что-то не так, — недоверчиво щурится на доску
Миклашевский.
— Не так, — соглашаюсь с ним, — и если написать ниже
верное определение, мы сразу обнаружим несходство. Но прежде
чем стирать неверное, давайте, ребята, попробуем разобраться —
что же написал Чюмин? Ведь что-то эта символическая фраза
да означает!
— Сейчас, сейчас, — принимает вызов Кочин. — Если
написано |/(х)| > е, значит /(х) лежит вне е-окрестности нуля...
— Существует х, — бормочет как будто совсем о другом
Кулагин, — «существует» — это мы часто пишем, когда что-то
отрицаем... Это какое-то отрицание.
— Ну, конечно! — осеняет Кочина. — Это отрицание того, что
функция стремится к нулю.
— Мы когда-то договаривались не давать негативных
определений. Начните лучше так: «Это утверждение о том...»
— Это утверждение о том, что при х, стремящимся к а, /(х)
не стремится к нулю.
— Отлично, Кочин! Как бы вы сами попробовали убедиться
в том, что правы? Я на вашем месте поступил бы так:
сначала написал бы утверждение о противоположном, то есть о том,
что функция /(х) стремится к нулю при х, стремящемся к а.
Помните его? Да, верно: Ve>035>0Vx((0<|x — а\ < 6) =>
^ (1/(х)1 < €))- Сравните эти утверждения: написанное Чю-
миным и написанное вами. Различия в кванторах и
заключительных неравенствах окончательно подтверждают вашу право-
126
ПРЕДЕЛЫ ФУНКЦИЙ
[Гл. 2
ту, Кочин: действительно, Чюмин сформулировал утверждение
о том, что при х, стремящемся к a, f(x) не стремится к нулю.
Правда, если бы он абсолютно точно строил отрицание
написанного вами, Дима, то что было бы у него по-другому?
— Тогда бы у него между двумя последними неравенствами
стояло бы «и».
— А как выглядело бы самое последнее неравенство? Верно,
\f{x)\ > е. Вы хорошо запомнили, как строится отрицание
следования. А самое главное — вы научились читать и понимать
записи на языке символов и доказали это тем, что нашли верное
толкование фразы из символов, которую написал Чюмин. Верно
сообразили и вы, Кулагин: вы очень точно подметили
отрицающий дух, сомневающуюся интонацию этой фразы из символов. А
теперь я обращаюсь к вам, Чюмин. Дайте мне то, чего я жду от
вас. Сформулируйте утверждение о том, что при х,
стремящемся к а, функция f(x) стремится к бесконечности. Постарайтесь
вложить в абстрактные символы сам дух стремления к
бесконечности. Почувствуйте этот дух, поймите: стремиться к
бесконечности — это значит не просто превысить один определенный
уровень, но превысить любой из предложенных уровней (я
отчеркиваю на вертикальной оси поперечный штрих и ставлю
рядом VM) — в определенной окрестности, разумеется
(огораживаю окрестность точки а скобками и сбоку поодаль ставлю 36),
но уж зато во всех точках этой окрестности (ставлю под нею Vx).
Соберите в логически стройную цепь написанные мною символы.
Ну вот, наконец-то вы пишете нечто похожее на правду: V М >
0 3 6 > 0 V х((0< \х-а\ < 6) =>> (|/(х)| > М)). Теперь напишите
еще раз определение неограниченности функции f(x) в точке а.
Так,так...УМ>0У<*>0 3 х((0< \х-а\ < 6) А (|/(х)| > М)).
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
127
Что ж, можно и так. Садитесь. Теперь, ребята, сравним между
собой два определения — одно, выражающее неограниченность
функции в точке а, и другое, выражающее стремление
функции к бесконечности при стремлении ее аргумента к а.
Определенные различия налицо. Но есть ли между ними какая-то
связь?
— Если функция стремится к бесконечности, то она и
неограниченна, это тривиально, — бросает Миклашевский.
— Настораживают меня эти ваши «тривиально»,
Миклашевский! И не без основания, как показывает опыт! Давайте-ка
к доске, докажите то, что вы сказали. Итак, пусть функция
стремится к бесконечности при стремлении аргумента к а. Я
взял некоторое произвольное е, подыскал Л — обозначу его в
виду его важности прописной буквой — подыскал Л такое, что
для всех х, удовлетворяющих неравенству 0 < |х — а\ < Л,
выполняется неравенство |/(х)| > М. Это стремление к
бесконечности. А неограниченность заключается в том, что
для некоторого произвольного М... продолжайте,
Миклашевский!
— И для любого произвольного 6 найдется х, который
удовлетворяет неравенству 0< |х — а\ < 6 и для которого
\f(x)\>M.
— Так вот: в силу произвольности S оно может быть либо
больше Л, либо равно Л, либо меньше А.
— Ну и что? Во всех этих случаях Л-окрестность и 6-
окрестность точки а перекрываются. Возьмем в 5-окрестности
точку х, которая принадлежит также и Л-окрестности, а раз
принадлежит, то в силу сказанного вами |/(х)| больше М. Вот,
значит, и нашелся в 5-окрестности а такой х, для которого
1/0*01 > м.
— Отбились. Ну, а верно ли обратное? Следует ли из
неограниченности стремление к бесконечности?
— Вряд ли.
128
ПРЕДЕЛЫ ФУНКЦИЙ
[Гл. 2
— Не подыскать ли опровергающий пример? Ну-ка, ребята,
поищем его все вместе!
Иду между рядами. Прежде всего — к Сынчикову. Как он
справился с моим заданием? Все верно. Он не так уж
безнадежен! Может быть, он просто не может работать у доски,
под взглядами стольких глаз? Теряется, когда мы навязы-
ваем ему свой напористый темп? Оставлю-ка его в покое на
некоторое время, не стану понукать — и не буду терять
надежды, что со временем он втянется в общий ритм. Пусть
пока присматривается к нашему стилю работы, привыкает,
прилаживается, насколько это ему удастся. Работать с ним
буду в основном на месте, а к доске вызывать временами, на
несложные задачи, которые он наверняка сможет решить,
вырабатывая и укрепляя тем самым свою уверенность в будущих
успехах...
Иду дальше: придумал ли кто-нибудь пример функции,
неограниченной в какой-то точке, но в то же время и не
бесконечно большой? У Костюка, Гарина, Стрельцова уже стоит
в тетрадях f(x) = ^sinj. Такое единодушие и такая быстрота
позволяет надеяться, что этот пример естественно вытекает
из наших предыдущих рассуждений и будет понятен многим.
Пишу эту формулу на доске.
— Аргунова, не нарисуете ли график такой функции?
График возникает, обретая верные черты, из
нервозного хаоса штришков — ну прямо как Афродита из морской
пены.
— Перерисуйте теперь набело. Как вы думаете, будет ли эта
функция неограниченной? И в какой точке? Сверьте ее
поведение с определением неограниченности.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
129
— Любое М... любое 6... и х в 5-окрестности... окрестности
нуля... вот этот, например... по модулю больше М. Неограничена
в окрестности нуля.
— А к бесконечности будет она стремиться при х,
стремящемся к нулю?
— Наверное, опять смотреть по определению?
— Разумеется.
— Любое М... найдется 5... и для любого х в 5-окрестности
f(x) по модулю больше М...
И замирает в молчании.
— Так для любого ли х? — легонько подталкиваю ее. Но у
нее уже готов верный ответ:
— Нет, не для любого! Вот f(x) равно нулю, — оборачивается
она ко мне, словно прося подтверждения.
— Что, не подходит под определение? Но тогда надо
попробовать подвести под отрицание определения, ведь так? Постройте
это отрицание. Помните, как это делается? Все кванторы
заменяются...
— Помню, — мягко отвергает она мою помощь. — Найдется
М... для любого 5... сколь угодно малого 6, да? — снова
оборачивается она ко мне.
— Ну, конечно! Продолжайте, все у вас правильно.
— Для любого сколь угодно малого 6 найдется х... f(x) по
модулю меньше М,..
130
ПРЕДЕЛЫ ФУНКЦИЙ
[Гл. 2
Кажется, дело у нее пошло на лад! Но в тот миг, как у
меня в голове пробегает эта мысль, Аргунова останавливается
опять:
— А как искать М?
Нет, радоваться рано: все ее успехи пока
заключаются в том, что она верно читает строчки символов,
сообразительно сверяет их с графиками... Правда, и это уже
кое-что. Но особых похвал это, конечно, не
заслуживает.
— Как искать М? Ребята, в самом деле — как его искать? А,
Меншиков?
— По картинке и искать, по графику.
— В принципе верно, если учесть, что график отражает
сущность функции, ее характер. Да, М определяется характером
функции. Какое же М годится в нашем случае?
— Да любое...
И, не дожидаясь нажима, сам — правда, со всегдашней своей
ленцой:
— Единица.
— Ну, вот, Аргунова, Меншиков нашел ответ на ваш
вопрос: существует М, равное единице и такое...
продолжайте!
— Такое, что для любой, для произвольной 5-окрестности
нуля в ней найдется х такой, что f(x) по модулю меньше
единицы. Лучше всего такой для этого взять х, чтобы f(x) равнялось
нулю.
— А найдется ли такой х в произвольной 5-окрестности нуля?
Вот в такой, например?
— Найдется, — она втискивает в очерченные мной тесные
границы все более сужающиеся и все более размашистые извивы
синусоиды и улыбается своей удаче.
— Итак, Аргунова, вы доказали, что функция f(x) = ^ sin ^
не стремится к бесконечности при х, стремящемся к
нулю. Стирайте все с доски. Мы будем сейчас решать
примеры.
— Подождите! — вскрикивает Мухин. — Как же это так —
не стремится к бесконечности? Но ведь на отдельных участках
все-таки стремится?
— То есть как это — на отдельных участках? Ну-ка,
идите к доске. Покажите-ка нам по графику, на каком
из его участков функция стремится к
бесконечности.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
131
Он тычет пальцем в одну из дуг синусоиды, взметнувшуюся
особенно высоко.
— Нарисуйте-ка её отдельно! Так в какой же точке эта дуга
стремится к бесконечности?
Он сконфуженно молчит.
— Может быть, вам все еще мерещится, что наша функция
стремится к бесконечности, когда её аргумент стремится к
нулю? Но что может означать такое утверждение? Только то,
что функция удовлетворяет строгому определению стремления
к бесконечности при стремлении ее аргумента к нулю. Вы его
помните?
-Да.
— Напишите. Что ж, написали верно. Теперь прочтем его по
складам: для любого М — отметьте его на графике! — найдется
такое 8 — отметьте и его! — такое 5, что для любого х из
5-окрестности точки а, в данном случае нуля, f(x) по модулю
больше М. Для любого х\ А как ведет себя наша функция? Вот
одной своей волной она вышла за рамки, которые я отметил
буквами М\ и —Mi, и тотчас вошла в них обратно, вышла,
приподнялась еще раз за рамки более широкие, сколь угодно
широкие — это-то и спровоцировало вашу неверную мысль! —
но все равно опять ушла к оси абсцисс. Так для любого ли
132
ПРЕДЕЛЫ ФУНКЦИЙ
[Гл. 2
аргумента из вашей 5-окрестности f(x) превышает по
модулю М?
— Нет.
— А раз нет — значит, рушится наша уверенность в её
стремлении к бесконечности. Функция не удовлетворяет
определению этого стремления. А ведь это определение. — основа
нашего четкого представления о стремлении к бесконечности.
Не график, а именно определение. И если график и определение
в конфликте, — доверяйте определению. Поняли? Всё поняли?
Согласны, что эта функция не стремится к бесконечности? Не
будете топать ногой, как Галилей: «А все-таки она бесконечно
большая!»? Ну, тогда стирайте все с доски — пора перейти к
примерам.
— Подождите! — снова умоляет кто-то. Буткус?!
— Мы ведь еще не всё посмотрели про функции и
последовательности, про их аналогии, — направляется он к доске, не
дожидаясь вызова. — Последовательность бывает монотонная и
функция тоже. Есть теорема: если последовательность
монотонная и ограниченная, то она имеет предел. А монотонная
функция? Я взял определение предела функции на языке
последовательностей. Чтобы последовательность f(xn) была монотонная,
надо, чтобы хп тоже была монотонная, тогда хп стремится к а
только с одной стороны. А разве так можно — стремиться только
с одной стороны?
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
133
— Юрий Васильевич, — почти возмущенно перебивает его
Рамзин, вполоборота глянув на него. О, сколько высокомерия
в этом взгляде! Сколько раз я замечал, с какой спесью глядит
он на тех, кого считает ниже себя по способностям! — Юрий
Васильевич, ну разве мы будем тратить время на эту заумь? А
примеры когда же?
Развожу руками:
— Придется нам с вами, Линас, отложить этот разговор
до лучших времен. Они наступят, обещаю. А пока садитесь на
место. Сейчас — примеры. Начнем с простого: найти предел
lim a;2ff J"3 • Чему он равен, Кочин?
— Минус единице, — рапортует он, выходя к доске.
— Как догадались?
— Предел частного равен частному пределов числителя и
знаменателя, если оба предела существуют и предел знаменателя не
равен нулю.
— Верно, есть такая теорема. Каков же здесь предел
знаменателя?
— Минус три.
— Как нашли?
— Предел суммы равен сумме пределов слагаемых, если они
существуют.
— Верно, есть и такая теорема. Чему же равен предел первого
слагаемого в знаменателе, предел х2?
— Нулю.
— Как нашли?
— Есть такая теорема: предел произведения, — чуть
улыбается он, подхватывая мою игру, — равен
произведению пределов сомножителей, если эти пределы
существуют. Можно представить х2 как произведение х • х, а
в нем оба сомножителя стремятся к нулю согласно
условию.
— Отлично. О числителе я уже не спрашиваю — уверен,
что вы расправитесь с ним так же ловко и покажете, что его
предел равен трем. Попробуйте теперь вычислить такой предел
limxl cosi|.
— Сейчас... а! Тут опять есть теорема! Произведение
бесконечно малой величины на ограниченную есть бесконечно малая.
Косинус — функция ограниченная, а х — бесконечно малый,
согласно условию. Значит, все произведение — бесконечно малое,
стремится к нулю.
134
ПРЕДЕЛЫ ФУНКЦИЙ
[Гл. 2
— Хорошо, садитесь. Попробуем теперь вычислить еще один
предел lim *2 Г^+^б • Как будем действовать, Мухин?
— Вычислим предел числителя и знаменателя — предел
числителя — девять минус пятнадцать плюс шесть — равен нулю...
предел знаменателя — девять минус — тоже нулю!
— Вывод?
— Наверное у этой функции нет предела!
— Сверимся с ответом. Вы знаете, автор задачника считает,
что предел у этой функции есть и он равен минус половине. Кто-
то из вас двоих неправ. Давайте, проверим еще раз свои
рассуждения. Насколько я заметил, вы почувствовали что-то неладное,
когда обнаружили, что предел знаменателя нашей дроби равен
нулю. Что же в этом плохого?
— Но ведь по теореме: если предел знаменателя не равен
нулю...
— Вот-вот: если предел знаменателя не равен нулю, мы
вычислим предел частного, применив соответствующую теорему. А
если равен, то что?
— Не вычислим, наверное, потому что теорема не применима.
— Вот в чем тут дело — теорема не применима! Не применим
основанный на ней прием вычисления предела! Только и всего!
А предел может существовать. Правда, его тогда придется
вычислять не привычным приемом, а иначе. Как же?
— Разложи на множители, — негромко подсказывает Гарин.
— Как, Мухин, — прислушаемся к совету знатока? — под-
держиваю дельное соображение. И когда Мухин зачеркивает в
числителе и знаменателе скобку (х — 3), обращаюсь к Чюмину:
— Почему он сделал это? Ведь сокращать можно лишь на
величину, не равную нулю.
— Если х стремится к трем, то он может не равняться трем.
— Неправильно! Как надо сказать, Аргунова?
— Если х стремится к трем, то х не может равняться трем.
— Почему?
— По определению предела функции.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
135
— Совершенно верно! Аргунова права, ребята, — обращаю
внимание остальных на сказанное ею. — Не зря ведь мы писали,
когда давали это определение: 0 < \х—а\ < 6. Если эта модульная
скобка строго больше нуля, то х действительно никак не может
равняться а — в нашем случае трем. Мы снова убеждаемся, как
важно было потребовать в определении предела функции, чтобы
её аргумент не совпадал со своим предельным значением, и тем
самым отделить друг от друга вопрос о существовании
предела функции в некоторой точке и вопрос о существовании самой
функции в этой точке. В только что разобранном примере при х,
стремящемся к трем, предел функции существует, а функция в
этой точке не определена. Какой же у вас получился ответ,
Мухин? Минус одна вторая? Как в задачнике? Хорошо, садитесь.
Вот еще пример: lim ^от^ёг. Как будем действовать, ребята?
Х—>1 Х *X-\-L
Пример не из легких — они это почувствовали сразу.
Растерянное молчание длилось чуть ли не минуту. Потом зазвучало:
«Разделить числитель и знаменатель на х1 ?» — «Толку-то» —
«На множители, может быть?» — «Попробуй!» — «Кажется, хп +1
разлагается...» — «Это хп—1 разлагается!» — «Тяжелый случай...»
— Разумных предложений, я вижу, нет, — резюмирую
стихийную дискуссию. — А из пройденного раньше ничего нам тут не
поможет? Не догадываетесь, на что я намекаю? Помните, как на
прошлом семинаре, в тех случаях, когда та или иная
последовательность не стремилась к нулю, мы вводили бесконечно малые
величины? Не сделать ли нам и сейчас что-нибудь подобное? Как
вы считаете, Лапиков?
— Заменить х на единицу плюс какая-то бесконечно малая?
— О, я вижу, вы освоили плодотворную дебютную идею!
Реализовать ее я попросил бы Кулагина. Хорошо, хорошо... На-
до только отметить, что эти хвосты из степеней у в числителе
136
ПРЕДЕЛЫ ФУНКЦИЙ
[Гл. 2
и знаменателе содержат конечное число слагаемых и потому в
пределе дают нуль. Взаимно уничтожились обе единицы и
минус двойка в числителе и знаменателе, дробь сократилась на у,
который не равен нулю, поскольку к нему стремится. Теперь мы
видим, что в получившейся дроби пределы числителя и
знаменателя уже ненулевые. Применима теорема о пределе частного...
Ответ? Верно, || или ||. Затвердите на будущее, ребята, как
удобно вводить бесконечно малую переменную в подобных
примерах на вычисление пределов. Если х стремится к конечному
числу а, то за новую переменную берем разность х — а; если х
стремится к бесконечности, то... продолжите, Кулагин!
— То за новую переменную нужно взять дробь j.
— Верно. Вот вам пример: lim X~(2x+\)™ ' Решайте!
Хорошо, хорошо... Ответ? Верно, (|)30.
Поглядываю за выкладками на доске, стоя рядом с Сын-
чиковым и наблюдая за его работой. Нет, в самом деле, он не
так уж плох: о многом догадывается сам, на доску смотрит
не часто.
— Еще пример, ребята: Hm^f •
— Что-то новенькое! — сразу замечает Миклашевский.
— Кажется, пахнет замечательным пределом: ^—^
стремится к единице, когда х стремится к нулю, — медленно говорит
Меншиков.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
137
— Точно! Может быть, вы и решите этот пример у доски?
Ответ верный, ^. Садитесь. Кстати, откуда вы знаете про этот
предел?
— Нам его еще в школе давали. И говорили: sinx при х,
стремящемся к нулю, ведет себя, как х.
— В школе вам давали один замечательный предел, а здесь
дадут целых пять сразу. Пишите, я вам продиктую. Доказывать
не буду — это сделает лектор. Запомните, ребята, накрепко эти
пять равенств. Замечательны они тем, что в выражениях под
знаком предела всюду и числитель и знаменатель стремятся к
нулю. Если где-то в ваших вычислениях возникнет подобная
ситуация — вспомните про замечательные пределы и попробуйте
применить один из них. А теперь пусть каждый загадает любое
число от 435 до 594 и скажет мне. Записываю: 455, 478, 522, 542,
577, 594... достаточно! Рамзин, это вы сказали 594? Великолепно!
Так вот, ребята, эти числа — номера тех примеров из
задачника, которые мы сейчас будем решать. Я напишу их условия на
доске.
138 ПРЕДЕЛЫ ФУНКЦИЙ [Гл. 2
I вст. % «»»** I
я+о cncosx
— Оригинально! — колокольно гудит бас Меншикова.
— Смотрите внимательно на эти примеры, ребята. У кого есть
идеи по их решению? — спрашиваю минут пять спустя. — Что
можно сказать, например, про второй, Мухин?
— Он сводится к первому замечательному пределу.
Иду к нему в надежде увидеть у него в тетради готовый
результат... но результата нет, хотя мучительные выкладки
заполнили уже целую страницу.
— Постойте, Мухин! Объясните: что вы сейчас делаете? И
почему вы решили, что этот пример сводится к первому
замечательному пределу?
— Но ведь синус же! И косинус! К чему еще он может
сводиться? Надо только вот этот косинус как-то перевести в синус —
синус минус косинус — есть такая формула? — нет, там ведь
синус от х плюс f ~ к нулю не стремится, нет! А единица плюс
синус? Единица — это sin | — если по формуле суммы, то будет
половина — то есть |-ис тем | сократится — там плюс или
минус?
И сбивчивая его речь — копия его писанины, где прямо
поверх только что написанной формулы жирно пишется другая,
потом все зачеркивается и исправления пишутся над и под
зачеркнутым, потом все густо заштриховывается и в том же духе
разукрашивается следующий кусок чистого листа...
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
139
Нет, надо его наконец отучить от такой манеры!
— Хватит, Мухин! Так вы ничего путного никогда не
добьетесь. Не спешите, я вас никуда не гоню. Обдумайте внимательно
план своих действий. Вы собираетесь получить в этой дроби одни
лишь синусы? Хорошо. Все ли пути к этой цели вы перебрали?
Вы объединяли синус с косинусом, потом синус с единицей. А
если объединить единицу с косинусом?
— Ну, конечно! Единица минус косинус х — это же 2 sin2 |!
Синус и синус! И в знаменателе так! Потрм делим числитель
и знаменатель на х — будет отношение §ijp... Нет, что-то не
sin2 —
то! Во втором слагаемом в числителе будет ведь 2! Такого
предела нет!
— Такого в нашем списке замечательных пределов нет, вы
правы. Но ведь эту дробь можно преобразовать тоже, своим
чередом и на свой лад. Подумайте об этом, обдумайте все до конца,
а уж тогда напишите окончательно и без единой помарки. Если
заметите ошибку — не исправляйте по десять раз одну и ту же
запись! Лучше зачеркните все, положите ручку, подумайте
снова, постарайтесь пояснее представить себе цель своих действий,
проговорить про себя путь к ней и начинайте писать все
заново, да повдумчивее, поаккуратней. И когда будете выходить к
доске, тоже не торопитесь: прежде все продумайте, а потом уж
излагайте. Договорились?
— Договорились, — отвечает Мухин, уверяюще глядя мне в
глаза.
Иду к другим ребятам, заглядываю в их тетради.
— В первом примере, если ввести бесконечно малую,
появляется что-то похожее на последний замечательный предел, —
скрестив руки на груди, по-наполеоновски взирает на доску
Миклашевский.
— Если знаете, как решать, решайте до конца, не сидите
сложа руки! Это, кстати, не такой уж и простой пример!
— А третий пример похож на второй замечательный
предел, — после долгой паузы говорит Кочин.
— Вы его уже решили!
— Нет.
— А что напомнило вам здесь второй замечательный предел?
— Мне просто показалось: основание стремится к единице,
показатель — к бесконечности, — все как в том пределе.
— Может быть, вы попытаетесь сделать это сходство
отчетливее? (Он пружинисто встает и выходит в доске). Во втором
замечательном пределе основание степени представляет собой сумму
140
ПРЕДЕЛЫ ФУНКЦИЙ
[Гл. 2
единицы и бесконечно малой величины. Нельзя ли в нашем
примере преобразовать основание к такому виду? Действуйте! (Он
только мусолит мел в туго сжатых пальцах). Да, обратите
внимание: х стремится здесь к ненулевой величине.
— Ага, значит та замена... ввести бесконечно малую...
у = х — |... В основании теперь дробь 1^|^... Выделить
единицу, вы говорите? Что-то не соображу, как.
— Вычесть и прибавить tg у в числителе, — своим
неоспоримым тоном советует Сутеев. Ну, наконец-то заработал опять!
— Верно, верно, — соглашается Кочин. — Получается
1 + ilfgy, то есть единица плюс бесконечно малая, как во
втором замечательном пределе.
— Но в этом замечательном пределе, — призываю его к
бдительности, — в показателе степени стоит дробь, и в ее
знаменателе — точно та же величина, что прибавляется к единице
в основании. А ведь у нас это не совсем так! Ведь tg2y равен
1Д||/ , а не ilfgy', к тому же у нас перед показателем степени
после замены х на у возник знак минус.
Кочин молчит. Почуяв проблему, отрываются от своих
тетрадей Горт, Костюк, Гарин, Синица...
— Здесь есть над чем подумать любителям головоломок! —
приглашаю их к размышлению, отослав Кочина на место. —
Желательно дать исчерпывающе общую постановку подобных задач
и четкую схему их решения.
Первым рвется в бой Горт:
— Я бы поставил задачу так: есть две функции f(x) и д(х),
бесконечно малые при а;, стремящемся к некоторому а, — и ис-
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
141
следуется предел lim [1 + /(х)]»(х). Я преобразую выражение под
х—>а
1 /(х)
знаком предела к такому виду: [[1 + /(ж)]'<х>]»<х> тогда
основание будет стремиться к числу е, и результат будет зависеть от
того, к чему стремится дробь Ц^1\ если к плюс бесконечности,
то туда же будет стремиться и все выражение; если к минус
бесконечности, то все выражение даст в пределе нуль; если к
конечному числу, то ответом будет е в степени, равной этому
числу. Если таким способом решить наш пример, то ответ
получается е-1.
Он показывает свои выкладки на доске, а я тем временем
спрашиваю у ребят:
— Понятно? Не трудно ли? Как, Миклашевский?
— Нормально. Я трудные задачи люблю.
— Сейчас посмотрим, как вы их любите. Помнится, на
прошлом семинаре мы с вами пришли к интересному и не слишком
,. i lim —
очевидному равенству limp* = р*-"*", и я попросил вас дока-
п—к»
зать его дома. Вы сделали это?
— Нет, — слегка краснеет он.
— Ненадежная, видать, у вас любовь! Так — шаляй-валяй... А
ведь сделай вы это — и сейчас легко заметили бы промах Горта.
— Что, я где-то ошибся? — мечется он встревоженным
взглядом по своим записям на доске.
— Давайте разберемся, — поворачиваюсь к ним и я. — Во-
первых, почему вы полагаете, что степень [1 + /(х)]^ будет
стремиться к числу е?
— Это можно доказать — если исходить из определения
предела функции на языке последовательностей: взять
произвольную последовательность хп, стремящуюся к а, тогда
последовательность г} ч будет стремиться к бесконечности, обозначим ее
qn — это как на прошлом семинаре: мы тогда разбирали выра-
142
ПРЕДЕЛЫ ФУНКЦИЙ
[Гл. 2
жение (1 + ~)9п и доказывали, что оно стремится к е, когда qn
бесконечно возрастает.
— Мы разбирали случай, когда qn стремится к плюс
бесконечности, — уточняю его ссылку. — А общий случай стремления
к бесконечности я просил вас разобрать дома. Вы это сделали,
Горт?
— Конечно! Все получилось.
— Что ж, поверим вам на слово. Но это еще не все мои
придирки к вам. Давайте заменим степень [1 + /(х)]^Т на функцию
р(х), и пусть эта функция при х, стремящемся к а, оставаясь
положительной, стремится к некоторому положительному
числу Р; тогда Р = е войдет в наши рассуждения как частный
случай. Дробь Д2* обозначим через q(x), и пусть она стремится
к числу Q. Вы уверены, что при этом выражение p(x)q^
стремится к Р^?
— Это, конечно, надо доказать, — розовеет теперь уже Горт. —
Сейчас, я докажу! Минутку! Все будет тогда обосновано!
Наверное, — торопливо гадает он, — это будет так, если функции р(х)
и q(x) непрерывны. Тогда предел р(х) равен р(а), а предел q(x)
равен q(a)...
— Тут, наверное, надо как-то свести все дело к теоремам
о непрерывности, — раздумывает вслух Стрельцов. — У нас
были теоремы о непрерывности суммы, произведения,
частного непрерывных функций... еще была теорема о том, что
суперпозиция непрерывных... Ой нет! — тут же машет он
рукой. — Что это я? Тут ведь совсем другое! Функция в степени
функция!
— По-моему, надо использовать стандартный прием, —
решительно шагает к доске Костюк, — представить то, о чем мы
рассуждаем, в каком-то другом виде — например, так: p(x)q^ =
= eq(x)lnp(x\ У нас р{х) стремится к р(а), значит, 1пр(х)
стремится к 1пр(а).
— Чем вы это обоснуете?
— Теоремой о том, что суперпозиция непрерывных
функций есть функция непрерывная. Функция f{x) непрерывна по
нашему предположению, про логарифм лектор говорил, что он
также непрерывен в каждой точке своей области существования.
Функция q(x) lnp(x) непрерывна как произведение
непрерывных функций. У нас это произведение играет роль показателя
степени, а показательная функция непрерывна при любом
значении показателя, об этом лектор тоже говорил. Следова-
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
143
тельно, функция eq^lnp^ непрерывна как суперпозиция двух
непрерывных — показательной и q(x) lnp(x) — и в пределе даст
eq(a)\nP(a)^ TQ естъ р(а)я(а) Короче говоря, l\mp(x)qW = p{a)q^a\
х—+а
Значит, — с горделивым лукавством улыбается он мне,
направляясь обратно, — все-таки есть такая теорема: степень,
образованная из двух непрерывных функций, непрерывна:
конечно, если основание степени р(х) — функция
положительная.
— Что вы скажете на это? — оборачиваюсь к Миклашевскому.
— Скажу, что все ясно: lim р* = р«-«>« = р° = 1. Доказать
п—юо
можно точно так же.
В спорах с Костюком Горт не любит оставлять за соперником
последнее слово:
— р(х) положительна? Можно потребовать меньшее: что бы
она была положительна только в самой точке а — ее
положительность в некоторой окрестности точки а будет следовать из
непрерывности р(х).
— Как это доказать?
— Очень просто. Сначала напишем условие непрерывности:
для любого положительного е найдется такая ^-окрестность
точки а, что для всех х из этой окрестности р(х) будет отличаться от
р(а) не более, чем на е, то естьр(а)—е < р(х) < р{а)+е. Положим
е = 12~'i это можно сделать, поскольку р(а) положительна. Тогда
из предыдущего неравенства вытекает: р{х) > р{а) —е= 4р > О
для всех х из ^-окрестности точки а.
— Все верно. Можно сформулировать более общую
теорему: функция, непрерывная в какой-то точке и не обращающаяся
там в нуль, сохраняет свой знак в некоторой окрестности этой
точки.
Не успел я закончить, как Костюк вновь порывается к
доске:
— Я тут подумал, что не нужно требовать от р{х) и q(x),
чтобы они были непрерывными — пусть имеют предел в точке а и
все. Рассмотрим выражение p(x)q^ и снова преобразуем его к
виду е?(я)1пр(я) Если р(х) стремится к Р, то 1пр(х) стремится к
In P по непрерывности логарифма. Про функцию р(х) и число
Р говорилось, что они положительны, так что логарифм от них
имеет смысл. Впрочем, — торопливо добавляет он, замечая, что
Горт вскинул было руку, прося слова, — можно доказать, что
если предел функции в какой-то точке а положителен, то в точ-
144
ПРЕДЕЛЫ ФУНКЦИЙ
[Гл. 2
ках, достаточно близких к а, функция тоже положительна, —
не вдаваясь в пояснения, он лишь указывает беглым жестом
на запись доказательства, только что проведенного Гортом. —
Предел q(x) мы обозначили через Q; тогда предел
произведения q(x) lnp(x) равен QlnP по теореме о пределе произведения
функций; eq^Xnp^ в силу непрерывности показательной
функции будет стремиться к е^1пР, а это не что иное как Р®. Что и
требовалось доказать.
— Очень хорошо. Разберемся с остальными примерами,
ребята.
Оглядываю аудиторию и перехватываю просительный взгляд
Кочина: ему хочется о чем-то спросить меня.
— Скажите, а в пятом замечательном пределе показатель
степени любой? Не обязательно целый? — почти шепчет он, когда
я сажусь рядом.
— Не обязательно, — так же тихо отвечаю ему. Встаю,
чтобы понаблюдать за теми, за кого особенно беспокоюсь.
Интересно, как там дела у Мухина? Подхожу к нему. Он
заканчивает решение четвертого примера. Правильные
вычисления, верный ответ. Подействовали мои наставления?
Или пример настолько прост и легок, что на пути к ответу
каждый шаг однозначно определяется результатом
предыдущего?
Склонившись над ним, говорю вполголоса, с усмешкой:
— Как мало недостает вам до уверенного успеха: аккуратного
почерка! А второе, что вам здорово помогло, это я говорю уже
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
145
серьезно, — спокойные, подробные, без вашей прежней
торопливости, выкладки. Покажите их на доске. Всегда бы так! Спасибо,
садитесь.
Иду дальше вдоль столов. Оставшиеся примеры так или
иначе, проще или сложнее, решаются применением замечательных
пределов. На доске демонстрирую красивые решения Гарина и
Стрельцова.
146
ПРЕДЕЛЫ ФУНКЦИЙ
[Гл. 2
— А ведь мы брали эти примеры наугад, ребята, Можно
подумать, что и для всего раздела задачника, откуда мы их брали,
пригоден все тот же подход: определить, к какому типу
относится пример, преобразовать его, чтобы был применим стандартный
прием решения, и, наконец, провести этот прием. Это очень
важный момент в нашей работе, учтите и усвойте его. Конечно,
восхищения и уважения заслуживает тот исследователь, который
создает новые методы для решения новых задач. Но не
меньшего заслуживает тот, кто в неизведанном сумел разглядеть черты
изученного, увидел, что новую задачу молено свести к старой,
уже решенной, заметил, что к новой задаче применимы старые
испытанные методы, сумел найти такое преобразование, после
которого сложная задача становится элементарной.
— Но ведь, — философствует Стрельцов, — мы никогда не
сумеем выработать полный набор методов для решения всех задач,
которые встретятся в будущем.
— Совершенно верно. Даже в том разделе задачника, откуда
я задавал вам примеры, попадаются такие экземпляры, для
решения которых недостаточно замечательных пределов, теорем о
пределе суммы, произведения, частного и о том, что
произведение бесконечно малой функции на ограниченную есть бесконечно
малая. Вы, Стрельцов, я вижу, полагаете, будто решили все, что
я задал? Вас и всех таких же быстрых я попросил бы
просмотреть в задачнике весь цикл примеров, над которыми мы
работаем, и найти среди них такие, которые не поддаются стандартным
методам.
Это будет неплохая тренировка для их математического
чутья. Впрочем, не лишне пройтись по аудитории —
проверить, всё ли из заданного сделали те, кто берется за поиск
нестандартных примеров.
— Рамзин, у вас, кажется, есть кое-какие недоделки. Не
согласны? Тогда, пожалуйста, к доске. Перепишите на ней из своей
тетради решение примера № 594. Ребята, присмотритесь вот к
этому переходу: судя по нему, Рамзин считает, что у/гр = у. Так
ли это, Лапиков?
— Нет, у/у1 = \у\.
— Точно! То есть результат извлечения корня зависит от
знака у. И ответ у примера будет двояким: один для х,
стремящегося к плюс бесконечности, другой — для х, стремящегося к минус
бесконечности. А когда мы переходим от х к у, то у оказывается
бесконечно малым и все будет зависеть от того, с какой
стороны у стремится к нулю — с положительной или отрицательной.
Ю. В. Пухначев] СЕМЬ СЕМИНАРОВ 147
Кстати, для различения этих случаев в математике есть
специальные обозначения: у —> +0 и у —> —0. И когда у функции
ищутся пределы при таком стремлении аргумента к предельной
точке, говорят, что это односторонние пределы — соответственно
предел справа и предел слева. Из решения Рамзина ясно, что он
получил ответ для случая у —> +0, то есть для х —► +оо.
Нетрудно видеть, что для случая х —> — оо, то есть у —► — 0, ответ просто
сменит знак и будет равен минус единице. А теперь вспомните,
Рамзин, как вы осадили Буткуса, когда он хотел заняться
исследованием таких явлений. Вы считали, что все это заумь, а
сейчас выясняется, что знание этой «зауми» уберегло бы вас от
ошибки. Так что мы с вами, Линас, — обращаюсь к Буткусу, —
можем теперь продолжить разговор о функциях, аргумент
которых стремится к предельной точке с какой-то одной стороны.
И на будущее я посоветовал бы вам не отказываться от
исследования интересных вам задач, как бы от них вас ни отваживали
неодобрение знатоков, текущие дела, неотложные поручения и
прочее. Разумеется, к мнению знающих людей следует
прислушиваться, порученные вам дела должны быть сделаны, но
старайтесь выкраивать время и на проблемы, которые интересны
вам сами по себе.
— А я так и думаю, — улыбается он, довольный. — Я
даже теорему придумал про эти... про односторонние
пределы.
— Интересно! А обязательные примеры решили?
- Решил.
— Хорошо. Так какую же теорему вы доказали?
— Если функция монотонна на отрезке, то она обязательно
имеет пределы на его концах.
148
ПРЕДЕЛЫ ФУНКЦИЙ
[Гл. 2
— Вот он, характер исследователя! Вы только подумайте,
ребята: мы с вами уже столько времени толковали о наших
примерах — а Линас под весь этот шум сумел, не отвлекаясь от
своих мыслей, придти к хорошему результату. «Как вы пришли
к своим открытиям?» — спросили однажды у Ньютона.
«Постоянно размышляя о них», — ответил Ньютон, директор
Монетного двора, член палаты лордов. Кулон находил время для
физических исследований, служа офицером во французской
армии, Ломоносов урывками занимался химией, состоя
придворным одописцем... Но довольно исторических примеров. Давайте-
ка докажем утверждение, которое сформулировал Буткус. Оно
совершенно справедливо: если f(x) определена и монотонна на
отрезке [а, Ь], то существует односторонние пределы lim f(x) и
х—►а+О
Ит /(х), — пишу на доске. — Для простоты докажем существо-
х—►Ь—О
вание лишь второго предела, функцию будем считать монотонно
возрастающей.
— Я как раз такой случай и рассматривал! — радуется
совпадению Буткус.
— И доказали?
-Да.
— Но я просил бы вас помолчать об этом. Я хочу, чтобы
ребята провели доказательство сами, без наших с вами подсказок.
Мне хотелось бы только напомнить те приемы решения задач,
о которых я говорил на прошлом семинаре. Поиск такого
решения, образно говоря, заключается в том, что мы стараемся
заполнить брешь между условием задачи и её заключением, вставкой
каких-то недостающих звеньев пытаемся сблизить условие и
заключение. И в этом нам помогают два основных приема. Первый:
стараться представить каждую деталь рассуждения во всех
возможных её вариантах. Второй: пытаться достраивать каждую
деталь, каждую совокупность деталей до встречавшихся ранее
завершенных логических комплексов, где эти детали
присутствуют поодиночке или участвуют в таких же сочетаниях, что и в
получившихся у нас совокупностях. Чтобы обеспечить себя
возможно более широким набором таких деталей, поиск следует
начинать с того...
Я обрываю свою речь и выжидательно гляжу на них.
Кажется я говорил с достаточным энтузиазмом, чтобы рассчитывать,
что они продолжат мое рассуждение, увлеченные им.
— С того, — чеканит Сутеев, — что мы внимательно
анализируем и условие, и заключение.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
149
— Разворачиваем, — продолжает Синица, — запись
условия и заключения. Что это значит, -- риторически вопрошает
она, — что функция монотонно возрастает? Что это значит, что
существует какой-то предел функции при х, стремящемся к Ь
слева?
— В самом деле — что? — подстраиваюсь под ее тон. — Пусть
кто-нибудь продиктует мне это!
И выжидающе гляжу на Лапикова:
— Егор, я вас спрашиваю!
Не быстро, но почти без ошибок дает он обе нужных
формулировки.
I Лапиков I
Vx« i [а,в] Voit [0.6] ((x, <*,) =>(f Cx,)< f (хж)))
((0<e-x<<S)=»(|fCx)-B|<£))
((0<e-3c<6)=>(B-6^f(3c)<S^6))
— Неплохо! — хвалю его. — Теперь я вижу, что вы
действительно выполняете наш уговор, хорошо заучиваете определения
основных математических понятий.
Аккуратно пишу на доске продиктованное Лапиковым.
Напомнив, что заключительное неравенство может быть выражено
иначе, пишу его также без модульных скобок. И тут же —
плавный голос Рамзина (видно, не держит на меня зла за то, что
дифирамбом в адрес Буткуса я косвенно осудил его слова про
«:*аумь»):
— Теперь, чтобы сблизить условие и заключение, надо
рассмотреть все то, что непосредственно следует из условия, и то,
in чего могло бы непосредственно следовать заключение.
— Верно! Это будут простейшие логические комплексы,
построенные на основе данного нам в формулировке задачи и
образованные с помощью причинно-следственных связей.
— Молено показать, — делает следующий шаг Костюк, — что
функция на всем отрезке ограничена. Она ведь монотонно
возрастает и, значит, не может быть больше f(b).
— А из ограниченности, — не отстает от соперника Горт, —
следует существование точной верхней грани.
150
ПРЕДЕЛЫ ФУНКЦИЙ
(Гл. 2
Пауза. Кто двинет дальше начатое доказательство?
Миклашевский:
— Надо бы расписать определение точной верхней грани.
— Продиктуете?
— Во-первых, для любого х наша f{x) меньше Q\ я предлагаю
обозначить буквой Q точную верхнюю грань.
— Вы говорили о своей любви к трудным задачам,
Миклашевский, а не знаете элементарных определений. А ведь это
краеугольные камни нашего рассуждения! Чтобы оно не
развалилось, пусть кто-нибудь сейчас же поправит Миклашевского!
— Не строго меньше Q, а меньше или равно, — поучающим
тоном замечает Меншиков. Киваю ему с выражением похвалы
во взгляде, чуточку даже преувеличенным. Мне кажется, что
в подобных его репликах сквозь кору застарелой лени
пробиваются искры какой-то активности, пусть еле тлеющие, но все же
не угасшие в нем, способные, на мой взгляд, сыграть роль
своеобразного запала. Подчеркнутыми похвалами по адресу любой
его верной поправки, любой разумной идеи, любой удачи в
решении задач я постараюсь раздуть эти искры, разжечь в нем
честолюбивое желание успеха — авось со временем оно растопит
его заскорузлую лень, а само перегорит в устойчивое
трудолюбие. А коли он затоскует о прежнем ленивом уюте, вздумает на
попятную — верну его на путь кнутом требовательности.
— А х откуда? — атакует Миклашевского новым вопросам
Кулагин. — Из какого множества?
— Разве не ясно из какого? Из отрезка [а, Ь], конечно, —
пожимает плечами Миклашевский.
— Внимательно анализируем условие и заключение — так
ведь мы говорили в самом начале, Миклашевский? Разве вы
не видите этого соотношения?— указываю на неравенство
0 < Ь — х < 6. — Разве не чувствуете, о чем оно говорит?
Пауза. И голос широко улыбающегося (догадался!) Мухина:
— Говорит, что х не доходит до Ь, не может равняться — это
же значит, что х строго меньше Ь. Надо, если искать верхнюю
грань — точную верхнюю грань — надо брать х из интервала.
Миклашевский хлопочет с реабилитации:
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
151
— Вы не дали мне договорить определение точной верхней
грани, второй пункт: для любого Q', меньшего Q, найдется х
такой, что f(x) > Qr.
По моей просьбе он пишет это на доске.
Снова томительная пауза.
— Второй пункт лучше написать по-другому, — не
выдерживает Буткус.
— Стоп! Я же просил вас молчать! — обрываю его и перевожу
взгляд на Миклашевского, все еще стоящего у доски: вспомнит
ли он другой вариант написанного? Вспомнил:
— Можно написать так: для любого положительного е
найдется х такой, что f{x) > Q — е.
Стирает и пишет заново. И тотчас голос Кочина:
— Второй пункт очень похож на то, что требуется доказать!
— Решающая догадка! — не выдерживаю на сей раз и я. —
Теперь вы поняли, ребята, как помогает умение выразить каждую
деталь рассуждения во всех возможных вариантах?
Миклашевский, садитесь. Кочин, хотите к доске?
Пример посложнее, чем он решал раньше, — я хочу оценить
пределы его возможностей.
Он поднимается, как в атаку:
— Последнее неравенство в заключении теоремы я бы
переписал по-другому: Q — е < f(x) < Q + е
— Постой, постой! Когда мы fix) сверху оценивали, у нас
было два неравенства: f(x) < f(b) и f(x) < Q. Ты что, уверен,
что пределом функции будет именно Q? — вонзается в Кочина
суровый взгляд Горта.
— Мне так кажется, — Кочин в смущении опускает мел.
Спешу ему на помощь:
— Догадка — хорошая вещь. Но что, если она не оправдается?
152
ПРЕДЕЛЫ ФУНКЦИЙ
[Гл. 2
— Тогда пойдем другим путем! — вновь вскидывает он мел. —
Но ведь у нас все сходится как раз к тому, что Q — предел f(x)
в точке 6. Осталось совсем немного!
— Ну-ну! — продолжаю накачивать его. —Давайте
сосредоточимся перед последним прыжком. Сначала присмотримся к
уже написанному. Нет ли там ошибок? Пробелов? Вот,
например, неравенство f(x)<Q + e. Откуда оно взялось?
— Оно следует из неравенства f{x) < Q.
— Что еще затрудняет вас?
— То, что в определении точной верхней грани, во втором
пункте стоит «найдется #»,а в заключении теоремы — «любое х».
— Не все! Не все! — настойчиво побуждаю его к вниманию.
— Ну да, еще в заключении есть 6...
— Что это за 81 Откуда её взять?
— Используй монотонность! — не удерживается от подсказки
Гарин. Но Кочин, кажется, умолк надолго. Нет, я не дам ему
покоя!
— Если не хватает догадки, пусть поможет рисунок.
Проиллюстрируйте им то, что вы сказали, глядите на него
внимательно, а при этом перебирайте вновь и вновь данные условия и
заключения теоремы — все ли из них вы использовали?
Между точками х и 6, которые он нанес на горизонтальную
ось графика, он отмечает еще одну, медленно тянет вверх от нее
пунктир и обрывает его на уровне между f(x) и /(b).
— Почему значение функции лежит в этом промежутке?
— Потому что функция монотонна.
Он замолкает опять.
— Не останавливайтесь на смутной мысли! Придавайте ей
максимальную четкость! Аргумент, который вы взяли между х
и 6 — произвольный? — напираю я. Но ему уже не нужна помощь,
хотя его слова еще нечетки и сбивчивы.
— Я все понял... Когда мы нашли это х, для которого
f(x) > Q — е... Подождите, я лучше обозначу его особо, через
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
153
х*... Когда мы нашли это х*... напишем для него /(х*) > Q — е...
то для всех х, которые больше х*, в силу монотонности тем
более будет /(х) > Q — £... а надо брать такие х, которые меньше
6... и тогда /(х) < Q < Q + е... все! Пусть х* будет той самой 6...
нет, S = 6 — х*, вот так... все!
— А коли все, то аккуратно повторите свое рассуждение с
самого начала.
И он, выждав время, чтобы успокоиться от напряжения
открытия, повторяет не без заминок доказательство теоремы, то
записывая на доске возникающие при этом соотношения, то
просто проговаривая их.
— Пишите полностью формульный протокол вашего
доказательства, Дима, последовательно и логично! Представьте, что вы
пишите книгу, где приводите это доказательство.
— Книгу! — с недоверчивой усмешкой повторяет он. — До
этого мне еще далеко.
— Не так далеко, Дима, как вам кажется. Через пять лет
вы должны выйти из этого вуза классным специалистом. Самое
главное для этого у вас уже есть — ваша математическая
одаренность. Не достает пока еще сноровки да знания некоторых
приемов, которые помогут вам быстрее достигать результатов и яснее
их излагать. За этим вы и ходите на занятия. Посмотрите, как
ваше доказательство написал бы я. Обратите внимание на цифры
в скобах, которыми я стану помечать формулы, на пояснения
логических переходов. Смотрите — я верно передаю ваши мысли?
— Верно.
— Но несколько доходчивее, правда? Вот теперь вы можете
садиться, Кочин. Теорема Буткуса доказана вами полностью:
154
ПРЕДЕЛЫ ФУНКЦИЙ
[Гл. 2
функция, определенная и монотонно возрастающая на
отрезке [а, 6], имеет в его правом конце односторонний предел,
равный точной верхней грани значений функции на
интервале (а, 6).
— Теорема Буткуса? — переспрашивает Чюмин. — Что, был
такой математик? — и с почтительным удивлением косится на
Линаса: уж не потомок ли это какого-то светила науки?
— Не был. Но будет, — отвечаю с доброй улыбкой, — если
Линас и дальше станет работать в том же духе, что сегодня...
Задержимся, ребята, еще немного на понятии одностороннего
предела. Мы столкнулись с ним, разбирая задачу, которую
не дорешал Рамзин. Она представила нам любопытный
случай, когда функция слева стремится к одному пределу, а
справа к другому. Я думаю, что с учетом такой возможности
мы можем дать более детальное, чем давали прежде,
определение непрерывности функции в точке. Не попробуете ли,
Стрельцов?
— Наверное, надо определить так: функция называется
непрерывной в точке, если она определена в этой точке, имеет в
ней предел справа и предел слева и все три величины — то есть
её значение в точке и оба предела попарно равны. Да,
наверное, так.
— А что значит, что функция не непрерывна в точке?
— Это значит: либо функция не определена в этой точке,
либо не существует хотя бы один из односторонних
пределов, либо не выполняется одно из равенств, про которые я
сказал.
Фразы его обдуманы и ясны, голос — негромкий и ровный.
По его манере говорить и держаться чувствуется, что он из
хорошей семьи, где считалось чем-то само собой разумеющимся
получать высокие оценки на уроках, закончить школу с
хорошим аттестатом, поступить в престижный вуз. У него неплохие
способности, и мои задачи он решает как бы в полсилы. А не
получается — поднапряжется чуть больше и все-таки решит.
Словом, за него можно не волноваться. Более того, можно смело
вызывать его к доске для показательного решения довольно
трудных задач, для безошибочного воспроизведения определений и
формулировок.
— Верно, — соглашаюсь с ним. — Замечу, что хороший
пример, когда левый и правый пределы не совпадают, дает
поведение функции у — sgnx в нуле. Говорят еще, что функция
непрерывна слева в некоторой точке а, если ее предел слева и
Ю. В. Пухначев] СЕМЬ СЕМИНАРОВ 155
ее значение в этой точке совпадают. Аналогично определяется
непрерывность справа. Эти понятия помогают дать
определение функции, непрерывной на некотором отрезке [а, 6]: функция
называется таковой, если она непрерывна в любой внутренней
точке отрезка, а в его концах а и b непрерывна
соответственно справа и слева. Но двинемся дальше, — обращаюсь уже ко
всей аудитории. — Или нет, вернемся на момент чуточку
назад. Помните, я просил вас поискать в задачнике нестандартные
примеры...
— Я нашел три, — отзывается Костюк.
— Покажите нам хотя бы один.
Его фразы кратки и вески:
— Сначала lim f^, где а больше единицы, а п натуральное...
х—►+ооа
Я его разобрал на языке последовательностей. Взял
произвольную бесконечно большую последовательность pk-> подставил ее
вместо х: ^^г- Это почти то же самое, что вы просили
посмотреть дома: ^-, где s > 0,р > 1. Вы просили доказать, что
такая дробь стремится к нулю. Это в самом деле так, я доказал.
В силу того, что последовательность pk произвольна, по
определению предела функции на языке последовательностей
утверждаем, что lim fr = 0.
х—►+оо°
— Хорошо. Может быть, продолжит кто-то другой? Вам
слово, Синица.
Вижу, что она так и ждет вызова.
— Тут вот есть такой предел: lim ^г, причем р > 0, — тара-
х—»+оо х
торит она. — Если сделать замену 1пх = у, то он сразу сводится
к предыдущему: lim т^г- И с пределом lim xp \пх так же по-
х—►+<хЛе ) х—>+0
ступаем, только замена здесь будет другая, 1пх = ^, а ответ
такой же, нуль.
156
ПРЕДЕЛЫ ФУНКЦИЙ
[Гл. 2
— Понятно? — оглядываю аудиторию. Многоголосое «да!»
звучит в ответ.
— Тише, ребята! Я повторю свой вопрос в духе нашего
прежнего уговора: те, кто все понял, молчат, а кто не понял — пусть
скажет об этом.
Напоминание о старом уговоре не подействовало: аудитория
безмолствует. Видимо, те, кто что-то не понял, стесняются в этом
признаться. Молчит Аргунова. Молчит Сынчиков, напряженно
всматриваясь в аккуратные, но предельно краткие пометки,
сделанные на доске Синицей.
Отослав ее на место, обстоятельно повторяю сказанное ею.
— Теперь, ребята, запишите в свои тетради обобщенные
варианты разобранных нами пределов: lim Щ^ = 0 и lim xp In9 x:
ж->+оо х х-*+0
здесь q > 0. Дома попробуйте доказать эти равенства и
хорошенько запомните их. Они еще пригодятся нам. Кто,
кстати, хотел бы потренировать свою память? Вы, Мухин?
Идите к доске. Напишите на ней быстренько все пять
замечательных пределов. Хорошо, хорошо... Четыре уже есть. А
пятый?
— Забыл. Помню только, что там в числителе был логарифм.
— Вспоминайте дальше, да не забывайте про хороших
помощников в таких затруднениях, про аналогии. Какая общая
особенность есть у функций, которые стоят в числителях написанных
вами замечательных пределов? Тех, которые представляют
собой дроби?
— Сейчас — sin х — потом ах — 1 и дальше — эти
функции — а х ведь стремится к нулю? — да? — они все стремятся к
нулю.
— Это вам ничего не подсказывает? Вспомните про других
своих помощников, про графики. Нарисуйте графики функций,
которые стоят в числителях. Смотрите: все эти графики про-
Ю. В. Пухначев] СЕМЬ СЕМИНАРОВ 157
ходят через начало координат. Что можно сделать с графиком
логарифма, чтобы он проходил через начало координат?
— Надо как-то его сдвинуть — на единицу — то ли вычесть
ее из х — то ли прибавить...
— Как же выбрать верный их двух возможных, на ваш
взгляд, вариантов? Напишите их на доске.
— Вот: 1п(х - 1) и 1п(х + 1).
— Какой же из двух этих логарифмов обратится в нуль при
нулевом х? Такой вопрос, Мухин, вы могли бы поставить перед
собой сами, без моей помощи, и сами ответить на него.
Насупившись, он стирает кривую логарифма, рисует её
заново, сдвинув влево, рядом пишет 1п(1 + х), подчеркивает чертой
158
ПРЕДЕЛЫ ФУНКЦИЙ
[Гл. 2
дроби и под нею быстро пишет х, слева от дроби — символ
предела, справа через знак равенства — единицу.
— Почему вы разделили 1п(1 + х) на х?
— Так ведь из графика видно, что этот логарифм в нуле ведет
себя как х.
— Вот этой фразы я от вас и дожидался. Как вы помните,
ребята, оборот «ведет себя, как х» произносил Меншиков, и, я
вижу, эти слова запали вам в память. Но я очень не хотел бы,
чтобы вы бросались ходячими словечками, не очень глубоко
понимая, что за ними стоит. Давайте поэтому разберемся, что это
значит — ведет себя, как х? Меншиков говорил это по
отношению к синусу, более знакомому вам, чем логарифм. Так что к
синусу и вернемся. Посмотрите на его график, Мухин, да
повнимательнее, и поясните с его помощью утверждение: «в начале
координат синус ведет себя, как х».
— Если нарисовать прямую у = х — вот так — ах пусть в
окрестности нуля — точнее, пусть стремится к нулю — то
синусоида при таких х все больше совпадает с этой прямой.
— Все больше совпадает? Как это понимать? Это, знаете ли,
напоминает фразу Марка Твена: «Слухи о моей смерти сильно
преувеличены». Нельзя быть более или менее мертвым — можно
быть либо мертвым либо живым. И точно так же нельзя
совпадать более или менее — можно либо совпадать, либо не
совпадать. Так совпадает ли синусоида с прямой у = х в окрестности
начала координат?
— Нет. У них расстояние — между ними расстояние
уменьшается — до нуля уменьшается — когда х стремится к
нулю.
— Не спорю. Но посмотрите: я провожу на том же
графике прямую у = |. расстояние между ней и синусоидой тоже
стремится к нулю по мере приближения к началу коорди-
Ю. В. Пухначев] СЕМЬ СЕМИНАРОВ 159
нат. Так почему же мы не говорим, что синусоида ведет себя
как |?
— Потому что прямая у = х касательная, а прямая у = |
секущая, она пересекает синусоиду.
— Боюсь, что вы просто заменили одно слово другим, а суть
не прояснили. Думайте над сутью и не забывайте про вашу
основную цель — объяснить слова «ведет себя, как х». Они
вырвались у вас, Мухин, по поводу замечательного предела с участием
логарифма. Но ведь синус, над которым мы бьемся сейчас,
тоже участвует в одном из замечательных пределов. Не привлечь
ли нам к делу этот предел? Перепишите-ка его рядом с
графиком, который мы разбираем: lim51^ = 1. Узловой пункт наших
недоразумений — расстояние между синусоидой и прямой у — х.
Не поможет ли осмыслить это расстояние переписанный вами
замечательный предел?
— Перенеси единицу в левую часть и внеси под знак
предела! — негромко командует Кулагин, и Мухин машинально
исполняет команду. Спрашиваю его:
— А вы уверены, что число можно вносить под знак предела?
Как вы понимаете выражение «предел единицы»? Не знаете? А
как понимаете это выражение вы, Кулагин?
— Если единица под знаком предела, то она понимается как
постоянная функция — такая, которая везде равна единице.
— Ну да, — сразу перевожу его слова для Мухина на
графический язык. — Предел функции, тождественно равной числу,
есть это же самое число: liml = 1. Это и означает, что мы
внесло
ли единицу под знак предела. Все верно. Продолжайте, Мухин.
Вероятно, обдумав свой шаг во время нашего разговора с
Кулагиным, он делает последнее решающее преобразование
полученного выражения к виду \[msm^-x = о. Оборачивается
ко мне:
— Вот в числителе расстояние между синусоидой и той
прямой, у = х. Знаменатель стремится к нулю — значит,
160
ПРЕДЕЛЫ ФУНКЦИЙ
[Гл. 2
и числитель к нулю — иначе вся дробь в пределе нуля не
даст.
— Расстояние стремится к нулю? И только? Разве мы не
знали этого раньше? И разве этот ваш вывод как-то отличил прямую
у = х от прямой у = |, о которой тоже известно, что расстояние
между нею и синусоидой стремится к нулю? Отправляйтесь к
своему столу, Мухин, и внимательно смотрите, как дела на
доске пойдут дальше. Ребята, кто поможет продвинуться вперед?
Руки вскидывают Горт, Костюк, Синица...
Гарин, не отрывая авторучки от тетради, лишь роняет:
— Относительное расхождение...
— Ну-ну! — тотчас настраиваюсь на его мысль. — Давайте-ка
к доске, Миша!
— Вот, — разжевывает он график Мухина, — расстояние от
прямой у = х до синусоиды, абсолютное расхождение между
ними: sin х — х. Вот расстояние от прямой у = | до той же
синусоиды: sin х — |. И то и другое расстояние стремятся к нулю.
Но предел, который получил Мухин, говорит не об абсолютном
расхождении между прямой и синусоидой, а об относительном.
— Ребята, — радуюсь удачному повороту беседы, — заметьте
себе это слово! Относительное расхождение!
И, чтобы было понятнее Мухину и иже с ним, комментирую
соображения Гарина на графике:
— Вот оно это относительное расхождение — отношение
этого маленького зазора между прямой и синусоидой (размашистой
вертикалью секу обе линии и горизонтальную ось, отступив
подальше от начала координат, и отмечаю стрелкой этот зазор)
ко всей вертикальной стороне этого прямоугольного
треугольника (отмечаю символом х оба его катета и рядом приписываю
sms-д^. Зазор, как видите, составляет почти четверть от верти-
кальной стороны треугольника, от х. Но приблизимся к началу
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
161
координат, уменьшим х (провожу вертикаль вдвое ближе к
точке 0) — зазор уменьшился тоже и даже сильнее: он составляет,
как видите, уже менее десятой доли х. Приблизимся к началу
еще — зазор уже совсем незаметен по сравнению с х, и это
воочию убеждает нас, что относительное расхождение между
синусоидой и прямой у = х стремится к нулю по мере уменьшения
х. Или строго: lim81"*"* = 0. Продолжайте, Гарин.
— А если взять прямую у = §, то предел относительной
погрешности будет не равен нулю: lim 1 s~2 = lim2smJc~a: =
х—>0 2 х—>0 х
= lim(2^-l) = l.
Поясняю на графике и эту выкладку:
— Очевидно, любая прямая, отличная от у = х, приведет нас
к тому же самому выводу: относительное расхождение между
нею и синусоидой при бесконечном убывании икса будет
держаться примерно на одном и том же уровне, не уменьшаясь до
нуля. И только в случае прямой у = х относительное
расхождение, как мы уже видели раньше, стремится к нулю. Именно
такое отношение к синусоиде отличает прямую у = х от любой
другой прямой. Именно поэтому мы и говорим, что в начале ко-
162
ПРЕДЕЛЫ ФУНКЦИЙ
[Гл. 2
ординат функция sinx ведет себя, как х. Такую же картину мы
увидим на графиках других кривых, которые рисовал Мухин:
функцию у = 1п(1 + х) в начале координат точно таким же
образом приближает та же прямая у = х; функцию у = ах — 1 —
прямая у = xlna. И каждая из этих прямых для соответствующей
функции будет касательной в начале координат. На следующем
семинаре, когда мы строго определим понятие касательной, мы
внимательнее проследим сходство между этим определением и
тем, как мы сегодня приближали кривые с помощью прямых.
Выдерживаю паузу, чтобы сказанное получше улеглось у них
в головах.
— Садитесь, Миша. Продолжаем. Мы говорили до сих пор о
приближении кривых с помощью прямых. Но можно поставить
вопрос шире — говорить о приближении одной кривой, одной
бесконечно малой функции /(х) с помощью другой, тоже
бесконечно малой д(х). Ради простоты будем по-прежнему вести
приближение в окрестности начала координат, то есть полагать
х бесконечно малой, стремящейся к нулю величиной, — рисую
поясняющий график. — Как и прежде, потребуем, чтобы стреми-
лась к нулю относительная погрешность приближения ^ Ьху ?
обозначим ее традиционным символом бесконечно малой
величины а(х). Рассмотрим теперь абсолютное расхождение тех же
функций /(х) — з(х); обозначим его h{x). Из предыдущего
следует: h(x) = а(х)д(х). Обратите внимание: /i(x) выражается через
д(х) с бесконечно малым множителем а(х). В таком случае
говорят, что h{x) есть бесконечно малая более высокого порядка,
чем з(х), и пишут: /i(x) = о(#(х)), а читают так: /i(x) равно о
малому от д(х).
Снова делаю паузу, давая понять, что далее последует нечто
важное.
- Этот новый термин «о малое» будет занимать
центральное место в наших ближайших рассуждениях и выкладках,
поэтому мы должны хорошо понимать его смысл. По существу это
обозначение некой специфической бесконечно малой функции от
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
163
бесконечно малого аргумента. Ее определяющее свойство
состоит в том, что ее отношение к своему аргументу есть опять-таки
бесконечно малая величина. В формульной записи это выглядит
так: lim^- = 0. Говорят еще, что величина o(z) стремится к
нулю быстрее, чем z. Записали это определение, ребята? Тогда
вернемся к нашим функциям f(x) и д{х). Используя новое
понятие, мы можем выразить результат приближения одной
функции с помощью другой в виде равенства: f(x) = д{х) + о(д\х)).
Тот, кто понаторел в о-символике, взглянув на это соотношение,
не станет спрашивать, как оно выводилось, — он сразу
понимает его суть: относительная погрешность приближения функции
f(x) функцией д{х) бесконечно мала. В самом деле, перенесем
д(х) в левую часть равенства и поделим обе части на д(х). Это
дает *\ (х) = Гх) • Затем устремим х к нулю, отчего д(х)
тоже устремится к нулю, — показываю это на графике,
поясняющем поведение функций f(x) и д(х). — И тогда в правой части
получаем по определению lim цГ*у = 0. Стало быть, предел
левой части q7x) тоже равен нулю, что и требовалось показать.
Возвращаюсь жестом к равенству f{x) = д{х) + о(д(х)).
— Всем было понятно, как я преобразовал это соотношение?
Тогда попробуйте сами пожонглировать с ним. Подумайте, какие
еще выводы можно из него извлечь.
— Я бы поделил обе части на д(х), если, конечно, д{х) нигде
не обращается в нуль, — начинает Горт. — Тогда в правой части
получилась бы единица плюс бесконечно малая величина, а в
левой — отношение f(x) к д(х). При стремлении х к нулю правая
часть стремится к единице, значит, отношение f(x) к д(х) тоже
стремится к единице.
Записываю на доске предложенное Гортом в кратком
формульном изложении.
164
ПРЕДЕЛЫ ФУНКЦИЙ
[Гл. 2
— А еще можно доказать, — не отстает Костюк, — что
если разность f(x) — д{х) есть о{д{х)), то она есть и о(/(х)). Я
представлю эту разность по-старому, в виде а{х) • д{х),
разделю ее и умножу на f(x) и перепишу все выражение как
произведение трех сомножителей: сначала а(х), которая бесконечно
мала, потом отношение д(х) к /(х), которое стремится к
единице и потому ограничено, потом f(x). Первые два сомножителя,
бесконечно малый и ограниченный, дают в произведении
бесконечно малую величину. Получается, что в правой части стоит
бесконечно малая, умноженная на /(х), то есть о(/(х)).
Кратко записываю в формульном виде и разъясняю
рассуждение Костюка.
— Теперь, ребята, я хочу ввести новый термин. Две
бесконечно малые функции, разность которых есть бесконечно малая
более высокого порядка, чем любая из них, называются
эквивалентными. То, что сказал Горт, позволяет дать еще одно
определение эквивалентных функций, равносильное первому: так
называются две функции, отношение которых стремится к
единице, когда они обе одновременно стремятся к нулю, — конечно,
при условии, что знаменатель такого отношения не
обращается в нуль. Мы видим теперь, что каждый из изученных нами
замечательных пределов служит выражением некоторого
отношения эквивалентности. Такое отношение обозначают особым
значком ~.
Переписываю столбиком четыре из пяти замечатедьных
пределов в виде отношений эквивалентности. Рядом пишу еще один
столбик, где эквивалентность выражается с помощью знака
равенства и о малого.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
165
— Нетрудно предвидеть, где можно использовать понятие
эквивалентности и какую пользу оно может принести. Бывает,
что для некоторой замысловатой функции f(x) удается
подобрать эквивалентную функцию д(х), более простую. Тогда во
всех выкладках, где участвует функция /(ж), делаем замену
f(x) = д(х) + о(д(х)), и выкладки упрощаются. В частности,
вычисляя предел отношения двух функций, скажем, jt-jt, мы
можем заменять их эквивалентными. Кто смог бы объяснить,
почему это так? Вы, Рамзин? Пожалуйста, к доске... Все верно,
садитесь. Кстати, ребята, именно так мы и поступали, если вы
помните, когда вычисляли предел lim ^™* . Теперь мы, конечно,
вычислили бы его быстрее: заменили бы sinrax эквивалентной
величиной тх, аналогично заменили бы sinnx, сократили бы
дробь ~ нахи сразу получили бы в ответе ^. Наибольшие
упрощения в выкладках подобного рода достигаются тогда,
когда в роли эквивалентных выступают степенные функции.
Разберем подробнее задачу их поиска. Пусть некоторая
функция f(x) стремится к нулю при х, стремящемся к а. Требуется
найти степенную функцию вида С(х — а)р, которая была бы
эквивалентна f(x) в точке а. Требуется, как еще говорят,
выделить главную часть функции f(x). Выделив ее, заменяем
f(x) суммой С(х — а)р + о((х — а)р). Если же речь идет лишь о
поиске степени р, говорят, что выясняется порядок малости
бесконечно малой функции f(x). Простейшие примеры такого рода
доставят нам все те же замечательные пределы — например,
такой: lim-^Ц—— = I. Этой несложной формуле можно дать
х—>о х
сразу три толкования. Во-первых: функция ln(l + x)
эквивалентна х. Во-вторых: главная часть функции ln(l + х) — это х.
166 ПРЕДЕЛЫ ФУНКЦИЙ [Гл. 2
В-третьих: 1п(1 + х) есть бесконечно малая первого порядка
относительно х,
— Но ведь в этой формуле, — медленно говорит Кочин,
пристально глядя на равенство 1п(1 + х) = х + о(х), выражение о(х)
это какая-то функция, верно?
— Верно.
— И чему же равно это о(х)? Хотя бы приблизительно?
— Приблизительно (—^-).
— А если взять sinx? Тут тоже sinx = х + о(х). Чему же
здесь равно о(х)?
— Приблизительно (—^-).
— Функции совершенно разные, но каждая есть о(х), так
получается?
— Совершенно верно. Что же вас здесь смущает? Ага,
кажется, я понял — сходство с законом арифметики: если а = Ь и
с = 6, то а = с. Здесь, на первый взгляд, то же самое: —\ — о(х)
и — ^ = о(х), стало быть, — ^- = — ^-, а это уже абсурд.
Разгадка парадокса в том, что здесь символ равенства имеет не
з
тот смысл, что в арифметике: утверждая, что — ^- = о(х), мы
говорим, что — ^- принадлежит к совокупности функций,
которые можно представить как произведение бесконечно малой
а(х) на х. Но эти бесконечно малые а(х) могут быть
самыми разными, так что под маской о(х) могут скрываться самые
разные функции: и — ^-, и — ^-, и 5х7, и 2х9. В самом деле,
Кочин, можно ли полагать, что 2х9 = о(х), если х стремится
к нулю?
— 2х9? Да, потому что 2х9 = 2х8 • х, а 2х8 стремится к нулю,
как и х.
— А можно ли сказать, что 2х9 = о(х3)?
— Тоже можно, потому что 2х9 = 2х6 • х3, а 2х6 бесконечно
малая.
— Верно. Надеюсь, ребята, — обращаюсь уже ко всем, —
что вы прислушивались к нашему разговору с Кочиным и
теперь лучше понимаете, что это за штука — о малое. Так
что перейдем к примерам посложнее. Кто хочет пойти к
доске?
Все молчат. Глянув по сторонам, встает Кулагин:
— Ну, давайте я.
— Скажите, Андрей: можно ли упростить сумму
o(xn) + o(xm), если п > т > 0 и х стремится к нулю?
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
167
— Сейчас посмотрим.
И он неторопливо ведет преобразования, приговаривая:
<<хп-т бесконечно малая, поскольку п — т > 0... произведение
бесконечно малых есть бесконечно малая, сумма тоже...» И
выписывает результат: о(хп) + о(хт) = о(хт).
— А если т = п?
— Тогда совсем просто: о(хт) + о(хт) = о(хт).
— Но алгебраическая сумма — это еще и разность. Верно ли,
что о{хт) - о{хт) = о(хт)?
— Вы что, ждете, что я напишу о(хт) — о(хт) = 0? Эти о
малые могут быть разными. Допустим, одна — это а(х) • хт,
другая (3{х) • хт. Подставим их в разность: а(х) • хт — /3(х) • хт =
= |а(х) — (3{х)]хт = 7(#) • ^т? где 7(^) тоже какая-то бесконечно
малая, как разность двух бесконечно малых. В общем, все ясно:
о(хт) ± о{хт) = о(хт).
— Не все ясно, Андрей, не все! Бывает и так, что разность
двух бесконечно малых одного порядка оказывается бесконечно
малой более высокого порядка. Вот смотрите: две функции
2sinx и sin2x. Обе бесконечно малы при х, стремящемся к
нулю. Легко показать, что они одинакового порядка, первого.
Составим их разность: 2sinx — sin2x = 2sinx — 2 sin x cos x =
— 2sinx(l — cosx). Составим далее отношение этой
разности к одной из наших функций, допустим, к первой:
2si^rSgn2x = 1 — cosx. Эта величина стремится к нулю при
х, стремящемся к нулю. Вот я и доказал вам таким примером,
что разность двух бесконечно малых одного порядка может
оказаться бесконечно малой более высокого порядка. Что скажете
на это?
Вместо ответа он пишет: о(хт) ± о(хт) = о(хп), где п > т.
С улыбкой беру другой кусок мела и завершаю эту строчку
резолюцией: «не возражаю».
— А раз так, — обретает он голос, — то я был прав!
И пишет ниже: о(хп) = а(х) • хп~т • хт = (3{х) • хт = о(хт).
— Хвалю вашу находчивость, Андрей, но ведь вы не
станете отрицать, что прав и я: возможны случаи, когда
о{хт) — о(хт) = о(хп), где п > т. Мой пример с синусами
заставляет в это поверить.
И ко всей группе, живо следящей за нашим турниром:
— Будьте осмотрительны, ребята, когда встречаете
сумму или разность о малых. У нас еще будет повод убедиться,
что такая встреча может обернуться неприятностью. Но,
как говорится, продолжим наши игры. Как упростить вы-
168
ПРЕДЕЛЫ ФУНКЦИЙ
[Гл. 2
ражение о(хт)о(хп)? Напишите его, Андрей, и садитесь:
пусть его исследует кто-нибудь другой. Хотите? — гляжу
на Лапикова. Тот молча поводит головой из стороны в
сторону.
— Останьтесь, Андрей! — зову Кулагина обратно. — Как вы
поступите с этим произведением?
— Наверное, так же, как с суммой... Получается о(хп+т).
— И притом весьма просто получается, — с упрекающей
усмешкой гляжу на Лапикова. — Чего ж вы испугались, Егор?
Только того, что я пообещал примеры посложнее? А вы уж
оробели! Значит, — возвращаюсь к результату Кулагина, —
когда перемножаются о малые от степеней х, можно заменить
их произведение о малым от суммарной степени. Запомните,
ребята, эти приемы сложения и умножения о малых.
Запишите их в своих тетрадях где-нибудь на отдельном листе.
Припишите к ним и такое соотношение: о(о(х)) = о(х).
Доказывается легко: о(о(х)) = а(х) • о(х) = а(х) • /3(х) • х =
= *у(х) • х = о(х); здесь а(х),(3(х) и у(х) = а(х)/3(х)
бесконечно малы. Садитесь, Андрей. Но прежде сотрите с доски
все то, что там написано. Мы возвращаемся к прерванной
теме.
Вновь пишу с краю доски: f(x) = С(х — а)р + о((х — а)р).
— Сейчас я задам примеры на выделение главной части
функций, бесконечно малых при стремлении их аргумента к
некоторой точке а. Напомню: если а не равно нулю, то для
облегчения выкладок удобна замена у = х — а. Мы уже
научились пользоваться ею на прежних примерах, и потому я
буду сразу давать вам функции бесконечно малые не в какой-то
произвольной точке, а в нуле. Я напишу на доске несколько
таких функций, причем не в том порядке, в каком их лучше
Ю. В. Пухначев] СЕМЬ СЕМИНАРОВ 169
решать, — вы сами должны будете угадать, с какого лучше
начать.
— Мне кажется, нужно начать со второго примера, —
изрекает Чюмин.
Предложение разумное, именно его я и ждал, но сдается мне,
что он ляпнул это наобум.
— Пожалуйста, к доске. Чему же, вы думаете, эквивалентна
вторая функция?
— Функции х3.
Он в своем амплуа: нарывается на новое фиаско.
— Иными словами, вы хотите сказать, что отношение
функции х + х2 sin х к х3 должно стремиться к единице, когда х
стремится к нулю. Покажите это. Второе слагаемое, которое у вас
получилось, действительно стремится к единице. А первое? К
чему стремится ^ при х, стремящемся к нулю?
— К бесконечности...
— Здесь ведь второе слагаемое более высокого порядка, чем
первое! — Горт удивлен, как можно было не заметить этого. —
Можно им пренебречь по сравнению с первым!
— Это функция не третьего, а первого порядка малости, она
эквивалентна х\ — посмеиваясь вместе со всеми, подсказывает
Рамзин. Чюмин проводит выкладки заново, следуя подсказке, и
получает в итоге единицу.
I Чюмин I
I ЗС + XZSinOC j . -*-•.-» I
= f + OCSVIZC
X
einv х+х2*пх=4+&*п*:Ыпэс=4\
зс-*о ж x+o I
Какой он все-таки чудак! Но в этом есть свой прок: потешаясь
над его ошибками, ребята учатся не повторять их. Со временем
он, вероятно, и сам научится работать без глупых оплошностей, а
до той поры надо строго следить за тем, чтобы снисходительное
170
ПРЕДЕЛЫ ФУНКЦИЙ
[Гл. 2
зубоскальство ребят по его адресу не переходило в унизительные
насмешки: такие, как Рамзин, на это горазды.
Гашу смешки деловым тоном:
— Этот пример подсказывает нам: сумма двух бесконечно
малых функций разного порядка малости эквивалентна
слагаемому, имеющему наименьший порядке малости.
Из желающих выйти к доске вызываю Синицу. По цепочке
сложных преобразований она приходит к выводу, что первая из
предложенных мною функций эквивалентна у/х.
— Хорошо, — одобряю ее искусство. — Но разве пример,
решенный Чюминым, не указал вам более простого пути к тому
же результату? Смотрите, вот сумма х + у/х. Какое из
слагаемых имеет наименьший порядок? Верно, у/х. Значит, сумма
эквивалентна ему, а квадратный корень из нее эквивалентен у/х.
Теперь смотрим на сумму х + у/х. Здесь наименьший порядок
имеет слагаемое у/х, и сумма эквивалентна ему, а квадратный
корень из нее эквивалентен у/х. Все!
— Как-то это все нестрого...
— Да, это лишь догадка, не отрицаю, ее еще нужно
подкрепить доказательством, показать, что полученный результат
удовлетворяет определению эквивалентности. Кстати сказать,
это вы уже сделали. Но согласитесь: угадать верный ответ и
проверить его достоверность — это все-таки легче, чем искать
его в полном неведении. Мастерство догадки — совсем не
лишнее для вас мастерство. Кто решил третий пример? Сутеев?
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
171
Прошу вас к доске. Эквивалентную функцию вы нашли
верно, это у. Но я все-таки хочу критически подойти к вашему
решению: оно могло быть изящнее. Смотрите: дробь, которую
вы получили после первого преобразования, далее можно было
бы преобразовать иначе, и тот же ответ подучился бы проще.
Перепишите ваше решение с учетом моих замечаний. Я снова
напоминаю вам: на каждом шагу ваших выкладок старайтесь
представить получившееся выражение во всех возможных его
формах.
— Непонятно! — вдруг слышится плачущий голос
Аргуновой.
— Что непонятно? Решение последнего примера?
— Нет, непонятно, почему у меня ничего не получается.
— А как вы решали этот пример?
— Я просто посмотрела: tgrr эквивалентен х, sinrr — тоже,
значит, их разность эквивалентна нулю.
— Да, после этого дело не сладится: из ничего и
получится ничего. Давайте разбираться, в чем причина неудачи.
Прошу вас к доске. Вспомните, когда мы с Кулагиным
рассуждали про о малые, я предупреждал, как осторожно нужно
обращаться в сомнительных случаях с разностями бесконечно
малых величин. Видимо, такой случай с вами и произошел. Итак,
tg х — sin x. Вы хотите использовать соотношения
эквивалентности tgrr ~ x,sinx ~ х. Как эти соотношения позволят
преобразовать разность tgrr — sinrr? Вы пишете за нею знак равенства?
Имеете в виду эквивалентность, а пишете равенство? Тем самым
вы обязываете себя использовать такое определение
эквивалентности, где употреблялся бы знак равенства. Есть у вас такое
определение? Определение, где одна функция выражается через
другую?
Подумав, она пишет lim Д|( = 1.
х—>а"\х)
— Равенство верное, но я ожидал другое. Ничего, сейчас
мы получим отсюда желаемое. Рассудим здраво: нам надо
выразить одну функцию через другую. Но обе стоят под
знаком предела, надо как-то убрать этот знак. Если
функция стремится к единице, то она может быть выражена в
виде...
172 ПРЕДЕЛЫ ФУНКЦИЙ
— Единица плюс бесконечно малая.
[Гл. 2
— Прекрасно! Ну-ка используйте это для выражения одной
функции через другую!
— Вспомнила: функция равна эквивалентной ей плюс о малое
от эквивалентной функции.
— Или, говоря иначе, равна своей главной части плюс о
малое от этой главной части. Как это будет звучать для тангенса
и синуса, о которых у нас идет речь? Напишите и подставьте
в разность tgrr — sinrr. Что получается в итоге? Иксы сократи-
лись, осталась разность о(х) — о(х), но это, как мы уже выяснили
с Кулагиным, тоже есть о малое от х. Но за таким выражением,
как мы знаем, могут скрываться весьма разнообразные
функции. Ответ не определен. То есть, этот путь нехорош. На одном
из следующих семинаров мы найдем самый эффективный метод
решения подобных задач. А сейчас, Аргунова, внимательно
просмотрите решение Сутеева, убедитесь, что вам все понятно в нем,
сотрите его и решайте на доске эту задачу заново. Ну вот, —
киваю, терпеливо дождавшись ответа, — все верно. Возвращайтесь
за свой стол.
Пока она добирается до своего места, прохаживаюсь у доски,
стараясь найти убедительное изложение мысли, которая только
что пришла мне в голову.
— Как вы неоднократно убеждались, ребята, путь от условия
задачи к ее решению редко бывает гладким и прямым. На нем
то и дело встречаются препятствия, котороые поначалу кажутся
непреодолимыми, или развилки, когда вы вместо верного пути
выбираете ошибочный. Таким уклоном был и шаг Аргуновой,
когда она в ответ на мою просьбу дать определение
эквивалентности написала не то, что подходило более всего. Не без моих
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
173
подсказок она вернулась на правильный путь. Но ведь я буду
рядом с вами не всегда. Рано или поздно вы должны
выработать в себе умение в случае ошибки возвращаться на путь
истинный самостоятельно, без посторонней помощи. Выработка такого
умения — вот, пожалуй, главное, ради чего вы ходите на наши
семинары — ведь теорию саму по себе вы можете изучать
самостоятельно, читая учебники. Надо заметить по поводу дальнейших
шагов Аргуновой, что к ответу они ее не привели.
Непреодолимым препятствием стало отсутствие необходимых знаний. На
одном из ближайших семинаров мы познакомимся с очень мощным
приемом, который позволил бы успешно развить подход,
выбранный Аргуновой. Накапливать арсенал эффективных приемов и
методов решения задач — еще одна важнейшая цель, ради
которой вы ходите на семинары и лекции, читаете учебники. А если
говорить образно — за годы учения в институте вы должны обре-
сти две силы, гарантирующие достижение успеха в любом деле:
силу движущую, ведущую через любые препятствия к
результату, и силу, возвращающую на путь к нему в случае отклонений,
ошибок, оплошностей, от которых не застрахован никто.
Произнося этот монолог, успеваю понаблюдать за работой
Сынчикова. Для последней функции х + х21п|х| он верно
угадал эквивалентную: х. Поделив одну на другую, написал
1 + xln|x| — и остановился, словно в тупике. Приписав под
этой суммой lira xphix и ниже р > О, шепчу: «Встречался ли
х—►+()
нам когда-нибудь такой предел?» Он листает тетрадь и через
шак равенства завершает гладеньким нулем написанное мною.
«Стало быть?» — жду ответа. И Сынчиков не без обычной своей
медлительности выписывает: х + х2 In \x\ ~ х.
— Покажите свое решение на доске, — прошу уже в полный
голос. Не проронив ни слова, он переписывает на доску выкладки
из своей тетради.
— Все хорошо. Садитесь, Сынчиков.
Похвалить его побольше? Нет, не буду. Спокойствие, с
которым я стану воспринимать его успехи, лучше, чем любая
похвала, будет убеждать его в том, что я считаю его ничуть не хуже
остальных.
174
ПРЕДЕЛЫ ФУНКЦИЙ
[Гл. 2
Зову к доске Стрельцова, доказываю вместе с ним, что
о(Схп) = о(хп),Со(хп) = о(хп) и если х ~ у, то о(хп) = о(уп).
— Эти соотношения тоже надо запомнить хорошенько,
ребята. Припишите их к списку равенств, которые
выражали приемы сложения и умножения о малых. Идем
далее. Лектор, вероятно, уже рассказывал вам про
свойства непрерывных функций и давал соответствующие
теоремы...
— Лектор давал теоремы о функциях, непрерывных на
отрезке, — уточняет меня Горт.
Молодец! Я намеренно обмолвился, чтобы проверить, не
устали ли они, по-прежнему ли внимательны.
— Да, я это и имел в виду. Не вспомните ли хотя бы одну из
этих теорем?
— Функция, непрерывная на отрезке и принимающая разные
знаки на его концах, обращается в нуль хотя бы в одной
внутренней точке отрезка.
— Верно. Кто вспомнит еще какую-нибудь теорему? Ко-
чин?
— Функция, непрерывная на отрезке, ограничена.
— Очень хорошо. Еще, еще теоремы! Говорил ли вам лектор
о равномерной непрерывности?
— Говорил, — не допуская и секундной паузы, но в то же
время с солидной неторопливостью отвечает Рамзин. — И
давал теорему: если функция непрерывна на некотором отрезке
[а, Ь], то она и равномерно непрерывна на нем. То есть для
любого е найдется такое 5, что для любых х' и х из [а, Ь],
удовлетворяющих неравенству \х' — х\ < 5, выполняется неравенство
\f(x') — f(x)\ < е. Это, если мне не изменяет память, так
называемая теорема Кантора.
— Верно. А ну, ребята, кому еще не изменяет память? Кто
вспомнит еще какую-нибудь теорему о функциях, непрерывных
на отрезке?
— Об обратной функции! — хлопает себя по лбу
Мухин. — Если монотонная, то у нее — это я про ту функцию
говорю, которая сначала дана — если она монотонная —
допустим , монотонно возрастающая — то у нее есть и
обратная.
И, заметив, что я беру мел с явным намерением в чем-то ему
возразить, поспешно поправляется:
— Если монотонная и непрерывная на некотором отрезке
[а, Ь], то у нее есть обратная. Вот, теперь точно.
Ю. В. Пухначев] СЕМЬ СЕМИНАРОВ 175
— Уж если быть точным, — рисую чертеж, — то надо бы
ваши слова пересказать так: пусть некоторая функция f(x)
определена, монотонно возрастает и непрерывна на некотором
отрезке [а, Ь]; тогда на отрезке ее значений [/(a), /(b)] существует
обратная функция х = д(у), также монотонно возрастающая и
непрерывная. Аналогично формулируется теорема для случая
монотонного убывания.
Кладу мел:
— Еще теоремы? Из тех, что вам давал лектор, осталась
забытой еще одна. Не вспомните ли ее, Буткус?
— Функция, непрерывная на отрезке, достигает своей точной
нижней и своей точной верхней грани.
— Я попросил бы вас к доске. Скажите, как вы понимаете
эту теорему?
Он рисует корявый чертеж:
Вот отрезок [а, Ь], вот множество значений функции. Оно
ограничено по предыдущей теореме. Значит, у этого множества
есть точная верхняя и точная нижняя грань, пусть Р и Q.
Теорема говорит, что на отрезке [а, Ь] есть точка с, в которой функция
176
ПРЕДЕЛЫ ФУНКЦИЙ
[Гл. 2
равна Р, и есть точка d, в которой функция равна Q. Это значит
«достигает».
— Хорошо. А можете ли вы придумать функцию,
определенную не обязательно на отрезке, а, скажем, на интервале, которая
не достигала бы точных граней множества своих значений? Хотя
бы нижней?
Он склоняет взгляд куда-то в угол доски и через несколько
секунд вновь вскидывает его:
— Могу! — и повторяет на доске график, который я видел у
него в тетради, когда он доказывал «свою» теорему. Повторяет
с одним лишь различием: не проставляет значения функции в
граничных точках интервала.
— Нельзя ли выразить эту функцию формулой?
У граничных точек области определения своей функции он
ставит отметки I и 2,рядом с ее графиком пишет равенство у = х:
— Точная нижняя грань значений — единица, а функция на
этом интервале не обращается в единицу.
— Хорошо, садитесь. Всем понятны, ребята, те теоремы,
которые только что были названы? Да? Тогда я попрошу вас
доказать несколько новых теорем. Запишите их формулировки.
Медленно диктую:
Теорема I. Функция f(x) определена и непрерывна для всех
неотрицательных х. Существует lira fix) = А. Доказать, что
х—>+оо
функция f(x) ограничена.
Теорема 2. Функция f(x) определена и непрерывна для всех
х. Существует lira f(x) = В < О и lira f(x) = А > 0. Дока-
х—►—оо х—>-+оо
зать, что существует £ такое, что /(£) = 0.
Теорема 3. Функция f(x) определена на отрезке [а, Ь]. Для
любого х из этого отрезка f(x) > 0. Доказать, что существует
такое число D > 0, что f(x) > D для любого х из отрезка [a, b].
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
177
Едва я успел продиктовать условия теорем, как Синица
радостно заявляет:
— Я доказала первую теорему!
— Как это вам удалось так быстро?
— Сама не знаю. Написала, что означает условие...
— Сделайте-ка это на доске.
— Сначала я написала, что значит lim fix) = А. Получа-
х—>+оо
ется, что для всех х > 8 функция удовлетворяет неравенству
А — е < f(x) < А + е. Это ведь какое-то ограничение, правда? Но
это неравенство справедливо для х > S. А какие еще остаются?
Очевидно, 0 < х < 6] но ведь это отрезок, правда? А
непрерывная функция на отрезке ограничена: Р < f(x) < Q. Значит, если
говорить про все х из области определения функции, то снизу
её можно ограничить числом min {P, А — е} а сверху — числом
max{Q, А + е}.
— Отлично! И главное — как просто! Достаточно было
выписать определения основных положений условия — и решение
возникло тотчас, как бы само собой. Да, теперь становится
ясной мудрость совета, который Паскаль дает желающим
научиться рассуждать: заменяйте определяемые понятия их
определениями. Кстати, именно благодаря такому приему Синица
сделал в свое время первый определяющий шаг, при
доказательстве теоремы Буткуса. Но перейдем к другим теоремам. Я
вижу, что многие уже доказали их; Миклашевский уже собирает
портфель... Куда вы торопитесь, Павел? Даже если сделано все,
можно улучшить сделанное. Возьмем, например, рассуждение
Люды: в нем присутствует некоторое е — произвольное, невесть
чем определяемое. Можно было взять в качестве е число, как-то
связанное с величинами из условия — скажем, е = ^Л. Тогда для
х > S можно было бы написать \f(x) \ < || А\ — не правда ли? Для
остальных х тоже можно было бы дать «классическое»
ограничение на функцию по абсолютной величине: \f(x)\ < М. Тогда
величина тах{М, \\А\) ограничивала бы функцию по модулю
для всех х из её области определения. Так ведь, Миклашевский?
Кстати, не покажете ли вы нам, как доказали вторую теорему?
— В общем-то, как Люда... Если функция стремится к
отрицательной величине при х, стремящемся к минус бесконечности,
то в какой-то достаточно удаленной точке функция будет
отрицательной...
— Строгость, Миклашевский, строгость! У Люды она была!
Так что держите марку, если обещаете работать, как Люда!
178
ПРЕДЕЛЫ ФУНКЦИЙ
[Гл. 2
— Ну да, вы хотите, чтобы я расписал определения... Для
любого е найдется 8 такое, что при х меньше 8 выполняется
В — £ < f(x) < В + £. Любое £ вам не нравится — возьмем у.
— Наверное — у, если уж В меньше нуля! Величина £
положительная, это вы забыли упомянуть!
— Ладно, пусть будет —у. Подставим такое е в наше
неравенство... получается |В < f(x) < у. И это для всех х, меньших
8. Выберем из них произвольное Ь, и для него будет выполняться
/(b) < у < 0. Аналогично найдем с такое, что /(с) > 0. Теперь
на отрезке [Ь, с] по теореме о промежуточных значениях найдется
точка £ такая, что /(£) = 0.
— Ну вот, теперь хорошо. А третья теорема? Докажете ее,
Лапиков?
— Там тоже вроде бы все просто, — с какой-то опаской
говорит он: вновь показаться оробелым перед сложной задачей ему
не хочется, но голос его выдает.
— Вы, наверное, боитесь, что это вам только кажется?
Смелее, Лапиков! К доске!
— Согласно условию теоремы, — осторожно начинает он,
поглядывая на меня, — функция определена на отрезке и
непрерывна в каждой его точке. Значит, она ограничена — есть такая
теорема для непрерывных функций, определенных на отрезке.
Значит, у её значений есть точная нижняя грань, обозначим её
через D. Получается f(x) > D. Все значения f(x)
положительны, — он снова глядит на меня.
— И это все доказательство? Но я, насколько вы помните,
просил найти положительное число, ограничивающее снизу
множество значений функции. Из того, что в этом множестве одни
положительные числа, не следует, что его точная нижняя грань
тоже положительна. Вспомните пример, который мы
разбирали на прошлом семинаре: дано множество {1,5,5,5,...}; все его
элементы положительны, а точная нижняя грань у него — нуль.
Что-то недоговорено в вашем доказательстве, Лапиков!
— Угу, — сокрушенно опускает он голову.
— Но ведь существует такая точка £, — пытается выручить
его Стрельцов, — значение функции в которой равно точной
нижней грани D.
— Напишите это! — даю новый толчок сникшему Лапикову. —
Как вы думаете, какой теоремой воспользовался Стрельцов?
— Теоремой о том, что непрерывная на отрезке функция
достигает своей точной нижней грани. У нас /(£)... Это ведь одно
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
179
из значений функции... и оно строго больше нуля! Ну да: D > 0;
значит, f(x)>D>0 для всех х из нашего отрезка.
— Вот-вот! Этого я и ждал от вас, Лапиков. Доказательство
доведено до конца, садитесь. И семинар наш тоже
закончился, ребята. На следующем займемся дифференцированием
функций.
Глава 3
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
— Тема нашего сегодняшнего занятия, ребята —
дифференцирование функций, вычисление производных...
— А мы это уже проходили в школе! — перебивает меня
Лапиков.
— Очень приятно. Тем не менее я хотел бы, как это
всегда у нас было при переходе к новой теме, напомнить
определения основных понятий, которые мы станем использовать в
дальнейшем: что такое производная, каковы условия ее
существования...
— Не надо! Мы это знаем! — звучат уже несколько голосов.
— Смотрите, ребята, как бы вам не раскаяться в своей
самонадеянности! Ну, а каковы производные элементарных функций,
вы тоже знаете? — оглядываю аудиторию. — Чему равна
производная... ну, скажем, синуса?
— Косинусу, — отвечает Стрельцов, на котором я
останавливаю взгляд.
— А производная косинуса?
— Минус синусу.
— Верно. Давайте-ка, — жестом зову его к доске, —
ради порядка выпишем производные основных элементарных
функций. Хорошо, хорошо... Заметим тут же, что производная
функции-константы равна нулю и что постоянный
коэффициент можно выносить за знак дифференцирования. Наконец,
перечислим правила дифференцирования суммы,
произведения, частного и суперпозиции двух функций и(х) и v(x). Все
правильно. Садитесь, Юра. Просмотрите внимательно эти
формулы, ребята, — вам действительно все это хорошо знакомо?
Все молчат —■ значит, все уверены в своих знаниях. Тогда
переходим к примерам. Кого бы вызвать к доске? Может быть, вас,
Мухин? Пишите: у равно дроби, у которой в числителе sin2x,
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
181
а в знаменателе sinx2. Попробуйте найти производную такой
функции.
Чувствуется, что Мухина в школе неплохо научили
дифференцировать: он сразу пишет производную от числителя в виде
sin2x, тотчас домножает ее на знаменатель... Мне даже
приходится сдерживать его:
— Пояснили бы, как получился sin2x.
— Квадрат синуса дифференцируем как сложную
функцию — берем сначала производную от квадрата — это будет
удвоенный синус — потом на производную синуса, то есть на
косинус, а 2 sin x cos x — это sin2x.
И, возвращаясь к своим вычислениям, быстро
заканчивает их.
— Легкий пример, — резюмирует Миклашевский.
— Сейчас будет посложнее. Напишите его условие, Мухин:
У = (f)x(|)a(f)b- Садитесь. Подумаем все вместе, как искать
производную такой функции.
Костюку, видимо, уже знакомы подобные примеры:
— Три сомножителя — значит, та формула, что у нас, с
двумя сомножителями, не годится. В общем виде надо делать
гак: производная первого сомножителя, умноженная на все
остальные, плюс производная второго на все остальные и так
далее, пока не дойдем до производной последнего
сомножителя.
182
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
[Гл. 3
— Три сомножителя? Разве? — возражает Горт. — Можно
так преобразовать, что будет только два. Показать? Я бы
сначала вынес все константы — Ьа из второго сомножителя, а~ь из
третьего, тогда осталось бы (|)х на хь~а. А это уже можно
дифференцировать по той формуле, которая у нас — с двумя
сомножителями.
— Сложно все это, — ворчит Костюк. — У меня все как по
нотам, никакой возни со всякими там преобразованиями ...
— Согласен, — киваю ему. — Я даже напишу на доске ваш
алгоритм, чтобы его запомнили все. Но согласитесь и вы: у способа
I [А (*) /,с*)... £(*)] = aW.£)~ Л&)А
Горта есть свои достоинства — простота используемой формулы
хотя бы. И притом учтите: сравнивая оба способа, мы вовсе не
ставим целью утвердить какой-то из них как единственно
верный и подлежащий применению в любых условиях. Наоборот: в
наших интересах освоить побольше подходов к каждой
пройденной задаче, чтобы.в будущем, если встретится нечто похожее,
выбирать среди различных подходов наиболее
предпочтительный в зависимости от обстоятельств. Так вот, Костюк, раз уж
вы так держитесь за свой способ, то я в порядке призыва к
многовариантному мышлению попрошу вас выйти к доске и решить
этот пример способом Горта. Ну вот — короткое решение,
красивый ответ. Кто хотел бы пойти к доске следующим? Не бойтесь,
на сей раз я дам пример полегче. Мне почему-то кажется, что
этот пример не прочь решить Аргунова. Ну, смелее, Галя!
Пишите: у = 1п(х + у/\ + х2). Решайте. Вы, конечно, видите, что это
суперпозиция.
— Да, я сначала дифференцирую логарифм...
— Потом корень... Так, так... Решение верное, садитесь. Но
прежде напишите условие следующего примера: у = tfx.
— То есть хП- осторожно спрашивает Лапиков.
— Точно.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
183
— Значит, можно дифференцировать как степенную
функцию? И в ответе будет х"1?
— А вот тут вы уже неправы. Так дифференцируется х,
возведенный в некоторую постоянную степень. А величина - —
непостоянная.
— Значит, как показательную? И ответ х*... умножить на
lnx...
— Опять неверно. Кто объяснит, почему?
— Потому что, — разъясняет Синица, — так
дифференцируется показательная функция с постоянным основанием. А здесь
основание — это х, это аргумент, величина переменная.
— Так что же делать? — обращаюсь к аудитории.
— Искать другие формулировки условия, — напоминает Рам-
зин, правоверный последователь моих советов.
— Разумно! Не попробуете ли, Лапиков? Пожалуйста, к
доске! Молчите? А помните, на прошлом семинаре нам встретилось
выражение p(x)q№ — что мы делали с ним?
— Не помню...
— Тогда запомните накрепко сейчас: как правило, действия с
подобными выражениями сильно упрощаются, если их
представить в виде eq^lnp^x\ Вот и теперь — сделайте такое
преобразование с нашей функцией.
— Получается е~... Ну да, это ведь е в степени!
Дифференцируем сначала экспоненту, у нее производная совпадает с ней
самой, потом показатель...
— Ну, конечно! Пишите же, пишите! Ответ в принципе
верный, e"^r(jj — ^г), только лучше бы его записать в более
простой форме: х*~2(1 — 1пх). Садитесь. Следующий пример:
у = arcsin(sinx). Чему равна производная этой функции?
Гляжу на Миклашевского, словно приглашая его к ответу.
Он уже уловил закон чередования моих заданий: за сложным
следует простое, стало быть, на сей раз опять дано нечто, не
требующее особых размышлений, — и отвечает на мой вопрос
незамедлительно и простодушно:
— Единице. Ведь arcsin(sinx) равен х, а производная х — это
единица.
Сработало! Ну-ка, как воспримут такой ответ ребята?
Неужели не запротестуют?
Первым, как я и ожидал, взрывается Горт: «Арксинус синуса
икс не равен икс!» — «Во всяком случае не всегда!» —
поспешно уточняет Костюк. «Ну, да», — пытается оправдаться Горт, но
184
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
[Гл. 3
его голос уже тонет в выкриках Буткуса, Меншикова, Чюмина...
Чюмина?! По выражению его лица, по интонации его голоса
(напрягаясь, успеваю различить ее в общем шуме) чувствую, что это
не подверженность общему настроению, а проблеск собственной
догадки. У него она не часто попадает в точку, но если на сей
раз оно так — это нельзя оставлять незамеченным!
— Чюмин, к доске! Скажите еще раз, с чем вы не согласны
в ответе Миклашевского. Не спешите, я не тороплю вас. Если
надо, нарисуйте какие-нибудь графики.
— Ну вот, значит, график синуса... (медленно, в темпе
проговариваемой мысли он рисует несколько волн синусоиды). Вот
график арксинуса.... Если возьмем какой-нибудь маленький икс,
вот такой, например (на графике синуса осторожный штришок
пересекает ось абсцисс неподалеку от начала координат), потом
возьмем от него синус (от штришка потянулся вверх шаткий
пунктир, преломился, достигнув синусоиды, и заковылял к оси
ординат), а от этого синуса возьмем арксинус (взгляд Чюмина
перекинулся два-три раза от одного графика к другому), тогда
для малого икс, если посмотреть на график арксинуса, это ведь
кусок синусоиды, только перевернутый (не отрывая взгляда от
графика синуса, он смешно кладет голову на правое плечо,
вероятно, чтобы лучше видеть тот самый кусок синусоиды) — для
такого икс мы снова получим икс... Значит (выпрямляется, уве-
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
185
ренный) для таких иксов arcsin(sinx) = x (прямо на графике
синуса он ведет из начала координат участок прямой у = х и
вновь кладет голову на плечо; мел в его руке движется по доске
все замедленнее, голос, сдавленный неестественным
положением головы, звучит еще глуше от сомнения). Но ведь арксинус не
может быть больше |! И прямую нельзя вести дальше!
— Верно, — соглашаюсь с ним и бросаю краткий взгляд на
Миклашевского: смотрите, мол, внимательно, в чем вы
сплоховали. — Равенство arcsin(sinx) = x справедливо лишь при
— | < х < |. Что же будет, Чюмин, если взять икс побольше,
чем |? Поглядите на график отсюда, — зову его к себе, чтобы
вывести из нелепой позы, и ставлю жирную точку на
нисходящем склоне синусоиды. — Вам когда-либо уже приходилось на
этом графике отмечать значение арксинуса для такого значения
синуса?
Поймет ли он мой намек? Жду секунду, другую...
— Конечно! — наконец вспыхивают улыбочкой стекла его
очков. И несколько звеньев ломаной линии стремительно
перечеркивают ось абсцисс.
— График совершенно верен. Отлично, Чюмин! Чему же
равна производная такой функции?
— Здесь (он указывает на участки возрастания) — плюс
единице, а здесь (указывает на участки убывания) — минус единице.
— Хорошо бы выразить этот ответ единой формулой. Не
можете? Кто мог бы это сделать?
Мой ровный тон не предвещает никаких принципиальных
трудностей, лишь призывает продемонстрировать хорошие
знания - и Рамзин не упускает шанса:
— Можно написать так: у' = sgn(cosx).
— Напишите это, — прошу Чюмина, — и садитесь на место.
Теперь, ребята, давайте сверим эту формулу с графиком
функции у = arcsin(sinx). Все правильно?
186
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
[Гл. 3
— Н-не совсем, — непривычно медленно выговаривает Горт,
напряженно смотря на доску. — Это что же получается — что в
точке | производная от arcsin(sin x) равна нулю?
— Да, именно такой ответ дает формула у' = sgn(cosx): в
точке ^ косинус равен нулю, а сигнум нуля есть нуль.
— А мне что-то кажется, что там производная от arcsin(sinx)
вообще не существует.
— Откуда же такие подозрения?
— Так это ж совсем так же, как у функции |х|: в нуле у нее
производной нет.
— А про |х| вы откуда знаете?
— Ну как «откуда»? Это нам еще лектор говорил, когда
объяснял понятие производной, когда давал определение.
— Вот оно! Понятие! Определение! Когда в самом начале
семинара я хотел поговорить об этом, вы все закричали: «Не надо!
Мы и так все знаем!» — а, оказывается, не знаете вовсе, иначе
не пропустили бы мимо глаз той чудовищной нелепости, которую
содержит формула Рамзина! Или вы думаете, что все
дифференциальное исчисление сводится к таблице производных от
элементарных функций? Допустим, вы ее знаете. Но разве это
оправдание для беспечности, которая так и пышет сегодня с ваших
лиц? Она прямо-таки парализовала ваши умы, судя по тому, что
вы без единого возражения переписываете с доски формулу, из
которой вытекает существование производной в изломах
ломаной линии. Боюсь, что с этакой вдумчивостью вы даже назубок
усвоенные правила дифференцирования не сумеете применять с
толком. Ну-ка, Костюк, к доске! Пишите: у = хз^л/\з+х)2'
Найдите производную этой функции. Что ж вы медлите? Пример
вполне подходит под ваш четкий алгоритм для
дифференцирования произведения: производная первого сомножителя на все
остальные плюс производная второго на все остальные... Но вы
с вашей догадливостью, очевидно, уже предвидите, что
необходимые по вашему алгоритму выкладки займут чуть ли не всю
доску, и чувствуете, что вряд ли такого размаха заслуживает
столь простенький пример, и потому не решаетесь применять
свой универсальный алгоритм. А между тем перечень основных
приемов дифференцирования, если в него вдуматься,
подсказывает остроумный выход из затруднительного положения. В
самом деле, посмотрите, что делается в результате
дифференцирования с произведением и с суммой функций? Любое
произведение после этого превращается в сумму из нескольких слага-
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
187
емых, а если продифференцировать сумму, то число слагаемых
останется неизменным. Так не стоит ли превратить произведение
в сумму, прежде чем его дифференцировать?
— Логарифм! — покаянным стоном откликается Горт.
— Да, надо, взять логарифм от произведения, и тогда
оно превратится в сумму логарифмов от сомножителей. Вот
выкладки, поясняющие такой прием — он называется
логарифмическим дифференцированием: F(x) = /i(x)/2(x).. ./п(х);
lnF(x) = In/:(*) + ... +In/n(z); fg = £g + ... + gg}.
Попробуйте применить этот прием к нашему примеру, Костюк.
Ну что ж, вроде бы все верно. Садитесь. Следующее задание:
вывести формулу для суммы: 1 + 2х + Зх2 + ... + (п + 1)хп.
— А если последнее слагаемое по-другому записать: nxn_1? —
после недолгого молчания поднимает на меня лукавый взгляд
Кулагин.
— Догадались? Идите к доске. Так, так ... Ответ верный, са-
дитесь. Надеюсь, ребята, что последние примеры возвратили вам
вдумчивость и мы с вами теперь готовы обстоятельно разобрать
все нужные нам определения. Так что же такое производная?
188
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
[Гл. 3
—Предел отношения приращения функции к приращению
аргумента, если такой предел существует, —четко отвечает Сутеев.
— Напишите это на доске.
В несколько отточенных движений он выписывает
лаконичную формулу: lim ^Щ1.
Дх-»0 ^Х
— Если такой предел существует, то его называют
производной функции f(x) в точке х и обозначают f'(x).
— Не поясните ли это на графике?
Столь же ловко он рисует две координатных оси и между
ними — изящно-извилистую кривую. И словно окаменела его
поднятая рука с зажатым в ней мелом; взгляд, обыкновенно прямой
и неподвижный, беспокойно перекинулся раз-другой от формулы
к графику и обратно.
Пытаюсь вывести его из внезапного оцепенения, не понимая
причин задержки:
— Напомните нам, что такое производная.
— Предел отношения приращения функции к приращению
аргумента, если такой предел существует, — повторяет он с
чеканной четкостью, но теперь она режет слух своей безмысленной
автоматичностью.
— Чему же это соответствует на графике?
С натужливой заторможенностью он наносит на ось абсцисс
невысокую засечку, отмечает ее буквой х, правее от прежней
засечки делает новую и приписывает рядом Дх, отмечает на
оси ординат соответствующие значения функции, пишет рядом
с первой отметкой у, стирает и пишет вновь у(х), рядом со
второй отметкой пишет у (Ах)... Тревожное недоумение все более
заметно в его взгляде, напряженно застывшем на этой
последней пометке.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
189
Осторожно поправляю его:
— Величина Ах — это приращение аргумента. И если
аргументу х, отмеченному на вашем графике, придано
приращение Дх, то в результате получится х + Ах: такое
выражение и должно стоять рядом со второй засечкой на оси
абсцисс.
— Да-да, — машинально соглашается он.
— А функцию, изображенную на графике, я посоветовал бы
обозначить как-то иначе, — пишу рядом с кривой у = f(x). —
Стоило бы еще отметить, что функция определена на
некотором интервале (а, Ь), и оба отмеченных вами числа, х и х + Дх,
принадлежат этому интервалу.
— Да-да, — глуховато повторяет он.
Он исправляет разметку графика и медленно, словно
впервые, со всеми подробностями расписывает формулу для
производной.
— Какой же геометрический смысл имеет выражение,
стоящее в написанной вами формуле под знаком предела?
— Тангенс угла наклона касательной.
Он, видимо, и сегодня не в лучшей форме. Привыкнув к
безупречной точности его ответов на первых семинарах, я особенно
болезненно ощущаю его срывы.
Оглядываюсь на аудиторию: как будет встречен неверный
ответ Сутеева? Ребята молчат, вглядываясь в нарисованный им
график: изящный сам по себе, он не очень-то приспособлен для
пояснения понятия производной. А, может быть, они молчат
190
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
[Гл. 3
оттого, что всем им, как и Сутееву, что-то не ясно в этом
понятии? Видимо, мне следует сказать несколько поясняющих
слов.
— Садитесь, Сутеев. Все, что вы написали, правильно.
Но ваш график я перерисовал бы, масштаб выбрал бы
покрупнее и приращение Ах для начала взял бы побольше. Я
отмечу его ради наглядности не только на оси абсцисс, но
и на самой кривой, и приращение функции отмечу тут же.
Треугольник, который при этом образовался, действительно,
Лт
позволяет истолковать отношение §^ как тангенс угла наклона
некоторой прямой, но не касательной, а... как вы думаете,
Гарин?
— Секущей.
— Правильно; ведь гипотенуза нашего треугольника — это
отрезок секущей, оба его конца лежат на кривой: заметьте это
себе, Сутеев! Возьмем теперь приращение Ах поменьше. Секу-
щая пройдет на этот раз в другом направлении и тангенс угла ее
наклона будет другим. Будем далее брать все новые, все меньшие
значения Ах — устремим его к нулю. Предельное положение
секущей при Дх, стремящемся к нулю, если оно существует,
определяет касательную к графику функции f(x) в точке х.
Следовательно, предел lim д^, то есть производная /'(х), — это тан-
Ах—>0
гене угла наклона касательной к оси абсцисс. Как подсказывает
график, в разных его точках касательная будет наклонена по-
разному. Таким образом, производная некоторой функции f(x)
также будет представлять собою некоторую функцию от того
же аргумента. Вот, скажем, функция sinx. Ее производная, как
мы хорошо знаем, — это cosx. Я нарисую оба графика один под
К). В. Пухначев] СЕМЬ СЕМИНАРОВ 191
другим. График синуса исходит из начала координат с
наибольшей крутизной, наклоненный к оси абсцисс под углом ^, тангенс
которого единица, — и в полном соответствии с этим косинус
принимает в нуле значение +1. Далее наклон синусоиды
падает — уменьшается и косинус, и когда касательная к синусоиде
становится горизонтальной, то есть тангенс угла ее наклона
обращается в нуль, косинусоида пересекает ось абсцисс. Наклон
синусоиды после этого становится отрицательным — косинус также
принимает отрицательные значения. И когда синусоида
пересекает горизонтальную ось под углом — j достигая максимальной
отрицательной крутизны, косинус принимает свое наименьшее
значение, равное минус единице. Все сходится, не правда ли? Но
давайте для пущей уверенности, пользуясь определением
производной, выведем сами, что производная синуса есть косинус.
('мотрите и запоминайте, как это делается. Все понятно?
Садитесь. Теперь, ребята, давайте подтвердим формулы
дифференцирования функций cosx, хп) ах) \пх.
Изобретая удачные преобразования, опираясь на
замечательные пределы, мои задания выполняют у доски Синица, Кочин,
Рамзин, Мухин.
Радует Мухин: усвоил-таки с прошлого семинара предел
п^ ', без запинки применяет его сейчас, при диффе-
Н11-
192
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
[Гл. 3
ренцировании логарифма. Неплох и Кочин: не расписывает
бином, а ссылается на соответствующий замечательный предел
и отмечает, что п — вообще говоря, не целое.
Поглядывая на доску, хожу между столами, наблюдаю за те-
ми, кто послабее. В действиях Лапикова чувствуется упорство,
но за вызванными к доске он при всем желании не поспевает:
боясь отстать, нет-нет да и глянет на их выкладки.
К доске между тем выходят Чюмин, Кулагин, Горт, Костюк:
из существования производных у функций f(x) и д(х) они
выводят формулы дифференцирования их суммы и произведения,
частного и суперпозиции.
Ю. В. Пухначев] СЕМЬ СЕМИНАРОВ 193
Аргунова пару раз подзывает меня к себе слезливым
«непонятно!», и я объясняю ей кое-что из того, что делается на
доске. А Сынчиков — молодец: сам старается справиться со своими
трудностями, на доску смотрит изредка, в самые безнадежные
моменты. Мне только однажды приходится помогать ему
советом, когда Горт дифференцировал частное и по своему
обыкновению перемахнул к выражению, готовому для предельного
перехода, от исходной разности, едва приведя ее к общему
знаменателю. Что делать с получившейся дробью, Сынчиков как
раз и забыл: сидит, напряженно вперившись взглядом в
доску... «Если в числителе, — говорю ему вполголоса, — прибавить
и вычесть ...» Хватит ли ему этого? Надолго погрузившись в
раздумье после моей подсказки, он все-таки догадывается сам,
что именно следует прибавить и вычесть, — и получает верный
ответ.
— Теперь, ребята, когда мы уже довольно много повозились
и с вычислениями, и с графиками, стоило бы для лучшего
запоминания еще раз кратко и четко сформулировать понятие
производной, усвоенное, надеюсь, теперь уже всеми. Не сделаете ли
но, Стрельцов? Пожалуйста, к доске.
194
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
[Гл. 3
— Пусть дана функция /(х), определенная на некотором
интервале (а, 6). Возьмем на нем точку х и еще одну, близлежащую,
х + Ах. Образуем разность f(x + Ах) — /(я), назовем ее
приращением функции f(x) на отрезке [х,х + А] и обозначим Af(x).
Образуем затем дробь -gjp и исследуем ее поведение при
стремлении Ах к нулю. Если она имеет предел, то он называется
производной функции f(x) в точке х и обозначается символом -^gp-
или /'(х), а сама функция при этом называется
дифференцируемой в точке х. Любая элементарная функция дифференцируема
в каждой точке своей области определения. Сумма и
произведение, частное и суперпозиция двух дифференцируемых функций
также дифференцируемы.
Речь его и движения при всей их точности подернуты какой-
то легкой, грациозной расслабленностью, весьма идущей ему,
впрочем.
— Спасибо, садитесь, все в вашем ответе верно. Только не
стоило так незаметно, без пояснений отождествлять
существование производной и дифференцируемость. Это все-таки разные
вещи, несмотря на их тесное родство. Чтобы вы понимали это,
ребята, я хотел бы сравнить их определения. Что такое
производная, мы знаем уже неплохо после стольких разговоров о ней.
А вот что такое дифференцируемость... Надеюсь, лектор давал
вам это понятие? Пусть кто-нибудь напомнит нам его —
например ... Меншиков.
Ленивый, но неглупый, он будет мне сейчас хорошим
собеседником: понаделает ошибок в тонких местах, которые не
удосужился продумать по своей лености, а его сообразительность
поможет быстро исправить эти ошибки, когда я укажу на них.
Так будут выявлены и тут же разъяснены типичные
заблуждения, которые возникают при знакомстве с понятием
дифференцируемое™.
— Функция f(x) называется дифференцируемой в точке х, —
начинает он, — когда приращение функции в этой точке можно
представить в виде Ау = А Ах плюс... а вот плюс что, я забыл.
— Приплюсуйте что угодно — потом вспомним поточнее. Вы
Меньшиков
ДЦ = Адх-ь ср(ос)
пишите (р(х)? Хорошо, пусть будет (р(х). А что обозначает в этой
формуле Ах?
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
195
— Приращение аргумента.
— Приращение... Вы хорошо запомнили это выразительное
словечко. Боюсь только, что выразительность его звучания
заслонила от вас свойство величины, им названной, а новизна
обозначения Ах не способствует его пониманию. Между тем,
ребята, нам в наших рассуждениях о дифференцируемости никогда
не следует забывать, что Ах — величина переменная, обычно
устремляемая к нулю. Чтобы лучше понять ее роль в формуле
дифференцируемости, давайте обозначим ее по-другому. Точку,
в которой мы будем исследовать на дифференцируемость
функцию /(я), назовем хо, рядом с нею возьмем точку х\ тогда
приращением аргумента будет... что Меншиков?
— Разность х — хо.
— Верно, Ах = х — хо- В таком же стиле переобозначим
левую часть формулы дифференцируемости: Ау = у — уо- И если
рассмотреть в этой формуле только то, что вспомнилось вам,
Меншиков, она примет вид у — у0 = А(х — хо). Вам когда-нибудь
встречалось такое выражение?
— Дайте вспомнить... Похоже на уравнение прямой.
— Верно! Это уравнение прямой линии с угловым
коэффициентом А, проходящей через точку с координатами (хо>Уо)- Вот
я нарисую график некоторой функции у = /(х), отмечу на нем
какую-то точку, обозначу ее координаты (хо, уо)> & вы проведите
через эту точку какую-нибудь прямую.
— Проведу касательную.
— О, я вижу, вам много что запомнилось из лекции о
дифференцировании функций! Прямая, как видим, расходится с
графиком функции f(x). Теперь я возьму на оси абсцисс рядом
со значением хо еще одно, обозначу его просто х. Затем я
отмечу приращение аргумента Дх, отмечу приращение функции
196
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
[Гл. 3
Д/ = f(x) — f(xo), наконец, отмечу величину А(х — хо) = ААх.
Как видите, две величины, отмеченные мною напоследок, не
совпадают, между ними остается некоторый зазор, некоторая
невязка. Как вы ее обозначите?
— Это ведь и есть то самое </?(#), которое мы прибавляли
к ААх.
— Совершенно верно! Что вы скажете про эту добавку (р(х),
если я устремлю х к xq, иначе говоря, устремлю к нулю
приращение Ах?
— Что эта... невязка, как вы говорите, стремится к нулю.
Он словно не был на прошлом семинаре, не слышал
того, что я втолковывал Мухину насчет касательной за
разговором об эквивалентности функций. Повторить все
заново? Да, надо бы: ведь если сказанное мною в прошлый
раз не запало в память Меншикову, того же можно
ожидать от других, менее сообразительных его товарищей по
группе.
— Просто стремится к нулю и только? Тогда я не понимаю,
зачем вам нужно было проводить именно касательную к
графику функции в точке (хо,Уо)- Проведите через эту точку
любую прямую — и зазор между нею и графиком функции будет
исправно стремиться к нулю. Смотрите: я покажу это на
новом чертеже. Если вы вглядитесь в него внимательнее, то
обнаружите, что зазор Д/ — ААх уменьшается так, что
остается приблизительно пропорциональным приращению аргумента.
В самом деле: вблизи точки (xq, Уо) график функции идет
почти прямолинейно, так что его скрещение с нашей новой
прямой можно рассматривать как угол, от которого вертикали,
соответствующие различным приращениям Ах, отсекают
подобные треугольники. Вертикальная сторона каждого такого
треугольника равна Д/ — ААх, а высота, опущенная на эту сторо-
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
197
ну, — приращению Дх. Теоремы о подобии треугольников под-
Af—AAx
сказывают, что отношение названных величин J Ax— при
изменении Дх остается примерно одинаковым и при стремлении
Ах к нулю будет стремиться к некоторой ненулевой величине.
Так оно будет — обратите на это серьезнейшее внимание, Мен-
шиков — почти с любой прямой, которую мы проведем через
точку (хо, Уо)- Почему почти? — спросите вы. Отвечаю и
прошу выслушать меня внимательнейшим образом: возможно, что
через данную точку графика функции /(х) можно провести
такую прямую, что дробь ' д х будет стремиться к нулю при
бесконечном уменьшении Ах. Тогда и говорят, что эта
функция f(x) в данной точке дифференцируема. Вглядитесь, Менши-
ков, в предыдущий график, который мы с вами рисовали
вместе в самом начале, постарайтесь увидеть и понять, как на этом
графике при подходе к точке (хо,уо) сближаются кривая и
нарисованная вами прямая: при Дх, отложенном мною поначалу,
расхождение между кривой и прямой составляло почти
половину Ах; взяли вдвое меньшее приращение аргумента —
расхождение уменьшилось чуть ли не до пятой доли этого
приращения; взяли еще вдвое меньшее приращение — расхождение уже
совсем ничтожно по сравнению с Дх, так что можно вполне
поверить, что для этой прямой при Дх, стремящемся к нулю,
дробь ' д х тоже будет стремиться к нулю, будет бесконечно
мала...
— А! — перебивает меня Меншиков, — Вы что-то похожее
уже рисовали... Когда? Совсем недавно когда-то ... не вспомню
точно...
— Ну, а как мы обычно обозначали бесконечно малую
функцию, — не вспомните? Символом а(х) — не так ли?
Давайте, так и сейчас обозначим нашу дробь ^дж ж, коль
скоро мы уже уверены в ее бесконечной малости. Обозначим ее
как функцию бесконечно убывающего аргумента Дх, вот так:
а(Дх). Как тогда представится приращение функции Д/,
Меншиков?
Он пишет: Д/ = ААх + а(Дх) • Дх. Донимаю его новыми
вопросами:
— А как мы когда-то вводили понятие о малого — помните?
Как истолковывали обозначение о(х)?
— Кажется, так: о(х) = а(х) • х... Я понял, что вы
хотите сказать! Функция называется дифференцируемой в точке
х, если ее приращение в этой точке можно выразить в виде
198
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
[Гл. 3
Д/ = ААх + о(Ах). Когда вы спросили об этом в первый раз, у
меня это из головы вылетело...
— Ничего, те, кто нас слушал, только поблагодарят вас за
забывчивость: иначе мы не разобрали бы так обстоятельно
понятие дифференцируемости. Я хочу теперь, ребята, напомнить
вам полное, строгое определение этого понятия. Садитесь, Мен-
шиков. Итак, функция называется дифференцируемой в точке
х, если существует некоторое число А такое, что приращение
функции в этой точке, то есть Д/, можно выразить в виде
линейной функции приращения аргумента с коэффициентом
пропорциональности А, то есть ААх, плюс некоторая величина,
которая представляет собою о малое от приращения
аргумента. Вся суть дифференцируемости именно в таком поведении
добавочного слагаемого, в том, что при определенном значении
коэффициента А оно стремится в нулю быстрее, чем
приращение аргумента, когда тот бесконечно уменьшается. Само по
себе представление приращения функции в виде ААх плюс
какое-то добавочное слагаемое еще мало что значит. В самом
деле, возьмите наугад какое-то А, выпишите разность значений
нашей функции f(x) в точках х и х + Ах, составьте разность
А/ — f(x + &х) — /(х)> составьте потом произведение ААх,
вычислите разность между Д/ и ААх, обозначьте ее как-нибудь —
хотя бы ip(Ax), как было у нас вначале, — и пожалуйста:
Д/ = ААх + ip(Ax). Внешне все, как в формуле
дифференцируемости. Но о дифференцируемости тут говорить еще рано.
Для этого надо еще исследовать функцию <р(Ах), а точнее — ее
отношение к Ах. И если при некотором А это отношение будет
стремиться к нулю при бесконечном уменьшении Ах — только
тогда мы назовем функцию дифференцируемой в точке х.
Слагаемое ААх мы назовем в таком случае ее дифференциалом
в этой точке. Всё ли было вам понятно, ребята, в моем
объяснении?
— Да! Все! — слышатся голоса.
— Тогда давайте займемся проблемой, которая скрывается в
том, что мы с Меншиковым говорили до сих пор о
дифференцируемости функций. Ну-ка, посмотрите внимательно то, что вы
записали по ходу того разговора.
Шелестят страницы... Спрашиваю минуты через две-три:
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
199
— Никто не находит ничего неясного? Как, Миклашевский?
Как, Горт? Нет? А помните, когда мы с Меншиковым разбирали
определение дифференцируемости функции в некоторой точке
хо, когда я сказал о существовании такой прямой, что
расхождение между нею и графиком функции есть о малое от
приращения аргумента, и попросил Меншикова проиллюстрировать
сказанное, то подходящей для этого прямой ему показалась
касательная к графику функции в точке xq (воспроизвожу этот
график).Но ведь мы знаем: как бы удачна ни была
иллюстрация, она не может заменить доказательства. Так ведь, ребята?
Теперь вы видите проблему, на которую я вам намекал?
— Надо доказать, что касательная и есть та самая прямая,
которая имеется в виду в определении дифференцируемости, —
улавливает мою мысль Синица. — Верно? Да?
— Угадали! Над доказательством думаем все вместе, — даю
сигнал к действию.
И пару минут спустя:
— Судя по тому, что никто из вас не брался за авторучки,
доказательство не найдено.
— Непонятно, с чего тут начинать, — жалуется Лапиков.
— Может быть, непонятно даже, в чем заключается
проблема? Как, Костюк?
— Да нет, тут-то все ясно: доказать, что расхождение между
касательной и графиком функции есть о малое от приращения
аргумента.
— Что же мешает вам развивать доказательство? Я
подскажу: мешает то, что при всей четкости, с которой вы описываете
проблему на словах, вы не видите ее математического описания.
11то такое, например, касательная, Костюк?
— Предел секущей.
— Опять слова! — с сожалением качаю головой. —
Напишите, пожалуйста, — указываю на график, — уравнение прямой,
которая касается графика функции у = f(x) в точке (хо, Уо)-
— Касательная — это прямая, которая... ну... это самое...
Дайте нам уравнение прямой, которая касается графика
функции в точке (яо>Уо)-
Его растерянное молчание длится еще несколько секунд — и
идруг:
— Все понятно!
И каскад равенств:
— Производная f'(xo) — это тангенс угла наклона
касательной, провведенной к графику функции f(x) в точке с
200
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
[Гл. 3
абсциссой хо- Значит, уравнение касательной выглядит так:
у - Уо = f(xo)(x — хо). С другой стороны, производная f'(xo) -
это предел отношения д£. Значит, само это отношение можно
представить в виде: производная плюс бесконечно малая
величина, а отсюда сразу получается формула дифференцируемости, и
производная /'(яо) играет в ней роль коэффициента А, который
мы писали, когда давали определение дифференцируемости.
— Окончательный ваш ответ верен, и преобразования
безошибочны, а вот в логике есть пробелы. О производной f'(x)
можно говорить лишь в том случае, если предел отношения д£
существует. Таким образом, вам вывод следует сформулировать
так: если у функции f(x) в точке xq существует производная,
то функция дифференцируема в этой точке и коэффициент А в
формуле дифференцируемости равен f'(xo). Запишите в своих
тетрадях, ребята, .рассуждение Костюка и мое резюме. Линас, —
поторапливаю некоторое время спустя Буткуса, все еще не
оторвавшегося от тетради, — вы что-то замешкались.
— Нет, я уже другое пишу, другое доказательство.
— Вы по-другому доказали то, что получил Костюк?
— Нет, я другое доказал.
— Тогда что же? Покажите на доске.
— Что такое дифференцируемость? Это когда приращение
функции допускает представить...
Он обрывает речь, стесняясь своего косноязычия и переходит
на язык формул, выписывает их тоже не очень каллиграфично,
но все же понятно.
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
201
— Вывод? — спрашиваю Буткуса, когда он кончает писать.
— Если функция f(x) дифференцируема в точке хо, то она
имеет в этой точке производную. Производная равна
коэффициенту А в формуле дифференцире ... дифферици...
— Дифференцируемости, — выручаю его. — Вывод верный.
Теперь мы можем утверждать, что дифференцируемость
функции f(x) в некоторой точке хо и существование производной
f'(xo) — вещи эквивалентные. Костюк доказал, что из
существования производной следует дифференцируемость, а Буткус
показал обратное. Показал правильно, только жаль, что так кратко:
появление символов предела в предпоследнем равенстве следует
оправдать. Априори не ясно, что его левая часть должна иметь
предел при бесконечном уменьшении Ах — так ведь, Линас?
— Она должна иметь предел, потому что правая часть имеет
предел — по определению о малого.
— Вот теперь все обосновано. Садитесь, Буткус, — вопрос
можно считать исчерпанным. И все-таки, ребята, меня
продолжает заботить та легкость, с которой вы применяете операцию
предельного перехода к отношению д£: ведь оно может и
не иметь предела. Разве вам неизвестны недифференцируе-
мые функции? Назовите какие-нибудь. Полистайте конспекты
лекций — лектор наверняка разбирал случаи, когда какие-то
функции недифференцируемы в каких-то точках.
Примеры следуют незамедлительно — я едва успеваю
набрасывать на доске соответствующие графики.
Сутеев:
— Модуль х, Он недифференцируем в нуле.
Кулагин:
202
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
[Гл. 3
— Синус j — недифференцируем там же.
Чюмин:
— Сигнум х — тоже нет производной при х = 0.
И некоторое время спустя — Гарин:
— Возьмем функцию х sin ^ и доопределим нулем при х = 0:
получается функция, недифференцируемая в начале координат.
— Хорошо, - подвожу черту. — Рассмотрим эти функции
в точках их недифференцируемости, познакомимся поближе с
этим явлением, а заодно лучше поймем, что такое дифференци-
руемость. Не зря пословица гласит: «Не узнавши горького, не
узнаешь и сладкого». Так почему функция |х| недифференци-
руема в нуле? Как вы думаете, Сутеев? Пожалуйста, к доске.
Выразите свое мнение четкими формулами.
В глухом, как его китель, безмолвии он пишет: |х| = xsgnx,
d\x\
-к? = ssnx-
— Ну и что? — удивляюсь, что вслед за этим он кладет мел. —
Из написанного вами не следует, что модуль х в нуле
недифференцируем: функция sgnx существует всюду; еще в начале
семинара она, если вы помните, ввела нас в заблуждение в
аналогичном случае. Попробуем подойти к модулю х иначе. Обратимся
от формул к графику. Давайте думать вместе, ребята, —
поворачиваюсь к сидящим.
— А нуль — это о малое? — направляет на меня свои окуляры
Чюмин.
— Не понял вашего вопроса.
— Я спрашиваю: если взять функцию v?(x), которая
тождественно равна нулю, то можно ли считать, что (р(х) = о(х)?
— Думаю, что на такой вопрос вы сможете ответить и без
моей помощи. Вы помните определение о малого? Что это значит:
ip(x) = о(х) при х —> 0?
— Это значит, что lim^^- = 0.
х-0 х
— Верно, — записываю сформулированное им условие на
доске. — Подставьте вместо <р(х) тождественный нуль — будет ли
тогда равен нулю такой предел?
— Будет.
— А вы не боитесь, что при предельном переходе знаменатель
дроби обратится в нуль и лишит ее смысла?
— Знаменатель? — переспрашивает Чюмин с осторожной рас-
становочкой: почувствовал, что я спрашиваю его об этом
неспроста. — Икс у нас стремится к нулю... Ну да, икс стремится к
нулю...
Ю В, Пухначев]
СЕМЬ СЕМИНАРОВ
203
Повторы, замедленный темп речи — все это для того, чтобы
в погоне за разбегающимися мыслями настигнуть ту, которая
напоминала бы слышанный когда-то верный ответ на подобные
вопросы... Настиг:
— Если икс стремится к нулю, то он не равен нулю, не
обращается в нуль!
— Может не обращаться или не может обращаться?
— Вообще не обращается. По определению предела
функции.
Вспомнил! Молодчина!
— Хорошо. Ну вот: наша дробь оказалась бесконечно малой,
и получается, что нуль — это о малое, если пользоваться вашими
выражениями, Чюмин. Но к чему вы об этом спрашиваете?
— Да я тут подумал: если приложить прямую к одной
половинке графика модуля, справа, например, зазор ведь будет равен
нулю, а нуль это о малое, вы сами сказали. Почему же мы тогда
говорим, что модуль в нуле недифференцируем?
— В самом деле, — оборачиваюсь к Сутееву, — почему?
— Потому что тогда зазор будет слева. Он будет равен 2Дх.
ЗдесьИт^ = 2.
Как быстро он пишет это равенство! Как непохоже это на
неловкость, которую он испытывал при действиях с формулами!
Правда, он забыл приписать Ах —> 0 под символом предела, но
это мелочь по сравнению с тем, как ловко и верно он получил
ответ. И как непривычно звучит его голос! Теперь он странно
прерывист и глуховат.
— А если приложить прямую к графику слева?
— Тогда зазор справа. И тут опять он такой же, 2Дх.
204
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
[Гл. 3
— Можно ли как-то еще провести прямую через начало
координат?
Он рисует ее сначала так, что она почти сливается с осью
абсцисс, потом так, что выше начала координат она пролегает
внутри прямого угла, образованного ветвями графика:
— Тут ненулевой зазор справа и слева. Тем более
недифференцируемость.
— То есть и справа, и слева отношение зазора к Дх равно
величине ненулевой и притом постоянной, так что не стремится
к нулю при бесконечном убывании Дх. Так?
-Так.
— Вы полагаете, что четыре характерных случая,
рассмотренные вами, исчерпывают все возможности? Что прямая,
проходящая через начало координат, больше никак не может
располагаться по отношению к графику?
-Да.
Потребовать, чтобы он повторил все снова языком формул,
предельно четко и строго? А вдруг снова откажется? В своих
отказах он стоек. Замкнется — и лишится ощущения успеха,
которое сейчас в нем есть наверняка. А оно не должно пропасть
ни в коем случае — это плацдарм для его дальнейшего
продвижения вперед. Аккуратно повторяю сам доказательство
недифференцируемости модуля в нуле, попросив Сутеева внимательно
следить за моим пересказом нашей с ним беседы.
— Все верно, да? Тогда садитесь. Добавлю только, что к
подобным примерам возможен еще один подход. Дифференциру-
емость функции в некоторой точке, как мы уже знаем,
эквивалентна тому, что у этой функции в данной точке
существует производная. Стало быть, недифференцируемость
равнозначна несуществованию производной, несуществованию предела у
отношения д£ при Ах, стремящемся к нулю. Проверим это на
примере все того же модуля х. Кто хотел бы это сделать? Вы,
Рамзин? Прошу.
— Я бы с вашего позволения сначала заметил, — не спеша
начинает он, методично сопровождая свои слова выкладками, —
что в нашем случае Д/ = |х — 0| = |х|, а Ах = х — 0 = х,
значит, д£ = 1^1. Данное отношение мы и должны исследовать на
существование предела при х, стремящемся к нулю. Легко
видеть, что указанное отношение при ненулевых значениях х
совпадает с функцией sgnx и подобно ей в нуле предела не
имеет. Стало быть, у функции |х| нет производной в начале
координат.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
205
— Можно, однако, заметить, — перенимаю у него слово, —
что предел отношения ^ существует, когда х, стремясь к. нулю,
остается либо положительным, либо отрицательным.
— Односторонние пределы! — Рамзин спешит показать мне,
что это понятие, поначалу не принятое им на прошлом семинаре
со слов Буткуса, теперь уже в его активе. — В первом случае
предел равен плюс единице, во втором — минус единице.
— Подобные случаи, когда отношение д£ имеет пределы при
стремлении Ах либо к плюс нулю, либо к минус нулю,
можно рассмотреть особо и назвать lim -тД, если он существует,
правой производной функции fix) в точке х, a lim дг» если
Ах—►—О
он существует, — соответственно левой производной. Попробуйте
применить эти понятия к функции |х|, Рамзин.
— В свете данных вами определений про функцию |х| можно
сказать, что в начале координат она имеет правую
производную, равную плюс единице, а также левую производную,
равную минус единице. Эти производные, однако, не равны друг
другу.
— Все сказанное до сих пор, — намечаю новую мысль, —
позволяет подойти к вопросу о существовании производной у
функции с новой точки зрения...
— Если у функции, — подхватывает Рамзин, — в некоторой
точке существует левая и правая производная и они равны друг
другу, то у функции существует и производная вообще, притом
равная тому же значению. Справедливо и обратное: если у
функции в некоторой точке существует производная, как мы ее
определили с самого начала, то в этой точке у функции существуют
равные той же величине левая и правая производные.
— Все верно, спасибо, садитесь.
Говорю это, отправляясь в обход аудитории. Задерживаюсь
в «глубинке» — между столами Мухина и Аргуновой с одной
стороны, Чюмина и Сынчикова — с другой: жду, пока они
запишут в свои тетради то, о чем говорили мы с Рамзиным. Потом
продолжаю:
— Рассмотрим теперь, ребята, остальные из предложенных
вами функций, у которых, как вам кажется, в начале
координат неблагополучно в смысле дифференцируемости. Поскольку
недифференцируемость эквивалентна несуществованию
производной, мы вправе доказывать либо то, либо другое, выбирая
в каждом случае из обоих подходов наиболее удобный.
206
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
[Гл. 3
На исследование функции sin ^ вызывается Кочин: не без
моих наводящих советов приходит к выражению ^sin^; воздев
взор к потолку, натужливо припоминает, как на прошлом
семинаре мы говорили, что такое произведение неограниченно в
начале координат и потому предела там не имеет, а уж из этого
быстро делает вывод о недифференцируемости функции sin ^ в
нуле. Отослав его с благодарностью на место, гляжу на
Лапикова: не хочет ли он пойти к доске следующим? Его, вижу, самого
подмывает попробовать: если уж у Кочина получилось... Встает,
идет к доске, рисует на ней чертеж и, сея вокруг сбивчивые
выкладки, показывает, что к графику сигнума х в начале
координат нельзя приладить прямую так, как того требует определение
дифференцируемости. Гарин решает вопрос о
недифференцируемости предложенной им функции обоими способами.
— Мне кажется, ребята, — сравниваю ответы всех троих, —
что есть некоторая неравноценность в том, как вы применяете
оба способа, которыми пользуетесь. Несуществование
производной — это несуществование предела некоторой функции, на этот
счет у нас есть четкое определение. А недифференцируемость
вы обосновываете одними лишь картинками. Разве вы не
можете сформулировать определение недифференцируемости? Как,
Мухин? Прошу вас к доске.
— Недифференцируемость — это когда приращение функции
нельзя представить в виде Д/ = ААх + о(Ах).
— Мы когда-то договорились не давать негативных
определений, то есть таких, где участвуют слова «нельзя», «не
существует» и им подобные.
— Без них — так вы хотите? Тогда вот что — сначала
возьмем определение дифференцируемости: Д/ = ААх — нет, не
так — существует А такое, что Д/ = ААх + о(Ах) — значит,
недифференцируемость — это когда для любого А — любого А —
Д/^ ААх + о(Ах).
— Как же прикажете понимать это неравенство? Представьте
себе: вот у нас есть некоторая функция f(x). Мы рассматриваем
ее в некоторой точке ее области определения, даем аргументу
какое-то конкретное приращение Дх, скажем, Ах = ^,
определяем соответствующее приращение функции Д/ — пусть оно
равно J*. Ну, а второе слагаемое в правой части вашего
неравенства: Откуда его брать? Не знаете? И я не знаю: в
обозначении о(Ах) нет указания ни на какую определенную функцию.
Но послушайте: если бы даже для выбранного нами конкретного
Ах мы и смогли определить значение слагаемого о(Ах) — пусть
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
207
оно равно ^ — это не избавило бы нас от ощущения парадокса:
ведь при каком-то А равенство Д/ = ААх + о(Ах) выполняется.
При выбранных нами значениях остальных величин,
участвующих в этом равенстве, оно справедливо при А = 2. В самом деле:
Yq = 2-^+^. А вы говорили, что неравенство Д/ ф ААх+о(Ах)
сохранится при любых А. Что же вы скажете теперь, Мухин?..
А вы, ребята?
Мёртвое молчание наступает вслед за моим вопросом. Такого
я не ожидал: мне казалось, что своими дотошными
разъяснениями дифференцируемости я снабдил ребят всем необходимым для
ответов на подобные вопросы. Почему же они молчат?!
Хоть растолковывай все заново! Я и впрямь собираюсь
сделать это, когда Стрельцов поднимает на меня просветленный и
чуточку виноватый взгляд:
— А ведь мы еще одним способом определяли дифференци-
руемость, точнее, по другому писали условие
дифференцируемости, исследовали дробь ' дд х. Если существует такое А, что
эта дробь стремится к нулю при бесконечном уменьшении Ах, —
функция дифференцируема, а если для любого А дробь к
нулю не стремится, когда Ах бесконечно уменьшается, — функция
недифференцируема. То есть это неравенство Д/ ф ААх+о(Ах)
надо понимать в предельном смысле, только так — проверка при
каком-то одном значении Ах здесь ничего не дает.
— Верно! Конечно! Только так! — раздаются несколько
секунд спустя все более громкие, все более уверенные голоса.
Я воспринимаю их, как оглушенный, к которому возвращается
слух, Нет, не впустую было то, что я говорил раньше!
— Вы поняли то, что сказал Стрельцов? — спрашиваю у
Мухина. И в ответ на его уверяющий кивок прошу его доказать
предложенным методом, что непрерывная функция, задаваемая
с помощью формулы xsin j, недифференцируема в нуле.
Что касается основной идеи метода и реализующих его
выкладок, то их Мухин и впрямь усвоил неплохо: дробь *дд х
быстро превращается в разность sin ~ — А. Но его логика...
— Конечно, недифференцируема! — пылко восклицает он,
еще не оторвав мела от доски. — Вот этот sin ^ — он же ни к
какому пределу не стремится — мы уже доказывали — у него в
нуле предела нет!
— Постойте, но ведь рядом с sin ^ у вас написана еще одна
величина!
Он смотрит на меня непонимающе. Мне стоит заметного
труда, чтобы он обратил внимание на букву А в полученной им
208
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
[Гл. 3
разности, сообразил, что это А, как величина постоянная, имеет
предел в нуле, вспомнил теорему о сумме сходящейся и
расходящейся величин... «Мы такое для последовательностей
доказывали, и сейчас можно доказать, если взять определение предела
функции на языке последовательностей», — торопливо
вставляет Горт. Я заставляю Мухина выслушать это еще раз, после чего
он уже без моей помощи заключает со ссылкой на сказанное
Тортом: разность sin ^ — А в нуле предела не имеет.
— Логика, Мухин, логика! — школю его, отсылая на
место. — В ней вся суть нашего давнего уговора о том, чтобы вы
продумывали свои рассуждения, прежде чем докладывать их.
В каждом своем умозаключении, если оно вам кажется верным,
постарайтесь выделить четкую логическую схему,
опирающуюся на уже известные определения и теоремы, дайте самому
себе строгий отчет в том, что в этой схеме все действительно
логично.
— Ну вот, — обращаюсь уже ко всем, — строгий подход к
вопросу о недифференцируемости нами наконец найден. Но то, что
вы не сразу нашли его, ребята, говорит о вашем слабом
понимании теории. Нажмем -ка на нее! Обратимся еще раз к
разобранным нами недифференцируемым функциям. Что можно сказать,
сравнивая их поведение в начале координат?
— Одни из них там непрерывны, другие разрывны, —
опережая всех, замечает Миклашевский.
— Непрерывность, разрывность, дифференцируемость,
недифференцируемость ... Существует ли какая-нибудь
взаимосвязь между этими понятиями? Что подсказывают нам на этот
счет решенные до сих пор примеры? — ставлю новые вопросы.
Тотчас же раздаются несколько ответов, разноречивые в
словах, единые по сути:
— Если функция разрывна в какой-то точке, то она там
недифференцируема.
— Согласен. Кстати, из этого утверждения чисто логическим
путем можно вывести еще одно...
— Если функция дифференцируема в некоторой точке, то она
там непрерывна, — догадывается Костюк.
— Тоже правдоподобно. Верно ли обратное?
— Нет, — отвечает он после секундного раздумья. —
Модуль х — функция в нуле непрерывная, но не
дифференцируемая.
— На этом же примере мы можем убедиться, что
недифференцируемость не гарантирует разрыва функции. Остается два
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
209
правдоподобных утверждения. Первое: из разрыва функции в
некоторой точке следует ее недифференцируемость в этой
точке. Второе: из дифференцируемости следует непрерывность. Как
будем их доказывать?
— Как прикажете, — с ноткой угодливости отвечает Рамзин.
— А я-то думал, что вы уже научились планировать свою
работу сами, без моих указаний. Логически оба утверждения
равносильны. Но, возможно, какое-то из них легче поддастся
доказательству...
— Конечно, второе! — не дает мне договорить Горт. — Надо
сначала...
— Минуточку! — останавливаю его. — Не лишайте других
удовольствия порассуждать!
Затем ко всей аудитории:
— Думаем все вместе, ребята: как доказать, что из
дифференцируемости следует непрерывность?
И некоторое время спустя:
— Кто доказал это? Ого, сколько рук! Интересно послушать
Кулагина.
— Непрерывность, — начинает он, — это когда при Дх,
стремящемся к нулю, приращение функции Д/ тоже стремится к
нулю. Теперь я возьму определение дифференцируемости. В
правой части равенства Д/ = ААх + о{Ах) и первое и второе
слагаемые стремятся к нулю, когда Ах уменьшается до нуля, значит,
и левая часть тогда тоже будет стремиться к нулю.
— Понял вас... Но все-таки еще раз: как вы представляете себе
непрерывность? Когда при стремящемся к нулю приращении
аргумента Ах к нулю стремится и приращение функции Д/... Этой
описательной фразой вы пользуетесь взамен строгого
определения непрерывности. Я не против подобных замен, которые часто
упрощают и облегчают рассуждения, — но только при условии,
если при этом вы не забываете стоящую за описательными
словами математическую сущность. Чтобы проверить это, я попрошу
вас вывести из определения дифференцируемости определение
непрерывности. Напишите-ка второе из них. Так, так ... для лю-
бого е существует 5... Вот и найдите зависимость S от е, опираясь
на то, что сумеете извлечь из определения дифференцируемости.
210
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
[Гл. 3
Опасаясь ошибки, он не спешит с ответом, скользит взглядом
по доске, пришептывая:
— Значит, 5 от £... Непрерывность... |Д/| < e...Af из
дифференцируемое™... модуль суммы...
И голосом погромче, поувереннее:
— Модуль правой части равенства в определении
дифференцируемое™ оценим сверху суммой модулей |АДх| + |о(Дх)|,
попробуем сделать то и другое меньше |. Очевидно, первое
слагаемое будет меньше | при |Дх| меньших ^гп• Второе слагаемое...
второе тоже можно сделать меньше |...
— Но несколько малым должно быть для этого | Дх|? Что ж
вы замолчали? Вам это не ясно? — стараюсь всмотреться в его
лицо, низко опущенное — в раздумьи? или в безнадежности?
— С первым слагаемым тоже не все ясно: если А = 0, дробь
2гп теряет смысл, — замечает Горт — без злорадного желания
добить поверженного, а из одной лишь своей ненасытной страсти
к строгости.
Но Кулагин вовсе и не повержен, не думает сдаваться:
— Если А = 0, то первого слагаемого просто не будет,
останется только о(Ах) — в нем вся штука. Сейчас я все сделаю, дайте
подумать ... Определение о малого... дд/ к нулю, значит, можно
меньше любого положительного числа... меньше |-А|... нет, не |Л|,
оно может в нуль... сейчас... не подсказывайте!., меньше любого
положительного... единицы?., тогда |о(Дх)| < |Дх|... Да,
существует S такое, что при |Дх| < 5 выполняется |о(Дх)| < |Дх|. И
тогда все оценки можно будет провести через Ах.
— Великолепно! — не могу не порадоваться его стойкости. —
Теперь до победного конца! И лучше — с самого начала.
Опять его речь осторожна, нетороплива:
— Оценим модуль суммы \ААх + о(Ах)\. Найдем S такое,
что при |Дх| < 5 получается |о(Дх)| < |Дх|. Тогда |Д/| =
= \ААх+о(Ах)\ < \ААх\ + \о{Ах)\ < |ЛДх| + |Дх| = (|Л| + 1)|Дх|.
Это выражение будет меньше е при |Дх| < \J+1- Теперь А = 0
уже не опасно. Из двух чисел 5 и \Af+1 возьмем минимальное и
обозначим его 5'. Если |Дх| < 5', то |Д/| < е. Все.
— Очень хорошо, садитесь. От теории вернемся, ребята, к
практическим задачам. Ради наглядности рассмотрим
поначалу уже знакомую нам функцию, равную нулю при х = 0, а в
остальных точках определяемую выражением xsin ^. В начале
координат, как мы уже знаем, эта функция недифференцируема.
А в остальных точках? Как вы думаете, Костюк?
Ю. В, Пухначев]
СЕМЬ СЕМИНАРОВ
211
— А что — в остальных? В остальных ничего
страшного. Если х ф О, то j дифференцируема, sin ^ тоже, как
суперпозиция дифференцируемых, а все вместе, х sin ^ — опять-
таки дифференцируемо, как произведение дифференцируемых
функций.
— И общий вывод, очевидно таков: при х = О наша функция
недифференцируема, а при х ф О — дифференцируема, —
подвожу итог. — Про каждую точку из области определения нашей
функции мы сказали, имеет она там производную или не имеет.
Исследование функции на дифференцируемость — вот как
называется подобный анализ. Поупражняемся в нем еще. Исследуем
на дифференцируемость функцию у = |(х — 1)(х — 2)2(х — 3)3|.
Не успел я дописать на доске формулу, как у Миклашевского
уже готов ответ:
— Не дифференцируема только в точках х = 1 и х = 3.
— К доске, Миклашевский! Обоснуйте свой вывод.
— Да тут все в общем-то тривиально. Все как с функцией
у = |х|. Модуль произведения — это произведение модулей:
|х — 1| • |(х — 2)2| • |(х — 3)3|. У второго сомножителя модульные
скобки можно стереть — квадрат всегда положителен, во
всяком случае, не отрицателен. На том же основании |(х — 3)3| =
= (х — 3)2|х — 3|. Значит, функцию можно переписать так:
у = (х - 2)2(х — 3)2|(х - 1)(х — 3)|. Теперь надо разбить
область ее определения на интервалы, на которых выражение
в модульных скобках будет сохранять знак; интервалы будут
такие: до единицы, между единицей и тройкой, за тройкой. На
каждом интервале функция выражается через полином, значит,
дифференцируема. А недифференцируема она будет на стыках
интервалов, в точках х = 1 и х = 3, там левая производная не
равна правой.
— Это еще надо проверить! — почти одновременно
вскидываются Горт, Рамзин, Кочин, Меншиков.
— Ну-ка, Миклашевский! — поддерживаю законное
требование. ,
—■ Сейчас... Слева от единицы у = |(х — 1)(х — 2)2(х — 3)3| =
= (х—1)(х—2)2(х—З)3 ... Значит левая производная функции у =
= (х — 1)(х — 2)2(х — З)3 в единице... (он поигрывает мелом в
раздумье: перспектива дифференцировать такую махину ему не
улыбается). А я вот что сделаю: напишу у = (х — 1)/(х). Тут
/(х) = (х - 2)2(х - З)3. Тогда у' = /(х) + (х - 1)/'(х) и, значит,
у'(1) = /(1) = (1 - 2)2(1 - З)3 = -8. А правая производная...
таким же образом... Получается +8, и выходит, что левая про-
212
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
[Гл. 3
изводная не равна правой, функция при х = 1 не
дифференцируема, как я и говорил!
— Хорошо. А в точке х = 3, там что?
— Тем же способом: между единицей и тройкой у = — (х—
-1)(х-2)2(х-3)3 = (х-3)3р(х), тогда у' = -3(х-3)2р(х)-(х-
—3)3р'(х), получается у'(3) = 0... Угу... Очевидно, если за
тройкой, то у = (х — 1)(х — 2)2(х — З)3 и у'(3) тоже нуль.
— И следовательно...
— Левая производная равна правой, дифференцируемость.
— А это и сразу видно! — вставляет Синица. — Из
графика! Давайте напишем, как было в самом начале: у = |(х — 1)(х—
—2)2(х — 3)3|. Здесь у нас в модульных скобках стоит полином,
который при х, стремящемся к минус бесконечности,
стремится к плюс бесконечности: ведь наибольшая степень х — шестая,
четная. Я график этого полинома на доске нарисую — можно?
Крутая, почти отвесная линия приближается сверху к оси
абсцисс.
— Как ведет себя этот полином в окрестности единицы? Как
линейная функция (х — 1), умноженная на какой-то
коэффициент; он получается, если в остальные сомножители подставить
вместо х единицу — Паша это уже показал. Значит, график
полинома в точке х = 1 пересечет ось абсцисс под каким-то углом
Паша его вычислил: — arctg8. А в окрестности двойки функция
будет вести себя как парабола (х — 2)2 с каким-то
коэффициентом, это легко Пашиным способом показать, с отрицательным
коэффициентом, по всей вероятности, раз она снизу к оси
абсцисс подходит — ведь верно? И график коснется этой оси, вот
так. А в окрестности тройки функция будет вести себя как
кубическая парабола: график пересечет ось абсцисс с касанием и
перегибом в точке х = 3. Когда мы возьмем модуль от полинома,
в единице получится излом, а в двойке и в тройке по-прежнему
будет касание.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
213
— Очень хорошее объяснение. Садитесь оба — и вы, Люда, и
вы, Павел.
И после того, как оба заняли свои места, обращаясь ко всем:
— Вы, наверное, ожидаете, ребята, что я опять разругаю
Миклашевского за торопливость, за верхоглядство. Нет, на сей раз
я не стану делать этого. Сегодняшние ошибки Миклашевского
требуют не категорического осуждения, а внимательного
разбора. Лозунг «не надо спешить, не надо выдвигать рискованных
гипотез», я уверен, не будет принят вами безоговорочно: вы
хорошо знаете, что истоками замечательных открытий очень часто
были смелые гипотезы. Остроумной гипотезой было заявление
Миклашевского о том, что функция у = |(х — 1)(х — 2)2(х — 3)3|
недифференцируема в точках х = 1 и х = 3, а в остальных
точках дифференцируема: этим вполне обосновано был очерчен
круг вероятных ответов. Поскользнулись же вы на том, Павел,
что не подкрепили догадку проверкой, выдвинули ее сразу как
окончательный вывод. Поверьте, ваши смелые пророчества
перестанут ставить вас в смешное положение, а наоборот станут
делать вам честь, если вы их будете не только выдвигать, но и
стараться строго обосновать — как вы это сделали, когда
должны были продифференцировать в единице громоздкое
произведение (х — 1)(х — 2)2(х- З)3 и представили его в виде (х — 1)/(х):
такой подход оказался надежным и плодотворным, он помог
Синице осмыслить поведение функции во всех интересующих нас
точках. Старайтесь использовать для обоснования своих гипотез
все средства — и преобразования формул, которые так удались
вам, и графики, о которых вам напомнила Синица.
Изощренность, которую вы будете приобретать при этом, со временем
придаст вашим рассуждениям и выкладкам ту легкость, к
которой вы так стремитесь, а опыт, подкрепляющий ее, убережет вас
от провалов. Но довольно поучений, вернемся к работе, к новым
задачам — на сей раз уже не аналитическим, а конструктивным.
Постройте, ребята, пример функции, не имеющей производных
в точках ai, а2, ...ап.
Иду между столами. Многие не медля пишут у = |(х — а\)(х—
—а2)...(х — ап)\. Среди них — Аргунова; вызванная к доске, она
воспроизводит схему рассуждений Синицы о
недифференцируемости функции |(х— 1)(х —2)2(х —3)3| в единице: рисует график
полинома (х — а\ )(х — а,2) •... • (х — an), потом график его модуля,
получая изломы в желательных точках.
— Хорошо, Аргунова, садитесь. На лекциях вы слышали,
ребята, что каждая элементарная функция дифференцируема в
214
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
[Гл. 3
каждой точке своей области определенности. Но если
обратиться к неэлементарным функциям — не припомните ли среди них
такую, которая в каждой точке своей области определения была
бы недифференцируема?
— Функция Дирихле! — тотчас отвечает Мухин и еще
многие вместе с ним. Увлеченный кажущимся единодушием,
я готов от каждого услышать обоснованное доказательство
недифференцируемости знакомой всем функции и, не
долго думая, с налету прошу об этом Сынчикова: мельком я
уже не раз замечал сегодня, что он живо следит за общим
разговором — авось, теперешнее мое задание будет ему по
силам.
К моему удивлению он стушевывается, опускает взгляд,
наливается краской.
Нехорошо получилось... Я забыл про свое давнее решение
вызывать его поосторожнее. Надо было перед тем, как его
вызывать, заглянуть в его тетрадь. Да и только ли в нем дело?
О каждом, кого я намереваюсь вызвать, я должен доподлинно
знать, на что он способен сию минуту, предвидеть его реакцию
и спрашивать так, чтобы неудачные ответы разжигали в нем
энергию, а не подавляли ее, удачные же — воодушевляли, но не
кружили голову... Нехорошо получилось.
Возвращаюсь к Мухину:
— Так как бы вы доказали, что функция Дирихле не имеет
производной ни в одной точке?
— Есть теорема: если функция в какой-то точке разрывна, то
она там недифференцируема. Функция Дирихле везде разрывна
следовательно, нигде не дифференцируема.
— Все логично! Теперь я прошу придумать функцию,
которая, наоборот, лишь в одной точке была бы
дифференцируема.
— Может быть, — приятно удивляет своей догадливостью
Лапиков, — та функция, которую на прошлом семинаре
придумал Виталик: х2, умноженный на функцию Дирихле? В
ненулевых точках она разрывна, значит,
недифференцируема, а в нуле у нее все точки... это... слипаются, разрыва
нет, к ней наверное, можно приставить горизонтальную
прямую...
— То, что вы имеете в виду, стоило бы пояснить графиком,
Лапиков. Прошу вас к доске ... Неплохо, очень неплохо, —
одобряю его рисунок. Напииште уравнение горизонтальной прямой,
которую хотите приставить к графику этой функции.
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
215
— Это же ось абсцисс, у = 0.
— Значит, коэффициент А в формуле дифференцируемости
Д/(х) = ААх + о(Дх) должен быть равен...
— Нулю: Д/(х) = 0 • Ах + о(Лх).
— Но, как легко видеть, А/(х) = /(х) — /(0) = /(х) — 0 =
= /(х); Лх = х — 0 = х. То есть формула дифференцируемости
приобретает вид...
— /(х) = о(х)
— Очень хорошо. Проверьте это для рациональных и
иррациональных х.
— Так и есть. Значит, /(х) в нуле дифференцируема.
— Отлично! Чтобы следующая задача была понятнее для вас,
ребята, я попрошу вас сначала придумать функцию,
определенную при сколь угодно больших значениях ее аргумента,
производная которой при бесконечном возрастании аргумента
стремилась бы к нулю.
— Гипербола у = j — тотчас откликается Сутеев.
— Хорошо. Рисуйте, Лапиков. Как видим, предложенная
функция стремится к нулю, убывая. Теперь я попрошу вас,
ребята, придумать функцию, у которой производная по-прежнему
убывала бы на плюс бесконечности до нуля, но которая при
этом возрастала бы и стремилась бы к положительной
величине.
216
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
[Гл. 3
Гляжу на Сутеева, который столь молниеносно выполнил мой
предыдущий заказ. Но он молчит, уставившись на меня
своими неморгающими глазами. Перевожу вопрошающий взгляд на
Синицу. Молчит и она, лишь смущенно прочерчивает в воздухе
пологую кривую.
— Вы поняли, Лапиков, — оборачиваюсь к доске, — что имеет
в виду Синица?
Он воспроизводит ее движение в графике.
— А как это выразить на языке формул? — допытываюсь у
Лапикова, у Синицы и, не дождавшись от них ответа, обращаюсь
за помощью ко всем.
— Да хотя бы так: у = 1 — j, — удивленно покосившись на
молчащих товарищей, предлагает Гарин.
— Уже не первый раз, ребята, — оглядываю аудиторию с
упрекающей усмешкой, — я подмечаю в вас этот недостаток:
вы всё понимаете, можете описать словами, обрисовать
графиками — а в математических понятиях выразить не умеете. Этот
порок надо изживать побыстрее! Ведь применение математики,
которая приобретает все большую роль в современных
исследованиях, начинается с того, что создаются математические
модели исследуемых явлений, установленные для этих явлений
закономерности формулируются в виде математических
соотношений. И дело тут не столько в том, чтобы ради каких-то
дополнительных выгод переводить на язык математики добытое в
рассуждениях на общепонятном языке, — нет, скорее наоборот:
для исследователей из очень многих областей современной
науки родным, привычным становится как раз язык математики,
в значительной мере не переводимый на житейскую речь. Все
вы, вероятно, слышали, как физики объясняют последние
достижения своей науки: мы, мол, научились понимать такие
вещи, которые невозможно вообразить. Суждение не совсем
точное: образотворческая способность присуща сегодня физике не
менее, чем когда-то, только ныне она пользуется в основном не
наглядными механическими образами, а абстрактными,
математическими. На какие же успехи вы можете рассчитывать в
своей будущей деятельности, ребята, покуда язык математических
формул, грамматика преобразований не станут для вас
привычными, родными? Давайте настойчивее овладевать этим языком!
Продолжим построение функций, у которых производная
стремится к нулю при стремлении аргумента к плюс бесконечности.
Но на сей раз попробуем придумать такие, которые в отличие от
прежних не имели бы предела на плюс бесконечности.
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
217
Мой вдохновляющий спич всколыхнул фантазию ребят:
Миклашевский предлагает In я, Стрельцов — у/х.
— Хорошо, — передаю их находки Лапикову на
иллюстрирование. — Обе эти функции неограничены на плюс бесконечности.
Попытаемся теперь изобрести ограниченную функцию, у
которой предела не бесконечности нет, а производная стремится к
нулю.
— Вы, кажется, что-то хотите сказать? — спрашиваю с
полминуты спустя Сутеева, медленно поднявшего на меня свой
неповоротливый взгляд.
— Да. Но я тоже — без формулы, только графиком.
— Ладно уж, рисуйте без формулы.
И он чертит на доске волны с одинаковой высотой и
неограниченно нарастающей длиной.
— Синус что ли? — морщит лоб Меншиков.
— Синус, говорите? — заинтересованно откликаюсь на эту
смутную мысль. -- Но...
— Но не от х, — моментально перехватывает слово Ко-
стюк. — Синус от чего-то, что растет неравномерно, все
медленнее...
— Но неограниченно, иначе не будет волн, — предостерегает
Гарин.
218
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
[Гл. 3
— Синус логарифма! — озаряется догадкой Синица.
— Или квадратного корня — правда? — с улыбкой киваю ей. —
Докажите-ка это на доске формулами, Сутеев. Все верно, сади-
тесь. Следующая задача: придумать функцию, которая при
бесконечном возрастании аргумента стремилась бы к пределу, а ее
производная — не стремилась бы.
Функция
отваживается рискнуть Рамзин.
— Докажите формулами.
— Функция стремится к нулю при бесконечном возрастании
аргумента, — начинает он еще на полдороге к доске, — вот оценка
на этот счет, а производная... Производная, к сожалению, тоже
стремится к нулю. Прошу прощения, — и берется за тряпку.
— Не стирай! — останавливает его Кулагин. Приглашенный
к доске, он возводит в квадрат аргумент синуса и в соответствии
с таким дополнением исправляет выкладки Рамзина. Потом
поясняет:
Функция 2 cos х2 не стремится на бесконечности ни к како-
— ™ ~2 стремится к нулю. Сходящееся и расходя-
му пределу, р sin x
щееся — их разность предела не имеет.
— Таким образом,— резюмирую я,
функция
при
стремлении аргумента к бесконечности стремится к нулю, а ее
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
219
производная (2cosx2 — §1^г-) не стремится. Хороший пример,
верное рассуждение, Кулагин. Садитесь, Андрей, и вы, Рамзин,
садитесь тоже, и вы, Лапиков. Мы переходим к новой теме. Речь
пойдет о дифференцировании функций, заданных еще мало
знакомыми для нас способами. Ну, например: у — esmy = х,
где О < е < 1. Здесь налицо зависимость х от у, но вряд ли мы
сможем вывести отсюда столь же короткую и простую формулу
для функции у(х). Можно лишь утверждать, что эта функция
существует как обратная по отношению к х(у). Нам известна
теорема: если на некотором отрезке задана непрерывная и
монотонная функция, то на отрезке ее значений существует обратная
по отношению к ней функция, притом также непрерывная и
монотонная. Ограничив для простоты изменение у пределами 0 и
|, мы легко применим эту теорему к функции х(у) = у — е sin у и
докажем существование обратной функции у(х). Функция х(у),
которую мы рассматриваем, дифференцируема по у.
Закономерен вопрос: следует ли отсюда дифференцируемость функции
у(х)? Оказывается, следует. Причем, если есть формула для
производной Ху, то можно получить и формулу для производной
у'х. Попробуйте это сделать, ребята, на примере нашей функции
х(у) = y-esiny.
Решение задачи долго не дается никому. Бродя между
столами, я не вижу в тетрадях у ребят ни одной стоящей выкладки.
И даже у Гарина пусто! Вопросительно всматриваюсь в его
глаза — и они отвечают мне знакомой затаенной улыбкой.
— Пожалуйста, к доске, Миша! — маню его за собою,
возвращаясь к столу.
Его идея проста и эффективна: начав с дроби ^, он
рассматривает ее как обратную по отношению к д| и получает в итоге
,/ = JL = I
•'я х'у 1-е cos у'
Когда я ставлю его решение в упрек остальным, те
оскорбленно шумят:
— Разве можно делать так, как он?
И Чюмин, выражая общее мнение, уточняет:
— Ведь ответ должен получиться как функция от х...
— Но разве я ставил такое условие? — удивляюсь в свою
очередь. — Вы полностью самостоятельны в своих поисках! Я
предупреждал вас, что мы приступаем к функциям нестандартного
кида, — значит, тут и подходы должны быть нестандартными.
11е надо зашоривать свою изобретательность привычками! Успех
Гарина призывает к этому весьма убедительно. И если вы спра-
220
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
[Гл 3
шиваете: «Разве можно делать так, как он?» — то под сомнение
следует ставить не оригинальность его подхода, а его
конкретные действия. Пусть он ответит, например: почему под знаком
предела он писал то Лу —► 0, то Лх —► 0? Ну-ка, Миша!
— Потому что х(у) функция непрерывная, и если
приращение аргумента Лу стремится к нулю, то к нулю же стремится и
приращение функции Лх.
— Вероятно, справедливо и обратное ...
— Да, потому что по теореме об обратной функции у(х) тоже
непрерывная, так что если приращение ее аргумента Лх
бесконечно убывает, то бесконечно убывает и приращение Лу. Можно
даже сказать, что в таком случае утверждения Лх —► 0 и Лу —> 0
эквивалентны.
— Вот-вот! Такая эквивалентность и обосновывает
взаимозаменяемость обоих утверждений. А почему вы перенесли в
знаменатель символ предельного перехода?
— По теореме о пределе частного двух функций. Надо было,
конечно, еще показать, что xfy ф 0.
— А это и так ясно: ведь функция х(у) монотонна, — не
раздумывая, замечает Кочин.
— Ого, — резко оборачивается к нему Горт. — Функция у = х3
монотонна, а в нуле у нее производная — нуль.
— Можно говорить об обратном: если производная нигде не
обращается в нуль, то функция монотонна, — уточняет Костюк.
— Теорема Костюка? — Меншиков растягивает губы в
иронической улыбке.
— А что? — отвергаю иронию. — Утверждение очень
правдоподобное и заслуживающее того, чтобы уделить ему то время,
которое будет оставаться у кого-нибудь из вас после решения
обязательных задач. Запишите его в свои тетради, — прошу
ребят, отослав Гарина на место.
Приятно, что в ответ на такие мои просьбы за ручки берутся
все. Даже Сынчиков, у которого вряд ли найдется время для
решения сложных дополнительных задач: ему успеть бы сделать
самое необходимое, самое простое! Но вслед за этой мыслью в
памяти моей звучит тихая, но твердая фраза, услышанная мной
от Сынчикова на первом семинаре: «...я все это обязательно
выучу!» И верится, что в глубине его души живет скрытая, но столь
же твердая уверенность: «Я буду не хуже других!»
А если не живет — ее должен вселить в него я.
На волне дискуссионного оживления вздымается голос Бут-
куса:
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
221
— А можно по-другому решать: продифференцировать по х
равенство у — е sin у = х. В правой части будет единица, а в
левой ух минус е производная sin у. Синус дифференцировать
как сложную функцию: будет cosy умножить на у'х. Потом найти
отсюда ух.
— Уверены ли вы, — испытующе смотрю на него, — что
равенство сохранится после дифференцирования?
Молчание. И убежденный голос Лапикова:
— Но ведь все получается верно!
— Это может оказаться и случайностью. Как же доказать,
что это закономерность? Не догадываетесь, Лапиков?
Скажите, когда по ходу дифференцирования левой части равенства
мы брали производную у по х, то мы ведь подразумевали под
у какую-то функцию от х, не правда ли? Какую же именно?
Как вы считаете, Лапиков? Молчите? А вы, Рамзин?
— По всей вероятности, ту, которая определяется равенством
у — е sin у = х.
— И если в это равенство вместо у подставить именно эту
функцию, то равенство обратится...
— Обратится в тождество! А производные от тождественно
равных функций равны друг другу.
— Вы совершенно правы, Рамзин. Вычислите-ка заодно
производные от функций arcsinx и arctgx — обратных по
отношению к синусу и тангенсу. Все верно, садитесь. Теперь, ребята, мы
наверное, сумеем вычислить производные и от функций,
задаваемых неявно. Так говорят, когда некоторая функция от х и у
приравнивается нулю или константе и для каждого допустимого
значения х подбирается такое значение у, при котором равенство
выполняется.
— А что это такое — допустимые значения х? — чуть
слышится негромкий вопрос Аргуновой.
222
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
[Гл. 3
— Значения, для каждого из которых существует такое у,
что равенство удовлетворяется. Может ведь случиться и так, что
для какого-то х такого у не найдется. (По ее глазам вижу, что
мои абстрактные рассуждения до нее не доходят). Это, пожалуй,
лучше пояснить на конкретном примере уравнения, задающего
неявную функцию, — скажем, на примере уравнения гипербо-
2 2
лы ^2 — р- = 1: если |х| < а, вы не добьетесь выполнения
равенства ни при каких вещественных у. Напротив, при |х| > а
легко получить у = Ьл/fs — 1; и если корень понимать в
арифметическом смысле, все будет так, как этого требует
определение функции: каждому числу х из некоторого множества
ставится в соответствие определенное число у. Вот и график такой
функции. Нетрудно заметить, что это лишь половина гипербо-
лы. Другую половину мы потеряли, выражая у через х в явном
виде и понимая корень в арифметическом смысле. Если же
сохранить неявное задание гиперболы, то оно позволит построить
график полностью. Как видим, у неявного представления
функций есть определенные преимущества перед явным — так что
его стоит изучать и применять. Поэтому давайте, не пытаясь
явно выражать ординаты гиперболы через абсциссы, сохраним
ее традиционное неявное задание и на этом примере
попробуем придумать общий способ, с помощью которого мы смогли
бы найти производную любой функции, заданной неявно. Я
вижу, Миклашевский, у вас уже есть кое-какие идеи на этот счет?
Пожалуйста, к доске. Но только смотрите — чтоб совершенно
строго! Можете?
Конечно, может — стоит только захотеть:
— Если в равенство, определяющее неявную функцию,
вместо у именно ее и подставить, оно будет выполняться
тождественно, то есть его левая часть будет тождественно
равно постоянной, в нашем случае — единице. И если те-
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
223
перь левую часть продифференцировать, то ее производная
будет равна нулю. После дифференцирования в левой части
появится производная у'х, которую можно будет выразить
через х и у — если решить получившееся равенство
относительно у'х.
Он подтверждает это, дифференцируя уравнение
гиперболы.
— Вот это — хорошее, толковое, строгое рассуждение.
Садитесь, Павел. Наконец, ребята, еще один нестандартный способ
задания функции. Мы разработаем его сами, рассматривая
движение точки окружности, катящейся подобно колесу по
прямой линии. Вид кривой, которую выписывает при этом
какая-либо точка окружности, вероятно, вам знаком, как и ее
название — это циклоида. Но каким уравнением описывается
>та кривая? Пусть прямая, по которой катится окружность,
будет горизонтальной осью прямоугольной декартовой
системы координат. Дополним эту ось вертикальной и расположим
окружность единичного радиуса так, чтобы интересующая
нас точка на ней совместилась с началом координат. А
потом прокатим окружность вправо, чтобы она повернулась на
угол (р. Каковы будут тогда координаты интересующей нас
точки?
Выждав некоторое время, вновь отправляюсь в путь из конца
и конец аудитории. Когда я даю задачу, непохожую на
предыдущие, нередки приятные сюрпризы: тот, кому еще совсем недавно
не везло, вдруг вырывается вперед, если задача ему по душе, по
складу ума.
Именно такой сюрприз на сей раз преподносит мне Мухин.
(Отчетливо, кратко и, пожалуй, лучше, чем у остальных,
выписывает он формулы, выражающие координаты точки катящейся
окружности через угол поворота (р. (Может быть, тут помогает
<чце и то, что, заметив его первые удачные попытки, я останав-
чпваюсь рядом с ним: под моим взглядом он старается работать
224 ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ [Гл. 3
внимательнее, аккуратнее). Подождав, пока он кончит писать,
зову его к доске.
— Только давайте обозначим угол поворота иначе, буквой
t. Теперь, ребята, обсудим внимательно способ задания функ-
циональной зависимости у от х, с которым мы познакомились
на примере циклоиды. Для некоторого значения величины,
называемой параметром и по традиции обозначаемой буквой
£, вычисляются значения функций x(t) и у(£); они и
образуют пару «значение аргумента — значение функции». Такое
задание функций называется параметрическим.
Предположим, что функции x(t) и y(t) дифференцируемы. Попытаемся
выразить через них производную у'х. Не сделаете ли это,
Мухин?
Пусть разовьет свой успех, насколько это ему по силам.
Урок Гарина пошел ему впрок: он начинает с дроби ^,
делит ее числитель и знаменатель на приращение Д£,
которое затем устремляет к нулю, и получает верный ответ:
t/ = ^
Ух X't'
— Проверить на циклоиде? — сам предлагает он и
подставляет в полученную формулу выражения для x(t)
и y(t).
— Проверка была бы еще более убедительной, —
всматриваюсь в выписанную им дробь, — если бы вы сумели подкрепить
свой результат с чисто геометрической точки зрения. Не
догадываетесь, как это можно сделать? Что могут предложить
остальные? — поворачиваюсь к аудитории. — Тоже ничего? Давайте-ка
я предложу вам в качестве косвенной подсказки один
простенький чертежик. Вот я беру окружность, ставлю на ней четыре
равноотстоящие точки A, J3, С, D и соединяю отрезками каждую
Ю. В. Пухначев] СЕМЬ СЕМИНАРОВ 225
пару этих точек. Скажите мне теперь: что представляет собою в
образовавшейся фигуре отрезок АС?
Ответы сыплются один за другим:
— Диаметр круга! Диагональ квадрата! Основание
треугольника АВС\ Гипотенузу этого треугольника — ведь он
прямоугольный! Сторону угла CAB, вписанного в круг! Биссектрису
угла DAB\ Перпендикуляр к DB\ Ось симметрии всей фигуры!
— Ого, какие мы сообразительные! — легкой улыбкой
отвечаю на эту лавину. — Тогда скажите мне: что представляет собою
на чертеже Мухина точка А?
— Основание перпендикуляра, опущенного из центра круга
на ось абсцисс! Нижний конец вертикального диаметра! — рьяно
бросаются ребята в новый поиск.
Ожидаемое мной толкование первым находит сам Мухин:
— Это ось вращения — точка, вокруг которой вращается
круг, — когда он в ней касается оси х, то вокруг нее и вращается.
Он соединяет отрезком точку А с точкой окружности,
которая выписывает циклоиду:
— Производная — это ведь тангенс утла наклона кривой —
пет, вернее, наклона касательной — или, можно сказать,
вектора мгновенной скорости — а я этот наклон и без производной
могу вычислить — точка окружности ведь движется так, как
Пудто вращается вокруг точки касания — перпендикулярно вот
угой прямой (он снова прочерчивает мелом проведенный им
отрезок) — движется под углом к горизонтали — сейчас — под
углом § — !• Тангенс этого угла — это котангенс | — а у нас
получилось — получилось то же самое — есть такая формула:
{ t _ sin*
— Отлично, садитесь, Мухин. Чюмин, вы что-то хотите
спросить?
— Скажите, а зачем вы рисовали тот вон квадрат? — он
указывает глазами на чертежик, который я предлагал ребятам как
подсказку.
226
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
[Гл. 3
— Деточка не понимает, что это тоже математика, — лице-
дейно сокрушается над его бестолковостью Рамзин.
— Послушайте, — резко оборачиваюсь к Рамзину, — если вы
еще раз, — стараюсь говорить как можно спокойнее, чтобы не
дать прорваться возмущению, — если вы еще хотя бы раз
позволите себе оскорбительные насмешки над кем-то из своих
товарищей, вы на моих семинарах больше не появитесь. Вы слышите?
— Слышу, — глухо продавливает он сквозь стиснутые зубы.
— Вот и хорошо. Вернемся к нашей задаче, ребята. Я хотел
бы, чтобы все посмотрели, как функцию, заданную
параметрически, продифференцировал Миклашевский: он поступил с ней
очень оригинально ... Но пусть об этом расскажет он сам.
— Я предположил, что для функции x(t) существует
обратная t(x), подставил ее в выражение для ординаты: y(t) = y(t(x))
и продифференцировал у по х как сложную функцию.
— Насколько же обосновано ваше предположение о
существовании функции t(x)? Что гарантирует ее существование?
— Что гарантирует? Очевидно, надо, чтобы x(t)
удовлетворяла условиям теоремы об обратной функции, чтобы она была
монотонной и непрерывной на каком-то отрезке.
— Можем ли мы утверждать это о функции x(t)?
— С непрерывностью у нее все нормально — она ведь
дифференцируема, это нам дано, то есть существует х'г... Да, и к тому
же ведь х[ не должна обращаться в нуль, иначе дробь |f
потеряет смысл! А мы уже говорили: если производная не обращается
в нуль, то функция монотонна.
— Да, что-то такое говорил Костюк, но лишь в порядке
гипотезы.
— Я доказал это! — то ли с упрямой, то ли с обиженной ноткой
в голосе перебивает меня Костюк.
— Доказали? Чудесно. Изложите свое доказательство на
доске. Садитесь, Миклашевский.
— Пусть на некотором интервале (а, Ь) определена функция
f(x) — уверенно начинает Костюк. — Пусть в любой точке х
этого интервала существует производная f'(x), не равная нулю, для
определенности положительная. Докажем, что на всем
интервале функция монотонно возрастает. Возьмем точку #о € (а>^).
Величина /'(#о) ~~ эт0 предел дроби ^1^ °' при х —> х$. Если
этот предел положителен, то сама дробь тоже положительна при
х, достаточно близких к хо, ближе, чем на некоторое 8 > 0.
Тогда при всех таких х, которые входят в левую 5-полуокрестность
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
227
точки хо, будет f(x) < /(хо) а ПРИ таких, которые входят в
правую полуокрестность, будет f(x) > f(xo).
— Простите, что я вас перебиваю, но, по-моему, перед тем, как
идти дальше, стоило бы напомнить определение возрастания.
Какую функцию мы назовем монотонно возрастающей на (а, Ь)?
— Такую, что для любых х\ и Х2 из этого интервала при
х\ < Х2 справедливо f(x\) < /(#2).
— Верно. Продолжайте доказательство. Если мне не изменяет
чутье, сейчас вы подведете под это определение функцию,
производная которой положительна в каждой точке интервала (а, Ь)?
-Да.
— Ну что ж, позвольте задать вам на этом интервале две
точки х\ и Х2 такие, что х\ <Х2- Докажите на основании сказанного
вами ранее, что f(x\) < /(£2).
— На основании сказанного ранее я отложу от точки х\,
вправо такую 5-полуокрестность, на которой все значения функции
больше f(x\). В этой полуокрестности возьму точку х' и отложу
вправо от нее полуокрестность такого же свойства. В ней
возьму точку х" и буду продолжать построение до тех пор, пока в
какую-то полуокрестность не попадет точка Х2-
— Если, разумеется, каждая новая полуокрестность не будет
целиком входить в предыдущую, — с приглушенным ехидством
вставляет Рамзин.
— Справедливое опасение — а, Костюк? — присоединяюсь к
Рамзину (пусть видит, что деловую критику я одобряю, в какой
бы манере она ни подавалась).
Костюк не находит, что ответить — стоит, набычившись,
бросая недовольные взгляды то на меня, то на Рамзина.
— Что ж, — обращаюсь ко всем, отослав его на место, —
если уж нам пришлось сделать остановку в решении этой задачи,
давайте оглянемся на пройденный путь — посмотрим, чего мы
достигли.
— По правде сказать, ничего, — пренебрежительно цедит
Меншиков.
— Не скажите! — возражаю ему. — Вы просто
невнимательно слушали Костюка, иначе заметили бы, что он выдвинул ни
много ни мало — новое понятие. Возрастание функции в
точке — вот как называется оно. Кто смог бы выделить строгую
формулировку этого понятия из сказанного Костюком?
— Функция f(x) называется возрастающей в точке хо, —
Горт торопится застолбить свой приоритет, — если... гм... если...
сейчас...
228
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
[Гл. 3
И медленнее, тише, словно чем-то мучимый — вероятно,
раздираемый противоречивыми желаниями быть самым первым и
в то же время быть абсолютно строгим:
— Функция называется возрастающей в точке хо, если для
любого 8... Нет, нет, не так! Сейчас я снова: если существует
5 > О такое, что для любого ... да, для любого х из
полуокрестности (хо, хо + 5) выполняется /(хо) < /(#)> а Для любого х из
полуокрестности (хо — 5, хо) выполняется f(x) < /(хо).
— Совершенно верно, Саша. Отмечу еще один результат,
полученный Костюком: если производная функции положительна
в некоторой точке, то функция в этой точке возрастает.
Аналогично определяется убывание в точке и доказывается, что оно
следует из отрицательного значения производной в этой точке.
Но ведь Костюк замахивался на большее — он хотел доказать,
что из ненулевого значения производной в каждой точке
некоторого интервала следует монотонность функции на всем
интервале. Первая попытка доказательства, предпринятая самим
Костюком, к успеху не привела. Но, может быть, теорема Костюка
неверна? Как это выяснить? Есть ли какая-нибудь логическая
связь между возрастанием функции на интервале и ее
возрастанием в каждой точке интервала?
— Если функция возрастает на всем интервале, то она
возрастает и в каждой его точке, это тривиально, — тотчас откликается
Миклашевский.
— Верно ли обратное? — допытываюсь у него.
— Вообще говоря, нет — судя по тому, что сказал Костюк.
— Неправда! — отстаивает справедливость молчавший до сих
пор Стрельцов. — Из того, что сказал Костюк следует, что таким
путем возрастание на интервале не докажешь, и все.
— Согласен с вами! — беру сторону Стрельцова.
— А если от противного? — подает голос надежды Буткус. —
Предположить, что в любой точке интервала (а, Ь) функция
возрастает, а на всем интервале — нет: существуют х' и х", что х'
меньше х", a f(x') больше /(х"). Отсюда надо вывести, что есть
хо, где /(х) не возрастает.
— Получившееся противоречие и докажет теорему, —
соглашаюсь с ним. — Вот, допустим, точки х' и х", а вот точка хо,
в которой функция не возрастает. Но определение возрастания
в точке включает в себя упоминание о некоторой 5-окрестности
этой точки, а она, эта окрестность, может оказаться совсем
крошечной, так что в нее не вместится отрезок [х', х"\. Что вы
скажете на это, Буткус?
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
229
— Надо как-то перейти от отрезка [х', х"\ к 5-окрестности хо.
— Сколь бы узкой она ни была! Есть ли у нас приемы такого
перехода?
Молчание.
— Перехода от макроскопических масштабов к
микроскопическим?
Молчание.
— Вспомните, как лектор доказывал теорему Больцано-Вей-
ерштрасса, теорему Коши о промежуточных значениях ...
— Деление пополам! — счастливо вскрикивает Синица.
— Совершенно верно! Я думаю, Люда, вам уже есть что
написать на доске. Прошу.
— Разделим пополам отрезок [х', х"]... Я его переобозначу
[х'^х'/], так надо, — увлеченно начинает она, — и посмотрим,
какое значение у функции в середине отрезка... Тут могут быть
три варианта, — заключает она после короткого раздумья и
рисует их на доске, — но всегда одна из половинок отрезка будет
такая, что на левом ее конце функция примет большее значение,
чем на правом, правда ведь? Этот отрезок обозначим [х^х^] и
сделаем с ним то же самое. Получим отрезок [хз,Хз] и с ним
поступим так же. Если дальше и дальше продолжать деление,
получится система вложенных, бесконечно убывающих по длине
отрезков. По теореме о вложенных отрезках они будут
стягиваться к какой-то точке хо, принадлежащей им всем. Ну, а тут
уж все ясно — я сейчас это докажу. В точке хо функция
возрастает согласно условно. Возьмем ту 5-окрестность, про которую
говорится в определении возрастания функции в этой точке. Из
построенной системы вложенных отрезков возьмем тот, который
целиком лежит в этой 5 - окрестности. Вот теперь смотрите: на
его левом конце х'п функция принимает большее значение, чем
на правом х^; и какое бы значение она ни приняла в точке хо, все-
230
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
[Гл. 3
гда, даже если xq совпадает с одним из концов отрезка [я4>хпЬ
будет выполняться одно из двух неравенств: либо /(хо) > f(x'n)
либо f{x'n) > /(xq). А это противоречит тому, что в точке xq
функция /(х) возрастает. Вот противоречие, которое мы хотели
получить. Все доказано!
— Отлично! — радуюсь вместе с ней. — Теорема Костю-
ка действительно доказана: возрастание некоторой функции
/(х) на интервале следует из ее возрастания в каждой точке
интервала, а оно — из положительности производной /'(х)
на рассматриваемом интервале, если та существует на нем.
Аналогично доказывается, что монотонное убывание функции
следует из отрицательности ее производной. Или в общем —
монотонность функции вытекает из того, что ее производная
не обращается в нуль. Так получает обоснование
предложенный Миклашевским метод дифференцирования функций,
заданных параметрически, — в будущем мы еще прибегнем
к нему. Теперь, ребята, перейдем к новой теме — к
производным высших порядков. Лектор ведь уже говорил вам о
них? Вспомним, как они определяются. Производную от
функции /(х) определенную обычным способом, изученным нами,
назовем первой производной. Продифференцируем ее, если
это возможно, и результат назовем второй производной;
обозначать ее станем /"(х) или rfyf'. Продифференцировав ее
еще раз, назовем результат третьей производной, обозначим
ее f"(x) или jffi' и так далее. Производные порядка
выше первого от функции /(х) называются ее производными
высших порядков и обозначаются собирательным символом
здесь буква п в скобочках, если заменить ее
конкретным числом, укажет порадок производной. Последовательное
вычисление производных все более высоких порядков,
очевидно, не составляет труда, если функция /(х) принадлежит
к разряду элементарных: ведь их дифференцирование всегда
приводит опять-таки к элементарным функциям. Ну, например:
f(x) = C\ sin Xx + C2C0S Ах. Ее первая производная...
диктуйте мне! Верно, /'(х) = CiA cos Ax — C2AsinAx. А вторая ее
производная... диктуйте! Да, f"{x) = —Ci A2 sin Ax — C2A2cos Ax.
— Колебание, — произносит Кулагин, когда я кладу мел.
— Вы о чем?
— Если умножить функцию на А2, потом сложить со второй
производной, сумма будет равна нулю. А у" — Х2у = 0 — это
уравнение колебания.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
231
— О, да вам, ребята, я вижу, не только из курса
математики, но и из курса механики уже знакома эта тема —
производные высших порядков. Что ж, тогда я не буду задерживаться
на совсем уж простых примерах и сразу перейду к сложным.
На лекциях вам, вероятно, давали формулы, которые
позволяют вычислить производную любого порядка п от некоторых
элементарных функций. Пусть кто-нибудь выпишет эти формулы
на доске.
— Разрешите? — вскидывает руку Кочин.
— Идите, Дима.
Для подстраховки он берет с собой конспект лекций, но
заглядывает в него нечасто. Оказывается, у него неплохая память!
— Все хорошо. Садитесь. Все, я думаю, понимают, что
формулы этого списка допускают вариации в своем прямом
применении. Например, вместо аргумента х в любую из них можно
подставить линейную функцию ах + Ъ: результат
дифференцирования усложнится лишь множителем ап. Используя эти
формулы, можно вычислять производные любого порядка п от
более сложных функций. По какому принципу это делается, вы
сейчас выясните сами, на конкретных примерах — вот они. Про-
232
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
[Гл. 3
буйте решать их один за другим; не получится первый —
переходите ко второму, второй не получился — беритесь за
третий... Рано или поздно вы откроете тот принцип, который я имею
в виду.
Медленно прохаживаюсь между столами. Чюмин упорно
пытается подогнать первый пример под невесть с чего
померещившуюся ему формулу ?/п) = (Ж2^зж+2)" и отклаДывает
ручку, видя бесплодность своих попыток. Мухин берет одну
за другой производные от sin я cos 2а;, тщетно пытаясь
подметить какую-то закономерность, связывающую полученные
в результате функции. Тем же безнадежным путем, притом
гораздо медленнее, идет и Аргунова. Сынчиков, занеся
ручку над чистой страницей, долго сидит так в неподвижности,
потом пишет логарифм дроби из последнего примера,
разворачивает его в разность логарифмов — и замирает вновь.
Стрельцов беззаботно продифференцировал по два-три раза
функции, стоящие первыми в списке, и добрался до
логарифма дроби. Маячу возле него: сейчас он сделает то же,
что и Сынчиков, а вслед за этим, конечно же, придет к
идее, которая поможет решить большинство заданных мною
примеров. Но он больше не пишет ни строчки. Не
выдерживаю:
— Стрельцов, неужели вы не знаете, что логарифм дроби
есть разность логарифмов числителя и знаменателя? А чему
равна n-ная производная разности двух функций — неужели
не догадываетесь? — добавляю, когда он раскладывает
логарифм.
— Ффу! — кривится он, сердясь на свою
несообразительность. — Ну, тогда все ясно!
— Что вам ясно?
— Что sin3x можно представить как сумму sin я и sin За;
с какими-то коэффициентами, не помню точно с какими, но
это неважно... И дробь Х2_\х+2 тоже> кажется, можно
разложить...
— Кажется? — говорю нарочито громко, чтобы мой вопрос
слышали все.
— Забыл, как это делается.
— Как это делается, ребята? — превращаю наш со
Стрельцовым обмен репликами в тему общей беседы.
— Разложение полиномиальных дробей на элементарные!
Метод неопределенных коэффициентов! — один за другим
выпаливают Костюк и Миклашевский.
Ю. В. Пухначев|
СЕМЬ СЕМИНАРОВ
233
Выясняю, кто еще знает этот прием, выбираю из
откликнувшихся Меншикова и зову его к доске. Получив разложение, он с
актерски пронзительной тоской глядит на меня:
— И производную брать?
— Конечно! Вы так хорошо начали — наверное и закончите
так же хорошо.
Обезоружено хмыкнув, он доводит вычисления до конца.
— Ну, как? — спрашиваю аудиторию, отослав Меншикова
на место. — Все понимают, что помогло нам решить этот
пример и, возможно, поможет решить остальные? Ключевая идея —
разлагать каждую из предложенных функций на сумму таких,
для которых n-ную производную можно вычислить по одной
из стандартных формул того списка, который написал на доске
Кочин.
Быстро находятся аналогичные решения третьего и пятого
примеров — их показывает Стрельцов. Предлагаю перейти к
оставшимся примерам.
И после достаточно долгой паузы:
— Все ли получилось?
— Нет, — честно признается Лапиков.
— Что не вышло?
— Второй и четвертый примеры. Никаких идей!
— А по формуле Лейбница не пробовали? Вам ее давали на
покции?
— Давали. Но ведь, — он глядит на меня разобижено, — ее
ист в списке!
— Верно, нет, — соглашаюсь с ним. — Я умышленно не
напоминал вам о ней.
— Зачем же так ... жестоко? — негромко, но весьма трагично
иосклицает Синица.
234
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
[Гл. 3
— А голова на плечах у вас есть? — отвечаю и ей, и
Лапикову, и всем. — Разве кто-то запрещает вам пользоваться тем, что
вы знаете? Что за глупое школярство! Когда же вы научитесь
самостоятельности? Идите к доске, Лапиков, добавьте к
нашему списку формулу Лейбница и решайте оба примера, второй и
четвертый.
Вместе обнаруживаем, что в применении к ним формула
Лейбница будет содержать лишь три слагаемых. Чтобы не
сбиться, Лапиков размечает обе заданные ему функции буковками
и и и, которые были в воспроизведенной им записи формулы
Лейбница, и, часто поглядывая на нее, решает оба примера.
I Лапиков
N(x2-7tx)cosx] =(cosx) V*2-7rx) + rt(cosx) C*-**H
+ Д^^соеэс/^х^х)1"- cos(x-^)(x2-7rx) +
Lri<*s(x+^-£)(2x-icJ + J^
= (x2-Tcx-n^-Yj)cos(x + ^-n(2x-7t)sin(x+^
— Все верно, садитесь. Теперь, ребята, давайте подумаем вот
над чем: как вычислять производные высших порядков от
функции, обратной к данной, и от функций, задаваемых
параметрически или неявно?
— Быть может, я заблуждаюсь, но для неявных функций, как
мне представляется, это делается просто, — несколько мгновений
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
235
спустя неспешно начинает Рамзин и по моему приглашению
выходит к доске. — Если вы не возражаете, я возьму уравнение той
же гиперболы ^- —^- = 1. Вот первая производная ух = ^|.
Чтобы получить вторую, эту дробь следует еще раз продифферен-
1 2
цировать по х: коэффициент ^, безусловно, выносится за
скобку, потом по формуле дифференцирования частного... Тут у нас
возникает у'х, вместо нее имеет смысл подставить ее выражение
через х и у. И тогда ухх тоже выразится только через х и у.
— Верно. Очевидно, таким путем можно вычислить сколь
угодно высокие производные для любой конкретной функции,
заданной неявно. Садитесь, Рамзин. Теперь перейдем к
функциям, задаваемым параметрически. Возьмем, например,
параметрическое уравнение циклоиды и попробуем вычислить ухх.
— Есть общая формула второй производной для функций,
задаваемых параметрически, — произносит Сутеев.
— Напишите ее на доске, — вручаю ему мел. — Так... Все
точно. Откуда же она берется?
— Вторая производная есть производная от первой, —
отвечает он после короткой заминки и по моей просьбе пытается
выразить это в выкладках.
— Но почему же у вас в знаменателе получилось (xj)2, а не
(xj)3, как прежде? Ну-ка, скажите еще раз, что такое вторая
производная ухх?
— Это производная от первой производной.
236
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
(Гл. 3
— Значит, чтобы вычислить вторую производную ухх, надо
продифференцировать ух — но по какому аргументу?
Вопрос остается без ответа.
— По х — подсказывает Горт.
— Конечно, по х\ Припишите, Сутеев, эту букву под штрихом,
../
которым вы обозначили дифференцирование дроби Щ-. Но эта
xt
дробь зависит от t, а не от х, и поэтому непосредственно по х ее
дифференцировать нельзя. Так ведь, Сутеев? Как же тогда нам
выполнить дифференцирование по х? Помолчите, Горт, — ведь
я спрашиваю не вас. Ладно, говорите, раз уж Сутеев не может
сообразить, — идите к доске.
— Надо дифференцировать эту дробь как сложную функцию:
сначала по £, а то, что получится, домножить на tx или, что то
же, разделить на х[. Чем я обосную существование производной
tx, вы спрашиваете? Когда мы разбирали дифференцирование
функции, заданной параметрически, мы говорили, что из
существования производной ух вытекает существование и дифферен-
цируемость функции t(x).
— Верно, — резюмирую итог его вычислений и отсылаю его
обратно. — Благодаря делению на х[ и получается (x't)3 в
знаменателе окончательной формулы для ухх. Теперь вы понимаете,
как она возникает, Сутеев? Ее вывод стоило бы запомнить. Это
я вам говорю не из абстрактных педагогических, а из
конкретных практических соображений. Дело в том, что для
вычисления второй производной от функции, заданной параметрически,
удобнее применять не окончательную, а промежуточную
формулу Ухх = P"(a^)t- В самом деле, при ее использовании нужно
выполнить три операции дифференцирования и два деления, а
окончательная формула предусматривает четыре операции
дифференцирования и четыре арифметических действия. К тому же
дробь !$- порой сокращается до очень простого выражения.
Убедитесь в этом, Сутеев, на примере циклоиды. Все правильно,
садитесь.
Что с ним сегодня? Уже в третий раз его ответы на
нынешнем семинаре озадачивают меня одним и тем лее: точность
начальных фраз сменяется полной беспомощностью в дальнейших
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
237
рассуждениях. Случайные срывы? Не много ли случайностей?
И, если уж честно, не только сегодня это с ним, бывало и
прежде. А я всё списывал такие провалы на плохое самочувствие,
считал нетипичными. Нет, я его определенно переоценивал! Но
почему? Меня подкупали четкие реплики, которые время от
времени он вставлял в общий разговор, они казались мне
свидетельством глубокого понимания. Как не прав я был, доверяясь
этой четкости и ни разу не удосужившись побеседовать с ним
поподробнее! Кстати, о чем были его реплики? С чем вообще
выступал он раньше? Еще на первом семинаре быстрее других
дал пример немонотонной последовательности. Построил
отрицание бесконечного возрастания. Успехи, нечего сказать... Нет-
нет, школьные знания у него действительно неплохие. Он без
запинки вспомнил определение предела последовательности. А
вычисление простейшего предела провел без всякого обоснования.
Это можно было объяснить либо прекрасным пониманием, либо
полным непониманием сути дела. Вторая версия мне почему-то
и в голову не пришла. Я было попросил его переделать тот
пример (это, вероятно, сразу обнаружило бы его слабости!) — но
увлекся и все сделал сам. Обольщаясь отчетливостью его
звучного голоса, строгостью прямого взгляда, всеми этими внешними
признаками, я пропускал мимо глаз его несостоятельность. Да,
несостоятельность! Только что он проявил ее воочию:
формулу написал безупречно, а откуда она берется и не представляет!
Обыкновенный зубрила? Похоже... Или дело в чем-то другом?
Я первый раз встречаю студента, который неплохо знает преды-
дущий, школьный материал и при этом неспособен усвоить
последующий. Достиг своего потолка? Пусть так, хотя и рановато.
Но тогда вопрос: почему он все-таки смог его достичь?
Откуда у него такие хорошие знания школьного курса? Наверное, в
школе у него был хороший учитель, который сумел подобрать
к нему ключик. А я? Неужели не сумею? Неужели не помогу
ему преодолеть еще одну ступеньку его роста? Обидно, что к
чтим размышлениям я пришел так поздно: безоглядно поверив
и него, я не уделял ему должного внимания, Надо побыстрее
наверстывать упущенное: почаще спрашивать его, на каждый
вопрос требовать досконального ответа, установить все его
надежные знания и умения, на которые можно будет надстраивать
дальнейшее, вспомнить, в чем до сих пор он был силен и
опираться на эти сильные стороны в моей дальнейшей с ним
работе... Додумаю все это потом, а сейчас надо вернуться к текущим
делам.
238
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
[Гл. 3
— Все поняли, ребята, как был решен последний пример?
Если да, то сходным образом вы сможете вычислять
производные все более высоких порядков от любой функции, заданной
параметрически, а также, зная производные высших порядков
от некоторой функции, найти производные тех же порядков для
функции, обратной к ней. Выразим, например, для функции
у(х) вторую производную ухх через производные обратной
функции х{у).
Дав это задание, отправляюсь в обход аудитории. По
выкладкам, которые набрасывает в своей тетради Сынчиков, оцениваю,
что на этот раз он имеет шансы на неплохое выступление — и
вызываю его. Да, вероятность неудач все еще никак не отступает
от него. И тем не менее мне верится, что за последнее время он
стал работать гораздо сноровистее по сравнению с первыми
семинарами. Мне кажется, что даже очки он быстрее укладывает
в очечник перед тем, как выйти из-за стола. Однако
медлительность, с которой он преодолевает путь до доски, тотчас
настраивает меня на прежний — с подсказками и понуканиями — стиль
общения с ним:
— Вторая производная ухх — это, согласно определению...
— Производная от первой, — по обыкновению глухо и
односложно, глядя в пол, продолжает он.
— Напишите это на доске. Да не забудьте отметить, что
производная берется по х\ Вместо ух подставляем ее выражение
через х'у, верно... Но теперь стоящую в скобках дробь нельзя будет
продифференцировать непосредственно по я, поскольку она
зависит от у. Значит, надо...
— По у и умножить на ух.
— Правильно. И окончательный ответ у вас верный. Очень
хорошо. Садитесь. Мы переходим теперь, ребята, к новой теме.
Суть ее в том, что для операции дифференцирования в
математике можно найти немало вычислительных приложений.
Давайте попробуем их поискать. Внимательно просмотрим под
таким углом зрения понятия, с которыми мы сегодня познако-
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
239
мились: производная, дифференциал... Кочин, вы что-то хотите
предложить?
— Да; я вот что подумал: если взять график синуса, то
прямая у = х в начале координат касается синусоиды, разность
между ними около начала маленькая, убывает быстро, быстрее, чем
х, то есть х и sinx близки...
Не очень много содержания в его словах — но сколько
желания сказать что-то содержательное! Поддержу это желание,
помогу придти к интересному результату по тому пути, на
который он ступил:
— То есть, если х мал, то sin я можно довольно точно
получить, не прибегая к таблицам: взять вместо синуса его аргумент.
Кстати, касательную к синусоиде можно провести не только в
начале координат, но и в любой точке хо- Покажите это на
чертеже, сделайте это на доске, Кочин. Хорошо, хорошо... Как
видите, и тут значение sinx можно приближенно заменить
значением некоторой линейной функции. Какой же именно? Не можете
сразу написать ее формулу? Подумайте, я не тороплю... Ну вот,
верно: sinx = sinxo + cosxo(x — xo). И если мы хотим вычислить
sin я, надо просто подставить в эту формулу х.
Он не склонен разделять звучащее в моем голосе убеждение
в простоте такого приема:
— Да, но... тут еще sinxo, cosxo... А их что — из таблиц? Тогда
зачем мы мудрим, если есть таблицы?
— Если аргумент хо — произвольный, то без таблиц, конечно,
не обойтись. Но ведь для некоторых значений аргумента
известны точные величины синуса и косинуса.
— Для некоторых? Ну, если для некоторых... Тридцать
градусов, наверное, сорок пять...
— Ну-ну!
— Шестьдесят...
— Теперь вы понимаете, куда я клоню?
— Можно, например, вычислить sin 29°.
— Вычислите! Ага: половина минус ifg • 2 ••• Чему жс ЭТ()
равно? Кулагин, у вас, кажется, есть калькулятор?
— Сейчас посчитаю, -- откликается он. — Если точно, то
0,4848851.
— Теперь сверимся с таблицами. Гарин, я у вас видел
справочник по математике — загляните туда... 0,4848? Совпадение
неплохое. Давайте, Кочин, вычислим теперь тем же манером
корень v^l,02. Чему он будет равен?
— Наверное, надо так: $Т702 = yfl + (\/Т)' • 0,02.
240
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
[Гл. 3
— Не очень удачно вы написали (y/l)': в скобках — константа,
а производная константы — нуль. Но я понимаю, что вы хотели
этим выразить: производную функции у/х в единице так? А коли
так — вычисляйте. Получается 1,007? А по справочнику, Гарин?
Тоже? Неплохо. Кстати, Кочин, нарисуйте-ка график
кубического корня у = tfx. И на том же чертеже нарисуйте еще график
кубической параболы у = х3. Садитесь. Какую задачу можно
поставить, глядя на такой чертеж, ребята?
— Под каким углом пересекаются кривые! — вносит свою
лепту Чюмин.
— А как бы вы определили угол пересечения кривых? Не
знаете? Я-то думал, что вы уже представляли себе это, когда
предлагали свою задачу, — с этими словами я провожу касательную
к кубической параболе в точке пересечения кривых.
— Как угол между касательными к кривым в точке их
пересечения, — догадывается Чюмин.
— Верно. Идите к доске и попытайтесь определить этот угол.
Все правильно, садитесь. Кто назовет еще какие-либо
практические выгоды от дифференцирования? Какие еще вопросы можно
решать с помощью производной?
— Можно выяснять, как ведет себя функция, — предлагает
Сутеев. — Если на каком-то интервале ее производная
положительна, то она возрастает, а если отрицательна — убывает.
Отличное предложение! Может быть, я поспешил с его
разжалованием? Сейчас посмотрим:
— Ну, а если в какой-то точке интервала производная
функции равна нулю? Что можно сказать о поведении функции в этой
точке? Как вы думаете, Сутеев?
— Что она имеет там максимум или минимум, — следует
уверенный ответ.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
241
— Отчасти верно, — берусь за мел. — У параболы,
например, в начале координат производная равна нулю, и там у нее
минимум. Но можно ли утверждать, что функция обязательно
достигает либо максимума, либо минимума там, где ее
производная обращается в нуль? Как, Сутеев? Молчите?
Опять всего лишь срыв? Нет, уже не верится.
— А что скажете на это вы, Кочин?
— Нет, нельзя. Говорили ведь: у кубической параболы в
начале координат производная равна нулю, но ни максимума, ни
минимума у нее там нет.
Молодец — он разобрался в том, на чем его когда-то подловил
Горт.
— Поправка правильная, я очень доволен вашим ответом. И
все же трудно отрешиться от мысли, что достижение экстремума
— так обобщено называют максимум и минимум — и обращение
производной в нуль как-то связаны друг с другом. Давайте
исследуем эту связь.
— Мы имеем теорему: если функция в какой-то точке
достигает экстремума и дифференцируема, то ее производная там
равна нулю, — заявляет Буткус.
— Верно, есть такая теорема, она называется теоремой
Ферма. Вдумаемся в нее: если хо -— экстремум, то /'(хо) = 0.
Иными словами, обращение производной в нуль — это
необходимый признак экстремума. А есть ли у него достаточные
признаки? Чем гарантируется достижение экстремума? Вот
вопрос! Кстати, давайте-ка сразу же повторим определение
экстремума. Говорят, что функция /(х) достигает
максимума в точке хо, если существует окрестность точки хо, в°
всех точках которой, не совпадающих с хо, значения
функции меньше, чем в хо- Или, говоря на символическом языке,
если существует такое 5 > 0, что для всех х,
удовлетворяющих первенству 0 < |х — хо| < £, выполняется неравенство
/(х) < /(хо). Если изменить знак последнего неравенства,
получится определение минимума. А теперь, ребята, давайте
разберемся в вопросе^ о достижении экстремума, используя те
понятия, которыми пользовались до сих пор: существование
и несуществование производной, а в случае существования —
равенство или неравенство ее нулю. Только что Кочин
показал: нулевая производная не может служить достаточным
признаком экстремума; имея нулевую производную в некоторой
точке, функция может достигать там экстремума, а может и не
достигать. Ну, а если функция в некоторой точке недифферен-
242
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
[Гл. 3
цируема? Может ли она иметь там экстремум? Как вы думаете,
Стрельцов?
— Может. Пример — функция у = |х|. В нуле у нее минимум,
а производной нет.
— Но обязательно ли функция достигает экстремума в той
точке, где не имеет производной?
— Да. То есть... постойте! Нет! Да, конечно, нет! И пример
можно привести: у = |х| +2х. В нуле недифференцируема и
возрастает.
— Может ли функция достигать экстремума в точке, где
имеет ненулевую производную?
— Нет. В такой точке функция либо возрастает, либо убывает,
мы об этом уже говорили.
— Все верно. Мы пришли, таким образом, к выводу:
функция может достигать экстремума лишь в тех точках, где она
имеет нулевую производную или недифференцируема. Мы еще
не получим точный перечень экстремумов функции, отобрав
такие точки из области ее определения, но можем поручиться, что
все без исключения точки экстремума входят в число
отобранных. Остается только выяснить, по каким признакам среди
подозрительных на экстремум точек можно безошибочно опознать
экстремальные. Что подсказывают на этот счет знакомые нам
примеры функций, у которых есть подозрительные точки
обоих сортов — точки без производной и с производной, равной
нулю?
— В точках экстремума меняется наклон графика! — осеняет
Меншикова.
— Как же он меняется?
— С положительного на отрицательный, если это максимум,
а если минимум — то с отрицательного на положительный.
— Прекрасно! Выразите этот факт в математических
понятиях.
— Попробую... Наклон — это производная. Слева от точки
экстремума производная одного знака, а справа — другого.
— Ах, Меншиков! Дискредитируете вы свои хорошие идеи
своей же нестрогостью! Если уж взялись говорить на
математическом языке, делайте это так, чтобы каждое ваше
высказывание можно было бы выразить в логических символах. Слева,
справа... Нечетко! Насколько далеко слева? Насколько далеко
справа?
— Понимаю: надо сказать, что существует такая окрестность
точки экстремума, что в левой половине этой окрестности, в лю-
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
243
бой ее точке, кроме самой точки экстремума, производная одного
знака, а в правой — другого.
— Ну вот, так оно лучше. Давайте ради максимальной
четкости выразим сказанное вами, Меншиков, на символическом
языке — пишите то, что я сейчас буду говорить, на доске, а
остальные пусть запишут в свои тетради. Я ограничусь
случаем максимума. Итак, пусть дана точка хо и существует 5-
окрестность этой точки, на которой определена функция /(х),
дифференцируемая в этой окрестности, за исключением, быть
может, точки хо- Пусть /'(х) > 0 при х Е (хо — 6, хо) и /'(х) < О
при х Е (хо, хо + 6). И пусть в самой точке производная либо
не существует, либо обращается в нуль. Я правильно
выразил ваши соображения? Да? Тогда садитесь, Меншиков. Так
вот, ребята, Меншиков утверждает, что при таких условиях
функция достигает максимума в точке хо- Прав ли он?
Подумайте.
Листаю задачник, оставляя их наедине со своими
раздумьями. Тишина. Но постепенно нарастает шум на правом
фланге среднего ряда. Аргунова что-то шепчет Синице, набрасывая
какой-то график в своей тетради. Почуяв что-то интересное, к
ним оборачивается Горт и Миклашевский; Мухин заглядывает
через плечо Аргуновой в ее тетрадь и поднимает на меня взгляд,
полный растерянности.
— Что там у вас, Аргунова?
— Сама не понимаю! Какая-то такая функция тут у меня
получилась — в одной точке у нее и максимум вроде и не
максимум.
— Нарисуйте ее на доске. Вы-то сами как считаете —
достигает она максимума в точке хо? Определению максимума она
здесь удовлетворяет? Вы помните это определение?
— Сейчас... Существует такая J-окрестность точки хо-..
существует 6 > О такое... что для любого х из окрестности
(хо — S,xo + 5)... выполняется /(х) < /(хо)... если х не равен хо-
Но ведь у нас-то все не так!
244
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
[Гл. 3
— Не так — то есть не удовлетворяется определение
максимума, то есть удовлетворяется отрицание этого определения.
Напишите его.
Это она делает уже попроворнее:
— Для любого 6 > О в окрестности (хо — 5, хо + 6) найдется
такой х, не равный хо, что /(х) > /(хо). Тут все х такие! Как в
минимуме!
Прошу ее показать, что функция удовлетворяет определению
минимума.
— Итак, в точке хо функция /(х) достигает минимума, а не
максимума. Так?
— Так. А признаку максимума удовлетворяет! Ведь наклон-
то у графика слева от хо положительный, а справа —
отрицательный!
— Ваша функция, Аргунова, действительно удовлетворяет
признаку который сформулировал Меншиков. Но ведь мы его
формулировку еще не приняли. Мы ее только обсуждаем. И вы,
Галя, своим примером, отличным примером, показали что в
признаке экстремума, предложенном Меншиковым, упущена какая-
то важная деталь. Какая же именно? Кто сообразит? Садитесь,
Галя, — негромко говорю Аргуновой.
— Я, кажется, понимаю, в чем тут дело, — приподнимает
руку Синица. — У Гали потому получилось противоречие, что она
взяла разрывную функцию, а мы до сих пор разбирали
непрерывные, с ними все было нормально.
— Нормально в том смысле, — разъясняю ее суждение, — что
к ним вполне применим достаточный признак экстремума,
высказанный Меншиковым. Недоразумение, с которым мы
столкнулись, ребята, снова напоминает, как опасно, формулируя
понятие, не отдавать себе отчета в свойствах конкретных примеров, с
помощью которых вы вырабатываете формулировку. Может
случиться, что некоторые свойства вы в ней не отразите, а в
дальнейших рассуждениях будете по-прежнему подразумевать — и
это приведет вас к парадоксам. Так оно с нами только что и
было. Чтобы устранить поводы для парадоксов, надо внести
упоминание о непрерывности в ту формулировку, которой я закончил
наш разговор с Меншиковым о достаточных признаках
экстремума. Конечно, тем самым мы сузили ее, но ведь непрерывные
функции многочисленны и важны, и если мы выработаем
достаточный признак экстремума, применимый лишь к ним, это тоже
будет кое-что из себя представлять. Так кто даст исправленную и
дополненную формулировку достаточного признака максимума,
Ю. В. Пухначев] СЕМЬ СЕМИНАРОВ 245
которую предложили мы с Меншиковым? Хотите вы, Рамзин?
Пожалуйста.
На доске возникает дуга, красиво выгнутая вверх над
точкой хо, отмеченной на горизонтальной прямой. Затем следуют
размеренные фразы:
— Пусть функция f(x) определена и непрерывна в
некоторой окрестности точки х$. Пусть в левой полуокрестности этой
точки у функции существует производная ff(x) > 0, а в правой
полуокрестности — производная /'(х) < 0. В самой точке хо
производная может не существовать. При таких условиях функция
/(х) достигает максимума в точке Хо- Это достаточный признак
максимума. Если поменять знаки неравенств на обратные,
получится достаточный признак минимума. Рисовать?
— Нет, ограничимся рассмотрением максимума. Садитесь,
спасибо.
После того, как Рамзин возвращается на место, спрашиваю
остальных:
— Будут ли еще у кого-нибудь какие-либо дополнения?
Поправки? Нет? Что ж, тогда попробуем доказать, что при
соблюдении всех перечисленных Рамзиным условий функция
/(х) действительно достигает максимума в точке хо- Для
простоты рассмотрим лишь правую ^-полуокрестность этой
точки, возьмем на ней произвольную точку х' и докажем, что
f(x') < /(хо).
Выжидаю минуту, другую, третью...
— Что, ни у кого не получается? А ведь у нас
налицо все, что необходимо для доказательства: функция /(х)
непрерывна на отрезке [хо,х'], дифференцируема на
интервале (хо, х')...
— Теорема Лагранжа! — стонет Горт с таким отчаянием,
которое можно истолковать как полное крушение веры в свои
способности.
— Вам ведь доказывали ее на лекциях? Да? В чем она
состоит? Напомните, Саша. А остальные пусть внимательно слуша-
246
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
[Гл. 3
ют! Формулировки теорем, которые сейчас будут приводиться,
рекомендую записывать. Итак, начинаем с теоремы Лагранжа.
Пожалуйста, Саша, к доске.
У доски он до забавного важен: лицо вздернуто, правая рука
с мелом в ней приподнята — готов дать немедленный и
исчерпывающий ответ на любой вопрос.
— Итак, теорема Лангража, — повторяет он, — Если функция
/(х) определена и непрерывна на отрезке [а, Ь] и имеет конечную
производную на интервале (а, Ь), то на этом интервале найдется
точка с такая, что /(b) — /(а) = f'(c)(b — а).
— У этой формулы есть запоминающееся наглядное
истолкование.
— Да, она означает, что касательная к графику функции в
точке с параллельна хорде, которая стягивает дугу графика над
отрезком [а,Ь].
— Теперь наметьте вкратце доказательство теоремы
Лагранжа.
— Оно опирается на теорему Ролля.
— Тогда сформулируйте ее. И не торопитесь, чтобы ребята
смогли записать.
— Если функция /(х) определена и непрерывна на
отрезке [а,Ь], принимает равные значения на его концах и имеет
конечную производную на интервале (а,Ь), то на этом интервале
найдется точка с, где производная функции обращается в нуль.
Он говорит в манере, явно перенятой им у лектора: медленно,
выразительно, этак даже важно.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
247
— Как же доказывается эта теорема?
— Сначала из непрерывности /(#) выводится, что она
достигает своей точной верхней и нижней грани. Если обе грани
совпадают, то функция на интервале (а, Ь) постоянна, и в
каждой его точке ее производная — нуль. Если не совпадают, то одна
из точных граней достигается во внутренней точке интервала, в
какой-то точке с, потому что /(а) = f(b). А отсюда по теореме
Ферма следует /'(с) = 0.
— По теореме Ферма... Ее стоило бы процитировать заново:
когда Буткус упоминал ее, это было как-то второпях.
— Пусть функция /(#) определена на некотором отрезке или
интервале, все равно, и во внутренней точке с этого промежутка
принимает наибольшее или наименьшее значение. Если в точке с
функция дифференцируема, то ее производная там равна нулю:
/'(с) = 0.
— А как доказывается теорема Ферма?
— От противного. Если бы /'(с) не равнялась нулю, то в точке
с функция возрастала бы или убывала, в зависимости от знака
/'(с), но то и другое противоречило бы тому, что в точке с
функция достигает одной из своих точных граней.
— Теперь осталось показать, как на основе теоремы Рол ля
доказывается теорема Лагранжа.
— Вводится вспомогательная функция F(x) = f(x) — /(a) —
bZa (x — °)- Она на отрезке [a, b] удовлетворяет условиям
теоремы Ролля, значит, на интервале (a, b) существует точка с,
где выполняется равенство F'(c) = 0 или, согласно
представлению функции F(x), равенство /'(с) — ' ь-а = 0> а эт0 по
существу то же самое, что требуется доказать.
— Отлично. По сходной схеме, насколько мне помнится,
доказывается еще одна теорема...
— Да, теорема Коши.
— Напомните ее формулировку.
— Если какие-то две функции f(x) и д(х) определены и
непрерывны на отрезке [a, b] и имеют конечные производные на
интервале (а, 6), причем д'(х) на всем интервале не обращается в нуль,
то на этом интервале найдется точка с такая, что q\b)Zq(a) = <?Ш'
— Это так называемая формула Коши. Для ее доказательства
опять-таки вводится вспомогательная функция...
— Да, вводится функция... сейчас... вот такая: F(x) =
- f(x) - /(a) - ^(^)-^(a)[g(x) ~ #(a)l- 0на Удовлетворяет услови-
248
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
[Гл. 3
ям теоремы Ролля, значит, на интервале (а, Ь) найдется точка с,
в которой выполняется равенство F'(c) = 0. Если сюда
подставить выражение для функции F(x), получится то, что требуется
доказать.
— Отлично. Садитесь, Саша, спасибо. Перечитайте, ребята,
формулировки теорем, которые вы записали со слов Горта: все
это стоит хорошенько затвердить. Я думаю, с таким
теоретическим багажом мы уже вполне смогли бы из условий
достаточного признака максимума, — отчеркиваю их на доске, —
вывести неравенства, определяющие максимум. Кто хотел бы это
сделать? Вы, Костюк? Прошу к доске. Можете рассмотреть только
правую полуокрестность.
— На отрезке [хо, х'\ выполняются условия теоремы Лагран-
жа. Следовательно, выполняется равенство f(x') — /(хо) =
= /'(с)(х' — жо), гДе точка с принадлежит интервалу (хо,х').
В правой части равенства первый сомножитель строго
отрицателен. Это по условию достаточного признака. Второй
сомножитель строго положителен. Следовательно, левая часть
строго меньше нуля. Что и требовалось доказать.
— Верно, садитесь, Виталий. Тем же путем нетрудно придти к
выводу, что для любой точки х* из левой ^-полуокрестности
точки хо выполняется /(х') < /(хо). Нетрудно провести подобные
рассуждения и для точки минимума. Таким образом,
сформулированный Рамзиным достаточный признак оказывается
верным — мы доказали его. Теперь, ребята, введем в
рассмотрение еще одну характеристику функции — ее вторую
производную...
— Прошу прощения! — перебивает меня Кочин. — А как же
с примером Аргуновой?
— А что в нем непонятного? Там в точке разрыва
удовлетворяется условие минимума.
— Нет, я хотел спросить, как быть в других таких
случаях? Если экстремум в точке разрыва — по каким признакам его
определять?
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
249
— Смотреть, удовлетворяется ли определение экстремума,
как это в свое время и сделала Аргунова, — никаких признаков
на этот счет не известно. Так что на подобных примерах
задерживаться не будем и пойдем дальше — к функциям, которые в
интересующих нас точках непрерывны и имеют там первую и
вторую производную. Подумаем, ребята: что можно сказать о
поведении функции /(х) в некоторой точке хо, если /'(х)
существует в некоторой окрестности точки хо и при этом /'(хо) = О,
a f"(xo) ф О? Хотите ответить вы, Миклашевский? Пожалуйста.
Только прошу — построже!
«Можете не напоминать», — читаю ответ на свою просьбу в
его подчеркнуто серьезном взгляде. Фразы его — кратки и
убедительны:
— Пусть /"(хо) > 0. Вторая производная — это производная
от первой. Если вторая производная в какой-то точке хо
положительная, значит, первая производная в этой точке возрастает.
Но в самой этой точке первая производная равна нулю. Значит,
при меньших х будет /'(х) < 0, а при больших будет f'{x) > 0.
Значит, в хо по достаточному признаку у /(х) минимум. Так же
доказывается, что при /"(хо) < 0 и /'(хо) = 0 у функции /(х) в
хо максимум.
— Правильно. Попутно я обратил бы ваше внимание, ребята,
на интересные особенности кривых, нарисованных Костюком и
Миклашевским. Вот график функции, первая производная
которой уменьшается с ростом х: кривая, выпуклая вверх.
Следовательно, отрицательный знак второй производной некоторой
функции — свидетельство того, что график этой функции
обращен выпуклостью кверху. И наоборот: если у функции в неко-
тором промежутке вторая производная положительна, то
график этой функции будет выпуклым вниз. Теперь представим
себе непрерывную и дифференцируемую функцию — хорошим
примером здесь может послужить синусоида, — график которой
на некоторых интервалах характеризуется выпуклостью вверх,
а на некоторых — выпуклостью вниз. Точки, в которых
стыкуются интервалы разноименной выпуклости, называются
точками перегиба. Как вы думаете, Паша, — вновь обращаюсь к Ми-
250
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
(Гл. 3
клашевскому, — какой математический факт мог бы послужить
признаком точки перегиба?
— Вторая производная равна нулю, — мгновенно отвечает он.
— Вы предполагаете, что в точке перегиба у исследуемой
функции существует вторая производная? Ладно, пусть
существует. И признак перегиба в некоторой точке хо вы
формулируете равенством /"(хо) = 0. Так?
— Так, — соглашается он. — Вот, например, у = х3: вторая
производная в нуле — нуль, и там как раз перегиб.
— Хорошо. Теперь возьмите функцию у = х4 и посмотрите,
какова у нее в нуле вторая производная. Равна нулю, верно. А
будет ли у этой функции перегиб в нуле?
— Нет, у нее там минимум, — сконфуженно отвечает
Миклашевский после секундного раздумья.
— Значит, нулевая вторая производная — это еще не
достаточный признак перегиба?
— Тут все, наверное, зависит от того, какая степень,—
торопливо подыскивает он объяснение загвоздки.— Если п— нечетное,
то у графика у = хп в нуле перегиб, если четное— перегиба нет.
— Ваш ответ, быть может, и верен, но мне он не нравится
тем, что вы очень уж резко сузили предмет нашего
обсуждения: я предполагал, что вы дадите признак перегиба для
любых дважды дифференцируемых функций, а вы все свели к
степенным.
— А что, если...
Его речь вдруг приобретает непривычный для него
пунктирный ритм, голос приглушен доверительностью заговорщика:
— А что, если для любой функции придумать что-нибудь
такое... как-то представить произвольную функцию степенной...
или полиномом... хотя бы приближенно как-то... и исследовать
тогда уже не саму эту функцию, а полином?
— Великолепная догадка! — вырывается у меня. — На
следующем занятии мы как раз будем говорить о формуле Тейлора, то
есть именно о таком представлении функций, которое вы сейчас
пытаетесь предложить. И тогда мы покажем: если в некоторой
точке хо функция /(х) имеет нулевые производные всех поряд-
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
251
ков от единицы до (п — 1), а /(п)(£о) Ф 0, то речь о перегибе
может идти лишь в случае нечетного п. Но это — на следующем
занятии. А сейчас, Паша, продолжаем выяснять, как искать
точки перегиба.
— Скажите, а можно все-таки предполагать, что в той точке,
где у функции перегиб... что в этой точке функция имеет вторую
производную?
— Я уже говорил об этом: если вам хочется,
предполагайте. Затем можете рассмотреть случай, когда вторая производная
функции существует не только в этой точке, но и в некоторой ее
окрестности.
— Ну, тогда все тривиально! Тогда все, как с экстремумами!
По теореме Ферма! Пусть по одну сторону от хо функция
выпукла, допустим, вверх, то есть f(x) убывает, а по другую —
вниз, то есть f{x) возрастает. Тогда, если существует /"(хо), то
обязательно /"(хо) = 0. Условие необходимое, но недостаточное,
конечно. И, наверное, еще бывает, что в точке перегиба f"{x) не
существует. Ну да: вот, например, две таких половинки парабол
усами вверх и вниз, у = х2 и у = —х2; вот графики их первых
производных; ясно, что в нуле второй производной нет. А
перегиб есть. Значит, надо перегибы искать так: сначала смотрим, в
каких точках f"(x) обращается в нуль или не существует. Потом
смотрим, существует ли f"(x) по разные стороны от каждой
такой точки. Если существует, то выпуклость по разные стороны
от такой точки можно определять по знаку f"{x).
Молчаливо дожидаюсь, пока кончится этот
захлебывающийся монолог. Потом вкратце, но последовательно повторяю
изложенное Миклашевским. И спрашиваю его с улыбкой:
— Я правильно понял вас?
— Правильно, — улыбается и он.
— Тогда садитесь, Павел. Следующий вопрос... Впрочем, мне
кажется, мы слишком увлеклись теоретизированием. Надо бы и
252
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
[Гл. 3
примеры порешать. Возьмем какую-нибудь функцию и
исследуем, где у нее точки максимума и минимума.
Пишу на доске: у = |x|e~lx_1L
— Не попробуете ли, Лапиков?
Он встает нерешительно, но безропотно. Взяв мел, начинает
с того, что избавляется от модульных скобок с помощью
сигнумов, затем дифференцирует преобразованную таким способом
функцию. Дождавшись, пока он допишет производную до
конца, спрашиваю:
— Что же дальше?
— Надо посмотреть, где эта производная обращается в нуль
или не существует.
— Ну и где же? Видите?
— Нет...
— Я тоже не вижу. Зато всем, надеюсь, отчетливо видно
другое: введение сигнумов может сильно затуманить даже
относительно простую формулу с модулями. Кстати, зачем вы их
убрали, Лапиков?
— Так ведь модуль нельзя дифференцировать!
— Нельзя, насколько я помню, лишь в одной точке, где он
обращается в нуль, а во всех остальных — можно. Ну да ладно,
если уж вам так не нравятся модули, устраните их, не возражаю.
Один способ устранения нам ничего хорошего не дал, давайте
искать другой.
— Никаких идей! — жалобно смотрит он на меня после
долгого томительного молчания.
— Неверно! Одна стандартная идея должна быть у вас
наготове всегда: если задача не решается, следует обратиться к
определениям тех понятий, которые фигурируют в условии задачи.
Определение функции |х| вы помните?
— Конечно: х, если х > О, и —х, если х < 0.
— Разве само это определение не подсказывает вам выход
из тупика? Модуль х оно представляет через простые,
дифференцируемые функции х и —х. Что напрашивается вслед за
этим? Подумайте, повспоминайте... Опять ничего не приходит в
голову? А помните, как совсем недавно Миклашевский исследо-
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
253
вал на дифференцируемость функцию |(х — 1)(х — 2)2(х — 3)3|?
Я, конечно, понимаю, что выхожу за рамки нашего с вами
договора заучивать все, что говорилось на прошлых
семинарах: то, на что я намекаю, Миклашевский делал не далее, как
сегодня...
— Представить по интервалам? — обрывает мои извинения
Лапиков.
— О, вы помните это! И, вероятно, понимаете мою подсказку...
Ну вот, появились и интервалы, и представление нашей функции
на них. Опять, как видите, дело свелось к простым и удобным
формулам. Взять хотя бы первую: не исследуете ли эту функцию
на экстремум?
— Производная обращается в нуль в минус единице, —
докладывает Лапиков после недолгих вычислений.
— Подозрительно на экстремум — правда? А достаточные
условия экстремума — вы запомнили их?
— Слева и справа производные разных знаков.
— Надо было еще отметить, что такое условие применяется
нами для функций, непрерывных в окрестности точки
экстремума...
— У модуля разрывов нет!
— Но есть точка недифференцируемости! Из-за этого такие
точки могут быть и у нашей функции. Взгляните на ее формулу:
йот |х|, вот \х — 1|. Значит, где наша функция может оказаться
недифференцируемой? При каких х?
— При х = О, х = 1.
— Могут ли такие аргументы навредить нам сейчас?
Замолчали? Опять оробели? А оснований для боязни пока что нет —
ведь мы сейчас исследуем функцию на промежутке (—оо, 0).
Входит ли в него хотя бы один из этих двух опасных иксов — нуль
и единица?
— Нет.
254
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
[Гл. 3
— Как вы сами показали, на этом промежутке можно
отождествить нашу функцию |х|е~1х_11 с функцией —хех~1.
— Это же элементарные функции! И минус икс, и экспонента.
Произведение — тоже элементарная функция. Значит,
непрерывна и дифференцируема.
— Мы рассматриваем ее на промежутке (—оо, 0) и
интересуемся точкой х = — 1. Можем ли мы окружить эту точку
окрестностью, лежащей целиком в этом промежутке?
— Можем.
— Хорошо... Ну-ка еще раз, полностью и четко,
формулировку достаточного признака экстремума,
Если сейчас он верно и полно повторит то, что я прошу,
можно будет поверить, что это въелось-таки ему в память.
— Если в какой-то точке хо производная у функции
обращается в нуль или не существует... а сама функция
непрерывна в какой-то окрестности хо... если производная... да, еще если
функция дифференцируема в левой и правой полуокрестности...
и если производная в левой полуокрестности одного знака, а в
правой другого...
— Точнее, — стараюсь говорить осторожно, как бы вплетая
свою поправку в его сосредоточенно-напряженные фразы, —
если для любого х из левой полуокрестности...
— Для любого х из левой полуокрестности производная
одного знака, а для любого х из правой — другого, то в точке хо
функция имеет экстремум. Если слева минус, а справа плюс, то
минимум, а если наоборот — то максимум.
— Очень хорошо! У вас неплохая память! Я уж подумываю,
не усилить ли наш договор новым обязательством с вашей
стороны: обязуюсь, мол, на каждом семинаре помнить все то, что
говорилось на нем, а не только на прошлых семинарах. Но
вернемся к нашей функции, у которой в минус единице вы
заподозрили экстремум. Попробуйте подойти к этой точке с нашим
признаком экстремума.
Выясняем: в минус единице у нашей функции максимум.
Переходим к интервалу (0,1) «Опять минус единица?»—
вполголоса удивляется Лапиков, получив в выражении для производной
множитель (х +1), но Костюк успокаивает его: минус единица не
принадлежит интервалу (0,1). «Тут функция монотонна», —
соображает Лапиков и обосновывает это постоянством знака
производной; переходя к следующему интервалу, сам замечает, что
единицу, хотя ее и подсказывает выражение для производной,
не следует брать в расчет: единица не принадлежит интервалу
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
255
(1, +оо), так что на нем функция строго убывает. Стыки
интервалов даются Лапикову намного легче (помнится, видно, подход
Миклашевского) — в обоих он распознает экстремумы: нуль —
минимум, единица — максимум.
— Запишите свои результаты рядом с формулой функции:
абсциссы точек экстремума, характер экстремума — максисум
или минимум, значение функции в каждой такой точке. Ну вот,
все верно. Садитесь, Лапиков. И впредь не спешите жаловаться
на отсутствие идей. Идеи приходят во время работы, как аппетит
во время еды. Продолжим нашу тему, ребята. Вам может
встретиться такая задача: определить наибольшее и наименьшее
значение функции на области ее определения. Если эта область —
отрезок, надо, очевидно, отыскать наибольший из максимумов и
наименьший из минимумов, но кроме того принять во внимание
значения функции в концах отрезка: наибольшее или
наименьшее ее значение может достигаться и там, вот соответствующий
пример, — рисую график. — Может быть поставлен и такой во-
прос: каковы точная верхняя и точная нижняя грань значений
функции? В таком случае, если область определения функции
неограничена, следует изучить поведение функции при
неограниченном убывании или возрастании аргумента. Именно перед
такой необходимостью ставит нас функция у = \х\е~\х~1К При
х, стремящемся к плюс бесконечности, она стремится... к чему,
Сутеев?
Он молчит, упершись взглядом в заново написанную мною
формулу.
— Не сообразите? А если написать так: у = J*}^ .
— Экспонента... Растет быстрее любой степени... Стремится
к нулю.
— Ответ верный. Но все же хотелось бы получить его
построже. Идите к доске, Сутеев.
В поисках строгого доказательства он лишь с моей
настойчивой помощью придумывает комбинацию е^- — вариант исход-
256
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
[Гл. 3
ной формулы, пригодный для достаточно больших аргументов,
и связывает его через определение предела функции на языке
последовательностей с упоминавшейся еще на первом семинаре
последовательностью —-.
— Вот теперь, — утверждаю достигнутое, — можно с
уверенностью говорить, что при х, стремящемся к плюс бесконечности,
наша функция стремится к нулю. И заметьте: при этом она
остается положительной. А как она ведет себя при х, стремящемся
к минус бесконечности?
— Тоже остается положительной... И тоже стремится к
нулю, — это он доказывает почти без моей помощи.
— Итак, наименьшее значение нашей функции на всей
оси равно... чему, Сутеев? Поглядите на результаты,
которые получил Лапиков, исследуя экстремумы нашей
функции.
— Ее наименьшее значение — нуль.
— И достигается в точке...
— В точке х = 0.
— А наибольшее значение?
— Наверное, у = 1 при х = 1.
— Наверное? Или точно?
— График бы нарисовать...
— Не возражаю. Но я советовал бы не рисовать, а, так
сказать, монтировать — то есть строить график функции,
исходя из ее поведения в характерных точках — граничных
точках ее области существования, точках разрыва,
экстремума, перегиба. Найти их можно уже знакомым нам путем —
анализируя формулу функции и ее производных, первой и
второй: их, разумеется, предварительно надо вычислить. Нелишне
учесть и другие точки, которые так или иначе
выявляются при исследовании функции. Например, когда мы хотели
представить функцию |х|е~1ж_11 формулами без модульных
скобок, мы разбили ось абсцисс на три части точками х = 0
и х = 1. Мы и их занесем в перечень характерных точек,
если будем строить график этой функции. Перед построением
графика все сведения о функции, полученные в
результате ее исследования, полезно свести в таблицу. В ее верхней
строке указываются абсциссы характерных точек: в первом
поле левая граница области существования (или
проставляется символ —оо, если функция определена в сколь угодно
далеких точках левой половины оси абсцисс), затем пропуск,
затем абсцисса следующей характерной точки, опять про-
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
257
пуск и так далее до правой границы области существования
(а если функция определена в сколь угодно далеких точках
правой половины оси абсцисс, то в последнем поле первой
строки проставляется символ +оо). В следующих строках
указывается, какие значения принимают в характерных точках
функция, ее первая и вторая производные, или, если они там
не существуют, описывается их поведение при приближении
аргумента к такой характерной точке. В самой левой
колонке таблицы и в самой правой указывается, к чему стремится
функция, ее первая и вторая производные при стремлении
аргумента к минус и плюс бесконечности соответственно.
В промежуточных клетках указывается знак первой и
второй производной. Положительное значение первой говорит о
возрастании функции, отрицательное — об убывании;
положительное значение второй — о том, что функция выпукла
книзу, отрицательное — о том, что функция выпукла кверху.
Давайте, чтобы далеко не ходить за примерами, построим
такую таблицу для функции у = \х\е~^х~^. Для этого нам
недостает второй производной yij.x. Пусть ее вычислит... хотите,
Сынчиков?
Прохаживаясь между столами, я заметил, как чисто
вычислил он первую производную на всех интервалах. Наверное,
сладит и со второй. И верно — сладил.
Сынчиков
— Все правильно, Сынчиков, садитесь. Начинайте строить
график, Сутеев.
Настраиваюсь, на долгую работу, готовый ловить
ошибки, разъяснять заблуждения, преодолевать заминки... Но что
это? Сутеев уже составил таблицу, размечает на графике
характерные точки и, поглядывая на таблицу, ведет через них
аккуратную кривую. Случайная удача? Нет, пожалуй, не
случайная — он и раньше бывал на высоте, когда мог выразить
свою мысль графиком: на предыдущем семинаре хорошо
разъяснил определение предела функции на языке окрестностей,
сегодня дал верный пример функции, у которой нет предела
258
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
[Гл. 3
на бесконечности, но производная при этом стремится к нулю...
Так сказать, визуальное мышление... И в то же время, начав
с хороших графиков, не смог доказать отсутствие предела в
нуле у функции sin^, не сумел объяснить понятие
производной... Опять какая-то загадка! Надо бы поскорее разрешить
ее: ведь если он действительно силен в этом своем
графическом, визуальном мышлении, за это обязательно следует
ухватиться!
А пока надо просто похвалить его за хорошее выполнение
моего задания.
— Очень хорошо! Садитесь, Игорь. Построим еще один
график, ребята. Кто хотел бы потренироваться в этом деле?
— Ну, давайте я, — поднимается Кулагин.
— Пишите формулу функции, график которой будете
строить: у — fa*\\2 - А дальше — по порядку: таблица, характерные
точки... Хорошо, хорошо... Что, вы уже кладете мел? А поведе-
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
259
ние функции при неограниченно возрастающем аргументе что ж
не показываете? Не представляете, как она себя при этом ведет?
Давайте разбираться вместе. Оказывается, ребята, у этой
функции есть характерная деталь, о которой мы еще не говорили. Это
так называемая асимптота — прямая, к которой неограниченно
приближается график функции по мере того, как ее аргумент
неограниченно возрастает по абсолютной величине. Вы можете
мне заметить, что на примере предыдущей функции уже
познакомились с горизонтальной асимптотой: ее роль играла ось
абсцисс — к ней стремилась нарисованная Сутеевым кривая при я,
стремящемся к минус или плюс бесконечности. Говорят также
и о вертикальных асимптотах, к которым приближается график
разрывной функции в точках бесконечного разрыва. Пример —
вертикаль х = О для гиперболы у = j. Но сейчас у нас речь
пойдет о наклонных асимптотах. Всякую такую асимптоту мы будем
выражать формулой вида Y(x) = кх + Ь; тогда поведение
функции при безграничном нарастании аргумента согласно
определению асимптоты можно описать так: у = кх + b + е(х), где
слагаемое е(х) бесконечно мало при я, стремящемся к бесконечности.
Как тке, зная формулу функции, найти уравнение ее
асимптоты, если та существует? Прошу всех высказывать свои
соображения.
После нескольких торопливых неудачных предложений —
рассудительный голос Гарина:
— Разделить обе части последнего равенства на х и
потом устремить х к бесконечности. Тогда справа
последние два слагаемых обратятся в нуль, и останется
только А;, а слева будет lim ^^. Если этот предел существу-
х—►оо х
от, то ему и равен коэффициент к в уравнении
асимптоты.
— А потом, — подхватывает Кулагин, — подставим в
равенство это А;, перенесем в левую часть кх и х опять
устремим к бесконечности. Тогда е(х) обнулится, и справа
останется Ь. То есть, если существует предел lim [у(х) — кх], то он и
£—►00
равен Ь.
— Верно, — даю свое согласие на оба предложения. —
Замечу только: бывают функции, для которых существует
предел lim №1 а предела lim \у(х) — кх] нет. Тогда, разу-
х—юо х х—>оо
меется, нет и асимптоты. Ну-ка, а как обстоит в этом
отношении дело с нашим примером? Разберитесь с ним, Кулагин.
Ну вот, выясняется, что у этой функции наклонная асимп-
260
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
[Гл. 3
тота имеется: Y(x) = х + 5. Рисуйте график с ее учетом,
Андрей.
Слежу за его работой до самого конца.
— Ну, что же, у вас все правильно. На будущее дам вам один
совет. Еще до того, как рисовать график функции у = /(х),
бывает полезно выяснить, с какой стороны он приближается
к асимптоте у = Y(x) — сверху или снизу. То есть
выяснить, каков знак разности /(х) — Y(x) в окрестности плюс и
минус бесконечности. Это можно указать в крайних клетках
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
261
самой нижней строки таблицы. Попробуем провести подобное
расследование на примере нашей функции. Уравнение
асимптоты у вас уже есть. Составьте разность f(x) — Y{x). Что
получилось? Верно, т^ш- Теперь очевидно, что на плюс
бесконечности эта дробь положительна, значит, график функции
приближается к асимптоте сверху, а на минус бесконечности
он приближается к ней снизу, поскольку там дробь
отрицательна. Садитесь, Андрей. Все было понятно, ребята, по части
построения графиков? Тогда подумайте дома над тем, как
строить графики функций, задаваемых параметрически и
неявно. А сейчас снова займемся теоремами о дифференцируемых
функциях.
— Разве мы их повторили не все? — удивляется Горт. — Нам
па лекциях давали только четыре: Ферма, Ролля, Лагранжа и
Коши.
— Уж не думаете ли вы, что больше и быть не может?
Давайте поразмышляем вот над чем, ребята: разговор о теоремах
Ролля и Лагранжа мы иллюстрировали функциями, которые
были определены на некотором отрезке [а, Ь] и принимали в
его концах конечные значения. Будем теперь рассматривать
функции, определенные, непрерывные и дифференцируемые на
некотором интервале (а, Ь) и стремящиеся к бесконечности того
или иного знака при стремлении аргумента к концам интервала.
Попробуйте сформулировать какие-нибудь теоремы о таких
функциях.
— Если функция стремится в этих точках к бесконечностям
разных знаков, то она в какой-то точке интервала обратится в
нуль, это тривиально, это следует из теоремы о промежуточных
значениях, — быстро соображает Миклашевский. — А если к
бесконечностям одного знака, то в какой-то точке у нее будет
нулевая производная. Что-то вроде теоремы Ролля.
— Как это доказать?
— Надо обрубить график на некоторой высоте, и тогда будет
применима теорема Ролля в чистом виде.
— Что значит «обрубить»?
— Провести горизонтальную прямую так, чтобы она
пересекла график хотя бы в двух точках.
— А как это сделать? Надо разработать алгоритм проведения
такой прямой! Не торопитесь, Павел, подумайте, подумаем все
имеете, ребята. Для определенности будем считать, что функция
стремится к плюс бесконечности при стремлении ее аргумента к
концам интервала (а, Ь).
262
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
[Гл. 3
— Надо взять на интервале (а, 6), — размышляет вслух Мен-
шиков, — какую-то точку xq....
— И чем поинтересоваться по поводу этой точки? —
завязываю разговор, быстрым своим откликом и тоном своим
показывая, что жду от него чего-то очень интересного.
— Какое значение имеет в ней f(x).
— Лучше уж тем, какая там производная: вдруг она
равна нулю — тогда теорема доказана, — ненавязчиво советует
Стрельцов.
— Хорошая мысль! — поддерживаю его. — На удачу
надеяться трудно, но отказываться от нее не стоит. Ну, а если /'(хо) не
равна нулю?
— Тогда она либо больше, либо меньше нуля! — возбужденно
(напал на плодотворную идею?) выкрикивает Мухин.
Зову его к доске. Не уверен, вытянет ли он доказательство,
но уж помуштрую его хорошенько! В крайнем случае сменю его
Буткусом: у того, как я заметил, бродя меж столами, назревает
более простое построение, поначалу не использующее дифферен-
цируемость функции.
Некоторое время Мухин стоит, не решаясь написать ни буквы:
— Мысль на языке крутится, а выразить не могу. Сейчас —
допустим, /'(хо) меньше нуля — если меньше нуля, то f(x) там
убывает...
Он проводит пунктирную горизонталь на уровне /(хо)>
затем, пересекая ее сверху вниз, прочерчивает кусочек графика
функции /(х), на нижнем его конце вырисовывает жирную
точку и отмечает ее абсциссу х\ на горизонтальной оси, продолжает
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
263
график еще чуть-чуть за жирную точку... Движения его все
более медлительны... и вдруг снова резко убыстряются: он
стремительно ведет график вправо, загибает его ввысь, вновь пересекая
пунктирную горизонталь, — и устремляет к бесконечности,
одновременно приближая к вертикали х = Ь.
— Все ясно! — восклицает Синица. — Найдется такое Х2, где
/(#2) > /(#о)> тогда на концах отрезка [xi,X2] функция слева
меньше, а справа больше /(хо) — ведь правда? И где-то
посредине найдется хз, где /(хз) = /(хо). А потом — теорема Ролля,
как Паша предлагал!
Эх, поспешила Люда! Я так хотел, чтобы Мухин сам
проложил весь путь от своей смутной идеи до ее окончательной,
логически безупречной реализации! Теперь этот путь намечен.
Правда в скоропалительном изложении Синицы он
обрисовался не очень ясно. Потребовать от Мухина, чтобы навел полную
логическую ясность? Да — в этом самый важный для него
аспект задачи, которую я хотел ему предложить: в логике ему надо
совершенствоваться в первую очередь.
— Вы поняли, Мухин, что сказала Синица? Да? Тогда
изложите ее рассуждение последовательно и строго с самого начала.
Как всегда, прошу вас хорошо продумать свои слова, прежде чем
говорить. Советую заранее назвать теоремы, на которые станете
ссылаться.
Пошевелив губами, он сосредоточенно пишет:
VM35 > OVx € (b - 5,b)(f(x) > М). Потом
оборачивается ко мне:
— Вот теорема — вернее, определение — функция стремится
к плюс бесконечности, когда х стремится к b — слева стремится.
Возьмем М = /(хо) — ах тогда можно уже взять любое из 6-
окрестности — возьмем любое и назовем Х2 — дальше все, как
Люда говорила — в точке Xi, функция...
— Стоп! — ловлю его. — От куда взялось это xi? Вы ничего
о нем раньше не говорили!
— В самом деле, — винится он. — Сейчас объясню — тут все
просто — это из того, что /'(хо) меньше нуля — да, надо и про
хо сказать — конечно, если с самого начала.
— Если с самого начала, — уточняю его исходную позицию,
то уж — с условия задачи, с того, что дано. Повторите-ка это! И
не спешите!
Отвешивая слово за словом, Мухин пересказывает то, что
говорили Меншиков и Стрельцов о проверке производной /'(х)
в выбранной наугад точке хо, предполагает /'(хо) < 0:
264
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
[Гл. 3
— Теперь надо показать, что справа от xq есть точка xi, где
/(xi) < /(хо). Опять, наверное, по определению? Ваять
определение производной — вот оно: /'(хо) = lim JZ^ ° — если
/'(хо) отрицательна, то дробь gig °' точке отрицательна — и
разность /(х) — /(хо) тоже — при каком-то х она отрицательна...
— При каком-то? — опять ловлю его на необдуманном
слове. — Как искать это х? И почему, если предел дроби
отрицателен, то и сама дробь тоже отрицательна?
Растерянно он подчеркивает шаткой линией выражение для
— Вот определение... Это же основа! Дальше я просто... нет,
не знаю.
— Не знаете, что определение производной само основывается
на определении предела? Напишите его для дроби IZxf и ее
предела /'(#о) на языке окрестностей. Так, так... Vs > 0 3 6 > 0...
так...Ух G (х0-^х0 + ^)(|/(а2:4(а;о) -/'0*0)1 < е). Для
заключительного неравенства была еще одна форма... так... /'(хо) — е <
< IZxo < /'(хо) + £• Если /'(хо) отрицательна, то можно
взять столь малое е > 0, что /'(хо) + £ тоже будет
отрицательным; для такого е найдется 6 такое, что для любого х из
интервала (хо —5, хо + 6) будет выполняться д!^ < /'(х°) + £ < 0-
Вы поняли то, что я сказал?
— Возьмем, — безвольно продолжает он, — любое такое х —
назовем х\ — для него д^Гдв < 0 — и /(xi) - /(хо)...
— Если х\ > хо, — досылаю примечанием; он кивает мне
вполоборота:
— Возьмем х\ справа — знаменатель положительный —
дробь отрицательная — числитель, значит, отрицательный:
f(xi) < /(хо).
— Ну, слава богу, отыскали-таки xi, — подбадриваю
улыбкой Мухина, расстроенного своими промахами и заминками. —
Теперь вы вроде ничего не упустили. Теорему можно считать
доказанной. Садитесь, — отпускаю его.
Когда Мухин приближался к концу доказательства, я
заглянул в тетрадь Буткуса: хотелось вызвать его следующим и
показать более простой подход к теореме. Но Линас застрял на
том, с чего начал. Это, разумеется, не удивило меня: от
невезения не застрахован никто. А вот потом было чему
удивиться: не построив своего доказательства, он не переписал в тет-
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
265
радь и мухинское! Сидел, нахохлившись, не глядя ни на доску,
ни по сторонам. Самостоятельность мышления, так
импонирующая в нем, показалась мне тогда чрезмерной, несколько
извращенной...
— Итак, ребята, мы доказали теорему, которую выдвинул
Миклашевский. Поищем другие.
Доброжелательный тон, которым я приглашаю аудиторию к
размышлению, развязывает язык Лапикову:
— Не знаю, может, это совсем уж простая теорема: если
функция стремится к бесконечности, то и ее производная тоже
стремится к бесконечности.
— Вот уж глупости! — стреляет в него презрительным
взглядом Горт.
— Горт! — возмущенно одергиваю его: в тот самый момент,
когда в Лапикове едва-едва начинает просыпаться инициатива,
он душит ее своей дурацкой борьбой за строгость!
— Но ведь действительно! — кипятится он, выскакивая к
доске и наскоро набрасывая на ней график. — Вот такая функция
стремится к бесконечности — так? Но стремится вот по таким вот
ступенькам, значит, ее производная в любой окрестности
предельной точки обращается в нуль, значит, к бесконечности не
стремится.
— Красивый пример, — не удерживаюсь от искренней
похвалы. — Он доказывает, что при стремлении дифференцируемой
функции к бесконечности ее производная может не стремиться
к бесконечности. Правда, ваш пример, Горт, задан пока лишь
иллюстративно. Хорошо бы выразить его в математических
образах. Попробуем сконструировать подобную функцию из
элементарных. Садитесь, Саша.
266
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
[Гл. 3
— Мне представляется, — крадется в наступившую тишину
голос Рамзина, — что подошло бы нечто такое: j + sin j.
— Проверьте у доски, подходит ли.
— Действительно, благодаря сомножителю (1 + cos j) в
выражении для производной она будет обращаться в нуль в любой
сколь угодно узкой окрестности нуля.
— Это всем понятно? — обращаюсь к аудитории. — Да?
Садитесь, Рамзин. Утверждение Лапикова опровергнуто
окончательно. Но я хотел бы, ребята, напомнить вам про нашу старую
договоренность: в любом суждении, которое выскажет каждый
из нас, искать рациональное зерно, а не забрасывать, — строго
заглядываю в глаза Горту, — обидными словечками неудачные
высказывания товарищей. Мне кажется, что неверное в общем
мнение Лапикова содержит намек на очень интересную теорему.
Итак, хотя при стремлении функции к бесконечности ее
производная к бесконечности не стремится, но ...
— Неограничена? — говорит Костюк каким-то
нехарактерным для него нетвердым голосом.
Поддержать его категорическим «совершенно верно»? Или
устроить ему тренировку в самостоятельном разрешении своих
сомнений? Второе, пожалуй, лучше:
— Проблема не так уж сложна, чтобы вы не смогли
разобраться в ней сами, — говорю, обращаясь ко всем.
И снова отправляюсь в обход. Покружив между столами,
направляюсь к Костюку. У него в тетради — интересный чертеж.
— Что это?
— Доказательство.
— Доказательство чего?
— Того, что производная неограниченна.
— Изложите на доске с самого начала.
— Если с самого начала, то нужно сказать, что функция f(x)
определена, непрерывна и дифференцируема на некотором
интервале (а, Х{)) и стремится к бесконечности при х, стремящемся
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
267
к хо- Мы хотим доказать, что /'(х) неограничена в точке xq.
Что это значит? Это значит, что для любого сколь угодно
большого положительного М в любой 5-полуокрестности хо должно
найтись такое £, что |/'(01 > М.
— Вы пользуетесь определением неограниченности в точке,
которое на прошлом семинаре предложила Синица?
— Да, — отрывисто отвечает он. — Я беру произвольное М,
потом произвольную левую 5-полуокрестность хо и в этой
полуокрестности — какую-то точку х\. Выясняю величину /'(xi).
Может оказаться, что \f{x\)\ > М. Тогда сразу полагаю £ = х\. В
противном случае провожу наклонные у = кх+Ь\иу = — fcx+&2>
которые пересекают график /(х) в точке с абсциссой х\, и пусть
наклон к у них будет больше, чем М\ к — положительное. Тогда
при некоторых х, которые ближе к хо, чем xi, график f(x) будет
заключаться в треугольнике между наклонными и вертикалью
х = xq. Функция стремится к бесконечности при х, стремящемся
к хо- Значит, ее график обязательно выйдет за пределы
треугольника, пересечет хотя бы одну из наклонных в какой-то точке Х2,
ближе к хо, чем х\.
Сдерживаю в себе недоуменное «откуда вы это взяли?» —
пусть договорит до конца.
268
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
[Гл. 3
— К отрезку [xi, £2] применю теорему Лагранжа: на нем
найдется точка £, в которой касательная к графику функции
параллельна одной из наклонных: |/'(01 = к > М. Что и требовалось
доказать.
— Но скажите теперь, Костюк: на каком основании вы
утверждаете, что одна из проведенных вами наклонных пересечется с
графиком функции /(х) в точке Х2, более близкой к хо, чем х\1
— Ну, это довольно очевидно, — небрежно заявляет он.
— Очевидно вам, но не мне.
— Пожалуйста, смотрите! Прямые у = fcx + bi, и у = — kx + b2
пересекают вертикаль х = хо так, что точки пересечения отстоят
от оси абсцисс на расстояния hi и /i2. Если график функции не
пересечет ни одну из наклонных, то на интервале (xi, хо),
значения |/(х)|, очевидно, не будут превышать максимального из
чисел hi и /i2, а это несовместимо со стремлением /(х) к
бесконечности.
— То есть вы хотите сказать, что на интервале (xi,xo)
найдется точка хз такая, что график функции в ней будет проходить
либо выше верхней, либо ниже нижней из ваших наклонных. Но
это еще не значит, что он будет пересекать ту или иную
наклонную, будет иметь с ней общую точку!
Он задумывается и через некоторое время вновь
поворачивается ко мне, глядит на меня с упрямым раздражением:
— Я же провел наклонные так, чтобы они ограничивали
график функции в некоторой окрестности точки xi, нет, лучше
сказать — чтобы хотя бы одна точка графика функции оказалась
между наклонными — хотя бы при одном значении аргумента
Х4- С другой стороны мы выяснили, что где-то ближе к хо, в
точке хз, график проходит вне угла, образованного
наклонными. Значит, где-то в промежуточной точке график обязательно
пересечет одну из наклонных!
— Это же теорема о промежуточных значениях! Наша
функция непрерывна, и к ней эта теорема применима, — заступается
за товарища Стрельцов.
— Извините! — оборачиваюсь к нему. — Если уж вам угодно
вести разговор на геометрическом языке, то в известном нам
доказательстве теоремы о промежуточных значениях график
непрерывной функции пересекал горизонтальную прямую, а у
нас обе прямые — сугубо наклонные!
— Не все ли равно? — со своей стороны напирает Костюк.
И Стрельцов вторит ему, обращаясь ко мне доверительно-
заигрывающим тоном:
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
269
— Мы то с вами понимаем, что это одно и то же.
— Мы с вами? Но разве научные истины носят договорный,
а не объективный характер?
— Сами говорили: искать нестандартные подходы, —
ввязывается Буткус.
— Да, говорил, и готов повторить сейчас, и в будущем не
стану сдерживать полет вашей фантазии: в поисках истины вы
вольны выдвигать любые гипотезы. Но когда истина найдена,
вы обязаны вымостить путь к ней крепкими доказательствами,
чтобы после вас ее могли достичь другие. В конце концов, вы
добываете научные истины не для одних себя. И еще я
напомнил бы вам, ребята, хорошее высказывание Спинозы: «Что такое
заблуждение? Истина одиночки. Что такое истина?
Заблуждение тысяч». Чтобы верилось в истинность нашего утверждения,
давайте поставим его на фундамент общеизвестных теорем
математического анализа. Вы ссылаетесь на теорему о
промежуточных значениях? Сведите к ней свое утверждение. Давайте
вспомним ее в той первичной формулировке, с которой мы
начинали свое знакомство с нею: на одном конце некоторого
отрезка непрерывная функция отрицательна, на другом —
положительна; утверждается, что в какой-то промежуточной точке
функция обращается в нуль. А что хотите доказать вы, Костюк?
Что если в некоторой точке х±, график функции f(x)
оказался под прямой у = кх + 6, а в некоторой точке Хз — над той
же прямой, то в какой-то точке £5, лежащей между хз и х^
этот график пересечет прямую, то есть /(£5) = ^#5 + &, то есть,
Стрельцов...
— Что /(хб) — кхь -6 = 0.
— Вот-вот! Так в нашем рассуждении появляется новая
функция F(x) = f(x) — кх — b. Давайте работать с ней,
Костюк.
Недовольный тем, что ему приходится действовать по
чужой указке, он показывает (не без нажима с моей стороны), что
F(x^) < 0, то есть /(£4) < ^х4 + b и что F(xs) > 0, то есть
/(хз) > кхз + Ь, а следовательно, по теореме о промежуточных
значениях найдется точка £5, лежащая между х± и хз, такая,
что F(xs) = 0, то есть f(x^) = кх$ + Ь.
— А это и есть пересечение, — вторю его выводу. —
Обратите внимание, Костюк: точка пересечения теперь обозначается
Х5, а не Х2, как было у вас раньше. Ее поиск, образно
говоря, потребовал в два с половиной раза больше труда, чем
казалось на первый, нестрогий взгляд. Далее рассуждения
270
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ
[Гл. 3
можно спокойно вести по той схеме, которую вы наметили
прежде. Займитесь этим, если хотите, дома, устраните все
остальные допущенные вами неряшливости и недоговорки —
и тогда ваше доказательство примет вполне приличный вид.
Садитесь.
Бросив взгляд на наручные часы Рамзина, замечаю, что
время семинара подходит к концу.
— Мне понравилось, ребята, как вы работали сегодня над
большинством моих заданий — инициативно, смекалисто.
Думаю, что в дальнейшем вы вполне сможете взять на себя часть
работы, которую обычно выполняет преподаватель: например,
излагать перед началом семинара основные положения темы,
которая на нем будет обсуждаться. На следующем семинаре мы
будем заниматься формулой Тейлора. Кто хотел бы рассказать
о ней в начале занятия?
Демонстративно равнодушно лицо Рамзина: риск — не
в его привычках. Костюк отводит глаза: не хочется и ему.
Усмешлив взгляд Стрельцова: «Попробовать, что ли?» И
только Горт смотрит просяще, почти умоляюще: «Разрешите
мне!»
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
271
— Пожалуйста, Саша! — отвечаю на эту немую просьбу. —
Итак, докладчиком на следующем семинаре будет Горт.
Остальным тоже будет задание: повторить все, что мы прошли до сих
пор.
Глава 4
ФОРМУЛА ТЕЙЛОРА
— Мы договорились, ребята, что сегодня будем заниматься
формулой Тейлора. Рассказать о ней вызвался Горт. Вы готовы,
Саша? Да? Тогда прошу вас к доске.
Чувствуется, что сегодняшний день для него торжественный:
он подтянут, тщательно причесан, и даже его скромный костюм
выглядит нарядным — такое впечатление создают отглаженная
белая рубашка и пестренький галстук.
— Рассмотрим функцию /(я), — степенно начинает он, —
имеющую в некоторой точке хо из своей области определения
производные всех порядков до n-ного включительно. Из этого,
в частности, следует, что функция определена и непрерывна
вместе с производными всех порядков до (га — 1)-го
включительно в некоторой окрестности точки х$. Составим многочлен
Рп(х) = /(х0) + Щ±(х-х0) + ^(х-хо)Ч... + £^(х-х0у.
Легко видеть, что он сам и его производные до n-ной вклю-
Горт I
Хг>Ы) = о((х-х0)п) (3)
чительно в точке хо такие же, как у функции f(x).
Составим разность rn(x) = f(x) — Pn(x)i назовем ее остаточным
членом и докажем, что для него справедливо утверждение
гп(х) = о((х-х0)п).
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
273
Он говорит солидно и назидательно, формулы помечает
аккуратными цифирками в скобках. Чувствуется, что роль лектора
ему нравится весьма.
— Из равенств (2) с очевидностью следуют соотношения
(4). Основываясь на этих соотношениях, мы и выведем
доказательство своего утверждения. Доказывать его будем по
методу полной математической индукции. Проверим, что наше
утверждение верно при п = 1. Иначе говоря, покажем, что если
п(#о) = ^(^о) = О? то п(#) = °(х — хо)- В самом деле:
lim ^tei = lim Г1(ж)~Г1(Жо) = r' (х0) = 0. Теперь предположим,
Х-+Х0Х Х° X-+XQ X Хо
что утверждение (3) вытекает из условий (4) при
некотором (п — 1), то есть из п условий rn_i(xo) = rn-i(xo) = ... =
rn-\ (xo) = 0 следует rn-\(x) = o((x — xo)n_1). Отсюда мы
получим, что из условий гп(хо) = г'п{хъ) = ... = Гп(хо) = 0 следует
гп(х) = о((х — хо)п). Легко видеть, что наше предположение
можно перенести на производную r'n{x) = f'(x) — /'(хо)—
-^ [х°'(х - х0) - ... - (^_i)°; (х - хо)п~1- ведь она тоже
представляет собой разность между какой-то функцией и
полиномом (п — 1)-й степени и для нее тоже выполняются
п условий г'п{хо) = ... = Гп хо] = 0. Перенос позволяет
написать: г'п(х) = о((х — хо) ). Теперь займемся
остаточным членом гп(х). Согласно условию гп(хо) = 0
представим его в виде разности: гп(х) = гп(х) — гп(хо). Далее
согласно теореме Лагранжа представим эту разность так:
гп(х) — Гп(#о) = гп(с)(х ~ хо)> где с лежит в интервале (хо,х).
Наконец используем представление г'п{х) в виде о малого:
г'п(с)(х - х0) = о((с - xo)n_1)(x - хо) = о((х - хо)п_1)(х - х0) =
= о((х — хо)71). А отсюда уже вытекает представление
функции Дх) в виде: /(х) = /(х0) + ^(х - х0) + ^(*-
-х0)2 + ... + ^г1^ - хо)п + о((х - х0)п). Эта
формула называется формулой Тейлора с остаточным членом в
форме Пеано.
274
ФОРМУЛА ТЕЙЛОРА
[Гл. 4
Он закругляет фразу подытоживающей интонацией и
смотрит на меня, ожидая оценку за начальную часть своего
выступления, — смотрит и горделиво и опасливо.
— Вы все изложили грамотно, Саша, — начинаю с
похвалы. — Но я хотел бы придраться к вашей манере изложения.
Мне показалось, что вы не очень заботились о том, чтобы все
ваши умозаключения были понятны слушающим вас.
Например, вы без единого комментария заменили о{{с — £о)п-1) на
о((х — xo)n_1). По-моему, такую замену стоило бы пояснить. Сде-
о((с-хо)п-1) o((c-xo)n_1) (c-Xo)n_1
лать это можно, скажем, так: fc_gnV = ^fr-i; • (Х-ХУ^
Если х стремится к хо, то и с, в силу своего положения,
стремится туда же. В последнем произведении первый
сомножитель бесконечно мал по определению о малого, а второй
ограничен опять-таки в силу положения точки с. Стало быть,
и все произведение бесконечно мало. А это и значит, что
о((с — xo)n_1) = о((х — xo)n_1). В вашем рассказе было еще
два-три подобных логических скачка. Вы совершали их
свободно и стремительно, иногда безотчетно, иногда с оговорками
«легко видеть», «очевидно». Но каждый ли из ваших
слушателей при этом столь же легко мог проследовать за вами? Вы
должны уметь ответить на этот вопрос, должны, что
называется, чувствовать аудиторию и вести свои умозаключения
достаточно короткими шажками, чтобы не растерять по дороге
тех, кто мысленно следует за вашей речью. Чтобы
сохранить их внимание и облегчить понимание ваших слов, надо
стараться использовать любую мелочь. Например, когда вы
переносили индуктивное предположение с функции гп-\{х) на
производную г'п(х) и писали цепочку равенств г'п(хо) = ... =
= Гп (хо) = О, то о выражении Гп (#о) можно было бы
сказать, что это (п — 1)-я производная от г'п(х) в точке х$. Тогда
перенос индуктивного предположения с гп-\(х) на г'п(х)
выглядел бы более отчетливым. И еще: на мой взгляд, когда вы
что-то собираетесь рассказать большой аудитории, то в целях
лучшего понимания исходным пунктом рассказа должен быть
какой-нибудь факт, хорошо известный вашим слушателям, но
вместе с тем такой, в котором вы вскрываете интересную
проблему — этот интерес увлечет за вами слушателей. Заводя речь
о формуле Тейлора, можно было бы вспомнить
общеизвестное представление функции, дифференцируемой в некоторой
точке х$, вот такое: /(ж) = /(яо) + Мх ~~ хо) + о{х — хо),
где А = f'(xo). Что это значит? То, что мы представили
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
275
функцию f(xo) с точностью до о(х — хо) в виде линейной
функции, которая в точке xq имеет то же значение и ту же
производную, что f(x). Можно было бы нарисовать при этом
график и показать, что такое представление — наглядно
выражаясь, приближение кривой линии с помощью прямой —
в общем-то довольно грубое. А затем можно было бы
поставить вопрос: нельзя ли приблизить функцию f(x) более
точно, какими-нибудь «криволинейными» функциями
достаточно простого вида? Кстати, так в свое время предлагал
поступить Миклашевский (Павел исподлобья вскидывает на
меня взгляд, гадая, что я скажу дальше по его поводу, и
улыбается, довольный, услышав окончание фразы) — это была
хорошая, смелая, перспективная идея. Ее можно развивать
во многих направлениях, с которыми мы познакомимся в
будущем, но сейчас проследуем лишь по одному пути,
который ведет к формуле Тейлора. Намечая этот путь, вы могли
бы, Саша, сказать так: попробуем приближать некоторую
функцию многочленами, к которым относится и линейная
функция /(хо) + А(х — хо) — Qi(х)- По аналогии с нею
вы написали бы искомый многочлен гс-ной степени в виде
qn(x) = А0 + А\(х - х0) + А2(х - х0)2 + ... + Ап(х - х0)п; такой
вид, пожалуй, сразу бы подсказали бы ваши слушатели, Саша.
Их живая реакция дала бы вам знать, что ваши слова доходят
до них. Если линейная функция q\{x) в точке хо совпадала
с f(x) вместе со своей первой производной, то от
многочлена qn(x) естественно потребовать большего: qn{xo) = /(яо);
q'n(xo) = f'(xo)\...;qn (хо) = f^n\xo). Если построенная нами
линейная функция q\(x) в окрестности точки хо отличалась
от f(x) на величину о(х — хо) то, развивая аналогию, на
многочлен qn(x) можно наложить условие: f(x) — qn(x) =
= о((х — xq)u). Выполнимы ли все эти требования? Условие
qn(xo) = f(xo) сразу приводит нас к равенству Aq = f(xo).
Продифференцируем qn(x) и подчиним его первую
производную условию q'n(xo) = /'(^o)- Отсюда получается,
что А\ = f'(x0).
Говорю вроде бы одному Горту, а сам то и дело кошу взглядом
на остальных: слушают ли? Я ведь заодно повторяю для них
рассказанное Гортом.
— Итак, А\ = /'(яо)- Дифференцируя многочлен qn(x) еще
и еще и последовательно ставя перед его производными в точке
xq выдвинутые нами требования, мы получим А2 = 1 ,
276
ФОРМУЛА ТЕЙЛОРА
[Гл. 4
^з = 2-з и во°бще Ak = fe|0', где значение fc мы
доведем наконец до п — то есть до степени нашего полинома. Так
мы полностью построим полином, удовлетворяющий
условиям, сформулированным нами для него и его производных до
n-ной включительно в точке х$. Как видите мои пролиномы
qn(x) совпадают с вашими рп{х). Но будет ли при этом
удовлетворяться последнее условие: f(x) — qn{x) = o((x — хо)п)?
Здесь я повторил бы, Саша, то что уже сказали вы.
Впрочем, мое вторжение в ваш доклад затянулось — извините.
Можете продолжать. Но прежде, пожалуй, резюмируйте все
сказанное о формуле Тейлора до сих пор. К чему мы пришли
в итоге?
— Мы пришли...
Он на секунду-другую замолкает, стараясь сосредоточиться.
Продолжает четко и неторопливо:
— Мы пришли к следующему выводу: пусть функция f(x)
определена в некоторой окрестности точки xq и имеет в этой
точке все производные до n-ного порядка включительно. Тогда
/(*) = /(*„) + £^(х - хо) + ^(х - хо)2 + ... + £$*!(*-
—хо)п+о((х — £о)п). Эта формула называется формулой Тейлора
с остаточным членом в форме Пеано.
Он отрывается. от доски и листает свой конспектик,
видимо, чтобы рассказать дальнейшее подоходчивее, как я
советовал:
— Форма Пеано не совсем удобна — она описывает
поведение остаточного члена при х, стремящемся к хо, выражает тот
факт, что остаточный член есть о малое от {х — #o)n, и все>
а оценить его не позволяет. Чтобы его оценить, нам
потребуется сделать одно предположение, потребуется предположить,
что функция f(x) имеет все производные, все до (п + 1)-го
порядка включительно, и притом не только в точке хо, но и в
некоторой ее окрестности. И еще, — запнувшись, он глядит на
меня с сомнением, — тут придется ввести одну хитрую
функцию...
— Вы смотрите на меня так, будто просите моего разрешения
на это. Конечно, для лучшего усвоения математических истин
было бы очень хорошо, чтобы в рассказе о них каждое
умозаключение логичным и понятным образом вытекало из
предыдущих. Но ведь поиск этих истин, как мы с вами хорошо знаем,
почти никогда не протекает подобным гладким путем, ищущая
мысль то и дело совершает внезапные «нелогичные» скачки. И
потому трудно надеяться, что достигнутое в таком поиске мо-
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
277
жет быть описано в безупречно гладком стиле. Однако, если в
остальном изложение будет предельно логичным и доходчивым,
то и отдельные неожиданные скачки будут усваиваться
слушателями наилучшим образом. Надо лишь следить, чтобы они не
следовали друг за другом слишком часто и чтобы все изложение
в целом не выглядело, как нечто ниспосланное с небес и не
имеющее никакой почвы в памяти и сознании слушателей; таким оно
было у вас, Саша, или по крайней мере казалось таким в самом
начале вашего выступление — это и вызвало мою критику. Так
какую функцию вы хотели ввести?
— Вот такую: (p(z) = f(x) - f(z) - Щг~(х-z)-...-f nJz'(x-
—z)n. Легко видеть, что <р(х) = 0, a <p(xo) — это rn(x),
остаточный член, расхождение между f(x) и рп(х), между функцией
f(x) и полиномом рп(х), который я строил раньше. Итак, гп(х) =
= <р(хо). Запишем это иначе: гп(х) = <р(хо) — <р(х). Такая замена
не нарушит равенства, потому что, как я уже сказал, <р(х) = 0.
И еще можно заметить, что ip'(z) очень просто выражается через
y(n+i) ^ _ я эт0 сейчас покажу.
Он аккуратно, медленнее, чем раньше, проводит выкладки, в
результате которых возникает цепочка равенств: rn(x) = <p(xq) —
-<р(х) = у?'(с)(хо ~ х) = f n+nl ^ (х - с)п(х - х0).
Горт I
<р(*)=fc*)■ и*)-4г Сж"7)- • - £Зг?^x-*)Л
— Ну вот, здесь есть разность между значениями функции
(p(z) и есть ее производная в точке с между х и х$. Такие
элементы встречаются в формуле Коши ^°Сц^ = £Щ • Что взять
в качестве гр(х), я скажу потом, а пока из формулы Коши
представим гп(х) в виде фчл ' п\ (х ~ С)П* И еще введем
обозначение с = хо + в(х — хо), где 0 < в < 1. Теперь, если
подставлять вместо ф(х) подходящие функции, мы станем
получать разные формы остаточного члена, более или менее удобные
278
ФОРМУЛА ТЕЙЛОРА
[Гл. 4
для тех или иных задач. Возьмем, например, ip(z) = (х — z)p,
где р > О, и получим остаточный член в форме Шлемильха-
Роша: rn(x) = f{n+1)(*о+в(х-х0)) ^ _ 0)n+i-P(x _ X())n+i Положим
в этой формуле р = 1 и получим остаточный член в форме
Коши: гп(х) = /(п+1)(^+^-хо))(1 _ 0)п(х _ Хо}п+1 д если по.
ложить в этой же формуле р = га + 1, то получится
остаточный член в форме Лагранжа: гп(х) = uXi)\~ (x ~ xo)n+1
/ х /(п+1)(с)/ чп+1
или короче гп(х) = ,п+1у/ (х — хо) , где с — какая-то точка
между хо и х.
— Спасибо, Саша. Все понятно, хотя и кратко. Но ведь, —
обращаюсь к аудитории, — я просил Горта не воспроизвести всю
лекцию о формуле Тейлора, а лишь напомнить основные
положения и выводы. Только в таком сжатом виде мы и повторяем
теорию на практических занятиях. На большее у нас просто нет
времени. Вот еще одна причина, по которой следует ходить на
лекции, читать учебники.
Горт тем временем смотрит в свои записки, бормоча:
— Кажется, все... Нет, забыл — еще теорема о
единственности разложения: если существует представление функции в виде
многочлена га-ной степени плюс какой-то остаточный член, то
есть /(х) = А0 + Ai(x - хо) +... + Ап(х - х0)п + гп(х), и для
остаточного члена справедливо утверждение гп(х) = о((х — хо)п), т0
коэффициенты полинома будут точно такими же, как в формуле
Тейлора: А$ = /(хо) и ПРИ любом к от единицы до га
включительно Ak = f £*°K
И складывает листки своего конспектика:
— Теперь все.
— Все? Нет, я не соглашусь с вами, Саша. Что касается
общетеоретических соображений, то их вы перечислили достаточно
полно. Но без конкретных примеров они выглядят как-то
безжизненно. Покажите нам тейлоровское разложение хотя бы
одной знакомой нам функции.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
279
— Пожалуйста! Могу даже не одной, а пяти! — и, вытерев
доску, молча пишет с левого ее края разложение функций
e^sina^cosx, (1 + х)Л,1п(1 + х).
Горт
| en(^x) = x-f,f,„4(-<r'.£.\0^ |
— Мы слушаем вас, — приглашаю его продолжать.
— А что тут, собственно, говорить? Все написано, — он
кивает на доску, — все ясно. Да я и не готовился про это
рассказывать.
— Гм ... не готовился ... Делать нечего — придется мне
объяснять самому. Напишите над списком основных разложений
формулу Тейлора в общем виде, напишите так, чтобы под ней
оставалась пустая строка, — и садитесь, Саша. Спасибо вам за доклад,
но если в будущем вам придется еще выступать в этой
аудитории, учтите, пожалуйста, замечания, которые я сделал вам
сегодня.
Проводив его взглядом, возвращаюсь к написанным им
формулам:
— Коэффициенты тейлоровского разложения функции
выражаются через ее высшие производные в некоторой точке xq.
Поэтому мы можем в явном виде написать сколь угодно
длинную формулу Тейлора для всякой функции, для которой умеем
вычислять производные сколь угодно высокого порядка.
Таковы синус, косинус, логарифм, показательная и степенная
функции. Вот, скажем, показательная функция ех. У нее все
производные совпадают с ней самой. Проще всего их вычислить
при xq = 0: это будут сплошь единицы. Подставим их в
формулу Тейлора. Выражение х — хо при этом обратится просто в
х. Остаточный член возьмем в форме Пеано. Получим, —
показываю на первое из написанных Гортом разложений, — что
ех = 1+х + §г + ... + ^т + о(хп). Теперь синус. Возьмем общую
формулу для его n-ной производной и подставим туда xq — 0.
280
ФОРМУЛА ТЕЙЛОРА
[Гл. 4
Ясно, что при четных п формула даст нам нули, а при
нечетных — последовательно плюс единицу, минус единицу, плюс
единицу, минус единицу и так далее. После подстановки этих чисел
в формулу Тейлора, мы получим второе из разложений нашего
списка: sinx = х - |f + ^ - ... + Д~^%:г2п+1 + о(х2п+2). Тем же
путем получим и третье разложение: cosx = 1 — §r + fr_•••+
+ feJx x2n + o(x2n+1). Примемся теперь за степенную функцию;
напишем ее поначалу в самом простом виде: хх. Вот формула ее
гс-ной производной: А(А — 1)...(А — п + 1)хх~п. Она
подсказывает нам, что для этой функции нуль неудобен в качестве точки
разложения. В самом деле, величина хх~п не существует в
нуле, если Х — п отрицательна. Какую же точку разложения здесь
лучше взять? Конечно, xq = 1: все величины хх~п тогда
обращаются в единицу. И получается: хх = 1 + Х(х — 1) Н—'27 < (х—
— I)2 + ... + MA-l)..jA-n+l)^ _ !)n + 0цх _ ^пу Более удобный
вид эта формула примет, если сделать замену х — 1 = t. Иными
словами, будем раскладывать не функцию хх в единице, а
бином (l+t)x в нуле. Его разложение будет таким, какое написано
у нас, если не обращать внимания на обозначение переменной:
(1 + t)X = 1 + Xt +.^^t2 + ... + A(A-lMA-n+l)tn + o(tn) Bnpo_
чем, лучше вернуться к более привычной, чем £, букве х, и тогда
формула в точности совпадет с той, что в нашем списке. Для
логарифма можно повторить те же, что и для степенной функции,
возражения против выбора нуля в качестве точки разложения и
те же доводы в пользу единицы. Но разлагать \пх в единице —
это то же самое, что разлагать 1п(1+х) в нуле. Вот это
разложение: ln(l +x) =x-f + f-... + (-1)п+1тг + °(хП)- я советую
вам, ребята, переписать в свои тетради на отдельной странице
всю таблицу из пяти разложений, которые написал Горт, вместе
с исходной формулой Тейлора в общем виде. Оставьте под этой
формулой такой же пробел, как на доске, а под таблицей — место
для ее продолжения.
Жду, пока ребята выполнят мою просьбу. Затем веду речь
далее:
— Итак, пять разложений. Каждое из них представляет
соответствующую функцию в окрестности нуля. Иными словами,
величина х в каждом из них предполагается малой. Это
подсказывает своей формой остаточный член: в выражении о{х)
аргумент х всегда подразумевается стремящимся к нулю,
бесконечно малым. Замечу попутно, что формула Тейлора в том случае,
Ю. В. Пухначев] СЕМЬ СЕМИНАРОВ 281
когда разложение производится в окрестности нуля,
называется формулой Маклорена (пишу ее в пустой строке, оставленной
Гортом и прошу ребят сделать то же самое). Казалось бы, в силу
привязанности к нулевой точке маклореновские разложения
находят довольно ограниченное применение. Это не так. По
формуле Маклорена перечисленные пять функций можно представить
в окрестности любой точки, где известны их значения. Скажем,
вам потребовалось представить функцию ех, где х близко к двум.
Величину, близкую к двум, не назовешь малой, однако,
пользуясь ее близостью к двойке, мы можем ввести новую переменную
t = х — 2. Тогда ех = e2+t = е2 • е*. Теперь второй сомножитель
мы уже сможем разложить по формуле Маклорена, а значение
первого нетрудно вычислить с помощью авторучки и листка
бумаги, не говоря уже о калькуляторе. Ну-ка, а как бы вы, ребята,
стали вычислять значение функции sinx в точке, близкой,
допустим, к j?
— Наверное, опять нужно начать с замены переменной? —
негромко спрашивает Лапиков.
— Совершенно верно! Сделайте ее на доске. Смелее, смелее!
Ну вот, получили sin(^ + t). Дальше что? Почему вы
остановились?
— Синус суммы, — вполголоса подсказывает Стрельцов.
Вспомнив тригонометрическую формулу, которая позволяет
выделить в чистом виде sint и cost, Лапиков аккуратно
переписывает их разложения из списка Горта и с довольным лицом
оборачивается ко мне.
— Вы считаете, что сделали все? Ошибаетесь. Поглядите на
любое из разложений, которые выписал Горт: задавшись
произвольной степенью аргумента хп, можно сразу выяснить, какой
при ней стоит коэффициент. А из написанной вами суммы это
определишь не сразу. Перепишите ее так, чтобы она кончалась
слагаемыми вида antn + o(tn), укажите , как определяется
коэффициент ak при любой степени tk — вот тогда вашу работу
можно будет считать законченной.
С живой готовностью вскинув мел, он через пару секунд
вновь оборачивается ко мне.
— Не знаете, как подвести под единую формулу
коэффициенты при четной и нечетной степенях tl — беру у него мел. —
282
ФОРМУЛА ТЕЙЛОРА
[Гл. 4
В таких случаях искомое выражают с помощью двух разных
формул, — пишу cik и правее рисую большую фигурную
скобку, еще правее нее, на довольно большом расстоянии ставлю две
пометки к = 2г + 1 и к = 2г, одну под другой, возвращаю мел
Лапикову, и он вписывает недостающее в пропущенные мною
промежутки.
— Вот теперь все. Садитесь, Лапиков. Следующий вопрос:
как вычислить значение функции In x в точке, близкой к десяти?
Не попробуете, Сутеев?
Он уверенно делает замену х = 10 + £, затем без задержек
пишет lnx = ln(10 + t)= ln[l + (9 + t)].
— И теперь, — перебиваю его, — если я правильно вас понял,
вы подставите в имеющееся у нас разложение функции 1п(1 + х)
вместо х сумму 9 + t?
— Да, — без тени сомнения отвечает он.
— Но глядите: в этом разложении величина х предполагается
малой. А разве можно сказать это про сумму 9+£? Своей заменой
вы добились, чтобы t было числом малым, а тогда уж 9+£ малым
никак не будет! Где-то в своих выкладках вы сделали неверный
поворот. Давайте разбираться, где. Замена х = 10 +1
возражений не вызывает: с ее помощью вы вводите в свои дальнейшие
построения бесконечно малую переменную, работать с которой
очень удобно. Не вызывает сомнений и равенство In х = 1п(10+£).
Значит, сомнителен лишь следующий переход.
— Но ведь нужно, чтоб под знаком логарифма стояла единица
плюс еще что-то!
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
283
— Не «что-то», а нечто малое! Значит, единицу следует
устроить каким-то другим способом. Каким же? Думайте, думайте!
Может быть, все его затруднения в рассуждениях и при
решении задач — от неловкости в преобразованиях, от неумения
увидеть каждую деталь рассуждения или выкладки во всех
возможных формах и мысленно скомбинировать логичную конструкцию
из подходящих друг к другу вариантов — подобно тому, как в
обыденной речи мы комбинируем связные фразы из слов во
взаимно соответствующих грамматических формах?
Не отрывая напряженно выжидающего взгляда от Сутеева,
вскидываю руку, прося ребят подождать со своими советами. Но
от него, видно, сейчас ничего не дождешься.
— Что тут можно сделать, ребята? Спросим об этом...
Аргунову.
— Вынести за скобку десятку? — отвечает она вопросом на
вопрос.
— Ну, разумеется! Получится сумма логарифмов: In 10, очень
употребительная константа, равная, насколько я помню, 2,303,
плюс ln(l + jq), который разложим по формуле Маклорена: ведь
в силу малости t мало и у^. Действуйте, Сутеев. Ну вот, все
сделано. Для полного совершенства стоило бы написать каждое
слагаемое так, чтобы степень переменной t стояла в самом конце,
а все остальное сгруппировалось в коэффициент при этой
степени... Есть! Все хорошо. Садитесь. А теперь давайте-ка вычислите
мне, ребята, v/T000 с точностью до четырех знаков после
запятой.
— Тысяча — это почти 1024, а 1024 = 210, — быстро смекает
Миклашевский и по моему пригласительному жесту выходит к
доске, приводит корень к виду 2 у 1 — y|g, начинает разлагать
его по формуле Маклорена — и останавливается на третьем
слагаемом.
Осторожно интересуюсь:
— Гадаете, достаточно ли? А как можно это выяснить?
Он приписывает к уже имеющимся слагаемым еще одно:
о(х2). Продолжаю донимать его расспросами:
— Можно ли оценить, насколько мала эта величина?
284
ФОРМУЛА ТЕЙЛОРА
[Гл. 4
— Наверное, меньше аг, — нерешительно бормочет он.
— Наверное? Или наверняка? Смотрите, — рисую две
параболы,— вот графики функций у = х2 и у = —х2. Покажите
на этом рисунке, как вы представляете себе поведение
величины остаточного члена, который вы взяли в форме о(х2). Вы
рисуете ее график между параболами. Но разве это вытекает
из определения величины о(аг)? Как она определяется? Верно:
о(х2) = а(х) • х2, где а(х) бесконечно мала при х, стремящемся
к нулю. В силу своей бесконечной малости а(х) при достаточно
малых х по абсолютной величине будет меньше единицы —
вот для столь малых х график величины о(х2) и будет
заключен между нарисованными мною параболами. Но можно
ли указать промежуток иксов, в котором а(х) по абсолютной
величине будет меньше единицы? Или нельзя? Попадет ли в
этот промежуток число y|g? Молчите? Вот теперь, надеюсь,
вы воочию убеждаетесь в невысоких достоинствах остаточного
члена формулы Маклорена, взятого в форме Псано, о чем в свое
время говорил Горт. А какие еще формы остаточного члена вы
знаете?
— Коши, Лагранжа.
— Напишите хотя бы одну. Не можете? Вы помните, я вижу,
только их названия. Опять вас подводит незнание элементарных
вещей! Вот заучите, пожалуйста, более простую из этих двух
форм — лагранжеву: rn(x) = /n+1v; (# — #o)n+1 или, поскольку,
f(ri + l)(c\ , 1
у нас хо = 0, гп{х) = /п+1ч; хni" , где с лежит между нулем
и х. Учтите: перед нашим разложением стоит еще двойка,
она умножится на каждое слагаемое и на остаточный член
тоже. Чтобы в своих вычислениях мы могли гарантировать
четыре верных знака после запятой, удвоенный остаточный
член должен быть меньше... какой величины,
Миклашевский?
— Меньше 10~5.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
285
— Совершенно верно. Каким же ради этого следует
выбрать п?
— Надо сначала вычислить /(п+1)(с).
— Вычисляйте.
— У нас /(*) = (1 + *)*, значит, /("+1>(с) = !(£ - 1)(^-
-2)...(±-п)(1 + с)Го-п-\
— А весь остаточный член — каким он будет по абсолютной
величине?
— Весь будет таким: |^(i - 1)(^ - 2)...(^ - п)(1+
i^\^T-n-l/ 3 \n-fl 1 I
+с)10 (ш) ^+ijil-
Вихлявая строчка вяло тянется по доске, понуро заваливаясь
вниз. С каким пылом порою сыпет он идеями — и как не любит
черной работы!
— Живее, Миклашевский, живее! И поаккуратнее,
пожалуйста! Ну вот, все. Громоздко получилось, правда? Оценивать
такое произведение нелегко, и вам, я чувствую, ужасно не хочется
этого делать. Знаете, что я посоветую вам? Старайтесь в
затруднительных случаях превращать каждую свою слабость в силу.
Ваша главная слабость — нежелание заниматься долгой нудной
работой. Так пусть оно движет вами в поисках хитроумного
ухода от такой работы, в поисках оригинального решения
поставленных перед вами задач. Хитроумием вас бог не обидел — пусть
оно помогает вам. Сейчас оно могло бы подсказать вам, что
требуемые оценки разумно провести для чуть большего по величине,
но менее сложного по виду выражения: ведь если оно не выйдет
за рамки назначенной точности, то в них уляжется и
оцениваемый вами остаточный член, величина меньшая. Давайте поищем
такие преувеличивающие упрощения. Скажем, -j|g можно
заменить дробью ^7). Не придумаете ли что-нибудь и для остальных
сомножителей:
— Модуль |(^ — 1)(^ — 2)...(yjj — п)\ меньше п факториал.
— Хорошо!
— Степень (1 + с)То~п_1 меньше единицы... Нет, стоп! Ведь
с отрицательное! А по модулю меньше ^... Сейчас, сейчас... Ну,
конечно! (1 + с)А—» = £$*■ < ^^ = (§)»+*
— Отлично! Огромное произведение таким образом
свернулось в простенькую дробь 10> +|ч39п+1. Удвоенная, она
должна быть меньше 10-5. Уж тут-то п можно найти даже
подбором!
286
ФОРМУЛА ТЕЙЛОРА
[Гл. 4
— При п = 1 получается немного меньше 10 , — постучав
по клавишам калькулятора, сообщает Кулагин. — При п = 2...
почти 10~6!
— А на самом деле еще меньше, — увидев, что все получается
просто, Миклашевский воспрянул духом. — Мы ведь
увеличивали остаточный член, когда упрощали!
— Смотрите, как удачно вышло! — стараюсь поддержать в
нем воскресший энтузиазм. — Неспроста вы, знать, с самого
начала писали в формуле Маклорена всего три слагаемых, если не
считать остаточного члена. Давайте вычислим их сумму. Помо-
гите нам, пожалуйста, Кулагин, Что получается?
— Получается 1,9952631.
— А если теперь вычислить точное значение 1000То? Есть у
вашего калькулятора, Андрей, такая операция — ху?
— Есть; сейчас посчитаю... вот: 1,9952623.
— Прекрасно! Садитесь, Миклашевский — вы получили свои
четыре знака после запятой. Решим, ребята, еще одну задачу
подобного рода. Определим интервал значений я, при которых
приближенное равенство cos х = 1 — \ выполняется с точностью
до 0,0001.
Еще стоя у стола, вижу по выкладкам в тетради Рамзина,
что ему удалось найти короткое и ясное решение,
непосредственно вытекающее из формулы Тейлора в ее общем виде. Именно
такой подход наиболее желателен сейчас, когда мы еще
только осваиваемся с этой формулой. Пожалуй, Рамзина я и вызову
сначала. Если найду в тетрадях остальных другие, более
оригинальные решения, разберем их потом.
— Рамзин, к доске! Изложите свои соображения.
— Что такое 1 — ^-? — проникновенно обращается он к
аудитории; видно, что мои советы Горту приняты им к руководству.—
Легко видеть, что это — начало маклореновского разложения
для косинуса. Расхождение между этим полиномом и
косинусом описывается остаточным членом формулы Маклорена, со-
f'"(c) ч
держащим х в следующей степени, в третьей: 3\ х° — возьмем
Ю, В. Пухначев)
СЕМЬ СЕМИНАРОВ
287
этот член в форме Лагранжа, она здесь удобнее. В нашем
случае f(x) = cos я, следовательно, /'"(с) = sine, где 0 < с < х.
Синус, как хорошо известно, никогда не превосходит по
абсолютной величине своего аргумента, поэтому написанному
нами остаточному члену можно дать весьма прозрачную оценку
сверху: | 3! Д^3| = |^р#3| < ^р А последняя величина меньше
0,0001... то есть меньше 10~4 при \х\ < -^. Это будет... корень из
шести...
— Ребята, ну-ка быстренько... на калькуляторе! —
просительно гляжу в аудиторию; без моей просьбы никто и не подумал
бы предлагать свою помощь Рамзину — я уже почувствовал: не
любят в группе этого надменного гордеца, несмотря на все его
таланты и успехи.
— Примерно 1, 57 — нехотя отзывается Кулагин.
— Значит, — моментально продолжает Рамзин, словно ничего
не заметив, — ответ такой: \х\ < 0,157.
— Вычисления вы провели верно, — говорю, отсылая его на
место, — но... в задачнике ответ не такой, как у вас. Там х
ограничен более широкими рамками. Почему это так, давайте подумаем
все вместе, ребята.
С этими словами я отправляюсь в свой обычный дозор —
посмотреть, как идут дела у каждого. Лапиков аккуратно и,
как мне кажется, с пониманием переписывает в свою тетрадь
с доски выкладки Рамзина. В тетради Мухина опять грязца:
видя, что я это заметил, он поспешно переворачивает
перемаранную страницу и на новой пишет осмотрительнее. Сынчиков
вопреки моим опасениям уже успел записать решение Рамзина
и, положив подбородок на составленные стопкой кулаки, замер в
раздумьи.
В тетради у Стрельцова несколько минут спустя
обнаруживаю более широкое, нежели у Рамзина, ограничение \х\ < 0,222 и
предшествующее ему неравенство ^ < 10~4. Просто взял
следующее слагаемое в тейлоровском разложении косинуса и бездумно
поставил его в оценочное неравенство? Нет, вызванный к доске,
он развивает более тонкие соображения:
— За квадратом икса в разложении косинуса идет четвертая
степень, |^. А дальше слагаемые будут все меньше и меньше:
степень икса растет, сам икс по модулю меньше единицы — я
это сначала, правда, только предполагал, но потом это
подтвердилось — да еще знаменатели у слагаемых увеличиваются. А
знаки у них чередуются. В общем получается вот такая картин-
288
ФОРМУЛА ТЕЙЛОРА
[Гл. 4
ка, — поясняет он скупым чертежиком, как складываются друг
с другом дальнейшие, начиная с |j, слагаемые в разложении
косинуса. — Значит, точное значение косинуса будет отличаться от
1 — ^- не более, чем на |j.
— Интересно, интересно! — оцениваю его построения. — Но
прежде, чем принять такую оценку, я хотел бы посмотреть, как
изобразится на вашем чертеже остаточный член формулы
Тейлора, оборванной на том или ином слагаемом.
— Остаточный член? — искоса смотрит он на меня, не
догадываясь, как сопрячь свою нестандартную идею с основными
понятиями тейлоровского разложения. — Я вообще-то
предполагал, что в формуле Тейлора можно взять бесконечное количество
слагаемых...
— Смелое предположение! Не скажу, что оно недопустимо,
но... оно уводит нас слишком далеко вперед, в один из
дальнейших разделов нашего курса, где речь пойдет о так называемых
функциональных рядах. Но разве мы не выйдем из положения
с помощью того, чем располагаем сейчас? Остановимся в нашем
разложении на интересующем нас слагаемом с четвертой
степенью икса, на |^ • Какой остаточный член должен стоять вслед за
4
ним? И каков он по сравнению с |j?
— Вроде бы меньше: степень икса выше, пятая, знаменатель
больше, пять факториал... производная... пятая производная от
косинуса... сейчас... минус синус... то есть минус Щ§х5.
— Минус! А сама дробь Щ§х5 положительна, поскольку
знаки у с и а; одинаковы. Значит в нашем разложении слагаемое
— Щ§хъ отличается по знаку от слагаемого f^ и меньше его по
абсолютной величине. То есть все укладывается в рамки вашей
схемы (поясняю это на чертеже) и можно утверждать, что
расхождение между cos х и 1 — ^- не превышает |^, а уже отсюда следует
и ваша оценка \х\ < О, 222. Так ведь? Так. Садитесь, Стрельцов.
Я надеюсь, ребята, — оглядываю аудиторию, — что мы вполне
освоились с пятью основными маклореновскими разложениями и
сможем с их помощью разлагать более сложные функции. Возь-
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
289
мем для примера такие: у = 3.2.334-2» 1П^Бх» У = s*n3 x*
Припомните, не встречались ли они вам когда-нибудь.
В беглой интонации, с которой я произношу свою просьбу,
чувствуется ожидание мгновенного ответа, — но ребята медлят
с ним, раздумывая, и это создает неловкое ощущение заминки.
— Встречались, — разрешает щекотливое молчание Гарин, —
когда искали производные высших порядков.
— А ведь действительно! — поддерживает его Костюк.
— Не хотите ли, — предлагаю Костюку, — разложить эти
функции по степеням х?
Он без промедления приписывает через знак равенства к
первой из заданных мною функций ее разложение на элементарные
дроби, выводит формулу для n-ной производной полученной
суммы, на момент задерживается с вопросом: «А икс нулевое
какое брать?» и тотчас отвечает себе: «Нуль, очевидно, чтобы икс
получилось... Да, нуль, конечно». Потом вычисляет
коэффициент при n-ной степени х и наконец пишет окончательное
разложение.
— Ваш результат верен. Но мне кажется, что вы шли к нему
не лучшим путем. Вот вы представили данную мною
полиномиальную дробь в виде суммы элементарных дробей. Неправда ли,
вторую из них, изменив перед нею знак с минуса на плюс,
можно переписать так: j^j. Это вам ничего не напоминает в связи с
задачей разложения? Нет? А вот такое равенство вам когда-либо
встречалось: j^ = 1 + х + х2 + х3 + ...
— Геометрическая прогрессия, что ли? — хмуро смотрит он
на меня.
— Она самая! Из формулы ее суммирования вы легко
получите: yz^ = 1 + х + х2 + ... + хп + о(хп).
— Вы хотите сказать, что это и будет разложение по формуле
Тейлора?
290
ФОРМУЛА ТЕЙЛОРА
[Гл. 4
— Проверьте! Перепешите j^j B виде (1-х) * и
разложите по формуле бинома (1 + х)л, в котором А = — 1, а вместо х
подставьте туда минус х. Все получилось, верно? Очевидно,
сходным образом можно разложить и дробь ^5. Как вы полагаете,
Меншиков?
— Если представить ^2 = (х "~ 2)-1... Но ведь в формуле
бинома стоит 1 + х...
— Неужели вы не сможете организовать в скобках единицу?
— Попробую... Так что ли: [1 + (ж — З)]-1?
— Неверно! Только что мы говорили: в подобных формулах
должно стоять не единица плюс что-то, а единица плюс...
Мою воспитательную атаку на Меншикова срывает своим
нетерпеливым выкриком Буткус:
— Тут надо по-другому! Опять, как с логарифмом: минус
два — за скобку!
— Разумеется! — с упреком гляжу на Меншикова. — И тотчас
подучим искомое. Пишите, Костюк.
Горт, неотрывно следящий за выкладками Костюка,
удивляется:
— А зачем ты пишешь о((§)п)? Это ведь то же самое,
что о{хп)\
— Я так и хотел написать дальше! — возмущается Костюк
преждевременной придиркой и оскорбленно глядит на меня:
неужели я не верю, что он знает это?
— Верим, верим, — успокаиваю его. — Вы только напомните
нам, чем обосновывается такая замена.
— Вот: о(Схп)= с(хп); на позапрошлом семинаре доказывали.
— Да, мы доказывали такое равенство. Доказывали и такое:
о(хп) = о(уп), если х эквивалентно у. И еще вот такое
доказывали: Со(хп) = о(хп). Вспоминаете? Эти равенства и
позволяют нам объединять о малые. Сделайте это, Виталий. Хорошо,
хорошо... Приведем теперь все подобные члены и получим то
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
291
самое разложение, которое вы однажды уже писали. Но теперь
мы пришли к нему более коротким путем, согласитесь, Виталий.
— Что-то он мне не показался короче...
— Не показался? Тогда пожалуйста — продолжайте идти
своим. Когда мы будем решать следующие примеры, стройте
разложения вычислением производных высших порядков. Посмотрим,
намного ли вы станете опережать тех, кто будет использовать
стандартные разложения. Садитесь. Итак, приступаем к
следующим примерам, ребята. Кто решит оба, пусть поднимет руку.
И когда об окончании работы докладывают Синица, Горт,
Рамзин, Стрельцов, Буткус, осведомляюсь у Костюка:
— А вы? Насколько вы продвинулись по своему пути?
— Я от него отказался. Я — как все...
— Убедились, значит, что выгоднее комбинировать
требуемые разложения из пяти основных? Все остальные, надеюсь,
тоже убеждены в преимуществах такого метода? Давайте
проследим и закрепим его основные положения. Пусть к доске пой-
дут Буткус и Синица и напишут решения следующих
примеров. Смотрите, ребята, — подход здесь всюду тот же самый, что
292
ФОРМУЛА ТЕЙЛОРА
[Гл. 4
при вычислении n-ных производных: каждая из данных
функций прежде всего преобразуется в сумму функций более
простых. Простых в том смысле, что нам известны их
тейлоровские разложения. Пишем эти разложения, потом из всех
разложений собираем одинаковые степени х, суммируем их
коэффициенты воедино, и получаем единое тейлоровское разложение,
где в формульном виде выражено слагаемое, содержащее
произвольную n-ную степень аргумента, найден, как принято
говорить, общий член разложения. Всем понятен такой подход?
Да? Тогда ответьте: не приведет ли он к другому результату,
нежели последовательное вычисление все более высоких
производных исходной функции в заданной точке разложения, как
это поначалу делал Костюк? Интересно, что скажет на это сам
Костюк?
— Я уже думал об этом, — уверенно отвечает он. — Так и
так разложения должны получаться одинаковые — по теореме о
единственности разложения.
— Совершенно верно. Мы уже убедились в этом на примере
функции х2_1х+2- Поэтому будем применять без опаски
предложенный мною метод. Напишите, — прошу стоящих у доски, —
условия трех следующих примеров. Функцию In 3-ж—
разложить в окрестности точки хо = 2, функцию х(х — 2)2Х ~2х~г — в
окрестности единицы, функцию (яг — ттх) cos(x + |) — в
окрестности |. Написали? Садитесь все трое. Решаем.
— Многие уже нашли верные решениям всех трех
примеров, — отмечаю, побродив несколько минут между столами. —
Но прежде чем демонстрировать безупречные ответы, я хотел
бы разобрать ошибочные. Ну-ка, Мухин, напишите на доске свое
разложение первой функции. Потом пусть Чюмин, Синица и Су-
Ю. В. Пухначев] СЕМЬ СЕМИНАРОВ 293
теев напишут свои разложения второй. Формы ответов, как ви-
Чюмин ^ _т^
Синица
x(x-2)2 =tf-<)2 =^3-i)2 -2 =
= £(<*-*) e e
(2-Lt"2)" /i"\\
Cymeee
дим, самые разнообразные, но среди них нет ни одной верной.
Написавшие все это, вероятно, не понимают, в чем заключается
суть тейлоровских разложений и чем они удобны. Но даже если
смотреть чисто формально — что собою представляет
формула Тейлора? — указываю на общее ее выражение, предваряющее
список разложений основных элементарных функций. — Как вы
ответили бы на мой вопрос, Чюмин?
— Это какие-то степени с коэффициентами из n-ных
производных, вернее, сумма степеней.
— Сумма степеней с коэффициентами... Для таких сумм в
математике есть особый термин.
— Всякое тейлоровское разложение представляет собой
полином, — словно не видя, что я жду ответа от Чюмина,
наставительно заявляет Рамзин.
— Совершенно верно, — приходится мне подтвердить его
ответ, хотя я не очень-то доволен его вмешательством в наш с
Чюминым разговор. — А у вас, Синица и Чюмин, произведе-
294
ФОРМУЛА ТЕЙЛОРА
[Гл. 4
ние полиномов — вот почему не годятся ваши ответы. Неверен
и ответ Мухина — здесь мы видим не единый полином, а
сумму полиномов, подобные члены не приведены, не выписан общий
член итогового разложения, слагаемое с £п, — а я уже говорил,
что без этого не буду считать разложение законченным.
Впрочем, ошибки Чюмина и Мухина исправить легко, мы в этом
скоро убедимся. А вот откуда взялся ваш странный ответ, Синица?
Покажите-ка свою тетрадь... Все ясно, вы неверно записали
условие: х(х-2)22х -2х-1, вместо х2 в показателе поставили 2х2. Мы
еще вернемся к вашей описке: к подобным примерам можно
найти свой разумный подход. Наконец, ошибка Сутеева. На первый
взгляд ее и ошибкой не назовешь: ответ получен в виде
полинома, каким и должно быть тейлоровское разложение. Но скажите,
Сутеев, подумайте и вы все, ребята: вас не удивляло, что
полиномы, представляющие собою тейлоровские разложения, всегда
записываются нами в порядке возрастания степеней, а не в
порядке их убывания, как вас учили в школе? Что это — дань
какой-то формальной традиции? Или нечто, связанное с сутью
тейлоровских разложений и их практического использования?
Не дождавшись ни слова от Сутеева, оборачиваюсь к
аудитории, и взгляд мой, скользящий по лицам ребят, отворяет уста,
давно готовые к ответу. Горт, Костюк, Рамзин вперемежку
вываливают свои суждения — я распутываю их фразы, выстраиваю
в логической последовательности:
— Если в формуле Тейлора стоят производные /(п)(£о)> то
разложение ведется в точке хо, и х берется в окрестности этой
точки. Разность (х — хо) тогда будет малой величиной. И в
формуле Маклорена аргумент тоже мал. Я бы обозначил его не
буквой х, а буквой t — это лучше напомнило бы вам, что
переход от одной формулы к другой можно совершить путем замены
t = х — xq. Мы этой заменой как бы смещаем начало координат
в точку xq. Вы понимаете то, что я говорю? — снова обращаюсь
к Сутееву. — Что же дает эта малость (х — хо) в первой
формуле, малость t во второй? Каким будет каждое новое слагаемое в
этих формулах по сравнению с предыдущим?
— Будет... будет меньше,— выдавливает он из себя.
— В принципе правильно, хотя здесь есть некоторые
тонкости, на которых стоило бы остановиться. Возьмем в маклоре-
новском разложении два последовательных слагаемых —
обозначим их atn и btn+l. Коэффициент Ь может оказаться
большим, чем а; но ведь переменная t — бесконечно малая, и
если она станет меньше, чем |, будет выполняться неравенство
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
295
|b£n+1| < |а£п|. Нетрудно показать, — набрасываю
соответствующие выкладки, — что с дальнейшим уменьшением t это
неравенство сохраняется, а потому уменьшением t можно добиться того,
что все слагаемые произвольного маклореновского разложения,
включая остаток, будут последовательно уменьшаться по
абсолютной величине по мере нарастания номера слагаемого. Вот,
пожалуй, как надо понимать утверждение о том, что каждое
новое слагаемое в разложении по формуле Тейлора или Маклорена
мало по сравнению с предыдущим. Так ведь? — напористо
побуждаю Сутеева к продолжению разговора, стараясь понять, как
уяснил он мое объяснение.
— Да это мы уже показывали, когда смотрели, как косинус
2
приближается выражением 1 — ^ вспоминает Кулагин.
— Было такое дело, — киваю ему, довольный столь
убедительным дополнением. — Выражение 1 — -| это, как тогда
сразу указал Рамзин, первые два слагаемых из тейлоровского
разложения косинуса в нуле, и покуда х не превышает 0.157, а
вернее — не превышает 0.222, как затем уточнил Стрельцов, их
достаточно, чтобы вычислять значение косинуса с точностью до
трех знаков после запятой. Последующие слагаемые с более
высокими степенями я, как отметил Стрельцов, вносят уточнения
лишь в дальнейшие знаки. Общий же вид функции, основные
особенности ее поведения в окрестности точки разложения
обрисовывают слагаемые с наименьшими степенями х — потому-то их
и помещают в начало тейлоровского полинома. Возьмем тот же
2
косинус и первые члены его разложения 1 — ^-. По ним сразу
видно, что косинус в окрестности нуля похож на параболу ветвями
вниз с вершиной, приподнятой на единицу над началом
координат. А вот первые члены разложения синуса: х — ^-. Легко
понять, что его график исходит из начала координат по
биссектрисе координатного угла с постепенно нарастающим уклонением к
оси абсцисс. Или возьмем первые члены разложения
логарифма в единице: х — ^-. За этой разностью четко видится кривая,
пересекающая ось абсцисс под углом 45° в начале координат и
загнутая вниз по обе стороны от точки пересечения. И каждая из
таких картин, набросанных первыми слагаемыми тейлоровских
разложений, очень хорошо согласуется с графиками упомянутых
функций. Надеюсь, Сутеев, теперь вы понимаете, сколь важно
выписывать тейлоровские разложения по нарастающим
степеням малых величин (х — хо), где хо — точка разложения. Ради
удобства мы вводим для этой разности особое обозначение t —
296
ФОРМУЛА ТЕЙЛОРА
[Гл. 4
смотрите, ребята, как быстро с помощью такой замены пришли
к верным ответам Кочин, Сынчиков, Горт.
И покуда те пишут свои решения на доске, комментирую:
-- Смотрите,ребята, как уверенно и быстро работает Горт,
какие короткие у него выкладки. Это оттого, что он хорошо
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
297
владеет формулами суммирования, где сложение однотипных
слагаемых выражается с помощью вот этой замысловатой
буквы — прописной греческой буквы «сигма»; за нею стоит
формула общего члена. Обратите внимание: первые
слагаемые, не охватываемые общей формулой, выписаны отдельно,
перед знаком суммирования дальнейших слагаемых. Те, кто
не знает таких формул, или не рискует ими
пользоваться, боясь запутаться, — те могут действовать с помощью
более подробных и наглядных выкладок, таких, как у Сын-
чикова. Смотрите, как осторожно и кропотливо приводит
он подобные члены, как изобретательно заменяет в
объединяемых суммах индексы суммирования: в первой полагает
п = m — 1, во второй п = т, Наконец, Кочин. Тот
упорно пытается угадать формулу общего члена по нескольким
первым слагаемым. С этим примером у вас все получилось
удачно, Дима, но должен вас предупредить: надежда на
подобную догадку иногда может и не оправдаться. Так что уж
постарайтесь освоить какие-нибудь приемы суммирования —
предельно лаконичные, как у Горта, или более пространные,
как у Сынчикова. Садитесь все трое. Подведем итог наших
рассуждений. Так какие же функции умеем мы разлагать по
Тейлору с указанием формулы общего члена? Спросим об этом
Гарина.
— Во-первых, — отвечает он, подумав, — те пять, для
которых мы написали разложения с самого начала. Во-торых,
выражаемые в виде суммы тех, которые «во-первых». В-
третьих, произведения полиномов на те функции, которые
«во-вторых».
— То есть, — подмечает Кулагин, — все те функции, для
которых мы вычисляли производные высших порядков.
— А вы ведь нам сегодня давали те же примеры, что на
прошлом семинаре! Это вы нарочно, да? — спрашивает
Лапиков.
— Вы правы, — утверждаю вывод Кулагина. — И вы
тоже, — киваю Лапикову. — Вам не откажешь в проницательности,
Егор.
— А что, другие функции по формуле Тейлора не
разлагаются? — с сомнением смотрит на меня Чюмин.
— Ну почему же? Речь у нас сейчас идет лишь про
такие разложения, где все слагаемые — кроме, быть может,
нескольких первых ■— задаются общей формулой. Для
элементарных функций, перечисленных Гариным, это можно
298
ФОРМУЛА ТЕЙЛОРА
[Гл. 4
сделать наверняка. Иногда это удается сделать для функций,
не входящих в перечень Гарина. Например, для exsinx —
пусть ею займутся на досуге любители трудных задач.
Предположим теперь, что вам встретилась элементарная функция,
для которой вы никак не можете отыскать общую формулу,
выражающую все слагаемые ее тейлоровского разложения в
заданной точке. Но ведь мы знаем, что все члены разложения
часто бывают и не нужны, в большинстве случаев
достаточно знать лишь несколько начальных членов, описывающих
разлагаемую функцию в общем, в главном. И если удастся
их найти — это будет значить многое. Кстати сказать,
хороший повод для подобных упражнений нам в свое время
создала Синица, когда неправильно списала с доски условие
одной из задач. Синица, к доске! На сей раз вы имеете
возможность выставить свои результаты в более выгодном свете.
Итак, функция х(х — 2)22х ~2х~1 или после замены переменной
(£2 — 1)е1п2(2*2+2*-1). Требуется разложить ее по степеням t
до... ну, скажем, до o(ir). Действуйте и поясняйте свои
действия.
Видимо, прежняя неудача крепко задела Люду:
похоже, что после этого она дотошно искала разумный подход
к подобным примерам, на который я намекал еще тогда,
и сейчас, когда я наметил его отчетливее, ухватила его
суть:
— Я сейчас все по-новому сделаю, не так, как раньше, —
проще. Сначала вынесу е~1п2, чтоб не мешалась — хорошо?
Вынесу в виде коэффициента ^, так проще. Тогда от
экспоненты останется eln2(2* +2t\ останется е в степени малая величина:
ведь если мы разлагаем по степеням £, то t мало — так ведь?
И 2£2 + 2£ тогда тоже будет мало. Ну вот, теперь стандартное
разложение экспоненты ех... нет, не х\ х уже было... лучше ez.
Выпишем это разложение до слагаемого... до слагаемого с
кубом, потому что нам нужно все, что с £3. А следующие
слагаемые можно не брать: ведь когда мы возведем в четвертую,
допустим, степень, то получатся степени t четвертая, пятая и еще
выше...
— Минуточку, Люда, минуточку! Мне что-то не совсем ясна
ваша фраза: «Выпишем разложение функции ez до слагаемого
с z3 потому что нам нужно все, что с £3». Как бы построже
обосновать такой выбор длины разложения? Не сообразите? Я
подскажу вам: все дело в том, что ваше z = 2t2 + 2t эквивалентно
2£, — доказываю это. — А отсюда, как мы недавно отмечали,
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
299
следует, что o(z3) = о(£3). После такой замены мы уже смело
можем подставлять в разложение ez вместо z сумму 2£2 + 2£,
выполнять возведение в степень, собирать степени t до третьей
включительно, а более высокие степени считать включенными в
выражение о(£3). Помните, как нечто подобное делал Кулагин?
Он доказывал, что о(хт) + о(хп) = о(хт) при п > т.
Продолжайте. Все верно, садитесь. Таким же образом, ребята,
вы сможете разлагать и другие подобные функции. В
качестве следующего примера такого же рода я предложу вам
получить разложение, которое не раз понадобится вам в
дальнейшем, — разложение тангенса в нуле. Прежде чем
приступать к работе, давайте вместе обсудим ее возможный
ход.
— Тангенс — функция нечетная, — начинает
Миклашевский, — значит, ее разложение будет содержать только нечетные
степени.
— Замечание кстати, — киваю ему. — Оно позволит точнее
намечать длину разложения. Давайте доведем ее до третьей
степени х плюс о малое... от чего, Миклашевский?
— Следующая степень — пятая... значит о(х4).
— Хорошо. Думаем дальше, ребята.
— Тангенс — это синус, деленный на косинус, — заходит с
другого бока Горт. - Надо написать такую дробь и подставить
вместо синуса и косинуса их разложения.
— Синус взять до третьей степени, а косинус — до
четвертой, — предлагает Костюк.
— Напишите все это, — приглашаю к доске Лапикова.
Он не пытается отказаться, к доске идет без дрожи в
коленках — уже достижение!
300
ФОРМУЛА ТЕЙЛОРА
[Гл. 4
— Лучше написать не §jj§, a sinx(cosx)~1, — негромко
советует Гарин.
— Что это даст? — оборачиваюсь к нему.
— Разложение косинуса — это единица плюс малая величина,
можно будет дальше разлагать по биному (1 + z)~l. И не нужно
брать четвертую степень в разложении косинуса — оно ведь
потом умножится на разложение синуса, то есть по меньшей мере
на х, тогда из четвертой степени получится пятая, а она нам не
нужна.
— Дельные соображения! Реализуйте их, Костюк.
Он пишет: cos я = 1 - \ + о(х3) = 1 — (^ + о(х3)).
— Выражение в скобках, насколько я понимаю, вы будете
рассматривать как z. Но это, Виталий, не совсем то, что предлагал
Гарин. У него (1 + z)~l, а у вас (1 — z)~l.
— Так удобнее: (1 — z)~l = 1 + z + z2 и так далее. A (l + z)~l =
= 1 — z + z2 — z3... Знаки чередуются.
— И надо следить за их чередованием, возрастает риск
ошибки — я так вас понял? Что ж, вы поступаете мудро,
когда нацеливаете свое преобразование на разложение более
простого вида. Но в этом преобразовании заметна
сомнительная деталь. Вот вы огородили скобками два последних
слагаемых в разложении косинуса. Если я раскрою скобки,
то получу —о(х3). А раньше, по левую сторону от знака
равенства, было +о(х3). Разница в знаках нарушает это
равенство.
— Нет, не нарушает. Мы уже говорили, что Со(хп) = о(хп).
Значит, (-l)o(x3) = о(х3).
— Убедили. Продолжайте, раскладывайте косинус по своей
схеме: (1 — z)~l = 1 + z + z2... Только заканчивайте разложение
не словами «и так далее», а о малым. Кстати, о малым от чего?
Какой длины разложение возьмете?
Он выписывает молча: (cosx)-1 = 1 + z + o(z) = 1 + ^-+
+о(х3) + о(х2) = 1 + % + о(х2).
— Не молчите, Виталий, поясняйте! Откуда взялось это
о(х2)? Как оно получилось?
— Из o(z). У нас z = \ + °(ж3)> значит, 2 ~ у. А у нас уже
было: если z ~ у, то o(z) = o(y).
— А как исчезло о(х3)?
— Тоже когда-то было: если т < п, то о(хт) +о(хп) = о(хт).
— Все ясно. Вычисляйте произведение sinx(cosx)-1. Так,
так... Все верно, садитесь. Но прежде припишите к списку
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
301
основных разложений еще одно — то, которое вы только что
получили: tgx = х + у + о(хг).
— А должно быть о(ж4), — перенимает у меня роль критика
Миклашевский.
— Верно, и мы убедимся в этом в недалеком будущем, когда
получим более длинное разложение тангенса, вот такое, —
стираю неугодное Павлу о малое и пишу вместо него ^- + о(х6). —
А вы, ребята, припишите это разложение в своих тетрадях в
дополнение к пяти основным. И в дальнейшем пополняйте этот
список сами, приписывайте к нему разложения, которые
станут особенно часто вам встречаться. Это будут важные
частные случаи формул основной пятерки — скажем, разложения
дробей (1 + х)~] и (1 — ж)-1, получаемые из разложения
бинома; они уже не раз пригождались нам и заслужили место в
нашем списке. Это будут употребительные комбинации
основных разложений — скажем, \ In у^| = \ 1п(1 + х) — ^ 1п(1 — х) =
x+^- + ^- + ... + 2n!_i +о(х2п). Это будут, наконец, совершенно
новые формулы, - например, разложения гиперболического синуса
и косинуса, shx и chx, сейчас я их напишу. Их легко запомнить:
302
ФОРМУЛА ТЕЙЛОРА
[Гл. 4
они напоминают формулы Маклорена для тригонометрического
синуса и косинуса.
Жду, пока ребята перепишут себе в тетради мои дополнения
к списку основных разложений. Потом продолжаю:
— В этом перечне разложение тангенса выглядит
исключением—в противоположность прочим разложениям здесь, если
писать все новые слагаемые, в чередовании коэффициентов не
просматривается простой закономерности. Впрочем, то, что
кажется исключением в учебных примерах, станет правилом в
дальнейшем, когда мы начнем решать с применением формулы
Тейлора задачи более практического характера. Из элементарных
функций, которые встретятся нам в формулировках этих задач,
там будут образовываться произведения, дроби, суперпозиции.
Для каждой элементарной функции мы сможем выписать сколь
угодно длинное разложение. Но когда мы станем перемножать и
делить эти разложения, использовать одно в качестве
аргумента другого, то простые закономерности, которым подчиняются
исходные цепочки, перепутаются настолько, что
коэффициенты полинома, образующегося в итоге, вряд ли удастся охватить
четкой формулой — поделив синус на косинус, мы уже
убедились в этом. В таких условиях повышается вероятность ошибки.
Для безупречного решения таких задач необходима
определенная сноровка. Вырабатывать ее мы будем в деле. А дела нам
сегодня хватит. Я не случайно просил вас перед нынешним
семинаром повторить все, что мы прошли до сих пор. Повторили?
Опущенные взгляды говорят красноречивее слов.
— Чувствую, моя просьба была опрометчивой: студент
всегда в цейтноте. Ну что ж, тогда попробуйте определить в одной
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
303
фразе предмет всех наших предыдущих занятий. Вы могли бы
это сделать, Миклашевский?
— В одной фразе? Разве что через запятую:
последовательности, пределы, функции, производные...
— Длинновато, — качаю головой. — К тому же вы
смешали в одну кучу объекты и операции: вычисление производных,
дифференцирование — это операция, а функция — это объект, к
которому эта операция применяется.
— Дифференцирование — частный случай предельного
перехода, — ищет Горт возможности сократить сумбурный список
Миклашевского.
— Последовательности нам были нужны только в самом
начале, только для того, чтобы познакомиться с понятием
предельного перехода, — бьет в ту же точку Костюк.
— А потом ведь опять мы про них говорили, когда определяли
предел функции, — вспоминает Мухин.
— Неважно, — бурчит Гарин. — Все равно
последовательности — не главное.
Дождавшись, пока утихнет это перепирательство, Стрельцов
говорит негромко и уверенно:
— Мы проходили средства для исследования поведения
функций.
Обвожу аудиторию удовлетворенным взглядом:
— Мне кажется, что с таким мнением можно согласиться. В
самом деле, какой практический смысл имеют понятия предела
функции или, скажем, ее главной части? Мы исследовали с
помощью этих понятий поведение функций в окрестности
отдельных точек. А для чего использовали мы на практике первую и
вторую производную? Чтобы исследовать поведение функции на
интервалах. Формулировка Стрельцова собирает к единой цели
изучавшиеся нами математические операции и приемы. Разумно
поставить вопрос: а существует ли математическое понятие, на
основе которого по единой методике мы могли бы решать как
можно больше из затронутых нами до сих пор проблем? Да,
уверенно ответим мы после сегодняшнего семинара,
существует — это формула Тейлора. Такое суждение нетрудно
подтвердить примерами. Вспомните, как на позапрошлом семинаре мы
определяли главные части различных функций — например,
таких: у = tg х — sin х\ у = у/\^2х — \J\ — Зж; у — х + ж2 sin ж.
Каждый из этих примеров требовал своего специфического
подхода. Теперь же, зная основные тейлоровские разложения, мы
выделим главную часть каждой из перечисленных функций со-
304
ФОРМУЛА ТЕЙЛОРА
[Гл. 4
вершенно единообразным приемом. Не сделаете ли это, Кулагин?
Энергично направившись к доске, он еще на полдороге
начинает:
— В разложениях тангенса и синуса первые слагаемые
одинаковые, ж, эти иксы сократятся, а следующие члены, с х3 —
разные: у тангенса делится на три, у синуса — на три факториал.
— Любопытно, — тут же подбрасываю ему вопрос, — что вы
напишете в разложении синуса — три факториал или шесть?
— Шесть, конечно; факториал я поставил бы, если бы
надо было вывести формулу общего члена, а ее в таких примерах
выводить без толку — вы сами говорили.
— Напишете члены с ж3, а потом что?
— А потом напишу о(ж4). И получу: tgx — sin а: = \ + о(хА).
Ну вот, ?j- и будет главная часть.
Он крупно пишет эту дробь на доске и снова поворачивается
ко мне, ожидая оценки.
— Все верно, Андрей. Ответ такой же, какой мы
получали и раньше. Мы подходим, — обращаюсь ко всем сидящим, —
к важному выводу, ребята: главная часть функции — это
начальное слагаемое ее тейлоровского разложения, если,
конечно, функция разложима по формуле Тейлора хотя бы в столь
куцом виде: С(х — хо)п + о((х — хо)п). Разумеется, если для
нее выполнимо более длинное разложение, его можно сократить
до кратчайшей суммы указанного вида. Составим отношение
С(х-х )п> заменим f(x) ee тейлоровским разложением, устремим
х к жо, перейдем к пределу в получившейся после замены дроби:
Ж—Хо С(Х-Хо)п X-+XQ 1
— Непонятно! — прерывает меня Аргунова. — Непонятно, как
у вас получились единички.
— Я разделил числитель и знаменатель на С(х — хо)п.
— Ах, да, конечно, — склоняется она над тетрадью, будто
съеживается от стыда за свою недогадливость.
Оборачиваюсь к дроби —у^-% смутившей Аргунову, и тут
меня пронзает неприятная догадка: ее вопрос наверняка был про
другую единичку, про ту, что появилась под знаком о малого.
В моих выкладках она возникла как-то исподволь, как нечто
привычное, само собой разумеющееся, — а ведь это выражение
о(1) могло показаться странным многим, не одной Аргуновой.
Надо было упомянуть и разъяснить такое выражение загодя, и
даже не сегодня, а на позапрошлом семинаре, когда мы знако-
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
305
мились с осимволикой. Надо было предвидеть, что рано или
поздно оно нам встретится. Недосмотр, что и говорить.
Оплошал. А еще поучал Горта: вы должны чувствовать аудиторию...
Чтобы убедительнее требовать чего-то от студентов, мне
следовало бы показывать пример требовательности к самому себе. Ну
да ладно — лучше поздно, чем никогда. Не выказывая своего
самобичевания, продолжаю в прежнем тоне:
— Тут еще появилось выражение о(1). Кто объяснит, как оно
возникло? И что означает? Горт? Пожалуйста.
— Давайте сначала посмотрим, откуда оно взялось. На его
месте в предыдущей дроби стояло о((х — яо)п)> то есть а * {х~
-хо)п. Когда поделили на (х — хо)п, осталось а, бесконечно
малая, которую можно записать так: а-1. И если мы обычно пишем
су. хп — о{хп), то сейчас можно формально записать а • 1 = о(1).
То есть о(1) — это просто еще одно обозначение бесконечно
малой величины.
— Верно, так и надо его понимать. Вернемся к отношению
сАх-х )п' ^го пРеДел оказывается равным единице. Иными
словами, f(x) и С(х — хо)п эквивалентны. Согласно определению,
принятому нами на позапрошлом семинаре, это означает, что
главная часть функции есть С(х — хо)п, начальное слагаемое
се тейлоровского разложения. Что и требовалось доказать. А
теперь, Андрей, — прошу Кулагина, — давайте еще раз, не
скороговоркой, как раньше, а подробно, шаг за шагом покажите на
доске, что \ действительно есть главная часть разности tgx — sin ж.
Ребята, — вновь поворачиваюсь к аудитории, — внимательно
следите за выкладками Кулагина: он никогда не забывает писать
о малое в конце каждого разложения.В подобных задачах это
спасает от многих ошибок. Советую брать пример с Андрея. В
будущем нам это ох как пригодится!
Сынчиков так прилежно переписывает себе в тетрадь все
написанное на доске, что мне хочется поставить в пример и его
ui такую чуткость к полезным соображениям и приемам. Жду,
пока он положит ручку.
306
ФОРМУЛА ТЕЙЛОРА
[Гл. 4
— Раз уж вы так четко работаете, Андрей, — вновь
возвращаюсь к Кулагину, — решите и другие примеры, чтобы
все посмотрели и запомнили, как надо выписывать тейло-
ровские разложения. Хорошо, хорошо... Ну вот, все верно,
садитесь. Возможно, ребята, последние примеры привели
вам на память решавшиеся нами когда-то задачи на
вычисление пределов функций. Я напомню вам некоторые:
lim.itf^r^^; lim^f; lim (л/1 + х + х2 - у/1-х + х2).
x_+0l+smpx-cospx> x_+a х-а > ж_юсГ '
Когда мы их решали, то каждый раз в поисках ответа вели
мудреные преобразования. А формула Тейлора и выполняемое
с ее помощью выделение главной части приведут нас к ответу и
на сей раз коротким и несложным путем. Покажите это, Буткус.
Ю. В. Пухначев] СЕМЬ СЕМИНАРОВ 307
Первый пример решен, беритесь за второй. Вы переходите к
бесконечно малой переменной? Очень хорошо! Это нам и сейчас
очень поможет, как и прежде. Так, так... Второй пример сделан,
теперь последний... Узнаете в нем функцию, у которой вы в свое
время обнаружили несходство пределов при х, стремящемся
к бесконечностям разных знаков? То, что казалось когда-то
замысловатым, сейчас представляется естественным и совсем
простым. Пример решен быстро и безошибочно. Садитесь. Идем
далее, ребята. Для вычисления пределов отношения двух
бесконечно малых функций лектор, очевидно, рекомендовал вам так
называемое правило Лопиталя. Кто напомнит его? Хотите вы,
Рамзин? Пожалуйста.
— Правило Лопиталя чаще всего применяется к отношению
двух функций f(x) и р(я), которые стремятся к нулю при
стремлении аргумента к какой-нибудь точке я?о, причем все
производные этих функций до (п — 1)-го порядка включительно
существуют и тоже обращаются в нуль в этой точке, а
производные f(n\xo) и д^(хо) существуют и д^п\хо) ф 0. Тогда
fix) _ /<">(яо)
дЩхо)'
lim -т-s
— Верно. А теперь проследите за моими выкладками,
ребята. Я строю для функций f(x) и д(х) тейлоровские разложения в
точке хо с остаточным членом в форме Пеано, выражаю
отношение функций f(x) и д(х) через их n-ные производные в точке хо
и в полученном выражении перехожу к пределу. Он
существует по теореме о пределе частного и равен %п) г°<, стало быть,
308
ФОРМУЛА ТЕЙЛОРА
[Гл. 4
существует равный тому же значению предел отношения ^t±-
Так коротко и ясно с помощью формулы Тейлора доказывается
важное правило, широко применяемое в задачах на отыскание
пределов. Скоро мы увидим, что по отношению к таким задачам
формула Тейлора имеет не только теоретическое, но и
практическое значение: во многих сложных случаях она ведет к
ответу быстрее, чем доказываемое с ее применением правило Лопи-
таля.
— Вы нам на прошлом занятии обещали разобраться с
функциями, у которых все производные... ну не все, а некоторые,
обращаются в нуль — у каких есть экстремум или перегиб, а у
каких нет, — напоминает Чюмин.
— Мы говорим про функции, у которых несколько начальных
производных в какой-то точке xq обращаются в нуль, — уточняет
Синица. — Вы обещали показать, как их исследовать на
экстремум и перегиб с помощью формулы Тейлора.
— Сейчас покажу. Вопрос, как вы помните состоял в
следующем: имеет ли такая функция f(x) экстремум в точке xq или не
имеет? Кстати: у кого на прошлом семинаре хорошо получались
графики? Кажется, у вас, Сутеев? Не поможете ли мне сейчас
с чертежами? Прошу вас к доске. Итак, функция f(x). Возьмем
ее разложение по формуле Тейлора в точке хо с остаточным
членом в форме Пеано и предположим, что f^n\xo) — это первая из
производных нашей функции, не обращающихся в нуль в точке
хо. Тогда разность f(x) — f(xo)...
Сутеев выражает ее, не дожидаясь, пока я договорю.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
309
— Очень хорошо. Теперь, — беру у него мел, — выразим о
малое в форме а(х)(х — хо)п и перепишем нашу разность так:
^— гс! (х ~ жо)п5 гДе Р(х) = п\а(х), то есть тоже
бесконечно мала. Поскольку а(х) стремится к нулю при ж,
стремящемся к жо, мы можем выбрать столь узкую окрестность
точки жо, в которой а(х) по абсолютной величине не превзойдет
/^(жо). Во всей этой окрестности сумма f(n'(xo) + a{x) будет
совпадать по знаку с f^n\xo)- А что можно сказать про знак
степени (х — хо)п в окрестности точки хо? Как вы полагаете,
Сутеев?
Молчит: вопрос для него слишком расплывчат.
— А как думаете вы, Синица?
— Все зависит от того, четное п или нечетное.
— У! — отрывистым глухим хрипом вырывается у Сутеева, и
вновь каменной маской застывает его лицо. Задело-таки, что не
смог сообразить?
— Нарисуйте, как выглядит график степени (х — хо)п при
четных и при нечетных п, — прошу его, сделав вид, что
ничего не заметил. — Оба графика верны. Очевидно, так же
ведет себя и разность f(x) — f(xo) в достаточно узкой
окрестности точки хо. Что можно сказать про эту разность в случае
нечетного п, Сутеев?
— Если х переходит через жо, то степень меняет знак и все
произведение, — он показывает взглядом на -—^—^-(х—
—хо)п — тоже.
Не чеканна его речь, как когда-то, но ведь на сей раз, это его
собственное, не вызубренное суждение.
— Значит...
— Перегиб.
— И экстремума нет. А если п четное?
— Экстремум.
310 ФОРМУЛА ТЕЙЛОРА [Гл. 4
И он ведет рядом с графиком степени (х — хо)п новый, выра-
жающии, очевидно, поведение произведения -—^—^-(х—xq),
несовпадение графиков, по всей вероятности, отражает его
представление о переменности функции а(х). Да, пожалуй, ему
свойственно то, что называют визуальным мышлением. Постараюсь
больше, чем до сих пор, специально для него подкреплять свои
объяснения графическими иллюстрациями. Боюсь только, что
не для каждого раздела программы они отыщутся в достатке...
Постараюсь внимательнее следить за тем, как он станет их
использовать. Я уже заметил: переходы от формул к их
графическим представлениям ему даются тяжелее, чем обратно. На
прошлом семинаре, точно написав на доске определение
производной, он затруднялся с построением соответствующего графика.
Но на том же семинаре, верно показав на графиках
недифференцируемость функции |х| в нуле, тотчас выразил это формулами.
Впрочем, может быть, я чрезмерно увлекаюсь такими
толкованиями, и все это теоретизирование о визуальном мышлении —
лишь моя фантазия, а на самом деле он мыслит совсем иначе?
Может быть... Но в одном я уверен твердо: у каждого
студента — своя, особенная, неповторимая манера мыслить, которую
хорошо бы разгадать и сообразно с нею подходить к каждому...
— Экстремум-то экстремум, — продолжаю между тем
разговор с Сутеевым. — Но какой? Максимум или минимум?
— Зависит от f(n\xo) + а(х) — какого знака.
— Вернее, зависит от знака /^(^о), — уточняю, не надеясь на
его сообразительность. — Мы говорили, что в достаточно узкой
окрестности точки xq знак суммы f^n\xo) + a(x) совпадает со
знаком f(n\xo).
— Если f(n\xo) положительная, то минимум, если
отрицательная, то максимум, — он поясняет сказанное на графике.
— Совершенно верно! Окончательно: если первая из
производных функции /(ж), не обращающихся в нуль в точке xq, есть
производная нечетного порядка, функция не имеет в точке xq ни
IO. В. Пухначев]
СЕМЬ СЕМИНАРОВ
311
максимума, ни минимума, а испытывает там перегиб. Если же
порядок такой производной четный, функция достигает в
точке хо максимума или минимума, смотря по тому, будет ли эта
производная отрицательна или положительна. Садитесь,
Сутеев. Вы хорошо поработали. Рассмотрим теперь новую задачу,
ребята. Попробуем доказать неравенство ех > 1 + х. Не правда
ли, формула Тейлора напрашивается в помощницы и тут: ведь
1 + х — это начало тейлоровского разложения экспоненты.
— А остаточный член лучше взять в форме Лагранжа, —
проворно завершает мою мысль Кочин.
— Верно! К доске! — мгновенно реагирую на его порыв. —
Решите этот пример, как вам хочется.
Мои надежды на его сноровистую работу не оправдываются.
Выражение для остаточного члена в форме Лагранжа, им же
самим предложенной, Кочин выписывает не сразу, ошибаясь и
поправляясь. Но в конце концов все пишет верно.
— Все правильно, садитесь. Я думаю, ребята, что даже после
этих примеров вы поняли: формула Тейлора служит
универсальным и мощным средством для исследования функций, имеющих
тейлоровское разложение. Более того, я бы даже сказал, что
приложения формулы Тейлора к задачам по исследованию функций
отличаются каким-то изяществом, какой-то красотой. Вижу, —
говорю, покосившись на Горта, — что некоторым из вас слово
«красота» кажется неприменимым к такой строгой науке, как
математика. Должен сказать, что многие видные математики
умели дать вполне четкое толкование понятию математической
красоты. Вот, например, что писал по этому поводу Пуанкаре:
«Каковы математические характеристики, которым мы
приписываем свойства красоты и изящества и которые способны
возбудить в нас своего рода эстетическое чувство? Это те элементы,
312
ФОРМУЛА ТЕЙЛОРА
[Гл. 4
которые гармонически расположены таким образом, что ум без
усилия может их охватить целиком, угадывая детали»
Формула Тейлора тем и замечательна, что способна охватить широкий
круг математических методов, столь богатых деталями, —
потому она и вызывает у искусного математика чувство прекрасного.
Крут математических методов, который я имею в виду, гораздо
шире того, что мы изучали до сих пор, и задачи, которые
можно решить при помощи формулы Тейлора, многообразны. Ради
развлечения давайте я покажу вам, как с ее помощью можно
подсчитать... число счастливых билетов в рулоне от номера 000000
до номера 999999. Хотите?
— Хотим! — отвечает хор оживившихся голосов.1
— Счастливым, как вы знаете, считается билет, в номере
которого сумма первых трех цифр равна сумме трех последних —
например, 359827. Теперь смотрите: каждому счастливому билету
я поставлю во взаимно однозначное соответствие
«дополнительный» билет, заменив для этого в номере счастливого билета
каждую из первых трех цифр ее дополнением до девятки — тогда,
например, номеру 359827 будет соответствовать 640827. Легко
видеть, что сумма всех цифр в номере любого дополнительного
билета равна 27. Поскольку счастливые и дополнительные
билеты связаны взаимно однозначным соответствием, вместо
подсчета первых я могу пересчитать вторые. Для этого я рассмотрю
полином (1 + х + хй + ... + х9)6 = (х° + х + х2 +... + ж9)6.
Шестикратно умножая на себя выражение в скобках, я стану получать
произведения вида х6х4х°х8х2х7. И если подсчитать все такие
произведения, где сумма степеней х равна 27, то их будет
столько, сколько дополнительных, а следовательно — и счастливых
билетов. Задача состоит, таким образом, в том, чтобы
определить коэффициент при х27 в полиноме (1 + х + х2 + ... + я9)6.
— Оригинально! — восторгается Меншиков.
— Перепишем этот полином несколько иначе: (1 + х + х2 + ...
+ *9)6 = С1^)6 = (1 - *10)6(1 - хГ6.
— Ага! — увлеченно восклицает Миклашевский. — Первый
сомножитель разложить по биному, второй — по Тейлору...
— Разложить, — неторопливо развиваю его разумную
идею, — по формуле Тейлора до достаточно большой
степени, превышающей 27. Ну, а теперь примемся за определение
коэффициента при х27 в произведении полученных разложений.
изложенное далее решение поставленной задачи принадлежит В. И. Бу-
ренкову
Ю. В. Пухначев) СЕМЬ СЕМИНАРОВ 313
— В разложении (1 — ж10)6 взять члены с я0, я10, я20, а в
разложении (1 — х)~6 — с я27, я17, ж7, — снова перебивает меня
Миклашевский, пристально шурясь на доску, — потом попарно их
перемножить и коэффициенты сложить.
— Верно, — утверждаю такой план действий, — Ну-ка, кто
сделает это быстрее?
— Есть! — буквально через минуту вскидывает руку
Кулагин. — Ответ — 55252.
— Правильно! — несколько секунд спустя подтверждает
Гарин.
— Интересный результат, ребята, правда? — обвожу
довольным взглядом аудиторию. — Хотя и несколько экзотический.
Вернемся к нашим прежним задачам, чтобы убедиться не
только в широте, но и в эффективности применений формулы
Тейлора. Помнится, когда на позапрошлом семинаре мы
занимались выделением главной части функций, некоторые из них
были очень непростыми — мы работали тогда, казалось, на пределе
своих возможностей. Но формула Тейлора позволит нам
выделять главную часть гораздо более сложных функций. Например:
у = е~х — ^55. Исследуйте ее на доске, Кочин.
Терпеливо наблюдаю, как он, преодолевая заминку за
заминкой, упорно продвигается к ответу. И вот ответ готов:
— Получается —\х2.
314
ФОРМУЛА ТЕЙЛОРА
[Гл. 4
— Точно! — заявляет Лапиков, довольный тем, что у него
получилось так же. И я отвечаю улыбкой на его улыбку:
— Верно. Садитесь, Кочин. Согласитесь, ребята: мы вряд ли
смогли бы решить этот пример без формулы Тейлора.
— Может и смогли бы, — с сомнением поднимает бровь
Костюк,— только провозились бы дольше.
— Вы так считаете? Тогда посмотрите пример из родственной
области, на вычисление пределов: lim х~*™ х. Несложная дробь,
правда? А подступиться к ней непросто. Теоремы о пределах,
связанные с арифметическими действиями, здесь непременимы:
знаменатель дроби, стоящей под знаком предела, стремится к
нулю, и поэтому нельзя использовать теорему о пределе
частного. Слагаемые, на которые естественным образом разлагается
дробь, стремятся к бесконечности, так что теорема о пределе
суммы не годится тоже. Замена синуса эквивалентной
величиной х приводит к неопределенному выражению ^^, о поведении
которого при бесконечно убывающем х ничего сказать нельзя.
При всей внешней простоте своей формулировки предел
оказывается неприступно сложным! Однако впечатление
неприступности пропадает тотчас, как только мы применяем к
исследованию этого предела формулу Тейлора. В самом деле,
разложим с ее помощью синус: sinх = х — ^- + о(ж4), следовательно
х — sin х = ^- + о(я4), и дробь под знаком предела приобретает
вид 6 жзХ = б + о(х). Теперь уже ясно, что искомый предел
равен g. Кстати, — гляжу на Аргунову, — всем ли понятно, как
я получил последнее равенство?
— Разделили числитель на знаменатель почленно —
поблуждав взглядом по моим выкладкам, отвечает она.
— А, может быть, проще по правилу Лопиталя? — оспаривает
мой способ Костюк. Приглашенный к доске, он показывает свое
решение.
Костюк
0:— У-Sin ас p. i-cosoc n. sinoc j
— Попробуйте теперь, — предлагаю ему же, — найти такой
1. l-(cosz)ainx тт.
предел: lim—N 3 —• Ьсли следовать вашему совету, деиство-
ж—►()
вать по правилу Лопиталя, то придется трижды
дифференцировать числитель и знаменатель. В знаменателе после этого воз-
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
315
никнет шестерка, а что получится в числителе?
Дифференцируйте его! Что ж вы медлите?
Он апатично пишет (cosx)sinx = esin:rlncos:E и
останавливается:
— Тут доски не хватит дифференцировать...
— А если определить главную часть числителя с помощью
формулы Тейлора? Попробуйте-ка разложить полученную вами
показательную функцию по степеням х. Работы здесь тоже
немало, но выполняется она с помощью одних лишь арифметических
действий, без дифференцирования. Да и не так уж много здесь
работы — это сразу выясняется из ваших выкладок. В самом
деле, вдумайтесь в них: главная часть функции In cos x — это
— %■; главная часть sinx — это х, стало быть, главная часть
всего показателя в целом — это — ^~. И если мы станем теперь
раскладывать экспоненту, то именно эта величина и будет стоять в
образующемся разложении вслед за единицей. Когда полученное
разложение мы поставим в числитель исследуемой дроби,
единицы взаимно уничтожатся, и останется Щ^ плюс о малое от х3 или,
пожалуй, даже от более высокой степени икса. Таким образом,
искомый предел равен ^. Как видите, с использованием
формулы Тейлора пример решается настолько просто, что я получил
ответ в уме. Проверьте теперь, Костюк, путем строгих
вычислений, прав ли я. Прав? Очень хорошо. Садитесь. Я думаю, всем
уже ясно теперь, каким эффективным средством оказывается
в подобных случаях формула Тейлора. Конечно, мой совет не
исключает использования других средств — правила Лопиталя,
соотношений эквивалентности, замечательных пределов. Но, как
поучал апостол Павел, «все испытывайте, хорошего держитесь».
А формула Тейлора в решении подобных примеров очень
хороша. Я, например, не знаю, что бы вы делали без нее, доведись
„ т l-(cosz)8inx гл
вам вычислять такой вот предел: lim —д_апа.—• ^ нею же,
повторяя уже проводившиеся нами выкладки, выделяя главную часть
числителя и знаменателя, легко преобразовать данный предел
к виду lim 3 ) 4у Миклашевский, я вижу, последний пример
привел вас в какое-то непонятное возбуждение. В чем дело?
— Очень похоже на примеры, которые были в прошлом году
на письменном экзамене по матанализу.
— Откуда они вам известны, если не секрет?
— Знакомые старшекурсники дали. Может, порешаем какие-
нибудь?
316
ФОРМУЛА ТЕЙЛОРА
[Гл. 4
— Что ж, порешаем. Для начала дайте нам пример попроще.
Записываю под его диктовку предел дроби, где собраны,
казалось, все элементарные функции.
— Ну-с, как будем вычислять? С чего начнем? —
оборачиваюсь к аудитории. — Что предложите, Меншиков? Пожалуйста,
к доске.
— Главная часть логарифма в первом слагаемом в
числителе — это я, — беззаботно размышляет он, поглядывая на таблицу
маклореновских разложений, — у гиперболического синуса
главная часть такая же, значит, у всего первого слагаемого тоже х.
Теперь у второго... Главная часть синуса... Главная часть
второго слагаемого — тоже х\
— Вы говорите это так, будто чем-то растревожены.
— Главные части обоих слагаемых сокращаются! —
втолковывает он мне.
— Сокращаются? Да, это печально. Может быть, это
вообще неразрешимая задача? Вроде квадратуры круга или
трисекции угла? А ведь что-то подобное уже было у нас на одном из
прошлых семинаров. Но вам это не припоминается. Или тут все
намного сложнее?
— Посмотрим... Это, — он стирает символ предела, — во
всяком случае пока уберем.
— И что будем делать с дробью?
— Преобразовывать, — заявляет он со всей решимостью, на
которую способен.
-Как?
— Как-нибудь по-другому.
Вслед за преобразуемым выражением он пишет знак
равенства, потом длиннющую черту дроби и над нею — короткую
строчку х + о{х) — х — о(х). Он словно не слышал то, что
мы с Кулагиным говорили по поводу разности tgx — sin x и
совсем недавно с Костюком, когда в разности х — sin x
пытались заменить синус его аргументом. Хоть начинай все
сначала!
...Если, следуя расхожему изречению, воображать
исследователя этаким альпинистом, карабкающимся по каменистым
тропам к вершинам науки, то в плане такого сравнения студенты,
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
317
вероятно, представятся новичками альплагеря, чинно
шествующими вслед за инструктором по давно освоенным и
порядком сглаженным дорожкам. Такое представление было бы
чересчур идиллическим; для большего соответствия
действительности следовало бы, пожалуй, вообразить эти гладкие
тренировочные дорожки то ли намокшими от дождя, то ли
оледеневшими, так что неопытная нога скользит по ним;
оглядываясь время от времени назад, инструктор видит, что многие из
его подопечных, только что осиливших вместе с ним сложную
дистанцию, соскользнули к ее началу... Надо возвращаться за
ними и опять тянуть их вверх. Надо уметь не раздражаться
этим и быть готовым повторять эту операцию снова и снова и
снова...
— Постойте! — останавливаю Меншикова, который уже
приготовился преобразовывать знаменатель дроби. — То
короткое выражение, которое вы написали, по-моему, поможет
предельно прояснить первопричину ваших затруднений. Для
большей ясности давайте сделаем это выражение еще короче.
Сократим х и —х. Остается о(х) — о(х). Разность двух о(х) —
это тоже о(ж), как совсем недавно говорилось. Но мы ничего
не можем о нем сказать кроме того, что это некая функция,
которая при бесконечном убывании х стремится к нулю быстрее,
чем х...
— А почему мы берем такие короткие разложения? —
вклинивается в наш разговор Буткус.
— Слышите? — кивком приглашаю Меншикова
прислушаться.
— Все ясно, — догадывается он без разъяснений. — Брать
такие разложения, чтобы какая-то степень икса не сократилась.
— То есть, чтобы получилась главная часть всего
разлагаемого выражения. Верно. Из нашего частного примера можно
сделать весьма общий и очень важный вывод: если в результате всех
подобных разложений у вас получается не какая-то степень икса
плюс о малое от этой или более высокой степени, а одно лишь о
малое, вносящее неопределенность в дальнейшие рассуждения и
вычисления, — разложения нужно взять более длинные, с
большим числом слагаемых, достаточно длинные для того, чтобы в
итоге получилось то, что нужно: какая-то степень икса с
ненулевым коэффициентом плюс о малое от этой или более высокой
степени. Но продолжаем, Меншиков. Пять основных
разложений помните? — указываю взглядом на их список в левом краю
доски.
318
ФОРМУЛА ТЕЙЛОРА
[Гл. 4
— Вроде бы помню. Могу стереть, если хотите.
— Может, подождем? — жалостливо просит Миклашевский,
видя, что я готов дать команду на это.
— Вы еще не выучили?! — с напускным изумлением гляжу
на него. — Не тяните с этим, а то, глядишь, на экзамене...
— На экзамене, — игриво улыбается он, — у нас будет... это
самое... вспомогательные материалы.
— Шпаргалки, — уточняю я. Игривая улыбка не сходит у него
с лица. Продолжаю, отправляясь в путь между столами:
— Вы, наверное, думаете, что я сейчас буду отчитывать
вас за такие мысли. Представляю и возражения, которые вы
приготовили в ответ: мол, все равно всего не упомнишь, мол,
даже самые образованные ученые, и те чего-то не знают и
заглядывают в книги, во всякие там справочники, когда нужно
уточнить в ответе задачи десятый или двадцатый знак после
запятой. Все это правильно, и глупо выглядело бы, если бы я
стал экзаменовать вас на знание, скажем, таблицы
логарифмов. Но согласитесь: чтобы уточнить какой-то результат, надо
прежде его получить, а для этого надо ясно представлять себе
существо решаемой задачи, алгоритм ее решения. Теоремы,
формулы и прочие сведения, которые помогают составлять
такое представление, лучше хранить в памяти, а не лазить
за ними в справочники — так быстрее, а время очень часто
бывает решающим фактором. В математических задачах, чтобы
уяснить их суть, часто требуется оценить по порядку величины
значения той или иной функции, характер ее поведения ...
Этим целям, как мы уже видели, хорошо служат тейлоровские
разложения. Потому я и требую от вас знать наизусть основные
из них.
Говорю, а сам не забываю поглядывать в тетради ребят.
У тех, за кого я беспокоюсь, дело по новизне идет не
блестяще. У каждого — свои беды: Мухин так и строчит, но ляпает
ошибку за ошибкой; Сынчиков продвигается вперед, слава
богу, без ошибок, но черепашьими темпами. Не очень
проворно, но, как мне кажется, с пониманием работает Лапиков.
Разок подзывает Кочин с каким-то пустяковым
недоразумением — разбираемся вместе. Аргунова запуталась — помогаю
ей. Сутееву и помогать-то не в чем — он ничего не пишет.
Абсолютный рекордсмен и по быстроте, и по точности — Бут-
кус. Он прозорливо начал со знаменателя и быстро выяснил,
что все разложение нужно доводить лишь до третьей степени
икса.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
319
— Что подсказало вам такой вывод? — спрашиваю его, когда
по моей просьбе он показывает свое решение на доске.
— То подсказало, что квадратные корни имеют одинаковые
разложения, только знаки у степеней — первой, третьей и
дальше — противоположные. Значит, когда вычесть, получается
сумма только из таких степеней, из нечетных. Разложение ех
имеет только четные степени; когда умножить на 2ж, опять будут
только нечетные. От первого корня первая степень х получается
с коэффициентом 1, от второго тоже — значит, вместе 2х. А от
последнего слагаемого — минус 2х. Они взаимно уничтожатся. А
третьи степени х — уничтожатся? Я проверил. Не уничтожатся.
Значит, разлагать до о(х3).
— Вы слышите, Миклашевский? Это урок для вас: знание
основных разложений плюс смекалка дают разительную экономию
времени, а в конечном счете — успех.
— Есть ответ! — с возбужденной улыбкой отрывается от
тетради Горт, и почти тотчас вслед за ним о том же рапортует
Синица и Рамзин.
— Хорошо, — призываю их к спокойствию. —
Подождем остальных. Чтобы не скучать, начните решать другой
пример.
Миклашевский диктует его по моей просьбе, и я записываю
его в свободном углу доски.
320
ФОРМУЛА ТЕЙЛОРА
[Гл. 4
Дождавшись, пока свой ответ получит Меншиков, прошу его
изложить решение.
— Главная часть числителя равна |ж3, — твердо заявляет он.
— Похоже, — соглашается с ним Рамзин.
— А у вас, Чюмин?
— А у меня ^-, — не очень уверенно откликается тот.
— А у меня %•, — с некоторым беспокойством произносит
Горт.
— У меня то же самое, — поддерживает его Синица.
— И у меня, — присоединяется Мухин. — Только почему-то
с минусом.
— Ну и разнобой! Давайте сверять вычисления, — предлагаю
я. — Прошу вас, Меншиков! Покажите сначала, как вы
раскладывали выражение ln(l + sin x).
— Сначала — синус; раскладываю его до я3; взял его
разложение и подставил в разложение 1п(1 + я), синус — вместо икса:
x-f + o(x3)-±(x-i)2.
— И все? — Горт изумленно смотрит сначала на Меншикова,
потом — вопросительно — на меня. И возмущенно:
— Типичный недобор!
— А если подробнее? — жестом приглашаю его к доске.
— Нельзя сразу подставлять sinx в разложение 1п(1 + х)\
Надо сначала выяснить, до какой степени этот логарифм
раскладывать! Как выяснить? Очень просто: синус эквивалентен х;
значит, если мы хотим учесть степени икса до xz включительно,
то в разложении ln(l + sinx) надо взять все слагаемые вплоть до
содержащего sin3 x.
— И чем закончить разложение? Слагаемым o(sin3x)?
— Можно написать его в виде о(х3) — ведь sin x эквивалентен
х. Потом вместо sinx надо подставить его разложение — взять
его опять-таки до о(х3). Подставить, раскрыть все скобки,
загнать все степени выше ж3 в о(ж3)... ну, и привести подобные.
— Предложенный вами порядок разложения верен. Однако,
мне кажется, его можно сделать еще нагляднее, если с самого
начала разложить sin x до нужной степени х и всю эту сумму
вместе с остаточным членом подставить вместо х в маклоре-
новскую формулу для 1п(1 + я), выписывая ее слагаемые одно
за другим. Тогда сразу будет видно, какое слагаемое в
формуле оказывается последним. Более того, приняв мой подход, мы
сможем лучше разобраться, чем определяется длина
разложения. Наберитесь терпения, ребята, я буду говорить долго, но
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
321
уж надеюсь, что после моего монолога вы станете подходить к
подобным задачам во всеоружии. Для начала давайте
вернемся к неудачному разложению Меншикова. Посмотрим, как оно
получилось из выражения ln(l + sinx). Меншиков верно
сообразил, что разлагать это выражение нужно, опираясь на
стандартную маклореновскую формулу ln(l + z) = ^ — у + tj— —+
+ ~(—l)n+1 +o(zn). Я намеренно, следуя Гарину — помните, как
мы раскладывали тангенс? — использовал здесь новую
переменную z: пример с тангенсом убедил нас, что опорные разложения
целесообразно писать со своими особыми переменными. Роль z в
наших дальнейших выкладках, как правильно отмечал Горт,
будет играть sinx. Для ясности последующих вычислений следует
сразу же выяснить порядок малости нововведенной величины:
z = sinx ~ х, то есть z имеет тот же порядок малости, что и
х, это Горт тоже правильно и своевременно отметил. Меншиков
сразу взял sin x в виде разложения до третьей степени икса,
поскольку именно до нее нужно довести итоговое разложение, и
про о малое не забыл: ln(l + sinx) = ln(l + х — ^- + о(х3)). Вот
тут было бы хорошо оградить скобками всю добавку к единице
под знаком логарифма: ln(l + sinx) = ln(l + (х — ^- + о(х3))).
Это служило бы постоянным напоминанием, что выражение в
круглых скобках мы станем подставлять вместо z в
разложение функции ln(l + z)y на которое нам придется опираться.
Собственно, такую подстановку и начал выполнять Меншиков,
когда писал х — ^g- + о(х3) — \{х — \)2- Поняв, откуда взялась
эта запись, нетрудно подметить ошибку Меншикова: в
последнем слагаемом, в скобках он упустил о(х3). Если бы
Меншиков сохранил это о малое, оно еще раз напомнило бы ему, что
в этом примере, по ходу разложения нельзя упускать ни
одного слагаемого, дающего степени икса до третьей включитель-
322
ФОРМУЛА ТЕЙЛОРА
[Гл. 4
но — иными словами, что в опорном разложении функции 1п(1+
+z) не следует пренебрегать слагаемым ~ = |(х — у- + о(х3))3.
Вы-то сами, — обращаюсь к Меншикову, — видите теперь, что
недоучли член с х3?
— Угу. Когда я в самом начале написал, мне показалось, что
куба больше не надо, и так уже есть.
— Избегайте таких ошибок! Не забывайте писать о малое
в конце каждого разложения, которое используете в подобных
выкладках! А теперь, ребята, заглянем дальше в разложение
функции ln(l + z) и зададимся вопросом: надо ли брать следу-
4
ющее слагаемое — ^-? Мы уже знаем что наше z эквивалентно
х. Выразим это формулой: z = х + о(х). Возведем обе части
равенства в четвертую степень по формуле бинома Ньютона:
z4 = х4 + 4х3о(х) + ... Уже второе слагаемое в получившейся
сумме представляет собой о(х4), да и остальные, как нетрудно
проверить, тоже. Получается, что г4 = х4 + о(х4) = о(х3). Итак,
последовательно беря из разложения функции ln(l + z)
начальные слагаемые, мы дошли до такого, которое оказалось о малым
от третьей степени икса — наивысшей степени, учитываемой
нами. На этом слагаемом, на — ^- давайте остановимся и напишем
так: ln(l+z) = z— у + у ~~ *4+°(*4)- Завершающее о малое
выразим в виде о(о(х3)) = о(х3). Не забыли, ребята, почему возможна
такая замена? В самом деле, о(о(хг)) = (3 • о(х3) = (3 • 7 • #3, где
/3 и 7 бесконечно малы. Итак, каждое из двух последних
слагаемых в правой части нашего последнего равенства представляет
собой о(х3). Собственно говоря, их сразу же можно было
записать в таком виде, и в будущем, когда вы понатореете в
подобных разложениях, вы так и станете поступать, совершая в уме
проведенные мною выкладки. Но сейчас, пока они еще не стали
для вас привычными, я решил продемонстрировать их во всех
деталях.
Новой паузой даю возможность проверить справедливость
моих оценок.
— Ну, а теперь уже можно охватить единым взглядом
пройденный до сих пор путь от опорного разложения к итоговому:
ln(l + z) = z-£ + f-$ + o(z*) = (x-f + o(x3))-l(x-?l-+
+о(х3))2 + 1(х- у+ о(х3))3 + о(х3) + о(х3). После этого остается
сделать совсем немногое: совершить возведение круглых скобок
в квадрат и в куб, все произведения вида xmo(xn), где т + п > 3,
заменить на о(х3) — попутно докажите, почему верна такая
замена — затем собрать все возникшие о малые в одно о(х3), и
Ю. В. Пухначев) СЕМЬ СЕМИНАРОВ 323
искомое разложение готово. Точно таким же образом вы може-
те удлинять подобные разложения до любой заданной степени.
Доделайте пример до конца, — прошу Меншикова, а сам вновь
отправляюсь в обход аудитории — заглянуть в тетради тех, у
кого при прежнем обходе заметил особенно много ошибок. Мухина,
чувствую, скоро придется опять подстегнуть: снова его тетрадь
заполнили грязь и путаница.
— Предел найден верно, минус одна треть, — говорю, увидев
на доске новый ответ. — Садитесь, Меншиков. Теперь я хотел
бы разобрать решение Чюмина. Напишите его на доске, Семен.
Прочтите повнимательнее то, что написали. Вы понимаете, что
ошиблись, когда заменили sinx на х?
— Я думал, раз sinx эквивалентен х ...
— Чтобы быть абсолютно уверенным в такой замене, можно
было бы выразить эту эквивалентность совершенно строго, как
324
ФОРМУЛА ТЕЙЛОРА
[Гл. 4
мы делали уже не раз: sinx = х + о(х). И тогда — смотрите! —
ваши выкладки потекли бы так: ln(l + sinx) = ln(l + х + о(х)) =
= х + о(х). Что же стало бы тогда с разложением предыдущего
слагаемого в числителе, функции shln(l + x)? Вы верно
написали это разложение: х—\+\+ о(х3) + ^-. Но ведь здесь каждое
слагаемое, кроме первого, есть о(х). И поэтому весь числитель
приобретает форму х + о(х) —х —о(х) = о(%). Ту неопределенную
форму, которая лишает смысла все дальнейшие выкладки.
Увидев это, вы спохватились бы: нельзя заменять sinx на х, надо
подставлять вместо синуса более длинное разложение! Садитесь
на место. Следующим пусть выйдет к доске Костюк.
Догадываетесь, Виталий, зачем я вас вызываю? Я хочу, чтобы вы
разложили тангенс в нуле до пятой степени икса. Сделайте это по той
же схеме, по которой вы получили разложение до третьей
степени. Только теперь, разумеется, в исходных разложениях синуса
и косинуса следует взять побольше слагаемых. То и другое вы
написали верно, теперь вычисляйте (cosx)"1. Следуя прежней
схеме, вы правильно пишете (cosx)-1 = [1 — (^г — §4 + °(#5))]~\
затем выписываете разложение по формуле бесконечно
убывающей геометрической прогрессии... так... единица... круглые
скобки... квадрат круглых скобок...
— Дальше, — ставит еще один плюс Костюк, — будет куб
круглых скобок, то есть сумма степеней х, которая
начинается с х6, а это уже о(х5), вот мы этим о малым и закончим. В
общем-то, как заканчивать такие разложения, вы только что
показывали, когда разбирали решение Меншикова. Дальше надо
писать о малое от куба круглых скобок, то есть о(о(х5)), но это,
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
325
как вы тогда же говорили, бесконечно малая не меньшего
порядка, чем о(х5), и в сумме с тем о(х5), — кивает на него, — даст
опять же о{хъ). Так что все правильно, после квадрата круглых
скобок напишем просто о(х5).
— Пишите. А как станем раскрывать квадрат круглых ско-
2
бок? Квадрат первого слагаемого, вот этого ^-, берем?
— Берем, это четвертая степень икса, она нам нужна.
— Квадрат второго слагаемого, величины |j, берем?
— Нет, это восьмая степень, то есть о(х5), а ее можно
включить в то о(х5), которое у нас уже есть, по формуле
о(хп) + о(хп) = о(хп).
— Хорошо. Доводите свои вычисления до конца. Ну вот,
разложение получилось точно таким же, каким я его написал когда-
то. Садитесь, Костюк. Решим теперь, ребята, второй пример из
тех, что дал нам Миклашевский.
— А как раскладывать арксинус? — спрашивает Лапиков.
— Где взять его разложение, если его нет на доске — вы об
этом, наверное, спрашиваете? — гляжу на него участливо, но
чуть с иронией, чуть с упреком. — Вы забываете, очевидно, что
все написанное на доске вывели мы сами.
— Но для этих функций у нас были формулы n-ной
производной! — напоминает Стрельцов, оправдывая затруднения
Лапикова.
— В данный момент, — уточняю ситуацию, — в нашем
положении нас устроили хотя бы несколько начальных производных
арксинуса в нуле: разлагать его придется, очевидно, до не очень
высокой степени.
— До о(х4), — бросает Костюк, не отрываясь от тетради.
— Вы, наверное, уже вычислили все нужные производные?
— Нет, я хочу без них — производные тут получаются
громоздкие...
— В таком случае, конечно, хорошо бы найти остроумный
обход вычислительных трудностей. Но если он не найдется —
будем атаковать задачу в лоб, последовательным
дифференцированием арксинуса. Каждый волен выбрать свой путь — там
посмотрим, кто быстрей придет к цели. Итак, объявляется
конкурс на скорейшее разложение арксинуса в нуле.
Брожу между столами и пару минут спустя возвращаюсь к
доске:
— Никто из вас, ребята, не пожелал решать задачу напрямик,
последовательным вычислением производных — все принялись
за разработку оригинальных идей. Некоторые получили инте-
326
ФОРМУЛА ТЕЙЛОРА
[Гл. 4
ресные заготовки — я покажу их на доске — но завершить их
почему-то не могут. Навалимся-ка на них всем миром — авось,
что-нибудь да выйдет. Вот, скажем, в тетради у Кочина
написаны такие равенства: у = arcsinx; затем х = siny = у — ^-+ о(у3).
А Буткус написал: arcsinx = ах + /Зх2 + ухг + 5х4 + о(х4). Не
догадываетесь, — спрашиваю Линаса, — чем могут вам помочь
равенства Кочина?
— Я своим способом делаю, — не поднимая головы,
отказывается он отвечать.
— Что же, воля ваша, делайте. А вы, Кочин, не видите, что
можно получить из всех трех равенств?
-- Честно говоря, нет.
— Кто сообразит? — гляжу на аудиторию. — Может быть, вы,
Миша? — спрашиваю Гарина.
Знакомая затаенная усмешка поигрывает в его глазах:
— Надо взять разложение х по степеням у, которое получил
Дима, и подставить в него вместо у то разложение, которое
получил Линас.
— Вот-вот! — одобряю его идею. Идите к доске, Дима, — зову
Кочина, — сделайте это. Чего ж вы остановились? Не знаете, что
предпринять дальше с этим равенством из степеней х и
неопределенных коэффициентов?
— Неопределенных коэффициентов? — быстро
переспрашивает он, бросив на меня острый взгляд. Затем приравнивает в
обеих частях равенства коэффициенты при х и пишет а = 1.
— Отлично! — подбадриваю его.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
327
— Теперь коэффициенты при х2, — ведет он уже сам линию
рассуждения. — Слева х2 вообще нет, справа — /Зх2.... Значит,
/3 = 0. С х3... слева опять нет, справа, если собрать все кубы,
7- g, то есть 7 = g.
— Отлично, отлично!
— Тем же путем можно показать, что 6 = 0. Получается, что
arcsinx = х + ^- + о(х4).
— А как дела у вас, Линас? — окликаю Буткуса.
— Никак, — мрачно бурчит он.
— Тогда обязательно перепишите себе в тетрадь то решение,
которое написано на доске!
— Хорошо, — отвечает он, не меняя мрачного тона.
— А что у остальных? — спрашиваю аудиторию. — Может
быть, кто-то получил разложение другим способом? Нет? Жаль
все-таки, ребята, что никто из вас не попытался
дифференцировать арксинус. Этот путь, конечно, не очень удобен, однако,
сделав по нему лишь один шаг, вы могли бы заметить заманчивое
ответвление от него. Смотрите: (arcsinx)' = , * 2 = (1—х2)~2,а
это уже функция, разложение которой нам знакомо:
проинтегрировав его, мы получили бы представление arcsinx более простым
способом, который к тому же позволит получать коэффициенты
при любых степенях х. Сделайте это, Дима, — прошу Кочина. —
Вы ведь проходили в школе интегрирование?
— Проходили..., — отвечает он с какой-то грустной
усмешечкой, в которой читается: «только когда это было...»
Получив в левой части равенства arcsin x + С, а в правой —
те же, что и прежде, начальные члены разложения, записав по
моему совету общий член через двойные факториалы, он
останавливается перед последним слагаемым:
— Не знаю, как интегрировать о малое...
— Непростая проблема, правда? — приглашаю к обсуждению
всех. — Как подойдем к ней?
328
ФОРМУЛА ТЕЙЛОРА
[Гл. 4
— Взять остаточный член в форме Лагранжа, — авторитетно
советует Костюк, и я пишу предложенное им на доске.
— А когда будем интегрировать, учесть, что производные
корня в окрестности нуля ограничены, — добавляет Горт.
— Ограничены какой-то константой, и интеграл будет
меньше, чем если вместо f^n\c) была бы эта константа, — с жаром
развивает наметившийся подход Миклашевский.
— А в школе разве вам давали такое неравенство для
интегралов? — испытующе гляжу на него.
— Не помню... но разве это не очевидно?
— Мне, во всяком случае, это очевидным не кажется.
Давайте, ребята, закончим такое решение на следующем семинаре,
когда речь пойдет об интегралах. Садитесь, Дима, — отпускаю
Кочина.
— С доски стирать?
— Нет, не надо. Ребята, все поняли второй из способов,
которыми пользовался Кочин? Да? Тогда давайте выведем таким
же способом разложение арктангенса. Пусть у доски это сделает
Сутеев.
Он получает ответ, копируя схему выкладок Кочина. Я
намеренно оставил их на доске, чтобы обеспечить этот успех,
подбодрить им Сутеева.
— Результат у вас правильный, Игорь, садитесь.
Припишите обе формулы к списку основных разложений, ребята.
Приписали? Продолжим решение нашего примера с пределом.
Я вижу, — приговариваю, проходя между столами, — что с
числителем справились уже многие. Но лучше всех, по-моему,
это получилось у Синицы. Покажите на доске, Люда, как вы
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
329
действовали. Смотрите, ребята, как основательно все делается —
как вводится опорное разложение корня \/1 + г, как тщательно
отслеживаются знаки перед слагаемыми... Садитесь, Люда,
спасибо за урок добротной работы. Некоторые, —
возвращаюсь к доске, — начали со знаменателя, но не все разлагают
его безошибочно. Самые фантастические результаты стоило
бы обсудить сообща. Вот что пишет, например, Сынчиков:
tgvT+д? = vTTx* + V***)^1*** + o((vTTx4)4). Под знаком
о малого, Сынчиков, в подобных формулах, как уже не раз
говорилось, мы всегда помещаем бесконечно малую величину —
а разве таков корень \/1 + х4 при х, стремящемся к нулю?
Нет ведь?
Признаться, перед тем как начать разбор неудачных
решений, я крепко сомневался, стоит ли включать Сынчикова в число
участников этого парада. Быть может, лучше было бы разобрать
его ошибку наедине с ним, в осторожной щадящей манере, как
я это делал раньше? Тогда, после его плачевных выходов к
доске, я составил весьма невысокое мнение о его возможностях. Но
потом, понаблюдав за его работой на месте, я стал гораздо
лучше думать о них. А требовательность к студенту всегда
должна соответствовать его способностям. Высокая требовательность
при скромных способностях ведет к разочарованиям и неверию в
свои силы, низкая требовательность при больших способностях
подрывает трудолюбие.
И, заглушив в себе сердобольную нотку, которая готова была
вкрасться в мое обращение к Сынчикову, перехожу к
следующему экземпляру коллекции ошибок:
— Странно выглядит и то, что написала Аргунова:
tg \/l + х4 = 1 + \ + -3-; в этой сумме как бы смешались
разложения корня и тангенса.
330
ФОРМУЛА ТЕЙЛОРА
[Гл. 4
— Очень остроумно! — с абсолютно невинным
видом и абсолютно нейтральной интонацией произносит Рам-
зин. Не отбил я ему, видно, охоту ехидничать!
Возмущение закипает во мне, но, сдержавшись, беру совсем другой
тон:
— А если по-деловому? Без издевки?
— Нужно сначала разложить корень по формуле
бинома: единица плюс малая величина х4 в степени одна
вторая; получится единица плюс несколько малых
слагаемых, — инструктивно излагает Рамзин; я между тем зову
его к доске. — К этой сумме применим формулу тангенса
суммы, возникнет тангенс малой величины, его разложим
по формуле разложения тангенса... а дальше уже дело
техники.
— Ну что ж, вы очень хорошо описали, Сергей, простой и
четкий подход к этой функции, — благодарю его. — Кстати,
такой же подход и у Синицы, и у Стрельцова... Но возможна и
более остроумная трактовка знаменателя: Миклашевский
вспомнил из школьного курса формулу для разности тангенсов, и она
быстро привела к ответу — покажите, как это у вас
получилось, Паша.
— Знаменатель эквивалентен дроби со^2 г, числитель, — он
показывает на завершающее равенство в вычислениях Синицы, —
дроби -у-. Ответ: -g2j^.
— Очень хорошо. Вот оно в действии — умение привлекать к
делу весь широкий арсенал своих знаний, полученных и когда-
то давно и только что. Пусть оно послужит нам образцом при
отыскании следующих пределов. Они будут посложнее
предыдущих — например: lim(j^^r)ctg2x. Еще парочку примеров я
напишу с краю доски. Пусть их решают те, кто раньше сделает
первый: начнем с него.
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
331
— Функция в степени функция — надо выразить в виде
экспоненты! — тотчас же начинает писать не доске Миклашевский
очевидное преобразование.
— Спасибо, — благодарю его, — но дальше думаем сообща.
Садитесь на свое место, Павел. Перед уходом сотрите формулы
основных разложений. Надеюсь, что все уже запомнили их. Или
скажем так: все должны были их запомнить. Ну-ну, не ропщите,
Лапиков, — не вечно же жить подсказками.
Иду между столами. Многие, в чьи тетради я заглядываю,
выделывают такое, что мне не придумалось бы и нарочно.
— Да, ребята, опять, я вижу, следует устроить паноптикум
вашей фантазии, чтобы заблуждения никогда больше не
повторялись, а верные подходы — запомнились.
Воспроизвожу на доске выдержки из тетрадей Чюмина,
Лапикова, Стрельцова, Кулагина:
332
ФОРМУЛА ТЕЙЛОРА
[Гл. 4
— Вы уже догадались, наверное, ребята, что я расположил
ваши подходы, начав с самых неудачных. Чюмин забыл формулу
Маклорена для логарифма — это тяжкий грех.
— Это опечатка! — оправдывается Чюмин. — Я точно помню,
что в каком-то разложении знаменатели без восклицательных
знаков, только забыл, в каком именно.
— Лапиков, — продолжаю я, — зачем-то брал логарифм от
ж2, вынесенного за скобки в числителе и знаменателе, хотя на
этот множитель разумно было бы сразу же сократить дробь.
Ненужные преобразования делал и Стрельцов — это особенно
ясно видно в сравнении его решения с решением Кулагина.
Чего, казалось бы, проще — логарифм дроби равен разности
логарифмов числителя и знаменателя. Но вас, ребята, все тянет
к ничем не оправданной сложности. Учитесь простоте!
Запомните простые подходы к примерам подобного типа!.. И наконец
я хотел бы еще раз поговорить о распространенной нестрогости,
которая может немало навредить вам при решении задач с
помощью тейлоровских разложений. Если же вы навсегда избавитесь
от нее, то обезопасите себя от многих ошибок. Я сейчас покажу
на доске, о чем идет речь. Смотрите, как поступила Аргунова
с последним примером после того, как представила
предложенную функцию в виде экспоненты; смотрите, как она преобра-
зовывает логарифм в показателе: In J^^ = In X2+JX3\ =
= 1П x4o(x3) = ln Aofr) = 1П(1 + ^ +0(Ж))-
Делаю паузу, предоставляя Гале возможность объясниться.
Но она сидит молча и понуро, подавленная своими последними
неудачами, что-то слишком уж частыми... На прошлых
семинарах шел разговор о вещах, которые так или иначе затрагивались
в школьном курсе, так что она худо-бедно справлялась с
задаваемыми мною примерами, а сегодня все ново для нее. Вызвать
ее к доске и вместе с нею разобрать ее ошибки? Нет, не
стоит: разговор с нею при всех угнетет ее еще сильнее. Поговорю с
ней наедине после занятий. И я отвожу глаза от ее печального
лица.
— Стоит сравнить два последних слагаемых в полученном
выражении под знаком логарифма, — веду далее разбор ее
результата, — и станет ясно, что ^- = о(х), а дальше выкладки
естественным путем пойдут так: 1п(1 + о(х)) = о(х).
Бессодержательный результат, правда? Получилось не какая-то степень
икса с ненулевым коэффициентом плюс о малое, а одно лишь о
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
333
малое. А это — вспомните наш разговор с Меншиковым! —
тревожный сигнал о том, что разложения были слишком короткими.
В самом деле, числитель последней дроби под знаком
логарифма разложен до о малого от третьей степени х, а знаменатель —
только до о малого от первой. Будьте внимательны, ребята, к
этому заключительному о малому, к этой неизменной концовке
ваших разложений, позволяющей должным образом поддерживать
и соразмерять их длину! Это же ваша техника безопасности!
Никогда не забывайте писать это заключительное слагаемое, а
когда выполняете с ним какие-нибудь арифметические действия —
не забывайте про то, что под ним могут скрываться весьма
различные функции — иначе вы рискуете повторить наивный
переход Сутеева: lim ctg2 x In 55^5755} = lim ctg2 x In 1 = НтО = 0.
Этот неожиданный вывод получился у Сутеева оттого, что он
счел равными величины о(х3) в числителе и знаменателе дроби
под знаком логарифма. Верно ли это? Как всегда, столкнувшись
с каверзным вопросом, обратимся к определению. Скажите,
Сутеев: что такое по определению о(х3)?
— Это произведение вида а(х)х3, — отвечает он со своей
подкупающей, но — увы! — обманчивой четкостью.
— Что же такое здесь а(х)?
— Бесконечно малая величина.
— Верно, бесконечно малая. Но больше про нее ничего не
скажешь, точное ее значение невозможно извлечь из
обозначения о(х3). Помня об этой неопределенности, мы не можем
отождествлять встречающиеся в наших выкладках величины о(х3).
И если одну выражаем в виде а(х)х3, то другую... продолжите,
Сутеев!
— Наверное, как-нибудь так: /?(х)х3, — тон его, заметно
потеряв в уверенности, приобрел тот глуховатый оттенок,
который чувствуется, когда он говорит что-то свое, не вызубренное,
а только что найденное им самим. — Наверное, тут будет другая
бесконечно малая.
— Точно! Покажите на доске, как тогда вы станете преобра-
зовывать дробь под знаком логарифма. Так, In X2,q)x\.X3 •
— Можно сократить на х2.
— Сокращайте.
— Логарифм дроби равен разности логарифмов числителя и
знаменателя, - его голос по-прежнему глух, но звучит
увереннее. — Получается \а{х) — (3{х)]х = 7(я) • я» разность бесконечно
малых — это опять бесконечно малая.
334
ФОРМУЛА ТЕЙЛОРА
[Гл. 4
Побуждаю его сделать следующий, все проясняющий шаг:
— Последнее равенство можно продолжить: *у(х) • х = о(х).
Мы снова получили не то, что всегда хотим получать в подобных
случаях, не икс в какой-то степени плюс о малое, а голое о малое.
А это, не постесняюсь повторить снова и снова, сигнал беды:
разложения недостаточно длинны. Какие разложения? Разберитесь
в этом сами.
— Надо оба... и числитель, и знаменатель... тянуть до такой
степени, которая не сократилась бы, чтобы не оставалось только
о малое от какой-то степени, а была какая-то степень с
коэффициентов, с ненулевым коэффициентом плюс о малое... Сначала
разложить 1п(1 + х2)... до х . И xshx тоже — до хА.
Как все-таки отличается невыразительный голос его
собственной мысли от магнитофонного звучания вызубренных им
фраз!
— До какой степени х надо при этом раскладывать shx?
— До третьей.
— Хорошо, продолжайте.
— В числителе и знаменателе получится х2 и еще какое-то
слагаемое... и еще какое-то о малое... Потом на х2 надо
сократить...
— Проведите все эти выкладки. Хорошо, хорошо. Получилось
, 1+^+о(х3) „ 9
In —V ) '. Что дальше г
— Логарифм дроби — это разность логарифмов. Там и там
будет логарифм единицы плюс малая величина. А это уже
раскладывается... у нас есть формула.
— Формулу помните? Нет? Возьмите тетрадку и перепишите
ту формулу оттуда на доску.
— Здесь в разложении логарифма квадрат... это будет х4,
можно включить в о(х3). Вот: |х2 + о(х3).
— И значит, наш предел в показателе экспоненты свелся к
виду: lim ctg2x(|x2 + o(x3)).
— Скажите, — вторгается в наш разговор Лапиков, — а до
какого члена раскладывать здесь котангенс?
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
335
— Не скажу, потому что сам не знаю, — начинаю с
притворной растерянностью. И продолжаю с доброжелательно-
хитроватой улыбкой, — но вы ответите на свой вопрос сами. Вы
и Паскаль. Помните его совет заменять определяемые понятия
их определениями? Очень помогает, когда понятия не очень
понятны. Вам не ясно, как разлагать? Напишите на доске
определение тейлоровского разложения. А вы, Сутеев, садитесь.
Спасибо за важный результат.
И к Лапикову, который словно не смеет начинать без
указаний:
— Вспомним теорему Тейлора. Пусть функция f(x)
определена в некоторой окрестности точки xq и имеет в этой точке все
производные до n-ного порядка включительно. При таких
условиях f(x) представима в виде... Продолжайте, Лапиков.
Он верно пишет: f(x) = f(x0) + f(x0)(x - х0) + ^f"(xo)(x-
-х0)2 + ... + ^f{n)(x0)(x - х0)п + о((х - х0)п)'
Повторить важную теорему никогда не лишне. И уместный
комментарий к ней стоит привести:
— Из упомянутых условий следует, что функция f(x)
определена и непрерывна вместе с производными всех порядков до
(га— 1)-го включительно в некоторой окрестности точки хо.
Впрочем, из этого нам достаточно того, что функция определена в
точке хо- Наша функция f{x) — это котангенс, хо — это нуль.
Чему же равно начальное слагаемое искомого разложения /(хо)>
то есть котангенс нуля?
— Он же в нуле не существует! — изумляется Горт, не
чувствуя розыгрыша в моих расспросах.
— У него там бесконечный разрыв! — поддакивает Костюк.
— Слышите, Лапиков? В нуле с котангенсом что-то
неладное. Опять надо просить помощи у Паскаля. Дайте определение
котангенса.
— Это косинус, поделенный на синус. Можно так и написать
в нашем пределе. Тогда все будет проще: Нт^^(|х2 + о(х3)).
А косинус в нуле — это единица. Может, вообще убрать этот
косинус?
— Нет, так было бы слишком уж просто. Лучше замените
косинус его разложением.
— Вот таким: 1 — ^- + о(х3)?
— Нет, на мой взгляд так будет слишком сложно. Достаточно
так: 1 + о(х). Возведите это в квадрат, умножьте на скобки. Вот
получилось так, как вы хотели, когда предлагали просто убрать
336
ФОРМУЛА ТЕЙЛОРА
[Гл. 4
косинус. Только на сей раз мы все сделали по науке. Ну, а с
синусом что будем делать?
— Синус икса в нуле ведет себя как икс.
— Сказать это было бы слишком просто. Мы уже давно в
таких случаях говорим иначе.
— Может, разложить синус?
— Можно, конечно, но, по-моему, теперь вы чуточку
усложняете дело. У нас ведь получилась дробь, а при нахождении
предела дроби мы ее части, как уже доказывалось, можем
заменять эквивалентными величинами. Последнее из написанных
вами равенств говорит, что синус икса, стремящегося к нулю,
эквивалентен иксу. И все выходит просто. Покажите, как.
о 2.
Он получает |, затем пишет искомый предел ез, и я с
похвалой отсылаю его на место.
— Тонкая это штука — простота, — изрекает Стрельцов.
— Тонкая, не спорю. С одной стороны, мы восхищаемся
простыми решениями, с другой — говорим: «Простота хуже
воровства». Как же определить грань простоты, которой следует
придерживаться в своих решениях? Надо помнить, что методы
решения задач должны быть адекватны содержанию задач. Если
вы применяете более сложные методы, чем того требует предмет
задачи, вас упрекнут в мудрствовании, если используете более
простые — обвинят в той самой простоте, которая хуже
воровства, в упрощенчестве. Но вернемся к теме нашего сегодняшнего
занятия, к тейлоровским разложениям. Собственно говоря, мы
ее уже заканчиваем. Меня заботит только то, ребята, что все
функции, которые нам до сих пор встречались, разлагались по
формуле Тейлора до сколь угодно высокой степени. Чего
доброго, вам могло почудиться, будто таковы все функции на свете. А
если бы нам встретилась, например, такая: f(x) = x2|x|? и вас
попросили бы разложить ее по формуле Тейлора в нуле, — что
вы сказали бы на это?
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
337
— Такая функция в нуле вообще не разлагается! —
отвечает Меншиков с понимающей улыбочкой человека, которого на
мякине не проведешь.
— Почему вы так думаете?
— Модуль ведь!
— Ну и что, что модуль?
— Модуль в нуле недифференцируем!
— А у нас тут, между прочим, не модуль сам по себе, а х2\х\.
Быть может, у такой функции производная в нуле существует.
— Существует, конечно! — вступает в разговор
Миклашевский. — Я сам что-то похожее на прошлом семинаре
дифференцировал.
— Вы это помните, Меншиков? Ну-ка, напрягите свою
память!
— Сейчас, — принимает он сосредоточенный вид. — Кажется,
мы брали производную слева, потом производную справа...
— К доске, Меншиков! Так что же получается?
— Производная слева и производная справа равны нулю, то
есть совпадают. Гм... Значит, существует производная в обычном
смысле и равна нулю.
— Может быть, и вторая производная существует?
— Поглядим... И вторая существует тоже — нуль! А третья...
Слева — минус шесть, справа — шесть., не равны. Третьей, как
говорится, не дано.
— Достаточно ли того, что мы нашли, для разложения нашей
функции по формуле Тейлора? Чувствуется, что этот вопрос
ставит вас в тупик, Меншиков. Кто мог бы ответить на него? Хотите
вы, Рамзин? Пожалуйста, к доске.
— Я бы прежде всего отметил, что мы всегда говорим о
формуле Тейлора с фиксированным количеством слагаемых. Если
речь идет о разложении в нуле, то есть о формуле Маклорена,
338
ФОРМУЛА ТЕЙЛОРА
[Гл. 4
то мы пишем ее так: f(x) = /(0) + фж+фх2 + ... + ^а;п+
+о(хп) — я взял остаточный член в форме Пеано. Такое
разложение можно написать, если в нуле у функции f{x) существуют
все производные до п-ной включительно. Если бы их не
существовало, написанное утратило бы смысл. Наша функция х2\х\
обладает в нуле производными вплоть до второй включительно.
Значит для нее позволительно написать формулу Маклорена
такую: /(х) = /(0) + ^г^х+ £^х2 + о(х2). Подставим вместо /(0)
и производных...
— Ну, ясно! — хамовато обрывает Рамзина Меншиков и
хоккейным движением оттесняет его в сторону, чтобы продолжть
самому.
— Это еще что за манеры?! — сурово одергиваю грубияна. А
сам втайне радуюсь: для Меншикова любая активность, пусть
даже такая невоспитанная — благо; была бы она, а уж за
воспитанием дело не станет.
— Так что вы хотели сказать, Меншиков? — спрашиваю
тоном помягче.
Он молча пишет: х2\х\ = 0 + 0 • х + 0 • х2 + о(х2). Потом,
повернувшись ко мне, поясняет:
— Получается, что х2|х| = о(х2), — вот искомое разложение.
— Правильно. Как ни странно оно выглядит, это именно то,
что требовалось получить. Садитесь, Рамзин, спасибо за
разъяснение. Вы, Меншиков, садитесь тоже, но прежде напишите на
доске функцию, которая уже встречалась нам на одном из
прошлых занятий: f(x) = х + х2\пх при х ф 0, а в нуле эта
функция равна нулю. Попробуем разложить ее в ряд Тейлора в точке
xq = 0. К доске я позвал бы Аргунову.
Она сидит, словно не слыша моих слов. И вдруг — с
капризным раздражением:
— Не пойду!
— Не пойдете?! Почему!
— Все равно у меня ничего не получится!
— Как вы можете знать это заранее?
— А так. Не получится — и все. Одним дано, а другим не
дано.
Бунт да и только!
— Вы устали, наверное, Аргунова. Давайте передохнем.
Поговорим о чем-нибудь постороннем, не о математике. О том,
например, как человеческий организм, зараженный инфекцией,
борется с нею. Смотрите, — рисую оси координат, — на горизонтальной
оси я стану откладывать количество инфекции, попавшей в оргн
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
339
низм, а на вертикальной — количество антител, которые в ответ
на это вырабатываются организмом. Предположим, что
количество проникшей инфекции невелико, совсем ничтожно. Какое
количество антител выработается в этом случае? Как вы
думаете, Аргунова?
— Тоже, наверное, немного.
В ее голосе нет горечи: ведь разговор — о постороннем.
— Ошибаетесь, Галя! Организм вообще не вырабатывает
антитела, если количество попавшей в него инфекции не
превосходит некоторого уровня. А вот если превосходит, то антитела
вырабатываются с некоторой постоянной интенсивностью, —
рисую ступенчатый график. — Постоянной, впрочем, лишь до тех
пор, покуда количество инфекции не превзойдет следующего
порога: тогда произойдет еще один скачок интенсивности. Мне
кажется, — убеждающе гляжу на Аргунову — что усвоение
знаний протекает по сходному механизму. Вы учите, учите,
учите какой-то материал, — отбиваю последовательные точки на
участке графика, сливающемся с осью абсцисс, — а результата
не ощущаете, не чувствуете, что ваши знания растут. Но от
этого не нужно впадать в отчаяние, нужно вгрызаться в материал
еще упорнее: настанет момент, когда внезапно вы обнаружите,
что владеете этим прежде неподатливым материалом свободно
и полно, — победным взмахом я перескакиваю на ступеньку, ведя
отстук новых точек уже по ней.
— Но могут быть всякие случайности , — недоверчиво глядит
Аргунова на мой аллегорический чертеж.
— Могут — принимаю ее возражение. — Могут быть
неудачи, провалы памяти и тому подобное, — отстукиваю пару точек
вспять, изображая такие срывы. — Но если вы уже на ступеньке,
нас так просто, случайными помехами с нее не сбросишь! Вы
понимаете меня, Галя? — заглядываю ей в глаза. — Напишите-ка у
себя в тетрадке определения производной. Это-то вам, надеюсь,
дано? И попробуйте все-таки исследовать функцию х + х2\пх —
340
ФОРМУЛА ТЕЙЛОРА
[Гл. 4
сколько производных существует у нее в нуле? Работайте
спокойно, не спеша — я подойду к вам попозже, посмотрю, как
у вас идут дела ... Но кто же пойдет к доске разобрать эту
функцию?
Вызывается Синица. Мел в ее руке так и скачет:
— У первого слагаемого все производные существуют: первая
равна единице, остальные — нулю. Теперь второе слагаемое...
По формуле дифференцирования здесь не выйдет — нуль в
выражение 2х1пх подставлять нельзя, логарифм в нуле не
определен — значит, надо по определению... Первая производная —
нуль, у всей функции, значит, единица. Вторая производная...
логарифм... логарифм в нуле предела не имеет, второй
производной нет. Значит, в формуле Маклорена будет только два
слагаемых и еще о малое: f(x) = /(0) + ^j # + о(х) — так ведь?
А если подставить все значения, то так: х + х2 \пх = х + о(х).
Странно... Выходит, х2\пх = о(х)... а вообще-то так оно и есть:
arlnx = (xlnx) * х, а х \пх — бесконечно малая... Малюсенькое
какое-то разложение... Но больше, наверное, уже нельзя?
— Нельзя, вы правы, — успокаиваю ее. — Садитесь, Люда.
Последними двумя примерами, ребята, я хотел призвать вас к
бдительности при разложении функций по формуле Тейлора:
она не для всякой функции может содержать столько
слагаемых, сколько душе угодно. Будъте же внимательны, когда ею
пользуетесь, не забывайте теоретический фундамент, на
котором она строится, и опирайтесь на него, если в каких-то случаях
эта замечательная формула откажется вам послужить. Желаю
успеха в ее применениях! На этом мы закончим сегодняшнее
занятие. На следующем поговорим об интегралах. Про них вам
уже рассказывали в школе, так что, может быть, сразу начнем
с примеров? Или все-таки стоит перечислить вначале основные
положения интегрального исчисления?
— Стоит! — отвечает аудитория.
— Кто хотел бы сделать краткий доклад на эту тему?
Поднимается несколько рук, но я словно не замечаю их.
Гляжу на Кочина:
— Может быть, вы, Дима? Вы что-то замялись сегодня, когда
я просил вас проинтегрировать разложение корня. Вам
необходимо хорошо обезопасить себя от подобных затруднений. А
лучший способ защиты — нападение. Вот и беритесь смелее за
работу, которую я предлагаю. Внимательно прослушайте лекцию,
на которой лектор объяснит операцию интегрирования,
разберитесь во всех тонкостях, это у вас получится, я уверен, все мы
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
341
обратили внимание, как четко вы сегодня написали формулы
производных высших порядков от элементарных функций;
составьте такой же четкий, краткий конспект своего доклада на
предстоящем семинаре — и вперед! Договорились?
— Договорились, — негромко, но решительно отвечает он,
глядя мне в глаза.
— Вот и хорошо. Итак, докладчиком на следующем
семинаре будет Кочин. Можете быть свободными, ребята. Все кроме
Аргуновой — ее я прошу остаться.
Глава 5
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
Вопрос Миклашевского меня не удивил — напротив, я удивился
бы, если бы этот вопрос не был задан мне в самом начале
семинара, как только я напомнил его тему, обещанную на предыдущем
занятии. «Повторим определение первообразной, потом
потренируемся в вычислении неопределенных интегралов», — начал
я, и тотчас Миклашевский вздернул брови, выкатывая наивно-
удивленные глаза:
— А зачем нам их вычислять? Есть ведь таблицы
интегралов, я сам видел — вот такие книжищи, — и он показал, какие,
расставив пальцы. — Понадобится вычислить какой-нибудь
интеграл — бери таблицы и смотри.
— Резонное соображение, — отвечаю с улыбкой. — Сейчас я
постараюсь обсудить его на подходящем примере... Напомните-
ка мне, Миклашевский, сколько будет двенадцать в квадрате.
— Сто сорок четыре.
— А четырнадцать в квадрате?
— Сто девяносто шесть.
— Скажите, пожалуйста, какие познания! Может быть,
вы и таблицу умножения знаете? Странно! Зачем вам ее
помнить? Ведь она напечатана на обложках ученических
тетрадей. Понадобится вычислить какое-нибудь произведение —
берите печатную таблицу и смотрите. Морщитесь?
Скажите, что я передергиваю? Мол, таблица умножения — совсем
другое дело, она нужна на каждом шагу, да и запомнить ее
нетрудно. Среди интегралов тоже есть несколько
простейших, которые наверняка будут встречаться вам на каждом
шагу.
— Вы о табличных интегралах? Я их знаю, можете
проверить, про них я не говорю. Я вот про какие, — он листает
задачник, подыскивая убедительный пример, — вот про такой хотя бы:
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
343
f х arctgx ln(l+x2)cte. Логарифм, да еще арктангенс, да еще икс!
Над такими-то интегралами зачем голову ломать? Их надо брать
из таблиц.
— А вы уверены, что в таблицах содержится любой интеграл
из тех, которые встретятся вам в будущем? Такая уверенность
была бы опрометчива. Вот почему необходимо знать приемы
вычисления неопределенных интегралов. Надеюсь, что в этом вы со
мной согласитесь, Миклашевский, — и все остальные тоже.
Запомнить эти приемы нетрудно — они просты и всего их по
существу четыре. Их назначение — сводить интегралы, подлежащие
вычислению, к простейшим, табличным. Но прежде чем
говорить обо всем этом, вспомним основные определения. Что такое
первообразная? Что такое неопределенный интеграл? Основные
положения темы сегодняшнего семинара обещал изложить Ко-
чин. Вы готовы, Дима?
— Готов.
— Тогда прошу вас к доске.
А сам сажусь на его место, с краю среднего ряда — такой же,
как и сидящие рядом со мной, слушатель.
Кочин несколько секунд стоит у доски молча, спиной к
аудитории; в сведенных его плечах и наклоненной голове — что-то
от курильщика, зажигающего на ветру спичку и ждущего, пока
она разгорится. В левой руке у него — несколько листков
бумаги, заполненных ровными строчками и аккуратными
графиками.
Он начинает с того, что чертит на доске две системы
координат, одну под другой, и в них
символами f(x) и F(x):
две кривые; их он помечает
344
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
[Гл. 5
— Пусть у нас есть функция /(х), определенная и
непрерывная на интервале (а, Ь). Пусть есть также функция F(x),
определенная и дифференцируемая на том же интервале,
причем F'(x) = f(x) для любого х из области определения
этих функций. При таких условиях F(x) называется
первообразной для f(x) на интервале (а, Ь). Если теперь к функции
F(x) прибавить функцию-константу, все равно какую, то и
такая функция F(x) + С (он прочерчивает еще одну кривую
точно над прежней) будет первообразной для /(х), это
легко показать (пишет поясняющее равенство). Получается, что
задача определения первообразной решается неоднозначно.
Совокупность всех первообразных для некоторой функции
f(x) называется ее неопределенным интегралом и обозначается
J f(x)dx. Раз любые две первообразные для данной функции
различаются на константу, то все их можно выразить через
какую-то одну в виде F(x) + С, где С — произвольная
постоянная.
В роли лектора он чувствует себя далеко не так уверенно,
как Горт, начинавший своим докладом прошлый семинар, —
говорит без менторской артикуляции и не поглядывает, как Горт,
на своих слушателей назидательным взглядом. Куда там! Он
почти не отрывает глаз от доски, опасаясь что-нибудь
напутать, а если и оглядывается изредка, то смотрит только на меня,
смотрит чуть боязливо, как и сейчас, замолкнув, ожидая моей
оценки.
Не спеша оглядываю его чертежи и выкладки:
— Вроде бы все верно. F'{x) = f(x) для любого
х из (а,Ь)... Если к F(x) прибавить константу, то ее
производная по-прежнему будет равна /(х)... Образно
говоря, — обращаюсь к сидящим, — если график
первообразной сдвинуть вверх или вниз вдоль оси ординат,
то такая «сдвинутая» функция останется
первообразной.
И снова Кочину:
— Да, все верно. Теперь стоило бы перечислить несколько
простейших неопределенных интегралов, называемых
табличными, о которых упоминал Миклашевский. Кстати, не
позвать ли его к доске, чтобы он сам написал эти
интегралы? А вы, Дима, станьте в сторонку и вместе со всеми
следите за тем, что станет он писать: потом будете
исправлять, если понадобится. Ну, как? — спрашиваю Кочина,
после того, как Миклашевский кладет мел и водворяется
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
345
на свое место. — Требуются ли здесь исправления?
Дополнения?
— Первая формула неприменима при п = — 1, — сразу
замечает Кочин.
— Стало быть, для такого п нужна особая формула?
Напишите ее, Дима. И не забудьте указать, что логарифм
берется от абсолютной величины х. Заодно внесите в нашу
таблицу уточнения аналогичного свойства: всюду, где Павел поставил
под знаком логарифма круглые скобки, замените их
модульными. Да, — укоризненно гляжу на Миклашевского, — не так уж
хорошо вы помните табличные интегралы, как хвастаетесь об
этом! До каких же пор вы будете блистать незнанием
элементарных вещей? Но продолжайте, Дима, — возвращаюсь взглядом
к доске.
— В пятом интеграле, — медленно говорит он, пристально
оглядывая написанное Миклашевским и сверяясь со своей
бумажкой, — под корнем можно написать не плюс, а плюс-минус:
формула верна и для разности.
— Точно, это нетрудно проверить.
— Для интеграла от показательной функции надо сделать
примечание что а больше нуля и не равно единице. Можно еще
особо указать случай а = е.
— Можно. Укажите. Что еще?
— Можно добавить интегралы с гиперболическими
функциями.
— Добавьте.
346 ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
— Теперь вроде все.
[Гл. 5
— Ну что ж, спасибо, Дима, — встаю с его места, — за хорошее
введение в тему семинара. Садитесь. Все остальное — я имею в
виду то, что относится к определенным интегралам, — доскажете
потом, когда мы к ним приступим.
И вновь к аудитории:
— Эти табличные интегралы, ребята, я попрошу вас знать
назубок. Перейдем теперь к рассмотрению основных приемов
интегрирования.
Выписываю на доске три примера: /(1 — ^)y/xy/xdx\
I T+x*^xi ftg2xdx. Их быстро решают, один за другим выходя
к доске, Костюк, Синица, Буткус.
Ю. В. Пухначев] СЕМЬ СЕМИНАРОВ 347
— В каждом из этих случаев, — комментирую их выкладки,
мы сначала преобразовали подынтегральное выражение.
Какова же была цель всех этих преобразований? Как вы считаете,
Сутеев?
— Свести интегралы к табличным.
— Свести-то свести, но каким образом? Что стало с
каждой из подынтегральных функций после проведенных
преобразований?
Надолго замолчавшему Сутееву по моей просьбе помогает
сметливый Стрельцов;
— После этих преобразований под интегралом всякий раз
получалась сумма таких функций, для каждой из которых мы
знаем неопределенный интеграл.
— А интеграл от суммы...
— Равен сумме интегралов от слагаемых, — заканчивает
Стрельцов.
— Это ясно всем?
— Конечно, —- мастито кивает Рамзин, на которого я
перевожу взгляд. — Это вытекает из определения неопределенного
интеграла и из того, что производная от суммы равна сумме
производных.
— Вы это поняли? — спрашиваю Сутеева. — Да? Тогда
покажите на доске, что интеграл от суммы двух функций равен
сумме интегралов, взятых от них по отдельности. Так, так...
все правильно. Еще покажите, что интеграл от функции,
умноженной на константу, равен константе, умноженной на интеграл
от этой функции. Садитесь, спасибо. Итак, ребята, мы с
вами разобрали первый основной метод интегрирования —
разложение подынтегрального выражения на слагаемые,
интегрировать которые проще, чем исходное выражение. Кто хочет ре-
348
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
[Гл. 5
шить следующий пример? Вы, Лапиков? Идите к доске, пишите:
f(2x — 3)1 dx. Решайте. Что ж вы медлите? Пример вполне
подходит под тот метод, который мы только что прошли, — можно
разложить подынтегральное выражение по биному Ньютона и
потом...
Смех всей аудитории не дает мне закончить фразу. Лапиков
смеется вместе со всеми:
— Тут проще не так: надо обозначить 2х — 3 через новую
переменную. Я вот только не соображу в уме, как тогда
выразится dx.
— Не можете сообразить в уме — пишите.
И после того, как он доводит решение до конца и садится,
обращаюсь ко всем:
— Понятна ли суть метода, которым был решен этот пример?
Кто мог бы сформулировать ее в общем виде? Никто не
отваживается? Что ж, придется для лучшего понимания решить еще
один-два примера. Скажем, такой: J ^r-dx.
— А ведь dx, деленное на я, — ловит идею Синица, — это
дифференциал от логарифма! Логарифм как-то обозначить —
нет, можно не обозначать — можно сразу как новую
переменную... Ладно, обозначу... Ответ: ^ In3 x + С. Верно?
— Верно. Еще пример: f (1 ~! ^. По его поводу, кажется,
хочет высказаться Кулагин. Пожалуйста.
Ю. В. Пухначев] СЕМЬ СЕМИНАРОВ 349
— Надо все под интегралом разделить и умножить на два,
там будет ^7=, это дифференциал от ^/х, корень взять за новую
переменную. Тогда интеграл... да, так: 2arctg у/х.
— Решить такой пример не фокус, а вот как описать
метод, которым мы вычислили уже три интеграла? Не
попробуете ли?
— Надо как-то так взять dx и что-то еще от
подынтегрального выражения, чтобы получился дифференциал от какой-то
хорошей функции, от такой функции, чтобы...
— От такой функции, — перехватывает Горт
споткнувшуюся мысль Кулагина, — через которую выразилось бы все
остальное...
— И в итоге подынтегральная функция, выраженная через
новую переменную, упростилась бы и в лучшем случае
получился бы табличный интеграл, — заканчиваю я. — Таков метод
введения нового аргумента, которым мы решили три последних
примера. Применять его можно, так сказать, с двух концов.
Иногда сама структура подынтегральной функции
подсказывает новый аргумент; мы пытаемся выразить через него эту
функцию, не забывая занести что-то под знак дифференциала,
чтобы под ним оказалась новая переменная интегрирования.
Именно так решался пример, предложенный мною Лапикову:
dx = \dflx = \d(2x — 3). Запомните, ребята: символ dx,
неизменную концовку всякого интеграла, никогда не следует
упускать из виду, вводя новый аргумент. Чтобы не забывать
об этом, я советую вам при пользовании этим методом
интегрирования всегда держать в голове второй его вариант:
вы объединяете символ dx и какие-то сомножители
подынтегральной функции в дифференциал от некоторого выражения
в надежде, что все остальное удастся представить как
функцию этого выражения. Хороший образчик такого подхода —
пример, решенный Кулагиным. Давайте закрепим навыки
подобных преобразований на новых примерах: f е*+е-х ' / 2-ьЗз:2'
Г ?osx dx.
J vcos2x
Иду между рядов в ожидании ответов. Сутеев в
формулировке первого примера записывает знаменатель в виде 2chx.
350
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
[Гл. 5
Довольно бесперспективная идея! Но пусть он убедится в этом
сам. Миклашевский, рядом с которым я останавливаюсь,
делится со мной своими предположениями: «Первые два интеграла
выразятся через арктангенс, последний — через арксинус».
«Получите окончательный ответ, тогда поговорим», — сухо
обрываю его. А как дела в противоположном углу? Меншиков,
быстро решив первый и третий примеры, никак не может совладать
со вторым — удивительно! И, пожалуй, даже кстати: пусть
расскажет о своих неудачных попытках у доски, и пусть выход из
тупика ему подскажут Сынчиков или Чюмин, у которых я
видел верные решения второго примера; это хорошо подействует
на тех, кто послабее — им сейчас очень нужно
приободриться, стряхнуть робость, которую нагнали на них наши
сегодняшние передовики, походя разделываясь с предлагавшимися до сих
пор примерами.
— Так как же вы намеревались решать второй пример,
Меншиков?
— Взять знаменатель за новую переменную, за какое-нибудь
там £...
— Ну вот, пожалуйста — вы делаете тот самый
просчет, о котором я только что предупреждал:
подынтегральную функцию преобразуете, а про dx забыли. И получится
у вас в итоге вашей замены нечто этакое: / ^f — ни то,
ни сё.
— Можно выразить х через t и подставить под знак
дифференциала...
— Но тем самым вы введете в подынтегральное выражение
квадратный корень и сильно усложните все дело.
Представляете, как это будет? 2 + Зх2 = £, х = л/^... Так ведь? Да?
Почему же вы это не предвидели до моей подсказки? Разве
это выше вашего разумения? Не поверю — вы неглупый
парень! Ленитесь думать? Стыдно, Меншиков! Так как же нам
свести этот интеграл к табличному? — перебрасываю взгляд
на Чюмина. — Что скажете, Семен? Нет ли в нашей
таблице простейших интегралов чего-нибудь похожего на этот
интеграл?
— Похоже на второй, на / х+^2*
— Ну, разумеется! Только там с квадратом складывается
единица, а в нашем примере — двойка.
— Единицу можно получить, если двойку вынести за скобки.
— И даже за знак интегрирования.
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
351
— Тогда в знаменателе будет единица плюс |х , то есть
единица плюс квадрат величины £л/§. А весь интеграл будет равен
арктангенсу от этой величины.
— Не совсем так, Семен, не совсем. — перед арктангенсом
появится еще некий множитель... Но пусть вас поправит Мен-
шиков — решить пример до конца я попрошу его. К доске, Мен-
шиков!
— В числителе, — начинает он, еще вставая со стула, — надо
получить дифференциал от этого ял/§.
I Ментиков
Г Ux. Г ctx.
— Вот-вот! Доделайте все до конечного результата. Ответ
верный. Садитесь. Вам все понятно в этом решении? — спрашиваю
аудиторию.
Нарочито замедляя темп обстоятельного разговора с Чюми-
ным и Меншиковым, даю возможность другим не торопясь
сделать два оставшихся примера. Эта своеобразная дотация не идет
впрок одному лишь Сутееву: мысль его так и остановилась над
записью/^.
— Давайте разбираться вместе, что можно сделать с этим
интегралом, — приглашаю его к доске. — Остальные пусть
решают другие задачи, которые я задал, а когда решат все, —
вполоборота поглядываю на Горта, — пусть попробуют взять
такой интеграл: / у th2 х + Ых. Мы же с вами начнем с небольшой
разминки. Нарисуйте на доске рядом друг с другом два
одинаковых равнобедренных треугольника с не очень большим углом
при вершине, градусов около тридцати. В первый треугольник
впишите окружность. Над нею впишите еще одну, чтобы с
боков она касалась боковых сторон треугольника, а снизу —
первой окружности. Над этой окружностью таким же образом
впишите еще одну и представьте, что подобные построения
продолжаются до бесконечности. Такую же
последовательность окружностей впишите во второй треугольник. Теперь
352
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
[Гл. 5
вернитесь к первому и в каждой окружности проведите
горизонтальный диаметр. Сможете ли вы подсчитать сумму длин
всех этих диаметров?
9= I
— Смогу, — уверенно отвечает Сутеев, подумав какие-то
считанные секунды. — Длины этих диаметров образуют бесконечно
убывающую геометрическую прогрессию. Знаменатель
прогрессии определяется из подобия треугольников, (между боковыми
сторонами первого треугольника через точку касания двух
нижних окружностей он проводит горизонтальный пунктир и
жестом обегает сначала отсеченную этим пунктиром верхушку
треугольника, затем весь треугольник). Этот знаменатель равен
отношению высоты треугольника минус диаметр нижней
окружности ко всей высоте. Высоту можно выразить через площадь
треугольника и его основание. Площадь треугольника можно
найти по формуле Герона, через полупериметр. Радиус вписанной
окружности можно определить через площадь треугольника,
если поделить ее на полу периметр.
Эти фразы, краткие и четкие, как и стоящие за ними простые
школьные формулы, он выкладывает, словно каменщик кладет
рядком гладкобокие кирпичи. И вслед за каждым термином
(знаменатель прогрессии, высота, площадь, полупериметр,
радиус) я проставляю в столбик в другой половине доски символы
g=,/i=,s=,p=,r=, оставляя между ними большие пробелы —
место для вычисления этих величин через длины сторон
треугольника. Сутеев уже пометил их буквами а и Ь, вопросительно
смотрит на меня:
— Вычислять?
— Подождите, — прошу его и обращаюсь к аудитории. — Я
хочу, чтобы все проследили за тем, что сейчас будет происходить
на доске. Только прошу вас — ни слова.
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
353
Кратко повторяю условие задачи и возвращаюсь к
Сутееву:
— Вы хотите использовать формулу для суммы бесконечно
убывающей геометрической прогрессии и выразить ее
знаменатель через высоту треугольника и диаметр вписанной в него
окружности. Проведите этот диаметр вертикально во втором
треугольнике. Молчите, молчите, — поднимаю руку, заметив,
как какая-то искра промелькнула в глазах Синицы,
Стрельцова, Горта, Гарина...
Если я верно разгадал стиль мышления Сутеева, то сейчас
он...
Его рука с зажатым в ней мелом, устремившись по моей
просьбе от первого треугольника ко второму, вдруг плавно
падает, словно подстреленная на лету птица, и вновь медленно
тянется вверх. Он прочерчивает снизу вверх диаметр самой нижней
окружности и продолжает все быстрее вести мел дальше, до
самой вершины треугольника.
— Высота, — глухо произносит он. — Сумма диаметров — это
высота треугольника.
— Здорово! — вполголоса восклицает Костюк, и вся
аудитория вторит ему кратким эхом не то удивления, не то восхищения.
— Да, — односложно резюмирую уже очевидный всем
вывод. — Искомая бесконечная сумма диаметров вписанных
окружностей равна высоте треугольника. Аккурат по ней
выстраиваются все эти диаметры, если их повернуть на 90 градусов. И те
громоздкие выкладки, которые намеревался совершить Сутеев,
провожу рукой сверху вниз по столбику написанных мною
символов, — оказались ненужными благодаря такому
простому повороту. О подобных «поворотах», очень типичных для ис-
12-2019
354
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
[Гл. 5
следовательской работы, выразительно говорил Гельмгольц на
праздновании своего 70-летнего юбилея. Он уподоблял
исследователя альпинисту, который карабкается по отвесной скале к ее
вершине, и в подобных случаях нередко, достигнув цели,
обнаруживает, что с другого направления, о котором он и не
подозревал, к вершине ведет широкая, пологая дорога... Гельмгольц
в этой речи говорил и о счастливых догадках, которые
сокращают путь к цели, но наступают они, как правило, после долгого
и напряженного исследования решаемой проблемы, и при этом,
отметил ученый в заключение, их появлению препятствуют
малейшие дозы алкоголя.
— А я слыхал, — шутовски улыбается Миклашевский, — что
многие художники и поэты любили творить «под этим делом» и
что у них неплохо получалось...
— Может быть, — пожимаю плечами. — Но это совсем
другая сфера деятельности и другой мир, о котором однажды
любопытно выразился Гильберт, когда ему сообщили, что один из
его учеников, притом не самый удачливый, решил бросить
математику и стать поэтом. Гильберт заметил по этому поводу:
«Наверное, для успешной работы в математике ему не хватало
воображения...» Но вернемся к интегралу, который мы
разбираем с Сутеевым. В формуле подынтегрального выражения
также можно сделать несколько «поворотов», после которой она из
непроглядной станет совершенно прозрачной. Вот, скажем, е~х.
Как это можно еще написать? Ну-ка, Сутеев! Верно, р.
Как бы невзначай приписываю под преобразованной
формулой t+ j:
— Кстати, какой еще вид вы предложили бы для такой
суммы? Верно, ^А. Нельзя ли и в нашем интеграле сделать нечто
подобное. Ну вот J ;й+/[• Мне кажется, тут есть новые поводы
потренироваться в умении представлять математические
объекты во всех возможных вариантах. Поглядите на числитель: exdx.
Как еще это можно написать? Не догадываетесь? Вспомните, как
мы говорили: -^= — это 2dy/x. Ага, догадались: exdx = dex. A
теперь поглядите на формулу J J*^ тем особым зрением, о
котором я всегда так настойчиво вам говорил, — поглядите на нее
так, чтобы каждая деталь виделась вам одновременно во всех
возможных вариантах, и старайтесь подметить наиболее
плодотворное сочетание вариантов. Числитель: exdx и dex.
Знаменатель: е2х + 1 и (ех)2 + 1. Ну, ничего не замечаете? Горт, помолчите,
я разговариваю не с вами! Внимательнее, Сутеев, внимательнее!
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
355
Совсем недавно мы говорили: «... объединить символ dx и
некоторые из сомножителей подынтегральной функции в
дифференциал от некоторого выражения, чтобы все остальное представить
как функцию этого выражения...»
Взгляд Сутеева, неподвижно упершийся в написанное на
доске, чуть качнулся в мою сторону, и мгновение спустя на доске
появилось ех = t. Ну! Какой-то азарт вспыхивает во мне:
неужели он не дотянет двух последних шагов до решения?! Ну же!!
Строчки преобразований медлительно текут по доске к
окончательному ответу: arctge* + С. Успех! Но еще далеко не такой,
чтобы звонить во все колокола.
— Хорошо, садитесь, — говорю Сутееву, стараясь выдержать
абсолютно бесстрастную интонацию. — Последний из
оставшихся примеров пусть решит на доске Миклашевский. Так... разло-
жение, замена, ответ, обратная замена... Как по маслу! Если бы
вы всегда работали так же, Павел! Все правильно, садитесь...
Нет, прежде напишите на доске еще один пример: J \/1 — x2dx.
С каким удивительным единодушием все берут за новую
переменную \Д — x2\ С каким упорством не желают отказаться от
такой замены, хотя ничего путного ни у кого из нее не выходит!
Здесь нужна моя подсказка — и я начинаю ее издалека.
— По-моему, ребята, ваши действия сковала инерция
мышления. Задумайтесь над методом интегрирования, который вы
12*
356
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
[Гл. 5
сейчас так рьяно и так безуспешно применяете — над методом
введения нового аргумента. В качестве такого аргумента в этом
методе берется некоторая функция от х. Скажите, никому из вас
не приходило в голову, что можно поступить и наоборот:
заменить х какой-нибудь функцией нового аргумента? В нынешнем
примере хорошо бы избавиться от корня — с рациональными
функциями дело идет лучше. Корень пропал бы, если бы мы
заменили х такой функцией, что разность между единицей и
квадратом этой функции была бы равна квадрату какой-то другой
функции. Что вы предложили бы для такой замены, Аргунова?
Вот в качестве намека я нарисую вам картинку: единица минус
цветочек в квадрате равна листочку в квадрате. Встречалось ли
вам когда-нибудь что-либо подобное? Попробуйте рассмотреть
различные варианты этого равенства.
— Единица равна листочек в квадрате плюс цветочек в
квадрате... Это тригонометрическое тождество! Синус квадрат плюс
косинус квадрат равно единице.
— Совершенно верно. Стало быть, х можно заменить...
— Синусом нового аргумента.
— К доске, Аргунова! Пишите: х = sint. Тогда dx... верно,
cos tdt. Теперь интеграл вычисляется без труда. Но он выражен
пока что через t. Надо вернуться к прежнему аргументу х. Еще
одна замена, t = arcsinx... и окончательный ответ: ^arcsinx +
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
357
|\/1 — х2 + С. Садитесь, Галя. Метод интегрирования, который
мы сейчас использовали, ребята, называется...
— Методом подстановки! — заканчивает за меня Рамзин.
— Вы знаете его? Почему же не применяли с самого
начала? Эрудиция немного стоит, если исчерпывается ориентацией в
терминологии. Лучше было бы наоборот: если бы вы, пусть не
очень зная мудреные термины, хорошо владели бы
разнообразными приемами интегрирования, догадывались, какие из них и
как применять в том или ином случае. А ну-ка, ребята,
поупражняемся в этом, подумаем все вместе: какие еще интегралы можно
вычислить методом подстановки?
— Например, / у/а2 — x2dx\ замена такая: х = asint, —
вызывается Кочин.
— А еще J у/а2 + x2dx, — тянет руку Мухин, — только здесь
не обычный, не круговой — ну, не тригонометрический синус, а
гиперболический.
Как кстати! Мухин сам предлагает упражнение для
тренировки в том искусстве, которого ему главным образом не
хватает, — искусстве составлять и продумывать логически строгий
план своих действий.
— К доске, Мухин! Напишите интеграл, который вы
придумали. А теперь изложите четко и последовательно, как вы
собираетесь его вычислять — шаг за шагом.
— Сначала замена х = asht. У нас есть тождество сейчас —
можно я его напишу? — боюсь напутать — да, вот так: ch2t—
— sh21 = 1, точно — значит, ch21 = 1 + sh21, ага — нет, х не sh t,
а по-другому, х = asht — теперь верно — подставляем...
— Минуточку, Мухин! Я просил бы вас продолжить устно.
Положите мел.
— Подставляем х — коэффициент а за корень — под
корнем 1 + sh2t — это ch2t — корень будет ch t — нет, а можно
даже за знак интеграла — интеграл от cht будет — не
помню знак — можно я посмотрю? — плюс — значит, интеграл
равен asht.
— Неверно. Посмотрите еще раз на формулу интеграла, еще
раз проговорите про себя то, что говорили вслух, и найдите свою
ошибку.
Он с полминуты шевелит губами:
— Ну, конечно! Ведь х еще заменяется в dx\ Если х = asht,
то dx = achtdt — еще одно a — то есть а2 — и еще один cht —
интеграл от ch2t? — гм! а как же -- наверное, через двойной
аргумент?..
358
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
[Гл. 5
— Возьмите мел, Мухин, дальше вы вряд ли сможете
вычислять устно. План вы составили верный, теперь реализуйте его
до конца.
Введение двойного аргумента вносит свои трудности,
однако Мухин справляется с ними почти без моей помощи. Но
вот трудность посущественнее: как провести обратную
замену переменной, выразить t через ж? Мухин догадывается
свести дело к квадратному уравнению — и надолго
останавливается, не зная, как быть со знаком плюс-минус. Помогу,
пожалуй:
— Подумайте, имеет ли тут смысл знак минус? Ведь в левой
части равенства стоит экспонента...
— А она всегда положительна! Если взять минус,
правая часть будет отрицательной — противоречие — минус
убрать.
— Если же взять плюс, то правая часть всегда будет
строго положительной при любом ж, даже отрицательном.
Так что напрасно вы заключили в модульные скобки выра-
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
359
жение под знаком логарифма. Достаточно обычных,
круглых.
— И In а можно не писать, рассматривать его как постоянную
интегрирования, — вставляет Котюк.
— Согласен. Теперь у вас все верно, Мухин.
С похвалой отсылаю его на место. Вертикальной чертой делю
доску пополам и вызываю Синицу и Буткуса, чтобы они взяли
еще два интеграла: / jl^y+1^ и I Х\/Т^^х-
Интегралы неравноценны; опасаюсь, что Линас вскоре
оставит Люду наедине с громоздкими выкладками. Однако к мое-
му удивлению на деле все выходит наоборот: странная замена
уз^ = tg2£ уводит Буткуса в чащу затяжных преобразований.
360
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
[Гл. 5
Синица уже давно получила свой ответ, глядит на маяту своего
напарника, пытается подсказать: «Тут проще х = sin2 £...»; вслед
за нею и я советую Буткусу то же самое, но он жестко отрезает:
— Дайте мне доделать!
И получив, наконец, ответ как функцию, зависящую от
£, sin2t и sin4£, еще долго выражает синус через тангенс, а тот
еще заменяет дробью yzj--- Когда он с удовлетворенным лицом
отрывается от доски и оборачивается к аудитории, никто и не
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
361
смотрит на него — все давно уже решили этот пример и теперь
занялись новым, который я дал Синице, чтобы время не уходило
впустую.
— Садитесь, Линас. Садитесь, Люда. Какие методы
интегрирования известны нам еще? — спрашиваю у аудитории.
— Интегрирование по частям, — звучит несколько голосов
— Видать, из-за характерного названия он хорошо
запомнился вам со школы. Кто изложил бы его у доски? Не хотите ли,
Стрельцов?
— Метод интегрирования по частям основан на формуле
дифференцирования произведения: d(uv) = udv + vdu. Он
выражается формулой / udv = uv — J vdu
И когда он садится, закончив, обращаюсь к аудитории:
— Кто мог бы привести примеры интегралов, которые берутся
по частям? Пусть это сделает Сынчиков.
Обходя аудиторию, я время от времени заглядывал в его
тетрадь, и мне показалось, что он хорошо помнит со школы все
относящееся к интегрированию. Предложенный им интеграл J In xdx
вычисляет без заминок, хотя страшно медленно. Испытать его
I Сынчиков
J&ixcrfx = эсблх- $-£с*х
= хблх -х + С
на знание теории? Или лучше пока не рисковать, подождать до
следующего семинара?
— Садитесь, Сынчиков, вы все сделали хорошо. Теперь
подумаем все вместе, ребята: для интегрирования каких еще функций
удобен такой метод?
— Для арксинуса, арктангенса, — убежденно высказывается
Костюк.
— Для арктангенса хорошо, а для арксинуса не очень, —
сомневается Горт.
— Почему? — оборачиваюсь к нему.
— Потому что тогда под интегралом появляется производная
от арксинуса, то есть квадратный корень, а он всегда усложняет
интегрирование.
— Во-первых, не всегда, а во-вторых = разве вся беда лишь
в том, что под интегралом появляется корень? — напористо
гляжу на него, потом на Костюка, потом, не дождавшись ответа от
обоих, — на Гарина: он не должен подвести!
362
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
[Гл. 5
Гарин не выдерживает моего взгляда, говорит нехотя:
— Не только... Корень — это еще полдела...
— Может быть, вы пойдете к доске? — предлагаю я,
подозревая, что ему есть что сказать, — и вижу, что не ошибся:
— Вот формула интегрирования по частям: f udv = uv—jvdu
— пишет он. — Когда от и мы переходим к du, могут возникнуть
сложности, это правда — например, арксинус превратится в
корень. Но ведь мы еще переходим от dv к v, об этом тоже надо
думать. А еще лучше смотреть в общем: было udv, стало vdu.
Какое из них проще? Вот, по-моему, как надо спрашивать. Может
даже случиться так, что и переход от и к du даст усложнение, и
переход от dv к v тоже, а вместе они компенсируются.
— Хорошо бы здесь привести какой-нибудь пример.
Возьмите задачник, раскройте его на соответствующем разделе,
посмотрите.
— Да тут, наверное, тот же интеграл с арксинусом
подойдет: J&rcsmxdx. Арксинус даст корень в знаменателе, а в
числителе получится xdx, то есть \d(x2 — 1), половина
дифференциала от подкоренного выражения, и все выйдет просто. И
потом: когда мы пишем подынтегральное выражение в виде udv,
мы ведь сами разбиваем его на и и dv, тут тоже надо угадать,
как лучше разбить. Вот тут в задачнике есть еще такой пример:
/ х arctg xdx. Можно и так его представить: / x • arctg xdx и так:
/ arctg x • xdx = \ /arctg xdx2. В первом случае, если arctg xdx
принять за dv, совершенно не ясно, как это v искать, а во
втором — сразу видно, что все будет просто: d arctg x — это значит
К). В. Пухначев)
СЕМЬ СЕМИНАРОВ
363
1 + х2 пойдет в знаменатель, а в числителе будет х2, прибавить
и вычесть единицу... Ну, в общем...
И, перейдя от слов к делу, он быстро получает решение.
— Спасибо, Миша, вы очень хорошо истолковали суть
интегрирования по частям. Садитесь. Но прежде запишите на
доске еще несколько примеров на применение этого метода:
/ х arctgх ln(l + x2)dx; Jx2 sin 2xdx\ j ex cosxdx. Первым из них,
как вы помните, ребята, нас совсем недавно пугал
Миклашевский. Но, если разобраться, он совсем не страшен, Давайте-ка с
него и начнем. Пусть к доске пойдет кто-нибудь не из робкого
десятка, например, Кулагин. Как мы уже могли заметить, метод
интегрирования по частям позволяет превратить логарифм и
арктангенс, стоящие под знаком интеграла, в рациональные
функции, более удобные для интегрирования. Отсюда нетрудно
заключить, что в качестве функции и, стоящей в общей формуле
интегрирования по частям, в данном конкретном случае следует
взять...
— Произведение arctgx 1п(1 + х2).
— А в качестве dv...
— Все остальное, xdx.
— Таким образом в качестве v у нас будет фигурировать...
— Функция ^-... Нет, подождите! Может, тут, еще что-то
можно выгадать... Когда будем дифференцировать arctg x получится
jt^2, когда 1п(1 + х2) — знаменатель тот же... v пойдет в
числитель... Лучше, пожалуй, взять v = ^-^-\ тогда многое сократится.
— Отлично! Дальнейший путь в общих чертах ясен.
Проследим его поподробнее. Дифференцирование произве-
364
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
[Гл. 5
дения arctgxln(l + х2) даст два слагаемых — покажите,
каких.
— Не надо дифференцировать! — останавливает начавшего
было писать Кулагина резкий голос Буткуса. — Лучше
воспользоваться, как Сынчиков взял интеграл от логарифма.
— Не соображу, что вы имеете в виду, — приглашаю его к
доске.
— Вот, — указывает он на последнюю из написанных
Кулагиным формул, — у нас получилось \ /arctgxln(l + x2)d(l + x2), a
ln(l+x2)d(l +х2) — это d[(l+x2) ln(l + x2)-(l+x2)]. Непонятно?
У нас было flnxdx = xlnx — х, то есть lnxdx = d(xlnx — х),
тут только заменить х на (1 + х2). Когда продифференцируем
arctgx, в знаменателе будет (1 + х2), и оно сократится с теми
(1 + х2), которые получились от логарифма.
— Прекрасно! — тотчас отказываюсь от прежнего плана
решения. — Вы согласны, Андрей, что так лучше? Да? Так и
действуйте. Хорошо, хорошо... Опять логарифм? Вы опять
избавляетесь от него, беря интеграл по частям. Продвигайтесь
дальше. Интеграл/ jHif ? Он у нас уже был, можете воспользоваться
прежним решением. Ну, вот и ответ. Садитесь, Линас, спасибо
за ценную идею.
I Кулагин
\ х atctgx 6п (4 «• х) doc =
*i J axctgxen(Y*xV ('♦**>
r il**ctfJCdL[(i+**)en(1+x*)-(4+**)] = I
= ±azct9X[(i+x*)en(i + x*)-(1 + x*)]-
-i№+**)e»(Ux*)-(Ux>)]^ =
-i atc^oc [...]- J- J &i(i+x*)dx + ± fcfx =
= £a*ctyx [...]- £&i^*x2j+x-aTctyx*2-*C =
Пока Кулагин доводит до конца решение примера, иду между
столами. Видно, что метод интегрирования по частям
действиЮ. В. Пухначев]
СЕМЬ СЕМИНАРОВ
365
тельно хорошо помнится ребятам со школьных уроков. Поэтому
меня интересуют уже не успехи в его применении, а ошибки,
которые было бы полезно разобрать на доске, окончательно
дошл ифовывая умение пользоваться эффективным методом.
— Чюмин, на что вы надеетесь, когда во втором интеграле
берете в качестве dv выражение x2dx? Ведь тогда под знаком
интеграла появится х3. Что же дальше? Если продолжать в том же
духе, степени х станут возрастать и конца этому не будет.
Покажите свои выкладки на доске, чтобы все научились не повторять
ваших ошибок. А как лучше решать этот пример, ребята?
— Взять х2 в качестве и, тогда du будет равно 2xdx, степень
х таким образом понизится, — берет слово Рамзин. — Тем же
путем мы понизим ее потом до чистой двойки. А в качестве dv
с самого начала возьмем sin2xdx, v будет тогда равно — \ cos2x;
никакого усложнения это ни даст ни сейчас, ни на следующем
шагу.
Он говорит, щеголяя своей сообразительностью, и в то же
время я ощущаю в его голосе какую-то новую ноту,
покровительственную, несвойственную ему раньше. Что ж,
покровительство — вполне пристойная отдушина для его чувства
превосходства. Надо время от времени предлагать ему оценить или
поправить товарищей, помочь им.
— Делайте, Чюмин, как вам советует Рамзин. Верно,
садитесь. Ну, а у кого получился третий пример?
Молчание. И несколько секунд спустя — смущенный голос
Синицы:
— А что, его тоже надо решать по частям?
— Его надо решать так, чтобы придти в верному результату.
Не выходит по частям -- применяйте другие методы.
366
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
[Гл. 5
— Другими я пробовала — получается что-то страшное.
— Например?
— Я попробовала заменить х через In t, тогда ех = t, но второй
сомножитель тогда приводится к виду cos Int. И если х положить
равным arccost, тоже не лучше...
— Метод интегрирования по частям, насколько я могу себе
представить, к таким сложностям не приведет.
— А он вообще ни к чему не ведет. Можно взять за
первый сомножитель ех, тогда v = sinx. И получается интеграл
fe*sinxdx.
— Разве вы не усматриваете здесь идею решения? Нет?
Только что мы с Сутеевым говорили про то, с чего начинать решение
любой задачи: проанализировать условие и каждый его элемент
попытаться представить во всех вариантах. А на самом первом
семинаре давалась наиболее общая формулировка этого
принципа: представлять каждый элемент условия не только во всех
вариантах, но и во всех формах, которые он может приобрести
после различных преобразований, относящихся к существу
задачи. Это принцип естественно развить: преобразованные
элементы можно вторично подвергнуть каким-то преобразованиям.
Посмотрите внимательнее на интеграл, над которым вы бьетесь:
f ex cosxdx. Вы применили к нему интегрирование по частям и
получили интеграл f ех sinxdx. А если и его проинтегрировать
по частям? Что получится?
— Наверное, опять f ex cos xdx — то же самое с чего начинали.
Какой смысл?
— То же самое с точностью до... Впрочем, идите-ка, Люда,
к доске и сделайте то, что я вам предлагаю. Так, так... ну вот!
К чему же мы пришли? К интегралу f ex cos xdx, но со знаком
минус! Это ничего вам не говорит? В левой части равенства —
исходный интеграл, в правой — он же, но с противоположным
знаком...
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
367
— Получилось уравнение для интеграла...
Ее голос все еще приглушен оттенком сомнения, словно она
не понимает, что решение неприступной задачи оказалось совсем
простым.
— Да, получилось уравнение для искомого интеграла.
Решайте его. Вот и ответ. Садитесь.
И обращаясь к аудитории:
— Сейчас я дам вам, ребята, четыре новых примера. Решайте
их, как хотите, выбирайте сами в каждом случае самый
подходящий метод интегрирования, напрягайте всю свою
сообразительность, мобилизуйте весь опыт, новый и старый!
Пишу на доске: / p™Z™lsxdx> /j^fe; fxexcosxdx;
f sinn xdx.
И вновь отправляюсь в дозор.
Мухин, оказывается, был на верном пути к решению
примера, над которым мучилась Синица, на том же пути, что
советовал и я, — но путался со знаками плюс и минус, перемарывал их
вновь и вновь и завяз в грязи своих помарок.
— Теперь-то вы видите, что решали правильно? —
полушепотом спрашиваю его. — Не все погубила ваша же неаккуратность.
Избавьтесь же наконец от нее!
А как дела у остальных? Лапиков преобразует интеграл
f х2^х+2 к ВИДУ / 2s-i"*" > заменяет трехчлен (х2 — х + 2)
на ег и вскоре безнадежно запутывается. Сутеев пытается взять
первый из интегралов по частям и запутывается тоже...
— Сутеев, вот вы нашли, что (sin я + cosx)dx = d(sinx —
cosx). Неужели вам не бросилось в глаза, что под знаком
дифференциала теперь стоит то же выражение, что и под корнем?
Неужели не догадались сделать замену sin х — cos х = t? Сде-
лайте ее на доске. Интеграл, как видите, тотчас сводится к
табличному и ответ получается немедленно. Садитесь... Итак, ре-
368 ИНТЕГРИРОВАНИЕ ФУНКЦИЙ [Гл. 5
бята, первый пример решен. Интересно, решил ли кто-нибудь
второй?
— А что его решать? — басит Меншиков. — Мы такие
примеры уже делали.
— Не понимаю вас.
— Да я говорю, что мы такие функции разлагали на
элементарные дроби — когда искали n-ную производную, например.
— Неплохая мысль! Ну-ка покажите, как такое разложение
помогает здесь. Очень хорошо! — оцениваю его прилежную
работу.
— Тут-то все просто, — приговаривает он, выписывая
окончательный ответ. — Вот третий пример — это в самом деле трудно.
— Даже труднее четвертого?
— Четвертый вообще пустяковый.
— Неужели? А ну, покажите! Вы до конца его решили? И
получили ответ в явном виде?
— До конца. И ответ получил.
— Не может быть! Покажите же!
— Пожалуйста, — переписывает он на доску решение из своей
тетради.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
369
— Начало разумное. Далее по частям ... так, так ...
действительно все получается! Но я ведь точно знаю, что этот интеграл
в явном виде так просто не берется! — растерянно оглядываю
выкладки Меншикова.
— Непонятно: когда Коля sin71-1 х дифференцировал —
почему он cosx не написал? — отчетливо слышится в наступившей
тишине слабый голос Аргуновой.
— В самом деле! — всплескиваю руками. — Мошенник вы,
Меншиков! Идите отсюда!..
— Как я вас напугал! — бормочет он с хмурой ухмылочкой,
бредя на свое место. Но я уже не слушаю его, я спешу расхвалить
Аргунову:
— Какая вы, оказывается, глазастая! Вы сегодня, я чувствую,
в ударе! Я жду от вас удач!
— А я придумал! — радостно улыбается Буткус. — Если
косинус не пропустить, то будет интеграл J sinn~2 dx cos2 xdx, потом
заменить cos2x на (1 — sin2 я) и в правой части будет такой же
интеграл, который мы вычисляем, fsinnxdx. Получится
уравнение для этого интеграла.
— Мысль верная, но по-моему, вы не совсем ясно
представляете, к чему она ведет. Идите к доске, покажите, что вы
хотите сделать. Действительно, получается уравнение для
интеграла fsinnxdx. Но через что он выражается? Через интеграл
/ sinn~2 xdx, вычислить который не намного легче, чем
исходный.
— Это же рекуррентное уравнение! — вскрикивает Горт.
370
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
[Гл. 5
— Термин кстати! Напомните нам, откуда он и что
означает.
— Из теории последовательностей — это когда n-ный член
последовательности выражается через несколько предыдущих,
чаще всего через один только (п — 1)-ый. У нас примерно так
и получилось: n-ный интеграл выразился через (п — 2)-ой,
его потом можно выразить через [п — 4)-ый и так далее — в
конце концов получим интеграл либо от sin я, если п нечетное,
либо от единицы, если п четное, а уж их-то мы умеем
вычислять.
— Очень неплохо. Напишите то, что вы сказали, на доске.
Садитесь. Остается третий пример, перед которым спасовал Мен-
шиков. Теперь-то вы его решили, Коля?
— Вы знаете, нет! — картинно разводит он руками.
— Удивительно! Мне этот пример кажется не труднее
первого, честное слово. Разве у вас не вызвала никаких воспоминаний
функция ех cos x? Разве вы видите ее впервые?
— Не впервые. Мы ее интегрировали.
— Но что это значит? То, что мы в явном виде нашли
функцию F(x), удовлетворяющую уравнению J ex cos xdx = F(x) + С.
Ведь так? А теперь представьте, пожалуйста, все варианты этого
равенства.
— Какие здесь могут быть варианты? Только такой:
excosx = F'{x).
— Нет, не только! Еще и такой: ех cos xdx = dF(x).
Буквально пять минут назад подобный прием блестяще применил
Буткус — спешите перенимать у товарищей хорошие идеи!
Как же с учетом такого варианта будет выглядеть наш
интеграл?
— Сейчас... JxdF(x)... Все понятно: интегрирование по
частям.
— Совершенно верно! И оно, как нетрудно догадаться,
приведет к интегралу J F(x)dx. Функцию F(x) = f ex cos xdx
мы уже вычисляли — она равна то ли полусумме, то ли
полуразности функций exsinx и excosx, точно уж не
помню. Но ведь это вам нужно помнить, Коля, а не мне!
Не пойдете ли к доске? Не возьмете ли весь интеграл до
конца?
— Да тут уж все ясно...
— Идите, идите, не ленитесь! Нет ответа — задача не решена.
Если не помните, как берется интеграл f ex cos xdx, посмотрите
в своей тетради.
К). В. Пухначев]
СЕМЬ СЕМИНАРОВ
371
Он повинуется не без показной неохоты, начинает
вычислять — и снова пытается бастовать:
— Тут интеграл, которого у нас не было: f exsmxdx.
— И вы не сообразите, как к нему подойти?
— Готов спорить, — негромко заявляет Кулагин, — что тут
опять будет какая-то линейная комбинация ех sin я и ех cos я.
— Попробуйте это доказать, — зову его к доске.
Он быстро реализует свою гипотезу.
Хорошо. Садитесь, Андрей. Продолжайте, Меншиков.
Доделав пример, он возвращается на место. Продолжаю:
372
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
[Гл. 5
— Каждый из взятых нами интегралов, ребята, требовал
особого подхода, порою весьма остроумного, побуждал нас к
изобретательности. Поистине, вычисление неопределенных
интегралов — это отличная школа искусства аналитических
преобразований. Неопределенные интегралы стоило бы изучать уже за
одно это, не говоря уж об их прямых приложениях, — гляжу
при этих словах на Миклашевского. — Но должен предупредить
вас, ребята: изобретательность при вычислении неопределенных
интегралов может оказаться бесплодной. Может случиться и
такое: функция под интегралом — совсем незамысловатая, а
первообразную для нее найти никак не удается. Это не то, что в
дифференциальном исчислении: производная любой
элементарной функции есть опять-таки элементарная функция. В
интегральном исчислении подобной закономерности не
наблюдается: задавшись какой-нибудь наугад составленной элементарной
функцией, вы далеко не всегда сможете выразить
неопределенный интеграл от нее в элементарных функциях, к каким бы
искусным приемам ни прибегали. Примеров тому можно привести
немало — тут и интеграл J e~x dx, играющий важную роль в
теории вероятностей, и так называемый интегральный логарифм
/ Шх> и интегральный синус J ^^dx, и эллиптический интеграл
/ / _J? . i , где к ф 1... Специальные названия, присвоенные
этим интегралам, говорят об их важности и широком
применении, говорят о том, как полезно было бы выразить их через
элементарные функции. Однако сделать это невозможно в
принципе, как невозможно разделить произвольный угол на три равные
части с помощью циркуля и линейки, — это доказано.
— Наверное, — с философской проницательностью во взгляде
замечает Стрельцов, — разумно поставить вопрос:
существуют ли такие классы элементарных функций, интегрирования
которых всегда приводит опять-таки к элементарным
функциям?
— Именно этим вопросом, — короткой паузой подчеркиваю
значительность реплики Стрельцова, — я и хотел бы заняться
сейчас. Но прежде, ребята, давайте вспомним пример, решенный
в свое время Меншиковым, когда подынтегральная функция
разлагалась на элементарные дроби. Оказывается, подобному
разложению поддается всякая рациональная функция. Кто мог бы
напомнить ее определение? Гарин? Пожалуйста.
— Когда мы выражаем значение функции у через значение
аргумента х и при этом совершаем только четыре арифметиче-
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
373
ских действия — сложение, вычитание, умножение, деление... ну,
и еще возведение в целую степень, частный случай умножения
и деления — то такая функция у(х) называется рациональной.
Ее всегда можно представить в виде отношения двух полиномов
от х.
— Или, как еще говорят, в виде полиномиальной дроби. Эта
дробь называется правильной, если степень полинома-числителя
меньше степени полинома-знаменателя. Если полиномиальная
дробь неправильна, то, деля ее числитель на знаменатель —
надеюсь, вы все умеете делить полином на полином? — можно
представить ее в виде: полином плюс правильная полиномиальная
дробь. Именно к такому виду целесообразно приводить
рациональную функцию, когда ее приходится интегрировать.
Интегрирование полинома при этом трудности не представит, а
всякую правильную полиномиальную дробь известным нам
методом неопределенных коэффициентов можно разложить на
элементарные вида (д,_^)т или (д.2^р^)п, где трехчлен x2+px+q не
имеет действительных корней и потому на линейные множители
не разлагается; показатели тип — натуральные. Для каждой
из элементарных дробей указанного вида первообразная
выражается через элементарные функции — степенную, логарифм,
арктангенс. Лектор показывал вам, как это делается? Да?
Тогда решим несложный пример на интегрирование рациональных
функций.
И я диктую интеграл: / {х+1){х$Пх+3)з.
— Видите, здесь все просто: знаменатель уже разложен на
множители, и все они линейные. Не хотите ли взять этот
интеграл, Миклашевский?
Быстро выйдя к доске в доверчивом порыве, с
простодушной энергией начав разлагать подынтегральную функцию на
элементарные дроби, он очень скоро убеждается, какая
большая и нелегкая работа скрывается за интегрированием такого
простого с виду выражения. Числитель дроби, образующейся
при суммировании элементарных дробей, не укладывается во
всю ширину доски, коэффициенты при иксах, возникающие
при приведении подобных членов, поражают своей
несуразностью. Бедняга старается не показывать своего разочарования
и, выписав систему уравнений для вычисления неопределенных
коэффициентов, оборачивает ко мне бодренько улыбающееся
лицо:
— Решать?
— А вы надеетесь решить эту систему до конца семинара?
374
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
[Гл. 5
— Если честно, то нет.
— А если нет, то садитесь на место.
Он проходит мимо меня и говорит вполголоса, как бы про
себя: «Нет ответа — задача не решена».
— Спасибо за напоминание, — ловлю его шпильку. — Я вовсе
не отказываюсь решать задачу. Я только думаю, что ее надо
решать иначе. В самом деле, если интегрирование весьма
несложной функции, которая стоит у нас под интегралом, приводит
к столь громоздкой системе уравнений, то что будет, если нам
встретится более сложный интеграл подобного рода? Тут очень
помог бы какой-то оригинальный обходный маневр. Честно
говоря, я думал, что у вас, Миклашевский, хватит остроумия, чтобы
его изобрести. Но, если вы так быстро убегаете от доски, мы
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
375
постараемся обойтись без вас. Итак, ребята, ищем новый
способ вычисления неопределенных коэффициентов, через которые
записывается разложение полиномиальной дроби на
элементарные.
— Новый — и только? — с усмешкой переспрашивает
Кулагин. — Пойди туда — не знаю куда?
— Да, пока что поставленная мной задача выглядит так. Но в
ваших силах уточнить ее. Давайте для этого разберемся, что не
устраивает нас в традиционном способе поиска неопределенных
коэффициентов? Как вы думаете, Сынчиков?
— То, что получается система уравнений... очень большая,
— не сразу и еле слышно, по своему обыкновению, отвечает он.
— Верно. А нельзя ли найти такой метод, при котором
каждый коэффициент вычислялся бы независимо от других,
выражался бы сам по себе?
Тишина. И в ней — непривычно нерешительный поначалу
голос Костюка:
— Кажется, есть способ ... Числитель левой, исходной
дроби — единица. Тогда числитель правой, которая получилась
после приведения к общему знаменателю тоже равен единице,
причем тождественно, при любых значениях х. Подставим туда
и туда х, равный минус единице, тогда в числителе правой
дроби обратятся в нуль все слагаемые, кроме первого, где
коэффициент А.
— Неверно, х не может равняться минус единице! — рубит
Горт. — В знаменателе обеих дробей стоит (х + 1), эта скобка
тогда обратится в нуль, дробь потеряет смысл.
И Костюк умолкает, упрямо хмуря брови, но не находя, что
возразить. Интересно, как после этого поражения он поступит
со своей идеей? Отбросит? Или сумеет найти и спасти ее
рациональное зерно?
— Ох, Саша, Саша! — вздыхаю в наступившей тишине. —
Когда же вы откажетесь от своей погромной манеры
дискутировать? Когда научитесь не громить сплеча неправоту чужих слов,
а стараться отыскать в них хоть какую-то правоту, развить ее?
Тишина... Но вот снова голос — Мухина:
— Не посмотрите, что у меня получилось?
Получилось, видимо, что-то сомнительное, с чем не
выступишь наверняка. Единственное, что может порадовать — это
аккуратность его почерка, заметная издалека: проняла его,
видно, неудача с интегралом от excosx, когда он сам загубил
свой близкий успех своей же небрежностью, и теперь он ста-
376
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
[Гл. 5
рается писать повдумчивее. Ан нет, он может похвастаться не
только четкостью, но и результатом выполненного
преобразования.
— Вы-то сами, Мухин, понимаете, чего добились?
— Выразил коэффициент А сам по себе.
— Это все, что вы можете сказать? А впрочем — давайте-ка,
ребята, оценим достижения Мухина все вместе. Напишите свой
результат на доске, Мухин.
— Может, не надо? — робеет он.
— Надо, Женя, надо.
И только он кончил писать, как Костюк взвивается:
— Я же говорил! Вот теперь можно подставлять вместо х
минус единицу, и А получается сразу — одна восьмая! А потом
и другие коэффициенты так же вычислим!
— О! Вот что значит коллектив! — радуюсь вместе с Костю-
ком. — Один выдвинул смутную идею, другой ее развил до чет-
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
377
кого результата. Я недоволен лишь тем, Виталий, что вы раньше,
самостоятельно не пришли к такому приему, недоволен тем, что
после возражений против вашей идеи не сумели отстоять того,
что было в ней ценного, и увидели эти ценности лишь с чужой
помощью. Но уж теперь, когда они выяснились, — развивайте,
развивайте их дальше! Все ли коэффициенты можно получить
тем же приемом?
— Нет, только А, С и F. Если таким же способам
попытаемся определить, скажем, J3, то в знаменателях некоторых дробей
появятся нули, а этого не должно быть.
— Верно. Думаем все вместе, как определить коэффициенты
B,D и Е.
— А их, по-моему, и не нужно определять, — внезапно
заявляет Миклашевский.
— То есть как это — не нужно?
— Я не так выразился: не нужно искать способ их
определения. У нас уже есть система из шести уравнений для
всех шести коэффициентов. Три мы уже знаем как найти —
А, С, F. Подставим их в систему и возьмем оттуда три
независимых уравнения для J3, D, Е. Три-то уравнения мы как-нибудь
решим!
— Остроумный выход из затруднительного положения! Если
понадобится, мы воспользуемся им. А пока все-таки разработаем
метод Костюка до такой степени, чтобы он позволял определять
все коэффициенты. Ну-ка, Чюмин, поглядите на равенство (4) и
скажите: что такое С?
— Коэффициент, числитель одной из элементарных
дробей.
— В этом контексте — да. А в каких контекстах еще
встречалась вам эта буква? Что ею обычно обозначается? Как бы вы
ответили на этот вопрос, ребята?
— Постоянная интегрирования, — отвечает Синица.
— Хорошо. Что еще?
— Постоянная величина, постоянная функция, — после
некоторого молчания добавляет Кочин.
— Что еще?
Ответа нет. Молчание затягивается.
— Надо продифференцировать равенство! — внезапно
вскрикивает в радостном возбуждении Рамзин. И тотчас взяв себя в
руки:
— Продифференцировать и подставить вместо х
минус два. Легко видеть, что правая часть при этом обра-
378
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
[Гл. 5
тится в J3, а левая даст численное значение этого
коэффициента. Таким же путем можно получить
коэффициенты D и Е, только дифференцировать следует уже
дважды.
Прекрасно! А я уж боялся — не додумаются ребята. Нет, что
ни говори, а голова у Рамзина на месте. Великолепно сообразил!
Похвалы так и рвутся у меня с губ, но все-таки что-то
удерживает меня от восторженных словоизлияний. Что же? Неужели
неприязнь? Но ведь это недопустимо! Я должен быть
совершенно ровен, совершенно беспристрастен по отношению ко всем
своим студентам. И все же — есть оправдание той холодноватой
критичности, с которой я отношусь к самовлюбленному,
заносчивому Рамзину.
Как-то раз, проходя по коридору мимо беседующих ребят из
этой группы, я услышал, как Рамзин высокомерно бросил Чю-
мину: «Ладно, когда я получу Нобелевскую, я тебе уделю один
процент на твое убожество». Нет, подумалось сразу, не получит
Нобелевской такой гордец! Крупный научный успех
предполагает максимальную самоотдачу, а чрезмерное внимание к
собственному «я» слишком снижает ее. И потому я должен настойчиво
выщелачивать гордыню из Рамзина — ради его же будущих
успехов.
Сдержанно приглашаю его к доске реализовать
предложенную идею. Он быстро получает В = 2, но потом темп
его выкладок быстро падает. И тогда раздается голос
Миклашевского:
— А дифференцировать-то трудно. Мой способ легче.
И я по сочувственным взглядам ребят в его сторону понимаю,
что они с ним согласны.
К). В. Пухначев]
СЕМЬ СЕМИНАРОВ
379
— Пожалуй, вы правы, Паша. Решайте пример до конца.
Садитесь, Рамзин на место и доделайте этот пример до конца своим
способом.
Пыхтя, ошибаясь, спохватываясь, поправляясь,
Миклашевский наконец получает решение.
— Спасибо, садитесь. С вашей помощью мы одним выстрелам
убили двух зайцев: во-первых, отыскали еще один путь к ответу,
во-вторых, потренировались в комбинировании различных
подходов к решению одного примера — такое комбинирование часто
бывает очень полезным. Кстати, какие коэффициенты
получились у вас, Рамзин? Такие же? Прекрасно.
Выдерживаю паузу, чтобы все могли переписать в свои
тетради и проверить написанное на доске. Потом
продолжаю:
380
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
[Гл. 5
— Известно немало приемов, так или иначе упрощающих
вычисление интегралов от рациональных функций.
Например, метод Остроградского. Он применяется, когда, разлагая
знаменатель подынтегральной функции на множители, вы
получаете их в степенях выше первой. Вот в чем суть
метода. Составляются две полиномиальных дроби. В знаменателе
первой — те же сомножители, что в исходной дроби,
интеграл от которой требуется взять, но каждый в степени на
единицу меньшей; если какой-то из них в исходной дроби
присутствовал в первой степени, то тут он, разумеется, будет
отсутствовать: ему в таком случае положено быть в нулевой
степени; а нулевая степень — это единица. В знаменателе
второй дроби — опять-таки те же сомножители, что в исходной,
но каждый — в первой степени. В числителях той и другой
дроби пишется полином с неопределенными коэффициентами,
имеющий степень на единицу меньшую, чем
соответствующий знаменатель. Интеграл от исходной дроби после этого
выражается суммой: первая из образованных дробей плюс
интеграл от второй — взять его легче, чем исходный: ведь
тут у знаменателя уже нет кратных корней. Для того, чтобы
отыскать неопределенные коэффициенты в числителях
составленных дробей, полученное равенство дифференцируют,
правую часть приводят к общему знаменателю, приравнивают
коэффициенты при одинаковых степенях икса в
числителях дробей в правой и левой частях равенства и решают
возникшую таким образом систему уравнений. Да, еще
примечание: составляя по методу Остроградского сумму из двух
полиномиальных дробей, вместо второй, стоящей под знаком
интеграла, удобно писать сразу ее разложение на элементарные
дроби.
Объяснив метод, даю пример на его применение — усеченный
вариант прежнего примера: / (х+2)Нх+з)3' ^ Д°ске приглашаю
Лапикова. В ответ — старая песня:
— Боюсь, что...
— Что не смогу? — заканчиваю в тон, слегка передразнивая
его. — Выбросьте из головы эту присказку, Лапиков! Меня вы
ей не убедите -- я уже не раз видел, что вы умеете решать очень
даже непростые задачи. Будьте решительнее, увереннее в себе,
работайте поэнергичнее — и успех всегда будет на вашей стороне.
Идите к доске.
Пример, что и говорить, требует немалых вычислений.
Правда, внеинтегральное выражение дифференцируется легко. Од-
1С). В. Пухначев]
СЕМЬ СЕМИНАРОВ
381
нако подынтегральные слагаемые при приведении всей суммы
к общему знаменателю вносят в числитель четвертые степени
икса, и Лапикова это пугает. Но я подсказываю, что это не во
зло, а во благо — сводя вместе эти степени, мы обнаруживаем,
что коэффициент при х4 равен D + Е, а поскольку числитель
дроби в левой части вообще не содержит никаких степеней х,
382
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
[Гл. 5
в том числе и х4, то D + Е = 0, так что во всех последующих
вычислениях можно заменить Е на —D. Более того, вслед за
этим выясняется, что после такой замены коэффициент при х3
обращается в (D — А), так что, в силу отсутствия х3 в числителе
дроби слева, получается D — А = 0, и потому далее можно
заменить D на Л, а это влечет дальнейшие упрощения. То-то
радости Лапикову с важным видом разруливать последнюю тройку
уравнений! Дождавшись ответа и отправив Лапикова на место,
резюмирую:
— Сложнее или проще, тем или иным способом,
рациональную функцию всегда можно проинтегрировать и выразить
интеграл от нее с помощью элементарных функций. Значение
такого вывода приумножается тем, что к интегрированию
полиномиальных дробей удается свести вычисление интегралов от
функций еще нескольких классов. Один из них — рациональные
функции от тригонометрических функций. Я напишу их в
виде i?(sinx, cosx), не упоминая в скобках другие
тригонометрические функции — тангенс и котангенс, секанс и косеканс,
потому что они выражаются через синус и косинус
рациональным образом. Если вам потребуется взять интеграл от такой
функции R и первые ваши попытки окажутся безуспешными
— не отчаивайтесь: у вас в запасе всегда есть универсальная
тригонометрическая подстановка t = tg|. Известно, что синус
и косинус выражаются через тангенс половинного угла в виде
несложных полиномиальных дробей, так что в итоге
подынтегральная функция превратится в рациональную функцию от
переменной t. Правда, под знаком интеграла стоит еще
дифференциал dx. He подпортит ли он нам дело? Нет — в результате
замены он превратится в выражение у^з, что не нарушит
рационального характера всей образующейся под интегралом
функции от новой переменной t. Все успели записать то, что
я объяснил? Тогда разберем еще один класс подынтегральных
выражений, которые в отдельных случаях удается упростить,
приходя к интегрированию рациональных функций. Бином-
ные дифференциалы — так называются эти выражения. Они
имеют вид хт(а + Ьхп)р, где га, п,р — рациональные числа.
Ясно, что при целом р интегрирование подобных выражений
не составляет труда: второй сомножитель надо разложить по
формуле бинома Ньютона и дальше интегрировать почленно.
Чебышёв доказал, что получение рациональных функций под
интегралом возможно здесь лишь еще в двух случаях, когда
либо т^-> либо ^^ + р равно целому числу. В каждом из
И >. И. Пухначев]
СЕМЬ СЕМИНАРОВ
383
■>тих случаев к успеху приводит своя подстановка,
соответственно t = у/а + Ьхп или t = >/^г + Ь, где г — знаменатель
дроби р.
Разделив доску на две части, пишу слева и справа несложные
интегралы того и другого рода. К одной половине доски
приглашаю Кочина, к другой — Сутеева.
Работа нетрудная — мел в руках Кочина без особых
задержек скользит по доске. Изредка поглядывая на выкладки
соседа, Сутеев не отстает от него. Дело спорится и у
остальных.
С усмешкой оглядываю аудиторию:
— Да, ребята, семинар у нас идет — любо-дорого
посмотреть. Я даю вам готовенькие методы — вы с их помощью
решаете задачки, одну за другой, почти не думая. С этим пора
кончать! Надо бы дать вам что-то такое, на чем вы
проявили бы свою сообразительность. В теме, которую мы сейчас
обсуждаем, можно найти кое-что подходящее для этого. Вам
рассказывал лектор про подстановки Эйлера? Еще нет? Ну
и чудесно. Рассмотрим интеграл, под знаком которого стоит
рациональная функция от двух аргументов: х и V'ах2 + Ьх + с.
Эйлер предложил для таких интегралов три подстановки, из
которых хотя бы одна применима, если только квадратный
трехчлен не всюду отрицателен, а это, как вы понимаете,
зависит от подбора его коэффициентов. Я подробно разъясню
вам первую эйлерову подстановку, а вы постарайтесь
разглядеть принцип, лежащей в ее основе. Если вы его уловите, вы
самостоятельно, без моих подсказок изобретете вторую и
третью подстановки — в их изобретении и состоит мое очередное
задание. Время его выполнения я не ограничиваю. До конца
семинара еще далеко, и я надеюсь, что открытия Эйлера мы
успеем повторить. Итак, первая подстановка. Она применима
в тех случаях, когда коэффициент а положителен. Новая
переменная t вводится равенством у/ах2 + Ьх + с = t ± у/ах; при
выборе знака (плюс или минус) следует учитывать особенности
конкретной подынтегральной функции и выбирать тот, при
котором дальнейшие выкладки будут проще. Возведя в квадрат
обе части равенства и произведя сокращение слагаемых ах2,
мы выразим х рациональным образом через £, а на основе
равенства, определяющего подстановку, подставив в него
выражение для х, рациональным же образом представим через
t и корень из квадратного трехчлена. Нетрудно видеть, что
подынтегральная функция в итоге превратится в рациональную
384 ИНТЕГРИРОВАНИЕ ФУНКЦИЙ [Гл. 5
функцию от £, дифференциал dx добавит к ней рациональный
же множитель.
— Оригинально! — не может не высказать своего мнения Мен-
шиков.
— Все было понятно в моем объяснении? Тогда приступаем
к конструированию второй и третьей подстановок.
Засекаю время: интересно, сколько провозятся ребята с моим
заданием, далеко не простым?
Прошло уже десять, пятнадцать минут. Все что-то
сосредоточенно пишут в тетрадях, и только Стрельцов, сложив руки
на груди, напряженно установился в чистые страницы, да Горт,
чего-то бормоча, мечет взгляды по сторонам: видать, никак не
может нащупать стоящую идею.
Чюмин прилежно вырисовывает: ах2 + Ьх + с = у/с± у^- к<^
где же у вас новая переменная?» — шепотом спрашиваю его. Он
конфузится и зачеркивает написанное.
В тетради у Кулагина — равенство: у/ах2 + Ьх + с = y/c + t.
— Зачем вы так написали? — наклоняюсь к нему.
— Чтобы что-то сократилось.
— Ну-ну, — и иду дальше вдоль ряда.
Аргунова придумала соотношение у/ах2 + Ьх + с = tx + с.
— Что это у вас написано? — указываю на последнее
слагаемое в правой части.
— Это? То же самое с, которое под корнем, — отвечает она.
— Значит, если возвести в квадрат...
Словно по рассеянности пишу результат возведения в
квадрат таким, каким он был бы, если бы в правой
части написанного Аргуновой равенства стояло не с, а у/с,
ах2 + Ьх + с = t2x2 + 2txy/c + с. Догадается ли она, что я
хочу сказать ей этим? Нет, она исправляет мою «описку»:
ах2 + bx + c = t2x2 + 2txc + с2. Я только вздыхаю: решил ведь не
подсказывать...
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
385
А время бежит — уже полчаса прошло с той минуты, как я
дал ребятам это необычное задание.
— Честно говоря, ребята, Кулагин и Аргунова наполовину
уже сконструировали вторую подстановку Эйлера, и если
соединить эти половинки, получится то, что требуется. Аргунова,
сядьте рядом с Кулагиным!
Разгуливая по аудитории, то и дело поглядываю в их
тетради. Видимо, не без помощи Кулагина в тетради у Аргуновой
появляется верная формула второй подстановки: у/ах1 + Ьх + с =
= tx + у/с, но что с ней делать, Галя не знает, а Андрей не
подскажет — он так и строчит авторучкой по чистым листам:
наконец-то угаданная формула открывает прямой путь к
желаемому результату.
Покуда он сводит подынтегральную функцию к
рациональной, Стрельцов внезапно берет ручку и без единой помарки тоже
пишет формулу второй подстановки.
Дело пошло! Может быть, того же успеха добился кто-то
еще? И точно: та же формула — в тетрадях Синицы и
Гарина.
— Ну что ж, ребята, — одна из поставленных целей
достигнута: вторую подстановку Эйлера самостоятельно открыли
Кулагин, Стрельцов, Синица и Гарин. Она применима, когда
коэффициент с в квадратном трехчлене неотрицателен. Покажите, как
она выполняется, Кулагин.
Он пробирается между стульев, и я, следя за ним, краем глаза
замечаю, как Синица, довольная, отчеркивает огромной
фигурной скобкой свои выкладки и аккуратно пишет вдоль
вертикального края тетради: «2-я подстановка».
— Все верно, Андрей, — просматриваю выкладки Кулагина
и, убедившись, что всем понятно написанное им, отправляю его
обратно и отпускаю на прежнее место Аргунову.
— Теперь, ребята, изобретаем третью подстановку.
13-2019
386
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
[IV*- 5
— А нужно? — сомневается закоренелый скептик Буткус. **
Костюк поддерживает его:
— Двух разве не хватит?
— Давайте разберемся, — предлагаю я. — Для применен^
первой подстановки необходимо, чтобы коэффициент а в квзЛ~
ратном трехчлене был больше нуля, для применения второй —
чтобы большим или равным нулю был коэффициент с. А вдрУг
оба они отрицательны?
Костюк пытается возражать:
— Но тогда квадратный трехчлен будет меньше нуля при jif°"
бом х, корень потеряет смысл и весь интеграл тоже...
— Не спешите с выводами! Покажите на доске, как зна^и
перед а и с определяют характер трехчлена, вид его графика. Да>
если оба коэффициента отрицательны, график может целике м
оказаться под осью абсцисс. Но...
— Но, — рисует он дальше, — тречлен может быть полол£и~
тельным, если у него есть действительные корни — если х при"
нимает значения между этими корнями, трехчлен будет поло^и"
тельным.
Ю. В. Пухначев|
СЕМЬ СЕМИНАРОВ
387
— Садитесь на место! — не даю его догадкке превратиться в
подсказку.
Стоило Костюку упомянуть о корнях квадратного трехчлена,
как тотчас в нескольких тетрадках появилась формула для
вычисления корней. Никто из написавших эту формулу, впрочем,
так и не может сообразить, какой от нее прок.
По-прежнему обильным потоком выкладок заполняется
тетрадь Кулагина. Он пробует соотношения у/ах2 + Ьх + с =
— Vbtx + у/с, у/ах2 + Ьх + с = y/atx + у/с.
— Но ведь они не представляют из себя ничего
принципиально нового по сравнению со второй подстановкой, — замечаю ему
и иду дальше.
Сынчиков догадался разложить на множители квадратный
трехчлен под корнем, но замена для корня у него неудачная:
у/а(х — х\)(х — Х2) = (t — x)(x — х\).
Разложить трехчлен на множители догадался и Кочин.
Он пишет сначала у/ах2 + Ьх + с = у/(х — xi)(x + £), потом
у/ах2 + bx + с = \Ja(x — х\)(х — хъ) = \J(x — xi)(|x + £),
возводит обе части равенства в квадрат, сокращает на (х — xi),
выражает х рациональным образом через t...
— Но вот корень из трехчлена вам уже не удастся выразить
рациональной функцией от £, — замечаю я.
— Да, не удастся, — невесело соглашается он, но не
отчаивается, продолжает писать все новые варианты равенства — и
опять с корнями в обеих частях.
— Подумайте: что вам мешает?
— Корень.
— А можно устроить сокращение на (х — xi) без корня в
правой части равенства? — и перехожу к другим ребятам.
Не успеваю сделать и трех шагов, как Кочин радостно
выкрикивает мне вдогонку:
— Есть!
И эхом — Синица:
— И у меня есть!
Смотрю в их тетради:
— Да, вы оба получили третью подстановку Эйлера.
Как все-таки неразборчива фортуна: Кочину, на
которого я особых надежд не возлагал, повезло, а Горту,
такому многознающему, такому многоопытному, и
похвастаться нечем: сидит, нахохлившись, над пустыми
страницами...
13*
388
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
[Гл. 5
Синица с гордым видом снова рисует в своей тетради
фигурную скобку с надписью «3-я подстановка», а Кочин получает
почетное поручение выписать на доске формулы, выполняющие
эту подстановку.
— Ну что ж, прекрасно, — отсылаю его на место. — Я
доволен вами, ребята. Потягаться силами с самим Эйлером —
дело не из легких, но вы справились с ним. И вообще я считаю,
что тему «неопределенный интеграл» мы с вами в целом
разобрали. Вы того же мнения? Тогда позвольте предложить вам
простенький пример для проверки ваших глубоких знаний.
Найдите первообразную для функции е'х1 Иными словами, возьмите
интеграл
Улавливаю удивленную гримасу, промелькнувшую на
лице Стрельцова, — чуть приподняв левую бровь, он словно
спрашивает: «А что, собственно, здесь трудного?» Зову его
к доске.
— Ответ краток и ясен, — комментирую его результат. Не
нарисуете ли график функции, которую вы получили?
Постоянную интегрирования для определенности возьмите равной
нулю. Нарисовали, отлично. Вас ничто не смущает в этом
графике?
Ю. В. Пухначев] СЕМЬ СЕМИНАРОВ 389
— Да вроде нет... Вот разве что разрыв в начале координат.
— А имеет ли эта функция право на разрыв, пусть даже
конечный?
Он молчит — и я жду. А в аудитории тем временем
нарастает глухой шум, прорывающийся наконец почти одновременными
возгласами Буткуса, Костюка, Горта, Рамзина:
— Это же первообразная! Функция, которая должна иметь
производную в каждой точке! И эта производная всюду
должна равняться подынтегральной функции! А эта функция в нуле
недифференцируема, потому что у нее там разрыв!
И когда утихает этот шквал, Стрельцов еще некоторое время
рокочет покаянно:
— Ах, дурень! Ну, идиот!
— Да будет вам каяться! Думайте-ка вместе со всеми, как
исправить график. У кого есть предложения на этот счет? Может
быть, у вас, Сутеев?
Если ему действительно свойственно то, что называют
визуальным мышлением...
Сутеев встает, идет к доске, берет мел и продолжает левую
ветвь графика вправо, на постоянной высоте над правой ветвью,
нарисованной Стрельцовым.
— Что это вы начертили? Поясните.
390
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
[Гл. 5
— Если первообразную сдвинуть вверх или вниз, она
останется первообразной.
Моя гипотеза, кажется, оправдывается: он способен
овладевать довольно сложными вещами, если их ему подавать на языке
графиков.
— Сдвинуть вверх или вниз — это значит, — добавляю
примечанием к его ответу, — прибавить или отнять
константу.
— Прибавить или отнять константу, — механически
повторяет он. — Первообразная останется первообразной, а вся кривая
станет непрерывной.
Голос его отдает магнитофонным тембром,
настораживающим отголоском бездумной зубрежки. Но ведь то, что он сказал,
сказано с толком!
— Как же это выразить формулами?
Он молчит. Формульный язык дается ему гораздо труднее,
чем графический. Посоветовать ему вызубривать формулы,
относящиеся к усвоенным визуальным математическим образам?
Нет, вряд ли такой путь приведет к успеху; я уже убедился
в этом, когда пытался разобрать вместе с ним у доски
понятие производной: верный график и верная формула стояли
рядом, а он никак не мог их связать. Значит, еще одна
проблема возникает в моей с ним дальнейшей работе: надо как-то
научить его переводу с формульного языка на графический
и обратно.
— Вот смотрите, — жестом приглашаю его поглядеть на
доску, — график, нарисованный Стрельцовым, а вот
соответствующая этому графику формула, — ради точного соответствия
стираю константу С. — Вы приподняли вверх правую ветвь
графика, подчеркиваю — е~х в формуле Стрельцова. — На языке
формул это выражается прибавлением некоторой константы. Какой
же именно?
Спустя несколько секунд тяжелой неподвижности он
приплюсовывает двойку к подчеркнутому мною
выражению.
— Правильно! Так представляется данная конкретная
первообразная. А чтобы получить всю совокупность
первообразных, неопределенный интеграл, надо... что надо сделать,
Сутеев?
Спустя еще несколько секунд томительного молчания он
прибавляет константу С к представлениям обеих ветвей
первообразной.
К). В. Пухначев] СЕМЬ СЕМИНАРОВ 391
— Все верно, Сутеев! Садитесь на место. Вы что-то хотите
сказать, Мухин?
— Да. Тут можно сделать еще красивее. Правую
половинку поднять не на два, а на единицу, а левую на единицу
опустить.
— Очень хорошо, в самом деле. А как это выразить
формулой? Не поможете, Рамзин?
— Сейчас, дайте только подумать.
Пауза, которую он выдерживает, должна показать всем, как
непрост вопрос и какую великую услугу он оказывает
Мухину своим ответом. Пишу на доске предложенную им формулу
(e-l*l - l)sgn(-x) + С.
— Формула не менее четкая, чем идея Мухина.
Спасибо, Сергей. Мы переходим, ребята, к новой теме, к
определенным интегралам. Снова начнем с основных
определений, и пусть их снова напомнит нам Кочин. Прошу вас,
Дима.
Он, как и прежде, несколько секунд молча стоит у доски: в
строгом, чуть нахмуренном его лице — желание
сосредоточиться. Потом берет мел, рисует систему координат, откладывает
на оси абсцисс отрезок [а, Ь] и над ним проводит волнообразную
кривую:
392
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
[Гл. 5
— Предположим, что нам потребовалось вычислить площадь
вот такой фигуры (Из концов отрезка, отложенного на
горизонтальной оси, он восставляет перпендикуляры и
заштриховывает образовавшуюся криволинейную трапецию). Сделаем это
так. Разобьем отрезок [а, 6] на п частей точками £i,£2, ...xn_i;
а и b назовем хо и хп соответственно. На каждом маленьком
отрезочке с концами Хг-i и^~ длину этого отрезочка
обозначим Ах{ — возьмем произвольную точку & и на высоте /(£i)
проведем над этим отрезочком горизонталь. У нас получится п
прямоугольников. Каждый г-тый прямоугольник имеет ширину
Дхг, высоту /(&)> значит, его площадь — f(£i)Ax{. Сумма всех
п
таких площадей S = Ylf(€i)^xi приближенно выразит площадь
г=1
заштрихованной фигуры. Максимальная ширина Ах{
называется мелкостью разбиения отрезка [а, 6]; обозначим ее А. Разобьем
отрезок [а, 6] еще и еще раз, чтобы мелкость разбиения
убывала, и каждый раз станем подсчитывать сумму S. Устремим А
к нулю и посмотрим, будет ли S стремиться к какому-нибудь
пределу, не зависящему от способа разбиения отрезка и выбора
точек &. Если будет, то этот предел равен площади
заштрихованной фигуры. Такие пределы... (Кочин аккуратно выписывает
п
lim J2f(£i)Axi и следующую фразу произносит, искоса погляды-
вая на своей конспектик: видимо, желает выразиться
понравившимися ему словами учебника) такие пределы играют большую
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
393
роль в математике, и их изучают не только с точки зрения
вычисления площадей. Можно взять произвольную функцию /(х),
заданную на каком-то отрезке [а, 6], и выяснить, существует для
нее такой предел или нет. Если существует, то функция
называется интегрируемой на отрезке [а, 6], а значение предела
называется определенным интегралом от функции f(x) на промежутке
от а до 6.
Справа от предела Кочин пишет через знак равенства
ь
Jf(x)dx и добавляет:
а
— Вот так обозначается определенный интеграл от а до Ь от
функции f(x).
— Может быть, у кого-то есть вопросы к Кочину? —
оглядываю аудиторию.
— У меня вопрос, — тянет руку Чюмин. — Чем
неопределенный интеграл отличается от определенного?
Да, с таким не соскучишься!
Кочин озадаченно смотрит на меня, не зная, что ответить.
Отвечаю сам:
— Неопределенный интеграл — это совокупность функций,
причем каждая из них по отношению к подынтегральной
функции является первообразной. Определенный интеграл — это
число. Вещи, как видите, совершенно разные. Но между ними есть
глубокая связь. Мы проследим ее, когда дойдем до формулы
Ньютона-Лейбница.
Снова Кочину:
— Вы можете сесть, Дима. Доклад вы сделали хороший.
Я бы только, пожалуй, внес несколько терминологических
дополнений к вашему последнему выступлению. Нарисованная
вами заштрихованная фигура обычно именуется криволинейной
трапецией. Числа а и b в обозначении определенного
интеграла называются соответственно нижним и верхним пределами
интегрирования, а суммы, предел которых вы ищите, —
интегральными суммами. Да, я бы сделал еще такое дополнение
к вашему докладу: если график функции проходит под осью
абсцисс, площадь ограниченной им криволинейной трапеции
будет отрицательной. Это с очевидностью следует из
определения определенного интеграла через интегральную сумму —
ведь в этом случае все ее слагаемые меньше нуля. И еще
следует уточнить одну вашу фразу, которую с использованием
введенных мною терминов можно пересказать так: предел
интегральной суммы равен площади криволинейной трапе-
394
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
[Гл. 5
ции. Я придрался бы здесь к слову «равен». Разве площадь
криволинейной трапеции уже известна вам? Разве ее можно
вычислить каким-то другим способом, не прибегая к
интегрированию? Хотя бы для некоторых фигур? Или спросим
иначе: площади каких фигур мы умели вычислять, еще не
зная про интегрирование? Как бы вы ответили на этот вопрос,
Аргунова?
— Площадь прямоугольника равна произведению основания
на высоту.
— Верно. Так определяется площадь прямоугольника.
Заметьте: определяется.
— Площадь треугольника равна половине произведения
основания на высоту, — добавляет Меншиков.
— Верно. Это вытекает из определения площади
прямоугольника — не так ли?
— И формула для площади параллелограмма из нее тоже
вытекает, — продолжает Меншиков, — и для площади трапеции
тоже.
— Точно, — поясняю беглыми чертежиками сказанное Мен-
шиковым.
— Площадь круга равна 7гД2, — вспоминает Лапиков.
— А как вычислялась эта площадь в школьном курсе
математики — помните? Крут рассекался на сектора все более узкие,
сектора заменялись треугольниками и отыскивался предел
суммарной площади треугольников при бесконечно
уменьшающейся ширине секторов. Это по существу интегрирование. И
когда чуть позже мы в порядке упражнения вычислим площадь
круга стандартными приемами интегрального исчисления и
получим в ответе 7гД2, не подумайте, что мы пришли к
ответу каким-то принципиально новым путем. В основе строгого
математического понятия площади криволинейной фигуры,
как бы ни реализовалось это понятие в конкретном
вычислении площадей, лежит процедура интегрирования. Стало
быть, неверно говорить, что предел интегральной суммы равен
площади криволинейной трапеции, — указываю на чертеж
Кочина. — Вернее сказать, что эта площадь по определению
равна пределу интегральной суммы, определяется через
определенный интеграл. Кто знает площади еще каких-нибудь
фигур?
— Я слыхал, — раздается после короткого молчания медный
голос Сутеева, — что если около параболы описать
прямоугольник, который касается ее в вершине, то парабола разделит пло-
IO. В. Пухначев]
СЕМЬ СЕМИНАРОВ
395
щадь прямоугольника в отношении один к двум. Наверное,
отсюда можно вывести площадь параболы.
— То, что вы сказали, совершенно верно. Любопытно, что
это знал еще Архимед. Способ, которым он вычислил площадь
параболы, для того времени был поразителен по смелости и
остроумию. Я повторю построения Архимеда в сильно упрощенном
ради наглядности виде. Представьте, — рисую, — что этот
горизонтальный отрезок с точкой О посредине — равноплечий рычаг.
На левое его плечо навесим параболу — представьте, будто она
вырезана из ткани, а на правое — лоскут, верхний обрез которого
сделан по точно такой же параболе, левый боковой — по
вертикали, правый боковой — по касательной к параболе. Во времена
Архимеда уже было известно, как ее строить: она отсекает ровно
одну четверть от основания прямоугольника, описанного около
сегмента параболы. На левой параболе проведем вертикаль,
отстоящую от левого конца рычага на расстояние х, а на правом
криволинейном треугольнике — вертикаль, отстоящую на точно такое
же расстояние от точки О. Архимед доказал, что по правилу ры-
396
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
[Гл. 5
чага (кстати, открытому им же) отрезки PQ и SL
уравновешивают друг друга. Чтобы вам было понятнее, я проведу
соответствующее доказательство не на манер древнегреческих математиков,
а в современных обозначениях. А затем Архимед утверждает:
поскольку парабола и этот криволинейный треугольник состоят из
всех своих линий, то они и в целом уравновешивают друг друга.
Затем на оба плеча рычага навешивается еще по одной
параболе, отчего справа возникает сплошной треугольник с
прямолинейными сторонами, и пишется условие равновесия по правилу
рычага: произведение общего веса фигуры на расстояние от
точки О до вертикали, проходящей через центр тяжести фигуры,
должно быть одинаковым и для правого треугольника и для
левой «сдвоенной» параболы. Вес фигуры пропорционален ее
площади. Центр тяжести параболы расположен на ее оси симметрии,
делящей пополам то плечо рычага, на котором повешена
парабола. Центр тяжести треугольника лежит на вертикальной линии,
отстоящей от точки опоры рычага на треть плеча, на котором
висит треугольник. Отсюда и получается площадь параболы.
— Парабола состоит из всех своих линий? — с театральным
восторгом переспрашивает Рамзин. — Гениально! В одной
фразе — вся суть интегрального исчисления! Архимед — вот кто его
изобрел!
— Еще не ясно, придавал ли он этой фразе тот смысл,
который в ней видим мы, — замечает Горт.
— Может быть, и не придавал, — отвечаю Горту. — Но
согласитесь: как удачно у него сказанулось! И что еще
любопытно: Архимед стыдился, что классическую для античных
математиков пару «циркуль и линейка» в его построениях
заменили весы — инструмент ремесленников и торговцев.
Конечно, столь непосредственное вторжение механики в
математику можно признать неожиданным и странным. Но
то, что математические открытия уходят своими корнями в
практическую деятельность человечества, извечно и
закономерно.
— А давайте, — перебивает меня Лапиков, — вычислим через
интеграл площадь параболы. И площадь круга.
— Давайте, — отвечаю ему с готовностью. — Но уверены ли
вы в интегрируемости функций, графиками которых служат
дуги окружности и параболы? Ведь не зря же, мы, когда давали
определенному интегралу определение через предельный
переход, говорили: если предел существует. Или вы думаете, что он
существует для всех на свете функций? Напрасно! Ну-ка, возь-
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
397
мите функцию Дирихле и попытайтесь ее проинтегрировать на
отрезке [0,1].
— Она вообще не интегрируема ни на каком отрезке. Нам это
на лекциях показывали.
— Повторите, как это делалось. Идите к доске.
— Ну, тут все довольно просто, — с небрежной легкостью
заявляет он. — Устраиваем произвольное разбиение отрезка. На
каждом отрезочке Ах*; найдется рациональная точка, функция
Дирихле в каждой такой точке равна единице, вся интегральная
сумма получается равной единице и ее предел тоже. На
каждом отрезочке есть и иррациональные точки, функция Дирихле
в каждой такой точке обращается в нуль, вся интегральная
сумма тоже будет равна нулю и предел суммы тоже.
— Очень хорошо! — хвалю столь четкое начало
рассуждения. — Не забываете про наш уговор, сразу заучиваете то, что
говорил лектор! Какой же вывод следует из того, что вы сказали?
— Получается, что определенный интеграл может принимать
разные значения. А это... ну... так не бывает.
— Как вы сказали? «Так не бывает?» Первый раз слышу,
чтобы математический вывод формулировался в таких словах!
Исправьтесь сейчас же! Напишите определение определенного
интеграла через интегральную сумму. Так... все правильно. Как
читается это определение?
— Определенным интегралом называется предел такой
суммы при А, стремящемся к нулю, если он не зависит от разбиения
и от выбора &.
— Тоже правильно. Вдумайтесь в то, что вы написали и
прочли, и скажите, почему функция Дирихле на отрезке [0,1] неин-
тегрируема.
Напряженные складки смяли розовый лоб Лапикова.
— Думайте! Думайте! — подстегиваю его. — Тут
действительно все просто!
И вот он расцветает смущенной улыбкой:
— Предел зависит от выбора &. Значит, интеграл не
существует.
— Точнее, в такой ситуации не существует сам предел, а
стало быть — и определяемый через него определенный интеграл.
Садитесь, Лапиков. Но перед тем, как сесть, напишите
определение еще одной функции — проверим, интегрируема ли она на
отрезке [0,1]. Для рациональных чисел, выражаемых
несократимой дробью ^, эта функция равна ^, для иррациональных —
нулю.
398
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
[Гл. 5
— Тоже вроде бы всюду разрывная, — заявляет Костюк.
— Во-первых, не всюду — докажите это, на досуге если
желаете, — а во-вторых, уверены ли вы, что любая разрывность —
помеха интегрированию?
Жду, пока ребята освоятся с диковинной функцией.
— Вы чем-то расстроены, Кочин?
— График не получается... Я ее график хотел построить.
— В виде привычной непрерывной линии график этой
функции, пожалуй, не получится. Но, может быть, здесь удастся
придумать какое-то нестандартное наглядное изображение?
— А что, если... — нерешительно приподнимается Мухин.
— Есть идея? Пожалуйста, — зову его к доске.
— Что, если попробовать порисовать по точкам, хотя бы
отдельные нарисовать точки? — с каким-то опасением заносит он
мел над вычерченными им осями координат. — Сначала все ра-
циональные, которые ^ — сначала даже только такие, у которых
п = 2 — их тут всего одна, ^ — и функция тут такая же... (Он
ставит жирную точку над серединой единичного отрезка).
Теперь, если знаменатель тройка — будет уже два числа, | и -^ —
а функция в них |...
Еще две точки возникают над единичным отрезком. И,
сминая свое пояснение в комок из слов, он с нарастающим
возбуждением ставит еще три точки на высоте | над торопливыми
штрихами, разбившими отрезок на четыре части, еще четыре — над
штришками, делящими отрезок на пятые доли... Горт пытается
что-то возразить, но я останавливаю его жестом...
— Вот такая пирамида, — с удовлетворением оглядывает
Мухин свое произведение.
К). В. Пухначев]
СЕМЬ СЕМИНАРОВ
399
— Ну и что дальше? — спрашиваю в надежде, что он перейдет
к рассуждениям.
— Дальше надо еще две точки — в нуле нуль — а в
единице, наверное, единица — это ведь | - а в нуле, наверное,
нуль — какой-то треугольник косой — некрасиво — если в
единице переопределить нулем, то ровно будет — или даже в нуле
единицей — зубец вот такой — как, все равно, у кремлевской
стены...
Треугольник, некрасиво, пирамида, зубец, красота... Что
кго?! Я смотрю на Мухина, словно вижу его впервые. Туда
ли он попал? Мысль, смутно шевелившаяся у меня в голове
при прежних с ним разговорах, сейчас звучит во мне со всей
отчетливостью: ведь у него же явно не математический, а
гуманитарный склад ума, то и дело выдающий себя своими
типичными проявлениями! Это и привязанность к конкретным
примерам, и стремление к цельным мыслительным образам:
если рассуждение не удалось ему сразу и целиком, он с великим
трудом дорабатывает его логически, особенно, если при этом
приходится раскидывать мыслью на несколько шагов вперед;
гак было с ним от самых первых наших занятий. Это и его
нпечатлительность, часто завораживаемая яркой деталью того
или иного построения: другие детали остаются при этом вне
поля зрения и все вместе никак не складываются в логическую
структуру. Так было, например, на позапрошлом семинаре,
когда он доказывал несуществование предела в нуле у разности
sin i — А: первое слагаемое завладело всем его вниманием,
а про второе он забыл... Может быть, ему следует, пока не
поздно, перейти в другой вуз? Но разве в математике не нужно
образное мышление? Красивая пирамида, которую он только
что построил, я уверен, сейчас кому-то подскажет убедительное
решение поставленной мною задачи... А логичность, которую
и стараюсь ему привить, конечно же, ему не помешает, даже
(*сли он изберет специальность, далекую от математики.
Воспитанный ею строгий стиль мышления укрепит его позиции в
любом деле: судьбы художника Ге и режиссера Эйзенштейна
дают прекрасные тому подтверждения.
— Кажется, я придумал, — вызывается к доске Кулагин. Взяв
мел, он несколько секунд молчит и только пожирнее
вырисовывает точки графика, набросанного Мухиным.
— Ты берешь |? — останавливает его Горт на той точке, о
которой порывался поспорить с Мухиным. — Это же сократимая
дробь, она равна \.
400
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
[Гл. 5
Кулагин стирает злополучную точку, медленнее перебирает
точки, соответствующие дробям со знаменателем 5...
— Дальше идут дроби с п = 6, из них много сократимых, —
предупреждает Горт.
— Да-да, — глухо отвечает Кулагин, погруженный в свои
мысли... И вдруг решительно:
— Все-таки я их возьму!
Крошащимся мелом он пропечатывает всю эту шестерку
точек, резким движением проводит горизонталь над единичным
отрезком и помечает ее высоту буквой е. И в полный голос,
уверенно смотря на меня:
— Пусть е — произвольно малое число. Посмотрим, в каких
точках отрезка [0,1] значения функции меньше е. Во-первых,
во всех иррациональных: там функция вообще равна нулю. Во-
вторых, в таких рациональных, которые выражаются
несократимыми дробями со знаменателем больше \. Таких дробей
бесконечно много. А остальных рациональных точек — конечное
число. Теперь... теперь надо взять разбиение таким мелким, чтобы
нам эти точки не помешали... Сейчас... Сколько их всего, этих
точек? Один раз ^, потом два раза \ и §... Я их умножу на А, а
сейчас просто подсчитаю, — бросает он на меня предупреждающий,
отводящий преждевременные возражения взгляд и опять
углубляется в свои подсчеты, — три раза |, | и |... ну, не три раза,
конечно, а два, потому что | не в счет, это ^, ее мы уже учли, но я
сейчас просто сверху... потом четыре раза ^, |, | и |, потом пять
раз g, g — я опять сверху оцениваю... Нет, я лучше по-другому.
Вот я выделю в интегральной сумме все слагаемые,
соответствующие отрезкам разбиения с такими точками, и соберу их в от-
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
401
дельную интегральную сумму, обозначу ее сигмой со штрихом:
^//(^i)Axi. Потом оценю эту сумму сверху, возьму на
отрезках разбиения точки & с абсциссами 5> 5> §> 5> 5> 5 и так Р&л^-
Ничего, что повторяются, это оценке сверху не повредит, даже
наоборот. Ну вот, если так выбирать &, то тогда слагаемые в
сумме ^2 примут самые большие из возможных значений, и оценка
будет такой: £'<[! + (! +i) + (I + I +I)...]A = [i + § +f + ...]A.
Тут в квадратных скобках все числа меньше единицы. А всего
их? Знаменатель меньше ^... А вот мы их и пересчитаем по
знаменателям: 2,3,4... Ну, в общем их меньше \. Каждое меньше
единицы, значит, сумма в квадратных скобках меньше ^. Если
Л = £2... Да, точно! Тогда X)' < £2 • \ = £•••
...Сколько раз, следя за его работой, я отмечал про себя: как
спорится у него дело! Конечно, он не сыплет идеями, как Горт
или Миклашевский, работает не быстро — но не отступит, не
добившись результата. Не удаются выкладки с формулами —
он построит график, не идет общее аналитическое
исследование он подыщет и рассчитает характерный частный случай, не
получается приближенная оценка — он быстренько вычислит
на калькуляторе точную величину, испробует все пути — и в
конце концов нащупает здравый и простой подход к любой
каверзной проблеме. Этот природный здравый смысл, эта
завидная уверенность в успехе притягивает к нему ребят — не зря он
староста.
Поймав на себе мой пристальный взгляд, он умолкает,
видимо, заподозрив во мне какое-то недоверие к его
рассуждению.
— Продолжайте, продолжайте, Андрей, — жестом отвожу его
подозрения.
— Теперь об остальных слагаемых /(^Дх*. Я обозначу
их сумму Y^!'• Для них /(&) < £•> а сумма всех таких Ах*
меньше единицы. Значит, ^!' < е. А вся интегральная сумма
Е = Е' + Е"<2е.
Он кладет мел и вытирает руки тряпкой, словно
мастеровой, закончивший работу у станка; странно выглядит он в этот
момент: высохшая тряпка пачкает еще сильнее его вымазанные
мелом пальцы.
— Теперь строго: мы доказали, — оглядывает он все свои
выкладки, — что если взять достаточно мелкое разбиение, то можно
сделать интегральную сумму сколь угодно малой. А это значит,
что ее предел при мелкости разбиения, стремящейся к нулю, ра-
402
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
[Гл. 5
вен нулю независимо от выбора точек f$. Функция интегрируема,
и интеграл от нее равен нулю.
— Отлично, садитесь, Андрей. Как видите, —
обращаюсь ко всем, — решение оказалось довольно трудоемким.
И вы, вероятно, почувствовали в этой трудоемкости нечто
настораживающее: неужели каждый раз, когда нам
придется вычислять какой-либо определенный интеграл, нам сначала
придется столь же долго и изобретательно выяснять, существует
ли он?
— Да ведь у нас и функция была какая непростая! — не
принимает моих чрезмерных опасений Миклашевский.
— В каком смысле непростая?
— В том, что она всюду разрывна.
— Не всюду, а только в рациональных точках — это можно
доказать.
— Пусть только в рациональных — все равно не
непрерывная.
— Вы произнесли слово, которое нам сейчас очень кстати.
Пример, решенный Кулагиным, естественным образом подводит
нас к вопросу: нельзя ли указать, какие-либо свойства функций,
из которых наверняка следовала бы её интегрируемость? Как
вы считаете, Миклашевский? Называл ли вам лектор какие-либо
классы интегрируемых функций? Не помните? А вы, Меншиков?
Не заглядывайте в конспект! Тоже не помните? Опять не были
на лекции?
— Да был я на ней! — с хмурой обидой в голосе отводит он
взгляд.
— А вы что скажете, Аргунова?
— Если функция непрерывна на отрезке, то она на нем
интегрируема.
— Неплохо! Однако я уверен, что лектор называл вам более
широкий класс интегрируемых функций, куда входят и
непрерывные. Вспоминаем, вспоминаем, ребята!
Во многих тетрадях возникают варианты графика кусочно-
непрерывной функции, которая, вероятно, разбиралась на
лекции, — их рисуют не только те, в чьей памяти я не сомневаюсь,
но и Сынчиков, и Сутеев, и Мухин...
— Мухин, не поможете?
— Зрительно-то я эти функции представляю, о которых
лектор говорил, — тянет он, одновременно прочерчивая пальцем в
воздухе ступенчатую линию, — а вот как они называются...
сейчас... нет, не помню.
К). В. Пухначев] СЕМЬ СЕМИНАРОВ 403
Воспроизвожу обрисованную им линию на доске:
— Так что же это за функции? Горт, помолчите, я спрашиваю
не вас. Не можете вспомнить, Мухин? А ведь лектор наверняка
называл их точным термином!
— Называл, — соглашается он. — Но ведь вы сами говорили —
не в терминах дело! Представлять-то я себе представляю, что это
*а функции!
— Я действительно говорил, что знание терминов немного
стоит, если не подкрепляется их пониманием, представлением,
что ими обозначено. Но и одно лишь представление, не
выраженное в четких формулировках, мало что дает: вспомните, как
Костюк из-за этого долго не мог доказать связь между диффе-
ренцируемостью функции и существованием производной. Как
бы вас получше убедить? Вот, — достаю из портфеля небольшой
гомик, — я сейчас перечитываю роман Владимира Богомолова
«Момент истины». Действие происходит в конце Великой
Отечественной войны. В тыл нашей армии заброшено несколько особо
опасных вражеских лазутчиков; их необходимо поймать в
кратчайший срок; один из наших контрразведчиков сидит в засаде
неподалеку от хаты, из которой должен выйти шпион — и вот
гот действительно появляется на дороге. Контрразведчик,
уверенный в своем успехе, все же не может полностью исключить
вероятность неудачи и на этот случай он... Что же он делает?
Как вы думаете, Мухин?
— Наверное, внимательно его разглядывает, этого шпиона,
старается лучше его запомнить, чтобы потом его разыскать, если
он убежит...
— Верно, но не до конца. Опытный контрразведчик знает, что
чисто зрительные представления стоят немного. А что он делает
и думает, я сейчас вам прочту: «Я хорошо разглядел его сильное,
нластное лицо и хотя ничуть не сомневался, ... что он от меня
уже не уйдет — я слеплю его как глинку! — все же по
обыкновению прикинул его словесный портрет: рост — высокий; фигура —
404
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
[Гл. 5
средняя; волосы — русые; лоб — широкий; глаза — темно-серые;
лицо — овальное; брови — дугообразные, широкие; нос толстый,
прямой, с горизонтальным основанием; рот — средний, с
опущенными углами; ухо — треугольное, малое, с выпуклым проти-
вокозелком». Как видите, контрразведчик закладывает в свою
память нужную информацию, оформляя ее в строгих терминах,
так она хранится дольше и надежнее, психологией хорошо
изучен этот факт. Его тем более следует учитывать, если вы хотите
не только запомнить какую-то информацию, но и использовать
ее в дальнейшем в своих рассуждениях. Вы поняли, что я сказал,
Мухин?
— Понял, — кивает он и указывает глазами на нарисованный
мною график. — Я вспомнил, как они называются — кусочно-
непрерывные — такие вот функции. А теорема была такая: если
на некотором отрезке функция кусочно-непрерывна, то она на
этом отрезке интегрируема.
— Не так! — прорывается-таки Горт. — Кусочно-непрерывные
лектор приводил только как пример; теорема была про...
— Горт, — останавливаю его, — не мешайте нам с Мухиным
разговаривать! Функцию, которую я нарисовал, — возвращаюсь
к Мухину, — вы назвали правильно. А вот формулировку
теоремы заузили, хотя я вас уже не раз предостерегал: нельзя
ограничивать понимание математического факта особенностями
конкретной иллюстрации, которой его можно пояснить. Это еще
одна причина, по которой нужно не останавливаться на
зрительных представлениях о математических понятиях, а идти глубже,
к их словесному выражению в строгих терминах: всякая
иллюстрация носит частный характер, наиболее же общую картину
могут обрисовать лишь абстрактные формулировки.
— Сейчас я получше вспомню, — просит Мухин о второй
попытке. — Если на некотором отрезке функция имеет конечное
число точек разрыва — конечного разрыва — в смысле не
бесконечного — то она на этом отрезке интегрируема.
— Нет, — качаю головой, — опять не совсем то. Кто поможет
вспомнить злосчастную теорему?
Руки поднимают Горт, Синица, Рамзин... Попрошу Рамзина,
чтобы почувствовал, каким я хочу его видеть:
— Помогите, пожалуйста, Мухину, Сергей.
Назидательно, но без высокомерия он диктует:
— Если некоторая функция /(х), определенная на некотором
отрезке [а, Ь], ограничена на нем и имеет на нем конечное число
точек разрыва, то она интегрируема на этом отрезке.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
405
— Очень хорошо. Если кто-то не помнит эту теорему, пусть
запишет ее себе еще раз и затвердит накрепко. Повторите
ее, пожалуйста, Рамзин! Она не раз поможет нам решать
вопрос об интегрируемости функций. Кстати, как доказывается
теорема, которую напомнил Рамзин? — перевожу взгляд на
Стрельцова.
— Да в общем-то просто, — отвечает он.
— Я спрашиваю не ваше мнение о доказательстве, а само
доказательство.
— Чтобы доказать эту теорему, надо привести еще три
других.
— Так каких же? Идите к доске и рассказывайте все по
порядку. А вы, ребята, внимательно слушайте и вспоминайте
определение понятий, формулировки и доказательства теорем, которые
будет приводить Стрельцов. Начинайте, Юра.
— Прежде всего, если функция интегрируема на отрезке
[а, Ь], то она на нем ограничена. В самом деле, предположим,
что функция f{x) неограничена на [а, Ь]. Тогда каким бы ни
было разбиение отрезка, функция не будет ограничена и на
каком-то одном из промежутков разбиения; значит, можно
сделать сколь угодно большим соответствующее этому
промежутку слагаемое интегральной суммы и всю сумму тоже. Таким
путем при последовательном делении отрезка [а, Ь] с бесконечно
уменьшающейся мелкостью мы можем построить бесконечно
возрастающую последовательность интегральных сумм, что
противоречит определению интегрируемости функции.
— Одна теорема есть, — отмечаю, когда он останавливается
для короткой передышки.
— Теперь введем понятие верхней и нижней сумм Дарбу.
Рассмотрим ограниченную функцию /(х), определенную на
отрезке [а, Ь]. При любом его разбиении функция будет
ограничена и на каждом промежутке разбиения Axi. Обозначим
через mi и М»; соответственно точную нижнюю и точную
верхнюю грань значений функции на промежутке Дхг. Суммы
п п
s = ^2miAxi и S = ^MiAxi называют соответственно нижней
г=1 г=1
и верхней суммами Дарбу. Легко видеть, что любая
интегральная сумма для данного разбиения заключена между обеими
суммами Дарбу. Есть теорема: для существования
определенного интеграла необходимо и достаточно, чтобы разность сумм
Дарбу стремилась к нулю, когда к нулю стремится мелкость
разбиения. Доказательство, извините, не помню.
406
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
[Гл. 5
Попросить кого-нибудь помочь? Гарин или Горт припомнили
бы все до мелочей. Впрочем, не стоит, пожалуй: сейчас лучше,
не зарываясь в глубины, дать сжатый и цельный обзор — с
птичьего, так сказать, полета — самых важных положений, которые
понадобятся в дальнейшем.
— Ладно, — дарую Стрельцову великодушную поблажку, —
пусть каждый — и вы в том числе, Юра, — проработает это
доказательство дома сам.
...Печать какого-то благодушия лежит на всем поведении
Стрельцова. И хотя по своим знаниям и навыкам он превосходит
многих в группе, нередко лучше других умеет вскрыть суть
предлагаемых мною задач и сформулировать необходимые для
их решения понятия (недаром я так часто обращаюсь к нему за
этим) все эти достоинства сильно обесцениваются в нем
абсолютным безразличием к собственным успехам, полным нежеланием
ставить себе какие-то цели и добиваться их. При всем при
этом он остается очень милым парнем: он хороший товарищ,
всегда готов помочь слабому, защитить его от несправедливых
нападок, всегда искренне радуется удачам друзей... К своим же
равнодушен совершенно! Конечно, противоположные черты —
жажда лавров, желание покрасоваться — отталкивают, Рамзин
яркий тому пример, но в должной мере стремление к успеху, а
вернее сказать, воля к победе для студента просто необходима!
Как импонирует она в Кочине! Явно уступая Стрельцову своей
математической подготовкой, часто не до конца представляя,
что требуется сделать в предложенной ему задаче, он смело
берется за нее — и верится: он и в жизни, в будущей работе
добьется большего.
А впрочем — кто знает, кто знает... Мне все почему-то
чудится: настанет час и, призванный к большому
захватывающему делу, Стрельцов проснется всем своим глубоким умом, как
дремавший лев...
— Так о чем еще вы хотели рассказать, Стрельцов?
— Следующая теорема — та, которую приводила Галя: если
функция непрерывна на отрезке [а, Ь], то она интегрируема на
этом отрезке.
— А вот ее доказательство хорошо бы повторить.
— Есть... Сначала берется разность сумм Дарбу и записыва-
п
ется в виде ^2 (Mi — mi)Axi. После этого надо вспомнить теоре-
г=1
му Кантора: если функция f(x) непрерывна на каком-то отрезке
[а, Ь], то она на нем и равномерно непрерывна, то есть для любого
IO. В. Пухначев]
СЕМЬ СЕМИНАРОВ
407
е найдется такое 5, что как только модуль разности любых двух
чисел х'и х" из [а, Ь] меньше 5, то \f(x') — f(x")\ < е. То есть, если
п
Axi < 5, то Mi—mi < е и, значит, величину ^(М^—m,i)Axi мож-
г=1
п
по оценить сверху величиной Yl£^xi = s(b — a), а она стремится
г=1
к нулю при бесконечном убывании е. Стало быть, разность сумм
Дарбу стремится к нулю, и по предыдущей теореме интеграл от
функции по промежутку [а, Ь] существует.
— Ну и наконец, — нетерпеливо напоминаю ему, — об
ограниченных функциях, имеющих на отрезке [а, Ь] конечное число
точек разрыва.
— Да, теорема о том, что всякая такая функция интегрируема
на [а, Ь]. Доказывать нужно?
— Очень желательно.
— Ладно, попробую, хоть не совсем хорошо помню. Как тут
но здравому смыслу? Разобьем отрезок на промежутки и
отберем из них все те, которые не имеют точек разрыва функции
\\ качестве внутренних или граничных. Все такие промежутки
сложатся в отрезки, на которых функция непрерывна и по
теореме Кантора равномерно непрерывна. Тогда по любому наперед
заданному е можно выбрать столь малую мелкость разбиения,
что на отобранных нами промежутках разность Mi — mi будет
меньше е и соответствующие величины (Mi — m,i)Axi в сумме
будут меньше е(Ь — а). Так... Теперь об остальных промежутках.
На каждом из них разность Mi — тп^ ограничена в силу
ограниченности функции на всем отрезке [а, Ь], ограничена каким-то
числом А... Надо сделать мелкость разбиения достаточно
малой... пусть она будет меньше того же е. И тогда
соответствующие величины (Mi — rrii)Axi] в сумме будут меньше кАе, где к —
число точек разрыва. Разность сумм Дарбу при этом
оказывается меньше е(Ь — а) + кАе, то есть может быть сделана меньше
любой наперед заданной величины, то есть стремится к нулю —
следовательно, наша функция интегрируема на [а, Ь].
— Очень хорошо. Не приведете ли еще какие-нибудь теоремы
об определенных интегралах, которые давал лектор?
— Ну, что еще? Вот такая, например, теорема: если f(x)
интегрируема на [а, 6], то на этом отрезке интегрируема также А:/(х),
б б
где к — какая-нибудь константа, причем Jkf(x)dx = kff(x)dx.
а а
Если на каком-то отрезке интегрируемы какие-то две функции
408
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
[Гл. 5
f(x) и д{х), то там интегрируемы их сумма и разность, причем
ь 6 6
f[f(x)±g(x)]dx = ff(x)dx±f. Если переставить пределы инте-
а а а
грирования, то интеграл изменит знак... Если изменить значение
интегрируемой функции в конечном числе точек на отрезке
интегрирования, то она останется интегрируемой и интеграл от нее
будет прежним... Что-то больше ничего не вспоминается.
— Кто поможет?
— Если на каком-то отрезке интегрируемы две функции, то
там интегрируемо и их произведение, — припоминает Костюк.
— Хорошо. Еще, еще теоремы! Буткус, поддержите разговор!
— Если функция интегрируема на отрезке, то она
интегрируема на любой его части. И наоборот...
— И наоборот, — подхватывает Стрельцов, — если она
интегрируема на каждой части отрезка, то и на всем отрезке тоже,
и весь интеграл по полному отрезку равен сумме интегралов по
всем частичным отрезкам.
— Видать, у вас восстановилась память, Юра. Тогда,
пожалуйста, еще какую-нибудь теорему.
— Если значения интегрируемой функции f(x) на [а, Ь]
ограничены снизу и сверху числами т и М соответственно, то
значение интеграла от этой функции по промежутку [а, Ь] заключено
между числами т(Ъ — а) и М{Ь — а).
— Отлично! Эта теорема имеет обширное развитие.
Прежде всего, надо заметить, что ей часто придают несколько иную
форму. Не вспомните, какую, Стрельцов?
— Можно подобрать такое число /i, лежащее между т и М,
б
что ff(x)dx = /i(b — a).
а
— Верно. В частности, если функция fix) непрерывна на
отрезке [а, Ь]...
— То можно найти такую точку с, принадлежащую [а, Ь], что
б
ff(x)dx = f(c)(b — а), — договаривает Стрельцов. — Это так
а
называемая теорема о среднем.
— У этой теоремы есть наглядная геометрическая
интерпретация, — рисую на доске поясняющий чертеж. — Площадь
криволинейной трапеции под графиком функции f[x) равна площади
прямоугольника с основанием {Ь — а) и высотой /(с). Скажите,
Юра, лектор давал эту теорему только в той формулировке, что
вы прочли?
К). В. Пухначев]
СЕМЬ СЕМИНАРОВ
409
— Насколько я помню, да.
— Но, может быть, — оборачиваюсь к аудитории, — кто-то
шает более общие формулировки теоремы о среднем? А ну,
Миша! — посреди всеобщего молчания обращаюсь с последней
надеждой к Гарину. И он не обманывает мою надежду:
— Если на [а, Ь] интегрируемы две функции, f{x) и д(х),
причем одна из них, для определенности д(х), не меняет знака на
ь ь
[а, 6], то ff(x)g(x)dx = /j,fg(x)dx. Тут /i — опять некоторое число
а а
между точной верхней и точной нижней гранью значений f{x)
па [а, Ь\\ оно равно одному из ее значений на [а, Ь] если она
непрерывна.
Записываю сказанное им на доске.
— Да, — снова берет слово Стрельцов, — я еще одну теорему
:*абыл: если у интеграла верхний и нижний пределы совпадают,
то он равен нулю.
— Еще одну... Только одну, вы думаете? Больше... Но
я надеюсь, что они не необходимости вспомнятся по
ходу решения примеров. Давайте перейдем к ним. Садитесь,
Стрельцов. Первый пример — по заявке Лапикова:
определить площадь под параболой. Или точнее: вычислить интеграл
1
fx2dx. Исходим в вычислениях из определения определенно-
и
го интеграла. Кто хочет пойти к доске? Что, нет ни
одного желающего? Тогда придется кого-то вызвать. Например,
Сутеева.
Ему сподручно будет решать эту задачу: она легко
переводится на графический язык. Сразу подсказываю ему такую
возможность:
— Рисуйте функцию х2 на отрезке [0,1], пишите интеграл,
который надо вычислить, и вычисляйте его с помощью
интегральных сумм. Что же вы стоите?
— Забыл, как это там... как пишется определение интеграла
через эти суммы.
— Можете взять свою тетрадь и переписать оттуда.
Выискав в своих записях нужное место, он сначала
перерисовывает на доску поясняющий чертеж, потом читает:
— Вот... функция f(x)... отрезок [а, Ь]... разбили отрезок на
п
эти Ах{... взяли на них &... сумма ^/(£г)Д#г--- А — это макси-
г=1
мальная длина Axi... она стремится к нулю... переходим к пре-
410
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
[Гл. 5
делу... если предел суммы существует, функция называется
интегрируемой.
— Да, называется интегрируемой на отрезке [а, Ь]. А значение
предела называется...
ь
— Интегралом ff(x)dx.
а
— Да, определенным интегралом. Все?
И, не дождавшись ответа, сам отвечаю на свой вопрос:
— Нет, не все. Еще надо предположить, что предел суммы
п
^2f(£i)Axi существует при любом способе разбиения отрезка
г=1
[а, Ь] и при любом выборе точек &; на промежутках Axi —
только в таком случае функция f(x) называется интегрируемой
на отрезке [а, 6]. Или совсем уж последовательно и четко: если
при любом разбиении отрезка [а, Ь] на промежутки Axi и при
любом выборе точек & на промежутках Axi и при стремлении к
нулю мелкости разбиения А = max{Axi} существует предел ин-
п
тегральной суммы ^2f(&)Axi, то он называется определенным
г=1
интегралом от функции f(x) по отрезку [а, Ь] и обозначается
ь
ff(x)dx, а функция называется интегрируемой на этом отрезке.
а
На первый взгляд я вдалбливаю трудно усвояемое
определение забывчивому и непонятливому студенту. Но есть у
происходящего и другой, более важный смысл: вслушиваясь в
наш с Сутеевым разговор, ребята исподволь троекратно
повторяют про себя важное определение и закрепляют его в своей
памяти: сначала — реконструируя его по отрывочным фразам
Сутеева, потом — уточняя пропущенное им, и наконец —
выслушивая все определение целиком в моей полной
формулировке.
— Итак, ребята, — несколько переиначиваю определение,
чтобы протянуть связующую нить от него к поставленной
задаче, — интегрируемость функции f(x) на отрезке [а, Ь] или, что то
ь
же, существование определенного интеграла ff(x)dx по опреде-
а
п
лению равнозначно существованию предела lim^/(^)Axi при
A^oi=1
любом разбиении отрезка на промежутке Ах*; и при любом
выборе на них точек &. Эту равнозначность можно трактовать с
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
411
двух как бы противоположных точек зрения. С одной стороны,
можно установить существование указанного предела, не
зависящего от разбиения отрезка и выбора значений функции, и отсюда
ь
заключить об ее интегрируемости; интеграл Jf(x)dx будет равен
а
этому пределу. С другой стороны, можно в силу каких-то свойств
функции установить ее интегрируемость — то есть существова-
71
ние предела Ит]Г/(&)Да;г при произвольном разбиении отрез-
Л—°г=1
ка [а,Ь] и произвольном выборе точек &. В силу такой произ-
ь
вольности мы будем вправе для вычисления интеграла ff(x)dx
а
через интегральную сумму проводить разбиение отрезка [а, Ь]
но наиболее удобной для дальнейших выкладок схеме, наиболее
удобным образом выбирать на промежутках разбиения точки &,
найти по такой схеме предел интегральной суммы — он и будет
равен искомому интегралу.
— Функция х2 непрерывна на отрезке [0,1], значит,
интегрируема на нем, — уверенно говорит Сутеев, уставив на меня свой
немигающий взгляд.
— Отлично! Какое же разбиение отрезка интегрирования
кажется вам наиболее простым и удобным с точки зрения
поставленной задачи?
Он молча делит отрезок [0,1] на равные части, восставляет
перпендикуляры в точках деления до пересечения с параболой,
412
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
[Гл. 5
как бы разрезая пространство между нею и осью абсцисс на
узкие полоски равной ширины.
— Что ж, проще равномерного разбиения придумать
нечего. Почему бы не попробовать взять его? Чему, кстати, тогда
будет равна длина каждого промежутка разбиения, если всего
их п? Верно, ^. А как станете выбирать точки &? Вы
берете их в серединах промежутков? Можно и так. Но, если вы
помните, еще на первом семинаре я советовал вам: на каждом
шагу математического рассуждения рассматривать все
возможные варианты этого шага. Варианты возможны и сейчас:
попробуйте-ка взять в качестве & правые концы промежутков
разбиения... так... а теперь на высоте /(&) проведите верхние
края вертикальных полосок. Так какой же будет при этом
•2
высота г-той полоски? Верно, ^. А если бы вы брали
значение функции в середине каждого промежутка разбиения?
Как выражалась бы высота полоски? Не можете даже
сообразить? Я помогу вам: середина г-той полоски имеет абсциссу
jj + 2^ — так ведь? А значение функции в этой точке... Верно,
(^jp)2. Выражение, как видите более сложное, чем ^. Значит,
я был прав, когда советовал выбирать точки & на правых
концах промежутков разбиения? Да? Ну, а чему равна в таком
случае площадь г-той полоски? Верно, ^. Теперь суммируем
п -2
площади всех полосок... так... ]>^^з... Сможете вычислить эту
г=1
сумму?
Терпеливо жду. Он наконец догадывается вынести за знак
суммы Дг:
— Получается ]>^г2, а для нее есть формула ——^-^—*. Да,
г=1
еще п3 внизу...
Догадается ли он разделить каждый сомножитель на п?
Догадался, неплохо!
Молча выполнив все нужные преобразования и в заключение
предельный переход, он кратко докладывает:
Предел — одна треть.
Итак, площадь под параболой.
К ) В. Пухначев]
СЕМЬ СЕМИНАРОВ
413
— Равна одной трети.
— Верно, равна третьей части единичного квадрата.
Отсюда нетрудно получить соотношение, о котором вы недавно го-
иорили: парабола делит площадь вот этого, — показываю на
чертеже, охватывающего ее прямоугольника в отношении один
к двум. Вас можно поздравить с успехом, Сутеев! Садитесь.
Вспомним теперь, ребята, вторую заявку Лапикова —
вычислить таким же способом площадь крута. Кто хотел бы это
сделать? Вы, Рамзин? Прошу к доске. Да, кстати, ребята, — наспо-
минаю, видя, как Рамзин рисует единичный крут с центром в
начале координат, — если график функции проходит под осью
абсцисс, площадь очерченной им криволинейной трапеции
отрицательна. Впрочем, в этой задаче, — указываю на чертеж Рам-
шна, — можно и не рассматривать нижнюю половину крута,
да и верхнюю вряд ли нужно брать целиком — достаточно
вычислить площадь его четвертушки, расположенной над
отрезком [0,1], в потом умножить ответ на четыре. Действуйте, Рам-
■шн. Ну вот, — гляжу на проворно составленную им интеграль-
ную сумму, — для получения окончательного ответа мы
должны просуммировать корни вида J\ — ^-, а для этого у нас, к
сожалению, нет соответствующей формулы. Но дело даже не
в ее нехватке, а... в чем? Кто ответит? - обращаюсь к
сидящим. — Почему определенные интегралы неудобно вычислять,
414
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
[Гл. 5
исходя непосредственно из их определения через интегральные
суммы?
— Каждый раз по-своему суммировать... Это плохо, да? —
после нескольких непринятых мной ответов пытает удачу
Кочин.
— Вот-вот! — одобрительно киваю ему. — Уже два
разобранных нами примера дают почувствовать, сколь
специфических выкладок требует вычисление каждого
интеграла, если он вычисляется с помощью интегральных сумм.
Разумно поставить вопрос: нет ли более универсального и
безотказного подхода к вычислению определенных
интегралов? Такой подход я и хочу сейчас вам напомнить. Садитесь,
Рамзин.
И после паузы, отмечающей начало новой темы:
— Рассмотрим всюду непрерывную и, стало быть, всюду
интегрируемую функцию f(x) на области значений ее аргумента £,
больших некоторого а или равных этому а. В области
определения этой функции возьмем произвольную точку х и подсчи-
х
таем интеграл ff(t)dt. В зависимости от выбора х этот инте-
грал будет принимать разные значения. Иными словами,
каждому значению верхнего предела в этом интеграле будет
соответствовать своя величина интеграла. Таким образом, он
будет представлять собою некоторую функцию от х. Обозначим
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
415
ее F(x). Наглядно ее можно истолковать так: вот мы
подсчитываем площадь под кривой у = /(£) в промежутке между а и
х; величину площади обозначаем F(x). Правая граница
промежутка [а, х] сдвигается, скажем, вправо, и соответственно
площадь F(x) изменяется — нарастает, если /(£) положительна, или
убывает, если f(t) отрицательна; напомню, что участки,
очерчиваемые кривыми, проходящими под осью абсцисс,
считаются имеющими отрицательную площадь. Естественно
поинтересоваться: как связаны друг с другом функции F(x) и /(х)? Для
ответа на поставленный вопрос можно рассмотреть несколько
участков кривой. Возьмем сначала такой, где значения
функции /(х) велики, где ее график проходит высоко над осью
абсцисс. Сдвиг точки х вправо дает здесь большую прибавку к
площади под кривой. А вот участок, где график функции /(£)
почти прилегает к горизонтальной оси, где значения /(х)
невелики. Здесь такой же, что и в предыдущем случае, сдвиг точки
х вправо дает сравнительно малый вклад в площадь под
кривой. Итак, если функция /(х) велика, то функция F{x)
нарастает быстро, если /(х) мала, то функция F{x) нарастает
медленно.
— Вы хотите сказать, — недоверчивым голосом, глядя
исподлобья, спрашивает Меншиков, — что производная от F{x)
равна /(х)?
— Да, именно это я утверждаю и прошу доказать
строго, что Ff(x) = /(x) или, иначе говоря, что F(x) является
первообразной для /(х). Над доказательством думаем все
вместе.
Чем объяснить недоуменный вопрос Меншикова? Он
говорил, так, словно впервые услыхал про интеграл с переменным
верхним пределом. Ясное дело, не был на лекции! Впрочем, по
глазам некоторых я заметил, что и они восприняли мой рассказ
как нечто новое. Может быть, лектор совсем по-другому
подавал этот раздел? Что ж, тем лучше! Идя к знакомым выводам
по незнакомым путям, напрягая мысль, ребята лишь прочнее
затвердят эти выводы.
Многие довольно быстро доказывают соотношение,
«открытое» Меншиковым. К доске вызываю Чюмина. Его решение
стоит того: на сей раз он получает ответ на редкость
удачно — исходит из определения производной, вычисляет ее
х+Ах
для функции F(x), получает при этом интеграл / f{t)dt,
х
применяет к нему теорему о среднем и, сославшись на непре-
416
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
[Гл. б
рывность функции /(£), заменяет этот интеграл
произведением /(£)Дх:
— Точка £ лежит на отрезке [х, х+Ах]. Если теперь устремить
Ах к нулю, £ будет стремиться к х, a /(f) — к f{x).
— В силу чего?
— Опять же в силу непрерывности.
— Верно.
— Значит, F'{x) = f(x). To есть F(x) — первообразная
для f(x).
— Правильно. Очень отчетливое, очень убедительное, очень
хорошее получилось у рас решение.
Может быть, я перехваливаю его, но он заслужил это:
впервые решил задачу без единой заминки.
— Садитесь, Семен, и внимательно слушайте, что я сейчас
буду говорить: речь пойдет о связи между понятиями
определенного и неопределенного интеграла, которую я когда-то обещал
вам разъяснить. Итак, ребята, мы видим, что определенный
интеграл, рассматриваемый как функция своего верхнего предела,
есть одна из первообразных для подынтегральной функции.
Этот вывод открывает перед нами удобную возможность для
х
вычисления определенного интеграла ff(t)dt. Вспомним, как
а
в начале сегодняшнего семинара мы тренировались в
нахождении неопределенных интегралов. Методами, которые мы
тогда отработали, отыщем какую-нибудь первообразную Ф(х)
для нашей подынтегральной функции f(x). Как мы
только что отмечали, интеграл с переменным верхним пределом
X
ff(t)dt = F(x) также является первообразной для функции
а
f(x). Любые две первообразные одной и той же функции разли-
К) В. Пухначев]
СЕМЬ СЕМИНАРОВ
417
х
чаются на константу: ff(t)dt = Ф(х) + С. Постоянную С в этом
а
равенстве нетрудно определить, положив х = а — тогда слева
получится нуль: 0 = Ф(а) + С. Отсюда находим С = —Ф(а).
X
Далее: Jf(t)dt = Ф(х) — Ф(а). Или в более привычном виде:
а
Ь
[/(х^х = Ф(Ь)-Ф(а).
а
— Формула Ньютона-Лейбница! — восклицает Горт, только
сейчас догадавшийся, ради чего я завел разговор об интеграле с
переменным верхним пределом.
— Она самая! — с улыбкой поворачиваюсь к нему.
— Лектор нам совсем по-другому ее доказывал. И про
функции f(x) и Ф(х) он тоже говорил по-другому: f(x)
просто интегрируема на [а, Ь], не обязательно непрерывна, а вот
Ф(х) — непрерывна и дифференцируема на этом отрезке
и равенство Ф'(х) = f(x) выполняется на интервале (а,Ь)
во всех точках, быть может, за исключением их конечного
числа.
— Не возражаю. Непрерывность функции /(#) понадобилась
нам лишь затем, чтобы проще доказать формулу Ньютона-
Лейбница. Подчеркну, что эта формула является надежнейшим
средством для вычисления интегралов, предельно простым и
универсальным. Повторю вкратце, как она применяется. Чтобы
ь
получить интеграл J/(x)cfx, берут какую-нибудь первообраз-
а
ную Ф(х) для подынтегральной функции f(x) и подсчитывают
разность ее значений в концах промежутка интегрирования:
ь
Ф(Ь) — Ф(а) = ff(x)dx. В достоинствах этой замечательной
а
формулы нетрудно убедиться на примерах. Кто из вас давно
7Г
не был у доски? Сынчиков? Прошу. Пишите: fsinxdx. Вычис-
о
ляйте. Верно, интеграл равен двум. А какой геометрический
смысл у этого результата — представляете? Нет? Я подскажу:
14 - 2019
418
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
[Гл. 5
площадь между положительной полуволной синусоиды у = sin x
и осью абсцисс равна двум. Но это так, к слову. Садитесь.
Прежде чем переходить к следующему примеру, ребята, я
хотел бы сделать небольшое примечание. Правую часть
формулы Ньютона-Лейбница обычно записывают в своеобразном
сокращении: не Ф(Ь) — Ф(а), а Ф(х)|д. И еще: легко видеть, что
для подстановки в эту разность годится любая первообразная
подынтегральной функции: ведь если взамен одной взять
другую, та будет отличаться от первой на константу, и когда мы
подставим ее в разность Ф(Ь) — Ф(а), константы сократятся при
вычитании, и разность получится та же самая. Кто пойдет к
доске следующим? Вы не хотите, Лапиков?
— Попробую, — отвечает он, вставая.
— Давайте решим заявленный вами же пример, вычислим
1
наконец площадь круга. Итак, fy/1 — х2 dx.
о
— Может быть, по частям?
— Пожалуйста.
1
В ходе преобразований Лапиков получает интеграл / J _ 2 и
надолго останавливается перед ним.
— Свой же пример и не можете решить? — подзадориваю
его. Но ничего не подсказываю: с таким простым примером он
должен полностью справиться сам. В конце концов он выходит
из тупика, но каким кружным путем! По школьному
избавляется от иррациональности в знаменателе, неправильную
полиномиальную дробь превращает в правильную, как это делалось
при вычислении неопределенных интегралов... Показываю, что
полученного им результата можно было бы достичь совсем про-
К). В. Пухначев]
СЕМЬ СЕМИНАРОВ
419
сто, с самого начала вычтя и прибавив единицу в числителе, —
II тут Лапиков берет реванш тем, что без наводящих вопросов
осмысливает сделанное: получилось уравнение для искомого
интеграла.
— Только странное какое-то уравнение, — с сомнением
разглядываю написанное им. — Смотрите: всюду в нем
определенные интегралы, то есть числа, за исключением слагаемого
х\/1 — х2. Это ведь функция, верно? Странно как-то: числа
складываются с функциями.
— Разве это функция? — робко спрашивает Аргунова.
— А если не функция, то что? — поворачиваюсь к ней.
— Не знаю, но... не функция это! — чуточку манерно
отвечает она. — Надо справа нарисовать черточку, вверху единичку
поставить, а внизу — нуль.
— То есть, — уточняю ее мысль, — надо поступить с этой
функцией, как с первообразной, — кратко доказываю, почему это
гак. — Заметьте это себе, ребята! Что же получится в результате
подстановки единицы и нуля, Лапиков?
— В единице эта функция — нуль, в нуле — тоже, разность
пуль... Это слагаемое можно просто выбросить.
И он решает уравнение, освобожденное от недоразумений:
/01VT=^dx=f.
— А вся площадь круга?
— В четыре раза больше, то есть 7г.
— Это для круга единичного радиуса. А для круга
радиуса Ю
— Площадь растет, как квадрат... 7гД2?
— Как и ожидалось. Все правильно, Лапиков. Перед тем,
как идти обратно, напишите следующий пример: J0 \Jex — 1 dx.
Кто подскажет, как его решать?
— Надо сделать замену ех = t2, — советует Миклашевский.
14*
420
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
[Гл. 5
— Лучше ех — 1 = £2, — настаивает Горт.
— Да, пожалуй, это лучше, — оцениваю его предложение. —
Не пойдете ли к доске, Саша?
— Когда будем делать подстановку, надо не забыть про
пределы интегрирования, — прозорливо подмечает он.
-- Заметьте себе, ребята, — гляжу в аудиторию, — это важное
соображение!
Горт между тем продолжает:
— Когда х равно нулю, t тоже нуль, когда х = In 2, то
t = 1. Значит, после подстановки получится такой интеграл:
2 f0 щг[ dt. Мы его когда-то уже брали.
Несколько секунд спустя он пишет ответ: 2 — |.
— Лихо! Не решите ли еще один пример? Пишите
интеграл fQ * sin4 x^cos4 x. Лихо, лихо, — приговариваю
под его стремительные выкладки.
Вот и ответ готов:
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
421
-4=arctg(^s^)|o7r. Что ж, подставляйте, вычитайте... Что-
получилось?
— Нуль! — бодро рапортует он.
— Великолепно. А подынтегральная функция, которую
вы представили в виде в|* а 2х, судя по такому представ-
2
лению, нигде не меньше единицы. Иными словами, график
этой функции на промежутке [0,27г] очерчивает отчетливо
положительную площадь. И в то же время, согласно вашему
окончательному результату, эта площадь равна нулю.
Великолепно!
— Парадокс, — обескуражено бормочет Горт.
Скольжу взглядом по лицам сидящих в первом ряду. Ни
малейшего проблеска здравого взгляда на суть проблемы! И
откуда-то издалека, из-за этой глухой стены непонимания —
спокойный голос Гарина:
— Первообразная рвется. Все как в примере с е"^'.
— Что же делать?
— Надо устранить разрывы. А лучше взять интеграл по
промежуткам, где первообразная непрерывна. Скажем, от 0 до j. И
умножить его на восемь. Тогда получится.
— А вас не смущает, что при j первообразная 4= arctg(^#)
не существует? Ведь при подстановке \ вместо х в функцию tg 2x
получается tg^, что не имеет смысла.
— Сейчас, — невозмутимо отражает Гарин мой полемический
наскок. — У нас подынтегральная функция непрерывна?
Непрерывна — что на [0, ^]> что на [0,27г], везде. А раз она
непрерывна, то первообразная для нее дифференцируема, Чюмин это
доказывал. Дифференцируема — значит, тоже непрерывна и
тоже везде. Там, где функция ^arctg(^f) сУш^ествУет и
непрерывна, можно через нее выразить первообразную. А в точке,
где она не существует, у нас это ^, ее надо доопределить так,
чтобы она там совпала с первообразной, то есть непрерывным
образом.
— Разгадали-таки мой обман! — посмеиваюсь, довольный.
И поясняю ребятам, — в чем он состоял:
— Когда я сказал «первообразная 4= arctg(^Jp)», то я
неправомерно отождествил две несовпадающие друг с другом вещи.
Вот первообразная для подынтегральной функции sin4 x+cos* х ? —
рисую на доске волнисто ползущую ввысь из нуля
непрерывную кривую, — а вот функция 4=arctg(^y^), то и дело рвуща-
422 ИНТЕГРИРОВАНИЕ ФУНКЦИЙ [Гл. 5
яся, — рисую ее график. — На полуинтервале [0, j) она совпа-
дает с первообразной для нашей подынтегральной функции. А
на дальнейших интервалах уже не совпадает, хотя во всех
точках имеет ту же производную и, следовательно, отличается на
константу. Ради полного совпадения ее дальнейшие ветви надо
приподнять и в точках стыка интервалов доопределить до
непрерывной. Но лучше это сделать лишь в точке ^, как предлагает
Миша, взять интеграл по промежутку [0, f ] и умножить его на
восемь - это и будет /0 п sin4 ДЖС054 х ■ Ну, а к чему же, —
возвращаюсь к Горту, — стремится функция 4= arctg(-^#) при х,
стремящемся к j?
— Стремится к -j=. Доопределим ее там этим числом.
— Ответ? Чему равен скомый интеграл от нуля до двух пи?
— 2тг\/2.
— Очень хорошо, садитесь. Ну вот, ребята, как видите, не так-
то все просто с формулой Ньютона-Лейбница: отыскивай, мол,
в таблицах первообразную да вычисляй разность ее значений.
Вот еще один пример на этот счет: интеграл /0 i+a.2 dx. Пусть
каждый поищет свой путь его вычисления.
Минут через пять встаю из-за стола, иду между рядами. И
еще минут через пять:
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
423
— Ну как, есть у кого-нибудь ответ?
— Нет, — за всех отвечает Лапиков.
— А как вы пытались вычислить этот интеграл?
— По формуле Ньютона — Лейбница.
— Понятно... Все стараются применить к этому интегралу
формулу Ньютона-Лейбница, а между тем первообразная этой
подынтегральной функции, — ради эффекта выдерживаю
секундную паузу, — не выражается через элементарные.
Оторвавшись от своих тетрадей, все смотрят на меня так,
будто хотят упрекнуть в каком-то подлоге.
— Зачем же так... жестоко? — изрекает свою излюбленную
трагическую фразу Синица.
— А что, собственно, плохого в том, что первообразная не
выражается через элементарные функции и потому мы не можем
выписать ее, не можем применить формулу Ньютона-Лейбница?
Разве на формуле Ньютона-Лейбница свет клином сошелся?
Разве, если она где-то отказывает, мы не можем преодолеть трудный
участок пути к ответу своей смекалкой, искусством
преобразований? Я посмотрел ваши попытки преобразовать
подынтегральную функцию и многих из вас заподозрил в недальновидности
— тех, кто заменял х через гиперболические функции, через sht
или ch t. Ассоциативная цепочка, ведущая к подобным заменам,
по-видимому, такова: натуральный логарифм — число е —
гиперболические функции. Но все эти функции выражаются суммами
экспонент, да и под знаком логарифма у нас стоит сумма. А
логарифм суммы, как известно, не преобразуется — того, кто это
не учел, я и упрекаю в недальновидности.
— А почему, — врезает Буткус свою реплику в мой монолог, —
обязательно брать в замену гиперболические функции? Можно
брать тригонометрические!
— Конечно! — поддерживаю его. — Тогда сумму под знаком
логарифма, по всей вероятности, удастся преобразовать в
произведение, а логарифм произведения можно будет разложить в
сумму логарифмов. Но через какую именно тригонометрическую
функцию лучше всего заменить х — через sint, cost или tgt?
Пусть каждый испытает ту, которая ему больше нравится, и
если получит ответ — пусть скажет.
— Лучше всего тангенс! — через несколько минут слышится
голос все того же Буткуса.
— Вы уже решили этот пример?
— Да. Те интегралы, которые не берутся, взаимно
уничтожаются. Функции под интегралом одинаковые, а пределы наоборот.
424
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
[Гл. 5
У первого от нуля до ^, у второго от j до нуля. От перестановки
пределов знак интеграла меняется. Это потому что в
определении от перестановки пределов меняется знак у всех Ах{.
И по моему приглашению он показывает свое решение на
доске.
— Все верно, садитесь. Еще раз напоминаю, ребята:
вычисление определенных интегралов не сводится к механи-
ческому использованию формулы Ньютона-Лейбница — точно
так же, как все задачи, решаемые с помощью операции
интегрирования, не сводятся к простому вычислению интегралов.
Ну, например: рассмотрим функцию, которая при ненулевых
х равна ^j5, а при нулевом — единице; требуется определить
знак интеграла JQ §1^ dx. Легко заметить, что в точке х = 7г
подынтегральная функция меняет знак, и задача сводится,
таким образом, к вопросу: какой из интегралов больше по
абсолютной величине — f£ §1^ dx или f n ^^-dxl Как мы уже
знаем, первообразная для подынтегральной функции — так
называемый интегральный синус через элементарные функции
не выражается, так что определить численные значения обоих
интегралов непросто. И тем не менее на поставленный мной
вопрос можно дать простой и строгий ответ. Как это сделать?
На размышление даю пять минут.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
425
Неожиданно для меня Миклашевский через десяток-другой
секунд вскидывает руку:
— Решил.
— Не может быть! Ну-ка к доске!
— Рисуем график подынтегральной функции, — набрасывает
он небрежную схему решения, — и в положительную полуволну
вписываем прямоугольник с шириной | и высотой ^; площадь
у него, стало быть, единица. А отрицательную полуволну
покрываем прямоугольником с шириной 7г и высотой ^ — у него
площадь тоже единица. Отрицательная полуволна не выходит
за пределы прямоугольника, потому что ее высота равна ^, она
достигается при х = ^7г, а у прямоугольника высота £.
Значит, у положительной полуволны площадь больше, чем у
отрицательной, и весь интеграл больше нуля, — заканчивает
Миклашевский.
— Архимед! — с царственной щедростью в голосе бросает ему
Меншиков.
Все верно? Или... всего лишь правдоподобно?
— Постойте, Миклашевский... Вы считаете, — что
минимальное значение подынтегральной функции достигается в точке
х = |7Г? Ну-ка вычислите производную. Так, так... Ну вот,
426
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
[Гл. 5
точка минимума функции §i^ определяется уравнением
xcosx — sinx = 0 или, что то же, tgx = x. Иными
словами, минимум достигается в той самой точке, где линия у = х
пересекает тангенсоиду у = tgx. Это очень близко к точке
х = |7г, но все-таки чуть левее ее — видите? Садитесь на место,
несостоявшийся Архимед. Ценю ваше остроумие, но оно, к
сожалению, оставило вас на полпути и передало эстафету вашему
обычному верхоглядству. Давайте, ребята, все вместе поищем
новое, точное решение.
— Я бы, — размышляет вслух Костюк, — разбил отрезок
[0,27г] на две половины, написал бы, как вы говорили, интеграл
в виде суммы интегралов по половинкам и во втором слагаемом
сделал бы замену х = тг + t.
— Пожалуйста, сделайте, — жестом зову его. — Так, вы
заменили переменную во втором интеграле... Пределы оказались
такими же, что у первого интеграла. Далее вы пишете х вместо
t. Можно ли так поступать?
— А почему нет? Не все ли равно, как обозначать
переменную интегрирования в определенном интеграле? Все равно
в конце концов получило число, ни от какой переменной не
зависящее. Если хотите, считайте, что я просто сделал замену
t на х.
— Согласен с таким толкованием. К чему вы придете,
суммируя оба интеграла? Обратите внимание: нижним пределом
интегрирования по-прежнему остается нуль, а подынтегральное
выражение содержит х в знаменателе...
— А в числителе-то sinx! Все как в исходном интеграле от
дроби §1^. Мы ее доопределили в нуле единицей. Когда мы
преобразовали интеграл, мы из этой дроби вычли дробь ^rpf, она в
нуле никакой особенности не имеет, она там равна нулю. Значит,
в нуле вся разность по-прежнему будет равна единице. Короче,
когда мы преобразовали исходный интеграл, мы пришли к инте-
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
427
гралу от положительной функции. Следовательно, этот интеграл
больше нуля.
— Во-первых, про новую подынтегральную функцию нельзя
сказать, что она везде строго положительна: в точке х = 7г
она обращается в нуль. Точнее было бы сказать, что она
неотрицательна. Во-вторых, на чем вы основываетесь, когда
говорите, что интеграл от положительной функции тоже
положителен? Что, есть такая теорема? Я что-то не помню ее
среди теорем об определенных интегралах, которые мы
перечисляли.
— Да это даже не теорема, а очевидный факт. Если в
интегральной сумме ^2f(£i)Axi все слагаемые положительны, то и
сумма положительны и ее предел тоже.
— И предел тоже? Но ведь еще в теории последовательностей
нам встречались примеры: все члены последовательности
положительны, а ее предел равен нулю. Вспомните: lim \- = О и в то
же время при любом п справедливо ^ > 0. Значит, вы можете
утверждать только то, что интеграл от неотрицательной
функции неотрицателен. Не знаете, что на это возразить? Подумайте,
сидя на месте.
И Костюк, упрямо потоптавшись у доски, направляется к
себе.
— Подождите! — пытается спасти товарища Стрельцов. —
Ведь наша подынтегральная функция непрерывна!
— Ну, конечно! — оборачивается на полдороге Костюк. —
Непрерывность все меняет!
И под улыбки ребят, наперебой перехватывая друг у друга
слово, они лепят импровизированное решение задачи:
— В нуле наша функция положительна, — указывает
Стрельцов.
— Значит, есть окрестность нуля, такой промежуток, где она
строго положительна, — продолжает Костюк.
— И даже больше определенной положительной величины.
— Мы такое доказывали.
— Значит, интеграл от нашей функции по этому
промежутку больше площади прямоугольника, основание
которого — этот промежуток, а высота — ограничение снизу для
функии.
— А площадь такого прямоугольника строго
положительна.
— Значит, и интеграл от нашей функции по этому
промежутку строго положителен.
428
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
[Гл. 5
— По оставшемуся промежутку он неотрицателен, это мы уже
знаем, поскольку функция там неотрицательна.
— Интеграл по всему отрезку [0,7г] равен сумме интегралов
по обоим промежуткам.
— А сумма строго положительной и неотрицательной
величин строго положительна.
Они наконец и сами понимают комичность своего дуэта и,
улыбаясь во весь рот, заканчавают хором:
— Значит, интеграл строго положителен.
— Отлично! — смеюсь и я. — А знаете, ребята, вы получили
больше, чем решение примера. По существу, вы доказали
теорему: если некоторая неотрицательная функция f(x) принимает
положительное значение в некоторой точке отрезка [а, Ь], на
котором она непрерывна, и на всем отрезке функция
интегрируема, то Ja f(x) dx > 0. Хвалю вашу сообразительность и в то де
время удивляюсь вашей забывчивости. Когда вы, Стрельцов,
перечисляли у доски теоремы об определенных интегралах, а вы,
Костюк, помогали Стрельцову, вы перечислили немало теорем,
выражаемых равенствами, и не вспомнили ни одной из тех, что
выражаются неравенствами. Приведи вы их — и вам сейчас не
пришлось бы изобретать велосипед. Но, как говорится, лучше
поздно, чем никогда. Вспомним эти теоремы сейчас. Начинайте,
Стрельцов!
— Мне, простите, вспоминается только одна: если f(x) < д(х)
и обе интегрируемы на [а, Ь], то f f(x) dx < Ja g(x) dx.
— Именно этой теоремой, — даю примечание, — не ссылаясь
на нее, воспользовался несколько минут назад Миклашевский,
когда утверждал, что площадь криволинейной трапеции больше
площади покрываемого ею прямоугольника. У этой теоремы
есть употребительное следствие: интеграл от положительной
функции положителен — это утверждение Костюк
пытался выдать за очевидный факт. Вот вам и вторая теорема,
Стрельцов. Но лектор наверняка давал еще и третью. Не
вспоминаете? В этой теореме сравнивались интегралы от некоторой
функции f(x) и от ее модуля. Может быть, вспомните вы,
Костюк?
— Кажется, было такое неравенство: | J f(x) dx\ <
<fba\f(x)\dx.
— Правильно: если функция f(x) интегрируема на [а, Ь] то
там интегрируема также функция \f(x)\ и справедливо
написанное вами неравенство. Этой теоремой — запишите ее формул и-
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
429
ровку, ребята! — мы будем широко пользоваться в дальнейшем.
Впрочем, она прояснит кое-что и в уже пройденном. Кочин, к
доске! Помните, как на прошлом семинаре вы искали
тейлоровское разложение арксинуса в нуле? Вы, в частности, — берусь
за мел, — написали тогда: > * 2 = 1 + \ + °(х3)> стали
интегрировать это равенство, в левой части получили arcsinx + С,
в правой интегрирование дало х + ^-... На этом вы
остановились и сказали: «Не знаю, как интегрировать о малое». Костюк
и Горт посоветовали вам взять остаточный член в форме Лагран-
f'"(c) ч 1
жа з! х , учесть, что производные корня , _ 2 в нуле
ограничены, стало быть, | з! ж31 — ^х3» а Миклашевский заметил по
поводу этого неравенства, что интеграл от его правой части
будет больше интеграла от остаточного члена, но обосновать такой
вывод не смог, и мы отложили окончательное решение вопроса
до сегодняшнего семинара. Надеюсь, что уж теперь-то вы его
решите, Дима.
Кочин вперяет напряженный взор в написанное мною, а Горт
и Костюк берут на себя, как и в тот раз, роль советчиков. «Надо
бы выяснить, будет ли интегрируема эта /'"(с)», сомневается
Костюк. «Производная от корня — функция элементарная,
значит, непрерывная, значит, интегрируемая», — тотчас отвечает
ему Горт. Успокоенный Костюк пускается дальше: «А константа
в левой части arcsinx + С равна нулю: если х устремить к
нулю...» «Секундочку, секундочку! — вдруг резко берет на
попятную Горт. — А как меняется с в выражении /'"(с), когда
х растет, — мы знаем? Что это будет за функция? И как себя
ведет f'"(c(x))? Может, она совсем не интегрируемая, и даже
разрывная!» Костюк вяло пытается возражать: «Ну, разрывная-
то она вряд ли...» — но, чувствуя серьезность замечания Горта,
останавливается: надо подумать.
Не видя ничего существенного в этих соображениях, Кочин
берется за дело сам:
— А, может, лучше взять остаточный член в форме
Пеано?
— Ну, конечно! — поддерживаю его, — и представить его
согласно определению в виде о(х3). А уж дальше
подсказывать не буду — с тем теоретическим заделом, который вы
наработали к сегодняшнему локладу, у вас все получится без
посторонней помощи. Если кого-то еще заинтересовала эта
проблема, пусть подумают над ней тоже. Правда, все это
придется делать уже дома — скоро звонок, занятие кончается. На
430
ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
[Гл. 5
следующем, ребята, будем заниматься приложениями
интегрального исчисления к вычислительным задачам из геометрии и
механики.
Глава 6
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
С самого начала семинара мы, как и было обещано в прошлый
раз, занялись приложениями интегрального исчисления к
геометрии и механике. Порядком поупражнялись в вычислении
площадей фигур и длин дуг, объемов и площадей поверхности
пространственных тел, в определении моментов инерции и центров
тяжести.
А до конца семинара еще далеко... Может быть, перейти к
новой теме?
— Ребята, про что рассказывал вам лектор на последней
лекции?
— Да про то же самое, что мы сейчас делаем — про площади,
про объемы, моменты, — отвечает Кулагин.
— И только?
— Еще пообещал, что на следующей лекции начнет
несобственные интегралы, — сообщает Кочин.
— Только пообещал? И ничего больше не успел?
— Ничего, — мотает головой Кочин. — Даже определение не
дал.
— Может быть, вы сами нам об этом расскажете? —
осторожно просит любопытный Миклашевский.
— Мне как-то неудобно брать на себя роль лектора...
Нерешительность, прозвучавшую в моем голосе, Меншиков
истолковывает по-своему:
— Мы вам поможем! — раздается с заднего ряда его задорный
бас.
— Поможете? Ну, тогда, — мгновенно сориентировавшись,
подхватываю его интонацию, — давайте уж не отступайтесь от
своего обещания! Будем вместе разрабатывать понятие
несобственного интеграла. Хорошо?
— Хорошо! Будем! - заверяет меня бодрый хор.
432
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[Гл. 6
«Да, — усмехаюсь про себя, — любопытно повернули
дело ребята! Он, конечно, не так уж неожидан, этот поворот:
я и раньше всегда, при решении каждой задачи
рассчитывал на их самостоятельность. Но решить задачу — это
одно, а вот разрабатывать целую, считай, теорию...
Справимся? Должны. Гарин, Буткус, Костюк, Горт — такие
вывезут».
Принимаю деловой тон:
— Понятие, к разработке которого мы приступаем, в
некотором смысле обобщает понятие интеграла, изучавшееся нами до
ь
сих пор, — пишу на доске ff(x)dx — Давайте вспомним и раз-
а
беремся, какими условиями мы ограничивали применение этой
формулы, и попытаемся изобрести более общее понятие
интеграла, свободное от тех или иных ограничений. Прежде всего: какой
должны быть функция /(х), чтобы написанный интегралл
существовал?
— Непрерывной? — с сомнением произносит Лапиков.
— Неверно! — тотчас откликается Горт. — Разрывные тоже
бывают интегрируемыми — сигнум, например.
— Саша, вы неисправимы, — выговариваю ему. — Сколько
раз я вам говорил: когда участвуете в дискуссии и оспариваете
чьи-то слова, обязательно прежде отметьте все положительное,
что в них есть, и возражения делайте скорее не в
опровержение, а в развитие сказанного до вас. А вы? Ваш единичный
пример с сигнумом явно рассчитан на то, чтобы опровергнуть
мнение Лапикова, — для опровержения достаточно
одного примера; но если бы вы хотели сделать содержательный
вклад в общую дискуссию, вы назвали бы целый класс
интегрируемых на отрезке [а, Ь] и при этом разрывных на нем
функций.
— Пожалуйста, — сбавляет он задиристый тон. — Это,
например, функции, ограниченные на отрезке и имеющие на нем
конечное число точек разрыва.
— Хорошо! После ваших слов нам будет легче ответить на
вопрос: какими свойствами необходимо обладает всякая функция,
интегрируемая на некотором отрезке?
— Она имеет на нем конечное число точек разрыва? —
тоном, утихнувшим до неуверенности, пытается продолжать
Горт.
— Конечное? Нет! — на той же, что когда-то и он,
бунтующей ноте вступает Костюк. — У нас на лекции был пример...
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
433
лектор разбирал на отрезке [0,1] функцию у = sin - при х ф 0...
нет, не совсем так, функция была такая: sgn[sin i] при х/Ои
нуль при х = 0. Она интегрируема на отрезке [0,1], лектор это
доказал, а у нее на этом отрезке бесконечное число точек
разрыва.
Где-то в середине его заявления Синица вскидывает руку и
тянет ее, всем своим видом стараясь показать, что ей пришла в
голову блестящая мысль.
— Пожалуйста, Люда.
— Мы на прошлом семинаре говорили: всякая функция,
интегрируемая на каком-то отрезке, ограничена на нем.
— Точно! И если мы хотим обобщить известное нам понятие
интеграла...
— Надо придумать, как интегрировать такие функции, у
которых на отрезке... которые неограничены на промежутке
интегрирования!
— Хорошо! Нарисуйте-ка нам на доске какую-нибудь
функцию, которая неограничена на некотором отрезке.
Почти в центре отрезка она восставляет пунктирный
перпендикуляр и с обеих сторон устремляет вдоль него ввысь выгнутые
вниз гладкие кривые.
— Неплохо. И все-таки я хотел бы кое в чем придраться к
вашему графику. Я ведь не просто так попросил вас нарисовать
его. Наглядные графики, конкретные примеры функций очень
помогут нам, когда мы станем искать обобщения известного
нам понятия интеграла. Чтобы поиск был успешнее,
вспомогательные образы и примеры должны быть как можно четче,
как можно проще. Вот я и интересуюсь: нельзя ли построить
более простой пример функции, неограниченной на
некотором промежутке? Вы, кажется, что-то хотите предложить,
Стрельцов?
— Вот такую функцию, — рисует он график, — повторяющий
своим обликом правую половину графика Синицы. — Правда,
434 НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ [Гл. 6
это будет функция, определенная уже не на отрезке, а на
полуинтервале...
— Ничего страшного! Придуманное вами упрощение стоит
таких изменений. Сотрите график Синицы...
Вместо этого галантный Стрельцов стирает свой, а на
графике Синицы легкими взмахами тряпки удаляет левую половину.
— Можно и так, — киваю ему с улыбкой.
Стрельцов между тем переобозначает концы интервала на
горизонтальным оси, оставшегося от графика Синицы числами
О и 1 и рядом с кривой пишет у = ^.
— А вот это, пожалуй, уже лишнее, Юра, — не соглашаюсь с
его дополнениями. — Не стоит сужать поле наших будущих
рассуждений до одного-единственного примера. Пусть у нас пока
остается общее представление о произвольной функции,
определенной на некотором полуинтервале и терпящей на открытом
конце этого промежутка бесконечный разрыв. А более
конкретные примеры будем подбирать, когда мало-мальски войдем в
курс дела, когда придумаем, как можно проинтегрировать
такую функцию, и тем самым укажем один из возможных путей
обобщения для известного нам понятия определенного
интеграла. Но прежде чем заняться этим, попробуем наметить другие
пути. Садитесь, Люда. Садитесь, Юра. Думаем все вместе,
ребята.
Молчание. И голос Рамзина:
— Надо, очевидно, отказаться еще от какого-то
свойства интегрируемой функции, так мне думается. От такого
свойства, которое вытекает из интегрируемости. Но у нас
на лекциях из нее не выводилось ничего, кроме
ограниченности.
— Согласен с вами. Но ведь мы развиваем не понятие
интегрируемости, а понятие интеграла. Вглядитесь в его обозначение.
Здесь кроме символа f(x) есть и другие детали, допускающие
обобщение.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
435
— Я где-то видел, — порывается к доске Миклашевский, —
вот такой интеграл, — и ставит вместо верхнего предела символ
оо
бесконечности: ff(x)dx.
а
— Такое обозначение действительно применяется в
математике. Как же, по-вашему, его можно истолковать графически?
Он отчеркивает вертикальный штришок на горизонтальной
оси, отмечает его буквой а и над правым из образовавшихся тем
самым лучей рисует пологую, стягивающуюся к нему кривую.
Придирчиво смотрит на свой рисунок, бормочет: «Интеграл —
это ведь площадь», — и аккуратно заштриховывает
пространство между кривой и осью абсцисс, двигаясь вправо от
перпендикуляра, восставленного в точке а:
— Графически это, наверное, будет так...
И вновь долго смотрит, о чем-то раздумывая, на эту
незамысловатую фигуру. Не спешу отправлять его на место.
Мухин чуть наклоняет голову и несколько раз
переводит взгляд с чертежа Синицы на рисунок Миклашевского и
обратно:
— Похожие вещи.
— Пожалуй, — соглашаюсь с ним. — Можно
надеяться, что существуют какие-то аналогии между двумя
обобщениями понятия интеграла, которые наметили Люда и
Павел. Правда, Женя, подмеченной вами аналогии еще
недостатет четкости, и вряд ли мы достигнем ее, пока не
располагаем строгими определениями интегралов,
которые нам обрисовали своими картинками Люда и Павел.
Надо сформулировать эти оба определения — вот
ближайшая наша задача. Быть может, одно из них отыщется легче,
чем другое. Поэтому, если дело не будет ладиться с одним,
перейдите к другому. И если нам удастся построить
одно определение, другое попытаемся написать по аналогии.
Думаем, ребята! Садитесь, — прошу Миклашевского
присоединиться к общей работе.
436
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[Гл. 6
Молчаливое раздумье длится минуту, другую...
— Никаких идей! — жалуется Лапиков.
— Сочувствую. Когда-то я говорил, что идеи приходят во
время работы. Но сейчас мы даже не можем приступить к делу.
Как же нам быть, ребята? Есть ли другие источники хороших
идей? Откуда они берутся?
— Из интуиции, — глуповато улыбается Чюмин.
— Допустим. Но тогда — что такое интуиция? Не знаете?
Что ж, вас нельзя в этом упрекать: среди психологов,
исследующих творческое мышление, тоже нет единого мнения на
этот счет. Одна из авторитетных точек зрения здесь такова:
почвой для творческих озарений служат впечатления человека,
в которых он не отдает себе отчета. По этой причине он не
может осознанно вовлекать их в свои размышления.
Однако они могут случайно попасть в сферу сознания, и при их
осмыслении возникают плодотворные идеи. Я расскажу вам
про один интересный психологический опыт. На листе бумаги
рисуются четыре точки, расположенные по вершинам квадрата.
Испытуемым предлагается провести замкнутую трехзвенную
ломаную линию так, чтобы она прошла через все четыре
точки.
— А, знаю! — перебивает меня Костюк. — Надо рисовать
ломаную так, чтобы она выходила за стороны квадрата!
— Да! Точно! — поддерживают его несколько голосов.
— Смотрите-ка, какие у нас собрались умники! — с усмешкой
оглядываю аудиторию. — В экспериментах, из описания
которых я узнал про этот опыт, таких было немного. Неудачникам
после первой безуспешной попытки давалась доска с четырьмя
шпеньками, расположенными по вершинам квадрата, и планки
с дырками, на которых были нарисованы кусочки эллипса.
Планки надо было надеть на шпеньки так, чтобы при этом
возникало целостное изображение эллипса. Это происходило
лишь в том случае, когда из планок складывался
треугольник, описанный вокруг квадрата, образованного шпеньками.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
437
Потом доска убиралась и испытуемым вновь предлагалась
задача о четырех точках. Теперь уже ее решали почти все,
располагая звенья искомой ломаной относительно точек
совершенно так же, как планки относительно шпеньков, — хотя,
судя по последующему опросу, лишь некоторые видели связь
между обоими испытаниями. Это и доказывало, что идея
решения задачи о четырех точках бралась из неосознанного
опыта.
— Оригинально! — издает Меншиков свой неизменный
возглас одобрения.
— Я вижу, вас заинтересовал такой способ наведения на
счастливые догадки, — гляжу на него. — Мы можем применить
его к своим проблемам. Ну-ка, Миклашевский, идите снова к
доске, нарисуйте еще раз то, что рисовали раньше и притом в
точно такой же последовательности. Так, так... Ну что,
Меншиков? Сообразили, как определить интеграл с бесконечным
верхним пределом? Нет? А вы сами, Миклашевский?
Сообразили? Тоже нет? А остальные? Тоже? Ну-ка, Павел, нарисуйте
свою картинку еще раз...
В каком-то заторможенном темпе, сконцентрировав все
свое внимание на кончике мела, он ведет прежнюю
кривую, начинает заштриховывать сужающуюся полосу под
ней...
— Есть! — вскрикивает Буткуе.
— Придумали? — оборачиваюсь к нему. — Пожалуйста, к
доске!
Он вычерчивает пунктирный перпендикуляр к оси абсцисс
за пределами заштрихованного поля, потом со всей
аккуратностью, на которую способен, доводит линии штриховки до этой
пунктирной границы.
— Отметьте как-нибудь точку, в которой восставили
перпендикуляр, скажем, буквой А, — негромко советую ему. Сделав это,
он продолжает:
438
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[Гл. 6
— Надо взять интеграл от а до Д потом устремить А к
бесконечности. Предел есть интеграл от а до бесконечности.
— При условии, что этот предел существует, — замечает
Кочин.
А
— И если при каждом А существует интеграл ff(x)dx, —
а
метнув в него взглядом, добавляет Горт.
— Если этот предел существует и при каждом А
существует интеграл, — автоматически повторяет Буткус, погруженный
в свои мысли. — Нет, не так: если при каждом А существует
А
интеграл ff(x)dx и при А стремится к плюс бесконечности
существует предел lim ff(x)dx1 то это будет интеграл от f(x) от
а до бесконечности — по определению.
— Интеграл от функции /(#), взятый в пределах от а
до бесконечности, — для лучшего запоминания повторяю
+оо de, А
его слова и пишу на доске: Г f(x)dx <£=*► lim ff(x)dx. —
Верно. Садитесь, Линас, спасибо. Теперь, надеюсь, мы
сможем определить и интеграл от функции, которая неограни-
чена в окрестности одного из концов промежутка
интегрирования. Кто хотел бы это сделать? Рамзин?
Прошу.
С величавой неторопливостью он рисует на доске числовую
ось, откладывает на ней отрезок [а, Ь].
Ю. В. Пухначев) СЕМЬ СЕМИНАРОВ 439
— Пусть это будет наш промежуток интегрирования. И
пусть в точке а подынтегральная функция неограничена, —
с этими словами он аккуратно рисует соответствующую
кривую. — Отступим от точки а вправо на малое расстоя-
6
ние е. Будем вычислять интеграл / f(x)dx при различных
а+е
значениях е. Затем устремим е к нулю и исследуем, будет
ь
ли существовать lim f f(x)dx. Если будет, то мы назовем
ь
его интегралом ff(x)dx.
а
— Непонятно! — раздается голос Аргуновой.
— Что именно? — поворачиваюсь в ее сторону.
— Почему, когда Линас писал про интеграл до бесконечности,
мы говорили: «Интегрируема на каждом промежутке», — а тут
не говорим?
— Справедливое замечание! — возвращаюсь взглядом к Рам-
зину.
— Безусловно справедливое, вы правы, — отвечает он мне.
— Не я, а Аргунова...
И понятливый Рамзин, повернувшись к ней, продолжает
заботливым тоном:
— Надо было сказать, что при любом е > О интеграл
ь
f f(x)dx существует.
— Припишите это, ребята, к тому, что вы записали во слов
Рамзина. Вот теперь все правильно, садитесь на место, Сергей.
Итак, ребята, мы с вами выработали весьма четкое
определение интеграла с бесконечным пределом и интеграла от функции,
неограниченной в некоторой точке. Такие интегралы, в отличие
от пройденных нами ранее «обычных» интегралов, и называют
интегралами в несобственном смысле или коротко —
несобственными интегралами. Про «обычные» же интегралы будем гово-
440
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[Гл. 6
рить, что они берутся в собственном смысле. И еще несколько
важных терминов. Определяя несобственные интегралы через
предельный переход, мы предусматривали две возможности:
когда существует конечный предел и когда он не существует. В
первом случае говорят, что несобственный интеграл сходится, во
втором — что он расходится. Точки на промежутке
интегрирования, из-за которых интеграл приходится брать в несобственном
смысле, называются особыми точками. Указывая их, говорят,
что интеграл имеет особенность в такой-то и такой-то точках.
Про интеграл с бесконечным пределом говорят, что он имеет
особенность на бесконечности. Итак, мы выработали
определение несобственного интеграла и его сходимости. Но существуют
ли математические объекты, удовлетворяющие нашему
определению? Это еще следовало бы проверить. В истории науки
бывали случаи, когда, разработав весьма отчетливые представления о
некоторых гипотетических предметах, ученые потом веками не
могли их создать или обнаружить в природе. Примеры —
философский камень, флогистон, теплород. Не случится ли нечто
подобное с тем, что придумали мы с вами? Давайте проверим.
Возьмем какую-нибудь функцию, определенную на
положительном луче оси абсцисс или неограниченную в какой-то точке, и
попробуем применить к ней наши построения. Какие
предложения будут у вас на этот счет?
— Стрельцов уже предлагал функцию у = j, — напоминает
Сутеев.
Не очень, честно говоря, удачный пример... Отвергнуть его
с порога? Или все-таки принять? Лучше принять. В таких
случаях важно не то, что высказал студент, а то, как высказанное
обыгрывается и осмысливается в дальнейшем разговоре.
Попробую сделать неудачный пример Сутеева затравкой
поучительного обсуждения.
— Ну что ж, рассмотрим функцию у = j. Она терпит
бесконечный разрыв в нуле. Она же может послужить и
примером функции, определенной на полубесконечном луче.
Нарисуйте ее на доске, Сутеев. А теперь, исходя из общего определения
1
несобственных интегралов, исследуйте на сходимость такие: f^-
о
и f ^. Можете взять тетрадь, если что-то забыли из нужных
1
вам определений. Помните оба? Отлично. Все же напишите их
на доске. Приступайте к разбору интегралов. Так, так... Ну вот,
Ю, В. Пухначев)
СЕМЬ СЕМИНАРОВ
441
и тут и там получается логарифм: в первом случае с бесконечно
малым аргументом, во втором — с бесконечно большим. Имеют
ли конечный предел такие логарифмы?
— Нет.
— Да, не очень обнадеживающее начало, ребята. Может быть,
и вправду не существует того, что мы так четко определили?
Ну-ка, как ответят на это наши корифеи? Что скажет Горт?
Буткус? Ответа не слышно ни от них, ни от Синицы, ни от Ко-
стюка...
Гарин раньше других превозмогает обескураживающее
впечатление первой неудачи:
— Надо брать не ^, надо брать единицу, деленную не просто
на я, а на х в какой-то степени, сейчас...
— Думайте, пожалуйста, молча! — предупреждающе
поднимаю руку. — А мы с вами, Сутеев, будем соображать сами.
Припишите в обоих интегралах к иксу в знаменателе показатель
степени s. Итак, когда s равно единице, то оба интеграла
расходятся. Рассмотрим теперь какой-либо из наших интегралов при в, не
равном единице, например, большем ее. Исследуем для начала
/ J?, где 5 > 1. Действуйте, Сутеев.
1
Пример достаточно прост, чтобы не вызвать у него
затруднений.
— Получается 1 — ;дт=т, — резюмирует он. — Если s > 1, дробь
дтгг стремится к нулю.
— Прекрасно. Рассмотрим тот же интеграл при s < 1.
Он начинает было вычислять - и догадывается, что дробь
получится та же самая: -тт^т-
442
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[Гл. 6
— Только степень уже отрицательная, это лучше так
написать: Al~s. Если s меньше единицы, то тут уже степень
положительная, А стремится к бесконечности... предел бесконечный.
— Иными словами, конечного предела в этом случае нет. Я
думаю, что про наш интеграл мы теперь знаем все, — пишу под
формулой разобранного интеграла в две строки слова
«сходится» и «расходится» с двоеточиями на конце:
— Укажите, Сутеев, когда будет то и другое.
Подумав, он пишет в первой строке 5 > 1, во второй 5 < 1.
Превращаю второе неравенство в нестрогое 5 < 1, и, дождавшись
от Сутеева замедленного: «Ах, да!», — заключаю:
— Два таких неравенства исчерпывают все возможные зна-
+оо
чения s. Вывод: интеграл / ~ сходится при 5 > 1, расходится
1
1
при s < 1. Переходите к интегралу /^?, Сутеев.
о
Сам, без единой подсказки он доводит исследование до конца
и пишет под формулой интеграла строчки «сходится: 5 < 1» и
«расходится: 5 > 1».
— Затвердите эти выводы, ребята! -- оборачиваюсь к
аудитории. — Они очень пригодятся нам в дальнейшем!
И снова Сутееву:
— Садитесь, Игорь, вы хорошо справились с заданием.
Отлично просто!
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
443
И, как конфетку отличившемуся ребенку, дарю ему в
заключение наглядную интерпретацию полученных им результатов —
она ведь ему ближе и понятнее, чем формулы:
— Я попробую выразить единым рисунком то, что вы только
что описали четырьмя неравенствами.
Вычерчиваю систему координат и в ней — графики функций
у = ^7 при различных значениях s — меньшем единицы, равном
ей и превышающем ее. Потом прочерчиваю пожирнее линию
У х'
— Интеграл от этой функции, ребята, как показал Сутеев,
расходится и на плюс бесконечности и в нуле. Это следует
знать твердо. И тогда известное нам положение с любой другой
функцией вида ~ с помощью этого чертежика можно запом-
нить так: если график такой функции лежит под гиперболой,
то интеграл от нее сходится, если над гиперболой —
расходится.
— А это в общем-то очевидно, — задумчиво произносит
Миклашевский, пристально щурясь на мой чертеж. — Площадь
под гиперболой растет неограниченно, а если кривая еще выше,
то под ней площадь растет еще быстрее и к пределу не
стремится...
Останавливаю его, подняв ладонь:
— В том, что вы говорите, есть свой резон, но этот
разговор я хотел бы начать попозже. А сейчас давайте обдумаем то,
что мы получили. Прежде всего порадуемся нашей удаче,
нашей счастливой находке: мы нашли функции, неограниченные
или даже терпящие бесконечный разрыв на некотором
интервале, и функции, определенные на бесконечном промежутке,
графики которых очерчивают тем не менее конечную площадь, —
заштриховываю на своем чертеже пространство под
соответствующими кривыми. — Иными словами, мы показали, что сходящи-
444
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[Гл. 6
еся несобственные интегралы существуют. А раз они
существуют, мы можем рассуждать о них, исследовать их свойства. Этим
мы и займемся в ближайшем будущем, — переписываю в
чистом углу доски из выкладок Буткуса определение
несобственного интеграла на неограниченном промежутке, из выкладок Рам-
зина — определение несобственного интеграла от
неограниченной на конечном промежутке функции. — Но прежде, ребята, я
хотел бы выяснить: всем ли понятно, что в обоих
определениях речь идет про предел некоторой функции? И всем ли
понятно, что за функция подвергается предельному переходу? Как,
Стрельцов?
— Да вроде бы понятно... В том интеграле, — он кивает
на выкладки Буткуса, — верхний предел А — переменный. То
есть интеграл рассматривается как функция верхнего предела,
как функция величины А. И это самое А потом устремляется к
бесконечности. А в том вон интеграле, — он переводит взгляд
на написанное Рамзиным, — изменяется нижний предел.
Можно было бы даже написать этот интеграл как-то по-другому,
допустим, от а' до 6, — я тотчас реализую это предложение
Стрельцова, — и рассматривать интеграл как функцию ниж-
него предела а', рассматривать его поведение при а',
стремящемся к а.
— Все правильно. Итак, в определении несобственного
интеграла, как мы видим, объединились два понятия: определенный
интеграл и предел функции. Оба хорошо знакомы нам. И если
мы станем вспоминать свойства этих понятий, то, пожалуй,
сможем предсказать многие свойства несобственных интегралов. Я
думаю, стоит начать с перечисления свойств определенного
интеграла — ведь мы проходили его совсем недавно. Жду ваших
предложений, ребята.
— Там, в интегралах было про константу — про функцию,
умноженную на константу — мы говорили, что константу
можно выносить за знак интегрирования, — торопливо говорит
Мухин.
— Вы имеете в виду случай, когда под интегралом стоит
функция, умноженния на постоянную, отличную от нуля?
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
445
В определениях несобственного интеграла обоих видов я
приписываю к подинтегральной функции коэффициент С.
— Да, — кивает Мухин.
— Посмотрите, — жестом зову его к доске, — что можно
сказать по этому поводу. Сотрите с доски все лишнее и пишите то,
что вам нужно.
Он начинает не сразу, памятуя мои советы, и выкладки
проводит последовательно: выносит С за знак интегрирования и
затем — за знак предела.
— А чем обосновано ваше второе преобразование? —
осведомляюсь я.
— Константу можно выносить за знак предела, — быстро
отвечает Мухин и тотчас добавляет:
— Если предел существует.
— Вот-вот! О существовании предела обязательно нужно
упомянуть в утверждении, которое вы подготовили своими
выкладками. Сформулируйте это утверждение окончательно и
полностью. Не торопитесь, подумайте.
— Наверное, нужно начать так: пусть сходится интеграл
+00
/ f(x)dx — медленно, осторожно произнеся эту фразу, Мухин
а
смотрит на меня, ожидая одобрения.
Я молчу. Потом говорю с улыбкой:
— Молчание — знак согласия, Мухин. Продолжайте. Пусть
+оо
сходится интеграл / f(x)dx...
а
+оо +оо
— Тогда сходится и f Cf(x)dx = С f f(x)dx. А если расхо-
а а
дится интеграл от /(ж), то расходится и интеграл от С/(я), —
бойко заканчивает он.
— Повторите доказательство от начала до конца, без
недомолвок. Так, так... Все правильно. Садитесь. Кто назовет еще
какие-нибудь свойства несобственных интегралов? Хотите вы,
Миклашевский?
— Если сходятся несобственные интегралы от функций f(x)
и д(х), то сходится интеграл от их суммы и равен сумме обоих
интегралов.
— Все интегралы берутся в одинаковых пределах?
— Да, конечно.
— Очень хорошо. Докажите свое утверждение на доске.
— Да это же тривиально!
446 НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ [Гл. 6
— Быть может. Но я хочу использовать ваши выкладки
Миклашевский
А А а
S (fС*) + $(*))cLoc = J f(x)rfx + JQWcioc
еще для одного утверждения. Скажите, — спрашиваю
Миклашевского, когда он заканчивает писать, — а если из двух
интегралов в правой части вашего равенства один имеет
предел при Л, стремящемся к бесконечности, а другой не имеет,
то что можно сказать про интеграл, стоящий в вашем
равенстве слева, то есть интеграл от суммы двух функций f(x)
и д{х)1
— Что он не имеет предела. Мы когда-то доказывали: сумма
сходящейся величины и расходящейся расходится.
— Верно, было у нас нечто подобное. Итак, если у нас
написан несобственный интеграл от суммы двух функций,
причем интеграл от одной сходится, а от другой
расходится...
— То весь интеграл расходится, — заканчивает
Миклашевский.
— Точно. Причем это можно сказать не только про интеграл
с бесконечным пределом, но и про интеграл от неограниченной
функции.
— Да. Доказательство совершенно аналогичное.
— Хорошо, садитесь. Кто продолжит перечень свойств
несобственных интегралов? Вспомните: мы разбивали интеграл на
сумму интегралов не только тогда, когда под интегралом стояла
сумма функций...
— Разбить промежуток интегрирования! — догадывается
Меншиков.
— Совершенно верно. Сделайте это, пожалуйста, на доске с
интегралом, у которого верхний предел будет потом
устремляться к бесконечности. Ну вот, сумма двух интегралов. К обоим сла-
Меншиков
А в А
J f(x)dx = Jf(х)Ыас + IfC*)dx
о» «• в
гаемым вы будете применять операцию предельного перехода —
так ведь?
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
447
— Ага. Первое слагаемое — обычный интеграл, то есть
некоторое число, в пределе будет то же самое число, — в неплохом
темпе начинает он рассуждение.
— Хорошо, хорошо! — одобрительно киваю ему.
— Значит, в этом равенстве будет только по одной переменной
величине справа и слева... Да, одна переменная справа и одна
слева...
Речь его катастрофически теряет взятый упругий темп,
грозя вот-вот переродиться в былой меншиковский расслабленный
говорок. Резко перенастраиваюсь с одобряющего тона на
понукающий:
— Что же вы можете сказать об этих переменных величинах,
исходя из полученного равенства? Ничего? Обещали помогать, а
сами... А какие соображения есть у остальных? — обращаюсь за
помощью к аудитории.
— Если одна сходится к какому-то пределу, то и другая тоже
сходится, — наконец произносит Синица.
— Верно! Как можно истолковать этот факт? — вновь
пытливо гляжу на Меншикова. — Снова молчите... Ну,
знаете, это на вас не похоже. Чтобы ни одной завалящей
идейки...
Отослав его на место, отвечаю на свой вопрос сам:
— Если исследуется на сходимость интеграл с бесконечным
верхним пределом, то нижний его предел можно изменять по
произволу. Можно также произвольно изменять значения
интегрируемой функции на любом отрезке, примыкакщем к нижнему
пределу интегрирования, — ни то ни другое не повлияет на
сходимость интеграла: сходящийся сохранит сходимость,
расходящийся так и останется расходящимся. Аналогично обстоит дело
с интегралом от функции, неограниченной в окрестности одного
из концов промежутка интегрирования: на любом участке
этого промежутка, не примыкающем к «опасному» концу, значения
подынтетральной функции можно изменять без последствий для
сходимости интеграла. Разумеется, такие изменения не должны
превращать функцию в неинтегрируемую. Запишите это себе в
тетради, ребята! Записали? Продолжаем перечислять свойства
несобственных интегралов.
Молчание, наступившее вслед за моим призывом, отдает
безнадежностью, и я стараюсь скрасить это ощущение:
— Ничего не приходит на ум? Раскиньте им пошире,
ребята! Я чувствую, что вы в своих поисках исходите лишь из
свойств определенного интеграла. Но ведь он представляет
448
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[Гл. 6
собою лишь одну из половинок определения несобственного
интеграла. Другая половинка — предел функции. Она тоже
могла бы нам подсказать кое-что. Вспомните: каждый раз,
как только мы определяли предел последовательности, предел
функции...
— Критерий Коши! — не дает мне договорить Кочин.
— Критерий Коши, — утвердительно киваю ему. — Идите
к доске, Дима, попробуйте сформулировать этот критерий
для несобственного интеграла с бесконечным верхним
пределом.
И, предчувствуя, что сделать это будет нелегко, советую:
— Начните с определения, для большей уверенности
распишите его на символическом языке.
— Тогда надо как-то обозначить предел интеграла, —
следует он моему совету, — допустим, Р. Интеграл мы
рассматриваем; как функцию верхнего предела... Может быть, ввести особое
обозначение для этой функции, какое-нибудь Ф(А)? — ждет он
нового совета.
— Давайте подумаем, стоит ли это делать. Я понимаю,
что задача нелегка, что без упрощающих переобозначений
с ней сразу не справиться. Но во всём должна быть мера.
Если новых обозначений окажется слишком много, вы
рискуете запутаться в них. Попробуем обойтись без этой Ф(А)
— хорошо? А не будет получаться — ввести ее мы всегда
успеем.
— Ладно, — соглашается он. — Значит, определение предела..
Для любого е существует А... нет, А уже занято... существует Ае
А
такое, что для любого А > А£ выполняется \Jf(x)dx — Р\ < е.
а
— Все правильно, — утверждаю этот промежуточный
результат. — Теперь критерий Коши.
Он откликается эхом:
— Теперь критерий Коши... Для любого е существует Ае
такое, что для любых А1 и А", больших А£, выполняется
А' А"
\ff(x)dx- ff(x)dx\<e.
а а
— Отлично! Получилась разность интегралов. На прошлом
семинаре мы встречали подобные разности, знаем, как их
упрощать.
Секунду-другую он смотрит на меня, не понимая, что я имею
в виду, потом догадывается:
Ю. В. Пухначев] СЕМЬ СЕМИНАРОВ 449
А"
- Это ведь интеграл f f{x)dx.
А'
— Верно. Перепишите заново, как можно четче
формулировку критерия, чтобы ее записали все. Посмотрите, нет ли в ней
I Кочин I
Ve>o ЗА VA'VA" д/,
((СА'>А)Л(А">А))=>(| JfG0rfx|< £))
чего-то лишнего? Может быть, вместо Ае для простоты лучше
написать А? Ну вот, все готово. Спасибо, садитесь. Теперь,
ребята, я предлагаю поупражняться в преобразованиях
несобственных интегралов и тем самым подготовиться к более
эффективному решению будущих задач. Какие еще свойства несобственного
интеграла подскажет нам наличие предельного перехода в его
определении? Если вам трудно рассуждать отвлеченно,
давайте привлечем в качестве опоры уже знакомые нам конкретные
примеры сходящихся и расходящихся несобственных интегралов
а +оо
вида /^7 и / jr. То, что мы знаем о них, в дальнейшем не раз
О а
поможет нам исследовать интегралы более сложные. Предполо-
2
жим, например, что нам встретился такой: Г /х . Как подойти
iVx l
к нему, Лапиков? Посмотрите, как ведет себя подынтегральная
функция...
— Неограничена в единице, я вижу, — спешит ответить Егор.
— И если брать этот интеграл, следуя определению
несобственного...
— Предел... от 1 + е до двух...
— Верно, от 1 + е до двух, где е стремится к нулю, или, что
то же, от некоторого А до двух, где А стремится к единице. А
при стремлении переменной величины к ненулевому пределу мы
раньше всегда...
— Сделать замену х — 1 = t — опять торопливо перебивает
меня Лапиков, чувствуя, что мое разжевывание выставляет его
в невыгодном свете.
— Пожалуйста, делайте, — вручаю ему мел, а сам
отправляюсь в обход по аудитории.
Лапиков аккуратно и безошибочно выполняет свой замысел,
не забывает и о том, чтобы изменить пределы интегрирования.
15-2019
450
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[Гл. 6
— Очень хорошо! — оцениваю его успех. — Интеграл принял
1 1
знакомый нам вид f-^j* = f^r. Сходится ли он?
— Сходится, — уверенно отвечает Лапиков, — потому что
показатель степени меньше единицы.
— О, да вы прогрессируете от семинара к семинару! Сразу
заучиваете то, что на них говорится! И применяете умело! Теперь
уж, — шутливо грожу ему пальцем, — я никогда в жизни не
поверю в ваши причитания: «Никаких идей...» Садитесь, Егор.
1
Рассмотрим теперь интеграл Г f* . Какую замену, — оборачи-
0vi х
ваюсь к Кулагину, — вы предложили бы здесь?
— Если х — 1 = t, то... х меньше единицы, значит, под корнем
отрицательное... Наверное, 1 — х = t то есть х = 1 — t.
— Верно. На доске пусть такую замену проведет Чюмин. Все
хорошо, Семен, садитесь. Опять, ребята, мы получили в ито-
1
ге хорошо знакомый нам интеграл с особенностью в нуле J-^-
Очевидно, по той же самой схеме, перенося начало координат в
особую точку, можно доказать общее утверждение: интегралы
6 а
J\х^а\а и Jij?x\a сходятся при s < 1, расходятся же при s > 1.
а Ь
— Мы и от бесконечности переходили к нулю, когда искали
пределы функций, заменой х = |, — замечает Мухин.
— Вы хотите испытать такую замену в несобственных инте-
+оо
гралах? Взять, скажем, интеграл / ~, с помощью замены х = \
1
перейти от особенности на бесконечности к особенности в нуле,
1
к интегралу J|f, написать зависимость между р и 5, а отсю-
о
да, зная при каких s сходится и расходится первый интеграл,
вывести условия сходимости и расходимости второго. Вот будет
забавно, если мы получим совсем не то, что раньше... Сделайте
это, Мухин. Впрочем, нет, сидите: вы сегодня уже выступали у
доски, лучше я вызову того, кто у нее нынче еще не был,
скажем... Сынчикова. Прошу!
Бродя между столами, я убедился, что он не теряет формы,
наработанной на прежних семинарах, — наверное, подтвердит ее
и сейчас. Не стану торопить его — пусть работает, как умеет,
не буду подсказывать... Да он и не нуждается в этом: требуе-
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
451
мые неравенства для показателя р выводит кратко и гладко: они
совпадают с ожидаемыми.
С похвалой отсылаю его обратно.
— А почему, — опережая мои новые вопросы, сам спрашивает
Буткус, — а почему мы брали бесконечный предел только плюс
бесконечность? Почему не брали минус?
— Этот пробел легко устранить, — приглашаю его к
доске. — Напишите соответствующее определение. Хорошо,
садитесь. Итак, в качестве пределов несобственного интеграла
могут выступать и плюс и минус бесконечность. А могут ли оба
этих знака встречаться в одном интеграле? Таким вот образом:
+оо
/ f(x)dx? Кто из нас сегодня вспоминал, что где-то видел ин-
—оо
тегралы с бесконечным пределом? Миклашевский? Скажите, —
оборачиваюсь к нему, — а такое вы видели? — кивав на только
что написанную мной формулу.
— Видел.
— А истолковать ее сможете? Нет? Кто поможет? Не
попробуете, Стрельцов?
— Можно взять сначала интеграл в конечных пределах:
в
J/(x)dx, а потом устремить В к плюс бесконечности, а А — к
А
минус.
в
— Вот так? — пишу на доске lim f/(x)dx, — Но это что-то
B^ + ooJA
новенькое для нас — две стрелки под знаком предела.
— Ну, конечно, конечно! — спешит откреститься от своего
опрометчивого предложения Стрельцов. — Это чепуха, мы
рассматривали пределы только с одной стрелкой!
— Нельзя ли здесь как-то обойтись «однострелочными»
пределами? — предлагаю ему исправиться. И, некоторое время
подержав взгляд на его неподвижно-сосредоточенной физиономии,
скольжу им по аудитории:
— Кто подскажет выход из положения?
— А если...
Это голос Аргуновой: ее рука взметнулась было вверх
и опустилась, легла на губы в жесте сомневающегося
раздумья.
— Ну-ну, смелее! — стараюсь воскресить ее робкий порыв.
— Если... как-то разбить интеграл на два, чтоб в каждом
была только одна бесконечность?
15*
452 НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ [Гл. 6
-- Какой интеграл? Этот? — словно не поняв, о чем она го-
в
ворит, подчеркиваю символ ff(x)dx.
А
— Да, — доверяется она моему, выбору.
— Ну что ж, — приглашаю ее к доске, — попробуйте с помо-
+оо
щью такого разбиения определить интеграл f f(x)dx.
—оо
У доски, где на нее глядят со всех сторон, она не
теряется, наоборот, — обнаруживает неплохую изобретательность:
+оо В С В
Г f(x)dx = lim ff(x)dx = lim ff(x)dx + lim ff(x)dx.
-oo tZ+ZA A^-°°A £^+ooc
Отослав ее на место, обращаюсь к сидящим:
— Кто отредактирует написанное Аргуновой?
Горт рассудительно замечает:
— Если мы не знаем, что такое предел с двумя
одновременными предельными переходами, то не надо его и упоминать.
+оо
Надо принять по определению, что интеграл вида J f(x)dx
—оо
есть сумма двух пределов, сумма двух несобственных
интегралов.
— Правильно. И сходящимся такой интеграл мы назовем
лишь в том случае, когда оба предела порознь существуют.
С такими поправками ваш ответ, — гляжу на Аргунову, —
становится безошибочным. Очень хорошо вы выступили. Я бы
советовал вам почаще вызываться к доске. Попробуем, ребята, —
даю новое задание, — разобрать выработанным нами способом
+оо
интеграл J e~^dx. Кто исследовал бы его на сходимость? Не
—оо
хотите, Чюмин?
Разбив область интегрирования надвое нулем, он довольно
быстро находит, что оба возникающих при этом предела
существуют, и вычисляет интеграл: он равен двум.
8
— А как бы вы подошли к интегралу f %=! — предлагаю
_1 Vх
ему еще один пример. — Обратите внимание: точка бесконечного
разрыва подынтегральной функции лежит внутри промежутка
интегрирования.
— Наверное, тут тоже надо разбить весь промежуток на два?
От минус единицы до нуля и от нуля до двух.
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
453
— Разумно. Так сходится ли интеграл?
— Сходится: показатель меньше единицы. Вычислить?
— Вычисляйте, если желаете. Ответ? Верно, |. Вероятно,
после этого примера вам ясен общий подход к исследованию
произвольного интеграла, у которого между пределами
интегрирования есть точка, где подынтегральная функция терпит
бесконечный разрыв. Нарисуйте такую функцию. Как станете
анализировать интеграл от нее?
— Сначала разобью промежуток интегрирования на два: один
левее точки разрыва, другой правее. Получится два интеграла.
Рассмотрю их по отдельности. Если оба сходятся, то сходится и
интеграл по всему промежутку.
— Верно. Так мы и определим его сходимость. Наконец,
разберем самый общий случай.
Я рисую на доске функцию, определенную на всей оси
абсцисс, бесконечно убывающую на бесконечностях обоих знаков, с
бесконечными разрывами в точках ai,a2, ...an.
— Как подойдете к интегралу от такой функции, Чюмин?
+оо
И пишу рядом J* f(x)dx.
—оо
Он уверенно расставляет точки 61,62? ---бп, Ьп+ъ так что они
перемежаются точками бесконечного разрыва, и расписывает
предложенный мною интеграл в виде длиннющей суммы.
— Снова верно.
Чюмина, до сих пор так часто городившего чепуху, надо бы
расхвалить за безошибочные ответы, а мне почему-то
становится грустно. Мне вспоминается старинная английская
эпиграмма: «Жму руку чудакам обеими руками. Как многим, в сущ-
454
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
(Гл. 6
ности, обязаны мы им! Ведь если б не были другие чудаками,
то чудаками быть пришлось бы нам самим». Нелепые
вопросы Чюмина не раз позволяли нам рассмотреть с новой,
неожиданной стороны и крепче усвоить многие нелегкие темы. Будет
жаль, если он навсегда перестанет задавать такие вопросы, —
если так, я и сам непрочь бы повыдумыватъ их для пользы
дела...
— Садитесь, Чюмин. Очевидно, — комментирую написанное
на доске, — каждый из этих интегралов-слагаемых мы сможем
определить с помощью одного-единственного предельного
перехода. Всем понятен такой подход? Может быть, у кого-то есть
вопросы?
Молчание. И удрученный голос Горта:
— Меня все-таки ужасно интригует то, что несобственный
интеграл от неограниченной функции в конце концов выглядит
совсем так же, как обыкновенный, собственный. А если к
собственному интегралу подойти так же, как к несобственному?
Так же попытаться его вычислить? Отступить от одного
конца — скажем, от верхнего — на е, вычислить интеграл по такому
неполному промежутку, потом устремить е к нулю...
— Заучился! — глядя на Горта, соболезнующе вздыхает Рам-
зин и в тот же миг умолкает под моим грозным взглядом.
— Устремить к нулю, — словно не слыша, продолжает Горт, —
и посмотреть, что будет с интегралом — станет он стремиться к
интегралу по полному промежутку?
— Конечно, станет! — моментально откликается Костюк. —
Это ведь у нас будет интеграл с переменным верхним
пределом. А он непрерывен, если функция интегрируема в
собственном смысле. Лектор это доказывал.
— Верно, верно! — угадываю в реплике Костюка импульс для
плодотворной дискуссии. — А если подынтегральная функция не
только интегрируема, но еще к тому же и непрерывна?
— Тогда, -- вспомнив нужные теоремы, Горт не желает
оставаться в долгу перед соперником, — интеграл с переменным
верхним пределом будет первообразной для подинтегральной
функции, это мы на прошлом семинаре показали.
— Поглядим теперь на дело с другой стороны, — увлекаю
моих собеседников вперед по намечающемуся пути. — Пусть на
интервале (а, 6), задана непрерывная функция f(x) и ее
первообразная F(z), то есть для любого х из (а, 6) справедливо
F'{x) = f{x). Пусть F(x) имеет предел в точке Ь. Что можно
Ю. В. Пухначев|
СЕМЬ СЕМИНАРОВ
455
Ь-е
сказать о поведении интеграла / f(x)dx при е, стремящемся к
а
нулю? Как вы думаете, Кулагин?
— Подумать можно? — просит тот.
— Конечно. Можно даже пойти к доске.
Неторопливо, вразвалочку Кулагин идет вдоль столов. В его
походке, в лице — полнейшая невозмутимость, но мысль его (это
угадывается по взгляду, прикованному к записям на доске)
бьется в поисках ответа на мой вопрос. Здраво сообразив, что ответ
должен найтись в рамках только что затрагивавшихся нами
понятий, он начинает прилаживать их друг к другу.
— Если е к нулю... верхний предел переменный... интеграл с
переменным верхним пределом... это первообразная...
— На константу! — не может не вставить своего соображения
Горт. Кулагин медлительно оборачивает к нему недовольное
лицо: «Что за манера перебивать?» — и в эти замедленные секунды
находит нужные слова. Произнесенные в абсолютно том же тоне,
что и предыдущие, они производят весьма достоверное
впечатление совершенно самостоятельных, ниоткуда не заимствованных
мыслей:
— Интеграл с переменным верхним пределом — это
первообразная для /(х)... Любые две первообразные различаются на
Ь-е
константу... Значит, F(x) и интеграл J f(x)dx... Тут даже по
а
Ь-е
формуле Ньютона-Лейбница можно: / f(x)dx = F(b — s) — F(a).
a
Если е стремится к нулю, то F(b — е) стремится к пределу, и
Ь-е
интеграл / f(x)dx тоже стремится к какому-то пределу.
а
Чувствуя, что ответ найден верный, он говорит со спокойным
достоинством, но подспудное сознание, что идея ответа
принадлежит не всецело одному ему, заставляет его говорить сверх
достаточного, выкладывать все, что родило напряжение поиска:
— Наверное, и с несобственным интегралом можно так же:
если у функции есть первообразная, которая имеет предел в особой
точке, то интеграл от этой функции сходится.
— Если вы говорите о несобственном интеграле, то, вероятно,
имеете в виду, что функция f(x) в особой точке стремится к
бесконечности, а ее первообразная F(x) стремится к конечному
пределу. А бывают ли такие функции? Можете ли вы представить
456
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[Гл. 6
нам хотя бы одну такую? Представить, быть может, и не
формулой — хотя бы графиком. Подумайте над моим вопросом — я не
требую немедленного ответа.
Минуты три спустя в первом квадранте координатной
системы он аккуратно рисует восходящую линию и заканчивает ее
жирной точкой, когда она круто направляется ввысь:
— Пусть это будет F(x). А вот /(х), — ниже он рисует
соответствующий график.
— Великолепно! Чего-то подобного я и ожидал от вас. От
себя добавлю к вашей кривой еще один штрих, —
подправляю ее так, чтобы она походила на график арксинуса. — И
еще замечу: если первообразная подынтегральной функции
не определена в особой точке, но имеет в ней предел, то ее
можно там доопределить до непрерывности. И тогда ваш вывод
можно сформулировать так: пусть функция f(x) интегрируема
в любом промежутке [а, Ь — е], где е > 0; если существует
функция F(x), которая на интервале (а, Ь) является
первообразной для /(х), а на отрезке [а, Ь] непрерывна, то интег-
ь
рал ff(x)dx...
а
— Сходится, — завершает Кулагин.
— А если исследуется сходимость интеграла от /(х) на
бесконечности?
— То для сходимости интеграла функция F(x) должна иметь
предел на бесконечности.
— Точно! Садитесь, Андрей.
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
457
Рядом с графиками, которые он набросал, я рисую еще два,
один под другим. Кривую на верхнем обозначаю F(x), на
нижнем — f(x).
— Внимательно поглядите, ребята, на обе кривые,
помеченные символом F(x), — те, что предложены Кулагиным и
мною, — и постарайтесь припомнить функции, которые ведут
себя подобным образом. Производные этих функций, возможно,
дадут нам новые примеры сходимости несобственных
интегралов.
Сутеев, указывая на мою кривую, называет арктангенс,
Синице же она напоминает выражение 1 — ^. Чюмин, показывая
на график Кулагина, предлагает рассмотреть арксинус — понял
мой намек! Записываю соответствующие интегралы со словами:
— Эти примеры, ребята, хорошо послужат нам на
предстоящем этапе нашего семинара. Но прежде, чем приступать к новым
примерам, я хотел бы вспомнить замечание Миклашевского,
которое я когда-то пресек, как преждевременное. Миклашевский
говорил примерно так: из того, что интеграл от функции ^
расходится на плюс бесконечности, следует, что там будет расходиться
и интеграл от всякой функции, график который пролегает над
гиперболой. Затем было несколько слов в доказательство этого
458
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[Гл. 6
утверждения, но я их повторять не стану: надеюсь, что мы сейчас
придумаем более строгое доказательство. Первую попытку для
этого следовало бы предоставить, конечно, автору утверждения.
Хотите, Павел? Да? Идите к доске и, прошу вас, — как можно
внимательнее и строже. Думаю, ради этого следует начинать с
определения несобственного интеграла.
— Можно, — покладисто отвечает он. — В этом определении
А
берется интеграл J/(x)dx, а потом А устремляется к бесконеч-
а
ности. Рассмотрим кроме функции f(x) еще и р(х), которая для
любого х больше /(х), — он поясняет сказанное простеньким
чертежиком. — Стало быть, для любого А выполняется неравенство
поддерживаю их, —
А А А
ff(x)dx < fg(x)dx. Когда А возрастает, интеграл ff(x)dx тоже
а а а
растет...
— Растет?! — вскидывает брови Горт, и Буткус вторит ему:
— Разве?
— С чего это вы взяли, Миклашевский,
что интеграл растет?
— Но ведь подынтегральная функция — положительная!
— Действительно, на вашем чертеже она положительна. Но
вы не оговаривали это условие.
— Да, пожалуй, это стоит оговорить...
— Я же просил вас: повнимательнее, построже!
После каждой такой оплошки Миклашевского меня
подмывает отругать его как следует, взять в ежовые рукавицы, следить
за каждым его словом, чтобы навсегда вытравить из него
верхоглядство. И всякий раз что-то удерживает меня от крутых мер.
Да, ошибок в его рассуждениях — хоть отбавляй. Но время от
времени в его скороспелых словоизлияниях встречаются
поистине блестящие мысли. Как здорово пришел он к идее формулы
Тейлора за разговором о пределах функций! Если я примусь за
него покрепче, приучу его контролировать каждое слово,
неряшливостей в его рассуждениях наверняка станет меньше. Но не
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
459
послужит ли такой контроль заслоном и для остроумных
догадок? Ладно уж, пусть выдает их в шелухе ляпов, если не может
иначе. Не стану заострять на нем требование строгости, — буду
понастойчивее создавать во всей группе атмосферу строгости,
дух строгости: он лучше исправит Миклашевского, не запугивая
его, не подавляя в нем творческой энергии. Она мне ценнее, и
следовало бы сильнее разжигать ее нетривиальными задачами,
которые так нравятся ему...
— Значит, — продолжаю разговор, — ваше рассуждение
годится только для всюду положительных функций?
-Угу.
— А, может быть, для более широкого класса — для
неотрицательных?
— Для неотрицательных, конечно, — соглашается он.
— Ну что ж, это тоже кое-что. Продолжайте.
— Значит так: в силу неотрицательности функции f(x) ин-
А
теграл ff(x)dx может лишь возрастать с ростом А. Здесь есть
а
две возможности. Первая: интеграл растет, но при этом ограни-
А
чен сверху. Тогде существует предел lim f/(x)dx, то есть ин-
А-+ооа
+оо
теграл J f(x)dx сходится. Вторая возможность: интеграл рас-
а
+оо
тет неограниченно. Тогда f f(x)dx расходится. Но в этом слу-
а
А
чае неограниченно будет расти и интеграл fg(x)dx, и интеграл
а
+оо
f g(x)dx тоже будет расходящимся.
а
— Так, так, — просматриваю его выкладки, — значит, если
для функций f(x) и д(х) при любом значении х > а
выполняется соотношение 0 < f(x) < д(х)... Вы не возражаете,если
я поставлю знак нестрогого неравенства между этими двумя
функциями?
— Нет, — пожимает он плечами, — выводы будут те же.
— Я тоже так считаю, потому и предлагаю. Значит, если f(x)
и д(х) при достаточно больших значениях х подчиняются
соотношению 0 < f(x) < g(x) и интеграл от f(x) расходится на плюс
бесконечности, то расходится и интеграл от д(х). Мне кажется,
было бы интересно изучить все возможные логические взаимо-
460
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[Гл. 6
связи между сходимостью и расходимостью интегралов от
функций /(х) и р(х), подчиняющихся указанному соотношению.
— Сейчас! — по его глазам вижу, что мое предложение его
увлекло. — Если интеграл от д(х) расходится, то про интеграл
от f(x) ничего сказать нельзя, он может и сходиться и
расходиться, это очевидно. Если интеграл от д{х) сходится... Тут кое-
А А
что интересное... ff(x)dx < fg(x)dx... Если у правого интеграла
а а
есть предел, то левый ограничен этим пределом, он к тому же
возрастает... и тоже будет иметь предел! Значит, если сходится
интеграл от д(х), то сходится интеграл от f{x). Теперь: если
сходится интеграл от f(x)... опять ничего нельзя сказать: от д{х)
интеграл может как сходиться, так и расходиться.
— Повторите-ка еще разок все эти «если... то», которые
вы нашли. Начните с условий, которым подчинены функции
f(x) и g(x).
— Пусть даны две неотрицательные функции, одна из
которых больше или равна другой, точнее, при достаточно больших
ж, больших какого-то а, выполняется неравенство 0 < f(x) <
+оо
< д{х). Тогда, если сходится интеграл / g(x)dx, то сходится и
а
+оо +оо
интеграл / f(x)dx. А если расходится интеграл / f(x)dx, то
а а
А
расходится и интеграл fg(x)dx.
а
— Очень хорошо. Запишите оба вывода в свои тетради,
ребята. Утверждение, которое продиктовал Миклашевский,
называется признаком сравнения. Он позволяет судить о сходимости
несобственных интегралов от неотрицательных функций на
основании исследования интегралов от других функций, как
правило, более простых. Мы увидим это на примере интеграла, ко-
торый я написал с подачи Сутеева: / т+^г- Догадываетесь, —
1
поворачиваюсь к Миклашевскому, — в чем тут суть дела? Как
объяснили бы ее?
— Элементарно: jq^2 < ^, а интеграл от ^ на бесконечности
сходится. Значит, от j^ тоже сходится.
— Совершенно верно. Садитесь, Миклашевский. А полное и
последовательное решение этого примера пусть даст на доске
Мухин.
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
461
Предупрежденный о четкости, которой я от него требую по
нашему давнему уговору, он сначала по моему совету повторяет
данную Миклашевским формулировку признака сравнения и
делает это неплохо. Потом столь же хорошо решает пример. Когда
же он научится работать так же хорошо без моих
предупреждений? Отсылаю его на место.
— Идем дальше, ребята...
— Мы не вычислили, чему равен интеграл / i+l*, —
замечает своим металлическим голосом Сутеев.
— А это, знаете ли, часто и не требуется при исследовании
несобственных интегралов. Как правило, важно выяснить лишь
вопрос об их сходимости. Для этой цели применяются различные
признаки сходимости. Один из них — признак сравнения — мы с
вами только что разработали. Правда, его формулировка носит
еще весьма частный характер...
— В том смысле, что не годится для интегралов от функций,
неограниченных в какой-то конечной точке? —
предупредительно спрашивает Рамзин.
— Для них проходит то же самое доказательство! — одним
махом закрывает вопрос Костюк.
— Все согласны с Костиком? — оглядываю аудиторию. — Кто
мог бы показать это строго?
Из поднявших руки выбираю Кочина. Терпеливо дожидаюсь,
пока он доберется до завершающего «что и требовалось
доказать». Чувствуется, что с легкокрылого говорка Миклашевского
он не совсем ясно усвоил, как обосновывается признак
сравнения, так что сейчас для него речь идет скорее не о
переформулировке, а о воссоздании доказательства, а это, конечно, стоит
ему немалых трудов.
Наблюдаю за его работой, стоя рядом с Сынчиковым. Тот без
задержек и, по-видимому, с ясным пониманием переписывает с
доски выкладки Кочина. Более того: когда Кочин надолго
останавливается в раздумьи, Сынчиков сам продолжает
доказательство! Он, пожалуй, уже не нуждается в моей неотрывной опеке.
Возвращаюсь к доске, помогаю Кочину довести рассуждение до
конца.
— Неплохо, — оцениваю сделанное им. — Теперь следовало
бы подкрепить общее рассуждение конкретным примером.
Среди трех несобственных интегралов, предложенных недавно
Сутеевым, Синицей и Чюминым, был один с особенностью в ко-
462
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[Гл. 6
1
нечной точке: [-===. Не подойдет ли он под доказательство,
J vi-x2
только что проведенное вами, Дима? Вы, очевидно, уже
заметили: когда мы применяем признак сравнения для исследования
несобственного интеграла от какой-то функции, то сравниваем
ее с одной из хорошо знакомых нам функций. А лучше всего
нам знакомы функции вида ^: мы разбирали интегралы от них
и на бесконечности, и в нуле; потом перенесли результаты
разбора на функции вида /х*ау и ,а}х\я с особенностью в ненулевой
точке а...
Замолкаю, надеясь, что он продолжит. И он продолжает —
не сразу, не громко, но довольно уверенно:
— Здесь особая точка единица... Для сравнения, наверное,
/1_ ... Нет, у нас ведь х меньше единицы; корень надо другой:
}_ . И чтоб подынитегральная функция была меньше... То есть
у/1 — х2 больше у/1 — х... у/{\ — х){\ + х)... х близок к единице,
положителен, 1 + х > 1... Все верно: \/1 — х2 > у/\ — х, , * 2 <
< }_ , показатель — половина, меньше единицы... По признаку
1
сравнения интеграл J-t== сходится.
о
— Очень хорошо, садитесь. Ну вот, ребята, теперь у нас готово
почти все для того, чтобы сформулировать признак сравнения в
наиболее общем виде. Стоило бы только еще отметить, что этот
признак применяется не только для всюду неотрицательных, но
и для всюду неположительных функций. Кто обоснует
возможность такого применения?
Ответ дает Синица:
— Неположительную функцию h(x) можно представить в
виде (—1)/(х), где f(x) уже неотрицательная: с ней и нужно
вести рассуждения, а минус единицу выносить за знак
интеграла, мы уже говорили, что это можно делать, это на сходимость
не влияет.
— А работать с неотрицательными функциями нам
привычнее, — продолжаю я. — Поэтому признак сравнения можно
применять к любой знакопостоянной функции, а
формулировать только для неотрицательных. Пусть нам даны две функции
f(x) и д(х), связанные неравенством 0 < f(x) < д(х) в
окрестности какой-либо особой точки, конечной или бесконечной.
Если несобственный интеграл от функции д(х) сходится в этой
точке, то там же сходится и интеграл от функции f(x). Если
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
463
же расходится интеграл от /(х), то расходится и интеграл от
д(х). Легко проверить, что те же выводы справедливы для
неположительных функций f(x) и д(х), связанных неравенством
д(х) < f(x) < о.
Выжидаю паузу, чтобы ребята успели записать
продиктованное мною.
— Записали? Тогда будем изобретать новые признаки.
— Скажите, — поднимает руку Синица, — нужно опять
придумать такой признак, который годился бы и для бесконечности
и для конечной точки, да?
— Если придумаете нечто, пригодное для интегралов лишь
одного из двух видов, то и это будет хорошо. Хотя, разумеется,
лучше бы изобрести что-то универсальное. Конечно, работать
сразу на два фронта нелегко. Но ведь вы можете действовать так
же, как при разработке признака сравнения: если вы помните,
мы сначала сформулировали его для интегралов с бесконечным
верхним пределом, а потом сумели перенести на случай
конечной особой точки. Можно действовать и наоборот, это дело
вкуса. Вам-то самой, Люда, какие интегралы больше нравятся — с
бесконечным верхним пределом или с конечной особой точкой?
— С бесконечным пределом: они как-то удобнее, нагляднее
что ли...
— Нагляднее? Это вы нам очень кстати напомнили про
наглядность. Мы забыли про нее, когда сравнивали функции j^-s
и -If. Давайте же ради наглядности задним числом нарисуем
графики обеих функций. Кто у нас в группе хорошо это делает?
Кажется, вы? — жестом зову к доске Стуеева. — Ну, что вы скажете
про эти два графика? — спрашиваю, когда он кончает рисовать.
— Очень близкие при больших х, почти сливаются...
— В этих словах что-то есть, не правда ли, Сутеев? А я не раз
говорил: если чувствуете, что напали на какую-то суть,
старайтесь выразить ее в строгих математических терминах. «Близки»,
«почти сливаются», «почти неотличимы» — как перевести все
это на математический язык? Не сообразите? А что скажете вы,
Синица?
— Эквивалентны!
— Не пахнет ли здесь каким-то признаком сходимости?
— Может быть, таким: если одна функция эквивалентна
другой и интеграл от одной сходится, то сходится и интеграл от
другой? — осторожно предлагает она.
— Утверждение довольно правдоподобное. Попробуем
доказать его сообща. Садитесь на место, Сутеев.
464
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[Гл. 6
Брожу между столами — минуту, другую... Никто не
вызывается довести до конца рассуждение, намеченное Синицей.
— Что же вас сдерживает, ребята? Наверное, все тот же
порок, от которого вы никак не можете избавиться: неумение
или нежелание выразить в математических терминах каждую
мысль, возникающую по ходу решения задачи. Функции f(x)
и д(х) эквивалентны, — говорим мы. А кто из вас записал на
языке формул, что это значит?
Мой упрек подхлестывает ребят. Буквально через минуту
покаянное «у-у-у!» Горта оповещает: решение найдено, оно совсем
простое — и как это оно сразу не пришло в голову?! В тетрадях
у Рамзина, Кулагина, Гарина тоже уже написаны соотношения,
необходимые для доказательства одновременной сходимости и
расходимости интегралов от f(x) и д(х). Вызываю Горта.
— Ну вот, опять! — негромко бурчит Гарин, когда Горт
умножает полученное им неравенство на д(х).
— Что «опять»? — оборачиваюсь к нему.
— Опять все справедливо только для знакопостоянных
функций: если д(х) положительная, все знаки неравенства
сохранятся, если отрицательная, — заменятся на обратные.
— Ради определенности, — делаю намечаемый его репликой
выбор, — будем считать д(х) неотрицательной при тех
аргументах, при которых справедливо неравенство для дроби ££■*.
— Надо даже потребовать, чтобы д(х) была строго больше
нуля: если бы она где-то обратилась в нуль, дробь потеряла бы
смысл, - уточняет бдительный Горт.
— Вы правы. Что же после всего перечисленного можно
сказать про интегралы от функций, которые вы подчинили своим
неравенствам?
— Сначала лучше рассмотреть второе неравенство. Тут все
как в признаке сравнения: две положительные функции, одна
Ю. В. Иухначев)
СЕМЬ СЕМИНАРОВ
465
больше другой; сходимость интеграла от f(x) следует из
сходимости интеграла от (1 +е)д(х), проще сказать — от д(х)\ (1 +е) —
постоянный множитель, его можно не учитывать, он на
сходимость не влияет, мы доказывали. Короче говоря, если сходится
интеграл от д(х), то сходится интеграл от f(x) — вот что
следует из второго неравенства. А из первого — тем же путем: если
сходится интеграл от /(х), то сходится и от д(х).
— В таких случаях говорят, что интегралы от обеих функций
сходятся одновременно.
—Они и расходятся одновременно. Из первого неравенства:
если расходится интеграл от д(х), то расходится и интеграл от f(x).
Из второго: если расходится от /(х), то расходится и от д(х).
— Как можно выразить все это в одной фразе? По-моему, у
вас все готово для формулировки нового признака сходимости.
Попробуете?
— Пусть даны две знакопостоянные функции f(x) и д(х), для
определенности — строго положительные. Пусть эти функции
эквиваленты на плюс бесконечности, то есть lim Ц%1 = 1. То-
x-+oo0W
+оо +оо
гда несобственные интегралы f f(x)dx и f g(x)dx сходятся и
а а
расходятся одновременно.
— Верно. Это так называемый признак эквивалентности. Мы
сформулировали его для интегралов с бесконечным верхним
пределом...
— Но можно перенести его на случай интегралов с конечной
особой точкой, — понимающе заканчивает Горт.
— Сделайте это. Хорошо, хорошо... Замечу, ребята, что при
использовании этого признака понятие эквивалентности
трактуется несколько шире, чем мы это делали до сих пор: отношение
функций предполагается стремящимся не к единице, а к любой
положительной константе. Доказательство проводится точно так
же, как оно было проведено Гортом, — двумя штрихами
превращаю единицу в его выкладках в прописную букву к и
приписываю рядом к > 0.
— А если к равно нулю? — любопытствует Лапиков.
— Нулю? — Горт тут же начинает набрасывать на доске
подходящее к такому случаю доказательство. — Тогда, значит...
меньше произвольного £...
— Остановитесь, Саша! — прерываю его. — И садитесь на
место — дальше, я думаю, Лапиков все сможет сделать сам. К
доске, Егор!
466
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[Гл. 6
Догадавшись умножить на д(х) последнее из написанных
Гортом неравенств, он наконец приходит к выводу:
— Если интеграл от д(х) сходится, то сходится и интеграл от
/(х), а если расходится от /(х), то расходится и от д(х).
— Все верно, садитесь. Теперь надо опробовать новый
признак в деле. Исследуем заново с его помощью интегралы,
предложенные Сутеевым, Синицей и Чюминым. Кто бы это сделал?
Аргунова, видимо, ободренная удачами Лапикова,
приподнимает руку над столом. Обрадованный ее желанием, я все-таки
стараюсь не обнаруживать своей радости: лучше вести себя так,
будто я воспринимаю это желание как нечто само собой
разумеющееся:
— Пожалуйста, Галя.
+оо 1
dx __ С dx
Без особых затруднений разбираем интегралы J Н^ и /-тг=
2 '
о
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
467
— Все хорошо, садитесь. Теперь три примера посложнее. В
каждом под интегралом будет стоять неотрицательное
выражение — ведь с помощью выведенных нами признаков можно
анализировать только такие случаи. Занесите это, ребята, на
видное место в своих тетрадях: признак сравнения и признак
эквивалентности применимы лишь к несобственным
интегралам от знакопостоянных функций! Ну, а теперь запишите
примеры: / ^*ff+1; / ^^dx; f -Jib;. Надо исследовать
l 1 о
эти интегралы на сходимость. Там, где встречаются
параметры — а, р, q — следует выяснить, при каких их значениях
интегралы сходятся.
Решение первого примера, как я и ожидал, отыскивается
быстро и единодушно: подынтегральная дробь эквивалентна
функции jj, интеграл от которой на бесконечности сходится, —
сходится, стало быть, и исходный интеграл. По второму
примеру затеваю дискуссию: Кулагин в своем решении опирается на
ограниченность арктангенса и применяет признак сравнения,
Гарин же предлагает использовать признак эквивалентности,
поскольку арктангенс на плюс бесконечности стремится к |.
— Какому подходу мы отдадим предпочтение, ребята?
Стрельцов удивленно приподнимает брови — в обоих
подходах он не видит существенной разницы:
— Ведь ^ — это и ограничение для арктангенса, и его предел.
Что по признаку эквивалентности, что по признаку сравнения —
ответ одинаковый: интеграл сходится при а > 1.
— Хорошо. Но такой ответ нельзя признать полным. Для
полноты надо еще доказать, что при всех остальных а интеграл
расходится.
— Да-да, — с полуслова понимает Стрельцов. — Чтобы
доказать расходимость, надо ограничивать арктангенс снизу... ^,
допустим...
— Во всяком случае, — развиваю его мысль, — надо делать
еще одну оценку. А когда мы сопоставляем с подынтегральной
функцией эквивалентную...
— То мы говорим: интегралы от них сходятся и расходятся
одновременно, — догадливо подхватывает он, напирая на слово
«расходятся». — При а > 1 интеграл / рг сходится, при а < 1
1
расходится, исходный интеграл, стало быть, ведет себя так же.
Значит, признак эквивалентности здесь удобнее.
468
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[Гл. 6
— И, как нетрудно догадаться, не только здесь: если какой-
то интеграл можно исследовать с помощью обоих признаков, то
признак эквивалентности, как правило, быстрее приводит к
результату, чем признак сравнения.
Беседуя со Стрельцовым, брожу между столами, смотрю как
продвигается работа у того, у другого... Хочется вызвать Сынчи-
кова: кажется, со своим решением последнего примера он может
рассчитывать на верный успех.
— Не хотите ли к доске, Сынчиков? Можете взять с собой
тетрадь. Итак, вы предполагаете р и q различными, причем р >
q, и разбиваете интеграл на два, чтобы в каждом было лишь
по одной особой точке, это понятно... А что вы делаете потом?
Например с тем интегралом, где особая точка — плюс
бесконечность?
— Если р больше q, то xq можно отбросить.
— Отбросить? Если не видеть того, что вы написали в своей
тетради, можно было бы подумать, что вы ничего не понимаете.
Прочтите-ка, что вы написали для дроби р* на бесконечности.
xp+xq
— Что она эквивалентна ~.
— Докажите это. Так, так... Ну вот! Эквивалентна ~ и,
следовательно, сходится в том случае...
— Когда р > 1.
— Верно. А что в окрестности нуля?
— В окрестности нуля хР+хЯ эквивалентно ^, — не дожидаясь
моих вопросов, он доказывает это и заключает:
— Сходится при q < 1.
— Все, в иринщпе, верно. Но все-таки, ребята, давайте еще
раз мысленно разберем сказанное Сынчиковым: быть может, он
чего-то недосказал? Не сделаете ли это, Рамзин?
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
469
Не зная, как вести себя в неожиданной для него роли
редактора, не успев сообразить, какую позу, какой тон ему
лучше принять, он останавливается на самых простых
выражениях:
— Надо было сказать, почему здесь применим признак
эквивалентности.
— Функция положительна, — отрывисто отвечает Сынчиков,
не поднимая взгляда.
— Вот-вот, — поддерживаю его. — Об этом всегда стоит
говорить в самом начале. А условие сходимости? Нельзя ли
сформулировать его иначе? Что скажете, Рамзин?
— Мне думается, лучше было бы записать его так:
max{p, q} > 1, min{p, q} < 1.
— Проще сказать, — предлагает Кулагин, — единица
принадлежит интервалу (q,p).
— Вот, на мой взгляд, самый удачный ответ на вопрос
задачи. — поддерживаю эту формулировку. — Садитесь,
Сынчиков. Следующий пример: исследовать на сходимость интег-
+00
рал / {-^dx.
1
— Только один? И все? — удивляются Лапиков и Кочин.
— Работы здесь на добрую пятерку примеров, — заверяю
их.
— Вы имеете в виду, что у этого интеграла не одна особая
точка? Наверное, не только бесконечность, но и единица? —
допытывается Меншиков.
— Возможно, возможно, — уклоняюсь от ответа, чтобы
ребята поискали его сами. — Кстати, если уж речь зашла об
особенности в единице, в точке, не совпадающей с нулем, — что
напрашивается в таких случаях?
— Замена переменных! — следует многоголосый ответ. На
доске замену проводит Синица:
— Получается 1п(1 + £), этот логарифм в нуле эквивалентен t.
Признак эквивалентности здесь применим, потому что при
положительных t подынтегральная функция в окрестности нуля
положительна.
— А чему эквивалентно в нуле 1 + t? — спрашивает Чю-
мин.
— В самом деле, чему? — передаю этот вопрос аудитории.
При всей своей простоте он озадачивает многих. Недоуменное
молчание лишь с полминуты спустя обрывается ворчливым
голосом Гарина:
470 НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ [Гл. 6
— Ну как это чему? Единице...
— Конечно! Разумеется! Отношение стремится к единице! —
подхватывают тут же Костюк, Рамзин, Стрельцов.
— Значит, — заключает Синица, — в нуле у подинтегральной
функции никакой особенности нет, она там стремится к нулю,
ограничена, интегрируется, как обычно, в собственном смысле.
— Правильно. Переходим к бесконечности. Думаем все
вместе. Садитесь, Люда.
Минута за минутой проходят безрезультатно. С усмешкой
гляжу на Лапикова:
— Что я говорил? За время, которое уже ушло на этот
пример, мы успели решить три предыдущих. Теперь я вижу,
насколько внимательно вы слушали то, о чем говорилось до сих
пор.
— О логарифмах мы сегодня не говорили, — оправдывается
Лапиков.
— Сегодня нет, вы правы. Но разве я требовал, чтобы вы в
своих рассуждениях применяли лишь то, о чем была речь
сегодня? Я уже подчеркивал однажды: в вашем активе — вся
пройденная вами математика, начиная с четырех арифметических
действий. И если вам не хватает упоминавшегося недавно —
значит, надо углубиться в более ранние занятия: когда-то, помнится,
у нас заходил разговор о дробях вида Щ^г, и я просил вас дома
исследовать их поведение на бесконечности.
— При любых положительных р и q такая дробь стремится
к нулю, это я доказал, — буравит наступившее безмолвие голос
Буткуса. — Но ведь если функция стремится к нулю, интеграл
от нее не обязательно сходится!
— Не обязательно, — соглашаюсь с ним. — Тут необходимы
еще какие-то соображения. Чтббы собрать их, я стану
записывать на доске каждую разумную идею, которая появится у кого-
либо из вас в тетради.
Мое обещание не доставило мне много работы: на доску я
занес лишь определение несобственного интеграла с особенностью
на бесконечности, которое старательно выписала на чистой
странице Аргунова. Никто из ребят не придал значения этой
общеизвестной формулировке: равнодушно глянули — и снова уткну-
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
471
лись в свои тетради. Но через минуту-другую Мухин вновь
впился в нее взглядом:
— А ведь... Я что хочу сказать — ведь когда мы брали
простой, обыкновенный интеграл — определенный или
неопределенный — от логарифма и еще чего-нибудь — мы логарифм — мы
ведь его убирали — по частям брали интеграл — ну, и убирали —
вместо логарифма получали j.
— Вы и здесь собираетесь интегрировать по частям? —
спрашиваю, стараясь выдерживать нейтральный тон. — Что это
даст? И как брать по частям несобственные интегралы?
— Не знаю, — мнется он, стушевавшись.
— Так давайте узнаем! — приглашаю его к доске и
указываю на свою последнюю запись на ней. — Возьмите
определение несобственного интеграла через определенный, который мы
умеем брать по частям, не забудьте, что подынтегральное
выражение записывается в виде... Словом, вспомните все, что нужно,
обдумайте, не торопясь...
А
Мухин пишет интеграл в виде lim fudv и преобразует его,
Л—+ооа
забыв поставить перед первым слагаемым в правой части
возникшего равенства символ предела.
— А почему вы переходите к пределу только во втором
слагаемом? — останавливаю его. — Я же говорил вам: не
торопитесь! Жертвуйте темпом ради качества, а не наоборот! Пишите
так, чтобы держать под контролем каждое свое преобразование,
каждое обозначение. И чтобы их понимали все, кто слушает вас.
Вот вы переписали первое слагаемое: lim uv\£. Что это такое?
А—>+оо
Можете объяснить? Давайте поподробнее, пологичнее, как мы с
вами договаривались когда-то: напомните сначала, что значит
472
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[Гл. 6
uv\q ... Ну вот, все верно — три слагаемых: значение uv в точке а
и еще два предела. Второй можно выразить знакомым нам сим-
+оо
волом / vdu. Первые два слагаемых после того, как мы разо-
а
брались с ними, тоже можно обозначить более кратко: гш|+°°,
теперь мы понимаем, что это такое.
— Это предел, — вставляет Мухин, чтобы ни у кого не
оставалось сомнений, понимает ли он такое обозначение и все, что
относится к вычислению несобственных интегралов по частям. —
Два предела — если оба существуют, то и интеграл сходится —
который мы берем по частям.
— Правильно, своими рассуждениями вы доказали такую
теорему. Давайте же применим эту теорему и выведенную вами
формулу к нашему интегралу с логарифмом.
В тот момент, когда Мухин получает под знаком предела
дробь ;^ггг, Буткус вскрикивает:
— Вот тот предел! Дробь стремится к нулю!
— Минуточку, Линас, — мягко притормаживаю его. — Пусть
Мухин все сделает сам.
Дождавшись, когда он выпишет оба предела, даю ему новые
задания:
— Выясните, когда существуют эти пределы. Не спешите,
обдумайте все...
Вероятно, выкрик Буткуса напомнил Мухину тот вывод, о
котором Линас сообщил раньше:
— Дробь j^^T стремится к нулю — когда а — 1 больше
нуля — когда а больше единицы... И интеграл, который дальше
получился, тоже сходится — когда а больше единицы!
— Правильно. Значит, и исходный интеграл сходится тогда...
— Когда а больше единицы.
— Запишите этот результат и садитесь на место.
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
473
Буткус не желает расставаться с удивительным интегралом:
— Получается как без логарифма!
— Да, получается, что логарифм не влияет на сходимость.
Такой вывод довольно неожидан, не правда ли, ребята? Те, кого
заинтересовал этот интеграл, могут рассмотреть его в усложнен-
+00i *
ной форме: J* -^^-dx, а затем исследовать, сходится ли в нуле
1
интеграл от такой усложненной функции.
— На бесконечности сходится, если р больше единицы, a q —
любое, — неймется Буткусу.
— Подумайте об этом дома, — ухожу от обсуждения. — А
сейчас мы переходим к новой теме. До сих пор мы
рассматривали несобственные интегралы от знакопостоянных функций,
в теперь речь пойдет о несобственных интегралах от
знакопеременных. Чтобы с самого начала наши рассуждения не
были слишком отвлеченными, давайте попробуем придумать
такую знакопеременную функцию, интеграл от которой сходился
бы... ну, скажем, на бесконечности — с ней, как мы уже
выяснили, работать удобнее, чем с конечной особой точкой. Так какую
же функцию мы придумаем? — выжидающим взглядом обвожу
аудиторию.
— Что-нибудь с синусом, — небрежно роняет Меншиков.
— С синусом? Давайте, — ухватываюсь за его предложение. —
Что еще, кроме синуса, должно находиться под интегралом?
Думайте, думайте! — не спускаю глаз с Меншикова. Но он молчит
— только чуть наморщен лоб, да пальцы приподнятой руки мнут
воздух...
— Надо, чтоб вся подынтегральная функция убывала!
Разделить синус на х, например, — подсказывает Кочин.
Ах, Дима, Дима! Испортил все дело! Мне так хотелось,
чтобы Меншиков без чьей-либо помощи довел до окончательного
выражения свою идею — тем более, что он и сам, как мне
показалось, хотел того же... Но делать нечего — надо переключаться
на Кочина.
— То есть умножить sin х на j, — перефразирую сказанное
им как бы вскользь, но в то же время достаточно настоятельно,
чтобы такая трактовка запала в память ребятам: пригодится,
когда станем изобретать признак Дирихле.
— Ну да, — повторяет Кочин, — умножить на j, в общем,
взять функцию ^f-.
— Нарисуйте-ка ее, — зову его к доске, — да поточнее:
мы ведь начинаем новую тему: сейчас каждое слово, каждый
474
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[Гл. 6
штрих могут направить нас либо на плодотворный путь, либо
в тупик.
Один за другим над и под осью абсцисс возникают
уменьшающиеся по высоте горбы синусоиды; касаясь их вершин, сверху
и снизу тянутся пунктирные гиперболы.
— Аккуратнее, Кочин, аккуратнее! Что это у вас узлы
синусоиды сближаются с ростом х? Перерисуйте все заново!
Он стирает с доски весь график, чертит вновь оси
координат, размечает горизонтальную ось равноотстоящими точками,
рисует синусоиду с убывающей амплитудой и помечает ее
формулой ^jp.
— Теперь хорошо. Садитесь.
Перед уходом, придирчиво оглядев свой чертеж, он ставит
рядом с пунктирными гиперболами, ограничивающими
синусоиду, пометки \ и -\.
— Единица на икс? — недоверчиво глядит на доску Гарин. —
Мы с такой функцией один раз уже обожглись...
— Слышите? — обращаюсь к Кочину. — Гарин, как
показывает история, хорошо чует слабые места. Может быть, и сейчас
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
475
стоит к нему прислушаться? Как, вы думаете, ребята? —
обращаюсь ко всей аудитории.
Синица порывисто вскидывает взгляд куда-то вглубь небес
за окном, видимо, захваченная какой-то интересной идеей, но
едва я, уловив ее движение, собираюсь вызвать ее, тотчас
отнекивается:
— Нет, не сейчас, я еще немножко подумаю, — но уже через
несколько секунд встает и уверенным шагом идет к доске;
возводит в квадрат иксы в знаменателях формул, написанных на
чертеже Кочина, и над каждым обращенным вниз горбом
синусоиды рисует точно такой же, но обращенный вверх:
— Если взять вот такую функцию, всюду положительную:
она ведь меньше ^-, а интеграл от -^ сходится, значит, и от
этой функции будет сходиться, по признаку сравнения, его
здесь можно применить, функции знакопостоянные, обе. Но
ведь от такой функции, — мел в ее руке скачет по аркам
нарисованного ею синусоидального акведука, — ему труднее
сойтись, чем от старой, — теперь мел плавно скользит по
волнам графика функции §*Ar, — потому что там каждая волна
положительная, а тут за положительной идет отрицательная,
когда они складываются, получается всего ничего, так потом по
чуть-чуть и суммируется, не то, что там — вон какие огромные
куски.
Перекидываюсь легкой улыбкой со Стрельцовым в
продолжение этого растрепанного монолога и, когда он кончается,
спрашиваю ребят:
— Все поняли то, что сказала Синица? Что значит,
например, то, что интегралу от введенной ею
знакопостоянной функции «труднее» сойтись, чем интегралу от исходной
функции?
476
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[Гл. 6
— В общем-то понятно, — раздумчиво произносит Горт. —
Она ввела функцию *s™2 .»
— Точнее l^rl, — перебиваю его. — Вам, идущему вслед,
надо бы говорить, обобщая.
Горт подтягивается тотчас же:
— Она, в сущности, сравнивала сходимость интегралов от
функций f(x) и |/(х)|...
— Вот-вот! — закрепляю это направление мысли. — Что же
+оо +оо
можно сказать, сравнивая интегралы J f(x)dx и / \f(x)\dx?
а а
— Дайте подумать! — не принимает столь стремительного
темпа осторожный Горт.
— Думаем все вместе! — призываю аудиторию. — Садитесь,
Люда.
— Наверное, справедливо такое утверждение: если сходится
интеграл / |/(x)|dx, то сходится и интеграл / f(x)dx, — вскоре
а а
предлагает Гарин.
Ситуация, на первый взгляд, обычная для семинара: один
наметил путь рассуждения, другой прошел по этому пути до
интересной гипотезы. И все-таки что-то неладное видится мне в
том, что гипотезу выдвинул не начавший рассуждение, не Горт.
«Дайте подумать...» Строгость, которая позволяет ему так
чутко улавливать чужие ошибки, — не обращается ли она порою
против него самого? Не стреножит ли его мысль? Не гасит ли в
нем творческую искру? Нет, не зря говорил Эйнштейн: «Если не
грешить против разума, то вообще невозможно придти к чему-
либо». Как бы не вышло так, что все творческие силы парня,
сдерживаемые его сверхбдительностью, уйдут лишь на
уточнение, оттачивание, интерпретацию найденного другими — такими,
как Гарин. Тот, как всегда, ухватил самую суть дела...
— Вы доказали свое утверждение? — спрашиваю его.
— Нет еще.
— А это разве не очевидно? Ведь для любой функции
справедливо неравенство f(x) < |/(х)|, — напоминает
Миклашевский.
— Ну и что? — предвидя его заблуждение, стараюсь выявить
его пояснее для всех.
— Если сходится интеграл от большей функции, то будет
сходиться интеграл от меньшей.
— Что мы скажем на это? — обращаюсь к аудитории.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
477
— Признак сравнения справедлив только для
знакопостоянных функций, — как бы про себя замечает Костюк.
— Ах да! — спохватывается Миклашевский.
— Все слышали, ребята, что сказал Костюк? — обвожу
взглядом аудиторию. — Не повторяйте подобных ошибок! Думаем
дальше!
Иду между рядами, задерживаюсь над тетрадями тех, кто
строчит особенно бойко. Фантазии ребятам не занимать! Буткус,
задавшись произвольной знакопеременной функцией, вводит на
ее основе две новых: одна совпадает с исходной там, где та
положительна, и обращается в нуль, где исходная функция
отрицательна; другая наоборот. Своеобразно, как многое из того, что он
придумывает. Жаль только, что его оригинальные идеи иногда
оказываются совершенно нецелесообразными. И что самое
плохое — в такие моменты он не умеет отказываться от выбранного
порочного направления, перейти на лучшую колею, уже
проложенную другими, настаивает на своем. О, своей строптивостью
он намного превосходит другого заядлого упрямца, Костюка!
Тот, хотя и ерепенится шумливее, и спорит подолгу, а в конце
концов все же примет разумный довод. Буткус — не то, его так
не уломаешь, с ним и спорить-то невозможно: любую попытку
увести его с избранного пути он встречает в штыки, а если даже
и согласится с тобою на словах, в душе останется при своем
мнении. Его твердокаменное упрямство коренится где-то в самых
глубинах характера. Как бы это не навредило ему в будущем!
Одно у него спасение — оказаться при таком деле, где столь
присущая ему самостоятельность мысли ценилась бы в первую
очередь и даже гипертрофированная не обращалась бы ему во вред.
С внезапной страстностью молитвы разгорается во мне эта
мысль, обращенная уже не к одному только Буткусу, а ко всем
сидящим передо мною. Как хотелось бы, чтобы каждый из этих
ребят нашел свое место в жизни, отыскал бы такую работу, где
решающими были бы его лучшие качества, а худшие не имели
бы повода проявиться!
По школьной привычке они еще рассматривают занятия, как
некое состязание, где нужно бороться за первое место. Такое
настроение заведомо сулит разочарование большинству
соревнующихся: ведь первое место только одно. Свое же может найти
каждый. Но я не стану до поры до времени отучать их от
школьной привычки: пока что она им на пользу, пока что речь идет о
выработке навыков, обязательных для всякого, и всякий должен
преуспеть в этом...
478
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[Гл. 6
Миклашевский упрямо разрабатывает свою прежнюю идею.
В его тетради — неравенство 0 < |/(х)| — f(x) < 2|/(х)|.
— Здесь уже все функции неотрицательные, и |/(х)| — /(я), и
2|/(х)|, — горячо шепчет он мне в ухо, когда я склоняюсь над его
тетрадью. — Пусть интеграл от \f(x)\ сходится. Предположим,
что интеграл от f(x) расходится. Тогда интеграл от |/(х)| — f(x)
тоже должен расходиться: сумма сходящегося и расходящегося
расходится, мы доказывали. Но тогда должен расходиться и
интеграл от большей функции, от 2|/(х)|, а это противоречит
условию. Значит, неверно предположение о расходимости интеграла
от /(х), интеграл от f(x) сходится.
Вызываю к доске Буткуса и Миклашевского, чтобы они
продемонстрировали свои подходы к задаче.
— Понятно? — с сомнением гляжу на Сутеева.
— Да, — кивает он, и многоголосый хор поддерживает его.
— Да, ребята, — качаю головой, — все-таки верно писал когда-
то Пастернак о простоте: «Она всего нужнее людям, но
сложное понятней им». Я отдаю должное изобретательности Линаса
и Павла, но, не говоря уж про неточности в их рассуждениях,
— честное слово, эта задача заслуживает гораздо меньших
умственных усилий: ее решение лежит совсем недалеко от
определения понятия сходимости.
— Критерий Коши? — чуть подается вперед Рамзин, готовый
тотчас сделать все, что ему будет приказано.
— Ну, конечно! — приглашаю его к доске. — Садитесь, Бут-
кус. Садитесь, Миклашевский. А вы, Рамзин, сначала напишите
формулировку критерия для интеграла, сходящегося на
бесконечности, — как для |/(х)|, так и для f(x).
— Для интегралов в обеих формулировках, — начинает он
в своей солидной манере, — справедлива теорема, которую мы
доказывали на прошлом семинаре: модуль интеграла от
некоторой функции меньше или равен интегралу от модуля этой
функции. Короче, Уе > 03АУЛ'УЛ"((Л' > А) А {А" > А)) =>
А" А"
=> (\ f f(x)dx\ < f\f(x)\dx < е). Таким образом, если сходится
А' А'
интеграл от |/(х)|, то сходится интеграл от /(#).
— Верно. Надо бы только еще быть уверенным в том, что все
написанное вами имеет смысл — ну, скажем, вот этот интеграл, —
А"
указываю на символ / f(x)dx.
А'
— А что не так с этим интегралом?
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
479
— Что? Сейчас поясню. Представьте себе функцию /(х),
которая равна — р- при ненулевых иррациональных х и -^ — при
рациональных. Легко видеть, что взятая по абсолютной
величине функция f(x) совпадает с функцией ^. Получается, что
интеграл от |/(х)|, очевидно, сходится на бесконечности, и если
мы рассмотрим равнозначное этой сходимости утверждение кри-
А"
терия Коши, то стоящий там интеграл f jf не вызовет никаких
А'
сомнений в своем существовании. Но если мы напишем подобный
интеграл для исходной функции, то он не будет иметь смысла ни
при каких А' и А", не совпадающих друг с другом.
— Понял, — полупокорно-полублагодарно склоняет голову
Рамзин, вежливо дождавшись конца моего разъяснения. — Вы
сегодня уже давали аналогичное указание. Надо потребовать,
А"
чтобы интеграл f f(x)dx существовал при любых А' и А".
А'
— Дело тут не столько в моих указаниях, — возражаю
ему, — сколько в формулировке используемой вами теоремы о
модуле интеграла и интеграле от модуля некоторой функции.
Вспомните-ка ее поточнее.
6
— Если существует интеграл ff(x)dx, то существует и ин-
а
Ь
теграл f\f(x)\dx... Да, действительно: существование интеграла
а
надо было потребовать с самого начала. Итак, — потвердевшим
от уверенности голосом заканчивает он, — если некоторая
функция f(x) интегрируема на любом конечном промежутке из обла-
+оо
сти ее определения и сходится интеграл J* |/(x)|dx, то сходится
а
+оо
и интеграл § f(x)dx.
а
— Теперь ваше утверждение сомнений не вызывает.
Запишите его, ребята. И запомните полезный термин: если сходится ин-
+оо
теграл J* \f(x) \dx, то про функцию f(x) говорят, что интеграл от
а
нее сходится абсолютно. То, что мы доказали, с помощью этого
термина можно выразить краткой фразой: если интеграл
сходится абсолютно, то он сходится и сам по себе. Вернемся теперь к
тому, с чего начинался наш разговор. Мы хотели исследовать на
480
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[Гл. 6
сходимость интеграл от ^^, однако по совету Гарина перешли
к интегралу от §рп. По предложению Синицы мы
исследовали интеграл от знакопостоянной функции |^г|, доказали, что
он сходится по признаку сравнения на основании неравенства
l^p^l < J3) а теперь, Рамзин, мы можем утверждать... что?
— Что сходится также и интеграл от §рг.
— На основании какой теоремы мы можем это утверждать,
Аргунова? — испытываю, насколько прочно усвоено только что
пройденное.
— Если сходится интеграл от модуля /(#), то от /(#) тоже
сходится.
— При условии, что f(x) интегрируема — не забывайте об
этом! Ну, а как же все-таки с интегралом от §*££? _ возвращаюсь
к Рамзину. — Что можно сказать про него? Или даже поставим
вопрос шире — это, думаю, нам уже по силам: что можно
сказать про интеграл от функции вида ~~? При каких а он будет
сходиться на плюс бесконечности, а при каких — расходиться?
Как вы полагаете, Рамзин?
+оо .
— Я полагаю, что при а > 1 интеграл J* ~~dx будет схо-
а
диться заведомо.
Он доказывает это по той же схеме, что применялась к инте-
+оо .
тралу J ^dx.
a
— Хорошо. Нарисуйте числовую ось, на которой мы станем
откладывать значения а, отметьте на ней нуль и единицу и очер-
тите область значений а, при которых заведомо будет сходиться
исследуемый нами интеграл. Что можем мы сказать про
остальные значения а? При любом ли из них наш интеграл будет
расходиться?
— Уж при отрицательных а он разойдется наверняка! —
безапелляционно заявляет Меншиков и чертит в воздухе синусоиду
с нарастающими по высоте горбами.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
481
— Начертите эту картинку на доске, — вызываю его.
Испуг — на сей раз отнюдь не притворный — пробегает по его
лицу, когда он встает со стула: высказался, видать, толком
не подумав, боится оскандалиться, когда я потребую
обоснований.
— Мне садиться? — учтиво осведомляется Рамзин.
— Нет, пока постойте... Так как вы думаете, Менши-
ков, — гляжу на чертеж, возникающий на доске, —
почему будет расходиться интеграл от ^г при
отрицательных а?
— Функция неограниченная, — только и находит он, что
сказать.
— Ну и что? Разве ее неограниченность подрывает
определение сходимости интеграла на бесконечности? Ну-ка напишите
его! Не вспоминается сразу? Напрягайте память, думайте,
думайте! Так, так... верно. Ну вот, в определении сходимости
А
речь идет о пределе выражения ff(x)dx при Д
стремясь
щемся к бесконечности. Вы думаете, что неограниченность
подынтегральной функции сама по себе наверняка сделает
это выражение расходящимся? Но ведь наша f(x)
знакопеременная, больше положительные ее горбы в какой-то мере
компенсируются отрицательными, быть может, даже в та-
А
кой мере, что будет существовать предел lim ff(x)dx. Что
А—+ооа
вы скажете на это? Молчите... Что-то вы начали сдавать по
сравнению с началом семинара. Раньше вы и соображали
лучше, и рисовали аккуратнее — а сейчас чертеж набросали
кое-как, хотя я подчеркивал, как сейчас для нас важна
аккуратность... Кстати, вы подозреваете расходимость интеграла
16-2019
482
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[Гл. 6
лишь при а, строго меньших нуля или при меньших или равных
нулю?
— При нулевом а все тривиально, — вместо замявшегося Мен-
шикова быстро отвечает Миклашевский. — Тогда у нас будет ин-
+оо
теграл / sinxdx] первообразная синуса — косинус, а косинус на
а
бесконечности ни к какому пределу не стремится.
— Напишите это, — зову его к доске. — Хорошо. А по-другому
+оо
вы не можете доказать расходимость интеграла / sin xdxl
а
— По-моему, я доказал проще всего, — в его голосе слышится
изумление.
— Сами ведь говорили, — напоминает Стрельцов, — что
надо всегда искать самое простое решение, предельно адекватное
задаче...
— Говорил. Но, во-первых, простота — не
самоцель; во-вторых, этот пример у нас не последний, и
хорошо бы решить его таким методом, который наметил бы
общие подходы к дальнейшим примерам такого типа. Так
что же еще можно предложить для анализа интеграла от
синуса?
Рамзин, оттертый от доски в угол и явно не
желающий ронять свое горделивое достоинство сотрудничеством
со столь непонятливыми коллегами, лишь коротко
бросает:
— Критерий Коши.
— Ну, конечно! — вновь призываю его к работе. — Станьте в
сторонку, Меншиков и Миклашевский.
Рамзин тем временем доказывает расходимость интеграла от
синуса на основании критерия Коши, направляется к чертежу
Меншикова, чтобы поточнее перерисовать график, но
Меншиков загораживает ему путь, повернувшись к нему могучей
спиной, сам исправляет свой чертеж, строго выдерживая расстояние
между узлами заново нарисованной функции, пририсовывает на
Ю. В. Пухначев] СЕМЬ СЕМИНАРОВ 483
том же графике синусоиду и, опираясь на только что проведен-
ное Рамзиным доказательство, выводит расходимость для
отрицательных значений а. Не знаю, в чем мотивы его достижения —
в неприязни к Рамзину или в пробуждающемся трудолюбии, но
результат хорош.
— Теперь вы поняли, Меншиков, почему я домогаюсь от
вас аккуратных чертежей? Будь они у вас такими, идеи Рам-
зина тотчас пришли бы в голову к вам, я уверен. Садитесь
все трое. Итак, ребята, мы доказали, что при а < О интеграл
от функции ^^г расходится на бесконечности, — я указываю
соответствующую область на числовой оси. —
Необследованным остался лишь промежуток 0 < а < 1. Что можно
сказать про интеграл при таких значениях а? Думаем все
вместе.
Брожу между рядами. И — нечаянная радость! — в тетради
Сынчикова вижу преобразование, которое открывает прямой и
ясный путь к успеху: он выписывает определение несобственного
интеграла и к фигурирующему там интегралу в конечных преде-
16*
484
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[Гл. 6
л ах применяет интегрирование по частям. Вот кого бы вызвать
к доске, если он все доделает до конца! Продолжаю разгуливать,
то и дело возвращаясь к нему — что же напишет он дальше? Но
он неподвижно вперился взглядом в свою лаконичную запись.
Была не была — вызову!
— Перепишите на доске то, что написано у вас в тетради,
Володя. Интересный ход! Правда, ребята? — говорю в тоне по-
хвалы, а сам при этом думаю с сомнением: «Но приведет ли он
к успеху Сынчикова?»
И снова ему:
— Пожалуйста, поясните то, что вы написали.
— Косинус ограничен. При а положительных -^
стремится к нулю, когда х стремится к бесконечности. И все
выражение ^pг тоже, — глухо и отрывисто говорит он,
наклонив голову и как бы украдкой поглядывая на
написанное им.
— А второе слагаемое? Сходится ли этот интеграл?
— Его можно ограничить: |р|т| < ^г+т-
— Не его, вы хотите сказать, а подынтегральную функцию.
— Подынтегральную функцию. Даже ее модуль. При
положительных а интеграл от -^z+т сходится. Потому что a + 1
больше единицы. От модуля сходится, значит и от самой
тоже.
Он говорит, прерывая свою речь долгими паузами.
Нетерпеливо ожидая итоговой фразы, не выдерживаю:
— И весь интеграл...
— Сходится.
— Верно. Садитесь, пожалуйста. Равенство, которое вы
написали, не стирайте — скоро пригодится. Спасибо за отличное
решение. Пора подвести некоторые итоги, ребята. Исследуя
интеграл J j§, мы выяснили, что он сходится при a > 1 и расхо-
а
дится при а < 1. Появление под интегралом знакопеременного
множителя sinx смещает границу между областями сходимости
+оо .
и расходимости: интеграл / ^rdx сходится при a > 0 и расхо-
а
Ю. В. Пухначев] СЕМЬ СЕМИНАРОВ 485
дится при а < 0. Таким образом, мы исчерпывающе исследова-
ли его на сходимость. Однако для интегралов от
знакопеременных функций принято выяснять также вопрос об их абсолютной
сходимости. В свое время мы уже доказали, что интеграл вида
+0°lsinxl
/ go cfa сходится при а > 1. А как он ведет себя при осталь-
а
ных а? Давайте подумаем.
— При неположительных а он расходится, — говорит
Лапиков словно ступает на тонкий лёд.
— Почему? — негромко и совсем ненастойчиво спрашиваю
его.
Чуть запнувшись, он отвечает:
— Так же доказывается... по критерию Коши.
— Совершенно верно, — киваю ему и показываю на
выкладки Меншикова. — Доказывается, как и в этом случае, по
критерию Коши. Покажите это, Егор. Так, так... добрались
27ГП+7Г
до интеграла f |sinx|dx, a |sinx| на таком промежутке
27ГП
интегрирования не отличается от sinx, и вывод Меншикова
естественно вписывается в ваше рассуждение. Все верно,
садитесь. С неположительными а все ясно. Кстати, о расходимости
+оо .
интеграла J I sl*ax* dx в этом случае можно было бы заявить
а
и без столь долгих разбирательств: ведь если бы он сходился,
+оо т
то сходился бы интеграл / ^J^dx, а мы уже доказали, что
а
он расходится при а < 0... Остается промежуток 0 < а < 1.
Что мы скажем про эти значения а? Думаем, думаем,
ребята!
Раздумье затягивается.
486
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[Гл. 6
— Чует мое сердце, — наконец подает голос Кулагин,
мое сердце, что при всех таких а интеграл расходится.
— Чем обоснуете свое предчувствие?
чует
— Так ведь на графике все так же почти выглядит, как для
чистого ^.
Не совсем ясно. Пожалуйста, поясните чертежом на доске.
— Тут что-то очень похожее на признак эквивалентности, —
говорит он, обводя еще раз мелом графики функции ^р и
р-. — Нет, не в том смысле, что их отношение стремится к
константе: | sinx|, понятное дело, ни к какой константе на
бесконечности не стремится. Но вот если отношение площадей под этими
графиками попробовать посмотреть: такое впечатление, что оно
примерно одинаковое на всех промежутках. Значит, если от ^
интеграл расходится при а < 1, то и от 's^x' тоже расходится...
— К сожалению, Кулагин, у нас нет в запасе признака
сходимости, где речь шла бы про отношение площадей. Попробуем
сконструировать такой признак? Или постараемся обойтись уже
надежно испытанными для знакопостоянных функций — а
наша такова — признаками? Их у нас всего два —
эквивалентности и сравнения. Первый из них, как вы сами сказали, здесь не
подходит. Остается второй — признак сравнения. Может быть,
попробуем как-то применить его? Может быть, найдется
неотрицательная функция, всюду меньшая или равная | sinx|, но
более привычная, более удобная, что ли, чья формула похожа на
| sinx|, но без модульных скобок?
— Найдется, — негромко вставляет Сутеев. — Это sin2x.
— Отлично! — награждаю его восхищенным взглядом. Он
найдет свое место в коллективной работе, даже оставшись при
одном лишь своем визуальном мышлении, если сумеет сопрячь
его с чьим-то аналитическим. Но все-таки я постараюсь
пробудить и развить в нем самом недостающие ему способности.
Попробую заставить его до конца решить ближайший пример, с
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
487
которым он выйдет к доске, от первого иллюстративного
наброска — до заключительных строгих формул.
И снова к Кулагину:
-- А ну, Андрей!
Сообразительный Кулагин не заставляет просить себя
дважды: написав
тотчас разлагает правую часть
неравенства в разность т^- - £25^г > 0.
— Интеграл от второго слагаемого сходится, доказывается
так же, как для интеграла с синусом; от первого — расходится.
Сумма сходящегося и расходящегося расходится.
+оо .
— Что скажем окончательно про интеграл вида / §prdx?
а
При каких а он сходится и расходится просто и
абсолютно?
— Сходится при а > 0, расходится при а < 0. Сходится
абсолютно при а > 1, расходится абсолютно при а < 1.
— Садитесь — вы дали совершенно верный и полный ответ.
Я хотел бы только сделать к нему небольшое примечание
терминологического характера: если интеграл сходится сам по себе, но
расходится абсолютно, то говорят, что он сходится условно. С
помощью этого термина мы так можем описать сходимость нашего
интеграла: при а > 1 сходится абсолютно, при 0 < а < 1
сходится условно, при а < 0 расходится. Обратите внимание на
исчерпывающую емкость такой терминологии: краткая фраза сказала
нам все про сходимость интеграла и от исходной функции и от
ее модуля. Сходится абсолютно — но это, по известной теореме,
означает и простую сходимость; расходится — значит, и
абсолютно расходится тоже. Впрочем, термины терминами, а прежде
всего — суть дела. Давайте, ребята, еще раз вглядимся в столь
488
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[Гл. 6
+оо я
дотошно разобранный нами интеграл / ^rdx и подумаем: в
а
чем суть его сходимости при а > О? Два множителя — sinхи^.
Какие их свойства обеспечивают сходимость интеграла? Если мы
выявим эти свойства, то на место sinx и ^ мы сможем в
дальнейшем ставить другие функции и(х) и v(x), обладающие теми
же свойствами, и утверждать сходимость подобных интегралов
без долгих разбирательств. А ну, кто что скажет на этот счет?
— При положительных а множитель ^ убывает, даже
стремится к нулю, — открывает дискуссию Мухин.
— Стремится к нулю, — соглашаюсь с ним. — А что
существенно в синусе?
— Ограниченность? — уже с меньшей уверенностью
продолжает он.
— Итак, если мы возьмем ограниченную функцию и(х) и
убывающую до нуля функцию v(x), то можно ли утверждать, что
интеграл от их произведения будет сходиться на бесконечности? —
обращаюсь к аудитории.
— Константа, скажем, единица — функция ограниченная,
-4= - убывающая, — безразличным голосом, но с ядовитой
искоркой в глазах произносит Рамзин. — Интеграл от их
произведения не сходится.
— Слышите, Мухин? — вручаю этот сюрприз
застрельщику. -- Неудачный мы с вами изобрели признак сходимости
несобственных интегралов. Если не хотите попадать впросак,
как сейчас, прислушайтесь, наконец, к моему совету: не
говорите, не подумавши; прежде, чем брать слово, старайтесь
проговорить про себя свою мысль, попытайтесь представить,
как вы излагаете ее у доски, как ее принимают слушатели,
попробуйте предвидеть их реакцию, их возможные возражения,
попробуйте сами поискать контрпримеры к своим суждениям...
У кого есть другие, лучше соображения? — обращаюсь к
аудитории.
— Может быть, — нерешительно предлагает Чюмин, —
сначала попробуем выяснить, какой должна быть хотя бы одна из
этих функций?
— Безотносительно другой? — не спешу одобрять такое
упрощение проблемы. — Ваше предложение можно сравнить с
желанием научиться ходить на одной ноге. Уж не думаете ли вы,
что при определенном характере функции v(x) интеграл будет
сходиться, какой бы ни была и(х)?
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
489
Язвительный Рамзин (когда он в ударе, то способен
перещеголять даже такого въедливого критика, как Горт) завершает
мои слова уничтожающим примером:
— Возьмем тогда и(х = ££-л), где f(x) такая, что интеграл от
+оо
нее расходится: с одной стороны f u(x)v(x)dx должен
СХОДИТЬСЯ
ся, а с другой — расходиться.
Горт не любит, когда у него отбивают хлеб:
— Не совсем точное рассуждение: не проходит, если v(x)
обращается в нуль.
Чюмин, внимательно слушавший эту летучую дискуссию,
подытоживает ее неожиданным выводом:
— Значит, v(x) знакопеременная.
Стою, не зная, что сказать, в дурацком положении
буриданова осла: с одной стороны, вывод совершенно нелогичен и я
должен указать на это Чюмину; с другой — функции, которые
в наших дальнейших рассуждениях станут выступать как
обобщение sinx, наверняка будут, как и синус, знакопеременными,
так что мне лучше промолчать, чтобы своими возражениями не
подтормозить, не запутать естественное развитие этих
рассуждений.
Молчу. И через пару минут бесплодного молчания:
— Я бы советовал вам, ребята, внимательно просмотреть то,
что вы сегодня записали в своих тетрадях: рассуждение,
проведенное одним из вас, допускает очень плодотворное
обобщение на случай сходимости интеграла от произведения функций
и(х) и v(x), обладающих подходящими для сходимости
свойствами.
Шуршат страницы перелистываемых тетрадей, то там то
здесь изредка слышится шепоток совещающихся, но сказать
что-либо в полный голос не решается никто.
— Может быть, вы нам дадите еще какой-нибудь пример,
чтобы лучше разобраться в этих самых свойствах? — просит
Лапиков.
— А, может быть, — отвечаю ему провокационным
предложением, — я вам без обиняков выложу эти свойства,
чтобы вы потом без труда щелкали интегралы из
задачника?
— Не надо! — умоляюще вскрикивает Миклашевский и еще
несколько голосов поддерживают его.
— Тогда, ребята, внимательно читайте свои записи!
490
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[Гл. 6
В детективном раже они извлекают из своих тетрадей явные
и домысливаемые суждения. Мы разбираем их одно за другим
и убеждаемся: нет, не то... пока, наконец, Синица не вспоминает
про удачное предложение Сынчикова проинтегрировать по
частям »
х
— Кажется, подходит! Пусть и(х) стремится к нулю, a v(x)...
— Пожалуйте к доске! — приглашаю ее.
Она первым делом выписывает определение несобственного
+оо А
интеграла через предельный переход: Г uvdx = lim fuvdx.
а Л-+ооа
Потом переводит взгляд на равенство, написанное Сын-
чиковым:
— Косинус - это ведь первообразная синуса... ограничен...
ага! Не сама v(x) должна быть ограниченной, а ее первообразная,
вот! Надо ее как-то обозначить, допустим V(x). Нет, постойте:
первообразная — это ведь еще и плюс С!
— Плюс С вам не помешает, — легонько увожу ее от
мнимого камня преткновения, — ведь она не сделает ограниченную
функцию неограниченной.
— Вообще-то да, — соглашается Синица и, продолжая свои
размышления, вскоре опять спотыкается на втором слагаемом
формулы интегрирования по частям. — Это ведь только V(x)
ограничена, а не интеграл от нее!
— Можно вынести V(x) за знак интегрирования, — советует
Гарин.
— Основание? — поворачиваюсь к нему.
— Теорема о среднем, самый общий вариант.
— Когда он применим?
— Когда функция, которая остается под интегралом, не
меняет знака.
— Производная и'{х) не меняет знака — что это означает? —
продолжаю допрашивать Гарина: еще одно его слово — и все
сделано.
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
491
— Монотонность.
... Что бы я делал без этих орлов — без Гарина, Горта, Ко-
стюка, Синицы, Буткуса? Наверное, мне оставалось бы лишь та
скучная для меня, да и для них безрадостная манера ведения
семинара, когда я диктовал бы им готовые рецепты решения
стандартных задач и требовал вызубривать продиктованное. А с
такими молодцами (я поверил в них с первого семинара!) можно
смело идти по тому заманчивому пути, когда математика словно
воссоздается в ходе наших разговоров, в пытливых вопросах и
находчивых ответах моих собеседников. Увлеченность сильных
расшевеливает и втягивает в этот своеобразный диспут самых
слабых, так что в аудитории не остается таких, кто не сказал бы
своего слова. Найденное в общей беседе становится достоянием
всех ее участников. И подобно тому, как сделанная своими
руками вещь дороже дареной им купленной, так знания, добытые в
самостоятельном поиске, на мой взгляд, надежнее
преподнесенных в готовом виде...
Ну, а если бы в группе не было звезд? Что ж, я и тогда
бы постарался создать в ней атмосферу живого диалога и
творческого поиска. Не потому, что такой стиль преподавания для
меня привычнее, а потому, что я считаю его наиболее
эффективным.
— Давайте, Люда, — снова обращаюсь к Синице, —
давайте учтем Мишины соображения и предположим функцию и(х)
монотонной. Тогда... продолжайте!
— Тогда, если V(x) непрерывная, то за знак интегрирования
вынесется V(£)... здесь £ лежит между а и А... все хорошо! По-
лучаются и(а) и и(А), а когда А стремится к бесконечности, то
и(А) стремится к нулю!
— Итак, — предлагаю ей подвести итог, — что требуется от
функций и(х) и v(x) для сходимости интеграла?
— От v(x) — ограниченность первообразной, от и(х) —
монотонное стремление к нулю. Ну и, конечно, обе они должны
быть интегрируемы на любом промежутке за точкой а. Да, ведь
первообразная V(x) должна быть непрерывной... Вот что: пусть
492
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[Гл. 6
обе функции и{х) и v(x) будут непрерыными. У нас еще есть
интеграл от и'(х) — тогда пусть и(х) будет еще и непрерывно
дифференцируемой.
— Пусть. И вы полагаете, что при соблюдении этих условий
+оо
интеграл J u(x)v(x)dx будет сходиться? То есть будет существо-
а
+оо
вать предел lim f u(x)v(x)dx?
Л—+00 а
— По-моему, мы это доказали.
— Доказали... И все-таки просмотрите свое доказательство
А
повнимательнее. Из интеграла fu(x)v(x)dx, стоящего под зна-
а
ком предела, получилась алгебраическая сумма четырех
слагаемых. Каждое ли из них имеет предел при А, стремящемся к
бесконечности? Проверьте!
— Первое, — медленно говорит Синица, — это произведение
ограниченной V(A) на бесконечно малую и(А), то есть стремится
к нулю. Второе — константа, у нее предел равен ей самой.
Третье — опять произведение ограниченной на бесконечно малую,
предел — нуль. Четвертое... и(а) — константа... V(£)...
— Что ж вы замолчали? V(£) — это переменная величина или
постоянная?
— Переменная... Когда А меняется, то £ тоже меняется,
вообще говоря, и V(£) меняется.
— Как же меняется величина V(f)? Стремится она к
некоторому пределу или не стремится? Не можете ответить? А ведь
вопрос важный, очень важный, вы это наверняка понимаете. Ведь
если V(£) не стремится ни к какому пределу, то и вся сумма
расходится тоже, поскольку в таком случае она образована тремя
сходящимися первыми слагаемыми и одним расходящимся,
последним. А мы не раз говорили: сумма сходящейся величины и
расходящейся расходится.
— Можно я сяду, подумаю? — тихо просит Синица.
— Сядьте, думать будем все вместе.
Проходит немало времени, заполненного и неудачными
суждениями, и новыми раздумьями, когда Костюк, наконец,
прозревает:
— Критерий Коши!
— Что он может здесь дать? Исследуем это сообща, ребята.
Брожу между рядами, заглядываю в тетради, выискивая
наиболее четкое решение. К доске вызываю Стрельцова. Он
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
493
тщательно выписывает формулировку критерия, потом пишет
А"
отдельно интеграл Ju{x)v{x)dx, преобразует его, повторяя
А1
схему выкладок Синицы и лишь переставляя некоторые
сомножители в произведениях функций и и v:
— Получилось, — заключает он, — четыре произведения, в
каждом из которых первый сомножитель ограничен по абсолют-
ной величине каким-то числом. Из этих чисел возьмем
наибольшее и обозначим его М. Второй сомножитель в каждом из
четырех произведений может быть сделан меньше любого наперед
заданного £, если взять достаточно большие значения А' и А":
ведь и(х) бесконечно убывает, когда х стремится к плюс
бесконечности. То есть для любого £, — ведет он взгляд по
формулировке критерия Коши, — найдется А такое, что при любых
А' > А и А" > А значения функции и{А') и и{А") будут по
А"
абсолютной величине меньше е и тогда интеграл J u{x)v{x)dx
А'
по абсолютной величине будет меньше AM е. То есть его
можно сделать меньше любого наперед заданного положительного
числа.
— Очень хорошо. Вот мы и разработали, ребята, так
называемый признак Дирихле для сходимости несобственных
интегралов на бесконечности: интеграл сходится, если один из
сомножителей, на которые разлагается подынтегральная функция,
непрерывен и имеет ограниченную первообразную, а другой
сомножитель непрерывно дифференцируем и монотонно
стремится к нулю на бесконечности.
Обвожу взглядом сидящих:
— Все записали формулировку признака? Да? Тогда
возвращайтесь, — оборачиваюсь к Стрельцову, — на место, запишите
и вы.
— А для конечной особой точки мы будем строить какие-
нибудь признаки? - интересуется Кочин.
494
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[Гл. 6
— Зачем? — опережая меня, отвечает ему Миклашевский.
— Такие интегралы можно переделать на бесконечность: замена
t = -^-.
х—а
— Мне нечего добавить к выступлению предыдущего
оратора, — с улыбкой развожу руками. — После долгих теоретических
рассуждений давайте, ребята, займемся примерами. Я буду
давать их вам по одному, поскольку исследование несобственного
интеграла от знакопеременной функции на сходимость, в
том числе абсолютную — дело трудоемкое. Первый пример:
+оо
/ xpsin(xq)dx, причем q ф 0. Решайте.
о
Когда почти у всех проклюнулись свои подходы к
решению, а у многих созрели результаты, начинаю «сбор урожая».
Левую половину доски отвожу исследованию интеграла в
нуле, правую — на бесконечности. Сначала вызываю к
доске авторов нерациональных решений, ведущих к неверным
ответам. (Обидно, что все они своими недавними успехами
позволяли надеяться на лучшее). Лапиков утверждает в нуле
эквивалентность rz^sinrr9 ~ жр+<7, Аргунова применяет оценку
xvsu\xq < xpsinx. Мухин дает оценку еще более жесткую:
xpsinx9 < хр.
— Три подхода — три ответа, — комментирую их решения. И
к каждому подходу можно придраться.
Почувствовав в моих словах сигнал к нападению, Горт тотчас
накидывается на Лапикова:
— Синус от xq эквивалентен хд только при положительных
д, при положительных!
Стыжу Лапикова взглядом, и он отводит глаза:
действительно стыдно!
Сразу за Гортом — уже по поводу решения Аргуновой — Ко-
стюк:
— Синус от хя меньше sin ж только при д, больших
единицы!
— Верно, — вежливо прерываю его, щадя Аргунову, и, чтобы
он не мог продолжать, принимаюсь за ошибки Мухина:
— Неравенство sin хя < 1 формально верно. Но ведь, если q
положительно, sin ж9 будет стремиться к нулю с приближением
аргумента х к началу координат, и это бесконечное убывание
синуса сможет дать свой вклад в сходимость интеграла. Зачем
же этим пренебрегать? Да и вряд ли вероятно, что сходимость
интеграла в нуле совершенно не зависит от д, как это следует из
ответа Мухина,,.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
495
Перехожу на правую половину доски:
— Теперь о сходимости интеграла на бесконечности. Тут у
вас, ребята, тоже не все ладно. Кочин и Сутеев, разбирая
абсолютную сходимость, опирались на неравенство |sinx9| > sin2 xq
и запутались в дальнейших выкладках. Меншиков искал
первообразную для sin xq, верно определил ее: — с^1, отметил ее
ограниченность. Вы, вероятно, имели в виду признак Дирихле,
Меншиков? Да? Чувствуется, что вы крепко заучили его
формулировку, добросовестно следовали ей и вывод ваш совершенно
+оо
справедлив: если q > 1 и р < О, то интеграл f xpsinxqdx cxo-
1
дится. Но можно ли гарантировать, что при всех остальных
сочетаниях р и q интеграл будет расходиться? Нет, нельзя: в
формулировке признака Дирихле нет и намека на подобные гарантии.
Давайте-ка вспомним, как мы выводили его по схеме, которую
предложил в свое время Сынчиков. Я воспроизведу те выклад-
а л
ки в обобщенном виде — смотрите внимательно на доску!
Замечаете, какую роль играет в оценке сходимости первообразная
V(x)l Согласитесь, что эту оценку значительно усиливает
убывание первообразной. А ведь у вас так оно и будет при q > 1.
Стало быть, можно подозревать, что из всех возможных
случаев сходимости нашего интеграла вы своим решением указываете
лишь часть. То есть повторяете ошибку Мухина.
Услышав вновь свою фамилию в неприглядном контексте,
тот не выдерживает:
— Когда Кулагин делал то же с чистым синусом, вы его
похвалили...
— С чистым синусом? Вы имеете в виду интеграл типа
+-оо ш
J ^rdx? Вспомни ли-таки наконец! Да и как не вспомнить то,
a
чему мы посвятили столько труда? И почему бы не опереться
на надежные, досконально обоснованные выводы, которые мы
получили при этом? Смотрите, как подошли к этому интегралу
Синица, Костюк, Гарин,
496 НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ [Гл. 6
Демонстрирую на доске их выкладки.
— Решающий шаг — замена xq = t. Она придает интегралу
хорошо изученную нами форму: «чистый» синус, как вы
говорите, Мухин, умноженный на «чистую» степень переменной
интегрирования. Правда, при отрицательных q особенности в нуле и
на бесконечности меняются местами, но это не слишком
усложняет исследование. А самое главное: опираясь в этом исследова-
+оо # 1
нии на типовые интегралы J* ^rdx и /^, мы предельно точ-
а О
но указываем случаи сходимости — ведь при разборе типовых
интегралов мы доказывали, что во всех остальных случаях име-
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
497
ет место расходимость. И все нужные нам выводы получаются
незамедлительно: абсолютная сходимость — когда — 1 < 2±^ < О,
условная — когда 0 < ^ < 1.
И, подождав пока все оформят в своих тетрадях решение
примера:
— Следующая задача: исследовать на сходимость, в том числе
+оо
абсолютную, интеграл J >/xsm(§1J^-)dx.
l
Сутеев за неимением других идей рисует графики — сначала
для функции ^^, потом для sin(§1~^)...
— Нарисуйте-ка последний график на доске, —
вызываю его. — Что подсказывает вн вам? Как описали бы вы
его характер? Не знаете, что сказать? А вычислить
значение этой функции в какой-либо точке смогли бы? Скажем, в
точке Ц*-1
— В точке Ц^? — хмуро переспрашивает он. — То есть 107Г+
+|? Синус равен сединице... Значит, sin^fj... Синус малой
величины... Может быть, по формуле Тейлора?
— Разумно! — поддерживаю его мысль, не очень представляя,
впрочем, насколько она осознанна: уж больно часто я восхвалял
замечательную формулу -- теперь она будет вспоминаться
ребятам к месту и не к месту. — По формуле Тейлора... А ну-ка,
поглядите на наш интеграл! Не замечаете ли вы в нем чего-то
такого, чего не видели раньше?
— Разложить sin(§~2-)? — с той же хмуростью в лице и в
голосе спрашивает он.
— А почему бы и нет? — уклоняюсь от прямого приказа —
пусть это придаст хоть какой-то оттенок
самостоятельности его действиям. И он пишет два первых члена
разложения. Потом оборачивается ко мне и смотрит мне в глаза
каким-то бездумным взглядом. Мне приходится его
подтолкнуть:
— Не знаете, до какого члена разлагать? Давайте
подумаем об этом. Остановимся пока на том, что вы сделали. Чтобы
формула Тейлора приобрела законченный вид, к ней надо
приписать... что, Сутеев?
— о малое.
— - Верно. Ну что ж, теперь внесите ваше разложение под знак
интеграла.
- Интеграл от первого слагаемого сходится по признаку
Дирихле, — продолжает он уже сам, — от второго... степень знаме-
498 НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ [Гл. 6
нателя больше единицы... можно оценить... от второго тоже
сходится... теперь, — показывает на остаточный член, — от этого...
— He знаете, как его проинтегрировать? — по
затянувшемуся молчанию Сутеева чувствую, что ему необходима помощь. И
оборачиваюсь к аудитории:
— Кто знает? Вы знаете, Миклашевский?
-Нет.
— А вы, Лапиков?
— Нет, тоже не соображу...
И добавляет поспешно:
— Разве только по определению... о малое это... если
разделить его на то, что стоит в скобках... стремится к нулю... значит...
сейчас... стремится к нулю...
Заметив, что Рамзин желает блеснуть сообразительностью на
фоне беспомощного Лапикова, упреждаю этот выпад:
— Вы, кажется, хотите нам помочь?
Смутившись, он говорит тоном весьма скромным:
— Нужно записать наше о малое в другой форме: а(ж), умно-
женное на =у-^.
— Возможно, такое преобразование, — комментирую
предложенную замену для Сутеева, — даст ответ на ваш вопрос. Вы
забыли мой старый совет: видеть каждый элемент задачи во всех
возможных его формах.
И снова Рамзину:
— Что такое а(х)?
— Бесконечно малая величина.
— Давайте напомним, что это значит. Определите на
символическом языке бесконечную малость а(х).
— Для любого £, большего нуля, найдется некоторое xq
такое, что при больших его значениях х выполняется неравенство
|а(х)|<е.
— При ж, больших некоторого xq... В свое время мы
отмечали, что поведение несобственного интеграла на бесконечности
не изменит своего характера, если изменить значение нижнего
предела в формуле интеграла. Так что мы можем рассматри-
Ю. В. Пухначев|
СЕМЬ СЕМИНАРОВ
499
вать интеграл не от 1, а от xq до бесконечности. Теперь насчет
того, что а(х) меньше е по абсолютной величине: поскольку мы
станем опираться именно на такую, на модульную оценку, мы
должны будем рассматривать не просто сходимость интеграла
от последнего слагаемого, а... какую сходимость, Сутеев?
— Абсолютную, наверное.
— Правильно. Ну-ка, возьмите модуль последнего слагаемого!
Обратите внимание: окруженная модульными скобками,
функция стала знакопостоянной, и к ней теперь применимы признаки
сходимости, выведенные нами для таких функций, — в
частности, признак сравнения. Не использовать ли нам его здесь,
Сутеев? Сразу учтем ограниченность |а(ж)|, правильно, —
комментирую его новые выкладки, — пишем неравенство и получаем в
его правой части абсолютную величину слагаемого, на котором
оборвали разложение, умноженную на е. Величину е можно, как
вы уже говорили, взять любую. Ради простоты и удобства
возьмем единицу. Упростите неравенство с помощью такого выбора,
Сутеев. Итак, L " /- • Что можно сказать про интеграл от такой
функции?
— Что он... сходится, пожалуй... sin3 ж меньше единицы... все
по модулю меньше -уЦ=... тут степень икса больше единицы...
значит, сходится.
— Итак, — ради четкости резюмирую сам. — сходятся
интегралы от всех слагаемых, на которые мы разложили
подынтегральную функцию, — стало быть, сходится и исходный
интеграл. Как вы, очевидно, догадываетесь, Сутеев, нам очень
повезло в том, что мы оборвали разложение на слагаемом, интеграл
от которого сходится абсолютно. И если при исследовании
подобных интегралов нам вновь придется разлагать подынтегральную
функцию по формуле Тейлора — до какого слагаемого мы станем
ее разлагать?
— До такого, интеграл от которого сходится абсолютно.
— И закончим разложение о малым от этого слагаемого. Все
слышали это, ребята? Запомните это правило! В дальнейшем,
думаю, оно не раз пригодится нам, поскольку формула Тейлора
500
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[Гл. 6
часто используется нами. Садитесь, Сутеев. Теперь надо
разобраться с абсолютной сходимостью нашего интеграла. Не
сделаете ди это, Стрельцов?
— Попробую...
Он начинает с того, что стирает написанное Сутеевым и
пишет все то же заново — пишет без спешки, в новом продуманном
расположении.
Умело оценив снизу модуль суммы функций, на которые
разложено подынтегральное выражение, он убедительно
истолковывает полученное неравенство. Начинает с дроби, которой оно
завершается.
— При х > хо величина а(х) по модулю меньше единицы.
Следовательно, сумма 1 + а(х) положительна, а по абсолютной
величине меньше двух. Квадрат икса — величина
положительная, квадрат синуса — тоже положительная и протом меньше
единицы. При х, больших единицы вся эта дробь меньше, чем
одна треть, ну и всегда остается положительной. Значит, эти
модульные скобки (он указывает на выражение, с которого начал
свои преобразования) больше, чем з^/s ' т0 есть больше
функции, интеграл от которой на бесконечности расходится. Выходит,
что абсолютной сходимости у нашего интеграла нет.
— Очень хорошо, садитесь. Еще один пример: при каких р
+оо
сходится на бесконечности интеграл J* xp+s^nx^x^
1
Привлеченный поспешностью, с которой Кочин что-то
пишет, едва взглянув на формулу предложенного мною интегра-
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
501
ла, выуживаю из его тетради и переписываю на доске
неравенство р > 0:
— Это условие сходимости?
— Да, по-моему, — отвечает он.
— Чем вы его обосновываете?
— При положительном р дробь хР_^йХ стремится к нулю,
первообразная sin я ограничена, по признаку Дирихле интеграл
должен сходиться.
Медлю с разбором его неточного ответа: может быть,
спохватится, сам вспомнит, какое еще условие накладывалось на
один из подынтегральных сомножителей в формулировке
признака Дирихле? Нет, не припоминает... Не уложился еще у него
в голове признак Дирихле всеми своими деталями, не
уложился... Случайный сбой, который может произойти с каждым?
Возможно, возможно... И все-таки что-то заставляет меня задержать
свое внимание на этой ошибке Кочина. Верно ли я оцениваю его?
Он заметно вырос по сравнению с первыми семинарами. Тогда
он то и дело звал меня на помощь. Совершенно не знал
логической символики. Но быстро освоил ее. Все лучше решал задачи.
Рассуждал все увереннее и четче. Все реже подзывал меня, а
когда я сам предлагал ему свою помощь, все чаще отказывался
от нее. Одним из немногих изобрел подстановку Эйлера — это
был успех настоящий! Я поверил тогда, что он способен выйти
на уровень если не лучших, то средних студентов группы,
поощрял его, чтобы это произошло скорее. Наверное, поэтому мне все
досаднее видеть его слабинки. Нало настойчивее изживать их —
буду требовать от него безупречного решения каждой
посильной ему задачи. Или, может быть, я не прав, предлагая время
от времени таким, как он, трудную первопроходческую работу?
Она ведь по плечу лишь немногим, самым сильным в группе —
остальные неизбежно отстанут от авангарда. Таким хватит и
того, чтобы стать хорошими исполнителями заученных
стандартных алгоритмов. Но ведь и в исполнительских ролях им хорошо
бы работать на пределе своих позможностей! В общем порыве
творческого поиска каждый из них вернее достигнет своего
рубежа, устремляясь за идущими впереди, стараясь подтянуться к
ним...
— Здесь можно по-другому! — прерывая мои раздумья,
вскидывает руку Буткус. Приглашенный к доске, он излагает свою
идею. С самого начала следует ограничиться лишь
положительными значениями р. При других р интеграл расходится, это легко
доказать по критерию Коши. Пользуясь бесконечным возраста-
502
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[Гл. 6
нием функции хр при положительных р, надо разделить
числитель и знаменатель подынтегральной дроби на хр и возникшее
таким образом выражение (1 + ^г)-1 разложить по формуле
Тейлора. Условие сходимости выражается у Буткуса
неравенством р> \-
— А у Кочина неравенство другое, р > 0. Кто же прав,
ребята? — обвожу взглядом аудиторию — Кочин или Буткус? Где
истинное и исчерпывающее условие сходимости? р > 0 или р > ^?
— Если р меньше или равна одна вторая, интеграл не
сходится, — отстаивает свою правоту Буткус, указывая на слагаемое
^^ в своем разложении.
— Вы правы, — соглашаюсь с ним, — поскольку опираетесь
на хорошо исследованный нами случай расходимости. Но ведь и
Кочин опирается на нечто строго доказанное — на признак
Дирихле. Смотрите: первообразная sin я ограничена, а дробь дР Лпд
при р > 0 стремится к нулю...
— Она должна монотонно к нему стремиться! — ловит
ошибку Костюк. — В признаке Дирихле говорится о монотонном
стремлении к нулю!
— При каких же р, — оборачиваюсь к нему, — эта дробь будет
стремиться к нулю монотонно?
— Надо взять производную.
Выясняем, что монотонность гарантируется неравенством
р> 1.
— Вот, Кочин, — подчеркиваю полученную оценку, — при
каких р вы вправе применять признак Дирихле и, основываясь
на нем, утверждать сходимость интеграла. Однако, как показал
Буткус, она будет наблюдаться еще при кое-каких значениях р.
Вы удивлены, что разные подходы к задаче приводят к разным
результатам? Я сообщу вам сейчас нечто еще более любопытное:
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
503
оказывается, разные результаты можно получить, исходя из
одного лишь признака Дирихле. В самом деле, применяя этот
признак, мы представляем подынтегральную функцию в виде
произведения двух сомножителей. Но ведь разложить ее на
сомножители можно по-разному. Не исключено, что при этом будут
получаться разные ответы — скажем, по-разному будет определяться
область параметров, входящих в исследуемый на сходимость
интеграл, при которых этот интеграл сходится. Вот почему в таких
случаях надо еще выяснять, будет ли интеграл расходитьея при
всех прочих значениях параметров. Буткус все это сделал, он
+оо .
строго показал, что при р > \ интеграл J др^д.^ сходится,
1
при 0 < р < \ — расходится, а еще раньше объяснил
расходимость интеграла при р < 0. Окончательно признаем верным его
+оо
решение. Садитесь, Кочин. Следующий пример: / хРх^+\ • Во-
1
прос все тот же: при каких р сходится на бесконечности этот
интеграл?
— Ну уж тут-то наверняка признак Дирихле, — заявляет
Миклашевский. — Дробь j^- эквивалентна £р~3, интеграл сходится
при р < 3.
— Признак эквивалентности применим только к
знакопостоянным функциям, — тихо, но отчетливо произносит Гарин
с какой-то болезненно-недовольной интонацией: сколько же
можно повторять элементарные истины!
— Ну так эта дробь знакопостоянная и есть! — не отступает
Миклашевский.
— Дробь — да, а вся подынтегральная функция — нет, —
беру сторону Гарина. — Перейдя от дроби -ф^ к степени хр_3, вы
заменили исследование интеграла от функции ^з!^
исследованием интеграла от функции хр~^ shirr. Чем вы обоснуете
возможность такой замены? Откуда следует, что выводы, справедливые
для одного интеграла, будут справедливы и для другого?
Извольте работать строго.
Сообща обсуждаем целесообразные подходы к этому
интегралу. (Миклашевский в обсуждении не участвует, в гордом
молчании листает задачник) Одни предлагают выяснить, при
каких значениях параметра р дробь ^f^y монотонно стремится к
нулю. Вывести соответствующее неравенство на доске
предлагаю Стрельцову. Большинство же считает необходимым вновь
использовать формулу Тейлора. Бродя между рядами, наблю-
504
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[Гл. 6
даю, как применяют ее те, в ком подозреваю ее нетвердое знание.
Аргунова справляется с примером неплохо, вполне качественно
работает и Сынчиков — он и выходит к доске вслед за
Стрельцовым. Ответ у обоих получается тот же, что предсказывал
Миклашевский: р < 3.
— Стоило огород городить! — ворчит Павел. — И так ясно...
— Стоило! — обрываю его. — Я постараюсь убедить вас в этом
чуть позже, а пока, ребята, давайте подведем итог тому, что мы
сегодня прошли. Мы познакомились с понятием
несобственного интеграла, отметили некоторые свойства таких интегралов и
способы их преобразования, узнали признаки их сходимости. Вот
вкратце, пожалуй, и все. Но я хотел бы особо отметить еще одну
деталь наших теоретических рассуждений, которой вы,
возможно, не придали того значения, какого она заслуживает.
Вспомните: как только мы начинали разговор про несобственные
интегралы от знакопостоянных функций, а затем — от
знакопеременных, мы каждый раз сразу же строили характерный пример того
и другого интеграла и постоянно обращались к нему,
иллюстрируя свои умозаключения. Для случая знакопостоянных функций
+оо а
роль таких модельных примеров играли интегралы f ^£ и J^f,
а О
для случая знакопеременных — интеграл f ^r-dx. Эти модель-
а
ные интегралы неизменно помогали нам и при решении
примеров. При интегрировании знакопостоянных функций дроби вида
р использовались нами в сравнительных оценках и
соотношениях эквивалентности, при интегрировании знакопеременных мы
старались придать подынтегральной функции вид произведения
или суммы произведений, где одним из сомножителей был бы
«чистый синус», как выразился Мухин, а другим — степень
икса. Надеюсь, теперь вы понимаете, какое значение имеют эти
модельные примеры для пройденной нами темы. Их значением
оправдывается та скрупулезность, с которой мы строили их, та
придирчивость, с которой я при этом требовал от вас точности
в словах, аккуратности в чертежах. Пожалуйста, запомните то,
что я вам сейчас сказал. И в будущем, когда вам придется
осваивать новые разделы математики, заботьтесь о том, чтобы каждое
новое понятие воплощалось в каком-то характерном примере,
который наглядно и по возможности полно отражал бы свойства
этого понятия, способы его применения. Разумеется, как я уже
не раз подчеркивал, общее понятие не должно засоряться
посторонними свойствами иллюстративных примеров — но это преду-
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
505
преждение отнюдь не умаляет значения хороших иллюстраций.
Нужно лишь быть разборчивым и требовательным в выборе
таких примеров. Этот совет я обобщил бы и на всю вашу
научную деятельность. Нынешние, студенческие ваши годы — это ее
начало. И они должны стать для вас своеобразным модельным
примером работы. Привычки и вкусы, которые вы выработаете
сейчас, останутся в вас на всю последующую жизнь, каким бы
новым содержанием она потом ни наполнялась. Очень важно,
чтобы эти привычки и вкусы не были бы дурными. Вот почему
я так настойчиво забочусь о строгости ваших умозаключений,
точности ваших суждений. Надеюсь, Паша, — оборачиваюсь к
Миклашевскому, — вы понимаете меня.
Он хмыкает, чуть краснея, и опускает голову, как бы кивая
в знак согласия.
Оглядываю лица ребят — дошло ли до них?
— Чюмин, вы что-то хотите спросить?
— Да. Про интегралы.
— Понятно, что не о смысле жизни. Слушаю вас.
— Вот вы говорили, что всякому интегралу от
знакопеременной функции мы стараемся придать вид интеграла от
произведения синуса на степень икса. Разве это всегда можно
сделать?
— Нет, конечно. Идите-ка к доске. Напишите интеграл:
+001 ' I-
J gins6^- Попробуйте определить, при каких а он сходится.
7Г
Понятен вам этот пример? Может быть, не совсем ясно, что
собою представляет выражение в числителе? Нарисуйте-ка
график этой функции для какого-нибудь конкретного а.
— Для а равного половине, например, — да?
— Возьмите половину.
Он медлительно рисует, напряженно глядит на
нарисованное — и косит взглядом на меня:
— Так это ж почти синус!
— Что значит «почти»?
506
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[Гл. 6
— Если такое взять альфа, чтоб интеграл был равен нулю
по каждой этой вот волне, это как от синуса по периоду, — то-
ропливыми графиками он поясняет свое сравнение, — если он
будет нуль по каждой волне, то первообразная числителя будет
ограничена...
— Непосредственно из ваших построений, — вношу
необходимое уточнение, — можно вывести лишь то, что ограничен
интеграл с переменным верхним пределом, взятый от числителя.
Но если после этого сказать, что интеграл с переменным верхним
пределом есть первообразная для подынтегральной функции,
станет справедливым и ваш вывод: первообразная числителя...
— Будет ограничена, — продолжает Чюмин, не видя особой
необходимости в моей поправке. — А ^-^ монотонно стремится
к нулю, и весь интеграл тогда сойдется.
— Основание?
— Признак Дирихле.
— Верно. Хотя здесь нет «чистого синуса», все же, глядя на
числитель подынтегральной дроби, вы непроизвольно
воскликнули: «Почти синус!» О чем это говорит? О том, что признак
Дирихле прочно связан в вашем представлении с модельным приме-
+оо .
ром f ^г, с этим примером вы невольно сверяете исследования
а
совсем не похожих на него интегралов. Так мы вновь убеждаемся
в его значимости. Хотя, разумеется, он не исчерпывает собою все
возможные примеры несобственных интегралов от
знакопеременных функций. Впрочем, и решение примеров не исчерпывает
нашу сегодняшнюю тему. Надо бы и теоретическими задачами
позаниматься. Садитесь, Чюмин. Может быть, ребята, —
обращаюсь к аудитории, — дать вам сразу задачу потруднее? Хотите?
— Хотим! — с энтузиазмом отвечают они.
— Ну что ж, докажите теорему: если f(x) всюду неотрица-
+оо
тельна и J f(x)dx сходится, то lim f(x) = 0.
Трудность задачи в том, что «теорема» неверна. Ребята
должны обнаружить это и привести противоречащий пример.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
507
Но они еще не чувствуют подвоха — работа кипит, идеи
«доказательств» появляются в их тетрадях одна за другой. Многие
подробно расписывают на символическом язнке определение
сходимости интеграла и стремления подынтегральной функции
к нулю, затем пытаются вывести из первого второе. Другие
отправляются от критерия Коши. Потерпев неудачу, иные
расписывают фигурирующий в формулировке критерия интеграл
через интегральную сумму...
Тем временем я вызываю к доске авторов наиболее четких
«доказательств».
— Пусть функция f(x) — излагает Мухин, — на плюс
бесконечности к нулю не стремится. Если по определению — нет,
по отрицанию определения — если по отрицанию стремления к
нулю, тогда — там для любого, а здесь — значит, существует —
тогда существует Ео такое, что для любого А — для любого
положительного А, если х > Д то f(x) > во- И для любых А' и А!',
А"
которые больше А, будет выполняться | J f(x)dx\ > eq(A"—A') —
А1
а это противоречит критерию Коши — а критерий должен
выполняться, если интеграл сходится.
— Вас нельзя не похвалить, Мухин, — начинаю
одобрительным тоном. — Хотя говорили вы сбивчиво, за вашими словами
просматривается довольно четкое доказательство. Жаль
только, — заканчиваю с грустью, — что оно неверно.
Горт и Синица быстро находят уязвимое место
умозаключений Мухина: для выполнения интегрального неравенства нужно,
чтобы соотношение f(x) > eq выполнялось на всем промежутке
интегрирования, а то, что f{x) на плюс бесконечности не
стремится к нулю, гарантирует это соотношение быть может только
для одной точки х, лежащей правее А.
— Если интеграл сходится, то выполняется критерий
Коши, — своим путем идет Костюк. — Тогда для любого
положительного е найдется А такое, что для любых больших его А' и
А"
А" справедливо | / f(x)dx\ < е. Возьмем эти А! и А!' такими,
А'
чтобы расстояние между ними равнялось единице, и применим к
интегралу теорему о среднем: из нее получим, что /(£) меньше...
И в ту же секунду, когда мел в его руке начинает
вычерчивать завершающую все рассуждение буковку е, настойчиво-
монотонный его голос срывается в разочарованном
выдохе:
508
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[Гл. 6
— Точка £ не любая ведь за А, а какая-то одна!
— А чтобы f(x) стремилась к нулю, — завершаю его мысль,—
нужно, чтобы она была меньше е для любого £, большего А.
Помрачневший Костюк кладет мел и идет обратно.
Вновь расхаживаю между рядами. Лапиков пытается
доказать от противного стремление f(x) к нулю и пишет намечаемое
к опровержению неравенство lim f(x) = А > 0. Не понима-
х—►+оо
ет, что предел f(x) может и не существовать?.. Ба, то же самое
условие пишет Буткус! Уж не повальное ли это заблуждение?
— Буткус, к доске! Изложите свою идею доказательства.
— Я по-другому доказывал: я предположил, что предел f(x)
не равен нулю, А ф 0. То есть больше нуля — функция
неотрицательная, А > 0. Тогда по определению предела найду такое, что
+оо
для любого х > хо будет f(x) > ^. Интеграл f ^dx расходится.
а
+оо
Значит, J f(x)dx тоже расходится. Получилось противоречие.
а
Значит, lim fix) = 0.
х—►-boo
— Рассуждение совершенно строгое, но исходит оно, к
сожалению, из неверного допущения.
Поворачиваюсь к аудитории в надежде, что кто-то
продолжит мое замечание. По лицам ребят вижу, что к этому
готовы многие и в их числе... Лапиков! Сам понял свою ошибку!
Чудесно!
— А ведь предел функции f(x) может и не существовать, —
тихо говорит он.
— Может и не существовать, — присоединяюсь к его
мнению. — Вы поняли это, Буткус?
— Да. Понял, — с оттенком неудовольствия в сдавленном
голосе отвечает он.
— Тогда садитесь.
И иду вслед за ним в очередной обход.
В тетради у Кулагина вижу небрежный график
своеобразной функции, способной послужить опровергающим примером.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
509
Неужели сообразил? Наклоняюсь к нему, и он едва слышно
шепчет мне на ухо:
— Кажется, теорема неверна.
— Да, — еще тише отвечаю ему. И мы улыбаемся друг другу,
как авгуры.
Перегибаюсь через задний стол: в тетради у Гарина — еще
один подходящий график. Показывая на него, Гарин что-то
шепчет Костюку.
— Вы, я вижу, уже все доказали, — обращаюсь к Гарину.
— Нет-нет, — отрицательно машет он рукой, но, когда я
отхожу и вновь оборачиваюсь на него, он с еще большим жаром
что-то втолковывает Костюку.
И тут Миклашевский — как младенец из сказки о голом
короле — громко, на всю аудиторию:
— А верно ли утверждение теоремы?
Играть дальше не стоит.
— Теорема действительно не верна, ребята. Это, точнее, не
теорема. Это неверное утверждение, ошибочность которого вы
должны были обнаружить и привести противоречащий пример.
— Ну, Юрий Васильевич! — раздосадованно тянет Стрельцов.
И Синица продолжает в той же тональности:
— Зачем же так... жестоко?!
Словно не слыша их, продолжаю:
— Такие примеры уже придумали некоторые из вас. Гарин,
пожалуйста!
Тот рисует свой график на доске.
— Функция разрывна! — возмущенно восклицает Рамзин.
— А кто говорил, — спокойно возражает Гарин, — что она
должна быть непрерывной?
— Надо еще доказать, что интеграл от такой функции
сходится! — требует Горт.
Гарин доказывает это, основываясь на критерии Коши и
напомнив, что интеграл сохраняет свою величину, если значения
510
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[Гл. 6
подынтегральной функции изменить в конечном числе точек на
промежутке интегрирования.
— Впрочем, — иду настречу Рамзину, — можно придумать и
непрерывную функцию того же свойства, — и вызываю к доске
Кулагина. Он излагает свой пример в слегка видоизмененном
варианте.
— Очень хорошие примеры. Садитесь, Миша. Садитесь,
Андрей. Спасибо. Любителям подобных диковинок я мог бы еще
предложить сходящийся на бесконечности интеграл от
знакопеременной функции, которая также не стремится к нулю при бес-
+оо
конечном возрастании ее аргумента: f cosx2dx. В самом деле,
1
+оо
проведем замену х2 = t и получим интеграл f irjtdt, который
сходится по признаку Дирихле. В дальнейшем этот интеграл от
cos я2 нам еще пригодится, запишите его, ребята, —
оборачиваюсь к аудитории. И замечаю кислую мину Стрельцова:
— Вы чем-то недовольны?
— После вашей «теоремы», — с наигранным негодованием
отвечает он, — у меня всякая охота пропала решать ваши
задачи.
-- Навсегда?
— Нет, — примирительно улыбается он.
— Вы, наверное, рассчитывали, что я всегда буду давать вам
задачи с предельно отчетливым условием и заведомо
существующим ответом? В таком случае я плохо готовил бы вас к вашей
будущей научной работе. На практике задачи редко рождаются
в рубашке четкой постановки. Напротив, они то и дело будут
возникать перед вами в неясной, отчасти даже запутывающей
форме. Хороший пример тому могла бы подсказать тема нашего
сегодняшнего семинара — несобственные интегралы. Представь-
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
511
те: в прямоугольной декартовой системе координат на
промежутке [—1; 0) задана функция у = j. Ее график — это полу ветвь
хорошо знакомой нам гиперболы. Если вращать эту линию
вокруг оси ординат, получится бесконечно глубокая воронка. Ее
емкость можно вычислить как интеграл 7г J -ff. Интеграл схо-
—оо
дится, стало быть, емкость воронки конечна. Вас просят
равномерно закрасить участок плоскости между вышеописанным
фрагментом гиперболы и осью ординат. Вы интуитивно
подозреваете, что выполнить такой заказ невозможно, но заказчик
и слышать не хочет про ваши сомнения, он вручает вам ту
самую воронку, доверху наполненную краской, и уверяет, что ее
должно хватить: глядите, мол, какой широкий раструб, его
диаметр больше, чем любая мыслимая толщина красочного слоя,
а горлышко у воронки бесконечно длинное... Делать нечего, вы
принимаетесь за работу. Как и следовало ожидать, краска через
какое-то время подходит к концу. Заказчик удивлен, он очищает
окрашенную поверхность, снова приносит вам в той же воронке
новую порцию краски и просит на сей раз наносить более
тонкий слой. Вы вновь беретесь за это безнадежное дело... та же
история! Краски не хватает! Заказчик, понятно, раздражен
таким непостижимым для него исходом — мол, как же так? Сама
форма воронки гарантировала, что краски должно хватить,
причем с избытком — широкий раструб, бесконечное горлышко... Не
объясните ли, ребята, воображаемому заказчику, в чем причина
неудачи?
Кулагин дает продлиться до конца минуте молчания, которой
группа почтила мой парадокс, и с легкой усмешкой спрашивает:
— Как, вы сказали надо красить? Равномерно?
512
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[Гл. 6
Горт не позволяет ему завершить догадку выводом:
— Равномерно — значит, толщина красочного слоя везде
одинаковая, объем краски пропорционален площади поверхности,
которую нужно покрасить. А эта площадь бесконечна, потому
-1
что интеграл J -^ расходится.
—оо
Костюк продолжает без промедления, в том же торопливом
темпе:
— И с воронкой все ясно: у нее толщина горлышка
уменьшается бесконечно, до нуля, рано или поздно его диаметр станет
меньше толщины любого слоя краски.
— И потому, — заканчиваю сам, — при любой наперед
заданной толщине красочного слоя равномерность покраски
обеспечить невозможно. Равномерно можно покрасить лишь конечный
участок площади, заключенной между бесконечной полуветвью
гиперболы и ее асимптотой. Будьте готовы к подобным
«заказам» в своей будущей деятельности, ребята. По поводу нелепо
формулируемых задач, с которыми приходится иметь дело
ученому, у известного физика Джинса есть поучительная притча,
которую я изложу вам в вольном пересказе. Некий князь сидит
на крылечке своего дворца и любуется природой — долиной,
которая расстилается перед дворцом, дальними горами... Недавно
прошел дождь, и над долиной поднимается радуга. Князь
призывает придворных ученых и велит им измерить расстояние до
радуги. Ученые устанавливают свои приборы, проводят
измерения и докладывают: расстояние до радуги — минус 93 миллиона
миль. И князь приказывает наказать ученых, как злостных
обманщиков: «Отрицательное расстояние? Что за абсурд? И уж во
всяком случае 93 миллиона миль — заведомая ложь: ведь
подножие радуги — я это вижу своими глазами! — находится между
дворцом и вон той горой!»... Если бы князь понимал, что
радуга — это оптическая иллюзия, он поставил бы вопрос иначе:
«Как далеко впереди лежит источник света, создающий
иллюзию радуги?» И тогда ответ ученых был бы совершенно понятен:
минус указывает, что источник света находится не впереди, а
позади, а величина 93 миллиона миль позволяет отождествить его
с Солнцем. «Часто труднее задать осмысленный вопрос, чем
получить ответ на бессмысленный», — пишет в заключение Джине.
Но вернемся к теме сегодняшнего семинара, ребята. На нем вы
познакомились с некоторыми методами решения новых для вас
и довольно трудных задач. Однако даже во всеоружии самых
эффективных методов ученый не застрахован от каверзной си-
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
513
туации, когда он не сразу может сообразить, как применить их
к решению стоящей перед ним задачи, потому что те, кто
поставил ее, могли сформулировать ее нечетко или некорректно, так
что ученому приходится самому отыскивать причины
недоразумений и ставить задачу заново. Чтобы убедительнее
предупредить вас об этом, я попросил вас сначала поискать
доказательство недоказуемой «теоремы», потом разобраться в парадоксе с
покраской. К тому же, ломая голову над этими заданиями, вы
обновили в своей памяти основные положения пройденной
сегодня темы. Мы часто будем вспоминать их, когда на одном из
будущих семинаров начнем заниматься числовыми рядами.
Глава 7
ЧИСЛОВЫЕ РЯДЫ
Семинар начинаю с расспросов:
— Как вам последняя лекция, ребята? Лектор ведь прочел
несобственные интегралы? Да? Не скучали оттого, что мы эту
тему уже разбирали сами?
— Наоборот! — звучно возражает Меншиков.
— Повторенье — мать ученья, — негромко замечает Кулагин.
— Всегда бы так! — соблазняюще ухмыляясь, смотрит на
меня Миклашевский.
— Всегда вряд ли получится, — отрицательно качаю
головой. — Темы наших семинаров все усложняются, и если какую-то
вы будете усваивать с трудом, мы задержимся на ней
основательно - вот тогда лектор надолго обгонит нас.
— Но пока-то мы еще впереди него! — не унимается
Миклашевский.
— А чем он закончил последнюю лекцию?
— Сказал, что такое числовой ряд, дал определение его
сходимости — и тут звонок... Может быть, мы опять дальше пойдем
сами?
— Что ж, попробуем: попытка — не пытка. Но давайте
сначала проверим, как вы уяснили те основные определения, которые
дал вам лектор. Пусть у доски их повторит кто-нибудь... ну,
допустим, Мухин.
Если уж ему они запомнились, то остальным и подавно.
Мухина мое предложение застает врасплох:
— Я?! — выкатывает он ошалелые от неожиданности
глаза. — Я же... вы... нет, пусть лучше кто-нибудь другой, кто лучше
знает.
— Знатоки поправят и дополнят вас, если потребуется, а
начните все-таки вы. К доске, Мухин! И давайте почетче! На
забывайте про наш уговор: сначала думать — потом говорить.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
515
Он все еще пытается увильнуть:
— А, может, все же...
— Нет уж, нет уж! Идите!
— Ну, я не знаю, — выбирается он наконец из-за стола. — Вы
уж тогда хоть вспомнить дайте...
оо
И замедленно пишет на доске: ^ ап. Потом с той же неуве-
71=1
ренной замедленностью:
— Значит так... Есть какие-то числа а\, o<i, аз — какая-то
последовательность. ..
Он пишет а,1+а2+аз+... и, не отрывая мела от доски,
несколько секунд молча смотрит на написанное... потом продолжает:
— Мы будем их суммировать — будем говорить, что задан
ряд.
— Члены последовательности, которые мы станем
последовательно суммировать, будем называть членами или слагаемыми
ряда, — ради пущей четкости пересказываю его мысль в
негромкой и ровной, словно звук камертона, интонации.
— Да, членами или слагаемыми ряда, — повторяет Мухин,
склоняясь к моему тону. — Первые N слагаемых — когда их
просуммируем, то будем называть это ЛГ-ной частичной
суммой — обозначим ее An — теперь рассмотрим
последовательность An — она может либо сходиться либо расходиться — если
сходится, то ряд называется сходящимся — если нет, то
расходящимся.
— И если последовательность An сходится к некоторому
пределу, — напоминаю Мухину про еще один важный термин, — то
этот предел...
— То этот предел называется суммой ряда.
— Ну вот, все вспомнили, и вспомнили верно. А еще
боялись! Садитесь на место, спасибо. Как видим, ребята, —
оглядываю аудиторию, — у нас есть немалая теоретическая база для
рассуждений о рядах: их сходимость определяется через
сходимость последовательностей, а с теорией последовательностей мы
уже знакомы. И если вам, — останавливаю взгляд на Миклашев-
17*
516
ЧИСЛОВЫЕ РЯДЫ
[Гл. 7
ском, — хочется самостоятельно развить теорию числовых рядов,
попробуйте вспомнить какие-нибудь теоремы о
последовательностях, по аналогии с которыми можно было бы сформулировать
сходные теоремы о числовых рядах.
— Предел суммы равен сумме пределов, — молниеносно
выдает Миклашевский.
— Если оба предела существуют, — заканчиваю, укоризненно
глядя на него: опять нестрогость! — Возьмем два ряда ап и Ьп
и образуем новый ряд Сп, каждое слагаемое которого
представляет собою сумму слагаемых исходных рядов с тем же номером:
с\ = а\ + bi,C2 = o>i + &2 и так Далее- Ряд Сп называется
суммой рядов ап и Ьп. Предположим, что ряды ап и Ьп сходятся.
Что можно сказать про ряд Сп? — перехожу с новым вопросом
к Стрельцову.
— Что он тоже сходится.
— Докажете?
Он аккуратно пишет ЛГ-ную частичную сумму ряда Си,
заменяет каждое слагаемое на ап + Ьп, разбивает сумму на две,
образованные из ап и Ьп:
— Обе эти частичные суммы по условию имеют пределы.
Значит, по известной теореме о последовательностях
частичная сумма ряда Сп тоже имеет предел, то есть ряд Сп
сходится.
— Верно, садитесь. Ну, а если ряд ап сходится, а ряд Ьп
расходится? — ставлю новый вопрос — Что можно тогда сказать про
ряд Сп? — гляжу на Рамзина.
— Ряд расходится как сумма сходящейся величины и
расходящейся.
— Поясните подробнее. Если хотите, пойдите к доске.
Не меняя уютной позы, он отвечает на мое предложение
жеманным жестом отказа:
— Да здесь и так все ясно. Выкладки — те же, что у
Стрельцова. Под сходящейся величиной нужно понимать частичную
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
517
сумму ряда ап, под расходящейся — частичную сумму ряда
Ьп. Тогда частичная сумма ряда Сп не будет иметь предела —
в теории последовательностей мы нечто подобное
доказывали.
— Доказывали, — подтверждаю эту ссылку. — Какие еще
теоремы о числовых рядах можно сформулировать по аналогии с
последовательностями?
— Можно посмотреть, что будет, если взять произведение
двух рядов, — предлагает Чюмин.
— Посмотрите, — передаю ему мел. — Постойте, что вы
пишете? Как вы понимаете произведение рядов?
— Ряд, у которого каждое слагаемое — это произведение
слагаемых каких-то рядов: с\ = а\Ь\, c<i = афч и так далее.
— Такое построение действительно применяется в теории
числовых рядов, и мы с ним еще познакомимся позже. Однако под
произведением рядов принято понимать нечто другое:
перемножаются суммы рядов, причем...
оо оо
Не дав мне договорить, Чюмин пишет: ^ ап ^ Ьп.
п=1 п=1
— Вы предполагаете ряды сходящимися? Ведь иначе симво-
оо оо
лы ^2ап и ^Ьп не имели бы смысла... А как вы собираетесь
п=1 п=1
перемножать суммы с бесконечным количеством слагаемых? Не
трудновато ли вам будет? Может быть, взять сначала частичные
суммы? По крайней мере, до сих пор мы именно с них начинали
рассуждения о сходимости рядов.
Он заменяет значок оо над символами суммирования
буквой N.
— Но от этого ваша запись, по-моему, не стала понятнее.
Может быть, ясности ради стоило бы записывать суммы без этой
вычурной сигмы, с помощью примитивных плюсов?
Он следует моему совету, умножает одну сумму на другую...
— Ой, зашьемся! — с притворным испугом громко шепчет
Меншиков.
— Похоже, что Меншиков прав, — с усмешкой гляжу в
аудиторию. — Как вы думаете, Чюмин? — вновь оборачиваюсь к
доске. — Боюсь, что вам не удастся вывести из сходимости исходных
рядов сходимость их произведения. Отложим этот вопрос до
поры до времени. Садитесь на место.
— А если умножить ряд просто на число? — предлагает
Синица.
— Попробуйте, - зову ее к доске.
518 ЧИСЛОВЫЕ РЯДЫ [Гл. 7
Все ее выкладки сводятся к единственному равенству, из
которого следует четкий вывод:
N N
— Если существует lim ]Гап, то существует lim с^ап =
N->°°n=l N-+°° 71=1
oo
= lim ]Г сап. То есть, если сходится ряд ап, то сходится и ряд
^-+°°п=1
сап. А если расходится ряд an, то расходится и ряд сап... это,
конечно, при с ф 0.
— Верный и полезный для будущего вывод, — оцениваю
полученный результат, отсылая Синицу на место. — Советую вам,
ребята, запомнить его. И два предыдущих вывода тоже
запомните: сумма двух рядов сходится, если сходятся оба ряда, и
расходится, если сходится лишь один из двух рядов, а другой
расходится. В будущем мы еще не раз сошлемся на эти утверждения.
Как видите, аналогия рядов с последовательностями оказалась
плодотворной. Собственно, это даже нечто большее, чем
аналогия. В самом деле, частичная сумма всякого ряда — это
последовательность в прямом смысле термина. И наоборот: всякую
последовательность ап можно представить в виде ряда, у
которого каждая n-ная частичная сумма равна n-ному члену
последовательности: ап = а\ + (а,2 — а\) + (аз — а>2) + ... + (ап — ап-\).
Становится понятным утверждение, встречающееся в некоторых
учебниках: рассмотрение рядов — это новая форма изучения
последовательностей. Конечно, у вас может возникнуть вопрос: а
есть ли необходимость в такой новой форме? Да, есть, и
сейчас я постараюсь убедить вас в этом. Начну с простого
примера. С первых занятий мы знаем, что число е определяется
как предел последовательности (1 + ^)п. После знакомства с
формулой Тейлора мы можем иначе представить число е: как
предел последовательности сумм вида 1 + jj + ^ + ... + ^, то
есть как сумму ряда ^ ^ — он, как мы увидим позже, схо-
71=0
дится. Какое же из этих двух представлений практичнее? Какое
стали бы мы использовать, если бы нам потребовалось выпи-
Ю. В. Пухначев|
СЕМЬ СЕМИНАРОВ
519
сать число е до некоторого определенного знака? Первое?
Тогда нам придется вычислять члены последовательности (1 + ^)п
один за другим, причем каждый раз целиком заново. Совсем
иначе пойдет дело, если мы воспользуемся вторым
представлением: е = l + if + «2F + -»+rir- каждое новое слагаемое ряда
будет лишь поправкой к полученному ранее значению
частичной суммы, поправкой все менее значительной. Ясно, что для
вычислений гораздо удобнее использовать второе представление
числа е — в виде ряда. Более того: остаточный член формулы
Тейлора, с помощью которой мы построили этот ряд, позволит
нам заранее установить, сколько слагаемых ряда следует взять
для достижения заданной точности. Подобная предварительная
оценка существенно облегчает применение рядов в
вычислительной практике. Впрочем, вряд ли стоит сейчас голословно
обсуждать все тонкости, все выгоды их применения: вы убедитесь в
их достоинствах в ближайшем будущем, на наших занятиях. Я
закончу соображением весьма общего характера. Вспомните не
раз слышанное вами по телефону, когда вы набирали номер
говорящих часов: «Точное время — столько-то часов столько-то
минут столько-то секунд». В некоторых спортивных
соревнованиях, в физических экспериментах, когда требуются более
точные данные о времени, указываются доли секунды — десятые,
сотые... В этом проявляется характерная особенность
человеческого сознания: всякое измерение начинается с грубой
оценки, а затем уточняется все более мелкими поправками,
дополнениями. Пожалуй, эта особенность и лежит в основе понятия
ряда.
Вглядываюсь в лица ребят: убедили ли их мои слова? И после
короткой паузы продолжаю:
— Надеюсь, теперь вы понимаете, как важно, располагая
теорией числовых последовательностей, построить еще и теорию
числовых рядов. Что же еще полезного могла бы нам
подсказать аналогия между последовательностями и рядами? Как вы
думаете, Кулагин?
— Да пока никак. Всех ведь тонкостей не упомнишь про эти
последовательности...
— Бог с ними, с тонкостями. Но очень стоило бы вспомнить
одно основополагающее понятие, которое на наших
предыдущих семинарах всегда сопутствовало понятию
сходимости...
— Фундаментальность? Критерий Коши? — ловит он мою
подсказку.
520
ЧИСЛОВЫЕ РЯДЫ
[Гл. 7
— Именно! Не попробуете ли перенести это понятие на
числовые ряды? Только будьте повнимательнее!
Он пишет формулировку критерия для некоторой числовой
переменной Ап и поясняет:
— Пусть это будет частичная сумма ряда. Разность Ап — Ат...
Лучше я распишу обе эти суммы... вот так... Значит, взяли п
слагаемых и га первых убрали... получается |am+i +am+2 +... + ап\.
И если для любого е найдется номер N такой, что для любых п
и т больших N, выражение |am+i + am+2 + ... + ап\ меньше £,
то ряд сходится. То есть из выполнения критерия Коши
вытекает сходимость ряда, из невыполнения — расходимость, это вещи
эквивалентные.
— Верно. Запишите формулировку критерия в свои
тетради, ребята. Повторите ее еще раз, Кулагин. Я прошу всех
твердо заучить ее: в теории числовых рядов критерий Коми
играет не меньшую роль, чем в теории последовательностей.
Садитесь Андрей. Какой еще математический объект можно было бы
использовать для проведения аналогий между ним и числовым
рядом?
— А если формулу Тейлора? — раздается ломкий голос Бут-
куса. — Там тоже сумма слагаемых.
— Хорошая мысль! Но она нам пригодится попозже, когда мы
станем изучать так называемые функциональные ряды. Ищем
дальше, ребята!
— Несобственный интеграл? — полувопросительно
произносит Гарин.
— Мысль интересная. Но прежде, чем мы станем ее
развивать, я хотел бы предупредить вас, ребята, о неполноте, о
нестрогости всякой аналогии. Чтобы мое предостережение
было понятнее вам, я поясню его на конкретных примерах.
Возьмем формулировку критерия Коми для числовых рядов —
прочтите ее еще раз. «Для любых т и п», — так говорится в ней.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
521
Положим п = т + 1. Тогда неравенство, завершающее
формулировку критерия, станет таким: \ап\ < е. Что это значит? Кто
сообразил?
Слово берет Стрельцов:
— Это значит, что слагаемые ряда должны убывать по
абсолютной величине. Ой, нет! Что за чушь я несу! Не
убывать, а стремиться к нулю при п, стремящемся к
бесконечности!
— Именно стремиться к нулю! — подчеркиваю я. — Итак, если
ряд сходится, то последовательность его слагаемых бесконечно
мала. Если же последовательность его слагаемых не стремится
к нулю, то... что будет тогда, Сынчиков?
— Тогда... ряд не будет сходиться, — после секундной паузы
отвечает он.
— Совершенно верно, ряд не будет сходиться. Итак,
бесконечная малость слагаемых ряда есть необходимое условие его
сходимости. Это очень важное положение, которое тоже
нужно заучить обязательно, ребята. Могла ли подсказать его нам
теория несобственных интегралов? Вряд ли. Я приведу по
этому поводу любопытный пример. В конце прошлого семинара мы
доказали, что из сходимости несобственного интеграла на
бесконечности не вытекает бесконечное убывание подынтегралъной
функции. В качестве одного из примеров мы разобрали тогда
+оо оо
интеграл J cosx2dx. Построим по аналогии ряд J^ cosn2. Ана-
а п=1
логия позволяет предположить, что он сходится. А между тем
это предположение неверно. Ряд расходится. Оказывается, его
слагаемое cosn2 не стремится к нулю с ростом п. Это нетрудно
показать.
Делаю небольшую паузу, как бы отсекающую ответвление
беседы от основной темы.
— Рассмотрим сначала последовательность cosn и докажем,
что она не бесконечно мала. Предположим противное. Тогда
бесконечно малой будет и ее подпоследовательность cos2n.
Преобразуем этот косинус, по известной тригонометрической
формуле в разность 2cos2n — 1. Она, согласно нашему
предположению о бесконечной малости cosn, должна стремиться
к минус единице. Полученное противоречие доказывает, что
последовательность cosn не бесконечно мала. Подобным же
образом поступаем с последовательностью cosn2: предполагаем,
что она бесконечно мала, выводим отсюда, что бесконечно мала
ее подпоследовательность cos(2n)2 = cos4n2; дважды применяя
522
ЧИСЛОВЫЕ РЯДЫ
[Гл. 7
использованное выше преобразование, выражаем этот косинус
суммой 8 cos4 n2 — 8 cos2 п2 + 1и видим, что согласно
предположению эта сумма стремится к единице. Полученное противоречие
опровергает бесконечнро малость последовательности cosn2.
оо
После этого становится понятным, что ряд ^2 cosn2 расходит-
п=\
ся: нарушено необходимое условие его сходимости. Выходит, что
+оо
аналогия со сходящимся интегралом J cosx2dx нас подвела.
а
Этот пример убедительно показывает неполноту аналогий и
призывает нас не терять из виду своеобразие тех вопросов,
в изучении которых мы опираемся на аналогии. Поэтому в
дальнейшем будем с осторожностью доверяться аналогиям и
все выводы, подсказанные ими, станем строго доказывать. Да
и проводить их будем повдумчивее, поразнообразнее, чтобы
всегда отыскивать среди них наиболее точную. Я вам не раз
советовал наряду с языком формул почаще применять в
своих рассуждениях язык более наглядный — графический. Для
несобственных интегралов мы использовали его с самого начала.
Быть может, нам удастся описать с его помощью и числовые
ряды?
Вскоре после моего вопроса к доске вызывается Костюк:
— Здесь можно так: вот несобственный интеграл, площадь
под бесконечной кривой, — он рисует в системе координат
ниспадающую линию, плавно приближающуюся к оси абсцисс, — вот
так можно изобразить ряд, — он рисует еще одну координатную
систему, размечает ось абсцисс целочисленными засечками и над
образовавшимися отрезками рисует прямоугольники. — Пусть
высоты этих прямоугольников численно равны членам ряда. Ос-
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
523
нования у них — единичные. Поэтому площади прямоугольников
численно тоже равны членам ряда, а площадь под всей этой
ломаной, несобственный интерграл от этой ступенчатой функции
равен сумме ряда. Если, конечно, ряд сходится, — поспешно
добавляет он.
— Хорошо, — одобряю его подход. — Аналогия между
числовыми рядами и несобственными интегралами стала зримой,
наглядной...
Перед тем, как отправить Костюка обратно, прошу, чтобы
он почетче перерисовал свой чертеж под выкладками Мухина,
с помощью которых определялся числовой ряд и его
сходимость.
— Если бы теперь, — с прекраснодушной улыбочкой
рассуждает Миклашевский, — придумать, как для произвольного ряда
выражать аналитически такую ступенчатую функцию, то
можно было бы всю теорию рядов свести к теории несобственных
интегралов...
— Такое представление поискать можно, — отвечаю ему, —
но вряд ли нам удастся сделать это за время семинара. Могу
заметить, что это не сделано за всю многовековую историю
высшей математики: теория числовых рядов до сих пор существует
сама по себе, не сливаясь с теорией несобственных интегралов.
Так что и нам придется развивать ее особо, а аналогия с
несобственными интегралами будет нам при этом советчицей.
Кстати, первый совет содержится уже в том чертеже, который
нарисовал Костюк. Обратите внимание: он провел график подинте-
гральной функции именно так (обвожу мелом плавную линию
на чертеже Костюка), а не так (рядом быстро рисую еде одну
систему координат и в ней — затухающую синусоиду). К чему
бы это?
— Он нарисовал самое простое, — пожимает плечами
Стрельцов.
— А вы как думаете, Миша? — спрашиваю Гарина, заметив
на его лице характерную еле уловимую усмешку.
524
ЧИСЛОВЫЕ РЯДЫ
[Гл. 7
— Костюк нарисовал знакопостоянную функцию. И ряд взял
тоже со знакопостоянными слагаемыми.
— Какую мысль подсказывает такое предпочтение? — не даю
ему остановиться на полуслове.
— Рассмотреть знакопостоянные ряды особо — так же, как
мы рассматривали несобственные интегралы от
знакопостоянных функций. Без ограничения общности можно считать
слагаемые таких рядов неотрицательными. Если встретится ряд с
неположительными слагаемыми, то минус единицу можно
вынести, это на сходимость не влияет, и ряд будет такой, как нужно:
с неотрицательными слагаемыми.
— Итак, — стираю свой график с затухающей синусоидой, —
аналогия на время сузилась: с одной стороны — ряды с
неотрицательными членами, с другой — несобственные интегралы
от неотрицательных функций. Что можно извлечь из такой
аналогии?
— Наверное, что-то вроде призкана сравнения и признака
эквивалентности, — тотчас откликается Горт.
— Разумно! Вот сразу две задачи, ребята: сформулировать
оба признака и попытаться их доказать. Думаем над этим все
вместе.
— Да тут все довольно очевидно, — порывается отвечать
Костюк.
— Подождите, — осаживаю его. — Если вы все понимаете
и уже нашли доказательство, напишите его в своей тетради, я
посмотрю, сравню с тем, что напишут другие, и вызову самого
понимающего.
Походив между столами, вызываю все-таки Костюка —
решимость нужно поощрять.
Он пишет неравенство для членов сравниваемых рядов
О < ап < Ьп, из сходимости ряда Ьп выводит ограниченность
его частичных сумм Bpj, а отсюда — и ограниченность
частичных сумм другого ряда, А^, указывает на возрастающий
характер последовательности А^, обусловленной
неотрицательностью слагаемых ап, и наконец применяет теорему о
пределе возрастающей и ограниченной сверху
последовательности:
— Значит, если ряд Ьп сходится, то ряд ап также сходится.
От противного легко доказать: если ряд ап расходится, то ряд
Ьп также расходится. Теперь признак эквивалентности.
Еще одна строка формул: предел lim ^ = к > О, затем це-
почка неравенств (к — е)Ьп < ап < (к + е)Ьп.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
525
— Выполняется, начиная с некоторого номера N, — замечает
Костюк по ее поводу.
Идя по этой цепочке справа налево, он на основании правого
неравенства выводит из сходимости ряда Ьп сходимость ряда
ап, на основании левого — из сходимости ряда ап сходимость
ряда Ьп. Затем — проход слева направо: на основании левого
неравенства из расходимости ряда Ьп выводится расходимость
ряда ап, на основании правого — из расходимости ряда ап
расходимость ряда Ьп.
— Таким образом, — следует четкий вывод, — если lim т*- =
п—+оо0п
= к > О, то ряды ап и Ьп сходятся и расходятся
одновременно.
— Все правильно, садитесь, Виталий. А теперь пусть к
доске пойдет Лапиков. Вы не догадываетесь, Егор, — смотрю, чуть
улыбаясь, в его настороженные глаза, — зачем я вас вызываю?
Помните, на прошлом семинаре мы доказывали признак
эквивалентности для несобственных интегралов, и именно вы
разобрали случай, когда предел отношения подинтегральных функций
равен нулю...
Не дожидаясь окончания моего объяснения, он встает,
идет к доске и сразу пишет lim f^ = 0. Как бы эта поспеш-
ность не привела его к срыву! Надо настроить его на более
рассудительный образ действий! Словно не замечая
написанного им, неторопливо набрасываю рядом в пояснение своих
+оо +оо
слов: J f(x)dx, f g{x)dx, lim ОЧ = 0. Оборвав свои
выкладки, Лапиков вглядывается в то, что я пишу.
Спрашиваю его:
— С чего мы начинали разбор случая с нулевым пределом,
когда говорили про несобственные интегралы?
— С определения... Расписали по определению, что это
значит: lim Щ = 0.
X—+OO0W
526
ЧИСЛОВЫЕ РЯДЫ
[Гл. 7
— Вот так же начните и сейчас, — говорю ему с
инструктивной размеренностью.
Приняв спокойный деловой темп, вспоминая этапы того
рассуждения, он ведет по отчетливой аналогии требуемое
доказательство: если lim т*- = 0, то из сходимости ряда Ьп следует
п—►оо071
сходимость ряда оп, а из расходимости ряда ап следует
расходимость ряда Ьп.
— Очень хорошо! — оцениваю его работу; вижу, что он и
сам доволен собою, что в жестах его и во взгляде уже весьма
заметна вера в свои силы, к которой я так настойчиво призывал
его когда-то. Конечно, к передовикам его не причислишь, но не
отнесешь уже и к тем отстающим, которые безнадежно запуганы
своим отставанием. Он сбросил с себя оцепенение робости, он в
движении — пусть же достигнет тех рубежей, которых способен
достичь.
— Садитесь, Егор. Теперь я хотел бы, ребята, —
обращаюсь к аудитории, — ненадолго вернуться к рассуждениям Ко-
стюка и вдуматься в одну фразу, сказанную им между прочим:
неравенства, с помощью которых доказывается признак
эквивалентности, могут выполняться не для всех номеров п, а лишь
начиная с некоторого N. Мне кажется, в этом есть намек на
еще одну аналогию с несобственными интегралами. Кто
чувствует ее?
— Там, в несобственных интегралах, — первым
откликается на мой вопрос Чюмин, — мы сначала писали пределы
«от единицы до плюс бесконечности», а потом по-другому —
«от а до бесконечности»; сначала брали в нижнем пределе
постоянную величину, единицу, а потом — переменную, какое-
то а.
— То есть... как это — переменную? — озадаченно смотрю на
него, готовый услышать в ответ очередную ересь.
— Переменную в том смысле, что сходимость интеграла на
бесконечности не меняется, если нижний предел изменить.
— Вот это уже вернее! — зову его к доске.
— Наверное, — продолжает он, — и тут ничего не изменится,
если от какого-то N проверять неравенства, а не от единицы.
Ряд как сходился, так и будет сходиться, если сходился, а если
не сходился, то и теперь не будет сходиться.
Потребовав от него строго доказать это, отсылаю его на место
одобрительным кивком:
— Все верно. Доказанное позволит нам дополнять
облегчающим примечанием те соотношения, из которых исходит любой
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
527
признак сходимости рядов: эти соотношения могут выполняться
лишь начиная с какого-то номера ЛГ, — приписываю такое
примечание к формулировке признака сравнения. — Теперь другой,
более существенный пункт в развитии нашего рассуждения,
который напрашивается при воспоминании о том, как мы
разбирали теорию несобственных интегралов. Сформулировав основные
положения о сходимости и расходимости интегралов от
знакопостоянных функций, мы тут же позаботились о характерных
примерах таких интегралов. По аналогии нам стоило бы
незамедлительно придумать характерыне примеры рядов со
знакопостоянными членами.
— Геометрическая прогрессия! — без дальних слов предлагает
Кочин.
— Напишите ее на доске! — вызываю его. — Хорошо.
Займемся сначала сходящейся прогрессией. Укажите, что в этом
случае ее знаменатель q меньше единицы... ну, и больше
нуля: ведь мы говорим пока о рядах с неотрицательными
членами. Тогда и начальное слагаемое прогрессии р тоже следует
считать положительным, отметьте это. Попробуйте сообразить:
0< <7< 4 , р>0
как могли бы фигурировать члены такой прогрессии в
признаке сравнения? Верно, ап < pqn. А теперь подумаем все вместе:
нельзя ли, варьируя форму этого соотношения, вывести какой-
нибудь новый признак сходимости? Что предложили бы вы,
Лапиков?
— Может быть, извлечь корень n-ной степени? —
прикидывает он.
— Давайте извлечем, — передаю его предложение Кочину. —
Что можно теперь сказать о правой части преобразованного
соотношения? Как вы полагаете, Кочин?
— Если п к бесконечности... Корень у/р стремится к
единице, если п стремится к бесконечности, q меньше единицы... Вся
правая часть рано или поздно будет меньше единицы.
— Это так. Нельзя ли вывести отсюда формулировку нового
признака? Не попробуете ли?
— Если ^/а^, начиная с некоторого номера, меньше
единицы... даже, пожалуй, меньше или равен единице, то ряд ап
сходится.
как могли бы фигурировать члены такой прогрессии в
признаке сравнения? Верно, ап < pqn. А теперь подумаем все вместе:
нельзя ли, варьируя форму этого соотношения, вывести какой-
нибудь новый признак сходимости? Что предложили бы вы,
Лапиков?
— Может быть, извлечь корень n-ной степени? —
прикидывает он.
— Давайте извлечем, — передаю его предложение Кочину. —
Что можно теперь сказать о правой части преобразованного
соотношения? Как вы полагаете, Кочин?
— Если п к бесконечности... Корень у/р стремится к
единице, если п стремится к бесконечности, q меньше единицы... Вся
правая часть рано или поздно будет меньше единицы.
— Это так. Нельзя ли вывести отсюда формулировку нового
признака? Не попробуете ли?
— Если ^/а^, начиная с некоторого номера, меньше
единицы... даже, пожалуй, меньше или равен единице, то ряд ап
сходится.
528
ЧИСЛОВЫЕ РЯДЫ
[Гл. 7
— Формулировка довольно четкая. Допустим, ваше
предположение о tfa^ выполнено. Докажите, что тогда ряд ап
действительно сходится.
— Возведем обе части неравенства в n-ную степень...
— Что же вы замолчали?
— Справа должен быть сходящийся ряд...
— А ряд из единиц, как вы хорошо понимаете, расходится,
потому что последовательность его слагаемых не стремится к
нулю. Конечно, это не опровергает сходимость ряда ап. Но и не
доказывает!
Сообразит ли он, как выйти из положения? Ничего от него
не дождавшись, оборачиваюсь к аудитории, чтобы попросить
о помощи, и вижу несколько поднятых рук — Рамзина,
Синицы, Мухина, Аргуновой... О, ее готовность меня особенно
радует!
— Помогайте, Аргунова!
— Надо в формулировке признака сказать: не меньше или
равно единице, а меньше или равно д, которое строго меньше
единицы.
— Исправьтесь, Кочин, — снова поворачиваюсь к доске. — Ну,
вот — теперь, если принять такую формулировку признака, то
он доказывается просто и быстро. Прочтите эту исправленную
формулировку еще раз.
— Пусть дан ряд с неотрицательными членами ап. И пусть,
начиная с некоторого номера, выполняется tfa^ < q < 1. Тогда
ряд ап сходится.
— Докажите это. Хорошо, хорошо... Все верно. Садитесь,
Кочин.
— А почему мы только про сходимость доказываем? —
слышится резкий голос Буткуса. — А про расходимость?
— Законный вопрос! — киваю ему. — Каждый признак,
разбиравшийся нами прежде, позволял судить как о сходимости, так
и о расходимости рядов. На сей же раз о расходимости ничего
не было сказано. Надо исправить этот недочет! Кто мог бы это
сделать?
— Надо там изменить знак неравенства! — раздается в ответ
твердый голос Костюка.
— Где «там»? В каком неравенстве? Выражайтесь точнее!
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
529
— Я имею в виду неравенство ^/а^ > 1; если оно
выполняется, начиная с какого-то номера TV, то ряд ап будет
расходиться.
Приглашаю его к доске, и он доказывает свое утверждение —
потом читает окончательную, полную формулировку нового
признака:
— Пусть есть ряд ап. Все его члены, начиная с какого-то
номера N, сохраняют знак. Без ограничения общности будем считать
их неотрицательными. И пусть выполняется, опять-таки
начиная с некоторого номера, неравенство tfa^ < q < 1. Тогда ряд
сходится. Но если, начиная с некоторого номера, выполняется
неравенство tfa^ > 1, то ряд расходится.
— Все правильно. Садитесь, Виталий. Признак, который вы
изложили, называется признаком Коши. Все записали его,
ребята? Тогда продолжаем. Геометрическая прогрессия способна
подсказать формулировку еще одного, не менее эффективного
признака сходимости и расходимости числовых рядов со
знакопостоянными членами. Поищите-ка его.
Чувствуя, что поставил непростую задачу, стараюсь
облегчить поиск решения наводящими вопросами:
— Скажите, Рамзин, как можно задать n-ный член нашей
геометрической прогрессии? Введем для него обозначение Ьп.
— Возвести q в n-ную степень и умножить на р, — отвечает
он, не понимая, куда я клоню.
— Верно, bn = pqn. Напишите это на доске. А еще какие
способы задания последовательностей вы знаете? Молчите... Помните,
когда-то у нас заходила речь про так называемый рекуррентный
способ.
— Это когда очередной член как-то выражается через
предыдущие...
— Или через один лишь непосредственно предшествующий
ему. Можно ли задать геометрическую прогрессию
рекуррентным способом?
— Ну, можно...
В интонации его ответа слышится недоговоренное: «Только
зачем?» Но все-таки он пишет: an+i = anq.
И тотчас — Мухин:
— Если слагаемые ряда — знакопостоянного ряда — если они,
начиная с какого-то номера N — если удовлетворяют
соотношению ^^ меньше или равно q — которое строго меньше
единицы — то ряд сходится.
— Правдоподобно. Согласны, Сергей?
18 - 2019
530 ЧИСЛОВЫЕ РЯДЫ [Гл. 7
— Это надо еще доказать! — косится тот на Мухина.
— Так пусть это докажет сам автор идеи! Возвращайтесь к
себе, Рамзин. К доске, Мухин! Сначала напишите-ка
поаккуратнее несколько неравенств, о которых вы говорили, — начиная с
некоторого номера N... Пишете вы, будто рисуете, — довольный,
оглядываю ровный столбик неравенств: с чем-чем, а с почерком
у Мухина, действительно, дело все лучше. — Но во всяком
рисунке важна не только техника, но и композиция. Попробуем-
ка расположить серию этих неравенств не в столбик, а в
строчку...
Пишу заново дроби ^^, -^- и далее, проставляю под ними
знаки неравенства уголками кверху, и под каждым из уголков
приписываю букву q.
— Не догадываетесь, — смотрю на безмолвного Мухина, —
что я имею в виду?
Синица вскидывает руку: сообразила? Я умолающим жестом
прошу ее помолчать. Молчат и остальные. Я мог бы дать слово
Рамзину с его законным правом на ответный ход... нет, он тоже
молчит. Но Сутеева прорывает:
— Надо перемножить эти неравенства!
Сработало-таки визуальное мышление! Мне бы ликовать
по поводу этой отличной находки — а у меня на душе
совсем не радостно, Расстраивает Мухин: когда же он научится
доводить до логически строгого выражения свои хорошие
идеи?
А ребят уже не уймешь:
— Перемножить все, от номера N до номера п, — продолжает
Синица. — И тогда получится...
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
531
— Что получится, пусть выяснит Мухин, — останавливаю ее.
Не без моей помощи он выводит неравенство ап < |#-gn.
Дальше — легче: путь доказательства уже проложен Костюком
при выработке признака Коши. Мухин заканчивает
рассуждение и диктует окончательную формулировку нового
признака:
— Если дан некоторый рад с неотрицательными членами ап и
выполняется неравенство ^^ < q < 1 — выполняется, начиная
с некоторого номера N — то ряд ап сходится. Если, начиная с
некоторого номера, выполняется неравенство ^±1 > 1, то ряд
расходится.
— Верно. Садитесь. Этот признак, ребята, называется
признаком Даламбера. Я хотел бы привести оба признака — Коши
и Даламбера — еще в одной форме, но для этого мне нужны
новые примеры знакопостоянных рядов. Дайте мне их!
— Мы когда-то говорили про гармонический ряд, —
напоминает Сутеев.
— Верно, говорили. Как, кстати, он определяется? —
обращаюсь с этим вопросом к Сынчикову.
— Один... плюс одна вторая, плюс одна третья... и так далее.
Пишу это на доске под его диктовку рядом с чертежиком,
который предложил Костюк в качестве графической иллюстрации
понятия числового ряда.
Горт как-то резко и странно прищуривается, перебрасывая
взгляд с этого рисунка на мою свежую запись, и отрывисто
говорит:
— Ряд ^г... при а > 1 сходится... при остальных а расходится.
— Уловили, на что я намекаю? — улыбаюсь ему. — Поясните
подробнее.
— Аналогия с интегралом J |§.
а
— То, что подсказывает аналогия, необходимо испытывать
строгими доказательствами.
— С расходимостью все ясно: при а = 1 будет гармонический
ряд, он расходится, это мы уже доказывали, при а < 1
расходится тем более — по признаку сравнения.
18*
532
ЧИСЛОВЫЕ РЯДЫ
[Гл. 7
Кратко записываю это на доске. Потом снова Горту:
— А как вы докажете сходимость ряда при а > 1?
Затрудняетесь с ответом? Тогда давайте внимательнее рассмотрим чертеж
Костюка...
— Подождите! — останавливает он меня; в его возгласе
слышится капризная интонация ребенка, когда тот кричит: «Я сам!»
— Жду, — моментально замолкаю я. — Может быть, вы
пойдете к доске, Саша?
... График, который должен проиллюстрировать
доказательство, давно уже нарисован на доске, а Горт все не может отвести
от него глаз.
— Мы слушаем вас, — стараюсь вернуть его к незаконченному
разговору.
Он оборачивается ко мне с сомнением во взгляде:
— Скажите, а если вот так, с помощью этих столбиков
доказывать, то как это считается — строго?
— Давайте разберемся, — подхожу к доске. — Если эти
столбики смущают вас, кажутся вам простоватыми, заменим их
вполне респектабельным графиком кусочно постоянной
функции, — рисую новый чертежик. — Эта функция всюду меньше
или равна функции рг, стало быть, то же неравенство связывает
и интегралы от той и другой функции. Мы берем их в целочис-
ленных пределах, так что промежуток интегрирования можно
разбить на единичные отрезки. На каждом из них интеграл
от ступенчатой функции численно равен соответствующему
слагаемому ряда. Отсюда и вытекает оценка для частичных
сумм ряда, выражающая их ограниченность, — и вытекает
совершенно логично, строго. Вы не возражаете?
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
533
— Пожалуй, — уклончиво соглашается Горт. — Дальше уже
все очевидно: в силу неотрицательности слагаемых ряда его
частичные суммы монотонно возрастают. Но при этом они
ограничены сверху площадью под кривой у = f(x). Эта площадь
конечна, поскольку интеграл от функции /(х) сходится на
бесконечности. Частичные суммы монотонно возрастают и ограничены —
значит, их последовательность имеет предел. Ряд сходится. Все
доказано.
— Пожалуй, — копирую его уклончивый тон. — Больше вы
нам ничего не скажете? Подумайте... Ничего? Честно говоря,
я ожидал услышать от вас, Саша, более широкое заключение,
нечто этакое: «С данным доказательством — все, но мне
кажется, что в этом рассуждении есть идея какого-то нового
признака сходимости». В том, что вы ее не заметили, конечно,
ничего страшного нет, общими усилиями мы этот признак выведем,
никуда он от нас не денется. Я сейчас о вашей будущей
работе беспокоюсь. Обидно будет, если вы всегда будете
удовлетворяться решением частных задач и ни в одной из них не увидите
зерно большой проблемы. Садитесь и думайте вместе со всеми
над формулировкой нового признака, которую можно извлечь из
проведенных вами рассуждений. Итак, предположим, что у нас
есть некоторый ряд, состоящий из неотрицательных членов ап...
Оглядываю аудиторию в надежде, что кто-то продолжит
начатую мной фразу.
— Надо найти такую функцию /(х), чтобы /(п) равнялась
ап, — предлагает Костюк.
— Например, вот так? — набрасываю заведомо негодный
график.
— Нет! — протестует он. — Надо, чтобы f(x) везде была над
этими ступеньками, как раньше.
— Начертите так, как вам хочется, — зову его к доске.
Он начинает было рисовать и останавливается, видя, что с
предложенным мною рядом нельзя сделать то, о чем ему
подумалось.
— Слабо! — с наигранным злорадством гудит Меншиков.
534
ЧИСЛОВЫЕ РЯДЫ
[Гл. 7
— А вот у Горта все получилось просто, — подигрываю ему,
подзадоривающе глядя на Костюка.
— Так ведь тогда, — хмуро отвечает Костюк, — и ряд был...
специфический.
— Ну-ка, в чем же заключалась специфичность того ряда?
Подумав, он кратко отвечает:
— В монотонности.
— Верно. Исправьте график с учетом требования
монотонности ряда. Как теперь вы будете строить функцию /(х)? Каким
условиям подчините ее?
— Первое условие — чтобы f(n) = ап... Второе — чтобы для
любого х такого, что п — 1 < х < п, выполнялось f(x) > ап...
— Не сложновато ли?
— Вторым условием можно просто потребовать от f(x)
монотонности, — замечает Гарин.
- Разумно, — одобряю его мысль. — Тогда автоматически
выполнится то,— поворачиваюсь к Костюку, — чего вам хотелось.
Согласны со мной?
- Согласен, - вяло кивает он: работать по чужой указке ему
не по нраву.
— Но это — далеко не единственный вывод, который можно
извлечь из совета Гарина, — стараюсь воскресить в нем
инициативу. — Подумайте: если ап — монотонная последовательность,
если f(x) — монотонная функция и для любого п выполняется
Дп) = ап, то разве для значений х из промежутка [п— 1, п]
можно написать лишь f(x) > an? Ну-ка, внимательнее всмотритесь
в свой график!
- Можно написать двустороннее неравенство... Вот такое:
ап-\ > f(x) > ап.
Ну, конечно! Вспомните, в каком еще признаке встречались
нам двусторонние неравенства.
•■- В признаке эквивалентности.
- Да, в том самом, формулировка которого оканчивалась
очень значительными словами: «... сходятся и расходятся
одновременно».
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
535
Он заменяет средний член своего неравенства интегралом,
суммирует крайние члены неравенства и резюмирует:
— Ряд и интеграл сходится и расходятся одновременно.
Доказывается так же, как в признаке эквивалентности.
Двойное неравенство, связывающее частичные суммы ряда с
интегралом от введенной им функции, он проходит вначале
справа налево, потом слева направо, наводя причинно-следственные
связи сначала между сходимостью интеграла и ряда, а затем —
между расходимостью того и другого.
— Вы вывели новый признак, — оцениваю его результат, —
признак Маклорена или, как его еще называют, интегральный.
Сформулируйте его окончательно.
— Можно подумать?
— Пожалуйста.
— Пусть дан ряд ап с неотрицательными, монотонно
убывающими членами. Пусть существует неотрицательная, монотонно
убывающая функция f(x). Причем для любого п выполняется
оо +оо
f(ri) = ап. Ряд ]Г ап и интеграл J f(x)dx сходятся и расходят-
п=1 a
ся одновременно.
оо
— Таким образом, сходимость ряда / —- при а > 1 и paCXO-
димость того же ряда при а < 1 вытекают из...
+оо
— Из сходимости интеграла J |§ при а > 1 и расходимости
а
того же интеграла при а < 1.
— Правильно. Садитесь, Виталий. Теперь, ребята, я хочу
ненадолго возвратиться к признакам Коши и Даламбера. Их
применяют иногда в так называемой предельной форме, если
последовательность ?/а^ или, соответственно, ^±L сходится к
v а,п
некоторому пределу — будем обозначать его в обоих случаях
одинаково, буквой Q. Что можно сказать о сходимости ряда,
если этот предел меньше единицы? больше единицы? равен
единице? Подумаем над этими вопросами.
Разгуливая между столами, замечаю в тетради Стрельцова
строчки символов, в которых угадываю доказательство
применимости обоих признаков для случая Q < 1: вводится новое
обозначение Q = 1 — а, где а > 0, потом отмечается, что, начиная с
какого-то номера iV, величины tfa^ или ^^ будут меньше 1 — f,
эта разность обозначается через q — видимо, с намерением
сослаться на признаки Коши и Даламбера в их первоначальной
536
ЧИСЛОВЫЕ РЯДЫ
[Гл. 7
формулировке. Вызванный к доске, Стрельцов именно так и
ведет свое рассуждение.
— Таким образом, — заканчивает он, — если lim ?/а^ = Q <
п—+оо
1 или lim ^^ = Q < 1, то ряд ап сходится.
п—>оо °п
— Сотрите все с доски и садитесь на место.
Следующим вызываю Сутеева. По моей просьбе, следуя
похожей логической схеме, он доказывает, что при Q > 1 ряд ап
будет расходиться.
— Теперь посмотрим, ребята, будет ли сходиться ряд,
если Q = 1.
Вместо молчаливого раздумья, которое я ожидал вслед
за этими словами, они огорошивают меня совсем иной
реакцией — незамедлительным единодушным возгласом: «Нет, не
будет!» И я догадываюсь, откуда эта убежденность: ведь в
первоначальной формулировке признаков Коши и Даламбера
расходимость ряда утверждалась тогда, когда величины фь^ и
соответственно ^^- были больше или равны единице — так что
и на сей раз слова «больше» и «равно» обещают одинаковый
исход.
— Не будет... Ну что ж, докажем это строго, — предлагаю я.
И через несколько минут бесплодных попыток:
— Что, никак не доказывается? Может быть, попытаемся
рассуждать не абстрактно, а на примере наших модельных ря-
оо
дов? Зря что ли мы их придумывали? Возьмем ряд J2 ^ с Р33-
п=1
ными а, при которых он сходится и расходится, и посмотрим,
что дает в том и другом случае попытка использовать признак
Коши в его предельной форме; признак Даламбера оставим на
потом.
Вскоре Миклашевский докладывает недоумевающим тоном:
— При любых а получается, что Q = 1.
И показывает это на доске. Затем получает тот же вывод,
применяя признак Даламбера.
— Очень хорошо. Ну, а теперь, Миклашевский, давайте
вернемся к вопросу: что можно сказать о сходимости ряда ап, если
lim ф^ = 1 или lim ^ = 1?
— Получается, что ничего нельзя сказать...
— Верно. Потому что к такому результату, к равенству Q = 1
оо
может привести как сходящийся ряд — например, Х^^7, где
Ю. В. Пухначев|
СЕМЬ СЕМИНАРОВ
537
оо
а > 1 — так и расходящийся — например, ^ ^-, где а < 1. Но
п=1
почему вы говорите об этом с каким-то смущением,
Миклашевский? Не можете объяснить? А я, кажется, понимаю, в чем тут
дело, и прошу всех вас, ребята, — оборачиваюсь к аудитории, —
внимательно выслушать мою версию: заблуждение, о котором
я буду говорить, носит очень распространенный характер. Мы
доказали: если выполняются признаки сходимости Коши или
Даламбера, то ряд сходится. Но справедливо ли обратное? Будет
ли выполняться хотя бы один из этих признаков, если ряд
сходится? Как вы думаете, Миклашевский? Вы медлите с ответом, и
это говорит за то, что вы не подметили достаточный, всего лишь
достаточный характер обоих признаков. Необходимого
характера они не носят. Запомните это, ребята! И учтите естественное
следствие из этого положения: исследуя сходимость того или
иного ряда, всегда приходится думать, какой признак здесь
сработает и притом наиболее убедительным образом. Об этом,
конечно, лучше поговорить на конкретных примерах — сейчас
мы к ним приступим. Но прежде уделим еще несколько минут
теории.
Небольшой паузой отмечаю новое задание.
— Мы разработали с вами, ребята, уже пять признаков
сходимости знакопостоянных рядов. Мне кажется, что рассуждения,
которые мы провели при этом, способны дать большее: привести
по крайней мере еще к одному-двум признакам сходимости.
Просмотрите внимательно то, что вы записали в своих тетрадях, и
попытайтесь извлечь что-нибудь новое из записанных вами
оценок и выкладок.
Расчет мой тот же, что и в прежних заданиях такого рода:
не придумают ничего интересного — так пусть хотя бы повторят
пройденное.
Затянувшуюся сосредоточенную тишину наконец нарушает
Стрельцов:
— Я что-то не совсем понимаю вашу просьбу. Вывести из
наших рассуждений о тех пяти признаках сходимости какие-то
новые признаки — так вы говорите? Да? Но ведь каждое
рассуждение приводит только к тем выводам, ради которых оно
велось!
— Вы правы, — киваю Стрельцову. — Каждое из наших
рассуждений о том или ином признаке сходимости вело лишь к
одному, вполне определенному выводу. Новые же выводы можно
из них получить, если из различных рассуждений извлекать от-
538
ЧИСЛОВЫЕ РЯДЫ
[Гл. 7
дельные характерные идеи и пытаться их скомбинировать.
Скажем, если мы говорим о признаке сравнения, то тут
характерная идея выражалась неравенством, которое связывает
слагаемые сравниваемых рядов ап и Ьп; если же взять признак Далам-
бера, то здесь суть в образовании и дальнейшем перемножении
дробей вида ^±1...
Называю как бы наугад детали прошлых построений —
авось, кто-нибудь догадается, что мой перечень подобран не
случайно.
— Минуточку, минуточку! — пытается поймать мою мысль
Горт. — Если взять an+i к ап и 6n+i к Ьп, взять такие
отношения...
— Взять такие отношения, — обгоняет его Костюк, — потом
перемножить...
И покуда еще звучат эти не очень-то связные размышления
вслух, раздается степенный голос Рамзина:
— Все ясно. Если для двух знакопостоянных рядов ап и
Ьп, начиная с какого-то номера JV, выполняется неравенство
^^ < -JjjtL, то из сходимости ряда Ьп вытекает сходимость ряда
ап, а из расходимости ап — расходимость Ъп.
Рамзин умолкает, горделиво глядя на меня. Что же, у него
есть все основания для гордости: приоритет в формулировке
признака — за ним. Когда я зову его к доске доказать свое
утверждение, у него, оказывается, уже готово и доказательство, краткое
и четкое, — то самое, которое наметили в своем бормотании Горт
и Костюк.
— Да, — удостоверяю его выкладки, — это один из тех
признаков, которые я имел в виду. Спасибо, Сергей. Садитесь.
Другие признаки искать уже не будем — приступаем к реше-
оо ? оо 1пп
нию примеров. Запишите, ребята, три первых: X) ^"5 S (inn)"'
п=1 п=2^ПП)
оо
J2 (inn)1""' Надо исследовать эти ряды на сходимость и
расходимость.
Ю. В. Пухначев|
СЕМЬ СЕМИНАРОВ
539
Видимо, оттого, что признаки Коши и Даламбера кажутся
проще прочих (для суждения о сходимости данного ряда не
надо привлекать еще один ряд), все пытаются использовать
именно их при решении первого примера. Многие
сообразили, что признак Даламбера здесь наиболее удобен — с его
помощью Кочин, вызванный к доске, довольно грамотно
проводит соответствующие вычисления и получает верный вывод
о сходимости ряда. Из немногих приверженцев признака Коши
вызываю к доске Меншикова. Он останавливается перед оценкой
корня \/п\: пытается огородить его неравенствами и так и этак
(надо отдать должное его настойчивости: за последнее время он
стал заметно старательнее!) — но ничего путного у него не
выходит.
— Поистине неприступное выражение! — сочувствую
бедняге. — Впрочем, может быть, кто-нибудь знает, как к нему под-
ступитъся? — обращаюсь за помощью к аудитории.
— Среднее геометрическое меньше или равно среднему
арифметическому, — напоминает школьное неравенство Сутеев. —
Сразу получается tfn\ < ^±^ = *±1.
— Такое неравенство есть в задачнике, на самых первых
страницах, — вспоминает Горт.
— А можно по формуле Стирлинга, — советует Гарин.
— Видите, сколько полезных советов, сколько выходов из
тупика! — оборачиваюсь к Меншикову. — Правда, совет Гарина вы
вряд ли сможете использовать — формулу Стирлинга мы не
проходили, ее вообще нет в нашей программе. Но самый полезный
совет: не старайтесь сами загонять себя в тупик. Если какой-
нибудь признак никак не приводит вас к результату, —
пытайтесь применить другие, и в конце концов вы найдете лучший для
каждого примера. Такой поиск, конечно, должен заключаться не
в простом переборе. С самого начала по формуле слагаемого
ряда надо постараться определить, какой признак здесь наиболее
подойдет. Взять хотя бы только что решенный пример: к
знаменателю так и просится, казалось бы, признак Коши — ведь
при его использовании исчезнет n-ная степень. Но вместе с тем,
как мы видим, возникает непростой вопрос об оценке
величины уп!. Если же применять признак Даламбера, то факториал
540
ЧИСЛОВЫЕ РЯДЫ
[Гл. 7
устраняется, а отношение n-ных степеней, как только что
показал Кочин, преобразуется в хорошо знакомое нам выражение
(1 + ^)п, поглядите на его решение этого примера и на ответ:
lim ^^±L = \, так что...
— Ряд сходится, — делает окончательный вывод Меншиков.
— Верный ответ, — отсылаю его на место. — Решаем
следующие примеры, ребята.
Мой совет внимательнее выбирать подходящий признак
не проходит впустую: второй пример почти все решают с
помощью наиболее уместного здесь признака Коши. Но как
неуклюже они его применяют! Числитель дроби, получившейся
после извлечения корня, Лапиков преобразует к виду (n«)lnn,
Аргунова и Мухин — к виду п1п ^™, Буткус выражает всю
дробь экспонентой с показателем In2 п — п In Inn и затем
через добрый десяток неравенств оценивает его сверху
величиной -77.
— Громоздко! — шепчу, склонившись над ним.
— Громоздко, но добрался! — упрямым шепотом отвечает он.
Вызвав к доске Лапикова, журю его за неудачное
преобразование числителя:
— Ведь еще на одном из первых занятий мы нашли
наилучшую во многих случаях форму для подобных выражений. Кто
ее напомнит, ребята? — оборачиваюсь к аудитории.
— Функция в степени функция — значит, е в степени, —
говорит Стрельцов голосом негромким, втолковывающим — будто
не мне отвечает, а подсказывает Лапикову.
— Ну, конечно! — быстро поправляется тот, виновато ежась,
In2 п
и, получив е « , сам нащупывает верную дорогу к решению:
I Лапиков 0 • I
— Показатель стремится к нулю, значит, вся степень в
числителе — к единице... знаменатель — к бесконечности... значит,
вся дробь — к нулю... и станет меньше любого числа, например,
половины... по признаку Коши ряд сходится.
— Верно, садитесь. Решаем третий пример, ребята.
Отправляюсь в обход аудитории. Задерживаюсь у
стола Сынчикова: за него можно порадоваться! Прошло время,
когда в решении примеров он неизменно был последним:
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
541
сейчас его темп работы близок к среднему по группе. Но,
может быть, все дело в том, что сам пример не очень-то
труден?
Почти все приходят к выводу о сходимости ряда опять-таки
через признак Коши. Но я предпочитаю этому направлению
подход Миклашевского: он оценивает слагаемое ряда дробью
jjy. Демонстрирую его решение на доске и добавляю в
заключение:
— Признаки сходимости надо знать назубок, ребята, но
для успешной работы одного этого, пожалуй, мало. Можно
сказать, что знание основных признаков носит необходимый,
но отнюдь не достаточный характер — сверх этого
желательны широта мысли, остроумие, чутье. В этом вас вновь
оо
убедят дальнейшие примеры. Запишите их: 5Z [е — (1 + ^)п];
71=1
00 ch- °° 1
nlnn'
71=1 п 71=2
— Есть первый пример! — буквально через полминуты трубит
Горт.
— Поздравляю! — отвешиваю ему шутливый поклон. —
Но давайте подождем остальных — а вам я пока дам еще
кое-что...
Пишу в его тетради формулировку еще одного примера,
посложнее. Когда свои подходы вырисовываются более, чем у
половины ребят, начинаю обсуждение примера. Первыми вызываю
к доске неудачников, Кочина и Сутеева — они пытались
использовать признаки Коши и Даламбера и, разумеется, застряли в
самом начале.
— Да и что вообще можно сказать, — комментирую их
попытки, - про эти непроглядные выражения — этот корень п-ной
степени, это отношение? Каким преобразованиям и оценкам их
можно подвергнуть? — спрапшваю Сутеева, потерпевшего
неудачу с признаком Коши. — Давайте разбираться в вашем решении.
Как ведет себя этот корень уе — (1 + ^)п? Не знаете... Ответить
542
ЧИСЛОВЫЕ РЯДЫ
[Гл. 7
на мой вопрос, действительно, трудно. Тогда давайте для начала
разберемся хотя бы в том, как ведет себя подкоренное
выражение. Опять молчите? Ну, а эта степень (1 + ^)п — как ведет
себя она?
— Возрастает...
— И только?
— Стремится к е.
— Как быстро стремится? По какому закону? Разве
упоминание о числе е, а еще раньше — явно присутствующее в
квадратных скобках число е не подсказало вам
эффективный подход к переменной (1 + ^)п? Чюмин, — спрашиваю
одного из тех, кто пошел более рациональным путем, —
подскажите, как было бы целесообразно преобразовать эту
степень.
— Функция в степени функция, — произносит Чюмин, как
заклинание.
— Понятно? — возвращаюсь к Сутееву.
Он выписывает enln^1_l"n) и останавливается.
— Присмотритесь к выражению 1п(1 + ^) — советую ему. —
Что вы можете сказать по его поводу? Как можете его
истолковать?
— Логарифм, — только и отвечает он.
— Логарифм от единицы плюс... какая величина?
— Величина £.
— А как бы ответили вы? — вновь обращаюсь к Чюмину.
— Логарифм от единицы плюс малая величина.
— Вот-вот!
Опять к Сутееву:
— Где вам встречалась эта комбинация — логарифм от суммы
вида единица плюс малая величина?
— Был такой замечательный предел: lim п' *ХК
х->0 х
— А еще где встречался? В каком контексте?
Сейчас он вспомнит про формулу Тейлора... Ну же! Ведь он
сам совсем недавно, на прошлом семинаре разлагал с ее помощью
синус малой величины. Что же не вспоминает теперь?! Опять к
Чюмину:
— Ваши предложения?
— Логарифм от единицы плюс малая величина можно
разложить по формуле Тейлора.
— Конечно! — передаю эту идею Сутееву. — Вы помните,
как раскладывается логарифм? Да? Помнить, значит, помните,
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
543
а где применить — не представляете. Примените его к нашему
примеру.
Когда Сутеев получает е1_2^+0(»', Чюмин советует:
— Надо вынести е за квадратные скобки.
— Вам, я вижу, не терпится самому порешать этот пример.
Что ж, идите к доске, сделайте несколько следующих
преобразований. Что же вы медлите? Получилось е~^г+0^Л Какой шаг
напрашивается далее?
— Разложить в ряд экспоненту.
— Так раскладывайте!
— А разве она при отрицательном показателе
раскладывается?
Час от часу не легче! Нет, напрасно я боялся, что Чюмин
вскорости остепенится и перестанет ошарашивать нелепицами
— его хватит еще надолго!
— А разве в теореме Тейлора были ограничения на этот
счет? — отвечаю изумленным вопросом на его вопрос. —
Конечно, раскладывается! Действуйте!
Подстегнутый нарочито строгим тоном моего приказания, он
быстро доводит разложение до конца; Сутеев вспоминает про
признак эквивалентности, и оба докладывают хором: ряд
расходится.
— Садитесь, Сутеев. Садитесь, Чюмин. Все верно. Решаем
второй пример, ребята.
Снова, как и при решении предыдущего примера, я вижу
в одних тетрадях завиральные идеи, которые хорошо было бы
разобрать сообща во избежание подобных ошибок в дальнейшем,
вижу четкие решения, разбором которых можно было бы
закрепить в памяти у каждого разумные подходы. Но вместо всего
этого я вызываю к доске Аргунову: отстававшая от остальных
в решении прежних примеров, сейчас она, применив
интегральный признак, нашла ответ одной из первых, нашла сама — ее
нельзя не отметить!
544
ЧИСЛОВЫЕ РЯДЫ
[Гл. 7
— Вы очень неплохо решили пример с логарифмом дроби,
Аргунова, — говорю ей. — Покажите ваше решение всем.
Хвалебный тон моего вызова неожидан для нее, свои
выкладки она пишет на доске отрывочно, сбивчиво, и странно смотрится
приписанное под знаком несобственного интеграла п = 1: в этой
описке запечатлелось ее взволнованное, недоверчивое ощущение
своего успеха.
— Отличное решение! — не скуплюсь на похвалу. —
Отличное, несмотря на то, что в нем масса огрехов: не сказано, как
выбирать длину того и другого разложения, потеряны о малые,
а уж последний интеграл... Что это за п = 1? При чем индекс п
в интеграле? Вы, очевидно, хотели написать так...
+оо
И пишу на доске: / Д-.
1
— A dxl — с легкой ехидцей спрашивает Костюк.
— Да, конечно, — сконфуженно поправляюсь я. И все
смеются; в этом счастливом смехе — радость за Галю, за ее успех,
и улыбка над безудержной восторженностью, с которой радуюсь
ее успеху я...
— Садитесь, Галя. Переходим к третьему ряду, ребята.
— Он расходится! По интегральному признаку! — шумят они.
Разбираем доказательство расходимости — его излагает
Кулагин.
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
545
— Легкий пример, — резюмирует Меншиков, довольный
собою — и не без основания: решение примера, которое я видел
у него в тетради, безупречно. И все-таки от его реплики мне
становится не по себе, хотя звучащая в ней уверенность, на
первый взгляд, должна радовать: пройденный теоретический
материал усвоен, затверждены вытекающие из него приемы решения
соответствующих задач... Однако отголосок самоуспокоенности,
ощутимый в реплике Меншикова, заставляет воспринимать ее
в ином значении: приемы решения разобранных задач
затверждены, теперь, ни о чем не думая, можно решать однотипные
примеры один за другим...
Вглядываюсь в лица ребят: самодовольная успокоенность,
похоже, закралась в душу не одному лишь Меншикову!
К счастью, предательское довольство аудитории действует
не только на меня — идиллическая тишина обычно пробуждает
бунтарскую натуру Буткуса. Вот и сейчас:
— А почему мы про признаки Коши и Даламбера не кончили,
когда предел равен единице? Ничего нельзя сказать — как это?
Нужно сказать! Если есть какой-то ряд, он обязательно или
сходится или расходится. Нужно что-то добавить к этим признакам!
Давайте говорить об этом!
— Поговорить можно, — живо откликаюсь на его запрос, —
только не совсем в том направлении, которое предлагаете вы.
Теория рядов не знает никакого усовершенствованного варианта
предельных признаков Коши и Даламбера. Когда они
отказываются служить, применяются другие признаки — Раабе, Гаусса...
Правда, ни один из них не входит в программу нашего курса. Так
что, если вам хочется их построить, вам придется работать
самостоятельно, одному, дома. Советую для этого поразмышлять
над сходимостью таких рядов...
00 (О Л\\\ °°
Пишу с правого края доски £ < g~,|" • ^т; £ ^т?;
71=1 71=1
п!
(р+1)(р+2)...(р+п)*
71=1
— Выясните, сходится ли первый ряд, а потом установите,
при каких значениях параметра р сходятся и расходятся второй
и третий ряды. Повторяю, ребята, — жестом привлекаю к
написанному желающих, — все эти примеры — факультативные, я
рекомендую взять их на дом, если для них у вас найдется
свободное время. А сейчас мы переходим к новой теме, где будем
рассматривать...
— Знакопеременные ряды? — догадывается Миклашевский.
546
ЧИСЛОВЫЕ РЯДЫ
[Гл. 7
— Да. Сначала разработаем признаки их сходимости...
— Признак Дирихле! — снова перебивает меня
Миклашевский.
— Можно подумать, — осуждающе гляжу на него, — что
вы в аудитории один. То, над чем мы будем работать, вы
угадали верно, но дальше будем работать все вместе. Само
название «признак Дирихле», — продолжаю, оглядывая аудиторию, —
говорит, что строить его можно по аналогии с одноименным
признаком сходимости несобственных интегралов. Как же это
сделать?
Мой выговор Миклашевскому приняли на свой счет и
другие «передовики»: аудитория молчит, ожидая, кого я
вызову.
— Как перефразировать признак Дирихле для рядов? Что
думает по этому поводу... Кочин?
— Надо представить слагаемые ряда в виде произведения
ЯпЬт — кратко отвечает он и умолкает, не решаясь продолжать
без моего нового вопроса.
— Хорошо. Какими свойствами должны обладать
сомножители? Что скажете, Сутеев?
— Один должен монотонно стремиться к нулю.
— Очень хорошо. Пусть таким будет сомножитель ап. А
каким должен быть тогда Ьп? Как вы полагаете, Синица?
Этот нелегкий вопрос я приберег для тех, кто
посильнее.
— А Ьп... Если рассматривать Ьп как ряд, то он... там
ограниченная первообразная... а здесь... у этого ряда должны быть
ограниченные частичные суммы. Да? Верно?
— Верно.
И поясняю для тех, кому могло показаться непонятным столь
стремительное умозаключение Синицы, — а заодно повторяю все
сказанное до сих пор, повторяю, не стесняясь утомить
длиннотами слишком сообразительных — должны ведь они учитывать,
что в группе есть и тугодумы:
— Итак, каждое слагаемое рассматриваемого нами
знакопеременного ряда мы представили в виде произведения апЬп —
по аналогии с несобственным интегралом от знакопеременной
функции, имеющей вид произведения f(x)g(x). И если в
теории несобственных интегралов одну из этих функций — скажем,
f(x) — мы считали монотонно стремящейся к нулю, то по
аналогии мы требуем того же от одного из сомножителей
произведения апЬп, допустим, от ап. В теории несобственных инте-
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
547
гралов у функции д(х) мы предполагали ограниченную
первообразную. Чего же мы потребуем по аналогии от сомножителя
Ьп1 Давайте разбираться. Когда мы применяли признак
Дирихле для несобственных интегралов и нам по ходу дела
приходилось отыскивать первообразные некоторых функций, это нам
удавалось без труда, поскольку функции были хорошо знакомые:
первообразная косинуса — синус, синуса — минус косинус... Но
вот однажды нам потребовалось определить первообразную для
«нестандартной» функции | sinx| — а. Сначала мы не знали, как
быть, но потом вспомнили, что, взяв от функции интеграл с
переменным верхним пределом, мы получим ее первообразную. Мне
кажется, что этот прием позволяет вполне отчетливо провести
искомую нами аналогию. Будем подыскивать аналог не к
первообразной, а к интегралу с переменным верхним пределом. Он
тоже представляет собой первообразную, но в плане наших
нынешних рассуждений может оказаться понятием более удобным,
чем она. Аналогом интегрирования функций в теории числовых
рядов служит суммирование слагаемых ряда. Аналогом
интеграла с переменным верхним пределом — частичная сумма
произвольной длины. И если в признаке Дирихле для несобственных
интегралов мы предполагали у функции д(х) ограниченную
первообразную, то бишь интеграл с переменным верхним пределом,
то от ряда из чисел Ьп потребуем ограниченность его частичных
сумм.
Вожу взглядом по аудитории: все ли приняли такое
обоснование?
— Я в каком-то учебнике читал, — вспоминает Горт, — что в
самой общей формулировке признака Дирихле говорится не про
первообразную, а просто, что функция — та, которую мы
обозначили д(х) — должна иметь ограниченный интеграл по любому
конечному промежутку. Тут аналогия с частичными суммами
совсем явная.
— Тоже верно. Давайте теперь окончательно сформулируем
признак Дирихле для числовых рядов.
Третьего повторения, думаю, будет достаточно для
заучивания.
- Кто хотел бы это сделать?
Из поднявших руки выбираю Чюмина:
- Можете говорить с места.
- Пусть ап — последовательность, которая монотонно
стремится к нулю. Пусть Ьп — ряд, у которого все частичные суммы
ограничены. Тогда ряд апЬп будет сходиться.
548
ЧИСЛОВЫЕ РЯДЫ
[Гл. 7
Ровный тон, короткие паузы между фразами — все
признаки неплохого усвоения. Наверное, так оно и есть, а что
касается его недавних нелепых сомнений по поводу экспоненты
с отрицательным показателем, то это был, возможно,
случайный заскок. Или все наоборот? И как случайность нужно
расценивать его нынешний удачный ответ? Нет, повременю
зачислять его в разряд благополучных. Но похвалить — конечно,
похвалю.
— Очень хорошо. Доказательство этого признака мы
провести не успеем — его дадут вам на лекции, ребята. А мы с
вами сейчас будем строить примеры сходящихся знакопеременных
рядов. Можно строить их сразу в той форме, к которой
удобно подходить с признаком Дирихле, — пишу на доске апЪп и
ставлю далее знак равенства, — то есть взять сначала какую-
нибудь типовую монотонную бесконечно малую
последовательность, — пишу ниже ап — потом придумать ряд с ограниченными
частичными суммами, — еще ниже пишу Ьп. — Кстати сказать,
никакого типового образца такого ряда у нас нет, в объектах
такого рода у нас до сих пор не было необходимости — их нам
срочно придется выдумывать самим. Кто предложит такой ряд,
ребята?
Молчание.
— Всем понятно, что требуется? Надо придумать ряд чисел,
при последовательном суммировании которых сумма колебалась
бы в определенных пределах.
— Минус единица в степени п? — гадает Кулагин.
— Давайте проверим, будут ли ограничены частичные
суммы такого ряда. Напишите на доске несколько его слагаемых,
Андрей. Суммируйте.
— Ноль, минус один, ноль, минус один... дальше все
повторяется. Суммы ограничены.
— Все хорошо, — отсылаю его на место и приписываю к Ьп
через знак равенства (—1)п. — Теперь поищем подходящие ап
и будем строить знакопеременные сходящиеся ряды апЬп. Жду
предложений.
— Минус единица в степени п, деленная на п в степени р, —
почти сразу отзывается Мухин. — Если положительное р — дробь
^ монотонно стремится к нулю — ряд сходится. Взять, допу-
(-1)п
стим, п в степени одна вторая — ряд s Л сходится.
Заношу это на доску: Ъп = (-1)п, ап = ^
Ю В. Пухначев]
СЕМЬ СЕМИНАРОВ
549
— А что будет при р < 0? — допытываюсь у Мухина.
— Расходимость, наверное, — с долей сомнения отвечает он
и жестом изображает слагаемые ряда в виде точек, ложащихся
все далее от воображаемой оси абсцисс.
— Но как доказать это строго?
Готовый преподать Махину очередной урок логического
мышления, я тотчас отказываюсь от своего намерения, едва
взглянув на Аргунову. По глазам вижу, что ей хотелось бы
высказаться. Очень кстати: последний ее успех, пусть
небольшой, но яркий и убедительный, не должен оставаться чем-то
мимолетным.
— Прошу вас, Галя.
— Наверное, здесь слагаемые ряда не стремится к нулю.
— То есть? — подталкиваю ее к завершающему выводу.
— Не выполняется необходимый признак...
00 ( л\п
— Точно! При неположительных р для ряда ^ пр не
71=1
выполняется необходимый признак сходимости, вы правы,
Галя.
— Следовательно, ряд расходится, — заключает она.
— Совершенно верно, расходится. Идем далее. Как и в
теории несобственных интегралов, в теории числовых рядов наряду
с их сходимостью в прямом смысле слова рассматривается
также и абсолютная сходимость, когда суммируются абсолютные
величины слагаемых ряда. Давайте исследуем на абсолютную
сходимость наш ряд J2 nJ ~ ПРИ каких р она будет иметь
71=1
место?
— При больше единицы, — мгновенно отвечает Буткус. —
Тогда ряд как раньше: ~. При р больше единицы ряд
сходится.
— Итак, — подтверждаю я, — мы получили условие
абсолютной сходимости нашего ряда: р > 1. При р, удовлетворяющих
неравенству 0 < р < 1, ряд будет сходиться, но не абсолютно. В
таком случае говорят об условной сходимости. Пользуясь
критерием Коши, нетрудно показать: если ряд сходится абсолютно, то
он сходится и просто. Обратно: если ряд расходится просто, то
он расходится и абсолютно. Стало быть, при р < 0 ряд ^ nJ
71=1
не сходится ни просто, ни абсолютно. Ясно, что абсолютная
сходимость ряда выясняется проще, чем условная: ведь взятые по
абсолютной величине слагаемые ряда неотрицательны, а в таком
550
ЧИСЛОВЫЕ РЯДЫ
[Гл. 7
случае применимы разнообразные признаки сходимости
знакопостоянных рядов. У абсолютно сходящихся рядов немало
замечательных свойств. На лекциях вам покажут, что сумма
абсолютно сходящегося ряда не меняется при любой
перестановке его членов; напротив, в случае неабсолютно сходящегося
ряда перестановкой его членов можно сделать сумму ряда равной
любому наперед заданному числу. На лекциях вам докажут, что
два абсолютно сходящихся ряда можно перемножить, и в
каком бы порядке мы ни суммировали попарные произведения их
членов, сумма всегда будет равна произведению сумм исходных
рядов...
Внезапно я спохватываюсь: не слишком ли много я говорю?
«Вам докажут... Вам покажут... Вам дадут...» Какое действие
могут оказать такие посулы? «Разжуют и в рот положат!».
Что касается признака Дирихле, то было еще
позволительно переложить его доказательство на лектора: проведенное
полностью, оно заняло бы значительную часть семинара,
оставив слишком мало времени для задач, без которых семинар
немыслим. Но вывод сходимости из абсолютной сходимости?
«Нетрудно показать...» Нетрудно — так надо показать! Тем
более, что сверхзадача сегодняшнего семинара в том и состоит,
чтобы все делать самостоятельно, самим развивать
теоретические положения, самим изобретать методы решения задач.
«Нетрудно показать...» Если бы такие заявления делались после
лекции, где это уже было показано, они служили бы
напоминанию, повторению, закреплению пройденного. А сейчас?
Сейчас они лишь склоняют к верхоглядству, против которого я
всегда так рьяно протестовал! И прямо на глазах в лицах ребят
проступает какая-то сонливость... Надо срочно выправлять
положение!
— Обратим внимание, ребята, еще на одну особенность
нашего модельного ряда z2 пр ' где Р > ®- ^г0 члены попе-
71=1
ременно меняют знак, а по абсолютной величине монотонно
стремятся к нулю. Ряды, обладающие такими свойствами,
называются рядами Лейбница. Из всех знакопеременных
рядов они, пожалуй, наиболее просты по структуре, наиболее
легко поддаются анализу. Непосредственно из их
определения можно, например, вывести простую оценку для остатка
ряда гп - так называется и обозначается разность между
полной суммой ряда и его частичной суммой, насчитывающей п
слагаемых.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
551
Делаю паузу и выжидательно гляжу на ребят:
— Не вижу, чтобы мои последние слова вызвали у вас
энтузиазм. Не ощущаю желания приняться за вывод
оценивающего неравенства для остатка ряда Лейбница. Вы не
уснули, ребята? Успокаиваться не время — мы скоро начнем
решать новые задачи. Пусть те, кто будет решать их быстрее
других, в освободившееся время попытаются вывести
искомую оценку для остатка гп. Возможно, попутно обнаружатся
кое-какие интересные свойства рядов Лейбница. А сейчас —
небольшая разминка. Продолжим серию рядов, имеющих
ограниченные частичные суммы. Пока что у нас имеется
единственный пример такого рода — это (—1)п. Придумаем еще
несколько.
Нелегко раздуть поугасшее рабочее настроение! Лишь после
моих советов опять воспользоваться аналогией с
несобственными интегралами, после косвенных подсказок появляются новые
идеи: Стрельцов предлагает ряд sin ™, а Сутеев вспоминает, как
в школе суммировали синусы последовательных натуральных
чисел — уловив суть дела, Рамзин быстро показывает
ограниченность частичных сумм ряда ап = sin п.
— Спасибо и на этом, ребята. Переходим к примерам. Вот
ОО . .nilLtll 00 ОО / i\n
первые три: £ <~V i Е ("1)п^; Е ln[l + <=g-]. На-
п=1 га=1 п=2
до исследовать эти ряды на сходимость и абсолютную
сходимость.
— Так... п на п плюс один пополам, — близоруко
щурится Миклашевский на первый пример. — Это, значит, как?
552
ЧИСЛОВЫЕ РЯДЫ
[Гл. 7
Если п единица, то показатель... тоже единица, числитель
минус единица... п двойка... опять числитель минус
единица... тройка... плюс единица... четыре... опять получается
плюс.
— Можете написать это на доске, — вручаю ему мел.
п(п+1)
Он выписывает несколько первых значений степени (—1) 2
и угадывает закономерность: за двумя отрицательными
единицами следует две положительных, потом опять две
отрицательных — и так далее.
— Всегда ли будет так? — спрашиваю с недоверием. — Это
следовало бы доказать.
Миклашевский молчит; молчат и все остальные. Внезапно
Синица:
— Что-то это напоминает... ^^—^... Что-то вроде
формулы для суммы натуральных чисел... Ну да! Если к нулю
прибавим единицу, то будет нечетное число, потом
прибавим двойку — снова будет нечетное, так ведь? Потом
тройку — будет уже четное, четверку — опять четное... В общем,
ясно.
— Пожалуй, — соглашаюсь с таким доказательством.
— А тогда ясно, что частичные суммы этого ряда, —
оживившийся Миклашевский указывает на написанную им
последовательность единиц, — будут ограничены. Дробь ^ монотонно
стремится к нулю, ряд сходится по признаку Дирихля. И
абсолютно он тоже сходится: ведь если взять модули, будет просто
геометрическая прогрессия.
— Хорошо, садитесь. Кто решил второй пример?
— Похоже на ряд Лейбница, — пристально глядя на доску,
медленно выговаривает Кочин. — Только вот... последователь-
■ 2
ность §1IJ-r?:... Будет ли она монотонной?
Взгляд мой, метнувшийся по лицам ребят навстречу
ответу на вопрос Кочина, резко обрывает свой разбег, приятно
удивленный находкой совсем другого рода: Сынчиков, никогда
еще не подававший голоса без моего вызова, робкий
Сынчиков, не распрямляя своих согбенных плеч, не поднимая глаз,
не произнося ни единого звука, чуть покачивает головой из
стороны в сторону. Этот жест отрицания едва заметен, но
во мне он отзывается горячим чувством: не зря я так
настойчиво старался пробудить инициативу в этом тихоне и
потом все больше стимулировать его активность; есть
надежда, что вскоре и он станет полногласным участником наших
дискуссий...
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
553
Голос Горта возвращает меня к общему разговору:
— Похоже, что не будет, — отрывисто бросает он (мельком
заглядываю в его тетрадь: он уже решил все три обязательных
примера и думает над одним из факультативных).
— Но уж дробь ^ — она-то наверняка монотонная! —
убежденно заявляет Мухин.
— Бесспорно, — соглашаюсь с ним. — Но этого, по-моему,
недостаточно для обоснованного вывода о сходимости нашего
ряда. Чем бы еще следовало поинтересоваться?
— Чем еще? — бросается он в дальнейшие рассуждения, но
тут же спохватывается:
— Нет, я сначала подумаю.
И сбавив темп, приглушив голос:
— Если бы доказать, что ряд (—l)n sin2 n имеет ограниченные
частичные суммы — тогда все по Дирихле — выразить sin2n
через косинус двойного угла...
— Напишите это на доске! — вызываю его. Он продолжает
все неувереннее:
— Одну вторую вынесем за знак суммирования — от
первого слагаемого останется просто (—1)п — тут частичные суммы
ограничены... А от второго — (—l)ncos2n...
И надолго замолкает, не зная, как сделать завершающий шаг.
Что ж, хорошо уже то, что он постарался представить себе путь
к ответу, логически обосновать свои действия.
— Минус единица в степени п — это ведь cos7rn, —
пытается помочь Синица. — Произведение косинусов разложить в
сумму...
— И опять будет то же самое, — отметает Кулагин
бесперспективное продолжение; вероятно, он уже обдумывал такое
преобразование.
Почувствовав, что дело зашло в тупик, Гарин отрывается от
своей тетради (он, видимо, тоже уже решил все обязательные
примеры и взялся за факультативные):
— А чего тут мудрить? Тут ведь все можно сделать, как у
Рамзина было, когда он сумму синусов преобразовывал. Сумма
у нас сейчас какая? Минус cos2 плюс cos4 минус cos6...
Для всеобщего понимания тотчас стенографирую на доске
его устные выкладки. Умолкнув в кратком раздумьи, он вскоре
продолжает:
— Умножим все это на cosl, получаются произведения
косинусов, каждое разложится в полусумму косинусов, косинуса
разности и косинуса суммы, то есть будет минус cos 1 минус
554
ЧИСЛОВЫЕ РЯДЫ
[Гл. 7
cos 3 плюс cos3 плюс cos 5 минус cos 5... Все поуничтожается
кроме первого и последнего слагаемого, а они в сумме не больше
двух...
Окружаю модульными скобками обе части получившегося
равенства, приписываю справа знак неравенства и передаю мел
Мухину. Он быстро оценивает преобразованную дробь:
— Все верно — сумма ограничена — значит, признак
Дирихле — сходится.
— А как у этого ряда насчет абсолютной сходимости?
Мухин снова надолго погружается в раздумья, и снова ему
на выручку идет Кулагин:
— Доказывается, как с несобственным интегралом. Сначала
sin2 п выражается в виде 1 — cos 2n; получается два ряда —
первый расходится, как гармонический, второй, навернео, сходится
по признаку Дирихле...
И я заставляю Мухина провести полное исследование вопроса
об абсолютной сходимости ряда — от проговоренного устно плана
действий до окончательного вывода: ряд абсолютно расходится.
— Хорошо, садитесь, — отсылаю его на место и даю сигнал к
новой работе:
— Третий пример!
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
555
— Формула Тейлора! — столь же громко, с торжественной
нотой в голосе откликается Рамзин.
— Решайте на доске, если знаете как, — приглашаю его.
Он деловито начинает расписывать тейлоровское разложение
логарифма: ^—^ 2п + з—Г' Расписав> подчеркивает, что на
третьем члене разложения можно остановиться, поскольку ряд
из таких слагаемых сходится абсолютно. Сославшись на
аналогичные примеры с несобственными интегралами, дидактическим
тоном напоминает, что подобные разложения всегда надо
заканчивать слагаемым, которое дает абсолютно сходящийся ряд.
Наконец, с многозначительной замедленностью пишет
завершающее o(-V).
П.2
— Итак, первое слагаемое — это ряд Лейбница, сходится.
Второе слагаемое — гармонический ряд, расходится. Третье
слагаемое — ряд сходится абсолютно по признаку сравнения | g~ L | <
< -V, значит, сходится и просто. Для тех, кто не понял, поясняю:
ряд \ — частный случай ряда ~, который сходится при 5 > 1.
п* п
Четвертое слагаемое — для него справедлива оценка по
модулю; абсолютная сходимость вытекает из признака сравнения, а
из нее получаем простую сходимость. Первый, третий и
четвертый ряды в сумме дают сходящийся ряд. Его затем
рассматриваем в сумме со вторым рядом, расходящимся. Сходящийся плюс
расходящийся в итоге дают расходящийся. Окончательно: ряд
оо
Y\ 1п(1 + ^~~Д ) расходится.
71=2
556
ЧИСЛОВЫЕ РЯДЫ
[Гл. 7
— А что вы скажете про абсолютную сходимость этого
ряда?
Он догадливо выделяет из четырех слагаемых тейлоровской
формулы первые два, показывает, что начиная с четвертого но-
мера абсолютная величина их суммы больше j^ — даже в том
худшем случае, когда они имеют разные знаки, потом
принимается за остальные слагаемые и находит, что при достаточно
большом п абсолютная величина их суммы меньше ^; все
это позволяет ему оценить снизу абсолютную величину каждого
слагаемого ряда дробью -^-д-
— Ряд абсолютно расходится, — заключает он.
— Отлично! — отдаю должное его отточенной технике. — Я
советовал бн всем, — оборачиваюсь к ребятам, — переписать эти
выкладки себе в тетради и стараться быть в своих оценках столь
же четкими и уверенными. Переписали? Просмотрите их
внимательно: все ли преобразования вам понятны? Если что неясно,
спрашивайте автора.
Приосанившись, Рамзин оглядывает аудиторию в ожидании
вопросов, но их ему никто не задает.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
557
— Садитесь, Рамзин. спасибо, — отправляю его на место. И
вновь ко всем:
— Советую вам, ребята, усвоить приемы подобных оценок и в
будущем умело применять их там, где они окажутся уместными.
Правда, здесь можно было обойтись без них, рассуждая от
противного: ведь если бы ряд сходился абсолютно, то он сходился
бы и просто, а это не так, мы уже доказали Получается что мы
пальнули из пушки по воробью.
— А что? Тоже неплохо, — вставляет реплику Кулагин, —
потренировались в стрельбе из пушки.
— Да, — соглашаюсь с ним, — и Рамзин показал себя бравым
бомбардиром. Потому я и призываю всех равняться на него...
А теперь давайте подумаем вот о чем: слагаемое нашего ряда
в исходной его формуле представляет собою логарифм от
суммы единицы и бесконечно малой величины. Такой логарифм мы
обычно заменяли этой малой величиной. Но что получается,
если мы сейчас поступим так же? Ряд ^ ^~Л сходится, как уже
п=1
отмечал Мухин, а ряд ^Г 1п[1 + ^~1 ], как показал Рамзин, —
71=2
расходится. В чем дело?
— Может быть, мы логарифм неверно разложили? — обеспо-
коенно вглядывается Лапиков в выкладки Рамзина.
— Все железно! — отгоняет его сомнения Меншиков. —
Просто, когда писали эквивалентность, то взяли мало членов
разложения.
Голос его горяч и отдает искренней готовностью по первому
моему зову выйти к доске и размолотить злополучный логарифм
по косточкам.
Посреди этих и дальнейших, не менее «разумных»
суждений (Горт, Костюк, Гарин и все, кто мог бы разрешить подобные
сомнения одной своей репликой, заняты факультативными
примерами) слышится монотонный и глухой, как падение капель,
голос Сынчикова:
— Не знакопостоянные ряды... не знакопостоянные ряды...
— Ну и что? - оборачиваюсь к нему.
— Нельзя использовать эквивалентность.
— Совершенно верно, — веско подтверждаю его слова. И уже
ко всем:
— Вы поняли, ребята, тот подвох, который скрывался в
моем сравнении решений Мухина и Рамзина? Что — не ожидали,
что я могу вас разыграть? А ведь я уже не в первый раз та-
558
ЧИСЛОВЫЕ РЯДЫ
[Гл. 7
ким способом испытываю вашу внимательность и
проницательности^ И говорю вам снова: не принимайте без критического
анализа никакую задачу, которая ставится перед вами, не
доверяйтесь слепо словам преподавателя, проверяйте собственным
разумением любое суждение, даже самое авторитетное. Так вам
следовало бы поступить и сейчас. Говоря об эквивалентности
величин, я протаскивал в рассуждения об этих знакопеременных
рядах признак эквивалентности, доказанный нами для
знакопостоянных рядов. К знакопеременным же рядам он, вообще
говоря, не применим, как убедительно показал разобранный нами
пример.
И вновь гляжу на Сынчикова — приветливо, ободряюще. И
он впервые за много занятий поднимает на меня свой взгляд —
гордость, уверенность видны в этом взгляде. И эта уверенность,
впервые заявившая о себе сегодня, пожалуй, дороже мне, чем
блистательная техника исполнительного Рамзина.
Что бы я делал, если бы не верил в то, что такой день
обязательно наступит для каждого из моих неудачников — для
безнадежного когда-то Сынчикова, для застенчивой Аргуновой
(сегодня у них праздник, пусть маленький, но знаменательный), для
нерешительного Лапикова (скоро такой праздник будет и у него,
я уверен: его растущая решимость тому порукой), для
чудаковатого Чюмина, для непостижимого Сутеева? Что делал бы я без
такой веры? Наверное, должен был бы оставить преподавание,
просто не имел бы морального права на роль преподавателя. А
коли не так, я обязан приближать день признания для каждого
из самых безнадежных, приближать неутомимо и
изобретательно, приближать на каждом занятии, каждым словом, каждым
взглядом, обращенным к идущим позади...
— Запишите, ребята, — вновь берусь за мел, — условия
еще трех задач: £ 8т(тг>/5*+Т); £ sinnnsitm ; £ *=$-—, здесь
га=1 га=1 га=1
квадратные скобки обозначают целую часть заключенного
в них числа. Прошу исследовать эти ряды на сходимость и
абсолютную сходимость.
— А первый ряд — он разве будет сходиться? У него ведь
слагаемые не стремятся к нулю! — бухает Чюмин, едва я кончаю
писать. — Нарушено необходимое условие сходимости!
В недоумении смотрю на него, готовясь к последовательному
разбору его заявления, — и во-время сдерживаюсь: у ребят оно
вызывает активные возражения, которые перерастают в
детальный анализ задачи.
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
559
— Как это не стремятся? — тотчас откликается Горт. —
Корень все ближе к п, все выражение в скобках — к 7гп, a sin nn —
это нуль, значит, слагаемое стремится к нулю.
— Стремится к нулю — это еще ни о чем не говорит! —
рассудительно замечает Костюк. — У гармонического ряда слагаемые
тоже стремятся к нулю!
— Надо оценить, как стремятся! — вступает Синица.
— Порядок малости! — выкрикивает Кочин.
— Формула Тейлора! — почти одновременно рявкает
Меншиков.
Оборачиваюсь к нему, поднеся мел к доске: говорите, мол, я
записываю. И он напористо продолжает:
— Вынести п из-под корня; под корнем тогда будет единица
плюс малая величина...
— Я вижу, вы и сами все можете сделать, — предлагаю ему
мел.
Доведя дело до разложения корня, он спотыкается: не
представляет толком, до какого члена разлагать.
— Помогайте, ребята! — обращаюсь за поддержкой к
аудитории. Знаю: Меншиков только раззадоривается пуще, когда я
навязываю ему помощников.
Заметив среди желающих высказаться Аргунову, приглашаю
к ответу ее.
— Надо еще один член разложения написать, — тихо советует
она, — такой член, у которого в знаменателе будет степень...
— Больше единицы! — молниеносно перекрывает Меншиков
своим басом ее слабый голос. — Я имею в виду: чтобы после
умножения на п в знаменателе получилась степень больше
единицы.
— Что это даст? — тотчас перевожу на него поощряющий
взгляд.
— Получится абсолютно сходящийся ряд. Надо всегда,
как в несобственных интегралах, заканчивать разложение по
Тейлору слагаемым, из которого получается абсолютно
сходящийся ряд.
— А от 7гп можно избавиться: добавить тгп к аргументу
синуса — это все равно, что умножить синус на (—1)п, —
споро подбрасывает Миклашевский еще одну идейку в общий
котел.
— Получается синус малой величины, — исправно учтя все
советы, заключает Меншиков. — Его снова можно разложить по
Тейлору.
560
ЧИСЛОВЫЕ РЯДЫ
[Гл. 7
— Зачем? — предостерегает от лишней работы Костюк. —
Получается ряд Лейбница, сходящийся ряд: (—1)п — это
чередование знаков, а синус монотонно стремится к нулю.
— Монотонно? — сомневается Горт. — Ты знаешь, как ведет
себя это о малое?
— Все-таки разложу, — не решаясь вступать в спор
знатоков, Меншиков смотрит на меня в ожидании одобрения своего
подхода. Я беззвучно киваю ему.
— Ну вот, — заканчивает он выкладки, — первый ряд
сходится по Дирихле, второй сходится абсолютно и, значит, просто
тоже, третий — тоже абсолютно. Исходный ряд, получается,
сходится.
— Очень хорошо! — с выразительной расстановкой
высказываю свое мнение о его результате. — А как у этого ряда насчет
абсолютной сходимости?
— А вот тут, — перехватывает слово упрямый Костюк, —
разлагать синус не надо! Когда возьмем модуль, получится
знакопостоянный ряд...
— Точно! — азартно подхватывает Меншиков, и я прошу его
продолжать, жестом остановив Костюка.
— Получится знакопостоянный ряд, — уверенно развивает
Меншиков начатое Костюком, — к нему можно применить при-
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
561
знак эквивалентности. Эквивалентный ряд здесь будет такой:
оо
^2 т^. Он расходится — и исходный ряд, значит, абсолютно не
71=1
СХОДИТСЯ.
— Все верно, исходный ряд сходится лишь условно, — с
улыбкой соглашаюсь с ним, — Все очень хорошо; садитесь,
Меншиков. Беремся за второй пример из тройки, ребята.
Может быть, кто-то уже сделал его, пока мы возились с
первым?
— Смеетесь? — наигранно оскорбленным тоном отвечает Рам-
зин. Я между тем начинаю привычное «хождение в народ»,
стараюсь по скупым записям, появляющимся в тетрадях ребят,
угадать различные подходы к примеру, пытаюсь выявить эти
подходы своими вопросами.
— У кого есть дельные соображения по поводу этого ряда?
Вы выделили в его слагаемом, — останавливаюсь рядом с
Сутеевым, — сомножитель sin п. Что можете сказать по его поводу?
N
Сутеев молча пишет сумму ^2 sinn, которую недавно упо-
71=1
минал.
— Чему же равна такая сумма? Не помните? Загляните в
свои записи, найдите соответствующую формулу. Нашли? Да?
В знаменателе 2sin^, величина постоянная, в числителе cos^,
тоже константа, минус cos 2iN^~1, величина уже переменная, но...
— Косинус всегда ограничен, — глухо вырывается у Сутеева
как бы против его воли, — по модулю меньше единицы...
— Так, так! Значит, частичные суммы ряда sinn...
— Ограничены? — каким-то странным, полуутвердительным-
полувопросительным тоном произносит Сутеев. И продолжает
опять как бы через силу:
— Признак Дирихле?
— Но остальное-то ведь не стремится к нулю монотонно! —
нетерпеливо предостерегает Миклашевский (со своим
неугомонным любопытством он, конечно, не мог пропустить мимо ушей
наш с Сутеевым разговор).
— Верно, — соглашаюсь с ним. — Есть в слагаемом ряда еще
сомножитель, sinn2, любопытный сомножитель, — правда?
— Да, что-то похожее уже было... Кажется, он тоже ни к
какому пределу не стремится, — задумчиво произносит в ответ
Павел.
— Произведение синусов... Разложить в сумму? — вскидывает
свою кудлатую голову Мухин.
19-2019
562
ЧИСЛОВЫЕ РЯДЫ
[Гл. 7
— Что это даст? — морщит лоб Горт.
— Мрак! — категорически отрубает Рамзин.
Как воспримет Мухин неверие «корифеев»? То и дело
заглядываю в его тетрадь, продолжая свое хождение. О, у него
хватило упорства выполнить свое намерение! Извлечь что-то полезное
для дальнейшего решения из получившейся формулы он,
правда, не смог. Но это его не обескураживает: он последовательно
подставляет в формулу вместо п единицу, двойку, тройку... И
наконец вновь подает голос:
— А ведь, если разложить числитель, кое-что получается...
интересное...
— К доске, Мухин! — зову его, направляясь к своему столу.
С первых же его слов, когда он демонстрирует подмеченную
закономерность на начальных слагаемых ряда, Рамзин спешит с
выводами:
— Все понятно! Если взять п2 + п, добавить и вычесть п + 1,
то будет...
— Я не давал вам слова! — строго обрываю его. — Подождем
сначала, что скажет автор идеи.
Мухин, к счастью, схватил суть сказанного Рамзиным и
пишет два равенства для sinn • sinn2 и sin(n + 1) • sin(n + l)2.
— Значит, косинусы всегда будут сокращаться! — с радостной
уверенностью заключает он, сравнивая эти равенства —
Частичные суммы этих вот sin n sin п2 будут, значит, ограниченными —
остальное, ^, монотонно стремится к нулю — ну и все: по
признаку Дирихле ряд сходится.
— Хорошее решение предложили вы, — просматриваю еще
раз его выкладки. — Садитесь, Женя.
И, обращаясь уже ко всем:
- Формула этого ряда поначалу казалась пугающей, а
решение получилось довольно простым. Такое бывает нередко,
поэтому не бойтесь громоздких формул, ребята. Решаем третий
пример.
Пример не из простых, и одни лишь призывы к бесстрашию
здесь не очень-то помогут: безнадежное молчание надолго
застаивается в аудитории.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
563
— Признак Дирихле не проходит, — словно про себя наконец
произносит Лапиков — не слезливым, как когда-то, а сердитым
голосом, в котором слышится желание осилить неподатливый
пример.
— Да, — подогреваю в нем энергию, — вполне возможно, что
этот ряд не укладывается ни в один из пройденных нами простых
рецептов — надо искать новые приемы!
— Я тут еще один рецепт вспомнил, — глядит на меня с
широкой улыбкой Буткус. — Вы говорили: когда не получается по
формулам, надо рисовать...
— Что ж, — зову его к доске, — давайте поглядим на ваши
художества.
Он вычерчивает систему координат и в ней изображает
слагаемые ряда в виде столбиков над и под осью абсцисс; потом в
той же манере изображает отдельно над отрезком [п2, (п + I)2]
группу слагаемых одного знака, обводит утолщенной линией
общую границу этой колонны столбиков:
— Я возьму новый ряд, у него слагаемые вот, — на
предыдущем графике он таким же образом охватывает общим контуром
каждую группу столбиков с ординатами одинакового знака,
затем возвращается ко второму графику, проводит на нем кривую
по вершинам уголков, обращенных внутрь жирно очерченной
фигуры, и заштриховывает площадь образовавшейся
криволинейной трапеции:
— Я сейчас докажу, что эта площадь равна двум, когда п к
бесконечности. Это значит — в новом ряде слагаемое не стремит-
19*
564
ЧИСЛОВЫЕ РЯДЫ
[Гл. 7
ся к нулю, ряд не сходится. И первый ряд тоже не сходится —
просто не сходится и абсолютно тоже.
Доказательство выражается короткой строчкой равенств.
— Неплохо, — просматриваю еще раз его построения. —
Неплохо, но... вашу идею можно реализовать гораздо проще,
если с самого начала явно высказать то фундаментальное
положение, которое лежит в ее основе. Мы в свое время
особо отмечали это положение и подчеркивали, что оно играет
важную роль в теории числовых рядов. Кто догадывается, что
я имею в виду? Никто? Тогда, ребята, я попрошу вас
внимательно просмотреть все, что вы записали в свои тетради во
время сегодняшнего семинара, и отыскать тот пункт, который
позволит наиболее кратко и просто развить идею Буткуса, дать
новое доказательство расходимости нашего ряда. Отыскав, не
заявляйте об этом вслух, а сразу принимайтесь за разработку
нового доказательства. Садитесь, Линас, и работайте вместе
со всеми.
Брожу между столами. Иные на первых же страницах
своих записей находят то, что я имел в виду. Другие все листают
и листают свои тетради: не очень-то прочно, видать, усвоили
пройденное сегодня — так пусть повторят еще и еще раз.
Из нашедших новый путь к ответу вызываю к доске Кочина:
— Сразу же укажите, какое положение берете за основу своих
рассуждений.
— Критерий Коши.
— Да, именно на него я и намекал. Да оно и само прямо-
таки вызывает о себе: из всех теорем, утверждений, принципов,
которые я в свое время советовал вам хорошенько затвердить,
накрепко запомнить, мы до сих пор не использовали ни разу
только критерий Коши.
— Как это ни разу? — удивленно спрашивает Мухин. — А
необходимый признак сходимости? Он разве не из критерия
Коши следует?
Молодец! Своим последним замечанием я хотел
спровоцировать именно такой отклик, который позволил бы естественным
образом напомнить несколько важных сведений.
— Пожалуй, вы правы, — отвечаю Мухину, как бы
спохватившись. — Ну-ка, Дима, — поворачиваюсь к доске, —
напишите нам формулировку критерия Коши и затем покажите, как из
него следует необходимый признак сходимости. Советую всем, —
выразительно гляжу на Буткуса, — занести к себе в тетради все,
что сейчас напишет Кочин.
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
565
С медлительной аккуратностью Кочин выполняет то, о чем
я прошу.
— То, что вы сказали, — веду его далее, — относится к
сходимости рядов. А мы будем доказывать расходимость. Значит, нам
понадобится не критерий Коши...
— А отрицание критерия Коши.
— Сформулируйте его для некоторого ряда ап.
— Существует е такое, что найдется... нет!... что для любого
N найдутся тип, больше N и такие, что |am+i+am+2+...+an| >
> е. Для нашего ряда я возьму е то же самое, как у Линаса, —
единицу. Теперь га и п; я их выберу тоже, как у Линаса...
— Минуточку! Выбор тип следовало бы объяснить.
В его присказке «как у Линаса» слышатся отголоски
былого ощущения своего отставания, внушенного успехами более
бойких друзей, и даже некоторой робости, которая порою
сковывала его на самых первых семинарах. Но теперь-то я
уже знаю, на что он способен! И постараюсь привить ему
стремление всегда работать на пределе своих возможностей,
доводить до посильного совершенства каждый свой
результат.
— Почему я такие тип беру, это нужно объяснить? —
переспрашивает он меня. И поясняет довольно спокойно:
— Я хочу, чтобы слагаемые ряда от т до п не меняли знака,
чтобы они шли от одного какого-то квадрата, от какого-то N2
до следующего, до (N + I)2, то есть т + 1 = iV2, а на (N + I)2
уже будет смена знака, значит п пусть будет на единицу меньше:
п = N2 + 2N.
И смотрит на меня: все ли понятно? все ли правильно? После
моего одобряющего кивка продолжает:
— Напишем теперь всю сумму от т + 1 до п... вот так...
Теперь, как в гармоническом ряде, все слагаемые заменим на
наименьшее, на у * , всего их 2ЛГ + 1, вся сумма больше /2JritlN
и эта дробь должна быть больше единицы. А это уже легко
показать.
— Покажите.
566
ЧИСЛОВЫЕ РЯДЫ
[Гл. 7
Повозившись с неравенством, он в конце концов сводит его к
виду: 2N2 + {N + 1)2 > 0.
— А это уже очевидно, — принимаю такое заключение.
По моей просьбе в отрицании критерия Коши он подставляет
под кванторы существования конкретные значения символов, и
и снова я прошу его придать неравенствам для тип предельно
ясную форму. Проявив неплохую изобретательность, он наконец
получает га = [(N — I)2 + (N — 2)] + N > N. И докладывает,
довольный:
— При N > 2 выражение в квадратных скобках положительно,
неравенство очевидно. И такое очевидно тоже: [N2+N]+N > N.
Выждав короткую паузу, подытоживает:
— Существует е, равное единице, такое, что для любого
N найдутся т = N2 - 1 > N и п = (N + I)2 - 1 > N и
при этом сумма членов ряда от т + 1 до п будет больше
единицы.
— Очень хорошо, Дима. Подождем, пока ребята перепишут
ваше решение, потом стирайте его и садитесь.
Нет, он все-таки молодец! В него можно верить. И вместе с
тем следует быть к нему потребовательнее. Как и ко всем
остальным, впрочем. На каждом занятии. При решении каждой задачи.
Вот тогда-то каждый из них и достигнет тех рубежей, которых
способен достичь.
Выжидая время, брожу между столами, заглядываю в
тетради ребят — и только сейчас замечаю, как успешно работает
Гарин над заданными мною когда-то факультативными
примерами, разбор которых, по моему мнению, мог бы привести к
формулировке признака Раабе.
— Не покажете ли всем, — приглашаю его к доске, — то, что
у вас получилось, Миша?
— Нет, — отказывается он, — нечего еще показывать.
Отрывистый его ответ отдает какой-то непривычной
резкостью. Наверное, думает, что другие — Горт, Костюк, кто-то
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
567
еще — тоже размышляют над этими примерами и достигли
большего, а показаться слабее их ему не хочется.
— Кто еще думал над этими примерами? — гляжу на Буткуса,
с подначки которого я их написал.
— Я думал, — тоскливо тянет тот, — и... ничего не придумал.
— Придется вам идти к доске, — снова поворачиваюсь к
Гарину. Он грузно прижался к столу, словно не замечая
ничего вокруг, не слыша моих слов. — Да сколько же вас можно
упрашивать?! Живо к доске! — повышаю голос. Потом помягче:
— Вы опасаетесь, Миша, что будете плохо выглядеть со
своими половинчатыми результатами? Считайте, что вы просто
высказываете свои соображения по поводу поставленной задачи
— с такой точки зрения даже скромные ваши результаты
будут смотреться очень выигрышно. А вы, ребята, — обращаюсь к
аудитории, — внимательно следите за тем, что станет говорить
Гарин.
— Ну, хорошо, — бурчит он, вставая. И, подойдя к примерам,
написанным мной когда-то с правого края доски:
— Здесь везде вроде бы годится признак Даламбера, но
предел во всех трех примерах получается равный единице, значит,
признак не работает. Но я вот что придумал: если предел
отношения ^^ равен единице, то само это отношение можно
представить в виде ^р1 = 1 + ^+о(^),то есть разложить по формуле
Тейлора по степеням ^... во всяком случае, так можно сделать в
этих примерах.
— Прекрасная мысль! — восклицаю в поддержку. И снова
обернувшись к Буткусу:
— Вам она не приходила в голову?
— Приходила. Но не в таком виде. А записать я не успел.
— Жаль. Записали бы — возможно, стали бы соавтором
открытия. Заметьте на будущее: с публикациями результатов
тянуть не следует. Во всяком случае, об успешном применении
формулы Тейлора сейчас докладывает Гарин, а не вы...
— У меня свой подход, — недовольно обрывает меня Буткус.
— Так что же, Миша, — гляжу на выписанное Гариным
разложение, — вы делаете с таким представлением дальше?
— Дальше я вспомнил про неравенство Бернулли...
Он знает неравенство Бернулли? Молодец. Значит, не
полагается на одни лишь лекции, читает учебники, и не самые легкие.
— А как оно выглядит, это неравенство?
— Вот: (1 + х)а > 1 + ах, — пишет Гарин в нижнем углу
доски. По его поутихшему голосу, по медлительности, с которой он
568
ЧИСЛОВЫЕ РЯДЫ
[Гл. 7
подносит мел к прежним выкладкам, чувствуется, что его
рассуждение подошло к какому-то щекотливому моменту. На доске
появляется: 1 + ^ + о(^) < С2^)**. Гарин недоверчиво смотрит
на написанное, напряженно размышляя. Мой вопрос про
неравенство Бернулли и его ответная беглая сноска остаются где-то
за пределами этих размышлений. Но я все-таки продолжаю
расспрашивать:
— А каким условиям подчинены в нервенвстве Бернулли эти
х и а?
Он нехотя переводит взгляд вниз:
— Про х я точно помню — больше минус единицы... Насчет
а не уверен... кажется, любое.
Откровенно говоря, я и сам смутно помню формулировку
этого неравенства. С тем, что х больше минус единицы, соглашусь,
это довольно очевидно, а вот а... оно должно быть то ли
положительным, то ли не меньше единицы... Впрочем, почему я должен
думать об этом больше, чем Гарин? Он предложил это
неравенство — так пусть и отвечает за него. Если мы обогнали лектора,
логично будет, если кто-то из них обгонит меня. В конце
концов, ученики должны идти дальше учителей — разве не так? И
я продолжаю разговор:
— Любое? Я готов принять ваше мнение — ведь если олно
неверно, это где-то приведет нас к ошибке — тогда мы его и
пересмотрим. А пока попробуем последовать за вами. Насколько я
понимаю, вы полагаете в неравенстве Бернулли х — ^ и
получаете 1 + ^ < (1 + ^)а = {г^)а- Но в том неравенстве, что вы
доказали, в левой части неравенства стоит еще слагаемое о(^),
так что это — не неравенство Бернулли, а несколько иное
соотношение, которое тоже нуждается в доказательстве. Вы
доказали его?
— Нет, — мрачнеет он.
— Не доказали... Ну, а если бы вам удалось его доказать —
что тогда?
— Тогда, — мгновенно вспыхивает в нем порыв к ясно
различимой цели, совсем уж теперь недалекой, — все сразу тогда
получилось бы: —^ < {j^)a — и дальше по теореме,
которую мы когда-то доказывали: если, начиная с какого-то номера,
Ц^ < "г111 и Рад Ьп сходится, то и ряд ап тоже сходится. Ряд
Ьп — это nQ, он сходится при а < — 1, расходится при а > — 1.
— Иными словами, — неторопливо и негромко говорю, как
бы вслух обдумывая сказанное Гариным, — если отношение ^^
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
569
раскладывается по формуле Тейлора в виде 1 + ^ + о(^)и
коэффициент а меньше минус единицы, то ряд ап сходится, в
противном же случае ряд расходится.
— Да, видно так, — в тон мне отвечает Гарин.
— Но неравенство, ведущее к такому выводу, — в той же
рассудительной манере продолжаю я, — вами не доказано.
— А, может, и не надо его доказывать? — шумно врывается
Костюк в наш с Гариным диалог. — Может, удастся получить
этот вывод по-другому? Если, конечно, он верен.
— По крайней мере, — оборачиваюсь к Костюку, — мы можем
проверить на наших примерах, насколько он правдоподобен. Кто
хотел бы применить к этим примерам признак
сформулированной Гариным?
И гляжу на Лапикова. Он с готовностью поднимается, бойко
решает первый пример и рапортует:
— Получается а = — |, то есть меньше минус единицы. Ряд
сходится.
— И в задачнике написано, что он сходится. Садитесь, Егор.
Кто решит второй пример? Может быть, Чюмин? — гляжу на
задний ряд. — Вы что-то хотите сказать? — замечаю
вздернувшуюся вверх руку Кулагина.
— Наверное, этот признак можно сформулировать как-то
короче, проще... Ну, в общем примерно так же, как признак
Даламбера — через предел. У нас есть разложение дроби:
^±i = 1 + ^ + о(^); надо единицу перенести влево... сейчас...
570
ЧИСЛОВЫЕ РЯДЫ
[Гл. 7
если умножить, то о(1)... да, перенести единицу влево, умножить
на п, в правой части остается а + о(1)...
— То есть, — нетерпеливо перебивает Кулагина Гарин («Что
это с ним? Он всегда был такая флегма!» — с усмешкой отмечаю
про себя), — то есть надо взять предел lim n(~±i — 1), если он
п—юо °п
меньше минус единицы, то ряд ап сходится, если больше или
равен минус единице, то расходится.
— Хорошо! — одобряю это рационализаторское
предложение. — Напишите, Чюмин, формулировку признака Гарина в но-
bom изложении. Решайте с помощью этого признака оставшиеся
два примера. Неплохо, неплохо... Итак, во втором примере: схо-
Ю. В. Пухначев)
СЕМЬ СЕМИНАРОВ
571
димость при р > |, расходимость — в остальных случаях. В
третьем: сходимость при р > 1, при остальных значениях р —
расходимость. В задачнике — те же ответы.
«Те же ответы», — мысленно повторяю про себя не без
удивления. Так, значит, на самом деле в неравенстве Бернулли
показатель степени а может быть любым? Но ведь я точно
помню, что он, как и слагаемое х, подчиняется какому-то
условию! Или я заблуждаюсь? И прав не я, а Гарин? Прав,
как всегда, когда он брал слово... Но ведь сейчас все
наоборот — он совсем не хотел отвечать, это я вытянул его к доске
с еще сырыми, почти интуитивными соображениями. Может
быть, на сей раз интуиция его подвела? Как говорится, и на
старуху бывает проруха... Надо срочно разобраться во всем
этом!
— Подождите минуточку, Чюмин, я хочу найти еще один
пример, — гляжу в задачник, а сам лихорадочно раздумываю:
«Может быть, разложить степень (1 + х)а по формуле Тейлора?
Начало будет таким же, как в другой части неравенства, l+ах...вот
на этом и оборвать разложение и взять остаточный член в
форме Лагранжа... вторая производная... то есть а(а — 1)... и на
(1 + вх)а~2... этот множитель положительный, как всякая
степень всякого положительного числа... потом х2, тоже
положительный множитель... а вот а(а — 1)... если а между нулем и
единицей...»
— А что, в самом деле есть такой признак? —
обрывает мои рассуждения Чюмин. Лучась чудаковатой улыбкой
сквозь стекла очков, он обводит почтительной рамкой формулу
limnf^1) < —1, которую записал на доске со слов Гарина.
п—юо fln
572
ЧИСЛОВЫЕ РЯДЫ
[Гл. 7
— Да, есть, — отвечаю, глядя в аудиторию так, чтобы
краем глаза следить за реакцией Гарина на мои дальнейшие слова.
— Он называется признаком Раабе. Только формулируется он
несколько иначе, чем у нас. Исследуется выражение п(^а— 1)...
— В принципе то же самое, — торопливо перебивает меня
Гарин.
— И если оно имеет предел при п, стремящемся к
бесконечности, — невозмутимо продолжаю, словно не расслышав, —
то вывод о сходимости и расходимости ряда делается, судя по
значению предела: если он больше единицы, ряд сходится,
если же меньше единицы, то ряд расходится. Обратите
внимание: последнее неравенство — строгое: если предел равен
единице, то признак Раабе ничего не говорит о сходимости ряда.
Кроме предельного варианта, признак Раабе имеет еще один
вариант...
— Ну, ясно! — опять не дает мне договорить Гарин (я еще
не видел его таким возбужденным!). — Наверное, так же, как
с признаками Коши и Даламбера: если выражение п(^а 1),
начиная с какого-то номера, больше какого-то q, которое
строго больше единицы... нет, больше или равно такому q, то ряд
сходится, а расходится он... расходится тогда, когда это
выражение меньше или равно единице, опять-таки начиная с какого-то
номера...
— Вы мыслите в верном направлении, Миша. Но вот что
смущает меня: формулировка неравенства Бернулли, которую вы
использовали в своих построениях, неверна. Поглядите на нее
еще раз: (1 + х)а > 1 + ах. Вы говорили, что х должен быть
больше минус единицы, и против этого я возражать не стану.
Но затем вы сказали, что величина а может быть любой. Нет,
Миша, не любой. Возьмите а = \. Что получается? Неверное
соотношение: у/1 + х > 1 + §. В самом деле, возведите его в
2
квадрат: 1 + х > 1 + х + ^-. Сокращая первые два слагаемых в
обеих частях неравенства, приходим к абсурду: 0 > ^-. Мне-то
самому кажется, что показатель а должен быть не меньшим
единицы... или натуральным... честно говоря, не помню. А значение
а = — 1, ключевое для вашего вывода, к таким числам не
принадлежит. И покуда мы не проверим на прочность это звено
вашего рассуждения, я не могу считать его обоснованным. Вижу,
вы расстроены. Напрасно! Ведь вашу формулировку признака
Раабе я не оспариваю, она совершенно верна. Надо лишь заново
выстроить путь к ней. Кстати, в науке не редкость такая ситуа-
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
573
ция, когда верный результат достигается путем нестрогих
умозаключений. Самый поразительный пример на этот счет дает сама
дисциплина, которую мы с вами изучаем, математический
анализ. После того, как его основные методы разработали Ньютон,
Лейбниц, их современники и ближайшие последователи, он
полтора века развивался и успешно применялся, не имея строгого
логического обоснования. Оно стало создаваться лишь в начале
девятнадцатого века трудами Коши, Больцано, Гаусса и других
видных математиков столетия... Да что вы так хмуримтесь,
Миша? Вы получили очень хороший результат, одержали крупный
успех, я это говорю без преувеличения. А то, что вы и просчет
допустили крупный — так это в порядке вещей. Надеюсь, моя
историческая ссылка вас в этом убедила. И та придирчивость, с
которой я указываю на вашу ошибку, тоже вполне правомерна.
Кому много дано, с того много и спросится. Дано будет и
счастье настоящих открытий, и признание, и, быть может, мировое
имя. А спросится так, что вы порой будете ощущать себя
проигравшимся в пух игроком. Но ведь это и будет означать, что вы
постигнете жизнь во всей ее полноте. Только не сворачивайте со
своего пути, не сдавайтесь, умейте держать удар! Для ученого
эта способносить важна не менее, чем для спортсмена. Так что
вот вам два задания на дом: во-первых, найдите где-нибудь и
заучите точную формулировку неравенства Бернулли, пригодится;
а во-вторых, докажите заново признак Раабе.
Докажет обязательно! В этом я не сомневаюсь ничуть!
Признаться, на первых семинарах, когда трудность разбиравшихся
нами задач была намного ниже его способностей, мне казалось,
что он заскучает, охладеет к занятиям. Но вот нашлись и для
него проблемы по плечу. С какой энергией сразу заработал его
ум! Таких, как он, всегда нужно загружать задачами на пределе
их возможностей! Кляну себя, что не думал об этом раньше. Свои
заботы я посвящал в основном самым слабым, добивался, чтобы
каждый мой студент обладал гарантированным минимумом
знаний и навыков. Но ведь нужно заботиться и о самых сильных,
о творчески одаренных, о будущих специалистах высшего
класса, чтобы каждый из них достиг гарантированного максимума в
расцвете своих способностей... Дар творчества — как редок он!
Гораздо более редок, чем дар понимания. Уж куда как понятлив
тот же Горт: о чем ни спроси его из пройденного — ответит
моментально и исчерпывающе, какую задачу ни напомни из
решавшихся когда-то — воспроизведет решение без погрешностей и
заминок. Вскрыть и разъяснить чью-нибудь ошибку — нет лучшего
574
ЧИСЛОВЫЕ РЯДЫ
[Гл. 7
детектива и критика, чем он; отточить и изложить чью-нибудь
удачную идею — нет лучшего, чем он редактора и
интерпретатора. Но вот настало время задач не школярских, таких в которых
требуется не применить уже известный, а изобрести новый прием
— где же наш блистательный Горт со своими богатейшими
знаниями? Такой задачей был поиск второй и третьей подстановок
Эйлера — Горт не нашел ни той, ни другой. Когда на прошлом
семинаре мы принялись за несобственные интегралы, он был на
высоте лишь при разработке одного из признаков сходимости -
да и тут не обошлось без моих намеков. Сегодня его тоже не
назовешь открывателем: проморгал признак Маклорена, который
так и плыл к нему, в руки... Боюсь, очень боюсь, что при всех его
способностях ему в будущей работе придется удовольствоваться
ролью исполнителя чужих замыслов, ролью ведомого,
идущего вслед за первопроходцами — такими, как Гарин, ролью, что
называется, «на подхвате»... В ком же еще, кроме Гарина, есть
искра творческого поиска? На кого я могу рассчитывать в этом
отношении? На Буткуса. Пожалуй, и на Кулагина. Отчасти на
Миклашевского — если сумею давать задачи в притягательной
для него постановке. С подобными оговорками круг кандидатов
в будущие лидеры расширяется: это и Стрельцов — если я сумею
вывести его из спячки благодушия, и Меншиков — если я
раздую чуть затеплившийся в нем азарт, и Рамзин — если я смогу
отвадить его от всепоглощающего эгоцентризма, и Горт — если
я претворю в нем дух исполнительства и придиренчества в дух
искания и конструктивного сотрудничества, и Костюк — если я
найду для его боевитости иной источник, помимо духа
противоречия...
— А сейчас, ребята, — возвращаюсь из мечтаний о будущем в
сегодняшний день, — обратимся к делам текущим: у нас их еще
немало. Да и в пройденном есть недоделки: с рядами Лейбница
мы так еще и не разобрались. Кто мог бы вывести оценочное
неравенство для остатка такого ряда? Не хотите ли, Стрельцов?
Вы, как я заметил, занимались этой проблемой? К доске!
Совсем недавно, заглянув в его тетрадь, я увидел, что он
додумался до плодотворной идеи: сгруппировать по двое
слагаемые остатка, начиная со второго. Отсюда сразу следует искомая
простая оценка: \гп\ < ап+ь Та же идея позволяет Стрельцову
предельно просто доказать сходимость ряда Лейбница: попарная
группировка его слагаемых, начатая с самого первого,
доказывает возрастание его частичных сумм, а начатая со второго — их
ограниченность. Отсюда и следует сходимость.
Ю. В. Пухначев]
СЕМЬ СЕМИНАРОВ
575
— Очень четкое доказательство! И очень любопытная схема
рассуждения, — утверждаю его результаты. — Интересно, как
это вы догадались сгруппировать слагаемые?
— Не знаю, — удивленно оглядывает свои выкладки
Стрельцов. — Как-то само собой получилось...
— А я, кажется, знаю — посмеиваюсь над его забавной
миной. — Помните, как на одном из прошлых семинаров, где
говорилось про формулу Тейлора, вы сами делали нечто похожее?
И рисую на доске характерную схемку, которой он в тот раз
иллюстрировал свои рассуждения.
— Ну, да, пожалуй, — смущенно улыбается Стрельцов.
— А как вообще оценивается остаток, если ряд совершенно
произвольный? — любопытствует Миклашевский.
— Ваш интерес к этому вопросу вполне оправдан, —
поворачиваюсь к нему. — В самом деле, числовые ряды
разрабатывается, очевидно, не только для того, чтобы рассуждать об их
сходимости и расходимости, но в основном затем, чтобы
проводить с их помощью какие-то вычисления. Скажем, в самом
начале нынешнего семинара мы упоминали про бесконечную сумму,
удобную для нахождения числа е = 1 + "п + ^г + --- + ^- Вот
ряды, с помощью которых можно вычислить число 7г, — смотрите:
2г_1_1.1_1. .2L_ J/X _l,l+i.i-I.l4- ^
4""1 3^5 7 ^ "•' 6 "" v/з^ 3 3 ^ 5 З2 7 З3 ^ —/•
Сколько слагаемых нужно взять в первом ряду для достижения
той или иной точности? Сколько во втором? Какой ряд проще
позволит достичь заданной точности? На эти и на многие другие
вопросы можно ответить, умея оценивать остаток ряда. Вот еще
один ряд: In2 = 1 — 5 + 5 — \+~- Здесь можно поставить тот же
вопрос с точности вычислений. Но к нему естественным образом
добавляется еще один: а нельзя ли построить такой ряд, чтобы
вычислять значения логарифма не от одного избранного, а от
любого значения аргумента? Отвечающий этой цели ряд должен,
очевидно, состоять уже не из чисел, а из функций. Такие ряды
576
ЧИСЛОВЫЕ РЯДЫ
(Гл. 7
тоже изучаются в математическом анализе — они называются
функциональными. К ним мы перейдем на одном из ближайших
занятий, там и поговорим про оценки их остатков...
Пронзительный звонок засыпает своим треском мои слова.
— И еще о многом другом поговорим. Наш сегодняшний
семинар окончен — но математика-то ведь продолжается!
ПРИЛОЖЕНИЕ
Собранные здесь тексты расположены в приблизительной
хронологической последовательности от настоящего к прошлому.
Александр ТВАРДОВСКИЙ
Вся суть в одном-единственном завете:
То, что скажу, до времени тая,
Я это знаю лучше всех на свете —
Живых и мертвых, — знаю только я.
Сказать то слово никому другому
Я никогда бы ни за что не мог
Передоверить. Даже Льву Толстому —
Нельзя. Не скажет — пусть себе он бог,
А я лишь смертный. За свое в ответе,
Я об одном при жизни хлопочу:
О том, что знаю лучше всех на свете,
Сказать хочу. И так, как я хочу.
СОБРАТЬЯМ ПО ПЕРУ
В деле своем без излишней тревоги
Мы затвердили с давнишней поры
То, что горшки обжигают не боги,
Ну, а не боги, так — дуй до горы.
Только по той продвигаясь дороге,
Нам бы вдобавок усвоить пора:
Верно, горшки обжигают не боги,
Но обжигают их — мастера!
Арсений ТАРКОВСКИЙ
СТАНЬ САМИМ СОБОЙ (отрывок)
Когда тебе придется туго,
Найдешь и сто рублей и друга.
Себя найти куда трудней,
Чем друга или сто рублей. (...)
Загородил полнеба гений,
Не по тебе его ступени,
Но даже под его стопой
Ты должен стать самим собой.
Найдешь и у пророка слово,
Но слово лучше у немого,
И ярче краска у слепца,
Когда отыскан угол зренья
И ты при вспышке озаренья
Собой угадан до конца.
578
ПРИЛОЖЕНИЕ
Давид САМОЙЛОВ
ВДОХНОВЕНЬЕ
Жду, как заваленный в забое,
Что стих пробьется в жизнь мою.
Бью в это темное, рябое,
В слепое, в каменное бью.
Прислушиваюсь: не слыхать ли,
Что пробиваются ко мне.
Но это только капли, капли
Скользят по каменной стене.
Жду, как заваленный в забое,
Долблю железную руду,
Не пробивается ль живое
Навстречу моему труду?
Жду исступленно и устало,
Бью в камень медленно и зло...
О, только бы оно пришло!
О, только бы не опоздало!
ТАЛАНТЫ
Их не ждут. Они приходят сами
И рассаживаются без спроса.
Негодующими голосами
Задают неловкие вопросы.
И уходят в ночь, туман и сырость
Странные девчонки и мальчишки,
Кутаясь в дешевые пальтишки,
Маменьками шитые на вырост.
В доме вдруг становится пустынно
И в уютном кресле неудобно.
И чего-то вдруг смертельно стыдно,
Угрызенью совести подобно.
И язвительная умудренность
Вдруг становится бедна и бренна.
И завидны юность и влюбленность,
И былая святость неизменна.
Как пловец, расталкиваю ставни
И кидаюсь в ночь за ними следом,
Потому что знаю цену давним
Нашим пораженьям и победам.
Приходите, юные таланты!
Говорите нам светло и ясно!
Что вам славы пестрые заплаты!
Что вам - низких истин постоянство!
ПРИЛОЖЕНИЕ
Сберегите нас от серой прозы,
От всего, что сбито и затерто.
И пускай бесстрашно льются слезы
Умиленья, зависти, восторга!
Евгений ЕВТУШЕНКО
Твердили пастыри, что вреден
и неразумен Галилей,
но, как показывает время,
кто неразумней, тот умней.
Ученый, сверстник Галилея,
был Галилея не глупее.
Он знал, что вертится Земля,
но у него была семья.
И он, садясь в свою карету,
свершив предательство свое,
считал, что делает карьеру,
а между тем губил ее.
За осознание планеты
шел Галилей один на риск.
И стал великим он... Вот это
я понимаю — карьерист!
Итак, да здравствует карьера,
когда карьера такова,
как у Шекспира и Пастера,
Гомера и Толстого... Льва!
Зачем их грязью покрывали?
Талант — талант, как ни клейми.
Забыты те, кто проклинали,
но помнят тех, кого кляли.
Все те, кто рвались в стратосферу,
врачи, что гибли от холер, —
вот эти делали карьеру!
Я с их карьер беру пример.
Я верю в их святую веру.
Их вера — мужество мое.
Я делаю себе карьеру
тем, что не делаю ее.
Борис ПАСТЕРНАК
Быть знаменитым некрасиво.
Не это подымает ввысь.
Не надо заводить архива,
Над рукописями трястись.
580
ПРИЛОЖЕНИЕ
Цель творчества — самоотдача,
А не шумиха, не успех.
Позорно, ничего не знача,
Быть притчей на устах у всех.
Но надо жить без самозванства,
Так жить, чтобы в конце концов
Привлечь к себе любовь пространства,
Услышать будущего зов.
И надо оставлять пробелы
В судьбе, а не среди бумаг,
Места и главы жизни целой
Отчеркивая на полях.
И окунаться в неизвестность,
И прятать в ней свои шаги,
Как прячется в тумане местность,
Когда в ней не видать ни зги.
Другие по живому следу
Пройдут твой путь за пядью пядь,
Но пораженья от победы
Ты сам не должен отличать.
И должен ни единой долькой
Не отступаться от лица,
Но быть живым, живым и только,
Живым и только до конца.
Николай ЗАБОЛОЦКИЙ
Облетают последние маки,
Журавли улетают, трубя,
И природа в болезненном мраке
Не похожа сама на себя.
По пустынной и голой аллее
Шелестя облетевшей листвой,
Отчего ты, себя не жалея,
С непокрытой бредешь головой?
Жизнь растений теперь затаилась
В этих странных обрубках ветвей.
Ну, а что же с тобой приключилось,
Что с душой приключилось твоей?
Как посмел ты красавицу эту,
Драгоценную душу твою,
Отпустить, чтоб скиталась по свету,
Чтоб погибла в далеком краю?
Пусть непрочны домашние стены,
Пусть дорога уводит во тьму, —
Нет на свете печальней измены,
Чем измена себе самому.
ПРИЛОЖЕНИЕ
ГРОЗА (отрывок)
Содрогаясь от мук, пробежала над миром зарница,
Тень от тучи легла, и слилась, и смешалась с травой.
Все труднее дышать, в небе облачный вал шевелится,
Низко стелется птица, пролетев над моей головой.
Я люблю этот сумрак восторга, эту краткую ночь вдохновенья,
Человеческий шорох травы, вещий холод на темной руке,
Эту молнию мысли и медлительное появленье
Первых дальних громов — первых слов на родном языке.
Леонид МАРТЫНОВ
Человек,
Которого ударили,
Человек, которого дубасили,
Купоросили и скипидарили,
Человек, которого отбросили,
Человек, к которому приставили
С четырех сторон по неприятелю,
Но в конце концов не обезглавили, —
Вот кто чувствует ко мне симпатию.
И к нему ее я тоже чувствую,
Потому что я над ним не властвую
И не то чтобы ему сочувствую,
Но в его страданиях участвую:
И меня пытались так когда-то ведь
Обрубать, обламывать, обтесывать,
Деликатно говоря — причесывать,
Говоря точнее — обрабатывать.
Чтоб признал их страшные законы я,
Убеждали и добром и злом они,
Но орудия, употребленные
Для всего для этого, изломаны,
Хоть и длились целые столетия
Эти бесконечные занятия.
И теперь в любой стране на свете я
Ясно чувствую твою симпатию,
Человек, которого мытарили,
Всячески трепали, зуботычили,
Купоросили и скипидарили,
Но в конце концов не обезличили.
Илья ЭРЕНБУРГ
САМЫЙ ВЕРНЫЙ
Я не знал, что дважды два — четыре,
И учитель двойку мне поставил.
А потом я оказался в мире
Всевозможных непреложных правил.
582
ПРИЛОЖЕНИЕ
Правила менялись, только бойко.
С той же снисходительной улыбкой
Неизменно ставили мне двойку
За допущенную вновь ошибку.
Не был я учеником примерным
И не стал с годами безупречным.
Из апостолов Фома Неверный
Кажется мне самым человечным.
Услыхав, он не поверил просто —
Мало ли рассказывают басен?
И, наверно, не один апостол
Говорил, что он весьма опасен.
Может, был Фома тяжелодумом,
Но, подумав, он за дело брался.
Говорил он только то, что думал,
И от слов своих не отрекался.
Жизнь он мерил собственною меркой,
Были у него свои скрижали.
Уж не потому ль, что он «неверный»,
Он молчал, когда его пытали?
Дмитрий КЕДРИН
АРХИМЕД
Нет, не всегда смешон и узок
Мудрец, глухой к делам земли:
Уже на рейде в Сиракузах
Стояли римлян корабли.
Над математиком курчавым
Солдат занес короткий нож,
А он на отмели песчаной
Окружность вписывал в чертеж.
Ах, если б смерть — лихую гостью —
Мне также встретить повезло,
Как Архимед, чертивший тростью
В минуту гибели — число!
Николай ГУМИЛЁВ
РОДОС
На полях опаленных Родоса
Камни стен и в цвету тополя
Видит зоркое сердце матроса
В тихий вечер с кормы корабля.
Там был рыцарский орден: соборы,
Цитадель, бастионы, мосты,
ПРИЛОЖЕНИЕ
И на людях простые уборы,
И на них золотые кресты.
Не стремиться ни к славе, ни к счастью,
Все равны перед взором Отца,
И не дать покорить самовластью
Посвященные небу сердца!
Но в долинах старинных поместий,
Посреди кипарисов и роз,
Говорить о Небесной Невесте,
Охраняющей нежный Родос!
Наше бремя — тяжелое бремя:
Труд зловещий дала нам судьба,
Чтоб прославить на краткое время,
Нет, не нас, только наши гроба.
Нам брести в смертоносных равнинах,
Чтоб узнать, где родилась река,
На тяжелых и гулких машинах
Грозовые пронзать облака.
В каждом взгляде тоска без просвета,
В каждом вздохе томительный крик, —
Высыхать в глубине кабинета
Перед пыльными грудами книг.
Мы идем сквозь туманные годы,
Смутно чувствуя веянье роз,
У веков, у пространств, у природы
Отвоевывать древний Родос.
Но, быть может, подумают внуки,
Как орлята тоскуя в гнезде:
«Где теперь эти крепкие руки,
Эти души горящие — где?»
СЛОВО
В оный день, когда над миром новым,
Бог склонял лицо свое, тогда
Солнце останавливали словом,
Словом разрушали города.
И орел не взмахивал крылами,
Звезды жались в ужасе к луне,
Если, точно розовое пламя,
Слово проплывало в вышине.
А для низкой жизни были числа,
Как домашний, подъяремный скот,
Потому что все оттенки смысла
Умное число передает.
ПРИЛОЖЕНИЕ
Патриарх седой, себе под руку
Покоривший и добро и зло,
Не решаясь обратиться к звуку,
Тростью на песке чертил число.
Но забыли мы, что осиянно
Только слово средь земных тревог,
И в Евангелии от Иоанна
Сказано, что Слово это — Бог.
Мы ему поставили пределом
Скудные пределы естества,
И, как пчелы в улье опустелом,
Дурно пахнут мертвые слова.
Иван БУНИН
РИТМ
Часы, шипя, двенадцать раз пробили
В соседней зале, темной и пустой.
Мгновения, бегущие чредой
К безвестности, к забвению, к могиле,
На краткий срок свой бег остановили
И вновь узор чеканят золотой:
Заворожен ритмической мечтой,
Вновь отдаюсь меня стремящей силе.
Раскрыв глаза, гляжу на яркий свет
И слышу сердца ровное биенье,
И этих строк размеренное пенье,
И мыслимую музыку планет.
Все ритм и бег. Бесцельное стремленье!
Но страшен миг, когда стремленья нет.
Редьярд КИПЛИНГ
ЕСЛИ...
О, если ты покоен, не растерян,
Когда теряют головы вокруг,
И если ты себе остался верен,
Когда в тебя не верит лучший друг,
И если ждать умеешь без волненья,
Не станешь ложью отвечать на ложь,
Не будешь злобен, став для всех мишенью,
Но и святым себя не назовешь,
И если ты своей владеешь страстью,
А не тобою властвует она,
И будешь тверд в удаче и несчастье,
Которым в сущности цена одна,
ПРИЛОЖЕНИЕ
И если ты готов к тому, что слово
Твое в ловушку превращает плут,
И, потерпев крушенье, можешь снова —
Без прежних сил — возобновить свой труд,
И если ты способен всё, что стало
Тебе привычным, выложить на стол,
Все проиграть и вновь начать сначала,
Не пожалев того, что приобрел,
И если можешь сердце, нервы, жилы,
Так завести, чтобы вперед нестись,
Когда с годами изменяют силы
И только воля говорит: «Держись!» —
И если можешь быть в толпе собою,
При короле с народом связь хранить,
И, уважая мнение любое,
Главы перед молвою не хранить,
И если будешь мерить расстоянье
Секундами, пускаясь в дальний бег, —
Земля — твое, мой мальчик, достоянье!
И более того, ты — человек!
(перевод С. Маршака)
Райнер Мария РИЛЬКЕ
И час этот пробил, ясен и строг,
и металлом коснулся меня.
Всё трепещет во мне: да, теперь бы я смог
дать пластический образ дня.
Здесь ничто без меня не завершено
и ничто не успело стать.
И мой взгляд все светлее: ему дано
этот мир, как невесту, обнять.
Даже малая вещь для меня хороша
и в картине моей цветет
на сияющем фоне, — и чья-то душа,
с нею встретившись, оживет.
(перевод Т. Сильман)
Фридрих НИЦШЕ
СЕ ЧЕЛОВЕК
Знаю, кто я. Ненасытен,
Как огонь, когда горит он;
Всё, что охвачу я, — в свет,
Всё, что отпущу я, — в уголь
Превращу — себе на убыль.
Я — огонь, сомненья нет.
(перевод Ю. Пухначева)
ПРИЛОЖЕНИЕ
Пауль ХЕЙЗЕ
СКОРО...
Будь терпеливей, ровней.
Скоро в каморке твоей
солнечный свет засияет.
Над коньком, где развешены колокола,
там давно уж заря взошла
и вошла в окно звонаря.
Он живет одиноко; раскатами грома
колокольного взорван покой его дома,
но его раньше всех утешает заря.
Кто внизу в переулочках поселился,
где уютно дом к домику прилепился, —
ливень холодный того не окатывал,
гром колокольный того не охватывал,
но зато и рассвет там позже теплился.
Высь и глубь - тут и боль, и радость.
Прочь гони неразумную зависть.
Всякая скорбь свой праздник скрывает.
Будь терпеливей, ровней!
Скоро в каморке твоей
солнечный свет засияет.
(перевод Ю. Пухначева)
Шарль БОДЛЕР
ПЛАВАНЬЕ (отрывки)
В один ненастный день, в тоске нечеловечьей,
Не вынеся тягот, под скрежет якорей,
Мы всходим на корабль, и происходит встреча
Безмерности мечты с предельностью морей.
Что нас толкает в путь? Тех — ненависть к отчизне,
Тех — скука очага, еще иных — в тени
Цирцеевых ресниц оставивших полжизни —
Надежда отстоять оставшиеся дни.
Но истые пловцы — те, что плывут без цели,
Плывущие — чтоб плыть! Глотатели широт,
Что каждую зарю справляют новоселье
И даже в смертный час еще твердят: вперед!
На облако взгляни: вот облик их желаний!
Как отроку — любовь, как рекруту — картечь,
Так край желанен им, которому названья
Доселе не нашла еще живая речь.
О странная игра с подвижною мишенью!
Не будучи нигде, цель может быть — везде!
ПРИЛОЖЕНИЕ
Игра, где человек охотится за тенью,
За призраком ладьи на призрачной воде...
(перевод М. Цветаевой)
Конрад Фердинанд МАЙЕР
ВЕСЕННЕЕ СТРАНСТВИЕ
Жар солнца полнит небосвод.
Вскипая, море рушит лед.
Вот парус врезался в прилив...
Как парус, сердце рвется, взмыв.
Оно блуждать обречено,
растратив молодости час,
весенним солнцем зажжено,
весеннею волной вспенясь.
Что годы юности пустой?
Томленья и скорбей оплот.
И сердце за своей весной
опять идет, опять идет...
И пусть седеет твой висок,
а сердцу дан последний срок —
пока волна кипит, оно
искать свою весну должно.
(перевод Ю. Пухначева
Каролина ПАВЛОВА
О былом, о погибшем, о старом
Мысль немая душе тяжела;
Много в жизни я встретила зла,
Много чувств я истратила даром,
Много жертв невпопад принесла.
Шла я вновь после каждой ошибки,
Забывая жестокий урок,
Безоружно в житейские сшибки:
Веры в слезы, слова и улыбки
Вырвать ум мой из сердца не мог.
И душою, судьбе непокорной,
Средь невзгод, одолевших меня,
Убежденье в успех сохраня,
Как игрок ожидала упорный
День за днем я счастливого дня.
Смело клад я бросала за кладом
И стою, проигравшися в пух;
И счастливцы, сидящие рядом,
Смотрят жадным, язвительным взглядом —
Изменяет ли твердый мне дух?
ПРИЛОЖЕНИЕ
Федор ТЮТЧЕВ
Когда дряхлеющие силы
Нам начинают изменять
И мы должны, как старожилы,
Пришельцам новым место дать, —
Спаси тогда нас, добрый гений,
От малодушных укоризн,
От клеветы, от озлоблений
На изменяющую жизнь;
От чувства затаенной злости
На обновляющийся мир,
Где новые садятся гости
За уготованный им пир;
От желчи горького сознанья,
Что нас поток уж не несет
И что другие есть призванья,
Другие вызваны вперед;
Ото всего, что тем задорней,
Чем глубже крылось с давних пор, —
И старческой любви позорней
Сварливый старческий задор.
Генрих ГЕЙНЕ
ДОКТРИНА
Бей в барабан, и не бойся беды,
И маркитантку целуй вольней!
Вот тебе смысл глубочайших книг,
Вот тебе суть науки всей.
Людей барабаном от сна буди,
Зорю барабань, не жалея рук,
Маршем вперед, барабаня, иди, —
Вот тебе смысл всех наук.
Вот тебе Гегеля полный курс,
Вот тебе смысл наук прямой:
Я понял его, потому что умен,
Потому что я барабанщик лихой.
(перевод Ю. Тынянова)
Фридрих ШИЛЛЕР
КОЛУМБ
Далее, смелый пловец! Пускай невежды смеются;
Пусть, утомившись, руль выпустит кормчий из рук.
ПРИЛОЖЕНИЕ
589
Далее, далее к западу! Должен там берег явиться:
Ясно видится он мысли твоей вдалеке!.
Веруй вожатому-разуму! Бодро плыви океаном!
Если земли там и нет, выйдет она из пучин.
В тесном союзе и были и будут природа и гений:
Что обещает нам он — верно исполнит она.
(перевод М. Михайлова)
Иоганн Вольфганг ГЁТЕ
САМОРОДКАМ
Он говорит: «Ничем я не обязан
Ни современникам, ни старым мастерам,
Я ни с какими школами не связан —
Учиться у кого-то — стыд и срам!»
Все это можно изложить и так:
«Никто не виноват, что я дурак...»
(перевод Б. Заходера)
Гаврила ДЕРЖАВИН
МОДНОЕ ОСТРОУМИЕ
Не мыслить ни о чем и презирать сомненье,
На всё давать тотчас свободное решенье,
Не много разуметь, о многом говорить;
Быть дерзку, но уметь продерзостями льстить;
Красивой пустошью плодиться в разговорах,
И другу и врагу являть приятство в взорах;
Блистать учтивостью, но, чтя, пренебрегать,
Смеяться дуракам и им же потакать,
Любить по прибыли, по случаю дружиться,
Душою подличать, а внешностью гордиться,
Казаться богачом, а жить за счет других;
С осанкой важничать в безделицах самих;
Для острого словца шутить и над законом,
Не уважать отцом, ни матерью, ни троном;
И, словом, лишь умом в поверхности блистать,
В познаниях одни цветы только срывать,
Тот узел рассекать, что развязать не знаем, —
Вот остроумием что часто мы считаем!
ЕВАНГЕЛИЕ ОТ МАТФЕЯ (отрывок)
Выйдя же в день тот из дома, Иисус сел у моря.
И собралось к Нему множество народа, так что Он вошел в лодку и сел;
а весь народ стоял на берегу.
И поучал их много притчами, говоря: вот вышел сеятель сеять;
и когда он сеял, иное упало при дороге, и налетели птицы, и поклевали
590
ПРИЛОЖЕНИЕ
иное упало на места каменистые, где немного было земли, и скоро
взошло, потому что земля была неглубока.
Когда же взошло солнце, увяло, и, как не имело корня, засохло;
иное упало в терние, и выросло терние и заглушило его;
иное упало на добрую землю и принесло плод: одно во сто крат, а другое
в шестьдесят, иное же в тридцать.
Кто имеет уши слышать, да слышит!
И, приступив, ученики сказали Ему: для чего притчами говоришь
им?
Он сказал им в ответ: для того, что вам дано знать тайны Царствия
Небесного, а им не дано.(...)
Вы же выслушайте значение притчи о сеятеле:
ко всякому, слушающему слово о Царствии и не разумеющему, приходит
лукавый и похищает посеянное в сердце его — вот кого означает посеянное
при дороге.
А посеянное на каменистых местах означает того, кто слышит слово и
тотчас с радостью принимает его;
но не имеет в себе корня и непостоянен: когда настанет скорбь или
гонение за слово, тотчас соблазняется.
А посеянное в тернии означает того, кто слышит слово, но забота
века сего и обольщение богатства заглушает слово, и оно бывает
бесплодно.
Посеянное же на доброй земле означает слышащего слово и
разумеющего, который и бывает плодоносен, так что иной приносит плод во сто крат,
иной в шестьдесят, а иной в тридцать.
КОНФУЦИЙ
БЕСЕДЫ И СУЖДЕНИЯ (отрывки)
Учитель сказал: «В пятнадцать лет я обратил свои помыслы к учебе.
В тридцать лет я обрел самостоятельность. В сорок лет я освободился от
сомнений. В пятьдесят лет я познал волю неба. В шестьдесят лет я научился
отличать правду от неправды. В семьдесят лет я стал следовать желаниям
своего сердца и не нарушал ритуала.»
Учитель сказал: «Учиться и не размышлять — напрасно терять время,
размышлять и не учиться — губительно.»
Учитель сказал: «Если я иду с двумя людьми, то у них обязательно есть
чему поучиться. Надо взять то хорошее, что есть у них, и следовать ему. От
нехорошего же надо избавиться.»
Учитель сказал: «В любви к учению опирайтесь на искреннюю
убежденность; стойте до смерти за правильное учение. Если в Поднебесной царит
спокойствие, будьте на виду; если в Поднебесной нет спокойствия, скройтесь.
Если государство управляется правильно, бедность и незнатность вызывают
стыд. Если государство управляется неправильно, то богатство и знатность
также вызывают стыд.»
Кто-то спросил: «Правильно ли отвечать добром на зло?» Учитель
ответил: «Как можно отвечать добром? На зло отвечают справедливостью. На
добро отвечают добром.»
Учитель сказал: «Не беспокойся о том, что люди тебя не знают, а
беспокойся о том, что ты не знаешь людей.»
Учитель сказал: «Благородный муж предъявляет требования к себе,
низкий человек предъявляет требования к людям.»
ПРИЛОЖЕНИЕ
Г><)|
Учитель сказал: «Благородный муж держит себя строго, но не устриц
вает споров с людьми, он умеет быть в согласии со всеми, но ни с кем иг
вступает в сговор.»
Цзы-гун спросил: «Можно ли всю жизнь руководствоваться одним
словом?» Учитель ответил: «Это слово — взаимность. Не делай другим того,
чего не желаешь себе.»
Учитель сказал: «Когда нет желания заниматься малыми делами, это
вредит большим замыслам.»
Учитель сказал: «Человек может сделать великим путь, которым идет,
но путь не может сделать человека великим.»
Учитель сказал: «Когда, совершив ошибку, не исправил ее, это и
называется совершить ошибку.»
Учитель сказал: «Те, кто обладает врожденными знаниями, стоят выше
всех. За ними следуют те, кто приобретает знания благодаря учению. Далее
следуют те, кто приступает к учению, встретившись с трудностями. Те же,
кто, встретившись с трудностями, не учатся, стоят ниже всех.»
Цзы-чжан спросил Кун-цзы о человеколюбии. Учитель ответил: «Тот,
кто способен проявлять в Поднебесной пять качеств, является
человеколюбивым.» Цзы-чжан спросил о них. Учитель ответил: «Почтительность,
обходительность, правдивость, сметливость, доброта. Если человек почтителен,
то его не презирают. Если человек обходителен, то его поддерживают.
Если человек правдив, то ему доверяют. Если человек сметлив, он добивается
успехов. Если человек добр, он может использовать других.»
Учитель сказал: «Ю, слышал ли ты в шести фразах о шести пороках?»
Цзы-лу ответил: «Нет.» Учитель сказал: «Садись! Я расскажу тебе. Любить
человеколюбие и не любить учиться. Порок в том, что это ведет к тупости.
Любить мудрость и не любить учиться. Порок в том, что это ведет к
тому, что человек разбрасывается. Любить правдивость и не любить учиться.
Порок в том, что это ведет к нанесению ущерба самому себе. Любить
прямоту и не любить учиться. Порок в том, что это ведет к грубости. Любить
мужество и не любить учиться. Порок в том, что это ведет к смутьянству.
Любить твердость и не любить учиться. Порок в том, что это ведет к
сумасбродству.»
Цзы-гун спросил: «Испытывает ли благородный муж отвращение к
кому-либо?» Учитель ответил: «Испытывает. Ему отвратительны те, кто
плохо говорит о людях. Он испытывает отвращение к тем, кто, будучи
внизу, клевещет на вышестоящих. Ему отвратительны те, кто, обладая
смелостью, не соблюдает ритуала. Он испытывает отвращение к тем,
кто, будучи решителен, действует не думая. А Вы, Сы, испытываете ли
отвращение к кому-нибудь?» Цзы-гун ответил: «Я испытываю отвращение
к тем, кто считает мудростью повторение чужих мыслей; кто думает, что
неподчинение есть смелость, а разоблачение чужих тайн — правдивость.»
(перевод В. Кривцова)
ДХАММАПАДА 1 (отрывки)
О! Мы живем очень счастливо, невраждующие среди враждебных:
среди враждебных людей живем мы, невраждующие.
1Один из возможных переводов слова дхамма — учение, слова пада —
путь.
592
ПРИЛОЖЕНИЕ
О! Мы живем очень счастливо, нетомящиеся среди томящихся: среди
томящихся людей живем мы, нетомящиеся.
О! Мы живем очень счастливо, небольные среди больных: среди
больных людей живем мы, небольные.
О! Мы живем очень счастливо, хотя у нас ничего нет. Мы будем питаться
радостью, как сияющие боги.
Если странствующий не встретит подобного себе или еще лучшего, пусть
он укрепится в одиночестве: с глупцом не бывает дружбы.
Если глупец связан с мудрым даже всю свою жизнь, он знает дхамму
не больше, чем ложка — вкус похлебки.
Если же глупец на свое несчастье овладевает знанием, оно уничтожает
его удачливый жребий, разбивая ему голову.
Что бы ни сделал враг врагу или же ненавистник ненавистнику, ложно
направленная мысль может сделать еще худшее.
Что бы ни сделали мать, отец или какой другой родственник, истинно
направленная мысль может сделать еще лучшее.
Если кто увидит мудреца, указывающего недостатки и упрекающего за
них, пусть он следует за таким мудрецом, как за указывающим сокровище.
Лучше, а не хуже будет тому, кто следует за таким.
Если хотя бы мгновение умный связан с мудрым, быстро знакомится он
с дхаммой, как язык со вкусом похлебки.
Не потому он мудр, что много говорит. Спокойного, свободного от
ненависти, не знающего страха называют мудрым.
Исполненного добродетели и проницательности, стойкого в дхамме,
говорящего правду, исполняющего свой долг — такого считает народ
приятным.
Если рука не ранена, можно нести яд в руке. Яд не повредит не
имеющему ран. Кто сам не делает зла, не подвержен злу.
Как ржавчина, появившаяся на железе, поедает его, хотя из него она
и возникла, так и собственные поступки приводят к несчастью того, кто
преступил нравственный закон.
Пусть он откажется от гнева, пусть он оставит самодовольство, пусть
он превозможет все привязанности. Никакие несчастья не случаются с тем,
кто не привязан к имени и форме.
Найдется ли в мире какой-либо человек, смиривший себя скромностью,
кто не нуждался бы в понукании, как хорошо тренированная лошадь — в
кнуте?
Подобно хорошо тренированной лошади, тронутой кнутом, будьте
энергичными и одушевленными. С помощью веры, добродетели и энергии,
самоуглубления и изучения дхаммы вы освободитесь от великого зла.
Строители каналов пускают воду, лучники подчиняют себе стрелу,
плотники подчиняют себе дерево, мудрые смиряют самих себя.
(перевод В. Топорова)