ТРИГОНОМЕТРИЯ
ДОПОЛНИТЕЛЬНЫЙ МАТЕРИАЛ
К КУРСУ ГЕОМЕТРИИ 9, 10 КЛАССОВ
1
ТРИГОНОМЕТРИЯ
ДОПОЛНИТЕЛЬНЫЙ МАТЕРИАЛ к курсу геометрии 9, 10 классов
ИЗДАНИЕ 5-е
ИЗДАТЕЛЬСТВО «ПРОСВЕЩЕНИЕ» Москва 1970
514 (075) Т67
ОТ ИЗДАТЕЛЬСТВА
В связи с тем, что в программу по геометрии для 9—10 классов включена тема «Решение треугольников», издательство «Просвещение» по предложению Министерства просвещения РСФСР выпускает дополнительное пособие по тригонометрии.
Представляемое пособие содержит соответствующий программе учебный материал, взятый из учебника С. И. Новосёлова «Тригонометрия», а упражнения из «Сборника задач по тригонометрии для 9 и 10 классов средней школы» П. В. Стратилатова.
В целях возможного использования полных изданий учебника С. И. Новосёлова и задачника П. В, Стратилатова в настоящем пособии введена двойная нумерация параграфов учебника и номеров задач. В скобках указана старая нумерация.
Данное пособие подготовлено к изданию П. В. Стратилатовым.
ТРИГОНОМЕТРИЯ
Дополнительный материал к курсу геометрии 9, 10 классов
Редактор В. Г. Долгополов	‘ 1	:
Технический редактор Л. К, Кухаревич Корректор В. Г. Соловьева
Подписано к печати с матриц 12/1Х 1969 г. 60x90’/ie. ТипографоСМ М 0.
Печ. л. 5. Уч.-изд. л. 4,07. Тираж 1000 тыс. экз. Заказ 4W,
Издательство «Просвещение»’ Комитета по печати при Сонет» Министров РСФСР. Москва, 3-й проезд Марьиной рощи, 41
Саратовский полиграфический комбинат Росглавполш рпфнромм Комитета по печати при' Совете Министров РСФСР. Саратов, ул. Чернышевского, 69.
Цена б коп.
6-6
ВВЕДЕНИЕ
§ 1 (35)., Элементы треугольника
В геометрии рассматриваются элементы треугольника: стороны, углы, периметр, площадь, биссектрисы, медианы, высоты и т. п. Стороны треугольника и его углы называются основными
элементами.
Если А, В, С — вершины углов треугольника, то принято этими же буквами обозначать и сами углы (и их величины); строчными
буквами а, Ь и с принято обозначать стороны (и их величины), противолежащие углам, которые обозначены теми же прописными буквами (черт. 1).
Допустимые значения основных элементов треугольника должны удовлетворять следующим условиям:
1°. Углы треугольника положительны и в сумме составляют 180°-.

В а
Черт. 1
Д>0, В >0, С>0 и А + В + С= 180°.
2°. Длины сторон треугольника положительны, и всякая сторона меньше суммы двух других сторон-.
0 <.а<,Ь + с\ 0 <Z b <с + а; 0 <с < а + Ь.
§ 2 (33)« Натуральные таблицы и таблицы логарифмов тригонометрических функций
Для практических вычислений пользуются таблицами приближённых значений тригонометрических функций и их логарифмов. В школьных вычислениях применяются четырёхзначные.таблицы В. М. Брадиса. В более точных вычислениях применяются таблицы значений функций с большим числом значащих цифр (например, пятизначные, семизначные таблицы).
Натуральные таблицы. Таблицы, в которых даются значения тригонометрических функций, называются натуральными
а
тригонометрическими таблицами. В таблицах VIII (см. таблицы Брадиса) даны приближённые значения с четырьмя десятичными знаками синусов и косинусов углов от 0 до 90° через каждые 6'. Формулы дополнительных аргументов:
sin (90° — а) = cos а; cos (90° — а) = sin а показывают, что для вычисления значений синуса и косинуса могут служить одни и те же таблицы. Так, например, sin 26° и cos 64° имеют одно и то же значение. В таблицах В. М. Брадиса значения аргумента синуса расположены в порядке возрастания сверху вниз, а значения аргумента косинуса — снизу вверх. Приближённое значение синуса или косинуса угла, содержащего целое число градусов, дано в таблице. Так, например, значение sin 33° » » 0,5446 помещено рядом с пометкой 33° в крайнем левом столбце «А». Значение cos 33°» 0,8387 помещено рядом с пометкой 33° в крайнем правом столбце «А».
Чтобы найти sin 33°12', отыскиваем в левом столбце «А» пометку 33°, а в самой верхней строке — пометку 12'. Значение sin 33°12'» 0,5476 находится на пересечении соответствующих строки и столбца. Значение cos 33°12'» 0,8368 находится так же, с той лишь разницей, что пометку 33° следует искать в крайнем правом столбце «А», а пометку 12' — в самой нижней строке.
Пусть требуется найти sin 33°14'. Из таблиц находим sin 33°12'» » 0,5476. Так как функция sin а в промежутке от 0 до 90° возрастает, то sin 33°14' > sin 33°12'. Следовательно, к значению sin 33°12' надо прибавить поправку на 2', которая помещена в таблице поправок справа от основной таблицы. В строке 33° и в столбце поправок с пометкой 2' находится число 5, которое следует прибавить к четвёртому десятичному знаку sin 33°12'. Таким образом, sin 33°14'» 0,5481. Если требуется найти sin 33°17', то из таблиц находим sin 33°18'» 0,5490 и из четвёртого десятичного знака вычитаем поправку на Г, равную 2. Итак, sin 33° 17'» » 0,5488. Значения косинуса находятся при помощи таблиц тем же способом, но со следующим отличием: функция cos а у б ы в'а ю-щ а я (в промежутке от 0 до 90°); поэтому, еёли косинус найден для меньшего значения аргумента, надо поправку вычитать (а не прибавлять); если же косинус найден для большего значения аргумента, то надо поправку прибавлять (а не вычитать). Так, например, чтобы вычислить cos 33Q14', находим по таб-. лицам cos 33°12'» 0,8368 и от последнего десятичного знака отнимаем поправку на 2', равную 3; итак, cos 33°14'» 0,8365. Чтобы вычислить cos 33°17', следует к последнему знаку cos 33’ 18'» » 0,8358 прибавить поправку на Г, равную 2. Итак, cos 33°17'» » 0,8360. -
В таблице IX В. М. Брадиса даны значения тангенса от 0 до 76° через каждые 6'. В таблице X даны эпичен и и тангенса от 76 до 89Q через Г. Наличие более подробной таблицы X для тангенсов
4
углов, близких к 90°, объясняется тем, что для этих углов разноси» между двумя соседними табличными значениями тангенса — зак называемая табличная разность — изменяется очень быстро. 11о тем же таблицам IX и X находят значения котангенса. Правила прибавления и вычитания поправок те же, что и для таблиц значений синуса и косинуса: следует помнить, что в интервале (0°, 90и) тангенс возрастает, а котангенс убывает.
Для нахождения угла по данному значению его тригонометрической функции применяются те же самые таблицы значений тригонометрических функций. Покажем это на примерах.
1. Найти острый угол а, зная sin а = 0,1016.
Решение. В таблице VIII находим число, ближайшее к 0,1016; это есть число 0,1011, помещённое в строке с пометкой 5° и в столбце с пометкой 48'. Заданное значение синуса 0,1016 больше, чем 0,1011; поэтому истинное значение угла больше, чем 5°48', так как sin а есть возрастающая функция в интервале (0°, 90°). В таблице поправок число 6 является ближайшим к числу 5, на которое отличаются последние десятичные знаки чисел 0,1016 и 0,1011. Прибавив соответствующую поправку, равную 2', получим;
а = arc sin 0,1016« 5°50'.
2. Найти 0 = arccos(— 0,5375).
Решение. Искомый угол оканчивается во второй четверти, так как cos — 0,5375 отрицателен. Вычислим острый угол а дополняющий искомый до 180°; имеем:
cos а = cos (180Q — р) = — cos Р = — (— 0,5375) = 0,5375.
Значению 0,5373, ближайшему к 0,5375, соответствует угол 57°30'. Разности 2 единицам четвёртого десятичного знака соответствует поправка на Г. Эту поправку следует вычесть. Итак,
а = 57°29' и р» 1809 — 57°29' = 122°ЗГ.
При вычислениях по натуральным таблицам целесообразно представлять произведение тригонометрических функций в виде суммы.
При вычислениях следует соблюдать правила приближённых вычислений.
Так, например, если приближённые числа даны с тремя значащими цифрами, то при выполнении умножения и деления значения функций, взятые из таблиц, следует округлить, сохранив четыре значащие цифры (четвёртая цифра сохраняется в качестве «запасной»), все промежуточные результаты вычислений следует округлять, сохраняя четыре значащие цифры, окончательный результат следует округлить до трёх значащих цифр'. При сложении приближённого числа, данного, например, с п я т ь ю десятичными знаками со значением тригонометрической функции, взятым из четырёхзначных таблиц, следует округлить приближённое число, сохранить в нём четыре десятичных знака. Если
5
;при вычислениях, требующих большой точности, такое округление недопустимо, следует воспользоваться более точными таблицами.
Примеры. 1. Вычислить по четырёхзначным таблицам sin 70° cos 55°.
Решение. Преобразуем произведение в сумму:
.	sin (70° + 55°) + sin (70° — 55°) sin 125* + sin 15°
sin 70 cos 55° =>------------------------=------------------.
&
По формулам приведения sin 125° —sin (180° — 125°) = sin 55°. Значения sin 55° ~ 0,8192 и sin 15° ~ 0,2588 находим по таблицам. Итак:
sin 70° cos 55° » ± (0,8192 + 0,2588) = 0,5390.
2.	Вычислить произведение S = 0,721 sin231°12'.
Решение. Преобразуем квадрат синуса в разность, воспользовавшись 1 — cos 2а формулой sin2 а =------; получим:
5 = 0,721 sin231°12' =	0,721 (1 — cos62°24').
По таблицам найдём cos 62°24'0,4633 и далее 1 — cos 62°24' « 0,5367. Следовательно,
5 =	0,721 -0,5367^0,1935«0,194.
Логарифмические таблицы. Для вычислений при помощи логарифмов составлены таблицы логарифмов значений тригонометрических функций. В таблицах Брадиса XV — XIX эти логарифмы даны с четырьмя десятичными знаками для значений аргумента в интервале (0°, 90°).
Логарифмическая функция при основании 10 является возрастающей; поэтому большему значению выражения, находящегося под знаком логарифма, соответствует большее значение логарифма. Так как в первой четверти функции sin х и tg х возрастают, а функции cos хи ctg х убывают, то и функции 1g sin х и 1g tg х также возрастают, а функции 1g cos х и 1g ctg х убывают.
Логарифмические тригонометрические таблицы устроены так же, как и натуральные; правила пользования ими те же.
1. Таблицы служат для вычисления значений логарифмов тригонометрических функций и для вычисления углов по значениям логарифмов их тригонометрических функций.
' 2. Для вычисления логарифмов синусов и косинусов (тангенсов и котангенсов) служит одна и та же таблица.
3.	Значения логарифмов даны для углов через каждые 6'. Поправки на Г, 2' и 3' даны в специальных таблицах справа от основной таблицы. Прибавление и вычитание поправок производителе учётом того, что в интервале (0, 90°) функции 1g sin х и 1g tg х возрастают, a 1g cos х и 1g ctg х убывают.
6‘
4.	Для промежутков, в которых табличная разность изменяется быстро, значения функций даны через Г, Такова, например, табли-ца XV значений логарифма синуса (косинуса} для углов от 0 до 14“ (от 76 до 90°).
5.	При вычислениях по четырёхзначным таблицам логарифмов приближённые числа следует округлить, сохранив четыре значащие цифры.
6.	При вычислении произведений, содержащих отрицательные сомножители, следует вычислить произведение абсолютных величин и взять его с надлежащим знаком (по числу отрицательных сомножителей).
На чертеже 2 представлен график функции у = 1g sin х. Этот график построен так: в I четверти 0 < х < , промежуточный аргумент и = sinx возрастает от 0 до 1, а функция у = 1g sin х = — lg и возрастает от — оо до 0. Для построения точек графика можно составить, например, следующую таблицу:
У
—0,81;—0,51 —0,34
—0,23—0,15—0,09
—0,05
—0,02
—0,01
0
взяв (с округлением) значения 1g sin х из таблицы XV Брадиса.
В промежутке — < х < л функция 1g sin х убывает от 0 до
— оо, так как во II четверти sin х убывает от 1 до 0.
Сегмент — л < х < 0 не принадлежит области определения функции, так как в нижней полуокружности sin х < 0 и 1g sin х не имеет смысла.
7
Функция Ig sin x периодическая с периодом 2л, так как lg sin (х + 2л)« Ig sin X.
График состоит из отдельных периодически повторяющихся линий.
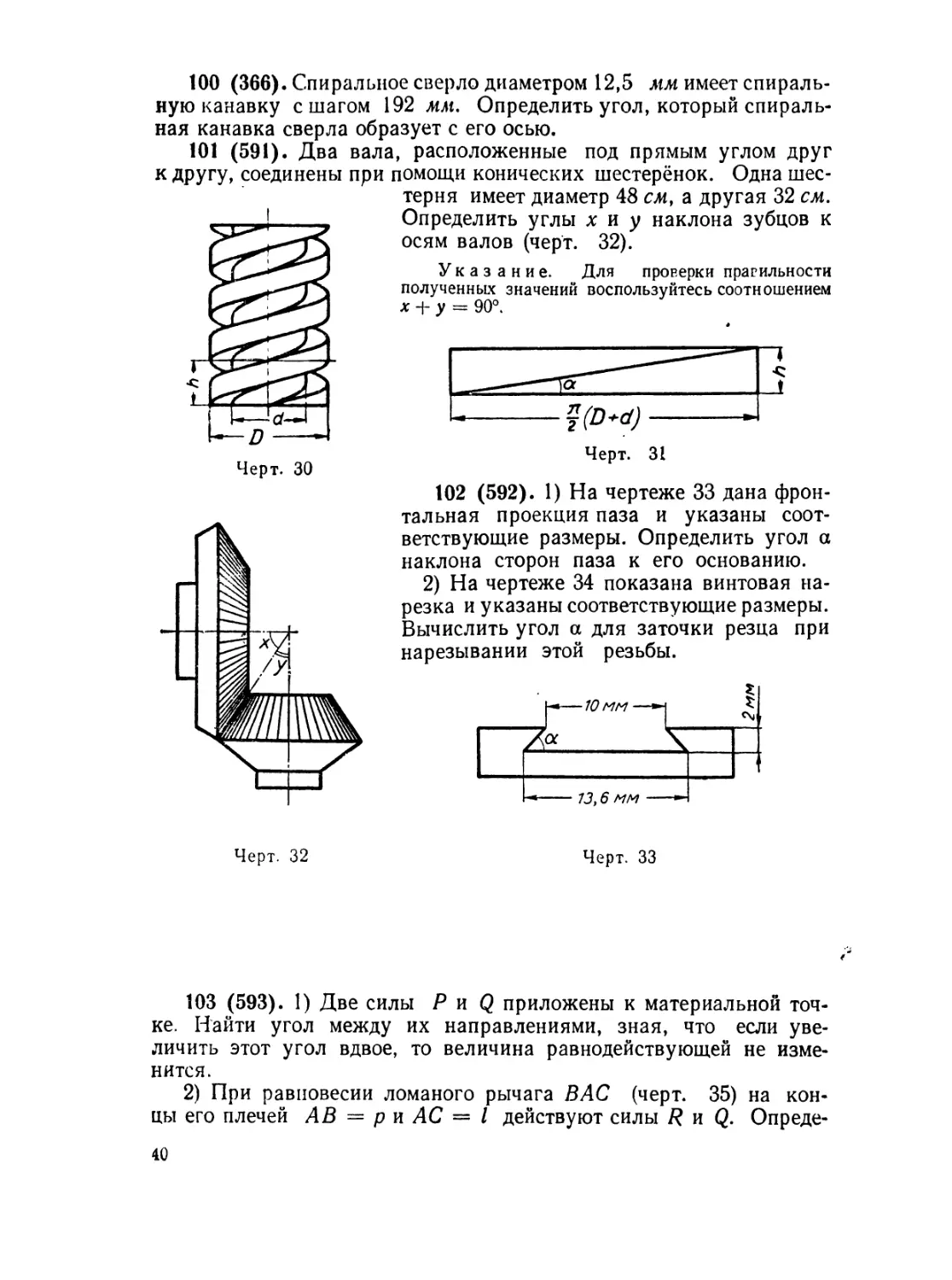
Упражнения.
1 (336). 1) Найти:
a) sin 17°23'; б) cos28°31'; в) cos-; г) cos(— 1,2538); 8
д) sin(— е) sin2,1730; ж) tg(—70°41'); з) tg^ ;
и) tg3,017; к) ctgл) ctg42°55'; м) ctg0,2613.
2)	Найти:
a) arc sin (—0,1217); б) arc sin 0,5670; в) arccos-^;
г) arc cos (— 0,7328); д) arc tg 10,35; ,е) arc tg ( —12, 31);
ж) arc etg 2,175; з) arc etg 0,6830.
3)	Найти наименьшее положительное значение а, если:
a) sin а ——0,7236; б) cos сс 0,3892; в) tga^0,7524;
г) etg a = — 1,340.
4)	Найти наиболее рациональным способом значения следующих выражений:
а) sin42°-cos 12°; б) cos38°-cos 52°; в) sin 82°-sin 66°;
г) sin27°40\cos70°48'; д) cos48° 14'-cos82° 16';
e) sin 72°26'-sin 17°34'; ж) sin 0,2347-cos 1,2459;
з) sin 1,3841-sin2,1176.
5)	To же:
\ sin 2 a	1 лог i	cos 3 x	г с о t t
a) ----- при a =12 51 ; o) ------при x = 55 11 ;
sin a	cos x
sin 2 a a = O)O124; r) 1>763 COS2 18" 16';
cos2a-tg a
д) 2,537 cos265°38'; e) x + sinx при x^2,5;
ж) x + cos — при x = л; з) x + cosx при к = 1,295; X
и) cos2a(l -f; cos a), sin2 при a = 126° 18'.
2	(337)« Найти по таблицам:
1)	a) lgcos21°37°; 6) lg cos 63°42'; в) lg cos 21° 11';
r) lgcos47°12'; д) lgcos53°15'; e) lgcosl°23'.
8
2)	a) 1g sin 12°8'; 6) 1g sin 50°22'; в) 1g sin 44°53';
r) 1g sin 62°47'; д) 1g sin 30°46'; e) 1g sin 88°34'.
3)	a) 1g tg 27°41'; 6) lg tg 16°7'; в) 1g tg 70°43';
r) lg tg 12°15'; д) 1g tg 84°19'; e) 1g tg 89°10'.
4)	a) 1g ctg 80°53'; 6) 1g ctg 20°26'; в) 1g ctg 77°21'; r) 1g ctg 15°38'; д) 1g ctg 87°59'; e) 1g ctg 15°40'.
Найти (положительный) острый угол х, если:
5)	1g cos х равен: £4001; £4634; J.6747;Т,9341;!,2711.
6)	lg sin х равен: £,8615; 2,9301; 1,9497; 1,3494; f.5080.
7)	lg tg x равен: £,7865; J),0066; 1,4608; 0,0771; 0,0002.
8)	lg ctg x равен: 1,0368; 1,5018; 0,3738; 1,3387; 1,2435.
3	(338). Решить каждое из данных простейших тригонометрических уравнений: а) найти главное значение угла х и б) выписать формулу множества всех решений:
1) sinx= 0,681; 2)sinx=jj; 3) sinx =— 0,3721;
4) tg x =	5) tg x = 1,45; 6) tgx =— 2,48;
7) cos x — 0,7621; 8) cos x = — 0,5688; 9) ctg x = 3;
10) ctg x= —0,731.
4 (339). Определить главное значение x из условий (использовать таблицы натуральных значений и логарифмов тригонометрических функций):
1) tg х = tg 40° + tg 70°; 2) cos x = 1 - ctg 66°12';
3) cos x = 1 tg 117°; 4) tg x = sin 44” cos 166’.
5 (340). Вычислить наиболее рациональным способом значения выражений:
1)	(а2 —	• sin (а + р) , если а = 7,386; Ь = 5,214; а = 42°26';
sin а • cos р
Р = 68°34';
2)	а2 . -L_ •	— tg 2а при а == 0,0204; а = 67°34'.
cos а	_____
3)	X = л • (sin30°53' + sin80°24'); 4) х =
7) х = /0,005 -(1 4- 2 sin 41 °); 8) х = (2,715)3-КЗ— 4 cos272°5'.
6 (346). Вычислить при помощи логарифмической линейки:
1)	а) 3,5 sin 25°; б) 8,3 sin 72°; в) 1,2 sin 3°.
2)	а) 2,8 tg 68°30'; б) 6,3 tg 29°; в) ?,4 tg 2°30'.
2 Тригонометрия
9
3)	а) -У_; 6) в)
sin 14м sin 43° sin 63°
их x 12,3	8,5	.	5,7 ч 12,8
7	tg53‘ 30'	tg 67°	tg!6° tg 28°30'
5)	a)	4,7	cos 37°;	6)	7,2 ctg 57°;	в)	—r)
’ ’	'	7	cos 71°	ctg623
6)	a)	sin	22° • sin 73°; 6) sin 41° •	tg 15°30';	в)	cos	29°	• sin 41°;
r) tg	32°	• tg 53°;	д)	tg 62°• cos	25°; e) cos 53° •	cos	64°;
ж) sin 4° • sin 57°; з) tg 12° • tg 4°30'.
4 sin 73° sin 8°	. sin 16°
7)	a ) ----; 6) -----; в) ----.
sin 31° sin 4°30' sin 8°
7 (343). Доказать, что тригонометрические функции углой косоугольного треугольника удовлетворяют следующим соотношениям:
1)	sin А + sin В + sin С = 4 cos — • cos — • cos —.
2	2	2
Указание. Воспользоваться формулами для преобразования суммы тригонометрических функции в произведение.
АВС
2)	4 sin - • sin — • cos— = sin A + sin В — sin C.
7	2	2	2
Указание. Воспользоваться формулами для преобразования произведения тригонометрических функций в сумму.
АВС
3)	cos А + cos В + cos С = 1 + 4 sin — - sin — - sin —.
7	2	2	2
ABC
4)	4 cos — • cos - * sin-1 = cos A 4- cos В — cos C.
7	2	2	2
5)	tg A + tg В + tg C = tg A • tg В  tg C.
6)	ctg^ + ctg^ + ctg^- = ctg4--ctg^-. ctg^-.
7)	sin 2A + sin 2B + sin 2C = 4 sin A • sin В • sin C.
8)	cos 2A + cos 2B + cos 2C = —1—4 cos A • cos В • cos C.
9)	cos2 A + cos2 В + cos2 C — 1 — 2 cos A • cos В • cos C.
10)	sin2 A -j- sin 2 В + sin2C = 2 '+ 2 cos A • cos В • cos C.
11)	Доказать, что если имеет место равенство
tgy ' tg | + tg | • tg У- + tg | • tg X = 1, где | и | - ост-рые углы, то a + p + у = 180°.
12)	Доказать, что если имеет место равенство
ctg a • ctg р + ctg a • ctg у + ctg p • ctg у = 1, где a, p, у — острые углы, то a + Р + Y = 180°.
10
Глава I
РЕШЕНИЕ ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ
§ 3 (37)< Основные соотношения и задачи
В тригонометрии рассматриваются задачи, в которых требуется вычислить те или иные элементы треугольника по достаточному количеству численных значений заданных его элементов. Эти задачи обычно называются задачами на решение	&
треугольника.	у
Пусть АВС—прямоугольный треугольник, С —пря- с / мой угол, а и Ъ—катеты, противолежащие острым углам	/ °
А и В, с — гипотенуза (черт. 3); тогда имеем:	/___
Косинус острого угла есть отношение при- д ь с лежащего катета к гипотенузе:	Черт, з
(1)
Синус острого угла есть отношение противолежащего катета к гипотенузе:
sin А = —, sin В =
(2)
Тангенс острого угла есть отношение противолежащего катета к прилежащему:
о	а
(3)
Котангенс острого угла есть отношение прилежащего катета к противолежащему:
ctgл = A, ctg = А a	b
Сумма острых углов равна 90°.
Основные задачи на прямоугольные треугольники.
Задача I. Даны гипотенуза и один из острых угловх вычислить прочие элементы.
Решение. Пусть даны с и А. Угол В = 90° — А также известен; катеты находятся, из формул (1) и (2):
а = с sin A, b = с cos А.
Задача IL Даны катет и один из острых углов, вычислить прочие элементы.
Решение. Пусть даны а и А. Угол В = 90° — А известен; из формул (3) и (2) найдём:
b =--- a tgB (= a ctg Л), с = ——. sin А
Задача III. Даны катет и гипотенуза, вычислить элементы.
Решение. Пусть даны а и с (причём а < с). Из равенств
(2) найдём угол А:
sin А = — и Л = arc sin—, затем В=90°—А и, наконец, катет Ь: с	с
b = с • cos А (= с sin В).
Задача IV. Даны катеты а и Ь, найти прочие элементы.
Решение. Из равенств (3) найдём острый угол, например Л:
tg Л = —, Л = arc tg—, угол В = 90° — Л, гипотенуза: b	ь
,Z= —=
sin А \ sin В cos В J
Ниже приводится пример решения прямоугольного треугольника при помощи логарифмических таблиц*.
* Вычисление элементов прямоугольных треугольников по натуральным таблицам известно из курса геометрии VIII класса.
12
При вычислениях по логарифмическим таблицам следует выписать соответствующие формулы, прологарифмировать их, подсп!-вить числовые данные, по таблицам найти требуемые логарифмы известных элементов (или их тригонометрических функций), вычислить логарифмы искомых элементов (или их тригонометрических функций) и по таблицам найти искомые элементы.
Пример. Даны катета = 166,1 и гипотенуза с = 187,3; вычислить острые углы, другой катет и площадь.
Решение. Имеем:
a	1g а = 2,2204
sin А = —; lg sin А = lg а — lg с\ ~ с = 2,2725
lg si пД=1,9479;
А 62°30'; Вх 9 О9 — 62°30' « 27°30'.
Вычисляем катет Ь:
1g а = 2,2204
&=atgS; lg &= lga+ IgtgB; +ig tg в = 1,7165
lg 6 = 1,9369; b x 86,48.
Площадь треугольника можно вычислить по формуле
S = ab = 0,5 a2 tgB;
1g 0,5 = 1,6990 । 2 Ig a =£,4408 lgtgB = 1,7165
lgS= 3,8563
lg a = 2,*2204
S = 7183.
Для контроля подсчитаем угол А на логарифмической линейке:
4	• а . 166	_
А = arc sin —= arc sin — « 62°.
с	187
Примечание. Катет b можно вычислить по теореме Пифагора, пользуясь таблицами квадратов и квадратных корней (табл. III и IV):
b = V 187;32— 166,12 = /3’508б^2759б' « 86,54.
Расхождение с ранее полученным значением b « 86,48 объясняется погрешностями таблиц, в которых даются приближённые значения функций. Результат 86,54 является более точным.
Упражнения
8 (341). Решить прямоугольные треугольники по данным основным элементам. Решение каждого примера следует выполнять при помощи таблиц логарифмов и логарифмической линейки.
1)	Даны гипотенуза и острый угол:
а) сж 9,35;	65°10'; б) сж 0,7979; А « 66°35';
в) сж 3,643;. Аж 50°10'.
2)	Даны катет и острый угол:
* а) аж 6,37; Аж 4°20';<б) Ьж 0,1738; Аж 35°55';
в) Ьж 0,2954; В ж 25°37'.	i
13
3)	Даны гипотенуза и катет:
а) ст 697, ах 528; t>) сх 113; Ьх 15;
в) с = 1710; Ьх 823.
4)	Даны катеты: ,
а) а«261; Ьх 380; б) ах 0,0978; Ьх 0,1003;
в) ах 12,01; Ьх 6,92.
9 (342). Решить равнобедренный треугольник по данным его элементам.
Обозначения: а = с — боковая сторона; Ь — основание; А = — С — углы при основании; В — угол при вершине; ha— высота, опущенная на сторону a; S — площадь треугольника.
])ах 797,9;	Д«66°35'.	4) А х 65°;	hax 20. '
2	) ах 8,76;	Ьх 13,96.	5) ах 627;	Вх 133°.
j3) Вх 73°14';	Sx 4504.	6) Ьх 925,2;	hbx 721,4.
10	(8). Вычислить площадь ромба по его стороне а = 7,5 см и острому углу а = 22°12'.
J 11 (9). Диагонали ромба = 28 см и d2 = 49 см\ вычислить углы ромба.
12	(10). По основанию b = 28,13 м и боковой стороне а = — 17,53' м равнобедренного треугольника вычислить, угол при основании.
13	(11). По основанию b = 31,26 м и высоте h = 20,75 м равнобедренного треугольника вычислить угол при его вершине.
•J 14 (12). Основания трапеции а и bt одна из боковых сторон с, острый угол, прилежащий к ней, а. Определить площадь трапеции.
15	(13). В круге радиуса R = 4,175 м вычислить длину хорды, стягивающей дугу а = 37°42'.
16	(14). Смежные стороны прямоугольника а = 75,2 см и Ъ = = 63,6 см\ вычислить, на какие части делит диагональ прямоугольника угол при его вершине.
17	(15). Смежные стороны прямоугольника а = 13,5 см и b = = 7,4 см. Вычислить угол Между его диагоналями.
х! 18 (16). В круге радиуса R = 35,8 см проведена хорда длиной а = 28,7 см. Найти число градусов и минут в меньшей дуге, стягиваемой этой хордой, и расстояние хорды от центра круга.
з
19	(17). Хорда равна у диаметра круга. Определить число градусов и минут в меньшей дуге, которая стягивается этой хордой.
20	(18). Угол а, вписанный в окружность, опирается на хорду, t длина которой а. Определить радиус круга.
21	(19). Дан круг радиуса R = 3,35 см. Из точки, отстоящей от центра на а = 8,32 см (а > R), проведены две касательные. Вычислить угол между касательными.
22	(20). Линия центров двух кругов, один из которых расположен вне другого, равна d = 6,245 м, а радиусы их равны R == = 3,065 м и г = 1,007 м. Определить углы, под которыми общие
J4
внутренняя и внешняя касательные этих кругов пересскаюг линию их центров.
23	(21). Боковая сторона равнобедренного треугольника и, угол при вершине 0. Определить радиусы описанной (/?) и вписан ной (г) в этот треугольник окружностей.
24	(22). Определить радиус круга, описанного около прямо угольного треугольника, катет которого равен а, а прилежащий к нему острый угол равен 0.
25	(23). С маяка, высота которого над уровнем моря Н& «150 лс, определяют расстояние до проходящего мимо парохода. Угол понижения а« 9° (черт. 4). Вычислить искомое расстояние.
26	(24). Самолёт радирует капитану рыболовецкого судна, что он находится над косяком рыбы на высоте Н« 950 м. С судна определяют угол а « 26°30' возвышения самолёта. Вычислить расстояние судна от косяка рыбы (черт. 5).
Черт. 5
27	(25). Чтобы измерить высоту башни главного входа здания Московского государственного университета имени М. В. Ломоносова, измерили угломерным инструментом угол возвышения а
15
(черт. 6). Расстояние угломера от главного входа равно а. Вычислить приближённое значение определяемой высоты, если высота угломерного инструмента h 53°; а ~ 180 м; hx 1,2 м).
Черт. 6
28	(26). Штурман на карте прокладывает курс корабля и при прохождении мимо маяка измеряет угол возвышения а. Вычислить отрезок, который на карте отложит штурман от точки, изображающей маяк, для установления местонахождения корабля. Высота маяка Я, масштаб карты —!— (а» 2°50'; Нж 150 jh).
F юооооv	7
29 (27). Чтобы определить ширину реки, проводят на одном берегу, непосредственно у воды, базис АВ, равный а (черт. 7); из конца А базиса, по перпендикулярному к нему направлению, на противоположном берегу у самой воды видно дерево С; из другого же конца В базиса это дерево видно под углом 0 к базису. Вычислить ширину реки, если аж 45 м и 0^ 25°.	i
30 (28). Горная железная дорога поднимается па — м на каждые 30 м пути. Найти угол подъёма.
— Д Q В
Черт. 7
31 (32). Поперечный разрез насыпи, при постройке которой . был применён наибольший воз- f можный откос ф, представляет равнобедренную трапецию. Нижнее основание трапеции а, высота ft. Вычислить верхнее основание трапеции, если
10,0 м, ИжЗ,0 м и ф^ 39°.
16
32 (33). Две точки выходят одновременно из вершины прямого угла и движутся равномерно первая по одной, а вторая по друюй стороне этого угла; первая проходит по а метров, а вторая -по b метров в секунду. Под каким углом ср к направлению движения первой точки видна из неё вторая точка?
33 (34). На прямой MN взята точка Л, и из неё под острым углом а к прямой MN проведён отрезок Л В длиной а. Определить проекцию отрезка АВ на прямую MN. Как изменяется величина этой проекции при увеличении угла а от 0 до 90°?
34 (35). Две силы: Рж 4,3 кГ и 5,6 кГ — направлены перпендикулярно друг к другу. Найти равнодействующую этих сил и угол, который она образует с направлением силы Р,
35 (36). Принимая Землю за шар с приближённым значением диаметра, равным 12 740 км, по широте места ф определить длину окружности параллели, соответствующей этому месту. Вычислить для г. Москвы при ф^56°.
36 (37). Вагонетка весом Р движется по рельсам в гору под углом а. Какую наименьшую силу нужно приложить, чтобы удержать вагонетку на месте, если Р ж 0,7 тиа^ 12°40'?
37 (224). Большее основание трапеции служит диаметром описанной около неё окружности, радиус которой равен R. Острый угол трапеции а. Определить площадь трапеции.
. 38 (225). В угол 2а вписан круг радиуса R. К этому кругу проведена касательная, перпендикулярная к биссектрисе угла (между вершиной угла и окружностью). Определить периметр отсечённого треугольника.
39 (252). К двум внешне касающимся друг друга кругам проведены две общие внешние касательные, образующие угол а. Радиус большего круга /?. Найти радиус меньшего круга.
40 (253). Радиус круга, вписанного в прямоугольный треугольник с острым углом а, равен г. С центром в вершине угла а построена окружность, касающаяся противолежащего катета. Определить длину этой окружности.
41 (254). Основание равнобедренного треугольника равно 6, угол при основании равен а. Определить периметр треугольника.
42 (255). 1) Определить площадь треугольника по двум его углам а и р и по высоте hc, опущенной из вершины третьего угла.
2	) Доказать, что площадь всякого четырёхугольника равна половине произведения его диагоналей на синус угла между ними.
43	(305). Хорда а, проведённая из конца диаметра круга, образует с диаметром угол а. Через другой конец’хорды проведена касательная к кругу и продолжена до пересечения с диаметром. Определить отрезок касательной от точки касания до общей точки её с продолжением диаметра.
44	(306). В равнобедренный треугольник с углом а при основании вписана окружность. Периметр треугольника, полученного
17
соединением точек касания, равен р. Определить периметр данного треугольника.
45	(307). В круговой сектор радиуса R с центральным углом а вписан круг. Определить радиус круга.
46	(308). Расстояние между центрами двух внутренне касающихся окружностей равно d. Касательная, проведённая к меньшей окружности из центра большей, составляет с линией центров угол а. Определить радиус большей окружности.
47	(309). Диагональ трапеции, вписанной в круг радиуса /?, образует с её боковыми сторонами углы а и 2а. Определить площадь трапеции.
48	(310). Определить длину наименьшей диагонали правильного n-угольника, сторона которого равна а,
49	(311). К окружности радиуса R из одной и той же внешней точки проведены две касательные, образующие между собой угол ср. Определить площадь фигуры, ограниченной отрезками касательных и меньшей дугой окружности, заключённой между точками касания.
50	(312). В данный угол а вписан круг радиуса R. Определить радиус такого круга, который, касаясь внешним образом данного круга, касается в то же время сторон данного угла (два случая).
51	(313). Острый угол ромба равен^а. Определить площадь ромба, если площадь вписанного в него круга К кв. ед.
52	(314). В круг вписан правильный n-угольник, сторона ко-торого равна а. Определить сторону правильного вписанного 2п-угольника.
53	(315). В сегмент вписан квадрат; две его вершины, лежащие на дуге, делят дугу на три равные части. Определить дугу сегмента.
54	(316). Две окружности пересекаются, отсекая друг от друга дуги 2а и 20. (2а — дуга большей окружности.) Определить угол между общими внешними касательными.
55	(317). Около правильного п-угольника со стороной а описана окружность, и в него вписана другая окружность. Найти площадь образовавшегося кольца.
56	(318). В равнобедренном треугольнике высота равна ft, а высота, опущенная на боковую сторону, равна ftP Определить угол при основании треугольника.
57	(319). Перпендикуляр, опущенный из середины основания равнобедренной трапеции на боковую сторону, равен ft и делит боковую сторону пополам; тупой угол трапеции равен а. Найти площадь трапеции.
58	(320). К плоскости восставлен перпендикуляр длиной р; из основания его как из центра описана в плоскости окружность радиуса г. Определить угол между перпендикуляром и наклонной, соединяющей вершину перпендикуляра с любой точкой окружности (р = 4,5; г = 8).
18
59 (321). Через центр О квадрата, сторона которого АВ а, проведён перпендикуляр к плоскости квадрата; на нём взят отргюк ОМ = d, а из М на АВ опущен перпендикуляр МС. Вычислить угол между МС и его проекцией на плоскость квадрата.
60 (322). Ребро куба а = 10 см. Вычислить угол, под которым диагональ куба наклонена к его грани. Изменится ли этот угол, если изменить длину ребра куба?
61 (323). В основании четырёхугольной пирамиды лежит квадрат со стороной 8 см. Высота пирамиды, равная 7 см, проходит через точку пересечения диагоналей основания. Под каким углом боковое ребро пирамиды наклонено к плоскости её основания?
62 (324). Из центра О правильного треугольника АВС, сторона
которого равна а, восставлен перпендикуляр к плоскости треугольника, на нём взята точка М так, что отрезок МА = а; из М на АС опущен перпендикуляр MD. Вычислить угол между MD и плоскостью треугольника АВС.
63 (325). Концы отрезка АВ = а удалены отданной плоскости на т и п. Определить угол, который отрезок составляет с плоскостью, и вычислить этот угол, если а = 13 см, т --= 5 см и п = 8 см. (Рассмотрите два случая.)
64 (326). Дан двугранный угол а. Из точки, лежащей на одной грани этого, угла на расстоянии а от ребра, восставлен перпендикуляр до пересечения с другой гранью. Определить длину этого перпендикуляра (а = 6,06; а = 41°50').
65 (327). Прямоугольный треугольник АВС расположен так, что-гипотенуза его АВ лежит в плоскости Р, а катеты образуют с плоскостью Р углы аир. Определить угол между плоскостью треугольника и плоскостью Р.
66 (328). В прямоугольном треугольнике даны гипотенуза а и острый угол а. Определить расстояние от вершины прямого угла
до плоскости, которая проходит через гипотенузу и составляет
угол ф с плоскостью треугольника.
67 (329). Одна сторона (АВ) треугольника АВС лежит на плоскости Р. Две другие стороны (С А и СВ) составляют с плоскостью о	1	1
углы а и р, тангенсы которых соответственно равны — и —, а
проекции этих сторон на плоскость Р взаимно перпендикулярны. Определить угол наклона плоскости треугольника АВС к плоскости Р.
68 (330). Параллелограмм и плоскость Р расположены так, что одна из меныних сторон параллелограмма находится в плоскости Р, а противоположная ей удалена от плоскости Р на расстояние, равное расстоянию между большими сторонами параллелограмма. Определить угол между плоскостью Р и плоскостью параллелограмма, если стороны параллелограмма относятся как 3 : 5.
69 (331). Наклонная образует с плоскостью угол а; через вершину этого угла проведена в данной плоскости прямая под углом 0
19
к проекции наклонной на плоскость. Определить угол между наклонной и прямой в плоскости.
70	(332). Прямая, находящаяся вне плоскости, пересекаясь с прямой, лежащей в плоскости, образует с этой прямой угол а, а ета последняя образует угол Р с проекцией первой прямой на плоскость. Определить угол первой прямой с плоскостью (а = 8°20'; ₽ = 5э40')
71	(333). Из двух точек плоскости, удалённых друг от друга на расстояние а, проведены две параллельные наклонные под углом <р к плоскости. Определить расстояние между ними, если расстояние между их проекциями на плоскость равно Ь.
72	(334). Отрезок АВ параллелен плоскости. Из его крнцов проведены к плоскости две наклонные: АС = с и BD = d. Наклонная АС составляет с плоскостью угол а. Определить угол наклона BD к этой плоскости.
.73 (335). Через концы трёх рёбер прямоугольного параллелепипеда, выходящих из одной вершины, проведена плоскость, образующая угол а с плоскостью основания. Смежные стороны основания имеют длины а и Ь. Определить площадь получившегося сечения.
74 (583). Общие внешние касательные к двум внешне касающимся окружностям между точками касания имеют длину а и составляют с линией центров угол а. Точки касания прямых каждой окружности соединены хордами. Определить площадь четырёхугольника, вершинами которого являются точки касания.
75 (584). Между двумя параллельными плоскостями проведены наклонная, образующая с ними угол а, и перпендикуляр, равный 2а. Определить расстояние между серединами этих прямых, если расстояние между их концами в каждой плоскости равно Ь.
Глава II
РЕШЕНИЕ КОСОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ
При решении прямоугольных треугольников мы использовали только определения основных тригонометрических функций. Для решения же косоугольных треугольников нам потребуется знание зависимостей между сторонами и тригонометрическими функциями углов косоугольных треугольников, известные как теоремы синусов, косинусов и тангенсов. К выводу этих теорем мы и переходим.
В дальнейшем мы будем пользоваться следующими обозначениями: а, b и с — стороны треугольника; Л, В и С — противолежащие им углы; S — площадь; 2р — периметр; R — радиус описанного круга; г — радиус вписанного круга; ha, 1а и та—высота, биссектриса и медиана, соответствующие стороне а.
§ 4 (38)« Теорема синусов
Теорема. Во всяком треугольнике стороны пропорциональны синусам противолежащих углов:
а ь с
sin A sin В sin С
Доказательство. Опишем круг около данного треугольника АВС (черт. 8). Пусть R — радиус этого круга. Возьмём одну из вершин треугольника, например Л; через одну из других вершин, например через В, проведём диаметр ВЛ' описанного круга. Вспомогательный треугольник Л'ВС прямоугольный, так как вписанный угол Л'СВ опира- -	-	д	д
ется на диаметр. Из вспомо-гательного треугольника най Л lVy\ дём:	( |/^)	\	1
а = 2 R sin Л'.	х___'
Если угол Л острый, то
Л = Л', так как вписанные
Черт. 8
21
углы А и А' опираются па одну и ту же дугу. Если угол А тупой, то угол Д' острый, измеряющийся половиной дуги ВАС:
А' = ВАС = - (2л — w ВА'С) = л —	= л — Д.
2	2	2
Итак, или А — Д', или Д' = л — Д, в обоих случаях sin Д' = sin Д, а потому
а = 2R sin А.	(1)
Если угол А прямой, то а = 2R, sin А = 1 и р'авенство (1) также справедливо.
Аналогичные равенства найдём и для прочих углов В и С. Итак, а =- 2R sin Д; b = 2R sin В\ с — 2 Afsin С, откуда
= Ь - = 	= 2R.
sin4	sin В	sin С
Следствие. Отношение стороны треугольника к синусу противолежащего угла равно диаметру круга, описанного около треугольника.
Упражнения
76 (344). 1) Чтобы определить расстояние между двумя пунктами Д и В, расположенными на разных берегах реки (черт. 9), выбрали произвольно пункт С, находящийся на том же берегу, что и пункт А, и произвели следующие измерения: базис ДС« 100 м; Z. СДВ« 749 и Z ДСВ« 44°.
При помощи указанных данных вычислить искомое расстояние.
Определить этим способом на школьном дворе расстояние между двумя какими-либо предметами.
2)	Чтобы определить высоту трубы, к основанию которой нельзя подойти, измерили базис AiB1na 11,0 м, продолжение которого упирается в основание трубы (черт. 10). Угол CAD = р as 49°;' угол CBD = а на 359. Высота угломерного прибора hna 1,4 м. Чему равна искомая высота трубы?
Определить этим способом высоту школьного здания.
3)	Для определения высоты вертикального предмета АВ от основания его А проведён базис АС, равный b и повышающийся от Д к С под углом а к плоскости горизонта.
22
Из конца С базиса верх предмета виден под углом высоты р. Определить высоту предмета (черт. 11).
4)	На горе, склон которой понижается к горизонту под углом 0, стоит дерево. Тень дерева, падающая вниз по склону горы при высоте солнца а ( а> 0), имеет длину /. Определить высоту дерева (черт. 12).
- 5) Чтобы	определить
ширину реки,	непосредственно у воды	по берегу
реки провели базис АВ длиной с метров и наметили дерево С, стоящее на другом берегу у самой воды; затем измерили /LCAB = = а и Z_ АВС = р.
Вычислить ширину реки против дерева С, если ся 400 м;	45°,0 и
0^ 30°,0 (черт. 13).
6)	Сила, равная Р~
23,0 яГ, разложена на две составляющие, которые образуют с её направлением углы а « 46°30' и р« 54° 10'. Вычислить величину каждой составляющей силы.
7)	Около треугольника описан круг. Найти отношение площади треугольника к площади круга.
Указание. Считать известными углы данного треугольника.
8)	Доказать, что в любом треугольнике сторона, лежащая против угла в 30°, равна радиусу круга, описанного около треугольника.
fi ™ с
Черт. 9
Черт. 13
23
§ 5 (39). Теорема косинусов
Теорема. Квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними:
а2 — Ь2 + с2 — 2Ьс с os Л Ь2 = с2 + а2 — 2са cosB с2 = а2 + Ь2 — 2ab cosC
Д о к а з С л у ч а
В
fl н с г
ательство. Докажем первое равенство.
й 1’. Угол А острый. Пусть ВН высота, опущенная из вершины В (черт. 14); из |L	геометрии известно, что
J	C|S< а2 = Ь2 +с2 — 2Ь  АН. (1)
ь. V	L	Из прямоугольного тре-
Н A b	С A	b	С угольника	АВН найдём
2°	3° АН = с cos	Л; подставив
Черт. 11	в формулу	(1), получим
доказываемое равенство.
Случай 2°. Угол А тупой. В этом случае
’ а2 -= Ь2 + с2 + 2Ь • АН.
(2)
Из треугольника АВН найдём:
АН = с cos Z_ ВАН = с cos (л — Л) = — с cos Л.
Подставив в формулу (2), получим доказываемое равенство.
Случай 3Q. Угол Л прямой. В этом случае (по теореме Пифагора): а2 = Ь2 + с2 =Ъ2-\-с2—2bc cos Л (так как cos Л = 0).
Итак, во всех случаях
а2 = Ь2 + с2 — 2bc cos Л.
Упражнения
77 (345). 1) Чтобы определить расстояние между пунктами Л и В, которое непосредственно измерить нельзя, выбрали третий пункт С так, что из него видны и доступны оба пункта Л и В; за- * тем измерили расстояние ВС = а, АС = b и Z. АСВ =у. Вычислить АВ (aw 100 jw; bw 80 м; yw 48°50') (черт. 15).
Определить этим способом расстояние между двумя предметами на школьном дворе.
2)	Смежные стороны параллелограмма равны 4,0 см и 5,0 см, угол между ними 52°. Найти диагонали параллелограмма.
24
3)	Две силы: Рт 100 кГ и Q« 200 кГ — приложены к материальной точке под углом а« 50° друг к другу. Определить поли-чину равнодействующей и углы, которые она составляет с силами Р и Q.
Черт. 15	Черт. 16
4)	Для определения расстояния между двумя пунктами А и В (черт. 16) измерили длину а выбранного базиса CD и углы: ACD = = у, BCD = a, ADC = 0 и BDC = 6. Найти АВ.
§ 6 (40). Формулы для вычисления площади треугольника
1°. Из геометрии известна формула Г е р о н а:
S — У'р (р — а) (р — Ь) (р — с) (где р =	— полупериметр)
позволяющая вычислять площадь треугольника по его сторонам.
2°. Теорема. Площадь треугольника равна половине произведения двух сторон на синус угла между ними;
S = — 6с sin А.
2
Доказательство. Из геометрии известно, что площадь треугольника равна половине произведения стороны треугольника на высоту, опущенную на эту сторону из противоположной вершины
5 = |б-Ай.	(1)
Если угол А острый, то из треугольника АВИ (черт. 14) найдём ВИ = hb = с sin А.
Если угол А тупой, то ВИ = hb — с sin (л — Д) = с sin А. Если угол А прямой, то sin А = 1 и hb = АВ = с — с sin А. Следовательно, во всех случаях hb = с sin А. Подставив в равенство (2), получим доказываемую формулу.
3 Тригонометрия	25
Точно так же получим формулы:
S — - ab sin С = — ас sin В.
2	2
3°. На основании теоремы синусов:
, a sin В а sin С Ь — ----, С= -----
sin A sin А ‘
Подставив эти выражения в формулу (1), получим следующую формулу:
__ a2 sin В sin С
2 sin Л ’
Упражнения
78 (346). 8) Вычислить площадь треугольника:
а) а = 40, b = 50 и Z. С = 50°; б) b = 64, с = 82 и Z. А = 65°; в) а = 32, b = 53 и Z. С = 61°; г) а = 95, Z. В = 35° и z£C=42°. 79 (345). 5) Доказать, что площадь вписанного в круг четырёхугольника равна — (ab + cd)  sin а, где a, b, с nd — стороны четырёхугольника на — угол между сторонами а и Ь.
80 (345). 6) Доказать, что площадь вписанного четырёхугольника равна ]f(p — а) (р — Ь) (р — с) (р — d), где р — полупериметр и а, Ь, с и d — стороны четырёхугольника.
Указание. Использовать предыдущую задачу. Найти по теореме косинусов cos а и выразить sin а через У 1 — cos2a.
§ 7	(41). Теорема тангенсов
Теорема. Разность двух сторон треугольника относится к их сумме, как тангенс полуразности противолежащих углов к тангенсу полусуммы этих углов:
lei-i a — b _	2
а + fg А В 2
(и две аналогичные формулы для прочих пар сторон а, с и Ь, с).
Доказательство. В силу теоремы синусов имеем: А +В А — В a — b — 2R (sin А — sin В) = 4 R cos —-— sin —-—;
4+ В А —В
aA-b = 2R (sin А + sin В) = 4 R sin —-— cos —-—е
Разделив почленно эти равенства, получим доказываемую формулу.
26
§ 8	(42). Решение треугольника по двум его углам и стороне
Задача. Даны два угла треугольника и сторона, прилежащая к ним-, вычислить другие стороны и угол.
Даны В, С и а-, требуется найти Ь, с и А.
Решение. Условие возможности построения треугольника по этим данным:^ А + В < 180° — будем считать выполненным.
Можно считать известными все три угла, так как
А = 180° — (B + Q.
Для вычисления сторон b и с достаточно применить теорему синусов:
=_5_,	откуда b = а-^, с =
sin В sin A sin С sin A	sin A sin А
Площадь вычисляется по формуле:
__ a2 sin Bsin С
2sin А
Пример. Решить треугольник по следующим данным: а « 17,4, В « «!4°30', С 64е».
Решение при помощи натуральных таблиц. Находим угол:
А = 180°‘ — (В + С) я 180q — (44°30' + 64°) я 71°30'.
Вычисляем стороны. Имеем:
sin В « 0,7009; sin С я 0,8988; sin А » 0,9483 и далее t a sin В	17,4-0,7009	12,20
Ь=  « —— ------------« —-— « 12,86 « 12,9;
sin Л	0,9483	0,9483
а sin С	17,4-0,8988	15,64	.	_ и
sin Л	0,9483	0,9483
Деление на sin Л можно заменить умножением на обратное число.
По таблицам Брадиса (см. табл. II) найдём: -« 1,055.
v,У4оо
Вычисления выполнены по правилам приближённых вычислений. Значения синусов взяты из таблиц Брадиса; во всех промежуточных результатах сохраняются четыре значащие цифры (правило запасной цифры), а окончательный результат округлён до трёх значащих цифр.
Решение при помощи логарифмических таблиц. Имеем:
a sin В sin Л ’
lg b= lg а + lg sin В — lg sin Л.
3*
27
По таблицам найдём:
1g а -_1,2405
+ lg sin В = 1,8457 — lg sin A 0,0230 lg£= 1,1092
Igsin A = 1,9770.
По таблицам Брадиса найдём b = 12,86. Однако в ответе следует оста вить три значащие цифры, так как значение а дано с тремя значащими цифрами; поэтому b а 12,9.
Сторона с вычисляется аналогично:
a sin С л	,	, . _	,	. „
с —-----lgс= lg а + Igsin С— lg sin Л;
sin А
lg a =J, 2405
+ lg sin С => 1,9537
— lg sin A = 0,0230
lgc= 1,2172; c « 16,5.
§ 9	(43). Решение треугольника по двум сторонам и углу между ними
Задача. Даны две стороны треугольника и угол между ними; вычислить третью сторону и два других угла.
Пусть, например, даны а, b и С, требуется вычислить Д, В и с.
Решение при помощи натуральных таблиц. Формула косинусов даёт выражение стороны с непосредственно через известные элементы:
с = |/а2 4- Ь2 — 2abcos С.
Для вычисления А можно также воспользоваться формулой косинусов:
а2 = Ь2 + с2 — 2bc cos А.
Так как 0 < А < 180°, то
А	Ь2 4- с2 — a2	D	а2 4- с2 — Ь2
А = arc cos--!------ и, наконец, В = arc cos ——------
2 be	2ab	'
Решение при помощи логарифмических таблиц.
Л 4- С	С
Известна сумма углов Л + В = 180° — С, откуда —-— = 90° — —. Раз-
ность углов Л — В можно вычислить, воспользовавшись теоремой тангенсов: tg^
------—= ?—откуда tg^------b ctg —
А + В а-\- b	2 а b 2 ‘
2
Углы Л и В определяются из системы уравнений: Л + В л С А— В [а — Ь С\
—-— = 90° — — —-— = arc tg ------- ctg 7-
2	2	2	*\аЛ- Ь2Г
28
Сторону с можно вычислить по теореме синусов:
a sin С с=> ’ -
sin Л
Пример. Дано: а я 49,4; Ъ « 26,4 и С « 47°20'; найти А, В и с. Решение при помощи натуральных таблиц. Имеем:
с2 = а2 + ь2 — 2ab cos С % 49,42 + 26,42 — 2 . 49,4 • 26,4 • cos 47°20'.
По таблицам квадратов найдём:
а2 » (49,4)2 » 2440; b2 « (26,4)2	697,0
и далее
2 • 49,4 • 26,4 • cos 47°20' « 2 . 49,4 . 2,64 . 0,6778 а 1768.
Следовательно, с2 « 2440 + 697 — 1768 « 1369.
По таблицам квадратных корней с « 37,0.
Далее
Ь2 + с^а2 cos А =---—----
2Ьс
697 4- 1369 — 2440 2-26,4.37,0
374
1954
« —0,191;
А « arc cos (—0,191); угол А — тупой. Находим дополнительный угол:
180° — А % arc cos (0,191) « 79°; А 180°—79° = 101°
(с округлением до 10'). Наконец,
а2 4- с2 - Ь2 2440 + 1369 — 697
cos В =------------ «-------------------
2аЬ	2 - 49,4-37,0
3112
3655,6
% 0,8513 и В = 31°40'.
Решение при помощи логарифмических таблиц. Вычислим углы А и В.
д__g	с
lg tg —-—= lg (а — 6)+ 1g ctg— — lg(a+6).
lg(a — b) = 1,3617
+ lg ctg-y= 0.3583
— Ig(a4-d) = 2,1203
Вспомогательные вычисления
a — b * 49,4 — 26,4 = 23,0;
a + b » 75,8;
-4" « 23°40';
2
lg(fl + d) = 1,8797.
lg tg Q~~ = 1,8403 и ~~~ ® 34°40'. z	z
Из системы уравнений
— 5 = 34°40';	-	- = 66’20'
2	2
найдём: A ss 101°, В и 31°40'.
29
§ 10 (44). Решение треугольника по двум сторонам и углу, противолежащему одной из них
Задача. Даны две стороны треугольника и угол, лежащий против одной из них\ вычислить третью сторону и два остальных угла.
Пусть даны а, b и Д; требуется вычислить В, С и с.
Р е ш е н и е. С л у ч а й 1°. а > Ь, т. е. заданный угол А лежит против большей стороны. Построение показано на чертеже 17, а.
Из точки С (как из центра), взятой на одной из сторон угла А на расстоянии b от вершины, описана окружность радиуса а; точка В есть точка пересечения этой окружности с другой стороной угла А.
Построение всегда возможно, задача имеет единственное решение.
Острый угол В, противолежащий меньшей стороне, находится по теореме синусов:
sin В = — sin Д,
а откуда В = arc sin (— sin А \а
~	a sin С
Сторона с находится по теореме синусов: с =-----
sin А
Случай 2°. a<Z b, т. е. угол А лежит против меньшей стороны; поэтому он не может быть тупым или прямым. Следовательно, при А > 90° задача не имеет решения. Пусть угол А острый. Из построения на чертеже 17, b видно, что окружность радиуса а с центром в точке С пересечёт другую сторону угла А в двух точках при условии а > CD, где D — основание перпендикуляра, опущенного из точки С на другую сторону угла Д. Так как CD = b sin А (из треугольника ACD), то условие запишется так: а > b sin Д. Для угла В возможны два значения: В = Bi (острый) и В = В2 (тупой). Задача имеет два решения.
Значения угла В вычисляются по теореме синусов:
• о ь . Л sin В = - sin А, а
откуда Bj = arc sin / — sin	и В2 = 180° — ВР
\ а /
Значения угла С и стороны с вычисляются так же, как в предыдущем случае (см. ниже, пример).
. 30
Из чертежа 17, с видно, что при CD = b sin А > а окружность не пересечёт другой стороны угла Д; задача не имеет решений. В этом случае sin В =----->1 и угол В вычислить нельзя.
а
При CD = b sin А задача имеет единственное решение: треугольник АВС прямоугольный.
Случай 3°. а = Ь. В этом случае треугольник АВС равнобедренный. Такой треугольник можно решить, разбив его высотой CD на два прямоугольных треугольника:
В = А; С = 180° — 24; с = 2AD = 2а cos А.
Пример. Вычислить стороны и углы треугольника, если дано:
а « 73,5; b я 86,4; А * 49°0'.
. Л 6sin4 sin В =-----
а
Решение:
(деление на 73,5 можно за-менить
86,4-0,7547	65,21 Л Л л „
—-«—2—« 0,8872 «0,887 73,5
— «0,0136, табл. II).
73,5
73,5
умножением на
Так как в данном случае а < Ъ и
b sin А
1, то
задача имеет два решения!
а
1) В, = arc sin 0,887 = 62°30';
(с округлением до 10');
a sin С, ~ 73,5-0,9304 Cl~ sin Л ~	0,755
2) В2 = 180°—В, я 117°30';
С, я 180° — (49° + 62°30') = 68°30'
68,38
я —-- х 90,56 я 90,6;
0,755
С2 я 180° — (49'’ 4- 117°30') = 13°30'}
asinC2 73,5-0,2334 ~ 17,15
Со —---------«---------------« _ ----- « 22, /2 « 22,/,
2 sin Л 0,755	0,755
§ 11 (45). Решение треугольника по трём сторонам
Задача. Даны три стороны треугольника; вычислить его углы.
Пусть даны длины трёх сторон треугольника. Обозначим через а меньшую сторону, через Ь — среднюю, а через с — большую: а < Ь < с. По трём данным сторонам можно построить единственный треугольник, если большая сторона меньше суммы двух других сторон: с < а + Ь. Если же с а 4- Ь, то треугольник с данными сторонами не существует. Будем считать, что с < а -(- Ь.
Решениепри помощи натуральных таблиц.
Углы треугольника можно вычислить по теореме косинусов: а2 = Ь2 + с2 — 2bc cos А; Ь2 = а2 + с2 — 2ас cos В, откуда
31
cos A =	—— и A — arc cos	—— (так как 0°<A <180°).
2 be	2 be
Аналогично найдём:
В — arc cos а +с ~b И) наконец, С = 180° — (Я 4- В). 2ае
Решение при помощи логарифмических таблиц. Вычислим сначала площадь треугольника (формула Герона):
S = /р(р —а)(р —6)(р —с), где р =
Имеем далее:
Sbc sin А	Л 2S
= —-—, откуда sin А =.
Угол А острый, так как он лежит против меньшей стороны; следовательно,
25
А = arc sin —.
be
25
Точно так же В = arc sin — и, наконец, С — 180° — (Л -|- В), be
Итак, при решении треугольника по трём сторонам при помощи логарифмических таблиц углы, лежащие против меньших сторон, находятся по формулам, а угол, лежащий против наибольшей стороны, вычисляется как разность между 180° и суммой двух найденных углов.
Пример. Решить треугольник, зная длины (приближённые) его сторон
24,7; 22,4 и 31,3. Обозначим а « 22,4; b « 24,7; с ~ 31,3.
Решение при помощи натуральных Имеем:
Л (24,7)2 + (31,3)2 — (22,4)а	610,1 +979,7 — 501,8
C0S ~	2-24,7-31,3	~	1546
откуда A « 45°20' (с округлением до 10')-
~ (22,4)2 + (31,3)а — (24,7)2 ~ 501,8 + 979,7 — 610,1
cosB~ 2-22,4-31,3	~	1402	'
откуда В «. 51°30' и, наконец, С « 180° — (45°20' + 5Г30') « 83°10'.
Решение при помощи логарифмических таблиц. Имеем:	t
2S sin А = —, lg sin А = lg 2S — lg b — lg c. be Вычисляем:
lg 2 S = lg2-f p(p —a) (p—b)(p — c) = lg 2 + -- lg p + -- lg (p — a) +
+ lg(p — b) + ~ lg(p—c),
таблиц.
«0,7038,
32
где
a + ti+c 22,4 4- 24,7 + 31,3
Р- 2	«	2	-39,2,
р — а к 39,2 — 22,4 = 16,8; р — 6 « 14,5; р— с « 7,9;
1g 2= 0,3010	
^lgp = 0,7966	Igp = 1,5933
7;lg (р — а} = 0,6126	lg(P —а) = 1,2253
4-1	
- 1g (р-6) = 0,5807	lg(P — i») = 1.1614
~lg(p —с) = 0,4488	lg (Р — с) = 0,8976
lg 2S = 2,7397.
Далее
lg 2S = 2,7397
, — lg b = 2,6073	lg b = 1,3927
— lg c = 2,5045	lg c = 1,4955
lg sin A = 1,8515; A ® 45°20'.
Вычисляем В. Имеем: lg sin В = lg 2S — lg a — 1 g c.
lg2S =2,7397
— lg a = 2,6498 lg a = 1,3502 — lg c =2,5045
Igsin В = 1,8940; В a 51°40' C = 180° — (4 + B) » 83°.
Упражнения
Решить косоугольные треугольники по заданным основным элементам. (Решение каждого примера следует выполнить при по-
мощи таблиц логарифмов и логарифмической линейки.)
81 (347). Даны сторона и два угла:
1)	ах 370,0;	В« 86°30';	С«	50°50'.
2)	а» 450,0;	Д«87°50';	10°50'.
3)	951;	В« 126°40';	С«	13°20'.
4)	Ьх 13,02;	Д«11°46';	В«	133°40'.
82 (348). Даны две стороны и угол между ними:
1)	а» 510;	317; С« 76°10'.
2)	ах 225;	Ьх 800;	Сх 36°40'.
3)	ах 2,296;	сх 1,687;	Вх 29°52'.
4)	Ьх 28;	сх42;	Ах 124°.
33
*83 (349). Даны		две стороны и угол против одной из них:			
'•'1) ал	J 87;	Ь;	» 65;	Ал	t 75°.
2) Ьл	i 360;	сх	; 309;	Сл	; 21°30'. *
ч)3) ал	г 13,89;	сх	; 8,42;	Ал	; 126°41'.
•> 4) а?	а 13,81;	сх	? 8,14;	Сл	; 14°37'.
5) Ьл	г 263,1;		; 215,4;	Вл	; 70°14'.
6) ал	; 19,06;	Ьх	; 88,19;	Ал	х 31°17'.
84 (350). Даны три стороны:
1) а	« 19;	Ьл	i 34;	ex	i 49.
2) ал	s 0,099;	Ьл	1 0,101;	сх	i 0,158.
3) ал	; 172,5;	Ьл	i 113,4;	ex	; 120,5.
4) ал	? 1,234;	Ьл	; 2,345;	ex	<. 3,457.
85 (351). Решить косоугольные треугольники по заданным элементам:
1)	Кл	# 7,92;	Ал	i 113°17';	Вл	; 48°16'.
2)	S»	501,9;	Ал	; 15°28';	Вл	; 45°23'.
3)	Ьал	s 5,37;	Вл	; 115°10';	Сл	5°33'.
4)		; 0,758;	Вл	98°30';	Сл	4°20'.
5)	a + bx 488,8;		Ал	; 70°24';	Вл	40°16'.
6)	a —	-	23;	Ал	108°;	Вл	18°.
7)	rxt	5,0;	Ал	; 22°;	Вл	39°.
8)	Sx	2420;	а л	i 42,5;	Вх	124°50'.
9)	ax	32;	Ь л	s 25;	Ал;	2В.
10)		15;	аЬл	«48;	sin		cos В.
H)	ax;	120,0;	Ь л	; 29,0;		23,7.
12)		« 8;	hb f	» 12;		18.
§12 (46). Применение тригонометрии к измерениям на местности и решению практических задач
С помощью тригонометрии решаются многие измерительные задачи на местности, как например вычисление расстояния между различными пунктами земной поверхности (если это расстояние нельзя измерить непосредственно), вычисление высоты данного предмета (горы, здания и т. п.), составление планов и карт и т. п. Будем предполагать, что измерения производятся на м а л о м участке, так что можно считать его плоским и не учитывать кривизны земной поверхности.
Измерение небольших расстояний производится непосредственно, при помощи, например, стальных измерительных лент.
Измерение углов на местности производится при помощи угломерных инструментов. Наиболее распространённым современным угломерным инструментом являетсятеодолит (черт. 18). Зрительная труба теодолита может вращаться как в горизонтальной,
34
так и в вертикальной плоскости. Если ось зрительной трубы, находящейся в горизонтальном положении в пункте С земной поверхности, направить сначала в пункт Л, а затем в пункт В, то угол её поворота есть угол С треугольника АВС\ под этим углом из пункта С видно расстояние АВ (черт. 19). При помощи поворота зрительной трубы можно измерять углы и в вертикальной плоскости (черт. 20).
Углы поворота зрительной трубы можно измерять с большой точностью при помощи де-
Черт. 19
Черт. 18
Черт. 20
лений на горизонтальном и вертикальном кругах и микрометрических винтов.
При отсутствии теодолита пользуются (например, в учебных целях) более простыми приборами. Один из таких приборов — астролябия — изображён на чертеже 21. Основные части астролябии следующие: круг, разделённый на градусы (лимб), и линейка (алидада), которая может вращаться вокруг центра круга. Для наведения линейки на данный пункт служат прикреплённые к её концам вертикальные пластинки с узкими продольными прорезями.
35
Рассмотрим несколько простейших задач на вычисление расстояний и высот.
Задача. Вычислить расстояние доступной точки А до недоступной точки В, видимой из точки А (точки А и В лежат водной и той же горизонтальной плоскости, черт. 22).
Разъяснение. Точка А считается доступной, если в ней । находиться измерительными ментами. “ тается ной, если расстояние не может быть непосредственно мер, река, овраг и т. п.).
Решение, вблизи точки ную точку С, видна точка В. непосредственно базис АС = Ь и С. Сторону АВС найдём по теореме синусов:
Черт. 21
в ней может наблюдатель с инстру-Точка В счи-н е*д о с т у п-АВ измерено (напри-имеется препятствие:
угольника
Выберем доступ-которой Измерим отрезок-и углы А х = с тре-
А из
с	b	„	6 sin С 6 sin С
------=---------, откуда х =	—------------------. sin С sin В-----sin В sin (Л-f-С)
Задача. Вычислять расстояние между двумя недоступными точками А и В, видимыми из доступной местности. Расположение точек дано на чертеже 23.
Черт. 22
Черт. 23
Решение. Выберем в доступной местности отрезок-базис, измерим базис и углы а = Z. AMN, 0 = Z. BMN, у = Z. ANM. 6 = Z. BNM между базисом и направлениями из его концов на
36
точки А и В. Вычислим расстояния МА и МВ (см. предыдущую задачу):
МА = -&sin't ; МВ =  *sin6 .
sin (а + *()	sin (Р + 6)
Зная две стороны треугольника АМВ и угол а — 0 между ними, можно вычислить третью сторону, например, по теореме косинусов:
X = АВ = У МА2 + МВ2 — 2МА-МВ cos (а — р).
Задача. Вычислить высоту вертикального предмета, основание которого недоступно (черт. 24).
Решение. Допустим, что можно выбрать горизонтальный базис АВ = fe, из концов которого видна вершина S измеряемой высоты. Пусть h—высота угломерного инструмента. Измерив углы аир треугольника 5ЛД, найдём (по теореме синусов):
AS ь
—> откуда sin р	sin (а — р)
- - ‘^14—
sin (а — р)
b sing sin p sin (а — P)
и, наконец,
OS = 001 + 0.S = h + since = h
У пражнения
86 (352). 1) Вычислить площадь земельного участка, имеющего форму треугольника, если при съёмке плана этого участка с масштабом 1 : 100000 две его стороны изображены отрезками 5,6 см, 7,5 см и угол между ними равен 48^.
2)	При съёмке плана участка полярным способом (за полюс взята вершина А многоугольника — участка) измерением были получены следующие данные: сторона АВ ж 250 м; диагонали АС ж 360 м AD « 430 лг, АЕ& 390 м и сторона AF ж 450 м; азимуты этих направлений соответственно равны Z_ NAB ж 25°; Z_ NAC^ 53°; Z. NAD ж 81°; Z. NAE& 125° и zl NAF& 140°.
Вычислить площадь участка ABCDEF.
3)	При съёмке плана участка ABCD полярным способом (за полюс взята точка О, одна из внутренних точек участка) измерением были получены следующие данные:
ОАж 28 м\ ОВ^ 31 м\ ОСж 24 м\ OD 37 м-, Z-AOB& «36°; Л-ВОСж 78°; Z_ COD ^110° и Z_DOA^ 136°.
37
Вычертить план участка A BCD и вычислить его площадь; угол NOA (азимут направления 0А)~ 280°.
4)	Вычислить площадь участка, имеющего форму пятиугольника, изображённого на прилагаемом плане в масштабе 1 : 10000 (черт. 25).
87 (353). Сила Р « 5,2 кГ должна быть разложена на две составляющие, действующие под прямым углом друг к другу, одна из которых составляет с направлением силы Р угол а« 469. Вычислить составляющие силы.
88 (354). Стропила В А и ВС (черт. 26) составляют углы а с горизонтальной балкой АС. К концу В подвешен груз Р. Определить: 1) силу S, прижимающую стропильную ногу к балке АС, и 2) силу F, растягивающую балку АС.
89 (355). Лодочник, переправляясь через реку, направлял лодку поперёк реки и грёб с такой силой, что в стоячей воде она подвигалась бы со скоростью « 0,3 —. На какой угол от этого сек
направления лодка будет отнесена течением реки, если оно составляет «1,0—?
сек
90 (356). Поезд идёт со скоростью «12 — , и пассажиру из вагона кажется, что капли дождя падают под углом а« 30° к отвесному направлению. Определить среднюю скорость падения дождя.
91 (357). Тело при свободном падении в первую секунду проходит « 4,9 м, а при скольжении с данной наклонной плоскости « 1,8 м. Вычислить угол наклона плоскости к горизонту (трение во внимание не принимать).
92 (358). На плечо, имеющее длину а, прямолинейного рычага под углом а к нему действует сила Р кГ. На другое плечо в противовес первой действует сила Q кГ под углом 0 к рычагу. Какова длина второго плеча рычага, если рычаг находится в равновесии (черт. 27)?
93 (359). Две силы Р кГ и Q кГ действуют на концы А и В прямолинейного рычага АВ длиной а см. Сила Р, действующая
38
на конец А, образует с рычагом угол а, сила Q, действующая на конец В, — угол 0. На каком расстоянии от А нужно подпереть рычаг, чтобы он находился в равновесии (весом рычага пренебречь)?
94 (360). К кронштейну (черт. 28) подвешен груз весом Р кГ. Вычислить силу, растягивающую стержень Ь, и силу, сжимающую стержень с, если угол между и с равен а.
Черт. 27
95 (361). Вычислить работу на пути ~ 20 м, если сила, равная « 10 кГ, действует на данный предмет под углом ж 40 Q к направлению движения.
96 (362). Труба диаметра СА& 100 мм при помощи конусообразного раструба переходит в трубу BD вдвое большего поперечного сечения (черт. 29). Определить длину раструба АВ, если противоположные образующие конической поверхности пересекаются под углом 40°.
Решите задачи, связанные с ‘винтовой линией. Обозначения: h — шаг винта; D — наружный диаметр; d — внутренний ди-u	D-\-d	v
аметр; а — угол подъема винтовой линии; — средний диаметр.
97 (363). Составить формулу, выражающую угол винтовой линии через шаг ее и диаметр цилиндра, на котором эта линия нанесена (черт. 30 и 31).
98 (364). Определить угол подъёма винтовой линии, если внешний диаметр винтовой нарезки 50 мм, внутренний диаметр 42 мм и шаг винта 6 мм.
99 (365). 1) Винтовая нарезка имеет 4,5 хода на дюйм (1 'дюйм ^25,4 мм), внешний диаметр 2,0
дюйма, внутренний 1,7 дюйма. Определить угол подъёма винтовой линии.
2) Внешний диаметр винта 25,4 мм, внутренний 21,3 мм, угол подъёма 2°20'. Найти шаг винта и число ходов на дюйм.
Черт. 29
39
100 (366). Спиральное сверло диаметром 12,5 мм имеет спиральную канавку с шагом 192 мм. Определить угол, который спиральная канавка сверла образует с его осью.
101 (591). Два вала, расположенные под прямым углом друг к другу, соединены при помощи конических шестерёнок. Одна шестерня имеет диаметр 48 см, а другая 32 см. Определить углы х и у наклона зубцов к осям валов (черт. 32).
Указание. Для проверки правильности полученных значений воспользуйтесь соотношением х н- у = 90°.
t— D------
Черт. 30
Черт. 31
102 (592). 1) На чертеже 33 дана фрон-
Черт. 32
тальная проекция паза и указаны соответствующие размеры. Определить угол а наклона сторон паза к его основанию.
2) На чертеже 34 показана винтовая нарезка и указаны соответствующие размеры. Вычислить угол а для заточки резца при нарезывании этой резьбы.
Черт. 33
103 (593). 1) Две силы Р и Q приложены к материальной точке. Найти угол между их направлениями, зная, что если увеличить этот угол вдвое, то величина равнодействующей не изменится.
2) При равновесии ломаного рычага ВАС (черт. 35) на концы его плечей АВ = р и АС = I действуют силы R и Q. Опреде-40
лить углы, образуемые плечами рычага с горизонтальной плоскостью, если плечо АС составляет угол, в два раза больший,
чем плечо АВ. (Вес рычага не учйыва- _ ется.)	9'
104 (581). На конце рычага АВ пер- д/ вого рода перпендикулярно к нему ; при- с. ч. креплён стержень АС (черт. 36) дли- а|	п
ной а см. Рычаг повернули на Z. а, д----------------------
и он занял положение AjBit причём	^*4.	1
AtD = AD — Ь. На какой высоте от	\
АВ, считая по вертикали, находится
теперь конец С стержня АС?	Черт. 36
Глава III
ПРИМЕНЕНИЕ ТРИГОНОМЕТРИИ К РЕШЕНИЮ ГЕОМЕТРИЧЕСКИХ ЗАДАЧ
§ 13 (47)< Образцы решения задач
Планиметрические задачи. Тригонометрия применяется к решению задач на вычисление элементов различных геометрических фигур. Обычно при вычислении элементов многоугольника его разбивают на треугольники с тем расчётом, чтобы искомые элементы можно было вычислить путём по-А следовательного решения ряда треугольников.
у/yia Задача. Вычислить площадь кругового сегмента, / Ч - дуга которого (в радианной мере) измеряется чис-0 В лом а; радиус круга равен R (черт. 37).
Черт. 37 Решение. Площадь S сегмента равна площади соответствующего сектора О АВ минус площадь треугольника О АВ. Из геометрии известно, что площадь кругового сектора вычисляется по формуле si = ~ RI* где I — длина ограничивающей его дуги. Так как I =aR, то st = ± R2a.
т-т	/?2sina
Площадь треугольника равна s2 =-------.
Искомая площадь сегмента равна	' ,
с	/?2а /?2sina R2 .	. ч
S —	$2 — —	-	— ~ (а sin а)-
Задача. Основания трапеции равны а и Ь, боковые стороны равны end. Вычислить углы трапеции.
Решение. Пусть а — большее основание, А — угол, образованный сторонами а и с (черт. 38). Проведём прямую, параллельную d\ тогда трапеция разобьётся на треугольник АВЕ и параллелограмм BCDE. В треугольнике АВЕ известны длины трёх сторон: с, d, a — b. По теореме косинусов найдём угол А: d2 = (а — b)2 + с2 — 2с(а — b) cos А, откуда cos А =	+ с ~
42
Аналогично вычислим:
cos D = ———— и, наконец, В = л — Л; С = л — D.
2d (а - Ь)
Стереометрические задачи. Тригонометрия применяется для вычисления различных элементов пространственных фигур: объёмов, поверхностей, площадей сечений, плоских и двугранных углов и т. п. Обычно производят вспомогательные построения (проведение сечений, линий и т. п.) с тем расчетом, чтобы искомые элементы можно было найти путем
последовательного решения ряда треугольников. В ь С При решении задач на вычисление с число-
в ы м и данными обычно сначала решают задачу / \	\
вобщемвиде, а затем подставляют данные д—□ j в условии числа. Общую формулу решения пред-
ставляют в виде, наиболее удобном для последу- Черт. 38
ющих вычислений.
Задача. Основанием пирамиды служит квадрат. Одна из боковых граней — равнобедренный треугольник и образует с основанием тупой угол а. Противоположная грань образует с основанием угол 0. Высота пирамиды равна Н\ найти объём пирамиды.
Решение. Пусть ABCD — основание пирамиды; S — вершина; OS — высота; ASB — грань, образующая с основанием угол a; DSC — грань, образующая с основанием угол 0 (черт. 39).
Наклонные SX и SB равны; поэтому их проекции ОА и ОВ на плоскость основания равны. Пусть L — середина стороны АВ. В равнобедренных треугольниках АО В и AS В медианы OL и SL
суть также и высоты; поэтому OL _1_ АВ и SL _1_ АВ. Следовательно, Z. OLS есть линейный угол двугранного угла OABS (с ребром АВ), а потому Z_ OLS = 180Q — а. Пусть /< — точка пересечения прямой OL со стороной СО; имеем: DK = КС и OK -L CD. Наклонная SK -L CD по теореме о трёх перпендикулярах. Так как OK JL CD и SK -L СО, то Z. OKS = 0. Полу
43
плоскости ABS и DCS пересекутся в том и только в том случае, если
180° — а > ₽, т. е. а + ₽ < 180°
(угол 180° — а есть внешний угол треугольника SLK, а ₽ — внутренний угол); это условие будем считать выполненным. Отрезок LK равен стороне основания а. Так как OL = Н ctg (180° — а) = = — Н ctg а (из треугольника SOL) и ОК = Я ctg Р (из треугольника SOK), тоа=ОК—OL=H (ctg P+ctga). Вычисляем объём.
V = -а2Н = ±Н3 (ctg ₽ + ctg a)2. 3	3
Эта форма ответа удобна для вычислений с помощью* натуральных таблиц. Если вычисления проводятся при помощи логарифмических таблиц или линейки, то следует сумму котангенсов преобразовать в произведение:
у _	s*n‘' (a ~Ь Р)
3 sin2a sin2р
Вычислим объём при следующих данных: Н « 12,53; a « 110°48';
Р = 32°30'.
1)	Н3 « (12,53)3 ~ 1967 (таблица V Брадиса).
2)	ctgР + ctg a х ctg 32°30' + ctg 110°48' = ctg 32Q30' — ctg 69Q12' л ~ 1,5697 — 0,3799 « 1,1898 « 1,190 (таблица IX Брадиса).
3)	(ctg P + ctg a)2 % (l,190)2 ж 1, 416 (таблица III Брадиса) H3 (ctg P + ctga)2 1967-1,416 и, наконец, V =------------------~	~ 928,4.
и	о
Упражнения
Задачи на многогранники
 105 (367). Углы, образуемые диагональю пря-Параллелепипед моугольного параллелепипеда с его рёбрами, и призма. исходящими из одной с ней вершины, равны а, --------------- 0 и у. Доказать, что cos2a + cos20 + cos2у = 1, ” и вычислить Zy, если а=ЗГ10' и 0 = 69°10' (преобразовать предварительно выражение для cos2 у в произведение).
106 (368). Даны в пространстве три взаимно перпендикулярных луча, выходящих из одной точки, и вектор, исходящий из этой же > точки. Доказать, что если вектор составляет с лучами углы а, 0* и у, то справедливо соотношение: cos2 a + cos20 + cos2y = 1.
Справедливо ли это соотношение, если направление вектора совпадает с направлением одного из трёх данных лучей?
107 (369). Диагональ'прямоугольного параллелепипеда образует с тремя его неравными гранями углы а, 0 и у. Доказать:
1) sin2a + sin20 -f- sin2y = 1; 2) cos2a -f- cos20 -f- cos2y — 2.
44
108 (370). 1) Стороны основания прямоугольного параллелепипеда а = 36 см и b = 15 см. Диагональ параллелепипеда составляет с плоскостью основания угол а = 38°. Определить площадь боковой поверхности параллелепипеда и его объём.
2) Основанием прямого параллелепипеда служит ромб со стороной а = 58 см и острым углом а = 63°. Большая диагональ параллелепипеда составляет с плоскостью его основания угол 0 = 52°. Определить объём параллелепипеда.
109 (371). Определить объём прямоугольного параллелепипеда, диагональ которого а составляет с плоскостью основания угол а, а с большей боковой гранью угол р. Исследовать полученную формулу решения.
• ПО (372). В прямоугольном параллелепипеде диагональ основания d, угол между диагоналями основания а, а угол, образуемый диагональной плоскостью, проведённой через большую сторону основания, с плоскостью основания, р. Определить объём параллелепипеда. (Вычислить при d = 7,5; а = 43° и 0 = 57°.)
111	(373). Каждое ребро параллелепипеда равно 1 см. У одной из вершин параллелепипеда, в гранях его, три угла острые, по 2а каждый. Определить объём параллелепипеда. Исследовать полученную формулу решения.
112	(374). В параллелепипеде длины трёх рёбер, выходящих из одной вершины, а , бис; рёбра а и b взаимно перпендикулярны, а ребро с образует с каждым из них угол а. Определить объём параллелепипеда и угол между ребром с и плоскостью основания.
113	(375). Высота правильной четырёхугольной призмы равна h. Из одной вершины основания проведены в двух смежных боковых гранях две диагонали, угол между которыми равен а. Определить площадь боковой поверхности призмы. Исследовать полученную формулу решения.
114	(376). Через диагональ нижнего и вершину верхнего основания правильной четырёхугольной призмы проведена плоскость, пересекающая две смежные боковые грани призмы по прямым, образующим угол а -= 58°. Сторона основания призмы а = 6,4 см. Определить объём призмы (вычисления произвести при помощи таблиц и логарифглической линейки; результаты сравнить).
115	(377). В правильной треугольной призме сторона основания равна а. Две вершины верхнего основания соединены с серединами противоположных им сторон нижнего основания. Определить объём призмы, если угол между проведёнными прямыми, обращённый к плоскости основания, равен а. Исследовать полученное решение.
116	(378). 1) Основанием .прямой призмы служит треугольник АВС, у которого сторона АС = Ь, сторона ВС = а, угол АСВ = = а. Боковое ребро призмы равно высоте треугольника АВС, проведённой из вершины С. Определить объём призмы.
2) Основанием прямой призмы служит равнобедренный треугольник/ в котором угол между равными сторонами а равен а. Из вер
45
шины верхнего основания проведены две диагонали равных боковых граней; угол между ними равен р. Найти площадь боковой поверхности призмы. Исследовать формулу решения.
(Вычислить при а = 97,84 см\ а = 63° 23' и р = 39°36').
117 (379). Основанием призмы служит Д АВС, в котором ВС = = аиАВ = АС. Ребро АА{ равно b и перпендикулярно ВС; двугранный угол при ребре АА{ равен а. Определить объём и площадь боковой поверхности призмы.
118 (380). Сторона основания правильной пятиугольной призмы
а, высота призмы равна — диагонали основания. Вычислить пло-
4 щадь поверхности призмы.
119	(381). В треугольной призме каждая сторона основания равна а. Одна из вершин верхнего основания имеет своей проекцией центр нижнего основания. Боковые рёбра наклонены к плоскости основания под углом а. Определить площадь боковой поверхности призмы. Исследовать формулу решения.
120	(382). Диагональ правильной четырёхугольной призмы равна d и наклонена к боковой грани под углом а. Определить площадь боковой поверхности призмы. Исследовать формулу решения.
121	(383). Определить объём прямой четырёхугольной призмы, если высота её й, диагонали её наклонены к плоскости основания под углами а и р и острый угол в пересечении диагоналей основания равен у.
122	(384). Плоскость, проведённая через ребро основания куба и составляющая с плоскостью основания угол а, делит куб на треугольную и четырёхугольную призмы. Определить объём каждой призмы, если ребро куба равно а. Исследовать формулу решения.
123	(385). Высота правильной треугольной призмы равна h. Через одно из рёбер основания и противоположную ему вершину другого основания проведена плоскость. Найти площадь получившейся в сечении фигуры, если угол её при взятой вершине призмы равен 2а. Исследовать полученную формулу решения.
124	(386)*. В правильной треугольной призме через сторону основания проведена плоскость под углом а к плоскости основания. Сторона основания призмы равна а. Найти площадь получившегося сечения. Исследовать полученное решение.
125	(387). 1) В прямой четырёхугольной призме площадь осно-вания т, площади диагональных сечений р и q, двугранный угол * между ними а. Определить объём призмы.
2) Площади двух боковых граней треугольной призмы равны /пип, двугранный угол между ними равен а. Определить объём призмы, если её боковое ребро а.
126 (388). 1) В основании прямой призмы лежит трапеция. Через противоположные основания трапеций верхнего и нижнего оснований призмы проведена плоскость под углом а к основаниям призмы.
46
Каждая диагональ получившейся в сечении фигуры равна d, а угол между диагоналями, обращённый к основаниям, 0. Определить объём призмы.
2) Высота h прямой призмы равна 20 см; основанием служит прямоугольная трапеция с острым углом а = 46°, описанная около круга радиуса г = 6 см. Найти объём призмы.
127	(389). В треугольной призме расстояния между тремя боковыми рёбрами последовательно равны а, b и с. Высота призмы Н и составляет с боковым ребром призмы угол а. Найти объем призмы и площадь её боковой поверхности.
128	(390). Основанием призмы служит правильный шестиугольник со стороной а. Боковое ребро составляет с плоскостью основания угол а, и его проекция на эту плоскость равна радиусу окружности, описанной около основания призмы. Определить объём призмы.
129	(391). Через сторону нижнего основания правильной треугольной призмы проведена плоскость, пересекающая две боковые её грани по прямым, составляющим между собой угол а. Определить наклон этой плоскости к основанию призмы.
130	(392). Через диагональ нижнего и вершину верхнего основания правильной четырёхугольной призмы проведена плоскость, пересекающая две смежные боковые грани призмы по прямым, угол между которыми равен а. Определить объём призмы, если ребро её основания равно а.
131	(393). В треугольной призме два угла основания а и 0, радиус описанного около основания круга R. Каждое боковое ребро а наклонено к плоскости основания под углом ф. Определить объём призмы.
132	(394). В правильной четырёхугольной призме через середины двух смежных сторон основания проведена плоскость, пересекающая три боковых ребра и наклонённая к плоскости основания под углом а. Сторона основания равна а. Определить площадь полученного сечения.
133	(395). В правильной четырёхугольной призме проведена плоскость через середину оси и середины двух последовательных сторон основания. Зная, что сторона основания равна а, а боковое ребро Ь, определить: 1) площадь полученного сечения и 2) угол между проведённой плоскостью и плоскостью основания.
134	(396). 1) Если правильную четырёхугольную призму пересечь так, чтобы в сечении получился ромб с острым углом а, то секущая плоскость окажется параллельной диагонали основания и составит с плоскостью основания такой угол ф, что cos ф = = tg Д Доказать.
2) Основанием прямой четырёхугольной призмы служит ромб с острым углом а. Если её пересечь плоскостью, параллельной большей диагонали ромба, под таким углом ф к плоскости основа-
47
ния, чтобы в сечении получился квадрат с вершинами на боко-
вых рёбрах призмы, то cos <р = tg^. Доказать.
Пирамида.
135 (397). 1) По данной модели правильной треугольной пирамиды рассчитать: угол наклона бокового ребра к плоскости основания; угол наклона боковой грани к плоскости основания; измерить транспор-
тиром плоские углы при вершинах.
2)	В правильной четырёхугольной пирамиде плоский угол при вершине равен а. Определить двугранный угол при ребре основания пирамиды.
3)	В правильной четырёхугольной пирамиде боковое ребро наклонено к плоскости основания под углом а. Определить двугранный угол при боковом ребре.
4)	В правильной треугольной пирамиде двугранный угол при ребре основания равен а. Определить угол наклона бокового ребра к плоскости основания.
136 (398). 1*) В правильной n-угольной пирамиде двугранный угол при боковом ребре равен 2а. Определить двугранный угол при ребре основания.
2*) В правильной n-угольной пирамиде двугранный угол при боковом ребре равен 2а. Определить угол наклона бокового ребра к
плоскости основания пирамиды.
3) В правильной n-угольной пирамиде угол между боковым ребром и смежным ребром основания равен а. Определить угол наклона боковой грани пирамиды к плоскости основания.
137 (399). Основанием пирамиды служит правильный треугольник; из боковых граней одна перпендикулярна к основанию, а две другие наклонены к нему под углом а. Как наклонены к плоскости основания боковые рёбра?
138 (400). В правильной n-угольной пирамиде, высота вдвое меньше стороны основания. Определить двугранный угол при ребре основания.
139 (401). В правильной треугольной пирамиде сторона основания равна а и составляет с боковым ребром угол а. Определить площадь сечения, проведённого через боковое ребро и высоту пирамиды. Почему угол а должен быть больше 30°?
140 (402). 1) В правильной четырёхугольной пирамиде боковое ребро равно Ь и образует с плоскостью основания угол а. Через диагональ основания параллельно боковому ребру проведена плоскость. Определить площадь сечения.
2) В правильной треугольной пирамиде SABC (черт. 40) ребро основания а и двугранный угол при ребре основания а.
Определить площадь сечения DEFK, проведённого через центр основания параллельно непересекающимся рёбрам ХЛ и ВС.
141 (403). В правильной треугольной пирамиде сторона основания равна а и боковое ребро образует с плоскостью основания
48
угол а. Через центр основания проведена плоскость параллельно двум непересекающимся рёбрам пирамиды. Определить площадь сечения.
142 (404). 1) В правильной четырёхугольной пирамиде сторона основания равняется а и двугранный угол при ребре основания 2а. Определить площадь сечения, которое делит данный двугранный угол пополам. Исследовать формулу решения.
2) В правильной четырёхугольной пирамиде двугранный угол при ребре основания равен а. Через ребро основания проведена плоскость под углом 0 к основанию (0 < а). Ребро основания пирамиды равно а. Определить площадь сечения.
143 (405). В правильной четырёхугольной пирамиде высота равна А, а двугранный угол при ребре основания равен а. Определить площадь сечения, образованного плоскостью, проходящей через середину высоты пирамиды параллельно боковой грани.
144 (406). 1) В правильной четырёхугольной пирамиде ребро основания равно а и боковое ребро накло
нено к плоскости основания под углом а. Через одну из вершин основания проведена плоскость перпендикулярно к противолежащему боковому ребру.
Определить площадь сечения. Исследовать формулу решения.
2) В правильной четырёхугольной пирамиде плоский угол при вершине равен а и ребро основания равно а. Через диагональ основания проведена плоскость, перпендикулярная к противолежащему боковому ребру. Определить площадь получившегося сечения. Исследовать формулу решения.
145 (407). 1) В правильной треугольной пирамиде боковое ребро равно а и наклонено к основанию под углом а. Найти площадь сечения этой пирамиды плоскостью, проведённой внутри пирамиды через её вершину, параллельно стороне основания и под углом 0 к плоскости основания. (Рассмотреть два случая.)
2) В правильной четырёхугольной пирамиде, высота которой h составляет с боковым ребром угол а, через диагональ основания проведена плоскость под углом <р к основанию. Определить площадь сечения.
146 (408). 1) В правильной четырёхугольной пирамиде через сторону основания проведена плоскость, перпендикулярная к противоположной боковой грани. Определить площадь получившегося сечения, если сторона основания пирамиды а и двугранный угол при основании а.
2) В правильной треугольной пирамиде сторона основания равна
49
а и плоский угол при вершине равен 2а. Определить площадь сечения пирамиды плоскостью, проходящей через одну из сторон основания перпендикулярно к противолежащему боковому ребру. Исследовать формулу решения.
147	(409). В правильной четырёхугольной пирамиде сторона основания равна а и боковое ребро наклонено к плоскости основания под углом а. Из центра основания пирамиды на две смежные боковые грани опущены перпендикуляры. Определить площадь сечения, образованного плоскостью, проведённой через два прстроен-ных перпендикуляра.
148	(410). Высота правильной четырёхугольной пирамиды равна й, и плоский угол при вершине равен 2а. Определить площадь боковой поверхности пирамиды.
149	(411). В треугольной пирамиде плоские углы при вершине а, аир. Боковое ребро, служащее общей стороной равных углов, перпендикулярно к плоскости основания и равно а. Определить площадь боковой поверхности пирамиды.
150	(412). 1) Основанием пирамиды служит квадрат со стороной а. Из боковых граней две перпендикулярны к основанию, а две другие образуют с ним угол а. Определить площадь поверхности пирамиды.
2) Основанием пирамиды служит прямоугольник. Две смежные боковые грани перпендикулярны к основанию, а две другие образуют с ним углы аир. Высота пирамиды равна h. Определить площадь боковой поверхности пирамиды.
151	(413). Основанием пирамиды служит ромб со стороной а и острым углом а. Две смежные боковые грани, заключающие угол а, перпендикулярны к основанию, а две другие наклонены к нему под углом <р. Определить площадь боковой поверхности пирамиды.
152	(414). Определить объём правильной n-угольной пирамиды, боковое ребро которой b наклонено к плоскости её основания под углом р. Вычислить при п = 8; b = 3,5 м; Р = 78°.
153	(415). В треугольной пирамиде две боковые грани — равнобедренные прямоугольные треугольники, гипотенузы которых равны й, и угол между ними а. Определить объём пирамиды.
154	(416). В правильной шестиугольной пирамиде сторона основания равна 2а и плоский угол при вершине равен 2а. Определить объём пирамиды.
155	(417). В правильной n-угольной пирамиде сторона основания равна 2а и двугранный угол при боковом ребре равен 2а. Опг ределить объём пирамиды. Исследовать формулу решения.
156(418). 1) Основанием пирамиды является прямоугольный треугольник с гипотенузой с и острым углом а. Боковая грань, проходящая через гипотенузу, перпендикулярна к плоскости основания, а каждая другая боковая грань образует с плоскостью основания угол р. Определить объём пирамиды.
2) Основанием пирамиды служит прямоугольный треугольник
50
с гипотенузой с и острым углом а. Боковая грань, проходящая через катет, прилежащий к углу а, перпендикулярна к плоскости основания, а две другие боковые грани наклонены к основанию под углом а. Определить объём пирамиды.
157 (419). Доказать, что если основание высоты пирамиды совпадает с центром окружности, описанной около основания пирамиды (т. е. вершина пирамиды проектируется в центр круга, описанного около основания пирамиды), то
а)	все боковые рёбра (/) пирамиды равны между собой;
б)	углы (<р) наклона боковых рёбер пирамиды к плоскости основания равны между собой;
в)	имеют место соотношения: Н = I • sin ф = R • tg ф; R = = I • cos ф;
Н — высота пирамиды;
R — радиус окружности, описанной около основания пирамиды.
В этом случае какие из известных вам четырёхугольников могут быть основанием пирамиды? '
Если основанием такой пирамиды является прямоугольный треугольник, то в какую точку проектируется вершина пирамиды?
158	(420). Определить объём пирамиды, имеющей основанием треугольник, два угла которого аир, радиус описанного круга R. Боковые рёбра пирамиды наклонены к плоскости её основания под углом ф.
159	(421). В основании пирамиды лежит прямоугольный треугольник, один из острых углов которого а, а каждое боковое ребро равно Ъ и образует с плоскостью основания угол р. Определить объём пирамиды.
160	(422). В основании пирамиды лежит прямоугольник. Каждое боковое ребро пирамиды равно tn и составляет со смежными сторонами прямоугольника углы аир. Определить объём пирамиды. Исследовать формулу решения.
161	(423). Основанием пирамиды служит трапеция, в которой каждая из боковых сторон и меньшая из параллельных имеют длину а, а острые углы равны а; боковые рёбра пирамиды образуют с плоскостью основания угол ф. Определить объём пирамиды.
162	(424). В треугольной пирамиде все боковые рёбра и два ребра основания равны а. Угол между равными рёбрами основания равен а. Определить объём пирамиды.
163	(425). Основанием пирамиды служит равнобедренный треугольник, боковые стороны которого равны а и угол между ними а. Боковые рёбра наклонены к плоскости основания под углом 0. В этой пирамиде проведена плоскость через её высоту и вершину угла а. Определить площадь полученного сечения.
164	(426). Доказать, что если основание высоты пирамиды совпадает с центром окружности, вписанной в основание пирамиды (т. е. вершина пирамиды проектируется в центр круга, вписанного в основание пирамиды), то:
51
а)	двугранные углы при рёбрах основания пирамиды равны между собой;
б)	высоты боковых граней пирамиды, проведённые из её вершины, равны между собой;
в)	имеют место соотношения: г = h • cos ф; Н = г - tg ср = = h • sin ф.
Н — высота пирамиды; h — высота боковой грани, проведённая к ребру основания; г —- радиус круга, вписанного в основание, и ф — двугранный угол при ребре основания.
В этом случае какие из известных вам четырёхугольников могут быть основанием пирамиды?
Указание. Если в треугольной пирамиде боковые грани наклонены к плоскости, в которой лежит основание пирамиды, под одинаковыми углами, то вершина пирамиды проектируется в центр вписанной или вневписанной окружности.
165	(427). Основанием пирамиды служит прямоугольный треугольник, катеты которого 6 см и 8 см. Все боковые грани пирамиды наклонены к плоскости, в которой лежит основание пирамиды, под углом 60°.
Найти площадь боковой поверхности пирамиды.
Указание. Рассмотреть четыре возможных случая решения, когда вершина пирамиды проектируется в центр вписанной и вневписанной окружностей в основание пирамиды.
166	(428). В треугольной пирамиде стороны основания 13 см, 14 см и 15 см и боковые грани пирамиды наклонены к плоскости, в которой лежит основание пирамиды, под углом в 45°. Вычислить площадь боковой поверхности пирамиды.
167	(429). Стороны основания треугольной пирамиды равны а, b и с\ каждый двугранный угол при рёбрах основания равен а. Определить площадь боковой поверхности и объём пирамиды.
168	(430). Основание пирамиды — ромб со стороной а и острым углом а. Каждый двугранный угол при рёбрах основания ф. Определить площадь боковой поверхности и объём пирамиды.
169	(431). В основании пирамиды лежит равнобедренная трапеция, параллельные стороны которой равны а и b (а > Ь). Все боковые грани пирамиды наклонены к плоскости основания под углом а. Определить площадь поверхности пирамиды.
170	(432). Основание пирамиды — равнобедренная трапеция, диагональ которой равна I и составляет с большим основанием угол а. Все боковые грани пирамиды наклонены к плоскости основания под углом ф. Определить площадь поверхности пирамиды.
171	(433). Если все боковые грани какой-либо пирамиды наклонены к плоскости основания под одним и тем же углом а, то
Збок = -2-и S = Q-tga.ctg^, cos а	2
где S — площадь поверхности, Q — площадь основания. Доказать.
52
172	(434). Дан правильный тетраэдр. Определить:
1) угол между двумя смежными гранями и 2) угол наклона ребра к плоскости противолежащей грани.
173 (435). Дан правильный октаэдр. Определить угол между двумя смежными гранями.
174 (436). 1) Дан икосаэдр (черт. 41). Определить угол между двумя его смежными гранями.
2) Дан додекаэдр (черт. 42). Определить угол между двумя его смежными гранями.
 175 (437). В правильной четырёхугольной Усечённая	усечённой пирамиде стороны нижнего и верхнего
пирамида.	оснований соответственно равны а и b (а > Ь),
-------------- двугранный угол при ребре нижнего основания равен а. Определить обьём и площадь боковой поверхности усечённой пирамиды.
176 (438). В правильной усечённой треугольной пирамиде рёбра нижнего и верхнего оснований соответственно равны а и b (а > Ь), двугранный угол при ребре нижнего основания равен а. Определить объём усечённой пирамиды и площадь её поверхности.
177 (439). В правильной п -угольной усечённой пирамиде даны боковое ребро с и стороны оснований а и Ь. Определить высоту усечённой пирамиды.
178 (440). В усечённой правильной четырёхугольной пирамиде стороны оснований относятся как т : п (т > п)\ боковые рёбра наклонены к плоскости большего основания под углом а. В этой пирамиде проведена плоскость через сторону большего основания и противоположную ей сторону меньшего основания. Какой угол образует эта плоскость с большим основанием пирамиды?
179 (441). В усечённой правильной четырёхугольной пирамиде даны высота Н и а и 0 — углы, образуемые боковым ребром и диагональю усечённой пирамиды с плоскостью её большего основания. Определить площадь боковой поверхности усечённой пирамиды.
53
Цилиндр.
180 (442). В усечённой правильной четырёхугольной пирамиде даны стороны оснований а и b (а > Ь) и острый угол а в боковой грани. Определить объём. Исследовать формулу решения.
181 4443). По данной модели правильной усечённой четырёхугольной пирамиды рассчитать:
1) угол наклона бокового ребра к плоскости основания и
2) угол наклона боковой грани к плоскости основания.
Задачи на круглые тела
182 (444). В равностороннем цилиндре точка окружности верхнего основания соединена с одной из точек окружности нижнего основания.
Угол между радиусами, проведёнными в эти точки, равен 30°. Определить угол между проведённой прямой и осью цилиндра.
183 (445). В равностороннем цилиндре, радиус основания которого равен /?, точка окружности верхнего основания соединена с точкой окружности нижнего основания. Проведённая прямая образует с плоскостью основания угол а. Определить расстояние этой прямой от оси цилиндра. Исследовать формулу решения.
184 (446). К цилиндру проведена касательная прямая под углом а к плоскости основания. Определить расстояние центра нижнего основания от этой прямой, если его расстояние от точки касания равно d и радиус основания равен R.
185 (447). Сечение цилиндра плоскостью, параллельное его высоте Н, представляет собой квадрат, отсекающий от окружности основания дугу а. Определить расстояние этого сечения от оси цилиндра.
186 (448). Цилиндр, высота которого Л, пересечён плоскостью, параллельной оси цилиндра и отстоящей от оси на расстояние d. Секущая плоскость отсекает от окружности основания дугу а. Определить площадь сечения.
187 (449). Высота цилиндра равна h. В развёртке его боковой поверхности образующая составляет с диагональю развёртки угол а. Определить объём и площадь поверхности цилиндра.
 188 (450). Радиус основания конуса равен 7?, Конус. а образующая наклонена к плоскости основания --------------под углом а. В этом конусе проведена плоскость через его вершину под углом <р к его высоте. Определить площадь полученного сечения. Исследовать формулу решения.	г
189 (451). Между двумя параллельными плоскостями заключён конус так, что его основание находится на одной из них, а вершина на другой. Угол между осью конуса и образующей равен а. Через середину оси проведена прямая, составляющая с ней острый угол 0 и пересекающая боковую поверхность конуса в двух точках. Отрезок этой прямой между параллельными плоскостями равен а. Определить отрезок её, заключённый внутри конуса.
54
190 (452). Площадь боковой поверхности конуса втрое больше площади основания. Найти угол между образующей и основанием.
191 (453). Через две образующие конуса, составляющие между собой угол ф, проведена плоскость, наклонённая к плоскости основания конуса по углом а. Площадь сечения равна S. Определить высоту конуса (ф = 52°16'; а = 33°10'; S = 618 cjw2).
192 (454). Высота конуса Я, образующая наклонена к плоскости основания под углом а. Перпендикулярно к высоте в конусе проведена секущая плоскость так, что она делит пополам площадь поверхности конуса. Определить расстояние секущей плоскости от вершины конуса.
193 (455). Угол при вершине в осевом сечении конуса равен а; определить .центральный угол в развёртке боковой поверхности конуса. Найти этот угол для равностороннего конуса.
194 (456). Через вершину конуса проведена плоскость, отсекающая от окружности основания дугу а и образующая с плоскостью
основания угол 0. Определить угол при вершине получившегося сечения.
195 (457). На плоскости основания равностороннего конуса (вне конуса) дана точка, удалённая от окружности основания на расстояние радиуса. Через эту точку проведены к конусу две касательные плоскости. Определить угол между ними (черт. 43).
196 (458). Через вершину конуса проведена плоскость, делящая боковую поверхность на две части; если развернуть эти части на плоскость, то получатся два сектора с углами а и 0 (а > 0). Определить угол при вершине проведённого сечения.
197 (459). Угол откоса для песка ф = 25°. Куча песка имеет вид конуса, длина окружности основания которого с ж 5,0 м. Узнать возможный наибольший объём кучи.
198 (460). Через две образующие усечённого конуса, составляющие между собой угол 0, проведена плоскость, пересекающая основания конуса по хордам, соответственно равным тип (т> п). Каждая хорда стягивает дугу а. Найти
площадь боковой поверхности усечённого конуса.
199 (461). В усечённом конусе, радиусы оснований которого/? и г, проведена плоскость под углом 0 к основанию. Эта плоскость отсекает от окружности каждого основания дугу б и не пересекает высоту усечённого конуса. Определить площадь сечения.
200 (462). В усечённом конусе высота равна ft; образующая составляет с плоскостью нижнего основания угол а и перпенди
Усечённый конус.
55
кулярна к линии, соединяющей верхний конец её с нижним концом противоположной образующей. Определить площадь боковой поверхности усечённого конуса.
201 (463). Площади нижнего и верхнего оснований усечённого конуса и боковой поверхности пропорциональны т, п ир. Определить угол между образующей и плоскостью нижнего основания.
202 (464). В усечённом конусе отношение площадей оснований равно 4, образующая имеет длину I и наклонена к плоскости основания под углом ф. Определить объём усечённого конуса.
203 (465). В усечённом конусе диагонали осевого сечения взаимно перпендикулярны, а образующая составляет с плоскостью большего основания угол а и равна /. Определить площадь поверхности и объём усечённого конуса (/ = 12; а = 70°).
204 (466). Через точку, данную на поверх-
Шар
ности шара радиуса /?, проведены две плоскости:
одна касательная к шару, другая под углом а
‘ к первой. Определить площадь сечения шара вто
рой плоскостью.
205 (467). Дан шар радиуса 7?; плоскость, пересекая диаметр под углом а, делит его на две части в отношении 3:1. На какие части разделилась поверхность шара?
206 (468). Высота шарового сегмента й; дуга в осевом сечении равна а. Определить площадь сферической поверхности сегмента.
207 (469). Дан шаровой сегмент; через середину его высоты проведена плоскость параллельно основанию; площади сечения и основания равны. Определить дугу в осевом сечении сегмента.
208 (470). Определить угол в осевом сечении шарового сектора, если плоскость, проведённая через середину среднего радиуса перпендикулярно к нему, делит коническую поверхность сектора на две равновеликие части.
209 (471). На поверхности шара радиуса R через данную её точку проведены два равных взаимно касательных круга; угол между их плоскостями равен а. Определить часть поверхности шара, заключённую между этим плоскостями.
210 (472). На поверхности шара даны четыре точки на одина-
ковом расстоянии друг от друга. Определить углы между радиусами шара, проведёнными в какие-либо две из них.
211 (473). 1) Радиус земного шара
равен » 6370 км. Найти длины окружностей тропика (широта» 23°30') и полярного круга (широта» 66°30').
Черт. 44
2) Наблюдатель, находясь на вершине горы в точке А (черт. 44), измерил угол DAC = а, составленный лучом зреция АС, идущим к горизон
56
с
Черт. 45
ту, и вертикальной линией AD. Зная радиус Земли л, определить высоту горы AD.
212 (474). Бак, имеющий форму шара радиуса R (внутренний размер), наполнен до некоторой высоты жидкостью, удельный вес которой равен d. Дуга АС В (черт. 45) равна <pQ. Найти вес жидкости.
213 (475). Резервуар для газа состоит из цилиндра, закрытого сверху шаровым сегментом. Внутренние размеры цилиндра: диаметр — 24,0 м, высота — 6,0 м. Дуга в осевом сечении шарового сегмента, покрывающего цилиндр, содержит 74°. Найти ёмкость резервуара.
Задачи на комбинации геометрических тел
Комбинации многогранников.
214 (476). В правильной четырёхугольной пирамиде сторона основания равна а, а боковое ребро образует с плоскостью основания угол а. В эту пирамиду вписан куб так, что четыре из его вершин лежат на апофемах пирамиды.
Определить ребро куба.
215 (477). В правильной четырёхугольной пирамиде боковое ребро а и составляет с плоскостью основания угол а. В эту пирамиду помещён куб так, что вершины одной его грани совпадают с серединами рёбер основания пирамиды, а каждое ребро противолежащей грани куба пересекает одно из боковых рёбер пирамиды. Определить объём части куба, расположенной вне пирамиды.
216 (478). Правильная треугольная пирамида с ребром основания а и двугранным углом а при этом ребре пересечена плоскостью, параллельной основанию, так, что площадь полученного сечения равна площади боковой поверхности образовавшейся усечённой пирамиды. Определить расстояние секущей плоскости от вершины пирамиды.
217 (479). В правильную треугольную пирамиду вписана другая правильная пирамида так, что её вершина лежит в центре основания первой, а вершины основания лежат на боковых рёбрах первой. Ребро основания первой пирамиды равно а, и боковое её ребро составляет с плоскостью основания угол а. Боковое ребро вписанной пирамиды наклонено к плоскости её основания под углом р. Определить объём вписанной пирамиды.
218 (480). Две правильные четырёхугольные пирамиды имеют общее основание, и одна из них находится внутри другой. Боковое ребро большей пирамиды наклонено к плоскости основания под углом а, а боковое ребро меньшей — под углом р. Радиус круга, описанного около общего основания пирамид, равен R. Определить
57
Черт. 46
объём части пространства, ограниченной боковыми гранями этих пирамид. Исследовать полученное решение.
219 (481). Две правильные треугольные пирамиды имеют общую высоту; вершина каждой пирамиды лежит в центре основания другой; боковые рёбра одной пересекают боковые рёбра другой. Боковое ребро I одной пирамиды образует с высотой угол а, боковое ребро второй образует с высотой угол 0. Определить объём общей части двух пирамид.
220 (482). В правильной усечённой четырёхугольной пирамиде сторона большего (нижнего) основания равна а\ боковое ребро также равно а и составляет со стороной нижнего основания угол а. Центр нижнего основания служит вершиной пирамиды, основание которой совпадает с верхним основанием данной усечённой пирамиды. Определить, разность объёмов усечённой и внутренней пирамид.
221 (483). Основанием пирамиды служит квадрат, сторона которого равна а. Две боковые грани пирамиды перпендикулярны к плоскости основания, а большее боковое ребро наклонено к пло
скости основания под углом 0. В пирамиду вписан прямоугольный параллелепипед так, что вершины его верхнего основания лежат на боковых рёбрах пирамиды, а вершины нижнего основания — в плоскости основания пирамиды. Определить объём параллелепипеда, если диагональ его составляет с плоскостью основания угол а (а = = 45,3 см; а = 41°30'; 0 = 43°54').
222 (484). Общим основанием двух параллелепипедов является квадрат со стороной а. Две стороны верхнего основания одного являются продолжением двух сторон верхнего основания другого. Две противоположные боковые грани каждого параллелепипеда наклонены к плоскости основания под одним углом а, а две другие боковые грани перпендикулярны к той же плоскости. Определить объём общей части двух параллелепипедов (черт. 46).
223 (485). Боковое ребро правильной треугольной пирамиды равно а и образует с плоскостью основания угол а. В эту пирамиду вписан равносторонний цилиндр, так что его нижнее основа*" ние лежит в плоскости основания пирамиды. Определить высоту цилиндра.
224 (486). Определить ребро куба, вписанного в конус, образующая которого равна I и наклонена к плоскости основания под углом а.
225 (487). В конусе даны радиус основания R и угол а между образующей и плоскостью основания. В конус вписана прямая тре
Комбинации цилиндров, конусов и многогранников.
58
угольная призма с равными рёбрами так, что её нижнее основание лежит в плоскости основания конуса. Определить длину её рёбер.
226 (488). Круг, радиус которого 7? = 5,38 м, служит общим основанием двух конусов, построенных по одну от него сторону. Образующая одного конуса составляет с плоскостью основания угол а=74°36', образующая другого составляет с той же плоскостью угол Р == 60°12' (а>Р). Определить объём части пространства, заключённой между боковыми поверхностями этих конусов.
227 (489). На чертеже 47 изображён продольный разрез доменной печи. Внутренность её состоит из двух усечённых конусов. Верхнее и нижнее отверстия имеют радиусы ri и г2. Углы наклона образующих к основанию аир. Общий объём V. Определить радиус общего основания конусов и их высоты.
228 (490). В усечённый конус вписан конус, имеющий с ним общее меньшее основание, общую высоту и образующие, соответственно параллельные образующим усечённого конуса. Определить объём части усечённого конуса, заключённой между поверхностями обоих конусов. Наибольший угол между продолжениями образующих усечённого конуса, из которых каждая а, равен а.
229 (491). Образующая конуса равна I и наклонена к основанию под углом а. Определить высо
ту вписанного равностороннего цилиндра, если Черт. 47 нижнее основание цилиндра лежит в плоскости основания конуса.
230 (492)» В конус вписан цилиндр, диагонали осевого сечения которого параллельны образующим конуса. Образующая конуса равна I и составляет с плоскостью основания конуса угол а. Найти объём части пространства, ограниченной боковыми поверхностями конуса и цилиндра.
231 (493). Два конуса имеют общую высоту Н и параллельно расположенные основания. Образующая одного конуса наклонена к плоскости основания под углом а, образующая другого — под углом р. Определить длину линии, по которой пересекаются их боковые поверхности.
232 (494). В равносторонний конус вписана правильная п-уголь-ная пирамида. Определить двугранные углы при рёбрах основания пирамиды.
233 (495). В конус вписана правильная n-угольная пирамида, плоский угол при вершине которой равен а. Определить площадь боковой поверхности конуса, если радиус основания его г.
234 (496). Два конуса имеют общую вершину, высота каждого из них лежит на боковой поверхности другого. Определить угол между линиями их пересечения, если угол между высотой и образующей в каждом конусе равен а (черт. 48).
59
235 (497). Около конуса описана треугольная пирамида. Боко
вая поверхность конуса линиями касания делится на три части пропорционально числам 5, 6 и 7. В каком отношении делят те же ли-
нии боковую поверхность пирамиды?
236 (498). Два конуса имеют общее основание. В общем осевом
сечении образующая одного из них перпендикулярна к противо-положной образующей другого. Объём одного вдвое меньше объёма
другого. Определить угол наклона образующих большего конуса к плоскости основания конусов.
237 (499). Внутри куба, ребро которого а, помещается конус так, что его вершина совпадает с одной из вершин куба, а окружность основания касается трёх граней куба, сходящихся в противоположной вершине. Образующая конуса составляет с его осью угол а. Определить радиус основания конуса (черт. 49).
238 (500). Радиус основания конуса равен г, а образующая наклонена к
плоскости основания под углом ф. Около конуса описана пирамида,
имеющая в основании прямоугольный треугольник с острым углом а. Определить объём и площадь боковой поверхности пирамиды.
239 (501)« В правильной четырёхугольной пирамиде боковое ребро равно Ь и образует с плоскостью основания угол а. В эту пирамиду вписан равносторонний цилиндр так, что одна из образую
щих расположена на диагонали основания пирамиды, а окружность каждого основания касается двух смежных боковых граней пирамиды. Определить радиус основания цилиндра.
240 (502)« Два конуса имеют концентрические основания и общую высоту й. Разность углов, составляемых образующими с осью, равна Р, угол наклона образующей внутреннего конуса к плоскости его основания равен а. Определить объём части пространства, заключённой между поверхностями конусов.
241 (503). Определить площадь боковой поверхности усечённого конуса, описанного около правильной треугольной усечённой пирамиды, если острый угол в боковой грани пирамиды равен а, а радиус вписанного . в неё круга равен г.
242 (504)« В конус, у которого площадь боковой поверхности т и угол наклона образующей к плоскости основания ф, вписана треугольная пирамида, имеющая основанием прямоугольный треугольник с острым углом а. Определить объём пирамиды.
60
243 (505). В цилиндр вписан параллелепипед; большая сторона
его основания а, угол между диагональю параллелепипеда и его большей боковой гранью 0, а угол между диагональю параллелепипеда и плоскостью его основания равена. Найти площадь боковой
поверхности цилиндра.
244 (506). На общем основании построены два конуса один вну-
три другого так, что их вершины находятся друг от друга на расстоянии а. Определить объём части пространства, ограниченной коническими поверхностями обоих конусов, если угол при вершине осе-
вого сечения большего конуса равен а, а меньшего конуса — 0 (а = 53° 17'; р =90°; а = 32,52 At).
245 (507). В правильной треугольной пирамиде вершина основания находится на расстоянии Ь от противолежащей боковой грани. Найти площадь поверхности конуса, вписанного в данную пирамиду, зная, что апофема пирамиды наклонена к плоскости основания под углом а (Ь = 10,16 м\ а = 61°16').
246 (508). Общим основанием пирамиды и прямой призмы, расположенных по одну
его сторону, является правильный треугольник со стороной а. Две боковые грани пирамиды перпендикулярны к плоскости
основания; равные боковые рёбра пирамиды образуют между собой угол а. Высота призмы в два раза меньше высоты пирамиды. Определить объём призмы (а = 3,52 м\ а = 41°20').
При обработке конических поверхностей на токарном станке играет роль понятие конусности. Конусностью называется отношение диаметра основания конуса к его высоте. Решить следующие за-
дачи:
247 (509). Определить угол при вершине в осевом сечении конуса, если конусность равна
248 (510). Из цилиндрического бруска меди требуется выточить деталь в форме конуса, образующая которого 125 мм, а конусность равна 1 : 20. Определить вес вытачиваемого конуса (удельный вес меди d % 8.9).
249 (511). На чертеже 50 изображено осевое сечение цилиндра (прямого кругового) и шара, описанного около цилиндра; считая, что радиус шара R, а диагональ прямоугольника в осевом сечении цилиндра составляет с основанием угол а, доказать, что Н = 2R • sin а и г = R - cos а,
где Н — высота цилиндра и г — радиус его основания.
Рассмотрите самостоятельно случай шара, вписанного в цилиндр.
Комбинации геометрических тел с шаром.
61
250 (512). 1) На чертеже 51 изображено осевое сечение конуса (прямого кругового) и шара, описанного около конуса. Считая, что радиус шара 7? и угол при вершине осевого сечения конуса ф, доказать, что -4 AOOt = ф; SO1 = Н = 2/? cos2 X;
/ = 2Rcos|; Н (2R — Н) = г2; г = R sin ф = I sin = H tg
2) На чертеже 52 изображено осевое сечение конуса (прямого кругового) и шара, вписанного в конус. Считая радиус шара рав-
ным R и угол при вершине осевого сечения конуса ф, доказать справедливость соотношений:
л — ф
27? cos2----
Z ОАО. = 45° - SOt = И =-----------------— = rctg Л rt = R cos
4	. ф	2	2
sin —
2
где — радиус окружности касания поверхности конуса с поверхностью шара; г = R ctg -; I = г + R ctg X
4	2
251 (513). На чертеже 53 изображено осевое сечение прямого
кругового усеченного
конуса и шара, описанного около конуса. Считая известным радиус шара R, образующую конуса / и угол <р наклона образующей конуса к плоскости нижнего его основания, доказать справедливость следующих соотношений:
d = 2R sin <р; Н — I sin <р;
(r2 + rj2 = sin2 ф (4/?2 — /2);
г2 — г, = I cos ф.
(/ — образующая, И—высота, d—диагональ осевого сечения, rt и г2 — радиусы нижнего и верхнего оснований).
62
252 (514). Г) Шар радиуса k вписан в усечённый конус. Угол наклона образующей к плоскости нижнего основания конуса а. Найти радиусы оснований и образующую усечённого конуса.
2	) Правильная n-угольная призма вписана в шар радиуса R. Ребро основания призмы а. Найти высоту призмы при п = 3;4; 6.
253	(515). Сторона основания правильной n-угольной пирамиды равна а, двугранный угол при основании равен <р. Определить радиус шара, вписанного в пирамиду.
254	(516). Определить радиус шара, описанного около правильной п-уголыюй пирамиды, если сторона основания равна а, а боковое ребро наклонено к плоскости основания под углом а. (Вычислить при п = 8; а = 3,5 м; а = 58°.)
255	(517). Основанием пирамиды служит ромб со стороной а и острым углом а, двугранные углы при основании равны <р. Определить радиус шара, вписанного в эту пирамиду.
256	(518). В конусе даны длина с окружности основания и угол а между образующей и основанием. Определить длину линии, по которой взаимно касаются боковая поверхность конуса и поверхность вписанного в него шара.
257	(519). В конус вписан шар; линией касания поверхность этого шара делится в отношении т : м. Определить угол наклона образующей конуса к его оси.
258	(520). Определить угол между образующей и плоскостью основания конуса, объём которого в т раз более объёма вписанного в конус шара. (Найти наименьшее значение т\ вычислить угол, если т = 2 — .
4 ]
259 (521). Сечение, перпендикулярное к высоте конуса, делит конус на две равновеликие части и проходит через центр описанного около конуса шара. Найти угол между образующей и плоскостью основания конуса.
260 (522). В конусе помещены два шара так, что они касаются друг друга и поверхности конуса. Отношение радиусов этих шаров равно т : п (т > п). Определить величину угла при вершине осевого сечения конуса.
261 (523). Определить угол при вершине в осевом сечении конуса, описанного около четырёх равных шаров, расположенных так, что каждый касается трёх других.
262 (524). Определить радиус шара, описанного около усечённого конуса, в котором радиусы оснований R и г, а образующая наклонена к плоскости нижнего основания под углом а (/? > г).
263 (525). В усечённый конус, радиусы оснований которого rt и r2 (fi > г2)> вписан шар. Определить: 1) площадь поверхности шара и 2) угол наклона образующей конуса к плоскости его основания.
264 (526). 1) Высота правильной четырёхугольной призмы равна й, а диагональ призмы наклонена к боковой грани под углом а. Определить радиус шара, описанного около призмы.
63
2) Сторона основания правильной треугольной призмы равна а, диагонали двух боковых граней, проведённых из одной вершины верхнего основания призмы, образуют угол 2а, обращённый к основанию. Определить радиус описанного шара.
265 (527). Около шара, объём которого V, описана прямая четырёхугольная призма; основание призмы — ромб с острым углом а. Определить объём призмы.
266 (528). В шар радиуса Z? вписана прямая призма; основание её — прямоугольный треугольник с острым углом а, а наибольшая её боковая грань — квадрат. Определить объём призмы.
267 (529). Призма, основание которой прямоугольный треугольник с острым углом а, описана около шара. Вычислить Ъбъём призмы, если перпендикуляр, опущенный из вершины прямого угла на гипотенузу в основании призмы, равен h.
268 (530)« В правильной четырёхугольной пирамиде боковое ребро b образует с плоскостью основания угол а. Определить радиус шара, описанного около пирамиды.
269 (531). В правильной четырёхугольной пирамиде сторона основания равна а и двугранный угол при ребре основания равен а. Определить радиус шара, вписанного в пирамиду.
270 (532). В правильной четырёхугольной пирамиде сторона основания а и плоский угол при вершине равен а. Определить: 1) радиус вписанного шара и 2) радиус описанного шара.
271 (533). В шар радиуса R вписана правильная треугольная пирамида с плоским углом а при вершине. Определить высоту пирамиды.
272 (534). Основанием пирамиды служит равнобедренный треугольник, каждый из равных углов которого а и сторона между ними а. Каждая боковая грань пирамиды наклонена к плоскости основания под углом 0. Определить радиус вписанного в пирамиду шара.
273 (535). 1) Около шара радиуса R описана четырёхугольная пирамида, в основании которой лежит ромб с острым углом а. Каждая боковая грань пирамиды наклонена к основанию под углом р. Определить объём и площадь поверхности пирамиды.
2) В шар радиуса R вписана правильная четырёхугольная пирамида, у которой двугранный угол при боковом ребре равен 2а. Определить ребро основания пирамиды.
274 (536). В правильной четырёхугольной пирамиде центры вписанного и описанного шаров совпадают. Определить двугран-, ный угол при ребре основания пирамиды.
275 (537). Основанием пирамиды служит прямоугольник с углом а между диагоналями, а боковые рёбра образуют с плоскостью основания угол ф. Определить объём этой пирамиды, если радиус описанного около неё шара равен R.
276 (538). Определить радиус шара, вписанного в’правильную n-угольную пирамиду, сторона основания которой равна а и плоский угол при вершине равен а.
64
277 (539). Определить радиус шара, описанного около треугольной пирамиды, стороны основания которой а, b и с, а боковые рёбра наклонены к плоскости основания под углом а.
278 (540). В правильную шестиугольную пирамиду с двугранным углом а при ребре основания вписан шар радиуса R. Определить площадь боковой поверхности усечённой пирамиды, которая отсечена от данной пирамиды плоскостью, касательной к шару и параллельной плоскости основания пирамиды.
279 (541). Около шара описана правильная четырёхугольная усечённая пирамида: объём восьмигранника, вершинами которого служат точки касания поверхности шара с гранями усечённой пирамиды, вчетверо меньше объёма шара. Определить двугранные углы при ребре основания пирамиды.
280 (542). В правильной четырёхугольной пирамиде плоский угол при вершине равен а; высота h пирамиды служит диаметром шара. Найти длину кривой пересечения их поверхностей.
281 (543). В конус вписан шар; сечение, касательное к шару и параллельное основанию конуса, делит конус на две равновеликие части. Определить угол наклона образующей к плоскости основания конуса.
282 (544). Вокруг шара радиуса R описан усечённый конус, образующая которого наклонена к плоскости большего основания под углом а. Определить длину линии, по которой шар касается боковой поверхности усечённого конуса.
283 (545). В усечённый конус вписан шар радиуса /?; из центра шара диаметр большего основания усечённого конуса виден под углом а. Определить объём усечённого конуса.
284 (546). 1) В шар радиуса R вписан конус, образующая которого составляет с высотой угол а. Определить объём конуса.
2) Определить площадь поверхности шара, вписанного в конус, высота которого h и угол наклона образующей к плоскости основания ср.
285 (547). Вычислить объём конуса, зная радиус R шара, вписанного в конус, и угол а, под которым из центра шара видна образующая конуса. Исследовать формулу решения.
286 (548). В полушар радиуса R вписан усечённый конус так, что его большее основание совпадает с основанием полушара, а образующая наклонена к плоскости большего основания под углом а. Определить площадь поверхности конуса.
287 (549). Шар касается боковой поверхности конуса по окружности основания. Поверхность шара делится при этом на две части, из которых одна в п раз больше другой. Определить угол наклона образующей конуса к плоскости его основания.
288 (550). Высота правильной четырёхугольной пирамиды равна Н\ перпендикуляр, опущенный из центра шара, описанного около пирамиды, на её боковую грань, образует с высотой угол а. Определить объём шара.
65
289 (590). Основание пирамиды — прямоугольный треугольник. Две боковые грани пирамиды перпендикулярны к плоскости основания и образуют острый двугранный угол а, а третья боковая грань наклонена к плоскости основания под углом а. Пирамида вписана в шар радиуса /?. Найти объём пирамиды.
290 (586). Около шара описан прямой параллелепипед, объём которого в tn раз больше объёма шара. Определить углы в основании параллелепипеда.
291 (587). Площадь поверхности шара, вписанного в конус, равна площади основания конуса. Определить угол при вершине осевого сечения конуса.
Задачи на тела вращения
292 (551). Треугольник, одна из сторон которого а = 6,5 м, и .прилежащие к ней углы В = 97° и С = 13°, вращается вокруг данной стороны. Вычислить объём и площадь поверхности тела, получившегося при вращении.
293 (552). Определить объём тела, образованного вращением треугольника АВС около оси, проходящей через вершину А и параллельной стороне ВС, зная, что ВС = а = 23,54 м, проекция стороны АВ на ось вращения Ь' = 7,33 м, а угол между АВ и осью а = 18°36'.
294 (553). Правильный треугольник, сторона которого а, вращается около оси, проходящей вне его через конец его стороны под острым углом а к этой стороне. Определить площадь поверхности тела вращения.
295 (554). Равнобедренный треугольник, у которого боковая сторона равна /?, а угол при вершине а, вращается около боковой стороны. Найти объём и площадь поверхности тела вращения.
296 (555). Ромб со стороной а и острым углом а вращается около оси, проходящей через вершину острого угла перпендикулярно к его стороне. Определить площадь поверхности и объём тела вращения.
297 (556). В треугольнике даны стороны Ь и с и угол между ними а; этот треугольник вращается около оси, которая проходит вне его через вершину угла а и равно наклонена к сторонам бис. Определить объём тела вращения.
298 (557). В треугольнике даны основание а и прилежащие углы а и (90° + а). Определить объём тела, полученного при вращении этого треугольника около его высоты.
299 (558). Два треугольника — равнобедренный с углом а = = 54°16' при вершине и равносторонний — лежат в одной плоскости и имеют общее основание а = 25,34 см. Определить объём и площадь поверхности тела, полученного при вращении треугольников около оси, проходящей через одну из общих вершин этих треугольников параллельно высоте равнобедренного треугольника.
66
300 (559). Определить объём и площадь поверхности тела, полученного при вращении прямоугольника ABCD около оси, проходящей через его вершину Л, перпендикулярно диагонали АС = d, если угол CAB = a (d = 34,06 см\ а = 56°14').
301 (560). Периметр прямоугольного треугольника 2р = 27,4 см, один из острых углов а = 41°10'. Определить объём тела, полученного при вращении треугольника около гипотенузы.
302 (561). В прямоугольной трапеции, описанной около круга радиуса /?, острый угол а. Определить площадь поверхности тела, полученного при вращении этой трапеции около меньшей из непараллельных её сторон.
303 (585). 1) Расстояние между основаниями перпендикуляров, опущенных из вершины тупого угла ромба на его стороны, равно d. Угол между этими перпендикулярами равен а. Определить объём тела, полученного при вращении ромба вокруг оси, проходящей через вершину его острого угла перпендикулярно к большей диагонали.
2) Острый угол прямоугольного треугольника разделён медианой, равной а, на части, из которых большая равна а. Определить объём тела, полученного при вращении данного треугольника вокруг оси, проходящей через вершину прямого угла параллельно данной медиане.
П риложение
ФОРМУЛЫ ТРИГОНОМЕТРИИ
Соотношения между единицами измерения углов
п° = рад ж 0,01745 п рад. а рад =	57,296 а°.
1°^ 0,017453 рад. 1 рад ^57° 17'44",8.
Соотношения между тригонометрическими функциями
_ sinx . cos х
tgX =-----. Ctgx = — .
cos х	sinx
14-tg2x = —L_. 1 +ctg*x = -rL-.
COS^X w	sin2x
sin2x + cos2x = 1.
Формулы приведения
Наименование функций	Значения аргумента				
	— a	Л	л ± a	3л	2л ± a
sin	— sin a	cos a	T sin a	— cos a	± sin a
cos	cos a	T sin a	— cos a	± sin a	cos a
tg	— tga	T etg a	± tga	T etg a	± tga
etg	— etg a	T tga	± etg a	T tga	T etg a
68
Преобразование сумм в произведения
Часто применяемые формулы
sin x + sin у ~ 2 sin — cos -— 7	2	2
sin x — sin у ~ 2 sin * — cos * 7	2	2
,	~ X 4- у X —у
COS X 4- cos у = 2 cos —— cos---------------
' y	2	2
• * — У
sin-------
2t4
sinx = ----------
1 + tg3 f
1 — tg2 -Ь 2 cos X =-----------
cos х — cos у = — 2 sin —- --7	2
.	. a	sln (х ± У)
tgx±tgy= ----*---—.
COS X • cos у ctgx±ctgy= sin(y-±"), sin x • siny
2
tg
х =
1	+ tg3 2
2	tg -
ь 2
1 - tg2 -в 2
Формулы для решения треугольников
Теорема синусов:
х? . = — = с = 2R.
sin A sinS sin С
Теорема косинусов: а2 = Ь2 + с2 — 2bc . cos А.
Формулы Мольвейде:
A — в cos------
_2_
~C
2
с
sin
sin — 2
Теорема тангенсов: tg±+* = 2 a — b ± A — В tg—
— c)
A —В sin------
a — b ________2
~c	C
COS — 2
fg = 1/ (p — b) (P—C) _ ё 2 К P(p-a) ~
b
— — cosC a
sin C
р—а
cos £ = УР(р~а)  ctg4
g  be sin A	g  b2 sin A sin C
2	’	2 sin В
с
-----cos В а
sin В
S	A aSin
^=(p-a)tg^= —
S = Vp (P — a) (p — b)(j> — c).
в . C
I — sln — 2	2	_ aba __ a
A ’ 4S 2sinH*
COS-
Выражение одних тригонометрических функций через другие
	sin x	cos X	fg*	ctgx
sin x		± У1— cos2x	tg x ±У1 +tg*x	1 ±V l+ctg3x
cos X	±У1 — sin2 x		I ±/l + tg2x		ctgx ±/1+ctg2 X
tgx	sin x ± У1—sin2 x	± У1 —COS2 X COS X		1 ctgx
ctgx	± У1—sin2 x sin x	COS X ± У1 —COS2 X	1 tg*	
Формулы сложения
Половинный аргумент
sin (х 4- у) = sinx • cos у 4- cos х- sin у.
sin (х — у) = sin х • cos у — cos х- sin у.
cos (х + у) = cos х • cos у — sin х sin у.
sin	—	=	+	1/ L=..cos.L,
2.	~	V	2
COS	-’=	+	]/1	+COSX
2	“	Г	2
cos (х — у) = cos х • cos у -Ь sin х • sin у.
f X ___ 1 — COS X
2 sin x '
tgf =
2	r	1 + cos x
. £  sin x
2	1 + cos x *
Кратные аргумента
sin 2x = 2 sin x • cos x.
cos 2x = cos3 x — sin3 x.
sin 3x = sinx (3 cos3 x — sin3x). cos 3x = cos x (cos3 x — 3 sin3 x). tg2x = —2t-gx .
l-tg3x
ctg2x = 5^=-1.
2 ctgx
Понижение степени sin2 x = -i (1 — cos 2x). cos3 x = -i- (1 + cos 2x). sin8 x = — (3 sin x — sin 3x). cos3 x = ± (3cos x 4- cos 3x).
70
Преобразование произведений в суммы
COS X • cos у = [cos (X — у) 4- COS (х + у)]-sinx • sin у = у [cos(x — у) — cos(x + у)], sinx • cos у = у [sin (х —у) + sin(x + у)|.
ОТВЕТЫ
4 (339). По натуральным таблицам. 1) « 74°25'; 2) « 56°Г; 3) » 164°22'; 4) 164° 36'. 5 (340). 1) « 104; 2) « 0,00109; 3)4,710; 4) 0,2248; 5) « — 1,191; 6) 342; 7) « 0,6151; 8) 32,16. 6 (346). 1) а) 1/78; б) 7,86; 2) а) 7,12; б) 3,48; 3) а) 22,3; б) 10,65; 4) а) 9,09; 6)3,60; 5) а) 3,75; 6)4,68; 6) а) 0,358; 6)0,1815; 7) а) 1,85; 6) 1,77; в) 1,978.
8 (341).
	а	b	с	Л	В	5
1) а)	8,49	3,93	9,35	65° 10'	24°50'	16.7
б)	0,7321	0,3172	0,7979	66°35'	23°25'	0,1161
в)	2,798	2,334	3,643	50е10'	39°50'	3,265
2) а)	6,37	84,07	84,29	4°20'	85°40'	268
б)	0,1259	0,1738	0,2146	35°55'	54°05'	0,01094
в)	0,6162	0,2954	0,6831	64°23'	25°37'	0,09101
3) а)	528	455	697	49° 15'	40°45'	120100
б)	112	15	113	82°22'	7°38'	840
в)	1499	823	1710	61°14'	28°46'	616800
4) а)	261	380	461	3-Г29'	55°31'	49590
б)	0,0978	0,1001	0,1399	44°2б'	45°40'	0,004905
в)	12,01	6,92	13,86	60°03'	29°57'	41,55
9 (342).
	а = с	‘ 1	А = С	В	S •	
1) 2) 3) 4) 5) 6)	797,9 8,76 97,0 26 627 856,7	634,4 13,96 115,7 22 1160 925,2	66°35' 37°10' 53°23' 65° 23°30' 57°19'	46°50' 105°40' 73°14' 50° 133° 65°22'	232200 36,9 4504 260 144000 333700	fta«20 hb «721,4
72
10 (8). a2 sin a; x 21 cm1. 11 (9). tg | = ^;	59’28'. 12(10). cos a ;
36’39'. 13 (11).	=	73’58'. 15(13). 2/? sin « 2,698. 16 (14). 40’13'.
17 (15). 57’27'. 13 (16). « 47’16';
Cl	ft /
----—; r = a sin - tg_ 45° -
2«4 k
я 32,8 cm. 19(17). 97’12'.	23 (21). R =
8\
— . 25 (23). H ctg a; я 947 m.
4 /
26 (24). Helga; « 1,91 km. 27 (25). ft + Htga; « 240 m. 28(26). « 3,0 cm. b
29 (27). atgP; « 21 m. 30 (28). « 57'. 31 (32). « 2,6 m. 32 (33). tg <p = a
34 (35). « 52°26'; «7,1 кГ. 35 (36). я 22380 км. 36 (37). Psina; «0,2m. л — a	a	a Iff 2a
39 (252). R tg3 -------. 41 (254). b tga-ctg -. 43 (305). x=± —-—; +, если
4	2	2 cos a
j	2p cos3 j
хорда стягивает дугу, большую — окружности. 44 (306). ---------------------------— •
4	/ а \
sin 2a cos2 45° — — ) \	4/
a
Я sin -r	,
2	/ a \	a
45 (307). ----------—. 46 (308). 2d cos2145° — - 1. 47(309). 2/?2 sin 3acos2-.
2 cos2 М5°—-- }
53 (315). 270°. Указание. Обозначить искомую дугу через 6х и провести sin ft — a
х	2	ла2
средний радиус. 54 (316). sin - =----------. 55(317). —. 57(319). —2Л2 sin 2a.
sin —
2
\
63 (325). Отрезок не пересекает плоскость ф- 13Э2Г; отрезок пересекает плоскость, <р = 90°. 64 {326). « 5,42. 65 (327). аге sin V sin2 a + sin2 ft .
a	_______
66 (328). —sin<p-sin2a. 67 (329). arc tg /tg2a+tg2ft; «22’37'. 68(330). я36°52'.
cos a
69 (331). arc cos (cos a • cos ft). 70 (332). cos x =---x « 6°12'.
cos ft
71 (333). /a3 sin3 <p -f- b1 cos3 q>. 72 (334). arc sin CSI-”° .	73 (335'.  —	.
a	2 cos a
74 (583). a3 cos a. 75 (584). /b2—a2 ctg2 a. 76(314). I) « 79 m; 2) я 21,1.и;
3) Й31п^ + Р)  6) 19 0 и 17>q	78 z34ei a) 765;	6) 2380; в) 742;
cos ft
r) 1780.
73
		а	b	с	А	1 5	С	S
81 (347).	1	370,0	545,0	423,4	42° 0'	86°30'	50°50'	78180	;
	2	450,0	84,6	445,1	87°50'	10°50'	81°20'	18820	I
	3	951	1187	341	40°	126°40'	13°20'	130200	|
	4	3,670	13,02	10,21	11°46'	133°40'	34°34'	13,56 |
82 (348).	1	510	317	532 .	68°30'	35°20'	76°10'	78500
	2	225	800 -	634	12°44'	134°06'	36°40'	53750
	3	2,296	1,184	1,687	104ъ54'	29°52'	45°14'	0,9647
	4	62	28	42	124°	21°56'	34°04'	488
83 (349).	1	87	65	77-	75°	46°,1 Г4	58°49'	2420
	2	614			Г33°14'	25°16'		40520
		55,4	360	309	3°46'	1Й4°44'	21°30'	’ 3660
	3	13,89	7,10	8,42	126°41'	24°13'	29°06'	23,99
	4	13,81	20,72		25°21'	140°02'		36,11
			6,01	8,14	154°39'	10°44'	14°37'	10,47
।	5	240,7	263,1	215,4	54°24'	70°14'	”50°22'	2'400
	6	19,06	88,19	—	31°17'	—	—	—
84 (350).	1	19	34	49	16°26'	30°24'	133°10'	235,6^
	2	0,099	0,101	0,158	37°22'	38° 16'	104°22'	0,00484
	3	172,5	113,4	120,5	95э	40°54'	44°06'	6806
	4	1,234	2,345	3,457	Ю°46'	20°50'	148°24'	0,7582
85 (351).
	а	b	с	А	В	С	S
1)	14,55	11,82	5,01	113°17'	48° 16'	18°27'	27,21
2)	20,75	55,39	67,95	15°28'	45°23'	119°09'	501,9
3)	52,76	55,52	-5,94	59° 17'	115°10'	5°33'	141,7.
4)	6,735	6,831	0,522	77° 10'	98°30'	4°20'	1,738
5)	289,9	198,9	287,8	70°24'	40° 16'	69°20'	26980
6)	34	11	29	108°	18°	54°	152,5
7)	17	29	40	22°	39°	119°	213,9
8)	42,5	166,7	138,8	12°05'	124°50'	43°04'	2420
9)	32	25	16	100°24'	50° 12'	29°24'	196
Ю)	10,0	4,8	6,9	115°40'	25°39'	38°41'	15
П)	120,0	29,0	134,4	54°48'	11°23'	113°49'	1590
			100,8	125° 12'		43°25'	1190
12)	34	23	15	127° 13'	32°04'	20°43'	136
86(352). 1) « 1560 га; 2) » 13,8 га; 3) « 1400 ла. 87 (353). 3,6 кГ;
3,7 кГ. 88 (354),—^—;	—etgа. 89 (355). яг 73°.	90 (356). 21 —.
2 sin а 2 -	сек
аР sin а	a О sin 6
91 (357). « 21°30'.	92 (358). —------ м. 93 (359). —	см.
17	v 7 Q sin fl '	7 Psina+Qsin p
94 (360).	(кГ)-, Petga (кГ)- 95 (361). « 150 кГм. 96 (362). ж 61 мм.
sin а
97 (363). a re tg —. 98 (364). яг 2°23'. 99(365). 1) яг 2°1 Г; 2) я 8,7 шага.
74
100 (366).
11°33'. 101 (591). « 56°19'; 33°41'. 102 (592).
1)
105 (367). « 67°55'.	108 (370). 1) « 3108
1) 48°Г; 2) 78 42'.
104 (581). a cos a -f-cm2. « 16450 cm1
103 (593).
+ £sina.
2) 2a3 sin a tg P cos «379 400 cm2. 109 (371). a2 sin a sin &Уcos (a+0) cos(a—
112 (374). abc К—cos 2а. 113(375).
4Л2 V 2 sin -| /cosa
a2b2 sin2 а
4а2 cos2
116 (378). 1) _	; 2)
' 2 У a2 + b2 — 2ab cos a
. p
sill 2
45°.
124 (386).
t f . a—ft	a 4-ft
I/ Sin —в sin -Of;
Г	Z
a3 К 3
—-------, сечение—тре-
4 cos a
)• 1) ^-p^msina;
p	4r2h	a\
\ ; 2) ~— cos2 (45° — - .
2	sin a	2 J
cos
34 700 cm2. 120 (382). 4d2 sin a /cos 2a, h2sin 2a 123 (385).	-------------------------.
8 sin (30° -f- a) sin (30° —a) 2H
угольник; tg a< » где л—высота призмы.
тп sin а .	1
2) ----------.	126 (388). 1) - d3 sin 2а • sin Р •
2а	4
уу
127 (389).-----У р (р — а) (р — Ь) (р — с) ; р — ’ (а + b + с),
cosa	2
130 (302). -“i-L2£0S±. 132 (394). - —
8 cos а
129 (391). arc cos
2 sin
а
2
3a r__________
133 (395). - У 2b2 + a2; arc
4) arctgf-^tgaj. 136 (398). 1) sin x = cosa
135
(397). 2)
± 180°
1) cos x = ctg-------ctg a.
n
180°
138 (400). ------. 139 (401).
n
—ST-2) sin sin-
n
arc cos f tg — 1;
+ 180°
x = ctg------ctga;
n
137 (399). arc tg tg a);
a* ___________________________________
-------/sin (a — 30°) sin (a + 30°). 4 cos a
arc
140 (402). 2)	/3 tg3 a + 12. 141(403).	.
a^acosp	. 15ft* ctg a
sin33a *	’ sinu(a-|-P) 1 \ 16sina
a2cos2tt  o’p^cosa 145/407) к Д*/3 sin a sin (P±a). sin a *	2	*	3sin2P
2) ~c ~_°aJ  146 (408). 1) a3 sin’a. 2) | a’ У sin (60° + a) sin (60° — a).
140 (402). 1)
142 (404). 1)
b2 cos a.
a2 sin2 2a cos a
144 (406). 1) — h2 sin a tga
75
2 •	a2 sin la + — j cos la— —
147 (409). - S‘n ”. 148(410). 2ft2 tg 2a. 149(411). ----------------7------------
2	cos2a
r— <x „	a + 0
а2 У 2 cos —	2/i2 cos —-—
2	2	/ B\ / av
150 (412). 1)-------------------; 2) —-------—- cos 45° — -4 cos 45°—-
/ a\ sin a sin p \	2 J \	2.
cos 145° -J- — I
151 (413).
155. (417). -------
3
/ Ф \	n	360°
a2 sin a ctg (45° — — I. 152 (414). •— fl3 sin 20 cos 0 sis-;
\	2/12	n
. . о 180°
ncr ctg2-cos a
n
1,71
156(418). 1)	2”tg-^; 2) | c3 sin3 a tg (450 —
48 sin (45° + a) 6	\	2 J
4	_______________________ 2	2
160 (422). — m3 cos a cos p У — cos (a-f-P) cos (a—P). 161 (423). —a3 tg <p cos3—. 3	3	a
162 (424). | a3 sin sin (60°+ sin (б0° -	«65 (427).	48 cm^
96 cm2; 144 cm2; 288 cm-. 166 (428). a) 84 /Y cm2; 6) 220,5 /T cm2;
___	a
У ab (a-{-b) cos2 —
-------------. 170. (432). cos a
173 (435). 109°28'.	174
cP — ft
-----;---tga. * 176(438).
6
в) 252 / 2 cm2. 169. (431). ---------
172 (434). 1) 70°32';	2) 54°46'.
a2 — b2
2)	116°34'. 175 (437). ---------;
cos a
I2 sin 2a cos2 —
cos Ф
(436). 1) 138°12'; fl3 — Z?3
~~24~ tga:
4c2 sin2 — (a — b)*
_________n ____________
. 180°
2sin----
n
—------ a*
2 cos a \
a	a \
cos2 — — b2 sin2 — ).
2	2/
177 (439).
----/ 2 tg a ). 179 (441). ——- /2 + ctg2 a.
m + n	)	tg p
fl" — z?3	-
180 (442). —---------У— cos 2a. 182. (444). arc tg (sin 15°) » 14°31z.
о cos a
183 (445). -Д- /— cos 2a. 184 (446). У R2 sin2 a + cP cos2a. 186 (448). 2dh tg-. sin a
л К2 tg2 a h2tga	/?2tga z-—-________________
187 (449).	-	;	-—(2л-j-tga). 188(450). ---------— }/cos((p-|-a)cos((p—a).
4 л 2л	cosacos2qp	7
>1W< a sin 2a sin 2p	--------
189(451).———	. ;-----190(452). 70°32'. 191 (453). sin a 1/Sctg*
sin (a + P) sin (P—a)	У 2
a	a
19,4 cm. 192 (454). ii cos -. 193 4455). 360° sin 180°.
2	2
76
194
196
198
201
203
204
207
211
212
216
219
221
223
226
228
231
(456). 2 arc tg (tg cos 195 (457). ж 82°49'.
/ a _l R 180° R \	c3 tg ф
(458). 2 arc sin sin .	197 (459). ------;
\ 360° a + P /	24ла
л л (m2— na)	Л (7?2— r2)sin6
(460).--------------7—. 199 (461). —-------------------. 200(462).
. a . p	2 cos p
0,25 (At3).
л/i2
cos a
(463). arc cos	.	202 (464).	л/3 sin 2ф cos ф. В	6 л/3 sin a	/	a\ t (465).	X(14-2sin2a); «1176; 2л/а sin I15Q+ —jcos	15°—7): 651,3.
(466). я/?2 sin2a. 205 (467). nR2 (2 + sin a); я/?2 (2 — sin a). 206 (468). -----
. „ a sin2-*
•»	4
(469). 218’54'. 208 (470). 90°. 209 (471). 4л??2 sin j . 210 (472). 2 arc cos iCi.
2r sin2 (45° — ~ j
(473).	1) « 36 750 km\ « 16 060 km\ 2) ---------------------\----------------
sin a
4	Ф /	Ф \	a sin a
(474).	- nd/?3 cos4 -3-2 cos2 - . 214 (476). —------------------------.
'	'	3	4 \	4 /	2 sin (45°+a)
(478).	a/6 tga 217 (479)< a3 sin3 a sin P cos2 p		2/?3 sin(a—6) . 218(480). —			
	a	12 sin* (a + p)	3 cos a cos p
	12 cos —		
	Z3 У 3 cos a sin2 2a sin (3 16 sin2 (a + 0)		4	a				
(481).		..	220 (482).	— a3 sin2 — 1/ — cos 2a. 3	2
(483).	У 2 a3 sin3 P sin a cos2 a	; 16 450 cAt3.	a3 222 (484). —tga. 4
	sin3 (a + P)		
	а У 2 sin 2a	Л v	/ У 2 sin a	Л	У 3 R sin a
(485).		. 224 (486). 4 sin (45°+a)	K"2+ tga	225 (487). 2	. 2sin(60°4a)
h=(r—rj tg a; 7i1=(r—r2) tgp.
(488). —л??2. S‘n (a «307 л<3. 227 (489).
3 cos a cos P
+ r? tg «+r2 *g 0 tga + tg P
(490).
(492).
a	2/sin a	10 _
ла3 sin a sin —. 229 (491). -------------—. 230 (492). “ лZ8 sin 2a cos a.
2	2 -f" tg a	81
„ , 180° n	_	nr2 sin----------
2лл cos a cos p а	дГ q	л _	n
--------------. 232 (494). tg x = -L d - . 233 K495).------------------
sin (a 4-P) 1 g	180’	a
cos-----	.sin —
n	2
77
234 (496). sin =
ctg 30°; ctg 20°.
sin sin ??
2	2/	x
---------- I или cos —
a 1'2 cos-
cos a \
------Y 235(497). ctg40°;
a I
cos - J
238 (500).
236 (498).' w 54°44'.
г2 Г	a	/	a \ 1
—~ 1 +cte 7 +ctg(45° — -I ;
cos <p L	2	\	2 / J
237 (499).	---zr-------•
/ 2 +ctga
r3 / a \ a
- tgq>tgl45° + -Jctg -.
239 (501). V 2 b sin £ sin (45° —	240 (502). л/г3
'	' '	2	\	2/	'	'	3 sin2 a sin3 (a — P)
241 (503). 8/Злг3 ,	242 (504).	l/.m3cof *?. tg <p sin 2a.
3sin2a	3 г л3
a 6 .	ка3 sin2 — sin2—
ла2 sin 2a	2	2
243 (505). -----------o---------. 244 (506). ---------------------;	36 510 л3.
2 cos (a + P) cos (a —P)	g P —a
2
a
4n62 cos2 —
2
245 (507). -----------.	246 (508). « 9,47 m3.	247 (509). « 18°54'.
9 sin a sin 2a
248 (510). x 11,4 г.
a	180°	ф
253 (515). - ctg--------tg 254 (516).
2 n	2
a	w	a	n —tn
5,09 л. 255 (517). - sin a tg 256 (518). 2c sin2 - . 257 (519). arc sin--------------
2	2	2	n -\-tn
258 (520).
2 arc tg
262 (524).
1 ; « 78°26'; 60°. 259(521). sin x = 2m.
s 52°32'. 260 (522). 2 arc sin “ n
V 7?2 r2 + 2/?r cos 2a"
sin 2a
266 (528).
261 (523).	» 70°32'.
V 2 /?3 sin 2a
271 (533). cos (30° + О
267 (529). __________/г3 /2___________ 268 (530) _L_ .
_ . a / Rrt a \	2 sin a
2 sin 2a cos— cos 45——
2	\	2)
2
— R3 sin3 2ф tg ф sin a. 3
2
abc	1
277 (539).	---------r__________—- - _____= . p = — (a 4- b 4- c).
4 sin 2a Yp (p — a)(p — b)(p—c)	2 k n*
78
278 (540). -8У 3 ^2. sin2 а
280 (542). ,/|а У^У.
45° cos ~
281 (543). 83°24'. 282 (544). 2лЯ$1па. 283 (545). - л/?’tg a (ctg3 £•—tg3-\
3	\	2	2 /
2	ср	1
284 (546). 1) -~nR3 cos2 a sin2 2а; 2) 4ji/i2 ctg2 <р tg2 —. 285 (547).—— n^3tg3atg2a. О	£>	О
279 (541). » 62°22'.
286 (548). л/?2 (1 + cos2 2а + 2 sin a sin 2а).
287 (549).	2arctg—7-=*
пН3
288 (550). — (1 + 2 ctg2 а)3.
лас
292 (551).	—
sin2 В sin2 С
sin2 (В + С) *
290 (586). arcsin —. 291 (587). » 73°44'’ пт
sin В sin Ceos ~(В—С)
ла2---------------j--------•
sin (В -|- С) cos — (В +С)
293 (552). nab2
,	л
tgaa. 294 (553). 2л«3 V 3 sin (30° 4- а). 297 (556). - Ьс(Ь+
О
лег* sin
а'	ла3 tg 2а
+ с) sin a cos —. 298 (557). --------—. 209 (558).
'	2	' 6cos2a
; 47 080 слР;
. а 2sin — 2
•а\ 8459 сл2. 300 (559).	— nd* sin 2а;
4 /	*
4 ла2	. /
--------• sin I 15° а \
sin 2
__	16л/?3
57 370 cjh3; 2/ 2 nd2 cos (45° + а) 10 110 см2. 302 (561).	— cos)
ЗМ(585)- 4 ~ 2 .1	; 2)—
ОГЛАВЛЕНИЕ
Введение ...........................................................3
§ 1	(35). Элементы треугольника...................................3
§ 2	(33). Натуральные таблицы и таблицы логарифмов тригонометрических функций.....................................................   3
Упражнения.................................................8
Глава I. Решение прямоугольных треугольников
§ 3	(37) Основные соотношения и задачи...........................11
Упражнения................................................13
Глава II. Решение косоугольных треугольников
§	4	(38).	Теорема синусов.......................................21
Упражнения................................................  22
§	5	(39).	Теорема косинусов.....................................24
Упражнения .....................................................24
§	6	(40).	Формулы для вычисления площади треугольника...........25
Упражнения..............,.......................................23
§	7	(41).	Теорема тангенсов.................................... 26
§	8	(42).	Решение треугольника	по двум его углам и стороне ....	27
§	9	(43).	Решение треугольника	по двум сторонам и углу между ними .	28
§	10	(44).	Решение треугольника	по двум сторонам и углу, противолежащему одной из них	30
§ 11	(45). Решение треугольника	по трём сторонам........................31
Упражнения......................................................33
§ 12	(46). Применение тригонометрии к измерениям на местности и решению практических задач ............................................ 34
Упражнения......................................................37
Глава III. Применение тригонометрии к решению геометрических задач
§ 13	(47). Образцы решения задач.............................42
Упражнения...........................................44
Задачи на	многогранники.............................44
Задачи на	круглые тела..............................54
Задачи на	комбинации геометрических тел.............57
Задачи на	тела вращения.............................G6
Приложение................................................,..68
Ответы..................................................    .	72