Dierck-Ekkehard Liebscher
Relativitatstheorie mit Zirkel und Lineal
Akademie-Verlag-Berlin 1977

ДгЭ.Либшер
ТЕОРИЯ
ОТНОСИТЕЛЬНОСТИ
с циркулем
и линейкой
Перевод с немецкого
В. Е. МАРКЕВИЧА
под редакцией
Н. В. МИЦКЕВИЧА
Издательство «Мир» Москва 1980

УДК 530,12 : 531.18
В книге ученого из ГДР Д.-Э. Либшера даяа
геометрическая интерпретация основных понятии и
соотношений частной теории относительности.
Рассмотрены применения известных простых
геометрических соотношений, а также понятия неевклидовой
геометрии. Дан наглядный геометрический, но
строгий вывод основных релятивистских эффектов, таких,
как изменение длин, замедление хода часов, эффект
Доплера, парадокс близнецов.
Книга рассчитана на самые широкие круги
читателей. Прочесть ее будет интересно каждому
физику и математику. Много интересных рассуждений,
примеров и построений найдут в ней преподаватели
и студенты вузов, учителя, а также учащиеся
старших классов средней школы.
Редакция литературы по физике
1704020000 © Akademie-Verlag Berlin 1977
л 20402-075 ?r o0
041@1)-80 J © Перевод на русский язык, «Мир», 1980

ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
Читатель держит в руках книгу, рассказывающую
о геометрическом представлении теории
относительности. По традиции мы представляем себе геометрию
как раздел математики, а теорию относительности как
физическую дисциплину. Однако в теоретической
физике математика является разговорным языком; в
свою очередь геометрия, если уж речь идет о реальном
мире, не является априорно аксиоматической наукой,
а подлежит опытной проверке, т. е. становится здесь
сама разделом физики. Такова диалектика
взаимодействия формы и содержания, метода и предмета, когда
более глубокое проникновение в сущность явлений
вскрывает их замечательную целостность. Теория
относительности потому и сыграла революционную роль
в физической науке, что раскрыла качественно новую
взаимосвязь материальных объектов — тел, частиц,
полей — и пространства-времени как формы их
существования. Сначала (в частной теории
относительности) эта взаимосвязь была лишь кинематической,
затем же (в общей теории относительности) она вполне
закономерно включила в себя и динамику. В этой
книге рассмотрена геометрическая сторона частной
теории относительности.
Эта теория — один из характерных признаков
современного этапа развития физики. Она не только
сделала понятным множество закономерностей, не
только позволила предсказать и инженерно
рассчитать многие эффекты и их приложения, но и внесла во
Dee это удивительную простоту. Впрочем, удивление
возникает только при первом знакомстве, а потом уже
нельзя себе представить, чтобы все могло быть иначе.
Частная теория относительности необходима как
тем, кто разрабатывает технические и практические

6
Предисловие редактора перевода
приложения ее на данном этапе развития физики, так
и тем, кто разведывает дальнейшие пути в области
реальности, где сегодняшняя теория относительности,
возможно, уступит место еще не известной, новой
теории. (Отметим, что такая разведка и трудна, и чаще
всего огорчительна, так как исследователей — множе*
ство, а новые принципы, в которые все должно вы*~
литься, можно будет пересчитать на пальцах.)
Наконец знание теории относительности для физика — это
просто вопрос элементарной грамотности.
У нас есть обширная литература по частной теории
относительности. Но каждое новое издание отнюдь не
копирует предыдущие, иначе было бы достаточно
просто повторять старые тиражи. В чем же специфика
данной книги? Она относится к разряду не слишком
элементарных, хотя, безусловно, популярна. Автор
стремится поднять читателя на более высокий уровень
не только в отношении чисто физической информации,
но и методически, предлагая интересный
математический аппарат (он опирается, в частности, на
проективную геометрию). Вместе с тем и физика представлена
здесь разбором целого ряда принципиальных
экспериментов и эффектов.
В издательстве «Мир» уже выходила книга [1],
в которой чисто графически и вполне строго
разбирались основания и стандартные эффекты частной
теории относительности. Тогда, однако, были
использованы лишь самые элементарные средства, так что
книга Д.-Э. Либшера может рассматриваться как
логическое развитие такого подхода. Кроме того, более
солидный уровень изложения делает ее
привлекательной и для математиков.
Какую литературу по этому предмету можно еще
порекомендовать читателю? Кроме уже упомянутой
книги Шварца, более солидное, также
геометризованное изложение Р. Неванлинны [2], отточенное в
математическом отношении. Ближе к физике и много
элементарнее отличная книга Г. Бонди [3]. Громадную
пользу может принести книга Э. Тейлора и Дж. Уи«
л ера [4], где, кроме педагогически совершенного
изложения, даны также упражнения с разбором реш^

Предисловие редактора перевода 7
ний. В более широком плане вместе с анализом
электродинамики теория относительности обсуждена в
книге М. Борна [5]. Наконец, детальный разбор
оснований теории и следствий из нее дал на современном
уровне Д. Бом [6]. Однако читателю следует
критически подходить к некоторым философским оценкам
автора (см. предисловие к этой книге).
Чтобы не утомлять читателя, из числа
отечественных работ такого рода мы укажем лишь немногие, в
которых, однако, приведена основная библиография
,[7-9].
Н, Мицкевич
ЛИТЕРАТУРА
1. Шварц Дж. Как это произошло? Иллюстрированный рассказ
о том, как теория относительности устанавливает связи
причин и следствий. — М.: Мир, 1965.
2. Неванлинна Р. Пространство, время и относительность. — М.:
Мир, 1966.
$. Бонда Г. Относительность и здравый смысл. — М.: Мир, 1967.
4. Тейлор Э., Уилер Дж., Физика пространства-времени. — М.:
Мир, 1973.
Б. Борн М. Эйнштейновская теория относительности. — М.: Мир,
1972.
. Бом Д. Специальная теория относительности. — М.г Мир, 1967.
. Угаров В. А. Специальная теория относительности. — М.:
Наука, 1977.
В. Терлецкий Я. П. Парадоксы теории относительности,—М.:
Наука, 1966.
?. Матвеев А. Н. Механика и теория относительности.— М.:
Высшая школа, 1977.

ПРЕДИСЛОВИЕ
Частная теория относительности Эйнштейна — это
основа физического учения о пространстве, времени и
движении. В рамках частной теории относительности,
согласно Герману Минковскому, удается объединить
пространство и время, в результате чего
эйнштейновская кинематика выражается через особую,
неевклидову тригонометрию. Частная теория относительности
позволяет в самом общем виде и весьма простыми
средствами представить физическое учение о
движении как проявление геометрии пространства-времени,
так что кинематика классической механики Галилея
и Ньютона оказывается следствием этой геометрии.
Поэтому синтетическое толкование неевклидовых
геометрий, которым мы обязаны Феликсу Клейну, яв*
ляется естественным и вместе с тем элементарным
введением в круг идей частной теории относительности.
Клейн неоднократно указывал на эту связь и развил
синтетическое представление эйнштейновской частной
теории относительности средствами элементарной
геометрии, что особенно полезно и желательно с
познавательной и методической точек зрения. В трудах
Клейна по элементарной математике и неевклидовым
геометриям содержатся основные методические
указания на этот счет.
Однако, насколько мне известно, эта программа,
состоящая в том, чтобы сделать теорию
относительности, описанную с помощью элементарной геометрии,
доступной всем интересующимся математикой и в то
же время порадовать физиков изящной простотой
построений, до сих пор не была осуществлена. Поэтому
к педагогическим достоинствам книги д-ра Д.-Э. Либ-
шера относится то, что в ней показано, каким образом
выводы теории относительности можно получить в

Предисловие 9
духе Клейна на основании элементарной геометрии с
помощью циркуля и линейки. Читателю предлагается
самому выполнить эти построения и тем самым
элементарным путем войти в мир эйнштейновской мысли.
Ганс-Юрген Тредер
От автора
Прежде всего я хотел бы поблагодарить проф.
Г.-Ю. Тредера за его стимулирующий интерес к
работе. Кроме того, я благодарен за прочтение рукописи
проф. Г. Рейхарду и моим коллегам д-рам Г.-Г. фон
Божешковскому, Г. Гюнтеру, Р. В. Иону и
дипломированному физику У. Блейеру. Дипломированному
математику К. Либшеру я обязан знакомством с
проективной геометрией, а Г. Шмидт выполнил чертежи. Им
я также благодарен.
Д.-Э. Либшер

1. Введение
Частная теория относительности особенно
привлекает интересующихся физикой, поскольку ее
выражения опираются на элементарные представления о
пространстве, времени и движении, что предполагает
простые средства построений и выводов. Однако часто на
пути к пониманию возникают трудности, суть которых
состоит в необычном поведении временной
координаты, в эйнштейновской относительности
одновременности ]).
Во многих случаях такие трудности удается
успешно проанализировать путем правильного изображения
временного хода процесса. Эту книгу нужно
рассматривать как руководство к описанию и оценке
ситуаций, в которых частная теория относительности
проявляется через конкретные явления. Поэтому здесь
делается попытка описать теорию относительности с
помощью евклидовой геометрии и геометрии галилее-
ва пространства-времени (пространства-времени
ньютоновской механики) и вывести простейшие формулы
и теоремы из геометрических представлений.
Читателю, желающему поупражняться в этом методе,
рекомендуется выполнить все построения самостоятельно.
В случае более громоздких изображений указывается
последовательность отдельных операций.
*) Два события, которые один наблюдатель фиксирует как
одновременные, всеми другими наблюдателями будут считаться
также одновременными только в том случае, если они
происходят в одном и том же месте. Такая относительность
одновременности является ключом к разрешению всех кинематических
парадоксов, которые возникают, если рассматривать
утверждения частной теории относительности, беспечно полагаясь на
«здравый смысл», ослепленный дорелятивисгекпмп
представлениями о пространстве-времени.

12
/. Введение
Фундаментом построения является теорема о
сохранении полного импульса при столкновении и распаде
частиц. Предполагается, что читатель знаком с этой
теоремой, а также с понятиями массы, импульса,
скорости и кинетической энергии (в том виде, в каком они
используются в классической механике). Из
геометрии в дальнейшем потребуются лишь теоремы
подобия и теорема Пифагора. Мы обсудим структуру инер-
циальной системы и ее физическую неоднозначность
(принцип относительности), продемонстрируем
явления распространения волн в среде, а также опыт Чем-
пени, Айзека и Хана, подтверждающий независимость
распространения света от выбора инерциальной
системы, сформулируем эйнштейновскую теорему сложения
скоростей, преобразования Лоренца, эйнштейновское
замедление времени, сокращение длин Лоренца и
Фицджеральда и эффект Доплера. Будет объяснен ряд
кинематических парадоксов, в том числе парадокс
близнецов, и построена зависимость эффективной
инертной массы от скорости, рассмотрена ее связь с
энергией и выведены простые кинематические правила
отбора для столкновений и распадов частиц. Так как
мы не выходим за плоскость чертежа, то будем всегда
ограничиваться двумя измерениями — временем и
одним пространственным измерением. Вследствие этого
нам не удастся рассмотреть некоторые разделы
релятивистской кинематики, которые не реализуются при
единственном пространственном измерении, такие, каН
свойства пространства скоростей Эйнштейна —
Лобачевского и прецессия Томаса.
Какое отношение имеет теория относительности к
геометрии? Каким образом мы можем что-то получить
при помощи циркуля и линейки? Свойства объектов
евклидовой геометрии плоскости остаются
неизменными, если эти объекты как целое перемещаются в
плоскости относительно осей декартовой системы
отсчета. Свойства же объектов проективной геометрии
плоскости сохраняются при таких «перемещениях»,
которые эквивалентны центральным проекциям. Ф. Клейн
в своей знаменитой эрлангенской программе в общем

1. Введение
13
виде установил, что геометрические объекты
характеризуются неизменностью свойств при обобщенных й
различным образом определяемых изменениях
положения. Эта программа отвечает структуре как
эйнштейновской, так и ньютоновской механики. Речь идег
о нахождении физических величин и законов, которые
не зависят от положения объектов в
пространстве-времени. При этом тела отсчета задаются масштабами и
часами, с помощью которых наблюдатель исследует
объекты в лаборатории (т. е. системами отсчета).
Надо отметить, что частная теория
относительности исследует здесь лишь особую взаимосвязь систем
отсчета, которая существует и в кинематике
Галилея — Ньютона, но имеет другой вид.
Подходя аналитически, мы можем привлекать при
построении циркуль и линейку только для решения
уравнений вплоть до квадратных и соответственно
получать решения, которые (за исключением
рациональных функций исходных величин) содержат только
квадратные корни. При решении этих задач
окружности заменяются коническими сечениями при заданных
направлении оси и эксцентриситете. (Определение
точек пересечения двух конических сечений с
одинаковым расположением главной оси и эксцентриситета
всегда представляет собой квадратичную задачу, т. е.
в конечной области существуют самое большее две
точки пересечения.) При конструировании мы должны
примириться с тем, что сможем явным образом
обнаружить лишь простые взаимосвязи, однако они
представляются более наглядными, чем при использовании
аналитических методов.
Предлагаемая книга ограничивается описанием и
иллюстрацией взаимосвязи между теорией
относительности и геометрией плоскости. При этом не
предполагается предварительное знакомство с основными
идеями теории относительности, которые
интерпретируются здесь преимущественно геометрически.
Поэтому читателя можно отослать к книге Ландау и Руме-
ра [13] и общедоступному изложению Эйнштейна [6],
Физические и аналитические выводы излагаются в
книге М. Борна i[3].

14 2. Диаграммы движения
Знание физики и геометрии предусматривается
приблизительно в объеме политехнического института.
Используемые теоремы проективной геометрии кратко
изложены в приложении. Читателю, желающему
получить более законченное введение в эту прекрасную и
увлекательную область геометрии, можно
порекомендовать книги В. Бляшке [1], К. Дёлеманна [5] или
О.-Х. Келлера [11]. Тем же, кто хотел бы более
подробно изучить возможности приложения неевклидовой
геометрии к проективным моделям, можно
предложить работы Ф. Клейна и Ф. Шиллинга [12, 19].
2. Диаграммы движения
Задача механики состоит в том, чтобы описать и
исследовать движение материальных тел. Основной
моделью такого тела является материальная точка.
При этом подразумевается лишь, что положение тела
можно свести к заданию места единственной точки.
Согласно третьему закону Ньютона, такой точкой
является центр тяжести. Модель, использующая понятие
материальной точки, работает тем лучше, чем меньше
движение внутренней структуры влияет на движение
центра тяжести.
Простейшим описанием движения является
диаграмма: она позволяет точно установить моменты
времени, в которые тело находится в определенных
местах. В качестве примера возьмем поезд, идущий с
постоянной скоростью1) из Берлина в Краков.
Пассажир садится в него непосредственно перед завтраком,
обедает в Герлице и к ужину прибывает на место
назначения. Пусть его диаграмма сначала имеет вид,
изображенный на фиг. 1.
Плоскость чертежа изображает
пространство-время, ибо она содержит временные и пространственные
координаты. Назовем точку в пространстве-времени
событием2), а кривую — мировой линией. Событие
*) Постоянство скорости обеспечивается здесь не измерением
отрезка пути, проходимого за единицу времени, а постоянством
условий, при которых работает двигатель.
2) Или мировой точкой.— Прим. перев,

2. Диаграммы движения
15
Ужин
Обед
Завтрак
. Мировая линия
поезда
Берлин Гер/шц Кряков
Фиг. 1. Пример обобщенной диаграммы движения.
Время А
Мировая линия
стоящего
поезда
МироВая линия
движущегося роеШ
-ф-^
берлш Герлиц Краков Место
Касательная к мировой линии
Фиг. 2. Диаграмма покоя и движения.
наряду с пространственными координатами всегда
имеет еще и временную координату. Иными словами,
в понятии события объединяются место и момент
времени. Кривая, соединяющая в пространстве-времени
все мировые точки, через которые проходит тело,
представляет собой мировую линию этого тела. Она
описывает историю его движения.
Мировая линия покоящегося тела — это прямая,
параллельная временной оси диаграммы. Если же
тело движется, то касательная к его мировой линии
образует с осью времени угол а, отличный от нуля
.(фиг. 2).

16
2. Диаграммы движения
Ииробая линия поезда А
И и роба я линия самолета F
Пиробая линия поезда В
оерлин Герлиц Кракоб
Фиг. 3. ]]римср диаграммы, иа которой не все равномерные
движения изображаются прямыми линиями.
Единицы
бремени
Ужин
О 1 1 5 Единицы длины
Берлин Герлиц Краков
Фиг. 4. Линейная система отсчета.
Все равномерные движения изображаются прямыми линиями. Диаграмма
фиг. 3 «выпрямлена».
На пашей диаграмме (фиг. 1) мировая линия
поезда А — прямая. Может показаться, что рисунок
отражает постоянство его скорости. Однако это не так.
Оказывается, мы неудачно выбрали координаты, так
как время между обедом и ужином почти вдвое
продолжительнее, чем между завтраком и обедом, а
расстояние между Герлицем и Краковом почти вдвое
длиннее, чем между Берлином и Герлицем.
Рассмотрим встречный поезд В, который идет с той же
скоростью; он не сможет прибыть в Герлиц к обеду, если

2. Диаграммы движения
17
Z 3 Расстояние
от поезда А
Фиг. 5. Диаграмма движения относительно поезда А.
расстояния отсчитываются не от неподвижного вокзала, а от поезда А.
3 Расстояний
от поезда В
Фиг. 6. Диаграмма движения относительно поезда В.
отправляется из Кракова во время завтрака и
развивает такую же скорость, что и первый поезд (фиг. 3).
Мировая линия поезда В в первоначально выбранных
координатах не является прямой. Не будет прямой-и
мировая линия самолета F (фиг. 3). Дело в том, что,
выбирая координаты, мы не приняли во внимание
описываемое движение, т. е. не измеряли промежутки
времени и расстояния. Но мы можем изменить
диаграмму так, чтобы все равномерные движения
изображались прямыми линиями (фиг. 4). Назовем такую
диаграмму линейной системой отсчета. Введение
такой системы отсчета соответствует измерению про-

18
2. Диаграмма движения
J Расстояние
от самолетов
Фиг. 7. Диаграмма движения относительно самолета F*
Расстояние
Фиг. 8. Диаграмма с часами, размещенными по ходу поезда.
Часы на каждой станции поставлены вперед на столько единиц, сколько
единиц длины укладывается в расстоянии от О до этой станции. При •foM
стрелки поставлены так, что поезд В всюду прибывает в одно и то же
время.
странственных и временных промежутков указанных
Событий. В нашем примере мы утверждаем, что
промежуток времени между обедом и ужином почти вдвое
продолжительнее, чем между завтраком и обедом, rt
что расстояние между Герлицем и Краковом почти

2. Диаграмма движения
19
вдвое длиннее, чем между Берлином и Герлицем. Учтя
этот факт при построении диаграммы, мы получим
линейную систему отсчета.
Прежде чем заняться вопросом о существовании
линейной системы отсчета (а для этого нам
потребуется точное определение понятия «равномерное
движение», которое не основывалось бы на определении
линейной системы отсчета), рассмотрим ее
однозначность.
Очевидно, мы снова получим линейные системы
отсчета, если будем откладывать расстояния не от
вокзала, а от поезда А (фиг. 5), от поезда В (фиг. 6) или
от самолета F (фиг. 7).
Впрочем, мы получим линейную систему отсчета и
в случае, если вдоль дороги расставим часы,
показывающие время, пропорциональное их расстоянию от
станции отправления (фиг. 8).
Такая на первый взгляд фантастическая ситуация
реализуется путем задания местного или поясного
времени. Нанесем на диаграмму поясное время в
направлении восток — запад, тогда получим мировые линии
обычных объектов, формально уходящие в прошлое:
можно скоростным самолетом вылететь из Хабаровска
после восхода солнца и прибыть в Москву до
восхода. Разумеется, в противоположном направлении
даже сверхскоростной самолет не может покрыть
разницу в поясном времени (фиг. 9).
Так как линейная система отсчета определяется
только тем, что мировые линии определенных
объектов— прямые, то каждое линейное (т. е. сохраняющее
прямые линии) отображение линейной системы
отсчета является опять линейной системой отсчета.
Линейное отображение плоскости в саму себя
осуществляется заданием трех соответственных пар точек (фиг. 10).
Обозначим координаты на исходной диаграмме через
(xt t), а на новой — через (х, ?), тогда переход к
новым координатам даст
x = al}x + a]2i + blf
t = a2ix + агг1 + b2.

20
2. Диаграмма движения
Поясное
Бремя
Обратный
рейс
ОпМироВое
Время
Рейс из Хабаровска
б Маскбу
О ' Москба
Фиг. 9. Поясное время на диаграмме движения.
Хабаровск Место
(Временные зоны)
Задавая шесть х — J-координат, относящихся к тре*м
событиям (заданным в х—^-координатах), мы тем
самым определяем шесть значений а^. Изображая эту
картину на чертеже, получим все линейные системы
отсчета, для чего нужно проложить все возможные
прямые оси в линейной системе отсчета (фиг. 11).
В дальнейшем из шести параметров aik и bi
линейного отображения A) нас будет интересовать один*
Прежде всего параметры Ь{ и Ь2 лишь сдвигают
систему отсчета, не изменяя расстояний и углов. Отбросив
их, мы тем самым устанавливаем для
определенного исходного события координаты х = 0, t = 0.
Теперь линейное отображение становится однородным и
имеет вид
х = а{{х + я12/,
t = a2\X + a22t.
Величина ац устанавливает связь между
пространственными, а величина а22 — между временными
B)

2. Диаграмма движения
21*
1[
,3
2
1
0
V
\^^ I
1 /
- 1
2
/Ei
3 X
[]
-/
it
4
3
z
i
0
\
\
-\
^-
!
;
ч
ё-
К
h
"
\
J
-*—- U
-=^ o3
1 m
4 1
Фиг. 10. Преобразование линейной системы отсчета.
Установив в новой системе отсчета события Е\, Е2 и ?3| соответствующие
Событиям Ei, E-2 и ?3. можно переносить фигуры с учетом всех соотношений
длин.
У*
Фиг. 11. Преобразование с помошью новых осей.
Для определения новых координат фигуры мы не делаем другого чертежа.
как на фиг. 10, а проецируем старую фигуру на новые осн.
единицами измерения обеих линейных систем отсчета.
Величина а21 определяет, какие события в новой
системе отсчета считаются одновременными (т. е.
обладают одной и той же временной координатой). На
чертеже она определяет направление оси х. Отношение
v = —%± C)
an

22
2. Диаграмма движения
представляет собой скорость, с которой объект,
покоящийся в новой системе (где его мировая линия
параллельна оси i), движется относительно исходной
системы отсчета.
Постараемся теперь ограничить свободу выбора
линейной системы отсчета. С этой целью будем
отдавать предпочтение таким системам отсчета, которые
особенно подходят для описания движения реальных
тел и которые к тому же наиболее просто описывают
неравномерное движение тел вследствие
взаимодействия. Однако оказывается, что такие ограничения с
помощью физики полностью наложить не удается, и
существует целый класс систем отсчета (так
называемые инерциальные системы отсчета), которые
физически друг от друга не отличаются. Это утверждение
называется принципом относительности. Примером
физически неприводимого параметра в преобразовав
иии B)является относительная скорость.
Как утверждает принцип относительности, одних
законов динамик** недостаточно для того, чтобы
отличить одну инерциальную систему от другой. Зато
существование материальных тел отсчета позволяет
выделить инерциальную систему, если законы движения
рассматриваемого процесса влияют на это тело
отсчета. Примером такого процесса является движение
волн в среде. Волновое движение — это внешнее
проявление внутреннего движения среды. Есл*и
рассматривается только волновое движение, система покоя
среды (инерциальная система, в которой среда в
среднем покоится) может быть выделена среди других
систем с помощью законов волнового движения,
имеющих в этой системе особенно простой вид (изотропия
распространения). Вообще говоря, для описания
внутреннего движения ансамбля частиц особенно пред-*
почтительной оказывается система покоя центра масс
этого ансамбля. Примером тому служит коперников-
екая планетная система. Описание же полного
движения, включающего в себя и движение тела отсчета, ни
в коем случае не позволяет выделить инерциальную.
систему.

2. Диаграмма движения
23
Таблица 1
Сравнение диаграммы, линейной системы отсчета
и инерциальной системы отсчета
тт u Инерциачьная система
Диаграмма Линсииая система отсчета отсчета
Частный случай днаграм- Частный случай ли-
мы нейной системы
отсчета
Обобщенное Описание событий с по-
описание собы- мощью координат. Равио-
тий (т. е. вре- мерное движение изобра-
мен н мест) жается прямыми линиями
Одновременность и
единицы измерения при
данном состоянии движения
системы отсчета не
устанавливаются
Одновременность и
единицы измерения
устанавливаются на
основе динамики
относительно состояния
движения системы
отсчета
Обобщенные линейные
координатные
преобразования содержат свойства
системы отсчета. Они
имеют на плоскости 6
свободных параметров:
2 сдвига
1 относительная
скорость,
1 одновременность,
2 единицы измерения
Преобразования,
сохраняющие свойства
инерцналыюй
системы, ограничиваются
динамикой. Они имеют
на плоскости 3
свободных параметра:
2 сдвига
1 относительная
скорость
Принцип относительности справедлив как в
частной теории относительности Эйнштейна, так и в
механике Ньютона, однако реализуется он в этих двух
случаях различным выбором инерциальных систем и
различными переходами между ними. Реализация
принципа относительности в ньютоновской механике

24
3. Инерциальные системы
оказывается непригодной для теории поля. Напротнв,
эйнштейновская реализация справедлива как для
механики, так и для теории поля. Об изменениях,
внесенных в механику частной теорией относительности, мы
будем говорить в следующих главах. Сначала же
рассмотрим реализацию принципа относительности в
ньютоновской механике.
3. Инерциальные системы
Как открытый пока вопрос о существовании
линейной системы отсчета (связанный с определением
равномерного движения), так и вопрос о возможности
сведения линейной системы отсчета к инерциальнои
системе решаются с помощью ньютоновских законов
механики. Частная формулировка этих законов под*
разумевает также и частные случаи реализации
принципа относительности. В ньютоновской механике он
реализуется в виде независимости массы от скорости.
Первый закон Ньютона утверждает, что имеется
класс особых (бессиловых) движений, которые в
подходящих системах отсчета (в нашем смысле
линейных) протекают прямолинейно и равномерно. Первый
закон Ньютона обеспечивает существование линейных
систем отсчета и определяет равномерное движение
как бессиловое. Таким образом, мы получаем
конструктивное предписание: нужно наблюдать за
движением материальных точек, удаленных на
значительное расстояние или экранированных от тел, которые
могут оказывать на них воздействие, и строить
систему отсчета, в которой четыре такие мировые линии
прямолинейны. В определенной таким образом
системе отсчета все мировые линии свободно движущихся
материальных точек будут прямыми.
Здесь не имеет смысла более подробно
останавливаться на вопросе о том, каким образом линейные
системы могут быть реализованы на практике. Примем
за основу следствия, вытекающие из этой концепции,,
чтобы в дальнейшем иметь возможность перехода к
инерциальнои системе. В предыдущей главе было
показано, что для этого нам нужны определения

3. Инерциальные системы
25
единицы времени, единицы длины и одновременности.
Снова обойдем рассуждения о техническом решении
и вернемся к законам Ньютона, которые непременно
лежат в основе даже самых сложных устройств. При
этом мы должны свести область применения законов
Ньютона к законам столкновения, чтобы при
нахождении реальных сил и взаимодействий с помощью
пространственных расстояний не возникло необходимости
в неявном определении эталонов длины, времени и
одновременности. При рассмотрении столкновений такой
опасности не возникает, так как каждое столкновение
является отдельным событием, которое в принципе не
имеет пространственной и временной протяженности.
Рассмотрим сначала полностью иеупругое
столкновение двух тел. До столкновения оба они движутся
свободно. После столкновения образуется одно тело,
которое опять движется свободно. Спрашивается:
какую скорость имеет тело, образующееся в результате
полностью неупругого столкновения? Опыт
показывает, что скорости, которыми обладают
сталкивающиеся тела до удара, не складываются, а
смешиваются по закону, напоминающему правило выравнивания
температур (правило смешивания Вихмана). Здесь
правило смешивания скоростей и называется теоремой
импульсов, причем теплоемкости соответствует
инертная масса М, а количеству теплоты — импульс Р =
= Ми:
Mu = mlul + m2u2, .
М = Ш\ + m2.
Легко понять, что таким образом — с точностью до
постоянного множителя — можно использовать массы
всех объектов данной системы отсчета. Множитель
устанавливается на основании определения эталона
массы (например, масса одного покоящегося атома
С12 равна 1,993-Ю-23 г).
Представим m и пги в качестве временной и
пространственной координат вектора х), тогда мы сможем
') Здесь под вектором мы понимаем направлении»! отрезок,
координаты которого определяются параллельным
проектированием на оси данной системы координат.

26
3. Инерциальные системы
Масса А Время
щц mzvz Mv Импульс
Фиг. 12. Параллелограмм импульсов.
Связь между вектором импульса и мировой линией частицы обусловливает
связь между диаграммой «масса-импульс» и диаграммой «пространство-
время». Тот факт, что теорема сохранения импульса справедлива во всех
системах отсчета, мы опишем наиболее удобным образом, а именно: нанесем
сеть векторов импульса и представим координатные преобразования по
образцу фиг. II. Вектор импульса пропорционален вектору скорости,
который строится из разностей координат. Поэтому выражения, записанные
с помощью векторов импульса, можно записать через координаты событий
в системах отсчета. В частности, линии «масса-временная компонента
импульса = const» параллельны линиям «временная координата = const».
проиллюстрировать теорему импульсов
параллелограммом (фиг. 12).
На х — ^-диаграмме проведем параллель g\ к оси
go через единичную точку на оси t. Мировая линия
равномерно движущегося объекта пересекает go при
х = х0 и g{ при х = Х\. Тогда v = Х\ — х0 есть
скорость объекта. Отложим на временной оси массу а и
найдем на мировой линии точку Р2У имеющую такую
же временную координату, тогда ее координата Х2
определит импульс р = X2 — х0. Далее, можно написать
fi = (mv, га), E)
где вторая компонента является массой. Для
обозначения числовых пар будем аналогично E)
использовать рукописные буквы. Числовые пары представляют
собой вектор в компонентном виде. Заметим, что
операции над обычными векторами трехмерного
пространства (скалярное произведение, векторное
произведение) еще не определены, поэтому мы не пользуемся

3. Инерциальные системы
27
Пасса А Время t
Место х
Импульс
Фиг. 13. Динамическое определение одновременности.
В заданной линейной системе отсчета x—t изобразим годограф возможных
векторов импульса данной частицы. Его точка пересечения Л с осью t
характеризует массу покоя частицы в х— f-системе. Теперь выберем новую ось X,
параллельную касательной а к годографу в точке А, т. е. выберем новое
определение одновременности, при котором а представляет собой
геометрическое место событий, одновременных с Л. В таком случае массу при малых
скоростях можно приближенно считать не зависящей от скорости. Это
определение одновременности назовем динамическим.
1 — обобщенная зависимость массы от скорости или импульса; 2—события,
одновременные с Л в г-системе (согласно динамическому определению);
3 — события, одновременные с Л в f-системе (согласно динамическому
определению); 4—вектор импульса частицы, которая покоится относительно
*-системы и движется относительно ^-системы; 5 — вектор импульса частицы,
которая покоится относительно f-системы и движется относительно ^-системы
обычным способом записи. Диагональ параллелен
грамма со сторонами р{ и /г2 дает нам мировую линию
ёР объекта после полностью неупругого столкновения,
а точки пересечения этой диагонали с go и gi — его
скорость.
Известно, что теплоемкости зависят от
температуры, но здесь мы не можем априори утверждать, что
массы тоже зависят от скорости. В принципе мы
измеряем зависимость от скорости на основании самой
теоремы импульсов и прежде всего устанавливаем,

28
3. Инерциальные системы
что зависимость от скорости для всех масс одна и та
же (в противоположность зависимости теплоемкостей
от температуры). Возьмем теперь эталон массы и
отметим конечные точки векторов импульса для всех
возможных скоростей этого объекта. Получится
кривая в плоскости х — t (фиг. 13).
Для другого объекта получается кривая,
геометрически похожая на первую. Заметим при этом, что не
всякая кривая m = m(v) удовлетворяет принципу
относительности. На стр. 52 мы, руководствуясь
принципом относительности и его конкретной реализацией в
виде зависимости массы от скорости, установим, в
каком случае экспериментальная проверка
подтверждает эту форму принципа относительности.
Теперь, имея кривую m = m(v), мы можем
определить динамическую одновременность: потребуем,
чтобы ось х была параллельна касательной к этой
кривой в единичной точке оси времени. Поскольку
зависимость массы от скорости не относится к какому-то
определенному объекту, то можно таким образом
выделить одно из определений одновременности,
допустимое в линейной системе отсчета. Это определение
одновременности назовем «динамической
одновременностью». Если мы принимаем это определение
одновременности, то все массы при достаточно малых
скоростях будут в первом приближении константами.
Рассмотрим снова переход от одной системы
отсчета к другой (фиг. 14). Числовые значения массы и
скорости, а также ход кривой m = m(v) зависят,
очевидно, от выбора системы отсчета. Для их получения
мы измеряем отрезки, представляющие вектор
импульса, в конкретной системе отсчета. При этом
отрезки, соответствующие векторам импульса, будут
жестко закреплены, так как соотношение различных
импульсов D), получаемое в результате процесса
столкновения, остается неизменным. Теперь мы видим,
что динамическое определение одновременности в
различных системах отсчета обусловливается ходом
зависимости инертной массы от скорости. Однако если
масса га объекта линейно зависит от mvy то в этом
случае динамическая одновременность двух событий

3. Инерциальные системы
29
1 mv 1 x
Фиг. 14. Зависимость массы от линейной системы отсчета.
Различные системы отсчета в соответствии с фиг. 11 представлены
различными осями. Установлена сеть векторов нмпульса. Координаты вектора
импульса в х — ^-системе суть mv и гп-
не зависит от выбора системы отсчета. Выберем в
каждой системе отсчета временную координату таким
образом, чтобы она описывала динамическую
одновременность (т. е. чтобы ось х была параллельна
прямолинейному годографу векторов импульса данного
объекта), тогда массы не будут зависеть от скорости.
Оказывается, что в диапазоне скоростей, технически
осуществимых для макроскопических объектов (v <,
|с<30 км/с), массы, по крайней мере с точностью 1 : 10г\
не зависят от скорости, если принимается
динамическая одновременность.
Если массы в одной системе отсчета не зависят от
скорости, то мы можем потребовать, чтобы они в
любой другой системе отсчета (а в последующем мы
будем использовать только инерциальные системы) не
зависели от скорости. Далее, будем рассматривать
лишь те системы отсчета, которые допускают такое
же определение одновременности, как исходная
система. Тогда временная единица во всех инерциаль-
ных системах может быть установлена через
временную единицу в этой системе. Поскольку теперь вопрос
одновременности двух событий решается независимо
от инерциальной системы, то можно также
унифицировать измерение длин. С помощью масштабов,
которые покоятся в исходной системе, можно прово-

30
S. Инерциальные системы
t=0
Годограф бектороб импульса
частицы постоянной массы
Фиг. 15. Специальные преобразования Галилея.
Независимость массы от скорости означает что геометрическое место
динамически одновременных событий не зависит от положения координатных
осей. Поэтому в инерциальиых системах вес х-оси имеют одинаковое
направление, так "как они должны совпадать с этим геометрическим местом.
Две инерциальные системы различаются только расположением /-осей. Для
произвольного события Е справедливо равенство^ {E) = t (?). Ввиду подобия
треугольников OSS и Е i.ti имеем
х (?) —* {E,= vt (E).
дить измерения во всех других инерциальиых
системах. Приложить масштаб — значит получить
одновременные данные па обоих концах объекта. Этот
механизм получения данных не зависит от движения
масштаба, если само определение одновременности не
зависит от этого движения.
Подведем итог. Теорема импульсов и условие
независимости массы от скорости могут относиться
только к специальным системам отсчета, которые
называются инерциальными, так как масштаб времени,
масштаб длины и одновременность в этих системах
относительны. Преобразование B) сводится к
следующему:
* = /,
F)
v = — al2.
Это специальные преобразования Галилея (фиг. 15),
Вопрос можно было бы сформулировать иначе:
имеются ли кроме лабораторной системы другие

3. Инерциальные системы
31
системы отсчета, в которых вполне справедлива
теорема импульсов, полученная в лаборатории, с
численным соотношением масс и разностью импульсов,
также полученными в лаборатории. Ответ будет тем же
самым: эти законы выполняются в классе так
называемых инерциальных систем, которые (при массах,
не зависящих от скорости) с помощью
преобразований Галилея выражаются одна через другую.
Теорема импульсов во всех инерциальных системах
имеет одну и ту же форму. Не существует выделенной
нперциальной системы So, обладающей каким-то
особым свойством, которое не зависит от движущихся
частиц, но тем не менее проявляется в законах этого
движения: не существует абсолютно покоящейся инер-
цнальной системы. Нет способа, который на основании
наблюдения законов столкновения в некоторой инер-
циальной системе S позволяет сделать заключение о
скорости системы S относительно гипотетически
абсолютно покоящейся системы S0. Но так как в
классической механике все движения состоят из движения
системы материальных точек и так как все силы,
действующие между материальными точками, связаны с
соответствующими законами столкновения, то в
классической механике не существует процесса, который
мог бы выделить некоторую инерциальную систему1).
В классической механике выполняется принцип
относительности: все инерциальные системы равноправны
в формулировании физических закономерностей.
Принцип относительности устанавливает преобразования
(формулы пересчета) между инерциальными
системами в виде преобразований Галилея, если масса не
зависит от скорости.
!) В аристотелевой механике не существует относительность
между системами отсчета, так как не выполняется теорема
импульсов: силы там пропорциональны не изменениям импульсов, а
самим импульсам. Состояние равновесия свободного объекта есть
покой, что выделяет определенную систему отсчета. При
наблюдении этого состояния равновесия можно в каждой системе
отсчета установить, какую скорость она имеет относительно
абсолютно покоящейся системы.

32
3. Инерциальные системы
Фиг. 16. Галилеево сложение скоростей.
Скорости еыражаются отрезками на линии / = 1 и складываются как эти
отрезки:
iT=u + v.
Преобразования Галилея F) образуют группу, что
означает: мы вновь получим преобразования Галилея,
если последовательно выполним два преобразования
Галилея. Для каждого преобразования Галилея
существует обратное, которое также является
преобразованием Галилея. Символически запишем F) в виде
S = G(o)-Z
(в дальнейшем будем всегда обозначать инерциаль-
иую систему через Е). Далее, если
2 = G(o,)S и I = G(o2)S,
то, следовательно,
1 = G(v{ + v2J G)
I!
2 = 0(-0,I (8)
При изображении на чертеже различные
инерциальные системы отличаются расположением
временной оси, которая представляет собой мировую линию
пространственного начала. Единичные точки всех этих
осей лежат на одной прямой (калибровочная кривая).
Относительные скорости систем отсчета являются
отрезками на этих прямых. Отсюда следуют выражения

3. Инерциальные системы
33
G) и (8) (фиг. 16). Выражение G) представляет
собой галилееву теорему сложения скоростей.
Безотносительно к преобразованиям Галилея
можно написать следующее:
из 2 = Г@!J и 1=Г(и2)!
следует
1 = 7(/@,,?))? (9)
где f{V\,V2) —обобщенная функция. Объект, который
движется со скоростью v2 относительно 2, движется
относительно 2 со скоростью f(v\,V2), если 2
движется со скоростью v\ относительно 2. Заметим, что в тео*
реме сложения скоростей речь идет не о сложении
скоростей различных объектов в одной заданной системе
отсчета, а о взаимосвязи скоростей, относящихся к
различным инерциальным системам, в частности о
взаимосвязи скорости в 2 и 2, если заданы скорости
системы 2 в 2 и системы 2 в 2.
Мы можем конкретно представить себе это па
примере Гюйгенса [8], рассматривая мяч, который
находится в лодке, плывущей по течению. Тогда 2
является системой покоя мяча, 2 — системой покоя лодки, а
2 — системой покоя наблюдателя, стоящего на берегу.
Наблюдатель видит движение лодки со скоростью v\
ц мяча со скоростью f(v\,V2)y если скорость мяча
относительно наблюдателя, находящегося в лодке,
равна v 2.
В случае преобразований Галилея имеем /(уь vz) =
= v{ + V2. Каждый равномерно движущийся объект
можно снабдить инерцнальной системой 20, в которой
этот объект покоится. Если же объект движется со
скоростью v относительно заданной системы 2, то
20 = G (- v) 2
есть искомая инерциальная система, которую мы
называем системой noKjfl объекта.
2 Зак. 224

34
4. Волновые явления
4. Волновые явления
В этой главе мы познакомимся с основными
понятиями, которые приводят к иному, эйнштейновскому,
выбору инерциальной системы. При этом
преобразования Галилея ньютоновской механики заменяются
преобразованиями Лоренца частной теории
относительности.
Рассмотрим некоторую среду (например, воздух),
в которой распространяются упругие волны (звук).
Возьмем простейший случай: в системе покоя среды,
где невозможно выделить направление движения
среды, звуковые волны распространяются с одинаковой
скоростью во всех направлениях (среда изотропна].
На фиг. 17 изображены мировые линии сигналов,
испускание которых задается событиями х = 0, t = nT
(п = 0, 1, .. .). Скорость сигналов в обоих
направлениях равна w. Мировые линии сигналов источника,
который движется в среде со скоростью и, изображены
на фиг. 18. Периодичность действия источника
задается величиной 7Y Оказывается, что для наблюдателя,
покоящегося в среде, период не будет тем же самым.
Находим
TM=TS^, A0а)
причем и считается положительной величиной, если
источник приближается к точке наблюдения.
Если наблюдатель движется в среде со скоростью
v и сигналы посылаются с периодом Тм> то
наблюдаемый период равен
Тв-Тм^: (Юб)
причем v считается положительной величиной, если
направления движения сигнала и наблюдателя
совпадают (фиг. 19).
Обе эти формулы вместе описывают эффект
Доплера в классической механике:
,_JL
TB=Ts—j-. A1)
w

4. Волновые явления
35
Мировая линия источника
Миробые линии
сигналоб
Фиг. 17. Изотропное распространение сигналов покоящегося
источника.
Период колебания Т представляет собой временнбй интервал между двумя
сигналами в одном и том же месте, длина волны К — пространственный
промежуток, относящийся к данному моменту времени. Скорость
распространения (при правой ориентации координатных осей)
Для частоты v=— выполняется равенство v • h=w. В нашем случае ху,
Л и Г одинаковы в обоих направлениях.
Эффект Доплера в случае движущегося
наблюдателя можно вычислить и иначе. В системе покоя
наблюдателя скорость сигнала уже не w, a w — v.
Поскольку длины волн равны во всех системах отсчета,
получим при
т м
1 м — —
И
г Ллг
снова равенство A0):
т —Т W
В системе покоя наблюдателя сигналы не будут
распространяться с одинаковой скоростью в обоих иа-
2*

зв
4. Волновые явления
Пиробая линия
источника
x=uTs x=wTs
Фиг. 18. Изотропное распространение сигналов движущегося
источника.
Г. л Хм означают периоды и длину волны (интервал) сигналов в тех
местах среды, от которых источник удаляется, ?м, и X . ~то же самое
в тех местах среды, к которым источник приближается. Так как скорость
распространения w одинакова в обоих направлениях, то мы получаем
Учет движения источника дает
Отсюда получается эффект Дсплсра для движущегося источника
V 4- и
Tm-=ts.
Тм + = т
S '
правлениях, так как скорость распространения в среде
складывается со скоростью среды в системе покоя
наблюдателя (фиг. 20 и 21).
Система покоя среды характеризуется
независимостью распространения волн от направления
(изотропией). Это не является нарушением принципа
относительности, поскольку распространение волн
связано с конкретной средой и как раз описывает
состояние среды. Волны распространяются относительно
частиц среды.

4. Волновые явления
37
Мировая линия
наблюдателя
Ииродая линия
сигнала
Фиг. 19. Эффект Доплера в случае движущегося наблюдателя.
Проведем мировую линию наблюдателя в поле мировых линий
сигналов. Выберем две последовательные точки пересечения и
проведем параллели к координатным осям. Тогда из выражений
и
следует формула
При этом и считается положительным, если направления
движения наблюдателя и сигналов совпадают.
Законы распространения света перечеркивают эти
рассуждения. Скорость света конечна (в дальнейшем
через с будем обозначать скорость света в средах с
коэффициентом преломления 1, т. е. в вакууме).
Следовательно, в соответствии с развитыми ранее
представлениями, исходящими из условия независимости
массы от скорости, распространение сигнала может быть
изотропным только в инерциальной системе. Таковой
являлась бы система покоя гипотетической среды.
Вопрос об изотропии распространения света может
быть проверен экспериментально (фиг. 22).
Опытная установка позволяет в принципе
исследовать сигналы любой природы. Мы рассматриваем

38
4. Волновые явления
Мировая линия точки,
покоящейся в среде
^Мировая линия сигнала,
^движущегося назад
Мировая линия
наблюдателя
Мировая линия
сигнала,
движущегося впередУ
Фиг. 20. Относительные скорости в случае движущегося иаблю*
дателя.
Расстояние от наблюдателя до сигнала, движущегося вперед, увеличивается,
со скоростью w — u, а расстояние до сигнала, движущегося назад, —со
скоростью w + и.
Мировая ^линуя точки,
покоящейся в среде
Пиробая линия
наблюдателя
x=-(w+u)
w-u
Фиг. 21. Распространение сигнала в случае движения среды.
Перенесем изэиражение с фиг. 20 в систему покоя наблюдателя по методу,
указанному на фкг. 10. Распространение сигнала изотропно, среда в этой
инерциальной. системе движется.
здесь световые сигналы лишь потому, что
распространение света дает экстремальный результат.
В каждой инерциальной системе обнаруживается
изотропия распространения света и не обнаруживают-
ся эффекты, которые должны были бы иметь место
при движении относительно системы покоя
гипотетической среды. -

4. Волновые явления 39
Фиг. 22. Схема опыта Чемпени, Айзека и Хана.
На симметричном стержне, который вращается вокруг своего центра, уста*
новлекы источник сигналов S и приемник сигналов Е. Среда движется
в плоскости вращения со скоростью и. Направление движения среды
указывает ось у. Время Т пробега сигнала зависит от положения стержня
относительно направления движения среды. В случае покоящейся среды
Время пробега всегда равно Г0 = 2Я/с, где с —скорость сигнала относительно
среды. При i>=?0 нужно учесть, что сигнал за время пробега увлекается
средой. Мы рассмотрим лишь случай, в котором скорость v среды очень
мала по сравнению со скоростью с распространения сигнала, поэтому можно
пренебречь углами C н $' по сравнению с остальными углами. Мгновенные
координаты S обозначим через хну.
Путь SE сигнала состоит из пути SE' в среде и Е'Е~вместе со средой.
Время пробега от S до Е в случае движущейся среды равно времени
пробега от S до Е' в покоящейся среде. Из подобия полученных треугольников
следует
с(Т-Т,) _ у / v у\-1 „т Л . LJL\
—5?—-~r ' т'т°V " т) ~ToV+TT)'
Сигнал, излученный в момент времени /, попадает в приемник в момент
времени
<^(-т^).

40
4. Волновые явления
Мы предлагаем, не обсуждая опытных данных, по-
новому выбрать инерциальную систему среди
линейных систем отсчета. Откажемся от гипотезы о
независимости массы от скорости и заменим ее
требованием, чтобы распространение света в любой инер-
циальной системе отсчета было изотропным, т. е. не
зависело от направления. Потребуем также, чтобы из
наблюдения зависимости распространения света от на-
правления нельзя было сделать вывод о состоянии
движения системы отсчета; иными словами, потребуем
соблюдения принципа относительности сначала для
скорости света. Тогда принцип относительности будет
справедлив в механике только в том случае, если
подвергнуть ее уточнению.
а сигнал, излученный в момент времени t + x , — в момент
Временному интервалу т_ излучателя соответствует временной интервал
приемника, равный
^ = ^0^(^5)-^)-
Для малых угловых скоростей (до < —) имеем а ~а н
»('+Ts)-"("_*
tfo)Ts R
Поэтому временной интервал
зависит от мгновенного положения стержня. Если сигнал является световой
волной частоты v то в приемник поступает частота
В S\ и с R )
Этот сдвиг частоты должен обнаружиться, если, во-первых, развитые в гл. 2
представления верны, и, во-вторых, если экспериментальная аппаратура
движется со скоростью — v относительно среды, в которой распространяется
сигнал. Однако такой сдвиг частоты ие наблюдается в случае
распространения света в земной лаборатории, хотя скорость Земли относительно
(гипотетической; среды, в которой распространяется свет, должна составлять по
меньшей мере 30 км/с.

5. Относительность одновременности 41
5. Относительность одновременности
В предыдущих главах мы установили, что
независимость массы от скорости эквивалентна абсолютному,
т. е. не зависящему от состояния движения иперциаль-
ной системы определению одновременности, и что
изотропное распространение волн возможно лишь в
отдельных инерциальных системах. Если мы будем
выбирать инерциальные системы из линейных систем
отсчета таким образом, чтобы распространение волн со
скоростью света в каждой инерциальной системе было
изотропным, то тем самым мы с самого начала будем
предполагать относительность одновременности и
зависимость массы от скорости. Как это осуществляется,
мы увидим в дальнейшем.
Прежде всего выберем в линейных системах
отсчета единицу времени так, чтобы мировые линии
световых сигналов имели наклон в 45° по отношению к
ортогональным осям, а затем запишем временную
координату через ct, где с — скорость света при обычных
временных единицах. С помощью ct время задается в
единицах длины (ct— это путь, который проходит
свет за время /). Скорости, выраженные через новую
единицу времени, безразмерны, так как теперь они
представляют собой отношение длин. Скорость света
в качестве скорости системы отсчета теперь
принимает значение, равное единице. Мировые линии
световых сигналов, выходящих из начала координат,
являются биссектрисами углов ортогонального
координатного репера (фиг. 23). В четырехмерном простран-
сгве-времени эти мировые линии образуют конус, ось
симметрии которого является временной осью. Он
называется световым конусом. Поэтому мы и в двумер*
ном пространстве-времени будем называть
биссектрисы координатного репера световым конусом.
Теперь построим к заданной новой оси времени
(координата ct) линии одновременных событий
(параллели к оси х). Для этого рассмотрим стержень,
который равномерно движется в исходной
инерциальной системе и центр которого (М) в момент времени
ct = 0 находится в точке х = 0 (фиг. 24). Тогда ми-

42
5. Относительность одновременности
Мцрадые линии световых сигналов,
испускаемых б миро бой точке'Е0
/ ct \
\ /
ч
ч
ч
\
ч
ч
7f
А
/
/
/
/
\ \
\ /
V
/
/
/
45° /
?У
V^
\
\
\
\
\
\
X
Фиг. 23. Мировые линии световых сигналов.
В дальнейшем временную ось будем всегда обозначать через с/. Этим мы
достигаем того, что мировые линии световых сигналов становятся
биссектрисами углов ортогонального репера, и численное значение скорости св^та
больше ие влияет на ее изображение hi чертеже; ct — это путь, который
проходит свет за время t. Таким образом, время задается в единицах длины.
ровая линия т фиксирует временную ось (х = 0)
системы покоя стержня. Конечные точки его движутся
вдоль мировых линий а и Ь, параллельных т.
Сигналы, излученные в мировой точке 0[(х, ct) = @, 0)],
должны в системе покоя стержня одновременно
пересекать а и ft, так как расстояния AM и ВМ равны, и
скорость сигнала по предположению в системе покоя
стержня также должна быть одинаковой в обоих на-
правлениях._Таким образом, прямая g, соединяющая
точки Л и Я, является геометрическим местом
событий, одновременных с Л и В в системе покоя стержня.
Поэтому прямая g параллельна оси х. Мы видим, что
мировые линии сигналов в системе 2 снова являются
биссектрисами. Итак, из множества линейных систем
отсчета мы выбираем те, в которых биссектрисы углов

5. Относительность одновременности 43
Пиробая линия
сдетодого сигнала
Пиробая линия
/ сбетодого сигнала*
Геометрическое
место событий,
одновременных 6 г
(cf=^ const)
Фиг. 24. Относительность одновременное и.
В инерциалыюй системе х — ct изобразим мировые линии Л и /2 двух
световых сигналов, излучаемых в мировой точке О. Затем изобразим
мировые лннин а, Ъ и т концов стержня Л и В и его середины М,
причем т должна_проходить через О. Мировые линии а и Ь пересекают /'
и /2 в точках А и в, которые в системе покоя стержня должны быть
одновременными, но в несходной системе одновременными не является.
Угол BOA прямой н^ВМ = АМ, поэтому_М является центром описанной
вокруг^греуго^ьника BOA окружности н МО = Л\А. Следовательно,
треугольники ОАМ и ВОМ являются равнобедренными _и_а = р\ Так как ось Я
системы покоя стержня должна быть параллельна АВ, то 1Х и /2 делят пополам
и угол между осями х и ей Мировые лннни световых сигналов во всех инер-
циальных системах являются биссектрисами углов между осями.
На чертеже изображена основная конструкция, которая в дальнейшем всегда
будет применяться^должны быть заданы произвольная ось ci, проходящая
через О, и точка М на ней. Требуется найти параллель к оси Jc,
проходящую через М, т. е. геометрическое место событий, одновременных с М в
системе х~ ей Для этого мы строим равнобедренные треугольники ОМ Л илн
ВОМ, описывая окружность радиуса МО с центром в точке М.
между осями отсчета для всех систем одинаковы.
Вопрос относительной калибровки осей пока еще открыт
(фиг. 25). Разумеется, единичные точки на обеих осях
системы отсчета должны находиться на одинаковом
расстоянии от начала.
Как уже было сказано, вопрос одновременности
существенным образом зависит от системы отсчета, в ко?
торой эта одновременность должна быть установлен^*

44
5. Относительность одновременности
Фиг. 25. Относительное положение и калибровка осей системы
отсчета.
Мировые линии световых сигналов всегда являются биссектрисами уиюв
между осями. Произведем относительную калибровку так, чтобы
формальная скорость светового сигнала, Ax/Act*=l, не изменялась. Таким образом,
единица времени определена как время, за которое свет проходит единицу
длины, независимо от численного значения скорости света. Следовательно,
мы сначала не утверждаем, что значение скорости света не зависит от
инерциалыюй системы, а говорим только об изотропии распространения.
Вопрос о численном значении требует к тому же стандарта отсчета для
скорости света. Этот вопрос будет обсуждаться иа стр. 116
Если два события (например, Л и В на фиг. 24)
одновременны в одной системе отсчета B на фиг. 2-1), то
они уже неодновременны в системе отсчета,
движущейся относительно первой B на фиг. 24).
Относительную скорость системы отсчета 2 (т. е. ее скорость
в 2) обозначим через v — отношение абсциссы к
ординате точки на оси ct в системе 2. Через б обозначим
скорость 2 относительно 2. Собственно, v есть
отношение абсциссы к ординате точки на оси ctt причем абс-

5. Относительность одновременности
45
Фиг. 26. Обратимость относительной скорости.
Изобразив в соответствии с фиг. 25 обе системы отсчета (т. е. четыре оси),
выберем точку А иа оси ct и проведем параллели к остальным трем осям.
Отметим точки пересечения этих параллелей с осями х act. Задание
относительной калибровки осей дает нам скорость системы 2 относительно 2
в виде v=*AB/OA и скорость системы 2 относительно 2 в виде — v = АС/ОС.
Но так как треугольник ABC подобен треугольнику АОС. мы получаем, чтф
ОС/ОА = АС/АВ и, следовательно, v= — v.
^цисса и ордината этой точки теперь относятся к осям
2 (фиг. 26). Следовательно, v = —v.
Проиллюстрируем теперь доказательство эйнштей-»
новской теоремы сложения скоростей (фиг. 27).
Скорость v системы 2 в системе 2 может быть
установлена, если заданы скорость v системы 2 относительно
2 и скорость v системы 2 относительно 2.
Находим
Приведенное на фиг. 27 доказательство, исходящее
из того, что оси системы отсчета 2 изображены
ортогональными, можно заменить доказательством,
которое уже не нуждается в таком предположений
(фиг. 28). Оно использует тот факт, что двойное отно-

46 5. Относительность одновременности
Фиг. 27. Эйнштейновская теорема сложения скоростей. Г.
Сначала изобразим оси систем 2, 2 и 2. При этом оси х и ct выберем
ортогональными. Затем отметим на оси ct точку Л, проведем через иее
параллель к оси х и найдем точки В и С. Проведя через точку В параллель
К оси х, найдем D и Е. Далее, опустив перпендикуляр из Е на ВС, найдем G.
Теперь скорость_системы 2 относительно 2 равна v=BD(OB — BA{OA, ско^
рость системы 2 относительно 2 равна v = AC/OA и скорость системы 32
относительно 2 равна ~и = ВЕ/ОВ. Ввиду подобия треугольников CGE н САО
Получаем GC/EG = AC[OA = v. Треугольники BGE и ОАВ также подобны,
откуда следует
\___ ОА BG BC — GC ВС = \ + vv
v ~~ AB EG ~~ EG ' EG ~~ v
Отнеся все величины к отрезку ОА, мы можем написать
EG v BG __ у + у
ОА {V V) 1 + vv ' О А ~ 1 + vv '
С другой стороны, также вследствие подобия имеем
BE = ОВ
BG~ ОА '
поэтому скорость системы 2 относительно 2 равна
=_ BE __ BG v-у v
V OB ~~ OA~ l-+vv *

5. Относительность одновременности 47
/ Сбегпсиой
у конус
cf=const,
Фиг. 28. Эйнштейновская теория сложения скоростей. II.
Изобразим трн оси н световой конус. Выберем на оси ct точку А и,
проведя через нее параллель к оси х (стандартное построение фиг. 24), найдем
точки пересечения В, С, D и В. Затем проведем через точку В параллель
к оси х и найдем точки D\, А\, Ci и Е\. Относительные скорости суть
ВА
ОЛ
АС
ОА
= ВС,
Заметим, что BO = 6Hi = D,B и ОЛ = Л? = ?Л.
Следовательно,
1 + р C,D) BE]
~ ~~ СХЕХ BDi
1 — v
= 3) {Си В, Di, Я,).
Но эго двойное отношение сохраняется, если прямая g проецируется из О
на g. Находим
-i±|«fl> (С, В, D, ?)--™ . 1L = A±± 1±1L.
\ — v СЕ BD \ — v l — v
Разрешая относительно v, получаем
= v+v
v =-
1 -jrvv
шение четырех точек прямой сохраняется при
проектировании на другую прямую. Изображая оси
системы отсчета и световой конус и затем проводя через
начало мировую линию равномерно движущегося тела,
получаем для точек пересечения прямой со световым

48
6. Относительность массы
конусом (Д Е), с осью времени (А) и мировой линией
рассматриваемой точки (В) соотношение
BD . АР __ 1 + v ( .
BE ' ЛЕ 1-и ' W
Согласно фиг. 28, отсюда вытекает теорема сложения
в виде
1+^ l+v 1+v
1-е 1-у !
A4)
Итак, при последовательном выполнении двух
преобразований складываются величины типа
*=4-1п-ппг- A5)
Величина qp описывает площадь / = qp/2 поверхности,
ограниченной обеими временными осями и
фиксированной гиперболой (гл. 7).
Эйнштейновская теорема сложения скоростей
означает, между прочим, что сложение двух движений со
скоростями, меньшими скорости света, снова дает
движение со скоростью меньше световой. Вопрос о
движении со сверхсветовой скоростью перенесем на
будущее (стр. 57 и далее).
Прежде чем исследовать геометрический смысл
параметра <р в уравнении A5), обратимся к
изменению массы, которое, как и относительность
одновременности, следует из изотропии распространения
света в выбранной системе отсчета. Затем мы сможем
произвести калибровку осей и опять считать
выбранную нами систему отсчета инерциальной.
6. Относительность массы
Относительность одновременности требует
относительности массы, т. е. зависимости массы,
определяемой как временная компонента импульса, от скорости
тела. Мы уже видели (фиг. 13), что одновременность
может быть определена на динамической основе
только в том случае, если все массы одинаковым образом

6. Относительность массы
49
ct A
ct^ const
' Ct=CGilSt
Фиг. 29. К релятивистскому изменению массы. I.
В системе отсчета 2 изобразим два вектора импульса для одинаковых масс,
движущихся в противоположных направлениях с одинаковыми скоростями
О А и ОВ). Далее, будем считать О А частью оси d системы покоя частицы /
и дополним '?> осью х. Проведем через точку В параллель к этой оси и
определим точкой С в системе отсчета 2 временную координату (массу)
импульса р2. скорость которой в этой системе равна v = CB/OC. Убеждаемся,
что угол ОВС прямой, и с учетом равенства АО = ВО приходим к выводу,
что
Следовательно,
/ од v / ов V 1 / вс V , ,
т2
ОС
О А
V"
Эта фигура симметрична. Для масс в системе покоя второй частицы имеем
1
т2
Vl — v2
зависят от скоростей. Будем искать зависимость от
скорости в виде
m{v) = m0f{v). A6)
Величина m0 = т@) называется массой покоя
объекта. Как и в гл. 2, произведем калибровку времен-

Ра=тж$\
Фиг. 30. К релятивистскому изменению массы. II.
Проведем в световом конусе мировую линию, в системе покоя которой будем
сравнивать две массы. Через точку А проведем параллель к оси X этой
системы отсчета н параллели к световому конусу. В, С, D и Е — точки
пересечения. Теперь выберем прямую, проходящую через А и пересекающую
конус в точках F и G; будем считать ее осью Я другой системы отсчете S.
Тогда все точки Р этой прямой определяют векторы импульса ОР, которые
в 2 имеют такие же массы, как ОА. На FG ищем точку Я, для которой
FA = HG. Тогда ОН имеет уже не только такую же массу, как ОА, по л
равную по величине, но противоположно направленную скорость
относительно 2. Напротив, отношение масс, соответствующих ОН и ОА в Е,
выражается как JO/АО. Точку J мы найдем, если через Я проведем
параллель к ВС. Теперь нужно найтн отношение JO/AO.
Обозначим через М и L точки пересечения ОН со световым конусом,
имеющим вершину в точке Л, и спроецируем точечный ряд О, М, К, Н н L из Д
на прямую ОВ. Постоянство двойного отношения дает
3) (М, О, К, L) =
KM LO
КО ' LM
= 3> (Р2, О, В, ?>) =
3) (М, О, Я, L)
Рг —несобственная точка прямой ОВ.
НМ LO
DO
НО - LM=®{P»°'F'D)—FO
Пусть Р\~несобственная точка прямой ОС, а Рз — несобственная точка
прямой OL. Спроецируем прямую OL параллельно (т. е. из Р2) на DL, а её
в свою очередь из О на ВС. Тогда
/ M 2v
-?$-*= & (OtM,Pit L) = 3> (D,A,Pi ,L = D (В, A, C,K) = j—-.
Далее получаем
FD FA __ I FA x GH __ IВ А _ С К [ \—v
DO *~ GA ~~ V GA ' FH ~\ CA ' BK \ l + v u
При учете относительных знаков отрезков все вместе дает
МК 1 Ш
JO
АО
НО
КО
1 + ¦
I +
ко
мн
но
LO
DO
FO
LM
LO
Vl— v*

Фиг. 31, Принцип относительности и коэффициент расширения.
Пусть Две инерцнальные системы_заданы своими временными осями. Еди.
ничными точками пусть будут Е и Е. Проведем через Е параллель FG к оси х
и через Е — параллель FG к оси х. Найдем точки пересечения В и В.
Точка В им^еет такую же /-координату, что и Е, а В —такую же
/—координату, что и Е. Теперь потребуем выполнения обратимости, т. е. ci (E)=?ct (Я).
Это означает, что ОВ!ОЕ = ОВ/ОЕ. Таким образом, соединяющая линия вЪ
оказывается параллельной ЕЕ. Треугольники EBB и EBB равновелик"»,
поэтому равновелики и треугольники ЕВО и ЕВО. Но ввиду обратимости
скорости (?i=s — v) треугольник ЕВО пропорционален треугольнику EGO
с таким же коэффициентом (v), с каким треугольник ВЕО пропорционален
треугольнику EGO. В таком случае мы можем установить равенство
площадей треугольников EGO и EGO:
Ol ."EI = OL. EL.
Это уравнение гиперболы с асимптотами 1\ и /2 (ср. с фиг. 45). Е и Е лежат
на одной н той же гиперболе. Теперь определим ОВ/ОЕ. Для этого из
точки В проведем параллель к FG и опустим перпендикуляр на 1и в
результате чего найдем точки М и /(. Согласно фнг- 24, имеем ОК = ОМ> Для
площади треугольника ОВМ получим
?Г №ОВМ) = ОК-ВК-
С одной стороны, теорема подобия дает
OK = FB
OL Т'Е
а с другой —
м.-Шг-1+v.
EL L О
Поэтому _
?Г (д ОВМ) = U — ^-) OL-EL =
= A-1;?) OL-EL =
= A-v*)<?r {AOEG).
Наконец, с помощью теоремы подобия получаем

52
6. Относительность массы
ных осей, требуя независимости массы покоя от
заданной системы отсчета. Кроме того, учитывая, что
принцип относительности обусловливает равноправность
всех направлений, ограничимся четной функцией f(v).
Рассмотрим систему отсчета, в которой два тела
с одинаковыми массами движутся с одинаковыми
скоростями в противоположных направлениях.
Следовательно, обе массы покоя m0i и т02 выбраны таким
образом, что
Woif (—*>) = tfW (и), откуда т01 = то2- A?)
Теперь рассмотрим временную компоненту импульса
второй массы в системе покоя первой массы. В этой
системе отсчета вторая масса, согласно A2), имеет
скорость
б = ТТ?" A8)
На основании доказательств, приведенных на
фиг. 29 и фиг. 30 (как и на предыдущих фигурах,
первое из них использует ортогональную исходную
систему отсчета, а второе — постоянство двойного
отношения четырех точек прямой, известное из
проективной геометрии), получаем для отношения обеих масс
в системе покоя пеовой:
/@) = -=1==- A9)
или
Ч I + v2 )
1 +V2
Калибровка осей системы отсчета производится таким
образом, что т@) не зависит от инерциальной
системы ]). Пусть Е — единичная точка на оси ct, тогда
i) Это требование инвариантности массы покоя
эквивалентно требованию, чтобы преобразования между инерциальными
системами образовывали группу. В данном случае это означает,
что преобразование, которое переводит из одной заданной
системы в другую, переводит из любой инерциальной системы в
другую инерциальную систему.

б. Относительность массы 53
В -единичная течка на оси ci, если Е имеет с/-коор-
динату
Теперь инерциальные системы полностью определены:
из изотропии скорости света во всех инерциалъных
системах следует определение одновременности; далее,
ось х прокалибрована относительно оси / таким
образом, что скорость света численно не зависит от
инерциальной системы. Наконец, временные оси так
прокалиброваны относительно друг друга, что численные
значения масс покоя не зависят от инерциальной
системы.
Результат B0) мы получим также и в том случае,
если, не обсуждая зависимость массы от скорости,
непосредственно применим принцип относительности к
кинематике систем отсчета, т. е. если потребуем, чтобы
кривая единичных точек во всех системах отсчета
имела одну и ту же форму (фиг. 31). Принцип
относительности представлен здесь требованием, чтобы
единичная точка на оси ci в системе 2 имела такую же
пременную координату, как и единичная точка на оси
ct в системе отсчета 2. Наряду с B0) получается, что
обе единичные точки лежат на одной и той же
равносторонней гиперболе с заданными асимптотами.
Теперь произведем калибровку (фиг. 32). Исходя
из инерциальной системы 2, определим единичную
точку системы 2. При этом используем уравнение
B0), чтобы с помощью теоремы подобия получить
ct (Е) = ct (В) = ct (Ё) ci {П)
ct (E)
с((В)= Vl — v!c~t(E).
Поменяем ролями системы 2 и 2. Тогда получим
ci (E) = ci (A) = ct (?) - ' .
Таким образом, единичная точка на оси ct отмечает
геометрическую середину отрезков ОА и ОВ.

54 0- Относительность массы
Фиг. 32. Определение калибровочных точек.
Пусть задана калибровочная точка Е на некоторой осн ct. Требуется найти
калибровочную точку на некоторой другой осн ct. Допустим, что начала
обеих координатных систем совпадают. Проведем через точку Е параллели
к осям х н х и найдем точки пересечения А и В. Мы знаем, что
калибровочная точка Е должна удовлетворять условию
_ОА_^_ОЕ_
ОЕ ОВ
Таким образом, ОЕ есть геометрическая середина отрезков ОА и ОВ.
Находим ОЕ как высоту прямоугольного треугольника, отрезки гипотенуза
которого суть О А и ОВ. Перенесем OBi = OB на ось ct, опишем окружность
вокруг отрезка В\А как диаметра, восстановим перпендикуляр из точки О
и найдем С. Получаем ОС^ОЕ.
Заметим на будущее, что с помощью ЕЕ найдена прямая, которая, согласно
определенной на фиг. 44 и 45 угловой мере, делит угол между ЕА н ЕЗ
пополам.
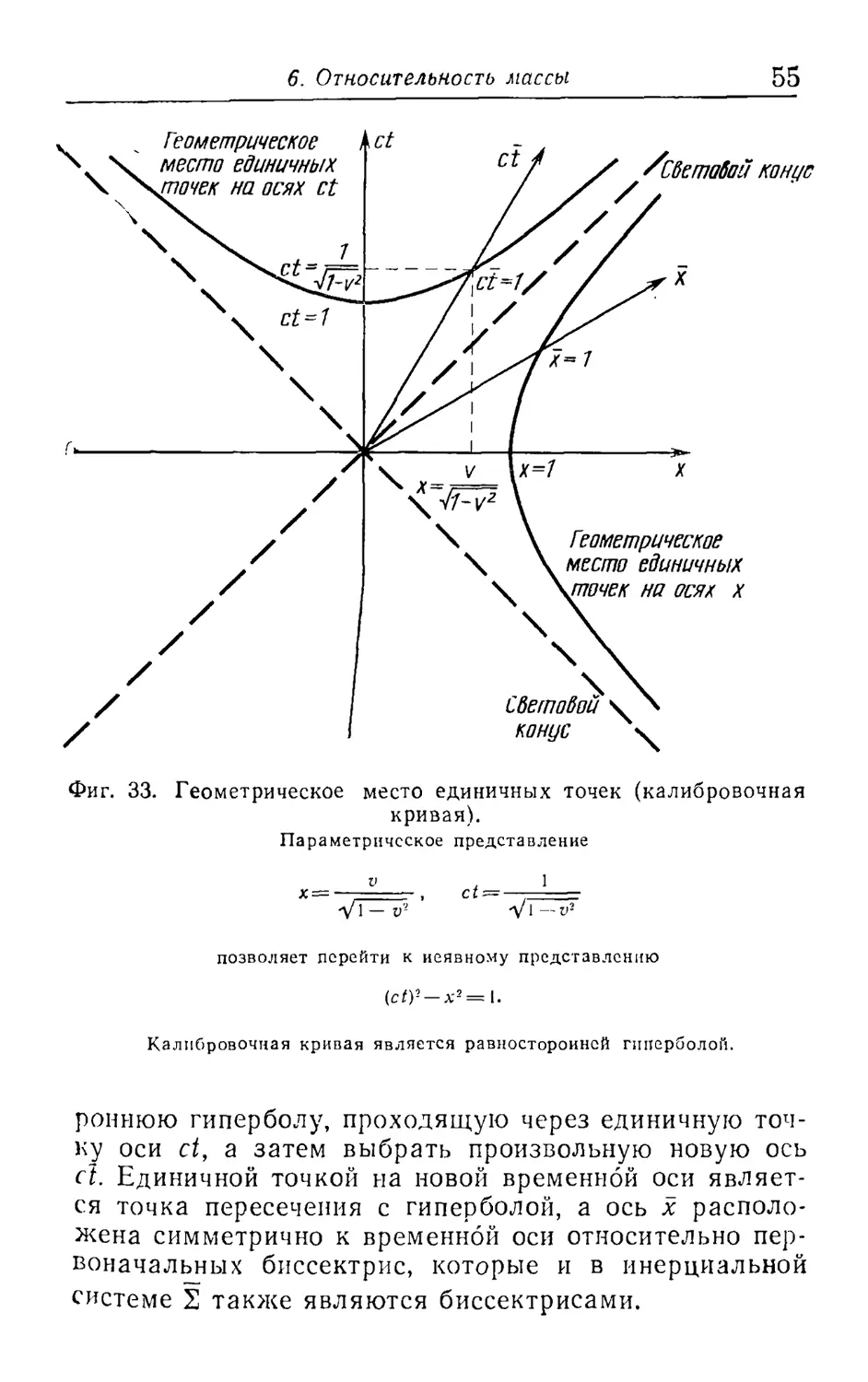
Теперь изобразим на фиг. 33 геометрическое место
всех возможных единичных точек. Им является
равносторонняя гипербола. Исходя из одной инерциальной
системы, которую мы изображаем ортогональными
осями, мы получим все инерциальные системы, для
чего нужно построить биссектрисы углов и равносто-

6. Относительность массы
55
v . Геометрическое ^ct
> \ место единичных
\ \/шуаг на осях ct
\
\
\
\
\
ct=1
\
\
\
/
/
/
/
/
/
/
ct
1/
/
/
/
/СВетобой конус
/
У
/
ГХ=7
\
\х=1
/
\ \ Геометрическое
\ \ memo единичных
\ \точек на осях х
\ \
\\
Сбетобой \\
конус ч
/
Фиг. 33. Геометрическое место единичных точек (калибровочная
кривая).
Параметрическое представление
ct^=-
1
V1 — v'- V1 —v2
позволяет перейти к неявному представлению
(cty-x2=l.
Калибровочная кривая является равносторонней гиперболой.
рониюю гиперболу, проходящую через единичную
точку оси ct, а затем выбрать произвольную новую ось
ct. Единичной точкой на новой временной оси
является точка пересечения с гиперболой, а ось х
расположена симметрично к временной оси относительно
первоначальных биссектрис, которые и в инерциальной
системе 2 также являются биссектрисами.

56 б- Относительность мессы
Cti
А
с.
Е
0
\
ct 4
у
г %
SF В
S*i
X
Фиг. 34. Частнорелятивистское преобразование Лоренца.
Изобразим оси двух систем отсчета и в первой из них установим единич*
ные точки Е и F. Затем найдем проекции Е{ и Л точек Е и ?\ так чтобы ЕЕ\
была параллельна оси х, a FFi — параллельна оси ci. Тогда, согласно B0),
получаем
x(F,) = cf (?,)=-
Vl-u2
Взяв некоторую произвольную точку Р, изобразим ее проекции А и В на
оси системы 2 и С и ?> — на оси 2. Эти проекции нужны нам для
определения точек Ci и ?>i на осях системы 2. Из формулы относительной ско
рост и
следует
" #р ов
с*(Р) сМС) _ ct «?')
Jt iP) __ X (Dj)
ci (?,)
x(P)
= ct (P)—DX (P),
x (Fi) x (Л) x (F)
= x{P)—vct(P).
Записав аргумент неявно, получим известную формулу частнорелятивист-
ского преобразования Лоренца
ct ¦¦
ct~vx
VT^T2
х — vet
VI — v'
Используя гиперболические функции (о=—tha), находим
ci^=ct ch a +• х sii a, x = ct bii a + x ch a.

6. Относительность массы
57
Теперь мы можем произвести пересчет координат
i\«
от одной инерциальной системы к другой (фиг. 34) -;
х — vet
VI_U2 B1)
7 Ct - VX V '
ct = ,
В честь Г. А. Лоренца они называются частнореляти-
вистскими преобразованиями Лоренца. Запишем
преобразования B1) символически:
2 = L(uJ;
отсюда _
и с учетом _
2 = L (и) 2
получим аналогично G)
Это уже знакомая теорема сложения скоростей
Эйнштейна.
В полученных формулах предполагается, что V <?
< с. Неравенство V > с означало бы, что ось cl
уходит в область, расположенную справа от обеих
биссектрис. Тогда оба сигнала, мировые линии которых
являются этими биссектрисами, больше не
распространялись бы вправо и влево от оси ct, и
предполагаемая изотропия распространения этих сигналов не
выполнялась бы. Поэтому мы связываем все инер-
циальные системы при помощи преобразований
Лоренца и можем утверждать, что относительная
скорость двух инерциальных систем всегда меньше с.
Таким образом, объект, обладающий мерой времени и
длины и, следовательно, реализующий систему отсче-
1) Заметим, что v — безразмерная величина, так как все
скорости с самого начала поделены на скорость света вследствие
введения координаты ct. В случае если имеется в виду обычная
скорость, мы будем употреблять большую букву V.

58
6. Относительность массы
Фиг. 35. Будущее и прошлое.
В будущем события О для каждого события Е\ имеется ииерциальная
система, в которой х {Е\) = х {О) = 0 и ct (Ех) > ct (О)=0. Временная ось этой
инерциальной системы —прямая, соединяющая О и ?|. В прошлом
события О для каждого события Е2 имеется ииерциальная система, в которой
ЗЙ?2) = 0 и ct (E2) < 0.
та, не может двигаться быстрее света. Иными
словами, предполагается, что принцип относительности и
принцип изотропии распространения света
справедливы во всех инерциальных системах и адекватно
описывают физическую реальность.
Рассмотрим теперь классификацию относительного
положения двух событий, которая осуществляется
биссектрисами осей инерциальных систем. Начало
координатных осей совместим с одним событием, а
другое обозначим через Е. Если Е лежит в области,
расположенной выше обеих биссектрис, то всегда имеется
ииерциальная система, в которой событие Е имеет ко-

6. Относительность массы
59
ординату х = 0, т. е. происходит в том же месте, что
и событие О. При этом сЦЕ) > 0, следовательно, Е
происходит позднее, чем О (фиг. 35, событие Е\). Если
же Е лежит ниже обеих биссектрис, то опять имеется
инерциальная система с х(Е) = 0, только теперь
ct < 0 и, следовательно, Е происходит раньше, чем О
(событие Е2 на фиг. 35). Если Е лежит выше одной,
но ниже другой биссектрисы, то всегда имеется
инерциальная система, в которой ct(E) = О и,
следовательно, Е происходит одновременно с О. Но тогда так-
же имеются инерциальиые системы, в которых
ci(E)<0 или с7(Е)>0.
Поэтому временная последовательность событий О и
Е относительна (фиг. 36).
На основании этих данных разделим пространство-
время на абсолютное прошлое относительно О
(содержащиеся в нем события независимо от инерциальной
системы происходят раньше, чем О), абсолютное
будущее относительно О (содержащиеся в нем события
независимо от инерциальной системы происходят
позже, чем О) и относительное настоящее 1) по
отношению к О (фиг. 35, 36). Если одно событие находится
в абсолютном будущем или абсолютном прошлом
относительно другого события, то они называются вре-
менноподобными друг другу. На фиг. 35 события Е\ и
Е2 временноподобны относительно О. Если одно
событие находится в относительном настоящем другого, то
оба они называются пространственноподобными друг
другу. На фиг. 36 события ? и О пространственнопо-
добны друг другу. Остается случай, когда два
события находятся на той или иной биссектрисе углов
между осями инерциальной системы, тогда эти события
называются светоподобными друг другу. События, све-
топодобные относительно О, изображаются точками на
биссектрисах, которые являются мировыми линиями
4) В отечественной литературе для обозначения этой
области употребительны также названия «абсолютно удаленная»,
«абсолютно безразличная», «нейтральная область квазиодновре*
менных событий». — Прим. перев%

60 & Относительность массы
Фиг. 36. Настоящее.
В настоящем события О для каждого, события Е имеется инерциальная
система, в которой ct {E^ = ct (О) = 0. Ось х этой инерциальной системы —
прямая, соединяющая О и Е. Наряду_ с этой имеются также системы
с ct (?) <0 net {Е)> 0.
световых сигналов, испущенных из точки О, т. е.
образующими светового конуса. Слово «конус» относится
к структуре этого множества событий в
четырехмерном пространстве-времени, как было уже замечено на
стр. 41.
Мировые линии, все события которых временнопо-
добны, называются временноподобными. Векторы,
имеющие направление временноподобной линии,
называются временноподобными. Соответственно
определяются светоподобные и пространственноподобные
векторы и мировые линии.
Рассмотрим теперь два события А и В на мировой
линии физического объекта. Если событие В простран-
ственноподобно /1, то временная последовательность
событий В и А зависит от системы отсчета. Более того,

7. Геометрия пространства-времени
61
в таком случае существует инерциальная система
отсчета, в которой А и В одновременны, так что объект
одновременно находится во многих точках
пространства. Мировые линии, на которых такая ситуация не
осуществляется, назовем кинематически причинными.
Все точки на кинематически причинной мировой линии
временноподобны или светоподобны друг другу.
Кинематически причинное движение никогда не происходит
быстрее света.
Закончим эту главу сводкой основных положений,
касающихся принципа относительности: .
1. Принцип относительности для распространения
света (изотропия не выделяет одну инерциальную
систему среди других) подразумевает
— относительность одновременности;
— существование светового конуса;
— положение координатных осей и их
относительную калибровку;
— определение относительной скорости как
двойного отношения;
— обратимость скорости как следствие
антисимметрии этого двойного отношения;
— теорему сложения скоростей как результат
последовательного использования этого двойного
отношения.
2. Принцип относительности для массы (вид
функции m(v) не выделяет инерциальную систему)
подразумевает
— изменение массы и формы калибровочной
кривой;
— преобразование Лоренца при переходах между
инерциальнымп системами.
7. Геометрия пространства-времени
Прежде чем заняться рассмотрением следствий
выполнения принципа относительности, который
соответствует установленной изотропии распространения св>
та do всех инерциальных системах, проведем
геометрическое сравнение галилеевой и новой,
эйнштейновской, кинематики с евклидовой геометрией плоскости.

62
7. Геометрия пространства-времени
Соответствующая эйнштейновской кинематике
геометрия названа в честь ее создателя геометрией Мин-
ковского1). В дальнейшем все понятия, относящиеся
к этой геометрии, будут обозначаться буквой М.
Геометрию, соответствующую галилеевой кинематике,
будем обозначать буквой Г, а евклидову геометрию—
буквой Е. Если же буква не указана, то мы будем
считать, что рассматриваемое понятие имеет обычный
евклидов смысл.
Геометрии, соответствующие эйнштейновской и
галилеевой кинематике, не являются евклидовыми,
однако они не идентичны геометриям, которые обычно
называют «неевклидовыми». Последние это
геометрии, в которых теряет силу евклидова аксиома
параллельных и которые описывают искривленное
пространство. В М- и Г-геометрии аксиома параллельных
евклидовой геометрии сохраняется, но аксиом:^
конгруэнтности имеют другую форму. Различают девять
геометрий плоскости [9, 12]. В трех из них действует
аксиома параллельных, о них уже упоминалось, и нас
интересуют здесь именно они.
В первой половине этой главы мы познакомимся
с основными понятиями М- и Г-геометрий, каждая из
которых описывает соответствующую кинематику. Это,
впрочем, не означает, что мы каким-либо образом
доказываем адекватность этих геометрий кинематикам.
Данная геометрическая система для описания
предлагаемой кинематики использует понятие не «истинный»,
а «применимый». Понятие «истинный» было бы здесь
неуместным. Внутреннее свойство геометрии,
описывающей кинематику, можно характеризовать
выражением «не противоречит».
Если мы хотим выразить в виде геометрической
конструкции кинематику, соответствующую
преобразованиям Галилея, и кинематику, соответствующую
преобразованиям Лоренца, мы должны представить
*) Имя Минковского упоминается в геометрии еще в
другом месте — оно связано с выпуклыми поверхностями. Здесь же
под геометрией Минковского мы всегда будем понимать псевдо-
евклидову геометрию пространства времени частной теории
относительности.

7. Геометрия пространства-времени 63
У*
A2)
о, я
х
% 7
/
/
/J
ft*;
/
ian (id
_i_
^ 1 X
Фиг. 37. Конгруэнтные фигуры в евклидовой геометрии.
tk
IX
\ (ггк
\
\ /hW7
\
A,2) (W B,2)
(V)(WB,J)B,V
1 х,х
Фиг. 38. Конгруэнтные фигуры в галилеевой геометрии.
основные геометрические понятия в форме,
позволяющей производить эти преобразования. Начнем с
понятия конгруэнтности. Элементарное представление о
конгруэнтности можно выразить так: две
геометрические фигуры, изображенные на бумаге, считаются
конгруэнтными, если, вырезав одну из них и наложив на
другую, мы обнаружим, что они полностью совпадают.
Не вдаваясь в тонкости безупречного определения,
сразу же перейдем к другим вариантам. Две фигуры
А и В конгруэнтны, если существует такая
координатная система 2, в которой В обладает такими же чис-

64 7. Геометрия пространства-времени
сГ
ct |
W7,J)
\
\ "Л
\
\
\ \™
\
(о,з) 0,3)
Ш) A,2) /
/
/
ч—
/
/
/
/
/
/
Фиг. 39. Конгруэнтные фигуры в геометрии Мннковского.
ленными значениями координат, какими А обладает
в 2 (фиг. 37, 38, 39).
Тогда в евклидовой геометрии преобразования
координат имеют вид
*=-'+^ + ?01
х =¦
Л/1 + v2
— vt -f х
B3)
V'l + v2
л"о,
где v — наклон оси i в системе отсчета 2. Обозначив
v через евклидов угол а, получим знакомый вид
преобразования (фиг. 40)
t = cos at — sin ад: + t0,
x = sin at + cos ax -\- x0.
B4)
Мы видим, что в обоих случаях коэффициенты ац,
«12, «21 и а<& линейного преобразования A) являются
функциями некоторого параметра (v или а), который
в свою очередь может быть произвольно представлен
в виде функции другого параметра, так что переход

7. Геометрия пространства-времени 65
Фиг, 40. Езклидов поворот.
Изобразим две прямоугольные координатные системы, повернутые
относительно друг друга на угол а < 0. В соответствии с принятой нами
терминологией назовем v = CC/OC скоростью. Далее, опустив из исследуемой
точки Р перпендикуляры на все четыре оси, найдем точки А, В, С, D,
С и D. Из равенства CC = v - ОС следует ОС~=л/\ +v* • ОС и из DD=vOD
следует OD = ^/\ + у2 • OD. Но, с другой стороны,
ОС = О А -г и АР = О A + vOB
и
OD = GB—vPB = OB — vOA.
Таким образом, находим
x(P) = OD = -
i(P) = OC --
1
1
-{x{P)-vt {P)),
{v-x(P) + t (P)).
V1 + V-
Используя тригонометрические функции (и = — t^ а), призодим эти формулы
к виду
л' = соз a»x + sin a*tt
t — — sin a-x+ cos d't.
3 Зак, 224

66 7. Геометрия пространства-времени
От B3) к B4) осуществляется путем подстановки
v = — tg a. B5)
Возникает вопрос: можно ли отличить один из
возможных параметров от других на основании его
геометрического смысла? Такая возможность имеется,
если учесть теорему сложения параметров при
осуществлении двух преобразований согласно выражению
(9). Мы можем отличить те параметры, для которых
теорема сложения имеет вид
f(Pl> P2)~Pl+P2- B6)
Угол а, взятый в качестве параметра в формуле B4),
удовлетворяет этому условию,
В данной системе отсчета каждому лучу,
проходящему через начало координат, приписывается
параметр, входящий в преобразование B3) или B4), так
что этот луч идентичен новой оси L Рассмотрим два
луча S\ и S2i проходящие через О (фиг. 41). Пусть
Т(а\) —преобразование Sj к оси t\ т. е.
преобразование, «переводящее S\ в положение S0, первоначальной
оси t». Преобразованием, переводящим S2 в
положение S0, пусть будет Т{а2). Тогда преобразование,
переводящее S2 в Si, будет
T2i = T-l(al)T(a2).
Если а— аддитивный параметр, т. е. если
выполняется соотношение B6), то
T2l = T(a2 — Q{)*=T(a),
и значение а = а2 — ai не зависит от выбора луча
отсчета 50. Таким образом, мы приходим к выводу:
относительное положение двух лучей, задаваемое с
помощью угла a = а2— ai, не зависит от положения
луча отсчета, если а — аддитивный параметр
преобразований, при которых координатные оси движутся
относительно геометрических фигур.
Если даны два луча (фиг. 42), то преобразование
Г(аз — ai) переводит S3 в S} и преобразование
Г(ос4 — а2) переводит S* в S2. Углы считаются кон-

7. Геометрия пространства-времени
67
Фиг. 41. К определению угла. I,
Фиг. 42. К определению угла. II.
груэнтными, если одно и то же преобразование
переводит S3 в S\ и S4 в S2, так что
или
а3 — а{ = а4 — а2
а4 — сц = а = а = а9 — а,.
Два угла конгруэнтны, если угловая мера, заданная
аддитивными параметрами преобразования,
одинакова.
3*

68 7. Геометрия пространства-времени
t,t-0
Фиг. 43. К определению угла в галилеевой геометрии.
Величина
(Zl2— —
1в-'м
не зависит от системы отсчета н является аддитивной для соседнего угла.
Поэтому она представляет собой угловую меру. Как и в евклидовой
геометрии, мы ориентируем углы таким образом, чтобы угол, образуемый
прямой gi no отношению к gt, был положительным, а угол, образуемый
прямой gi по отношению к g2, —отрицательным. Считая g\ и gi временными
осями систем отсчета 2t и 22, находим, что угол, образуемый прямой gi по
отношению к g2, соответствует отрицательному значению относительной
скорости системы 2i по отношению к системе 22.
Опираясь на эти результаты, мы можем также
определить углы в Г- и М-геометрии: угол есть
соответствующая разность аддитивных параметров
преобразований F) или B1). Следовательно, в Г-геометрии
угол идентичен относительной скорости, так как
относительная скорость является здесь аддитивным
параметром (фиг. 16, 43). В М-геометрии угол задается
логарифмом двойного отношения двух лучей и двух
асимптот в вершине, так как это двойное отношение
представляет собой мультипликативный параметр
(фиг. 28,44, 45).
Во всех трех случаях можно показать, что
определяемый таким образом угол пропорционален
поверхности между обоими лучами и кривой с расстоянием 1
от вершины. Эта поверхность, очевидно, аддитивна, но
она также не зависит от положения луча отсчета, так
как все три преобразования [B4), F) и B1)]
оставляют поверхности неизменными, т. е. поверхности
сохраняются. Можно показать, что
ЯЦ#22 — #12^21 = 1

7. Геометрия пространства-времени
69
Фиг. 44. К определению угла в геометрии Минковского.
Двойное отношение
АС ВС
&(С, D, А, ?) =
AD ' BD
характеризует четыре луча, проходящие через точки А, В, С и D. Оио не
зависит от конкретной прямой, пересекающей эти лучи. Эта прямая в
качестве параллели к оси х представляет систему отсчета, от которой к тому же
не зависит двойное отношение. Последнее является положительным, и его
логарифм —вещественной величиной. Согласно фиг. 28, для соседних углов
эти двойные отношения перемножаются. Если бы точка А находилась справа
от D, то знак отрезка AD изменился бы, двойное отношение стало бы
отрицательным, а его логарифм — невещественным. В геометрии Мннковского
углы между времеиноподобными и пространственноподобиыми прямыми
невещественны. В качестве угловой меры получим
ct32=-~ In 3> (С, D, А, В) = -
¦In
1+0
1 — V
Ориентация углов между времеиноподобными прямыми устанавливаете:!
так же, как на фиг. 43; v является скоростью системы 2j относительно ->,
если gi и gi — временные оси системы отсчета.
представляет собой условие того, что A) сохраняет
поверхность и что это условие обеспечивается
равенствами B4), F) и B1). Здесь мы откажемся от
общего доказательства и приведем лишь представление
преобразований Лоренца, из которого можно сразу же
установить сохранение поверхности преобразования
(фиг. 46).
Наконец, дадим сводку соотношений между углом
и относительной скоростью:
в Е-геометрии v = —tg а,
в Г-геометрии v = —а,
в М-геометрии v = —th а.

70
7. Геометрия пространства-времени
Фиг. 45. К определению угла между простраясг^енноподобными
прямыми.
На плоскости Минковского угол между двумя пространствеиноподобными
прямыми определяется аналогично фиг. 44 с помощью двойного отношения
а,2 = 4- In 3) (С, D, А, В).
Теперь определим, что мы будем понимать под
длиной отрезка. Для этого рассмотрим треугольник с
двумя равными углами при основании. Мы знаем, что в
обычной евклидовой геометрии такие треугольники
называются равнобедренными, т. е. соответствующие
стороны имеют одинаковую длину (фиг. 47). Определим
теперь длины в Г- и М-геометрии так, чтобы и здесь
треугольники с равными углами при основании были
равны. Тогда определение угла порождает
определение длины с точностью до коэффициента
пропорциональности. Так как определение угла строится
независимо от координатного представления, то определение
длины, полученное таким образом, также не зависит
от инерциальнои системы. В Г-геометрии в качестве
меры длины получаем
1ав = I' л — h I
B7)

7. Геометрия пространства-времени 71
Фиг. 46. Световые координаты.
Спроецировав точки плоскости на световой конус, найдем координаты
u = ct + x, v=ct~-x.
Для калибровочной кривой справедливо соотношение но=(с/J—х2=\. Все
прямоугольники, относящиеся к точкам одной и той же гиперболы, имеют
одинаковые площади. Если для двух точек выполняется равенство U\V\=u?z>2,
2 2 2 2
То, следовательно, справедливо и равенство (?^) -xi-(d2) —#2-
Координаты «и о при лоренцевых преобразованиях изменяются таким образом,
что произведение uv остается неизменным:
VT^o _ ж /Т+Т
1+и V 1-я
Все фигуры в направлении и сокращаются в такой же степени, в какой они
вытягиваются в направлении v.
(фиг. 48), а в М-геометрии длина временноподобного
отрезка равна (фиг. 49)
lAB = <s/(ctA - ctBf - (хА - хвJ. B8)
Напротив, в евклидовой геометрии длина равна
1лв = л/Ца-*вУ + (Ха-хвJ. B9)
Согласно формуле B8), длина нространственнопо-
добного отрезка является мнимой величиной, но так
как она чисто мнимая, то мы можем для сравнения
пространственноподобных отрезков использовать и
вещественные величины
1ав = л/(ха — *вJ ~ (с(а — ctBJ.

пространственно-
подобный

Фиг. 47. Треугольник с равными базисными углами в евклидовой
геометрии.
Если длина определяется по Евклиду:
1АВ = Л/AА-'ВУ+(ХА-*ВУ-
то стороны такого треугольника при зеркальном отражении равны н имеют
одинаковые длины.
Фиг. 48. Треугольник с равными базисными углами в галилеевой
геометрии.
Выражения для углов суть
*С~*Л
Р=
Ъ-'в
Ввиду абсолютной одновременности (*с = *0) имеем a=fl для/-— ic—
e=:iC~tB' Таким °бРазом, АС конгруэнтно СВ. Если длина определяется
выражением
!ЛС=<С-*А-
то длины обеих отрезков равны.

7. Геометрия пространства-времени
73
Фиг. 49. Треугольник с равными базисными углами в геометрии
Минковского.
Изобразим треугольник ABC с временноподобными сторонами и проведем
через А и В световые конусы, которые пересекаются в Е и F. Соединяющая
линия пересекает АВ в точке D. Углы а н C равны тогда и только тогда,
когда а и 6 пересекают прямую EF в одной точке С; только тогда будут
равны соответствующие двойные отношения. При а = Р точка С лежит
на EF.
Теперь проведем световой конус через Сив силу теоремы подобия находим
для точек Q и Я.
EQ AR
¦U^TF- T'e- BQ.RF=.AQ.AR.
Если С лежит на EF, то прямоугольники ARCQ и BR'CQ' равновелики
На основании фиг. 46 приходим к выводу, что
(с'с-с{аУ-(хс-хаУ=(с'в-с(сУ-(хв-хсУ
в любой координатной системе. Длина временноподобного отрезка
определяется выражением
После того как мы определили угловые и линейные
меры, рассмотрим обобщение понятия
перпендикуляра. В евклидовой геометрии (фиг. 50) справедливы
следующие утверждения:
1. Перпендикуляр является кратчайшим
расстоянием между точкой и прямой.

74 7. Геометрия пространства-времени
Крибая
постоянного
расстояния
от О
Фиг. 50. Перпендикуляр в евклидовой геометрии.
Основание F является точкой касания кривой постоянного расстояния от
точки О, а так как это окружность, то F представляет собой точку на
прямой g, находящуюся на кратчайшем расстоянии от О.
t~t@)= const
X
Фиг. 51. Перпендикуляр в галилеевой геометрии.
Кратчайшее Г-расстолние между точкой F на прямой g и точкой О равно
нулю. Перпендикуляры —это всегда прямые t = const.
2. Основание перпендикуляра является точкой, в
которой прямая касается кривой постоянного
расстояния от точки Р.
3. Перпендикуляр образует с прямыми линиями
прямой угол.
4. Перпендикуляр и прямая образуют оси
декартовой системы отсчета, или (применительно к излагае-

7. Геометрия пространства-времени
75
мому материалу) систему отсчета, в которой
справедливо выражение B9).
Последнее свойство обобщается наиболее просто,
так как мы уже знаем, какие системы отсчета в Г- и
М-геометриях мы должны рассматривать как декар*
товы: это инерциальные системы, ибо в них
справедливо выражение B9), являющееся аналогом
определения длины [B7) или B8)]. Следовательно, в
М-геометрии «прямой угол» уже не является, собственно,
углом, так как мы определили вещественный угол
только между двумя временноподобными или двумя про-
странственноподобными лучами, а не между одним
временноподобным и одним пространственноподобным
лучами. Заметим только, что в М-геометрии стороны
прямого угла, образованного световым конусом,
выходящим из вершины угла, имеют двойное отношение,
равное —1. Следовательно, прямой угол
характеризуется здесь гармоническим делением. В Г-геометрии
прямой угол — это просто бесконечный угол. Согласно
четвертой формулировке определения перпендикуляра,
одна сторона здесь имеет направление, выделяемое
осью х. На фиг. 51 приводится построение
перпендикуляра в Г-геометрии: это всегда параллель к оси х.
Таким образом обобщается четвертое свойство
прямого угла. Пункт 3 удовлетворяет новому
определению прямого угла. Пункт 2 не поддается аналогичной
интерпретации. Пункт 1 гласит: в Г-геометрии
расстояние между основанием перпендикуляра и
точкой Ру к которой он восстанавливается, всегда равно
нулю.
Фиг. 52 иллюстрирует построение перпендикуляра
в М-геометрии. Перпендикуляр из точки О к данной
прямой g проводится так, что (евклидов) световой
конус, построенный из основания перпендикуляра, делит
пополам угол между перпендикуляром и прямой. Все
четыре пункта, полученные при определении
евклидова перпендикуляра, в М-геометрии выглядят
по-другому:
1. Перпендикуляр является (локально)
наибольшим расстоянием между точкой и прямой.

76
7. Геометрия пространства-времени
/
Кривая постоянного '
расстояния от О
Фиг. 52. Перпендикуляр в геометрии Минковского.
Даны прямая g и точка О, из которой на эту прямую опускается
перпендикуляр. Построим перпендикуляр как ось х системы отсчета, в. которой g
параллельна оси ct. С этой целью изобразим световой коиус 1\, /? с
вершиной в точке О и найдем точки пересечения А и В. Середина F этого отрезка,
согласно фиг. 24, отмечает направление оси х. Таким образом, F является
основанием перпендикуляра. Гипербола с асимптотами U и /2, проходящая
через точку /-', касается g в точке F. Но эта гипербола представляет собой
кривую постоянного расстояния от О. Отсюда следует, что F является
наиболее > леченной от О точкой отрезка АВ. ПространственнопоДобшш
прямая (g) перпендикулярна времеииоподобной прямой (OF).
2. В основании перпендикуляра прямая касается
кривой постоянного расстояния от определенной точки
(в данном случае гиперболы).
3. Перпендикуляр и прямая образуют «прямой
угол».
4. Они образуют оси инерциальной системы.
Обратим внимание на отличие в первом пункте, где
«кратчайшее расстояние» в Е-геометрии заменено
«(локально) наибольшим расстоянием» в М-геомет-

7. Геометрия пространства-времени
п
рии. Мы вернемся к этому при обсуждении роли
времени в частной теории относительности (гл. 8).
Исходя из определения угла, перпендикуляра и
длины, можно многие теоремы перенести из
евклидовой геометрии в Г- и М-геометрию. Для
подтверждения укажем, что эти теоремы касаются только
проективных свойств рассматриваемых конструкций:
пересечения многих прямых в одной точке, отношения
отрезков на одной прямой и тому подобного. Роль
окружности в обеих неевклидовых плоских геометриях
выполняют кривые, которые проективно эквивалентны
окружности. В случае геометрии Минковского — это
гипербола (с фиксированными направлениями
асимптот), а в случае галилеевой геометрии—парабола (с
фиксированными направлениями осей) и две
параллели, т. е. обобщенное коническое сечение. Читателя,
который незнаком с проективной геометрией,
приложение в конце книги введет в круг этих проблем в той
степени, в какой это используется в данной главе.
Общим для всех трех геометрий является то, что
существуют конкретные конические сечения, которые
при определенных допустимых движениях в
соответствующей геометрии переходят сами в себя. Все три
геометрии являются частными случаями проективной
геометрии, в которой конические сечения не
выделяются. В евклидовой геометрии выделяются
окружности, в геометрии Минковского — гиперболы.
Окружности при обычном повороте вокруг центра переходят
сами в себя; введенные на стр. 54 в качестве
калибровочных равносторонние гиперболы переходят сами в
себя при лоренцевых поворотах, т. е. при лоренцевых
преобразованиях вокруг центров этих гипербол.
В проективной геометрии параллельность,
ортогональность и длина не определяются. Если мы выделим
несобственные прямые, т. е. оставим лишь такие
преобразования, которые переводят несобственные точки
в несобственные точки (линейные, преобразования), то
тем самым ограничимся аффинной геометрией. Две
прямые параллельны, если точка их пересечения
лежит на несобственной прямой. Аффинное
преобразование не меняет этого свойства.

Таблица 2
Сравнение трех плоских геометрий плоскости** и соответствующих им кинематик
Реальные выделяемые
направления
Калибровочная кривая2)
Угол3) и относительная
скорость
Длина 4)
Перпендикуляр 5)
Евклидова геометрия
Отсутствуют
Окружность
0 = —tga
/2 = Д/2 + Дл:2
Обычная
ортогональность на прямых отсчета
Галилеева геометрия
Направление осей
параболы (двойная точка на
несобственных прямых)
Прямая с выделенным
направлением
v=s — a
I2 = At2
Параллель к выделенному
направлению независимо
от прямых отсчета
Геометрия Мииковского
Направления асимптот
гиперболы (две точки на
несобственных прямых)
Гипербола с
выделенными асимптотами
v = — th a
I2 = Act2 - Ax2
Гармонически делит
выделенные направления
прямыми отсчета
Теорема сложения ско- v -\- 0 = = i> + а
ростей") « — , _ об v = v + v v= { + vS

Уравнение
треугольника 7) и экстремальные
свойства прямых
АВ ^ АВ + ВС
Прямые являются
кратчайшими линиями
АС^АВ + ВС
Все кинематически
причинные линии,
соединяющие две точки, имеют
одинаковую длину
АС^АВ + ВС
Времениоподобные
прямые являются линиями
наибольшей длины
Геометрическое место Описанная окружность,
вершины прямого угла, отрезок — диаметр
опирающегося на данный
отрезок
Пара прямых,
направление которых выделяется
конечными точками
Гипербола с заданными
асимптотами, отрезок —
диаметр
Кривая со свойством
вписанных углов
Окружность
Парабола с выделенным
направлением оси
Гипербола с
выделенными направлениями
асимптот
') Плоскостью здесь называется двумерное пространство, а плоской геометрией — геометрия, требующая выполнения
аксиомы о параллельных. Неплоской геометрией плоскости является геометрия сферической поверхности или геометрия
Лобачевского.
7) Кривая постоянного расстояния от заданного центра.
л) Определяется как обычная поверхность между лучами и калибровочной кривой вокруг вершины.
*) Соотношение обычных длин отрезков и сегмента, выражаемого калибровочной кривой вокруг конечных точек.
5) Связь экстремальных длин н прямых отсчета.
6) Получается как теорема сложения угловых функций, заданных в третьей строке.
7) Справедливо в обеих неевклидовых геометриях для кинематически причинной последовательности отрезков АЗС.
«^J

80 7. Геометрия пространства-времени
Фиг. 53. Теорема о вписанных углах окружности.
В круге с центром в точке М выберем хорду АВ и точку Р. Мы хотим
сравнить углы АМВ и АРВ. Так как треугольники РМА и РМВ
равносторонние, то Х = 2|5 и Ц = 2\\ следовательно,
г АМВ = K3^Tfi = 2(pTY}s2a^2Zi4PB.
Угол АРВ независимо от положения точки Р на окружности всегда имеет
одно и то же значение (пока Р и М находятся по одну сторону от хорды АВ).
Из этих точек хорда АВ всегда видна лод одним и тем же углом.
Установление ортогональности соответствует
заданию двух фиксированных точек на несобственных
прямых. Обе эти точки являются неподвижными точками
инволюции, которая определяется парой
ортогональных направлений. Тогда угол между двумя прямыми
равен логарифму двойного отношения, образованного
несобственными точками обеих прямых и двумя
неподвижными точками. В М-геометрии неподвижные
точки вещественны и представляют собой направления
асимптот калибровочных гипербол. Каждая из
гипербол проходит через обе неподвижные точки. Две
прямые ортогональны, если их несобственные точки делят
обе неподвижные точки гармонически. В случае Г-гео-
метрии обе неподвижные точки совпадают. В Е-гео-

7. Геометрия пространства-времени
81
Фиг. 54. К теореме о вписанных углах параболы.
Мы хотим показать, что Г-угол, под которым хорда АВ параболы видна из
точки Р, не зависит от положения этой точки иа параболе. Отложим на
л/юскости хорду АВ и две точки Pi и Р2 и покажем, что эти точки тогда и
только тогда будут лежать иа одной параболе (с заданным направлением
осей Fi = F2) с точками А и В, когда Г-углы АР\В и APiB будут равны.
Сначала проведем через точки Pi и Р2 параллели к оси параболы.
Несобственная точка этих прямых совпадает с иесобствеииой точкой параболы.
Соединяющая прямая АВ пересекает gx в Si и g2 в S2. Спроецируем АВ из
F\ на Q2R2 и из Р2 на QiRi. Г-углы АрхВ и АР2В равны, если отрезки Q\Ri
и QiRi имеют одинаковую длину. Но тогда и только тогда длина отрезка QiSi
равна длине отрезка #2S2, т. е. отрезки QiRi и АВ параллельны. Покажем
это, используя постоянство двойного отношения. Взяв в качестве центров
перспективы точки Pi и Р2, получим
S2R2
'-& (S2, Q2, Я2, Л) = «0 (S2, А, 5, 50 = <2) (Fu Qi. Ru Si) =
QxSx
Q\R\
Параллельность Q\R2 и АВ является непосредственным условием того, что
точки А, В, Р\ и Р2 лежат иа одной и той же параболе с направлением
оси Fi = F2. Проиллюстрируем это с помощью теоремы Паскаля (фиг. 80).
Для этого рассмотрим шестиугольник FiPlBAP2F?.. Прямая F1F2 пересекает АВ
в несобственной точке прямой АВ, F|Pt пересекает АР? в точке Qi и PiS
пересекает P2-Fi в точке R2. Эти три точки лежат на одной прямой, если R2Qi
проходит через несобственную точку прямой АВ, т. е. параллельно АВ.
Но это имеет место в случае равенства углов, следовательно, шесть точек
лежат на одном коническом сечении параболы, проходящей через Pi, А. В
и Р2 с несобственной точкой F]t если рассматриваемые углы в галилеевой
мере равны. Таким образом, теорема о вписанных углах параболы доказана.
метрии неподвижные точки мнимы. Каждая
окружность проходит через эти две мнимые точки.
С установлением ортогональности определяются
также и единицы измерения на осях относительно друг
друга. Их абсолютное и инвариантное определение
дополняет основы метрической геометрии. Теорема
Пифагора, которая может рассматриваться как
определение правила размерностей, в трех геометриях прини-

82 7. Геометрия пространства-времена
мает формы B9), B7) и B8). Далее, можно называть
евклидову геометрию дефинитной, галилееву —
полудефинитной, а геометрию Минковского —
индефинитной (табл. 2).
В качестве примера аналогии трех геометрий
рассмотрим теорему о вписанных углах для окружности
(фиг. 53), параболы (фиг. 54) и гиперболы (фиг. 55).
Мы видим, что Г-геометрия в этом отношении
представляет собой вырожденный случай: только часть
кривых, удовлетворяющих теореме о вписанных углах,
представляет собой кривые постоянного расстояния от
данной точки (пары параллелей к оси х). В М-гео«
метрии гипербола является основной фигурой, которая
всегда задает две вещественные бесконечно удаленные
точки. Вообще параболы можно называть Г-окружно*
стями, а гиперболы — М-окружностями. Все построен
ния, осуществляемые с помощью Е-окружностей и
прямых, осуществимы также с помощью М-окружностей
и прямых. Так как приведенные здесь построения
большей частью содержат нахождение точек
гиперболы, что их весьма упрощает, предположим, что
вместо Е-окружности задана М-окружность. Тогда мы
можем выполнять построения с помощью инвариантных
в М-геометрии конических сечений, которые к тому же
имеют не зависящий от системы отсчета
геометрический смысл.
Укажем, наконец, на аналогию трех особых точек
плоского треугольника. Три высоты треугольника
пересекаются в одной точке независимо от того, в
соответствии с какой из трех возможностей определен
перпендикуляр. В случае Г-геометрии точка пересечения
высот всегда является бесконечно удаленной точкой
оси х, так как все высоты являются параллелями к
оси х. Три биссектрисы и три перпендикуляра к ним,
проведенные из вершин, пересекаются в четырех
точках, которые в случае евклидова определения
являются центрами вписанной и вневписанной 1) окружно*
*) Вневписанная окружность — окружность, касающаяся од«<
ной стороны треугольника и продолжений двух других сторон*—4
Прим. перев. --"

7. Геометрия пространства-времени
83
Фиг. 55. Теорема о вписанных углах гиперболы.
Мы хотим показать, что хорда гиперболы АВ видиа из точек Pi и Р2 под
углами, которые в мере Минковского равны. Выберем отрезок АВ (хорду)
и две точки Pi и Р2. Кроме того, зададим направления асимптот F| и F2
гиперболы. Покажем, что условие Л1-равенства углов -APiB и АР2В
равносильно условию, что F]PiBAP2f,2 есть шестиугольник с углами иа
коническом сечении, которое ввиду определенных несобственных точек является
гиперболой с заданными направлениями асимптот.
Условие УИ-равенства углов, согласно фиг. 45, дает
-^- «3 10, Q,, Я,, Ft) = 3> (F2, Q2, R2, 0) = -^2- .
Вследствие постоянства двойного отношения при проецировании из Pi н Рг
имеем
& (О, Qlf Ri, S,) = 5) (S2f A, B, S,)=»5) (S?1 Q2, R2, 0),
Что означает
Ofli _OiSi = S-.fi? QoO Q,Si ^/?2
05t ' CMt ^0 " Q-Лг ИЛИ OSi S20 "
Последней формулой мы аналогично фиг. 54 подтвердили, что Qifi? и S\S.
параллельны, если рассматриваемые углы в мере Минковского равны.
Но Qifi2 проходит через несобственную точку соединяющей прямой АВ тогда
и только тогда, когда F,, Рь В, А, Р-> и F2 лежат на коническом сечении.
Теорема о вписанных углах гиперболы доказана.
стей. Три медиатрисы т) пересекаются в одной точке
независимо от определения прямого угла. Через три
середины сторон и три основания высот проходит
особое коническое сечение — окружность Фейербаха в
евклидовой геометрии (фиг. 56, 57, 58).
*) Медиатриса — перпендикуляр к отрезку, проходящий
через его середину. — Прим. перев.

84 7. Геометрия пространства-времени
Фиг. 56. Окружность Фейербаха.
Через произвольные точки L, Л1 и К (не лежащие на одной прямой)
проведем окружность и треугольник, причем треугольник построим так, чтобы
указанные точки были серединами его сторон. Ввиду подобия треугольников
угол MLK равен углу СВА—р\ С другой стороны, опустив перпендикуляр
из вершины С в точку HQ, получим прямоугольный треугольник ВСНС. Так
как точка К делит его гипотенузу ВС пополам, треугольник Н СВК будет
равнобедренным и, следовательно, угол MHQK равен р. Из теоремы о
вписанных углах следует, что точка Н лежит на окружности, проходящей
через К, L и М. Те же рассуждения можно применить и к остальным
основаниям высот треугольника, для чего нужно только сменить обозначения
и повторить такие же построения. Высоты пересекаются в одной точке,
обозначенной через Н. Треугольники АСН, АВН н СВН имеют те же
основания высот, что и треугольник ABC, Поскольку середины сторон этих
треугольников также лежат на названной окружности, то она называется
еще окружностью девяти точек.
Центр гиперболы, соответствующей окружности
Фейербаха, делит пополам отрезок между точкой
пересечения М-медиатрисы и М-высоты, и эта гипербола
также делит пополам линии, соединяющие вершины
углов с точкой пересечения высот. Эта аналогия в Г-
геометрии получается тривиально, так как все
упомянутые точки совпадают с несобственной точкой оси х.
В этом сказывается вырождение для случая Г-геомет-

7. Геометрия прост ранет в а-в реме ни
85
Фиг. 57. Парабола Фейербаха.
Построим параболу с бесконечно удаленной двойной точкой /^ = /^,
проходящую через три Г-основания высот треугольника ABC, и покажем, что
середины сторон лежат иа параболе. Высоты параллельны направленক
оси параболы, которое указывается точкой F\. Выберем середину стороны М
Линия #^//^, пересекает высоту hQ в точке D, ИQM пересекает высоту Л.
в точке Е. Из теоремы подобия имеем DAIHcC = AHcjHcB = AtijHcCt т. v.
DA = AH и ЕВ = АН . Таким образом, DE\\AB. Но это является условием
того, что точки F Я , М, И^, Ht. и F2 лежат иа одном коническом
сечении, которое представляет собой искомую параболу. Это утверждение
следует из теоремы Паскаля. Противоположные стороны образованного этими
сторонами шестиугольника пересекаются в точках D, Е и несобственной
точке прямой АВ. Эти три точки лежат на одной прямой, так как DE\\AB.
т. е. DE проходит через несобственную точку прямой АВ.
¦рии. Отметим к тому же, что окружность, парабола и
гипербола являются конкретными кривыми
постоянной кривизны (кривизна равна углу изменения
направления касательной, деленному на длину отрезка
кривой), если углы и длины соответствуют
конкретной геометрии.
Теоремы об окружности в Е-геометрии и теоремы
о равносторонней гиперболе в М-геометрии являются
частными случаями обобщенных теорем о коническом
сечении. Указанное выше коническое сечение
Фейербаха представляет собой геометрическое место
центров таких конических сечений, которые проходят через
три угла и точку пересечения высот треугольника.
Если высоты определены по Евклиду, то это
геометрическое место — окружность, если по Минковскому—

86 7. Геометрия пространства-времени
В
1?
.и УЪ
/,
/
/
/\
/
\Н,
'//
^
\
\
\
\
\
&

7. Геометрия пространства-времени
87
Фиг, 58. Гипербола Фейербаха.
Мы хотим показать, что гипербола с заданными направлениями F| и F?
асимптот, проходящая через середины сторон К, L и М некоторого
треугольника, содержит точку Н' , являющуюся основанием Л4-высоты па стороне с.
Поскольку обозначение точек треугольника произвольно, то каждое
основание высоты лежит на гиперболе. Вместе с серединами высот мы опять
получаем девять точек, через которые проходит эта гипербола. Аналогично
доказательству в евклидовой геометрии добавим к точкам А, В и С
треугольника основание высоты Я, тогда можно получить четыре треугольника.
Не включенной в эту четверку остается точка пересечения высот
треугольника. Основания высот одни и те же, только они меняются местами. В таком
Случае середины сторон одного треугольника являются серединами высот
другого, поэтому на гиперболе, проходящей через основания высот, наряду
с серединами сторон лежат и середины высот.
Изобразим треугольник ABC с серединами сторон К, L и М и основанием
высоты Н . Через точки L, С и К проведем параллели к асимптотам
(т. с. линии, проходящие через несобственные точки F, и F2 гиперболы).
Онн пересекают сторону с в точках L\, L2, C\, C2. К] и /С2- Как и на фиг. 52,
точка Нс делит отрезок СуС2 пополам. Ввиду подобия треугольников
выполняются равенства ACi~2AL2, AC] = 2ALi, ВС2 = 2ВКъ ВС\ = 2ВК\ и
CiC2 —2/(i/B = 2LiL2. Продолжим теперь прямую LL, до пересечения ее с КК2
в точке Q. Точку V найдем как пересечение LL{ с Кп a W — как
пересечение КК2 с LM. Сначала покажем, что VW\\AB, и, исходя из полученных
данных, используем теорему Паскаля для шестиугольника FlLMH(,KF2.
Прежде всего спроецируем из К на с точки Q, V, L и Fj и получим точки К2,
И , Z и К,, причем через Z обозначим несобственную точку прямой АВ.
Отсюда получаем
— = 2> (Q, V, L, Fl)es> (К2. Ис, Z, К,)—j^ •
Проекция точек Q, W, К и F2 из /, на с дает точки Ц М, Z и L2 и двойное
отношение
-?§- = & (Q, W, К, F,) = 3> (Llf м. Z, LJ = ~- .
С помощью установленных выше соотношений получаем
Vi=i-c2s=tfcK,.
Следовательно, все приведенные двойные отношения равны, и, вспомнив
теорему подобия, мы обнаружим, что VW\\LK н VW\\AB. Точки Z, V и W
лежат "на одной прямой. Но эти три точки являются точками пересечения
противоположных сторон шестиугольника F {LMH CKF 2. Шесть точек лежат
на одном коническом сечении, которое является гиперболой с направлениями
асимптот F, и F2.
Заметим еще, что центр гиперболы F делит пополам отрезок между
основанием высоты Н и точкой U пересечения М-перпеиднкуляров,
восстановленных из середин сторон. Эта точка U — аналогично центру описанной
окружности в евклидовой геометрии — является центром гиперболы, которая
проходит через вершины треугольника ABC.

88 8- Время в частной теории относительности
гипербола. Вообще справедливо следующее: пять
точек определяют коническое сечение. Четыре точки (Аг
В, С и D) определяют пучок конических сечений.
Геометрическое место центров этих конических сечении
снова является коническим сечением. Это коническое
сечение делит пополам шесть соединяющих линий
четырехугольника и проходит через три диагональные
точки. Оно является окружностью, если D
представляет собой точку пересечения Е-высот треугольника
ABC. Тогда диагональные точки четырехугольника
являются основаниями высот треугольника.
8. Время в частной теории относительности
После экскурса в чистую геометрию вернемся к
обсуждению частной теории относительности. Геометрия
здесь приобретает физическое содержание: так как
одна из координат является временем, то геометрия
становится кинематикой, т. е. учением о движении.
В кинематике Галилея время — абсолютная величина:
временной интервал между двумя событиями не
зависит от инерциалыюй системы. В каждый данный
момент времени имеется однозначное множество
событий — трехмерное пространство, которое в нашем
двумерном пространстве-времени представляет собой
прямые, параллельные оси х.
Мы привыкли к такому абсолютному ходу
времени, так как скорости, с которыми движется человек,
используя или не используя технические средства,
чрезвычайно малы по сравнению со скоростью света.
Даже ракеты, выводящие спутник на орбиту вокруг
Солнца, достигают скорости (относительно Земли)
всего в одну десятитысячную скорости света, хотя, с
другой стороны, эта скорость в сто раз больше
скорости звука в воздухе на Земле. Тем более
удивительным кажется нам релятивистское изменение хода
времени, что с геометрической точки зрения вовсе не яв«
ляется неожиданным.
Получаемая в М-геометрии длина временноподоб-
пого отрезка — это разность времен, измеряемая
часами, мировая линия которых содержит эти отрезки.

8. Время в частной теории относительности 89
\Х=Х(А) = const
Фиг. 59. Евклидов аналог замедления времени.
Изобразим х-оси двух систем отсчета с общим началом О и отметим
калибровочные точки А и Д. Через каждую__из этих точек проведем Е-перпенди-
куляр к другой оси и найдем точки_А и ~В. ОА является J-координатой
точки A. OS — х-координатой точки 5. Неравенство ОА < ОВ не противо*
речит неравенству ОВ~ < О А.
Сославшись на фиг. 31, заметим, что условие обратимости
ОА
oW
ОВ
ОА
требует равенства площадей подобных треугольников ОАА и ОВВ, а
следовательно, и равенства ОА = ОВ\ в Е-геометрии единичные точки лежат на
окружности, если перпендикуляр определяется но Евклиду.
Мы знаем, что любая временноподобпая прямая
является осью времени определенной инерциальной
системы. Но в этой инерциальной системе объект,
мировая линия котрого является данной прямой, покоится,
т. е. не меняет своего положения. На временной оси
все события имеют нулевую пространственную
координату. Из формулы для получения длины временно-
подобного отрезка B8) следует, что длина отрезка
временной оси равна Ub = ctB — ctA. Таким образом,
длина временноподобного отрезка равна разности
времен в инерциальной системе, где отрезок является
частью временной оси, т. е. в инерциальной системе,
где часы, мировая линия которых является этим
отрезком, покоятся. Время, которое они показывают, равно
М-длине соответствующих отрезков мировой линии
этих часов. Поэтому М-длина временноподобного от-

90 #• Время в частной теории относительности
резка называется собственным временем. Если
мировая линия часов не прямая, то для определения
собственного времени нужно использовать такие же
конструкции, как и для опредления длины дуги в Е-гео-
метрии. Собственное время в частнорелятивистской
кинематике аналогично длине дуги в Е-геометрии:
между двумя событиями существует различная разность
собственных времен, так же как между двумя точками
кривой можно провести дуги, различные по своей
евклидовой длине. Прямая, которая в Е-геометрии
является кратчайшим расстоянием между двумя
точками, в М-геометрии становится кривой наибольшей
разности собственных времен. Перед дальнейшим
рассуждением исследуем и сравним несколько простых
ситуаций.
Рассмотрим ортогональную проекцию отрезка ОА
на прямую g (фиг. 59). Очевидно, проекция О А короче
самого отрезка ОА, тогда, согласно B9), получаем
О А2 = О А2 + А А2 > О А2. C0)
Точно так же ортогональная проекция ОВ отрезка ОБ
на прямую g короче ОБ: ортогональная проекция
всегда короче проектируемого отрезка, и это не зависит от
прямых, на которые производится ортогональное
проектирование; разумеется, проекция, ортогональная
данной прямой, изменяется вместе с этой прямой.
Перейдем теперь к аналогичной конструкции в М-
геометрии (фиг. 60). Проекция на прямую g является
ортогональной, если световой конус делит пополам
угол между проекционными лучами и прямой g, т. е,
если прямая и проекционный луч образуют оси инер-
циальной системы. Теперь проекция ОА отрезка ОА
на прямую g будет длиннее, чем ОА, ибо ввиду
равенства B8) выполняется соотношение
ОА2 = ОА2 - АА2 < ОА2. C1)
Аналогично и проекция ОВ отрезка ОБ на прямую g
длиннее ОБ, В противоположность евклидовой
геометрии здесь изменяется знак в соотношении между
отрезком и его проекцией.

8. Время в частной теории относительности 9
ct-ct(A) /
/°\
Фиг. 60. Эйнштейновское замедление времени.
Изобразим мировые линии двух наблюдателей. Они представляют собой
временные оси соответствующих систем отсчета. Единичные точки А и В
лежат на калибровочной^ гиперболе. Проводя М-перпендикуляры, определим
f — координату точки В_ и f-координату точки А. Устанавливаем, что
неравенства ОА > ОВ и ОВ > ОА непротиворечивы. Временная координата
единичной точки на временной оси инерциальной системы, движущейся со
скоростью и, есть OBlOA = OA!OB = \H\-v\ Эта единичная точка отме1*
чает единицу времени на часах, система покоя которых является этой ииер-
циальиой системой, движущейся в исходной системе со скоростью v. Оче«
видно, что движущиеся часы идут медленнее часов этой исходной системы.
Создается странная ситуация, когда мы
обнаруживаем, что длина временноподобного отрезка равна
временному интервалу, который мы измеряем часами,
движущимися вдоль этой мировой линии. Событие,
которому часы, движущиеся вдоль ?, приписывают
время т, есть Л. Событие, которому часы, движущиеся
вдоль gt приписывают время т, есть В. Л и В лежат на
одной гиперболе, соответствующей калибровочной
кривой (см. фиг. 32).
Но у события Л имеется rf-координата
ci(A)>ci(B) = cr9 C2)
так же как и у события В имеется с/-координата,
большая, чем у Л:
d (В) > ct (Л) = сх. C3)

92 Я- Время в частной теории относительности
Поэтому кажется, что_ в инерциальной системе 2
(временная координата ct) 2-время на gy т. е. время
часов, движущихся относительно 2, течет медленнее,
чем 2-время, которое показывают часы, движущиеся
вдоль мировой линии g. Событие А B-время I = х)
происходит в момент 2-времени i > т. То же самое
справедливо и для обратного направления: кажется,
что в инерциальной системе 21 2-время на g, т. е.
время часов, движущихся относительно 2, течет
медленнее, чем 2-время, которое измеряется часами,
движущимися вдоль мировой линии g. Событие В B-время
т) происходит в момент 2-времени t > т. Кажется,
что движущиеся часы идут медленнее, чем
покоящиеся, точнее: движущиеся часы идут медленнее по
сравнению с покоящейся системой часов, ход которых
задается временной координатой. Этот факт
называется замедлением времени. Такое эйнштейновское
замедление времени геометрически аналогично
укорачиванию отрезков при евклидовых ортогональных
проекциях. Причина кроется в относительности
одновременности. В системе 2 события А к А одновременны (так
что Б происходит раньше, чем Л), а в 2 нет: там,
наоборот, одновременны В к В (В происходит позже,
чем Л).
При абсолютной одновременности не существует
замедления времени. Рассмотрим галилееву
геометрию: в ней положение лучей Г-ортогональной
проекции не зависит от прямых, на которые происходит
проецирование, и длина проекции отрезка идентична
длине самого отрезка. Эквиваленты событий А и В
совпадают, так же как совпадают эквиваленты
событий Лий.
Замедление времени становится значительным,
когда сравниваются показания быстро движущихся
часов. Такими часами могут быть нестабильные
частицы, так как их среднее время жизни т определяет
единицу времени в их системе покоя. Согласно галилее-
вой кинематике, они могут за это время пройти путь
5 = ут, если их скорость равна у. Но, согласно М-гео-

8. Время в частной теории относительности 93
метрии (фиг. 60), координатное время распада есть не
t = т, а 1)
и пройденный за это время путь
с- 1/т
Когда частица движется медленнее света (V<?c), то
и тогда она может за определенное время жизни
пройти любой произвольный путь, если скорость V
вплотную приближается к с:
s
~ct v
Нам известны частицы космического излучения,
которые рождаются в верхних слоях атмосферы и
достигают поверхности Земли (s « 30 км), хотя
продолжительность их жизни в состоянии покоя меньше s/c
(т « 10"8 с, s/c « 10~4 с). Отсюда можно сделать два
вывода: либо частицы движутся в 104 раз быстрее
света, либо собственное время частиц (т. е. время в
их системе покоя) течет в 104 раз медленнее земного
времени, что происходит в результате замедления
времени, вызываемого движением. Измеряя скорость
частицы, мы устанавливаем, что она не превышает
скорости света, так что первый вариант приходится
исключить. Замедление времени правильно описывает
результаты наблюдения.
Замедление времени позволяет за время жизни
человека достичь удаленных звезд в космосе, если ра-
*) Для того чтобы облегчить сравнение с Г-геометрией,
сделаем скорость безразмерной величиной, т. е. разделим ее обычное
тг / путь \ V
выражение V I размерность — J на скорость света: v = —.

94 8- Время в частной теории относительности
кета развивает скорость, достаточно близкую к
скорости света. Разумеется, в космических масштабах
структура пространства изменяется благодаря
гравитационному полю, поэтому при определенных уело?
виях мы должны ожидать достаточно сложных
взаимосвязей. Геометрию Минковского можно
использовать тогда, когда размеры рассматриваемой области
пространства не очень велики.
Легко оценить отклонение от М-геометрии,
вызванное гравитационным полем. Обозначим через Ф
ньютоновский гравитационный потенциал, а через ДФ —
разность между его максимальным и минимальным
значениями в рассматриваемой области:
АФ = Фмакс-ФМин-
Этой разности потенциалов соответствует, как и в
гидродинамике, скорость
Дф= \/%-
Считая Уф погрешностью скорости, на основании
закона распространения ошибок получим погрешность
определяемой величины в М-геометрии. Эта
погрешность имеет такой же порядок, что и эффект,
вызываемый гравитационным полем.
Симметрия утверждения о замедлении времени
вызывает попытки найти подход, при котором эта
симметрия приводила бы к противоречию. Рассматривать
противоречивость утверждения о том, что при
определенных обстоятельствах одни часы идут медленнее
других, можно в том случае, если эти часы через
известное время снова встречаются и позволяют
непосредственно сравнивать показания, причем без отказа
от симметрии. Такая возможность, по-видимому,
представляется нам при рассмотрении парадокса
близнецов. Суть этого парадокса (называемого также
парадоксом часов) можно понять из фиг. 61. Здесь мы
видим три мировые линии часов, которые движутся
прямолинейно и равномерно, т. е. без ускорения. Первые
часы движутся вдоль прямой АС, вторые — вдоль А5,
третьи — вдоль ВС. В мировой точке А
непосредственно сравниваются показания часов / и 2, в мировой

8. Время в частной теории относительности 95
Миробая линия часов I'
Прибой постоянного
М-расстояния до С
Мировая линия часоб 1 \w МиробаЯ линий Часов 2
Фиг. 61. К парадоксу близнецов.
Изобразим мировые линии трех наблюдателей. Эти мировые линии
пересекаются в исходной мировой точке А, промежуточной точке В и конечной
точке С. Опустим М-перпендикуляр из точки В на АС, тогда точка Е даст
нам событие, одновременное с В в системе покоя первых часов.
Восстановим М-перпендикуляр из точки В к прямым АВ и ВС, тогда точки D и D'
дадут иам события, одновременные с В в системах соответственно вторых
и третьих часов. На чертеже отрезок BE пришлось изобразить так, будто
он является перпендикуляром не к АС, а к АВ. Дальнейшие разъяснения
в тексте.
точке В — часов 2 и 3, в мировой точке С — часов 3
и /. Таким образом, мы имеем возможность
сравнивать течение времени вдоль мировой линии АС со
временем вдоль АВ и ВС.
Рассмотрим ситуацию в системе покоя первых
часов. Двое других часов находятся в движении и
поэтому, согласно замедлению времени, идут медленнее,
чем часы /, так что сравнение в точке С дает
тас > тав + хвс*
C4)
Парадокс заключается вовсе не в неравенстве. Мы
знаем, что время соответствует М-длинам сторон
треугольника; в евклидовой геометрии также сумма длин
двух сторон не равна длине третьей стороны.
Парадокс заключается в том, что можно считать часы 1
движущимися относительно часов 2 и <3, и на
основании тех же рассуждений получить замедление времени

PQ S. Время в частной теории относительности
в виде
ТАС < ХАВ + *ВС- C5)
Чтобы разрешить парадокс, нужно учесть
относительность одновременности, учесть точные выражения C2)
и C3) для замедления времени. Это означает, что
время %pQ, показываемое часами, мировая линия
которых содержит прямой отрезок PQ, меньше, чем
разность временных координат точек Р и Q в инерциаль-
ной системе:
Рассмотрим снова систему покоя часов /. Проведя
через В параллель к оси х этой инерциальной системы,
т. е. опуская перпендикуляр на ЛС, найдем мировую
точку ?, одновременную с В в системе покоя часов /:
t\E = t\B. Теперь, согласно C2),
%АС = ХАЕ + ТЕС — ME — МЛ + he ~~" ME ~
= мв мл 4" he — мв > тлв + твс-
Если же рассматриваются системы покоя часов 2 и 3,
то перпендикуляры к ВС и А В даются соответственно
прямыми D'B и DB, и с учетом равенств t2B = hn и
Чв = *ъъ' получается
ХАВ + ТВС == he ~~ ^2Л + ^ЗС — 'з.9 =
= ^2?> — t-2A + ^ЗС — t$D' > T.4D + tr,-c
Но отсюда следует, что
*АВ + ХВС > *АС — T/>D'.
Это не противоречит C4). При качественной
формулировке парадокса вклад %DD, исчезает, и результат
сравнения хода часов в точке С есть C4).
Заметим следующее: на основании неравенства C4)
нельзя ничего сказать об ускорении системы часов
2—3 — рассматриваемая конструкция использует
только неускоренные часы. Естественно, возникает
вопрос: можно ли заменить систему 2—3 одними
часами, которые в точке В испытывают краткое и доста-

8. Время в частной теории относительности 97
точно сильное ускорение, и оказывает ли эта фаза
ускорения существенное влияние на результаты
сравнения конкретных часов? При этом нужно выделить два
момента. Во-первых, данная фаза ускорения может
внести лишь вклад, который не зависит от длины нс-
ускоренного участка мировой линии от Л до Б и от В
до С, в то время как релятивистская разность
пропорциональна этим длинам (теорема подобия). Таким
образом, фаза ускорения не может внести в разность
времен вклада, который компенсировал бы
релятивистский эффект. Во-вторых, мы можем
непосредственно оценить эффект ускорения: для этого нам
нужно сравнить ускорение bQ часов, находящихся в пути,
с типичным ускорением Ь\ в (периодическом)
механизме часов и умножить его на продолжительность f0
внешнего ускорения. Ход часов определяется
внутренним движением, которое нарушается из-за ускорения
часов. Эта помеха в первом приближении
пропорциональна внешнему ускорению и обратно
пропорциональна ускорению, возникающему при внутреннем
движении. Чем больше последнее, тем прочнее часы и тем
менее чувствительны они к внешним ускорениям.
Таким образом, отношение обоих ускорений
устанавливает относительную погрешность хода часов; общая
погрешность в определении времени получается путем
умножения на продолжительность помехи:
дт« *„-?:* IT- C6)
Рассмотрим три примера. В каждом из них под
влиянием ускорения происходит изменение скорости
па величину Av = 100 км/с относительно
первоначального движения. Возьмем маятниковые часы, маятник
которых длиной / = 100 см колеблется с амплитудой
а = 10 см в силовом поле, соответствующем земному
ускорению силы тяжести g = 981 см/с2. Для этих
часов Ь\ « 100 см/с2 и Дт » 105 с, т. е. около суток.
В атомных часах b\ ^ аВцУтр/период ~ с/период.
Для аммиачных часов с периодом около 4- Ю-11 с
следует ожидать Дт ^ 10~14 с. Для углеродных часов
(правда, они непригодны для таких точных измерений
4 За к. 224

98 & Бремя в частной теории относительно ста
времени) это значение было бы еще меньше, так как
здесь в качестве периода мы должны установить
время, в течение которого свет пересекает атомное ядро
(^10-23 с) : Ат — 3-Ю-27 с.
Следующий вопрос касается хода биологических
часов: что произойдет, если два близнеца расстанутся
и один из них совершит путешествие, в то время как
другой будет ожидать его в исходной системе без
ускорения? Вернется ли путешественник меньше
состарившимся, чем домосед? Так во всяком случае
утверждает формула C2). Прежде всего нужно учесть тот
факт, что биологическое старение не устанавливается
какими-то определенными часами, так что живые
организмы и без больших релятивистских путешествий
стареют по-разному. То же самое справедливо и для
возможности определения биологического возраста в
отдельном случае. Поэтому вопрос сводится к
влиянию фазы ускорения на ход биологического старения.
Наряду с постоянной погрешностью Ат,
рассмотренной нами в предыдущем абзаце и ожидаемой в часах
обычной конструкции, здесь не исключается само
изменение биологических часов. Подобные изменения
можно наблюдать лишь как изменение структуры
обычных физических часов и исключить их. Однако
может получиться, что биологические часы после
фазы ускорения пойдут быстрее, чем прежде, т. е. живой
организм будет стареть несколько быстрее, как это
бывает, например, после болезни. Такие изменения в
биологической функции часов мы можем исключить,
постоянно сравнивая биологические часы с
соответствующими физически контролируемыми часами. Но
можно установить изменения в биологическом процессе
и благодаря тому, что их нельзя повернуть вспять при
возобновлении ускорения, т. е. они необратимы.
Поэтому изменения в биологических часах можно
отделить от релятивистского замедления времени
благодаря тому эффекту, что замедление времени исчезает,
если движущееся тело снова приходит в состояние
покоя относительно сравниваемой инерциальной
системы. В соответствии с этим релятивистское замедление
времени не может быть полностью компенсировано та-

8. Время в частной теории относительности 99
кими изменениями в биологических часах, которые
могут встретиться в фазе ускорения.
Наконец, остается часто задаваемый вопрос о роли
гравитационного поля и общей теории
относительности при разрешении парадокса близнецов. Скажем
сразу: гравитационное поле не играет никакой роли.
Гравитационное поле описывается такими же
средствами, как и поле сил инерции, появляющихся при
ускоренном движении, — это лежит в основе принципа
эквивалентности, устанавливающего равенство
инерционной и пассивной гравитационной масс. Поэтому
лишь в особых случаях гравитационное поле является
причиной ускоренных движений. Парадокс близнецов
является частнорелятивистской задачей и
формулируется кинематически, так что истинное решение не
должно выводиться средствами общерелятивистской
(т. е. эйнштейновской) кинематики. Истинное решение
не может состоять ни в обобщении частной теории
относительности, ни в прямом рассмотрении динамики
часов. Как мы показали, существует также чисто
кинематическое решение. Гравитационное поле входит
сюда лишь в качестве дополнительной конструкции:
если мы рассматриваем часы 2 и 3 как одни часы,
которые меняют направление своего движения в точке 5,
то предлагается реализовать необходимое ускорение
через гравитационное поле, так как мы знаем, что
свободное падение в гравитационном поле не может
вызвать никаких внутренних ускорений в часах—все
части часов ускоряются гравитационным полем
одинаково1). Общая теория относительности возводит это
в принцип и тем самым получает возможность такого
описания гравитационного поля, при котором
свободное движение в гравитационном поле оказывается не*
ускоренным движением, и объединенная одними
часами система 2—3 формально не отличается от часов
1. Но для этого должна быть задана плоская
геометрия частной теории относительности: частная теория
относительности справедлива в заданной области толь-
') Если это гравитационное поле достаточно однородно; в
противном случае возникнут приливные эффекты. — Прим, ред4
4*

100 8. Время в частной теории относительности
ко с точностью, задаваемой с помощью
гравитационного поля (смотри также стр. 94). Гравитационное
поле, которому соответствует ньютоновский потенциал
Ф, вызывает эффекты такого же порядка, что и
скорость
Скорость Уф для потенциала Земли па поверхности
составляет около 8 км/с, для потенциала Солнца на
земной орбите — около 30 км/с. Таким образом, в
любом случае возвращение близнеца в В
осуществляется через гравитационное поле. Разумеется, результаты
сравнения часов в С всегда однозначны. Но временная
разница сильно зависит от конкретного распределения
гравитационного поля, которое осуществляет
возвращение. В общей теории относительности
рассматривается ситуация, когда один близнец остается на
земной орбите (т. е. движется вокруг Солнца), а другой
в это время летит в баллистической ракете по орбите
кометы к Плутону и затем возвращается под
действием силы притяжения Солнца; в результате
сравнения часов получается, что путешественник стал
старше, чем землянин. В конце нашей дискуссии
подчеркнем еще раз: все, что получается из фиг. 61, с
парадоксом, строго говоря, не связано и получает
определенный смысл только при введении дополнительных
построений.
Замедление времени и парадокс близнецов
являются чисто кинематическими, т. е. геометрическими
эффектами. Имеются и соответствующие евклидовы
аналоги. Для замедления времени это было уже описано
на фиг. 59. Перенесем теперь в евклидову геометрию
и построение парадокса близнецов (фиг. 62).
Ортогональная параллельная проекция отрезка короче
самого отрезка. Следовательно, третья
сторона-треугольника короче суммы двух других (неравенство
треугольника):
АС = АЕ + ЕС<АВ + ВС. C7)
Как и при построении парадокса близнецов,
возникает вопрос: нельзя ли также обе стороны (АВ и ВС)

8. Время в частной теории относительности \§\
В
Кривая постоянного"
Е-расстояния до А
А
Фиг. 62. Евклидов аналог парадокса близнецов.
Изобразим треугольник ABC, опустим Е-перпсидикуляр из В на АС и
восстановим из В Е-периендикуляры к АВ и ВС. Аналогично фиг. 61 заданные
точки Е, D и D' не совпадают.
считать проекциями третьей стороны и показать
противоречивость неравенства C7)? Ответ аналогичен
решению парадокса близнецов: ВС является проекцией
D'C, и АВ— проекцией AD, следовательно,
AB + BC<AD + D'C = AC + D'D,
и никакого противоречия с неравенством треугольника
C7) не возникает.
В галилеевой геометрии не существует парадокса
близнецов: так как все перпендикуляры имеют
определенное направление, то Д Е и D' совпадают.
Наиболее длинная сторона треугольника всегда равна
сумме длин двух других. Если неравенство C0)
означает, что прямая — это Е-кратчайшая линия,
соединяющая две точки, то неравенство C7) означает, что
прямая—это М-длиннейшая временноподобная
линия, соединяющая два временноподобных события.
В галилеевой же геометрии длина дуги кривой
зависит только от своих конечных точек, а не от своего
конкретного образа.

102 & Длина & частной теории относительности
9. Длина в частной теории относительности
Относительность одновременности заметна и при
обычном изменении длин. Длина стержня измеряется
путем приложения линейки и отметки на этой линейке
положения двух концов стержня. Если стержень
движется относительно линейки, то тогда, естественно,
нужно снимать показания с обоих концов стержня
одновременно, чтобы результат имел смысл. Таким
образом, мы уже коснулись существа проблемы: то, что
одновременно, зависит от выбора инерциальной
системы, поэтому измеряемые длины движущегося
стержня зависят от инерциальной системы, в которой они
измеряются. Два примера: мы можем измерить длину,
одновременно снимая показания с обоих концов
стержня в его системе покоя, но мы также можем сделать
это, одновременно снимая показания с обоих концов
в системе покоя линейки. Результаты будут разными,
так как определение одновременности в этих двух
случаях различно. На фиг. 63 изображены мировые линии
концов линейки и стержня, движущегося относительно
этой линейки. Длина стержня в его системе покоя есть
х(Б) и равна длине линейки в ее системе покоя, т. е.
х(А), Сравним стержень и линейку в момент t = 0
системы покоя линейки, тогда стержень будет короче
линейки: х(В) <. х(А). Если же мы будем сравнивать
длины в момент t = 0 системы покоя стержня, то
стержень, наоборот, будет длиннее линейки, х(Б) >\
> х(А). В обоих случаях движущийся объект
кажется короче покоящегося. Это явление называется
сокращением длин Лоренца и Фицджеральда.
Можно привести целый ряд примеров сокращения
длин, которые выделяют в этом явлении самое
существенное. Предположим, что линейка заменена трубой,
концы которой закрываются практически мгновенно.
Стержень входит в трубу слева и выходит из правого
конца. Как только задний конец стержня (мировая
линия bo) достигнет левого конца трубы (мировая
линия а0), левый и правый концы закрываются.
Окажется ли тогда стержень запертым в трубе или нет? Стер*

9. Длина в частной теории относительности ЮЗ
Фиг, 63. Сокращение длин.
Изобразим в системе покоя линейки мировые линии а^ и а ее концов. Мы
знаем, что калибровочная кривая к О А является гиперболой. Проложим
мировые линии bo и b концов движущегося стержня. Эти мировые лини л
параллельны. Если Ь^ и а3 проходят через иачало, то b касается
калибровочной гиперболы, когда длины покоящихся стержня и линейки равны.
жень движется относительно трубы, стало быть, он
сокращается и поэтому оказывается запертым. Но, с
другой стороны, труба также движется относительно
стержня и, следовательно, сокращается по сравнению
со стержнем: часть стержня уже вне трубы, когда
левый его конец исчезает в трубе, — теперь уже
стержень оказывается незапертым. Нет ли тут
противоречия? «К моменту времени, когда левый конец стержня
исчезает в трубе, правый конец закрывается». Из этой
формулировки ясно, что необходимо определение
одновременности. Но одновременность зависит от инер-

104 0 Длина в частной теории относительности
Стержень
i
—•-
Препятствие
Фиг. 64. К парадоксу масштабов. I.
Объяснения в тексте.
циальнои системы, в которой она задается равенством
временных координат двух событий. Отнеся все к
трубе, мы выясним вопрос с одновременностью в системе
покоя трубы. Стержень сокращается, и событие
запирания трубы есть А (фиг. 63): стержень заперт. Если
мы будем рассматривать все относительно стержня,
то ввиду иного определения одновременности событие
запирания будет А: стержень не заперт. Это не
противоречие, ибо очевидно, чтр событие А происходит
позже Л, и не удивительно, что правый конец стержня
вышел из трубы. Классические примеры ([22], стр. 94)
также совершенно не меняют этот результат.
Пожалуй, более сложной является следующая
постановка вопроса. Рассмотрим стержень, который
движется вдоль ряда точечных препятствий (фиг. 64).
Длина стержня и расстояние между препятствиями
должны быть равными в каждой рассматриваемой
системе покоя. Стержень приближается к препятствиям
с очень малой дополнительной скоростью е. Стержень
и ряд препятствий параллельны. При таких
обстоятельствах стержень должен встретиться с рядом
препятствий. Но здесь возникают две, казалось бы,
противоречащие друг другу возможности описания
происходящего.
Случай 1. Движение стержня рассматривается из
системы покоя ряда препятствий. Стержень
кажется укороченным и поэтому может
миновать ряд препятствий, если попадет в
промежуток между ними.

9. Длина в частной теории относительности 105
Случай 2. В системе покоя стержня ряд препятствий,
наоборот, кажется укороченным, т. с.
промежутки между препятствиями сужаются,
поэтому стержень никак не может миновать
ряд, не столкнувшись хоть с одним
препятствием.
В чем же заключается решение? Что же
укорачивается, стержень или ряд препятствий? Для того
чтобы решить эту задачу, стержень и ряд препятствии
должны быть параллельны друг другу. В случае 1 они
должны быть параллельны в системе покоя ряда
препятствий, в случае 2, наоборот, параллельность
требуется в системе покоя стержня. Но физически это
разные ситуации. Две движущиеся относительно друг
друга прямые могут быть параллельными только
водной инерциальной системе. Это становится очевидным,
если заменить, что параллельность в нашей ситуации
означает, что оба конца стержня пересекают ряд
препятствий одновременно. Это решающий пункт.
Параллельность двух прямых, движущихся относительно
друг друга, связана с определением одновременности
и поэтому не может не зависеть от выбора системы
отсчета. Если концы стержня одновременно пересекают
ряд препятствий в системе покоя этого ряда, то мы
имеем случай У, и стержень может проскочить.
События, соответствующие прохождению концами стержня
ряда препятствий, на фиг. 65 обозначаются через Л и
В. Описание этого случая в системе покоя стержня не
идентично случаю 2. Если смотреть со стержня, то
укорачивается как раз ряд препятствий, но он уже не
параллелен стержню (фиг. 65). Передний конец
стержня первым достигает ряда препятствий. В системе
покоя стержня событие В происходит раньше Л, и
стержень минует ряд препятствий благодаря повороту
этого ряда. В случае 2 мы имеем параллельность в
системе покоя стержня. В этой системе оба конца
стержня достигают линии препятствий одновременно
(события Л и С на фиг. 65). Поэтому случай 2 не
эквивалентен случаю 1, а представляет собой иную фи-

106
9. Длина в частной теории относительности
Миробия линия
переднего рдщц,
стержня * ¦ *
Мировая линия-
прерятстШ
Фиг. 65. К парадоксу масштабоз. 1Г.
Аналогично фиг. 63 изобразим мировые линии ряда препятствий в системе
покоя препятствий и проложим мировые линии концов движущегося стержня.
События А и В одновременны в системе покоя ряда препятствий, события А
и С одновременны в системе покоя стержня. Дальнейшие разъяснения
в тексте.
зическую ситуацию, так что нет никакого
противоречия в том, что результат звучит иначе: стержень hq
минует ряда препятствий. Если смотреть из ряда
препятствий, то стержень в случае 2 укорачивается, но
оба конца достигают линии препятствий не одновре-:
менно. Точнее, задний конец достигает этой линии
первым. В системе покоя ряда препятствий событие С
происходит позже события А. Таким образом,
стержень поворачивается относительно параллельного
положения таким образом, что непременно наталкивает*
ся на одно из препятствий, хотя он и короче
расстояния между препятствиями.
В предыдущем изложении мы установили, что
относительная ориентация движущихся относительно
друг друга объектов в различных системах отсчета
оказывается разной. Поэтому ответ на вопрос о
параллельности стержня и ряда препятствий в двух рассма*
триваемых системах всегда будет разным. Эта зависим

9. Длина в частной теории отндсительности 107
мость относительной ориентации от системы отсчета и
есть камень преткновения при вычислении попереч-
ного эффекта Доплера. В связи с замедлением
времени можно также наблюдать эффект Доплера в
направлении, перпендикулярном направлению движения
источника. Не входя в подробности, отметим только,
что формулировка «в направлении, перпендикулярном
направлению движения источника», касается
относительной ориентации, которая в системе покоя
источника понимается иначе, чем в системе покоя
наблюдателя. Таким образом, если мы не учтем этой разницы,
мы получим разные формулы. Поперечный эффект
Доплера, отражающий замедление времени,
определяет направление наблюдения перпендикулярно
направлению движения источника в инерциальной
системе наблюдателя.
Зависимость относительной ориентации от системы
отсчета лежит также в основе прецессии Томаса.
Последняя наблюдается у гироскопа, движущегося
ускоренно. В заданной мировой точке Е\ этот гироскоп
имеет трехмерную скорость V, а в несколько более
поздней точке Еч— скорость V + ДУ. Направление его
оси вращательного момента дается вращательным
моментом L и соответственно L + ДЬ. Теперь на вопрос
о получении этого (трехмерного) вращательного
момента в зависимости от системы отсчета можно
ответить по-разному. Если AL = 0, то вращательные
моменты параллельны в мировых точках Е\ и Еч в
системе отсчета наблюдателя, но в системе покоя
гироскопа в мировой точке Е\ в общем не параллельны.
Наоборот, если вращательные моменты в (мгновенной)
системе покоя гироскопа параллельны, то они не
параллельны для наблюдателя, относительно которого
движется этот гироскоп, что означает: если сила,
ускоряющая гироскоп, действует таким образом, что
трехмерный вращательный момент в системе покоя
гироскопа не изменяется, то из некоторой
инерциальной системы наблюдается изменение вращательного
момента, т. е. прецессия Томаса4

108 10. Эффект Доплера в частной теории относительн.
10. Эффект Доплера в частной теории
относительности
Обратимся еще раз к уже рассмотренному в гл. 4
эффекту Доплера. Полученную там формулу A1),
являющуюся выражением галилеевои геометрии, нужно
заменить частнорелятивистской формулой. Эта частно-
релятивистская формула при подходящем выборе
координат оказывается эквивалентной преобразованию
Лоренца.
Фиг. 66 иллюстрирует рассматриваемую ситуацию.
Излучатель и приемник движутся неускоренно, и
излучатель посылает сигналы с постоянным периодом
cts = ct(A). Если приемник движется по
направлению к излучателю, то он улавливает период сТВ- =
= —ct(D), если же он удаляется от излучателя, то
принимаемый им период равен сТв+ = сЦВ).
Рассматривая треугольник О А В на фиг. 67, получаем
-T7=77W = Vi^r. C8)
где v — скорость, с которой приемник удаляется от
излучателя. Чтобы распространить результат на случаи
их сближения, можно использовать две возможности.
Прежде всего, если излучатель также удаляется от
наблюдателя со скоростью v (фиг. 26), то, согласно
фиг. С6,
ct(E) = /Т+^
ci (В) V 1 — v '
Для случая сближения со скоростью v получаем
Тв_ ci (О) cl (В) I1 -v
~TJT = ct(C) = ct(E) = V Т+~?" ^
Такой же результат мы получим, если в формуле C8)
для случая сближения заменим скорость на
отрицательную. Формула C9) —это обратное выражение
формулы C8). Эффект Доплера зависит только от от-

10. Эффект Доплера в частной теории относительн. Ю9
Пиродые линии
сигналов, посланных
вслед приемнику
/
/
Мировые линии
сигналов, посланных
излучателем набстре
чу приемнику /
/
/
Мировая
линия наблюдателя
\
Миробая линия
' излучателя
Фиг. 66. Релятивистский эффект Доплера. I.
Изобразим мировые линии источника и наблюдателя и в точке их
пересечения— световой конус. Затем на мировой линии источника определим
мировые точки, в которых излучаются сигналы (в том числе С, О и А). Ьсли
источник и наблюдатель движутся навстречу друг другу, то
Тв ct (D) ct (В)
Ts ~~ ct {С) ~~ ct (Е) '
если удаляются друг от друга,
TQ ct (В)
Т5 — ~ct (Af
то
носительной скорости излучателя и приемника. В га-
лилеевой кинематике A1) это не так. Там в решение
с точностью до второго порядка скорости входит
скорость относительно среды:

]10 10. Эффект Доплера в частной теории относитсльн.
Ниробыв
линии '
сигналов
/
Фиг. 67. Релятивистский эффект Доплера. II.
Изобразим световой конус с вершиной в точке пересечения мировых линий
источника и наблюдателя. На мировой линии источника выберем точку А.
соответствующую периоду let {А) = сТ$\, и изобразим мировую линию
сигнала, излученного в этой точке, которую продолжим до точки С, затем
найдем точку В. Равенство cj {В) — сТq представляет собой наблюдаемый
период. Отметим точку D, которая должна удовлетворять условию DC = CO,
Тогда DB является параллелью к оси х и DA — параллелью к оси х.
Точки пересечения назовем как указано на чертеже. Мы знаем, что двойное
отношение равно
ВК ЕР __ ?у
BD ' ЕК~~ 1 + v '
причем v представляет собой скорость системы 2 относительно 2, Это
двойное отношение сохраняется при проецировании на прямую DH:
GA ND
GD
2и
НА
l + v
Симметрия относительно прямой СВ порождает равенства
tGA
GD
КА
КО
HA = yHD'
К А
КО
Теперь находим
v КО
l+v ' АО
и тогда
ct (К)
= 1 + 0,

JO. Эффект Доплера ъ частной теории относительн. "~'" 111
Разницу между выражениями C8) и D0) можно
проверить экспериментально. Оказывается, формулы C8)'
и C9) (эйнштейновская кинематика) подтверждаются.
Приведем пример, показывающий, насколько
полезным оказывается графический анализ ситуации на
х — /-диаграмме. Попытаемся получить эффект
Доплера путем измерения расстояния между сигналами.
Определим пространственное расстояние между
сигналами, для чего измерим расстояние между двумя
наблюдателями, которые одновременно принимают
соседние сигналы. Очевидно, мы можем определить
расстояние между сигналами в движущейся системе от*
счета, потому что наблюдатели движутся, и расстоя*
ние между ними измеряется в движущейся системе
отсчета. Затем ввиду сокращения длин (фиг, 63)
получаем
Расстояние в сопутствующей
системе отсчета 1
Расстояние в исходной ^J\ _ v2
системе отсчета
Если бы это были расстояния между сигналами, это
противоречило бы формуле C8). Из фиг. 68 видно,,
что это не так. При движении наблюдателей должна
учитываться относительность одновременности. В
исходной системе сигналы достигают наблюдателей од*
новременно (события О и G), Но для того чтобы
расстояния между наблюдателями являлись и расстоя*
ниями между сигналами, сигналы должны одновре*
менно достигать наблюдателей в сопутствующей си*
стеме отсчета (события О и К).
Приступим теперь к построению преобразования
Лоренца B1) из эффекта Доплера и принципа
относительности [2].
Введем следующие предположения:
1. Мировые линии рассматриваемых сигналов за«
даны в системе отсчета и представлены там двумя
семействами параллелей.
2. Время на неускоренных часах течет так, что
сШ_ = ШЁ1 = к D1)
ctlA) cilB) v '

112 tO. Эффект Доплера в частной теории относительна
Фиг. 68. Ложный вывод при определении (продольного) эффекта
Доплера.
Чтобы определить длину волны в движущейся системе, относительно которой
два наблюдателя А н В покоятся, поступим таким образом, чтобы в
исходной системе однооременно принимали два последовательных сигнала, и
затем измерим пространственное М-расстояиие между ними. Это есть не что
иное, как длина L отрезка О/ в системе покоя А и В. Мы знаем, что
L = h V1 — у2« Но эта формула не описывает эффект Доплера. Как
показывает чертеж, А, —это длина покоящегося отрезка О К, она равна
Я, = 's/OiW — KM* = О.VI V(l — V').
С другой стороны,
OM=l + KM = X + vOM, ОМ = -j"Z7-
Теперь получим верную формулу
в соответствии с фиг. 67. При этом значение k зависит
только от двух рассматриваемых мировых линий.
Синтез этих двух предположений осуществляется
путем построения на фиг. 69. Формулу D1) можно
понимать двояко. Во-первых, эффект Доплера при
сближении всегда равен обратной величине эффекта при
удалении. Во-вторых, эта формула означает, что
наблюдатель I видит излучатель на мировой линии II в
той же частоте, что и наблюдатель II видел бы этот
излучатель, движущийся вдоль мировой линии I. Итак,
предположим, что в случае световых сигналов эффект
Доплера зависит только от относительного движения

10. Эффект Доплера в частной теории относительн. ИЗ
Фиг. 69. Эффект Доплера и принцип относительности.
Изобразим мировые линии четырех наблюдателей, причем три из них пере
секаются в точке О. Проложим мировые линии сигналов через точки В и
найдем Л, ? и Я. Мировые линии сигналов изображены здесь не в виде
биссектрис углов между вертикалью и горизонталью, так как положение и
калибровка координатных осей заранее не предполагаются, а выводятся-
Проведем через Е параллель к АН, через А и С —параллели к BE и найдем
точки К, F, D, J и G. Сигнал, испущенный в мировой точке А и
отраженным в мировой точке В, снова принимается наблюдателем I в мировой
точке Е. Соответствующие мировой точке G мировые точки отсчета суть А
и С на мировой линии наблюдателя I и В н / — на мировой линии
наблюдателя II. Дальнейшее разъяснение в тексте.
наблюдателей I и II. Теперь определим
пространственные и временные координаты относительно
наблюдателя I через время пробега сигналов, которые
излучаются в этой мировой точке или принимаются в ней.
Координаты событий В определяются выражениями
ctl(B) = ^r(ctl(E) + ctl(A))>
[ D2)
X{{B) = ^(ctl{E)-ctl(A)).
7г5 Зак. 224

114 №• Эффект Доплера в частной теории относительн.
Это определение координат означает, что все скорости
установлены в единицах скорости сигнала. Теперь
скорость сигнала всегда равна единице. Тогда скорость
наблюдателя II относительно I равна
ct} {E)-ct} (Л)
V— ctl (?) +с/, (Л)
Ввиду D1) получаем
ctl{E) = kctu{B) = k2ctl(A)
и
k2- 1
v = ¦
Vl*7- <43>
k2 + 1 *
Эйнштейновскую теорему сложения получим как
правило дифференцирования произведения или цепное
правило для k:
ctlv{H)_ct„(H) ctuW
* ах(А) ctn{B) ct{(A) K R' [^V
Наконец, выведем неравенство треугольника —
эквивалент парадокса близнецов. Для этого сравним
время cti(C) с временем
cf(C) = ctm(Q-ctlu(B) + ctu(B).
Ввиду D1) имеют место равенства
ctin (С) - ctiu (В) = k (с/, (С) - с/, (?)) =4" X
и
ctu(B) = kctl(A) = -]rctl(E).
Параметры }. и Л. мы можем выбрать произвольно, и
тогда
сС (С) = (I - я) k (<*i (Q - cix (E)) +
+ X-j-(cl1(C)-dl(A)) +
+ (l-X)kctl(A) +
+ А+С/,(?).

10. Эффект Доплера в частной теории относительн. 115
Теперь выберем л и Я так, чтобы вклады величин
cU(A) и cti(E) исчезли:
kk
1 + kk
Кстати, отметим, что k и k больше единицы, так что
ввиду неравенства A —k) A —k) >> 0 получим
k + к <С 1 + kk- Следовательно, для ct* (С) имеем
cf (С) = -?±А- с/, (С) < с/, (С). D5)
Это выражение для парадокса близнецов.
Далее, мы видим, что F и В одновременны для
наблюдателя I, но не для наблюдателя II. Для
наблюдателя II одновременной с F была бы середина отрезка
KD. Одновременность оказывается относительной.
Наконец, из сравнения положений мировой точки G,
отмечаемых наблюдателями I и II, получается
преобразование Лоренца. Определим координаты события G,
согласно D2),
ctl(E) = ctl(G) + xl(G),
ctx (A) = ct} (G) - х{ (G),
ctu(J) = ctu(G) + xu(G),
ctn(B) = ctu(G)-xu(G).
Теперь заметим, что ctu (В) = kct\ (А) и ctu(J) =
= (\/k)cti(E). Тогда получим формулы
преобразования Лоренца
ctu— 2k Vi k2+ 1 ХЧ*
— А1±1 ( _ ь2- х \
*п — 2k \Xi k2 + 1 Ч'
Построение координат с помощью светового конуса
наводит на мысль, что преобразования Лоренца и вся
частная теория относительности содержат явное
соглашение о величине скорости света и изотропии
распространения светового сигнала. Это обнаруживается,
72б*

116 Ю- Эффект Доплера в частной теории относительн.
когда мы выбираем координаты таким образом, чтобы
средняя скорость светового сигнала всегда
равнялась с. Но нам нужно учесть, что предлагаемое
построение координат предусматривает особые свойства
эффекта Доплера: наблюдатель, движущийся со
скоростью v\, обнаружит такой же эффект Доплера (k\)
у излучателя, движущегося со скоростью v2, какой
наблюдатель, движущийся со скоростью V2, обнаружил
бы у излучателя, движущегося со скоростью V\(k2).
Это и есть принцип относительности для эффекта
Доплера. Он не является априорно необходимым и
требует экспериментального подтверждения.
Согласно галилеевой кинематике, получается не
k\/k2 = 1, а
^L = ] ~ "'
k, 1 - v\
и в Е-геометрии
kx _ 1 -Pf i + vj
k2~ \-v\ \+v\'
Таким образом, упомянутое выше построение
координат не является вопросом соглашения, оно лишь воз-
можно, поскольку принцип относительности
справедлив для света, изотропное распространение и
постоянная скорость которого должны быть проверены путем
измерения.
Возникает вопрос: на какой другой скорости
можно проверять постоянство скорости света; другими
словами: определяются ли единицы измерения
времени и длины таким образом, чтобы получаемые из
них единицы измерения скорости не зависели от
скорости света? Наконец, измерение пространства и
времени исторически производилось не так, как мы это
делали при абстрактном построении инерциальной
системы в частной теории относительности (ср. стр. 52).
Временная координата уже ориентирована на
равномерное движение, когда мы измеряем ее с помощью
вращения Земли. Длина же задается посредством
переноса стандартного масштаба. Поэтому нам нужно

11. Импульс, масса и энергия
117
рассмотреть этот стандартный масштаб более
подробно. Размеры твердого тела определяются
взаимодействием атомов, составляющих это тело. Масштаб
длины в этой области равен боровскому радиусу, г =
= ft2m_1e~2 (т и е — масса и заряд электрона, ft «
^ 10~27 эрг-с — постоянная Планка). Сравнивая его
с атомной единицей времени, которая задается
постоянной Ридберга (R = me4/4nh3 — частота
излучения, при которой ионизуется водород), получим
эталон скорости, который не зависит от скорости света:
rR = e2/4nh. Изменение скорости света по сравнению
с этой единицей означает изменение постоянной
тонкой структуры Зоммерфельда a = e2/hc. Точное
измерение расщепления спектральных линий космических
объектов показывает, что признаков такого изменения
не наблюдается. В заключение следует добавить, что
определение временной и пространственной единиц по
спектральным линиям точнее, чем на основании
вращения Земли и стандартного масштаба. Используя
для этой цели единственную спектральную линию, мы
определим постоянную с (скорость света) по крайней
мере для этой спектральной линии.
11. Импульс, масса и энергия
Импульс — это величина, закон сохранения которой
сводится к правилу «смешивания» скоростей при
полностью неупругом столкновении. Вычисляя скорость
как отношение (координатного) пути к
(координатному) времени, мы обнаружим, что масса зависит от
скорости, как это было установлено в выражениях
A6) и A9). Эта масса является компонентой
импульса в направлении времени. Запишем
где т0—масса объекта в сопутствующей инерциаль-
ной системе, т. е. в системе покоя объекта. Она
называется массой покоя. Согласно Минковскому, квадрат

118 /Л Импульс, масса и энергия
модуля импульса есть
|/.|2 = т§Л D8)
В соответствии с этой конструкцией численное
значение массы покоя не зависит от инерциальной системы,
в которой измеряется объект, и не зависит от скорости
объекта.
Разлагая временную компоненту импульса по
скоростям, получим
т0с (Л . V2 , \
тс = —^==- = т0сA +1?-+ ...) =
Для малых скорстей временная компонента импульса
с точностью до постоянной суммирования
пропорциональна кинетической энергии объекта, так что в этом
случае можно записать
тс2 = m0c2 +^-V2 = E0 + EK№ D9)
Справедлива ли эта формула для больших
скоростей? Если не опираться на формулу ?Кнн = (l/2)mV2,
а определять кинетическую энергию как работу,
которую нужно совершить над объектом, чтобы вывести
его из состояния покоя (в заданной инерциальной
системе) и разогнать до скорости V, то для
произвольных скоростей имеет место равенство
?кин = тс2 — т0с2. E0)
Является ли Е0 = тос2 просто константой или Е0
описывает энергию, которая может превратиться в
кинетическую энергию? Говоря о взаимном превращении
форм энергии, мы приходим к закону сохранения
энергии, который исходит из сохранения энергии при
упругом столкновении. В ньютоновской механике мы
наблюдаем неупругое столкновение, при котором
кинетическая энергия соударяющихся тел уменьшается.
Но мы можем установить механический эквивалент

11. Импульс, масса и энергия
119
теплоты, т. е. сказать, что чисто кинетическая энергия
превращается в тепловую, т. е. обобщенную
внутреннюю энергию. Но закон сохранения для четвертой
компоненты импульса, который содержится в правиле
смешивания скоростей, означает, что
Сумма кинетических энергий + Сумма членов
Е0 — const.
Поэтому член ?0 должен содержать внутреннюю
энергию объекта; Е0 называется энергией покоя.
Согласно выражению D8), частицы, движущиеся
со скоростью света, имеют нулевую массу покоя.
Такими частицами являются кванты электромагнитного
поля — фотоны, которые ради более наглядного
представления эйнштейновской кинематики могут
пониматься и как волновые пакеты света. Для них
справедливо соотношение
Модуль р пространственной компоненты
импульса = временной компоненте импульса.
Экспериментально обнаруживается, что энергия этих
частиц пропорциональна импульсу и что для них
выполняется равенство Е = р-с. Для этих же частиц
временная компонента пропорциональна полной
энергии, которая в данном случае является чисто
кинетической. Таким образом, мы имеем право написать, что
полная энергия равна
Е = тс2. E1)
Подтверждением того, что полная энергия частиц
действительно может перейти в кинетическую энергию,
служат реакции столкновения элементарных частиц, в
результате которых образуются только частицы с
нулевой массой покоя, т. е. частицы, движущиеся со
скоростью света (фиг. 73).
Формула ?Кин = тс2— т0с2 выражает зависимость
инертной массы от скорости

120
П. Импульс, масса и энергия
и, стало быть, гиперболическую форму калибровочных
кривых (фиг. 13 и 33). Если бы в Е-геометрии
калибровочные кривые были окружностями, то
соответствующая им зависимость инертной массы от
скорости }) имела бы вид
и кинетическая энергия выражалась бы как
?Кин = ™>qC2 — тс2-
Какая геометрия применима — решает эксперимент.
Мы уже рассматривали кинематику и динамику,
которые соответствуют М-геометрии (см. наши
рассуждения на стр. 62).
Формула E1) —выдающийся результат частной
теории относительности. Она означает, что закон
сохранения энергии является частью закона сохранения
импульса и содержится в правиле смешивания
скоростей. В ньютоновской механике это не так. Там массы
не изменяются, и, естественно, не выполняется закон
сохранения механической энергии: механическая
энергия при неупругих ударах теряется, и необходимы
дополнительные теоретические построения, чтобы можно
было сохранить сам закон сохранения для неупругих
столкновений. В частной теории относительности
закон сохранения инертной массы идентичен закону
сохранения энергии. Каждый вид энергии имеет
инертную массу, и коэффицент пропорциональности равен
с*. Укажем еще раз на различие между инертной
массой и массой покоя. Инертная масса является
множителем между импульсом и координатной скоростью V;
напротив, масса покоя является инертной массой
только в сопутствующей инерциальной системе. Таким об-
*) В евклидовой геометрии с не означает абсолютной
скорости особого физического процесса, так как такого процесса
не существует. Величина с здесь представляет собой
естественную постоянную, которая сама должна быть определена
посредством зависимости массы от скорости.

12. Процессы столкновения
121
разом, масса покоя не зависит от инерциальной
системы и от скорости объекта в ней, а инертная масса
зависит от скорости. Частица, движущаяся со
скоростью света, не имеет массы покоя. Нет такой
инерциальной системы, в которой эта частица покоилась
бы. Свойство двигаться со скоростью света не зависит
от инерциальной системы. Это предположение лежит
в основе частнорелятивистской кинематики. Однако
такая частица обладает инертной массой, которая
соответствует присущей этой частице энергии.
Формула E1) отнюдь не означает, что энергия
может превращаться в массу и наоборот. Полная
энергия и полная масса всегда сохраняются.
Превращаться друг в друга могут энергия покоя (и,
следовательно, масса покоя) и кинетическая энергия. Рассмотрим
теперь примеры, иллюстрирующие сказанное.
12. Процессы столкновения
Цель этой главы — на различных примерах столк-
новительных процессов объяснить закон сохранения
энергии-импульса и превращение энергии покоя и
кинетической энергии. Рассмотрим процессы, в которых
частицы взаимодействуют друг с другом в
ограниченном временном промежутке, так что ни до, ни после
они ие подвергаются влиянию, и получим полную
энергию, полный импульс и т. д. путем суммирования
этих величин по отдельным частицам. Такие процессы
называются процессами столкновения. Здесь мы
рассмотрим лишь простейшие результаты.
При комптоновском рассеянии частица, не
имеющая массы покоя, упруго соударяется с массивной
частицей (т0 ф 0). Упругое столкновение означает, что
характеристики частиц (число, масса покоя, заряд,
собственный вращательный момент1)) сохраняются.
Наблюдения показывают, что сохраняется не только
полная энергия, но и отдельно энергия покоя и
кинетическая энергия. Изобразим рассеяние Комптона в
системе покоя массивной частицы до удара (фиг. 70).
1) Спин. — Прим. псрев.
6 Зак. 224

122
12. Процессы столкновения
/°\
Фиг. 70. Упругое столкновение частицы без массы покоя с
покоящейся частицей.
Построим сначала полный импульс <Р=ОВ с помощью Pi — OA и qi = AB-
Из & вычтем qz = DB и найдем p-,= OD. Так как pi и рг должны
относиться к одинаковым массам покоя, то можно найти D как такую
точку гиперболы, проходящей через А, в которой эта гипербола
пересекается с прямой, параллельной асимптоте и проходящей через точку В.
Эту точку мы находим с помощью построения гиперболы посредством двух
проективных пучков параллелей (фиг. 84). Проведем через А и В параллели
к асимптотам, найдем точку С как пересечение параллели к асимптоте с ОВ,
и точку D как пересечение параллелей к асимптотам, проходящих через В
и С. Вычисляя с помощью временных компонент четырех импульсов
BD
_??.. mi = BGY2, m2+2qi = OG^2, qi = -~r
= HG
Я1 V2"
на основании теоремы подобия BD/BG = HG/OG получим формулу
1 +
2<?i
т,
Замечая, что временная компонента импульса фотона (не обладающая
массой покоя) представляет собой произведение q = h"v частоты на постоянную
Планка h, находим формулу для эффекта Комптона (в случае обратного
рассеяния, так как мы оперируем здесь только одним пространственным
измерением):
v2=
1 +
2/zv,
Массивная частица (импульс р\) испытывает удар со
стороны частицы без массы покоя (импульс yi) и
забирает часть ее импульса и энергии, причем так, что
масса покоя массивной частицы остается неизменной.
Таким образом, вектор импульса /г2 массивной
частицы после столкновения должен заканчиваться на той

12. Процессы столкновения 123
же калибровочной гиперболе, что и р\. Для энергии
частицы без массы покоя после столкновения находим
где Ш\ — масса покоя первой частицы. Эта формула
подтверждается экспериментально. В качестве частиц
без массы покоя используются фотоны, энергия
которых пропорциональна их частоте, так что формулу
E2) можно проверить путем измерения частоты света,
рассеянного на свободных (заряженных) частицах.
Если рассеянный фотон летит дальше в некотором
направлении, образующем угол а с направлением
падения, то формула E2) обобщается и принимает вид
I ТП\Ц\ COSCI I
'2 | Щ\ 4- <1\ U — cos а) |"
Формула же E2) —это частный случай а = л.
А что произойдет, если частица без массы покоя не
рассеется, а полностью поглотится? В этом случае
процесс уже не будет упругим — число частиц и масса
покоя массивной частицы не сохраняются.
Образующаяся в результате такого столкновения частица, согласно
фиг. 70, имеет импульс, изображаемый отрезком ОВ.
Этому импульсу соответствует масса, большая, чем
импульсу р\. Обратным этому процессу является
излучение частицы без массы покоя. Фиг. 71
иллюстрирует этот процесс в системе покоя частицы до
излучения. Излучение сопровождается потерей массы покоя
и отдачей. Излученная частица черпает свою энергию
из энергии покоя. В обратном процессе поглощенная
энергия вызывает прирост внутренней энергии
поглощающей частицы: ее энергия покоя и масса покоя
должны расти.
Потеря массы покоя характерна для излучающего
атома, а также для элементарной частицы, которая
распадается на фотон и частицу меньшей массы покоя
B°—^Л° + у). Без потери массы невозможно
излучение кинематически причинных частиц (т. е. частиц со
скоростью, меньшей или равной скорости света)
(фиг. 72). Две точки на кривой постоянной массы по-
6*

124 /?• Процессы столкновения
/77 А
Фиг. 71. Излучение частицы без массы покоя.
Импульс pi = OE состоит из импульса p2=OD заданной массы покоя и
и импульса qr=DE без массы покоя. Масса покоя импульса р2 определяет
гиперболу, которая неявно задается точкой А. Отрезок О А представляет
собой массу покоя. Точка D—-точка пересечения гиперболы, заданной
точкой А, с параллелью к асимптоте, проходящей через точку Е. Найдем D
так же, как н на фиг. 70. В системе покоя импульса р, для временных
компонент импульса аналогично фиг. 70 будут выполняться равенства
V^ л/я У ^
Находим
BD ОН LD OG-\0(f m\ — m-2
ЬЬ ='00 ' "сВ UU ' q=s 2tnx *
Здесь гпч означает массу покоя импульса р>. По предположению Ш\ равна
массе покоя, так как мы производили построения в системе покоя
импульса рх.
коя (гиперболы в верхней полуплоскости) всегда
расположены временноподобно друг другу. Таким
образом, процесс, сопровождающийся изменением
импульса без изменения массы покоя, может происходить
только при рождении или поглощении частицы,
движущейся со сверхсветовой скоростью; в противном
случае в процессе должно участвовать больше частиц,
как это имеет место в эффекте Комптона.
Изобразим теперь распад массивной частицы на
две частицы без массы покоя (фиг. 73). В системе
покоя распадающейся частицы оба продукта распада
обладают одинаковой энергией и разлетаются в
противоположных направлениях. Эта энергия в системе

12. Процессы столкновения
125
Место вектороб импуша,
\ ^^относящихся
\
\
ш
\
\
А
/
/
/
/
/
/
/
пг /
/
/
/ \ р
Фиг. 72. Реакции без изменения массы покоя.
Реакция р = р2 + ^ возможна лишь для пространственноподобного
импульса q, когда массы покоя, относящиеся к р\ и р2, равны. При излучении
кинематически причинной частицы (временноподобный импульс) масса покоя
всегда уменьшается.
/ \
Фиг. 73. Рассеяние излучения массивной частицы.
Частица, оиладающая кассой покоя, может полностью распасться на
частицы без массы покоя, если этого не запрещают правила отбора. Энергия
покоя распавшейся частйиЫ полностью переходит в (кинетическую) энергию
излучения. Полная энергия и сумма инертных масс (т. е. сумма временных
компонент импульсов) остаются неизменными. Примерами таких продетой
являются распады л°-»2у и е"*~+е— -»2у. Эта диаграмма является
элементарным особым случаем, изображенным иа фиг, 71, при тг=0.
покоя распадающейся частицы определяется
исключительно ее массой покоя. Процесс называется
рассеянием излучения, продукты распада — аннигиляцион-
ным излучением. В этом процессе полная энергия
покоя превращается в кинетическую энергию. В
результате рассеяния электрон-позитронной пары (масса по-

126 12. Процессы столкновения
коя около 1 МэВ ж 2 -10-27 г) образуются два фотона
с частотой
v=-^« 1,23-КРс-1
Другой пример; распад л°-мезона на два фотона.
Наоборот, массивные частицы могут образовываться
за счет энергии частицы без массы покоя, но не без
участия массивной частицы, которая воспринимает
избыточный импульс: как только образуются массивные
частицы, полный импульс становится временноподоб-
ным, так что массивные частицы не могут
образовываться из одной частицы без массы покоя.
Наконец, изобразим распад массивной частицы на
две массивные частицы (фиг. 74). Полный импульс
разлагается на две части, масса покоя которых
задана. Далее, третья вершина треугольника,
построенного на векторах импульса ОМ, ОР и РМ, является
точкой пересечения гипербол, соответствующих
массам покоя продуктов распада. Вычислим координаты
этой точки в системе покоя распадающейся частицы,
используя уравнения обеих гипербол:
tri1 — р2 = т],
(т-МJ-р2 = т2г.
Здесь т\ и т,2 — массы покоя продуктов распада. От*
сюда
р = д/m2 — т\.
К тому же точка пересечения обеих гипербол строится
с помощью циркуля и линейки, так что координаты
точки пересечения наряду с рациональными
выражениями содержат только квадратные корни. Однако
само построение выполняется не так просто, как
предыдущие, и мы укажем здесь лишь общие его черты.
Интересующемуся читателю нужно обязательно взять в
руки книгу по проективной геометрии и более
подробно ознакомиться с методами выводов и построений, ,

12. Процессы столкновения - 127
Геометрическое место
импульсоб с массой
покоя шуточка отсчета О)
Геометрическое место
импульсоб с массой
пот /я (точка отметя М)
Фиг. 74. Распад на две массивные частицы.
Вектор импульса распадающейся системы есть ОМ, импульсы продуктов
распада, р1^=ОР и р2=РМ, обладают массами покоя т\ и т2, которые
отмечаются отрезками ОС и ВМ. Теперь построим световые конусы с
вершинами в точках О и М. Точка пересечения гипербол, проходящих через В
и С, с этими асимптотами дает точку Р*

128
12. Процессы столкновения
Из фиг. 74 мы узнаем, что точки пеленга точек н^
гиперболе гармонически делят точки пересечения обе»
их ветвей гиперболы с осью отсчета. Так как точк$:
пересечения лежит и на гиперболе I (с центром в точ-
ке О), соответствующей массе покоя пги и на гипер»
боле II (с центром в точке М), соответствующей
массе покоя m2t то ее точки пеленга Е и F гармонически
делят точки пересечения осей отсчета как с
гиперболой I (Си D), так и с гиперболой II (Ли В). Теперь
точки Е и F осуществляют инволюцию на прямых
отсчета: каждой точке Pi прямой отсчета ставится в со«.
ответствие точка Ря, которая вместе с Pi гармоничен
ски делит точки Е и F, называемые неподвижными
точками инволюции. При изображении известны пары
точек Л, В и С, D. Если мы по этим данным
определим неподвижные точки инволюции, то можно
построить точки пересечения обеих гипербол, для
чего через точки Е и F проведем параллели к
асимптотам. Определение неподвижных точек
инволюции является стандартным построением
проективной геометрии (фиг. 87). Эта операция объясня*
ется в приложении.
Теперь мы выполнили все построения для реакций
двух частиц, т. е. для случаев, в которых полный
импульс разлагается на два светоподобиых импульса
(фиг. 73), один временноподобный и один светоподоб-
ный (фиг. 71), и на два временноподобных (фиг. 74)
импульса. В заключение обсудим некоторые
качественные аспекты.
Объект только тогда может самопроизвольно
распадаться на несколько частиц, когда сумма масс
покоя этих частиц меньше массы покоя распадающегося
объекта (фиг. 74), так как кинетическая энергия
разлетающихся продуктов расщепления черпается из
энергии покоя. То, что мы здесь формулируем для
импульсов, является эквивалентом кинематического вы*
ражения C4) в динамике. Если нам известны массы
покоя объекта и продуктов его расщепления, то
можно подсчитать кинетическую энергию последних. Так,
при расщеплении ядра UJjf {mo ~ 235 ат. ед.) кине-

12. Процессы столкновения
129
тическая энергия составляет около 0,2 ат. сд. *), т. е.
3-Ю-11 Вт-с/атом, или 5 млн. кВт-ч/моль.
При неупругом столкновении двух частиц не может
возникнуть стабильный объект, в таком случае
возникает вторая частица. Простейший процесс,
приводящий к системе, в которой сталкивающиеся частицы
стабильно связаны, образует из сталкивающихся
частиц связанную систему и частицу без массы покоя;
при этом последняя поглощает энергию. Тогда без
подвода энергии образованная система не сможет
распасться. Минимальное значение энергии, которую
нужно сообщить связанной системе, чтобы расщепить ее
на составные части, называется энергией связи. Она
пропорциональна разности между суммой масс покоя
продуктов распада и массой покоя системы. Эта
разность называется дефектом массы. Если подводится
энергия, соответствующая дефекту массы, то система
может распасться, но не останется дополнительной
кинетической энергии для продуктов распада. Наоборот,
если образуется связанная стабильная система, то
дополнительно остается энергия, соответствующая
дефекту массы, которая может излучаться в виде частиц
без массы покоя (нейтрино, фотоны) или же
массивных частиц. Так, при образовании ядра гелия (масса
покоя 4,00275 ат. ед.) из четырех протонов (масса
покоя 4-1,00795 ат. ед.) возникают еще два позитрона
(масса покоя 2-0,00549 ат. ед.). Остаток @,028 ат.
ед. = 4,8- Ю-26 г на ядро Не, или 0,7 млн. Кзт-ч на
моль Не) входит в кинетическую энергию позитронов
и частиц без массы покоя, которые возникают в этом
процессе. Процесс 4р^Не!* + 2e+ + 2v + 2y всегда
проходит много промежуточных этапов, на каждом из
которых взаимодействуют две частицы.
При столкновении двух массивных частиц могут
образоваться также и другие массивные частицы. При-
!) ат. ед. — атомная единица массы определяйся как одна
двенадцатая массы атома 12С: 1 ат. ед = A,660531 rh
rh 0,000033) Ю-27 кг.

130
12. Процессы столкновения
мер: процесс, в котором при столкновении двух
протонов дополнительный л-мезон образуется из
кинетической энергии, которой обладали оба протона до удара.
Так как полная масса покоя после удара равна
2mp + тл, то кинетическая энергия в системе покоя
центра масс должна равняться по меньшей мере
тЛс2, а это означает, что каждый протон в системе
покоя центра масс должен обладать скоростью по
меньшей мере 0,361 с. Если этот процесс рассматривать в
системе покоя одного протона, то второй должен
обладать скоростью по меньшей мере 0,638 с. Это
соответствует энергии Е = тс2 = 1,3т/с2, которая
ускоряет протон разностью потенциалов около 300 млн.
вольт. Эта энергия является пороговой энергией для
ускорителя протонов, когда протоны из ускорителя
при столкновении с протонами в водородной
пузырьковой камере образуют я-мезоны. Ввиду
определенных правил отбора (сохранение барионного числа,
лептонного числа, электрического заряда и др.) ниже
этого порога частицы, обладающие массой покоя (ju,
е), могут образовываться лишь парами (например,
р + р -> р + р + е+ + е~). Эти процессы весьма
редки, так как, с одной стороны, должны появиться две
частицы, а с другой — их рождение длится в 10м раз
медленнее, чем рождение л-мезона.
Далее, первое возбужденное состояние протона
имеет массу покоя, большую, чем тр + тл, так что
ниже указанного порога не могут происходить
неупругие столкновения без рождения частиц.
13. Заключительные замечания
Кинематика частной теории относительности — это
геометрия, причем такая, в которой мы используем
иные предположения, чем в евклидовой геометрии.
Однако во всех вопросах, касающихся проективных
взаимосвязей, эта геометрия аналогична евклидовой.
Таким образом, установлено, что частная теория
относительности в такой же мере непротиворечива, как и

13. Заключительные замечания 131
геометрия. Следовательно, мы можем быть
уверенными, что все «парадоксы» заключаются в
непоследовательной формулировке утверждений и
предположений частной теории относительности. Чаще всего это
связано с относительностью одновременности, смысл
которой при формулировке парадокса затемняется,
так как смысл определения одновременности во
многих случаях не так очевиден.
Другой вопрос: правильно ли представляет
частная теория относительности описываемые ею подходы?
При обсуждении экспериментов, подтверждающих
теорию относительности, нельзя останавливаться на тех,
которые исследуют изотропию распространения света.
Эти эксперименты согласуются с изотропией скорости
света, хотя могут быть объяснены и другими
вспомогательными гипотезами. К тому же, постоянство и
изотропия распространения света не составляют полного
содержания частной теории относительности.
Физические свойства массивных объектов (инвариантность
массы покоя — см. стр. 52 — и связанное с ней
существование объективных масштабов длины и времени)
так дополняют условия, накладываемые на системы
отсчета, что инерциальные системы могут строиться
на основе рассуждений, приведенных на стр. 52.
Прежде всего теория относительности характеризуется
такой многосторонней взаимосвязью.
Существует много опытов, проверяющих
простейшие следствия кинематики частной теории
относительности, такие, как изменение массы и замедление
времени (поперечный эффект Доплера, спутниковые
часы, масс-спектрографы, ускорители частиц). Все эти
опыты еще ни разу не вошли в противоречие с частной
теорией относительности. Однако наиболее отчетливо
результаты частной теории относительности
проявляются в косвенных и качественных следствиях,
которые опираются не на тот или иной частный эффект, а
непосредственно на независимость формы закона
природы от инерциальных систем, получающихся одна из
другой с помощью преобразований Лоренца. Такими
следствиями являются существование античастиц для

132 №• Заключительные замечания
электронов, нейтронов, протонов и т. п., нарушение
зеркальной симметрии ввиду существования нейтрино,
нарушение симметрии реакций между элементарными
частицами при одновременной замене их
античастицами и отражении процессов в пространстве и
времени (СРГ-теорема). При выводе этих законов
используется только часть свойств, характеризуемых группой
Лоренца. Качественные выводы из теоретических
построений, обусловленных частной теорией
относительности, и результаты наблюдений убеждают нас в
правильности этой теории.
Однако частная теория относительности вовсе не
является неограниченно применимой формой описания
природы. Рассмотрение гравитационного поля требует
ее модификации. При этом частная теория
относительности не полностью заменяется, а становится
стержнем новой теории. Обобщение частной теории
относительности заключается во введении пространственной
кривизны в М-геометрию, что приводит к отказу от
аксиомы параллельных в М-геометрии. Кривизна
зависит от силы гравитационного поля в исследуемой
мировой точке. На поверхности Земли гравитационное
поле очень слабо. Для солнечной системы поправки
минимальны, да и то в области, значительно
превосходящей размеры земной лаборатории. Локально
частная теория относительности справедлива без
изменений. Эффекты гравитационного поля становятся
ощутимыми лишь тогда, когда соответствующий этому
полю ньютоновский потенциал становится порядка с2,
т. е. когда ньютоновская энергия объекта в
гравитационном поле сравнима с энергией покоя (см. также
стр. 95). Это имеет место только в космических
масштабах и в очень тяжелых и плотных космических
объектах. Вопрос о том, каких качественных
корректив требует гравитационное поле в микроскопической
области, в физике элементарных частиц остается
открытым, и не потому, что нет никаких соображений
на этот счет, а потому, что этот вопрос технически
очень трудно решить. Здесь нам предстоит еще много
работы.

Приложение
133
Приложение
Сводка основ проективной геометрии плоскости
Мы приводим здесь лишь основные определения и
теоремы, причем ровно столько, сколько их требуется
для усвоения материала предлагаемой книги. При
этом внимание уделяется не исчерпывающему
методическому или аксиоматическому изложению
проективной геометрии, а возможности получить отчетливые
соотношения в случае, если под рукой нет пособия по
этой дисциплине. Необходимая литература указана
в конце книги.
Основой всех построений является двойное
отношение точек прямой и лучей пучка (фиг. 75). Для
данных четырех точек прямой двойное отношение имеет
вид
GГМА А А А\ М. М МАъ . A2.'h /rn\
При отсчете расстояний следует учитывать знаки: для
этого одно из направлений на прямой принимается
положительным, и направления отрезков
сравниваются с ним. Двойное отношение не зависит от того, какое
из двух возможных направлений считается
положительным. Существенно то, что это двойное отношение
сохраняется при проецировании. Чтобы показать это,
проведем из произвольной точки Q четыре луча через
четыре точки прямой. Теперь двойное отношение на
прямой можно представить как свойство углов между
лучами (фиг. 75):
ЙНАч А, А, А \— Л'Лз ¦ ^3 —
= y(A/M«g) • *-(АЛ2Л4<3) =g>(flbfl2,fl3,fl4). E4)
Следовательно, четыре луча, проходящие через точку
Q, имеют такое же двойное отношение, как и четыре
луча, проходящие через точку Q', если точки
пересечения соответственных лучей лежат на одной прямой:

134
приложение
Фиг. 75. Инвариантность двойного отношения.
Через четыре точки прямого точечного ряда проведены четыре луча
к центру Q, расположенному вне этой прямой. Покажем, что двойное
отношение четырех точек есть величина, зависящая только от относительного
направления лучей, а не от их длин.
Прежде всего двойное отношение отрезков иа прямой равно двойному
отношению площадей треугольников с общей вершиной Q. Все эти
треугольники имеют одну и ту же высоту, поэтому их площади пропорциональны
длинам оснований:
&<А А А л ч_ А^ . А*А\ _ & (A;M,Q) . QT (A A,A,0)
{Al' Аи Ли Аа)~ТХ * "аЯГ~~ «gr (AA,A,Q) ¦ <?¦ (А А.А4) ¦
С другой стороны, если мы зафиксируем углы с вершинами в точке Q
то площади треугольников, образованных двумя лучами, будут
пропорциональны длине каждого из двух отрезков лучей, например,
JT (Д А,А Q) = -24- . -?4- ?Г (ЛВ,Яз<2).
Но тогда получается, что двойное отношение четырех площадей можно
представить как двойное отношение четырех лучей, поскольку оио зависит
не от выбора на этих лучах точек, образующих вершины треугольника,
а от образуемых этими лучами углов:
ъ,а л л л\ ел ¦ ~ ~ ч & <АЯ,В^ <?""(Afl,fl<Q)
* М„ А,. А. *>-в ,»,. а, «,. °.>=^(Afl,B^ '¦ #-{АВ\В%
\В\ ?<— произвольные точки иа соответствующих лучах). Одновременно
мы показали, что двойное отношение точек, в которых прямая пересекает
четыре луча, не зависит от положения этой секущей прямой. Таким образом,
двойное отношение сохраняется при проецировании одной прямой на другую
(перспективное отображение двух прямых одна на другую). Дуальным
к этому является двойное отношение четырех лучей, которые проведены из
четырех точек прямой к некоторому центру Q, независимо от положения
этого центра. Если мы расположим лучи, исходящие из точек Q и Q'.
таким образом, чтобы точки пересечения соответствующих друг другу лучей
лежали на одной прямой, то и в этом случае двойное отношение
сохраняется (перспективное отображение двух пучков лучей).

Приложение
135
- Ы
Фиг. 76. Перспективное и проективное отображения.
Чертеж дает пример таких отображений. Пучок лучей с центром в точке Q
осуществляет перспективное соответствие точек прямых g Hg(. Точка
пересечения этих двух перспективных рядов точек является
самосоответственной точкой {F=F ). Точка Q называется центром перспективы этого
соответствия. Прямая gi в свою очередь осуществляет перспективное
соответствие пучков лучей, исходящих из точек Q и Q'. Она называется осью
перспективы этого соответствия. Прямая gz опять перспективна к gu но уже
не к g. Прямые g2 и g называются проективными друг к другу, двойные
отношения соответственных точек опять-таки не изменяются. Аналогично
Q" опять перспективна к Q', но уже ие к Q, а пучки с центрами в Q и Q"
теперь проективны друг к другу. Прямая, соединяющая центры Q' и Q" двух
перспективных пучков, является самосоответственным лучом {b' = bn).
двойное отношение обеих групп лучей равно двойному
отношению точек пересечения, лежащих на этой
прямой. Аналогично четыре точки на одной прямой g
имеют такое же двойное отношение, как и четыре
точки на другой прямой g\ если линии, соединяющие
соответственные точки, пересекаются в одной точке
(фиг. 76): оба двойных отношения равны двойному
отношению соответственных лучей, проходящих через
эту точку.
Два точечных ряда g и gf называются
перспективными друг к другу, если все линии, соединяющие
соответственные точки, проходят через одну точку,
называемую центром перспективы. Перспектива из этой
точки отображает обе прямые одна на другую. Два.

] 36 Приложение
Фиг. 77. Построение проективного отображения двух точечных
рядов по трем заданным парам точек.
Пусть на двух прямых g и g' выделены три пары соответственных точек
Требуется с помощью обоих точечных рядов определить два перспективных
друг к другу пучка лучей. Линия, соединяющая центры Q и Q' этих лучей,
должна быть самосоответственным лучом, поэтому мы выбираем Q и Q'na
прямой, проходящей через Л и А'. Теперь ось перспективы q должна
проходить через точки пересечения QB с Q'B' и QC с Q'C. Для некоторой
точки Р на прямой g найдем ее образ на прямой g', для чего из Q
спроецируем Р на Р", а затем из Q' — P" иа Р'.
пучка лучей Q и Q' называются перспективными друг
к другу, если точки пересечения соответственных
лучей лежат на одной прямой, называемой осью
перспективы. Дальнейшие последовательные перспективные
отображения хотя и дают отображение, сохраняющее
двойное отношение четырех элементов, но оно уже не
является перспективным отображением. Такие
отображения называются проективными. Проективные
отображения образуют группу, т. е. два проективных
отображения, выполненные последовательно, дают снова
проективное отображение. Проективная геометрия

Приложение
137
Фиг. 78. Построение проективного отображения двух пучков
лучей из трех заданных пар лучей.
Это построение дуально предыдущему. Мы хотим отобразить оба пучка на
две прямые, перспективные друг к другу. Эти прямые должны иметь
самосоответственную точку—точку их пересечения, так что выберем две прямые,
проходящие через точку пересечения лучей а и а'. Центр перспективы Q"
прямых g и g' должен быть точкой пересечения линий, соединяющих В
с В' и С с С.
имеет дело с конфигурациями, свойства которых при
проективных отображениях не изменяются.
Так как при проективном отображении двойное
отношение четырех элементов не изменяется, то
проективное отображение определяется полностью, если
заданы три соответственных друг другу пары точек или
три пары лучей. Образ четвертой точки находится с
помощью построения уже имеющегося двойного
отношения. В общем случае проективность является
следствием перспективных отображений (фиг. 77 и 78).
Два проективных точечных ряда расположены
перспективно друг к другу, если точка пересечения пря-

138
Приложение
Фиг. 79. Порождение двух проективных пучков лучей.
Пусть два пучка лучей с центрами в точках Q и Q' проективно соотв*Т«
ствуют друг другу и проективность осуществляется двумя взаимно
перспективными прямыми g и g' с центром перспективы Q" в соответствии с фиг. 78.
Точки пересечения взаимно соответственных лучей образуют коническое
сечение, проходящее через точки Q и Q'. В качестве иллюстрации изобразим
несколько лучей, проходящих через Q". точки пересечения которых с
прямыми g и g' соединим соответственно с точками Q и Q'. Точки пересечения
этих соответственных линий образуют гиперболу.
Заметим к тому же, что точка пересечения С двух прямых лежит на
коническом сечении. Точка Q" является пересечением двух линий, одиг из
которых соединяет точку Q с точкой В (пересечением конического сечения
с прямой g*), а вторая — точку Q' с точкой D (пересечением конического
сечения с прямой g).
мых является самосоответственной точкой. Два
проективных пучка лучей расположены перспективно друг
к другу, если прямая, соединяющая их центры,
является самосоответственным лучом.
Чтобы при проективном отображении каждая
точка прямой и каждый луч имели свои образы, нужно

Приложение
139
Фиг. 80. Теорема Паскаля.
БаЯВ шесть точек лежат на коническом сечении, то противоположные пары
tT4toCH образуемого ими- шестиугольника пересекаются на одной прямой.
Сначала выделим пять точек А, В, С, D и Е и образуем коническое сечение
с помощью проективных пучков с центрами в точках А и Е, Аналогично
фиг. 79 построим проективное отображение таким образом, чтобы Л было
перспективно к Q с осью a = CD, а ? — перспективно к Q с осью е — ВС.
К тому же Q должна быть точкой пересечения АВ и DE. Все другие точки
Конического сечения )Можно получить, проводя через Q произвольные прямые,
пересекающие а в точке R и е — в точке 5. Точка F пересечения взаимно
соответственных лучей AR и ES принадлежит коническому сечению. Точки Q,
R и S являются пересечениями противоположных сторон
шестиугольника ABCDEF: в точке Q пересекаются АВ и DE, в точке S — BC и ?F,
а в точке R—CD и FA. Но Q, /? и 5 по построению лежат на одной прямой.
Это и есть теорема Паскаля.
формально ввести несобственные (бесконечно
удаленные) точки. Эти точки следует понимать как точки
пересечения параллельных, так что несобственная точка
соответствует направлению прямой. Совокупность всех
несобственных точек обладает проективными
свойствами прямой. Она называется несобственной прямой.
Пучок параллельных прямых обладает свойствами
пучка лучей; его центром является несобственная
точка, соответствующая направлению параллельных.
На фиг. 76 G' является перспективным образом
несобственной точки на прямой g. Несобственные прямые и
несобственные точки по своим проективным свойствам
не отличаются от обычных (собственных) прямых и
точек плоскости.
Совокупность точек пересечения соответственных
лучей двух пучков называют порождением этих
пучков. Порождение двух перспективных пучков пред-

140
Приложение
Фиг. 81. Построение конического сечения по пяти точкам.
Из пяти заданных точек две (А и В) выбираются в качестве центров
проективных пучков лучей, третья (С) — как самосоответственная точка обоих
перспективных точечных рядов. Итак, проводим через точку С две
произвольные прямые а и Ь. Две остальные точки, D и Е, суть проекции из А
на а и из В на Ь. Точка пересечения Q прямых, соединяющих
соответствующие точки, является центром перспективы прямых а и Ь.
В предыдущей фигуре мы выбрали а и b так, чтобы они проходили через
две последние точки из пяти. Здесь же мы выбираем их так, чтобы они
проходили через две первые точки (центры проективных пучков). Каждому
лучу, проходящему через точку Q, соответствуют две точки пересечения Р
и Р^ с а и с. Соединяющие линии АРа и ВР^ пересекаются в точке Р
конического сечения. Условие того, что D и Е должны получаться таким же
образом, н дает нам положение точки Q. Соединяющие лннни QA и QB
являются касательными к коническому сечению в точках А и В, если А
н В, как и прежде, лежат на а и Ъ.
ставляет собой прямую — ось перспективы.
Порождение двух конгруэнтных равнонаправленных пучков,
согласно теореме о вписанных углах, образует
окружность; порождение двух конгруэнтных неравнонаправ-
ленных пучков образует равностороннюю гиперболу.
Порождение двух произвольных проективных пучков
является коническим сечением (фиг. 79).
Огибающая двух рядов точек, соответственных
соединяющим прямым, является порождением этих
точечных рядов. Можно показать, что порождение двух
проективных точечных рядов снова образует
коническое сечение, т. е. может быть представлено в виде
порождения двух проективных пучков лучей.
К порождению двух пучков принадлежат также их
центры. Поэтому коническое сечение можно построить
в том случае, если заданы пять точек: две из них
выбираются в качестве центров пучков, проективность

Приложение
141
Фиг. 82. Построение параболы по трем заданным точкам и
направлению оси.
Направление оси выделяет бесконечно удаленную точку параболы, licjjit
мы примем во внимание, что несобственная прямая является касательной
к параболе в своей несобственной точке, то увидим, что задача сводится
к построению конического сечения по четырем точкам и касательной в
первой точке. Это построение можно выполнить по предыдущей фигуре, если
там точки D и А совпадают, а касательная в точке А представляет собс.1
линию AQ. В случае параболы точки А и Q принадлежат несобственное
прямой, поэтому пучкн с центрами в А и Q являются параллельными
пучками. Прямая b параллельна направлению оси А в точке С. Линии АЕ
также параллельны направлению оси. Направление Q определим аналогичю
предыдущей фигуре. Отыскиваем точки Е и Е^. Точка Q является
несобственной точкой соединяющей прямой Е'Ей. Параллель к этой прямо»!
в точке В является касательной к параболе в этой точке.
которых можно определить, поскольку тремя осталы
ными точками конического сечения задаются три соот-
ветственных пары лучей (фиг. 80 и 81). Из этих
построений получается также доказательство очень
важной теоремы Паскаля: шесть точек Л, В, С, Z), Е и
F тогда и только тогда лежат на одном коническом
сечении, когда точки пересечения соединяющих линии
АВ с DEy ВС с EF и CD с FA лежат на одной прямой.
Если все точки конического сечения лежат в
конечной области, то оно является эллипсом (или кругом).
Если одна точка лежит в бесконечности, то коническое
сечение является параболой, и касательная к
параболе в несобственной точке является несобственной

142
Приложение
Фиг. 83. Построение гиперболы по трем заданным точкам и обоим
направлениям асимптот.
Направления асимптот дают две несобственные точки гиперболы, поэтому
мы должны выполнить построение по пяти точкам. Для построения
воспользуемся фиг. 81. Пусть пентры проективных лучей совпадают с
несобственными точками гиперболы. Следовательно, гипербола есть пересечение
двух проективных пучков параллелей, направление которых определяется
заданными направлениями асимптот.
прямой. Несобственная точка указывает направление
оси параболы. Если две точки конического сечения
лежат в бесконечности, то оно представляет собой
гиперболу. Обе несобственные точки указывают
направления асимптот.
Если задано направление оси параболы, то для ее
определения требуется только три собственные точки
(фиг. 82). Два остальных однозначно определяемых
элемента суть заданная несобственная точка и
касательная к ней, которая совпадает с несобственной
прямой. Если обе несобственные точки гиперболы, т. е.
направления асимптот, заданы, то для ее определения
необходимы также еще три точки в конечной области
(фиг. 83). Если асимптоты, т. е. несобственные точки
и касательные в них, полностью заданы, то
необходима еще только одна точка, чтобы можно было по*
строить остальные точки гиперболы (фиг. 84).
Закончим сводку изложением некоторых свойств
гармонического деления. Пара точек Л3 и Л4
гармонически разделяет пару точек А\ и Л2, если точки Аг и
Л4 лежат на прямых, соединяющих точки А\ и Лг, и

Фиг. 84. Построение гиперболы по одной точке и обеим
асимптотам.
Если заданы сами асимптоты, а не просто их направления, то тем самым
мы имеем не только несобственные точки, но и касательные, проходящие
через эти точки. Поэтому задача является частным случаем построения
конического сечення по трем точкам и касательным к двум из них.
Эта задача решается с помощью фиг. 81, если D совпадает с Л, а В — с В.
Точку Q будем считать пересечением касательных в Л и В. Пусть теперь
А н В уходят в бесконечность. Тогда точка Q является пересечением
асимптот гиперболы, т, е. ее центром. Проведем через С прямые а и Ь,
параллельные асимптотам. Они являются осями перспективы между пучком
с центром в Q и пучками параллелей к асимптотам. Каждому лучу р,
проходящему через Q, соответствуют точки пересечения PQ и Р^. Параллели
к асимптотам, проходящие через эти точки, пересекаются в точке Р,
принадлежащей гиперболе.
Дополнительно_докажем следующую теорему. Прямая QC пересекает
гиперболу в точке С, причем CQ — QC. Параллели к асимптотам, проходящие
через произвольную точку Р гиперболы, пересекают QC в двух точках Р\ н
Ра, которые гармонически делят отрезок СС. Назовем точки Р{ и Р2 точками
пеленга точки Р, так как параллели к асимптотам, проходящие через Р,
соответствуют сигналам, которые испускаются в точку Р наблюдателем,
находящимся на мировой линии QC, и соответственно принимаются в точке Р.
Двойное отношение равно 3) (Я,, Я2, С, С) = — 1. Чтобы убедиться в этом,
заметим сначала, что точка Рл пересечения PC и PQPu делит пополам как PC,
так и PQPfr Поэтому прямая РаР^ параллельна PC. Обозначим через U
несобственную точку этой прямой. Теперь можно спроецировать точки Pi,
?2> С* С на Pq; Pfr V> *V Ho Двойное отношение последних точек есть

Фиг. 85. Полный четырехугольник.
Через четыре вершины А, В, С и D проведем шесть соединяющих линий И
отмотим точки их пересечения Е\, Е2 н Е. Соединяющие линии этих точек
образуют точки пересечения Л F2 F% и Ft. Четыре луча, проходящие через
каждую из трех точек Е\, Е2 и Ез, имеют двойное отношение, равное — 1.
Покажем, что на прямой АВ двойное отношение есть 3> (А, В, Е? Л) = —1.
Для этого спроецируем А, В, Е2, F2 из Е\ на D, С, Е2, Л. а последние —из
Ei иа В, А, Е2 и Ег. По построению двойные отношения SD (А, В, Е2 Л)
и 3) {В, А, Е2, Fi) равны. С другой стороны, согласно правилу E3),
3> (А, В, Ег, Fa) • 3> {В, А, Е2, /=4=1. Этим и доказывается, что 3) (А, В,
Е2, F2) = -l.
Фиг. 86. Гиперболическая инволюция.
Выделим на прямой q две точки, Е и F, и для произвольной точки А\
найдем четвертую гармо шческую точку А2 в соответствии с фиг. 85. Для
этого выберем точку Q и прямую g\, проходящую через F. Затем проведем
соединяющие линии QE и g2~QF. Прямая g\ пересекает QE в некоторой
точке R. Спроецируем А{ из Q на Д., Д.—из Е на Aj и, наконец, А{— тлз R
на Л2- Геометрическая фигура FERA.— это знакомый нам по фиг. 85

Приложение
М5
Фиг. 87. К определению неподвижных точек инволюции.
Пусть инволюция задается двумя парами точек, ЛВ и CD, причем В = Л\
A = Bf, C~D' н ?>=С'. Изобразим произвольную окружность и выберем
на ней точку So, нз которой спроецируем четыре заданные точки на
окружность (Aq=Bq и так далее). К Sq построим два конгруэнтных пучка
в 51 = Ло и S2=Aq. Лучи из Sj будут соответствовать точкам Bq% Cq и.
Dq, а из $2 — точкам Bq, Cq и Dq« Определенные таким образом лучи S[ и
S2 вследствие конгруэнтности с обоими проективными пучками в So проек-
тивны друг к другу. Более того, ввиду существования самосоэтветственного
луча SB0 — S2BQ лучи Si и S2 даже перспективны друг к другу. Будем искать
ось q как соединение точек пересечения обоих прежних соответствующих
пар лучей. Соответственные друг другу лучи оказываются на ц. Точки
пересечения этой оси перспективы q с окружностью суть Ео н /v Онн, очевидно,
являются неподвижными точками окружности, так как лучи SiEo и S2Eo
(;-;а фигуре не изображены) в случае точки ?о соответствуют Друг
другу. Они выделяют одну и ту же точку ?0 на окружности.
Спроецировав E^ и Fq из So на прямую g, найдем с помощью Е и Е неподвижные
точки инволюции.
двойное отношение есть 2D(AU Аъ Л3, А4) = —1.
Гармоническое деление — это проективное обобщение
обычного деления пополам: если Л3 является
несобственной точкой прямой, то четвертая гармоническая
точка делит отрезок АХА2 пополам. Четвертая точка,
гармоническая к трем точкам, строится с помощью
полного четырехугольника (фиг. 85). Если на прямой
заданы две точки Е и F и если каждой точке Pi
поставлена в соответствие точка Р2, такая, что Р2} Р, Е

146
Приложение
и F образуют гармоническую четверку, то мы получим
проективное отображение прямой на саму себя
(фиг. 86), при котором образ образа точки является
исходной точкой. Такие отображения называются
инволюциями. В нашем случае инволюция имеет две
неподвижные точки (? и F). В общем случае
инволюция определяется с помощью круга Штейнера
{фиг, 87).

ЛИТЕРАТУРА
1. Blaschke W.t Projektive Geometrie, Wolfenbuttel und Hannover,
1947.
2. Bondi //., Relativity and Common Sense, London, 1962.
[Имеется перевод: Бонда Г. Относительность и здравый смысл. —«
JVU Мир, 1967.]
3. Born М., Die Relativitatstheorie Einsteins, Berlin, 1920.
[Имеется перевод: Борн М. Эйнштейновская теория
относительности.—М.: Мир, 1972.]
4. Champeney D. С, haak G. R., Khan A M , An Aether Drift
Experiment Based on the Mossbauer Effect, Physics Letters,
7, 241 A963).
5. Doehlemann K., Projektive Geometrie in synthesischer Behand-
lung, Berlin und Leipzig, 1924.
6. Einstein A., Cber spezielle und allgemeine Relativitatstheorie,-
21. Aufl., Berlin, Oxford und Braunschweig, 1969. [Имеется
перевод: Эйнштейн А. О специальной и общей теории
относительности. Собрание научных трудов, т. L—М.: Наука, 1966.]
7. Einstein A., Grundzuge der Relativitatstheorie, 5. Aufl., Berlin,
Oxford und Braunschweig, 1969. [Имеется перевод: Эйн*
штейн Л. Сущность теории относительности. Собрание
научных трудов, т. II.— М.: Наука, 1966.]
8. Huygens Ch., De motu corporum ex percussione, Opuscula
posthuma, Leiden, 1703, Ostswald's Klassiker Band 138,
Leipzig, 1903. [Имеется перевод: Гюйгенс X. О движении тел
под влиянием удара. — В кн.: Три мемуара по механике. М.з
изд-во АН СССР, 1951.]
9. Яглом И. М. Принцип относительности Галилея и
неевклидова геометрия. — М.: Наука, 1969.
10. Розенфелъд Б. А., Яглом И. М. Неевклидовы геометрии.
Энциклопедия элементарной математики, кн. V, с. 294.
И. Keller О.-Н., Analytische Geometrie und lineare Algebra,
Berlin, 1957.
12. Klein F., Vorlesungen uber nichteuklidische Geometrie, Berlin,
1928. [Имеется перевод: Клейн Ф. Неевклидова геометрия.—•
М. —Л.: ОНТИ, 1936.]
13. Ландау Л. Д., Румер Ю. Б. Что такое теория
относительности? — М.: Советская Россия, 1963.
14. Nevanlinna /?., Raum, Zeit und Relativitat, Basel und
Stuttgart 1964. [Имеется перевод: Неванлинна Р. Пространство!
время и относительность. — М.: Мир. 1966.]
15. Nevanlinna R.t Kustaanheimo P.t Grundlagen der Geometrie,
Basel und Stuttgart, 1975.

148
ЛИТЕРАТУРА
16. Papapeirou Д., Spezielle Relativitatstheorie, Berlin, 195o
17. Reichardi //., Kleine Enzyklopadie Mathematik, Leipzig, 1974.
18. Reichardi #., Vorlesungen uber Vektor- und Tensorrechnung,
Berlin, 1957.
19. Schilling /\, Projektive und nichteuklidische Geometrie, Leipzig
und Berlin, 1931.
20. Steiner /., Vorlesungen uber synthetische Geometrie, Bd. 1.
Leipzig, 1887 C. Aufl.), Bd. 2, Leipzig, 1898 C Aufl.)
21. Synge J. L.f Relativity: The special theory, 2. Aufl. Amsterdam,
1958.
22. Taylor E. /\, Wheeler J. Л., Space-time physics, San
Francisco, 1966. [Имеется перевод: Тейлор Э. Ф., Уилер Дж. А.
Физика пространства-времени. — М.: Мир, 1969.]
23. Treder H.-J., Relativitat und Kosmos, Berlin, Oxford und
Braunschweig, 1968.
24. Wissenschaft und Fortschritt, Jahrgang, 1965, Heft 11.

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Абсолютное будущее 59
— прошлое 59
Вектор 25
Временноподобный 59, 88
Время поясное 19
— собственное 90
Гармоническое деление 142
Гравитационное поле 94, 99,
132
Двойное отношение 133
Дефект массы 129
Диаграмма движения 14
Длина 70, 71, 90
Зависимость массы от
скорости 27
Замедление времени 92
Изотропия распространения
света 37
Импульс 25, 117
Конгруэнтность 63
Коническое сечение 140
Масса 25, 117
Материальная точка 14, 24
Мировая линия 14
Несобственная прямая 139
— точка 139
Одновременносуь абсолютная
92
— динамическая 28
— относительная 11, 41, 92,
102
Относительное настоящее 59
Парадокс близнецов (часов) 94
Перпендикуляр 73, 75
Перспективность 135
Правило смешивания 25, llf)
Преобразование Галилея Ю
— Лоренца 57, 111, 115
Принцип относительности 22,
31, 53, 61
Причинность 61
Проективность 136
Простраиственноподобнып 59
Рассеяние Комптона 121
Световой конус 40, 60
Светоподобный 59
Система отсчета инерциальпая
22, 24, 41, 53
линейная 17
покоящаяся 31
Скорость света 119
— относительная 32, 44, 78
— системы отсчета 41
Событие 14
Сокращение длин 103
Столкновение неупругое 25,
129
— упругое 121
Теорема импульсов 25
— о вписанных углах 82
— сложения скоростей 33, 45,
114
Угол 66, 67, 78
Ускорение 96
Энергия кинетическая 118
— покоя I19
— полная 119
— связи 129

ОГЛАВЛЕНИЕ
Предисловие редактора перевода .... 5
Предисловие 8
{. Введение 11
2. Диаграммы движения 14
3. Инерциальные системы . . . . * 24
4. Волновые явления - 34
5. Относительность одновременности 41
6. Относительность массы 48
7. Геометрия пространства-времени 61
8. Время в частной теории относительности 88
9. Длина в частной теории относительности 102
10. Эффект Доплера в частной теории отиосительиостй . . 108
11. Импульс, масса и энергия 117
32. Процессы столкновения 121
13. Заключительные замечания 130
Приложение 133
Литература . . 147
Предметный указатель 149

УВАЖАЕМЫЙ ЧИТАТЕЛЬ!
Ваши замечания о содержании
книги, ее оформлении, качестве перевода и
другие просим присылать по адресу:
129820, Москва, И-110, ГСП, 1-й
Рижский пер., д. 2г изд-во «Мир».

Д.-Э. Либшер
ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
С ЦИРКУЛЕМ
И ЛИНЕЙКОЙ
Научный речактор В. Самсонооа
Мл. научи, редакторы Г. Сорокина, Р. Зацепина
Художник А. Ясинский
Художественный редактор Л. Безрученкоз
Технический редактор И. Кренделева
Корректор С. Денисова
ИБ № 1935
Сдано в набор 18.05.79. Подписано к печати
10.12.79. Формат 84X1087-2- Бумага
типографская Ni 2. Гарнитура латинская. Печать высокая.
Объем 2,38 бум. л. Усл. печ. л. 7,98.Уч.-нзд. л.
6,96. Изд. № 2/0335. Тираж 123 000 экз. Зак. 224.
Цена 35 коп.
ИЗДАТЕЛЬСТВО «МИР»
Москва, 1-й Рижский пер., 2.
Ордена Трудового Красного Знамени
Ленинградская типография № 2 имени Евгении
Соколовой «Союзполиграфпрома» при
Государственном комитете СССР по делам
издательств, полиграфии и книжной торговли.
198052, Ленинград, Л-52, Измайловский
проспект, 29

35 коп