Концепции современной математики - Стюарт Ян

Автор: Стюарт Ян

Теги: математика

Год: 1980

Похожие

Концепции современной математики

Современная математика и ее творцы

Случайный Бог или божественная случайность? Математика неопределённости

Мысли о современной математике и ее изучении

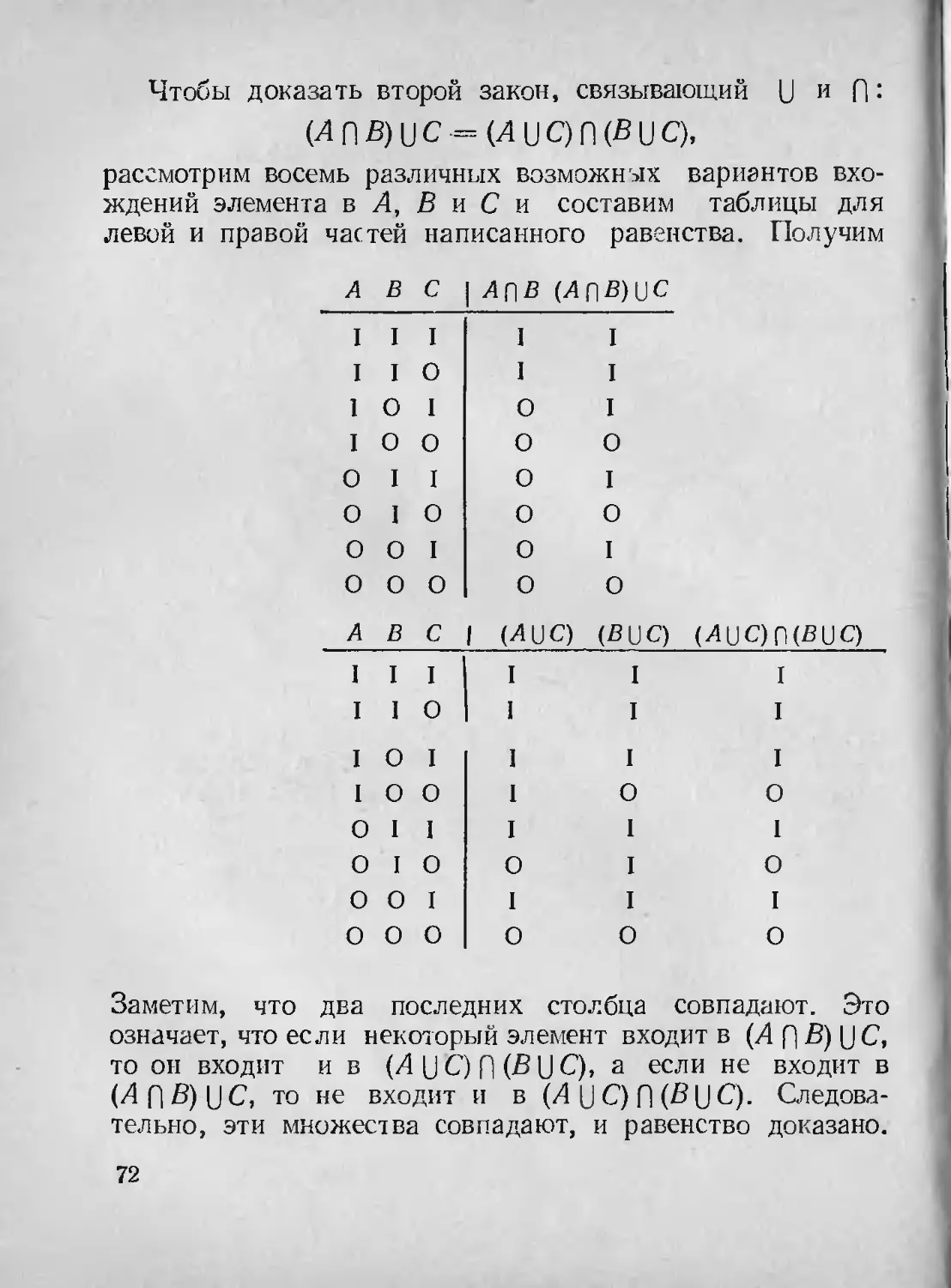
Текст

Ян Стюар-
КОНЦЕПЦИИ
СОВРЕМЕННОЙ
МАТЕМАТИКИ
Перевод с английского
Минск, «Вышэйшая школа», 1980
ББК 22.1 Г
С 88
УДК 51(023)
Ian Stewart
Concepts of Modern Mathematics
Penguin Books
Перевод с английского H. И. Плужниковой (предисловие,
гл. 1—5, 9—14, 16—20, примечания, указатель) и Г. М. Цу-
керман (гл. 6—8, 15); предисловие к русскому изданию
Э. И, Зверовича, д-ра физ.-мат. наук, проф.
Я
с
н
о
н
и.
п
и
Г1
К]
Ч(
и:
ее
ж
м
(<
гл
ПС
141
Of
м<
20201—009
С М 304(05)—80 28—79
1702010000
Copyright (g) Ian Stewart, 1975
(^Предисловие к русскому изданию,
перевод на русский язык, издательство
«Вышэйшая школа», 1980
। е
с к
ПС
пс
ль
14
с я
су
Предисловие к русскому изданию
Предлагаемая вниманию советских читателей книга
Яна Стюарта при сравнительно небольшом объеме отличается
очень широким охватом материала. В ней автор на конкрет-
ных математических объектах и в популярной форме излагает
основные понятия, а также некоторые идеи и методы современ-
ной математики. Книга состоит из 20 небольших глав, первая
из которых имеет характер введения и посвящена общим во-
просам методологии математики (абстрактность и общность,
интуиция и формализм, цели математики, ее полезность и дру-
гие). В остальных 19 главах книги рассматриваются более кон-
кретные вопросы. Во второй главе автор обсуждает геометри-
ческие преобразования (в основном, движения) и показывает
их роль при доказательстве геометрических теорем. В следу-
ющей главе рассматривается арифметика вычетов и некоторые
ее теоретико-числовые приложения. Глава 4 посвящена изло-
жению теоретико-множественного языка и элементов алгебры
множеств. В главе 5 обсуждается общее понятие отображения
(функции) и связанная с ним терминология. Две следующие
главы посвящены элементам общей алгебры. Здесь вводятся
понятия кольца и поля, приводятся примеры и даются интерес-
ные приложения. Понятие группы и элементы теории групп
обсуждаются на примере групп симметрий, демонстрируются
методы теории групп, позволяющие классифицировать группы
с точки зрения изоморфизма. В главе 8 на геометрическом ма-
гериале обсуждается аксиоматический метод в математике, рас-
сматриваются понятия непротиворечивости, независимости и
полноты систем аксиом. В следующей главе рассматривается
понятие мощности конечных и бесконечных множеств, устанав-
ливается существование трансцендентных чисел. Главы 10—
14 посвящены популярному изложению топологии. Обсуждает-
ся топологическая эквивалентность, топологические теоремы
существования, теорема Эйлера о многогранниках и ее прило-
3
Be
книга
Это ;
с гуде
ся сс
нрепс
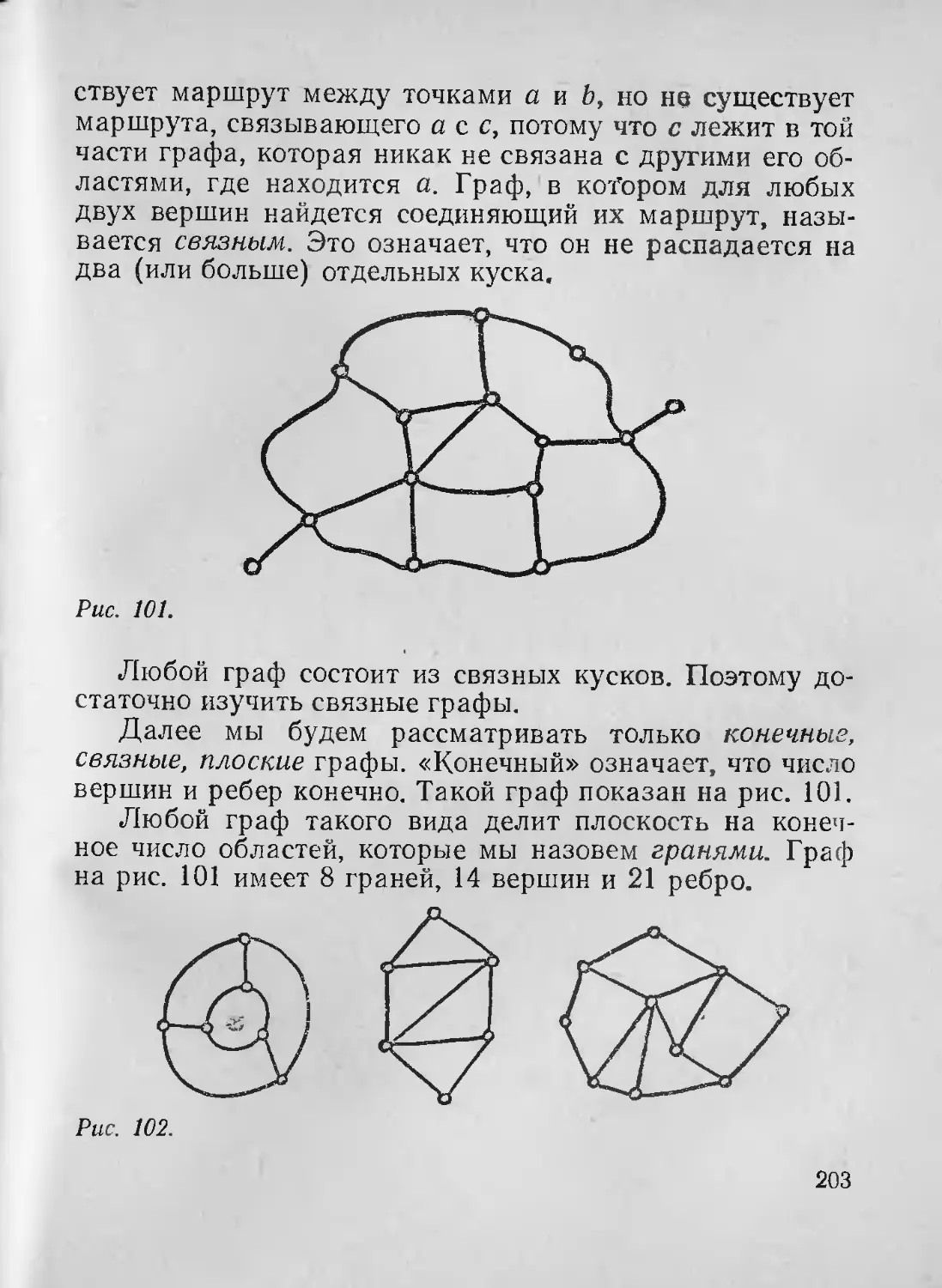
жения к теории графов и к проблеме четырех красок. Дале,
рассматриваются топологические инварианты поверхностей
эйлерова характеристика и свойство ориентируемости, на этс|
основе дается топологическая классификация конечных поверх
костей. Затем автор переходит к элементам алгебраическо!
топологии. Вводится понятие гомотопных путей, гомотопические
классов, фундаментальной группы топологического простран
ства, показывается ее топологическая инвариантность, рассма-
триваются примеры на вычисление фундаментальных групп
Рассмотрены также формула Эйлера для пространств высшие
размерностей, гомотопические группы высших размерностей
Эта часть книги окажется наиболее интересной для советской;
читателя, так как наша научно-популярная литература по то
пологий крайне бедна, особенно в той части, которая касаетс!
алгебраической топологии. Остальные главы книги посвящень
соответственно элементам линейной алгебры, вещественной,
анализа, теории вероятностей, вычислительным машинам i
программированию, некоторым приложениям современной ма
тематики (линейное программирование, катастрофы) и осно
ваниям математики. Каждая из перечисленных дисциплин са
ма по себе достаточно обширна, однако автор касается не
столько наиболее ярких, сколько некоторых популярных во-
просов этих наук. Очевидно, по своим научным интересам
автор стоит ближе к алгебре и топологии, поэтому последние
пять глав книги читаются с меньшим интересом, чем преды-
дущие.
Не все в книге представляется бесспорным. Например, в пер-
вой главе автор утверждает, что математическая теория про-
ходит путь, начиная от задачи, которую «математик решает ра<
ди удовольствия», и до приложений ее в практике, в производ-
стве. Здесь автор склонен идеализировать ситуацию
пренебрегая тем фактом, что задача, которую «математик ре
шает ради удовольствия», сама в конечном счете появилась ич
практики (возможно, в результате относительно самостоятель-
ного развития математики).
Книга написана простым, ясным языком, хорошо иллюстри-
рована и не лишена юмора. Удачен подбор примеров, на кото
рых демонстрируются математические понятия и идеи. Все это
делает чтение книги не только полезным, но и увлека-
тельным.
Докт
наук.
4
Ввиду разнообразия материала и доступности изложения
ьл,-е книга, несомненно, будет с интересом встречена читателями.
I —
ТС .1
фХ-
коп
ких
Это учащиеся и преподаватели средних учебных заведений,
студенты и преподаватели вузов и вообще все, кто интересует-
ся современными концепциями математики и вопросами ее
। [реподавания.
ISH-
ма-
inni
НИХ
гей.
Доктор физико-математических
наук, профессор
Э. И. Зверович
ог)
то
тс я
ны
ОГС|
1 I
ма •
I о-
са-
н
во-
:ам
ив
цы-
ер-
ро-
ра-
V
!1Ю,
ре
и 1
ль-
ри-
то
эт«
ка-
Предисловие
Е
ПОСТ
Мат
пред
она
и ни
Когда-то давным-давно родители могли помогать своим детя1
делать уроки. «Модернизация» школьного курса математик!
сильно уменьшила эту возможность: родителям, которые во
же не захотят отказаться от таких намерений, придется сами»
осваивать массу нового материала, который будет казаться им
как правило, странным и ненужным. Один мой друг — учц
тель — рассказывал, что его ученики шумно требовали, чтоб!
их учили «настоящей математике,— той, которой учили их ма1
и пап». Этот интересный факт, кстати, проливает дополнитель
ный свет на то, как у детей формируются мнения. Многие учи
теля тоже считают, что научиться математике нового стил
ком,
зани
ческ
ренг
1
очень трудно.
И это весьма печально. Новые программы по математик
вводились с целью содействовать лучшему пониманию этоп
предмета взамен бездумного манипулирования символами
Ведь настоящий математик работает не с числами, а с поня
тиями.
Данная книга — попытка рассеять предубеждение. Пр|
встрече с неизведанным всегда возникают опасения, и лучший
способ их побороть состоит в том, чтобы посмотреть, как эт
новое работает, что оно умеет делать и почему ему это удается
Когда новое становится привычным, страхи рассеиваются са
ми собой. Разумеется, эта книга не есть «справочник по соврс
менной математике». Автор попытался описать цели, методы
проблемы и применения современной математики, раскрыт
повседневную деятельность работающего математика.
Я предпочел бы не требовать от читателя никаких предвл
рительных знаний из области математики, но здесь мне при
шлось пойти на компромисс. Читателю понадобится кос-каке»
знакомство с алгеброй, геометрией и тригонометрией, а такж
некоторое представление о графиках. Я старался избегать диф
ференциального и интегрального исчисления; хотя оно кое-гд
и упоминается, это несущественно для изложения.
6
етяь
Ithki
5 ВС
fiMIIA
Ч им
учи
тобь
ма»
Важнее любых предварительных знаний я считаю готов-
ность воспринимать новые идеи и искреннее желание понять.
Математика не относится к числу легких предметов — стоящие
предметы не бывают легкими, зато как щедро вознаграждает
она усвоившего! Математика стала частью нашей культуры,
и никто не вправе считать себя истинно образованным челове-
ком, не имея представления, что такое математика и чем она
снимается. Более того, математика — наука глубоко челове-
ческая, в ней есть свои триумфы и падения, крушения и оза-
рения.
Итак, приступим!
Автор
учи
тпл
тик,
?ТО: <
!ам>1
'Оня
Пр
1ШИ1
1 эт<
*тся
са
>вр<
рдь
ЭБ Г
га
П[ ч
а ко
|КЖ(
1иф
гд
Благодарности
Цитата в гл. 2 из книги А. Милна «Винни-Пух» и эпиграф
к гл. 9 из книги того же автора «Дом на Пуховой опушке»
(A. A. Milne, Winnie-the-Pooh; The House at Pooh Corner) при-
ведены с разрешения издательства Methuen and Co. Ltd н г-на
I\. P. Милна, которому принадлежит авторское право на эти
произведения. Эпиграф к гл. 8 из книги Ст. Темерсона «Фак-
тор Т» (Stefan Themerson, Factor Т) печатается с разрешения
издательства Gaberbocchus Press Ltd. Классификация поверх-
ностей в гл. 12 приводится в сокращенном виде по книге
Э. К. Зимана «Введение в топологию» (Е. С. Zeeman, Introduc-
tion to Topology), которая готовится к изданию, и включена с
разрешения проф. Зимана, однако любые неточности, которые
могли возникнуть в результате сокращения, лежат на совести
автора. Всем упомянутым лицам и издательствам автор выра-
жает свою искреннюю благодарность.
Глаза 1 МАТЕМАТИКА В ЦЕЛОМ
Трудно дать представление о
том, сколь обширна современ-
ная математика.
А. Кэли, из речи 1883 г.
Внезапный переход в наших школах к «современной
математике» мог создать впечатление, что математика
утратила контроль над собой, отбросила все свои тради-
ционные идеи и понятия и вместо них вывела на сцену
странные и нелепые создания, которые вряд ли кому-ни-
будь и когда-нибудь понадобятся.
Это не совсем точная картина. Большая часть «совре-
менной математики», которой сейчас учат в школах,
существует, по самым скромным оценкам, уже более
века. Дело в том, что в математике как науке новые идеи
естественным путем развивались из старых и впитыва-
лись постепенно с течением времени. В школьные же кур-
сы целый ряд новых понятий был введен сразу и, как
правило, без всякого обсуждения их связи с традицион-
ными понятиями.
Абстрактность и общность
Одна из наиболее заметных особенностей современ-
ной математики — это тенденция ко все более высокой
степени абстракции. Каждое сколько-нибудь важное по-
нятие охватывает не один, а много различных объектов,
которые, однако, имеют какое-то общее свойство. Абст-
рактная теория выводит следствия из этого свойства,
которые затем можно применить к любому из рассматри-
ваемых объектов.
Так, например, понятие «группы» относится и к жест-
ким движениям в пространстве, и к симметриям геомет-
9
рических фигур, и к аддитивной структуре на множестве
целых чисел, и к деформациям кривых в топологическом
пространстве. Общим свойством во всех перечисленных
случаях является возможность составить такую комбина-
цию двух данных объектов, которая дает в результате
объект той же природы. Два жестких движения, выпол-
ненные последовательно одно за другим, снова дают
жесткое движение; сумма двух целых чисел — целое
число; две кривые, смыкающиеся концами, образуют
новую кривую.
Абстракция и обобщение идут рука об руку. Главным
достоинством обобщения является экономия работы. Не-
лепо доказывать одну и ту же теорему четыре раза в
четырех разных ситуациях, когда ее можно доказать
один раз в общей постановке, не зависящей от конкрет-
ного типа объектов.
Вторая характерная черта современной математи-
ки — широкое использование в ней языка теории мно-
жеств. В сущности это всего лишь здравый смысл,
облеченный в математические символы. Математику, в
особенности когда она становится более общей, интере-
суют уже не столько конкретные объекты, сколько их
совокупности. То, что 5=4+1, не так уж важно. А вот
то, что всякое простое число вида 4п+1 является суммой
двух квадратов, — гораздо более содержательно. Это
последнее утверждение касается всей совокупности про-
стых чисел, а не какого-то отдельного простого числа.
Множество — это и есть совокупность. Другое слово
используется скорее из психологических соображений,
чтобы избежать ненужных ассоциаций *. Множества
можно различными способами комбинировать и получать
другие множества, подобно тому как разные операции
над числами (сложение, вычитание, умножение...) приво-
дят к другим числам. Общую теорию арифметических
операций называют алгеброй; по аналогии можно разра-
ботать алгебру множеств.
10
Множества имеют перед числами определенные пре-
имущества, особенно с точки зрения обучения. Они могут
оказаться более конкретными. Скажем, нельзя показать
ребенку какое-то число («Я держу в руках число 3»),
зато можно показать ему какое-то число определенных
предметов: три конфетки, три шарика, т. е. по существу
множество конфет, множество шариков. И хотя, как пра-
вило, рассматриваемые в математике множества не кон-
кретны — обычно это множества чисел или функций,—
основные операции теории множеств можно продемонст-
рировать на конкретном материале.
Теория множеств играет в математике более сущест-
венную роль, чем арифметика, и хотя основные принци-
пы — не всегда лучшая отправная точка, для понимания
современной математики без теории множеств не обой-
тись. По этой причине в гл. 4 и 5 обсуждаются основные
понятия теории множеств, а в последующих главах сво-
бодно используется язык теории множеств, хотя я старал-
ся держаться на самом элементарном уровне. Но было бы
неправильно переоценивать теорию множеств саму по
себе: это всего-навсего удобный язык, и если вы в совер-
шенстве владеете им и больше ничего из математики не
знаете, едва ли от вас будет много проку. Наоборот, если
вы знаете «много математики» и совсем незнакомы с
теорией множеств, вы, возможно, достигнете крупных
успехов. Но если вы знаете что-то и из теории множеств,
вы будете значительно лучше понимать язык мате-
матики.
Интуиция и формализм
Тенденция ко все большей общности сопровождается
ростом требований, предъявляемых к логической строго-
сти. Евклида теперь критикуют за отсутствие в его систе-
ме аксиомы о том, что всякая прямая, проходящая через
точку внутри треугольника, должна где-то пересечь тре-
11
угольник. Эйлерово определение функции как «кривой,
свободно проведенной от руки» портит математикам всю
игру и страдает к тому же неопределенностью (что такое
«кривая»?). Однако в заботе о логической безупречности
легко хватить через край, заменив словесные рассужде-
ния потоком логических символов и слепым применением
стандартных приемов. В этом направлении можно далеко
зайти (а тут и не слишком далеко — уже весьма далеко)
и вместо того, чтобы углубить понимание, начисто его
утратить.
В то же время требование большей строгости — не
пустая прихоть. Чем сложнее и обширнее становится
предмет, тем важнее выработать критический подход к
нему. Социолог, пытающийся осмыслить массив стати-
стических данных, вынужден отказаться от тех из них,
которые получены в результате недобросовестных экспе-
риментов или сомнительных выводов. То же происходит
и в математике. Слишком часто «очевидное» оказыва-
лось неверным. Существуют геометрические фигуры, не
имеющие площади. Согласно Банаху и Тарскому2, мож-
но разрезать круг на пять частей и сложить из них два
круга того же размера, что исходный. С точки зрения по-
нятия площади это невозможно, но дело в том, что эти
части не имеют площади.
Логическая строгость оказывает сдерживающее воз-
действие, неоценимое в опасных обстоятельствах, а так-
же тогда, когда речь идет о тонкостях. Существуют тео-
ремы, в справедливости которых убеждены большинство
математиков, и тем не менее, пока их кто-нибудь не дока-
жет, они останутся необоснованными предположения-
ми и могут применяться только в роли предположений.
Особое внимание к строгости необходимо при доказа-
тельстве невозможности чего-либо. То, что невозможно
сделать одним способом, иногда легко выполнить другим,
поэтому на всех этапах такого рода доказательств тре-
буется большая аккуратность. Существуют доказатель-
12
ства неразрешимости в радикалах уравнений пятой сте-
пени и доказательства невозможности трисекции угла
при помощи циркуля и линейки. Это важные теоремы,
так как они перекрывают пути бесполезных изысканий.
Но если нам нужна уверенность в том, что подобные
поиски действительно бесплодны, наша логика должна
быть безупречной.
Доказательства невозможности весьма характерны
для математики. Ведь это, пожалуй, единственный пред-
мет, который полностью отдает себе отчет в своих огра-
ничениях. Временами это становится наваждением, и
люди тратят больше сил на то, чтобы доказать невозмож-
ность какого-то построения, чем на то, чтобы найти спо-
соб его выполнить! Если бы самопознание было добро-
детелью, математики могли бы образовать племя святых.
Однако логика — это еще не все. Никакая формула
сама по себе никогда еще ничего не подсказала. Логика
может применяться для решения задач, но она не под-
скажет нам, какие задачи стоит решать. Никому еще не
удалось формализовать значение. Чтобы понять, что
имеет значение, а что нет, требуется опыт, а еще то труд-
но определимое качество интеллекта, которое называют
интуицией.
Я не могу объяснить, что я сам понимаю под интуи-
цией. Просто это то, чем живет настоящий математик
(или физик, инженер, поэт). Интуиция позволяет ему
«ощущать» свой предмет, видеть, что теорема верна, еще
не зная ее формального доказательства, а потом приду-
мывать это доказательство.
Практически каждый человек в какой-то мере обла-
дает математической интуицией. Ею наделен ребенок,
складывающий картинку из кубиков, ею обладает вся-
кий, кому удалось уложить вещи в багажник автомобиля,
перед тем как всей семьей отправиться на нем в отпуск.
Главной целью подготовки математиков следовало бы
сделать оттачивание их интуиции до такой степени, что-
13
бы она превратилась в управляемое орудие исследо-
вания.
Много бумаги истрачено на споры о преимуществе
строгости перед интуицией и, наоборот, интуиции перед
строгостью. Обе эти крайности бьют мимо цели: вся сила
математики — в разумном сочетании интуиции и строго-
сти. Контролируемый дух и вдохновенная логика! Все мы
знаем людей блестящих способностей, идеи которых ни-
когда не воплощались в конкретные результаты, и дру-
гих — организованных и аккуратных, которые так и не
создали ничего стоящего, потому что были слишком за-
няты тем, чтобы все было аккуратно и организованно.
Надо избегать обеих крайностей,
О картинках
При изучении математики психологический аспект
часто важнее логического. Мне приходилось присутство-
вать на лекциях, в которых все было потрясающе логич-
но, но слушатели ничего не понимали. Интуитивные со-
ображения должны выступать первыми и лишь потом
подкрепляться формальным доказательством. Интуитив-
ные рассуждения позволяют нам понять, почему должна
быть верной та или иная теорема, а затем уже при помо-
щи прочных логических обоснований можно убедиться,
что она действительно справедлива.
В последующих главах я буду стараться подчеркивать
интуитивную сторону математики. Вместо строгих дока-
зательств я попытаюсь дать читателю представление о
лежащих в их основе идеях. В хороших учебниках долж-
но было бы быть и то, и другое, но, к сожалению, лишь
немногие из них отвечают этому идеалу.
Некоторые математики, может быть 10 из 100, мыслят
формулами. Такова их интуиция. Но остальные мыслят
образами: их интуиция геометрическая. Картинки несут
гораздо больше информации, чем слова. В течение мно-
14
гих лет школьников отучали пользоваться картинками,
потому что «они не строгие». Это печальное недоразуме-
ние. Да, они не строгие, но они помогают думать, а тако-
го рода помощью никогда не следует пренебрегать.
Зачем!
Имеется множество причин для занятий математикой,
и едва ли кто-нибудь из читателей станет требовать, что-
бы ему тут же немедленно доказали правомерность су-
ществования математики, а не то он дальше читать не
будет. Математика красива, стимулирует интеллектуаль-
но и даже полезна.
Большинство вопросов, которые я собираюсь рассмот-
реть, взяты из чистой математики. Чистая математика
ставит перед собой в качестве цели не практические при-
менения, а интеллектуальное удовлетворение. Этим она
напоминает изящные искусства: мало найдется людей,
которые требовали бы практической пользы, например,
от живописи. (Однако в отличие от искусства в матема-
тике существуют повсеместно принятые критерии.) Но
вот что замечательно: почти вопреки самой себе чистая
математика полезна! Позвольте привести пример.
В начале 18 в. математики затратили много усилий на
изучение волнового уравнения — уравнения в частных
производных, описывающего колебания струны или рас-
пространение волн в жидкости. Несмотря на физическое
происхождение, это была чисто математическая зада-
ча — о практическом применении волн никто не думал.
В 1864 г. Максвелл предложил систему уравнений для
описания электрических явлений. Из этих уравнений пу-
тем несложных преобразований получилось уже извест-
ное волновое уравнение. На основе этого факта Максвелл
предсказал существование электромагнитных волн.
В 1888 г. Герц экспериментально подтвердил предсказа-
ние Максвелла, осуществив в своей лаборатории прием
45
радиоволн. И, наконец, в 1896 г. произошла первая
радиопередача.
Ход событий весьма типичен: именно таким путем,
как правило, становится полезной чистая математика.
Все начинается с задачи, которую математик решает
ради удовольствия. Затем приходит теоретик, который
применяет математический результат, но не делает ника-
ких попыток проверить свою теорию. Его сменяет уче-
ный-экспериментатор, который подтверждает теорию, но
не предлагает ей никакого употребления. И наконец,
появляется человек практики, который на этой базе вы-
дает товар жаждущему миру.
Та же последовательность событий наблюдалась при
открытии и разработке атомной энергии, теории матриц
(которая нашла применение в технике и экономике), тео-
рии интегральных уравнений.
Обратите внимание на интервалы времени: от волново-
го уравнения до радиопередатчика— 150 лет; от диффе-
ренциальной геометрии до атомной бомбы — 100 лет; от
первого появления матриц (в работах Кэли) до их приме-
нения экономистами — 100 лет. Интегральным уравнени-
ям понадобилось 30 лет, чтобы пройти путь от момента,
когда Курант и Гильберт превратили их в полезный ма-
тематический инструмент, до момента, когда они приго-
дились в квантовой теории, а это произошло за много лет
до того, как сама квантовая теория нашла практические
применения. В те времена никто и подумать не мог, что
математика, которой они занимаются, понадобится сто-
летие или более спустя!
Означает ли это, что надо приветствовать занятия
любыми математическими задачами, даже теми, которые
сейчас кажутся не представляющими ни малейшего инте-
реса, ибо есть небольшой шанс, что именно они понадо-
бятся физикам к 2075 г.?
И волновое уравнение, и дифференциальная геомет-
рия, и матрицы, и интегральные уравнения признавались
16
важными в математике уже в то время, когда они только
появились. Математика устроена так, что ее части тесно
связаны между собой, и развитие одной части затрагива-
ет другие. Это позволяет говорить о некоем «теле» мате-
матики, имеющем свои главные и второстепенные
«органы». Важным признается то, что затрагивает глав-
ную часть «организма». Даже совсем новые методы до-
казывают свою важность на проблемах «главного на-
правления». Почти вся математика, нашедшая практиче-
ские применения, относится именно к главной части
организма.
Получается, что торжествует математическая интуи-
ция? Или просто то, что не признано важным, никогда не
развивают до такого уровня, когда бы оно могло стать
полезным? Не знаю. Однако бесспорно, что те математи-
ческие теории, которые по единодушному мнению мате-
матиков считаются тривиальными или несущественными,
никогда не окажутся полезными. Теория обобщенных
левых псевдоскопищ не держит в своих руках ключей от
будущего.
И все же некоторые очень изящные и важные матема-
тические результаты не находят практического примене-
ния просто потому, что реальный мир устроен иначе.
Один физик-теоретик заработал себе прочный авторитет
тем, что, исходя из весьма общих математических сооб-
ражений, вывел формулу для радиуса Вселенной. Это
была очень впечатляющая формула, щедро начиненная
константами е, с, h, несколько раз в ней встречалось чис-
ло л и много квадратных корней. Поскольку он был
убежденным теоретиком, его не беспокоили численные
значения. Прошло несколько лет, пока нашелся человек,
которому захотелось узнать, чему равен радиус Все-
ленной.
Оказалось, 10 сантиметрам.
17
Глава 2
ДВИЖЕНИЕ БЕЗ ПЕРЕМЕЩЕНИЯ
Геометр — разновидность гусе-
ницы.
Старый словарь.
Геометрия — одно из самых мощных средств челове-
ческого мышления. Мы воспринимаем окружающий мир
в основном при помощи зрения, а геометрическая интуи-
ция тесно связана со зрением. В геометрии часто в бук-
вальном смысле можно увидеть то, что происходит. На-
пример, теорема Пифагора становится почти очевидной,
если посмотреть на рис. 1.
Более того, вызываемое этой картинкой интуитивное
ощущение справедливости теоремы нетрудно превратить
в логически строгое доказательство, и благодаря привле-
чению на помощь интуиции это доказательство очень
убедительно.
Геометрия в стиле Евклида (а до недавнего времени
только с ней и сталкивалось большинство людей) не одо-
бряет обращения к картинкам и пользуется вместо этого
высокопарными рассуждениями по существу алгебраиче-
ского характера, основанными на понятии конгруэнтно-
сти треугольников. В итоге все геометрические идеи
сводятся к свойствам треугольников.
Понятие конгруэнтности достаточно наглядно: два
треугольника конгруэнтны, если они одинаковой формы и
одного размера. Однако дети часто находят трудными те
рассуждения с конгруэнтными треугольниками, которые
применяются для доказательства теорем. Первая «труд-
ная» теорема евклидовой геометрии стала камнем пре-
ткновения как раз из-за сложных манипуляций конгру-
энтными треугольниками в ее доказательстве. (Были и
другие проблемы; в 50-е годы 18 в. от школьников требо-
валось не только воспроизводить доказательства самого
18
Евклида, но и пользоваться его обозначениями на
чертежах.)
Оказывается, у Евклида были веские причины избе-
гать картинок. Его переполняло желание вывести всю
геометрию чисто логически из нескольких простых основ-
ных принципов. Правда, позднее в его логике обнаружи-
Рис. 1.
лись пробелы, но их удалось заполнить. Однако боль-
шинство детей не способны оценить эту жажду строгих
доказательств. При занятиях математикой на любом
уровне за «логически строгое» принимается то, что
«убеждает», хотя, конечно, требуется немало работы,
чтобы «убедить» профессионального логика! Значитель-
ная часть обучения • математике состоит в том, чтобы
выявить дефекты вполне убедительных на вид рассужде-
ний и показать ученику, что они не должны его убеждать.
Если мы хотим научить детей геометрии, нам придется
либо снизойти до таких доказательств, которые они най-
дут приемлемыми, либо быть готовыми потратить много
времени на усовершенствование их критического мышле-
ния, причем в последнем случае больше пользы, возмож-
но, принесет не курс геометрии, а курс логики!
Однако объяснять ребенку доказательство, которое
лишь выглядит убедительным, а потом оказывается в
корне неверным, — очень вредно. Это только выработает
замешательство и недоверие. Нужны такие способы
убеждения, которые позднее удастся превратить в стро-
гие доказательства. Примером того, что я имею в виду,
19
служит приведенный выше рисунок. Его можно превра-
тить в строгое доказательство теоремы Пифагора, после
того как будет разработано понятие площади. Иными
словами, математика должна отражать интуицию.
Евклид (кто бы он ни был), несомненно, обладал
сильно развитой геометрической интуицией, иначе его
книга никогда не была бы написана. Но он не владел еще
средствами, пригодными для прямого выражения его
интуитивных идей. И тогда с гениальной изобретатель-
ностью он пустил в ход атрибуты конгруэнтности и т. д.
Теперь такие средства есть. Появившись в математике
19-го в., они проникли сейчас в новые школьные програм-
мы под названием «геометрия преобразований» или «гео-
метрия движений».
Опрокидывая Евклида
Теорема, которую мы упомянули выше как «первую
трудную теорему у Евклида», гласит: в равнобедренном
треугольнике углы при основании равны. Я хочу привести
сначала доказательство самого Евклида. В отличие от
обычного школьного доказательства в нем не применя-
ются никакие построения, связанные с серединой осно-
вания, ибо в том месте, где Евклид ее доказывает, еще
не установлено, что отрезки имеют середины, и поэтому
понятием середины пользоваться нельзя.
На рис. 2 мы продолжили АВ до некоторой точки D,
а АС— до точки Е, причем так, что AD = AE. Затем
провели отрезки DC и ЕВ. Дальше доказательство Евк-
лида строится так.
1. Треугольники ACD и АВЕ конгруэнтны (по двум
сторонам и углу между ними).
2. Следовательно, 2.ABE=ZACD.
3. Значит, DC=EB.
4. Поэтому конгруэнтны треугольники DBC и ЕСВ
(по трем сторонам).
5. Отсюда Z.DCB=Z_EBC.
20
6. Из 5 и 2 вычитанием получаем, что Z.ABC= г^АСВ,
что и требовалось доказать.
Отдельные шаги доказательства, возможно, станут
яснее, если составить из них не- л
что вроде комикса, как на рис. 3. Л
Сразу бросается в глаза (осо- / \
бенно на комиксе), что все здесь / \
встречается парами. Сторона АВ J. \
слева, АС справа, и они равны. J \
Треугольник ACD слева, АВЕ / \
справа, и они конгруэнтны, и т. д. р/ \
Наконец, Z.ABC слева, Z.ACB / \
справа: они равны, и теорема до- / \
казана. / s' X. \
Возникает твердое ощущение, rJs' 'Д
что если найти способ превращать
правое в левое, а левое в правое, 2-
то все станет очевидным. Дока-
зательство прямо-таки требует этого. Но как это осу-
ществить?
Когда вопрос поставлен так, ответ простой: перевер-
нем треугольник. Сделайте из картона равнобедренный
треугольник, обведите его контуры, затем переверните и
приложите к рисунку. Вы увидите, что он точно занял
свое прежнее место. Можно и не экспериментировать, а
рассуждать следующим образом: перевернем треуголь-
ник так, чтобы точка А осталась на месте, а сторона АС
легла на прежнюю сторону АВ\ тогда, поскольку угол А,
в каком направлении его ни измеряй, равен самому себе,
сторона АВ ляжет на бывшую сторону АС. Так как рас-
стояния АВ и АС равны, новая точка С совпадет с преж-
ней точкой В, а новая точка В — с прежней точкой С.
Таким образом, В и С поменялись местами. Теперь все
определено и новые стороны совпали со старыми. Новый
ЕАВС лег точно поверх старого Е_АСВ, следовательно,
они равны.
21
а. Эти два треугольника конгру-
энтны, поэтому отмеченные углы
равны.
б. Следовательно, эти два тре-
угольника конгруэнтны, и отме-
ченные углы равны.
в. Сравним отмеченные углы ...
г. ... и убедимся, что они равны.
Что и требовалось доказать.
Рис. 3.
Доводы против перемещения
Ч. Л. Доджсон в одной из своих математических ра-
бот 1 приводит следующую беседу:
МИНОС: Предлагается доказать [эту теорему], взяв равнобед-
ренный треугольник, перевернув его и опустив на самого себя
ЕВКЛИД: В таком доказательстве слишком много нелепицы,
чтобы его можно было поместить в строго философском трак-
тате; не напоминает ли оно о том человеке, который спускал-
ся вниз по собственной глотке?
МИНОС: Я полагаю, защитники этого доказательства могут
сказать, что треугольник оставляет за собой след и что пере-
вернутый треугольник кладется на этот след.
Так можно «расправиться» с одним из возможных
возражений. Но имеется другое, более глубокое возраже-
ние, которое, вероятно, казалось древним грекам особен-
но веским: само понятие перемещения из-за парадоксов
Зенона несет в себе неясность. Возможно, именно поэто-
му Евклид обратился к более надежному понятию кон-
груэнтности.
Зенон перечислил четыре парадокса. Чтобы передать
их специфику, достаточно привести здесь один 2. Допу-
стим, нам надо попасть из точки А по прямой в точку В.
Для этого сначала надо попасть в точку С на полпути
между А и В. Но прежде чем попасть в С, надо достичь
точки D на полпути между А и С, и так до бесконечно-
сти... Создается впечатление, что движение никогда не
сможет начаться!
Проблема не так проста, как кажется, и древние гре-
ки это хорошо понимали. Получается, что всякая ссылка
на движение в строгом доказательстве выглядит как его
изъян. В реальном мире перемещения, конечно, проис-
ходят, однако экспериментальное подтверждение не
является логически строгим доказательством.
Поправка к понятию движения
Мы сможем полностью обойти проблемы, поднятые
парадоксами Зенона, если позаботимся о более аккурат-
ных формулировках.
23
Возьмите свой картонный треугольник, переверните
его и положите на прежнее место. Зависит ли приведен-
ное выше доказательство от того, где он побывал в про-
межутке между действиями? Зависит ли что-нибудь от
того, как вы его перевернули: ловко подбросив, как блин,
или помахав им сначала в воздухе, или покружившись
по комнате в вальсе «Голубой Дунай»? А если вы выйде-
Рм. 4.
те из дому, доедете поездом до Ливерпуля, вернетесь
оттуда на попутной машине и только после этого положи-
те свой треугольник на место, что-нибудь изменится?
Коль скоро треугольник лег на прежнее место, не
имеет никакого значения, где он побывал до этого. Ему
вообще не надо было никуда деваться: взмахните вол-
шебной палочкой, — и он мгновенно перейдет из одного
положения в другое. Выразим эту мысль точнее: раз нам
не важно, где треугольник побывал, то нечего и говорить
об этом, а следовательно, нечего и предполагать, что он
где-то побывал. Все, что нам действительно нужно
знать, — это куда в конце концов попала каждая его
точка.
Для этого нужно придумать какой-то способ пометить
все точки треугольника, а еще проще — пометить раз и
навсегда все точки плоскости, чтобы для какого-нибудь
24
другого случая не пришлось делать все заново. В прин-
ципе не очень важно, какой способ выбрать, но особенно
удобно воспользоваться координатами: каждая точка ев-
клидовой плоскости задается парой своих координат
(х, у) относительно двух фиксированных осей.
Рис. 5.
Допустим для определенности, что наши оси разме-
чены в сантиметрах, и мы хотим передвинуться на 5 см
вправо. Куда попадет данная точка (х, г/)?
Посмотрим на рис. 4. Легко заметить, что координата
у не изменилась, а координата х увеличилась на 5. Таким
образом, на 5 см вправо от точки (х, у) находится точка
(х + 5, у).
Теперь заметим, что точка (х, у) на самом деле нику-
да не переместилась. Взгляните на точку (2, 3), а затем
на точку (7, 3). Разве точка (2, 3) после этого куда-то
делась? Ничего подобного. И это для нас очень сущест-
венно. Точки плоскости не перемещаются, перемещается
наш взгляд. Если бы треугольник с вершинами (1,1),
(2,1) и (1,4) сдвинулся на 5 см вправо, его вершинами
стали бы (6,1), (7,1) и (6,4), как на рис. 5.
Теперь у нас не один треугольник, а целых два, при-
чем один лежит на 5 см правее другого. Переводя взгляд
с одного треугольника на другой, мы без всякого переме-
щения достигаем того же эффекта, что и при реальном
25
перемещении. (Между прочим, это помогает понять вы-
сказанную Миносом мысль о том, что треугольник остав-
ляет «след». Мы пошли еще дальше и сохранили весь
треугольник!)
Способ, которым мы переводим взгляд, можно опи-
сать такой схемой:
(1. 1)
(2, 1)->(7, 1)
(1, 4)->(6, 4)
и вообще
(х, {/)->(% +5, у).
Введем для обозначения выражения «точка на 5 см
вправо от» специальный символ, скажем, Т. Тогда фор-
мула
Г(1, 1) = (6, 1)
читается так: «точка на 5 см вправо от (1,1) есть (6,1)»,
а формула
Т(х,у) = (х + 5,у) (*)
читается так: «точка на 5 см вправо от (х, у) есть
(х + 5, у)».
Этот новый символ Т по существу равносилен коман-
де: «подвинься на 5 см вправо», но на самом деле он ни-
чего не двигает. Он лишь сообщает нам, где какие точки
оказались бы, если бы они и впрямь вздумали переме-
щаться. Все, что нам нужно знать о Т, заключено в фор-
муле (*), которую можно рассматривать как определе-
ние Т, т. е. определение действия: «подвинься на 5 см
вправо».
Символы действия, подобные Т, называются преобра-
зованиями плоскости. Преобразование F считается за-
данным, если для каждой точки (х, у) известна точка
F(x, у). Можно задавать преобразование формулой вро-
де ( * ) или любым другим, но четко определенным спо-
26
собой нахождения F(x, у), Всякому перемещению (в ип<
туитивном смысле) соответствует преобразование F та-
кое, что
F(x, гД=точка, в которую переместится объект, рас-
положенный в точке (х, у).
Преобразования обладают тем преимуществом, что,
возникнув благодаря идее перемещения, они потеряли с
ней прямую связь, и потому им не угрожает опасность
парадоксов Зенона. Пользуясь преобразованиями, мож-
но создать такую разновидность математики, в которой
действие: «перевернем треугольник и опустим его на са-
мого себя» — имеет четкую интерпретацию, не опасную
никакими логическими ловушками.
Свойство жесткости
Интересно разобраться, какие преобразования каким
движениям соответствуют. Например, зеркальному отра-
жению относительно оси х отвечает преобразование G:
6(х, у) = (х, -у),
а повороту на 90° по часовой стрелке — преобразова-
ние Н:
Н(х, у) = (у, -х).
Это легко установить по рис. 6 и 7.
Можно, наоборот, сначала задать преобразование, а
потом выяснить, какое движение ему отвечает. Напри-
мер, если
К(х, у)=(х+3, у-2),
то преобразованию К соответствует движение, которое
перемещает все точки на 3 см вправо и на 2 см вниз.
Для исследования более сложных преобразований
полезно отметить на чертеже, куда перешли несколько
выбранных точек. Так, для J:
У) = (х2, ху)
27
можно сосчитать: /(1,1) = (1, 1), /(2, 3) = (4, 6) и т. д. и
нанести полученные точки на лист в клеточку. Это преоб-
разование переводит квадрат с вершинами (1, 1), (1, 3),
(3, 1) и (3, 3) в фигуру, показанную на рис. 8.
Мы видим, что преобразование / искажает форму фи-
гур, закручивая и растягивая их. В обычной геометрии
28
такие преобразования не рассматриваются. Если допус-
тить изгибания и растяжения, то треугольники будут сво-
бодно переходить один в другой, и ничего хорошего не
получится.
Нам нужны такие преобразования, которые соответ-
ствуют жестким движениям, не изменяющим форм фи-
гур и их размеров. Наши рассуждения о равнобедренном
треугольнике потеряют силу, если перевернутый тре-
угольник окажется другой формы. Определенные выше
преобразования G, Н, К соответствуют жестким движе-
ниям, а преобразование J — нет.
Основное свойство жесткого движения состоит в том,
что оно ничего не вытягивает и не сжимает. Никакие две
точки не сближаются и не отдаляются, т. е. остаются од-
на от другой на том же расстоянии. При помощи коорди-
нат на евклидовой плоскости это свойство можно выра-
зить алгебраически. Расстояние между двумя точками
(х, у) и (и, v) определяется по формуле
V +
которая выводится из теоремы Пифагора. Если при пре-
образовании F
F(x, у) = (х', у'), F(u, v) = (u', v'),
то расстояние между F(x, у) и F(u, v) равно
Если F соответствует жесткому движению, эти два рас-
стояния должны быть равными для любых выбранных
точек (х, у) и (и, v). Записывая это равенство и возводя
в квадрат обе его части, получаем, что для всех (х, у)
и (и, v)
(x-u)2+(y-v)2=(x'-u')2 + (y'-v')2.
Преобразование F соответствует жесткому движению то-
гда и только тогда, когда оно удовлетворяет этому урав-
29
нению, пели угодно, это свойство можно рассматривать
как определение жесткого движения, отождествляя тем
самым формальное понятие с интуитивным.
Поработав над этим уравнением, можно было бы по-
лучить более простые определяющие свойства жестких
движений. Однако это завело бы нас в сторону от основ-
ного пути. Здесь нам важно то, что жесткое движение
можно охарактеризовать как преобразование некоего
определенного вида.
Параллельный перенос, вращение, зеркальное отражение
Рассмотрим теперь три частных вида жестких дви-
жений.
Параллельный перенос (или сдвиг) перемещает каж-
дую точку на заданное расстояние в заданном направле-
нии (рис. 9).
Вращение поворачивает каждую точку вокруг неко-
торой фиксированной точки Р (центра вращения) на за-
данный угол 6 (рис. 10),
Рис. 9.
30
Зеркальное отражение (осевая симметрия) отражает
каждую точку плоскости относительно некоторой фикси-
рованной прямой I (оси симметрии) так, как будто вдоль
этой прямой поставлено зеркало (рис, 11).
Пользуясь координатным методом, легко записать
соответствующие преобразования. Например, повороту
на угол 6 относительно начала координат отвечает пре-
образование R.
R(x, У) = (х cos Q—y sin 6, х sin Q+y cos 6),
По формулам для трех перечисленных преобразований
легко проверить различные их свойства, подсказывае-
мые интуицией: то, что они действительно задают жест-
кие движения, что вращение на угол 6, а затем на угол <р
дает вращение на угол 6 + <р, и т. д.
Мы выделили именно эти три типа движений пото-
му, что они действуют по-разному, имеют довольно про-
стой вид и отвечают преобразованиям с простыми форму-
лами. Оказывается, никаких других и не нужно: любое
жесткое движение плоскости можно получить при помо-
31
Рис. 12.
щи последовательного выполнения параллельных пере-
носов, вращений и зеркальных отражений. Наглядно в
этом можно убедиться при помощи рис. 12.
1. Начнем с произвольного треугольника АВС и про-
извольного жесткого движения С.
2. При помощи параллельного переноса Т можно со-
вместить Т(А) и U(А).
3. Вращение S вокруг точки U(A) позволяет совмес-
тить Т(В) и U(B).
4. Наконец, зеркальное отражение относительно пря-
мой U(A) U(В) переводит S(T(C)) в U(C).
(Конечно, в некоторых случаях какой-то из этих ша-
гов, возможно, не понадобится.)
Мы не случайно воспользовались треугольником. Де-
ло в том, что плоскость двумерна, и потому всякое жест-
кое движение на ней однозначно определено, если из-
вестно, куда оно переводит некоторый (невырожденный)
треугольник3. Итак, мы показали, что всякое жесткое
движение на плоскости можно получить при помощи по-
следовательного выполнения параллельного переноса,
вращения и зеркального отражения (причем некоторые
из них могут не понадобиться).
Ясно, что зеркальное отражение потребуется только
тогда, когда движение переворачивает фигуры. Поэтому
движения, при которых этого не происходит, получаются
лишь переносом и вращением. (Дальнейшие исследова-
ния позволят выяснить нечто большее.) Допустим, что
выполняются два зеркальных отражения относительно
двух (быть может) различных прямых. Первое все опро-
кидывает, а второе переворачивает обратно, и в итоге
все остается неперевернутым. Отсюда видно, что резуль-
тат двух отражений можно получить переносом и враще-
нием. Этот факт менее очевиден, чем упомянутые выше,
однако и он без труда выводится из наших рассуждений.
Полученный выше результат можно выразить так:
для каждого жесткого движения U найдется такой па-
2 Я- Стюарт
33
раллельный перенос Т, такое вращение S и такое зер-
кальное отражение R, что для любой точки Х=(х, у)
U(X) =R(S(T(X)))
(с обычной оговоркой, что в некоторых случаях любое из
R, S, Т может отсутствовать). Здесь напрашивается бо-
лее краткое обозначение. Пусть заданы два преобразо-
вания Е и F, Определим преобразование ЕЕ формулой
EF(x, y)=E(F(x, у)).
Если Е соответствует жесткому движению (которое мы
тоже обозначим Е), a F — жесткому движению F, то ЕЕ
отвечает движению: «сначала F, потом Е». (Это объяс-
няется тем, что, когда мы ищем E(F(x, у)), мы сначала
находим Е(х, у), а потом уже E(F(x, у)). Жаль, конеч-
но, что движения выступают не в том порядке4. Подобное
же явление происходит при вычислении log sin х: снача-
ла мы находим sin х, а затем его логарифм.)
Выше мы рассмотрели два жестких движения, кото-
рым соответствовали преобразования G, ЕЕ
G(х, у) = (х, -у), Н(х, у) = (у, -х).
Найдем GEE
GH(x, y) = G(H(x, y))=-G(y, -х) = (у, х),
(Чтобы получить последнее равенство, нужно помнить,
что символы хи у совершенно произвольны: с тем же
успехом можно написать G(u, v) = (u, —v) и затем под-
ставить у вместо и и х вместо и.)
Сделав чертеж, мы обнаружим, что GEE соответствует
зеркальному отражению относительно диагонали у=х
(рис. 13).
Обозначим его D-.
D(x, у) = (у, х).
34
Мы доказали, что для любой точки (х, у)
GH(x, y)=D(x, у).
В этом смысле мы и будем понимать равенство
GH=D.
Если вернуться к соответст-
вующим движениям, то мож-
но проверить его эксперимен-
тально: вращение на 90° по ча-
совой стрелке и зеркальное от-
ражение относительно оси х
приводят к тому же результа-
ту, что и отражение относитель-
но прямой у=х. Наши вычисле-
ния согласуются с экспери-
ментом!
Теперь вместо GH рассмот-
рим HG:
HG(x, y)=H(G(x, у))=Н(х, -у)={-у, -х).
Это преобразование отвечает отражению относительно
другой диагонали у =—х. Заметим, что GH=^HG. На
самом деле нет никаких причин (кроме привычки) думать,
что они должны совпадать. Данный пример это подтверж-
дает. Поэтому-то нужно твердо знать, что означает EF:
«сначала F, потом Е» или наоборот.
Теперь мы можем переписать прежнее равенство
U(X) =R(S(T(X))) в очень простой форме
U=RST,
Тот факт, что удалось определить «произведение» EF,
наводит на мысль о построении «алгебры» преобразо-
ваний. Развитая в одном направлении, эта идея приво-
дит к линейной алгебре, которую мы обсудим в гл. 15, а
в другом — к теории групп (гл. 7).
2*
35
Назад к теореме
Мы немного отклонились от равнобедренных треуголь-
ников, которые толкнули нас на этот путь, зато построи-
ли аппарат, который позволит теперь сделать вполне
респектабельным «опрокидывающее» доказательство. То-
му, кто имел дело с преобразованиями, достаточно то-
го, что уже сказано. Более предусмотрительно следова-
ло бы рассуждать примерно так.
Существует преобразование Т, отвечающее зеркаль-
ному отражению относительно биссектрисы угла ВАС.
Поскольку при жестких движениях не меняются рассто-
яния (а значит, и углы), Т(А)=А, Т(В) = С и Т(С)=В.
Следовательно, применение Т к углу АВС дает угол АС В.
Так как величины углов не меняются, то
ZABC=Z_T(A)T(B)T(C) = ААСВ,
что и требовалось доказать.
Это доказательство, когда оно станет для вас обыч-
ным, проще того, которое дал Евклид, потому что в нем
логика следует за интуицией.
Теперь, владея аппаратом преобразований, мы можем
спокойно говорить о движениях, не ощущая за спиной
призрака Зенона. Это открывает доступ к новым, более
простым доказательствам многих теорем стандартного
курса геометрии. Приведем два примера.
1. Если в треугольнике два угла равны, то он равно-
бедренный.
Пусть в треугольнике АВС равны углы А и В. Выпол-
ним зеркальное отражение относительно перпендикуля-
ра, проведенного через середину стороны АВ. На первый
взгляд, должно получиться то, что изображено на
рис. 14.
Однако из равенства углов А и В следует, что преоб-
разованный треугольник ляжет точно поверх прежнего,
36
так что АС совпадет с ВС. Значит, треугольник равно-
бедренный.
2. Равным дугам окружности соответствуют равные
хорды.
Пусть А, В, X, У — точки на окружности с центром О
и дуга АВ равна (по длине) дуге XY (рис. 15).
Рис. 14.
Выполним вращение вокруг точки О, так чтобы точ-
ка А перешла в X. Тогда в силу равенства длин дуг точ-
ка В совпадет с У и, значит, хорда АВ совпадет с хордой
XY, откуда видно, что они равны.
Теперь вы наверняка вспомните и другие теоремы из
геометрии, которые можно доказать таким путем. Если
бы мы задумали провести эту программу для всей гео-
метрии, пришлось бы более тщательно сформулировать
основные понятия; при этом выяснилось бы, что далеко
не каждая геометрическая теорема есть прямое следст-
вие свойств жестких движений. Те теоремы, которые мо-
гут быть сразу доказаны, исходя из этих свойств, станут
тривиальными, и мы сможем сосредоточить внимание на
более тонких геометрических результатах. Так приме-
нение жестких движений помогает нам отсеять тривиаль-
ное и заняться тем, что по-настоящему интересно.
37
Глава 3 кратчайшие пути
В ВЫСШЕЙ АРИФМЕТИКЕ
Поразительно, до каких пре-
мудростей могут дойти матема-
тики, чтобы только поменьше
трудиться.
Мэтью Пордейдж
Представление о числах впервые возникло у перво-
бытных людей скорее всего из желания как-то уследить
за важными событиями их жизни. Сколько у меня овец,
наконечников для стрел, жен? Скоро ли наступит весен-
нее половодье? Подобные вопросы фокусируют внима-
ние на именованных числах, которые первыми нашли
практическое применение. Абстрактное понятие «отвле-
ченного числа» сложилось значительно позднее. Тот факт,
что две овцы и две жены имеют нечто общее — то что их
«две» — совсем не очевиден. Очень маленькие дети этого
еще не понимают, хотя они прекрасно отличают одну ов-
цу от двух овец.
По мере развития человечества к этим первым. числам
для счета предметов добавились другие. Каждая эпоха
изобретала числа, отвечающие ее нуждам. Индусы изо-
брели нуль. Чтобы сделать возможным деление на части,
пришлось ввести дроби. Затем понадобились отрицатель-
ные числа. В результате сложилась сначала система
целых чисел: ..., — 3, —2, — 1, 0, 1, 2, 3, ... , а затем,
после введения отрицательных дробей, система рацио-
нальных чисел, т. е. чисел вида p/q с целыми р и q, на-
пример 1/2, 17/25, — 11/292. Геометрия (та, что была
разработана еще греками), а затем потребности анализа
(дифференциального и интегрального исчисления) привели
к понятию действительного числа, вобравшему в себя и
те числа, которые не являются рациональными (например,
38
V2). Наконец, попытки научиться решать алгебраичес-
кие уравнения породили уже вовсе загадочные комплекс-
ные числа, для создания которых пришлось считать, что
существует квадратный корень из — 1.
Каждый шаг по ступеням этой лестницы сопровож-
дался бурными дебатами о том, являются ли эти ново-
модные штуки числами.
Комплексные
Действительные
Рациональные
Дрова
Целые
Натуральные
Именованные^
Рис. 16,
Оказалось, что все эти числа укладываются в одну
стройную схему (рис. 16).
Стрелки, ведущие от одной системы чисел к другой,
означают, что вторая содержит все числа из первой и
какие-то еще.
Более того, в каждой из этих систем можно выпол-
нять арифметические действия. Это в какой-то мере объ-
ясняет, почему столь разные объекты упорно называли
числами. Выбор такого названия все же в большой
степени произволен, однако позднее об этом забыли
и «числу» стали приписывать мистические качества срод-
ни божественному откровению.
Ни одно из чисел ни одной из этих систем не сущест-
39
вует в реальном мире. Я еще никогда не встречал в своих
путешествиях число 2. Как-то я проходил мимо двух
овец и, насколько я понял, их поведение вполне отвечало
свойствам этого числа, но самого числа я так и не видел.
В то же время числа удачно описывают некоторые свойст-
ва реального мира; поэтому они и были выделены как
абстрактные понятия, отражающие его поведение.
Различные физические ситуации требуют разного ма-
тематического описания. Чтобы сосчитать своих жен,
человеку хватит натуральных чисел; чтобы взвесить свое
золото, он воспользуется дробями. Греческому геометру,
который захотел узнать, чему равна гипотенуза равно-
бедренного прямоугольного треугольника, понадобились
числа вроде У2, а математик эпохи Возрождения, ре-
шавший кубическое уравнение1, нашел применение числу
Существует много важных математических объектов,
которые по каким-то историческим или психологическим
причинам не называют числами, хотя они и возникли из
столь же практических потребностей. Эти объекты обла-
дают многими свойствами чисел и даже применяются
для их исследования. Различие между числовым и не-
числовым столь же иллюзорно, как и вера в то, что числа
даны нам богом.
Арифметика в миниатюре
Интересную математическую систему представляет
собой так называемая арифметика вычетов.2 Подобная
система возникает тогда, когда мы рассматриваем ци-
клически повторяющиеся события: чередование дней не-
дели, часов в течение суток, величин углов по окружности
(при этом дни недели повторяются каждые 7 дней, время
дня — каждые 24 часа, а углы по окружности — каждые
360°).
Занумеруем дни недели от 0 до 6, начиная от воскре-
40
сенья, и расположим цифры по кругу, как на рис. 17.
Если мы будем продолжать нумерацию, то 7-й день
снова окажется воскресеньем, 8-й — понедельником,
9-й — вторником и т. д. Таким образом, в каком-то смыс-
ле 7 = 0, 8=1, 9 = 2 и т. д„ хотя, конечно, знак равенства
здесь нужно понимать не совсем так, как обычно! Можно
пойти в обратном направлении и установить, что -1-й
день, предшествующий воскресенью,— суббота, так что
— 1 = 6; аналогично —2=5. В итоге вся совокупность
целых чисел «наматывается» на круг дней недели, как по-
казано на рис. 18.
Нетрудно вывести общий признак, какие числа како-
му дню отвечают.
Воскресенье: ..., —14, —7, 0, 7, 14.. т. е. числа
вида 7/г.
Понедельник: ..., —13, —6, 1, 8, 15, ..., т. е. числа вида
7п+1.
Вторник: ..., —12, —5, 2, 9, 16, ..., т. е. числа вида
7м 4-2.
Среда: ..., —11, —4, 3, 10, 17, ..., т. е. числа вида
7п+3.
41
Четверг: — 10, —3, 4, 11, 18. т. е. числа вида
7п+4.
Пятница: ..., — 9, ~—2, 5, 12, 19, ..., т. е. числа вида
7п + 5.
Суббота: — 8, — 1, 6, 13, 20, ..., т. е. числа вида
7п + 6.
(Числа вида 7п+7 суть ви-
да 7(п + 1), т. е. 7п.)
Итак, день недели, соответ-
ствующий данному числу, опре-
деляется по остатку при деле-
нии на 7. Такими остатками
могут быть только 0, 1, 2, 3, 4,
5, 6. А теперь построим для
них «арифметику остатков
(вычетов)». Условимся пони-
мать формулу
4+5=2
в том смысле, что «если к чет-
вертому дню прибавить пять
дней, то получится второй
день». Такая интерпретация
вполне естественна и позволяет
нам построить следующую таб-
лицу сложения «чисел» от 0 до 6:
-р | 0 1 2
о
1
2
3
4
5
6
0
1
2
3
4
5
6
1 2
2 3
3 4
4 5
5 6
6 0
0 1
3 4 5 6
3 4 5 6
4 5 6 0
5 6 0 1
6 0 12
0 12 3
12 3 4
2 3 4 5
42
Эта таблица отражает структуру 7-дневного цикла. До-
пустим, нас интересует, какой день недели наступит че-
рез 751 день после вторника. Сформулируем задачу так:
4 + 751 = ?
Числа 751 в нашей таблице нет, но мы замечаем, что
751 = 7- 107+2 = 7п+2,
т. е. 751 =2. Итак задача принимает вид
4+2=?
и из таблицы мы находим, что ? = 0, т. е. через 751 день
после вторника наступит суббота.
Это «сложение» имеет свои причуды: например,
1 + 1 + 1 + 1 + 1 + 1 + 1=0,
однако если истолковать эту формулу так, как сказано
выше, то смысл ее ясен, и к подобным причудам можно
быстро привыкнуть.
Воодушевленные своими успехами, попробуем ввести
для этой системы умножение. Конечно, трудно приписать
какой-нибудь смысл умножению воскресенья на поне-
дельник, но мы и не собираемся этим заниматься 3. Что-
бы произведение 3-6 имело хоть какой-то смысл, оно
должно равняться 6+6+6, т. е. 4 по нашей таблице.
Поэтому мы, по определению, полагаем
3-6=4.
Не менее разумно потребовать, чтобы 3-6 равнялось
З+З + З + З + З+З. Не приведет ли это к другому от-
вету? Нет, мы снова получаем 4. Можно еще рассуж-
дать так: поскольку 3= 10, 3-6 должно равняться 10-6,
или 60,— но 60 снова равно 4. Итак, как бы ни называ-
лось это действие, оно по крайней мере приводит к со-
гласованным результатам, и это очень приятно.
43
Построим теперь таким же способом (повторным
сложением) таблицу умножения (проверьте ее!):
х | о 1 2 3 4 5 6
о
1
2
3
4
5
6
О О
О 1
О 2
О 3
О 4
О 5
О 6
ООО
2 3 4
4 6 1
6 2 5
1 5 2
3 1 6
5 4 3
О О
5 6
3 5
1 4
6 3
4 2
2 1
Конечный результат наших усилий — числа от 0 до 6
и две таблицы — называют системой целых чисел по мо-
дулю 7 или для краткости числами по модулю 7. Затей-
ливое словечко «модуль» употреблено здесь только для
того, чтобы отметить роль числа 7. Вместо 7 можно, ра-
зумеется, взять любое другое целое число. Если исходить
из чисел на циферблате часов, получится арифметика по
модулю 12 (или по модулю 24, если часы электронные).
В общем случае годится любое целое число. Нужно толь-
ко вообразить «неделю» с таким числом дней и дальше
поступать точно так же, как выше.
Сравнения
В 1801 г. Карл Фридрих Гаусс, которого считают
одним из трех самых великих математиков, когда-либо
живших на земле, опубликовал свои «Арифметические
исследования» (Disquisitiones Arithmeticae). Это был
трактат по теории чисел, т. е. речь шла о свойствах обыч-
ных целых чисел. Гаусса интересовали, конечно, более
глубокие идеи, чем те несложные вычисления, которые
составляют элементарную арифметику. Поскольку теория
чисел занимается лишь целыми числами, можно поду-
44
мать, что это очень простая наука. Дело обстоит как раз
наоборот. Теория чисел — одна из самых трудных облас-
тей математики, изобилующая нерешенными пробле-
мами.
Вводный раздел своего трактата, на котором основано
все дальнейшее, Гаусс начинает таким определением:
Если некоторое число а лепт разность чисел b и с, будем назы-
вать b и с сравнимыми 4 относительно а ... Число а называется мо-
дулем.
(Под «числом» Гаусс понимает «целое число».)
Если b и с сравнимы по модулю а, будем писать
b=c (mod а)
или просто Ь==с, если ясно, о каком модуле идет речь.
Посмотрим, как это связано с тем, что мы делали
выше. Пусть b и с сравнимы по модулю 7. Тогда сущест-
вует такое целое число k, что
b — c=7k или b = 7k+c.
Мы видим, что числа, сравнимые по модулю 7 с задан-
ным числом с,— это числа вида 7k + с и только они. На-
пример, с 1 сравнимы числа вида 7&+1.
Любое заданное число b можно разделить на 7 и най-
ти остаток г:
b = 7q + r\
отсюда следует, что b сравнимо с г (mod 7). Так как
остатками могут быть только числа от 0 до 6, мы заклю-
чаем, что любое целое число сравнимо по модулю 7 с
одним из чисел 0, 1,2, 3, 4, 5, 6.
Посмотрим еще раз на рис. 18. Числа, лежащие на
спирали над нулевым днем, воскресеньем, имеют вид 7п,
т. е. сравнимы с 0. Числа, лежащие над первым днем,
сравнимы с 1, и вообще числа, лежащие над d-м днем,
сравнимы с d.
Далее оказывается, что сравнения можно складывать
45
и перемножать, совсем как обычные равенства. Точнее,
если
ct^a' (mod m); Ье==Ь' (modm),
то
a+b=a'+b' (mod m)'j ab = a'b' (modm),
Давайте это докажем. Для этого не требуется ничего,
кроме самой элементарной алгебры. Из двух первых
сравнений мы знаем, что существуют целые / и k, для
которых
а = т] + а', b = mk+b't (*)
Чтобы убедиться в сравнимости а-\-Ь и а'^-Ь', нужно по-
казать, что их разность
(а + Ь) - (а'+Ь')
делится на т. Подставим выражения для а и b по фор-
мулам ( * ). Получим m(j—k), т. е. число, явно делящее-
ся на т. Чтобы доказать второе утверждение, нужно
рассмотреть разность ab — a'b', которая равна
mfka+jb—jkm)
и, следовательно, тоже делится на т.
Из двух доказанных утверждений следует, например,
что если 1 = 8 и 3^ 10 (mod 7), то 1 + 3=4 сравнимо
с 8+10=18, а 1-3 = 3 сравнимо с 8-10 = 80. И действи-
тельно, обе разности 14 и 77 делятся на 7.
Полученное нами раньше, в арифметике дней недели,
«равенство» 4+5 = 2 теперь можно сформулировать бо-
лее точно
4 + 5=2 (mod 7),
И наши таблицы сложения и умножения относятся по
существу к сравнениям. Например, 4-5=6 означает, что
если какое-то число, сравнимое с 4, умножается на число,
сравнимое с 5, то их произведение сравнимо с 6. Ариф-
46
метика сравнений по модулю 7 позволяет нам отбрасы-
вать при желании часть, кратную 7, и это находит при-
менение в тех случаях, когда продвижение на 7 позиций
вперед возвращает нас к исходному положению.
При помощи сравнений по модулю 10 легко объяс-
нить, почему все полные квадраты кончаются на 0, 1, 4,
5, 6 или 9 и не могут кончаться на 2, 3, 7 или 8. Любое
целое число сравнимо по модулю 10 с одним из чисел от
0 до 9 поэтому все квадраты сравнимы с квадратами
этих чисел. Квадраты чисел от 0 до 9 сравнимы соответ-
ственно с 0, 1, 4, 9, 6, 5, 6, 9, 4, 1. Только этими цифрами
и может кончаться любой квадрат, поскольку остаток от
деления целого числа на 10 равен его последней цифре
(в десятичной системе записи).
Подобным же образом можно объяснить и многие
другие арифметические закономерности.
Деление
В арифметике по модулю п числа можно складывать
и умножать почти так же, как в обычной арифметике,
А вот проблема деления намного интереснее, потому что
ответ зависит от того, какой взять модуль.
Допустим, мы хотим придать смысл дроби 4/3 (mod 7).
Пока этот символ не имеет никакого смысла, и мы воль-
ны приписать ему любое значение, какое нам заблаго-
рассудится. Однако мы пожелали, чтобы он имел какое-
то отношение к делению, а это уже налагает на наш вы-
бор определенные ограничения. Наиболее естественно
было бы определить 4/3 как любое число х, удовлетво-
ряющее сравнению
Зх=4 (mod 7).
Из соответствующей таблицы умножения находим един-
ственное подходящее значение х, а именно х=6, Поэтому
47
в арифметике по модулю 7 можно положить по опреде-
лению
4/3 = 6.
Точно так же для любых других двух чисел р и q от
О до 6 естественно полагать p/q равным такому у, для
которого
ЯУ—Р (mod 7).
Число qy стоит в нашей таблице на пересечении строки q
и столбца у. Для того чтобы это сравнение имело реше-
ние у, где-то в строке q должно встретиться число р.
А для того чтобы решение было единственным, это число
р должно встретиться в строке q ровно один раз. (Если
решений будет несколько, мы не будем знать, какое из
них взять в качестве p/q.)
Таблица умножения по модулю 7 устроена так, что
в каждой ее строке, за исключением строки 0, каждое
число встречается один и только один раз. Значит, для
любого ненулевого q наше сравнение имеет единственное
решение. Поэтому мы можем определить p/q при любом
<7=7^0. Последнее условие не является серьезным ограни-
чением, поскольку мы и не надеялись найти способ де-
лить на 0.
А что произойдет в арифметике по модулю 6? Вот
соответствующая таблица умножения:
X 0 1 2 3 4 5
0
1
2
3
0 0 0 0 0 0
0 1 2 3 4 5
0 2 4 0 2 4
0 3 0 3 0 3
4 0 4 2 0 4 2
5 0 5 4 3 2 1
Здесь дело обстоит по-другому.
Все числа встречаются
48
только в строках 1 и 5. В строке 2 стоят только 0, 2 и 4,
причем каждое из них дважды. В строке 3 — только
О и 3. Следовательно, на 5 и на 1 делить можно, а вот
определить 1/2 или 3/4 не удастся. На роль 4/2 имеются
два кандидата (2 и 5), а на роль 3/3 — целых три. Ну и
кутерьма! И ничего похожего на предыдущий случай!
Из этой дилеммы нет выхода. Приходится признать,
что в случае модуля 6 деление возможно не всегда. Си-
туация гораздо хуже, чем с обычными целыми числами
(правда, не при всех модулях). Хотя при делении одного
целого числа на другое и не всегда получается снова це-
лое число, систему целых чисел можно расширить до си-
стемы рациональных чисел, в которой деление выполни-
мо. Более того, в этой расширенной системе выполняются
все те же «законы арифметики» (вроде a + b = b + a), что
и в системе целых чисел.
Систему целых чисел по модулю 6 не удастся так
расширить, чтобы стало возможным деление и выполня-
лись законы арифметики (о которых мы еще будем много
говорить в гл. 6). Под словом «расширить» я понимаю
«добавить еще несколько «чисел». Заметим, что эту си-
стему нельзя расширить до множества всех обычных
целых чисел, ибо тогда пришлось бы изменить таблицы
сложения и умножения, а это было бы уже не расшире-
нием, а уничтожением.
В чем же здесь дело? А в том, что в таблице умно-
жения слишком много нулей. Иногда нулю равно про-
изведение двух чисел, отличных от нуля, например
2-3=0 (mod 6).
Допустим, нам удалось расширить систему так, что в ней
можно определить число 1/2, скажем 1/2 = а. Тогда по
законам 6-арифметики должно быть
3=l-3=(a-2)-3=a-(2-3)=a-0=0 (mod 6),
что неверно. Таким образом, в расширенной системе за-
коны 6-арифметики не выполняются,
49
Та же неприятность ожидает нас в случае любого мо-
дуля т, для которого произведение ненулевых сомножи-
телей может обращаться в нуль.
Выписав таблицы умножения для модулей 2, 3, 4,
5, нетрудно убедиться, что для модулей 2, 3, 5, 7, 11,
13, 17, деление возможно всегда (кроме деления на
нуль), а для модулей 4, 6, 9, 10, 12, 14, 15, 16, ...— не всег-
да. Не обязательно быть гением, чтобы обнаружить здесь
закономерность. Первая последовательность состоит из
простых чисел (которые не имеют делителей, кроме са-
мих себя и 1), вторую образуют составные числа (кото-
рые разлагаются в произведение меньших чисел).
Легко доказать, что в случае составного модуля де-
ление возможно не всегда. Допустим, что модуль m
имеет вид m=a-b, где a<m, b<m. Тогда ни а, ни b не
сравнимо с 0 по модулю т, а их произведение а- b сравни-
мо с 0 (точно так же, как 2'3=0 (mod 6)). Подобно
тому как раньше мы вывели, что в 6-арифметике нельзя
определить 1/2, можно убедиться, что в этом, более об-
щем, случае нельзя определить 1/и (или 1/й).
Итак, с составными модулями все ясно, а как
быть с простыми? Пока мы знаем только, что несколько
первых простых модулей годятся для определения деле-
ния, а вдруг для какого-то очень большого простого чи-
сла (слишком большого, чтобы составить для него табли-
цу умножения) все будет по-другому?
Возьмем какое-нибудь простое число р. Пусть t не-
сравнимо с 0 (mod р). Вспомним, что деление на t
возможно тогда и только тогда, когда каждое число по
модулю р встречается ровно один раз в строке t таблицы
умножения. Установим сначала, что ни одно из чисел не
встречается в ней дважды. Допустим, что это не так
и какое-то из чисел (mod р) встретилось дважды. Тогда
найдутся два различных числа (mod р), скажем и и о,
для которых
tu^tv (mod р).
50
откуда
t(u — и)=0 (mod р).
В применении к обычным числам это означает, что
произведение t(u— v) делится на р. Но если произведе-
ние делится на простое число, на него должен делиться
один из сомножителей. Если t делится на р, то
(mod р), что невозможно в силу нашего выбора t. Если
и—v делится на р, то (mod р), что тоже невозмож-
но. Итак, наше предположение, что какое-то число встре-
чается в строке t дважды, привело к противоречию.
Следовательно, оно неверно, и остается единственная
возможность: ни одно число не встречается дважды в
строке t.
Но в строке t имеется ровно р мест, на каждом из
которых должно стоять одно из чисел 0, ..., р— 1. По-
скольку ни одно из них не может встретиться дважды,
остается единственный способ их размещения: каждое
по одному разу. (Это соображение называют «принци-
пом ящиков (или клеток)» Дирихле.) Итак, в строке t
каждое из чисел по модулю р встречается точно один раз.
Но тогда из сказанного выше следует, что деление на t
однозначно определено.
Л вот любопытное приложение этого факта к знаме-
нитым «числам Ферма». В 1640 г. Ферма высказал
утверждение5, что все числа вида
22П+1
простые, однако отметил, что доказать это он не может.
Первые числа такого вида 3, 5, 17, 257 и 65 537 действи-
тельно простые. В 1732 г. Эйлер показал, что Ферма
ошибся: следующее число в его последовательности
232+1 делится на 641. Эйлер обнаружил это прямым вы-
числением. Теперь, когда ответ известен, можно прийти
к нему более простым способом,
51
Заметим, что число 641 простое и что 641 = 24+54=
= 1+5-27. В арифметике по модулю 641
27=-1/5,
так что
28s-2/5,
откуда
2з2=(_2/5)4=24/54^-1
(последнее получается, если воспользоваться равенст-
вом 641 =24 + 54). Следовательно, 232+1 делится на 641.
Две знаменитые теоремы
Сравнения применяются не только для вычислений.
Они играют очень важную роль в теории чисел. В качест-
ве иллюстрации я приведу здесь доказательства двух
знаменитых теорем. Эти доказательства нетрудно понять,
стоит только увидеть их, но, как сказал Э. Т. Белл,
«... можно смело держать пари, что среди миллиона лю-
дей любых возрастов с нормальными умственными спо-
собностями не наберется и десяти таких, которые, зная
математику лишь в объеме обычной средней школы, су-
меют найти доказательство за разумное время, скажем
за год6».
Если составить ряд степеней какого-нибудь числа по
модулю 7, то обнаружится, что в нем все время повто-
ряется одна и та же последовательность. Например,
степени числа 2 равны
2°н=1, 23=1, 28=1,
91 = 9 94 = 9 97 =9
22=4; 25=4,’ 28=4,’... (mod 7);
здесь повторяется набор 1, 2, 4. В последовательности
степеней числа 3 повторяется набор 1, 3, 2, 6, 4, 5, и лег-
52
ко проверить, что подобный набор есть и для любого
другого числа.
Ясно, что если какая-то степень оказалась равной 1,
то дальше все начнет повторяться. Поскольку 36== 1, то
37= 31, 38=32 и т. д. В случае модуля 7 любое число,
кроме 0, удовлетворяет сравнению
л6=1 (mod 6)
(хотя при некоторых значениях х единица получается
и для меньших степеней).
Проделав вычисления, можно убедиться, что в случае
mod 5 всякое отличное от нуля число удовлетворяет
условию
x4==l (mod 5),
для mod 11
х10=1,
а для mod 13
х'М.
Я останавливаю внимание на простых модулях, посколь-
ку здесь лучше видна закономерность. Итак, очень
похоже на то, что для любого простого р и любого це-
лого х, не сравнимого с 0 (mod р),
(mod р).
Поясним на примере модуля 7 один из способов до-
казательства этого утверждения. Отличные от 0 числа
(mod 7) таковы:
1, 2, 3, 4, 5, 6.
Удвоив каждое из них, получим
2, 4, 6, 1, 3, 5,
т. е. те же числа в другом порядке. Значит, произведения
1-2-3-4-5-6; 2-4-6-1 -3-5
53
сравнимы по модулю 7. Но второе из них сравнимо так-
же с произведением
(1 -2) (2-2) • (3-2) • (4-2) • (5-2) - (6-2) (mod 7),
которое можно записать как
26 • (1 2 • 3 • 4 5 6) (mod 7).
Отсюда
1-2-3-4-5-6=26 • (1-2-3-4-5-6) (mod 7),
и после деления получим
1=26 (mod 7) ,
То же самое произойдет, если утроить все числа:
3, 6, 2, 5, 1, 4;
аналогичные рассуждения покажут, что
1==36 (mod 7).
Теперь перейдем к общему случаю модуля р. Поскольку
р простое, в строке х таблицы умножения по модулю р
каждое число встречается ровно один раз. Поэтому числа
(1 -х), (2-х), ..., ((р-1) -х)
есть 1, ..., р—1, взятые в другом порядке. Перемножая
их, получим
ХР-1 • (1 • 2 <... • (р— 1)) = 1 • 2 •... • (р— 1) (mod р);
деление обеих частей на 1 • 2 •... • (р — 1) дает
хг-'sl (mod р),
и теорема доказана.
При помощи этой теоремы можно, к примеру, сразу,
не выполняя никакого деления, сказать, что число
7|8-1 = 1 628 413 597 910 448
Б4
делится на 19. В общем виде эта теорема широко приме-
няется в исследованиях по теории чисел 1. Ее называют
теоремой Ферма (не путать со знаменитой последней тео-
ремой Ферма!8).
Вторая теорема относится больше к произведению
1-2..... (р-1),
которое встретилось в доказательстве теоремы Ферма,
Можно ли вычислить его по модулю р?.
При р = 7 это есть произведение
1 • 2 • 3 • 4 • 5 • 6.
Переписав его в виде
Ь (2-4) • (3-5) -6,
обнаружим, что оно сравнимо с
1’Ы. (-1),
т. е. с — 1. Мы специально собрали в пары те числа, ко-
торые дают в произведении 1.
То же самое можно проделать в случае модуля 11;
1• 2 • 3 • 4 • 5 • 6 • 7 • 8 9 • 10 =
= 1 • (2-6) • (3-4) • (5-9) - (7-8) • 10=
= 1 • 1 • 1 • 1. 1 • (-1) = -1
или модуля 13:
1 • 2 • 3 4 • 5 • 6 • 7 • 8 • 9 10 11 • 12 =
= 1 • (2-7) • (3-9) • (4- 10) • (5-8) (6 - 11) -12 =
= 1 . 1 . 1 . 1 . 1 . 1 . (-1) = -1.
В общем случае возьмем числа 1, 2, ,,р—1 и разо-
бьем их на пары взаимно обратных, т. е. дающих в про-
изведении 1. Тем самым мы избавимся от всех чисел, кро-
ме тех, которые совпадают со своими обратными, т. е.
удовлетворяют условию
х=1/х (mod р),
55
или
х2=1 (mod р),
или
х2 —1 = 0 (mod р),
откуда
(х—1)(х+1)=0 (mod р).
Таким образом, либо х=1, либо х= — 1. Поэтому можно
написать.
1 -2-....(p-l)Sb (?.?).....(?•?)• (-1)^-1.
Мы доказали, что для любого простого р
1-2 •... • (р—1)е= — 1 (mod р)}
эта теорема известна под названием теоремы Вильсона.
Для составного числа пг теорема не верна. В самом
деле, раз m составное, у него есть делитель d^m— 1. Он
должен содержаться в произведении 1 • 2-...• (m— 1). Но
тогда число 1 2 •... • (т— 1) +1 при делении на d даст
остаток 1, а отсюда следует, что это число не делится
на т.
Теоретически мы получили признак простых чисел.
Чтобы узнать, простое или не простое данное число q,
мы находим
1-2-...- (<7-1) + 1
и делим на q. Если делится без остатка, то q — простое,
если получается остаток,—-составное. Так, число
1 • 2 - 3 • 4 - 5 - 6+ 1 =721
делится на 7, значит, 7 — простое. Число
1 -2-3-4-5+1 = 121
не делится на 6, значит, 6 — составное. Правда, даже для
сравнительно небольшого числа 17 приходиться находить
56
число 1 • 2 ... • 164-1 =20 922 789 888 001 и затем делить его
на 17. Поэтому такой критерий не имеет практической
ценности даже при применении ЭВМ с очень большим
быстродействием.
Однако он представляет собой замечательный теоре-
тический результат, ибо с его помощью можно устано-
вить, простое заданное число или нет, даже не пытаясь
искать его делители.
Глава 4
ЯЗЫК МНОЖЕСТВ
Почти каждая книжка по «современной математике»
толкует о множествах и пестрит странными символами
вроде С , s, J, П, 0. Не будет исключением и эта,
хотя я и старался вводить как можно меньше символов.
Такое нашествие множеств имеет свои причины. Дело в
том, что теория множеств — это своего рода математичес-
кий язык. Без него невозможно не только заниматься
математикой, невозможно даже объяснить, о чем вообще
идет речь. Это все равно, что изучать французскую лите-
ратуру, совсем не зная французского языка. В остальной
части книги мы не сумеем обойтись без языка теории
множеств, поэтому и понадобилась эта глава.
Множество — это некоторый набор объектов; напри-
мер, множество всех графств Англии, множество всех
эпических поэм, множество всех рыжеволосых ирланд-
цев. Объекты, принадлежащие множеству, называются
его элементами. Так, «Потерянный рай» — это элемент
множества всех эпических поэм, а Кент — элемент мно-
жества всех графств Англии. Если для первоначального
ознакомления с теорией множеств удобно работать с кон-
кретными множествами, элементы которых — реальные
объекты, то в математике интерес представляют множе-
ства, состоящие из абстрактных математических объек-
тов: множество всех окружностей на плоскости, множест-
во точек на сфере, множество всех чисел.
Многие понятия теории множеств наглядно иллюстри-
руются при помощи несложных приспособлений. Доста-
точно иметь несколько маленьких предметов (каранда-
ши, ластик, точилку, несколько бусинок, сахарного мы-
шонка и т. д.). Эти предметы (или часть из них) будут
58
элементами множества; само множество будет состоять
из выбранных предметов, помещенных в мешок (крайне
важно иметь мешок). Чтобы узнать, является ли дан-
ный предмет элементом множества, нужно просто загля-
нуть в мешок и посмотреть, лежит он там или нет. По
этой причине самый лучший мешок—полиэтиленовый!
Для дальнейшего изложения он будет весьма полезен.
Мы будем строить алгебру множеств. Как и в обыч-
ной алгебре, множества и их элементы обозначаются
буквами. Мы используем маленькие буквы для обозначе-
ния элементов, а большие — для обозначения множеств,
однако строго придерживаться этого’правила невозможно,
ибо множества сами могут стать элементами других
множеств (вложите один мешок в другой). Если X — мно-
жество всех эпических поэм, а х — «Потерянный рай», то
х является элементом X. Фраза «является элементом»
повторяется столь часто, что удобно заменить ее каким-
то символом. Общепринятым является символ СТа-
ким образом,
х € X
означает, что «х является элементом X».
Множество считается известным, если мы знаем его
элементы или в принципе можем их найти. Задать мно-
жество можно многими способами; простейший из них —
перечислить его элементы. Так список избирателей опре-
деляет множество лиц, имеющих право голоса. Перечень
элементов множества заключают обычно в фигурные
скобки. Например, {1, 2, 3, 4} —это множество, элемен-
тами которого являются числа 1, 2, 3, 4 и только они;
{весна, лето, осень, зима} — это множество времен года.
На рис. 19 изображено множество {карандаш, бусинка,
сахарный мышонок}; фигурные скобки играют здесь роль
полиэтиленового мешка.
Два множества равны, если они состоят из одних и
тех же элементов. В полиэтиленовый мешок мы можем
положить два карандаша, но не можем дважды поло-
59
жить один и тот же карандаш (не вынув его предвари-
тельно оттуда). К сожалению, взятие в фигурные скобки
не создает такого чисто физического ограничения, и впол-
не можно написать что-нибудь вроде {1, 2, 3, 4, 4, 4}.
Буквально это означает множество, элементы которого
1, 2, 3, 4, 4 и 4. В книге про Винни-Пуха 2 есть место, где
Кролик перечисляет жите-
лей Леса и Пух несколь-
ко раз повторяет: «И еще
Иа, я про него чуть было
не позабыл». И хотя об
Иа упоминают несколько
раз, в Лесу есть всего
один Иа. Точно так же,
хотя число 4 написано не-
сколько раз, в нашем
множестве всего одно чи-
Рис ело 4, т. е. это множество
равно {1, 2, 3, 4}. При ис-
пользовании фигурных скобок подразумевается, что эле-
менты, указанные более одного раза, входят в множест-
во один раз.
Далее, предметы в мешке никак не упорядочены, а фи-
гурные скобки вводят искусственный порядок, поскольку
мы читаем слева направо. Множество {1, 3, 2, 4} состоит
из тех же самых элементов, что и {1, 2, 3, 4}, и, следова-
тельно, это то же самое множество, т. е. порядок внутри
фигурных скобок не имеет никакого значения.
Может возникнуть вопрос: что, если включить в мно-
жество два карандаша? Если это разные карандаши —
пожалуйста, кладите их оба. Поскольку они разные, вам
не придется класть какой-то предмет дважды, вы поло-
жите просто два сходных предмета. Если же это один и
тот же карандаш, то у вас нет двух карандашей.
Эти соглашения в высшей степени разумны. В самом
деле, если ваше имя дважды встретилось в списке избн-
60
рателей, разве это дает вам два голоса? И разве порядок
в этом списке предполагает какие-нибудь привилегии?
В более общем случае символ
{все эпические поэмы}
означает множество всех эпических поэм. То же самое
множество можно обозначить еще так:
{х | х — эпическая поэма}.
Вертикальную черту можно читать как «такой, что»; то-
гда множество всех х, таких, что х — эпическая поэма,
совпадает с множеством всех эпических поэм, Мно-
жество
{п | п — целое число и 1^н^4}
совпадает с множеством
{1, 2, 3, 4}.
Итак, вместо того чтобы перечислять все элементы мно-
жества, мы указываем свойство, в точности определя-
ющее, какие элементы мы хотим в это множество вклю-
чить. Если делать это аккуратно, заботясь о том, чтобы
точно указать требуемое свойство, то этот способ ничуть
не хуже предыдущего и, как правило, удобнее. Множе-
ства, содержащие бесконечно много элементов, напри-
мер {все натуральные числа}, вообще невозможно зада-
вать первым способом; то же относится к множествам с
конечным, но достаточно большим числом элементов.
Слово «набор» наводит на нежелательные ассоциа-
ции. Математическое понятие множества допускает мно-
жества, состоящие из одного элемента, и даже множест-
ва, вообще не имеющие элементов, в то время как «на-
бор», «совокупность», «коллекция» всегда подразумевает
какое-то довольно большое количество предметов. Вы
были бы, вероятно, разочарованы, если бы вас пригласи-
ли посмотреть коллекцию марок и оказалось бы, что она
состоит всего из одной марки (а если бы ею оказалась
61
та самая, выпущенная в 1856 г. в Британской Гвиане
черно-красная марка в один цент, только один экземп-
ляр которой известен?).
Если мы задаем множество каким-то свойством, по-
том может оказаться, что этим свойством обладает лишь
один объект, а то и вообще такого объекта нет. Но сразу
это может быть не оче-
видно, и глупо было бы
\ л J иметь какие-то перемен-
J'A / рЛ f чивые «множества», ко-
[ Г // I \ торые при ближайшем
\J ) { J \ рассмотрении могут не
J оказаться множествами.
Так, множество {п\п —
х Iх* натуральное число, боль-
Рис. 20. пие 1 и такое, что уравне-
ние xn+yn=zn имеет ре-
шение в ненулевых целых числах} содержит по крайней
мере один элемент, а именно 2, но есть ли у него еще
элементы, никто не знает. Это очень трудная проблема
теории чисел 3, уже более 300 лет остающаяся нерешен-
ной. Является такое множество собственно множеством
или нет, не должно зависеть от решения этой проблемы,
а если она когда-нибудь будет решена, может оказаться,
что 2 — единственный элемент. Поэтому нам придется
допустить множества, состоящие из одного элемента.
Такие множества не следует путать с самим этим
элементом: х и {%} — не одно и то же. В этом легко убе-
диться при помощи аналогии с мешком (рис. 20). Кро-
ме того, это подтверждается и таким соображением:
{х} состоит ровно из одного элемента, а х может содер-
жать сколько угодно элементов — ведь он сам может
оказаться множеством!
62
Пустое множество
По тем же причинам, которые заставили нас при-
знать множества из одного элемента, мы должны допус-
тить и множества, не имеющие вообще ни одного элемен-
та. Насколько мне известно, таковым является множе-
ство всех единорогов, обитающих в настоящее время в
окрестностях Бексхилла.
Множество, не содержащее ни одного элемента, на-
зывается пустым. (Представьте себе пустой полиэтиле-
новый мешок.)
А теперь многие, наверное, удивятся] существует толь-
ко одно пустое множество, т. е. все пустые множества
равны между собой (полная демократия!). Вспомним,
что два множества равны, если они состоят из одних и
тех же элементов. Если они не равны, значит, они состо-
ят не из одних и тех же элементов, т, е, в одном из них
должен содержаться по крайней мере один элемент, ко-
торого нет во втором. В данном случае одно из множеств
должно содержать элемент. Если они оба пусты, это
невозможно, следовательно, ойи не являются неравны-
ми. Отсюда вытекает, что они равны.
Странно, не правда ли? Это рассуждение часто при-
меняется в математике и не содержит ничего непонят-
ного. Тривиальные идеи иногда трудно осознать. Мы
думаем, что ищем что-то существенное, а на деле там
ничего нет, и тогда кажется, что мы не нашли того, что
искали. Любые два пустых множества равны потому,
что нет элементов, по которым их можно было бы разли-
чить (ведь содержимое двух пустых мешков одинаково).
Но тогда получается, что сахарный мышонок, который
тоже не имеет элементов, равен пустому множеству? Нет,
не получается. Доказательство относится только к мно-
жествам. Вот если сахарный мышонок — это какое-то
множество и если (что выглядит вполне правдоподоб-
63
ным) оно не имеет элементов, тогда оно равно пустому
множеству.
Установив, что имеется одно-единственное пустое мно-
жество, можно ввести для него специальное обозначе-
ние. Сейчас, как правило, для этого используется сим-
вол 0 (знак диаметра) или 0 (перечеркнутый нуль).
Нельзя сказать, что пустое множество — это «ничто» или
что оно не существует. Оно существует точно так же, как
любое другое множество, не существуют его элементы.
Не следует путать его с 0, ибо 0 — число, а 0 — мно-
жество 4.
Пустое множество широко используется в математи-
ке. В частности, оно применяется для того, чтобы выра-
зить в компактной форме отсутствие чего-либо. Пусть
17 — множество единорогов, обитающих в Бексхилле.
Тогда равенство U=0 говорит нам о том, что в Бекс-
хилле нет единорогов.
Подмножества
Нередко одно множество оказывается частью (не пу-
тать с элементом!) другого множества. Так, множество
всех женщин составляет часть множества всех людей, а
множество всех четных чисел — часть множества целых
чисел. Слово «часть», как мы увидим ниже, не совсем
удобно, и математики вынуждены были придумать для
точного обозначения этого понятия новый термин.
Множество S называется подмножеством множества
Т, если каждый элемент S является элементом Т. Так,
элемент множества IV всех женщин — женщина, т. е.
человек, а следовательно, элемент множества Н всех
людей. Значит, W—подмножество множества Н. Для
64
обозначения этой ситуации используется специальный
символ £= : запись5
W^H
означает, что W является подмножеством Н, или, как
иногда говорят, W содержится в Н.
Воспользуемся снова по-
лиэтиленовым мешком.
Здесь все уже не совсем так
просто, как в наших преж-
них примерах. Допустим,
что S состоит из каран-
даша и ластика, а Т содер-
жит тот же карандаш и ла-
стик и вдобавок три бусин-рис 21.
ки. Тогда прямая иллюстра-
ция, как на рис. 21, никуда не годится. В самом деле, по
этой картинке можно подумать, что у нас есть одно мно-
жество, элементами которого служат: 1) три бусинки;
2) множество, состоящее из карандаша и ластика.
Рис. 22 дает картинку получше, хотя для ее практи-
ческого осуществления нужны «взаимопроникающие»
мешки.
Из самого определения «подмножества» сразу выте-
кает несколько следствий. Всякое множество есть под-
множество самого себя, ибо все его элементы являются
3 Я- Стюарт
65
его же элементами. Пустое множество является подмно-
жеством любого множества, какое бы вы ни назвали.
В этом можно убедиться опять при помощи применен-
ного выше рассуждения. Если бы оно не было подмноже-
ством какого-то заданного множества S, оно содержало
бы некоторый элемент ; 0 < не принадлежащий S. По-
скольку 0 не содержит элементов, это невозможно.
(По этим двум причинам неудобно слово «часть»: полу-
чается, что часть может совпасть с целым, а может ока-
заться пустой.)
Вот еще приятное свойство подмножеств: подмножест-
во подмножества само является подмножеством, т. е.
если A s В и В £ С, то А <= С. Действительно, если
каждый элемент А является элементом В, а каждый
элемент В является элементом С, то каждый элемент А
есть элемент С.
Когда в начале гл. 3 мы говорили о «системах» чисел,
на самом деле речь шла о множествах и подмножествах.
В дальнейшем мы будем пользоваться следующими
стандартными обозначениями6 числовых множеств!
N — множество натуральных чисел 0, 1, 2, 3, ...|
Z — множество всех целых чисел ...—2, —1, О,
1,2, ...;
Q — множество рациональных чисел (вида plq, где р
и q целые и ^у=0);
R — множество действительных чисел (представимых в
виде десятичных дробей, не обязательно конечных и не
обязательно периодических; чисел вроде J/2 или л);
С — множество комплексных чисел (о нем тоже сле-
дует здесь упомянуть, хотя дальше оно встречается
редко).
Все эти множества фигурировали выше, где мы го-
ворили о «системах», а «стройную схему», в которую они
все укладываются, теперь можно представить в виде
66
N <= Z c= Q c= R <= c.
Отсюда по доказанному выше свойству получаем
NeQ, Z s R и т. n.
Очень важно не путать символы и С . Соответст-
вующие понятия имеют мало общего. Подмножества
множества {1, 2, 3} — это множества 0 ,{1}, {2}, {3}, {1,
2}, {1, 3}, {2, 3} и {1, 2, 3}; его элементы — это 1, 2 и
3. Кроме того, утверждение: если А С В и В£С, то
А б С, пе имеет места7.
Объединения и пересечения
Множества можно комбинировать между собой и по-
лучать другие множества. Среди бесчисленного количе-
ства мыслимых способов комбинирования очень мало та-
ких, которые оказались полезными, и самые замечатель-
ные из них — объединение и пересечение.
Объединением двух множеств S и Т называется мно-
жество, элементами которого являются элементы S и эле-
менты Т. Это обозначается так:
SUT.
Например, если S={1, 3, 2, 9}, а 7={1, 7, 5, 2}, то
SU^ = {К 3, 2, 9, 7, 5}.
Если
Р = {все женщины моложе 35 лет},
Q = {все кондукторы автобусов},
то Р J Q — множество всех людей, каждый из которых
представляет собой либо женщину моложе 35 лет, либо
кондуктора автобуса (либо и то, и другое).
Пересечением S{\T называется множество, состоящее
из общих элементов множеств S и Т, т, е, элементов, при-
з*
67
надлежащих обоим этим множествам. В приведенных вы-
ше примерах
Sf]T = {l, 2},
Р П Q = {все женщины моложе 35 лет, работаю-
щие кондукторами автобуса}.
Рис. 23.
Рис. 25.
Рис. 24.
Для множеств S и Т на рис. 23 SIJT получится, если
сложить все предметы в один мешок (рис. 24), a SC|T
состоит из предметов, лежащих в обоих мешках (рис. 25).
Можно нарисовать мешки не сбоку, а сверху (рис. 26).
Тогда SJT и SQT—множества объектов в заштрихо-
ванных областях на рис. 27.
Теперь можно забыть о содржимом мешков. Общая
картина объединения и пересечения двух множеств S и
Т выглядит так, как показано на рис. 28.
68
Такого рода диаграммы, на которых множества пред-
ставлены в виде кругов и те области, где лежат нужные
элементы, заштрихованы, называют диаграммами Венна
по имени их изобретателя.
Операции (J и f] подчиняются некоторым общим
законам, подобно тому как обстоит дело со сложением
Рис. 26.
SnT
Рис. 27.
и умножением чисел. Так, например, каковы бы ни были
множества А и В, всегда
A (J В = В (J А,
ЛПВ = ВПЛ.
Действительно, A (J В состоит из всех элементов А и всех
элементов В, а это все равно, что все элементы В и все
элементы А. Если нарисовать диаграмму Венна, то на
ней оба множества A U В и В U А изображаются областью,
которая получится, если заштриховать оба круга, соот-
G9
ветствующие множествам А и В. Точно так же А П В и
В А изображаются областью, общей для А и В.
Если А, В, С — три множества, то
(Л U В) U С = A U (В U С),
ИПВ)ПС = ЛП(ВПС).
Первое из этих равенств означает, что, когда мы объеди-
няем элементы трех множеств, безразлично, в каком по-
SuT
SnT
Рис. 28.
рядке это делать; точно так же не играет никакой роли
порядок и тогда, когда берутся элементы, общие для
всех трех множеств. Можно нарисовать соответствующие
диаграммы Венна. На этот раз понадобится три пересе-
кающихся кружка. Я проиллюстрирую этот метод на
примере другого закона.
Существует два закона, связывающие между собой
операции J и П • Для любых трех множеств А, В, С
(Лий)ПС=(ЛПС)и(ВПС),
И пв)ис = (xuc)n(B'uQ.
70
Диаграммы Венна, демонстрирующие первое равенство,
показаны на рис. 29.
Есть и другой способ проиллюстрировать теоретико-
множественные законы — при помощи специальных таб-
лиц8. Элемент содержится в S(JT, если он входит в S,
или в Т, или в оба эти множества. Он содержится в
Рис. 29.
SftT, если входит и в 5, и в
ву I (от in), если элемент
и букву О (от out), если не
ставить такие таблицы:
Т. Будем писать бук-
входит в множество,
входит. Тогда можно со-
st । s и т
I I I
I 0 I
0 I I
О 0 0
S Т | S n 7
I I I
I О О
О I о
0 0 о
(Скажем, третья строка таблицы S (J Т читается так: если
элемент не входит в S, но входит в Т, он входит в
SU71.)
71
Чтобы доказать второй закон, связывающий U и f] •
(ЛПВ)иС -=(ЛиС)П(ВиС),
рассмотрим восемь различных возможных вариантов вхо-
ждений элемента в Л, В и С и составим таблицы для
левой и правой частей написанного равенства. Получим
А в с лрв (Лрв)ис
I I I I I
I I О I I
1 О I О I
I О О О О
О I I О I
О I О О О
О О I О I
О О О О О
А в с | (Лис) (BUQ (ЛиС)П(ВиС)
I I I I I I
I I О I I I
I О I I I I
I О О I О О
О I I I I I
О I О О I О
О О I I I I
О О О О О О
Заметим, что два последних столбца совпадают. Это
означает, что если некоторый элемент входит в (Л П В) JC,
то он входит ив (Л UC) П (BUQ, а если не входит в
(ЛПВ)иС, то не входит и в (Л J Q П (SUQ- Следова-
тельно, эти множества совпадают, и равенство доказано.
72
На диаграммах Венна (если вы поняли, как они пред-
ставляют множества общего вида) можно увидеть, поче-
му выполняется то или иное тождество, а таблицы вхож-
дений позволяют доказать его.
Дополнения
Еще один полезный метод комбинирования двух мно-
жеств— взятие их разности А —В, которая состоит из
элементов, лежащих в А, но не лежащих в В. Диаграмма
Венна для разности показана на рис. 30. Соответствую-
щая таблица принадлежности выглядит так;
А В
А—В
J I
I О
О I
о о
о
I
о
о
Рис. 30.
Рис. 31.
Дополнением S' некоторого множества S называется
множество всех элементов, не лежащих в S. Если обо-
значить через V множество всех на свете элементов —
всего, что могло бы быть элементом какого-то множест-
ва, то дополнение S' окажется равным V—S. Таким об-
73
разом, S' изображается заштрихованной областью на
рис. 31.
Как-то страшновато представить себе это множест-
во V! Так много всего там содержится! Все числа, все
собаки, кошки, люди, книги, все возможные понятия, все
множества. А так как и само V может быть элементом ка-
кого-то множества, то и V содержится в V. Во многих от-
ношениях V слишком велико. Так, если разговор идет о
собаках и кому-то захотелось высказаться обо всех, кро-
ме овчарок, то не стоит беспокоиться о верблюдах.
В каждой конкретной задаче множества, имеющие к
ней отношение, лежат обычно в некотором универсаль-
ном множестве, уже не являющемся столь необъятным.
Когда мы говорим о собаках, разумно считать таким
универсальным множеством множество всех собак; это
удобнее, чем рассматривать множество всех животных.
Для выбора универсального множества нет какого-то раз
и навсегда установленного способа. Но если выбор сде-
лан, этим множеством можно пользоваться вместо V. То-
гда дополнение S7 состоит из тех элементов универсала
ного множества, которые не лежат в S, т. е. тех элементов
рассматриваемого типа, которые не вошли в S. Если уни-
версальное множество указано, никаких недоразумений
не возникнет.
Когда берутся дополнения множеств, отношения вклю-
чения между ними меняются на противоположные: если
S^T, то Т's S'. В самом деле, в Т содержится больше
элементов, чем в S, значит, элементов, которые не входят
в Т, меньше, чем тех, которые не входят в S. На диа-
грамме Венна это сразу видно (рис. 32).
Взятие дополнений тесно связано с отрицанием утвер-
ждений. Поэтому с помощью теории множеств удается
решить некоторые логические задачи. Рассмотрим такой
набор утверждений:
1. Животные, которых не видно в темноте, серы.
2. Соседи не любят тех, кто не дает им спать.
74
3. Кто крепко спит, громко храпит.
4. Соседи любят животных, которых видно в
темноте.
5. Все слоны крепко спят.
6. Кто громко храпит, не дает спать соседям.
Рис 32.
Эти утверждения можно перевести на язык теории мно-
жеств, если ввести следующие обозначения:
А = множество тех, кто будит соседей,
В = множество тех, кто крепко спит,
С=множество тех, кто громко храпит,
D = множество животных, которых видно в тем-
ноте,
Е = множество слонов,
/^множество тех, кого любят соседи,
G = множество тех, кто серы.
Тогда в утверждении 1) говорится, что не лежащее в D
содержится в G, т. е.
1. D'<= G.
Остальные утверждения принимают такой вид:
2. A^F',
3. В<=С,
4. DsF,
5. Е<=В,
6. С е А.
Взяв дополнения D и F, из (4) можно вывести, что F'^
Е D'. А теперь соединим все утверждения в цепочку;
75
EczB<=C<=A<=F' sD’ sG.
Так как подмножество подмножества само является под-
множеством, из этой цепочки получим, что Е s G, т. е.
все слоны серы.
Связь между теорией множеств и логикой гораздо
шире. Исследованием этой связи впервые занимался
Джордж Буль (1815—1864), работы которого вылились
в теорию, называемую ныне булевой алгеброй9.
При помощи дополнений можно объяснить одно явле-
ние, на которое вы, возможно, уже обратили внимание.
Различные теоретико-множественные тождества, или «за-
коны», встречаются как бы парами. Если взять какой-
нибудь закон, содержащий знаки (J и П, и заменить
все [J на П, а все f] на (J, получится другой закон.
Упомянутые выше законы, в которых речь шла об объ-
единениях и пересечениях, были выписаны как раз та-
кими парами.
Таким образом, наша работа по доказательству тео-
рем сокращается вдвое: доказав одну, мы одновременно
доказываем и вторую.
Это отнюдь не совпадение, а следствие двух других
тождеств, называемых законами де Моргана: для любых
двух множеств А и В
(A U В)' = А' П В',
(дпв)' = л'и в'.
И опять пара. Далее, все, что не не лежит в S, лежит в S,
и наоборот. Поэтому (S')' = S. Следовательно, можно
переписать наши тождества в виде
лив = Ц'пв/)'.
ЛПВ=(Л'иву.
Возьмем теперь любой теоретико-множественный закон,
скажем,
(лие)пс = ипс)и(впс).
76
Поскольку это справедливо для любого набора множеств
А, В, С, то оно справедливо и для их дополнений А',
В', С':
(А'I) В') ПС' = (А' ПС') U (В' ПС').
Теперь возьмем дополнения с обеих частей последнего
равенства:
((Л' U В') 0 С')' = ((Л' П С') U (В' 0 С'))'
и упростим полученные выражения, пользуясь законами
де Моргана в форме (*). Левая часть примет вид
(Л'J ВТ U С,
и окончательно
(лпв)ис
(нужно вспомнить, что (А')' = А, (В')' — В, (С'У = С).
Правая часть примет вид
(А' П СТ П (В' (}С'У
или
(ЛиС)П(В11С).
Итак, мы показали, что
(ЛПВ)иС=(ЛиС)П(ВиС),
т. е. доказали закон, в котором знаки (J и (] поменя-
лись местами по сравнению с исходным законом. Тот же
метод применим к любому другому закону, содержащему
только объединения и пересечения.
Геометрия как теория множеств
Евклид пытался дать определения некоторых основ-
ных геометрических объектов, таких, как «точка» или
«прямая». Например, точка — это нечто, имеющее опре-
77
деленное положение, но не имеющее размеров. Однако
если проанализировать понятие «положение», окажется,
что дать его определение ничуть не легче, чем дать опре-
деление точки, и два эти определения кругами ходят
друг за другом.
Ведь всякое определение должно на чем-нибудь осно-
вываться. В словаре английского языка the определяет-
ся как the definite article, и если вы не знаете, что такое
the, это вам мало поможет 10. Евклид пытался соотнести
своим идеализированным точкам и линиям объекты фи-
зического мира, но, к сожалению, ничто в реальном ми-
ре не ведет себя точно так, как его идеальные объекты.
Даже совсем маленькие элементарные частицы имеют
какие-то размеры. (И если права квантовая теория, то
на очень маленьких расстояниях само понятие размера
становится туманным: физически невозможно измерять
расстояния, меньшие, скажем, одной триллионной сан-
тиметра. Это потребовало бы такой огромной энергии,
что вы бы разнесли на куски то, что измеряли.) Наилуч-
ший способ обойти это затруднение — считать понятия
точки и прямой неопределимыми исходными понятиями,
а затем сформулировать их свойства. Такова современ-
ная версия аксиоматического метода, о котором мы еще
будем говорить в гл. 8.
Очень привлекательно понятие плоскости, составлен-
ной из отдельных точек. Другой способ сделать эти по-
нятия логически ясными — определить их при помощи
уже известных математических объектов. Нельзя опре-
делить нечто, являющееся плоскостью в физическом
смысле, однако можно определить объект, который ведет
себя так, как должна была бы вести себя идеализиро-
ванная евклидова плоскость.
Как мы уже отмечали в гл. 2, метод координат по-
зволяет сопоставить каждой точке плоскости единствен-
ную пару (х, у) координат. Таким образом, таинствен-
ный объект «точка» становится просто «парой действи-
78
тельных чисел», и эти последние ведут себя именно так,
как требуется от таинственных точек. Если мы не хотим
удариться в мистику, мы можем по определению считать
точкой пару (х, у) действительных чисел. А раз плос-
кость состоит из всевозможных точек, мы можем опре-
делить ее как множество всех пар действительных чисел.
А как быть с прямыми? И здесь на помощь приходит
метод координат. Оказывается, всякая прямая состоит
из таких точек (х, у), которые удовлетворяют уравнению
вида
ах+Ьу=с
с некоторыми фиксированными а, Ь, с. Например, урав-
нение 1 • х+ ( — 1) • у=0 определяет диагональ, проходя-
щую через начало координат из положения снизу слева в
направлении вправо вверх. Значит, прямую можно опре-
делить как множество всех пар (х, у), удовлетворяющих
какому-нибудь уравнению указанного вида. Подобным
же образом для определения геометрического понятия
окружности можно воспользоваться задающим ее уравне-
нием.
Точка лежит на прямой, если она является элемен-
том множества точек этой прямой. Точка лежит на двух
прямых L и М, если она является элементом множества
L и элементом множества М, т. е. элементом их пере-
сечения L Q М. Значит, геометрическое пересечение со-
ответствует теоретико-множественному.
Продолжая рассуждать таким образом и черпая вдох-
новение из источника, который открывает метод коорди-
нат, можно сформулировать всю евклидову геометрию
как часть теории множеств. Задавшись определенным на-
бором требований к поведению геометрических объектов,
можно построить чисто математическую теорию. И те-
перь, вместо того чтобы погрузиться в бездну метафи-
зических рассуждений о «реальной» геометрии, можно
сказать; вот некоторая математическая теория. Она опе-
79
рирует объектами, которые я называю «точками» и «пря-
мыми». Я думаю, что примерно так в реальном мире ве-
дут себя очень маленькие точки и очень тоненькие пря-
мые. После этого, чтобы узнать, так это или нет, можно
делать эксперименты. И даже если при помощи очень
точных измерений будет установлено, что вы ошибались,
у вас все-таки останется красивая теория.
В
(ДХ)
(Д,$) ca.fiCoJ)
ЛхВ
Рис. 33.
Теперь я хочу обобщить понятие пары чисел. Важно
отметить, что те пары, которые мы рассматривали выше,
упорядочены., т. е. пара (1, 3) — это не то же самое, что
пара (3, 1). Отметим их на миллиметровке. (Здесь дело
обстоит не так, как при рассмотрении множеств {1, 3} и
{3, 1}. Эти множества, как мы выше условились, сов-
падают.) Для любых двух заданных множеств А и В мы
можем определить11 упорядоченные пары (а, Ь), где
а £А и Ь£В. «Упорядоченные» .означает, что
(а, Ь) = (с, d)
тогда и только тогда, когда а = с и b = d. Затем опре-
делим декартово произведение А х В множеств А и В
как множество всех упорядоченных пар (а, Ь), где а б А
80
и b £ В. (Оно называется так в честь Декарта, который
придумал метод координат.)
Допустим, что А = {Л, □, Q) и В={£,$) . Мно-
жество А х В можно изобразить, как на рис. 33.
Заметим, что АхВ не совпадает с ВхА, ибо послед-
нее содержит, например, элемент (£, д) , который не вхо-
дит в Ах В.
Вспомним обозначение R для множества действитель-
ных чисел; в свете сказанного выше плоскость — это мно-
жество RXR. Принято пользоваться более простым
обозначением R2. Тогда евклидову геометрию можно
представлять себе как изучение подмножеств плоскос-
ти R2.
Глэвэ S
ЧТО ТАКОЕ ФУНКЦИЯ!
В элементарной математике мы встречаемся с разны-
ми объектами, которые называют словом «функция»: ло-
гарифмическая функция, тригонометрическая функция,
показательная функция. Эти объекты характеризуются
одним общим свойством: для каждого числа х функция
принимает некоторое определенное значение, а именно
log х, sin х, cos х, tg x, ex и т. д.
Кроме того, нас учат строить графики функций: над
точкой х отмечать значение функции в ней. На рис. 34
показаны графики четырех общеизвестных функций.
Рис. 34.
82
По традиции х называют переменной (или аргумен-
том), и функция сопоставляет каждому значению пере-
менной х некоторое значение у. Если функция обознача-
ется каким-то символом, например f, то мы пишем
y=f(x).
Если под f понимается функция log, то y = logx, если
f — функция sin, то г/ = sin х.
Ни х, ни у не являются функциями, и очень трудно
точно сказать, что они собой представляют. Не являет-
ся функцией и f(x), ибо это есть значение функции в х.
Функция — это f. «Переменные» х и у существуют только
затем, чтобы сообщить нам, что делает f. Так, например,
функция «возведения в квадрат» принимает значение х1 2
для любого заданного значения х. Это обстоятельство
можно кратко выразить формулой
У=х2,
однако если нам заранее не скажут, то мы не будем
знать, что это за формула — определение функции или
уравнение, которое нужно решить.
О формулах
Большинство функций в школьной математике выра-
жаются какой-нибудь формулой: у = х2, у = Д/гх, у = |х|
или посложнее
1 + X
Отсюда берет начало заблуждение, что математика —
это формулы, а смысл жизни математика — выводить все
более сложные формулы и применять их для все более
трудных вычислений. Это совсем не так. Более того, без-
думная манипуляция формулами не раз приводила к раз-
ным нелепостям. Я приведу один пример из дифферен-
83
циального исчисления, но пусть не пугается тот, кто не
знает, что это такое,— он тоже сможет уловить суть дела.
Когда-то я давал своим ученикам такую задачу: про-
дифференцировать функцию
z/ = log (log (sinx)).
Если, не думая, следовать стандартным правилам диф-
ференцирования, в ответе получится
1 1
• • COS X
log (sin х)--sin х
или
ctg х
log (sin x)
Большинство учеников были очень довольны таким от-
ветом. Когда же я просил их нарисовать график функции
log (log (sinx)), они пугались, поскольку тут выясня-
лось, что формула не имеет смысла. В самом деле, sin х
при любом х не превосходит 1 и, значит, log (sin х) ^0,
а так как логарифм отрицательного числа не определен,
то log (log (sin х)) не существует; формула оказывается
с подвохом.
С другой стороны, полученная «производная»
ctg x/Iog (sin х) имеет смысл для тех значений х, для
которых sin х>0.
Некоторым, может, и нравится жить в мире, где из не-
существующих функций получаются существующие про-
изводные, но я не из их числа.
Любая данная формула может не иметь смысла для
некоторых значений переменной х. Так, 1/х не определено
при х=0, log х не определен при х^О, a tg х не опреде-
лен при значениях х, равных нечетным кратным 90°. Для
более сложной формулы условия, при которых она не
имеет смысла, могут оказаться более хитрыми. Напри-
мер, выражение
84
log(x2— 1)
x'1 — 5x + 6
не определено, когда — l^x^l, или х=2, или х=3.
К тому же есть много полезных функций, которые не-
легко задать формулами. (И тут возникает еще вопрос:
какими формулами? Скажем, для функции «синус» при-
шлось придумать спе-
циальный символ sin.)
Широко применяются в
математике такие функ-
ции, как, например, «це-
лая часть х», обозначае-
мая [х]:
[х] = наибольшее целое
^х,
или функция, изображен-
ная на рис. 35:
при х < — 1,
при — 1 ^х 1,
при 1 < х.
В теории рядов Фурье встречаются функции наподо-
бие квадратной волны (рис. 36).
Математики долго спорили, считать ее функцией или
нет. Она не похожа на привычные функции, и для нее,
85
как будто бы, нет подходящей формулы. Положение
ухудшилось, когда удалось доказать, что бесконечный
ряд
sin х+ -o-sin Зх+ sin 5х+...
о о
можно просуммировать, и его сумма будет как раз та-
кой квадратной волной. Подумать только, как могли та-
кие приятные и понятные тригонометрические функции
породить это нелепое угловатое создание!
Чтобы уладить этот спор, потребовалось больше ста
лет. Отчасти это было вызвано тем, что проблема: «Функ-
ция это или нет?» — переплеталась с другими подобны-
ми проблемами, например: «Что такое бесконечный ряд?»
Однако главная причина состояла в том, что каждый ма-
тематик по-своему представлял себе функции и не согла-
шался с другими.
Белее общие функции
Мы уже видели, что функция f не обязательно опре-
делена при всех значениях переменной х. Если значе-
ние f(x) задается формулой, эта формула при некото-
рых х может не иметь смысла.
Значения х, при которых функция определена, обра-
зуют подмножество множества R действительных чисел.
Это подмножество называется областью определения
функции f; оно сообщает нам, к каким значениям х мож-
но применять функцию f.
Из всех свойств, общих приведенным выше примерам
функций, выделим одно, особенно важное: каждому эле-
менту х области определения функции f сопоставлено
единственное значение f (х).
Кроме области определения, с каждой функцией свя-
зано еще одно множество — область значений. Оно со-
стоит из всех значений, которые функция принимает на
86
элементах своей области определения. Так, область зна-
чений функции sin состоит из всех действительных чисел
от —1 до +1, а областью значений функции «возведения
в квадрат» является множество всех неотрицательных
действительных чисел.
Область значений даже простой функции может ока-
заться очень сложной. Например, функция f, определен-
ная на множестве положительных целых чисел формулой
/ (л) = УхГ
(положительный квадратный корень), имеет в качестве
области значений множество всех квадратных корней из
факториалов. Трудно придумать более «удобное» описа-
ние множества, не правда ли?
По этой причине нас не будет особенно интересовать
точная область значений заданной функции. Часто важ-
нее знать, куда попадают эти значения, т. е. уметь на-
звать какое-нибудь удобное множество Т, в котором они
все содержатся. В таком случае мы будем говорить, что
f есть функция из области определения D в множество Т.
Итак, понятие функции состоит их трех неотъемлемых
частей:
1) области определения D;
2) множества Т, содержащего область значений;
3) правила, которое для каждого х £ D задает един-
ственный элемент f (х) С Г.
Суть дела изложена в пункте 3. Важно, что f(x) опре-
делено однозначно, так что с ним не связано никакой не-
определенности. Взятие квадратного корня не определя-
ет функции, пока не сказано, какой берется корень —
положительный или отрицательный. Важно также, что
f(x) определено для каждого х из D. Знание области
определения говорит нам о том, где безопасно применять
функцию f В то же время необязательно знать точную
область значений f: часто ее трудно описать, а мы хотим
пользоваться функцией f, не занимаясь подобными проб-
87
лемами. Поэтому нам предоставлена возможность выби-
рать Т любым удобным способом.
Осталось еще одно слово в пункте 3, которое требует
пояснения: «правило». Пока будем считать, что все мы
знаем, что такое «правило»: некий способ получить f(x)
для заданного конкретного х. К этому нужно добавить
следующее: достаточно, чтобы f(x) в принципе можно
было вычислить по х. Практически такое вычисление
может оказаться невыполнимым: либо слишком трудо-
емким, требующим слишком много времени, либо свя-
занным с решением какой-то очень трудной задачи.
До сих пор область определения и область значений
были у нас множествами действительных чисел. Однако
понятие функции в смысле 1, 2 и 3 пригодно для любых
множеств D и Т. Более того, правила, предусмотренные
в пункте 3, совершенно естественно проявляются во мно-
гих ситуациях, когда D или Т не являются множествами
действительных чисел. Это замечание весьма важно для
всего последующего, поэтому я приведу несколько при-
меров.
1. Пусть D—множество всех окружностей, а Т —
множество действительных чисел. Для каждой окружнос-
ти х положим
f(x)= радиус х.
2. Пусть D — множество положительных целых чисел,
а Т включает в себя все множества, составленные из
простых чисел. Для любого х € D положим
f(x) = множество простых делителей X.
3. Пусть D — некоторое множество на плоскости, а
Т — вся плоскость (подразумевается множество R2). Для
х £ D положим
Дх)=точка, лежащая на 5 см вправо от х.
4. Пусть D — множество всех функций, a Т — множе-
ство всех множеств. Для любой функции х положим
88
f(x) = область определения х.
В каждом из этих примеров указано лишенное дву-
смысленности правило, по которому определяется f(x).
Особенно интересен пример 3. В гл. 2 мы определили пре-
образование Т:
Т(х, у)= (х+5, у).
То же самое правило определяет функцию f в примере 3:
по существу между Т и f нет никакой разницы.
Современное понятие функции сформулировано так,
что оно подходит ко всем этим примерам. Отныне функ-
цией будем считать все, что удовлетворяет условиям 1, 2
и 3, где D и Т могут быть множествами вполне общего
вида. Наши прежние функции относились к специально-
му типу функций действительного переменного — их
области определения и значений принадлежат множест-
ву действительных чисел.
Функция [, для которой f (х, у) = (х+5, у), зависит от
двух переменных. Таким образом, функции двух перемен-
ных, известные из анализа, тоже подходят под наше об-
щее определение. Для них областью определения служит
множество пар (х, у) действительных чисел, т. е. под-
множество из R2.
В связи с такой «всеохватностыо» понятие функции
служит серьезным претендентом на роль самого важного
понятия в современной математике. По мере нашего про-
движения вперед понятие функции будет снова и снова
появляться перед нами в своих разнообразных обличь-
ях, поэтому стоит остановиться на некоторых относящих-
ся к функциям общих понятиях.
Сзойстза функций
Если область определения и область значений функ-
ции не являются подмножествами R, то график такой
функции нарисовать невозможно. Да и вообще график не
89
слишком помогает при работе с нашим обобщенным по-
нятием функции. Лучше представлять себе функции так,
как показано на рис. 37. Стрелки на рисунке соответст-
вуют правилу, задающему Не-
общепринятое обозначение, отражающее тот факт,
что f — функция из D в Т, таково:
/: D->T,
и здесь стрелка используется в том же качестве.
На рис. 37 мы видим, что в Т есть элемент, на который
не указывает ни одна стрелка. Это свидетельствует о
том, что область значений f не заполняет все Т. Если об-
ласть значений f совпадает с Т, то говорят, что f — функ-
ция из D на Т. Такую функцию называют также сюръек-
тивной (или сюръекцией). На рисунке в таком случае к
каждому элементу Т ведет хотя бы одна стрелка (рис. 38),
90
При этом к некоторым элементам Т могут вести не-
сколько стрелок. Если же к любому элементу Т ведет не
более одной стрелки, то f называется инъективной (или
инъекцией). Инъективные функции не обязательно сюръ-
ективны (стрелки ведут не ко всем элементам Т, как на
рис. 39),
Рис. 39.
Если функция f: D->T одновременно инъективна и
сюръективна, то стрелки соединяют по два элементы D
и Т. При этом выполняются следующие условия. Ника-
кие два элемента из D не соединяются с одним и тем же
элементом Т, ибо / инъективна. Никакие два элемента
из Т не соединяются с одним и тем же элементом D по
условию 3 определения функции (из-за требования един-
ственности). Каждый элемент из D попадает в такую
пару, поскольку D •—область определения. Наконец,
каждый элемент из Т тоже участвует в одной из пар,
ибо f сюръективна. Хотя это и не очевидно из наших
обозначений, роли D и Т совершенно одинаковы, и если
повернуть все стрелки вспять, получится другая функ-
ция g: T->D, которая тоже инъективна и сюръективна
(рис. 40).
Функции, допускающие такое обращение, будут играть
большую роль в некоторых наших дальнейших исследо-
ваниях. Их называют биекциями или взаимно однознач-
ными соответствиями.
91
Ничто не мешает нам попробовать повернуть все
стрелки обратно и в том случае, когда f не биективна. Од-
нако при этом функция не получится. Если f не инъек-
тивна, то от некоторого элемента из Т начнутся две стрел-
ки, и «обращенная» функция не будет однозначно опре-
деленной, если же f не сюръективна, то в Т найдутся эле-
менты, в которых она вообще не определена.
Рис. 40.
В гл. 2 мы рассматривали композицию преобразова-
ний F и G: новое преобразование FG, состоящее в том,
что сначала выполняется G, а затем F. Но преобразова-
ния — это разновидность функций. Нельзя ли тем же спо-
собом комбинировать функции?
Возьмем две функции f и g и попробуем определить
функцию fg. Как и в случае преобразований, мы хотим,
чтобы
fg(x)=f(g(x)).
92
Эта формула имеет смысл, если выполняются несколь-
ко условий. Во-первых, чтобы было определено g(x),
1. х должно лежать в области определения g.
Во-вторых, чтобы можно было образовать f(g(x)),
2. g (х) должно лежать в области определения /. До-
пустим, что /: А -> В и g: С D. В силу условия (1)
Рис. 41.
самое большее, на что можно надеяться, —это что fg
имеет область определения С. Чтобы fg была определена
на всем С, для всех х € С должно выполняться условие
(2). Иными словами, область значений функции g должна
лежать в области определения А функции /. Если это
так, то fg, определенная написанной выше формулой,
будет функцией из С в В (рис. 41).
Итак, функция fg реализует идею: «применяй g, за-
тем применяй f». Если у нас есть три функции f, g и h и
их области определения и области значений нужным об-
разом соответствуют друг другу, мы можем применять
по порядку все три: сначала h, затем g, затем f. При этом
можно двумя способами комбинировать их в пары: при-
менить h, а затем fg либо применить gh и затем f, что
соответствует выражениям
(fg)h и f(gh).
К счастью, результат не зависит от выбранного способа
(рис. 42). Проверим это:
93
(fg)h(x) = (fg) (h(x)) = f(g(h(x))),
f(gh) (x)4(Sh(x)4(g(h(x))).
Итак, всегда
(fg)h^f(gh),
Будем говорить, что операция композиции функций удов-
летворяет закону ассоциативности.
________g/t Выше было сказано,
LJ— . 5»Z-A что f, g н h можно комби-
\ \ нировать, при условии
х^£^ / \ что их области определе-
^xV^, уГ ния и области значений
\ нужным образом соответ-
/8 х. \ ствуют друг другу. Легко
/ понять, что это означает:
Q область значений h долж-
fg на быть подмножеством
рис 42 области определения g, а
область значений g —•
подмножеством области определения f, Вернемся к на-
шей «незаконной» формуле
log (log (sin х)).
Она отвечает композиции функций sin, log и снова log.
Положив /i = sin и f"=g = log, получим log(log(sin х)) =
^fgh(x).
Область определения синуса —• все множество R, а об-
ласть значений — множество действительных чисел от
— 1 до +1. Область определения логарифма — множест-
во положительных действительных чисел, его область зна-
чений— все множество R. Таким образом, условия
позволяющие составлять композицию функций, наруша-
ются сразу в нескольких местах: область значений сину-
са не содержится в области определения логарифма, а об-
ласть значений логарифма не содержится в его области
определения. Не удивительно, что формула бессмыс-
ленна!
94
Наконец, вернемся к идее обращения стрелок и при-
дадим ей строгую математическую форму.
На любом множестве D определена функция, называ-
емая тождественной. Она обозначается 1D, имеет область
определения D, область значений D и задается формулой
1 £> (х) = х для всех х б D.
Ее действие состоит в том, что она оставляет все на сво-
их местах. Много ли проку от такой функции? Конечно,
это не слишком сложная функция. Но она нам очень при-
годится именно тогда, когда мы захотим выразить то, что
какая-то композиция функций оставляет все на своих
местах.
Выше мы рассмотрели биекцию /: D-*-T. Обратив все
стрелки, мы получили другую функцию g: T->D. Если
выполнить сначала g, а затем /, то все останется, как
было: каждый элемент «пропутешествует» по одной и той
же стрелке туда и обратно и вернется на свое прежнее
место. Этот факт и выражается формулой
fg= It-
Точно так же (*)
Два этих равенства означают, что fug получаются од-
на из другой обращением стрелок. В этом случае f на-
зывают обратной функцией Kg (a g — обратной к f). Лег-
ко показать, что обратная функция единственна: имеет-
ся только один способ обращения стрелок.
Выводы
Эта глава носила несколько учебный характер. Пере-
числим основные моменты, которые важно помнить.
Функция определена на некотором множестве.
Она принимает значения в некотором множестве.
Она задана, если известно правило, позволяющее
05
найти ее значение на каждом элементе, причем
единственным образом.
Биекции, или взаимно однозначные соответствия,—
это те и только те функции, для которых сущест-
вуют обратные.
Я не стал распространяться здесь по поводу слова
«правило». Более изощренное теоретико-множественное
определение функции помещено в примечаниях *, ибо
оно представляет интерес лишь с чисто формальной точки
зрения.
Глава 6
ОСНОВЫ АБСТРАКТНОЙ АЛГЕБРЫ
С самого начала изучения алгебры возникает потреб-
ность упрощать выражения типа 2x4-(у—х). Постепенно
приобретаются навыки в такого рода вычислениях, и вам
уже достаточно взглянуть на это выражение, чтобы, не
задумываясь, написать х+у.
С привычкой приходит пренебрежение. Вы забываете,
как много трудных этапов пришлось пройти, как много
сложных идей потребовалось воспринять, прежде чем
вы обрели эту легкость. Если попытаться выписать под-
робно все шаги, необходимые для упрощения выражения
2x4- (у—х), их окажется порядочно.
Вот как я упрощаю это выражение (со всеми подроб-
ностями) :
2х 4- (у — х) = 2х 4- (у + (— х)) (1)
= 2х 4- ((- х) +у) (2)
= (2х 4- (—х)) 4- У (3)
= (2х 4-(—1)х) 4-у (4)
-(2 + (-1))х4-«/ (5)
= 1-х 4- У (6)
= х 4 у. (7)
(1) и (4) —второстепенные шаги, состоящие в исполь-
зовании определений элементов ( —х) и (у—х), а шаг
(6) — это простая арифметика. Но каждый из осталь-
ных шагов использует справедливость некоторых общих
арифметических законов (вероятно, их было бы лучше
назвать алгебраическими). На шаге (2) я предполагаю,
что а + Ь = Ь + а. На шаге (3) использую закон, согласно
которому а+(Ь + с) — (а + Ь)+ с, на шаге (5) —пра-
вило ах + Ьх— (а + Ь)х, а на шаге (7) —-правило 1 -х = х.
4 Я- Стюарт
97
Мы можем перечислить самые важные из этих зако-
нов, оставляя пока в стороне законы, связанные с деле-
нием:
(1) закон ассоциативности сложения:
(а + b) +с=а+ (Ь + с)-,
(2) закон коммутативности сложения:
a + b = b + a;
(3) существование нуля:
существует число 0, такое, что a+0=a=0+fl для
любого числа а;
(4) существование обратного по сложению:
для любого числа а найдется число —а, такое, что
а+(-а) =0= ( — а) +а-
(5) закон ассоциативности умножения:
(ab)c = a(bc)\
(6) закон коммутативности умножения:
ab = ba-t
(7) существование единицы:
существует число 1, такое, что 1о = а1 = с для любого
числа а;
(8) законы дистрибутивности:
a(b + c) =ab+ac,
(a + b)c=ac + bc.
Такое обилие законов не усложняет алгебру. На са-
мом деле, чем больше законов, тем лучше, потому что
у нас больше способов упрощать выражения.
На справедливости этих законов основаны даже неко-
торые из наших алгебраических обозначений, Мы можем,
не опасаясь двусмысленности, писать
а -|- b -|- с
98
лишь потому, что выполняется закон ассоциативности.
Большую часть элементарной алгебры составляет до-
казательство различных формул с помощью этих зако-
нов (хотя она не всегда предстает перед нами в этом све-
те), Формулу
(х+у)2=х2+2ху+у2
можно вывести следующим образом. Отметим сначала,
что для любого числа с мы определяем а2 как а • а, а
2а — как а + а. Далее, а + Ь + с — это сокращенная запись
для (а + b) +с. Теперь сам процесс вычисления:
(обозначение)
(закон 8)
(закон 8)
(обозначение)
(закон 6)
(закон 1)
(закон 1)
(обозначение)
(обозначение)
(х+у)2 = (л'+у) (х+у)
= (х(х+у)) + (у(х+у))
= (хх+ху) + (ух+уу)
= (х2+ху) + (tjx+y2)
= (х2+ху)+)ху+у2)
= ((х2+ху) +ху) +у2
= (х2 + (ху + ху)) +у2
= (х2+2ху) +у2
=х2 + 2ху+у2
Приложив чуть больше усилий, мы могли бы доказать,
что обычные формулы верны и для (х+у)3, (х+у)4, и
даже вывести формулу бинома (для целых показате-
лей) — и все это лишь с помощью законов (1) — (8),
Кольца и поля
Обычные числовые системы (Z, Q и R) —это еще не
все системы, в которых выполняются законы (1) — (8).
Они также, например, справедливы (хотя я пока не буду
приводить доказательство) для целых чисел по модулю 6.
Рассмотрим несколько выражений:
(1+4)+3=5 + 3=2= 1+ 7= 1 + (4 + 3),
2-5=4 = 5-2,
4*
99
1.4 = 4 = 4- 1,
3(2 + 5) =3- 1 = 3=0 + 3= (3-2) + (3-5).
Как следствие для целых чисел по модулю 6 справед-
лива формула (х+у)2 = х2 + 2ху+у2 (ведь для ее вывода
использовались лишь правила (1)- (8)).
В числе 6 нет ничего особенного. Целые числа по мо-
дулю 2, 3, 4, 5, 6, 7, наконец, по модулю п для произ-
вольного п удовлетворяют законам (1) — (8). И для
всех этих систем справедлива формула (х+у)2~
= х2 + 2ху+у2, причем с тем же доказательством.
Математики в глубине души — лентяи. Труд, затра-
ченный на доказательство данной формулы в каждой
из систем целых чисел по модулю 2, по модулю 3, по мо-
дулю 4, по модулю 5, ..., кажется неоправданно большим
по сравнению с результатами, особенно, если для всех
случаев годится одно и то же доказательство. Почему бы
не сказать просто, что это доказательство проходит во
всех системах, удовлетворяющих требованиям (1) — (8)?
А чтобы еще прояснить ситуацию, почему бы как-нибудь
не назвать такие системы, и тогда не надо будет пере-
числять каждый раз все эти восемь правил.
Общепринятое название для таких систем —• комму-
тативное кольцо с единицей — термин несколько громозд-
кий. Кольцо — это множество S с двумя определенными
на нем операциями + и •, такими, что если s и t лежат
в S, то $ + / и s • t тоже лежат в S, и выполняются законы
(1) — (5) и (8). Дальше мы будем писать st вместо s • t.
Кольцо называется коммутативным, если выполняется
еще закон (6). Оно обладает единицей, если выполняется
закон (7). Наиболее короткий термин «кольцо» исполь-
зуется для объектов, с которыми мы сталкиваемся чаще
всего. Но в этой книге некоммутативные кольца встре-
чаться не будут, поскольку область, из которой мы чер-
паем примеры, весьма ограниченна.
Использование символов ху и ху для «сложения»
100
и «умножения» в кольце — это всего лишь соглашение —
хотя очень удобное! Если бы мы взяли вместо + и • сим-
волы □ и з, то потребовали бы, чтобы выполнялись
соответствующие законы: закон (8) в этом случае выгля-
дел бы так:
аз (Ь □ с) = (а з Ь) □ (а з с),
(а □ Ь) з с = (а э с) □ (Ь з с).
Исходное множество S для кольца не обязательно
должно быть множеством чисел. Даже когда рассматри-
ваются целые числа по модулю 7 и в качестве S берется
множество {1, 2, 3, 4, 5, 6, 0}, то его элементы — не на-
стоящие числа; на самом деле не важно, что собой пред-
ставляют эти элементы, если сложение и умножение для
них задано с помощью таблиц на с. 42 и 44. Можно,
например, рассмотреть произвольное множество Т и
взять в качестве S множество всех его подмножеств.
Определим операции так:
а + b = (a [J b)\(a fi b),
ab = а Ь,
где а, b € 5 (рис. 43).
Остается проверить, что все законы (1) — (8) для
этих операций на S выполняются,— это громоздкое, но
простое упражнение по теории множеств. Пустое множе-
ство 0 играет роль 0 в правиле (3), в. то время как все
Т—это 1 в законе (7). Обе части равенства (1) пред-
ставлены на рис. 44.
Что такое в этом кольце х2? Напомним, что х2 = хх.
Элементы множества хх — это те, которые лежат одно-
временно в х и в х, т. е. все элементы из х. Таким образом,
хх—х. Это кольцо обладает любопытным свойством —
в нем х2 = х для всех элементов! Если в качестве Т мы
101
взяли множество, содержащее ровно п элементов, то X
содержит 2П элементов, и у нас получилось кольцо, в ко-
тором квадратное уравнение
х2 — х=0
имеет 2п решений. Если Т бесконечно, то это уравнение
имеет бесконечно много решений!
а + Ь
Рис. 43.
ab
Рис. 44.
Мы говорили выше, что в любом кольце справедливо
равенство (х-\-у)2=х2-\-2ху+у2. Если же каждый эле-
мент рассматриваемого кольца удовлетворяет условию
х2=х, то указанное равенство примет вид
х+у = х + 2ху+у,
а отсюда (с помощью законов (4), (1) и (3)) получает-
ся, что
2ху = О
для любых х, у. На самом деле в нашем кольце верно и бо-
лее сильное утверждение. Для любого элемента х из 5
2х — х -j- х = (х U х) — (х[}х) — х — х = 0 =0.
Ну и, разумеется, 2хг/=0. Хотя это кольцо обладает мно-
гими специфическими свойствами, обычная формула
для (х+у)2 ничему не противоречит.
102
Ветвь математики, известная под названием теории
колец, состоит из всех утверждений, которые можно
вывести из законов (1) — (5) и (8),— это те теоремы, ко-
торые верны для всех колец. Если в ходе своих исследо-
ваний математик наталкивается на систему, удовлетворя-
ющую всем этим требованиям, он говорит себе: ага, коль-
цо! — и понимает, что из этого замечания уже вытекает
определенный набор свойств. (Правда, это редко решает
все его проблемы.)
Если мы введем в рассмотрение деление, то появятся
еще два важных закона:
(9) существование обратного по умножению:
если а 7^=0, то существует элемент а~1 , такой, что
аа~~1 = 1 = а~1а;
(10) 0 7^=1. (Это для того, чтобы исключить некоторые
тривиальные системы.)
ЛЪюжество S, обладающее операциями сложения и
умножения, которые удовлетворяют законам (1) — (10),
называется полем. Результаты гл. 3 о делимости показы-
вают, что целые числа по модулю п образуют поле тогда
и только тогда, когда п — простое число. Таким обра-
зом, возникает масса примеров колец, не являющихся по-
лями,— сюда относятся все кольца целых чисел по мо-
дулю п, где п не является простым числом.
Исторически понятия кольца и поля возникли при
изучении алгебраических чисел, т. е. чисел, удовлетво-
ряющих уравнениям, левые части которых являются
многочленами, таким, например, как х2 — 2 = 0 или
17х23 — 5х5 4- 439= 0. Первому из них удовлетворяют
числа ±1^2 (относительно решения для второго у меня
нет никаких соображений!), и на некотором этапе раз-
вития теории полезно рассмотреть всю совокупность чи-
сел вида a -f- b | 2 для целых а и Ь. Поскольку
(а 4- b Y2)(с 4- d ]/2) = (ас 4- 26d) 4-
103
+ (ad + be) 1 2,
оказывается, что они образуют котьца.
Если считать теперь а и b рациональными, то для лю-
бого элемента мы сможем найти обратный:
Таким образом, мы получили поле. С помощью тео-
рии колец и теории полей были обнаружены многие глу-
бокие свойства алгебраических чисел. В частности, эти
теории применяются в современных изложениях нераз-
решимости в радикалах уравнения общего вида степе-
ни 5 *.
Применение к геометрическим построениям
Серьезное исследование уравнения пятой степени уве-
ло бы нас слишком далеко в сторону. Но некоторые
возможности названных выше теорий можно проиллюстри-
ровать на примере проблемы, использующей менее слож-
ный аппарат. У древних греков существовала известная
геометрическая задача (ее часто приводят в виде легенды,
связанной с оракулом острова Делос2): как построить
отрезок длины -j/ 2, если дан отрезок длины 1? По-
строение должно быть выполнено лишь с помощью цир-
куля и линейки (платоново ограничение). Греки не смог-
ли найти решение этой задачи (хотя открыли полезное
коническое сечение).
Мы покажем, что такое построение осуществить не-
возможно.
Если даны отрезки длины г и s, то указанным на
рис. 45 способом можно построить отрезки длины r+s,
г—s (если r^s), rs и r/s. (Мы считаем, что отрезок дли-
ны 1 задан, чтобы фиксировать масштаб.)
104
Будем говорить, что число а можно построить, если
можно построить отрезок длины |а|. Множество К всех
таких чисел является подмножеством множества R
всех действительных чисел. Нетрудно видеть (см.
рис, 45), что, не выходя за пределы этого множества, его
Рис. 45.
элементы можно складывать,
вычитать, перемножать, и де-
лить друг на Друга; отсюда
легко получить, что К — поле.
Оно является подполем по-
ля R.
Кроме того, в рамках этого
множества можно извлекать
корни из его положительных
элементов, как показано на
рис. 46.
105
Если начать с отрезка заданной длины 1, то, исполь.
зуя указанные на рис. 45 построения, мы сможем по-
112
строить числа 2, 3, 4, ... , -у, -р ... , и вообще
любые положительные рациональные числа. Далее, для
любого такого числа г мы можем построить ]/7”(рис. 46).
Тогда можно построить все числа вида
p + qVr
для любых рациональных р и q. Множество всех чисел
такого вида образует поле (обозначим его через Ех), по-
скольку формула
(р+9 щг'- М-М+
\ ра — rq* ] \ р2 — rq2 )
обобщающая соответствующую формулу для р + q ]/?,
позволяет находить обратный по умножению элемент.
Теперь можно повторить этот процесс, начиная с по-
ложительного элемента s С Ех, и построить J/^s, а затем
все числа вида p-}-q]fs, где р, q принадлежат Тем
самым мы получим большее поле F2. Проведя этот про-
цесс еще раз, но уже исходя из поля Е2, мы получим
поле F3. Вообще получается возрастающая последова-
тельность полей
Q — Л — ^2 — ^3 — ••• — Pk — Fk-\A — • • I
и любое число из любого поля Fi может быть построено.
Существуют ли еще какие-нибудь числа, которые мож-
но построить?
Конечно, мы могли бы брать различные элементы г,
s, .... когда строили квадратный корень. Но это ведет
лишь к аналогичной последовательности полей. Есть ли
числа, которые можно построить, но с помощью нашей
процедуры получить нельзя?
106
Любое геометрическое построение можно разбить на
последовательность шагов следующих трех типов:
1) нахождение точки пересечения двух прямолиней-
ных отрезков, концы которых уже построены;
2) нахождение точки (точек) пересечения прямоли-
нейного отрезка и окружности, если уже построены кон-
цы отрезка, центр окружности и отрезок, длина которого
равна радиусу окружности;
3) нахождение точки (точек) пересечения двух
окружностей, если уже построены их центры и отрезки,
длины которых равны их радиусам.
Исследуя все это с помощью метода координат, мы
видим, что шаг 1 позволяет найти числа, которые можно
получить из уже построенных чисел с помощью сложе-
ния, вычитания, умножения и деления. Шаги 2 и 3 позво-
ляют находить квадратные корни из известных положи-
тельных чисел, но ничего больше. Таким образом, любое
число, которое можно построить, лежит в одном из полей
Fi при подходящем выборе чисел г, st ..., из которых мы
извлекаем квадратный корень.
Теперь мы переходим к задаче построения j^2. Если
это возможно, то 1^2 лежит в одном из полей F.. На
первый взгляд, непохоже, чтобы 1^2 можно было выра-
зить, используя лишь квадратные корни, но внешность
бывает обманчива. Уверены ли вы, что не существует ка-
кого-либо сложного выражения, вроде
з + -у- /(5 + 6]/7) - VТз,
которое равно у42?
Это, конечно, маловероятно, потому что корень-то ку-
бический. Кубические корни и квадратные корни — ве-
щи разные. Это различие и надо использовать.
107
Сначала докажем, что |/2 — не рациональное число.
Доказательство очень похоже на стандартное доказатель-
ство того, что ]/г2 — не рациональное число.
3 Л
Предположим, напротив, что число у 2 рационально,
и, следовательно, существуют целые числа с, d, для ко-
торых
3 г—
у 2 — ad.
Возможно, что с и d имеют общие делители. Если это
так, сократим на них. Иными словами, мы можем найти
целые числа е, f, не имеющие общих делителей, и такие,
что
1/2 = elf.
Возведя это равенство в куб и умножив на /3, получим,
что
2/3 = е3.
Значит е3—четное число. Куб нечетного числа нечетен,
поэтому е не может быть нечетным числом. Таким обра-
зом, е четно и существует такое целое число g, что
e = 2g.
Тогда
2р = е3 = (2g)3 = 8g3, Р = 4g3,
т. е. р четно. Отсюда, как и выше, получаем четность
числа f. Значит, существует целое число А, для которого
f=2h.
Но тогда e( = 2g) и [( = 2Л) имеют общий делитель 2, а
е и f не имеют общих делителей!
Если ей/ существуют, то они обладают свойствами,
которые противоречат друг другу. Следовательно, их не
существует, но тогда не существует и чисел с и d, а от-
сюда следует, что число ]/2 не рационально. Допустим
108
теперь, что у 2 может быть построено. Мы уже видели,
что это не рациональное число. Значит, оно должно ле-
жать в поле Fk при подходящем выборе элементов г,
s, ... Без ограничения общности можно взять k наимень-
шим из возможных.
Запишем х=]Л2. Поскольку х С Fk, то
х = Р + <7 УК
где р, q и t лежат в Fk^\, а УТ—нет, (Если J/Тлежит
в Е*-!, то Fk — Fk-i, а значит, х С Fk-i, что противоре-
чит нашему выбору наименьшего k.) Элемент х удовле-
творяет уравнению
х3 —2 = 0.
Подставляя сюда его выражение из (»), получаем, что
а + b J/7" = 0,
где
а=р3 + 3р<72^—2, & = Зр2<7 + <?3/.
Это означает, что и а, и b должны быть равны нулю, по*
скольку если бы b было отлично от нуля, то выполнялось
бы равенство
УТ ~ — alb,
т. е. yt лежал бы в Fk—i. Но мы уже отмечали, что
Уt не лежит в Fk-i. Значит, b = 0. Но тогда и а = 0.
Рассмотрим теперь число
У = P — qyt.
Нетрудно убедиться, что
у3—2 = а —Т>]/7,
где а и b те же, что и выше. Но они оба равны нулю,
следовательно,
у3—2 = 0.
109
Это означает, что у — другой кубический корень из 2.
Как х, так и у — действительные числа, но существует
лишь один действительный кубический корень из 2. Оста-
ется лишь возможность х=у, но тогда
p + qVt=p — qVi,
так что <7 = 0. Из (*) мы теперь получаем, что х=р, но р
лежит в Fk-t. Таким образом, х лежит в F^-i- Но это сно-
ва противоречит нашему выбору наименьшего возможно-
го k.
Действуя в согласии со строгой логикой, мы пришли
к противоречию. Единственное сомнительное место — это
з,-
предположение, что число у 2 —может быть построено,
значит, здесь и находится источник наших затруднений:
мы можем избежать противоречия, лишь отказавшись от
з.—
этого предположения. Итак, у 2 нельзя построить.
Другие задачи о геометрических построениях можно
рещать подобным же образом. Задача о трисекции угла
60й ведет к построению такого х, что
х3 — Зх= 1,
и аналогичные рассуждения показывают, что это невоз-
можно сделать.
Задача о квадратуре круга требует построения х=л.
Поскольку элементы из F{ получаются с помощью извле-
чения лишь квадратных корней, то можно убедиться, что
они должны удовлетворять некоторому уравнению типа
апхп + an-ixn~l + +aix+ao = O,
коэффициенты сц которого рациональны. Любопытная и
трудная теорема Линдемана 3 показывает, что л не удов-
летворяет никакому уравнению такого вида. Иначе гово-
ря, нельзя построить квадрат, площадь которого равня-
лась бы площади данного круга.
В этой связи следует упомянуть задачу о построении
по
правильных многоугольников. Построение правильного
п-угольника тесно связано с уравнением типа
хи-Ч-хи-2+ ... +%+1 = 0.
Глубокое исследование показывает, что правильный п-
угольник можно построить тогда и только тогда, когда
п = 2а-р1-...-рь,
где Рг — различные нечетные простые числа вида
22С + 1.
Известны лишь простые числа этого вида с с = 0, 1, 2, 3, 4,
а именно: 3, 5, 17, 257, 65 537. Правильные многоугольни-
ки с таким числом сторон можно построить. 17, 257 или
65 537 сторон — это впечатляет!
Все эти замечания относятся к теоретически точным
построениям. Для практических же целей нужны лишь
хорошие приблизительные построения, которые сущест-
вуют для всех разумно малых п, например достаточно
малых для того, чтобы сторону получающегося много-
угольника можно было разглядеть.
Снова сравнения
Теперь я хочу доказать, что арифметика по модулю п
определяет кольцо.
Одно препятствие сразу бросается в глаза — законы
кольца основаны на равенствах, а у меня пока есть лишь
сравнения. Но если я сумею получить равенства вместо
сравнений, останется еще одна задача — доказать, что
законы кольца здесь справедливы.
Как обычно, рассмотрим частный случай арифмети-
ки по модулю 7. В гл. 3 мы установили, что множество Z
целых чисел разбивается на семь подмножеств, соответ-
ствующих семи дням недели. Среда, например, соответ-
ствует множеству чисел {..., —11, —4, 3, 10, 17, ...}, со-
стоящему из чисел вида 7п+3,
111
Это в точности числа, сравнимые с 3 по модулю 7,
Если обозначить через [х] множество чисел, сравнимых с
х. то множества чисел, соответствующие дням недели,
будут выглядеть так: [0]. [1], [2], [3], [4], [5], [6]. Множества
И называются классами вычетов. Кроме того, [7]=[0],
[8]=[1], [9] = [2] и т. д., поскольку число сравнимо с 7 тог-
да и только тогда, когда оно сравнимо с 0.
В гл. 3 у нас встречались «равенства» вроде 7 = 0, 8 =
= 1, 9 = 2; но мы отмечали, что « = » — нс настоящее ра-
венство. Но вот [7] = [0] — действительно равенство: мно-
жества [7] п [0] совпадают. Это наводит на мысль, что, по-
ставив всюду квадратные скобки, мы превратим сравне-
ния в равенства.
Flo тогда надо определить сложение и умножение
классов вычетов. Это намерение может показаться слиш-
ком смелым. С другой стороны, в этой главе мы уже вво-
дили подобные операции на подмножествах некоторого
множества Т, так что мысль складывать и умножать мно-
жества не совсем неожиданна.
Чтобы определить эти операции, воспользуемся таб-
лицами умножения и сложения по модулю 7, только рас-
ставим везде квадратные скобки. Тогда
[4] + [5] = [2],
[3]+[1]=[4],
[5]Х[2]=[3]
и т. д.
Это шаг в правильном направлении, но в таком виде
незаметно одно важное упрощение. Ведь [2] — это то же
самое множество, что и [9], так что [4]+[5]=[9]. А [3] =
= [10], значит, [5] X [2] = [ 10]. И мы возвращаемся к обыч-
ной арифметике. Вообще
[а]+[Ь] = [а+й], (**)
[а]Х[6]=[а6].
Можно проверить, что в результате получаются те же
112
таблицы сложения и умножения, что и раньше. Если вы
все аккуратно проделаете, то убедитесь, что даже вычи-
сления в обоих случаях проводятся по существу одинако-
во, только в одних есть скобки, а в других •— нет.
Не прошли лй мы весь этот путь лишь для того, чтобы
в конце концов вернуться к обычной арифметике? К сча-
стью, нет. Законы сложения и умножения здесь такие же,
как в обычной арифметике, но есть еще дополнительные
свойства, такие, как [7]=[0], т. е. мы имеет обычную
арифметику плюс право отбрасывать числа, кратные 7.
А это и есть арифметика по модулю 7.
Теперь мы знаем, что арифметика по модулю 7 под-
чиняется по существу тем же законам, что и обычная
арифметика. Поэтому неудивительно, что возникает коль-
цо. Чтобы доказать справедливость закона (8), проведем
такие вычисления:
[а]- ([й] + [с]) =[а] • ([й + d) (определение сложения)
= [а(й + с)] (определение умножения)
= [ай + ас] - (закон 8 для обычных целых
чисел)
=[ай]+[ас] (определение сложения)
ь= ([а] • [й] + ([а] • [с]). (определение умножения)
Другие законы проверяются столь же легко. Все сво-
дится к обычным целым числам.
Те же рассуждения подходят и для модуля п при лю-
бом п. Сначала определяем классы вычетов [х], затем —
сложение и умножение, пользуясь ( **), и, наконец,
проверяем правила (1) — (8).
Надо отметить, что правила ( »* ) коварнее, чем мо-
жет показаться. По ним получается, что [1]+[3] = [4]. Но
по ним же получается, что [8]+[10]=[18]. А так как [1]=
=[8] и [3] = [10], то наступает опасный момент—- у нас
есть два значения одной и той же суммы. Но — и здесь
можно вздохнуть с облегчением — [4] = [18], так что в ко-
нечном счете ответ лишь один.
113
Не всегда дело обстоит так удачно. Если разбить Z
на два подмножества Р и Q, где
Р = {целые числа 0},
Q= {целые числа > 0},
и определить [х] как то из этих двух множеств, которому
принадлежит х (это похоже на то, как мы выбирали в
качестве [х] тот класс вычетов, которому принадлежал
х), то сразу же возникнут неприятности.
Используя формулы (** ), чтобы найти P + Q, полу-
чаем
P + Q=[-5]+[l]=[-5+l]=[-4]=F,
P+Q = [-3]+[6]=[-3+6] = [3]=Q.
Таким образом, для этих Р и Q определение ( * * ) аб-
солютно бессмысленно. Это вообще не определение!
Однако для классов вычетов ( * * ) не приводит к не-
однозначности. Проверить это можно без особых усилий.
Действительно, если в арифметике по модулю п имеем
[а] = [а'] и [й]=[й/], то a~a'=jn и b — b'=kn, где / и k —
целые числа. Значит, (п-рй) — (a' — b') = (j + k)n, откуда
[о + й]=[п' + й'], и все в порядке. Операции + и • для клас-
сов вычетов определены корректно.
Введение в комплексные числа
Комплексные числа 4 появляются при попытке решить
уравнение х2 + 1 = 0. Мы вводим новое число i такое, что
р= — 1. Чтобы складывать и умножать, нам необходимы
числа вида a + bi для действительных а и Ь. Наконец, за-
метим, что если предположить, что для них выполняются
обычные законы арифметики, то уже никаких неприятно-
стей возникнуть не должно. И, более того, в этой системе
мы сможем также делить.
Все это очень хорошо, но не слишком обоснованно,
не доказано даже, что законы арифметики действи-
114
тельно должны выполняться. И само число i кажется
таинственным: почему действительные числа названы
действительными, а мнимые — мнимыми? Это очень пе-
чально — не столько потому, что в этих названиях выра-
жено неуважение к мнимым числам, сколько из-за того,
что они приписывают действительным числам значитель-
ность, которой те никоим образом не заслуживают!
Существует способ введения комплексных чисел, ко-
торый ставит их наравне с целыми числами по модулю
п. Поскольку для целых чисел по модулю 7 нам требуется
равенство 7 = 0, то мы рассматриваем сравнения по моду-
лю 7. В системе комплексных чисел мы хотим, чтобы х2+.
+ 1 = 0, значит, надо брать сравнения по модулю х2 + 1.
Такова во всяком случае общая идея. Теперь нам надо
найти нечто, на чем можно рассматривать сравнения.
Это «нечто» должно содержать х. Мы хотим, чтобы в
окончательную систему входили действительные числа,
значит, их надо сразу включить в рассмотрение. По-
скольку мы хотим задать арифметику, нам нужно опре-
делить х+х, ххх, xxxx+lx—З и тому подобное. Эти вы-
ражения похожи на многочлены (и на самом деле ими
являются) от х с действительными коэффициентами. Мы
уже знаем, как складывать, вычитать и умножать много-
члены, и знаем, что для них выполняются законы ариф-
метики. Во всяком случае мы всегда предполагали, что
они выполняются, хотя это и не одно и то же! Но, если
захотим, мы можем доказать, что они выполняются. Это
означает, что многочлены образуют кольцо. Мы обозна-
чим это кольцо через R[x], Здесь R показывает, что коэф-
фициенты — действительные числа, а х — что именно
берется в качестве переменной, но квадратные скобки не
имеют отношения к сравнениям.
В кольце R[x] мы можем взять сравнения по модулю
х2 + 1. Скажем, что два многочлена сравнимы, если их
разность делится на х2+1. Каждый многочлен сравним
со своим остатком от деления на х2+1, Например,
115
х3+х2-2х+3=(х2+1) (х+1)+ (-Зх+2),
так что
х3+х2 —2х+3= —Зх+2 (modx2 + l).
Действительно, каждый многочлен сравним с единствен-
ным многочленом вида ах+Ь, где а и Ь — действитель-
ные числа. Все члены более высокой степени можно
исключить, вычитая подходящие кратные х2+1.
Многочлены-константы практически не отличаются от
обычных действительных чисел, несмотря на то что вве-
дены сравнения по модулю х2 + 1. Многочлен х удовлетво-
ряет условию
х2= —1 (modx2+l)
и, значит, ведет себя как мнимое число I. Тогда много-
члены ах+Ь ведут себя именно так, как должны вести
себя комплексные числа ai+b.
Законы (1) — (8) для классов вычетов по модулю х2 +
+ 1 можно проверить точно так же, как и для классов вы-
четов по модулю п, с тем лишь исключением, что здесь
мы опираемся на соответствующие законы кольца много-
членов R[x],
Наконец, заметим, что
(ах + Ь) (—ах + Ь) — —а2х2+Ь2=в
= a2+b2 (modx2 + l),
и, таким образом, если ах + Ь += 0, то мы можем найти
для него обратное
Это уже просто подарок, так как кольцо R[x], с которого
мы начинали, не является полем. Но то же самое проис-
ходило, когда мы рассматривали сравнения по модулю
п. Мы начинали с кольца Z, не являющегося полем, а за-
тем обнаружили, что, когда п — простое число, целые чи-
116
ела по модулю п образуют поле. И практически так же
обстоит дело здесь: многочлен х2+1 прост в кольце мно-
гочленов, его нельзя разложить на множители.
Мы могли бы продолжить рассмотрение и вывести все
обычные свойства комплексных чисел.
Я не утверждаю, что изложил наилучший способ вве-
дения комплексных чисел в школе. Но для тех, кто сво-
бодно владеет арифметикой по модулю п и имеет опыт
работы с комплексными числами, этот подход многое мо-
жет прояснить.
Я могу даже так сформулировать: комплексные чи-
сла — это классы вычетов кольца многочленов по моду-
лю х2 + 1. Немножко непривычно, но в сущности ничего
непостижимого!
В более легком жанре
Теория колец и полей может быть полезна и в обла-
стях, весьма далеких от абстрактной алгебры.
Для игры в солитер, как вы, вероятно, знаете, нужна
доска с отверстиями, образующими такую конфигу-
рацию:
ООО
ООО
О О О О ООО-
ООО О О О О
О О О О О О О
ООО
ООО
В начале игры в каждое отверстие, кроме центрального,
вставлен колышек. Играющий может переносить любой
колышек в свободное отверстие через любой соседний по
горизонтали и по вертикали, причем последний при этом
117
вынимается из своего отверстия. Движения по диагонали
не допускаются. Цель игры — освободить все отверстия,
кроме одного. Обычно требуют, чтобы последний колы-
шек находился в центральном отверстии. Любой, кто до-
статочно много играет в солитер, заметит, что, если и не
требовать, чтобы последний колышек оказался в центре,
представляется маловероятным, чтобы он мог оказаться
в любом другом месте. Существует ограниченное число
окончательных позиций.
В каких же отверстиях может находиться последний
колышек? Мы ответим на этот вопрос с помощью метода
де Брёвна 5, использовавшего поле из четырех элементов.
Это элементы 0, 1, р и q со следующими таблицами сло-
жения и умножения:
+ 1 о 1 р q X 0 J Р q
0 0 1 р q 0 1 1 0 q р . 1 р р q о 1 р <7 <7 р 1 0 q 0 0 0 0 о 1 р q о р q 1 о q 1 р
Мы не будем проверять здесь, определяют ли эти табли-
цы поле, но это так. Проделайте соответствующие вычи-
сления, если не верите.
Заметим, что имеет место равенство
р2+р+1=0. (***)
(Именно поэтому мы и выбрали такое поле.) Действи-
тельно,
p2+p+\ = q+P+ I
= 1 + 1
= 0.
Поставим в соответствие отверстиям на доске цело-
численные координаты следующим образом:
118
(—3,1) (-2,1)
(—3,0) (—2 0)
(-3,-1) (-2, -1)
(-1.3)
(-1.2)
(-1.1)
(-1.0)
(-1.-1)
(-1, -2)
(-1,-3)
(0.3)
(0,2)
(0,1)
(0,0)
(0,-1)
(0,-2)
(0,-3)
(1,1) (2,1)
(1.0) (2,0)
(1,-1) (2,-1) (3,-1)
(1,-2)
(3,1)
(3,0)
(1.-3)
Ситуация определяется как некоторое множество ко-
лышков на доске. Определим значение для каждой ситуа-
ции S по формуле
A (S) =
где знак S означает, что мы складываем все рк' 1 для
всех координат (k, I) колышков из S. (Отметим, что А—
функция с множеством возможных ситуаций в качестве
области определения и с полем из четырех элементов
в качестве области значений.) Таким образом, ситуация
(колышки отмечены черным)
ООО
О О Ф
о о о о о о о
о о © в о в о
о ф о в о о о
ООО
ООО
описывается множеством 5 = {(-2, -1), (-1, 0), (0,
(0, -1), (2, 0), (1, 2)} и
/1(5') =р-2~!+р-1+0 + р0+°+ р0-1 -рр2 + 0_|_р1+2
= Р“3 + р"1 +р° + р~1+р2+р3
^l+q+1+q+q+l
= l + q
119
Функция А обладает очень хорошими свойствами: если
допустимое преобразование переводит ситуацию 5 в си-
туацию Т, то A(S) = A(T). Значение ситуации не меня-
ется при допустимых преобразованиях и остается, сле-
довательно, постоянным на протяжении всей игры.
Чтобы убедиться в этом, рассмотрим «прыжок» влево.
Колышки в (k, /) и в (k — 1, /) заменяются одним колыш-
ком в (k—2, 1\. Значение ситуации изменяется на
ph-2+l _ — ph+1 —
=pft+'(p-2-p-1-l)
= pft+1(p2+p2 + l)
= 0 (в силу ( * * * )).
Аналогично рассматриваются «прыжки» вправо, вверх и
вниз.
Существует еще одна функция, обладающая этим
свойством, а именно
В (S) = 2рк~1
(суммирование также проводится по (k, I) из S). Значит,
каждой ситуации мы можем поставить в соответствие
пару
B(S))
элементов нашего поля. Существует 16 таких пар, и
каждую из них можно получить, подобрав соответству-
ющим образом ситуацию <S. Они разделяют ситуации на
16 множеств, так что никакая последовательность «прыж-
ков» не выводит ситуацию за пределы множества, кото-
рому она первоначально принадлежала.
Для исходной позиции нашей игры A(S) = B(S) = 1.
Поэтому для любой позиции, которая может возникнуть
в течение игры, = B(S) = 1. Для единственного ко-
лышка (k, I) получим:
ZlfS)=pM'
B(S)=p^',
120
т. е.
дй-Н = р*-Г — J
для любой допустимой конечной позиции. Степени эле-
мента р, которые равны 1, это р~6, р~3, р°, р3, и вообще
р3п. Значит, k + l и k — I кратны трем. Отсюда следует, что
k п I также кратны трем. Таким образом, мы можем прий-
ти лишь к следующим пяти позициям с единственным ко-
лышком: ( — 3, 0), (0, 3), (3, 0), (0, — 3) и (0, 0).
Эти рассуждения не показывают, что все эти пози-
ции достижимы, но они в сущности исключают возмож-
ность, чтобы какая-либо из них оказалась недостижи-
мой. И в действительности все они достижимы.
Подобные рассуждения годятся для досок любой
формы, лишь бы отверстия располагались по строкам и
столбцам. Можете, если хотите, рассмотреть точно так же
трехмерные доски.
Глава 7
СИММЕТРИЯ: ПОНЯТИЕ ГРУППЫ
И теперь мы можем решить за-
дачу вообще без всякой мате-
матики — с помощью одной
лишь теории групп.
Профессор из Кембриджа,
В природе существует много видов симметрии, и об-
наружены они были в самые древние времена. Челове-
ческая фигура приблизительно симметрична относитель-
но вертикальной оси (точнее, вертикальной плоскости),
и это одна из причин, почему нам кажется, что зеркало
меняет местами правое и левое. Этот вид симметрии из-
вестен как зеркальная симметрия.
Символ острова Мэн, изображающий три бегущие
ноги, обладает поворотной симметрией (рис. 47).
Фигура может быть симметричной относительно не-
скольких прямых одновременно или обладать одновре-
менно зеркальной и поворотной симметриями. Квадрат
обладает зеркальной симметрией относительно диагона-
лей и относительно прямых, проходящих через его центр
параллельно какой-нибудь из его сторон; его можно так-
же поворачивать на 90°.
©Совсем другой вид симметрии
демонстрируют настенные орнамен-
ты, которые целиком можно пере-
мещать в различных направлениях,
так, чтобы на вид ничего не изменя-
лось. Тот факт, что объект симмет-
ричен, необычайно важен с точки
зрения математики.
Рассмотрение равнобедренных
треугольников в гл. 2 сводится к
Рис. 47. утверждению, что они обладают зер-
122
калькой симметрией. В математической физике законы
типа закона сохранения энергии вытекают из априорно-
го предположения о симметрии Вселенной. Такое важ-
ное свойство, как симметрия, должно поддаваться мате-
матическому анализу и поддается ему на самом деле.
Прежде всего нужно выработать рабочее определение
Рис. 48.
симметрии, чтобы быть уверенными, что все мы говорим
об одном и том же. Иначе мы можем спутать, например,
«симметричный» с «красивый». Симметрия фигуры опи-
сывается теми движениями, в результате которых она
совмещается сама с собой. Отдельные точки при этом,
однако, могут смещаться. Если повернуть квадрат ABCD
вокруг его центра на 90°, как это показано на рис. 48, то
вершина А переместится в В, В — в С, С — в D и D —
в А.
Важно здесь не положение точек, а операция, их пе-
редвигающая. «Вращение на 90°» описывает симметрию
квадрата, и ее же описывает «отражение относительно
вертикальной прямой». Но это то, что мы раньше назы-
вали жесткими движениями. Их можно описать как не-
которые функции, у которых как область определения,
так и область значений совпадает с плоскостью R2.
Таким образом, для любого подмножества S плоско-
сти R2 можно определить его симметрию как сохраняю-
щую расстояние биекцию f: R2->R2, такую, что f(x), т. е.
123
результат применения f к точке х, принадлежит S для
любого х £ S. Последнее условие можно переписать так:
f (S) — S На языке геометрии симметрия подмножества А—
это жесткое движение плоскости, которое оставляет S на
месте, хотя может перемещать отдельные точки из S.
Нет необходимости ограничиваться рассмотрением
плоскости, трехмерное пространство ничем не хуже.
Для «бегущих ног» существует очевидная симмет-
рия— вращение на 120° вокруг центра, скажем, по часо-
вой стрелке. Обозначим соответствующую функцию (или
жесткое движение) через w. Другая симметрия, скажем,
v — это вращение на 240°. На первый взгляд этим исчер-
паны все возможные симметрии, но мы всегда должны
помнить также о тривиальном случае. Это третья
симметрия; тождественная функция. При ней все точки
остаются на месте, и, значит, она подходит под наше
определение. Для нее мы используем символ I, напоми-
нающий о природе этой функции. Таким образом, {/, w,
tz} — множество симметрий для «бегущих ног».
Повернуть на 240° — это все равно, что дважды по-
вернуть на 120°. Иными словами, ге = и, где умножение
определено, как в гл. 5. Чтобы упростить обозначения,
будем писать w2 вместо ww, w3 вместо www и т. д., т. е.
ьу2 = о. Аналогично t|2 = w: дважды повернуть на 240° —
это все равно, что повернуть на 120°, поскольку 360° —
это полный поворот, в результате которого все точки воз-
вращаются на свои места. На самом деле, произведение
любых двух симметрий из этих трех — снова одна из
этих симметрий.
Приведем таблицу:
X | I w у
I I W V
ull W V I
О V I W
124
Из этой таблицы видно, что w3 — I. И это правильно, так
как в результате трех последовательных вращений на
120° все точки возвращаются в исходное положение.
Тот факт, что произведение двух симметрий также
является симметрией, обычно формулируют так; множе-
ство симметрий замкнуто относительно умножения.
Если бы мы не включили в число симметрий /, то лиши-
лись бы этого свойства. Это было бы нечто вроде ариф-
метики, в которой сумма двух чисел не обязательно
является числом. Иными словами, мы могли бы обойтись
без I, но удобнее этого не делать.
Это множество симметрий
X
Рис. 49.
: заданным на нем умноже-
нием представляет собой
пример математической
структуры, именуемой
«группой». Группа будет
определена позже, пока
же нам нужен лишь тер-
мин. Мы нашли группу сим-
метрии «бегущих ног».
Каждая фигура имеет
группу симметрии. Чело-
веческая фигура имеет
две симметрии: тождест-
венное преобразование и
отражение относительно
вертикальной прямой.
Вот соответствующая та-
блица умножения:
г
г
I
и снова множество симметрий замкнуто относительно
умножения. Рассмотрим более сложный пример. Равно-
сторонний треугольник (рис. 49) имеет шесть симметрий.
125
Это тождественное преобразование вращения но часовой
стрелке w и v на 120° и 240° соответственно, а также
отражения х, у, z относительно прямых X, Y, 1 (предпо-
лагается, что при движениях треугольника прямые
остаются неподвижными). Когда мы рассматриваем «бе-
гущие ноги», отражений не возникает, так как после от-
ражения ступни окажутся направленными не в ту сторону.
Множество w, v, х, у, z} симметрий замкнуто
относительно умножения (если симметрии перемножать
как функции), и мы получаем такую таблицу:
X ] I w у х у z
I I W V
w w v I
V V / W
X X у Z
У У г х
Z Z X у
X У Z
Z X у
у Z X
I W V
V I W
W V 1
Что такое, например, wx (проделать wx — это сначала
проделать х, а затем да)?
Треугольник
А
С В
переходит при х в
А
В С
а затем при w — в
В
С А
Но это все равно, что применить г. Таким образом,
wx=z.
Рассмотрим теперь yz. При z наш треугольник пере-
ходит в
В
С А
126
а при у переходит в
С
В А
(вспомним, что прямые X, У, Z остаются на месте). Но
то же действие производит и w, т. е. yz=w.
Теперь уже можно проверить, что таблица составлена
правильно. Для большей наглядности сделаем треуголь-
ник из картона и пометим его углы. Обведем его конту-
ры на листе бумаги и нарисуем на этом листе прямые
X, У, Z.
Вообще, чтобы определить группу симметрии некото-
рой фигуры, надо
1) отыскать все ее симметрии;
2) составить для них таблицу умножения.
Всякий раз мы будем убеждаться, что полученное
множество замкнуто относительно умножения. Исключе-
ний здесь нет. Если f и g — жесткие движения, то жест-
ким движением будет и fg. Если как f, так и g оставля-
ют S на месте, то и fg оставляет S на месте, поскольку
f(g(S)) =f(S) =S. Если применение f и g по отдельности
не меняет очертания фигуры, то его не изменит и приме-
нение их обоих.
Те же соображения применимы и к более сложным
фигурам. Куб имеет 24 поворотные симметрии или 48,
если считать отражения. Мы можем перевести каждую
вершину в любую другую и повернуть ребра, исходящие
из этой вершины, тремя способами. Додекаэдр имеет
60 поворотных симметрий или 120, если считать отраже-
ния. Естественно, здесь уже невозможно выписывать
таблицы умножения. Вычислить все возможные произве-
дения симметрий — это не единственно возможный спо-
соб выразить отношения между ними. Но мы не будем
здесь углубляться в этот вопрос
127
Понятие группы
Понятие группы возникает на основе рассмотренных
выше, а также других примеров таким же образом, как
при рассмотрении арифметик возникло понятие кольца.
Вместо того чтобы ходить вокруг да около, я приведу
сначала определение, а уже затем мы будем его об-
суждать.
Группа состоит из:
(1) множества G;
(2) операции *, которая ставит в соответствие лю-
бым двум элементам х и у из G элемент х * у, также
принадлежащий G.
Эта операция удовлетворяет трем следующим за-
конам:
(3) она ассоциативна: для любых х, у, z^G
(4) существует единичный элемент I такой, что
I *х = х = х*1
для любого х £ G;
(5) существуют обратные элементы: для любого
X £ G существует х' € G такой, что
х*х'=1—-х' *х.
Группы возникают в самых разнообразных ситуациях.
Вот несколько примеров:
a) G — множество симметрий «бегущих ног», а * —
умножение симметрий, указанное в табл, на с. 125. Не-
трудно проверить свойства (1)—(5). Выполнение свойства.
!1) очевидно — мы взяли в качестве G множество. Пункт
2) имеет место, поскольку наше множество замкнуто
относительно умножения. Операция ассоциативна, так
как операция умножения ассоциативна для любых функ-
ций — выполняется (3). Что касается пункта (4), то тут
128
мы предвосхитили события, обозначив через I тожде-
ственную функцию. Наконец, пункт (5): можно положить
/'•=/, v'=w, w'=v;
б) Пусть О — множество целых чисел, G = Z. Тогда
выполняется (1). В качестве * возьмем операцию сложе-
ния +,. Тогда справедливо (2), поскольку сумма а+Ь
двух целых чисел а и b — целое число. Условие (3) — это
закон (1) арифметики (с. 98), (4) — это закон (3) (где
О играет роль /), а (5) — это закон (4);
в) Пусть G — R, т. е. G — множество действительных
чисел, а *—это + . Рассуждения проводятся так же, как
в предыдущем примере;
г) Пусть G — множество ненулевых рациональных
чисел, а * — операция умножения. G является множе-
ством, а произведение двух ненулевых рациональных
чисел — ненулевое рациональное число. Это относится
к пунктам (1) и (2). Условие (3) —просто закон (5)
со с. 98, который справедлив для рациональных чисел,
а (4) —это закон (7) (где 1 играет роль /). Рациональ-
ные числа образуют поле, а условие (5) — это закон (9)
(см. там же), который справедлив в любом поле;
д) Пусть S — произвольное подмножество плоско-
сти, G — множество его симметрий, а * — умножение
функций. Тогда, как и в примере «а», легко убедиться,
что G — группа.
Следует подчеркнуть, что если не соблюдено хотя бы
одно из перечисленных пяти условий, то рассматривае-
мый объект не есть группа.
Если взять в качестве G множество целых чисел меж-
ду — 10 и 10, а в качестве * —сложение, то закон (2) не
будет выполняться: 6 + 6 не является элементом мно-
жества G.
Множество целых чисел, больших 1, с операцией сло-
жения не обладает элементом / из пункта (4).
Множество целых чисел с операцией вычитания не
В Я. Стюарт
129
удовлетворяет условию (3), так как вычитание неассо-
циативно:
(2—3)—5 = —6^4 = 2—(3—5).
Множество всех рациональных чисел с операцией
умножения — не группа. Единственный элемент, пригод-
ный на роль I,— это 1, Но тогда мы не сможем найти
элемент О', такой, чтобы 0'0=1; поскольку гХ0 = 0 для
любого рационального г, то 0'0 равно 0, а не 1.
Таким образом, ни в одном из рассмотренных случаев
мы не получаем группы.
Хотелось бы остановиться подробнее на операции *.
Для любой пары элементов (х, у), где х, у £G, мы полу-
чаем единственный элемент х * у С G. Это означает, что
* задает функцию с областью определения G*G (множе-
ство всех пар (х, у)) и областью значений, лежащей в G (на
самом деле совпадающей с G).
Операцию можно определить как функцию
*: G х G —> G,
если воспринимать х * у как сокращение для *(х, у),
При таком определении условие (2) выполняется авто-
матически, и его можно опустить, но в каждом конкрет-
ном случае необходимо проверять, что * действительно
является функцией из GXG в G.
Коль скоро эти понятия усвоены, можно упростить
обозначения и писать вместо х * у просто ху (но следует
помнить, что это не обязательно обычное умножение)
и х-1 вместо х'. Если мы употребляем эти обозначения,
но имеем дело с группой целых чисел относительно сло-
жения, то ху означает х+у, а х-1 означает —х. Тут важно
не запутаться!
130
Подгруппы
Если из шести симметрий треугольника отобрать три:.
I, w и v, то легко убедиться, что они составляют меньшую
группу, лежащую в большей группе. Мы можем прове-
рить это как с помощью таблицы умножения, так и о
с помощью геометрических соображений: это симметрии,
которые не переворачивают треугольника, и если мы
перемножаем две такие симметрии, то снова получаем
симметрию, которая также не переворачивает треуголь-
ника.
Эта меньшая группа в большей дает пример подгруп-
пы. Если G — группа с операцией * , то подмножество Н
из G является подгруппой, если оно образует группу от-
носительно операции *.
Не каждое подмножество Н оказывается подгруппой.
Совокупность Н={х, у, ?} не будет группой, так как
xy=w, a w не лежит в Н. Если h и k лежат в подгруп-
пе Н, то должны выполняться такие условия:
a) h*k £ Н-,
б) h~l е н,
а отсюда следует, что
в) I = h*h~1 С Н.
Обратно, если выполняются условия «а», «б», то
можно утверждать, что Н — подгруппа, поскольку закон
ассоциативности обязательно выполняется в Н, если он
выполняется в G.
Подгрупп чрезвычайно много. Группа целых чисел
относительно сложения содержит подгруппы, состоящие
из всех четных чисел, из всех чисел, кратных 3, из всех
чисел, кратных 4, из всех чисел, кратных 5, ... Каждая
группа G является своей собственной подгруппой. Под-
группой в любой группе оказывается множество {/}, со-
131
стоящее из одного элемента, с тривиальной таблицей
умножения
х | /
Группа симметрии равностороннего треугольника обла-
дает шестью разными подгруппами:
{/, w, v, х, у, z},
{I, w, v},
{1,4,
{Л у},
{1, г},
{/}•
Число элементов группы (если их конечное число) на-
зывается порядком группы. Мы уже нашли группу по-
рядка 6 с подгруппами порядков 1, 2, 3 и 6. Не требуется
особых способностей, чтобы заметить, что все эти числа
делят 6.
По рассмотрении еще ряда примеров естественно
предположить, что порядок подгруппы всегда делит по-
рядок группы.
Это предположение верно: соответствующая теорема
была доказана Лагранжей раньше, чем возникло аб-
страктное понятие группы!
Пусть К = {/, w, v, х, у, z), и рассмотрим подгруппу
J — {/, х). Для любого элемента а £ К определим смеж-
ный класс J*a как
{I * а, х » о},
т. е. умножим каждый элемент из J на а и объединим
полученные элементы в одно множество. Выпишем
их все:
/ * х — {/, х},
J *z = {v, z},
/ * y={w, у}.
] * /={/,х},
J * v= {v, z},
J * ЙУ= {w, у),
132
Отметим, что:
а} существуют лишь 3 различных смежных класса;
б) один из смежных классов — сама подгруппа /;
в) никакие два различных смежных класса не имеют
общих элементов:
г) каждый элемент из К лежит в некотором смежном
классе;
д) все смежные классы содержат одинаковое число
элементов.
Из пунктов «б» и «д» следует, что все смежные клас-
сы содержат по 2 элемента. Из пунктов «в» и «а» выте-
кает, что все смежные классы вместе содержат 2-3 = 6
элементов. В соответствии с пунктом «г» К состоит из
6 элементов. Это не только объясняет, почему порядок
подгруппы J делит порядок К, но и показывает, что
частное от деления равно числу смежных классов.
Доказательство теоремы Лагранжа идет по тому же
пути. Сначала доказывается, что пункты «а»—«д» спра-
ведливы для любой группы К и любой подгруппы J
(за исключением того, что в пункте «а» фигурирует
какое-то число с смежных классов). Если порядок под-
группы J равен /, а порядок группы К равен k, то
k — jc. Таким образом, / делит k. Свойства «б»— «д»
получаются из аксиом группы с помощью не очень слож-
ных рассуждений.
Это замечательная теорема. Из не очень на первый
взгляд ясных (но на самом деле сверхточных) абстракт-
ных понятий группы и подгруппы мы извлекли конкрет-
ные численные соотношения. Если дана группа поряд-
ка 615, то без всякой информации об ее таблице умно-
жения можно сказать, что порядками ее подгрупп мо-
гут быть лишь числа 1, 3, 5, 15, 41, 123, 205 и 615.
Возникает вопрос, все ли эти числа действительно
оказываются порядками каких-либо подгрупп. Поря-
док группы вращений додекаэдра равен 60, но она не
имеет подгрупп порядка 15, хотя 15 делит 60. Все, что
133
мы знаем по этому Поводу в общем Случай,*— это теоре-
ма Силова-. если Й**-степень простого числа и делит по-
рядок группы 6, то О имеет подгруппу порядка h. Та-
ким образом, наша группа порядка 60 обязательно
имеет подгруйпы порядков 2, 3, 4 и 5, а любая группа
порядка 616 имеет подгруппы порядков 3, 5 и 41,
Изоморфизм
Существуют другие способы построения группы из 6
элементов. Для множества S = {а, Ь, с} имеется 6 биекций
S->S, а именно функции р, q, г, s, t, и, записанные в
следующей таблице:
| р q г s t и
a a a b b с с
b b с а с а b
с с b с а Ь а
где, например, значение s(b) функции s на элементе b —•
это элемент й-й строки и s-го столбца, т. е. с.
Биекции множества на себя называются перестанов-
ками этого множества.
Эти шесть биекций образуют группу относительно
обычного умножения функций с такой таблицей умно*
жения:
X р q г s t и
р р q г s t и
q q р t и г s
г г s р q и t
s s г и t р q
t t и q р s г
и и t s г q р
134
Например, чтобы найти rs, проведем следующие вычис-
ления:
rs(cz) =r(s(a)) =r(b) =а,
rs(fe) =r(s(b)) = г(с) =с,
rs(c) =r(s(c)) = r(a) = b,
t. e, rs действует на всех элементах как q. Таким обра-
зом, rs*=q.
Эта группа не совпадает с группой симметрии пра-
вильного треугольника, поскольку у нее другие элемен-
ты, Но между этими группами есть большое сходство,
помимо того, что они обе имеют порядок 6.
Каждая симметрия правильного треугольника пере-
упорядочивает вершины А, В, С следующим образом!
I
А
В
С
А
В
С
w v х у г
В С А С В
С А С В А
А В В А С
Это наводит нас на мысль сопоставить движения с пе-
рестановками (заменяя заглавные буквы А, В, С строч-
ными а, Ь, с):
р q г s t и
1 t t t t f
;+!!!!
/ X Z W V у
Если переписать таблицы умножения для обеих групп
так, чтобы соответствующие друг другу элементы при
этом сопоставлении стояли на одинаковых местах и в
верхней строке и в самом левом столбце таблиц, а за-
тем вписать в таблицы значения произведений, взятые
из исходных таблиц, то получим;
135
X I I W V X у 2
I I W V X у z
W W V I Z X у
V V 1 w у Z X
X X у Z I W V
у у z x v I w
2 z x у w v 1
X | p s t q U
p p s t q и
s s I p r q
t t p s и r
q q a r p s
и и r q t p
r r q и s t
r
r
и
<1
t
s
P
В этих таблицах соответствующие друг другу элементы
стоят на одинаковых местах не только в верхней стро-
ке и левом столбце, но и в основной части таблицы,
Например, I и р расположены так:
*
*
*
*
«
а х, q — так:
*
*
«
*
*
Это не должно вас удивлять, поскольку способ пере-
множения перестановок очень близок к способу пере-
множения симметрий. Таким образом, две группы мо-
гут иметь одинаковую структуру, не будучи тожде-
ственны одна другой. Разница состоит в наименовани-
ях элементов.
Чтобы эти соображения приняли более строгую
136
форму, рассмотрим функцию f, которая устанавливает
соответствие между элементами двух рассматривае-
мых групп, такую, что f(I)=p, f(x)=q, ... Областью
определения функции / служит первая группа, а об-
ластью значений — вторая. Пусть аир — элементы пер-
вой группы. На пересечении строки а и столбца р лежит
элемент а * р. На пересечении соответствующих строки
f (а) и столбца f (Р) находится элемент f(a)*f(P).
Но это, как мы уже отмечали, должен быть элемент,
соответствующий элементу а * р, т. е. f(a*p). Таким
образом, тот факт, что соответствующие элементы стоят
на одинаковых местах, означает, что
Р)=/ (а) 4(₽) (*)
для любых а и р из первой группы.
Конечно, формулу (*) гораздо удобнее использовать,
так как она не зависит от «геометрии» таблицы умноже-
ния. Две группы G и Н называются изоморфными, если
существует биекция f; G-> Н, такая, что для всех а, р б G
выполняется (*). Изоморфные группы имеют одинаковую
абстрактную структуру и различаются лишь элементами.
Так как вся существенная информация о структуре груп-
пы заключена в способе перемножения ее элементов, то
в большинстве случаев изоморфные группы можно не
различать.
Мы уже знаем, что первая из рассматриваемых нами
групп имеет 6 подгрупп. Из этого непосредственно вы-
текает, что вторая, изоморфная ей, группа тоже содер-
жит 6 подгрупп. Например, подгруппе {I, w, v} первой
группы во второй группе соответствует подгруппа
{Р. s.t}.
Группы одного порядка не всегда изоморфны. Рас-
смотрим еще одну группу порядка 6, а именно группу
целых чисел по модулю 6 относительно сложения. Ее
таблица «умножения» — это таблица сложения по мо-
дулю 6, т. е.
137
4» j О 1 2 3 4 5
0 0 1
1 1 2
2 2 3
8 3 4
4 4 5
5 5 0
2 3 4 5
3 4 5 0
4 5 0 1
5 0 12
0 12 3
12 3 4
Обозначим эту группу через Л1. Будет ли она изоморфна
группе симметрий К равностороннего угольника?
Один из способов решить такую задачу — просмотреть
все биекции из М в К и выяснить, выполняется ли для
какой-нибудь из них равенство ( *). Попробуем задать
f так:
f(0)=7, f(V)=w, f(2)=v, f(3)=x, f(4) =y, f(5)=z.
Тогда
f (1+2) (3) =x,
f(l) * f(2) — wv = I.
Это означает, что функцию мы выбрали неудачно. Пере-
брать нужно всего лишь 720 биекций. Так можно было
бы осуществить этот первый подход.
С другой стороны, можно попытаться найти свойство
группы М, не зависящее от наименований ее элементов.
Одно из них мы знаем — это число подгрупп в группе.
Нетрудно убедиться, что подгруппами группы М будут
{0}, {0, 2, 4}, {0, 3} и М. Значит, М имеет всего четыре
подгруппы и не может быть изоморфной группе /С, у
которой 6 подгрупп.
Это приятнее, чем исследовать 720 функций. Но су-
ществует еще более простой способ. Сложение по моду-
лю 6 удовлетворяет закону коммутативности (см. закон
(2) на с. 98), а + р = р а. Предположим, что
f: М -> — изоморфизм. Тогда
f («+P)=F (Р + а)>
138
так что, согласно (*),
f («)f (₽)=/ (₽)f (a).
Иными словами, группа К также должна удовлетворять
закону коммутативности, только относительно умноже-
ния. Но vx=y, xv = z, что ему противоречит. Таким
образом, между группой М и группой симметрии К нель-
зя установить изоморфизм.
Изоморфизмы позволяют во многих случаях значи-
тельно упростить ситуацию. В математике очень важно
иметь возможность выяснить, когда две на первый
взгляд различные задачи по существу совпадают. Если
в двух задачах возникают изоморфные структуры, то
это может навести на мысль о связи между двумя ука-
занными задачами.
В предыдущем примере мы установили изоморфизм,
используя уже известную нам связь между симметри-
ями треугольника и перестановками на множестве из
трех элементов. Иногда МЫ сталкиваемся с противопо-
ложной ситуацией: мы видим, что группы изоморфны,
и хотим понять, почему это так. С общим уравнением
пятой степени можно связать некоторую группу пере-
становок на множестве из пяти элементов. (Перестав-
ляемые элементы — это 5 корней рассматриваемого урав-
нения.) Эта группа содержит 60 элементов. Группа
вращений додекаэдра тоже состоит из 60 элементов.
Можно показать, что две эти группы изоморфны. Оттал-
киваясь от этого совпадения, Феликс Клейн раскрыл
глубокие связи между тремя теориями:
уравнений пятой степени,
групп вращений,
комплексных функций.
Среди прочего это объяснило один уже отмеченный
факт: уравнение пятой степени можно решить с по-
мощью особого рода комплексных функций—-так назы-
ваемых эллиптических функций, До открытия Клейна
139
это можно было доказать лишь «неизящными вычисле*
ниями, и выглядело все это случайным, КдеЙН^рбъясниЛ^
почему так происходит.
Классификация орнаментов
Теория групп возникает везде, где мы сталкиваемся с
симметриями. Она позволяет описывать симметрии объ-
екта с помощью подходящей группы. Например, говоря о
додекаэдральной симметрии данного объекта, мы имеем
в виду, что его группа симметрии изоморфна группе сим-
метрии додекаэдра.
Но, кроме того, она позволяет нам классифицировать
симметрии. В некоторых ситуациях можно утверждать:
здесь возможны эти и только эти симметрии.
Рисунки (орнаменты) на обоях — это в сущности
просто симметричные конфигурации на плоскости. Группа
симметрии такого орнамента состоит из некоторых жест-
ких движений и является подгруппой группы всех жест-
ких движений плоскости. Здесь нам следует более строго
определить, что мы понимаем под орнаментами: они
должны простираться как угодно далеко и быть дискрет-
ными в том смысле, что самосовмещение происходит
«скачками». (Существует точное, но формальное мате-
матическое описание.) Можно провести классификацию
соответствующих групп и убедиться, что существует
всего 17 типов таких плоских орнаментов (9 из которых
подходят скорее для бордюров, чем для обоев). Некото-
рые из них изображены на рис. 50—52.
Когда вы держите в руках каталог обоев — сотни и
сотни различных узоров,— вам трудно представить себе,
что их можно каким-нибудь разумным образом класси-
фицировать. Их так много! Но если отвлечься от рас-
цветки, размера, качества бумаги (все это относится к
практической стороне производства обоев!) и сконцент-
рировать внимание лишь на основной структуре, то мож-
140
Рис. 50.
141
Рис. 51.
142
Рис, 52.
143
но убедиться, что имеется лишь 17 существенно различ-
ных типов структур. Говорят, что в работах арабских
гончаров встречаются все 17 видов. Было бы интересно
изучить современные каталоги обоев и выяснить, столь
же ли они исчерпывающи. Вероятно, нет.
Аналогичная задача в трехмерном пространстве
(здесь получается 230 возможных групп симметрии3)
очень важна в кристаллографии: с помощью этих групп
можно описывать молекулярное строение кристаллов.
144
Глава 8
АКСИОМАТИКА
Лишь слоны и киты произво-
дят на свет детенышей, кото-
рые весят больше 70 кг. Пре-
зидент весит 75 кг. Значит, его
мать — либо слониха, либо ки-
тиха.
Стефан Темерсон
Математика насчитывает много уровней. Ребенок
чйтся решать задачи с одним или несколькими числами.
Позднее он изучает общие свойства всех чисел ( в неко-
тором смысле объект его изучения изменился, это уже не
Число, а кольцо Z всех целых чисел). Далее, в теории
колец он вместо одного конкретного кольца изучает
классы колец. Целая область математики становится
Одним объектом, а он, в свою очередь, является лишь од-
ним из многих объектов другой области. И так далее.
В этой главе мы поднимемся на ступеньку выше.
Объектами наших рассмотрений будут целые теории:
теория колец, теория полей, теория групп, геометрия.
В наших определениях группы, кольца, поля много
общего. Вводятся основные понятия. Эти понятия никак
не определяются, Вместо этого перечисляется ряд зако-
нов, которым они должны удовлетворять. Эти законы
суть аксиомы, а вся система в целом — аксиоматическая
система.
Не требуется «верить» аксиомам. Даже поднимать
этот вопрос и бесполезно, и бессмысленно — ведь за ни-
ми не стоит никакой реальности.
Всякий раз, когда вы сталкиваетесь с некоторой
аксиоматической системой, кто-то другой сообщает вам,
какими свойствами он наделил эту систему. Аксиомы —
145
это как правила игры. Если их изменить, вы будете
играть уже в другую игру.
Основываясь на некоторой системе аксиом, можно
далее строить некоторые логические выводы. Все они
(явно или неявно) принимают такую форму: если данные
аксиомы выполняются, то выполняется что-то еще.
«Истинность» аксиом не обсуждается. Тот факт, что
Римская империя распалась, не имеет отношения К дис-
куссии о том, что могло бы произойти, если бы она не
распалась. Обсуждению подлежит лишь правильность
вывода.
Можно обсуждать также пригодность данных аксиом
в каждом конкретном случае. Соответствует ли происхо-
дящее в реальном мире тому, что утверждают аксио-
мы,— это уместный вопрос, когда речь идет о попытке
применить соответствующую теорию к реальному миру,
но этот вопрос не является частью рассматриваемой
теории. Ответить на него можно лишь с помощью экспе-
римента. Аналогично, чтобы применить теорию групп к
какой-либо ветви математики, необходимо проверить,
являются ли соответствующие объекты группами. Если
это не так, то теорию групп применять нельзя, Но на
саму теорию групп это не оказывает никакого влияния.
Верны ли аксиомы теории групп — бессмысленный воп-
рос, Аксиомы не являются истинными ни в каком абсо-
лютном смысле; но они могут быть истинными в некото-
рых конкретных ситуациях.
Сила аксиоматического метода состоит в том, что он
позволяет построить из небольшого числа допущений
огромное здание теории. Если нечто удовлетворяет этим
допущениям, то оно должно удовлетворять и всем заклю-
чениям, которые из них выводятся. Мы можем применить
все результаты нашей теории для получения различных
свойств: нам не надо заново проделывать всю работу для
каждого приложения.
Представление об аксиоматической системе как о
146
чем-то оторванном от реальности сложилось сравнитель-
но недавно. По-видимому, древние греки, устанавливая
аксиомы геометрии, считали, что они выражают подлин-
ные физические истины, хотя и для несколько идеализи-
рованной природы. Разумеется, аксиома определялась
как очевидная, не требующая доказательства истина, и
сейчас еще в имеющемся у меня словаре приводится та-
кое определение, Но в математике это слово приобрело
совсем иное значение. Обратимся к аксиомам группы.
Очевидны ли они?
Аксиомы Евклида
Евклид дал список аксиом геометрии. Вот наиболее
важные из них'
(1) Через любые две точки можно провести прямую
(2) Любые две прямые имеют не более одной общей
точки.
(3) Любой конечный отрезок прямой можно неогра-
ниченно продолжать.
(4) Вокруг любой точки можно описать окружность
произвольного радиуса.
(5) Ёсе прямые углы равны между собой.
(6) Для любой прямой и любой точки, не лежащей на
этой прямой, существует прямая и притом единственная,
параллельная первой и проходящая через эту точку.
(Формулировки не совсем такие, как были у
Евклида.)
В течение долгого времени считалось недостатком,
что аксиома (6) выглядит не вполне очевидной. Было
предпринято множество попыток доказать ее, основы-
ваясь на других аксиомах, и все безрезультатно.
Позже мы увидим, что доказать таким образом ак-
сиому (6) невозможно. Но вот существенный вопрос-
истинна ли эта аксиома в реальном мире? Этот вопрос
выходит за рамки математики. Чтобы ответить на него,
147
надо провести эксперимент. Вообразим, однако, что такой
эксперимент осуществляют древние греки. Они проводят
две «параллельные» прямые, например меридианы, че-
рез Рим и Афины, и те сходятся в Южном полюсе.
В геометрии поверхности земного шара аксиома о парал-
лельных неверна.
На самом деле это жульничество: мы знаем, что
земной шар круглый, а евклидова геометрия прилагает-
ся к плоскости, а не к сфере. В действительности, если
всерьез задуматься, наша уверенность, что земной шар
круглый, основана именно на том, что на нем нарушают-
ся законы евклидовой геометрии. Значит, если Евклид
был неправ, то, быть может, земной шар совсем и не
обязан быть круглым.
Более правильный эксперимент можно было бы по-
ставить с помощью лазерных лучей или еще чего-нибудь
подобного. Вы направляете лучи лазеров в межзвездное
пространство, причем настолько параллельно, насколько
сможете, и затем пытаетесь выяснить, пересекаются ли
они. К сожалению, подобный эксперимент невозможно
осуществить на практике. (А если верны некоторые кос-
мологические теории, то и его осуществление не подтвер-
дило бы справедливости евклидовой геометрии.)
Похоже на то, что Евклид гораздо лучше понимал,
что он делает, чем те, кто позднее его критиковали. Он,
по всей видимости, подозревал, что аксиому о параллель-
ных доказать нельзя, и потому явно ее сформулировал.
Непротиворечивость
Приступая к разработке аксиоматической теории, вы
имеете в своем распоряжении лишь аксиомы (постольку,
поскольку это касается логических выводов; психологи-
чески у вас могут быть некоторые интуитивные сообра-
жения о том, как должна развиваться эта теория). Вы их
используете, чтобы доказать некоторые теоремы, а затем
148
Применяете $Ти теоремы для доказательства других.
Аксиомы становятся источником широко распространяю-
щейся волны теорем, каждая из которых в конечном сче-
те от них зависит.
Все идет хорошо до тех пор, пока вы не получите на
э^ом пути две противоречащие друг другу теоремы. Но
если в вашей теории можно доказать две противоречащие
друг другу теоремы, то вся она бесполезна. Ведь тогда
в ней можно доказать все, что угодно.
Когда однажды на обеде известный математик
Дж. Харди сделал подобное замечание, кто-то из при-
сутствующих потребовал обосновать его: предположив,
например, что 2 + 2 = 5, доказать, что Мак-Таггарт —
папа римский. Харди ненадолго задумался и ответил:
«Мы знаем также, что 2 + 2=4, значит, 5 = 4. Вычитая 3,
получаем 2=1. Мак-Таггарт и папа римский — это два
человека, следовательно, Мак-Таггарт и папа римский —
это один человек».
Чтобы перейти к более общей ситуации, надо вспом-
нить, прежде всего, метод доказательства от против,-
ного. Мы хотим доказать утверждение р. Начнем с пред-
положения, что р неверно, и выведем из него два проти-
воречащих друг другу утверждения. Но этого не может
быть. Значит, наше предположение, что р неверно, явля-
ется ошибочным. Законность этого метода основывается
на современной математической логике. Мы использовали
з —
его в гл. 6 для доказательства иррациональности | 2 .
Предположим теперь, что в некоторой аксиоматической
системе можно вывести две противоречащие друг другу
теоремы г и s. (Например, г—«масло дешево», as—«мас-
ло не дешево».) Этим можно воспользоваться, чтобы по-
лучить противоречие в предыдущем доказательстве, ка-
ково бы ни было р. Теоремы г и s можно вывести из р,
поскольку их можно вывести из аксиом. Мы не обязаны
действительно использовать р в этом выводе.
149
Например, чтобы доказать утверждение «страна ра-
зоряется», предположим противное, т ё. что она не разо-
ряется. Выведем теперь оба противоречащих друг другу
утверждения «масло дешево» и «масло не дешево». Тогда
наше предположение оказывается неверным, и страна
разоряется.
Совершенно так же можно доказать, что страна не
разоряется, предположив, что она разоряется, и проведя
'те же самйе рассуждения.
Это полная катастрофа. Быть может, и возможно
примириться с оракулом, который время от времени дает
Два ответа: «да» и «нет» на один и Тот же вопрос. Но что
за польза от оракула, который на все вопросы отвечает
«да»?
Система аксиом, из которой нельзя вывести противо-
речащих друг другу утверждений, называется непроти-
воречивой, Непротиворечивость — важнейшее свойство
аксиоматической теории. Его важность была впервые
дтмечена Давидом Гильбертом, основоположником сов-
ременной формальной аксиоматики.
Противоречивость противоречивой теории не всегда
очевидна, Это очень тонкий вопрос. Аксиомы поля непро-
тиворечивы. Но если слегка видоизменить закон (9), по-
требовав, чтобы каждый (а не каждый ненулевой) эле-
мент имел обратный по умножению, то система станет
противоречивой. Действительно, если бы 0 имел обрат-
ный О-1, то
(о-о) • о-1=о • о-1=1,
О - (О- О-1) =0- 1=0,
что противоречит закону ассоциативности, поскольку
аксиома (10) на с. 103 утверждает, что 0=^=1. (Вот почему
вы никогда не станете делить на нуль! Это нарушает
законы арифметики.)
Таким образом, произведя очень небольшие измене-
ния, мы превратили непротиворечивую систему в противо-
150
речивую. И противоречивость второй системы неочевид-
на (если вы не знаете заранее, где должны возникнуть
неприятности). Каким бы безобидным ни показалось за-
данное множество аксиом, непременно возникает вопрос
об их непротиворечивости.
Модели
Гильберт сформулировал также еще два важных для
аксиоматических систем свойства: полноту и независи-
мость.
Для того чтобы объяснить, что такое полнота, надо
ввести понятие доказательства в аксиоматической систе-
ме. Если р — некоторое утверждение этой системы, то
его доказательством называют конечную последователь-
ность утверждений, каждое из которых является либо
аксиомой, либо логическим следствием некоторых из
предыдущих, утверждений этой последовательности, при-
чем последним в этой последовательности стоит р. При-
мером может служить доказательство утверждения
(х+у)2 = х2 + 2ху+у2
в гл. 6. Система полна, если для каждого утверждения
р в ней можно найти или доказательство этого утвержде-
ния, или доказательство утверждения не -р. Иными
словами, в нашем распоряжении имеется достаточно
аксиом, чтобы доказать истинность или ложность любо-
го мыслимого утверждения этой системы.
К полной системе никоим образом нельзя добавить
еще одну аксиому — или она будет следствием из уже
имеющихся (т. е. лишней), или будет им противоречить
(т. е. система станет бессмысленной).
Множество аксиом независимо, если ни одну из этих
аксиом нельзя вывести из других.
Доказать полноту системы (если она действительно
волна) всегда нелегко, поскольку нужно рассмотреть все
151
возможные доказательства. Но существуют простые ме-
тоды, позволяющие доказать независимость (при подхо-
дящих условиях), а иногда и непротиворечивость. Свя-
заны они с понятием модели.
Модель аксиоматической системы — это некоторый
объект, в котором аксиомы этой системы при подходя-
щей интерпретации истинны. Любая группа является мо-
делью для аксиом группы: абстрактная операция из этих
аксиом интерпретируется как некоторая вполне опреде-
ленная операция в рассматриваемой конкретной группе.
Это может быть, например, сложение или умножение
функций. Аналогично любое кольцо — это модель для
аксиом кольца, а поле — модель для аксиом поля. Ана-
литическая геометрия на плоскости дает алгебраическую
модель аксиом евклидовой геометрии, если интерпрети-
ровать точки как пары (х, у) действительных чисел, а
прямые, окружности и т. п.— обычным образом.
Если для некоторой системы аксиом можно подобрать
модель, то эта система должна быть непротиворечивой.
Таблица умножения любой группы определяет некото-
рую модель; можно взять самый тривиальный пример:
X 1
1 I
Если бы система аксиом была противоречивой, то можно
было бы доказать любую теорему, например, что каждая
группа имеет 129 элементов. И так как эти аксиомы вы-
полняются в нашей модели, то и все следствия из них
также выполняются. Таким образом, наша модель долж-
на содержать 129 элементов. Понятно, что это не так.
Значит, система была непротиворечивой.
Это можно подтвердить и несколько иначе: любое
противоречие между теоремами, выведенными из аксиом,
найдет отражение в модели. Мы сумеем доказать и то,
152
что модель обладает некоторым свойством, и то, что она
им не обладает. Но это невозможно — модель или обла-
дает данным свойством, или нет, и одновременно обла-
дать и не обладать им она не может.
Модели бывают полезны и для доказательства неза-
висимости. Чтобы доказать, что закон ассоциативности
умножения в группе независим от других аксиом груп-
пы, надо лишь найти модель, в которой закон ассоциа-
тивности не выполняется, а все остальные аксиомы груп-
пы справедливы. Если бы закон ассоциативности выво-
дился из других аксиом, то можно было бы доказать
ассоциативность умножения в выбранной модели, но она
выбиралась именно так, чтобы умножение не было ассо-
циативным,
Мы построим необходимую нам модель с помощью
таблицы умножения. Нужно, чтобы в ней были справед-
ливы аксиомы (1), (2), (4), (5) со с. 128, но не (3).
Для аксиомы (1) нам необходимо множество G. Что-
бы облегчить задачу, возьмем маленькое множество, но
не слишком маленькое, чтобы иметь некоторую свободу
действий. Попробуем взять G= {о, Ь, а}.
Аксиома (4) утверждает существование единичного
элемента. Если мы примем за единицу элемент а, то тем
самым определим часть таблицы умножения:
X | а Ь с
а а b с
b b
с с
Далее, согласно аксиоме (5), у каждого элемента дол-
жен быть обратный. Наш единичный элемент а уже име-
ет обратный, так как а2 = а. Если положить be = cb = а, то
тем самым определятся обратные для b и с. Теперь наша
таблица выглядит так:
153
a b с
a b с
b a
c a
и аксиомы (1), (4) и (5) выполняются.
Чтобы выполнялась аксиома (2), нужно определить
произведение для любых двух элементов. Для этого нам
осталось лишь заполнить пустые места в нашей таблице
с помощью элементов а, b и с, причем неважно, как имен-
но мы их расположим. По нам еще нужно, чтобы была
неверна аксиома (3), и именно на это последнее требо-
вание мы будем ориентироваться, производя выбор. По-
ставить на оба оставшихся места элемент с нельзя — у
нас получилась бы такая же таблица умножения, как
для симметрий «бегущих ног», а умножение этих сим-
метрий удовлетворяет закону ассоциативности, Попробу-
ем сделать так:
X а Ь с
а а Ь с
b b Ь а
с с а b
После нескольких
попыток найдем
(cc)b = bb=bf
c(cb) =са—с,
то, что нам нужно:
т, е. закон ассоциативности не верен.
Таким образом, нужная модель построена. Построе-
ние моделей — это скорее искусство, чем наука. Оно тре-
бует опыта, склонности и «нешаблонности мышления»
де Боно. Наилучший способ научиться строить модели —
это пытаться их строить.
К вопросам непротиворечивости и полноты мы вер-
154
немея в гл. 20. Наша ближайшайЗщдГ^Нрйменйть ме-
тод моделей к вопросу о евклидовой аксиоме о парал-
лельных.
Евклид был лрав
Проблему можно сформулировать так: является ли
аксиома Евклида о параллельных независимой от дру-
гих его аксиом? Сформулировав таким образом, мы ее
уже наполовину решили, так как наибольшая трудность
заключается в том, чтобы осознать возможность незави-
симости этой аксиомы. МоЖет оказаться, что она выво-
дится из других аксиом, может оказаться, что не выво-
дится, но этим еще не исчерпываются все возможности.
Чтобы приступить к решению этого вопроса, необхо-
димо сделать одно допущение, а именно — предполо-
жить, что аксиомы евклидовой геометрии непротиворе-
чивы. Ведь мы собираемся использовать евклидову гео-
метрию как «сырье» для модели. И если ее аксиомы
противоречивы, то вопрос независимости отступает на
второй план.
Построение моделей — это, как я уже говорил, искус-
ство, но в данном случае искусство становится магией:
мне не остается ничего иного, как взмахнуть волшебной
палочкой и извлечь из шляпы кролика.
Проведем на плоскости окружность Г. Наша модель —-
это та часть евклидовой геометрии, которая попадает
внутрь круга, ограниченного этой окружностью. Чтобы
избежать путаницы, для обозначения интерпретаций в
модели стандартных понятий евклидовой геометрии мы
будем использовать курсив:
точка — точка плоскости, лежащая внутри Г;
прямая — часть некоторой прямой на плоскости, ле-
жащая внутри Г;
окружность — часть некоторой окружности на пло-
скости, лежащая внутри Г;
155
прямой угрл — обычный црдмой угол внутри Г;
(Вер это изображено на рис. 53.)
Проверим аксиомы (см. с. 146).
(Г) Через любые две точки можно провести прямую.
Это верно. Любые две точки внутри Г — это точки на
плоскости. Соединим их прямой на плоскости, а затем
Рис. 53.
ртбросим ту часть, которая не лежит внутри Г, и тем
самым получим прямую (рис. 54).
(2) Любые две прямые имеют не более одной общей
точки. Это верно. Две прямые являются частями двух
прямых на плоскости, которые имеют не более одной об-
щей точки, а значит, и не более одной общей точки
(рис. 55).
(3) Любой конечный отрезок прямой можно неогра-
ниченно продолжать. Это уже не столь бесспорное утвер-
ждение. На первый взгляд кажется, что это просто не-
верно, поскольку как только прямая выходит за пределы
Г, она перестает быть прямой. Но ведь и Евклид не имел
156
б виду, чтобы прямую продолжали за пределы плоско-
сти — за край, так сказать. Построение должно ограни-
чиваться рассматриваемой областью, т. е. мы должны
рассматривать понятие продолжения, а не продолжения.
Смысл аксиомы (3) состоит в том, что если у нас есть
отрезок прямой с концами, его можно продолжить за эти
Рис. 54.
концы. Эго также верно в нашем круге, если, говоря
«внутри» Г, мы исключаем из рассмотрения все точки,
лежащие на Г. Действительно, как показано на рис. 56,
мы можем последовательно продолжать отрезок прямой
до точек 1, 2, 3, 4, 5, ..., и этот процесс никогда не прекра-
тится
157
Сама прямая не имеет концов: те точки, которые
могли бы служить ее концами, лежат на окружности Г,
а не внутри нее и, значит, не являются точками. В этой
модели все прямые продолжаются неограниченно,
(4) Вокруг любой точки можно описать окружность
произвольного радиуса, Это следует из соответствующей
аксиомы для плоскости (как всегда, отбрасывается все,
что находится на окружности Г и вне ее. Конечно,
окружность уже не всегда будет «круглой» (рис. 57),
Но это не влияет на истинность аксиомы.
(5) Все прямые углы равны между собой опять-таки
потому, что на плоскости все прямые углы равны между
собой.
Таким образом, аксиомы (1) — (5) в рассматривае-
мой модели выполняются. Однако аксиома (6) в ней не
выполняется: на рис. 58 показаны прямая, точка и не-
сколько прямых, параллельных первой и проходящих че-
рез данную точку. Здесь, разумеется, мы «параллель-
ные» понимаем как «непересекающиеся». И неважно,
что если продолжить наши прямые за пределы рассмат-
риваемого круга, то они пересекутся,— все точки, нахо-
дящиеся вне круга, не принадлежат нашей модели.
158
Отсюда следует, Чтд аксиома (6) ревЫвддима из ак-
сиом (1) — (Б), Если бы она была выводима из них, то
поскольку аксиомы (1) — (5) в рассматриваемой моде-
ли истинны, то и аксиома (6) как их логическое следст-
вие должна была быть истинной в этой же модели. Но это
не так. Можно провести рассуждение несколько иначе{
любое доказательство аксиомы ----jt
(6) в евклидовой геометрии ста-
Йовится доказательством этой Z—
аксиомы в рассматриваемой мо-
дели, если ааменить везде «точ- Г
ка» на «точка», «прямая» на I I
«прямая» и т. п. Так как аксио- V /
ма (6) в модели ложна, То пред- \ "у
полагаемое евклидово доказа-
тельство Не может существовать,
lot факт, что «точки» — это не рис. 58.
то же самое, что «точки», ничего
не меняет! ведь аксиомы (1) — (5) для них истинны.
Это я имел в виду, когда озаглавил раздеЛ «Евклид
был прав». Не то, что евклидова геометрия — единствен-
но возможная, а что Евклид был совершенно прав, вве-
дя свою аксиому о параллельных как исходную посылку,
невыводимую из его остальных аксиом.
Другие геометрии
Выбрав другую модель, можно несколько улучшить
доказательство, сделав, в частности, аксиомы (3) и (4)
более убедительными. Для этого нужно так переопреде-
лить понятие длины внутри Г, чтобы все прямые стали
бесконечно длинными (однако тогда они должны стать
кривыми). Подробнее см. книгу Сойера2.
Можно устроить и так, чтобы параллельных прямых
не было вовсе. Такая модель построена Клейном, В этой
модели мы используем прописные буквы,
169
Рассмотрим сферу S в трехмерном пространстве. (Она
будет играть ту же роль, что и внутренность Г.) Пусть
ПРЯМАЯ — это большая окружность на S (т. е. та
окружность, центр которой совпадает с центром самой
сферы);
ТОЧКА — пара диаметрально противоположных точек
на 2.
Рис. 60.
Проверим аксиомы. Аксиома (2) истинна, поскольку лю-
бые два больших круга пересекаются в двух диаметраль-
но противоположных точках. Другие аксиомы (1), (3), (4),
(5) тоже выполняются (без всяких тонкостей по поводу
(3)). Но поскольку любые две большие окружности пере-
секаются, параллельных прямых нет вообще! (См. рис. 59.)
Теперь в нашем распоряжении три различных рода
геометрии: евклидова геометрия, гиперболическая гео-
метрия, где через точку проходит много различных па-
раллельных прямых, и эллиптическая геометрия, где па-
раллельных прямых не существует.
Риман ввел общую геометрию, которая может быть
эллиптической в одних областях и гиперболической в
других. Ее двумерный вариант можно представлять как
геометрию некоторой искривленной поверхности (рис. 60).
Возле точки А геометрия эллиптическая, а возле В —
гиперболическая. (Это объясняет терминологию: сечение
160
рассматриваемой поверхности возле точки А близко к
вллипсу, а возле точки В — к гиперболе.)
Идея Римана развивается дальше. Существуют про-
странства размерности (три или более), геометрия ко-
торых также меняется от точки к точке: «искривленное»
пространство! Согласно Эйнштейну, обычное простран-
ство — время имеет именно такую геометрию. Мы можем
считать, что кривизна вызывается гравитационным по-
лем вещества или же, наоборот, вещество и тяготение
есть следствие искривления пространства.
Если геометрия пространства — времени в некоторой
области эллиптическая, то не исключена возможность
отправиться в путь по прямой и в конце концов вернуть-
ся в исходную точку. Хуже, если это случается со вре-
менем: вы можете вернуться раньше, чем выйти. Это
кажется неправдоподобным. Но некоторые астрономы
заявляют, что слишком большое количество радиозвезд
расположено в диаметрально противоположных точках
неба, чтобы это могло оказаться случайным. Быть может,
такая пара звезд — это одна звезда, видимая с двух про-
тивоположных направлений.
6 Я. Стюарт
Глава 9
СЧЕТ. ПОНЯТИЕ О БЕСКОНЕЧНОМ
«Четырнадцать»,~~ сказал Пух.
«Входите. Четырнадцать. Или
пятнадцать? Ох. Я совсем за*
путался».
А. А. Милн
Никто не станет учить ребенка считать, объясняя ему,
что такое число. Вместо этого ему будут показывать двух
собак, два яблока, две книги, и постепенно он выделит
свойство, общее всем этим примерам, и сам выработает
какое-то свое представление о «числе».
Числа — это свойства множеств. Из двух элементов
состоит множество яблок, собак и т. д., и в процессе сче-
та мы как раз устанавливаем количество элементов мно-
жества. Когда математики всерьез задумались над во-
просом, что же такое число, они прежде всего обнару-
жили этот факт. Кроме того, им стало ясно и другое:
легче установить, совпадают или нет два числа, чем ска-
зать, каковы они.
Если ребенок видит две чашки, каждую со своим
блюдцем, то наступит день, когда он поймет, что и блю-
дец тоже два. Если у нас семеро гостей, а стульев всего
шесть,— кто-то останется без стула. Если администратор
театра видит, что каждое кресло занято одним зрителем,
он понимает, что зрителей ровно столько, сколько мест
в зале, и для этого ему не надо знать само количество
мест.
Это означает, что понятие «равные числа» не связа-
но с понятием «число» (несмотря на причуды языка).
Подобным же образом, приложив друг к другу два куска
веревки, можно установить, что они имеют одинаковую
длину, так никогда и не узнав, чему она равна, или при
162
помощи равноплечих весов убедиться, что два тела име-
ют одинаковую массу,
Во всех этих случаях легче сказать, обладают или нет
два данных объекта общим свойством, чем объяснить в
общем виде, что это за свойство. Все, что требуется,—
придумать способ сравнения объектов по отношению к
этому (пока не определенному) свойству.
Метод сравнения длин или масс выбрать нетрудно, а
как сравнивать числа?
Вернемся к примеру о зрителях в театре. Чтобы знать
наверное, что число зрителей в точности равно числу
мест в зале, нужно знать две вещи:
а) каждый зритель занимает ровно одно место;
б) каждое место занято ровно одним зрителем.
Пусть S—множество мест, а Р—множество зрителей
и выполнены эти условия. Тогда для каждого зрителя
р С Р мы можем определить f(p)£S как место, которое
он занимает. Тем самым будет задана биекция /: P->S.
В самом деле, во-первых, f—функция: Р—ее область
определения, S — множество, содержащее ее область зна-
чений, и указанное выше правило однозначно (в силу усло-
вия «а») задает f (р) для каждого р. Во-вторых, f сюръ-
ективна, так как, по условию «б», каждое место занято,
и инъективна, так как, по тому же условию, каждое ме-
сто занято только одним зрителем.
И в общем случае два множества имеют равное число
элементов тогда и только тогда, когда между ними су-
ществует биекция (взаимно .однозначное соответствие),
Эту ситуацию иллюстрирует рис. 61.
Во избежание лингвистических проблем назовем два
множества равночисленными, если между ними суще-
ствует биекция. Тогда станет несколько яснее, что, говоря
о «равных числах», можно пока не знать, что такое чи-
сло. Подобно тому как мы разбивали целые числа на
классы сравнимых по некоторому модулю, разобьем
теперь множества на классы равночисленных: два мно-
6»
163
жества отнесем к одному классу тогда и только тогда,
когда они равночисленны. Каждый класс можно задать,
указав один из его членов. Например, класс, содержа-
щий множество {a, b, с, d, е), включает в себя любое
равночисленное с ним множество, а таковыми являются
те и только те множества, которые состоят из пяти эле-
ментов. Эту ситуацию иллюстрирует рис. 62.
Рис. 61,
Рис. 62.
164
В этом смысле число 5 будет задано, если
а) задано некоторое множество и сказано, что оно со-
стоит из 5 элементов;
б) сказано, что любое множество, равночисленное с
заданным, тоже состоит из 5 элементов.
Как заметил Фреге, мы попадаем в весьма занятную
ситуацию. С одной стороны, имеется загадочное и уди-
вительное понятие: «число», которому мы не можем дать
определение. С другой стороны, есть вполне земное по-
нятие: класс, к которому относится данное множество.
Двум множествам отвечает одно и то же число тогда и
только тогда, когда они из одного класса. Отсюда следу-
ет, что если знать все о классах, то будешь знать все и
о числах.
На этом этапе можно занять одну из следующих двух
позиций:
А) каковы бы ни были эти дурацкие классы, я пре-
красно знаю, что они не числа, а только ведут себя, как
числа;
В) я не знаю, что такое числа, я просто пользуюсь
этим словом. Эти классы ведут себя точно так же, как
мои гипотетические числа, и имеют то преимущество, что
я знаю, что они такое. Я мог бы сказать, что классы и
есть числа.
Какую именно из этих позиций занять,— не очень су-
щественно, важно только понимать, что позиция «В»
имеет одну привлекательную сторону: классами можно
воспользоваться для определения чисел, и это определе-
ние будет вполне удовлетворительным *. И действитель-
но, показывая ребенку двух собак, два яблока, две кни-
ги, мы как раз и демонстрируем ему элементы класса,
отвечающего числу 2.
Вот все, что нам требуется знать о числах: каждому
множеству отвечает нечто, называемое числом, причем
двум множествам отвечает одно и то же число тогда
и только тогда, когда они равночисленны.
165
Существование чисел можно принять за аксиому,
А дальше можно построить всю арифметику. Сначала
определим несколько чисел:
О отвечает пустому множеству 0
1 отвечает множеству {х},
2 отвечает множеству {х, у},
3 отвечает множеству {х, у, z},
4 отвечает множеству {х, у, г, ш}
Конечно, все х, у, z, w, ... выбираются различными.
Затем введем сложение и умножение. Вспомним, как
это делают в начальной школе: чтобы сложить 3 и 2,
берут три фишки, потом еще две, выкладывают их все
в ряд и считают, сколько получилось (рис. 63).
Важно, чтобы фишек хватило! Если две новые взять
из трех старых, ответ получится неправильный!
Таким же способом можно определить сложение лю-
бых двух чисел. Возьмем два числа т и п. Найдем отве-
чающие им множества М и N (соответственно), причем
такие, которые не пересекаются, т. е. не имеют общих эле-
ментов (в теории множеств это обозначается так!
MHN=0 )• Образуем объединение Л4 (J N. Ему отвечает
166
какое-то число. Это число и будем, по определению, счи-
тать суммой т + п (рис. 64).
По поводу этого определения нужно сделать два за-
мечания. Во-первых, всегда можно найти непересекаю-
щиеся множества М и N. В самом деле, если они пере-
секаются, можно заменять по одному общие элементы
другими, и сам способ замены определяет биекцию меж-
ду старым и новым множеством, которая гарантирует,
что они остаются в одном классе.
Во-вторых, сложение должно быть «корректно опре-
делено». Взяв другие множества М' и N', отвечающие
числам т и п, придем ли мы к тому же результату?
Если нет, то наше определение бесполезно. Что же это
за сложение, если одним способом получается 2 + 2 = 4,
а другим 2+2 = 5?
Допустим, что выбраны другие множества М' и N',
которые не пересекаются и отвечают числам т и п. То-
гда М и М' отвечают одному и тому же числу, и, значит,
существует биекция /: М-^-М'. По той же причине су-
ществует биекция g: N->N'. Тогда можно построить би-
екцию h: М (J N -> М' (J N', если положить
лж = Jпри хеМ’
1 g (х) при х 6 N.
(Нужно еще проверить, что это действительно биекция.
Интуитивно это очевидно из рис. 65.)
Теперь у нас достаточно информации, чтобы дока-
зать знаменитую теорему: 2+2 = 4.
Сначала нужно найти непересекающиеся множества
Л4 и 7V, каждое из которых отвечает числу 2. По опре-
делению, можно взять М — {х, у}. В качестве N возьмем
множество {а, Ь}, где х, у, а, b все различны. Существует
биекция f: М -> N, при которой f (х) = a, f (у) = Ь, так что
М и N равночисленны. Значит, N тоже отвечает числу 2.
Затем образуем М (J N = {х, у, а, Ь}. Существует биекция
167
между этим множеством и множеством {х, у, г, го}, опреде-
ленная формулами g (л) = х, g (у) = у, g (о) = z, g (b) — w.
Множество {x, у, г, то}, по определению, отвечает числу 4,
значит, и Л4 J N отвечает числу 4. По определению сло-
жения, 2 4-2 = 4.
Схема этого рассуждения представлена на рис. 66.
Немного легче определить умножение, поскольку при
этом не придется заботиться о том, чтобы соответствую-
щие множества не пересекались. Чтобы перемножить
числа т и п, возьмем соответствующие множества М
и N, построим их декартово произведение MxN (гл. 4)
и отвечающее ему число будем, по определению, считать
произведением тп. В том, что это правильное определе-
Рис. 66.
168
ние, можно убедиться при помощи рис. 67. (Здесь снова
необходимо проверить, что при другом выборе Л'1 и N
получится тот же ответ, и это нетрудно сделать.)
Еще более впечатляет то, что при таком подходе
можно доказать законы арифметики, по крайней мере
для положительных целых чисел (а из них уже можно
Рис. 67.
вывести эти законы для отрицательных целых, для ра-
циональных и для действительных чисел 2), Возьмем, к
примеру, закон дистрибутивности:
(т + п)р = тр + пр.
Пусть множества А4, N, Р отвечают числам т, п, р
причем М и N не пересекаются. Тогда (т + п) р отвеча-
ет множеству (Л! U N) х Р, а тр + пр — множеству (Л1 х
xP)U(-MxP). Но эти два множества совпадают: первое
состоит из всех упорядоченных пар (х, у), где М или
х С N, а у £Р', второе состоит из всех упорядоченных пар
(х, у), где х 6 М и у£Р или N и у 6 Р (рис. 68).
Раз эти множества совпадают, то между ними су-
ществует биекция, определяемая в данном случае тож-
дественным отображением. Следовательно, они равно-
169
численны, отвечающие им числа равны, и закон дистрнч
бутивности доказан.
Аналогично доказываются другие законы арифмв*
тики.
В заключение этого раздела попробуем по-новому
истолковать способ счета,, применяемый ребенком*

Рис. 68.
Обычно он указывает по очереди на каждый предмет
и произносит: «один, два, три, ...». Если в качеств^ стан-
дартных множеств для определения чисел мы возьмем
0 ,{1}, {1, 2}, {1, 2, 3},{1, 2, 3, 4} и т. д. (где 1, 2, 3,
Рис. 69.
170
...— какие-то символы), то этот детский счет удиви-
тельно нй'поминает установление биекции между дан-
ным множеством предметов и одним из наших стандарт-
ных множеств (рис. 69).
Арифметика бесконечного
Все предыдущие рассуждения, как обнаружил Георг
Кантор, пригодны не только для конечных, но и для бес-
конечных множеств. (А мы нигде и не говорили, что
рассматриваем лишь конечные множества, но умышлен-
но приводили конечные примеры.) Понятие биекции
вполне подходит для бесконечных множеств, поэтому
можно говорить об их «равночисленности», а это позво-
ляет ввести бесконечные «числа», считая, как раньше,
что равночисленные множества определяют одно и то
же число, и наоборот.
Чтобы никого не шокировать, математики придумали
для этих «чисел» другое слово, точнее, воспользовались
уже существующим словом «мощность». Их называют
также кардинальными или трансфинитными числами, а
вместо слова «равночисленные» пользуются термином
«равномощные». Для конечного множества мощность —
это число его элементов; мощность бесконечного мно-
жества также обладает многими свойствами, напоми-
нающими о происхождении этого понятия. Данные выше
определения сложения и умножения также годятся и для
кардинальных чисел, и для них справедливы законы
коммутативности, ассоциативности и дистрибутивности,
Однако за выход в бесконечность приходится кое-чем
и поступиться.
Одно любопытное свойство кардинальных чисел было
отмечено Галилеем в 1638 г.: оказывается, существует
биекция между бесконечным множеством и его меньшим
подмножеством. Например, функция f, для которой
f (п)=п2} является биекцией между множеством N нату«
171
ральных чисел и его подмножеством — множеством пол-
ных квадратов. Значит, бесконечное множество может
иметь ту же мощность, что и какая-то его часть. Таким
образом, евклидов принцип: целое больше своей части —
следует несколько уточнить: целое больше или равно
своей части (где под «равно» понимается «равно-
мощно»)
Изменив немного наши прежние диаграммы для
функций, мы получим подходящий способ изобразить
эту биекцию:
0 1 2 3 4 5 6 ... п ...
t t t t t ♦ t t
444**44 *
0 1 4 9 16 25 36 ... n2 ...
Существуют и другие подобные биекции: между N и мно-
жеством четных натуральных чисел, или нечетных, или
всех целых, или простых. Вот эти биекции:
0 1 2 3 4 5 6 ...
t t t t t t t
i i ♦ i i * 4
0 2 4 6 8 10 12 ...
0
t
4
1
12 3 4
5
t
г
11
6 ...
t
i
13 ...
t
3
t
i
5
t
4
7
t
4
9
0
t
4
0
1
t
I
1
2 3 4 5 6 ..
1 1 t 1 г
4 4 4 4 1
— 1 2 —2 3 —3 ...
0 1
t t
4
2 3
2
t
4
5
3
1
4
7
4 5 6 ...
t t t
4 4 4
ll 13 17 ...
Это означает, что все перечисленные множества имеют
одну и ту же мощность. Мощность множества N нату-
172
ральных чисел обозначается (алеф-нуль). Кантор
предполагал, что имеется целая система бесконечных
кардинальных чисел Ко К* , из которых Ко “
наименьшее.
Всякое множество мощности Ко называется счет-
ным (поскольку биекция с N позволяет его «пересчиты-
вать», хотя этот счет никогда не кончится). Бесконечные
множества, которые не являются счетными (а бывают и
такие), называются несчетными.
Только что мы показали, что множества А и В четных
и нечетных чисел оба счетны. Они не пересекаются, и их
объединение есть N. По определению сложения карди-
нальных чисел, мощность N равна сумме мощностей
А и В. Но N тоже счетно, поэтому
Ко+Ко = Ко •
Итак, мы удвоили Ко , а оно осталось тем же. Это еще
одна жертва, которую приходится принести, если мы
хотим рассматривать бесконечные множества. (Заметим,
что отсюда не следует равенство Ko=Q поскольку вы-
читать мощности мы не умеем.)
Большие и маленькие бесконечности
Мощности можно сравнивать по величине. В случае
конечных множеств М и N, если в М меньше элементов,
чем в N, существует инъекция М в N (как на рис. 70).
Обобщим этот факт. В случае бесконечных кардиналь-
ных чисел аир будем говорить, что а меньше или рав-
но р, если найдутся такие множества А и В мощностей
соответственно а и р, для которых существует инъекция
/: А-+В. Иначе говоря, это условие означает, что неко-
торое множество мощности а можно поставить во взаим-
173
но однозначное соответствие с подмножеством некоторого
множества мощности р. Как обычно, мы пишем
Будем говорить, что а меньше р, если а р и а р.
Это отношение порядка кардинальных чисел обладав
ет несколькими приятными свойствами:
а) аа для любого а;
б) если а^р и Р^у, то
в) если а^р и р^а, то а=р.
Свойство «в» доказать очень нелегко. Оно составля-
ет содержание известной теоремы Шредера Берн-
штейна 3.
i 4г
ООО
Рис. 70.
До сих пор мы познакомились только с одним беско-
нечным кардинальным числом . Существуют ли
другие?
Можно было бы думать, что множество Q рациональ-
ных чисел имеет большую мощность; ведь между любы-
ми двумя целыми числами лежит бесконечно много ра-
циональных. Однако это не так.
Представим себе, что все рациональные числа p/q
(g^O) расположены в виде бесконечной квадратной таб-
лицы;
174
1 ! | 1 1
• • • 3/—3 3/-2 3/-1 3/1 3/2 3/3 • . •
• • • 2/—3 2/—2 2/-1 2/1 2/2 2/3
• • • 1/-3 1/-2 1/-1 1/1 1/2 1/3
».. 0/—3 0/—2 0/-1 0/1 0/2 0/3
•.« —1/—3 -1/-2 -1/-1 -1/1 —1/2 -1/3
• • • —2/—3 —2/—2 -2/-1 —2/1 —2/2 —2/3
• « • —3/—3 —3/—2 —3/—1 -3/1 —3/2 —3/3
А теперь пойдем по спиральному пути, начиная от точки
0/1 (рис. 71),
Двигаясь по этому пути,
мы рано или поздно достиг-
нем любого рационального
числа p/q. Определим функцию
f: N -> Q так: положим f(n)
равным n-му по порядку чис-
лу вдоль нашего пути, считая
только те рациональные чис-
ла, которые не встретились
раньше. Это правило одно-
значно определяет f (п) и, еле- рис_ 71
довательно, задает функцию.
Она сюръективна, так как путь проходит через каждое
рациональное число, и инъективна, так как учитываются
только различные рациональные числа. Значит, установ-
лена биекция между N и Q, а следовательно, мощность
Q тоже равна .
Несколько первых рациональных чисел на нашем
пути таковы: 0/1, 0/2, 1/2, 1/1, 1/—1, 0/—1, — 1/—1, —1/1,
-1/2, -1/3, 0/3, 1/3, 2/3, 2/2, 2/1, .„ Некоторые из них
175
повторяются: 0/1 =0/2 = 0/—3 = 0/3 = 0; 1/1 = — 1/—3=
= 2/2=1 и т. д. Исключив эти повторения, получим
0123 4 5 6 78...
ftttf t t ft
I I t I I 4 4 II
0 1/2 1 —1 —1/2 —1/3 1/3 2/3 2 ...
Закономерность, по которой нижняя строка получается
из верхней, не очевидна, но мы тем не менее знаем, как
продолжить эту строку, двигаясь дальше по спирали.
Получить формулу n-го рационального числа трудно, но,
поскольку функция не обязательно должна задаваться
формулой, нас это не волнует.
Другой возможный кандидат на роль множества,
мощность которого больше ,— множество R дейст-
вительных чисел. Поскольку каждое действительное чи-
сло допускает приближение рациональными числами с
любой точностью, можно было бы думать, что мощности
этих множеств одинаковы. Однако на этот раз это не так.
Мощность множества R — обозначим ее с — больше,
чем Ко1.
Это доказывается методом от противного. Допустим,
что существует биекция между множествами N и R. Каж-
дое действительное число записывается в виде
где А — целое, а каждое а, равно одному из чисел от 0
до 9. При этом следует помнить, что в десятичной запи-
си имеется неопределенность: 0,1 000... = 0,0999... . Она
возникает тогда, когда бесконечно повторяются нули
или девятки, поэтому давайте договоримся не пользо-
ваться записью с повторяющимися девятками. Тогда
каждое действительное число будет единственным обра-
зом записываться в указанном виде.
17G
Биекция N->R выглядела бы так:
Оч- 1 Р с? к? о «я
1ч > В, bL b2 Ь3 Ьц Ь6
2 ч- Су Сл
Зч- -+-D, d1 d2 d3 dt d6
4ч- £> C2 ^3 ^4 ^6 '
где слева стояли бы все числа из N, а справа — все чи-
сла из R.
Теперь мы выпишем число из R, которого справа нет.
Возьмем число
О, Z1Z2Z3Z4Z6...,
ГДе Zi отлично от ab z2 отлично от b2, z3 отлично от с3
и т. д., z„ отлично от n-й цифры после запятой числа,
стоящего напротив п—1. Кроме того, во избежание не-
определенности будем выбирать наши zb z2, ... отличны-
ми от 0 и 9.
Полученное число будет действительным. Однако оно
не совпадает ни с одним из чисел правого столбца, по-
скольку отличается от каждого из них хотя бы в одном
десятичном знаке: от первого — в первом, от второго —
во втором и т. д., от н-го (стоящего напротив и—1) —
В /1-м.
Итак, мы нашли число, которое не вошло в нашу
диаграмму. Но мы утверждали, что в нее входят все
действительные числа. Значит, мы пришли к противо-
речию.
Остается сделать вывод, что такой диаграммы не су-
ществует, а значит, не существует биекции N~>R. От-
сюда видно, что мощность множества R не равна ^0.
Но существует очевидная инъекция N—>R (тождествен-
ное отображение N), так что ^0^с, Хо*с
то есть $о<с. Таким образом, судя по мощностям,
177
действительных чисел больше, чем рациональных, а ра-
циональных ровно столько же, сколько целых.
Итак, у нас появилось новое кардинальное число с,
большее, чем .Не является ли это с канторовским
?Ответ зависит от того, существует или нет карди-
нальное число, меньшее, чем с,но большее, чем .Эта
г»
проблема была решена Коэном в 1963 г., но решение
Оказалось настолько неожиданным, что мы отложим
разговор о нем до гл. 20.
Существуют кардинальные числа, большие с. Самого
большого кардинального числа вообще нет: для любого
кардинального числа а можно найти большее карди-
нальное число.
Возьмем какое-нибудь множество А мощности а.
Пусть Р — множество всех его подмножеств и 0 — мощ-
ность Р. Покажем, что 0>а.
Сначала заметим, что формула f (х) — {х} определяет
инъекцию А->Р. Поэтому заведомо а^0. Если а ==
то существует биекция h: А->Р. Для каждого х£ А эле-
мент h(x) является подмножеством А. При этом х либо
принадлежит h (х), либо не принадлежит. Определим мно-
жество Т условием Т = {х| х не принадлежит й(х)}. Это
подмножество множества А, так что Т € Р. Поскольку h—
биекция, найдется t^A, для которого h(t) = T.
Посмотрим теперь, принадлежит t множеству /i(/) или
нет. Если да, то Т. Но Т состоит из тех х, для ко-
торых х£ h (х), откуда следует, что h(f). С другой сто-
роны, если то t удовлетворяет условию, опреде-
ляющему Т, и, значит, Т. Но Т = h(t), поэтому h(t).
В любом случае мы приходим к противоречию. Следова-
тельно, неверно исходное предположение о существовании
h. Тогда 0=^=а, и остается единственная возможность: а<0.
Этот факт позволяет дать другое доказательство не-
счетности множества R. Всякому подмножеству S мно-
178
жества натуральных чисел можно поставить в соответ-
ствие действительное число
О,
где а„=1, если п С S, и ап = 2, если п С S. При этом
разным подмножествам S соответствуют разные числа. Зна-
чит, определена инъекция множества подмножеств мно-
жества N в множество R. Но мощность множества под-
множеств N больше , следовательно, и мощность R
больше .
Трансцендентные числа
Если бы бесконечные кардинальные числа годились
только для того, чтобы доказывать теоремы о бесконеч-
ных кардинальных числах, вряд ли они бы кого-нибудь
особенно заинтересовали. Обратить на них внимание за-
ставила математиков возможность применять их для
доказательства теорем, не относящихся к кардинальным
числам.
Некоторые действительные числа удовлетворяют
уравнениям вида
апхп + On-iX”-1 +... + а0 = О,
где в левой части стоит многочлен с целыми коэффици-
ентами az . Например, число ~]/~2 удовлетворяет уравне-
нию
х2—2 = 0.
Такие числа называются алгебраическими. Любое дей-
ствительное число, не являющееся алгебраическим, на-
зывается трансцендентным.
В гл. 6 мы отмечали, что все числа, для которых воз-
можно построение, удовлетворяют уравнению такого
вида, но с рациональными коэффициентами. Умножив
179
такое уравнение на общий знаменатель всех коэффи-
циентов, мы получим уравнение с целыми коэффициента-
ми. Следовательно, всякое такое число является алгеб-
раическим. Кроме того, мы там утверждали, что число л
не удовлетворяет никакому уравнению такого вида, ина-
че говоря, оно трансцендентно.
Математики в течение многих лет подозревали, что л
трансцендентно, но не могли это доказать. Хуже того,
ни для каких чисел вообще не удавалось доказать, что
они трансцендентны. Затем в 1844 г. Лиувилль доказал
теорему, которая давала способ построения трансцен-
дентных чисел. Это доказательство отнюдь не отличалось
простотой! В 1873 г. Эрмит доказал трансцендентность
числа е (основания натуральных логарифмов), а в
1882 г. Линдеман установил трансцендентность числа л.
И вот в 1874 г. Кантор нашел очень простой способ
доказать существование трансцендентных чисел, не ука-
зывая ни одного из них. Он воспользовался бесконечны-
ми кардинальными числами.
Допустим, что задан многочлен
апхп +ап-iXn~ * +... + Gq.
Назовем его высотой числа
| ао | + | 1 +... + | ап | + п.
Например, высота многочлена х2 — 2 равна
|-2| + |1|+2 = 2+2+1 = 5.
Всякий многочлен с целыми коэффициентами имеет
конечную высоту. Более того, имеется только конечное
число многочленов любой заданной высоты h. В самом
деле, степень п меньше высоты, а каждый коэффициент
может принимать лишь одно из значений — h, —h + 1, ...,
— 1, 0, 1, 2, ..., h. Итак, многочленов высоты h во всяком
случае не больше, чем
(2h+1 )'*+>,
180
(Эту оценку можно было бы улучшить, но здесь нас
устраивает любая оценка.)
Таким образом, все многочлены с целыми коэффи-
циентами можно расположить в последовательность:
сначала перечислить многочлены высоты 1 (в любом
порядке), затем высоты 2, высоты 3 и т. д. Поскольку
многочленов каждой высоты конечное число, мы не за-
стрянем навсегда на какой-то определенной высоте, и
каждый многочлен с целыми коэффициентами где-то
в нашей последовательности обязательно появится.
Многочлены высоты 1—это 1 и —1. Многочлены
высоты 2 —это 2, —2, х, — х; высоты 3 — это 3, —3, 2х,
—2х, х+1, х—1, — х+1, — х— 1, х2, — х2. Значит, наша
последовательность начинается так: 1, —1, 2, —2, х, —х,
3, —3, 2х, —2х, х+1, х—1, —х+1, —х—1, ... . Обозна-
чим n-й многочлен в этой последовательности рп(х); то-
гда она примет вид:
Pi(x), Рг(х), Рз(Х), ..., рп(х), ....
причем здесь встречается каждый многочлен с целыми
коэффициентами.
Алгебраические числа — это корни уравнений
Рп(х)=0.
Если степень многочлена рп(х) равна d, это уравнение
имеет не более d корней, которые можно написать в
каком-нибудь порядке:
«1... CLd-
Записав подряд корни каждого многочлена Рп(х), мы
получим новую последовательность, содержащую каждое
алгебраическое число:
Pi, р,, Р<+1, ••• Р/, •••» Ра , .... Р/, ...
корни корни корни
А (*) = 0 р2 (х) = 0 рп (х) = 0
181
При stom, конечно, всякое алгебраическое число может
встретиться в этой последовательности не один раз.
Теперь для всякого натурального т определим f(m)
как (m-f-l)-e число в нашей последовательности, считая
только различные алгебраические числа. Тем самым
будет задана функция f из N в множестве алгебраиче-
ских чисел. Она сюръективна, потому что в нашу по-
следовательность входит каждое алгебраическое число,
и инъективна, потому что учитываются только различ-
ные алгебраические числа. Значит, / — биекция, откуда
следует, что множество алгебраических чисел имеет
мощность $0, т. е. счетно.
Но, как мы знаем, множество действительных чисел
несчетно. Значит, некоторые действительные числа не
являются алгебраическими. Тем самым доказано суще-
ствование трансцендентных чисел.
Короче; трансцендентные числа существуют, потому
что действительных чисел больше, чем алгебраических.
Перед нами пример чистого доказательства су-
ществования. Из него мы не узнаем ни одного трансцен-
дентного числа. В частности, оно не поможет установить
статус л. Из него понятно лишь одно: невозможно, что-
бы трансцендентных чисел совсем не было.
На самом деле оно показывает, что трансцендентных
чисел больше, чем алгебраических. Если бы их было
столько же, т. е. их число равнялось бы , то посколь-
ку каждое действительное число либо алгебраическое,
либо трансцендентное, выполнялось бы равенство
t^o + Ko = C,
где с — мощность R. Но мы уже знаем, что
а не равно с.
До того как Кантор доказал свою теорему, матема-
тики привыкли думать, что трансцендентные числа —
182
большая редкость, поскольку они, казалось, почти не
рспользущтся. Выло настоящим ударом узнать, что они
весьма обычны и что почти все действительные числа
Франсцендентны. Если вы наугад выберете какое-то
Действительное число, оно почти наверняка окажется
1*рансцендентным,
Глава 10
топология
«Тополог — это тот, кто наби-
вает чучела?»
Из разговоров
Одним из самых неожиданных явлений в развитии
математики 20 в. стал головокружительный взлет науки,
известной под названием топология. Желая пояснить,
что такое топология, иногда говорят, что это «геометрия
на резиновой поверхности». Это малопонятное и туман-
ное описание позволяет тем не менее уловить суть пред-
мета. Топология изучает те свойства геометрических
объектов, которые сохраняются при непрерывных пре-
образованиях. Непрерывные преобразования характери-
зуются тем, что точки, расположенные «близко одна к
другой» до преобразования, остаются такими и после то-
го, как преобразование закончено. При топологических
преобразованиях разрешается растягивать и изгибать, но
не разрешается рвать и ломать. (Однако, с одной ого-
воркой: когда речь идет о преобразованиях, нас не инте-
ресует, что происходит в процессе этих преобразований,
важны только начальное положение и конечный резуль-
тат. Поэтому допускаются, скажем, разрезы по каким-
то линиям, которые потом склеиваются по тем же ли-
ниям. Например, если шнурок завязан узлом и его кон-
цы соединены, можно разрезать его где-то, развязать
узел и снова соединить на месте разреза. В этом смысле
выражение «геометрия на резиновой поверхности» не
слишком удачно.) Можно было бы дать строгое опреде-
ление «непрерывности», однако пока мы ограничимся
интуитивным представлением о ней. Этот вопрос будет
поднят еще раз в гл. 16.
Какого рода свойства являются топологическими?
Ясно, что не те, которые изучаются в обычной евклидо-
184
вой геометрии. Прямолинейность не есть топологическое
свойство, потому что прямую линию можно изогнуть,
и она станет волнистой. Треугольность — тоже не явля-
ется топологическим свойством, ибо треугольник можно
непрерывно деформировать в окружность (рис. 72).
Итак, в топологии треугольник и окружность — одно
и то же. Длины отрезков,
величины углов, площа-
ди — все эти понятия из-
меняются при непрерыв-
ных преобразованиях, и о
них следует забыть. Очень
немногие привычные по-
нятия геометрии годятся
для топологии, поэтому
приходится искать новые.
Этим топология трудна
для начинающего, пока
он не постигнет сути дела.
Образцом топологиче-
ского свойства объекта
служит наличие дырки у Рис 72
бублика (причем доволь-
но тонкая сторона этого дела — тот факт, что дырка не
является частью бублика). Какую бы непрерывную де-
формацию ни претерпел бублик, дырка останется. Дру-
гое топологическое свойство — наличие края. Поверх-
ность сферы не имеет края, а пустая полусфера имеет, и
никакое непрерывное преобразование не в состоянии
это изменить.
Существует очень много различных непрерывных пре-
образований, поэтому топологам что бублик, что какая-
нибудь другая штука с одной дыркой — все едино (в этом
мы убедимся в следующем разделе). У тополога меньше
объектов изучения, и в этом смысле предмет изучения в
топологии проще1 чем в большинстве других разделов
185
математики (хотя сама топология как предмет отнюдь
не проще других). В этом одна из причин того, что то-
пология превратилась в мощный инструмент математики
в целом: ее простота и общность обеспечили ей широкий
круг применений.
Топологическая эквивалентность
Основные объекты изучения в топологии называются
топологическими пространствами. Интуитивно их можно
представлять себе как геометрические фигуры. Матема-
тически это — множества (иногда — подмножества евкли-
дова пространства), наделенные дополнительной струк-
турой под названием топология, которая позволяет фор-
мализовать понятие непрерывности. Поверхность сферы,
бублика (правильнее — тора) или двойного тора — это
примеры топологических пространств (рис. 73),
Рис. 73.
Два топологических пространства топологически эк-
вивалентны, если можно непрерывным образом перейти
от одного из них к другому и непрерывным же образом
вернуться обратно, Часто говорят, что тополог не отли-
186
чает бублика от кофейной чашки. Это как раз и есть при-
мер топологической эквивалентности (рис, 74),
На языке теории множеств можно сказать, что у нас
есть два топологических пространства А и В и требу-
ется, чтобы существовала функция fi А -+В, удовлетво-
ряющая условиям:
a) f биективна,
б) f непрерывна,
в) обратная к f функция тоже непрерывна.
Нам приходится вводить требование непрерывности
как функции f, так и обратной к ней, по следующей при-
чине. Возьмем два куска глины и слепим их вместе. Та-
Рис. 74.
кое преобразование непрерывно, поскольку близкие друг
к другу точки останутся таковыми (рис. 75). Однако при
обратном преобразовании один кусок распадается на
Рис. 75.
Рис. 76.
два (рис. 76), и, следовательно, близкие точки по разные
стороны от линии раздела окажутся далеко друг от дру-
га, т. е. обратное преобразование не будет непрерывным.
Такие преобразования нам не подходят.
В качестве упражнения попытайтесь разбить тополо-
гические пространства, изображенные на рис. 77, на клас-
сы топологически эквивалентных.
187
Рис. 77.
Некоторые необычные пространства
Если бы все топологические пространства были таки-
ми удобными, как сфера или тор, вряд ли стоило бы за-
ниматься топологией. Несколько более экзотических при-
меров, возможно, помогут разбудить вашу интуицию.
188
Вы, наверное, слышали о ленте (или листе) Мёбиуса,
которую можно получить из бумажной полоски, склеив
ее края после поворота на 180° (рис. 78).
Лента Мёбиуса топологически не то же самое, что
цилиндрическая лента, склеенная из той же полоски. Она
имеет только один край (посчитайте!). Поскольку коли-
Рис. 78.
чество краев — топологическое свойство, а цилиндриче-
ская лента имеет два края, эти две ленты топологически
неэквивалентны.
Известно еще одно свойство ленты Мёбиуса — то, что
она имеет лишь одну сторону. Цилиндрическую ленту
можно раскрасить двумя цветами — одну сторону крас-
ным, другую синим. Проделать то же самое с лентой Мё-
биуса не удастся.
К сожалению, свойство односторонности трудно опи-
сать математически строго и в то же время достаточно
наглядно. Ведь наша лента не имеет толщины, и каждая
ее точка находится «на» обеих сторонах, подобно тому
как каждая точка плоскости лежит «на» обеих ее сторо-
нах. В топологии мы должны рассматривать эту ленту
как некое пространство, а не подмножество евклидова
пространства, и тогда не совсем очевидно, является ли
количество сторон топологическим свойством.
Чтобы пояснить эту мысль, позвольте мне задать во-
прос: сколько сторон у трехмерного евклидова прост-
ранства?
189
Думаю, большинство ответит: «ни одной». Ведь наше
пространство продолжается до бесконечности в любом
направлении, какие же у него могут быть стороны?
Но представьте себе, что вы плоское существо, живу-
щее на двумерной плоскости и не имеющее больше ни о
чем понятия, Сколько сторон у вашего «пространства»?
_____ Если вы раньше ответили
S’"1 (^*4 «ни одной», вы непременно
( \ 1 д должны повторить тот же
I v—x r—J j ответ и теперь: ведь плос-
। ) х. 1 кость тоже продолжается и
I f A. I продолжается во всех на-
\ I \ J правлениях.
Иначе говоря, количество
Рис. 79. сторон зависит от того, рас-
сматривать ли плоскость са-
му по себе или как часть трехмерного пространства. То
же самое относится и к трехмерному пространству: если
в качестве четвертого измерения ввести время, то ока-
жется, что наше пространство имеет две стороны — про-
шлое и будущее.
Надеюсь, теперь понятно, насколько трудно даже
объяснить, что понимается под числом сторон, не говоря
уж о том, чтобы понять, топологическое это свойство
или нет.
Однако существует все-таки одно явление, которое
могут наблюдать воображаемые жители ленты Мёбиуса,
не выходя за пределы своего «пространства», и которое
позволяет дать математическое описание «односторон-
ности». Предположим, что эти создания имеют две руки,
причем их большие пальцы направлены в разные сторо-
ны. Тогда им доступны понятия «правый» и «левый».
Кроме того, допустим, что они носят варежки (рис. 79).
Однажды просыпается такое существо и видит, что
все его правые варежки куда-то подевались и остались
одни левые. Проявив находчивость, оно берет одну ва-
190
режку и переносит ее вдоль ленты, как показано на
рис. 80.
К большому нашему (но не его!) удивлению, левая
варежка превратилась в правую. Правда, при этом и ле-
вая рука воображаемого существа превратилась в пра-
вую, а правая — в левую, но зато оно получило годную
пару варежек.
Рис. 80,
Можете сами убедиться в этом, склеив ленту Мёбиуса
из бумаги (и тогда, чтобы увидеть, что делается «на дру-
гой стороне» бумаги, придется смотреть на свет сквозь
нее), а лучше из прозрачной пленки. Вместо этого може-
те воспользоваться своими двумя руками и воображае-
мой лентой Мёбиуса. Поскольку руки не двумерны, сле-
дите только за их очертаниями. Держите руки перед со-
бой ладонями наружу, пальцы вверх, большие пальцы
прижаты друг к другу. Левую руку оставьте на месте, а
правую двигайте вдоль воображаемой ленты Мёбиуса
следующим образом. Поднимите правый локоть, чтобы
ладонь наклонилась, затем поворачивайте ее вниз от се-
бя, поднимайте локоть еще выше, пока рука не окажет-
ся в положении тыльной стороной к вам, пальцами вниз.
Теперь сдвиньте ее влево на уровень левой руки и отве-
дите от себя большой палец, чтобы ладонь стала к вам
ребром. В идеале следовало бы поворачивать и дальше
нравую руку, но анатомия не позволяет, поэтому повер-
191
ните левую руку большим пальцем к себе и соедините
ладони ребром к ребру, левая вниз, правая вверх.
Вот это неудобное положение и получается после то-
го, как ваша правая рука опишет ленту Мёбиуса (а левая
немного продвинется ей навстречу). Чтобы стало полег-
че, держите руки в том же положении одну относительно
другой, но передвиньте правую немного вправо, а левую
за ней следом. Теперь нужно перевернуть правую руку
снизу вверх на поверхности ленты Мёбиуса. Для этого
опустите правый локоть, продолжая держать руку ла-
донью наружу. Теперь обе кисти направлены вверх, ле-
вая ладонью внутрь, правая — наружу. Сложите их вме-
сте. Вы убедились в том, как точно они совпали.
Если говорить только об очертаниях, то ваша пра-
вая рука, описав ленту Мёбиуса, стала левой (а за-
одно вы получили превосходный пример стиля рассужде-
ний, известного у математиков под названием «размахи-
вание руками»).
Жители двустороннего мира (к которым относимся и
мы с вами, согласно современным представлениям нау-
ки) не смогли бы проделать этот фокус с варежками: для
них правая останется правой, а левая — левой. Для су-
щества с ленты Мёбиуса понятие правого и левого име-
ет смысл лишь до тех пор, пока предметы не передви-
гаются, и невозможно дать определение правого и лево-
го, которое годилось бы для всей поверхности в целом.
В таком случае говорят, что эта поверхность неориенти-
руема. А пространство вроде нашего, в котором можно
дать глобальное определение правого и левого, называ-
ется ориентируемым. Ориентируемость соответствует дву-
стороннее™, а неориентируемость — односторонности, и
оба этих свойства являются внутренними топологически-
ми свойствами, не зависящими ни от какого внешнего
пространства.
Если соединить края двух лент Мёбиуса, получится
поверхность, называемая бутылкой Клейна (рис. 81).
192
У нее нет краев, и она неориентируема, потому что не-
ориентируемы ленты Мёбиуса. Кроме того, ее нельзя вло-
жить в трехмерное пространство так, чтобы не было са-
мопересечений.
Бутылку Клейна можно описать по-другому: пред-
ставьте себе квадрат, стороны которого склеены так, как
Рис. 82.
показывают стрелки на рис. 82. (Сначала верхняя сторо-
на склеивается с нижней и получается цилиндр. Затем,
чтобы правильно склеить края цилиндра, его надо со-
гнуть и протолкнуть сквозь самого себя.) При помощи
этой же диаграммы можно убедиться в том, что бутылка
Клейна действительно получается из двух лент Мёбиуса:
разрежем ее, как показано на рис. 83.
+
Рис. 83.
Иногда можно услышать какие-то утверждения о
внутренней и наружной стороне бутылки Клейна. Они
бессмысленны: в трехмерном пространстве ее построить
нельзя, а в четырехмерном (о котором мы будем гово-
7 Я. Стюарт
193
рить в гл. 14), где ее можно сделать без самопересече-
ний, говорить о внутренности бутылки Клейна — все рав-
но, что говорить о внутренности окружности в трехмер-
ном пространстве,— можно в нее войти и из нее выйти
без всяких препятствий.
Склеиванием сторон квадрата можно получить еще
два интересных пространства: тор и проективную плос-
кость (называемую так из-за ее связи с проективной гео-
метрией) (см. рис. 84).
О торе мы уже говорили — это ориентируемая по-
верхность. Проективная плоскость, подобно бутылке
Клейна, не имеет края, неориентируема и не допускает
вложения в трехмерное пространство.
Проективная плоскость представляет собой ленту Мё-
биуса, приклеенную край в край к кругу. Чтобы по-
строить ее в трехмерном пространстве, надо превратить
край ленты Мёбиуса в окружность. Лента при этом бу-
дет перекручиваться и самопересекаться, образуя так
называемый скрещенный колпак (рис. 85). Закрыв его
отверстие, получим проективную плоскость (рис. 86).
Наконец, познакомимся еще с одним занятным про-
странством — рогатой сферой Александера (рис. 87). Оно
строится так. Вытянем из сферы два рога, расщепим на-
двое их концы и переплетем их между собой, расщепим
надвое новые концы и снова переплетем их, и так далее
до бесконечности. Хотите — верьте, хотите — нет, но то,
194
что получается, топологически эквивалентно сфере: спо-
соб вытягивания рогов можно задать при помощи подхо-
дящей функции, которая определяет топологическую
эквивалентность. Однако наружное пространство рогатой
сферы уже не будет топологически эквивалентно прост-
ранству вне обычной сферы.
В самом деле, с обычной сферы соскакивает любая
надетая на нее петля
Рис. 86.
Рис. 88.
Рис. 89.
7»
195
может запутаться в рогах (рис. 89). И здесь снова забо-
ты причиняет не сама поверхность, а окружающее ее про-
странство.
Теорема о волосатом шаре
Рис. 90.
Мы немного поговорили о понятиях, которые вводят-
ся в топологии, и объектах, которые в ней изучаются.
Теперь приведем пример топологической теоремы.
Если внимательно по-
смотреть, как растет шерсть
у собаки, можно обнару-
жить, что вдоль спины она
разделяется «на пробор», а
другой «пробор» идет вдоль
живота. С точки зрения топо-
логии собака — это шар (ес-
ли считать, что пасть у нее
закрыта, и пренебречь внут-
ренними органами); чтобы в
этом убедиться, достаточно
«втянуть» ей ноги и немного
ее «раздуть» (рис. 90).
Можно задаться таким вопросом: удастся ли так «при-
чесать» собаку, чтобы не стало «проборов». В результа-
те получился бы волосатый шар, не имеющий ни «про-
боров», ни «макушек», изображенный на рис. 91.
Этот вопрос относится к топологии, ибо при любой
непрерывной деформации такого шара гладкая шерсть
Рис. 91.
196
останется гладкой, а «пробор» останется «пробором». То-
пологические методы позволяют установить (хотя это не-
легко), что гладко причесать шар невозможно. (В пра-
вильной формулировке задачи говорится о «векторных
полях» на сфере, но этому вполне соответствует интуи-
тивное представление о волосатом шаре.)
Рис. 92.
Лучшее, чего можно добиться,— причесать волосы
так, что останется лишь одна «макушка» — точка, в ко-
торой нарушается гладкость (рис. 92).
Не будем углубляться здесь в доказательство этой
теоремы, однако заметим, что ее значение выходит дале-
ко за рамки причудливых применений к воображаемым
гладким собакам.
Рис. 93.
197
Поверхность Земли представляет собой сферу. Если
для какого-то момента времени изобразить на сфере на-
правления воздушных потоков в атмосфере Земли, т. е.
направления всех ветров, дующих над поверхностью Зем-
ли, то получится своего рода «прическа» на этой сфере,
где роль волос будут играть линии, изображающие пото-
Рис. 94.
ки. Наша теорема утверждает, что не существует глад-
кой системы ветров (за исключением случая полного без-
ветрия, что, однако, невозможно, но по другим причинам),
т. е. где-то всегда есть циклон.
Таким образом, зная только форму Земли, мы уже
можем делать заключения о поведении ветров без вся-
ких сведений о том, куда они дуют на самом деле.
А вот на тороидальной планете возможен постоянный
ветер без циклонов, поскольку волосатый тор можно
причесать требуемым образом (рис. 93).
Дальнейшее изучение, основанное уже на более под-
робных сведениях о ветрах, показывает, что гладкий по-
ток скорее будет обвиваться вокруг тора, кац на рис. 94.
Известны и многие другие приложения теоремы о во-
лосатом шаре. Например, в алгебре она применяется для
доказательства теоремы о том, что каждое уравнение,
левая часть которого — многочлен, имеет корни в поле
комплексных чисел (так называемая «основная теорема
алгебры»),
198
Глава 11
УМНЫЙ В ГОРУ НЕ П ЖДЕТ
Идти напролом — не всегда самый быстрый путь к
успеху. Иногда лучше обойти препятствие, чем очертя
голову бросаться ему навстречу. Так же обстоит дело и
в математике. Часто задача кажется неодолимой, и даже
хорошо представляя себе, каким должен быть ответ, ни-
как не удается придумать способ решения. В таком слу-
чае все может изменить какая-то новая точка зрения, све-
жая идея.
Где же взять эту свежую идею?
Первопроходец, пробивающий путь в джунглях, обыч-
но видит лишь то, что его непосредственно окружает.
Если у него на пути оказывается гора, он взбирается на
нее, если река,— переплывает через нее. Позднее, когда
люди начинают прокладывать через джунгли дороги, они
не обязательно идут теми же тропами. У них есть карты.
Они знают, где река, а где гора, и потому обойдут гору,
а на реке найдут удобное место для постройки моста.
Если бы первопроходец имел более широкий обзор мест-
ности, например с борта самолета, он сэкономил бы мас-
су усилий и, возможно, преуспел бы там, где без этого по-
терпел неудачу.
В математике очень легко сосредоточиться на какой-
то конкретной задаче. Если ваши методы к ней не под-
ходят, а вы продолжаете упорно ломать над ней голову,
то в конце концов возникает ощущение растерянности и
поражения. В таком случае иногда полезно отступить,
забыть о конкретной задаче, осмотреться и подумать: нет
ли в близлежащих областях каких-то общих признаков,
особенностей, которые могут пригодиться для выбора
правильного направления.
Д99
Грефы
Известна одна старая задача, которая в одном из ва-
риантов формулируется так. Имеется три дома и три ко-
лодца (рис. 95). Можно ли проложить дорожки от каж-
дого из трех домов к каждому из трех колодцев так, что-
бы они не пересекались между собой?
Взяв карандаш и бумагу,
вы довольно скоро убеди-
тесь, что сделать это каким-
нибудь простым способом не
удается. Однако, если вы
попытаетесь доказать, что
Рис. 95.
В решения не существует, вы
столкнетесь с трудной про-
блемой: ведь способов про-
водить линии так много! Кто
знает, может, если сначала
одну линию заставить опи-
сать шесть или семь петель, то это приведет к цели. Вро-
де нет, но как это доказать?
Перед нами как раз такая ситуация, о какой говори-
лось выше, и лучший способ дальнейших действий —
спокойно сесть и оглядеться.
Тогда станет ясно, что для задачи неважно, дома это
или не дома, и рядом они с колодцами или за тридевять
земель. Отбросив лишние подробности, условие можно
сформулировать так: есть два множества на плоскости,
каждое из трех точек; нужно соединить каждую точку
одного с каждой точкой другого так, чтобы линии соеди-
нения не пересекались одна с другой.
Такого рода задачами занимается раздел математи-
ки, известный под названием теории графов.
Граф состоит из двух главных частей:
1) некоторого множества N, элементы которого назы-
ваются узлами или вершинами-,
200
2) некоторого способа установить, когда две вершины
соединены одна с другой.
При помощи теории множеств это абстрактное опре-
деление можно было бы сделать более строгим. Од-
нако понимать различные утверждения о графах намно-
го проще, если изображать вершины в виде точек на
Рис. 96.
плоскости и соединять их линиями. Последние называют-
ся ребрами графа. Точное расположение точек и линий
несущественно, но важно, чтобы соединения были сдела-
ны правильно.
Две фигуры на рис. 96 служат изображениями одно-
Рис. 97.
го и того же графа (вершины отмечены кружочками; пе-
ресечение без кружка на второй фигуре не считается).
Каждая фигура имеет четыре вершины, и каждая пара
вершин соединена линией. Передвинув вершины и линии,
как показано на рис. 97, можно перевести одну фигуру в
другую.
Совсем не обязательно проводить прямолинейные от-
201
резки; фигуры, показанные на рис. 98,— это изображе-
ния того же самого графа.
Топологическая структура графа — вот что суще-
ственно.
Нарисовать граф на плоскости так, чтобы его ребра
пересекались только в вершинах, не всегда возможно.
Графы, для которых это возможно, называются плоскими.
Рис. 98. Рис. 99.
Теперь нашу задачу о домах и колодцах можно сфор-
мулировать так: плоский или нет граф, одно из изобра-
жений которого дано на рис. 99?
Для того чтобы ответить на этот вопрос, нужно изу-
чить свойства плоских графов.
Формула Эйлера
Маршрутом на графе между вершинами а и b назы-
вается последовательность ребер с началом в а и концом
в Ь, в которой каждое следующее ребро начинается там,
где кончается предыдущее. На рис, 100, например, суще-
Рис. 100.
202
ствует маршрут между точками а и Ь, но не существует
маршрута, связывающего асе, потому что с лежит в той
части графа, которая никак не связана с другими его об-
ластями, где находится а. Граф, в котором для любых
двух вершин найдется соединяющий их маршрут, назы-
вается связным. Это означает, что он не распадается на
два (или больше) отдельных куска.
Рис. 101.
Любой граф состоит из связных кусков. Поэтому до-
статочно изучить связные графы.
Далее мы будем рассматривать только конечные,
связные, плоские графы. «Конечный» означает, что число
вершин и ребер конечно. Такой граф показан на рис. 101.
Любой граф такого вида делит плоскость на конеч-
ное число областей, которые мы назовем гранями. Граф
на рис. 101 имеет 8 граней, 14 вершин и 21 ребро.
203
Интересующие нас графы (конечные, связные, плос-
кие) напоминают карту некоего воображаемого острова,
поэтому будем ради краткости называть такие графы
картами.
Нарисуйте теперь несколько карт и сосчитайте число
граней (Г), вершин (В) и ребер (Р). Для начала займи-
тесь теми, которые показаны на рис. 102.
Составьте таблицу результатов:
Г В Р
8 14 21
4 6 9
4 6 9
6 10 15
Подметили вы какую-нибудь связь между этими чис-
лами?
Сразу видно, что Р всегда наибольшее из них. Числа
Г и В меньше, но в сумме они дают примерно то же, что
и Р: 22, 10, 10, 16. Эти суммы на 1 больше соответствую-
щего Р, и похоже, что для всякой карты выполняется ра-
венство
Р+В=Р+1
или
В —Р + Г=1. (*)
Первым, кто доказал, что эта формула имеет место
для любой карты, был Эйлер (1707—1783). На первый
взгляд нет никаких оснований ожидать, что Г, В и Р как-
то связаны между собой. Но если не полениться и посчи-
тать их для дюжины карт, появится уверенность, что
формула («) ив самом деле выполняется. Однако это
нисколько не поможет ее доказать.
204
Если подумать, само выражение В — Р+Г подсказы-
вает способ действий. Раз оно одно и то же для всех
карт, значит, оно не меняется, когда вместо одной карты
берется другая.
Рассмотрим простейшие случаи, когда не меняется
В — Р+Г; во-первых, если Р и Г оба уменьшаются на 1,
и во-вторых, если В и Р оба уменьшаются на 1 (в обоих
случаях их разность не изменится).
Первому случаю соответствует удаление одной из
граней путем стирания одного из ограничивающих ее ре-
бер (рис. 103).
Второй осуществится, если убрать вершину, которая
«болтается» на конце одного ребра, как на рис. 104.
Эти операции назовем стягиваниями. Наше наблюде-
ние состоит в том, что величина В — Р+Г не меняется при
Рис. 104.
205
двух типах стягиваний; значит, она не меняется и в ре-
зультате любой последовательности стягиваний.
Допустим теперь, что океан, омывающий наш остров,
очень суров. День за днем он разрушает береговую ли-
нию, вызывая стягивания то одного, то другого вида. Все
это время величина В — Р + Г невозмутимо сохраняет
с с
О
©
Рис. 105.
свое значение. Океан продолжает свою разрушительную
работу..., пока не останется никакого острова.
Я сказал никакого острова? Это было неосторожно.
Давайте посмотрим на рис. 105.
На самом деле остров превратился в точку: 1 верши-
на, 0 ребер, 0 граней. Значит, В — Р + Г= 1 — 0 + 0= 1. Но
величина В — Р+Г не изменялась при стягиваниях. Сле-
довательно, формула В — Р+Г=1 выполнялась и для
исходного острова!
По существу мы провели доказательство. Каждую
карту при помощи стягиваний можно превратить в точ-
ку, не меняя величины В — Р+Г, а для точки она равна 1.
Следовательно, формула ( ) имеет место для любой
карты. Эта формула — так называемая формула Эйле-
ра — имеет удивительно широкий круг очень ценных при-
менений. Прежде всего рассмотрим ее применение к за-
даче о трех домах и трех колодцах.
206
Неплоские графы
Итак, наша задача — узнать, плоский или нет граф,
изображенный на рис. 99.
Применим прием, который на языке шахмат можно
было бы назвать «гамбитом математика»: пожертвуем
утверждением, что этот граф не плоский, а на основе
этой жертвы попробуем прийти к противоречию. Если
это удастся, отсюда будет следовать, что он не плоский.
Для этого графа В = 6, Р = 9. Число граней сосчитать
невозможно, поскольку понятие грани введено только
для плоских графов (карт), а у нас нет плоского изоб-
ражения этого графа. Но если бы оно у нас было в ка-
кой угодно форме, оно имело бы Г граней, где
6 —9+Г=1.
Значит, Г<=4.
Теперь, хотя мы и не будем пытаться нарисовать
плоское изображение нашего графа, нам придется все же
выяснить кое-что о его гранях.
Каждая грань плоского графа окружена замкнутой
цепью, или циклом, из его ребер (рис. 106). Цикл обра-<
зован периметром этой грани (береговой линией). Не-
трудно проверить, что циклы графа на рис. 99 состоят
либо из 4, либо из 6 ребер. Перечислим все возможные
случаи:
4 4 4 4
4 4 4 6
4 4 6 6
4 6 6 6
6 6 6 6.
А теперь посчитаем ребра другим способом. Каждое
ребро, за исключением наружных, принадлежит двум
207
граням. Допустим, что наружная часть — это еще одна
очень большая грань; она тоже имеет 4 или 6 ребер, и
мы получаем 5 граней:
4 4 4 4 4
4 4 4 4 6
4 4 4 6 6
4 4 6 6 6
4 6 6 6 6
6 6 6 6 6
причем каждое ребро принадлежит двум из них. Тогда
сумма ребер, принадлежащих всем граням, равна удво-
енному общему числу ребер, и, значит, число ребер в
указанных выше случаях должно равняться соответст-
венно 10, 11, 12, 13, 14, 15. Но, как мы знаем, Р = 9.
Итак, получено противоречие. Значит, наше допу-
щение неверно, и рассматриваемый граф не является
плоским. «Гамбит математика» снова окупился. Таким
образом доказано, что задача о трех домах и трех колод-
цах не имеет решения.
В этом доказательстве замечательно то, что не делает-
ся никаких попыток разобраться, как могли бы прохо-
дить линии соединения. Оно оставляет подобные заботы
в стороне, сначала допуская возможность проведения та-
208
ких линий, а затем показывая, что она неосуществима.
Подобным образом можно поступить и с графом, по-
казанным на рис. 107. Для него В = 5, Р=10, и, значит,
если бы он был плоским, Г должно было бы равняться
6 (или с учетом дополнительной внешней грани 7). Да-
лее, каждая грань ограничена по крайней мере тремя
ребрами, а каждое ребро принадлежит двум граням, по-
этому общее число ребер должно быть больше, чем
(3-7) : 2=21 : 2, т. е. больше 10. Но мы уже знаем, что
их ровно 10. Таким образом, снова получено противоре-
чие, и данный граф не плоский.
Два рассмотренных графа — важные прототипы всех
неплоских графов. Как показал Куратовский, всякий не-
плоский граф обязательно содержит в себе один из этих
двух графов. Результат в принципе прост, но несколько
страниц занимает проверка разных случаев, и мы не ста-
нем приводить здесь его доказательство '.
Способы установления, плоский граф или нет, нахо-
дят практическое применение к электронным схемам, в
частности к печатным схемам и микроминиатюрным ин-
тегральным схемам, однако там приходится учитывать и
другие факторы: например, иногда имеет значение длина
соединительных линий, а в некоторых случаях компонен-
ты схемы могут взаимодействовать, хотя они и не пере-
секаются.
Другое применение формулы Эйлера
Из формулы Эйлера можно извлечь почти все, что из-
вестно к настоящему времени о знаменитой (или скорее
бесславной?) проблеме четырех красок: можно ли лю-
бую заданную карту раскрасить четырьмя красками так,
чтобы никакие две соседние (имеющие общее ребро)
страны (грани) не были одного цвета?
Четыре краски понадобятся наверняка (рис. 108).
Кроме того, можно показать, что не существует карты,
209
L
имеющей 5 граней, каждая из которых граничит по реб-
ру с остальными четырьмя. Однако из этого еще не сле-
дует, что четырех красок хватит.
Известно, что пяти красок достаточно, а вот запол-
нить дыру между 4 и 5 никак не удается. (Прежде чем
вы побежите пробовать, позвольте вас предостеречь, что
Рис. 108.
это очень тонкая задача. Ду-
маю, она не устоит лишь перед
очень глубоким пониманием
теории плоских графов.)
Под картой до сих пор по-
нималась карта на плоскости
в нашем прежнем смысле. Од-
нако задача на плоскости име-
ет тот же ответ, что и задача
на сфере. В этом можно убедиться с помощью приема,
который мы назовем «трюк с апельсиновой коркой».
Если задана карта на сфере, делаем дырочку на одной из
граней и раскрываем сферу на плоскость. С другой сторо-
ны, если есть карта на плоскости, свертываем ее в сферу,
и та область, которая лежала вне исходной карты, обра-
зует лишнюю грань. Если каждую карту на плоскости
можно раскрасить четырьмя красками, то же самое вер-
но для сферы и наоборот. По той же причине, по которой
нам пришлось в предыдущем разделе ввести лишнюю
грань, удобнее рассматривать сферу, а не плоскость.
Появление еще одной грани отражается на формуле
Эйлера: она принимает вид
В-Р+Г=2.
Докажем, что пяти цветов достаточно для раскраши-
вания любой карты на сфере (а значит, и на плоскости).
Доказательство будет построено следующим образом:
сначала мы найдем способы превращать данную карту в
новую карту с меньшим числом граней, при которых мож-
но получить нужную окраску исходной карты из окраски
210
новой; проделав несколько таких превращений, мы при-
дем к карте с 5 или меньше гранями, которую заведомо
можно раскрасить в 5 цветов. Вернувшись к исходной
карте, получим ее окраску в 5 цветов.
1. Можно исключить вершины, где сходятся более
трех граней. Если в какой-то точке сходятся четыре гра-
Рис. 109.
Рис. ИО.
ни или больше, среди них найдутся две, которые больше
нигде не примыкают друг к другу, и их можно слить в
одну (рис. 109). Если новая карта допускает раскраску
в 5 цветов, та же раскраска годится для старой карты,
ибо эти две грани могут быть одного цвета.
Если вершина, с которой мы начали, окружена боль-
шим количеством граней, нам придется много раз выпол-
нить эту операцию, до тех пор пока останутся только три
грани.
2. Можно исключить треугольные грани (ограничен-
ные тремя ребрами), сливая их с одной из соседних (рис.
ПО). Из раскраски новой карты получается раскраска
старой, если выбрать для треугольной грани цвет, не сов-
падающий с тремя окружающими.
3. Точно так же можно слить четырехугольные грани
с одной из соседних. Для раскрашивания исключенной
области воспользуемся пятым цветом, отличным от че-
тырех занятых (рис. 111).
4. В итоге у нас получится карта на сфере, все грани
которой окружены не менее чем пятью ребрами. Дока-
211
жем, чти по крайней мере одна грань имеет ровно
5 ребер.
Пусть у нашей карты В вершин, Р ребер и Г граней.
Согласно шагу 1, в каждой вершине встречаются три
ребра, а каждое ребро принадлежит двум граням, по-
этому
Рис. 111.
ЗВ = 2Р=аГ,
где а — среднее число ребер
у грани, Поскольку
В—Р + Г=2,
имеем
откуда
т. е. а меньше шести. Если среднее число ребер у грани
меньше шести, то найдется грань, у которой меньше
шести ребер. Но каждая грань имеет не меньше пяти
ребер. Значит, есть грань, у которой ребер ровно 5.
5. Рассмотрим такую грань Р с 5 ребрами и обозна-
чим соседние с ней грани Q, R, S (рис. 112).
Среди них найдется пара несоприкасающихся граней;
выберем наши обозначения так, чтобы это были Q и S.
Сольем теперь грани Р, Q и S (рис. 113).
Если полученную в результате карту можно окрасить
в 5 цветов, то можно окрасить и исходную: после слия-
ния грани Q и S стали одного цвета, значит, грань Р
окружена 4 цветами и на нее можно истратить пятый.
6. После каждого слияния количество граней умень-
шается. В конце концов мы получим карту с 5 или мень-
ше гранями. Такую карту, разумеется, можно раскрасить
212
5 красками: достаточно выбрать свой цвет для каждой
грани.
Проделав теперь все перечисленные шаги в обратном
порядке, получим требуемую раскраску исходной карты.
Итак, наши действия, коротко говоря, сводятся к сле-
дующему. Мы применяем к исходной карте процесс ре-
Рис. 113.
дукции, в результате которого она постепенно упрощает-
ся. На каждом шаге этого процесса, если мы умеем рас-
крашивать новую карту, то умеем раскрашивать и
старую. Доказательство гарантирует, что в конце кон-
цов получится новая карта, которую мы сумеем раскра-
сить. Значит, мы сможем раскрасить и предыдущую, и
ту, из которой получилась предыдущая, и т. д. В итоге мы
сумеем раскрасить и исходную карту.
Чтобы понять, как работает этот процесс, нарисуйте
какую-нибудь карту (не берите слишком много граней!)
и, следуя указанным путем, найдите способ ее раскраши-
вания.
Для поверхностей, отличных от сферы, анало-ичная
проблема решена. Мы кратко расскажем об этом в гл. 12.
Однако для сферы — простейшей из поверхностей — из-
вестно только, что 5 цветов достаточны, а 4 необходимы.
В каком-то смысле было бы жаль, если бы эту задачу
удалось решить. Мы лишились бы великолепного приме-
ра задачи, которую так легко сформулировать и так не-
вообразимо трудно решить 2,
213
Глава 12
ТОПОЛОГИЧЕСКИЕ ИНВАРИАНТЫ
«Настоящий традиционный
пончик имеет топологию сфе-
ры. Дело вкуса — считать, что
у него есть внешняя и внутрен-
няя поверхности. Важно лишь
то, что пространство внутри
должно быть заполнено души-
стым малиновым вареньем. Но
это тоже дело вкуса».
П. Б. Фелгет
Если два топологических пространства топологиче-
ски эквивалентны, то обычно доказать это нетрудно. Все,
что требуется, — найти между ними нужное соответствие.
Гораздо труднее доказать, что два неэквивалентных
пространства действительно неэквивалентны. Ведь для
этого нужно убедиться в том, что из бесконечного мно-
жества всевозможных функций ни одна не удовлетворяет
требуемым условиям. Так, например, две поверхности,
изображенные на рис. 114, явно топологически различ-
ны, но как это доказать?
Мы видим, что тор имеет дырку, а сфера — нет. Но
трудность состоит в том, что дырка эта вовсе не на са-
Рис. 114.
214
мом торе, а в окружающем его пространстве, а мы уже
знаем, как опасно делать заключения, основанные на
свойствах окружающего пространства. Как топологиче-
ское пространство, рассматриваемое само по себе, тор не
содержит ничего такого, что можно было бы назвать
Рис. 115.
дыркой, и эта дырка, которую мы видим, не является его
частью.
Единственный способ различить два неэквивалентных
топологических пространства — найти какое-то тополо-
Рис. 116.
гическое свойство, которым обладает одно из них и не
обладает второе. Например, всякая замкнутая кривая на
сфере разделяет ее на два куска (рис. 115), а на торе
есть замкнутые кривые, которые не разрезают его на от-
дельные куски (рис. 116).
Такие свойства, как замкнутость кривой, связность,
215
несвязность, являются топологическими. Значит, мы до-
казали, что сфера и тор топологически различны.
Подобным же, но более тонким методом можно было
бы, скажем, отличить поверхность с 19 дырками от по-
верхности с 18 дырками, однако для этого пришлось бы
проделать много «грязной» работы и, хуже того, убе-
диться, что такой метод не вполне удовлетворителен.
Обобщенная формула Эйлера
Свойство сферы, состоящее в том, что В—Р+Г=2,
является топологическим. Любое непрерывное преобра-
зование сферы переводит всякую заданную на ней кар-
ту в другую карту с теми же значениями В, Р и Г,
Если мы попробуем рисовать карты на торе, то обна-
ружим, что В—Р+Г уже не равно 2. Например, для кар-
ты, показанной на рис. 117, В=4, Р=8, Г=4, так что
В—Р + Г=о.
То же равенство выполняется для любой другой кар-
ты на торе, в основном по тем же причинам, по которым
Рис. 117.
для любой карты на плоскости и на сфере имеет место
формула Эйлера. Это свойство карт на торе также явля-
ется топологическим.
Подобные формулы можно получить для широкого
216
класса топологических пространств, называемых поверх-
ностями.
И сферу, и тор можно триангулировать, т. е. покрыть
треугольниками, примыкающими друг к другу вдоль
сторон (рис. 118).
Рис. 118.
Неважно, что эти треугольники не плоские, а их сто-
роны не прямолинейны; требуется только, чтобы они бы-
ли топологически эквивалентны обычным треугольникам.
Любое пространство, которое можно построить из ко-
нечного множества треугольников, причем так, что два
треугольника могут иметь общими либо одну (целую)
сторону, либо одну вершину, называется триангулируе-
мым. Поверхность — это топологическое пространство,
которое:
а) триангулируемо;
б) связно (т. е. состоит из одного куска, как в случае
графов);
в) не имеет края.
Сфера, тор, бутылка Клейна, проективная пло-
скость— все это примеры поверхностей. На рис. 119 по-
казана триангуляция проективной плоскости.
Лента Мёбиуса не является поверхностью в этом
смысле, так как у нее есть край. Плоскость тоже не
является поверхностью, ибо ее нельзя построить из ко-
нечного числа треугольников.
217
На любой поверхности, точно так же как на сфере,
можно рисовать карты и считать количество вершин, ре-
бер и граней. Можно доказать, что для каждой данной
поверхности S число В—Р + Г не зависит от выбранной
карты. Оно называется эйлеровой характеристикой по-
верхности S и обозначается % (S). Поскольку оно не
зависит от выбранной карты,
это число будет одним и тем
же для всех топологически
эквивалентных пространств,
' т. е. оно является топологиче-
ским инвариантом. (Топологи-
ческий инвариант — это общее
свойство всех топологически
эквивалентных поверхностей.)
Еще один топологический
инвариант — ориентируемость
Тор не эквивалентен бутылке
Рис. 119. Клейна, так как он ориенти-
руем, а бутылка Клейна — нет
Эти два инварианта—эйлерова характеристика и
ориентируемость — позволяют различить все поверхно-
сти, о которых мы до сих пор упоминали:
S
Сфера
Тор
Двойной тор
Проективная
плоскость
Бутылка Клейна
I Ориенти-
I руема?
Да
Да
Да
Нет
Нет
1
О
218
Построение поверхностей
Наша конечная цель — классифицировать все воз-
можные поверхности с точностью до топологической
эквивалентности. Первым шагом будет построение набо-
ра стандартных поверхностей.
Рис. 120.
Методика нашего построения известна под названием
хирургиш мы будем разрезать пространства на куски, а
затем соединять в одно целое. Такие приемы оказывают-
ся очень полезными в топологии.
Стандартные ориентируемые поверхности получаются
пришиванием ручек к сфере. За исходную поверхность
берем сферу без ручек. Чтобы пришить ручку, мы выре-
заем в сфере две дырки и вшиваем в нее цилиндр, соеди-
няя его края с краями дырок (рис. 120).
Одна ручка дает тор, две ручки — двойной тор и т. д.
Стандартная ориентируемая поверхность рода п — это
Рис. 121.
219
сфера с п пришитыми к ней ручками. (Слово род служит
просто-напросто гвоздиком, на который можно «пове-
сить» число п.)
Стандартные неориентируемые поверхности получа-
ются пришиванием лент Мёбиуса. Для этого в сфере вы-
резаем одну дырку. У нее один круглый край, у ленты
Мёбиуса тоже один круглый край, и мы соединяем их
вместе. Если пытаться сделать это в трехмерном прост-
ранстве, то лента Мёбиуса будет пересекать самое себя,
образуя скрещенный колпак. Однако мы рассуждаем
абстрактно и можем не беспокоиться об этом( рис. 121).
Пришивая одну ленту Мёбиуса, получаем проектив-
ную плоскость (как на рис. 86), две — бутылку Клейна
(как на рис. 83).
Эйлерова характеристика стандартной поверхности
Наш следующий шаг — найти эйлерову характери-
стику стандартных поверхностей. В ориентируемом
случае действуем так: считаем вырезанные из сферы два
кружка гранями некоторой карты (ее часть показана на
рис. 122).
Для этой карты В—Р + Г=2, ибо все происходит на
сфере. Добавление ручки, как показано на рис. 123, меня-
ет дело: мы теряем две грани на сфере, зато получаем
две грани на ручке с темп же вершинами, но с двумя но-
выми ребрами. Итак, эйлерова характеристика умень-
шается на 2. То же самое происходит при добавлении
Рис. 122.
220
каждой новой ручки, значит п ручкам соответствует
уменьшение на 2п. Таким образом, эйлерова характери-
стика стандартной ориентируемой поверхности рода п
равна
2—2п.
В частности, это показывает, что стандартные ориентиру-
емые поверхности разных родов не являются топологиче-
ски эквивалентными, поскольку имеют разные эйлеровы
характеристики.
Рис. 123.
Рис. 124.
Теперь займемся неориентируемым случаем. Допу-
стим, что вырезанный кружок есть часть карты, изобра-
женной на рис. 124.
Пришивание ленты Мёбиуса (рис. 125) ликвидирует
одну грань на сфере и добавит одну грань и одно ребро
221
на ленте. Поэтому теперь эйлерова характеристика для
каждой новой ленты Мёбиуса уменьшается на 1 и, сле-
довательно, для стандартной неориентируемой поверх-
ности рода п она равна
2—п.
Это позволяет различать стандартные неориентируемые
поверхности.
Рис. 125.
Эти два инварианта вместе — эйлерова характеристи-
ка и ориентируемость — показывают, что все стандарт-
ные поверхности топологически различны. Теперь пока-
жем, что всякая поверхность топологически эквивалент-
на одной из стандартных.
Классификация поверхностей
Метод доказательства, которым мы воспользуемся,
принадлежит Э. К. Зиману *. При помощи «хирургиче-
ского вмешательства» мы разрежем заданную поверх-
ность на куски, из которых затем соберем стандартную
поверхность, причем и разрезать, и собирать будем так,
чтобы не терять топологическую эквивалентность, т. е.
все куски будем соединять по линиям разрезов.
Пусть S — некоторая поверхность. Нарисуем на ней
222
замкнутую кривую (если это возможно), не разбиваю-
щую S на два куска. (Если это не удастся, остановимся.)
Узкая полоска поверхности по обе стороны от такой
кривой топологически эквивалентна полосе со склеенны-
ми концами, следовательно, это либо цилиндр, либо лен-
та Мёбиуса.
Рис. 126.
Теперь начнем «операцию». Если полоска цилиндри-
ческая, удалим ее и вошьем по кружочку в каждую из
двух образовавшихся дырок. Чтобы не забыть, как вста-
вить цилиндр обратно, пометим каждый кружок стрел-
кой. Если полоска представляет ленту Мёбиуса, удалим
ее и вошьем один кружок.
При помощи тех же рассуждений, что и выше, при
вычислении эйлеровой характеристики стандартных по-
верхностей (только в обратном порядке), можно убе-
диться, что каждая «операция» увеличивает эйлерову
характеристику: на 2 в случае цилиндра и на 1 в случае
ленты Мёбиуса. Теперь сошлемся на
Недоказанное утверждение А. Эйлерова характери-
стика любой поверхности не превосходит 2.
Отсюда вытекает, что последовательность «операций»
после конечного числа шагов оборвется. Но она обрыва-
ется только тогда, когда больше не удается найти замк-
нутую кривую, не разбивающую поверхность.
Недоказанное утверждение В. Поверхность, кото-
223
рую каждая замкнутая кривая на ней разбивает на
отдельные куски, топологически эквивалентна
сфере.
Теперь проделаем обратную процедуру. При этом
потребуются три типа «операций».
Рис. 127.
1. Имеются два кружка с противоположно направлен'
ными стрелками, и вместо них пришивается цилиндр. Это
все равно, что пришить ручку (рис. 126).
2. Имеется один кружок, и вместо него пришивается
лента Мёбиуса.
3. Имеются два кружка с одинаково направленными
стрелками; в таком случае пришить обратно цилиндр —
это все равно, что пришить бутылку Клейна (рис. 127),
а это в свою очередь равносильно пришиванию двух лент
Мёбиуса (см. рис. 83). Таким образом, операцию треть-
его типа можно заменить двумя операциями второго
типа.
Если исходная поверхность ориентируема, то потре-
буются только операции первого типа. Значит, в резуль-
тате мы придем к сфере с каким-то количеством ручек,
т. е. к стандартной ориентируемой поверхности. Все, что
мы делали, — разрезали S на куски и потом складывали
их обратно, следя за тем, чтобы они правильно соединя-
лись. Значит, S топологически эквивалентна стандартной
сфере с ручками.
Если исходная поверхность неориентируема, то могут
224
потребоваться операции всех трех типов. Третий тип
можно исключить так же, как выше. Поскольку рас-
сматривается неориентируемый случай, потребуется по
крайней мере одна операция второго типа. Далее, если
возникнет ситуация первого типа (два кружка с противо-
положно направленными стрелками), можно взять и про-
нести один из кружков по ленте Мёбиуса. Как и в случае
с варежкой (гл. 10), направление стрелки изменится на
противоположное, и мы окажемся в ситуации третьего
типа. Но операцию третьего типа можно заменить двумя
операциями второго типа. Таким образом, все сведено к
операциям только второго типа — пришиванию ленты
Мёбиуса, и в результате получается стандартная неорп-
ентируемая поверхность.
Итак, опираясь на два недоказанные утверждения,
мы показали, что всякая поверхность топологически эк-
вивалентна стандартной ориентируемой поверхности рода
п^О или стандартной неориентируемой поверхности ро-
да п^1. (Значение п=0 во втором случае рассматривать
не нужно, ибо ему отвечает сфера, которая ориентируема
и охватывается первым случаем.)
Утверждения А и В мы не доказали, потому что не
хотели прерывать ход изложения. Теперь настало время
ими заняться.
Доказательство утверждения А
Эйлерову характеристику графа N можно определить
как
%(N)=B—P,
поскольку граф сам по себе не имеет граней. (Грани
можно определить только тогда, когда граф нарисован
на некоторой поверхности, поэтому мы их не принимаем
в расчет.)
8 Я. Стюарт
225
Покажем, что эйлерова характеристика всякого гра-
фа N не превосходит 1.
Если N содержит циклы, один из них можно разор-
вать, отбросив одно ребро. При этом Р уменьшится, и,
следовательно, % (N) увеличится. Повторяя эту операцию
до тех пор, пока не останется ни одного цикла, мы полу-
чим граф без циклов. Такой граф
? л называется деревом (рис. 128).
о [у Теперь воспользуемся стяги-
X. / f / ваниямй (как в гл. 11). Отбросив
веРшинУ ни конце «ветки» и при-
/\. летающее к ней ребро, мы не
\ уменьшим эйлерову характери-
I стику. После достаточного числа
I стягиваний останется одна точка,
а для точки эйлерова характери-
стика равна 1 — 0=1. Итак, пре-
/ ь Ъ образуя исходный граф W, мы
сначала увеличивали % (7V), а за-
Рис. 128. тем оставляли ее без изменения.
Следовательно, % (N) 1.
Отсюда видно также, что эйлерова характеристика
любого дерева равна 1.
Теперь вернемся к нашей поверхности S и докажем,
что %(S) =С2. Она триангулируема, значит, на ней можно
нарисовать карту с треугольными гранями. Определим
новую, двойственную к ней карту, так, как показано на
рис. 129: поместим вершину в центре каждого треуголь-
ника и соединим ребрами каждые две вершины, лежащие
в смежных треугольниках.
Вершины и ребра двойственной карты образуют граф.
Это-f граф содержит деревья (например, каждая отдель-
ная вершина является деревом). Среди всех этих де-
ревьев выберем максимальное, т, е. дерево, которое нель-
зя увеличить так, чтобы оно осталось деревом. Назовем
его максимальным двойственным деревом. (Пример та-
226
кого дерева нарисован жирными линиями на рис.
130.)
Максимальное двойственное дерево содержит все
вершины двойственной карты. В самом деле, если это не
так, можно присоединить к нему новую вершину при по-
мощи какого-нибудь маршрута. Этот маршрут достигнет
Рис. 129.
Рис. 130.
8*
227
двойственного дерева в какой-то вершине Р, а предшест-
вующая вершина Q ему не принадлежит. Тогда, добав-
ляя к дереву вершину Q и ребро PQ, мы вновь получим
дерево, что противоречит максимальности нашего исход-
ного двойственного дерева. Значит, ему уже принад-
лежат все вершины двойственной карты.
Та часть двойственного графа, которая не вошла в
максимальное дерево, не может развалиться на отдель-
ные куски, ибо это означало бы, что наше дерево пол-
ностью окружило какую-то часть двойственного графа,
а тогда оно должно было бы содержать цикл. Но деревья
не содержат циклов.
Допустим, что М — максимальное двойственное де-
рево, а С — остальная, не вошедшая в него часть двой-
ственного графа. Тогда имеют место биекции между:
а) гранями на S и вершинами М\
б) ребрами на S и ребрами М и С (поскольку каждое
ребро определяет единственное двойственное ребро, а М
и С вместе исчерпывают двойственный граф);
в) вершинами на S и вершинами С. (Каждая верши-
на на S соответствует грани двойственной карты, и в
точности одна вершина этой грани принадлежит С, так
как, если бы их было больше одной, можно было бы
увеличить М.)
Это означает, что
x(S)=xW+x(Q.
Поскольку М — дерево, % (М) = 1. Граф С связен, поэто-
му х(О^1- Следовательно,
x(S)^2,
что и требовалось доказать.
228
Доказательство утверждения В
Пусть S •— поверхность, которую любая замкнутая
кривая на ней разбивает на отдельные части. Покажем,
что S — сфера.
Сначала докажем, что x(\S) = 2. Пусть М и С обо-
значают то же, что и выше. Тогда из равенства
следует, что если х(5)¥=2, то
Х(С)¥=1» т. е. С не является де- Г \
РеВ0М ’ \ \ уГ)
Значит, С содержит цикл. Этот \ | ya^^Z^
цикл является замкнутой кривой \ Х_\
на S и, по предположению, разби- —“X | Г\”/
вает S на куски. Каждый кусок 1 (
обязательно содержит двойствен- /z"'z\ \
ную вершину. Эти вершины дол- [ Г | \
жны быть соединены маршрутом I А | J
в М, значит, этот маршрут где- х—/
то пересечет цикл, принадлежа- Рис- 131-
щий С. Но множества М и С, по
определению, не пересекаются. Таким образом, мы пришли
к противоречию. Следовательно, предположение % (S) 2
неверно, поэтому х (•$) = 2.
Отсюда видно также, что x(Q) = l> т. е. С—-дерево.
Если взять какое-то дерево и немного его «раздуть», как
на рис. 131, то полученная фигура будет топологически
эквивалентна кругу: достаточно, чтобы ветки «съежи-
лись» по направлению к некоторой заданной точке.
Разобьем S на два подмножества X и У: к первому
отнесем те точки, которые лежат ближе к М, чем к С,
а ко второму — те, которые ближе к С, чем к М.
Тогда X и У—«раздутия» М и С, т. е. топологиче-
ски — круги. Края X и У совпадают. Следовательно, по-
верхность S топологически эквивалентна двум кругам,
сшитым друг с другом по краям, а это и есть сфера.
229
Раскрашивание карт на поверхностях
Посмотрим теперь, сколько нужно красок для рас-
крашивания карт на стандартных поверхностях.
Можно показать (примерно тем же способом, каким
мы доказали, что для сферы достаточно пяти красок),
что в случае эйлеровой характеристики
(а это верно для всех поверхностей, кроме сферы) до-
статочно иметь
4 (7 + V 49 —24п )
красок.
По этой формуле, например, для тора (п = 0) полу-
чаем число 7. Такое количество красок является и необ-
ходимым, как показывает рис. 132.
В результате недавних исследований2 установлено,
что эта формула дает точное число красок во всех слу-
чаях, кроме двух. Для сферы она дает ответ 4 — то ли
правильный, то ли нет, неизвестно 3. Для бутылки Клей-
на получается ответ 7, заведомо неверный: для нее тре-
буется только 6 красок.
Эти результаты ставят проблему четырех красок в
довольно странное положение: точный ответ неизвестен
только для сферы — простейшей из поверхностей,
230
Глава 13
АЛГЕБРАИЧЕСКАЯ ТОПОЛОГИЯ
Эйлерова характеристика представляет собой числен-
ный инвариант, позволяющий различать топологически
не эквивалентные пространства. При поисках других ин-
вариантов открылась замечательная связь между двумя
областями современной математики — топологией и аб-
страктной алгеброй. Оказалось, что с топологическими
пространствами связано огромное количество алгебраи-
ческих инвариантов. Чаще всего пространству ставится в
соответствие некоторая группа, причем так, что тополо-
гически эквивалентным пространствам отвечают изо-
морфные группы.
Поиски инвариантов ведутся в надежде на то, что
когда их накопится очень много, удастся классифициро-
вать большие совокупности топологических пространств.
За исключением поверхностей (где оказалось достаточно
эйлеровой характеристики и ориентируемости), по-
строить классификацию не удалось, однако в процессе
этих поисков математики, как никогда, приблизились к
истинному пониманию возникающих здесь задач.
Дырки, пути и петли
Предположим, что мы хотим найти различие между
кругом и кругом с дыркой.
Нетрудно заметить, что в круге любой замкнутый
путь можно стянуть в точку; если же в круге есть дырка,
то никакой замкнутый путь вокруг дырки стянуть в
точку не удастся — дырка помешает.
«Стягиваемость» замкнутой кривой — это, безусловно,
топологическое свойство, и наша цель достигнута: мы
231
сумели отличить круг от круга с дыркой. Попробуем
теперь развить дальше содержащуюся здесь ключевую
идею: пользоваться для обнаружения дырок изучением
путей в пространстве и способов их деформации.
Во-первых, приведем в порядок нашу терминологию.
Путь в топологическом пространстве — это линия, соеди-
Рис. 133.
няющая две точки пространства. Неважно, насколько
она извилиста и есть ли на ней самопересечения. Важно
только, чтобы она не разрывалась: мы хотим, чтобы пути
были непрерывны.
Однако если путь имеет самопересечение, нужно ука-
зать, каким способом его проходить: два пути на рис. 133
следует рассматривать как разные.
Рис. 134.
Это важно: ведь мы хотим при помощи путей обна-
руживать дырки, а способ обхода влияет на то, как путь
обвивается вокруг дырки. Например, на рис. 134 один
путь можно «сдвинуть» с дырки, а другой — нет.
232
Простейший способ задать обход пути — вообразить
движущуюся по нему точку. В момент времени t точка
занимает положение p(t). Она начинает двигаться в не-
который момент t0, а заканчивает в момент Посколь-
ку путь нигде не разрывается, тем самым задается не-
прерывная функция р, область определения которой —
Рис. 135.
множество действительных чисел в интервале
а область значений лежит в данном топологическом про-
странстве. Каждая такая функция определяет некоторый
путь, а каждый путь — такую функцию.
Если конец одного пути совпадает с началом друго-
го, можно составить композицию этих путей, пройдя
сначала один, а потом другой, как показано на рис. 135.
Для путешествия из А в В воспользуемся путем р;
затем установим на часах время отправления для q и
продолжим движение из В в С. Пройденный в резуль-
тате путь обозначим
/’* Я-
Если р определен на интервале a q — на ин-
тервале t2^.x^.t3, то р* q определен на интервале
— t2+t3 в результате того, что мы перевели
часы в точке В.
Композиция * определяет операцию на множестве
путей. Она приводит к другому пути, следовательно,
множество путей замкнуто относительно этой операции.
Далее, операция * ассоциативна (рис. 136).
233
Пройти от Л к В, а затем от В к С и к D
(т. е. р *(q *г)) — это все равно, что пройти от А к В и
С, а затем от С к D (т. е. (р * q) * г). (Это напоминает
ситуацию с композицией функций, которая тоже ассо-
циативна. Однако следует заметить, что р * q для пу-
тей — совсем не то же самое, что pq для функций. Обла-
Рис. 136.
сти определения и значений для р и q не соответствуют
друг другу, и композицию pq вообще нельзя определить.)
Не всякие два пути допускают композицию: конец
одного должен совпадать с началом другого. Поэтому
сделаем так: выберем некоторую точку А — она назы-
вается отмеченной точкой — и сосредоточим внимание
на петлях в А, т. е. путях с началом и концом в А. Теперь
у нас нет никаких забот: всякая петля начинается и кон-
чается в А, так что можно составить композицию любых
двух петель. Множество петель в А замкнуто относитель-
но операции*, и выполнен закон ассоциативности.
Итак, выполнены аксиомы (1), (2), (3) группы
(см. гл. 6). Значит, мы уже получили какую-то алгебраи-
ческую структуру. Легко видеть, что выполняется и ак-
сиома (4): тривиальная петля, которую мы опишем, если
просто останемся в точке А и не затратим на обход ника-
кого времени, в композиции с любой другой петлей даст
эту последнюю,
234
Единственное, чего нам еще не хватает,— аксиомы
(5) о существовании обратного элемента. Но что такое
обращение? Это способ сделать что-то в обратную сто-
рону. Тогда естественно попробовать обойти петлю в об-
ратном направлении.
К сожалению, это не очень помогает. В самом деле,
композиция р-1 с р должна давать тривиальную петлю.
Но обход тривиальной петли не занимает времени, а для
того, чтобы пройти по петле р * р~1, требуется уж во
всяком случае не меньше времени, чем для того, чтобы
пройти по р.
Обойти эту трудность, выбрав другой единичный
элемент, не удастся: ведь если р * х должно равняться р,
то обход по х не должен занимать времени, иначе мы не
успеем обойти р.
И все-таки то, что мы получили, так похоже на груп-
пу! Неужели нельзя найти какой-то выход из создавше-
гося положения?
Г омотопия
Вспомним, что в кольце Z целых чисел нет обратных
элементов по умножению. Однако стоит разбить его на
классы чисел, сравнимых по какому-нибудь простому
модулю, как обратные элементы неким загадочным обра-
зом появляются.
Сейчас мы попали в аналогичную ситуацию: обрат-
ных элементов нет, а нам они очень нужны. Попробуем
выйти из положения таким же способом: разбить мно-
жество петель на какие-то классы и затем оперировать
этими классами.
Требуется ввести нечто вроде «конгруэнтности»
петель, хотя конгруэнтность в смысле евклидовой гео-
метрии здесь явно не подойдет. Подсказку надо искать
в том, для чего мы вообще занялись петлями: чтобы с их
235
помощью обнаруживать дырки. Вспомните: когда речь
шла о дырке в круге, мы говорили о «стягивании» петель.
Назовем две петли в пространстве S гомотопными,
если одну из них можно непрерывно деформировать в
другую, оставаясь в S.
На этот раз нам нужны действительно деформации,
а не просто непрерывные функции. Здесь уже не важно,
что способ вложения в окружающее пространство может
изменить всю картину. Ведь наши петли уже вложены
в S, а нас интересует само пространство S.
Понятие гомотопии легче пояснить не для петель, а
для путей общего вида. Определение остается тем же,
только гомотопные пути должны, конечно, иметь одни и
те же концы. Пример гомотопных путей приведен на
рис. 137. (Последовательность пунктирных линий изо-
бражает деформацию.)
Пути на рис. 138 не гомотопны: дырка мешает де-
формировать их один в другой.
Вместо путей мы будем рассматривать их гомотопи-
ческие классы. Для данного пути р обозначим через [р]
множество всех путей, гомотопных р. Это и есть гомото-
пический класс пути р. Такие классы ведут себя подобно
классам целых чисел, сравнимых по некоторому мо-
дулю.
Если р~1 — путь р в обратном направлении, то путь
236
р *р~х, хотя и не равен тривиальной петле, зато гомото-
пен ей. Как показано на рис. 139, мы можем постепенно
стягивать р * р~1 к отмеченной точке, двигаясь по нему
все быстрее и быстрее. В конце концов получится путь,
, который так и не выходит из этой точки и не требует
совсем никакого времени для своего обхода. (Для ясно-
сти мы на рисунке слегка раздвинули р и р~1.)
Рис. 139.
Ну вот, почти все и сделано. Композицию гомотопи-
ческих классов определяем формулой
fph[<7]=[p *9]
(и проверяем, имеет ли определение смысл). А затем
убеждаемся, что множество гомотопических классов
образует группу относительно операции * .
Эта группа называется фундаментальной группой
пространства S и обозначается л (S). Построил ее Пуан-
каре.
Если S и Т — топологически эквивалентные прост-
ранства, то, как мы знаем, существует такая функция
f: S Т, что и она сама, и обратная ей функция g обе
непрерывны.
Непрерывная функция переводит пути в пространст-
ве S в пути в пространстве Т. Понятие композиции путей
является топологическим, понятие гомотопии тоже. По-
237
этому f определяет функцию F на множестве гомотопи-
ческих классов:
F([p])=[f(p)]-
При этом
F([p]‘ Ы)= F(W)*F([?]), (*)
Подобным же образом функция g: Т -> 5 опреде-
ляет функцию G, которая является обратной к F.
Поэтому F — биекция, а из формулы (») следует, что
F — изоморфизм.
Итак, группы л(5) и л(Т) изоморфны, и в этом
смысле л (S) — топологический инвариант.
С группой л (S) связаны и числовые инварианты,
например ее порядок, однако, если ограничиться лишь
числовыми инвариантами, можно потерять много цен-
ной информации.
Фундаментальная группа окружности
Мы не сможем эффективно пользоваться фундамен-
тальными группами, если не научимся их вычислять.
В общем случае это не простая задача, и для ее реше-
ния и обобщения требуется много теории.
Для некоторых пространств, таких, как R, R2, круг,
шар и т. д., найти фундаментальную группу легко. Это
пространства без дырок, и любая петля в них стяги-
вается в тривиальную (рис. 140).
Поэтому их фундаментальная группа — тривиальная
группа, состоящая из одного элемента /, такого, что
72 = /.
Воспользовавшись «трюком с апельсиновой коркой»
(см. с. 210), можно вычислить л (S) для сферы S. Выбе-
рем на S какую-нибудь петлю р и не лежащую на ней
точку и вырежем из сферы маленький кружок с центром
в этой точке, не пересекающийся с р. Оставшуюся часть
сферы можно «расплющить» в круг. Внутри этого круга
238
путь р стягивается в точку. «Завернув» круг обратно, мы
получим способ стягивания р в точку на S. Значит,
п (S) тоже тривиальна.
Другой простейший случай — когда S — окружность.
Любая петля на S оборачивается вокруг S то или иное
число раз. Это число называется степенью петли. Петли
на рис. 141 имеют соответственно
степени 1, 2 и 0 Если условиться
считать положительным направ-
ление против часовой стрелки, то
обратные им петли имеют степе-
ни -1, -2, 0.
Мы покажем, что степень пет-
ли определяет ее гомотопический
класс: две петли гомотопны тог- Рис
да и только тогда, когда они име-
ют одинаковые степени.
Интуитивно это понятно: не видно, как можно было
бы изменить степень петли простой деформацией. Три-
виальная петля, разумеется, имеет степень 0; третью
петлю на рис. 141, тоже имеющую степень 0, можно
стянуть в точку.
Чтобы получить доказательство, введем вспомога-
тельное пространство, в котором хорошо видны гомото-
пические свойства и которое тесно связано с окружно-
стью. Это поможет нам вывести гомотопические свойства
окружности.
239
Представим себе кривую L, восходящую над окруж-
ностью подобно винтовой лестнице, и отметим над точ-
кой А на окружности точку О на кривой. Любую петлю
в S можно «поднять» и получить некоторый путь в L,
Действительно, возьмем какую-нибудь точку .в S и ле-
жащую над ней точку в L. Когда первая описывает пет-
лю в S, вторая, двигаясь точно над первой, описывает
непрерывный путь в L. Например, петлям на рис. 141
соответствуют пути, изображенные на рис. 142.
Поднятый путь не обязательно кончается в точке О,
но всегда точно над (или под) ней на спирали. Коли-
чество витков, на которое он поднимается (или опуска-
ется), равно в точности степени соответствующей петли.
Если угодно, можно считать это определением.
Теперь настал решительный момент: два пути в S го-
мотопны тогда и только тогда, когда их «поднятия» гомо-
топны в L. В самом деле, имея гомотопию в L, мы можем
240
«спроектировать» ее и получить гомотопию в S. И наобо-
рот, любую гомотопию в S можно поднять в L: дефор-
мируя путь в S, мы деформируем соответствующий
путь в L.
Но в L гомотопические свойства тривиальны, посколь-
ку L — линия, и мы уже знаем, что группа л(Ь) три-
виальна. Два пути в L гомотопны тогда и только тогда,
когда они имеют одни и те же концы. Ясно, что это усло-
вие необходимо; ввиду тривиальности л(Ь) оно являет-
ся и достаточным.
Все поднятые в L пути начинаются в О. Концы их
совпадают, когда они делают одинаковое число витков
над (или под) О. Но это происходит тогда и только то-
гда, когда соответствующие петли в S имеют одну и ту
же степень.
Возьмем петлю в S степени п и составим ее компози-
цию с петлей степени т; мы получим петлю, которая
делает сначала п оборотов по окружности, а потом еще
т оборотов. Значит, ее степень равна п + т. Отсюда вид-
но, что группа л(5) изоморфна группе Z целых чисел по
сложению.
Проективная плоскость
Возьмем в качестве S проективную плоскость. Ее
фундаментальная группа n(S) состоит из двух эле-
ментов:
I 1 г
1 1 г
г г 1
Элемент г — это гомотопический класс пути, показанно-
го на рис. 143. (Вспомним, что проективную плоскость
можно представить как квадрат с отождествленными
диаметрально противоположными точками.)
241
Соотношение г2=/ означает, что, хотя путь на
рис. 143 не стягивается в точку, путь, который получает-
ся, если пройти по нему дважды, обладает этим свой-
ством.
В этом можно убедиться геометрически (рис. 144£;
возьмем один экземпляр нашего пути и вытянем его по
направлению к левому верхнему уг-
лу; пройдя через край квадрата, он
в силу наших отождествлений вер-
нется через правый нижний угол в
обратном направлении, и мы стянем
его к отмеченной точке.
Этот забавный факт имеет неко-
торое отношение к «фокусу с глу-
бокой тарелкой». Возьмите глубо-
кую тарелку, желательно не из фа-
242
мильного сервиза, и держите ее перед собой на кончиках
пальцев правой руки. Опускайте локоть и двигайте его
назад, пронося тарелку под мышкой. Продолжайте вы-
ворачивать руку в том же направлении и поднимайте
локоть, пока тарелка не займет исходное положение.
Теперь ваша рука вывернута локтем вверх.
Но вы на этом не останавливайтесь. Продолжайте
тем же способом выворачивать руку, пронося тарелку
над головой, а локоть перед собой. Вы вернетесь в исход-
ное положение. На полпути рука была вывернута. Каза-
лось бы, после следующего оборота должно стать еще
хуже. Но этого не случилось: вы вернулись в исходное
положение с невывернутой рукой.
Именно это происходит на проективной плоскости:
после одного оборота все закручивается, а после вто-
рого — приходит в нормальное состояние.
Глава 14
В ГИПЕРПРОСТРАНСТВО
Меня спрашивают: «Можете вы
показать нам это четвертое из-
мерение?» А я отвечаю- «А вы
можете показать мне первое,
второе и третье?»
Аноним
Часто случается так, что какое-то математическое
обобщение, которое сначала развивают ради него само-
го, позднее приобретает важное значение для математи-
ки в целом.
В гл. 4 мы установили, что евклидову плоскость мож-
но представлять как множество всех упорядоченных пар
действительных чисел, которое мы обозначили R2. По-
добным же образом трехмерное пространство можно
рассматривать как множество R3 всех упорядоченных
троек (х, у, х) действительных чисел. Наконец, линия
R — это одномерное пространство. Таким образом, мы
получаем:
1-мерное пространство= R = множество действитель-
ных чисел х,
2-мерное пространство= R2 = множество пар действи-
тельных чисел (х, у),
3-мерное пространство = R3 = множество троек дейст-
вительных чисел (х, у, г).
На этом реальные пространства кончаются. Но реаль-
ность так часто разочаровывает... А что, если попытать-
ся уйти от нее:
4-мерное пространство = R4 = множество четверок дей-
ствительных чисел (х, у,
г, и),
5-мерное пространство = RE = множество пятерок дей-
244
ствительных чисел (х, у,
z, и, v),
и вообще
«-мерное пространство= Rn = множество «-наборов
("М, Хп).
В самом деле, почему бы и нет? Мы вольны давать
любые определения, какие захотим. Правда, говоря о
пространствах, обычно подразумевают не просто мно-
жества точек. В пространствах определено расстояние
между точками.
Так, расстояние d между двумя точками (х4, х2) и
(i/i, У2) по теореме Пифагора определено формулой
d2= (xi-t/i)2+ (х2-у2)2.
Соответствующая формула в 3-мерном пространстве
имеет вид
d2= (м-!/1)2+ (Хг-р2)2+ (Хз-Уз)2.
И в 1-мерном пространстве можно написать такую же
формулу
d2= (М-У1)2.
Если мы на верном пути, то, вероятно, в 4-мерном про-
странстве расстояние между (хь х2, х3, х4) и (z/i, у2, уз,
у4) должно определяться формулой
d2 = (xi-tji)2+ (х2-у2)2+ (хз-уз)2+ (х4-у4)2,
и аналогичную формулу мы вправе ожидать для «-мер-
ного пространства.
Вопрос не в том, верна эта формула или нет. Посколь-
ку о 4-мерном пространстве нам ничего не известно, у
нас нет возможности проверить ее справедливость. Мы
находимся во владениях абстрактной математики и мо-
жем пользоваться любой формулой, какой захотим.
Правильнее поставить вопрос так: «Все это прекрасно,
и я согласен, что напрашивается именно такая формула,
245
но можно ли с ее помощью получить что-нибудь ра-
зумное?»
Для того чтобы некую величину можно было считать
«расстоянием», она должна удовлетворять трем усло-
виям:
1) расстояние между любыми двумя точками поло-
жительно;
2) расстояние от точки
А до точки В равно рассто-
янию от В до Л;
3) расстояние от А до В
не превосходит суммы рас-
стояний от Л до С и от С
до В.
Условие 3 говорит о том,
что сторона треугольника
меньше суммы двух других
его сторон, н, грубо говоря,
оно отражает наше представление, что «прямая опреде-
ляет кратчайшее расстояние между двумя точками».
Проверим, удовлетворяет ли наша формула этим
условиям.
Условие 1 выполняется, если для определения d взять
положительный квадратный корень, причем извлечение
корня допустимо, так как правая часть есть сумма квад-
ратов и, следовательно, неотрицательна.
Условие 2 заключается в том, что d не изменится,
если поменять местами все Xi и у,. Но (х, —у,)2=
= (yi — Xi)2, поэтому условие 2 выполнено.
Условие 3 приводит к важному алгебраическому не-
равенству. Рассмотрим частный случай п = 2. Из рис. 145
видно, что дело сводится к доказательству неравенства
V а2 + b2 +V с2 + d2 > V(а + с)2 + (b + d)2.
Возведя его в квадрат, получим неравенство
246
а2 + ь2 + С2 + d2 + 2 / (й2 + Ь2) (с2 + d2)
>(й + с)2 + (b + d)2,
которое верно при условии, что
2 V (a2 + b2) (c2 + d2) > 2 (йс + bd).
Последнее в свою очередь верно, если
(й2 + &2) (c2+d2) (ac+bd)2,
или, что то же самое,
(й2 + 62) (c2 + d2) — (ac + bd)2^0.
Преобразуем левую часть и убедимся, что она равна
(ad—be)2.
Но квадрат всегда неотрицателен. Поэтому в 2-мерном
случае условие 3 выполняется.
В n-мерном случае проводятся аналогичные, но более
громоздкие выкладки. Таким образом, наша попытка
обобщения сразу привела к важному неравенству.
Это означает, что наше определение расстояния по
крайней мере не лишено смысла. Свойства абстрактно-
го 4-мерного пространства начали изучать геометры
19 века (которым стало почти нечего доказывать в про-
странствах меньшей размерности). К своей великов
радости они обнаружили, что концепция 4-мерного про-
странства не только не бессмысленна, но и весьма пло-
дотворна и приносит с собой много красивых идей и
теорем.
Политопы
В 3-мерном пространстве существуют ровно 5 пра-
вильных многогранников: тетраэдр, куб, октаэдр, до-
декаэдр, икосаэдр. Соответствующий объект в 4-мерном
247
пространстве называется правильным политопом. Его
«грани» — трехмерные правильные многогранники, гра-
ни последних — правильные многоугольники. Располо-
жение «граней» одинаково в каждой вершине. Во избе-
жание путаницы будем называть эти трехмерные «грани»
ячейками, а название «грани» сохраним за двумерными
гранями этих ячеек.
Геометры (в частности, Шлефли) установили, что
в 4-мерном пространстве имеется ровно 6 правильных
политопов:
Число ячеек Число граней Число ребер Число вершин Тип ячеек Название поли топа
5 10 10 5 Тетраэдр Симплекс
8 24 32 16 Куб Гиперкуб
16 32 24 8 Тетраэдр 16-ячейка
24 96 96 24 Октаэдр 24-ячейка
120 720 1200 600 Додекаэдр 120-ячейка
600 1200 720 120 Тетраэдр 600-ячейка
(К вопросу о закономерностях появления этих чисел мы
вернемся позднее.)
В пространствах более высоких размерностей —
5-мерном, 6-мерном и т. д.— насчитывается всего три
правильных политопа: это аналоги тетраэдра, куба и
октаэдра.
Итак, числа правильных фигур в пространствах раз-
мерности 1, 2, 3, 4, 5, ... равны соответственно оо, 5, 6,
3, 3, ...
Политопы невозможно нарисовать на бумаге. Но и
3-мерные фигуры тоже невозможно нарисовать на бума-
ге. При изображении 3-мерных объектов на плоском
листе мы пользуемся определенными соглашениями, ко-
торые обусловлены анатомическим строением нашего
глаза. Можно научиться делать изображения и 4-мерных
248
фигур, однако без достаточной практики их трудно будет
«читать», подобно тому как трудно понять технический
чертеж, не будучи инженером.
Четырехмерные изображения
Четырехмерные фигуры можно, например, изобра-
жать с помощью проекции. Именно таким способом ху-
дожник рисует трехмерную натуру на двумерном холсте.
При этом «натура» сплющивается либо радиально, либо
перпендикулярно (рис. 146).
Рис. 146.
Аналогичным способом можно строить проекции
4-мерных фигур в 3-мерное пространство. Чтобы получить
плоское изображение, приходится преодолеть еще одну
трудность: полученную 3-мерную проекцию спроектиро-
вать в 2-мерное пространство. На рис. 147 показаны две
проекции гиперкуба.
При интерпретации этих картинок следует принимать
во внимание действие перспективы. Маленький кубик
внутри левого рисунка на самом деле того же размера,
что и внешний куб. Однако из этой картинки легко ви-
деть, что гиперкуб составлен из 8 кубов (на левой кар-
249
L
тинке: из одного маленького, одного большого и шести
искаженных, которые выглядят как усеченные пирами-
ды). Каждый из этих кубов соприкасается с 6 другими —
по каждой своей грани, и к каждой вершине примыкают
4 куба.
Существуют программы для вычислительных машин,
которые выдают на экран проекции 4-мерных фигур.
Рис. 147.
Оператор может менять направление проекции, «пово-
рачивая» фигуру. Говорят, что по мере накопления опыта
оператор начинает угадывать, как будут выглядеть про-
екции после поворота,— он начинает думать в 4-мерном
пространстве. Топологи, изучающие пространства выс-
ших размерностей, также овладевают этим уменьем.
Есть еще один, по-видимому более наглядный, способ
изображать 4-мерные объекты: при помощи поперечных
сечений. Подобным способом изображаются на карте
горы и долины: местность расслаивается воображаемы-
ми горизонтальными плоскостями и на карту наносятся
контуры пересечений (рис. 148),
Вырезав из картона куски в форме этих контуров и
расположив их друг над другом на правильной высоте,
можно восстановить форму поверхности.
Жители 2-мерного мира могли бы пользоваться этими
сечениями для изображения 3-мерных объектов, а обита-
тель 1-мерного пространства при помощи ряда линейных
250
сечений мог бы составить представление о форме пло-
ской фигуры.
Во всяком случае сечение уменьшает размерность.
Сечения 4-мерной фигуры 3-мерны.
Обобщив алгебраическое определение сечения в трех-
мерном пространстве, можно точно сказать, что пони-
Рис. 148.
мается под сечением объекта в R4, R5 и т. д. В некото-
рых случаях по аналогии можно угадать, как выглядят
эти сечения, а затем проверить правильность догадки
при помощи алгебры. Мы здесь не будем морочить себе
голову алгеброй.
Сечениями сферы являются окружности, вырастаю-
щие от точки до большого круга и затем стягивающиеся
Рис. 149.
ОЙО(Э
Рис. 150.
251
снова в точку. Значит, сечениями гиперсферы (4-мерно-
го аналога сферы) будут сферы, вырастающие от точки
до максимума и затем сжимающиеся, как на рис. 149.
Сечения куба (параллельные граням) всегда квад-
раты, поэтому сечениями (аналогичными) гиперкуба
должны быть кубы (рис. 150).
Укладка сечений
Поскольку мы живем в 3-мерном пространстве, наша
главная проблема — мысленно уложить сечения в одно
целое. Здесь снова помогает аналогия с воображаемыми
обитателями плоскости. Как они стали бы укладывать
двумерные сечения?
Они могли бы, например, считать, что секущая плос-
кость равномерно движется. В каждый момент време-
ни t в сечении получается некоторый двумерный объект.
Если бы удалось снять кинофильм, в котором чередова-
ние кадров соответствовало бы последовательным мо-
ментам времени, его можно было бы использовать для
воссоздания трехмерной картины. Эти существа пред-
ставляли бы себе шар как вырастающий из точки кру-
жок, который затем снова сжимается в точку.
Подобным образом могли бы поступать и мы: укла-
дывать 3-мерные сечения 4-мерных объектов во време-
ни, создавая 3-мерный кинофильм. Гиперсфера тогда
выглядела бы как растущий, а затем снова сжимающий-
ся пузырь. Вместо гиперкуба перед нами внезапно воз-
никал бы куб, который, пробыв некоторое время без
всяких изменений, внезапно исчезал бы. А если бы вдруг
появилась сфера, побыла некоторое время, а потом про-
пала, мы знали бы, что это был гиперцилиндр со сфери-
ческим сечением.
Это уже лучше, но еще не совсем то, что нужно. Нам
приходится смотреть этот кинофильм в строго опреде-
ленной последовательности, и мы попадаем в положение
252
слепого, которому разрешено ощупывать предметы лишь
одним движением — сверху донизу. А хотелось бы пово-
дить руками вверх и вниз, изучить подробнее каждую
непонятную (или особенно интересную) деталь.
Короче говоря, требуется машина времени — или по
крайней мере кинопроектор с обратным ходом и разными
скоростями.
Рис. 151.
Эта машина должна иметь педаль управления вре-
менем и особый экран для воспроизведения 3-мерных
изображений. К счастью, нас устроит воображаемая
машина: двигайте ногой, как будто нажимаете на пе-
даль, и представляйте себе изображения!
Изменяя степень нажима на педаль, вы сможете
перемещаться во времени. В качестве первого упражне-
ния в управлении педалью развяжем в 4-мерном про-
странстве узел, не разъединяя концов шнура. Для про-
стоты займемся самым простым узлом, хотя годится и
любой другой. В кадре А на рис. 151 изображен такой
узел; он «обитает» в 3-мерном пространстве в момент
времени t = 0.
253
Схватите шнурок покрепче вблизи точки самопере-
сечения X. Ослабьте нажим на педаль и продвиньтесь
немного вперед во времени, протащив за собой малую
петлю шнура, но так, чтобы большая часть узла оста-
лась в прежнем положении во времени и пространстве
(показанном пунктиром), как в кадре В. Теперь опусти-
те эту петлю ниже того места, где раньше был другой
Рис. 152.
участок шнура, как в кадре С. Наконец, вернитесь обрат-
но во время t=Q, захватив с собой все ту же петлю. В ре-
зультате (кадр D) узел будет развязан.
В качестве второго упражнения попробуйте вложить
без самопересечений в 4-мерное пространство бутылку
Клейна. Начните с рис. 81 в момент t=0. Возьмите уча-
сток «трубки» около пересечения и немного передвиньте
его во времени.
А теперь попытаемся сцепить окружность со сферой.
Сначала воспользуемся аналогией: рассмотрим две сцеп-
ленные окружности в 3-мерном пространстве (для удоб-
ства одну из них сделаем прямоугольной, см. рис. 152)«
Введем временную ось, как показано на рисунке.
Можно считать, что это зацепление получилось так:
в момент t=0 точка начала двигаться из центра окруж-
ности вперед во времени, в сторону в пространстве, назад
во времени до момента, предшествующего t=0, снова
в сторону в пространстве до некоторой точки, лежащей
254
непосредственно под центром окружности (относительно
оси времени), и, наконец, вперед во времени, после чего
петля замкнулась.
Чтобы сцепить в 4-мерном пространстве сферу с
окружностью, поступим аналогично. Вообразим сферу
в момент £=0. Пусть точка начинает движение из центра
сферы. Она перемещается вперед во времени (не пере-
секая сферы, которая исчезла, как только точка пошла
вперед), огибает сферу во времени и в пространстве,
достигая точки, лежащей непосредственно под центром
сферы относительно оси времени, и, наконец, двигается
вперед во времени, замыкая окружность.
Вместо зацеплений можно рассматривать заузлива-
ния. Сфера в 4-мерном пространстве может быть завяза-
на в узел, точно так же как окружность в 3-мерном про-
странстве. Топологи потратили много усилий на решение
такой задачи: может ли заузливаться m-мерная сфера
в n-мерном пространстве? В момент написания этой
книги первый, еще не решенный случай касался 10-мер-
ной сферы в 17-мерном пространстве.
Космонавты в 24-мерном пространстве
Представьте себе маятник, качающийся с небольшой
амплитудой. В любой данный момент времени t он зани-
мает некоторое положение р, и его скорость равна q.
Если нарисовать график зависимости р от q (выбрав для
измерения времени некоторую подходящую единицу), по-
лучится окружность, и, когда маятник качается, точка
(Р> У) движется по окружности равномерно (рис. 153).
В точке А у нас р = 0, 9>0; в точке В имеем q = 0 и р>0;
в точке С — снова р = 0, но 9<0; в точке D — наоборот,
9=0, а р<0; все это согласуется с колебаниями маятни-
ка (рис. 154).
График зависимости р от q называют фаговой диа-
граммой, а плоскость (р, q) -— фазовым пространством.
255
В рассматриваемом случае оно 2-мерно, так как состоя-
ние маятника определяется двумя величинами; коорди-
натой и скоростью.
Любой динамической системе соответствует фазовое
пространство, размерность которого определяется коли-
чеством пространственных координат и составляющих
скорости.
Рис. 153.
Так, например, динамическая система, состоящая из
Солнца, Луны и Земли, движущихся по законам грави-
тационного притяжения, имеет 18-мерное фазовое про-
странство: по три пространственные координаты и по
три составляющие скорости для каждого из трех небес-
Рис. 154.
256
ных тел (ибо в 3-мерном пространстве и положение, и
скорость задаются тремя координатами). Состояние этой
системы в целом в каждый момент времени задается
одной-единственной точкой фазового пространства. При
изменении времени эта точка описывает некоторую тра
екторию, полностью задающую движение всей системы
Чтобы вычислить орбиту
космического корабля, дви-
жущегося в этой системе,
нужно добавить еще 6 изме-
рений (положение и ско-
рость корабля), и тогда по-
лучится задача 24-мерной
геометрии! Такой подход
позволяет не только описать
задачу. Последовательно и
основательно разработан-
ный, он становится мощным
математическим методом:
геометрической динамикой. Рис. 155.
Движение заданной ди-
намической системы может начинаться различными
способами. Например, космический корабль можно за-
пускать из любых начальных положений с разными на-
чальными скоростями. Каждому начальному состоянию
отвечает некоторая точка фазового пространства. Когда
система движется, эта точка описывает некоторую тра-
екторию; так мы получаем семейство траекторий — по
одной для каждого начального состояния. Вообразим,
что фазовое пространство заполнено жидкостью, причем
каждая частичка жидкости соответствует некоторому
состоянию системы. Тогда жидкость будет течь по тра-
екториям. Для нашего маятника линиями тока служат
концентрические окружности, а стационарная точка в
центре отвечает вертикально висящему маятнику, нахо-
дящемуся в состоянии покоя (рис. 155).
6 Я. Стюарт
257
Из ньютонова закона сохранения энергии следует,
что эта воображаемая жидкость ведет себя в точности,
как настоящая; более того, она несжимаема. Это позво-
ляет применять к общей теории динамических систем ме-
тоды гидродинамики. Без использования многомерной
геометрии такое применение было бы неосуществимо.
Дальнейшее обобщение формулы Эйлера
Формула Эйлера сначала давала нам соотношение
между числом граней, числом ребер и числом вершин
карты на плоскости. Затем мы обобщили ее на другие
поверхности. Теперь посмот-
Рис. 156.
рим, нельзя ли обобщить ее
на пространства высших
размерностей.
«Карта» в «-мерном про-
странстве состоит из «-мер-
ных «областей» с («— 1)-
мерными «гранями»; пос-
ледние имеют (п—^-мер-
ные «грани» и т. д. вплоть
до вершин, которые пред-
ставляют собой 0-мерные
«грани», Обозначим число
«-мерных «граней» карты
символом Fn. Например,
для политопа в 4-мерном
пространстве Fq — число вершин, Fi •— число ребер, Fz —
число граней, F$—число ячеек и Ft — число 4-мерных
областей, которое для правильного политопа равно 1.
В 2-мерном случае формула имела вид
В-Р+Г=1
или в новых обозначениях
F9-Fi+F2~1.
258
Вспомним, как доказывалась эта формула: посредством
«стягиваний» мы добивались того, чтобы изменения чи-
сла «граней» соседних размерностей компенсировали
друг друга. Это наводит на мысль рассмотреть в 4-мер-
ном пространстве выражение
Fo—Fi +F2—F3 + F4.
Рис. 157.
Испробуем его на правильных политопах, помня, что для
них +4=1. Воспользовавшись таблицей на с. 248, найдем:
5-10+10-5+1 = 1,
16-32 + 24-8+1 = 1,
8-24 + 32-16+1 = 1,
24-96+96-24+1 = 1,
600-1200 + 720-120+ 1 = 1,
120-720 + 1200-600+ 1 = 1.
Невероятно, что это простое совпадение.
9*
259
Для 3-мерной карты соответствующее выражение
имеет вид
Fo~ Fi +F2—F3.
Испробуем его на чем-нибудь не очень правильном
(рис. 156). Имеем Fa — 14, Fi = 22, Р2= И, Fs=2 и
14-22 + 11-2=1.
И опять это мало похоже на совпадение.
Итак, естественно ожидать; что для карты в «-мер-
ном пространстве выполнена формула
Fo~ Fi + F?—...±Fn= 1.
Ее нетрудно доказать все тем же методом стягиваний,
Можно одновременно избавиться от вершины и ребра,
или от ребра и грани, или от грани и ячейки и т. д., т. е.
от m-мерной и (т +1)-мерной «граней» (рис. 157).
Каждое такое стягивание не меняет левой части фор-
мулы. В конце концов мы приходим к одной точке, для
которой эта левая часть равна 1. (Чтобы такое доказа-
тельство работало, нужно еще делать стягивания в пра-
вильном порядке, но мы хотели лишь дать главную
идею.)
Итак, в этом случае допускают обобщение и сама
теорема, и метод ее доказательства.
Впервые «-мерный вариант формулы Эйлера доказал
Пуанкаре, поэтому ее называют формулой Эйлера —
Пуанкаре.
Еще немного алгебраической топологии
Понятия гомотопии и фундаментальной группы
(гл. 13) допускают обобщения на пространства высших
размерностей. Для получения «путей» вместо отрезка ис-
пользуется «-мерный гиперкуб. Вместо соединения конца
с концом используется соединение грани с гранью, как
260
показано на рис. 158. Чтобы получить группу, мы рас-
сматриваем гиперкубы, граница которых стягивается в
одну точку.
В результате соответствующего обобщения понятия
гомотопии получается группа, состоящая из гомотопиче-
ских классов n-мерных «путей». Она называется n-й го-
Рис. 158.
мотопической группой itn(S) пространства S. Фундамен-
тальная группа л(3) становится, таким образом, груп-
пой Л](S)—первым членом целой последовательности
алгебраических инвариантов.
Высшие гомотопические группы способны обнаружи-
вать такие различия между пространствами, которые не
улавливает группа Ль Допустим, что из большего шара
выброшен шар поменьше, т. е. пространство S представ-
ляет собой'что-то вроде утолщенной апельсиновой корки.
Тогда любая петля соскользнет с дырки, и группа Я1(5)
тривиальна. Но если мы окружим дырку квадратом из
пленки, граница которого стянута в точку (так ска-
зать, упрячем дырку в пакет), то нам не удастся стянуть
его в точку внутри S. Таким образом, группа яг(5) нетри-
виальна и обнаруживает дырку, которую «пропустила»
группа ль
Казалось бы, зная все гомотопические группы яДЗ),
Лг(3), мы должны были бы знать, что представляет
261
собой пространство 5 с точностью до топологической
эквивалентности. К сожалению, это не так. Пуанкаре вы-
сказал гипотезу, что верен хотя бы частный случай этого
утверждения; если пространство 5 имеет ту же последо-
вательность гомотопических групп, что и «-мерная сфера,
то S и есть n-мерная сфера. В случае п=2 это наше
утверждение В из гл. 12. При п^5, как доказал Смейл *,
это тоже верно. Однако справедлива или нет эта гипо-
теза при п=3ип=4 — никто не знает.
Выходит, что топология в больших размерностях
иногда проще, чем в меньших! И правда, в топологиче-
ском фольклоре самой плохой считается размерность 4.
Что такого особенного в 4-мерном пространстве — не-
разгаданная тайна.
Глава 15
ЛИНЕЙНАЯ АЛГЕБРА
Задача
В школе на уроках алгебры нас учат решать системы
уравнений вроде
х + 2у = 6,
Зх — у = 4
следующим методом (или какой-нибудь его разновид-
ностью): умножить первое уравнение на 3, получив
Зх+6у= 18,
и вычесть из него второе уравнение. В результате мы
приходим к уравнению
7у=14,
откуда у=2. Далее надо подставить это значение в пер-
вое уравнение и получить х=2.
Теперь предположим, что вместо рассмотренной
системы нам задали уравнения'
х + 2у = 6,
Зх -|- бу = 4.
Согласно изложенному методу, умножаем первое уравне-
ние на 3, получив
Зх+6у= 18,
и вычитаем из него второе. Это дает равенство
0=14.
(1)
(2)
Мы пытаемся найти из него у и впадаем в уныние.
263
В школе с нами такого не случалось: нас оберегали
от такого рода неприятностей, тщательно подбирая урав-
нения. Не сталкивались мы и с ситуацией, которая возни-
кает при решении уравнений
х + 2у = 6, |
Зх + бу = 18. J W
Здесь обычный метод дает
0=0.
Мы могли бы покачать головой, заявить, что системы
уравнений типа (2) и (3) бессмысленны, и не обращать
на них больше внимания. Но всегда ли мы сумеем во-
время догадаться, что возникнет такая бессмыслица?
Во всех рассмотренных случаях нетрудно дать объяс-
нение происходящему. Уравнения (2) противоречат друг
другу, поэтому-то решения и не существует. В системе
(3) второе уравнение по существу совпадает с первым,
т. е. на самом деле у нас есть лишь одно уравнение с
двумя неизвестными. Это не значит, что система (3) не
имеет решений: напротив, их много. Например, х=2,
у=2\ х=4, у=1; х=6, у=0; х = 1/2, у=11/4. С другой сто-
роны, не всякая пара чисел годится: х=1, у= 1 не будет
решением. Полное множество решений можно найти так:
выбрать х произвольным образом, скажем, взять х—а,
а тогда у=1/г(6 —а). И это будут все решения.
Итак, система может:
{иметь единственное решение,
не иметь решений,
иметь бесконечно много решений,
и этим исчерпываются все возможности. Не существует
системы уравнений, которая имела бы точно 2 решения,
или точно 3, цли 4, или вообще какое-нибудь конечное
число (кроме 0 и 1) решений, (Я ие хочу проводить
264
здесь доказательство, но из дальнейших рассуждений
будет ясно, что это так.)
Аналогично ведут себя системы с большим числом
неизвестных, но это значительно труднее обнаружить.
Вполне простительно, имея дело с системой уравнений
х 4- 4у — 2z 4~ 3/ = 9,
2х— у —z — t = 4,
5х + Ту + г — 2/ = 7,
Зх— 2у —8г + 5/ = 21,
не сразу заметить, что удвоенное первое уравнение плюс
утроенное второе минус третье равно
Зх—2у—8г + 5/=23,
а это уравнение противоречит четвертому. Если же за-
менить в четвертом уравнении 21 на 23, то у нас по суще-
ству получится система из трех уравнений с четырьмя
неизвестными, 'Которая, как выясняется, имеет бесконеч-
но много решений.
Но, вообще говоря, если у системы больше неизвест-
ных, чем уравнений, то это еще не значит, что у нее есть
решения: система
2х 4- 2у 4- 2г + 2/ = О J
решений не имеет.
Таким образом, системы уравнений оказываются
совсем не такими «ручными», как мы думали. Их по-
ведение «дико» и (на первый взгляд) непредсказуемо.
Если бы мы были уверены, что все системы уравнений,
которые встречаются на самом деле, имеют единственное
решение, мы могли бы не обращать внимания на эти не-
приятности. К сожалению, это не так. Но системы урав-
нений, по счастью, обладают некоторыми тайными при-
знаками, которые позволяют разрешить большую часть
проблем.
265
Геометрическая точка зрения
Обратимся к графическому изображению уравнений.
Это поможет нам разобраться, в чем состоит разница
между системами (1), (2) и (3). На рис. 159 изображе-
ны прямые, соответствующие уравнениям системы (1):
точка пересечения этих прямых и есть единственное ре-
шение рассматриваемой системы.
Уравнения системы (2)
определяют две параллель-
ные прямые (рис. 160), которые никогда не пересекутся.
Соответствующие системе (3) прямые совпадают, и,
таким образом, все их точки определяют решения систе-
мы (рис. 161).
Очевидно, что этим исчерпываются все возможности
взаимного расположения
двух прямых. Теперь ясно,
почему система должна или
не иметь решений совсем,
или иметь одно решение, или
иметь их бесконечно много.
При изучении общей за-
дачи более полезным оказы-
вается другой геометриче-
ский подход к системам
уравнений. Введем две си-
266
стемы координат: (х, у) и (X, Y). Каждой точке (х, у) по-
ставим в соответствие точку (X, Y) такую, что
х -\-2у — X, 1
Зх— 2у = У. J
Чтобы решить систему (1), надо найти такую |очку
(х, у), чтобы для соответствующей ей пары (X, Y) вы-
полнялось равенство (X, У) =(6,4).
Что получается? Вычислим (X, Y) для некоторых
(х, у)'.
(х, у) (X У)
(0,0) (0,0)
(0,1) (2,-1)
(0,2) (4,-2)
(1,0) (1,3)
(1,1) (3,2)
(1,2) (5,1)
(2,0) (2,6)
(2,1) (4,5)
(2,2) (6,4)
Ясно, что преобразование (х, у) в (X, Y) превращает
квадраты на (х, у)-плоскости в параллелограммы на
(X, У)-плоскости.
Последняя строчка выписанной выше таблицы дает
решение нашей системы: Х—6, У=4 при х=2, у=2. Но
так вышло случайно. Гораздо большую ясность вносит
рисунок. Рассмотрим произвольную точку (а, р) на
(X, У)-плоскости. Очевидно, что некоторая точка (х, у)-
плоскости переходит в (а, Р), поскольку мы нашу плос-
кость лишь несколько растянули и повернули. Паралле-
лограмм, содержащий (а, р), получился из некоторого
квадрата, и одна из точек этого квадрата переходит в
(а, Р). Например, пусть (а, Р) = (472, 3) —центр одного
267
из изображенных на рис. 162 параллелограммов. Центр
соответствующего квадрата — это (Р/г, Р/г), И, конеч-
но, единственным решением системы
х + 2t/ = |
Зх — у = 3 J
будет х=Р/2,у=Р/2.
Рис. 162.’
Далее ясно, что это решение должно быть единст-
венным, поскольку преобразование квадрата в парал-
лелограмм происходило так, что две различные точки
(х, у)-плоскости не могли перейти в одну. Построенное
преобразование не производит склейки.
Однако когда мы переходим к системам (2) и (3), то
должны положить
х+2 у=JC,
Зх+6у= У,
Нетрудно видеть, что все получающиеся таким путем
точки (X, Y) лежат на прямой, а именно на прямой
У=ЗХ (рис. 163).
Соответствующее преобразование стягивает всю
268
(х, у)-плоскость в единственную прямую. В системе (2)
у нас Х = 6, У=4. Но точка (6, 4) не лежит на получен-
ной прямой. Значит, решения не существует, так как все
точки (х, у) отображаются только в эту прямую. С дру-
гой стороны, для системы (3) Z=6, У= 18, и эта точка
лежит на полученной прямой. Более того, в нее стяну-
лось бесконечно много точек (х, у).
Рис. 163.
Далее все возможные значения (х, у) образуют на
(х, гд)-плоскости прямую, задаваемую уравнением
x+2z/=6.
Таким образом, особенности поведения рассматри-
ваемых систем зависят от геометрических свойств пре-
образования Т такого, что
Т(х, у) = (X, У) = (х+2у, Зх-у),
и преобразования S такого, что
S(x, у) = (X, У) = (х+2у, Зх+бу).
Чтобы исследовать систему уравнений общего вида
ax -j- by = X, |
ex -|- dy = У, J
нужно рассмотреть преобразование
269
U(x, у) = (ax+by, cx+dy).
Для системы из трех уравнений с тремя неизвестными
ах 4- by 4- cz — X, )
dx 4- еу 4- fz = Y, >
gx + hy 4- kz— Z J
нам потребуется преобразование
V(x, у, z) = (ax + by+cz, dx+ey+fz, gx+hy+kz).
Все это так называемые линейные преобразования; их
изучением занимается линейная алгебра.
Некоторые соображения о поведении систем
Используя введенное выше преобразование Т, мы
можем найти для системы (1) теоретико-множественную
формулировку: является ли точка (6,4) элементом обла-
сти значений преобразования Т? Напомним, что об-
ластью значений преобразования Т называется множе-
ство значений Т(х, у), которые принимает Т. Таким
образом, точка (6,4) лежит в этой области в том и толь-
ко в том случае, если найдутся х и у такие, что (6, 4) =
= Т(х, у) — (х+2у, Зх—у), и это иная формулировка си-
стемы (1).
Аналогично обстоит дело с двумя другими система-
ми: они выясняют, принадлежат ли точка (6,4) или точ-
ка (6, 18) области значений линейного преобразова-
ния 3.
Поскольку Т преобразует квадраты в параллелограм-
мы, то из геометрических соображений ясно, что об-
ластью его значений является вся плоскость. Как мы
уже установили, областью значений преобразования 3
служит одна прямая.
Чтобы изучать системы уравнений общего вида, надо
попытаться побольше разузнать об областях значений
270
линейных преобразований. Мы уже знаем, что ими могут
быть плоскости и прямые. Есть ли другие возможности?
Да. Тривиальная системй
Ох + Оу = X, 1
Ох 4- Оу = Y J
соответствует линейному преобразованию F такому, что
F(x, у) = (0, 0). Его область значений — единственная
точка {(0, 0)}. (Область значений — это множество,
поэтому мы, как это принято в теории множеств, заклю-
чили (0, 0) в фигурные скобки.)
Однако теперь для системы из двух уравнений с дву-
мя неизвестными исчерпаны все возможности. Соответ-
ствующая область значений — это или плоскость, или
прямая, или точка. Разумеется, если она является плос-
костью, то это вся плоскость R2.
Если область значений соответствующего преобразо-
вания оказывается плоскостью, то решение системы су-
ществует, и оно единственно. Если область значений —
прямая, то система может иметь решения и может их не
иметь; они существуют тогда и только тогда, когда
(X, У) лежит на этой прямой, и при фиксированной паре
(X, У) сами решения составляют прямую. Если область
значений — точка, то решения существуют только при
(X, У) = (0, 0), и тогда они составляют целую плоскость,
т. е. решением служит любая точка из R2.
Будем называть множество решений системы (если
они у нее есть!) пространством решений. Тогда описан-
ные выше сЛучаи можно свести в такую таблицу;
Область значений
Плоскость
Прямая
Точка
Пространство решений
Точка
Прямая
Плоскость
271
Естественно ожидать, что для систем трех уравнений
а тремя неизвестными области значений и пространства
решений могут быть точками, прямыми, плоскостями или
всем пространством R3. И это действительно так. Все
возможные случаи отражены в следующей таблице(
Область значений
R8
Плоскость
Прямая
Точка
Пространство решений
Точка
Прямая
Плоскость
R8
Иначе говоря, чем меньше область значений, тем
больше пространство решений, но, с другой стороны,
чем меньше область значений, тем меньше шансов, что
система вообще имеет решение.
Так же обстоит дело и в общем случае. Если все про-
исходит в Rn, то можно доказать, что сумма размерно-
стей области значений и пространства решений равна п.
Таким образом, если линейное преобразование в прост-
ранстве R7 имеет трехмерную область значений, то соот-
ветствующее пространство решений должно иметь раз-
мерность 4.
Конечно, мы до сих пор не определили точно, что
такое размерность. Здесь действительно начинается ли-
нейная алгебра, но подробнее об этом лучше прочитать
в специальном учебнике *, Однако теперь уже ясно, что
кажущаяся «дикость» поведения систем уравнений укла-
дывается в четкую схему,
Матрицы
Существует очень удобный способ записи линейных
преобразований (ввел его Кэли), Если Т[х, у) = [Х, У),
где
272
ax + by => X, 1
ex + dy = Y, J
(4)
то, отделив коэффициенты при неизвестных и записав их
в виде квадратной таблицы, получим
/а
\е d/
Такое выражение называется матрицей, в данном слу-
чае это матрица преобразования Т. Если она известна, то
известно и Т при условии, что мы знаем, какие исполь-
зуются неизвестные х, у, X, Y. Их тоже можно включить
в нашу схему, введя вектор-столбцы
(Й и
и записать (4) в следующей компактной форме:
(°d)Q=(v). <5>
где, по определению, «произведение» в левой части есть
вектор-столбец
lax -р Ьу\
+ dy/’
а два вектор-столбца равны тогда и только тогда, когда
совпадают их компоненты.
Это обозначение легко распространить на случай трех
или более неизвестных. Система общего вида из трех
уравнений с тремя неизвестными примет вид
а b о\ (х\ (Х\
d е f Ь = Г .
,g h k) \z J \Zj
Часто нам приходится последовательно применять
несколько преобразований. Пусть, например, имеются
273
другие переменные X и Y и преобразование U такое, что
U(X, У) = (X, Y), где
АХ + BY = X, 1
CXA-DY—Y j
(6)
или в матричных обозначениях
(А В\(Х\ /Х\
D)\Yj = \Y/
Мы уже определили произведение преобразований!
UT(x, y) = U(X, У) = (X, Y),
Теперь UT в свою очередь можно представить матрицей.
Из систем (6) и (4) получаем
X=AXa-BY=
’=*A(ax + by') A-B(cxA-dy) =*
•= (AdA-Bc)x + (Ab + Bd)y,
Y=CX+DY=
= C(ax+by) +D(cx+dy) =
= (Ca+Dc)x+ (Cb+Dd)y.
Отделив коэффициенты при неизвестных, можно записать
(Ad + Вс Ab + Bd\ (х\ /Х\
tCa + De Cb + Dd) \y) ~ \Y)>
т. e. матрицей преобразования UT служит
Ad -|- Be Ab -J" Bd\
Cd A- De Cb A- Dd)‘
С другой стороны, мы можем, поступив формально, по-
лучить из систем (5) и (7) уравнение
(A B\(d b\(x\ _ /Х\
Dj[c d)\y) [Yp
и это nodcKd3bieder нам, что если определить произведе-
ние матриц по формуле
1А В\ (d b\ _ (Ad + Вс Ab + Bd\
\С D) V? d) ~ \Cd A- De Cb A- Dd)>
274
то получится корректная алгебраическая операция. На-
пример, в гл. 2 у нас появились преобразования G и Н,
где G(x, у) = (х, -у) и Н(х, у) = (у, —х). Если (X, У) =
= Н (х, у), то
Х=»/ = 0-х+1-у,
У = — х= ( — 1) - х + 0-t/,
и матрицей преобразования Н служит
( 0 П
1 о/-
Если G(X, У)-(Х, Y),to
Х = Х=ЬХ+0-У,
У=-У = 0-Х+(-1)-У,
и матрицей преобразования G будет
/1 0\
\0 —1/
По нашей формуле матрицей GH должна служить
Л 0J 0 1\
V) —1Д—1 от-
равная
/1 • 0 + 0 • (—1) 1 • 1 + о . о \
^0 - О + (—1) • (—1) О - 1 +(-!)• 0)’
или после упрощения
/0 1\
\1 о}
Получилось GH(x, у) = (у, х), так что
Х = 0-х +1 -у,
Y = 1 -x+0-y,
а это проверяется.
Фактически, вводя такое определение, мы получаем
удобную алгебру, что позволяет нам производить вычи-
275
сления с линейными преобразованиями. Я не хочу гово-
рить об этом подробнее, поскольку уже существует за-
мечательное изложение этих вопросов, принадлежащее
Сойеру 2.
Однако мне хочется проделать еще одно вычисление и
показать, какую пользу можно извлечь из матриц в три-
гонометрии. В гл. 2 я привел формулу для поворота на
угол 6. В матричной форме она приобретает вид
/cos 0 —sin 0\
\sin0 cos О/"
Тогда произведение поворота на угол 6 и поворота на
угол ф имеет матрицу
/costp —sin ф\/cos О —sin 0\
\sin ф СОБфДзшб COS0/
или
/cos ф cos 0 — sin ф sin 0 —cos ф sin 0 —з!пфсо5 0\
\sin ф cos 0 -ф- cos ф sin 0 — sin ф sin 0 -|- cos ф cos 0/'
Но, разумеется, это произведение означает поворот на
угол ф -ф 0 и имеет матрицу
/cos (ф -г 0) — sin (ф -ф 0)\
\sin (ф -ф- 0) cos (ф -ф 0)/"
Сравнение двух полученных матриц дает равенства
cos (ф4-0) = cos ф cos 0 —sin ф sin 0,
sin (ф4-0) =sin ф cos 04-cos ф81п 0,
т. е. формулы сложения из курса тригонометрии.
Абстрактные формулировки
В настоящее время изучение линейных преобразова-
ний составляет часть абстрактной алгебры. Это про-
изошло из-за желания избежать применения координат.
276
Если заданы две точки (р, q) и (г, s) из R2, то можно
определить их сумму формулой
(Р, Р) + (г, s) — (p + q, r+s).
Если а — действительное число, то можно также опреде-
лить произведение
а (р, q) = (ap, aq).
С помощью этих операций мы можем охарактеризовать
линейные преобразования: это такие функции Т (R2->R2),
что для всех р, q, г, s и а
q) + (r, s)) = T(p, q)+T(r, s),
T(a(p, q)) = аЦр, q).
(Можете проверить это, если хотите.) Первое равенство
очень напоминает условие, которому подчиняется изо-
морфизм в смысле теории групп. Это наводит на мысль,
что абстрактный подход с позиций, близких к теоретико-
групповым, может оказаться полезным. Основываясь на
свойствах сложения и умножения на действительные
числа в R2 и на свойствах аналогичных операций в R3,
R4, R5, .... математики дали следующие ниже опреде-
ления.
Векторное пространство над R — это множество V
с двумя операциями, называемыми сложением и умноже-
нием на скаляры. Если и и v — элементы из V, а а —
действительное число, то результаты этих операций обо-
значаются через
u + v, а и,
где u + v и а и — элементы множества V.
Кроме того, должны выполняться следующие ак-
сиомы:
(1) V — коммутативная группа относительно сложе-
ния с единичным элементом О,
(2) ссО = 0 для всех а Q R,
(3) Оц = 0 для всех v С V,
277
(4) lo — v для всех о £ V,
(5) (а + Р) v = ао -J- ро для всех а, р £ R, о С V,
(6) а (о + w) = ао + aw для всех а С R, о, w С V,
(7) аро = а (Ро) для всех а, р £ R, о g V.
Можно привести много примеров векторных прост-
ранств. Самые обычные — это R, R2, R3, ... , но есть и
другие. Кольцо многочленов R[x] от одной переменной
является векторным пространством, векторными про-
странствами будут и R[x, у], R[x, у, г] ... . Это бесконечно-
мерные пространства. Векторные пространства возника-
ют при решении дифференциальных уравнений, в не-
которых разделах теории групп и в современных
изложениях математического анализа.
Линейное преобразование теперь определяется как
функция Т: V -> IF, где V и W — произвольные вектор-
ные пространства, со следующими свойствами:
Т (u+v) ==Т (и) +Т (у),
Т(аи) = аТ (w)
для всех и, v £ V, а С R.
В этой абстрактной форме можно доказать все необ-
ходимые теоремы о линейных преобразованиях. По-
скольку не выбираются конкретные координаты, дока-
зательства изящны и естественны.
Однако при выполнении вычислений в конкретных
случаях используют матричные обозначения.
Для глубокого, понимания линейной алгебры необхо-
димо совместить все три подхода:
1) основные геометрические обоснования;
2) абстрактное алгебраическое изложение;
3) технику теории матриц.
Поначалу это затрудняет изучение предмета. Вероятно,
поэтому большинство учебников концентрирует внима-
ние на каком-нибудь одном аспекте. Но из-за такой одно-
278
сторонности по мере продвижения встает больше про-
блем, чем решается: вид студента, сражающегося с
громадными матрицами, в то время как несложные
геометрические соображения позволяют решить задачу
в две строчки, отнюдь не воодушевляет,
Глава 16
ВЕЩЕСТВЕННЫЙ АНАЛИЗ
В математике едва ли есть
хоть один бесконечный ряд,
сумма которого была бы стро-
го определена.
Н. Г. Абель, в письме 1826 г.
Алгебра, топология и анализ являются тремя крае-
угольными камнями современной математики. (Матема-
тическая логика — это скорее строительный раствор,
который их скрепляет.) Я довольно подробно остано-
вился на двух первых; теперь не грех сказать что-нибудь
и о третьем.
Печальный факт состоит в том, что об анализе нельзя
говорить сколько-нибудь содержательно, не введя пред-
варительно большого количества технических понятий.
Наивный подход к анализу наталкивается на непреодо-,
лимые препятствия — в истории математики есть немало
тому примеров.
Анализ можно описать как исследование бесконечных
процессов, таких, как бесконечные ряды, пределы, диф-
ференцирование, интегрирование. Маячащий перед нами
призрак бесконечного — вот что вызывает трудности.
Бесконечное сложение
Бесконечными рядами называются выражения типа
1 +4* + ~Г + 4" + — w
Самое существенное здесь — многоточие. Эти точки как
будто приглашают нас прибавлять все новые члены, и
так до бесконечности. Здравый смысл заставляет нас
отнестись к подобному выражению скептически, ибо оно
280
требует, казалось бы, невозможного: ни человек, ни са-
мая быстродействующая ЭВМ не в состоянии произвести
бесконечно много сложений за конечное время. На па-
мять приходит парадокс о включении и выключении
света: если включить свет через секунду, выключить
через полсекунды, снова включить через четверть секун-
ды, выключить через одну восьмую секунды, что бу-
дет через две секунды — включен свет или выключен?
Таким образом, у нас нет никакой гарантии, что вы-
ражение (1) вообще что-нибудь означает, однако это
простое соображение ускользнуло от внимания почти
всех, кто занимался этим предметом в 18 в. Тогда каза-
лось, что любая комбинация математических символов
имеет математический смысл,— наивное представление,
с которым математикам пришлось со временем распро-
щаться, причем совсем не безболезненно.
Если выражение (1) что-нибудь и означает, то, конеч-
но, наилучшей отгадкой служит число 2, ибо
1 + 2 + 4 + 8 + + 2Л 2”'
Если считать, что эта сумма равна 2, то, остановившись
на (п+1)-м члене, мы сделаем ошибку 1/2”. С ростом п
знаменатель 2" растет еще сильнее, и 1/2” быстро умень-
шается. Взяв п достаточно большим, мы можем сделать
1/2” сколь угодно малым.
В 18 в. рассуждали бы примерно так. В формуле для
суммы п + 1 членов положим п = оо. Тогда левая часть
есть сумма оо + 1 членов, и так как оо-Н = оо, это есть
281
не что иное, как ряд (1), С другой стороны, правая часть
равна
2----L = 2----5-= 2—0 = 2.
2°° оо
Тем самым доказано, что сумма равна 2.
На самом деле ровным счетом ничего не доказано, по
крайней мере по трем причинам. Во-первых, нужно пред-
положить, что (1) принимает какое-то значение. Во-вто-
рых, нужно предположить, что над бесконечными сумма-
ми можно производить алгебраические операции так же,
как над конечными. В третьих, такое использование сим-
вола оо предполагает, что он ведет себя, как число, но
законно ли такое предположение?
Бездумная манипуляция бесконечными рядами при-
водит ко всякого рода парадоксам; некоторые из них
просто прелестны, но математически они все губительны.
Пусть, например,
5=1-1 + 1 — 14-1 — 1+’..;
Тогда
S= (1-1) + (1-1) + (1-1) +..,
=о+о+о+. .. = 0.
Запишем иначе:
s = i- (i-i) - (1—1) - (1-1>-„.
— 1 — (0 + 0 + 0 + ...)
= 1-0=1,
Или
1 — S = 1 — (1 — 1 +1 — 1 + 1 — 1 + ...)
= 1 —1+1—1 + 1—1+..,
= S,
откуда S= 1/2.
Один подающий надежды умник заявил, что полу-
282
ценное при помощи S равенство 0 и 1 символизирует со-
творение из ничего, и это не только служит обоснованием
всяческих манипуляций бесконечными процессами, но
дает математическое доказательство существования
бога!
На заре анализа у математиков было гнетущее ощу-
щение, что все эти три значения S в каком-то смысле
«правильны». Математика не сразу научилась отметать
подобный вздор. Постепенно было осознано, что сами
по себе бесконечные процессы ничего не означают, пока
им не придан какой-то определенный смысл. Как только
это сделано, на выражения, которые встречаются в этих
процессах, можно налагать определенные ограничения.
Кроме того, нельзя считать, что для них выполняются
обычные законы действий, хотя, к счастью, кое-что и
удается спасти.
Что такое предел!
Рассмотрим подробнее этот причиняющий столько
хлопот ряд S. Подсчитаем суммы одного, двух, трех,
четырех, пяти его членов:
1 =1,
1-1 =0,
1-1 + 1 =1,
1-1 +1-1 =0,
1 —1 + 1 —1 + 1 = 1.
Мы видам, что они поочередно принимают значения 0
и 1. С ростом п эти суммы не «успокаиваются» на каком-
то «предельном» значении, а продолжают весело пере-
прыгивать от 0 к 1 и обратно.
Если счесть эту сумму равной 1, то при четном коли-
честве членов получится ошибка, равная 1; если счесть
ее равной 0, ошибка, равная 1, получится при нечетном
283
количестве членов. Тогда уж лучше считать ее равной
1/2 — по крайней мере ошибка будет минимальной!
Запишем бесконечную сумму в общем виде!
а1 + й2 + йз +
где а,— действительные числа. «Приближенные» сум-
мы равны
bi = «i,
Й2 = О1
Ьз = О[ Ч-йг + йз,
^4 = 1 Т ^2 Т «3 “Ь ^-4,
Если значения Ьп стремятся к некоторому «пределу»,
когда п становится очень большим, то этот предел мож-.
но было бы, по определению, считать значением беско-
нечной суммы. Что же понимается под «пределом»?
Первая мысль — посмотреть, какую ошибку мы со-
вершаем, останавливаясь на сумме п членов: если предел
существует, эта ошибка должна становиться очень ма<
лой. Но ошибка равна
Un+I +йП4-2 + йп+з +... ,
т. е. опять бесконечному ряду. Пока что это нам не по-
могает.
Итак, нужно сосредоточить внимание на последова-
тельности частичных сумм
bi, b2, Ь3, Ь4, ...
и подумать, нельзя ли придать смысл «пределу» этой по-
следовательности.
Выражение (1), пожалуй, может помочь, поскольку
мы вправе ожидать, что этот ряд имеет сумму и она
равна 2. Для него
Ьп = 2 • •
284
Разность bn — 2 можно сделать сколь угодно малой,
выбрав п достаточно большим. Например, чтобы выпол-
нялись неравенства
_____1 I) ________2 < -I_____1
1 000 ООО *=* " ~ 1 000 000 ’
достаточно взять н^>21, и тогда
1 'Г' 1
2«_i j ооооОО •
А чтобы выполнялись неравенства
_________!_____<; __2 < -I________-_____
1 000 000 000 000 п ^5 г ! ооо 000 000 000’
достаточно взять и^41, и т. д.
Подобные примеры подсказывают общее определе-
ние. Последовательность Ьп называется стремящейся к
пределу I, если разность
Ьп I
можно сделать сколь угодно малой, выбрав п достаточ-
но большим
Последовательность, которая ртремится к какому-то
пределу, называется сходящейся. (Предел I должен
быть действительным числом; пока мы не говорим о оо.)
Определив понятие предела последовательности Ьп,
мы можем придать значение бесконечному ряду
+ П2 + П3 + П4 + ...
Им будет предел I последовательности частичных
сумм Ьп при условии, что этот предел существует. Если
это так, ряд называется сходящимся. Как показывает
пример ряда S, предел частичных сумм существует не
всегда.
Теперь мы можем говорить о сумме бесконечного
ряда, но только после того, как докажем, что этот ряд
сходится. (Существуют, правда, другие, менее естествен-
285
ные определения, позволяющие приписывать суммы и
таким рядам, которые в нашем смысле не сходятся. На-
пример, в некоторых из таких теорий ряд S оказывается
вполне благополучным и имеет сумму 1/2. Однако здесь
мы не будем обсуждать эти теории.)
Раз можно говорить о суммах, посмотрим, как обстоит
дело с законами алгебры. Можем ли мы поставить скоб-
ки, где захотим, или поменять местами какие-то из сла-
гаемых?
Даже для сходящихся рядов это возможно не всегда.
Например, можно доказать, что ряд
д=1_____L + J___L + J____± +
Х 2 Г 3 4 г 5 6
сходится к числу In 2, которое равно примерно 0,69.
А теперь найдите ошибку в следующей выкладке 2:
9А'_О 2 । 2 2 । 2 2i2 2i2 2 ।
2 2 г 3 4 г 5 6'7 8'9 10 + •"
__ ___1-Д-—_L । 2___1__i_ __L л 2___!_i_
Z 1 г 3 2'5 3 + 7 4'9 5 *"
e 1__L_lJ__L + _L
2'3 4 5
= к,
откуда следует, что 1,38=0,69.
Аксиома полноты
Наше определение сходимости обладает одним не-
достатком — прежде чем доказать сходимость ряда, мы
должны угадать предел I, к которому он сходится. Так,
сравнительно легко доказать сходимость ряда (1) после
того, как мы угадали, что его пределом должно быть чис-
ло 2. А кроме угадывания предела, никакого другого
способа убедиться в сходимости ряда у нас нет,
286
Вернемся снова к «ошибке»
йп+1 + йп+г + йп+з+... ,
которую мы выше сочли бесполезной. В случае сходя-
щегося ряда такие ошибки «малы». Можно ли сделать
это соображение точным и положить его в основу крите-
рия сходимости?
Попробуем приближенно найти ошибку. (Казалось
бы, такая попытка обречена на неудачу, ибо тогда при*
дется учитывать ошибку уже в этом приближении, но
все-таки посмотрим, что из этого выйдет.) Получим
Йп+Ь
йп+1 +Пп+2,
• йП4-1 + Пп+2 + йп+3»
йп+1 + .-. + йп+т-
• а w9 я « S
йп+1 +... +йп+т.
Допустим, что все эти суммы малы, т, е. существует
малое положительное число k такое, что
— йп+1 + ... + йп+т^Й
при любом т. Тогда имеет смысл говорить о «малой»
ошибке, не превосходящей k.
Иными словами, всякий сходящийся ряд обладает
таким свойством. Пусть задано некоторое fe>0. Найдет-
ся такое целое п (зависящее от /г), что при любом т
«приближенная ошибка»
йп+1 + ... + йп+т
меньше k.
Если это свойство выполняется для некоторого ряда,
то ошибки становятся произвольно малыми, и естествен-
но ожидать, что этот ряд сходится.
Приятная сторона этих рассуждений состоит в том,
что в них не участвуют бесконечные суммы и что не надо
угадывать предел. Речь идет только о конечных суммах
287
членов ряда. Правда, взамен приходится прибегать к
утверждению с довольно сложной логикой, но это не
страшно.
Вот здесь-то и вступают в игру действительные числа.
Если бы мы думали, что все числа рациональны, мы
могли бы определить предел последовательности рацио-
нальных чисел как такое рациональное число /, к кото-
рому сколь угодно близко подходят члены последова-
тельности. Могли бы мы провести и анализ ошибки.
Но рассмотрим десятичное представление числа 2 :
/Т = 1,414213
которое можно считать суммой бесконечного ряда
1 1__4 1__!__1 4 I 2 I__________1 _|____3_____,
г 10 г100“г 1000 “ 10 000 *" 100000 "г 1 000 ООО ‘г •"
Оценим теперь ошибку, которая получается, если оста-
новиться на сумме п членов. Она не превосходит числа
0,00 ... 099 ... 9,
п тп
которое меньше 1/10", как бы велико ни было т. Но 1/10"
при достаточно большом п становится сколь угодно ма-
лым. Поэтому естественно ожидать, что этот ряд схо-
дится.
С другой стороны, если он сходится, в пределе
должно получиться У" 2, что не является рациональ-
ным числом.
Итак, все члены нашего ряда рациональны, и мы
в своем невежестве полагаем, что и сумма его рацио-
нальна, но это, увы, не так. Интуитивное ощущение под-
сказывает нам, что это происходит из-за отсутствия сре-
ди рациональных некоторых чисел, вроде V 2 . Чтобы
восполнить эти пробелы, и вводятся действительные
числа.
288
Ради логической строгости к аксиомам рациональ-
ных чисел добавляется еще одна, называемая аксиомой
полноты. Она гарантирует существование действитель-
ного числа, которое является пределом заданной после-
довательности, если для этой последовательности «ошиб-
ка» становится произвольно малой. '
Непрерывность
В главе, посвященной топологии, мы уже коснулись
понятия непрерывности функции. В анализе это понятие
приобретает первостепенную важность.
Посмотрим на график какой-нибудь функции, вроде
f (х) = 1 — 2х—х2
(рис. 164). Мы увидим, что
этот график — плавная кривая,
не имеющая «скачков». X >
С другой стороны, если по- / \
строить, скажем, график поч- / \
товых сборов за отправление ----- / ------1 V- •-
заказных писем в зависимости / \
от веса, такой график содер- / . \
жит определенное число скач- / \
ков (рис. 165). / . \
Первая из этих функций не- 1
прерывна, вторая разрывна.
На заре анализа ученые ду-
мали, что любая функция, опре- рис. 164.
деленная красивой формулой,
обязательно непрерывна. Праведная, но тщетная на-
дежда! Посмотрите на изображенный на рис. 166 график
функции
g (х) = х 4- V (х — 1) (х — 2) .
Итак, следует соблюдать осторожность в подобных
10 я. Стюарт
289
высказываниях. Эйлер пытался определить непрерыв-
ную функцию как «кривую, которая рисуется свободным
движением руки», но такое определение не слишком
подходит. Коши сначала определял ее как «функцию,
для которой бесконечно малое изменение аргумен-
та приводит к бесконечно малому изменению значения»,
Рис. 165.
Это прекрасно, если вы знаете, что такое «бесконечно
малое», однако тогда этого никто не знал. Наивные по-
пытки оперировать этим понятием попали в водоворот
парадоксов, точно так же, как это случилось с понятием
бесконечного.
290
Определение, которым пользуются сейчас, опирает-
ся на идею «отсутствия скачков».
Со скачками дело обстоит так же, как с ребенком
служанки: маленький он или большой — одинаково пло-
хо! Иными словами, разглядывая скачки, мы разрешаем
себе, образно говоря, пользоваться микроскопом. Под
микроскопом всякий скачок выглядит примерно так, как
показано на рис. 167.
Этот скачок имеет определенную ширину w. Поэтому,
если мы возьмем точку р0 немного левее х и точку pi
немного правее, значения f (ро) и f (pi) будут разли-
чаться примерно на w. Если же взять точки р0 и pi дале-
ко друг от друга, то о f (р0) и f (pi) едва ли удастся
что-нибудь сказать.
Стандартное определение непрерывной функции на
множестве действительных чисел формулируется так,
чтобы исключить скачки. Функция f называется непре-
рывной в точке х, если путем выбора р0 и pi достаточно
близкими к х можно добиться того, чтобы f (ро) и f (pi)
были сколь угодно близки друг другу 3. Функция f назы-
вается непрерывной, если она непрерывна во всех точ-
ках х.
Преимущество этого определения перед определе-
нием Эйлера состоит в том, что оно позволяет доказать
непрерывность той или иной функции. Рассмотрим, на-
пример, функцию
f (х) =х2
и докажем ее непрерывность в точке 0. Заметим, что если
выбрать р0 между —k и 0, a pi — между 0 и k (k — не-
которое положительное число), то
--2k2 :С Ро-Р1 :С 2А2.
Таким образом, размер разности не превосходит 2k2,
и, выбирая k достаточно малым, мы можем сделать ее
меньше любого наперед заданного числа, Например,
ю*
291
чтобы выполнялось неравенство 1/1 000 000, доста-
точно взять 1/10 000, и т. д. Проделав то же самое
для каждой точки х, а не только для точки 0 (вычисле-
ния немного более громоздкие, но проводятся так же
легко), можно убедиться в непрерывности функции f.
Функции могут быть в одних точках непрерывны, а в
других разрывны. Например, функция почтового сбора
разрывна при х = 2, 4, 6, 8, 10, 12, 14, 16, 24, 32 унциям
и непрерывна во всех других точках в пределах от 0 до
32 унций.
Однако есть функции, которые ведут себя очень стран-
но, и отсюда видно, что, хотя наше определение и хоро-
шее, оно не совсем такое простенькое, как может
показаться. Так, например, функция
, , f 0, если х иррационально,
и W — ( j/g, если х _ р/д рационально,
согласно этому определению, непрерывна во всех ирра-
циональных точках и разрывна в рациональных. А функ-
ции, непрерывной во всех рациональных точках и раз-
рывной во всех иррациональных, не существует!
Конечно, это весьма необычайная функция.
Оказывается, несмотря на такие странности, данное
определение непрерывности вполне пригодно для того,
чтобы построить весь аппарат анализа. Однако не исклю-
чено, что существует лучший способ действий. Не так
давно при помощи одной довольно сложной конструкции
из математической логики удалось формализовать поня-
тие «бесконечно малого» и тем самым сделать строгим
определение Коши. Тем не менее я не советовал бы
учить школьников так называемому «нестандартному
анализу» с его слишком уж тонкой логикой.
На самом деле вполне удовлетворительный способ
строгого изложения анализа, особенно на школьном
уровне, еще не найден.
292
Доказательство теорем в анализе
Известна следующая занимательная задача. Ровно в
0 часов утра в понедельник один человек начинает взби-
раться на гору и в 6 часов вечера достигает горной хи-
?кины, где остается ночевать. На следующее утро в
9 часов он начинает спускаться по той же тропе и в 6 ча-
сов вечера прибывает на то место, откуда начал восхож-
дение. Требуется доказать, что в какой-то момент вре-
мени первого дня и в тот же момент второго дня он
находился в одном и том же месте.
Немного подумав, можно прийти к такому решению.
Допустим, что на второй день в гору поднимается при-
зрак, который делает все то, что человек в первый день.
Так как призрак двигается вверх, а человек — вниз, они
неизбежно где-то встретятся — это и будет искомый мо-
мент времени.
За этим рассуждением скрыта теорема анализа, ибо
предполагается, что продвижение человека непрерывно.
Если бы при помощи какого-нибудь чуда техники он мог
перепрыгивать с одной части горы на другую, минуя
промежуточные участки, ему удалось бы избежать
встречи с призраком.
Нарисуем график продвижения человека в первый и
293
второй день (рис. 168). На нем легко проследить идею
доказательства: эти две кривые обязательно пересе-
каются.
Для разрывных кривых это не обязательно (рие. 169),
Однако картинки обманчивы, и в анализе нельзя на
них опираться. Наши выводы должны логически следо-
Рис. ПО.
вать из определений (о картинке, конечно, тоже не надо
забывать!). Теорема, которую нам хочется установить,
должна звучать примерно так: допустим, что заданы две
непрерывные функции f и g, определенные на действи-
тельной прямой и такие, что в двух точках а и b выпол-
нены неравенства
f(a)<g(a), f(b)>g(b)-
тогда в некоторой точке с между а и b имеет место ра-
венство (рис. 170)
f(c)=g(c).
Эту теорему можно было бы доказать так. Разделим
интервал между а и b на 10 частей. На некоторых из
них f меньше g (рис. 171.) Возьмем первый из малых
интервалов, где f становится больше g, и разобьем его
на 10 частей. Выберем среди них первый интервал, где
294
f становится больше g, разделим его на 10 частей, ...
и т. д. Концы выбранных интервалов образуют последо-
вательность pi, р2, рз, и в силу аксиомы полноты эта
последовательность сходится к некоторому действитель-
ному числу р между а и Ь. Воспользовавшись определе-
нием непрерывности и еще немного поработав, убедимся,
что f(p)=g(p).
Допустим, что 61=0, Ь = 1 (см. рис, 171), Тогда
pi = 0,5,
р2=0,58,
рз = 0,583,
* • я f
и наша процедура приводит, вообще говоря, к бесконеч-
ной десятичной дроби
р = 0,583...
Аксиома полноты как раз и узаконивает бесконечные де-
сятичные дроби. И, разумеется, деление на 10 частей
делалось только для того, чтобы удобно было пользо-
ваться десятичной записью. С таким же успехом можно
было делить на 2 части, или на 19, или 1066.
Аксиома полноты используется здесь по существу;
над полем рациональных чисел теорема неверна. Рас-
смотрим, например, функцию
f (х) = 1 — 2х —х2.
Она непрерывна на множестве рациональных чисел,
f(0) = l, f(l) = —2. Если бы теорема была верна для
рациональных чисел, то между 0 и 1 нашлось бы ра-
циональное число р такое, что
1- 2р-р2 = 0.
Но р = V 2— 1, а это число не рационально. Таким
образом, без полноты нам не обойтись.
Можно было бы, конечно, счесть излишним строгое
доказательство: если теорема геометрически очевидна,
295
зачем ее доказывать? Именно такая позиция была при-
нята в 18 в. Результатом явились неразбериха и пута-
ница в 19 в., ибо не подкрепленная логикой интуиция
обычно создает впечатление, что все обстоит гораздо
более «гладко», чем на самом деле.
В математике никогда не следует отвергать хорошие
идеи только потому, что для них еще нет строгого обо-
снования. Однако, пока обоснование не найдено, нельзя
позволять им «заходить слишком далеко» — обычно это
плохо кончается.
Глава 17
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Статистика — это ветвь тео-
логии
Ученый муж из Кембриджа
Источниками теории вероятностей послужили задачи,
связанные с азартными играми. При каких условиях я
имею большую вероятность выиграть в карты, в кости?
Каковы шансы?
Поскольку игры, как правило, конечны, для решения
подобных вопросов требуются комбинаторные методы,
т. е. методы, основанные на подсчете количества вариан-
тов, Если, например, мы хотим найти вероятность того,
что при выбрасывании монеты три раза подряд выпада-
ет «орел», мы перечисляем все возможности:
ООО, OOP, ОРО, ОРР,
POO, POP, РРО, РРР.
Их восемь, и только одна из них нас устраивает; значит,
вероятность равна 1/8.
При таком рассуждении, конечно, предполагается, что
выпадения «орла» или «решки» равновероятны. Понятие
«равновероятны» нельзя определить словами «с вероят-
ностью 1/2» пока не определено, что означают эти слова,
а последнее нельзя сделать, не определив понятия «рав-
новероятны». Так по крайней мере выглядит эта ситуа-
ция на первый взгляд.
Пытаясь обойти эту трудность экспериментальным
путем, мы сталкиваемся с другой трудностью. Если вы-
падения «орла» и «решки» равновероятны, то естествен-
но ожидать, что в длинной серии бросаний выпадет при-
мерно одинаковое число «орлов» и «решек». Конечно, не
точно одинаковое: если число бросаний нечетно, то ра-
венство вообще невозможно, но и при четном числе
297
бросаний будут небольшие расхождения. Подбросьте мо-
нету 20 раз и посмотрите, выпадет ли «орел» ровно 10
раз. (А если это случится, повторите этот эксперимент
еще несколько раз и посмотрите, как часто это проис-
ходит.)
Можно надеяться лишь, что в пределе отношение чис-
ла «орлов» к числу «решек» стремится к 1. Однако горе
в том, что этот «предел» не является пределом в смысле
анализа. Даже если монета правильная, мыслим и та-
кой случай, когда вся последовательность состоит из
одних «орлов». Конечно, это маловероятно. Но чтобы
ввести понятие «предела», не исключающее и такую воз-
можность, требуется установить точно, что понимается
под «маловероятным», а для этого, как видно, опять-
таки нужно дать определение «вероятности».
С этими трудностями удалось справиться только в
30-е годы нашего века, когда была разработана аксиома-
тическая теория вероятностей. Отдельно от приложений
математику можно развивать без малейших логических
изъянов, и уже потом опытным путем проверять, на-
сколько она отвечает фактам. Аксиоматическая теория
вероятностей достигла успехов по тем же причинам, что
и аксиоматическая геометрия.
Комбинаторная вероятность
Допустим на время, что нам известно, что понимает-
ся под словом «равновероятны». Тогда «грубое рабо-
чее» определение вероятности р(Е) некоторого события
Е таково:
/р, _ Число исходов, когда реализуется событие Д
' ' ' Общее число возможных исходов
(при условии, что все исходы равновероятны).
Так, например, при выбрасывании двух игральных
костей общее число возможных исходов равно 36, при-
298
чем в 5 из них в сумме получается число 6 (1 + 5, 2 + 4,
3 + 3, 4+2, 5+.1). Значит, вероятность этого события
(т. е. что выпадет сумма 6) равна 5/36.
Поскольку рассматриваемые числа неотрицательны,
а число исходов, при которых реализуется событие Е,
не превосходит общего числа исходов, р(Е) всегда удов-
летворяет неравенствам
0Cp(£)<Sl.
Равенство /?(£)= О означает, что событие Е невозмож-
но, а равенство р(Е) = 1—что оно происходит всегда.
Методы комбинаторной вероятности относятся в ос-
новном к разным комбинациям событий. Допустим, на-
пример, что есть два различных события Е и F. Какова
вероятность того, что происходит Е или £?
Рассмотрим выбрасывание игральной кости. Пусть
событие Е состоит в том, что «выпало число 6», a F —
что «выпало 5». Тогда фраза «произошло Е или £» озна-
чает, что «выпало 6 или 5». Этому отвечают два случая
из шести, следовательно,
р(Е или F) = 1/3.
Вообще пусть N(E) (соответственно N(F)) — число исхо-
дов, в которых реализуется событие Е (соответствен-
но F), а Т — общее число исходов. Тогда
р(Е или F)=N (Е или F)IT,
Чему равно N (Е или £)? Допустим, что события Е и F
«не перекрывают» одно другое (позднее мы к этому вер-
немся). Тогда
N (Е или £)=/V (£)+#(£),
так что
р{Е или F) = (N(E)+N (F))/T=
=N(E)/T+N(F)/T=
~p(E)+p(F). (1)
299
Если же Е и F «перекрываются», то все, что входит в их
общую часть, считается в N(E)+N(F) дважды, а в
N(E или F) — только один раз.
Допустим, например, что
Е = «выпало простое число»,
F—«выпало нечетное число».
Тогда Е осуществляется тремя способами: 2, 3, 5 (за-
метьте, что 1, по определению, не является простым
числом), a F — тоже тремя способами: 1, 3, 5. Однако
Е или F реализуется четырьмя способами: 1, 2, 3, 5.
Поэтому
р(Е)=1/2, р(Г) = 1/2, р(Е или Е)=2/3,
В общем случае имеет место формула
N (Е или F)=A'(E)+/V(F)-7V(E и F), (2)
ибо, вычитая N (Е и F), мы как раз избавляемся от
удвоения. В нашем примере Е и F осуществляются дву-
мя способами: 3, 5, и формула дает
4 = 3 + 3—2,
т. е. правильное равенство.
Разделив (2) на Т, получаем соотношение для ве-
роятностей:
р(Е или F) = р(Е) +p(F) — р(Е и F). (3)
Вмешательство теории множеств
Все перечисленные выше понятия гораздо лучше
выражаются на языке теории множеств. Всевозможные
исходы бросания кости образуют множество
Х={1, 2, 3, 4, 5, 6}.
События Е и F отвечают подмножествам (рис. 172):
Е={2, 3, 5},
Е={1,3, 5}.
300
Событие «Е или F» отвечает множеству {1, 2, 3, 5} —
объединению EIJF. Событие «£ и £» отвечает множеству
{3, 5} — пересечению Ef\F. Вероятность р—это функ-
ция, определенная на множестве Е всех подмножеств
множества X, со значениями в R, а точнее, в отрезке
[О, 1], т. е. множестве всех действительных чисел меж-
ду 0 и 1.
Рис. 172.
Исходя из этих соображений, можно ввести более
абстрактное понятие конечного вероятностного про-
странства. Оно состоит из:
а) конечного множества X;
б) множества Е всех подмножеств множества X;
в) функции р:£->[0, 1], обладающей тем свойством,
что дл я всех Е, F £Е
р(Е[)Е) = р(Е) + p(F) — p(E(]F).
Аксиоматическая теория вероятностей и занимается
вероятностными пространствами. Однако для того, чтобы
рассматривать бесконечное вероятностное пространство,
нужны более тонкие определения. Во многих практиче-
ских приложениях требуются бесконечные множества X;
301
например рост человека может измеряться любым дей-
ствительным числом (в определенных пределах), и в
этом случае имеется бесконечно много возможностей.
Независимость
Другая важная операция в теории вероятностей —
определение исхода двух последовательных испытаний:
какова вероятность того, что результатом первого испы-
тания будет событие Е, а второго — событие F? Напри-
мер, дважды выбрасывается кость и спрашивается: ка-
кова вероятность того, что сначала выпадет 5, а затем 2?
Из 36 возможных комбинаций нас устраивает только
одна: 5, затем 2. Значит, вероятность равна 1/36.
Если Е и F — события, рассмотренные в предыдущем
разделе, то каждому из трех способов реализации Е со-
ответствует один из трех способов реализации F, так
что всего благоприятных исходов 3-3 = 9. Следовательно,
вероятность того, что сначала происходит событие Е,
а затем F, равна 9/36=1/4.
В общем случае допустим, что первый опыт имеет Ту
возможных исходов и в N (Е) из них происходит собы-
тие Е, а второй имеет Т2 исходов и в N (F) из них про-
исходит событие F. Тогда два этих опыта в совокупности
имеют ТуТ2 исходов, так как за каждым из Ту исходов
первого может следовать каждый из Т2 исходов второго.
По той же причине число исходов, при которых сначала
происходит Е, а затем F, равно N(E)-N(F). Поэтому
р (Е, следом за ним F) = •—• ДД- =
= р(Е)р(Е). (4)
При этом подсчете мы должны предполагать, что Е и F
независимы, т. е. что исход первого опыта не влияет на
вероятности исходов второго.
302
Если бы второе событие F состояло в том, что в сумме
выпало число 4, это условие не соблюдалось бы. В самом
деле, если бы при первом бросании выпало 4 или больше,
вероятность успеха при втором была бы равна 0, а если
бы при первом выпало 1, 2 или 3, вероятность успеха
при втором бросании равнялась бы 1/6.
В теории вероятностных пространств понятию неза-
висимости можно дать строгое определение. В прило-
жениях независимость изучаемых событий реального
мира вводят в качестве предположения, затем приме-
няют теорию, а потом проверяют полученные результа-
ты экспериментально.
Парадоксальные кости
Когда дело касается вероятностей, интуиция часто
нас обманывает. Допустим, например, что 4 игрока А, Б,
В, Г бросают каждый свою кость, причем кости помечены
следующим образом:
А- 0 0 4 4 4 4
Б: 3 3 3 3 3 3
В: 2 2 2 2 7 7
Г: 1 1 1 5 5 5
(порядок граней не имеет значения).
Какова вероятность того, что при одном бросании
игрок А выбросит число большее, чем игрок Б? Игрок Б
всегда выбрасывает число 3. У Л четыре раза из шести
выпадает 4, и в этих случаях он побеждает Б. Если же
выпадает 0, что происходит два раза из шести, он про-
игрывает. Следовательно,
А выигрывает у В с вероятностью 2/3.
Если Б соревнуется в В, он выиграет, когда В вы-
бросит 2, и проиграет, когда В выбросит 7. Следова-
тельно,
Б выигрывает у В с вероятностью 2/3.
303
Если В играет с Г, дело несколько осложняется. С ве*
роятностью 1/2 у Г выпадает 1, и в этом случае В всегда
выигрывает; если же Г выбрасывает 5 тоже с вероят*
ностью 1/2, то В победит в случае, когда он выбросит 7,
т. е. с вероятностью 1/3. Таким образом, вероятность того,
что выиграет В, равна
i
2
1 1 _ 2
2 3 “ 3 '
Следовательно,
В выигрывает у Г с вероятностью 2/3.
Наконец, допустим, что Г выступает против А. Если
он выбросил 5 с вероятностью 1/2, он наверняка выиг-
рал. Если же он выбросил 1 тоже с вероятностью 1/2,
он выиграет, когда у А выпадет 0, что происходит с ве-
роятностью 1/3. Вероятность выигрыша Г равна
+ 1 2
2 ‘ 2
3 3 •
Итак,
Г выигрывает у А с вероятностью 2/3.
Будем считать ту кость, которая чаще выигрывает,
чем проигрывает, «лучше» той, которая чаще проигры-
вает. В этом смысле
А лучше Б,
Б лучше В,
В лучше Г,
Г лучше А.
Все наши вычисления правильны. Попробуйте сы-
грать в эту игру! Предоставьте противнику выбирать
кость, которую он захочет, и тогда вы всегда сможете
выбрать ту из остальных, которая даст вам шанс выиг-
рать 2:1.
304
Казалось бы, последовательность «Л лучше Б лучше
В лучше Г» должна означать, что А лучше Г, но это не
так. Значение слова «лучше» зависит здесь от выбора
костей; на самом деле играются 4 разные игры. Ситу-
ация такая же, как если бы, скажем, Альфред выиграл
у Бертрана в теннис, Бертран — у Вильяма в шахматы,
Вильям — у Грегори в бадминтон, а Грегори обыграл
Альфреда в орлянку.
На это явление стоило бы обратить внимание тем
экономистам, которые считают, что товары можно упо-
рядочить по принципу их предпочтения большинством.
Биномигшьцсг смещение
Представим себе неправильную монету, которая вме-
сто того чтобы с одинаковой частотой падать то «орлом»,
то «решкой», отдает предпочтение одной из своих
сторон.
Такая монета служит моделью многих вероятностных
процессов. Если, к примеру, бросая кость, мы заинтересо-
ваны лишь в выпадении 6, то в сущности мы имеем дело
с неправильной монетой, для которой р(«орел») = 1/6,
р («решка») =5/6. Если нас интересует пол новорожден-
ных младенцев, то р (мальчик) =0,52, р(девочка) =
= 0,48.
В общем случае положим
р = р(«орел»)
<7=р («решка»).
Разумеется, р + <7=1, так как, согласно приведенной вы-
ше формуле (1),
р(«орел») +р(«решка») =р(«орел» или «решка») = 1.
Применяя теорию независимых событий, легко вы-
числить вероятности конечных последовательностей выпа-
дения «орла» и «решки»:
305
О poo р2 ООО р3
Р q OP pq OOP p2q
PO pq OPO p2q
PP q2 OPP pq2
POO p2q
POP pq2
PPO pq2
PPP q3
Какова вероятность того, что выпадет заданное число
(О, 1,2 или 3) «орлов»? Сгруппируем вместе последова-
тельности с одинаковым количеством «орлов». Тогда для
выпадения двух «орлов» при трех бросаниях получаем
три последовательности OOP, ОРО, РОО, каждая с ве-
роятностью p2q. Следовательно, вероятность выпадения
двух «орлов» при трех бросаниях равна 3p2q. Аналогич-
ные вычисления приводят к такой таблице:
(q+p)x = q+p,
(q+pr=q2+2pq+p2,
(q+p)3=q3+3pq2 + 3p2q + p.
Члены правых частей как раз и стоят в нашей таблице.
Следующая строка, должно быть, выглядит так:
(<7+Р)4=<74+4р<?3+6p2q2+4p3q+р^,
и убедиться в этом было бы хорошим упражнением.
306
Вообще, n-ю строку таблицы составят члены разложения
бинома
('7+Р)п-
Это, конечно, не простое совпадение, и его легко
объяснить. Чтобы разложить, скажем (q+p)5t нужно
выполнить умножение
lQ+P) (<7+р) (q+p) (q+p) (q+p).
Члены, содержащие ровно 3 сомножителя q, получаются
из следующих произведений:
q q q р р
q q р q р
q q р р q
q р q q р
q p q p q
q p p q q
p q q q p
p q p q q
p p q q q
Эти произведения как раз соответствуют 10 возможным
последовательностям трех «решек» и двух «орлов»:
Р Р Р О О
Р Р О Р О
Р Р О О Р
Р О Р Р о
Р О Р О Р
Р О О Р Р
О Р Р Р о
О Р Р О Р
О Р О Р Р
О О Р Р Р
Та же картина наблюдается и в общем случае. Обозна-
чим число последовательностей из п букв О и Р, со дер-
307
жащих г букв О и (п— г) букв Р, через ^.J. Тогда
роятнссть г «орлов» при п бросаниях равна
ве-
Нетрудно выяснить, чему равно —число способов
выбрать г предметов из их общего числа п, т. е. число
сочетаний из п по г. Можно показать, что
_п(п—1)(п — 2) ... (п — г + 1)
~ 7(г— 1)(г —2) ... 1 '
Отсюда для последовательностей двух «орлов» и трех
«решек» получаем

5 • 4
2 • 1
= 10,
и это число совпадает с полученным нами раньше.
Разложение бинома в общем случае выглядит так:
(<7 + Р)п = дп + npqn-' + ... + [Р] prqn~' ... + рп.
В этом состоит биномиальная теорема, приписываемая
обычно Ньютону. Совпадение это или нет, но одно время
Ньютон занимал пост начальника монетного двора!
По этой формуле можно найти среднее число «орлов»,
выпадающее при п бросаниях, которое оказывается ра-
вным пр. Таким образом, частота, с которой выпадает
«орел», равна пр/п, т. е. р. Итак, описав полный круг,
мы вернулись к представлению о вероятности как о
«средней частоте появления». Соответствующая теорема,
выраженная в строгой форме, называется законом боль-
308
ших чисел-, она наглядно показывает, как математиче-
ские модели устанавливают связи с наблюдениями из
окружающей действительности.
Случайные блуждания
В заключение этой главы я хочу рассмотреть еще
один тип теоретико-вероятностных задач. Такие задачи
возникают при изучении движения электрона в кристал-
ле или частицы в жидкости.
Представим себе частицу, начинающую двигаться из
точки х = 0 на оси х в момент времени 1=0. В момент
t=l она оказывается в точке х= — 1 с вероятностью 1/2
либо в точке х= + 1 с вероятностью 1/2. Если в момент t
она находилась в положении х, то в момент 1+1 она с
вероятностью 1/2 переходит либо в положение х— 1, либо
в положение х+1. Что можно сказать о последующем
движении такой частицы?
Например, она может двигаться вправо и влево в со
ответствии с последовательностью
лппппллплплллпллллллпплпп
и тогда ее путь, для ясности слегка вытянутый в направ-
лении t, будет выглядеть, как показано на рис. 173. Это
довольно типичный путь. Если хотите, можете сами
построить другие пути, воспользовавшись для выбора
направления подбрасыванием монеты.
Вместо движения по прямой можно рассмотреть дви-
жение по плоскости: на единицу длины вверх, вниз, впра-
во либо влево с вероятностью 1/4 или изучить трехмер-
ное блуждание в шести возможных направлениях, в
каждом с вероятностью 1/6.
Особенно интересен такой вопрос: пусть задана лю-
бая другая точка X; какова вероятность того, что части-
309
ца в конце концов (не важно, сколько времени для этого
потребуется) достигнет точки X?
Казалось бы, эта вероятность должна уменьшаться
по мере удаления X от начала координат. Ничего подоб-
ного! Она одинакова для всех X. Если случайное блуж-
дание происходит достаточно долго, всякая точка для
него так же хороша, как и любая другая.
Рис. 173.
Для одномерных и двумерных случайных блужданий
эта вероятность равна 1, т. е. частица почти наверняка
достигает любой заданной точки X. (Я говорю «почти»,
поскольку может оказаться, что это и не так: частица
может «кинуться» вправо и навеки исчезнуть. Однако
вероятность такого события равна 0. Для бесконечных
процессов утверждение, что «с вероятностью 1» означает
«наверняка», а «с вероятностью 0» — «никогда»,—уже
не совсем верно 2.)
Однако в трехмерном пространстве эта вероятность
310
равна уже только 0,24, Если вы заблудитесь в одномер-
ном или двумерном пространстве и начнете случайно
блуждать, то с вероятностью 1 вы найдете в конце кон-
цов дорогу домой. В трехмерном пространстве ваши
шансы вернуться домой меньше, чем 1 : 4.
Однако во всех случаях вам потребуется для этого
бесконечное время. Точнее, выберем любой отрезок вре-
мени t0 — возможно, 5 секунд, а может быть, 3000 лет.
Тогда, продолжая блуждать, в большинстве случаев вы
будете находиться вдали от дома в течение большего
промежутка времени, чем tQ.
Глава 18
КОМПЬЮТЕРЫ И ИХ ПРИМЕНЕНИЕ
Один специалист по гидроди-
намике, читая научную статью
в переводе с английского, был
весьма озадачен упоминанием
о какой-то «водяной овце».
Оказалось, что перевод был вы-
полнен при помощи компью-
тера, а речь шла о «гидравли-
ческом таране» (hydraulic ram,
ram — баран)
Из поучительных историй
Строго говоря, вычисления при помощи компьютеров
не относятся к математике, а составляют отдельную на-
учную дисциплину. Вычислительная машина — это не
понятие современной математики, а продукт современ-
ной техники. Тем не менее во многие школьные програм-
мы по математике сейчас входят элементы программи-
рования и методы вычислений, и это совершенно пра-
вильно, ибо компьютеры — мощное средство применения
математики в современном мире, имеющее громадное
практическое значение.
В теоретической математике компьютеры не играют
почти никакой роли. Чтобы иметь возможность передать
задачу машине, необходимо в принципе уметь точно опи-
сать каждый шаг ее решения. С теоретической точки
зрения это означает, что задача уже решена, особенно
если главной заботой было — найти метод. Однако для
получения конкретных результатов (которые в практи-
ческих применениях являются, конечно, главной целью)
создания метода, пригодного в принципе, недостаточно:
нужно, чтобы он работал на практике. Ценность компью-
теров в том и состоит, что они способны «возвести мост»
312
над пропастью между принципиальным и практическим
решением задачи.
Но компьютеры представляют интерес для матема-
тика еще и потому, что их действие основано на опреде-
ленных математических идеях.
В этой главе я хочу дать небольшое представление
как о математических, так и о практических соображе-
ниях, которые лежат в основе конструирования и приме-
нения компьютеров. Технические подробности читатель
найдет в специальных книгах
Двоичная запись
Компьютер — это прежде всего устройство для вычи-
слений. Иначе говоря, в него вводятся данные — обычно
в числовой форме, указывается, как с ними обращаться,
и он, поработав, выдает результаты. В настоящее время
применяются в основном электронные цифровые компью-
теры, где для запоминания и операций над числами в ци-
фровой форме используются электронные схемы. Однако
имеются и другие возможности: бывают оптические ком-
пьютеры (в них используются пучки света), струйные
компьютеры (в которых используются струи жидкости
или газа). А немного ниже я собираюсь проиллюстриро-
вать некоторые идеи устройства компьютеров на простом
механическом устройстве с шариком.
Никакой компьютер не может оперировать непосред-
ственно числами, поскольку числа как таковые не суще-
ствуют в реальном мире. Чтобы ввести числа в машину,
их нужно представить в какой-то конкретной физической
форме. В аналоговых компьютерах число х представля-
ется, например, величиной силы тока — ему соответству-
ет х единиц силы тока. Однако такие машины действуют
недостаточно быстро, не обладают необходимой гиб-
костью и зависят от точности физических измерений, ко-
торую трудно поддерживать на должном уровне. Поэто-
313
му аналоговые компьютеры годятся лишь для ограничен-
ного круга задач. Необходимо было придумать нечто
более совершенное.
Простейшее устройство, способное представлять чи-
сла, — это устройство, которое имеет два устойчивых
состояния. Например, выключатель может быть либо
включен, либо выключен. Ток может либо идти, либо
нет. Магнит может быть намагничен двумя способами!
север — юг или юг — север. Использование таких
устройств для запоминания чисел и действий над ними
возможно благодаря двоичной системе записи.
В повседневной жизни мы применяем для записи чи-
сел десятичную систему. Так,
365= (3-102) +(6-10)+ (5-1),
1066= (1 • 103) + (0-102) + (6-10) + (6-1).
Степени числа 10 выступают здесь скорее по традиции,
чем по необходимости. Для этого нет никаких особых
причин. С тем же успехом можно взять, скажем, число
6 и получить натуральный ряд в виде
1=(1-1),
2= (2-1),
3= (3-1),
4= (4-1),
5= (5-1),
10= (1-6) + (0-1),
11= (1-6) + (1-1),
12= (1-6) + (2-1),
55= (5-6) + (5-1), *
100= (1-62) + (0-6) + (0-1),
Такую систему могли бы выдумать существа, у которых
не 10, а только 6 пальцев.
Простейшей системой такого типа является двоичная
314
система, в которой для представления чисел используют-
ся степени двойки. Такую систему мы бы давно изобре-
ли, если бы считали не на пальцах, а на своих двух
руках. В двоичной системе нужны только две цифры
О и 1, а последовательность натуральных чисел выгля-
дит следующим образом;
1 = (1 1) [= 1]
10 = (1 • 2) + (0 • 1) [= 2]
11 = (1 • 2) + (1 • 1) [= 3]
100 = (1 - 22) + (0 2) + (0 - 1) [= 4]
101 = (1 - 22) + (0 • 2) 4- (1 • 1) [= 5]
110 = (1 • 22) 4- (1 • 2) 4- (0 - 1) [= 6]
111 = (1 • 22) 4- (1 • 2) 4- (1 1) [= 7]
1000 = (1 • 23) 4- (0 • 2я) 4- (0 2) + (0 • 1) [= 8]
1001 = (1 • 23) 4- (0 22) 4- (0 - 2) 4- (1 • 1) [= 9]
(числа в квадратных скобках справа даны в обычной
десятичной системе).
В двоичной системе применимы все обычные приемы
сложения, вычитания, умножения, только все, что боль-
ше 1, остается «в уме». Вся информация, необходимая
для сложения, содержится в таблице
0 + 0=0,
1+0=1,
0+1 = 1,
1 + 1 =0 (1 в уме).
Таблица умножения еще проще:
0-0=0,
0-1 = 0,
1-0=0,
1-1=1.
(+)
(X)
315
Если бы дети учились считать в двоичной системе, им
не пришлось бы мучиться с таблицей умножения!
На основе этих двух таблиц можно выполнить любые
арифметические расчеты. Умножим, например, 11 011 на
1010, как обычно, столбиком:
11 ОН'
1010
11011
11011
100001110
ни
(маленькие единички внизу — это единицы, которые мы
при сложении держим «в уме», а затем переносим в дру-
гой разряд).
Для проверки переведем эти числа в десятичную
систему: 11011 = 16 + 8 + 2 + 1=27, 1010=8+2=10,
100 001 110 = 256 + 8 + 4 + 2 = 270.
Таким образом, арифметика в двоичной и десятичной
системах различается лишь способом записи: в обоих
случаях речь идет об одних и тех же числах.
Компьютер на шариках
Я хочу продемонстрировать, как можно было бы вы-
полнять на машине сложение и умножение, задаваемые
таблицами (+) и (X). Чтобы не засорять голову пре-
мудростями электроники, воспользуемся механическим
устройством, в котором катаются шарики. Общие прин-
ципы здесь те же, что и в ЭВМ, только в ЭВМ вместо
шариков применяются электрические импульсы.
Сначала нужно изобрести элемент, который будет
действовать в соответствии с таблицей ( + ). Он должен
иметь два устойчивых состояния (которые мы для удоб-
ства обозначим 0 и 1) и должен реагировать на «входные
316
сигналы», тоже принимающие значения 0 и 1, следую-
щим образом:
На входе Начальное состояние Конечное состояние На выхо- де
0 0 0 0
0 1 1 0
1 0 1 0
1 1 0 1
(Начальное состояние представляет одну из цифр, кото-
рые складываются, на вход подается вторая цифра, ко-
нечное состояние задает сумму, на выход поступает
цифра, которая переносится в следующий разряд.)
Допустим, что цифре 1 на входе отвечает 1 шарик, а
цифре 0 — отсутствие шарика. Тогда устройство, изо-
браженное на рис. 174, будет осуществлять нужное нам
сложение. Оно снабжено заслонкой в виде буквы Т, ко-
торая может находиться в одном из двух положений,
отвечающих прибавляемой цифре. Движение шарика
происходит под действием силы тяжести.
Легко видеть, что:
а) если устройство находится в состоянии 0 и на вхо-
де тоже 0 (шарик не подается), то оно остается в состоя-
нии 0;
б) если оно находится в состоянии 1, а на входе 0, оно
остается в состоянии 1;
в) если устройство находится в состоянии 0, а на
входе 1, то в него вкатывается шарнк, опрокидывает
заслонку и выкатывается через канал сброса; на выходе,
как и в предыдущих случаях, остается 0;
г) если устройство находится в состоянии 1 и на входе
тоже 1, то шарик переводит заслонку в положение 0 и
выкатывается через канал выхода, т. е. на выходе полу-
чается 1.
317
Итак, наше устройство точно выполняет все требуе-
мые действия.
Теперь, соединяя вместе нужное количество таких
«суммирующих элементов», можно построить «полно-
масштабную» машину для сложения. Будем изображать
суммирующий элемент так, как показано на рис. 175.
Рис. 174.
Рис. 175.
318
Тогда «цепь» таких элементов, представленная на
рис. 176, будет действовать как сумматор.
Допустим, мы хотим сложить числа ПОПОООи НО НО,
которые выше перемножили. Первое число введем в ма-
шину, приводя суммирующие элементы в состояния, от-

Рис. 176.
вечающие его цифрам, а цифры второго подадим на
входы соответствующих элементов (рис. 177).
Представим себе, что шарики последовательно вка-
тываются по одному в соответствующие элементы справа
налево. Это даст нам возможность проследить каждый
шаг вычисления суммы. В первый справа желобок шарик
17 0 7/0
Рис. 177.
не поступает, и состояние первого элемента не меняется
Во второй вкатывается шарик, изменяет 0 на 1 и выкаты-
вается через канал сброса, оставляя машину в состоянии
0 110 110 10.
319
То же самое происходит на третьем шаге, после которого
устанавливается состояние
0 110 11110.
На четвертом шаге ничего не меняется. В пятый желобок
вкатывается шарик, изменяет 1 на 0, проходит через ка-
нал выхода в шестой элемент, изменяет 0 на 1 и сбра-
сывается:
0 110 0 1110,
о 1 1 Го 1 1 1 0.
Наконец, шарик, падающий в шестой желобок, вызывает
следующую серию изменений:
0 110 0 1110,
0 10 0 0 1110,
1<-
0 0 0 0 0 1 1 1 0,
Го 0 0 0 1 1 1 0,
и мы получили правильный ответ.
Читателю рекомендуется проверить, что перечислен-
ные операции точно соответствуют обычному сложению
столбиком, и испробовать несколько других примеров.
Интересно также решить практическую задачу: найти
такое взаимное расположение элементов, чтобы машина
работала только за счет силы тяжести. Такую машину
действительно можно построить.
Разумеется, в электронных компьютерах вместо ша-
риков используются электрические импульсы, а вместо
Т-образных заслонок — электронные приборы. Однако
их действие основано на том же принципе.
На такой машине можно выполнять и умножение
(например, путем многократного сложения). Используя
небольшое количество многократно повторяющихся
320
основных элементов, можно создать счетную машину с
довольно широкими возможностями, а поскольку элект-
ронные приборы действуют весьма быстро, то эта маши-
на будет также и быстродействующей.
Структура SBM
Идеи, которых мы коснулись выше, позволяют скон-
струировать арифметическое устройство. Но одно ариф-
метическое устройство не обладает достаточной
гибкостью и еще не составляет ЭВМ как таковую. ЭВМ
состоит из следующих основных частей:
t
АРИФМЕТИЧЕСКОЕ
УСТРОЙСТВО
Память ЭВМ выполняет две функции. Во-первых, в
ней хранятся числа, поданные на вход, промежуточные
результаты вычислений и окончательные результаты,
которые вот-вот попадут на выход. Во-вторых, в ней
хранится программа, из которой машина «узнает», как и
в какой последовательности должны выполняться вычис-
ления. Машина, так сказать, «считывает» команду,
содержащуюся в программе, выполняет ее и запоминает
ответ; затем она переходит к следующей команде и т. д.
Эти команды должны быть сформулированы на ма-
шинном языке, т. е. в специальном коде, «понятном» ма-
шине. Формулировки должны быть очень конкретными и
точными, например: «Взять содержимое ячейки 17 из
памяти и поместить его в арифметическое устройство»;
И Я. Стюарт
321
«Сложить два разряда в арифметическом устройстве»
и т. п Даже для перемножения двух чисел требуется
множество команд на машинном языке.
По этой причине для программирования были приду-
маны другие языки, более близкие к тому, которым обыч-
но описываются соответствующие действия. Например,
инструкция
С=А + В
должна сообщить машине, что требуется сложить два
числа, хранящиеся в ячейках А и В, и поместить резуль-
тат в ячейку С. Для этого машина снабжается специаль-
ной программой-компилятором, написанной на машинном
языке и переводящей каждую инструкцию с языка более
высокого уровня в серию команд на машинном языке.
Сейчас известно много разновидностей языков про-
граммирования, носящих экзотические названия, вроде
АЛГОЛ, ФОРТРАН, КОБОЛ (для коммерческих задач).
Машины поступают от изготовителя вместе с нужными
программами-компиляторами.
Именно использование программ придает ЭВМ боль-
шую гибкость. Машина выполняет последовательность
инструкций, которую задает ей программист. Поэтому
одна и та же машина может «решать» много различных
задач. Программист должен выучить один или несколько
стандартных языков программирования, что не так уж
трудно. Гораздо труднее овладеть искусством програм-
мирования, т. е. умением применять эти языки экономно
и продуктивно.
Составление программы
Предположим, что вы выучили какой-нибудь из язы-
ков программирования и у вас есть задача, которую вы
хотите решить при помощи ЭВМ, Как составить про-
грамму?
322
Первый шаг состоит в том, чтобы выделить в процедур
ре решения отдельные блоки, доступные машине, а затем
приступить к написанию программы, связывающей их
воедино.
Допустим, например, что вы хотите решать при помо-
щи машины квадратные уравнения. Известно, что корни
уравнения
ах2 + Ьх+с = 0
задаются формулой
— b + У Ь2 — 4ас
* =--------------'•
Однако в качестве инструкции для ЭВМ эта формула не
подходит. Ведь может случиться, что разность Ь2 — 4ас
отрицательна, а ЭВМ этого «не поймет» и будет пытать-
ся извлечь корень. Или а может обратиться в 0, и тогда
деление на а утратит смысл.
Предположим, что наша ЭВМ умеет выполнять все
арифметические действия, включая извлечение квадрат-
ных корней, и может различать положительные и отри-
цательные числа. Тогда процесс вычислений, расчленен-
ный на отдельные блоки, можно представить в виде
диаграммы, изображенной на рис. 178. Такая диаграмма
называется блок-схемой.
В блок-схеме предусмотрено несколько различных
ситуаций: если а = 0, то наше уравнение, возможно, ли-
нейное; может не быть действительных решений, или
быть одно действительное решение, или два действитель-
ных решения.
Следующий шаг — превратить процедуру, представ-
ленную блок-схемой, в программу. Здесь имеются труд-
ности, ибо программа должна состоять из определенной
последовательности инструкций, а в нашей процедуре
имеются разветвления и альтернативы. Чтобы выйти из
положения, различным частям программы присванвают-
11»
323
Рис. 175.
ся буквенные индексы (А, В, С, D, Е в описываемом ниже
примере) и машине даются специальные инструкции о
том, как переходить от одной части программы к другой
в зависимости от того, какой ответ: ДА или НЕТ — полу-
чен на тот или иной вопрос.
Сейчас мы приведем одну из возможных программ
для нашего примера, записанную на некоем гипотетиче-
ском языке типа АЛГОЛа. Его нетрудно понимать, если
поглядывать иногда на блок-схему.
ПРОГРАММА РЕШЕНИЯ КВАДРАТНЫХ
УРАВНЕНИЙ
А: начало действительные а, b, с, k, и, и, w, х, у
ввести а, Ь, с
если а = 0, то перейти к В
у = Ь2 — 4ас
если у 0, то перейти к С
напечатать ДЕЙСТВИТЕЛЬНЫХ КОРНЕЙ НЕТ
конец
В: если b = 0, то перейти к Е
х = —с/Ь
напечатать х
конец
С: если у — 0, то перейти к D
k = / у
и = (—b + k)i"2a
v = (—b — k)/2a
напечатать и
напечатать ИЛИ
напечатать v
конец
D: w = —Ы2а
напечатать w
конец
Е: напечатать КОРНЕЙ НЕТ
конец
325
Инструкцию «действительные a, b, с, k, и, v, w, х, у»
называют описанием- она указывает машине, какие сим-
волы заняты для чисел и какие рассматриваются числа
(действительные). Инструкция «ввести» предписывает
считать значения, а, Ь, с с приготовленной заранее ленты
данных. Инструкция: «если Р, то перейти к X» означает,
что в случае ситуации Р нужно перейти к части програм-
мы, помеченной символом X. Если же ситуация Р не
осуществилась, то выполняется следующая строка про-
граммы. Остальные инструкции очевидны: машина вы-
полняет их строка за строкой по порядку, за исключением
случаев, когда ей предписывается перейти к другой части
программы.
Это довольно типичная простая программа, и я при-
вел ее для того, чтобы объяснить, как составляются
программы. Читателю рекомендуется выбрать несколько
вариантов конкретных значений а, Ь, с и посмотреть, как
эта программа справляется со своей задачей.
Дальнейшие подробности, касающиеся программиро-
вания на специальных языках программирования, чита-
тель найдет в многочисленных руководствах, посвящен-
ных этим вопросам 2.
Применения компьютеров
Говоря попросту, компьютеры можно применять то-
гда, когда требуется выполнить большой объем вы-
числений, которые допускают точное описание. А вот
вопрос о том, нужно ли их применять, решается обычно
исходя из экономических соображений: поскольку это
дорого, окупит ли полученный результат необходимые
затраты?
Компьютеры используются в бизнесе и в управлении,
в основном для ведения счетов и накопления информа-
ции. Об этих применениях я говорить не буду, замечу
только, что распространенное оправдание «ошибка ком-
326
пьютера» на деле часто оказывается «ошибкой программ
миста».
Ученые-исследователи могут с успехом пользоваться
компьютером для обработки опытных данных, вычерчи-
вания графиков, расчета таблиц результатов, применения
статистических методов. Они могут решать численными
методами «неприступные» уравнения. Есть даже опас-
ность, что под впечатлением огромного потока информа-
ции, которую можно получить в результате машинных
вычислений, утратится трезвый взгляд на вещи: никакое
количество вычислений самих по себе не приведет к по-
лезным результатам, если задача или эксперимент плохо
поставлены. И все же возможности, которые предостав-
ляют компьютеры, поистине огромны. Они позволили
нам заглянуть в структуру белка, раскрыть генетический
код, изучать свойства элементарных частиц и строение
звезд. Они помогли человеку осуществить посадку на
Луну.
Даже в области чистой математики на счету у ком-
пьютеров имеется ряд замечательных достижений, осо-
бенно в теории конечных групп. Однако в этой области
мало задач, пригодных для машинных вычислений, и
даже среди этих немногих большинство требует для ре-
шения слишком много времени; быстродействия совре-
менных (а скорее всего, и завтрашних) компьютеров для
решения таких задач еще недостаточно.
Применение компьютеров не ограничивается числовы-
ми задачами. Существуют программы, позволяющие
компьютерам играть в шашки (хорошо), в шахматы
(плохо), переводить с одного языка на другой (отврати-
тельно), сочинять музыку (в некотором роде) и стихи.
Некоторые недавние достижения в производстве «умных»
машин весьма впечатляющи.
Это, естественно, заставляет меня обратиться к тра-
диционному вопросу: могут ли машины мыслить? Как
сказал бы Подай, все зависит от того, что понимается под
327
словом «мыслить». Пока что компьютеры умеют выпол-
нять некоторые функции человеческого мозга быстрее и
точнее, а другие не могут выполнять вообще. Но если по-
ставить вопрос так: существуют ли в способе мышления
человека какие-то особенности, которые никакая маши-
на в принципе никогда не сможет воспроизвести? — то,
по моему личному мнению, на него нужно ответить: нет.
Разумеется, в настоящее время мы не умеем дубли-
ровать функции мозга, и сходство между мозгом и су-
ществующими компьютерами примерно такое же, как
между коровой и автоцистерной «Молоко». Быть может,
наша техника так никогда и не приблизится к созданию
«мыслящей» машины: не исключено, что человеческий
мозг для этого слишком «глуп». Однако я не думаю,
что существуют принципиально непреодолимые препят-
ствия, не позволяющие создать машину, выполняющую
функции человеческого мозга, такие логические пре-
пятствия, которые мешают У 2 быть рациональным чис-
лом и не дают человеку поднять самого себя за шнурки
ботинок. И вот почему: ведь человеческое тело явно
представляет собой некую машину в том смысле, что оно
состоит из той же материи, что и все остальное, и под-
чиняется тем же законам движения материи. Это очень
сложная и удивительная машина, в которой мы еще мало
что понимаем. Однако, если бы существовали принципи-
альные препятствия для создания машин, ведущих себя,
как люди, то и люди никогда бы не появились.
Это утверждение вовсе не сводит человека до уровня
простейшего механизма. Многие люди настойчиво пропо-
ведуют, что сложность человеческого поведения, его эмо-,
циональные, творческие и духовные атрибуты определя-
ются чем-то «высшим», нежели физические законы. Это
замечательная концепция. Однако насколько более за-
мечательно было бы, если бы даже эти свойства были
следствиями физических законов. Это нисколько не уни-
зило бы человечество, зато как возвысило бы физику!
328
Глава 19
ПРИМЕНЕНИЯ СОВРЕМЕННОЙ
МАТЕМАТИКИ
Хотя выше я вел речь о различных разделах матема-
тики — алгебре, анализе, логике, геометрии, теории чи-
сел, топологии, теории вероятностей — однако надо иметь
в виду, что никаких четких границ между ними провести
нельзя и что такое разделение во многом условно. Когда
Декарт впервые установил связь между геометрией и ал-
геброй, это было встречено с удивлением. Когда Галуа
применил теорию групп к алгебраическим уравнениям,
это тоже было удивительно. Когда Адамар и Валле Пус-
сен, используя анализ, доказали важные гипотезы о про-
стых числах, это опять вызвало удивление. Теперь мате-
матики больше не удивляются таким событиям. Наобо-
рот, они намеренно ищут встречи с ними. Стало уже
обычным, когда, начав с какой-то задачи анализа, ее
превращают в топологическую, затем сводят к алгебраи-
ческой и, наконец, решают при помети теории чисел.
Именно это единство позволяет говорить о «теле ма-
тематики», как в гл. 1. Отдельные его части столь тесно
связаны, что любое серьезное изменение в одной из них
оказывается важным для всего «организма». Математи-
ка есть гармоничное целое, несмотря на то что это неза-
вершенная гармония, ибо в наших знаниях всегда есть
пробелы, и на каждом этапе мы смутно догадываемся о
новых и новых взаимосвязях.
В этом смысле любое применение какого-либо разде-
ла математики есть применение математики в целом.
Если придерживаться той точки зрения, что математи-
ка оправдывает свое существование в той мере, в какой
она находит применение, тогда следует признать, что лю-
329
бое применение какой бы то ни было ее части оправды-
вает существование всего остального. Не станем же мы
утверждать, что скрипачу нужно ампутировать ноги, на
том основании, что для игры на скрипке они ему не нуж-
ны. По тем же соображениям не стоит отвергать теорию
групп только потому, что она «не рентабельна».
По традиции выделяют два вида математики — «чи-
стую» и прикладную. У тех, кто занимается «чистой ма-
тематикой», мысли витают в облаках абстракций, они
изучают науку ради нее самой, не интересуются приме-
нениями и не придают им значения. Те же, кто занима-
ется прикладной математикой, прочно стоят на земле и
приносят пользу обществу.
Как и в большинстве других традиций, в этой тради-
ции есть доля разумного. Математика столь обширна,
что каждый математик вынужден ограничиться опреде-
ленным направлением исследований. Если выбранное
направление не имеет непосредственных применений в се-
годняшнем реальном мире, то его отнесут к «чистым» ма-
тематикам, если же имеет, он попадет в категорию «при-
кладников». Но очень часто оказывается, что результа-
ты «чистой» математики находят важные практические
применения, а результаты, задуманные как прикладные,
не находят вообще никаких применений. Мне вспомина-
ется человек, который разрабатывал математическую
теорию малярной кисти. Чтобы написать уравнения, ко-
торые он смог бы решить, ему пришлось ввести предпо-
ложение, что каждый волосок кисти представляет собой
бесконечную полуплоскость. Таким образом, его теория
утратила всякую связь с реальной кистью. В то же вре-
мя она не имела почти никакой ценности и для матема-
тики, поскольку он умышленно выбирал такие уравне-
ния, которые можно было решить уже известными мето-
дами.
Я бы предпочел сказать иначе: имеется математика и
применения математики. Дело математиков — создавать
330
мощные средства для решения математических задач, и
эти задачи могут быть выдвинуты возможными примене-
ниями (потребностями практики), могут возникать в хо-
де абстрактных исследований в виде камней преткнове*
ния при разработке каких-то математических методой
или, наконец, это могут быть важные нерешенные задачи.
Как я уже говорил в гл. 1, обычно применения находятся
с большим запозданием: чистая математика Одного сто-
летия может оказаться теоретической физикой следую-
щего. Конечно, применения важны, но в этом вопросе
необходимо проявлять достаточную дальновидность.
Я хочу привести ниже три примера применений совре-
менной математики, Первый показывает, как можно ис-
пользовать линейную алгебру для решения некоторых
типов экономических задач; правда, к вопросам рента-
бельности он имеет примерно такое же отношение, как
теория групп. Второй иллюстрирует современные приме-
нения теории групп к исследованию физических свойств
элементарных частиц. Третий пример — совсем новая
теория скачкообразных (разрывных) процессов, которая
основана на совсем свежих математических результа-
тах. Может оказаться, что она получит важные примене-
ния в биологии и медицине; она уже с успехом использо-
валась для изучения распространения нервных им-
пульсов.
Эта последняя теория столь нова, что многое в ней
пока чисто умозрительно и большая ее часть еще требу-
ет разработки. Чтобы преодолеть «эффект запаздывания
применений» и предсказать будущее, мне придется вос-
пользоваться магическим кристаллом. Однако вспо-
мним, что анализ был разработан в основном для изуче-
ния непрерывных процессов и в течение двух столетий
считался главным средством всей теоретической науки.
Сейчас в науке имеется огромная необходимость постиг-
нуть именно разрывные, скачкообразные процессы, кото-
рые встречаются в физике, химии, технике, метеорологии.
331
биологии, экономике, социологии, политике, геофизике,
аэродинамике и т. д„ поэтому следует признать по мень-
шей мере правдоподобным, что теория таких процессов
имеет большое будущее.
Как добиться максимальной прибыли
Предположим, что некий завод выпускает два вида
изделий: «штучки» и «дрючки». Каждое сначала обтачи-
вается на токарном станке, а затем на сверлильном в
нем проделывают отверстия. Обработка каждого изделия
на каждом станке требует определенного времени, при-
чем каждый из станков можно занимать только установ-
ленное время (в неделю). Известна также прибыль от
продажи каждого вида изделий. Сведем все эти данные
в таблицу:
Обработка Штучка Дрючка Время доступа к станку
Обточка 3 5 15
Сверление 5 2 10
Прибыль с одного изделия 5 3
Требуется выяснить, как сделать прибыль максимальной.
Предположим, что каждую неделю выпускается х
штучек и у дрючск. Тогда, исходя из затрат времени, по-
лучаем следующие условия:
3.v + 5y<15, 1 (1)
5л -Ь2«/< 10; J (2)
при этом, разумеется,
х>0, (3)
f/^0. (4)
342
Прибыль от продажи изделий за неделю равна
5х+3г/. (5)
Задача состоит в том, чтобы найти максимум выражения
(5) при выполнении условий (1) — (4).
Мы не знаем методов решения неравенств, поэтому
нарисуем график. Точки (х, у), удовлетворяющие усло-
вие. 179.
ВИЯМ (1) —(4), лежат в заштрихованной области на
рис. 179. Последние два условия означают, что х и у по-
ложительны, условие (1) говорит о том, что точки (х, у)
лежат ниже прямой 3x+5z/= 15, а условие (2) — что они
лежат левее прямой 5х + 2у= 10.
Прямая 5х+3у — р, отвечающая некоторому конкрет-
ному значению прибыли р, показана на рисунке. Когда р
меняется, прямая перемещается параллельно самой се-
бе, оставаясь под тем же наклоном к оси. Чем левее пря-
мая, тем меньше прибыль.
Наша задача состоит в нахождении наибольшего зна-
333
чения р, при котором прямая проходит через заштрихо-
ванную область, поскольку только в этой области лежат
допустимые точки (х, у). Ясно, что этому значению р от-
вечает прямая, проходящая через точку А на рисунке —
правый верхний угол заштрихованной области.
Чтобы найти точку А, решим систему уравнений
5х 4- 2у = 10, 1
Зх -j- 5 у = 15. J
Получим
х=20/19, г/=45/19.
Тогда прибыль за неделю равна 5х+3у, т. е.
100+ 135 235.
19 “ 19'
Итак, чтобы получить максимальную прибыль, завод дол-
жен выпускать 20 штучек и 45 др точек каждые 19 недель.
Аналогичные соображения применимы в масштабах
целой отрасли хозяйства или экономики всей страны, хо-
тя в реальных ситуациях число изделий и машин будет
очень велико. В общем случае задача сводится к нахож-
дению максимума некоторой линейной комбинации не-
известных, удовлетворяющих системе линейных нера-
венств. Эти неравенства определяют некоторую область в
многомерном пространстве. Можно показать, что:
а) эта область выпукла;
б) максимальное значение, если оно существует, при-
быль принимает в одном из углов этой области.
Для доказательства этих утверждений не обойтись
без линейной алгебры; она требуется и для нахождения
того угла, в котором принимается максимальное значе-
ние. При большом числе неизвестных эти вычисления
проводятся при помощи ЭВМ.
Чтобы достаточно полно и подробно изучать эконо-
мику всей страны, нужно составить так много уравнений,
что даже самые быстродействующие из существующих
834
ЭВМ. едва ли справятся с этой задачей. Поэтому придет-
ся сделать упрощающие предположения, а тогда появят-
ся сомнения в достоверности результатов.
Подобные методы, известные под названием линейно-
го программирования, широко применяются в экономи-
ке; их описание можно найти во многих учебниках по
математической экономике
Восьмеричный путь
Когда-то теория атома была довольно проста. Счита-
лось, что все атомы состоят из трех различных видов эле-
ментарных частиц: протонов, нейтронов и электронов.
В результате более тонких исследований обнаружилось
существование уймы других элементарных частиц: ней-
трино, пионы, мюоны и т. п. Однако теории, которая по-
зволяла бы их как-то систематизировать, не было.
В 1964 г. было обнаружено, что для такой системати-
зации может быть использована теория групп. Приводи-
мое ниже описание этой идеи по необходимости очень
сжато, поэтому не надейтесь извлечь из него больше, чем
самое общее понятие о том, как это делается.
Технической основой для осуществления этой идеи
послужили представления групп. Для данной группы G
ее представления находятся так: ищется векторное про-
странство V, допускающее некоторые линейные преобра-
зования, составляющие группу G', изоморфную G. Эта
группа G' (или, точнее, этот изоморфизм) и называют
представлением группы G.
Рассмотрим, например, группу G, состоящую из двух
элементов {I, г}, причем г2 = 1. В качестве V возьмем
плоскость R2 и рассмотрим зеркальное отражение Т от-
носительно некоторой фиксированной прямой, проходя-
щей через начало координат. Присоединив к нему тож-
дественное отображение I, получим группу {/, Т} линей-
ных преобразований пространства V, Более того, Т2—1,
335
поэтому группа G'= {I, 7} изоморфна G, т. е. является ее
представлением.
Размерность пространства V называют размерностью
представления (на страх педантам).
В квантовой механике данный физический объект мо-
жет существовать в различных энергетических состоя-
ниях Например, в атоме водорода, состоящем из прото-
на и электрона, энергия электрона может принимать бес-
конечно много значений, хотя весь набор этих значений
можно вполне точно рассчитать. Электрон может перехо-
дить из одного энергетического состояния в другое, по-
глощая или испуская фотон, так что сохраняется полная
энергия системы.
Из законов квантовой механики вытекает такое мате-
матическое следствие: возможные состояния физического
объекта точно описываются представлениями его группы
симметрий.
Например, один атом, находящийся в некоторой точ-
ке Р пустого пространства, обладает полной поворотной
симметрией: его группа симметрий — это группа О3 всех
жестких движений 3-мерного пространства, оставляющих
на месте точку Р. Эта группа имеет 3-мерное представ-
ление (физики называют его триплетным представлени-
ем), поскольку она сама уже является группой линей-
ных преобразований 3-мерного пространства (ибо жест-
кие движения — это линейные преобразования).
Если теперь приложить магнитное поле, симметрия
нарушится: направление поля выделит в 3-мерном про-
странстве некоторую прямую, и группой симметрий ста-
нет группа О2 вращений, оставляющих неподвижной эту
прямую. Оказывается, что при этом триплетное представ-
ление группы О3 распадается на 3 различных 1-мерных
представления группы О2. Спектроскопическое исследо-
вание показывает, что одиночная спектральная линия,
наблюдаемая в отсутствие магнитного поля, расщепля-
ется при включении поля на 3 расположенные поблизо-
336
сти одна от другой линии. Соответствующие энергии мож-
но вычислить, и они согласуются с экспериментальными
данными.
Такое применение теории групп в квантовой механике
общепринято. Оно позволило предсказать в 1938 г. суще-
ствование и различные свойства пионов. Пионы были об-
наружены экспериментально в 1947 г., и оказалось, что
предсказанные свойства вполне отвечают действитель-
ности.
Среди известных элементарных частиц имеется неко-
торое количество более тяжелых, чем остальные. Эти тя-
желые частицы образуют семейство, известное под общим
названием барионы. В семейство барионов входят: ней-
трон п°, протон п+ и ряд более загадочных, называемых
по присвоенным им греческим буквам Л (ламбда), 3
(кси), 2 (сигма) и Д (дельта). Каждая из частиц обла-
337
дает определенными массой и электрическим зарядом,
всегда целым кратным основной единице заряда, которая
равна 4'1 для протона и 0 для нейтрона (заряд элек-
трона равен —1, но электрон не относится к семейству
барионов).
Элементарные частицы обладают и другими физическими
характеристиками, менее наглядными, чем масса и заряд.
Вот некоторые из них: спин, изотопический спин, гипер-
заряд, странность.
Наиболее известно семейство 8 барионов, состоящее
из Е-дуплета, 2-триплета, А-синглета и n-дуплета. Их
массы, заряды, изотопические спины (/) и гиперзаряды
(У) указаны на рис. 180.
Это семейство может быть описано на языке пред-
ставлений некоторой группы, называемой SU3. Ее наи-
более естественное представление имеет размерность 8.
Поскольку в природе идеальная 5Д3-симметрия всегда
несколько нарушена, группа симметрий сводится к неко-
торой подгруппе U2, а исходное 8-мерное представление
распадается на 4 части размерностей соответственно 3,
2, 2, 1. Эти части в точности соответствуют 2-триплету,
Е- и n-дуплетам и Д-синглету.
Далее было замечено, что наблюдаемые значения У,
I, массы и заряда согласуются с предсказываемыми
5{73-теорией. Получается, что все эти барионы — как
бы различные состояния одной элементарной частицы,
которая превратилась в 8 разновидностей вследствие
асимметрий в природе.
Эта теория известна под названием «восьмеричный
путь».
Была осуществлена решающая проверка. Следующее
представление группы SU3 имеет размерность 10. Све-
денное к U2, оно распадается на 4 части размерностей
4, 3, 2 и 1. Девять известных частиц отвечали этой си-
туации: Д-квадруплет, 2-триплет и Е-дуплет (рис. 181).
(Массы частиц 2 и Е несколько отличаются от тех, ко-
338
торые указаны на рис. 180, поскольку здесь мы рас-
сматриваем другие состояния.)
Знак вопроса в верхнем кружке относится к частице,
которой недоставало для полноты картины. Теория пред-
сказала несколько ее характеристик: она должна была
иметь заряд —1, гиперзаряд —2, изотопический спин 0,
г - ...W г- ' -'I
-1 О 1 +2
заряд
Рис. 181,
массу около 1700 МэВ. Совершенно неожиданная комби-
нация!
В феврале 1964 г. в специально разработанном экспе-
рименте эта частица была найдена. Ей дали название
омега-минус (Q-).
Так, теория, основанная на свойствах абстрактных
групп, правильно предсказала существование ранее не-
известной элементарной частицы 2.
839
Теория катастроф
Не всегда бывает так, что непрерывные воздействия
приводят к непрерывным изменениям. Чтобы зажечь
свет, вы плавно переводите выключатель из положения
«выключен» в положение «включен», но на этом пути
он проходит через точку, когда внезапно вспыхивает
свет. Непрерывное движение по краю скалы может обор-
ваться, если вы свалитесь вниз.
До недавнего времени большинство исследований в
математике и почти все в физике были посвящены непре-
рывным изменениям. Однако один ИЗ выдающихся мате-
матиков нашего времени Рене Том разработал глубокую
теорию скачкообразных изменений, которые он назвал
катастрофами3.
Возможные применения такой теории широки и раз-
нообразны. Самым важным полем применения станет,
вероятно, биология. Вспомним, что по мере своего раз-
вития зародыш претерпевает много скачкообразных
изменений: в результате деления клеток начинают фор-
мироваться конечности, образуются нервы, кости и мыш-
цы. Выяснение механизма этих процессов могло бы
привести к небывалым успехам биологии. И, возможно,
наступит день, когда мы окажемся в состоянии приме-
нить эти новые знания в медицине, и в частности научим-
ся предотвращать врожденные уродства.
Такие применения, если они окажутся возможными,
далеко впереди — это дело десятилетий или даже сто-
летий. Однако пока теория Тома — единственная теория,
позволяющая хоть как-то исследовать скачкообразные
процессы, и потому заслуживает того, чтобы заняться ее
разработкой.
Читателю будет значительно легче понять дальней-
шее, если он построит или хотя бы вообразит машину Зи-
мана4, схематически представленную на рис. 182. Она
состоит из вращающегося диска, к краю которого при-
340
креплены две одинаковые пружины: конец одной за-
креплен в точке F, коней другой можно свободно пере-
мещать, каждый раз фиксируя ее положение. (Диск мож-
но сделать из картона и приколоть в центре булавкой
к деревянной доске. Если диаметр диска 5 см, то точка
F должна быть примерно в 12 см от центра. Тогда пру-
жины нужно взять примерно по
8 см и не слишком тугие. Желатель-
но, чтобы устройство, закрепляю-
щее пружины на краю диска, сво-
бодно вращалось вместе с диском.)
Путем экспериментов с этой ма-
шиной можно обнаружить, что су-
ществует ромбовидная область
PQRS со следующим свойством: ко-
гда свободный конец пружины на-
ходится вне этой области, у диска
есть лишь одно положение равнове-
сия; когда же этот конец попадает
внутрь области, положений равно-
весия два.
Более того, диск можно заста-
вить перескочить из одного положе-
ния равновесия в другое непрерыв-
ным перемещением свободного кон-
ца пружины. Например, в случае,
показанном на рис. 183, диск пово-
рачивается скачком, когда свобод-
ный конец выходит из области
Рис. 182.
PQRS (однако когда он входит в эту область, ничего
подобного не происходит).
Чтобы установить причину этого явления, проанали-
зируем изменение энергии натяжения пружин. Допустим,
что мы силой вывели диск из положения равновесия,
повернув его на некоторый угол 6. Когда мы его отпу-
стим, он скачком вернется в некоторое положение равно-
341
весия. Это происходит потому, что система, в которой
энергия запасена в растянутых пружинах, стремится
перейти в состояние с минимальной энергией (или, гово-
ря более строго, в состояние со стационарной энергией
в том смысле, как это поясняется ниже).
Вне области PQRS график энергии в зависимости от
угла 0 выглядит так, как пока-
зано на рис. 184. Кривая имеет
единственный минимум, чтб и
соответствует одному положе-
нию равновесия.
Внутри области PQPS гра-
фик энергии выглядит, как по-
казано на рис. 185. На этот раз
имеется два минимума, соот-
ветствующих двум разным
углам 6; отсюда и два положе-
ния равновесия.
Между двумя минимумами
отвечает равновесию, но не-
устойчивому. Даже слабый толчок приведет к тому, что
система «покатится вниз по склону», т. е. энергия устре-
мится к минимуму. Теоретически иголка может стоять на
342
острие, однако такое положение равновесия для нее не-
устойчиво.
Когда свободный конец пружины проходит путь, по-
казанный на рис. 183, кривая энергии претерпевает ряд
изменений (рис. 186). Поведение диска иллюстрирует
шарик, катающийся по желобку. Сначала он пребывает
LW
Рис. 186.
«на дне», в минимуме, и остается там до тех пор, пока
этот минимум существует. Когда этот минимум исчезает,
шарику не остается ничего другого, как скатиться в един-
ственную оставшуюся ямку. Так же и диск срывается в
другое положение равновесия, вынужденный к тому не
зависящими от него обстоятельствами.
Поведение диска можно описать более наглядно, если
нарисовать в 3-мерном пространстве график, изобра-
жающий возможные равновесные состояния для разных
положений свободного конца. Можно доказать, что он
имеет такой вид, как показано на рис. 187. На рисунке
отмечены точка Р и часть ромбовидной области (кото-
рая для большей ясности повернута). Над точками обла-
сти, ограниченной кривой К с острием, мы видим три
положения равновесия; одно на верхнем слое складки,
343
одно посредине и одно на нижнем слое. Среднее положе-
ние неустойчиво. Над точками вне этой области лежит
один слой поверхности.
Когда свободный конец пружины, пересекая кривую
К, входит во внутреннюю область, диск «старается» со-
хранить равновесие, отвечающее верхнему слою склад-
Рис. 187.
кн. Когда же он выходит из области, диск «срывается
с края» и перепрыгивает в другое положение равно-
весия.
Все это можно описать количественно. Выберем си-
стему координат (а, Ь) с началом в точке Р. Введем
третью переменную х, описывающую угол поворота ди-
ска в равновесном состоянии. Для малых а, Ь, х энергию
натянутых пружин можно считать равной
V = -^-х* +-^-ах2 + Ьх.
Чтобы найти состояния равновесия, нужно опреде-
лить стационарные значения энергии. Это те точки, где
344
кривая энергии горизонтальна, т. е. максимумы, миниму-
мы и так называемые «точки перегиба». Все эти возмож-
ности иллюстрирует рис. 188. Из дифференциального
исчисления известно, что стационарные значения соот-
ветствуют тем точкам, в которых производная обращает-
ся в нуль:
~ = х3 + ах + b = 0.
Рис. 188.
Если нарисовать «график» этого уравнения, выбирая
значения а и b и откладывая соответствующие значе-
ния х, получится поверхность, изображенная на рис. 187.
Рене Том исследовал общую ситуацию, с точки зре-
ния которой все описанное выше — лишь частный случай.
Он рассматривал любую динамическую систему, поведе-
ние которой можно измерять переменными
х, у, z, ...
и которая «управляется» другим набором переменных
а, Ь, с, ...
Переменные х, у, г, ...— это, так сказать, координаты
пространства поведения (внутренние переменные), а, Ь,
с, ...— координаты пространства управления (внешние
переменные). Поведение системы задается ее потенциа-
345
лом (или энергией). В общем случае рассматривается
потенциал вполне общего вида
V=V(x, у, z, ..., а, Ь, с, ...),
подчиненный лишь таким условиям, которые позволяют
применять к функции V операции дифференциального
и интегрального исчисления.
В случае машины Зимана мы имеем дело с системой,
у которой одна внутренняя переменная х и две внешние
а, Ь; потенциал V этой системы задается написанной вы-
ше формулой.
Ясно, что подобную систему можно построить для
любого потенциала V, и, значит, существует бесконечное
множество различных систем такого рода. Однако мно-
гие из них переходят одна в другую при «замене коорди-
нат». Например, в случае машины Зимана, если заме-
нить х на 2Х, то потенциал V станет другим:
4Х4 + 2аХ+Ь,
но если мы узнали все о новой системе, нам станет изве-
стно все и о старой, ибо такие изменения несущественны.
Простейший способ избавиться от несущественных раз-
личий — обращать внимание только на топологические
свойства соответствующих поверхностей.
Все события в физическом мире можно описывать
при помощи 4 переменных: трех пространственных коор-
динат и одной временной. Поэтому, если иметь в виду
физические применения, достаточно ограничиться 4-мер-
ным пространством управлений.
Для этого случая Том доказал удивительную теоре-
му: в динамической системе с 4 внешними переменными
могут встретиться ровно 7 топологически различных
типов скачка. Любое физическое нарушение непрерыв-
ности относится к одному из 7 типов.
Том перечислил эти 7 типов и назвал их элементар-
ными катастрофами. Вот они:
346
Название Потенциал V
Морщина — л3 + ах 3
Складка -L х* + - - ах2 + Ьх
Ласточкин хвост -1. х5 + -L ах3 +-L Ьх2 + с О о Z
Бабочка —L х6 + —1- axi +—L. Ьх3 + J— сх2 + d 6 4 3 2
Гиперболическая омбилика Эллиптическая омбилика Параболическая омбилика х3 + у3 + ах + by + сху х3 — Зхг/2 + сх + by + с (х2 + у2) х2у + yi + ах + by + сх2 + dy2
Эта таблица не подсказывает никакой очевидной за-
кономерности, никакой очевидной причины, почему встре-
чаются только эти 7 катастроф. В доказательстве Тома
существенно используются весьма глубокие результаты
топологии, анализа, абстрактной алгебры — как я уже
говорил, математика есть гармоничное целое — и даже
если все это знать, оно очень трудное.
Геометрические формы элементарных катастроф
очень красивы. На рис. 189 показано построенное
компьютером сечение части параболической омбилики 5.
Легко видеть, что машине Зимана соответствует вто-
рая катастрофа — складка. Эта же катастрофа позво-
ляет показать, как можно было бы применить теорию
Тома в биологии.
Живая клетка есть не что иное, как трехмерная ка-
пелька вещества. Для простоты будем считать, что это
двумерная капелька — тогда легче рисовать картинки.
347
Соответственно будем предполагать, что клетка живет
в двумерном внешнем пространстве.
Мы будем наблюдать за поведением клетки, измеряя
концентрацию в ней некоторого химического соединения
(неважно, какого — это может быть хлорид натрия, ДНК
или что-нибудь другое). Поскольку клетки претерпевают
Рис. 189.
скачкообразные изменения (именно это нас и интересу-
ет), то в способе зависимости химической концентрации
от внешних параметров должна проявляться одна из ка-
тастроф Тома. Возможной моделью служит складка.
С течением времени концентрация фиксированного
вещества в клетке постепенно изменяется («дрейфует»).
Этот процесс можно описать как медленное движение
клетки в пространстве управления. На рис. 190 показа-
ны 4 стадии развития клетки.
Положения клетки показаны на нижних рисунках, по-
верхность со складкой представляет ее химическое со-
стояние. На последнем рисунке вдоль клетки проходит
четкая линия раздела. Та часть, которая лежит слева от
этой линии, отвечает верхнему листу поверхности и, сле-
довательно, имеет высокую концентрацию рассматрива-
емого вещества. Часть, лежащая справа, имеет низкую
концентрацию.
Но такая резкая разница концентраций может озна-
чать только одно: фактически клетка разделилась на две
различные клетки.
348
Как уже говорилось, это очень грубая и упрощенная
модель. Процесс деления клетки совсем не так прост.
Однако он относится к скачкообразным процессам типа
рассмотренных Томом и, значит, на каждой стадии дол-
жен описываться одной из 7 элементарных катастроф.

Рис. 190.
Это позволяет совершенно по-новому ответить на
вопрос: почему делятся клетки? Потому что топологиче-
ские свойства описывающей их химическое состояние
поверхности таковы, что не делиться им невозможно.
349
Представим себе картину развития зародыша: вот он
медленно скользит по немыслимо изогнутой поверхности
своих химических изменений, испытывая новые и новые
деления; там начинают формироваться клетки конечно-
стей, тут — нервов, мышц или костей. И каждая ступень
этого процесса происходит одним из 7 различных спо*
собов!
Глава 20
ОСНОВАНИЯ МАТЕМАТИКИ
Рассказывают, что однажды астроном, физик и мате-
матик проводили отпуск, путешествуя по Шотландии.
Выглянув из окна вагона, они увидели черную овцу на
лугу. «Как интересно! — заметил астроном.— Оказы-
вается, в Шотландии все овцы черные!» «Э, нет! — ото-
звался физик.— В Шотландии некоторые овцы черные».
На что математик скорбно воздел глаза к небу и тоном
проповедника провозгласил: «В Шотландии есть по край-
ней мере один луг, на котором пасется по крайней мере
одна овца, у которой по крайней мере один бок черный».
Математики (когда они говорят всерьез) предпочи-
тают выражаться осторожно. Вот перед математиком
теорема, которая по всем признакам должна быть вер-
ной. Он вспомнит множество случаев, когда «очевидное»
оказывалось неверным, и затрепещет от страха. И кто
осудит его за это, если в его науке можно построить (с
циркулем и линейкой) правильный 17-угольник и нельзя
построить правильный 19-угольник, если сферу можно
вывернуть наизнанку *, а рациональных чисел столько же,
сколько целых? Нет уж, он лучше подождет, пока теоре-
ма будет доказана.
Я должен, однако, добавить, что не все математики
проявляют подобную предусмотрительность и меньше
других — некоторые из самых великих (как в минувшие
времена, так и теперь) 2. Но даже они обычно понимают,
что стоят на зыбком основании. И, кроме того, есть боль-
шая разница между сомнением в справедливости теоре-
мы и ее игнорированием. Каждый изучающий математи-
ку должен быть готов к тому, чтобы сказать: «Я не со-
всем понимаю, почему это так, но допустим, что это дей-
ствительно так, и посмотрим, куда это нас приведет».
851
Иногда трудность легче понять, если продвинуться впе-
ред и посмотреть на нее издали. Тот, кто настаивает на
полном понимании каждого мелкого шага рассуждений и
не хочет без этого двигаться дальше, рискует попасть в
положение человека, который слишком пристально раз-
глядывал, куда ступить, и не заметил, что идет не в ту
сторону. Вначале всегда позволительно игнорировать
частные трудности: так легче понять генеральную стра-
тегию атаки. А потом, когда станет ясно, что в целом она
правильна, можно вернуться к проработке деталей.
Настало время и нам заняться обсуждением деталей
некоторых наших предыдущих рассуждений. Овца с одно-
го боку белая, с другого черная — большая редкость, да
и вообще не так уж важно, является ли данная овца та-
кой, какой она кажется. Однако математике свойственна
устрашающая тенденция громоздить умозаключения
одно на другое, сооружая нечто вроде карточных доми-
ков. Выньте одну карту — и постройка рухнет. Когда в
США начинали разрабатывать программу космических
исследований, был такой случай: одна ракета стоимостью
в несколько миллионов долларов, как показала провер-
ка, должна была взорваться сразу же после запуска.
Выяснилось, что в записанной на пленку программе
управления полетом (которая выполняется при помощи
компьютера) пропущена точка с запятой. Чем сложнее
сооружение, тем более ужасными могут оказаться по-
следствия даже самой мелкой ошибки.
На рубеже 19 и 20 вв. у математиков возникли со-
мнения в прочности фундамента их науки. Сейчас модно
рассуждать о «пирамидальных» структурах. Математика
напоминает пирамиду, стоящую на своей вершине. Почти
все ее результаты покоятся на небольшом числе исходных
предположений. Обыкновенное благоразумие требует
присмотреться к ним повнимательнее и сделать их на-
столько прочным фундаментом, насколько это возможно.
352
Получерная овца в стаде
В гл. 9 мы упоминали о попытке Фреге поставить на
твердое основание понятие числа. До тех пор адекватная
трактовка этого понятия в математике отсутствовала.
В качестве краеугольного камня было взято разбиение
множеств на классы равномощных. Согласно прагмати-
ческой позиции В, эти классы ведут себя, как числа, и
потому можно считать, что они и являются числами.
Однако мы не приняли эту позицию и предпочли счи-
тать существование чисел аксиомой. Это было удачно, по-
тому что, как выяснилось, рассматривать множество всех
множеств, обладающих определенным свойством,— со-
всем не такое безобидное дело, как кажется. Бертран
Рассел указал Фреге на это обстоятельство сразу, как
только тот закончил свой шедевр.
Представим себе огромную библиотеку. Среди книг,
стоящих на полках, есть каталоги, в которых перечисля-
ются книги стихов, справочники, книги по математике,
книги нестандартного размера и т. д. В некоторые из ка-
талогов (например, в каталог справочных изданий) вхо-
дят и они сами, другие (например, каталог стихов) сами
себя не включают. Библиотекарь решает навести полный
порядок и составить еще один каталог (обозначим его С)
всех каталогов, не включающих самих себя.
Возникает вопрос: включает ли каталог С сам себя?
Если включает, то он входит в С и, значит, сам себя
не включает. Если нет, то С является каталогом, кото-
рый сам себя не вктючает, и, значит, он должен содер-
жаться в С.
Помните деревенского брадобрея? 3
Если бы этот парадокс касался только библиотека-
рей, мы не стали бы особо огорчаться и попросту выбро-
сили бы из математики любые упоминания о них. К со-
жалению, это явно не так: ведь любое множество — это
по существу каталог его элементов.
12 Я. Стюарт
353
Теоретико-множественная формулировка этого пара-
докса такова: пусть В — множество всех множеств, ко-
торые не содержат себя как элемент множества. Содер-
жит множество В себя в качестве элемента или не содер-
жит? Рассуждение такое же, как и в случае каталогов,
и что бы мы ни предположили, мы выведем противопо-
ложное.
Итак, теория множеств в том виде, в каком ею поль-
зовался Фреге, противоречива. Худшая судьба не может
постичь теорию!
У нас есть только один выход: отказаться от предло-
женной Фреге наивной теории множеств и найти ей не-
противоречивую замену. В наивной теории мы позволили
себе слишком много вольностей, вот и получили по заслу-
гам.
Два выхода
Чтобы обойти парадокс Рассела, нам придется так
изменить ход рассуждений, чтобы к подобным выводам
невозможно было прийти. Однако наши новые правила
не должны вводить слишком много ограничений, иначе
нам грозит опасность вместе с водой парадоксов выплес-
нуть и математического ребенка.
В приведенном выше рассуждении есть по крайней
мере два места, где логика чуточку сомнительна.
Во-первых, возможно, что мы позволили себе слиш-
ком большую свободу в построении множеств. Ведь если
В не является множеством, то теряет смысл вопрос о
«вхождении» В в В, и рассуждение не может продол-
жаться.
Во-вторых, возможно, что доказательство от против-
ного не заслуживает такого полного доверия, какое мы
ему оказали. Ведь если двойное отрицание не-не-р не
совпадает с р, то доказательство от противного рушится:
в этом случае мы доказали только, что В не содержится
354
в В и не не содержится в В, но второе нисколько не про-,
тиворечит первому.
Приверженцы второго тезиса, так называемые интуи-
ционисты, особенно подняли голос в ЗО-е годы. Предло-
женный ими выход был весьма радикальным; отбросив
доказательства от противного, математика понесет огром-
ные потери. Интуиционисты предприняли большие уси-
лия по перестройке математики без использования дока-
зательств от противного, и можно только удивляться,
сколь многое удалось спасти. Однако потери все же есть.
Например, в такой математике все функции непрерывны.
Рассуждения интуиционистов строятся примерно так.
На первый взгляд правдоподобно, что не-не-р — это то
же самое, что р. Иначе эту мысль можно выразить так:
верно в точности одно из двух
либо р, либо не-р.
Разумеется, если р относится лишь к конечному числу
объектов, то это так и есть, и мы можем просто прове-
рить р для каждого из имеющихся объектов. Закончив
проверку, мы либо убедимся в том, что все они удовлет-
воряют р, и тогда р имеет место, либо найдем такой объ-
ект, который не удовлетворяет р, и тогда р неверно, т. е.
имеет место не-р.
Но если объектов бесконечно много, такой перебор
уже невозможен. Мы проверим р на любом количестве
объектов, найдем, что оно верно для этих объектов, и все
же не получим никакого способа узнать, не нарушается
ли р для тех, для которых оно осталось непроверенным.
Если не удастся найти доказательства р (или не-p), от-
носящегося ко всем объектам, то все пропало. Мыслима
и такая ситуация, когда р верно для каждого объекта, но
каждый раз по разным причинам (нечто вроде бесконеч-
ного числа совпадений). Если так, мы не сможем опро-
вергнуть р, но не сможем и доказать, поскольку нельзя
написать бесконечно длинное доказательство.

355
В качестве примера рассмотрим известную гипотезу
Гольдбаха: каждое четное число, большее 2, является
суммой двух простых. Это утверждение не было ни до-
казано, ни опровергнуто. Если начать проверять его на
первых четных числах, кажется, что оно верно:
4 = 2 + 2
6 = 3 + 3
8 = 3+5
10 = 3 + 7
12 = 5+7
14 = 3+11
16=5+11
18 = 5+13
20 = 7+13
22 = 3+19
24 = 5+19
26=3 + 23
28 = 5+23
30 = 7+23
С другой стороны, уловить здесь какую-то закономерность
не удается. Весьма возможно, что никакой закономер-
ности и не существует, а гипотеза тем не менее верна.
Сама эта возможность уже означает, что наше уве-
ренное утверждение: либо верно р, либо верно не-р — от-
носится скорее к метафизике, чем к математике. Оно ос-
новано на предположении, что бесконечно много объек-
тов ведут себя так же, как и их конечное число. А нам
уже известно достаточно примеров (особенно из гл. 9)
странного поведения бесконечных множеств, чтобы при-
знать такое предположение сомнительным.
Если это предположение неверно, то парадокс Рассе-
ла становится просто одной из теорем, которую нельзя ни
доказать, ни опровергнуть. Конечно, и сам смысл слова
«неверно» в таком контексте становится предметом ис-
следования, ибо неясно, есть ли в нем какое-нибудь по-
лезное содержание.
Интуициониста радуют высказывания типа «всякое
четное число, меньшее 10'100, является суммой двух про-
стых», и он согласен, что они либо верны, либо неверны.
Но высказывание типа «всякое четное число есть сумма
двух простых» с его точки зрения не может быть ни вер-
356
ным, ни неверным; оно попадает в новую категорию истин
сомнительных.
Менее радикальной кажется идея ограничить свободу
образования множеств. В одной из разновидностей тео-
рии множеств 4 различают два типа объектов, подобных
множествам. Первые называют классами-, они имеют
элементы и во многом напоминают наивные множества.
Однако класс не обязательно способен быть элементом
другого класса. Тс классы, которые на это способны,
являются множествами.
Это означает, что определение класса в форме
С = {х | х обладает свойством Р}
нужно интерпретировать так: С есть класс всех мно-
жеств х, обладающих свойством Р. Если х обладает
свойством Р, отсюда еще не следует, что х С С; мы не
можем сделать такой вывод, если не знаем, что х —
множество.
В рассуждении, которое привело к парадоксу Рассела,
показывалось, что если В б В, то В само обладает тем
свойством, которое определяет его элементы (а именно,
не быть элементами самих себя), и, следовательно, лежит
в В. В повой теории множеств к такому выводу прийти
нельзя—ведь В может не быть множеством.
Тем самым мы поставили на место парадокс Рассела:
он доказывает (методом от противного) всего-навсего то,
что В не является множеством. В самом деле, если бы
оно было множеством, парадокс вступил бы в действие,
и мы бы пришли к противоречию.
Классы, которые не являются множествами, называют
собственно классами. Парадокс Рассела доказывает, что
они существуют. С другой стороны, о существовании
множеств нам ничего не известно.
Единственный способ приобрести уверенность в их су-
ществовании — написать аксиомы, которые это утверж-
дают. В простых аксиомах, необходимых всякой теории
12 Я- Стюарт
357
множеств, говорится о том, что 0 является множеством,
что объединение двух множеств есть множество и пере-
сечение двух множеств есть множество. Таким путем
Строится аксиоматическая теория множеств.
Фреге создал свою наивную теорию множеств по об-
разцу поведения совокупностей реальных объектов. Мы
не ждем от реального мира, что он станет противоречить
самому себе (убеждение, которое может оказаться столь
же необоснованным, как и многие другие взлелеенные че-
ловечеством принципы), поэтому мы надеемся, что тео-
рия Фреге непротиворечива. Напрасно, потому что это не
так. Правда, в конечном итоге это случилось с ней пото-
му, что она заблудилась и вышла за пределы реального.
С другой стороны, аксиоматическая теория множеств
не претендует ни на какую связь с реальным миром.
Прежде чем она сможет стать приемлемым фундаментом
для математики, следует убедиться в ее непротиворечи-
вости. Реальный физический мир не дает нам никакой
уверенности на этот счет. Требуется доказательство не-
противоречивости,
Программа Гильберта
Прежде всего нужно было решить, какие методы до-
казательства непротиворечивости считать допустимыми.
Ведь ясно, что нельзя пользоваться методами, которые
сами вызывают сомнения.
Давид Гильберт, который первым занялся этим во-
просом, пришел к заключению, что удовлетворительным
будет лишь такое доказательство, которое расчленяется
на конечное число шагов (как мы теперь сказали бы, его
может проводить компьютер). Не должно быть никакой
неопределенности, каждый шаг должен быть совершен-
но ясен и все возможности учтены.
Кроме того, Гильберт понял, что для получения тако-
го доказательства нужно отказаться от приписывания со-
358
держательного смысла математическим символам и дей-
ствовать чисто формально, как бы играя в некую игру по
определенным правилам. Например, правило может го-
ворить нам, что последовательность символов 1 + 1 допу-
скается заменять символом 2. Если удастся показать, что
никакая последовательность дозволенных ходов никогда
не приведет к комбинации символов вида
0^0,
и если это будет установлено конечным числом конструк-
тивных шагов, то тем самым будет получено доказатель-
ство непротиворечивости.
Если же комбинация 0=^=0 встретится в нашей игре,
то приведшие к ней ходы можно интерпретировать как
шаги доказательства того, что 0 0, и тогда аксиомати-
ческая теория множеств окажется противоречивой. С дру-
гой стороны, если аксиоматическая теория множеств про-
тиворечива, то существует доказательство того, что
0^=0; его шаги дадут нам те ходы, которые приводят к
такой комбинации символов в нашей игре.
На основе этих соображений Гильберт сформулиро-
вал полную программу проведения такого доказательст-
ва. После этого, чтобы дать математике столь желанный
прочный логический фундамент, оставалось лишь выпол-
нить эту программу.
Гильберта интересовал еще другой вопрос: всякая ли
задача может быть в принципе решена? Он возник в свя-
зи с убеждением интуиционистов, что это не так. Про-
грамма Гильберта предусматривала еще и получение
ответа на этот вопрос. Он считал, что существует совер-
шенно определенная процедура, позволяющая узнать
заранее, разрешима или нет данная задача, и надеялся,
что ее удастся найти.
В то время Гильберт был признанным лидером мате-
матического мира. Но один никому не известный молодой
человек Курт Гёдель (инженер по образованию) пришел
359
к выводу, что Гильберт нс прав. В 1930 г. он направил в
печать работу5, которая превратила программу Гильбер-
та в руины. Другой великий математик Джон фон Ней-
ман читал тогда курс лекций о программе Гильберта.
Прочитав работу Гёделя, он тотчас перестроился и по-
святил ей оставшиеся лекции.
Гёдель доказал две вещи:
1) если аксиоматическая теория множеств непротиво-
речива, то существуют теоремы, которые нельзя ни до-
казать, ни опровергнуть;
2) не существует никакой конструктивной процедуры,
при помощи которой можно было бы доказать непроти-
воречивость аксиоматической теории множеств.
Первый результат показывает, что не всякая задача
разрешима даже в принципе, второй полностью зачерки-
вает предложенную Гильбертом программу доказатель-
ства непротиворечивости. Говорят, что, услышав о рабо-
те Гёделя, Гильберт «очень рассердился».
В дальнейшем выяснилось, что нанесенный ущерб был
даже больше, чем воображал Гёдель. Любая аксиомати-
ческая система, достаточно обширная, чтобы содержать
формализованную арифметику, страдает теми же недо-
статками, и, значит, в этом «виновата» не та или иная
конкретная аксиоматизация, а сама арифметика!
Гёделезские номера
В этом и следующем разделах дается краткий обзор
доказательства теоремы Гёделя. Те читатели, у которых
кет желания в этом разбираться, могут спокойно их про-
пустить.
Начнем с простого вопроса: много ли существует
арифметических формул? (Под «арифметической фор-
мулой» я понимаю любую комбинацию символов +, —,
X,:, (,),=, 0, 1,2, 3, 4, 5, 6, 7, 8, 9.)
Ясно, что таких формул бесконечно много. Однако,
360
вспомнив о том, что говорилось в гл. 9, мы сразу спро-
сим: а какова эта бесконечность — счетна или несчетна?
Оказывается, множество таких формул счетно: существу-
ет биекция между ним и множеством N натуральных
чисел.
Чтобы установить эту биекцию, начнем с того, что
«закодируем» символы:
+ — ><:()= 0 1 2 3 4 56 78 9
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
(под каждым символом стоит его код). Далее, чтобы за-
кодировать цепочку символов, например
4 + 7=11,
образуем число
2’2-3*-515-77-119-139,
где 2, 3, 5, 7, 11, 13, ...— последовательность простых
чисел, а показатели степени 12, 1, 15, 7, 9, 9 — коды сим-
волов 4, +, 7, = , 1, 1, составляющих нашу цепочку.
Таким способом каждой цепочке можно поставить в
соответствие ее код, который является натуральным
числом.
Поскольку всякое натуральное число единственным
способом разлагается на простые множители, цепочку
можно восстановить по ее коду. Допустим, например, что
кодом является число 720. Разлагаем его на множители:
720 = 24-32-51.
Числа 4, 2 и 1 являются кодами символов :, —, +. Зна-
чит, 720 есть код цепочки
: - +
(хоть и не очень содержательная, но все же цепочка).
Такие коды называют гёделевскими номерами^
361
Для более сложных цепочек номера становятся очень
большими, но всякая цепочка имеет некоторый номер,
и различным цепочкам отвечают разные номера. Распо-
ложив цепочки в порядке возрастания номеров, можно
убедиться, что множество цепочек счетно.
В аксиоматической теории множеств у нас становится
больше символов: добавляются С , U > П, { , }• Кроме
того, появляются еще символы «переменных» х, у, z, ...
Однако применима та же процедура: кодируем символы,
затем при помощи простых чисел кодируем цепочки. Та-
ким образом, в аксиоматической теории множеств мно-
жество цепочек тоже счетно.
Доказательства теорем Гёделя
В этом разделе мы будем «работать» с двумя различ-
ными системами: некоторой аксиоматической теорией
множеств (обозначим ее М) и обычной арифметикой А.
Система Л1 будет представлять собой формализацию
арифметики. В М будут входить некоторые символы, из
них мы будем строить цепочки. Правила обращения
с этими цепочками мы узнаем из аксиом системы М.
Предположим, что система М устроена так, что в нее
входят все арифметические символы, которые подчи-
няются тем же правилам, что и в арифметике; так, на-
пример, цепочка 2 + 2 = 4 имеет две интерпретации: а) как
цепочка в М, лишенная всякого значения; б) как ариф-
метическая формула. Далее, если некоторая последова-
тельность допустимых преобразований цепочек в М при-
вела нас, скажем, к цепочке 2 + 2=4, то соответствующая
последовательность арифметических формул в А соста-
вит доказательство равенства 2 + 2 = 4.
В системе М имеются цепочки, содержащие одну чи-
словую переменную х, например
х+1 = 1+х, х(х— 1) =хх—х, х+х=43, (*)
362
Именно такие цепочки нас особенно интересуют. Цепоч-
ки, содержащие одну числовую переменную для
краткости будем называть сайнами.
Если а — некоторый сайн, a t — положительное целое
число, то можно образовать новую цепочку [а : /], под-
ставив в а вместо х число t (которое рассматривается
адесь как цепочка символов 0, 1,2, 3, Пусть, напри-
мер, а — сайн х+1 = 1 +х, а ?=31; тогда [ct: 31] — это це-
почка 31 +1 = 1 + 31.
Каждый сайн имеет определенный гёделевский номер.
Расположим их по порядку, и пусть
R(n)
есть n-й сайн. Тогда всякий сайн совпадает с некоторым
R(n), отвечающим какому-то п.
Определим теперь в А множество К, состоящее из
натуральных чисел, удовлетворяющих следующему усло-
вию: п£К. тогда и только тогда, когда цепочка
[7? (п): и] недоказуема в М.
Выясним, к примеру, верно ли, что З^К. Для этого
найдем R (3); пусть это будет сайн х + 4 — 0. Подставив
в него 3 вместо х, получим 3 + 4 = 0. Если эта цепочка
недоказуема в М, то 3 С К.
Теперь формулу х С К из А можно формализовать
в М\ получится некоторая цепочка S в М. Она содер-
жит одну числовую переменную и, значит, является сай-
ком. Для любого конкретного значения п цепочка [S: п]
является формальной версией арифметического утвержде-
ния п£ R.
Поскольку S —сайн, найдется такое q, что S=R{q\.
Покажем, что цепочка
(1)
недоказуема в М и что в то же время ее отрицание
не-[/?(/7) : <?] (2)
тоже недоказуемо в М,
363
Если бы (1) можно было доказать в М, то в Л была
бы верна ее интерпретация, поскольку М является фор-
мализацией А. Значит, q^K. Но, по определению мно-
жества Л, цепочка (1) недоказуема в М.
Если бы (2) можно было доказать в Л4, то в 4 было
бы верным утверждение не - (q С Л')- Тогда q £ К, и не-
верно, что [A* (q) : q] недоказуема в М; значит, [R(q): q]
доказуема в М. В предположении непротиворечивости М
отсюда вытекает, что (2) недоказуема в М.
Итак, цепочка [R(q) : </] (вполне определенная цепоч-
ка в М) дает нам теорему, которую нельзя ни доказать,
ни опровергнуть в М. Тем самым доказана первая теоре-
ма Гёделя.
«Распутав» цепочку [R(q) : 9], можно обнаружить,
что она по существу как бы сама утверждает свою недо-
казуемость. Ведь она звучит примерно так: «эта теорема
недоказуема», почти совсем как «это утверждение не-
верно». Однако высказывание «эта теорема недоказуе-
ма» нельзя формализовать в М, поэтому нам и при-
ходится метаться из М в А и обратно.
Теперь попробуем доказать вторую теорему Гёделя.
Пусть Т — цепочка [R(q) : q], которая, как мы видели,
утверждает свою собственную недоказуемость. Пусть
W — любая формула в М, утверждающая непротиворе-
чивость М. Мы хотим показать, что W нельзя дока-
зать в М.
Первая теорема Гёделя говорит: «если М непротиво-
речива, то Т недоказуема в М». Это высказывание можно
выразить внутри системы М. «Л1 непротиворечива» —
это наша формула W\ «Т недоказуема в М»— это сама
цепочка Т, раз она утверждает свою недоказуемость.
Значит, первая теорема Гёделя внутри системы М при-
нимает вид
W влечет за собой Т.
Если бы W можно было доказать в М, то это позволило
364
бы доказать Т. Но мы знаем, что Т недоказуема; значит,
нельзя доказать и №. Поскольку W утверждает непроти-
воречивость М, отсюда следует, что доказать непротиво-
речивость М, оставаясь в рамках самой этой системы 7И,
невозможно. Это доказывает вторую теорему Гёделя.
Неразрешимость
Полное доказательство теорем Гёделя (включая
подробное описание того, что понимается под «конструк-
тивной процедурой») удовлетворяет самым высоким тре-
бованиям строгости6. Хотя вторая теорема означает
полный крах программы Гильберта, первая теорема ин-
тереснее. Она показывает, что в самой обычной арифме-
тике существуют утверждения Р, для которых нельзя
доказать ни Р, ни не-Р. Такие утверждения называются
неразрешимыми.
В каком-то смысле это подтверждает правоту интуи-
ционистов, но лишь до тех пор, пока мы приравниваем
«истинное» к «доказуемому». А доказательство теоремы
Гёделя сохраняет силу и для интуиционистской матема-
тики.
Участь, постигшую проблему непротиворечивости
арифметики, разделили с ней и некоторые другие из
проблем, поднятых Гильбертом, например проблема раз-
решимости диофантовых уравнений. Диофантовым урав-
нением называется алгебраическое уравнение наподобие
х2 + </2 = гз/31
для которого ищутся целочисленные решения. Гильберт
поставил задачу придумать такой метод, который позво-
лял бы для каждого данного диофантова уравнения
определять, имеет оно решение или нет. Как показал
недавно Ю. Матиясевич7 (следуя более ранней работе
Дэвиса, Путнама и Робинсона), такого метода не сущест-
365
вует: вопрос о том, имеет или нет решение данное дио-
фантово уравнение, может оказаться неразрешимым.
Из доказательства Матиясевича вытекает любопыт-
ное следствие: существует многочлен
Р(*ь х2...х2з)
от 23 переменных такой, что если вместо переменных
подставлять в него положительные целые числа, будут
получаться простые числа и только они. Выходит, что
найдена «формула простых чисел»! 8 В принципе возмож-
но выписать этот многочлен в явном виде, однако прак-
тически очень трудно сделать больше, чем описать про-
цедуру, посредством которой можно было бы получить
явную формулу. И главное, весьма маловероятно, что
такая формула пригодится в теории простых чисел.
В гл. 9 мы упоминали о такой проблеме; является ли
мощность с множества действительных чисел кардиналь-
ным числом, следующим за jf > ? В этом состояла так
называемая гипотеза континуума. Проблему: верна или
нет гипотеза континуума —• Гильберт включил в свой
знаменитый список 23 наиболее актуальных, по его мне-
нию, проблем математики (хотя первым этот вопрос по-
ставил Кантор). Ответ был получен П. Коэном9 в 1963 г.
и оказался таким: и да, и нет. Гипотеза континуума не
зависит от других аксиом теории множеств. Вы можете
добавить аксиому, утверждающую, что гипотеза конти-
нуума верна, и теория не станет от этого противоречивой
(если она была непротиворечивой с самого начала!),
а можете добавить аксиому, утверждающую, что гипо-
теза континуума неверна, и это тоже не нарушит непро-
тиворечивости. Получился вариант неевклидовой геомет-
рии 20 в.: отвергая гипотезу континуума, можно строить
неканторовы теории множеств,
366
Эпилог
Быть может, следовало с самого начала понять, чтр
программа Гильберта обречена на неудачу. Уж слишком
она похожу на попытку поднять самого себя за шнурки
ботинок! Существуют ли вообще знания, истинные в
абсолютном смысле? Но в том-то и дело, что значение
работы Гёделя выходит за рамки подобных умозритель-
ных рассуждений: она доказывает невозможность ариф-
метического доказательства непротиворечивости самой
арифметики.
Это не значит, что нельзя найти другие пути доказа-
тельства непротиворечивости арифметики. И действи-
тельно, Генцен 10 доказал ее, но его методы основаны на
трансфинитной индукции. Я не стану объяснять здесь,
что это такое, но вопрос о непротиворечивости самой
трансфинитной индукции остается открытым.
Итак, математика по-прежнему стоит на шатком
основании, несмотря на все усилия укрепить его. Быть
может в один прекрасный день кто-нибудь найдет такое
неразрешимое противоречие, что рухнет все здание це-
ликом. Но даже тогда найдутся неутомимые математики,
которые, копаясь среди руин, что-то разыщут, как-то
починят и вернут к жизни все, что смогут.
Истина состоит в том, что интуиция всегда будет
сильнее логики. Если теоремы хорошо согласуются меж-
ду собой, углубляют понимание и дают пищу любозна-
тельности, никто не решится отбросить их только пото-
му, что они немного грешат против логики. В таких слу-
чаях всегда возникает ощущение, что можно изменить
саму логику, а теоремы лучше не трогать.
Когда-то Гаусс назвал математику «королевой
наук». Я скорее дал бы этому предмету титул короля.
И даже если когда-нибудь обнаружится, что этот король
голый, все равно он будет одет лучше, чем его при-
дворные.
867
Примечания
Глава I. Математика в целом
1. Мне рассказали, что в голландском языке привилось как раз
другое употребление: там, где мы говорим «множество», использует-
ся слово, соответствующее нашему слову «совокупность».
2. См. W. Sierpinski, On the congruence of sets and their equiva-
lence by finite decomposition, Lucknow University Studies, 1954,
а также E Kasner, J. Newman, Mathematics and the imagination,
Bell, 1949.
3. Чтобы решить в радикалах алгебраическое уравнение
ап хп+... + а^х 4- По=О,
нужно найти формулу, выражающую его корни через коэффициенты
а0, аь ..., ап с использованием только операций сложения, вычитания,
умножения, деления и извлечения корня. Примером служит стан-
дартная формула корней квадратного уравнения
ах2+йх + с=0,
имеющая вид
— b + Д/b2— 4ас
Было установлено, что для корней общего уравнения 5-й степени
(и выше) такой формулы не существует. Доказательство проводится
средствами теории Галуа и требует солидных познаний в области
абстрактной алгебры. Подробнее см. Е. Artin, Galois theory, Notre
Dame, 1959; I. T. Adamson, Introduction io field theory, Oliver and
Boyd, 1964; Ian Stewart, Galois theory, Chapman and Hall, 1973.
(См. также: M. M. Постников. Основы теории Галуа,— М., Физмат-
гиз, 1960.— Перев.)
Глава 2. Движение без перемещения
1. С. L. Dodgson, Euclid and his modern rivals, Macmillan, Lon-
don, 1879, p. 48. (4. Л. Доджсон более известен советскому читателю
под псевдонимом Льюиса Кэррола как автор книг «Алиса в стране
чудес» и «Алиса в Зазеркалье».— Перев.)
2. Остальное можно найти в работах: F. Cajory, The history of
368
Zeno’s arguments on motion, American Mathematical Monthly, 22,
1915, E. Kasner and J Newman, Mathematics and the imagination,
Bell, 1949; Russel, Mysticism and logic.
3 Поясним это утверждение. Пусть заданы три точки А, В, С
(все три различные и не лежащие на одной прямой) и три расстоя-
ния а, Ь, с. Тогда существует не более чем одна точка, лежащая на
расстояниях а от А, b от В и с от С. В самом деле, окружности ра-
диуса а с центром А и радиуса Ь с центром В пересекаются не более
чем в двух точках, которые находятся на разных расстояниях от С.
Значит, не более чем одна из них находится от С на расстоянии с.
Поскольку жесткие движения пе меняют расстояний, отсюда сле-
дует, что, зная, куда переходит какой-нибудь треугольник, мы знаем
эго и про все остальные точки.
В 3-мерном пространстве понадобится еще одна точка, так как
придется рассматривать сферы.
4. Это неудобство можно обойти, если писать преобразование
справа; XT плп (Х)Т. Тогда можно, по определению, положить
(X)EF=((X)E)F,
и все станет па свои места: ЕЕ будет означать «сначала Е, затем
F». К этому нужно немного привыкнуть (хотя такая запись для не-
которых преобразований давно применяется, например п!). Матема
тики часто пользуются этим приемом.
Глава 3. Кратчайшие пути в высшей арифметике
1. Хотя в нынешние времена мы впервые встречаемся с комплекс-
ными числами при решении квадратных уравнений вида
№+3=0,
когда обычная формула дает ответ х = + V—3, исторически комп-
лексные числа впервые привлекли к себе внимание при решении ку
бических уравнений.
Формула Тартальн для корней кубического уравнения
Xs + рх + q = 0
имеет вид
«-|/ ?+/£+£
В случае уравнения
х3 — 7х + 6 = 0 (,)
мы имеем р = —7, q — 6, и получается ответ
369
Юг
з/Т ’
где
С другой стороны, уравнение (*) можно разложить на мно-
жители:
(х—1) (х—2) (х+3) =0,
и, значит, его корнями являются х=1, 2 и —3.
Чтобы «примирить» эти два результата, допустим, что с i можно
обращаться, как с неким числом. Тогда можно извлечь кубические
корни. В самом деле,
2i 3 • 2i 3 + 4i2 ( 8i3
1 + УТ/ = 1 + У~+ 3 + 3 УТ =
= 1-4 +
18 — 8
ЗТ/Т
i = — 3
10t
зут
и аналогично
1 21 \3 о 10t'
Уз) зУ з '
Подставив эти значения кубических корней в выражения для х, по-
лучим
т. е. один из корней уравнения. А где два других? Они получатся
при другом выборе значений кубического корня: в области комплекс-
ных чисел каждая величина имеет три кубических корня.
Итак, использование комплексных чисел позволило прийти к пра-
вильному результату в области действительных чисел. Это впечат-
ляющее достижение подсказывало, что комплексные числа стоит
изучать
2. Эта фраза — образец стиля современных школьных учеб-
ников.
3. Это проще простого. Мы вольны давать любые определения,
^ажно только потом строго их придерживаться. Во всяком случае
умножение или вычитание натуральных или отрицательных чисел
вводятся тем же методом: забудьте, откуда они возникли, действуй-
те по аналогии и затем убедитесь, что получаются согласованные
результаты.
4. В понятии сравнимости есть нечто общее с конгруэнтностью
треугольников: в обоих случаях не принимаются во внимание раз-
370
.чичия определенного вида. Треугольники одинаковы, если они по-
лучаются один из другого жестким движением, а числа — если дают
один и тот же остаток при делении на фиксированный модуль.
5. Нетрудно видеть, что если k не является степенью числа 2,
то 2'4-1—не простое. Быть может, именно это обстоятельство
ввело в заблуждение Ферма. Из всех сделанных Ферма недоказан-
ных утверждений только про одно известно, что оно неверно, и надо
сказать, оно же — единственное, в котором Ферма сомневался.
6. Е. Т. Bell, Men of Mathematics, v. 1, Penguin Books, 1965, p. 73.
7. Cm. Hardy and Wright, An introduction to the theory of num-
bers, Oxford University Press, 1962, ch. 6
8. «Последняя теорема» Ферма (называется так потому, что
это его последняя теорема, о которой еще неизвестно, верна она
или нет) утверждает, что при целом и>2 уравнение
xn+</n=zn
не имеет ненулевых целочисленных решений. При ге=2 существует
бесконечно много решений, например 32+42=52. Известно, что при
л^25 ООО теорема верна (см. Selfridge and Pollock, Notices of the
American Mathematical Society, 11, 1964, p. 97).
Глава 4. Язык множеств
1. Символ € представляет собой стилизованный вариант гре-
ческой буквы е (эпсилон) — начальной буквы слова «элемент». Во
многих книгах (особенно более старых) использована сама эта
буква.
2. А. А. Милн. Винни-Пух и все остальные. М., 1960, гл. 7.
3. Это снова последняя теорема Ферма См. примечание 8 к
гл. 3.
4. В некоторых арифметических теориях 0 определяется как 0,
1 — как {0}, 2 — как {0,{0}} и т. д. Поэтому утверждение, что 0
и 0 — разные вещи, не совсем верно. Однако мы думаем о них,
несомненно, по-разному, а здесь нам только это и важно.
5. Символ с произошел от но был специально искривлен,
чтобы напомнить, что речь идет не о числах, а о множествах. В не-
которых книгах вместо него используется символ с.
6. Обозначения N, R и С происходят от начальных букв латин-
ских названий соответствующих чисел. Буква Z — от немецкого
слова Zahl — число. Обозначение Q, я думаю, произошло от слова
quotient -— отношение. Иногда вместо N используют букву Р — от
слова positive (положительный).
7. Рассмотрим множество С = {{1, 2},{3, 4}}. Тогда 1 С {1, 2}
и {1, 2}ёС, но ЙС.
371
8. Единственное место, где я видел напечатанными таблицы
принадлежности,— это статья «Venn Vili They Ever Learn?» Фрэнка
Эллиса (Frank Eliis, Manifold 6, 1970, p. 44).
9. Булева алгебра применяется при разработке логических схем
компьютеров (см., например, Rutherford, Introduction to lattice theo-
ry, Oliver and Boyd, 1965, pp. 31—40, 58—74). Кроме связи с тео-
рией множеств, она имеет мало отношения к основному руслу мате-
матики. Тем не менее существует глубокая теория булевых алгебр.
См. Р. R. Haimos, Lectures on Boolean algebras, Van Nostrand, 1963.
10. Существует даже такая игра «visli» (сокращение от «vicious
circle»- порочный круг): берут наугад какое-нибудь слово в тол-
ковом словаре, из его дефиниции выбирают какое-нибудь другое
слово и т. д. Выигрывает тот, кто раньше вернется к исходному
слову.
I1. Первое удовлетворительное определение упорядоченной пары
было дано К. Куратовским в 1921 г. Трудность состояла в том, чтобы
избежать ссылок на способ изображения такой пары в виде (а, Ь).
Нельзя говорить «а — левый элемент», потому что «левый» не явля-
ется понятием теории множеств. Ранние философы совершенно за-
путались в этом вопросе (см. Russel, The principles oj Mathema-
tics, 1903).
«Является ли упорядочение свойством а?» Нет, оно зависит
также и от Ь, ибо, скажем, упорядочения (1, 2) и (3, 1) различны.
«Является ли оно свойством й?» Нет, по той же причине. «Тогда
это свойство а и Ы» Тоже нет, потому что а и b не отличается от
b и а, и тогда получается, что (а, Ь) и (Ь, а) — одно и то же.
Требуется как-то избавиться от симметрии между а и Ь. Фило-
софы оказались здесь бессильны, потому что не понимали разницы
между х и {х}. Они не хотели различать эти вещи. Однако стоит
только осознать эту разницу, как открывается целый ряд разнооб-
разных путей решения задачи. Например, можно, по определению,
положить
(а, Ь)={{а}, {а, Ь}}.
Асимметрия в правой части гарантирует, что (а, Ь) равно (с, d)
тогда и только тогда, когда а —с и b=d-, это вытекает из элементар-
ных теоретико-множественных соображений. Поскольку в этом со-
стоит единственное важное свойство упорядоченных пар, такое опре-
деление является вполне подходящим, хотя психологически не осо-
бенно привлекательным.
Глава 5. Что такое функция?
1. Используя понятие упорядоченной пары можно дать чисто
теоретико-множественное определение функции. Обычно оно с трудом
372
воспринимается учащимися, ибо па первый взгляд лишено всякой
связи с идеей «правила» и, кроме того, очень непривычно, поскольку
до этого они встречались лишь с числовыми функциями, которые
задавались формулами.
Проблема состоит в том, чтобы построить единый объект f,
который однозначным образом связывает с каждым элементом х
области определения соответствующее f(x) Для каждого конкрет-
ного х это достаточно хорошо осуществляет упорядоченная пара
(*,
если, например, у нас есть пара (7, 24), то мы знаем, что /(7) =24.
Чтобы задать f на всей области определения D, можно воспользо-
ваться множеством, состоящим пз всех пар (х, f(x)), где х про-
бегает всю область D.
Если Т — множество, в котором лежат все f(x), то множество
упорядоченных пар (х, f(x)) является подмножеством декартова
произведения D'/. T. В силу свойства (3) функций, это подмножество
удовлетворяет двум условиям:
1) для всякого х £ 7) существует y(LT такое, что пара (х, у)
содержится в рассматриваемом подмножестве;
2) если (х, у) и (х, г) содержатся в этом подмножестве, то
f/=z.
Условие (1) говорит о том, что [(х) определено для всех х,
а условие (2) обеспечивает однозначность.
Теперь начнем с конца. Для заданных множеств D и Т опреде-
лим функцию из D в Т как подмножество f произведения D X Т,
удовлетворяющее условиям 1 и 2. Если нам задано х С D, мы най-
дем f (х) так: сначала найдем какое-нибудь у, для которого (х, у) g f
(это возможно в силу 1), а затем положим
f(x)=y,
что однозначно определяет f(x) в силу условия 2.
Иными словами, любое «правило» эквивалентно некоторому мно-
жеству упорядоченных пар. Это ие сразу очевидно (было бы ужас-
но, если бы все на свете стало очевидным), однако, как говорил
один известный политик, «это делает свое дело».
Дальнейшую информацию можно получить из книг: Halnios,
Naive set theory. Van Nostrand, 1964; Hamilton and Landin, Set
theory, Prentice Hall, 196 k
Глава 6. Основы абстрактной алгебры
1. См. примечание 3 к гл. 1.
2. См. Rouse Ball, Mathematical recreations and essays, Macmil-
lan 1959, ch. 12. (См. также: Ф. Кымпан. История, числа л.— М„
Наука, 1971, с. 214,— Перев.)
373
3. Линдеман доказал свою теорему в 1832 г. См. Stewart, Galois
theory, Chapman and Hall, 1973, p. 74. (См. также указанную выше
книгу Ф. Кымпана.— Перев.)
4. Читателям, которые незнакомы с комплексными числами, реко-
мендуется обратиться к книге W. W. Sawyer, Mathematician’s delight.
Penguin Books, 1943. (См. также: А. И. Маркушевич. Комплексные
числа и конформные отображения.— М., Физматгиз, 1960.— Перев.)
5. См. de Bruijn, A Solitaire game and its relation to a finite
field, Journal of recreational Mathematics, 5, 1972, p 133.
Глава 7. Симметрия; понятие группы
1. См., например, Ledermann, Introduction to group theory, ОИ«
ver and Boyd, 1973.
В журнале Bulletin of the London Mathematical Society l,pp. 79—•
88, 1969, опубликована статья Конвея (J. H. Conway) под названием
«Группа порядка 8 315 553 613 086 720 000». Такую группу едва ли
можно определить при помощи таблицы умножения! (Однако не сле-
дует думать, что математики специально проводят время, строя все
большие и большие группы. Сам по себе размер группы Конвея
неважен, важны те несколько замечательных свойств, которыми она
обладает.)
2. См. Klein, Lectures on the icosahedron and the solution of
equations of the fifth degree, Kegan Paul, 1913 (имеется также изда-
ние 1956 г.).
3. См. Г. С. М. Кокстер. Введение в геометрию. Пер. с англ.—
М., 1966, с. 404. В этой интересной книге содержатся также сведения
о 17 типах симметрии на плоскости (см. с. 85—99).
Глава 8. Аксиоматика
1. В реальном мире точки в конце концов становятся настолько
близкими, что различить их невозможно. Однако можно пустить
в ход алгебру. Рассмотрим для простоты радиальную прямую и пред-
положим, что радиус Г равен d. Любая точка, лежащая строго
внутри Г, находится от центра на некотором расстоянии е, где е
строго меньше d. Отсюда следует, что точка, находящаяся от центра
на расстоянии, скажем, (e+d)/2, все еще лежит строго внутри Г,
хотя уже дальше от центра, чем на е. В самом деле,
d — -j- (е + d) = -у (d — е) > 0, -у- (е + d) — е = (d — е) > 0.
2. У. У. Сойер. Прелюдия, к математике. Пер. с англ.— М., 1965,
с. 135.
374
Глава 9. Счет. Понятие о бесконечном
1. С точностью до некоторых теоретико-множественных трудно-
стей, о которых пойдет речь в гл. 20.
2, Отнюдь не без тяжкого труда! См. Hamilton and Landin, Set
theory, Prentice Hal!, 1961, pp. 133—238.
3. Birkhoff and MacLane, A survey of modern algebra, Macmillan,
1963, p. 362.
Глава 10. Топология
1. В предположении, что все материалы, из которых сделаны
эти предметы, имеют толщину, а все внутренние полости чем-нибудь
заполнены, получим такую классификацию: А, Е, G, 1 — шары; С,
D и F — заполненные торы; В, Н — двойные заполненные торы.
Если (как это чаще бывает в реальной жизни) A, D и Е полые внут-
ри, а коробка / пустая, то различных топологических типов стано-
вится больше: А, Е, I — сферы; G — по-прежнему шар; С и F—
заполненные торы; D — полый тор; В и Н — по-прежнему двойные
заполненные торы. Если придумать еще больше подробностей, на-
пример дырочки в хлебе, придется делать еще больше различий.
2. У Дж. Гамова есть научно-фантастический рассказ (G. Ga-
mow, The heart on the other side, in The expert dreamers, Gollancz,
1963), в котором предполагается, что реальная Вселенная неориенти-
руема. Герой пытается произвести революцию в обувной промышлен-
ности, но попадает в беду, когда все белки его организма превра-
щаются в свои зеркально симметричные формы.
Ориентируема или нет физическая Вселенная, сказать трудно.
Дело здесь в том, что ориентируемость — это такое свойство, кото-
рое топологи называют «глобальным»: чтобы его обнаружить, нужно
посмотреть на все пространство. Лента Мёбиуса локально почти не
отличается от цилиндра: вблизи каждой точки их свойства практи-
чески одинаковы. Вселенная так велика, что у нас очень мало све-
дений о ее глобальной структуре. Но если астрономические наблю-
дения, о которых говорилось в конце гл. 8, подтвердятся, то она,
скорее всего, неориентируема!
Глава 11. Умный в гору не пойдет
1. См. Ore, The four-colour problem, Academic Press, 1967.
2. [По-видимому, автор настоящей книги был сильно огорчен,
когда узнал, что проблему четырех красок удалось решить при по-
375
мощи компьютера; см. К. Appel and W. Flaken, Every planar map is
four colorable. Bulletin of the American Mathematical Society, 82,
1976. См. также: Наука и жизнь, № 3, 1979, с. 80.— Перев.)
Глава 12. Топологические инварианты
1. См. Е. С. Zeeman, Introduction to topology, Penguin Books.
Я признателен проф. Зимапу за разрешение изложить здесь некото-
рые его идеи.
2. См. статьи Рингеля и Янгса в Proceedings of the National
Academy of Science (USA), 1968, а также книгу: A. T. White Graphs,
groups and surfaces, Amsterdam, London and New York, 1973. (Ha
русский язык переведена книга Г. Рингеля «Теорема о раскраске
карт».— М., 1977. См., кроме того, примечание 2 к гл. 11.— Перев.)
Глава 13. Алгебраическая топология
1. Другой важный класс алгебраических инвариантов образуют
группы гомологий, впервые увидевшие свет в рудиментарной число-
вой форме под названием числа Бени.
Глава 14. В гиперпростраиство
1. См. К. Рурк, Б. Сандерсон. Введение в кусочно линейную то-
пологию. Пер. с англ.— М., 1974.
Глава 15. Линейная алгебра
1. Учебников по линейной алгебре очень много. Хорошее неслож-
ное введение имеется в книге У. Сойера «Путь в современную ма-
тематику». (Пер. с англ.— М., 1972.) С практи щекой точки зрения
много полезного содержится в книге: Fletcher, Linear algebra through
its applications, Van Nostrand, 1973. (См. также: А. И. Мальцев.
Основы линейной алгебры.— М., Наука, 1970; А. Г. Курош. Кура
высшей алгебры.— М., Физматгиз, 1963.— Перев.)
2. У. У. Сойер. Прелюдия к математике. Пер. с англ.— М.,
1965, гл. 8.
Глава 16. Вещественный анализ
1. Подозрительно нечеткие фразы типа «сколь угодно малый»
или «достаточно большой» иа самом деле имеют вполне точный
смысл. Первая означает, что, каково бы ни было положительное
число е, мы можем сделать Ьп—1 меньше е. Для этого нам нужно
376
взять п большим некоторого числа N, зависящего от е. Таким обра-
зом, точная формулировка сходимости последовательности такова:
hn стремится к пределу I, если для всякого 8>0 существует такое N,
что при всех n>N
2. Перестановка членов ряда предполагает справедливость тако-
го закона, который нарушается даже для некоторых сходящихся
рядов,— это наглядно демонстрирует приведенный парадокс!
Для сходящихся рядов с положительными членами перестановка
членов допустима.
3. Как и в примечании 1, от кажущейся нечеткости можно изба-
виться, если пользоваться обычным формальным определением:
функция f непрерывна в точке х, если для всякого е>0 найдется
такое б>0, что при
|х-р| <6
мы имеем
Отсюда понятно, почему учащиеся считают анализ трудным. Ведь
такое определение непрерывности весьма далеко от интуитивного
представления о непрерывной кривой как «состоящей из одного ку-
ска». Однако е-6-определение окупается тем, что позволяет доказывать
непрерывность различных функций, таких, как х2 или sin х; поэтому
его и применяют. Придумать более простой подход к этому вопросу,
не впадая при этом в серьезные логические ошибки, никому пока
не удалось. Отсюда, разумеется, не следует делать вывод, что при-
меняемая сейчас теория непрерывности — последнее слово в этой
области.
Глава 17. Теория вероятностей
1. См. W. Weaver, Lady Luck, Doubleday, 1963, и D. Huff, How
to take a chance, Penguin Books, 1965.
2. Рассмотрим, к примеру, опыт, состоящий в том, что выби-
рается наугад число на действительной прямой. Вероятность выбрать
любое конкретное число, скажем 2 или л, равна 0. Тем не менее
это событие — выбор числа 2 или числа л — не является невоз-
можным.
Глава 18. Компьютеры и их применение
1. Большое количество интересного материала имеется в сбор-
нике Computers and computation, Freeman, San Francisco.
2. По поводу, языка ФОРТРАН см. Kreitzberg and Schneiderman,
377
The elements of Fortran style, New York, 1972, или McCracken, A guide
to Fortran programming, New York, 1961. По поводу языка АЛГОЛ
см. Wooldridge and Ratcliffe, An introduction to Algol programming,
English Universities Press, 1963.
Глава 19. Применения современной математики
1. См., например, Allen, Mathematical analysis for economists,
Macmillan, 1970, и A. Battersby, Mathematics in Management, Pen-
guin Books, 1966.
2. Подробнее об этом см. в статье Ф, Дайсона «Математика в
физических науках».— Математика в современном мире, М., 1967,
с. 111—127. (Сборник представляет собой перевод на русский язык
тематического номера журнала Scientific American.— Перев.)
3. См. R. Tom, Stabilite structurelie et morphogenese, Reading,
Massachusetts, 1972 (готовится английский перевод).
4. См. Poston and Woodcock, Zeeman's catastrophe machine,
Proceedings of the Cambridge Philosophical Society, 74, 1973,
pp. 217—226. (На русском языке описание машины Зимана приво-
дится в журнале «Наука и жизнь», 1977, № 12, с. 82—87. Кроме
того, готовится русский перевод посвященной теории катастроф
книги Т. Постона и Я. Стюарта «Теория катастроф и ее прило-
жения».— Перев.)
5. Большое количество сделанных компьютером рисунков ка-
тастроф приводится в книге: Woodcock and Poston, A geometrical
study of the elementary catastrophes, Lecture Notes in Mathematics,
Springer, 1974. (См. также T. Брекер, Л. Ландер. Дифференцируе-
мые ростки и катастрофы. Перевод с англ.— М., 1977.— Перев.)
Глава 20. Основания математики
1. См. A. Phillips, Turning a surface inside out, Scientific Ameri-
can, May 1966, pp. 112—120.
2. Об их именах мы скромно умолчим!
3. Который бреет всех тех, кто сам не бреется. Кто побреет
брадобрея?
4. А именно, теория фон Неймана — Бернайса — Гёделя. См.
Bernays and Fraenkel, Axiomatic set theory, North Holland, 1958,
p. 31
5. Uber forma! unentscheidbare Satze der Principia Mathematica
und verwandter Systeme I, Monatshefte file Mathematik und Physik
38, 1931, pp>. 173—198. См. примечание 6.
6. Статья Гёделя вместе с комментариями вышла под ориги-
нальным названием в английском переводе (Oliver and Boyd, 1962),
378
7. См. 10. В. Матиясевич. Диофантовость перечислимых мно-
жеств. ДАН СССР, 191, 1970, с. 279—282. Диофантово представле-
ние множеств простых чисел. ДАН СССР, 196, 1971, с. 770—773.
8. На поиски формул, дающих все простые числа или хотя бы
принимающих только простые значения, были затрачены огромные
усилия. Это пытался сделать Ферма, предложивший формулу
22п+1,
а также Эйлер. Его формула
n2-79п + 1601
принимает простые значения при п=0, .... 79 (однако при я=80
получается составное число). Разные истолкования слова «формула»
дают большой простор всякого рода «жульничеству». См. об этом
Dudley, History of a Formula for Primes, American Mathematical
Monthly 76, 1969 p. 23.
Такие формулы вряд ли пригодятся при изучении простых чи-
сел, потому что из них мало что можно увидеть: как правило, они
еще более «неподатливы», чем простое бесформульное определение.
Результаты Матиясевича свидетельствуют скорее о сложности мно-
гочленов, чем о «доступности» простых чисел.
9. На самом деле Гёдель доказал, что гипотеза континуума не
приводит к противоречивости теории множеств (см. К. Гёдель, Со-
вместимость аксиомы выбора и обобщенной континуум-гипотезы с
аксиомами теории множеств.— Успехи математических паук, 3, 1948,
Кб 1, с. 96—149). Коэн же доказал, что предположение о невер-
ности гипотезы континуума тоже не приводит к противоречиям
(П. Дж. Коэн. Теория множеств и континуум-гипотеза. Пер. с
англ.— М., 1969).
10. См. Mendelson, Introduction to mathematical logic, Van
Nostrand, 1964.
Обозначения
(mod с) € сравнимость (целых чисел). по модулю с. принадлежность (элемента множеству). множество, состоящее из элементов ...
W-J 0 с N Z R С и л / 5' лхв (а, Ь) R’ х! f-.D-+T fg Id К л W RM £ Ж / х', X-1 «0 • а^₽ а<р множество всех х таких, что ... пустое множество. включение множеств. множество натуральных чисел. множество целых чисел. множество действительных чисел. множество комплексных чисел. объединение. пересечение. разность (множеств), дополнение множества S. декартово произведение множеств, упорядоченная пара. евклидова плоскость. х факториал (= 1 -2 - 3 •... (х— 1) • х). функция [ из D в Т. композиция функций. тождественная функция па D. множество чисел, которые можно построить» 3,14159... множество целых чисел, сравнимых с х. множество многочленов от переменной х. знак суммирования. операция в группе. единичный элемент группы, элемент, обратный х. бесконечные кардинальные числа. неравенство для мощностей. строгое неравенство для мощностей.
380
с е И мощность множества действительных чисел 2.7J828... абсолютная величина х (=л, если х^О, =— х
Г В Р x(S) l(N) [-.] Р*<7 М R3, R4, лп(3) С 5) (?) (?) если х<0). число граней карты. число вершин карты. число рсбер карты. эйлерова характеристика поверхности S. эйлерова характеристика графа N. наибольшее целое, не превосходящее... композиция путей. гомотопический класс пути р. Фундаментальная группа пространства 3. К , R" евклидовы пространства размерности 3, 4, 5, п. п-я гомотопическая группа пространства S. матириа. вектор-столбец. вероятность события Е. биномиальный коэффициент.
В м А [а :/] R(n) множество Рассела. аксиоматическая теория множеств. обычная арифметика. результат подстановки 1 в а n-ii сайн в гёделевской нумерации.
Оглавление
Предисловие к русскому изданию 3
Предисловие 6
Благодарности 8
Глава 1. Математика в целом 9
Глава 2. Движение без перемещения 18
Глава 3. Кратчайшие пути в высшей арифметике 38
Глава 4. Язык множеств 58
Глава 5. Что такое функция? 82
Глава 6. Основы абстрактной алгебры 98
Глава 7. Симметрия: понятие группы 122
Глава 8. Аксиоматика 145
Глава 9. Счет. Понятие о бесконечном 162
Глава 10. Топология 184
Глава 11. Умный в гору не пойдет 199
Глава 12. Топологические инварианты 214
Глава 13. Алгебраическая топология 231
Глава 14. В гиперпространство 244
Глава 15. Линейная алгебра 263
Глава 16. Вещественный анализ 280
Глава 17. Теория вероятностей 297
Глава 18. Компьютеры и их применение 312
Глава 19. Применения современной математики 329
Глава 20. Основания математики 351
Примечания 368
Обозначения 380
382
Ян Стюарт
КОНЦЕПЦИИ СОВРЕМЕННОЙ МАТЕМАТИКИ
Редактор Л. С. Румянцева
Мл. редактор Т. С. Капелян
Худож. редактор Ю. С. Сергачев
Техн, редактор М. Н. Кислякова
Корректор В. В. Неверко
ИБ 621
Сдано в набор 04.07.79. Подписано в печать 20.11.79. Формат
70Х108’/з2. Бумага типогр. № 2. Гарнитура литературная. Высо-
кая печать. Усл. печ. л. 16,8. Уч.-изд. л. 15,52. Тираж 35 000
экз. Изд. № 77-127. Зак. 2386. Цена 75 коп.
Издательство «Вышэйшая школа» Государственного комитета
Белорусской ССР по делам издательств, полиграфии и книж-
ной торговли. 220048, Минск, Парковая магистраль. II.
Полиграфический комбинат им. Я. Кол аса Государственного ко-
митета Белорусской ССР по делам издательств, полиграфии и
книжной торговли. 220005, Минск, ул. Красная» 23.
Стюарт fl.
С88 Концепции современной математики. /Пер. с
англ. Н. И. Плужниковой и Г. М. Цукерман.— Мн
Выш. школа, 1980.— 384 с., ил.
75 к.
В увлекательной форме с помощью множества примеров рассмаг
риваются цели, методы, проблемы и области применения многих ва
нейших отраслей современной математики. Для понимания основы;
идей достаточно знания школьного курса математики.
Предназначена для широкого круга читателей.
с 2020 009 98—70 1702010000
М 304(05)—80
ББК 22.1
51
КОНЦЕПЦИИ
СОВРЕМЕННОЙ
МАТЕМАТИКИ
Ян Стюарт