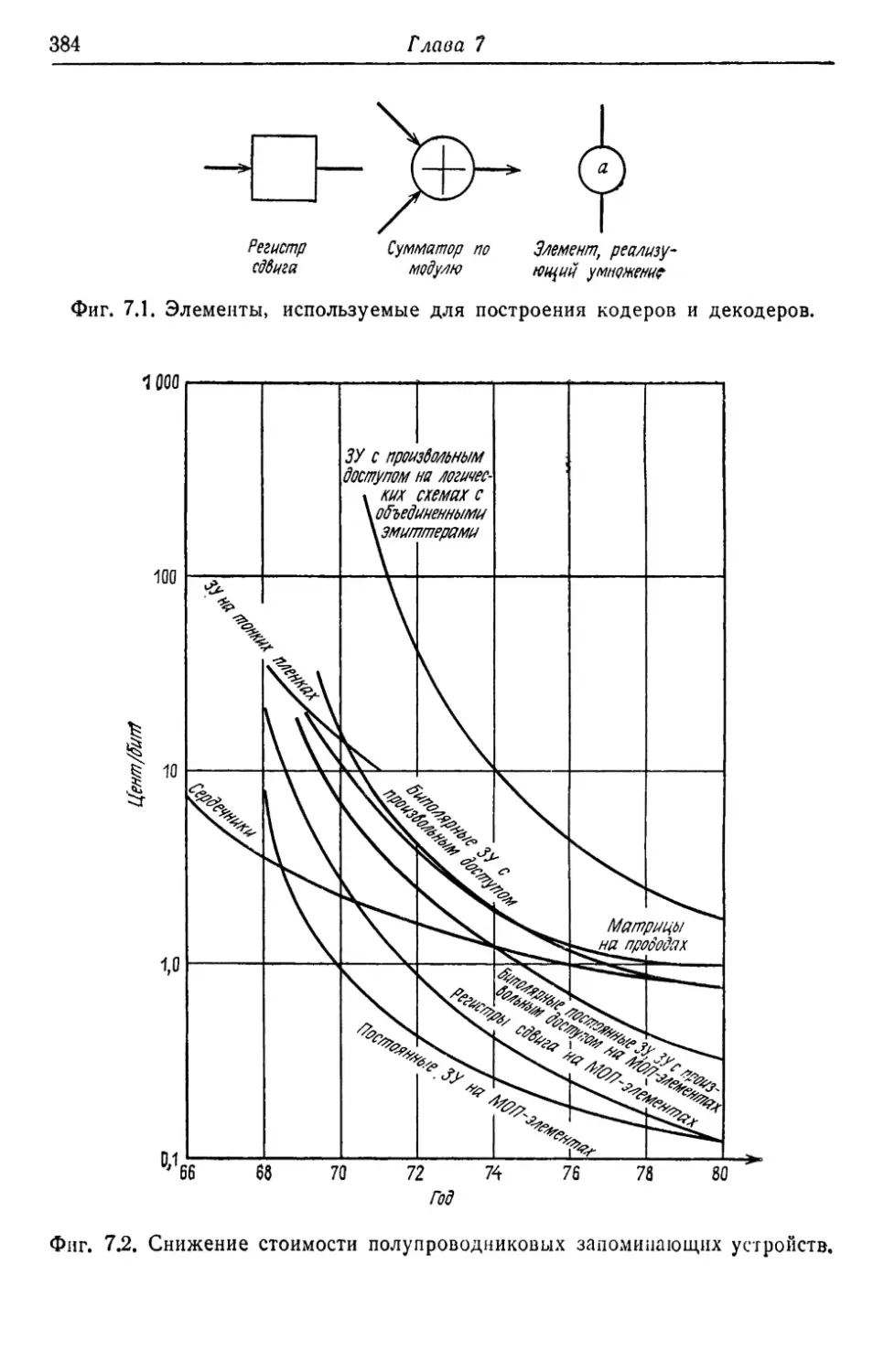
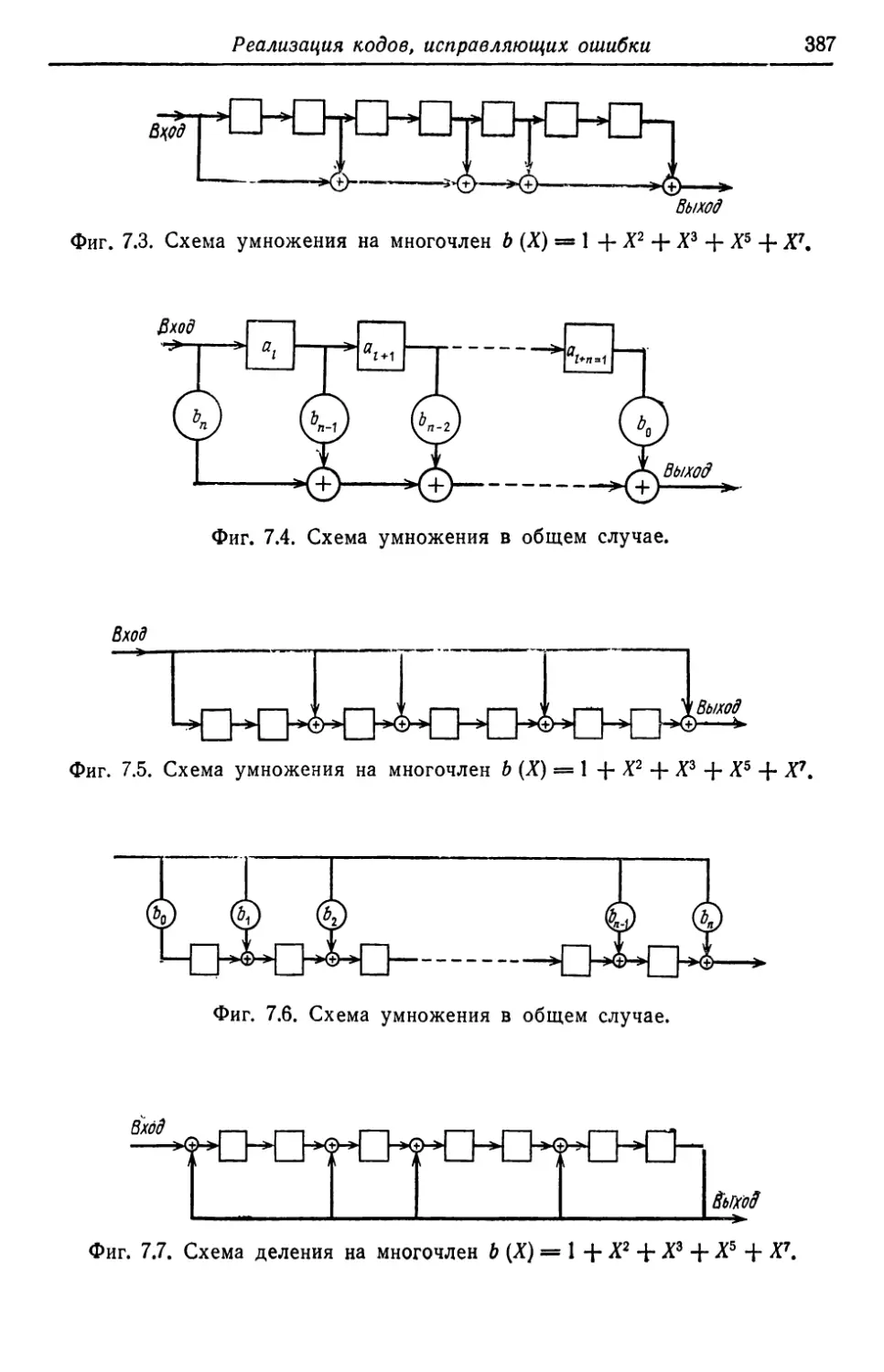
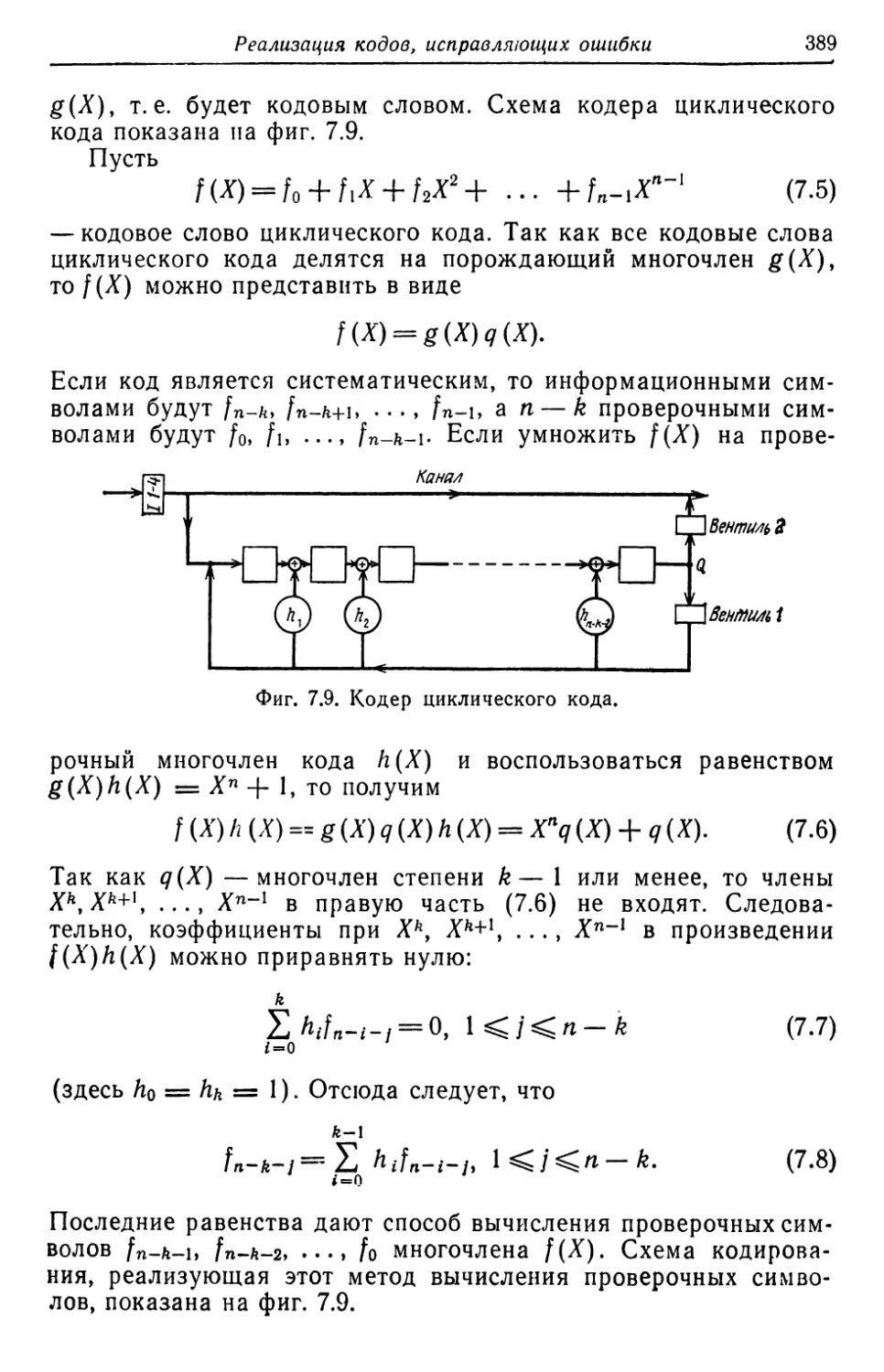
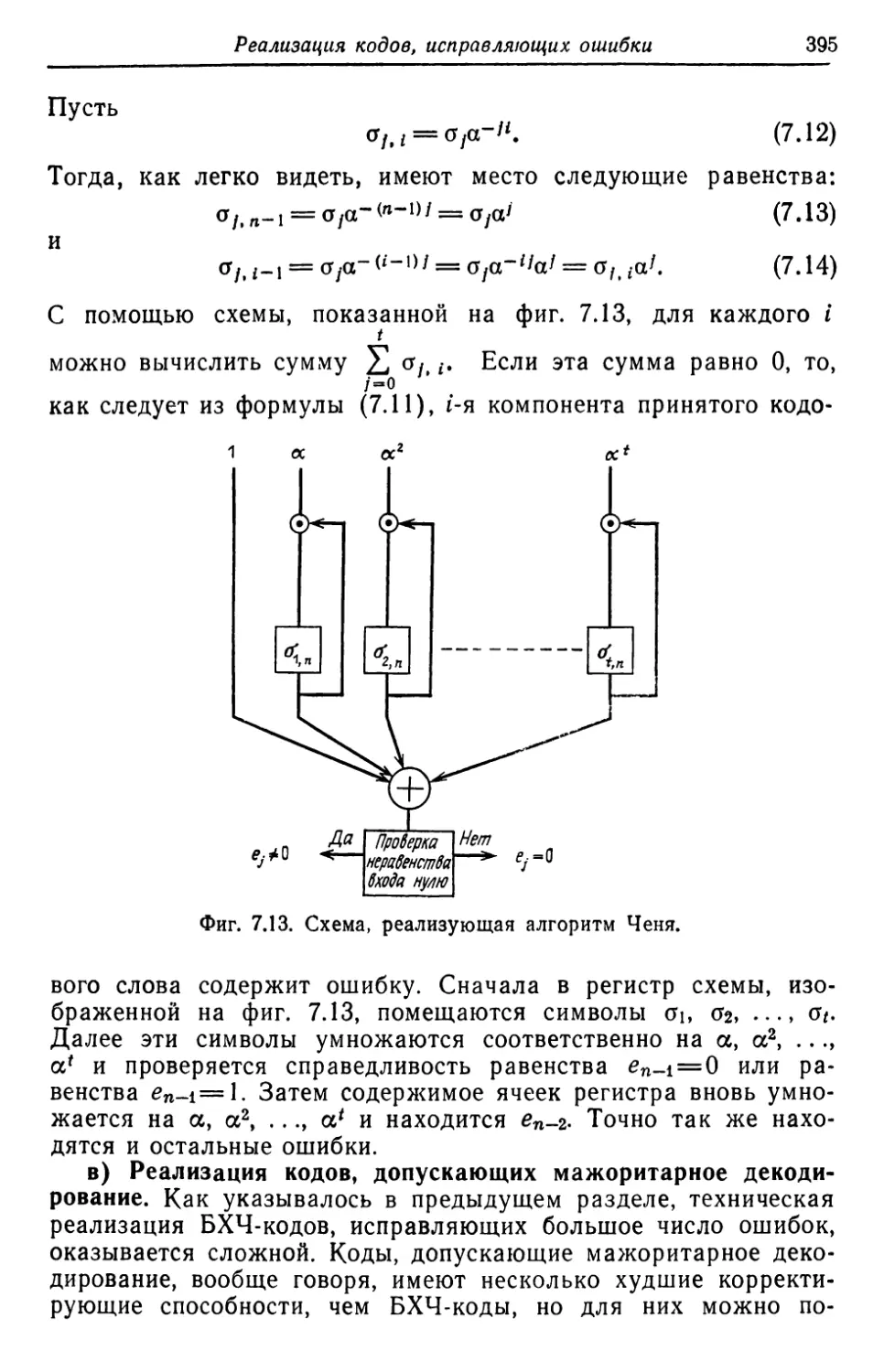
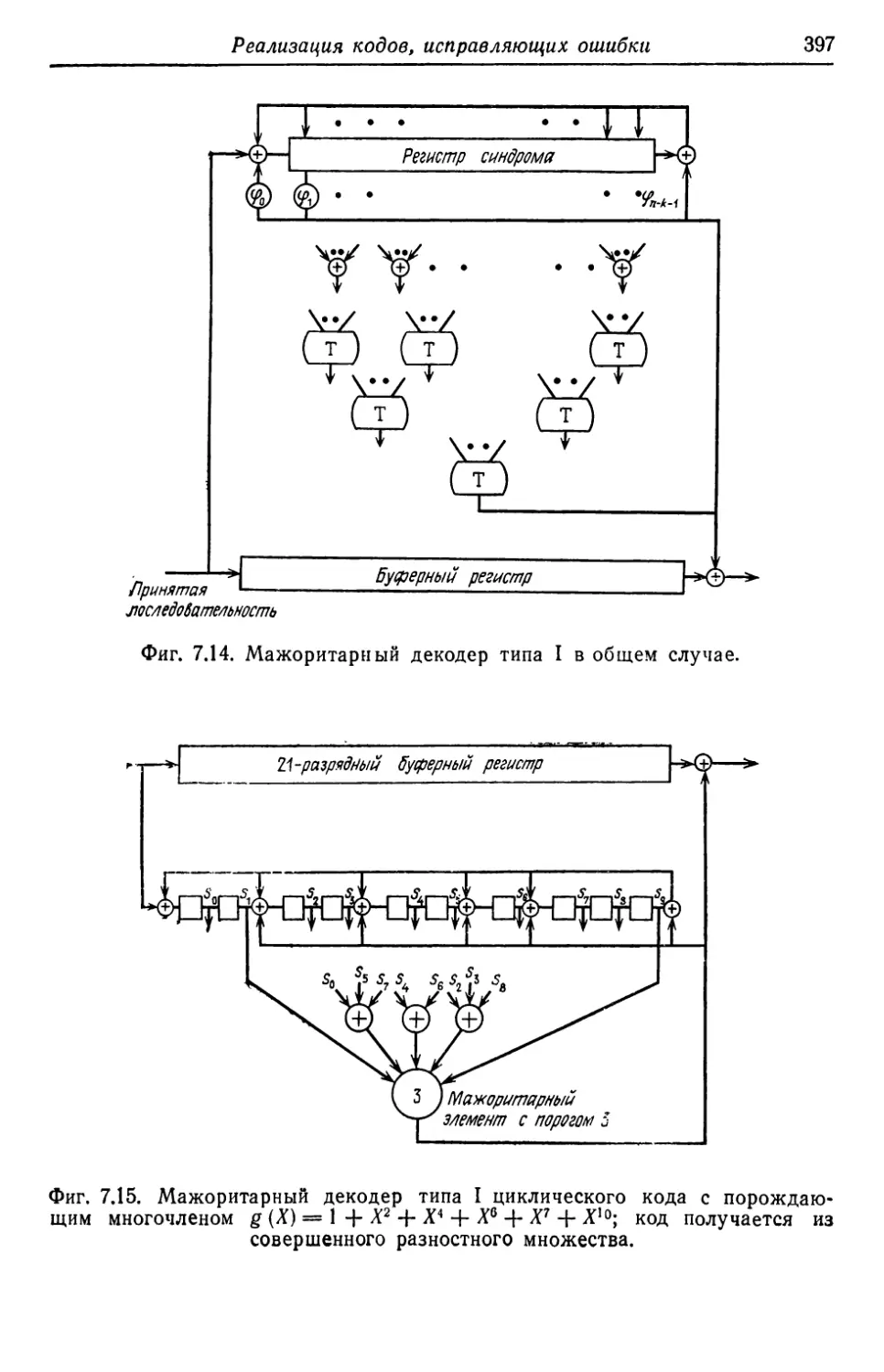
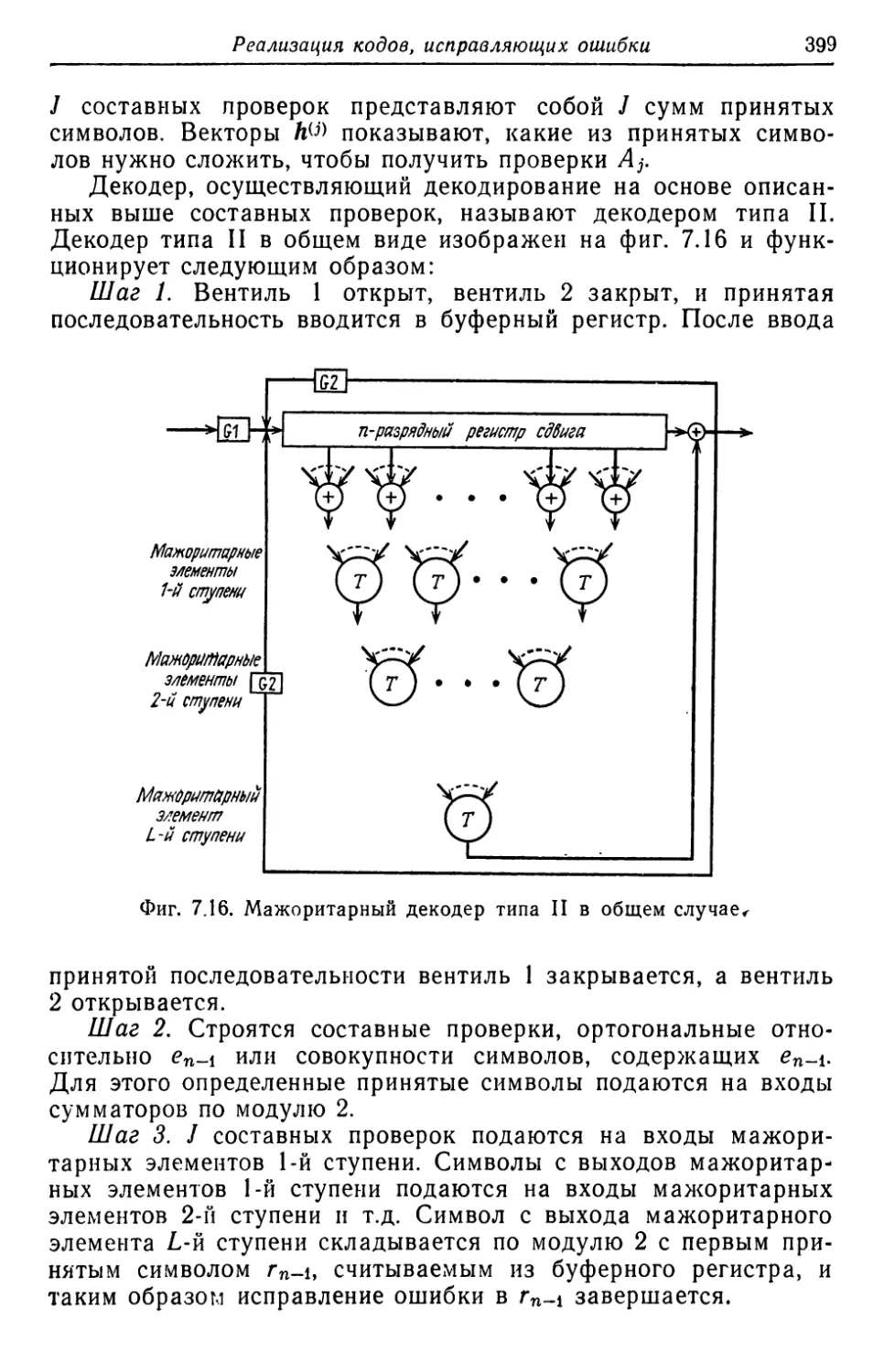
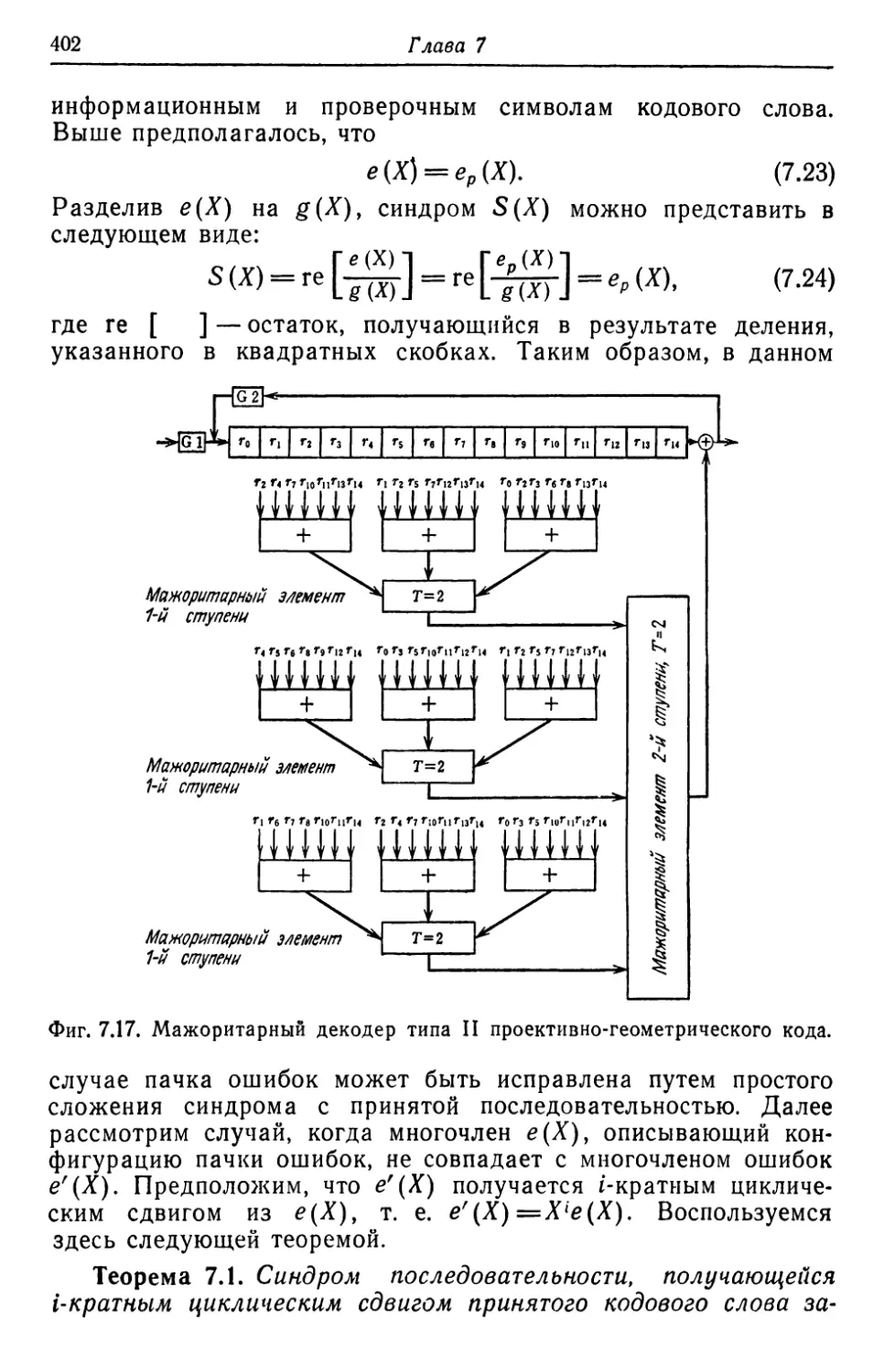
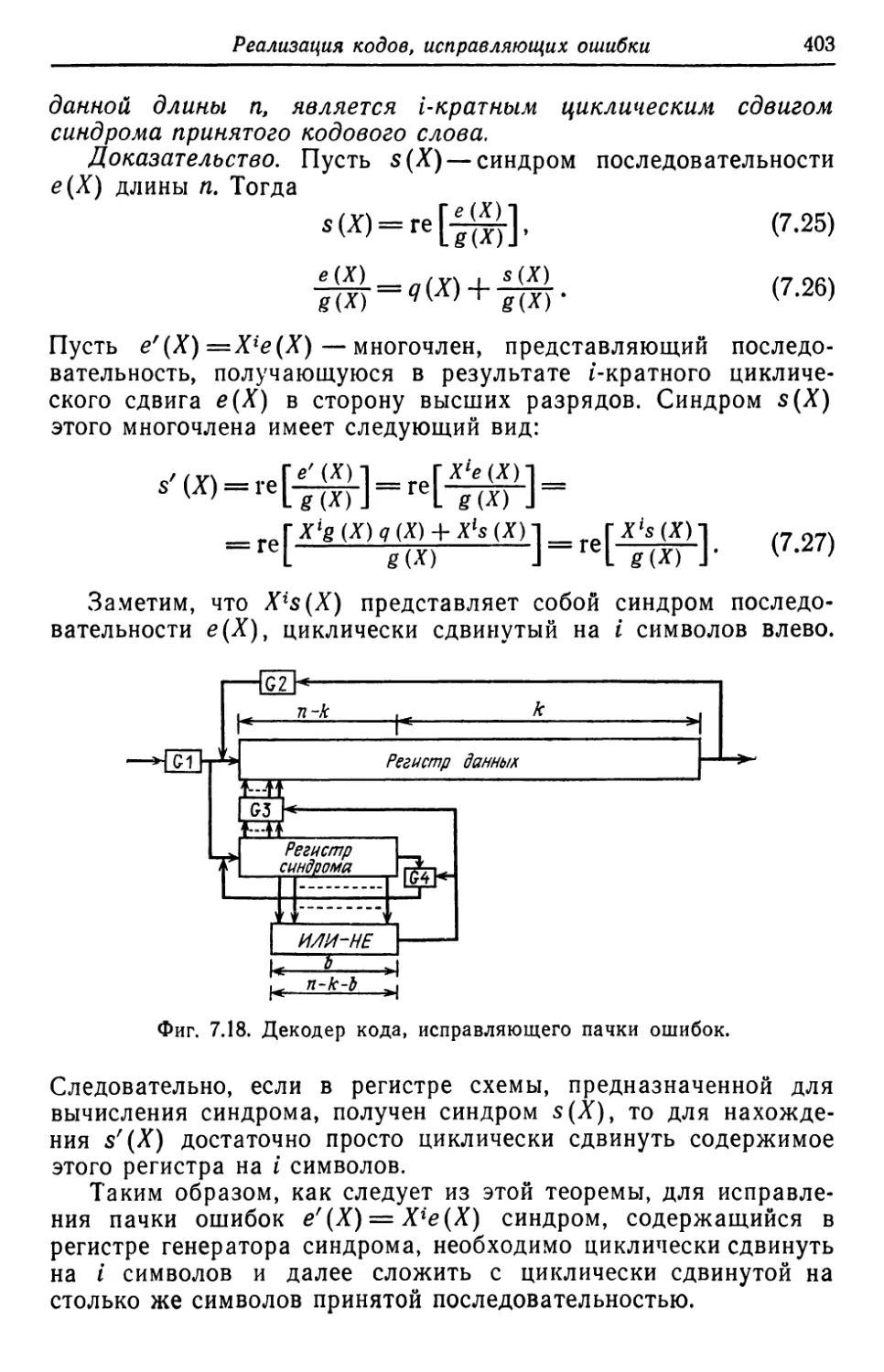
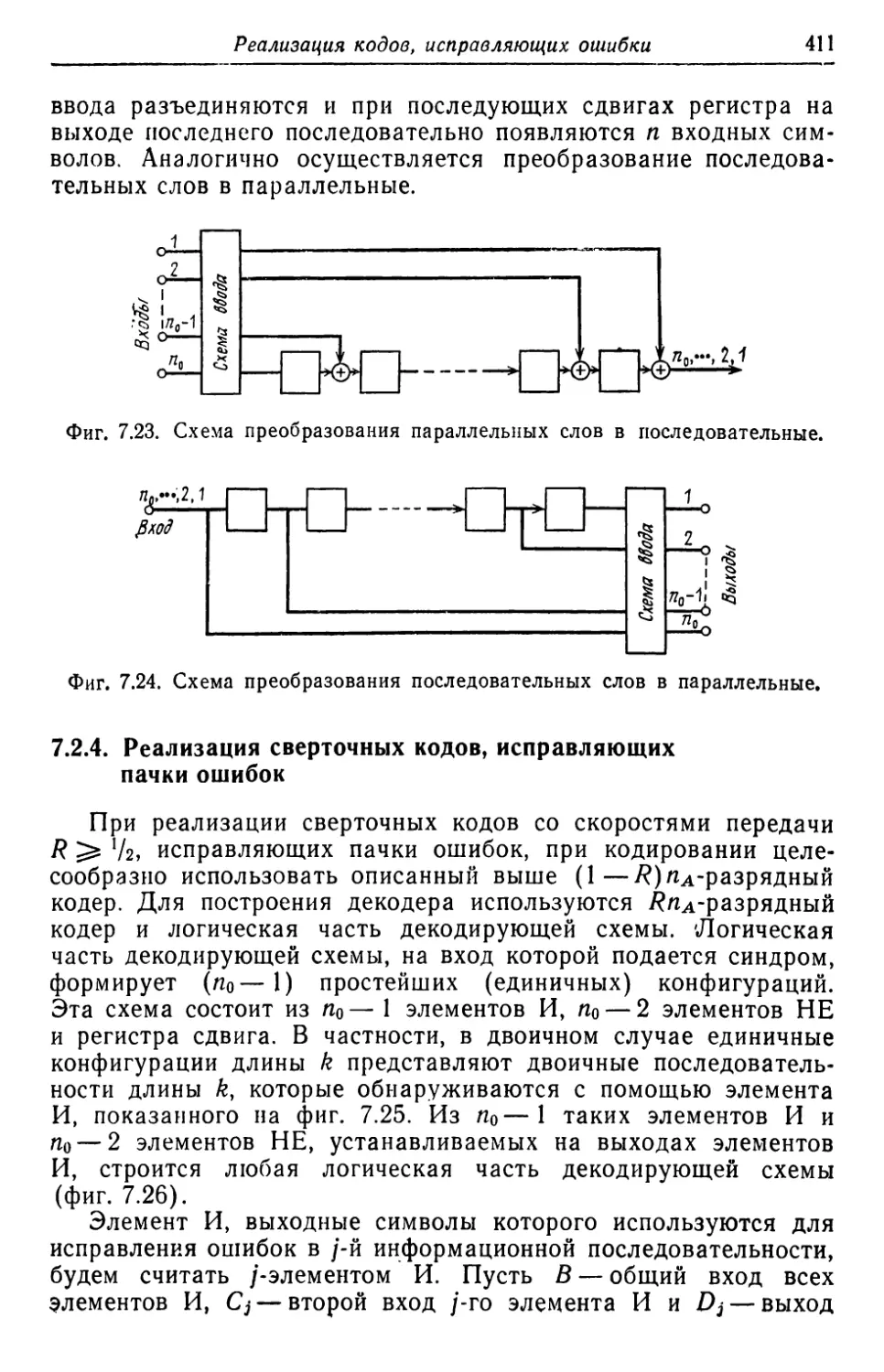
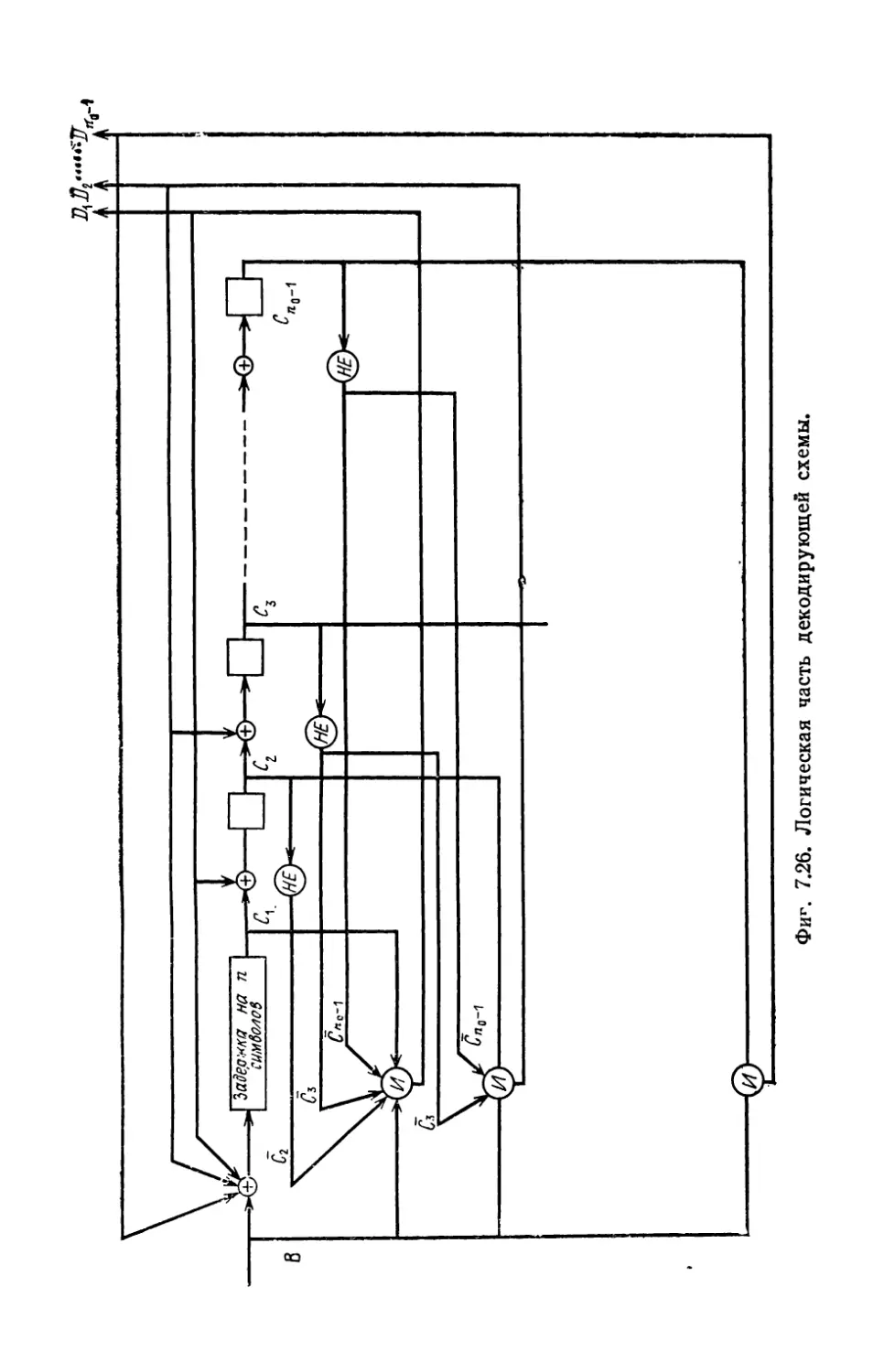
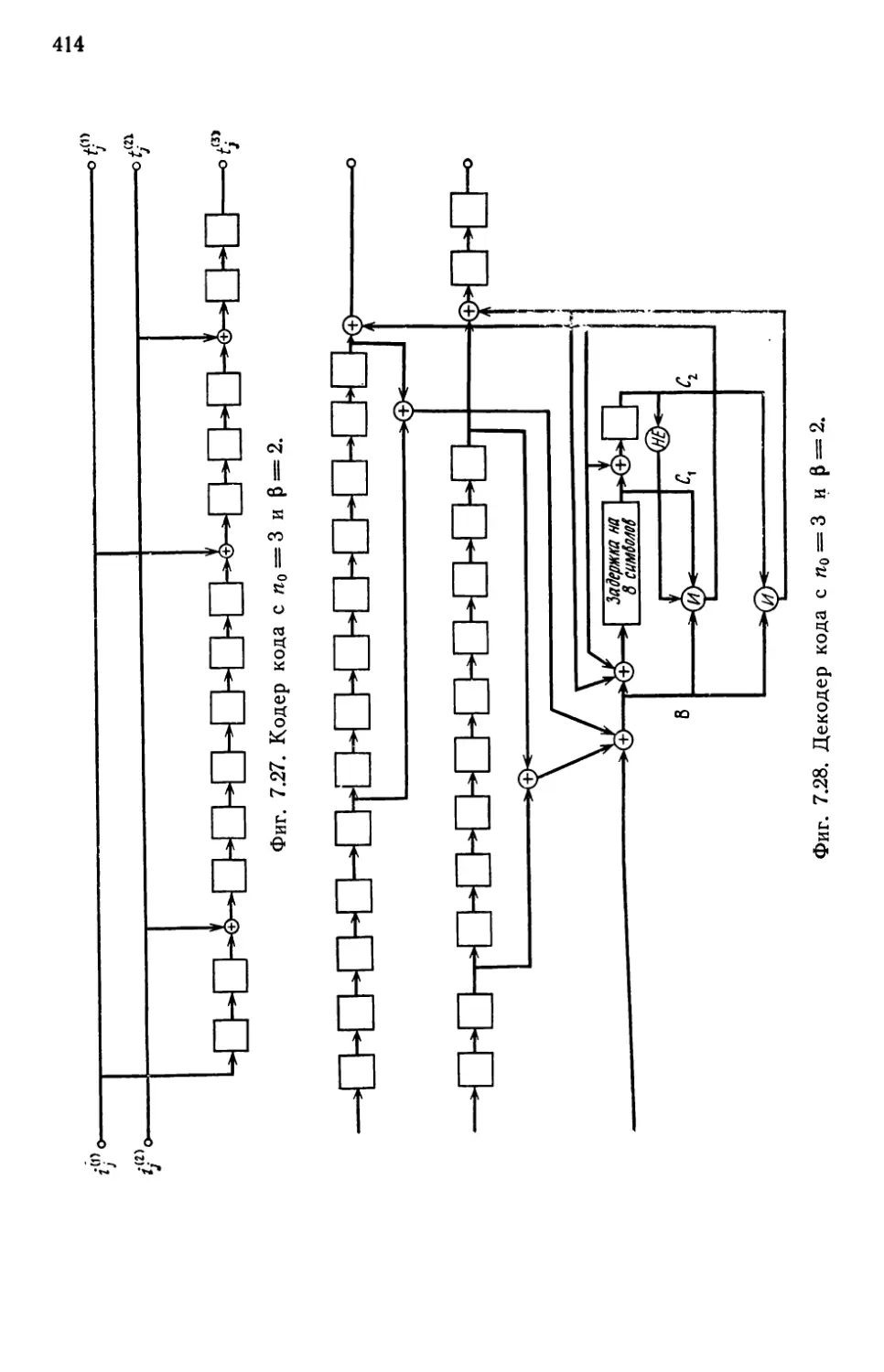
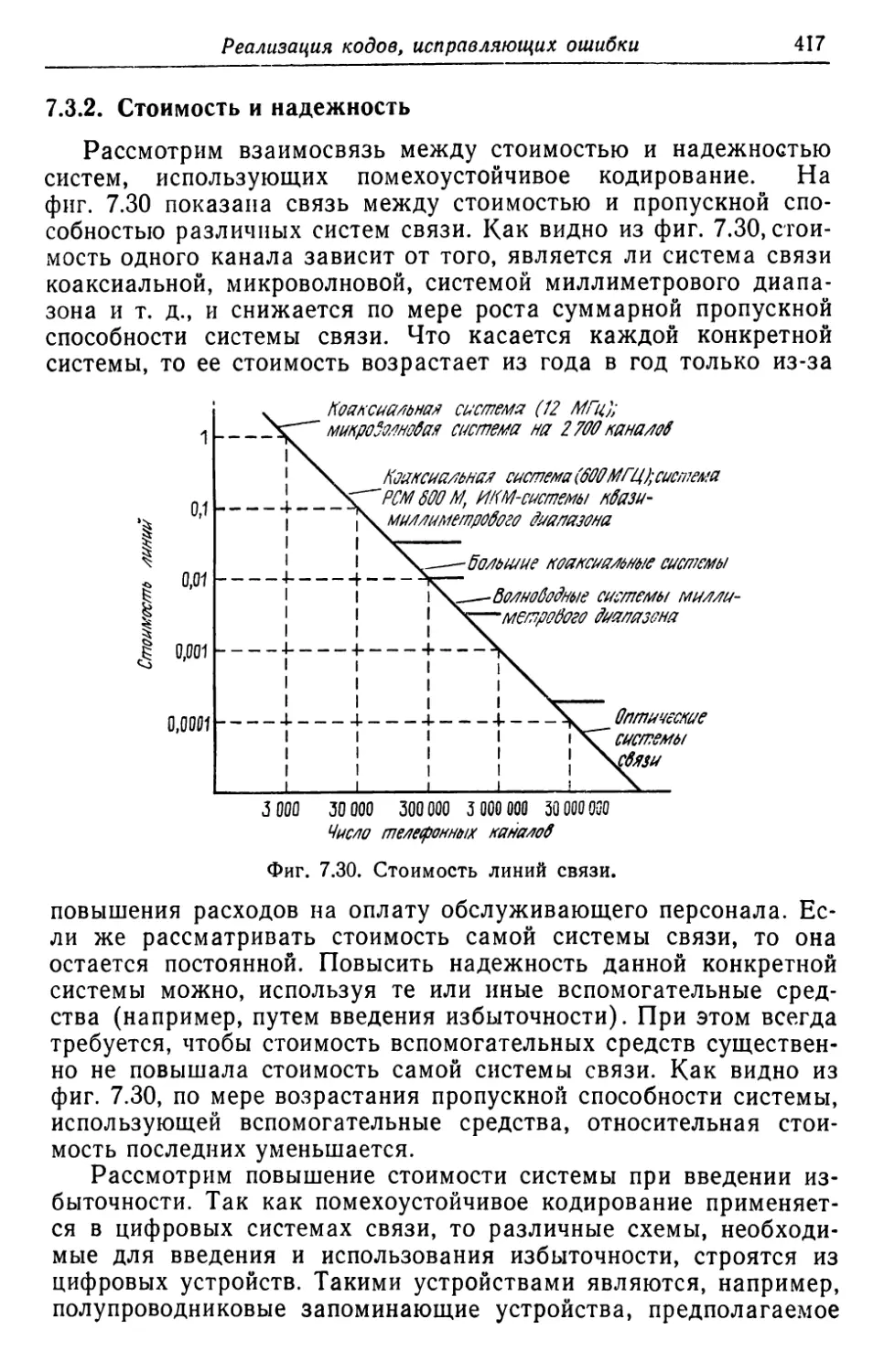
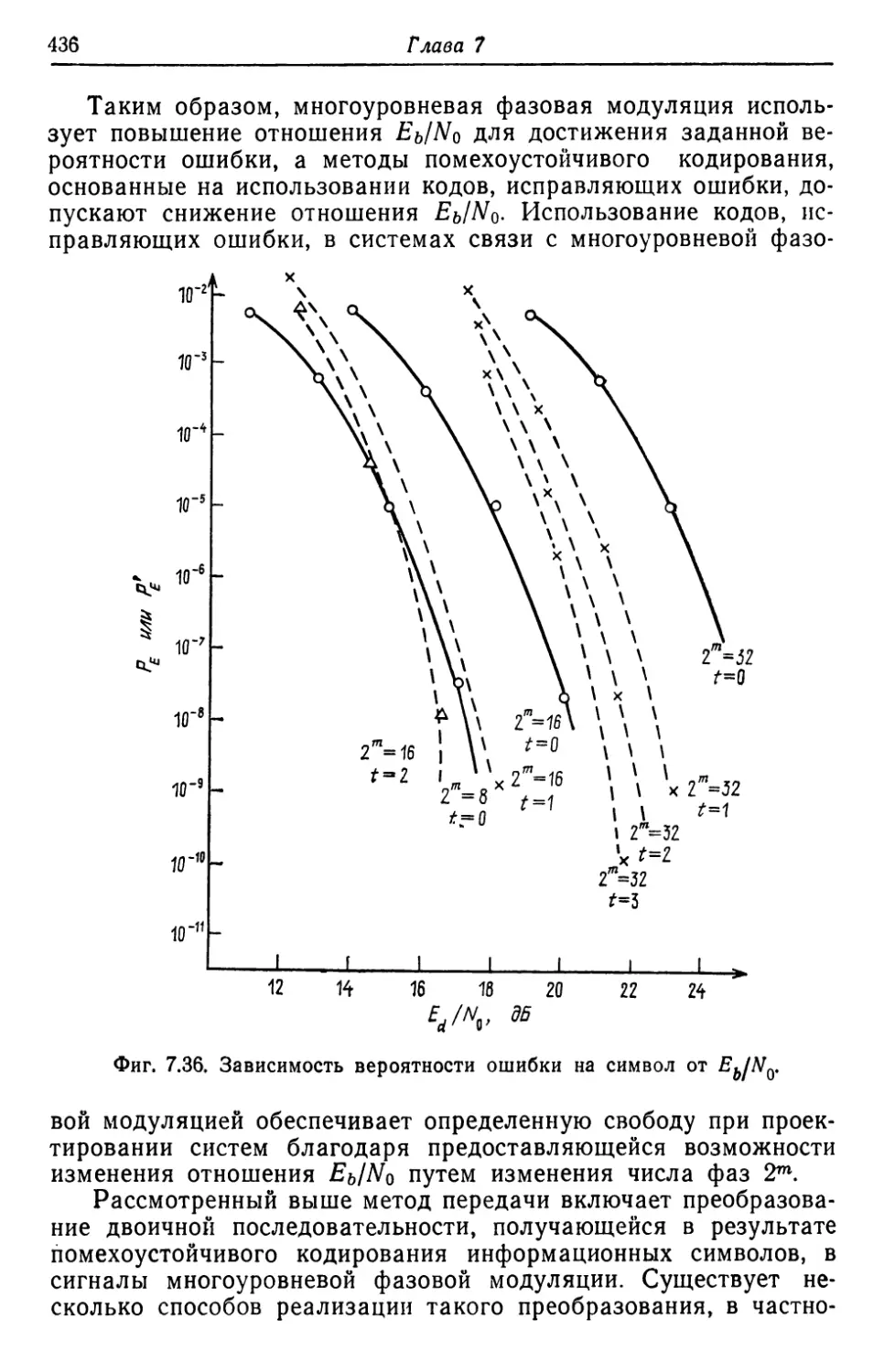
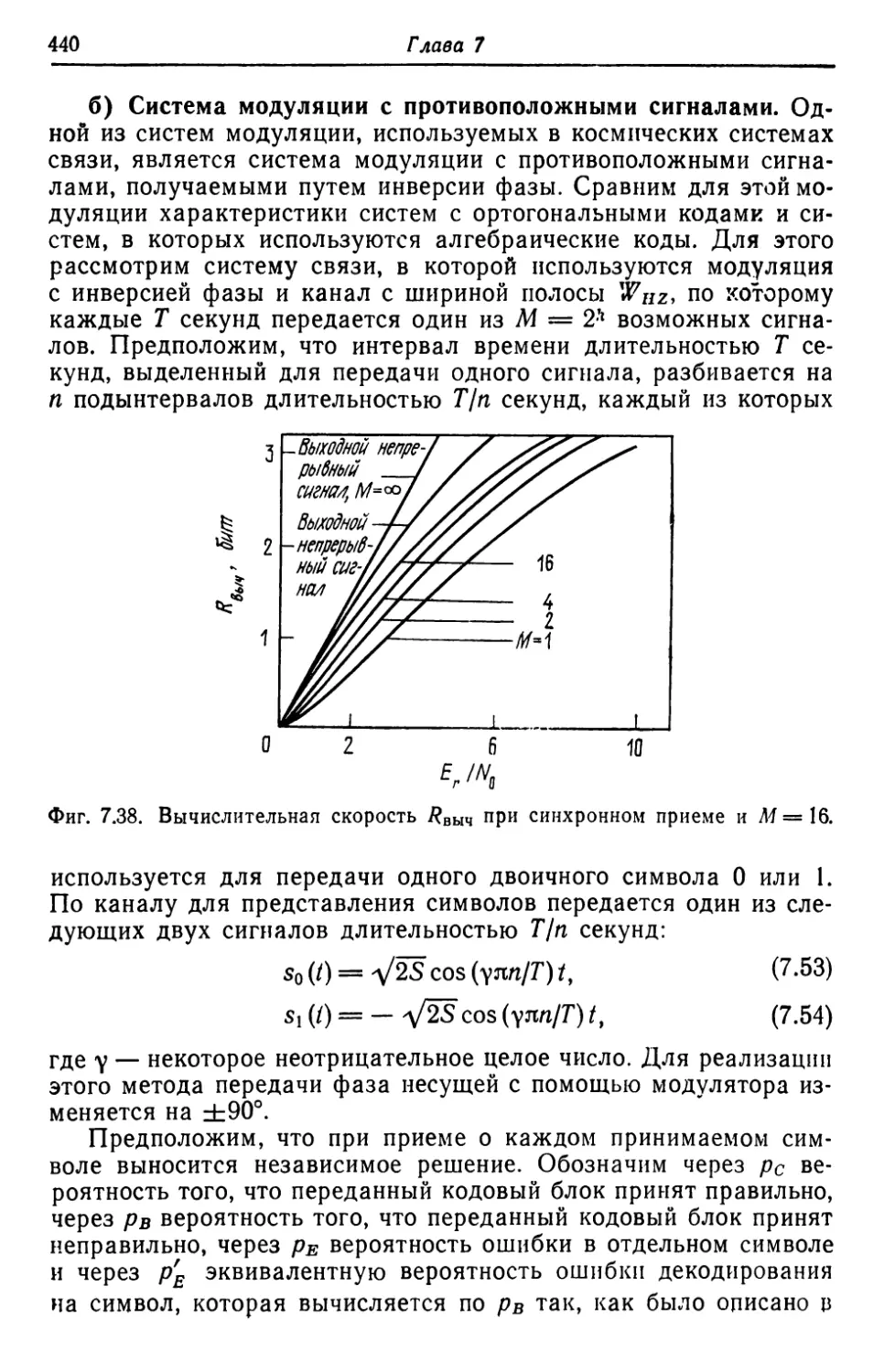
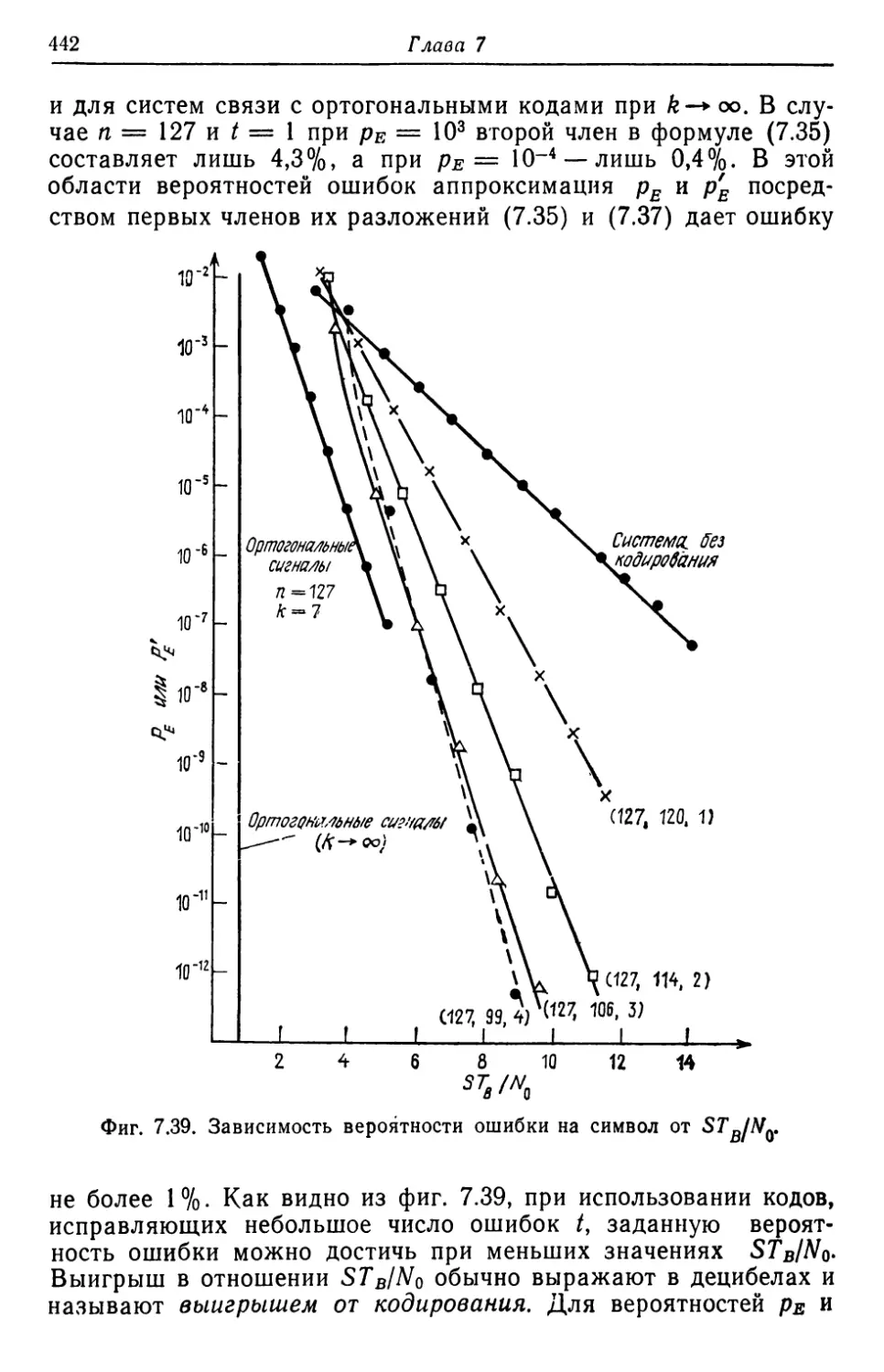
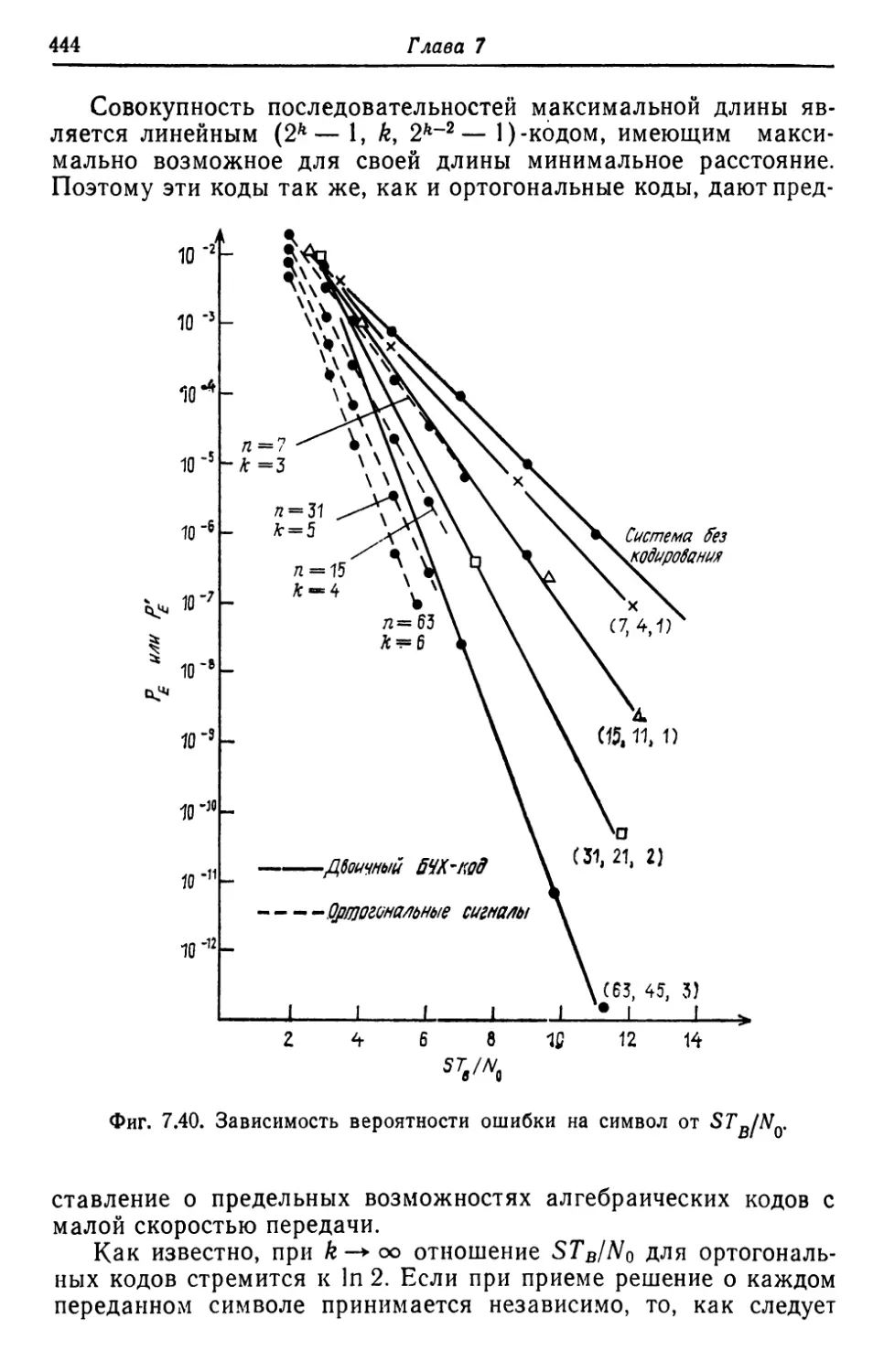
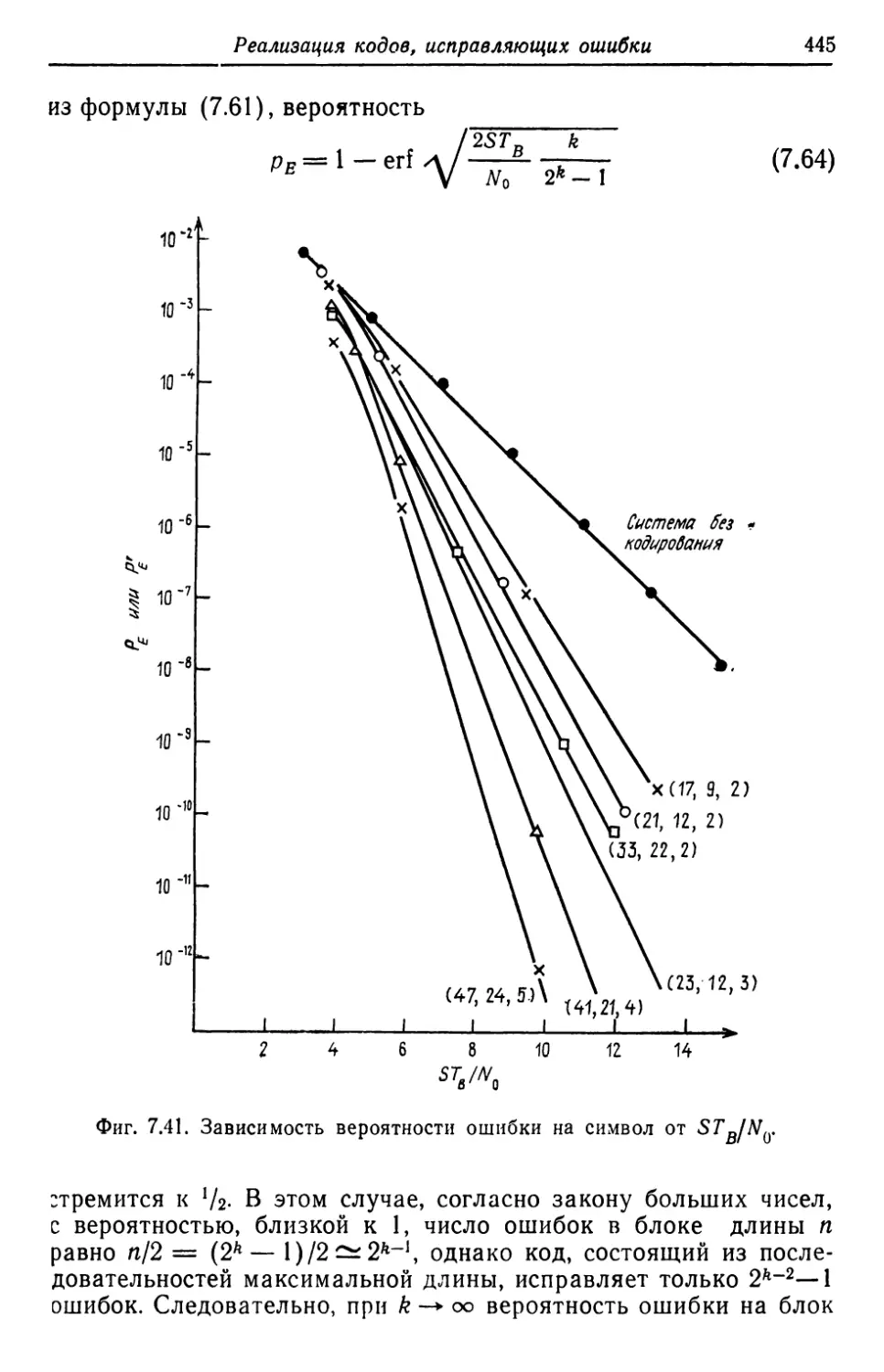
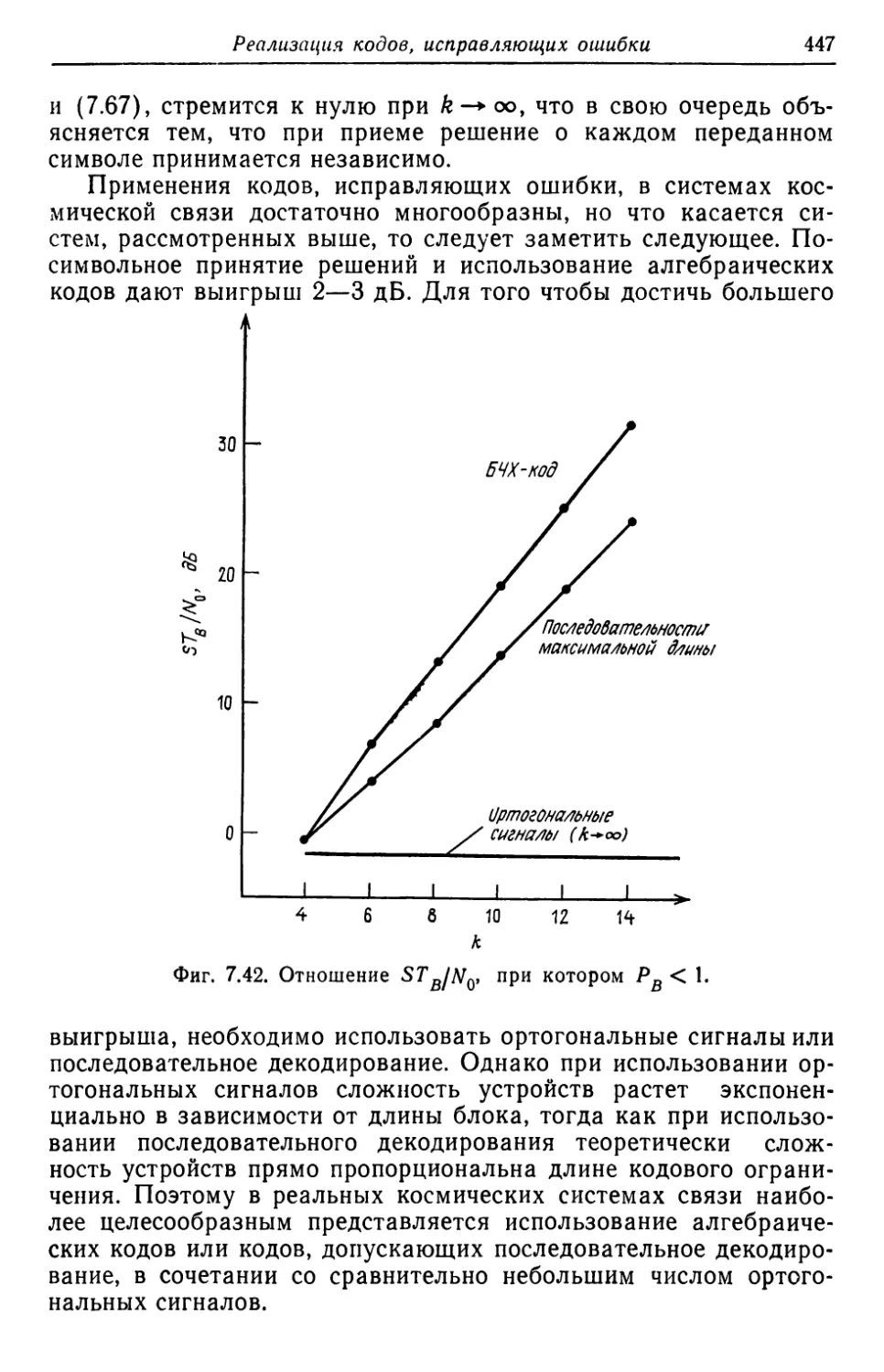
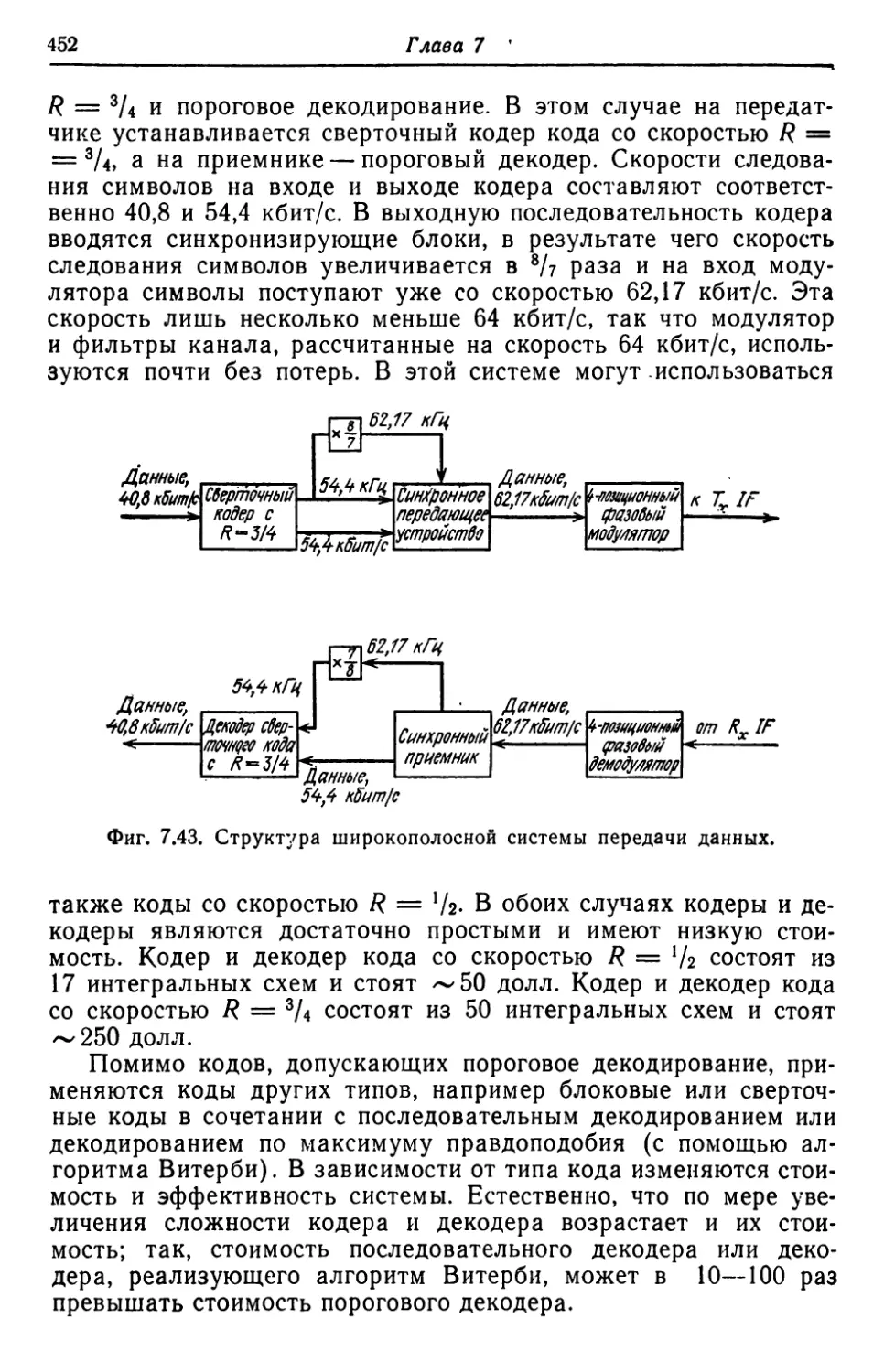
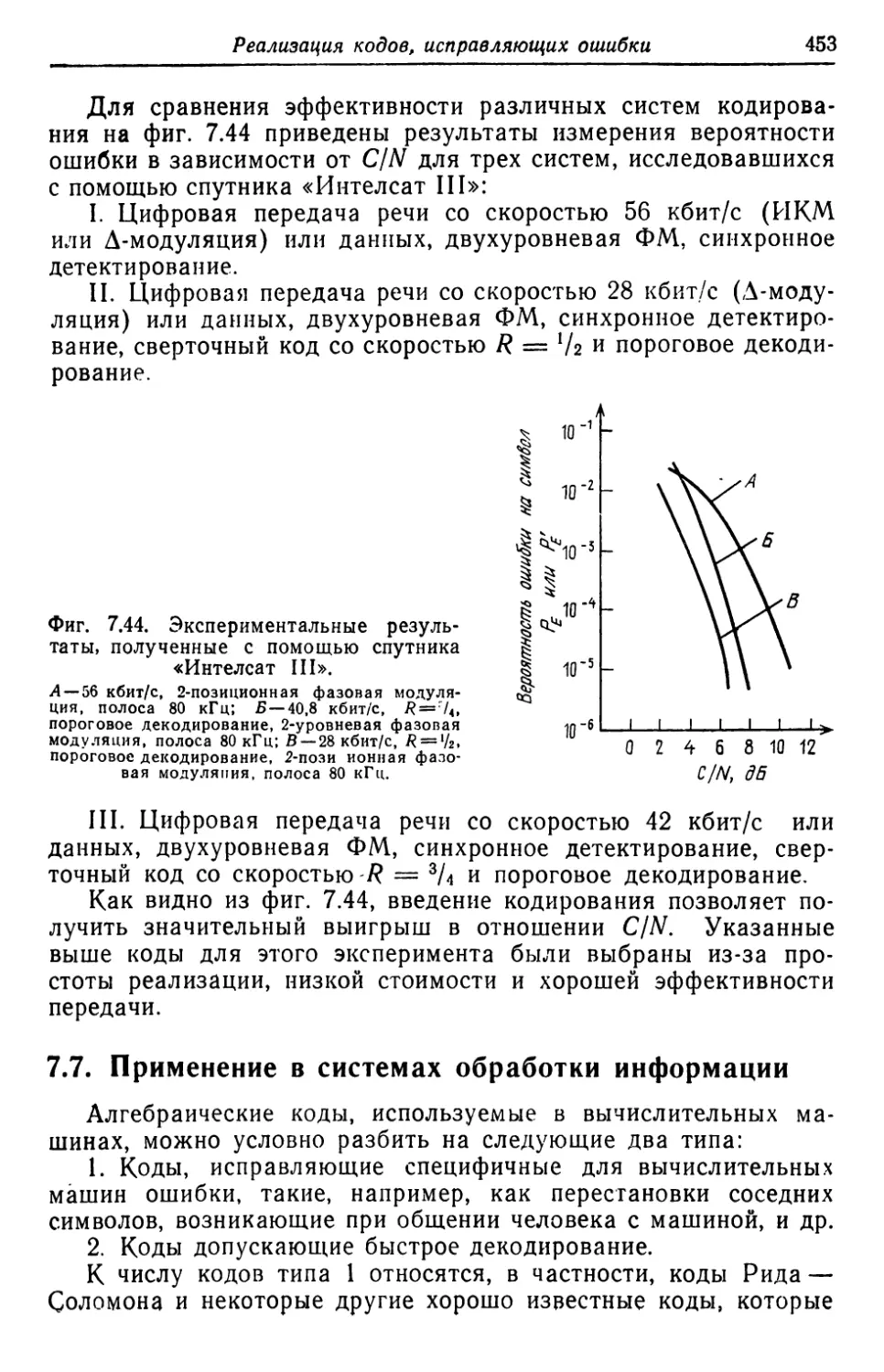
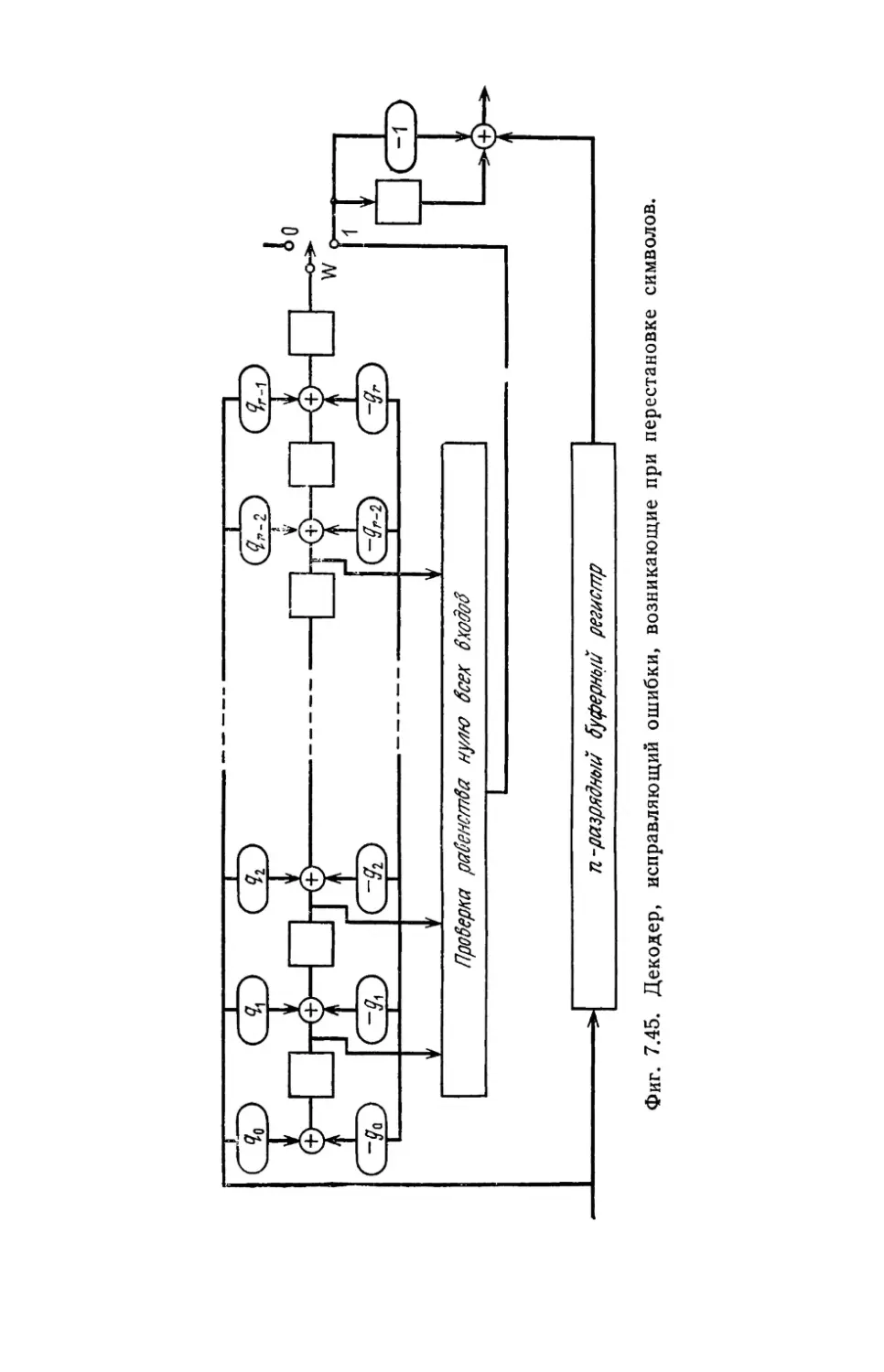
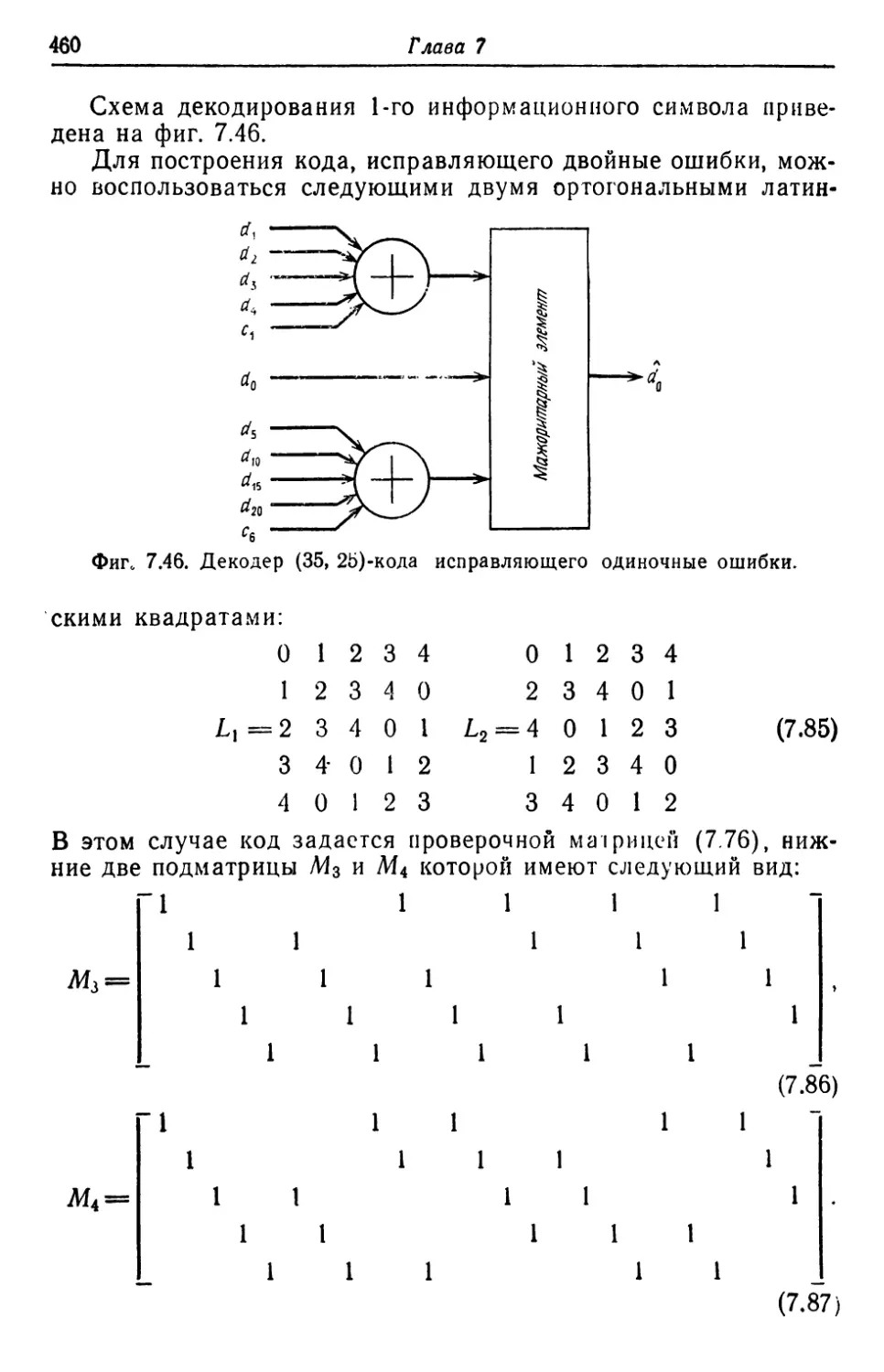
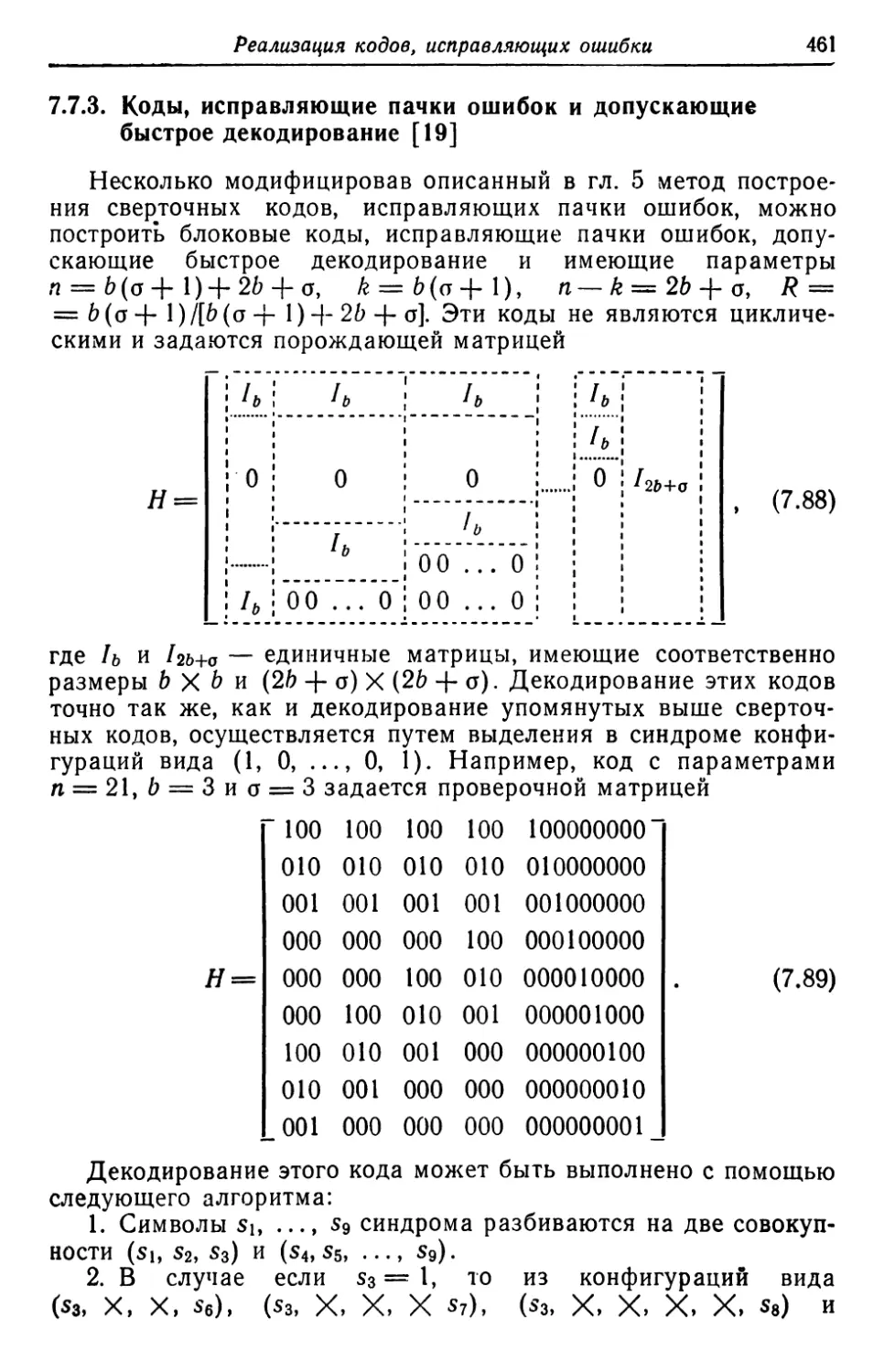
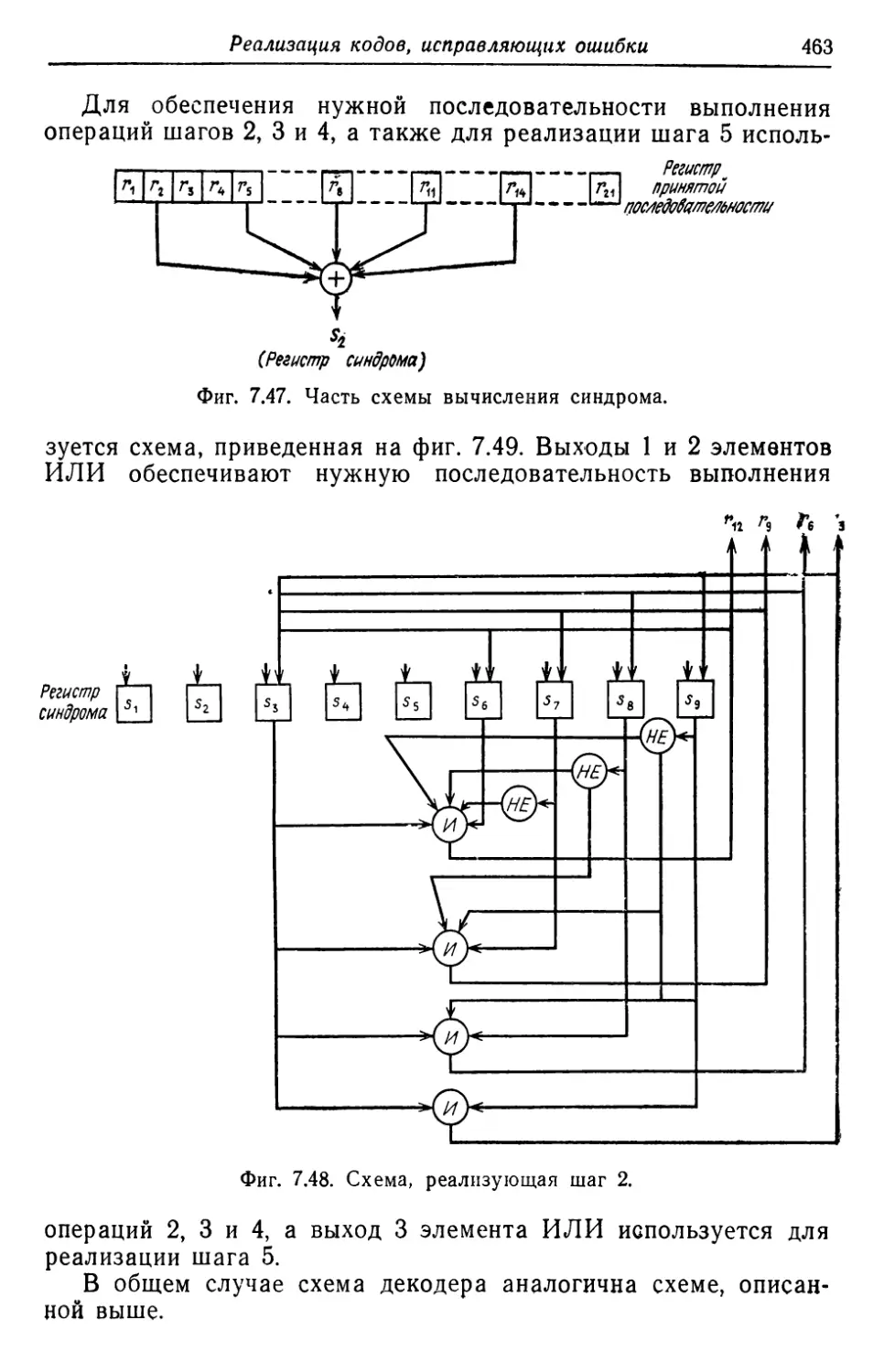
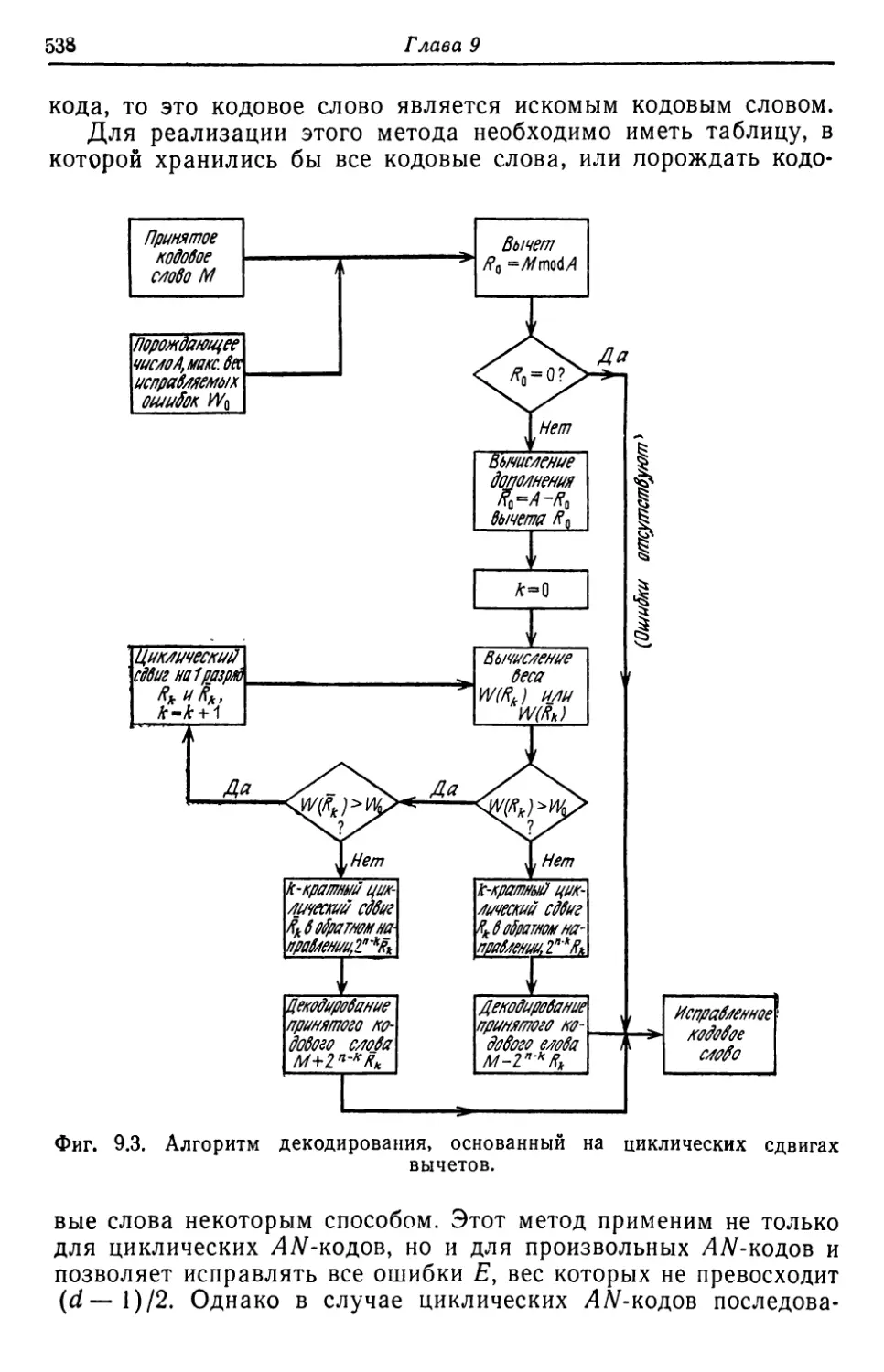
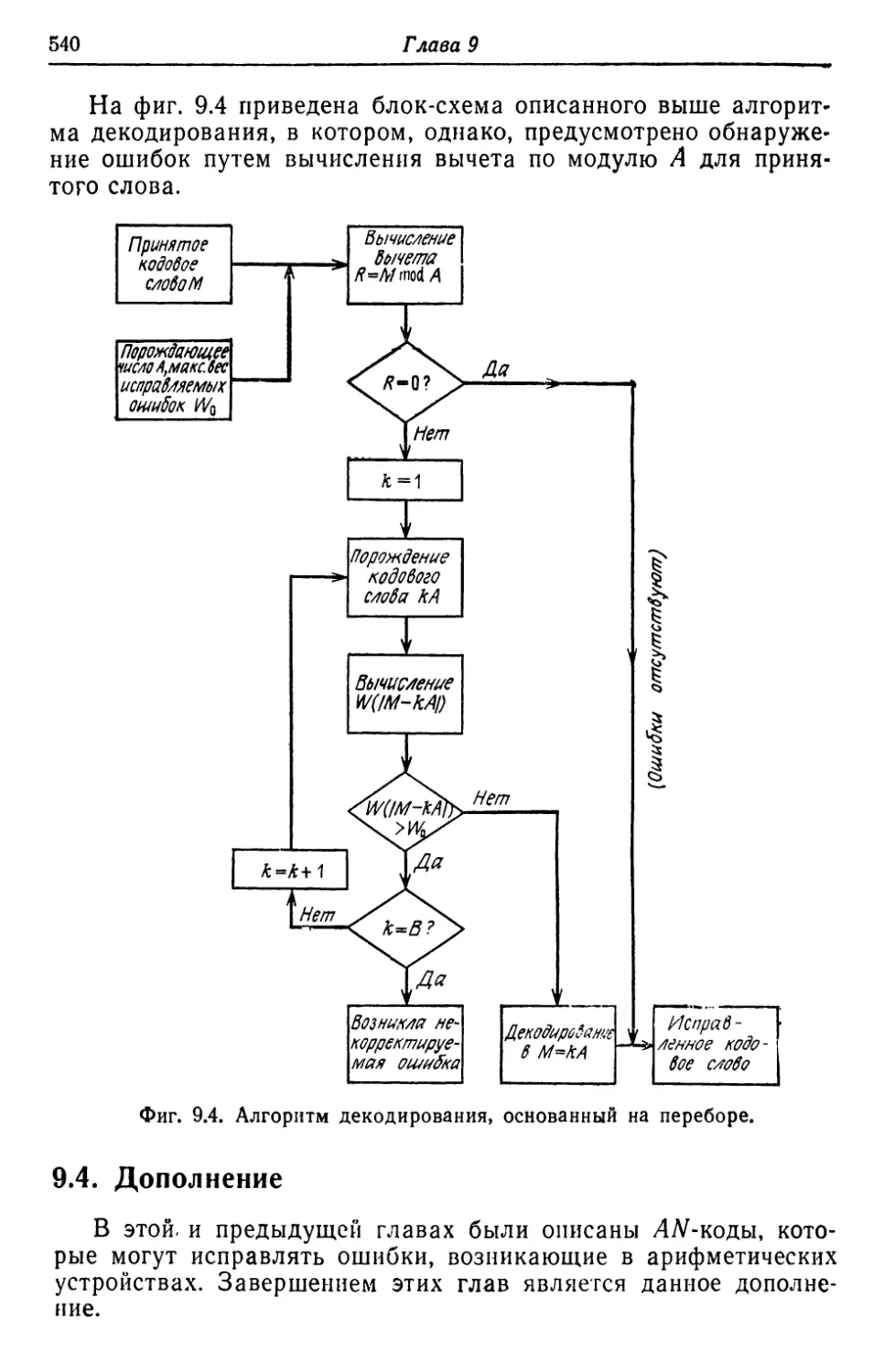
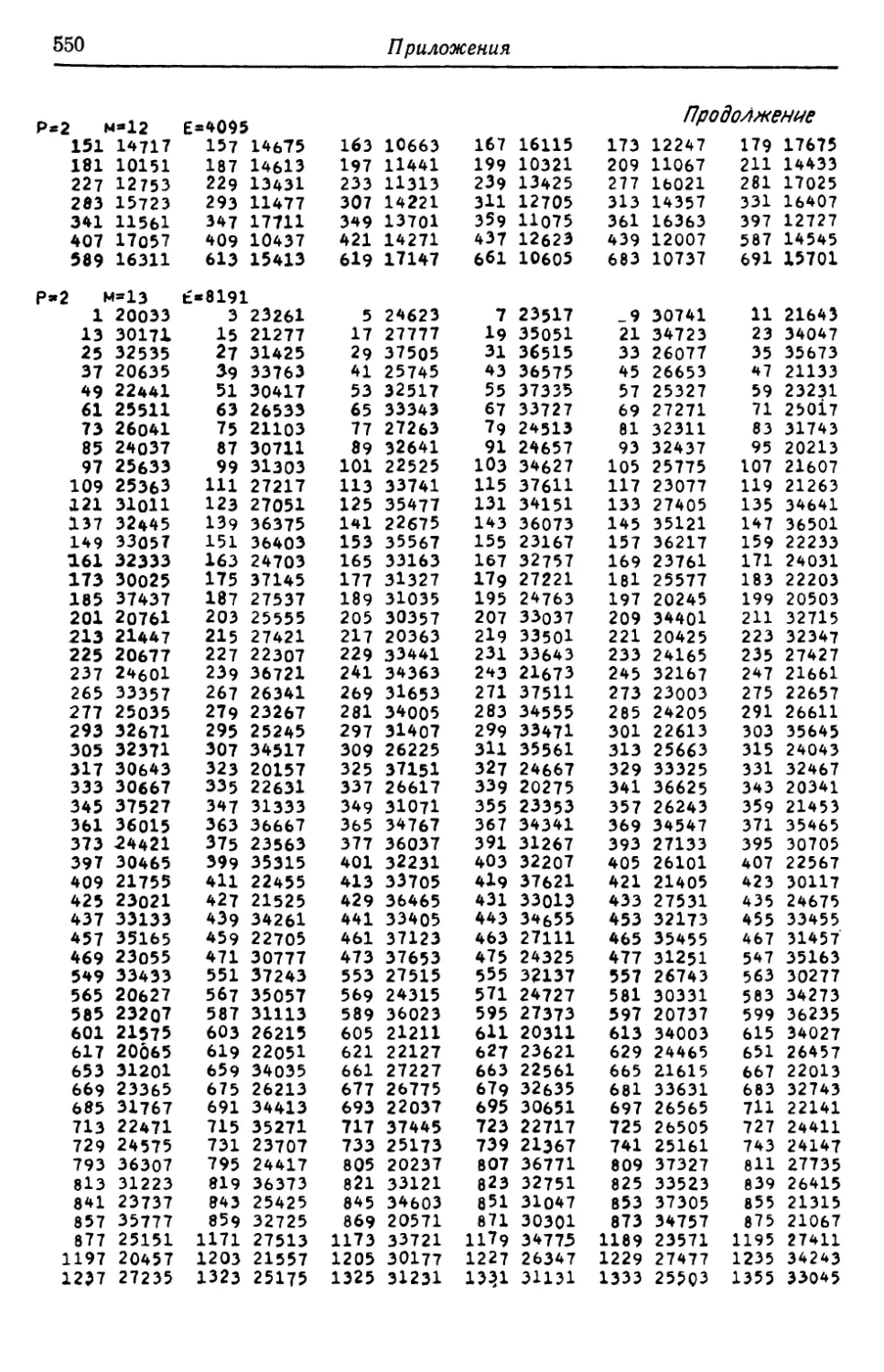
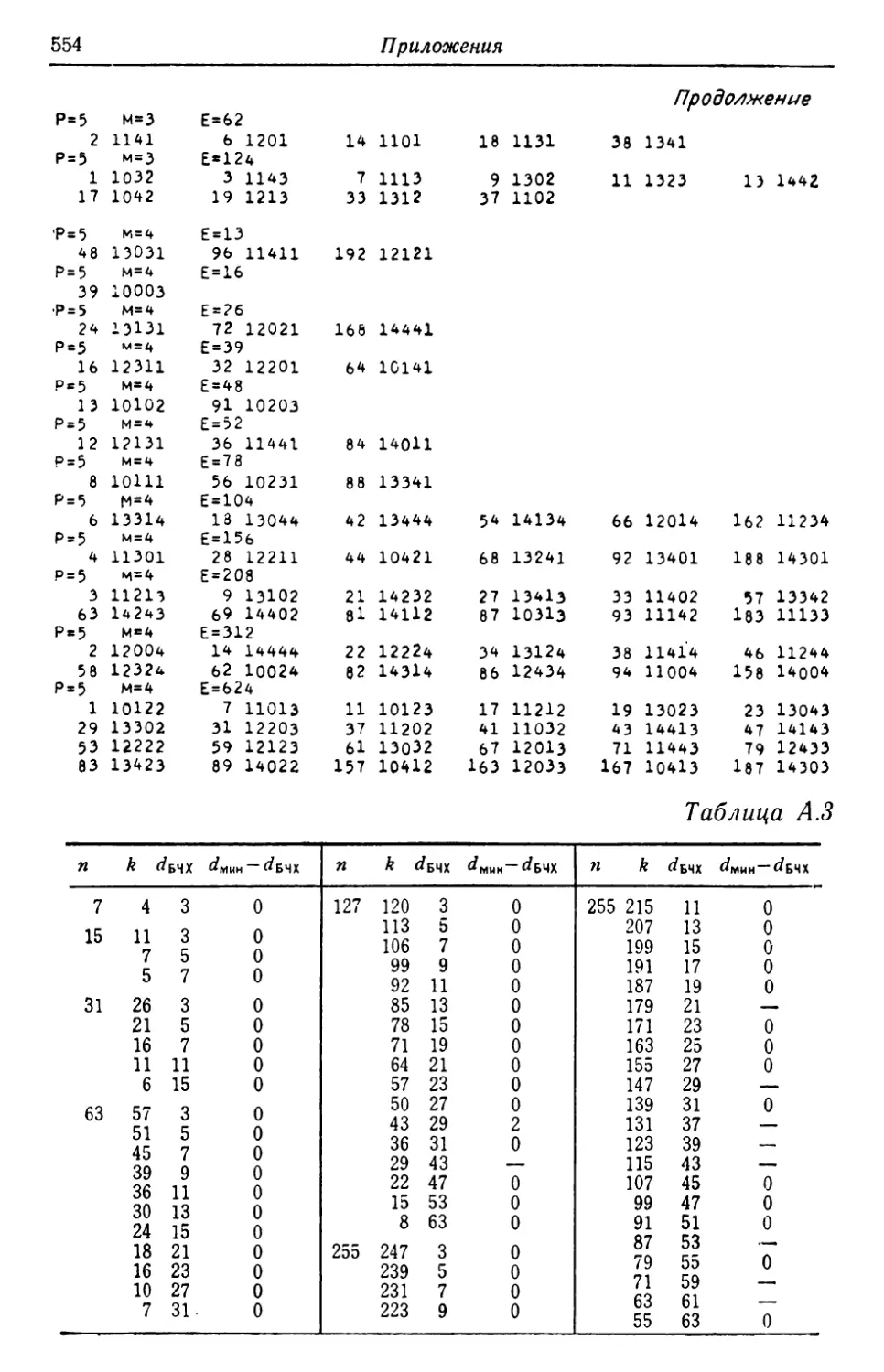
Автор: Касами Т. Токура Н. Ивадари Ё. Инагаки Я.
Теги: компьютерные технологии математика кибернетика
Год: 1978
Текст
ТЕОРИЯ
КОДИРОВАНИЯ
т КАСАМИ.
Н.ТОКУРА.
Е. ИЕАДАPV1.
Я. ИНArАКИ
Т. КАСАМИ,
Н. ТОКУРА,
Ё. ИВАДАРИ,
я. ИНАr АКИ
ТЕОРИЯ
КОДИРОВАНИЯ
Перевод с японскоrо
А. В. КУЗНЕЦОВА
под редакцией
Б. С. ЦЫБАКОВА И с. и. rЕЛЬФАНДА
ИЗДАТЕЛЬСТВО «мир»
MOCI<BA 1978
УДК 681.32
в КНИf'е систематически излаrается теория кодов, исправляющих ошибки,
и рас.:сматриваеrся их применение в системах связи и вычислительной технике.
В последние rоды интерес к BO!JpOC8M использования кодовых методов защиты
от ошибок значительно возрос в связи с развитием сетей передачи данных и
особенно сетей с коммутацией пакетов. В книrе рассматриваются важнеЙlllие
классы кодов: блоковые, свеРТОЧllые и арифметические. Приводятся последние
достижения теории I{одирования. Подробно обсуждаются возможности исполь-
зования кодов в практических системах.
Книrа полезна специалистам, работающим в области систем связи, вычис-
лительной техники и автоматизированны
систем управлrния, математикам и
кибернетика м, интереСУIОЩИМСЯ теорией кпд ирования, а так}ке аспирантам и
студента м соответств УIОЩИХ специальностей.
Редакция литературы по новоа технике
30401..374 @ Т. Касами, Н. Токура, Е. Ивадари, Я. Инаrаки, 1975
К 041(01)-78 146-77 tri\ П u М 1978
ереnод на русскии язык,« ир»,
Предисловие редакторов
PYCCKoro издания
Предлаrаемая советскому читатеЛIО книrа посвящена од-
ному из центральных разделов теории информации
кодам,
исправляющим ошибки. Она написана японскими учеными
Т. Касами, Н. Токура, Е. Ивадари и Я. Инаrаки. Первые два
автора приобрели мировую известность блаrодаря своим рабо
там по теории кодов.
Из переводных книr по теории кодирования наибольшую из..
вестность в нашей стране получила книrа У. Питерсона «Коды,
испраВ.тIяющие ошибки» (издательство «Мир», 1964). В 1976 r.
издатеJIЬСТВО «Мир» выпустило перевод BToporo издания этоЙ
книrи, I10дrотовленноrо У. Питерсоном совместно с э. Уэлдо
ном. Во мноrих отношениях эта замечательная книrа основана
На работах, выполненных до 1970 r. Однако в семидесятых ro
дах учеными разных стран был получен ряд новых результатов,
существенно обоrативших теорию кодирования и в известноrvl
смысле изменивших некоторые ее общие концепции. Данная
книrа японских авторов ВКЛlочает наиболее важные из этих pe
зультатов, такие, как коды Юстесена, коды rоппы, каскадные
коды, циклические арифметические коды и др.
Теория кодирования является прикладной наукой. Она чер
пает задачи из техники связи, радиолокации, измерительной, BЫ
числительной и управляющей техники. Поэтому ва}l{ное. значе-
ние имеют применимость получаемых результатов, их KOHKY
рентоспособность по сравнению с некодовыми методами защиты
от ошибок. Практические достижения теории кодирования сей
час хорошо известны. Однако наиболее широкое применение
получили лишь самые примитивные способы кодирования, та-
кие, как проверка на четность, коды Хэмминrа, циклические
проверки для обнаружения ошибок, простейшие сверточные ко-
ды и Т. П. С точки зрения специалистов по теории кодирования,
отставание в использовании более мощных и нетривиальныIx
кодовых конструкций происходит из-за сложности восприятия
инженерами математическоrо аппарата теории и из-за HeДOCTa
точной разработанности вопросов взаимосвязи кодирования и
модуляции.
Книrа японских авторов помоrает преодолеть это OTCTaBa
ние. Авторы излаrают математические вопросы весьма обстон
тельно, неторопливо, сопровождая текст мноrочисленными
примерами и задачами учебноrа характера. Восточная
6
п редuсловuе редакторов рУССКО20 издания
v о
медлительность здесь выступает удачнои альтернативои запад-
ной лаконичности, образцом которой служат произведения
Н. Бурбаки. В книrу помещена специальная r лава (rл. 7), по-
священная реализации и применениям кодов. В этой rлаве рас-
сматриваются принципы построения кодирующих и декодирую-
щих устройств для циклических и сверточных кодов. Приводятся
способы использования двоичных и друrих дискретных кодов в
реальных каналах, которые по своей физической природе яв"
ляются аналоrовыми. Обсуждается проблема соrласованноrо
выбора методов кодирования и модуляции. Вводится новый па..
раметр, измеряющий выиrрыш при использовании кодирования
в канале. Эта не претендующая на математическую cTporocTb
rлава призвана cbIrpaTb важную роль связующеrо звена между
v
теориеи кодов и ее практическими применениями.
Хочется отметить, что теория информации сейчас находит я
в процессе развития. Поэтому ее достижения и тенденции за
u
время, прошедшее после выхода в свет даннои книrи, не моrли
быть в ней отражены. К вопросам, не включенным в книrу, от-
носятся, в частности, коды дл мноrоисточниковых, широкове-
щательных и мноrосторонних каналов, коды, исправляющие дe
фекты и ошибки, и коды, повышающие скрытность передачи.
В настоящее время с этими достижениями можно ознакомиться
лишь по журнальным и обзорным статьям.
При переводе и редактировании были исправлены некото-
рые опечатки, имеющие место в японском издании. Часть из
них была любезно указана нам авторами, которым приносим
rлубокую блаrодарность.
С. И. fельфанд, Б. С. ЦыбаКО(J
Предисловие авторов
К настоящему времени по теории кодирования вышли сле-
дующие моноrрафии: книrа Питерсона [1] и ее расширенный Ba
риант
моноrрафия Питерсона и Уэлдона [2], ориrинальная
книrа по алrебраической теории кодирования Берлекэмпа [З]t
книrа Ван-Линта, систематизирующая алrебраическую теорию
кодирования [4], прекрасное введение в теорию кодирования
Лина [5] и большой труд Миякавы, Ивадари и Имаи [6]. Однако
уже после выхода в свет этих книr rоппа, Юстесен и др. полу-
чили ряд новых важных результатов.
В теории кодирования можно выделить следующие три раз-
дела: теорию алrебраических кодов, теорию сверточных кодов
и теорию кодов, используемых в арифметических устройствах.
Все эти разделы тесно связаны друr с друrом, но в то же время
характеризуются собственным подходом к проблеме кодирова-
ния. В данной книrе этим разделам посвящены соответственно
rлавы 1
4; 5, 6; 8, 9. Каждый раздел, как правило, начинается
введением основных понятий и заканчивается изложением срав-
нительно новых результатов. Авторы не претендуют на исчер-
пывающее изложение Bcero материала теории кодирования, ско-
рее, они преследуют цель рассмотреть все наиболее важные мо-
менты в развитии методов теории.
В rл. 7 подробно исследуются различные вопросы, связанные
с применением теории кодирования. При первом знакомстве с
теорией кодирования затруднения, как правило, возникают там,
rде используются понятия и результаты теории конечных полей.
Поэтому в эту книrу было решено включить rлаву, в которой
кратко рассматриваются основные понятия и результаты теории
конечных полей, используемые в теории кодирования. Для по
нимания содержания книrи достаточно знакомства с универси-
тетским курсом математики.
Разд. 1.1
1.4 rл. 1, а также rл. 3, 4 написаны Касами,rл.2.........
Токура, разд. 1.5 rл. 1 и rл. 5............7
Ивадари, rл. 8 и 9
Ина-
rаки. rлавы 1
4, 5
7 и 8, 9 можно читать почти независимо.
Кроме Toro, читатели, знакомые с конечными полями, MorYT про-
пустить rл. 2 и приступить К чтению последующих rлав, обра
щаясь к rл. 2 лишь по мере необходимости.
В rл. 1 вводятся основные понятия теории кодирования, в
частности понятия, связанные с блоковыми кодами, определяе'r..
ся ряд rраниц, характеризующих предельные характеристики
8
Предисловие авторов
блоковых кодов; в разд. 1.5 методом rаллаrера доказана теоре-
ма кодирования Шеннона, которая в свое время ПОСлужи.па от-
правной точкой теории кодирования.
В rл. 2 рассматриваются rруппы, кольца, поля, векторные
пространства, мноrочлены и друrие понятия и результаты тео-
рии конечных полей в том объеме, который необходим д.пя чте
ния статей по теории кодирования. Мноrие результаты теории
кодирования формулируются в виде задач или утвеР)l{дений.
В rл. 3 рассматриваются свойства линейных кодов и методы
их кодирования и декодирования, свойства циклических кодов,
tt
являющихся подклассом линеиных кодов, а также методы за.
дания таких кодов. При этом подчеркивается значение алrе-
браической теории кодирования, которая изучает классы кодов
с определенной алrебраической структурой и использует эту
структуру для детальноrо описания свойств кодов и построения
для них эффективных алrоритмов кодирования и декодиро-
вания.
Алrебраическая теория кодирования содержит MHoro ре-
зультатов, которые заслуживают подробноrо рассмотрения, и
поэтому выбрать материал для данной книrи было довольно
трудно. В rл. 4 основной акцент был сделан на пояснение раз-
личных методов теории кодирования, в соответствии с чем 11
отбирался материал для этой rлавы. В эту rлаву включены наи-
более детально исследованные к настоящему времени БЧХ-коды
u
и методы их декодирования, важные с практическои точки зре-
ния методы мажоритарноrо декодирования, иrрающие важную
роль в теории l\Iноrочлены Матсона Соломона, полиномиаль-
ные коды, содер)кащие в качестве своих подкодов БЧХ коды,
некоторые классы кодов, допускающих мажоритарное декоди-
рование, их двойственные коды, каскадные коды, строящиеся
на основе нескольких кодов с меньшими значениями napaMer-
ров, каскадные коды Юстесена, представляющие собой первыЙ
класс кодов, свойства которых не ухудшаются н области боль
ших значений параметров. Она содержит также интенсивно
исследуемые в наСТОЯLl.tее время коды rоппы (вообще rоворя,
не являющиеся циклическими), включаЮIl{ие I<aK подкласс
БЧХ коды, методы декодирования кодов rоппы 1) и несколько
отличающиеся от кодов, перечисленных выше, коды, испраJJ
ляющие пачки ошибок. К сожалению, в этой книrе не удалось
рассмотреть квадратично-вычетные коды [2, 3], нелинейные ко-
ды [6], обстоятельные работы, посвященные исследованию струк-
1) Уже после Toro, Kal{ книrа была написана, Хелrерт, Суrияма Каса-
хара, Чень Чоу опубликовали метод зад ния кодоп rоппы. несколько от-
личныЙ от метода rоппы, а так}ке итераТIII3НЫЙ алrоритм де;{однрования по-
с.педннх.
Предисловие авТОрО8
9
туры весов [3, 4], проблему синхронизации [2] и некоторые друrие
важные вопросы.
Читателям, которые впервые хотели бы ознакомиться с
основами теории блоковых кодов, рекомендуется изучить сле-
дующие разделы: 1.1 1.3, 1.4.1, помеченные знаком * разделы
r л. 2, 3.1 3.3, 3.5 3. 7, 4.1, 4.2.1, 4.3, 4.8.
rл. 5 и 6 посвящены сверточным кодам. Рассматриваемые
в начале rл. 5 коды, которые допускаIОТ пороrовое декодирова
ние, имеют простые алrоритмы декодирования и MorYT быть
леrко реализованы, что очень важно с практической точки зре
ния. Методы построения и декодирования таких кодов rлав-
ным образом являются алrебраическими и основаны на теории
автоматов. Особое внимание в этой rлаве уделяется возмож
ности практической реализации декодирования. Простое дeKO
дирование допускаIОТ рассматриваемые здесь oды, исправляю
щие независимые ошибки, коды, ИСIIраВЛЯIощие пачки ошибок,
диффузные коды, исправляющие независимые ошибки и пачки
ошибок, равномерные коды, похожие на блоковые коды, обра
зоnанныIe последовательностями максимальной длины.
При последовательном декодировании, которое рассматри-
вается в r л. 6, число операций изменяется в зависимости от
уровня шума, действующеrо в канале. Блаrода{АЯ этому после-
довательное декодирование по своим характеристикам прибли-
жается к декодированию по максимуму правдоподобия и ши-
роко используется в реальных системах космической связи.
Алrебраические методы для анализа этоrо метода декодирова-
ния не подходят. С помощью вероятностных методов для
последовательноrо декодирования выводятся различные rpa-
ницы, в частности верхние и нижние rраницы для распределения
выполняемых декодером операций, вероятности переполнения
буфера, вероятности ошибки при декодировании и др. Анализ
последовательноrо декодирования оказывается весьма слож-
ным. Кроме алrоритмов последовательноrо декодирования, в
этой rлаве рассматривается также алrоритм декодирования Ви
терби, который представляет собой алrоритм декодирования по
максимуму правдоподобия. Сравнение сверточных кодов с бло-
ковыми кодами показывает, что первые при декодировании с
помощью алrоритма Витерби имеют лучшие характеристики;
это один из важных выводов теории кодирования. Кроме Toro,
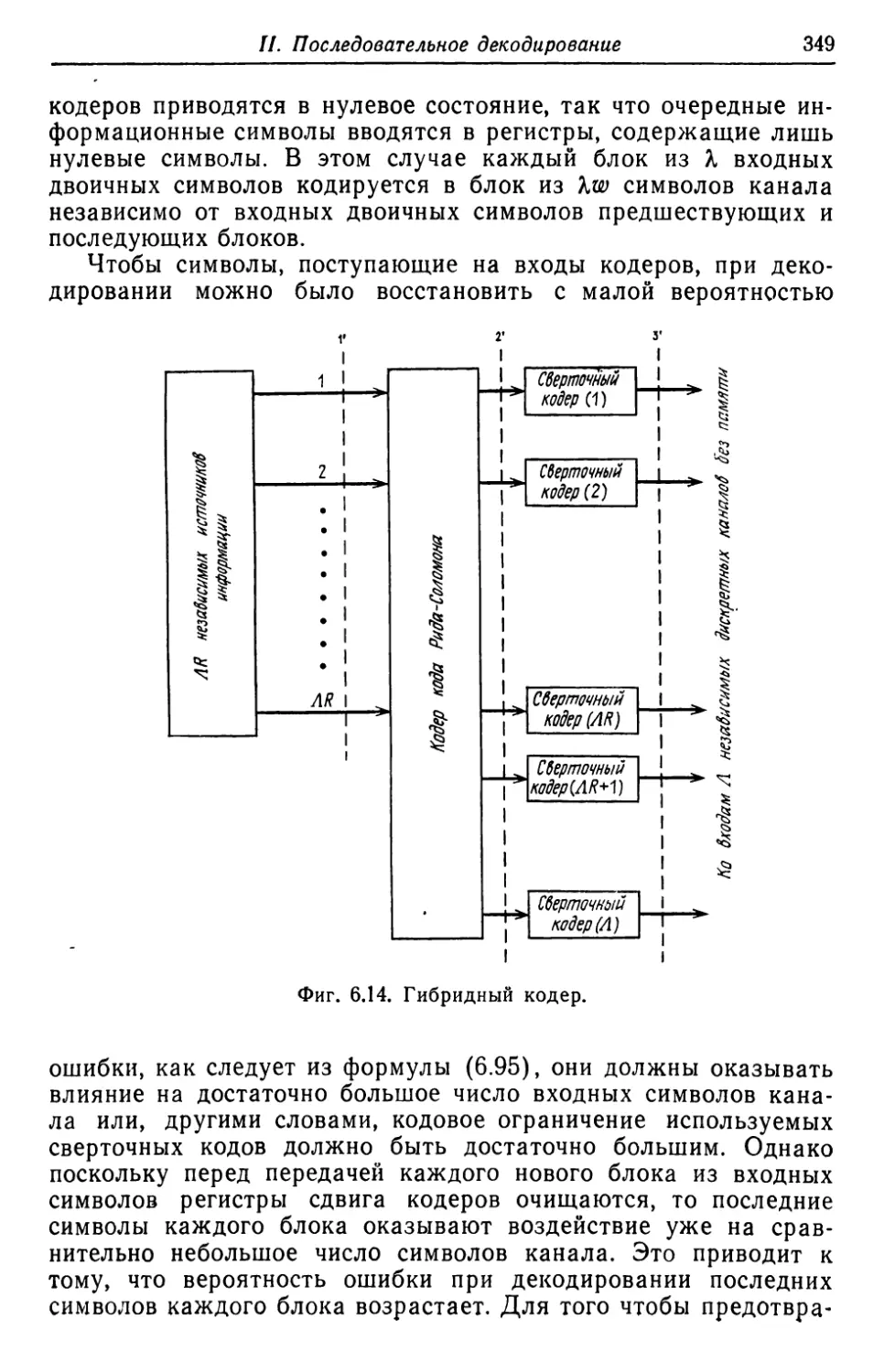
в этой l'лаве рассматривается rибридный метод декодирования,
представляющий собой объединение последовательноrо и алrе-
браическоrо декодирования, а также исследуется структура pac
стояний сверточных кодов.
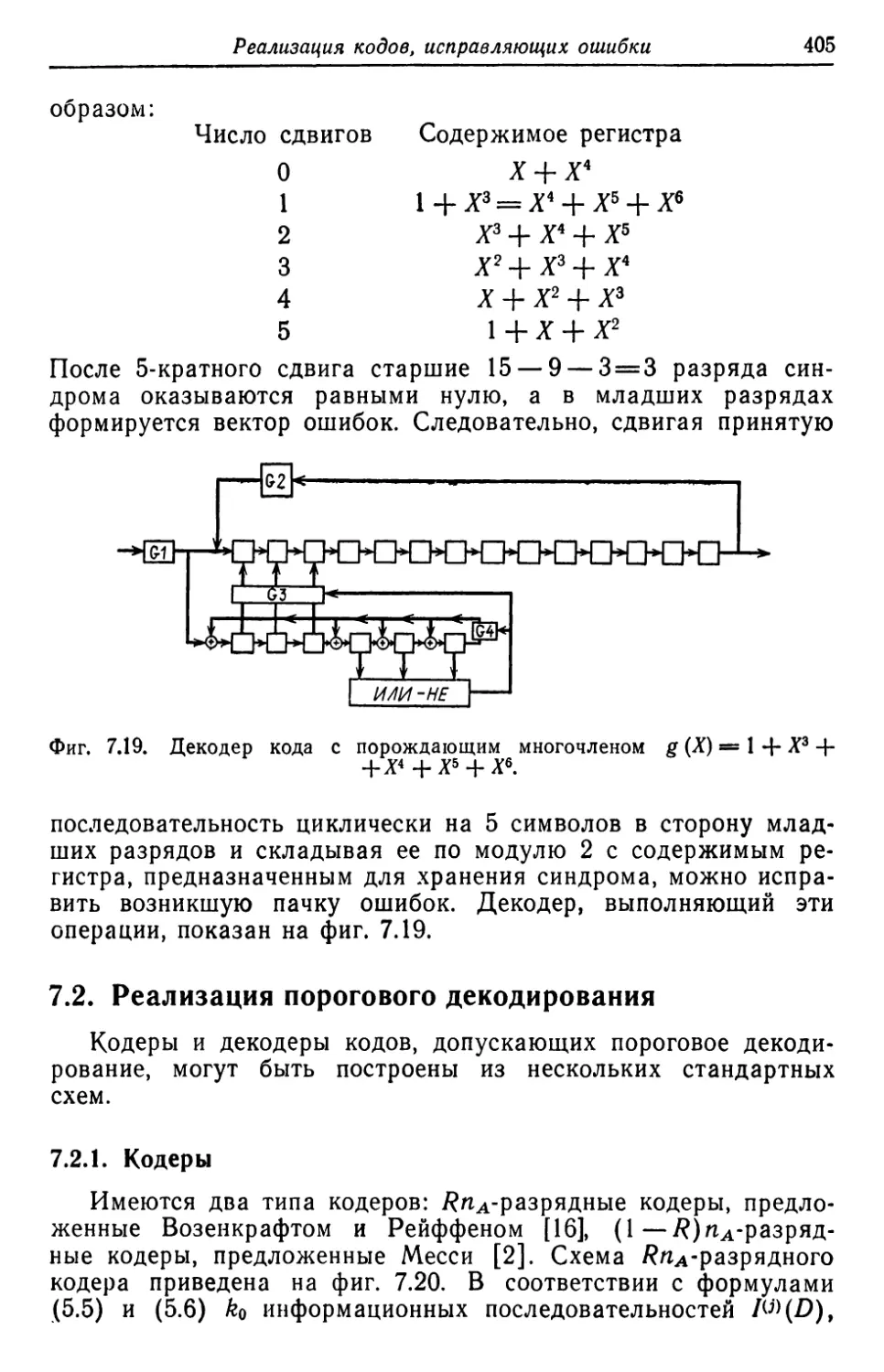
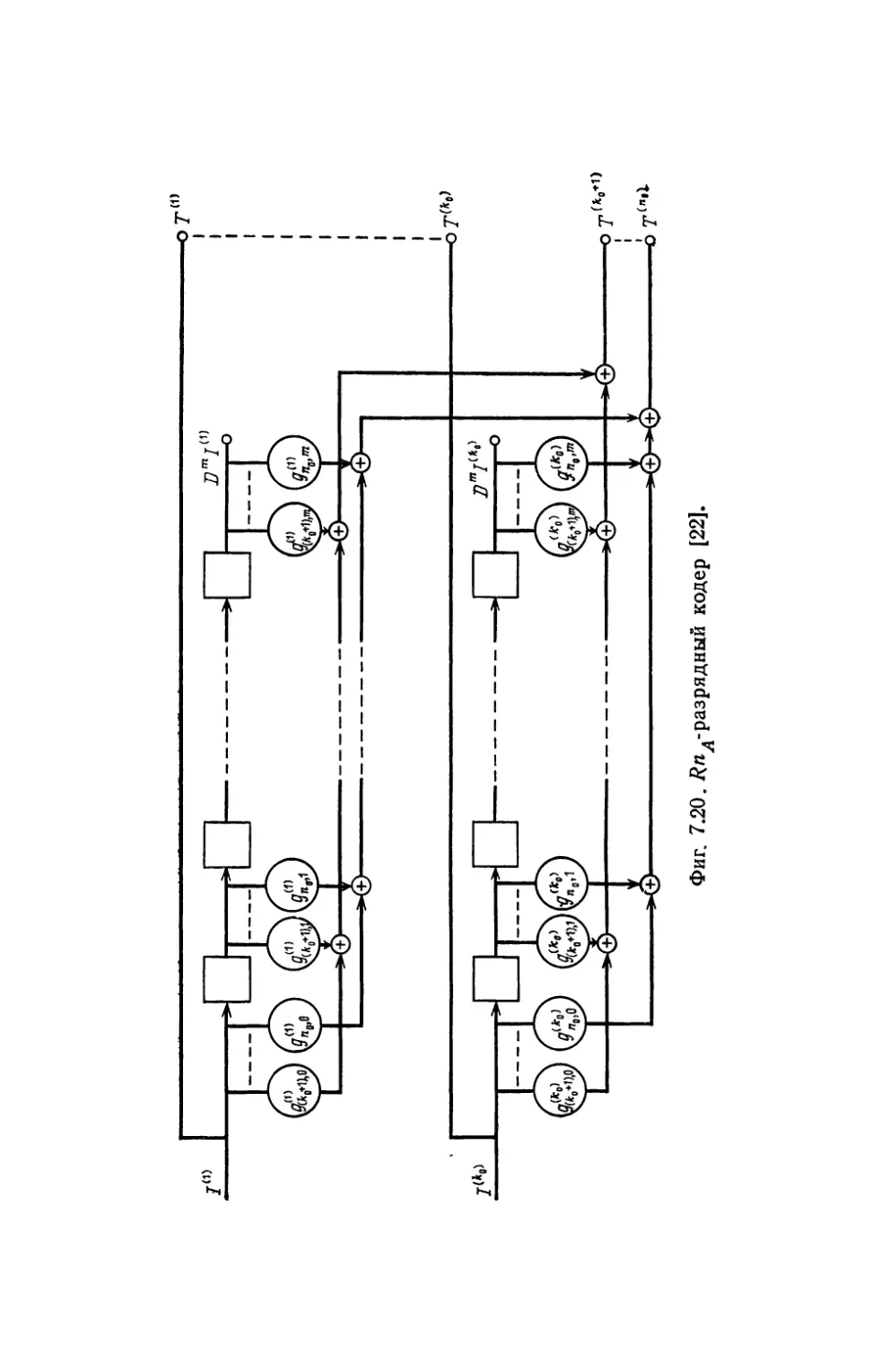
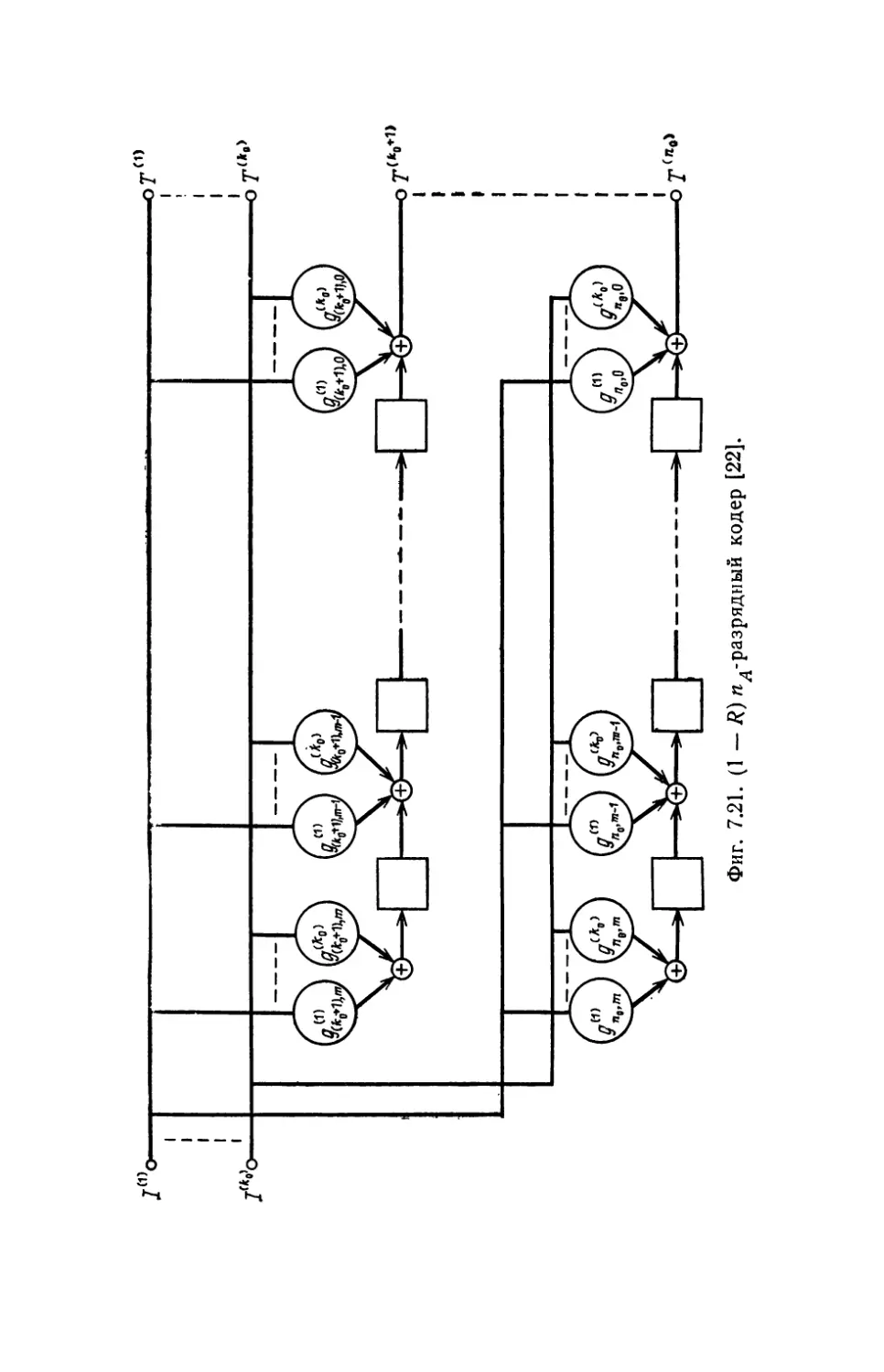
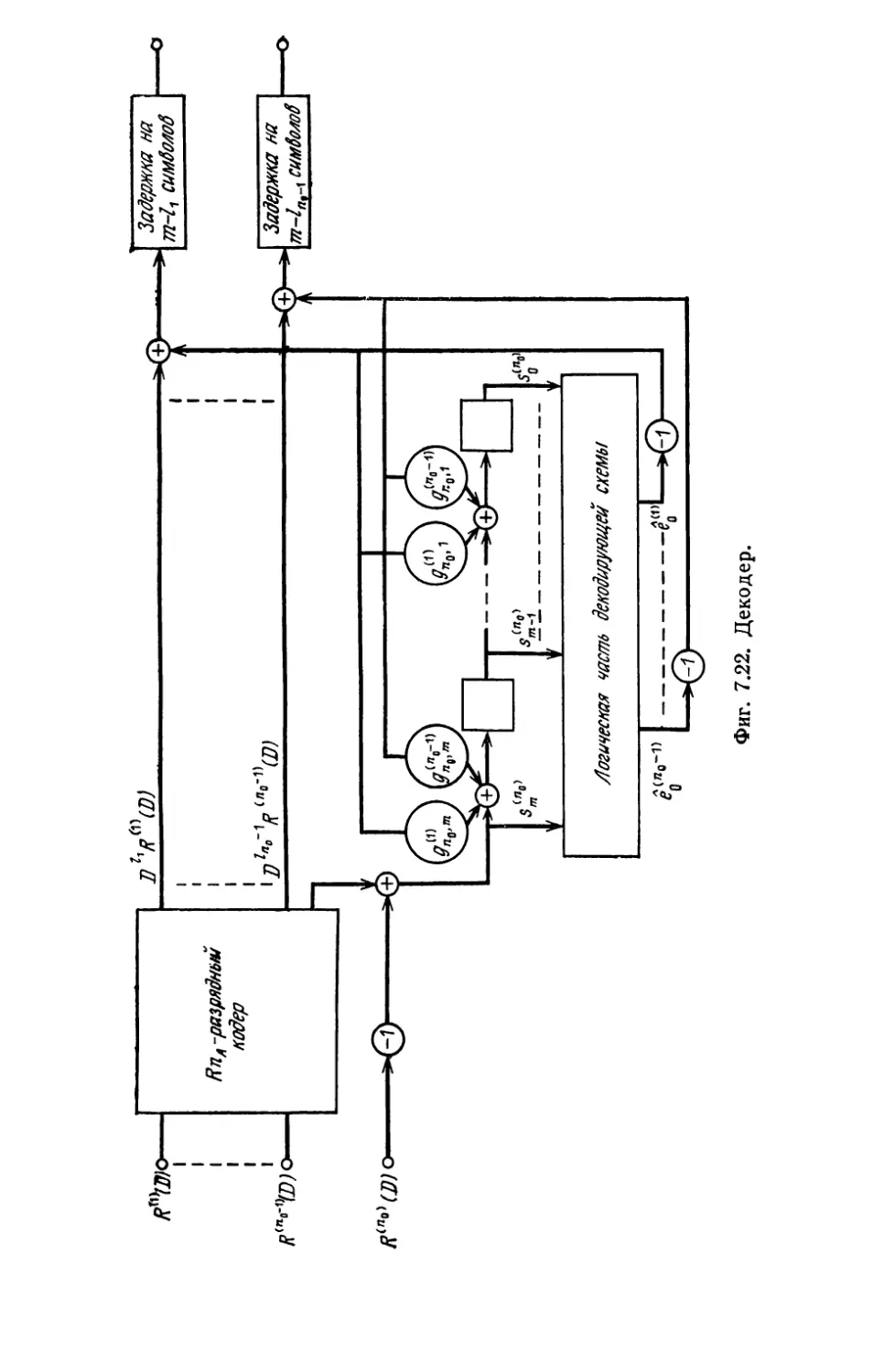
В rл. 7 сначала описываются основные компоненты, входя
щие в состав I\ОДИРУIОIЦИХ и декодирующих устройств, а также
схемы КОДИРУIОLЦИХ и декодирующих устройств для некоторых
10
п редuсловuе авторов
кодов. Вторая часть этой rлавы посвящена проблемам, связан-
ным с применением теории кодирования. Для развития теории
v
кодирования использовались в основном методы современнои
алrебры и различные методы получения оценок; из-за сложно-
сти этих методов существуют трудности в пони мании связи тео-
рии с теми реальными задачами, которые она призвана решать.
Чтобы преодолеть эти трудности, в rл. 7 исследуется адекват-
ность математических моделей их реальным прообразам и
исследуются rраницы применимости теории кодирования. Основ-
ными объектами применения теории кодирования ЯВЛЯIОТСЯ си-
стемы связи и вычислительные машины. В этой rлаве введено
понятие выиrрыша при ПРИl\fенении кодирования в системе свя-
зи, дано несколько примеров систем связи с кодированием и по-
казана целесообразность введения этоrо понятия. В разделаХ t
посвященных применениям теории кодирования в вычислитель-
ных машинах, рассмотрены коды, исправляющие ошибки
оператора при вводе информации в машину, а также коды,
допускающие быстрое декодирование.
Тем, кто хочет ознакомиться лишь с основами сверточных
кодов, рекомендуем прочитать разделы 5.1
5.8, 6.1 и 6.2. Чи-
татели, которые интересуются лишь применениями теории ко-
дирования, MorYT читать rл. 7 независимо.
В rл. 8 и 9 рассматриваются коды, предназначенные для об-
нару}кения и исправления арифметических ошибок, возникаю-
щих в арифметических устройствах, в частности АN
коды. Ко..
довыми словами АN-кодов являются двоичные представления
целых чисел, кратных числу А. Эти коды отличаются от всех
кодов, рассматривавшихся до rл. 8. Поскольку для изложения
теории таких кодов требуются дополнительные сведения о свой-
ствах целых чисел и их двоичных представлений, то в начале
rл. 8 приводятся основные понятия и результаты теории целых
чисел, используемые в дальнейшем. Далее в rл. 8 дается опре-
дсление АN
кода, описываются особенности ошибок, возникаю-
щих при выполнении арифметических операций, в частности при
сложении и вычитании чисел, вводится арифметическое расстоя-
ние, иrрающее в теории арифметических кодов ту iKe роль, что
и расстояние Хэмминrа в теории алrебраических кодов, описыl-
вается несколько классов кодов, исправляющих одиночные и
кратные ошибки, и исследуются их свойства.
rл. 9 посвящена циклическим АN
кодам. Как и алrебраиче
ские циклические коды, циклические АN
коды обладают рядом
достоинств и особых свойств. С помощью разложения целых чи-
сел на простые множители и приведенной системы вычетов по
ее подrруппе циклические АN-коды мо}кно разложить на cTporo
циклические коды и таким образом исследовать их структуру.
Кроме Toro, это разложение указывает на систематический ме-
Предисловие авторов
11
тод построения циклических АN кодов и позволяет оценить рас-
пределение весов кодовых слов. В конце rлавы кратко рассмот-
рены АN-коды, исправляющие пачки ошибок, арифметические
коды с несколькими модулями, q-ичные АN коды и проведено
сравнение АN кодов и алrебраических кодов.
В заключение нам хочется поблаrодарить С. Адзуми за со-
ставление табл. А. 1 и А.2 приложения и внесение исправлений
в rл. 1 4.
Авторы
Литература
1. Peterson W. W., Error Correcting Codes, М 'Т Press, Саш bridge, L'Лаss. 1961.
2. Peterson W. W., Weldon Е. J., Jr., Error Correcting Codes, 2nd ed., MIT
Press, Cambridge, Mass., 1972; есть русский перевод: Питерсон У., Узл-
дон Э., Коды, исправляющие ошибки, ИЗД DО «Мир», 1976.
З. Berlekamp Е. R., Algebraic Coding Theory, McGraw Hi11, N. У., 1968; есть
русский перевод: Берлекэмп Э., Алrебраическая теория кодирования, изд во
«Мир», 1971.
4. Van Lint J. Н., Coding Theory, 5pringer V erlag, Berlin, Heidelberg, N. У.,
1971.
5. Lin 5., 1 пtrоduсtiоп to Error Correcting Codes, Prentice Hall, Englewood
C1iffs, N. J., 1970.
6. Миякава, Ивадари, Имаи, Теория кодирования, изд во "Сёкодо", 1973.
1. Основные понятия
теории кодирования
1.1. КОДЫ, обнаруживающие и исправляющие ошибки
Если взять достаточно длинное предложение анrлийскоrо
или японскоrо текста и исказить ero, заменив в некоторых ме-
стах одни буквы на друrие, исключив ряд букв (символов) или
добавив новые, то, используя знание структуры отдельных слов
и предложения в целом, предыдущий и послеДУIОЩИЙ тексты,
а также наши обычные познания о предмете, о котором идет
речь, можно в большом числе случаев полностью восстановить
исходное предложение или по крайней мере безошибочно уло-
вить ero смысл. Это показывает, что анrлийский, японский н
друrие естественные языки обладают очень большой избыточ
ностью. В технике также часто устанавливают по два или три
одинаковых устройства, чтобы при выходе из строя одноrо из
них ero можно было заменить друrим. В некоторых случаях
с помощью одноrо устройства выполняются дважды одни и те
же вычисления, и если результаты этих вычислений совпадают,
то принимается решение о том, что вычисления выполнены без
ошибок. Если же результаты вычислений не совпадают, то это
означает, что в процессе вычислений ПРОИЗОШЛа ошибка. BLI
числения проводятся еще раз, и обнаруженная ошибка устра-
няется. Во всех рассмотренных выше случаях наличие избыточ
ности позволяет провести обнаружение ошибок и повыIитьь на-
дежность устройств.
Однако проблема состоит не в том, чтобы просто повысить
надежность за счет введения очень большой избыточности, а в
том, как с помощью ПО возможности l\lеньшей специальным об..
разом вводимой избыточности достичь нужной степени HaдefК-
ности.
В некоторых предложениях, взятых из eCTeCTBeHHoro языка,
достаточно сильно исказить небольшое число букв (например,
считать эти буквы неопределенными), чтобы смысл был пол
ностыо искажен. Известно [1] 1), что избыточность анrЛИЙСКОI'О
языка достиrает 700/0, однако нельзя сказать, что избыточность
v v
вводится в анrлиискии текст оптимально с точки зрения B03
можности исправления и обнаружения ошибок. Основной зада-
чей теории кодирования в настоящее время является повыше-
ние надежности систем связи и вычислительных систем
1) Цифры В квадратных скобках указывают номер работы в СПИСI<е лите-
ратуры, помещенном в конце книrи.
J4
r лава 1
с ПОМОЩЬЮ целенаправленноrо эффективноrо введения избыточ-
ности в процессе представления информации (в процессе преоб-
разования информации). Введение избыточности приводит к сни-
жению количества сообщений, которые MorYT быть переданы или
обработаны за определенный период времени, а кроме Toro,
предполаrает использование в системе дополнительных YCT
ройств для целенаправленноrо введения избыточности (ко-
деров), устройств для обнаружения и исправления возникаю-
щих ошибок (декодеров) и ряда друrих дополнительных
устройств. Само собой разумеется, что проектирование таких
избыточных систем должно выполняться с учетом стоимости
этих дополнительно вводимых устройств (см. rл. 7). Поскольку
От источника Преоораз
иНфОрМQции Ватель ер
оащении
tlCтOflHII
ка 6 880
И'Iную по
слеQо6а
mel/6HIJCТ6
Кооер
МООУ/lЯ
тор
Шум КаНIlЛ
f( nОIlУ'IRmе/fЮ rpeooPaJo
информации 6gтelf! 180
ЧНОIJ пoc
ioIQTeAS
ности 6
соооще
НIIЯ пO/1Y
., чатеllЯ
Демоиу
/1ятор
tt иr. 1.1. Модель системы связи.
в теории обычно рассматриваются идеализированные модели
реальных систем, в которых из большоrо числа факторов, влияю-
v
щих на поведение реальнои системы, учитывается лишь часть,
то теоретические результаты должны использоваться для реше-
ния задач, связанных с построением реальных систем, только
после Toro, как будут определены rраницы применимости этих
теоретических результатов.
На фиr. 1.1 показана типичная модель системы связи, в ко-
торой используются коды, исправляющие ОllIибки [2]. В этой мо-
дели каналом является простейший двоичный канал. Эта же
модель может быть использована и в качестве модели заломи-
нающеrо устройства (например, запоминающеrо устройства на
маrнитной ленте или интеrральной памяти), если среду, в ко-
торой хранится информация, рассматривать как канал связи.
Поступающая от источника информация вначале с помощыо
преобразователя «источник информации двоичная последова-
тельность» преобразуется в последовательность двоичных сиы-
Основные понятия теории одирования
15
волов, которая подается на вход кодера, rде в нее вводится из-
быточность. Символы с выхода кодера с помощью модулятора
преобразуются в сиrналы, которые MorYT быть переданы по ка-
налу. Эти сиrналы поступаIОТ в канал, rде они обычно иска-
жаются шумами. На приемном конце искаженные сиrналы
канала с помощью демодулятора преобразуются в последова-
тельность двоичных символов, содер}кащую избыточные сим-
волы. Используя эту избыточность, декодер обнаруживает и
исправляет возникшие ошибки. Двоичная последовательность
символов на выходе декодера уже не является избыточной. Если
о
воздеиствие шума в канале не слишком сильное и декодер может
исправить все ВОЗНИI{шие ошибки, то двоичная последователь-
ность на выходе декодера будет совпадать с двоичной последо-
вательностыо на выходе преобразователя «источник информа-
ции двоичная последовательность». И наконец, двоичная
последовательность, получающаяся на выходе декодера, преоб-
разуется в сиrналы, приемлемые для получателя информации,
и передается последнему.
Ниже рассматривается несколько примеров простых кодов,
обнаруживающих или исправляющих ошибки.
Пример 1.1. Рассмотрим канал, по которому за время t o
может быть передан один импульс типа «О» или типа «1 ». До-
пустим, что при передаче MorYT происходить случайные ошибки,
так что импульсы О и 1 MorYT быть приняты с некоторой вероят-
ностью 1 РО соответственно как 1 и О. Предположим, что
ошибки при передаче различных импульсов возникают незави-
симо. Пусть информацией, подлежащей передаче, является по-
следовательность двоичных символов. Каждый символ ai этой
последовательности передается по каналу с помощью последо-
вательности из пяти импульсов О О О О О, если ai == О, и 1 1 1 1 1,
если ai == 1. На приемном конце принимаемая последователь
ность импульсов разбивается на rруппы по пять импульсов,на
зываемые блоками, в соответствии с разбиением передаваемой
последовательности. Если в принятом блоке содержится два и
менее импульса О, то принимается решение о том, что переда
вался символ ai == 1. Если в принятом блоке содержится три и
более импульсов О, то считается, что ai == О. Очевидно, что пе-
реданный символ ai будет декодирован верно тоrда и только
тоrда, коrда число ошибочно принятых импульсов в соответ-
ствующем блоке не больше двух. Следовательно, вероятность
ошибочноrо декодирования любоrо символа ai равна ')
1) Через (:) обозначено число сочетаний из п по m. Прuм. ред.
16
r лава 1
5
L ( ) pg l (1 ро)'. Этот метод передачи является простым,
i==3
но для передачи одноrо бита информации он требует интервала
времени длительностью 5t o . В то же время существуют коды
(см. теорему кодирования из разд. 1.5), которые позволяют П:
редавать по тому же самому каналу один бит информации в
среднем за меньший интервал времени с вероятностью ошибки,
не превосходящей указанную выше величину. При этом, однако,
процедуры кодирования и декодирования оказываIОТСЯ более
сложными. В тех случаях, коrда «убытки» Из за ошибочноrо
декодирования оказываются больше убытков, возникающих
Из за Toro, что часть символов ai вообще не декодируется и
считается неизвестной (как это имеет место, например, в си
стемах с переспросом) , часто оказывается более целесообраз-
ным использовать друrой алrоритм декодирования. Этот алrо-
ритм состоит в том, что если в блоке нет символов 1 или со-
держится только один символ 1, то считается, что ai == О, если
же в блоке содержатся четыре или пять символов 1, то счн-
тается, что ai 1. Во всех остальных случаях решение не при-
нимается. Для этоrо алrоритма вероятность ошибочноrо дeKO
5
дирования равна L ( ) pg l (1 РОУ, а вероятность отказа от
i==4
з
декодирования равна I ( ) Pg ' (1 ри(
i==2
Пример 1.2 В вычислительных l\fашинах информация обычно
представляется в виде двоичных последовательностей. При этом
используется несколько способов представления десятичных
цифр О, 1 ..., 9. Одним из таких способов является код «два
ИЗ пяти», показанный в табл. 1.1. Любая из цифр в этом коде
представляется в виде двоичной последовательности длины 5,
в которой два из пяти символов всеrда равны 1 (заметим, что
( ;) == 10 ). При возникновении одиночной ошибки, т. е. при
искажении одноrо из двоичных символов, последовательность
содержит один или три символа, равных 1, а это позволяет обна-
ружить возникновение ошибки. В общем случае для представ-
ления каких либо ( : ) сообщений MorYT использоваться двоич-
ные ПОСJIедовательности длины n, ка}кдая из которых содер-
жит w символов 1. Совокупность таких двоичных последова-
тельностей называется равновесным кодом. Коды этоrо типа
оказываются эфq)ективными, в частности, в тех случаях, коrда
l,3ероятность ВО3IIНJ(lIопения ОIllибки типа «переход символа О в
Основные понятия теории кодирования 17
Таблица 1.1
Пример представления десятичных цифр
Десятич СИМВОЛ проверки
вые КОД «2 из 5» 842 1
uифры на четность
О 00011 О О О О О
1 О О 1 О 1 О О О 1 1
2 О О 1 1 О О О 1 О 1
3 О 1 О О 1 О О 1 1 О
4 О ] О 1 О О 1 О О 1
5 О 1 1 О О О 1 О 1 .о
6 1 О О О 1 О 1 1 О О
7 1 О О 1 О О 1 1 1 1
8 1 О 1 О О 1 О О О 1
9 ] 1 О О О 1 О О 1 О
символ 1» значительно больше (или значительно меньше), чем
вероятность возникновения ошибки типа «переход символа 1 в
символ О» (т. е. при так называемых несимметричных ошиб-
ках), а также в тех случаях, коrда «убытки» из за ошибочноrо
принятия символа 1 вместо символа О значительно больше
(меньше) убытков при принятии символа О вместо символа 1
[17 19]. Рассмотренные здесь коды являются примерами так
называемых нелинейных кодов.
Пример 1.3. Предположим, что некоторые 2n 1 или менее
сообщений представлены в виде двоичных последовательностей
(XI, Х2, ..., Xn 1) длины n 1 и это представление взаимно
однозначно. Пусть
X n ==XI+X2+ ... +Xn 1,
(1.1)
rде в данном с,пучае знак + означает сложение по модулю 2,
т. е. Х N == О, если сумма в правой части (1.1) четна, и Х N == ],
если она нечетна. Предположим, что вместо последовательно-
стеЙ (XI, ..., Xn 1) длины n 1 ИСПОЛЬЗУIОТСЯ последователь
ности (XI, ..., Х n ) длины N. Допустим, что в процессе переда 4И
или обработки одной из таких последовательностей, содержа
щей один избыточный двоичный символ, возникла ошибка в
одном из двоичных символов. Как видно из формулы (1.1), в
неискаженной последовательности (Хl,..., Х n ) число симво
лов 1 всеrда четно, а при возникновении ошибки в одном ИЗ
символов это число становится нечетным. Это позволяет обна
руживать возникновение одиночIIыIx ошибок. Символ Х п
18
r лава 1
называют символом nроверки на четность. Рассмотренный здесь
метод обнаружения одиночных ошибок блаrодаря своей простоте
применяется очень широко. В табл. 1.1 показан способ пред-
ставления десятичных цифр с помощью пяти двоичных симво-
лов, первые четыре из которых являются двоичным разложе-
нием соответствующей десятичной цифры, а пятый символом
проверки на четность.
Пример 1.4. Предположим, что имеется 16 сообщений, каж-
дому из которых взаимно однозначно поставлена в соответствие
двоичная последовательность (хз, Xs, Хв, Х7) длины 4. Вместо
последовательности (Хз, XS, Хв, Х7) для представления сообщений
будем использовать двоичную последовательность (XI, Х2, . . . ,Х7 >:
длины 7, символы XI, Х2 И Х4 которой определим следующим об-
разом:
[ 1010101 ]
0110011
0001111
Xl
Х 2
Хз
Х4
Х5
===0
,
т. е.
{ XI == Хз + Xs + Х 7 ,
Х2 === Хз + Х6 + Х7,
Х4 === Х5 + Х6 + Х 7 .
( 1.2)
Х 6
X7
Здесь знак +" означает сложение по модулю 2, а остальные обо-
значения имеют тот же смысл, что и в обычных матричных со-
отношениях. Поскольку в процессе передачи или хранения по-
следовательности (Х], Х2, ..., Х7) MorYT возникнуть ошибки, то
принимаемая последовательность (x , X , . . ., х;), вообще rоворя,
будет отлична от исходной. Рассмотрим задачу восстановления
исходной последовательности (Х], Х2, ..., Х7) по известной по-
следовательности (x , X , . . ., Х;). Предположим, что верояr-
ность возникновения двух и более ошибок в двоичных символах
одной последовательности длины 7 настолько мала, что этим
событием можно пренебречь. Положим
. I
x l Т X l z::::e l ,
rде знак + обозначает сложение по модулю 2. Если ei == 1, то
это означает, что в i-M двоичном символе произошла ошибкз;
если ei == О, то i й двоичный символ передан без ошибок. Ис-
пользуя матрицу из левой части (1.2), определим '1,'2 И 'з сле-
Основные понятия теории кодирования
19
ДУЮЩИМ образом:
[ 1010101 ]
0110011
О О О 1 1 1 1
,
Х 1
х'
2
х'
1 == [ : ].
)С'
6
х'
7
(1 .3)
Из формул (1.2) и (1.3) получаем
el
е2
[1010101] ез == [ ].
0110011 е4
00 01111 еБ 'з
е6
e7
(1.4 )
По предположению только один ИЗ символов eI, е2, ..., е7 MO
жет быть равен 1. При отсутствии ошибок, коrда el == е2 ==
== ... == е7 == о, имееI '1 == '2 == 'з == о.
Далее рассмотрим случай, коrда ei == 1, а остальные шесть
символов ej, j =1= i, равны о. Заметим, во-первых, что все столб-
цы матрицы
[ 1010101 ]
р== 0110011
0001111
из левой части (1.4) различны, а BO BTOpЫX, что k..й столбец
этой матрицы представляет собой двоичную запись номера k
(самый младший разряд двоичноrо представления числа k ЯВ
ляется верхним элементом столбца). При сделанных выше пред-
положениях вектор-столбец ( :) совпадает с i-M столбцом
матрицы Р. Следовательно, номер i искаженноrо двоичноrо сим-
вола может быть найден следующим образом: i=='l + 2'2 + 4,з.
С ПОМОЩЬЮ равенства X i == X + e i находим правильные двоич-
ные символы XI, ..., Х7. Множество двоичных последовательно-
стей (Xl, Х2, ... ,Х7), удовлетворяющих соотношению (1.2} и
20
r лава 1
называемых обычно кодовыми векторами, называется кодом
Хэмминzа длины 7 [3].
Утверждение 1.1. Если последовательности Х === (Xl, Х2, ..., Х7)
и у == (YI, У2, ..., У7) удовлетворяют соотношению (1.2) (Т. е.
РХТ == О и рУТ == О) и Х =1= У, то число d(X, У) значений индек-
са i, таких, что Xi =1= Yi (это число называется расстоянием ХЭМ-
минzа [3] между векторами Х и У), не меньше трех, (символ Т
означает транспонирование).
Краткое доказательство. Число ненулевых компонент векто-
ра называют весом этоrо вектора. Пусть Z произво.ПЬНЫЙ век-
тор веса 1 или 2. Так как все столбцы матрицы Р разJlичныI и
ни один из них не является нулевым, то PZT =1= О. Вместе с тем
по условиям утверждения Р (Х У) т == о. Наконец, заметим,
что вес вектора Х У совпадает с d (Х У, О) и d (Х У, О) ==
== d (Х У) (здесь О нулевой вектор).
Утверждение 1.2. Для любосо двоичносо вектора У длины 7
найдется такой кодовый вектор X что d (Х, У) 1.
Краткое доказательство. Если У кодовый вектор, то Х ==: У.
Предположим, что У не является кодовым вектором. Пусть
РУТ == r (, двоичный вектор длины 3, r =1= О). Среди столбцов
матрицы р существует ровно один столбец, в точности совпа-
дающий с '. Пусть i номер этоrо столбца. Возьмем в качестве
вектора Х вектор, отличаЮIЦИЙСЯ от У только i й компонентоЙ.
Тоrда РХТ == О И d(X, У) == 1.
Для представления в двоичной записи К различных сооб-
щений достаточно [log2 К] двоичных символов ([А] минимаJlЬ-
ное целое число, не меныпее А). Однако, как показывают при-
веденные выше примеры, использование HeKoToporo числа до-
полнительных избыточных символов позволяет осуществить ис-
правление или обнаружение части возникаrощих ошибок или
упростить схемы, осуществляющие обработку этих сообщений.
Число n [10g2 К], rде n общее число двоичных символов,
используемых для представления каждоrо сообщения, назы-
вают числом проверочных или избыточных символов. ECTeCTBeH
но, что всеrда хотелось бы достичь нужных свойств кода (на-
пример, способности исправлять так называемые ОДИНОЧНI.)IС
ошибки, т. е. ошибки в одном двоичном символе), используя по
возможности меньшее число избыточных символов.
Утверждение 1.3. В случае К == 16 никакой код, имеющий два
или менее проверочных символа, не может исправлять одиноч-
ные ошибки. В этом СЛl,ысле код Хэмминса длины 7 является
наилучшим среди кодов, исправляющих одиночные ошибки.
Краткое доказательство. Для Toro чтобы код исправлял оди-
ночные ОIIIибки, множества векторов, находящихся на расстон-
Основные понятия теории Kol}upoBaHQ,jf
21
нии Хэмминrа 1 и менее от каждоrо кодовоrо слова, не должны
пересекаться. Если длина кода равна п, то число векторов, на-
ходящихся на расстоянии 1 и менее от кодовоrо слова, равно
n + 1. Так как общее число двоичных векторов длины п равно
2 n , то для любоrо кода, исправляющеrо одиночные ошибки,
ДОЛ)I(НО выполняться неравенство (п + 1) К
2 n , откуда сле-
дует справедливость доказываемоrо утверждения.
По матрице Р из примера 1.4 построим матрицу р' следую..
щим образом:
р' ==
о
р о
о
1 1 ... 1
............ -..----
8
Совокупность всех двоичных векторов Х длины 8, удовлетво-
РЯIОЩИХ УСЛОВИIО Р' ХТ == О, называется расширением кода из
ПРИ1\1ера 1.4.
Утверждение 1.4. Расширение кода из примера 1.4 исправ-
ляет одиночные ошибки и в то же время обнаруживает двойные
ошибки (то ео ошибки в любых двух KO}rf,nOHeHTax кодовосо ве!,,-
тора) .
И дея доказательства. В начале, используя утверждение 1.1,
нужно показать, что расстояние Хэмминrа между любыми дву-
мя различными кодовыми векторами не меньше четырех. OCHO
вываясь на этом, далее следует доказать, что рассматриваемыЙ
код исправляет одиночные и обнаруживает двойные ошибки (в
общем случае связь между минимальным значением расстоянии
Хэмминrа и способностью кода исправлять и обнаруживать
ошибки устанавливается в разд. 1.3).
При изучении корректирующей способности кода Хэмминrа
из примера 103 и ero расширения из утверждения 1.4 для нас
существенным было лишь то, что все СТО"ТIбцы матрицы Р раз.
.пичны и все они являются ненулевыми. Аналоrично можно по
строить коды для любоrо К == 2т. В общем случае коды Хэм
минrа и их расширения рассматриваются в задаче 3.2, приме-
ре 3.5 и разд. 4.1.
1.2. Блоковые коды. Систематические коды
Рассмотрим q
ичный канал (q
2), по которому MorYT пе-
редаваться сиrналы (импульсы) q типов определенной длитель-
ности. Для обозначения этих сиrналов будем использовать q
22
r лава 1
различных символов, которые назовем символами канала; мно-
жество q символов канала обозначим через V 1 . Пусть V n ........ мно-
жество всех последовательностей длины п из символов V 1 , т. е.
V n == {(al, а2, ..., а n ) I ai Е V], 1 i п}. Расстояние Хэм-
минrа d (А, В) между последовательностями А == (al, а2, ,..
. . ., а n ) и В == (b l , Ь 2 , ..., Ь n ) длины n определим l<aK число
пар компонент ai и b i , таких, что ai =1= b i . Заметим, что это рас-
стояние зависит лишь от Toro, совпадаlОТ или нет соответствую
щие символы последовательностей А и В. Расстояние Хэмминrа
может быть использовано в системах модуляции с ортоrонаЛ1>
ными сиrналами [4]. Это связано с тем, что, коrда q символов
канала представляют q взаимно ортоrональных сиrналов с рав-
ной энерrией, а шум в канале является аддитивным белым и
rауссовским, вероятность ошибки (т. е. вероятность перехода
одноrо символа канала в друrой) для всех сиrналов одна и та
же. Расстояние Хэмминrа применяется также для описания про-
цесса возникновения ошибок в запоминающих устройствах вы-
числительных машин, в которых разные двоичные символы сло-
ва хранятся в различных матрицах [5].
Для описания возникновения ошибок в системах с фазовой
модуляцией может быть использовано расстояние Л и [6]. Чтобы
ввести это расстояние, необходимо установить взаимно одно-
значное соответствие между элементами множества V 1 и целы-
ми числами от О до q 1. Здесь для простоты будем считать,
что V 1 == {О, 1, ..., q........ l}. Для каждоrо элемента а Е V 1 опре-
делим число I а I L следующим образом: I а I L == а, если О а
(q 1) /2, и I а I L == q ........ а в противном случае. Расстояние
Ли d L (А, В) между последовательностями А == (al, а2, ..., а n )
и В == (b 1 , Ь 2 , ..., Ь n ) определяется равенством d L (А, В) ==
n
== L I ai b i ILe При q, равном 2 или 3, расстояние Хэмминrа со-
l==l
совпадает с расстоянием Ли. Поскольку в теории кодирования
результаты, полученные для расстояния Ли, не являются столь
значительными, как результаты, полученные для расстояния
Хэмминrа, то в данной книrе вопросы, связанные с расстоянием
Ли, почти не рассматриваются (детальное изложение этих BO
просов можно найти в книrе Берлекэмпа [4]).
Для описания и исследования методов кодирования в систе-
мах с амплитудной модуляцией наиболее подходящим является
евклидово расстояние (см. r л. 7), однако в теории кодирования
получено лишь несколько частных результатов, посвя[ценных
этому вопросу, и они в основном связаны с некоторыми идеЯ\1:И
устранения недостатков кодов, построенных для расстояния
Хэмминrа [7,8].
Основные понятия теории кодироваНllЯ
23
Подмножество С множества V п, состоящее из К последова-
тельностей длины n, назовем q-ичным блоковым кодом длины n.
Последовательности длины n, входящие в С, будем называть
кодовыми словами. Число R == (logqK) /n называется скоростью
передачи кода С. Минимальное значение расстояния Хэмминrа
(расстояния Ли) между различными кодовыми словами кода С
назовем минимальным расстоянием Хэмминrа (минимальным
расстоянием Ли) или просто минимальным расстоянием кода С.
Если К == qk (1 k n) и в блоковом коде для любой по-
следовательности al, а2, ..., ak из k символов V I (символы Н
этой последовательности MorYT повторяться) найдется ровно
одно кодовое слово, первые k компонент KOToporo есть al, а2, ...
. . ., ah, то этот блоковый код называется систематическим. Боль
шинство используемых на практике и обычно исследуемых ко-
дов пВЛЯЮТСЯ систематическими. Кодер систематическоrо кода,
на вход KOToporo с выхода преобразователя «источник инфор
мации q-ичная последовательность» поступает q ичная после..
довательность символов множества V 1 , разбивает входную по-
следовательность на блоки длины k и для каждоrо TaKoro бло-
ка Wi (а., а2, ..., ak) из k символов находит кодовое слово
<J>e(Wi), первые k символов KOToporo совпадают с Wi (по опреде-
лению существует ровно одно такое кодовое слово). Далее, к
k символам al, ..., а,! кодер приписывает в конце n k симво-
лов a't+l, ..., а п и полученное таким образом кодовое слово по
сылает на выход как единый блок. Первые k компонент TaKoro
кодовоrо слова называются информационными СИМВОЛQ.Аtи, а по
следние n k компонент nровеРОЧНblМИ символами. При этом
параметры k и n k называются соответственно числом инфор
мационных и числом nровеРОЧНblХ (или избыточных) символов.
Как мы видели в приведенных в предыдущем разделе примерах,
избыточные n k символов MorYT использоваться для исправ
ления или обнаружения ошибок. Отношение k/n обычно обозна-
чаIОТ через R и называют скоростью передачи. Скорость пере
дачи является параметром, характеризующим эффективность пе-
редачи.
Описанный BbIllIe кодер обрабатывает каждый поступающий
блок независимо от друrих, так что каждое новое кодовое слово
на ero выходе оказывается не связанным с предыдущими KOДO
выми словами. Это является особенностью блоковых кодов.
Кроме блоковых I{ОДОВ, имеются друrие типы кодов, в частности
сверточные коды, которые детально рассматриваются в rл. 5 и 6.
Каждый новый блок на выходе кодера сверточных кодов зави
сит от предыдущих блоков. Блоковые коды по сравнению с KO
дами друrих типов являются более простыми с точки зрения их
математическоrо описания, и, кроме Toro, они лучше исслеДQ
ваны.
Входные символы канала, которые являются в то же время
выходными символами кодера, преобразуются в модуляторе в
сиrналы, которые MorYT быть переданы по каналу. Демодулятор
выполняет обратную операцию, а именно каждому принятому
сиrналу, подверrшемуся воздействию шумов, он сопоставляет
наиболее подходящий символ канала. Последовательность сим-
волов с выхода демодулятора поступает на вход декодера. )1е-
кодер блоковоrо кода С разбивает эту последовательность на
блоки в соответствии с разбиением последовательности на вы-
ходе кодера 1) И далее для каждоrо принятоrо блока, используя
свойства кода С, выбирает одно из наиболее вероятных кодовых
слов, которые моrли быть переданы. Это кодовое слово появ-
ляется на выходе декодера (в действительности на выходе дe
кодера MorYT быть лишь информационные символы I(ОДОВОI"О
слова). В некоторых случаях декодер может не принимать ре-
шения о том, какое кодовое слово передавалось, а послать на
выход специальный символ D, означающий обнаружение ОШИQ-
ки. Таким образом, функция декодера заКЛlочается в реализа-
ции отображения (f)d множества V n В множество С U {D}. Это
отображение в принципе можно задать с помощью таблиt,ы де-
кодирования, которая каждой последовательности из V n сопо-
ставляет некоторое кодовое слово или символ D. В тех случаях,
коrда код С используется как код, исправляющий ошибки, то
значениями (f)d(W r ), W r Е V, являются только кодовые слова.
Если же код С используется как код, обнаруживающий ошиб-
ки, то (f)d(W r ) == D для всех последовательностей W r ДЛИНbI n,
не являющихся кодовыми словами. Как видно из примера 1.1,
существуют также коды, которые часть ошибок испраВЛЯIОТ, а
друrие ошибки обнаруживают (вопросы целесообразности ис
пользования таких кодов будут рассмотрены в rл. 7).
В теории кодирования обычно предполаrается, что кодер 11
демодулятор, точно так же, как и декодер и демодулятор, пред-
ставляют собой отдельные устройства; при этом каждый СИМВО.11
канала преобразуется и передается независимо от друrих. Та-
кое построение системы приводит не только к упрощению
устройств, но, как мы увидим в rл. 7, и к некоторому снижени!о
пропускной способности канала. Соrласно теореме Шеннона Л.'IЯ
дискретноrо канала r9] (этот канал будет рассмотрен ниже в
разд. 1.5), в случае использования ПОДХОДЯIl ИХ (блоковых) ко-
дов, исправляющих ошибки, при всех скоростях, l\fеНЫllИХ про-
пускной способности канала, информаЦИIО можно передавать со
1) Из за воздействия шумов разбиение последовательности на блоки м 0--
жет оказаться неправильным. В таких случаях rоворят, что ПрОIIЗОIlIла ОIIJи6.
ка синхронизации. Для борьбы с ошибl<НМИ СИIJХРОНlIзации разработаны раз
,11ичные методы [2].
Основные понятия теории кодирования
25
сколь уrодно малой вероятностыо ОILlиБI{И. Однако теорема
Шеннона является так называемой теоремоЙ существования и
не дает конкретных методов построения таких кодов. Разра-
ботка практически приемлемых методов кодирования является
задачей теории кодирования. Для Toro чтобы эффективность
использования кодов была ВЫСОI{ОЙ, необходимо усреднить воз-
действие шумов. Это приводит К необходимости выбирать длину
кода достаточно большой, что в свою очередь обычно связано
с чрезмерным усложнением кодеров и декодеров. Например, в
случае q === 2, R == 1/2 И n === 200 число кодовых слов достиrает
приблизительно 1030, а общее число последовательностей дли-
ны n приблизительно 1060, так что практически построить опи-
caHHYlo таблицу деl{одирования просто невозможно. Этот при-
мер показывает, что построение кодов, которые имели бы
достаточно большую длину (а следовательно, и высокую эф-
фективность), но в то же время были бы практически реализуе-
мыми с точки зрения сло)кности кодера и декодера, является
непростой задачей. Коды, удовлетворяющие этим условиям,
должны иметь хорошую (алrебраическую) структуру, которая
rарантировала бы нужные корректирующие способности и по-
зволяла бы найти практически реализуемые процедуры кодиро-
вания и декодирования. Эта точка зрения на цели теории коди
рования и пути их достижения была положена в основу исследо-
ваний, которые велись и ведутся в настоящее время в области
алrебраической теории кодирования.
Утверждение 1.5. Если А 1 , А 2 , Аз е: V n,
d(AI,A2) +d(А 2 ,А з ).
Утверждение 1.6. Пусть D(AI) =={Ald(A 1 ,A) t, Ae:V n }
и D (А 2 ) == {А I d (А2, А) t, А е: V n}. Tozaa необходимым и до-
статочным условием TOZO, что D (А 1) и D (А 2 ) не содержат об-
щих элементов, является выполнение соотношения d(AI, А 2 )
21 + 1.
Краткое доказательство. 1) Допустим, что d (А 1, А 2 ) 2t.
Пусть ip i 2 , .. ., (/ (А 1 . А 2 ) номера компонент, в которых разли-
чаются последовательности AI и А 2 . Тоrда если обозначить че
рез Аз последовательность, получающуюся из А 1 заменой КОМ-
понент последней с номерами i., i 2 , ..., i(d(A 1 , А 2 )/2] на cOOTBer-
ствующие компоненты А 2 , то Аз е: D (А 1 ) и Аз Е D (А 2 ).
2) Пусть d(A 1 , А 2 ) 2! + 1. Предположим, что существуеr
последовательность Аз, принадлежащая одновременно и D(Al}
и D (А 2 ). Тоrда d (А 1 , Аз) f и d (А 2 , Аз) '. Но в таком слу-
чае, как следует из' утверждения 1.4, d(AI' А 2 ) 2f, что ПРОТII-
воречит преДI10ЛО)l(еНИIО,
то
d (А], Аз)
26
r лава 1
1.3. Двоичный симметричный канал
Чтобы оценить эффективность использования кодов, необхо-
димо знать статистические свойства используемоrо канала. При
этом в состав канала входят также модулятор и демодулятор.
Простейшей приближенной моделью канала является так назы-
ваемый двоичный симметричный канал (ДСК). В ДСК приня-
тый символ С вероятностью РО совпадает с переданным симво-
лом и с вероятн'остью qo == 1
Ро, Ро > qo, отличается от послед
Hero; при этом считается, что ошибки при передаче различных
символов происходят независимо (фиr. 1.2). Такие каналы,
в которых ошибки возникают независимо, называют каналами
без памяти. Ошибки, возникающие в дск, называются случай
ными ошибками. Для дек вероятность Toro, что при передаче
Q
о
1
1
РО
Фиr. 1.2. Двоичный симметрич
ный канал.
Фиr. 1.3. Расстояние Хэмминrа
и исправление ошибок.
HeKoToporo кодовоrо слова кода длины n ошибки возникнут в
определенных i компонентах из n, равна pg
iqb. Поско.пьку
Ро > Qo, то чем меньше i, тем больше эта вероятность. Следова-
тельно, если предположить, что все кодовые слова передаются
с равными вероятностями, то наилучшим решением при приеl\lе
является такое, при котором переданным считается кодовое сло-
во, отличающееся от принятой последовательности длины n в
наименьшем числе компонент. Такое правило принятия решений
называется декодированием по максимуму nравдоnодобия. Из
вышеизложенноrо видно, что введенное в предыдущем разделе
расстояние Хэмминrа является понятием, важным дЛЯ ДСI(.
Чтобы можно было исправлять ошибl{И в t и меньшем числе
компонент (далее такие ошибки называются ошибками веса t
и меньше или t-кратными ошибками), необходимо и достаточ-
но, чтобы для любых двух различных кодовых слов Wl И W2
множество различных двоичных последовательностей длины п,
отличающихся в t или меньшем числе компонент от WI, т. е.
{wld(w, Wl)
t, w Е V n }, И множество различных двоичных
последовательностей длины n, отличающихся в t или меньшем
числе компонент от W2, т. е. {w I d (w, W2)
t, w Е V n}, не имели
оБLlJ.ИХ элементов (фиr. 1.3). Друrими словаl\fИ, как следует из
утвеР,I
ДСIIНЯ 1.6, необходимо и достаточно, чтобы d(Wl, W2)
Основные понятия теории кодирования
27
2t + 1. Таким образом, код исправляет ошибки веса t и ме-
нее тоrда и только тоrда, коrда минимальное расстояние кода
больше или равно 2t + 1. Аналоrично можно показать, что код
обнаруживает любые ошибки веса t и менее (т. е. ошибки в t
и меньшем числе компонент) тоrда и только тоrда, Коrда ми-
нимальное расстояние кода больше или равно t + 1.
Утверждение 1.7. ДЛЯ Т020 чтобы код исправлял любые
ошибки веса t 1 u менее и обнаруживал любые ошибки веса от
t 1 + 1 до t 2 (t l < t 2 ), минимальное расстояние должно быть не
меньше чем t 1 + t 2 + 1.
Краткое доказательство. Пусть WI и W2 два произвольных
различных кодовых слова, а D t1 (Wt) {lCJ I d (w, Wt) t], W Е V n}
и D tJ (W2) == {ш I d (w, Ш2) 12, W Е V п}. Для TOrO чтобы код удов-
летворял указанному в утверждении 1.7 свойству, необходимо
и достаточно, чтобы множества Dt. (Wt) и Dt'l (W2) не имели об-
щих элементов.
Таким образом, как видно из вышеизложенноrо, минималь-
ное расстояние d кода является важным параметром, показы-
вающим, насколько хорошим является КОД в дск. Здесь сле
дует заметить, что при d == 2t + 1 и d == 2t + 2 обычно удается
исправлять также часть ошибок веса t + 1 и более (см. при-
мер 3.1 в разд. 3.2).
В некоторых случаях удается более или менее точно устано-
вить зависимость вероятности правильноrо декодирования от
вероятности ошибки в канале, но полностью определить коррек-
ТИРУЮЩУIО способность кода только через минимальное pac
стояние кода d, вообще rоворя, нельзя. Однако, поскольку, за
исключением ряда случаев, коrда значения параметров п и k
очень малы, описать более детальные свойства кода почти не-
возможно, то обычно корректирующую способность кода харак-
теризуют минимальным расстоянием d. Исходя из вышеизло-
женноrо, rоворят, что: 1) среди кодов с одинаковыми парамет-
рами п и k (т. е. в классе (п, k) -кодов) лучшим является код,
КОТОрЫЙ имеет большее минимальное расстояние d; 2) среди
кодов с одинаковыми параметрами п и d лучшим является код,
который имеет большее число информационных символов k, и
3) среди кодов с одинаковыми параметрами k и lt лучшим яв
ляется код, который имеет меньшую длину п, а следовательно,
и меНЫllее число избыточных символов r == n k. Заметим, что
здесь при сравнении качества кодов не учитываlОТ сложность
кодирования и декодирования. Поэтому иноrда rоворят более
точно: «код имеет лучшие параметры».
Существуют аналоrи двоичноrо симметричноrо кана lIa и в
случае q > 2. Для этих каналов, точно так же, как и для дек,
можно получить необходимые и достаточные условия Toro, что
28
r лава 1
код исправляет (обнаруживает) ошибки веса t и менее (при вы-
воде этих условий для дек мы не пользовались тем, что q== 2).
Однако при q > 2 эта модель является адекватной моделью
лишь тех каналов, в которых вероятность Toro, что переданныiI
символ S будет ошибочно принят как некоторый символ 8', от-
личный от 8, является величиной, не зависяtцей ни от 8, НИ
от 8'.
Современные цифровые системы БО"ТУЫIJеЙ частыо являются
двоичными, поэтому двоичный случай является на
более важ-
ным. Однако, поскольку, во-первых, мноrие алrебраичеСКИf KO
дЫ MorYT быть достаточно просто обобщены с двоичноrо случая
на случай q == рт (р
простое число), BO
BTOpЫX, из 2l.ичных
кодов MorYT быть получены некоторые превосходные двоичные
коды [2], а в-третьих, и сами q
ичные коды (q > 2) MorYT найти
практическое применение, то в данной книrе рассматривается и
случай q == рт там, rде это не усложняет изложение.
Корректирующая способность блоковых кодов, предназна-
ченных для исправления случайных ошибок, не зависит от по-
рядка следования компонент блока. В силу этоrо блоковые ко-
ды С и С' длины n, для которых существует такая перестаноп-
ка П упорядоченноrо множества {l, ..., n}, что С' == {(аП(1),
ап (2), . . ., ап (n)) I (UI, а 2 , ..., а n ) Е С}, называются эквивалент-
ными.
дек, как и друrие каналы без памяти, не дает адекватной
модели некоторых реальных линий связи. В частности, в теле-
фонных каналах и в запоминающих устройствах на маrнитной
ленте явно выражена тенденция. к rруппированию О[l1ибок [2].
При этом в среднем ошибки возникают сравнительно редко, од-
нако в некоторые интервалы времени, коrда [LlYMbI очень силь-
ны, они появляются часто, а в друrие интервалы, коrда шумов
почти нет, ошибки практически OTCYTCTBYIOT. Если ошибки BO.l
никли в пределах rруппы из Ь соседних компонент, то rоворят,
что возникла пачка ошибок длины Ь. ДЛЯ корреl<UИИ таких па-
чек ошибок разрабатываются коды специальных типов (см..
r л. 4).
1.4. Верхние rраницы для минимальноrо расстояния
кодов
Предельные возможности кодов, исп раВЛЯIОЩИХ ОIlJибки, He
обходимо знать, во
первых, при оценке Toro, насколько реально
используемые коды хуже «идеальных» кодов, BO
BTOpЫX, при
определении характеристик систем в целом и, в
третьих, для
сравнения систем различных типов. В данном разделе будут
получены простейшие верхние rраницы для минимаЛЫIоrо рас-
Основные понятия теории КОдирования
29
стояния [2, 4, 10]. Рассмотрение этих rраниц, кроме Toro, позво-
u
лит ознакомить читателеи с некоторыми принципиальными идея
ми теории информации.
Вначале получим zранuцу Чернова [4], которая будет необ-
ходима в дальнейшем.
Лемма 1.1. Пусть t < (q I)n/q. Tozaa
t
:п; ) ('; ) (q l)t I ( ; ) (q l)i qnr' (tIn),
i==O
еде <p(x)==xlogq(q l) x]ogqx (l x)]ogq(1 x).
n
Доказательство. Пусть А (z) === (1 + (q 1) z)n === L Aizi; ясно,
i==O
ЧТО A i == (; ) (q 1)/. Ее.пи О < z 1, ТО
t t t t
I (;) (q 1)/ == I А/ I Alzi t == z / I AiZl z iA(z). (1.5)
i-=O i==O i==O 1-=0
с друrой стороны, поскольку ОТНОlllение Ai/Ai+l ==
== (i + 1)/[(tt i) (q 1)] является монотонно возрастающей ФУНК-
цией i при 0< i < n и, кроме Toro, t < (q l)n/q, то найдется
такое число Z, о < 2 1, что
At 1 .. At
А z A ·
t t +1
Так как Ai I/Ai At J/4t<z при O<:i<t и 2 At/At+l
A,/Al+l при t < i, то для всех i
А t............ А l
t Z i Z ,
n
и, следовательно, А (2) == A i 2 1 (n + 1) Atz t . Отсюда и из
i==O
формулы (1.5) получаем
t t
min Z: \Z) At < I А ! min z tA(z). (1.6)
О < z 1 i==O O<z l
ПОЛО}I{ИМ t/п === т. Значение z, при котором достиrается экстре
мум ФУНКЦИИ z n'tA (z) == "n't (1 + (q 1) z) n, находится из
уравнения
...... n't'z nt I(1 + (q...... l)z)n + пz nt (q 1)(1 + (q...... l)z)n ' == о.
Отсюда следует, что экстремум достиrается в точке Ze ==
== т/[ (1 1') (q 1)]. Поскольку исследуемая (рункция ЯВ
ляется монотонно убывающей при О < Z < Ze И монотонно
30
r лава 1
возрастающей при ze < Z, то в точке Ze она достиrает МИНИМума.
Так как t< (q
l)n/q, то ze< 1. В точке Ze рассматриваемая
функция равна
't
nt [(1 ........ 't) (q........ l)]n't (1
't)
n == qnФ('t).
Отсюда и ИЗ формулы (1.6) получаем доказательство леммы 1.1.
Введенная выше функция ер (х) при q == 2 совпадает с энтро-
пией Н (х).
1.4.1. Верхняя rраница Хэмминrа
Здесь будет получена так называемая верхняя zраница Хам-
минzа rЗ].
Теорема 1.1. Е ели существует q
UЧНblЙ блоковый код длины п
со скоростью R и минимальным расстоянием Хэмминzа 2/ + 1
или более, то
t
L (
) (q
1/
qn(l
R).
i==O
Доказательство. Для каждоrо кодовоrо слова w рассмотрим
следующее множество D (w) последовательностей длины п:
D (w) === {w' I d (w, w')
t, w' Е V n} ,
т. е. D (w) включает все последовательности w', ОТJ!ичающиеся
от w не более чем в t компонентах. Следовательно, число после-
довательностей длины n, входящих в D (w), равно
f
L (
) (q
1)1,
i-=O
Так как множества D (w), соответствующие различным кодо-
вым словам, не имеют общих элементов, то
t
" ( n ) i n
К I.....J i (q........ 1)
q ,
i..O
rде К
общее число кодовых слов. Отсюда и из равенства
К == qnR следует справедливость теоремы.
Если для HeKoToporo кода верхняя rраниuа Хэмминrа вы-
полняется со знаком равенства, то код называется совершен-
ным. Как можно видеть из вывода rраницы Хэмминrа, для co
Основные понятия теории кодирования
31
вершенных кодов введенные выше множества D (w), или, дру-
rими словами, «сферы» радиуса t, центрами которых являются
кодовые слова, попарно не пересекаются и заполняют все про-
странство V n. В силу этоrо совершенные коды ИНоrда называют
также плотноупакованными кодами.
Кроме тривиальных двоичных кодов из примера 1.1, код()-
вые слова которых получаются повторением одноrо и Toro же
символа некоторое фиксированное число раз, со.вершенными ко-
дами являются также следующие: 1) q-ичные совершенные коды,
испраВЛЯIощие одиночные ошибки и имеющие длину п ==
== (ql 1) / (q .......... 1), q == рт, rде р.......... простое число (обобщенные
коды Хэмминzа из утверждения 3.2 rЗ, 11). нелинейные коды Ва-
сильева [12] и Шёнzеuма [13] с теми же параметрами), 2) двоич-
ный (23, 12) Koд [олея, исправляющий тройные ошибки (при-
мер 4.2) и 3) троичный (ll,б)"код [олея. исправляющий двой-
ные ошибки (пример 4.3'. Если q является степенью простоrо
числа, то не существует друrих q ичных совершенных кодов, за
исключением кодов, эквивалентных указанным выше, и триви-
альных нелинейных кодов, получающихся сложением каждоrо
кодовоrо слова указанных выше линейных совершрнных кодов
с некоторой фиксированной последовательностью длины п. Это
было доказано Титвайненом [15] 1).
Утверждение 1.8. Если существует q ичный систематический
совершенный код длины n, то
п (q' ....... 1 )/(q 1),
еде , число проверочных символов.
Идея доказательства. Поскольку код систематический, то
R == k/n. Далее следует воспользоваться верхней rраницей Хэм-
минrа в частном случае t == 1.
Как будет ПОI<азано ниже (утверждение 3.2), если q яв-
.пяется степеныо простоrо числа, q-ичные совершенные коды
длины п == (qT l)/(q 1) всеrда СУlцествуют.
Утверждение 1.9. (Фарр [2, 4]). Если q ичный блоковый код
длины п == q1n 1 со скоростью R 1 .......... mt/п такой, что
(! + 1 )1 (t + 1) (t + 2) т
1+1 + q t
(q 1) 2
ТО d МИI1 < 21 + 2.
') В работе f26*] ()ПlIспны все COBepllIeHHbIe КОДЫ над а.пфавитами из
q == 2't3 l Э.'lСМСll"l ОН. J 1 pllJt. ред.
32
r лава J
к ратк,ое доказательство.
"+1 t+1
( q
ll ) (q
1)1+1 == [(q 7t
i
)l 11 (1
iq
т);;:::
i==1
2 [(q...... 1) qт)t+l ( 1
i q
т )
(1+1)1 i...J
i == 1
[(q
l)qт)t+l ( q
т(t+2)(t+)) )
и+l)! 1
2
qтt
qn(l
R).
Отсюда и из теоремы 1.1 непосредственно следует, что нера-
венство d мин
2t + 3 не может иметь места. Это утверждение
используется для получения верхней оценки минимальноrо рас-
стояния некоторых двоичных БЧХ
кодов (см. rл. 4) [2, 4].
ВеРХНIОЮ rраницу Хэмминrа можно записать следующим
образом:
R
1
logq [t, (; ) (q
I)i].
Используя неравенство Чернова, мо)кно показать, что при фик-
сированном отношении t/n и достаточно БОЛЫlIИХ n rраница
Хэмминrа имеет вид
R
I
<p(
).
( 1 .7)
Так как <р' (х) == logq (q
1)
logqx + logq (1
х), то в интер-
вале О
х
(q
1) /q функция <р (х) монотонно возрастает от
О до 1. Поэтому для любоrо R, О < '
< 1, существует единст
венное значение х, при котором qJ (х) == 1
R. Обозначим это
значение х через б (R). ИЗ формулы (1.7) непосредственно сле-
дует справедливость следующеrо утверждения.
Следствие 1.1. Для люБО20 блоковоzо кода со скоростью R
u минимальным раССТОЯflие.k1 d мин при достаточно больu
их n
d;:"
() (R). (1.8)
1.4.2. Верхняя rраница Плоткина
В области малых значений R верхняя rраница Хэмминrа яв.
ляется довольно rрубой. При малых R более точной, чем rpa-
ница Хэмминrа, является верхняя rраница Плоткина [16J, olIpe
деляемая слеДУIощей теоремоЙ.
Основные понятия теории кодирования
33
Теорема 1.2. Если существует q ИЧflЫЙ блоковый код длины п
с общи/уt числом кодовых слов К и минимальным расстоянием
d мин , ТО
(q 1) пК
d мин q (К 1) ·
Доказательство. Эта rраница получается путем оценки свер-
ху среднеrо расстояния между кодовыми словами [4]. Пусть
w(l), W(2) ..., W(K) кодовые слова кода, существование кото-
poro предполаrается в теореме, и пусть и' ) т я (1 т n)
компонента кодовоrо слова W(i). Сумма попарных расстояний
Хэмминrа между кодовыми словами определяется следующими
равенствами:
к к к к n
Dt== L L d(w(i), w(j») L L L d(w ), w(j/)===
1=:11 /==1 1-=1 /::аl т==1
n К l(
== L L L d (w<;}, w<,!1),
m::z:1 1==1 1==1
rде ФУНКЦИЯ d (w ), w ) равна 1, еС"lИ W =1= w<J2, и равна О,
если w(i) === w(j). П у сть J m) число Р авных i символов канала
т т t
среди ко мпонент w (, w ), . . ., w<,:>. Тоrда имеют место следую-
щие равенства:
q
L J т> == К,
1 -= I
к к q q
L L d (W ), w » == L L бiIJ т)J т),
1=:11 1==1 i==1 1==1
(1.9)
rде б l / == 1, если i =1= j, и б l / == О, если i === j. Обозначим через q
q q
максимум квадратичной формы L L б1jХlХ/ при следующих
i==1 /==1
q
условиях: L Х! === К И Xi О (1 i т) (здесь будем считать,
i == I
что переменные Xi принимают действительные значения). MeTO
дом индукции по q покажем, что q == K2(q 1)/q. В случае
q == 2 справедливость последнеrо равенства проверяется леrко.
Полученные с использованием метода неопределенных множи
телей Лаrранжа значения XI, ..., Xq, при которых достиrается
эксrремум рассматриваемой квадратичной фОрМhI, должны
удовлетворят& следующим условиям:
q
L бijХj == Л, 1 i q.
j..l
34
r лава 1
Отсюда следует, что Xi == K/q (1
i
q). в этой точке значе-
ние квадратичной формы равно K2(q
1)/q. Поскольку рас-
сматриваемая область значений переменных Xi является orpa
ниченной и замкнутой, то максимум квадратичной формы дo
стиrается либо в этой точке, либо на rранице. На rранице по
крайней мере одна из переменных оказывается равной НУЛIО,
так что мы переходим к случаю, коrда число переменных равно
q
1 или меньше. По предположению индукции значения функ-
ции в таких точках не превосходят К2 (q
2) / (q
1). Следо..
вательно,
q === K2(q
1)/q. с друrой стороны, минимальное
расстояние d МИII дол}кно удовлетворять неравенству
(К 2
К) d мин
Dt
n/(2 (q
l)/q,
так как число пар различных кодовых слов равно К2
К. Тео-
рема 1.2 доказана.
Аналоrичная rраница может быть получена и для расстон-
ния Ли [4]. Из вывода rраницы Плоткина можно видеть, что ко-
дами, минимальное расстояние которых достиrает rраницы
Плоткина, MorYT быть лишь коды, в которых расстояние между
любыми двумя различными кодовыми словами одно и то }ке; та-
кие коды называются эквидистантными. Примерами двоичных
эквидистантных кодов являются коды, состоящие из nоследова
тельностей максимальной длины (СМ. пример 3.4), и коды, полу-
чающиеся из матриц Адамара.
1.4.3. Верхняя rраница Элайса
Используя идеи доказательства верхних rраниц Хэмминrа
и Плоткина, Элайс получил новую rраницу для минимальноrо
расстояния, которая оказалась лучше обеих исходных rраниц
по крайнеЙ мере при средних скоростях r2,4]. Эта rраница в
дальнеЙIlJем получила название zраницы Элайса 1). Рассмотрим
q
ичный блоковый код С Д,,1ИНЫ n с К кодовыми словами, ско-
ростью R и минимальным расстоянием Хэмминrа d мин .
Предположим, что все последовательности длины п из V'B
перенумерованы каким
либо образом числами от 1 ДО qrt. Пусть
S
произвольное целое положительное число и К i
число кодо-
ВЫХ С.пов кода С, наХОДЯUIИХСЯ на расстоянии Хэмминrа s или
менее от i
й последовательности длины п. ПОСКОЛЬКУ каждое
кодовое слово находится на расстоянии s или менее or
1) Этот результат получен Элпi'IСОМ, ДОI<азатеЛЬСТВQ было даllО Бассалыrо
[27] .
п рим. ред.
Основные понятия теории кодирования
35
s
I ( ) (q 1)1 последовательностей длины n, то
i..O
n
q
I К/ == КС п . q (S), rде
i==1
s
Cn.q(s)=== I ( )(q 1)/,
i==O
Учитывая, что К == qnR, получаем из последнеrо равенства сле
ДУЮЩУIО оценку снизу для К' ===тах K i :
i
к' КС n , q (s)/qn === Сп. q (s)/qn(l R).
( 1.1 О)
Предположим, что К} == К'. Без оrраничения общности можно
считать, что V 1 == {О, 1, ..., q 1}. Пусть (al, а2, ..., а п )
j я последовательность длины n. Рассмотрим далее BMe
сто блоковоrо кода С код С' == {(Ь 1 al), (Ь 2 а2), ...
. . ., (Ь n а n ) , (b 1 , Ь 2 , ..., Ь n ) Е С}, rде знак означает вы-
читание по модулю q. Если каждому кодовому слову (b 1 ,..., Ь n )
кода С сопоставить кодовое слово (bl al, b2 a2, ..., bп an)
кода С', то расстояние Хэмминrа между кодовыми словами KO
да С будет совпадать с расстоянием Хэмминrа между COOTBeT
ствующими словами кода С'. Следовательно, код С' имеет те же
параметры n, К и d мин , что И код С, и содержит К' кодовых
слов, находящихся на расстоянии s или менее от последователь-
ности (О, О, ..., О) длины n. Поэтому вместо кода С с caMoro
начала можно было рассматривать код С', так что мы просто
будем считать, что указанные К' кодовых слов существуют в
коде С. Обозначим через J\т) число таких кодовых слов среди
К' кодовых слов кода С, находящихся на расстоянии s или Me
нее от последовательности (О, О, ..., О) длины n, у которых
т я компонента равна i. Но тоrда, как и при определении rpa
,
ницы Плоткина, получаем, что сумма Dt попарных расстоя
ний Хэмминrа 'между указанными выше кодовыми словами оп
ределяется равенством
n q 1 q l
D; === L L L бiJJ т) 11т),
т:::81 i==O j==O
rде
q 1
К , === " J ( t . т ) , 1
L.J =:::::::: т =:::::::: n.
i==O
Так как расстояние Хэмминrа между любым из К' кодовых слов
и кодовым словом (О, О, ..., О) не превышает s, то
n q l
L L J m) :::;;;, 1(.' s.
т==} l::al
36
r лава 1
,
Поскольку Dt и амин, как и раньше, связаны между собей не.
равенством
( '2 ' ) ,
К К d мин Dt, (1.11)
то следует оценить сверху D;. Возьмем произвольное действи-
тельное число у(т), О у(т) К', И найдем максимум 1 ==
q 1 q 1
=== L L бljХlХj при следующих оrраничениях:
l..O 1..0
q 1
LXl==K',
l==O
q 1
L Х; === у(т),
l..1
Х; О, О i < q.
Поскольку, как следует из формул (1.12) и (1.13), xo==K' y<т),
то
( 1.12)
( 1 .13)
q 1 q l q l
1 == I I бijХ/Хj + 2 (К' у(т» I Xi ==
l..1 /"1 ["1
q 1 q 1
=== " ,,() .x x' q 1 (К' у(т»)2
i...J i...J l} t / q 2 '
1..1 /..1
rде X == Х 1 + (К' ........ y(т»)/(q 2). Оrраничения на х; имеют сле-
дующий вид:
q l
" х' == у(m) + q 1 (К' у(m»).
i...J l q 2
1..1
Таким образом, задача свелась к той же самой задаче нахож-
дения максимума квадратичной формы, что решал ась и при оп.
ределении rраницы Плоткина. Искомый максимум 1 (у(т») квад-
ратичной формы 1 определяется равенством
1 (у(т» == [(q 1) К' у(т)]2 q l (К' у(т»2 ==
(q 2)(q 1) q 2
== (2К' q l у(т») у(т),
п
Так как L 1 (у(т») является выпуклой вверх функцией y(I), i',
m..l
. . . , у(n>: то С помощью метода множителей Лаrранжа можно
n n
показать, что максимум L 1 (у(m») при условии L у(т) /('s
т..1 т..l
Основные понятия теории кодирования
37
достиrается в точке
у(т) == К' s/n, 1 т n,
и равен
K'2 S ( 2 (q sl) n ) ·
ОТСlода и из неравенств (1.1 О) и (1.11) получаем
K's ( q S ) sC ( s )q n(I R) ( Q S )
d 2 n, q 2 ........
МИН К I 1 (q 1) п Сп. q (S) Q n (I R) 1 (q 1) п ·
Далее l1араметр s следует выбрать так, чтобы он минимизиро-
вал праВУIО часть последнеrо неравенства. Однако, поскольку
в обиtем случае это сделать сложно, рассмотрим здесь случаЙ
БОЛЫlJlIХ n. Из леммы 1.1 имеем
qnФ(S/n>/(n + 1) Сп. q (8).
Если выбрать отношение s/n несколько большим, чем б (R), и
фиксировать, то при n 00 произведение
Сп. q (8) q n (1 R)
будет стремиться к бесконечности, так что при больших пот-
ношение К'/ (К' 1) можно считать равным единице. Таким
образом, мы доказали следующую теорему.
Теорема 1.3. Для любой скорости передачи R и люБО20 пO
ложительносо числа в при достаточно большой длине кода n
d мин < б (R) ( 2 ......... qб (R) ) + в
п q l'
еде б (R) функция, введенная выше в следствии 1.1.
Утверждение 1.10. При фиксированном отношении t/n и дo
статочно больших n полученная выше верхняя сраница лучше
верхней сраницы (1.8).
Утверждение 1.11. При малых скоростях R и достаточно
больших n полученная выше верхняя сраница u сраница П лот-
кина почти совпадают.
Идея доказательства. Как указывалось выше (при введении
функции б(R)), б(R) (q 1)/q при R O. С друrой стороны,
К == qnR 00 при n -+ 00.
В следующем разделе будет получена нижняя rраница для
вероятности ошибки, а в разд. 3.3 нижняя rраница Барша-
мова rилберта для минимальноrо расстояния кодов. На
38
r лава 1
фиr. 3.1 приведены rрафики полученных выше верхних rраниц,
а также нижней rраницы Варшамова ......... rилберта при доста-
точно больших п 1) .
1.5. Теорема кодирования
Теория кодирования насчитывает уже более чем двадцати-
v
летнюю историю и сеичас можно указать очень MHoro примеров
ее применения. Ученые и инженеры, которые работали в обла-
сти теории кодирования на начальном этапе ее развития, счи-
тали основной своей задачей разработку практически приемле
мых методов реализации теоремы кодирования Шеннона [9].
Соrласно этой теореме, для широкоrо класса каналов при пере-
даче информации со скоростью, меньшей пропускной способно-
сти канала, путем увеличения длины кода можно достичь сколь
уrодно малой вероятности ошибки при передаче. Известно, что
в дискретном канале' без памяти (предполаrается, что шумы 8
канале являются случайными) вероятность ошибки при пере-
даче Ре для кода длины п оценивается следующим образом:
e
n [Esp {R
Ol (n)}+О2 (n)]
Ре
Ae
nE (R),
(1.14)
rде Е (R) и Евр (R)
некоторые функции скорости передачи R
и переходных вероятностей канала, 01 (п) и 02(п)
функции,
стремящиеся к нулю с ростом п, а А
константа. В области
скоростей R, близких к пропускной способности канала, Функ
ции Е (R) и Евр (R) совпадают, т. е. Евр (R) == Е (R). Как видно
из неравенств (1.14), если значения функций E(R) и Esp(R) по-
ложительны, то, выбрав длину кода п достаточно большой, ве-
роятность ошибки можно сделать сколь уrодно малой.
Верхняя rраница вероятности ошибки в (1.14) была полу-
чена UПенноном путем определения средней вероятности ошиб-
ки в ансамбле кодов. Этот метод сравнительно сложен. I
алла
rep [1 О, 20] предложил более простой метод получения этой rpa-
ницы. Метод rаллаrера оказался применимым не только для
упрощения доказательства теоремы кодирования, он, в частно-
сти, широко используется при изучении поведения алrоритмов
последовательноrо декодирования.
Функция Евр (R), входящая в нижнюю rраницу для вероят-
ности ошибки в (1.14), была найдена Шенноном, rаллаrером и
Берлекэмпом методом, в основном аналоrичным методу нахож-
дения функции Е (R) [21].
1) Отметим, что в последнее время рЯДОМ авторов получены верхние
rраницы минимальноrо расстоS!ния, УЛУЧШЗIОЩliе rpaHIlUY Элайса.
П рu.м.
ред.
Основные понятия теории кодироваllИЯ
39
I1a основании вышеизложенноrо можно считать, что рас-
смотрение здесь метода rаллаrера и друrих вопросов, связан-
ных с верхней и нижней rраницами (1.14) для вероятности
ошибки, буде,т полезным для понимания методов, которые ока-
зали сущест
енное влияние на развитие теории кодирования.
С друrой стороны, этот материал потребуется нам в дальней
шем.
1.5.1. rраница случайноrо кодирования
Поскольку верхняя rраница для вероятности ошибки в (1.14)
получается методом случайноrо кодирования, то она называется
zраницей случайносо кодирования.
Теорема 1.4. (Шеннон, rаллаrер). п усть задан дискретный
канал без памяти с входным алфавитом из К символов Ul, и2, . . .
. . ., ик, выходным алфавитом из J символов VI, V2, ..., VJ (,
переходными вероятностями Pjk == рт (Vj I Uk). ТОсда для любой
длины кода п, любосо числа кодовых слов М == e nR и л/обосо
распределения вероятностей на множестве этих кодовых слов
существует код длины n, вероятность ошибки для КОТОРОсО в
указаННОJ.t выше канале оценивается сверху следующиJ.t обра-
зом:
Ре
ехр [
n {
vR + Ео (v, Q)}],
( 1.15)
zae
J ( К ) I+V
Ео (v, Q) ===
In L L q pI.I(I+V) ,
1==1 k==1 k Jk
( 1.16)
'V
nроизвольное число из интервала О
v
1, Q == (ql, Q2,...
. . ., qk)
nроизвольный вероятностный вектор 1) .
Доказательство. Обозначим через и n множество всех после..
довательностей длины n, которые MorYT быть переданы по кз-
налу, а через V n
множество последовательностей длины n, KO
торые MorYT быть приняты на выходе канала. Пусть Pr(VI и)
вероятность Toro, что на выходе канала принято слово V Е V fl
при условии, что было передано слово U Е V n.
Вначале рассмотрим некоторый фиксированный код, состоя
щий из М кодовых слов. Допустим, что целым числам 1, 2, ...
. . ., м сопоставлены соответственно кодовые слова U 1 , и 2 , . . .
#.., и т , ..., им, и т С и n , 1
т
М. Предположим, что
декодирование производится по максимуму правдоподобия.
1) Вероятностным вектором называется вектор Q == (q l' .. ., q k)' у КОТО-
k
poro q i
о, L q i == 1.
П рим. ред.
i
1
40
r лава 1
А именно осли принято слово V и целое число {1l таково, что
при всех т' =F т, 1 т' М,
Р, (V I и m ) > Р, (V' и m ,),
( 1 . 1 7)
то декодер максимальноrо правдоподобия декодирует V в т.
Если же принято СЛО80 V, такое, что ни при каком т нера-
8etl TBa (1.17) однозременно для всех т' =1= т, 1 т' М, не
ВltIПОЛНЯЮТСЯ, то считается, что произошла ошибка декодирова-
ни". Вероятность возникновения ошибки декодирования при пе-
редаче m ro кодовоrо слова обозначим через Рет. Эта вероят-
ность определяется равенством
Реm === L Р, (V I и m ) W т (V),
УеУ n
( 1.18)
rде
{ 1, если Pr(V\ Um) Pr(VI и m ,) при некотором т' =1= т',
W (V)
т О В остальных случаях.
( 1.19)
Первым шаrом на пути вывода верхней rраницы для Рет ЯВ-
ляется следующая оценка сверху для W т (V):
[ L Р, (У I и m,)l/(l+V) ] V
т' =1= m
W т (V) р, (У I u т )IЮ+ V ) ," > о. (1.20)
в спра8едливости этоrо неравенства леrко убедиться, если за-
метить, что
1) правая часть ero всеrда положительна, и, следовательно,
оно выполняется всеrда, коrда W п1 (V) === о;
2) в случае коrда W 1п (V) == 1, одно из слаrаемых в числи-
теле правой части (1.20) больше знаменателя, а следовательно,
и весь числитель больше знаменателя (при возведении числи-
теля и знаменателя в v ю степень по прежнему первый остается
больше BToporo).
Подставив (1.20) в (1.18), получим
Рет L Р, (У I и т)I/(l+V) [ L Р, (V I и m/)I/(1+V) ] V, V > о. (1.21)
V Е V n т' =1= т
Это неравенство дает rраницу сверху для Рет В случае, коrда
множество кодовых слов задано, т. е. для фиксированноrо кода.
Однако если число кодовых слов велико, то непосредственное
вltIчисление rраницы (1.21) оказывается чрезвычаЙно затрудни..
тел.ным или вообще невозможным. В силу этоrо па слеДУlощем
шаrе осуществляется усреднение (1.21) 110 ансамблю кодов, BI)I
бранному некоторым специаЛЬНLIМ образам.
Основные понятия теории кодирования
41
Зададим вначале на множестве и n сообщений на входе ка-
нала распределение вероятностей Q (и) и рассмотрим ансамбль
кодов, в котором каждое кодовое слово выбирается независимо
с распределением вероятностей Q (и). А именно рассмотрим
ансамбль кодов, в котором код, состоящий из М кодовых СЛОВ
м
и 1 , и 2 , ..., им, имеет вероятность П Q(U т ) '). Оценим сверху
т==l
среднюю по этому ансамблю вероятность ошибки. Поскольку в
любом ансамбле кодов всеrда существует по крайней мере один
код, вероятность ошибки для KOToporo не больше, чем средняя
по ансамблю вероятность ошибки, то таким образом можно дo
казать существование кода, для KOToporo вероятность ошибки
по крайней мере не больше, чем вероятность ошибки, средняя
по ансамблю.
Итак, усредняя вероятность ошибки по ансамблю кодов, из
формулы (1. 21) получаем
Рет <. L: p,(V1uт)I/O+V) [ L: p,(V\u m ,)l/(I+V) ] V, (1.21')
УЕ V n т' =1= т
rде черта сверху означает усреднение. Оrраничим область зна-
чениЙ параметра v интервалом v 1 и следующим образом
упростим формулу (1.21'):
1) Все слаrаемые под чертой в формуле (1.21) ЯВЛЯIОТСЯ
случайными величинами. А именно каждое из слаrаемых яв-
ляется функцией случайно выбираемых кодовых слов, прини-
мающей действительные значения. Поскольку среднее значение
суммы случайных величин равно сумме средних значений, то
Peт L: p,(V\uт)I/(I+V) [ L: p,(Vlum,)I/O+V) ] v. (1.21")
V Е V n т' + m
2) Аналоrично, поскольку среднее значение произведения не-
зависимых случайных величин равно произведению средних
значений сомножителей, то из формулы (1.21 ") получаем
Pe L: p,(V I и т)l/O+V) [ L: р, (V I и m,)1/0+V) ] V. (1.21 "')
УЕУ n т'+m
3) Положи м === L: р, (V I и т') 1/( 1 +v) И воспользуемся тем,
т' =Р т
что " " при О v 1. В справедливости последнеrо нера-
венства леrко убедиться, если заметить, что " при всех O V 1
1) Заметим, что среди КОДОВЫХ СЛОВ U t , ... и 1tf MorYT быть и совпct-
дающие. Прим. ред.
42 а
r лава 1
является выпуклой вверх функцией арrумеита . Тоrда
Рет L р, (У I U т)I/(1+V) [ L Р, (У \ и т,)I/O+V) ] V. (1.21"")
VeV n т'=р m
4) Пользуясь опять тем, что среднее значение суммы слу-
чайных величин равно сумме средних значений слаrаемых, по-
лучаем
L p,(V\Uт,)I/(J+V)== L p,(V\U т ,)1/0+V).
т' =1= т т' =р m
Отсюда и ИЗ формулы (1.21"") следует, что
.
р ет L Р, (У \ и т ) 1/( 1 +v) [ L Р, (У \ U т') 1/( 1 +V) ] V . ( 1.22)
УеУ n т'=Рт
Поскольку кодовые слова в рассматриваемом ансамбле кодов
выбираются с распределением Q (и), то
р, (У \ U т)l/(1 +v) == L Q (и) р, (V I U)I/(l +V).
иеи n
( 1.23)
Правая часть последнеrо равенства не зависит от т, и, следо-
вательно, ее можно подставить в формулу (1.22) вместо соот-
ветствующих выражений как с индексом т, так и с индек-
сом т'. Так как сумма по т' в (1.22) является суммой М 1
одинаковых слаrаемых, то
Рет (М ---- 1)" L [ L Q (и) р, (V I U)I/(I+V) ] V+l . (1.24)
УеУ n иеи n
Оценка (1.24) справедлива для произво.пьноrо дискретноrо
канала, задаваемоrо распределением pr (V I и), а та кже произ-
вольноrо распределения Q (и) и .пюбоrо О \' 1. Если пред-
поло)кить дополнительно, что канал ЯВ"lяется кана.пом без па-
мяти, то оценку (1.24) MO}l{HO упростить.
Пусть UI, и2, ..., u w , ..., и n компонснты входноЙ после
довательности и, а VI, V2, ..., V W , ..., V N компоненты выход-
ной последовательности V. По определению в канале без па
мяти для любых U Е и n И V Е V n
n
р, (У \ и) == П р, (v w I u w )'
w==1
( 1.25)
Наложим на ансамбль кодов еще одно оrраничение, а именно
предположим, ЧТО СИ1\1ВОЛЫ ксдовых слов выбираются незаDН
ОСНОАные понятия теории кодирования
43
симо С распределением q(u), ue:U 1 (Ul ВХОДНОЙ алфавит
канала). Тоrда
n
Q (и) === П q (u w ), и === (UI. . · ., u w , . . ., и п ).
w==1
( 1.26)
Подставляя фор мулы (1.25) и (1.26) в (1.24), получаем
[ n ] 1 +V
Peт «Nl 1)" L L П q(uw)p,(Vw\uw)I/(I+V) . (1.27)
VEV п UEV n w==1
Представляя далее сумму произведе,н.ий в квадратных скобках
в (1.27), как обычно, в виде произведения сумм, находим
[ n ] I+V
Peт (M 1)" L П L q(Uw)p,(VwIUw)I/(I+V) . (1.28)
VE V п w=aI UWE и}
Аналоrично, вынося знак произведения в формуле (1.28) за
квадратные скобки, имеем
n
Peт (M 1)" П L [ L q(U w )Pr(V w I U w )I/(I+V) ] I+V t (1.29)
w==I VWEV} UWEU}
O v l.
Правую часть этой формулы можно упростить следующим
образом. Совокупность К входных символов Ul, ..., Uk, ..., ик
обозначим через U 1 , а совокупность J выходных символов
Vl, ..., Vj, ..., VJ через V I . Обозначим также через РЛt пе-
реходную вероятность канала рт (Vj I uk), а через qk вероят-
ность q(Uk) выбора символа uk в ансамбле кодов. Эти обозначе-
ния подставим в формулу (1.29) и, заметив, что все сомножи-
тели произведения в правой части (1.29) равны, получим
Peт (J\;1 .I)v [ t ( f qkP} I+v) ) I+V ] n, 0 'V 1. (1.30)
fraal k==1
Пусть R скорость передачи информации в натуральных еди-
ницах (натах) на один символ канала (по определению e nR ==
== М). Если оценить сверху М 1 величиной М == e nR , то со",
отношение (1.30) можно представить в виде
Реrn exp [ n { 'VR 1" /tl ( l QkP}k<I+V)Y+V} ]. (1.31)
Поскольку правая часть (1.31) не зависит от т, то она является
также rраницей сверху для средней по ансамблю кодов вероят-
ности ошибки декодирования. Так как в ансамбле кодов имеет-
ся по крайней мере один код, вероятность ошибки декодирова-
ния для KOToporo не больше средней по ансамблю вероятности
ошибки декодирования, то таким образом теорема 1.4 доказана.
44
r лава 1
Если провести минимизацию правой части формулы (1.31)
по v и Q, то можно получить более точную оценку для Ре.
Следствие 1.2. При выполнении условий теоремы 1.4 суще-
ствует код, для KOTOpOZO
Ре
ехр [
пE (R)],
Е (R)
тах [
vR + Ео (v, Q)],
'V,Q
( 1.32)
( 1.33)
zae максимум берется по всем 'v из интервала О
'v
1 и всем
вероятностным векторам Q.
Функция Е (R) называется функцией надежности, и ее свой-
ства оказывают большое влияние на поведение верхней zpaHU-
ЦЫ для Ре.
1.5.2. Свойства ФУНКЦИИ надежности
Нахождение максимума по v и Q в формуле (1.33), естест-
венно, зависит от Toro, как ведет себя функция Eo(v
Q). ПО..
этому вначале исследуем свойства Eo(v, Q) как функции v и Q.
Поведение Eo(v, Q) как функции v описывается следуrощей
теоремой, доказательство которой было получено rаллаrе-
ром [12].
Теорема 1.5. П усть задан канал с входным алфавитом из К
символов, выходным алфавитом из J символов и переходными
вероятностями Pjk, 1
k
К, 1
j
J. Будем счuтать, что ве-
роятностный вектор Q == (q 1, ..., q'i) задает распределение ве-
роятностей на множестве входных символов канала. П редполо-
жим, что средняя взаимная информация между входом и выхо-
дом канала
I( J
1 (Q) == L L QkP/k \п к P/k
kC81 jr=sl L QlP jl
ic:al
положительна. Tozaa при 'v
О функция Ба (v, Q) обладает сле-
дующими свойствами:
(1) Ео (v, Q) == О, v==O
,
(11) Ео (v, Q) > О, v > О,
(111) дЕ о (v, Q) > о v > О,
а" '
(IV) дЕ о ('\1. Q) I == 1 (Q),
а" 'V
O
(V) д 2 Е о (v, Q)
о
av 2
.
( 1 .34)
( 1.35)
( 1.36)
( 1.37)
( 1.38)
Основные понятия теории кодирования
4б
Равенство 8 (1.38) имеет место Tozaa и только Tozaa, Kozaa при
всех j и k, таких, что QkPjk > О, имеет место равенство
ln Pjk == 1 (Q),
L q k P J k
k
Т. е. если случайная величина, являющаяся взаимной информа-
цией, имеет нулевую дисперсию.
Доказательство опускается (см. работу [12]).
Соотношения (1.34) (1.38) показывают, что Eo(v, Q) как
функция v ведет себя так, как показано на фиr. 1.4.
[о( v, Q)
v
о
Фиr. 1.4. Типичный rрафик ФУНКЦИИ Ео (,\" Q).
Используя теорему 1.5, можно достаточно просто провести
максимизаЦИIО Е (R) по v при заданном Q. Для этоrо введем
функцию
E(R,Q)=== тах [ vR+Eo(v,Q)]. (1.39)
O V l
Продифференцировав выражение в квадратных скобках в
(1.39) по v и приравняв ero затем к нулю, получим
R == дЕ о . Q) . (1.40)
Если значение параметра v, являющееся решением уравне-
ния (1.40), лежит в интервале О v 1, то оно максимизи-
рует выражение (1.39). Так как, соrласно формуле (1.38), пра-
вая часть (1.40) является невозрастающей функцией v, то в си-
лу равенства (1.37) уравнение (1.40) имеет решение всеrда,
коrда
дЕ о (,\" Q) I R 1 (Q) . (1.41)
а'\' v..1
в этой области значений скорости передачи R функцию Е (R, Q)
удобно задавать параметрически следующими соотношениями:
Е (R, Q) == Ео ('\1, Q) '\1 дЕ о . Q) ,
R == дЕ о (,\" Q) О 1
д ' V::::::-.....
'\'
( 1.42)
( 1.43)
46
r лава 1
в случае коrда R < aEo(v,Q)/avlv==l, параметрическое задание
E(R, Q) посредством формул (1.42) и (1.43) не имеет смысла.
В этой области скоростей передачи ФУНКЦИЯ vR + Eo(v, R)
возрастает с ростом V, О v 1, и достиrает максимума при
'v == 1. Следовательно,
E(R , Q)==Eo(I,Q) R, R< aEo(v,Q) ! . (1.44)
дv v=1
На фиr. 1.5 показан rрафИI( E(R, Q) как функции R, построен-
ный на основании формул (1.42) (1.44).
Рассмотрим R и Е (R, Q) как функции v, задаваемые фор-
мулами (1.42) и (1.43). С одной стороны, из СООТНОIllениЙ (1.38),
(1.40) и (1.43) можно видеть, что R является невозрастаIощей
Е(Я, Q)
Е(О) Q)
Е 11 Q ) aEo(v, Q)
а" } ov
О
R
аЕ о (v, Q) I
0 11 lJ'I:'t
Фиr. 1.5. Типичный rрафик ФУНКЦIIИ Е (R, Q)
функцией v. С друrой стороны, дифференцируя выражение
(1.42) по v, получаем, что производная E(R, Q) по v равна 1,
а следовательно, в силу (1.40) Е (R, Q) является неубываIощей
функцией v при v о. Кроме Toro, заметим, что Е (R, Q) == о
при v == о. Отсюда приходим к выводу, что Е (R, Q) > О при
всех R < 1 (Q). При этом если выбрать в качестве Q распре-
деление вероятностей, на котором достиrается пропускная спо
собность канала, то функция Е (R, Q) будет cTporo положи-
тельна при всех R < С. Это означает, что при всех R < С
вероятность ошибки убывает экспоненциально с ростом длины
кодовых слов. Взяв отношение производных (1.42) и (1.43), по-
лучаем
дЕ (R, Q) ( 1. 45)
aR == v,
Т. е. параметр v в формулах (1.42) и (1.43) можно интерпрети-
ровать как наклон rрафика функции Е (R, Q) к оси R.
Из замечания к неравенству (1.38), приведенному в теоре-
ме 1.5, видно, что a 2 E o (V, Q)/av 2 == О при всех v о, если ТО.пько
a 2 E o (V, Q)/av 2 == О при каком либо одном значении v о.
в этом случае связь между R и Е (R, Q) задаеlСЯ форму.
Основные понятия теории кодирования
47
лай (1.44). Каналы, для которых a 2 E o (v, Q)/aV 2 === О, являются
довольно искусственными и представляют собой каналы без
шума. По этим каналам при всех скоростях, меньших пропуск
ной способности, можно вести передачу с нулевой вероятностью
ошибки.
Рассмотрим еще один способ максимизации Е (R, Q) по v.
Заметим, что при фиксированном v функция 'VR + Ео (v, Q)
является линейной по R, имеет наклон " и пересекается с
осью ординат в точке Eo(v, Q). Таким образоrvI, Eo(R, Q) яв-
ляется оrибающей сверху семейства указанных выше прямых
линий, соответствующих различным значениям параметра р из
интервала [О, 1]. ОТСlода следует, в частности, что Е (R, Q) ЯВ
..1Jяется выпуклой вниз функцией R.
После Toro как проведена описанная выше максимизация
по \' и В результате получена функция Е (R, Q), дЛЯ нахожде-
ния функции E(R) необходимо максимизировать E(R,Q) по Q,
а именно
Е (R) === т а х Е (R, Q), ( 1.46)
Q
rде максимум берется по всем K MepHЫM вероятностным Be'KTO
рам. Как видно из формулы (1.46), функция Е (R) является
оrибаIощей сверху семейства выпуклых вниз функций Е (R, Q).
ЭТО позволяет доказать следующую теорему.
Теорема 1.6. Для любосо дискретносо канала без памяти
функция надежности Е (R) является положительной HenpepЫB
ной выпуклой вниз функцией R при О R < С.
Доказательство. Если С == О, то теорема тривиальна. Если
С =1= О, то при том Q, на котором достиrается пропускная спо-
собность канала, функция Е (R, Q) будет положительной при
всех О R < С. Очевидно, что в этоЙ области скоростей будет
по/Iо)l(птелыIйй и функция Е (R). Кроме Toro, как мы уже ви-
де..ТIИ выше, при любом вероятностном векторе Q функция
E(R, Q) является непрерывной выпуклой вниз функцией R,
производная которой изменяется в интервале от О до 1. От-
сюда следует, что и оrибаlощая этоrо семейства кривых также
является непрерывной выпуклой вниз функцией.
Далее рассмотрим, каким образом можно аналитически мак-
симизировать Е (R, Q) по Q. Соотношение (1.33), задающее
Е (R), можно переписать в виде
E(R)=== тах [ vR+maxEo(v,Q)]. (1.47)
0 'V 1 Q
Введем функцию
(J (\', Q) == ( q kP} I+V)Y+V.
( 1.48)
48
r лава 1
Тorда, как видно из формулы (1.16), Eo(v, Q) == ln G(v, Q)",
и, следовательно, минимизируя G (v, Q) по Q, можно максими-
зировать Ео (v, Q) по Q. Следующая теорема дает необходимые
и достаточные условия, которым должен удовлетворять век-
тор Q, минимизирующий G (v, Q).
Теорема 1.7. Функция G (v, Q), задаваеАtая формулой (1.48),
является выпуклой вниз функцией вероятностноzо вектора Q ==
== (ql, ..., qK). Необходимыми и достаточными условиями TOZO,
ЧТО на вероятностном векторе Q достиzается .минимум G (v, Q)
[или максимум Ео (v, Q)], являются следующие неравенства:
p} I+V)v'j;::: v}+v. (1.49)
еде
1\, q P I/(l +v)
, I k Jk ·
( 1.50)
Эти неравенства при всеХ k, для которых qk =F О, переходят 8
равенства.
Доказательство этой теоремы здесь опускается, однако ero
можно найти в работе rаллаrера [20]. в случае коrда все qk по-
ложительны, соотношение (1.49) является простым следствиеj\1
метода неопределенных коэффициентов Лаrранжа максимиза-
ции G (v, Q) при условии L qk === 1. Неравенства (1.49) почти
не облеrчают задачу явноrо нахождения максимума Eo(v, Q),
но позволяют леrко проверить, максимизирует ли тот или иной
вероятностный вектор Q функцию Ео (v, Q). Практически наибо-
лее простыми методами максимизации Eo(v, Q) оказываются
численные методы.
После Toro как максимизация Ео (v, Q) по Q проведена, функ-
ция Е (R) может быть найдена любым из указанных ниже трех
способов:
1) Функция Е (R) может быть задана с помощыо фОрl\IУ-
лы (1.47) совокупностью прямых
vR+maxEo(v,Q), O v<l. (1.51)
Q
2) Построив rрафик тах Ео (v, Q) в зависимости от v, Е (R)
Q
можно найти rрафичеСI{И.
3) ФУНКЦИIО Е (R) можно найти также с помощыо соотноше-
ний (1.42) и (1.43), взяв для каждоrо v то значение Q, на ко-
тором достиrае,тся максимум Eo(v,Q).
Пример 1.5. Рассмотрим двоичный симметричный канал с
переходными вероятностями Pl2 == Р21 Р == 0,001 и PII ==
== P2 === 1 р == 0,999. Параметр р == 0,001 это вероятность
ошибки при передаче по каналу одноrо ДВОИЧII rо символа il
Основные понятия теории кодирования
49
случае, если кодирование не проиэводится. ОчевИДНО, что в ЭТОf\.f
частном случае все компоненты вектора вероятностей Q, мак-
симизирующеrо Eo(v, Q), равны 1/2, а именно ql == q2 ==01/2.
Для Toro чтобы убедиться в этом, достаточно подставить эти
величины в формулу (1.49). Функция Eo(v, Q) при таком зна-
чении Q имеет вид
Ео ('\', Q) === ln t ( t q pIJ O + V ) ) I+V ===
j==1 k==I k ]k
===" ln 2 (1 + v) ln [pI/(I+V) + (1 р)l/(1 ")] ==
=== v In 2 (1 + ,,) In [0,001 1/(1+v) + O,9991/(l+V)]. (1.52)
Е(Я, Q)
0,634
о 089
,
о
0,5556
OJ993 R
Фиr. 1.6. rрафик функции Е (R, Q) дЛЯ двоичноrо симметричноrо канала.
Дифференцируя (1.52) и используя параметрическое
E(R, Q), из соотношений (1.42) и (1.43) получаем
R ln 2 Н (Pv),
Н (Pv) == р" ln р" (1 Pv) ln (1 ---- pv),
Е (R, Q) === Pv ln Р; + (1 Pv) ln \ --=..Ppv ,
задание
( 1 .53)
( 1 .54 )
( 1.55)
rде
pl/(l+v)
Pv === pl/(I+V) + (1 p)I/(1+V) · (1.56)
Эти равенства справеДtJIИВЫ при О v 1, или, что то же
самое, при
ln 2 Н [ p/( + 1 р )] === 0,5556 R С == 0,993.
При меньших скоростях E(R, Q) нахо дим по формуле (1.44)
Е (R, Q) == 111 2 ..... 2 ln ( 'p + 1 ..... Р ) ..... R == 0.634 ..... R. (1.57)
50
r лава 1
rрафик функции E(R,Q), задаваемой формулами (1.55) и
(1.57), предста' лен на фиr. 1.6.
1.5.3. rраница сферической упаковки
Выше была получена верхняя rраница для вероятности
ошибки, и мы не рассматривали нижней rраницы вероятности
ошибки в формул
(1.14). Вывод нижней rраницыI, называе.моЙ
rраницей сферической упаковки, несколько отличается от BЫ
вода верхней rраницы и детально рассмотрен в работах rаллз
repa [10] и Шеннона, rаллаrера и Берлекэмпа [21}. Поэтому
здесь мы только сформулируем результаты, относящиеся к IIИЖ
ней rранице.
Теорема 1.8. (rраница сферической упаковки.) Для любоzо
кода длины n со скоростью передачи R в дискретном канале
без памяти
Ре
ехр [
n {E sp (R
01 (n) + 02(n)}]'
( 1.58)
( 1.59)
zae
Esp (R) == sup [тах Ео (v, Q)
vR]
v>O Q
и E(v, Q) определяется формулой (1.16). Функции 01 (п) II
02 (n) стремятся к нулю с ростом n и определя/отся равенствами
01 (n) == ln 8 + к ln п ,
n n
(1.60)
О ( ) ln 8 + V 2 1 е2
2n==
п ,
n n Рмин
zae Рмин
наименьшая ненулевая переходная вероятность ка-
нала, а К
число входных символов.
Доказательство опускается.
Как видно из формул (1.47), (1.51) 11 (1.59), всличина
тах Ео (v, Q) входит в показатели экспонент как верхней, Tal{
Q
и нижнеЙ rраниц для вероятности ошибки и иrрает основную
роль в поведении эти х rраниц. Введем для ЭТО{I величины спе-
циальное обозначение
(1.61 )
Ео (v) === тах Ео (v, Q). (1.62)
Q
Как известно из работы Шеннона, rаллаrера и Берлекэмпа,
теорему кодирования можно упростить, если ввести ВЫПУКЛУIО
вверх функцию Eo(v), примыкающую сверху к Eo(v) 1). Так,
{) То есть Ео (v) == inf f (х), r де НIПКНЯЯ rpaHl) берется по всем выпукльп,
воерх функциям f, для которых f (v)
Ео (v) при всех v
О.
П pllJf. ред.
Основные понятия теории кодироваНllЯ
51
например, через Eo(v) функция Esp(R), задаваемая форму-
лой (1.59), МО}l{ет Быьb выра}кена следующим образом:
Esp (R) == sup {Ео (\') vR} == sup {Ео (v) vR}.
v>o V>O
(1.63)
в действительности функция Ео (v) очень часто используется
вместо Eo(v), поскольку для большоrо числа каналов Eo(v) ==
== Eo(v). Функцию Eo(v) называют внешним замыканием.
rраница сферической упаковки в области малых скоростей
является неточной. В этой области скоростей следует пользо
ваться следующей прямолинейной rраницей.
Теорема 1.9. (Прямолинейная rраница.) Пусть задан проuз
вольный дискретный канал без памяти, и пусть ESl (R) линей.
о
R
Фиr. 1.7. Типичные rрафики ФУНКЦИЙ Esp (R) и ESl (R) дЛЯ двоичноrо сим-
метричноrо канала.
ная функция, которая касается кривой Евр (R) и в. eCTe с тем
удовлетворяет условию ESl (О) == Е ОО} еде
к к J
Еоо == тах L L qiqk ln L PiiPkJ.
Q i==1 k==1 j==l
( 1.64)
Пусть RI значение R, при котором ESI (R) == Евр (R). Tozaa
для люБОеО кода со скоростью R < Rl вероятность ошибки Ре
удовлетворяет неравенству
Ре 2 ехр [ п [E s1 {R Оз (п)} + 04 (п)]],
(1.65)
еде Оз(п) u 04(п) функции, стремящиеся к нулю с ростом n.
Доказательство опускается.
Поведение кривых Esp (R) и ESl (R) дЛЯ двоичноrо сим мет-
ричноrо канала показано на фиr. 1.7.
52
r лава 1
1.5.4. Декодирование списком
В основе концепций, развиваемых в предыдущем разделе, ле-
жит декодирование по максимуму правдоподобия, коrда приня
той последовательности символов сопоставляется одно из цe
лых чисел. В данном разделе рассматривается более оБLцая кон..
цепция декодирования, а именно декодирование списком. При
декодировании списком принятой последовательности символов
ставится в соответствие некоторый набор (СПИСОI<) целых чисе"l
из интервала от 1 дО М. Если целое число, соответствующее
переданному сообщению, не входит в список целых чисел, по
лученный в результате декодирования, то rоворят, что произо-
шла ошибка при декодировании списком.
Допустим, что код и декодирование списком заданы. Пусть
V т
совокупность последовательностей длины п, которые мо-
rYT быть приняты и которым сопоставляются списки сообще-
ний, содержащие целое число т; пусть V
дополнение V tn ..
Тоrда условная вероятность возникновения ошибки при пере-
даче сообщения т и декодировании списком определяется ра-
венством
Ре, т == L Р, (V I V т).
Уеу С
т
( 1.66)
Полаrая, что подлежащие передаче сообщения и
леют равные
вероятности и усредняя Ре. т по т, можно ввести среДНЮIО ве-
роятность ошибки Ре для заданных кода и декодирования спис-
ком.
Пусть Ре(n, М, [)
минимальная вероятность ОILlибки, кото-
рая может быть достиrнута в заданном канале при декодирова
нии списком из L сообщений и при использовании кодов дли-
ны п, содержащих М кодовых слов. В этих обозначениях
Ре(n, М, 1)
минимальная вероятность ошибки при обычном
декодировании. Скорость передачи при декодировании списк
м
определяется равенством
R == lп (M/L) === 1" М ..... lп L . (1.67)
ппп
При L == 1 это определение совпадает с обычным определением
скорости передачи.
Таким образом, декодирование списком является одним из
методов принятия промежуточных «мяrких» решений. Для деко-
дирования списком Шенноном, rаллаrером и Берлекэмпом [1.3]
была получена следующая rраница сферической упаковки.
Теорема 1.10. В дискретном канале без памяти с переходны-
.ми вероятностями Pkj, 1
k
К, 1
j
J,
Ре (п, М, IJ)
ехр [
n [E sp {R ...... 05 (п)} + 06 (n)]] , (1.68)
Основные понятия теории кодирования
53
еде
Esp (R) == sup [Ео (v) vR],
v>o
05 (п) === 1: 8 + к П п , (1.69)
О ( ) V 8 I е + In 8
6 n == n .
n Рмин n
Доказательство опускается.
Эта rраница будет использована в дальнейшем при опреде
лении различных rраниц, характеризующих поведение алrорит
l\10B последовательноrо декодирования.
Метод, основанный на построении rраниц для средних по
некоторому ансамблю кодов характеристик и используемый при
доказательстве теоремы кодирования и исследовании алrорит-
мов последовательноrо декодирования, является полезным по
следующим причинам. Обычно с увеличением длины кода n
число кодовых слов возрастает экспоненциально. При этом, как
правило, ничеrо нельзя сказать о поведении характеристик I<аж-
доrо кода в отдельности. В то же время, вычислив средние по
некоторому ансамблю кодов характеристики, можно утвер-
ждать, что характеристики по крайней мере одноrо из кодов
этоrо ансамбля не хуже средних характеристик. Таким образом,
метод исследования, основанный на вычислении rраниц для
средних характеристик HeKoToporo ансамбля кодов, оказывает-
ся полезным при анализе систем связи, характеристики которых
зависят от очень большоrо числа случайных величин. В послед-
ние rоды этот метод широко используется, кроме Toro, для по-
лучения оценок вероятности ошибки в системах передачи дан-
ных с межсимвольной интерференцией r22, 25]"
2. Конечные поля
в данной rлаве рассматриваются теория rрупп, колец и по-
лей, в частности конечных полей, в том объеме, который необ-
ходим для чтения литературы по теории кодирования. Для по-
нимания материала этой rлавы необходимо знакомство с обо-
значениями, используемыми в теории множеств (но не с самой
теорией множеств), а также с основными понятиями линейной
алrебры. Основной текст и упражнения в этой rлаве одинаково
важны. Упражнения MorYT быть примерами или задачами, мо-
ryr входить в основной текст. Разделы, помеченные знаком .)ft,
при первом чтении MorYT быть опущены и прочитаны в даль-
нейшем, если в этом возникнет необходимость.
Запись А
В означает, что из А следует В. Через Z обозна-
чается множество целых чисел {О, + 1, + 2, ...}.
2.1. rpYnnbI
Важнейшими объектами, изучаемыми в алrебре, являются
алrебраические системы. При мерами алrебраических систем яв
ляются rруппы, кольца, поля и др. Вообще rоворя, под алzеб-
раическuМ,и системами в алrебре поним аются множества, в ко-
торых определены одна или несколько операции, таких, напри
мер, как сложение или умножение. Операция в самом широком
понимании
это закон, по которому некоторым упорядоченным
парам элементов данноrо множества S ставятся D соответствие
один или несколько элементов из S. Алrебраическую систему,
образованную множеством S, в котором определены операции
а,
, ..., будем обозначать через (S, cx,
, .. .). Однако в тех
случаях, коrда ясно, каковы операции в системе, алrебраиче-
ская система (S, сх, р, . ..) будет обозначаться просто через S.
rруппы. Алrебраическая система (а, О), образованная непу-
стым множеством G и операцией О, определенной для любых
двух элементов а и Ь из а, называется zpynnou, если выполнены
следующие четыре аксиомы:
а. 1. Для любых двух элементов а и Ь из G однозначно оп-
ределен элемент аОЬ Е а.
6.2. Для любых трех элементов а, Ь и с из G
а О (Ь О с) == (а О Ь) О с.
Конечные поля
55
G.3. В G существует элемент е, называемый единичным, Ta
кой, что ДLlIЯ ЛIобоrо элемента а из G
а О е == е О а == а.
а.4. Для любоrо элемента а из О существует эле.мент х, на-
зываемый обратным к а, такой, что
Х О а === а О х == е.
Если операция (Х такова, что для любых двух элементов Q
и Ь из S определен один элемент а(ХЬ Е S, то rоворят, что опе
рация (Х замкнута. Таким образом, аксиома О. 1 постулирует
замкнутость операции О в rруппе. Свойство операции, сформу-
лированное в виде аксиомы О. 2, называется ассоциативностью.
Ассоциативность операций означает, что последовательность вы-
полнения ряда операций не влияет на результат. Аксиома а. 3
постулирует существование единичноzо элемента. Во мно)кестве
целых чисел О является единичным элементом по сложению, а
1 по умножению. Аксиома О. 4 требует для каждоrо элемента
множества G существования обратноrо элемента. Например, при
сложении целых чисел обратным к чис.пу а является a.
rруппа (О, О) называется коммутативной или абелевОll,
если, кроме аксиом О. 1 О. 4, справедлива также следующая
аксиома коммутативности:
Аа.5. Для двух произвольных элементов а и Ь из G
а О Ь == Ь О а.
Если для обозначения rрупповой операции rруппы (О, О),
дЛЯ которой выполняются аксиомы О. l G. 4 и АО.5, вместо
знака О используется знак +, то rруппа (О, +) называется по
традиции аддитивной zруппой. Часто для обозначения rрупп.:)-
воЙ операции, вообu{е rоворя некоммутативной, используется
мультипликативная запись, т. е. вместо знака О испо.пьзуется
знак " а вместо записи аОЬ запись а. Ь или аЬ. При мульти-
пликативноЙ записи обратныЙ элемент к а обозначается че
рез a l. В результате Toro, что одни и те же стандартные обо-
значения, например знаки + и., используются Д.ТIЯ разных опе
раuий в различных rруппах, возникает некоторый сознательно
создаваемый беспорядок в использовании обозначений. С дpy
rой стороны, это можно рассматривать и как некоторыЙ KOH
структивный способ расширения смысла знаков. Так, например,
евклидово расстояние в двумерном случ ае определяется prt-
венством d (Х, У) == \1' (XI Yl)2 + (Х2 !1'2)2, Х === (Xl, Х2), у ==
== (Yl, У2), и обоб щается на n - мерный случа й следующим обра-
зом: d(X, У) ==\I'(Xl Yl)2 + . .. + (Х п УпУ'. Однако замеТИ:VI,
что аналоrично в rл. 1 были определены TaK)I{e расстояния
56
r лава 2
Хэмминrа и Ли. В общем случае расстояние можно определить
как функцию двух переменных, обладающую следующими тремя
свойствами:
D. 1. d (Х, У) == O X == У,
D.2. d(X, У) == d(Y, Х),
D.3. d(X, Z) d(X, У) + d(Y, Z).
Понятие расстояния возникло в результате абстраrирования
общих свойств «частных» расстояний. Однако после Toro, как
расстояние определено указанным выше образом, все функции
двух переменных, обладающие указанными выlеe тремя cBoii
ствами, MorYT быть названы единым термином расстояние.
В дальнейшем будем придерживаться следующеrо правила
в использовании знаков + и.. Будем считать что + есть знак
замкнутой операции, для которой а + ь == ь + а (т. е. KOMMYTa
тивной операции), а · есть знак замкнутой операции, которая,
вообще rоворя, может не быть коммутативной.
Утверждение 2.1. Алzебраuческая система < z, +) представ-
ляет собой zpynny, тоеда как (Z, .) zpynnou не является (oпe
рации + u · здесь являются соответственно обычными сложе
нием и умножением целых чисел).
Доказательство. Можно проверить, что (Z, +) удовлетво-
ряет аксиомам О. 1 o. 4 и АО. 5. Следовательно, (Z, +) яв-
ляется rруппой, и, более Toro, коммутативной. Для алrебраи-
ческой системы (Z, .) аксиома О. 4 не выполняется, в частности,
хотя бы потому, что уравнение 2 · а == 1 не имеет решения в
множестве Z.
Утверждение 2.2. Если в множестве SЗ == {О, 1, 2} oпpeдe
лить операцию + с помощью табл. 2.1 (заметим, что эта oпepa
ция коммутативна), то множество SЗ становится zpynnou отно-
сительно введенной операции (друzими словами, (Sз, +) есть
еруппа) .
Таблица 2.1
+ 012
о о 1 2
1 1 2 О
2 2 О 1
Этот пример интересен здесь по следующим причинам. Bo
первых, он иллюстрирует использование знака 1 для обозна
чения коммутативной опе{МlЦИИ. Во-вторых, операция + не яв-
Конечные поля
57
ляется обычным сложением. Так, в данном случае 2 + 2 1,
тоrда как при обычном сложении 2 + 2 == 4. Если бы опера-
ция + была обычным сложением, то не выполнялась бы аксио-
ма а. 1. Таким образом, введенная операция не является обыч-
ным сложением, но для нее выполняются аксиомы О. 1 O. 4 и
Аа.5, и, как и при обычном сложении, справедливы следующие
равенства:
2 + (О + 1) === (2 + О) + 1, 2 + 1 === 1 + 2.
с помощью таблиц, аналоrичных табл. 2.1, MorYT быть за-
даны и друrие rруппы. Такие таблицы называются rрупповыми.
Табл. 2.1 обладает следующими свойствами:
1) Она состоит лишь из элементов множества {О, 1, 2}.
2) Строки и столбцы ее являются перестановками последо-
вательности (О, 1, 2); все строки (столбцы) различны.
Аналоrичными свойствами обладают все rрупповые таблицы.
Утверждение 2.3. Множество комплексных чисел {1, 0), 0)2},
zae о) корень третьей степени из единицы, образует zpynny от-
носительно обычной операции умножения комплексных чисел.
Доказательство. Следует непосредственно проверить спра-
ведливость всех аксиом rруппы. Кроме Toro, доказательство мо-
жно леrко получить, если воспользоваться rрупповой табл. 2.2.
Таблица 2.2
.
о)
0)2
1
о)
0)2
0)2
о)
0)2
о)
0)2
1
о)
rомоморфизм и И30МОР'фИ3М rрупп. Если отображение f мно-
жества S в S' таково, что для любоrо элемента у Е S' сущест-
вует элемент Х Е S, такой, что f(x) == у, то rоворят, что f сюръ
ективно. Если отображение f таково, что f(xl) =1= '(Х2) дЛЯ лю-
бых двух элементов Х} и Х2 из S, то rоворят, что f инъектuвно.
Отображение f биеКТИ8НО, если оно одновременно сюръективно
и инъективно } 3]. Пусть даны две rруппы (а, а) и (а', а'). Если
отображение множества G в й' таково, что для любых двух
элементов а, Ь Е G
f (ааЬ) === f (а) a'f (Ь),
то f называется ZОМ,ОМ,ОРФНblМ, или ZОМ,ОМОРФUЗМ,Оhl < О, а) в
.< О', а'). Далее, если, кроме Toro, отображение f множества Q
58
fлава 2
в О' сюръективно или инъективно, то rоворят, что rомоморфизм
соответственно сюръективен или инъективен. Если rOMoMop
физм f одновременно и сюръективен и инъективен, то отображе-
ние f rруппы (О, а) в (О', а') называется изоморфным или изо-
МОРфИЗМОМ. Две rруппы G и О' называются изоморфными, если
существует изоморфное отображение G в О'. Две изоморфные
rруппы идентичны с точки зрения их свойств и отличаются лишь
формой представления элементов. С помощью биективноrо OTO
бражения f можно установить взаимно однозначное соответ-
ствие между элементами изоморфных rрупп так, что их rРУПI10-
вые таблицы будут иметь одинаковый вид (с точностью до
обозначения элементов). rруппы, задаваемые табл. 2.1 и 2.2,
изоморфны. Чтобы убедиться в этом, достаточно между элемен-
тами этих rрупп установить следующее взаимно однозначное
соответствие:
О 1 == юО
,
1 (j) === (j)l
,
2 ю2 == ю2.
Число элементов в rруппе G называется порядком О. rруп-
па, порядок которой конечен, называется конечной. Если поря-
док rруппы бесконечен, то она называется бесконечной. Так как
изоморфизм задает отношение эквивалентности, то Асе rруппы
можно разбить на классы эквивалентности, каждый из которых
можно было бы назвать абстрактной rруппой. При этом rруппы,
принадлежащие одному классу эквивалентности и имеющие
одинаковую «структуру», можно назвать КОНI<ретными rруппа-
ми. Определение числа классов эквивалентности rрупп задан
Horo конечноrо порядка n является одной из нерешенных про-
блем те()рии конечных rрупп. В то же время, как это будет дo
казано ниже, все конечные поля, имеющие одинаковое ЧИС 10
элементов, изоморфны. Структура всех конечных полей также
хорошо известна. Здесь мы не будем rлубоко вникать в про-
блемы теории конечных rрупп, однако для справок YKaiKeM
число классов эквивалентности rрупп порядка n 10:
Порядок rрупп п: 1 2 3 4 5 6 7 8 9 1 О
Число классов: 1 1 1 2 1 2 1 5 2 2
Задача 2.4. Показать, что все rруппы обладают следую-
щими свойствами:
1. В rруппе содержится только один единичный элемент
(единственность еДИничноrо элемента).
2. Для каждоrо элемента а rруппы обратный элемент опре-
деляется единственным образом (единственность обраТllоrо эл -
мента) .
Конечные поля
59
3. Из аЬ == ас следует, что Ь == с. Из Ьа == са также сле
дует, что Ь == с.
4. Пусть а и Ь два произвольных элемента rруппы. Тоrда
решениями уравнений ха Ь и ау == Ь являются соответствен-
но элементы х == ba 1 и у a lb, и эти решения единстве,нны.
5. (ab) 1 b la l.
Решение. Предположим, что rруппа О содержит два единич-
ных элемента е и е'. Тоrда ИЗ аксиомы О. 3 имеем
ее' === е и ее' === е' .
Следовательно, е == е'. Таким образом, единичный элемент
единственный. Доказательство свойств 2 5 предлаrается про-
вести читателю самостоятельно.
Подrруппы. Пусть (О, О) rруппа, а Н подмножество а,
ЯВЛЯЮUlееся rруппой относительно той же rрупповой опера-
ЦИИ о. Тоrда Н называется noazpynnoa rруппы а. Соrласно
этому определению, сама rруппа и rруппа \ {е}, О), состоящая
только из одноrо единичноrо элемента rруппы О, являются ПОl(-
rруппами rруппы О. Все подrруппы О, за исключением двух
вышеуказанных (если они существуют), называются собствен-
ными. Например, множество Е всех четных чисел является под
множеством множества Z, а (Е, +) собственная подrруппа
rруппы (Z, +). Множество {О, 1, 2} является подмножеством
MHo eCTBa Z, но rруппа, задаваемая табл. 2.1, не является под-
rруппой rруппы (Z, +), так как эти rруппы определяются раз-
личными операциями.
Утверждение 2.5. Н еобходимым и достаточным условием
TOZO, ЧТО непустое подмножество Н элементов zpynnbt G являет
СЯ noazpynnoa zpynпbl О, является каждое из следующих СООТ-
ношений:
1) а, Ь Е Н =7 а. Ь Е Н и a 1 Е Н;
2) а, Ь Е Н =7 ab 1 Е Н.
Пусть Н подrруппа rруппы О, а g произвольный эле
мент из о. Множество {xl х == gh, h Е Н}, обозначаемое ниже
через gH, называется левым смежным классом rруппы G по под
rруппе Н, порождаемым элементом g. Аналоrично множество
{xlx == hg, h Е Н}, обозначаемое через Hg, называется праВЫА-f
смежным классом rруппы О по подrруппе Н, порождаемым эле
ментом g.
Задача 2.6. Пусть G == ({О, 1,2,3, 4, 5}, +) rруппа поряд-
ка 6, задаваемая табл. 2.3, а Н == < {О, 3}, +) подrруппа rpYI1-
пы О, задаваемая табл. 2.4. Найти все правые смежные классы
rруппы G по подrруппе Н. Показать, что любые два левых смеж
ных класса либо совпадают, либо не имеют общих элементоз.
60
r лава 2
Кро.ме 'Юf{), проверить, чте объединеиие всех смежных классов
совпадает с множеством й.
Таблица 2.3
+ о 2 3 4 5
О О 1 2 3 4 5
1 1 2 3 4 5 О
2 2 3 4 5 О 1
3 3 4 5 О 1 2
4 4 5 О 1 2 3
5 5 О 1 2 3 4
Таблица 2.4
+ о 3
О О 3
3 3 О
Решение. Поскольку в этой задаче используется аддитивная
запись, то смежные классы также будем обозначать через H+g.
Находя смежные классы, порожденные всеми элементами gEG,
получим
н + О == Н + 3 === {О, 3} === Н,
Н + 1 === Н + 4 === {l, 4},
Н+2===Н+5=={2,5},
(Н+О)П(Н+ 1)===</>, (Н+0)П(Н+2)===ф,
(Н +. 1) n (Н + 2) == </>, (Н + О) U (Н + 1) U (Н + 2) == а.
Отсюда не.посредственно следует справедливость указанных вы-
ше свойств.
в приведенном выше примере каждый смежный класс содер-
жит столько же элементов, сколько и подrруппа Н. Это своЙство
присуще любой конечной rруппе G и любой ее подrруппе 11,
а именно для произвольноrо смежноrо класса Н g rруппы G по
подrруппе Н имеем
IHgl==IHI.
(2.1 )
Здесь и в дальнейшем через I S I обозначается число элемен-
тов в множестве s. Равенство (2.1) доказывается следующим
Конечные поля
61
образом. Пусть Н == {hl' "', h n }. Тоrда, пользуяеь опр@деЛQ-
нием Hg, можно установить следующее соответствие меж.ltу ЭJIе-
ментами Н и Н g:
н : h 1 h 2 '" h n ,
Н g : h l g h 2 g . .. hng.
Отсюда следует, что IHgl IHI. Предположим, что IHgl<
< 1 н 1. Тоrда найдутся два различных элемента h i и h j , таких,
что hig == hjg. В силу свойства 3 rруппы, указанноrо в зада
че 2.4, получим h i == h j , что противоречит предположению о том,
что элементы h i и h j различны. Следовательно, справедливость
равенства (2.1) доказана. В приведенном выше упражнении
Н + о == н + 3 и т. д. Эти равенства являются следствием сле-
дующеrо общеrо свойства rрупп. Если смежные классы На и
НЬ rруппы О по подrруппе Н имеют хотя бы один общий эле-
мент, то они совпадают, т. е. На == НЬ. В самом деле, если два
смежных класса На и НЬ имеют хотя бы один общий элемент,
то h1a == h 2 b, rде h 1 , h 2 Е Н. Умножая обе части последнеrо ра-
венства слева на /zjl, получим а === h 1 1 h 2 b, rде h J 1 h 2 Е Н. Тоrда
На == {ha I h Е Н} == {h (h 1 I h 2 b) I h Е Н} === {h'b I h' Е Н} еНЬ,
rде h' === hh1lh() Е Н. Точно. так же можно доказать, что
НЬ с:: На. Следовательно,
На == НЬ.
Отсюда следует справедливость следующей теоремы Лаr-
ранжа.
Теорема 2.1. (Лаrранж.) Порядок любой noazpynnbt KOfle'l-
ной zpynnbl является делителем порядка 2руппы.
Доказательство. Пусть Н произвольная подrруппа rpyn-
пы О. Обозначим через т и n соответственно порядки G и /1.
Если пz === n, то .0 == Н и теорема доказана. ЕСJIИ т > n, ВОЗh-
мем некоторый элемент al Е О, не входящий в Н, и построим
правыЙ смежный класс Hal. Общее число элементов, входящих
в Н и Hal, равно 2п. Если m > 2n, возьмем некоторый элемент
а2 Е О, такой, что а2 Ф. Н U Hal, и построим смежный класс
На2. Число элементов в Н U Hal U На2 равно 3n. ПРОДОЛiКИl\f
эту процедуру до тех пор, пока все элементы О не будут ВКЛIО-
чены .пибо в /1, либо в один из смежных классов rруппы G по
подrруппе /1. Если число смежных классов, включая Н, равно 1,
то т == ln.
Число левых смежных классов rруппы G по подrруппе /!
равно числу правых смежных классов. Это число обозначается
через [О : н] и называется индексом подrруппы Н в rруппе а.
62
r лава 2
Из теоремы Лаrранжа непосредственно следует справедливосrь
следующеrо утверждения.
Следствие 2.1. Если G конечная zpynna, то
I G I === [О : Н] I l! 1.
Задача 2.7. Доказать, что rруппа О, которая рассматрива..
лась в предыдущей задаче, мо)кет содерясать подrруппы поряд-
ка 1, 2, 3 и 6, но не 4 и 5.
Решение. Порядок О равен 6, и все ero делители это чис-
ла 1, 2, 3 и 6. Подrруппой порядка 1 ЯВЛЯ6ТСЯ подrруппа {О},
а подrруппой порядка 6 сама rруппа а.
Нормальные делители. Подrруппа Н rруппы G называется
нормальным делителем, если для любоrо элемента g Е G
Hg===gH или gHg I===H===g lHg.
Если Н подrруппа rруппы О, то, вообlце rоворя, левый смеж-
ный класс rруппы О по подrруппе Н не совпадает ни с l{аКИ l
правым смежным классом. Однако если Н нормальный дели..
тель, то, как следует из вышеприведенноrо определения, Hg ==
== gH и, следовательно, необходимость в различении левых и
правых смежных классов отпадает. В этом случае можно rOBO
рить просто о смежном классе, порождаемом элементом g.
В коммутативных rруппах все подrруппы являются нормальны-
ми делителями.
Факторrруппа. Пусть подrруппа Н rруппы G является нор-
мальным делителем. Факторzруппа О/Н rруппы по нормаль
ному делителю Н определяется следующим образом. Обозна-
чим через Hg смежный класс rруппы О по ПОllrруппе Н, coдep
жащий элемент g, а именно Hg == {hg I h Е Н}. Конечно, такое
представление смежных К,,1ассов не однозначно в том смысле,
что для представления одноrо и Toro же смежноrо класса MorYT
использоваться различные элементы g. Введем во множестве
смежных классов операцию · следующим образом:
Hgi.Hgj==={g'g"\g'EHg i , g"EHg j }. (2.2)
Факторrруппа rруппы G по нормальному делитеЛIО Н опре-
деляется как алrебраическая система, элементами которой яв-
ляются смежные классы rруппы G по нормальному делитеЛIО Н
с операцией ., задаваемой соотношением (2.2). Как будет по
казано ниже, эта алrебраическая система является rруппой.
Прежде Bcero покажем, что для этой алrебраической систе
мы выполняется аксиома О. 1. Для этоrо вначале покажем, что
множество Н g i · f/ g j, определяемое СООТНОLlIснием (2.2), являет
ся ОДНИ!vI из смежных классов rруппы G по нормальному деЛII"
Конечные поля
63
телю Н. В самом деле,
Н g i · Н g j == {g' g" I g' Е Н g i === g i Н, g" Е Н g I} ===
== {gihlh2gjl h 1 , h 2 Е Н} == {gihgjl h Е Н} ==
{gigj (gj1hg j ) I h Е Н}.
Так как Н является нормальным делителем, то {gj1hg j I hEH}===H.
Следовательно,
Hg i · Hg j === {gigjh I h Е Н} == Hg k ,
rде g'l == gigj. Таким образом, справедливость аксиомы о. 1 до-
I{азана. I1спользуя вышеприведенные результаты, можно пока-
зать справедливость аксиомы о. 2. Действительно,
(Н gl · Н g2) · н g:j === Н glg2 · Н gз == Н glg2gз ===
== Hg 1 · Нg 2 g з === Hg 1 . (Hg 2 . Нg з ).
Точно так же можно показать, что сама подrруппа а выпол-
няет роль единичноrо элемента, а элемент Н g l является обрат
ным к элементу Hg. Таким образом, а/н удовлетворяет всем
аксиомам rруппы.
Утверждение 2.8. Пусть G == (Z, +). Обозначим через (п)
множество кратных цеЛ020 положительноzо числа п, а именно
(п) == {nzlz Е Z}. Так как сруппа а коммутативна, то алzеб-
раическая система Н == «( n), +) является нормальным делите-
лем сруппы о. Следовательно, можно определить факторzруппу
О/Н. Эту факторzруnпу часто обозначают через Zn.
Доказательство. То, что Н является подrруппой rруппы А,
проверяется леrко. Рассмотрим несколько более детально rруп-
пу Zn. Обозначим через [х] смежный класс, содержащий х. Все-
ro имеется n следующих смежных классов:
[О] == {О, + п, ::1:: 2n, . . .} == (n),
[1] === {1, 1 + п, 1 + 2n, .. .},
[п 1] == {п 1, п 1 + n, п 1 + 2п, . . .}.
Элемент, используемый для представления Toro или иноrо
смежноrо класса, называется представителем этоrо смежноrо
класса. В данном случае в качестве представителей смежных
классов используются минимальные неотрицательные целые чис
па, входящие в соответствующие смежные K..1JaCCbI. Если ввести
операЦИIО сложения смежных K..Т"l3CCOB с помощью соотношеНИ>I
64
r лава 2
[i] 1: [j] == [i + j], то эти смежные классы будут образовывать
rруппу.
rрупповую таблицу rруппы Z6 можно получить из табл. 2.3,
если заменить в последней элементы i на [i]. .
Циклические подrруппы. Рассмотрим один элемент а rруп-
пы а. По примеру обычных экспоненциальных выражениЙ эле
менты а · а, а · а · а, ... будем обозначать соответственно через
а 2 , аЗ, ... (при использовании аддитивной записи эти же эле-
менты обозначаются через 2а, 3а, ...). Предположим, что rруп-
па G конечна, и рассмотрим следующую последовательность
элементов:
2 З
а, а , а , . . . .
(2.3)
Так как rруппа G конечна, то существуют такие числа i и j,
что
а l == а}
(i < j).
(2.4)
Но тоrда, поскольку
а ! == а/ == a i · aj i
,
aj i == е. Минимальное целое ПОJIожитеJIьное число т, такое,
что а т == е, называют порядком элемента а. Если rруппа G KO
нечна, то порядок каждоrо элемента rруппы G также конечен.
Однако в бесконечных rруппах порядок каждоrо элемента rруп
пы не обязательно должен быть конечным. Например, рассмот-
рим rруппу (Z, +). Для элемента 1 этой rруппы последова
тельность (2.3) имеет следующий вид:
1, 2, 3, 4, ... .
в этом случае равенство ,п · 1 === т == О не выполняется ни при
каком целом положительном т. В подобных случаях rоворят,
что порядок элемента беСI{онечен.
Задача 2.9. Определить порядок каждоrо элемента rруппы G
из задачи 2.6.
Решение. о: О == О Порядок 1
1: 1, 2, 3, 4, 5, О 6
2: 2, 4, О 3
3: 3, О 2
4: 4, 2, О 3
u: 5, 4, 3, 2, 1, О 6
В данном случае порядок каждоrо элемента определялся по
числу различных элементов А соотвеТСТВУIОlцеi.t I ПОС.rIедоватеu1Ь
насти (2.3). Хотя 110 определению порядок элемента это ми-
Конечные поля
65
нимальная разность j i чисе ТI j и i, удовлетворяющих (2.4) J
использованный здесь метод нахождения порядка приводит к
правильным результатам.
Наконец, заметим, что если m есть порядок элемента а, то
все m элементов а, а2, ..., а т == е различны. В противном слу-
чае мы имели бы a i == aj (1 i < j т) и, поскольку a i ==
== a i · aj i, получили бы aj i == е, rде j i < т. Это противо-
речит определеНИIО т.
Теорема 2.2. Пусть а элемент порядка т zpynnbt О. Tozaa
Н== {а,а 2 , ..., а т } == {е,а,а 2 , ..., aт l} noazpynna zpyn-
nы О.
Доказательство. В Н содержится единичный элемент е. Оче-
видно, что в Н выполняется так)ке аксиома ассоциативности.
Кроме Toro, поскольку равенство a i . a1n i == а т == е справедли-
во при всех О i т, то для любоrо элемента a i Е Н в Е/ су-
ще.ствует обратный элемент. Пусть a i и a j два произвольных
элемента из Н. Если i + j т, то a i . a j == a i + j Е f/. Если
i + j > т, то a i . a j == ai+j т · а т == ai+j 1п(i +j m < т),
а это вновь означает, что a i · a j Е Н. Таким образом, в Н вы-
полняется и аксиома О. 1, а следовательно, Н есть rруппа.
Рассмотренная выше подrруппа Н называется циклической
noazpynnou. В частности, если в rруппе G существует элемент а,
такой, что о== {е, а, а 2 , ..., aп l}, и n===IGI(an==e), то сама
rруппа G называется циклической rруппой, поро)кденной элс-
ментом а.
Заметим, что слово порядок употребляется в следующих co
четаниях: порядок rруппы и порядок элемента rруппы, приче \I
порядок элемента rруппы равен порядку циклической подrруп-
пы, порожденной данным элементом. Из теорем 2.1 и 2.2 BЫTe
кает справедливость следующеrо утверждения.
Следствие 2.2. Порядок каждоzо элемента конечной zpyп-
пы G является делителем порядка О.
Утверждение 2.10. Для nроизвольноzо целоzо числа р суще
ствует циклическая zpynna порядка р.
Доказательство. Рассмотрим rруппу Zn из утверждения 2.8с
Леrко убедиться в том, что Zn порождается элементом [1], а
с.педовательно, является циклической. rруппа, рассмотренная в
задаче 2.6, есть не что иное, как частный случай rруппы Zn при
n == 6. Заметим, что элемент 1 является не единственным эле-
ментом, порождающим эту rруппу. В частности, rруппа Z6 мо-
жет быть поро)кдена также элементом 5 (СМ. задачу 2.9). Та-
кие элементы, ПОРО)l{даlощие rруппу, называIОТСЯ порождающн-
ми элементами.
66
r лава 2
Утверждение 2.1 1. Все циклические zpynnbt OaHOZO и Т020 же
порядка т ( < 00) изоморфны.
Доказательство. Пусть G == {а, а 2 , ..., aт 1, е} и Н ==
== {Ь, Ь 2 , ..., bт l, е} две циклические rруппы порядка т.
Введем следующее отображение G в Н:
f (a i ) === b l , i === 1, .. ., nz.
Очевидно, что отображение f биективно. Поскольку для любых
двух элементов a i и а; из G
f (a l · а 1 ) ===
{ ' (a i + i ) === b i + 1 == blb l , если i + j (1l,
== f (ai+j m . а m ) == f (ai+J m) == bi+j m == bib l ,
если
i + j > т,
то f является rомоморфным отображением G в Н. Следова-
тельно, G и Н изоморфны.
Вообще rоворя, две конечные rруппы одноrо порядка не обя-
зательно должны быть изоморфными (см. задачу 2.4). Однако
если оrраничиться только циклическими rруппами, то, как м 1)1
видели выше, из равенства порядков rрупп следует их изомор-
физм. Если rруппы G и Н изоморфны, обычно одну из этих
rрупп, например Н, называют nредставлением о. Так, rруппа
Zp, введенная в утверждении 2.8, является одним из представ-
лений циклических rрупп порядка р. Обычно удается получить
несколько представлений rрупп, и выбор используемоrо пред-
ставления определяется соображениями удобства.
Утверждение 2.12. Все конечные zpynnbl, порядок которых
является простым числом, циклические.
Доказательство следует из утверждения 2.2.
Утверждение 2.13. Пусть т порядок циклической еруnnы,
nорожденной элементом а. Tozaa порядок элемента a i равен
т/ (т, i), rде (т, i) наибольший общий делитель чисел т и i.
Доказательство. Используемая ниже запись ylx означает,
что у делит х. Пусть 1 порядок элемента a i . По определению 1
является минимальным целым числом, таким, что a i1 == е. От-
сюда и из Toro, что порядок а равен т, следует, что 1 мини-
мальное целое число, такое, что т I il. Это означает, что 1 ==
== m/ (т, i) .
Утверждение 2.14. Пусть т и n соответственно порядки
элементов а и Ь zpynnbt о. Если аЬ Ьа и n 1 т, то в G суще-
ствует элемент порядка тn/ (т, n).
Конечные поля
67
Доказательство. Предположим сначала, что (т, п) == 1, т. е.
что числа т и п взаимно простые. В этом случае элемент аЬ
является искомым. В самом деле, поскольку (аЬ) тn ==
== атnЬ тn === е, то порядок I элемента аЬ делит тп, т. е. I1 тn.
С друrой стороны, поскольку е == (аЬ) 1711 === a lm b ,т == b lm , то п 11т.
Аналоrично т Iln. Однако, поскольку (т, n) == 1, получаем, что
п II и т 11, а следовательно, тп 11. Отсюда и из Toro, что II тn,
имеем I == тn. Рассмотрим СJ1учай, коrда (т, n) > 1. Разлаrая
числа т и п на простые множители и упорядочивая последние
специальным образом, получаем
е 1 e s e S + 1 е,
т == р 1 ... р s р s+ 1 ... р r
п P f 1 P fs p fs+l P f,
1 ... s s+1 '" ,
(el O, i==l, "', ,),
(f l О, i === 1, "', '),
rде
el fl, '.', es fs, es+t<fs+t, "', e,<f,.
Поскольку по предположению п..r т, то ei < fi для HeKOTOpOrO i
и, следовательно, s < '. Положим 1ft === p l ". p s И fi == pf s + 1. . .
s+1
. .. p;r. Поскольку ( т , п) == 1, элементы а == а т / т и Б == Ь n / п
имеют соответственно порядки т и п, а в силу первой части
настоящеrо доказательства порядок элемента с == аБ равен т n.
3 ( ) f 1 fs. e S + 1 е, Н ........
аметим, что т, n P I ... Ps PS+l ... р,. о тоrда тn........
== тп/(т, п), т. е. порядок элемента с равен тп/(т, п).
Дополнение. Здесь приводятся некоторые обозначения и
краткие сведения из теории чисел, знание которых необходимо
для чтения этой и последующих rлав. Будем обозначать через
Ь 1 а тот факт. что Ь делит а; запись Ь l' а означает. что Ь не де-
лит а. Наибольший общий делитель чисел а и Ь обозначим че-
рез (а, Ь). Если (а, Ь) == 1, то будем rоворить, YO числа а и Ь
взаимно просты. Если п' (a Ь), то rоворят, что а сравнимо сЬ
по модулю п, и обозначают это следующим образом:
аааЬ (mod п). Таким образом, записи nl (а Ь) и а == Ь (mod п)
эквивалентны. Остаток от деления числа а на целое положи-
тельное число п обозначим через Rn (а).
N.I. ДЛЯ произвольноrо целоrо числа а и произвольноrо иe
JIoro положительноrо числа Ь существуют такие числа q и " что
a==bq+r, O r<b,
и притом единственные.
N.2. Если bla, то (а.Ь)== Ь.
N.3. Если а == bq + с, то (а, Ь) (Ь, cJ,
68
r лава 2
N.4. Алсоритм' Евклида. Этот алrоритм хорошо известен как
алrоритм нахождения наибольшеrо общеrо делителя.
Предположим, что а Ь, и рассмотрим следующую после-
довательность равенств:
а === bql + '2,
Ь === '2Q2 -+. 'з,
'2 === 'зq'j + '4,
0<'2 < Ь,
О < 'з < '2,
О <; '4 < 'з,
....... .
'n 2 == 'n lqn . + 'n,
'n 1 === 'nqn + 'n+l,
O<'n<'n l,
O 'n+..
Число равенств в этой последовательности всеrда конечно, по-
скольку /
а Ь > '2 > , > . . . о.
Соrласно свойствам N. 2 и N. 3 целых чисел,
(а, Ь)===(Ь, (2)===('2' 'з)== ... ===('n l, rn)==r n .
Друrими словами, наибольший общий делитель чисел а и Ь ра-
вен последнему ненулевому остатку в вышеприведенной после-
довательности равенств.
N.5. ДЛЯ Лlобых двух целых чисел а и Ь существуют такие
целые числа х и у, что ах + Ьу == (а, Ь).
Доказательство. Воспользуемся последовательностью ра-
венств, введенной выше при рассмотрении свойства N. 4. А имен
но подставим '2 из nepBoro равенства во второе. В полученное
таким образом равенство подставим 'з из TpeTbero равенства.
Продолжая эту процедуру, исключим все остатки '2, ..., 'n 1 И
придем: к равенству ах + Ьу == 'п == (а, Ь).
Свойство N.5 можно также сформулировать в следующем
виде:
N.5'. Если числа а и Ь взаимно простые, то существуют та-
кие целые числа х и У, что ах + Ьу == 1.
N.6. Если Ql == Ь. (mod т) и а2 == Ь 2 (mod т), то
1) аl + а2 == Ь. + Ь 2 (mod nl),
2) al а2 == Ь 1 Ь 2 (mod т),
3) ala2 == b 1 b 2 (mod т).
N.7. Если (с, т) == 1 и са == сЬ (Пl0d /п), то
а == Ь (mod т).
Конечные поля
69
Доказательство. Так как са == сЬ (mod т), то тlc(a
Ь).
Так как т и с взаимно простые, то тl(a
b), т. е. а ==
== Ь (mod т).
Функция Эйлера ер (п) определяется для всех натуральных п
как количество чисел между 1 и п, взаимно простых с п. Поло
жим <р (1) == 1. Если п == ре, rде р
простое число, то среди
всех целых чисел от 1 до ре содержится pe
l чисел, кратных р.
Отсюда следует, что
<р (ре) == ре
pe
1 == р! (1
+ ) .
в общем случае, коrда п === p
lp;2 f .. р;' (Pl' ..., Р,
простые
числа), имеем [4]
<p(n)==<p(p
I)... <p(p;r)==n(1
+) .., (1
J .
L{оказательство последнеrо равенства здесь опускается 1).
2.2. Кольца и поля
rруппа
это алrебраическая система с одной операцией,
а рассматриваемые ниже кольца и поля ЯВЛЯIОТСЯ алrебраиче..
скими системами с двумя операциями.
Кольца. Пусть R
множество, для любых двух элементов
KOToporo определены две операции + и.. Алrебраическая си
стема (R, +, .) называется кольцом, если выполнены следую
щие три аксиомы: /
R. 1. (R, +)
коммутативная rруппа.
R.2. (R,.)
полуrруппа, т. е. алrебраическая система, для
которой выполняются о. 1 и G. 2.
R. 3. Аксиома дистрибутивности. Для любых трех элементов
а, Ь u с из R
а(Ь+с)==аЬ+ас,
(а + Ь) с === ас + Ьс.
Заметим, что в кольце для операции ., вообще rоворя, мо-
rYT не выполняться аксиомы О.3, О.4 и АО.5. Если же опера-
ция · коммутативна в кольце, то такое кольцо называется KOM
мутаТИ8НЫМ. Если в кольце существует единичный элемент OT
носительно операции ., т. е. если выполняется аксиома а. 3, то
это кольцо называется кольцом с eaUflUl{eu.
1) СМ. rл. 8. разд. 8.1.5.
П ptUrt. ред.
70
rлава 2
Задача 2.15. Доказать следующее утверждение. Алrебраи-
ческая система (Z, +, .), rде + и · есть обычные сложение и
умножение целых чисел, является коммутативным кольцом С
единицей.
Задача 2.16. Доказать следующее утверждение. Пусть М п
множество всех квадратных матриц размера n Х n, элементами
которых являются действительные числа, и пусть + и · есть
обычные операции сложения и умножения матриц. Тоrда алrеб..
раическая система (М п , +, .) является кольцом с единицей. Это
кольцо называется кольцом матриц.
Указание. Единичным элементом относительно операции ·
в М п является единичная матрица. Поскольку умножение мат-
риц, вообще rоворя, неКОМl\fутативная операция, то кольцо
матриц является, таким образом, примером некоммутативноrо
кольца.
Задача 2.17. Пусть дано кольuо R. МИОiкество всех MHoro-
членов
/'
aoXn+aIXn J+ ... +an lX+an, aiER, n O,
с коэффициентами из R является кольцом относительно обыч-
ных операций сложения и умножения мноrочленов. Это кольцо
называется кольцом мноzочленов от неизвестноrо х над коль-
цом R и обозначается через R[x].
Подмножество 1 кольца R называется идеалом кольца R
если оно удовлетворяет следующим двум условиям:
1.1. Для любых двух элементов а и Ь из 1 элемент а + ь при-
надлежит 1.
1. 2. Для любоrо элемента х кольца R и любоrо а из 1 оба
произведения ах и ха лежат в 1.
Задача 2.18. Множество целых чисел Z является коммутатив-
ным кольцом с единицей. Какой вид имеют идеалы кольца Z?
Решение. Пусть 1 некоторый идеал кольца Z, 1 с Z, и
пусть n минимальное целое положительное число из 1. Для
любоrо элемента а Е 1 однозначно определяются такие числа q
и " что
а === qn + " О r < n.
Так как n Е 1, то ( q) n Е 1. Следовательно, а + ( q) n ==
== а qn == r Е 1. Если допустить, что, > О, то сразу получаем
противоречие, так как по предположению n минимальное чис-
ло в 1. Следовательно, , == о и
а == qn.
Конечные поля
11
Это означает, что каждый элемент идеала J делится на п. Та-
ким образом, идеал 1 это множество всех чисел, кратных n
Будем обозначать этот идеал через (п).
В теории rрупп с помощью нормальных делителей строятся
факторrруппы. В теории колец роль нормальных делителей вы..
полняют идеалы.
Если 1 идеал кольца R, то в R можно ввести НОБое бинар-
ное отношение следующим образом:
а == Ь (mod 1) # а ....... Ь Е 1.
Это бинарное отношение является отношением эквива.пентности.
Для Toro чтобы убедиться в этом, проверим справедливость
аксиом отношения эквивалентности:
1) Так как а а == О Е 1, то а == а (mod 1).
2) Пусть а == Ь (Лl0d 1). Тоrда, поскольку а Ь Е 1 и
( I) Е R, имеем (a Ь) == Ь а Е 1, а это означает, что
Ь == а (mod 1).
3) Пусть а == Ь (mod 1) и Ь == С (mod 1). Тоrда, поскольку
a bEI и b CE/, то из 1.1 получаем, что (a b)+(b c)==
== a CE 1. Это означает, что а == c(mod 1).
Классы эквивалентности, определяемые отношением ==, на-
зываются классами вычетов КО.i1ьца R по модулю 1. Операции
сложения и умножения классов вычетов кольца R по модулю 1
определяются следующим образом. Обозначим через (х) и (у)
классы вычетов, содержащие соответственно элементы х и у.
По определению
(х) + (у) == (х + у),
(х) · (у) == (х · у).
Эти определения были бы некорректными, если бы для некото-
рых элементов х' и у', таких, что (х) == (х') и (у) == (у'), ока.
залось, что (х + у) =1= (х' + у') или (х. у) =1= (х' · у'). Однако,
как показано ни'же, это случиться не может, так что введенные
определения корректны. Действительно, пусть х' и у' таковы,
что (х) == (х') и (у) == (у'). По определению
х х' Е 1 и у ....... у' Е 1.
Отсюда следует, что
(х + у) (х' + у') == (х....... х') + (у у') Е It
ху х' у' == ху ....... ху' + ху' х' у' === х (у ........ у') + (х ....... х') у' eg 1,
а именно
(х + у) === (х' + у') и (ху) == (х' у').
Введя таким образом операции + и · в множестве классов вы..
четов кольца R, порожденных идеалом 1, мы построили новое
72
r лава 2
КОЛЬЦО. Это {{ОЛЬЦО называется КОЛЬЦО.Аt классов вычетов и обо-
значается через RjI.
Утверждение 2.19. Как следует из задачи 2.18, идеалы коль
ца Z ЭТО множества вида (п) == {nzlz Е Z}. Выберем одно из
чисел n и с помощью идеала 1 == (n) построи.А! кольцо классов
вычетов Zj(n). Аддитивная срупnа ЭТОсО кольца изоморфна фак
торсруnпе Zn из утверждения 2.8. J1 множение определяется ра-
венством (i). (j) == (i · j) == (Остаток от деления i · j на n).
Задача 2.20. Построить таблицы сложения и умножения для
кольца класса вычетов Zj (6).
Реи1ение:
+ \ (О) (1) (2) (3) (4) (5)
(О) (О) (1) (2) (3) (4) (5)
(1) (1) (2) (3) (4) (5) (О)
(2) ( 2) ( 3 ) (4) (5) ( О) (1)
(3) (3) (4) (5) (О) (1) (2)
(4) (4) (5) (О) (1) (2) (3)
(5) (5) (О) (1) (2) (3) (4)
· I (О) (1) (2) (3) (4) (5)
(О) (О) (О) (О) (О) (О) (О)
(1) (О) (1) (2) (3) (4) (5)
(2) (О) (2) (4) (О) (2) (4)
(3) (О) (3) (О) (3) (О) (3)
(4) (О) (4) (2) (О) (4) (2)
(5) (О) (5) (4) (3) (2) (1)
Как видно из этих таблиц, кольцо Zj (6) относительно опера-
ции · не ЯВ.J1яется rруппой. В частности, в Zj (6) произведение
двух HeHy..ТIeBЫX элементов может оказаться равным (О), напри
мер (2) · (3) == (6) === (О). Если произведение двух элементов
кольца равно нулю, то каждый из них называется делителем
нуля. Коммутативное кольцо без делителей нуля, обладающее
единичным элементом по умножению, называется областыо це-
лостности.
. Поля. Пусть Р множество, содержащее по крайней мере
2 элемента, такое, что для любых двух элементов а и Ь из F
определены две операции + и.. Алrебраическая система
(Р, +, .) называется полем, если она удовлетворяет следующим
аксиомам:
F. 1. (Р, +) коммутативная rруппа.
Пусть О единичный элемент rруппы (Р, +), а Р*.......... мно-
жество, полученное из Р удалением элемента о.
F.2. (р*, .) коммутативная rруппа.
F. 3. Закон дистрибутивности. Для любых трех элементов а,
Ь и с из F
а . (Ь + с) == а · Ь + а · с,
(а + Ь) · с == а · с + ь · с.
к. онечные поля
73
Утверждение 2.21. Л1ножество R действительных чисел и
множество С комплексных чисел являются полями относительно
обычных операций сложения u умножения и называются СООТ-
ветственно полем действительных чисел и nолеА! КОJ,.ttnлексных
чuсел. Однако KOAlMYTaTUBHoe кольцо с единицей (Z, +, .) nо-
леАt не является.
Утверждение 2.22. Свойства полей. (Единичный элемент поля
по сложению обозначается через О.)
1) Д ля любосо элемента а поля а · О === О · а === О.
2) Для любых двух ненулевых элеАtентов а и Ь поля а. Ь + О.
3) Для любых двух элементов а и Ь поля (а. Ь) ===
== ( a) · Ь == а . ( b).
4) Ec,,'lu а . Ь == а · с и а =1= О, то Ь == с.
Доказательство.
1) По определению единичноrо элемента аддитивной rруппы
Ь == Ь + О. в силу закона дистрибутивности а · Ь == а · (Ь+О) ==
== а. Ь + а. о. Так как поле является I'рУППОЙ по сложению, то
из единственности единичноrо элемента аддитивной rруппы (СМ.
задачу 2.4) имеем а. 0==0. Аналоrично доказывается, что
О · а == О.
2) Аксиома F.2 устанавливает, что множество Р* == P {O}
является rруппой относительно операции .. Сформулированное
выше свойство 2 поля есть просто следствие свойства замкнуто
сти операции · в rруппе (Р*, .).
3) Справедливость слеДУIОЩИХ равенств следует непосред-
ственно из определения поля: О == О . Ь == (а + ( a)) · Ь ==
== а · Ь + ( a) . Ь. Из существования и единственности обрат..
Horo элемента (см. задачу 2.4) имеем ( a) · Ь == (а · Ь). AHa
лоrично доказывается, что а · ( b) == (а · Ь).
4) Так как а =1= О, то существует обратный к а элемент по
умножению a l. Умно}кая обе части равенства а · Ь == а · с сле-
ва на a l, ПОJIучаем Ь == с.
Таким образом, поле это алrебраическая система, в кото-
рой можно выполнять, как обычно, сложение, вычитание, умно..
жение и деление ЭJlементов.
Алrебраические системы (Р, +) и (Р*, .) поля (Р, +, .) на-
зываются соответственно аддитивной и 1\1ультипликативной rруп-
пами поля. Единичные элементы относитепьно операций + и а
называются соответственно нулевым элементо;11, поля и единич'"
ным элемеНТО}r! поля и обозначаIОТСЯ через О и 1 в тех случаях"
коrда их нельзя спутать с числами О и 1. По аналоrии с rруп
пами число элементов в поле называется порядком поля. Поля,
порядок которых конечен. называются конечными nол.[lм'U.
74
r лава 2
Задача 2.23. По определению поле содержит по крайней мере
два элемента О и 1. Построить таблицы сложения и умножения
для поля, состоящеrо только из двух элементов О и 1.
Решение. Сначала воспользуемся свойствами 1 и 2 поля,
сформулированными в утверждении 2.19. Три rрафы таблицы
умножения можно заполнить, воспользовавшись первым из этих
свойств. В силу BToporo свойства произведение 1 · 1 не может
быть равно о, а следовательно, 1 · 1 === 1. Три rрафы таблицы
сложения, за исключением той, которая соответствует сумме
1 + 1, можно сразу же заполнить, воспользовавшись тем, что О
является единичным элементом по сложению. Сумма 1 + 1 мо-
жет принимать два значения О и 1. Однако, поскольку {О, 1}
есть rруппа по сложению, то, соrласно свойствам rрупповых таб-
лиц, 1 + 1 == о.
+ 101
О О 1
110
· I о 1
О О О
1 О 1
п римечанuе. Операция сложения в данном случае представ-
ляет собой так называемое сложение по модулю 2. Часто для
обозначения этой операции используется знак ЕВ.
Если порядок поля задан, то степень свободы при составле-
нии таблиц сложения и умножения элементов поля в действи-
тельности не столь уж велика, как это моrло бы показаться с
первоrо взr ляда (см., например, последнюю задачу). Способы
построения полей MorYT быть различными, но если порядок поля
фиксирован, то конечное ПО.не определяется однозначно с точ-
ностью до изоморфизма. Друrими словами, каким бы образом
не было построено конечное поле, результат будет одним и тем
же. Конечное поле может быть изоморфно друrим полям, т. е.
может быть представлено различными способами, и выбор удоб-
Horo представления поля это в действительности очень важ-
ная проблема.
Если существует биективное отображение f поля F на поле F',
такое, что для любых двух элементов а и Ь из F
f (а + Ь) == f (а) + f (Ь),
f (а · Ь) == f(a). [(Ь),
1'0 поли F и Р' называются изоморфными. В подобных случаях
rоворят, что отображение f сохраняет операции + и..
Рассмотрим здесь конкретный способ построения конечных
полей.
Утверждение 2.24. Если Р простое число, то Z/ (р) поле.
Доказательство. Выше уже было доказано, что Z/ (р) коль-
110 (утверждение 2.19). Чтобы доказать, что Z/ (р) являет я пg-
Конечные поля
75
лем, достаточно показать, что для каждоrо класса вычетов (а)
кольца Zj (р), за ИСКЛlочением класса вычетов (О), существует
обратный элемент (а) I. Рассмотрим смежные классы (1), (2), . . .
. . ., (р 1). Заметим, что если р простое число, то равенство
(а, р) == 1 справедливо для всех а == 1, ..., р 1. Следова-
тельно, в силу свойства N.5' целых чисел существуют такие чис-
ла х и у, что ах + ру == 1. Отсюда следует, что (а). (х) ==
== (а · х) == (1 ру) == (1), т. е. обратным элементом к (а) я а..
ляется элемент (х). Таким образом, если из кольца Z/ (р) исклю..
чить элемент (О), то оставшиеся элементы образуют мультипли.
кативную rруппу (очевидно, коммутативную), а это означает,
что l/(p) является полем. Порядок этоrо поля равен р.
Итак, для каждоrо простоrо числа р мы построили конечное
поле порядка р. Элементами этоrо поля являются классы выче
тов (0)== (р), (1), ..., (p l) кольцаZпо модулю (р). Опе-
рации сложения и умножения Э,лементов этоrо поля задаются
равенствами
(i) + (j) (i + j) == (R p (i + j»),
(i) · (j) == (i · j) == (R p (i · j»),
rде R p (а) остаток от деления числа а на число р.
Задача 2.25. Построить таблицы сложения и умножения эле-
ментов конечных полей порядков 3 и 5.
Решение. Для простоты элементы (i) поля будем обозна-
чать просто символом i:
Поле порядка 3 .!
+1012 .1012
О 012 0000
1 120 1012
220 1 2 021
По.ле порядка 5
+101234 .101234
О 01234 000000
1 1 2 340 1 О 123 4
22340 1 2 024 1 3
3 340 1 2 3 О 3 142
440 1 2 3 4 043 2 1
Как леrко видеть из описанноrо выше метода построения
конкретных полей, для любоrо простоrо числа р существует KO
вечное поле порядка р. Если же р не является простым числом,
76
r лава 2
то построить поле порядка р тем же методом, а имеНIIО вводя
сложение и умножение классов вычетов кольца Z с помощью
операции Вhlчисления остатка при делении ЧИССJl на МОДУJIЬ р,
нельзя. Это, в частности, связано с тем, что если р составное
число, то произведение двух ненулевых элементов а и Ь может
оказаться равным р. В этом СJIучае R p (а · Ь) == R p (р) == О, а
следовательно, в силу свойства 2 полей, сформулированноrо в
утверждении 2.22, мно)кество классов вычетов по модулю р не
может быть полем. Однако, как будет показано ниже, для лю
боrо простоrо р и любоrо це.поrо положительноrо числа m cy
ществует поле порядка рт. В силу вышеизложенноrо операции
сложения и умно)кения по модулю рт для построения полей не
используются. Как строить поля порядка рт, будет описано
ниже. Вначале докажем существование ПО.пей порядка рт.
Если подмножество РО элементов поля F само является по-
лем, то Fo называется подполем Р, а F расширением РО. По-
скольку операции в подполе ро те ,ке, что и в поле Р, то единич-
ный элемент по сложеНИIО О и единичныЙ элемент по умноже-
нию 1 оба входят в РО.
Утверждение 2.26. Н еобходимы.,ии и достаточными условия-
ми Т020, чтобы неnустое от личное от {О} подмножество РО поля F
было nодполел,t поля Р, являются следУl0lцие:
1) если а, Ь Е РО, то а Ь Е РО;
2) если а, Ь Е РО, Ь =1= О, то ab l Е ро.
Теорема 2.3. Любое конечное поле является расширениеАl пo
ля Z/ (р), zae р "'Ростое число (или поля, uзоморфноzо Z/ (р)).
Доказательство. Пусть ро == {О, 1, 1 + 1, ...} подrруппа
(по сложению), порожденная элементом 1 поля Р, и пусть т.......
порядок ро (т порядок элемента 1 в аддитивной rруппе по
ля Р). Тоrда
1 + 1 + ... + 1 =t= О, 1 l < ,п,
i ла r аемых
1 + 1 + ... + 1 == о.
т слаrаемых
Допустим, что т не является простым числом, т. е. т==mJт2,
rде тl > 1 и т2 > 1 некоторые положительные числа. Тоrда
из аксиом дистрибутивности поля получаем
(1 + 1 + ... + 1) (1 + 1 + ... + 1) === 1 + 1 + ... + 1 == О,
.. \..... .. - -
m( т'l т
что противоречит свойству 2 полей, сформулированному в УТ-
верждении 2.22. Таким образом, т ДОJIЖНО быть простым чис-
лом. Поставим в соответствие элементу 1 + 1 . .. + 1 поля F
........
,
i
Конечные поля
77
класс вычетов (i) ПОJIЯ Z/ (р). Так как это отображение взаим-
но однозначно и сохраняет операции, то ро и Z/(p) изоморфны.
В любом конечном поле F ПОРЯДОК Р единичноrо по умноже
нию элемента 1 как элемента аддитивной rруппы поля F опре-
деляется однозначно и называется характеристикой поля Р.
В поле F характеристики р для любоrо элемента а поля F сумма
(а + а + ... + а) всеrда равна О, так как
.. - ---
1J
а + а -+ ... + а == а . (1 + 1 . .. + 1) == а · О === о.
......
---.--I'
ТJ
."... ...............
р
Более Toro, для Лlобоrо ненулевоrо элемента а поля F мини
мальное число n, для KOToporo а + а + ... + а === О, равно р.
'-'-'__.... .J
n
в самом деле, "fJerKO проверить, что
а + а + ... + а == О 1 + 1 + ... + 1 == о.
J
....................
n
n
Таким образом, порядок любоrо элемента аддитивной rруп-
пы поля Р, за исключением элемента О, равен р.
Задача 2.27. Пусть F поле характеристики р. Доказать, что
для любых двух элементов а и Ь из F и любоrо натуральноrо
числа m
(а + ь)рт == а рт + ь рт , (а ь)рт === а рт ь рт .
Решение. Сначала покажем справедливость первоrо из этих
равенств в случае т == 1. Раскрывая двучлен (а + Ь) р по фор-
муле бинома Ньютона, получаем
(а + Ь)Р == аР + ( ) aP lb + (;) aP 2b2 + ... + ( f) abP 1 + Ь Р .
rде через ( ) aP lbl обозначена сумма aP ibi + . . . + aP lbl
(( ) слаrаемых). а ( ) биномиальный коэффициент,
равный р!/п (р i)!. Так как при О < i < Р знаменатель послед-
Hero выражения не делится на р, то все биномиальные коэффи-
циенты ( ). о < i < р, делятся на р. В поле характеристики р
для любоrо элемента а поля сумма а + а + ... + а при любом
. ....,
р
натуральном р равна О, так что все слаrаемые в приведенном
выше разложении, за ИСКЛlочением двух крайних, равны нулю.
Следовательно,
(а + Ь)Р === аР + Ь Р .
78
rлава 2
Далее, в случае т == 2 имеем
(а + ь)р2 === ((а + Ь)Р)Р === (аР + ЬО)Р == aO
+ ь рl .
Аналоrично доказывается справедливость первоrо равенства и
при остальных m. Доказать второе равенство читателям предла-
rается самостоятельно.
Соrласно теореме 2.3, любое конечное поле является расши-
рением HeKoToporo поля Zj (р), rде р
простое число. В связи
с этим возникает вопрос о структуре конечноrо поля, если по-
следнее рассматривать как расширение HeKoToporo друrоrо поля.
Сразу отметим, что расширение F поля Fo является векторным
пространством над полем ро. Прежде чем ДОI<азать это, напом-
ним определение BeKTopHoro пространства и кратко рассмотрим
свойства последнеrо, а кроме Toro, введем понятие кольца мно-
rочленов. Тем самым мы завершим подrотовку к доказательству
указанноrо выше утверждения. Можно, однако, перейти здесь
непосредственно к разд. 2.5, возвращаясь к разд. 2.3 и 2.4 в слу-
чае необходимости.
2.3. Векторные пространства
Векторные пространства. Определим векторное пространство
V над полем F как алrебраическую систему, удовлетворяющую
указанным ниже аксиомам:
v. 1. V является аддитивноЙ rруппой. .
V.2. ДЛЯ любых двух элементов х Е V И а Е F определено
произведение ах, являющееся элементом v.
v. 3. Если х, у Е V, а Е F, то а (х + у) == ах + ау.
V.4. Если х Е V, а,
Е Р, то (а +
)x == ах +
x.
V.5. Если ХЕ V, а,
Е Р, то (a
)X == a(
x).
v. 6. 1 · х === х (1
единичный элемент поля F).
Утверждение 2.28. Векторное пространство V над полем. F
обладает следующими свойствами:
1) О. Х === О (О в левой части равенства
элемент поля F,
а О в правой части
элемент v, являющийся единичным элемен-
том аддитивной zpynnbt V и называемый нулевым вектором);
2) (
l) х ===
x (
l в левой части равенства
элемент по-
ля Р, а .........х в правой части
элемент V, обратныЙ х;
3) ах == О Е V, а =1= О
Х == О.
Доказательство. Соrласно определеНИIО нулевоrо элемента
поля Р, для любоrо элемента а Е F имеет место paBeHCI'BO
О + а == а. Тоrда
(О+а)х==О.х+а.х==а.х (ввиду V.4).
Конечные поля
19
Так как V является аддитивной rруппой и в этой rруппе су-
ществует единственный единичный элемент (в данном случае
это нулевой вектор О), то О · Х == О.
Доказательство свойств 2 и 3 опускается.
Утверждение 2.29. Пусть V n (Р) множество всех последо-
вательностей (Xl, ..., Х n ) длины n с компонентами из поля Р,
т. е.
Vn(F)==={xlx===(XI, .,., Х n ), Xl ЕР, i=== 1, ..., п}.
Пусть Х == (Xl, . . ., Х n ), У === (Yl, . . ., Уn) Е V n (Р), а Е F и
Х + у === (х 1 + l' 1, · · ., Х п + у n),
ах == (ах 1, ..., ах n ).
Тоеда V n (Р) является векторным nространством над полем Р.
Если еl == (1, О, ..., О), е2 == (0,1, ..., О), ..., е n ==
== (О, О, ..., 1), то
Х === (XI, . . ., х n ) === Xlel + ... + хnе n .
Рассмотрим векторное пространство V над полем Р. Век-
торы Vl, V2, . . . , Vk из V называются линейно зависимыми, если
в F существуют такие элементы CXI, (Х2, ..., CXh (по кр.?йней мере
один из которых не равен нулю), что
alvl + ... + akvk == О, (2.5)
и линейно независимыми в противном случае. А именно векто-
ры Vl, ..., Vk являются линейно независимыми, если равенство
(2.5) выполняется лишь коrда (1,1 == . . . ==(1,k == О. Максималь
ное число линейно независимых векторов в V называется раз-
мерностью BeKTopHoro пространства V над полем F 1 обозна-
чается через dim v. Пусть dim V == т и Vl, ..., V m линейно
независимые векторы из V (по определению в V существует хо-
тя бы одна такая совокупность векторов). Тоrда любой вектор V
из V можно представить как линейную комбинацию векторов из
этой совокупности:
V == lVI + ... + тvт, (2.6)
rде l, ..., т Е Р. Действительно, как следует из определе-
ния т, совокупность из т + 1 векторов v, VI, '.., V m линейно
зависима, и, следовательно, существуют такие элементы V'l Е Р,
i == О, 1, ..., т, что
VoV + VIVl + ... + VтVm === О
и не все Vi равны нулю (в частности, 'Уо =1= О 1).
1) Поскольку иl, ... t V m лин йно независимы. ПРU'м'. ред.
80
r лава 2
Умножая обе части ПОСJIеднеrо равенства на элемент V 0 1 Е Р,
явлRющийся обратным по умножению к элементу Уо, получаем
V V l V V ......... V l V V V ---1 V V
О 1 1 О 2 2 · 8 · О т т 8
Таким образом, rvlbI показали, что любой вектор V из V можно
представить в виде линейной комбинации векторов Vl, ..., V m .
Любая совокупность таких линейно независимых векторов из V,
что любой вектор из V может быть представлен в виде их ли-
нейной комбинации, называется базисом. Базис BeKTopHoro про
странства V можно выбрать различными способами. Однако мо-
жно доказать, что число векторов в ЛIобом базисе равно размер-
ности т BeKTopHoro. пространства v. Если размерность вектор-
Horo пространства V конечна, то подмножество W векторов из
V является базисом тоrда и только тоrда, коrда W состоит из
т == dim V линейно независимых векторов.
Утверждение 2.30. Пусть Vl, . . . , V m один из базисов вeKTOp
НОсО пространства V. Представление (2.6) любосо вектора VE '!
единственно.
Доказательство. Предположим, что вектор V из V может
быть представлен в виде (2.6) двумя различными способами, а
именно V == alVl + ... +amvm == b1vI + . . . + bmv т . Тоrда
(al b 1 ) VI + . 8. + (а т Ь т ) V m о.
Так как векторы Vl, ..., V т . линейно независимы, то ai b i == О
(i == 1, . . . , т), т. е. ai == Ь i (i == 1, . . . , т).
Подмножество W BeKTopHoro пространства V, удовлетворяю-
щее следующим двум условиям:
1) WI, W2 Е W Wl + W2 Е W,
2) для любых а Е F и W Е W э.лемент aW Е W,
само является векторным простраНСТВОl\f над F и называется
nодnространством веКТОРНО20 пространства V.
Пусть VI, ..., V m базис BeKTopHoro пространства V над
полем Р, т == dim v. Скалярное произведение а 8 Ь двух век-
т т
торов а :=: L alvl и Ь == L biVi определяется равенством
l l i 1
а 8 Ь == ( f aiVi ) · ( f: biVi ) f: aibi е Р.
1 1 i 1 1 1
Если скалярное произведение двух векторов а и Ь и V равно
н'улю, то rоворят, что эти векторы ортосонаЛЬНbl. Ортосональное
дополнение WJ.. подпространства W BeKTopHoro пространства V
определим следующим образом:
J..
Х е: W # х · у == о для B e у Е W,
Конечные !10ЛЯ
81
Кроме Toro, введем сумму V 1 Е9 V 2 двух подпространств V I
и V 2 BeKTopHoro пространства V:
X E V t EВV 2 #x==y+z, YEV tt ZEV 2 ,
Утверждение 2.31. Пусть W t II U 7 2 подпространства V.
ТОсда W 1 n W 2 также является nодnространством' V.
Доказательство. Проверим справеД"lИВОСТЬ свойств 1 и 2 в
опреде.пении подпространства дЛЯ W I n W 2 :
1) w 1, W2 Е \\7 1 n W 2 9 w 1, W2 Е W 1 И W 1, W2 Е W 29 w 1 + W2 Е \\7 1 ,
Wl + W2 Е \V 2 9(WI + te'2) Е W I n \\72;
2) Свойство 2 проверяется анаJ10rично.
Утверждение 2.32. Если W t и W 2 подпространства V, то
W 1 ffi W 2 также является nодnространством' V.
Доказательство. Kal( и при доказательстве предыдущеrо
утверждения, проверим справедливость свойств 1 и 2 в опреде-
лении подпространства:
1) u,' === W 1 + и'2, и == U t + и2 Е \\7 1 ЕВ w 2, W 1 , иl Е W 1, W2, и2 Е
Е W 29 w + U == (Wl + Ut) + (и'2 + и2) Е \\71 ЕВ W 2;
2) свойство 2 проверяется анаJ10rично.
Утверждение 2.33 *. dim (и п W) + dim (и ЕВ W) == dim и +
+ dim W.
. Доказательство. Пусть dim и ==k 1 , diln W ==k 2 и dim (и n W) ==
== ko. В U П W существует базис из ko векторов. Присоединив
к этим ko векторам k 1 ko дополнительных векторов, можно по-
строить базис дЛЯ U. Точно так же, присоединяя к тем же ko
векторам k 2 ko векторов, можно построить базис дЛЯ W. в Ka
честве базиса для и ED W можно взять базис W из ko векторов,
присоединив к нему (k 1 ko) дополнительных векторов из ба-
зиса и и (k 2 k{J) дополнительных векторов из базиса w. Тоrда
dim (и ЕВ W) == ko + (k l ko) + (k 2 k o ).
Утверждение 2. 4. * Пусть и u W подпространства вектор-
НОсО пространства V. Т 02да и 1.. ЕВ W 1.. === (и n W) 1..
Доказательство. Так как
UnW c: U, w,
и , W (U n W)J..,
ТО
(U ф \ ? ) с:: (и n W.)J...
82
r лава 2
с друrой CTOPOHbl t
и1., W1. c: U1.EВW.L,
(и.1 ЕВ w 1.)1. с: и1.1., w 1.1.,
(и1. ЕВ W.1)1. с: и1.1. n W.1.l == и n w,
(и n w).1 с: (( и .1 ЕВ w 1. )1.)1. == U 1. ЕВ W .L.
Утверждение 2.35. * Пусть V
векторное пространство раз-
мерности n над полем порядка q, U и А
nодпространства раз-
мерностей j и k соответственно веКТОРНО20 пространства V, W ==
=== и.1 и В == А.1. Tozaa
I W n А I == qk
J I U n в 1,
еде через I S I обозначено число элементов в множестве S.
Доказательство. dim (U.l n А) == n
dim (и.1 п А).1. Со-
rласно предыдущему утверждению,
(и.1 n А)1. == и.1.1 ЕВ А1. === U ЕВ A.L,
dim (и ЕВ А1.) == dim U + dim А1.
dim (и n А1.).
Тоrда
dim (W n А) == n ----- dim U ----- dim В + dim (и n В) ===
=== k
j + dim (и n В).
2.4. Мноrочлены
Пусть F
поле, а Р[Х]
множество всех М,ноzочленов
f (Х) == ао + alX + ... + ak xk , ai Е F t i == О, 1, . . ., k, (2.7)
от переменной Х над поле,м Р. Если в (2.7) ah =1= О, то rоворят,
что мноrочлен '(Х) имеет степень k. Степень мноrочлена f бу-
дем обозначать через deg'. Множество всех мноrочленов, имею-
щих степень k и менее, обозначим через F(k{X].
k l
Два мноrочлена f (Х) == L ai X' и g(X)
L ь,х' называют-
i
O '
O
ся равными, если они имеlОТ одну и ту же степень, Т. е. k == 1,
а кроме Toro, ai == b i при всех О
i
k. (При этом считается,
ЧТО ХО == 1, rде 1
единичный элемент поля Р.) Мноrочлен, все
коэффициенты KOToporo равны нулю, будем называть нулевым
мноrочленом и обозначать через О.
Задача 2.36. Перечислить все мноrочлены степени 2
M
Hee
над полем F :;::;:: Zj (2) === {О, ,} и указа ть их степеНI1,
. .
/(онечные пОАЛ
83
Решение.
f 111 (Х) == 1 + Х + Х 2
/101 (Х) == 1 + Х2
/011 (Х) == + Х + Х2
/001 (Х) == Х 2
fllo(X) == 1 + Х }
f 010 (Х) === Х степень 1,
f 100 (Х) === 1 степень о,
fooo (Х) == о степень не определена.
П рuмечанuе. Степень нулевоrо мноrочлена не определена, но
коrда rоворят о мноrочленах степени, меньшей HeKoToporo це-
лоrо k, то обычно к ним относят также и нулевой мноrочлен.
Если в мноrочлен fOll === Х + Х 2 из последней задачи под-
ставлять вместо Х элементы О и 1 поля Р, то он будет прини-
мать те же значения, что и мноrочлен fooo(X) == о. Однако как
мноrочлены 'ООО(Х) и f011 (Х) различны. Заметим, что число раз-
личных мноrочленов степени k и меньше над полем порядка q
равно qk+l.
Введем далее операции сложения и умножения мноrочленов
следующим образом. Для любых двух мноrочленов f (Х) === L /IX'
И g (Х) === L giXi положим
/ (Х) + g(X) == L (fl + gi) Xl,
f (х). g(X) === (to flgl /) Xl.
В частности, если а Е Р, то
af (Х) === L (а' i) Xl.
1
степень 2,
(2.8)
(2.9)
(2.1 о)
Введя таким образом сложение и умножение в Р[Х], мы получи-
ли, как нетрудно проверить, кольцо, называемое кольцом МНО-
rочленов.
Утверждение 2.37. МноzочлеНbt из Р[Х] обладают следую-
щими свойствами:
1) '(Х). о == о для любоzо '(Х) Е Р[Х];
2) если '(Х) =1= О u g(X) * о, то f(X)g(X) =#= о;
3) [f(X)g(X)] == [ f(X)]g(X) == f(X)[ g(X)];
4) (f(X) + g(X)]h(X) == f(X)h(X) + g(X)h(X);
5) если '(Х) =р О u f(X)g(X) == f(X)h(X), то g(X) == h(XJ..
84
r лава 2
Доказательство. Свойства 1 4 мо)кно доказать точно так же,
как и соответствующие свойства из утвержденШI 2.28. Дока}кем
свойство 5. Из предположений и свойства 4 непосредственно сле
дует, что О == f(X)g(X) f(X)h(X) == f(X)[g(X) h(X)]. Так
как f (Х) =1= о, то в силу свойства 2 g (Х) h (Х) == о, так что
h(X) == g(X).
П римечание. Метод доказательства своЙства 4 из утвержде-
ния 2.22 здесь неприменим, так как элемент, обратный к f (Х),
может и не cyulecTBoBaTb.
Утверждение 2.38. Для любых двух ненулевых мноzочленов
f (Х), g (Х) Е F[ Х], таких, что f (Х) + g (Х) -=1= о,
deg (f + g) шах (deg [, deg g),
deg (У · g) == deg f + deg g.
Утверждение 2.39. Для любых двух мноеочленов {(Х),
g(X) Е F[X], g(X) =1= о, существуют, и притом единственные,
мноzочлены а (Х), , (Х) Е Р[.Х], такие, что
f (Х) == а (Х) g (Х) + r (Х), deg g > deg,. (2.1)
Доказательство. Для нахождения частноrо а (Х) и остатка
,(Х) следует провести деление f(X) на g(X) точно так же, как
производится деление мноrочленов над полем действительных
чисел. Докажем единственность разложения (2.11). Предполо-
жим, что сущеСТВУIОТ два частных а (Х) и а' (Х) и два остатка
, (Х) и r' (Х), такие, что
а (Х) g (Х) + r (Х) === а' (Х) g (Х) + " (Х).
g (Х) [а (Х) ....... а' (Х)] === " (Х) ..... , (Х).
Тоrда
Поскольку степень мноrочлена в правой части последнеrо ра-
венства меньше, чем степень g (Х), то это равенство может иметь
место лишь в том СЛ.учае, коrда а (Х) а' (Х) == о, и, следова-
тельно, , (Х) ,'(Х) == о.
Если в формуле (2.11) остаток ,(Х) равен НУЛIО, то rоворят,
что g(X) деJIИТ f(X). Если в Р[Х] нет ни одноrо мноrочлена сте-
пени, большей О, который делил бы f (Х) (за исключением ска-
лярных кратных f (Х) ), то f (Х) называется неnриводимым. Эле-
мент а поля Р, такой, что [(а) == О, называется корнем '(Х).
в этом случае также rоворят, что уравнение f (Х) == о имееr
корень а в поле F.
Утверждение 2.40. Если уравнение f(X) == о, {(Х) Е Fk[X],
имеет корень а в поле Р, то существует такой МНОZО'lлен g(X) Е
Е Fk---l[Х], что f(X) == (X a)g(X). Если степень f(X) равна k,
то уравнение f (Х) == о имеет не более k корней.
Конечные поля
85
Доказательство. Из предыдущеrо утверждения следует cy
ществование и единственность таких мноrочленов g (Х) Е
Е Fk I[X] И r (Х) Е F (поскольку deg r < 1), что
f (Х) == (Х а) g (Х) + r (Х), r (Х) Е Р.
Подставляя в обе части последнеrо равенства Х === а, получаем
f (а) == О . g (а) + r (а) == r (а).
Поскольку а является корнем f (.У), то f (а) == r (а) === о, т. е.
,(Х) == о. Следовательно,
f (Х) == ()( а) g (Х).
Далее, если уравнение f (Х) == о имеет v раз.ПИЧНЫХ корней
al, ..., ау Е Р, то существует такой мноrочлен h (Х) Е Fk v[X],
что f (Х) === (Х aI) . . . (Х ау) h (Х). Это означает, что f (Х)
имеет не более k корней.
Мноrочлены f (Х), g (Х) Е Р[Х] называются взаимно npOCTЫ
ми, если в Р[Х] нет ни одноrо мноrочлена степени, большей чем 1,
который делил Бы одновременно и f (Х) и g (Х).
Утверждение 2.41. Д ЛЯ двух проuзвОЛЬНblХ взаимно простых
мносочленов f(X), g(X) Е Р[Х] существуют такие мносочлены
а(Х) и Ь(Х), что
а (Х) f (Х) + ь (Х) g (Х) == 1.
(2.12)
Это свойство мноrочленов аналоrично свойству N.5' целых
чисел. ДОI<азательство последнеrо было основано на алrоритме
Евклида для целых чисел, однако для доказательства утверж-
дения 2.41 мы воспользуемся друrим методом. Этим методом
можно было бы доказать и свойство N.5' целых чисел точно
так же, как и для доказательства вышеприведенноrо утвержде-
ния можно было бы воспользоваться алrоритмом Евклида ДЛЯ
мноrочленов. Для доказательства существования обратных эле-
ментов в полях по умножению нам будет вполне достаточно свой-
ства мноrочленов, сформулированноrо в утверждении 2.41. Од-
нако в тех случаях, коrда обратный элемент для Toro или иноrо
KOHKpeTHoro элемента требуется найти в явном виде, необходимо
использовать непосредственно а.пrоритм Евклида.
Доказательство. Пусть 1== {a(X)j(X) + b(X)g(X) la(X},
ь (Х) Е Р[Х]} {о} и h (Х) один из мноrочленов минимальной
степени из J. Предположим, что deg h (Х) 1 и в I имеется хотя
бы один мноrочлен, который не делится на fl (Х). Тоrда остаток
от деления этоrо мноrочлена на h (Х) принадлежит J и имеет
степень, меньшую степени h (Х), что противоречит тому, что
h(X) мноrочлен минимальной степени в 1. Следовательно, все
мноrочлены из J должны делиться на h(X). Это означает. в
86
r лава 2
частности, что мноrочлены f (Х) Е J и g (Х) Е J оба делятся на
мноrочлен h (Х) не нулевой степени. Мы получили противоречие.
поскольку по условию h(X) и g(X) взаимно просты. Таким об-
разом, любой мноrочлен минимальной степени в J является мно-
rочленом нулевой степени, т. е. элементом поля F. Пусть с...:....
один из таких элементов, с Е F. По определению
с === ао (Х) f (Х) + Ь о (Х) g (Х),
rде ао (Х), Ь о (Х) Е F[X]. Умножая обе части последнеrо равенст-
ва на c l, получим равенство (2.12).
Мноrочлены из F[X], коэффициенты при наивысшей степе-
ни Х которых равны 1, называются нормированными "w'ноzочле-
нами.
Утверждение 2.42. Любой hlноеОflлен степени 1 и выше над
полем F можно представить в виде произведения элемента по-
ля F и нормированных неnриводимых мноzочленов над тем же
полем. Это разложение единственно с точностью до порядка сле-
дования сомножителей (доказательство см. в [3]).
Выше были рассмотрены основные свойства мноrочленов из
Р[Х]. Поскольку F[X] является кольцом, можно рассматривать
кольца классов вычетов, порождаемые идеалами кольца F[X].
По существу именно так строятся конечные поля, однако вопро-
сы построения конечных полей будут рассмотрены в следующем
разделе. Для построения конечных полей необходимы неприво-
димые мноrочлены и следующая задача посвящена нахождению
некоторых из них.
Задача 2.43. Найти все неприводимые мноrочлены степени 4
и менее над полем Z/ (2) .
Решение. М н о r о ч л е н ы пер в о й с т е n е н и. Имеется два
мноrочлена первой степени Х и Х + 1. По определению оба они
неприводимы.
Мн о r о ч л е н ы в т о рой с т е n е н и. Мноrочлен р (Х) ==
=== Х2 + аХ + ь второй степени неприводим тоrда и только то-
rда, коrда он не делится ни на Х, ни на Х 1 1). Это эквива-
лентно тому, что р (О) == Ь :1= О и р (1) == 1 + а + ь =1= О. Следо-
вательно, лишь один из мноrочленов второй степени, а именно
Х 2 + х + 1, является неприводимым.
М н о r о ч л е н ы т р е т ь е й с т е n е н и. Мноrочлен р (Х) :::::1
== Х3 + аХ2 + ЬХ + с является неприводимым тоrда и только
тоrда, коrда он не делится ни на Х, ни на Х + 1. Это эквива-
лентно тому, что р(О) == с =1= О и р(l) == 1 + а + ь + с =р О, или
t) Заметим, что Х ........ 1 =о. Х + 1. П рим. ред.
Конечные поля
87
с == 1 и а + ь == 1. Следовательно, Иl\tlеются два неприводимых
мноrочлена третьей степени Х 3 + Х 2 + 1 и Х 3 + Х + 1.
м н о r о ч л е н ы ч е т в е р т о й с т е п е н и. Мноrочлен
р(Х) == Х 4 + аХ 3 + ЬХ 2 + сХ + d является неприводимым тоrда
и только тоrда, коrда он не делится ни на один из неприводи-
мых мноrочленов первой и.пи второй степени. Поскольку имеется
только один неприводимый мноrочлен второй степени, то все
мноrочлены четвертой степени, не являющиеся неприводимыми,
за исключением мноrочлена (Х2+Х + 1)2 == Х 4 +Х2+ 1, дол-
жны делиться на один из мноrочленов первой степени. Следова-
тельно, для неприводимых мноrочленов четвертой степени
р(О) == d =1= О, p(l) == 1 + а + ь + с + d =1= о. Мноrочленами,
удовлетворяющими этим условиям, являются следующие: Х 4 +
+ Х 2 + 1, Х 4 + Х3 + Х 2 + 1, Х4 + х + 1 и Х 4 + Х 3 + 1. Все они,
за исключением Х 4 + Х 2 + 1, являются неприводимыми.
Прuмечание. Таблица неприводимых мноrочленов до 34-й
степени включительно над полем порядка 2 приведена в [1]. В
[2] описан способ нахождения неприводимых мноrочленов и под
счета числа последних. В приложении в конце данной книrи дa
H таблица неприводимых мноrочленов до 14 й степени вклю
чительно над полем порядка 2, до 6 й степени над полем поряд-
ка 3 и до 4 й степени над полем порядка 5.
Задача 2.44. Показать, что мноrочлен Х 2 + 1, рассматривае-
мый как мноrочлен над полем Zj (3) порядка 3, является непри-
водимым.
Решение. В данном случае необходимо проверить, что Х2+ 1
не делится ни на один из мноrочленов первой степени. Для этоrо
достаточно убедиться в том, что f ( (О) ) * (О), f ( (1)) * (О) - и
f ( (2)) =1= (О). Действительно,
f (О)) === (О) · (О) ---t (1) === (1),
f (1)) == (1) . (1) + (1) == (2),
f ((2)) === (2) . (2) + (1) == (2).
Производная мноrочлена. Как мы уже видели выше, для по-
троения полей Z/ (р) используются классы вычетов по простому
модулю. Такой прием, коrда некоторое множество элементов
разбивается на классы по некоторому модулю, используется в
,а.пrебре чрезвычайно эффе,ктивно. Путем разбиения кольца мно-
rочленов на классы вычетов по модулю HeKoToporo неприводи-
Moro мноrочлена в следующем разделе строятся поля порядка
рт (р простое число). В заКЛlочение этоrо раадела введем по-
Hs.IT e произво ной мноrочлеН,а l:I ра смртрим некоторые e ой
88
r лава 2
ства. Приведенные здесь результаты используются при доказа-
тельстве различных утверждений следующеrо раздела.
Заменим в мноrочлене f (Х) переменную Х на Х + У. Если
теперь рассматривать f (Х + У) как мноrочлен от У, то коэффи-
циентами последнеrо будут мноrочлены от Х:
f (Х + У) == L f i (Х) Yi.
Если считать эквивалентными 1ноrочлены, сравнимые по MO
дулю У2, то
f (Х + У) == f о (Х) + f 1 (Х) У (mod у2),
rде fo (Х) == f (Х + О) == f (Х). Обозначив /1 (Х) через f' (Х), по-
лучим
f (Х + У) == f (Х) + f' (Х) у (mod у2).
Введенный таким образом мноrочлен f' (Х) называется произ-
водной f(X).
Утверждение 2.45. Для любоео элемента а Е F и любых
IItноеочленов f, g Е Р[Х] UАtеют место следу/ощие равенства:
1) (af)' == af', (а)' == О, (Х)' == 1,
2) (f + g)' == f' + g',
3) (f. g)' === f'. g + f. g',
4) если f (Х) == L ai Xl , то f' (Х) == L iaiXi l.
Доказательство. Справедливость первых двух равенств про-
веряется леrко. Докажем третье равенство:
f (Х + У) == f (Х) + f' (){) . у (mod у 2 ),
g (Х + У) == g (Х) + g' (Х) . у (mod у2),
f (Х + У) . g (Х + У) == (, (Х) + f' (Х) У) (g (Х) +
+ g' (Х) У) (lnod у2) f (Х) g (Х) + (f' (Х) g (Х) +
.+ f (Х) g' (Х)) у (mod у2).
Третье равенство доказано. В частности, если f(X) ==Хп (п 2),
то из TpeTbero равенства леrко получить, что
(Х + у)n == х n + nxn 1y (mod у 2 ).
Отсюда в свою очередь следует, что
5) (Xi)' === iXi l (i 1).
Из первоrо, BToporo и пятоrо равенств получаем четвертое ра-
венство.
Задача 2.46. Пусть F поле характеристики 2. Найти произ..
одную мноrочлена
f (Х) == L a Xi Е F [Х].
Конечные поля
89
Решение. Так как характеристика поля коэффициентов рав-
на двум, то из четвертоrо равенства имеем
f' (Х) == L iaiXi l == L aiXi l.
по четным i
Например, если f (Х) === 1 + Х + Х3 + Х1 + Х 8 , то
f' (Х) === 1 + Х2 + Хб
и deg f' == 6 < (deg f) 1 === 7. Этот пример показывает, что
правила вычисления производной мноrочлена с коэффициента-
ми из конечноrо поля несколько отличаются от обычных правил
дифференцирования в поле действительных чисел. Однако ра-
венства 1 5 сохраняются без изменений. Таким образом, по-
нятие производной l\fноrочлена мо,кно ввести, не прибеrая к пре-
дельному нереходу, а основываясь JIИШЬ на понятии сравнимости
мноrочленов. Этот l\1етод часто называют формальным диффе
ренuированием.
Утверждение 2.47. Пусть F поле, а g(X) Е Р[Х] не-
приводимый Мflоzочлеfl, такой, что g' (Х) =1= О. Мноеочлен,
f(X) Е F(X] делится на g(X)2 тоеда и только тоеда, коеда наи-
больший общий делитель (f (х), {' (Х» Jиноеочленов f (Х) и f' (Х)
делится на g (Х).
Доказательство. Допустим, что f (Х) == g (Х) h (Х). Тоrда
f' (Х) == g' (Х) h (Х) + g (Х) h' (Х).
Если g(X) If'(X), то g(X) Ig'(X)h(X). Однако, поскольку
g(X){g'(X) (так как degg>degg'), то g(X)lh(X), т. е.
g (Х) 21 f (Х). Это означает, что необходимым и достаточным ус-
ловием Toro, что (g (Х) ) 2 делит f (Х), является наличие общеrо
множителя g (Х) в раЗЛО)I{ениях f (Х) и f' (Х), что эквивалентно
сфОРl'4улированному выше утверждению.
Утверждение 2.48. Пусть F конечное поле порядка q.
Каков бы ни был двучлен XQl Х Е F [Х], в Р[Х] не существует
ни одноео неnриводимоео мноеочлена g (Х), такоео, что
(g (Х))21 (X Q1 ..... х).
Доказательство. Так как (XQl..... х)' == 1, то справедли-
вость утверждения 2.48 непосредственно следует из утвержде-
ния 2.47. Доказанное утверждение означает, что двучлен X Q1 ........ Х
не имеет кратных корней.
Утверждение 2.49 *. МНО20член
(X Х ) X all X a12 X aln +
I 1" · · , n а 1 1 2 ... n
+ а xa21Xa . х а2n + + а X akl X ak2 X akn О а <
2 J 22 · · n · · · k 1 2 . '. n' i j q,
90
r лава 2
над полем F == G F (q) равен О ТОЛЬКО в том слуttае, если все
еео коэффициенты ai равны О 1) .
Доказательство. Пусть R
произвольное кольцо. Тоrда ясно,
что мноrочлен g(X) == ао + a1X + ... + атХт Е R[X] может
быть равен О только в том случае, если ао==аl == . . . ==ат==О.
Докажем сформулированное выше утверждение индукцией по
числу неизвестных. rруппируя слаrаемые f(X I , ..., Х п ), ИМею-
щие одинаковые степени Х n, запишем равенство f (X I , ,.., Х п ) ==
== о в виде
А 1 (X I , ..., Xn
l) X':I + A 2 (X 1 , ..., Xn
1)X
2 + ...
. .. + А[ (Х р . . ., х n
1) Х:l == о.
Каждый коэффициент мноrочлена от Х п В левой части послед-
Hero равенства является элементом кольца F[Xl' ..., Xn
l].
Если это кольцо рассматривать как кольцо R, а Х п
как Х, то
из сформулированноrо в начале доказательства утверждения бу-
дет следовать, что
A 1 (X 1 , ..., Xn
1)==A2(Xl, ..., Xn
l)== ...
· .. == Аl (Х 1, . . ., Xn
1) === о.
Но тоrда по пре.дположению индукции все коэффициенты MHoro-
членов A i (Х 1, ..., Xn
l) должны быть равны О, а следователь..
но, равны О и коэффициенты ai.
2.5. Конечные поля
Выше мы несколько отклонились от изучения полей, перейдя
к рассмотрению векторных пространств и колец мноrочленов.
Однако сейчас, коrда все необходимые понятия уже введены,
попытаемся более детально рассмотреть структуру конечных
полей.
Теорема 2.4. Конечное поле F является векторным nростран-
ством над любым своим подполем РО.
Доказательство. Возьмем любой элемент XI Е F
{О} и рас-
смотрим множество FI == {alxll aIEFo}, FI с Р. Если F
Р 1 =l=Ф,
то выберем произвольным образом элемент Х2 Е F
Р 1 И рас-
смотрим множество Р 2 == {аl Х l + a2X21al, а2 Е РО}. Если продол-
жить эту процедуру дальше, то в силу конечности поля F при
некотором целом т множество Р т == {al X I + ... + amxmlai Е
Е РО, 1
i
т} совпадает с Р. По построеНИIО элементы
1) Здесь предполаrается, конечно, что приведены все подобные члены, т. е.
наборы степеней (ан, ai2, ..., ain) различны при различных i.
Прuм.. ред.
Конечные поля
91
XI, ..., Х 1n поля F линейно независимы. Следовательно, поле F
является векторным пространством размерности т над полем Р О ,
в качестве базиса KOToporo можно взять элементы XI, ..., Х т .
Выбрав в качестве РО поле Z/ (р) из утверждения 2.24, леrко
доказать следующую теорему.
Теорема 2.5. Если F поле характеристики р, то еео порядок
Я8ляется степенью р.
ДоказатеЛЬСТ80. Как было показано при доказательстве пре-
дыдущей теоремы, поле F всеrда можно представить в виде
F == {alXI + ... + атХ т I ai Е РО, 1 i т}. Поскольку каждый
элемент Х поля F можно представить в виде линейной комбина-
ции базисных элементов единственным образом (см. утвержде-
ние 2.30), то число различных векторов в Р, очевидно, равно
рт, ['де р порядок РО, в данном случае совпадающий с харак-
теристикой поля. Отсюда следует доказательство теоремы.
Как мы уже знаем, характеристика любоrо конечноrо поля
должна быть простым числом. Выше было доказано, что порядок
конечноrо поля характеристики р равен рт, rде т некоторое
це.пое число (т 1).
Из теоремы 2.4, в частности, следует, что любое конечное
поле является векторным пространством над некоторым полем
Z/ (р), порядок KOToporo есть простое число. Элементы этоrо
BeKTopHoro пространства, называемые ниже векторами, можно
представить различными способами. Например, их мо}кно пред-
"
ставить в виде последовательностеи из n элементов поля
(утверждение 2.29). С друrой стороны, каждому вектору
(ао, йl, ..., an l) можно сопоставить мноrочлен
ао + alX + а2х2 + ... + an IXn l.
Если ввести операции сложения мно,"очлснов и умножения МНО-
rочлена на константу посредством соотношений (2.8) и (2.10),
то эти операции будут в точности соответствовать сложению и
умножению на константу соответствующих последовательностей
символов длины N. Э10 позволяет рассматривать множество мно-
rочленов степени n 1 и менее и последовательности символов
длины n как различные представления одноrо и Toro же вектор-
Horo пространства. Представление произвольной бесконечной
последовательности (50, 51, ...) элементов HeKoToporo множества
S в виде формальноrо мноrочлена
80 + 51Х + 52 Х2 + ...
является хорошо известным и широко применяемым приемом.
Такие мноrочлены иноrда называют nрои380дящuмu функциямu
ИJlИ фор.маЛЬНblМU степенными рядамu. При представлении по-
92
r лава 2
слсдоваrельностей в виде формальных мноrочленов символ Х
используется лишь для указания поло)кения элементов в исход-
ной последовательности и не является некоторым «неизвестным
элементом». В силу этоrо СИМRОЛ Х был назван формальной
переменной. Как мы у)ке знаем, конечное поле F является BeK
торным пространством размерности k над полем РО, порядок
KOToporo есть простое число. Поэтому любой элемент (вектор)
поля F можно представить в виде мноrочлена степени k 1 над
ПО,,'1ем РО. Однако само по себе это преДС1авление будет не очень
интересным, если не указать, каким образом следует складывать
и умножать элементы поля Р, преДСlавленные в виде мноrочле-
нов. Выше мы ввели сложение векторов, но не касались их умно-
жения. Если представить векторы в виде мноrочленов, то можно
ввести операцию умножения векторов, используя для этоrо
умножение мноrочленов. Однако, как показывает доказатель-
ство свойства 5 из утверждения 2.37, при таком определении
умножения злементы F [Х] MorYT не иметь обратных, т. е. f [х]
не является полем. Более 10ro, при представлении элементов
поля F в виде мноrочленов степени k 1 из F l [Х] при обыч-
ном умножении мноrочленов из F l [Х] может получиться мно-
rочлен степени k или выl1е а это означает, что обычное умноже
ние мноrочленов оказывается не замкнутой в F l [Х] операцией.
Ключом к построению конечных полей порядка рт (т 1,
р простое число) является разло)кение кольца мноrочленов на
классы вычетов по некоторому специально выбранному модулю.
Аналоrичный прием использовался и при построении полей вида
Z/ (р), коrда были введены операции по модулю р.
Построение полей путем разложения кольца мноrочленов на
классы вычетов по модулю неприводимоrо ноrочлена
Пусть g (Х) Е F [Х] некоторый неприводимый мноrочлен
степени m. Используя g (Х), разложим Р[Х] на классы сле-
дующим образом. Отиесеl\f к одному классу все мноrочле-
ны, которые дают один и тот )ке остаток при делении на
g (Х). Класс, содержащий мноrочлен f (Х), обозначим через
(f (Х) ). Два мноrочлена fl (Х) и f2 (Х) принадлежат одному клас-
су тоrда и только тоrда, коrда fl(X) f2(X) делится на g(X).
Это мы будем записывать в виде fl(X) == f2(X) (modg(X»).
flолученные таким образом классы будем называть классами
вычетов по модулю g(X). Множество всех классов вычетов по
модулю g (Х) обозначим через F [g]. Поскольку существует
взаимно однозначное соответствие между классами вычетов из
F [g] и мноrочленами из Frп 1 [Х], то ясно, что число классов BЫ
четов равно 1 F 1 1n . Введем в F[g] операции сложения и умножения
Конечные поля
93
следующим образом. Для любых (f (Х) ), (h (Х) ) Е F [g] положим
(f (Х» + (h (Х» === (f (Х) + h (Х»,
(f (Х» · (h (Х) === (f (Х) · h (Х».
При таком определении сложения и умножения классы вычетов
(1) и (о) оказываются соответственно единичным и нулевым
элементами F[g]. Пусть (f(X» =1= о. Так как мноrочлены f{X} Jf
g (Х) взаимно просты, то, соrласно утверждению 2.41, СУlцествуст
единственный мноrочJiен а (Х), такой, что
а (Х) f (Х) == 1 Ь (Х) g (Х) == 1 (mod g (Х».
Следовательно,
(а (Х» · (f (Х» == (а (Х) · f (Х» == (1).
Это означает, что в F [g] существует элемент (а (Х», обратный
к (f (Х) ). Следовательно, F [g] поле. В частности, если
F == Z/ (р), р простое число, то, допустив существование в
F [Х] неприводимоrо мноrочлена степени т, мы доказали суще..
ствование поля порядка рт (суще ТВОRание неприводимых мно"
rочленов для любых т и р будет следовать из приведенной ниже
теоремы 2.11).
Описанный выше способ построения полей порядка рт В
общем аналоrичен рассмотренному ранее способу построения
полей вида Z/ (р). Действительно, множество (g (Х» мноrочле
нов в Р[Х], которые делятся на неприводимый мноrочлен g (Х),
ЯВJlяется одним из идеалов кольца F [Х]. Кольцо классов выче..
тов F [Х] / (g (Х», порожденное идеалом (g (Х» кольца F [Х], KaI{
было показано выше, есть поле. Неприводимый мноrочлен вы..
полняет в данном случае ту же роль, что и простое число р в
кольце целых чисел.
Обозначим через сх. класс вычетов (Х), содержащий MHoro
т
член Х. Пусть g (Х) === .L giXi. Тоrда
i==O
go + gla + ... + gm am === go + gl (Х) + ... + gm (Х т ) ==
=== (go + glX -t ... + gm Xт ) ===
=== (g (Х» == (О) === Ну левой элемент.
Это означает, что мноrочлен g (Х) имеет корень (Х в поле
F[g]. Мноrочлен g (Х) является неприводимым над полем Р, и
уравнение g (Х) == О не имеет решений в поле Р. Однако, как мы
только что показали, уравнение g(X) == о имеет решение в поле
F [g]. В этом смысле поле F [g] является расширением поля Р,
94
r лава 2
полученным присоединением к F корня уравнения g (Х) == о.
Каждый элемент р поля F [g] можно представить в виде
p==aт laт l+ ... +ala+aO, atEF, l i т.
Это так называемое .мНО20членное представление элементов
поля. Кроме Toro, выбрав в качестве базиса элементы am l,
an' 2, ..., 1 поля F [g], каждый элемент поля F [g] можно пред-
ставить также в виде последовательности
(aт 1, aт 2, · · ., ао).
Последнее представление называется векторным nредставленuеJd
элементов поля.
Задача 2.50. Показать, что элементы cx.т l, cx.т 2, . . . t 1 обра-
зуют базис F [g].
Построим несколько конечных полей указанным выше спо-
собом.
Задача 2.51. Построить поле порядка 32.
Решение. В качестве неприводимоrо мноrочлена второй сте-
пени над F==Z/(3) возьмем мноrочлен Х 2 +1 (задача 2.44).
Каждый элемент поля F [g] имеет вид (а + ЬХ), rде а, Ь Е Р.
Найдем сумму и произведение элементов (а + ЬХ), (с + dX) Е
Е F [g]:
(а + ЬХ) + (с + dX) == (а + с + (Ь + d) Х),
(а + ЬХ) · (с + dX) == (ас + (Ьс + ad) Х + Ь dX 2 ) ==
== (ас....... bd) + (Ьс + ad) Х.
Эти формулы напоминают соответствуюшие формулы для вычис-
ления суммы и произведения КОМI1лексных чисел. Отличие со-
стоит лишь в том, что в последних вместо Х обычно стоит мни-
мая единица i.
С точки зрения алrебры поле комплексных чисел полностью
идентично описанному выше полю, поскольку оно может быть
построено путем разбиения на классы вычетов по модулю не-
"
приводимоrо над полем деиствительных чисел МlIоrочлена
Х2 + 1 кольца мноrочленов над полем действительных чисел.
Поэтому формулы для нахождения суммы и произведения эле-
"
ментов этих полеи полностью идентичны.
В поле комплексных чисел используется соотношение i2=== 1.
т. е. i 2 + 1 == О. Понижение степеней слаrаемых вида i a , а > 1,
с помощью этоrо соотношения эквивалентно вычислению остатка
при делении на i 2 + 1. При этом в поле КОVfплексных чисел для
обозначения корня уравнения Х 2 + 1 == О используется специ-
аJlЬНЫЙ символ i. . .
Конечные поля
95
Задача 2.52. Построить поле порядка 2 З t используя неприво-
ДИМЫЙ мноrочлен Х 3 + х + 1.
Решение. Положим g (Х) == ХЗ + х + 1 и рассмотрим сле-
дующие восемь классов вычетов по МОДУJIЮ g (Х) :
{(О), (1), (Х), (Х + 1), (Х 2 ), (Х 2 + 1), (Х 2 + Х), (Х2 + х + 1 )}.
Определим сложение и умножение этих классов вычетов сле-
ДУЮЩИМ образом:
(/ (Х)) + (h (Х)) === (f (Х) + h (Х)),
(/ (Х)) · (h (Х)) == Остаток от деления f (Х) h (Х) на g (Х).
Поскольку складывать элементы леrко, ниже приведена лишь
таблица умножения элементов введенноrо поля. В таблице эле-
менты поля представлены в виде мноrочленов. Элемент О из
этой таблицы исключен.
1 а а+l а 2 а 2 + 1 а 2 + а а 2 +а+ 1
1 1 а а+l а 2 а 2 + 1 а 2 +а а 2 +а+ 1
а а а 2 а 2 +а а+l 1 а 2 + а + 1 а 2 + 1
а+l а+1 а 2 +а а 2 + 1 а 2 + а + 1 а 2 1 а
а 2 а 2 а+l а 2 + а + 1 а 2 +а а а 2 + 1 1
а 2 + 1 а 2 + 1 1 а 2 а а 2 + а + 1 а+l а 2 +а
а 2 + 1 а 2 +а а 2 + а + 1 1 а 2 + 1 а+l а а 2
а 2 +а+l а 2 +а+l (12 + 1 а 1 а 2 +а а 2 а+1
Составление таблиц, подобных приведенной выше, является
довольно трудоемким. Представление элементов поля в виде
мноrочленов или векторов удобно с точки зрения простоты сло-
жения и, наоборот, неудобно с точки зрения умножения. Избе-
"
жать затруднении, связанных с умножением элементов поля,
представленных в виде мноrочленов или векторов, позволяет
представление элементов в виде степеней HeKoToporo элемента
этоrо поля. Если. с помощью вышеприведенной таблицы найти
мноrочленные представления элементов поля 1, а, а 2 , ..., то
МОЖНО ПОС1рОИТЬ друrую таблицу:
Степенное
представление
1==
Мноrочленное
представление
1
а=== а
а 2 == а 2
аЗ === а + 1
а" == а 2 + а
а 5 === а 2 + а + 1
а 6 == а 2 + 1
(а 7 == 1)
96
r лава 2
Итак, все ненулевые элементы поля оказались представленными
в виде степеней элемента сх,. В этом случае произведение любых
двух элементов поля, представленных соответственно в виде a i
и а), можно найти следующим простым способом:
a i . af === ai+i == aR1 (i+Л
,
r де R7 (i + j) остаток от деления {+ j на 7 (здесь мы поль-
зуемся свойст,вом ассоциативности мультипликативной rруппы
поля и тем, что а? == 1). Как мы только что видели, в случае
"
представления элементов поля в виде степенен одноrо из них
умножение осуществляется очень просто. При наличии таБJIИЦЫ
соответствия различных представлений можно обойтись без таб-
лиц сложения и умножения. Нулевой элемент поля иноrда по
традиции обозначают через сх,ОО. Описанный выше способ умно-
жения элементов поля применим только в том случае, коrда все
ненулевые элементы поля MorYT быть представлены в виде сте-
пеней одноrо из них. Однако, как с.ледует из приведенной ниже
теоремы, такое представление элементов в виде степеней всеrда
возможно.
Теорема 2.6. В любом конеЧНОll1, поле F найдется по крайней
Atepe один. элемент сх" такой, что все элементы F* == F {О}
MOZYT быть представлены в виде степеней cx,i (1 i 1 F 1)
элемента сх,. Друеими словами, р* цuклиtlеская еруnnа. Эле-
мент сх" степени котороео nробееаl0Т .все flенулевые элементы по-
ля, называется nримитивным.
Доказательство. Пусть а произвольный элемент мульти-
пликативной rРУППhI F* поля F порядка m (по определению m
все элементы сх" сх,2, . . . , сх,т раЗЛИЧНbI и а т == 1). Если m == I р* 1,
то теорема доказана. Предположим, что m < 1 F*I. Тоrда, так
как элементы Р*, порядок которых делит т, являются корнями
уравнения Хт 1 === О, то их число не превышает m (утвержде-
ние 2.40). Следовательно, в F* существует элемент, порядок
KOToporo не является делителем 1n. Пусть один из таких
элементов порядка n. Соrласно утверждению 2.14, в F* суще
ствует элемент порядка {nп/(т,п). Заметим, что тn/(т,п»т.
Повторяя эту процедуру достаточное количество раз, всеrда
можно доказать существование в F* элемента порядка I Р* 1.
Теорема 2.7. Любой элемент конечноzо поля порядка рт яв-
т
ляется корнем уравнения Х Р Х === о.
Доказательство. Пусть а один из примитивных элементов
поля I"C} а произвольньтй элемент F* == F {О}. Элемент
можно представить в виде неКQrорой степени элемента а, т. е.
Конечные поля
97
== cx,i. Тоrда pт l == a l (pт l) === 1. Следовательно, любой эле
т
мент из Р* является корнем уравнения х р I 1 == о.
Утверждение 2.53. Пусть а целое положительное число,
n........ минимал ьное целое положuтеЛЬ1l0е число, такое, что
al (qn 1). Тоrда
1) al (qт 1) nlm;
2) (qn I)I(qт I) пlт;
3) (а, q) == 1 существует такое n, что а I (qn 1).
Доказательство. Пусть т == ln + " о r < n. Тоrда qт l==
==(qln l)qr+qr 1. Так как (qn 1) I (qln 1), то al (qln l).
Если r =1= о, то а f (qт 1), поскольку по определению
а 1 (qr 1). Второе утверждение следует из первоrо.
Чтобы доказать третье утверждение, рассмотрим следующую
последовательность целых чисел: R n (I), Ra(q), Ra(q2), ..., rде
Ra (i)' остаток от деления i на а. Так как число различных
остатков при делении на а не может превышать а, то найдутся
таl{ие i и j (i < j), что Ra(qi) === Ra(qj), т. е. qi == qj (mod а).
Так как (а, q) == 1, то в силу свойства N.7 целых чисел
1 == qj i (mod а), т. е. а I (qj i 1). Таким образом, мы ДOKa
зали, что если (а, q) == 1, то существует такое целое n, что
al (q'n 1). Использованный здесь метод доказательства будет
применяться в дальнейшем неоднократно. Доказательство об-
paTHoro утверждения предоставляется провести читателю само-
стоятельно.
Запись g (Х) I h (Х), часто используемая ниже, означает, что
мноrочлен g (Х) делит мноrочлен h (Х).
Утверждение 2.54.
1) (Xn I)I(Xm I) nlт.
Пусть g (Х) Е F [Х] и n минимальное целое число, такое,
что g (Х) I (Хn 1) (п называется nоказателем g (Х) ). Tozaa
2) g(X) I (.)(т 1) nlm.
Пусть F поле, РО подполе поля F и сх, элемент муль"
типликативной rруппы Р {о} поля Р. Обозначим через / а мно-
жество всех мноrочленов над РО, корнем которых является сх"
а именно
[« == {f (Х) Е РО [Х] {О} I f (а) == О}.
( т 1 )
Если порядок F равен рт, то, соrласно теореме 2.7 х р .......х Е
Е /а. Пусть ,п а (Х) нормированный мноrочлен минимаЛЬе
ной степени в 1 а; этот мноrочлен называется минимальным MHO
20ЧЛР1l0М элемента а над ро. Минимальный мноrочлен пza. (Х)
98
r лава 2
является неприводимым. Действительно, если преДПОЛО}I{ИТЬ, что
та(Х) == fl(X)f2(X)' fl(X), f2(X) Е Ро(Х), deg fl l и dcg f2 1.
то из определения та (Х) непосредственно будет следовать, что
та(а) == fl (a.)f2(a) == О. Но тоrда в силу свойства 2 поля из
утверждения 2.22 либо fl (а) == О, либо f2 (а) == О, т. е. в 1 а со-
держится мноrочлен, степень KOToporo меньше, чем степень
та (Х), т. е. мы получили противоречие. Далее заметим, что все
мноrочлены из 1 а должны делиться на та (Х). Действительно,
допустим, что в 1 а содержится мноrочлен f (Х), который не де-
лится на та (Х). Тоrда, как мы знаем, существуют мноrочлены
q (Х) и r (Х), такие, что
f (Х) === та (Х) q (Х) + r (Х), deg r < deg та-
Подставим в последнее равенство вместо Х элемент а. Тоrда,
так как r (а) == О, опять получаем, что в 1 а содержится MHO
rочлен, степень KOToporo меньше, чем степень та (Х), что про-
тиворечит определению та (Х). Следовательно, все мноrочлены
из 1 а это мноrочлены вида ат а (Х), а Е Ро[Х] {О}. В част-
ности, отсюда следует, что минимальный мноrочлен элемента а
определяется однозначно.
Теорема 2.8. Пусть РО поле порядка q, g (Х) Е РО [Х] HOp
мированный неnриводимый мноеочлен степени т и n nоказа-
тель g (Х). Тоеда т .минимальное целое число, такое, что
n 1 (qm 1). в частности, если n == qm 1, то g (Х) называется
nримитивным мноеочленом.
Доказательство. Пусть F == РО [g] и cx. элемент (Х) поля Р.
Как мы уже видели выше, g(a) == О. Так как g(X) неприводи-
мый мноrочлен, то та(Х) === g(X). Соrласно теореме 2.7, а яв-
ляется корнем уравнения Xqm 1 1 === О, так что g (х)1 (Xqm l ......... 1).
Отсюда и из утверждения 2.54 следует, что n l (qт 1). Допус-
ТИМ, что n I (ql......... 1), О < 1 < т. Т or да a q === а, поскольку
g (Х) I (Xql l 1). Как указывалось выше, любой элемент поля
ро [g] может быть представлен в виде
== ао + аl а + ... + aт laт l, ai Е РО (О i < т).
Из теоремы 2.7 имеем а1 == a t . Поскольку, кроме Toro, a q1 == а,
ПОJ)учаем (см. задачу 2.27)
Aql ql + ql ql + + {/1 (т l)ql
t-' ао а 1 а . . . ат 1 а
=== ао + ala + ... + aт laт 1 === .
Это означает, что порядок любоrо ненулевоrо элемента поля
Р"О [g] является делителем ql......... 1. Получили противоречие. Сле-
довательно, 1 == т.
Конечные поля
99
Теорема 2.9. Пусть РО поле порядка q и пусть g (Х) не-
приводимый М1l0еочлен степени т из РО [Х]. Тоеда
g (Х) I (xi 1 1)#т 11.
Доказательство. Соrласно утверждеНИIО 2.53,
т 11#(qт 1) I (ql ....... 1).
flo тоrда из утвер}кдения 2.54 получаем
т 11#(Xqт J 1) I (Xi 1 1).
Из теоремы 2.8 следует, что минимальное k, для KOToporo
g (Х) I (Xi l 1), равно т.
Из единственности разложения любоrо мноrочлена на не-
приводимые множители (утверждение 2.42), из Toro, что MHoro
т
член x q ....... Х не имеет кратных множителей (утверждение 2.48),
и из теоремы 2.9 следует справедливость следующей теоремы.
Теорема 2.10. Пусть ро поле порядка q. ТОсда двучлен
т
X q Х равен произведению различных неnриводимых норми-
рованных мноеочленов из РО [Х], степени которых делят m.
Обозначим через N i число неприводимых нормированных
мноrочленов степени i, входящих в Ро[Х]. Очевидно, что N I == q.
Из теоремы 2.1 О непосредственно получаем, что для любоrо
целоrо 1 2
ql L iN i ,
i Il
rде сумма берется по всем делителям i числа 1 (включая 1 и 1).
Отсюда следует, что
ql iNi ( ПОСКОЛЬКУ qi===LiN,===iNi+ LiN,;З:iNi ) .
/ I l i 1 i
i+i
Но тоrда
ll2
ql==lNL+LiNl lNl+L iNi INl+q+ ...
ill 1==1
i+l
. . .
+ qll2 < lN l + lqll2,
откуда
и
N 1 > (ql ..... lq l I2)/1
Nt>O (1 1).
(2.13)
Таким образом, для Лlобоrо целоrо положительноrо числа
т в РО [Х] существует неприводимый мноrочлен степени т.. ОТ-
100
rлава 2
Сlода и описанноrо выше способа построения полей следует
справедливость следующей теоремы.
Теорема 2.11. Для любоео nростоео числа р u любоео целоео
положuтельноео т существует конечное поле порядка рт.
В случае конечных rрупп, как мы уже видели выше (за-
дача 2.4), из равенства порядков rрупп еще не следует их изо-
морфизм. Однако все поля одноrо и Toro же порядка изо-
морфны. Дока}l{ем это.
Пусть F произвольное конечное поле, являющееся расши-
рением поля РО. Пусть IFol == q == рт И If'l == ql. Возьмем
произвольный мноrочлен g (Х) из F о [Х], степень KOToporo яв-
ляется делителем 1 (как следует из теорем 2.4 И 2.10, это всеrда
можно сделать). Этот мноrочлен g (Х) является минимальным
мноrочленом та (Х) HeKOTOpOrO элемен ra сх. поля Р. Пусть n
степень g(X). Рассмотрим следующее пuдмножество ро(сх)
поля Р:
Fo(a)==={al+a2a+ ... +anan 11aiEFo, l<i<n}.
Сопоставим каждому элементу аl + а2сх. + ... + ancx.n 1 Е РО(а)
элемент (аl + а2Х +... + anXn l)E Fo[g]. Заметим, что это ото-
бражение <р является взаимно однозначным, и если
А == al + а2а + ... + anan l Е РО (а),
B==b l +b 2 a+ ... +bnan IEFo(a),
то
А + в === (аl + b l ) + (а2 + Ь 2 ) а + ... --t (а n + Ь n ) a tt "' l Е РО (а),
т. е. отобра)кение ер сохраняет операцию сложения. Пусть
g(X) == go + glX + . . . + х n . Поскольку g(cx.) == О, то
а n ==........ go ---- gla........ ... ....... gn lan l Е Ро(а).
Пока}l{ем, что все элементы вида cx. i , i n, поля F принадле-
жат РО (сх.). Так,
а n + I == а · а n == ........ g оа ....... g I а 2 ....... ... ....... g n 1 а n ==
== gOgn l + (glgn 1....... go) а + ... + (gп lgn 1 gn 2) aп 1 Е ро (а).
Аналоrично можно доказать, что и остальные элементы a,i,
i> n, принадлежат Ро(сх.). Отсюда следует, что если А, В Е
е Ро(сх.) , то А'ВЕРо(а). С друrой стороны, в Fo[g]
(х n ) == (go + gtX + ... + gп IXn I),
и, следовательно, отобра}l{ение ер сохраняет так}ке и операцию
умножения. Таким образом, Ро(сх.) и Fo[g] изоморфны. Элементы
q> (О) и ер (1) являются соответственно HYJleBbIM и единичны,"
элементами РО [g]. Поэтому для любоrо А Е РО (сх.) элементы
Конечные поля
101
.......А и A l (если А =1= О) также принадлежат Ро(сх,). Следова
тельно, РО (сх,) является подполем поля Ро. Порядок РО (сх,) ра-
вен qп И п является одним из делителей 1. Поле Ро(сх,) является
минимальным подполем поля Р, содержащим РО и сх,. В частно-
сти, если сх, выбрать таким образом, что n === 1, то Ро(а) == Р.
П.олаrая Fo == Z/ (р), rде р простое число, получаем следую-
щую теорему.
Теорема 2.12. Все KOHe'tHble поля одноео и тоео же порядка
изоморфны. Друеими словами, конечное поле заданноео по-
рядка единственно с точностью до обозначения .9леАtентов.
Поле порядка рт будем обозначать через ор(рт) (первые
две буквы являются сокращением анrлийскоrо термина Galois
Field) .
Следовательно, ор(рт) изоморфно Fo[g] (здесь РО == Z/(p),
р простое число, а g (Х) нормированный неприводимый МНО-
rочлен степени т над Р{) [Х]). Этот изоморфизм имеет место при
любом выборе мноrочлеllа g (Х). Однако различным мноrочле-
нам g(X) соответствуют различные представления. выIеe было
доказано, что если поле существует, то оно единственно. Далее
рассмотрим некоторые свойства ПОJIей, которые потребуются
нам в дальнейшем.
Теорема 2.13. Пусть F поле, являющееся расширением
поля Ро, IFol==q, IFI==qт, и пусть EP {O}. Тоеда nока-
затель минимальноео А-tноеочлена пir. (Х) элемента равен по-
рядку v элеhtента . Степень n АtноеочлеНа т13 (Х) является
минимальным целым положител ьным числом, таким, что
vl (qn 1); при этом nlт. КОРНЯАtи уравнения mj3(X)== О ЯВ-
ляются следующие п различных элементов: , q, .. ., 8qn '.
Доказательство. Так как v 1 == О, то тj3 (Х) I (Xv 1).
С друrой стороны, если (пв (Х) I (Xl 1), то l == 1. Следова-
тельно) показатель тв (Х) равен v. Из теоремы 2.8 следует, что
степень мноrочлена т (Х) является минимальным целым поло-
жительным числом, таким, что v I (qп 1). Кроме Toro, из Teo
ремы 2.6 следует, что v I (qт 1). Но тоrдз, cor ласно утверж'де-
n
нию 2.53, п 1т. Пусть т(3 (Х) == L C1Xi. Тоrда, так как т(3 ( ) ===
1==0
n
=== L Cl i И
l O
n n
(т ( ))q == L cq ( l)q == L С ( q), == т ( q) === О,
в [-=о 1 1==0 l IЗ
то q также является корнем уравнения lпв (Х) == О. Аналоrично
можно дока1ать, что все элементы , q, q2, ... являются KOp
нями уравнения тв (Х) == О. Среди этих корней элементы
102
r лава 2
, qt .. ., qn 1 являются различными. Для TOrO чтобы убе-
ДИТЬСЯ в справедливости последнеrо утверждения, предположим
противное, а именно что qi::::: ql, О i < j < n. В этом случае
т 1 т /
=== qт === ( q/) q == ( qi) q == pqт+ 1 / t
И, следовательно, порядок v элемента делит qт+i j 1. Но
тоrда, соrласно утверждению 2.53, n I (т + i j). С друrой CTO
роны, так как nlm и m..........n<m j+i m..........l, то
n1 (т........ j + i), и мы пришли к противоречию.
Как следует из теоремы 2.13 и доказательства теоремы 2.8,
неприводимый мноrочлен g (Х) степени nl из Ро[Х] имеет т
различных корней в поле Fo{g], т. е. в силу теоремы 2.12 в ПО.не
(iF(qт). Таким образом, мноrочлен g(X) не имеет корней в поле
РIQ и в то же время имеет m различных корней в РО [g].
Утверждение 2.55. Пусть та (Х) минимальный мноеочлеll
элемента (1,. Если является корнем уравнения т'а (Х) === О, то
т (X)===тa(X). Все корни минимальноео МН020члена та(Х)
имеют один u тот же порядок.
Доказательство. Если тa( ) == О, то тр(Х) Ima(X). Тоrда,
так как та (Х) неприводимый мноrочлен, то т (Х) == та (Х).
Если мноrочлен та (Х) имеет степень п, то ero корнями яв
ляются элементы а, a Q , а q2, .. ., aqn l. Пусть I FI === q и
та (Х) Е F [Х]. Тоrда, если элемент сх имеет порядок v, а элемент
a ql ...... порядок v', то
( 1 ) " j ql I
pq === vq == ( v) == 1 q === 1, так что 'V I 'У',
'\/' === ( qn) ,\/' === qiqn 1,\/' === (( ql/Yn 1 === 1 qn I === 1,
так что v' I v. Следовательно, v === v'.
Утверждение 2.56. Пусть (1, nроизвольный элемент из
Р* === р.......... {О}. Тоеда, если порядок (1, равен v, то порядок эле-
мента a,i равен v/ (i, v).
Доказательство следует из утверждения 2.2 и теоремы 2.6.
Утверждение 2.57. Пусть IFI == q. Тоеда Р имеет Р08НО
ер (q 1) nримитивных элементов (ер функция Эйлера).
Доказательство. Множество Р* == F {О} является цикличе-
ской rруппой порядка q.......... 1. Порядок любоrо элемента из Р*
является делителем q.......... 1. Порядок элемента a i равен
(q ........ 1) / (i, q 1). Отсюда B ДHO, что == q ..........! тоrда толька
Конечные поля
103
тоrда, коrда (i, q ...... 1) == 1, но количество целых чисел i, для
которых выполняется последнее неравенство, равно по опреде-
лению fP(q 1).
т
Пусть f (Х) == L CiXl ....... мноrочлен степени т. Мноrочлен
ic:aQ
т
f. (Х) == L Cт iXI называется двойственным к мноrочлену f (Х).
ic:O
Мноrочлен f (Х), дЛЯ KOToporo f* (Х) == f (Х), называется само-
двойственным. Если f (Х) == П (Х ...... (Xi), то f* (Х) == П (Х ..... a I 1 ),
rде ai l элемент, обратный к cx,i.
Утверждение 2.58.
1) Мноzочлен f(X) неnриводим ТО2да и только тоеда, КО2да
неnриводим мноеочлен f* (Х) .
2) МНО20член f (Х) является nримитивным ТО2да и только
тоеда, коеда nримитивным является МНО20член f* (Х).
Пусть 1 и q взаимно простые целые положительные числа.
Пусть О i < 1 и целые числа i, iq, ..., iqn l попарно несрав-
нимы по модулю 1 (Т. е. среди остатков от деления этих чисел
на 1 нет одинаковых), но iqj == iqn (mod 1) при некотором
О j n 1. Так как (q, 1) == 1, то iqn j ЕЕ i (mod 1) (здесь
мы воспользовались свойством N.7 целых чисел). Следовательно,
при сделанных выше предположениях j == О. Если числа i, iq, ...
. . ., iqn 1 заменить на их остатки от деления на 1, то получен-
ная таким образом совокупность чисел назы,вается (q, 1) -цик-
лом, содержащим i. Количество чисел, входящих в цик.п, назы-
вается длиной цикла. Длина n цикла, содержащеrо i, представ-
ляет собой минимальное целое положительное число, удовлетво-
ряющее уравнению iqn == i (mod 1).
Пусть F == GF(q). Разобьем числа от О до qm 1 на
(q, qт ---- 1) ..циклы. Пусть i 1 , i 2 , ..., i n циклы, содержащие i.
Возьмем некоторый примитивный элемент а поля ОР (qm) и рас-
смотрим минимальный мноrочлен т(3 (Х) Е F [Х] ЭJlемента
== cx,i. Тоrда, соrласно теореме 2.13, корни уравнения
. 1 l
т(3 (Х) == о это элементы a l, а 2, ..., а n. Степень т(3 (Х)
равна длине цикла. Таким образом, мы установилй соответствие
между циклами и минимальными мноrочленами (фиксировав
предварительно примитивный элемент).
Задача 2.59. Рассмотрим поле ОР(2 4 ). Используя неприво-
.димый над G F (2) мноrочлен четвертой степени g (Х) == Х4 +
+ х + 1, составить таблицу соответствия представлений ЭJlе-
ментов поля ОР (24) В виде степеней примитивноrо элемента
и мноrочленов. Найти минимальный мноrочлен элемента
a==(XJ.
104
r лава 2
Решение. Таблицу соответствия следует составлять последо-
вательно так, как это было описано при доказательстве тео-
ремы 2.12:
а О ==
а 1 ==
а
') 2
a == а
аЗ == аЗ
а 4 == а + 1
а 5 == а 2 + а
а 6 == аЗ + а 2
а 7 == аЗ + а + 1
1
а 8 == а 2 + 1
а 9 == аЗ + а
a 10 == а 2 + а + 1
a ll == аЗ + а 2 + а
a l2 == аЗ + а 2 + а + 1
a l3 == аЗ + а'2 + 1
a l4 == аЗ + 1
(a I5 == 1)
Как видно из доказательства теоремы 2.8, минимальным MHoro-
членом та (Х) элемента сх. является сам мноrочлен g (Х) ==
== Х 4 + Х + 1. Однако mа(Х) можно найти также следующим
образом. Так как, соrласно теореме 2.13, все корни ma(X) это
248
элементы а, сх. , сх.. , сх. , то
та(Х) === (Х а) (Х а 2 ) (Х а 4 ) (Х ....... ( 8 ) ==
== Х 4 (а + а 2 + а 4 + а 8 ) Х3 + (аЗ + а 5 + а 9 + а 6 +
+ a lO + a 12 ) Х 2 (а 7 + a ll + a l3 + a J4 ) Х + a l5 ===
== Х 4 ........ О · Х 3 + о · х 2 Х + 1 == Х 4 + х + 1.
Задача 2.60. В случае q == 2 и т == 4, разбив совокупность
це.ПЫХ чисел от О до 24 2 на (2, 24 1) .циклы И выбрав в ка-
честве минимальноrо мно['очлена, соотвеТСТВУЮJцеrо циклу, со-
держащему 1, мноrочлен q (Х) === Х 4 + х + 1, найти минималь
ные мноrочлены, соответствующие друrим циклам.
Решение. Совокупность целых чисел от О до 24 2 разби-
вается на циклы следующим образом:
.
о
1, 2,
3, 6,
5, 10
7, 14
4, 8
12, 9
13, 11
Циклу, содержащему О, соответствует I\fинимальный мноrочлен
Х + 1. Циклу, содержащему 3, соответствует минимальный MHO
КонеЧllые поля
105
rочлен
(Х ........ аЗ) (Х ( 6 ) (Х а r 2) (Х ........ а 9) ==
== Х4 ........ (аЗ + а 6 + а 9 + ( 12 ) х з + (а 9 + a l2 + a l5 +
+ a l5 + аЗ + ( 6 ) Х2....... (а 6 + аЗ + а 9 + a 12 ) Х + 1 ==
=== Х 4 + Х3 + Х 2 + х + 1 (так как а 15 == 1)
(поскольку в этой и предыдущей задачах поле ОР(2 4 ) строится
С ПОМОIЦЬЮ одноrо и Toro же мноrочлена, то для вычисления
суммы сх,З + сх,6 + сх,9 + (Х12 в данном случае можно воспользо-
ваться таблицей соответствия из предыдущей задачи).
Полученные выше мноrочлены ЯВЛЯIОТСЯ само двойственными.
Поэтому наряду с корнем cx,i они имеют в J<ачестве корня также
и cx, i. Так как в данном случае (ХЗ.сх,12 === сх,6.сх,9 === cx,15 === 1, то
a 3 == сх,12 И (X 6 == сх,9. Из таблицы циклов леrко видеть, что ми-
е е
нимальныи мноrочлен, соответствую щи и циклу, содержащему
числа 5 и 10, также является самодвойственным и имеет сте-
пень 2. Имеются два мноrочлена, удовлетворяющие этому усло
вию: Х2 + 1 и Х 2 + х + 1. Однако Х2 + 1 == (Х + 1 )2, т. е. мно-
rочлен Х 2 + 1 не является неприводимым. Следовательно, мини-
мальным мноrочленом, соответствующим циклу, содержащему
5, является Х 2 + х + 1. Наконец, рассмотрим последний цикл,
содержащий число 14. Поскольку (X14 == cx, I, то минимальные
мноrочлены, соответствующие циклу, содержащему 1, и циклу,
содержащему 14, двойственны друr друrу. Следовательно, мини-
мальным мноrочленом, соотвеТСТВУЮlЦИМ пиклу, содер)кащему
14, является мноrочлен Х 4 + Х 3 + 1.
в приведенном выше примере
X l6 + Х === х (Х + 1) (Х 2 + х + 1) (Х 4 + х + 1) (Х4 + Х З +
+ Х 2 + х + 1) (Х4 + Х З + 1).
о
{, 2, 4, 8:
3, 6, 12, 9:
5, 10
7, 14, 13, 11 :
Это соответствует случаю, коrда в теореме 2.12 q === 2 и т == 4.
Порядок каждоrо сомножителя является делителем числа 4.
Найдем порядки элементов (Xi, коrда числа i принадлежат
различным циклам. Из утверждения 2.55 получаем
1
15 == 15/(2, 15) === 15/(4, 15) == 15/(8, 15)
5 == 15/(3, 15) === 15/(6, 15) == 15/(12, 15) == 15/(9, 15)
3 == 15/(5, 15) == 15/( 1 о, 15)
15 === 15/(7, 15) === 15/(14, 15)===15/(13, 15)==15/(11, 15)
Пусть сх,0, сх,1, ..., cx,n 1 совокупность корней уравнения
ХN ........ 1. Разбив эту совокупность на rруппы элементов, имеющи
106
r лава 2
один и тот же IIОРЯДОК, и введя мноrочлены
'i'd (Х) == П (Х a l ),
1, ПОРЯДОК а ' d
получим
х n 1 == П d (Х).
dln
Мноrочлены, имеющие своими корнями все элементы одноrо
и Toro же порядка, называются круеО8ыми. В приведенном
выше при мере
(2.14 )
Х 1 == 'i'1 (Х),
Х З 1 == I (Х) 'i'з (Х), 'l'з (Х) == Х2 + Х + 1,
Х 5 1 == 'i'1 (Х) 'i'5 (Х), 'i'5 (Х) === х 4 + ХЗ + Х 2 + Х + 1,
X 1 5..... 1 == 'i'1 (Х) 'i'з (Х) 'i'5 (Х) 'i'15 (Х),
15(X)==(X4+X+ 1)(Х 4 +ХЗ+ 1).
в общем случае KpyroBble мноrочлены представляют собой
произведения минимальных мноrочленов. Соrласно теореме 2.13,
(jJ,
<fз
Фиr. 2.1.
« 0 8 ((!
(Х9
cx 1t
'Рб
0 «0 О ОС5
cX O
d является минимаЛЬНЫ!\1 мноrочленом в том и только том
случае, если степень 'Фd является минимальным целым числом n,
таким, что d I (qn 1). в приведенном выше примере '1'1, Фз, '1'5
минимальные мноrочлены. Однако поскольку минимальное
число n, такое, что 151 (2 n 1) равно 4, то '1'15 (Х) представляет
собой произведение двух неПРИВОДИ!\1ЫХ мноrочленов.
Разделим окружность на 15 равных частей с помощью 15 то-
чек, которые обозначим в порядке их расположения на окруж-
ности через а О , а 1 , ..., a 14 . Исследуем взаимосвязь между по-
ложением на окружности корней 1ноrочленов '1'1, Фз, '5 И '1'15
И полученными выше соотношениями (фиr. 2.1).
Составляя таблицу ЦИК.пов, как показано на фиr. 2.1, любой
двучлен ХN 1 можно разложить в произведение неприводимых
мноrочленов. Рассмотрим пример.
Задача 2.61. Разложить на множители мноrочлен Х 8 1 над
олем GF(З)..
Конечные поля
107
Решение. Сначала построим все (3, 8) -циклы:
О
1 3
2 6
4
5 7
Двучлен Х 8 1, рассматриваемый как мноrочлен над полем
Ор(3 2 ), имеет своими корнями все ненулевые элементы этоrо
поля. Поле G F (32) было построено в задаче 2.51. Однако, по
скольку ни один из корней неприводимоrо lноrочлена Х2 + 1,
использованноrо в этой задаче, не является примитивным эле-
ментом поля G F (32), то сначала нужно найти один из таких
элементов. Возьмем элемент == (Х + 1) и, обозначив элемент
(Х) через i, найдем все степени :
p==i+ 1,
2 === i,
З == ...... i + 1,
4 == 1,
5 == i 1,
6 == i,
7 == i ......... 1,
8 == 1 .
Отсюда видно, что примитивный элемент G F (32). Используя
u
этот примитивныи элемент, наидем минимальные мноrочлены,
соответствующие каждому циклу. Результат будет следующим:
Следовательно,
1) (X2 X 1).
Эта задача дает пример разложения в простом поле [поле
u
называется простым, если оно не содержит друrих полеи, кроме
caMoro себя; как мы видели выше, поле может содержать только
одно подполе, изоморфное Z/ (р), р простое число (тео-
рема 2.3)]. Остано:вимся I\l'эr'1<о На полях, не Я:ВЛ$IЮЩИХся
простыми.
о Х.........l
1, 3: Х 2 + х ...... 1
2, 6: Х 2 + 1
4 Х+l
5, 7: Х 2 Х ......... 1
(Х8 1) == (Х 1) (Х + 1) (Х2 + 1) (Х 2 + Х
108
rлава 2
Задача 2.62. Поле GF(qk) является подполем поля GF(qj)
тоrда и только тоrда, Kor да k I j.
Задача 2.63. Разложить двучлен X 15 1 в произведение не-
приводимых над ОР(2 2 ) мноrочленов.
Решение. Будем считать, что, кроме элементов О и 1, поле
ОР(2 2 ) содержит также корни и у мноrочлена Х 2 +Х+l.
Элемент (а следовательно, и у) является примитивным эле-
ментом поля G F (22). Представление элементов поля G F (22)
В виде степеней ПрИМИТИI ноrо элемента будет слеДУIОIl ИМ:
,
2 + 1 +у,
( 3 == 1).
Чтобы разложить Х 15 1 в произведение неприводимых над
Gf"(4) мноrочленов, необходимо построить все (4, 15) циклы:
О
1, 4
2, 8
3, 12
5
6, 9
7, 13
10
11, 14
Если сравнить эту таблицу циклов с таблицей (2,15) -циклов из
задачи 2.60, то можно замеТИ1Ь, что первая таблица получается
разбиением каждоrо ЦИКJIа второй таблицы (за исключением
цикла О) на два цикла. Используя примитивный элемент а из
задачи 2.60, мноrочлен, соответствующий (2, 15) циклу, содер-
жащему число 3, MOII<HO преобразопать следующим образом:
Х 4 + Х З + Х 2 + Х + 1 (Х аЗ) (Х ( 6 ) (Х ( 12 ) (Х ( 9 ) ===
== (Х аЗ) (Х ( 12 ) · (Х ( 6 ) (Х ( 9 ) ==
(Х2 (аЗ + ( 12 )X + 1)(X2 (a6 + ( 9 )Х+ 1).
Из вышеизложенноrо (см. задачу 2.59) имеем аЗ + a 12 === а 2 +
+ а + 1 == а 1О И а 6 + а 9 === а 2 + а == а 5 . Оба элемента а 5 и а 1О
имеют порядок 3 и являются элемеНТ(:iМИ и 'у поля GF(4).
Следовательно,
Х 4 + х з + х 2 + х +. 1 === (Х 2 X + 1) (х 2 " Y + 1).
Конечные поля
109
АнаЛОI"ИЧНО преобразовывая мноrочлены, соответствующие дру-
rИ:М uиклам, получим
X15 1==(X 1)(X2 X+y)(X2 X+ )(X2...... X+ I)Х
х (Х 2 уХ + 1) (Х ....... у) (Х 2 уХ + у) (Х ) (Х 2 ....... X + ).
Выше достаточно подробно было описано, каким образом
с помощью таблицы циклов можно находить те или иные мини
мальные мноrОЧJIены. Нахождение минимальных мноrочленов,
как мы увидим в следующей rлавс, является одним из этапов
построения цикличtсКих кодов. Например, часто приходится BЫ
" v
по.пнять следующую последовательность деиствии:
1. Выбирается q (q ичный код).
2. Выбирается n (длина кода).
3. Находится минимальное т, такое, что nl (qm 1), и бе-
рется поле GF(qm).
4. Из элементов поля GF(q1n) выбирается один, имеющий по
рядок п. Этот элемент обозначается через и считается фикси-
рованным; (q, п) циклу, содержащему 1, сопоставляется MHoro-
член mf3 (Х). После этоrо находятся минимальные мноrочлены,
соответствующие друrим интересующим нас циклам.
Задача 2.64. Разложить двучлен Х 23 1 в произведение не-
приводимых над ОР(2) мноrочленов.
Решение. Построим таблицу (2, 23) циклов:
о
1, 2, 4, 8, 16, 9, 18, 13, 3, 6, 12
5, 10, 20, 17, 11, 22, 21, 19, 15, 7, 14
Следовательно, двучлен Х2З 1 являеrся произведением (Х 1)
и двух неприводимых мноrочленов 11 й степени, двойственных
друr друrу. Эти неприводимые мноrочлены в принципе можно
найти так же, как и раньше, но такоЙ способ очень сложен. Для
нахождения двух сомножителей 11 й степени воспользуемся
таблицами, помещенными в приложении. Поскольку порядок
корня двучлена Х 2З 1 равен 23, то сначала найдем такие це-
лые числа i, что 23 == (211 1) / (211 1, i). Поскольку, как сле-
дует из табл. А.l, 211 1 === 23 Х 89, то i === 89. Если (1, прими-
тивный элемент поля G F (211), то а 89 будет элементом по-
рядка 23. Из табл. А.2 находим, что неприводимым мноrочленом
11 й степени, имеющим своим корнем элемент (1,89, является мно-
rочлен Х1I + Х 9 + Х 1 + Х 6 + Х 5 + х + 1. Этот мноrочлен соот-
ветствует указанному выше циклу, содеря{ащему 1. Друrой ие-
110
r лава 2
комый мноrочлен является двойственным к уже найденному мно-
rочлену. Таким образом,
Х 23
1 == (Х + 1) (X l1 + Х9 + Х7 + Хб + Х 5 + х + 1) (X 11 + X IO +
+ х 6 + Х 5 + Х 4 + Х 2 + 1).
Неприводимы
МНQrочлены l1-й степени в правой части послед-
HeI'o разложения явJIяются порождающими мноrочленами кода
rолея.
2.6.* Дополнительные сведения о конечных полях
2.6.1 Вычисления в конечных полях
В конечных полях, как обычно, можно складывать, вычи-
тать, умножать и делить.
Задача 2.65. Решить следующую систему уравнений над
ОР(2 4 ):
х + абу == а 3 ,
а,3Х + аllу == а 4 .
(Следует воспользоваться таблицей соответствия из задачи
2.59. )
Решение. Используем метод подстановки. Из первоrо уравне-
ния находим Х == аЗ + а 6 У и, подставляя ero во второе уравне-
ние, получаем
(19 + a I1 ) у == а 4 + (16,
а 2 у == а 2 , откуда
Х == а 3 + а === а 9 .
Для решения указанной выше системы уравнений можно вос-
пользоваться так)ке методом Крамера:
у == a 10
,
аЗ
а 4
Х==
I
з
I N 1з
у==
I а 1з
а 6 I
a ll a l4 + а 1О a l1
.......
а 9
а б I
all + а 9 ....... а 2
,
а 11
:: l' а 4 + а 8 a l2
6 1 == 2 ==
==aIO.
а а а
а 11
Утверждение 2.66. П усть а
nроизвольный ненулевой эле-
AteHT поля ор(рт). Если существует такой элемент
Е Ор(рт),
что а ==
2, то а называется квадратичным вычетом. В nротив-
Конечные поля
111
НОМ случае, т. е. если в ОР (рт) не существует TaKOZO элемента
, что а ==
2, сх. называется квадратичным невычетом.
1) Е ели р == 2, то любой элемент поля, за исключением эле-
hteHTa О, является квадратичным вычетом.
2) Если р
нечетное число, то четные степени nримитиВН020
элемента являются квадратичными вычетами, а нечетные сте-
пени
квадратичными невычетамu (следовательно, имеется
(рт
1) /2 квадратичных вычетов u столько же квадратичных
невычетов) .
2.6.2. Матрицы Адамара
Матрицы Адамара используются в теории планирования ЭК-
спериментов, теории кодирования, теории связи и друrих обла
стях. Хорошим введением в теорию матриц Адамара является
работа Киясу [8]. Матрицей Адамара Н n порядка n называется
квадратная матрица размера nх n с элементами
l и
l из
поля действительных чисел, такая, что
HnH;==nI,
т
rде /
единичная матрица, а Н п
матрица, транспонирован-
ная к Нn. Например,
Hl===[l],
H2==[
].
1 1 1 1
1
l 1
1
Н 4 == 1 1
1
1
1
1
1 1
Утверждени
2.67. Если Нn
матрица Адамара и n > 2, то
n == О (mod 4 ).
Доказательство. Если Нn == (al/)
матрица Адамара, то
НnН;==n/. Это значит, что
п { О
L alkajk ===
k:a 1 n
при
при
i=l=j,
i==j,
112
r лава 2
Отсюда следует, что
ппп
L (a 1k + a 2k ) (a 1k + а зk ) == L aTk + L a 1k a 2k +
k:;::1 kz=l k:lal
n n
+ L аlkаЗk + L а2k й Зk == n.
k==1 k...J
Так как каждое слаrаемое в левой части последнеrо равенства
равно О, 4 или 4, то n кратно четырем.
Высказываются предположения, что существуют матрицы
Адамара любоrо порядка n, KpaTHoro четырем. Однако эта rипо
теза не доказана и не опроверrнута. Для всех п 200, кратных
четырем, за исключением п == 188, матрицы Адамара найдены
(для этоrо частично использовались вычислительные машины).
Кроме Toro, известно также несколько конструктивных способов
построения матриц Адамара. Один из этих способов дается сле-
ДУIОЩИМ утверждением.
Утверждение 2.68. Если существуют матрицы Адамара Н т
u H 1t , ТО существует u матрица Адамара порядка тn.
Доказательство. Пусть Н п == (ан). Тоrда матрица Н тп ==
== (aijH т) является искомой.
Этим методом можно построить последовательность матриц
i\.дамара, взяв, например, за основу матрицы Н 2 и Н4.
Рассмотрим еще один способ построения матриц Адам ара,
предложенный Палеем. Ряд друrих методов построения матриц
Адамара мо}кно найти также в книrе Холла [7].
Пусть q простое число. Введем функцию 1) Х, определив
ее на множестве элементов поля GF(q) следующим образом:
х(о)==о,
{ 1 а квадратичный выIет,'
х(а)== 1 : . .
а квадратичный невычет.
Утверждение 2.69.
1) %(a )==%(a)%( ).
2) % ( 1) == 1.
3) L х(а)==О.
aeGF(q)
4) Если q == 3 (mod4), то x( l)== 1.
Доказательство. Докажем утверждение 4. Пусть а....... прими-
тивный элемент поля GF(q). Тоrда
aq l 1 === (a(q I)/2 1) (a(q 1)/2 + 1) == о.
1) Х называется символом Лежандра; СМ. также разд. 8.1.9. Прuм.. ред.
Конечные поля
113
Однако так как все Э.nементы 1, а, а 2 , . . ., aq 2 различны, ТО
a(q 1)/2 =1= 1. Следовательно,
a(q 1)/2 === 1.
Но тоrда
{ + 1 , q === 4t + 1,
x( I)== 1, q===4t 1, Т. е. q == 3mod4.
Утверждение 2.70. Если =1= О, то
L х (а) Х (а + ) === ....... 1.
а Е аР (q)
Доказательство. Если а===О, то ;«0);«0 + ) === О. Допустим,
что а =1= О. Тоrда в поле GF(q) найдется, и притом единствен-
ный, элемент у, такой, что а + == ау. КОI'да а пробеrает все
ненулевые элементы поля GF(q), у пробеrает также все нену-
левые элементы поля G F (q), за исключенирм 1. Следовательно.
Lx(a)x(a+ )=== L x(a)x(a+ )== L х(а 2 )х(у)==
а а:#:О а+О
== L х(у) === L х(у)....... x(l) == О 1 == 1.
'У+ 1 V
Используя приведенные выше утвеР}l{дения и отождествляя
элементы поля G F (q) с вычетами 1, ..., q 1, q ( == О), по мо-
дулю q, построим следующую квадратную матрицу Н == (aij)
порядка q + 1:
alO === а/о === 1, О < i, j q,
ан ==....... 1, О i q,
ai / == Х (j ....... i), О < i, j < q , i =1= j.
Утверждение 2.71. Если q простое число, такое, что
q ::::: 3 (mod 4), то построенная выше матрица Н является мат-
рицей А дам ара.
Доказательство. Ну}кно ноказать, что ННТ == (q + 1)/. Оче-
видно, что диаrональные элементы b ij матрицы В === Н 1fT ==
== (Ьи) равны q + 1. Из части 3 утверждения 2.69 непосред-
ственно следует, что
b iO == Ь О / == О, О < i, j q.
Покажем, что все остальные элементы b ij (О < i, j q, i =1= j)
матрицы В равны нулю Имеем
n П
b lJ == L а{ k a jk == 1 + L х (k ....... i) Х (k ....... j) + '.......1) Х (i ....... j) +
k O k l
+ ( ....... 1 ) Х (j ---- i).
114
r лава 2
[Iоложим 1 === k i и == i j. Коrда k пробеrает все значения
от 1 до q, то 1 также пробеrает все элементы поля РО (q). Заме-
ТИI\1, что В данном случае =1= о. Кроме Toro, соrласно утвержде-
нию 2.69, ( I)X(j i)==X( I)X(j i)==X(i j). Тоrда из
утверждения 2.70 следует, что
bl/ l+ L X(l)X(l+ )===I l==O.
1 Е а F (q)
Как известно (см., например, [4]), существует бесконечная
последовательность простых чисел q, таких, что q == 3 (mod 4).
Это означает, что описанная выше конструкция дает бесконеч-
ный класс матриц Адамара.
С помощью матриц Адамара можно строить некоторые
двоичные коды. Один из таких классов кодов это эквидистант-
ные коды, описанные в разд. 1.4.2. Друrой класс кодов, которые
rvlorYT быть построены с помощью матриц Адамара, это коды
Рида Маллера, рассматриваемые в разд. 4.5.1.
Утверждение 2.72.
1 ) При одновременной nерестановке строк и столбцов, а
такЖе при умножении строк и столбцов матрицы Адамара на
1 опять получается MaTpUl{a Адамара. В случае необходимости
с nОАtощью операций этих двух типов всееда можно получить
приведенную матрицу AaaAtapa, все элементы первой строки II
nервоео столбца которой равны + 1. Рассмотрим матрицу раз-
мера n Х (n 1), riолучающуюся из nриведенной матрицы Aдa
мара порядка n удаление.lU nервоео столбца. Заменим в этой
матрице элементы + 1 на о, а 1 и каждую строку nолучаю-
щейся .Аtатрицы будем рассматривать как кодовое слово блоко
воео кода длины n 1. Совокупность таких п кодовых слов
представляет собой эквидистантныu код. Заметим, что этот код,
вообще 20ВОрЯ, не является линейным.
2) Рассмотрим совокупность из 2n векторов, первые n из
которых VI, ..., V N являются строками матрицы Адамара по-
рядка n, а вторые n nолуttаются умножением первых на 1.
Аналоеично тому, как это мы сделали выше, заменим элементы
+1 на О, а элементы 1 на 1. Полученная таким образом сово..
куnность из 2n двоичных векторов представляет собой блоковый
код длины n с кодовым расстоянием n/2. Вообще 20воря, этот
код также не является линейным. Однако коды этоео типа, по-
строенные на основе матриц Адамара Н 2т, являются не че J 11
UHbtAt, как кодами Рида Маллера nервоео порядка. Существо-
вание матриц Адамара Н 2т для люб020 целоео 'п следует из
утверждения 2.68.
Конечные nоАЯ
115
2.6.3. Конечные rеометрии
В этом разделе рассматриваются rлавным образом конечные
евклидовы rеометрии на языке их конечных представлений. Ко..
нечные rеометрии так же, как rруппы и поля, являются систе..
мами, которые определяются совокупностью аксиом, однако в
данном случае вполне МО)I{НО отказаться от общности изложения
и рассмотреть конечные rеометрии в одном из их конкретных
представлений. Детальное изложение теории конечных reoMeT..
рий можно найти в [5]. Конечные rеометрии используются в Teo
рин планирования экспериментов [6], в теории кодирования для
введения проективно
rеометрических кодов и для друrих целей.
Конечные евклидовы rеометрии. Последовательности из т
элементов поля GF(q)
Х == (XI, Х2, . . ., Х т ), Xi Е ОР (q),
будем называть далее точками. Пусть Х == (Х1, ..., Xп
) И
у == (YI, ..., Ут)
две различные точки. Совокупность точек,
rде сх,
элемент поля GF(q),
аХ + (1
а) У == (аХ1 + (1
а) У1, . . ., аХ т + (1 ...... а) Ут, а Е ОР (q),
назовем прямой, проходящей через Х и У, и обозначим через
Х V У. Следовательно, одна прямая содержит q точек. Множе..
ство из qт точек и систему прямых, определенных указанным
выше способом, назовем е8клидО80Й ееометрией размерности т
и будем обозначать через БG (т, q). Параметр q евклидовой
I'еометрии ОР(т, q) указывает не на то, что последняя «берется
над полем GF(q)>>, а определяет число точек, содержащихся в
одной прямой. Использованный здесь способ описания конечной
евклидовой rеометрии, при котором каждая точка задается
своими координатами, являющимися элементами поля ОР (q),
представляет собой не более чем один из способов представле..
ния БG (т, q). Некоторые авторы обозначают введенную выIеe
конструкцию не через БG(т, q), а через АО(т, q). При этом
они исходят из Toro, что rеометрию БG (т, q), в которой не вве..
дено расстояние, следует называть аффинной ееометрией.
Определим k"пространство в БG (n-l, q) как множество из qh
точек Х == (XI, ..., Х т ), удовлетворяющих соотношению
АХТ == Ь Т
,
rде ХТ и Ь Т
вектор
столбцы, полученные транспонированием
последовательностей Х и Ь == (b l , ..., bт
k), а А
матрица
размера (т
k)Xm с элементами из поля GF(q), имеющая
paHr т
k. В частности, О
пространство называется точкой,
l
пространство
прямой, 2"ПРОСтранство
плоскостью, а (m
1)-
пространство
2uпер.плоскостью в БG (т, q). Друrими словами,
116
rлава 2
rиперплоскость это MHO}l{eCTBO решений (Xl, ..., Х т ) одноrо
"
линеиноrо уравнениия
atXl + а2 Х 2 + ... + атХ т == Ь.
Поэтому k пространство это пересечение т k rиперплоско-
стей. Вначале прямая была определена как совокупность линей-
ных комбинаций двух точек, а затем прнмой было названо также
l пространство. Покажем, что в действительности оба эти опре
деления эквивалентны. Пусть Х == (Xl, ..., Х т ) и У == (YI, ...
..., Ут) две различные точки, принадлежащие I пространству.
Рассмотрим ВСС линейные комбинации (Х.\' + (1 а) У этих двух
точек. Так как АХТ === Ь Т И АУТ === Ь Т , то
А [аХ + (1 ...... а) У]Т == аЬ Т + (1 а) Ь Т == Ь Т ,
Т. е. все линейные комбинации Х и У принадле}l{ат l простран-
ству. Далее рассмотрим совокупность точек Z == (ZI, ..., Zm),
являющихся линейными комбинациями аХ + (1 а) У точек Х
и У. В этом случае
ZI == ах! + (1 ....... а) YI,
Zm === аХ т + (1 ....... а) Уте
Отсюда следует, что
(Х2 У2) ZI (XI ....... YI) Z, == YIX2 ....... XIY2.
Таким образом можно получить т 1 везависимых соотноше
ний, связывающих координаты Zl, ..., Zm точек z.
Сформулированные выше утверждения MorYT быть распро-
странены на произвольные k-пространства. Действительно, рас-
смотрим k + 1 точек ХО == (XOl, ..., Хот), ..., X k == (Xkl, ...
. . ., Xkт), таких, что paHr матрицы Х === (Хц) равен k; такие точ-
ки называются линейно незаВИСИМblМИ. Определим k npocTpaH-
ство как множество из qk точек следующеrо вида:
k
L atXl, L ai === 1, al Е ОР (q).
' o
Это определение k-пространства эквивалентно приведенному
выше; k пространство, порождаемое k + 1 независимыми точ-
ками Ха, X 1 , ..., X k , будем обозначать через ХО V X I V ...
. .. V X k .
Задача 2.73. Найти все 2-пространства в E O (3,2).
PelueHue. В данном случае 2 пространства являются rипер
плоскостями и задаются одним линейным уравнением. С друrой
Конечные поля
117
стороны, выбор трех линейно независимых точек Х, У и Z также
задает 2 пространство, которое в этом случае представляет
собой множество из четырех точек {Х, У, Z, Х + У + Z}. Bcero
имеется 14 различных 2 пространств:
b O b 1
х] == Ь (О, О, О), (О, О, 1), (О, 1, О), (О, 1, 1) (1, О, О), (1, О, 1) (1, 1, О), (1, 1, 1)
Х2==Ь (0,0,0),(0,0,1), (1,0,0),(1,0,1) (0.1,0),(0,1, 1),(I.I,о),{I.. 1,1)
хз Ь (0,0.0),(0,1,0),(1,0,0),(1,1,0) (0,0,1),(0,1,1),(1,0,1),(1,1,1)
х} + X2 b (О, О, О), (О, О, 1), (1,1, О), (1,1,1) (0,1. О), (0,1,1), (1, О, О), (1, 0,1)
Хl+ХЗ==Ь (0,0,0),(0,1,0),(1,0,1),(1,1,1) (0,0,1),(0,1,1),(1,0,0),(1,1,0)
Х2+ХЗ==Ь (0,0,0),(1,0,0),(0,1,1),(1,1,1) (0,0,1),(1,0.1),(0,1,0),(1.1,0)
х} + Х2 + хз == Ь (О, О, О), (0,1,1), (1, 0,1), (1,1, О) (О, 0,1), (0,1, О), (1, о, О), (1,1,1)
Мы установили, что в ЕО (3, 2) сущ ствует 14 различных 2 про-
странств. Попробуем найти число W (m k, q) различных k-про-
странств в ЕО (т, q) в общем случае.
Утверждение 2.74. Число W(rп,k,q) различных k-nростраflСТ8
8 ЕО (т, q) определяется следующей фОРАtулой:
W ( т k ) == т k (qт 1) ... (qт k+1 1) .
, , q q (qk 1) ... (q 1)
Доказательство. Вначале определим число способов выбора
точек Х о , ..., X k , поро}кдающих k-просrранство Ха V X I V ...
. .. V X h . Из множества всех qh точек точку ХО можно выбрать
qffl способами. Исключив из множеС1 ва всех qrп точек точку Х О ,
точку Х} можно выбрать qт 1 способами. Так как точка Х 2 не
должна входить в ХО V X I , то ее можно выбрать qm q спосо-
бами и т. д. Таким образом, число способов выбора точек
Х о , ..., X k равно
qт(qт l)(qт q) ... (qт qk I).
Однако ХО V X I V ... V X h === X I V ХО V ... V X h === ... . Эти
равенства показывают, что одно и то же k-просrранство имеет
различные представления. Аналоrично тому, как выше было под-
считано число способов выбора Х О , ..., X k , можно найти также
и число способов представления одноrо фиксированноrо k-про
странства. Это число оказывается равным
qk (qk...... 1) (qk q) . . . (qk ____ qk l).
Следовательно, искомое число различных k-пространств опре-
деляется равенством
W (т, k. q);:: qт k «: : q: qi ... ?k т k ;> ·
q q q...q q
118
rлава 2
Как показывает пример евклидовой rеометрии ЕО (3,2), пе-
ресечение двух 2 пространств является либо прямой, либо пу-
стым множеством. Для доказательства утверждения 2.76 потре-
буется следующее обобщение этоrо факта.
Утверждение 2.75. Два (k + 1) npOCTpaHCT8a, содержащие
некоторое k-nростраНСТ80, не имеют общих точек, отличных от
точек этоzо k npoCTpaHCT8a.
ДоказатеЛЬСТ80. Пусть X 1 , ..., X k + 1 линейно независимые
точки, порождающие общее k простраНСТIВО С, и пусть DI И D 2
два различных (k + 1) -пространства, содержащих с. Предполо-
жим, что Dl И D 2 имеют общую точку Х о , которая не входит в
с. Тоrда точки Ха, X I , ..., X h + 1 задают одно (k + 1) простран
ство, т. е. DI == D2, И мы получили противоречие.
Утверждение 2.76. Число различных (k + 1) npOCTpaHCTв в
ЕО (т, q), содержащих заданное k npoCTpaHCTBo, равно
т k 1
q
q 1
Доказательство. Число точек, не принадлежащих рассмат-
риваемому k пространству С, равно qffi qh. Любое (k + 1) про-
странство задается k + 1 линейно независимыми точками, одна
из которых не принадлежит С, а остальные k входят в С. Число
точек (k + 1) пространства, не я.вляющихся точками С, равно
qh+1 qh. Пусть I число (k + 1) -пространств, содержащих С.
Тоrда, принимая во внимание утверждение 2.75, получаем
/ (qk+l qk) == qт qk.
Конечные проективные rеометрии. Как и в случае евклидовых
rеометрий, будем представлять точки (а точнее объекты, назы-
ваемые точками) посредством координат. Конечную nроектив-
ную ееометрuю, каждая прямая которой состоит из q + 1 точек,
будем обозначать через РО (т, q). Конечная проективная reo-
метрия РО (т., q) состоит из конечноrо числа точек, ка,кдая из
которых может быть представлена своими координатами:
х == (Хо, XI, . . ., х т ), Xi Е ОР (q).
Однако в случае проективной rеомеrрии это представление точки
не однозначно, а именно считается, что последовательности
Х==(ХО,Хl, ..., Х т ) и аХ=== (СХХо, ..., (ХХ т ) , aEGF(q) {O},
опр деJtЯЮТ одну и ту же точку. СледоваТ JIЬНО, ка,кдая точка
в Ра (т, q) может быть представлена q 1 способами. Последо-
Конечные поля
119
вательнасть (О, ..., О) в данном случае из рассмотрения исклю-
чается. Таким образом, число точек в РО (т, q) равно
qm+1 1
q 1
Пусть Х == (хо, . . . , Х т ) и У === (Уо, . . . , Ут) представления двух
различных точек. Множество точек, которые MorYT быть пред-
ставлены в виде
аХ + y === (ахо + Yo, . . ., аХ т + Yт)
[а, Е G F (q), сочетание (1, === == О исключается], называется
прямой, проходя щей через точки Х и У (или l-пространством) II
обозначается через Х V У. Поскольку пара ((1" ) может быть
выбрана q2 1 различными способами, то одна прямая co
стоит из
q2 1
==q+l
q 1
точек, на что и указывает параметр q в обозначении РО (k, q)
проективной rеометрии.
Пусть Z == (Zo, ..., Х т ) точка, не лежащая на прямой
Х V У. Множество всех точек вида
аХ + y + v z ,
rде (1" и V не равные одновременно нулю элементы поля
GF(q), называется ПЛОСКОС1ЬЮ (или 2 пространством), проходя-
щей через точки Х, У и Z, и обозначается через Х V У V z. Каж-
дая плоскость состоит из
q3 1
==q2+q+l
q 1
точек.
Задача 2.77. Представьте PG (2,2) в указанном выше виде.
Решение. Так как размерность РО (2, 2) равна 2, то РО (2, 2)
представляет собой проективную плоскость, состоящую из
(2 З 1) / (2 1) == 7 точек. В качестве представлений этих семи
точек MorYT быть взяты следующие последовательности 1):
(О, 0,1), (0,1, О), (0,1,1), (1, О, О), (1,0,1), (1,1, О), (1,1,1).
В РО (2, 2) имеется семь прямых, каждая из которых состоит
из трех точек:
{(О, 0,1), (0,1, О), (0,1, 1)}, {(О, 1, О), (1, О, О), (1, 1, О)}, {(О, 1, 1),
(1, 0,1), (1, 1, О)}, {(О, 0,1), (1, О, О), (1, О, 1)}, {(О, 1, О), (1, 0,1),
(1,1,1)}, {(О, 0,1), (1,1, О), (1,1, 1)}, {(О, 1, 1), (1, О, О), (1, 1, 1)}.
1) Поскольку ОР(2) {О} состоит из одноrо элемента, любая точка пред-
ставляется в данном случае однозначно. П рим. ред.
. . '
120
fлава 2
На фиr. 2.2 показано расположение точек и прямых РО (2,2)
на плоскости.
Леrко видеть, что проективная ПJ10СКОСТЬ РО (2, q) суще-
ствует, если q является простым числом или степенью простоrо
числа. Если же q составное число, не являющееся степенью
npocToro числа, то о существовании проективной плоскости
РО (2, q) в общем случае ничеrо сказать нельзя. Известно, что
проективная плоскость РО (2, 6) Не существует, а вопрос о cy
ществовании РО (2, 10) является открытым.
В РО (т, с;) точно так же, как в ЕО (т, q), k пространство
может быть определено и как пересечение rиперплоскостей, и
100
001
011
010
Фиr. 2.2.
как совокупность линейных комбинаuий (k + 1) линейно неза-
висимых точек. При этом rиперплоскость определяется как мно-
жество решений (хо,. . ., Х т ) следующеrо уравнения первой
степени:
аохо + alxl + ... + атХ т == О
(тривиальное решение (О, ..., О) ИСКЛlочается). Второе из ука-
занных выше определений k npocTpaHcrBa более cTporo MOil<eT
быть сформулировано слеДУЮlltиМ образом: k пространство
это совокупность всех линейных комбинаций (k + 1) линейно
независимых точек Хо, ..., Х т следующеrо вида:
аоХо + al X l + ... + akXk,
rде сх.о, (Хl, ..., cx.h элементы поля G F (q), одновременно не paB
ные нулю. Оба эти определения полностью эквивалентны.
Утверждение 2.78. Число V(f1'I, k, q) k npOCTpaflCT8 8 РО(т, q)
определяется формулой
V т k == (qт+l 1)(qm 1) ... (qm+l k 1)
( , ,q) (q н 1 1)( qk 1) .., (q 1) ·
Между РО (т, q) и ЕО (т, q) существует тесная связь. Сопо
ставим точке Х == (Xl, ..., Х т ) цЗ ЕО (т, q) ТОЧКУ из РО (т, q)
Конечные поля
121
по следующему правилу:
(хl, ..., Х т )....(I, XI, ..., Х т ).
Обратное отображение при хо =1= О задаеrся формулой
(Хо, XI, . . ., Х т )
(XJ/XO, · · ., xmlxo).
Точки в РО (т, q) с Ха == О называются бесконечно удаленными.
При описанном выше соответствии k
пространства переходят в
k
пространства.
2.6.4. Разностные множества
Множество из k цеЛI)IХ чисел (d l , ..., d k ) называется (совер-
шенным) раЗflОСТНЫМ (v, k, л)
множеством, если при делении
разностей d i
d j , i =1= j, на целое число v каждый из остатков
1, 2, ..., v
1 встречается ровно л раз.
Из определения непосредственно следует, что
k (k
1) == л (v
1). (2.15)
Утверждение 2.79. Пусть (d l , ..., d k )
разностное (v, k, 1)-
множество, Р == {О, 1, ..., v
1} u
L I === {j + d i (т od v); i == 1, . . " k} , j == О, 1, . . ., v
1.
Тоеда множество Р, рассматриваемое как множество точек, II
система прямых Lo, ..., Lv
1 являются конечной nроективн.ой
ееометрией размерности k
1.
Пример. Множество (О, 1, 3) является разностным (7, 3, 1)-
множеством.
Р === {О, 1,2,3,4,5, 6},
Lo == {О, 1, 3}, L 1 === {1, 2, 4},
L4 == {4, 5, О}, L5 === {5, 6, 1},
L 2 =={2,З,5},
L6 === {6, О, 2}.
L3 == {З, 4, 6},
Получающаяся из эrоrо разнuстноrо множества проективная reo-
u "
метрия совпадает с рассмотреннои выше проективнои rеомвr-
рией РО (2, 2).
Рассмотрим один из способов построения разностных MHO
жеств. Заметим, что, кроме этоrо способа существует MHoro дру-
rих способов, подробное описание которых можно найти в [7].
Утверждение 2.80. Пусть v == 4л + 3
простое число, такое,
ЧТО v == 3 (mod 4). Тоеда множество D л квадратичных вычетов
по модулю v является разностны"u (4л + 3, 2л + 1, л)
множе-
ством.
122
r лава 2
Доказательство. Нужно показать, что при любом d (О < d <
< v) сравнение х 2
у2 == d (mod v), О < х, у < v, имеет одно
и то же число решений (х, у). Предположим, чТо сравнение
x2
y2 == 1 (mod v) имеет
решений (al, b l ), ..., (a
, bJ.L),
О < ai, b i < V. Если d
квадратичный вычет, то d == е 2 и реше-
ниями сравнения х 2
у2 == d являются (eal, eb 1 ), . .., (ea
, ebJ.L) ,
Если d
квадратичный невычет, то, соrласно утверждению 2.69
(4), квадратичным вычетом является
d. Полаrая
d == е 2 , по-
лучаем, что решениями сравнения х 2
у2 == d являются (eb t ,
eal), ..., (eb
, eaJ.t). Таким образом, мы доказали, что для каж-
доrо d сравнение х 2
у2 == d (mod v) имеет ровно
решений, а
это означает, что D'A....... разностное множество. Как следует из
формулы (2.14),
=== л.
Пример. л == 2, v == 11, k == 5. Так как в этом случае 12 == 1,
22 == 4, 32 == 9, 42 == 5, 52 == 3, 62 == 3, 72 == 5, 82 == 9, 92 == 4,
102 == 1, то D 2 == {1, 3, 4, 5, 9}. Если найти все разности, то
можно непосредственно убедиться, что каждое из чисел, отлич-
ное от О и меньше 11, входит в множество разностей ровно 2
раза. Действительно,
...... I 1 3 4 5 9
1 О 9 8 7 3
3 2 О 10 9 5
4 3 1 О 10 6
5 4 2 1 О 7
9 8 6 5 4 О
2.6.5. ДОПОЛНЯЮЩИЙ базис
Пусть Е == aF(q), q == pt, р.......простое число. След Тq(л) элс-
мента л Е GF(qт) относительно Е определяется соотношением
т q (л)==л+л q +л q2 + ... +л qт .... 1 .
Утверждение 2.81. Для Лl0боео базиса aI, ..., СХ т векторноео
пространства GF(qm) над полем Е существует двойственный ба-
зис AI, ..., лт, обладающий следующим свойством:
{ О, i=l=j,
Т q (л Ja J) == 1 ·
·
, t
].
Конечные поля
123
Доказательство. Рассмотрим
a l
a Q
1
матрицу
aQm 1
1
a f! a qm 1
2 ... 2
а 2
А==
a Q aQm 1
а т т. · · m
Матрица А является невырожденной, поскольку элементы
(Хl, ..., сх. т линейно независимы над Е. Следовательно, матрица
А имеет обратную матрицу A I. Определитель А обозначим через
I А 1. Пусть м == (ан) квадратная матрица порядка n, и пусть
Ан определитель матрицы, получающейся из матрицы М уда-
лением i й строки и j ro столбца; Ан называется минором. При
этом величина ( 1) i+j ij называется алеебраическим дополне
1lием элемента ан и обозначается через Ао. Матрица
А 11 А 21 ... А nl
A I2 А 22 А n2
A 1t А 2п Ann
называется дополнительной матрицей матрицы М и обозначается
через adj М. Матрица adj М обладает следующим свойством:
(adj М). М == М. (adj М) == 1М 1. [n'
rде 1 n единичная матрица порядка n.
Попробуем найти матрицу adj А:
I aQ aQт 1
2 2
а 2
a Q2
2
т 1
a Q
2
AII ==
А 12 ==
Q Qт 1
а т ... а т
а т
Q2
а т
aQm 1
т
и т. д. Имеют f\.feCTO также следующие равенства:
) т' Q А A Q2 А т' Q3
AI2===( 1 A II , IЗ== 11, 14==( 1) Ан,
А ( 1 ) т' A Q А A q2 ( т' q1
22 == 12, 23 == 12, А 24 == 1) A12,
. . . ,
. . .,
...................... .
еде т' == т 1. Докажем, например, справедливость paJ;3e CTBa
т' q
А\2 === ( 1) AlI. Cor ласно определению определителя"
А,. == L (] (Рl' .. ., Р т ) а 1Р а 2Р ... а mр ,
I .:l Щ
124
r лава 2
rде сумма берется пu всем набора", чисел (PI, ..., Рт), полу-
чающимся в результате перестановки чисел (1, 2, ..., т), а
(J (Рl, ... ,Рт) знак перестановки.
Воспользовавшись вышеизложенным (см. задачу 2.27), по-
лучим
Ail==L:O(PI' .... pт)a Pl "0 a Pm
q2 qm 1
а 2 ... а 2 а 2
а 2
a q2
2
. . .
qm 1
а 2
.
т'
==( 1)
a q2
m
. . .
т I
a q
m
а т
а a q2
т т
. . .
m I
a q
т
т'
==( l) А 128
Аналоrично доказываются и остальные иведенные BbIUle ра-
венства. Из этих равенств следует, что I А q == ( l) т' I А 1. Сле-
довательно, первым столбцом матрицы 1 == adj А/ I А I явля-
ется вектор
(АIlЛ А 1, (.......l)m' A11/1 А 1, AY:/I А 1, ...)Т ==
== (АIIЛ А 1, Arl/I А I q , Ai;/\ А \q2, . . .)Т ==
( q q2 qm l ) l
=== л'1, л'I, ЛI , ..., ЛI
rде Лl==А 11 /IАI. Аналоrично через Лi==А1i/IАI можно выра-
эить и остальные столбцы матрицы A I. Таким образом,
л'1 . .. Л m
л,{ ... л,in
A--- I ==
л, qm--- 1 Л m qт 1
I · · ·
Очевидно, что элементы ЛI, ..., Л т линейно независимы (если
допустить, что они линейно зависимы, то должны существо
вать такие элементы Ci Е Е, ЧI0 L: СlЛI == О и (Сl, . . . , С т ) =Р
:;= (О, ..., О)). в этом случае L: СlЛl === L: Сlлt == о и L: с iлi; ===
==0, j== 1, 2, ..., т 1, но это противоречит тому, что A I..........
невырожденная матрица).
Из равенства АА I == 1 n получаем
m / / m I 1t
L Лt а, == 1, L: л1 a ===0 (j =1= k).
l I 1 1
УтвеР)J{дение 2.81 доказано.
Конечные поля
125
2.6.6. Некоторые понятия, необходимые для
определения кодов rоппы
Пусть L
некоторое подмножество ЭJlементов поля ОР (2т).
Элементы множества L обозначим через cx,1, ..., сх n , n
2т.
Пусть S
векторное пространство размерности п над G F (2).
Каждому вектору х == (al, ..., а n ) Е S поставим в соответствие
рациональную функцию
n
I al
Rx (z) == ·
z
a
l=sl l
Это отображение является rомоморфным отображением S в ад-
дитивную rруппу рациональных функций над ОР(2 т ).
Если вектору х, у KOToporo al) === ai 2 == ... == al k == 1 t а oc
тальные компоненты равны О, сопоставить мноrочлен f (z) ==
==(z
all) ... (z
alk)' то Rx(z) можно представить 13 виде
f' (z)
Rx (z) == f (z) ,
rде f'(z)
формальная производная f(z) (см. разд. 2.4).
Рассмотрим один из мноrочленов g (z) с коэффициентами
из поля G F (2т), среди корней KOToporo нет элементов множе-
ства L. Имеет место следующее .соотношение:
n n
Rx(z)===" a i =sO(modg(z»#" al{(z......al)
I}т==Ot (2.16)
f...J z
а f...J
[=-I l l-=I
rде {(z
(Xi)
I}т
элемент кольца мноrочленов по МОДУЛIО
g(z), обратный к (z
cx,i), который имеет следующий вид:
{(
)
1 } === g(z)
g(al)
I ( )
Z al т
Z
а. g al.
l
Действительно, {(z
cx,i)
I}т (z
ai) == g
1 (cx,i)g(Z)
1 ==
==
1 (mod g (z) ). в справедливости (2.16) можно убедиться,
если заметить, что
(2. 1 7)
1
g (z)
g ( а )
== 1 g
1 (al) (mod g (z».
z
a
1
z
a
1
[Последнее соотношение имеет Me('fo потому, что степень мно-
rочлена в правой части (2.17), меньше, чем степень g (z).]
Задачи
1. (rруппы.) Привести примеры f'рУПП порядка n
3 (по-
строить таблицы rрупповой операции). Построить таблицы rруп-
повых операций зсех неизоморфных rрупп порядка n == 4 (с.пе
126
r лава 2
дует воспользоваться пояснениями, приведенными перед зада-
чей 2.4).
2. (Конечные поля). Найти значения ( l), ( 1)2, ( 1)3,...
в поле характеристики р (р простое число) (к задаче 2.27).
3. (Конечные поля.) Решить уравнение BToporo порядка над
G F (2) : аХ2 + ЬХ + с === О. в случае если оно не имеет решений
в поле ОР (2), найти корни, расширив соответствующим образом
поле ОР(2).
4. (Неприводимые мноrочлены.) Ниже указаны неприводи
мые над Z/ (3) мноrочлены второй, третьей и четвертой степеней:
второй степени: Х 2 + 1, Х2 + х + 2, Х 2 + 2Х + 2,
третьей степени: Х З + 2Х + 1,
четвертой степени: Х 4 + Х З + Х2 + 2Х + 2.
Доказать, что эти мноrочлены неприводимы. Каждый элемент
(i) поля Z/ (3) для простоты можно обозначать через i (к зада-
чам 2.43 и 2.44).
5. (Построение конечных полей.) Построить поле ОР (32), ис
пользуя для этоrо неприводимый мноrочлен Х З + 2Х + 1 (к за-
даче 2.51).
6. (Представление конечных полей.) Поле ОР(2 4 ) можно по
строить как с помощью неприводимоrо мноrочлена Х З + Х + 1,
так и с помощью неприводимоrо мноrочлена ХЗ + Х2 + Х + 1.
Получить таблицу соответствия представлений элементов (к Тео-
реме 2.12).
7. (Примитивный элемент.) Попробуйте найти примитивные
элементы поля Z/ (р) простоrо порядка в случае, если р == 3, 5,
7,11,13,17,19,23 (при р==7 имеются два примитивных эле..
мента 3 и 5, утверждение 2.57).
8. (Конечные проективные rеометрии.) Исследовать струк"
туру РО (4, 3) (определить числа точек, прямых, плоскостей,
3"пространств; определить числа точек, входящих в указанные
множества) .
9. (Разностные множества.) Построить описанным в утверж..
дении 2.80 методом разностные множества в случаях л == 3 и
'А == 4.
10. (Условие неприводимости мноrочлена степени 2.) Пусть
элемент GF(qm). След элемента относительно GF(q) был
определен следующим образом:
т 1
т q ( ) == L qt.
i =-1
Если Е ОР(2 т ) и T2( ) =1= О, то мноrочлен Х 2 + х + явля..
ется неприводимым над G F (2т). Это можно доказать следую'
{Дим образом. Пусть
Х 2 + х + == (Х + 1) (Х + 2), 1, 2 Е ОР (2т),
Конечные пОАЛ
127
Тоrда l + 2 === 1, 1 2 == . Поэтому I + T и
т 2 ( ) === Т 2 ( 1 + ) == т 2 ( 1) + Т 2 ( 1) == Т 2 ( I) + Т 2 ( I) == О.
Установить, какими свойствами следа Tq мы пользовались выше.
11. (Условие приводимости мноrочлена второй степени.)
Если Е аР(2 т ) и T2( ) == О, то мноrочлен Х 2 + х + приво-
дим над полем аР(2 т ). В самом деле, рассмотрим отображение
ОР(2 т ) в себя, задаваемое мноrоч.пеном f(X) == Х 2 + х. При
этом отображении каждый элемент 6 поля ОР (2т) переходит
в элемент (62+6), след KOToporo равен нулю. В аР(2 т )
имеется ровно 2m 1 элементов, след которых равен О. Пусть А
множество этих элементов.
Поскольку рассматриваемое отображение аР(2 т ) в Е сюръ-
ективно, то для дюбоrо Е аР(2 т ), TaKoro, что T2( ) === О, спра-
ведливо равенство f (Х) == . Это означает, что в G F (2?Yi) суще-
ствуют элементы Х (их два), такие, что Х 2 + х + === О, т. е.
Х 2 + х + неприводимым не является.
12. (Преобрэзование неприводимых мноrочленов.) Пусть
о элемент ОР(2 т ), такой, ЧТОТ2( 'О)== 1, и пусть g(X) ==
== Х2 + уХ + мноrочлен, неприводимый над G F (2т). Пока-
зать, что при соответствующем выборе ' преобразование Х ==
== уУ + ' переводит мноrочлен g(X) в g(Y) === у2(У2 + у + ).'
3. Линейные и циклические коды
3.1. Линейные коды
Линейные коды составляют лишь небольшой подкласс бло
ковых кодов, однако, поскольку они образуют такую хорошо
известную структуру, как линейное пространство, то сразу же
после их построения Киясу [1] и Слепяном [2] они стали OCHOA
ным объектом исследования в теории кодирования. Предполо-
жим, что число символов на входе канала q является некоторой
степенью простоrо числа р. Входные символы канала представ-
ляют собой обозначения для реальных сиrналов в канале; для
удобства обращения с ними возьмем в качестве входноrо алфа-
вита V 1 канала конечное поле GF(q) из q элементов. Введенное
выше предположение о том, что q является степенью простоrо
числа, обусловлено тем, что, как указывалось в разд. 2.5, число
элементов в любом конечном поле есть степень простоrо числа
И, наоборот, для любоrо q, являющеrося степенью простоrо чис
ла, существует поле из q элементов.
Пусть V n
векторное пространство размерности n над полем
G F (q). Подпространства размерности k пространства V n назы
ваются q
ичными линейными кодами длины n с k информацион-
ными символами [или (n, k)
кодами]. Если С
линейный код, то
подпространства линеЙноrо пространства С будем называть (ли-
неЙными) подкодами кода с.
Коды из примеров 1.3 и 1.4 являются линейными. В случае
линейных кодов кодовые слова называют также кодовыми ве/\'-
торами. При q == 2 линейные коды называют zруnnовыми.
Как было замечено выше, линейные коды представляют со-
бой лишь подкласс класса блоковых кодов; известны примеры
нелинейных кодов, число кодовых слов в которых больше числа
кодовых слов в любом линейном коде с теми же параметрами n
и d (3
7]. Однако линейные коды обладают более простой
структурой, что позволяет выявить более тонкие их свойства и
делает их перспективными при построении простых процедур
кодирования и декодирования. Кроме Tor'o, следует заметить, что
коды Препараты [4], являющиеся типичными представителями
нелинейных кодов, тесно связаны с циклическими кодами (см.
разд. 3.5), являющимися В свою очередь подклассом класса ли-
v
ненных кодов.
Назовем весом Хэ.мМИН2а вектора v (или просто весом BeK
тора v) из V n число ненулевых компон
нт этоrо вектора; вес
л инейные u ЦUКАuческuе коды
129
вектора v будем обозначать через )(и). Расстояние Хэмминеа
d (и, и) между векторами и, v Е V n определим как вес их разно..
сти, а именно ПОЛОЖИIvI d(v,u)==w(v u). Пусть d мини"
мальное расстояние линейноrо кода с. Тоrда для любоrо не..
нулевоrо вектора v Е С
W (и) === w (и О) d,
та1\: как нулевой вектор также принадлежит коду С (нулевой
вектор обозначен здесь символом О).
С друrой стороны, из определения d следует существование
векторов и, и Е с, таких, что d(v, и) == ш(и и) == d. Но тоrда,
поскольку V и Е С, минимальный вес кода С (который опрс..
деляется как минимальный из весов ненулевых векторов, входя
щих В с) в точности равен минимальному раССТОЯНИIО кода с.
Для задания линейноrо кода удобно пользоваться опреде
ляемоЙ ниже матрицей а. Пусть gl, ..., gk некоторый базис
(n, k) Koдa С, и пусть G матрица из k строк и п столбцов,
i й строкой которой является базисный вектор gi. Матрица G
называется nорождающей матрицей кода С. Из свойств базиса
непосредственно следует, что любой кодовый вектор может быть
представлен в виде линейной комбинации строк gl, ..., gk MaT
рицы G и, наоборот, что любая линеЙная комбинация строк
gl, ..., gk матрицы G представляет собой кодовый вектор и, бо
лее Toro, различные линейные комбинации задают различные
кодовые векторы.
Поскольку каждый из k коэффициентов линейной комбина..
ции может принимать q значений, общее число кодовых BeKTO
ров в коде С равно qk. Наоборот, задав матрицу G размера
k Х п и paHra k с элементами из поля GF(q), мы задаем линей..
ный код, для KOToporo G является порождающей матрицей. Об
удобстве задания линейных кодов с помощью порождающих
матриц свидетельствует, например, тот факт, что двоичный ли..
нейный (40, 20) KOД содержит более Ч I\i 106 слов, а задается
порождающей матрицей размера все]"'о лишь 20 Х 40.
Для задания линейных кодов используются также Iатрицы
Н, КО10рые определяются следующим образом. rlYCTb сп мно"
жество всех векторов U === (UI, ..., lln) Е V n' таких, что для лю
боrо v == (Vl, ..., и п ) Е С
uо Т === О ( То е. t Ui V / == О ) t
L == 1
rде индекс Т означает транспонирование. Как известно, Сп яв-
ляется подпространством размерности (п k) пространства V n .
Это подпространство называется кодом, двойственным коду с.
Порождающую матрицу двойственноrо кода назовем nрове-
130
r лава 3
рочн,ой матрицей (или просто матрицей Н) исходноrо кода с.
Матрица Н имеет размер (n k) Х п. По определению
Но Т === О # v Е с. (3.1)
В частности, если взять в качестве векторов v базисные векторы
кода с, то получим
НОТ == О,
rде О........... нулевая матрица. С помощью матрицы Н, например,
задавался код в примере 1.4. Поскольку по определению paHr
матрицы Н равен (п........... k), то Н содержит невырожденную под-
матрицу Н' размера (п k) Х (п k). Путем перестановки
столбцов Н и соответствующеrо изменения нумерации компо-
нент кодовых векторов всеrда можно добиться Toro, чтобы мат-
рица Н' была образована последними (п k) столбцами Н.
Как хорошо известно, с помощью элементарных операций над
строками [умножения строк на ненулевые элементы поля GF(q)
и сложения одной строки с друrой] матрица Н всеrда может
быть приведена к следующему виду:
Но == [Р, 1 n k],
rде р........... некоторая матрица размера (п k) Х k, а 1 n h еди-
ничная матрица размера (п k) Х (п k).
Поскольку НО получена посредством элементарных операций
над строками, то
(3.2)
Hv T == о # Hov T === О,
(3.3)
Т. е. Но также является проверочной ма1рицей кода с. Обозна-
чим через Pij элемент подматрицы Р матрицы Но, стоящий в
;-й строке и j-M столбце. Очевидно, что необходимым и доста-
точным условием принадлежности вектора v == (V}, ..., v n ) коду
с является выполнение следующей системы равенств:
k
Vk+l == ....... L PljV " 1 i п k. (3.4)
j }
Таким образом, если компоненты vl, . . . , Vk Е ОР (q) заданы, то
существует ровно один кодовый вектор, первыми k компонен-
тами KOToporo являются аl, ..., Vk, И равенства (3.4) задают
остальные компоненты этоrо кодовоrо вектора. Друrими слова-
ми, мы показали, что любой линейный код является системати-
ческим, и получили при этом равенства (3.4), которые описывают
процедуру кодирования. В самом деле, первые k компонент ко-
д.овоrо вектора можно считать информационными и использо-
вать для передачи блоков длины k, поступающих от источника,
а остальные (п k) компонент можно вычислять с помощыо
равенств (3.4).
л инеn'ные и циклические коды
131
Утверждение 3.1. Пусть проверочная матрица линейНО2()
(n, k) Koдa С имеет вид Н,о == [Р, / n k]. Тоеда матрица 00 ==
== [1 k РТ] является nорождающей матрицей кода С. Справед-
ливо TaK;JlCe и обратное утверждение.
Краткое доказательство. PaHr O(J равен k. Поскольку Н о О6 ==
== Р/ k ......... 1 n kP == О, то каждая строка 00 является кодовым
вектором кода С.
Вернемся к примеру 1.4. Изменяя нумерацию компонент ко-
довых векторов, можно привести проверочную матрицу рас-
смаrриваемоrо кода к виду (3.2). В данном случае
[ 1 1 О 1 1 О О ]
Но == 1 О 1 1 О 1 О .
0111 О 01
Но тоrда, как следует из утверждения 3.1, проверочная MaT
рица кода, двойственноrо (7.4) KOДY Хэмминrа из примера 1.4,
имеет следующий вид:
1 О О О 1
О 1 О О 1
О О 1 О О
О О О 1 1
1 О
О 1
1 1
1 1
Пример 3.1. Пусть С линейный q"ичный (n, k)-код. Линей-
ный q ичный (п + 1, k )"код
С ех :=: { ( /t. О/. О.. ,. '. Оn) (о.. ,. '. оп) Е С }
называется расширением кода с. Исходный код С при этом
называют укорочением расширенноrо кода С ех . Множество
{ (Оl. . . '. оn) t О/:=: О. (о,. ',.. оn) Е С } является (n, k 1)..под-
t == 1
кодом кода С и называется четным nодкодОА! кода С. Если С еХ
содержит вектор (1, .. *, 1), то двойственный код C exD кода С еХ
является расширением двойственноrо кода C ) четноrо подкода С(е)
кода С.
Доказательство. Пусть (ио, UI, ..., и n ) Е C eXD . Поскольку
(1, 1, ..., 1) Е С ех, то
п
ио + L иi === о.
1..1
Следовательно, C exD ......... расширение кода c SlD == {(Ur, и2, ...,
и n ) I (ио, UI, . . ., и n ) Е C exD ). Число информационных символов
132
,;.
r лава 3
кода C D совпадает с числом
кода C exD И равно n k 1.
(v V V ) с..=:=. С (е) то
1, 2,..., n ,
информационных символов
Если (и:,..., и n ) Е C D И
( t и/ ) ( f VI ) + t щv/==о.
ic::l 1==1 i==1
п n
Так как L Vi === о, то L UiVi == о, а это значит, что
[ o i==I
(UI, и2, . . ., И n ) Е C ). Далее, поскольку число информационных
символов кода сь равно n k + 1 и совпадает с числом ин-
формационных символов кода C D, то C ) === c slD.
Приведенные выше положения теории кодирования пред
ставляют собой достаточно хорошо известные факты линейной
алrебры. Однако с введением понятия веса, которое иrрает
центральную роль в теории кодирования, теория линейных кодов
приобретает собственные характерные черты. Приведенная ниже
теорема показывает, каким образом :минимальный вес кода MO
жет быть связан с классическими понятие f линейной зависи-
мости.
Обозначим через h i i й столбец проверочной матрицы Н ли..
нейноrо кода С. Пусть v == (Vl, ..., V 1t )......... кодовый вектор веса
w, ненулевые компоненты KOToporo имеют номера i}, ..., lш.
Из формулы (3.1) имеем
w
L v//h//==O.
/...}
Следовательно, столбцы Н с номерами i}, ..., i ю должны быть
линейно зависимыми. Наоборот, предположим, что w столбцов
Н с номерами i t , ..., iw линейно заВИСН fЫ, но любая совокуп
ность меньшеrо числа из них оказывается линейно независимой.
Из определения линейной зависимости следует существование
ненулевых элементов aj Е GF(q), 1 j w, таких, что
w
L ajh lj == о.
J-=I
(3.5)
Пусть V == (V}, . . . , V n ) вектор, у KOToporo компоненты с HOMe
раr\1И i j , 1 j w, равны aj, а друrие рапны О. Тоrда в силу
равенства (3.5)
н v T == О
,
Т. е. V кодовый вектор веса w.
Таким образом, мы доказали слеДУЮЩУIО Teope iY.
Лuнейные и циклические коды
133
Теорема 3.1. Минимальный вес линейноео (n, k) Koдa С pa
вен d Т02да и только тоеда, коеда любые (d 1) столбцов npo
верочноu матрицы 9Т020 кода линейно независимы, но некото-
рые d столбцов nроверочН,оu матрицы линейно зависимы.
Прямым следствием этой теоремы является следующее.
Следствие 3.1. d n k + 1.
Линейный код, для KOToporo последнее соотношение выпол-
няется со знаком равенства, называется разделимым кодом
с достиЖИА!ЫМ максимаЛЬНЫhl раССТОЯfluе.Аl. Примерами таких
кодов являются описанные ниже коды Рида Соломона, а TaK
же БЧХ коды из примера 4.5.
Доказанная простая теорема указывает способ прямоrо по-
строения проверочных матриц Н кода с заданными парамет-
рамп п, k и d. Она оказывается полезной при построении и ис
следовании не только БЧХ кодов и кодов rоппы, но и кодов
Сриваставы [9] и друrих кодов. Кроме Toro, на основании этой
теоремы выводится rраница Варшамова rилберта. До сих пор
V I считалось конечным полем, однако в действительности можно
рассмотреть более общий случаЙ, коrда V 1 является конечным
кольцом. Однако, поскольку в этом более общем случае не
удается получить I{аI(ие либо полезные результаты, далее мы
будем по пре}l{нему считать, что V 1 конечное поле.
Утверждение 3.2. Пусть q степень nростоео числа и n ==
== (qm 1) / (q 1), II пусть сх, nримитивный элемент поля
GF(qm). Представим !f-аждыu элемент a,i, О i < n, поля
GF(qт) в виде
т
aJ === L aliaJ I, аи Е ОР (q).
/::::1
Пусть Af == (a 1i , a 2i , . . " a тi ). Тоеда q uчный линейный (n,
II "l) Koд, задаваемыu проверочной матрицей Н === (AoAI . . .
... Aп l) раЗ/l4ера т Х n, является совершенным кодом, исправ-
ляющим одиночные ошибки.
Доказательство. Пусть v == (vo, V], . . . , Vn l) вектор из V n'
таI{ОЙ, что все ero компоненты, за ИСКЛIочением Vl 1 и Vi 2 (i 1 < i 2 ),
равны нулю. Если предположить, что Hv T == О, то
vl 1 A i1 + vl 2 A l2 о.
Но тоrда, если один из элементов Vl 1 или Vl 2 равен нулю, то
и друrой элемент также должен быть равен нулю. Если же
Vl 1 , Vl 2 =1= О, то из определения A i имеем
vl 1 a l1 + vl'!a l2 === О,
......... v. V ) == ai2 11
'1 12 '
134
r лава .']
rде О < i 2
i 1 < n и ....... ViLV
1 Е ОР (q)....... {О}. Возводя обе части
п6следнеrо равенства в степень q....... 1, получаем
1 === a(q
l) ({2
(1).
Это приводит К противоречию, ПОСI{ОЛЬКУ О < (q
1) (i 2
i l ) <
< qm ....... 1. Следовательно, минимальное расстояние рассматри"
BaeMoro. кода не меньше 3. Более Toro, поскольку этот код ле..
жит на rранице Хэмминrа при t == 1, он является совершенным.
Этот код называется q
ичным (обобщенным) кодом Хэммuнеа.
3.2. Методы декодирования линейных кодов
Рассмотрим далее методы декодирования линейных кодов.
Пусть V
переданный кодовый вектор, а и
соответствующий
ему принятый вектор (получающийся 'в результате разбиения
последовательности символов на выходе демодулятора на блоки
длины п в соответствии с разбиением на блоки передаваемой
последовательности). Вектор е == и
V называется вектором
ошибок, а вектор иНТ Е V n
h
синдромом, соответствующим
вектору и Е V n. Как следует из формулы (3.1), VHT === О. По
этому
иНТ == (и
v) НТ == еНТ.
(3.6)
Векторы х, у
v n называются сравнимыми по модулю С, если
(х....... у) Е С {12]; сравнимость векторов обозначается следую
щим образом: х == у (mod С). Из определения сравнимости век-
торов непосредственно слеДУЕ=Т, что: 1) х == х (mod С); 2) если
х == у (mod С), то у == х (mod С) и 3) если х == у, у == z (rnod С),
то х == z (mod С). В этом случае, как хорошо известно, множе..
ство V n мо)кно разбить на непересекающиеся классы таким об..
разом, что любые два вектора из одноrо класса будут сравнимы
,по модулю С, но любые два вектора из разных классов не будут
.сравнимыми по модулю С. Эти классы называют смежными
классами (см. утверждение 2.5 и раздел, посвященный нормаль
ным делителям). Смежный класс, содержащий вектор х, будем
обозначать через (х). Заметим, что смежный класс (О) совпа..
дae
' с кодом С. в общем случае
(х) == {у I у == х + v, V Е С}.
Это соотношение показывает, что каждый смежный класс со..
стоит из qk векторов. Число различных смежных классов равно
qn
k. Так как в силу (3.1)
х == у (mod С)#х
у Е С#хНТ == уНТ,
то необходимым и достаточным условием Toro, что векторы
Ц у принадлежат одному смежному классу, является раве»ство
Лuнеtlные и циклические "оды
135
соответствующих им синдромов хНТ И уНТ. Друrими словами,
синдром 5 вектора х однозначно определяет смежный класс, ко-
торому принадлежит х. Обозначим смежный класс, соответ-
ствующий синдрому s, через С(5).
ПреДПОЛО}l{ИМ, что все кодовые векторы передаются с рав-
ными вероятностями и вероятность получить при приеме вектор
v + е, rде v переданный кодовый вектор, зависит только от
вектора ошибок е. Пусть e(l) и е(2) векторы ошибок, принадле-
жащие одному смежному классу (e(l») == (е(2»). Предположим, что
передавался кодовый вектор v, а был принят вектор v + еР).
Так как e(l) е(2) Е С, то В деЙСТВИ1ельности при приеме есть все
основания предположить, что пеРЕ'давался кодовый вектор
u == v + еР) е(2), вектор ошибок был равен е(2), а принят вектор
tl + е(2) (== v + еР»). При этом должно быть принято то решение,
которое имеет наибольшую вероятность оказаться правильным.
СлеДОJ3ательно, из всех векторов ошибок, принадлежащих од-
ному смежному классу, должен быть выбран тот, который
имеет наибольшую вероятность. Этот вектор называется преД-
ставителем или лидером cBoero смежноrо класса. Как указыва..
лось выше, в дек или канале, являющемся обобщением дск
на q ичный случай, лидером смежноrо класса является вектор
минимальноrо веса.
Для декодирования линейноrо кода можно построить таб-
лицу декодирования, которая каждому вектору 5 Е V n k сопо-
ставляет лидер смежноrо класса С (5). При этом декодирование
линейноrо кода осуществляется следующим образом:
1) По принятому вектору u вычисляется синдром 5 === ufJT.
2) е помощью таблицы декодирования находится вектор
ошибок е, соответствующий данному 5; кодовое слово u е по-
сылается на выход декодер"а.
Задача 3.3. Описать таблицу декодирования в случае, если
часть ошибок декодируется (исправляется), а друrая часть об-
наруживается.
Пример 3.2. Рассмотрим двоичный линейный (6, 3) KOД, за-
v v
даваемыи проверочнои матрицеи
[ 1 О 1
Н=== О 1 1
1 1 1
1
О
О
о
1
О
].
Этот код получается из (7, 3) -кода Хэмминrа, описанноrо в при-
мере 1.4 из разд. 1.1, удалением третьей компоненты во всех
кодовых словах и изменением нумерации остальных компонент.
В первой строке табл. 3.1 перечислены все кодовые векторы рас-
сматриваемоrо кода. Поскольку таблица имеет большие раз-
136 (лава 3
Таблица 3.1
Смежные классы кода из примера 3.2
Синдром Лидеры смежных классов
000 (00) ( 17) (23) (34) (45) (52) (66) (71 )
001 (01 ) ( 16) (22) (35) (44) (53) (67) (70)
010 (02) ( 15) (21) (36) (47) (50) (64) (73)
100 (04) ( 13) (27) (30) (41 ) (56) (62) (75)
111 (1 О) (07) (33) (24) (55) (42) (76) (61 )
011 (20) (37) (03) ( 14) (65) (72) (46) (51 )
101 (40) (57) (63) (74) (05) ( 12) (26) (31 )
110 (06) ( 11 ) (25) (32) (43) (54) (60) (77)
меры, то двоичные векторы записаны в восьмеричном представ-
лении; например, вектору (101110) соответствует запись (56).
В каждой из друrих строк этой таблицы перечислены векторы
одноrо из смежных классов. Так как этот код исправляет все
одиночные ошибки (см. пример 1.4), то все векторы веса 1
можно взять в качестве лидеров смежных классов. В последнем
смежном классе вектор (000110) является вектором минималь-
Horo веса, так что ero можно выбрать в качестве лидера этоrо
смежноrо класса. Таким образом, рассматриваемый код исправ-
ляет все одиночные ошибки и одну ошибку веса 2. При исполь-
зовании этоrо кода в ДСК дЛЯ исправления ошибок вероятность
правильноrо декодирования равна
p + 6pgqo + P q6
(предполаrается, что все кодовые векторы посылаются с paB
ными вероятностями).
Так как сам код С как сме}I(НЫЙ класс соответствует отсут.
ствию ошибок, то в качестве лидеров qn k 1 остальных смеж.
ных классов желательно иметь BeI{TOpbI, которые как векторы
ошибок имеlОТ наибольшие вероятности появления. Если в Ka
честве лидеров qn k смежных классов удается взять все векторы
веса t и меньше и только их, то код С является совершенным,
так как
t
L ( ) (q......... l)l === qn k 1.
i=sl L
Как указывалось в разд. 1.4.1, совершенных {{ОДОВ существует
Не очень MHoro. Более широким является класс так называеl\1ЫХ
кваэисовершенных кодов. КвазuсовершеННblМU называются та-
кие линейные коды, в качестве лидеров qп k смежных классов
которых можно взять все векторы веса t и менее и несколько
Линейные и циклические коды
137
векторов веса t + 1. Если канал является дск или обобщением
ДСК на q ичный случай, то в классе линейных кодов содинако..
выми параметрами квазисовершенные коды имеют минимальную
вероятность ошибки декодирования. I(вазисовершенные коды,
так же как и совершенные коды, MorYT не существовать при не-
которых значениях n и d (например, двоичные квазисовершен"
ные коды с параметрами n == 15, d === 5 и n === 17, d === 5 суще..
u
ствуют, а двоичныи !{вазисовершенныи код с параметрами
n == 16, d == 5 не существует [1 О]), однако квазисовершенных
кодов существует rораздо больше, чем cOBepIlIeHHbIx. Например,
квазисовершенными являются код из примера 3.2 и все двоич"
ные БЧХ коды, исправляющие ошибки веса 2 [11]. Кроме Toro,
при d == 5 и q == 2 всеrда существует по крайней мере один
квазисовершенный код с любым наперед заданным числом про..
верочных символов (утверждение 3.9).
Число строк описанной выше таблицы декодирования ли..
нейноrо кода равно qп h. По сравнеНИIО с числом qn строк таб..
лицы декодирования произвольноrо блоковоrо кода число qn h
строк В описанной таблице значительно меньше, однако, на..
пример при q === 2 и n k == 30, таблица декодирования линей..
Horo кода содержит более чем 109 строк, что, конечно, остается
практически неприемлемым. Вполне естественно поэтому пе..
рейти к исследованию более полезных кодов, для которых суще..
ствуют практически приемлемые алrоритмы нахождения вектора
ошибок по СИНДРО 1У. Ниже в разд. 3.5 рассматривается один из
таких классов кодов.
Утверждение 3.4. Если в линейном двоичном (n, k) ..коде су.
ществуют кодовые векторы нечеТН020 веса, то их число равно
2h 1. Более Т020, множество всех кодовых векторов чеТН020 веса
образует подкод Се размерности k 1.
Краткое доказательство. Сначала следует доказать вторую
часть утвер}l{дения. Далее, если Vнечетн один из кодовых век..
торов нечетноrо веса, то множество {Vнечетн + и I и Е Се} является
смежным I{лассом по подrруппе Се. Этот смежный класс состоит
только из кодовых векторов нечетноrо веса, а их число
равно 2h l.
Утверждение 3.5. Если хотя бы один из кодовых веКТОрОВ
q"UЧНО20 линеUНО20 (n, k) Koдa имеет ненулевую i ю KOMnO
ненту, то число кодовых векторов, i я компонента которых равна
элементу а поля G F (q), составляет qk l.
Краткое доказательство. Мно)кество всех кодовых векторов,
i..я ко понента которых равна нулю, является подпространством
размерности (k 1). Для доказатель тва утверждения следует
]38
r лава 3
рассмотреть порождаемое этим подпросrранством разложение
рассматриваемоrо кода на смежные классы. Множество кодовых
векторов, имеющих одну и ту же i ю компоненту, является одним
из смежных классов этоrо разложения.
Утверждение 3.6 [8]. Если для каждоео целоео i, 1 i п,
8 коде существует хотя бы один кодовый вектор, i я компонента
КОТОР020 не равна нулю, то сумма весов всех кодовых векторов
q ичноео линейноео (n, k) Koдa равна n (q 1) qh l.
Идея доказательства. Следует воспользоваться тем, что, co
rласно утверждению 3.5, число кодовых векторов, i я компо-
нента которых не равна нулю, состаВJlяет (q l)qk l.
Утверждение 3.7. Пусть С представляет собой q ичный Лll-
нейный (n, k) -код. Тоrда:
1) если код С обнаруживает пачки ошибок длины Ь и Ate-
нее, то
n ........ k Ь;
2) если код С исправляет пачки ошибок длины Ь и менее, то
n k 2Ь.
Эти соотношения известны как нижние ераницы Рейд-
жера {12].
Краткое доказательство. Пусть V множество векторов из
V n' все компоненты которых с (i + 1) й ПО Il Ю равны нулю.
Рассмотрим случай 1. Предположим, что два различных вектора
из V принадлежат одному и тому же смежному классу по
Ilодrруппе с. Тоrда существует ненулевой вектор v Е \' , при.,
надлежащий коду С, т. е. код С не обнаруживает по крайней
мере одну пачку ошибок длины Ь или менее, какой является
вектор и. Следовательно, число смежных классов не может быть
меньше, чем qb. Отсюда следует, что n k Ь. Рассмотрим
случай 2. Аналоrично можно доказать, что никакие два различ-
'12b "
ных вектора из 'n не должны входить в один смеЖНЬiИ класс.
Следовательно, число сме)I{НЫХ классов не может быть меньше,
чем q2b, т. е. n k 2Ь.
Утверждение 3.8 [13]. Пусть С двоичный линейный (п,k)-
код с минимальным расстоянием d и nорождающей матрицей а.
Предположим, что среди лидеров смежных классов (в качестве
которых берутся векторы lинимаЛЬН020 веса) существуют век-
торы веса d 1 или более; пусть и один из таких лидеров.
То?да . Ul1имальное расстоянце дВQuчноео лuнеUf(оео (п + 1,
Линейные II циклические коды
139
k + 1) Koдa С', задаваемоzо nорождающей матрицей
O
а' ==
G
, равно d.
о
и 1
К ратк ое доказательство. Пусть V === (VI, V2, . . . , V N , Vп+l) KO
ДОВЫЙ вектор кода С'о Если Vn+1 == О, то .вес V не меньше чем cl,
так как (Vl' . . ., V n ) Е с. Если Vn+l === 1, то (Vl' V2, ..., v n ) ===
==(иl' и 2 , ..., и n ) +(V t V , о. о, V ), rде (v , V o ..., V ) Е Со
Это равенство показывает, что вектор (V}, V2, . . . , V n) принадле-
}кит тому же смежному классу, что и вектор (и}, и2, . . . , и n ),
а следовательно, вес (Vl, V2,..., v n ) не меньше чем d 1.
Утверждение 3.9 {13]. В утверждении 3.8 положим d == 5.
Если код С не является квазисовершенным, то условия утверж-
дения 3.8 выполняются, так что существует код С' с d == 5.
Если в свою очередь код С' не является КВGзtlсовеРUlенным, то
по С' описанным в утверждении 3.8 способом можно построить
новый код и т. д. Эта nроцедура всееда приводит к квазисовер-
шенному коду.
Краткое доказательство. Заметим, что каждый вновь по
строенный код имеет то же число проверочных символов, что
и исходный код. rраница Хэмминrа в этом частном случае
u
имеет следующии вид:
log2 ( 1 + n + п (п 2+ 1» ) '.
Из этоrо неравенст,ва видно, что описанная выше процедура
построения последовательности кодов должна закончиться че..
рез конечное число шаrов.
Утверждение 3.10 [8]. Двоичные квазисовершенные коды
длины n, исправляющие одиночные ошибки, существуют для
всех n, заключенных в пределах 2m/2+1 2 n < 2т, еде т
произвольное четное число, и 2(m+I)/2 + 2(nl 1)/2 2 n 2т, еде
т. произвольное нечетное число.
Краткое доказательство. Квазисовершенными кодами длины
n == 2m/2+1 2 при четном т и n == 2(1)1.+1)/2 + 2(т 1)/2 2 при He
четном т являются коды, столбцами проверочных матриц раз-
мера т Х n которых являются: 1) все вектор"столбцы, первые
(m/2] компонент которых равны нулю, и 2) все вектор столбцы,
последние т [mj2] компонент которых равны нулю (нулевые
векторы в число столбцов проверочной матрицы не вклю"
чаIОТСЯ). Поскольку произвольный вектор столбец длины т мо"
жет быть представлен в виде суммы вектор столбца первоrо
140
r лава 3
типа и вектор
столбца BToporo типа, то для Лlобоrо двоичноrо
вектора v длины n найдется вектор и длины n веса 2 или менее,
такой, что их сумма v + и будет кодовым словом. Следова.
тельно, все лидеры смежных классов рассматриваемоrо кода
имеют вес 2 или менее.
3.3. Нижняя rраница Варшамова
rилберта
в разд. 1.4 выше были получены верхние rраницы для про..
извольных блоковых кодов. Здесь мы получиrvf нижнюю rраницу
Варшамова
rилберта, которая rарантирует существование ли
"
неиноrо кода с заданным числом проверочных символов r ==
== n ......... k и заданным минимальным расстоянием d, число ин..
фОР
lационных символов KOToporo больше определенной вели..
чины (вначале rилберт получил Э1У rраницу для блокозых
кодов (14]; Варшамов улучшил результат rилберта, получив
аналоrичную rраницу для линейных кодов [15, 16]).
Теорема 3.2. Пусть q
степень простосо числа, а , и d
не-
которые целые положительные числа. Тоеда существует q
ичный
линейный код длины n с r nроверОЧНblМU символами и кодО8ЫJИ
расстоянием, не меньши.Jt d, nараJлетры КОТОрОсО удовлетворяют
неравенству
d
2
q'
L (
) (q
1)1.
i =:0 1
И сnользуя функцию ер из неравенства Чернова, неравенство
(3.7) можно заменить следующиАt:
.!..
( d
2 ) .
n
ep n
В частности, при q == 2 последнее неравенство имеет вид
!..
H ( d
2 ) .
n
n
Доказательство. Как следует из теоремы 3.1, построение мат..
рицы Н, любые d
1 столбцов которой линейно независимы,
эквивалентно построению кода с минимальным расстоянием, не
меньшим d. Построим матрицу Н, удовлетворяющую указанному
выше свойству, следующим образом. Вначале произвольныы
образом выберем в множестве v; == V,
{нулевой вектор}
l..й столбец h 1 матрицы Н.
В качестве 2
ro столбца h 2 матрицы Н возьмем произвольный
вектор из v;, не являющийся произведением ah l , ае: GF(q).
Если в v; существует хотя бы один вектор, не ЯВЛЯIОЩИЙСЯ
линейной комбинацией h l и h 2 , то выберем один из этих векто..
(3.7)
(3.8)
(3.8')
J1 инецные и циклические коды
141
ров (произвольныЙ) В качестве h з . Предполо}ким, что таким оп-
разом мы выбрали j векторов h i , О i j; по построению h i
не является линейной комбинацией никаких d 2 или менее
СТО.lIбцов из h 1 , ..., hi l. Поскольку i (О i d 2) векторов
из h}, ..., h j можно выбрать ({) способами, а число способов
выбора i ненулевых коэффициентов линейной КО!\1бинации равно
(q 1) i, то число векторов, являющихся линейными комбина-
циями d 2 или менее столбцов из h l , ..., h j не больше
d 2
L ( ) (q l)l.
i } L
I I
Если это число меньше общеrо числа векторов в V r, то В V r
v v
существует вектор, не совпадающии ни с однои из указанных
выше линейных комбинаций. Этот вектор можно выбрать в ка-
. честве hj+l. К тому моменту, коrда новый вектор hn+l выбрать
уже нельзя, общее число п выбранных ранее векторов h i удов-
летворяет неравенству (п является длиной кода)
d 2
l: ( ;)(q 1)I qT l.
t ..1
Из этоrо неравенства и rраницы Чернова получаются неравен-
ства (3.8) и (3.8').
На фиr. 3.1 показано поведение верхних rраниц Плоткина,
Хэмминrа и Элайса, а также нижней rраницы Варшамова
rилберта при достаточно БОJIЬШИХ n (здесь по вертикальной оси
откладывается скорость кода R == k/п, а по rоризонтальной
отношение минимальноrо расстояния d мин к 2п [8].
Вывод неравенства (3.7), как мы видели выше, допускает
.пюбой способ выбора векторов h}, . . . , h i , . . . , удовлетворяющих
условиям теоремы 3.1. Поэтому если задан линейный (n,k) код
с минимальным весом d, параметры n, k и d KOToporo удовле-
творяют неравенству (3.7), то к проверочной матрице этоrо
кода всеrда можно добавить еще один столбец, не нарушая
при этом условий теоремы 3.1. Друrими словами, сохраняя по-
стоянным и число проверочных символов, и минимальный вес
и увеличивая число информационных символов, можно расши-
рить исходный код. Как показывают несло}кные расчеты, ми-
нимальный вес почти всех линейных кодов близок к величинс,
rарантируемой неравенством (3.7) [8]. Из неравенства (3.8')
следует, что при фиксированном отношении d/n « 1/2) и n oo
существуют линейные коды, для которых 01ношение k/n больше
1 Н (d/n). Здесь следует заметить, что для БЧХ кодов, обла-
дающих хорошими свойствами с точки зрения кодирования
и декодирования, при фиксироваННОI\f d/n и n 00 отношение
142
[лава 3
k/n стремится к нулю (СМ. разд. 4.1). За исключением кодов
lOcTeceHa [14], все известные к настоящему времени алrебраи-
ческие коды обладают этим недостатком. Однако и для кодов
Юстесена отношение k/n значительно меньше величины, rapaH-
тируемой rраницей Варшамова
rилберта. Построение лежа-
щих на rранице Варша
ова
rилберта (или близко к ней)
кодов, способ построения которых можно было бы задать явно
(конструктивно) и которые обладали бы хорошими проuедурами
кодирования и декодирования, является одной из нерешенных
проблем теории кодирования 1). Так как параметры двоичных
1,0
06
J
0,4
0,2
0,8
о 0,1 0,156 0,2 0,3 0,4 О,!;
Поло8ина MUHUMQ/lbHOZO расстояния
Фиr. 3.1.
А
верхняя rраница Плоткина; Б
верхняя rраница Хэмминrа; В
верхняя rраница
Элайса; r
нижняя rраНИI
а Варшамова
rи.пберта.
БЧХ
кодов С ДЛИНОЙ порядка нескольких тысяч являются не
столь уж плохими [8] по сравнению с параметрами, задавае-
мыми (3.8), то исследование асимптотических евойств кодов
при больших длинах представляет rлавным образом теоретиче-
"
скии интерес.
3.4. Распределение весов
Рассмотрим q-ичный линейный (n, k)
KOД, содержащий A i
кодовых векторов веса i. Совокупносrь чисел Ао, A 1 , ..., А п на.
1) Эти вопросы более подробно освеlцеllЫ в книrе Э. J1. Блоха и
В. 13. Зяблова [39] 1I в статье л. А. Бассалыrо [40].
П рим. ред.
л инейные u цtlклuческuе коды
143
зывается распределением весов, а мноrочлен
n
А (z) == L AlZI
i=sO
нумератором весов кода с.
Предположим, что код С является линейным, имеет мини...
Аtальное расстояние d и используется в двоичном симметричном
канале (ДСК) с вероятностью ошибки в символе Ро. Выразим
вероятность ошибочноrо декодирования Р de И вероятность об
наружения ошибки (отказа от декодирования) P df через HYMe
ратор весов кода С [9, 17]. Сначала рассмотрим следующую
процедуру декодирования: принятые кодовые векторы декоДи-
руются в самих себя, а при получении любоrо друrоrо вектора,
не являющеrося кодовым, констатируется лишь факт обнару-
жения ошибки. В этом случае вероятность ошибочноrо декоди-
рования совпадает с вероятностью Toro, что вектор ошибки
является одним из ненулевых кодовых векторов, которая в свою
очередь равна
n
L AiP (1 Po)п l === (1 Ро)n А [Р о /( 1 Р О )] (1 РО)n.
lc::::l
Поскольку вероятность обнаРУ}I{ения ошибки (отказа от деко-
дирования) Р df может быть получена вычитанием Р de из ве-
роятности TOI'O, что вектор ошибок является ненулевым, то
Р df === 1 (1 Ро)n А [Ро/( 1 Ро)].
Далее предположим, что d 2t + 1, и рассмотрим следующую
процедуру декодирования. Если принятый вектор находится на
расстоянии t или менее от одноrо из кодовых слов (такое кодо-
вое слопо, если оно существует, может быть только одно), то
он декодируется в это кодовое слово. В остальных случаях
ошибки обнаруживаются, но декодирование не про изводится.
Так как в это случае вероятность правильноrо декодирования
P dc равна вероятности Toro, что в канале возникнет не более
че А t ошибок, то
t
Р dc == { O ( ;) p (1 po)n ! ·
(3.9)
Вероятность ошибочноrо декодирования равна вероятности
Toro, что вектор ошибок в канале принадлежит смежному классу
с минимальным весом t или менее (или, друrими словами, смеж
НОМУ классу лидер KOToporo имеет вес t или менее), но не яв
ляется лидером этоrо смежноrо класса. Рассмотрим совокуп
ность векторов и Е V n веса w, находящихся на расстоянии j от
вектора v веса i. Число таких векторов обозначим через N ) и"
144
r лава 3
Очевидно, что Nj )w не зависит от Toro, какие компоненты v рав..
ны 1. Для простоты В качестве v возьмем вектор, у l<oToporo все
компоненты с l й по i ю равны 1, а остальные равны О. Заметим,
что если 1 число равных единице компонент вектора u с HOMe
рами от 1 до i, то 21 === w + i ........ j. Поэтому 1)
(О ( i ) ( n ........ i )
Ni.w (w+i j)/2 (w i+j)/2'
Введем мноrочлен N(i) (х, у) == L L N )wx/yw. Леrко про..
j w
верить, что
N (i) (х, у) == t I ( i ) ( n ........ i ) Xi v +11 У v + J.t === (х + у) i (1 + х у) n i .
v == О IJ. == О 'v f..t
(3.1 О)
Так как 2t + 1 d, то при j t ни один вектор не может
находиться на расстоянии j или меньше сразу от двух кодовых
векторов. Поэтому общее число векторов веса w, находящихся
на расстоянии j (j t) от кодовых векторов, равно
n
" А N (i) .
L..J i j,w, J t.
i==O
Отсюда в свою очередь следует, что общее число векторов
веса w, принадле)кащих смежным классам с минимальным Be
сом t и менее, равно
t п
" " а)
L..J L..J AiN /' w, j t.
/z=Oi O
Но тоrда вероятность Toro, что вектор ошибок принадлежит
смежному классу с минимальным весом t и менее, т. е. вероят"
ность Toro, что принятое слово будет неправильно декодировано,
равна
n t n
L L L AiN(i) pW ( 1 ........ р ) n w .
О / О . J /. w о о
и'== == t===
Для удобства расчета последней вероятности часто используется
мноrочлен
t n n
Р t (Х) === L AiN :) wP (1 ........ Po)п W х/ .
J == 'J w==O t ==0
t) В случае коrда п < т или т < о, полаrаем ( ) == о.
Линейные и ЦUl\,лutl.еСКllР коды
145
Из определения Pt (х) непосредственно следует, что
P dc + P de == Pt (1).
(3.11)
Мноrочлен Pt (х) является суммой первых t членов вида Ajx J
(степени j < t) следующеrо мноrочлена:
ппп
Р n (х) == L L AiN :) wP (1 po)n w х/.
J O w==O t==O
11спользуя формулу (3.1 О), мноrочлен Р n (х) путем несложных
преобразований МО)I{НО привести к виду
n
Р п (х) == I A i (х ХРо + PO)i (1 Ро + xpo)n i ==
i O
=== (1 Ро + хро)n А ( Х ХРо + Ро ) .
I Ро + ХРо
Так как Р df == 1 Р dc Р de, то, зная А (х), с помощью фор
мул (3.9) и (3.11) можно найти P dc , P de И Pdf. Это показывает,
что нумератор весов является одной из важнейших характерис-
тик кода. Однако нумераторы весов не дают полной информации
о распределении весов лидеров смежных классов веса d/2 ибо..
лее. Более Toro, существуют коды с одним и тем же HYMepaTO
ром весов, имеющие, однако, различные распределения весов
лидеров сме}кных классов [9].
Для некоторых классов кодов, например разделимых кодов
с максимально достижимым расстоянием, БЧХ кодов, исправ
ляющих t KpaTHbIe ОlIlибки (только при t 3), и ряда друrих,
известны общие формулы для распределения весов {9, 18 26].
Однако определение распределения весов произвольноrо кода
является непростой задачей. Конечно, для кодов с неБОЛЬШИ l
числом информационных символов, используя вычислитеЛЬНУIО
машину, с помощью порождающей матрицы можно механически
породить все кодовые слова и найти таким образом распределе
ние весов. При небольших значениях числа проверочных сим..
волов (п k) для нахождения распределения весов можно BOC
пользоваться следующим тождеством Мак Вильямс [17].
'JeopeMa 3.3. Пусть С представляет собой q uчный линейный
(n, k) Koд, C D код, двойственныЙ к С, а А (z) и В (z) соот-
ветственно нумераторы весов кодов С и C D . Tozaa
А (z) == qk п (1 + (q 1) z)n В ( I + 1(;- 1) z ) .
Доказательство. Множество векторов, у которых ФИI{сирован-
НЫе j компонент равны О, очевидно, является подпространством.
Выбирая различными способами положение этих j компонент,
146
r лава :1
можно построить ( ; ) таких подпространств S(m), 1 :::::; т :::::; ( ).
Обозначим через Sb m ) подпространство, двойственное к S(m);
sb m ) состоит из векторов, фиксированные п j компонент ко-
торых (дополнительные к j нулевым фиксированным компонен-
там: векторов из S(т» равны о. Положим I v n S(m) 1=== 1, если
вектор v принадлея{ит S(m), И I v n S(rn) 1== о в противном случае.
Если вектор v имеет вес i и п i j, то для подпространств
S(m), которые определяются выбором j компонент из п i ну-
левых компонент вектора v, имеем I v n S(n1) 1== 1; I v n S(m) 1== о
для всех остальных подпространств S(т). Следовательно,
(;) ( n i )
L I v n S(т) 1 === j ·
m=sl
Но Tor да
(n) (n)
t I с n S(т) I == L t I v n S(т) I == L A i ( n i ) . (3.12)
m==1 ОЕС m=sl i /
Аналоrично получаем
(;) (7) .
L ICDns )I== L L 'vns )I=== L B i ( n ) . (3.13)
m==1 V ECD m 1 i n /
с друrой стороны, из утверждения 2.35 следует, что
I СП s(m) I === qk /I C D n Sb т ) 1.
Из формул (3.12) и (3.13) имеем
( n i ) ( п i )
L A i . == qk / L B i . .
i J i n ]
Заметим, что j в последнем равенстве является произвольным
целым числом из интервала (о, п]. Умножим обе части (3.15) на
x j и просуммируем по j. При ЭТОМ в левой части получим сле
дующую сумму:
L L A i ( n i ) Х/ == L A i (1 + x)n l .
/ l J i
(3.14)
(3.15)
в то же время сумма в правой части будет равна
Iqk IIBi(:= )xl==qk ( ; )пIBi(1 + : )п i.
I i t
/1 инейные II циклические ,соды
147
Разделив обе части получаЮIЦеrося в результате равенства на
(1 +х)n, получим
I А ! ( 1 х У == qk n ( i t: )n I В ! ( q х у.
l i
Замена z == 1/ (1 + х), х == (1 z) /z переводит последнее равен-
ство в то}кдество Мак Вильямс.
Если часть параметров A i и В; известна, то для нахождения
оставшихся можно воспользоваться то}кдествами Плесс [8, 9, 27],
представляющими собой модифицированные тождества Мак-
Вильямс.
Понятие двойственноrо кода может быть обобщено на слу-
чай нелинейных кодов. При этом также удается получить ана-
лоr тождества Мак Вильямс [28].
Утверждение 3.11 [8]. Пусть G матрица размера т Х
Х (2т 1) с элемента"м'и из поля ОР(2), все столбцы которой
являются различными и ненулеВbtми. Тоеда все ненулевые ко-
довые векторы двоичноzо линейноео (2 n 1. 1, lп) Koдa, для ко-
тороео матрица G является nорождающей, имеют вес 2т 1.
Краткое доказательство. Пусть Vl, V2, ..., V m строки О.
Рассмотрим линейную комбинацию
V 11 + V 12 + ... + V 1/ (i 1 < i 2 < ... < i 1, 1 j т).
Число столбцов матрицы О, компоненты которых, расположен-
ные в строках с номерами i l , i 2 , ... i j , равны заданным двоич-
ным символам al, а2, ..., aj, составляет 2т ; 1, если аl ===
== а2 == ... == а; == О, и 2т ; во всех остальных случаях. Общее
число наборов значений al, а2, ..., aj, таких, что al + а2 + ...
. .. + aj == 1, равно 2j l. Отсюда следует, что вес вектора
Vl 1 + Vi 2 + ... + Vi j всеrда равен 2m l.
Задача 3.12. Обобщить предыдущее утверждение на случай
произвольноrо q.
Утверждение 3.13. Н умератором весов кода, двойственноео
к коду из утверждения 3.11, является Мflоеочлен
2 т {(1 + z)2m 1 + (2т 1) (1 + Z)'2т l I (1 Z)2т I}.
(Для доказательства этоrо утверждения следует воспользо..
ваться утвер}кдением 3.11 и тождеством Мак-Вильяме.)
148
r лава а
3.5. Циклические коды (1)
Циклические коды являются линейными кодами, которые не
v
изменяют своих своиств при циклическои перестановке компо-
нент кодовых слоев. Блаrодаря этому свойству они обладают
сравнительно простыми процедурами кодирования и декодиро-
вания и, кроме Toro, имеют удобные алrебраические своЙства.
Все совершенные линейные коды, коды Рида
Мал.пера
(СМ. разд. 4.5) и друrие коды, построенные еще до Toro, как
Прейндж ввел понятие циклическоrо кода и описал свойства по
следнеrо, являются кодами, которые после перестановки компо
нент или незначительной модификации оказываются цикличе
скими. Все важнейшие блоковые коды, открытые поз}ке, также
оказались либо циклическими кодами, либо кодами, получаю-
ЩИМИСЯ из циклических, либо тесно связанными с последними.
Пусть С представляет собой q-ичный линейный (п, k)
KOД.
Если вместе с каждым кодовым BeI{TOpOM и == (vo, Vl,..., Vn
l)
(в циклических кодах удобно нумеровать компоненты, начиная
с нуля) коду С принадлежит также вектор Pv === (Vn
l, VO, VI,...
.. . , Vn
2), то код С называется циклическим. При изучении цик
лических кодов векторы (vo, V}, . . . , t'n
l) У добно представлять
в виде мноrочленов V (Х) == Vo + vlX + V2X2+ ... + Vn
IXn
1 от
неизвестноrо Х с коэффициентами из поля GF(q). При этом век-
тору Ра == (Vn
l, Vo(), . . . ,Vn
2) соответствует мноrочлен
Xv (Х)
Vn
1 (JY fl
1).
Первая и последняя компоненты кодовых слов циклических ко-
дов рассматриваются как соседние компоненты. Поэтому при
представлении кодовых слов циклических кодов в виде MHoro-
членов степени Х'п И ХО == 1 неизвестноrо Х должны рассматри-
ваться как тождественные. Друrими словами, если два MHoro
члена а (Х) и Ь (Х) при делении на )(n
1 имеют равные
остатки, т. е. если а (Х) и Ь (Х) принадлежат одному классу BЫ
четов в кольце мноrочленов по МОДУЛIО Хп
1, то они paCCMaT
риваIОТСЯ как тождественные. Различные мноrочлены степени
n
1 и менее принадлежат различным классам вычетов по мо-
ду.пю Хп
1. Класс вычетов по модулю ХN
1, содержащий
мноrочлен f (Х), будем обозначать через (, (Х». Как было опи-
сано в разд. 2.4, можно определить операции сло}кения, выЧита
"
ния И умножения классов вычетов так, что для этих операции
будут выполняться обычные правила арифметики. Множество
всех классов вычетов по модулю х n
1 далее будем обозначать
через Rn.
Резюмируя вышеизложенное, заметим, что сопоставление
кодовым векторам (vo, Vl,. .., Vn
l) классов вычетов
(VO+VI X + ... +Vn
lXn
I)E/
п
л uнейные и циклические коды
149
Д lЯ циклических КОДОВ является вая{ным по существу. Действи
тельно, это отображение является взаимно однозначным. Далее,
вектору Ро соответствует класс вычетов (Xv(X))==(X) (v(X)).
И наконец, если при представлении кодовых векторов в виде
последовательностей для нахождения линейной комбинации He
обходимо рассматривать циклические перестановки (соответ..
ствующие операциям над матрицами), то при представлении
кодовых векторов в виде элементов Rn нахождение линейной
, u
комоинации осущестВляtтся только с помощью операции сложе..
ния, вычитания и умно)кения мноrочленов.
Пусть 1 подмножество Rn, соответствующее коду С,
а именно
1 == {( v (Х)) Е R n I v Е С}.
Так как С является линейным подпространством, то для
вольных (v(X)), (и(Х))Е/ и аЕ GF(q)
(v (Х) и (Х)) == (v (Х)) + (и (Х)) Е [,
(аи (Х») == (а) (и (Х)) Е 1.
произ-
(3.16)
( 3. 1 7)
Кроме Toro, как указывалось выше,
( Х) (v (Х») Е [. (3. 18)
Из формул (3.16) (3.18) следует, что для произвольноrо
(f (Х») Е R n
(f (Х)) (v (Х)) Е 1.
(3.19)
Таким образом, из соотношений (3.16) и (3.19) видно, что [ яв-
ляется идеалом Rn (см. разд. 2.2).
Пусть g (Х) нормированный мноrочлен (т. е. мноrочлен,
коэффициент при наивысшей степени Х KOToporo равен 1) ми-
нимальной степени, не являющийся нулевым и такой, что
(g (Х)) Е 1. Пусть f (Х) произвольный мноrочлен, принадлежа-
щий /. Тоrда, если , (Х) остаток от деления f (Х) на g (Х), то
f (Х) == а (Х) g(X) + ,(Х)
(, (Х)) == (f C:r)) ....... (а (Х)) (g (Х)).
Из формул (3.16) и (3.17) следует, что (, (Х) ) Е 1. Но Tor да,
соrласно определению g (Х), мноrочлен r (Х) должен быть ну-
левым, так как степень r (Х) меньше, чем степень g (Х). Это
означает, что f (Х) делится на g (Х). в частности, на g (Х) дол-
жен делиться двучлен Хп 1, поскольку (Хn 1) == (О) Е [.
Обратно, пусть f (Х) произвольный мноrочлен, который де..
.П и ТСЯ Н а g ( Х) . То r Д а, со r л а с н о фор м у л е ( 3.19) , (f (Х) ) Е 1.
Пусть степень g (Х) равна 1. Так как имеется ровно qп l MHoro..
членов степени п 1 и меньше, которые делятся на g (Х), ТО
и
150
r лава 3
число классов вычетов, порождаемых идеалом 1, равно qn l.
Поскольку соответствие между С и 1 является взаимно одно..
значным и С содержит qk векторов, то 1 == n k. Далее, если
предполо)кить, что существуют два мноrочлена g (Х), удовле..
творяющих описанным выше свойствам, то из Toro, что эти мно-
rочлены должны делить друr друrа и их старшие коэффициенты
равны 1, будет следовать, что эти мноrочлены совпадают. Это
означает, что g (Х) определяется однозначно. Таким образом, мы
доказали следующую теорему {8, 29 31].
Теорема 3.4. П усть С циклический (п, k) Koд и 1 == {( t' (Х) ) Е
Е Rn I V Е С}. Тоеда существует такой нормированный MHoeo
член g (Х) степени п k, делящий Хп 1, что выполнение cpaв
не1tия
f (Х) :== О
(mod g (Х))
является необходимым u достаточным условием тоео, что
(f(X»e::/.
Мноrочлен g (Х) определяется однозначно и называется по-
рождающим мноrочленом циклическоrо кода с.
Наоборот, пусть g (Х) произвольный нормированный мно-
rочлен степени п k, которыЙ делит Х N 1. Рассмотрим мно.
жество 1 сме}кных классов из Rn вида (а (Х)) (g (Х)). в Ka)K
дом смежном классе из 1 возьмем мноrочлен v (Х) == Vo +
+ vlX + ... + Vn IXn l степени п 1 или менее, принадлежа
щий этому смежному классу (такой мноrочлен только один),
и поставим ему в соответствие вектор (vo, VI, . . . , Vn l) из V n.
Пусть С множество всех таких векторов. Леrко проверить,
что С является циклическим (п, k) KOДOM и g (Х) порождаю
щий мноrочлен этоrо кода.
Пусть g (Х) == go + glX + ... + gn kXn h поро}кдающий
мноrочлен циклическоrо кода С, и пусть G матрица следую-
щеrо вида:
+ n
go gl · gn k О . O r
о go gl · · gn k О ... о
о=== k (3.20)
О 1
о . . . go gl . gn k
'f ак как строки матрицы G это кодовые слова кода С,
а paHr G равен k (поскольку gn h == 1), то матрица G является
порождающей матрицей кода С. При этом порождающий мно-
rочлен g (Х) можно рассматривать как краткое представление
л инеl1ные и циклические коды
151
матрицы о. Мноrочлен h(X)==(Xn 1)/g(X) называется nро-
верочным МНО20членом кода. Рассмотрим код C D , двойственный
к коду С. в силу Toro что код С вместе с каждым кодовым
вектором v содержит также вектор pn IV, для произвольноrо
вектора и Е C D (pn lv) и Т === О, или, что то же самое,
v (Ри)Т === о.
Это означает, что Рu Е C D , т. е. код C D также является цикли
ческим. Порождающий мноrочлен KOД C D обозначим через..
gD(X). Пустьh(Х)===hо+hIХ+ ... +hkXk и
h * === (h k, h k 1, ..., h o , О, · · ., О) .
-...-....""'"
n k 1
Тоrда
h*GT == ( Е hk tgt. 'r' hk i lgl. · · .. h,go ) ,
1 с:аО {==о
rде gi == О, i > n k. Так как g (Х) h (Х) == Х N 1, то
k k 1
L hk igi==L hk i lgi== ... ===hlgo==O, goho== l.
iz::O l=sO
Следовательно,
h*GT == о
,
т. e.ll*EC D . Мноrочлен h o 1 h*(X) должен делиться на gD(X), но
он, так же как и gD (Х), имеет степень k, а ero старший коэф-
фициент равен 1. Таким образом,
gD (Х) == hOI h* (Х) == hC;l Xk/l (X I).
Из вышеизложенноrо следует справедливость следующей
теоремы.
Теорема 3.5. Двойственный код C D циклическоео (n, k) -кода
также является циклическим. Порождающим мноеочленом кода
C D является мноеочлен hOlX' h(X I), еде h(X) nроверОЧНblЙ
мноеочлен кода С, а ho свободный член /1 (Х).
Из этоЙ теоремы непосредственно следует, что матрица
n )
hk
О
hk 1 ·
h k
hk 1
. ho О
ho ·
. . .
. о
i
n.......k
!
(3.21 )
Н==
о
о ... о h k h k 1 . ho
ЯВ.,'1яется поро)кдающей матрицей кода C D и проверочной
рицсй кода С.
мат-
Поскольку вопросы реализации кодов детально будут рас..
сматриваться в rл. 7, то здесь кратко остановимся лишь на Me
тодах кодирования и декодирования, приложимых ко всем цик
лическим кодам. Условимся, что последние k компонент кодовоrо
слова являются информационными символами, а первые n k
компонент проверочными символами (для конкретности pac
смотрим последовательные системы, коrда обработка символов
ведется последовательно по мере их поступления; случай парал
лельных систем принципиально не отличается от случая после..
довательных систем). Представим совокупность информацион
ных символов в виде мноrочлена Xn hfo (Х) [fo (Х) мноrочлен
степени k 1 или меньше, коэффициентами KOToporo являются
информационные символы]. Совокупность проверочных симво.
лов представим в виде мноrочлена r (Х) [r (Х) мноrочлен CTe
певи n k 1 или меньше, коэффициентами KOToporo являются
проверочные символы]. Соrласно теореме 3.4, мноrочлен f (Х) ==
== Xn hfQ(X) + r(X) является кодовым тоrда и только тоrда,
КОl"да он делится на порождающий мноrочлен g; (Х), т. е. тоrда
и только тоrда, коrда выполняется следующее равенство
Xn hf,o (Х) == а (Х) g (Х) r (Х). Из Э10rо равенства видно, что
в качестве r(X) можно взять остаток из деления Xn kfo(X) на
g (Х), заменив все ero коэффициенты на противоположные. Это
отображение {о (Х) в r (Х) является линейным и фактически pea
лизует метод нахождения проверочных символов с помощью
порождающей матрицы и соотношения (3.4).
Остановимся далее на декодировании. Предположим, что пе
редавался мноrочлен f (Х), а был принят мноrочлен f (Х) +
+e(X)l). Так как f(X) делится на g(X), то, вычислив OCTaTOI(
,(Х) от деления f(X)+ е(Х) на g(X), можно однозначно опре
делить класс вычетов по модулю g (Х), которому принадлежит
е (Х). Из взаимнооднозначности отображений V 11 в Rn и С в 1,
а также описанных выше свойств идеала 1 леrко видеть, что
классы вычетов по модулю g(X) соответствуют сме)кным клас
сам V n ПО подrруппе С. При этом мноrочлены r (Х) COOTBeT
ствуют синдромам.
Пороrовые методы декодирования и алrебраические методы
декодирования БЧХ кодов будут описаны в следующей rлаве.
В оставшейся части этоrо раздела рассмотрим ряд друrих MeTO
дов декодирования, которые MorYT быть использованы при He
больших длинах кодов и малых скоростях передачи 1[8, 32 36].
При этом понадобится следующая теорема.
Теорема 3.6. Пусть С циклический (n, k) Koд с nорождаю
ЩUАt М1l0еочлеНО,Л,l g (Х) и МИllИАtаЛЬНblМ весо/и d 2t + 1. Пусть
е (Х) мн оеочлен ошибок веса t или менее, а r (Х) остаток от
1) е (х) соответствующиЙ вектору ошибок мноrОЧ.ТIен, которыЙ назы-
вается мноrочленом ошибок,
Линейные и циклические коды
153
деления е (Х) на g (Х). Пусть 'i (Х) остаток от деления Xi, (Х)
на g(X), O i n. Если вес W('i(X)) (число ненулеВblХ коэф"
фицuентов) i eo остатка 'i (Х) меньше или равен t, то
e(X) == Xn i'i(X) (modXn 1).
Доказательство. Пусть е' (Х) остаток от деления Xn i'i (Х)
на Хп 1. Так как
x i [е (Х) е' (Х)] == Xlr (Х) 'i (Х) == о (1110d g (Х)),
то Xi[e(X) е'(Х)], а следовательно, е(Х) е'(Х) кодовый
мноrочлен. Поскольку е (Х) и е' (Х) имеют вес, меньший чем
t,Toe(X) == е'(Х).
Пусть t < n/k и е(Х) произвольный мноrочлен, соответ-
ствующий вектору ошибок веса t или менее. Тоrда выбором под-
ходящеrо i, О i < n, можно добиться Toro, что
х ' е (Х) == е, (Х) (mod Х n ........ 1),
deg ei < n k,
rде deg ei степень ei. С друrой стороны,
ei (Х) == Xie (Х) == X l ,(Х) == 'i (Х) (mod g (Х)).
Отсюда СJIедует, что ei (Х) == 'i (Х). Вычисляя по ,(Х) последо
вательно '1 (Х), '2 (Х), ..., всеrда можно найти такое целое чис-
ло i, что W ('i (Х)) t, и, пользуясь предыдущей теоремой, оп-
ределить е(Х). Последовательное вычисление мноrочлеНОВ'i (Х)
можно реализовать с помощью реrистров сдвиrа (см. разд. 7.1).
в случае коrда t n/k, целое число i, удовлетворяющее указан
ным выше условиям, l\10жет и не существовать. Предположим,
что выбором подходящих мноrочленов So(X) == О, 51 (Х),
52 (Х), ..., S[ (Х) можно добиться Toro, что для любоrо MHoro
члена ошибок е(Х) веса t или меньше будет существовать по
крайней мере одна пара целых чисел i и j, такая, что, во пер
вых, слаrаемые 5j (Х) с ненулевыми коэффициентами будут вхо-
дить в качестве слаrаемых с ненулевыми коэффициентами TaK
же и в ei (Х) и, BO BTOpЫX, deg (ei 5 j) < n k. Tor да е i (Х)........
........ 5/ (Х) == , l (Х) 5; (Х), rде s; (Х) остаток от деления 5j (Х)
Н а g ( Х). Т а к к а к W ( е i (Х) S j ( Х)) t, то w ( 'l (Х) ........ s; (Х)) t.
Обратно, если можно найти такие целые числа i и j, что
W ('i (Х)........ 5; (Х)) t, то точно так же, как и при доказательстве
теоремы 3.6, можно показать, что
Xie (Х) ........ 8/ (Х) == 'i (Х) 5; (Х) (mod Х N 1).
В этом случае из сравнения
е (Х) == Xn i [, i (Х) s; (Х) + 5/ (Х)]
(mod Х n ....... 1)
154
r лава !J
находится е (Х). Поясним на примере способ выбора мноrочле-
нов 51 (Х), 52(Х)' ... .
Пример 3.3 [34]. Рассмотрим двоичный циклический код с
параметрами n == 23, k == 12, t == 3. Как будет показано ниже
в примере 4.2, кодом с такими параметрами является только код
rолея. Рассмотрим конфиrурации ошибок веса 3. Конфиrурации
ошибок удобно изображать на окружности длины 23, как ПОl{а
зано на фиr. 3.2. Предположим, что на окружности имеются три
символа 1, показывающие положение ошибок, и между ними
находятся al, а2 и аз символов О (а} а2 аз). Если аз 12,
то, выбрав надлежащим образом i, можно добиться Toro, что
deg ei < 11 и deg (ei 50) < 11. ПреДПОЛО)I{ИМ, что аз < 12.
18 Х 17
х 19 Х 51 = 16
Х %0 х.... х х..... х 51 Xs
х11 /(0 О О О 1 [х<,1 1lt
.0 О х Х
Х 21 /0 о\х 13
xoJ x О x1%
X1lx О J X 11
\х 'Хх' Х 1О
Х 2 \ Х Х /
х зх ,'f- х х х .,ХХ 9
X lt '" х..... х..... . "" х 8
x s х' х 7
Фиr. 3.2.
в этом случае al + а2 > 8. Тоrда, так как 02 aI, то а2 5.
С друrой стороны, аз 7. Поэтому по крайней мере один из
трех символов 1 обладает тем свойством, что с одной стороны
от Hero располаrается по меньшей мере пять символов О, а с
друrой более шести. Тоrда, положив 51 (Х) ==X16 И 52(Х) ===X11,
получим, что для любоrо е (Х) веса w (е (Х)) == 3 существуют
такие целые числа i и j (О i < 23, О j < 3), что
deg (ei 5/) < 11.
Рассмотрим конфиrурации ошибок веса 2. Пусть аl и а2......... числа
символов О между символами 1, определяющими положение
ошибок (al (2). Если а2 12, то при некотором i
deg (ei 50) < 11.
Как леrко видеть, в случае, коrда а2 == 11, 0"1 == 10, при веко..
тором i
deg (el ...... 51) < 11.
Если w (е (Х» == 1, то при некотором i
d е g (е i 50) < 11.
Линейные и циклические коды
155
Итак, как видно из вышеизложенноrо, 51 (Х) И 82(Х) удовлет
воряют нужным условиям. Декодер, основанный на использо
вании 80, 81 И 82, описан в работах [34, 36].
Утверждение 3.14. Пусть ql(X) IXn
1 и gl(X)g2(X) IXn
1.
Tozaa циклический код С 2 длины n с nорождающuм МН020чле
ном gl(X)g2(X) является подкодом циклuчеСКО20 кода той же
длины с nорождающим МН020членом gl (Х).
Краткое доказательство. Так как из Toro, что gl (Х) g2 (Х) I v (Х),
следует, что gl (Х) I v (Х), то кодовые векторы кода С 2 принадле
жат также коду C I .
Утверждение 3.15. 1) Если g(X) не содержит в качестве co
множителя Х
1, то циклический код С длины п с nорождаю
щим мноzоtlленом g (Х) содержит кодовое слово (1,1, ..., 1).
2) Подкод Се кода С, задаваемый порождающим МН020членом
(Х
1) g (Х), является четным подкодом кода С.
Краткое доказательство. 1) Так как g (Х) I Хп
1 t (Х
],
g(X»== 1 и ХN
1 === (Х
1) (Xn
1 + Xn
2 + ... + 1), то
g(X) 'Xn
I+Xn
2+ ... + 1. 2) Если V(X)EC e , то (Х
1) Iv(X).
Но тоrда v (1) == О. Так как справедливо также и обратное YT
верждение, то Се является четным подкодом кода С.
3.6. Циклические коды (11)
Рассмотрим q
ичный циклический (п, k)
KOД. Порождающий
мноrочлен g(X) этоrо кода можно разложить единственным об
разом в произведение нормированных неприводимых мноrочле-
нов над GF(q). Пусть это разложение имеет вид
g 1 (Х) r 1 . . . g 1 (Х) r 1.
Так как для важнейших кодов '1 === '2 == . . . ::::: 'l == 1, то ниже
для простоты рассмотрим случай, коrда кратные сомножители
отсутствуют. Пусть mi
степень gi (Х) И
т == НОК (тl, т2, ..., ml),
rде НОК
обозначает наименьшее общее кратное. Соrласно за-
мечанию, сделанному после теоремы 2.13, gi (Х) имеет mi раз-
личных корней в поле GF(qmi), а следовательно, и в GF(qm).
mi
J
Если
i
один из этих корней, то
7,..., р1
остальные
корни gi (Х). Пусть ni
порядок элемента
i. Соrласно Teope
ме 2.13, показатель gi (Х) равен ni, так что
g t (Х) I (Xпi
1).
(3.22)
156
rлава 3
Поскольку gi (Х) I (Хn 1), то из части 2 утверждения 2.54 сле-
дует, что ni I n. Следовательно,
НОК (nl, n2, ..., n/) 'п.
Обозначим HOI, (nl' n2, ..., nz) через по. Из формулы (3.22) и
части 2 утверждения 2.54 следует, что
g (Х) I (Х ПО ..... 1) .
Если n > по, то вектор ХNО 1 [ниже вектор, соответствующий
(f (Х) ), будем называть просто вектором f (Х)] является KOДO
вым вектором веса 2, так что минимальное расстояние этоrо KO
да не больше чем 2, и последний не может исправлять даже
одиночные ошибки. Для обнаружения одиночных ОIl1ибок можно
обойтись, например, кодами с одной общей проверкой на чет-
ность. Учитывая это, в дальнейшем всеrда будем предполаl"'ать,
что n == По.
Покажем, что можно сделать и обратное, а именно задать
циклический код, задав корни g (Х). ДЛЯ этоrо вначале зада
дим m. Пусть сх. один из примитивных элементов поля GF(qт).
Далее зададим 1 неотрицательных не превосходящих qm 2 це-
лых чисел J.11, ..., J.1z, никакие два из которых не принадлежат
одному (q, qт 1) циклу. Пусть gi (Х) минимальный MHoro
член элемента atJ.i с коэффициентами из поля GF(q). Степень
mi мноrочлена gi (Х) равна длине (q, qт 1) ЦИКJIа, которому
принадлежит J.1i. Соrласно утверждению 2.13, порядок ni эле-
мента aJJ.i равен (qm 1)/(J.1i,q'n 1). Тоrда в качестве поро-
ждающеrо мноrочлена циклическоrо кода можно взять произве
дение gl(X)q2(X) ... gz(X). Длина n полученноrо таким обра-
зом кода равна НОК (nl, n2, ..., nz), а число информационных
1
символов составляет n...... L mi.
1==1
Пример 3.4. Пусть q === 2 и m == 4. Выберем J.11 == I и J.12 == 3.
Как следует из утверждения 2.60, в этом случае тl == т2 == 4,
nl == 15, n2 == 5. Но тоrда п === 15. Используя конкретное пред-
ставление поля ОР(2 4 ) и элемент сх. из задачи 2.59, получим, что
gl(X) ==X4+X+l, g2(X) ==Х 4 +ХЗ+Х2+Х+l И g(X) ==
==gl(X)g2(X) ==Х8+Х7+Х6+Х4+ 1. Построенный здесь код
является примером БЧХ кода, испраВЛЯIощеrо двойные ошибки
(произвольные Б ЧХ коды будут описаны в разд. 4.1).
Предположим, что g (Х) является произведением различных
неприводимых мноrочленов gl(X), g2(X), ..., gl(X) с коэффи
циенrами из поля GF(q). Пусть mi степень gi(X), а сх.'i ОДИН
1
из корней gi (Х). Степень g (Х) равна L ml. Поскольку любой
i ..1
л инейные и циклические коды
157
КОДОВЫЙ вектор v (Х) == ио + vlX + ... + иn lXn l q-ичноrо ЦИК-
лическоrо кода С длины n с порождающим мноrочленом g (Х)
делится на g (Х), то
v(ai)==O, 1 i l,
(3.23)
или, что то же самое,
1 2 п I .......
a l а 1 ... аl и о
1 2 п 1
а 2 а 2 ... 0.;2 V 1
== о.
(3.24)
1 а 2 aп l v
аl /. .. 1 n 1
Наоборот, как следует из свойств МИНИl\lальноrо мноrочлена, лю
бой вектор V (Х), удовлетворяющий указанны! выше условиям,
делится на g (Х), а следовательно, является кодовым вектором.
В этом смысле вышеприведенная матрица похожа на провероч-
ную матрицу кода. Элементами ЭТОЙ матрицы являются элемен
ты поля GF(qт). Однако, используя любой базис поля GF(qmi)
каждый элемент а{ можно представить в ниде вектор столбца
Ац, компонентами KOToporo являются элементы поля GF(q).
Заменяя a на A ij , получаем матрицу размера, Х n с элемента
ми из поля GF(q):
А 10 AII... АI (n 1)
м == А 20 А 22 ... А 2 (n 1)
А/о A/I'.. А/ (n 1)
которая обладает тем свойством, что вектор V === (ио, иl,..., Vn l)
удовлетворяет условию (3.24), т. е. является кодовым тоrда
и только тоrда, коrда
Ми Т о.
Следовательно, М является одной из проверочных матриц.
Пример 3.5. Пусть q == 2, а примитивный элемент поля
OP(2п ) и g(X) flvfинимальный мноrочлен элемента а. Тоrда
g(X)1 X2т 1 1. Пусть С циклический (2т 1,2т 1 m)
КОД с поро}{{дающим мноrочленом g (Х). Соrласно равенству
(3.24), каждый I<ОДОВЫЙ вектор V == (и о , и Р .. ., V т 2) должен
удовлетворять следующему УСЛОВИIО:
2т 1
L Vi<I t == о.
i==O
(3.25)
158
r лава 3
Предположим, что вес V меньше или равен 2 и все компоненты
Vi вектора V, за исключением Vl 1 и Vl 2 (i 1 < i 2 ), равны нулю.
Тоrда, так как
Vl 1 a l1 + Vl 2 a i2 == О,
то
V . :::::: V . al2 ll
II l2 ·
Поскольку О < i 2 i 1 < 2т 1 и (Х примитивный элемент
поля, то ai2 il Ф ОР (2), так что Vl. == Vl 2 == о. Таким образом,
минимальный вес d кода С не меньше трех. С друrой стороны,
если i l и i 2 произвольные целые числа, такие, что О i l <
< i 2 < 2т 1, то a l1 + a i '! Е ОР (2т). Следовательно, существует
такое целое число j, О j < 2т 1, что
a il + a i ! == а/.
Очевидно, что j =1= i l , i 2 . Если V вектор, компоненты KOToporo
ViI, Vi2 и Vj равны 1, а остальные равны О, то V удовлетворяет
соотношению (3.24) и, следовательно, является кодовым. Таким
образом, минимальное расстояние кода С в точности равно 3.
Этот код лежит на rранице Хэмминrа и является совершеННЫl\l.
Код С называется двоичным циклическим кодом ХЭМА-lинеа;
коды, эквивалентные с, называют просто двоичными KoaaAtU
Хэммuнеа. Если в матрице коэффициентов (сх,0, (XI,..., cx,2т 2) из
(3.25) каждый элемент а,.; заменить на вектор"столбец, получаю..
щийся транспонированием вектор строки, который является
представлением cx,j в базисе 1, сх" сх,2, ..., cx,m l, то получится
матрица Н размера т Х (2т 1) с элементами из поля ОР (2),
У которой все столбцы различные и ненулевые. Следовательно,
утверждение 3.13 дает нумератор весов кода С. Если в случае
т == 3 взять в качестве минимальноrо мноrочлена элемента сх,
мноrочлен Х З + Х + 1, то получим
[ 1 О О 1
Н== О 1 О 1
О О 1 О
о
1
1
1
1
1
].
Изменяя подходящим образом нумерацию компонент кодовых
слов, можно получить код из примера 1.4.
Утверждение 3.16. В примере 3.5 оценка сх, 3 была nолу
чена на основании равенства (3.25). Однако эту оценку можно
также получить исходя из Т020, что если g (Х) I aX l1 + bx i \ еде
а, Ь Е ОР(2), О i l < i 2 < 2т 1, то а == Ь == О.
Краткое доказательство. Сначала заметим, что g (Х) Xi.
Так как g (Х) минимальный мноrочлен примитивноrо эле-
мента сх" то g (Х) является ПРИМИТИВНЫМ а а следовательно,
g(X) Xi 1, О < i < 2т 1.
Линейные и циклические коды
159
Пример 3.6. Пусть h (Х)........ примитивный мноrочлен степени т
над полем ОР (2). Рассмотрим двоичный циклический код
длины n == 2т 1 с порождающим мноrочленом g (Х) == (Хn +
+ 1) /h (Х). Так как порождающий мноrочлен X n1 ,h (X I) двой-
CTBeHHoro кода также является примитивным мноrочленом
(СМ. утверждение 2.58), то двойственный код является кодом
Хэмминrа из примера 3.5. Рассматриваемый код имеет т ин-
формационных символов и состоит из 2:т кодовых векторов.
Мноrочлены g (Х), Xg (Х), ..., Xn lg (Х) являются различными
кодовыми векторами. В самом деле, допустим, что Xig (Х) ==
== XJg(X) (mod Хп + 1), О i j < n. Тоrда Хп + 1 )Xig(X) Х
X(Xi j+ 1) и h(X) IXj i + 1. lio это противоречит тому, что
h (Х) примитивный мноrочлен. Следовательно, 2т кодовыми
векторами являются нулевой вектор, вектор g (Х) и все цикли-
ческие сдвиrи последнеrо. Проверочным мноrочленом этоrо кода
является h (Х). Если V == (v.o, Vl, . . . t Vn l) ненулевой кодовый
вектор и h(X) == 1 + h1X + h 2 X2 + ... + Хт, то из (3.21) имеем
т l
L hт lVj+l === Vj+т, О j < п,
1==0
(3.26)
rде индексы вычисляются по модулю n, а ho === h m == 1. Следова-
тельно, ес.НИ 'Ol+i == Vj+i (О i < т) при некоторых 1 и j,
1 Ф j (mod п), то Vl+i == Vj+i при всех i, т. е. последовательность
'00, Vl, ..., Vn l, Vo является периодической. Однако это проти-
воречит тому, что n векторов, получаемых с помощью последо-
вательных циклических перестановок компонент кодовоrо слова,
являются различными. Следовательно, при всех i и j
(i j (mod п»)
(Vl t Vi+l, ..., Vl+т r) =1= (Vj, 'Vj+lt ..., Vj+т I).
Если (Vi, Vi+l, ... t Vi+m l) == (О, О, ..., О) при некотором i, то,
соrласно (3.26), вектор V должен быть нулевым, но по предполо
жению v ненулевой вектор, поскольку (Vi, 'Oi+l, . . ., Vi+т, l) =#=0
при всех i. Так как число т MepHЫX ненулевых двоичных BeKTO
ров над ОР(2) равно n == 2т 1, то для произвольноrо вектора
(ао, аl, . . . ,aт l) =1= О над ОР (2) найдется ровно одно такое целое
число i, О i < п, что
( V 1, V l + 1 t · · · t V l + т 1) == (ао t а I t ... t а т 1).
Последовательности '00, '01, ..., Vn l, Vo, ... t обладающие этим
свойством, называют последовательностями максимальной дли-
ны. Как следует из вышеизложенноrо, общее число символов 1, co
держащихся в последовательностях (Vi, 'Oi+l, . . . , Vi+m l), i == О,
1, ..., n 1, равно общему числу символов 1, содер)кащихся
в ненулевых векторах размерности т над полем ОР (2), которое
160
r лава 3
в свою очередь равно m2m 1. Если Vj == 1, то число символов 1
среди Vo, Vl, ..., Vn 1 равно 2т 1, а следовательно, вес любоrо
ненулевоrо кодовоrо слова равен 2m 1. Таким образом, рассмат"
риваемый код является эквидистантным (это можно было бы
также показать, используя результаты примера 3 5 и утвержде
ние 3.11). Этот код называют кодом максимальной длины.
В разд. 4.3 будет описан алrоритм пороrовоrо декодирования
кодов fvlаксимальной длины.
Для примера рассмотрим случай, коrда т == 3 и }l (Х) ==
== ХЗ + Х2 + 1. При этом g(X) === (Х + 1) (Х 3 + Х + 1). Соrласно
(3.21), матрица Н имеет следующий вид:
Н==
1 1 О 1
О 1 1 О
О О 1 1
О О О 1
о о
1 О
О 1
1 О
о
о
о
1
До сих пор в процессе всех построений предполаrалось, что
выбор одноrо из примитивных элементов или одноrо из элемен
то.в порядка п уже сделан. Рассмотрим, какое влияние выбор
этих элементов оказывает на получающиеся коды. Пусть
и 'у различные элементы порядка п поля GF(qm). Тоrда 1,
, ..., n l, у корни уравнения ХN 1 === О. Так как это урав..
нение имеет не более чем п корней, то найдется такое целое
положительное число ", что у === " И
n 1 n 1
V (V i ) === L V/yl/ == 0# V ( Vi) == L V/ Vi/ === о.
/ O j O
Поскольку порядок у также раврн п, то, соrласно утверж
дению 2.13, (п, ") == 1, так что найдется такое целое положи
тельное число , что " == 1 (mod п). Пусть Т.... преобразова..
ние, переводящее вектор (vo, VI, . . ., Vn l) Е V n В вектор (V o , Vu.'
V 2 J..L' · · · t V(n 1) IJ.) (индексы вычисляются по модулю п). Заметим,
что это преобразование приводит лишь К перестановке компо..
нент векторов. Если Т IJ. (v o ' v p · · · t vn l) == V' == (v , V , ..., V l)t
то V; === VJ..LI (о j п). Следовательно, V J == V j (о j < п). Тоrда
n l n 1 n l
L V I Vil == L V / iV/ == L V; i/.
1==0 j O j==o
Таким образом, использование вместо элемента элемента V
приводит лишь К некоторой перестановке компонент кодовых
векторов. Это означает, что построенные в обоих случаях коды
эквивалентны, имеют одинаковую весовую структуру, а следо-
вательно, и о инаковую. способность исправлять независимые
Линейные и циклические коды
161
ошибки. Однако, вообще rоворя, эти коды обладают различными
способностями исправлять пачки ошибок. Кроме Toro, описан-
ные в разд. 7.1 кодирующие и декодирующие устройства имеют
различные коэффициенты в цепи обратной связи, а значит,
и различное число сумматоров.
Утверждение 3.17. Пусть g(Х)
АtНО20член степени т, такой,
что g (Х) == Xmg (X
I). ТО2да, если С
циклический код с пo
рождающим М1l020членом g(X) и (VO,VI,...,Vn
I)EC, то
(Vп
J, Vп
2,...) VO) Е с.
Утверждение 3.18. Пусть V == (VO, VI,..., Vn
I)
кодовое слово
q
UЧНО20 цикличеСКО20 кода с. ТО2да вектор ПqV, получающuйся
из V циклической перестановкоЙ компонент П q : i --+ qi (mod п),
также принадлежит коду с.
Краткое доказательство. Если V (Х)
представление V в виде
мноrочлена, то vq (.Х")
представление ПqV в виде мноrочлена.
Утверждение следует из Toro, что если g (Х) I V (Х), то
g(X) IvQ(X).
Методы декодирования циклических кодов, основанные на
утверждении 3.18 и теореме 3.6, описаны в работах (33, 37].
3.7. Укороченные коды
Предположим, что линейный (п, k)
KOД С имеет порождаю-
IЦУЮ матрицу, первые i столбцов которой являются линейно He
зависимыми (i < k). Множество кодовых векторов, первые i
компонент которых равны О, образует подпространство размер
ности (k
i) пространства (кода) с. Множество С' векторов
длины п
i, полученных удалением первых i компонент из Ta
ких кодовых векторов, образует линейный (п
i, k
i)
KOД. Эта
процедура называется укорачиванием, а код С'
укорочением
кода С. Минимальное расстояние С' не меньше, чем минималь-
ное расстояние С. В частности, если С
циклический код, то С'
называется укороченным циклическим кодом. Порождающая
матрица О' кода С' получается из порождающей матрицы G
вида (3.20) кода С путем удаления первых i строк и i столбцов.
Проверочная матрица кода С' получается удалением первых i
столбцов из проверочной матрицы кода С. Если вектору
(v о, Vl, ..., V n '
l) (здесь п' == п
i) поставить в соответствие
n' 1
мноrочлен Vo + VI Х + ... + V n '
IX
(а не класс вычетов по
n'
модулю Х
1, как в случае циклических кодов), то, как сле-
дует из (3.20) и ука.занноrо выше способа построения О' [8,31],
V (Х) будет кодовым вектором тоrда и только тоrда, коrда V (Х)
делится на ПОРО)I<дающий мноrОЧ.,1ен g (Х) кода С. Так как
162
r лава 8
в отличие от случая циклических кодов здесь не требуется,
n'
чтобы мноrочлен g (Х) делил Х 1, то класс укороченных
циклических кодов значительно шире, чем класс циклических
кодов. В то же время методы кодирования и декодирования цик-
лических кодов почти без изменения MorYT использоваться
и для укороченных циклических кодов.
Утверждение 3.19 [38]. Пусть n, r и d - целые числа, удовле-
творяющие следующему неравенству:
d 2
[(п l)/r(I (n --; I ) < Ф И,
i==O
еде Ф (r) число неnриводимых мноеочленов степени r над по-
лем G F (2). ТОсда существует двоичный укороченный цикличе-
ский код длины n с минимальным расстоянием d или более, nо-
рождаемый неnриводи.мым мноеочленом степени '.
Краткое доказательство. Число мноrочленов над ОР(2) сте-
пени не выше n 1 со свободным членом, равным 1, и не более
d--2
чем с d 1 ненулевыми коэффициентами равно I (n -; I ) .
i..O
Каждый такой мноrочлен делится не больше чем на {(n 1) /r]
неприводимых мноrочленов степени r. Следовательно, если при-
веденное выше соотношение выполняется, то найдется по край-
ней мере один неприводимый мноrочлен g (Х) степени " кото-
рый не делит ни один мноrочлен ошибок веса d 1 или менее.
Минимальный вес уксроченноrо циклиqескоrо кода, порождаю-
щим мноrочленом KOToporo является g (Х), болыпе или
равен d.
Утверждение 3.20 [38]. Н еравенство в формулировке nреды-
дущеzо утверждения можно заменить на неравенство
Н (d/n) (r/n) (1 ---- О (n)),
еде О (n) О при n 00 и фиксированных отношениях d/n и ,/n.
Друсими словаМll, при больших п укороченные циклические
коды достиеают нижней ераницы BaptUaMoaa fилберта.
Jfдея доказательства. Следует воспользоваться верхней rpa-
ницей Чернова инеравенством (2.13).
4. Важнейшие коды
4.1. КОДЫ Боуза
ЧОУДХУРИ
Хоквинrема
Коды Боуза
Чоудхури
Хоквинrема [1
4] (БЧХ-КQДЫ) со-
ставляют один из оольших классов кодов, исправляющих неза-
висимые ошибки веса t, метод построения которых может быть
задан явно. Свойства и методы декодирования этих кодов до-
статочно подробно исследованы. Пусть т
произвольное целое
ПО.пожительное число и п
один из делителей qт
1. Соrласно
теореме 2.6 и утверждению 2.13, в поле GF(qm) всеrда суще-
ствует элемент порядка п; пусть
один из таких элементов.
Заметим, что все элементы
i (О
i < п) различны. Справед-
лива следующая теорема.
Теорема 4.1. Если порождающий мноеочлен g (Х) цикличе-
скоео кода длины n имеет своими корнями
l+l,
l+2, ...,
l+r
(1
r < п), еде 1 (О
1 < п)
не.1(оторое целое число, то ми-
нимальное расстояние этоео кода не Аtеньше чем r + 1.
Доказательство. Если в (3.24) положить cx.1 ==
l+l, (Х2 ==
=== Al+2 N
Al+r то
t' ,. · ., I..Nr
t" ,
1
l+1
2 (l+I) . ..
(n
l) (1+1)
Vo
1
l+2
2 (l+2) . ..
(n
1) 0+2) Vl
===0. (4.1)
1
l+'
2 (l+r) ...
(n
o (l+r)
Vn
l
Определитель любой подматрицы из r столбцов матрицы в ле-
вой части (4.1) имеет следующий вид:
/. (l+1) р/2 (l+l)
f, (l+I)
/. и+2)
j2 и+2)
jr и+2)
r/ 1 (l+r)
/2(l+r)
/, (l+,)
1 1 1 .
. . .
/.
/2 . . .
/,
(/1+/2+ .../,) О+1), .
===
/. (,
1)
/2(r
l)
/r (r
l)
164
r лава 4
Определитель в правой части последнеrо равенства известен как
определитель Вандермонда [4, 5], который, как известно, равен
П ( fи jv) И В данном случае отличен от нуля, поскольку
и>о
/и =F fv (и =1= v). Отсюда и из первой части теоремы 3.1 следует
справедливость теорем:ы 4.1.
Расстояние r + 1, rарантируемое этой теоремой, называется
нижней БЧХ ераНllцей минимальноrо расстояния. Циклические
коды с минимальной степеныо g (Х), или, что то )I{e самое,
с Аинимальным числом проверочных символов, УДОВJlетворяю
щие указанным в этой теореме условиям при заданных п, 1 и "
называются БЧ X KoдaMи. Друrими словами, БЧХ"код это цик
v
лическии код, корнями порождающеrо мноrочлена KOToporo
являются элементы i, rде i пробеrает все числа из (q, п) "цик"
лов, содер}кащих 1 + 1, ..., 1 + " и только они. Чтобы тео..
рема 4.1 rарантировала исправление кодом ошибок веса t, сле..
дует ПОЛО)l{ИТЬ r == 2t. Так как, соrласно теореме 2.13, длина
ка){{доrо цикла, содержащеrо число 1 + j (1 j ,), равна т
или некоторому делителю т, то степень g (Х), т. е. число прове..
рочных символов кода, не превосходит 2mt. Если оба элемента
l и r+l+1 не являются корнями g (Х") , то r + 1 называют KOH
структи8НЫМ расстоянием данноrо БЧХ J{ода. В частном случае
q == 2, п == 2т 1, l == О, r == 2t БЧХ коды называют также при
митивными БЧХ кодами (или БЧХ кодами в узком смысле).
В случае t == 1 эти коды представляют собой не что иное, как
циклические коды Хэмминеа. В табл. А.3, помещенной в прило..
жении, для т 10 приведены возможные значения КОНСТРУК"
тивноrо расстояния БЧХ кодов, соответствующие им числа ин
формационных символов И, коrда это извесrно, фактическое
минимальНое расстояние и разность между фактическим и KOH
структивным минимальными расстояниями. ОДИН из алrебраи
ческих методов нахождения числа информационных символов
БЧХ"кодов описан в работе [3]. Как показано в при мере 4.6,
нижняя БЧХ rраница может быть несколько обобщена.
Пример 4.1. Рассмотри).1 ПРИМИТИВНЫЙ БЧХ код с парамет..
рами пl == 4, n == 15, t == 3. В этом случае (2, 15) циклами, co
держащими числа 1, 2, 3, 4, 5, 6, являются следующие множе
ства: {1, 2,4, 8}, {3,6, 12, 9}, {5, 10}. Следовательно, рассматривае
мы.й код имеет 1 О проверочных символов. Конструктивное рас..
стояние эrоrо кода равно 7. Выбирая в качестве корень MHoro..
члена Х 4 + х + 1 и основываясь на задаче 2.60, находим g (Х):
g (Х) == (Х 4 + Х + 1) (Х 4 + ХЗ + Х 2 + х + 1) (Х 2 + Х + 1).
Пример 4.2. Пусть Il == 23, t === 2, 1 == О. Минимальное целое
число т, такое, что 231 (2 rп ......... 1), cor л асно табл. A.l, равно 11.
Важнеutuuе коды
163
Совокупность чисел {1, 2, 3, 4} в данном случае содержится
в (2, 23) ЦИl{ле: {l, 2, 4,8,16,9,18,13,3,6, 12}. Следовательно,
рассматриваемый код имеет 11 проверочных символов и KOH
структивное расстояние, равное 5. Если в качестве взять KO
рень неприводимоrо мноrочлена g (Х) === XII + Х 9 + Х 7 + Х 6 +
+ Х 5 + х + 1 с показателем 23. то, как следует из задачи 2.64,
g (Х) будет порождаIОЩИМ мноrочленом кода. Вместо g (Х) в Ka
честве порождаlОIцеrо l\1ноrочлена мо)кно также взять Xllg(X I).
Этот код им('('т минимальное расстояние 7 (см. пример 4.11),
которое не совпадает с конструктlIвныIM расстоянием, равным 5.
ПреЙНД)I\ показал, что TOT код эквивалентrн двоичному COBep
llICIIHOMY (23, 11) KOДY I" олея [7]. Поскольку Х23 1 ==
== (Х l)g(X)Xllg(X I), то по рождающим мноrочленом кода,
двойственноrо к этому циклическому коду r олея, является
(Х 1) g (Х). Следовательно, минимальный вес двойственноrо
кода равен 8.
Пример 4.3. Пусть q == 3 и элемент порядка 11 поля
Ор(3 5 ) (Tal< как 35 1 делится на 11, то такой элемент суще
ствует). В данном случае (3, 11) циклом, содержащим 1, яв"
ляется множество {l, 3, 9, 5, 4}, нижняя БЧХ rраница равна 4.
Однако, как известно [3, 4], минимальное расстояние получаlО"
щеrося кода в действительности равно 5, и этот код эквивален"
тен троичному (11, 6) KOДY rолея. Посколы<у мноrочлены
g(X) == Х 5 + Х4 + 2Х З + Х2 + 2 и X5g( X I) ЯВЛЯIОТСЯ неприво
димыми мноrочленами над ОР (3) Сlепени 5 с показателем 11
(см. табл. А.2), то любой из них может быть взят в качестве
порождающеrо мноrочлена.
Утверждение 4.1. Пусть m минимальное целое число, та-
кое, что n 12т 1. Тоеда число проверочных символов двоuчноео
БЧХ кода длины n с конструктивНЫА! расстоянием 2t + 1 и
с 1 == О не nревосходит mt.
Краткое доказательство. Числа 2i (О i t) и i всеrда
принадлежат одному циклу. Так как длина цикла, содеря{а-
щеrо i, равна m или некоторому делителю т, то количество це-
лых ПОЛО)l{ительных чисел, не превосходящих n 1 и входящих
в циклы, содержащие числа 1, 2, ..., 2t, не превосходит mt.
Утверждение 4.2. Пусть n == (qm 1)/(q 1) и (п, q 1) === 1.
Пусть oдиH uз эле.ментов порядка n поля ор(цт). Если j
такое целое число, что (q l)j == 1 (lnodn), O<j<n, то no
рядок j равен n, так как (j, n) == 1. Циклический код С длины
n, nорождающим МНО20членом котороео является МUНllЛ1,альныu
.чноеочлен g (Х) элемента j, является совершенным KOaO/vt, ис..
nравляюu uм oaUHOtlHble ошибки.
Краткое доказательство. Так как элемент qJ === j+1 также
ЯВ"ТIяется корнем g (Х), ТО, cor ласно TeopeM 4.1, миним альное
166
r лава 4
расстояние кода С не меньше 3. Так KaI{ этот код лежит на
rраниuе Хэмминrа, то он является совершенным.
Пример 4.4. БЧХ-коды, для которых п == q 1 и 1 == О, на-
зываются кодами Рида Соломона [8]. Точнее, коды Рида
Соломона это q-ичные циклические коды длины q 1 с по-
r
рождающим мноrочленом g (Х) == П(Х i), rде один из
i == 1
примитивных элементов поля GF(q). В этом случае минималь-
ное расстояние d r + 1, а число информационных символов
k === q ........ 1 ........ '. В то же время, cor ласно следствию 3.1, d r + 1.
Следовательно, для кодов Рида Соломона
d==r+ 1.
Поскольку соотношение в следствии 3.1 для кодов Рида Соло-
мона выполняется со знаком равенс'Тва, то эти коды являются
разделимыми кодами с максимально достижимым расстоянием.
Если gD (Х) порождающий мноrочлен кода, двойственноrо
К коду Рида Соломона, то
xq l rgD(X l)===(xq l 1)/g(X) ===
q 1 r q l
== П (Х l)/П (Х l) == Т1 (Х l)t
i==l [=sl i==r+l
q 2 r
так что gD (Х) === П (Х........ i). Следовательно, миним альное
[==0
расстояние двойственноrо кода равно q 1 '. Коды Рида
Соломона используются для построения кодов Юстесена
(разд. 4.6) и кодов, исправляющих пачки ошибок (разд. 4.8).
Пример 4.5. Рассмотрим БЧХ коды с параметрами n == q + 1,
1== t 1, '== 2t+ 1. Так как nlq2 1, то т == 2. Кроме Toro,
заметим, что q == ........1 (mod п). Отсюда следует, что qi ==
== ........i (mod п) для всех i, О i t. А именно если i =1= О, то
(q,q+ 1) циклом, содержащим i, является мно}кество {i,q+
+ 1 ........ i}. Tor да, если один из элементов ПОРЯДI<а q + 1
в поле ОР (q2), то
i==t
g (Х) === П (Х l)
i == t
........ МНОI'очлен над G F (q), являющийся порождаIОЩИМ мноrочле-
ном рассматриваемоI'О БЧХ кода. Как и в примере 4.4, из след-
ствия 3.1 получаем, что этот код является разделимым кодом
с максимально достижимым расстоянием d == 2t + 2. Этот код
имеет на два информационных символа больше, чем код Рида
Соломона С теми же параметрами q и d [51].
ВажнеЙUluе коды
167
Задача 4.3. Проверить, что аналоrичный результат можно
получить, если в примере 4.5 положить 1 == (q 2t + 1)/2, q > 2,
и , == 2t.
Утверждение 4.4 [4]. Пусть q == 2 и gl (Х)........ неnриводимый
МНО20член степени т, удовлетворяющий условию X1ng 1 (X l) ==
== gl (Х). ТО2да мини,Л,tальное расстояние цикличеСКО20 (п, n
m 1) ..кода, 2де n показатель gl (Х), С nорождающим мно-
еочленом g(X)===(X l)gl(X) не меньше 6.
Краткое доказательство. Пусть один из корней gl (Х).
Так как q == 2, то 2 также корень gl (Х). Из Toro, что
Xтg 1 (X l) == gl (Х), следует, что l, а следовательно, и 2
также будут корнями gl (Х). Таким образом, g (Х) имеет своими
корнями 2, l, O, l, 2, так что, соrласно теореме 4.1, мини-
мальное расстояние рассматриваемоrо кода не меньше 6. По
табл. А.2 можно установить, что мноrочлен gl (Х) == Х8 + Х7 +.
+ Хб + Х4 + Х2 + х + 1 является неприводимым и имеет пока..
затель 17. Если рассмотреть циклический (17, 8) KOД спорож..
дающим мноrочленом (Х + 1) gl (Х), то из верхней rраницы
Хэмминrа будет следовать, что минимальный вес этоrо кода
не может быть больше. Следовательно, d == 6.
Утверждение 4.5. 1) М инимальное целое число 1, такое, что
2т + 1/2 l 1, равно 2т. 2) Минимальное расстояние цикличе-
СКО20 (2т + 1,2 т + 1 2т) Koдa С, порождающим МНО20членом
g (Х) КОТОРО20 является неприводимый Мflоzочлен степени 2пz
над G F (2) с показателем 2т + 1, не ме,ч'ьше 5.
Краткое доказательство. 2т + 1122т 1. Если 1 < 2т, то
21 + 1 не делится на 2т + 1, поскольку 2 l ........ 1 == 21 т (2 1n + 1)........
21 m 1. Это означает, что существует по крайней мере один
неприводимый мноrочлен, указанный в уrверждении 4.5. Если
один из ero корней, то порядок должен быть равен 2т + 1,
т 1
так что 2 == . Таким образом, корни g (Х) это элементы
:!:2i) О i < ,п. Следовательно, X 2т 'g (X l) == g (Х). Соrласно
утверждеНИIО 4.4, минимальный вес четноrо подкода кода С не
меньше 6. Если допустить, что минимальный вес кода не
больше 4, то вес четноrо подкода также будет не больше 4, что
противоречит доказанному выше.
Конструктивное расстояние является rраницей снизу для ми-
нимальноrо расстояния и, как показывает пример циклическоrо
(23, 11) Koдa rолея, вообще rоворя, может не совпадать с ми-
нимальным расстоянием. Для примитивных БЧХ кодов при
m 6(п 63) эти два параметра совпадают [4], однако мини
мальное расстояни , равное 31, примитивноrо (127, 43) БЧХ-
кода превышает конструктивное расстояние этоrо кода, рав-
ное 29. Вообще rоворя, конструктивное и фактическое мини
168
r лава 4
мальное расстояния БЧХ"кодов различаются редко, но тем не
менее существует бесконечно MHoro примитивных БЧХ кодов,
минимальное расстояние которых больше конструктивноrо рас-
стояния (см. табл. Л.3) [9]. Известно несколько достаточных
условий Toro, что минимальное и конструктивное расстояния
совпадают [3, 4, 1 o 13). Одно из таких условий дает приведен..
ное ниже утвеР.ll{дение 4.14. А именно из утвер,кдения 4.14 сле..
дует, что минимальное расстояние q ичноrо БЧХ кода длины
п == qт. 1 с 1 == О и конструкти.вным расстоянием (R+ 1) qQ 1
(rде о Q < т, О R < q 1) равно конструктивному рас..
стоянию. Рассмотрим произвольный q ичный БЧХ код С пара..
метрами n === qт 1 и 1 == о. Пусть d вчх конструктивное
расстояние этоrо кода. Если минимальное целое число вида
(R' + 1) qQ', такое, что d Бчх + 1 (R' + 1) qQ', то /( d вчх + 1) <
< 2. Поскольку минимальное расстояние d этоrо БЧХ"кода не
может быть больше минимальноrо веса d 1 БЧХ кода той )ке
длины с конструктивным расстоянием (R' + l)qQI 1, то
d /). 1 < 2d вчх + 1.
Для примитивных кодов последняя rраница может быть не-
сколько улучшена [13]:
d < 1 ,5d вчх + 0,5.
Существует rипотеза, что эта оцен:ка является не очень хорошей.
Для примитивных БЧХ кодов при фиксированной скорости
R == k/n и n --+ 00 имеют место слеДУЮlцие асимптотические ра-
венства: d/n d вчх /n 21п R 1/10g2 n (ln обозначение на..
туральноrо лоrарифма) [52]. Следовательно, при фиксированной
скорости k/n и п --+ 00 ОТНОllIение d/n стремится к нулю.
С помощыо описанноrо в слеДУIощем разделе алrебраиче-
cKoro алrоритм а декодирования МО)I{НО исправить все конфиrу-
рации ошибок, исправление которых rарантируется конструктив-
ным расстоянием (но не минимальным расстоянием). Для бсс
конечноrо числа наборов значений параметров в работе [9]
показано существование циклических кодов, минимальное рас-
стояние которых несколько больше минима льноrо расстояния
БЧХ кодов с теми же параметрами п и k. Однако, поскольку
при длинах n до нескольких тысяч параметры БЧХ-кодов не
хуже параметров друrих кодов, для которых известны конструк-
тивные методы построения, а кроме Toro, блаrодаря существо-
ванию эффективноrо алrоритма декодирования БЧХ коды яв-
ляются одим из ва)l{неЙllIИХ классов блоковых кодов.
Пример 4.6 [14]. flycTb элемент порядка Il поля GF(qт) и
С представляет собой q ичныЙ ЦИКJlический J{ОД длиныI п с мини-
l\1альным расстоянис:vI d 11 ПОр() I(даl0ЩIl 1 мноrочленом g (Х)..
Важнеllшuе коды 169
Пусть g (
l+l,+CiJ) == о, О
i l < d o ...... 1, О
i 2
s, (n, с) == 1.
Тоrда
d
d o + s.
Доказательство. Из теоремы 4.1 следует, что d
d o . Пусть
v (Х)
кодовый вектор, вес w KOToporo удовлетворяет неравен-
ствам d o
w < d o + s. Осуществляя в случае необходимости
циклическую перестановку, получаем
w
1
V (Х) == 1 + L у/ха"
j==1
rде 0<aJ<a2< ... <aw
l<n, YjEGF(q)
{O}.
а
Х 1 ==
/ и введем величины
w
1
SI == L y/xJ.
j
1
Положим
Если R (рЁ) === О, то
51 ===
1,
поскольку v (B I ) === о. Кроме Toro, положим
d(l
2 do
2
<1 (Х) == П ( Х
Х ) == L <1
l)Xi ,
1 f::=I I 11==0 L,
w
l w
do+1
<12 (Х) == П (Х
Xj) == .L <1
)XI2,
/ == d o
1 L О == О
<1 (Х) == <11 (Х) <12 (Х).
Так как a j =1= О, (п
с) == 1, ТО Х/ =/::: 1 и Xj =1= 1. Следовательно,
()' (1) =1= о. С дру rой стороны,
w
l т
l ( dO
2 ) ( W
dO+I )
L У IX
<11 (Х j) <12 (x
) == L у ,X
.L <1
) X
I .L <1
) X
l2 ==
1==1 j=sl tl=SO t:!==O
dt
2 w
do+l
== L L <1(I)<1
2)S . === о.
i..
О i
== О t 1 t
1 + l J + с t:.?
Так как Sl+i.+ci! ===
1, то приведенное выше выражение равно
а (1), но это противоречит тому, что (J (1) =1= о. Поэтому d
d o + s. Положив s == О, найдем нижнюю БЧХ
rраницу. Это
покаЗI>Iвает, что полученная выше rраница является обобщс
ни ем НИ}l{ней БЧХ-rраНИllЫ. Известен так}ке ряд друrих обоб
ЩСНИЙ БЧХ
rраницы [14].
4.2. Декодирование БЧХ"кодов
4.2.1. Основные этапы
Процедура исправления t и менее ошибок для q
ичноrо цик-
Лliческоrо кода, КОРНЯМИ поро}({даЮlдеrо мноrочлена KOToporo
170
r лава 4
являются элементы 1+1, 1+2, . . ., 1+2t, rде элемент по-
рядка n поля ОР (q), впервые была предложена Питерсоном для
q == 2 [15]. Цирлер и rоренстейн [16] обобщили эту процедуру
на случай произвольноrо q.
Пусть v (Х) переданный кодовый вектор, е (Х) вектор
ошибок и r(Х)==v(Х)+е(Х) принятый вектор. Так как
v ( l+i) == О (О < i 2t), то
r ( l+i) == е ( l+i), О < i 2t. (4.2)
Вместо Toro чтобы вычислять эти величины непосредственно
по r (Х), можно с помощью схемы деления, описанной
в разд. 7.1.3, вначале найти остаток от деления ,(Х) на g(X)
и подставить в Hero элементы l+i. Вектор ошибок е (Х) можно
задавать, указывая положение ero ненулевых компонент и зна-
чения последних. Для обозначения положения ненулевых ком-
понент введем так называемые локаторы ошибок, а именно co
поставим j й компоненте е(Х) элемент j 1 поля GF(qm), I{OTO-
рый назовем ее локатором. Каждую ненулевую компоненту
вектора ошибок будем задавать с помощью пары (Х, У), rде
ХЕGF(qт) локатор этой компоненты, а Y ee значение. Та-
ким образом, если вектор ошибок имеет v ненулевых компонент,
то он может быть задан совокупностыо v пар (Х 1 , Y I ),
(Х 2 , У2), ..., (X v , Yv), все элементы X 1 , Х 2 , .. , Xv которых раз-
личны, а элементы Y 1 , У2, ..., У v не равны нулю. В частности,
если q == 2, то Y i == 1 и для задания вектора ошибок достаточно
задать лишь локаторы. Если X i === J..LI, то В соответствии с опре-
делением
v J v
( / ) lJ.i " I
е === L..J Yi === L.J YiXi.
i==O i:z=1
Положим
v
5/ == L YiX{,
i==1
О j < п.
(4.3)
Величины 5 j (1 < j 2t + 1) MorYT быть наЙдены по приня
тому пектору с помощью (4.2). Если 5 j == О при всех 1 < j
1 + 2t, то синдром оказывается нулевым и принимается ре-
шение об отсутствии ошибок. Если хотя бы одна из указанных
выше величин Sj не равна нулю, то принимается решение о том,
что
l 'V t.
Дальнейшая задача заключается в том, чтобы каким либо спо
собом найти пары (X I , Y I ), (Х 2 , У 2 ), ..., (X v , Y v ) по известным
величинам Sj, 1 < j 1 + 2t. Основная идея решения этой за-
"
дачи состоит в том, что вначале ну}кно попытаться наити v, за
тем локаторы Х., ..., Xv и далее по локаторам с помощью фор-
Важнейшие коды
171
мулы (4.3) найти Y 1 , ..., Yv. Для нахождения локаторов X 1 , ...
. . . , Xv введем мноrочлен
v
О' (z) == П (1 Xiz) == 0'0 + O'lZ + 0'2Z2 + ... + CJvz v , (4.4)
i==l
v
rде 0'0===1 и CJv===ПХi=l=О. Из формулы (4.4) следует, что
i == 1
v
У iX{O' (Xi 1 ) == L O'sY iX{ s == О,
8==0
о j < n.
Если левыIe и правые части последнеrо равенства просумми-
ровать по i от 1 до ", ТО, В частности, получим
O'vSj+O'v lSI+l+ ... +O'lSI+V l+S/+V===O,
1 < j 1 + 2/ ".
Матрица коэффициентов
Sl+t Sl+2
Sl+2 Sl+З
(4.5)
Sl+V
Sl+V+l
М===
Sl+V Sl+V+l . . . S 1 + 2v'" 1 ......
как леrко проверить, может быть разложена в произведение
трех матриц:
1 1 1 Ylxf+l о . . . о
X I Х 2 . . . Xv о Y2x +1 . . . о
М=== Х
.
XV J X; 1 . . . XV J О О . . . У Xl+l
.... 1 V V V
1 XI . . . Xi ll
1 Х 2 . . . x; 1
Х (4.6)
.
1 Х v ... X 1
Определители первой и третьей матриц в правой части (4.6)
являются определителями Вандермонда. Если все элементы
X 1 , ..., Xv различны, а кроме Toro, YiX i =1= О, 1 i ", то
матрица М не вырождена. Таким образом, задача свелась к
тому, что необходимо найти ". Берлекэмп [3,4, 17] предложил ал-
rоритм одновременноrо нахождения v и решения 0'1, 02, ..., Оу
172
r лава 4
уравнения (4.5). Если мноrочлен а (z) найден, ro, подставляя
В Hero вместо z послеДовательно элементы i, О i < п, можно
найти корни X 1 , Х 2 , ..., Xv уравнения а (z) == О (для реализа-
ции этой процедуры можно воспользоваться методом Ченя, ко-
торый будет описан в разд. 7.1.3). Далее, реlIIая СИСТ 1У урав-
u
пении
v
L YiX +J === 8/+1,
i == 1
можно найти Y 1 , У2, ..., У v (для решения этой системыI мо)кно
воспользоваться методом, предложенным Фор ни [18]). ОIIреде
литель матрицы коэффициентов последней системы уравнений
является определителем Вандермонда, который в данном слу
чае отличен от нуля. При q == 2 последняя операция не НУ)l(на;
следует лишь заменить символы пrИНЯ10rо кодовоrо Bt\I\Topa,
соотвеТСТВУIощие найденныrvl локаторам ОIIIибок Х}, Х 2 , ..., х у,
на противополо)кные.
Если tjп == const и п 00, то число операциЙ при декодиро-
вании для описанноrо выше алrориrма растет ПРОПОРЦИОНClЛLНО
n 2 10g q n.
Утверждение 4.6. Матрица
81+1 81+2
81+2 81+3
l<j<v,
Sl+i
8 1 + i + 1
. . .
M l ==
v i<t,
.
s 1 + 1 81+ 1 + 1 ... 8/ + 21 1
является вырожденн'ОЙ при любом i > ".
Идея доказательства. По аналоrии с выводом
M i можно представить в виде
1 1 . .. 1 У } X + 1 О
(4.6) матрицы
Х 1 Х 2 . . . Xv о
М , ==
X l --- I x l . . . Xl---l О
1 v ...
Y2X +}
. .. о
о
х
о у Х'+)
'v 'v
1 X I . . . Xf l
1 Х 2 Xi }
. . . 2
Х .
.
.
1 Xv . . . Xl l
V
в ажнеtiUluе коды
173
Используя это разложение, можно проверить, что все матрицы
Л1 i , i> \', являются вырожд нными.
Для нахождения числа ошибок \' мuжно последовательно
анализировать матрицы Mt, Mt l, ..., M i . Как следует из
утверждения 4.6, искомое v равно наибольшему индексу i (i t),
такому, что матрица M i не вырождена. Этот способ нахожде
ния \' использовали Питерсон [15], а также rоренстейн и Цир-
лер [16]. Определив таким образом ", они решали систему урав-
нений (4.5) и находили значения 0'1, 0'2, ..., O'v.
Пример 4.7. Рассмотрим (15, 5) БЧХ-код, исправляющиЙ
тройные ошибки, из примера 4.1. Для этоrо кода 1 == О и t == 3.
В качестве возьмем корень примитивноrо мноrочлена Х 4 +
+ х + 1. ПреДПОЛО)l{ИМ, что ошибки ВОЗНИI{ЛИ в 1, 3 и 9 й ком-
понентах. Тоrда локаторами явля.ются O, 2, 8. Используя
таблицу из задачи 2.59, получаем
S 1 === r ( ) === 1 + 2 + 8 === О,
SJ === r ( З) === 1 + 6 + 9 === 10,
85 === r ( 5) === 1 + 10 + 10 1,
Находим N1t === м з :
82 === 8Т === о,
84 === 8 =-= О,
S6 === S === 5.
[ о о IO ]
1'-'13 === О 10 О .
IO О 1
Так как det М з =1= О, то, соrласно лемме 4.6, \' == 3. Система
уравнений (4.5), в данном случае ПРИНИ 1ающая вид
1°0'1 === О,
100' 2 === 1,
IОО'з + о' 1 == 5,
имеет следующее решение: 0'1:== О, 0'2 == 10 == 5, О'з == 5 ==
== lO. Следовательно,
о' (z) == 1 + 5Z + IOZ2.
С помощью таблицы из задачи 2.59 можно проверить, что
корнями этоrо уравнения являются 1, 2 == IЗ И 8 == 7. Рас-
смотренный КОД совпадает с кодом Рида Маллера первоrо
порядка длины 15, для KOToporo известен простой алrоритм по-
poroBoro декодирования (утверждение 4.23).
Задача 4.7. Рассмотреть декодирование двоичноrо цикличе-
CKoro кода Хэмминrа.
174
r лава 4
Решение. Так как t == 1, то ,,== 1, если только e(
) =1= о.
В этом случае e(
) сразу определяет локатор. Поскольку код
Хэмминrа является вырожденным кодом, исправляющим пачки
ошибок (длина пачки ошибок равна 1), то, кроме Toro, он мо-
жет быть декодирован так, как описано в разд. 4.7.
4.2.2. Итеративный алrоритм Берлекэмпа 1)
Опишем итеративный алrоритм Берлекэмпа в модификации,
предложенной Месси [17]. Пусть 50, 51, .", SN
I
последова
тельность элементов поля Р. ПоследоватеJlЬНОСТЬ с}, С2, ..., CL
элементов Toro же поля, удовлетворяющую УС"ТIовию
L
8,+ L Ci8/
i===0,
i == 1
L
j < N, с i Е Р, 1
i
L, (4.7)
назовем порождающей последовательностью длины L для по
следовательности 5.0, 51, ..., 5N
I. Порождающую последователь-
ность минимальной длины будем называть минимальной по-
рождающей последовательностью.
Утверждение 4.8. Пусть Si == О (О
i < ио
1 < N) u
8иo
1 =1= О. При ио == N порождающей последовательности не су-
ществует. При ио == N
1 порождающая последовательность
существует и ее минимальная длина равна N ........ 1.
Идея доказательства. В случае сели uo == N, то при j ==
== N
1 равенство (4.7) не может иметь места. Если же прсд
положить, что ио == N
1 и L < N ........ 1, то равенство (4.7) при
j == N
2 не справедливо ни при каких CI, ..., CN
2. В то же
время, полаrая CI ==
5N
I/5N
2, Ci === О (2
i < N), получаем
порождающую последовательность длины L == N
1.
Следующая лемма устанавливает связь между последова-
тельностями 8l+1, Sl+2, '.', Sl+2t и 0'1, 0'2, ..., О'у, введенными
в разд. 4.2.1.
Лемма 4.1. Последовательность 0'1, 0"2, ..., O'v является един-
ственной минимальной порождаl0щей последовательностью для
последовательности 8 l + l , 8l+2' ..., 8 l + 2f .
Доказательство. Положим 5j == Sl+l+j, О
j < 2t, N === 2t.
Из формул (4.5) и (4.7) следует, что 0'1, 0'2, ..., O'v
порождаю-
щая последовательность для последовательности 8'+1, 8l+2' ...
. .., Sl+2t. Предположим, что существует друrая порождающая
" , L а
последовательность о' l' 0'2' ..., о' L длины ,меньшеи или paB
{) Для поля действительных чисел аналоrичный алrоритм был наЙден
ранее Тренчем [19].
Важнейшие коды
175
ной 'У. Тоrда
L
81 + (J;S j....i === О,
1 с::: 1
1 + L < j 1 + L + v.
Однако это противоречит тому, что матрица М является невы.
u
рожденнои.
Наша задача сейчас состоит в TOf\1, чтобы получить эффек-
тивный алrоритм нахождения минимальной порождающей по-
следовательности. Если существует минимальная порождающая
последовательность для префикса so, SI, ..., Su 1 (О U < N)
заданной последовательности S(), 51, ..., SN l, то будем обозна-
чать ее через c и), c и), .. ., ct U). Для удобства представим эту
последовательность коэффициентов в виде мноrочлена
с(и) (D) === I + c U)D + ... + ct U)DL (и).
Если порождающая последовательность не существует, будем
полаrать
L (и) == и.
По определению L (и + 1) L (и).
L (и)
Лемма 4.2 [17]. Если Su + L c tl)su i =1= О, ТО
i::aJ
L (и + 1) u + 1 L (и).
Доказательство. Предположим, что
L (и) u L (и).
(4.8)
По определению
L (и)
"с(и), . == S.
1 I t l'
1==1
L (и+ 1)
" c(U+l)s === S
L..J h ' h l'
h::al
L (и) j < и,
(4.9)
L (и + 1) j < и + 1.
(4.1 О)
Отсюда и из формул (4.8) (4.10) получаем
L (и) L (и) L(u+ 1)
L C(U)S . == L с(и) L c(u+1)s . ==
1=-1 1 a " i=:s1 i hc:::l h U L h
L (и+О L (и) L (и+О
== L с(и+1) L C(u)S == L C(u+l)S == s
h==J h i=-I 1 и....i....h hcal h " h и,
но это противоречит предположению.
Основываясь на вышеизложенном, рассмотрим следующий
итеративныЙ алrОРIlТМ построения минимальной порождающей
последоватеJIЬНОСТИ для последовательности so, SI, ..., SN l'
176
r лава 4
Обозначим через сх'и подпоследовательность 5f), SI, ..., Sи l по-
следовательности 5Q, 51, ..., SN l. Можно, очевидно, оrрани-
читься рассмотрением случая, коrда среди символов Si, О i <
< N, имеется хотя бы один, отличный от нуля. Пусть ИО 1
минимальное значение i, такое, что 5i =1= о. Из утвержде
ния 4.8, следует, что
1) если ио == N, то порождающей последовательности не су-
ществует;
1') если ио < N, то для аио+l существует минимальная по-
рождающая последовательность длины ио, а именно
с(ио+ 1) ( D ) === 1 s S 1 D.
ио иO 1
в этом случае
L (ио + 1) === ио.
Для удобства положим
L (ио 1) === о, L (ип) == llu. (4.11)
2) Предполо)ким, что для cx'j, ио < j и < N, найдена по..
рождающая последовательность c j (D). Введем следующие ве-
личины:
БU) 1 === suo 1,
L(f)
б. == S I + L C<. , i)S. .,
J i==1 t J t
и о < j и.
Кроме Toro, предположим, что
L (j) == m а х [1--1 (j 1), j L (j 1)],
(4.12)
если ио < j u < N и бj l =1= о. Справr,ПЛИБОСТЬ равенства
(4.12) при j == ио, ио + 1 очевидна. Так как L (ио 1) < L (ио)
== ио == L (ИQ + 1) L (и), то существует целuе й, такое, что
L (й) < L (Й + 1) === L (и), ио 1 <. й < и. ( 4.13)
При этом либо й === ио 1, либо й > [[о. Если п === 1I0 1, то
б й == sUo 1 =f= о. Допусти М, что б й === о, й > и о . Tor да c )й\ c й), . . .
. . " Ctulu) порождающая последовательность для (Xa+l' но это
противоречит (4.13). Следовательно,
ба =1= о.
Лемма 4.3. МНОёочлен
с(и+l) (D) == с(и) (D) + бuб й J DU Йс(Й) (D), (4.14)
ёде c(и') 1) (D) === 1, определяет nорождающую последовательность
для а и + 1. Если c(u+l) (D) =1= с(и) (D), то L (и + 1) == тах [L (и),
и+l IJ(u)J.
Важнейшие коды
177
Доказательство. Соrласно соотношейИЯIvI (4.12) и (4.13),
L(u)===L(u+ 1)==й+ 1 L(Й). (4.15)
Если б u === О, то c(U+l) (D) == с(и) (D), L (и + 1) == L (и). Если ба =1= О,
то, полаrая
IJ === mах [L (и), u + 1 L (и)] , (4.16)
из формулы (4.15) получаем, что L == mах [L (и), и........ й + L (й)].
Из (4.14) в свою очередь следует, что
L L (и)
S + L C(tl+1)5. . === s. + L c(.u)s. .
I . 1 t J t J . 1 t J t
t l
[ L (й)
б б I + " (й) ]
........ и й S/ u+u L..J C i S/ u+u l '
/==1
( 4. 1 7)
rде L j U. ИЗ определения с(и) (D) и Toro, что L (и) L,
имеем
L (и) { О
(и) '
s. + L с. s. .
J . 1 t J t U
t== а,
L j < и,
] == и.
(4.18)
Если j меняется между L и и, то j u + й меняется от L U + й
до й. Тоrда, так как L u + й й + 1 L (и) :=:: L (й) (это сле
дует из (4.15) и (4.16), то L (й) :::;; j II + й :::;; й. Если й > ио,
то, соrласно определению с(й) (D),
L (й) { О L ] . < и ,
+ L (й) '
S. с.. .
, и+1l . 1 SJ u+u t б ] '===и .
t==1 и,
(4.19)
Поскольку Sl === О (О i < ио 1), это равенство справедливо
также при й == иo 1.11з формул (4.17) (4.19) получаем
L
S + L c(u+l)s .==0
/. i==1 t / t '
L j<u+l,
т. е. с(и+1) (D) задает ПОРО)I<дающую последовательность
длиныI L для С'Х и +l. Соrл асно лем ме 4.2 и равенству (4.16),
длина L является минимальной и опредрляется равенством
L (и + 1) == m а х [L (и), u + 1 1--1 (и)].
Из этой леммы следует, что c(N)(D) определяет минималь-
ИУIО порождаIОЩУIО ПОС,,1сдовательность для 50, 5}, ..., SN I.
Пример 4.8. Рассмотрим случай исправления трех ОDlибок
кодом из примера 4.7. Здесь
(S., S2, . . ., 56) === (su, SI, .. .1 55) == (О, О, IO, О, 1, 5).
178
r лава 4
Сначала положим U,О == 3. Из утверждения l' имеем
с(4) (D) === 1,
L(4)==3.
При этом, cor ласно соотношению (4.11),
L (2) == О, L (3) == 3.
Поэтому если u == 4, то й == 2. В то же время, так как 62 ==
10
И 64== 1, то из формулы (4.14) и равенства c(2)(D)== 1 имеем
с(5) (D) == 1
IOD2C(2) (D) == 1
_
5D2,
L (5) == тах [L (4), 5
L (4)] === 3.
Далее, если II == 5, то й == 2 и
з
() == S + L с(5) S . ==
5 O&
5 · О ==
5.
5 5 . 1 t 5---L
L::JI
ИЗ формулы (4.14) имеем
с(6) (D) == с(5) (D)
10
5D3C(2) (D) == 1
5D2
10DЗ,
L (6) == тах [L (5), 6
L (5)] == 3.
Таким образом, 0'1 == О, 0'2 ==
5, АЗ ==
10.
В случае q == 2, используя вместо системы уравнений (4.5)
'v
равенства Ньютона [20], связывающие величины Sj === LX{ (l <
[=-1
< j
1 + 2/) с элементарными симметрическими функциями
Х 1 +Х 2 + ... +Xv==+al, Х t Х 2 +Х 2 Х з + ... +XV
lXV==0'2, ...
..., Х 1 Х 2 ... Xv==(
I)'VO'v переменных Х 1 , Х 2 , ..., XVt можно
определить 0'1, 0"2, ..., О''' по Sj (1 < j
1 + 2t). Питерсон [15]
использовал именно этот метод. В этом случае мо)кно приме
нить такой же рекуррентный метод решения, как и ранее, и сни
зить таким образом число шаrов с 2/ до t [3, 4].
Методы декодирования, описаНН[>lе в разд. 4.2.1 и 4.2.2, пред"
назначены для исправления ошибок, вес которых не превосхо
дит (d
1) /2, [де d
конструктивное расстояние даже в том
случае, если фактическое минимальное расстояние кода больше
конструктивноrо. Были разработаны алrоритмы декодирования
ошибок более высокой кратности, но их эффективность оказа-
лась не очень высокой [21].
4.3. Методы мажоритарноrо декодирования
В некоторых случаях оказывается более предпочтительным
использовать коды, корреКТИРУl0щая способность которых HC
сколько хуже, чем у лучших известных кодов, но которые Moryr
Важнейшие коды
179
быть просто реализованы. Типичными представителями таких
кодов являются коды, допускающие мажоритарное декодирова-
ние (см. разд. 4.5.2). В некоторой области значений параметров
эти коды имеют корректирующую способность, незначительно
уступающую корректирующей способности БЧХ кодов, но зато
их можно проще реализовать [3, 4, 22 24].
Определим q-ичную мажоритарную фУНКЦИ10 Maj (Х}, Х2, ...
. . . ,Х т ) от т переменных Х}, Х2, ..., Х т , принимающих значения
в GF(q), следующим образом:
1) Если некоторые 1 > m/2 переменных Xi , Х ,, ' , . . ., Х. при-
1 2 t 1
u
нимают одно и то }I{е значение а, то значение ма}l{оритарнои
функции также равно а.
2) Во всех остальных случаях мажоритарная функция при
нимает нулевое значение.
При q == 2 и нечетных т введенная функция является обыч-
ной мажоритарной функцией и может быть реализована с по-
мощью пороrовоrо элемента. В случае четных т предпочтение
отдается символу О.
Вначале поясним метод пороrовоrо декодирования на про-
стом примере.
Пример 4.9. Рассмотрим (7, 3) KOД маI{симальной длины.
Матрица Н в данном случае имеет слеДУfОЩИЙ вид:
... 1 1
О 1
О О
О О
о 1
1 О
1 1
О 1
о о
1 О
О 1
1 О
о
о
о
1
Пусть е == (e , еl, . . . , ев) вектор ошибок, а 80, 81, 82 И 5з ком-
поненты синдрома. Тоrда
80 == ео + еl + ез,
8} == е( + е2 + е4,
82 === е2 + ез + ев,
8з == ез + е4 + е 6 .
Положив S === 80' s; === 80 + 81 + 82 и 8 == 80 + 81 + 8 з , получаем
8 == е о + е( + е з ,
8 == е о + е 4 + e s ,
8 == е о + е 2 + е 6 .
180
t лава 4
Заметим, что каждая из компонент ei вектора ошибок, за
исключ.ением ео, входит только в ОДНу из сумм So' 8;, 8 . Пред-
положим, что произошла только одна ошибка. Тоrда, если
ео == О, то одна из сумм S , S и 8 будет равна 1, а остальные
две будут равны О. Если ей === 1, то S === S === S; === 1. Слсдопа-
тельно, при отсутствии ошибок, а так)ке при одиночных ошибках
е о == klaj (S , S , 8 ) == Maj (80' 80 + S( + 82' 80 + SI + SЗ).
Так как рассматриваемый код является циклическим, то анало-
rичные соотношения имеют место и для остальных i:
el == Maj (Si, 81 + 81+1 + Si+2, 8l + SI+l + 8i+З),
rде индексы вычисляются по МОДУЛIО 7. Таким образом, вычис
.пяя 80, 81, 82, 8з И осуществляя их сдви['и, с помощью вышепри
веденной формулы мо,кно провести декодирование. Вопросы
технической реализации этой процедуры декодирования будут
рассмотрены детально в разд. 7.1.3в.
Пуст.ь С q ичный линейный (п, k) KOД и пусть C D код,
двойственный к С. Обозначим через у == (уо, YI, . . . ,Yrt l) И е ==
(ео, el, ..., en 1) соответственно принятый вектор и вектор
ошибок. Тоrда для любоrо вектора а == (ао, al,..., an 1) Е
n 1 п 1
Е Сп {О} выполняе1СЯ равенство L ajYi === L ajej; послед
/ o /==0
нне суммы называются nровеРОЧНbtми суммами. Пусть линеНllые
n 1
комбинации 8i===L aijej(aijEGF(q), I i l) символов ео,
j==O
eI, ..., en 1 (ни)ке эти линейные комбинации называются Tal()f(e
линейными е суммами) инепустое ПОДМНОll<ество J множества
{О, 1, . . . , п 1} удовлетворяют слеДУЮIЦIl м двум условиям:
1) для любоrо jEJ cYll{eCTByeT такое азЕ GF(q) {О}, что
al/==aj, O i l;
2) для любоrо j Ф. J все символы аlЗ, a2j, ..., аи, за исклю-
чением, быть может, одноrо, равны О. Такие линейные e CYMMЫ
Sl, 82, ..., 81 называются ортоеонаЛЬНbt.А-IU относительно L a/e j .
/е/
Л v " , 49
ннеиные е-суммы 80' 81 И S2 из примера . ортоrональны
относительно ео.
Вес вектора е будем, как обычно, обозначать через w(e).
Лемма 4.4. Если линейные e CYMMЫ 81,82, ..., 8[ ортоеональны
относительно линейной е-суммы s и w (е) [1/2], то
8==Maj(81, 82, ...,81). (4.10)
Доказательство. Пусть 8 == L a/ej, а/ =1= О (j Е J). Если
/ е /
Важнейшие кооы
181
ej == о (j Е J), то, соrласно условию 2 ортоrональности, среди
51, 52, ..., 5l самое большее [1/2] линейныIx e CYMM отличны от
нуля. В этом случае справедливость соотношения (4.20) непо
средственно следует из определения Maj. ЕСJIИ ej =1= О хотя бы
для одноrо j Е J, то количесrво компонент ei =1= О, i Ф J, не пре
вышает [//2] 1. 110 тоrда из определения ортоrональности IlО
лучаем, что не меньше чем 1 + 1 [//2] линейных e CYMM среди
51, 52, ..., 5, равны 5. Таким образом, в этом случае равенство
(4.20) также выполняется.
Если в лемме 4.4 5 == ej, то формула (4.20) принимает сле-
дующий вид:
eJ === /vlaj (51, 52, . . ., 51). (4.21)
Если линейныc e CYMMЫ 51, 52, ..., 5, ЯВЛЯIОТСЯ проверочными,
то после Toro, как по принятому вектору у найдены значения
51, 52, ..., 51, С ПОМОll ЬЮ вышеприведенной формулы можно
определить значение ej. Если для ка)кдоrо О j < п суще
CTBYIOT проверочныIe сум 1\1 1)1 5jl, 5)2, ..., S j, 2t, opToroH альные OT
носительно ej, то rоворят, 4 ro Оluибкu веса до t можно иcпpa
вить с пОМОlЦЬЮ 1l0pO OBOZO декодирования в один шае. Если
код является циклическим, то достаточно потребовать существо..
вания ортоrональных проверОЧllЫХ сумм только для ео.
Указанную выше идеIО пороrовоrо декодирования в один шаr
можно развить дальше слеДУЮlIJ.И.М образом. Выше предполаrа-
лось, что 5jJ, 5j2, ..., 5j,2t являются проверочными суммами.
Здесь же будем считать, что 5j1 это просто линейные e CYMMЫ,
для каждой из которых, однако, существуют 2t проверочных
сумм 5jil, 5ji2, ..., 5ji,2l, ортоrональных относительно 5ji. Тоrда,
если w (е) t, то, вычисляя по принятому вектору у значения
всех проверочных сумм 5jilt, С помощью леммы 4.4 можно найти
значения всех линеЙных e CYMM 5н и, днлее, вновь обращаясь
I( лемме 4.4, найти ej. В этом случае rовuрят, что ошибки веса
до t можно исправить с помощью пороеовоео декодирования
в 2 шаеа. Совершенно аналоrично МО)КНО описать декодирова
ние в 3, 4, ..., L ш arOB. В последнем СJIучае rоворят, что
ошибки веса до t включительно можно исправить с помощью
пороеовоео декодирования в L шаеов.
Этот метод первоначально был предложен Ридом [25] для
декодирования I{ОДОВ Рида Маллера (см. разд. 4.5). Имеет
место следующая теорема [4, 24].
Теорема 4.2. Пусть код С допускает исправление ошибок
веса до (1 С помои{ыо пОРОёовоео декодирования в один шае.
Тоеда, если код C D , двойственный к коду С, имеет минимальное
расстояние d D , то
п 1
tl 2(dD I) '
182
r лава 4
Доказательство. По предположению существуют 2t 1 прове-
рочных сумм 801' 802' · · ., 80, 2t l ' ортоrональных относительно ео.
Пусть а(О == (аьО, a O, . . ., a I) вектор, компонентами KOTO
poro являются коэффициенты проверочной суммы 80i. По пред-
положению аьо =1= о. Если вес a(i) равен 1, то d D == 1, поскольку
a(i) Е C D . Следовательно, в этом случае теорема справедлива.
Предположим, что d D > 1. Тоrда каждый вектор аи) содер}кит
по крайней мере (d D 1) компонент a O =1= О, j =1= о. С друrой
стороны, при каждом О < j < п из символов a l), a 2), .. ., a
только один может быть ненулевым. Отсюда следует, что
2(dD l)t 1 п 1.
Из этой теоремы видно, что возможности пороrовоrо декоди-
рования в один шаr очень оrраничены. Например, как следует
из примера 4.2, в случае двоичноrо (23, 12) Koдa l"олея d D == 8,
так что t 1 22/14. Таким образом, (23,12) -код rолея, который,
вообще rоворя, позволяет исправлять ОIlIибки веса 3 11 менее,
при пороrовом декодировании в один шаr позволяет исправлять
только одиночные ошибки. Это же можно сказать и о кодах
Рида Соломона (СМ. пример 4.4). Если минимальное pac
стояние кода равно d и он позволяет исправлять ошибки веса
до [(d 1) /2] с помощью пороrовоrо декодирования в L шаrов,
то rоворят, что код допускает полную ОрТОёонализаЦtlю в L ша
rOB. Для произвольноrо L имеет место следующая теорема.
Теорема 4.3. Пусть код С допускает исправление ОUlибок
веса t L и менее с помощыо пОРОёОВОёО декодирования в L ша
20В. Если d D минимальное расстояние кода, двойствеННОёО
к коду С, тоl)
n (d D /2)
t L 2 [d D /2] ·
Доказательство. По предположению существуют 2t L прове-
рочных сумм 81, 82, .. ., 82tL' ортоrональных относительно неко-
торой линейной e CYMMЫ 8. Пусть а, а(1), . . ., a(2tL) векторы,
компонентами которых являются коэффициенты сумм S, Sl, ...
..., 82tL' Без оrраничения общности можно предположить, что
w (аО) а) w (a(i) а), О < i 2t L . Из определения opToro-
нальности следует, что при любом О j < п только одна из
· (1) (2) 2tL
компонент с номером J векторов а, а а, а а, .. ., а ...... а
{) Через [А] здесь обозначено наибольшее целое число, меньшее или рав-
ное А (целая часть А), а через ] А [ наименыlееe целое число, БолыlJееe или
равное А.
Важнейшие коды
183
может быть отл,ичной от нуля. Следовательно,
2tL
w (а) + L w (а(О а) n,
i а: 1
( 4.22)
(4.23)
(4.24)
w (а(О) === w (а) + w (а(1) а),
w (а(О аО») === w (а(О а) + w (a(l) а), 1 < i 2t L.
Так как а(l), аи) a(l) Е С D, то
W (а(1») d D, (4.25)
w (а(О a(I») d D, 1 < i <. 2t L. (4.26)
С друrой стороны, по предполо)кению w (а(1) а) :::;; w (аи)
...... а). Из формул (4.24) и (4.26) имеем
w (а(О а) [d D /2] , 1 < i <.2t L .
Отсюда и из соотношений (4.22), (4.23), (4.25) в свою очередь
следует, что
(2t L 1)] d D /2 [<. п d D ,
а поэтому
2t L [d D /2] <. n (d D /2).
Если сравнить верхние rраницы для t l и t L , то можно за
метить, что оцеНI{а для t L при6лизительно в 2 раза меньше
оценки для t l .
Пример 4.10. Рассмотрим (7, 4) KOД Хэмминrа. Проверочная
матрица этоrо кода 6ыла построена в примере 3.5:
[ 1 О О 1 О 11 ]
Н=== О 1 О 1 1 1 О .
О О 1 011 I
Обозначим через 51, 52 И 5з проверочные суммы, коэффициен
тами которых являются элементы соответственно 1, 2 и 3-й строк
матрицы Н. Так как
51 + 52 == ео + еl + е4 + е6,
51 + 52 + 5з === ео + eJ + е2 + еБ,
10 проверочные CYM IЫ 51 + 52 и 51 + 52 + 5з ортоrональны OTHO
сительно ео + el. Поскольку этот код является циклическим, то
двойственный к нему код также циклический. Отсюда, 060зна..
чая циклический сдвиr вектора v на одну компоненту вправо
через Pv, а сдвиr на i компонент вправо через piv, получаем
p6(Sl + 52) == е6 + ео + ез + es,
р6 (51 4- 52 + 5з) === е6 + ео + еl + е4.
184
r лава 4
Это означает, что проверочные суммы P6(Sl + S2) и P6(SI +:
+ S2 + 5з) ортоrональны относительно е.о + е6. Поскольку суммы
ео + el и ео + ев ортоrональны в свою очередь относительно ео
и этот код является циклическим, то, таким образом, мы пока
u
зали, что рассматриваемыи код допускает исправление одиноч-
ных ошибок с помощью пороrовоrо декодирования в 2 шаrа
и, следовательно, является полностью ортоrонализуемым
в 2 шаrа. Этот код представляет собой один из укороченных
циклических кодов Рида
Маллера, а описанный здесь метод
ero декодирования является частным случаем известноrо об-
щеrо метода декодирования таких кодов (см. пример 4.12).
Задача 4.9 [26]. Как следует изменить формулировку лем-
мы 4.4, если свойство 2 в определении ортоrональности заме-
нить следующим:
2') ДilIЯ любоrо j Ф J среди символов alj, a2j, ..., alj отлич-
ными от нvля являются самое большее 'л символов.
Краткое решение. Величину [1/2] следует заменить на [l/2'Л].
Доказательство леммы 4.4 в этом случае проводится анало-
rично.
Методы декодирования, основанные на лемме 4.4, изменен
ной указанным в задаче 4.9 способом, называIОТСЯ методами по
poroBoro декодирования с помощью неортоеонаЛЬНblХ проверок...
Область применения этих методов достаточно широка, но они
обладают тем недостатком, что при их использовании значи
тельно возрастает число входов мажоритарных элементов [4].
Обобщению методов м:ажоритаРНОI'О декодирования и их моди-
фикации посвящен ряд работ [4, 27
31]. Наиболее типичные
классы кодов, допускающих мажоритарное деI{одирование, бу.
дут рассмотрены в разд. 4.5.2 и 7.7.2.
4.4. Мноrочлены Матеона
Соломона
Некоторые способы задания циклических кодов основаны на
использовании мноrочленов Матеона
СОЛОАtона (MC
MHoro-
членов) [3, 4, 32]. Пусть q
число, яв.пяющееся степенью неко-
Toporo простоrо числа р, т
целое ПО.lIО)l{ительное число, п
целое поло)кительное число, которое делит qln
1, и
эле-
мент порядка п поля GF(q1n). Обозначим через V n ReI{TOpHOe
пространство размерности п над GF(q). Сопоставим BeI{Topy
v === (v,o, Vl, .. ., иn
1) Е V n мноrочлен V (х) === ио + vlX + ...
.,. + [}n
IXn
l. МС-мноrочлен вектора и, обозначаемый ниже
через MS (и, Х), определяется СJIедующим образом:
n
/И S ( V,
Y) === п
I L S I Х N
i,
j==1
(4.27)
Важнейшие коды
185
rде
Sj == v (p/).
( 4.28)
Так как v1 == V i ' то
51 == Ct Vi ijY === :t Vi ijq === 5qj
(4.29)
(индексы у 8/ вычисляются по модулю n). Таким образом,
n
1\18 (v, ') == n 1 L S/ /[ ===
j l
n n l ... n l n
=== n l L jl L Vi il === п l L Vi L (l l) J.
j==1 i==O i==O j;:1
Ниже нам понадобится следующая лемма.
Лемма 4.5. П усть элемент порядка n поля аР (qт), U
пусть i целое число. Тоеда
1) если i =1= O(mod п), то
n 1
n l L ll === о;
j==O
2) если i == O(mod n), то
n l
n l L il === 1.
j==O
Доказательство. Справедливость части 2 леммы очевидна.
Для доказательства части 1 достаточно заметить, что в этом
случае ; 1 =1= О и
n l
( ; 1) L il === n 1 === о.
/==0
n n !
Из леммы 4.5 и равенства L (/ !) j == L (i l) / следует, ЧТО
j==l j==O
л,lS (v, l) === V[, О 1 < n. (4.30)
Это равенство показывает, что есл и среди элементов l, 2, ...
.. ., п == O имеется r корней MS (v, Х), то вес и' (v) вектора V
равен ll r.
Пусть С q ИЧНЫЙ циклическиЙ (п, k) KOД с порождающим
мноrочленом
g(X) == ТI (х...... ;зi),
iER
rде R с:: {О, 1, . . . , п l}. Как было пока:lано в разд. 3.6, MHO)I(e
ство R замкнуто относительно перестаНО8КИ П q : i iq (mod п)
множества {О, 1,..., п 1}. Пусть dвчх fинимаЛЫlое целое
число, не IIринадле)кащее R. Если v . произвольный кодовый
186
r лава 4
вектор кода С, то
81 === V ( f) === О, j Е R,
поскольку g (Х) I V (Х). Следовательно, степень MS (и, Х) не
больше чем п dвчх. Если v ненулевой вектор веса w (v), то
ИЗ формулы (4.30) получаем
dвчх w(v). (4.31)
l"аким образом, d вчх является не чем иным, как нижней
БЧХ rраницей для минимальноrо расстояния.
Обратно, выберем произвольным образом СОВОI{УПНОСТЬ
(SI, S2, . . . ,Sn) элементов ОР (qm), удовлетворяющую слеДУIО"
щим условиям:
S I == О,
S] === Sqj,
jER,
1 j n.
( 4.32)
Пусть
n
а (Х) == n ---1 L 8,Xn---l,
j==l
va==(a( O), a( l), ..., a( n I)).
Тоrда из леммы 4.5 для всех О 1 < п имеем
n l n I n
V a ( l) === L а ( i) H == п I L H L SJ (n j) i ===
i O i==O j l
n n 1
== n --- 1 L S J L (! J) i == S 1,
j 1 i==O
т. е. V a Е О. Отсюда и из равенств (4.27) и (4.28) следует, что
MS (v a , Х) == а (Х).
Пусть МS(С) множество всех мноrочленов над GF(q1Yt)
n
вида n l L SIXn j, удовлетворяющих соотношениям (4.32). Из
j == 1
вышеизложенноrо следует справеДЛИDОСТЬ следующей теоремы.
Теорема 4.4. Отображение С 8 MS (С)
ер: v MS(v, Х)
и обратное отображение
ep l: a(X) >Va==(a( O), a( I), ..., a( n I))
устанавливают взаимно однозначное соответствие между эле-
ментами С u MS(C). Число КОРllей мносочлена MS(v,X)
(j GF(qт) {О} равно n w(v).
Важнейшие коды
187
Это отображение Иёрает в теории кодирования важную роль,
поскольку позволяет сводить задачи о весах кодовых векторов
к задачам о числе корней МНОёочленов.
Пример 4.11 [32]. Рассмотрим двоичный (23, 13) KOД rолея
из примера 4.2. В этом случае п === 23, т == 11, R == {1, 2,3, 4,
6, 8, 9, 12, 13, 16, 18} и ......... элемент G F (211) порядка 23. Множе
ство {О, 1, ..., п I} R состоит из следующих (2, 23) циклов:
{О} и { 1 == 22, 2 == 21, 4 == 19, .........8 == 15, .........16 == 7, 9 ==
== 14, 18 == 5, 13 == 10, 3 == 20, 6 == 17, 12 == 11}.
В последнем цикле i e целое число сравнимо с 2i 1 по модулю
23 (это связано с тем, что все (2, 23) циклы это {о}, цикл
длины 11, содержащий 1, и цикл той же длины, содержа
щий 1 == 22]. Следовательно, полаrая S22 == S, получаем
821 == 82, S19 == S2\ 815 === S2', 87 == 824, 8]4 == 825, 85 == 82\ 810 == 827,
28 29 210 С ( ) 2
820 == S , SI7 == S, SI1 == S. оrласно 4.32, So == 8o, т. е.
80 е:: G F (2). Как следует из вышеизложенноrо, для любоrо KOДO
Boro вектора
MS (и, Х) === 80 + 8Х + S2X2 + S2 8 X 2 8 22 Х 4 + S2 9 X6 + S2'X8 +
+ S2 5 X9 + S2 1 0X 12 + S2 7 X13 + S2 4 X16 + S2 6 X]8,
SoEGF(2), Se::GF(2]]). (4.33)
Так как v ( O) == So, то So == о при четном w (t!) и 80 == 1 при
нечетном w (и). Ниже будем считать, что v =1= О. Поскольку CTe
пень MS(vX) не больше 18, то w(v) не меньше 23 18 == 5.
Предполо)ким, что w (и) == 5. Тоrда 80 == 1 и все корни
MS (и, Х) ЭТО корни уравнения Х23 1 == О вида i. Произве-
дение этих 18 корней, соrласно 4.33, равно S 26, так что (s 26)2З ==
== 1. Следовательно, (S2 6 )2 5 == S также является корнем Х2з......... 1,
и показатель S следует вычислять по модулю 23. Равенство
(4.33) перепишем в виде
1\18 (и, Х) == 80 + 8Х + (SX)2 + (SX)3 + (SX)4 + (SX)6 + (8Х)8 +
+ (8Х)9 + (SX)12 + (8Х)13 -f- (8Х)]6 + (8Х)18.
Тоrда, поскольку М8(v,S IХ) мноrочлен над ОР(2), то, если
i......... I{OpeHb, 2i также корень. Так как длина (2, 23) llИКЛОВ,
отличных от {о}, равна 11, то число корней MS (и, S 1 Х) вида i
не больше 12. В то же время мноrочлен MS (и, Х) также имеет не
более 12 корней вида i. Получили противоречие. Следовательно,
w(v) 6. Предположим, что w(v) == 6. Тоrда So == v(l) == о, и
все корни мноrочлена MS (и, Х) x 1 == 8 + 8 2 х + ... + S2 b X I7
должны иметь вид i. Произведение этих корней равно 81 26.
Элемент SI 2б, а следовательно, и 826 ! являются КОРНЯМИ
уравнения Х 2З 1 == о. Так как числа 26 1 и 211 1 взаимно
188
r лава -1
простые, то сам элемент S также имеет вид
i. Вновь получили
противоречие. Следовательно, w (v)
7. Поскольку кодовый BeK
тор v, для KOToporo мноrочлен v (Х) является порождающим
мноrочленом g(X)=== I+X+X5+X6+X7+X9+XII, имеет вес
7, то минимальное расстояние (23, 12)
Koдa rолея равно семи.
Утверждение 4.10. Рассмотрим код Рида
Соломона, oпpe
деленный в примере 4.4. Множество MS (С) представляет собоЙ
множество всех МНО20tfленов над G F (q) степени (q
2
') и
менее. Следовательно, С == {(а (ВО), а (
I), ..., а (
ч
2)) I а (Х)
МНОёочлеНbl над GF(q) степени (q
2
') и AtCHee}.
Краткое доказательство. Так Kal{ qi == i (mod q
1), то ДOKa
u
зательство непосредственно следует из определении и Teo
ремы 4.4.
4.5. Полиномиальные коды
4. 5. 1. Обобщенные коды Рида
Маллера
Как следует из TeOpel\tlbI 4.4 и утверждения 4.1 О, код можно
задать, указав мно)кество F мноrочленов, удовлетворяющих
определенным условиям, и сопоставив далее каждому MHoro
члену f Е F вектор, компонентами KOToporo являются значения
f, получающиеся при подстановке в мноrочлен f определенных
значений переменной. Впервые этот способ использовал Митани
[33] для изучения кодов Рида
Маллера [34].
Обозначим через Pv, т множество всех мноrочленов степени
\' и меньше от ln переменных Х 1 , Х 2 , ..., Х т , принимающих зна
чения в поле GF(q) 1). Так как Xq === }( для любой переменной Х.
принимающей значения в GF(q), то ЛIuбой одночлен из Р\',III С
коэффициентом 1 имеет следующий вид:
X i1 X i2 X im
1 2... ln'
O
il<qt
1
j
"1.
Любой мноrочлен f Е Pv,т мо)кет быть .представлен в виде ли
ней ной комбинации таких (нормированных) одночленов с I<ОЭф
фициснтами из поля G F (q). Так [{ак различные одночленыI ли
ней но независимы (утверждение 2.49), то коэффициенты этой
линейной комбинации определнются однозначно. Мно)кество
всех линейных комбинаций нормированных одночленов степени
" и меньше с коэффициентами из поля GF(qт,) будем обозначать
через p
. m.
1) Коэффициентами этих мноrочленов также являются элементы GF(q).
Важнейшие коды
189
Лемма 4.6. Сумма L L L afla 2 . . . a т
йl Е GF (q) а 2 е rJF (q) й т Е йР (q)
равна ( I)т, если il==i2 ... ;)п===q l, и равна О 80
всех остальных случаях.
т
Доказательство. Указанная выше сумма равна II L ail.
1..1 Й/ЕGF(q) 1
Поло)ким 5. == L a i . Если а =1= О, то Sq -l == 1, так что
t й с= ОР (Q)
aq 1 == 1. Очевидно, 50 == О. Если О < i < q 1 и В один из
примитивных элементов поля ОР (q), то, полаrая а == j, из
леммы 4.5 получаем
q---2
Si == L и.
1880
Отсюда следует справедливость леммы.
Пусть а оДИН из примитивных Э.ЛеМеНТОБ GF(qnt). Тоrда
m---l
i /
а === L.J ai la ,
j==O
О i qт 1 ,
( 4.34 )
rде aijEGF(q). Для простоты значение f(aiO, ai1, ..., ai,т l
мноrочлена f (Х 1, ..', Х т) Е p , т будем обозначать через f (ex,i) ,
а значение f (О, ..., О) через f (О). Положим
v е (f) === (f (О), f (а О ), f (а 1 ) , ..., f (а q т 2 ) ).
Вектор, получаемый из ve(f) удалением первой компоненты, бу-
дем обозначать через v (f). Пользуясь леммой 4.6, можно ПрОБе-
рить справедливость следующей леммы.
Лемма 4.7. Пусть" < 'n (q 1) u f Е p , т. Тиёда
L т f (а) == о.
ЙЕGF(q )
Множество {v(f) IfE Pv,т}, О v < т(q 1), называется
q uЧНЫМ обобщенным кодом Рида Маллера длины п == qт 1
порядка v (или сокраlцеино OPM KoдOM) [3, 4, 34, 35]. Очевидно,
что этот код является линейным. Расширение OPM Koдa назо.
вем p OPM KoдOM. Как следует из леммы 4.7, p OPM KOД это
мно)кество {ve{f} If Е Pv,т}. в случае q == 2 p OPM KOД назы
вается кодом Рида Маллера, а OPM KOД укороченным цu
кличеСКllМ кодом Рида Маллера. В случае т 1 OPM KOД
совпадает с кодом Рида Соломона (см. утверждение 4.1 О) .
Исследуем основные свойства OPM KOДOB и p OPM KOДOB.
Утверждеllие 4.11. Ч аСАО информационных символов kv
p OPM Koдa порядка v и OPM Koдa порядка v равно общему
190
r лава 4
числу совокупностей целых чисел (i}, i 2 , ..., i m ), удовлетворяю-
щих следующим условиям:
O il<q,
т
L i/ 'V.
Ir=al
'v
В частности, kv == L ( 7) при q == 2.
1==0
Краткое доказательство. Как указывалось выше, MHoro
член f Е Pv,rп является линейной комбинацией одночленов
т
X lX 2 ... x т, O i/ q, l j m, Li/ 'V. Так как все
1==1
одночлены линейно независимы, то число информационных сим-
волов p OPM Koдa порядка " равно оБIцему числу таких одно-
членов. Так как" < m(q 1), то, соrласно лемме 4.7, р-ОРМ-
код является расширением OPM Koдa и имеет то же число ин-
формационных символов.
Утверждение 4.12. kv + kт(q l) V l == qт.
Краткое доказательство. Соrласно утверждению 4.11,
kт(q l) V l равно числу совокупностей целых чисел (i 1 , i 2 , . . . , i m },
удовлетворяющих условиям
О i 1 < q, 1 j т,
т
L i/ m(q 1) 'V 1.
1== 1
Полаrая i; == q 1 ...... i/, получим, что это число равно числу со-
вокупностей целых чисел (i , i , . . ., i ), удовлетворяющих усло-
виям
О ij < q,
1 j т,
т
L ij 'V + 1.
1==1
Следовательно, kv + kт(q I) -V l равно общему числу qт всех со-
вокупностей (i 1 , ..', i т ), для которых О ij < q, 1 j т.
Теорема 4.5. Код, двойственный p OPM Koдy порядка v, яв-
ляется p OPM KoдOM порядка m(q l) ,, 1.
Доказательство. Если f Е Pv,m, f' Е pт(q 1) V' I, т, то по опре-
делению
v e (f) [v e (f')]T === L f (а) [' (а).
(t Е йЕ (qт)
Важнейшие !Соды
191
Поскольку степень f. f' не превышает т (q..-...a 1) 1, то, как сле
дует из леммы 4.7, вышеприведенное выражение равно о. Это
означает, что p OPM KOД порядка m(q I) v 1 является
подкодом кода, двойственноrо p OPM KOДY порядка ". I1з
утверждения 4.12 в свою очередь следует, что этот подкод сов-
падает с двойственным кодом.
Определим вес Wq(h) целоrо числа h, О::::;; h < qm, q ичное
разложение KOToporo имеет вид
т l
h Lhlq', O hl<q, O l<m,
1:=0
( 4.35)
по формуле
т l
Wq(h) L h 1 8
1==0
Теорема 4.6. OPM Koд порядка" является циклическим ко-
дом, .множествОАt корней порождающеGО МНОёочлена КОТОрОёО
является множество {ahIO< Wq(h)<lп(q I) v, O<h<qm}.
Доказательство. Пусть h произвольное целое число, такое,
что O<Wq(h)<m(q I) ", O<h<qm, и пусть выражение
(4.35) ero q ичное разложение. Как следует из утверждения
4.11, имеется km(q 1) v l 1 чисел h, удовлетворяющих указан..
ным выше условиям ( 1 появляется из за Toro, что число h == О
исключается). Учитывая, что п == qm 1, из утверждения 4.12
находим, что количество h равно п kv. Следовательно, цикли
ческий код С длины п с порождающим мноrочленом g (Х) ==
........ п (Х аh)имеет то же число проверочных сим
O<h<n
O<W q (h)<т(q---1}---v
волов, что И OPM KOД порядка ". Таким образом, для заверше
ния доказательства теоремы достаточно показать, что OPM KOД
порядка v является подкодом кода С. Рассмотрим следующий
мноrочлен fh от переменных X 1 , Х 2 , ..., Х т :
( т---l ) '1
fh == aiX 1 + 1 ·
}==о
Так как Х' == X j , то
m 1
( т l ) h,ql т l ( т l 1 ) hl
fh == L а/ X/+ 1 1==0 == Т1 L a jq X j + 1 ·
I O 1==0 I O
Степень t/t не превышает W q (h) и, следовательно, не больше
т (q 1) " 1. уlз формулы (4.34) имеем
J'h (a i ) === ( 1: I aija i ) lI === a ih .
}==о
192
r лаtа 4
Отсюда следует, что V (/ h) == «(ХО, (Xh, (X2h, ..., (X(п l)lt). ЕСJI И f
произвольный вектор из Р 'У, т И V (f) == (f «(ХО) , f «(Х 1), . . . , f ((Xn 1)) ==
== (Vo, Vl, ..., Vn l), ТО
n 1
L Vi aih === L f (а) f h (а).
1...0 а Е GF (qт)
а:рО
Так как степень f.fh меньше m(q 1) и fh(O)==f't(O, ...,0)==0,
то, соrласно лемме 4.7, сумма в правой части последнеrо paBeH
ства равна О. Отсюда и из формулы (3.24) следует, что V (f) Е С.
Таким образоYl, OPM KOД порядка v является подкодом ({ода С,
так что они совпадают.
Теорема 4.7. Пусть m(q I) v Q(q l) +J , O Q<lп,
О R < q 1. ТОёда ОРjИ код порядка v UA,teer МUНUfitальное
расстояние
d МИII === (R + 1) qQ 1
и является подкодом Б Ч Х Koдa с конструктивным расстоянием
d мин 1) БЧХ кода с 1 == О).
Доказательство. Так как {h 10< W q (h) < Q (q 1) + R, О <
<. h < qт} { h/h === }=:1 h,q' + hQqQ, O h,<q (O ,l<Q), O hQ<R,
1==0
h =1= О }, то порождаlOЩИЙ мноrочлен OPM Koдa порядка 'V имеет
среди своих корней элементы (XI, (Х2, ..., (X(R+l)qQ 2. Это означает,
что OPM KOД порядка v является подкодом БЧХ кода с ({OH
СТРУКТИВНblМ расстоянием (R + 1) qQ 1. уlз нижней БЧХ-rра-
ницы получаем
( 4.36)
Пусть один из примитивных элементов ОР (q). ПОЛО)l{ИМ
q 2 R
f мин == (X1 1 ...... 1) (x "'1 1) . . . (X I lQ 1 1) L (х т Q i).
i==O
d MIIII (R + 1) qQ 1.
Так как (q 1) (1n Q 1) + q 1 R == ", то необходимым
условием Toro, что fмин Е P v , т, f II1H =1= О, является выIолнениеe
равенств Х 1 == Х 2 == ... == Xт, Q 1 == О. Поскольку Х т , Q =1=
=1= i (О i q 2 R), число совокупностей значений
Х 1, ..., Х т , для которых fмин =1= О, равно (R + 1) qQ. Тчитывая,
что в число этих совокупностей входит и (О, О, ..., О), полу-
чаем, что вес V (f мин) равен (R + 1) qQ 1. Таким обраЗОМ t в
формуле (4.36) в д йствительности имеет место 311аl< равенства.
1) БЧХ-код С L == О.
Важнейtuuе коды
193
Пусть U подмножество GF(qт). Для каждоrо O:::;i<
< qm 1 определим величину Ui, положив Ui == 1, если а)Еи,
и Ui == О, если r.x,i Ф. И; положим и оо == 1, если О Е и, И и оо == О,
если О Ф. U. Вектор и е == (и оо , и о , U 1 , .. ., Uqm 2) называется ха
рактеристическим вектором подмножества U (вектор и == (и о ,
l' l' . . ., Uqт 2)' получающийся из и е удалениеl\1 первой компо
ненты, называется укороченным характеристическим вектором).
Теорема 4.8. Пусть U аффинное подпространство 1) над
GF(q) пространства GF(qт) размерностu '. Укороченный xa
рактеристический вектор II U характерuстuческuй вектор и е noд
пространства и ЯВЛЯ10ТСЯ кодовыми векторами соответственно
OPM Koдa U p OPM Koдa порядка (1n ') (q 1).
Доказательство. ИЗ разд. 2.6.3 следует существование (m r)
строк Ь(1), Ь(2), ,.., b(т T) длины ln с КОl\lпонентами из
G F (q) и n1, r элементов Cl, С2, ..., Cт T поля ОР (q), таких,
что
и === { f: al IXII ЬЩХТ === Ci, 1 i m ' } ,
lr:al
rде Х == (X 1 , Х 2 , .." Х т ). Положим
m r
f и == П (1 (Ь(О хт ....... Cl)q J).
i == I
Тоrда выражение (Ьи)ХТ Ci) q l равно О, если b(i)XT == Ci, И
равно 1 во всех остальных СJlучаях, так что v(fu) == и. Тбtдз,
очевидно, v e (fu) == и е .
Утверждение 4.13. Четный подкод укорочеННОёО цuклическо"
20 кода Рида Маллера l ёO порядка является кодом MaKcи
мальноu длины. Укороченный цuклический код Рида Маллера
порядка (т 2) представляет собой код ХЭММUНёа.
Это утверждение непосредственно следует из теоремы 4.6.
Утверждение 4.14. М uнимальное расстояние q UЧНОёО Б Ч Х..
кода длuны n == q'n 1 с конструктивным расстояние.лt
(R+l)qQ I (2де O Q<m, O R<q l) U [==0 совпа-
дает с конструктивным расстоянuем.
Краткое доказательство. Справедливость данноrо утвержде-
ния непосредственно следует из доказательства теоремы 4.7.
Выше были описаны OPM KOДЫ длины n == q'n 1, но Mory-r
быть построены и OPM KOДЫ длины nl == (qm 1) jb, rде Ь
произвольный делитель q 1.
1) См. разд. 2.6.3.
194
r лава 4
т
Утверждение 4.15. Пусть f == X:IX 2 . .. x т и Ь L i,. Тоеда
1:=1
вектор v (f) получается Ь"кратным повторением первых (qm 1) /Ь
своих компонент.
Краткое доказательство. Так как a(q l) n1 == a(qт... 1 ) (q l)lb == 1,
то а n \ Е ОР (q). Из форму ль! (4.34) для произвольных О i < пl
и О 1 < Ь получаем
т---l т....l
a l + 1nl == а 'n1 L alla l == L ai+ln1' ja/.
1==0 1-=0
Так как a 1n1 Е ОР (q), то al+lпl, 1 == a1n1ail, О j < т. Следова-
тельно,
т ....1
ln i m...1
f (al+l п ,) == а I /..0 / П a == f (a l ).
/r=a0
Пусть Р", т, ь множество всех линейных комбинаций одно-
членов степени" и меньше с коэффициентами из ОР (q), YДOB
летворяющих условиям утверждения 4.15. Тоrда для произволь
Horo f Е Р", т, ь вектор v (f) получается b KpaTHЫM повторением
первых nl своих компонент. Если v' (f) вектор длины nl, со-
стоящий из первых nl компонент v (f) , то множество
{v'(f) 11 Е P vb , т, Ь} называют OPM KOДOM длины пl порядка 'У.
Утверждение 4.16. OPM Koд длины nl порядка " является
циклическим кодом, множеством корней nорождаl0щеео мн,оео-
члена котороео является множество {rx h 1 0< W q (h) < т (q 1)........
"Ь, О < h < qт, Ь I Wq(h)}.
Краткое доказательство. Утверждения 4.11 и 4.12 можно леr-
ко обобщить. Тоrда, если заметить, что для любых мноrочленов
f Е Pb'V, т, Ь, f' Е pт(q l) ('V+I)b, т, ь
имеет место равенство
bv' (f) [v' (f')JT == V (f) [v (f')]T == О,
то справедливость данноrо утверждения будет следовать непо-
средственно из доказательства теоремы 4.6.
Утверждение 4.1.7. Теорема 4.7 остается справедливой, если
длину кода заменить на пl, 'v на "Ь u d мин на
[(R+l)qQ I]/b.
Идея доказательства. Воспользоваться утверждением 4.16,
положить == (х Ь и далее воспользоваться нижней БЧХ rра
ницей.
Рассмотрим частный случай, коrда Ь == q 1. При этом
111==(qп" 1)/(q 1). Для любоrо O i<nl МНО)l{ество
Важнейшие коды
195
{( a l + 1n1 , О, a i + 1nl , l' · · ., a i + 1nt , т...t) I о
1 < q.... 1} из q
1 век-
торов представляет собой некоторое множество совпадающих
точек проективной rеометрии РО (т, q) 1). с помощью отображе
ния, задаваемоrо формулой (4.34), этим векторам MorYT быть
сопоставлены элементы a i + 1n1 , О
1 < q
1. С помощью та-
Koro отображения устанавливается взаимно однозначное соот-
ветствие между точками РО(т, q) и множествами {(XiIO
i<nl}.
Ниже точки Ра (т, q) будем представлять с помощью сооТ-
ветствующих элементов (Xi. Пусть U
проективное подпростран-
ство размерности r проективноrо пространства Ра (т, q). Для
каждоrо О
i < nl определим величину Иi следующим обра-
зом: Иi == 1, если (Xi Е и, И Ui === О, если (Xi Ф. и. Назовем вектор
и === (ио, UI, .. " Un1
1) характеристическим вектором и.
Утверждение 4.18. Пусть U
проективное подпространство
раЗlltерности r проеКТИВНОёО пространства Ра (т, q). Характери-
стuческий вектор подпространства U является кодовым векто..
ром OPM
Koдa длины nl == (qт
1)/(q
1) порядка m
r
].
Краткое доказательство. Соrласно определению проективно
ro подпространства размерности " существует такое подпро-
странство [J размерности r + 1, что U === {(Xi I a,i Е tJ, O
i<nl}.
в свою очередь в О существуют такие (т
r
1) BeKTop
CTpOK
(ЬО), Ь(2), ..., b(т
T
l» размерности т с компонентами из G F (q) ,
что (см. разд. 2.6.3)
U === { i: a.l
1 Xll ьи) ХТ == О, 1
i < т
r } ,
1==0
rде Х == (Х 1, Х 2 , . . ., Х m ). Положим
т---r---l
f и == П (1...... (ЬО) XT)q
l).
i == 1
Тоrда fи Е P(т
r
l)(q
l), т, q
l И v' (fи) совпадает с характеристи-
ческим вектором подпространства и.
4.5.2. Полиномиальные коды и двойственные к ним коды
Множество СО всех кодовых слов кода С над ОР (qs), все
компоненты которых являются эле.ментаl\1И подполя G F (q), на
зывается ОР (q)
пoдKoдOM кода С или подкодом над подполем.
Если С
линейный код, то СО также является линейным кодом;
если С
циклический код, то циклическим является также и
код СО.
Теорема 4.9. Пусть
элемент порядка п поля GF(qsm), и
пусть С
циклический код длины п над GF(qs) с порождающuм'
1) См. разд. 2.6.3.
196
r лава 4
М1tосочленом g (Х) === П (Х....... i). Тоада nорождающий мноео..
ieR
член аР (q) пoдKoдa Со кода С имеет следующий вид:
go (Х) === П (Х ---- i),
lERq
еде R q минимальное множество, содержащее R и замкнутое
относительно перестановки П q : i -+ iq (mod п).
Доказательство. Если v произвольный вектор над а F (q) ,
принадлежащий С, то v ( i) == О, iER, так что v q ( i) == V ( iq) ==
== О. Следовательно, go (Х) I v (Х).
Обратно, пусть v произвольный вектор длины п над aF(q),
и пусть go (Х) I v (Х). Тоrда, так как g (Х) I go (Х), то g (Х) I v (Х),
а следовательно, v Е С.
Например, БtIХ коды с l == О являются подкодами над под
полем кода Рида Соломона.
Подкоды над подполем OPM KOДOB 1) называIОТСЯ полино..
миаЛЬНblми кодами [37]. БЧХ коды при 1 == О и укороченные
циклические коды Рида Маллера ЯВЛЯIОТСЯ полиномиальными
кодами. Кроме Toro, как будет показано ниже, евклидово rео
метрические коды [27, 35] и проективно rеометрические коды [27,
39, 40] ЯВЛЯIОТСЯ кодами, двойственными к полиномиальным KO
дам [4, 37, 41]. Основные свойства полиномиальных кодов можно
вывести из теорем 4.6 4.9 [4, 37].
Утверждение 4.19. Множеством корней nорождаЮl-l{еео МНО-
еочлена GF(q) noдKoдa qs ичноео OPM Koдa длины (q'ns l)jb
(Ь делитель qs I) порядка" является множество {a 'Z 10<
< min W q$ (hqt) < т (qS....... 1) ---- "Ь, О < h < qт, Ь I W qS (h)}.
O l s
Идея доказательства. Это утверждение леrко доказать, ис-
пользуя утверждение 4.16 и теорему 4.9.
Утверждение 4.20. П усть т (qs 1) ........" == Q (qs 1) + R,
О Q < т, О R < q 1, u пусть минимальный вес q tlчноео
БЧХ кода Со длины qs l С конструктивным расстоянием R + 1 и
1 == О совпадает с еео конструктивным расстоянuеJ1,. Тоеда
1) минимальный вес d мин а F (q) пoдKoдa qS UЧl-lоео О Р М Koдa
длины qтs l ....... 1 порядка" равен (R + 1) qsQ ....... 1;
2) минимальный вес q uчноео БЧХ-кода длины qтs 1 с
конструктивным расстояние.Аt (R + 1) qsQ I и 1 == О равен еео
конструктивному расстоянию.
Идея доказательства. Доказательство теоремы 4.7, за ИСКЛIО-
чением Toro, что вектор v (fмин) дол}кен быть вектором над
1) В общем случае длина кода равна (q'm l)/Ь, rде Ь........ делитель q 1.
Ва JlСflеЙlllllе коды
197
GF(q), полностью сохраняется и для подкода над подполем.
Пусть f (Х) МС мноrочлен кодовоrо вектора минимальноrо Be
са Иl Со. Степень f (Х) по определению l\tlеньше чем qs 2 R.
Пусть В один из примитивных элементов поля GF(qs). Тоrда,
так Kal{ вес вектора (1 ( O), f ( I), . . ., f (B qS 2)) равен R + 1, то
мноrочлен f (Х) имеет степень qs 2 R и ровно qs 2 R
корней в поле G F (qs). Если ПОЛО}l{ИТЬ
m Q l
fмин=== П (X7 1 1)f(Xm Q),
ic:::1
то v(f JI1JI) будет вектором над GF(q). Доказательство части 2
утвер)кдеllИЯ 4.20 а налоrично ДОI{азательству утверждения 4.14.
Пример 4.12. Пусть Р простое число и q == ps. Код, двой
ствеНIIЫЙ GF(р) подкоду q ичноrо p OPM кода длины п == qт
И порядка r (/n r 1) (q 1)], называется расширенным eвK
лидово zеометрuческиАt KOaOht размерности (r, s) (сокращенно
р Еr кодом). Эти коды явJlяются раСIlIирениями евклидово rео
метрических кодов (Er KOДOB), введенных Уэлдоном [38]. Как
следует из теоремы 4.5, в случае q == 2 и s == 1 р Еr I{ОД являет
ся кодом Рида Маллера порядка '. Поле GF(qm) является
векторным пространством размерности ,п над GF(q), но xapaK
теристический BeI{TOp произвольноrо аффинноrо подпростран
ства размерности (, + 1) этоrо пространства, соrласно Teope
ме 4.8, принадлежит p OPM KOДY порядка [(m r 1) (q 1)].
Так как вектор и является вектором над GF(q), то он также
принадлежит подкоду над подполем. Рассмотрим произвольное
аффинное подпростраIIСТВО и размерности r над ОР (q) про
странства G F (qт). Из утверждения 2.76 следует, что число
аффинных подпространств размерности r + 1, содер}кащих и
и не имеIОЩИХ друrих общих точек, кроме точек и, равно
(qrп r I)/(q 1). Пусть иО), и(2), ..., u(d r }, d r == (qm r 1)/
/ (q 1) характеристические векторы этих подпространств.
Проверочные суммы, коэффициентами которых являются KOM
поненты этих ха рактеристических векторов, ортоrональны OTHO
сительно линейноЙ e CYMMЫ, коэффициентами которой являются
компоненты характеристическоrо вектора аффинноrо подпро
странства U. Аналоrичными свойствами обладают и аффинные
подпространства меньшей размерности. Так как d r < dr l <. . . ,
то р Еr код размерности (r, s) допускает исправление ошибок
веса до [( qт r 1) /2 (q 1)] с помощью пороrовоrо декодиро
вания за (, + 1) шаrов.
Утверждение 4.21. МножествОАt корней порождающеzо MHO
20члена р uчноzо Er Koaa длины n == рта 1 и размерности
198
r лава 4
(r, s) является множество
{all О < тах \V р$ (ipl) (т r 1) (pS 1), О < i < pтS}.
O l<s
Краткое доказательство. Как следует из примера 3.1, Er KOД
размерности (r, s) является кодом, двойственным четному под
коду Се подкода над подполем OPM Koдa размерности
[( m r 1) (ps 1)]. Множеством корней порождающеrо MHO
rочлена кода С, соrласно утверждеНИIО 4.19, является множество
{a h I о min W pS (hp') < (, + 1) (ps 1), О h < pтS}.
O l<s
Чтобы элемент a.,i был корнем порождающеrо мноrочлена двой
ствепноrо кода, необходимо, чтобы элемент a., i == a.,pтs i 1 не
принадлежал этому множеству; соответствующее условие На i
заключается в том, что m (р' 1) > min \f' pS ((pтS 1 i) р')
о 1 <s
(, + 1) (pS 1). Кроме Toro, заметим, что W pS ((pтS 1
i) р') == m(pS 1) W pS (ip'). Отсюда следует справедливость
утверждения 4.21.
Утверждение 4.22. Er KOa может быть декодирован точно
так же, как и p Er KOa.
и дея доказательства. В примере 4.12 следует рассмотреть
только такие аффинные подпространства GF(qт), которые не
содержат О. При этом ошибки веса до [(dT 1)/2] MorYT быть
исправлены с помощью пороrовоrо декодирования за (, + 1)
шаrов.
По определению р Еr кода двойственный к нему код coдep
жит характеристические векторы всех аффинных подпространств
размерности r + 1, однако совсем не очевидно, что он может
быть натянут только на эти векторы. В действительности же это
так [42, 43]. Это означает, что из всех кодов, допускающих поро
rOBoe декодирование, основанное на описанных выше свойствах
аффинных подпространств, Еr коды имеют максимальное число
информационных символов.
Утверждение 4.23. П римитивный Б Ч Х Koд с nараметрами
п ::::: 15, 1 == О U t == 3 из примера 4.1 является укороченным цик-
лическим кодом Рида Маллера nервОёО порядка и допускает
исправление ошибок веса 3 и менее с помощью nopozoeozo дe
кодирования в 2 шаzа.
Краткое доказательство. Корнями порождающеrо мноrочле
на этоrо кода являются элементы множества {a.,i I i == 20, 21, 22,
23, 20 + 21, 21 + 22, 22 + 23, 20 + 23, 20 + 22, 21 + 2 З }. С друrой
стороны, как следует из примера 4.12, укороченный циклический
код Рида Маллера длины 15 первоrо порядка является двоич-
Важнейluuе коды
199
ным Er KOДOM размерности (1, 1). Полвrая в утверждении 4.21
т == 4, Р == 2 и s == 1, получаем, что корнями порождающеrо
мноrочлена этоrо кода являются элементы множества {rx i I о <
< W(i) 2}. Следовательно, оба кода совпадают и, соrласно
примеру 4.12, допускают исправление ошибок веса 3 и менее
с помощью пороrовоrо декодирования в 2 шаrа.
Пример 4.13. Пусть р простое число и q == рз. Код, двой
ственный ОР (р) подкоду СО q ичноrо OPM Koдa С длины nl ==
== (qт 1) / (q 1) и порядка (т r 1), называется nроек-
тивно zеометрическим кодом размерности (r, s) (или COI{pa-
щенно пr KOДOM) }). Соrласно утверждению 4.18, характеристи
ческие векторы и проективных подпространств раЗl\lерности r
проективноrо пространства РО (т, q) принадлежат С. Так как
и вектор над ОР (р), то он принадлежит также и СО. PaCCMOT
рим произвольное проективное подпространство и размерности
r ] проективноrо пространства РО (т, q). Существует d r ==
== (qт T 1) / (q 1) проектных подпространств размерности "
содеР}l{ащих U и не имеIОЩИХ друrих общих точек, кроме точек
из и. Проверочные суммы, коэффициентами которых являются
компоненты этих характеристичеСI{ИХ векторов, ортоrональны
относительно линейной e CYMMЫ, коэффициентами которой яв
ляются компоненты характеристическоrо вектора подпростран
ства и. АнаЛОI'ИЧНЫМИ свойствами обладают и проектные под-
пространства меньшей размерности. Это означает, что пr код
размерности (r, s) допускает исправление ошибок веса до
[( qт 7' 1) /2 (q 1)] с помощью пороrовоrо декодирования в r
шаrов.
В случае р == 2 и s == 1 проективно rеометрические коды яв-
ляются четными подкодами укороченных циклических кодов Ри..
да Маллера.
Утверждение 4.24. КОРНЯМИ nорождаюu{еёО МНОёочлена р-
UЧНОZО flроективНО ёеометрическоzо кода размерности (r, s) и
длины n} == (ртв 1) / (ps 1) являются элементы множества
{а ё ,О шах W pS (ipl) <:. (т r 1) (ps 1), О < i < pтs,
O l<s .
(ps...... 1) I W р!; (i)}.
ёде элеhtент ОР (ртэ) порядка nl.
Идея доказательства. Вывод этоrо утверждения из утверж-
дения 4.16 почти аналоrичен доказательству утверждения 4.21.
Утверждение 4.25. Код максимальной длины с блоковой дли-
ной 2т 1 является двоичным nроективно zео.метрическим ко-
дом размерности (11 1) и, следовательно, допускает исправление
1) Иноrда парамстры пr -кода вводятся несколько отличным способом.
200
r лава 4
ошибок веса до 21п
2
1 с поJt,tощью nОРО20ВО20 декодирования в
один ша2. Код из примера 4.9 является одНИht из таких кодов.
Идея доказательства. Следует воспользоваться приме
ром 4.13 и утверждением 4.24.
Циклические разностные коды [44] также ЯDЛЯIОТСЯ кодами,
двойственными полиномиальным кодам [37]. l-1зучены расшире-
ния кодов, основанных на конечных rеометриях [45, 46], и Me
тоды пороrовоrо декодирования кодов, двойственных произволь
ным полиномиальным кодам [43]. Нахождение числа информа
ционных символов полиномиальных кодов в общем случае яв
,,1Jяе,тся трудной задачей, а полученные формулы ЯВЛЯIОТСЯ очень
сложными [47, 48].
Задача 4.26. Пусть f(X 1 , Х 2 , ..., Xт)e::PV,Нl'
Iайти для
v (f) мноrочлен Матсона
Соломона MS (и (f), Х).
Краткое решение. По определеНИIО i
я компонента вектора
т
1
V (f) равна f (aiO, ai1, ..., ai, т
I), rде а/ == L aija/. С друrой
j==O
стороны, из свойств MS (и (f), Х) и формулы (4.30) имеем
MS (v (f), a i ) == f (aiO, аи, . . ., ai, m
I), О
i < qт
1. (4.37)
Пусть '\'0, '\'1, ..., ,\,т
1
базис, двойственный базису 1, а,
а 2 , ..., a1п
1 (см. утверждение 2.81). Тоrда
. { .0, i =1= j,
T q ( a1 Vi)== 1, · .
t===J,
( 4.38)
rде о:::;;; j < т, О
i < m. Если положить ф(Х)
f(Tq(VoX}',
Т q (VIX), .
., т q (Vm
IX) ), то из формул (4.34) и (4.38) будет
следовать, что
Ф (a i ) === f (aiO, ап, . , ., ai, ln
I), О
i < qт
1.
Мноrочлен, удовлетворяющий равенству (4.37), определяется
однозначно (теорема 4.4), TaI{ что ф(Х)
MS(v(f), Х).
4.6. Каскадные коды и коды Юстесена
4.6.1. Каскадные коды 1)
Пусть Со
Jlинейный (nо,kо)-код над GP(qk/) и Сl
ЛИ
нейный (n], k]) -код над ОР (q). КаскадНЫА! кодОА! [49] с внеШНИl\1
кодом СО и внутренним кодом С] называется линейныЙ q
ичныЙ
1) Каскадным кодам посвящена книrа Э. Л. Блоха и В. В. Зяб.rIова
[72].
П рим. ред.
Важнеuutuе коды
201
(поп], kok]) KOД, который строится следующим образом. Век-
тор V длины поп] в данном разделе будет удобно представлять
в виде матрицы размера поХп] с элементами Vij (О i < по,
О j < п]); элемент Vij этой матрицы будем также называть
(i, j) компонентоЙ вектора V.
1) Информационные компоненты кода С представляют co
бой вектор длины kok[, который мы таI{же представим в виде
матрицы размера koXk[ (ка}кдую строку этой матрицы можно
рассмаТРИRать как представление HeKoToporo элемента поля
ОР (qkl) в виде вектора над ОР (q), пусть Vi элемент ОР (qkl),
предстаВJIением KOToporo является i я строка).
2) Пусть (V O ' VI' . . ., Vno l) кодовый вектор кода Со, ин-
формаЦИОIIIIьте компоненты KOToporo совпадаIОТ с V O ' V 1 , ...
..., Vko l (по определеНИIО существует ровно один такой вектор).
3) Пусть 11' взаимно однозначное отображение 1) ОР (qkl)
в С[ (например, ка}кдому элеl\lепту из ОР (qkl) можно взаИl\-IНО
однозначно сопоставить кодовый вектор кода С], информацион-
ные l<омпонеНТbJ {{OTOpOro представляют собой k[ компонент век-
тора, ЯВ.тIЯIОIП,еrося представлением этоrо элемента в виде BeK
тора над ОР (q)). Матрицу размера поХn[, i й строкой которой
является 'Ф(Vi), О i < по, будем считать КОДОВЫl\1 вектором
кода С.
Пусть {/О и d/ соответственно минимальные веса кодов СО
и С[. Как видно из описания построения каскадноrо кода, вес
вектора (и о , Vl' . . ., V no 1) Е Со' не все компонентыI V O ' V 1 ....
..., VkO l KOToporo равны Hy.TIIO, не меньше d o , а следовательно,
не меныIеe d o строк ЯВЛЯIОТСЯ ненулевыми строками н их вес в
CBOIO очередь не меньше d[. Таким обраЗОl\I, минимаJIЬНЫЙ вес
каскаДIiОI О кода не МСНЫllС tICM dud [.
lIСI10ЛЬЗУЯ В качестве BHelllHcro кода код Рида Соломона
и подбирая специальным образом внутренний код, Форпи по{{а
зал, что в двоичном симметричном I{анале при Лlобых скоростях,
меныIlихx пропускной способности, вероятность ошибочноrо дe
кодирования для каскадноrо кода с ростом по стремится экспо
ненцнально к НУЛI() [49].
Все строки I<одовоrо слова описанноrо выше каскаДJ-Iоrо !{ода
ЯВЛЯI0тrн кодовыми словаl\1И одноrо и Toro же кода С[. МО)I{НО,
однако, рассматривать так)ке каскадные коды, в которых для
каждоЙ строки используется свой линейный (n[, k[) KOД С li.
Коды Юстесена ЯВЛЯIОТСЯ {(одами TaKoro типа [50].
1) Поле G F (q k 1) эдеСI) р ('сматривается КЯI{ линеiiное пространство над
GF(q) раЗf\1СрIlОСТИ k J .
202
r лава 4
Что касается декодирования каскадных кодов, то сначала
проводится декодирование каждой принятой строки (v;o' V;I' . . .
. .., v;. nJ---I); при этом используются методы декодирования ко-
да С]. Информационные части векторов, полученных в резуль-
тате этоrо декодирования (пе,рвые k] компонент), можно рас-
сматривать как элементы V d) поля GP(qk/). Далее, используя
методы декодирования кода Со, следует провести декодирова-
ние вектор а (Vb d ), v1 d ), ..., V 6---1) [49].
Пример 4.14 [69]. Пусть п положительное нечетное число,
т минимальное целое число, такое, что п 12т 1, V эле!\1ент
ОР (2т) ПОРЯДI<а п и С] двоичный циклический код длины п,
проверочным мноrочленом KOToporo является минимальный мно-
rочлен h] (Х) элемента 'У. Поскольку корни ПОРО}I{дающеrо MHO
rочлена представляют собой элементы множества {v o , v l , . . .
..., Vn l} {V l , ,, 2 , V 22 , ..., V 2т "' I },TO мноrочлен MS(v, Х),соот-
ветствующий кодовому вектору V кода С], имеет вид
1S (v, Х) == SlXn l + (SlXn 1)2 + (SIXn l )22 + ...
т
. .. + (SIXn 1)2 ...1 === Т 2 (Sl X "' l ), SI Е ОР (2т). (4.39)
Cor ласно теореме 4.4, отображение '1': S 1 MS (v, Х) v яв
ляется взаимно однозначным линейным отобра}кением т-мер-
Horo линейноrо пространства GF(2 rn ) над полем ОР(2) в С].
В качестве СО возьмем 2т ичный БЧХ код длины по == 2т + 1
с ko информационными символами из примера 4.5 или утверж-
дения 4.3. Пусть MS (СО) множество всех МС мноrочленов ко-
довых векторов кода СО и элемент ОР(2 2т ) порядка 2т + 1
(поскольку 2т + 1122т 1, то такой элемент существует). Обо-
значим через С каскадный код с внеJlJНИМ кодом СО и BHYTpeH
ним кодом С] (получаемый с помощью отображения 'Ф). Код С
является q-ИЧНЫl\1 линейным (поп, kom) KOДOM. Если фИI{СИрО
вать один из кодовых векторов v(o) кода СО, то, соrласно опреде-
лению кода С, фиксируется кодовый вектор 'Ф (v(o») 1), соответ-
ствующий v(o). Элементу Ф Е MS (СО) сопоставим вектор
v(o) (ф) == (ф ( O), Ф ( 1), ..., ф ( no 1)) из Со. При этом (i, j) KOM-
понента кодовоrо вектора v(o) (ф) (для простоты обозначаемоrо
ниже через v(ф)), соrласно формуле (4.39), равна
т 2 (ф ( i) v"' / ). (4.40)
Если использовать у lф Е MS (СО) вместо ф, то (i, j) компо-
t Кодовый вектор, который получается путем замены каждой компоненты
V O) вектора V(O) на '1' ( V O)).
Важнейшие коды
203
нента v(v lф) будет равна
Т 2 (ф ( l) V / l).
Так как у Н == 1, то вектор v (v lф) может быть получен с помо
щью однократноrо циклическоrо сдвиrа каждой строки v (ф).
Аналоrично, рассматривая ф' (Х) == ф( Х) Е MS (СО), можно убе
диться в том, что v (ф') является вектором, получающимся OДHO
кратным циклическим сдвиrом каждоrо столбца v (ф). Следова
тельно, код С инвариантен относительно циклических перестано
вок строк и столбцов. Так как п нечетное число и п 12т 1, то
(п, 2т + 1) == 1. Если положить а == y, то порядок элемента а
будет равен п(2 т +l). Пусть I(h) и J(h) остатки от деления h,
О h < п (2т + 1), соответственно на 2т + 1 и n. Тоrда a,h ==
== 'lVh == I(/l)VJ(h). Отображение, сопоставляющее h пару чисел
(1 (h), J (h)), переводит двумерные матрицы в одномерные BeK
торы. Если П ........... перестаНОВI<а. предстаВЛЯЮlI ая собой последова
тельность однократных циклических перестановок строк или
столбцов, то при этой перестановке h h + 1, и это COOTBeT
ствует циклической перестановке одномерноrо вектора. Следова
тельно, при таком расположении компонент код С оказывается
цикличеСI{ИМ. Так как, соrласно примеру 4.5, минимальный вес
СО равен 2'n+2 ko, то минимальный вес С равен (2n1+2 ko)dI'
rде d I минимальный вес C 1 . Необходимым условием Toro, что
a,h представляет собой корень проверочноrо мноrочлена кода,
является наличие в С хотя бы одноrо кодовоrо слова, MC MHoro
член KOToporo содерл(ит Xп h С ненулевым коэффициентом. Пусть
а элемент, обратный элементу п по модулю 2т + 1, и пусть
Ь элемент, обратный элементу 2т + 1 по модулю n. Так Kal{
а :........ y, то
::=: а,аn,
V а,Ь (2 т +l).
Следовательно, из определений 1 (h) и J (h)
I (h) == a,anh,
VJ(h) == а,Ь (2 т +l) h.
Преобразуя выражение (4.40), получаем,
понента v(ф) равна
имеем
что
(/(h), J(h)) KOM
Отсюда следует,
с MS (v (1))). Если
т 2 (ф (a,anh) a, b (2 т +l) h).
что f (Х) == т 2 (ф (х аn ) x b (2 т +l)) совпадает
h (Х) == П (Х l) ....... проверочный MHoro-
iERO
,k (Х) " SIX 2т+l i ,
так как I имеет вид L..J
iERO
член кода СО, то,
204
r лава 4
S2i == si, ролучае
1
lп
1
f (Х) == L L SlIXn(2т+l)
(ani+b (i т +I))2).
j==O iE R o
Следовательно, корнями проверочноrо мноrочлена кода С ЯВ
ляются элементы мно)кества
{ а ( аn i + Ь (
т + 1 ))
j , i Е R о, о
j < т}.
Выбирая подходящим образом коды C r , Берлекэмп и Юсте-
сен показали существование большоrо числа кодов, ДJIЯ которых
при достаточно больших их длинах отношение минимальноrо
расстояния к длине кода больше, чем у БЧХ
I(ОДОВ, имеfОIЦИХ
приблизительно такую )I<e скорость передачи [51].
4.6.2. КОДЫ Юстесена
Бесконечную последовательность систематических кодов
C 1 , С 2 , ... будем называть асuм.птотuчеСКll ХОрОlllей, если выпол-
нены следующие условия:
n! < ni+l,
R i
R,
di/пi
б,
rде пi, Ri, d i
соответственно длина, скорость и минимальное
расстояние кода C i , а О < R < 1 и О < б < 1
некоторые чис
ла. Из rраницы Варшамова
rилберта следует СУIП,ествование
асимптотически хорошей последовательности систематических
кодов, параметры б и R котороЙ в двоичном случае удовлетво-
ряют условию Н (б) < 1
R. Однако здесь утверждается только
существование асимптотичеСI{И хорошей последовательности KO
дОВ и ничеrо не rоворится о том, как конкретно строить коды
C i . Если попытаться строить коды C i , следуя выводу rраницы
Варшамова
rилберта, то нужно последовательно выбирать
каждый столбец матрицы Н. Юстесен предложил метод построе-
ния асимптотически хорошей последовательности кодов, кото-
рый является столь же конструктивным, как и методы построе
ния БЧХ
кодов или OPM
KOДOB [50]. Для простоты будем рас-
сматривать двоичные коды. Код Юстесена является каскадным
КОДОМ, в качестве внешнеrо кода Со KOToporo используется
(2т
1, kо)
код Рида
Соломона над ОР(2 т ). Положим по ==
== 2т
1. Пусть (Х
примитивный элемент ОР(2 т ), <p(
)
представление элемента
Е ОР(2 т ) в виде вектора над аР(2)
относительно HeKoToporo фиксированноrо определенноrо базиса
и (CP(
l), CP(
2)' ..., CP(
l)J
BeKTOp ДЛИНЫ 1т) являющийся
Важнеt"ltUllе коды
205
последовательностью векторов (j) ( l), ер ( 2), ..., ер ( l). Множе
с тв о Д в о и ч 11 Ы Х В е к то р о в { ( ер ( V о), ер ( (Х о V о), ер ( V 1 ), ер ( (Х 1 V 1 ), ...
о.., qJ(Vi). qJ(aiVi) ,..., qJ(Vno l)' qJ(a.no IVno l))I(vo, Vl,..o
. . ., VnO---l)Е со} Н азывается кодом Юсrесена. Очевидно, что код
Юстесена является линейным (2т (2 пt ....... 1), koln) KOДOM. Как и
раньше, кодовые векторы будем представлять в виде матриц
размера поХ2т, (i+ 1) й строкой которых является (ep(Vi),
ер ((XiVi) ). CTpoI<a матрицы является нулевой только при V == О.
JIюбые две ненулевые строки (ep(Vi)' ep((XiVi)) и (ep(Vj), cp(a}Vj))
обладают тем свойством, что если Vi == Vj, то
(ер (Vt), ер (aIVi) :#: (ер (t'/), ер (a/Vj)),
так как (XiVi =1= (Xjv} (здесь Vi =1= О, О i < j < по). Минималь
ный вес кода СО, СОI'ласно примеру 4.4, равен по + 1 ko. Сле
довательно, если только кодовый вектор является ненулевым, то
по меньшей мере по + 1 ko ero строк также являются ненуле
выми, а значит, и различными. Поэтому минимальный вес кода
Юстесена не меньше суммы весов по + 1 ko ненулевых двоич
ных векторов длины 2т минимально возможноrо веса, а именно
w w
d/ j ( 2;) + (w + 1) (по ko + 1 ( 2 j т )). (4.41)
w+l w
rде I (2[1) ;;:; по ko + 1 ;;:; I ( 2;п) .
I l i l
Пусть п1 > 2 и л == H l (( 1/2) (1/1og 2т)), rде H l функция,
обратная энтропии 1). Из леммы 1.1, положив в ней q == 2, по..
лучаем
2 m
L ( 2 j т ) 2 2тН ( ) === 2т 2m/log 2т о
/ 1
Тоrда
2Ат
( 2tn ) I( k + 1) 1 ( 1 + t ) 2 ....2тlIog 2т
р === l...J j / по...... о ::::::::: 1 2R 2 пz 1 '
j == 1
rде R == k o /[2(2 /n ........l)]. Заметим, что параметр R является CKO
ростью рассматриваемоrо кода. Из формул (4.41) и (4.42) сле
дует, что
d J ;;з:. (по....... ko + 1) (1 ....... р) 2mл > 2тnо (1 ....... 2R) (1 ....... р) л >
> 2тnо(1 ....... 2R) (1 ....... р) H l ((1/2)....... (1/1og 2т)).
1) Для простоты log22m обозначается здесь через log 2т.
206
r лава 4
Поскольку длина кода п равна 2тnо и р стремится к нулю с po
сто м т при фиксированной скорости R, то
d,:
H
[ (
) (1
2R)(1
О[ (т))
0,11 (1
2R), (4.43)
rде 01 (т)
О при т
00 и фиксированном R. Это означает, что
бесконечная последовательность кодов Юстесена (при т
00)
является асимптотически хорошей. Однако правая часть фор-
мулы (4.43) значительно меньше rраницы Варшамова
rил-
берт а H
l (1 ....... R) .
Описанные выше коды имели скорость О < R < 1/2. Однако
если модифицировать описанную выше конструкцию, а именно
в качестве (i + 1)
й строки кодовых матриц использовать век-
торы (CP(Vi), ep(s)((XiVi)), rде <p(s)(
)
BeKTOp длины s, компонен-
тами KOToporo являются первые s компонент ер (s), то получается
линейный ((т + s) (2т
1), mko) -код, который может иметь
скорость R > 1/2. Используя ту же технику, что и раньше, мож
но найти следующую нижнюю оценку для минимальноrо рас-
стояния модифицированных кодов:
d J ( R ) ]
n
1
a H
(1
a)(1
02(т)),
rде a==т/(2m
s), а 02(т)
O при т
oo.
Методы декодирования кодов Юстесена описаны в работе
[50]. Как указывалось в разд. 3.3, рассматривавшиеся выше
асимптотические свойства кодов представляют rлавным образом
теоретический интерес. Одной из нерешенных проблем является
построение последовательности кодов, которые можно было бы
задать столь же конструктивно, как и коды Юстесена, но KOTO
рые лежали бы на rранице Варшамова
rилберта. Кроме
Toro, открытым остается вопрос о существовании асимптотиче-
ски хороших последовательностей циклических кодов.
4.7. Коды rоппы
4.7.1. Определение
Коды rоппы представляют собой очень широкий класс ли
нейных кодов, включающий все БЧХ
коды. Известно, что среди
этих кодов есть коды, лежащие На rранице Варшамова
rил
берта. Однако такие коды не задаются конструктивно. Для ко-
дов rоппы в обла.сти «конструктивных расстояний» известны
алrебраические методы декодирования, подобные методам де-
кодирования БЧХ
кодов. Коды rоппы
это один из вая{неЙIIIИХ
классов линейных КОДОВ, не являющихся, вообще rоворя, цикли-
ческими.
Важнейшие коды
207
При рассмотрении кодов rоппы будем следовать работе [53],
оrраничившись случаем двоичных кодов 1). Пусть О < n 2т и
L == {(Хl, (Х2, ..., (Хn} множество элементов поля ОР (2т). Обо-
значим через V n n MepHoe векторное пространство над G F (2).
Вектору v == (Vl, V2, ..., V n ) Е V n сопоставим рациональную
функцию переменноrо z (z будет принимать значения в ОР(2 т ) >.:
n
I v.
Ro (z) t .
z a
. 1 l
t==
Пусть g(z) мноrочлен от z с коэффициентами из ОР(2 т ),
среди корней KOToporo нет элементов из L. Код Fonпbt, задавае-
мый парой (L, g), определяется следующим образом:
{v' Rv (z) == О (mод g(z)), V 6 V п}. (4.44)
Мноrочлен g (z) называется мноrочленом rоппы. Очевидно, что
введенный код являеl'СЯ линейным. Пусть {i 1 , i 2 , .... i l } мно-
жество индексов i компонент t'i вектора v == (Vl, V2, ..., V n ) Е
Е V n' равных единице. Пусть
f v (z) == ( z а i 1) ( z а i 2) · · · (z а i 1). ( 4.45)
Тоrда, как указывалось в разд. 2.6.6, Rv (z) можно представить
в виде
Rv (z) == f (z)/f v (z), (4.46)
rде f производная f v.
Для любоrо (Xi Е L справедливо следующее соотношение 2):
z а/ == g (Z = :/(a i ) g 1 (ад (mod g (z)). (4.47)
Заметим, что правая часть последнеrо уравнения является MHO
rочленом степени deg g 1 (deg g степень мноrочлена g).
lfспользуя (4.47), условие Rv(Z) == О (modg(z») из (4.44)
можно переписать в слеДУlощем виде:
п
I g (z) g ( а )
V i g 1 ( а ) == о
i z a i
. 1 1
t
(mod g (z).
Поскольку левая часть этоrо сравнения является мноrочленом
степени deg g . 1 или менее, то оно эквивалентно выполнению
1) Случай q > 2 рассмотрен в работе [55].
2) Так как используется поле G F (2т), то знак ниже может заме
няться на знак +. Поскольку g{CXi) =1= О, то z CXi И g(z) ЯВЛЯIОТСЯ взаимно
простыми МlJоrочленами, так что 1/(z ai) элемент, обратный z. (Х. В
кольце мноrОЧ.rIеllОВ по МОДУЛIО g (z).
208
r лава 4
следующеrо равенства:
n
I g (z) ..... g (a i ) l ( ) О
V;, g а;, .
z .w::.. а l
i ::::11
( 4.48)
t
Пусть g (z) L biz i И deg g с::: t. Без оrраничения общности
i==O
будем счита:rь, что b t === 1. Приравнивая суммы коэффициентов
при zt l, zt 2, ..., z, 1 в (4.48) нулю, получим систему из t ли-
нейных уравнений относительно VI, V2, ..., V п . Матрица коэф
фициентов этой системы имеет вид
btg l (аl) ...
(bt l+btal)g I(CLl) ...
btg l (а п )
(bt 1 + bta n ) g I (а п )
(bl +Ь 2 а 1 + ... +bta "'l) g....l (а 1 ). .. (b 1 + Ь 2 а n + ... + bta I) g 1 (an)
(4.49)
Из этой матрицы с помощью операций над строками (учи-
тывая, что b t == 1) можно получить следующую матрицу:
g I (а 1 ) . . . g I (а п )
alg 1 (аl) ang l (а n )
Н==
.
( 1
== а1
at 1
1
a "'lg 1 (а 1 ) ... a lg 1 (а п )
.... g I (а 1 ) О ... о -
о g I (а2) О... о
о
1
. .. 1 ]
. .. а п
t l
· · · а п
( 4.50)
а2
at l
2
. .
. .
о
.
о
о . . . о g l (а п )
. .
Как следует из вышеизложенноrо, Н проверочная матрица
(заметим, однако, что еСЛИ каждый элемент этой матрицы пред
ставить в виде вектор столбца над G F (2), то строки полученноЙ
таким образом матрицы над ОР (2), вообще rоворя, MorYT
оказаться линейно зависимыми). Следовательно, если k число
ин(рормационных символов этоrо кода, то
n k Пl deg g. (4.51)
Важнейшие коды
209
в частности, если п 12т......... 1, элемент IIорядка n поля G F (2т),
L == { O, 1, ..., n l} И g(z) == zt, то
1 t 2t. . . (n"'l) t
1 ...(t""l) "'1 (t....1) ... (n 1) (t....1)
H . . . .
. . .
.
1 ...l ...2 .... (n...1)
. . .
Если заменить I на и поменять порядок следования строк
на противоположный, то можно леrко увидеть, что эта матрица
является не чем иным, как проверочной матрицей БЧХ кода с
1 О. Следовательно, !{ласс кодов rоппы ВI{лючает БЧХ"коды
с 1 == О.
Пусть g (z) мноrочлен минимальной степени, являющийся
полным квадратом [Т. е. имеющий вид ср2 (z)], такой, что
g (z) I g (z). Если v вектор, принадлежащий коду rоппы, то,
со.rласно формулам (4.44) и (4.46),
Поэтому
f (z)/f v (z) == О (mod g (z).
f (z) == О (mod g (z)).
(4.52)
Так как рассматривается поле характеристики 2, то мноrочлен
f состоит только из слаrаемых четных степеней и, значит, ЯВ-
ляется полным квадратом. Следовательно,
f (z) == О mod g (z).
(4.53)
l'ЗI{ как w(v) == deg fv, то из последнеrо СООТНОIllения получаем
оценку снизу для минимальноrо веса d I1III:
dMIIH degg+ 1.
(4.54)
Если все корни g(z) различны, то g == g2 И В этом случае
d МИII > 2 deg g + 1.
( 4.55)
ДЛЯ задания кода rоппы нужно задать т, L и g. Однако
код rоппы MO)l{HO также определить, если вместо g задать про-
из вольным образом вектор а == (al, а2, ..., а n ), ai Е OP(2т)
{О}, 1 i п. Действительно, в этом случае мноrочлен g (z)
минимальной степени, такой, что g 1 (CXi) == ai (1 i п) опре-
деляется едннствеННЫ!\1 образом. Матрица Н кода rоппы, зада-
210
r лава 4
вземоrо этим мноrочленом, имеет вид
1 1 . . . 1 аl О . . .0--
аl а2 . . . а п О а2
.
. . . . .
. о
at l at l t 1 О О а п
1 2 · · · а п . . .
Утверждение 4.27 [53J. Пусть элемент порядка п поля
G F (2т), u пусть L == { l, 2, ..., n}. Если код Топпы, опреде-
ляемый этим множеством L, является циклическим, то он пред-
ставляет собой БЧХ код.
Идея доказательства. Пусть v произвольный кодовый BeK
тор, и пусть v(i).......... вектор, получающийся из v i KpaTHbIM цикли
l
ческим сдвиrом. Положим f v (z) == П (z ........ ! 1). По определению
1,.1
l
f(O (z) ==: П (z i+i 1) == llf v ( ...fz).
v 1==1
Так как при всех О i < п вектор V(i) является кодовым векто-
ром, то из формулы (4.52) получаем
f (i) (z) == О (mod g (z)).
Следовательно,
f (z) == О (mod g ( iZ)).
Если g (z) имеет своим корнем ненулевой элемент 'У, то n раз
личных элементов '\', '\' , ,\, 2, ..., 'Y n 1 должны быть корнями
f , а это противоречит тому, что deg f < п. Следовательно,
g(z) == zt. Но тоrда, как уже указывалось выше, код rоппы яв-
ляется БЧХ кодом.
Пример 4.15 [56]. Пусть (х примитивный элемент GF(2 m )
и L == {(Хl, (Х2, ..., (Xn 1, О}. В этом случае длина кода п равна
2111 и мноrочл н rоппы g (z) не имеет корней в ОР (2т). В част..
ности, рассмотрим случай, коrда g(z) является неприводимым
мноrочленом над ОР(2 т ) степени t. Корни g(z) в этом случае
принадле}кат GF(2 mt ). Из формул (4.51) и (4.55) имеем
n k тt,
d мин 2/ + 1.
Аналоrичные оценки имеют место и для параметров примитив-
ных БЧХ кодов длины 2т....... 1, однако длина кодов rолпы на
единицу больше.
Важнеtllllllе коды
211
Предположим, что для представления кодовоrо вектора
v == (VI, V2, ..., V n ) используется мноrочлен C V (Х) над G F (2т),
u
такон, что
C v (a i ) == Vi,
C V (О) === v n .
Далее вместо BeKTopHoro представления будем использовать
представление мноrочленами (для простоты мноrочлен C V (Х)
будем обозначать через с (Х)). Используя проверочную матрицу
(4.50), получаем
L X; i ) == о, о i < t. (4.56)
Хе йР (2т)
Рассмотрим расширение этоrо кода rоппы. Обозначим добав-
ленный символ индексом 00. Полаrая L == L U {оо}, имеем
L с (Х) == О. (4.57)
XeL
1 i < n,
Если условиться, что в формуле (4.56) Xi/g(X) == о при Х == 00,
то можно считать, что Х в (4.56) пробеrает все элементы Е. 1;0
тоrда, соrласно равенству (4.57),
L g ( )( iX) == О. (4.58)
Хет.
Из формул (4.56) и (4.58) имеем
" xlc (х) == О
i.J g (Х) ,
XeL
о i t.
(4.59)
Пусть h (Х) мноrочлен, получаемый из g (Х) с помощью
аффинноrо преобразования Х ---+ (АХ + В) / (СХ + D) (А, В, С,
D Е GF(2 nt ) , AD=FBC) множества ОР(2 т ) I U {оо} в себя. Тоrда,
как следует из вышеизложенноrо, расширенный код rоппы, за-
даваемый мноrочленом rоппы h (Х) и тем же множеством L,
может быть получен из расширенноrо кода rоппы, задаваемоrо
мноrочленом rоппы g (Х), с помощью Toro же аффинноrо пре..
образования множества двоичных символов 1). Если мноrочлен
g(X) инварианте относительно аффинноrо преобразования ТА,
то расширенный код rоппы, задаваемый мноrочленом rоппы
g (Х), тоже является инвариантным относительно этоrо аффин-
Horo преобразования множества двоичных символов. Так как
1) Так как между множеством двоичных символов и множеством
G F (2т) U {оо} имеется взаимно однозначное соответствие, то llреобраэование
множества ОР(2 т ) U {ос} можно рассматривать как преобразование соответ"
ствующеrо множества двоичных символов,
212
r лава 4
в случае t == 2, СОI"'ласно утверждению 2.12, произвольный не-
приводимый мноrочлен может быть получен из ЛIобоrо друrоrо
неприводимоrо мноrочлена с помощью аффинноrо преобразова-
ния (с точностью до постоянноrо множителя), 1'0 все расширен
ные коды rоппы с параметрами 11 2 rn + 1 и t 2 попарно
эквивалентны. Без оrраничения общности (см. YTBep)l\дe
ние 2.10) будем считать, что g (z) === Z2 + Z + и Т 2 ( ) === 1.
Если V корень уравнения g (z) == О, то V + 1 и /" также
являются корнями этоrо уравнения. Следовательно, код инва-
риантен относительно аффинных преобразований
PI:X X+l,
Р2: Х /X.
Покажем, что при соответствующем выборе элемента преоб-
разование р Р2Рl: Х / (Х + 1) является циклической пере-
становкой множества [. Действительно, как известно, в общем
случае для любоrо преобразования о' мно)кества [ существует
такое разбиение [1, [2, ..., [l множества Е, что о' мо)кет быть
представлено как произведение циклических преобразований
0"1, 0'2, ..., (Jl lVIножеств [1, [2, ..., [l соответственно. Если п'
число элементов, входящих в [1, то преобразование <1 n ' остав-
ляет на месте элементы [1. Следовательно, для Toro чтобы по
казать, что о' является циклическим преобразованием, а именно
что 1 == 1, следует показать, что ни одно из преобразопаниЙ a i ,
О < i < 2т + 1, Не имеет неподвижных точек. rlсобходимым ус-
ловием Toro, что аффинное преобразование (АХ + В) / (СХ + D)
имеет неподвижную точку, является существованиие среди элс..
ментов мно}кества [ решения уравнения (АХ + 8)/(СХ + D) ==
х. Как следует из уrвер}кдения 4.28, это условие эквива
лент но тому. что собственные значения Лl и Л2 матрицы [ ]
принадлежаr ОР (2т). С друrой стороны, если положить
<1: (АХ + В)/(СХ + D),
0": (А' Х + В')/( с' Х + D'),
<10": (А"Х + В")/(С"Х + D"),
ТО
[ А" В" ] [ АВ ] [ А' В' ]
С" D" === С D С' D' ·
Следовательно, необходимым условием Toro, что O'i имеет ста-
ционарную точку, является принадлежность собственных З113-
Важнеr'lUluе коды
213
l l [ А В ] i
ченнй ""1 и ""2 матрицы С D ПОЛIО G F (2т) 1). Итак, co
rласно выIеизло)кенному,' чтобы показать, что р является цик
личеСI{И 1 преобразованием, следует доказать, что ""i Е
Е GF(2 1n ) i == 0(mod2 'n + 1), rде л собственное значение
матрицы [ i] (л является корнем уравнения Z2 + Z + == о
и принадлежит ОР(2 21n )). Пусть v элемент ОР(2 2т ) порядка
,n fIп
2 ,п + 1, и пусть 1 == '\' + ,\, 1. Так как ,\,2 == v l, то i === l'
Т. е. l Е GF(2 m ). Если заПИС31Ь равенство l == y+y l в виде
( 1,\,)2 + B lV + 2 == О
И положить === 2, то уравнение Z2 + Z + === о будет иметь
своими корнями элементы 1,\" l,\, l. Тоrда i,\,:i:i Е ОР (2 т )#
<=>,,:t:i Е ОР (2т). Так KaI{ порядок 2 rn + 1 элемента '\' и 2т 1
являются взаимно простыми числами, то y:!:i Е ОР(2 т )
i == О (rl1od 2т + 1). Таким образом, при подходящем BЫ
боре преобразование р оказывается циклическим и, следова
тельно, в этом случае расширенные коды rоппы эквивалентны
циклическим кодам.
Утверждение 4.28. Н еобходUМbtМ условием существования
среди элеА'lСНТОВ },lножества L решения уравнения (АХ +
+ В) j (СХ + D) == Х является прuнадлеJJCНОСТЬ корня уравнения
A z В
,
=== о полю ОР (2т).
С D z
,
Краткое доказательство. Если С == о, то утверждение оче
видно. В случае С =1= О без оrраничения общности МО)l<НО поло
жить С == 1. В этом случае первое уравнение принимает вид
Х 2 + (А + D) Х + В === о, а второе Z2 + (А + D) z + В + AD == о.
При А + D === О оба эти уравнения имеют корни в ОР (2т).
Предположим, что А + D =1= о. Если вместо Х и Z ввести COOT
ветственно (A+D) lX и (A+D) lZ, то придем 1{ следующим
уравнениям: X2+X+(A+D) 2B==0 и z2+z+(A+D) 2X
Х (AD В) == О. Так как [А! (А + D)]2 + А/ (А + D) == AD/ (А .+J
+ D) 2, то Т 2 ((А + D) 2AD) == О. Поэтому
Т 2 ((А + D) 2 AD + (А + D) 2 В) == Т 2 (А + D) 2 В).
1) Как хорошо известно, собственные значения матрицы [ ]/ равны
i-hI степеням собственных значений матрицы [ ] [5J,
214
r лава 4
Но тоrда, как СJlедует из утверждений 2.10 и 2.11, если одно из
уравнений Иf\.1еет корень в ОР (2т), то и друrое также имеет
корень в ОР(2 т ).
Утверждение 4.29 [54]. Рассмотрим подкласс кодов Топпы
длины п == 2т, для KOTOPblX L == GF (2т), а мноrочлены rоппыI
g(z)
неприводимые МНОZОtlлены над ОР(2 1n ). Для люБО20
О < R < 1/2, люБО20 цеЛО20 k, п/k
R в ЭТОАt подклассе суще
ствует код Топпы с любым наперед заданным минимальным
расстоянием d, удовлетворяющим неравенству
н (d/n)
[(n
k)/n] (1 ...... О (n)).
Идея доказательства. Доказательство почти аналоrично до-
казательству утверждений 3.19 и 3.20.
4.7.2. Метод декодирования
Пусть v и е
соответственно переданный кодовый вектор
и вектор ошибок. Принятый вектор v + е обозначим через и.
Положим и == (иl, и2, . . . , ии). Определяя мноrочлен f и (z) с по
мощью формулы (4.45), из соотношения (4.46) получаем
, , ,
f и (z)
fv (z) + fe (z)
fи (z)
fv (z) fe (z) ·
Так как fv не имеет кратных !{орней, то, соrласно формуле
( 4.43) ,
,
f v (z)
fv(z) ==0 (modg(z)).
Следовательно,
Положим
, ,
fe(z)
fи(z)
f е (z) == f и (z) (mod g (z)).
g"(z)
g ( а )
s(z)===
и! z
a i g....l(ai).
. 1 i
t==
(4.60 )
Мноrочлен s (z) MO}l{eT быть найден по принятому вектору.
Имеет место следующее соотношенйе:
, ,
fи(z) fe(z)
s (z) == f и (z) == f е (z) (mod g (z)).
[ак как deg g
четное число, то положим deg g == 2t. Далее
будем предполаrать, что О < w (е)
t, или, что то же самое,
Важнейшие коды
215
о < deg 'е t. Задача заключается в том, чтобы найти по за-
данному мноrочлену s (z) ::F О такой мноrочлен fe (z), что
f (z) == f е (z) s (z) (mod g (z)).
Сначала покажем, что мноrочлен, являющийся решением этой
задачи, определяется однозначно с точностью до свободноrо
члена. Пусть Ф (z) мноrочлен с коэффициентами из аР (2т),
не имеющий кратных корней. Если предположить, что
dеgф tи
ф' (z) == Ф (z) s (z) (l110d g (z)),
то ф' (z) == Ф (z) (f (z)/f е (z)) (mод g (z) ), а следовательно,
( Ф (z) f е ( z) ) , == о (m od g (z) ). т а к к а к d е g ( ф ( z) f е ( z) )' 2 t, то
(ф (z) fe (Z) )' === о, так что ф' (z) f е (Z) === Ф (Z) f; (z). Так как fe (z)
не имеет кратных корней, то fe (z) и f (z) взаимно простые,
а поэтому fe (z) I Ф (z). Аналоrично получаем, что Ф (z) I fe (z)
и, зн а ч ит, f е (z) === сф (z), С Е а F (2т) .
Далее для простоты рассмотрим лишь случай, коrда g(z)
не имеет кратных корней. При этом, определяя s (z) с помощью
равенства (4.60), предварительно заменив в нем g на g, по-
лучим
f: (z) == f е (z) s (z) (mod g (z)).
Если Ф (z) мноrочлен степени не больше t, такой, что
ф'(z) == ф(z)s(z) (mod g(z)), (4.61)
то (Фfе)' =: о (modg(z)). Так как (фfе)' является полным квад-
ратом, то (Фfе)' == о (mod g2 (z». Следовательно, (фfе)' == о
и с точностью до свободноrо члена решение определяется одно-
значно. Решение сравнения (4.61) имеет следующий вид:
Ф (z) === аО + z<p (z), deg <р < t, аО Е аР (2).
fIодставляя это решение в формулу (4.61), после несло)кных
преобразовапий получаем
(zep' (z) + <р (z)) (1 + zs (z») === aos (z) (mod g (z)). (4.62)
t l t l t l
Пусть ер (z) === L CP1ZI; s(z) r::: L Sjz/; (1 + zs (Z))Zl == L C/lZ/
1==0 /=:JO 1==0
(mod g (z) ), о i < t; D матриuа размера t Х t, у которой
диаrона.пьные элементы с четными номерами равны 1, а осталь-
ные элементы равны о; Ts матрица размера t Х t, (i, j) й эле
м е нт кото рой р а в е н с j 1, i 1; ер == (ера, ер 1, . · · , qJ t 1); s === (s О, S 1, . . .
. . . ,St l). В этих обозначениях уравнение (4.62) будет иметь
следующий вид:
(D + Ts) фТ === aos T .
(4.63)
216
r лава 4
Из единственности решения следует, что матрица D + Ts яв
ляется невырожденной, если ао == 1, и вырожденной, если
ао == О. Таким образом, мы получили следующий алrоритм дe
кодирования. (Если О Е L, будем считать, что (хn == о.)
1) По принятому вектору находится s (z). Если s (z) О, то
принимается решение о том, что ошибок при передаче не было.
Если s (z) =1= О, то переходят к шаrу 2"
( 1
2) Для каждоrо О i < t находится остаток L CijZ' от дe
j==O
ления (1 + zs (z) ) Zi на g (z).
3) Строится матрица D + Ts. Если полученная матрица яв
ляется вырожденной, то к n й компоненте прибавляется единица
и осуществляется переход к шаrу 1. Если полученная матрица
оказывается невырожденной, то находится решение Ф уравнения
(D + т s) фТ == ST
и далее определяется ер (z) .
4) Подставляя в Ф (z) === 1 + zcp (z) последовательно элементы
L {О}, находят все корни aip (Xi 2 , ..., ai v Е L {О} уравнения
Ф (z) О. Компоненты принятоrо вектора с номерами i 1 , i 2 , ...
. . . , i" заменяются на противоположные.
Как следует из утвер)кдения 4.29, минимальный вес d MIIH
«хороших» кодов rоппы значительно превышает правые части
(4.54) и (4.55). Однако хороших методов исправления ошибок
веса более чем t + 1 неизвестно. В тех случаях, коrда ошибки
веса до t исправляются, а ошибки большеrо веса обнаружи
ваются, вероятность ошибочноrо декодирования обычно тем
меньше, чем больше d мин , так что с этой точки зрения «хорошие»
коды rоппы более предпочтительны, чем ПрИ IИТИВНЫС БЧХ-
коды, для которых dыIIп/d БЧХ мсныпе приблизительно в пол-
тора раза.
Пример 4.16 [53]. Пусть пl == 4 и L == GF(2 4 ). Так I{aK в этом
случае мноrочлен g (z) не дол}кен иметь корней среди элементоп
G F (24), то он должен выбираться из мноrочленов, неприводи
мых над G F (24) или их произведений. Пусть (х примитивный
элемент ОР(2 4 ), а X4+X+l ero минимальный мноrочлен.
Упорядочим элементы L слеДУЮIЦИМ образом: L == {(Хl, (Х2,...
. . . ,a 15 , О).
Так как элемент (ХЗ имеет ПОРЯДОI{ 5 И ero минимальный
мноrочлен есть Х 4 + х з + Х 2 + х + 1, то сумма корнеЙ Т 2 ((ХЗ)
равна 1. Тоrда, соrласно утверждеНИIО 2.10, мноrочлен Z2 +
.+ Z + (ХЗ является неприводимым над G F (24) И ero МО}I{НО ис
пользовать в качестве g (z). С по лощью таблицы из задачи 2.59
1\1 о)к Н О про в е р ить, что g ( (Х) == 2 + CG + (Х 3 == (Х 11 , g 1 ( (Х) == а 4,
Важнейшие коды
217
g ( (Х 2) == (Х 4 + (х 2 + аЗ == 1 + а + (Х 2 + а 3 == (Х 12 , g 1 ((Х 2) == (Х 3, ...
..., (1 + a)g 1 (а) == а 8 , (1 + (2)g 1 (а 2 ) == а 11 , ... .
в этом случае матрица (4.49) имеет вид
[:: : I :: :: :11 :: 6 :: ::3 :6 : '! ::3 ::4 ::2 12 :::].
Если представить эту матрицу в ДВОИЧНОМ виде, то она будет
u
иметь слеДУIОЩИИ вид:
O 1 1 О О О 1 1 1 О О О О 1 1 1
О О О О О 1 1 О 1 О 1 1 1 О 1 1
1 О 1 1 1 О О О О 1 О О О 1 1 1
1 О О 1 О 1 О О О О О О 1 О 1 1
О 1 О О 1 1 О О 1 1 1 1 1 1 О 1 .
1 1 1 1 1 1 О 1 1 1 О 1 О 1 О 1
О 1 О 1 1 О О 1 О О О О О 1 О 1
1 О 1 О О О 1 О 1 О 1 1 1 1 О 1
Так как paHr этой матрицы равен 8, то код имеет 8 проверочных
и 8 информационных символов.
Предполо}ким, что ошибки возникли в l й и 5 й компонен-
тах. Тоrда
s (z) == (а + (1,4) Z + а 8 + а 11 == а 7 + z,
1 +zs(z)==z2+a 7 z+ 1 ==(а 7 + l)z+a 3 + 1 (modg(z)) ==
== a l4 + a 9 z (mod g (z)),
(1 + zs (z)) z == a 9 z 2 + a l4 z == а 9 (z + аЗ) + a 14 z ==
== (а 9 + ( 14 ) Z + а 12 == а 12 + a 4 z (тод g (z)),
D Т == [ а14 a l2 ] == [ a14 а 12 ]
+ s а 9 а 4 + 1 а 9 а '
5==(а 7 , 1), Ф==(<Ро, ерl). Уравнения (4.59) имеют вид
а 14еро + а 12ер 1 == а 7 ,
а 9 <ро + аерl == 1.
<Ро == (а 8 + a I2 )/(1 + ( 6 ) == a ll , <Рl == (a 14 + a)/(l + а 6 ) == а 9 .
Следовательно, ф(z) == 1 + (XIIZ + a 9 z 2 . В ЭТО f случае, как леrко
проверить, ф(а) == ф(а. 5 ) == О. Из примера 4.15 следует, что рас-
ширенный КОД кода rоппы, paccMoTpeHHoro в данном примере,
эквивалентен циклическому (17, 8) KOДY с минимальным весом 6
(принадле}кащему KJlaccy БЧХ l{ОДОВ из утвер}кдения 4.4)"
218
fлава 4
4.8. КОДЫ, исправляющие пачки ошибок
Для любоrо линейноrо (п, k)
Koдa, исправляющеrо пачки
ошибок длины Ь и меньше, должно выполняться следующее со-
отношение Рейджера [57] (утверждение 3.7):
n ........ k
2Ь.
Важнейшими известными кодами, исправляющими пачки оши-
бок, являются коды, получающиеся из циклических кодов, уко-
роченных циклических кодов или кодов Рида
Соломона. Рас-
смотрим сначала укороченные циклические коды (ВКЛIочая цик-
лические коды). Пусть g(X)
порождающий мноrочлен. Пачку
ошибок длины Ь или менее можно представить в слеДУIощем
виде:
Xie (Х),
rде е(О) =1= О, deg е < Ь, О
i < п....... deg е. Следовательно, для
Toro чтобы код исправлял пачки ошибок длины Ь и менее, He
обходимо, чтобы для произвольных мноrОЧJIенов еl (Х) и е2 (Х),
таких, что ej (О) =1= О, deg ej < Ь, и любых целых чисеJI i 1 и i 2 ,
О
i j < п
deg е.1 (1 ::::;;; j
2), выполнялось соотношение
X i1 el (Х) +"Xi2e2 (Х) ф О (mod g (Х)).
Если последнее соотношение выполняется при i 1 == О, то, как
следует из свойств укороченных циклических кодов, оно выпол-
няется и для произвольноrо i 1 0 Поэтому указанное выше условие
эквивалентно тому, что
еl (Х) + Xie2 (Х) == О (mod g (Х)),
О
i < n
deg е2.
В частности, в случае циклических кодов, если п
deg е2
::::;;; i < п, то Xn
i (еl (Х) + Xie2 (Х) ) == е2 (Х) + Xn
iel (Х) Х
Х (mod Хп
1), п
i
deg е2 < ь < п
Ь, так что можно
оrраничиться следующими значениями i: О
i < п. Следующая
теорема дает так называемый метод перемежения, IlОЗВОЛЯЮ-
щий по кодам небольшой длины строить более длинные
коды [4].
Теорема 4.10. Если (укороченный) циклический (п, k)
Koд С
с порождающиht А1НОёочленом g (Х) исправляет пачки ошибок
длины Ь и менее, то (укороченный) циклический (пl, kl)
Koд с<о
с порождающим МНОёочленом g (Xl) исправляет паtlКИ ошибок
длины bl и Jиенее.
Д оказатеЛЬСТ80. Так как G
циклический код, то g (Х) I
'(n
1.
Следовательно, g (x 1 ) I X nl ...... 1, так что C(l) так)ке является
Важнейшие коды
219
n---l
циклическим КОДОМ. ДЛЯ любоrо мноrочлена f (Х) === L '/Х} и
j==O
1---1
любоrо h, О h < [, имеет место равенство f (Х) == L Xhf(h)(X'),
h==O
(n---h)/l
rде f(h) (Х) == L fh+l/X/. Если мноrочлены еl (Х), е2 (Х) и
1==0
целые числа i, io такие, что еl (О) =1= О, deg еl < Ы, е2 (О) =1= О,
deg е2 < Ы, О il + io < nl deg е2, О i < п/l, О io < [, ТО
1---1
еl (Х) + X il + i oe2 (Х)::=: L Xh [e1 h ) (х 1 ) + Xile h---io) (х ' )]
h==O
(здесь индекс h io У e h---io) вычисляется по модулю [). Обо-
значим левую часть последнеrо равенства че рез е (Х). Заметим
что g (Х/) I е (Х) только в том случае, если g (Х/) I (e\h) (Х/) +'
+ Xile h---io) (Xl)), О h < 1. Следовательно, g (Х) I [e1 h ) (Х) +
+ Xle h---io) (Х)]. Поскольку это противоречит тому, что код С
исправляет пачки ошибок длины Ь и менее, то
е (Х) Ф О тод g (X 1 )),
Т. е. код С(О исправляет пачки ошибок длины bl и менее.
Следующая теорема принадлежит Файру (9, 58].
Теорема 4.11. П усть СО циклuческ'uй код длины по с по-
рождающим МНОёочленом g,o(X) , исправляющий пач.ки ошибок
длины Ь и менее, и пусть gl (Х) неприводимый взаимно про-
стой с go (Х) МНОёочлен с периодом пl, степень КОТОрОёО не
меньше Ь. ТОёда циклический код длины п == паnl/ (по, пl) с nо-
рождающим МНОёочленом g (Х) ::=: go (Х) gl (Х) исправляет пачки
ошибок длины Ь и менее.
Доказательство. Предположим, что для мноrочленов еl (Х),
е2 (Х) и целоrо i, таких, что el (О) =1= О,
degel < Ь, е2(0) =1= О, dege2 < Ь, О i < n,
имеет место следующее сравнение:
el (Х) + Xie2 (Х) == О (mod go (Х) gl (Х».
Пусть Ёо остаток, а 1 частное от деления i на По. Так как
go (Х) I х n ) ........ 1, то
el (Х) + Х! е2 (Х) == еl (Х) + X1oe2 (Х) ==
== О (mod go (Х», О io < па-
Поскольку СО исправляет пачки ошибок длины Ь и менее, то
io == О и
el (Х) ::=: ........е2 (Х),
220
r лава 4
а поэтому
(x 1nfJ ....... 1) еl (Х) == о (mod go (Х) gl (Х)).
Так как gl (Х) неприводим и deg gl Ь > deg el, то
gl (Х) I Xlno 1.
По предположению go (Х) I ХnО 1 и (go (Х), gl (Х)) == 1, так что
g (Х) I х 1 n\)....... 1.
Поскольку О i == lno < п, то это противоречит тому, что fl
является минимальным целым ЧИСЛОl\1, таким, что g (Х) I Хп 1.
Следствие 4.11. Пусть gI (X) HeпpUBoaUhtlJlil hlносочлен с пе-
риодом nl, степень КОТОр020 не меньше Ь, взаи1f,tно nрОС1'ой
с х 2Ь ....... 1. Тоеда цикличеС1СUЙ ,(од длины (2Ь 1) пl/ (2Ь 1, пl)
с порождаЮЩU.Аt мноеочленом (X2b l 1) gl (Х) исправляет
пачки ошибок длины Ь и .AteHee.
КОДЫ, введенные в этом следствии, наЗЫВRIОТ кодаА'Еи Файра
[58]. Код Файра имеет более чем 3Ь 1 проверочных символов,
что на Ь 1 больше, чем нижняя rраница РеЙД)l{ера, равная 2Ь.
ДЛЯ длин кодов до нескольких тысяч построены «вручную» или
С помощью вычислительных маlJlИН таблицы порождающих мно-
rочленов лучших циклических и укороченных циклических Ко-
ДОВ, исправляющих пачки ошибок [60 65].
Утверждение 4.30 [66]. Пусть С укороченный циклический
код с порождаЮЩИht мноеочленом (Xl....... 1) go (Х), исправляющий
пачки ошибок длины Ь и меньше. Если минимальный вес С pa
вен 2t + 2, то код С исправляет все случайные ошибl(,и веса t
и менее, а кроме Т020, все пачки ошибок длины min (Ь, 1) и менее.
Краткое доказательство. Если t min(b, 1), то утверждение
очевидно. Предположим, что t < min (Ь, 1). Пусть e(X) MHoro-
член ошибок. Положим
е (Х) == r 1 (Х) (mod X 1 ....... 1),
degrl<l.
1) Если вес w (е (Х)) мноrочлена е (Х) не больше чем t, то
w (rl (Х)) (.
2) Если w(e(X))>t или если е(Х) пачка ОIlIибок длины
min (Ь, l) или менее, то
и' (rl (Х)) >. t.
Следовательно, остатки от деления векторов ОLllиБОI{ типа 1
и типа 2 на (Xl 1) go (Х) различны, а поэтому принадлежат
различным смежным классам.
Важнейшие коды
221
Кодами, подобными кода м из утвеР)l{дения 4.30, которые MO
rYT исправлять как случайны ошибки, так и паЧI{И ошибок,
являются коды, описанные НИ}l{е, а также коды, которые полу
чаются, коrда в качестве мноrочленов go (Х) в утвер}кдении 4.30
используются порождающие мноrочлены БЧХ кодов, а также
некоторые друrие мноrочлены [66, 67].
Вообще rоворя, если в (п, k) Koдe над ОР (qт) элементы
GF(qт) заменить на их представления в виде векторов размер
ности т над GF(q), то мо}кно получить (тn,mk) код над
ОР (q). Если исходный код линейный, то полученный таким об
разом код также будет линейным. Однако если исходный код
является циклическим, то получающийся код MO}l{eT не быть
циклическим. Возьмем в качестве исходноrо !{ода qт ичный
(qт 1, qln 1 2t) KOД Рида Соломона, испраВЛЯIОЩИЙ t
ошибок. Пусть С q-ичный линеЙный (т (qт 1), т (q1n ----- 1
2t) KOД, получающийся указанным выше способом. Непосред
ственно из построения кода С можно видеть, что он исправляет
все пачки ошибок длины lп (t 1) + 1 и менее, а также все
случайные ОIllибки веса t и менее. Аналоrичные коды можно
построить, если BMtCTO кода Рида Соломона использовать
коды из примера 4.5.
Утверждение 4.31. Описанный BblUle код С исправляет лю-
бые 1 или менее пачек ошибок длины m ( (t/ [) 1) + 1 u менее.
5. Сверточные коды
1. Методы пороrовоrо декодирования
5.1. Общий обзор сверточиых кодов
Сверrочные (или рекуррентные) коды были введены Элай
сом [1] из Массачусетскоrо технолоrическоrо института (МТИ).
В отличие от блоковых кодов, коrда каждый символ на выходе
кодера зависит лишь от конечноrо числа информационных сим
волов на входе кодера, в случае сверточных кодов символы на
выходе кодера, вообще rоворя, MorYT зависеть от бесконечноrо
числа информационных символов. В этом смысле сверточные
коды можно рассматривать как обобщение блоковых кодов.
Развитие теории сверточных кодов происходило в трех Ha
правлениях в соотве,тствии с тремя важнейшими методами дe
кодирования сверточных кодов: метода пOPOZOB020 декодиро-
вания [2], метода декодирования по максимуму правдоподобия
[25] и метода последовательноzо декодирования [14]. Метод по
poroBoro декодирования сверточных кодов в принципе аналоrи
чен методу l\1ажоритарноrо декодирования блоковых кодов. Дo
стоинством этоrо метода является простота алrоритма, а следо
вательно, и реализующих ero устройств. Точно так же, как и
для блоковых алrебраических кодов, число операций, необходи
мых для декодирования одноrо информационноrо символа, для
этоrо алrоритма не превосходит некоторой постоянной величи
НЫ. Метод декодирования по максимуму правдоподобия Teope
тически более эффективен, чем метод пороrовоrо декодирования,
однако сложность устройств, необходимых для ero реализации,
возрастает экспоненциально с ростом длины кода. И наконец,
метод последовательноrо декодирования является методом Be
u
роятностноrо декодирования, при котором число операции, He
обходимых для декодирования одноrо символа, является слу
чайной величиной. При практически приемлемой сложности
устройств метод последовательноrо декодирования по своим xa
рактеристикам приближается к методу декодирования по мак-
симуму правдоподобия.
5.1.1. Метод nopor080ro декодирования
Метод пороrовоrо декодирования, предложенный Месси [2],
состоит в том, что при приеме вычисляются синдромы и ЭТИ
синдромы или последовательности, полученные в результате ли-
нейноrо преобразования синдромов, подаются на входы поро
1. Методы nОрО208020 декодирО8ания
223
rOBoro элемента; исправление ошибок осуществляется далее
с помощью символов, поступающих с выхода пороrовоrо эле
мента. Коды, которые допускают декодирование этим методом,
должны обладать введенным Месси свойством ортоrональности.
Ряд кодов со скоростью 1/2 И меньше, обладающих этим свой
ством, был построен Месси. В дальнейшем Робинсон и Берн
стейн [3] на основе совершенных разностных множеств построи
ли самоортоrональные коды, для которых проверочные после
довательности обладают свойством ортоrональности и .MorYT
быть непосредственно поданы на входы пороrовых элементов.
К числу кодов, которые допускают пороrовое декодирование,
относятся также равномерные коды [36], аналоrи кодов Рида..........
Маллера [2] и др.
Сверточные коды, исправляющие пачки ошибок, впервые
были предложены Хеrельберrером [4]. В дальнейшем Вайнер и
Эш [6], Препарата [7], Берлекэмп [5], Месси [8] и др., основываясь
rлавным образом на теории матриц, построили ряд квазиопти
мальных кодов, исправляющих пачки ошибок и требующих для
этоrо защитный интервал, близкий к минимально возможному.
Ивадари [10.........12]' разлаrая синдромы на простые конфиrура
ЦИИ, построил класс кодов, допускающих очень простое коди
рование и декодирование. ·
Для исправления случайных ошибок и пачек ошибок Колен
бурr разработал так называемые диффузные коды, допускаю
щие пороrовое декодирование [9]. Относительно реrулярный Me
тод построения самоортоrональных диффузных кодов предло
жил TOHr [13].
Методы пороrовоrо декодирования основаны на простых
идеях, и они находят широкое применение на практике. Работы
в этой области оказали большое влияние на развитие исследо
ваний не только сверточных кодов, но и блоковых кодов, допу
екающих мажоритарное декодирование.
5.1.2. Методы последовательноrо декодирования
Последовательное декодирование было введено Возенкраф
том [14] раньше, чем пороrовое декодирование, и на начальном
этапе исследования в этой области велись rлавным образом в
МТИ. Этот метод, приближающийся по своим характеристикам
к методу декодирования по максимуму правдоподобия, требует
для декодирования одноrо символа тем меньше операций, чеl\1
меньше уровень шума в канале; в отличие от этоrо при декоди
ровании по максимуму правдоподобия число операций постоян
но И достаточно велико, поскольку оно определяется макси
мальным уровнем шума в канале. Это свойство последователь
Horo декодирования позволяет упростить требующиеся для ero
224
r лава 5
реализации устройства. Предложенный Возенкрафтом аJlrоритм
был положен в основу экспериментов по передаче данных по
телефонным каналам, проводившихся в Линкольновской лабо..
ратории МТИ и получивших название SECO [15].
Алrоритм Возенкрафта, предназначавшиЙся первоначально
для Д130ичноrо симметричноrо канала, был обобщен РеЙффеном
[16] на случай произвольноrо ДPlскретноrо канала без nа/vlЯТll.
Крупным успехом исследований в этом направлении было OT
крытие алrоритма Фано [17]. Среднее число операций, требую..
щееся для декодирования одноrо символа при использовании
аЛI"оритма Фано, не зависит от кодовоrо оrраничения. Допуская
простую техническую реализацию, а также обладая рядом дpy
rих достоинств, этот алrоритм до настоящеrо времени остается
одним из основных алrоритмов. Поскольку алrОРИТivlЫ последо
вательноrо декодирования являются вероятностными, то анализ
их работы связан с рядом сложностеЙ. Один из путеЙ преодо.пе..
ния этих сложностей заключается в том, чтобы, как и при дo
казательстве теоремы кодирования Шеннона для канала с П1У
мом, найти характеристики алrоритма, средние по некоторому
ансамблю кодов, и далее, воспользовавшись тем, что по крайней
l\1lepe для одноrо из кодов в этом ансамбле характеристики алrо
ритма не хуже средних, сделать вывод об эффективности Toro
или иноrо алrоритма. Метод определения rраницы случаЙноrо
кодирования, предложенный rаллаrером и подробно рассмот"
ренный в r л. 1, TaK}I{e широко применяется для анализа алrо
ритмов последовательноrо декодирования. Этим методом BHa
чале Севадж [18] нашел среднее число операциЙ для алrоритма
Фано; затеl\11 вновь Севадж [19], Джекобс и Берлекэмп [20] и др.
показали, что распределение числа операций при декодирова
нии является распределением Парето. Еще одним способом aHa
лиза сложных алrоритмов является их моделирование на вычис
лительной машине. Большая работа по моделированию алrорит"
мов последовате,льноrо декодирования была выполнена Джор
даном [21] и др. Кроме этих методов для исследования поведе
ния алrоритмов последовательноrо декодирования ИСПОЛЬЗУЮ1
ся также качественные и общие методы.
При последовательном декодировании желательно исполь
зовать коды с большим минимальным расстоянием и по возмож
ности меньшим кодовым оrраничениеl\1. Удобно представ.пять
коды в виде кодовоrо дерева. Буссrанr [22] опубликовал список
кодов со скоростями R === 1/2 И l/ з , которые MorYT использоваться
в сочетании с последовательным декодированием, а Лин [23]
предложил реrулярный l\1етод построения таких кодов. I<poMe
Toro, КостеJIЛО [24] предло}кил простоЙ алrоритм, при НСПОJIЬЗО
вании KOToporo с помощью вычислительной маU1ИНЫ можно
строить I ОДЫ С БОЛblllИМ минимальным расстоянием.
1. Методы поросовосо декодирования
225
При последовательном декодировании число операциЙ, He
обходимых для декодирования одноrо символа, возрастает по
мере увеличения уровня шума в канале. При сильном шуме
принятые, но еще не декодированные символы накапливаIОТСЯ
в буферной памяти декодера. В тех случаях, коrда о)кидающая
обработки последовательность символов переполняет буферную
память, декодер перестает работать правильно. Это явление
характерно для последовательноrо декодирования и известно
под названиеl'vI переполнения буфера. Вероятность переполнения
буфера можно вычислить или оценить с помощью распределе
ния Парето для числа операций при декодировании, получен
Horo Севаджем [181, а также Джекобсом и Берлекэмпом [20].
В деЙствительности вероятность переполнения буфера часто OKa
зывается rораздо больше, чем вероятность ошибочноrо декоди-
рования, и именно она определяет возмо)кности последователь
Horo декодирования. Фальконер [38] предложил rибридный Me
тод декодирования каскадных кодов, сочетающий в себе эле-
менты алrебраическоrо и последовательноrо декодирования.
В качесТве внешних кодов он использовал коды Рида
Соло
мона, а в качестве внутренних кодов
коды, допускающие по
следовательное декодирование. При этом в случае, если при
последовательном декодировании число операций превышает He
который определенный пороr, то соответствующий символ внеш-
Hero кода считается стертым. Как показал Фальконер, такой Me
ТОД декодирования позволяет уменьшить вероятность перепал-
нения буфера.
Как уже указывалось выше, алrорит
.1 Фано занимает цент-
ральное полохсение среди алrоритмов последовательноrо дeKO
дирования. Зиrанrировым [27] и Джелинеком [26] независимо
был преД,,'10жен друrоЙ алrоритм последовательноrо декодиро-
вания, известный под названием стек
аЛZОрUТм'а. Этот алrоритм
во мноrих случаях лучше алrоритма Фано; он очень просто опи
сывается и помоrает проникнуть в существо различных прин-
ципиальных вопросов последовательноrо декодирования 1).
5.1.3. Методы декодирования по максимуму правдоподобия
После введения Элайсом сверточных кодов встал вопрос
о том, какие коды (сверточные или блоковые) потенциально луч-
ше. Ответ на этот вопрос был дан Витерби [25], который полу-
чил верхние и нижние rраницы вероятности ошибки для CBep
1) Последовательному декодированию посвящена выпущенная в 1974 r.
издательством «Связь» книrа К. Ш. Зиrанrирова «Последовательное декоди
рование». В этой Кllиrе дан историческиЙ обзор дости}кений но последователь
ному декодированию, объективно отражающий как советские, так и зару.
бе}кные р<iботы.
Прuм. ред.
226
r лава 5
точных кодов и с их ПОМОЩЬЮ показал, что характеристики
оптимальных сверточных кодов как функции кодовоrо оrрани-
чения лучше соответствующих характеристик блоковых кодов
той же длины. Для получения этих rраниц Витерби использовал
алrоритм декодирования сверточных кодов, которыЙ, как ока-
залось, действует как а.,1rОрИТl'vl декодирования по максимуму
п.равдоподобия. Этот алrоритм впоследствии стал называться
аЛ20рUТ.мом Вuтербu.
Если на начальном этапе сверточные коды были лишь объ
ектом теоретических исследований, то в дальнейшем они стали
применяться сначала в сочетании с последовательным декоди
рованием в КОСl'.1ическоЙ связи, а затем в сочетании с пороrовым
декодированием в спутниковых системах передачи данных, си
стемах морской радиосвязи и друrих системах. Кроме Toro, aHa
лиз структуры сверточных кодов связан с теорией автоматов.
Несомненно, что в будущем будет наблюдаться дальнейшее
уr.,7Jубление взаимосвязи между теоре'тическими исследованиями
в области сверточных кодов и практическим использованием
последних. В этой rлаве будут рассмотрены лишь методы по
poroBoro декодирования сверточных кодов и используемые при
этом коды. Методам последовательноrо декодирования сверточ
ных кодов посвящена следующая rлава.
5.2. Представление сверточных кодов
Известно несколько способов представления сверточных ко-
дов: представление с помощью оператора задержки, использо
ванное Месси [2], ПРЕдставление с помощью матриц, использо
ванное Вайнером и Эшем [6], представление с помощыо дерева,
обычно используемое при последовательном декодировании и др.
Ответить на вопрос о том, какое из этих представлений является
самым удоБНЫ
f, нельзя, поскольку все зависит от решаемой за-
дачи. В данном разделе будут рассмотрены представление CBep
точных кодов с помощью оператора задержки и представление
с помощыо матриц, а также будет установлена связь между
ним:и. Представление с помощыо дерева будет описано в rлаве,
посвященной последовательному декодироваНИIО.
5.2.1. Представление с ПОМОЩЬЮ операторов задержки
На фиr. 5.] показан сверточный кодер в общем виде. В каж
дый момент времени на вход кодера поступают ko информа..
ционных символов и С выходов декодера по выходных символов
посылаIОТСЯ в канал. Вообще rоворя, символами MorYT быть
элементы произвольноrо конечноrо поля ОР (q), и тоrда инфор-
r.1ация передается со cKopocTыo R == (ko/no) 10g2 q двоичных еди
1. Методы nОрОёовОёО декодирования
227
ниц на один выходной символ. Далее, ес.ПИ это не oroBopeHo
особо, предполаrается, что все операции с входными и BЫXOД
ными символами кодера выполняются в поле GF(q).
Удобный способ представления временных последовательно
стей предложен Хаффменом [31]; он основан на использоваНИJ1_
оператора задержки D. При этом ko входных пос.педователынj...
стей информационных символов представляются в виде rHoro
членов
[и) (D) == ibf) + i f) D + i&Л D 2 + ...,
j==1,2,
. , . ,
ko,
(5.1)
rде i ) информационный символ, поступивший на j й ВХОД
кодера в момент и. Аналоrично ПО выходных последовательно-
1
,,2
ii
I
"о
С6ертОI/НЬ/Й
коВер
1
2 .....
:
I
'
I.CQ
ПО
Фиr. 5.1. Сверточный кодер.
стей представляются в виде мноrочленов
Т(О (D) === ib i ) + ' O D + i i) D + ..., i == 1, 2, .. ., ПО, (5.2)
rде ' ) символ, ПОЯВЛЯIОЩИЙСЯ на i M выходе кодера в MO
мент и.
Связь между выходными последовательностями T(i)(D) и
входными последовательностями I(j> (D) задается для HeKOTO
poro т с помощью мноrочленов
т
GЧ) (D) == L gЧ) Dk
(t) k==O (t), k
(5.3)
степени пl или меньше с коэффициентами из поля ОР (q). Эта
связь выражается равенством
k
1'(0 (D) == L G П (D) [<j) (D). (5.4)
j==l
( ')
Мноrочлены оа) (D) называются порождаIОЩИ IИ мноrочленами;
выбор порождающих МlIоrочленов oH (D) полностью опреде-
ляет сперточныЙ код.
Пример 5.1. Рассмотрим показанный на фиr. 5.2 кодер све.р-
точноrо кода со скоростью 1/2, имеlОЩИЙ один вход и два BЫ
хода. Если входная последовательность
j(1) (D) == ibl) + i\1) D + i l) D 2 + ...
228
r лава 5
задана, то две выходные последовательности
т(1) (D) == tb1) + tP)D + t 1)D2 + ...,
т(2) (D) == tb 2 ) + t\2) D + t ) D 2 +
определяются порождаЮЩИl\iИ мноrочленами
a B (D) == 1 + D,
O (п) == 1 + D + D3
слеДУIОIll,ИМ образом:
T(l) (D) == o B (D) z(1) (D),
т(2) (D) == o M (D) Z(1) (D).
Если т наибольшая из степеней порождающих мноrочле-
нов, то произвольный фиксированный информационный символ
t (1) t (1) t (1)
..., 2 1 1, О
.(1) . (1) . (1)
...,12. ,11 I 10
... t(2) t(2) «2)
, 2 , 1, О
Фиr. 5.2. Кодер сперточноrо кода со скоростью R == 1/2.
мо}кет оказывать влияние на ВЫХОДНУIО последовательность в
течение не более чем т + 1 единиц времени. За это время ко-
дер выдаст Bcero (т + l)по символов, а поэтому rоворят, что
кодовое оrраничение ПА этоrо кода составляет (т + 1) по сим-
в ол О в.
По аналоrии с систеl\fатическими блоковыми кодами можно
рассматривать так)ке систематические сверточные коды. В слу-
чае систематических кодов первые ko выходных последователь-
ностей совпадают с входными последовательностями:
Т(О (D) == [Н) (D), i == j === 1, 2, . . ., ko. (5.5)
Остальные по ko выходных последовательностей, которые MO
жно рассматривать как проверочные последовательности, яв
ЛЯIОТСЯ линейными комбинациями входных последовательно
стеЙ, т. е.
ko
Т(О (D) == L a H (D) /(f) (D) == a B (D) /(1) (D) + aa (D) /(2) (D) +
jr=ao
. .. + G f)o) (D) /(k o ) (D), i == ko + 1, .. ., по- (5.6)
1. Методы пОРО20вО20 декодирования
229
Друrими словами, каждыЙ передаваемый по каналу символ про
верочноЙ последовательности является линейной комбинациеЙ
преДllIеСТВУIОЩИХ информационных символов. Систематический
сверточныЙ код определяется уже выбором ko (по ko) порож
дающих мноrочленов o H (D), i == ko + 1, ..., по, j == 1, ..., ko.
Проверочные последовательности сверточноrо кода при
приеме MorYT быть найдены следующим образом. Приняты е по
с.педовате.пьности R(i) (D), i == 1, 2, ..., по, MorYT быть прсд
ставлены с помощью оператора задеР)l{КИ в виде
R (i) (D) (1) + ( I) D + (i) D 2 + · 1 2 (5.7)
== r о r 1 r 2 . . . , t == , ,..., по,
rде ' ) символ i й принятой последовательности, поступивший
в l\10MeHT времени и. Точно так же MorYT быть представлены и
шумовые последовательности E(i) (D) :
Е (О (D) (i) + (i) D + (i) D 2 + · 1 2 (5.8)
=== ео е} е2 . . . , t == , ,..., по,
rде e ) шумовой символ, оказавшийся в момент u в".i й при
нятой последовательности. При этом
R(i) (D) === ТО) (D) + Е(О (D), i == 1, 2, . . ., по. (5.9)
Произвольные CYMl\1bI шумовых симво.пов, вычисляемые при
приеме, для сверточных кодов так же, как и в случае блоковых
линейных кодов, будем называть проверками или проверочными
суммами. По аналоrии с блоковыми линейными кодами после
довательности коэффициентов мноrочленов
S(i) (D) == [o B (D) R(1) (О) + . . . + a ;)o) (D) R(k o ) (D)] R(i) (D), (5.1 О)
i == k о + 1, . . ., по,
будем называть CIl1-lарОJtаМtl. Заметим, что синдромы являются
последовательностями проверочных сумм, которые MorYT быть
вычислены при приеме. Синдромами будем также иноrда Ha
зывать и сами l\lноrочлены (5.10). Подставляя выражения (5.6)
и (5.9) в (5.1 О), получаем
s(i) (D) === [o B (D) Е(1) (D) + ... + a ;) (D) E(k o ) (D)] Е(О (D), (5.11)
i == ko + 1, . . ., по.
Если СИНДРОМ!>I S(i) (D) представить в виде
s(i) (D) === sb i ) + s i) D + s i) D 2 + ..., i == ko + 1, . . ., по, (5.12)
rде s ) проверочная cYl\IMa последовательности s(i) (D), BЫ
чис.пяемая в момент и, то с учеТОl\1 формулы (5.1 О) имеем
s(i) == [g (1) е(1) + g (I) е(1) + + g (I) е(1) ] +
и (i), u О (О, и 1 1 · · · (i), О u · · ·
+ [g (ko) e (ko) + g (ko) e(ko) + + g (ko) e (kQ) ] е (О (5 .13)
· · · (О, U О (о. " 1 1 · · · (О, о u и ·
230
r лава 5
Поскольку при рассмотренном выше методе кодирования пере
даваемые последовательности и синдромы получаются в резуль-
тате свертки порождающих мноrочленов соответственно с ин-
формационными последовательностями и шумовыми последова
тельностями, то рассматриваемые коды получили название CBep
точных.
5.2.2. Представление с помощью матриц
Рассмотрим, каким образом мо}кно задавать сверточные ко-
ДЫ с помощью матриц. Символ t
) i
й передаваемой последова-
теJlЬНОСТИ, поступающий на вход канала в MOl\leHT и, соrласно
формуле (5.4), определяется равенством
t
) === [g
B, ui
1) + g
B, u
l i
1) + ... + g
B, oi
1)] + ...
+ [g (ke) t .(ko) + g (ko) t .(ke) + + g (k.) l '(ko) ] ==
· · · (О, u О (1), u
J 1 · · · (О, о u
[g (I) t 8(1) + + g (ko) ;(ko) ] +
........... (О, и О · · · (1), и"о
+ [g
H, и
li
J) + ... + g
f)'! U
li
k.)] + ...
· .. + [g
B, Oi
) + ... + g
f)o! Oi
ko)].
(5.14)
Следовательно, вектор-строка из символов передаваемых по-
следовательностей
Т == (t (l) t (2) t (n a ) t ( 1) (2) (по) (1) (2) (nJ' )
о, о, ..., о , 1, /1, ...,1, ,.'., 1т, 1т, ...,Im, ... ===
=== (t o , t 1 , .. ., t m , .. .), (5.15)
rде
( 1) (2) .(n()))
t u
t u , t u , . . ., Еи /,
и===О, 1, ..., т, ..., (5.15')
и BeKTop
CTpOKa из СИ
IВОЛОВ ИНфОр
1ационных ПОС.педователь-
ностей
1 == ( ; 0 (1) , '(2) t '(ko) .(!) '(2) .(ko) '(1) '(2) 8(k o ) )
.. lo, ..., О ,ll' II ,..., lj ,..., [m' 1т' ..., t m , '"
== (i o , i 1 ,
. . . ,
i m , . · · ),
(5.16)
rде
J
( '(1) '(2) .(ko»
"и
t u ' lи ' · · ., l u ,
u === О, 1, . . ., т, .. . ,
(5.16')
связаны между собой (!леДУIОIЦИМ rvlатричным равенством
т == 1000'
(5.17)
1. Л1етоды nopozoBozo декодирования
231
rде 000 полубесконечная матрица, которая задается с по-
мощью матриц
Ои==
и имеет следующий вид:
[ 00,
о === ·
00
о
g (l) g o)
(1), и... (па), и
(5.18)
g (k e ) g (ko)
(1), и... (по), и
01, ..., От. ]
00, 01, ..., От . О .
. о о, 01, . . ., о m .
(5. 19)
(Обозначенные символом О области матрицы 000 состоят ПОJI
ностыо из нулеЙ.) Матрица 000 называется порождающей MaT
рицеЙ сверТQчноrо кода.
В случае систематических кодов ko информационных симво
лов входят в первые ko передаваемых последовательностей без
изменений, так что порождающая матрица 000 систематичс
cKoro сверточноrо кода задается матрицами
l
О
0...0
1 ... о
Об ===
о . . . 1
о
о ... о
a ==
о
о ... о
g (])
(ko+ 1), О · · ·
(1)
g (ni), О
== [1, O ],
g (k o ) g (ko)
(ko+ 1), О · .. tn,,), о
g (1)
(k Q + 1), и
. . .
g(l)
(по), и
== [ О О" ]
, и,
и 1
g (k()
(k,)+ 1), u
. . .
g (k o )
(Па), и
(здесь 1 и О соответственно единичная и нулевая матрицы
размера ko Х ko) и имеет следующий вид:
[ . 00
G ·
OQ
О
O O
00 ...
. о ].
.
О , ·
In
(5.19')
232
r лава 5
Пример 5.2. Поро)кдающая матрица кода, paccMoTpelIHoro
в при м ере 5.1, имеет DИД
11 1 1 00 01 00 ...........
G == 00 1 1 1 1 00 01 00 .......
00 00 00 1 1 1 1 00 01 00
. . .
. . . . . . . . . . . . . . .
в случае систематических кодов символы синдромов за-
даются равенством (5.13), которое МО)КНО записать в виде
S i) == [g B, ue l) + gП , ue 2) + ... + g :): ue o)] +
+ [g B, и Jei I ) -+- ... + g :) и 1 e ko)] +
+ [ 0'(1) е О) + + g (ko) e (ko) ] е (О (5.20)
· · · б (i), О u · · · (i), О и и ·
Если ввести вектор столбцы 800 и Еоо:
S T == [S (k o + 1) S (k o +2) S (no) S (k/)+ 1)
00 о ' о ,. · · , о ,..., т ,
S (k J +2) S fпo) ]
m ,..., ,...,
Е Т == [е (l) е (2) е (nо) е О) е (2) е (nо)
00 о J О'... , о , l' 1'... J 1 ,
. . . ,
е( 1)
т'
е (2) е (nо) ]
т'...' т'....
rде Т символ транспонирования, то равенство (5.2()) МО)КНО
записать в матричных обозначениях слеДУIОIЦИМ образом:
800 == н 00800,
(5.21)
rде Н 00 полубесконечная матрица, которая задается матрицей
- ( 1) (2, g( ko) l О О
g(llo+I), О g(.llo+l), О (.ko+ 1), о
g(l) ( ) g(k o ) О 1 О
(k o +2), О g(llo+2), о (k o +2), о
. . . . . . . . . . . . . . . . . . . . . .
g(t) g(2) g(k o ) О О l
(по), о (по), О ( по), о
g( ]) (2) g( ko) О О О
(k..+ 1), J gUlo+l), 1 (ko+ 1), 1 (5.22)
В== . . . . . . . . . . . . . . . . . . .
g(] ) ( ) g( ko) О О О
(по), 1 gitLo), 1 (по), 1 . . .
. . . . . . . . . . . . . . . . . . .
g(1) (2\ g(k a ) О О О
(ko+ 1), m g(llo+ 1), m . . . <ko+li.m . . .
. . . . . . . . . . . . . . . . . . . . .
(' . g(2) g(k oJ О О О
g( o), т (по), т . . . (по). т . . .
Т. Методы пopozoBozo декодирования
233
и имеет следующий вид:
по
Н .
CID
в )по ko
В
В
о
о
(5.23)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
l v \атрица Н 00 называется проверочноЙ матрицей системати
ческоrо сверточноrо кода и, как и в случае блоковых кодов,
ПО.тIностыо задает код.
Ошибка, возникшая внекотором СИМВО.пе в MOl\1eHT BpeMe
ни О, 10жет оказывать влияние на символы синдромов ЛИllIЬ до
момента ,п. Ilоэтому при изучении вли ния ошибок, возникших
в момент времени О, можно не рассматривать СИl\fВОJ1Ы синдро
мов В момент времени т + 1 и далее, а оrраничиться началь
ными участками синдромов и шумовых последовательностей,
а именно рассматривать лишь совокупности из первых (т + 1)
СИIНВОL10В синдромов И шумовых последовательностей. Такие
укороченные синдромыI, состоящие из первых (1n + 1) симво
.:10В, называются усеченными сuндРО.Л1,амu. Прове-рочная матри
ца Н, соотвеТСТВУIощая таким усеченным синдромам и шумо-
вым последоватеЛЬНОСТЯl\1, имеет вид
Н==
) по ko
Во
В 1
В 2
Q
.
.
.
.
.
.
.
.
.
.
о
..
.
.
.
.
.
............
( 5.24 )
[де B i матрица, получающаяся из матрицы В удалением ниж
них i (по ko) строк (i == О, 1, ..., т). Заметим) что для yce
234
r лава 5
ченной передаваемой последовательности Т! имеет место ра-
венство
HTt==O,
(5.25)
так что при приеме, умножая усечеННУIО ПРИНИf\1аемую последо-
вательность
R T === [t (1) + e (l) t (2) + е (2) t (n.) + е (nе) t (l) + е О)
t о О, О О , ..., о О, 1 J ' ...
t (no) + е (nо) t (l) + е О) / (2) + е (2) t(n ) + е(nо) ] (5 .2 6)
· · · , 1 l' · · · , 'n т' т т' ..., т т
на матрицу Н, можно вычислить укороченный синдром St'
поскольку
HRt == н (Tt + Et) == HTt + HEt == St.
( 5.27)
в некоторых случаях удобнее пользоваться векторами
S T == [S (k o + 1) S (ko+ 1) S (k. I +2) S (ko+2)
00 О ' ..., т ,..., О ,..., т'...
E === [ еь О , . . . ,
еО)
т'
(2)
· · ., е о , .. · ,
..., s п ), ..., S Q}, ...], (5.28)
е (2) e (niJ) е (110) ]
т'...' О ,..., т'....
(5.29)
При этом
800 == [H : 100] Еоо,
(5.30)
rде 1 00 полубесконечная единичная матрица,
Hf:1 Hf:1 H l \
1, kб+l 2, ko+l ... k J , k'j+/
Н!1 ==
00
(5.31)
fl H
1. n1 2. n')
a(j)
Б (О, О
fI
k.). n;)
Нп ==
(J(j) o.(j)
б и). 1 б и), о
[Т(j)
<:'>(i). т
g (j)
(О, о
Л'1атрицы Н ji оБЫЧIlО паЗЫВ310Т проверочными треуrольиикаМII 1).
1) ПроверочIТЫМИ треуrолыIкамии авторы ИНОJ'да называIОТ так ж,: 'IaT
рицы [H : I 00]. п рим. перев.
1. Методы пopo(?OвOZO декодироваНllЯ
235
Пример 5.3. Двоичный систематический све.рточный код со
скоростью R == ko/no == 2/3 И кодовым оrраничениеl'vl ПА ==
== (т + 1)110 == 12, задаваемый порождающими мноrочленами
a (D) == 1 + D),
a (D) === 1 + D 2 + D З ,
и i\1 еет порождаIОЩУЮ матрицу
1 О 1 О О 1 О О О О О О О О О .........
О 1 1 О О О О О 1 О О 1 О О О .........
G == 1 О 1 О О 1 О О О О О О О О О
00 О 1 1 О О О О О 1 О О 1- О О О
. .
в этом случае
1 1 1
1 О О
В=== О 1 О
О 1 О
1I
1 1 1
1 1 О 1 1
О 1 1 О 1 О 1 О 1 О
[H : 100] == о о 1 1 1 1 О 1 1
О О О 1 1 О 1 1 О 1
Выше рассматривались синдромы с момента времени О дО
MO:\IE:H [а времсни nl. В то )ке время иноrда возникает необходи
мость рассматривать синдромы с МОl\леита вреl'vIени t до MO
мента времени ,п. В этих случаях l'vIОЖНО достаточно просто
обобщить поро}кдаIО НС l\!ноrочлены, поро)кдающие l\'Iатрнцы и
проверочные матрицы, за:\1енив индекс О, показываIОЩИЙ время,
на t.
236
r лава 5
Пример 5.4. Если КОД, задаваемый в интервале времени от О
до 3 проверочныl'Л треуrольником
н/1 ==
1
110
1 1 1
О 1 1 1
рассматривать в интервале времени от
3 до 3, то проверочная
матрица будет иметь следующий вид:
l 1 1
1 1 1
Н!1 == 1 1 1
О 1 1
1
о
1
1 1
Число ненулевых элементов проверочных и ПОРО}I{дающих
матриц сверточных кодов по сравнеНИIО с числом нулевых эле
.;.
ментов обычно сравнительно неве.пико. Поэтому такие матрицы
можно просто задавать, УI<азыпая для каждоrо столбца лишь
номера СТРОК, в I{OTOPbIX раСПОЛО}I{ены ненулсI3ЫС элементы это-
ro столбца.
Пример 5.5. Следуя указанному выеe способу, матрину В
из примера 5.3 1\10ЖНО просто задать слеДУIОЩПМ образом:
111
В ==
== [
1]. (5.32)
О 1 О
Это представление особенно удобно для матриц большпх раз-
r
IepoB.
5.3. Пример noporoBoro деl<одирования
Пороrовое декодирование сверточных кодов основано на тех
же принципах, что и
Iажоритарное декодирование блокопых
кодов. Прежде чем рассм:отреть эти принципы в общем случае,
приведем простой пример, попутно ВЕОДЯ необходимые ПОНЯТИЯ.
Пример 5.6. РаССl\10ТрИМ сверточныЙ код со скоростью R :=::
<== ]/2 И КОДОВЫМ оrраничением ПА == 12, испраВЛЯIОЩИЙ лIоБыIe
1. Методы поросовОёО декодирования
237
две случаЙные ошибки в пределах кодовоrо оrраничения и
имеющий слеДУIОЩИЙ проверочный треуrольник:
[H , 16]
1
О 1
О О 1 О
1 О О 1
1 1 О О 1
1 1 1 О О 1
1
1
1
о
.
1
(5.33)
1
1
Кодер и декодер этоrо кода показаны соответственно на фиr. 5.3
и фиr. 5.4. I(аждыIй ИIнрормационныЙ двоичный СИl\IВОЛ посту
'(1 )
z.
J
::. t 1)
J
t 2)
J
Фнr. 5.3. Кодер (R == J/ 2 , J == 4).
пает в кодер с .певой стороны, выходит из кодера с правой CTO
роны и передается по каналу. В это же время в кодере фОрМИ
руется проверочный символ, которыЙ так)ке передается по Ka
валу. Этот кодер, соrласно вводимой в rл. 7 терминолоrии, Ha
зывается RпА разрядным кодерОl\1. Декодер по принятой инфор
мационной последовательности сначала вычисляет точно так )ке,
как и при кодировании, проверочные СИМDОЛЫ. ДЛЯ вычислеНIIЯ
l' (1)
,.
;;
Фиr. 5.4. Декодер (R == 1/2, J == 4).
этих проперОЧlIЫХ символов декодер содержит RnA разрядный
кодер. Далее, полученная с ПОl\IОЩЫО этоrо кодера проверочная
ПОСJlедовательность складывается покомпонентно по модулю 2
с принятоЙ провеРОЧlIОЙ последовательностью, и в результате
получается СИНДрОl\1
S Т === [8 (2) S (2) 8 (2) S (2) ]
О, l' 2'...' 5.
23
r лава 5
Символы этоrо синдрома подаются в реrистр сдвиrа, показан
ный на фиr. 5.4 в нижней части декодера. Соrласно Форму
.не (5.33), синдром S и Iпумовые символы e ), II == О, ..., 5,
i == 1, 2, связаны между собой слеДУIОЩИМ матричным COOTHO
шениеl\1 :
1
eO'
u
e(I)
1
е(1)
2
eil)
u
е(l)
4
e 1)
( 5.34 )
е(2)
о
е(2)
1
1 е(2)
2
е(2)
з
е(2)
4
e 2)
(2)
So 1 1
S(2) О 1 1
J
S(2) О О 1 О 1
2
s== (2) 1 О О 1
Sз 1
S(2) 1 1 О О 1
4
S(2) 1 1 1 О О 1
5
о
ИЛИ, что
то же самое,
Sb 2 ) === еь 1 )
S (2) е (})
1 1
S(2) == e(l)
2 2
S 2) === e l) e l)
S 2) == еы) + еР) + ei1)
S 2) == еъ l ) + e O + e O + e l)
+ е(2)
о ,
+ е(2)
1 ,
+ е (2)
2 ,
+ е(2)
з '
+ е(2)
4 '
+ e 2).
"
синдрома S находятся
(5.35)
С ПОi\10ЩЫО линейноrо преобразования
величины Av, V == 1, 2, 3, 4:
А 1 == sb 2 ) == eb 1 ) + е&2),
А 2 == S 2) == eb 1 ) + e l) + e 2),
Аз == S 2) == e 1) + ер) + e 1) + е\2) ,
А == S(2) r.:-(2) === е( 1) + е О ) + е(1) + е(2) + е(2)
4 5 I uJ О.; 3 1 5 .
Линейное преобразование, с помощыо KOToporo по СИНДРО IУ S
находнтся величины Av, называется п,оааUЛО.А-t ортосонализациu,
(5.36 )
1. Методы nopozoвozo декодирования
239
а получаемые с ero помощью величины Av называJОТСЯ COCTaв
ными проверками. Если посмотреть на составные проверки
(5.36), то можно заметить, что они обладают слеДУЮIЦИМ свой
ством: шумовой символ e
l), воздействующий на информацион
ныЙ символ в момент О, входит во все составные проверки Av,
v == 1, 2, 3, 4, и в то же время Лlобой друrой шумовой символ
входит не более чем в одну из этих проверок. Такая совокупность
составных проверок {Av} называется ортоzональной относи
тельно e
1).
Если еъ 1 ) === 1 и остальные шумовые символы равны нулю, то
составные проверки, задаваемые формулами (5.36), равны 1,
а И!\1енно А 1 === А 2 == Аз == А 4 == 1. Если же один иэ ШУi\10ВЫХ
СИl\fВОЛОВ, отличных от ChJ), равен 1, то среди проверок по край
ней мере три будут 1. И наконец, если e
1) === О и среди остальных
шумовых символов имеется не более чем две единицы, то среди
проверок Av равными единице будут самое большее две про-
верки. Если эти составные проверки подать на вход пороrовоrо
элемента с пороrом 2,5, то СИl\IВОЛ на выходе ПОС,,1еднеrо будет
равен еы) всеrда, коrда число случайных ошибок в пределах
кодовоrо оrраничения не больше двух. Далее, СКII1адывая сим
вол с выхода пороrовоrо элемента с припятым двоичным СИl\IВО
лом i
l) + еь!), которыЙ хранится в ячейке памяти, показаННОI U '
на фиr. 5.4 в верхнеЙ части декодера, шумовой символ eb l }
всеrда MOiKHO исправить. При этом: выходной символ пороrовоrо
элемента по цепи обратной связи подается на схему вычис
е
ния синдрома 11 корректирует последний, устраняя влияние e
I).
Такая процедура называется декодированием с обратной
связЬ/о. Следовательно, ана.поrИЧIIЫС рассуждения можно про
вести и для моментов времени tl == 1, 2, ... .
ЕС,,1И I.ПУМЫ не выходят за пределыI допустимых, то испраD
lенпе ошибок ОСУIl
ествляется праВИ,1ЬНО. Если ПIУМЫ превы-
I.llaIOT ДОПУСТИМУIО пС:'лпчиау, то MorYT возникнуть естественные
ОIJlибки деКОJI.ировапип. Однако ПОСКО.,lЬКУ декодер содеР)I{ИТ
це!lЬ обратноЙ СПИЗII, то однократная ошибка декодирования
приводит '{ ист{а)кеНИIО синдрома и дальнеЙIUИМ ОIlIибкам дeKO
дирования. Это ЯI3"l€НИС характерно для сверточных кодов и
известно KaI{ распространение ошибок. Конечно, всеrда хотелось
бы использовать КОДЫ, не спосоБСТВУlоп
ие распространеНИJО
ошибок.
5.4. ПРИНI(ИП noporoBoro де!'
одирования
Равенстпо (5.13), которое задает СИl\fВОЛЫ СИ:НДрОl\-IОВ 8 Ы0
менты времени а? О, заПИ!llем в несколько БО"lее обlцеl\1 B!i.1e,
считая, что символы синдромов поро)кдаIОТСЯ D моментьу Bpe
210 '
r лава 5
мени и от t до т:
S ) == [g B, u+te )t + g B, tl+t le +1 + ... + g B, и me ] + ...
+ [g (ko) e (k() + g (ko) e (ko) +
· .. (О, и+t t (i), u+t 1 t+l ...
+ g (kf) e(ko) ] е (О ( .37)
· · · (О, и m т и. u
Рассмотрим проверку
n т
А === L L Ь. s(i), V == 1, 2 . . ., J, (5.38)
v . k +1 t ,и u
t== о И==
являющуюся линейноЙ комбинацией символов синдромов. Эта
проверка называется составной проверкой. Поскольку СИМВОЛЫ
S ), задавае t1ые формулой (5.37), являются линейными I{OM
бинациями ШУl\10ВЫХ символов e O, i == 1, ..., ПО, возникающих
за время t и т, то составные проверки А1' также яв
ЛЯIОТСЯ линейными комбинациями этих символов e ). ПРИIlЦИП
пороrовоrо деI{одирования был сформулирован Месси [2] с.пе
дующим обраЗО I.
Определение 5.1. Система из J составных проверок {Av,
v == 1, ..., J}, контролирующих e :), называется ортосональной
относительно e ), если никакой друсой шумовой символ, отлич
liblЙ от e ), не контролируется более tleAt одной проверкой этой
системы (шумовой символ контролируется проверкой Av ТОсда
и только ТОёда, КОсда он входит в эту провер'ку с ненулеВЫ.А'l KO
эффuциентом) .
Рассмотрим один И3 методов мажоритарноrо декодирования,
который позволяет определить e ) из систе\1Ы J проверОI{ {Av},
ортоrональных относительно e ). Здесь и далее через [J] будем
обозначать наибольшее цепое число, не преВОСХОДЯlцее J.
Теорема 5.1. П усть отличны от нуля не более r J /2] lllУЛIОВЫХ
сиЛ,tво.лов в совокупности {e f,)}, ! =:::;: w ,n, 1 j по,
контролируеJrZЫХ системой из J составных проверок {Av}, v ==
== ], 2, ..., J, ортосонаЛЬНblХ относительно (! O (Т. е. иЛ1,еется
не более J /2 ошибок в cootbeTCTBY'0l-цих nрuнятыlx символах).
ТОсда e ;) есть значение, пPUHU.A,taeMoe 60ЛblUUНСТВОМ COCTaB
ных проверок (в случае, КОсда ни одно значение uз GF(q) не
nринuмается аБСОЛЮТНbl.А-t БОЛЫllинствОАt составных проверок,
считается, что e :) == О).
Доказательство. ПОЛО)l(Иl\1 e /) == v и допустим, что все дpy
rие шумовые символы, ВХОДЯПLие в проперки системы {Av},
имеют значение О, Тоrда
..4 v == V , v === 1, 2, . . ., J. (5. 39)
1. Методы пOPOZOB020 декодирования
241
Если V == О, то [! /2] шумовых СИМВОJIОВ MorYT изменить значе.
ния не более чем [! /2] проверок Av из (5.39), а поэтому не менее
чем J [! /2] проверок среди {Av} равны нулю. Таким образом,
нуль является либо наиболее часто встречающимся (при нечет
ном J), либо одним из двух одинаково часто встречаlОЩИХСЯ зна
чениЙ проверок из {Av}, однако в любом случае указанное в
теореме правило декодирования дает правильное значение шу
MOBoro символа.
Далее предположим, что V =1= О. В этом случае e ) == V =1= О
и среди друrих ПIУМОВЫХ символов e ) отличными от нуля MorYT
быть самое БОЛЫllее [! /2] 1 символов. Следовательно, не Me
нее чем J [J/2] + 1 проверок Av в (5.39) равны V, так что
указанное в теореме правило декодирования вновь дает пра
ВП"lьное значение шумовоrо символа e O.
Если J == 2f, то из теоремы 5.1 следует, что сиl\tIВОЛ e ) MO
жет быть праDИЛЬНО определен во всех случаях, коrда число
ошибок не превыIаетT [. Если J == 2/ + 1, то символ e O снова
l\Iожет быть правильно определен во всех случаях, коrда произо
ШLТJО не более / ошибок; при этом дополнительно MorYT быть об.
наружены любые / + 1 ошибок. Это означает, что расстояние
ХЭ:vIминrа между любыми двумя кодовыми словами не меньше
чем J + 1. Таким образом, имеет место слеДУIощее утвержде
нне.
С,,1едствие 5.1. Е сли линейный код допускает образование
CUCTeJ tbl из J проверок, ОРТОёонаЛЬНblХ относительно e ), то ми",
ниJtальНое расстояние d FD ЭТОсО кода не меньше tleM J + 1, Т. е.
dFD J+l.
(5.40)
Параметр J называется числом ОРТОёонаЛЬНblХ провеРОl(,.
}\1етод ма)l{оритарноrо декодирования в случае двоичных KO
дов сводится К слеДУЮlцему.
Теорема 5.2. Если {Av} система из J проверок, ОрТОёональ
ных относительно C :), ТО алсориТlI1, IvlажорuтарНОёО дeKoдиpOBa
ния таков: выбирать e :) == 1 Tozaa и только Tozaa, КОёда сумма
всех Av (рассматриваемых как действительные числа) пpeBOC
ходит пopoz J /2, если J четное, и (! + 1) /2, если J нечетное.
Теорема 5.2 указывает очень простой способ декодирования.
А именно ССJIИ задан код, ортоrональный относительно ( ), то
при приеме следует сначала вычислить синдромы, а зате.м пу
те!\! .:1инеЙноrо преобразования полученных синдромов найти co
ставные проперки. Далее составные проверки с"туедует подать на
входы noporODoro элемента, иl\tlеющеrо пороr (! /2) + 1, и испра
242
r лава 5
вить возникшие ошибки с помощыо выходноrо символа этоrо
пороrовоrо элемента.
Приведенные выше две теоремы касались ЛИIJJЬ исправления
шумовоrо СИМВОJIа e
), воздействующеrо на информационныЙ
символ в момент u. Однако сверточные коды таковы, что, BЫ
полняя В точности те же самые операции только в моменты вре.
мени и + 1, и + 2, ..., можно провести исправление также и
(О (i) U .
шумовых символов е u + 1 , е и + 2 , .. ., деиствующих в моменты Bpe
мени и + 1, u + 2, ... . За начало отсчета времени обычно вы-
бирают момент и == О, однако при пороrовом декодиропзнии Д..1Н
исправления шумовоrо символа eb i ) ИСПОЛЬЗУIОТСЯ СIlМВО..1Ы
синдромов от момента О до момента т. При этом после нахо-
ждения ШУМОБоrо символа иноrда с помощью цепи обратноЙ
связи «воздействие» e6 i ) на синдром устраняется, а в друrи\
случаях цепь обратной связи отсутствует и синдром остается
искаженным шумовым СИ1\1ВОЛОМ е6О Д3)I{е после нахождения
последнеrо. В последних случаях декодирование называlОТ дe
ФUНUТНblМ,. Коды, используемые при дефинитном декодированип,
имеlОТ приблизительно в 2 раза болыпее кодовое оrраничеНllе,
чем коды, используемые при декодировании с обратноЙ связыо.
При этом, вообще rоворя, УХУДI.1I3ЮТСЯ корреКТИРУlощие спо
собности кодов, но блаrодаря ОТСУТСТВИIО цепи обратной спя зи
при возникновении шумов, превосходящих допустимыЙ уровень,
возникшие ошибки MorYT распространяться ЛИПIЬ на конеЧНУIО
r.пубину.
5.5. CaMoopTOrOHa,,'1bHbIe КОДЫ
5.5.1. ОпредеJlение самоортоrональноrо кода
При пороrовом декодировании сверточных кодов Оlllибl{lf
исправляются последовате.ПЬНО сначала в l-M принятом блоке
Д,,1ИНЫ по, затем во 2-1\1 и Т. Д. При этом корреКТИРУIОI.цие спо-
собности кода определяются re1\1, как испраВЛЯIОТСЯ ОIllиБI<И в
1
M блоке, так как после Iiсправления ОIlIибок в l-м блоке IIС
прав.пение ОIlIибок в послеДУIОПLИХ блоках ОСУI.I
еСТП.:I51СТСЯ т()чно
так же, как и испрап.пение ОllIиБОJ
R 1
M БЛОl(С. Следопате\1
!!О,
при изучении пороrовоrо деКОДИРОRаI:ИЯ свер10ЧJ!ЫХ кодоп !\10
iKIlO оrраничиться исс.педова lIием ВЛИ5II1 ия структурыI СИI1ЛРО\IОiЗ
И матрицы 11 на декодирование лишь l
ro БJJОКCl. Среди КО,l,ОП,
допускаюш,ИХ пороrовое декодирование, самыми ПРОСТI)IМИ яп
J1
I()ТСЯ так называемые саJilООрТОсОНQЛЬНblе коды.
Определение 5.2. (Месси.) СверТОЧ1-lblU код, для КОТОрОсО
'
Lpи Лl0боМ, i == 1, 2, ..., ko система проверок, КОНТРО/lUРУ'0u(ая
1. Методы поросовО20 декодирования
243
шу.мовой символ еь О , воздеiiствующий на i й информационный
сиАlВОЛ в AtOMeHT BpeAteHU О, ортоzональна относительно e ), Ha
зывается самоортоzональны.lИ кодом.
Все самоортоrональные коды допускаIОТ полную ортоrонали-
заUИI0, т. е. с помощыо мажоритарноrо декодирования лоrут
быть исправлены все ошибки, исправление которых rаранти-
руется минимальным расстоянием. Коды этоrо типа первым ис
следовал Месси [2]. Метод построения таких I{ОДОВ с высокой
корректирующей способностью, а им:енно кодов, имеIОЩИХ при
заданном J неБОЛbllIое кодовое оrраничение ПА, был предло)кен
Робинсоном и Бернстейном [3]. Декодирование самоортоrональ
ных кодов осуществляется крайне просто, и это связано с Te I,
что соотвеТСТВУIОЩИlVl образом выбранные символы синдроl\tl0В
ортоrональны относительно e ) и при декодировании нет необ
ходимости проводить линейное преобразование символов синд
ромов для получения составных проверок. Следующая теорема
дает необходимые и достаточные условия Toro, что код является
самоортоrональным.
Теорема 5.3. (Месси.) Код является самоортоzональным TO
2да и ТОЛЬКО ТОёда, КО2да совокупность символов синдромов,
контрОЛUРУ,0f.,цtlХ каждый информационный шумовой символ
еа), О Р ТО20нальна относительно еи).
u и
Доказательство. Очевидно, что если при любом u 1 COBO
купность символов синдромов, контролирующих e ), opToro
на.пьна относительно e ), то, в частности, это свойство opToro
нальности выполняется и при и == О, т. е. код является caMOOp
тоrональным. ДОI{ажем обратное утверждение. Предположим,
что при некотором и > О совокупность СИl\fВОЛОВ синдромов,
КОНТРОЛИРУIОЩИХ e O, не ЯВJIяется ортоrональной относительно
е:/). Тоrда ДОJIЖНЫ существовать два символа синдрома, напри
мер s j) и s (), контролирующих один и тот же информационный
ИlУ.МОВОЙ символ e ,') (т. е. шумовой СИl\IВОЛ, воздействующий
на информационный символ), отличный от e ). Из равенства
(5.13), опредеЛЯlощеrо способ построения символа синдрома,
непосредственно следует, что t, t' и, и'. Кром:е Toro, без orpa
lIнчения общности можно преДПОu10)l{ИТЬ, что и' > u. Вновь обра
щзясь '( способу построения символа синдрома, получаем, что
Сll v1ВОЛbl синдромов s u И S ( ll КОНТРО,,1ИРУIОТ И (! и == еь О , 11
e ;,' и. С.тlедовательно, совокупность сиr..IВОЛОВ синдромов, конт-
ролирующих e O, не является ортоrональной относительно едп,
что в CBOIO очередь означает, что код не является caMoopToro
налыlм..
241
r лава 5
5.5.2. Простой пример
Прежде чем перейти к методам построения самоортоrональ-
ных кодов, попытаемся сначала исследовать структуру самоор-
тоrональных кодов.
ПРИl\1ер 5.6. Рассмотрим самоортоrопальныIй код со ско-
ростью передачи R == 2/3 И J == 3, задаваемый порождаIОЩИМИ
l\'1ноrочленами
G
l
(D) == 1 + D + D 4 ,
a
(D) === 1 + D 2 + D 7 .
Проверочная матрица Н/1 этоrо кода для интервала времени
7
u
7 имеет следующий вид:
lJ!1 ==
1 О О 1.1
1 О о. 1 1
10:0 1 1
1.0011 О
.1 О О 1 1
.
О .0 1 О О 1 1
.0 О 1 О О 1 1
00010011
1000010.1
1 О О О О 1'0 1
10000:1 о 1
1 О О 0.0 1 О 1 О
1 О 0.0 О 1 О 1
.
1 0.0 О О 1 О 1
1.00001 01
1 О О О О 1 О 1
1
1
1
1
1
1
1
1
(5.41 )
.lvl0ЖНО построить слеДУIОIl
ие три составные проверки, opToro-
нальпые относительно eb l ):
А 1 === 8
1) === e
)4 + e
)l + eb l ) + e
j + e
)2 + e
2) + e
3),
А 2 == sP) == е
)з + eb l ) + eil) + e
)6 + e
\ + ei 2 ) + ei 3 \ (5.42)
А === 8(3) == е( 1) + е(l) + e(l) + е(2) + e(
) + е(2) + е(З)
3 4 О ;3 4
3 2 .1 4 '
2
И три составные проверКII, ортоrональные относительно eo
А' == 8(3) === е(2) + e(.
) + е(2) + е(!) + е( 1).
ell) + е(З)
1 о
7
2 О
4
J I О U '
A
== 8
З) == e
)5 + е6 2 ) + ei
) + e
k + e
\
r e;l) + еi З ), (5.43)
А I === S(З) === е(2) + е(2) + е(;2) + е О ) + е( 1) + е О ) + е(Э)
j 7 О 5 7 4 ] 8 ].
Очевидно, что для этоrо кода J == 3.
Как можно видеть из формул (5.42) и (5.43), симво.ттаi\'1И
СИНДрО
10В, ОрТОf'она.пьными относительно е61), НВЛНIОТС51 си
f
1. А-lетоды пOPOZOBOZO декодирования
245
волы, порождаемые в моменты времени О, 1, 4, а СИ1\1волаl\fИ
синдромов, ортоrопальными OTHOCHTeJIbHO e 2), ЯВЛЯIОТСЯ СИМ
волы, поро)кдаемые в моменть} времени О, 2, 7. MorvreHTbI обра
зования этих символов синдромов cooTBeTcTBYIOT ПОI<азате.пям
{О, 1, 4} и {О, 2, 7} степеней неизнестноrо D с ненулевыl'ЛИ KO
эффициентами поро)кдаЮЩlIХ мноrочленов OH (О) и O (D).
Пусть {d o , d 1 , d 2 } показатели степеней неизвестноrо D с пе
нулевыми коэф(рициентами порождающеrо мноrочлена. Pac
смотрим совокупность
{d} d o , d 2 d u , d 2 d 1 , d o d 1 , d o d 2 , d 1 d 2 }
разностеЙ этих показателей степеней. А именно для введенных
выше мноrочлепов оы: (D) и O (D) раССМОТРИ 1 совокупности
чисел {l, 4, 3, I, 4, 3} и {2, 7, 5, 2, 7, 5}. Совокуп
ность {l, 4, 3, 1, 4, 3} представляет собой совокупность
значениЙ индексов tl информационных шумовых символов e l),
входящих в проверки (5.42) и отличных от e&I). Точно так же
СОВОКУПНОСТЬ {2, 7, 5, 2, 7, 5} совпадает с совокупностыо
значений индексов u информационных шумовых символов e ),
входящих в проверки (5.73) и отличных от е&2). Следовательно,
неоБХОДИМЬ1М условием ортоrональности систеl\I проверок (5.42)
и (5.43) относительно соответственно e l) и eb ) является OTCYT
ствие в кз){{доЙ из указанных выше совокупностей одинаковых
чисел. I<poMe Toro, если обозначить совокупности {О, 1, 4} и
{О, 2, 7} через {d o , d 1 , d 2 } И {d , d , d;}, то целые числа d o
d' === О d d' == 2 d d' === . 7 d d' == 1 d d' ==
о ,о 1 ,о '1 v ' } 1
=== 1, d 1 d === 6, d: d == 4, d 2 d === 2, d 2 d == 3 оказы..
ваются ЗI1ачеНИ51МИ индексов u шумовых символов e ), входя
щих в cj)ормулы (5.42). АнаJIоrично целые числа, ПОЛУЧ3Iощиеся
в результате выIитапияя из каждоrо числа {d , d;, d } кажд()rо
числа {d o , d}, d 2 }, ЯПll1ЯIОТСЯ значениями индексов u шумовых
символов e I), входящих в (5.43). С.педовательно, друrИl\1 необ
ходимым условием ортоrона.пьНОСТИ систем проверок (5.42) и
(5.43) относитеЛilIIО соответственно еы) и еь 2 ) является также OT
CYTcTBlIe одинаковых чисел и в последних указанных совокупно
стях. В деЙствительности, как леrко видеть, эти условия яв
ЛЯIОТСЯ И достаточными, а именно если совокупности целых чи
сел {d o , d l , d:z} и {d , d , d } удовлетворяют указанным выше
условиям, то задаваемый ими код является самоортоrонаЛЬНЫl\1.
В общем случае пусть целые числа d 1 < d 2 < ... <d q + 1
являются ПОI\азателями степенеЙ в порождающем мноrочлене
246
r лава 5
O H (D), Иl\1еющем q + 1 ненулевых коэффициентов, Т. е. пусть
a п (D) == D d } + D d 2 + ... + Ddq+ J. (5.44)
Множество {d i djli >j} из q(q + 1)/2 разностей целых чисел
d i , i == 1, 2, ..., q + 1, будем называть совокупностыо разно
стей порождающеrо мноrочлена o H.
Теорема 5.4. (Маси и Робинсон.) СверточJ-tblе коды с ko == 1
или ko === по 1 являются саМООРТОсОНQЛЬJ-tbl.А-tu ТОсда u только
ТОёда, КОёда совокупности разностей их по 1 nорОJlсдаJОUfllХ
МНОёочленов не пересекаются, а КрОЛl,е ТОёО, ни одна llЗ них не
содержит одно u ТО :JlCe число дважды.
Доказательство. РаССМОТРИl\-I случай ko == ПО 1, КОI'да cy
ществует только один синдром S(n;,) (1). Пусть d 1 < d 2 < ...
. .. < d y и d; < d < ... < d , показатели степеней неизвест
Horo с ненулевыr и коэффициентами ПОРО)l{даЮIЦИХ мноrочленов
G J) (D) и a :) (D). Соrласно фОрl\1улам (5.11) и (5.13), симво
лаl\1И синдрома, контролирующими шу овой СИМВОЛ e p, яв
ляются символы, появляющиеся в моменты времени t === и d},
u + d 2 , ..., и + d y . Индексы символов j й и j' Й информацион
ных шумовых последовательностей, контролируемых ЭТИ IИ сим
волами синдромов, MorYT быть найдены с помощыо слеДУЮlltей
таблицы:
СИМ
вол Индексы контролируемых си во..тIОВ j й.
синд информа ' ионной ШУМОВОII последовательности
рома
и IIдексы КОIIТРО-
.тшруемых снм::,олов
I' й Иllформа.щонной
последоuательносrн
S -)d2 II + d 2 d y , и + d 2 dy l' и, и + d 2 d 1
,
u + d} d y " ...,
,
и d} d 2 ,
,
и + d 1 d 1
и + d 2 d " ...,
,
и + d 2 d}
s(п o ) u + d 1 d y , u + d 1 d y l' ..., tt + d 1 d 2' l!
и+d t
s(пo)
n+dy
и, u+dy dy l' .... u+dy dl
,
u+dy {ly',
. . .,
,
u+dy dl
Эти СИYIволы синдромов орто['онаЛЫIЫ относите.,'1ЬНО e :) TO
rда и ТОЛЬКО тоrда, коrда ВЫПОЛНЯIОТСЯ С.пеДУIощие два УСЛ0
пия:
1. Методы nОрОёовОёО декодирования
247
1) Никакой индекс, отличный от и, не входит сразу в две
строки BToporo столбца таблицы. Действительно, если при He
которых i, j, k, 1, i > k имеет место равенство u + d i d j ==
=== u + d h d l , то d i d j == d 1t d l , а это означает, что HeKO
торое число входит в совокупность разностей G Q.) (D) по крайнеЙ
мере дважды.
2) Никакой индекс не входит сразу в две строки TpeTbero
С10лбца таблицы. Действительно, если при некоторых i, j', k, 1ft
i > k имеет место равенство u + d i . d t , == u + d k d", то d i
d k === d 1 , d j , и совокупности разностей O '!) (D) и G Q ) (D) co
держат одно и то )ке целое число.
Это доказывает теорему в случае ko == по 1. Аналоrично
теорема доказывается и в случае ko =1= ПО 1.
Из этой теоремы непосредственно следует, что после опреде
ления по 1 порождающих мноrочленов, для которых все co
вокупности разностей состоят из различных чисел и не пересе
каются, сразу получаем самоортоrональный код.
СУlцествует бесконечно MHoro совокупностей целых чисел
{d 1 , d 2 , ..., d q + 1 }, множества разностей {d i d.i I i > j} которых
состоят из различных целых чисел. Однако для построения KO
дОВ с наивысшими корректируюu.{ими способностями, а именно
для ДОСТИ}I{ения минимально возможноrо КОДОRоrо оrраничения
при заданном J, необходимы такие совокупности целыIx чисел,
для которых максимальное целое число, ВХОДЯlцее R Iножество
разностеЙ {d i d j I i > j}, имело бы минимально ВО.1можное зна
чение.
Простое cOBeplIleHHoe разностное множество порядка q пред"
ставляет собой СОВОКУПНОСТЬ q+ 1 целых чисел (d 1, d 2 , ... dq+l},
к a)l{ д а н из q2 + q раз II ОС Т ей d i d j, i =1= j, i, j == 1, 2, ..., q + 1,
которой сравнима по МОДУЛfО q2 + q + 1 с одним из чисел 1.
2, ..., q2 + q. Синrер r 37 1 доказал СУlцествовапие простыIx co
вершеНIlЫХ разностных мно)кеств ЛJобоrо порядка q, ЯВЛЯЮIlLе
rося стrпсныо простоrо ЧIIсла, и более Toro, указал метод их
построения. Например, как показано ниже, при q == 3 совокуп-
ность целых чис л {О, 1, 3, 9} ЯDляется простым соверrПСННЫ!\I
разностныIl\1 м но)кеСТВОl\l:
I O===l O 9 == 4 3 9 == 7, O 3 == lO
....
3 1 == 2 1 9 == 5 9 1 == 8 1 3 == 11 (mod 13).
,
3 O 3 9 3 == 6 9 O==9 о........ 1 === 1 ')
, ' '-
248
r лава 5
5.5.3. Коды, строящиеся с помощью простых
совершенных разностных множеств
Если задано простое совершенное разностное множество, то
теорема 5.4 позволяет сразу построить самоортоrональный код
со скоростью R == 1/2 И J == q + 1. Для этоrо достаточно в каче-
стве порождающеrо мноrочлена этоrо кода взять мноrочлен
GП
(D) == D d l + D d 2 + ... + Ddq+l. (5.45)
Коды со скоростью R === (по
1) /nо или l/no MorYT быть по-
TpoeHЫ с помощью слеДУlощей процедуры.
Если из простоrо совершенноrо разностноrо мно)кества
{d l , d 2 , ..., d q + 1 } выделить подмножество {d;, d
, . . ., d;}, r
:::::;; q+ 1, из r слеДУIОЩИХ ДРуr за ДРуrом целых чисел и построить
совокупность {d;
d; I i > j} из r (,
1) /2 разностей этих чисел,
то все эти разности будут различными цеЛЫ\1И числами. Это
означает, что указанное выше подмножество само является про
TЫM совершенным разностным мно)кеством. Следовательно,
разбивая простое совершенное разностное множество на по
1
непересекающихся подмножеств слеДУIОЩИХ подряд целых чисел
и рассматривая 'эти подмножества как совокупности показате
леЙ степеней неизвестноrо с ненулевыми коэффициентами no
l
ПОRождающих мноrочленов, можно построить самоортоrональ
ный код со скоростью R == (по
1) /nо или l/no. Если задано
простое совершенное разностное множество, то, ВЬiчитая из
каждоrо элемента этоrо мно)кества 1\1инимальныЙ элеl\1ент, опять
получаем разностное множество. Пользуясь этим свойством раз
ностных множеств, можно понизить степени порождающих мпо
rочленов, а следовательно, и объем памяти, используемый Koдe
ром и декодером.
Пример 5.7. Простое совершенное разностное множество
{О, 1, 3, 9} с q == 3 позволяет построить самоортоrональный код
со скоростью R == 1/2 И J == 4. Для этоrо достаточно взять по
ро)кдающиЙ мноrочлен
o
M (D) === 1 + D + D 3 + D 9 . (5.46)
Разбивая это разностное множество на два ПОДМНО}I<ества {O,l}
и {З,9} и вычитая из элементов последнеrо минимальный эле
мент 3, получим подмно)кествз {О, 1} и {О, 6}. С ПОМОЩЬЮ этих
подмножеств можно построить код со cKopocTыo R === I/ з и J ==4,
положив
G
(D)== 1 + D,
o
M (D) === 1 + D 6 ,
(5.47)
1. Методы поросовОёО декодирования
249
и код СО скоростью R === 2/3 И J == 2, поло)кив
a M (D) === 1 + D,
O (D) === 1 + D 6 .
Таким образом, с ПОМОIЦЫО простоrо совершенноrо раЗIIОСТ-
Horo мнол(ества всеrда мо)кно построить самоортоrонаJIыIыIй код
СО скоростью R == (по 1) jпo и 1/nо. Однако при построении
необходимо стремиться уменьшить кодовое оrраничение при фИК
сироваНIIОМ J, поскольку это повышает корректирующие способ
ности кода и позволяет уменьшить объем памяти кодера и дeKO
дера. Учитывая это, оптималы-IыIM кодом будем называть код,.
который при заданных скорости передачи R, числе ОрТОI'ональ
ных проверок J и длине блока по имеет минимаJIЬНО возмо)кное
кодовое ОI"'раничение ПА == (fп + 1) /nо. Робинсон и БернстеЙн
преДЛО)l{ИJIИ следующую эффеКТИВНУIО процедуру оптимизации
построения самоортоrональных кодов на основе совершенных
разностныlx множеств [3]:
1) Строится слеДУIощее разбиение множества разностей про
cToro совершеНIIоrо разностноrо множества порядка q на q под
MHO)l{eCTB. rIepBoe ПОДМНО)l{ество:
(5.48 )
al. i === d i + 1 d i , i=== 1,2, "', q,
аl. q+ 1 === d 1 d q + 1 + q2 + q + 1.
Остальные q 1 подмно}кеств разбиения {ai,l,
2 :::::; j :::::;; q, определяются равенством
i+j l
ai, I === L аl. k,
k==-j
, . , ,
ai, q+l}
(5.49)
rде ас k == ас 'i. q l, k > q + 1, 1 i q, 1::::;; j ::::; q + 1. Ha
пример, с ПОМОЩЫО простоrо COBeprueHHoro разностноrо множе
ства (О, 1, 3, 9) получается слеДУlощее разбиение множества
разностеЙ:
1, 2,
3, 8,
9, 12,
6, 4
10, 5
11, 7
(5.50)
КаждыЙ элемент этоrо разбиения равен по МОДУЛIО q2 + q + 1
одной из разностей двух элементов простоrо совершенноrо раз
HOCTHoro 1\1 НО)l{ества :
i+/ 1 i+/ l
а l, J === d r ........ d J == L а 1, k L а 1, k ( m о d q2 + q + 1), (5.51 )
k==J k==-/ l
r == i + j (тод q + 1). (5.52)
250
r ла а S
Например, в (5.50)
а2З == 10 == d l d.з == 1 4 (mod 13).
в силу OCHoBHoro свойства простоrо совершенноrо разностноrо
l\lножества каждое из целых чисел от 1 до q2 + q входит в это
разложение ровно один раз.
2) Рассмотрим множество {аО; === О, alj, ..., aqj}, aOj==O <
< alj < . . . < aqj. Из формул (5.51) и (5.52) получаем
ai+k./ al, / == (d,' d/) (d, d J ) === d r , d, (mod q2 + q + 1),
(5.53)
" == i + k + j (mod q + 1),
r == i + j (mod q + 1),
i===O, '.', q, k== 1, ..., q.
Из этих соотношений видно, что совокупность разностей чисел
из рассматриваемоrо множества совпадает с совокупностыо
q2 + q разностей d i d j , i =1= j, i, j == 1,2, ..., q + 1, чисел про..
CToro совершенноrо разностноrо множества {d 1 , ..., d q + 1 }. Сле
довательно, множество {аО; == О, alj, ..., aqj} так}ке является
просты ! совершенным разностным множеством. Например, MHO
жество целых чисел, образующих 2 й столбец разложения
(5.50), таково, что
0 12 == 1 12 8==4
2 0 == 2 0 8 == 5
2 12 == 3 8 2 == 6
2 8===7
8 0 == 8
8 12 == 9
12 2 == 10
O 2 == 11
12 0 == 12
(mod 13),
и является простым COBepI.lIeHHbIM разностным мно)кеством. Та-
ким образом, если задано одно совершенное разностное множе
ство, то можно С ero помощью построить q + 1 совершенных
разностных множеств {О, alj, a2j, ..., aqj}, j == 1, ..., q + 1.
3) Если из построенных таким образом q + 1 простых совер-
шенных разностных множеств
(О, all,..., aqt) == (О, d 1 , .. ., d q ),
(О, a12,,'" a q 2),
(О, al, q+l, . . ., a q , q+l)
выбрать множество, максимальное из чисел KOToporo является
наИ:\1еньшим из максимальных чисел aql, a q 2, ..., a q , q+1 ука-
занных выше множеств, то можно построить порождающий MHO
rоч.пен кода минимальной степени.
1. Методы пОРО20вОёО декодирования
251
rlапример, разложение (5.50) позволяет построить следую
щие четыре порождающих мноrочлена кодов со скоростью R ==
== 1/2 И J == 4:
aЫ
(D) === 1 + D + D З + D 9 ,
a
M (D) == 1 + D 2 + D 8 + D 12 ,
а:М (D) == 1 + D 6 + D 10 + D 11 ,
a
M (D) == 1 + D 4 + D 5 + D 7 .
Из этих мноrочленов следует выбрать мноrочлен
O
(D)
1 + D 4 + D 5 + D 7 ,
имеющий минимальную степень.
5.5.4. Примеры кодов
Робинсон и Бернстейн, используя описанную выше процедуру
понижения степеней поро)кдающих мноrочленов, методом пере
бора с помощью простых совершенных рззностных множеств,
порядки которых являются степенями простых чисел, не пре
восходящими 30, нашли порождающие мноrочлены кодов со
скоростями R == (по
1) /nо и Ro == 1/nо, имеющие минимальные
степени. Полученные ими результаты приведены в табл. 5.1.
5.5.5. Оптимальность кодов
Один из путей определения оп rимальности построенных YKa
занным выше способом кодов заключается в том, чтобы найти
нижнюю rраницу кодовоrо оrраничения и далее сравнивать с ней
кодовые оrраничения построенных кодов. Уэлдон [40] получил
следующие ни}кние rраницы кодовоrо оrраничения.
Для любоrо кода со скоростью передачи R == (по
1) /пО И J
ортоrональными проверками (по
1) совокупностей разностей
порождающих мноrочленов из различных целых чисел и каж
дая из этих совокупностей разностей содержит по крайней мере
J (!
1) /2 элементов. Следовательно, максимальное число, BXO
дящее в эти (по
1) совокупностей разностей, по крайней мере
не меньше чем (по
1) J (!
1) /2. Добавляя к этому числу еди
ницу и умно)кая полученную сумму на по, получаем следующую
нижнюю rраницу для кодовоrо оrраничения:
............ [ (по
1) J (1
1) + 1]
ПА:;::::::; по 2 .
(5.54)
Рассмотрим самоортоrональные коды со скоростью R == 1/nо.
Поскольку для каждоrо из этих кодов MorYT быть построены
252
fлава 5
Таблица 5.1
Самоортоrональные КОДЫ
R li2
J
ПА
Невулевые коэффициенты порождающих МllоrОЧJlенов,
nо==2
4
6
8
10
12
14
16
18
14
36
72
1 ] 2
]72
255
360
о, 2, 5, 6
О, 2, 7, 13, 16, 17
о, 7, 10, 16, 18, 30, 31, 35
о, 2, 14, 21, 29, 32, 45, 49, 54, 55
О, 2, 6, 24, 29, 40, 43, 55, 68, 75, 76, 85
0,5,28,39,41,49,50,68,75,92,107,121,123,127
о, 6, 19, 40, 58, 67, 78, 83, 109 132, 133, 162, 165, 169,
177, 179
о, 2, 1 О, 22, 53, 56, 82, 83, 89, 98, 130, 148, 153, 167,
188, ] 92. 205, 216
О, 24, 30, 43, 55, 71, 75, 89, 104, 125, 127, 162, 167, 189,
206, 215, 272, 275, 282, 283
О, 3, 16, 45, 50, 51, 65, 104, 125, 142, 182, 206, 21 О, 218,
228, 237, 289, 300, 326, 333, 356, 358
о, 22, 41,57,72,93,99, 139, 147, 173, 217. 220, 234, 273,
283, 285, 296, 303, 328, 387, 388, 392, 416, 425
434
20
568
22
718
24
852
R==2/ R==I/ S ПА Нену левые КОЭФфИIlиенты порождающих мноrочленов,
J J no 3
2 4 9 о, 1
О, 2
6 27 о, 1, 7
о, 3, 8
4 8 42 о, 8, 9, 12
о, 6, 11, 13
10 69 О, 2, 9, 21, 22
о, 4, 10, 15, 18
6 12 120 о, 14, 21, 23, 36, 39
О, 8, 27, 28, 32, 38
14 165 О, 1, 28, 31, 44, 46, 52
О, 7, 17, 29, 40, 49, 54
8 16 237 0,19,21,45,63,73,74,78
о, 27, 39, 47, 61, 64, 70, 77
18 309 о, 16, 37, 44, 47, 70, 82, 83, 97
О, 22, 24, 30, 41, 73, 93, 98, 102
10 20 393 о, 1, 6, 25, 32, 72, 100, 108, 120, 130
О, 23, 39, 57, 60, 74, 101, 103, 112, 116
22 507 О, 5, 12, 53, 72, 81, 135, 136, 146, 159, 167
О, 17, 46/ 50, 52, 66, 88, 125, 150, 165, 168
12 24 588 О, 17, 46, 50, 52, 66, 88, 125, 150, 165, 168, 195
О, 26, 34, 47, 57, 58, 112, 12], 140, 181, 188, 193
1. Методы nоросовосо декодирования
253
Продолжение табл. 5.1
R==2/ з R== I/!
J J
ПА
Ненулсвые коэффициенты порождающих мноrО'lле:юз.
nо==3
26
753
14 28
867
О, 16, 64, 104, 122, 124, 146. 159, 167, 171, 178, 237, 240
О, 30, 39. 53. 68. 129, 139, 165, 170, 216, 222, 249, 250
О, 2, 7, 42, 45, 117, 163, 185, 195, 216, 229, 246 255, 279
О, 8, 12, 27, 28, 64, 113, 131, 154, 160, 208, 219, 233,288
1l.=='If. R== 1/.
J J
ПА
Ненулевые коэффициенты порождающих hfноrочленов,
nо==4
4 12 80 о, 3, 15, 19
О, 8, 17, 18
О, 6, 11, 13
6 18 248 О, ]2, 16, 42, 48, 61
о, 3, 5, 14, 34, 58
О, 15, 22, 23, 40, 50
8 24
512
10 30
812
о 16, 31, 34, 48, 75, 85, 124
О, 28, 35, 47, 58, 71, 80, 100
О, 2], 25, 26, 81, 87, 89. 127
О, 7, 27, 76, 113, 137, 155, 156, 170, 202
О, 8, 38, 48, 59, 82, 111, 146, 150, 152
о, 12, 25, 28, 78, 83, 100, 109, 145, 199
R==4/ S R==I/ 6
J J
ПА
Не нулевые КОЭффИllиенты порождающих мноrочленов,
ПО == 5
4 16 135 О, 1 О, 20, 21
о, 2, 1 О, 25
О, 14, 17, 26
О, 11, 18, 24
6 24 415 О, 5, 26, 51, 55, 69
О, 6, 7, 41, 60, 72
О, 8, 11, 24, 44, 82
О, 10, 32, 47, 49, 77
8 32 895 О, 19. 59, 68, 85, 88, 103, 141
О, 39, 87, 117, 138, 148, 154, 162
о, 2, 13, 25, 96, 118. 168, 172
О, 7, 65, 70, 97, 98, 144, 178
254
r лава 5
(no
1)! ортоrональных проверок для одной информационной
последовательности, то число ортоrональных проверок кода по
меньшей мере равно J' == (пo
I)J. Так как кодовое оrраниче
ние одно и то же, то, подставляя J из последнеrо равенства и
опуская для простоты штрих, получаем следующую нижнюю
rраницу:
ПА
ПО [; ( по
1
1) + 1].
(5.55)
5.6. Ортоrонализируемые КОДЫ
ОРТОёоналuзuруемые коды были введены Месси как KOДЫ
допускающие пороrовое декодирование [2]. По сравнению с caMO
ортоrональными кодами эти коды MorYT иметь при заданном
минимальном расстоянии (или числе ортоrональных проверок)
меньшее кодовое оrраничение и в этом смысле обладают более
высокими корректирующими способностями. Однако эти коды
имеют и ряд недостат:к.ов, в частн()сти они строятся методом
перебора и, как указывается ниже, MorYT иметь бесконечную
rлубину распространения ошибок.
Ортоrонализируемый код с минимальным расстоянием d
(или J ==d
1 ортоrональными проверками)
это код, который
допускает построение для каждоrо информационноrо символа,
входящеrо в декодируемый блок, J составных проверок, являю
щихся линейными комбинациями символов синдромов.
5.6.1. П ростейшие примеры
Примером ортоrонализируемоrо кода является код, paCCl\10T
ренный в начале разд. 5.3 и имеющий скорость R == 1/2 И кодовое
оrраничение ПА == 12. Рассмотрим этот код более детально. При
пороrОВО
1 декодировании с обратной связью этоrо кода посред
ством линейноrо преобразования символов синдрома Sb 2 \ s
2), . . .
. .., S
), формирующихся В А-I0мен rbI времени от О до 5, MorYT
быть построены составные проверки:
А 1
А 2
Аз
А4
100000
000100
О О О О 1 О
О 1 О О О 1
(2)
So
S(2)
1
S (2)
2
S (2)
3
S(2)
4
(2)
..... S 5
(5.56)
1. Методы nopOZOB020 декодирования
255
Заметим, что следующее линейное преобразование синдрома
[который определяется в данном случае соотношением (5.34)]:
А 1
А 2
Аз
А4
1 О О О О О
О О О 1 О О
010010
О О О О О 1
..... (2)
80
8(2)
1
8(2)
2
8(2)
3
8(2)
4
8(2)
5 ......
(5.57)
также позволяет построить систему составных проверок, opToro"
нальных относительно еъl).
Линейное преобразование, с помощью KOToporo по синдрому
находятся составные проверки, при декодировании с обратной
связью обычно задается с помощью матрицы размера /Х (m+ 1).
Ка}l{ДЫЙ столбец этой матрицы линейноrо преобразования co
держит не более одноrо ненулевоrо элемента, а для caMoopToro
нальных кодов не более чем один ненулевой элемент входит
также и в ка}l{ДУЮ строку этой матрицы.
В случае самоортоrональных кодов матрица линейноrо пре
образования определяется однозначно построением CTPYI{TypbI
синдрома. В то же время, как показывает вышеприведенный
"
пример, для друrих ортоrонализируемых кодов матрица линен..
Horo преобразования может определяться и неоднозначно. Сле
довательно, при задании ОР10rонализируемоrо кода необходимо
указывать не только 110рождающие мноrочлены, но и линеЙное
преобразование, с помощью KOToporo по синдрому вычисляются
составные проверки. Поскольку последнее преобразование за
КjIIочается в вычислении некоторых сумм строк проверочноЙ
матрииы, то преобразование (5.56) можно задать слеДУЮllLИМ
образом: 02, 32, 42, 5212, rде основные цифры указывают момент
формирования символа синдрома, а верхние индексы
синдром,
к которому они принадлежат. Символы синдромов, участвующие
в формировании различных проверок, ра.зделены запятыми.
5.6.2. Способ построения кодов
Построение ортоrонализируемых кодов и линейных преобра
зований для их ортоrонализации осуществляется полностью Me
тодом перебора. Исключение состаВЛЯIОТ лишь коды со СКОРО-
256
rлава 5
стыIo R === 1/2, при построении I(OTOPbIX можно воспользоваться
следующим приемом:
1) Пусть элемент проверочноrо треуrОЛЬНИI{а, раСПОЛО)I{ен
ный в l
й строке и 1
l\1 столбце, равен 1, а элементы, распо,,10
)кенные в l
M столбце и в строках со второЙ по (пА/4)
ю, равны
о. Тоrда шумовые символы с e
/4 по e(
A/2)
1 MorYT иметь OT
личные от нуля коэффициенты только в одной строке треуrоль
ника.
2) Каждая из строк проверочноrо треуrольника со BTOpOli по
(пА/4)
ю мо}кет быть использована для ИСI{лючения ОДНОI
О He
иу,аевоrо коэффициента при одном ИЗ шумовых символов
(1) (1) На ример (5 r::: 6) ... ложеllllе 8 (2) С S (2) позво
е 1 ' · · ., е (n А/4)
1. П ,в. и с '1 ;)
ляет исключить шумовой символ e\l), входящий в 8
2). Заметим,
что первая строка проверочноrо треуr'ОЛhника H
дает проверку,
контролирующую eb 1 ) и e
). Таким образом, задача построения
кодов со скоростью R == 1/2 свел ась к выбору последних пА/4
строк проверочноrо треуrольника H
, таких, что из них мо)кно
составить J
1 проверок, контролирующих eb 1 ) и обладаIОЩИХ
тем свойством, что ни один из шумовыIx СИМIЗолов еР>, ...
..., e(
A/4)
1 не контролируется трижды.
5.6.3. Примеры КОДОВ
в табл. 5.2 приведены ортоrонализируемые кодыI' построен
ные 1\1есси [2] описанным выше способом.
Рассматриваемые в этом разделе ор10rонализируемыIe КОДЫ
и самоортоrональные I{ОДЫ из предыдущеI'О раздела являются
основными сверточными кодами, исправляющими случайные
ошибки и допускающими пороrовое декодирование. Поскольку,
как уже указывалось выше, поросовое декодирование сверточ
ных кодов в принципе аналоrично мажоритарному декодирова
нию блоковых кодов, то попробуем уст ановить вза имосвязь
1ел{-
ду указанными выше кодами и блоковыми кодами, допускаю-
щими мажоритарное декодирование.
5.6.4. Связь с блоковыми кодами
Одним из больших классов блоковых кодов, допускающих
пороrовое декодирование, является класс обобщенных кодов
Рида
Маллера, построенный Уэлдоном [44]. Следует заметить,
что если обобщенные коды Рида
Маллера, вообще rоворя,
1. Методы пОРО20вО20 декодирования
257
являютсн кодами, ортоrонализируемыми за L шаrов, то сверточ-
ные коды, !{ак самоортоrональные, так и ортоrонализируемые,
являются кодами, ортоrонализируемыми за один шаr. В частно-
Таблица 5.2
R
1/2
10
12
1/3
10
1/5
4
6
8
10
J
2
4
6
8
104
4
6
8
33
Ортоrонализируемые КОДЫ (22)
ПА
Код 1)
Правило ортоrОllализации 2)
02, 1 2
02, 32, 42, 1252
02, 62, 72,92, 1232102, 4282112
02, ] 12, 132, 162, 172, 223262192 J
42142202, 125282152212
02, 182, 192, 272, 1292282, 10222292,
112302312, 132212232322, 142332342,
2232162242262352
02,262,272,392,12132402,142282412,
152422432,172292312442, 182452462,
2232202322342472, 212352482492502,
242302332362382512
02, 03, 12, 23
02, 03, 12, 2 J , 1233, 2243
02,03, 12,23,1333,2243,72,32526263
02, 03, 12, 2223, 92, 3343, 325253,
134 6263, 8283, 739 103
02, 03, 0\ 05
1214, 1315
2223, 2125
35, 3233
1) ЗаШIСЬ (il' i 2 , ..., i k )2 ... и.. /2' ..', /т)n означает, Что ненулевыми коэффици-
CIIta:-'lII ПОI'ОЖJ а ющнх МlIOI'ОЧJIенов кода со скоростью I/п ЯВЛЯЮТСЯ g 2). g 2), ..., g 2).
1 2 k
(п) (п) (n) П
gjl' gj2 ' .'., gjт' (JtlM. перев.
2) ИСIJО:lьзуемая в таб:шце заl1llСЬ праВII l ортоrонзлизаЦIIИ ПОЯСlIнется в KOHue
разд. 5.6.1. п ри,м. перев,
4
12
24
44
(О, 1)2
(О, 3, 4, 5)2
(0,6,7,9, 10, 11)2
(о, 11, 13, 16, 17, 19,
20, 21)
(О, 18, 19, 27, 28, 29,
30, 32, 33, 35)2
(О, 26, 27, 39, 40, 41,
42, 44, 45, 47, 48,
51 )2
72
9
(О, 1)2
(о, 2)3
(О, 1)2
(о, 2, 3, 4)J
(0,1,7)2
(о, 2, 3, 4, 6)2
(0,1,9)2
(О, 1, 2, 3, 5, 8, 9)3
(O) (0)3 (0)4 (0)5
( 1)2 (1) 3
(2)2 (2)1
(3)2 (3)5
сти, Месси [2] показал, как описано ниже, что если системати
ческий сверточный код со скоростью передачи R == l/по явля
стся кодом, ортоrОIlализируемым за L шаrов, то он допускает
T<lI()Ke ортоrонализацию и за один шаr.
15
2,1
5
10
15
20
58
rлава 5
Действительно, проверочный треуrольник На
кода со скоростью R == 1/nо имеет следующий вид:
.... (1)
g (2), О
(1)
g(2), 1
сверrочноrо
g (l)
(2), О
g(I) g(l)
(2), т ..... (2), О
H == (5.58)
(1)
g(no), о
g(l) (1)
(по), 1 g (по), О
g (1)
.....
(по), т
(1)
g(no). о
Предположим, что существует система J проверок, ортоrональных
относительно некоторой суммы информационных шумовых сим-
волов e O + e O + ... + e 1). Это означает, что существует J под-
1 2 l
множеств строк матрицы H , сумма строк каждоrо из которых
имеет символы 1 на позициях, соответствующих информацион
ным шумовым символаI\1 e H, e l), ..., a l) и обладаIОЩИХ тем
I 2 J
ct
своиством, что никакие две суммы строк этих подмножеств не
содержат символ 1 на одной и той же позиции, отличной от ука-
занных ВЫШе. Друrими словами, J составных проверок, по рож-
даемых этими подмножествами, контролируют символы е(Н, ...
al
.. ,e O, но никакой друrой шумовой символ не КОНТРОЛИ-
J
руется ими два}l{ДЫ. Предположим, что al < а2 < ... < aj.
Рассмотрим матрицу, полученную из H удалением всех столб-
цов слева вплоть до столбца, соответствующеrо e ). Строки этой
I
усеченной матрицы ПОЗВОЛЯIОТ построить J про верок, ортоrональ-
ных относительно e ). Из симметрии проверочноrо треуrольника
J u u
следует, что расположение коэффициентов в этои усеченнои мат-
рице такое же, как и в матрице, получающейся путем отбрасы-
вания нижних строк проверочных треуrольников в количестве,
равном числу отброшенных столбцов. Следовательно, из строк
lатрицы H можно построить J проверок, ортоrональных OTHO
сительно е6Н. Друrими словами, число проверок, ортоrональных
относительно е61), не меньше, чем число провеРОI{, ортоrональных
относительно ЛIобой суммы шумовых информационных символов.
1. Методы nОрО208020 декодирования
259
Это означает, ЧТО если некоторый КОД допускает ортоrонализа-
ЦИIО за L шаrов, то он ортоrонализуем и в один шаr, а следо-
вательно, сверточные коды со скоростью R === 1/n,о, ортоrонали
зируемые за L шаrов, рассматривать не имеет смысла.
5.6.5. Сопоставление с циклическими кодами,
построенными на основе разностных множеств
При первой же попытке установить взаимосвязь мел{ду ЦИК-
лическими разностными кодами и самоортоrональными кодами
сразу можно увидеть, что и те и друrие строятся на основе
простых совершенных разностных мно}кеств и допускают орто-
rонализацию за один Шаr. Однако эти коды имеют и принци-
пиальные различия. В частности, свойство цикличности разно-
стных циклических кодов требует, чтобы число т, определяю
щее модуль т,2 + т + 1 простоrо совершенноrо разностноrо
множества, было степенью числа 2, raK что длина п этих кодов,
равная модулю, имеет вид п == 228 + 28 + 1, rде s
целое поло
жительное число. В то же время кодовое оrраничение самоор-
тоrональноrо кода определяется максимальным элементом
простоrо совершенноrо разностноrо множества, на основе кото-
poro строится код, и непосредственно не связано с модулем
т 2 + т + 1 этоrо разностноrо множества. Далее, если при по
строении самоортоrональных кодов простые совершенные разно-
стные множества используются для удобства оптимизации ха-
рактеристик кодов, то при построении разностных циклических
кодов простые совершенные разностные множества обеспечи-
вают цикличность кодов, являющуюся одним из важнейших
свойств последних. В табл. 5.3 приведены для сравнения пара-
метры самоортоrональных кодов со скоростью R == 1/2 И разно-
стных циклических кодов, имеющих одно и то же значение
d == J + 1 и строящихся на основе одноrо и Toro }I{e простоrо
совершенноrо разностноrо множества или двух различных про
стых совершенных разностных мно}кеств, имеющих один и тот
же максим альный элемент. Простые совершенные разностные
множества, использующиеся для построения самоортоrональных
кодов со скоростью R == 1/2, при фиксированном J приводят К
эквивалентным кодам, если только они имеют одинаковые MaK
симальные элементы. Следовательно, самоортоrональные коды
со скоростью R == 1/2 И разностные циклические коды, имеющие
одинаковое расстояние d == J + 1, MorYT быть построены на
основе одноrо и тoro же простоrо совершенноrо разностноrо
множества.
Самоортоrональные коды и разностные циклические коды
строятся на основе одних и тех же разностных МНО}l{еств, однако
методы их построения совершенно различны. В то }I{e время
260
r лава 5
Таблица 5.3
Самоортоrональные коды и разностные циклические коды
(обозначаются соответственно через S и D)
n Простое или сопсршенно(' разностное
d Код или R
ПА множеСТАО
4 D 7 3/7 О, 2, 3
S 8 4/8 О, 2, 3
6 D 21 ) ) /21 О, 2, 7, 8, 11
S 24 12/24 0,2,7, 10, 11
10 D 73 45/73 О, 2, 1 О, 24, 25, 29, 36, 42, 45
S 92 46/92 О, 3, 9, 16, 20, 21, 35, 43, 45
18 D 273 191/273 О, 18, 24, 46, 50, 67, 103, 112, 115, 126,
128, 159, 166, 167, 186, 196, 201
S 404 202/404 О, 18, 24, 46, 50, 67, 103, 112 115, 126,
128, 159, 166, 167, 186, 196, 201
самоортоrональные коды и квазициклические самоортоrОlIаль-
ные коды, предложенные Таунсендом и Уэлдоном [40], очень по
хожи друr на друrа. Так, квазициклический самоортоrональный
код можно построить по самоортоrОIIальному коду слеДУIОЩИМ
образом. Входные последовательности /(Л (D) оrраIIИЧИМ по мо-
дулю степени М
1, а И1\1енно будем рассматривать лишь Mko
информационных символов. ПроверОЧНУIО последовательность
ko
L йH
(D) j(J) (D)также оrраничим по МQДУЛIО степени М
1, по..
JraO
.лаrая DM == 1. Полученный таким образом блоковый код длины
Мпо с Mko информационными символами и скоростью R == ko/пo
является квазициклическим самоортоrональным кодом. Однако
в случае квазициклических кодов моду.пь М должен выбираться
таким образом, чтобы совокупности разностей разностноrо мно-
жества не пересекались. Поэтому разностные множества, исполь..
зуемые для построения самоортоrональных кодов, и разностные
множества, используемые для построения кпазициклицеских са-
моортоrональных кодов с той }I{e СI{ОРОСТЬЮ передаflИ R и тем }ке
числом ортоrональных проверок " часто оказываlОТСЯ различ-
ными.
5.7. Распространение ошибок
При декодировании сверточных кодов часто наб;нодается ПВ
ление распространения ошибок, которое состоит в том, что oд
нажды возникшая ошибка декодирования мо)кет привести к
1. Методы nОрО20аОёО декодирования
261
возникновению ошибок в последующие моменты времени. В слу
чае блоковых кодов, коrда информационные символы разби
ваются на блоки и ка}l{ДЫЙ блок кодируется независимо от
друrих, ВОЗНИКIllая ошибка декодирования может ОI{азать влия
вне на декодирование СИМВОJlОВ лишь в пределах одноrо блока.
В случае же сверточных кодов, коrда при кодировании каждый
информационный символ воздеЙствует на несколько блоков, воз-
никновение одиночноЙ ОIllИUI{И при декодировании оказыва
т
влияние на декодирование нескольких послеДУIОЩИХ блоков, а
при HeKoTopuIX неблаrоприятных условиях и на бесконечное
число блоков. В частности, в системах кодирования, ИСПОЛЬЗУIО
И!IIХ декодирова вис с обр атной связью, пр и возникновении
ОllIибкн декодироваНIIЯ по непраВИJ1ЬНЫМ оценкам значений оши
бок еь", j == 1, 2, . . ., ko, осуществляется коррекция синдром а
(естественно, неправильнан), что может привести к новой
ошибке деI{одирования. Таким образом, при построении сверточ
ных кодов необходимо стремиться достичь не только высокой
корректирующей способности, но и по возмо)кности минималь
ной r.пубины распространения ошиБОI<'
rлубина распространения ОllIибок при декодировании с об-
ратной связью определяется структурой лоrических схем дeKO
дера, и поэтому анализ этой структуры обычно сводится к aHa
лизу функционирования реrистров сдвиrа с нелинейной обратной
связью, образующих декодирующие .лоrические схемы. В случае,
если шумы превышают корректирующую способность кода и это
приводит I{ появлению ошибки декодирования, то обычно в тече-
ние HeKoToporo периода времени ошибок не возникает, декоди-
РУЮlцая лоrическая схема автомзтичеСI{И возвращается в нор-
мальное рабочее состояние и распространение ошибок прекра-
щается. В этом случае rоворят о конечной rлубине распростра
нения ОIllибок. Если }ке декодирующая лоrическая схема в нор-
мальное рабочее состояние не возвращается, то rлубина рас-
пространения Оlllибок считается бесконечной. Таким образом,
анализ распространения ошибок сводится к анализу работы pe
rистров сдвиrа с нелинейной обратной связью, коrда на их входы
подаются нулевые символы, т., е. в ре}l{име самоконтроля.
5.7.1. Анализ rлубины распространения ошибок
Для простоты рассмотрим случай, коrда ko == по
1. Реrистр
сдвиrа, предназначенный для хранения сим:волов синдрома, и
лоrицеская декодирующая схема декодера показаны на фиr. 5.5.
В данном случае синдром
s(пo) (D) == sъn
) + s
no) D + s
no) D 2 + ... (5.59)
262
rлйвй 5
вычисляется в декодере соrласно правилу
no l
s(n o ) (D) == L G Qo) (D) ви) tD) ..... В(n О ) (D)
j 1
. (5.60)
и подается на вход реrистра синдрома, показаННОI'О на фиr. 5.5.
При исправлении случайных ошибок с помощью пороrОБоrо
декодирования лоrическая декодирующая схема в момент вре.
мени т по исправленному синдрому, символы KOToporo полу-
чаются из символов синдром а S nJ), s n.), .. ., S J) вычитанием
информационных шумовых символов, возникающих до момента
"'(1) л (n 1)
ей ей о
s(ll a )
т 1
5("0'
о
д еКОUIIРУЮЩClЯ /lОёl/l.ffСffая схема
Фиr. 5.5. Реrистр синдрома и лоrическая часть декодирующеЙ схемы.
о, формирует оценки ebl),..., e no 1) значений информационных
шумовых символов в момент времени о. Используемый при этом
исправленный синдром
() (т) == [()О (т), () I (т), ..., () т (пl)]
(5.61)
определяется слеДУIОЩИМИ равенствами:
ПО 1 т
(). (пz) == s(.no)....... L L g(j) e(.f) ===
. 1 . + 1 (по) t и
J== u==t
no 1 т no 1 lп
== L L g(j) е(l) ....... e(n ) ---- L L g(f) e<.j).
/==1 и==О (n,). u t U 1==1 u==i+1 (nJ)' II t U
(5.62)
Если предположить, что предшествующие оценки шумовых сим
водов были верными, то последнее равенство сведется к сле-
дующему;
ПО ....1 i
6 i (т) === L L g(J) e(f) ........ e(nu).
/==1 и=-О (по), u и
(5.63)
1. Методы пOPOZOB020 декодирования
263
Величина б i (т), задаваемая этим равенством, равна символу
синдрома
по 1 l
s(no) == L L g(f) еи) е(nо) .
/1181 и==О (по), и i u
(5.64 )
Если функцию Р, реализуемую декодирующей лоrической
схемой, выбрать таким образом, чтобы значение F (s&no> , ...
. .., s o») давало правильные оценки символов е&О, ..., e o l), то
А(/) А(Л. 1
при условии, что предыдущие оценки e p . · ., e m' 1 , ...
. . ., по 1, правильные, эта функция будет давать правильные
значения и е&О, . . ., ebnO O. Однако если хотя бы одно из значе-
ний предшествующих оценок было правильное, то значения Be
личин бi (т) будут отличаться от значений, даваемьrх формулой
6,'
т
//оеическая схема
Фиr. 5.6. Нелинейный реrистр сдвиrа.
(5.63), и при декодировании с большой вероятностью оценки
еЬО, ..., ebno l) будут неверными. Это в свою очередь ПОРО}l{дает
тендеНЦИIО к возникновению последоватеJIЬНОСТИ новых ошибок.
В подобных случаях, коrда конечное число ошибок в канале
при водит к возникновению бесконечной последовательности
ошибок декодирования, rоворят, что декодирующая лоrическая
схема с обратной связью имеет бесконечную rлубину распро-
странения ошибок.
Внутреннее состояние декодирующей лоrической схемы, по
казанной на фиr. 5.5, определяется состояниями (т + 1) ячеек
реrистра сдвиrа. Поэтому если после момента возникновения
ошибки декодирования в течение т последующих моментов
ct
времени декодирование происходит правильно. то влияние этои
ошибки декодирования исчезает и схема оказывается в нор-
мальном рабочем состоянии. Следовательно, необходимым усло
вием возникновения бесконечноrо распространения ошибки яв"
ляется возникновение после каждой ошибки декодирования в те-
чение т последующих MOM HTOB времени новой ошибки деко..
дирования.
264
r лава 5
Далее для простоты рассмотрим работу схемы, изобра)кен
ной на фиr. 5.6, коrда на ВХОД реrистра сдвиrа снелинейной
обратной связью подается последовательность из одних нулей,
т. е. в режиме самоконтроля. Пусть б == (б,о, 61, . . . ,бп
)
BHYT
реннее состояние реrистра сдвиrа и О
вектор, BC
компоненты
KOToporo равны нулю. Если обозначить через Т оператор сле-
дующеrо состояния, то функционирование cxeMhI, показанной на
фиr. 5.6, можно описать равенством
Т6 == F (6), (5.65)
rде F
некоторая векторная функция (Р (о) == о). Вектор Тб
представляет собой состояние нелинейноrо реrистра сдвиrа
после однократноrо сдвиrа, а ТNб
состояние после N последо
вательных сдвиrов. Из Toro, что F (О) == о, следует, что То == о,
т. е. О является равновесным состоянием реrистра сдвиrа с He
линейной обратной связью.
Определение 5.3. Если для каждоzо состояния б существует
такое N, что ТNб == о, то ресистр сдви2а с нелинейной обратной
связью называется устойчивым. В противном случае этот pe
еистр называют неустойчивым.
Для самоортоrональных КОДОВ существуют простые доста-
точные условия устойчивости, которые оказываются полезными
и с практической точки зрения. Для произвольных кодов .про
стых общих критериев УСТОЙЧИВОСfll не существует. В наСТОЯll{ее
время известны два метода определения устойчивости: метод
Ляпунова, использованный Месси и Лиу [32], и метод, предло-
)кенный Робинсоном [3] для дефИНIIТIIоrо декодирования.
5.7.2. Критерий устойчивости пороrО80Й декодирующей
лоrической схемы
Обозначим через W(б) вес внутреинеJ'О состояния реrистра
сдвиrа с нелинейной обратной связью, который определим как
число ненулевых компонент вектора б == (60,61, . . . , 6 т ). Необхо
димое условие устойчивости пороrовой декодирующей лоrиче-
v
скон схемы состоит в слеДУIQшем.
Критерий устойчивости. Если каждыЙ шаz декодирования,
при котором значение оценки шумовоzо символа равно 1, при-
водит к уменьшению веса внутреннесо состояния, т. е. если при
каждом таком шаzе W(Тб)
W(б), то поросовая декодuруто-
щая лоzическая схема является устойчивой.
Доказательство. Распространение ошибки будет иметь место
только в том случае, если после ка)l{ДОЙ ОIlIибки леI(одирования
Прll декодировании пz последующих БЛОI(ОВ ВОЗНИКНСТ хотя бы
1. Л1етодbl nOpOi!080eO декодирования
265
одна новая ошибка декодирования. Однако в данном случае при
этом вес BHYTpeHHero состояния обязательно будет уменьшаться.
Максимальный вес BHYTpeHHero состояния равен т, так что
если вес BHYTpeHHcro состояния становится равным [//2] или
меньшим, то значение оценки декодирования ни на каком из
последующих шаrов не может равняться 1. Следовательно, ca
мое большее после т (т + 1 ...... [//2]) сдвиrов вес BHYTpeHHero
состояния будет [J/2] или меньше. Если вес BHYTpeHHero состоя-
ния не превышает [! /2], то после самое большее (т + 1) сдвиrов
внутреннее состояние реrистра сдвиrа с нелинейной обратной
связыо будет нулевым. Из вышеИЗ..ттоженноrо следует, что
N ln (т ...... [J/2] + 2) + 1. (5.66)
Таким образом, мы доказали, что пороrовая декодирующая
лоrическая схема является устойчивой.
То, что самоортоrональные коды имеют конечную rлубину
распространения ошибок, было показано Робинсоном и Берн
стейном [3] непосредственно с помощью этоrо достаточноrо yc
ловия. Действительно, пусть V минимальное число ненулевых
значений входов пороrовоrо элемента, при котором выход по-
poroBoro элемента равен 1. В случае самоортоrональных кодов
на входы пороrОВОI О элемента подаются J символов синдромов.
Если среди этих символов синдромов V или более равны 1, то
выход декодирующей лоrической схемы оказывается равным 1
и используется для исправления ошибок и J символов синдро
мов. После исправления этих символов синдрома равными 1
будут не более чем 1...... V из них. Поскольку в режиме caMO
контроля на ВХОД поступают только символы О, то в результате
таких операций ни один из этих вводимых по пепи обратной
связи в синдром СИМВОЛОВ 1 не уничто)кится, так что число сим-
волов 1 среди символов синдрома уменьшится по крайней мере
на v...... (1 ...... V) == 2V ...... 1. Следовательно, необходимые условия
устойчивости пороrовой декодирующей лоrической схемы для
самоортоrональных КОДОВ выполнены. Как показали Робинсон
п Бернстейн, число L ошибочных символов, которые должны
следовать за произвольной ошибкой декодирования для caMOOp
тоrональных кодов, удовлетворяет следующему соотношению:
L (ПА...... По) t + 2nА, (5.67)
r де t максимальное целое число, удовлетворяющее HepaBeH
ству
( v 1 ) + ( 2V ;- J ) ;;?;: (N J + V 1) [ J -; V J .
Неравенство (5.66) rарантирует также устойчивость pac
сматриваемых в слеДУlощем разделе сверточных кодов, исправ
266
rлйвй 5
ляющих пачки ошибок. Однако для ортоrонализируемых кодов
это достаточное условие может и Не выполняться. Например,
для рассматриваемоrо в разд. 5.3 кода со скоростью R == 1/2
И кодовым оrраничением ПА == 12 при e61) == e
l) == 1 символы си-
ндрома 5ь 2 ) == 5
2) == 5
2) == 1 и вес BHYTpeHHero состояния равен 3.
В эrом случае ebI) == 1, но после сдвиrа внутренним состоянием
реrистра сдвиrа оказывается ПОС"ТIедовательность 1001100, имеIО-
щая также вес 3. В подобных случаях необходимо пользоваться
более сложными критериями устойчивости. Одним из таких кри-
териев является раССlVIатриваемыЙ ниже критериЙ, основанныЙ на
использовании функции Ляпунова.
5.7.3. Критерий, основанный на использовании функции
Ляпунова [32]
Пусть с
произвольное множество векторов, а с
MHO)Ke
ство, являющееся дополнением с. Пусть D(б)
функция, прини
мающая два значения и такая, что D (б) == О, если б Е с, И
D (б) == 1, если
Е С. Изменение Функuии D (б), связанное с из
менением состояния б при сдвиrе, обозначим через
D. Вели
чина
D == 1 тоrда и только тоrда, коrда состояние переходит
из с в с или, наоборот, из с в с. Следовательно, если состояние
'6 == О не изменяется, то
D == О. Аналоrом теоремы Ляпунова
об асимптотической устойчивости является следующая теорема.
Теорема 5.5. Пусть Do({))
функция, такая, что Do(O) == О
и D,o(6) == 1 при всех б =1= О. ТОсда ресистр сдвиса с нелuнеuноu
обратной связью является неустоuчивым, если
Do == О при всех
6, и УСТОЙttИВЫМ, если
Do == 1 при всех б =1= О.
Эта теорема ПОI{азывает, что реrистр сдвиrа с неJIинеЙной
обратноЙ связью ЯВJIяется устойчивым, еСJIИ при сдвиrе любое
ero ненулевое внутреннее состояние переходит в состояние О,
и неустойчивым, если при сдвиrе никакое состояние, кроме, быть
может, нулевоrо, не переходит в состояние О. Однако, как пра-
вило, в действительности часть ненулевых состояний при сдвиrе
переходит в состояние О, но существуют также так называемые
неопределенные состояния, которые при сдвиrе в состояние О
не переходят. Для определения устойчивости при наличии таких
неопределенных состояний можно воспользоваться следующим
алrоритмом:
1) Пусть со
множество, включающее только состояние Q.
2) Определим функцию D.о(б) так, как указано в теореме 5.5.
3) Пусть 51 .
множество всех таких б, что dDo (б) == 1, и пусть
CI == с.о U 51. Состояния, принадлежащие 51, обладают тем свой
TBOM, что при сдвиrе они переходят J;J состояние О. Если ё] яв
Т. Аlетоды nОРО20вО20 декодирования
267
J1яется пустым множеством, т. е. если Cl == ф, то из теоремы 5.5
следует, что рассматриваемая схема устойчивая, а если 81 == ф,
то эта cxe a неустойчивая. Если ни одно из этих условий не
выполняется, то переходим к следующему шаrу:
4) Определим ФУНКЦИЮ D 1 (б): DI (б) == О, если бl Е Cl,
И DI (б) == 1, если 6 Е CI.
5) Пусть 82 множество всех состояний б, для которых
дD 1 (б) == 1, и пусть С2 == Сl U 82. К 82 относятся те состояния,
которые переходят в состояние О в результате двух сдвиrов.
6) Этот процесс будем продолжать до тех пор, пока одно из
множеств CAI или 8м не окажется пустым (заметим, что для
этоrо потребуется конечное число шаrов М, а именно М 2т).
Если СМ == ф, т. е. ссли все состояния после М или менее сдви
rOB переходят в состояние О, то схема является устойчивой. Если
8м == ф, то существует некоторое ненулевое с()стояние, которое
никоrда в состояние О не переходит, что означает неустойчи-
вость исследуемой схемы.
Используемые в этом алrоритме функции D i можно опреде
лить также следующим образом. Пусть
Do=== lЕБП(б i ЕБl)
i
(5.68)
и
Тоrда
Р/(6)== L П(6 i 6Э Ь iЕ91).
беSJ i
(5.69)
и
n
Dn (6) == D о (6)EfЭ L P J , n === 1, 2, . . ., М,
f l
Dn (6) == Р n (Т6).
(5.70)
(5.71 )
Эти формулыI позволяют упростить вычисления при определении
u u u
устоичивости тои или инон схемы с ПОМОЩЬЮ описанноrо выше
алrоритма.
Пример 5.8. Воспользуемся описанным выше алrоритмом
для определения устойчивости декодирующей лоrической схемы
ортоrонализуеМОI'О кода из примера 5.6. Реrистр сдвиrа с нели
нейной обратной связью в этом случае имеет вид, показанный
на фиr. 5.7. В целях упрощения внутренние состояния этоrо pe
rистра будем представлять в десятичной записи, а именно co
стоянию б == (б о , 61, б 2 , бз, б 4 , 65) сопоставим десятичное число
01 + б 2 2 + б з 2 2 + б 4 2 З + б52 4 (б о в режиме самоконтроля всеrда
равно О). Состояния ячеек реrистра, которые MorYT принимать
значения и О и 1, будем обозначать через Х. Основываясь на
фиr. 5.7, можно установить следующее:
268
rлава 5
1) fIри однократном сдвиrе только состояние Ь == (О, О, О, О, 1),
десятичным представлением KOToporo является число 16, пере
ходит в состояние О.
2) При однократном сдвиrе в состояние 16 переходят лишь
состояния вида == (О, О, О, 1, Х), т. е. состояния 8 и 24.
3) При однократном сдвиrе в' состояние 8 или 24 переходят
лишь состояния вида б == (О, О, 1, Х, Х), т. е. состояния 4, 20, 12
и 28.
4) При однократном сдвиrе в состояния 4, 20, 12 и 28 пере-
ходят лишь состояния вида б == (О, 1, Х, О, 1), б == (О, 1, Х, 1, О)
и б === (О, 1, Х, О, О), т. е. состояния 2, 18, 1 О, 6, 22, 24.
Фиr. 5.7. РеrиС'тр синдрома (12,6) Koдa,
Продолжая этот процесс даJIьше, построим табл. 5.4 и най
дем, что 89 === ф. Это 0значает, что рассматриваемая схема ЯВ-
ляется неустойчивой.
Однако выIодд о неустойчивости схемы, изобра)l{СННОЙ на
фиr. 5.7, не означает, что эта схема имеет бесконеЧНУIО rлу-
бину распространения ошибок. Декодирующая лоrическая
схема всеrда начинает работать с нулевоrо виутреннеrо co
стояния и в зависимости от значений СИl\1ВОЛОВ синдрома, посту-
паIОЩИХ на ее вход, проходит те или иные внутренние состоЯ
иия. Следовательно, из всех внутренних состояний реrисrра
сдвиrа с нелинейной обратной связью с распространением оши-
бок связаны лишь так называемые дости)кимые состояния, т. е.
состояния, в которых ре)"'истр может оказаться при всевозмож-
ных синдромах на ero входе. Здесь BJ\.lecro определения 5.3, ко-
торое понятие устойчивости связывало со всеми внутренними
состояниями, рассмотрим следующее определение.
Определение 5.4. (Месси, Лиу.) Ресистр сдвиса с нелинейной.
обратной связью называется устойчивым по отношенu/о к Bxoд
HCJAty воздействию ТОсда и только ТОсда, КОсда для любосо co
стояния 6, которое этот ресистр может достичь из состояния О
1. Л1етоды пОРО20вОёО декодирования
269
Таблица 5.4
Определение устойчивости схемы, изображенной на фиr. 5.7
Число
j sJ ЭJ1емеНТОВ р I (9)
ё j
1 16 30 65 (64 + 1) (63 + 1) (62 + 1) (61 + 1)
2 8, 24 28 64 (6з + 1) (62 + 1) (61 + 1)
3 4, 20, 12, 28 24 6з (62 + 1) (61 + 1)
4 2, 18, 1 О, 6, 22, 14 18 (6465 + 1) 62 (61 + 1)
5 1, 17, 9, 5, 21, 3, 7 11 6. [( 62 + 1) (6з + 1) 64 (65 + 1) +
+ 62 (6 1 + 1) (65 + 1) + (6 2 + 1) (64 + 1)]
6 25, 17, 11, 27, 23 6 6. [62 (6з + 1) 64 + 62 + 6з (64 + 1) 65 +
+ 6265 (6з + 1) (6з + 1) + 6 65 (6з+1) (62+1)]
7 26, 30, 15, 31 2 б-16 2 [б 5 (61 + 1) + б з б 1 ]
8 13 1 б 1 (б 2 + 1) б 4 б з (б 5 )
9 Ф 1 Вывод: неустойчива
при той или иной входной последовательности, существует такое
число N, что TN{) == О.
Если реrистр сдпиrа с нелинейной обратной связью является
устойчивым по ОТНОL1IеНИIО 1( входному воздействию, то rлубина
распространения ОLuибок бесконечной быть не мо)кет. Наоборот,
если реrистр СДВИi"'а с не.линейной обратной связью не являетс
УСТОЙЧИI3ым по отношеНИIО к входному воздействию, то rлубинз
распространения ошибок мо)кет оказаться и бесконечной. 3aMe
тим, что если реrистр СДВИI"'а с нелинейной обратной связью яв
ляется просто устойчивым, то он устойчив и по отношению
к входному воздеЙСТВ}I10. Обратное утверждение неверно. Дей-
ствительно, как было показано BbIlue, реrистр сдвиrа, изобра
,кенный на фиr. 5.7, не является устойчивым, поскольку из со-
стояния 29 нельзя достичь состояния О. Из состояния 29 этот
реrистр вновь переходит в состояние 29, т. е. это состояние яв
лястся равновесным состоянием. При определенных последова-
тельностях на входе в состояние 29 можно попасть из состоя-
ний 30 и 14. В состояние 14 можно попасть только из состоя
ния 7, но состояние 7 является недостижимым (т. е. в Hero
нельзя попасть из состояния О). Кроме Toro, недостижимым
является и состояние 30. Следовательно, реrистр сдвиrа с нели
ней ной обратной связью, изображенный на фиr. 5.7, является
устойчивым по отношению к входному воздействию и имеет ко-
нечную rлубину распространения ошибок.
270
r лава 5
5.7.4. Дефинитное декодирование
Друrим методом борьбы с распространением ошибок ЯВ-
ляется так называемый метод дефинитноrо декодирования. При
этом декодировании обратноrо воздействия на синдром нет
(т. е. исправление синдрома не проводится) и оценка значения
информационноrо символа в момент и осуществляется по ин
формационным символам, принятым с момента времени и
т
до момента времени и + т, и проверочным символам, принятым
с момента времени и до момента времени и + т.
Поскольку кодовое оrраничение TaKoro кода пDIJ равно
mko + (т + 1) n{) и обратная связь 01 сутствует, то в,,'!ияние воз-
никшей ошибки декодирования распространяется не более чем
на декодирование nDD символов. Однако при таком декодиро-
вании и достат()чно больших кодовых оrраничениях корректи-
рующие способности кодов обычно оказываются хуже, чем при
декодировании с обратной связью.
Различные свойства дефинитноrо декодирования методами
теории матриц установил Робинсон [33]. По существу эти }ке
методы теории матриц использовали Вайнер и Эш [6] для ана-
лиза корректирующих способностей сверточных кодов при де-
кодировании с обратной связыо. Этот анализ интересен по MHO
rим причинам, но так как коды специально для дефинитноrо
декодирования почти не разрабатывались (ввиду их несколько
худших корректирующих способностей), то эдесь эти вопросы
подробно не рассматриваются.
Как было показано выше, для сверточных кодов характерно
распространение ошибок. Поэтому всеrда хотелось бы исполь-
зовать коды, для которых r.nубина распространения ошибок не-
большая. Следует, однако, заметить, что реально возникновение
ошибок в количестве, превышающем корректирующие способно
сти кода, не всеrда приводит к распространению ошибок; воз-
никнет или не возникнет распространение ошибок, зависит от
Toro, какова конфиrурация ошибок, появившихея в канале.
5.8. Сверточиые коды, исправляющие пачки ошибок
Несколько раньше, чем было введено пороrовое декодирова
ние, Хеrельберrер [4] построил сверточные коды, испраВЛЯlощие
пачки ошибок. В дальнейшем Вайнер и Эш [6], Препарата [7],
Берлекэмп [5] и Месси [8] получили нижние rраницы для длины
свободноrо от ошибок защитноrо интервала, необходимоrо для
исправления ошибок, разработали методы кодирования, осно-
ванные на теории матриц, и методы декодирования, использую-
щие структуру систематических кодов.
1. Методы nОРО20вО20 декодирования
271
в данном разделе будут paCC1\10TpeHbI так называемые коды
Ивадари, исправляющие пачки ошибок и асимптотически дости
rающие нижней rраницы для кодовоrо оrраничения (или для
длины защитноrо интервала) кодов, исправляющих пачки оши
бок [10
12]. Эти коды MorYT быть очень просто реализованы,
поскольку метод их декодирования является самым простым, KO
торый только может быть при пороrовом декодировании.
При построении кодов, исправляющих пачки ошибок, как
и в случае блоковых кодов, очень важно иметь НИ}l{НЮЮ rраницу
для кодовоrо оrраничения ПА (или длины защитноrо интервала).
Защитным интервалом называют последовательность свободных
от ошибок символов, следующих за пачкой ошибок. Защитный
интервал необходим для Toro, чтобы пачки ошибок можно было
исправлять. Вайнер и Эш [6] получили следующую rраницу для
одовоrо оrраничения (и длины защитноrо интервала g) кода,
исправляющеrо пачки ошибок длины Ь:
ПА
g + ь
2Ь/(1
R). (5.72)
Рассматриваемые в этом разделе коды Ивадари представ
ляют собой подкласс сверточных кодов, в котором для любых
целых чисел по
2 и
1 существует код со скоростью
R == (по
1) /по, исправляющий любые пачки ошибок длины
Ь === пo
и менее. Любой код из этоrо класса, исправляющий
пачки ошибок длины Ь == по, называется основным кодом. Коды
со скоростью R == (по
1) /nо, исправляющие пачки ошибок
длины Ь ==
nO, Ь > 1, получаются из OCHoBHoro кода методом
чередования.
5.8.1. Метод чередования
Существуют два типа метода чередования: простой и обоб
щенный. При простом чередовании с периодом х кода с порож
дающими мноrочленами o
H (D), j == 1, ..., ko, i == 1, ..., по,
все показатели степеней в каждом порождающем мноrочлене
умножаются на число х. В результате простоrо чередования
кода с проверочной матрицей Н получается новый код, прове
рочная матрица KOToporo может быть получена из матрицы Н
путем введения между любыми двумя соседними строками по-
следней х
1 нулевых строк. Если )I{e на х умножаются не все
показате.пи степеней в порождающих мноrочленах, а только
те, которые принадлежат некоторому заданному множеству, то
такое чередование называется обобщенным. При обобщенном
чередовании проверочная матрица получающеrося кода строится
из проверочной матрицы исходноrо кода путем введения х....... 1
ct u
нулевых строк между каждои строкои из HeKoToporo заданноrо
подмножества строк и следующей строкой.
272
rлава б
Пример 5.9. Рассмотрим сверточный код из примера 5.6 со
скоростью R === 1/2 И кодовым оrраничением nл == 12, которыЙ
задается порождающим мноrочленом
G M(D)=== 1 +D3+D4+D5.
(5.73)
Матрица Н для этоrо кода имеет следующий вид:
Н===
... 1 1
О О 1 1
О О О О 1 1
1 О О О О О 1 1
1 О 1 О О О О О 1 1
1 О 1 О 1 О О О О О
1 1
в результате простоrо чередования с пеРIl()ДО l 2 эrоrо кода
получается код с поро)кдающим мноrочлеНОIН
aH (О) === 1 + D 6 + D 8 + D 10 .
(5.74)
Этот код имеет следующую матрицу:
1 1
О О 1 1
000011 О
О О О О О О 1 1
О О О О О О О О 1 1
Н== О О О О О О О О О О 1 1
1 О О О О О О О О О О О 1 1
О О 1 О О О О О О О О О О О 1 1
1 О О О 1 О О О О О О О О О О О 1 1
О О 1 О О О 1 О О О О О О О О О О О 1 1
1 О О О 1 О О О 1 О О О О О О О О О О О 1 1
При обобщенном чередовании исходноrо кода, а именно при
чередовании членов с нулевой, второй и третьей степенью, по
лучается код с порождающим мноrочленом
aЫ (D) 1 + О · D + О · D 2 + О · D 3 + о · D 4 + о · D 5 +
+ О · D6 + Di + [)8 == 1 4- D:j + п7 + D8.
1. Методы пopo
oв020 декодирования
273
Матрица Н получаlощеrося кода имеет следующий вид:
1 1
О О 1 1
О О О О 1 1
О О О О О 1 1 О О
Н=== О О О О О О О О 1 1
1 О О О О О О О О О 1 1
О О 1 О О О О О О О О О 1 1
1 О О О 1 О О О О О О О О О 1 1
1 О 1 О О О 1 О О О О О О О О О 1 1
Как видно из этоrо примера, при обобщенном чередовании
HYi-I\НО вссrда указывать, какие слаrаемые порождающеrо MHO
['ОЧJIена пли какие строки матрицы участвуют в чередовании.
5.8.2. ПРИНЦИП построения кодов
Основная идея, использованная Ивадари, заключалась в TO
I,
чтобы построить коды, удовлетворяющие следующим требова-
ниям. При отсутствии ошибок в канале синдром должен быть
нулеВЫl\I. ЛIобая ошибка, возникшая в Лlобой передаваемой по
следовате.пьности, должна иметь в синдроме так называе1\1УIО
собственную часть, не пересекающуюся с собственными частями
друrих ошибок. Кроме Toro, код ДОЛ)l{ен быть построен таким
образом, чтобы деI{одер Mor выделить собственную часть любой
ошибки, а следовательно, обнаружить и исправить эти ошибки.
При построении кодов Ивадари по
1 информационным по-
следовательностям сопоставляются различные последователь
ности веса 2 вида (е,е), (е,О,е), (е,О,О,е), ..., rде е
ЭЛемент
поля GF(q); единственной про вер очной последовательности при
этом сопоставляется последовательность (е, О,.. . , О) веса 1. По-
следовательности (е, О, . . . , О, е) длиныI k называются единич
ными конфиrурациями длины k, а последовательности (е, О,...
. . . , О) длины k
проверочными конфиrурациями длины k.
ЕСЛII информационным последовательностям сопоставить двоич
вые представления (О 11), (1 О 1), ... нечетных целых чисел,
а ПрОВСрОЧI-IОЙ последовательности
проверочную конфиrура
UIIIO, то точно таI{ )I{е, как и коды Ивадари, можно построить
коды Хеrельберrера. Метод декодирования всех этих кодов
один и тот )I{e.
Проще Bcero коды Ивадари можно ввести, если описать
структуру синдрома этих кодов. Поскольку при возникновении
пачки ошибок длины
пo в каждой из передаваемых последова-
274
r лава 5
тельностей может оказаться
ошибок, то при возникновении
такой пачки ошибок
собственных конфиrураций ошибок для
u v
каждои из по передаваемых последовательностеи должны по-
явиться в синдроме. Задача построения 'кода, удовлетворяющеrо
указанным выше требованиям, сводится I{ тому, чтобы размес-
тить эти конфиrурации в синдроме так, чтобы они не наклады-
вались друr на друrа и при декодировании их можно было бы
безошибочно выделить. В целях упрощения последовательность
ошибок, возникаIОlЦИХ в j
й передаваемой последовательности
с момента времени О до момента времени
1, будем обозна
чать в дальнейшем как
е (Л е (Л е (Л == Е и)
о 1 ... f3
1 ,
(5.75)
rде e
f)...... ошибка в момент времени i в j
й передаваемой после-
довательности.
5.8.3. Способ построения кодов
Рассматриваемые в этом разделе I{ОДЫ большей частыо
строятся методом проб и ОIIIибок; общим достоинством этих ко-
дов ЯВJlяется то, что их структура позволяет сначала исправлять
ошибки, возникшие в (по
1)
й информационной последователь-
ности, затем ошибки, появившиеся в (по....... 2) -й информацион-
ной последовательностя, и наконец ошибки, возникшие в l
й ин-
формационной последовательности. Это позволяет правильно
исправить ошибки даже в случае, если они возникли за преде
лами l
й информационной последовательности. При этом ис
пользуется свойство ошибок возникать пачками. Следует также
обратить внимание на то, что если при декодировании paCCMaT
риваемых здесь кодов ошибки раЗ
7JИЧНЫХ информационных по
следовательностей исправляются раздельно, то при декодиро
вании рассмотренных ранее самоортоrональных и ортоrонали-
зируемых кодов, предназначеliНЫХ для исправления случайных
ошибок, сначала исправляются ошибки, возникшие в момент
времени О во всех по
1 информационных последовательностях,
затем одновреl\1енно исправляются ошибки, ВОЗНИКIllие в по
1
информационных последовательностях в момент времени 1,
и т. д.
Сначала рассмотрим коды типа 1, на основе которых
строятся коды типа 11. Сопоставив по
Й передаваемой последо
вательности проверОЧНУIО конфиrурацию длины
+ 1,
(:t (по
j)
й передаваемой последовательности единичную KOH
фиrураТLIНО длины
+ j, j == 1, 2, ..., по
1, сq)оrмируем
Т. Методы поросовосо декодироваflllЯ
275
синдром следующим образом:
s no) (D) === В(n О ) О О . . . о о о . . . о E(nO 1) E(nO I) E(no 2) О E(no 2) . . .
........ ..... ........ -...----
х
. . . Е(1) О О . . . о E(l).
......-...-......
nJ 2
(5.76)
Заметим, что в эту формулу входят все п конфиrураций
ошибок. Предполаrая, что используется метод декодирования
с обратной связью, выберем параметр х такиt\.1 образом, чтобы
в синдроме можно было при деl{одировании выделить без оши-
бок собственные конфиrурации каждой передаваемой последо
вательности.
Чтобы разло>кить при декодировании ненулевой синдром на
ПО 1 различных единичных конфиrураuий, используется сле
дующий алrоритм декодирования. С появлением каждоrо HeHY
левоrо символа в синдроме начинается поиск единичных конфи
rураций, образованных этим и предшесТ'вующими ненулевыми
символами, хранящимися в ячейках памяти декодирующей ло
rической схемы.
1) Если ни одну из n:О 1 единичных конфиrураций обнару-
жить не удается, то этот ненулевой символ синдрома сдвиrается
в реrистр.
2) Если обнару>кена одна из по 1 единичных конфиrура-
ций, по длине этой конфиrурации определяется номер передан
ноЙ последовательности, в которой возникла ошибка, породив
шая эту конфиrурацию, а символ, входящий в эту конфиrура
ЦИIО, дает значение ошибки. Это позволяет исправить обнару-
женную ошибку и провести исправление синдрома.
3) Если одновременно можно построить несколько единич
ных конфиrураций, то с помощью указанноrо ниже правила за
прета выбирается одна из этих конфиrураций и осуществляется
переход к шаrу 2.
Правило запрета: «Если обнаружено несколько единичных
КОНфИI"ураций, то IЗыбнрается та, которая имеет б6ЛЬШУIО
длину».
Последовательность ошибок Е<n о ), возникших в по й переда
ваемой последовательности (проверочной последовательности),
для исправления ошибок в информационных передаваемых по
следовательностях не используется. Величину х следует BЫ
брать так, чтобы указанные выше операции 1 3 выполнялись
без ошибок и длина синдрома была бы по возможности мини
мальной. Этим условиям удовлетворяет х == ПО 2. Таким oo
разом строятся коды 1ипа 1.
276
rлава 5
5.8.4. Конкретные коды
Код типа 1 [10
12]:
s
no) (D) === Е(n О ) О О . . . о E(no
OE(пo
l) О E(nl)
2) О E(nlJ
'2) .. .
........ ---.......
+ по ........ 2
. . . Е< 1) О О . . . о Е< 1).
.........---
пo
2
ПорождаЮJЦИМИ мноrочленами этоrо кода НВЛЯIОТСЯ MHoro-
члены
(5.77)
ПО
2
I
no
2+213 <no
j) +
1
a
) (D) === D i=-I (1 + DB+no
J
l).
(5.78)
Используя тот же самый метод декодирования, что и для
кода типа 1, но несколько изменяя расположение в синдроме
последовательностей Еи), мо)!{но получить слеДУIОЩИЙ код.
Код типа 11 [11, 12]:
s\lo) (D) === в(n о ) E(no
1) О E(no
2) О . . .
. . . о B(I) О О . . . о E(na
I) Е(nз
2) . . . E(l). (5.79)
'---'
---
по +
---- 1
ПОРО)l{даIОЩИМИ мноrочленами кода типа 11 ЯВЛНIОТСЯ MHoro-
члены
a
) (D) == D B (no
j)+no
/
1 (1 + DnJ (B+1)+j'
2).
(5.80)
Принцип декодирования кодов типа 1 и типа 11 один и тот }I{е,
но тем не менее эти коды несколько отличаIОТСЯ друr от л.руrа.
Пример 5.10 иллюстрирует процесс декодирования рассмот-
ренных выше кодов.
Пример 5.10. Рассмотрим код Ивадари типа 11 с парамет-
рами ПО == 3,
== 2, q === 2. Соrласно формуле (5.80), этот код
задается порождающими мноrочленами
a
M (D) == D 5 (1 + D8) == D 5 + D 13 ,
a
(D) == D 2 (1 + D9) == D 2 + D Il .
(5.81 )
(5.82)
Пр
дположим, что возникли следующие ошибки:
E(l) (D) == e)l)D + e
l)D2,
Е(2) (D) === еъ 2 ) + e
2) D,
Е(З) (D) == е
З) + е\З}D.
(5.83)
1. Методы пОРО20вО20 декодирования
277
Конечно, на приемном конце эти мноrочлены неизвестны, но
может быть вычислен синдром, который, соrласно формулам
(5.81)
(5.83), в данном случае имеет следующий вид:
2
8(З) (D) === L Е(/) (D) аи) (D) ....... Е(З) (D) ===
11 . 1
J==
== ....... е
З) ....... e
3)Doe(2)D2 + e
2)D3 + e
I)D6 + e
l)D7 +
+ eb 2 )D 1J + e
2)D12 + ep)D 14 + e
l)D15 ==
== Е(З)Е(2)ООЕ(1)ОООЕ(2)ОЕ(l) ===
== e(3)e(3)e(2)e(2)OOe(l)e(l)OOOe(2)e(2)Oe(1)e(I) ( 5.84 )
о 1 01 12 01 12.
Из формул (5.81) и (5.82) следует, что единичные конфиrура-
ции второй и первой информационных последовательностей
имеют длину соответственно 1 О и 9.
Соrласно шаrу 1 алrоритма декодирования, до появления
2
ro символа e
) eI'o единичная конфиrурация образована быть
не может и до этоrо момента поступаIощие символы ошибок
просто направляются в реrистр сдвиrа. При появлении 2
ro
символа еь 2 ) алrоритм обнаружит две единичные конфиrурации
д.пины 1 О и 9, образованные этим символом соответственно
с I
M символом e
) и с I
M СИl\IВОЛОМ e
2). Соrласно пра
ви..пу запрета, алrоритм выбирает конфиrурацию длины 1 О, ис
правляет еь 2 ) и устраняет воздействие e
) на 8\31 (D). После
этоrо синдром принимает следующий вид:
5\31 (D) ==
е
З) ....... е
З) (D) + еь 2 ) D2 (1 + D9) +
+ e
2)D3 (1 + D9) + e\J)D6 (1 + D8) + e
l)D7 (1 + D8).
Разлаrая этот синдром дальше, можно исправить остаВIl.IИССН
ошибки.
5.8.5. Оценки кодов и сравнение их параметров
Обычно используются следующие критерии оценки качества
!{одов, исправляющих пачки ошибок:
1) Достиrает (быть может, асимптотически) или нет кодовое
оrраничение (пли длина защитноrо интервала) нижней rраницы
(5.72). Свойства сверточных кодов таковы, что соотношения
(5.72) для этих величин со знаком равенства выполняться не
MorYT. Так, Вайнер и Эш [3], рассма'I'ривая случай, коrда пачка
ошибок начинается за первой информационной последователь
ностью, получили следующую более точную rраницу для CBep
точных кодов:
2Ь
ПА > g + ь
1
R + по ---- 1 == 2Ьпо + по ---- 1 (5.85)
278
rлава 5
и назвали оптимальными коды, для которыIx эти соотношения
выполняются со знаком равенства. Следуя этому определению,
будем называть квазиоптимальными коды, ДЛЯ которых
ПА === 2Ьпо + const,
const > по 1,
т. е. нижняя rраница (5.85) достиrается асимптотически при
большой длине исправляемых пачек ошибок.
2) Экономичность можно характеризовать числом каскадов
реrистров сдвиrа, используемых в кодере и декодере.
3) В случае возникновения ошибки декодирования rлубина
распространения последней ДОJI)l(на быть по возмо)кности мень-
шей. При декодировании рассматриваемых здесь кодов реше-
ние о наличии или отсутствии ошибки в символе принимается
элементом И. Поскольку этот элемент MO)l{HO рассматривать
как пороrовый элемент с двумя входам и и пороrом 1,5, то
в данном случае можно воспользоваться критерием устойчиво
сти пороrовой декодирующей лоrической схемы. Так как при
каЖДОl\1 срабатывании декодирующей лоrической схемы вес
BHYTpeHHero состояния этой схемы уменьшается на 1 или 2,
то, следовательно, схема устойчива. Что касается rлубины pac
пространения ошибок, то обычный защитный интервал длины g
rарантирует, что влияние возникшей ошибки распространяется
только на последующие ошибки в синдроме, а дополнительныЙ
ct
защитныи интервал gдоп rарантирует, что все ненулевые сим
волы будут из декодирующей лоrической схемы удалены. Сле-
Таблица 5.5
Необходимое число ячеек реrистров сдвиrа
и длина защитных интервалов кодов,
исправляющих пачки ошибок
КОД Ilсобходимос ЧИСJlO
Защитный интервал ячеек реrистров
СДВllrа
Длина 11 I1
пачки
ошиБОI{
3 23 26 23 30
30 158 161 167 192
300 1 508 1 511 1607 1 812
5 94 84 94 92
50 499 489 508 542
500 4549 4539 4648 5042
10 639 369 639 387
100 2349 2079 2358 2 187
1000 1 9 449 19 179 19 548 20 187
1. Методы пopo
oв020 декодирования
279
довательно, rлубина распространения ошибок не превышает
g + gдоп.
в табл. 5.5 приведены значения указанных выше характе-
ристик для кодов типа 1 и 11.
5.8.6. Друrие коды
Выше был ОПIIсан метод построения кодов со скоростью
R == (по
l)j п o, 110
2. Известно, что при R == l/по эти коды
оказываются почти тривиальныIи,, допускающими мажоритар-
ное декодирование [10, 12].
Рассмотренные коды позволяют исправлять любые пачки
ошибок длины Ь и менее. Однако известны коды [41], которые
позволяют исправлять почти все пачки ошибок длины до Ь ==
==
no, имеют скорость R == (по
1) /по и защитный интервал,
несколько больший чем по (по
1)
. Эти коды имеют несколько
лучшие корректирующие способности, блаrодаря чему необхо-
дим меньший защитный интервал. Кроме Toro, эти коды позво
ЛЯIОТ исправлять TaI{}I{e и случайные ошибки.
Найти реrулярный метод построения циклических кодов
с числом проверочных символов т == 2Ь + 0', о'
2Ь, довольно
трудно. Как указывается в rл. 7 и как в этом дей,ствительно
нетрудно убедиться, рассмотренные коды соответствуют бло-
ковым кодам с числом проверочных символов т == 2Ь + 0',
а
2Ь. То, что эти кодыI можно строить реrулярным методом,
объясняется тем, что они имеют очень простые алrоритмы ко-
дирования и дскодирования и, кроме Toro, позволяют изменять
избыточность. Коды с числом избыточных символов 2Ь яв-
ЛЯIОТСЯ наилучшими среди кодов, имеющих ту же длину и ис
правляющих пачки ошибок длины Ь. Известно, что если число
проверочных символов болыпе 2Ь, то вероятность возникнове
ния в пределах одноrо блока или кодовоrо оrраничения двух
пачек ошибок становится большой, а следовательно, становится
большой и вероятность ошибочноrо декодирования.
5.9. Сверточные коды, исправляющие пачки ошибок
и незави
имые.ошибки (диффузные коды)
Рассматриваемые в этом разделе коды позволяют с по
мощью пороrовоrо декодирования исправлять как пачки оши
бок, так и независимые ошибки. ЭТИ I{ОДЫ требуют для исправ-
..пения пачек ошибок несколько больший защитный интервал,
чем коды, исправляющие только па'[ки ошибок, и в этом
смысле они несколы{о хуж
последних, но MorYT исправлять
любые две независимые ошибки. Коленбурr [9] и Месси пер
280
r лава 5
выми исследовали такие коды и назвали их диффузными. BHa
чале эти коды были построены лишь для скорости R == 1/2
И J == 4, однако в дальнейшем TOHr- [13] предложил относи-
тельно реrулярный метод их построения и при друrих значе-
ниях параметров R и J.
5.9.1. Два типа пачек ошибок
Диффузные коды в отличие от кодов, рассматриваВIПИХСЯ
в предыдущем разделе, все ошиБI{И, ВОЗНИI{шие в блоке, исправ-
ляют одновременно точно так же, !{ак самоортоrональные коды
исправляют независимые ошибки. При изучении таких кодов
удобно пользоваться следу[ощим определением пачки ошибок.
f(ОНФU2урация 1, Ь = 5 х х х х х
/(ОНСРИ2урацuя 2, Ь = 2 О О х х О
КОНСРИ2ураu,ия 3, Ь = 2 О О О О х
о о о о о
о о о о о
х О О О О
..........
Фиr. 5.8. Па чки ошибок типа В 1 и В2.
Определение 5.5. Пачкой ошибок типа В2 длиной В назы
вается совокупность ошибок, расположенных в В следующих
подряд блоках, первыЙ и последний из которых содержат co
ответственно первый и последний Оlиибочные символы.
Чтобы отличать пачки ОllIибок типа В2 от обычных пачек
ошибок, последние называют пачками ошибок типа В 1. На
фиr. 5.8 показано несколько примеров па'lек ошибок в случае
п{) == 5. Здесь через Х обозначеныI ошибочные символы, а че
рез О
символы, свободные от ошибок. Конфиrурация 1 на
фиr. 5.8 представляет собой пачку ошибок типа В 1 длиной 5 бит,
но в то же время является пачкой ошибок типа 82 длиноЙ
1 блок. КонфиrураЦIIЯ 2 представляет собой пачку ошибок
типа В 1 длиной 2 бита и пачку ошибок типа В2 длиной 1 блок.
И наконец, конфиrурация 3, как и конфиrурация 2, является
пачкой ошибок типа В 1 длиной 2 бита, но как пачка ошибок
типа 82 она имеет длину 2 блока. Друrими словами, пачка
ошибок длиной Ь бит является пачкой ошибок типа В2 длиной
]bjno[ или ]bjno[ + 1 блоков. И, наоборот, любая пачка ошибок
типа 82 длиной В блоков является пачкой ошибок типа В 1
длиной Ь бит, rде Впо
Ь
(В + l)по.
5.9.2. Корреl{тирующая способность
Корректирующая способность диффузных кодов опреде
дяется следующей теоремоц.
1. Методы nОрО208020 декодирО8ания
281
Теорема 5.6. Сверточный код исправляет конфиzурацию оши
бо1\, Е, если шумовые символ bl е
Л, j == 1, 2, ..., по
1, воздей-
ствующие на информационные симвОЛbl нулевоzо блока, удов-
летворяют следующим условиям:
1) при e
) === О воздействию Е подвержены не более чем 1/2
проверОЧНblХ соотношений, в которые входит e
);
2) при e
) == 1 не более чем (! /2)
1 проверочных соотно-
шений, в которые входит e
), подвержены воздействию шумовых
символов, входящих в Е и отличных от e
).
Доказател ьство.
1) В этом случ ае число сост авных проверок А з, j == 1, 2, ...
.. ., " принимающих отличные от нуля значения, самое большее
равно J /2 и не достиrает пороrа (! /2) + 0,5.
2) Число проверок Aj, принимающих ненулевые значения,
эдесь не меньше чем J
(J/2)
1 == (J/2) + 1, и, следовательно,
ошибка исправляется.
5.9.3. Простой пример
Примером диффузноrо кода со скоростью R == 1/2, исправ
ляющеrо любые две независимые ошибки или пачки ошибок
длиной 2 при наличии защитноrо интервала длины 6Ь........ 2, ЯВ
ляется код, задаваемый поро)кдаlОЩИМ lVIноrочленом
oa
(D) == 1 + D b + D 2b + D ЗЬ + I . (5.86)
Декодер этоrо кода, показанный на фиr. 5.9, формирует четыре
составные проверки:
AI === S
) == e
l) + еь 2 ),
А 2 == S
) == e
l) + e
l) + e
2),
Аз == S
+ S
== e
l) + e
+ e
+ e
,
А4 == S
+l === е61) + e
l+1 + e
V+l + e
+1 + e
+1'
ортоrональные относительно e
I). Эrо означает, что с помощью
пороrОБоrо декодирования такой код позволяет исправить лю-
бые две или менее случайные ошибки. Предположим, что по-
явилась пачка ошибок длиной 2Ь или менее. Как видно из фор-
мул (5.87), в процессе движения пачки ошибок по декодеру
u
слева направо, коrда она еще не достиrла выхода, ее воздеи
СТВИIО подвеР)I<ены не более двух составных про верок A i , i == 1,
2, 3, 4, и, следовательно, в этот период времени выход пороrо
Boro элемента вссrда равен нулю. В частности, вначале, коrда
(5.87)
282
r лава 5
пачка ВХОДИТ в декодер, она оказывает влияние лишь на про
верки Аз и А4. После Toro как пачка достиrнет выхода декодера,
ct
отличными от нуля шумовыми символами, воздеиствующими
на составные проверки, оказываются лишь символы еь о и e
2),
поскольку символы ebl), e
) и все остальные символы, сле
дующие за ними, равны нулю. Следовательно, ошибка ebl) MO
жет быть исправлена с помощью пороrовоrо декодирования.
Аналоrично исправляются остальные ошибки еР>, .. . J e
I
I.
Фиr. 5.9. Декодер диффузноrо кода.
5.9.4. Самоортоrональные коды
В то время как рассмотренный в последнем примере код
представляет собой ортоrонализуемый код, коды, преДЛОjкенные
l'oHroM [13], являются самоортоrонаЛЫiЫМИ и строятся следую
щим образом:
1) Сначала строится код, испраВJlЯЮЩИЙ пачки ошибок
и имеющий J проверок для ка}l{доrо информационноrо символа
нулевоrо блока.
2) Далее этот код с помощью TeoprMbI 5.6 модифицируется
таким образом, чтобы он Mor исправлять [! /2] и менее незави-
симых ошибок.
Поскольку в действительности построение кодов осуще-
ствляется rлавным обраЗО
1 методом проб и ОllIибок, то детали
построения этих кодов здесь не рассматриваются (с ними
можно ознакомиться по ориrинальной работе TOHra [13]). Коды,
построенные TOHroM, приведены в табл. 5.6.
TOHrOM была получена также следующая нижняя rраница
для кодовоrо оrраничения самоор rоrонаЛЫiЫХ кодов, исправ-
ляющих пачки ошибок типа В2 [13].
Теорема 5.7. Кодовое осраниченuе саJtоорrО20нальносо кода,
uсправЛЯ10щесо пачки ОUluбок типа 82 длиной В блоков, должно
t::S
::t
;:s
'с
t::S
......
.....
.с)
,а.>
:s:o
::::
:s: .0
....=--
?
::Е
:о
::
d>
t;
:r
о
'-
О
::с
:.:Е
d>
:s:
g
s!
t::(
:Е
о
о-
О
t:
q:
....
a:I
Q
t:{
Q
:!
=
.g.
.g.
=
t:{
:!
а::
..а
=
е
""
е
f-t
с-
е
е
:Е
u
=-
=
1;:
\о
...... OOM
+
>ос:)
CD
О +
м
1+
CD >ос:)
и"
+
+
>ос:) +
и" >ос:)
..,.
+ +
t--- +
+ С'I
+ +
>oC:)
м м
t +
Q+ +
+
+
м -с\
+ + +Q
t--- +
'o:t" +
..с CD
++
+ ++
..c м 'o:t"
++QQ
..с - +++
Q C)
+++++
...... ..... ...... ...... .......
.........
.................. ....... <=>
...... u",) ...... C\I
+++++
..C;) ..C;)
М t..QФt--
..................
..... м t..Q
........
м
t--
.......
о')
+
>ос:)
t---
+
и"
......
>ос:)
C':I
+
C':I >ос:)
+ C':I
=
Q+
+
м +
..с
+ о
..с ......
о')
о t--- +
:+ t +......
..с:. C'J C':I ......
О ...... +
...... +..с
+..с '....
+ 00
L") + + +
+ =
Q= +
++
+ +
..c + +
+ Q+ +t---
..с t--- +
Q + +1
++ +C'
..с + C':I i + +
'O:t",..... C':I t-..
""'-I..c 'O:t"
+.t>+ + +
..с C':I C':I C':I
Q
++++++
Ф
ф
t--
t-..
'o:t" +
+..с
:!: 00 +
""' Q + cg
........ Q
+ + +
м + +
+ >ос:) +
..с м ..с ..с
о t--- 00
QQ
++++
..с) >ос:) ..t:)
..(:) C':I М и"
++++
...... ...........
+
-t:)
00
.........
......
.........
t--
C'I
+
..с)
......
+
..t:::>
<=>
.......
м
м
м
м
м
........
+ t---
>ос:) +
Q oo
+ +1
t---
+ и"
>ос:) + Q
C':I ..с
OO +
и" + ++
+ ..с
CD М о')
...... + +
+ 1:З +
+Q Q ..........с
м + + +Q
+ + м
:з ..t:) м + +
..с ...... t--- + ..с
CD ,.....,.....,::) ..с
Q........""'-IC':I Q
+ ""+ .,,+ + +
..с C':I 'o:t" C':I М
Q QQ
++++++
.........
Ф
+
.........
м
+
-t:)
.....
t..Q
м
........
м
.........
ф
+
-t:)
Ф
.........
LC
t..Q
........
284
r лава 5
удовлетворять следующе.л.tу неравенству:
пA
(пo
l)(
+2)Ь== l
R (
2)b.
(5.88)
КОДЫ, кодовое оrраничение которых достиrает этой rраницы
при больших длинах пачек ошибок Ь, называются квазиопти-
мальными. В частности, квазиоптимальными ЯВЛЯIОТСЯ коды,
приведенные в табл. 5.6.
Построенные TOH['O
l коды имеlОТ скорость R == (по
1) /по,
однако аналоrично можно построить коды со cKopocTыo R ===
== l/nо. Блоковые коды, испраВЛЯIОlцие пачка ОIllиБОI< 11 lIеза
висимые ошибки, были построены TaK}I{C XCIO, Касами 1I Чене
1
[43]. Эти коды предназначены ДJlЯ составных каналов; асимпто
тически достиrая ни}кней rраницы для длины блоковых кодов,
исправляющих одиночные пачки ошибок, они позволяют исправ-
лять несколько независимых ошибок. Указанная выше нижняя
rраница (5.88) для кодовоrо оrраничения самоортоrональных
кодов больше, чем нижняя rраница для КОДОI30rо оrраничения
кодов, испраВЛЯIОЩИХ одиночные пачки ошибок. Однако слож-
ность декодирования для кодов, построенных Хсю, Касами и Че
нем, Toro же порядка, что и для БЧХ. кодов, тоrда как рассмот-
ренные выше коды допускают более простое пороrОБое дeKO
дирование.
5.10. Равномерные сверточные коды
Друrим классом кодов, допускающих пороrовое декодирова-
ние, является класс равномерных сверrочных кодов. Эти коды
имеют низкую скорость передачи, но их минимальное расстоя
ние совпадает со средним расстоянием. Обладая приблизительно
такой же корректирующей способностью, как и блоковые коды
максимальной длины, они тем не менее имеют небольшую rлу-
бину распространения ошибок. Однако этот класс кодов ЯВ-
ляется небольшим, поскольку строится лишь для скоростей
вида R == 112т. Эти коды, впервые построенные Мссси [2] для
ko == 1, в дальнейшем были обобщены Робинсоном [36] и на
случай IlO> 1. Однако здесь в целях упрощения
1Ы оrrани-
чимся рассмотрением только кодов над ОР(2) с ko === 1.
5.10.1. Определение paBHoMcpHoro кода
Определение 5.6. Д вОUЧНblМ равНо,Л,tеРНblЛ1, кодом называется
код СО скоростью R == 1/2 rп , nОрОJ!сдаЮЩUМll MH020 t lJ1Cf-lамU
a
B (D), i === 2, 3, . . ., 2т, КОТОрО20 являются все 2т
1 раЗolltlч
1. Л1етоды пОРО20вО20 декодирования
285
НЫХ ненулевых МflоаочлеНО8 вида 1 + fJID + ... + gn
Dт над
G F (q) степени т и менее.
l;апример, равномерным кодом является код со cKopocTыo
R === '/4, порождаемый мноrочленами G
l) (D) == 1 + D, a
ы (D) ==
==1+D2, G
I)(D)==1+D+D2.
5.10.2. n ранило ортоrонализации
Равномерные коды имеют кодовое оrраничение ПА ===
== (т + 1) 2т, минимальное расстояние d FD === (т + 2) 21п
1 И до-
пускаIОТ построение J == d FD ....... 1 проверок, ортоrональных OTHO
сительно e
l). Последовательность символов синдрома, обра-
зующихся за время w
i
w + т, определяется матричным
соотношением (5.89), rде H
ма1рица, задаваемая Форму
лай (5.90).
Матрицу R/j. будем называть провеРОЧНblМ параллелоzрам-
МОМ. Подматрица в правой части H d, выделенная пунктирной
линией, является проверочной матрицей H
.
8(2)
w
8(2)
w+'
......
"(1)
ew
m
8(2)
w+т
8(З)
w
......
'"' (I )
ew
1
e(l)
w
( З)
sW+11l
e(l)
/j.. w+т
=== [ f/ · 1 (m+ 1) (2m
1)] е(2)
w
(5.89)
(2т)
8w
(2)
e w + m
2 пl
e w
8(
т)
w+m....
2т
е
..... w+т
286
r лава 5
(1)
g (2), т.. ·
g (l)
(2), О
.
(1) g(l)
g (2), т (2), О
(1) (1)
g (З), т . . . g(З), о
н tз.== g() (1) (5.90)
. (3), т g (3), О
.
(1) (1)
g(2 m ), т . . . g (2т), О
.
(1) () )
g (2'n)' т.. · g(2 m ). О
,..
Величины e I), i == w ........ nl, ..., w 1, в (5.89) будучи CYM
.......
мами e 1) == e l) + e l), i === w ........ т, ..., w........ 1, преДILIествующих
шумовых информационных символов e 1) и оценок e l) послед-
них, равны О, если e l)==e l), т. е. если символ e l) был декоди
рован верно, равны 1 в противном случае и отражают воздей-
ствие на символы синдрома ошибок декодирования.
Месси предложил следующее правило ортоrональности paB
номерных кодов, позволяющее построить систему составных
проверок, ортоrональных относительно e ):
1. В качестве 2т 1 первых составных проверок выбираются
S ), j == 2, 3, ..., 2т.
2. Пусть S i' i =1= О, символ синдрома, которому COOTBeT
ствует строка OQi матрицы Н/). (Qi последовательность из i
символов О и 1, оканчивающаяся символом 1). Тоrда найдется
по крайней мере один символ S i' которому В матрице H/j. co
ответствует строка lQi. Все суммы S )+i + S ] относятся
к числу искомых составных проверок.
3. В качестве остальных т составных проверок берутся сим
волы S i' которым соответствуют строки матрицы Н/). вида 11,
101, 1021, ..., 10 i l, rде Oi последовательность символов О
длины i. Заметим, что каждый из шумовых символов e i'
i == 1, 2, ..., т, контролирует только одну составную проверку.
1. Методы поросовО20 деl(одироваНllЯ
287
Пример 5.11. Проверочный параЛJIелоrрамм paBHOMepHoro
кода со скоростью R == 1/8 задается формулой (5.91).:
o о 1
О О
О
о 1 О
О 1
О
о 1 1
О 1
О
1 О О
1 О
1
H ' ==
1 О 1
1 О
1
1 1 О
1 1
1
1 1 1
1 1
1
1
1 1
О 1 1
О О 1 1
1
О 1
1 О 1
О 1 О 1
1
1 1
111
О 1 1 1
1
О 1
О О 1
1 О О 1
1
1 1
О 1 1
1 О 1 1
1
О 1
1 О 1
1 1 О 1
1
1 1
111
1 1 1 1
(5.91 )
Метод ор rоrонализации Месси дает следующую систему opToro-
нальных проверок:
1) S ), j == 2, 3, .. ., 8;
288
r лава 5
2) (2) + (3) (4) + )
SW+l SW+l' SW+l S
+l'
S
2 + S
2' S
? + s
t2'
s (2) + S( 6) S(З) + S(7)
w+з w+З' w+з l
+З'
3) S (З) S (7) S \5)
w+p w+2' w+з.
S{6) + S(7)
w+l w+l'
(6) + (8)
Sw+2 SW+2'
S(4) + S(8) ·
w+з w+З'
5.10.3. Метод ортоrоналиэации, обеспечивающий
небольшую rлубину распространения ошибок
Одной из характеристик равномерных кодов является rлу-
бина распространения ошибок. Анализируя явление распростра
нения ошибок, Салливан [35] разработал следующий алrоритм
ортоrонализации, позволяющий минимизировать rJlубину рас-
пространения ошибок:
1) В качестве 2т
1 первых составных проверок берутся
символы синдром а S
), j === 2, 3, ..., 2т.
2) Пусть S
i
символ синдрома, которому соответствует
строка Rm
ilQi матрицы H
, содержащая не менее трех симво
JIOB 1 (здесь Rт
i
последовательность из I1l
i си
волов О
И 1). Тоrда среди строк матрицы H
всеrда можно найти строку
вида Rт
iOQi, соответствующую некоторому СИМВОJlУ синдрома
S
i. Действительно, это всеrда можно сделать, ПОСКОЛЬКУ все
заканчивающиеся символом 1 строки с номером i + 1 провероч
ных параллелоrраммов образуют совокупность, в которую каж-
дая двоичная последовательность длины т + 1, содеря{аlцая не
менее двух единиц, входит ровно один раз. Суммы S
i + S:!Jl
образуют составные проверки, которые содер)кат только символ
e
).
3) В качестве остальных т составных проверок берутся
символы синдрома, которым в матрице H
cooTBeTcTBYIOT СТРОКИ
вида oт
il Oi
l, 1
i < т.
Пример 5.12. Если применить метод Салливана для opToro
нализации кода из примера 5.1 1, то получим следующую си
стему составных проверок:
1) S
), j == 2, 3, . . ., 8;
2) S
l + s
p S
I + S
l'
S
2 + S
2' S
2 + S
2'
S
)+з + S
з, S
з + S
t-З'
3) s
)+p S
2' S
з.
Метод ортоrонализации СаЛЛIIвана является чаСТIII)1
1 слу
чаем метода орrОI'онализации .l\'lecclI, но он 13иII'ОДНО ОТ.JIll"
(7) + (8)
SW+I SW+l'
(6) + (8)
SW+2 SW+2'
S(4) + S(8) ·
w+з w+З'
1. Методы пOPOZOBOZO декодирования
289
чается от последнеrо СЛСДУЮIЦИМ. Использование метода OpTO
rона.пизации Месси в примере 5.11 приводит, наПРИl\.fер, к тому,
""'"
что от e 1 оказываются зависящими восемь составных про
верок. Но в этом случае возникновение ошибки декодирования,
......
коrда e 1 =1= О, эквивалентно появлению пачки ошибок
длины 8, что резко ухудшает корректирующую способность кода
по отношеНИIО к символу e ). В то ){{е время при использовании
метода ортоrонализации Салливана ни одна из составных про
верок, полученных на втором и третьем шаrах, не содержит ни
один ИЗ символов O, i == w т, ..., w 1. Поэтому с точки
зрения уменьшения rлубины распространения ошибок метод
Салливана является оптимальным методом ортоrонализации.
Поскольку при использовании метода ортоrонализации Сал
...... ......
ливана величины e m' ..., e 1 контролируются лишь провер
ками S ), j == 2, 3, .. ., 2т, то их воздействие на составные про
верки может быть задано следующим простым соотношением:
""'"
S(2) ...... е(l) (2)
(1)
w ew m w e w
8(3) e(I) е(З)
w w w
==А + + (5.92)
...... .
8(2 m ) ...... е(О е(2 т )
e(I)
w w l ...... w ___ w
rде Л матрица размера (2т 1) Х т, строками которой яв
ляются всевозможные ненулевые последовательности длины
т + 1.
Будем rоворить, что декодер в момент времени w + т на-
""'" ......
ходится В нормальном рабочем состоянии, если т ==e m+l
......
== ... == e l == о. Пусть Ew ..... множество ошибок, контролируе-
мых составными проверками, т. е. Ew === {e J): i == w, . . ., w + т,
j == 1, 2, ..., 2т}.
Теорема 5.8. П усть при использовании равно.меРНО80 свер-
ТОЧНОсО кода u оптuмальносо правила ОРТОсОНQлизации HeKOTO
рая некорректuруе.м,ая совокупность ошибок в канале приводит
к ошибочном у декодированию символа e l) . Пусть rv MиHи
мальное целое число, такое, ЧТО ни одно из .множеств Ew,
EW+I' ..., Ew+т 1 не содержит У(т) или более символов 1
290
r лава 5
(w > i), еде
{ О, m=== 1,
у (т) === т2m
2
1, т
2.
ТОеда декодер к моменту времени w + 2т перейдет в нормаль-
ное рабочее состояние.
Доказательство. Сначала преДПОЛО)J{ИМ, что e
) === О и НИ
один из элементов Ew не равен 1. В этом случае в правой части
(5.92) ненулевым является только первый вектор, а следова
тельно, ровно 2т
1 символов множеств {s
), j == 2, 3, . . ., 2т}
будут равны единице 1). Допустим, что в Е ш равны 1 не более
У(т) символов (e
)==O). Тоrда изменить свое значение с О на
1 MorYT самое болыпее У (т) составных проверок. Следова-
тельно, общее число составных проверок, принимающих значе
ние 1, не больше, чем целая часть [(2 + m)2т
1
1]/2, и реШе
ние о e
) принимается правильно.
Далее предположим, что e
) == 1, и все элементы Ew, за ис-
ключением e
), равны нулю. Тоrда среди элементов множества
{s
), j === 2, 3, ..., 2 n }} будут равны О самое большее 2т
1 эле-
ментов. Если допустить, что среди символов Ew равны 1 не
больше чем У(m), то число символов Ew, равных 1 и отличных
от e
, cTpor'o меньше чем У(т), а следовательно, CTporo меньше
чем У (т) составных про верок изменяют свое значение с 1 на О.
В этом случае не менее [(2 + т) 2т
1
1]/2 составных про верок
по-прежнему будут оставаться равными единице и решение
о e
) ОПпТЬ будет принято правильно.
Из доказанной теоремы следует, в частности, что декодер
кода из примера 5.11 принимает правильное решение о e
) при
наличии в Ew не более девяти символов 1, если ошибок декоди-
рования раньше не было, и при наличии в Ew не более пяти
символов 1, если перед этим произошла ошибка декодирования.
5.10.4. Пер,форированные равномерные КОДЫ
Равномерные коды имеют очень высокую корректирующую
способность при низкой скорости передачи. Скорость передачи
можно повысить путем выбрасывания некоторых проверочных
символов, ухудшив при этом несколько корректирующую спо
собность. Этот метод построения кодов был использован Робин
соном [36]. Рассмотрим решетку, узлами котороЙ являются дво-
t) Это связано с тем, что сумма Лlобоrо lIенулевоrо числа столбцов
матрицы i\ всеrда является вектором веса 2т
1.
П pU.4t. перев.
Т. Л1еrоды пOP020BOZO декодuрования
291
ичные векторы, соответствующие различным проверочным co
отношениям (порождающим мноrочлеtIам) и соединенные
определенным образом друr с друrом стрелками. Например,
решетка paBHoMepHoro кода с параметрами по == 4, ko == 1
и т == 2 имеет вид
1 1 0/1 1 1 \ 1 О 1
Узел 111 этой решетки представляет следующие три провероч
ных СООТНОllIения:
S(2) == e(l) + e(l) + е(О
w w 2 w l w'
S(2) ==
w+1
е(О + е(О + е( 1)
w l w w+l'
S(2) ==
w+2
е(1) + е(О + e(l)
w w+1 W+28
Стрелка, соединяющая у лы 111 и 101, указывает шаr про
ct
цесса ортоrонализации кода, позволяющии путем сложения сим-
вола синдрома
S(3) == еО) + е(!)
w+1 w 1 w+t
с S(2) пол у чить так у ю составн у ю П р ове р к у что s(?) + s(: ) +
w+ I ' w+ 1 w+ I
+ e ) === о. Аналоrично стрелка, соединяющая узлы 110 и 1 11,
указывает шаr процесса ортоrонализации, позволяющий путем
сложения символа синдрома
S(4) == е(О + е(Н
w l w 2 w l
с S ) получить такую проверку, что
S(4) + S(2) + s(1) == О
w 1 w w 8
Последняя стрелка указывает шаr ортоrоналиэации, позволяю-
щий путем сложения символа синдрома
S(4) == е(1) + е(О
w+2 w+1 w+2
с S 2 получить составную прове,рку, такую, ЧТО
S(2) + S(4) + e(l) == о
w+2 w+2 w 8
Общее правило построения решетки состоит в следующем:
вектор V j ro яруса соединяется с вектором W (j + 1) ro яруса,
если покомпонентная сумма по модулю 2 этих векторов или
292
r лава 5
одноrо из них с некоторым сдвиrом дрУI'оrо является вектором
веса 1. Вектор, расположенный на самом высоком ярусе, имеет
вес ko(т + 1), а векторы, располо)кенные На самом нижнем
ярусе, И lеIОТ вес 2.
Рассмотрим, каким образом можно повысить скорость пе-
редачи за счет выбрасывания проверочных символов. На
фиr. 5.10 показана решетка кода с параметрами пz == 4 и ko == 1.
Удали л вектор 11111, располо)кенный в четвертом ярусе. Заме
тим, что в этом случае оставшимся узлам решетки соответ-
ствуют символы синдрома, ортоrон;злизация которых осуще-
ствляется без использования символов синдрома, соответствую
щих вектору 1 1 111, а следовательно, ортоrонализацию получен
Horo кода можно п.ровеСТJ1 точно так ){{е, как и исходноrо кода.
Фиr. 5.10. Решетчатан структура кода с т == 4 и ko == 1.
Пас.кольку выброшенный узел имел вес 5, то минимальное pac
стояние кода уменьшается с 48 до 43; скорость передачи при
этом возрастает с 1/16 до 1/15. Далее без нарушения процесса
ортоrонализации можно выбросить l1РОИЗВОЛЬНЫЙ вектор, pac
положенный в 3 M ярусе. После Toro как будут выброшены все
векторы 3 ro яруса, можно пер.ейти к выбрасыванию векторов
2 ro я руса.
Однако можно воспользоваться друrой процедурой выбра
сывания, позволяющей получить коды с большим минимальным
расстоянием. Эта процедура заключается в следующем. При
выбрасывании любоrо узла решетки число проверочных симво
лов кода уменьшается на единицу, а минимальное расстояние
на вес 'элемента, соответствующеrо выброшенному узлу. Если
обратиться к проuессу ортоrонализации, коrда в результате сло
жения двух символов синдромов образуются составные про
верки, то можно заметить, что узел решетки можно выбросить,
если он не связан с оставшимися узлами более высоких ярусов.
Рассматривая каждый вектор как двоичную запись HeKoToporo
дссятичноrо числа (старшим разрядом будем считать самый
правый символ) t упорядочим узлы решетки в порядке убывания
1. Л1етодbl пОРО20восо декодирования
293
этих десятичных чисел (номеров). При построении кода узлы
решетки буде
1 выбрасывать в порядке убывания их номеров.
Это всеrда МО}l{НО дслать, поскольку вектор j
ro яруса, имею
щий номер Ь, не связан ни с одним из векторов (i + 1)
ro яруса,
имеIОЩИМ номер, i\1сIIыIlнйй че
1 Ь. Например, с помощью этоrо
алrоритма выбрасывания может быть получен код с парамет
рами R == 1/11, d == 28, пА == 55 (при этом из решетки, изобра
жен ной на фи r . 5. 1 О, в ы б Р а с ы в а 10 т с н узлы 11111 , 1 О 111 , ] 1 О 1 1,
1 1101). ПОJlучающиеся таким образом коды называются nep
форuроваН1-tыл,tll pa8HOAtepHblMU Koaa.
tи.
Задачи
1. Построить кодер и декодер кода из табл. 5.1 со скоростью
передачи R == 2/3 И J == 6 ортоrональными проверками.
2. а) Показать, что совокупности целых чисел
{2, 10, 7, 6, 5, 3, 1},
{З, 6, 8, 2, 13, 7, 4, 1}
задают порождаlощие мноrочлены самоортоrональных кодов со
скоростью R == 1/2 И соответственно J == 8 и J == 9 ортоrональ
НЫМИ проверками.
б) Сравнить кодовое оrраничение указанноrо в п. «а» кода
с параметрами R == 1/2 И J == 8 с кодовым оrраничением COOT
ветствующеrо кода из табл. 5.1.
(Приведенные выше две совокупности целых чисел были He
давно найдены Робинсоном [45].)
3. Сверточные коды, испраВЛЯЮIJl.ие одиночные ошибки [6].
Эти коды имеют параметры
2 т
1
ПО == ,
ko === ПО ---- 1,
d==З
и строятся следуюi.ЦИМ образо
.
В качестве первых по столбцов матрицы Н, т. е. столбцов
матрицы В, берутся 2т
1 лвоичных векторов длины т, первая
компонента которых равна 1 (по
й СТОJIбец матрицы ВО, соот-
ветствующий проверочному символу, дол)кен быть вектором, все
компоненты KOToporo, за исключением первой, равны О).
а) Показать, что опредрляемый таl(ОЙ матриuей {пl2т
l,
т (21n
1
1)) -код исправляет одиночные ошибки.
б) flостроить матрицу /;30 в случа
по . 2
1 == 8.
294
r лава ,;
4. Коды, исправляющие две независимые ошибки [6]. Пусть
а примитивный элемент поля ОР(2 т ), HI и Н2 матрицы
размера mX(2 т .......l):
Н 1 == [а 2т 2 , ?т 3 1 О ]
а'" ,. . ., а, а ,
н 2 == [аЗ (2т 2), аЗ (2т З), . . ., аЗ, а О ],
1 BeKTop CTpOKa, все 2т 1 компонент KOToporo рапны 1,
а О BeKTop CTpOK8, все 2т 1 компонент KOToporo равны О.
Показать, что сверточный код, который задается матрицей
Н===
1
Н 1
О
H2
1
H2
мо)кет исправлять любые две независимые ошибки.
5. БПМ коды [5, 7, 8].
Берлекэмп, Препарата и Месси построили коды, исправляю-
щие пачки ошибок типа 82 длины Ь == по. Рассмотрим случай
по == 6. Пусть Во матрица следующеrо вида:
1 О О О О O
О 1 О О О О
О О 1 О О О
О О О 1 О О
О О О О 1 О
О О О О О 1
ВО== О О О О О О ,
О О О О О 4
О О О О СВ
OOOFED
00 J 1 на
OONMLK
rде А, В, С, . . . двоичные переменные, которые нужно выбрать.
Проверочной матрицей этоrо кода является матрица (5.93). Пу-
тем сложения столбцов O ro блока со столбцами последующих
блоков можно превратить в нули все единичные символы, ле
1. /у1етоды пOPOZ080Z0 декодироваНllЯ
295
жащие выше rоризонтальной линии.
О 1 2 3 4 5
100000
01 О О О О 10000 О
001 О 0101000 0100000
00 О 1 О О 00100 О 010000 100000
00 О О 1 О 00010 О 0010 О О 01000 О 100000
00 О О 0100001 00001000010000100001100000
00 О О О О 00000 О 0000 1 О 00010 О 001000 010000
00 О О ОА 00000 000000100001 0000100001000
ООООСВОООООАОООООО 000001000010000100
00 О FED 0000е8 ОООООА 000000000001 000010
00 J 1 НО OOOFED ооооев 00000 А 000000 000001
ООNл,1LК 00JIНG OOOFED ооооев ОООООА 000000
(5.93 )
а) Пусть М 1, М2, М з , М4, Мб подблоки матрицы, получаю
щейся из (5.93) в результате выполнения указанных выше опе
u u
рации, расположенные ниже rоризонтальнои линии и соответ-
ствующие блокам 1 5 матрицы (5.93). Найти MI' М2, М з , М4,
Мб.
б) Найти необходимое и достаточное условие Toro, что этоr
код исправляет пачки ошибок типа 82.
в) В результате указанных в П. «а» операций неизвестный
символ А появляется в левой верхней подматрице размера
2 Х 2 матрицы Мб:
О 1
А О
Если выбрать А == 1, то эта подматрица будет невырожденной.
Неизвестный символ 8 входит в подматрицу
О 1 О О 1 О
АОl==101
БОО 800
..Если выбрать 8 == 1, то эта подматрица также будет невырож-
денной. Аналоrично найти остальные символы С, D, . .. .
r) Определить защитный интервал этоrо кода.
д) Пусть этот код используется для исправления пачек оши
бок типа В 1. Определить необходимый защитный интервал
296
r лава 5
и сравнить ero с защитным ИН1ервалом соответствующеrо кода
Ивадари. .
6. а) Построить матрицу Во кода Хеrельберrера с парамет-
рами по == 4, Ь == 4.
б) Начертить схемы кодера и декодера для этоrо кода.
в) Сравнить защитный интервал этоrо кода с rраницей (5.72).
7. а) Найти порождаЮLllИЙ мноrочлен кода уIвадари типа 11
со скоростью R === 3/4, исправляющеrо пачки ошибок длины
Ь == 8.
б) Построить кодер и декодер для этоrо кода.
т(2)
R;'} ' i(1)'
Я(2) : + А
R ) +
1(1)
......о т (1)
т (3)
Kof1 [! Деlfоиер
Фиr. 5.11. Кодер и декодер кода, исправляющеrо пачки ошибок Длины Ь == 3
(скорость R == 1/ з).
в) Рассмотреть работу декодера при коррекции следующей
пачки ошибок дJII1ныI [8]:
Е(l) (D) == e I)D + e I)D2,
Е(2) (D) === еь 2 ) + e 2) D,
Е(З) (D) == еь З ) + е1 З ) D ,
Е(4) (D) == еь 4 ) + e 4) D.
8. Известны коды r12], исправляющие пачки ошибок типа Bl,
которые задаются синдромами
s(no)(D)==E(no)OO ... OE(nQ l)O ... OE(no I)E(nu 2)O ... OE(no 2) ...
8+no 2 no 2 nо з
. . . ВО) B(l)
и
s(no) (D) ==
== Е(nо)ОО . . . ОЕ(nо'" I) Е(nо"'2)
n,... ]
. . . ЕО >00 . . . OE(no 1) ОЕ(nо"'2) ОЕ(nо"'З) О ...
(3+n() 1
. . . OE(I).
а) Рассмотреть работу декодера в случае по == 3, == 2.
Т. Методы nОрО208020 декодирования
297
б) Определить неоБХОДИ:\fЫЙ заlltИТНЫЙ интервал и число
ячеек реrистров сдвиrа, необходимых для построения кодера и
декодера.
9. Коды, испраВЛЯlошие пачки ошибок со скоростью R== I/пo
[1 О].
а) Показать, что изобра}кенные на фиr. 5.1) кодер и деко-
пер ПОЗВОЛЯЮl исправлять пачки ошибок длины Ь == 3 и менее.
б) Обобщить указанные в п. «а» методы кодирования и де..
кодирования на случаЙ произвольных кодов со скоростью R ==
== 1/nо.
10. а) Выписать поро)кдающие мноrочлены paBHoMepHoro ко-
да со скоростью R == 1/16.
б) Провести ортоrонализацию этоrо кода методом Салли-
вана.
6. Сверточные коды
Н. Последовате.пьное декодирование
Последовательное декодирование было предложено Бозен-
крафтом [1]. и, как уже укззывалось выше, на начальном этапе
исследования в этой области велись rлавным образом в Macca
чусетском технолоrическом институте. Кодирование и декоди-
рование блоковых кодов и рассматривавшихся до сих пор CBep
точных кодов основано rлавным образом на использовании
алrебраических методов. Основные достоинства метода после
довательноrо декодирования связаны с тем, что при этом MeTO
де число операций, необходимых для декодирования одноrо
символа, является случайной величиной в отличие от Toro, что
имеет место при алrебраических методах.
Если простота алrоритмов пороrовоrо декодирования и, сле-
довательно, простота их реализации стимулировали исследова
ния сравнительно коротких кодов и повышение их корректиру
ющих способностей, то проводившиеся параллельно исследова-
ния методов последовательноrо декодирования имели одной из
своих rлавных целей практическую реализаЦИIО теоремы Шеи-
нона Д.ля канала с шумами [2]. При доказательстве теоремы ко-
дирования Шеннон и rаллаrер [3] использовали деI{одированис
по максимуму правдоподобия. Алrоритм декодирования по мак-
симуму правдоподобия применительно к сверточным кодам
предложен Витерби [4]. Однако при декодировании по макси-
муму правдоподобия сложность устройств с увеличением длины
кода растет экспоненциально. Достоинством методов последо-
вательноrо декодирования является то, что они требуют для
своей реализации приемлемоrо по стоимости оборудования и
при этом позволяют достичь приблизительно той же вероятно-
сти ошибки, что и методы оптимальноrо декодирования ПО мак-
симуму правдоподобия, стоимость реализации которых является
очень высокой. Это связано с тем, что при последовательном де-
кодировании число операций, которые должен выполнить деко-
дер для Toro, чтобы декодировать один символ, изменяется в
зависимости от уровня шумов в канале. Число операций при
последовательном декодировании является функцией скорости
передачи и шумов в канале. При всех скоростях передачи, мень-
ших определенной скорости Rвы,' среднее число операций при
декодировании оказывается небольшим. Последовательный дe
кодер состоит из лоrической схемы, позволяющей проводить вы-
ч
сления со средней СКОРОСТЬЮ t в несколько раз большей ско-
//. Последовательное декодирование
299
рости Ilередачи символов, и буферноrо заПОМИllающеrо устрой-
ства, предназначенноrо для хранения поступающих данных при
повышении уровня шумов в канале. В случае если число воз
никших В канале ошибок превысит корректирующую способ-
ность кода, при последовательном декодировании и друrих Me
тодах декодирования MorYT возникать ошибки. Однако при по-
следовательном декодировании ошибки MorYT возникать также
и из
за Toro, что оказываются занятыми все ячейки памяти бу-
ферноrо запоминаIощеrо устройства, т. е., друrими словами, из
за
переполнения буфера. Конечно, если вероятность возникновения
ошибки из
за переполнения буфера оказывается значительно
болыпе, чем вероятность возникновения ошибки из
за невоз
можности исправить или обнаружить ошибку, то именно она и
будет определять характеристики алrоритма последовательноrо
декодирования.
Число операций, необходимых для деКОДИР9вания одноrо
символа, при последовательном декодировании является слу-
чайной величиной, и поэтому важным методом анализа последо
вательноrо декодирования является метод, использованный rал
Лаrером [3], а также Шенноном, rаллаrером и Берлекэмпом [5]
для получения rраницы случайноrо кодирования. Однако даже
при использовании этоrо эффективноrо метода провести пол
ный теоретический анализ не удается, и поэтому важным Me
тодом анализа последовательноrо декодирования остается ero
моделирование.
6.1. Древовидные коды и принцип последовательноrо
декодирования
6.1.1. Древовидные коды
Рассмотрим кодер сверточноrо кода, схема KOToporo изобра.
жена на фиr. 6.1. Последовате.ТIЬНОСТЬ информационных симво-
лов поступает в реrистр сдвиrа, состоящий из пяти ячеек; сдвиr
реrистра производится со скоростью R бит/с. Через каждые I/R с
на выход кодера поступают два символа, один из которых яв-
ляется информационным, а второй
проверочным. Каждый
проверочный символ в данном случае является суммой по мо-
дулю 2 текущеrо и пяти предыдущих информационны.х симво-
лов.
Одним из способов представления сверточных кодов являет
ся представление их в виде кодовых деревьев. На фиr. 6.2 НО-
казано кодовое дерево сверточноrо кода, порождаемоrо описан-
ным выше кодером. Символы (i j , Cj), показанные на этом дe
реве, ЯВЛЯIОТСЯ соответственно информационным и проверочным
//. Последовательное декодирование
301
символами на выходе кодера в момент времени j. Верхнее реб..
ро, выходящее 113 каждоrо узла на фиr. 6.2, соответствует зна
чению О информационноrо символа, а нижнее ребро
значе-
нию 1. Если последовательность информационных символов за
дана, то полностью определенными оказываются и проверочные
символыI' и, следовательно, они MorYT быть указаны на соответ-
ствующих ребрах вместе с информационными символами.
Структура древовидноrо кода такова, что каждой передаваемой
информационной последовательности соответствует определен-
ный путь на кодовом дереве.
Рассмотрим кодер, схема KOToporo изображена на фиr. 6.3.
Этот кодер построен таким образом, что после Toro как первый
информационный символ поступит в верхний реrистр сдвиrа,
а второй информационный символ
в нижний реrистр сдвиrа,
с помощью трех сумматоров по МОДУЛIО 2 формируются три сим-
вола канала. Каждая последующая пара информационных сим-
волов также направляется в верхний и нижний ретистры сдвиrа,
после чеrо осуществляется вычисление очередных выходных
символов. В данном случае каждым двум информационным сим-
волам сопоставляются три символа канала и, следовательно,
рассматриваемый код имеет скорость R == 2/3. Так как каждый
информационный символ оказывает влияние на 12 последую-
щих выходных символов, то кодовое оrраничение этоrо кода
равно 12.
Аналоrично, используя ko m
разрядных реrистров сдвиrа и
по сумматоров, мо)кно построить кодер кода со скоростью R ==
== ko/no и кодовым оrраничением ПА == по (т + 1). в двоичном
случае из каждоrо узла кодовоrо дерева, соответствующеrо та-
кому коду, выходит 2 k \J ребер, каждому из которых сопостав-
лено по двоичных символов. Кодовое дерево кода, кодер кото-
poro изображен на фиr. 6.3, показано на фиr. 6.4. Коды, пред-
ставляемые в виде кодовоrо дерева, называIОТСЯ древовидными.
Вообще rоворя, древовидными кодами MorYT быть названы
произвольные коды, имеющие древовидную структуру, подоб
ную показанной на фиr. 6.2 или фиr. 6.4. При таком широком
определении древовидных кодов коды, порождаемые сверточны
ми кодерами, ЯВЛЯIОТСЯ лишь подмножеством множества древо"
видных кодов.
6.1.2. Принцип последовательноrо декодирования
Предположим, что задан некоторый древовидный код и по..
пытаемся по принятой последовательности определить переда-
вавшуюся последовательность. Для этоrо сначала будем пере-
двиrаться поочередно вдоль каждоrо пути кодовоrо дерева,
сравнивая I1рИНЯТУIО последовательность с последовательностью,
302
fлава 6
соответствующей пути, по которому мы ДВИiкемся. Если при
этом удается обнаружить некоторый путь, которому COOTBeT
е
ствует последовательность, почти совпадаlощая с принятои по
следовательностью, то естественно считать, что эта последова-
тельность и передавалась. Метод декодирования, предложенный
Возенкрафтом, предусматривает вначале поиск на кодовом де-
реве пути из (т + 1) ro ребра, соотвеТСТВУlощая которому ко-
довая последовательность находится на KaKOM TO определенном
расстоянии от переданной последовательности, и далее декоди
рование первоrо информационноrо си:vrво.па (первым передан-
О К О 01
10
1
000
000 101
110
101 111
000 .
110
.
111
.
110
.
010
101 .
000
.
101
..... .
111
.
010
110 .
001
100 .
с
001
.
100
111 110 ,
с
010
. . . .
.
Фиr. 6.4. Пример древовидноrо кода скоростью R 2/3.
.
ным информационным символом считается первый ИНфОРf\.fаци
онный символ первоrо ребра найденноrо пути). Посколы{у далее
декодирование BToporo и последующих информационных симво
лов осуществляется точно так же, как и первоrо информаuион-
Horo символа, то этот алrоритм был назван алrоритмом после..
довательноrо декодирования.
Одним из критериев близости пути на кодовом дереве к при-
нятой последовательности является расстояние Хэмминrа ме-
жду ними; если расстояние Хэмминrа между последователы-I
стями длины n не превышает определенный пороr [n, то после
довательности можно считать совпадающими. В случае двоич-
Horo симметричноrо канала пороr [n выбирается таким обра-
зом, чтобы вероятность Toro, что расстояние ХЭММИIн'а ме,кду
Т/. Последовательное декодирование
303
передававшейся и принятой последовательностями было больше
чем [n, не преВЫlпала величины 2 L, rде L некоторая задан
ная постоянная. При этом вероятность Toro, что расстояние ХЭМ-
минrа между правильным путем дерева и принятой последова-
тельностью больше чем [n, при больших L оказывается чрезвы-
чайно малой.
Предположим, что этот метод декодирования используется
в двоичном симметричном канале с вероятностью перехода р.
Тоrда, поскольку в этом случае в канале ошибки в различных
символах возникают независимо с вероятностью перехода р, то
расстояние Хэмминrа, вычисляемое вдоль правильноrо пути, как
показано на фиr. 6.5, почти всеrда будет возрастать со ско-
ростью р вместе с числом обработанных символов. В то же время
1
(..)
о...
} Непра6иt1ьныi/
'" путь
" " (НClКI10Н 0,5)
"
",
'" ", Пра8t1l1ьныif пjт6
(НClклон Р)
",
'"
"
Число оораоотаннЬ/х абоичных
симболо8 п
Фиr. 6.5. Число декодированных символов и расстояние Хэмминrа ДЛЯ по-
следовательноrо декодера.
расстояние Хэмминrа, вычисляемое вдоль любоrо друrоrо пути
кодовоrо дерева, будет возрастать со скоростью 1 , поскольку
различные пути кодовоrо дерева отличаIОТСЯ друr от друrа при-
близительно в половине символов. Таким образом, расстояния
Хэмминrа, вычисленные вдоль праВИJlьноrо и ошибочноrо пути
кодовоrо дерева, оказываются различными. При этом, даже
если на начальном этапе декодирования путь кодовоrо дерева
был выбран неправильно, то через некоторое время ошибка бу-
дет обнаружена, поиск правильноrо пути будет продолжен и в
конце концов правильный путь будет найден.
Этот алrорит последовательноrо декодирования был обоб-
щен Рейффеном r6] на случай произвольноrо дискретноrо кана-
ла без памяти. Обобщение было сделано путем замены расстоя-
ния Хэмминrа на друrую функцию, являющуюся обобщением
расстояния Хэмминrа.
Дискретный канал без памяти с входным алфавитом из К
символов и выходным алфавитом из J символов определяется
<;овокупностью переходных вероятностей Р (Vj I Ui), i i К,
304
[лава 6
1 j J, rде p(tJjIUi) вероятность Toro, что при передаче
входноrо символа Ui на выходе канала будет принят символ Vj.
Расстояние между путем кодовоrо дерева (т. е. и п == (UI, и2, . . .
. . ., и п ), содержащим п символов, и принятой последователь-
ностью бп == (V}, V2, ..., V n ) определяется равенством
n
" p(V i I"i)
1 (и n . V n ) == IOg2 Q ([/) ,
. 1 i
1.==
(6.1 )
rде
n
Q (Vi) == L QiP (Vi I Ui).
i 1
(6.2)
Величина Q (Vi) представляет собой вероятность появления на
выходе канала символа Vi в случае, если на входе канала сим-
вол Ui появляется с вероятностью Qi, 1 i К. Расстояние,
определяемое формулой (6.1), является количеством информа-
ции между последовательностями й N И дп В случае, коrда пары
(Ui, Vi) статистически независимы и символы Ui на входе канала
появляются с вероятностями Qi, 1 i К. Если правую часть
(6.1) представить в виде JIоrарифма произведенин, то можно за
метить, что величина I(й n , дn) определяется вероятностью
р (бп I й n ), которая в случае двоичноrо симметричноrо канала яв
ляется монотонно убывающей функцией расстояния Хэмминrа
между последовательностями й N И б n . Следовательно, в случае
двоичноrо симме-rричноrо канала введенное выше расстояние
эквивалентно расстоянию Хэмминrа. Однако поскольку в случае
произвольноrо дискретноrо канала без памяти введенная функ-
ция не может быть интерпретирована в терминах расстояния
Хэмминrа, то будем называть ее в дальнейшем ценой пути.
Алrоритм последовательноrо декодирования, предложенный
Фано [23], предусматривает вычисление и использование при дe
кодировании наряду с ценой пути также некоторых пороrов.
Этот алrоритм является алrоритмом Toro же типа, что и алrо-
ритм Возенкрафта, но если среднее число операциЙ, необходи
мых для декодирования одноrо символа, в случае использова
ния алrоритма Возенкрафта при скоростях передачи, меньших
определенной скорости Rвы,' растет как небольшая степень KO
довоrо оrраничения, то для алrоритма Фано это среднее число
в тех же условиях не зависит от длины кодовоrо оrраничения.
Это упрощает анализ алrоритма декодирования Фано. Кроме
Toro, достоинством алrоритма Фано является также то, что он
ДОПУСI{ает более простую техническую реализацию, чем алrо-
ритм Возенкрафта. В силу этоrо приблизительно с 1964 r. ис
следования алrоритмов последовательноrо дек дирования взна
чительной степени были связаны с исследованием алrоритмц
//. Последопательное декодирование
305
Фано. По тем же причинам алrоритм Фано будет детально pac
смотрен в данноЙ книrе. В пос.nедние rоды независимо ДжеJIИ
нек [7] и Зиrанrиров r8] предложили алrоритм последовательноrо
декодирования, часто называемый стек
аЛ20рUТМОМ. Нельзя
сказать, что этот алrоритм во всех отношениях лучше алrо-
ритма Фано, но так как ero описание значительно проще опи-
сания алrоритма Фано и поскольку он хорошо иллюстрирует
принцип последовательноrо декодирования, то этот алrоритм
также будет кратко рассмотрен ни)ке.
6.2. Алrоритм Фано
При декодировании сверточных кодов с помощью алrоритма
Фано точно так же, как и в случае аJIrоритма Возенкрафта, де-
кодер всякий раз вычисляет цену пути для принятой последо
вательности и одноrо из путей на кодовом дереве. В случае, если
найденная цена пути превышает определенный пороr, то ocy
ществляется декодирование очередноrо информационноrо сим
вола. Если же иена пути оказывается ниже пороrа, то декодер
полаrает, что он попал на ошибочный путь, и начинает поиск
правильноrо пути. ОСУIЦествляя декодирование таким образом,
декодер Фано постепенно приближается к правильному пути
кодовоrо дерева, а следовательно, и к правильному декодиро-
ванию информационных символов. Прежде чем перейти к опи
санию алrоритма, рассмотрим, что в данном случае понимается
под ценой пути.
6.2.1. Цена пути
Будем предполаrать, что для каждоrо пути й N на кодовом
дереве декодер может вычислить вероятность р (а n I бп) Toro, что
передавалась последовательность и п при условии, что принята
последовательность и n . Здесь а п И б п
последовательности
длины п:
й п == (иl, и2, ..., и n ),
б п == (v J, V2, . · ., V n ).
РаССl\fОТРИМ а.пrоритм, который, сравнивая эту вероятность
Р (Й п I й n ) с некоторым пороrом, принимает решение о том, яв-
ляется ли данная ветвь правильной или неправильной. Вероят-
ность р (й n I б n ) можно представить в следующем виде:
(
I
)
Р (й п , б п )
Q (й п ) Р (д п I й п ) (6. 4)
Р а п v n
Q (й n )
Q (й n ) ·
Если предположить, что капал является каналом без памяти, то
(6.3)
'1
Р (Й п I й n ) == П Р (Vll Ul).
. 1==-=1
(6.5)
306
rлава 6
Для простоты рассмотрим случай двоичных кодов и, кроме Toro,
предположим, что все пути кодовоrо дерева порождаются с рав-
ными вероятностями. В этом случае
Q (й п ) == 2 Rп,
rде R скорость передачи, выраженная в битах на символ ка-
нала. Таким образом,
n
( I ) == 2 Rп П Р (v i I U i )
Р и п V п Q (v.) ·
i == I t
Если взять лоrарифм обеих частей равенства (6.6), то получим
(6.6)
[ Р (v i I U i ) ]
log р (и n I v n ) == log Q (v i ) R ==
п
== L log Р (v i I U i ) nR. (6.7)
i==1 Q (v i )
Заметим, что сумма по i в правой части этоrо равенства яв
ляется взаимной информацией 1 (й n , йn) между последователь-
€
ПраВtlльныil
путь} искаженный
ШУМОМ
::::r
Непра8И17ЬНЬlU путь
])0
Чис//о 05ра50танных 060Jll/HbIX Сtlмбо//о8 п
Фиr. 6.6. Изменение цен путей для алrоритма Фано.
ностями й n И б n . Следовательно, при ПОДХОДЯlцем выборе ско-
рости передачи R среднее значение (6.7) для правильноrо пути
будет положительным, а для неправильноrо пути отрицатель-
ным. Более Toro, вдоль правильноrо пути это среднее значе-
ние (6.7) является возрастающей функцией n. Поэтому в общем
случае определим цену пути следующим образом:
'У(Й п , vn)==I(u n , дn).......nи, (6.8)
11. Последовательное декодирование
307
rде U
коэффиuиент сноса, который будет определен ниже.
В качестве HoporOB, с КОТUрЫМИ сравниваются цены путей, pac
смотрим совокупность прямых, парал.JIельных оси абсцисс и рас-
положенных друr от друrа на расстоянии Do (эта совокупность
noporoB удобна с точки зрения практической реализации алrо-
ритма). flри подходящем выборе величины и цены правильноrо
и неправильноrо путей изменяются обычно так, как показано на
фиr. 6.6. Рассматриваемый здесь алrоритм Фано в конце концов
позволяет найти путь кодовоrо дерева, вдоль KOToporo цена пути
возрастает. Поскольку при этом неправильные пути, вдоль KO
торых цена пути в течение длительноrо промежутка времени
постоянно возрастает, встречаются очень редко, то оказывается
очень БОJIЬШОЙ вероятность Toro, что путь кодовоrо дерева, вдоль
KOToporo цена пути возрастает, определяет переданную последо-
вательность.
6.2.2. Поведение декодера
Решение о том, возрастает или не возрастает цена пути, дe
кодер принимает, проводя сравнение цены пути с пороrом. При
этом в каждом узле кодовоrо дерева декодер упорядочивает у
ребер, выходящих из этоrо узла, в порядке приращения цены
пути вдоль этих ребер. Декодер может находиться в слеДУIОЩИХ
состояниях:
1. «Смотри вперед» (СВ).
Находясь в этом состоянии, декодер считает, что путь й N ,
ведущий к узлу, в котором он находится в настоящий момент,
является правильным, и принимает решение о переходе к пути
Un+l, получающемуся присоединением к а n следующеrо ребра 1).
11. «Смотри назад» (СН).
Декодер считает, что правильным является префикс ат ИЗ
некоторых т первых ребер пути й n , и принимает решение про
должить поиск правильноrо пути среди друrих путей, являю
щихся продолжением И т .
ТеКУпtее значение пороrа в состоянии СВ выбирается непо
средственно под текущим значением у (и n , б n ). Предположим,
что декодер ДОСТИI" HeKoToporo узла, которому соответствует
путь u'rt на кодовом дереве, и находится в состоянии СВ. В этом
узле декодер выбирает первое по порядку ребро (как указыва
лось выше, ребра упорядочены), вычисляет приращение цены
пути вдоль этоrо ребра и смотрит, превышает ли цена пути
(пути, включаlощеrо присоединенное ребро) текущий пороr.
Если иена пути, включающеrо присоединенное ребро, превы-
1) Здесь индекс п обозначает ЧИСJIО ребер, составляющих путь, а не число
симuолов, как в (6.1).
П рим. ред.
308
r лава 6
шает текущий пороr, то проведенное обследование считается
удачным и декодер переходит вдоль этоrо ребра в новыЙ узел.
При этом присоединенное ребро записывается в память деко-
дера, а пороr с шаrом Do поднимается вверх до максимально
возможной величины, меньшей, чем цена пути с присоединенным
ребром. Далее, точно так же деI{одер выбирает одно из ребер,
являющихся продолжением ребра, присоединенноrо на преды..
дущем шаrе, сравнивает новую цену пути t:, пороrом, и если эта
новая цена пути превышает пороr, то новое ребро считается
правильным и декодер переходит к обследованию последующих
ребер. До тех пор пока цены исследуемых путей не опускаются
ниже соответствующих пороrов, декодер движется вперед по
дереву.
Предположим, что декодер в состоянии СВ обнаружил, что
цена пути, вычисленная вдоль ребра, выходящеrо из HeKoToporo
(п + 1) ro узла, лежит ниже текущеrо пороrа. В этом случае
декодер принимает решение о том, что он оказался на невер-
ном пути, и переходит в состояние СН. При этом декодер тем
не менее считает правильным путь до «caMoro cTaporo» узла т,
цена пути в котором еще лежит выше текущеrо значения по-
pora. Последнее значение пороrа фиксируется, и декодер пы
u u u
тается наити друrои путь, ПРОХОДЯIЦИИ через узел т, но лежа
щий выше фиксированноrо значения пороrа. Для этоrо декодер
сначала возвращается из узла, в котором он перешел в состоя-
ние СН, на одно ребро назад и осуществляет поиск друrоrо
ребра, лежащеrо выше замороженноrо пороrа. Если такое реб-
ро удается найти, то декодер ВОЗВРqщается в состояние СВ и
начинает вновь двиrаться вперед. Если указанное ребро обиа-
ружить не удается, то декодер возвращается из (п + 1) -ro узла
на два ребра назад и вновь пытается найти путь, лежащий
выше фиксированноrо пороrа. При неблаrоприятных условиях
декодер може.т вернуться в узел т, так и не найдя пути, про
ходящеrо через узел m и лежащеrо выше фиксированноrо по-
pora. В этом случае декодер вновь переходит в узел n + 1, сни-
жает значение пороrа на Do, переходит в состояние СВ и пы-
тается продвинуться вперед при пониженном пороrе. Если все
ребра, выходящие из узла n + 1, пересекают это новое значение
nopora, то декодер повторяет указанные выше действия с этим
новым фиксированным пороrом. Будем считать, что, выполняя
достаточно большое число раз указанные выше действия, деко-
u u
дер в конце концов наидет правильныи путь.
Фиr. 6.7 иллюстрирует описанный выше алrоритм. Рассмот-
рим изменение величины V (й n , и n ) при движении слева направо.
Так как вначале величина у(й n , иn) возрастает, то декодер На-
ходится в состоянии СВ и считает пройденный путь правильным.
В узле (1) знач ние V(u n , д n ) несколько уменынается, но тем не
//. последовательное декодирование
309
менее оказывается выше пороrа и декодер остается в состоя-
нии СВ. Однако в узле (2) значение V(U n , й n ) становится MeHЬ
ше текущеrо значения пороrа, paBHoro 3Do. Декодер переХОДll [
в состояние СН, но путь до caMoro левоrо узла, лежашеrо выlеe
Toro пороrа [т. е. узла (3)] считает правильным. Вначале дe
кодер возвращается из узла (2) в узел (4) и начинает поиск
правильноrо пути из этоrо узла, но ни одно ребро, ВЫХОДЯlцее
из узла (4), не лежит выше пороrа. Декодер возвращается в
узел (3') и продолжает поиск из этоrо узла. Путь, оканчиваIО
щийся в узле (5), оказывается лежащим выше пороrа, и дeKO
дер переходит в состояние СВ. Однако в узле (6) цена пути
вновь оказывается ниже пороrа, декодер возвращается в состоя
иие СН, но путь до узла (3) по прежнему считает праВИЛЬНЫl\'I.
I r::
...
l';:;;sfl:
::::r
Чuс//о оораоотанны.1 880ИЧНЫХ СИМВО/lОВ. п
Фиr. 6.7. ПрН:\lер к описанию а.тrrоритма ФаIlО.
После Toro как становится ясным, что все пути, выходящие из
узла (3), пересекают пороr 3Do, декодер возвращается в узел (2),
понижает пороr до веJlИЧИНЫ 2Do и возвращается в состонние
СВ. Выполняя последние операции, декодер предполаrает, что
в окрестности узла (2) возникли сильные шумы, в результате
чеrо правильный путь оказался похожим на неправильные пути.
В этой ситуации декодер пытается найти путь, выходящий из
узла (2) и лежащий выше пороrа 2Do. Если, выполняя про
цедуру, аналоrичную описанной выше, декодер не находит узла,
лежащеrо выше пороrа 2Do, то он понижает пороr до величи
ны Do, переходит в состояние СВ и начинает движение вперед
из узла (7).
На фиr. 6.8 показана лоrическая блок схема алrоритма Фано.
Смысл операций СВ, СН, «переход вперед в просмотревный
узел», «возвращение назад в просмотренный узел», «увеличе
ние пороrа», «понижеllие пороrа» ДОЛiкен быть понятен из при..
веденноrо выше описания алrоритма. Так как в каждом узле
ребра упорядочены в соответствии с прираUlением вдоль них
цены пути, то ясными оказываIОТСЯ и операции «выбор первоrо
310
rлава 6
Декооер ч(/хоrJllтСfI 8
!/СI'lClЛЫ/О1J1 УЗJfе(порoz=О/
УбеЛtl'lеНllе ,
110РОёа
Дa
'1'
РеОро IIClk";1bЗY быOt.7jJ перБОZ{l по
етСfI dлерdые?Нет ЛОРJ1JI(У рш5ра
l' YrJo'llloe ООСl1еио НеУОСТ'lное
f1ejJeJoи dпе/lеи 8 OOIl e Смотри оослеgоdаНllе
просмотрен бпереtJ (СВ)
ный узе/!
It
I
I
;:s; "
c:::s
ВЫО0Р С/lеuующе о
!!.Е3!ряо/(у реорст Отсутст6ие
реора
!70Н/lжt'НIlt'
пОрОёll
I
HtyoCl'lHOe
o c/leJ(J8oHl/e
СмотРII
HCl3ClU (СН)
УQClчное
ООС/lеQобаНJlС
ВозdjJllЩfNuе
нtlJCltJ 6 Лр(JС
lttотреННЫIi YJfA
Фиr. 6.8. Лоrическая схема алrоритма Фа но.
У6е//JlЧСНJlе
nОрО2а
ПО/lО
жить
р=о
Да
ЗНQчение
межrJу п
и IJ+IJ o ?
Нет
Выоор пер6020
по лоgж}к.У
РСЬИl
Неуdl1чное
ООС'l1еоо-
Смотр" 811НйС ЛО//О
BпepetJ 71'/'{6
Р=D
Р=1
Oтcyтcт#lI(
р!оди
ЛОН/I)Кt'Нllе
пOpO fl
f/еуоtlчное
ot5Cl!eOOdClN/I
Смотр"
6перео
пO/lO tl
ЖJlт6 3Н(lчеНJlС'
р=о меж#у ]}
и II t- ло?
.
"'s
s::::
-..;::
..
.
СЗ
Нет
Фиr. 6.9. Лоrическая схема аЛl'оритма Фано (с функцией Р).
//. Последовательное декодирование
311
по порядку ребра» и «выбор слеДУЮLuеrо по порядку ребра».
Наличие вопроса «ребро используется впервые?» связано с He
обходимостью фиксировать пороr в состоянии СН и предотвра
тить остановку алrоритма из
за зацикливания. Фано предложил
ориrинальный способ получения ответа на этот вопрос, который
иллюстрируется на фиr 6.9. .
Функция Р определяется таким образом, что Р == 1 в состоя-
нии СН и р == О в остальных случаях. Если Р == О, то любой
путь, не пересека ющий текущее зна чение пороrа, исследуется
впервые. В случае Р == 1 декодер впервые переходит узел в
следующих случаях:
1) После продвижения вперед цена пути оказывается лежа
щей между текущим значением пороrа D и величиноЙ D + Do,
например в приведенном выше примере при переходе из узла (3')
в узел (5).
2) Декодер возвращается назад к некоторому пути, цена KO
ct
Toporo лежит между текущим значением пороrа и величинои
D + Do. Так, в приведенном выше примере при переходе в
узел (7) цена пути оказывается лежаll
ей ниже пороrа 2Do, дe
кодер возвращается в узел (2) и начинает поиск друrоrо пути.
Не наЙдя пути, исходящеrо из узла (2), декодер продолжает
поиск из узла (4). Если и в этом случае ПОИСJ{ также оказы
вается безуспешным, декодер начинает поиск из узла (3'). Путь
из узла (3) в узел (5) уже исследовался раньше, и это леrк()
обнаружить, поскольку цена пути в узле (5) лежит между зна
чениями пороrа 3Do и 4Do, а не 2Do и 3Оо.
Путь с узлом (7) не может быть достиrнут при значении
пороrа D + Do, и, следовательно, он является новым. При пе
реходе в Hero значение Р изменяется с 1 на о.
6.3. Среднее число операций при декодировании
6.3.1. Среднее число операций
При последовательном декодировании с помощью а.пrоритма
Фано среднее число операций при декодировании является слу-
чайной величиной, зависящей от принятой последовательности,
подверrшеЙся воздействию шумов в канале, переданной инфор
мационной последовательности и сверточноrо кода. В силу
этоrо определение среднеrо числа операций для HeKoToporo за
данноrо кода является очень трудной задачей. Олнако с по
МОЩЫО rраницы случайноrо кодирования Сэвад}ку [9, 10] уда-
лось получить rраницу для среднеrо по некоторому ансамблю
кодов числа операциЙ при декодироваНfI И .
312
r лава 6
Уточним сначала ряд терминов. Путь на кодовом дереве, со-
ответствующий переданной информационной последовательно-
сти, будем называть правильным путем. Пути, начинающиеся в
узлах правильноrо пути, но отличающиеся от правильноrо пути,
будем называть неправилыlмии путями. Совокупность непра-
вильных путей, начинающихся в X OM узле правильноrо пути,
назовем X ЫM подмножеством неправильных путей. На фиr. 6.10
показано 2 e подмножество неправильных путей.
00
k 01
1'1 10
000
000 101
101
101 111
000 .
110
.
111
.
/11 О" / / / / / / / / /
/ .
010 Непр.
101 / . пр;м.
/ 000
11 a1т: ;;;;
... 111 nym/J
.
010
110 .
ОО1
о
1ОО
.
001
.
10а
111 .
11О
.
010
...................
'tl6I1/1IJHOf
'Н{JЖfстlи (' х =2
'IIHIJlli
. . .
.
Фиr. 6.10. Неправильное подмножество с х == 2.
Вывод rраницы для среднеrо числа операций условно моя{но
разделить на две части. Сначала в предположении, что де колер
достиr x ro узла правильноrо пути, находится верхняя rраница
для среднеrо числа операций, выполняемых декодером при ДВИ
жении из x ro узла по правильному пути и подмножеству He
правильных путей. Далее с помощью rраницы случайноrо КО-
о u
дирования находится rраница для среднеrо числа операции.
Каждый путь в X M подмножестве неправильных путей OДHO
значно определяется двумя числами: числом t, показывающим
ero длину в ребрах, и числом т, показываIОIЦИМ ero положение
среди путей той же длиныI. Если число ребер, выходящих из
каждоrо узла кодовоrо дерева, обозначить через у, то число пу-
Т 'Й длины t и менее 't(t), содержащихс.:я в X M подмножестц
11. Последовательное декодирование
31з
неправильных llутей, будет определяться равенством
{ (у....... l)yt l, t 1,
't' (t) 1 t == О
(равенство t (О) == 1 принято для удобства).
Ниже для простоты будем предполаrать, что х === 1. Пусть
U t , т....... путь, задаваемый парой целых чисел (t, т); и пра
вильный путь длины w ребер; V t принятая последователь
ность длины t ребер. Допустим, что текущее значение пороrа
декодера равно jDo. Тоrда если V(U t , т, V t ) < jDo, то декодер
достичь пути (t, т) не может. Попытаемся найти среднее число
операций, выполняемых декодером на пути (t, т) в случае, если
V(Ut,m, V t ) jDo.
1) Если декодер достиr пути (t, т) впервые, то он нахо-
дится в состоянии СВ, и для Toro, чтобы пройти одно следую
щее ребро, он должен выполнить одну операцию.
2) Допустим, что двоичная переменная Р алrоритма Фано
равна 1 и декодер при поиске коrда то возвращается к пути
(t, т). В силу Toro что Р == 1, декодер не может вторично вы-
брать ребро, указанное в п. 1, и пытается найти какое либо дpy
roe ребро, чтобы пройти вперед. Если этот поиск оканчивается
неудачно, то декодер возвращается в узел, предшествующий
началу (t, т). Следовательно, при значении пороrа jDo и усло
вии, что V(Ut,m, V t ) jDo, на пути (t,m) декодер может вы-
полнить самое большое (у + 1) операций.
Далее, для Toro чтобы получить оценку сверху для числа
операций с, рассмотрим необходимые условия достижения пути
(t, т). Пусть r минимальная цена правильноrо пути, а именно
r==minv(U , v w ), (6.10)
o w
(6.9)
и пусть Dr значение пороrа, лежащее непосредственно под
ценой r. Необходимым условием дости}кения пути (t, т) яв-
ляется выполнение следующеrо неравенства:
V(Ut,m, Vt) (r+jDo) O. (6.11)
Действительно:
1) в случае j 1 путь (t, т) может быть достиrнут при зна-
чении пороrа jDo;
2) .если j == О, то V(U t , т, V t ) r Dr и путь (t, т) мо-
жет быть достиrнут при значении пороrа Dr;
3) так как при j== l V(Ut,m, V t » r Do и r Do:ii!!:Dr,
то V(U t . т, V t ) > 1"" Do > D 1 , И путь (t, т) может быть до-
стиrнут при значении пороrа r Do.
Таким образом, путь (t, т) может быть достиrнут только
при значениях I1opora r + jDo, j 1.
314
rлава 6
Величины t и т, определяющие путь (t, т), MorYT принимать
значения соответственно от О до 00 и от 1 до t(t). Таким обра
зом, вводя ступенчатую функцию
{ 1, x O,
W (х) О, х < О,
( 6.12)
число операций с можно оценить сверху следующим образом:
00 00 't (t)
С (у + 1) L: L: L: w [)' (U t . т, V t ) r...... jD o ]. (6.13)
jC8 1 t==o m==l
Далее оценим сверху правую часть (6.13). Величина r, со-
rласно формуле (6.10), определяется равенством
r == min V (и:, V w)'
O w
(6.14)
т. е. r является значением V (и , V w) при некотором W == О,
1, ..., 00. Так как W (х) является ступенчатой функцией, при-
нимающей значения О и 1, то среди значений W'rV(U t . т' V t )....
......)' (и , V w) ...... jD o ]' w ==0, 1, . . . , 00, содержится и W[y (U t , т, V t )
......... r jD o ]. Таким образом, для с получаем следующую оценку:
00 00 00 't (t)
c (y+ 1) L: L L L: \V[V(Ut,m, Vt) V(U , Vw)......jDo].
j 1 w=-I t==O m==l
(6.15)
Аналоrичную оценку можно получить для произвольноrо
х 1, если несколько изменить определения величин
V(Ut,m,V t ), V(U , V ) И др. Действительно, пусть vх значе
ние правильноrо пути из х первых ребер, V (U t , т, V t ) значе-
ние пути из t последних ребер пути (t, т), входящеrо в x e под-
множество неправильных путей. Тоrда 'Ух + V (U t , т, V t ) ......... пол-
ная цена этоrо пути. Пусть V (и , V w) цена пути из W послед-
них ребер правильноrо пути длины х......... 1 + r ребер. Тоrда V х +
+ V (и , V w) ...... полная цена правильноrо пути. Следовательно?
число операций, выполняемых декодером на пути (t, т), входя
щем в x e подмно}кество неправильных путей, зависит от цены
'Ух + 'у (U t , т, V t ) и минимальной цены правильноrо пути 'Ух + r.
rде r == min V (и:, V w). Однако так как 'Ух + 'Y(U t , т, V t ) 'Yx
w O
r == V(U t , т, V t ) f, то, используя опред ленные вышеука-
занным образом величины у (U t , т, V t ) и v (и Ц!," V rv)' можно до-
казать справедливость соотношения (6.13) и для x ro подмно..
жества непраВИJlЬНЫХ путей.
/1. П оследоватеЛhное декодирование
315
6.3.2. Свойство независимости в древовидном коде
На слеДУIощем этапе вывода верхней rраницы для среднеrо
числа операций при декодировании используется метод случай
Horo кодирования и проводится усреднение (6.15) по ансамблю
кодов, шумам в канале и информационным последовательно
стям. Чтобы можно было применить метод случаЙноrо кодиро
вания, потребуется ансамбль древовидных кодов, обладающий
слеДУЮll
ИМИ свойствами:
1. Кодовые слова, или, точнее, символы ребер, принадлежа
щих различным путям кодовоrо дерева, должны быть статисти
чески независимыми. А именно для любых двух путей U 1 и и 2
должно выполняться равенство
Q(U I , U 2 )===Q(U I ) Q(U 2 }.
11. Символы канала каждоrо кодовоrо слова должны быть
статистически независимыми. А именно для любой кодовой по
следовательности И п == (UI, и2, ..., и п ) длины n должно BЫ
полняться равенство
Q (и n) === Q (UI) Q (и2) · . . Q (и п ).
Приведенная несколько ниже лемма, принадлежащая rалла-
repy [11], дает метод построения ансамбля древовидных кодов,
обладающих указанными выше свойствами.
Пусть а....... некоторое целое число; рассмотрим двоичный
сверточный кодер с ko входами и аnо выхода ми. Пусть i
l), ...,
.(ko). [ '(I) l .(k
). И t (l) ' (апо). / (1) ' (апо). .......
lo, ],..., 1 ,... о ' .. ., О' l' .. ., 1 ,...
последовательности символов соответственно на входах и BЫXO
дах этоrо кодера. Соrласно формуле (5.14), входные и BЫXOД
ные символы сверточноrо кодера связаны между собой следую
щим соотношением:
т kl)
t(i) == L L gЧ) i(f) .
u 1s:=0 j=z:1 (t) u
l
( 6.16)
в целях упрощения далее будем считать т равным бесконеч
ности. Выходную последовательность кодера сложим с произ-
вольной двоичной последовательностью Z === zы), ..., zъ апо ); z
l), ...,
z
ano); ... и построим таким образом последовательность
t (I) m Z (1) t (ano) ffi Z (ano). t (l) ffi Z (l) [ (апо) ffi Z (ano) Эту
о Q] о ' · · · , о w О' 1 W I ' .. ., 1 Q7 1 ·
последовате,,1ЬНОСТЬ разобьем на блоки по а двоичных сим-
волов, и каждый из полученных блоков будем передавать по
каналу с помощью одноrо из ero символов. Вероятность появ-
ления на входе канала k
ro символа канала обозначим через
Qk. В данном случае ПО символов канала порождаются ko двоич-
316
fлавй 6
ными информационными символами, и, следовательно, рассмат-
риваемый код имеет скорость передачи R == ko/пo.
ПреДПОЛОЖИ 'I, что параметры k o , по и а, а также COOTBeT
ствие между двоичными последовательностями длины а и сим-
волами канала заданы. Рассмотрим ансамбль кодов, который
получается в ТОМ случае, если все коэффициенты g H, ( в фор-
муле (6.16) и все компоненты последовательности z являются
независимыми ДВОИЧНЫl\'IИ случайными величинами, принимаю-
щими значения О и 1 с равными вероятностями.
Лемма 6.1. (rаллаrер.) в рассмотренном выше ансамбле ко-
дов кодовая последовательность ис\о , . . ., u ko); и l), . . ., ll koJ; ...,
соответствующая произвольной, но заданной информа-
ционной последовательности, является случаЙной после-
довательностью, символы которой являются независиМ,ыМ,u слу-
чайными величинами, nрuнимающими значение k с вероятностью
qk, k === 1, ..., К. Если информационные последовательности I
и }' совпадают лишь в первых Ь 1 блоках, то соответствую-
щие им кодовые последовательности также совпада/от в первых
Ь 1 блоках, а символы остальных блоков этих кодовых после-
довательностей являются статистическu незавuсuмыМ,u.
)10казательство. Так как последовательность Z является по-
ct
следовательностью независимых двоичных случаиных величин,
принимающих значения О и 1 с равными вероятностями, то при
произвольной фиксированной последовательности на выходе
двоичноrо сверточноrо кодера последовательность Т ЕВ z также
ct
является последовательностью независимых двоичных случаи-
ных величин, принимающих значения О и 1 с равными вероятно-
стями. В силу ЭТОFО кодовая последовательность на входе ка-
нала представляет собой последовательность независимыхсим
волов канала, k й из которых имеет вероятность Qh, k == 1, ...
. . ., К.
Далее, пусть 1 и [' информационные последовательности,
символы которых начинают различаться лишь в b M блоке. Если
т и Т' соответствующие им последовательности на выходе
двоичноrо сверточноrо кодера, то Т" == Т' ЕВ т выходная по-
ct
с.педова тельность кодера, соответствующая входнои последова
тельности [" == [' Е9 [. Так как первые Ь 1 блоков последо
вательности }" нулевые, то нулевыми являются также и первые
Ь 1 блоков последовательности Т". Если только при некото-
ром значении j, например j', имеет место равенство iV') == 1, то
для произвольноrо u Ь
'1 /lll
[" (l) == gU') + 2: g(j) i" и) + L: L: g(f) i". (6 17)
и (l), (и....Ь} '+/' (l). (u b) (Ь) l..b+\ /--1 (О, (n o 1 ·
11. Последовательное декодирование
317
Так как gH;
(и
Ь) ...... случайные величины, статистически незави
сящие от друrих веJIИЧИН gИ
, 1 и принимающие значения О и 1
с равными вероятностями, то символы t; (О также оказывают
ся двоичными случайными величинами, принимающими значе
ния О и 1 с равными вероятностями. Более Toro, так как при
i =1= i' случайные величины t
(О И gH;
(u
b) статистически неза
висимы, то статистически независимыми являются величины
t; (О и '; (i) при всех s < и. Следовательно, все блоки после
довательности Т", за исключением первых Ь
1, являются ста-
тистически независимыми, принимающими с равными вероят-
ностями все возможные значения. Таким образом, символы по
следовательностей Т ЕВ z и т' ЕВ Z, за исключением символов
первых Ь
1 блоков, статистически независимы. Отсюда в
свою очередь следует, что символы последовательностей Т и Т',
за исключением символов первых Ь
1 блоков, также ЯВЛЯIОТ-
ся независимыми.
Выше в целях упрощения предполаrалось, что кодовое orpa
ничение имеет бесконечно большие значения. Поскольку KOДO
вое оrраничение сверточных кодов, порождаемых реальными KO
дерами, является конечным, то из
за этоrо, как описывается в
следующем разделе, MorYT возникать необнаруживаемые ошиб
ки. Однако при определении среднеrо числа операций предполо-
жение о бесконечности кодовоrо оrраничения позволяет упро
стить анализ, проводимый методом случайноrо кодирования, и,
как будет показано ниже, получить для алrоритма Фано верх-
ct
нюю rраницу для среднеrо числа операции, не зависящую от
длины кодовоrо оrраничения ПА. ЭТО показывает целесообраз
ность предположения о бесконечности кодовоrо оrраничения
ct
при анализе среднеrо числа операции.
6.3.3. Верхняя rраница для среднеrо числа операций
В этом разделе оценку среднеrо числа операций, задавае-
мую формулой (6.15), усредним по ансамблю кодов, обладаю
щих указанными выше свойствами. Для этоrо нам понадобит
ся следующее неравенство Чернова, которое позволяет оценить
сверху ступенчатую функцию W (х) с помощью экспоненциаль
ной функции (фиr. 6.11)
W (х) < e
X, л
о. (6.18)
Здесь докажем следующую теорему.
Теорема 6.1. (Сэвадж.) В дискретном канале без памяти
при ttспО,llьзованuи аЛсОрUТА1Q Фана среднее по ансамблю кодов
число операций при декодировании (nриходящееся на одно дe
318
r лава 6
кодированное ребро) оеранuчено сверху константой, не завuся
щей от длины кодовоео 02раничения, если ТОЛЬКО и < R выч и
R < И/2 + R выч /2, еде
R выч тах [ \п t ( t qk [р (v ,1 V k )]1/2 ) 2 ] . (6.19)
{qk} j==1 k==1
Доказательство. Подставим (6.18) в (6.15). Тоrда
00 00 00 't (t) [ ( ) ( * ) D ]
c (y+ 1) L L L L еЛ v U t , т' v t v и ш , V w f О. (6.20)
I == 1 ш==о t==O т== 1
,
'-.:.
.........
e X
w(x)
о х
Фиr. 6.11. е ЛХ и w (х).
Так как каждому ребру кодовоrо дерева соответствует ПО сим-
волов канала, то в данном случае
V(Ut,m, Vt) /(Ut,m, Vд tnоU,
у (и:, V w) == 1 (и , V ш) wnou.
Из формул (6.20) (6.22) имеем
00 00 00 't (t) *
С (y+ 1) L L L L е JЛDое tnоUЛеWnоUЛелI (Ut,m' Vt)е Л/ (и ш , V w ).
f== l ш==О t==o m==1
(6.21 )
(6.22)
rде
'Л/ (U t т' V t ) == е (Л/lп 2) ln / (и ! т' V t ) == [ Р (Vt, т I Ut, т) ] Л!lП2
е.. Q (V t) ,
е л/ (и;'. V ш) == е( л/lп 2) In / (и . V w) === [ Q (V w) ] Л/lП?
p(VwIU w )
Суммируя по j в правой части последнеrо неравенства,
получаем
00 00 't (t)
С (у + 1) в L L L e tn.uv ln 2e wn . uv ln 2 Х
w==O t==o m==1
х [ р (V t I U t. т) ] v [ Q (V w) . ] ", (6.23)
Q(V t ) p(VwIU w )
rде 'v == л/lп 2 и В == елDо/(l е ЛDо).
/1. Последовательное декодирование
319
Далее зафиксируем правильныЙ путь и и усредним (6.23)
по принимаемым последовательностям V w. Так как cpeд
нее значение суммы равно сумме средних значений и, кроме
Toro, V t входит только в два последних сомножителя пра
вой части последнеrо неравенства, то усреднение (6.23) CBO
дится К нахо)кдению среднеrо значения [Р]ср произведения
[р (V t I U t , т)/Q (V t)]V [Q (V w)/p (V w I U;')]v. Имеет место следующее
равенство:
[ P(VtIUt.m) ] V [ Q(Vw) ] V
[Р]ср Q (V t ) Р (U W I и:)
Ip(VtIUt) [ P(VtIUt.m) ] V [ Q(Vw). ] V, (6.24)
v Q(V t ) p(VwIU w )
t
Так как канал является дискретным каналом без памяти, то при
всех t ,
,, ( * ) ( * )[ P(VtIUt.т) ] V [ Q(Vw) ] V
[p]CP fP Vt wIUt wp VwlU w Q(V t ) p(VwIU:)
t
( V и* ) .
== " р t w I t w [ ( V I u* )] I....V [ ( V I и )] V
f...J [Q (V t....w)]V Р w w Р t t, т ,
V t
tfc
rде через Ut w и Vt w обозначены соответственно последние
t ....... w ребер путей и; и V t .
Далее проведем усреднение (6.25) по ансамблю кодов. Если
воспользоваться свойствами рассматриваемоrо ансамбля кодов,
даваемыми леммой 6.1, а именно тем, что различные пути KOДO
Boro дерева статистически независимы и, кроме Toro, незави-
симо с распределением вероятностей {Qk, 1 k К} выби
раюrся и символы канала для каждоrо фиксированноrо пути, то
* *
усреднение (6.25) по Ut w, U w И U t , т можно провести LЗЗ-
дельно. Обозначим искомое среднее значение через [Р]ср.
В силу вышеИЗЛО)l{енноrо
(6.25)
1 ( * ) [ ( * )] I V V
[p]cp L.J [Q(Vt 'W)]V P Vt ",IUt w Р V",IU", [p(VtIU tт )] .
v t
(6.26)
rде
p(Vt wIU; w)== L Q(U; w)p(Vt wIU; w)===Q(Vt w) l.
*
Ut w
( 6.27)
320
rлава 6
Следовательно,
[Р] ср L [p -( V w I U:)]l V [р (V t I Ut U!')]",
V t
(6.28)
Правую часть (6.28) оценим сверху, воспользовавшись Hepa
венством Шварца:
L [р (v w I U )]l V [р (V t I U t , m)]V
v t
[ { ( * ) 1 'У } 1) ] 1/2 [ { ] 1/2
Р VwlU w · p(VtIUt,т),,} .
(6.29 )
Так как в случае дискретноrо канала без памяти вероятности
р (V w I и:) и р (V t I U t , т) являются произведениями соответствую-
щих вероятностей для пар символов Ui и Vt из и и V, то
[ { * I V } 2 ] 1/2 [ J { К } 2 ] Wn Q /2
p(VwIU w ) == j 1 l:lqkР(V/lщ)l " .
1/2 [ J { К } 2 ] t nо/2
[ {P(VtIUt,m)"}2] == / I- k lqkр(v/lщ)" ·
(6.30 )
Выше был рассмотрен случай, коrда t '. В действительности
аналоrичные оценки имеют место и при w [. В силу этоrо
[Р]ср, а следовательно, и е можно оценить сверху с помощью пра-
вых частей (6.30).
Чтобы получить по возможности более точную rраницу, пра-
вые части (6.30) необходимо минимизировать по v и распреде
лению вероятностей {Qk, 1 k К}. Однако здесь минимиза
цию по v мы проводить не будем, положим просто v == Ч2
И минимизируем правые части (6.30) только по Qk. Пусть
R выч == mах [ In t (qk [p(v/I Uk)]1/2)2l- (6.31)
{qk} /=:01 ..:J
Тоrда
[ / ( К ) 2 ] 1
mах L L Qk [Р (Vj I Uk)]1/2 ==
{qk} 1::11 k::ll
тах [ log2 ( qk [р (v/I Uk)]I/2YJ
== e{qk} J::II kз:1 == еRвыч.
Отсюда и из неравенств
't (t) === (у 1) yt 1 yt е(nо 10 2) R
(6.32)
//. П оследовQтельное декодирование
321
получаем
с
(у + 1) В ( f: 't' (t) е
tпoи (ln 2/2) etno (ln 2/2) (
RBbl"» ) х
t--O
Х ( f: e Wnou ln 2/2е
wn o lп 2/2R BbIq )
w .... О
(Ут 1) В {l........e
(no ln 2/2) (R8ыч+U
2R)}
I {1
e
(По 102/2) (Rвыч
И)} (6.33)
Из этоrо неравенства, в частности, следует справедливость тео-
ремы 6.1.
6.4. Распределение числа операций и вероятность
переполнения буфера
Как будет показано ниже, при последовательном декодиро-
вании в некоторой области скоростей передачи вероятность
ошибки стремится экспоненциально к нулю с ростом длины КО-
довоrо Оl'раничения. Однако вероятность ошибки при декоди-
ct
ровании не является тем парамЕ'ТРОМ, которыи определяет пове-
дение алrоритмов последовательноro декодирования. Чтобы
ct ct
наити правильныи путь при наличии сильных шумов, приемник
должен обследовать большое число ребер, а для этоrо он дол-
жен хранить в памяти достаточно большое число принятых
символов. Емкость памяти декодера в реальных системах orpa
ничена, и поэтому при возникновении пачки шумов все эле-
менты памяти MorYT оказываться занятыми, т. е. возникает так
называемое переполнение буфера. Вероятность переполнения
буфера является обычно тем параметром, который определяет
поведение алrоритмов последоватеЛhноrо декодирования.
В предыдущем разделе было найдено среднее число опера-
ций, необходимых для декодирования одноrо ребра, однако Be
личиной, определяющей переполнение буфера, является не сред-
ct ct
нее число операции, а распределение числа операции, а именно
вероятность р[с
L] Toro, что число операций при декодирова
нии с превысит значение L. Как уже было показано выше, слу-
ct ct
чаиная величина с, определяющая число операции, выполняемых
декодером внеправильных подмно)кествах кодовоrо дерева,
связана с ценами путей всех возможных длин; поскольку эти
ct
пути являются зависимыми, то нахождение точных значении ве-
роятности р [с
L] является трудной задачей. Поэтому очень
важно попытаться обойти статистическую зави('имость непра-
ct .
вильных путеи кодовоrо дерева и получить верхнюю и нижнюю
rраницы для вероятности р [с
L], которые бы достаточно точно
описывали ее поведение. Ниже такие rраницы будут получены,
и из этих rраниц будет следовать, что распределение числа
322
rлйва б
операций при декодировании является распределением Парето,
а именно р[с
L]
L
v.
Исследование вероятности переполнения буфера проведем
в три этапа. Сначала рассмотрим структуру буфера и ero функ
ционирование, затем получим верхнюю и нижнюю rраницы для
вероятности р {с
L] и наконец установим связь ме)кду вероят
ностью переполнения буфера и вероятностью р[с
L].
6.4.1. Структура и функционирование буфера
Структура буфера показана на фиr. 6.12. Как видно из этой
фиrуры, часть емкости буфера используется для хранения сим-
волов принимаемых последовательностей, которые вводятся
1-=
приНllтая
пOC4fdOdllтfllbllllCт6
в
1
В J1НфОРAftl/{/I:JIIJI/l,f
/!IlC//fPtJ!/l/1lft. "t'HtJCтi
IJlf.!ОdV{JJld{lН
IIНФ!!рМ{l
rr!.11!f16
t
'-
v
Резерdl1illl
Руфер
:>;
Фиr. 6.12. Стандартная структура буфера.
в буфер слева блоками в порядке поступления последних (каж-
дый блок соответствует определенному ребру кодовоrо дерева),
а друrая часть емкости буфера используется для хранения ре-
зультатов предварительноrо декодирования принятых блоков.
Буфер содер)кит два указателя Один из них, так называе
мый указатель предела, указывает первое слева ребро, обследо
ванное декодером. Друrой указатель, так называемый указатель
поиска, указывает положение, в котором в данный момент Bpe
мени декодер осуществляет поиск. Соrласно фиr. 6.12, декодер
может хранить В ребер. Защитная память, показанная на
фиr. 6.12 справа, устанавливается для Toro, чтобы при перепол
нении буфера можно было выделить ненадежно декодированные
данные.
При слабых шумах оба указателя находятся, как правило,
вблизи левоrо конца буфера, а также близко друr к друrу. По
мере возрастания уровня шумов, действующих в канале, оба
указателя обычно смеlцаются вправо. При этом указатель по-
//. Последовательное декодирование
323
иска псеrда располаrается справа от указателя предела и pac
стояние между этими указателями возрастает медленнее, чем
расстояние между указателем предела и левым концом буфера.
Так как при малом уровне шумов цены правильноrо и непра-
ct
вильноrо путеи сильно различаются, то в результате проводи
ct
Moro поиска сразу удается разделить правильныи и неправиль
ный пути. При пачке шумов цены правильноrо пути начинают
падать и декодер, исследуя как падающий участок правильноrо
пути, так и неправильные пути, цены которых лежат выше ми
нимальной иены правильноrо пути, постепенно понижает пороr.
С умеНЫlIением уровня шумов цены правильноrо пути начинают
возрастать и декодер движется вперед, вновь повышая значения
пороrа. Однако, возвращаясь к фиr. 6.7, заметим, что до этоrо
декодер должен обследовать неправильные пути между узлами
(7) и (9). Так как число ребер неправильных путей, лежащих
в этой области, растет экспоненциально с ростом длины этоrо
участка, то резко возрастает и объем ПрОБОДИМЫХ вычислений.
В результате указатель предела перемещается вправо на значи
тельное расстояние от левоrо конца буфера, однако при этом
расстояние между указателями предела и поиска оказывается
несколько меньшим.
6.4.2. Нижняя rраница для р[с
L]
Распределение р [с
L] числа операций
двоичных информационных символов было
и Берлекэмпом [12]:
при декодировании Z
найдено Джекобсом
p[c
L]
L
V.
(6.34 )
Точнее, ими была получена нижняя rраница для распределения
р [с
L] числа операций С, необходимых декодеру для декоди
рования Z первых информационных символов, из которой следо
вало приведенное выше приближенное равенство. Эта нижняя
rраница была получена методом, в основных чертах совпадаю-
u
щим с методом получения нижнеи rраницы для вероятности
ОUlибки при декодировании списком, использованным Шенно-
нам, rаллаrером и Берлекэмпом [5].
Пусть задан дискретный канал без памяти, и пусть
{ J ( К ) 1+" }
Ео (v) == тах
ln L L QkP (VJ I Uk)l/l+V .
{qk} I
I k==1
Верхнюю оrибающую Eo(v) будем обозначать через Eo(v). Для
большоrо числа реальных каналов 20(v) == E,o(v) И вместо
Eo(v) всеrда можно использовать Eo{v). Использование 2o(v)
в подобных случаях позволяет упростить нижнюю rраницу.
(6.35)
324
fлава 6
Рассмотрим передачу по дискретному каналу без памяти 1
равновероятных сообщений с помощью блоковоrо кода из М KO
довых слов, каждое из которых состоит из N входных символов
канала. Приемник обрабатывает последовательности длины lV,
поступающие с выхода канала, и сопосrавляет каждой из них
список из L сообщений. Вероятность Toro, что в этом списке со-
общений отсутствует действительно передававшееся сообщение,
обозначается через Pe(N,M,L). Пусrь v произвольное целое
число. Если число кодовых слов М и число сообщений L, ВКЛIО-
чаемых при декодировании в список, удовлетворяют неравенству
1 ехр{NЕо(v)+ОI(-v' N )}.
(6.36)
ТО, соrласно формулам (1.68) и (1.69),
Ре (N, М, L) ехр [ ---- N {Ео (v) ...... vЕб (v)} ...... 02 (-v' N )], (6.37)
rде Еб(v)==dЕо/dv, а 01(-v' N ) и 02(-v' N ) функции, стремя-
щиеся к нулю с ростом -v' N .Эта rраница справедлива для про-
извольноrо блоковоrо кода длины N и произвольноrо декодера
со списком объема L.
Прежде чем применитъ эту rраницу для нахождения распре
деления числа операций при декодировании, введем следующие
величины:
R == ln M/N (Т. е. М == e NR ),
Rv == Ео (" )/" .
Пока>кем, что вероятность Pe(N, М, L) можно оценить сверху
функцией, которая имеет тот же вид, что и распределение
Парето.
Для этоrо рассмотрим блоковый КОД со скоростью R > Rv,
зафиксируем L и выберем некоторым специальным указанным
ниже образом N так, чтобы выполнялось неравенство (6.36).
Сначала запишем неравенство (6.36) в следующем виде:
(6.38)
(6.39)
L м ехр { ---- N Еб ( ") ...... 01 ( -v' N )}.
(6.40 )
Далее, подставим e NRv в правую часть (6.40) вместо М ==
== eNR. ( eNRv) и выберем минимально возможное N, такое, что
L ехр [N {Rv ---- E (v)} ---- 01 (,yN)].
(6.41 )
Пусть Х некоторая постоянная и N минимальное I{paTHOe
Х, дЛЯ KOToporo выполняется неравенство (6.41). При таком
выборе N наряду с (6.41) имеет место и друrо е нера венство:
L ;;;: ехр [(N ..... Х) {Rv ...... E (v)} 01 ( -v' N ---- Х]. (6. 2)
//. Последовательное декодирование
325
При этом справедливы также неравенства (6.36) и (6.37). Под
ставляя выражение (6.39) в (6.37), получаем
Ре (N, М, L) ехр [ Nv {R" ...... E (v)} ...... 02 (,yЛr)]. (6.43)
Возьмем натуральный лоrарифм от обеих частей (6.42):
ln L + 01 ( N ....... х) (N ....... Х) {Rv ....... E (v)}.
(6.44 )
Используя эту формулу, преобразуем неравенство (6.43) к виду
Р, (N, М, L) ехр[ ; {In L + 01 ( N х)} 02( .y N )] ==
===exP[lnL ; +v v N X O.( N X ) 02( N )]==
=== L V ехр [ ; In L N N....\ о. ( N х) 02 (-V'N)]. (6.45)
Как следует из формулы (6.44), N имеет пор ядок ln L:
N lп:, +Оз( lпL).
R" Ео (v)
(6.46 )
Используя это соотношение, запишем формулу (6.45) в виде
Pe(N, М, L) L Vexp{ 04( lnL )}. (6.47)
Эта оценка MO}l{eT быть использована следующим образом.
Предположим, что в начале принятой последовательности
возникла пачка ошибок длины N. Допустим, что длина этой
пачки является целым числом, кратным некоторой постоянной Х
и удовлетворяющим неравенствам (6.41) и (6.42). Обозначим
через {и Ni} совокупность передаваемых последовательностей
длины N, выходящих из начальноrо узла кодовоrо дерева. Эту
совокупность, содержащую М == e NR последовательностей,
мо}кно рассматривать как блоковый код длины N со CKO
ростью R. Обозначим через V N первые N символов принятой
последовательности. Для каждой фиксированной последователь
ности V N совокупность М вероятностей р (V lV I и N) упорядочим
В порядке их убывания. Пусть 1 в (V N) совокупность индексов
М L последних вероятностей из этоrо списка. Если принята
последовательность V N, то 1 в (V N) указывает М...... L наименее
правдоподобных сообщений или, друrими словами, 1 в (V N) BЫ
деляет совокупность сообщений, которые при декодировании
списком по максимуму праядоподобия не включаются в список,
326
r лава 6
Условная вероятность Toro, что при передаче последователь-
ности U Ni , индекс i которой принадлежит IB(V N ), будет принята
последовательность V N , равна
I p[VNIUNl], (6.48)
le/B(VN)
и, следовательно, при декодировании списком по максимуму
правдоподобия вероятность ошибки определяется равенством
Pe(N, М, L)== I I p[VNIU Ni ]. (6.49)
VN i Е/В (VN)
Неравенство (6.47) представляет собой нижнюю rраницу для
этой вероятности.
Далее, предположим, что принята последовательность V N,
и рассмотрим, каким образом последовательный декодер осу-
ществляет поиск правильноrо пути, выходящеrо из начальноrо
узла кодовоrо дерева. Поведение любоrо последовательноrо
декодера характеризуется следующими особенностями:
1) Поиск ребер осуществляется последовательно. Если в He
котором узле кодовоrо дерева декодер выберет ребро, которое
раньше не обследовалось, то это решение не зависит от приня-
той последовательности, соответствующей ребрам, лежащим на
кодовом дереве rлубже.
2) Декодер выполняет по крайней мере одну операцию на
каждом обследуемом пути.
В резулыа re этоrо поиска передаваемые последовательности
{и Ni} обследуются до полной длины N, и декодер после N ro
символа продолжает двиrаться вперед; здесь мы рассмотрим
лишь пути кодовоrо дерева длины N.
На время допустим, что на месте (N + 1) -ro символа имеется
некий учитель, который указывает декодеру, выбрал ли он пра
вильную последовательность и Ni или некоторую неправильную
последовательность. Если последовательность и Ni является He
правильным путем, то декодер установленным для данноrо ал
rоритма порядком возвращается назад и начинает обследование
друrоrо пути и Nj до длины N. ЕСJIИ И этот путь является непра-
вильным, то учитель вторично указывает декодеру на ошибку.
eKoдep вновь возвращается назад в исходное состояние и Ha
чинает обследование третьей последовательности и т. д. Дру-
rими словами, эти действия декодера для каждоЙ фиксирован-
ной принятой последоватеЛЬНОС1И V N длины N мо)кно интерпре
тировать как один из способов упорядочения последовательно
стей из {и Ni}.
Результат упорядочения зависит от принятой последователь-
ности V N, передаваемых посдедовательностей U Ni и алrоритма
//. Последовательное декодирование
327
последовательноrо декодирования. Однако результирующий по-
рЯДОК, соrласно особенности 1, не зависит от символов переда-
ваемой и принятой последовательностей, находящихся на pac
стоянии N и более от начальноrо узла кодовоrо дерева. Пусть
1 s ( V N) множе-ство индексов i последних М L последователь
ностей из {и Ni}, упорядоченных указанным выше образом.
Соrласно особенности 2 последовательноrо декодирования,
в любом узле кодовоrо дерева, который обследуется в процессе
u u
декодирования, декодер должен выполнить по краинеи мере
одну операцию. Следовательно, в случае, если передается после
довательность, индекс которой принадлежит 1 s ( V N), а принята
последовательность V N, то декодер с учителем на rлубине N
кодовоrо дерева должен выполнить по крайней мере L опе
u
рации.
Таким образом, вероятность QN (L) Toro, что декодер с учи-
телем выполнит по крайней мере L операций при обследовании
кодовоrо дерева до rлубины N, должна удовлетворять нера..
венству
QN (L) I L р (V N I U NI ). (6.50)
VN lE/s(VN)
Для каждой фиксированной последовательности V N наборы
1 в (V N) И 1 s ( V N) задают подмножества из М ----- L кодовых слов
множества {и Ni}, Так как 1 в (V N) определяет подмножество
наименее правдоподобных кодовых слов, то
L p[VNIUNI]
iEJS(VN)
и, следовательно,
QN(L) L L p[VNIUNi] Pe(L)==
VN iE/N (VN)
L p(VNIU Nl ]
iE/B(VN)
== L v ехр { 04 ( ln L )}. (6.51)
Эта оценка показывает, что распределение числа операций
при декодировании является распределением IlapeTo. Заметим,
u u
что полученная оценка является оценкои снизу числа операции,
выполняемых декодером в узлах кодовоrо дерева, лежащих на
rлубине N и менее. Так как в число этих операций входят
также и операции, выполняемые декодером в подмножестве не-
правильных путей, то левая часть (6 51) также является oцeH
кой снизу для распределения числа операций с, выполняемых
в подмножестве неправильных путей, r. е.
p[c L] ON(L) L Vexp{ 04 lnL }. (6.52)
Таким образом, нижняя оценка для р [с L] получена.
328
r лйва 6
6.4.3. Верхняя rраница для р [ с
L]
.
Для вывода верхней rраницы для р [с
L] поrребуются сле-
дующие два неравенства:
1) Неравенство Чебышева.
Пусть W
произвольная случайная величина, W
ее cpeд
нее значение и 02
дисперсия. Тоrда
0'2
Р [1 w ---- w I
е]
.
f,
(6.53)
Справедливо также следующее неравенство:
t'V
Р [t
б]
v '
6
(6.54)
rде t
случайная величина, принимающая только отрицатель
ные значения.
2) Неравенство Минковскоrо.
Пусть al, ..., ак
неотрицательные случайные величины,
принимающие с вероятностыо Qj соответственно значения
аjl, ..., ajK. Тоrда для любоrо , > 1
[
QJ (
aJkY/T
(
QJаЖ)'
(6.55)
и, кроме Toro,
[(
) ' ] I/r "
I/r
ak
[a
J.
(6.56)
Используя эти два неравеНСТl3а и верхнюю rраницу для
числа операций при декодировании, даваеМУIО соотношением
(6.15), СэваД)l{ [9] получил следующую верХНЮIО rраницу для
р[с
L].
Теорема 6.2. (Сэвадж). Существует сверточный код со ско-
ростью передачи R, для КОТОрО20 распределение р [с
L] числа
операций с для тuпичноzо подмножества неnравиЛЬНblХ путей
в дискретном канале без памяти удовлетворяет неравенству
р [с
L]
G L
R.выч/R.. (6.57)
Доказательство. Рассматривая суммы по j, W, t и 'n в (6.15),
т. е. внеравенстве
00 00 00 't (t)
c
(y+ 1) L L L L W[V(U t . т , Vt)
V(U:, Vw)
jDo],
j==
l L:.'==U L==U m==1
/1. Последовательное декодирование
329
как суммы по k неравенства (6.56), получаем
со 00 00 't' (t)
[C
]l/
(y+ 1) L L L L
f=a
1 ШС::;О t..o m==I
{[W [" (U t . т, V t)
,,(U:V, v ш)
jDo]
}I/
,
(6.58)
rде черта сверху означает усреднение по принимаемым последо
вательностям и ансамблю кодов. Здесь воспользуемся ансамб-
лем кодов, в котором все символы кодовых слов являются не-
зависимыми величинами с распределением {QK, 1
k
К}.
Аналоrично тому, как было получено неравенство (6.33), можно
показать, что
[ C
]l/
(у + 1) в {1
e
(no 'п 2/2J.1) (Rвыч
U)}
1 Х
Х {l
e
(no ln 2/2
) (Rвыч+U
2R
)}
I, (6.59)
rде
e Do / 2
B
1
e Do/2 ·
(6.60)
1/
При и < R вЪ1ч И R < (и + RFЪ1Ч) /2fJ- ве
ТIиqина [c
] и, следо-
вательно, [ c
] сходятся. Это означает, что существует код, для
KOToporo момент JA.
ro порядка величины с не превышает HeKO
торую константу а. Из неравенств и < R въtч и R < (и +
+ R выч ) /2JA. получаем, что f.1 < Rвыч/R. Соrласно нер авенству
Чебышева, типичное для ансамбля кодов распределение р [с
L]
величины с должно уд овлетво рять неравенству
р [с > L]
GL
Rвыч/R. (6.61)
Это доказывает существование по крайней мере одноrо кода,
распределение величины с для KOToporo удовлетворяет (6.57).
ТаКИ
1 образом, мы получили верхнюю и нижнюю rраницы
распределения р [с
L] числа операций при декодировании С.
ЭТИ rраницы показывают, что рассматривае
10е распределение
является распределением Парето.
6.4.4. Связь с вероятностью переполнения буфера
jt7становить связь между распределением р [с
L] и вероят
ностью переполнения буфера точно очень трудно. Поэтому здесь
сначала обсудим эту связь качественно, а затем покажем, как,
следуя подобным качественным рассуждениям, можно получить
нижнюю rраницу для вероятности переполнения буфера.
Операции, которые выполняются декодерО!\-f в узлах непра
вильноrо подмно)кества кодовоrо дерева, обычно являются опе-
330
rлйвй 6
рациями, связанными с обследованием коротких путей этоrо
неправильноrо подмножества. Действительно, длинные пути
имеют цены, значительно отличающиеся от цен правильноrо
пути. В силу этоrо вероятность Toro, что выполняемые декоде-
ром операции связаны с обследованием длинноrо пути, яв-
ляется очень малой. Это позволяет предположить, что операции,
выполняемые декодером в lIеправильных подмножествах KOДO
Boro дерева, являются операциями, которые, как правило, деко-
дер выполняет в небольших локальных «впадинах», обраЗУIО
щихся на траектории правильноrо пути. Поэтому, если HeKOTO
рая впадина правильноrо пути содержит N ер неправильных под-
множеств, то суммарное число операций, выполняемых декоде-
ром при обследовании этой впадины, является суммой чисел
операций, выполняемых декодером в ка}l{ДОМ из неправильных
подмножеств, а поэтому естественно предположить, что эта
сумма имеет то же распределение, что и число операций, выпол
няемых декодером в каждом из упомянутых выше неправильных
подмножеств. Обозначим через ст суммарное число операций,
необходимых для обследования каждой впадины, и пусть с
число операций, выполняемых декодером в ОДНОМ неправильном
подмножестве кодовоrо дерева. Тоrда в силу вышеизложенноrо
при больших значениях с и Ст имеем
Р [Ст L] р [с L/N cp ].
(6.62)
Предположим, что пики числа операций, обусловленные
этими неправильными ПОДМНО}l{ествами, появляются независимо.
Пусть Рбуф (N) вероятность Toro, что буфер переполнится при
декодировании N ro ребра или ранее, а Lo число операций,
необходимых для заполнения пустоrо буфера. Тоrда, так как
Bcero образуется N/N cp пиков числа операций, то
N
Рбуф (N) р [с Lo/N cp ]. (6.63)
ср
Обозначим через (J число операций, выполняемых декодеРО1\1
за время получения одноrо ребра, и через В объем реrистра
в ребрах. Тоrда
Lo == аВ
и, следовательно,
N
Рбуф (N) ---r Р [с aB/N ер].
ер
(6.64)
Приведенные выше качественные рассуждения подтверж-
даются результатами моделирования. Кроме Toro, теоретиче
ским подтверждением правильности этих качественных рассуж.
дений является нижняя rраница для Рбуф (N), полученная с их
помощью Джекобсом и Берлекэмпом [12] на основании оценки
11. Последовательное декодирование
331
(6.50). в оставшейся части этоrо раздела остановимся на этой
нижней rранице.
Предположим, что емкость памяти декодера такова, что в ней
MorYT храниться все данные, необходимые для декодирования е
двоичных информационных символов. Тоrда, если за время по
ступления и + 8 двоичных информационных символов по краЙ-
ней мере u символов оказались не декодированными, то возни..
кает переполнение буфера. За время поступления u + 8 двоич-
ных информационных символов декодер может выполнить не
более чем (J (и + 8) операций. Следовательно, всеrда, коrда для
декодирования u двоичных информационных символов необхо-
димо выполнить более чем (J (и + 8) операций, возникает пере-
полнение буфера. Пусть
L === о' (и + 8)
(6.65)
и u число двоичных информационных символов, cooTBeTcTBYIO
щих N символам канала. Тоrда при любой скорости передачи
R Rv имеет место следующее равенство:
II === [N R/ln 2]+,
(6.66 )
(6.41 )
и (6.42) (через [х]+ ([xr) здесь и ниже обозначается мини-
мальное (максимальное) целое число, большее (меньшее) или
равное х).
Далее рассмотрим случай декодирования Z двоичных инфор-
мационных символов. Эти символы можно разбить на [Z/u]
подблоков по u двоичных символов в каждом (N символов ка-
нала). Предположим, что декодер имеет учителя, и всякий раз,
коrда он начинает декодирование подблока неправильноrо пути,
учитель указывает на это. Декодер возвращается по этому под-
блоку назад, начинает обследование следующеrо пути и, таким
образом, в конце концов обнаруживает правильный подблок.
Друrими словами, предположим, что декодер с учителем всеrда
следует по [Z/u] подблокам правильноrо пути. Таким образом,
в случае декодера с учителем вероятность ro возникновения пе-
реполнения буфера во время декодирования любоrо из [Z/u]
подблоков оrраничена снизу вероятностью Toro, что для обнару-
жения правильноrо пути для этоrо подблока потребуется
(J (8 + и) или более операций, т. е.
(J) Q.v (L).
rде u целое число, удовлетворяющее соотношениям
(6.67)
Так как в данном случае рассматривается канал без памяти,
то шумы, деЙСТВУЮlllие на тот или иной фиксированный под
блок, не зависят от шумов, действующих на друrие подблоки.
Поскольку вероятность ошибки при обработке Z двоичных ин
формационных символов равна нулю для декодера с учителем,
332
fлава 6
то, используя разложение бинома, для вероятности PG (Z) пере-
полнения буфера для одноrо подблока получаем следующую
оценку:
Ра (Z) == 1 (1 (j)[Zlи] [Z/u] (j) ( [Z/;] ) ф2
> (Z/u....... 1) (i) (1 Z ro/2u). (6.68)
Далее рассмотрим случай декодера без учителя. Всякий раз,
коrда декодер с учителем переполняет буфер, декодер без учи-
теля либо также переполняет буq)ер, либо возникает ошибка.
(При отсутствии ошибки декодер без учителя выполняет все
операции, которые выполняет декодер с учителем, и, кроме
Toro, при выходе за пределы начальных подблоков неправиль
"
ных путеи он должен также выполнять операции на последую
щих подблоках. Эти операции ВЫПОЛНЯI0Т функuии учителя и при
отсутствии ошибок указываlОТ декодеру на то, что он выше.п из
подблока неправильноrо пути.) Следовательно, вероятность, пе
реполнения буфера декодером с учителем является rраницей
сверху для вероятности переполнения буфера декодером без
учителя или возникновения ошибки, т. е.
Ро (Z) Ра (Z).
(6.69)
СлеДУlощее неравенство следует непосредств енно и з (6.42):
ln L > (N ....... Х) (Rv ....... Вб (v») 01 (v N ....... х). (6.70)
Из формул (6.65) и (6.66) для In L получаем следующую оценку:
InL==ln{()'8+()'[NR/ln2]+} ln()'8+ln{1 + ( + 1)}.
(Здесь мы ВОСПОЛЬЗ0вались также тем, что [NR/ln 2]+
(NR/ln 2) + 1.) Разлаrая второе слаrаемое в правой части
последнеrо неравенства, получаем
In L In а8 + (N R/8 ln 2) + 1/8.
(6.71)
Из формул (6.69) и (6.71) н епосре дственно следует, что
(N Х) [Rv Eo(v)] 01 (vN...... Х) < In L
ln а8 + (N R/8 In 2) + 1/8.
Объединяя слаrаемые, содержа lцие N , имеем
N (Rv Ба (v) ....... R/8 ln 2) ..... 01 ( ,у N ...... Х)
In а8 + Х {Rv Еб(v)} + 1/8. (6.72)
11. Последовательное декодирование
333
Отсюда следует, что если
8 > R/{Rv....... Еб (v)} ln 2,
N == 05 (lп (8).
(6.73)
(6.74)
т)
Заметим, что условие (6.73) в большинстве практически инте
реСIIЫХ случаев выполняется.
Соrласно формулам (6.66) и (6.73),
II == [N R/ln 2]+ == 06 (ln (8). (6.75)
Отсюда, а также из формул (6.52), (6.65), неравенства ro
QN (L) JI формулы (6.75) получаем
(J) L v ехр { о А (In L) 1/2} ==
==(ae) v(l + ) VexP{ 04vtnae+[1 + ;] }==
( 8) v { 1 ( 1 + 06 (1 n 0'8) )
=== а ехр v n е
04 ,ytn ае + tn [1 + 06 ( иВ) ] } ;;:::
(а8) v ехр { 07 ln а8 }. (6.76)
Предположим, что (J) и Z таковы, что Z > 2и == 2 Х 06 (ln (8)
и (roZ/2u) 1/2. При этих предположениях из формул (6.68)
и (6.69) получаем
( Z ) ( Z(j) ) (j)l ( Z(j) ) Z(j)
Ро (Z) Ра (Z) и 1 u 1 2u 2u 1 2u 4u
z (а8) v ехр { 07 l n 0'8 ln [406 (ln (8)]} (6.77)
Z (a8) V ехр { 08 lna8}. (6.78)
Таким образом, сравнительно просто была получена нижняя
rраница для вероятности ошибки или переполнения буфера.
Этот результат не является столь же сильным, как верхняя rpa-
ница. Ни)княя rраница и верхняя rраница, полученная с по-
МОЩЫО качественных рассу){{дений, похожи друr на друrа. Из
формул (6.64) и (6.57) следует, что
Рбуф(N) : p[c;;:::a8/Ncp] NN G(аВ/Nср) Rвыч/R==
ср ср
N G ( в) RвычIR
=== ] ( R / 1< ) а ·
N выч
ер
(6.79)
334
fлйва 6
ПолаI'ая в нижней rранице Z == N, е == в, v === RиыJR, полуqае
1
Ро (N)
!!... (а В)
Rвыч/R G ехр {
07 ( ,yln а В )}
и
.!:!... G ( а в)Rвыч/R . (6.80)
и
Таким образом, вероятность переполнения буфера линейно ВОЗ
растает с N и убывает с ростом аВ.
6.5. Вероятность необнаружения ошибки
При исследовании среднеrо числа операций для алrоритма
Фано использовалось предположение о бесконечности кодовоrо
оrраничения сверточноrо кода, но полученная в результате
верхняя rраница для среднеrо числа операций оказалась неза
ct
висящеи от длины кодовоrо оrраничения, и это позволило cдe
лать вывод о том, что предположение о бесконечности КОДОВОI'О
оrраничения допустимо.
Однако кодовое оrраничение сверточных кодов, ПОРО)l{дае-
мых реальными кодерами, конечно и поэтому MorYT возникать
необнаруживаемые ошибки. Например, вернемся к показанному
на фиr. 6.1 сверточному кодеру кода со скоростью 1/2. Этот KO
дер содержит 5
разрядный реrистр сдвиrа, и информационный
ct .
символ, поступающии в момент времени t, еlце влияет на прове
рочный символ, формируемый в момент времени i + 5, но У}I(е
не оказывает влияния на последующие проверочные символы.
В силу этоrо две выходные последовательности кодера, COOTBeT
ствующие двум двоичным входным последовательностям, отли-
чаlОЩИМСЯ в первых s символах и совпадающим в остальных
символах, MorYT отличатьсSl лишь в первых 2(8 + 5) символах,
но обязательно совпадают в последующих символах. Предпо
ложим, что при передаче одной из этих выходных последова..
тельностей по каналу шумы исказили первые 2 (8 + 5) символов
таким образом, что эта выходная последовательность перешла
в друrую указанную выше последовательность. В этом случае
возникшую ошибку декодер не может ни обнаружить, ни ис
править. Такие ошибки называют необнаруживаемыми ошиб
ками.
Известно несколько rраниц вероятности ошибки для алrо
ритма Фано. В частности, для всех скоростей, меньших про
пускной способности канала, верхняя rраница для вероятности
ошибки была получена Юдкиным [13]. Однако здесь мы pac
смотрим верхнюю rраницу для вероятности ошибки, получен-
ную Сэваджем (9] из соотношений, приведенных в разд. 6.3.
Вообще rоворя, двоичная последовательность длины k 0 8, по-
ступающая на вход сверточноrо кодера, содеР}l{ащеrо ko т
раз
//. Последовательное декодирование
335
рядных реrистров сдвиrа, порождает 8 ребер и оказывает влия-
ние на формирование t == 8 + т + 1 ребер. Предположим, что
задан некоторый фиксированный правильный путь, и попробуем
наЙти число 1;(S) путей в первом неправильном подмножестве,
отличаIОЩИХСЯ от заданноrо праВИJlьноrо пути в первых ребрах
и совпадающих с ним в последующих ребрах. Сначала заметим,
что из каждоrо узла кодовоrо дерева выходит Ь == 2 k ) ребер.
Чтобы путь принадлежал первому непранильному подмноже-
ству, ero первое ребро должно отличаться от первоrо ребра пра-
вильноrо пути. При этом для Toro, чтобы путь отличался от
правильноrо пути самое большее в s ребрах, ero 8-е ребро
должно отличаться от 8 ro ребра правильноrо пути. Отсюда сле-
дует, что
,; (8) === (2 k o ...... 1) (2ko)S 2 2 sko . (6.81)
В случае если путь U t длины t == 8 + п1 + 1 ребер, лежащих
в неправильном подмножестве, начинающемся в начальном
узле кодовоrо дерева, имеет цену, превыIающуюю максимальное
значение пороrа, которое лежит ниже минимальной цены пра
ВИ.пьных путей длины tпo или менее символов, декодер Фано
MO)l{eT по ошибке идентифицировать путь U t как правильный
и породить таким образом 8 или менее ошибок. Друrими сло
вами, если путь U t такой, что
V (и t, V t) ---- ( min V (и , V w) ....... Do) О, (6.82)
o w t
то декодер Фано может декодировать этот путь ошибочно. Сле
довательно, вероятность Ре (8 I И*) возникновения 8 или менее
необнаруживаемых ошибок при передаче правильноrо пути
мо)кно найти, используя почти те же рассуждения, что и
в разд. 6.3. Пусть W (х) ступенчатая функция, определенная
выше [см. формулу (6.12)]. Тоrда
't (s) t
Pe(8IU;) LP(V;'U;) L L W[V(U t , Vt)......V(U , V )+Do].
v t m==1 w==O
(6.83)
Далее, точно TaI{ же, как и в разд. 6.3, воспользуемся rраницей
Чернова
w (х) е ЛХ ,
л> О,
(6.84)
(6.85)
(6.86)
подставим
v (U t , V t) == 1 (U t , V t) fnоИ,
V (и , v w) == 1 (и , v w) ---- wnoU
в правую часть (6.83) и проведем усреднение по ансамблю ко-
дов. Здесь следует заметить, что в разlJ,. 6.3 допускались бес-
конечные кодовые оrраничения, а среднее значение по ансамблю
336
rлава 6
вычислялось для ансамбля кодов бесконечно большой длины.
В данном же случае кодовое оrраничение кода ПА равно
(т + 1) по, а длина кодов в ансамбле, по которому производится
усреднение, составляет (t + т + 1) по == tno + ПА символов. Если
на длине tno + ПА символов кодовые последовательности из
этоrо ансамбля статистически независимы, то в друrих местах
эти последовательности оказываются, вообще rоворя, уже ста-
тистически зависимыми. Как показал rаллаrер [11], ансамбль
кодов, обладающих этими свойствами, можно построить, выби
рая всякий раз, коrда в реrистры сдвиrа кодера поступаlОТ но-
вые информационные символы, случайным образом связи и осу-
ществляя сложение выходной последовательности кодера с не-
которой случайной последовательностью.
Теорема 6.3. Для люБО20 R < R nыч существует сверточный
код со скоростью передачи R и вероятностью необнаружеНtLя
ошибки, эксnонеНLfиально убывающей с ростом длины кодОВО20
оераничения ПА. Показатель экспоненты этой вероятности
меньше чем R выч .
Доказательство. Подставляя (6.84) (6.86) в (6.83), ПО.,'JУ.
чаем
't (s) t
Pe(sIU*) 2: L LP(VtIU;)exp{I(U t , \It)
m..1 w-=O v t
....... 1 (и , v w) tnoU + wnoU + Do} ===
t
"" ( V I и* ) лDо л (w t) nои [ Р (Vt I Ut) ] Л [ Q (V w) ] . ==
i..J i..Jp t t е е Q(Vt) p(VwIU w )
w==O V t
t 't' (s) 'Л
== L L L e'A.Doe'A. (w t) lIoи [ [р (Vt I Vt))'A. ] Х
,==О т== 1 V t [Q (V t w)]
Х [р (V w I и )]I 'Л [р (V w I и )I Л] [р (Vt w I U; w)]. (6.87)
't' (5)
==2:
т==l
Проводя усреднение по ансамблю кодов, полаrая
[Е ns]cp ===
== L Р (V t w J U; w) [р (V w I и:]I Л [р (V t I Ut)]Л (Q(V t w)]Л (6.88)
v t
и используя соотношения р (v t w I U; w) == Q (V t w) 1, получаем
[Ens]cp L [р (V w I и:)] 'A. [р (V t I U t))'A..
\'
t
(6.89)
11. Последовательное декодирование
337
Соrласно неравенству UUварца,
(Eпs]cp [ {[р (v w I u:)]I Л}2Т2 [ {(p (\1 t I ut})Л }2Т2.
Далее, вводя Rпыч с помощью равенств (6.30) и (6.31)
водя суммирование по т, находим
( I И * ) ( 'AwnoU лwпоRвыч ) sko ln 2 'ADo Лt (nо+R выч )
Ре s ::::::::::: L...J е е е е е .
Ш С8 О
(6.90)
и про-
(6.91 )
Если это неравенство усреднить по И*, то получим rраницу
для средней вероятности ошибки Ре (s). Однако правая часть
(6.91) не зависит от И* и, следовательно, (6.91) дает верхнюю
rраницу также для Pe(S). Вводя величины t == s + т + 1, R ==
== ko/пo, ПА == по (т + 1), получаем
Ре (s) < ( S+f:+1 iwпo (и RBbl") ) eSno (R ln 2 лU лRвыч)е (n A no) л (U+R BbI1J )
w==o
(6.92)
Вероятность Ре возникновения по крайней мере одной необнару-
живаемой ошибки в неправильном подмножестве, начинаю-
lцемся в начальном узле кодовоrо дерева, оrраничена сверху
суммой по s вероятностей ps(S):
00
Ре L Ре (s) ==
S=:a)
00 ( s+m+) )
лпоw(U Rвыч) snо(RIП2 ЛU лUвыч) (пА по) ..(U+Rвыч) 'ADo
L...J L...J е е е е ·
s== 1 w==o
(6.93)
Правая часть этоrо неравенства сходится, если и < R выч
И R < (л(U + Rвыч)/lп 2). В случае, если R > R выч , то, как
видно из разд. 6.3, среднее число операций расходится. Если
положить л== (ln 2)2, то при R<R вЪJч правая часть неравенства
(6.93) будет сходиться. Если в этой области значений R сумми-
рование по w и s в правой части (6.93) провести независимо,
положив верхние пределы равными бесконечности, то получим
следующее неравенство:
Ре < {1 е по (In 2/2) (U Rвыч)} I {1 е по In 2 (R U/2 Rвыч/2)} I Х
Х еОП2/2) (Dо+2Rвыч)е пА 'П2/2) (U+R выч ). (6.94)
Обозначив через А произведение первых трех сомножителей
в правой части (6.94), последнее неравенство перепишем в виде
Ре /le пA In 2/2 (U+R выч ) Ae пA In 2R выч . (6.95)
338
r л ава 6
Отсюда следует справедливость доказываемой теоремы.
Таким образом, для алrоритма Фано в случае R < R nыч
были найдены rраницы для вероятности ошибки, среднеrо
числа операций и вероятности переполнения буфера. Чтобы
получить представление о порядке этих параметров, paCCMOT
рим следующий пример.
Пример 6.1. Рассмотрим двоичный симметричный канал с ве-
роятностью ошибки Р == 0,01 и сверточный код со скоростью
передачи R == 1/2 == 0,974R пыч и кодовым оrраничением ПА. == 120.
Пусть и == 0,974R в ыч и То == 2R выч о При PI === Р2 == 1/2 И V == 1
получаем
R выч == v ln 2
(1 + v) ln [0,99 1 /(I+V) + O,Ol l /(l+V)] === 0,512.
Верхняя rраница для вероятности ошибки имеет с.п:еДУЮIЦИЙ вид:
Ре
{l
е
0.026Iп 2Rвыч}
1 {1
e 1n2 (1
1.974Rвыч}
1 Х
Х е Rвыч In 2 е
60.ln 2.1.974R выч
8 . 1 0
17.
Пусть о' == 20 и В == 1000. Полаrая ехр {
08 ,.yln 0'8)}
ехр {
'\I'ln аВ}, v
Rвыч/R, из формулы (6.78) находим Be
роятность переполнения буфера
N
Ро (N)
460 000 ·
При передаче со скоростью 2400 бит/с переполнение буфера
возникает в среднем один раз за 460 000/2400
200 с. В то же
время ошибка появляется в среднем один раз за 1014 с.
Как показывают приведенные выше численные результаты,
поведение алrоритмов последовательноrо декодирования опре-
де
яется rлавным образом вероятностью переполнения буфера.
6.6. rраницы Витерби и декодирование
по максимуму правдоподобия
Начало этой rлавы, за исключением вывода нижней rраницы
для вероятности переполнения буфера, посвящено исследова-
нию вероятности ошибки, среднеrо числа операций и распреде
ления числа операций для алrоритма последовательноrо дeKO
дирования, предложенноrо Фано. В этом разделе находятся
верхняя и нижняя rраницы для вероятности ошибки при дeKO
дировании методом Витерби, который не связан с алrоритмом
Фано. Верхняя rраница будет получена с помощью вероятност
Horo (но не последовательноrо) алrоритма декодирования, пред
ложенноrо Витерби, а вывод нижней rраницы вообще не связан
с каким-либо конкретным адrоритмом декодирования, и нижняя
1/. П оследоватеЛЫ-lое декодирование
339
rраница справедлива для произвольноrо сверточноrо кода. По
лученные ниже rраницы Витерби показывают, что характери-
стики сверточных кодов лучше, чем у блоковых кодов той же
длины. Это утверждение неоднократно высказывал ось после
введения Элайсом сверточных кодов, но cTporoe доказательство
оно получило лишь с появлением rраниц Витерби.
Форни [14] показал, что использованный Витерби для полу-
чения верхней rраницы алrоритм декодирования является алrо
ритмом декодирования по максимуму правдоподобия, и таким
образом еще раз отметил ero важность.
6.6.1. Верхняя rраница для вероятности ошибки
Верхняя rраница Витерби так же, как и полученная выше
верхняя rраница вероятности ошибки для алrоритма Фано, BЫ
водится методом СJlучайноrо кодирования. Использованный в
СКClлярнь/ Х nроиз6fОf!НИЙ
Вхоо
Фиr. 6.13. Кодер.
разд. 6.6 ансамбль сверточных кодов можно построить также
следующим образом.
Входная последовательность, символами которой являются
элементы поля ОР (2), как показано на фиr. 6.13, подается на
вход т
разрядноrо реrистра сдвиrа, входящеrо в состав кодера.
С каждым поступлением в реrистр сдвиrа очередноrо входноrо
символа с помощью схемы вычисления скалярных произведений
формируется nо! выходных символов. Схема вычисления ска-
лярных произведений выбирается случайным образом с по
мощью ансамбля 2(m+}) по матриц с равномерным распределе
нием 1). Выходная последовательность f складывается со слу
1) На фиr. 6.13 каждый элемент, обозначенный кружком с точкой внутри,
выполняет умно}кение символа из соответствующеrо разряда реrистра на
двоичныЙ символ, котоrый для этоrо элемента выбирается случайно, незавн
симо и равновероятно среди {О, 1}. Все произведения вдоль каждой rоризон-
талыlйй строки складываются и подаюrся на соответствующий вход преобра-
зователя параллельных слоев в последовательные.
П pи
H. ред.
340
rлава 6
чайной последовательностью Z независимых равновероятных
символов. В результате все символы на выходе устройства фор
мирования символов канала оказываются равновероятными.
После Toro как на вход кодера будет подано В информацион-
ных символов, сюда подается последовательность из 'n + 1 ну-
лей. Порождаемый таким кодером код обладает слеДУIОIIlИМИ
свойствами:
1. Если т + 1 информационных символов двух различныIx
путей кодовоrо дерева совпадают, эти информационные сим
полы порождаIОТ одну и ту же последовательность из по сим
волов.
2. Все символы канала вдоль любоrо пути кодовоrо дерева
являются равновероятными.
3. Символы канала вдоль любоrо пути кодовоro лерева ста-
тистически независимы.
4. Если с вводом в реrистр сдвиrа каждоrо информаIlионноrо
символа матрица из (fn + I)no элементов, используемых для
вычисления скалярных произведениЙ, выбирается случайно и
независимо, то символы канала различных двух ПРОИЗ130ЛЬНЫХ
путей кодовоrо дерева оказываIОТСЯ независимыми.
Поскольку каждому информационному символу описанныЙ
выше кодер сопоставляет ПО символов канала, то порождаемые
этим кодером КОДЫ Иl\rfеIОТ скорость передачи
R === In 2/по (6.96)
и кодовое оrраничение ПА == (т + 1) по.
Далее, как было сказано, булем предполаrать, что после вве-
дения в реrистр сдвиrа В информационных символов в Hero
вводятся 'n + I нулей. При выводе верхней rраницы для вероят
ности ошибки будет использоваться следующий алrоритм дeKO
дирования.
Каждое ребро заданноrо пути кодовоrо дерева будет обозна
чаться посредством соотвеТСТВУlощеrо информационноrо симво
ла Ui, Ui Е ОР(2), а соотвеТСТВУlощие этому ребру символы при
нятой последовательности через Vi.
1) Для каждоrо из 2 т + 1 путей кодовоrо дерева, образован-
ных первыми т + 1 ребрами, вычисляются значения 2m+1 ФУНК-
т+l
ций правдоподобия П Р (Vi I и{). Далее проводится сравнение
1 =r 1
значений функций правдоподобия путей
(О, , . . ., и т +l),
(1, и2, . . ., и т + 1)
для всех 2т возможных векторов (и2, ..., и т +l). При ПрОБе-
дении каждоrо из этих 2т сравнений путь, имеющиЙ наиболь-
(6.97)
//. Последовательное декодирование
341
шее значение функции правдоподобия, оставляется, а друrой
путь отбрасывается. После выполнения 2т сравнений остается
2т векторов, и для каждоrо из них вектор (и2, Uз, ..., И т +l)
определяется однозначно.
2) Для каждоrо из оставленных на шаrе 1 путей вычисляют
ся значения функций правдоподобия двух ребер, выходящих из
(т + 2) ro узла кодовоrо дерева; ПО"ТIученные значения YMHO
жаются на значение функции правдоподобия исходноrо пути, и
таким образом находятся 2т значениЙ функций правдоподобия
путей, состоящих из 'n + 2 ребер. Эти последовательности
(и2, Uз, ..., и т +2) определяются однозначно. Пусть J..L
(w 1, 2) символ Ul последовательности, оставленной на I M
шаrе. Для различных пар путей
(J..L 11)' О, tl з , и 4 , · · ., и т + 2 ),
(f.I. ?, 1, llз, и 4 , .. ., llт+2)
(6.98)
находятся 2 т + 1 значений функциЙ правдоподобия. Далее, как и
на 1 YI lllare, 2т из этих путей оставляются, а остальные отбра-
сываlОТСЯ.
Этот шаr процедуры декодирования повторяется В т раз.
В частности, на (w + 1) M шаrе декодер выполняет 2т cpaBHe
ний функций правдоподобия для следуюIЦИХ пар путей:
( II(W) II(W)
rl1 , rl2 , · · .,
( 11. (w) 11. (w)
r 21 , r 22 , .. · ,
J..L , О, и ш + 2 , .. · t U w + т + I ),
t ), 1, U W + 2 ' ..., и ш + m + 1)'
(6.99)
rде J..Lk ), . . " J..L (k == 1, 2) символы, полученные в резуль-
тате сравнений на предыдущих шаrах декодирования.
3) На (8 т + 1) M шаrе на вход декодера подается сим-
вол О, проводится сравнение значений функций правдоподобия
следующих 2т 1 пар путей:
( (B т) II(B т) О U U О)
J..L" ,'.', rl.B m' , B т+2"." в' ,
( (B т) ..(B т) 1 U U О)
J..L 21 ,..., r2.B m' , B т+2"'.' в'
(6.100)
при всевозможных Bel{TOpaX иB т+2, ..., ив И по результатам
этих сравнениЙ оставляются 2m 1 путей. Так как на вход ре-
rистра сдвиrа с момента 8 + 1 подаются нулевые символы, то
число выполняемых сравнений с каждым шаrом уменьшается
вдвое. Перед B M шаrом остаются два пу"'и:
( 11. (8 1)
t"'11 ,'.',
( ..(В 1)
r H " · · ,
f.t B Jt О, О, . . " О),
J..L B!!l' 1, О, ..., О).
(6.101)
342
r лава б
На B M шаrе из этих двух путей выбирается TOT t который имеет
большее значение функции правдоподобия, и этот путь остав-
ляется как правильный.
При использовании этоrо алrоритма декодирования шибка
при декодировании возникает в том случае, если при проведе-
нии В сравнений для пар путей, содержащих правильный путь,
оказывается, что значение функции правдоподобия правильноrо
пути меньше, чем значение функции правдоподобия HeKoToporo
друrоrо сравниваемоrо пути. В целях упрощения предположим,
что правильный путь является последовательностыо, состоящей
из одних нулей. РаССl\fОТРИМ случай, коrда ошибка возникает
на (ш + 1) M шаrе декодирования. На (w + 1) M шаrе декоди-
рования первые w + 1 ребер правильноrо пути обозначим через
(О) === (О, О, ... t О). Векторы, сравнение которых проводится
на этом шаrе декодироваНИЯ t задаются формулами (6.99) t но
правильный путь входит лишь в следующие пары:
(О, О, . . ., О, О, О, . . ., О),
(f1 ), f1 ), "', f1 , 1, О, . . ., о),
(6.102)
rде f1 ), u== lt .'., { , символы, найденные на предыдущих
шаrах и являющиеся элементами поля ОР (2). Следовательно,
число путей, которые сравниваются на (ш + 1) M шаrе с пра
вильным путеМ t равно 2 w . Эти 2 w путей можно разбить на rруп
пы слеДУЮЩИh-I образом.
Пусть (О, . . ., О, 1, О, . . " О)......... вектор, обозначаlОЩИЙ путь,
w т
ответвляющийся от правильноrо пути в (ш + 1) -м узле, а
(О, ..., О, 1, 1, О, . . ., О) вектор, обозначающий путь, ответ-
ш l т
вляющийся от правильноrо пути в ш м узле. По аналоrии пусть
(О, . . ., О, 1, б, 1, О, . . ., О) BeKTOp, обозначаIОЩИЙ путь, OTBe
ш 2 т
вляющийся от правильноrо пути в (ш 1)-м узле (б == О, 1);
Bcero имеются два таких пути. В общем случае число путей, OT
ветвляющихся от правильноrо пути в (ш + 1 k) M узле, равно
2k 1 (k == 1, ..., ш), а число путей, ответвляющихся в (ш+ 1) M
узле, равно 1. Общее число указанных выше путей равно 2 ю ,
и оно является общим числом векторов, которые MorYT состав-
лять вторую строку (6.102).
Однако все эти векторы не имеют прямоrо отношения к BЫ
бору правильноrо пути. В силу свойства I кодера, если два
пути, отличающиеся в некотором заданном ребре, совпадают в
последующих т + 1 информационных символах, то они также
совпадают в следующем за ними ребре. Если два пути с про-
//. Последовательное декодирование
343
извольными фиксированными информационными символами не
имеют никаких т + I совпадающих подряд идущих информа
ционных символов, то они не имеют совпадающих ребер. Такие
пути будем называть полностью несовпадающими. В СИ,НУ этоrо
свойства кодера при рассматриваемом алrоритме декодирова
ния векторами, которые сравниваются с правильным путем на
(ш + 1) M шаrе, ЯВЛЯIОТСЯ не все векторы вида (6.99), а только
те из них, которые полностью не совпадают с правильным пу-
тем. Следовательно, математическое ожидание вероятности
ошибки при проведении сравнений на (ш + 1) M шаrе можно
оценить сверху суммой математических ожиданий вероятностей
возникновения ошибок при проведении сравнений с векторами,
отличающимися от правильноrо пути соответственно в
(ш + 1) м, ..., 1 M ребрах:
w { ошибка происходит из-за пути, }
р (w + 1) < L Pr ответвляющеrося от правильноrо .
k-=O _ на (w + 1 k) M ребре
(6.103)
С,паrаемое с k == О в правой части этоrо неравенства можно оце-
нить сверху вероятностью ошибки для блоковоrо кода длиной
ПА == (т + 1)nо, состоящеrо из одноrо кодовоrо слова; k e сла
raeMoe в правой части (6.103) можно оценить сверху вероят-
ностью ошибки для блоковоrо кода длиной ПА + (ln 2/R) k сим
волов канала, состоящеrо из 2k 1 кодовых слов. Используя
свойства 2 4 кодера и rраницу случайноrо кодирования, полу-
чаем
w
р (ш + 1)<ехр [ nAEo (v)] + I {2k 1}V exp[ ( nА+ 1 2 k ) Ео (v)]<
k== 1
00
< ехр [ nAEo (v)] I 2 k [v E.(v)/RI == I ФIR ехр [ NEo (v)] , (6.104)
k==O
rде
<р === Б о (v) vR > о.
(6.105)
Верхняя rраница для вероятности ошибки при декодировании
древовидноrо кода РЕ длиной В получается суммированием
(6.104) по ш. Так как правая часть неравенства (6.104) не за
висит от Ш, то имеем
B l
РЕ < I Р(Ш+ 1) < I : (fIR exp[ nAEo(v)], О < " 1.
w...o
(6.106)
в силу Toro что в ансамбле кодов, для KOToporo справедли
вы lIеравенства (6.106), существует по крайней мере один код,
344
r лава 6
для KOToporo РЕ < РЕ, а Eo(v) является монотонно возрастаю-
щей функцией ", получаем следующую теорему.
Теорема 6.4. (Витерби) В дискретном канале без памяти ве-
роятность ошибки при декодировании В ребер двоиЧНО20 дре-
ВОВllдноzо кода удовлетворяет следующему неравенству:
rде
в
РЕ < 1
2
ФIR ехр [
ПАЕ (R)],
{ Ro, О
R == Ro
ер < Ro,
Е (R) == Е ( ) R
R
Ео (,,)
с
ov, 0
<P
" < с,
Ro == Ео (1) == тах {
ln L [ L Q (и) ,у р (и I и) ] 2 } .
Q (и) v и
(6.107)
(6.108)
6.6.2. Нижняя rраница для вероятности ошибки
в этом разделе получим нижнюю rраницу для вероятности
ОllIибки. Для этоrо воспользуемся декодером с учителем, для
исследования KOToporo применим rраницу сферической упаков-
ки и прямолинейную rраницу.
В данном случае будем предполаrать, что учитель указы-
вает декодеру все ребра правильноrо пути кодовоrо дерева, за
исключением 1 следующих друr за друrом ребер w + 1,
w + 2, ..., w + 1 (О
w
8
1). Друrими словами, учитель
указывает все передаваемые информационные символы Vi, за
исключением 1 символов, соотвеТСТВУIОЩИХ указанным выше реб
рам. Таким образом, задача деl{одера сводится к тому, чтобы
по принятой последовательности V == (Vl, и2, ..., ив+т), co
стоящеЙ из (8 + m)nо си
волов, определить, какая из 2 l двоич-
ных последовательностей передавалась. (Здесь Vi
совокупность
принятых символов, соотвеТСТВУIОЩИХ i
MY ребру.) Итак, по-
скольку в данном случае символы, передаваемые в моменты
времени i < и', даются учителем, то декодеру необходимо ис
следовать лишь символы Vi, i
w + 1. Исследуемые 21 путеЙ
MorYT различаться лишь в (w + 1)
M И послеДУIОIЦIIХ ребрах,
но если рассматривать только информационные IIОС.}1едователь
ности, имеющие одни и те же символы Vi при i
w + 1 + ], то
состояния реrистра сдвиrа при порождении (w + 1 + 1)
ro и
последующих ребер будут совпадать и, следовательно, при i
w + 1 + 1 кодер будет порождать всеrда одну и ту же ПОСJIе-
довательность. Таким образом, исследуемые 2 l путей MorYT от-
личаться друr от друrа самое бо.пьшее в 1 + т ребрах.
Будеl\1 считать, что приеМIIИК Д,,1Я каJl<доrо из этих 2' путеЙ,
имеющих равные априорные вероятности, вычисляет значение
11. Последовательное декодирование
345
функции правдоподобия Р (v I и), v == (Vw+l' ..., VW+l+ т ) ' и ==
== (Utc+l' ..., Uw+l) , и выбирает из них тот путь, для KOToporo
значение функции правдоподобия максимально. Здесь и век-
тор, определяющий путь. Полаrая
получаем
11 === [/(m + 1),
nА==(m+ 1)nо
lln 2 == 11nAR.
(6.109)
(6.110)
(6.111)
из равенства
Длина вектора v равна (.., + 1) ПА + 110. Следовательно, вероят-
ность ошибки для УI<азанноrо выше декодера можно оценить
снизу любой нижней rраницей для вероятности ошибки блоко-
Boro кода длиной (.., + 1) ПА по, содержащеrо 21 === ef\n AR кодо-
вых слов.
Как следует из соотношений (1.59) и (1.63) первой rлавы,
rраниuа сферической упаковки для блоковоrо кода длиной n
со скоростью R' имеет следующий вид:
Ре ехр [...... п {E sp (R' ...... 01 (n) + 02 (п)}],
.....
Esp (R') == тах [Ео (v) ........ vR'] ,
0<\7<00
(6.112)
(6.113)
rде Ео (v) верхняя оrибающая Ео (v, Q). Так как
Е s р (R' ...... О 1 ( .vn)) == m ах {Е о ( v . v (R' ....... 01 ( n) ) }
0<\7<00
и параметр v здесь является некоторой фиксированной постоян-
ноЙ, то "Оl ( n) стремится к нулю с ростом п и, следовательно,
Ре ехр[ n {E sp (R') + Оз ( n)}].
(6.114)
Подставляя п == (11 + 1) ПА ....... по, получаем
PEf\ ехр [ {(1l + 1) ПА ........ по} {E sp (R') + Оз ( пA )}]
ехр [ {(1l + 1) ПА} {E sp (R') + Оз ( nA )}]. (6.115)
Так как aprYMeHT R' функции Esp (R') удовлетворяет нера--
венству
, ln Л1 1111 A R т)
R п === (11 + 1) п А по > 11 + 1 R,
то
[ .... 1, ]
Esp (R) < E spL (R, п) == тах Eo(v) v + 1 R ·
0 \7<00 т)
(6.116)
346
fлава б
Как следует из результатов UJeHHoHa, rаллаrера и Берлекэм-
па [5], функция E SPL (R, Т)) может быть задана параметрически:
E spL (R, 11) == Б о (v) ...... "E (v),
R == f) + 1 Е' ( v )
11 о ,
( 6. 11 7)
(6.118)
rде т) == l/(tп + 1), а 1 любое из чисел 1, ..., В. ПРОВОДЯ
максимизацию РЕТ1 по ", получаем следующую нижнюю rраницу
для вероятности ошибки РЕ:
РЕ (ПА, R) тах РЕ (ПА, R) >
l/(m+l) 1'1 B/(m+l) 1'1
> ехр {...... ПА min (11 + 1) [E spL (R, ,,) + о (11, 11А)]}. (6.119)
l/(т+ 1 ) Т1<B/(т+ 1)
Здесь необходимо найти функцию
E spL (R) === min (" + 1) E spL (R, ,,). (6.120)
)/(т+ 1) 1'1 В/(т+ 1)
Для этоrо, выбрав В/ (т + 1) достаточно большим, сначала про
ведем минимизацию по всем действительным положительным
числам Т), а после этоrо оrраничим область минимизации для
чисел 11, кратных l/(т + 1).
Дифференцируя (Т) + I)E SPL (R,11) по 11, получаем
д [(1] +1) : PL (R. 1])] == Б о (v) vБ (v) + (" + 1) [vB; (v)] : .
(6.121)
Из равенства (6.118) имеем
Е" ( ) av д 1'} R R
о v дl1 == дl1 1'} + 1 === (1') + 1)2 .
(6.122)
Подставляя последнее равенство в формулу (6.121) и прирав"
нива я далее (6.121) к нулю, находим 11 + 1:
vR
11 + 1 == ,,;-, (6.123)
Ео (v) vE o (v)
Повторно дифференцируя равенство (6.121), используя (6.118)
.....
и то, что вторая производная E ' (v) выпуклой вверх функции
Eo(v) отрицательна, получаем
д 2 [(!) + 1) spL (R, 1'})] == о ( 6.124 )
дТ}2 (Т) + 1)2E (v) ·
Следовательно, в точке, определяемой соотношением (6.123) ,
достиrается минимум исследуемой функции. Подставляя v из
//. последовательное декодирование
347
формулы (6.123) в (6.118), имеем
R ('\7R ....... E ('\7)) == о.
(6.125)
Отсюда находим R:
R === Ео (,,) .
"
(6.126)
Так как Ео ('\7) ........ выпуклая вверх функция, то R === Ео ('\7)/'\7 E ('\7)
и, следовательно,
"R
1') == ,.. , 1 O,
ВО (,,) "Во (,,)
т. е. .., неотрицательная величина. Из формул (6.117), (6.123)
и (6.126) получаем
(6.127)
min (..,+ I)E spL (R, ..,)==vR==Eo(v). (6.128)
O l'I OO
Далее, предположим, что 'YI кратно 1/ (т + 1), введем «коррек-
тирующее слаrаемое» б < 1/(т + 1) и исследуем ero влияние.
Изменение.., на величину порядка I/(m + 1) приводит к из
менению показателя экспоненты на величину порядка
nА/(т + 1) == по. Обозначим ПО/ПА через О(nА). Величина R
связана с n следующим образом:
1'1 + 1 + т 1 I (11 + 1) (1 + (т + 1)\11 + 1)) I I"V
R 1 Е о ('\7) ( 1 ) Eo(v)
11 + т + 1 11 1 + (т + 1) 11
1I 1 E ("){ 1 + (т+l (11+1) }(l (m I)1I )
rv Ео (,,) { 1 1 }
" (т+l)11(11+ 1 ) ·
Чтобы учесть влияние б, в показатель экспоненты оценки дЛЯ
РЕ достаточно ввести слаrаемое О(nА). Из формул (6.119),
(6.120), (6.126) и (6.128) получаем следующую теорему.
Теорема 6.5. (Витерби.) В дискретном канале без памяти ве-
роятность ошибки при декодировании nРОUЗВОЛЬНОZО сверточ
Ч,ОZО кода с кодовым оzраничением ПА оzраничена снизу сле-
дующим образом:
РЕ > ехр { ПА [E spL (R) + о (ПА)]}, (6.129)
дe
......
E spL (R) === Ео ('\7), О '\7 < 00,
......
R === Ео ('\7)/'\7.
(6.130)
(6.131)
348
r лава 6
в случае малых скоростей, используя прямолинейную ара-
ницу, для РЕ можно получить более сильную нижнюю 2раницу.
Эту араницу мы приведем здесь без доказательства.
Утверждение 6.1. В области малых скоростей имеет место
следующая 2раница:
РЕ> ехр {
nA [EspL(R) + о (N)]},
( Eo(v) (6.132)
E spL R)==E и , O
R
,
'v
Е и == тах { ........ Iiт [ " ln L L Q (и) Q (и') Х
Q (и) 'У+ОО и и'
Х (
-Ур (v I и) р (v I и') ) T/V}' (6.133)
rде v
решение уравнения Eo(v) == Еоо и
Еоо == тах
Е L Q (и) Q (и') lп L -V р (v I и) р (v I и'). (6.134)
Q (и) и и' v
6.7. rибридные методы кодирования
Как было указано выше, важнейшей характеристикой алrо-
ритмов последовательноrо декодирования является вероятность
переполнения буфера. Вероятность переполнения буфера можно
понизить, если установить для последовательноrо декодера мак-
u
симально допустимое число операции, а символы, для опреде
ления которых декодер должен выполнить большее число опе
раций, декодировать друrим методом, например одним ИЗ алrе-
браических методов, для которых число операций при декоди-
ровании всеrда оrраничено. Возможность уменьшения вероят
ности переполнения буфера указанным выше образом cTporo
обосновал Фалконер [16], воспользовавшись для этоrо рассмат-
риваемым ниже rибридным методом кодирования и декодиро
вания.
6.7.1. Системы rибридноrо кодирования
Предположим, что по Л независимым дискретным каналам
без памяти каждые 'V секунд передается один символ канала
(фиr. 6.14). Будем считать, что на вход каждоrо из этих KaHa
лов символы подаются с выхода относящеrося к этому каналу
сверточноrо кодера. Если используемые в этой системе свер-
точные коды имеют скорость передачи r == 1/ш, то на вход лю-
боrо сверточноrо кодера информационные двоичные символы
ДОЛЖНЫ поступать каждые Wv секунд. Наконец, предположим,
что через I<аждые 'Лwv секунд реrистры сдвиrа всех сверточных
[ J. Последовательное декодирование
349
кодеров приводятся в нулевое состояние t так что очередные ин
формационные символы вводятся в реrистры, содер)кащие лишь
ну.певые символы. В этом случае ка}кдый блок из л входных
двоичных символов кодируется в блок из ЛW символов канала
независимо от входных двоичных символов предшествующих и
последующих блоков.
Чтобы символы, поступающие на входы кодеров, при дeKO
дировании можно было восстановить с малой вероятностью
l' 2' 3'
1 СВерточныи
кооер (1)
t:::
С8ертОllНЫЙ
2
I /(оОер (2)
.
. I
I
.
C::) . I
I
.
I I .
.
I
.
. I
I
AR I С6ертОl/НIJ/Й
коиер (AR)
С6ерточныii
/(oQep(AR+1 )
С6ерточный
/(ооер (11 )
Фиr. 6.14. rибридный кодер.
ошибки, как следует из формулы (6.95), они должны оказывать
влияние на достаточно большое число входных символов KaHa
ла или, друrими словаМИ t кодовое оrраничение используемых
сверточных кодов должно быть достаточно большим. Однако
поскольку перед передачей каждоrо HOBoro блока из входных
символов реrистры сдвиrа кодеров очищаются, то последние
символы каждоrо блока оказывают воздействие уже на cpaB
нительно небольшое число символов канала. Это приводит к
тому, что вероятность ошибки при деI{одировании последних
СИМВО 10В каждоrо БЛОI{а возрастает. Для Toro чтобы предотвра"
350
r лава б
тить возрастание вероятности ошибки в конце блока, в качестве
последних J..L(f.t < л) входных символов в каждом блоке берется
некоторая фиксированная последовательность, известная деко-
деру. В этом случае входные символы каждоrо кодера, которые
декодеру неизвестны априори, оказывают влияние по крайней
мере на JlW символов канала. Однако в результате последние f.t
символов каждоrо входноrо блока оказываются избыточными и
реальная скорость передачи сверточных кодеров становится
равной (1 J..L/л) /w. Вообще rоворя, если выбрать л J..L, то
этим уменьшением скорости передачи можно пренебречь.
л. 51/т Jl Otlт
'< I 1< I t
х х х х х .......,, X Х Х Х Х Х Х
ххххх ххххххх
r.: .. ...
X x J 2<2<"}< .i'2< х...х ..
. . .. .. ...
. ... .. ...
. . .. . . ...
ххххххх
:::t . . ...
;(5 l xxxxxxx
ххххххх
х х х )( )( )()(
. . ... ti:
ххх)(ххх
х)(ххххх
.
Фиr. 6.15. Структура кода (фиrуры а, б, в соответствуют сечеНhЯМ 1', 2' и
3' на фиr. 6.14).
a BXOДHыe символы кодера кода Рида Соломона; б параллельный блок; в супер-
блок.
а
5
а::
1<
tJ
.1ш СJlмБО/108
КС/НйЛй
>/
ХХхххххххх
хххххххххх
[ x:x---....x x x.J<Xx::.
)
CQ
хххххххххх
ХХХХхххххх
ХХхххххххх
Хххххххххх
хххххххххх
хххххххххх
а) Структура кодов. Структура кодовоrо слова при rибрид
ном кодировании показана на фиr. 6.15. Как видно из фиr. 6.15, в,
Л внутренних блоков формируются при кодировании OДHOBpe
менно и передаются по Л дискретным каналам без памяти. Эти
Л внутренних блоков образуют один'суперблок. Как указано
На фиr. 6.15, в, Лл символов, поступающих параллельно на вхо-
ды последовательных декодеров, образуют параллельный блок.
Верхние ЛR л символов параллельноrо блока составляют неза-
висимые подблоки, каждый из которых состоит из л J..L инфор-
мационных двоичных символов и f.t известных фиксированных
символов. Остальные Л(1 R) л символов пара.плельноrо бло
ка являются проверочными и формируются алrебраическим ко-
дером по ЛR верхним независимым л символам, с которыми ал-
rебраичеGКИЙ кодер оперирует !<зк с элементами поля ОР (2')-)..
11. Последовательное декодирование
351
Параллельные блоки образуют 2л ичный блоковый код дли-
ны Л, содержащий 2 лАR кодовых слов.
Скорость передачи для всей описанной выше системы коди-
рования, выраженная в битах на один используемый символ ка-
нала, равна
R' === R (1 Il/'A)/w [бит].
Так как по предпо.пожеНИIО по ка}кдому дискретному каналу без
памяти передается один символ канала каждые " секунд, то
скорость передачи информации равна ЛR'/" [бит/с].
Далее остановимся на выборе блоковоrо кода. При средних
и больших длинах блоков наиболее эффективными кодами яв
ляются коды Рида Соломона. Эти коды MorYT быть построе-
ны для ЛlобоЙ скорости передачи R и любой длины А, не пре
вышающеЙ объема алфавита символов, и имеют минимальное
расстояние d == dMal\C == (1 R) Л + 1. Если рассматривать ко-
ды над полем ОР (2) или ero расширением, то размер алфавита
является степенью числа 2 и должен быть не меньше Л + 1.
Последнее условие эквивалентно следующему: 'А log (Л + 1).
Для построения кодера Рида Соломона требуется число
элементов, линейно растущее с Л. Каждый из Л сверточных
кодеров содержит самое большее " разрядов реrистра сдвиrа.
Следовательно, общее число элементов, необходимых для по-
строения rибридноrо кодирующеrо устройства, пропорциональ-
но "л.
б) Декодер. Как показано на фиr. 6.16, rибридный декодер
состоит из А параллельно работающих последовательных дeKO
деров и декодера кода Рида Соломона. При декодировании
каждоrо суперблока Л независимых последовательных декоде-
ров Фано осуществляют декодирование соответствующих внут-
ренних блоков. Декодирование различных внутренних блоков,
вообще rоворя, может продолжаться различное время. Здесь
будем предполаrать, что после окончания декодирования после-
довательными декодерами некоторых Л D внутренних блоков
декодирование остальных D блоков прекращается и все А по
следовательных декодеров начинают декодирование внутренних
блоков следующеrо суперблока. При этом л символы, декодиро-
вание которых не было завершено, воспринимаются далее дe
кодером кода Рида Соломона как стирания.
Таким образом, после завершения декодирования супербло
ка последовательными декодерами он переходит в параллель
ный блок (параллельный блок это кодовое слово Рида Co
ломона, быть может, искаженное в канале), состоящий из
(А D) л символов, последовательное декодирование которых
было завершено, и D 'А символов, которые рассматриваются как
352
r лава б
стирания. Этот параллельный блок подается на декодер кода
Рида Соломона. Предположим, что используемый код Ри-
да Соломона имеет минимальное расстояние d и что среди
Л D л символов, последовательное декодирование которых
было завершено, имеется не более чем Т неправи.rIЬНО декоди-
рованных л символов. Как хорошо известно, если выполняется
соотношение 2Т + D == d 1 между числом ошибок Т, числом
стираний D и минимальным расстоянием кода d, то декодер ко-
да Рида Соломона может декодировать данный блок пра-
вильно. Итак, при rибридном кодировании и декодировании
число операций при декодировании всеrда конечно и прибли
женно оценивается величиноЙ порядка Л log Л или Т log л. Как
ПОСllfРо&!тf.tfЬ/lЫР
ие/(о#ер (1)
'-:.
!1oCAfPodtlтe.tfIJNblii
> иe/(oJe,o (2)
1
.
. . .
......'
. . .
. .
....
'(JClff#u!g me.tf611b/#
иеl(оиер (А)
't
Фиr. 6.16. rибридиый декодер.
было указано, если даже последовательное декодирование He
которых D внутренних б.1JОКОВ не завершено, но друrие Л D
внутренних блоков уже декодированы, то начинается процесс
коррекции всех этих блоков с помощью алrебраическоrо деко-
дера. Таким образом, использование алrебраическоrо декодера
позволяет не допустить резких возрастаний объема вычисле
ний, время от времени возникающих при последовательном дe
кодировании внутренних блоков, и таким образом уменьшить
вероятность переполнения буферов последовательных декодеров.
В заключение заметим, что так как минимальное расстояние
кода Рида Соломона равно (1 R)A + 1, то всеrда можно
положить 2Т + D == (1 R)A, т. е. число исправляемых оши-
бок и стираний при фиксированной скорости передачи R прямо
пропорциональноЛ.
/1. последовательное декодирование
353
6.7.2. Характеристики rибридноrо кодирования
Найдем вероятность ошибки, распределение числа опера-
ций, среднее число операций и вероятность переполнения буфе-
ра для описанноrо выше rибридноrо метода кодирования. CHa
чала рассмотрим случай, коrда половина минимальноrо pac
стояния кода Рида
Соломона используется для исправления
стираний, а друrая
для исправления ошибок. Будем исполь
зовать код Рида
Соломона для коррекции Т == (Ав/2)
1 оши..
бок и D == Ав
1 стираний, rде в
некоторое число из интер-
вала О < е < 1/2. Подставляя эти значения Т и D в равенство
2Т + D == (1
R)л, находим 8:
l
R 3 l
R
в === 2 + 2А
2 .
(6.135)
Заметим, что при больших значениях Л параметр в не зависит
от л. Полаrая Il/л == в, получаем
R'==rR(1
11/л)==r(l
8)(1
2e+
) >r(1
8)(1
28).
(6.136)
а) Вероятность ошибки. Начнем с отыскания вероятности
ошибки. СоrлаСllО результатам Юдкина [13], связанным с иссле-
дованием вероятности ошибки для алrоритма Фано, вероятность
РЕи ошибки при последовательном декодировании одноrо BHYT
peHHero БЛОI{а можно оценить сверху экспоненциальной функ-
цией, стремящейся к нулю с ростом числа избыточных двоичных
символов, содсржащихся в каждом л
символе, поступающем на
вход кодера. Используя то, что f.l == лв, получаем
РЕи < p
== лG е ехр [
лвЕ u (r)],
(6.137)
{'де О е
постоянная, а Еu (r)
функция скорости передачи ,..
дреВОRидноrо кода и переходных вероятностей дискретноrо ка-
нала без памяти. Вероятность РЕ ошибки для rибридноrо дeKO
дера равна вероятности Toro, что Лв/2 или более внутренних
блоков декодированы неверно; она определяется равенством
л
Р В == I (
) P
и(1
Рви)Л
V'
v == 1.8/2
(6.138)
Правая часть (6.138) представляет собой функцию распределе
ния суммы lIезависимых двоичных случайных величин, и ее MO
,кно оцеНИТl) сверху с помощью неравенства Чернова (см., на
354
rлава 6
пример, Возенкрафт и Джекобс [24]) 1). Используя это нера-
венство, находим
Рв ехр ( л. {Т е [8/2, Рви] ...... Н (е/2)}),
о РВи 8/2, (6.139)
rде
Те (и, v) ===...... и lп V...... (1 ....... и) lп (1....... v),
Н (и) === и ln и (1 и) ln (1 ....... и).
Как нетрудно проверить, при V < и < 1/2
Т е (и, V) Н (и) > о.
(6.140)
От-сюда следует, что вероятность ошибки РЕ с ростом А ЭI{СПО-
ненциально стремится к нулю. Так как при РЕи < 8/2
д
д Т е [8/2, PEul < о, РВи < 8/2, (6.141)
РВи
то показатель экспоненты в формуле (6.139) является MOHO
тонно убывающей функцией РЕи. Следовательно, в (6.139) BMe
,
сто РЕи можно подставить верхнюю rраницу РЕи' задаваемую
формулой (6.137). В результате дЛЯ РЕ получаем следующую
верхнюю rраницу:
PE<exp[ A{Te(8/2, p и) H(e/2)}], p и<8/2. (f.142)
б) Распределение числа операций. Далее найдем распределе
вие числа операций. Пусть с число операций, которое необхо-
димо последовательному декодеру для Toro, чтобы без помощи
алrебраическоrо декодера декодировать один внутренний блок.
I(aK следует из разд. 6.4, эта величина имеет распределение
Парето
р (с L) < G [.J r выч/ r ,
(6.143)
rде G некоторая постоянная. Этим неравенством MO/l(HO BOC
пользоваться для Toro, чтобы получить веРХНIОЮ rраНИllУ для
числа операций, необходимых rибридному декодеру для декоди-
рования одноrо суперблока.
Чтобы упростить последующий анализ, предполо)ким, что
последовательные декодеры всех внутренних блоков не начи
нают декодирование очередноrо суперблока до тех пор, пока
1) не закончат декодирование предыдуrцеrо суперблока;
2) в буферы последовательных декодеров не поступит после
окончания приема весь суперблок.
Эти предположения означают, что все суперблоки декодп
руются независимо и, кроме Toro, в процессе декодирования
t) в частном случае неравенство Чернова выводитс!] таI{же в разд. 6.5
: '1J1I10Й книrи.
//. Последовательное декодирование
355
последовательные декодеры не простаивают в О)l{идании поступ
ления новых ребер. При этих предположениях последователь-
ные декодеры работают несколько медленнее, чем обычно,
и полученные ни {е значения вероятности переполнения буфера
оказываются завышенными.
Итак, при декодировании каждоrо суперблока сначала с по
мощыо последовательных декодеров декодируются А D из Л
внутренних блоков, после чеrо параллельный блок декоди-
руется декодером кода Рида Соломона. Так как число опера-
ций при декодировании, выполняемых декодером кода Рида
Соломона, конечно, то здесь это число мы учитывать не будем.
Сначала введем понятие приведенноrо числа операций с, необ
ходимоrо для декодирования одноrо суперблока. Пусть С;
число операций, необходимых j MY последовательному декодеру
для декодирования j ro BHYTpeHHero блока. Если величины
сl, ..., СА упорядочить В порядке их убывания, то по определе
нию С это (D + 1) e из этих чисел. Определив таким обра-
зом С, MO {HO утверждать, что при декодировании любоrо супер-
блока ни один из последовательных декодеров не выполняет бо-
лее чем С операций. Если D + 1 или больше чисел Сl, С2, ...
,. . ., С превышают L, то приведенное число операций с также
будет превышать L. Как следует из неравенства (6.143),
p[Cj L] Pl===O.L v, (6.144)
rде V == rпыч/r. Точно так же, как при выводе неравенства
(6.142), полаrая D + 1 == Ав, ИЗ формулы (6.138) получаем
p[c L] exp[ A{Te(B, Pe) H(B)}], Ре <в. (6.145)
Более простую rраницу можно получить, если воспользоваться
тем, что Т е (в, Ре) Bln Ре. Действительно, используя это не-
равенство, находим, что при всех Ре < е
р [С L] ехр [АН (в)] рАе == (01/ L)A8 V , (6.146)
rде
01 == ехр [Н (B)/VB] Ol/V.
(6.147)
Как следует из определений О 1 и Н (в), а также определения Pl
(см. формулу (6.144)], при L > G 1 условие Pl < В всеrда выпол-
няется. Учитывая, что величина р [С L] является вероятностью
и поэтому не больше 1, получаем
р [С L] { [OI/L l ]A8'V, L > а" (6.148)
, L О 1 .
Используя это неравенство, оценим среднее число операций, He
обходимое для декодирования одноrо суперблока при условии,
356
r лава б
что о::::;)'::::; 1 и лвv> 1. Сначала найдем среднее значение
приведенноrо числа операций с:
00 00
(С)ср == L Lp [с == L] == L L {р [с L] р [с L + l]} ==
L l L l
00
===LP[c / J.
L I
Отсюда и из формулы (6.148) следует, что
00
(С)ср 01 + L (ОI/ L )Ле v .
La:G 1 +1
Так как (G 1 /L)A8 V является положитсльной монотонно убываю-
щей функцией L, то сумму в правой части послеДIlеI'О неравен-
ства можно заменить интеrралом по L от 01 до 00:
00
(С)ср 01 + (OI/ L ) AB V dL <== A V " ==
01
== Aev [ехр {Н (e)/VB } 01{У]. (6.149 )
Aev 1
При Ав)' > 1 правая часть (6.149) ПОJlожительна и дает оценку
сверху для среднеrо приведенноrо числа операций, необходи-
Moro для декодирования одноrо суперблока. Заметим, что для
любой скорости передачи, сколь уrодно близкой к пропускной
способности канала, при достаточно больших Л и выполнении
неравенства Ав)' > 1 приведенное число операций на один су-
перблок является оrраниченным.
в) Вероятность nереnолненuя буфера. Остановимся на ве-
роятности переполнения буфера при rибридном декодировании.
Каждые 'Aw'V секунд в деКодt:р поступает один суперблок.
КаждыЙ из последовательных декодеров имеет буфер, кото-
рый он использует для хранения последних Bw символов, по-
ступивших с выхода соответствующеrо дискретноrо канала без
памяти. Так как ранее предполаrалось, что перед началом де-
кодирования очередноrо суперблока все символы последнеrо
должны быть приняты, то буферы должны иметь объем, доста-
точный для хранения по крайней мере одноrо суперблока. Сле-
довательно, параметр В должен быть не меньше 'А. Часть су-
перблоков, хранящихся в буфере и еще не декодированных, об-
разует очередь.
Если очередь превышает В/л суперблоков (или Bw символов
канала на каждый дискретный канал без памяти), то возникает
переполнение буфера. Интересующей нас величиной является
РL(В) вероятность возникновения переполнения буфера за
время декодирования L первых суперблоков при условии, что
11. Последовательное декодирование
357
декодер начинает декодирование очередноrо суперблока, имея
свободный буфер. Верхняя rраница для вероятности PL (8)
была получена Фалконером. Эта rраница имеет вид
[ G е ] Аеу
PL(B) < (1 + е 6 ) L 0'(8 Л) J
(6.150)
rде а некоторая постоянная, зависящая от скорости вычис-
.пений.
r) Численный пример. В заключение приведем численный
пример, ИJIЛIОСТРИРУЮЩИЙ характеристики rибридноrо декодера.
Фалконер и Ниссен [26] провели моделирование последова-
re"lbHOI"'O декодирования, используя сверточный код со скоростью
r == 1/7 И осуществляя в канале с отношением сиrнал/шум, рав-
ным 6,5 дБ, квантование сиrнала На восемь уровней. При
этом "( 1 и, следовательно, rвыч I/7. Будем считать, что
длина BHYTpeHHero блока 'V равна 360 ребрам, из которых
ln == 24 ребра являются избыточными. Если кодовое оrраниче-
ине сверточноrо кода выбрать равным 24 ребрам, то истинная
скорость передачи будет равна
J 360 24
7"' 360 == 0,133 бит на одно использование канала. (6.151)
Код Рида Соломона выберем длины Л === 31 == 25 1 со СКО-
ростыо R == 26/31 и алфавитом из 25 == 32 символов. В этом
случае каждый суперблок будет состоять из 72 кодовых слов
кода Рида Соломона. Из 31 BHYTpeHHero блока каждоrо су-
перблока пять внутренних блоков являются проверочными.
ПреДПОЛО)I(ИМ, что код Рида Соломона используется только
для исправления стираний.
Фалконер и Ниссен экспериментально исследовали распре-
деление cYMMapHoro числа операций при декодировании одноrо
BHYTpeHHero блока. Соrласно полученным ими данными, для Ka
нала, отношение сиrнал/шум в котором равно 6,5 дБ, вероят-
ность Toro, что суммарное число операций с при декодировании
одноrо суперБЛОI<а превысит 36000, приближенно равна 10 2.
Следовательно, вероятность р, (с 36 000) Toro, что приведен-
ное число операций, необходимое для декодирования одноrо су-
перблока, превысит 36000, равна вероятности Toro, что среди
31 BHYTpeHHero БЛОI<а шесть или более блоков требуют для
CBoero дскодирования более 36 000 операций. Эта вероятность
находится по формуле
Зl
Р,(с 36000) == I (з; ) (10 2)V (1 10 2)Зl V 6. 10 1. (6.152)
v==6
Если для каждоrо последовате.,1ьноrо декодера (J == 50, то
за время ввода в буфер HOBorQ внутреинеrо блока декодер можеt
358
rлава 6
выполнить 360 (J == 18000 операций. Следовательно, если каж-
дый последовательный декодер имеет буфер, способный хранить
три внутренних блока, то переполнение буфера будет возникать
только в том случае, если приведенное число операций, необхо
димых для декодирования nepBoro суперблока, превышает
2 Х 18000 == 36000. Если ДОПУСТИ1Ь, что переполнения буфера
возникают достаточно редко и являются статистически незави
симыми, то вероятность переполнения буфера при декодирова-
нии одноrо суперблока будет величиной порядка 6.10
7. Так как
буфер каждоrо последовательноrо декодера позволяет хранить
3 Х 360 ребер, то общее число ребер, которые MOI'YT храниться
в памяти декодера, равно 1080Л == 33480. Общее число двоич-
ных символов, входящих в один суперблок, равно 360 Х 31 ==
== 11 160.
Полаrая АЕ == т == 24, w == 7, Еu (r) 10g2
Rвыч
1/7 И В
(6.137) а е
1, для вероятности ошибочноrо декодирования од-
Horo BHYTpeHHero блока получаем следующую rраницу:
РВи
360 Х 2
24 == 2,23 · 10
5. (6.153)
С
помощью несложных расчетов, основанных на результа-
тах моделирования, можно оптимизировать различные пара-
метры rибридных систем кодирования и при этом учесть требо-
вания к стоимости и друrим характеристикам системы в целом.
6.8. Стек..алrоритм
Выше было проведено детальное исследование алrоритма
Фано. Этот алrоритм обладает рядом несомненных достоинств,
но, как можно было убедиться выше, анализ мноrих ero харак-
теристик очень сложен. Рассматриваемый в этом разделе так
называемый стек-алrоритм, найденный независимо Джелинеком
[7] и Зиrанrировым [8], по сравнению с алrоритмом Фано может
быть описан rораздо проще, а кроме Toro, он достаточно прост
для понимания. Этот алrоритм не всеrда лучше алrоритма Фано
(rейст [15]), но блаrодаря своей простоте он позволяет rлубже
понять сущность последовательноrо декодирования. Для про
стоты рассмотрим здесь этот алrоритм применительно к двоич
ным кодам.
Для пояснений будем использовать двоичный древовидный
код со скоростью R == 1/з, кодовое дерево KOToporo изобра)l{ено
на фиr. 6.17. Пусть it........... двоичный информационный символ, по-
ступающий в момент времени t на вход кодера. Пути длины t
будем обозначать с помощью соответствующих им векторов
i t == (i 1 , i 2 , ..., it). Через Uj (i t ), j < 1, обозначим символы, ис
пользуемые для передачи по каналу j
ro ребра пути i t . Так как
J 1. Последовательное декодирование
359
передаваемые символы, соответствующие ребрам показанноrо
на фиr. 6.17 кодовоrо дерева, пред,ставляют собой последова
тельности из трех двоичных символов, то для них удобно ис-
пользовать восьмеричное представление, например ИЗ (О 1 О i 4 ) ==
== 7, И2(1, О, i з , i 4 ) == 2. Предположим, что на выходе канала при-
нята последовательность v P , rде р длина этой последователь-
ности в ребрах кодовоrо дерева. Задача состоит в том, чтобы по
этой последовательности восстановиrь входную последователь-
ность ip.
110
101
O
о
t
+
1
L.110
111
ОI0
101
010
000
11
100
001
001
00
11
101
010
OUl
110
101
011
000
111
101
010
001
110
101
011
Фиr. 6.17. Пример древовидноrо кода со скоростью R == ] /3.
Предположим, что символ канала И, и === О, 1, ..., 7, посту-
пает на вход канала с вероятностью р (и). Тоrда вероятность
p(v) появления на выходе канала символа v будет задаваться
равенством
р (v) == L Р (v I и) р (и).
tl
(6.154)
При декодировании принятой последовательности v P нахо..
дятся функции правдоподобия L (i t ) для различных путей i t ==
( .8 . . )
== " lS+l J ... J tt :
t
L (i t ) == L л s (lS).
s==l
(6.155)
Для этоrо используются функции правдоподобия Л S (i s ) ребер,
соединяющих узлы is l и i s :
л ( i S ) == lo g [ Р [v s I Us (iS)] ] N R
s 2 Q (vs) о ·
(6.156)
360
r лава б
Поскольку в процессе декодирования последовательность v P
не изменяется и символы U s (i s ) для ка}l{доrо i 8 определяются
кодовым деревом, которое считается заданным, то величины
L (i t ) и лs(i s ) являются функциями только путей. Рассмотрим
следующий алrоритм декодирования:
1. Вычисляются функции правдоподобия L (О) == Лl (О) И
L (1) == Лl (1) двух ребер, выходящих из начальноrо узла KOДO
Boro дерева. Эти значения помещаются в память декодера.
2. Если L (О) L (1), то L (О) извлекается из памяти деко-
дера и вычисляются значения L (00) == L (О) + Л2 (00) и L (01) ==
===L(0)+Л2(01). Если L(O)<L(I), то из памяти извлекается
L (1) и вычисляются значения L (1 О) == L (1) + Л2 (1 О) и L (11) ==
== L (1) + Л2 (11). Величина L (1) (L (О) ) удаляется из памяти дe
кодера, а вновь найденные значения функций правдоподобия
помещаются в память декодера. На этом шаr 2 заканчивается.
Таким образом, перед следующим шаrом в памяти декодера
хранятся значения функций правдоподобия трех путей, а именно
двух путей длиной 2 и одноrо пути длиной 1.
3. Значения функций правдоподобия трех путей, храня
щиеся в памяти декодера, упорядочиваются в порядке их убы
вания, после чеrо находится путь, соотвеТСТВУIОЩИЙ наиболь-
шему из этих значений. Для двух путей, которые получаются из
указанноrо выше пути присоединением следующеrо ребра, BЫ
числяются значения функции правдоподобия. Значение функпии
правдоподобия пути, который был только что удлинен, из па
мяти удаляется, а в память помещаIОТСЯ вновь выIисленньlеe зна
чения функций правдоподобия. Например, преДПОЛО)l(ИМ, что в
памяти декодера хранятся значения L(O), L(10) и L(II) и
L(10) L(O) L(11). В этом случае из памяти удаляется L(O),
а помещаются в память значения функций правдоподобия
L ( 1 00) === L ( 1 О) + Аз ( 1 00) и L ( 1 О 1 ) == L ( 1 О) + Аз ( 1 01 ). Н а это м
шаr декодирования заканчивается. Перед следующим шаrом
декодирования в памяти декодера хранятся значения функuий
правдоподобия четырех путей, среди которых два пути имеют
длину 3, один длину 1, и еще один длину 2 (возможно, что
все четыре пути будут иметь длину 2).
4. Каждый последующий шаr алrоритма декодирования aHa
лоrичен описанным выше шаrам. После k ro шаrа в памяти
декодера хранятся k + 1 значений функций правдоподобия
k + 1 путей, которые MorYT иметь раЗЛИЧНУIО длину, но ни один
из которых не является началом друrоrо. На (k + 1) -м lпаrе на-
ходятся наибольшее содержащееся в памяти значение функции
правдоподобия и соответствующий этому значеНИIО путь. Значе-
ние ФУНКЦИIl правдоподобия этоrо пути из памяти деI{одера
УД,аляется, а : начения функций правдоподобия днух IJУТ Й) полу-
/1. Последовательное декодирование
361
чаlОЩИХСЯ из указанноrо выше пути присоединением следующеrо
ребра, помещаются в память.
5. Процесс декодирования заканчивается, коrда длина пути,
который должен быть удлинен, оказывается равной некоторому
заданному числу р.
Так как содержимое памяти декодера постоянно упорядочи-
вается, то этот алrоритм получил название стек алrоритма.
Понсним этот алrоритм на примере. Рассмотрим кодовое де-
рево, узлыI KOToporo пронумерованы так, как показано на
фиr. 6.18. Для обозначения путей будем использовать номера
6
о
t
о
1 1
Фпr. 6.18. Пример распределения значений функций правдоподобия по раз-
личным путям.
узлов, в которых они оканчиваются. Числа, приведенные над
ка,кдым ребром, являются значениями функции правдоподобия
соотвеТСТВУIощеrо ребра для некоторой принятой последова-
тельности v 3 . Так, значение функции правдоподобия пути с но-
мером 13 равно 6 + 1 + 1 == 4. В рассматриваемом примере
состояние памяти деI{одера меняется следующим образом (но-
мера путей n }{а)кдой cTpOI<e упорядочены таким образом, что
значение ФУНКЦИИ правдоподобия пути, номер KOToporo зани-
мает крайнее левое положение, максимально):
Состояние Путь
1 О
2 1 , 2
3 4, 3, 2
4 3, 2, 1 О, 9
5 2, 1 О, 9, 8, 7
6 6, 1 О, 9, 8, 7, 5
7 13, 1 О, 9, 8, 7, 14, 5
362
rлава 6
Так как путь с номером 13, занимающим крайнее левое поло-
жение в последней строке, имеЕТ длину 3, то декодер на шаrе 7
декодирование прекращает.
Таким образом, стек
алrоритм действительно значительно
проще алrоритма Фано. В работе [7] приведено обобщение этоrо
алrоритма на случай недвоичных кодов. Анализ вероятности
ошибки и среднеrо числа операций при декодировании можно
найти в работе [25]. Методы расчета этих характеРИСТИI{ для
стек
алrоритма аналоrичны методам расчета соответствующих
характеристик алrоритма Фана и здесь рас,сматриваться не
б у дут 1 ) .
6.9. Структура расстояний сверточных кодов
Исследование расстояний между кодовыми словами является
важным при анализе свойств кодов. Следуя Месси [17, 18], полу-
чим сначала аналоrи верхней rраницы Плоткина и нижней rpa-
ницы Варшамова
rилберта для минимальноrо расстояния си-
стематических сверточных кодов. Далее остановимся на введен-
ном Костелло [19] понятии свободноrо расстояния, !{оторым
удобно пользоваться для описания расстояния кодов, исполь
зуемых при последовательном декодировании, и в заКЛlочение
рассмотрим несколько алrоритмов построения сверточных кодов
со скоростью 1/nо.
Как y)l{e указывалось выше, существуют два типа методов
алrебраическоrо декодирования сверточных кодов: декодирова-
ние с обратной связью и дефинитное декодирование. При выводе
кодовых rраниц для минимальноrо расстояния сверточных кодов,
допускающих декодирование одним из этих методов, КОДЫ
удобно задавать с помощью порождающих мноrочленов, как
это было описано в разд. 6.2. Если совокупности провеРОЧIIЫХ
и информационных символов на выходе систематическоrо CBep
точноrо кодера в момент времени u обозначить соответственно
через
ti< == (t (k o + 1) t (k o +2) t (no» )
u и 'и ,..., u
: === (t .(I) t .(2) l '(kll» )
.и и' и' ..., u ,
(6.157)
(6.158)
и
u u
то систематическии сверточныи код моя{но задать с помощью
порождающих мноrочленов следующим образом:
t * · О " + . о " + + · О "
u == 'и О 'и
1 1 · · · 'о u.
При рассмотрении декодирования с обратной связью всеI"да бу-
дем считать, что itt === О при и > О.
(6.159)
t) См. также книrу К. Ш. 3иrанr'ирова «Процедуры llоследовательноrо
декодирования», изд
во «СВЯЗЬ», 1\1., 1974.
ПРU/vt. ред.
//. последовательное декодирование
363
6.9.1. Верхняя rраница Плоткина при декодировании
с обратной связью
Как указывалось выше, при декодировании с обратной свя-
зью без оrраничения общности всеrда можно рассматривать лишь
декодирование подблока io (декодирование остальных подблоков
iu осуществляется аналоrично). Миним альное расстояние свер-
точноrо кода d FD при декодировании с обратной связью есте-
ственно определить следующим образом.
Минимальное расстояние d FD сверточноrо кода есть наимень-
шее число символов, в которых различаются две кодовые после-
довательности длиной пА == nFD, порождаемые кодером с мо-
мента времени О до момента времени т и имеющие отличные
первые информационные подблоки io.
В силу свойства линейности систематических сверточных
кодов определенное таким образом минимальное расстояние
совпадает с минимальным весом начальных кодовых слов:
d pD === min W н (io, i l , · . ., i m , t
, t
, . . ., t
),
/} =1= О ..
(6.160)
rде W I-I ( · )
вес Хэмминrа вектора, заключенноrо в круrлые
скобки. В целях упрощения далее будем рассматривать лишь
двоичные коды.
Из равенства (6.160) непосредственно следует, что макси-
мальное значение d FD в клас.се всех сверточных кодов со скоро-
стью R == ko/no, порождаемых кодерами с т
разрядными реrи-
страми сдвиrа, является верхней rраницей для d FD . Это макси-
мальное значение обозначим через maXFD (т, па, ko). Для
maXFD (т, по, ko) Месси была получена следующая верхняя rpa-
ница:
maXPD(m, па, ko)
[ тi5 ](no
ko)+ 1. (6.161)
Для доказательства этоrо неравенства нам понадобятся следую-
щие свойства величины maxFD(т, по, ko) как функции т, па и k:
Свойство 1.
maxPD(т, по, ko)
maxPD(т, no
ko+ 1,1). (6.162)
Так как минимум в (6.160) берется по всем кодовым после-
довательностям, ка)кдый подблок из ПО символов которых содер-
кит ko информационных символов, то естественно, что минимум
в (6.162) берется и по всем кодовым последовательностям, по-
рождаемым информационными подблоками iu, последние ko
1
символов которых равны нулю. Минимизация только по таким
кодовым последовательностям эквивалентна нахождению мини-
мальноrо расстояния сверточноrо кода, на вход кодера KOToporo
в каждый момент времени подается один информационный сим-
364
r лава 6
вол, на пыходе кодера формируется по (/lo 1) символов и
порождающие матрицы 07, j === О, 1, ..., и, KOToporo представ-
ляют собой первые строки соответствующих порождающих мат-
риц исходноrо кода. Максимум минимальных расстояний по
всем таким кодам равен правой части (6.162). Это доказывает
справедливость неравенства (6.162).
Свойство 2. Для ЛIобоrо нечетноrо по
( 1) + Ilо 1
maxpD т, по, no т 2 ·
(6.163)
Сначала дока)кем существование кода с Il o == 1 и d FD ===
=== maXFD (т, по, k o ), для KOToporo O T == (1, 1, . . ., 1). Пусть
k == 1, ..., по 1 произвольное целое число. Пока}l{ем, как
по коду, k й элемент матрицы O KOToporo равен О, можно по
строить код, k Й элемент порождающсй матрицы 00 KOToporo
равен 1 и минимальное расстояние d FD KOToporo не меньше, чем
минимальное расстояние исходноrо кода.
ПреДПОЛО)I{-ИМ, что задан некоторый код, k й элемент поро-
ждающей матрицы O KOToporo равен О. Если k e элементы всех
остальных матриц 07, j =1= О, этоrо кода равны О, то k e эле-
менты всех блоков t в формуле (6.159) также будут равны
О. СJIедовательно, если k й элемент матрицы O , равный О, за-
менить на 1, то минимальное расстояние d FD можно увеличить.
Допустим, что k e элементы матриц 01 не все равны о.
Пусть ОТ....... порождающая матрица, имеющая наименьший ин
декс 1 в множестве матриц 07, k й элемент КОТОРЫХ отличен ОТ
нуля. Если k й элемент матрицы 07+1, j == о, 1, ..., т n, по-
местить на место k ro элемента матрицы Oj, j == о, 1,..., т n,
то в результате k й элемент блока ti+/ просто переместится на
место k ro элемента блока tj. Из ОIIределения d FD и формулы
(6.159) следует, что новый КОД имеет минимальное расстояние,
по крайней мере не меньшее, чем исходный код, а k й элемент
ero матрицы О({ равен 1. Так как k произвольное число из
множества {1, 2, ..., по}, то при ko === 1 существует код с мини-
lальным расстоянием d FD === maXFD(m, по, ko) и O T===(I, 1, ...
...,1).
Следующий шаr на пути доказательства неравснства (6.163)
заключается в том, чтобы показать, что для Лlобоrо сверточноrо
кода с ko == 1 и О;Т == (1, 1, ..., 1) информ аЦИОНIII)те символы
i 1 , ..., i m всеrда можно выбрать так, что соответствующий им
кодовый вектор (io, i J , ..., i m , t , t;, ..., t ), iu== 1, будет
иметь вес, не превышающий правой части (6.163). Сначала за-
меТИ f, что подблок (io, t ) вектора (i o , il' . . ., i 17P t , t , . . ., t )
такой, что (io, t ) === (1, O T), т. е. является вектором веса по.
//. Последовательное декодирование 365
Далее, произвольный подблок (iu, t:), и > О, предстаВИ 1 в сле
дующем виде:
(iu, t:) == ( i u . t [и P7 ) == ( i u , iuG; + t iu P'f ) ==
/ o J l
== ... i u ) + (о, jtl iU JG7 ). (6.164)
n.
Второе слаrаемое в правой части (6.164) представляет собой
вектор длины по, не зависящий от iu. Следовательно, векторы
(iu' t:), соответствующие i и . == О и i и == 1, являются дополни-
тельными. Так как ПО по предположению нечетное число, то,
выбрав iu равным О или 1, МОЖНО добиться Toro, что вес no Mep-
Horo вектора (iu' t:) не будет превыIатьb (по 1)/2. Поскольку
вышеизложенное справедливо при любом и == 1, 2, '.', т, то в
любом коде с O T == (1, 1, . . " 1) Bcer да существует кодовое
слово, вес KOToporo не преВОСХОДИ1 по + т (по 1) /2. Это дока-
зывает свойство 2.
Свойство 3. При любом четном т
maxpD (т, по, ko) maxpD (т/2, 2nо, 2ko).
(6.165)
Чтобы доказать это свойство, рассмотрим код с параметрами
2 , k u О " О " О "
т == т, по, о, пор о JI( Д а е м ы и м а т р и Ц а м и О ' 1'. · · , 2т' , И
ностроим по нему новый код с параметрами т', n === 2n о ,
k == 2k o , определив порождаlощие матрицы последнеrо сле
дующим образом:
О"
О* 2/
j О"
2/....1
О"
2/+ 1
О"
21
j == О, 1, . . ., т',
(6.166)
О " О " О
rде ___1 и rn+l матрицы, все элементы которых равны .
Обозначим через
l; === (i2/' i2/+ 1)
t;===(t;/, t;l+l)
(6.167)
(6.168)
и
векторы соответственно из k == 2ko информационных и n
........ k === 2 (ПО........ ko) проверочных двоичных символов HOBoro кода
в момент времени j. По определению
t ' ., О * + ., о '" + + ., 0 *
и == t и 10 'u+l 1 · · · 'и т т.
(6.169)
366
rлава 6
Блоки t КОДОВЫХ слов HOBoro кода, как леI ко видеть, являются
также блоками КОДОВЫХ слов исходноrо кода, порождаемоrо
матрицами 07, и MorYT быть найдены с помощью равенства
(6.159). Соrласно равенству (6.160), минимальное расстояние
HOBoro кода определяется равенством
d ' ·
PD === mlП
10 ер О ИЛИ t, + о
(либо 10 + о, t 1 + о)
WH(i o , il'
. . .,
i m + 1 , t , t;, ..., t +1).(6.170)
Можно показать, что правая часть равенства (6.170) к тому же
является минимальным расстоянием d FD исходноrо кодз. Дей
ствительно, минимум W н (i1), i 1 , ..., i т + 1 , t , t;, .. " t;n+l) по
всем информационным последовательностям, для. которых io == О
(в этом случае t О) и i 1 =1= О, равен минимальному расстоя
нию d FD по определению. Так как при io =1= О вектор (io,..., i т ,
t , ..., t ) не может иметь вес, меньший d FD , то, очевидно, что
( · .. t * t * t * )
вес вектора '0'...' 'т' ' т + 1 , о,..., т' т+l также не меньше
d FD . Следовательно, правая чаrть равенства (6.170) раАна d FD .
Отсюда следует неравенство (6.162).
Свойство 4.
max pD (т, по, ko) maxpD (т + 1, по, ko).
(6.171)
Это свойство очевидно.
Используя приведенные выше свойства, докажем слеДУЮЩУIО
теорему.
Теорема 6.6 (Месси.) Величина max[I'D(m, по, ko) удовлетво-
ряет следующему неравенству:
maXPD(m, по, ko) [ тt5 ](no ko)+ 1. (6.172)
Доказательство. Сначала рас,смотрим случай, коrда па ko
нечетно. Из свойств 1, 3, 4 непосредственно следует, что
maxpD (т, по, ko) maxPD (т, по....... ko + 1, 1)
тах ( [ т 1 ], 2no 2ko + 2, 2).
Отсюда и ИЗ свойств 1 и 2 получаем
maXPD(m, по, ko) maXPD([ тil ]. 2no 2ko+ 1. 1)
2 (по ko) + 1 + [ т i I ] (по k o ).
//. Последовательное декодирование
367
Предположим, что (по
ko) четное. Тоrда, соrласно свойствам
1 и 2,
тахр D (т, по, ko)
mахр D (т, па........ ko + 1)
(по
ko + 1) + '; (по
k o ).
Подставляя пFD == (fn + 1) по и R == ko/no в (6.172), получаем
следующее асимптотическое неравенство:
1 . maxpD (т, 110' ko)
1 (1 R) (6.173)
1т
2
·
т
oo п pD
6.9.2. Нижняя rраница rилберта для сверточных кодов
при деКОДllровании с обратной связью
Нижняя rраница rилберта для с.верточных кодов, исполь
зуемых при декодировании с обратной связью, для произвольных
скоростей передачи R == ko/пo была получена Возенкрафтом [1],
коrда Ilo == ko + 1. в общем случае нижняя rраница выводится
аналоrично, в частности, использованный ни}ке метод вывода
этой rраницы может быть непосредственно обобщен на случай
произвольных кодов.
В случае по == ko + 1 блоки t
представляют собой просто
двоичные символы t
ko+l), а матрицы 07 вырождаются в BeKTOp
столбцы
g "T == (g ko+l) g (ko+I) ) .
и 1, и , · · · , ko I U
При этом
t<ko+ 1)
I f\k,+ [)
i o ,
О, ...,
O
,,
go
g;'
i l'
i o , · · ., о
(6.174)
t<k,j+ 1)
т
i m ,
iт
1'
. . . ,
i g"
o
т
Вектор в левой части (6.174) назовем t
BeKTopoM, матрицу
раЗ
1ера (111 + 1) Х (т + 1) ko в правой части
информационной
матрицей, а вектор (i o , i l , ..., iп
)
информационным вектором.
BeKTop
CTPOKY, компонентами KOToporo являются компоненты ин
формационноrо вектора и t
BeKTopa, связанные между собой ра-
венством (6.174), будем называть начальным кодовым вектором.
Начальный кодовый вектор состоит из пFп === (ko + 1) (т + 1)
двоичных символов, ko (т + 1) из которых являются компонен-
тами информационноrо вектора, а остальные (т + 1)
компо-
нентами t
Bel{TOpa. rоворят, что некоторый код имеет минималь-
368
rлава 6
ное расстояние d FD , cTporo меньшее d, если вес HeKOToporo ero
d 1
начальноrо кодовоrо вектора меньше d. Bcero имеется L (п jD )
j O
двоичных векторов длиной nFD и веса d 1 или менее. Далее
ц
потреоуется слеДУЮIцая известная оценка сверху для указаННОII
BbIIlIC CYM?\fbI n следующей лемме.
Лемма 6.2.
u
I ( ) 2 11Н (Щn) ,
j==O
ёде Н (х) функция, называемая энтропией и определяемая ра-
венством
(6.175)
н (х) == ........ х log х ........ (1 х) log (1 ...:... х).
(6.176)
Доказательство. Лемму 6.2 можно доказать различными спо
собами. Здесь, следуя Парку [20], дока)кем ее методом MaTeMa
тической индукции. Для этоrо положим
и
А (п, и) === I ( ) ,
j==O
(6.177)
в (n, и) === 2 nН (и/n) == (п/и)и [n/(п ........ ll)]n a. (6.178)
1. В случае u == о: А (n, о) == в (n, о) == 1 и (6.175) выполня-
ется со знаком равенства.
2. В случае n == 2и: А (2и, и) < А (2и, 2и) == 2 2и == В (2и, и).
3. В случае О < и < n/2 справедливость неравенства (6.175)
докажем индукцией. ПреДПОЛО)l(ИМ, что неравенство (6.175)
имеет место при (n, и) и (п, и + 1), и докажем ero справедли-
вость при (n + 1, u + 1). Сначала заметим, что
(:t:)==(U l)+(:)
и, следовательно,
А (n + 1, u + 1) == А (n, и + 1) + А (n, и).
(6.179)
Оценивая слзтаемые в правой части (6.179) с ПОМОI.ЦI)IО Hepa
венства (6.175), которое ПО предполо}кению ИНДУКЦИJI выполня-
ется при данных (п, и) и (п, U + 1), и полаrая
а == [ п 1 ]11 [ t : ][ II 1 Т ' (6.180)
[ п ] n [ п и ] n U 1 [ п fl ]
== . п + 1 Il U 1 fl + l _ '
(6.1 1)
/1. Последовательное декодирование
369
после неСЛОЖI-lЫХ преобразований находим, что
А(п+ 1, u+ 1) B(n+ 1, u+ 1)[a+ ].
(6.182)
Покажем, что а + 1, и этим завершим доказательство лем
мы. JIоrарифмируя выражения (6.180) и (6.181) и используя
неравенство ln х х 1, получаем
1 (п II 1) (6.183)
па п+l '
и
ln п + 1 ·
(6.184)
Отсюда следует, что
а + [e (n u 1) + e U]l/n+l. (6.185)
Так I<aK n и 1 1 и tl 1 при всех 1 и :::;; п 2, то
e (H u l) + c ц, e l + e l == 2/е < 1 и, следовательно, a+ < 1.
JlcMMa 6.2 доказана.
dpD 1
Используя нсраВСIIСТВО (6.175), сумму L сп jD ) можно оце-
/r::::o
. НIIТЬ сверху слеДУЮIДИМ образом:
dpD 1
L ( п jD ) :::;;;; 2 nPDH (d/nPD) .
/==0
Так как в случае io =1= О информационная матрица в (6.174)
имеет paHr ln + 1, то доля кодов, таких, что заданный информа
llИОННЫЙ всктор с io =1= О и произвольный фиксированный t BeK
тор ЯВЛЯIОТСЯ решением (6.174) (т. е. доля кодов, содержащих
на'Iальнос кодовое слово, образованное заданным информацион
HЫ вектором с io =1= О и заданным t BeKTopOM), равна
2(т+,) (ko I)/2(т+l,> ko == 1/2 т + 1 . Следовательно, доля кодов, coдep
жаIДIIХ по краЙней мере одно из начальных кодовых слов веса
d PD или менее, не превосходит 2nPDH(d/nPD)X (1/2 т + 1 ) (здесь мы
ВОСIIо.пьзовались неравенством (6.186)). Отсюда в свою очередь
npDH (d/nPD) ( m+l ) u u
следует, что ссли 2 Х 1/2 < 1, то по краинеи мере
однн из кодоп имеет минимальное расстояние d FD или более.
Jl0rарнq)мируя последнее неравенство и учитывая, что пFD ==
== (пl + 1) (ko + 1), R == ko/ (ko + 1), указанное выше услови
существования кода с минимальным расстоянием d FD или более
перепишем в виде (/n + 1) (ko + 1) н (dFD/пFD) < т + 1, или, что
то )I{е самое, Н (dFп!пРD) < 1/ (ko + 1) == 1 R. Если этот ре-
зультат обобщить на случаЙ произвольных кодов, то получится
с.пеДУlощая теорема.
(6.186)
370
rлава 6
Теорема 6.7. Существует по крайней мере один сверточный
код со скоростью передачи R, кодовым оzраничением ПА и мини-
мальным расстоянием d FD , ёде d FD
наибольшее целое число,
удовлетворяющее условию
н (dPD/nPD) > 1
R.
(6.187)
Траница, задаваемая формулой (6.187), называется ёрани-
цей Тилберта для сверточных кодов.
6.9.3. Верхняя и нижняя rраницы минимальноrо расстояния
при дефинитном декодировании
Как опи,сывалось выше, при дефинитном декодировании с
целью подавления распространения ошибок решение об инфор
мационном символе, передаваемом в момент времени и, прини
мается по информационным символам, принятым с момента вре-
мени и
m до момента и + т, и проверочным символам, при
нятым с момента времени и до момента времени и + т. Число
этих символов называется кодовым оrраничением при дефинит-
ном декодировании nDD, а именно по определению
nDD == (2т + 1) ko + (т + 1) (по
k o ).
(6.188)
инимальное расстояние кода d DD при определенном дeKO
дировании определяется Kal{ минимальное число символов в
пределах кодовоrо оrраничения, в которых различаются две ко-
довые последовательности, соответствующие различным значе
ниям io. В силу свойства линейности сверточных кодов в данном
случае минимальное расстояние d DD можно также выразить
через веса Хэмминrа кодовых последовательностей:
d DD == min П7н(i
m' i---m---l' ..., 1т' t
, t;, ..., t
). (6.189)
10 + о
Если сравнить формулы (6.160) и (6.189), то сразу же можно за-
метить, что d DD
d FD . Следовательно, верхняя rраница для
d FD является также верхней rраниuей и для d DD . Однако ни}l{няя
rраница для d FD нижней rраницей d DD не является.
Задача нахождения нижней rраницы для d DD была постав-
лена и решена
есси [18].
eTOД, использованный
есси для
вывода этой rраницы, довольно сложен и основан на использова
нии периодичности последовательностей на выходе реrистра
сдвиrа. Поэтому здесь приводится лишь сама rраница.
Теорема 6.8 (Месси.) Для nроизвОЛЬНО20 по > ko и достаточно
БОА ЫllllХ п 1)О сусцествует по крайней Al«!pe один cBeproflflblll код
//. Последовательное деl(одированuе
371
со скоростью R == k.o/no и кодовым оzраничение.м nDD, .мини.маль
ное расстояние d DD КОТОрОёО удовлетворяет условию
( d DD ) 1 1
R
Н п DD
10 1 + R ·
(6.190)
6.10. КОДЫ, используемые при декодировании
с обратной связью
Важнейшей характеристикой сверточных кодов, исправляю
щих случайные ошибки, точно так же, как в блоковых кодах,
является их минимальное расстояние. Однако сверточным Koдa
1
не присущи алrебраические свойства, подобные свойствам uик.пи
ческих кодов, и С1рОИТЬ сверточные коды с большим минималь
ным расстоянием методами, подобными методам построения
БХЧ
кодов, не удается. Ряд сверточных кодов с большим мини
мальным расстоянием для скоростей передачи R == 1/2 И I/ з был
построен Бусrанrом [21]. Относительно реrулярный метод по
строения таких кодов предложен также JIином [22]. Здесь бу
дет описан метод поиска сверточных кодов с помощью HeKOTO
рых простых алrоритмов, предложенных Костелло [19], и приве
дены получающиеся коды. Класс построенных Костелло кодов
является наиболее широким из всех известных в настоящее
время. При этом Костелло ввел два важных понятия: столбцо-
вое расстояние, используемое при декодировании с обратной свя
зью, и свободное расстояние, используемое при последователь-
ном декодировании.
Порождающая матрица 000 сверточноrо кода, введенная в
разд. 5.2, при скорости передачи R === 1/nо имеет следующий вид:
[ 1, g
M, о' ..., g
J), О, О, g
Ы. l' ..., g
o. 1)' о, g
M, 2' ... ]
rr(I) 1 g (1) g (1) О (1) (1) .
..., f
(no), 2' ..., , (2) о' ..., (по), о' , g(2, 1)' ..., g(no), Р ...
........................... .
(6.191)
Подматрицу матрицы 000' состоящую из первых tl + 1 строк и
(и + 1) (по + 1) столбцов, обозначим через O
:
1, g
Ы. О, ..., g
o)t О' · · ., О, gH
, и'
. . . ,
аО)
:''> (п,,), и
a
===
. (6.192)
Пусть
1, g
Ы, О, .. ., g
o), О
i и == [i o , i 1, . . ., iuJ
(6.193)
372
r лава 6
информационный BeKlop. Введенное в разд. 6.9.1 минимальное
расстояние d FD сверточноrо кода определяется равенством
d pD == rnin,dH[imG:, i G:]== min WH[imG:]. (6.194)
io =1:: io 10 =1:: о
Используемое ниже столбцовое расстояние определяется еле-
ДУI{)ЩИМ образом.
Определение 6.1. Столбцовое расстояние порядка и сверточ-
НОёО кода со скоростью передачи R === 1/nо равно
d · W ( . О и .' о и )
и тlП, " и 00' 'и 00.'
10 =1= io
и == О, 1, .... (6.195)
Сравнивая формулы (6.194) и (6.195), можно заметить, что
d FD == d т . Введенное столбцовое расстояние обладает следую
щими свойствами:
1)
2)
d и == in W н (i/O:');
to =1:: о
d" WH(g"),
(6.196)
(6.197)
rде gи первая строка матрицы O ;
3)
dи dи+l' и==О, 1,2, ....
(6.198)
Свойство 1 непосредственно следует из определений мини-
мальноrо расстояния кода и минимальноrо песа. Полаrая io === 1,
.. . О · G tt u
tl == t2 == ... == t и == , получаем " и 00 == gu; ОТСlода и из сВОН....
ства 1 следует справедливость свойства 2. Свойство 3 следует
из Toro, что вектор iиo всеrда является префиксом вектора
С . · ] O и+1 · 0 "+1
'u, Еи+ 1 00 === " u + 1 00 ·
Как указывалось выше, сверточный код тем лучше, чем боль-
шее отношение dFD/nFD он имеет. Одним из критериев, позволяю
щих судить О том, является ли отношение d FD /nJ4'D плохим или
хорошим, является близость этоrо отношения к rранице rилбер-
та, определяемой формулой (6.187). Так как число сумматоров
по модулю 2, содержащихся в показанном на фиr. 6.5 Rпл раз-
рядном кодере сверточноrо кода со скоростью R == l/по, в точ-
ности равно W н (gm) по, то при заданных параметрах d FD и
прп более предпочтитеЛЬНЫf\1И оказываются коды, которые имеют
меньшее значение W н (gm).
а) КОДЫ СО скоростью R === 1/2. Коды С такой скоростью мо-
J'YT быть построены с помощью слеДУЮIцеl"О алrоритма:
//. П оследоваtеЛЬflое декодирование
373
Алrоритм I.
О) Положить g Mf О === 1, d o === 2, U == 1.
1) Положить g M. u === 1.
2) Вычислить d u . Если d u > dи l, то перейти к шаrу 4.
3) Положить g Ы, u == о.
4) Если U == т, то построение кода заканчивается; в против
ном случае положить U == U + 1 и перейrи к шаrу 1.
Свойство 1..1. WH(gи)== d u , U == 0,1, ..., т.
Доказательство. Из Toro, что W н (go) == d o == 2, и из свойства
2 следует, что W1:l (gu) d u . С друrой С10рОНЫ, шаrи 2 4 алrо
ритма таковы, что при d u > du l И только в этом случае вели
чина W н (gи) увеличивается на единицу, но не больше. Следо
вательно, W л (g1J) d u , а поэтому WH(gu) === d .
В силу свойства 2 столбцовоrо расстояния W н (gm) d m ==
== d FD , но, ка к следует из свойства 1 1, в да нном случае вели-
чина W н (gт) принимает минимальное возможное значение, а
это означает в свою очередь, что число сумматоров по модулю 2
в кодере также минимально.
Свойство 1..2. Если g M. u == 1, то g . u+l == О для всех U =1= о.
Доказательство. Предположим, что g Ы. u === 1 при некотором
U 1 и g J;. и+l == 1. В этом случае информационная последова
тельность io == iu === 1, i 1 == i 2 == ... == iu ..l == iU+l == О Bcer да бу-
дет порождать кодовое слово веса d и , так что d и + 1 == d u . Однако
это противоречит тому, что в силу свойства 1 при сделанных
предположениях d u + 1 == W (gu+l) > W (gu) == d u . Следовательно,
если g:Ы. u 1, U 1, то для алrоритма I всеrда g . u+l == О.
Из свойства I 2 следует, что всякий раз, коrда коэффициент
g C u полаrается равным 1, следующий коэффициент g M. u+l дол-
х<ен равняться О. Это свойство алrоритма I позволяет сократить
число операций 1 и 2 при построении кода.
Свойство 1..3. Пусть gт, порождаlОЩИЙ вектор, получаю-
щийся при построении кода с помощыо алrоритма I. Пусть g
u u u
друrои порождающии вектор тои же длины, что и gт, но отлич-
НЫЙ от последнеrо и такой, что \\7 н (g ) == d при любом целом
II == О, 1, ..., т, а именно g вектор, любой символ 1 кото-
poro увеличивает минимальное расстояние ровно на единицу.
Тоrда существует такое целое число ио, 1 ио т, что d l == d;
при i == О, 1, ..., II О 1 и d ио > d o .
374
rлава ()
Доказательство. Пусть ио, О ио ln, начальная rочка, в
которой начинаlОТ различаться по рождающие векторы gm И g .
Допустим, что g , ио == О и g M: и о == 1. Tor да d o == d un + 1 > d uo .
Это означает, что столбцовое расстояние в точке ио увеличи-
вается, а следовательно, соrласно алrоритму 1, следовало бы
положить gt , и о == 1, но это противоречит предположению о том,
что g , === о. Следова тельно, в точ ке ио, r де порождающие век-
торы grn' И gm впервые начинают различаться, g( : ио == О, g , ио ===
=== 1 и d и о > d o ·
Коды, которые MorYT быть построены с помощью друrих алrо-
ритмов, отличаются от кодов, алrоритм построения KOTOPIJIX был
описан выше, тем, что их порождаIощие последовательности МО-
rYT не содержать символ 1 на позиции, rде он Mor Бы быть
введен.
Коды с R === 1/2, полученные с ПОМОll{ЬЮ а.тll"оритма 1, и их
минимальное расстояние, удовлеТВОРЯЮJlJее rранице rилберта,
приведены в табл. 6.1.
т аблuца 6.1
КОДЫ со скоростью R == 1/2
и ( 1 ) d u u I I ) d u u ( 1 ) d u " ( I ) d и
B{ ), и g(2). и g(2), и R(2), и
о 1 2 17 О 8 34 О 12 50 О 16
1 1 3 18 О 8 35 1 13 51 О 16
2 О 3 19 О 8 36 О 13 52 О 16
3 1 4 20 1 9 37 О 13 53 1 17
4 О 4 21 О 9 38 О 13 54 О 17
5 1 5 22 О 9 39 О 13 55 О 17
6 О 5 23 О 9 40 1 14 56 1 18
7 О 5 24 1 10 41 О 14 57 О 18
8 1 6 25 О 10 42 О 14 58 О 18
9 О 6 26 О 10 43 1 15 59 О 18
10 О 6 27 1 11 44 О 15 60 О 18
11 1 7 28 О 11 45 О 15 61 О 18
12 О 7 29 О 11 46 О 15 62 1 19
13 О 7 30 О 11 47 О 15 66 О 19
14 О 7 31 1 12 48 1 16 61 О 19
15 О 7 32 О 12 49 О 16 65 1 20
16 1 8 33 О 12
б) Коды со скоростью R == 1/3. Коды со скоростью R == l/по,
по > 2, также можно получить, строя порождающие последо
В2тельности, удовлетворяющие условию d1.L == Wл(gи), U ==.
== О, 1, ..., т, путем присоединения к уже построенной после-
довательности gи l совокупности из ПО 1 символов, по край-
ней мере один из которых равен 1, если при этом не нарушается
//. Последовательное декодирование
375
условие d u == WH(gи), и совокупности из no 1 нулевых сим-
волов в противном случае. При этом для каждоrо значения
и приходится определить уже ПО 1 символов g Ы, и' ..., g o), ".
В случае по === 3 удлинить порожде-нную последовательность
можно тремя указанными ниже способами. Для построения по
рождающеЙ последовательности gu, удовлетворяющей условию
d u == W H (gu), при каждом значении u в пеРВУIО очередь ис
пользуется тот способ, который не при водит к нарушеНИIО усло-
вия d u == W H (gu) И В то же время позволяет повысить мини-
мальное расстояние.
Алrоритм 11.
О) Положить g , о == gB , о === 1, d o === 3 и и == 1.
1) Положить g , и === 1, gH , rt == о.
2) Вычислить d u . Если d u > du l, то rерейти к шаrу 6.
3) Положить g Ы, u == о, gi . u == 1.
4) Вычислить dllo Если d и > dи l, то перейти к шаrу 6.
5) Положить g M, и == gH;, и == о.
6) Если u == т, то построение кода заканчивается; в про-
тивном случае положить и == и + 1 и перейти к шаrу 1.
Заметим, что описанный алrОРИТ 1 исключает возможность
удлинения порождающей последовательности путем присоедине
ния символов g J , и == 1 и g M, и == 1. Как показали Лин и Лайн
[22], для данноrо алrоритма всеrда d u dи l + 1.
т аБЛllца 6.2
Коды со скоростью R == l/ з
u (?) ( ) d u II (2) (1) d u
g( i), U gt 1): и g( 1), U g{I), u
о 1 1 3 14 О О 14
1 1 О 4 15 О О 15
2 1 О 5 16 О О 15
3 О 1 6 17 1 О 16
4 1 О 7 18 О 1 17
5 О 1 8 19 О О 17
6 О 1 9 20 1 О 18
7 О 1 10 21 О О 18
8 О О 11 22 1 О 19
9 1 О 11 23 6 1 20
10 1 О 12 24 О О 20
11 О О 12 25 О О 20
12 1 О 13 26 1 О 21
13 О О 13
............. -....... .... -............... ....
376
r лава 6
КОДЫ, построенные с ПОМОЩЬЮ алrоритма 11, а также значе-
ния минимальноrо расстояния, найденные из rраницы rилбер-
та, приведены в табл. 6.2.
в) КОДЫ со скоростью R === 1/4. В этом случае для каЖДоrо
значения и должны быть определены у}ке три символа g
, и'
g
M, u и g
, и. Кроме Toro, следует заметить, что здесь при ка/к-
дом значении tl минимальное раССТ05Iние может увеличиться не
только на 1, но и на 2. Как и все преДЫДУlltие алrоритыы, описан
ный ниже алrоритм позволяет построить I(л(
сс поро}кдаfОIЦИХ по.
следовательностей gu, удовлетворяющих условию d и == W п (gu),
путем присоединения к построенной последовательности gu
1 co
вокупности трех символов g
Ы, и' g
M, и' g
, и' однн из !{ОТОРЫХ ра-
вен 1, если при этом нарушается условие (1и== WH(gu), и трех
символов О в противном с.лучае.
Алrоритм 111.
О) Положить g
, о === g
M, о === g
, о == 1, d o
4, j == 1.
1 ) Положить g o) === g (1) === 1 a(l) === О i == 1 и пе р ейти
(2),и (З), и 'Ь(4).u ,
К шаrу 8.
2) Положить g
M, u == О, g
. u == 1, i === 2 и перейти к шаrу 8.
3) Положить g
Ы. u == О, gЫ
. и == 1, i === 3 и перейти к шаrу 8.
4) Положить g
M. и === О, i == 4 и перейти к шаrу 8.
5) Положить gH
. и === 1, gti
. и === О, i == 5 и перейти к шаrу 8.
6) Положить g
M, u == 1, g
M. и === 1, i == 6 и перейти к шаrу 8.
7) Il0ЛОЖИТЬ g
M. и == О И перейти к шаrу 9.
8) Вычислить d u . Если d u === dU
I, то перейти I{ i + 1.
9) Если u === т, то построение кода заканчивается; в про-
тивном случае положить и == и + 1 и перейти к шаrу 1.
КОДЫ, построенные с помощью этоrо алrоритма, приведены
в табл. 6.3.
6.11. КОДЫ, используеl\lые при последовательном
декодировании
При последовательном и друrих аналоrичных методах деко-
дирования декодер принимает решение о том или ином пере
данном СИМВО
lIе, основываясь не обязательно лишь на симво-
лах, ле}кащих в пределах кодовоrо оrраничения. Как мы ви-
дели выше в разд. 6.2, в процессе поиска прави.пьноrо пути на
1/. последовательное декодирование
377
т аблиц а 6.3
Коды со скоростью R === J /4
u (1) (3) (4) d и U (2) (3) (4) d и
R(I ), и R( I ). t1 R(I ), и R(l ), и R(l). и R(I ), и
о 1 1 1 4 14 О 1 О 21
1 1 1 О 6 15 О О 1 22
2 1 О 1 8 16 О О 1 23
3 О О 1 9 17 О О 1 24
4 О 1 О 10 18 О 1 О 25
5 О О 1 11 19 О 1 О 26
6 О О 1 12 20 1 О О 27
7 1 О 1 14 21 О О 1 28
8 О О 1 15 22 О О 1 29
9 О 1 О 16 23 О О 1 30
10 О 1 О 17 24 О 1 О 31
11 О О О 17 25 О О 1 32
12 1 1 О 19 26 О 1 О 33
13 О О 1 20 27 О 1 О 34
кодовом дереве декодер может обследовать пути, длина KOTO
рых HaMHoro превышает кодовое оrраничение. В подобных слу
чаях параметр d FD , характеризующий расстояние Хэмминrа Me
жду кодовыми последовательностями в пределах одноrо KOДO
Boro оrраничения, не очень интересен. Друrой более подходя
щеЙ в подобных случаях характеристикой кода является так
называемое свободное расстояние, введенное Ме.сси.
Определение 6.2. Свободное расстояние dсвоб равно d oo , т. е.
столбцовому раССТОЯНU10 порядка и === 00. Свободное расстояние
обладает слеДУIОЩИ:VIИ своЙствами:
Свойство 1. Для Лlобоrо и d u dсвоб W н (g) И, В частно
сти, d m === d мии d своб W н (g), rде g ПОРО)l{дающий вектор
кода.
Доказательство. Неравенство d u d oo == d своб следует непо
средственно из свойств столбцовоrо расстояния. Неравенство
d своб == d oo W н (g) является следствием свойства 2 столбцо-
Boro расстояния.
Свойство 2. Для всех кодов, которые строятся с помощью
алrоритмов 1, 11 и 111, dсDоб == d FD == d т .
Доказательство. СправеДJIИВОСТЬ свойства 2 непосредственно
следует из Toro, что для всех кодов, которые строятся с по
мощью указанных аЛI"'ОрИТМОВ, d PD == d 1n == WH(gn ) === WH(g).
Свойство 3. Для систематических кодов со скоростью пере
дачи R == l/no свободное расстоннне dсDоб равно d(no 1) (т+1) т.
378
r лава б
Доказательство. Минимальное расстояние кода не может
быть достиrнуто На кодовых последовательностях, информа-
ционные подпоследовательности которых имеют ненулевой пер-
вый символ (io =F О), но содержат т или более С 1Jедующих друr
за друrом символов О. Это связано с тем, что при наличии т
и более следующих друr за друrом символов О в информацион-
ной подпоследовательности вес соответствующей кодовой по-
следовательности можно увеличить на 1. Cor ласно свойству 1,
свободное расстояние dсвоб систематическоrо кода со скоростью
R == 1/nо не может превышать число единиц в порождающей
последовательности, которое в свою очередь не превышает
(по 1) (т + 1) + 1. Кодовая последовательность, на котороЙ
достиrается минимальное расстояние, должна содер)кать по
крайней мере один символ 1 в O M подблоке и по крайней мере
один символ 1 в любых следующих друr за друrом подблоках.
Это означает, что все такие кодовые слова с io =F О в пределах
первых (по 1) (т + 1) т подблоков имеют вес не менее
(по 1) (т + 1) + 1. Следовательно, d своб == d(no lHт+l) т.
Свободное расстояние является характеристикой кода, кото-
рая представляет интерес не только в тех случаях, коrда рас-
сматривается rипотетический декодер с u === 00, но и при после-
довательном декодировании, коrда перед принятием решения
о том или ином переданном символе MorYT обследоваться по-
следовательности длиной в несколько кодовых оrраничений.
Коды с большими значениями d своб MorYT быть построены
с помощью описанноrо ниже алrоритма, предстаВЛЯIощеrо со-
бой модификацию алrоритма 1.
Алrоритм IV (предполаrается, что L т).
О) ПОЛО'жить g M. О == 1, Do == 2, u == 1.
1) Положить g M. u == 1.
2) Вычислить d L . Если d L > Du t, то положить Du == d L И
перейти к шаrу 4.
3) ПОЛО)I{ИТЬ g M. u === О, Du == Du t.
4) Если и == т, то построение кода заканчивается: в про-
тивном случае положить и == tl + 1 и переЙти к lllary 1.
Коды, построенные с помощью этоrо алrоритма, обладают
следующими свойствами:
Свойство IV..l. WH(gu) == Du для всех и.
Свойство IV..2. Если на шаrе 2 оказывается, что d L > DU I,
то Du == Du l + 1.
Теорема 6.9. При всех и: W н (gu) ==: Du < d споб , zae d с в об"""""
свободное расстояние «усеченноzо» кода с палtЯТЫО на Пl AtO"
Atte1-lТОВ BpehteHU.
//. Последовательное декодирование
379
Доказательство. Соотношение W н (gи) == Du
W СБоб сле
дует из свойства IV
1 и свойства 1 свободноrо расстояния. Из
свойства 1 свободноrо расстояния также следует, что d своб <
.< W I1 (gи) И, следовательно, d своб == d H (gu) при всех и.
Таблица 6.4
КОДЫ, построенные с помощью алrоритма IV
и ('2) d и (2) d и (2) d
R(I), и g(I), и g( 1), u
о 1 2 7 1 7 14 О 10
1 1 3 8 О 7 15 О 10
2 1 4 9 1 8 16 О 10
3 О 4 10 О 8 17 О 10
4 1 5 11 О 8 18 I 11
5 1 6 12 1 9 19 1 12
6 О 6 13 1 10 20 1 13
Коды, построенные с помощью алrоритма IV, приведены в
табл. 6.4. Костелло вычислил для сравнения вероятности оши
бок при последовательном декодировании в случае R == Rвыч
для двух кодов: кода с d FD == d своб == 13 и кода с d FD == 13 11
d своб == 17. Оказалось, что в первом случае Ре == 0,073, а во
втором случае Ре == 0,017. Это показывает, что при последова
тельном декодировании коды с большими значениями d СВоб яв
ляются более предпочтительными.
Задачи и упражнения
1. На фиr. 6.19 приведен пример поиска правильноrо пути
на кодовом дереве с помощью алrоритма Фано. Для этоrо при-
мера заполните приведенную ниже таблицу.
Текущее 11 Текущее Действие
Узел значение Действие 11 Узел значение
IIopora декодера nopora декодера
О С
А D
В С
С F
D G
С Н
2. Для двоичноrо симметричноrо канала с р === 0,02 найти
верхнюю rраницу среднеrо числа операций в случае, если и ==
== 0,95Rвыч, R == 1/3 И ПО == 2 (постоянным членом пренебречь).
380
r лава 6
3. Для двоичноrо симметричноrо канала с р === О,О2, сверточ-
Horo кода со скоростью R == 1/3 И КОДОВЫМ оrраничением ПА ==
== 200 при и === О,95Rвыч,
а) вычислить значение верхней rраницы для вероятности
ошибки при и пользовании алrоритма Фано;
7 по
б по
1J о
4- ])0 Н
3 ПО
Z ])0
])0
О
])
о
Фиr. 6.19. Пример поиска пути с помощью алrоритма ФаJlО.
б) вычислить вероятность переполнения буфера при (J == 30
и В === 2000;
в) рассмотреть передачу со скоростыо 4800 бит/с и вычис-
лить приближенные значения частоты возникновения перепол
нения буфера и частоты ошибок.
и f/{pOPMQl1lJdHHb/C
CIIMdQt/ /
+
.
8ыхоаНIJ/е
СIIм60АЫ
Фиr. 6.20. СверточныЙ кодер кода с по === 2, ko == 1 и т === 2.
4. Для кодов с относительно небольшим кодовым оrраllиче-
нием, используя диаrрамму переходов из состояния в состояние,
можно сравнительно просто провести анализ алrоритма Витер-
би [27].
а) Построить кодовое дерево кода, порождаемоrо сверточ-
НЫМ кодером, показанным на фиr. 6.20 (до rлубины, коrда у}!<е
обнаруживается периодическая структура кода)..
/ 1. Последовательное декодирование
381
б) Используя четыре состояния упомянутой выше периоди-
ческой структуры, построить диаrрамму переходов из состояния
в состояние.
в) Показать, что при декодировании описанноrо выше кода
с помощью алrоритма Витерби вероятность Pk возникновения
ошибки при сравнении правильноrо пути с любым друrим пу-
тем, наХОДЯIЦИМСЯ от Hero на расстоянии k, определяется pa
венством
Pk == I
I
[
k
L (:) ре (1 p)k e, k четное число,
е == (k + l) /2
k
(k 2)pkI2(1 p)kI2+ L (:)pe(1 p)k e,
e==k/2+ 1
k нечетное число.
r) Доказать справедливость следующеrо неравенства: Pk <
r< 2kphl2, rде р вероятность перехода символа О в символ 1
(или 1 в О) в двоичном симметричном канале.
д) Показать, что вероятность ошибки на символ для рас-
сматривае-моrо кода можно оценить сверху следующим обра
зом:
00
р в < L (k...... 4) 2 k --- 5 [4р (1 ...... р )]k/2.
k==5
5. Доказать неравенства (6.53).......... (6.56).
6. Пусть ql, q2, ..., qJ распределение вероятностей на BЫ
ходе дискретноrо канала без памяти с К входными и J выход-
ными символами. Если переходные вероятности этоrо канала
таковы, что
р (j I k) == q 1 (1 + 81 k),
и 18j/ll 1 для всех j и k, то этот канал называется каналом с
сильным ШУМОМ.
а) Показать, что для блоковых кодов функция надежности
E(R)== тах [......vR+maxEo(v, Q)]
O<" l Q
для канала с сильным шумом имеет слеДУIОЩИЙ вид [3]:
с
R T'
с
R<4'
E(R) (vc ,yR)2,
С
Е (R) 2: ..... R,
rHe С пропускная способность канала.
382
rлава 6
б) Показать, что для сверточных кодов функция надежно
сти канала с сильным шумом определяется равенствами [4]
Е (R) ("/2, О R С/2,
E(R) C R, C/2 R<C.
7. Месси и др. [28], исс.педуя коды со скоростью R == l/no, по
ЛУЧИJ1И ряд интересных результатов, которые сформулированы
ниже в виде задач.
а) Пусть
1 (D) === i l) + ip>D + i 1)D2 + ...
информационная последовательность. Показать, что если по-
рождающий мноrочлен кода имеет вид
а (D) === a B (D no ) + а И (Dno) + ... + Dno la o> (Dno),
то кодовая последовательность T(D) будет определяться ра-
венством
т (D) == 1 (Dno) а (D).
б) Пусть g (х) порождающий мноrочлен циклическоrо KO
да нечетной длины над полем аР (2 т ). Показать, что свободное
расстояние d своб 2r ичноrо сверточноrо кода со скоростью R ==
== l/no (rде по == 2т и m произвольное целое положительное
число), порождаемоrо мноrочленом а (D) == g(D), удовлетво"
ряет неравенству
d своб min {d g , 2d h },
rде d g минимальное расстояние циклическоrо кода, порож-
даемоrо мноrочленом g (х), а d (h) минимальное расстояние
циклическоrо кода, порождаемоrо мноrочленом h (х) ==
== (х n + 1) / g ( х) .
в) Показать, что свободное расстояние d своб 2 т ичноrо свер-
точноrо кода со скоростью R === l/no, по === 4m, порождаемоrо
мноrочленом a(D) ==g(D)2+h(D)2, удовлетворяет неравенству
d своб min {d g + d h , 3d g , 3d h }.
7. Реализация и применение КОДОВ,
исправляющих ошибки
7.1. Реализация КОДОВ, исправляющих ошибки
Кодирующие и декодирующие устройства MorYT быть по-
строены из показанных на фиr. 7.1 реrистров сдвиrа, суммато-
ров по модулю 2 и элементов, реализующих умножение. В ре-
зультате проrресса интеrральной техники, в частности техники
изrотовления больших интеrральных схем, стоимость этих ди-
скретных элементов в настоящее время быстро снижается.
На фиr. 7.2 показано, например, каким образом происхо-
дило и происходит снижение стоимости полупроводниковой па-
мяти. Если стоимость полупроводниковоrо триrrера вначале со-
ставляла около 1 О долл., то в настоящее время стоимость па-
мяти составляет несколько центов за 1 бит. Ожидается, что
к концу семидесятых rодов она достиrнет 0,1 цента за 1 бит.
Поэтому, если на начальном этапе развития теории кодирова
ния реализация кодирования и декодирования с помощью аппа
ратурных средств из
за их сложности и высокой стоимости пред
ставлялась почти нереальной, то сейчас можно привести боль-
шое число примеров, коrда аппаратура для кодирования и дe
кодирования используется в реальных системах (rлавным обра
зом в системах связи). Как правило, эта аппаратура строится
из обычных широко используемых интеrральных и так назы
ваемых больших интеrральных схем и выполняет относительно
простые стандартные операции.
Кодирование и декодирование MorYT быть реализованы как
с помощью специализированных устройств, так и в некоторой
области скоростей передачи проrраммными методами на УНИ
версальных ЭВМ. В последние rоды для проrраммной реализа
ции стали широко использоваться мини
ЭВМ. Для выполнения
простых стандартных операций относительно просто MorYT быть
построены небольшие специализированные вычислительные
устройства. При передаче данных между вычислительными ма-
шинами для выполнения кодирования и декодирования можно
использовать также часть вычислительной мощности BЫCOKO
скоростных ЭВМ С большой емкостью памяти.
Применение проrраммных методов позволяет снизить вес ко-
деров и декодеров. Например, если строить специализированное
устройство для декодирования БЧХ
кода с большим ЧИС.l0М
исправляемых оrllибок t, то при использовании алrоритма Пи.
терсона и алrоритма Берлекэмпа
Месси приходится приме
Реализация кодов, uсnравЛЯIОЩUХ ошибки
385
нять сложные устройства. В подобных случаях проrраммные
методы являются эффективным средством СНИ)l{ения сложности
устройств.
В этом разделе будут рассматриваться rлавным образом
стандартные схемы, используемые при аппаратурной реализа-
ции кодирования и декодирования, а также ряд друrих вопро
сов, связанных с реализацией БЧХ
кодов и кодов, допускаю
щих пороr'овое декодирование.
7.1.1. Стандартные схемы
Сначала раССМОТРИl\1 простой пример, а именно показанную
на фиr. 7.3 схему умножения фиксированноrо мноrочлена
Ь(Х)==I+Х 2 +Х З +Х5+Х7 (7.1)
на входной мноrочлен
а (Х) == ао + alX + ... + атх т .
(7.2)
Все ячейки памяти показанноrо на фиr. 7.3 реrистра сдвиrа
вначале содержат нулевые символы. Будем считать, что на
вход реrистра сдвиrа первыми подаются старшие члены BXOД
Horo мноrочлена (т. е. члены с высшими степенями неизвест
Horo). Член атХт, поступивший на вход реrистра сдвиrа, без
изменениЙ передается на выход. Точно так же без изменений
передается на выход схемы и aт
lX1n
1. После Toro как на вход
реrистра сдвиrа поступит aт___2Xт
2 с помощью крайнеrо JIenOrO
сумматора, он складывается с поступившим ранее атХт, и их
сумма
а т ___2 хт --- 2 х 7 + атх т х 5 === (а т ---2 + а т ) х т + 5 (7.3)
поступает на выход схемы. Точно так же вычисляются и после-
дующие члены искомоrо произведения
(1 + Х 2 + Х З + Х5 + Х7) (ао + alX + ... + атх т ) ==
== ао + a1X + (а2 + ао) х 2 + ... + (а т ---2 + а т ) х т + 5 +
+ а т ___l хт + 6 + а т х т + 7 . (7.4)
В общем случае умножение входноrо мноrочлена
а (Х) == ао + alX + + aпJX m
на фиксированный мноrочлен
Ь (Х) == Ь о + blX + + ьпх n
можно выполнить аналоrично. Соответствующая схема пока-
зана на фиr. 7.4. Существует еще один тип схем, предназначен
ных для нахождения указанноrо выше произведения. Вначале
раССl\10ТРИМ пример такой схемы, выполняющей умножение BXOД
386
rлава 7
Horo мноrочлена а (Х) на фиксированный м ноrочлен
Ь (Х) == 1 + Х 2 + Х З + Х5 + Х7.
Схема умножения в данном случае имеет вид, показанный на
фиr. 7.5. При поступлении а т Х ,п на вход реrистра сдвиrа это
слаrаемое без изменений передается на выход схемы как
а т Хт+7. Одновременно а т Х1п вводится во 2, 4, 5 и 7 й разряды
реrистра сдвиrа. Точно так же со входа без изменений на BЫ
ход CXel\1bI передается am lXт 1 (Kal{ am IXln+6); при этом
aт lXm l вводится в реrистр сдвиrа точно так же, как атХт.
Далее после Toro, как на вход поступит alп _2Xln 2, член а 1n Хт,
поступивший на два момента времени ранее во 2 IO справа нчей
ку реrистра сдвиrа, складывается с помощью крайнеrо правоrо
сумматора с aт 2Xт 2 и полученная сумма поступает на выход
схемы как (а т + aт 2)xт+5. Точно так же схема работает при
поступлении последующих членов входноrо мноrочлена. В об
щем случае схема, выполняющая умножение указанным выше
образом, имеет вид, показанный на фиr. 7.6.
Так как схемы умножения описанных выше двух типов co
держат одинаковое число разрядов реrистров сдвиrа и одина
ковое число сумматоров по модулю 2, то на первый взrляд с
точки зрения сложности они представляются эквивалентными.
Однако в схеме, изображенной на фиr. 7.6, сумматоры по MO
дулю 2 располаrаются между разрядами реrистра сдвиrа, TO
rда как в схеме, изображенной на фиr. 7.4, сумматоры распо
лаrаются отдельно от реrистра сдвиrа. При использовании ин
теrральных схем для построения таких устройств умножения
мноrочленов схема, изображенная на фиr. 7.4, является более
предпочтительной, поскольку она может быть проще реализо
вана.
Рассмотрим далее CXel\IY, выполняющую деление мноrочле-
нов. Сначала рассмотрим пример такоЙ cxeMI>I, а именно пока-
занную на фиr. 7.7 схему, предназначеННУIО для деления вход-
Horo мноrочлена а (Х) на мноrочлен
Ь (Х) == 1 + Х 2 + х з + Х 5 + Х7.
Пусть
а (Х) == 1 + Х + Х З + Х 4 + Х7 + Х 8 + XIO.
а (Х) на Ь (Х) «уrлом» проводится следующим обра-
Деление
зом:
Х 1О + о + Х 8 + Х 7 +О + 0+ Х 4 + ХЗ+О+Х+1
Х 1О + о + Х 8 + () + Х 3 + Х5 + о + х з
о + о + о + Х 7 + х о + Х 5 + Х 4 + о + О+Х+l
Х 7 + о + Х 5 + о + х з + Х2 +0+ 1
о + Хб + о + Х- 1 +Х 3 + Х 2 + х +0
I Х7 +О+Х 5 +О+Х3+Х 2 +О+ 1
IX3 + о + о + 1
Реализация кодов, исправляющих ошибки
387
Bx.QU
+
8b/XOtJ
Фиr. 7.3. Схема умножения на мноrочлен Ь (Х) == 1 + Х 2 + Х 3 + Х 5 + Х 7 .
Вход
а !
Фиr. 7.4. Схема умножения в общем случае.
Вход
:)
8ыхоВ
. + + + +
Фиr. 7.5. Схема умножения на мноrочлен Ь (Х) == 1 + Х 2 + Х 3 + Х 5 + Х7.
Фиr. 7.6. Схема умножения в общем случае.
ВхМ
н + + + - Ь U
Фиr. 7.7. Схема деления на мноrОЧJIен Ь (Х) == 1 + Х 2 + х э + Х 5 + Х 7 .
388
fлава 7
При делении а (Х) на Ь (Х) с помощью схемы, ноказанной
на фиr. 7.7, сначала в реrистр сдвиrа последовательно вводятся
коэффициенты входноrо мноrочлена при Х 1О , ..., Х 4 . При по.
ступлении на вход реrистра коэффициента при Х3 коэффициент
при XIO на входе поступает на выход схемы как коэффициент
при Х З частноrо. Одновременно коэффициент при XJO С выхода
реrистра подается на входы трех сумматоров по модулю 2,
установленных на выходах 3, 4 и 5
й слева ячеек памяти ре-
rистра сдвиrа, и складывает их с выходными символами этих
ячеек. При следующем сдвиrе коэффициент О при Х 9 входноrо
мноrочлена выводится как О при Х 2 частноrо. При следующем
сдвиrе символ О, получающийся в результате сложения коэф-
фициента 1 при Х8 входноrо мноrочлена с коэффициентом 1 при
вхоа
Фиr. 7.8. Схема деления в общем случае.
Х 1О , поступающим по цепи обратной связи, выводится как ко.
эффициент О при Х 1 частноrо. После ввода всех символов вход-
Horo мноrочлена в реrистре остается остаток Х + Х 2 + Х З +
+ х 4 + о + Х 6 (т а бл. 7.1).
В общем виде схема, выполняющая деление входноrо мно-
rочлена на некоторый фиксированный мноrочлен, изображена
на фиr. 7.8.
7. J .2. Кодеры циклических кодов
Все кодовые слова циклическоrо кода делятся на порожда-
ющий мноrочлен кода g (Х). Если цикличе-ский код является
к тому же систематичеСI{ИМ, то в каждом кодовом слове можно
выделить информационные символы и слеДУIощие за ними из-
быточные символы. Поэтому при использовании циклических
кодов сначала по каналу связи передаются информационные
СИl\IВОЛЫ и одновременно эти символы вводятся в схему деления
мноrочленов, описанную в предыдущем разделе. После Toro как
все информационные символы будут введены в реrистр сдвиrа,
в последнем оказывается остаток от деления информаIlионноrо
мноrочлена на порождающий мноrочлен. Если этот остаток пе-
редать по каналу связи вслед за информационными символами,
то полная переданная последовательность будет делиться на
Реализация кодов, uсnравЛЯjоu их ошибки
389
g (Х), Т. е. будет КОДОВЫМ словом. Схема кодера циклическоrо
кода показана на фиr. 7.9.
Пусть
f(X)==fo+f1X+f2X2+ ... +fn lXn l (7.5)
кодовое слово циклическоrо кода. Так как все кодовые слова
циклическоrо кода делятся на порождающий мноrочлен g (Х),
то f (Х) можно представить в виде
f (Х) == g (Х) q (.Х).
Если код является систематическим, то информационными сим
волами будут fn h, fn k+l, "., fn l, а n k проверочными сим-
волами будут fo, fl, ..., f n h l. Если умножить f (Х) на прове-
KaHIlII
8eHmll1l6 а
8СНII!/lII' 1
Фиr. 7.9. I(одер циклическоrо кода.
рочный мноrочлен кода 11 (Х) и воспользоваться равенством
g(X)h(X) == Хn + 1, то получим
f (Х) /1 СУ) == g (Х) q (Х) h (Х) == XnQ (Х) + q (Х). (7.6)
Так как q (Х) мноrочлен степени k 1 или менее, то члены
Хп, Xk+l, ..., Xn 1 В правую часть (7.6) не входят. Следова-
тельно, коэффициенты при Xk, Xk+l, ..., Xn l В произведении
f (Х) h (Х) можно приравнять нулю:
k
L hifп i /==O, 1 j n k
1==0
(7.7)
(здесь ho == hh == 1). ОТСlода следует, что
k l
fn k J===L hifn i J' l j n k.
i==O
(7.8)
Последние равенства дают способ вычисления проверочных сим-
волов fn k l, fn k 2, ..., fo мноrочлена f (Х). Схема кодирова-
ния, реализующая этот метод вычисления проверочных симво-
лов, показана на фиr. 7.9.
390
r лйва 7
Таблица 7.1
Состояния реrистра сдвиrа
Число СИМВОЛ СИМВО.Т'lЫ СИМВОЛ
СостояНие на выходе на выходе
СДВИ- после l СДвиrов после 1 обратной связи при l-м
rOB 1 сдвиrов после 1 сдвиrов <.'двиrе
О 0000000 О ---
1 1000000 О 0000000 1
2 0100000 О 0000000 О
3 1010000 О 0000000 1
4 1101000 О 0000000 1
5 О 11 О 1 00 О 0000000 О
6 0011010 О 0000000 О
7 1001101 1 0000000 1
о)
8 0111100 О о 1011010 1
0000000
9 00 1111 О О CJ О
::r
10 1001111 1 0000000 1
11 10111]01 I 1 1011010 1
Остаток
Сначала вентиль 1 закрыт, а вентиль 2 открыт. Инфор-
мационные символыI передаются по каналу и одновременно вво-
дятся в реrистр сдвиrа. После Toro как все k информационных
символов будут введены в реrистр, вентиль 1 открывается, а
вентиль 2 закрывается. В этот момент в точке Q, показанноЙ на
фиr. 7.9, появляется первый проверочный символ fn k---l. При
очередном сдвиrе содержимоrо реrистра первый проверочный
символ вводится в крайний JIевый разряд реrистра и OДHOBpe
менно передается по каналу. При этом в точке Q появляется
второй проверочный символ. Точно так же формируются, BBO
дятся В реrистр сдвиrа и передаются по каналу все n k про-
верочных символов. После этоrо вентиль 1 закрывается, BeH
тиль 2 открывается и в реrистр сдвиrа вводятся слеДУЮIцие k
информационных СИl\1ВОЛОВ.
В тех случаях, I{оrда допустимо использование несистемати
ческих кодов для реализации кодирующеrо устройства, MO)l{HO
воспользоваться описанной в предыдущем разделе схемой YMHO
жения мноrочленов. Заметим что с точки зрения простоты pea
лизации более предпочтительными часто оказываются схемы
умножения мноrочленов изображенные на фиr, 7.4 и исполь-
зующие сумматоры.
Реализация кодО8, llсnравляющих ОUlllбкu
391
7.1.3. Декодеры циклических кодов
Если кодеры обычно относительно просты и однотипны, то
декодеры, KaI{ правило, rораздо сложнее кодеров и их CTPYK
тура сильно зависит от используемых кодов. В этом разделе
сначала рассматриваIОТСЯ простейшие декодеры, а именно дe
кодеры кодов, обнаруживающих ошибки. Далее рассматри
ваIОТСЯ декодеры БХЧ
кодов, деI{одеры для кодов, допускаIО
щих пороrовое декодирование, декодеры для кодов, исправляю
щих пачки ошибок, и некоторые друrие декодеры.
а) Декодеры, обнаруживающие ошибки. Декодер этоrо типа
состоит обычно из буферноrо реrистра, предназначенноrо для
хранения принятоrо кодовоrо слова, и схемы деления приня
Toro слова на порождающий мноrочлен кода g (Х). Если полу
ченный. в результате деления остаток равен нулю, то считается,
буq:;еРНЬltl ре,tlстр
Фиr. 7.10. Декодер, обнаруживающий ошибки.
что ошибок при передаче не было. В противном случае, Т. е.
если хотя бы один из коэффициентов остатка отличен от нуля,
принимается решение о том, что произошла ошибка при пере
даче; при этом прием прекращается и на передающую сторону
посылается запрос на повторную передачу этоrо кодовоrо слова.
В показанном на фиr. 7.1 О декодере принятое кодовое слово
одновременно вводится в буферный реrистр и изображенную
под реrистром схему деления мноrочленов. После введения
принятоrо слова в схему деления в реrистре сдвиrа последней
оказывается остаток от деления принятоrо слова на порождаю
щий мноrочлен кода; в зависимости от Toro, равен ли остаток
нулю или нет, принимается решение об отсутствии или наличии
ошибок в принятом слове.
Эта схема обнаружения ошибок очень проста, и устройства
обнаружения ошибок с этой схемой широко ИСПОЛЬЗУIОТСЯ в ре-
альных системах. Следует заметить, что при использовании
этой схемы необходим канал обратной связи, буферное запоми-
нающее устройство для хранения данных и ряд друrих
устройств. .
б) Декодер БЧХ"кода. Как уже указывалось выше, БЧХ
ко-
ды MorYT иметь достаточно большое кодовое расстояние. Одна-
892
fлава 7
o их техническая реализация оказывается сравнительно слож-
ной.
Алrоритм декодирования БЧХ кода включает следующие
пять операций:
1. Вычисление синдрома.
11. Вычисление мноrочлена, имеющеrо своими корнями ло
каторы ошибок.
111. Нахождение корней этоrо мноrочлена.
IV. Вычисление значениЙ Оlllибок (в двоичном случае эта
операция не нужна).
V. Исправление ошибок.
В двоичном случае операции 111 и V MorYT выполняться од-
новременно с помощью описанноrо ниже алrориrма Ченя.
Фиr. 7.11. Схема для вычисления r (а).
При декодировании БЧХ кодов сначала находится синдром;
Ta операция может быть реализована с помощью схемы, ocy
ществляющей вычисления в поле rалуа. Чтобы найти синдром,
необходимо для принятоrо слова
r (Х) === 'о + r1X + ... + rn lXn l
(7.9)
вычислить ero значение r(a j ) в некоторых точках а.1. Эту опе
рацию можно выполнить посредством следующей последова
тельной схемы.
Рассмотрим схему вычисления синдрома для кода, корни
порождающеrо мноrочлена KOToporo лежат в поле ОР (24). CHa
чала рассмотрим схему вычисления ((а). Пусть а прими
тивный элемент поля GF(2 4), являющийся корнем мноrочлена
Х 4 + х + 1. Если в крайний левый разряд реrисrра схемы, изо-
браженной на фиr. 7.1] t ввести символ 1 и начать ero сдвиrать,
то, как леrко проверить,' блаrодаря цепи обратной связи в раз-
рядах реrистра ПОС4едовательно будут формироваться двоич
ные представления а 2 , а,З, ... . Таким образом, чтобы вычислить
r(a)==rO+rla+ ... +rn lan l,
в рассмотренную схему следует последовательно ввести сим-
волы rn l, 'n 2, ... .
Далее рассмотрим случай, кот'да j =1= 1. На фиr. 7.12 при-
веден пример схемы вычисления r (аЗ) с помощью реrистра
сдвиrа с четырьмя разрядами [(Х примитивный элемент поля
РеализаЦllЯ кодов, uсправЛЯ10lЦllХ ОUluбкu
393
ОР(2 4 )]. Так как, соrласно таблице умножения в поле ОР(2 4 ),
1 · а == аЗ
,
а · аЗ == а 4 == 1 + а,
а 2 . аЗ == а 5 == а + а 2 ,
аЗ . аЗ == а 6 === а 2 + аЗ,
ТО
а,1 (aJ' аlа + а2а2 + азаЗ) == аоа З +
+01(1 +а)+а2(а+а 2 )+аз(а 2 +а З )===
== al + (al + а2) а + (а2 + аз) а 2 + (ао + аз) аЗ.
Если обозначить через a , а;, a , a соответственно коэффициенты
BeKTopHoro представления ао, al, а2, аз элемента поля ао + аl а +
Вхоо
Фиr. 7.12. Схема для вычисления, (аЗ).
+ а2а2 + азаЗ после умножения последнеrо на аЗ, то будем иметь
I
а о == а 1 ,
a == a 1 + а 2 ,
a == а 2 + аз,
a ==ao+ аз.
Эти CYf\1MbI MorYT быть вычислены с помощью изображенной на
фиr. 7.12 схемы, представляющей собой реrистр СДвиrа с об-
ратной связью. Таким образом, если ввести последовательно в
этот реrистр символы принятой последовательности rn l,
'n 2, ..., то в результате в реrистре окажется r(а З ). При ис-
пользовании этой схемы вычисление синдрома кончается в тот
момент, коrда завершается прием слова.
После Toro как синдром вычислен, следующей операцией
при декодировании БЧХ кодов является нахожд ние мноrочле-
На, корнями KOToporo являются локаторы ошибок. Эта опера-
ция является наиболее сложной при технической реализации.
При использовании для этой цели как алrоритма Питереона,
39
r лава 7
так и преДЛО)l{енноrо позже алrоритма Берлекэмпа Месси
при большом числе исправляемых ошибок достаточно простоrо
устройства, реализующеrо эту операцию, построить не удается.
В то же время как в том, так и друrом случаях математически
сложные расчеты MorYT быть относительно леrко выполнены
проrраммными методами. Поэтому использование постоянных
и полупостоянных памятей и друrих подобных устройств для
построения специализированных вычислительных устройств,
предназначенных для декодирования БЧХ кодов, позволяет сни-
зить стоимость и упростить структуру декодеров.
Однако, коrда скорость передачи информации велика, бы-
стродействие универсальной вычислительной машины может
оказаться недостаточным для выполнения декодирования по
ступающих слов. В этих случаях для реализации декодирования
часто применяются специализированные устройства. Вопрос
о том, какой из алrоритмов Питерсона или Берлекэмпа.........
Месси в этом случае лучше, должен в каждом конкретном
случае исследоваться специально.
Как уже указывалось выше, вычисление синдрома осуще-
ствляется параллельно с приемом слова и завершается после
ввода последнеrо в буферный реrистр. Как будет показано
ниже, определение положения ошибок при использовании алrо-
ритма Ченя выполняется при считывании принятоrо слова из
буфера. Таким образом, нахо}кдение мноrочлена, корнями ко-
Toporo ЯВЛЯIОТСЯ локаторы ОIIIибок, дол}кно выполняться неза-
висимо от приема переданноrо слопа и считывания последнеrо
из буфера. Поэтому к быстроте ВЫПОJIнения этой операции,
а Иl\1енно времени вычисления мноrочлена локаторов ошибок,
предъявляются повышенные требования.
Если число исправляемых ошибок невелико, коэффициенты
мноrочлена локаторов ошибок а(Х) сравнительно просто опре-
делить, выразив их через символы синдрома и подставив в по-
лученные формулы конкретные значения символов синдрома. При
этом соотвеТСТВУlощие схемы оказываются не очень сложными.
Если мноrочлен
t
а (Х) == 0'0 + O'lX + ... + O't xt == L О'/х/, (7.10)
/==0
корнями KOToporo являются локаторы ошибок, наЙден, то не-
посредственное исправление ошибок можно осуществить, на-
например, воспользовавшись следующим алrоритмом Ченя.
Предположим, что при передаче кодовоrо слова БЧХ кода про-
изошло t ОIlIибок. Тоrда, если i я компонента принятоrо слова
является ошибочной, то
t
а (а i) === L о' /a---/ 1 == О.
/==0
(7 .11 )
Реализация кодов, исnравля/ощих ошибки
395
Пусть
(J 1. l === (1 /а /l .
Тоrда, как леrко видеть, имеют место следующие
(J /. n --- 1 === (J /а'" (n...l) / == (J ja i
(7.12)
(J/.l l == а,а--- (i J)/ == (1/a i/a/ === (1,. ia/.
равенства:
(7 .13)
(7 . 14)
и
с помощью схемы, показанной на фиr. 7.13, для каждоrо i
t
можно вычислить сумму L а/. i. Если эта сумма равно О, то,
j::O
как следует из формулы (7.11), i я компонента принятоrо кодо-
1
(х
0;2
()(.t
,
е."О
J
е. ==0
J
Фиr. 7.13. Схема, реализующая алrоритм Ченя.
Boro слова содержит ошибку. Сначала в реrистр схемы, изо-
браженной на фиr. 7.13, помещаются символы (11, (12, ..., (1t.
ДаJIее эти символы умножаются соответственно на а, а 2 , ...,
a t и проверяется справедливость равенства en 1==O или ра-
венства en 1 == 1. Затем содеря{имое ячеек реrистра вновь умно-
жается на а, а 2 , ..., a t и находится en 2. Точно так же нахо-
дятся и остальные ошибки.
в) Реализация КОДОВ, допускающих мажоритарное декоди-
рование. Как указывал ось в предыдущем разделе, техническая
реализация БХЧ кодов, исправляющих большое число ошибок,
оказывается сложной. Коды, допускаlощие ма}коритарное деко-
дирование, вообще rоворя, имеют неСI<ОЛЬКО худшие корректи-
рующие способности, чем БХЧ коды, но для них можно по-
396
rлава 7
строить простые декодирующие устройства. Заметим, что эти
коды также являются цикличеСI<ИМИ. Поэтому будем считать,
что в принятой последовательности 'n 1, 'n 2, ..., 'о символы
'n 1, 'n 2, ..., 'n k являются информационными, а символы
'n k 1, ..., '0 проверочными. При декодировании таких кодов
удобно вначале вычислять составные проверки, ортоrональные
относительно шумовоrо символа en 1, воздеЙствующеrо на при-
нятый символ 'n 1. При этом декодирование происходит следую-
щим образом:
Шаz 1. Вычисляется синдром.
Шаz 2. По n k символам синдрома строятся J составных
проверок, ортоrональных относительно en 1; полученные J со-
ставных проверок подаются на входы мажоритарНОI'О элеI\lента.
Эта операция повторяется L раз, и если выход последнеrо
мажоритарноrо элемента оказывается равным 1, то декодер
принимает решение о том, что в первом символе принятой по
следовательности содержится ошибка. Если же выход послед-
Hero мажоритарноrо элемента равен О, то декодер принимает
v u
решение о том, что первыи символ принятои последователь
ности является правильным.
Ша2 3. Первый символ принятой последовательности считы-
вается из буфера и складывается по модулю 2 с выходным
символом последнеrо мажоритарноrо элемента; этим завер-
шается исправление ошибки в первом символе.
Шаz 4. Осуществляется сдвиr синдрома и буферноrо ре-
rистра. На этом шаrе необходимо устранить воздействие en 1
на синдром. Если обозначить шумовую последовательность
через Е (Х), сумму членов Е (Х) степени п 2 и менее через
En 2 (Х), то синдром S (Х) можно представить в виде
S (Х) == re [ ; ] == re [ en l n) 1 + En;(i ) ] (7.15)
(здесь re [ ] остаток выражения, стоящеrо в квадратных
скобках). Следовательно, воздеЙствие en 1 на синдром можно
устранить, сложив синдром с мноrочленом
<р (Х) == <Ро + <Р} Х + ... + СРn'" k Ixn"'k ], (7.16)
представляющим собой остаток от деления Xn 1 на g (Х). Эту
операцию называют коррекцией синдрома. После коррекции
синдроrvIа в реrистре синдрома содержится синдром приняrоЙ
последовательности, сдвинутой на один символ.
Ш аа 5. Новый синдром, полученныЙ на шаrе 4, используется
для декодирования 2 ro символа принятой последовательности.
Вновь выполняя операции 2, 3 и 4, можно декодировать
2 й символ принятой последовательности точно так же, как и
I й символ.
Реализация кодов, исправляющих ошибки
397
. . .
. .
Ре2истр CJlHtJptJMt1
.
.
.
. -K 1
t '(.
.
. .
ЛРJlнятая
Л(JслеО(J6атеI1IJНtJсть
5усрерныу ре2истр
Фиr. 7.14. Мажоритарн ый декодер типа 1 в общем случае.
.
21 разр.qаIlыl1 5усрерНЬ/i1 ре8t1стр
МажорvmUРНIJ/i/
ЭllfМfнт с ntJpP20/r1 .5
Фиr. 7.15. Мажоритарный декодер типа 1 циклическоrо кода с порождаю..
ЩИМ мноrочленом g (Х) == 1 + Х 2 + Х 4 + ха + Х7 + Х 1О ; код получается из
совершенноrо разностноrо множества.
398
r лава 1
Ша2 6. Точно так же декодер осуществляет декодирование
остальных символов принятой последовательности.
Блок-схема декодера, осуществляющеrо декодирование при-
нятой последовательности описанным выше обраЗО I, приведена
на фиr. 7.14. Изображенный на фиr. 7.14 декодер называют
декодером типа 1. На фиr. 7.15 показан декодер типа 1 цикли-
'leCKoro кС'да с порождающим мноrочленом g (Х) === 1 +Х 2 +Х"+
+ Х 6 + Х 7 + Х 1О , получающеrося из совершенноrо разностноrо
множества.
Еще один споособ декодирования рассматриваемых кодов
можно получить, построив составные проверки на основе про-
верочной матрицы кода Н. Обозначим здесь через
h (f) === (h (f) h (j) h (f) )
о, 1,... , n 1
элементы пространства строк провероtrНОЙ матрицы Н, а чере.J
Т == (t o , /1, ..., tn--д,
Е == (ео, el, . . ., en I),
R===(ro, '1, ..., 'п 1)
соответственно передаваемый кодовый вектор, вектор ОIIIибок
и принятьнi вектор. Скалярное произведение R и hU) имеет вид:
Rh(j) == (Т + Е) h(j) == Th(j) + Eh(f). (7.18)
Так как Th(f) О то
,
(7.17)
Rh(f) === Eh(J),
(7.19)
ИЛИ, что то же самое,
h )'o+h\f)rl+ ... +h lrn l==hbf)eo+
+ h Л е 1 + ... + h 1 е n 1. (7 . 2а)
Как видно, отыскание J составных проверок, ортоrональных
( ')
относительно eп 1, эквивалентно отысканию J векторов h J ==
===(h ), h1j), .. ., h l) В пространстве строк матрицы /1; (п 1) e
элементы h 1' j == 1, 2, ..., J, строк равны 1, и строки таковы,
что ни при каком i =F п 1 среди элементов h l), h 2), . .. h J)
нет двух единиц. Соrласно формуле (7.15), в качестве состав-
ных проверок, ортоrональных относительно е п ---1, МО)I{НО взять
следующие проверки:
Аl == Rh(1) h l)ro + h l)rl + ... + h lr n---I'
А 2 === Rh(2) h 2),O + h 2)'1 + ... + h lr n 1'
А == Rh(l) == h(J), + h(l)r +
J о О 1 1
+ I (1)
... 1п lrп---l.
Реализация кодов, исправляющих ошибки
399
J составных проверок представляют собой J сумм принятых
символов. Векторы h<j) показывают, I{акие из принятых симво-
лов нужно СЛО}I{ИТЬ, чтобы получить проверки A j .
Декодер, осуществляющий декодирование на основе описан-
ных выше составных проверок, называют декодером типа 11.
Декодер типа 11 в общем виде изображен на фиr. 7.16 и функ-
ционирует следующим образом:
Шаz 1. Вентиль 1 открыт, вентиль 2 закрыт, и принятая
последовательность вводится в буферный реrистр. После ввода
G2
. . .
МажоРtlтllfJNIJ/е
ЭАсменты
' II Clпj'nCHJI
. . .
{i)...(i)
/v/IlжьрJllflllрныe
Зl1tменты G 2
2 t1 СlПj'nени
Мй ЖОРilтtl/lIl/J/#
з/!!'меllт
L й ступени
Фиr. 7.16. Мажоритарный декодер типа 11 в общем случае
принятой последовательности вентиль I закрывается, а вентиль
2 открывается.
Шаz 2. Строятся составные проверки, ортоrональные отно-
сительно en 1 или совокупности символов, содер)кащих en 1.
Для этоrо определенные принятые символы подаются на входы
сумматоров по МОДУJIIО 2.
Шаz 3. J составных проверок подаются на входы мажори
тарных элементов l й ступени. Символы с выходов мажоритар-
ных элементов I й ступени подаются на входы ма)l{оритарных
элементов 2 Й ступени п Т.д. Символ С выхода мажоритарноrо
элемента L й ступени складывается по модулю 2 с первым при-
нятым символом 'n 1, считываемым из буферноrо реrистра, и
таким образом исправление ошибки в 'n 1 завершается.
400
fлава 7
Шаz 4. После выполнения шаrа 3 содержимое буферноrо
реrистра сдвиrается на один символ вправо. При этом 2 й при
нятый символ переходит на место l ro принятоrо символа и
декодируется точно так же, как и 1 й принятый символ.
Шаz 5. Повторяя указанные выше операции 2, 3 и 4, дeKO
дер точно так же декодирует остальные принятые символы.
После окончания декодирования всех принятых символов
в буферном реrистре содержится кодовый вектор и на входы
l\rIажоритарных элеl'лентов подаются символы о.
в качестве примера декодера типа 11 рассмотрим декодер
кода над Ра (3, 2) с параметрами п== 15, k== 10, t== 1, opToro
нализируемоrо в два шаrа. Этот код задается нуль матрицеЙ
(проверочной матрицей), в качестве которой берется матрица
инцидентности D, строками которой являются в свою очередь
всевозможные циклические сдвиrи последовательности коэффи-
циентов мноrочлена 1)
w (Х) == 1 + х + Х 2 + Х 4 + Х 6 + Х8 + ХI1. (7.21)
Заметим, что каждой строке матрицы D соответствует одно из
15 проективных пространств РО (2, 2), содержащихся в
РО (3, 2) :
111011001010000
011101100101000
001110110010100
О О О 1 1 1 О 1 1 О О 1 О 1 О
000011101100101
1 О О О О 1 110 1 1 О О 1 О
О 1 О О О О 1 1 1 О 1 1 О О 1
D== 1 О 1 О О О О 111 О 11 О О
О 1 О 1 О О О О 1 1 1 О 1 1 О
О О 1 О 1 О О О О 1 110 1 1
1 О О 1 О 1 О О О О 1 1 1 О 1
1 1 О О 1 О 1 О О О О 1 110
011001010000111
101100101000011
1 1 О 1 1 О О 1 О 1 О О О О 1
Среди подпространств Ра (1, 2) существуют три подпро-
странства (а 14 , а 13 , ( 2 ), (а 14 , а 12 , ( 5 ) и (а 14 , аН, а 1О ), содержа-
щие элемент а l 4, соответствующий '14. Следовательно, строками
(7.22)
1) N\.атрица D выполняет роль проверочной матрицы кода. Она содержит
больше чем п k строк, но поскольку среди них есть линейно зависимые, то
задает код размерности k.
Реализация кодов, исправляющих ошибки
401
матрицы D, ортоrональными относительно е14+е1з+е2, являют-
ся 10, 13 и 14 я строки. Кроме Toro, 5, 11 и 13-я строки матрицы
D ортоrональны относительно e14+ e 12+ e s, а 7, 1 О и l1-я строки
ортоrональны относительно е14+ен+е10. Вычисляя следующие
три суммы по модулю 2, в каждую из которых входит по 7 сим-
волов:
'2 + '4 +'9 + '10 +'11 + 'lJ + '14,
'1 + '2 + '5 +'7 + '12 + 'IЗ + '14,
'о + '2 + 'з +'6 +'8 + 'IЗ + '14
и подавая их на вход пороrовоrо элемента с пороrом 2, получаем
составную проверку, ортоrональную относительно '2+'1З+'1 .
Вычисляя суммы
'4 + '5 + '6 +'8 +'9 + '12 + '14,
'о + '.i + '5 + '10 + '11 + '12 + '14:
'. + '2 + '5 +'7 + '12 + '13 + '14,
получаем составную проверку, ОрТОI'ональную относительно
'5+'12+'14. Аналоrично, вычисляя суммы
'1 + '6 + '7 +'8 + '10 + '11 + '14,
'2 + '4 + '9 + '10 + 'lt + 'IЗ + '14,
'о +, +'5 + 'to + '11 + '12 + '14,
получаем составную проверку, ортоrональную относительно
'10+'11+'14. Если выходы этих трех пороrовых элементов по-
дать на вход четвертоrо пороrовоrо элемента, пороr KOToporo
также равен 2, то на выходе последнеrо пороrовоrо элемента
получим проверку, ортоrональную относительно e1 . Схема де-
кодера, выполняющеrо описанные выше операции, приведена
на фиr. 7.17.
r) Декодирование циклических кодов, исправляющих пачки
ошибок. Как циклические коды, так и укороченные циклические
КОДЫ, предложенные Касаl\1И и друrими авторами для исправле
ния пачек ошибок, задаются либо порождающим мноrочленом
go (Х), ,1Iибо порождающим мноrочленом g (Х) ===go (Xi), полу-
чающимся перемежением go(X) с шаrом i. .
Декодирование таких кодов, исправляющих пачки ошибок,
осуществляется следующим образом. Предположим, что кор-
ректируемая пачка ошибок длины Ь >п k возникла в прове-
рочных символах кодовоrо слова. Пусть е (Х) мноrочлен,
описывающий конфиrурацию данной пачки ошибок, а ei (Х) и
ер (Х) мноrочлены ошибок, соответствующие соответственно
402
fлава 7
информационным и проверочным символам кодовоrо слова.
Выше предполаrалось, что
е (х) === ер (Х). (7.23)
Разделив е (Х) на g (Х), синдром S (Х) можно представить в
следующем виде:
S (Х) === re [ ; ] == re [ е; ( : ] == ер (Х), (7.24)
rде re [ ] остаток, получающийся в результате деления,
указанноrо в квадратных скобках. Таким образом, в данном
"2"41'71'101'111'1з1'14 1'11'21'5 1'71'121'1з1'14 1'0 r21'з 1'б 1'8 1'lз1'l
МажорvтllРНIJ/Й Эllемент
1 й ступени
1'41'51'61'81'91'121'14 1'01',1'51'101'111'121'14 Т1 1'2 1's 1'71'121'1з1'14
Мажоритарный Э/!fмент
1 ;; ступени
1'2 1'4 Т7 1'101'11 1'1з1'14 1'0 1'3 1' 1'lU 1' ll 1' l2 1' l4
МажорuтпРН/JIU JlleMBH/f1
1 i/ ступени
N
11
: ..
CIi
[
Фиr. 7.17. Мажоритарный декодер типа 11 проективно rеометрическоrо кода.
СJIучае пачка ошибок может быть исправлена путем простоrо
сложения синдрома с принятой последовательностью. Далее
рассмотрим случай, коrда мноrочлен е (Х), описывающий кон-
фиrурацию паЧI{И ошибок, не совпадает с мноrочленом ошибок
е' (Х). ПреДПОЛО}l{ИМ, что е' (Х) получается i KpaTHbIM цикличе-
ским сдвиrом из е(Х), Т. е. e'(X) Xie(X). Воспользуемся
здесь следующей теоремой.
Теорема 7.1. Синдро ! последовательности, nолучающеЙся
i KpaTftblM ЦUКЛUflескuм сдвиёОМ nрИНЯТОZО кодовОёО слова за-
Реализация кодов, исправляющих ошибки
403
данной длuны n l является i KpaTHbtM ЦUКлu t tеСКUАI, сдви20м,
синдрома nрUНЯТО20 кодовоzо слова.
Доказательство. Пусть s (Х) синдром последовательности
е(Х) ДJIИНЫ n. Тоrда
[ е (Х) ]
s(X)==re g(X) ,
е(Х) s(X)
g(X) ==q(X) + g(X) .
(7.25)
(7.26)
Пусть е ' (Х) ===Xie (Х) мноrочлен, представляющий последо-
вательность, получающуюся в результате i KpaTHoro цикличе-
cKoro сдвиrа е (Х) в сторону высших разрядов. Синдром s (Х)
этоrо мноrочлена имеет следующий вид:
s' (Х) == 1.е [ е' (Х) ] == re [ Xie (Х) ] ==
g(X) g(X)
[ Xig(X)q(X)+xtS(X) ] [ XiS(X) ]
re g (Х) re g (Х) ·
(7.27)
Заметим, что Xis (Х) представляет собой синдром последо-
вательности е (Х), циклически сдвинутый на i символов влево.
1..:
k
:.1
Pe ",cтp OClHHIJIX
И/lИ НЕ
1< :.1
1< п k b :.1
Фиr. 7.18. Декодер кода, исправляющеrо пачки ошибок.
Следовательно, если в реrистре схемы, предназначенной для
вычисления синдрома, получен синдром s (Х), то для нахожде-
ния s' (Х) достаточно просто циклически сдвинуть содержимое
этоrо реrистра на i символов.
Таким образом, как следует из этой теоремы, для исправле-
ния пачки ошибок е' (Х) == Xie (Х) синдром, содержащийся в
реrистре reHepaTopa синдрома, необходимо циклически сдвинуть
на i символов и далее сложить с циклически сдвинутой на
столько же символов принятой последовательностью.
404
rлава 7
Декодер кода, исправляющеrо пачки ошибок описанным
выше образом, показан на фиr. 7.18. Элемент ИЛИ НЕ этоrо
декодера имеет n........ k ........ Ь входов, на которые подаlОТСЯ сим-
волы с выходов реrистра синдрома. Если все эти символы
равны нулю, то это означает, что Ь младших разрядов синдрома
представляют собой пачку ошибок длины Ь или менее, которая
может быть исправлена. В этом случае цепь обратной связи
реrистра синдрома с помощью вентиля 04 разрывается, приня-
тая последовательность, сдвинутая циклически на HY)l(HOe число
символов, складывается с синдромом, и таким образом пачка
ошибок оказывается исправленной.
Для примера рассмотрим код длины n== 15 с k==9 инфор-
мационными СИМВОJlами, испраВJIЯIОЩИЙ пачки ошибок длины 3
и менее. Соrласно табл. 7.1, этот код имеет следующий порож-
дающий мноrочлен:
go (х) == Х 6 + Х 5 + Х 4 + ХЗ + 1.
Для исправления пачек ОllIибок длины 9 и менее этот код сле-
дует «проредить» С шаrом з. В этом случае код будет задавать-
ся порождающим мноrочленом
g(X) == X l8 + xI5 + Xl2 + Х9 + 1.
Рассмотрим код, задаваемый мноrочленом go (Х). Предпо
ложим, что передавалось нулевое кодовое слово и при передаче
возникли ошибки в О, 1 и 2-м символах. В этом случае
е (Х) === 1 + Х + Х2,
а синдром
s (Х) === re [(1 + х + Х 2 )/(1 + х з + Х 4 + Х5 + Х 6 )] == 1 + х + Х 2 .
Далее предположим, что при передаче возникла пачка ошибок
длины 3 в 5, 6 и 7-м символах. В этом случае
е' (Х) == Х5 + Х6 + x:r == Х 5 (1 + Х + Х 2 ),
а синдром
8' (Х) == re [(Х 5 + Хб + X')/(l + Х3 + Х 4 + Х5 + Х 6 )] == Х + . 4.
Если этот синдром сдвиrать влево, в сторону младших разря-
дов, то содержимое реrистра будет изменяться следующим
Реализация кодов, исправляющих ошибки
405
обраЗОtvl :
Число сдвиrов СодеРЖИl\rlое реrистра
О Х + Х 4
1 1 + Х 3 == Х 4 + Х 5 + Х 6
2 х з + Х 4 + Х 5
3 х 2 + х з + Х 4
4 Х + Х 2 + Х 3
5 1+Х+Х 2
После 5
KpaTHoro сдвиrа старшие 15
9
3==3 разряда син
драма оказываются равными нулю, а в младших разрядах
формируется вектор ошибок. Следовательно, сдвиrая принятую
Фиr. 7.19. Декодер кода с порождаIОЩИМ мноrочленом g (Х) == 1 + Х З +
+Х4 + Х 5 + Х 6 .
последовательность циклически на 5 символов в сторону млад-
ших разрядов и складывая ее по модулю 2 с содержимым ре-
rистра, предназначенным для хранения синдрома, можно испра-
вить возникшую пачку ошибок. Декодер, выполняющий эти
операции, показан на фиr. 7.19.
7.2. Реализация noporOBoro декодирования
Кодеры и декодеры кодов, допускающих пороrовое декоди-
рование, MorYT быть построены из нескольких стандартных
схем.
7.2.1. Кодеры
Имеются два типа кодеров: RnА
разрядные кодеры, предло-
женные Возенкрафтом и Рейффеном [16], (I.........R)nA-разряд-
ные кодеры, предложенные Месси [2]. Схема RnA -разрядноrо
кодера приведена на фиr. 7.20. В соответствии с формулами
.<5.5) и (5.6) ko информационных последовательностей [(j)(D),
....
....
- .-.
,...
....
h.t
roo,
со
01(
h
+0
1:
h h
+
со
.......
.
......
.......
Q..
о)
D::S:::
:а
:х:
D::
Q..
(1')
ro
I
о
r...:
::S:::
ее
Реализация кодов, исправЛЯ10щих ошибки
407
j == 1, . .., ko, подаIОТСЯ на ko ВХОДОВ m разрядных реrистров
сдвиrа и одновременно на выходы кодера для передачи по
каналу. Построение по ko проверочных последовательностей
Т<Л (D), j == ko+ 1, ..., по, осущеСТВJlяется с ПОМОIЦЬЮ сумм ато-
ров по модулю 2 по порождающим мноrочленам кода.
Покажем, что проверочные последовательности на выходе
этоrо кодера действительно порождаются в соответствии с ра-
венством (5.6). Для этоrо сначала преДПОЛО)l{ИМ, что i l) == 1,
а все остальные входные символы равны нулю. В этом случае,
как леrко убедиться, i я выходная последовательность будет
совпадать с o B (D) (i == ko+ 1, . .., по). Аналоrично f\10ЖНО
убедиться, что. при поступлении символа 1 на любой друrой
j й, j =1= 1, вход кодера и символов О на остальные входы i я вы-
ходная последоватеJIЬНОСТЬ будет совпадать с порождающим
мноrочленом a H (lJ) используемоrо кода. В силу линейности
кодера при любом входе последовательности на выходе кодера
будут определяться равенством (5.6). Поскольку для построе-
ния описанноЙ схемы требуется ko реrистров СДВИI'а, каждый из
которых должен иметь т разрядов, то общее число разрядов
реrистров в схеме равно mko==R (ПА no) RпA. Поэтому эту
схему называют RпA разрядным кодером.
Друrой кодер называется (1 R) ПА разрядным кодером и
показан на фиr. 7.21. В этом кодере сумматоры устанавливают-
ся между ячейками памяти реrистра сдвиrа и, следовательно,
каждый из них имеет не более k+ I входов. Определив отклики
схемы на единичные воздействия и воспользовавшись своЙством
линейности точно так lI{е, как и в случае RпА разрядноrо ко-
дера, MO)I{HO проверить, что последовательности на выходе
(1 R) nА разрядноrо кодера определяются равенствами (5.5)
и (5.6). Последний кодер содержит m разрядныЙ реrистр сдвиrа
для каждой из по ko проверочных последовательностей и, сле-
довательно, требует для построения т (по ko) == (1 R) (ПА .........
по) (1 R) ПА разрядов реrистров сдвиrа.
Если сравнивать описанные выше кодеры по числу разрядов
реrистров сдвиrа, необходимых для их построения, то, как леrко
видеть, при R > 1/2 лучше иметь (1 R) ПА разрядный кодер,
а при R < 1/2 ЛУЧlllе иметь RпA разрядный кодер. При R== 1/2
оба :)TII кодера треБУIОТ одно и то же число разрядов реrистра
сдвиrа. Однако здесь следует заметить, что в RпA разрядноы
кодере информационные символы после поступления хранятся
еще т интервалов времени без изменений, в частности, этот
кодер имеет выходы D т {(I), . . ., D т I(k ), Tor да ка к в (1 R) пА-
разрядном кодере такие выходы отсутствуют. По этой ПРИ(lине
В описанном ниже декодере используется RпА разрядный, а не
(1 ....... R) ПА разрядный кодер.
'--
h
,...
....
.....
t-.;
,..
о
OIiC
.....
.....
+
са
.....
(.....
".,
о
""
h
--.-,..----- ---
N
.
.......
I Q)
t:{
I о
i D:S::
I :iS
I ::;::
1::{
I
CI')
р.
I
;:
........
I
......
......
с'!
t'--
.....
....
ее
o
....t--.;
i
t:
t'
...:
I
""
St::t
\')
--- -
.....
...
....а
<
I .
I Q..
I Q)
t:{
I о
.....
о.... I Q)
.!: I I t:i
CI)
I
I I
I
I
==
,.... е
,
,....'-.; Q
I ....."" '""'а
а
t:: (Q,)
'J
-......; fJ')
ro
I
Q
N
...... ---
)
?-
Q:::
........
gз
I
""
Q::
-......:
са
t::
'J
Q::
410
r лава 7
7.2.2. Декодер
Схема декодера приведена на фиr. 7.22, rде для простоты
ko ===n
1. Принимаемые информационные последовательности
подаlОТСЯ на входы содерх{ащеrося в декодере RпА
разрядноrо
кодера, который точно Tal{ же, как и при I<ОДИрОI33НИИ, вычис
ляет для поступающих на ero входы последовательностей про
верочную последовательность. Эта проверочная последовате.пь
ность СI{ладывается с принимаемой проверочноii послеДОDатсль
востью и таким образом формнруетсSl СИНДРО
1 Sb no ) t ..., S
J).
Синдром вводится в m
разрядный реrистр сдвиrа, с т+ 1 BЫXO
дОВ KOTOpOrO в свою очередь символы поступают на входы
.поrической части декодирующей схемы. При использовании
самоортоrональных кодов лоrическая часть декодирующей
схемы представляет собой совокупность пороrовых элементов
с пороrом (! /2) + 1. в случае же использования ортоrоанализи
руемых кодов лоrические части декодирующеЙ схемы, кроме
пороrовых элементов, содержат так)ке сумматоры по модулю 2t
предназначенные для линейноrо преобразования синдрома. На
выходах лоrическоЙ части декодирующеЙ схемы формируются
оценки eb1)t. . . t ebn()
1) шумовых символов ebl)t. . ., e
no
O.
Эти оценки складываются с соответствующими выходными
символами RпA
разрядноrо кодера, и таким образом процесс
исправления ошибок завершается. Пос.пе устранения с помощью
цепи обратной связи воздействия символов eb 1 \... t ebnO
!) на
синдром в последующие моменты времени 1, 2, . . . точно так же
осуществляется исправление ошибок e
I),..., e
n)---O, e
l), ...
е (nо ---1)
...t 2 t....
7.2.3. Схема преобразования параллельных слов
в последовательные и обратная схема
Если канал один и передача n СИМВОЛОВ t формирующихся
на выходе кодера в каждый момент времени, осуществляется
последовательно, то на передающем конце используется схема
преобразования параллельных слов в последовательные, а на
приемном конце
схема преобразования последовательных
слов в параллельные. Эти схемы показаны соответственно на
фиr. 7.23 и 7.24. Рассмотрим функционирование схемы преоб-
разования параллельных слов в последовательные, предполо.
ЖИВ, что передача по каналу п символов осуществляется за
время Т. Схема ввода соединяет одновременно по своих входов
с соответствующими выходами на время Т/по, 11 в течение этоrо
времени, как показано на фиr. 7.23, входные символы вводятся
в ячейки реrистра сдв'иrа. После этоrо входы и выходы схемы
Реализация кодов, исправляющих ОUJ.ибкu
411
ввода разъединяются и при последующих сдвиrах реrистра на
выодеe поrлсднсrо последовательно появляются n входных сим-
волов. Аналоrично осуществляется преобразование последова-
тельных слов в параллельные.
n о ,---' 2, 1
+
Фиr. 7.23. Схе:\1а преобразования параллелыIхx слов в последовательные.
.......
Фиr. 7.24. Схема преобразования последовательных слов в параллельные.
7.2.4. Реализация сверточных кодов, исправляющих
пачки ошибок
При реализации сверточных кодов со скоростями передачи
R
1/2, исправляющих пачки ошибок, при кодировании целе-
сообразно использовать описанныЙ выше (1
R) ПА
разрядный
кодер. Для построения декодера используются RnA
разрядный
кодер и Jlоrическая часть декодирующей схемы.
оrическая
часть декодирующей схемы, на вход которой подается синдром,
формирует (по
1) простейших (единичных) конфиrураций.
Эта схема состоит из ПО
1 элементов И, ПО
2 элементов НЕ
и реrистра сдвиrа. В частности, в двоичном случае единичные
конфиrурации длины k представляют двоичные последователь-
ности длины k, которые обнаруживаются с помощью элемента
И, показанноrо на фиr. 7.25. Из по
1 таких элементов И и
ПО
2 элементов НЕ, устанавливаемых на выходах элеl\rlентов
И, строится Лlобая лоrическая часть декодирующей схемы
(фиr.7.26).
Элемент И, выходные символы KOToporo используются для
исправления Оlllибок в j
й ин.формационной последовательности,
будем считать j-элементом и. Пусть В
общий вход всех
элементов И, cj....... второй вход j
ro ЭJIемента И и D j
выход
412
rлава 7
последнеrо. выIодд D j называется функцией исправления оши-
бок и определяется следующим образом:
DJ == BC1C j + 1 ... CnJ
I, (7.28)
rде BC j соответствует единичной конфиrурации l
й прини м ае
мой последовательности, а черта над символами С 1+1, . . ., C no --- 1
означает инверсию последних. Число элементов задержки, по-
. казанных на фиr. 7.26, равно
для кодов типа 1 и Ь+по
1
для кодов типа 11.
Кодер и декодер кода, paccMoTpeHHoro в примере 5.1 О, по..
казаны соответственно на фиr. 7.27 и 7.28. Функции исправле-
Фиr. 7.25. Элемент И.
ния ошибок в этом случае определяются равенствами
DI
BC 1 C 2 ,
D 2 == ВС 2 .
Если синдром содержит символ еь 2 ) и еь 2 ) === e
2) == 1, то тем не
менее с 1 ==о и С 2 ==1 (так как А==:В 1 ===В 2 ===1) и ошибка e
)
мо}кет быть исправлена.
7.3. Обсуждение связи теории кодирования
с реальными техническими проблемами
В первых шести rлавах рассматривались различные КЛассы
кодов, испраВЛЯЮIl!ИХ ошибки. Эта часть книrи носила матема-
тический, rлавным образом алrебраический характер. Данная
rлава посвящена применениям результатов теории кодирования,
в частности применениям кодов, исправляющих ошибки. Здесь
математические алrоритмы рассматриваются под друrим уrлом
зрения, а именно описываются их применения в реальных усло
виях И те стороны, которые не всеrда удается достаточно полно
учесть в теории. Ниже рассматриваются вопросы стоимости и по
вышения надежности при использовании кодирования, различ-
ные принятые в теории кодирования условности и друrие воп
росы.
,
a
'1:
..
.
.
.
J::f
CIC::)
):.
_f...
t:$
(
I
а
:а
::s
Q)
(J
0=
о)
Ef
g
>.
Q.
=
t:(
/") о
о)
t:(
..Q
f-4
с,)
ro
tr
ro
с,)
Q)
tr
=
о
cd
.
r.
=
ее
I
CI
'
I
а
'
.
со
414
,...... ,..
.... N .
':i.:.. .... "'" ,....
,...
'.....,.
'N
,...
N
,;",,.:,.
-.... """' .. .
N
11
11 C:Q.
со. :s=.
::s::
C'I':) 11
11 о
i} ;:
о Q(:)
;: с)
()
ro о
t:::( ::s:
о
::s:
Q)
Q) о
t:::( DQ
О Q)
r:::r
00
с\1
r--:
:s:: ::s::
е ее
Реализация кодов, uсправЛЯIОЩll,« ошибки
415
7.3.1. Задача теории кодирования
в теории кодирования изучаются п предлаrаются методы
борьбы с ошибками при обработке информации на ЭВМ и Me
тоды помехоустойчивой передачи информации по каналам с шу
мами, т. е. задача этой теории
повышение надежности работы
вычислительных систем и систем связи. В теории кодирования
эта задача решается путем введения избыточности в передавае
мую информацию или вычислительные устройства. Nlетоды по-
вышения надежности путем введения избыточности широко ис
по.пьзуются l<aK при повседневной деяте.J1ЬНОСТИ людей, так и в
различных технических устройствах. НаПРИl'vIер, в анrлийском,
японском и друrих естественных языках всеrда имеется избы
точность, обусловленная rрамматикой, а также структурой слов
и предложений данноrо языка. Используя эту избыточность, мы
решаем кроссворды, исправляем ошибки и т. д. Известно, напри
мер, что избыточность анrлийскоrо языка достиrает 70 О/о. Точно
так же в технике устройства M()rYT дублироваться, и при выходе
одноrо из них из строя система перек.пючается на друrое. В дру-
rих случаях используется одно устройство, но каждая операция
с помощью этоrо устройства выполняется дважды, и если pe
зультат операции в обоих случаях один и тот же, то считается,
что этот результат правильный. Если же результаты различны,
то это означает, что произошла ошибка и для ее исправления
операция выполняется еще один раз. Во всех этих случаях Ha
личие избыточности позволяет обнаруживать и даже исправлять
ошибки и, следовательно, повышает надежность систем связи
или вычислительных систем. Поскольку теория кодирования при
меняется rлавным образом при построении систем связи и вы-
числительных систем, то ниже мы оrраничимся только их рас-
смотрением.
Сначала остановимся на системах связи, хотя в настоящее
время теория кодирования в этих системах достаточно широко
еще не применяется. Это связано с тем, что до настоящеrо вре-
мени, как правило, системы связи проектировались таким обра-
зом, чтобы можно было достичь нужной степени надежности без
применения кодов, исправляющих ошибки. Кроме Toro, в случае
передачи речи и изобра}кений при наличии небольших шумов
качество передачи хотя и снижается, но остается приемлемым
для получателя. Отдельные ошибки и искажения получатель,
кроме Toro, может исправить, используя естественную избыточ
ность, содержащуюся в информации TaKoro тИпа. В то же время
в тех случаях, коrда естественная избыточность, вводимая ис-
точником информации, невеJlика, например в системах передачи
416
fлава 7
данных, для достижения нужной достоверности передачи необ
ходимо вводить избыточность в передаваеМУIО информацию ис
кусственно методами теории кодирования. I/fMeHHo в подобных
системах и находят широкое применение методы теории кодиро
вания. Методы теории кодирования применяются rлавным обра
30М в системах связи ДBYX Tpex типов, но по мере роста ВОЗ IОJl{
ностей разработчиков, увеличения числа видов передаваемой
информации и типов систем связи, а также снижения стоимости
интеrральных и больших интеrральных схем область примене
ния теории кодирования постоянно будет расширяться и методы
помехоустойчивоrо кодирования, используемые в настоящее Bpe
мя, найдут применение в системах связи также и друrих типов.
Исто'lНUК
IIhфОflМ(lt{1I1I
Уст/1ОIIст
60 преоо.
PI1JOdllHUII
соо!щеllVR
6 и6Ulllf-
НjЮ JОЛl/а
Mooy
/ТятО/l
RОЛУI//JI!lt'1f6
IIНфt1fJAlRII"JI
Шум Кllllа//
t'KotJeJl,
IItllfJtld
АiЮЩIIU
ОШJlОКJI
eMoиy
/IятОfl
Фиr. 7.29. Модель системы связи.
На фиr. 7.29 показана простейшая модель системы связи, в
которой ИСПОЛЬ3УIОТСЯ коды, исправляющие ОIlIибки. Информа
ция, поступающая от источника информации, с помощью преоб.
разователя «информация двоичная последовательность» пре
образуется в двоичную последовательность, которая направляет
ся на вход кодера некотороео кода, исправляющеrо ошибки.
Двоичная последовательность с выхода этоrо кодера, в KOTOPYIO
введена избыточность, с помощь модулятора преобразуется
в сиrналы канала и передается по нему. При передаче по ка.
налу на сиrналы канала воздействуют шумы, которые искаJl(ают
их. На приемном конце искаженные шумом сиrналы поступают
на вход демодулятора, который преобразует их в двоичную по
следовательность, часть символов которой является избыточной.
Декодер, используя эту избыточность, осуществляет исправление
ошибок и восстанавливает исходную двоичную информационную
последовательность. Эта информационная последовательность
преобразуется к виду, удобному для получателя информации, и
направляется к нему.
Реализация кодов, исправЛЯЮlЦUХ ошибки
417
7.3.2. Стоимость и надежность
Рассмотрим взаимосвязь между стоимостью и надежностью
систеlVl, использующих помехоустойчивое кодирование. На
фиr. 7.30 ПОl<азана связь между стоимостью и пропускной спо
собностыо различных систем связи. I(aK видно из фиr. 7.30, стои
масть одноrо канала зависит от Toro, является ли система связи
коаксиальной, микроволновой, системой миллиметровоrо диапа
зона и т. д., И снижается по мере роста СУl\1марной пропускной
способности системы связи. Что касается каждой конкретной
системы, то ее стоимость возрастает из rода в rод только из
за
0,Ой01
Ir'Оtl/r'СИClIiЬНtll1 Си'стем:; (/2 Mfi'h'
ми/(роJа111t?I1Оi1 CIICтeMtl 11/1 21(/(/ ffPHtl/1Q!
I
I !(Jй/(Сlltl/1Ьh'tlJ1 систеМIl (6'lllllr1rLl
'cllcI77e""'{/
... ....
1.... ....
РСМ 8IJtl #1, И!( M
cpcтeMb/ /(tfPJJI
0,1 I I MJI/!/!/f;,.ttf/1,11
tftlt(/ t1l1lllJnJ(/!ltl
I I
I I
ОО//ЫРllе 1((/(//(C/l/14(;1I6/t' еиС/11СМЬ/
0,01 ....
.... ....
-+ -- ....
I I I
8IJ/llltJlJtJdIl6/e C'1I:;тt'M6/ /'r1I1/1/1/.1
I I I меl:l,Й7(}Оё(/ tllltlll{{J(/lf.q
I I I
....
-I--............+....
+
--
I I I
I I I
I I I I
+
........+
....
+
I I I I
I I I I
I I I I
1
'
0,001
Ullтй !{с"с/(ие
СJlСIl'6'МЫ
r:6I1JJI
j ООО зо 000 300 000 J 000 000 50 000 оаа
ЧИСl10 тellftpoHHbI,f KIlHIlIIO!
Фиr. 7.30. Стоимость линий связи.
повышения расходов на оплату обслуживающеrо персонала. Ес-
ли же рассматривать стоимость самой системы связи, то она
остается постоянной. Повысить надежность данной конкретной
системы можно, используя те или иные вспомоrательные cpeд
ства (например, путем введения избыточности). При этом всеrда
требуется, чтобы стоимость вспомоrательных средств существен-
но не повышала стоимость самой системы связи. Как видно из
фиr. 7.30, по мере возрастания пропускноЙ способности системы,
использующей вспомоrательные средства, относительная стои
мость последних уменьшается.
Рассмотрим повышение стоимости системы при введении из-
быточности. Так как помехоустойчивое кодирование применяет-
ся в цифровых системах связи, то различные схемы, необходи-
мые для введения и использования избыточности, строятся из
цифровых устройств. Такими устройствами являются, например,
полупроводниковые запоминающие устройства, предполаrаеl\10е
418
Fлава 7
ИЗlVIенение стоимости которых показано на фиr. 7.30. Соrласно
проrнозам на ближайшие [оды, стоимость цифровых устройств
будет по
прежнему быстро снижаться. KaI< следствие СНИ)I(ения
стоимости цифровых устроЙств будет сни}каться стоимость CXel\f,
используемых для введения и использования избыточности; в
свою очередь это приведет к раСlllиреННIО области применеНIIЯ
помехоустойчивоrо кодирования.
7.3.3. Применение в вычислительных системах
Остановимся здесь на применении теории кодирования ввы-
числительных системах. Первым кодом, исправляющим ошибки,
который стал ПРИl\Iеняться в вычислительных машинах, был раз
работанный еще на заре теории кодирования в 1950 r. код ХЭМ
минrа. Как указывалось ранее, этот код был разработан спе
циально для приrvIенения в вычислительных машинах. Код ХЭI\f
минrа стал применяться в вычислительных машинах не сразу, и
это объясняется тем, что после появления кода Хэмминrа по-
стоянно совершенствовались сами запоминающие элементы; CHa
чала использовались электронные лампы, далее появились пара
метроны, полупроводниковые элементы и наконец интеrральные
схемы. При этом надежность запоминающих элементов постоян
но и быстро росла. Первой вычислительной маIllИНОЙ, в которой
использовался код Хэмминrа, была вычислительная машина
IBM 7030, а в Японии
машина DIPS фирмы Japan Telephone
and Telegraph Public. Однако если первая была построена спу
стя 1 О лет после появления кода Хэмминrа, то вторая
спустя
20 лет. До этоrо времени в вычислительных машинах ИСПОJIЬЗО
вался лишь простейший способ повышения надежности, а Иl\1ен
но проверка на четность (или на нечетность).
В последние rоды различные достаточно сложные коды, ис
правляющие большое число ошибок, начали применяться как в
самих вычислительных машинах, так и в их периферийном обо
рудовании, в частности в накопителях на маrнитной ленте. По
мере развития вычислительной техники коды, исправляющие
ошибки, будут иrрать все большую роль в повышении Haдe)KHO
сти вычислительных систем 1). Соr,пасно Чену [2], для этоrо
имеются следующие предпосылки:
1. При повышении скорости вычислений и плотности MOH
тажа уменьшается отношение сиrналjшум.
11. Целесообразность использования с экономической точки
зрения несовеРlпенных элементов, в частности больших иите-
rральных с хем.
t) Обзор достижений в области надежных вычислений и надежноrо хра-
нения информации читатель может найти в статье Б. С. Цыбакова, С. И. rель-
фанда, А. В. Кузнецова, С. М. Артюкова «Reliable computation and
reliable storage of information», Proc. of 1975 IEEE
USSR Joint Werkshop
оп Inform. Theory, IEEE Press, N. У., 1976, р. 216.
Прu
и. ред.
Реализация KOaOB 1 исправляющих ошибки
419
111. По мере увеличения числа вычислительных машин, ие..
пользующих каналы связи, т. е. по мере раСlIIирения сетей BЫ
числительных {аIIIИН, возрастает объем информации, передавае-
мой в режиме «оп lirie».
УI{азанные выше закономерности связаны между собой. Так,
например, существует хорошо известный закон rроша [3], YCl'a
навливающий связь между стоимостью и скоростью обработки
информации в вычислительных маIIIинах. Соrласно этому за
I{OHY, стоимость вычислений пропорциональна корню KBaдpaT
ному из скорости вычислений. Так, например, для снижения
стоимости вычислений в 1 О раз скорость вычислений должна
быть увеличена в 100 раз. Однако если повышается скорость
вычислений, то уменьшаются отношение сиrналjшум и, eCTe
ственно, надежность. В этом случае обычно возникает необходи
мость вновь повысить надежность путем введения избыточно
сти, которая существенно не повлияла бы на стоимость системы
в целом. Еще одно обстоятельство, связанное с предпосылкой
11, на которое следует обратить внимание, это то, что в каче..
стве оперативной памяти современных вычислительных машин
начали использоваться полупроводниковые запоминающие YCT
ройства, стоимость которых, как указывалось, быстро снижается.
Для сравнения надежности полупроводниковых запоминаю
щих устройств и запоминающих устройств на f\,lаrнитных эле-
ментах рассмотрим, например, ЗУ средней емкости, состоящие
из накопителей и периферийноrо оборудования. В ЗУ на маrнит
ных элементах доля отказов из за неисправности накопителя co
ставляет 10 400/0, а доля отказов из за неисправности перифе
риЙны схем от 60 до 90 О/о. в то же время в ПОЛУllРОВОДНИКО
вых ЗУ доля отказов из за неисправности наI{опителя достиrает
70 950/0 и лишь 5 300/0 составляют отказы периферийноrо обо
рудования [4]. Таким образом, при использовании полупровод
никовых ЗУ в качестве оперативной паl\IЯТИ возникает необходи
мость повышения надежности последней. rлавным образом
именно в связи с этим в настоящее время обсуждаIОТСЯ раЗ,J1ИЧ
ные способы ПОВЫlпения надежности оперативноЙ паl\tIЯТИ с по-
мощью кодов, исправляющих Оlllибки. Конечно, введение избы-
точности приводит к повышению стоимости памяти периферий
Horo оборудования, но если учесть, что это повышение позволяет
резко понизить стоимость накопителей, то в целом стоимость
вычислений понижается. С точки зрения возможности пониже
ния стоимости вычислений применение кодов, исправляющих
ошибки, в вычислительных машинах также представляется целе-
сообразным.
Выше rлавныI\11 образом раССl\1атривалось применение в вы-
ЧIlслительных системах кодов, исправляющих ошибки. Однако
для повышения надежности вычислительных систем используют
420
r лава 7
ся также «саl\lокорректирующиеся» схемы, изучаемые в теории
автоматов, а также так называемые арифметические коды, опи
сываемые в последующих двух rлавах и используемые в HeKOTO
рых арифметических устройствах, в частности в сумматорах. Что
касается кодов, исправляющих ошибки, то они в общем случае
применяются в системах, про которые достаточно знать лишь
то, что в них информация вводится и выводится. При этом ис
следуемая система часто оказывается сложнее, чем изображен
ный на фиr. 7.29 канал связи. В действительности, как показаJlО
на фиr. 7.31, ЛIобую систеl\1У можно раССl'vIатривать как некий
«черный ящик» и, сравнивая входыI с выходами, найти распре
деление ошибок. Зная это распределение, из всех известных KO
дОВ можно выбрать тот, который исправляет наиболее часто воз
никающие конфиrурации ошибок; кроме Toro, можно построить
новый код специально для данноrо распределения ошибок. Ha
пример, в процессе общения оператора с вычислительной маши
ной при выполнении ручных операций возникает большое число
«паер
ЧерныtlllЩIIК
еЛ'О8ерr
Фиr. 7.31. Система связи с каналом, рассматриваемым как «черный ящик».
ошибок, связанных с перестановкой соседних символов. Эти
ошибки представляют собой специальные пачки ошибок длины
2, и для их исправления MorYT быть разработаны специальные
коды, учитывающие этот характер ошибок.
Для определения ухудшения качества и эффективности пере
дачи существующих систем связи широко используются анали
тические методы, с помощью которых разрабатываются методы
улучшения характеристик систем связи. Что касается диалоrа
человека с машиной, то для определения причин возникновения
ошибок здесь необходимо анализировать сложные процессы, про
текающие от клеток мозrа до нервных окончаний человека, что,
конечно, практически сделать невозможно. Для борьбы с ошиб
К8l\IИ оператора можно использовать алrебраические коды, рас-
сматривая при этом тракт ввода как «черный ЯLЦИК» и просто
устанавливая на ero входе кодер, а на выходе
декодер.
7.4. Различные предположения, используемые
в теории кодирования
Рассмотрим здесь различные предположения, используемые в
теории кодирования. В теории кодирования применяются rлав
ным образом а.п:rебраические методы, в частности теория rалуа,
Реализация кодО8 1 исправЛЯ10щих ошибки
421
и это позволило достаточно быстро достичь значительных успе
хов. При этом некоторые проблемы, для реlllения которых алrе
браичеСI(ие методы применить было трудно, остались в значи
тельной степени нерешенными. ВОЗМО}l(НОСТЬ решения алrебраи
ческими методами одних проблем и трудности решения друrих
не менее важных проблем оказали существенное влияние на
формирование теории I(одирования. Для Toro чтобы l\10ЖНО было
применить алrебраические методы, в теории кодирования вводи
пись различные предположения, что оrраничивало область при
менения полученных результатов. Знание этих предположений
очень важно для понимания взаимосвязи теории кодирования с
теми реальными проБJIемами, которые она призвана решать.
7.4.1. Дискретные величины
В теории кодирования подлежащая передаче, хранению или
какой
либо обработке ИНфОРl\lация обычно представляется в ви
де последовательностей целых чисел, в частности в простейшем
случае в виде последовательностей символов О и 1. Поэтому
при изучении передачи информации в теории кодирования pac
сматриваются лишь дискретные каналы. Чтобы коды, исправ
ляющие ошибки, можно было применить в реальных непрерыв
ных каналах, непрерывные величины с помощью аналоrо
циф
ровых преобразователей должны преобразовываться в дискрет"
ные величины.
7.4.2. Методы принятия решений
Предположим, что для передачи СИi\ЛВО.;10R О и 1 используются
прямоуrольные импульсы длительности Т единиц времени с aM
плиту дам и соответственно
V и v. При передаче по каналу с
аддитивным rауссовским шумом эти символы искажаются и на
вход приемника поступают СИl\fВОЛЫ, имеющие случайную aM
плитуду. В качестве рсшающеrо элемента при приеме может
использоваться пороrовый элемент с пороrом О, I(ОТОРЫЙ класси
фицирует принятый импульс как О, если ero амплитуда меньше
нуля, и как 1, если амплптуда больше нуля. Такой способ при
нятия решения о переданном символе называется жестким. K.po
ме Toro, существует так}ке так называемыЙ МЯZКUU способ при
нятия решений, коrда решаlОЩИЙ элемент Иl'vlеет два пороrа VjЗ
и
Vj3, l(aK показано на фиr. 7.32, б. При ЭТОl'vI выход решаю
щеrо элемента принимает значение 1, если амплитуда принятоrо
импульса больше v/з
значение О, если амплитуда принятоrо Иl\rl
пульса меньше
V /3, и решаIОЩИЙ элемент не принимает НИКа
Koro решеНIIЯ относительно О и 1, ес
'IИ аl\fплитуда импульса Ha
ходится между Vj3 и
VjЗ. Ilри этом, кроме ошибок типа I1ере
422
r лава 7
ХОД символа 1 в символ О или наоборот, MorYT возникать также
так называемые стирания, коrда решающий элемент решения о
переданном символе не принимает. В этом случае на выходе pe
шающеrо элемента формируется так называемый символ стира
ния. При передаче последовательности символов место возник
новения ошибок типа переход символа 1 в О или наоборот апри
ори неизвестно. В то же время положение стираний при прие fе
известно, а поэтому исправить их оказывается значительно про
ще, чем исправить ошибки. Поскольку в канале с аддитивным
rауссовским lIIYMOM стираний возникает значительно больше,
чем, ошибок, то путем использования мяrкоrо способа принятия
решений можно упростить процесс исправления ошибок в цe
лом.
Далее рассмотрим случай, коrда описанные выше импульсы
передаются по каналу блоками по К импульсов в каЖДО 1, но о
t t
v v
v
о о
1 1
v ... -- --
:. --у
т +
а
о'
Фиr. 7.32. Импульсы 1 и О и значения noporoB.
каждом отдельном переданном. символе принимается жесткое
решение, не зависящее от друrих принятых импульсов. Предпо
ложим, что шум В канале является аддитивным и rауссовским.
Обозначим через Ре вероятность возникновения ошибки в OT
дельном символе. Тоrда вероятность Toro, что в принятом блоке
нет ни одной ОII1ибки, равна (1 Ре) к и убывает с ростом К.
Это связано с тем, что при увеличении К расстояние между «со-
седними» сиrналами остается постоянным, равным 2V
(фиr. 7.33, а), а число соседних сиrналов возрастает пропорцио-
нально К; в результате вероятность возникновения ошибки по
крайней мере в одном из передаваемых символов возрастает.
В данном случае для передачи одноrо блока используется энер
rия, равная KV 2 T, а число сиrналов равно 2 К .
Далее раССl'vIОТРИМ систему связи с 2 К ортоrональными сиr
налами 'Фi, i == 1, 2, . . . , 2 К , длительности 2КТ; i й сиrнал пред
ставляет собой положительныЙ начинаIОЩИЙСЯ в момент i им
пульс длите,,1ЬНОСТИ Т с энерrией KV 2 T, которыЙ используется
для передачи блока из 2 К двоичных СИ:\IВО.пов) предстаВJ1яющеrо
двоичную запись ero номера i (фиr. 7.33, б). Такие сиrналы ие-
Реализация кодов, исправляющих oUlu6KU
423
пользуются, например, в системах с время импульсной 1\10ДУЛЯ
цией (ВИМ). Один из описанных выше сиrналов при К == 3 по
казан на фиr. 7.33, б. Как видно из фиr. 7.33, в, расстояние l\tle
жду соседними сиrнала ми (в данном случае все сиrналы являют-
ся соседними) равно ,y2KTV. Поскольку здесь с ростом К число
соседних сиrналов растет как 2К, а расстояние меж.ду сиrна-
лами как ,у К , то при достаточно больших значениях отноше-
ния сиrнал/шум ошибку между блоками можно сделать сколь
1< 2V I
. . SU;
о 1
К= 1
I I I
t з (t)
1
1 01
О 00
3HefJ lIlIc= зv 2 Т
р;
т
1
а
К=:2
1 234 5 б 7 8 t
C/1Yf{(11l к а: j
5
';3TV
IJТv
6
ljJ'j
Фиr. 7.33. Расстояние между блоками.
уrодно малой, выбрав достаточно большое К. Таким обра'З0М,
при наличии оrраничений лишь на среднюю мощность методы
передачи, коrда при приеме решение принимается о переданном
блоке в целом, позволяют достичь лучших результатов, чем Me
тоды передачи, при использовании которых двоичные символы
передаются независимо и при приеl\lе решение о каждом из них
принимается независимо.
Как показывают приведенные выше примеры, методы приня-
тия решения о символах существенно влияют на вероятность
ошибки в символе и посредством этоrо они связаны с методами
исправления ошибок. N\ноrообразие методов принятия решений
приводит к мноrообраЭИIО методов исправления ошибок в тео-
рии кодирования. Однако в теории кодирования, как правило,
424
r лава 7
предполаrается, что метод принятия решения является жестким
и ЛИJl1Ь часть получающихся результатов обобщается на системы
с исправлением ошибок и стираний.
7.4.3. Расстояние Хэмминrа
Одной из условностей, принятых в теории кодирования, яв
ляется понятие расстояния. UUироко используемое в теории KO
дирования расстояние Хэмминrа между векторами (al, а2, ...
. . . , а n ) и (b 1 , Ь 2 , . . . , Ь n ) определяется как число пар несовпа
.....
)
1
........,..-
-...,..---
о
z
1
а
l>i
j
1
t
1
1 1 1
б
Фиr. 7.34. Троичные импульсы.
дающих компонент этих векторов. Например, расстояние ХЭМ
минrа между векторами (О, О, О) и (о; 1, 1) длины 3 с компонен-
тами О и 1 равно двум. В то же время равно двум расстояние
Хэмминrа между троичными векторами (2, 1, О) и (О, 1, 1) с ком-
понентами О, 1 и 2. Кроме Toro, равно двум расстояние ХЭМ-
минrа между векторами (2, 1, О) и (1, 1, 1).
Расстояние Хэмминrа между двумя векторами определяется
лишь числом пар несовпадающих компонент векторов и COBep
шенно не учитывает, насколько сильно различаются несовпадаю
щие компоненты. Слабые стороны TaKoro определения расстоя
ния становятся очевидными, если рассмотреть передачу по ка-
налу с аддитивным rауссовским шумом компонент О, 1 и 2 TpO
Реализация кодов, исправляющих ошибки
425
ичных векторов с помощью импульсов фиксированноЙ длитель
ности с амплитудами соответственно О, 1 и 2 В, как показано на
фиr. 7.34, а. ПреДПОJ10ЖИМ, например, что по каналу передается
последовательность импульсов, соответствующая вектору (2, 1,
О). В результате воздействия шумов эта последовательность MO
жет быть воспринята приемником и как последовательность, co
ответствующая вектору (О, 1, 1), и как последовательность, co
ответствующая вектору (1, 1, 1). Однако поскольку шум в Ka
нале является аддитивным и rауссовским, то, очевидно, что Be
роятность принять символ 2 как О меньше, чем вероятность при
нять символ 1 как О. В то же время расстояние ХЭl\rIминrа ме.
жду вектором (2, 1, О) и векторами (О, 1', 1), (1,1, 1) одно и
то же.
Однако это пеестествеllное с первоrо взrляда понятие pac
стояния Хэмминrа позволяет упростить модель системы связи, а
следовательно, и теоретический анализ последней. Расстоянием,
которое определяется не только числом пар несовпадаIОЩИХ
компонент, но и учитывает величину различия последних, яв
ляется расстоянием Ли. Однако сразу следует заметить, что
часть теории кодирования, основанная на расстоянии Ли, cpaB
нительно невелика. Если же использовать еще более общее по-
нятие расстояния, а именно евклидово расстояние, как показано
на фиr. 7.33,8, то построить теорию кодирования оказывается
почти невозможным.
7.4.4. Положительные стороны теории кодирования
Таким образом, в теории кодирования достаточно MHoro yc
ловностей, но, с друrой стороны, она имеет и ряд существенныIx
достоинств. Одно из них заключается в том, что при увеличении
длины кода или числа информационных символов, несмотря на
то, что число кодовых слов в коде, а следовательно, и число BHY
тренних состояний кодера и декодера растут экспоненциально,
для их обработки, как правило, требуется линейно растущее с
ДЛIIНОЙ кода число операций (шаrов). Заl\Jlетим, что в теории
конечных автоматов, как правило, экспоненциальное возраста
вне числа внутренних состояний сопровождается таким же экс
поненциальным ростом числа операций (шаrов, циклов), необхо
димых для обработки.
Таким образом, из вышеизложенноrо следует, что при приме.
нении теории кодирования к тем или иным системаl\1 необхо
димо, во
первых, ясно понимать rраницы применимости этих
результатов, а во.вторых, для достижения высокой эффективно.
сти и оптимальности систем умело соrласовывать методы приня
тия решений с используемыми кода 1\.1 И, исправляющими ошибки.
426
rлава 7
7.5. Применения в системах связи метода
u
повторнои передачи
Так как обнаружение и исправление ОIlIибок обычно вво-
дятся с целью повышения достоверности передачи данных за
счет HeKoToporo увеличения времени декодирования и стоимости
системы, то естественно, что решение вопроса о выборе помехо
устойчивых кодов и методов их использования в системе связи
должно составлять один из этапов проектирования системы в цe
лом. В существующих системах связи для обнаружения и ис
правления ошибок широко ИСПОЛЬЗУIОТСЯ различные методы, oc
нованные на повторной передаче данных. Для реализации этих
методов обычно требуется достаточно простое устройство обна-
ружения ошибок, но при ЭТОl\1 функционирование схем, необхо
димых для орrанизации повторной передачи при обнаружеНIIИ
ошибок, оказывается очень тесно связанным с управлениеl\1 си
стемой связи в целом, что, конечно, является недостатком этих
методов.
7.5.1. Системы с полной обратной связью
и системы с дублированием передачи
Существуют различные типы систем связи с повторной пере-
дачей данных, такие, например, как системы с полной обратной
связью, системы с дублированием передачи, системы с обнару
жением ошибок посредством продольных или поперечных про
верок на четность, системы с обнаружением ошибок посредством
циклических кодов и др. В системах с полной обратной связью
подлежащие передаче данные посылаются в канал связи и одно-
временно вводятся в буферное заполняющее устройство или ли-
нию задержки. На приемном конце принятый сиrнал также за-
поминается в буферном запоминающем устройстве и возвра-
щается без изменений по KaHaJ1Y обратной связи на передатчик.
На передающем конце полученный от при
емника сиrнал сравни-
вается с сиrналом, хранящимся в буферном запоминаIощем YCT
ройстве, и если сравниваемые сиrналы не совпадают, то обычно
выполняется одна из следующих операций: 1) формируется сиr-
нал ошибки и передача данных прекращается; 2) на приемник
посылается сиrнал, указывающий ПОJlожение ошибки; 3) исход
ный сиrнал передается вторично. Достоинством этой системы яв.
ляется то, что она позволяет без заметноrо снижения скорости
передачи очень эффеI{ТИВНО обнаруживать ошибки. Ее недостат"
ками являются низкая эффективность схем, необходимость со-
rласования времени хранения сообщениЙ на передающем конце
u
с задержкои сиrнала в линии связи, неВОЗМОЖIIОСТЬ ИСПОЛЬ30ва
ния в сетях передачи данных с коммутацией пакетов.
Реализация кодов, исправляющих ошибки
427
в системах с дублированием передачи каждый сиrнал пере
дается по каналу два раза. На приемном конце принятые сиr
налы сравниваются, и если они совпадают, то считается, что при
передаче ошибок не было. В противном случае на передатчик
посылается запрос на повторную передачу. Такая система также
очень хорошо обнаруживает ошибки, но скорость передачи ин
формации уменьшается в два раза.
7.5.2. Обнаружение ошибок
Методы обнаружения ошибок с помощью продольных и попе.
речных проверок на четность или циклических кодов позволяют
хорошо обнаруживать ошибки при сравнительно небольшой из-
быточности, требующейся для их реализации. При использова
нии продольных и поперечных проверок на четность подлежащие
передаче данные располаrаются в виде прямоуrольной таблицы,
к которой добавляются один проверочный столбец и одна про
верочная строка так, чтобы число единиц в каждой строке и Ka
ждом столбце такой расширенной таблицы было четным (нечет
ным). Расширенная таблица передается по каналу связи. При
приеме подсчитывается число единиu в каждом столбце и Ka
ждой строке принятой таблицы и таким образом обнаруживаIОТ
ся uшибки.
В случае использования циклических кодов для обнаружения
ошибок подлежащие передаче данные представляются в виде
мноrочлена. Этот мноrочлен делится на порождающий MHoro
член g (Х) циклическоrо кода, и полученный в результате этоrо
деления остаток передается по каналу вслед за информацион-
ными символами, так что кодовый мноrочлен, коэффициентаl\lИ
KOToporo являются переданные информационные и проверочные
символы, делится на g (Х). При приеме принятый мноrочлен дe
лится на g (Х), и если остаток от деления оказывается равным
нулю, то считается, что при передаче ошибок не было. Если же
полученный остаток оказывается отличным от нуля, то это оз
начает, что при передаче в кодовом мноrочлене возникли ошиб
ки. В этом случае передача данных либо прекращается, либо на
передатчик посылается запрос на повторную передачу искажен-
ных данных. Поскольку при обнаружении ошибок с помощью
циклических кодов на передающем и приемном концах ДOCTa
точно иметь ЛИIIIЬ схемы деления мноrочленов, то этот метод мо-
жет быть реализован технически сравнительно просто. В настоя-
щее время в системах связи с небольшой скоростью передачи
обычно используются продольные проверки на четность. В син
u
хронных системах связи с высокои скоростью передачи, как пра-
вило, для обнаружения ошибок применяются циклические коды,
а для исправления ошибок
повторная передача.
428
r лава 7
7.6. Применения в системах связи кодов,
исправляющих ошибки
7.6.1. МОДУЛЯЦИЯ и кодирование
Системы с обнаружением ошибок почти всеrда обладаlОТ
очень хорошей способностью обнаруживать ошибки и в настоя-
щее время широко используются на практике. Однако для pea
лизации таких систеl\1 необходимо иметь обратный канал связи,
реrулировать время задержки сообщениЙ в буферном запоми
нающем устройстве; при реализации некоторых из этих систем
значительно СIIИ}l{ается скорость передачи. Кроме Toro, в ли-
ниях связи между вычислительными машинами при работе по-
следних в режиме «оп line» осуществить ПОВТОРНУIО переда чу в
случае обнаружения ошибки крайне сложно, поскольку это свя
зано с необходимостью ИIvlеть схему задержки на большое время.
В подобных случаях для повышения достоверности передачи це-
лесообразнее использовать коды, исправляющие ошибки.
Модель системы связи, которая обычно берется за основу
при разработке подсистем контроля и исправления ошибок, по-
казана на фпr. 7.29. Функции каждоrо БЛОI{а, представленноrо
на фиr. 7.29, описаны выше. rлавная трудность, возникающая
при введении этой модели, связана с обоснованием разделения
функций модуляции (в широком смысле) и кодирования. В Ha
стоящее время даже теоретичеСКII трудно установить, насколько
это разделение ухудшает эффективность передачи. Однако на
практике такое разделение ОСУll
ествляется, и поэтому реально
существуют два Kpyra проблем:
1. Проблемы модуляции (в широком смысле), связанные с
выбором типа модуляции (амплитудной, фазовой и т. д.), пере-
дачей реальных непрерывных сиrналов, обнаружением сиrналов,
интерференцией, квантованием, искажениями и т. д.
11. Проблемы кодирования, связанные с обнаружением и ис-
правлением ошибок.
Параметрами, характеризующими эффективность цифровой
связи, являются отношение энерrии принимаемоrо сиrнала, не-
обходимой для передачи одноrо бита информации, к мощности
шумов Eb/No, отношение амплитуды сиrнала к амплитуде шумов
C/N, отношение W/R, устанавливающее связь между полосой и
скоростью передачи, и др. Взаимосвязь между этими парамет-
рами и параметрами, характеризующими поведение канала свя-
зи ( к последним относится, например, вероятность ошибки), оп-
ределяет эффективность цифровых систем связи.
Джордан [10] показал, что отношение Eb/No характеризует
взаимосвязь модуляции и кодирования. Если обозначить через
S мощность ПРИНИIvlаемоrо сиrнала в системе связи, показанной
Реализация кодов, исправляющих ошибки
429
на фиr. 7.20, через N o мощность белоrо шума в прямом канале и
через ffl скорость передачи информации в битах в секунду, то
отношение необходимой для передачи одноrо бита информации
энерrии принимаемоrо сиrнала к мощности ШУl\10В можно пред
ставить в следующеlVl виде: i:
Еы N о === (51 N о) (1/Ш). (7.29)
Даи1ее, если предположить, что каждые l' секунд по каналу пе
редается один из М различных сиrналов, 1'0 скорость передачи
ИНфОРl\fации в битах на один сиrнал будет равна
R == шт [бит/сиrнал].
Так как энерrия Er одноrо принимаемоrо сиrнала равна ST, то
(Eb/No) === (E,/N o ) (l/R). (7.30)
При передаче данных по телефонным каналам скорость пе-
редачи информации R определяется интерференцией в канале.
В то же время, как указывалось в rл. 6, в каналах связи, в KO
торых применяется последовательное декодирование, скорость
передачи R всеrда выбирается меньшей вычислительной скоро-
сти Rвыч С тем, чтобы среднее число операций при декодирова
нии оставалось постоянным. Как видно из формулы (6.19), BЫ
числительная скорость Rвыч определяется только переходными
вероятностями канала. Вообще rоворя, скорость передачи ин-
формации всеrда оrраничена сверху некоторой постоянной,
определяемой системой модуляции (в широком смысле) и свой
ствами канала. Если эту предеЛЬНУIО скорость передачи обозна-
чить через Rмаис (бит/сиrнал], то для каналов без устройств об
наружения и исправления ошибок будет иметь место следующее
равенство:
Eb/ N 0== 1) === (E,IN о) (lIR мзкс ).
(7.31 )
(Здесь 11 некоторая константа, определяемая системой MOДY
ляции (в широком смысле), но не зависящая от кодирующих и
декодирующих устройств, используемых для обнаружения и ис
правления ошибок.)
Ес.Н:И ввести кодирование информации с целью обнаружения
или исправления ошибок, то скорость передачи будет меньше,
чем Rмаис. При этом величины
а === R/R MaKc (7.32)
и 11 можно рассматривать как независимые переменные и полу-
чить
Eb/No== (E,/N o ) (I/R MaKc ) (RMaKc/R) == ·
(7.33)
В процессе проектирования систем связи при заданных требо
ваниях к сложности реализации, вероятности ошибки и друrим
430
rлава 7
характеристикам системы желательно использовать минимально
возможное значение 11 и максимально возможное значение а.
При проектировании систем связи отношение Eb/No является
rлавным параметром, определяющим взаимосвязь модуляции и
кодирования. Отношение Eb/No является rлавным парамеТрОl\'1
при передаче информации с помощью маломощных сиrналов,
как, например, в системах космической связи. В системах назем
ной связи вследствие переrрузки каналов связи, а также по др у-
rим причинам наиболее жесткие требования предъявляются к
пиковым напряжениям; требования к мощности передаваемых
сиrналов являются менее жесткими. В этих случанх rлаВНJ)Il\IИ
параметрами являются Eb/No и отношение C/N. Поэтому при
проектировании систем связи в соответствии с их целями и на-
значением желательно учитывать оба параметра Eb/No и C/N.
Параметр W/R, характеризующий полосу, для систем космиче
ской связи может быть выбран очень большим, а в большинстве
систем наземной связи на полосу наI{ладываIОТСЯ оrраничения,
часто очень жесткие.
7.6.2. Вероятность ошибки при использовании
алrебраических кодов
Найдем вероятность ошибки на блок Р в и эквивалентную
,
вероятность ОIIIибки на символ Р Е, которые понадобятся в даль-
нейшем [6].
Блоковые коды длины n с k информационными символами,
исправляющие ошибки кратности t и менее, будем называть (n,
k, t)
кодами. Предположим, что при приеме о каждом передан-
ном символе принимается независимое решение. В этом случае
вероятность Р в ошибки в кодовом слове (n, k, t)
Koдa опреде-
ляется paBeHCTBOl\I
n
" n! pt+1 ( 1 Р ) n
t
1 Х
Р в == f...J Р Е /== (t+l)!(n.....t.....l)f Е
Е
jr:::a t+1
{ n ..... t ..... 2 РЕ (n ..... t ..... 2) (n ..... t ..... 3) ( РЕ ) 2 + }
х 1 + t
2 1
РЕ + (t + 2) (t + З) 1
РЕ ' .. <
n!pk+ 1 { n РЕ п ( РЕ ) 2 }
< (t + 1)1 (п
t
1)1 1 + t + 2 1
РЕ + (t + 2)2 1
РЕ +. ., ,
(7 . 34 )
rде
PEj == ( 7 ) pf, (1
PE)n
J,
(7.35)
Реализация кодов, uсправляюu{uх ошибки
431
а РЕ вероятность ошибки при принятии решения о каждом
отдельном символе.
Чтобы cTporo определить эквивалентную вероятность ошибки
на символ, необходимо знать полные статистические свойства
ошибок, а не только то, что среди п двоичных символов воз
никает t + 1 или более ошибок. Вместе с тем каких либо алrе-
браических законов, описывающих поведение ошибок для алrе-
браических кодов, не существует, и поэтому должны исследо..
ваться и определяться вероятности различных конфиrураций
ошиБОI<' Однако даже при использовании вычислительных Ma
шин эта задача весьма трудоемкая, так как требует очень боль
шоrо числа операций. В данном разделе будет получена верхняп
rраница для вероятности ошибки на символ при следующих
предположениях.
В случае возникновения t + 1 или более ошибок в результате
ошибочных действий декодер может породить еще t ошибок.
Если среди п символов появилось t + 1 и "более ошибок, та
2t + 1 или более ошибок возникают случайно. Предположение
о случайном возникновении 2t + 1 или более ошибок вводится
по следующим причинам:
1. Почти для всех алrебраических кодов при таком декоди-
ровании не существует каких либо оснований к тому, чтобы pe
зультат ошибочных действий сказывался на каких либо Bыдe
ленных символах.
11. В процессе декодирования почти всех алrебраических KO
дов ошибки в информационных символах и ошибки в провероч-
ных символах не разделяются. Следовательно, если результат
ошибочных действий связать с некоторыми определенными сим-
волами и вероятности ошибок в символах считать различными,
то путем расположения проверочных символов на позициях
с высокой вероятностью ошибки можно понизить среднюю Be
роятность ошибки в информационных символах в случае, коrда
распределение вероятностей ошибок в символах неизвестно.
Итак, при сделанных выше предположениях х 2t + 1 оши
бок в п символах возникают независимо, так что среднее число
ошибок в информационных символах равно kx/n. Отсюда сле-
дует, что среднее число (математическое ожидание) ошибочных
информационных символов равно
n t
I
I==t+l
n
(j + t) k Р + k " Р
n Е! i...J EJe
f ==n t+l
(7.36)
Следовательно, для ЭI{вивалентноЙ оероятности ошибки на сим
вол p (после деления на k и замены (1 Pe)n t l на 1) полу
432
rлава 7
чаем следующую верхнюю rраницу:
P ' E« 2t+l) t+l ( n )[{ n РЕ
II РЕ t + 1 1 + t + 2 1
Р +
Е
+ ( t
2 I
Ер Е У + ...} +
+{ 2t
1 t:2 I
EPE +... + n;
1 C
21
EPE y
t
I}].
(7 .37)
Вероятность РЕ в .реальных системах обычно имеет значения
порядка IO
3+IO
IO. В случае коrда nPE/(t+2)(1
PE)
1,
т. е. при РЕ
(t + 2) / (п + t + 2), правые части формул (7.35)
и (7.37) достаточно точно аппроксимируются их первыми или
несколькими первыми членами.
Вероятность возникновения ошибки в отдельном символе при
передаче по каналу (входящая в эти формулы) зависит от мо-
дуляции и должна определяться для каждой системы отдельно.
7.6.3. Мноrоуровневая фазовая модуляция и кодирование
Как указывалось в разд. 7.6.1, установление взаимосвязи M
-
жду вероятностью ошибки и необходимым для передачи одноrо
двоичноrо символа отношением энерrии принимаемоrо сиrнала
к мощности шумов позволяет рассматривать проблемы модуля-
ции и кодирования на единой основе. Ниже мы продемонстри-
руем еще раз взаимосвязь модуляции и кодирования и покажем,
что использование кодирования в системах с мноrоуровневоЙ
фазовой модуляцией позволяет улучшить отношение сиrнал/шум
при фиксированной вероятности ошибки.
При мноrоуровневой фазовой модуляции и отсутствии orpa-
ничения на выбор отношения сиrналjшум в канале можно повы
сить Rмаис за счет увеличения числа фаз. Однако с увеличением
числа фаз увеличивается отношение Eb/No, необходимое для
достижения заданной вероятности ошибки. Задача состоит
в том, чтобы найти точку, в котороЙ возрастание отношения
Eb/No за счет увеличения числа фаз компенсируется уменьше-
нием Eb/No за счет введения кодов, исправляющих небольшое
число ошибок; решив эту задачу, мы покажем на ее примере
эквивалентность систем модуляции (в широком смысле) и си-
стем кодирования при обеспечении помехоустойчивости.
Система связи с мноrоуровневой фазовой модуляцией и поме
хоустойчивым кодированием информации показана на фиr. 7.35.
Двоичные символы с выхода источника информации сначала
поступ
ют на вход блоковоrо кодера, который разбивает их на
. Реализация кодов, исправляющих ОUlllбки
433
блоки и преобразует в кодовые слова HeKoToporo блоковоrо кода,
исправляющеrо ошибки, например БЧХ кода. Далее последова
тельность символов с выхода блоковоrо кодера поступает на
вход фазовоrо кодера, который преобразует ее в последователь.
ность символов кода rрея, каждый из которых содержит т
двоичных информационных символов. Символы кода rрея пе
редаются по каналу посредством импульсов фиксированной дли-
тельности с модулированной фазой. При приеме сначала ocy
ществляется синхронное детектирование каждоrо принятоrо
импульса и далее берется отсчет в максимуме выхода детектора.
После декодирования фазовыЙ код преобразуется в двоичный
ИстОl/НV/(
и60P'lNtJiI
'НфОjJМf1ЦИtl
/(оиср
БЧХ
/(ооп
lfotJep
!рея
ФпЗIlВЬА"
MOOY/lJl-
тор
/(nНОА
1117//1'111 rf,fj
UНФ()РNО-
ЦJlи
е/(оиер
бl.j%
/(0011
д ек(}иер
/(оио
(рен
Фоз(}б6/iI
rJCA1IlUY
lIJ1тор
Фиr. 7.35. Модель системы связи с мноrоуровневой фазовой модуляцией.
код. С помощью БЧХ-декодера проводится исправление ошиБОI<
в двоичных словах, после чеrо информационные символы на-
праВЛЯIОТСЯ получателю информации.
Следуя Кану [7], рассмотрим более детально систему связи
с 2 1n сиrналами вида
s (t) === V 2S cos (000/ + 8),
е == , о k 2т 1,
(7.38)
rде S мощность принимаемоrо сиrнала. Предположим, что
R канале действует аддитивный белый rауссовский шум
n (t) == х (t) COS U>ot + у (t) sin u>o/,
(7.39)
rде х(t) п у(t) низкочастотпые случайные компоненты n(t);
ii == О, п 2 == N. В этом случае распределение фазы на выходе
434
fлава 7
синхронноrо детектора имеет следующий вид:
{ (1/ v nN /S ) е e2/(N/S)
р (8) ==
О,
j'[
181 <2'
j'[
I е 1> 2'
(7.40)
а вероятность ошибки в символе Ps может быть вычислена по
формуле
1t/2 т
Р а ;:::: 1 р (8) d8 ;:::: 1 2 erfc ( 2 ,-J ).
1t/2m
(7.41 )
rде
х
erfc х === -v'k- e u'12 du.
о
Амплитуда сиrнала с модулированной фазой при наличии
оrраничений на ширину полосы не является постОянной п,
вообще rоворя, канал связи необходимо рассматривать вместе
с фильтром. Однако здесь, следуя Беннету и Дэви [12], в целях
упрощения при проведении анализа будем считать амплитуду
сиrнала постоянной.
Фазовый код, задаваемый таблицей rрея, обладает тем свой-
ством, что кодовые слова, соответствующие сиrналам с coceд
ними фазами, различаются лишь в одном двоичном символе.
При воздействии сильных шумов в результате сильноrо искаже-
ния фазы передаваемоrо сиrнала Moryr возникать ошиБКJI
в двух И большем числе символов кодовых слов кода rрея. Как
будет видно ниже, в наиболее ва}I{НОЙ с практической точки
зрения области вероятностей ошибок в отдельном символе,
а именно при РЕ Ps IO 3 10 10, такими кратными ошиб
ками можно пренебречь.
Положим, например, т == 4 и SjN =:Е: 18 дБ. В этом случае
р s == 1 2 Х 0,4860966 === 0,278068, а вероятность ошибки, об-
условленная переходом сиrнала в соседний, равна 2 [erfc (6,603).........
erfc(2,201)] == 0,0278066. При этом вероятность ОПIибки из-за
выхода сиrнала за пределы соседнеrо равна 2. 1 0 7, т. е. при-
близительно в 105 раз меньше вероятности Ps === 2,78.10 2. Ана-
лоrично можно убедиться в том, что и во всех остальных случаях
в практически важной области вероятностей ошибок в символе
РЕ Р s 1 0 3 1 0 10 С поrрешностью, не превышающей 1 O 5,
Ps === РЕ'
В области вероятностей ошибок в символе, для которых
справедливо указанное выше предположение, по аналоrии с вы-
водом формул (7.35) и (7.37) в предыдущем разделе для ве.
роятностей ошибок на блок и на символ можно получить сле-
(7.42)
Реализация кодов, исправЛЯ10щих ошибки
435
дующие оценки сверху:
Р в < [ ]! p +1 (1 PE)[ ] t 1 Х
(t + 1)1 ([ : ] / 1)!
х [1 + t 11 Ep +...],
Е
(7 . 43)
р' < (2/+1) pt+I ( [ ] )X
Е n Е t+l
Х [{ 1+ [';'] РЕ + ( [,';]
t+2 l P t+2
в
{ 1 [ : ] РЕ 2 ( [ : ]
+ 2/+1 /+2 I PE + 2/+1 t+2
1 Ер У + ...} +
Е
1 EPE У + ...}].
(7 .44)
Здесь через [х] обозначено наименьшее целое число, большее или
равное х. В случае Р Е (' + 2)/([ : ] + t + 2 ) правые части по-
следних равенств достаточно точно аппроксимируются первыми
членаlVIИ.
Равенство (7.41) определяет отношение сиrнаJI/ШУМ, необхо
димое для передачи одноrо символа. В системах связи с MHoro
уровневой фазовой модуляцией и помехоустойчивым кодирова-
нием информации для нахождения отношения сиrнал/шум, KOTO
рое требуется для передачи одноrо двоичноrо символа, необхо-
димо внести поправку, обусловленную ростом числа фаз и избы-
точностью кодов, исправляющих ошибки. При наличии оrрани-
чений на ширину полосы поправка вносится путем умножения
времени Т в на n/k. Таким образом, если Eb/No вычислять в де-
цибелах,то
10 19 (Eb/NO) == 10 19 (S/N) ....... 10 19 т + 10 19 (n/k),
rде N == NoT, а Т время, необходимое для передачи одноrо
двоичноrо символа. На фиr. 7.36 приведены результаты вычис-
лений с учетом указанной выше поправки отношения сиr-
нал/шум и вероятности ошибки в случае k == 100, 2т == 8, 16, 32
(t == О) при использовании БЧХ кодов с параl\fетрами (127, 120,
1), (127,114,2) и (127,106,3). Как видно из этих данных, си-
стемы без кодирования с 2т == 8 и системы с 2т == 16, исполь-
зующие (127, 114, 2)-код, в области практически ваЖНbIХ значе-
ний РЕ почти эквивалентны.
436
rлава 7
Таким образом, мноrоуровневая фазовая модуляция исполь-
зует повышение отношения Eb/No для достижения заданной ве-
роятности ошибки, а методы помехоустоЙчивоrо кодирования,
основанные на использовании кодов, испраВЛЯЮIЦИХ ошибки, до-
пускают снижение отношения Eb/No. Использование кодов, IIС-
правляющих ошибки, в системах связи с мноrоуровневоЙ фазо-
х
10 2 , Х
, ,
" х'
" \'
1a 3 " \'
\\ х\ '
\ \ \ \ \
\ \ \ \ х
10 4 \ \ \ \ \
\ \ \ \
\ \ \ \
\ \ \ \
10 5 \ \Х \
\' \
\ \ \ \
\ ,\ )(
х \ ,
... \ \ , \ \
I:l , \ \ \ \
' \ \ \ \
::t \ \ \ \ \
ct.1.ц \ \ \ \ \ 2 т =j2
\ \ , , \ t=D
\ \ ,
1D 8 \ \ , ,
\ \ \ ,
, , t=O
2 т == 16 I \ , \
t==2 , т 'х zт==1б \ \ \ т
1D 9 2 ==8 (==1 \ \ )( Z =32
t .. О \ \ t=1
, 2 т ==32
')( (=2.
2т =32
t=3
10 11
12 14 16 18 20 22 24
Еа / N o ' дБ
Фиr. 7.36. Зависимость вероятности ошибки на символ от Eb/No.
вой модуляцией обеспечивает определенную свободу при проек-
тировании систем блаrодаря предоставляющейся возможности
изменения отношения Eb/No путем изменения числа фаз .
Рассмотренный выше метод передачи включает преобразова-
ние двоичноЙ последовательности, получающейся в результате
помехоустойчивоrо кодирования информационных символов, в
сиrналы мноrоуровневой фазовой модуляции. Существует не-
сколько способов реализации TaKoro преобразования, в частно-
Реализация кодов, исправляющих ошибки
437
сти С ПОМОЩЬЮ использованноrо выше кода rрея. Друrой способ
описывается в работе Имаи и др. [8]. Как показывают расчеты,
последний способ в некоторых случаях приводит к лучшим ре-
зультатам, чем код rрея.
7.6.4. Применения кодов в космических и спутниковых
системах связи
а) Применение последовательноrо декодирования. Наиболее
ранними работами, в которых начали рассматриваться примене-
ния последовательноrо декодирования в космических системах
связи, являются работы Возенкрафта и Кеннеди [9], а также
Джордана [10]. Алrоритмам последовательноrо декодирования
s(t}
.
c::::t
.
ч hn(t}
h,. (t) = х,.{ '['
t) Устрорст6а
1<61lHтo61l1f1l11
Фиr. 7.37. Декодер максималыlrоo правдоподобия для raYCCOBCKoro канала
СВЯЗИ.
rllуссоdс/(иll
шум
МОЩlfосmll
N a /2
.
.
.
.
и вычислениям их характеристик в этой книrе посвящена rл. 6.
В данном разделе будут кратко описаны некоторые системы MO
дуляции
используемые в сочетании с последовательным декоди
рованием.
Рассмотрим систему связи, в котороЙ передача последова-
тельности двоичных информационных символов осуществляется
блоками по NR символов в каждом. Каждому блоку из NR сим-
волов сопоставляется одна из 2 NR последовательностей S[, 1 == 1,
2, ..., 2 NR , из N сиrналов, каждый из которых в свою очередь
выбирается кодером из СОВОI<УПНОСТИ М ортоrональных сиrналов
Xi, i == 1, . . . , М. ДЛЯ каждоrо ортоrональноrо сиrнала модуля
тор формирует сиrнал Xi (t), который передается по каналу к
приемнику. При приеме, как показано на фиr. 7.37, с помощью
фильтров, соrласованных с ортоrональными сиrналами, осуще-
ствляется декодирование принятоrо сиrнала по максимуму пра-
вдоподобия. Так как выход системы соrласованных фильтров
представляет собой совокупность М действительных величин,
438
Fлава 7
то ero можно представить в виде вектора У == (Уl, . . . J Ум). Та-
ким образом, входом рассматриваеl\lоrо канала являются СИМ-
волы из конечноrо алфавита, а выходом ;\1 действительных
величин. С выходов фильтров эти действительные величины по-
даются на входы решающеrо устройства, с помощью KOToporo
они вновь преобразуются в дискретные сиrналы, поступающие
далее на вход деI{одера. ПростеЙшим решающим устройством
является устройство выделения сиrнала, имеющеrо наибольшую
апостериорную вероятность. На выходе решающеrо устройства
появляется последовательность lоg21И двоичных символов.
Как было показано в rл. 6, поведение алrоритмов последо-
вательноrо декодирования определяется значением Rвыч. Най-
дем Rвыч для описанной выше системы модуляции. По определе-
нию
R выч == X { log2 dy [t. Pk ,у Р (У I k) Т},
(7.45)
rде Ph вероятность передачи по каналу k ro ортоrональноrо
сиrнала (1 k М), Р (YI k) условная плотность распреде-
ления вектора У при условии передачи по каналу k ro opToro
нальноrо сиrнала. Если предположить, что при фиксированном
входе выходы соrласованных фильтров ЯВЛЯIОТСЯ статистически
неэависимыми, то
м
р (У I k) == Ps+n (Yk) П Рn (У J)'
/=-1
J+k
(7 .46)
rде ps+n (Yk) плотность распределения вероятностей на выходе
фильтра, соответствующеrо передаваемому сиrналу, а Рп (Yj) .........
плотность распределения вероятностей на остальных выходах.
Подставляя выражение (7.46) в (7.45), после несложных пре-
образований для Rвыч получаем следующую формулу:
R выч === тах { log2 [ t P +
,Pk k==l
+ ( ktl PkP, ) ( [ ,у PS+fI (у) Рп (у) d y )2J}. (7.47)
k+l
Максимум по РА в правой части (7.47) достиrается при Pk ==
=== 11М, 1 k М. Подставляя эти значения Pk в формулу
Реализация кодов, исnравЛJlющих ошибкu
439
JI
(7.47), находим
М
R выч == 10g2 2 ·
1 + (М 1)[ r -v Ра+n(У) pn(y) dy ]
oo
(7.48)
При М....... 00 последнее выражение принимает следующий вид:
R obl ', == 2 IOg2 [ r -v Ра+n (у) Рn (у) dy ] ·
oo
(7.49)
Далее предположим, что шум в канале является rаУССОВСI{ИМ
и при приеме ОСУlll.ествляется синхроничация фазы. Оптималь
ный приемник содержит совокупность показанных на фиr. 7.37
соrласованных фильтров, с выходов которых берется отсчет в
момент окончания передачи каждоrо ортоrональноrо сиrнала.
Плотность распределения вероятностей сиrнала на выходе филь
тра, на который поступаlОТ сиrнал и шум, и плотность распреде
леt-IИЯ вероятностеЙ с-иrнала на выходе фильтра, на который по-
ступает только шум, имеют соответственно следующий вид:
1
Р ( х ) == e (x a)2/2
s+n 2л '
2
Рn (х) == -Y e X'/2,
2л
(7.50)
rде
а=== .& / 2E r .
V N o
Подставляя эти выражения в формулу (7.49), для вычислитель-
ной скорости в rayccoBCKOM канале получаем выражение
М
R выч ==10g2 1+(M I)exp( ErI2No) . (7.51)
Зависимость Rвыч от Er/No 110казана на фиr. 7.38. Если с по
мощью фиr. 7.38 и формулы (7.31) найти Eb/No == fI и взять до-
статочно большое значение 1\1, то ! также можно сделать доста-
точно большим. В пределе при М ....... 00 имеем
liт R оыч == ;; IOg2 е [бит/сиrнал). (7.52)
м . 00 о
Это асимптотическое значение Rвыч также показано на фиr. 7.38.
Установив таким образом связь между Eb/No, вероятностью
ошибки и вероятностыо переполнения буфера, l\fОЖНО оценить
характеристики системы связи с последовательным декодирова
нием.
440
r лава 7
б) Система модуляции с противоположными сиrналами. Од-
о
нои из систем модуляции, используемых в КОСМIIческих системах
связи, является система модуляции с противоположными сиrна-
лами, получаемыми путем инверсии фазы. СраВНИl\I для этt.)Й мо-
дуляции характеристики систем с ортоrональными KoдaM и си-
стем, в которых используются алrебраические коды. Для этоrо
рассмотрим систему связи, в которой IIСПОЛЬЗУЮТСЯ модуляция
С инверсией фазы и канал с шириной ПО.посы W IIZ , по r(OTvpoMY
каждые т секунд передается один из М == 2!! возможных сиrна
лов. Предположим, что интервал времени длительностью Т ce
кунд, выделенный для передачи ОДноrо сиrнала, разбивается на
n подынтервалов длительностью Т/n секунд, каждый из которых
j 8ЫlОQНШI lIt'пflt'
PbIdHb/1i
сиеНIl/? М=ОО
J
8bIAOQH(J/l
2 HeпpepыB
... Н6/и Cl/ 16
11М
4
2
1 М=1
б
Е r / N a
Фиr. 7.38. Вычислительнап скорость R выч при синхронном приеме и Аl == 16.
о
2
1а
используется для передачи одноrо двоичноrо символа О или 1.
По каналу для представления символов передается один из сле
дующих двух сиrналов длительностью Т/n секунд:
50 (t) == 2S cos (v'Лn/Т) t,
81 (t) == cos (v'Лn/Т) t,
(7.53)
(7.54)
rде V некоторое неотрицательное целое число. l ля реализаЦlI1I
этоrо метода передачи фаза несущей с помощыо модулятора из-
меняется на :f:90°.
Предположим, что при приеl\1е о каждом принимаемом сим-
воле выносится независимое решение. Обозначим через Ре ве-
роятность Toro, что переданный кодовый блок принят правильно,
через РВ вероятность Toro, что переданный кодовыЙ блок принят
неправильно, через РЕ вероятность ошибки в отдельном символе
и через P эквивалентную вероятность ошиБКII декодирования
На символ, которая вычисляется по Рв Tal{, как было описано 13
Реализация кодов, исправляющих ошибки
441
предыдущем разделе. Витерби [21] определяет вероятность ошиб-
ки для ортоrональных кодов (у которых кодовые блоки попарно
ортоrональны) и вероятность ошибки в системе без кодирования
следующим образом:
А. Вероятность ошибки для ортоzонаЛЬНblХ кодов
r ехр ( vi/2) [ ( (2SТ )] .M 1
1 Рв == Ре ==.\ -v'21t erf v\ + dv\. (7.55)
oo
, 2k 1
Рв === 2 k ..... 1 Рв' (7.56)
rде
х
erf х == k e r'/2 dr.
oo
(7.57)
Б. Вероятность ошибки 8 системе без к одирования
РЕ === 1 erf ( лJ 2 : в ).
При передаче блока из k двоичны х сим волов
Ре === 1 Рв == ( erf V 2 : в у.
(7.58)
(7.59)
rде
ТВ == T/k [с/бит].
(7.60 )
Эквивалентная вероятность ошибки на символ при исполь
зовании алrебраических кодов определяется равенством (7.37).
Однако для нахождения входящей в формулу (7.37) вероятно
сти ошибки в отдельном символе РЕ в формулу (7.58) необхо
димо внести поправку, поскольку из за расширения полосы шум
возрастает в n/k раз В этом случае
... / 2ST в k
Рв == 1 ...... erf N o 11'
(7.61 )
а полоса характеризуется параметром
W /R == n/21og 2 м === n/2k.
(7.62)
Таким образом,
Еь ST B
N o == N o ·
(7.63)
На фиr. 7.39 показана заВИСИl\10СТЬ вероятности ошибки от
STB/N o для систем связи, в которых используются (127, 120, 1),
(127, 114, 2), (127, 106, 3) и (127, 99, 4) БЧХ-коды, длины п ==
== 127 с k 99, для систем связи без кодирования, для систем
связи с ортоrональными кодами той же длины n == 127 (k :=; 7)
442
fлава 7
и для систем связи с ортоrональными кодами при k 00. в слу-
чае n == 127 и t == 1 при РЕ == 10 З второй член в формуле (7.35)
составляет лишь 4,3 О/о, а при РЕ == 1 O 4 лишь 0,4 О/О. в этой
области вероятностей ошибок аппроксимация РЕ и P посред-
ством первых членов их раэложений (7.35) и (7.37) дает ошибку
8 10
З /N o
Фиr. 7.39. Зависимость вероятности ошибки на символ от ST B/N o .
10 2
10 3
10 4
10 5
10 6
10 7
.....
'"
10 8
Q..
10 -9
1 О 10
10 11
10 1Z
ОртfJёtJНtlllЬНЬ/4
сиёна//61
п :=;: 127
/(-=7
i Орт-. О31l h'/,-r/JЫlдIС C'1/?/11l;16/
(If oo)
\
\
\
\
\
\ (127, 114, 2)
(127, 99, it) (127, 10б, 3)
2
4
6
12
14
не более 1 о/о. Как видно из фиr. 7.39, при использовании кодов,
исправляющих небольшое число ошибок t, заданную вероят-
ность ошибки можно достичь при меньших значениях ST B/N o .
Выиrрыш в отношении ST B/N o обычно выражают в децибелах и
называют 8bluzрышем ОТ кодирования. Для вероятностей РЕ и
Реализация кодов, исправляющих ошибки
443
p порядка lO 6 значения выиrрыша от кодирования и необхо
димой для этоrо ширины полосы приведены в табл. 7.2. Как
видно из этой таблицы, при использовании алrебраических KO
дОВ при незначительном увеличении ширины полосы выиrрыш
от кодирования составляет 2 3 дВ.
Таблица 7.2
Выиrрыш от кодирования и необходимая ширина полосы
Без коди- t . t ===2 t===з t===4 oртоrональ-
РОВ3НlfЯ I ные коды
Выиrрыш от KO
дирования, дБ
W/R
1,67 2,53 3,28 3,14 4,13 (k===7)
0,53 0,55 0,6 0,64 9,0 (k == 7)
0,5
Зависимость вероятности ошиб[{и от отношения ST B/N o при
использовании БЧХ кодов показана также на фиr. 7.40 и 7.41.
Приведенные rрафики хорошо иллюстрируют взаимосвязь
iОДУЛЯЦИИ и кодирования. Для систем без кодирования rрафики
вероятности ошибки были построены в предположении, что при
передаче отсутствуют интерференция между словами и друrие
линейные искажения. При этом предположении поведение кри
вых вероятности ошибки определяется системами модуляции (в
узком смысле) и выделения сиrналов. Ilри наличии искажениЙ
кривые вероятности ошибки смещаются вверх по отношению к
кривой вероятности ошибки для системы без кодирования. Раз
личные методы подавления искажений применяются для Toro,
чтобы приблизить, насколько это возможно, реальную кривую
вероятности ошибки к идеальной кривой системы без кодиро
вания. В то же время введение помехоустойчивоrо кодирования
позволяет достичь вероятностей ошибок, лежащих ниже кривой
вероятности ОIlIибки системы без кодирования. Сложность аппа
ратурной реализации кодов с алrебраическим декодированием
обычно возрастает линейно или как небольшая степень длины
кода n.
Приведенные на фиr. 7.39 rрафики вероятности ошибки для
t === 3 и t == 4 в важноЙ с практичеСI{ОЙ точки зрения области
значений отношения сиrнал/шум почти совпадают, но обычно
бывает задан нижний предел числа информационных СИl\1ВОЛОВ,
и интерес представляет поведение вероятности ошибки при YBe
личении числа проверочных символов. Рассмотрим возможность
использования в системах космической связи последовательно
стей маКСИl\1альной длины, занимающих в теории кодирования
особое положение, а также очень похожих на них равномерных
сверточных кодов, введенных в r л. 5.
444
fлава 7
Совокупность последовательностей м ксимальной длины яв-
ляется линейным (2 k 1, k, 2k 2 1) KOДOM, имеющим макси-
u
мально возможное для своеи длины минимальное расстояние.
Поэтому эти коды так же, как и ортоrональные коды, дают пред-
10 -2
10 -3
10 eft
п ""
10 5 I
10 6
, 10 7
ч.,
10 8
ц"
10 -э
---- д60''''iI(Ьlй 5'fX''J(08
2)
.. ... .. .000юоеCiНf1/1IJНIJlе ClIlHl1l1bI
(63, 45 J 3,
, · I r
1D 12 14
>-
z
Б 8
S /Na
4
Фиr. 7.40. Зависимость вероятности ошибки на символ от ST B/N o '
ставление о предельных возможностях алrебраических кодов с
малой скоростью передачи.
Как известно, при k 00 отношение STB/N o для ортоrональ
ных кодов стремится 1{ 1n 2. Если при приеl\1е решение о каждом
переданном символе ПРИНИ 1ается независимо, то, как следует
Реализация кодов, исправляющих ошибки
445
ИЗ формулы (7.61), веронтность
/ 2ST в k
Р в == 1 erf N о 2 k I
(7.64 )
10 "1
10 3
С",стеМIl Of3 i!'
/(ОUtlро6аНИII
10 4
"
t:t.1ц
10 7
CL..ч"
(23,1213)
I I , 141,21, 4) I
I I I :.
2 4 6 8 10 12 14
S /No
Фиr. 7.41. Зависимость вероятности ошибки на символ от ST B/N(J'
тремится !{ 1/2. В этом случае, соrласно закону больших чисел,
с вероятностью, близкой к 1, число ошибок в блоке длины n
равно n/2 == (2 k 1) /2 2k J, однако код, состоящий из после
довательностей максимальной длины, исправляет только 2k 2........1
ошибок. Следовательно, при k....... 00 вероятность ошибки на блок
446
r лава 7
РВ стремится к 1. Для Toro чтобы достичь вероятности ошибки
РВ < 1, необходимо, чтобы выполнялось условие РЕ (2k 2
1) / (2 k 1) 1/4. Это условие может выполняться лишь в том
случае, если
( 2STB k ) 3
erf k ,
N o 2 1 4
(7.65)
т. е. если отношение ST B/N o удов.петворяет следующему неравен"
ству:
ST в 2 k 1
N o 0,456 2k
(7.66)
Последнее неравенство показывает, что при k 00 отношение
ST B/N o также должно стремиться к бесконечности.
Анализ равномерных сверточных кодов из за xapaKTepHoro
для н"х явления распространения ошибок оказывается более
сложным. Однако поскольку эти коды являются .(k2k l, k, ((k +
+ 1) 2k 2 1) /2) кодами, то для достижения вероятности ошиб
ки РВ < 1 необходимо, чтобы выполнялось следующее HepaBeH
ство: РЕ < (k + 1)2k 2/k2k 1/4.
Далее для сравнения рассмотрим БЧХ коды с малой ско-
ростью передачи. Примитивные БЧХ-коды имеIОТ длину п ==
== 2т 1 11, как следует из rраницы для БЧХ-кодов, при нали-
чии mt проверочных символов они MorYT исправлять t и менее
ошибок. При m == k ПРИl'vIитивные БЧХ коды являются (2 k 1,
k, ((2 k 1) /k) 1) кодами. Для Toro чтобы с помощыо этих KO
дОВ MO)l{HO было достичь вероятности ошибки Рв < ], необхо-
димо, чтобы выполнялось неравенство РЕ < ((2ft l/k)
1) /2 k 1 l/k. Это неравенство в свою очередь может вы-
полняться лишь в случае, если
erf ( · / 2ST в k k ) > 1 k l .
rv N o 2 1
(7.67)
Однако, как леrко видеть, при k 00 левая часть (7.67) стре-
мится к 1/2, т. е. неравенство (7.67) не выполняется. ТаI{ИМ обра
зом, и для этих кодов в пределе также необходимы бесконечно
большие значения ,,)Т B/N o .
Неравенства (7.65) и (7.67) при БОЛЫIIИХ значениях k имеют
хорошие приближенные решения; поведение этих решений при
малых k, а также при k 00 показано на фиr. 7.42. Как видно
из фиr. 7.42, во всех рассмотренных выше случаях отношение
ST B/N o 00 при.k 00. Это связано с тем, что выражение
Il/ (2 k 1), входящее в aprYMeHT функции erf в формулах (7.65)
РеаЛllзаЦllЯ кодов, исправляющих ОUlибкu
447
и (7.67), стремится к нулю при k 00, что в свою очередь объ-
ясняется тем, что при приеме решение о каждом переданном
символе принимается независимо.
Применения кодов, исправляющих ошибки, в системах кос-
мическоЙ связи достаточно мноrообразны, но что касается си
стеl\l, рассмотренных выше, то следует заметить следующее. По
символьное принятие решений и использование алrебраических
кодов дают выиrРЫllI 2 3 дВ. Для Toro чтобы достичь большеrо
30
БЧХ J(оа
CtS 20
...
............
,,",СО
CI)
ЛОС/7еQоВumе/70NоС'тu
Мс/КСJlма.4IJНО;; d/lUNO/
10
о
IJртОёОfltl/lЬflЫf
/ Clltlitl/l/J/ (k oo)
8 10
k
Фиr. 7.42. Отношение ST B/N o ' при котором Р в < 1.
4
6
12
14
выиrРЫlпа, необходимо использовать ортоrональные сиrналы или
последовательное декодирование. Однако при использовании ор-
тоrональных сиrналов сложность устройств растет экспонен-
циально в зависимости от длины блока, тоrда как при использо-
вании последовательноrо декодирования теоретически слож-
ность устройств прямо пропорциональна длине кодовоrо оrрани-
чения. Поэтому в реальных космических системах связи наибо-
лее целесообразным представляется использование алrебраиче-
ских кодов или кодов, допускающих последовательное декодиро-
вание, в сочетании со сравнительно небольшим числом opToro-
нальных сиrналов.
448
fлава 7
7.6.5. Основные понятия о проеК'fировании систем
связи с помехоустойчивым кодированием
Используя результаты, полученные выше в этой и предыду-
щих rлавах, остановимся на некоторых ОСНОВIIЫХ моментах про-
ектирования систем соязи с помехоустойчивым кодированием
информации. Сначала рассмотрим системы с исправлением слу
чайных ошибок. Подставляя R
lal(c/R == n/k в формулу (7.33) и
выражая отношение сиrнал/шум в децибелах, получаем
10 19 (Eb/NO) == 10 19 (Er/No)
10 19 R MaKc + 10 19 n/k. (7.68)
Рассмотрим по отдельности каждое слаrаемое в правой части
этоrо неравенства. Ilервое слаrаемое, как указывалось в
разд. 7.6.3 и 7.6.4, связано с системой модуляции, выбором сиr-
налов канала, обнаружением сиrналов и т. д. И оказывает влия-
ние на отношение мощности несущей к f\.10ЩНОСТИ шумов C/N.
Следовательно, если на величину G/N накладываIОТСЯ жеСТI<ие
оrраничения, например, обусловленные высокой заrруженностью
каналов, то значения G/N оказываются небольшими. Второе сла-
raeMoe отражает влияние скорости передачи при фиксированном
отношении Eb/No и зависит от выбора сиrналов, искажений при
передаче, интерференции между кодовыми словами и системы
модуляции (в широком смысле). Например, путем компенсации
канала можно устранить интерференцию между кодовыми сло-
вами и, таким образом, повысить RMal(c. Третье слаrаемое OTpa
жает влияние кодирования и показывает, что путем увеличения
времени или ширины полосы, используемых для передачи, мож-
но понизить вероятность ошибки.
В тех случаях, коrда мощность источника питания передат-
чика мала, как это имеет место, например, в космической связи,
очень важно достичь заданной верности передачи при малых
отношениях мощности сиrнала (приходящейся на 1 бит пере
даваемой информации) к мощности шума в канале. Чтобы MO
жно было достичь значительноrо снижения вероятности ошибки
при возможно малых отношениях сиrнал/шум, должны быть пол-
ностью использованы все возможности, представляемые указан-
ными выше тремя слаrаемыми
Как следует из разд. 7.6.3 и 7.6.4,
отношение Eb/No можно уменьшить путем использования кодов,
исправляющих небольшое число ОIIIибок t. Однако следует за
метить, что при больших t отношение Eb/N() может увеличиться
из
за необходимости дополнительной значительной мощности
для передачи избыточных символов или из
за увеличения МОЩ
ности шума при увеличении ширины полосы. Если решение о
каждом переданном символе принимается независимо, то коды
с алrебраическим декодированием нельзя заменить на opToro-
нальные сиrналы. При использовании ортоrоналъных сиrналов
Реализация lCодов# исправляющих ошибкu
449
с !\орреЛЯЦИОllliЫМ приеМОl\1 отношение Eb/No при k 00 стре-
мится к ln 2, однако при этом с ростом k экспоненциально YBe
личивается сложность устройств, что, конечно, не приемлемо с
практической точки зрения. В реальных космических системах
связи наиболее целесообразным представляется использование
небольшоrо числа ортоrональных сиrналов в сочетании с алrе-
браическими кодами или последовательным декодированием.
В наземных систеl\lах связи (а также в системах космической
связи некоторых типов) iкесткие мощностные оrраничения на-
кладываются сравнительно редко. В этих системах часто имеют-
ся жесткие оrраничения на отношение C/N, обусловленные пере-
rрузкой диапазонов. Наиболее важной характеристикой систем
связи в этих условиях является то, насколько мал первый член
в правой части равенства (7.68); малость всей CYMl\lbI в этом ра-
венстве оказывается менее важным фактором. В подобных слу-
чаях для достижения заданной вероятности ошибки целесооб
разно уменьшить насколько возмо}кно первое слаrаемое в пра-
вой части (7.68), понизив скорость передачи путем введения со-
ответствующих кодов, исправляющих ошибки, и увеличив третье
слаrаемое настолько, насколько это позволяет ширина полосы.
Следовательно, в этих случаях можно использовать код с не-
большим числом исправляемых ошибок t, минимизирующий пер-
вый член равенства (7.68), но, быть может, несколько увеличи
вающий отношение Eb/No. Даже при использовании кодов со CKO
ростыо R == 1/2, коrда ширина полосы увеличивается, а скорость
передачи уменьшается в два раза, отношение ST B/N o УJ3еличи
вается приблизительно на 3 дБ и существуют достаточно широ
кие возможности для использования кодов, исправляющих
ошибки. Так, например, в приведенном ниже примере 7.6.7 BЫ
бор кода, который не приводит к ухудшению отношения Eb/No
по сравнению со случаем отсутствия кодирования, позволил
улучшить отношение C/N.
Таким образом, важным этапом проектирования оптималь-
ных систем связи является выбор значений трех слаrаемых в
правой части равенства (7.68) в соответствии с назначением си-
стемы связи, требованиями к качеству передачи и, следователь-
но, к стоимости системы. Введение обнаружения и исправления
ошибок, что учитывается третьим членом в правой части (7.68),
обеспечивает широкие возмо {ности при проектировании систем
связи.
Далее рассмотрим случаЙ, коrДа шум является импульсным.
Импульсный шум обычно имеет амплитуду, значительно превы"
шающую уровень сиrнала в канале. Поэтому понизить вероят-
ность ошибки путем повышения мощности сиrнала в канале чао.
сто не удается. В таких случаях единственным методом борьбы
450
fлавй 7
с импульсным шумом является обнаружение ошибок или ис-
пользование кодов, исправляющих пачки ошибок.
При введении кодов, исправляющих пачки ошибок, обычно
сначала берется модель rИJlберта, хорошо описывающая шум
в канале, далее выбирается соответствующий код и в заверше-
ние оценивается получающаяся вероятность ошибки. Однако им-
пульсные шумы чрезвычайно разнообразны и в некоторых слу-
чаях плохо описываются с помощью модели rилберта. в этом
случае одним из способов определения длины кода и длины па
чек ошибок, которые должны исправляться для Toro, чтобы
можно было достичь заданной вероятности ошибки, является
измерение шума, действующеrо в канале. Коды, удов.петворяю
щие определенным таким образом условиям и имеющие мини
мальную избыточность т === 2Ь, являются оптимальными с точки
зрения повышения скорости передачи.
Если длина кода п, найденная по результатам измерений
шума в канале, оказывается настолько большой, что реализация
соответствующеrо кода будет очень дороrой, то можно понизить
длину п, несколько уменьшив при этом скорость передачи R.
Пусть п и Ь
найденные по результатам измерения шума в ка-
нале соответственно длина кода и длина пачек ошибок, которые
должны исправляться. Тоrда соответствуюll.
ИЙ код с минималь
ной избыточностью имеет скорость передачи
R === 1
. (7.69)
n
Если длину кода уменьшить до величины п' «п), то скорость
пере,дачи кода длины п' с минимальной избыточностью будет
равна R' == 1
2bjn', и, следовательно, это уменьшение длины
кода достиrается за счет уменьшения скорости передачи на ве-
личину
R
R' == 2Ь (
f ) ·
(7.70)
в заключение заметим, что проектирование систем связи, в ко-
торых должны использоваться коды, исправляющие пачки оши-
бок, упрощается при использовании моделирования.
7.6.6. Проблемы, возникающие при проектировании систем связи
с помехоустойчивым кодированием информации
В предыдущем разделе кратко были даны основные идеи,
используемые при проектировании систем связи в случае приме-
пения кодов, исправляющих ошибки. Однако эти идеи в том
виде, в каком они были представлены выше, редко применяются
при проектировании реальных систем связи. Одной из причин
этоrо является то, что ШУl'v1 В реальных каналах не является чи
Реализация кодов, uсправЛЯ10ЩUХ ошибки
451
сто rауссовским или чисто импульсным и характеристики канала
связи и шум часто ИЗ
lеняются во времени. Например [11], в BЫ
сокочастотных каналах шум не является ни rауссонским, ни им
пульсным, а представляет собой смесь rayccoBCKoro и импульс
Horo шумов. Известно несколько классов кодов, исправ.п:ЯЮIJJ,ИХ
независимые ошибl{И и пачки ошибок одновреl\1енно, но при про
ектировании систем СRЯЗИ, в которых должны применяться эти
коды, пользоваться непосредственно описанными выше принци
пами нельзя. Кроме Toro, характеристики затухания в высокоча
стотных каналах MorYT изменяться в течение дня. Следователь-
но, обнаружение или исправление ошибок необходимо проводить
в одни периоды времени, тоrда как в друrие периоды времени
необходимости в этом нет. Поэтому при проектировании очень
важно использовать системы обнаружения или исправления
ошибок, которые можно адаптировать к действующему в канале
шуму по результатам ero измерения. rIриведенные в этой rлаве
некоторые соображения о проектировании следует рассматри-
вать лишь как одни из подходов к решению сложных реальных
проблем. При проектировании реальных систем всеrда необхо-
димо следить за тем, насколько отвечает реальным условиям
получающаяся система.
7.6.7. Пример применения пороrовоrо декодирования
u
В спутниковои связи
В качестве примера применения теории кодирования paCCMO
трим систему SPADE, в которой используется пороrовое декоди
рование [13].
Эта система является системой спутниковой связи с несколь
кими каналами, работающими на разных частотах. При поступ
лении требования на установление связи каждая станция может
использовать любой свободный накал. В этой системе для теле
фон ноЙ связи используется импульсно
кодовая модуляция фазы.
Способ связи, допускающий занятие любоrо свободноrо канала,
позволяет эффективно использовать суммарную пропускную спо-
собность каналов спутниковоrо ретранслятора [14].
Для передачи ИК1\1
сиrнала (который представляет данные,
идущие с выхода кодера со скоростью 54 кбит/с) со скоростью
на выходе модулятора 64 кбит/с в рассматриваемой системе ис
пользуется четырехуровневая фазовая модуляция (ФМ) и син
хронное детектирование. Скорость передачи информации в би-
тах в секунду равна 32 000.
Эта система предназначена для передачи речи, но после не-
сложной модификации ее можно использовать для передачи
данных. На фиr. 7.43 показана CXel\la одноrо канала этой си-
стемы, в котором используется сверточный код со скоростью
452
r лава 7 '
R === 3/4 И пороrовое декодирование. В этом случае на передат-
чике устанавливается сверточный кодер кода со скоростью R ==
== 3/4, а на приемнике пороrовый декодер. Скорости следова-
ния символов на входе и выходе кодера составляют соответст-
венно 40,8 и 54,4 кбитjс. В выходную последовательность кодера
вводятся синхронизирующие блоки, в результате чеrо скорость
следования символов увеличивается в 8/7 раза и на вход моду-
лятора символы поступают уже со скоростью 62,17 кбит/с. Эта
скорость лишь несколько меньше 64 кбит/с, так что модулятор
и фильтры канала, рассчитанные на скорость 64 кбит/с, исполь-
зуются почти без потерь. В этой системе моrУТ.ИСПОЛЬ30ваться
Данные, 54" п Д аННIJ/е,
«),8 конт C6epi770l{HbJU ' /( ц СlIн,(ронное 6217коит/с РJIIl/lIоНН6Ii1 /( т... /F
кооер с переОflНJЩfl' ФfJJо61J/Ji.
R--5/4 1:/. J:: ,1 ycтpoucтDo моиУl1l1т()р
J'Тj /(IЛlт, с
ит Hr IF
Фиr. 7.43. CTPYKTjTpa широкополосной системы передачи данных.
также коды со скоростыо R == 1/2. В обоих случаях кодеры и де-
кодеры являются достаточно простыми и имеют низкую стои-
мость. Кодер и декодер кода со скоростью R == 1/2 состоят из
17 интеrральных схем и стоят 50 долл. Кодер и декодер кода
со скоростью R == 3/4 состоят ИЗ 50 интеrральных схем и стоят
250 дол.п.
Помимо кодов, допускающих пороrовое декодирование, при-
меняются коды друrих типов, например блоковые или сверточ-
ные коды в сочетании с последовательным декодированием или
декодированием по максимуму правдоподобия (с помощью ал-
rоритма Витерби). В зависимости от типа кода изменяются стои-
мость и эффективность системы. Естественно, что по мере уве-
личения сложности кодера и декодера возрастает и их стои-
мость; так, стоимость последовательноrо декодера или дeKO
дера, реализующеrо алrоритм Витерби, может в 10 lOO раз
превышать СТОИМОсть пороrовоrо декодера.
Реализация кодов, исправляющих ошибки
453
Для сравнения эффективности различных систем кодирова-
ния на фиr. 7.44 приведены результаты измерения вероятности
ошибки в зависимости от G/N дЛЯ трех систем, исследовавшихся
с помощью спутника «Интелсат 111»:
1. Цифровая передача речи со скоростью 56 кбит/с (YIKM
И"rIИ Ll
модуляция) или данных, двухуровневая ФМ, синхронное
детектирование.
11. l\ифровзS1 передача речи со скоростью 28 кбит!с (,
MOДY-
ляция) или данных, двухуровневая ФМ, синхронное детектиро
вание, сверточный код со скоростью R == 1/2 И пороrовое декоди
рование.
Фиr. 7.44. Экспериментальные резуль-
таты, полученные с помощью спутника
«Интелсат 1 1 1».
A
56 кбит/с, 2-позиционная фазовая модуля
ция, полоса 80 кrц; Б
40,8 кбит/с, R==
/4,
пороrовое декодирование, 2
уровневая фазопая
модуляция, полоса 80 кrц; B
28 кбит/с, R.==1/ 2 ,
пороrовое деl(одирование, 2-пози ионная фазо
вая МОДУЛЯIIИЯ, полоса 80 Krtt.
10
1
10
2
...
10
3
10
't
Q... "ч
10
s
10
б
о 2 4 б В 10 12
C/N, 8Б
111. Цифровая передача речи со скоростыо 42 кбит/с или
данных, двухуровневая ФМ, синхронное детектирование, CBep
точный код со скоростью
R === 3/4 и noporoHoe декодирование.
Как видно из фиr. 7.44, введение кодирования позволяет по
лучить значительный выиrрыш в отношении GjN. Указанные
выше ({оды для этоrо эксперимента были выбраны из
за про
стоты реализации, низкой стоимости и хорошей эффективности
передачи.
7.7. Применение в системах обработки информации
Алrебраические КОДЫ, используемые в вычислительных Ma
шинах, можно условно разбить на следующие два типа:
1. Коды, исправляющие специфичные для вычислительных
машин ошибки, такие, например, как перестановки соседних
символов, возникающие при общении человека с машиной, и др.
2. Коды допускаЮlцие быстрое декодирование.
К числу кодов типа 1 относятся, в частности, коды Рида
Соломона и некоторые друrие хорошо изнестные коды, которые
454
rлава 7
используются на практике для исправления различных специ-
фичных для вычислительных машин ошибок {15]. В тех случаях
коrда необходимы коды, допускающие быстрое декодирование,.
циклические коды, занимающие в теории кодирования централь--
ное место, не всеrда оказываются наилучшими. Это связано с
тем, что алrоритмы декодирования циклических кодов, как
правило, являются последовательными, т. е. они сначала исправ--
ляют ошибку в некотором одном символе, далее осуществляют
циклический СДВИI' декодируемоrо слова, затем исправляют
ошибку в следующем символе и т. д. Устройства, реализующие
такие алrоритмы, являются очень простыми, но проведение n
циклических сдвиrов значительно увеличивает время декодиро
вания, что при использовании этих алrоритмов в вычислительной
машине снижает эффективность работы последней. В этом раз
деле будут рассмотрены класс кодов, предназначенных для ис
пользования при общении человека с маlllИНОЙ, и класс кодов,
допускающих быстрое декодирование.
7.7.1. Применение кодов при общении человека
с машиной
В процессе общения человека с ма
иной иноrда не удается
точно установить источник возникновения ошибок и принять
соответствующие меры к их устранению; в этом случае для
повышения надежности обычно используются !{оды, исправляю
щие ошибки. Модель процесса общения человека с машиной
сложнее, чем модель канала связи.
К числу наиболее типичных ошибок, возникающих в процессе
общения человека с машиной, можно отнести следующие: nepe
становкu соседних символов, замена символов, вставки симво
лов, выпадения символов и др.
Рассмотрим класс кодов, исправляющих перестановки coceд
них символов [13]. Перестановку соседних символов всеrда мож-
но рассматривать как пачку ошибок длины 2. Так как при
перестановке соседних символов значения ошибок в них всеrда
совпадают, то эти ошибки можно исправить значительно проще,
чем обычные пачки ошибок длины 2. Описанные ниже коды
являются кодами, которые исправляют ошибку из
за переста-
новки символов как обычную одиночную ошибку.
Предположим, что передаваемые и принимаемые символы
являются элементами поля GF(q). Рассмотрим q
ичный цикли
ческий код длины n, задаваемый порождающим мноrочленом
g (Х) степени r. Кодовыми словами 3Toro кода являются MHoro-
члены степени п
1 или менее, которые делятся на g (Х). Пусть
g (Х) является неПРИВОДИf\,fЫМ мноrочленом, корнем KOTOPOI'Q
является элемент
== (Xq
l, r де ,,
примитивный элемент G F (q).
Реализация кодов, исnраВЛЯlощих ошибки
455
Так как произвольный вектор столбец из r символов поля ОР (q)
всеrда можно представить в виде произведения элемента поля
GF(q) и одноrо из столбцов проверочной матрицы рассматри-
U .
BaeMoro кода, то существуют единственныи элемент J поля
G F (q) и целое положительное число 1, 1 < n, такие, что
х 1 == jX ' (mod g (Х».
(7. 71 )
Это сравнение можно переписать в виде
Xn l 1
j === х 1 (mod g (Х».
(7.72)
Так как ошибкам из за перестановки символов соответствует
мноrочлен ошибок вида
ei (Х l)x l ,
то синдром определяется равенством
s (Х) == ei (Х 1) Х ! (mod g (Х».
(7 . 73)
Поскольку Х 1 и g (Х) являются взаимно простыми MHoro-
членами, то можно установить взаимно однозначное соответ-
ствие между значениями синдрома, соответ'ствующими различ-
ным пачкам ошибок, возникающим при перестановке символов,
и значениями синдрома, соответствующими простым одиночным
ошибкам. Чтобы схему испраВJlения одиночных ошибок можно
было использовать для исправления ошибок, возникающих из за
перестановки символов, достаточно воспользоваться следующим
соотношением:
. + 1 Xr+l Xn l+r+l
S' (Х) == ejX I + r == Х I S(X) == j S(X) (mod g(X)). (7.74)
При этом синдром s' (Х) можно получить умножением синдрома
s (Х), вычисленноrо по принятому кодовому вектору, на MHoro..
чден
r l Xn l+r+l ( d ( » ( )
q(X)==qo+qIX+ ... +qr IX == . то q Х . 7.75
/
Декодер, реализующий описанный выше алroритм исправле...
ния ошибок, возникающих при перестановке символов, показал
на фиr. 7.45. Переключатель W находится в положении О до тех
пор, пока левые r 1 разрядов реrистра сдвиrа не будут со...
держать нулевые символы.
Реализация кодов, uсправля/оu{uх ОUluбки
457
7.7.2. КОДЫ На оснопе ортоrональных латинских квадратов
Используя ортоrональные латинские квадраты Сяо, Воссев
и Чень [14, 18] построили класс кодов для исправления незави-
симых ошибок, ортоrонализируемых в один шаI' и, следова
тельно, допускаlОЩИХ пороrовое декодирование [14, 18]. Этим
кодам посвящен данный раздел. Обычно достичь большой ско-
рости дскодирования кодов, исправляющих независимые ошибки,
при небольшой избыточности бываеr очень трудно. Это связано
с тем, что эффективные с точки зрения избыточности коды
u
IIмеют очень сложные декодирующие УСТРОИСТВ8, а в результате
и низкую скорость декодирования. В подобных случаях часто
возникает необходимость повысить скорость декодирования з;]
счет использования более простых алrоритмов декодирования 11
HeKoToporo увеличения избыточности кода. Пороrовые методыI
декодирования являются как раз такими методами, которые
позволяют достичь высокой СI{ОРОСТИ декодирования. Из осо-
бенностей рассматриваемых ниже кодов следует ОТ
1етить то, что
они не являются циклическими и что введение избыточности для
повышения корректирующей способности кода осуществляется
целыми модулями.
I<aK указывалось в rл. 5 при описании пороrовоrо декодиро
вания, каждый соответствующий информационному символу
столбец проверочной матрицы кода, испраВЛllющеrо t независи-
мых ошибок, должен содержать по крайней мере 2t символов 1.
Матрицу Н, обладающую этим свойством, мо)кно построить на
основе лаТИНСI{ИХ квадратов.
Определение 7.1. Латинским квадратом порядка 'n наЗbl-
вается квадратная матрица раЗАtера т Х т с элеАtентами
О, 1, ..., т
1, каждая строка и каждыЙ СТО
1беlf которой яв-
ляются перестановками последовательности О, 1, ..., т
1.
Два латинских квадрата называются ортоzональными, если при
наЛО:J/Сении друz на дРУ2а каждая упорядоченная пара соответ-
ствующих элемеllтов этих квадратов появляется ровно один раз.
Проверочная матрица кода, построенноrо на основе латин-
ских квадратов, имеет следующий вид:
M 1
М 2
Н === М з 1
2tm. ,
7. 76)
..
A1 2t
458
r лова 7
rде 1 2tm единичная матрица размера 2tm Х 2tm,
1 1...1 О
1 1. .. 1
M 1 ==
.
, (7.77)
.
о
1 1. .. 1 тXт2
1\12== [Iml m ... Iт]mхт н
(7.78)
а М з , ..., M 2t матрицы, которые строятся указанным НИ)I{е
образом на основе ортоrональных латинских квадратов:
LI == [1}j]M8KCJ
L 2 == [17j]MaKc'
(7.79)
L 2t 2 == [1 2]макс'
r де 1 ij Е {1, 2, ..., т}.
Для каждоrо из введенных выше латинских квадратов по-
рядка m и каждоrо элемента латинскоrо квадрата можно по-
строить матрицу инцидентности, которая определяется следую-
щим образом.
. Определение 7.2. Пусть L == [l ij ]MaHc латинский квадрат, и
пусть f.1 nроиЗВОЛЬНvtЙ еёО элемент. Матрица инцидентности
QJ.t === [q /] элемента f.1 определяется равенством
11/ == J.L,
11/ =1= J.L.
{ 1,
qi/ == О,
(7.80)
Для каждоrо латинскоrо квадрата порядка m можно по-
строить m матриц инцидентности Ql, Q2, ..., Qm' Каждой из
этих матриц сопоставим вектор
V J.t === [q l ... q mq l ... qim ... q J ... q m].
(7.81 )
Подматрица M i , i 3, проверочной ма рицы Н строится сле-
дующим образом;
V 1
У 2
Mt==
(7.82)
v
8""!8 т...
Реализация кодов, исправляющих ошибки
459
rде V 1 , V 2 , ..., Yт BeKTOpы, определяемые формулой (7.81)
и соответствующие i MY латинскому квадрату L i .
Теорема 7.2. Линейный код с проверочной матрицей Н, no
строенной описанным выше образом по Л т (Л т т 1) орто..
20нальным латинским квадратам порядка т, исправляет любые
t или менее Оluибок, zae
t === m + 1.
(7 .83)
Доказательство. Для доказательства этой теоремы доста-
точно показать, что проверки, порождаемые матрицей Н и конт-
u
ролирующие данныи символ, попарно ортоrональны относитель-
но последнеrо. Ортоrональность пр-оверок, порождаемых подмат-
рицами M 1 и М2, очевидна. Далее заметим, что каждый столбец
матрицы Mi, i 3, содержит ровно один ненулевой элемент. До-
пустим, что некоторая строка матрицы M i и некоторая строка
матрицы M j пересекаIОТСЯ более чем в одном символе (i, j ==
== 3, 4, ..., 2t). В этом случае при наложении латинских квад-
ратов Ll и Lj по крайней мере две упорядоченные пары символов
будут одинаковыми. Это противоречит определению ортоrональ-
ности латинских квадратов. Наконец, если допустить, что одна
из строк матрицы М 1 (или М 2 ) совпадает с какой либо строкой
матрицы Mi' i =1= 1, 2, то мы придем к тому, что L i не является
латинским квадратом. Вновь получили противоречие. Teope 1a
ДОI<азана.
Все коды, которые строятся описанным выше способом, со-
держат m 2 информационных и 2trn проверочных символов.
Пример 7.1. Рассмотрим коды с k == т 2 == 25 информацион
ными символами. Используя только матрицы М 1 и М2, можно
построить (35, 25) KOД, исправляющий одиночные ошибки. Про-
верочная матрица Н этоrо кода имеет следующий вид:
1 1 1 1 1 1 ....
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1
1 1 1 1 1 1. (7.84)
1 1 1 1 1 1
1 1 1 1 1 1
111 1 1 1
111 111
460
r лава 7
Схема декодирования l-ro информационноrо символа Прllве-
дена На фиr. 7.46.
Для построения кода, исправляющеrо двойные ошибки, мож-
но воспользоваться следующими двумя ОрТОI'она.пьными латин-
cl s
ct ro
d 15
d 20
С б
Фиr" 7.46. Декодер (35, 2Ь)-кода
d 1
а 2
d '
.3
а,
.,
'1
а о
)
1\
ай
исправляющеrо одиночные ошибки.
'с КИМ И квадратами:
О 1 2 3 4 О 1 2 3 4
1 2 3 4 О 2 3 4 О 1
L) == 2 3 4 О 1 L 2 == 4 О 1 2 3 (7.85)
3 4' О 1 2 1 2 3 4 О
4 О 1 2 3 3 4 О 1 2
В этом случае код задастся проверочной мао, риасii (7.76), ниж-
ние две подt\tатрицы М з и М4 КОТОlJОЙ имеют СJlедук)щий вид:
1 1 1 1 1
1 1 1 1 1
M J == 1 1 1 1 1
1 1 1 1 1
1 1 1 1 1
(7.86)
l 1 1 1 1
1 1 1 1
М 4 == 1 t 1 1 1
1 1 1 1 1
1 1 1 1 1
(7.87 )
Реализация кодов, исправляющих ошибки
461
7.7.3. КОДЫ, исправляющие пачки ошибок и допускающие
быстрое декодирование [19]
Несколько модифицировав описанный в rл. 5 метод построе..
ния сверточных кодов, исправляющих пачки ошибок, можно
построить блоковые коды, исправляющие пачки ошибок, допу
екающие быстрое декодирование и имеющие параметры
п==b(a+I)+2b+a, k==b(a+l), n
k==2b+a, R===
== Ь (а + 1) j[b (а + 1)
2Ь + а]. Эти коды не являются цикличе-
скими и задаются порождающей матрицей
i
Т - . - - /
-
- т - . - -
ib- - - - - !
........ I _
_
_
_ -.
_
I
t
I
,
,
I
.
1...... ..
1 ь :
I
.........,
1 ь :
.........1
.0
О
О
О 1 2Ь +0
(7.88)
H
Iь
Ib
I
1
,
:Zb'OO ...0:00... О
'. ..
..
_
..
_ .:. _ .. .. _ 18 .. .. ..
... .. __
О О ... О
rде lb и 1 2ь + о
единичные матрицы, имеющие соответственно
размеры Ь Х Ь и (2Ь + а) х (2Ь + а). Декодирование этих кодов
точно так же, как и декодирование упомянутых выше сверточ-
ных кодов, осуществляется путем выделения в синдроме конфи
rураций вида (1, О, ..., О, 1). Например, код с параметрами
n == 21, Ь == 3 и а == 3 задается проверочной матрицей
1 00 1 00 1 00 1 00 1 00000000
010 010 010 010 010000000
001 001 001 001 001000000
000 000 000 100 000100000
Н === 000 000 100 О 1 О 000010000
000 100 010 001 000001000
100 010 001 000 000000100
О 1 О 001 000 000 000000010
001 000 000 000 000000001
(7.89)
Декодирование этоrо кода мо}кет быть выполнено с помощью
следующеrо алrоритма:
1. Символы 51, ..., 59 синдрома разбиваются на две совокуп-
ности (51, 52, 8з) И (54, 55, ..., 59).
2. В случае если Sз == 1, то из конфиrураций вида
(5з, х, х, 56), (Sз, Х, Х, Х 57), (sз, Х, Х, Х, Х, 58) и
462
r лава 7
(sз, Х, Х, Х, Х, Х, S9) выбирается та, которая имеет наиболь-
шую длину (знаком Х обозначены символы, значения которых
на данном этапе не существенны). С помощью этой конфиrура-
ции исправляются ошибки в 12, 9, 6 и 3-М символах. После
исправления указанных символов полаrаются paBHbIMj1 нулю и
соответствующие символы синдрома.
3. Из конфиrураций вида (S2, О, Х, S5), (S2, О, Х, Х, S6),
(S2, О, Х, Х, Х, S7), (S2, О, Х, Х, Х, Х, S8) выбирается та, KO
торая имеет наибольшую длину. С помощью этой конфиrурации
исправляются ошибки в 11, 8, 5 и 2 M символах, после чеrо так-
же осуществляется коррекция синдрома.
4. Из конфиrураций (SI, О, о, S4), (SI, О, О, Х, S5), (SI, О, О,
Х, Х, S6) и (81, О, О, Х, Х, Х, S7) выбирается та, которая имеет
наибольшую длину. С помощью этой конфиrурации исправля-
ются ошибки в 10, 7, 4 и l-м символах, после чеrо осуществля-
ется коррекция синдрома.
5. Если некоторые символы синдрома отличны от нуля, то
осуществляется восстановление.
Предположим, например, что ошибки возникли в 3 M И 5 M
символах 'з и '5 кодовоrо слова кода, задаваемоrо порождаю-
щей матрицей (7.89). Обозначим через ei значение ошибки в i-й
компоненте кодовоrо слова. В данном случае синдром имеет
следующий вид:
8 == Ое5езОООеsОез == 0110001 О 1.
При декодировании принятоrо кодовоrо слова с помощью опи-
caHHoro выше алrоритма на шаrе 2 выделяется конфиrурация
(S3, Х, Х, Х, Х, Х, S9) и осуществлнется исправление ошиБКII
ез. На шаrе 3 выделяется конфиrурация (S2, О, Х, Х, Х, S7) и
исправляется ошибка е5.
Рассмотрим декодер, реализующий описанный выше алrо-
ритм декодирования. Этот декодер состоит из схемы вычисления
синдрома, схемы исправления ошибок и схемы (оррекции синд-
рома. Схемы кодеров здесь рассматривать не будем, поскольку
они аналоrичны соответствующим схемам вычисления синдрома,
входящим в состав декодеров.
t..IacTb схемы вычисления синдрома, используемая для вы-
числения символа S2, приведена на фиr. 7.47. Остальные символы
синдрома вычисляются с помощью аналоrичных схем.
Для реализации шаrов 2, 3, и 4 описанноrо алrоритма ис-
пользуются почти идентичные cxeMbl. На фиr. 7 48 приведена
схема, используемая для реализации шаrа 2. В этой схеме эле
менты И используются для выделения конфиrураItИЙ вида
(1, Х, ..., Х, 1), а элемеНl ы НЕ для определения наиболее
длинной из них.
Реализация кодов, исправляющих ошибки
463
Для обеспечения нужной последовательности выполнения
операций шаrов 2, 3 и 4, а также для реализации шаrа 5 исполь-
.. ее .. ... ... .. ... .. .. .. @J Рееистр
711 ?14 r Z1 пРlIнято;;
... .. ... .. .. .. (l(Jt'4fQQ'"тfIl6110cтll
$,'
(Ре2l1стр с/,/нВрьма)
Фиr. 7.47. Часть схемы вычисления синдрома.
зуется схема, приведенная на фиr. 7.49. Выходы 1 и 2 элементов
ИЛИ обеспечивают нужную последовательность выполнения
"11 rg .,& "!
· GJ
Pezwcтp h
СlIнирома L::J S 2
5JbJ
Фиr. 7.48. Схема, реаЛИЗУlощая шаr 2.
операций 2, 3 и 4, а выход 3 элемента ИЛИ используется для
реализации шаrа 5.
В общем случае схема декодера аналоrична схеме, описан-
ной выше.
.,.
"'
....
80
v)
<
Q
f и!/и 3Н
t:$
e:
in-'
:=
c'i
.:=
:=
::r
Q)
t::
О
tJ::
==
:t:
а.>
:t:
&;:
О
=
.Q
CJ
О
:t:
..Q
&;:
Q)
са
о
Q)
о
t::
D::
S
2
c\s
са
:s::
J::
:I:
CJ
J, И//И 3/-1
с ИI/И' 3Н
ci
:I!
Q)
u
с)
:=
е
Реализация кодО8, исnра8АJlЮЩUХ ОШllб.кu
465
Так как рассмотренные здесь коды, исправляющие пачки
ошибок, допускают быстрое декодирование, то они MOrYT исполь-
зоваться в вычислительных машинах. В качестве кодов, исправ-
ляющих пачки ошибок и допускающих быстрое декодирование,
MorYT также использоваться коды Файра и их обобщения (алrо-
ритм быстроrо декодирования этих кодов предложен Ченем [20]).
Задачи
1. Пусть а
примитивный эле
1ент ОР(2 4 ). ДЛЯ декодера
БЧХ
кодов найти схему вычисления r(cx?).
2. Рассмотрим (псевдо) циклический код длины n
14 с
k == 11 информационными символами, испраВЛ1lЮЩИЙ пачки
ошибок длины 4 и менее. Исследовать процесс исправления
следующей пачки ошибок длины 4: X 12 + Х13 + X15.
3. Вычислить и сравнить между собой вероятности ошибок
на символ при РЕ == IO
3 И 10
5 для кодов со следующими пара-
метрами: а) n == 23, k == 12, d == 6; б) n === 45, k == 23, d == 7.
4. Вычислить и сравнить между собой вероятности ошибок
при РЕ == 1 о
з и 1 O
5 для самоортоrональноrо сверточноrо кода
с R == 3/4, J == 6, ПА == 248 и БЧХ
кода с n == 255, k == 191,
d == 17.
5. Пусть задан код максимальной длины с n == 32, k == 6.
Найти связь между вероятностыо ошибки на символ при алrе
браическом декодировании этоrо кода как циклическоrо кода
и отношением Eb/No. Установить связь между вероятностью
ошибки при корреляционном приеме, кurда заданный код pac
сматривается как биортоrона.пьный, и ОТНОllIением Eb/No. Полу
ченные результаты сравнить [21].
6. а) Построить проверочную матрицу кода длины n == 55
с k == 25, получающеrося из ортоrональных латинских квадратов
и исправляющеr'о три ошибки.
б) Описать аппаратурную реализацию этоrо кода.
7. а) Найти проверочную матрицу кода с параметрами
n == 33, Ь == 5, а == 3, исправляющеrо пачки ошибок и допускаю
щеrо быстрое декодирование.
б) Рассмотреть процесс исправления ошибок в случае воз
никновения пачки ошибок ДЛИНhI 5.
в) Определить числа ячеек реrистров сдвиrа элементов И,
ИЛИ и НЕ, необходимых для построения декодера этоr() кода.
8. Коды для
арифметических
u
устроиств
Излаrавшаяся до сих пор теория кодирования представляет
собой теорию кодов, предназначенных для обнаружения и
исправления ошибок в каналах связи, т. е. для повышения Ha
дежности связи. Методы повышения надежности вычислений,
выполняемых вычислительными машинами и ДР'уrими устрой-
ствами, развивались независимо в двух следующих направле-
ниях.
Первое направление восходит к работам фон Неймана [1] и
связано с построением надежных устройств из ненадежных эле-
ментов. Результаты развития этоrо направления были подыто
жены Виноrрадом и Коэном [2]. Во всех работах, относящих
я к
этому направлению, ПОВЫllIение надежности достиrается различ-
ными методами введения так называемой структурной избыточ
ности.
Если задачей первоrо направления является повышение Ha
дежности вычислений путем повышения надежности caMoro вы-
числительноrо устройства, то отличительной особенностью BTO
poro направления является то, что само вычислительное
устройство не модифицируется, а данные, которые в Hero BBO
дятся, кодируются так, чтобы на выходе можно было осуще-
ствить обнаружение и исправление ошибок, возникших в про
цессе вычислений. Как показал Элайс [3], такое кодирование
эффективно не для всякоrо вычислительноrо устройства; однако
оно с успехом применяется, например, в устройствах, которые
оперируют с целыми числами. В данном случае речь идет об
арифметических кодах, называемых также А N
кодами, начало
иеследованию которых было положено работами Дайямонда [4]
и Брауна [5]. К числу кодов этоrо типа относятся таI{же так
называемые коды в остаточных классах (residue class code) и
линейные вычетftые коды (linear residue code).
В случае АN
кодов сообщения (данные) обычно представ-
ляются в виде целых чисел. Кодовыми словами АN
кода яв-
ляются r
ичные представления чисел
сообщений, УМНО)J{еиных на
некоторое фиксированное число (модуль) А, так что кодовое
слово суммы и разности двух чисел всеrда будет соответственно
суммоЙ и разностью кодовых слов, соответствующих исходным
числам. Блаrодаря этому АN
коды MorYT обнаруживать и ис
пра6ЛЯТЬ как обычные ошибки, возникающие в каналах связи,
Коды для арифметич.еских устройств
467
так и ошибки, возникающие в вычислительных устройствах. По
этому такие коды MorYT применяrься в каналах передачи дан-
ных, соединяющих вычислительные машины. В данной книrе
АN
кодам посвящены эта и следующая rлавы.
8.1. Основные понятия теории чисел
Для исследования АN
кодuв необходимо знать основы теории
чисел. Настоящий раздел является вспомоrательным и содер)кит
краткое изложение основных понятиА и результатов теории чи-
сел, используемых в пос.ледующих разделах при рассмотрении
АN
кодов. Более детальное изложение этих вопросов можно
найти, например, в книrах Такаrи [6] и Виноrрадова [7].
8.1.1. Делимость целых чисел
Пусть m > О
целое положительное число. Произвольное
целое число а единственным образом может быть представлено
в виде
а == mq + r (О
r < т).
(8.1 )
Целое число q называется частным, а целое число r
остатком
от деления а на m или наименьшим неотрицатеЛЫ-tЫМ вычетом
по модулю т. Равенство (8.1) иноrда записывают также в виде
r т (а) == " или а mod m == '. (8.2)
Очевидно, что в тех случаях, коrда ,п делит а, остаток r == о.
в этом случае будем писать m I а. Для произвольных целых чи-
сел а и Ь имеlОТ место слеДУlощие равенства:
' т (а + Ь) == ' т (r m (а) + ' т (Ь)), или
(а + Ь) mod m == (amod m + Ь mod т) mod т;
(8.3)
кроме Toro,
,т(аЬ) == rm(r m (а) ' т (Ь)), или
(аЬ) mod т == (а mocl,n · Ь mod т) mod т.
(8.4)
8.1.2. Наименьшее общее кратное и наибольший
общин делитель
Общим кратным ненулевых целых чисел al, а2, ,..., ak Ha
зывается любое целое число, которое делится на каждое из
этих чисел. Iiаименыпее положительно
из общих кратных Ha
зывается наименьшим общим кратным и обозначается через
НОК (al, а2, ..., ah) или [al, а2, ..., ak].
Целое число, которое делит ка)кдое из чисел al, а2, ...., al:t.
назыIаетсяя их общим делителем. Наибольший из общих дели
488
r лава 8
телей называется наиБОЛЬUlUМ общим делителем и обозначается
через НОД (al, а2, ..., ан) или (al, а2, ..., ak).
Если (al, а2, ..., ak) == 1, то числа а1, а2, ..., ah называются
взаимно простыми. Очевидно, что для взаимно простых чисел
k
[al, а2, . .. ak] === П al == аl · а2. ... · ak. (8.5)
i =-1
Любое общее кратное двух целых чисел а и Ь всеrда делится на
наименьшее общее кратное [а, Ь]. KpO
1e Toro, имеет место ра-
венство
[а, Ь] === (a
bb) ·
(8.6)
8.1.3. Простые числа и разложение на простые
сомножители
Любое цe
1I0e число р > 1 всеrда имеет по крайней мере два
делителя, а именно 1 и р. Если, кроме этих делителей, число р
не имеет друrих положительных делителей, то оно называется
npOCTblAt. Числа, большие 1 и имеющие положительные делители,
отличные от 1 и caMoro себя, называются составными.
Произвольное целое число а > 1 единственным с точностью
до порядка образом разлаrается в произведение попарно раз-
личных простых чисел Pi (или их степеней p;t):
k
а а a k П a l
а == р l. р 2. . р == Р
J 2 ... k 1.
1..1
(8.7)
в разд. 9.1 и 9.2 рассматриваются, в частности, разложения
TaKoro типа для целых чисел вида 2 n ....... 1.
8.1.4. Функция Эйлера
Для любоrо натуральноrо а функция Эйлера ер (а) опреде-
ляется как количество чисел х среди 1, 2, 3, ..., а, взаимно
простых с а. Например, <р(I)=== l(x=== 1), <р(2)== l(x== 1),
<р ( 3) == 2 (х == 1, 2), ер ( 4) == 2 (х == 1, 3), <р ( 5) == 4 (х === 1 , 2, 3, 4),
<р (6) == 2 (х == 1, 5). Пусть р
простое число. Поскольку все
целые положительные числа, меньшие р, взаимно просты с р, то
q> (р) == р
1.
(8.8)
Кроме Toro, леrко проверить, что для любоrо целоrо а > О
q> (ра) === pa
1 (р
1).
(8.9
Коды для арифметических УСТРОЙС1'8
469
Если представить произвольное целое а в виде (8.7), то из при-
веденноrо ниже свойства мультипликативности функции Эйлера
с учетом формул (8.8) и (8.9) получаем
<р (а) == а (1
"* ) (1
;2 ) ... (1
* ). (8.10)
Упомянутая мультипликативность функции Эйлера означает, что
для любых взаимно простых чисел а й Ь
<р (аЬ) == <р (а) <р (Ь). (8.11)
Еще одно важное свойство <р(а) состоит в том, что для произ-
вольноrо целоrо числа а
L <p(d) == а,
dla
ИЛИ, что то же самое J), L <р ( : ) == а. (8.12)
O<d
a
Друrими словами, сумма значений cp(d) по всем d, которые де-
лят а, равна а.
8.1.5. Сравнимость и кл ассы вычетов
Если задано целое число т, называемое модулем, то, как
можно видеть из формулы (8.1), для любоrо целоrо числа а
определен остаток ,т(а) == '. Если целые числа а и Ь имеlОТ
один и тот же остаток, т. е. если ,т(а) == 'т(Ь) == (, ТО они назы-
ваются сравнимыми по модулю т, и это записывается так:
а == Ь (mod т). (8.13)
в тех случаях, коrда модуль сравнения понятен из контекста,
вместо формулы (8.13) иноrда пользуются также упрощенной
записью а == Ь. Очевидно, что а == f И Ь == (. В действительности
существует бесконечно MHoro чисел, сравнимых с (. Множестоо
{а I а ==, (mod т)} всех чисел, сравнимых с " называется клас-
сом вычетов, содержащим (. Леrко видеть, что существует т
попарно непересеl{ающихся классов вычетов в соответствии с т
значениями остатка " ,== О, 1, 2, ..., т
]. Каждое целое
число принадлеiКИТ одному из этих т классов вычетов. .ЕСJlИ
взять по одному представителю каждоrо И:-i этих классов выче-
тов, то получится полная система вычетов по модулю т. Полная
система вычетов является коммутативным кольцом с операциями
сложения и УМНО>l<ения по МОДУЛIО nl. Более Toro, если т яв-
ляется простым числом, то 9'10 кольцо является полем. Часто
в качестве полной системы вычетов используется совокупность
наименьших неотрицательных остатков О, 1, 2, 3, ..., т
1.
1) В этой формуле предполаrается, что q>(x) == О для нецелых Х, ..... ПриМ,.
ред.
470
r лава 8
Если некоторый класс вычетов по модулю т содержит число,
взаимно простое с т, то и все целые числа, входящие в этот
класс вычетов, будут взаимно простыми с т. Как леrко видеть
из определения функции Эйлера, существует ер (т.) таких классов
вычетов. Если у каждоrо из этих КЛассов вычетов взять по од-
ному представителю, то получится nриведенная система вычетов
по модулю т. Приведенная система вычетов является rруппой
относительно операции УМНО}l{ения по модулю т.
8.1.6. Теоремы Эйлера и Ферма
Теорема Эйлера. Если т > 1 и (а, т) == 1,
a
(т) == 1 (mod т),
(8.14 )
Т. е. а'Р (т) ....... 1 делится на т.
Эта теорема является обобщением следующей теоремы
Ферма.
Теорема Ферма. Если р
простое число и а Не делится на
р, то
aP
1 == 1 (mod р).
(8.15)
Умножив обе части последнеrо равенства на а, получим
аР == а (mod р).
Последнее равенство справедливо для любоrо а.
8.1.7. Показатели экспоненты и примитивные корни
Пусть (а, т) == 1. Рассмотрим бесконечную последователь-
ность
1 2 3 4 5
а, а, а, а, а, ....
Соrласно теореме Эйлера, существует целое положительное
число е, такое, что а е == 1 (mod т). Минимальное целое положи-
тельное число е, удовлетворяющее этому условию, называется
nоказателем числа а по модулю т. ИНОI"'да е называется также
порядком а по модулю m. Показатель а по модулю т обозна-
чают следующим образом:
е==Е(а, т).
Если e
E(a,т), то числа 1 == а О , a 1 , а 2 , ..., ae
l являются
попарно несравнимыми по модулю m. Далее, если a k == 1
(mod т), то е делит k. Очевидно, что е делит <р (т). Наконец,
если показатель а по модулю т равен е и (k, е) == d, то показа
тель a h по модулю т равен e/d.
Для примера в табл. 8.1 указаны вычеты (остатки) по MO
дулю т :::::: 45, взаимно простые с т (т. е. дана приведенная си-
Коды для арифметических устройств
471
Таблица 8.1
Приведенная система вычетов по модулю
т == 45 и показатели этих выч етов
е == Е (а, 45) {а I a e 2!l1 ( m о d 45), (а, 45) == 1}
1 1
2 19 26 44
3 16 31
4 8 17 28 37
6 4 11 14 29 34
8
12 2 7 13 22 23 32 38 43
24
стема ВЬJчетов) и их показатели. В этом случае <р(45) == 24 и из
таблицы видно, что не существует целых чисел с показателем
ер (45). Это означает, что никакое число, при надлежащее приве-
денной системе вычетов по модулю 45, не порождает эту си
стему. Друrими словами, не существует TaKoro целоrо числа а,
что {a l , а 2 , аЗ, ..., aq>(45)} является приведенной системой выче-
тов по модулю 45. Кроме Toro, не существует и целоro числа,
которое имело бы показатель 8 по модулю 45. Таким образом,
следует заметить, что не каждый делитель числа <р (45) является
показателем kaI{oro-либо целоrо числа по модулю 45.
Если показатель а по модулю т равен <р (т), т. е. если
<р (т) == Е (а, т), то а называется прuмuтивным элементом по
модулю т. Как показывает приведенный выше пример, прими
тивные элементы существуют не для всех целых чисел. Извест
но, что примитивные элементы существуют только для целых
чисел т вида
т == 2, 4, ра, 2ра,
rде р простое нечетное число и r.J., ]. Более Toro, для каж-
доrо из этих чисел существует <р (<р (т)) примитивных элемен
тов. Если g является примитивным элементом по модулю р
и gp 1 О (mod р2), то g является примитивным элементом
также и по модулю ра (а 1). l(poMe Toro, если g один из
примитивных элементов по модулю т, то все примитивные эле
менты по модулю т представляют собой числа gkmod т,
(k, <р (т)) == 1.
Например, минимальным положительным примитивным эле
ментом по модулю р == 13 является 2. Следовательно,
212 IВE 1 (mod 13).
472
r лава 8
Дtйствительно, как видно из табл. 8.2, элементы 2 i mod 13 об
разуют приведеННУIО систему вычетов по модулю 13.
Таблица 8.2
i
1 2 3 4 5 6 7 8 9 10 11 12
2 i mod 13
2 4 8 3 6 12 11 9 5 10 7 1
Так как <р(<р(13)) == <p(12) 4, то СУlцествуют четыре прн-
l\fИТИВНЫХ корня для 13, а имен но 21 == 2, 25 == 6, 21 == 11.
211 == 7.
Необходимое условие существования в привед-енной системе
вычетов по модулю т числа а, принадлежаlцеrо показателю е,
10ЖНО получить, используя определеННУIО ниже Л фУн'КЧUЮ
Кармайкла. Эта функция определяется на множестве целых чи-
сел т следующим образом:
1) eColl и т 211, n == О, 1, 2, то л ( т) == <р ( т) ;
2) если т 2 n , 11 > 2, то л(m) === <p(m)j2;
3) если т == ра, сх > О, rде р простое число, то л(m) ==
== <р (р а ).
4) если т == 2np 1p 2 . . . p k, n О, CXi > О, И Pi попарно
различные нечетные простые числа, то
л(т)==ноК(л(2 n ), л(р I), ..., л(р k)).
Из апреде-ления л(т) и теоремы Эйлера следует, что
аЛ (т) == 1 (mod т).
(8 .1 б)
Известно, что целое число а < т, взаимно простое с т Ii
имеющее показатель е (друrими словами. элемент а приведен
ной системы вычетов показателя е), существует тоrда 11 ТО,,1ЬКО
тоrда, коrда е является делителем л(т). Например, при m==45
л (т) == л (45) == НОК (л (32), л (5)) == НОК (6, 4) == 12,
и для каждоrо делителя числа л(45) == 12 (и только для таких
делителей) существует целое число, взаимно простое с т и
имеющее своим показателем этот делитель. Это соrлаеуется
с табл. 8.1. .
Е ел и е == Е (а, т), (а, т) == 1 и 'n == р 71 Р 7 . . . Р k, то
е(а, m)==HQK(E(a, р7 1 ), Е'(а, p ), ..., Е(а, p k)). (8,17;
Коды для арифметических устроаств
473
8.1.8. Мультипликативные rруппы и их разложение
Приведенная система вычетов по модулю m является КОМ-
мутативной rруппой с операцией умножения по модулю т. Обо-
значим эту rруппу через G (т), а именно
G(m)=={rIO<r<m, (r, т)===l}.
(8.18)
Если m
нечетное число, то в G (т) входит число 2. Если по-
казатель 2 по модулю n1, равен б, т. е. если 2 б == 1 (mod т), то
б является делителем л (т), а следовательно, и делителем ер (т).
МНО}l{ество {2 0 , 21, ..., 2б
1} степеней числа 2, вычисленных по
модулю т, образует подrруппу порядка б rруппы G (пl). Как
хорошо известно, rруппу G (т) можно разложить на непересе-
кающиеся смежные классы по этой подrруппе. Число таких
смежных классов будет в точности равно ((J(m)/б.
Рассмотрим, например, разложение rруппы G (105) (nl ==
== 105). в этом случае т == 105 == 3.5. 7 и ((J ( 1 05) == 48, т. е. в
G (105) входит 48 целых чисел. Показатель числа 2 по моду-
лю 105 определяется из соотношений
Е (2, 105) === НОК (Е (2, 3), Е (2, 5), Е (2, 7)) == НОК (2, 4, 3) === 12.
Разложение rруппы G (105) на ((J(105)/12 == 48/12 == 4 смеж-
ных класса по подrруппе {2 i mod 1051i == О, 1, ..., 11} поряд-
ка 12 задается табл. 8.3.
Таблица 8.3
Разложение G (105) по подrруппе
{2 i m od 105 I i == О, 1, ..., 11}
21 20 21 22 23 24 25 26 27 28 29 210 211.
2' mod 105 1 2 4 8 16 32 64 23 46 92 75 53
11.21 mod 105 11 22 44 88 71 37 74 43 86 67 29 68
13 · 2 ! mod 105 13 26 52 104 103 101 97 89 73 41 82 69
17 · 2 i mod 105 17 34 68 31 62 19 38 76 47 94 83 61
Предположим опять, что m
нечетное число. Если m не яв-
ляется простым, то существуют вычеты по модулю т, не яв-
ляющиеся взаимно простыми с т. Пусть а
один из этих вы-
четов. Заметим, что сх не. является элементом G (т). ОднаКQ
если (сх, т) == d, то (cx/d, m/d) == 1 и, следовательно,
а ( пl )
([Е G ([ ·
474
r лава 8
rруппу G (m/d) точно так же, KaI{ и О (т), можно разложить на
q> (m/d) /6' смежных классов по подrруппе {2 0 , 21, . . ., 26' 1} по-
рядка 6', rде б' показатель числа 2 по модулю т. Эту про
цедуру можно выполнить для всех делителей d модуля m/d. При
этом исходный вычет сх может быть найден путем умножения
вычета, принадлежащеrо G (m/d), на делитель d. Таким обра-
зом, для произвольноrо нечетноrо т множество вычетов по мо-
дулю т (т. е. полная система вычетов) разлаrается на смежные
классы, не имеющие общих элементов. Отсутствие общих эле-
ментов следует из формулы (8.12) и Toro, что при d 1 =1= d 2 мно-
жества d1G(m/d l ) == {d1ala Е G(пl/d l )} и d 2 G(m/d 2 ) не имеют
общих элементов. Сле.дует также заметить, что поскольку по-
казатели числа 2 по модулю m/d для разных d различны, то в
разных смежных классах содержится неодинаковое число эле-
ментов.
Пусть, например, m == 105 и d == 3. Рассмотрим мультипли-
кативную rруппу 0(105/3) == 0(35). В данном случае б' ==
== Е(2, 35) == 12, ср(35) == 24, и, следовательно, 0(35) состоит
из 24 элементов. rруппа 0(35) разлаrается на 24/12 == 2 смеж-
ных класса, как показано в табл. 8.4.
Таблица 8.4
Разложение G (35)
2' 20 21 22 23 2 25 26 27 28 29 210 211
2 t mod 35 1 2 4 8 16 32 29 23 11 22 9 18
3 . 2 i m od 35 3 6 12 24 13 26 17 34 33 31 27 19
Соответствующие вычеты а по модулю 105, такие, что
(а, 105) == 3, представлены в табл. 8.5.
Таблица 8.5
Вычеты по модулю 105, соответствующие двум смежным
классам rруппы G (35)
3 . 2 i m od 105
9 · 2 i mod 105
3 6 12 24 48 96 87 69 33 66 27 54
9 18 36 72 39 78 51 102 99 93 81 57
Аналоrично, рассматривая мультипликативную rруппу
G(105/21):::: 0(5) при d == 21, получаем, что Е(2, 5) == 4,
<р (5) == 4. rруппа о (5) из четырех элементов и соответствую-
щие вычеты по модулю 105 приведены соответственно в
табл. 8.6а и 8.6б.
Коды для арифметических устройств
475
Таблица В.ба
G (5)
2 i
20
21
22
23
2 i mod 5
1
2
4
3
т аблuца 8.66
Вычеты по модулю 105,
соответствующие G (5)
21 .2' mod 105
21
42
84
63
8.1.9. Квадратичные вычеты и символ Лежандра
Пусть а и т
такие целые числа, что (а, т) == 1. Если
сравнение
х 2 == а
(mod т)
(8.19)
имеет решение в целых числах, то число а называется K8aдpa
ТUЧНblМ вычетом по модулю m. В противном случае, т. е. если
(8.19) не имеет решения в целых числах, число а называе,тся
квадратичным невычетом.
Для Toro чтобы целое число а было квадратичным вычетом
по модулю простоrо числа р, необходимо и достаточно, чтобы
выполнялось следующее сравнение:
a(p
1)/2 == 1 (mod р). (8.20)
Для всех целых чисел а, которые не делятся
на р, опреде
лим величину (а/р) следующим образом:
I 1,
( а ) J
р
I
1,
I
если
u
а ....... квадратичныи вычет
по модулю р,
а
квадратичный невычет
по модулю р.
(8.21 )
eCJI и
Введенная величина называется
место следующее сравнение:
( ; ) == a(p
1)/2 (mod р)
символом Лежандра. Имеет
(критерий Эйлера),
(8.22)
включающее как частный случай также сравнение (8.20). Для
произвольных нечетных простых чисел р и q справедливы TaK
же следующие законы:
476
r Айва 8
1) Первое дополнение к закону взаимности
( р 1 ) === (
l)(P
1)/2.
(8.23)
2) Второе дополнение к закону взаимности
( ; ) == (
l)(рЧ)f2.
3) Закон взаимности
( ; ) ( : ) == (
l){(P
1)/2}{q
I)f2).
(8.24)
(8.25)
в заключение сформулируем еще одно необходимое и до-
статочное условие для произвольноrо модуля т === 2ap
1 р;2 ...
ak Д
. .. Pk' rде Pl, Р2, ..., Pk
нечетные простые числа. ля Toro
чтобы число а, взаимно простое с модулем, было квадратичным
вычетом, необходимо и достаточно, чтобы выпnлнялись следую:-
щие условия: 1) а == 1 (mod 4), если (Х == 2, и 2) а == 1 (mod 8)
и (а/Рl) == 1, (а/Р2) == 1, ..., (a/pk) == 1, если ct
3. Кроме
Toro, заметим, что если 2 является квадратичным вычетом по
модулю р, то 2 будет также и ({вадратичным вычетом по мо-
дулю Р а (сх, > 1).
8.1.10. KpyroBble мноrочлены и их сомножители
Как хорошо известно, алrебраическое уравнение
xd
l==O
(8.26)
имеет d различных корнеЙ cx,1, сх,2, ..., ad. Эти корни называют-
ся корнями степени d из 1 и часто представляются в виде комп-
лексных чисел:
2тt"' + .. 2тtт ( О 1 2 d 1 )
а т == cos
J SIП d т == , , ,... , ..... ·
(8.27)
Если корень ат обладает тем свойством, что все элементы a
,
a
, .. ., a
1 различны, то он называется nримuтuвным корнем
степени d из 1. Элемент (Хт является примитивным корнем сте-
пени d ИЗ 1 тоrда и только Torna, коrда (т, d) == 1. Следова-
тельно, Bcero существует <р (d) прим итивных корней из 1. Если
ат является примитивным корнем степени d из 1, а кроме Toro,
и корнем HeKoToporo уравнения Х N
1, то число d ДОЛ)l{НО Д
-
ЛИТЬ n,
Коды для арuф.метuческuх устройств
477
Если ао, СХl, ..., ak, ..., CXn l различные корни п й CTe
лени из 1 1), то
Х N 1 == (х ......... (10) (х ......... (11) . . . (Х......... (1 k) .. . (Х......... (1n 1). (8.28)
Те из корней ak, для которых (k, п) == 1, являются примитив
ными корнями п й степени из 1. Каждый из остальных корней
является корнем некоторой степени d из 1, rде d один из де-
лителей числа п (1 < d < п). Пусть Фd(Х) мноrочлен от Х,
корнями KOToporo являются только примитивные корни d й сте...
пени из 1, а именно пусть
Фd (х) == П (х (1k),
(k, d)""1
rде П произведение по всем примитивным корням d-й
(k, d)..l
степени из 1 2).
Заметим, что Фd (х) имеет степень {{) (d). Поскольку каждый
корень n й степени из 1 является примитивным корнем сте-
пени d из 1 для HeKoToporo делителя d числа п, то
(8.29)
х n ......... 1 == П Ф d (Х),
litn
(8.30 )
rде П произведение по всем делителям d числа n.
dln
Мноrочлен Фd (х) называется KPYZOBblM мноzочленом поряд-
I{а d. Он обладает рядом интересных свойств, однако здесь для
нас будет представ.пять интерес rлавным образом значение
этоrо мноrочлена Фd (2) при х 2, называемое KPYZ08blM чис-
ЛОМ порядка d. KpyroBbIe числа иrрают важную роль при раз-
ложении на сомножители целых чисел ВИда 2 n 1.
Приведем два свойства KpyroBbIx чисел и примеры таких
чисел:
1) Если Р простое число, не являющееся делителем d, то
необходимым и достаточным условием Toro, ЧТо Фd (2) имеет
в качестве простоrо сомножителя число Р, является выполнение
равенства Е (2, Р) == d. Кроме Toro, pf3 является делителем
Фd (2) тоrда и только тоrда, коrда pf3 является делителем 2d 1.
2) Пусть р простое число, являющееся делителем d, а
именно пусть d p a d 1 (р не делит d l ). Тоrда необходимым и
достаточным условием Toro, что Фd (2) и еет в качестве про-
CToro сомножителя число р, является выполнение равенства
Е (2, р) == d 1 . При этом Фd (2) де Т'IИТСЯ на р, но не делится на р2.
1) Пронумерованные, KRI< в (8.27). П pllAt. перев.
2) Заметим, что Фd (х) мноrочлен с целыми коэффициеf:Iтами. - П рим.
ред.
478
r лава 8
Для примера рассмотрим разложение числа 218
1 на кру-
rOBbIe числа:
X 18
1 == П Фd (х),
d 118
218
1 == Фl8 (2) · Ф g (2) · Ф 6 (2) · Ф З (2) · Ф 2 (2) · Фl (2) ==
== (3 · 19) · (73) · (3) · (7) · (3) · (1).
Примеры KpyroBbIx чисел приведены в табл. 8.7.
Таблица 8.7
Примеры KpyroBblx чисел
d Фd (2) d Фd (2) d Ф d (2) d (D d (2) d Фd (2)
1 1 5 31 9 73 13 8 191 17 131 071
2 3 6 3 10 11 14 43 18 3 Х 19
3 7 7 127 11 23 Х 89 15 151 19 524 287
4 5 8 17 12 13 I 16 257 20 5 Х 41
8.1.11. Минимальное представление дроби
Как известно, любую дробь а/В (О < а < В) можно пред-
ставить в виде
О, а 1 а 2 аз . . . .
Пусть В
произвольное заданное целое число, и пусть n.......... по.
казатель числа, по модулю В. Тоrда
,n == 1 (mod В),
т. е. можно подобрать такое целое число А, что
,n
1 == АВ.
Следовательно, для любоrо а < В
В а == аА ( n
1 ) === а.4 (О, 00 ... о i) 1).
r
.........
период n
Это равенство показывает, что дробная часть является перио-
дической последовательность!? с пер
одом п.
Например, дробь 1/13 == 0,076923 является десятичной пос-
ледовательностью с периодом 6. Это следует из Toro, что
Е(10, 13) == 6 и 106 == 1 (mod 13). При этом 10/13 == 0,769230;
100/13 == 7 + 9/13 == 7,692307, 9/13 == 0,692307; 1000/13 == 76 +
I} Точки над цифрой означают периодичность.
П рим. рвд.
Коды для арифметических устройств
479
+ 12/13 == 76,923076; 12/13 == 0,923076; 10000/13 == 769 + 3/13,
3/13 == 0,230769; 100 000/13 == 7692 + 4/13; 4/13 == 0,307692. 3a
метим, что в данном примере дробные части 1/13, 10/13, 9/13,
12/13, 3/]3, 4/13 получаются циклическими перестановка-
ми 076923.
В общем случае, если взять В так, что Е (r, В) == В
1,
а именно чтобы число r было примитивным корнем В, то пред-
ставление в виде десятичной дроби числа а/В (О < r.J., < В) по-
лучается путем циклических перестановок символов в представ-
лении в виде десятичной дроби числа I/В. Это широко при-
меняется в теории циклических АN
кодов и ниже будет исполь-
зовано в частном случае r == 2.
8.2. Определение АN"кода
АN
код представляет собой отображение целых чисел О, 1,
2, ..., N o в целые числа О, А.l, А.2, ..., A.N o , rде A
HeKO-
торое фиксированное для каждоrо кода целое положительное
число, называемое порождающим числом. Числа О, А -1, ..., Ао
называют кодовыми числами, а их представления в системе
счисления по основанию r
кодовыми словами. В этой rлаве
рассматривается случай двоичной системы счисления, коrда
r == 2, хотя мноrие результаты леrко обобщаются и на случай
произвольноrо '.
Очень важным свойством АN
кодов являе,тся то, что сумма
кодовых чисел также является кодовым числом, а именно для
любых двух целых чисел N 1 и N 2
А (N 1 + N 2) == AN 1 + AN 2.
(8.31 )
Следовательно, если N 1 + N 2
N o , то число А (N 1 + N 2 ) ===
== AN 1 + AN 2 также является одним из кодовых чисел. По-
этому, если закодированные числа сложить с помощью обыч-
Horo сумматора, то полученная в результате сумма будет кодо-
вым ЧИСJ1,ОМ суммы исходных чисел. Блаrодаря этому АN
коды
MorYT обнаруживать и испраВJlЯТЬ ошибки, возникающие в сум-
маторах.
Если r является делителем А, т. е. если r является делите-
лем каждоrо кодовоrо числа AN, то в представлении чисел по
основанию r самый младший разряд всеrда будет равен О. Да-
ле
, если А и r не являются взаимно простыми, то в младших
разрядах, начиная с HeKoToporo, будут появляться только опре-
деленные символы, тоrда как друrие цифры никоrда не по-
явятся. Поскольку это неже.пательно, будем предполаrать, что
А и r взаимно просты. В случае r == 2 это означает, что число А
480
r лава 8
ДОЛЖНО быть нечетно. АN коды с r == 2 называются двоичными
АN-кодами 1).
Пример 8.1. АN код с параметрами А == 13, N o == 4 и , :z= 2,
Т. е. двоичный 13N код, приведен в табл. 8.8.
Таблица 8.8
Двоичный 13 N -КОД
N AN Кодовые слова
О О 000000
1 13 00 11 О 1
2 26 011010
3 39 100111
4 52 110100
Например, сумме 1 + 2 === 3 соответствуют следующие сум-
мы кодовых чисел и кодовых слов этоrо кода: 13 t-- 26 == 39 и
001101 + 011010 == 100111. Если при переносе 1 из разряда 23
в разряд 24 происходит ошибка, в результате которой эта еди-
ница переноса превращается в О, то результатом вычисления
будет число (010111)2 == (23)10 (нижний индекс показывает ос-
нование системыI счисления). Остаток от деления этоrо числа
на 13 равен 10, а это означает, что полученная сумма не ЯВ
ляется кодовым числом 13N кода. Следовательно, возникшая
ошибка будет всеrда обнаружена. В действительности, как мы
покажем ниже, эта ошибка может быть и исправлена (см. при-
мер 8.6).
Так как максимальное кодовое число равно AN o , то для
представления чисел О, А. 1, А. 2, ..., А. N о в двоичной системе
счисления требуется n двоичных символов, причем
2n 1 ANo < 2 n ,
Т. е.
n == [(log2 AN о) + 1].
(8.32)
(Здесь [х] наибольшее целое число, не пре'восходящее х, или,
друrими словами, целая часть х 2).) Это число n называют дли-
ной двоичноrо АN кода. Для представления исходных некоди-
рованных чисел О ,1, 2, .." N о в двоичной системе счисления
1) Ниже, если это специально не oroBopeHo, рассматриваются двоичные
АN коды.
2) Для любых двух действительных чисел х и у имеют место следую..
щие неравенства: а) х 1 < [х] х < [х] + 1 и б) [х] + [у] [х+у]
[х] + [у] + 1.
Коды для арифметических устроl1ств
481
достаточно иметь
k == [log2No + 1]
(8.33)
двоичных знаков. Таким образом, разность
r==n.........k
(8.34)
представляет собой число избыточных двоичных символов, не-
обходимых для Toro, чтобы множество целых чисел {О, 1,2, ...
. . ., N o } можно было представить с помощью АN
кода. Из фор..
мул (8.32)
(8.34) получаем
log2 А ......... 1 < r < log2 А + 1. (8.35)
Следовательно, величина IOg2 А является мерой избыточности
АN
кода.
Пример 8.2. Избыточность 29N-кода равна
log 2 29 == 4,8.
Например, для представления целых чисел от О до 29 == 512
включительно в двоичной системе счисления необходимо 9 раз
рядов, а для их представления в виде кодовых слов 29N-кода
требуется уже 14 двоичных символов. Следовательно, факти-
чески необходимая избыточность равна пяти двоичным сим-
волам.
Избыточность 3N
кода равна
log23 == 1,6.
Если этот код используется для представления десятичных
цифр О, 1, 2, ..., 9, то избыточность этоrо кода будет равна 1,
поскольку в данном случае длина кода равна 5, а минимальное
число двоичных символов, необходи
ых для представления тех
же цифр в двоичной системе счисления, равно 4.
8.3. Арифметический вес и арифметическое
,
расстояние
Определим сначала арифметический вес W (N) ПРОИЗ:SоЛЬ-
Horo целоrо числа N. Арифметический вес является одним из
основных понятий В теории арифметических кодов и иrрает ту
же роль, что и вес Хэмминrа в теории алrебраических кодов.
Целое число N в двоичной системе счисления всеrда может
быть представлено единственным образом в следующем виде:
N === а о 2 0 + а121 + а222 + ... + a l 2 i + ..., ai Е {О, 1}, (8.36)
i == О, 1, 2, ... .
482
r :!'ll
8
Если разрешить коэффициентам в этом представлении прини-
мать значения О, 1 и
1, то целое число N может быть также
представлено в друrом виде:
N==b 0 2°+b 1 21+b 2 22+...+b t 21+ ..., bIE{
1,0,+1},(8.37\
i -== О, 1, 2, . . .
Наприме.р, (1111) 2 === 23 + 22 + 21 + 20, и в то же время
(1111) 2 == 24
20. Этот пример показывает, что второе из ука-
занных выше представлений может иметь меньшее число нену-
левых коэффициентов. Представление (8.37), имеющее наимень-
шее число ненулевых коэффициентов, называется пРlfдставле-
нием с минимальным весом или просто минимальным представ-
ление.м.
Число членов с ненулевыми коэффициентами в минималь-
ном представлении числа N называется арифметическим весом
W(N) числа N, Т.е.
W (N) == [ Число нену левых коэффициентов ]
в минимальном представлении N ·
(8.38)
Ниже в Данной rлаве арифметический вес будем называть про-
сто
eCOM.
В отличие от обычноrо двоичноrо представления в мини-
мальном представлении коэффициенты Moryr принимать три
значения + 1, О и ...........1. Не следует, однако, смешивать мини-
мальное представление с представлением в троичной системе
счисления.
Кроме Toro, следует заметить, что минимальное представле-
ние не однозначно. Например,
43
1 О 1 О 1 1 == 1 1 О Т о Т === 1 О r о т о 1,
rде через Т обозначены символы
l. Имеет место следующая
лемма.
Лемма 8.1. Если целое число N удовлетворяет условию
I N I
2т, ТО во всех минимальных представлениях вида (8.37)
числа N
bJ==O, j
m+l.
Доказательство. Предположим, что представление
Ь о 20 + b l 2 1 + Ь 2 2 2 + .., b L 2 L , b L + О,
Числа N является минимальным представлением. Если b L "' 1 =- О,
То
(8.ЗQ)
2т > I N 1== I ь020 + b 1 21 + ... + ь L
22L
2 + Ь L2 L I > 2L
1.
Коды для арифметических устройств
483
Кроме Toro, если Ь L
l === Ь L, то очевидно, что
2т
I N 1== 1 Ь02О + b 1 2 t + ... + bL
22L
2 + bL2L
1 + b L 2 L 1 > 2L
1.
Следовательно, в любо
{ из этих случаев
2т > 2 L --- 1 .
ЭТО означает, что т> L..... 1, т. е. т + 1 > L.
При этом, если Ь L
1 == ........ ь L, то
bL
12L
1 + b L 2 L == (bL
1 + 2Ь L) 2 L --- 1 == Ь L2 L --- 1
и, следовательно, два слаrаемых представления можно заме-
нить одним. Это означает, что такое представление не является
минимальным.
Из доказательства леммы 8.1 следует, что если в минималь-
ном представлении произвольноrо числа N два соседних коэф-
фициента Ь ; и b j + 1 отличны от нуля, то Ь ; == b j + 1 .
Еще одно важное свойство арифметическоrо расстояния со-
стоит в том, что для произвольных целых чисел N 1 и N 2
W (N 1 ::i:: N 2 ) <W (N 1 ) + W (N 2 ). (8.40)
Действительно, если ненулевые коэффициенты при некоторой
степени основания в минимальных представлениях чисел N 1 и
N 2 отличны от нуля, то при сложении N 1 и N 2 они Moryr либо
уничтожиться, либо может возникнуть перенос. В силу этоrо
число ненулевых коэффициентов в сумме может быть лишь
меньше суммы чисел ненулевых коэффициентов исходных ми-
нимальных представлений.
Пример 8.3. Так как 15 === 24 ....... 20, то арифметический вес
W (15) числа 15 равен 2. Кодовым словом, соотвеТСТВУIОЩИМ
этому числу, является последовательность 1111, вес Хэмминrа
которой равен 4.
4рuфмеruческое расстояние между целыми числами N 1 и N 2
определяется как арифметический вес абсолютноrо значения их
разности и обозначается через d(N 1 , N 2 ). А именно
d (N 1, N 2) == W ( 1 N 1 .... N 21). (8.41)
Отсюда непосредственно следует, что
d (N 1, N 2)
о.
(8.42)
Равенство в (8.42) имеет место только при N 1 == N 2 . Заметим
также, что
d{N 1 , N 2 )==d(N 2 , N 1 ).
(8.43 )
484
r лава 8
Для введенноrо расстояния выполняется также неравенство
треуrольника
d (N 1 , N з )
d (N 1 , N 2 ) + d (N 2 , N з ).
(8.44 )
Действительно,
d (N 1, N 3) == W ( I N 1
N 2 + N 2 ...... N 3 I )
W (1 N 1
N 2 1) + W (N 2 ...... Nзl) == d (N 1 , N 2 ) + d (N 2 , N з ).
Как видно из формул (8.41)
(8.43), d(N 1 , N 2 ) определяет рас-
стОЯние в произвольном множестве целых чисел. В этой и сле-
дующей rлавах арифметическое расстояние будем называть
просто расстоянием.
Введенные выше арифметические вес и расстояние в теории
арифметических кодов аналоrичны весу и расстоянию Хэмминrа,
используемым в теории алrебраических кодов. Это связано с тем,
что если при сложении двух чисел в двоичном представлении
возникает ошибка в некотором разряде, в результате которой
символ О переходит в 1 (или, наоборот, 1 переходит в О), или
ошибка переноса, то полученная в результате сумма будет от-
личаться от правильной суммы на величину +2 j или
2j, rде
j
некоторое целое число. В результате этоЙ ошибки в двоич
ном представлении искомой суммы MorYT оказаться искажен
выми несколько разрядов и расстояние ХЭМl\fинrа между этим
представлением и правильным представлением будет больше 1,
хотя арифметическое расстояние между правилыlйй и непра-
вильной суммами равно в точности 1. Друrими словами, для
арифметических кодов арифметические вес и расстояние более
удобны по следующим двум причинам:
1) В арифметических устройствах ошибка из
за переноса MO
жет привести к искажению нескольких -последующих разрядов.
В арифметических кодах в отличие от алrебраических кодов
ошибки в раЗЛИЧI1ЫХ разрядах не являются независимыми.
2) В сумматорах и устройствах, осуществляющих вычита-
ние, ошибки бывают двух типов; с переходами 1 в О и перехо-
дами О в 1 нельзя обращаться совершенно одинаково.
Эти причины хорошо иллюстрирует следующий пример.
Пример 8.4. Пусть N 1 == 31 и N 2 === 32. Эти числа имеют сле
дующие двоичные представления: N 1 == 31 == 011111 и N 2 ==
== 32 == 100000. Расстояние Хэмминrа между этими последова-
тельностями равно 6. Если в результате аРИфl\lетической ошибки
в разряде 20 к N 1 прибавляется 20 (конфиrурация ошибки
000001), то N 1 == О 11111 перейдет в LV 2 == 100000. Поскольку
31 == 25
20 и 32 == 25, то, как следует из приведенных выше
Коды для арифАtетuческuх устройств
485
определений арифметическоrо веса и арифметическоrо расстоя...
ния, W(31) == 2, W(32) == 1 и
d (31, 32) == W (32
31) == W (1) == 1,
что соответствует ошибке в одном разряде.
Если в результате арифметической оши бк и в разряде 22 из
N 2 вычитается 22 (конфиrурация ошибки 000100), то N 2 == 32 ==
== 100000 переходит в 28 == 011100. Расстояние Хэмминrа м е...
жду двумя последними последовательностями равно 4, а ариф-
метическое расстояние между 32 и 28 равно
d (32, 28) === W (32
28) == W (4) == 1.
Это соответствует ошибочному вычитанию 22.
Рассмотрим, далее, методы нахождения минимальноrо пред-
ставления числа N. Как уже указывалось выше, минимальное
представление не единственно. Однако известно, что если в пред-
ставлении (8.37) никакие два соседних коэффициента OДHOBpe
менно не являются ненулевыми, т. е.
Ь i Ь i + 1 == О, i === О, 1, 2, . . . (8.45)
(ниже это условие называется условием М), то представление
(8.37) является минимальным и, более Toro, единственно [8].
МинимаЛЫlОСТЬ и единственность представления, удовлетворяющеrо
условию М, может быть доказана следующим образом.
Предположим, что представление (8.37) целоrо числа N:
п
N == Ь о 20 + Ь 1 2 1 + ... + Ь п 2 n == L b[2
, Ь[ Е {О. +1, .......1}, (1)
ir::aO
удовлетворяет условию М, а именно
lJibi+l == О, i == О, 1, ..., n....... 1. (2)
Сначала докажем единственность представления вцда (1} заданноrо це-
лоrо числа N. Допустим, что существуют два различных представления чис
па N 8 виде (1), т. е.
п п
't
IIt ' 11 1
N === L..J b i 2 == L.J b t 2, b i , b i Е {О, +1,
},
[==о [==о
(3)
и П р идем к противоречию. Действительно, пусть т
мипимал.ьный из индек.
, 11 .
сов i, таких, что Ь t =1= Ь [ . т or да
, "
Ь т
Ь т == :i: (1 + а), (4)
rде а==О или 1, и
т т
L b;2 i
L Ь;'2 ё == :i: (1 + а) 2т.
iсзО [..о
(5)
4В6
r лава 8
Если т == n, равенство (3) не может выполняться. При т < n и а === 1 из
, "
равенства (4) следует, что Ь т + о :;ь Ь т . Но тоrда, соrласно формуле (2),
, "
b т + I === О ::z Ь т + 1 . Из равенства (5) слеДУiТ, что s этом случае
т+а т+а
L b;2 1 ...... L b72i == ::1: (1 + а) 2т,
i..O 1
0
(6)
Очевидно, что при т < n и а == О равенство (6) можно ПО.ТIучить непосред-
ственно из (5). Таким образом, при т < n равенство (6) справедливо как
при а == О, так и при а с:: 1. При т + а
n получаем противоречие с ра-
венством (3). Рассмотрим случай т + а < п. Равенства (3) и (6) Moryr
выполняться одновременно только в том случае, если
n
L Ь;2 ! ......
l"m+a+1
n .
L b
'2i == =F (1 + а) 2т == =F 2 т + а ,
Ic:т+a+1
(7)
но это невозможно, поскольку левая часть последнеrо равенства является
целым положительным кратным 2 m + a + I ,
тоrда как правая часть равна
=F2 m + a . Таким образом, если представление, удовлетворяющее условию М,
существует, то оно единственно.
Далее для произвольноrо целоrо числа N докажем существование пред-
ставления, у довлетворяющеrо условию М, а также минимальность числа
n
т n
L I bll
1..0
(8)
ненулевых коэффициентов в нем.
Представим число N в виде (1):
n
N
"" b
V) 2 1 , .................... О
L..J. n
V:;::::; ,
1
0
(9)
и положим
п
T
) == L I b
V) 1.
1-0
(10)
При п
О существование и минимальность этоrо представления очевидны.
Рассмотрим случай n > О. Предположим, что {b
V)}
совокупность коэф-
фициентов b
V) (i == О, 1, ..., n; п > v
О), которые удовлетворяют усло-
вию М до разряда 2", и найдем совокупность {b
v+l)} коэффиuиентов пред-
ставления (9) числа N, которые удовлетворяют условию М до разряда 2 v + I .
Совокупность {b
O)} удовлетворяет одному из следующих трех взаимоисклю-
чающих условий:
b(V) b(v) == + 1
v+I V '
(1Iа)
b(V) b(v)
О
v+I V
,
(116)
b(V) b(v) ==а
1
v+l v ·
(11 В)
Коды для арифМIтических устройств
487
При выполнении равенств (1Iа) и (11в) имеIОТ место также следующие два
соотноШения:
ь(о)
ь(о) а:: ь(о) -= -= ь(с) == :1: 1 n
и '" v + 2
и ,.. и
l и
2 ... о t::J:ii'
,
:ж: 1 == b
O
l + b
C) == :ь 1.
( 12а )
(12в)
Следовательно,
и
Ь(О)2' == ( ь(о) + ь(о» ) 2"
Ь(О)2 и
1 и V о'
i V
v+1
L b
O)2' == О · 20+1
b
O)20,
iro::::v
( 1 За)
(13в)
rде и
индекс, значения KOToporo лежат в области n
и
v + 2. Для
каждоrо ИЗ трех возможных случаев, определяемых равенствами (11 а), (11 б:)
и (11в), соответственно по формулам (116), (IЗа) и (13в) находим
Ь(О+О == ь(о) + ь'О)
и и О '
b
O+ I) == О, и > i > о,
( 14а)
ь(о+ 1) == ..... ь(о)
V v ,
Ь (о+ 1)
b (v)
1 .......... i '
b
v+l)==b
v), n
i
O, (146)
ь(о+ I) == о
0+1 '
ь(о+ 1) ==
ь(о) ( 140 )
о V '
Ь (о+ 1)
Ь (о)
l
l ·
Очевидно, что при данном методе построения ПОЛУЧ8ющаяся совокупность
{b
o+l)} удовлетворяет условию М до разряда 21'+1 и при этом
T
+I)
T
). (15)
Таким образом, проиэвольное заданное представление (9) при v &::а О удо-
влетворяет условию М до разряда 20. Далее, взяв за основу множество {b
O)}
и строя с помощью описанной выше процедуры последовательно множества
{b
1)}, ..., {b
п)}, можно найти {b
п)}
При этом
Т (О) .......... Т < 1) .......... .......... Т (п)
п :::;::; п :::;::; ...:;:::; п'
(16)
Т. е. T
) меньше соответствующеrо параметра любоrо друrоrо множе.
ства {b i }.
Алrоритм нахождения представления,
удовлетворяющеrо условию М
Рассмотрим простой алrоритм нахождения представления,
удовлетворяющеrо условию М, по обычному представлению цe
JIoro числа N в двоичной системе счисления. Пусть
N -= aп
laп
2 . . . alaO, а, Е {О, l}, aп
1 =1= О (8.46)
488
t лава 8
и
n
1
N === L a i 2 i .
[==о
(8.47)
Так как 3N == 2N + N, то, сдвиrая праВУIО часть (8.46) на
1 разряд влево и прибавляя N, получаем
3 N
Ь п + 1 Ь п Ь п
1 .. . ь 1 Ь о, Ь i Е {о, I}, (8.48)
rде
Ь О
ао
коэффициент при 20 в представлениях N
и 3N,
ы l == ai + at--l + С 1 (mod 2), 1 <. i <. n ........ 1,
СI равен 1 при наличии переноса из (i
1)..ro раз..
ряда и О в остальных случаях,
Ь п == an
l + Сп,
Ь п + 1 == С п +l.
(8.49)
Далее, пользуясь тем, что 2N == 3N
N, и вычитая (8.46)
поразрядно из (8.48), получаем
b n + 1 Ь п bn
l bп
2 . .. Ь ! ... b l Ь о
а п
1 а п
2 · · · а i · · · а 1 а О
d п + 1 d n d п
1 d n
2 . .' d 1 ... d 1 d o
(8.50)
rде
{ 1,
d 1 == ........ 1 ,
О,
Ь ! > GI,
ь i < ai,
b l == ai.
(8.51 )
Лемма 8.2. Представление dn+1d n . . . d i . . . d1d o числа 2N, за-
даваемое формулами (8.50) и (8.51), удовлетворяет условию М.
Доказательство. Очевидно, что d o == О. Следовательно, для
доказательства леммы достаточно показать, что если d i =1= О при
некотором 1
i
n, то d i + 1 == О. Предположим, что d i =1= о.
Пусть ai == 1 и b i == О (при ai == О и b i == 1 доказательство про-
водится аналоrично). Тоrда
ы l :ЕЕ ai + al
l + Cl == 1 + al
l + С! == О (mod 2).
Так как 1
al
l
О, 1
СI
О, то CI+I == 1. Следовательно,
b l + 1 === al+l + аl + Cl+l == al+l + 1 + 1 == al+l (mod 2),
так что
d l + 1 == о.
Коды для арифметических устройств
489
Таким обраЗО
f, как утвер)кдается в лемме 8.2, представление
dn+1d n . . . d 1 d o числа 2N удовлетворяет условию М и, следова
тельно, является минимаЛЬНLIМ. Число ненулевых слаrаемых в
.. n+1
9ТОМ представлении L I d i I является весом W (2N) числа 2N,
i==()
который равен весу' W (N) числа N. Действительно, так как 2N
является результатом деления 2N на 2, то последовательность,
полученная сдвиrом предстаilления 2N на один разряд вправо,
будет представлением N. fIоскольку d o == О, то в результате
этоrо преобразованин вес не изменяется.
Из этой леl\1МЫ, кроме Bcero прочеrо, непосредственно сле-
дует, что ]) число разрядов в минимальном представлении чис-
ла, обычное двоичное представление KOToporo имеет п разрядов,
не превышает п + 1 и 2) вес ДВОИЧlIоrо п-разрядноrо числа не
превышает [nj2] + 1.
Пример 8.5. 11спо.пьзуя лемму 8.2, найдем вес числа N ==
== 3673. Так ка l{ N .== 011100] 011001 и 3N:::; 1 О 1 О 11 0000 1 011,
то
3N == 1 О 1 О 11 0000 1 011
N == 0111001011001
2N == 10010101010010
N== 1001010101001
и, следовательно, W (N) == 6.
8.4. Минимальное расстояние и корректирующая
способность АN"кода
Если в процессе передачи или некоторых вычислений целое
число N в результате ОIllибок переходит в число N' и расстояние
d (N, N') == W ( I N
N' 1) между N и N' равно t, то будем rOBO-
рить, что произошла ошибка веса t.
Пусть 1
целое число, совпадающее с кодовым числом AN
при отсутствии ошибок и, БыIьb может, отличающееся от AN при
наличии ошибок. Например, 1 может быть выходом сумматора,
суммы на выходе KOTOpOI'O в отсутствие ошибок являются KO
довыми числами АN
кода. В этом случае
1 == AN + Е, (8.52)
rде Е
целое число, называемое ошибкой. Если W (Е) == t, ТО
Е называется ошибкоЙ веса t.
Минимальное расстояние d мин кода
это по определению ми-
нимальное значсние расстояния между различными кодовыми
UИ(
Л2МИ. Точнее, МИНИl\lал
ное расстояние АN-кода, который cq.
490
r лава 8
поставляет числам О, 1, ..., N o кодовые числа О, А .1, ..., А .N o ,
определяется следующим образом:
d МIIИ == min W (ANl AN 2 ), O Nl, N 2 <N o . (8.53)
N 1 + N 2
Теорема 8.1. .4N Koд исправляет все ошибки веса t и JtteHee
ТОёда и только ТОёда, КОсда еёО минимальное расстояние d мин не
.меньше чем 2t + 1. A1V KOa может обнаруживать все ошибк'и
веса d и менее ТОёда и только ТОёда, КОёда еео минимальное рас-
стояние не меньше чем d + 1.
Доказательство. Если ни для каких двух различных кодовых
чисел AN 1 и AN 2 не существует пары ошибок EI и Е 2 веса t или
менее, такой, что
AN 1 + El == AN 2 + Е2'
(8.54)
ТО по /1 == AN 1 + EI всеrда можно однозначно восстановить
AN 1 . Верно и обратное; в самом деле, из формул (8.54) и (8.40)
имеем
d (AN 1, AN 2) == \\,/ ( I AN 1 AN 2 I ) c:z
=== W (1 Е 2 E11) W (E 1 ) + W (E2) 2t.
(8.55)
Следовательно, условие d мин 2t + 1 является достаточным
для Toro, чтобы АN код Mor исправлять все ошибки веса t и
менее. Наоборот, если допустить, что d (AN 1 , AN 2 ) ::::;; 2t, то чис-
ло AN 1 AN 2 будет иметь минимальное представление веса 2t
или менее. Пусть El сумма t ненулевых членов высших раз
рядов этоrо минимальноrо представления, а Е 2 сумма остав-
шихся членов этоrо представления. Вес определенных таким об-
разом ошибок El и Е 2 не превосходит t, и El' Е 2 удовлетворяют
равенству (8.54). Следовательно, они не MorYT быть исправлены.
Далее, АN код может обнаруживать все ошибки веса d и ме-
нее тоrда и только тоrда, коrда ни для каких двух различных
кодовых слов AN 1 И AN 2 не существует ни одной ошибки веса d
именее,такой, что
AN 1 + Е === AN 2 .
(8.56 )
Вторая часть теоремы доказывается точно так же, как и пер-
вая.
Аналоrично можно ДОI<азать, что А1V КОД может испраВJ1ЯТЬ
ошибки веса t и менее и одновременно обнаруживать ошибки
веса d (> t) и менее тоrда и только тоrда, коrда ero минималь
ное расстояние не меньше чем t + d + 1.
Эти соотношения между коорректирующей способностью и
минимальным расстоянием АN кодов совершенно аналоrичны
соответствующим соотношениям для алrебраических кодов. Они
Коды для арифметических устроиств
491
,
подтверждают сделанное в примере 8.4 и ранее утверждение о
том, что арифметический вес, арифметическое расстояние и ми-
нимальное расстояние являются понятиями, которые иrрают в
теории арифметических кодов очень важную роль.
Теорема 8.2. Расстояние d (AN 1 , AN 2 ) между дВУАfЯ nРОUЗ80ЛЬ-
ными различными KOa08blAfU числами AN 1 и AN 2 AN-Koaa равно
весу HeKoTopoZO ненулевоzо KOaOBOZO числа АiV з . Наоборот, для
любоzо ненулевоzо KOaOBOZO числа АN з Веса W (АN з ) найдутся
такие два различных кодовых числа AN 1 и AN 2 , что расстояние
между ними будет в точности равно \V (АN з ).
Доказательство. Пусть AN 1 и AN 2 различные кодовые чис-
ла. Так как О N 1 N o и О N 2 N o , то число N з == I N 1
N 2 1 также удовлетворяет неравенству О < N з N o . Следова-
тельно, АN з ненулевое кодовое число и W(АN з ) == d( 4Nl,
AN 2 ) .
Наоборот, вес W (АN з ) любоrо ненулевоrо кодовоrо числа
АN з совпадает с расстоянием между АN з и кодовым числом
А.О == о.
Еще одной важной характеристикой АN кодов является пара-
метр М (А, d), который определяется следующим образом:
М (А, d) === [ минимальное целое число т, ] . (8.57)
такое, что вес тА меньше d
Непосредственным следствием TeOpel'vlbI 8.2 является следую-
щее утверждение.
Утверждение 8.2.1. АN код {О, A.l, А.2,..., A.N o }, для кото-
poro N o == М (А, d) 1, имеет минимальное расстояние d.
Пример 8.6. Если А == 13 и d == 3, то M(13, 5) == 5. Действи-
тельно,
13 Х О == 0==0000000,
13 Х 1 == 13 == 00 1 О 1 О 1 ,
13 Х 2 == 26 == 0101010,
13 Х 3 == 39 === 0101001,
13 Х 4 == 52 === 1010100,
13 Х 5 == 65 == 1000001,
w (О) == о;
w (13) == 3;
W (26) == 3;
W (39) == 3;
W (52) == 3;
W (65) === 2.
Таким образом, минимальное расстояние АN-кода, описанноrо
в примере 8.1, равно 3, и, следовательно, cor ласно TeOpel\'le 8.1,
он может исправлять любые ошибки веса 1.
Как следует И3 утверждения 8.2.1, вычисление значений
ФУНКЦИИ м (А, d) является одной И3 важнейших проблем т.еорнн
0\
00
;:s-
if
'о
fo-..
ID
С
J:(
С
II1II
I
:в
:1
11
с..
с:
...... .... .... .... .... ...... .... .... ...... ......
11) + + I + I + + + + + I I I
:!
Q)
==
= C\I О
D: .-... 00 Il) ... Il) ...,. .
О tr.) C'II
... I + + + + I + I
(J S
(J
... ...,. о C\I
Q. ... .... N ...
:!
:lJ + I + + I I + I I
:с
.а о ...,. 11) '.о т О ;; м
1:; т ... . ('1 N
со
2
==
:с
== G LC .... Ф tr.) r--- ф LQ ...... r--- ...... ф r---
::r ...... ф 00 о 00 r--- 00
(J ...... C' tr.) 00 .... о')
.......
:8 ....
1::{
О
.
.... uj r--- LC tr.) ф r--- ф ф ф r---
"( "( t--- О LC Ф 00 ф .... 00 о') ф о
.... LC tC 00 Ф о 00 ф ф 00
...... ...... ...... ....
.... .... .... .... ...... ..... ...... ...... ...... ...... ...... .... ......
. + + I I I + I I + I + + I I I
:1 .
Q)
== ... Q) C\I 00
:с 1'00 N N N
D: .......
О
t + + + + I I +
(J
... N 10 N М с\? ...,. со со C\I с\?
Q. 1'00 ос) ... ... C\I N C\I N N C\I М ...,. ...,.
::s
:8
:с
LC Ф LC r--- ф tr.) ф \.1.) ...... r--- ф
.... ...... <::> <::> ф r---
:1 r--- ф ф ...... 00 .....
== .-...
. .... tr.) LC Ф tr.) 00
:с ..... 00 ...... ф
= "( .... 00 .....
:1
...... r--- .....
(J ф 00
:8 .... ф ф
1::{ tr.) о
О
.
"( c'r,) .... о') LC с"':) LC r--- ...... r--- r--- LC r---
LC 00 О LC 00 Ф tr.) tr.) tr.) ф tr.) о
...... .... .... tr.) tC r--- 00
.-... .... .... .... .... ..... .... .... ..... .... ...... ...... ......
+ + + I + + I + + + + I I + +
s
... .,. 00 м со т о с": 11) т ;Q о
:1 11) со т ... ... N C\I N с\? М cf) tQ со
:! "(
=
.а
:1:1 LC r--- ф LC tr.) ...... tr.) ....... tr.) ф r--.. ...... 1.0
==а.> 00 ф 00 00 <::> <::> r--.. r--- LC ф
:С== LC О h":) о) ф <::> ......
==:с t--- (х) Ф Ф r--.. ф ф <::>
:lD: .-...
r-..... ф ф <::> <::> LC
С)О .... C'I О Ф Ф о') 00
...
:! ...... Q) r--- 00 00
.... 00 LC Ф
I::{ .... ф LC
OQ.
:.: с1:) ф о')
ф
о
LC
...... c'r,) о') ф r--- r--- C'Ij о') ...... r--- ..... о) с"':) ......
...... ...... ...... LC LQ Ф Ф r--- t--- 00 О
......
Коды для арифметических устройств
493
арифметических кодов. Эта проблема полностью решена только
при d === 2, 3. Соответствующее решение приводится в разд. 8.5.
За исключением этоrо частноrо случая, общих методов ВЫЧИСJ1е
ния М (А, d), которые требовали бы небольшоrо числа операций,
нет. В табл. 8.9 приведено несколько примеров АN
кодов.
8.5. Обнаружение и исправление независимых
ошибок веса 1
Как следует из теоремы 8.1, код с l'vlинимальным расстоянием
d мин == 2 является кодом, обнаруживающим независимые ошиб-
ки веса 1. СлеДУlощая теорема дает простой способ построения
таких кодов.
Теорема 8.3. Если А (> 1)
нечетное число, те
м (А, 2) == 00.
(8.58)
Доказательство. Если допустить существование конечноrо цe
лоrо положительноrо числа N, TaKoro, что W(AN) == 1, то при
некотором целом положительном j будет иметь место равенство
AN == 2j. Следовательно, А делится на 2, но этоrо не может
быть, поскольку по условию теоремы А
нечетное число. Это
доказывает (8.58).
Соrласно этой теореме, при люБОl\1 нечеТНОl\I А (> 1) и любом
сколь уrодно большом N o минимальное расстояние А1V
кода {О,
А.l, А. 2, А. 3, ..., А. N о} не меньше 2, и, Сlllедовательно, при
любой кодовой длине такие АN-коды MorYT обнаруживать неза-
висимые ошибки веса 1. Среди этих кодов код с А == 3 имеет
минимальную изБI>IТОЧНОСТЬ. Для этоrо кода Iog 2 А == log23 ===
== 1,5849... и число избыточных разрядов не провосходит 2.
Коды с минимальным расстоянием d мин === 3 являются ко-
дами, которые либо исправляют ошибки веса 1, либо обнаружи-
вают ошибки веса 2. Как показывают две следующие теоремы,
коды с минимальным расстоянием 3 также MorYT быть построе
ны сравнительно просто.
В разд. 8.1.7 было дано определение показателя е === Е(а, т)
целоrо числа а по модулю т. Для взаимно простых а и т BBe
дем величину d == D(a, т) следующим образом. По определе
пию D (а, т)
минимальное целое положительное число d, 1'a
кое, что
a d ==
1 (mod т).
Если D (а, т) существует, то
2D (а, т) == Е (а, т).
(8.59)
8.60)
494
r лава 8
Последнее равенство следует из TOrO, что если a d == 1, то
a 2d == 1 и ни при каком е ( < 2d) сравнение а е == 1 выполняться
не может.
Теорема 8.4. Если А (> 1) нечетное число, то
{ (2е l)/A, е === Е (2, А), если d == D (2, А)
М(А, 3) == не существует, (8.61)
(2 d + l)/A, d == D (2, А).
Доказательство. Сначала предположим, что D (2, А) не суще-
ствует. По определению е
2 е == 1 (mod (А),
или, что то же самое, 2 е 1 == О (mod А). Следовательно, суще-
ствует целое положительное число N 1 , такое, что AN 1 == 2 е .... 1.
Отсюда и из определения М (А, 3) имеем
1
""1 (А, 3) N 1 А · (8.62)
Покажем, далее, что целые положительные числа N, такие,
что W (AN) 2, удовлетворяют неравенству N N 1 . Во пер-
вых, очевидно, что W (AN) =1= О. Далее, поскольку А нечетно,
то, соrласно теореме 8.3, W(AN) =1== 1. Если же W(.4N) === 2, то
существуют такие целые числа i и j (i > j О), что
AN == 2' ::l:: 2/ == 2/ (21 J ::l:: 1).
Так как А нечетно, то (A,2 j ) == I и, следовательно, А должно
делить 2i j + 1, т. е. 2i j ::J:: 1 == О (mod А). Из определения е ==
== Е (2, А) имеем i j е. Следовательно 1), .
AN == 21 (21 1 .... 1) 2 е 1 == AN 1t
и, таким образом, мы показали, что N N 1 .
Если d == D (2, А) существует, то доказательство проводится
аналоrично.
Лемма 8.3. AN-КОа {ANIO N < М} имеет .минимальное рас-
стояние d мив == 3 Tozaa и только Tozaa, Kozaa
а2 ' Ф 21 (mod А) (8.63)
для всех i и j (i =р j), таких, что 2 i + 2j < АМ и а, р Е {+I,
1}.
Д оказатеЛЬСТ80. l CG2 i 2; I 12 i + 2j l < АМ. Т ак как, со-
rласно формуле (8.63), a2 i ......... 2j О (mod А), то в число кодо-
вых чисел рассматриваемых АN-кодов не входят целые числа
t) По предположению 2i j + 1 :;s О (mod А.) П рu,м. перев.
Коды для арuф},(,етuч ск.их устройств
495
веса 2. Кроме Toro, если существует целое i, такое, что 2 i < АМ
и a2 i I!!! О (modA), то А == 2 k , kli (k i) и 12i 2kl < 4M.
В этом случае 2 i 2 k == О (mod А), что противоречит условиям
леммы. Следовательно, в чис.ПО кодовых чисел рассматриваеrvIЫХ
АN кодов не входят и числа веса 1. I(poMe Toro, заметим, что су-
ществует только одно число веса о, а именно А. О 3Шr О. Сладова
тельно, минимальное расстояние рассматрива@мых кодов не
меньше 3.
Предположим наоборот, что a2 i aiII 2j (mod А) дЛЯ некото-
рых i и j (i j), таких, что 2 i + 2} < АМ. Тоrда, так как D ==
=-la2i 2jl< 12i+2jl<AM и la2i 2jl ==0 (modA), то
число D является кодовым числом рассматриваемоrо АN кода,
и, следовательно, последний имеет минимальное расстояние 2
или меньше.
Теорема 8.5. П УСТЬ А (> 1) нечетное простое число. Тоеда
полная система вычетов по модулю А образует конечное поле
ОР(А). Если 2 является nримитивным ЭЛiiМВНТОМ 1) ОР(А), то
2(A 1)/2 + 1
м (А, 3) == А . (8.64а)
Если 2 не является примиТИ8НЫМ элементом ОР(А), Ho 2 Я8
ляется nримитивным корнем ОР (А), то
2(A O/2 1
1\1 (А, 3) == А . . (8.64б)
Верно и обратное, а именно если выполняется (8.64а), то.4
нечетное простое число и 2 nримитuвный корень по модулю А.
Далее, если выполняется равенство (8.646), то А нечетное
простое число, 2. примитивный корень, а 2 nримитивным
корнем не является.
Доказательство. Так как А нечетное простое число, то (2,
А) == 1 и, соrласно теореме Ферма,
2A 1 1 == (2(A I)/2 + 1) (2(A O/2 1) === О (mod А). (8.65)
В разд. 8.1.5 указывалось, что полная и приведенная системы
вычетов по простому модулю А являются соответственно полем
ОР(А) и ero мультипликативной rруппой 0(..4).
Если 2 является примитивным элементом G (А), то 2(A I)/2 9s
1 (mod А). в этом случае 2(A 1)/2 + 1 == О, т. е. 2(A I)/2 == ...... 1,
и так как 2 примитивный элемент а (А), то множество чисел
2 0 === 1 2 1 2 2 2 (А З)/2 2 (A 1)/2:s: ....... 1 2 1 2 2 2 (А""З)/2
, "..." " ,...,
будет приведенной системой вычетов по модулю А. Следователь-
1) ТQчнее, предполаrается, что 2 является образующей мультипликативной
rруппы а (А).
496
r лава 8
но числа ::J::2 j (j (А 3) /2) при делении на А имеют различ-
ные остатки. Замечая, что 2 (A 1)/2 + 1 == О (mod А), и полаrая
АМ == 2(A I)/2 + 1, получаем, что a2i =1= 2; (mod А) дЛЯ всех i
и j, удовлетворяющих условию 1 2i + 2; I < АМ (здесь а, Е
Е {+1, I}). Отсюда и из леммы 8.3 следует справедливость
равенства (8.64а).
Далее рассмотрим случай, коrда примитивным элементом
ОР(А) является число 2. Если (А 1)/2 четное число, то
2(A I)/2 == ( 2)(A 1)/2 Ф 1 (mod А), и, поскольку А простое
число, то, используя формулу (8.65), вновь приходим К сравне-
нию
2 ( А 1)/2 + 1 === О
, т. е.
2(А 1)/2 == ......... 1.
Так как 2 является примитивным элементом, то числа
20, 21, 22, .. ., 2(A 3)/2, 2(A I)/2 == 1, 21, 22, ..., 2(A 3)/2
принадлежат различным классам вычетов. Это означает, что
число 2 также является примитивным корнем и, следовательно,
в этом случае применима формула (8.64а).
Если 2 является примитивным корнем, а 2 не является при-
митивным корнем, то, как следует из вышеизложенноrо, число
(А 1) /2 должно быть нечетным. Кроме Toro, ( 2) (A 1)/2
o =1= О (modA). Так как ( 2)(A I)/2 1 === 2(A I)/2 1 Ф
=/=0 (modA), то 2(A I)/2+1 =1=0 (modA). Вновь обращаясь к
формуле (8.65), получаем, что 2(A I)/2 1 == О (mod А), а имен
но 2(A 1)/2 == 1 (mod А). Отсюда следует, что приведенной систе
мой вычетов является также множество чисел
1 2 22 23 2(A 3)/2 2(A O/2 == 1 2 22 2(А З)/2
, " ,.,., ",...,.
Таким образом, числа + 2; (j (А 3) /2) являются попарно
несравнимыми по модулю А. Так как 2(A I)i2 1 == O(mod А), то,
полаrая АМ == 2(A I)/2 == 1, получаем, что a2 i =1= 2; (mod А) дЛЯ
всех i и j (i =1= j), удовлетворяющих условию 1 2i + 2j I < АМ.
Отсюда из леммы 8.3 следует справедливость равенства (8.64б).
Наоборот, если имеют место равенства (8.64а) или (8.646),
то из леммы 8.3 следует, что a2 i =1= 2j (mod А) дЛЯ всех i и j
(i =1= j), удовлетворяющих соответственно условию
12 i + 2/1 < 2(A l)/2 + 1
или
12 i + 2 i I < 2(A I)/2 1,
и любых а, Е; {+ 1, l}. Эти условия выполняются только в
том случае, если (А 1) /2 чисел + 2 i (О i ( 4 3) /2), а
именно
2 (} 2 i 2! 2 (A 3)/Z
, J ,..., ,
Коды для арифметических устройств
497
пробеrают все элементы приведенной системы вычетов по мо-
дулю А. Следовательно, вычеты по модулю А имеют вид ::I::2 i и
А является нечетным числом. Отсюда в свою очередь следует,
что число А взаимно просто с числом 2 И, кроме Toro, со всеми
вычетами по модулю А, т. е. А является нечетным простым чис-
лом. Это означает, что система вычетов по модулю А является
конечным полем. Так как все степени числа 2, не превосходящие
(А 1) /2, различны, то порядок числа 2 не меньше (А 1) /2.
Кроме Toro, заметим, что порядок числа 2 должен делить А 1.
Следовательно, порядок числа 2 равен либо (А 1) /2, либо
А 1. Для числа 2 рассуждения полностью аналоrичны. В лю
бом конечном поле существует примитивный элемент а 1). Если
порядки чисел 2 и 2 равны (А 1) /2, то числа вида ::J::2 j дол-
жны быть нечетными степенями а, но этоrо быть не может. Сле-
довательно, по краЙней мере одно из чисел 2 или 2 имеет по-
рядок А 1, т. е. одно из чисел 2 или 2 ЯВ.lIяется примитивным'
корнем.
По аналоrии с совершенными кодами Хэмминrа, исправляю-
щими ошибки веса 1, даваемые теоремой 8.5 АN-коды, исправ-
ляющие ошибки веса 1, также можно назвать совершенными в
указанном ниже смысле. АN код длины n, исправляющий ошиб
ки веса 1, дол}кен обладать способностью различать посредст-
вом вычетов по модулю А каждую из 2т возможных ошибок
+ 20, + 21, ..., + 2т 1 веса 1 и правильное кодовое число, т. е.
Bcero 2т + 1 различных исходов. Соrласно лемме 8.З, каждому
из этих 2т + 1 исходов должен соответствовать «собственный»-
вычет, что возможно только в случае, если А 2т + 1. Тео-
рема 8.5 дает необходимые и достаточные условия для Toro, что-
бы выполнялось точное равенство. Условия теоремы таковы, что'
у даваемых ею кодов число А вычетов О, 1, 2, ..., А 1 по MO
дулю А равно 2т + 1 возможным различным исходам. В этом
смысле эти коды являются совершенными. Все АN коды с мини-
мальным расстоянием d мин == З, приведенные в табл. 8.9, яв-
ляются кодами этоrо типа.
Чанr и Рид [12] ДОI{азали следующую теорему, из которой
следует, что, за исключением кодов, указанных в теореме 8.5,-
друrих совершенных АN кодов, исправляющих ошибки веса 1-,
не существует.
Теорема 8.6. AN KOa длины т, исправляющий ошибки веса 1,
является совершенным Tozaa и только Tozaa, Kozaa А простое
число, А == 2т + 1 и одно из чисел 2 или 2 является nрими-
тивным корнеА! по модулю А.
t) Доказательство этоrо факта можно найти, например, в работе [6] вц
стр. 74,
498
r лава 8
Пример 8.7. Если А:;:::: 11, то 2 является примитивным
корнем GF(ll). Из теоремы 8.5 следует, что М(11,З)=::
== (2(11...1)/2 + 1) /11 == 3. Следовательно, llN код с N o == 2 имеет
минимальное расстояние d мин == 3 и может исправлять ошибки
веса 1. Этот код имеет три кодовых числа 11. О == О, 11. 1 ::CI: 11
и 11. 2 == 22, которым соответствуют следующие кодовые слова:
00000, О 1 О 11 и 1 О 11 О.
При этом ненулевыми вычетами по модулю А == 11 являются
следующие числа:
2 i 1 20 21 22 23 21 25 26 27 28 29
2' mod 11 I I 2 4 8 5 10== 1 9== 2 7== 4 3== 8 6 S!E б
Действительно, ::J::2 i ф + 2 j (modA) для всех i и j (i=#=j), таких,
что 12 i + 2j I < АМ == 11. 3 == 33. Каждому из этих вычетов co
ответствует одна из ошибок + 20; ::J::2 1 ; + 22; + 23; ::J::2 4 или пра
вильное кодовое слово. Для справок ниже приведена таблица, в
которой сопоставляются указанным выше 11 возможным оiпиб
кам (Е == О указывает на отсутствие ошибок) вычеты по мо.
дулю 11.
Е 24 .......23 ......22 21 20 О 20 21 22 23 2'
Е mod 11
6
3
7
9
10 О
2 485
в заключение обратим внимание на аналоrию АN кодов и
обычных циклических кодов.
Пусть А (Х) мноrочлен степени r над ОР (2), и пусть n
минимальное целое число, такое, что А (Х) делит ХоП 1. Тоrда
циклический код j ro порядка, порождаемый А (Х), будет пред-
ставлять собой совокупность последовательностей (fo, fl, /2, ...
. . . , fjn l), fi Е GF (2), 1 i jn, длины jn, таких, что l'vIHOrO-
член
f (Х) == fo + f1X + '2 х2 + ... + fJn IXln 1
делится на А (Х). Следовательно, все мноrочлены f (Х), соответ-
ствующие кодовым словаl\1, имеют вид
f (Х) == А (Х) N (Х),
rде N (Х) мноrочлен степени jn . r 1 или менее.
Если А (Х) имеет четное число ненулевых членов, то А (1) == о.
в дейстВ'иtельности верно и обратное. В этом случае для всех
Коды для арифметических устройств
499
КОДОВЫХ слов А (1) == О, т. е. все кодовые слова имеют четный
вес. Такие коды имеют минимальное расстояние Хэмминrа, не
меньшее 2, и, следовательно, MorYT обнаруживать ошибки веса I
(в смысле расстояния Хэмминrа). Мноrочлен А (Х) == 1 + х по-
рождает код этоrо типа, имеющий минимальную избыточность,
равную 1 при любом j. Такие коды полностью соответствуют
АN
кодам, описанным в теореме 8.З.
Если мноrочлен А (Х) является примитивным, то п::::: 2 Т ....... 1,
и поро}кдаемые А (Х) циклические КОДЫ первоrо порядка имеют
минимальное расстояние З и ЯВЛЯlоrся кодами Хэмминrа, ис-
правляющими одиночные ошиБI{И. Эти коды полностью соответ-
ствуют АN
кодам, даваемым теоремой 8.5. Кроме Toro, как было
замечено сразу же после доказательства этой теоремы, И те и
друrие коды являются совершенными.
8.6. АN"коды, исправляющие нратные ошибки
в предыдущем разделе были описаны коды, исправляющие
одиночные ошибки. Как показывают теоремы 8.4 и 8.5, такие
коды MorYT строиться систематическим образом. Что касается
АN
кодов, исправляющих кратные ошибки, то, за исключением
специальноrо случая описанных ниже циклических АN
кодов,
обrцих методов их построения неизвестно.
В табл. 8.9 приведено несколько примеров АN
кодов с мини
мальным расстоянием d МИII === З, 4 и 5. Эти коды были построены
с помощью утверждения 8.2.1, а именно путем последовательноrо
вычисления весов кодовых чисел А. О, А. 1, А. 2, ..., А. N с це-
лью нахождения минимальноrо числа М (А, d), TaKoro, что
А.М (А, d)
d. Однако объем вычислений резко возрастает с
ростом А и d.
В настоящее время одним из полезных методов построения
АN
кодов, исправляющих кратные ошибки, является построение
по известным кодам с некоторым минимальным расстоянием d
кодов с тем же минимальным расстоянием d, имеющих большую
длину. Здесь приведем следующую теорему, принадлежащую
И. Л. Ерошу и С. Л. Ерошу [10].
Теорема 8.7. Если АI nорождает AN
Koa длиной nl с .мини-
АtаЛЬНbtМ расстоянием d] и А 2 nорождает AN
KOa длиной
n2 (n2
nl) с минимальным расстоянием d 2 == [( d + 1) /2], то при
выполнении люБО20 из следующих двух условий:
2 n1 == 1 (mod A 1 ), }
(2 n1 ..... 1, А 2 ) === 1
(8.66)
500
r лава 8
и
2 п1 == ........ 1 (mod A 1 ), }
(2 п1 + 1, А 2 )=== 1
(8.67)
чuсло А == AIA2 порождает AN KOa длиной n(n 2nl) с МИНU-
мальным расстоянием d J .
Доказательство. Докажем теорему в предположении, что
выполняется условие (8.66). При выполнении условия (8.67)
доказательство про водится аналоrично.
Предположим, что по крайней мере для одной совокупности
чисел CXi или 'i, CXi Е (О, +1, 1}) О 'i 2пl 1, имеет место
сравнение
dl l
L a l 2 r1 == О (mod A 1 A 2 ).
1..1
(8.68)
Пусть 'l == nl Х l + Pl, rде Хl === О, если 0< '1 < nl ....... 1, и Х! == 1,
если nl 'l 2пl 1, а Pi Е {О, 1, ..., (nl....... 1)}. Тоrда фор..
мулу (8.68) можно переписать в виде
dl 1
L a l 2 п1 +х л +Pi == О (mod A 1 A 2 ).
1....1
(8.69)
Эта система сравнений должна иметь место также по модулю
А 1 И по модулю А 2 . Поэтому
dl l
L а[2'" == О (mod Ад.
1..1
(8.70)
(Здесь мы воспользовались также условием (8.б6).) Так как А 1
порождает АN код длиной nl с минимальным расстоянием d t ,
то последнее сравнение может иметь место только в том случае,
если
dl 1
L a l 2 Pl == о.
1..1
(8.71)
Кроме Toro, имеется еще система сравнений по мудулю А 2 :
d.....t
L al2пiXt+Pi == О (mod А 2 ).
i ..1
(8.72)
Если в формуле (8.72) Xi === О для d' слаrаемых и Xi == 1 для
d" слаrаемых (d' + d" == d 1 ...... 1), то
d' d"
L aJ2PJ + L a l 2 п1 +Pl == О (mod А 2 ).
/..1 1"1
(8.73)
Коды для "арифметических УСТРОйСТВ
501-
Если предположить здесь, что d' d", то d' [(d 1 1) /2]. При-
d'
бавляя к обеим частям (8.73) L aJ2nJ +Р, и принимая во внн-
. 1 r:::a 1
мание равенство (8.71), получаем
d'
(2 n1 1) L aJ29J == О (mod А 2 ). (8.74)
1:::)
Так как, соrласно формулам (8.66), числа 2 п , 1 и А 2 взаимно
просты, то обе части последнеrо сравнения можно разделить на
2 пl .... 1. В результате имеем
d'
L aJ2PJ == О (mod А 2 ), (8.75)
/..)
rде О Pi nl 1 и rJ,j Е {О, +1, l}. Однако это сравнение
не может выполняться, так как по условию теоремы А 2 поро-
ждает АN код длиной n2(n2 пl) с минимальным расстоянием
d 2 == [(d 1 + 1) /2]. Следовательно, не выполняется и система
сравнений (8.68).
В случае если d" < d', прибавляя к обеим частям (8.73)
d"
число L a , 2° 1 , приходим к тому же выводу.
[..)
Теорема 8.8. Пусть Al' А 2 , Аз l{елые числа. Если целое
число AI nорождает AN Koa длиной n'l с минимальным расстоя-
нием d l == 5, А 2 nорождает AN Koa длиной n2 (n2 nl) с мини-
мальным расстоянием d 2 == 3 и А2Аз nорождает AN Koa длиной
n2.З (n2,3 2nl) с .Аtuнимальным расстоянием d 2 ,з == 3, то при вы-
полнении люБО20 из следующих двух условий:
2 n1 == 1 (mod A 1 ),
(2 n1 + 1, А 2 ) == 1, (8.76)
2 n . == .... 1 (mod Аз)
2 п1 == 1 (mod Ад,
(2 пi :i: 1, А 2 ) == 1, (8.77)
2 n1 == 1 (mod Аз)
число А == А 1 А 2 А з nорождает AN KOa длиной n (n 3nl) с ми-
нимальным расстоянием d == 5.
Теорема 8.9. Пусть А 1 , А 2 , Аз и А. 1 целые числа. Если А 1
и А 2 nорождают AN Koabt длиной по с минимальным расстоянием
d == 5, такие, Ч7'О 2 n !) == 1 (mod А 1 ) и 2 n а == .... 1 (mod А 2 ) J Аз nо-
и
502
r лава 8
рождает AN"Koa длиной nз
4nо с минимальным расстоянием
d з == 3, Аз взаимно просто с 2 2n , ---- 1 и 2 2nо + 1 и А4 является
делителем 2 2по + 1, то А == А 1 А 2 А з А 4 nорождает AN"KOa длиной n
(n
6no) с минимальным расстоянием d == 5.
Теоремы 8.8 и 8.9 MorYT быть доказаны точно так же, как и
теорема 8.7, но здесь эти доказательства опускаются 1). Пр иве-
дем некоторые утверждения, полезные при построении кодов
с помощью этих теорем.
Сначала заметим, что любое целое ЧИС,,'10 А вида
2 kd + 1
А === d ---- нечетное число,
2 k + 1 '
(8.78)
или
А
2 kd
1
d ...... четное число,
2 k + 1 '
rде k === 2, 3, 4, ..., порождаеr АN
код длиной n == kd с мини-
мальным расстоянием d. Действительно, леrко доказать, что для
любоrо целоrо числа А указанноrо выше вида М (А, d) == 2 k + 1
и W (АМ (А, d) ) == 2.
Далее, при любом целом положительном d число
А == (2 kd
1)/(2 k ........ 1)
(8.79)
(8.80)
порождает АN
код длины n == kd с минимальным расстоянием
d. При этом М (А, d) == 2 k ........ 1 и W (АМ (А, d) ) == 2.
Минимальным целым положительным числом, имеющим вес
d, является
А == (22d
1 + 1)/3, (8.81)
но для таких А М (А, d) == 3.
В табл. 8.1 О приведено несколько кодов с минимаЛЬНЫ
1
расстоянием 5, построенных с помощью теорем 8.7
8.9.
8.7. Синдромы и методы декодирования АN-кодов
Предположим, что кодовое число AN в результате арифмети-
ческой ошибки Е переходит в число 1 == AN + Е. Минимальный
вычет по модулю А числа 1:
r А (/) == r (AN + Е) == r А (Е)
(8.82)
определяется только ошибкой Е. Этот вычет бу,nем называть
синдромом числа 1. Естественно, что при отсутствии ошибок,
т. е. при Е == о, r А (1). == о.
{) СМ. [10].
Коды для арифметических иСТРОЙСТ8
503
Таблица 8.10
примеры АN-кодов с минимальныM
расстоянием 5
А А 1 А 2 Аз А. I Длина
кода п
27 531 171 23 7 27
39 215 341 23 5 30
14 145 205 23 3 30
62 715 565 37 3 42
98 635 955 205 341 83 17 60
463 185 1 971 47 5 54
199 797 1 417 47 3 54
11 163 506 255 3641 4681 131 5 90
7739 145297 1 417 1 971 163 17 108
Связь между свойствами синдрома и корректирующей спо-
собностью кода устанавливается следующей теоремой, являю-
щейся обобщением леммы 8.3.
Теорема 8.10. Пусть а некоторое множество ошибок. Для
ТОёО чтобы AN-КОа исправлял все ошибки из множества s, необ-
ходимо и достаточно, чтобы любые две ошибки E i и Ej, такие,
что E i =1= Е; и
I Е i ......... Е J i AN о,
(8.83)
имели различные синдромы.
Доказательство. Пусть Е 1 И Е 2 две различные ошибки.
Если допустить, что эти ошибки нельзя исправить, то найдутся
такие кодовые числа AN 1 и AN 2 , что
AN1+E 1 . AN 2 +E 2 .
Так как O Nl No и O N2 No, то IEl E21==IA(N2
N 1 ) I AN o . Однако r А (E 1 ) == r А (AN 1 + E 1 ) == r А (АН 2 + Е 2 ) ==
== r А (Е 2 ).
Следовательно, код исправляет все ошибки из тоrда и толь-
ко тоrда, коrда r А (E 1 ) =1= r А (Е 2 ) дЛЯ любых двух различных
ошибок Е 1 и Е2, удовлетворяющих неравенству (8.83) 1).
Казалось бы, что в данной формулировке этой теоремы усло-
вие (8.83) можно исключить, а необходимое и достаточное усло-
вие исправления кодом ошибок заданноrо множества сформули-
ровать следующим образом: «все ошибки из 6 имеют попарно
различные синдромы». В действительности, как следует из тео-
{) Необходимость условия (8.83) не доказана. П рим. ред.
504
r лава 8
ремы 8.1 О, это не так; последнее условие является достаточным,
но не необходимым.
Рассмотрим АN код с А == 11 и N o == 2 из примера 8.7. Пусть
множеСтво, состоящее из ошибок Е веса 1, таких, что I Е I <
< А.М (11,3) == 33, и числа О. Этот АN код имеет минимальное
раестояние 3 и, следовательно, может исправлять все ошибки
веса 1. Ошибки из множества удовлетворяют условиям тео-
ремы 8.10, но не обязательно все они имеют различные синдро-
мы. Например, ошибки El == 25 И Е 2 == 1 входят в s, но
rA(E 1 )==rA(E 2 )== 10. Однако поскольку IEI E21 ==33>
> AN o == 22, то условия теоремы 8.10 в действительности и не
требуют, чтобы ошибки имели различные синдромы. Тем не Me
нее обе эти ошибки рассматриваемым АN кодом испраВЛЯIОТСЯ.
Это происходит потому, что ни для каких двух кодовых чисел
AN 1 и AN.2 из трех кодовых чисел О, 11 и 22 не выполняется
равенство AN 1 + El == AN 2 + Е 2 . Рассмотрим, например, уравне-
ние 1 == 11 + Е 1 == 11 + 32 == 43. В этом случае r А (1) === r А (11 +
+Е 1 )== 'А(43)== 10 и, следовательно, возникла одна из двух
ошибок 25 или 1. Однако число 43 ( 1) == 44 > 33 не явля-
ется кодовым числом рассматриваемоrо кода, и, значит, ошибка
.........1 возникнуть не моrла. Допустим, что произошла ошибка 25.
Тоrда 43 25 == 43 32 === ] 1. В результате приходим к выводу,
что ошибка равна 25, а правильное кодовое число равно 11.
Таким образом, исправляемые ошибки не обязательно долж-
ны иметь различные синдромы. Кроме Toro, непосредственным
следствием теоремы 8.1 О является следующее утверждение.
Утверждение 8.10.1. AN 1\,oд исправляет все ошибки из за
даННОёО множества s ТОёда и только ТОёда, к'Оёда при любом
фиксированном целом i все ошибки из S, удовлетворяющие
условию
i Е < i + AN o ,
имеют различные синдромы.
Это утверждение непосредственно следует иэ теоремы 8.1 О,
если 3 !v1етить, что коrда Е, и Ej' удовлетворяют неравенству
(8.84) при одном и том же i, то они удовлетворяют TaKiKe и
(8.83) .
Последнее утверждение оказывается полезным, коrда J.IЗ Be
личину ошибок устанавливается оrраничение. Так как число
1 == AN + Е лежит вобл асти О 1 2 n ......... 1, rде п........ длина
кода, задаваемая равенством (8.32), то
AN < Е < 2 n ....... 1 ....... AN.
Однако поскольку О N N o , то это неравенство можно заме-
нпть на следующее неравенство, не связанное с N:
ANo E 2п 1.
(8.84 )
l8,,8Б)
Коды для арифметических устройств
505
Ошибки Е, удовлетворяющие (8.85), называlОТСЯ реально" воз-
можными ошибками. Для paccMorpeHHoro выше АN-кода с
А == 11 и N o == 2 реально возможными ошибками являются
ошибки, удовлетворяющие неравенству
22 E 31.
KaI{ видно из таблицы, приведенной в примере 8.7, целые числа
веса О и 1, лежащие в этой области (это множество обозна...
чается через 6), имеют различные синдромы. Действительно,
ля АN кодов, даваемых теоре lОЙ 8.5 из разд. 8.5, реально воз-
можные ошибки веса О и 1 имеют различные синдромы, и, более
Toro, эти синдромы «пробеrают» все вычеты по модулю А. .
Однако, вообще rоворя, различные синдромы MorYT иметь не
только исправляемые реально возможные. ошибки. Например,
в приведенном выше примере Е 1 == 17 является исправляемой
ошибкой веса 2. Если эту ошибку ввести в 6, то все элементы 6
будут исправляемыми ошибками и 6 по прежнему останется
множеством реально возможных ОIIJибок. flри этом синдром
r А (E 1 ) == r А (17) == 6 равен синдрому r А ( 16) == 6 ошибки
E2== 16. Однако поскольку IEl E21==33>ANo==22, то
теорема 8.10 и не требует, чтобы ошибки EI и Е 2 имели различ-
ные синдромы.
Остановимся здесь кратко на декодировании АN кодов. Про-
стейший способ состоит в том, ЧТобы построить таблицу декоди-
рования, в которой каждому из 2 n возможных чисел 1 == AN + Е
сопоставлялось бы правильное кодовое число. Однако при дo
статочно больших п для хранения этой таблицы требуется па-
мять большой емкости, а кроме Toro, большим оказывается и
время обращения к этой таблице. Декодирование значительно
упрощается при использовании синдрома. Вычислив синдром
'А (1) == r А (Е) и найдя по таблице ошибку Е, соответствующую
этому синдрому, мо}кно восстановить правильное кодовое число
AN, вычитая Е из 1. Так как Bcero имеется не более А различных
вычетов, то в этом случае используемая таблица имеет не более
А разделов. Если синдрому r А (1) соответствуют две или более
ошибки, то из этих ошибок необходимо выбрать ту ошибку,
после вычитания которой из 1 получается кодовое число (такая
ошибка единственна).
Как можно видеть из этоrо краl Koro пояснения, желательно,
чтобы соответствие между реально возможными исправляемыми
ошибками и соответствующими им синдромами было взаимно
однозначным. Такие коды известны [11], но даже если это усло-
вие не выполняется, можно использовать друrие описанные НИЖЕ!
методы декодирования. Кроме Toro, в случае, если длина кода
такова, что 2 n 1 == О (mod А), ПО.lIезным оказывает я алrоритм
декодирования, описанный в разд. 9.3.
9. Циклические АN"коды
9.1. Структура циклических АN-кодов 1)
9.1.1. Определение циклическоrо АN-кода
Если множество кодовых слов замкнуто относительно цикли-
ческих caeuzoa, т. е. если циклические сдвиrи любоrо кодовоrо
слова вновь приводят к кодовым словам, то такой АN
код на"
зывается циклическим АN
кодом. В частности, если любое ко-
довое слово АN
кода может быть получено циклическими сдви-
rами из любоrо друrоrо кодовоrо слова, то такой код назы
вается сильно циклическим.
Например, рассмотрим АN
код с А == 9 и N o === 6. Кодовыми
числами этоrо кода являются О, 9, 18, 27, 36, 45, 54, которым
соответствуют кодовые слова 000000, 001001, 010010, 011011,
100100, 101101, 110110. Это множество кодовых слов является
замкнутым относительно циклических сдвиrов, и, следовательно,
раесматриваемый АN
код является циклическим.
Циклические АN
коды впервые исследовал Мандельбаум [1].
После этоrо они были предметом большоrо числа публикаций
друrих авторов. В этом разделе рассматриваются основные свой-
ства этих кодов.
9.1.2. КОЛЬЦО целых чисел ПО модулю 2 е ....... 1
и ero идеалы
Если целые числа 2 и В взаимно просты, Т. е. (2, В) == 1 и
показатель 2 по модулю В равен е, то, как следует из изложен
Horo в разд. 8.1.7,
28 == 1
(mod В).
(9.1)
Следовательно, при подходящем выборе целоrо числа А
2 е ....... 1 == А · В. (9.2)
Полная система вычетов по любому модулю является коммута-
тивным кольцом (см. разд. 8.1.5). Пусть Rе
кольцо целых
чисел по модулю 2 е
1. Рассмотрим подмножество кольца Re,
состоящее из чисел, кратных А:
{О, А. 1, А. 2, ..., А. (В.......l)}.
1) Все изложенное в этой rлаве справедливо для системы счисления с
произвольным основанием " используемой для представления кодовых чисел,
но, как и в предыдущей r лаве, оrраничимся лишь случаем ДВОИЧНОЙ системы
счисления, коrда r == 2.
ц uклuчеСl(uе AN -коды
507
Используя равенство (9.2), леrко покаэать, что это подмноже-
ство, состоящее из В целых чисел и включающее О, является
идеалом. Обозначим этот идеал черiЗ 1, а число А назовем ero
порождающим элементом 1) .
Каждый элемент идеала / является числом, которое делится
на А, и, следовательно, идеал 1 является АN"кодом. Следующая
теорема показывает, что этот АN код является циклическим.
Теорема 9.1. Циклический сдвиё двоичноzо представления
произвольноzо цеЛО20 числа идеала 1, т. е. к,одОВОёО слова, также
принадлежит идеалу /2). Друёими словами, идеал 1 замкнут ОТ-
1l0сительно циклических сдВUёОВ.
Доказательство. Так как 2 е == 1 (mod (2 е 1)), то двоичное
представление произвольноrо числа N, входящеrо в 1, имеет Не
более е разрядов. Пусть
е.... 1
N == L а , 2'.
1..0
Вновь пользуясь тем, что 2 е == 1, получаем
e 1 e l e 1
2N == L ai 21 + 1 == L a 1 2 i + 1 + а е ....1 2е == ae 1 + L al"'1 2'
i=-O [..о 1881
(тod 2 е 1).
Таким образом, двоичное представление 2N (mod (2 е 1) яв-
Jlяется циклическим сдвиrом двоичноrо представления N. Так
как 2 является элементом Re и N принадлежит /, то 2N
(mod 2 е 1) также принадлежит 1. Следовательно, двоичное
представление 2N (mod 2 е 1) является кодовым словом.
Введенный таким образом циклический АN код является
идеалом кольца целых чисел по модулю 2 е 1, и все ero эле..
менты являются кратными порождающеrо элемента А. Сумма
по модулю 2 е 1 произвольных двух кодовых слов идеала также
принадлежит идеалу и, следовательно, является кодовым сло-
вом. Кроме Toro, KaI{ видно из выIеизложенноrо,' е определяет
длину кода, а В чИСло кодовых слов.
1) Подмножество S кольца R называется идеалом кольца R, если оно
удовлетворяет следующим трем условиям: 1) S замкнуто относительно сло-
жения; 2) для произвольноrо элемента из S в S существует обратный элемент
по сложению; 3) произведение произвольноrо элемента из S и ПРОИЗFольноrо
элемента из R принадлежит S. Идеалы кольца Re являются rЛRВНЫМИ идеа-
лами. Детальное изложение этих вопросов можно найти, например, в [3].
2) Ниже кодовые числа часто называются также кодовыми словами.
В этом случае имеется в виду двоичное представление этоrо числа
508
r лава 9
9.1.3. Задание циклических кодов
Из предыдущеrо раздела следует, что все кодовые слова ци-
клическоrо АN
кода длины е == Е (2, В), содержащеrо В кодовых
слов, можно построить по двоичному представлению поро}кдаю-
щеrо числа А, которое определяется из равенства 2 е
1 == АВ.
Произвольное кодовое слово может быть построено путем про-
ведения циклических сдвиrов двоичноrо представления А и вы-
числения определенных линейных комбинаций кодовых слов,
получающихся в результате указанных циклических сдвиrов.
В этом разделе, преДСТ8ВИВ порождающее число А в виде
e
l
А == L а / 2/, а / Е {О, 1},
/..0
докажем следующие сравнения 1):
ae
IB ==
21 mod В (mod 2), 1
i
е,
а кроме Toro, укажем простой способ определения коэффициен-
тов ai, О
i
е
1, двоичноrо представления числа А.
Обращаясь к разд. 8.1.11 и равенству (9.2), имеем
ir == 2е
I == А (О, 6 О · . . О i). (9.3)
\. .J
..,
период е
Так как А < 2 е
1, то длина двоичноrо представления А не
превосходит е. Полаrая
А == (ae
lae
2 . · .
alao)t
И3 формулы (9.3) получаем
== О, ae
lae
2 . . . a2 a l a O'
Следовательно, при лю()ом целом i, 1
i
е, имеет место сле-
дующее равенство:
2 ; . . + 2
mod В
8 == ae
lae
2 · · · ae
l, ae
l
l... aOae
l ... ао == q В'
rде q и 2 i mod В/В являются соответственно целой и дробной ча-
стями числа 2i/B. Отсюда в свою очередь следует, что
2 i 2' mod В
q === ae
lae
2 · · · ae
l === В
в
и
(ae
lae
2 . . . ae
i) В == 2' ......... 2' mod В.
(9.4)
1) Напомним, что под 2 i 1110d 8 понимается наимеНЬUIИЙ неотрицательный
вычет 2 i по модулю В.
ц uк;лuческuе А N
к.oды
509
Переходя к сравнению по модулю 2, получаем
ae
IB ==
21 mod В (mod 2) (9.5)
или (поскольку 2 mod 2 == О)
ae
iB == (2
21 mod В) mod 2. (9.6)
Так как (2, В) == 1, то В mod 2 == 1 и, следовательно,
ae
iB mod 2 == ae
i mod 2 · В mod 2 == ae
i mod 2. Так как при
этом ae
iE {О, I}, то ae
i mod 2 == ae
i. Кроме Toro, (2
2imod В) ·
· mod 2 == (2 i mod В) mod 2. Таким образом,
ae
i == (21 mod В) mod 2, (9.7)
т. е. ae
i == 1, если 2 i mod В
нечетное число, и ae
i == О, если
2 i mod В
четное число.
Например, при В == 13, 212
1 == О (mod 13) получаем дво-
ичное представление А, приведенное в табл. 9.1.
т аблuца 9.1
Двоичное предстаВJIение А при В == 13
l
2
3
4
5
6
7
8
9
10 11 12
21 mod В
А
2 4 8 3 6 12 11 9 5 10 7
О О О 1 О О 1 1 1 О 1
1
I
Действительно, 12
разрядным двоичным представлением
А == (212
1) / в == 4095/13 == 315 является 000100111 О 11. Путем
деле
ия ДВОИЧН
IХ чисел можно проверить, что 1/8 == 1/13 ===
== 0,000100111011.
Произвольное ненулевое кодовое слово' этоrо АN-кода мо-
жет быть получено путем циклическоrо сдвиrа А · 1.
9.1.4. Разложение и структура циклических АN-кодов
Циклические АN
l{ОДЫ разлаrаются на подкоды, каждый из
которых в свою очередь может быть разложен на несколько
простых кодов. Простые коды являются cTporo циклическими,
и, следовательно, путем циклических сдвиrов их кодовых слов
можно построить исходный код. Это широко используется при
определении минимальноrо расстояния АN
кодов. В данном
разделе на основе разложения мультипликативной rруппы,опи-
caHHoro в разд. 8.] .8, будет проведено разложение цикличе-
cKoro АN
кода и таким образом описана структура последнеrо.
В результате циклических сдвиrов кодовоrо числа А · 1 ==
== (ae
l, ae
2," " '" al, ао) получаются кодовые слова
510
r лава 9
А2} mod (2t'....... 1), о j е 1. Пользуясь тем, что kA8 ==.
3CI: k (2 е ....... 1) == о (mod (2 е ....... 1)) при любом целом k, все эти ко-
довые слова можно представить в виде
А2/ == А (2/ mod 8 + k8) == А (21 mod 8) (mod 2 е ....... 1). (9.8)
Попытаемся найти аналоrичное сравнение в общем случае,
Т. е. для кодовых слов, получающихся в результате циклических
сдвиrов кодовоrо слова Аа (О < а < В). Пусть (be l, be 2, ...
.. ., b 1 , Ь о ) двоичное представление Аа. Следуя выводу фор-
мулы (9.5) (соответствующему случаю А · 1), можно проверить,
что
be lB == ....... a2 i mod В (mod 2).
(9.9)
Далее представим кодовые слова, получающиеся в результате
циклических сдвиrов Аа, в виде
Аа2 1 == А (а2 1 mod В) (mod (2 е 1)).
(9.1 О)
Следовательно, если а выбрать так, что а a2j mod В, то
всем ненулевым кодовым словам будут соответствовать ненуле-
вые вычеты по модулю 8.
Далее, как описывалось в разд. 8.1.8, приведенная система
вычетов по модулю 8, т. е. множество вычетов, взаимно про-
стых с 8, образует мультипликативную rруппу G (В), и если
G (8) имеет хотя бы одну нетривиальную подrруппу, то G (8)
можно разложить на непересекаIощиеся классы. Так как между
вычетами по модулю В и кодовыми словами существует опи-
санное выше соответствие, то циклические АN коды также МО-
rYT быть разбиты на подкоды, как описывается ниже. Мно-
жество кодовых слов, соответствующих вычетам, входящим в
G (В), назовем подкодом и обозначим через S (В). Путем разло-
жения G (В) на смежные классы по подrруппе можно разло-
жить S (8) на простые коды. S (8) может разлаrаться на не-
сколько простых кодов, каждый из которых будет сильно uик-
лическим и состоять из кодовых слов, получающихся цикличе-
ским сдвиrом HeKoToporo Аа, а Е G (В). Этот простой код бу-
дем обозначать через Са (8).
Очевидно, что подкод S (8) состоит из ер (В) кодовых слов.
Так как е == Е (2, В) по опреJТ.рлению является минимальным
целым числом k, таким, что а == a2 k (mod 8), то каждый про-
стой код содержит е кодовых слов. Следовательно, S (В) со-
стоит из 'V == <p(B)je простых подкодов.
Если 8 является простым числом, то G (8) содержит все вы-
четы по модулю 8, и, следовательно, S (В) содержит все кодо-
вые слова и друrих подкодов, кроме S (8), не существует. Да-
лее, если при этом число 2 является примитивным корнем В, то
е == <р (В) и, следовательно, существует один простой код, кота..
Циклические AN KOabl
бll
рый к тому же совпадает с S (В). Таким образом, если В про-
стое число и 2 примитивный корень В, то может быть по-
строен cTporo циклический АN код.
Однако если В не является простым, то существует вычет
а по модулю В, не являющийся взаимно простым с В. Предпо..
ложим, что (а, В) == d. Тоrда, поскольку (rx/d, B/d) == 1, то
a/d ;Е G (B/d). В этом случае множество кодовых слов, соответ"
ствующих вычетам по модулю В, получающимся умножением
на d вычетов по модулю B/d, взаимно простых с B/d, образует
подкод. Обозначим этот подкод через S (В) d. В S (В) d входит
q> (B/d) кодовых слов. Если показатель 2 по модулю B/d равен k,
а именно если 2 k =:; 1 (mod B/d), то каждый простой код в S (B)d
содержит k кодовых слов. Само собой разумеется, что k яв-
ляется делителем е. Следовательно, S (В) d состоит из Vd ==
=z q>{B/d)/k простых кодов. Здесь следует заметить, что S{B)d
равно (e/k) KpaTHOMY повторению подкода S (B/d), соответству-
ющеrо вычетам из G (B/d).
Таким образом, циклический АN код раскладывается на под-
коды S (B)d.' соответствующие различным делителям d i чис..
t
ла В и содержащие q> (B/d i ) кодовых слов. При этом в каждом
из кодов S (B)d l существует V d l ер (B/d l )/ k l cTporo циклических
простых кодов, каждый из которых содержит k i == Е (2, B/d i )
кодовых слов. Подкод S (B)d i содержит ровно V == 'V d i простых
кодов:
S (B)d l == {Са! (В), С а2 (В), ..., Oak (В), .,., C av (В)},
rде a k (k == 1, . . ., v == V d i ) ........ целые числа, удовлетворяющие
условию (rxk, В) == d i . Схема разложения циклическоrо АN"кода
на подкоды, а подкодов на простые коды показана на фиr. 9.1,
которая позволяет также понять структуру циклическоrо AN-
кода.
Если разложению подкода на простые коды соответствует
разложение мультипликативной rруппы на смежные классы по
ее подrруппе, то разложение циклическоrо АN кода на подкоды
является одним из применений равенства (8.12):
L q> (1-) == в.
l d B
8то равенство дает суммарное число кодовых слов В (вклю-
чая кодовое слово О, соответствующее случаю d == В). Разло-
жение на подкоды соответствует разложению целоrо числа на
слаrаемые. Остановимся на этом несколько более подробно.
;:;- ........
CI)
.л..... ..А.. "'
r "' r
...........
""-- ""--
I
Q ,
't:s 'd
. '"' 1 :а
CIQ
>
.
....
t!
t::,
I
I
CI) I
...
J
I
'-- '-=
.. ...-.. ... . ..........
.",.
'""'
се .
'i
:-)
........
cr)
Q::) I '"
cf)
f
I
l ""
./
v
........
I
,....
У:а.:
'=8
1:{
о
=-=
о)
:2s
Е-8
(J
&.
=
=
о
=-=
1:{
о
=
(Ij
==
(Ij
.
о
to4
О
(.)
си
:=
=-=
:s::
::t
о)
:=
==
о)
о
t:;:
(1')
(Ij
.
....
а)
Циклические AN-КОаbl
513
в целях упрощения рассмотрим случаЙ, коrда В разлаrается в
произведение 1 различных простых чисел, а Иl\lенно коrда
В == Р 1 · Р2. ... · р 1 ,
rде Pi (1 i l) ......... простые числа. От этоrо случая леrко пе..
рейти к друrим ВОЗМОЖНЫl\-I ситуациям. Исходя из разложе-
ния В на простые сомножители, можно построить следующую
каСI<аДНУIО схему подкодов. Начиная с 5 (В), соответствующеrо
случаю d === 1, рассмотрим S (B)d==Pi' 5 (B)d==Pi P /' .. ., 8 (B)d B.
Подкоды можно классифицировать следующим образом: 8 (В)..........
подкод O-ro порядка, 5 (B)Pi (i === 1, ..., l)........ подкоды 1 ro по-
рядка, 5 (B)PiPj (i =1= j, i, j === 1, ..., l) подкоды 2..ro поряд-
ка, ..., 8 (В) в подкод l..ro порядка. Подкоды m-ro порядка,
О т l, представляют собой коды 5 (В) d, rде d произве-
дение тсомножителеи из разложения В; Bcero существует ( )
подкодов т ro порядка. В частности, подкод l..ro порядка со-
стоит только из одноrо нулевоrо кодовоrо слова. Такая струк-
тура называется «пучковой» конструкцией. Пучковая конструк-
ция подкодов В случае В === РIР2РЗР4 показана на фиr. 9.2.
Приведем пример, показывающий, каким образом ЦИК.пиче-
ский АN код разлаrается на подкоды и простые коды.
Пример 9.1. Рассмотрим случай В == 105. При ЭТО I е ===
== Е(2, 105) == 12, АВ == (2e 1) == 212 1 == (3 Х 13) Х
Х(3Х5Х7), А==39. Как следует из изложенноrо в разд.9.1.2,
рассматриваемый код имеет длину е === 12 и содержит 105 KO
довых чисел. Поскольку В является составным числом, у кода
существует несколько подкодов. Подкод O ro порядка 5 (В) ==
== 5 (105) приведен в табл. 9.2. Кодовые слова, приведенные в
этой таблице, были вычислены с помощью формулы (9.7) или
(9.9). Каждый простой код является cTporo циклическим, и все
ero кодовые слова MorYT быть получены путем циклических
сдвиrов кодовоrо слова, помещенноrо в соответствующей rрафе
формулы. Каждый простой код содержит 12 кодовых слов; Bcero
в S (В) содержится ер (В) == ер (3) · ер (5) · ер (7) == 48 кодовых
слов.
Существуют три подкода l-ro порядка: 5(В)з, 8(В)з, 8(В)7;
эти подкоды приведены в табл. 9.3.
Существуют три нодкода 2 ro порядка: 5 (В) 15, S (В)21,
8 (8)35; эти подкоды приведены в табл. 9.4.
В подкоды l-ro и 2 ro порядка входят кодовые слова, соот-
ветствующие ненулевым вычетам по модулю В, которые не яв-
ляются взаимно простыми с В; Bcero имеется (В 1) ер (В) ==
== (1 05 1) 48 == 56 таких кодовых слов. Эти подкоды экви-
валентны подкодам, соответствующим вычетам, которые Прl:
l
llклuческuе AN
KOabt 515
Таблица 9.2
ПОДКОД O-ro порядка S (В)
S (В) === S (105) === {С 1 (8), С 11 (В), С 13 (В), C J7 (В)}
I 2 .l 4 5 6 7 8 9 10 11 12
С 1 (В) 21 mod 105 2 4 8 16 32 64 23 46 92 79 53 1
А · 1 О О О О О О 1 О О 1 1 1
С 11 (В) 11 . 21 m od 105 22 44 88 71 37 74 43 86 67 29 58 11
А . 11 О О О 1 1 О 1 О 1 1 О 1
С 1З (В) 13 . 2/ m о d 105 26 52 104 103 101 97 89 73 41 82 59 13
А .13 О О О 1 1 1 1 1 1 О 1 1
C 17 (В) 17 . 21 mod 105 34 68 31 62 19 38 76 47 94 83 61 17
А .17 О О 1 О 1 О О 1 О 1 1 1
Таблица 9.3
ПОДКОДЫ 1-ro порядка: S (В)з, S (B)s, S (В)7
а) S (В)з === {С З (В), C g (В)}
С з (В) 3.21 mod 105 6 12 24 48 96 87 69 33 66 27 54 3
А.3 О О О О О 1 1 1 О 1 О 1
C g (В) 9.21 mod 105 18 36 72 39 78 51 102 99 93 81 57 9
А.9 О О О 1 О 1 О 1 1 1 1 1
б) S (8) 5 === {С 5 (8), С 25 (В)}
C S (В) 5 . 21 mod 105 10 20 40 80 55 5 10 20 40 80 55 5
А.5 О О О О 1 1 О О О О 1 1
С 25 (В) 25.2/ mod 105 50 100 95 85 65 25 50 100 95 85 65 25
А.25 О О 1 1 1 1 О О 1 1 1 1
В) S (8)7 === {С 7 (8), С 49 (8)}
С 7 (В) 7 . 2/ m od 105 14 28 56 7 14 28 56 7 14 28 56 7
А.7 О О О 1 О О О 1 О О О 1
С 49 (В) 49. 2/ mod 105 98 91 77 49 98 91 77 49 98 91 77 49
А.49 О 1 1 1 О 1 1 1 О 1 1 1
516 r лава 9
Таблица 9.4
ПОДКОДЫ 2-ro порядка: S (В).5' S (В)21 , S (В)З5
а) S (В)15 === {С 15 (8), С 45 (8)}
С 15 (8) 15.21 mod 105 30 60 15 30 60 15 30 60 15 30 60 15
А . 15 О О 1 О О 1 О О 1 О О 1
С 45 (8) 45. 21 mod 105 90 75 45 90 75 45 90 75 45 90 75 45
А.45 О 1 1 О 1 1 О 1 1 О 1 1
б) S (В)21 == {С 21 (В)}
С 21 (В)
21 · 2/ mod 15 42 84 63 21 42 84 63 21 42 84 63 21
А · 21 О О 1 1 О О 1 1 О О 1 1
В) S (8)35 == {С З5 (В)}
с 35 (В)
35. 2/ mod 105 70 35 70 35 70 35 70 35 70 35 70 35
А · 35 О 1 О 1 О 1 О 1 О 1 О 1
надлежат G (B/d). Например, ПОДКОД S (В) з эквивалентен под-
коду S (В/3) == S (35), кодовые слова KOToporo соответствуют
вычетам, принадлежащим G (35) (B/d == 105/3 == 35). Как вид-
но из табл. 9.5, подкод S (35) состоит из двух простых падко-
дав С 1 (35) и С з (35).
Таблица 9.5
S (35) == {С. (35), С З (35)}
С 1 (35) 2/ mod 35 2 4 8 16 32 29 23 11 22 9 18 1
А' · 1 О О О О О 1 1 1 О 1 О 1
С 3 (35) 3 · 2/ m od 35 6 12 24 13 26 17 34 33 31 27 19 3
А' · 3 О О О 1 О 1 О 1 1 1 1 1
Простые подкоды С з (105) и C g (105) совпадают соответст-
венно с С 1 (35) и С з (35). Далее, поскольку k==E(2,35) == 12,
то, как известно, в C 1 (35) и С з (35) содержится по 12 подкодо-
вых слов. Рассмотрим подкод S (В) 21, соответствующий случаю
d==21, B/d==5, k==E(2,5) ==4. Этот код порождается 4-
кратным повторением подкода S (5), приведенноrо в табл. 9.6.
Так как 4 кратный циклический сдвиr приводит к тому же ко-
довому слову, ТО этому ПОДl{ОДУ. принад.тIеЖlIТ Bccro ср(5) == 4
кодовых слова.
ц uклuческuе AN
Koды
517
Таблица 9.6
Построение S (105)21 повторением S (5)
2 i mod 5
А' · 1
243
О О 1
243 1 243 1
О 011 О 011
9.2. Минимальное расстояние циклических АN"кодов
В преДЫДУlдем разделе был описан способ построения цик-
лических АN
I{ОДОВ. После Toro как здесь будут получены oцeH
ки МИlIимальноrо расстояния этих кодов, с ПОl\lОЩЬЮ теоремы 8.1
можно будет оценить их способности исправлять и обнаружи
вать ошибки. Как следует из теоремы 8.2, минимальное расстоя
ние АN-кода равно минимальному из весов кодовых слов, при-
надлежащих этому АМ-коду. Кроме Toro, как мы уже знаем,
простые коды являются cTporo циклическими, и, следовательно,
rрубо rоворя, вес одноrо кодовоrо слова простоrо кода опреде
ляет МlIнимальный вес последнеrо 1). Таким образом, взяв по
одному кодовому слову из каждоrо простоrо кода, определив
веса этих кодовых слов и выбрав среди них минимальный, мо-
жно узнать минимальное расстояние циклическоrо АN-кода.
В соответствии с равенством (3.2) здесь будем считать, что
2 n
1 === А · В. (9.11)
9.2.1. Минимальное расстояние простых кодов
Рассмотрим простой код Са (В). Предположим, что кодовые
слова этоrо кода представлены в каноническом виде, т. е. имеют
представления, удовлетворяющие условию М 2. Для пояснения
возьмем к()д С1з(В) == С 1з (105) из примера 9.1:
А · 13 == (000 111111 О 11) == (00 1 000000 1 О 1 ).
Следовательно, W (А · 13) == 3. Очевидно, что кодовые слова,
получающиеся в результате любых циклических сдвиrов KOДO
Boro числа А · 13, представленноrо в каноническом виде, имеют
одинаковый вес. В этом смысле все кодовые слова, принадле
жащие С 1З (В), имеют один и тот же вес 3.
Следует однако, обратить внимание на одну трудность, свя
занную с тем, что среди кодовых слов, получающихся в резуль
тате циклических сдвиrов каноническоrо представления, имеют
1) Этот вопрос требует дета.пьноrо ИСС"Т'lедования и будет подробно рас-
смотрен ниже.
2) См разд. 8.3.
518
r лава 9
ся слова, являющиеся представлением отрицательных чисел.
Это связано с тем, что, хотя числа А · (а · 2 j ) П1оd В и ЯВЛЯЮТ-
ся положительными, существуют отрицательные числа, сраnни"
мые с ними по модулю 2 n 1. Поэтому, если выписать пред-
ставления минимальноrо веса для всех кодов, получающихея
в результате циклических сдвиrов обычноrо двоичноrо представ
ления ЧИС.па А · а, и определить их веса, то может оказаться,
что некоторые кодовые слова имеIОТ вес, отличный от веса дру-
rих кодовых слов, принадлежащих тому же простому коду. На-
пример,
4 · (13 · 25 mQd 105) == А · 1 О 1 == (1111 О 11 000 11) == ( 1 0000 Т 01001 01)
и w (А · 101) == 5. С друrой стороны,
А · (13 · 211 mod 105) == А · 59 == (100011111101) == (10010000101)
и W (А · 59) == 4. Однако, как видно из табл. 9.2, А · 101 и
А · 59 получаются циклическим сдвиrом А · 13.
Причина этоrо «cTpaHHoro» явления, очевидно, состоит в том,
что число 2 n 1 хотя и представляет О, но имеет вес 2 (так
как кодовые слова являются вычетами по модулю 2 n .......... 1) 1).
Это явление возникает из за Toro, что (00 ... О) и (11 ... 1)
используются для представления одноrо и Toro же кодовоrо
числа. Следовательно, если вернуться к приведенному выше
примеру и из А · 1 О 1 и А · 59 вычесть 2 n .......... 1, то полученные Ka
нонические представления будут иметь уже равный вес. Дей-
ствительно, вычитая 2 n .......... 1 == (11 ... 1) из А. 101 ==
....... .........
== (1111 0 1 !0001 1), получаем кодовое слово (000010011100) ==
== (000010100100), которое является циклическим сдвиrом
А · 13 == (001000000101). Друrими словами, если циклические
сдвиrи каноническоrо представления А · а приводят к кодовому
слову, являющемуся представлением отрицательноrо числа N,
то, поско.п Ьt<у абсолютное значение N меньше, чем 2 n .......... 1, сло-
1) Обратив на это внимание, Рао и rарсиа [11] ввели понятия модуляр-
НОёО веса и м.одулярноzо расстояния. Они определили модулярный вес по мо-
дулю т uелоrо числа 1 слеДУIQ'ДИМ образом:
W m (1) == min {W (1), W (е l)},
rде W(8I) == W(т l) == W(/ т). При этом модулярное расстояние по
модулю т между целы и числами 11 и 12 определяется равенством
D m (/1,/2) == W m (/1 е 12),
rде /1 е/ == (/1 1 2 )modm. Для модулярноrо расстояния по модулю
т === 2 n 1 описанное выше «странное» явление не возникает. В то же вре:\fЯ
известно, что при любых т, равных 2 n 1, 2 n , 2 n + 1, минимальное ариф-
метическое расстояние АN-кодов, для которых m == А. В, совпадает с мини-
мальным модулярным расстоянием. Детально эти вопросы рассмотрены в ра-
ботах [8] и [11] . (Эти вопросы подробно разбираlОТСЯ так}ке в работе
r. А. Кабатянскоrо [13]. Прuм.. ред.)
ц UКЛllческuе A1v Koды
519
жением N с 2 п 1 ( == о (mod (2 n 1))) можно получить по-
ложительное число А · (a2 j ) mod В. Вес этоrо числа можно оце-
нить сверху следующим образом:
W (N + 2 n 1) W (N) + W (2 n 1) == W (Аа) + 2.
в приведенном выше примере W (А · 13) === 3 и W (А · 1 01)
== 5 W(A. 13) +2==5, W(A. 59) ==4<5.
ЕСJ1И выбрать а таким образом, что
а < а2/ mod В, О < j n 1,
то, как следует из вышеизложенноrо, W (А · а) дает минималь..
ный вес кодовых слов простоrо кода, содержащеrо А · а. Та..
ким образом, если определить вес TaKoro кодовоrо слова А · а,
то можно оценить минимальное расстояние простоrо кода Са (8).
Пусть задано двоичное представление А · а:
А · а == (an la n ....2 ... ао).
Тоrда, так как (2,8)== 1, Т.е. В== 1 (mоd2),и 1 == 1 (mod2),
то, заменяя Ь и е соответственно на а и n, формулу (9.9) можно
переписать в виде
an i == a2 l mod В == Xi (mod 2), (9.12)
rде Xi ненулевой вычет по модулю В.
Далее введем понятие центральноrо интервала СВ нечетноrо
числа 8, положив
CB {XlnodBIB 3x<2B}. (9.13)
Как показывает теорема 9.2, центральный интервал иrрает важ-
ную роль при оценке минимальноrо расстояния АN кодов.
Однако, прежде чем перейти к теореме 9.2, сформулируем в
виде лемм два важных свойства центральноrо интервала 1).
Лемма 9.1. В Св существует ((В + 1) /3) целых чисел, сле-
дующих подряд.
Лемма 9.2. Пусть В О (mod 3). Тоrда, если Xi Е СВ, то
(В Xi) Е Св. Друrими словаl\tlИ, если 8 < 3Xi < 2В, то
В < 3 (В Xi) < 2В.
Теорема 9.2.2). Вес кодО8020 слова А. а == (an l, an 2, ...
. . ., ао) равен числу ненулевых, входящих в Св вычеТО8 XiJ та..
ких, что
an l == Xi == a2 l mod В (mod 2), 1 i n.
(9. 14)
1) Так как доказательства этих лемм являются простыми, то провести
их читателям предлаrается самостоятельно.
2) Эта теорема была независимо ДОI<азана rOTO и Фукумура [4], а также
Ченом, XOHroM и Препарата [5].
520
r лава 9
llоказатеЛЬСТ80. Рассмотрим двоичное представление числа
А · За:
А · За == (bn lbn 2 ... Ь о ),
b n ..... l == 3а · 21 mod В == 3Xi mod В (mod 2).
Используя алrоритм нахождения каноническоrо представления,
задаваемый соотношениями (8.50) и (8.51) (см. разд. 8.3), по-
лучаем
А · 2а == (dn ldn 2 ... d o ),
rде dn i == bn i an i. Следовательно, вес W (А · 2с-х) числа
А · 2с-х равен весу W (А а) числа Аа. Отсюда и из леммы 8.2
имеем
rде
n
W (А · 2а) == W (А · a) L , dn i 1.
i == 1
Докажем, что I dn i f =1= О, а следовательно, и an i =р bn l
тоrда и только тоrда, коrда Xi == a2 i mod В является ненулевым
вычетом, принадлежащим Св. Отсюда непосредственно будет
следовать справедливость теоремы.
Сначала дока}кем необходимость. Допустим, что Xi Е св.
Так как по определению
B 3xi < 2В
и В является нечетным ЧИСJJОМ, то
bn i == ЗХl mod В (mod 2) == 3Xi В (mod 2):::=
== ximod2........1 (mod2)*an i.
Следовательно, I dn i I =1= О.
Далее докажем достаточность. Предположим, что Xi Ф CB
Тоrда
а) если 3Xi < В, ТО
bn l == ЗХi mod В (mod 2) ==
== 3Xi (mod 2) == Xi (mod 2) == an l;
б) если 2В ЗХi < 3В, то
bn l == 3Xl 28 (mod 2):=! Xi (mod 2) == an l'
Таким образом, dn i =1= О тоrда и только тоrда, коrда нену"
певой вычет Xi принадлежит Св и, следовательно, вес кодовоrо
слова Ас-х равен числу таких вычетов Xi == a2 i mod В.
В заключение укажеf\.I неоБХОДИl\Iые и достаточные условия
Toro, что код является дОnОЛНЯ/ОlЦUМ, а именно что для любоrо
кодовоrо слова Ас-х == (an lan 2 ... ао) при всех j nj2 имеет
место сравнение
aп } + aп и+n/2) == 1 (mod 2). (9.15)
11.uклtlческuе AN
KOabt
521
Выполнение сравнения (9.15) rарантирует, что оба КОДОВЫХ
слова АС"Х и
Aa принадлежат простому коду Са (В). Это яв
ляется следствием Toro, что кодовое слово
AC"X может быть
получено из Аа путем n/2 циклических сдвиrов.
Если же код не является ДОПОЛНЯIОЩИМ, то для любоrо про
cToro кода Са (8) существует простой КОД C
a (В). Эти два
простых кода являются взаимно дополняющими в том смысле,
что число, дополнительное к произвольному кодовому слову oд
Horo из этих кодов, является кодовым словом друrоrо простоrо
.
кода.
Лемма 9.3. Двоичное представление Аа === (an
1an
2 ... ао)
числа Аа обладает тем свойством, что аn
з + an
и+n/2) == 1
(mod 2) ТО2да и только Tozaa, КО2да 8 делит 2 ni2 + 1 (2де 2 n
........ 1 == А · 8).
Доказательство. Если 2 n / 2 + 1 == О (mod В), то
an
1 + an
(/+n/2) == а2' mod R + a2 f + n/2 mod В (mod 2) ==
== а2/ mod В + (....... а2/) mod В (mod 2) ==
== а2/ mod В + (В ....... а2') mod В (mod 2) ==
== 1 (mod 2).
Наоборот, если аn
з + an
(j+nI2) == 1 (mod 2), 1
j
n/2,
то при подходящем выборе целоrо числ а k имеем (2 n / 2 + 1) Аа==
== k(2 n
1). Так как С"Х < В, то В делит 2 n / 2 + 1.
9.2.2. Минимальное расстояние АN"кодов,
удовлетворяющих специальным условиям
Минимальное расстояние произвольноrо циклическоrо AN
кода можно оценить, используя результаты разд. 9.1 и 9.2.1.
В этом разделе будет рассмотрено неСI(ОЛЬКО случаев, коrда для
минимальноrо расстояния КОДОВ, удовлетворяющих определен
ным условиям, удается получить явные оценки.
Длина n, число кодовых слов В и порождающее число А
всех рассматриваемых здесь кодов удовлетворяют условию
2 n
1 === А · В, и, кроме Toro, n == Е (2, В) делит ер (В). Все
результаты, приведенные ниже в п. «а»
«Ж», получаются He
посредственно из лемм 9.1, 9.2 и теоремы 9.2.
а) В == Р (р
простое число, для KOToporo число 2 являет-
ся примитивным корнем).
Так как В
простое число, то в данном случае n == <р (В) ==
== В
1. Далее, поскольку 2 является примитивным корнем В,
то существует (В
1) ненулевых вычетов, порождающих муль
типликативную rруппу G (В), порождаеМУIО числом 2. Поэтому,
как уже указывалось в разд. 9.1.4, существует толы<o одна под.
522
r лава 9
rруппа S (В), соответствующая G (В). Произвольное кодовое
слово из S (В) может быть получено путем циклических сдви-
rOB А · 1 == (an lan 2, ..., ао) и имеет вес [(8 + 1) /3].
Это можно показать следующим образом. Так как 2 являет
ся примитивным корнем В, то числа Xi == 2 i mod В при измене
нии i от 1 до n «пр,обеrают» все ненулевые вычеты. Следова
тельно, соrласно лемме 9.1, в Св входит [(В + 1)/3] вычетов.
Отсюда и из теоремы 9.2 в свою очередь следует, что вес А · 1
равен ((В + 1) /3), а минимальное расстояние рассматриваемых
АN кодов равно
[ В+l ]
d МИII == 3 .
(9.16)
Далее, так как 2 n 1 == О (Пl0d В) и п == В 1 является
четным числом, то (211/2 1) (2 n / 2 + 1) == о (rпоd В). Если дo
пустить, что 2 п / 2 1 == О (mod В), ТО это противоречило бы TO
r y, что n == Е(2, В) (== ер(В) == В 1). Следовательно, 2 n / 2 +
+ 1 == О (mod В). Но тоrда, соrласно лемме 9.3, рассматривае-
мые коды являются сам'одополняющими.
т аБЛU1 а 9.7
Циклический AN код с В == 13
l 2 3 4 5 6 7 8 9 10 I1 12
2 i mod В 2 4 8* 3 6* 12 11 9 5* 10 7* 1
А · 1 О О О 1 О О 1 1 1 О 1 1
А.3 О О 1 1 1 О 1 1 О () О 1
А.2 О О 1 О 1 О О О 1 О 1 О
в табл. 9.7 приведен код с В == 13 и n == Е(2, 13)==ер(13)==
== 12. Так как 212 1 == (3 Х 3 Х 5 Х 7) Х 13, то А == 315.
Вес А · 2, а следовательно, и вес А.] можно определить по
3, 4 и 5 й строкам этой таблицы или по числу вычетов Xi ==
== 2 i mod В, являющихся элементами С 13 == {5, 6, 7, 8} (в таб
лице эти вычеты отмечены знаком *).
б) В == Р простое число, n == ер (р) /2 и n нечетное число.
Так как в этом случае 2(p 1)/2 == 1 (mod р), то 2 является
квадратичным вычетом по модулю р. Следовательно, соrласно
формуле (8.24), р == 8т::!: 1, rде т целое число. Если р ==
=== 8т 1, то n == (р 1 )/2 нечетное число. Таким образом,
в даННОl\Л случае В == р является простым числом вида Вт 1.
Если n нечетное число, то, соrласно лемме 9.3, код не яв
ляется самодополняющим. Кроме Toro, заметим, что по условию
ер (р) /2 === n. Следовате Т}ьно, в S (В) существуют два простых
кода C 1 (В) и C l (В). Однако, Ka следует из леммы 9.2. если
Циклические AN-КОаbt
523
вычет Xi == 2 i Inod В принадлежит Св, то Xi == 2i mod В Е
Е Св, а поэтому веса равномерно раСП1?еделяются по С 1 (8) и
C l (В). Это означает, что минимальный вес равен [(В + 1) /3]/2
и минимальное расстояние кода определяется равенством
1 [ 8+1 ]
d мин == 2 3 .
(9.17)
Аналоrично определяется минимальное расстояние кодов,
рассматриваемых ниже в п. «в» «ж» 1).
в) В === ра (а > 1), р простое число, 2 примитивный Ко-
рень ра.
В этом случае
d мин { [ р2 i 1 ] [ Р t 1 ]} pa 2.
(9.18)
в частности, если р имеет вид 3k + 1, то все подкоды имеют
один и тот же минимальный вес, равный 1/3 длины кода.
r) В == ра (а > 1), р простое ЧИСLТIО, 2 квадратичный
вычет по модулю р, n === ер (ра) /2 нечетное число.
{ [ р2 + 1 ] [ р 1 ] } a 2
d МИII 2 3 3 р.
(9.19)
д) В === PIP2, Рl И P2 ' простые числа, имеющие своим при-
митивным корнем число 2, В не делит 2 n / 2 + 1, (Pl 1,
Р2 1) == 2.
d мин ; {[ PIP + 1 ] [ РI i 1 ] [ Р2 : 1 ] } . (9.20)
е) В == PIP2, PI И Р2.......... простые числа, 2 примитивныи ко-
рень P и квадратичtIый вычет по модулю Р2, В не делит
2 n tl + 1 и (Р 1 .......... 1, (Р2 1)/2) == 1.
d мин f {[ РIР2 з + 1 ] [ РI i 1 ] [ Р2 i 1 ]} . (9.21)
ж) В Pf'P 1 (ар а 2 > 1), Р 1 И Р 2 простые числа, 2 является
примитивным корнем pfl и p I, (p l l (Р 1 1), p 2 l (Р2 1)) == 2.
В не делит 2 nп + 1. Предположим, что Р2 > Рl.
1) Если Рl == 1 (mod 3), Р2 == 2 (mod 3), то
== pfl ]p 2(PI 1) {[ p + 1 ] ....... [ Р2+ 1 ]}
d мин 2 3 3 .
2) В остальных случаях
d lИlI p , lp I :(P2 1) {[ p ; 1 ] [ Р! i I ]}.
(9.22)
(9.23)
1) Подробно ЭТII вопросы рассматриваiОТСЯ в [2].
b
4
t лава 9
9.2.3. Минимальное расстояние циклических АN"кодов
(В
простое число)
В разд. 9.2.2 были получены точные формулы для минималь-
Horo расстояния кодов, удовлеТВОРЯЮIЦИХ одному из следующих
двух условий. Первое условие состояло в ТОМ, что каждый из
подкодов содержит лишь один простой код. Друrое условие тре..
бует, чтобы длина кода была нечетной, а число простых кодов
не превышало двух. При выполнении этих условий леrко 'найти
распределение весов, а следовательно, и минимальное расстоя-
н ие кода.
В этом разделе рассматриваются оценки минимальноrо рас-
стояния циклических АN-кодов, параметр В которых является
произвольным простым числом. Оценки минимальноrо расстоя
иия таких кодов представляют интерес не только сами по себе,
но и используются для оценки минимальноrо расстояния про-
извольных циклических кодов, для которых 8 является состав-
ным числом. Это связано с тем, что минимальное расстояние
произвольноrо циклическоrо АN"кода не может быть больше,
чем минимальное расстояние какоrо
либо ero подкода S (Pi), па-
раметр Pi KOToporo является делителем В.
Общую формулу для минимальноrо расстояния произволь-
Horo циклическоrо AM
Koдa, число кодовых слов В KOToporo
является простым числом, явно записать не удается. Можно,
однако, указать простой способ вычисления не только мини-
мальноrо расстояния, но и распределения весов.
Как уже неоднократно указывалось выше, длина п цикличе-
CKoro АN"кода определяется из сравнения
2 n ....... 1 == О (mod 8).
При этом n == Е(2, В) и n делит ср(В) == В
1. Положим
B
I
n
(9.24)
'У==
Из разд. 9.1.4 следует, что существует v простых кодов. Все
вычеты по модулю В образуют мультипликативную rруппу
G (В), которая может быть разложена на v классов, каждому из
которых соответствуют v простых кодов С Ui (8), как указано
в табл. 9.8. Вычеты ai выбираются последовательно таким об-
разом, чтобы ai не принадлежал ни одному из i уже построенных
классов.
Если множество {2 1 , 22, ..., 2n
l, 2 n == 2 0 } рассматривать как
подrруппу порядка n rруппы G (В), то разложение, задаваемое
табл. 9.8, будет не чем иным, как разложением G (8) на смеж-
ные классы по подrруппе {21, 22, ..., 2 n }. Следовательно, если
Циклические AN Koды
525
Таблица 9.8
Последовательное разложение G (В)
21
а 21
1
2n l
a12n 1
2 n == 2 0 1
а]
С 1 (В)
С а1 (8)
a'V 121
а 2n 1
" 1
a'V l
Са (В)
" 1
g примнтивный корень В, то, выбирая элементы cti следующим
образом:
а i == gl m о d В, О < i v ...... 1,
аО == gO == 1,
(9.25 )
разложение, задаваемое табл. 9.8, можно построить реrУЛЯРНЬП 1
способом, как показано в табл. 9.9. Разложение, полученное та-
ким образом, и разложение в виде табл. 9.8, полученное после-
Довательным выбором элементов ai, MorYT отличаться порядком
"
следования строк и порядкоr следования элементов в каЖДОII
строке, Но тем не менее они определяют одно и то же разложе-
ние 0(8).
т аблuца 9.9
Разложение G (В) при выборе a l с помощью
формулы (9.25)
I == gO
g.l
g'V ... gV(n l)
g'V+1 g'V(n 1)+1
С. (8)
Cgl шоd В (8)
.
g'V 1
g2'V I
n" .... 1
g
Cg'V 1 mod В (8)
Действительно, 2 я можно представить в виде 2 я == gJ
(mod В), rде j некоторое целое число, такое, что j < в 1.
Следовательно, так как 2 Яn == gjn. == 1 (mod В), то jn
== 1 (В 1), rде 1 некоторое целое число. Отсюда и из фор-
мулы (9.24) получаем, что j == lv. Э ro означает, что 211 имеет вид
gl'V и 1 == О только в том случае, коrда k === О. Покажем, что если
а, Ь < v, то ga И gb не MorYT принадлежать одному и тому же
смежному классу. Действит льно, ес.ли бы эти элементы вхо-
дили в один смежный класс, то, предполаrая, что Ь > а, мы при..
526
r лава 9
шли бы к равенству gb === ga+l'V (О < 1 < v). Однако этоrо быть
не может, так как Ь > v.
Таким образом, каждый простой код является одним из ко-
дов Са. (В), a l === gi mod В, и, соrласно теореме 9.2, ero минималь-
t
ное расстояние равно числу вычетов gi+jV mod В, О j n 1,
входящих в центральный интервал Св === {х mod 8 I 8 3х <
< 2В} числа В. Следовательно, определив минимальные рас-
стояния всех простых кодов C ai , i === О, 1, ..., v 1, и выбрав
среди них минимальное, можно определить минимальное рас-
стояние подкода S (В), а следовательно, и исходноrо кода.
Пример 9.2. Определ'им минимальное расстояние цикличе-
CKoro АN кода с В == 89. Для этоrо кода n == Е (2, 89) == 11,
,,==(B 1)/n==88/11 ==8 и табл. 9.8 переходит в табл. 9.10.
Таблица 9.10
Вычисление минимальноrо расстояния циклическоrо AN "кода
с В === 89 (таблица соответствует табл. 9.8)
l 2 3 4 5 6 7 8 9 10 11 Вес
21 mod 89 2 4 8 16 32* 64 39* 78 67 45* 1 3
3 · 2& mod 89 6 12 24 48* 7 14 28 56* 23 46* 3 3
5 · 2& mod 89 10 20 40* 80 71 53* 17 34* 68 47* 5 4
9 · 21 mod 89 18 36* 72 55* 21 42* 84 79 69 49* 9 4
11.2 mod89 22 44* 88 87 85 81 73 57* 25 50* 11 3
13.2 1 mod89 26 52* 15 30* 60 31* 62 35* 70 51* 13 5
19.2 i mod89 38* 76 63 37* 74 59* 29 58* 27 54* 19 5
33 · 21 m od 89 66 43* 86 83 77 65 41* 82 75 61 33* 3
в этой таблице знаком *' обозначены вычеты, входящие в
множество Св == {зо, 31, 32, ..., 59}; число таких вычетов ука-
зывается в последнем столбце таблицы.
То же самое разложение можно получить с помощыо
табл. 9.9. В данном случае 6 является примитивным корнем
В == 89 и табл. 9.9 переходит в табл. 9.11.
Табл. 9.1 О и 9.11 дают одно и то }I{e распределение весов:
3, 3, 4, 5, 3, 3, 4, 5. Следовательно, раССl\lаrриваемый код имеет
lинимальное расстояние d мин == 3 и может исправлять любые
ошибки веса 1.
В табл. 9.12 приведены значения минимальноrо расстояния,
вычисленные указанным выше образом для В < 300. Кроме ми-
нимальноrо расстояния, в этой таблице приводятся также число
простых кодов v, длина кода n, число исправляемых ОUlибок t
И вычет Xi == gi mod В, соответствующий lIpOCTOMY !{оду Сх i (8),
"
которыи дает минимальное расстояние.
ц uклuческuе А N к:oды 527
Таблица 9.11
Определение минимальноrо расстояния циклическоrо А1V-кода
с В == 89 (таблица соответствует табл. 9.9)
Вычеты 61 mod 89 r=
J
о 2 3 4 5 6 7 8 9 10
60 t- iv 1 8 64 67 2 16 39* 45* 4 32* 78 3
6 1 + i \' 6 48* 28 46* 12 7 56. 3 24 14 23 3
62 + fv 36* 21 79 9 72 42* 69 18 55* 84 49* 4
63+ Jv 38* 37* 29 54* 76 74 58* 19 63 59* 27 5
6 4 + 1 \' 50* 44* 85 57* 11 88 81 25 22 87 73 3
65+ I\' 33* 86 65 75 66 83 41* 61 43* 77 82 3
6 6 +/ V 20 71 34* 5 40* 53* 68 10 80 17 47* 4
6 7 + /v 31* 70 26 30* 62 51* 52* 60 35* 13 15 5
т аблuца 9.12
Минимальное расстояние циклических AN - кодов, соответствующих
простым В « 300) и не относящимся к кодам, рассмотренным
в разд. 9.2.2, а, б
в \' d м.и 11 Х. t n В \' d мин xl t n
t
17 2 2 1 О 8 157 3 14 5 6 52
31 6 1 1 О 5 193 2 28 1 13 96
41 2 6 1 2 20 223 6 10 1 4 37
43 3 4 1 1 14 229 3 22 1 10 76
73 8 2 1 О 9 233 8 8 9 3 29
89 8 3 1 1 11 241 10 4 1 1 24
97 2 14 1 6 48 251 5 14 1 6 50
109 3 10 6 4 36 257 16 2 1 О 16
113 4 6 1 2 28 277 3 28 1 13 92
127 18 1 1 О 7 281 4 20 9 9 70
137 2 20 1 9 68 283 3 28 9 13 94
151 10 4 1 1 15
в заключение приведем верхнюю rраницу для минимальноrо
расстояния циклических АN кодов, параметр В которых является
простым числом. Вывод этой rраницы основан на том, что cpeд
нее арифметическое совокупности чисел является верхней rрани
цей для минимальноrо числа в этой совокупности. Определим
среднее значение минимальноrо расстояния v простых кодов.
Так как общее число вычетов, входящих в Св, равно [(8 + 1 }/3]
Ji эти вычеты распределяются по v прость м кодам, то среднее
528
r лава 9
арифметическое минимальноrо расстояния равно
..!. [ В+l ] == n [ 8+1 ]
,,3 В
1 3 .
(9.26)
Приближенно эта величина равна n/3. Эта rраница справедлива
не только для кодов, рассматривавшихся в этом разделе, но и
является достаточно хорошей верхней rраницей минимальноrо
расстояния циклических АN
кодов, характеристики которых
определяются подкодом S (р) (р
простое число).
9.2.4. Минимальное расстояние циклических АN-кодов
(В
составное число)
Минимальное расстояние кодов, для которых В является со-
ставным числом, определяется почти так же, как и в рассмот-
ренном в разд. 9.2.3 случае простоrо В. Отличие состоит лишь
в том, что если при простом В существует лишь один подкод
S (В), то при составном В необходимо рассматривать уже He
сколько мультипликативных rрупп G (B/d), соответствующих
подкодам S (В) d, для различных делителей d числа 8. I<poMe
Toro, если В не является простым числом, то G (8) не имеет
порождающеrо элемента, подобноrо элементу g, использован
ному в разд. 9.2.3.
Первое из этих отличиЙ приводит лишь К увеличению ЧИС,lIа
подкодов, которые должны быть рассмотрены, и увеличению
в связи с этим объема вычислений, но не создает каких
либо
принципиальных трудностей.
Рассмотрим особенности определения J\fинимальноrо расстоя
ния, связанные со вторым из указанных выше отличий. Так как
В является нечетным числом, то мно)кество степеней 2 h числа
2, взятых по модулю В, является подrруппой rруппы G (В). Если
разложить G (В) по этой подrруппе на v === ер (В) /n смежных
классов, KaI{ было описано в разд. 8.1.8, то можно получить
таблицу, аналоrичную табл. 9.8 из предыдущеrо раздела, т. е.
Таблица 9.13
Классификация выче"тов G (В) (последовательное разложение)
20== 1
а 1
й 2
21 22 23 ... 2n
1
a 1 2 1 a 1 2 2 a 1 2 3 ... a12n
1
а 2 2 1 а 2 2 2 а 2 2 3 ... a22n
1
с ай (В)
С а1 (8)
С a'l (8)
а,,___!
а 2 1 а 2 2 а 2 3 а 2 n
1
"
1 "
l "
1... v
l
Са (8)
"
1
ц иклuцеСf{uе А N -коды
529
расположить Вblчеты входящие в G (8), так, как показано в
табл. 9.13. Лидер ai (О i ::::;; \' 1) каждоrо смежноrо класса
этой таблицы выбирается из элементов, не вошедших ни в один
из смежных классов, ПОРО)I<даемых предшествующими лидерами
(1,j, j < i (ао == 1). Соrласно теореме 9.2, минимальное расстоя
иие просrоrо кода С аё (В) определяется числом вычетов
(1,i. 2 h nl0d В, О k n 1, лежащих в центральном интервале
Св == {х mod В I в 3х < 2В} числа В. Следовательно, вычис
лив минимальные расстояния всех простых кодов Са. (В) И вы.
t
брав из них минимальное, можно определить минимальное pac
стояние S (В).
Вычисленные таким образом значения минимальноrо рас-
стояния некоторых циклических АN кодов, параметр В которых
является составным числом, приведены в табл. 9.14.
Таблица 9.14
Минимальное расстояние d мин и длина n В (2, В) циклических
AN -кодов с составным В « 150)
в п d мин В n d мин В n d мин
15 4 1 77 30 10 117 12 3
21 6 2 85 8 2 119 24 6
33 10 2 87 28 9 123 20 6
35 12 4 91 12 3 129 14 2
39 12 4 93 10 2 133 18 5
45 12 3 95 36 12 135 36 9
51 8 2 99 30 6 141 46 15
57 18 4 105 12 3 143 60 20
69 22 7 111 36 12 ]45 28 6
75 20 5 115 44 14 147 42 14
в заключение этоrо раздела остановимся на связи между
разложением чисел вида 2 n 1 на множители и построением
различных циклических АN кодов, имеющих одну и ту же длину
n. Обычно в разложение числа
2 n 1 Р а 1 р а2 P ak == А · В ( 9.27 )
12 ... k
входит несколько простых делителей. Распределяя эти делители
между А и В так, чтобы выполнялось условие n == Е (2, В),
всеrда будем получать коды одной и той же длины n. Как было
указано в разд. 8.1.11, число 2 n 1 может быть представлено
J3 виде произведеНJ1S{ !{pyroBbIx чисел, а именно
2 n ........ 1 == П Ф d (2),
"I '
(9.28)
530
r лава 9
Е.ели среди делителей В существует простое число, большее n,
КОТорое делит Фn (2), то n == Е (2, В). Если В имеет такой сомно-
житель, то независимо от Toro, каковы друrие сомножители В,
получающийся код будет иметь длину n. Следовательно, выби-
рая В по возможности большим, но так, чтобы выполнялось ука-
занное выше условие, можно максимизировать число кодовых
слов в коде, не увеличивая длину последнеrо. Однако вполне
естественно, что при этом может уменьшиться минимальное рас-
стояние. Как можно видеть из формулы (9.28), число различных
делителей 2 n 1 не меньше ч'исла делителей у n. Поэтому всеrда
можно построить циклические АN коды одной и той же длины
с различным числом кодовых слов и различным минимальным
расстоянием.
Например, рас.смотрим разложение 228 1:
228 1 == Ф28 (2) Ф14 (2) Ф7 (2) Ф4 (2) Ф2 (2) Фl (2) ==
== (29 Х 113) Х 43 Х (127) Х (5) Х (3) Х (1).
Некоторые возможные с.пособы распределения простых делите-
лей ме}l{ДУ А и В приведены в табл. 9.15.
Таблица 9.15
Распределение делителей 228 --- 1 и минимальное расстояние
получающихея кодов
А
8
d мнн
1
127
127 Х 113
127 Х 113 Х 43
127 Х 113 Х 43 Х 5
127 Х 113 Х 43 Х 5 Х 3
29 Х 3 Х 5 Х 43 Х 113 Х ] 27
29 Х 3 Х 5 Х 4::\ Х 113
29 Х 3 Х 5 Х 43
29 Х 3 Х 5
29Х 3
29
1
2
4
6
9
10
Все задаваемые табл. 9.15 коды содержат в качестве под
кода S (29). Так как 2 является примитивным корнем 29, то
минимальное расстояние подкода S (29) равно [(29 + 1) /3] ==
== 10. Как видно из табл. 9.15, по мере введения в число COMHO
жителей В друrих делителей 228 1 , отличных от 29, число ко-
довых слов возрастает, а минимальное расстояние dJ\ПfН YMeHЬ
IlJается. В этой таблице в качестве СОМНО)I{ителя В. который де-
лит Ф28 (2), используется число 29. Поскольку Е (2, 113) ==
== Е (2,29) === 28, то вместо 29 можно использовать также и
113. Однако минимальное расстояние S (113) равно 6, а поэтому
минимальное расстояние кодов, параметр В которых имеет Б ка-
честве сомно)кителя 113, не MO)l{eT превышать 6.
Циклическuе AN
KOabt
531
Наконси, ]а
lСТИЫ, что если отказаться от TOrO, что В должно
содержать в качестве одноrо из своих сомножителей простое
число, которое делит Фп (2), то, определив все делители В числа
2 п
1, УДОВvlетворяющие условию п == Е (2, В), можно найти
максимально возможное значение В, по рождающее циклический
АN
код заданной длины п с заданным минимальным расстоя
ние
1 d. Этот код имеет наибольшее число кодовых слов из всех
кодов заданной длины с заданным минимальным расстоянием и
в этом смысле является оптимальным.
9.3. Декодирование циклических АN"кодов
Так как при декодировании арифметических кодов все вы-
числения выполняются в поле действительных чисел, то обнару-
жение и исправление ошибок леrко можно реализовать с помо-
щью универсальной вычислительной машины, разработав для
нее специальную проrрамму. Это является одним из достоинств
арифметических кодов. Арифметические коды MorYT исправлять
ошибки, возникающие в арифметических устройствах, при пере-
даче данных между вычислительными машинами, во входных и
выходных устройствах, и друrие ошибки, результатом которых
является арифметическая ошибка. Декодер арифметическоrо
кода рассматривает все ошибки независимо от причин, породив-
ших их, как арифметические, и если эти ошибки лежат в об-
ласти корректирующей способности используемоrо кода, то он
правильно восстанавливает исходное кодовое слово. В разд. 8.7
был описан метод декодирования произвольных арифметических
кодов по синдрому. В этом разделе будут описаны два эффек-
тивных алrоритма декодирования циклических АN
кодов, ис-
пользующие специальные свойства последних.
9.3.1. Вычеты по модулю А и конфиrурации ошибок
Тоrда как при построении и вычислении минимальноrо рас-
стояния циклических АN
кодов важную роль выполняют вычеты
по модулю В, при исправлении ошибок более важными оказы-
ваются вычеты по модулю А. Установим сначала связь ме}I{ДУ
ошибками и вычетами по модулю А, а также укажем некоторые
свойства ошибок.
Ошибка всеrда может быть задана с помощью двоичноrо
представления целоrо числа Е:
n
l
Е === L Ci2l, Ci Е {О, 1} (9.29)
ir=O
(здесь п
длина кода). Ошибка 2jE получается сдвиrом двоич-
Horo предстаВJlСНИЯ ошибки Е на j разрядов влево и имеет ту
532
r лйва 9
же КОНфИI'урацию, что и Е. Здесь и ни)ке конфиrурациями оши-
бок называIОТСЯ двоичные ПlJеДСl авления нечетных чисел Е,
меньших А 1). Зададим конфиrурацию Ео =1= О и будем рассмат-
ривать только такие ошибки, которые представляются в виде
2;Е о (О j n 1). При рассмотрении АN кодов с минималь-
ным расстоянием d ошибки Е веса W (Е) (d........ 1) /2 будем
называть исправляемыми ошибками. уJначе rоворя, исправляе
мыми ошибками называются ошибки Е, вес W (Е) которых не
превышает корректирующей способности кода. Далее, если кон-
фиrурация ошибок Ео удовлетворяет условию W (Ео) (d 1)/2,
то она будет называться исправляемой конфиrурацией Оlпибок.
Если в процессе передачи в арифмеrическом устройстве воз-
никает ошибка, в результате которой вместо кодовоrо слова
(ХА (а < В) принимается друrое слово, 10 последнее всеrда
можно представить в виде
аА + 21Ео.
(9.30 )
Взяв остаток от деления числа, СООl'веТСТВУЮlцеrо этому слову,
на А, получим
r А (аА + 2/ во) == (аА + 2/ во) mod А == 2 i Ео mod А. (9.31)
Этот остаток зависит только от ошибки 2;Е о и, как указывалось
в разд. 8.7, часто называется синдромом. Если синдром равен
нулю, то ошибка не обнаруживается (это имеет место, если
ошибки не возникают или если возникаIОТ необнаРУ)l{иваемые
ошибки). Если синдром отличен от нуля, то это означает, что
произошла ошибка.
Чтобы исправить эту ошибку, необходимо определить кон-
фиrурацию ошибки Ео и число j, указывающее место, в котором
она возникла.
Следующая лемма устанавливает взаимно однозначное со-
ответствие между ошибками 2;Е о и вычетами по модулю А.
Лемма 9.4. Если Ео является исправляемой конфuеурацией
ошибок, Т. е. если
w (ВО) (d 1)/2,
то ни при каком j, О < j < n, вычет
R == 2/ Ео mod А
не совпадает с Ео. Кроме TOZO, если i=l=i, 0< i, j < п. то
2'Е о mod A=I=2i Ео mod А.
{) Особой конфиrурацией ошибок является конфиrурация Ео::а: О, соот-
ветствующая отсутствию каких либо ошибок.
ц uклuческuе AN Koды
533
Доказательство. Поскольку R === 2 i Ео mod А, то
R == 21 Ео аА.
Если R == Ео, то
2 j Ео Ео == аА.
Так как минимальное расстояние кода равно d, то W (аА) d
для всех О < а < В. Следовательно,
W (2 i Ео Ео) ;;:: d.
Однако W (2 j E o Е()) W (2jEo) + W (Ео) d 1, и мы полу-
чили противоречие. Таким образом, равенство R === Ео выпол-
няться не может. Если а == О, то
21 Ео Ео == О (mod А).
Так как j < n, то Ео и А не являются взаимно простыми. Пусть
(Е. о , А) == g. Тоrда
2/ == 1 (mod A/g).
Отсюда можно найти минимальное значение j, удовлетворяю
щее приведенному выше сравнению. Так KaI{ в этом случае
ошибка 2 j E o совпадает с конфиrурацией ошибки Ео, то вычет
R === 2 j E o mod А может совпадать с Ео. Вторая часть леммы дo
казывается аналоrично.
Пример 9.3. Циклический АN код ДJIИНЫ n == 18, содержа-
щий В == 19 кодовых слов (А == 13797), является кодом, ис
праВЛЯIОЩИМ ошибки веса 2. Рассмотрим следующую исправ"
ляемую конфиrурацию ошибок:
000000001000000001.
Эта конфиrурация является двоичным представлением числа
513. JlerKo проверить, что (513, А) === 27. Ошибка 29. 513 совпа
дает с приведенной выше конфиrурацией и 2 9 .513 == 513(modA).
Лемма 9.5. Если исправляемая ко1tфиzурация ошибок Ео
(W(Eo) (d 1)/2) удовлетворяет условию 2 j E o > А, ТО вычет
2 j E o mod А исправляемой ошибкой не является.
Доказательство. Если предположить, что R === 2 j E o mod А, ro
при подходящем выборе (Х > О будет иметь место равенство
21 Ео R == аА.
Следовательно,
w (2 1 Е о R) == W (аА) d.
Однако так как \fI (21 Ео) + \V (R) \r! (21 Ео R), то W (2' Ео) +
+ w (R) d
и
\V (R) d W (21 Ео).
534
r лава 9
Таким образом, для веса R мы получили следующую верхнюю
rраницу:
w (R)
d
d;- 1 ::=: d
I .
Эта rраница показывает, что R == 2ЗЕо rnod А не является ис-
правляемой ошибкой.
Пример 9.4. В табл. 9.16 приведены результаты вычисления
вычетов 2ЗЕо mod А для кода из примера 9.3 и конфиrурации
ошибок Е,о === 3, W (Ео) === 2. Эта таблица служит хорошим при-
мером к лемме 9.5.
Таблица 9.16
ЦИКJIические сдвиrи конфиrурации ошибок Во == 000000000000000011
и вес соответствующих вычетов
R === 2fEo mod А
i R
2jEo mod А W (R) j R === 2fEo mod А W (R)
9 1 536 2
10 3072 2 21 Ео < А
11 6 144 2
12 12 288 2
13 1 О 779 7
14 7761 5
15 1 725 5 2 j E o >А
16 3450 5
17 6900 5
о 3 2
1 6 2
2 12 2
3 24 2
4 48 2 2iEo< А
5 96 2
6 192 2
7 384 2
8 768 2
9.3.2. Метод декодирования, основанный
на циклических сдвиrах вычетов
в этом разделе описывается алrоритм декодирования, ис-
пользующий циклический сдвиr вычетов. Сначала заметим, что
если R == Е2; (mod А), то
2 n --- ! R == Е (mod А),
так как 2 п
1 == О (mod А). Отсюда и из леммы 9.5 получаем
следующий алrоритм декодирования. Сначала ВЫЧИСЛЯIОТСЯ вы-
чет Ro == 2ЗЕ-о mod А по модулю А принятоrо кодовоrо слова
(ХА + 2ЗЕо и ero вес W (Ro). Если W (R o ) не превышает
(d
1)/2, то Ro является ошибкой. Если п{е W(R o ) > (d
1)/2,
то Ro сдвиrается влево на один разряд, НаХОДИТСЯ вычет Rl ==
=== 2Ro mod А полученноrо в результате сдвиrа числа 21 Ro и ero
вес W(R 1 ) сравнивается с (d
1)/2. Если W(RJ)
(d
1)/2,
Циклические AN KOabl
535
то Rl является конфиrурацией ошибок. Тоrда, осуществляя сдвиr
на ОДИН разряд вправо, можно определить положение ОIlIибки.
Если W(R 1 ) > (d 1)/2, то осуществляется новый сдвиr, вычис-
.пяется вес полученноrо вычета по модулю А, принимается ре-
шение о том, принадлежит или нет этот вес области корректи
рующей способности, и т. д. Если после HeKoToporo сдвиrа BЫ
численный вес оказывается лежащим в области корректирующей
способности, то это означает, что конфиrурация ошибок найдена
и дальнейшие сдвиrи влево не производятся. При этом опреде
ляется число сдвиrов, потребовавшихся для нахождения конфи
rурации ошибок, и путем осуществления TaKoro же числа сдви
rOB в обратном направлении устанавливается положение ошибки.
Если ни один из сдвиrов не приводит к вычету, вес KOToporo
лежит в области корректирующей способности кода, то это
означает, что произошла обнаруживаемая, но не исправляемая
данным кодом ошибка. Заметим, что некоторые неисправлпемые
ошибки MorYT декодером не обнаруживаться и декодироваться
ошибочно.
Пример 9.5. Вновь рассмотрим ЦИКЛИЧЕСКИЙ АN-код с пара..
метрами n == 18 и В 19, использованный ранее в примерах 9.3
и 9.4. Этот код исправляет ошибки веса 2. Предположим, что
вычет по модулю А (== 13797) принятоrо кодовоrо слова pa
вен 7761. Ero вес равен 5 и превышает 2. Поэтому, соrласно
описанному алrоритму декодирования, будем сдвиrать этот BЫ
чет влево, вычисляя после каждоrо сдвиrа вычет по МОДУЛIО А
и ero вес. Результаты этих вычислений приведены в табл. 9.17,
т аблuца 9.17
Rk и W (RIl) при Ro == 7761
k
Rk W (Rk)
7761 5
1725 5
3450 5
6900 5
3 2
о
1
2
3
4
rде Ro вычет по модулю А принятоrо кодовоrо слова, а Rk
вычет по модулю А после k сдвиrов. Так как W (R 4 ) == 2 лежит
в области корректирующей способности кода, то 5-й и после-
дующие сдвиrи проводить не нужно. Конфиrурация ошибок
J3 данном случае имеет вид
OOOOOOOOOOOOOOOOJJ,
536
r лава 9
Осуществляя четыре сдвиrа в обратном направлении, находим
ошибку
001100000000000000.
Вычитая эту ошибку из принятоrо кодовоrо слова, получаем ис-
ходное кодовое слово.
Если бы в действительности возникла ошибка 7761, имею-
щая двоичное представление
Е == 000001111001010001
и вес которой превышает корреКТИРУТОЩУIО способность кода, то
при декодировании принятоrо кодовоrо слова с помощью опи
caHHoro выше алrоритма декодирования было бы получено то
же кодовое слово, что и ранее, т. е. произошла бы ошибка деко..
дирования.
Однако, как уже указывалось в разд. 8.З, аРИфl\-Iетические
ошибки бывают двух типов: ошибки сложения и ошибки вычи
тания. Ошибки сложения MorYT быть исправлены с помощью
описанноrо выше алrоритма, но в действительности существуют
еще ошибки вычитания. Хотя ошибка вычитания Е является OT
рицательным числом, вычет по модулю А принятоrо кодовоrо
слова по определению всеrда положителен. Действительно, вы..
чет определяется числом А Е или полученным в результате
ero циклических сдвиrов числом 2j (А Е) mod А == А
2jE mod А. Поэтому для каждоrо поло}кительноrо вычета
2JE mod А, соответствующеrо ошибке 2 j E, существует вычет
А 2jE mod А, соответствующий ошиБI{е 2; ( E). Ilервый вычет
будем обозначать через R+, а второй через R . Очевидно, что
R+ и R связаны равенством R == А R+.
Например, в табл. 9.18 приведены вычеты R+ и R дЛЯ кода
из примера 9.5 и ошибок Е == + з.
т аБЛUI{а 9.18
Вычеты R+==2 J BmodА и R ==2J(---Е)mоdА==А""R+
j R+ ==2 j E mod А R == А R+ j R+ == 2 i E mod А R == А R+
О 3 13 794 9 1 536 ] 2 261
I 6 13 791 10 3072 1 О 725
2 12 13 785 11 6144 7653
3 24 13 773 12 12 288 1 509
4 48 13 749 13 1 О 779 3018
5 96 13 701 14 7761 6036
6 192 13 605 15 1 725 12 072
7 384 13413 16 3450 1 О 347
8 768 13 029 17 6900 6897
ц uклuческuе AN
Koды
531
Таким образом, если задан только вычет Ro, то сначала He
известно, соответствует ли он ошибке сложения или ОIlIибке BЫ
читания. Поэтому алrоритм декодирования должен включать
вычисление Ro == А
Ro и определение весов вычетов в про
цессе проведения циклических сдвиrов как для Ro, так и для R.o.
Если вес оказывается в области корректирующей способности
кода,Т. е. если
\V (R k)
(d ........ 1 )/2,
то ошибка является ошибкой сложения. Если проведение цик
лических сдвиrов заканчивается, коrда в области корректирую
щей способности кода оказывается W (Rh), то ошибка является
ошибкой вычитания. В последнем случае для восстановления ис-
ХОДноrо кодовоrо слова наЙденная ошибка должна быть сло
жена с принятым кодовым словом.
Таким образом, при использовании описанноrо ВЫlпе алrо-
ритма декодирования необходимы веса как вычета Rk' так и дo
полнительноrо вычета Rk == А
Rh. Для вычисления весов MO
жно использовать метод, описанный в разд. 8.3. Ilри вычислении
весов полезно знать следующее. Так как нес вычета 2 j R o соnпа
дает с весом вычета Ro, если только 2 j R o < А, необязате.пыlo
вычислять W (2 j Ro). Однако, как леrко видеть, если 2Ro < А, то
2Ro > А. Верно и обратно"е. Следовательно, после каждоrо цик-
лическоrо сдвиrа достаточно вычислить вес лишь одноrо из вы-
четов Rh или Rh В зависимости от Toro, какое из неравенств
2Rk
1 > А или 2Rh
1 < А имеет место. Само собой разумеется,
что если W (Ro) или W (Ro) оказывается в области корректирую
щей способности кода, то необходимости в проведении дальней-
ших циклических сдвиrов нет. [Iри этом искомой конфиrурациеЙ
ошибки является двоичное представление Ro или Ro в заВИСИlVIО
сти от Toro, какое из неравенств W (R o )
(d ........ 1) /2 или
W(Ro)
(d
1)/2 имеет место. Если W(Ro)
(d
1)/2, то
возникшая ошибка является ошибкой сложения, в противном
случае
ошибкой вычитания.
На фиr. 9.3 приведена блок
схема алrоритма декодирования,
детально описанноrо выше.
9.3.3. Метод декодирования, основанный на переборе
Более простым методом декодирования по сравнению С тем,
что был описан в предыдущем разделе, является метод декоди"
рования, описанный ниже. Эт'от метод предусматривает Вычис-
ление расстояний между ПрИНЯ1'Ыl\tl словом И КОДОВЫl'vIИ словами
и основан на том, что если расстояние между принятым словом
и некоторым кодовым словом оказывается меlIыпе или равным
(d....... 1)/2, rде d
минимальное расстояние используемоrо
538
r лава 9
кода, то это кодовое слово является искомым кодовым словом.
Для реализации этоrо метода необходимо иметь таблицу, в
которой хранились бы все кодовые слова, или по рождать кодо-
ЛРJlнятое
KotJodoe
('/7060 М
ВlJlчет
Ro ==MmodA
Rfl/lОЖ r/Н1Щff
'IIIC/fflA,AfIlKC.
IIСЛ/lIl!lItffМ';/ Х
ОИ/I/doк W o
....
6/'IlIt/7t'Hllf
tJ!jttJ//HfHII/I
о с:А Ho
ВЬJl.lетр /f
-....;,
JlKIII/'1t'C/(1I1l В 61'1I/С/1еlI/1С'
c/du! HIl1IlflJp, 6ecll
Rfr 11 Н,р W(l1'k) J.Y111
k-k + 1 W(Rk)
Нет
k-КрtlI!lННР I/IIK
//lIlftrK/l1i cl!lI
d IJl;Jtl TIfIlH 1111
I! /lfl!tft'H/l1I. 2." .k
Да
fKlltllljlll!/lllllf
п,QlIlI/1тOtO /(0-
{}оВuео C'/!o!g
М+2 п /( К"
lIeffotllljlll!tllflA
I!flllll$1110tll KIl
r1tJ!Ot С/Ш!IJ
М z "-К Hk
#t'n,uCl!II!IIIfQe
KIlt7llllle
c4C'lo
Фиr. 9.3. Алrоритм декодирования, основанный на циклических сдвиrах
вычетов.
вые слова некоторым способом. Этот метод применим не rо.ПЬКО
для циклических АN кодов, но и Д,,1]Я произвольных АN кодов И
позволяет исправлять все ошибки Е, вес которых не превосходит
(d 1) /2. Однако в случае циклических АN кодов последова-
Циклические AN KOabl
539
тельное построение кодовых слов может быть реализовано cpaB
нительно просто.
Для Toro чтобы декодировать этим методом одно принятое
слово, необходимо провести сравнение этоrо слов приблизи
тельно с половиной всех возможных кодовых слов. Более Toro,
все эти сравнения необходимо проводить даже в том случае, ec
ли ошибок не было. Чтобы избежать этоrо, можно сначала BЫ
числить вычет принятоrо кодовоrо слова по модулю А, провести
таким образом обнаружение ошибок и лишь после этоrо при
ступать к их исправлению. 11РИВОДИl\Iая ниже леМJ\ilа rаранти
рует, что при использовании указанноrо алrоритма исправляют
ся все указанные BbIllle ошибки. Эта .пемма утвержд.ает, что если
расстояние между принятым словом и некоторым кодовым сло
вом не превышает (d 1) /2, то это кодовое слово является ис-
комым кодовым СЛОВОl\1 И никакое друrое кодовое слово не ле
жит ближе к принятому слову.
Лемма 9.6. Пусть (XIA u а2А два различных кодовых слова
(al =1= (2). Если принято слово аА + Е,
W (Е) d -; l
u d......... минимальное расстояние кода, то неравенства
d (аА + Е, alA) (d ......... 1 )/2,
d (аА + Е, а2А) (d ......... 1 )/2
одновременно выполняться не мосут. Кроме ТОсО, если вы/ол--
няется первое из этих неравенств, то аА == a1A.
Доказательство. Если оба приведенных выше неравенства вы-
полняются одновременно, то
d (аlА, а2А) == W (1 a1A......... а2 А 1) ==
== w (1 al А ......... аА ......... Е а2 А + аА + Е 1) ==
== w (1 alA ...... аА ....... Е) ...... (а2 А аА ...... Е) 1)
w (1 a1A ...... аА Е 1) + w (1 а2 А аА ...... Е 1) ==
== d (аА + Е, alA) + d (аА + Е, а2А) d 1.
Однако так как код имеет минимальное расстояние d и аl =1= !Х2,
то d (alA, a2 4) d, и мы получили противоречие. Следователь
но. если al =1= а2, то приведенные в формулировке леМ 1Ы два
неравенства одновременно выполняться не MorYT. Справедли
вость равенства аА == a1A при условии, что d (аА + Е, a1A)
(d 1) /2 и W (Е) (d 1) /2, доказывается аналоrично.
540
r лава 9
На фиr. 9.4 приведена блок
схема описанноrо выше алrорит"
ма декодирования, в котором, однако, предусмотрено обнаруже..
нне ошибок путем вычисления вычета по модулю А для приня-
Toro слова.
Прwннтое
КОdобое
слобо М
ВЫЧIIС/7еН/JС
6bI'lt'mtl
R=Л4 rnоа А
пQрожtlllЮЩ
'/.IС;10 А,маКс'6ес
tlСnРCZ!;fяеМIJI к
ОНlИООК Jlv'o
Да
nОрfJжrJеНIlt'
кооо80ёО
слоВа kA
/J6/ЧllСАt'Нllе
W(/M
"A/)
<:)
........
Нет
8{lJflи
I(ЛCl Hf
/(oppexт"pye
МС1Н ОИIIlОКО
Декои"рVI}(lll.'.
6 M==kA
Y!c';p'
/1
HHoe KOQO
I
60е c/i1J8Q
Фиr. 9.4. Алrоритм декодирования, основанный на переборе.
9.4. Дополнение
в этой, и предыдущеЙ r.павах бы,ни описаны АN
коды, KOTO
рые MorYT исправлять ошиuки, возникаЮlцие в арифметических
устроЙствах. Завершение
1 этих rлав является данное ДОПОJlне
нне.
Циклические А N Koды
541
До сих пор рассматривались АN кодь" предназначенныIe для
исправления независимых ОIIIибок. Эти коды MorYT использо-
ваться также и для исправления пачек ошибок, но их эффектив
ность в этом случае будет невысокой. Действительно, так как
А не делит никакой сдвиr 2 j E, rде Е произвольная пачка ОIlJИ
бок ДЛИНЫ Ь == [log 2 А] или менее, то этим кодом всеrда MorYT
быть обнаружены произвольные конфиrурации пачки ошибок
длины Ь == [log2 А] и менее.
Далее, так как число ненулевых членов каноничеСI{оrо пред
ставления, описанноrо в разд. 8.3, определяет минимальный вес,
для максимальноrо веса пачки ошибок Ь' длины Ь имеет место
следующая верхняя rраница:
W (Е) [ ] + 1. (9.32)
Следовательно, произвольный циклический код, исправляющий
[Ь/2] + 1 независимых Оlllибок, может исправлять пачки ошибок
длины Ь. Друrими словами, циклический АN код с минимальным
расстоянием d может исправлять любые пачки ОIlIибок длины Ь
и менее, rде Ь определяется равенством
{ d..... 2, d....... нечетное,
Ь==
d ....... 3, d..... четное.
(9.33)
АN-коды, обнаруживающие пачки ошибок и подобные I{одам
Файра, были предложены Мандельбаумом [6]. Эти коды имеют
порождающие числа А вида
А == (20 ....... 1) р.
(9.34 )
При выполнении указанных ниже трех условий всеrда MorYT
быть обнаружены произвольные пачки ошибок Е == 2 i E 1 +
+ 2 j E 2 веса 2.
1) Длины Ь} и Ь 2 конфиrураций пачек ошибок El и Е 2 yдo
влетворяют неравенству
с ....... 1 Ь 1 + Ь 2 .
(9.35)
2) Число р является простым и
[log2 р] min (Ь}, Ь 2 ).
(9.36)
3) Длина кода n НОК (с, е), rде е == Е (2, р).
542
r лава 9
Если с нечетное чис.по, с;;:: 2Ь, [log2 р] == Ь, n НОК (с,
е), то коды с таl{ИМИ параl'летрами MorYT обнаруживать произ-
вольные пачки ошибок веса 2, длины Ь и менее. Кроме Toro, эти
коды MorYT исправлять произво.пьные пачки ОllIибок веса 1,
длины Ь и менее.
rOTO и Фукумура [7] установили необходимые и достаточные
УС.повия Toro, что I{ОД исправ.пяет пачки ОIIIибок веса 1 или обна-
руживает пачки ошибок веса 2. Они показали, что этим усло
виям удовлетворяют АN коды, испраВЛЯЮlцие ОIlIиБI{И веса 1
с порождающими числами вида р (2 с :f: 1), р (2 2hm 1) / (2'l +
+ 1), р (2h(2m l) + 1) / (2 h + 1), rде р простое число.
К числу кодов, используеl\1ЫХ в арифметических устройствах,
относятся также как называемые A1,J-lО200статочные коды. MHoro
остаточныЙ код определяется k целыми поло)китеЛЬНhIМИ чис
лами тl, т2, . . . , mk и сопоставляет каждому числу N (О N
пz 1, т == 2 n 1) СОВОI<УПНОСТЬ (k + 1) це.пыIx чисел (N,
C1(N), C 2 (N), ..., Ck(N)), rде Ci(N) вычет N по модулю т.i
и mi поло)кительный делитель т. Кодовое слово TaKoro кода
представляет собой последовательность двоичных представле
ний числа N и вычетов С 1 (N), С 2 (N), . . . , C h (N). Так как
C i (N 1 :f: N 2 ) == (N 1 :f: N 2 ) mod тi == (C l (N 1 ) + C i (N 2 )) mod /nl (9.37)
и
C l (N 1 · N 2) == (N 1 · N 2 ) mod тi === (C i (N 1) · C i (N 2)) mod пZi, (9.38)
то сумма, разность и произведение кодовых слов также являют-
ся кодовыми словами. Отметим также, что в кодовых словах
мноrоостаточных кодов можно выделить информационные сим-
волы, представляющие число N, и проверочные СИl\1ВОЛЫ, пред-
ставляющие k остатков C i (N), что является одним из достоинств
этих кодов.
Между мноrоостаточными кодами и АN кодами существует
тесная связь. Мноrоостаточному коду, порождаемому целыми
числами mI, т2, ..., тh, можно поставить в соответствие AN..
код, взяв в качестве порождающеrо числа последнеrо НОК (тI,
т2, . . . , тh)' Число кодовых слов В этоrо AN Koдa определяется
из равенства АВ == m == 2 n 1. При этом по k вычета i
С 1 (N), ..., C k (N) произвольноrо числа N (О N т 1)
однозначно может быть определен вычет N mod А по модулю А
и, наоборот, по вычету N mod А MorYT быть определены OДHO
значно вычеты С 1 (N), . . . , C k (lV) 1). В силу этоrо мноrоостаточ
ные коды и соответствующие им .AN KOДЫ имеют одинаковую
корреКТИРУЮЩУIО способность.
1) Это является следствие I теоремы теории целых чисел, известноЙ под
названием китайской теоремы об остатках.
Цu"лuческuе AN-КОаbt
543
Опубликовано несколы<о работ, посвященных мноrоостаточ-
ным кодам [8, 11], в которых затронутые выше вопросы paCCMO
трены БОJIее детально.
На большое сходство АN кодов И циклических алrебраиче-
ских кодов у>ке УК3Зblвалось в конце разд. 8.5. Однако если рас-
сматривать циклические АN коды, то это сходство оказывается
еще более rлубоким. Этот вопрос подробно рассматривается в
работе Месси и rарсиа l8]. в последние rоды было проведено
несколько исследованиЙ, посвященных поиску циклических А.ЛJ-
кодов, соотвеТСТВУЮIЦИХ некоторым хорошим циклическим алrе-
браическим кодам и исследованию их свойств 1).
В заключение I<ратко остановимся на применении рассмо-
тренных кодов. В настоящее время для повышения надежности
вычислительных устройств применяются слеДУЮll{ие методы:
1) использование трех идентичных устройств (тройное дублиро
вание) для выполнения одноЙ и тоЙ же операции и мажоритар..
ное декодирование их выходов; 2) использовние двух идентич
ных устройств (двойное дублирование) с целью обнаружения
неисправностей и 3) использование арифметических устройств,
предусматривающее кодирование подлежащей обработке ин
формации и контроль последней после обработки. Последний из
этих методов не rарантирует исправления ошибок при всех воз-
можных арифметичеСI{ИХ операциях, но стоимость аппаратуры,
необходимой для ero реализации, меньше, чем стоимость допол-
нительных устройств, необходимых для реализации первоrо и
BToporo методов. Кроме Toro, использование арифметических KO
дОВ позволяет проводить одними и теми же методами исправле-
ние ошибок, возни]{аЮII ИХ как при передаче данных, так и при
их обработке в арифметических устройствах. Блаrодаря этому
арифметические коды эффективно MorYT использоваться в COBpe
менных системах связи и друrих устроЙствах.
Наиболее rлубоким исследованием, ПОСВЯll{енным примене
нию АN кодов в реальных системах, по видимому, является ис..
следование, проведенное Авидзинисом и др. [9] в рамках проекта
JPL STAR Лаборатории реактивных двиrателей, имевшеrо
своей целью создание сверхнадежной вычислительной машины
для космических кораблей. Авидзинис и друrие исследовали эф
фективность AN KOДOB не только при исправлении ошибок, воз
никающих при обычных арифметических операциях, но и при
сдвиrах чисел, вычислении дополнительных чисел и др. Кроме
Toro, были проведены экспериментальные исследования процес-
сора с длиной слова 4 байта (32 бита), использовавшеrо AN..
код с А == 24 1, который может быть реализован с ПОJ\iIОЩЬЮ
относительно простых и недороrих устройств. Результаты нселе-
1) ЭТll вопросы рассмотрены в КНИl'е Рао [12].
544
r лйва 9
дования проведенноrо Авидзинисом и друrими, в частности, до-
казываlОТ высокую эффективность использования АN кодов с по
рождающими числами А вида 2 Ь 1 для обнаружения ошибок
в вычислительных машинах с параллельной обработкой бантов
длины Ь.
Предполаrается, что АN коды, рассмотренные в этой и пре
дыдущей rлавах, будут неоБХОДИМЬt д.пя достижения CBepXBЫ
сокой надежности вычислительных маLUИН, состаВЛЯIОЩИХ основу
бо.льших ИНфОрl\1ационных систем, которые будут созданы в бу
дущем.
Приложения
ПРИJ10жение 1. Разложение чисел вида 211.......1
на простые множители и таблица
неПрИ80ДИМЫХ мноrочленов
в табл. А.l содержатся разложения чисел 2 п
1, О < n
50, на простые множители. В этой таблице рядом с числом п
стоит разложение 2 п
1 на простые множители. Отмеченные
знаком .
.:. сомножители MorYT не быть простыми, но ни на одно
простое число, меньшее 25013, они не делятся.
В табл. А.2 помещены неприводимые мноrочлены над ОР(р),
р == 2, 3, 5, в следующей записи:
Р==р NI==m E
e
i fi ...
rде fi
минимальный мноrочлен ЭЛе
ента a,i, сх
некоторый
примитивный ЭJlемент. В случае р == 2 для записи коэффициен-
тов мноrочленов используется восьмеричное представление (ко-
эффициенты двоичноrо представл
ния разбиваются на rруппы
по три символа, начиная с младших разрядов, и каждая rруппа
записывается с помощью одноrо в()сьмеричноrо числа; напри-
11 11 11
мер, двоичному представлению 011 101 001 соответствует вось-
меричное представление 351; от двоичноrо представления леrко
перейти к восьмеричному представлению и наоборот).
Пример. В случае р == 2, f1l === 4 и е
15 число 23 в паре
(1, 23) является восьмеричным представлением неприводимоrо
lноrочлеlIа Х 4 + х + 1 над GF (2), поскольку число 23 является
u
восьмеричным представлением двоичнои последовательности
010011.
В случае р === 3, т === 2 и е == 8 последовательность 112
в паре (1,112) является непосредственно последовательностью
коэффициентов неприводимоrо МНОJ'очлена Х 2 + х + 2.
Для любых Р и т мноrочлен 'l пары (1 t fl) является прими-
тивным мноrочленuм, и ero показатель е равен рт
1. Если
существует несколько примитивных мноrочленов заданной сте-
пени над GF(p), для данной таблицы выбирался тот из них, ко-
торый имеет минимальное число ненулевых коэффициентов,
а при наличии нескольких таких мноrочленов
тот, последова-
тельность коэффициентов KOToporo, рассм атриваемая как р
ичное
"
число, является наименьшеи.
Для любых р и т в таблицу помеlI
ены только неприводи-
мые мноrочлены, степень которых в точности равна т. По этоft
546
п рuложеНll.'l
,., u"
таОЛllце мо,кно опреде,пить
IИIIИ
lаv1ЬНЫИ
1IIоrОЧ.,1СIl Лlоооrо Э1l1е
leHTa a,i, 1
i ::::;; рт
20 Если i не указано, в таблице следует
найти одно из чисел i k или i[, таких, что i k == ip/{ mod (р1n
1)
и i[ ==
ip[ mod (рп!
1). Если в таблице приведено (ik' fi k ), то
искомым минимаЛЬНЫ
1 :VIноrочленом элемента a,i ЯВ,,1яется
fik. Если указана пара(il' f i /), то ИСКОМЫ
1 минимаЛЬНЫ
1
IHO
. I'!' U U ('
rочленом элемента a.
l оудет мноrочлен, двоиствеНlIЫИ 1\ 1..
l[
При проведении подобных вычислений удобно пользоваться
,.
таолица:VIИ циклов.
Пример. Случай р == 3, т === 2.
Из таблицы берем примитивный мноrочлен Х 2 + х + 2. НаЙ
дем минимальные мноrочлены fi над GF(3) элементов a i :
1) f2: по таблице находим (2, 101); с.педовательно, 12 ==
== Х 2 + 1.
2) iз: так как 3 в таблицу не входит, то строи
таблицу
циклов:
3,9(== 1);
следовательно, tз == {l.
3) f4: аналоrично строим цикл
4,2(==4);
так как этот цикл имеет длину 1, то искомый мноrочлен имеет
степень 10
4) f5: в это.\! случае таблица ЦИКЛОВ 11 \1еет 13И,.1
5, 15(===7==
1);
мноrочленом, двойственным к fl, является X2(X
2 + X
l + 2) ==
==2X2+X+l==2(X2
X
I) (поскольку 2==
1); значит,
f 5 == f 7 == Х 2
Х
1.
5) f6: 6, 18 === 2; следовательно, f6 == f2.
Табл. А.l и А02 были построены С. Адзуми. l'абл. А.l построена
с помощью ЭВМ NEAC 2200
500 TSS, а табло А.2
с помощью
ЭВМ FACOM 230
45 S.
Приложение 2. Параметры ДВОИЧНЫХ БЧХ"кодов
В узком смысле ДЛИНЫ 1 023 и менее
в табло А.3 приведены следующие параметры двоичных
БЧХ
кодов в узком смысле длины 1023 и менее: п
длина кода,
k
число информационных символов, d вчх
rраница БЧХ
л рuложенuя
547
If разность d мин d БЧХ , rде d мин истинное минимальное pac
стояние кода. Для кодов, истинное минимальное расстояние KO
торых не определено, в rрафе d мин dвчх стоит знак . Зна
чения параметров 11, k и dвчх , приведенные в табл. А.3, взяты
из табл. 9.1 книrи Питерсона и Уэлдона. Значения d мин полу
чены на основании результатов работ [9, 10, 12, 13] из списка
литературы к rл. 4.
Таблица А.l
2 з 27 7.73.262657
3 7 28 3.5. 29.43.113.127'
ц 3.5 29 233.1103.2089
31 30 2
3 .7.11.31.151.331
6 32.7 31 214748з647
7 127 32 3.5.11.257.65537
8 3.5.11 33 7.23.89.599479
9 7.73 з4 3.43691.131071
10 3.11.31 35 31.71.127.122921
J.1 23.89 з6 3
3 .5.7.13.19.37.7З.109
12 2 З7 22з.616318177
3 .5.1.13
13 8191 з8 3.91625968981*
14 3.43.127 39 7.19.8191.121369
15 1.31.151 40 2
3.5 .11.17.31.41.6168]
16 3.5.17.251 41 13367.164511353
.17 131071 42 2 2
3 .7 .43.127.337.5419
18 3 4з 4З1. 9719. 209986з
3 .7.19.73
19 524287 44 3.5.23.89.397.683.2113
20 2 45 7.31.73.151.631.23311
3.5 .11.31.41
21 2 46 з.47.49906910164з.
7 .127.337
22 3.23.89.683 47 2351.4513.13264529
23 47.118481. 48 2
3 .5.1.13.17.97.241.257.673
24 2 .. 4 49 121.4432676798593.
3 . .7.1З.17.2 1
25 31.601.1801 50 3.11.31.251.601.1801.4051
26 З.2731.8191
548 П рuложенuя
Таблица А.2
Р=2 =2 Е=3
1 7
Р=2 м=3 Е-7
1 13
Р=2 М-4 Е='
Э 31
Р=2 м-4 Е=15
1 23
Р-2 M=S Ее'l
1 45 Э 75 67
Р=2 м-Б Е=9
7 111
Р=2 м=6 Е=21
3 127
Р=2 м=6 Е=63
1 103 , 141 11 155
Р=2 м.7 Ez121
1 203 Э 253 5 217 7 375 9 211 11 211
13 345 19' 351 21 313
Р=2 м=8 Е=17
15 727 45 4'1
Р.2 м=8 Е-51
5 76.3 25 43з
Р.2 м=8 Е=85
3 567 9 675 21 613 21 477
Р=2 м-в Е.=255 23 4)
1 4.35 7 551 11 747 1) 453 19 545
31 537 43 703
Р=2 M z 9 Е=73
1 1231 21 1027 35 1401 71 1511
Р=2. tA=9 Е='11
1 1021 3 11з1 5 1461 9 1423 11 1"';5 13 1167
15 1541 17 1333 19 1605 23 1751 25 1143 21 1617
29 1553 37 1157 39 1715 l 1563 43 1713 45 1175
51 1725 S3 1225 55 1275 15 1173 83 1425 85 1267
Р=2 M-=lO Е=11
93 ,777
Р=2 м с 10 Е=33
31 3043 155 22';1
Р=2 м=10 Е=93
11 2065 55 3453 71 2413
Р=2 м.10 Ее3"1
3 2017 9 2257 15 2653 21 3753 27 3573 39 2107
45 3061 51 2547 57 3121 69 2701 75 2431 81 2311
105 3607 147 2355 171 3315
Р=2 м-10 Е=1023
1 2011 5 2415 7 3171 1, 2151 11 3515 19 2773
23 2033 25 2443 29 2461 Э, .3023 37 3543 41 2745
'43 2431 47 3177 49 3525 '3 2617 9 3471 71 3323
13 3507 83 3623 85 2707 89 2321 r;1 3265 101 2055
103 3575 107 3111 109 20'+7 149 з025 173 3З37 179 3211
Р-2 M c ll Е=23
8, )4'
п рuложенuя 549
ПроВо//жеНIIС
Р=2 M-ll Е=89
23 4757 69 6771 115 7311 299 4303
Р.2 м=11 Е-2047
1 4005 3 4445 5 4215 7 4055 9 6015 11 7413
13 4143 15 4563 17 4053 19 502 21 5623 25 4577
21 6233 29 6673 31 1237 33 1З35 35 4505 37 5337
.39 5263 41 5361 43 5171 45 6637 47 7173 49 5711
,1 5221 53 6307 55 6211 57 5747 59 4533 61 4341
67 6711 71 7715 73 6343 15 6227 77 6263 79 5235
81 7431 83 6455 85 5247 87 526'; 91 4761 93 5607
99 603 101 6561 103 7107 105 1041 107 4251 109 5675
L11 4173 113 4707 117 546З 119 5755 137 6675 139 7655
L41 55З1 147 7243 149 7621 "151 7161 153 4731 155 4451
L 7 6557 163 7745 165 7317 167 5205 169 4565 171 6765
L7Э 7535 179 465.3 181 5411 18з 5545 185 1565 199 6543
201 5613 203 6013 205 7647 211 6507 213 6037 215 7'з6)
217 7201 219 7273 293 7723 ЗО1 5007 З07 7555 309 4261
331 6447 333 5141 339 7461 З41 5253
Ра:2 М=12 Е=1З
315 11771
Р=2 м=12 Еас35
117 16475
Р=2 м-12 ЕаЗ9
105 13617
Р.2 М=12 Е-45
91 10011
Р=2 "1=-12 Е-65
63 10761 189 13535 441 15353 693 12345
Рс2 м=12 Е=91
5 15173 135 10571 405 13003
Ра2 M za 12 E=-105
39 13321 429 11073
Р.2 м-12 E.=117
.35 10377 175 16757 595 13413
Р=2 м а 12 Е=195
21 10065 147 17651 231 10167 351 15347
РIC2 м=12 Е=273
15 13077 75 16267 1&5 10621 285 17141 345 14537 435 10743
р ас 2 M=-12 Е=31.,
13 12513 143 12111 169 16547 221 17513 299 16401 403 14373
Р-2 М=12 Е-455
9 11165 27 14405 81 17545 99 17323 153 13517 171 10213
207 10603 219 16137 291 17073 ЗЗЗ 11703 423 14313 603 14411
Р=2 м=12 Е=585
7 1215.3' 49 17103 77 15115 119 14з15 133 11433 203 13157
217 13563 ЗО1 12315 329 11637 343 12673 311 14043 427 10245
Р=2 М с 12 Е=819
5 10115 25 13377 55 10201 85 11673 95 11705 115 13223
145 16535 155 14241 185 14037 205 14513 215 10653 235 11411
275 14601 295 11463 355 10461 з65 11265 425 14155 685 16355
Р-2. t-1:11 2 Е=1З65
3 12133 ЭЗ 13311 51 10355 57 12331 69 16663 81 17361
93 14755 111 15415 123 13475 141 13511 177 16011 183 14111
201 14067 213 16457 219 11657 237 13137 291 15715 309 11763
321 17233 339 1ьооз 363 11045 411 10071 597 1226'; 717 16571
Р=2 М=12 Е-4095
1 10123 11 15647 11 16533 19 1Ь047 23 11015 29 14127
.31 17673 37 13565 41 15341 43 15053 '+7 15621 5.3 15321
59 11417 61 13505 67 1327'; 71 11411 .73 16231 79 12515
83 12255 89 11271 91 17121 101 14227 103 12111 107 14135
109 14711 113 13131 121 16S21 lJ7 15437 139 12067 149 121lt1
550 П рuложенuя
Р=2 м=-12 Е=4095 ПроооАжение
151 14717 151 14675 16з 10663 167 16115 173 12247 179 1167S
181 10151 187 14613 197 11441 199 10321 209 11067 211 14433
227 12753 229 134з1 233 11313 239 13425 277 1Ь021 281 17025
283 15723 293 11477 307 14221 311 12705 313 14357 з31 16407
341 11561 347 11711 349 13701 з59 11075 361 16363 397 12127
407 17057 409 10437 421 14271 437 12623 439 12007 587 14545
,89 16311 613 15413 619 1711+7 661 10605 683 10131 691 15701
Р=-2 м=1з '::-8191
1 20033 3 23261 5 2"623 7 23517 9 30741 11 2164'
13 30171 15 21277 17 27177 19 35051 21 34723 23 34047
25 32535 27 31425 29 37505 31 36515 33 26077 35 35673
37 20635 39 33763 41 25745 43 36515 45 26653 47 21133
Ч9 22441 51 30417 53 32517 55 373ЗS 51 25321 59 23231
61 25511 63 26533 65 3334Э 67 33727 69 27271 71 2 oi7
73 26041 75 21103 11 27263 19 24513 81 32311 83 )1143
85 24037 87 30711 89 з2641 91 2't651 93 32437 95 20213
91 25633 99 31303 101 22525 10з 34627 105 25715 107 21607
109 2S363 111 21217 113 33741 115 31611 111 23017 119 21263
121 31011 12.3 27051 125 35477 131 34151 133 21405 135 34641
137 32445 139 36375 141 22675 143 36073 145 35121 147 36501
149 33057 151 36403 153 з5567 155 23167 157 36217 159 22233
"161 32333 163 24703 165 33163 167 ,21')7 169 23761 171 24031
173 30025 175 37145 117 .31327 179 27221 181 25577 183 22203
185 374Э7 187 21537 189 31035 195 24763 191 20245 199 20503
201 20761 203 25555 205 30351 201 33037 209 34401 211 32115
213 21,.47 215 21421 217 20363 219 33501 221 20425 223 32347
225 20677 221 22307 229 ,33441 231 33643 233 24165 235 21421
237 24601 239 36721 241 34363 24t3 21673 245 32167 247 216Ь!
265 33351 261 26341 269 31653 271 31511 273 23003 215 22657
277 25035 279 23267 281 34005 283 34555 285 24205 291 26611
293 32671 295 25245 291 31407 299 33471 Э01 22613 303 35645
305 32371 307 34517 309 26225 311 35561 .31.3 25663 315 24043
317 30643 323 20157 325 37151 з27 24667 329 33325 з31 32 61
З33 30667 335 22631 337 26617 339 20275 341 36625 343 20341
З45 37527 31+7 31зЗЗ 349 31071 .355 23353 351 26243 359 21453
361 36015 363 .36661 ЗЬ5 34767 3б7 34341 369 34547 371 35465
373 24421 375 23563 317 36037 з91 31267 393 27133 395 30705
Э97 30465 399 35315 401 32231 403 32207 405 26101 407 22567
409 21755 411 22455 413 33705 419 37621 421 21405 423 30117
425 23021 427 21525 429 36465 431 3301З 433 27531 4)') 2467')
437 33133 439 34261 441 33405 443 3lt655 453 Э2173 455 33 55
457 35165 459 22705 4&1 31123 463 27111 "65 35455 461 3145?"
469 23055 411 30777 473 37653 415 24.325 477 31251 547 35163
54t9 334'3 551 37243 553 27515 55 32137 ,57 26743 563 30217
565 20621 567 35057 569 24315 511 24727 581 30331 583 34273
585 232а7 581 31113 589 36023 595 27373 597 20737 599 36235
601 21575 603 2621, 605 21211 611 20з11 61з 34003 615 34027
617 20065 619 22051 621 22127 627 23621 629 24465 651 26457
653 31201 659 34035 661 27227 663 22561 665 2.1615 667 22013
669 23365 675 26213 677 26775 619 32635 681 33631 683 32743
685 31767 691 34413 693 22037 695 30651 691 26565 711 22141
113 22471 715 35271 717 37445 723 22717 725 2Ь505 721 24411
729 24575 731 23707 7З3 25173 739 21367 741 25161 743 24147
193 36301 795 24417 805 20237 807 36771 809 37327 811 21735
813 31223 819 36313 821 33121 823 32751 825 33523 839 26415
8 1 23731 в43 25425 845 34603 851 31047 853 37305 855 21315
857 35777 859 32725 869 20511 871 30301 873 3 757 875 21067
877 25151 1171 21513 1173 33721 1179 34775 1189 23571 1195 27411
1191 20457 1203 21 57 1205 З0177 1227 26347 1229 21477 1235 34243
12 1 27235 132з 25175 1325 31231 1) 1 Эl1З1 1333 25'03 1355 33045
п рuложенuя
551
/7,ооiJОАженuе
Р.2 М-1З E-8191
1357 24253 1363 35351 1365 260 3
Р.2 M:z14 Е=43
381 41771 1143 64213 2667 52225
Р а 2 м-14 Е-129
127 51145 635 17211 889 42721 1391 41241 1651 71147 2413 62123
Р=2 м-14 Е=381
43 72127 215 40621 з01 43353 473 67665 559 65013 731 73305
811 51161 1333 40207 1591 50133
Р=2 М-14 Е=5461
3 44741 9 63155 15 57521 21 63747 27 60111 33 64707
39 17741 45 62055 51 50471 57 63163 63 15505 69 ,.2403
15 41001 81 64003 87 50357 93 65763 99 44121 105 72501
111 45257 117 76175 123 52423 135 72203 141 47755 141 10627
153 4603.3 159 64157 165 52547 171 63217 177 56155 183 61065
189 776з1 195 67627 201 52131 207 50313 213 57161 219 42111
225 41111 231 72513 237 47043 243 54423 249 74121 261 51467
267 1З655 213 62603 279 55217 285 17643 291 54021 291 74641)
303 57745 .309 62225 315 46605 327 55643 333 71323 339 62261
345 52553 351 7770"з 357 44037 363 54055 369 51547 375 63001
393 50441 399 66361 405 57653 411 66735 417 53525 423 67267
429 71001 435 45131 441 44545 45з 62731 459 77661 465 71057
471 43503 477 56061 483 44367 489 46053 495 5477'5 531 15761
537 51143 549 14351 555 11141 561 50343 567 15167 573 64475
579 13225 585 45275 591 17211 597 54175 603 40653 615 46145
621 51371 621 43243 633 50433 651 ,6601 651 53513 663 602 1
669 62761 675 41403 681 70443 687 77727 693 44221 699 43665
711 14117 717 43225 723 64033 729 17307 741 64311 147 70065
753 7661 7 783 41551 789 65373 795 56711 807 47513 813 65043
819 60523 825 47601 837 64407 843 44307 849 52737 855 71557
861 41441 867 54371 873 67541 819 40555 885 65315 909 62251
915 45437 921 6'Ь37 933 45021 939 64633 945 64215 951 61353
1095 56741 1101 51353 1107 40145 1113 66141 1125 62511 1131 54321
1173 67533 1179 46761 1191 44501 1197 44375 1203 43215 1209 73603
1221 2361 1227 51123 1239 56421 1245 61115 1251 51215 1257 40327
1305 74463 1317 66103 1323 624)1 1335 71501 1353 55651 1365 46047
1311 71255 1383 5031 1389 41263 1395 41163 1431 76511 1431 72465
1443 71217 1449 72325 1461 70535 1479 6ч715 1485 74133 1581 53135
159.3 71765 1611 71233 1623 47727 1641 70053 1683 52353 1689 63667
1701 67115 1.707 77217 1719 42567 1737 44361 1749 15473 1755 70261
2349 .57743 2355 ,5363 2379 74105 2469 4207 2475 63351 2643 40413
2133 535lt') 2739 53763 2763 56637
P 2 M=14 Е=16383
1 40071 5 53727 7 55031 11 76715 13 47067 17 52431
19 63331 23 67137 2S 70641 29 40635 31 51737 35 ,.5145
37 43035 41 65403 47 71367 49 57017 53 45715 55 40423
59 40473 61 45553 65 61757 67 7225) 71 67047 73 70665
77 1613 19 67517 83 54641 85 42631 89 47121 91 76571
95 76371 97 52621 101 64167 10з 75273 107 11411 109 53477
11З 63247 115 50351 119 41357 121 61207 125 63253 131 51305
133 46505 137 63073 139 50007 1't3 54641 145 51647 149 64635
151 4 641 155 560З1 151 50523 161 43017 163 73143 161 44651
169 54517 17з 51633 175 67333 119 70063 181 50325 185 74313
181 67335 191 55165 193 57365 197 46101 199 41753 203 61237
205 61473 209 41015 211 40415 217 42763 221 63265 223 76621.
227 60575 229 56315 2.33 72753 235 55427 239 6Ь301 241 56111
245 41667 2ч1 74661 251 71637 263 54257 265 714lt7 269 72117
271 56615 275 5:3061 217 4l+567 281 42163 283 64237 287 66127
289 40665 293 50765 295 55301 299 56135 305 64563 307 51415
.311 72643 313 74711 .317 75077 323 6S4S3 325 43305 329 50631
331 71121 335 51213 337 Q241 341 13;)21 31+3 1 66 ) 7 17015
552 П рuложенuя
Р:а2 м=14 E=16383 проаОАж нuе
.:349 10035 353 41711 355 40731 359 40503 361 51541 36' 714,3
367 66551 311 61461 З73 77525 377 73527 319 61225 389 4 137
391 46517 395 4Ь11З 391 70633 401 65165 403 47111 407 10467
409 43751 41з 51261 415 61565 419 66163 421 53575 425 42705
427 40137 431 61443 433 53253 437 54065 439 47551 443 50753
445 60421 451 65601 455 41117 457 77721 461 51055 463 65203
467 72375 469 72023 415 45713 479 75161 481 60411 485 41025
481 57347 491 70251 493 54353 529 65427 533 51443 535 5&171
539 75053 541 71037 547 44343 551 55265 553 60025 551 57505
563 57431 565 65155 569 47351 571 40641 581 54665 583 51055
587 77411 589 64223 593 53025 595 66545 599 52571 601 47155
605 55013 611 '56345 61з 43131 617 52701 619 63531 623 7261)
625 63227 629 41343 631 73125 647 51231 649 75033 65.3 62011
655 67131 659 46.355 661 10425 665 45371 667 42 .3 2"3 677 45563
679 117'i7 683 63153 685 63015 689 40257 691 43745 695 55567
697 52751 701 71361 707 70553 109 5З651 713 15 43 715 60673
719 16707 721 54317 725 63601 727 ,+2531 733 4720) 739 2453
743 '76321 745 52457 749 44141 751 74.331 755 70173 781 5 571
785 41351 787 45243 791 55331 79з 76005 797 56557 803 70317
805 65277 809 73353 811 54&11 815 65575 821 67621 823 51243
827 64653 839 51017 841 12573 845 64553 847 62401 8 l 64641
853 6215 851 40251 859 75653 869 70461 871 62725 815.57333
877 47233 881 11117 883 44133 881 7.3131 905 52215 907 43'701
911 41607 913 50135 917 42013 919 45653 923 70767 925 70.311
931 65755 935 51107 931 72117 941 55705 943 66075 941 61063
949 56111 953 53703 955 52027 1093 77343 1097 74557 1099 5013.3
1109 77561 1111 61335 1115 52655 1117 56-2 О 3 1123 53623 1127 45213
1129 57401 113з 62107 1139 55105 1141 41753 1163 66661 1165 542 3
1171 67425 1175 56241 1177 60651 1181 45555 1181 55417 1189 60325
1193 56625 1195 74025 1205 71331 1201 40053 1211 51321 1223 44031
1225 61533 1229 73125 1235 65133 1237 41127 1241 54627 1243 50717
1253 62677 1255 67151 1259 72721 1301 57003 1303 51303 1307 511,.5
1309 62461 1315 76505 1319 70415 1321 76303 1325 45065 1331 67371
13.31 52131 1351 45335 1355 60147 13'7 61 O1 1363 555lt3 1367 17235
1369 62767 1.373 63203 1379 67011 1з81 57201 1385 51617 1381 71623
1421 7lt601 1421 61Ь21 1429 52237 1433 54003 1435 62671 1445 5703
1447 47103 14 1 45511 1453 75617 1459 lt5467 1463 56463 1 65 40273
1481 53057 1483 41755 1589 51347 1607 72133 1609 62 13 1613 76223
1619 72631 1621 66523 1625 62655 1627 4З161 1631 41625 1639 46565
1643 71477 161+5 51671 1685 51005 1681 75003 1691 51231 17.03 15123
1 705 11061 1109 4715.3 1715 41651 1717 55103 1721 53233 1735 73231
1139 Ь4457 1141 75267 1747 61363 1751 46077 1753 61ЗЗ3 2341 41441
2341 76621 2357 53367 2381 41205 2з87 7.32lt3 2389 43511 2395 42557
2405 72351 2411 1.3563 2453 64305 2459 44203 2417 64035 2645 75'71
2731 67451 21 1 11613 2765 11615 711 41417 2061 43173 2867 ,5111
Р::3 M 2 Е-4
2 101
Р=3 м=2 Е-8
1 112
Р=3 М=3 Е-1Э
2 1112 1+ 110
Р:3 м=3 Е-26
1 1021 , 1211
р.з м=4 Е-5
16 11111
п рuложенuя 553
f!pооt//lжение
Р-3 f.4-4 E-1O
8 12121.
Р:аЗ М=4 Е-16
, 10102
Р:а3 М='+ Е-20
4 12011
р=з М-4 Е-40
2 10121 14 10111
р з М-4 Е-80
1 10012 7 11222 11 12112 13 11002
Р=3 M-S Ez11
22 112102
Р:а3 М-5 е:-22
11 102221
р.з Mz:S Е-121
2 101012 4 120212 8 120022 10 112022 1,. 11212 16 121112
20 102112 32 112202 34 100112 эв 101102 O 110002
р:а) MZ:S Е=242
1 100021 5 121111 7 102101 13 111011 17 122101 19 1120О1
23 111211 31 120221 41 101011 43 110021 41 102211
р.з м=6 Е=7
] 04 1111111
Ра3 м:а6 Е=14
52 1212121
РаЗ м=6 Ez:28
26 1101011 130 1202021
Р э =6 Е-52
14 1020001 70 1010201
РаЗ М=б Е=56
13 1022102 65 1100012
Pz:3 м=6 Е а 91
8 1011001 16 1211201 з2 1112011 40 1122001 64 1102121 128 1210211
РаЗ М=5 Е=104
7 1001122 35 1121122 49 1221112 11q 1221002
р=з М=6 Ez:1B2
4 1001221 20 1110221 44 1211021 68 1112201 92 1111021 124 1012001
р-з м:а6 Е-З64
2 1001021 10 1110011 22 1011011 34 1210001 Э8 1202101 46 1021021
50 1022011 8 1000111 62 1122221 94 1200121 122 1002011 142 1221211
р.з м=6 Ez:728
1 1000012 5 1211212 11 1222102 17 1202002 19 1012112 23 1222022
25 1220 12 29 1222222 31 1110202 37 1010212 41 1112222 43 1121012
47 1102202 59 1201202 61 1120102 67 1022122 71 1101212 95 1101002
97 1202222 101 1020112 103 1212122 113 1110122 115 1122202 121 1100002
p= М=2 Еа)
8 111
Р=5 =2 Еа6
4 141
Р-5 м=2 EsB
3 103
Р=5 м=2 Е-12
2 134
p- м:а2 Е=24
1 112 7 123
.Р с 5 м=з Е=31
4 121+41 8 1404 12 111lt 16 1434 32 102'+
554 П рuложенuя
ПродО/1жение
Р=5 М=З Е=62
2 1141 6 1201 14 1101 18 1131 З8 1341
Р=5 М=3 Е=124
1 10.32 .3 1143 7 1113 9 1302 11 1323 1} 144Z
17 1042 19 1213 33 1312 37 1102
'Р=5 М=4 Е=l.3
48 13031 96 11411 192 12121
Р=5 М=4 E=16
39 1000.3
'Р=5 М=ц Е=?б
24 1.)1.31 72 12021 168 14441
р=; М=4 Е=39
16 12311 32 12201 64 1G141
Р=5 М=4 Е=48
1 :3 10102 91 10203
Р=5 M= Е=;2
12 12131 36 11441 84 14011
Р=5 М=ц Е=78
8 10111 56 10231 88 13341
p= М=4 Е=104
6 13314 18 13044 42 13444 54 14134 66 12014 162 11234
Р=5 М=4 Е=156
4 11301 28 12211 44 10421 68 13241 92 13401 188 14301
Р=5 rv,=4 Е=208
.3 1121-, 9 13102 21 14232 27 13413 33 11402 1}7 13342
63 14243 69 14402 81 14112 87 1031з 93 11142 183 11133
Р=5 М=4 Е=312
2 12004 14 14444 22 12224 )4 13124 38 11414 46 11244
58 12324 62 10024 82 14314 86 12434 94 11004 158 14004
Р=5 М=4 Е=Ь24
1 10122 7 1101з 11 10123 17 11212 19 13023 23 13043
29 13302 31 12203 37 11202 41 11032 43 14413 47 14143
53 12222 59 12123 61 13032 67 1201) 71 11443 79 12433
8.3 13423 89 14022 157 10412 163 12033 167 10413 187 14303
Таблица А.3
п k dБчх d MIAH d БЧХ п k d Бчх dMWH d Бчх 1l k d Бчх dМИН d&чх
...
7 4 3 О 127 120 3 О 255 215 11 О
15 11 3 О 113 5 О 207 13 О
106 7 О 199 15 О
7 5 О 99 9 О 191 17 О
5 7 О 92 11 О 187 19 О
31 26 3 О 85 13 О 179 21
21 5 О 78 15 О 171 23 О
16 7 О 71 19 О 163 25 О
11 11 О 64 21 О 155 27 О
6 15 О 57 23 О 147 29
63 57 3 О 50 27 О 139 31 О
51 5 О 43 29 2 131 37
45 7 О 36 31 О 123 39
39 9 О 29 43 115 43
22 47 О 107 45 О
36 11 О 15 53 О 99 47 О
30 13 О 8 63 О 91 51 О
24 15 О 87 53
18 21 О 255 247 3 О .
79 55 О
16 23 О 239 5 О 71 59
10 27 О 231 7 О
7 31 . О 223 9 О 63 61
55 63 О
ПрuложеНllЯ
555
Проt10//жеflJlt'
п k d Бчх dмин dБЧХ п k d Бчх d"'Н4н dБЧХ 11 k d Бчх dмuw dБЧХ
255
47 85
45 87
37 91
29 95
21 111
13 119
9 127
3
511 502
493
484
475
4()6
457
448
439
430
421
41
403
394
385
76
367
358
349
: .H)
3;)1
322
31З
304
293
286
5
7
9
11
13
15
17
19
21
23
25
27
29
31
33
37
39
41
13
45
47
51
53
55
57
277
263 59
259 61
63
250 73
241
2 . )( 'i ;)
,):)
4')2ч , "' 77
J:. 79
220 83
211 85
202
19 87
184 91
175 93
166 95
157 103
143 107
139 109
1Зt) 111
121 112
112 119
103 123
94 125
85 127
7G 171
о
511 67 175
58 183
49 187
40 191
31 219
28 223
19 239
10 255
о
о
о
о
о
о
о
о
о
о
о
1023 1013 3
1003 5
993 7
983 9
973 11
96 13
953 15
943 17
933 19
923 21
913 23
903 25
893 27
883 29
873 31
863 33
858 35
848 37
838 39
828 41
813 43
808 45
798 47
788 49
778 51
768 53
758 55
748 57
738 59
728 61
718 63
708 69
698 71
688 73
678 75
668 77
658 79
648 83
638 85
628 87
618 89
608 91
598 93
588 95
578 99
2 0 ' I 573 101
563 103
553 105
_ J . .
о
о
о
о
о
о
о
2
О
2
О
2
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
1023 543 107
533 109
523 111
513 115
503 117
493 119
483 121
473 123
463 125
453 127
443 147
433 149
423 151
413 153
403 157
393 159
383 165
378 167
368 171
358 17:3
348 175
338 179
328 181
318 183
308 187
298 189
288 191
278 203
268 207
258 213
248 215
238 219
228 221
218 223
208 231
203 235
193 237
183 239
173 245
163 247
15З 251
143 25:)
133 255
123 34 1
121 343
111 347
101 3'51
91 363
86 367
76 375
66 379
56 383
46 439
36 447
26 479
16 495
11 511
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
о
4
О
о
о
о
о
Литература 1)
1( rлаве 1
1. Киясу, lV\ypora, Теория информации, Серия «Соnременная прикладная
математика», изд-во «Иванами», 1957.
2. Peterson W. W., Weldon Е. J., Jr., Error-Correcting Codes, 2nd ed., л.\IТ
Press, Cambridge, Mass., 1972; есть русский перевод: Питерсон У., Уэл-
дон Э., Коды, исправляющие ошибки, изд
во «Мир», 1976.
3. Hamming R. W., Error Detecting and Error Correcting Codes, 8ST J, 29,
147
160 (1950); есть русский перевод: Хэмминr Р. В., Коды с обнару-
жением и исправлением ошибок, в сб. Коды с обнаружение.м и иcпpaв
ление.м ошибок, ИЛ, 1956, стр. 7
22.
4. Berlekamp Е. R., Algebraic Coding Theory, McGra\\T "Hill, N. У., 1968; есть
русский перевод: Бер.пекэмп Э., Алrебраическая теория кодирования.
изд-во «
\ир», 1971.
5. Hsiao М. У., А Class оС Optinlal Minilnunl Odd- \\;eigth-Column SEC
DED
Codes, / ВМ J. Res. Develop., 14, 395
40 1 (1970).
6. Lee С. У., Some Properties of Nonbinary Error-Correcting Codes, /ЕЕЕ
Trans., 'T
4, 77
82 (1958).
7. Forney а. О., Jr., Concatenated Codes, MIT Press, Cambridge, Mass., 1966;
есть русский перевод: Форни r. Д., Каскадные коды, изд
во «Мир», 1970.
8. Weldon Е. J., Jr., Decoding Binary Block Codes оп Q-ary Output Chan-
nels, /ЕЕЕ Traпs., 'T
17, 713
718 (1971).
9. Shannon С. Е., Weaver \V., Mathematical Theory of Communication, Uni\T.
of Illinois Press, Urbana, Il1inois, 1949; есть русский перевод: Шеннон К.,
Работы по теории информации и кибернетике, ИЛ, 1962, стр. 7
32.
10. Callager R. G., Information Theory зпd Reliable С')П1Inuпicаtiоп, Wiley,
N. У., 1968; есть русский перевод: rаллаrер Р., Теория информаЦИII 11
надежная связь, изд
во «Советское радио», 1974.
11. Cocke J., Lossless Symbol Coding with Nonprimes, /RE Trans., 'T
5, 33
34 (1959).
12. Васильев Ю. Л., о неrрупповых плотно упакованных кодах, П роблеМbl
кибе рнетики, H
8, 337
339 (1962).
13. Sсhбпhеim J., Оп Linear and Nonlinear Single-Error-Correcting q
nary
Perfect Codes, /nform. and Control, 12, 23
26 (1968).
14. Golay Л\. J. Е., Notes оп Digital Coding, Proc. /RE, 37,657 (1949).
15. Тiеtаvаiпеп А., Оп the Nonexistence of Perfect Codes over Fiлi1е Fields,
S/AM J. Appl. Math., 24, 88
96 (1973).
16. Plotkin М., Binary Codes ,vith Specified МjпirЛUln Distance, /RE T,"ans.,
IT
6, 44
450 (1960); есть русскиЙ перевод: ПДОТI(ИН л.\.. Двоичные коды
с заданным минимаЛЫIЫМ расстоянием, КибернетическиЙ сборник, вып. 7,
ИЛ, 1963, стр. 60
73.
17. Freiman С. У., Optimal Error Detection Codes for Completely Asymmetl'ic
Binary Channels, /nforпz. and Control, 5, 64
71 (1962).
18. Tokura N., Kasami Т., Hasimoto А., Failsafe Logic Nets, / ЕЕЕ Traпs.,
C
20, 323
330 (1971).
19. Икэно, Тамура, Намура, Равновесные коды и блок-схемы, ДЭНСll чусuн
ёаккай рОА
бунси, 54-А, 12, 671
678 (1971).
{) Литература, отмеченная эвеЗДОЧJ<ОЙ, добавлена переводчнком.
П Рll.".
ред.
Литература
557
20. Gallager R. G., А Simple Derivation of the Coding Theorem апс! Some
Applications, /ЕЕЕ Traпs., IT
11, 3
18 (1965); есть русский перевод:
rаллаrер Р., Простой вывод теоремы кодирования и некоторые примене
ния, Кибернетический сборник, новая серия, вып. 3, изд -во «Мир», 1966.
21. Shannon С. Е., GalIager R. G., Berlekamp Е. R., Lo,ver Bounds to Error
Probability for Coding оп Discrete Memoryless Channels, lnforт. and Con
trol, 10, 65
103 (Part 1), 522
552 (Part 11) (1967); есть русский перевод:
IПеннон К., rал.паrер Р. r., Берлекэмп Е. Р., Нижние rраницы вероятно-
сти ошибки кодирования в дискретных каналах без памяти, Зарубежная
радuоэлект роника, 2, 41
64 (1968).
22. Saltzberg В. R., Intersymbol Interference Error Bounds with Appli
ations
to Ideal Bandlimited Signaling, /ЕЕЕ Trans., 'T
14, 563
568 (1968).
23. Yeh У. S., Но Е. У., IПlрrоvеd IntersY111bol Interference Error Bounds in
Digital Systerns, BST J, 50, 2585
2598 (1971).
24. Prabhtl lJ. К., SOnle Considerations of Error Bounds in Digital Systems,
8ST J, 50, 3127
3151 (1971).
25. Glave F. Е., Ап Upper Bound оп the Probability of Error due to Intersym-
bol Interference for Correlated Digital Signals, I ЕЕЕ Trans., 'T
18, 356
363 (1972).
26*. Бассалыrо Л. А., Зиновьев В. А., Леонтьев В. К., Фельдман Н. И., Не-
существованне совершенных кодов для некоторых составных алфавитов,
J/роблеМbl передаЧll информации, 11, N2 3, 3
13 (1975).
27*. Бассалыrо Л. А., Новые верхние rраницы для кодов, испраВЛЯЮIЦИХ
ошибки, П робле
ff,bl передачи информаЦ!lU, 1, N
4, 41
44 (1965).
1( rлаве 2
1. Peterson W. W.. Weldol1 Е. J., J., Error-Correcting Codes, 2nd ed., MIT
Press, Cambridge, Mass., 1972; есть русскиЙ перевод: Питерсон У., Уэл-
дОН Э., Коды, исправ..1ЯlOщие ошибки, изд-во «Мир», 1976.
2. Berlekamp Е. R., Algebraic Coding Theory, Jv\:.Graw-Нill, N. У., 1968; есть
русский перевод: Берлекэмп Э., Алrебраич
ская теория кодирования, изд-во
«Мир», 1971.
3. Янаrи, Кодаира, Введение в современную математику, 1, изд-во «Ивана-
ми», 1961.
4. Виноrрадов И. М., Основы теории чисел, изд
во «Наука», 1965.
5. Carmichael R. О., Introduction to the Theory of Groups of Finite Order,
Dover, N. У., 1956.
6. Масияма, Планирование экспериментов, Второе издание, изд-во «Иванами».
7. Hall М., Jr., Combinatorial Theory, Blaisdell Pub. Со., 1967; есть русский
перевод: Холл М., Комбинаторика, изд
во «Мир», 1970.
8. КIIЯСУ. !v\атрицы Адамара и их применение, Дэнси цусин zaKi(au ромбунеи,
57, 17
27 (1974).
1( rлаве 3
1. Киясу, Mypora, Теория информации, Серия «Современная прикладная ма-
темаТlIка», изд-во «Иванами», 1957.
2. Slepian О., А Class of Binary Signaling Alphabets, BST J, 35, 203
234
(1956); eCTl> русский перевод: Слепян Д., Класс двоичных сиrнальных
алфаВIIТОВ, в сб. «Теория передаЧII сообщений» ИЛ, 1957, стр. 82
113.
3. Nordstrom А. W., Robinson J. Р., Ап Optimum Nonlinear Code, /nforпz.
Qпd Control, 11, 613
616 (1967).
4. Preparata Е. Р., А Class of OptiInum Nonlinear Double Error Correcting
Codes. /nforпz. aпd Control, 13, 378
400 (1968); есть русский перевод:
Препарата Ф. П., Класс оптимальных нелинейных кодов с исправлением
558
Литература
ДВОЙНЫХ ошибок, Кибернетический сборник, новая серия, вып. 7, lIЗД-ВО
«Мир», 1970, стр. 18
42.
5. Миякава, Имаи, Накадзима, Модифицированные коды Препарата как СН-
стематические оптимальные нелинейные КОДЫ, исправляющие двоЙные
ошибки, Дэнсu ЦУСUН ёаккаu ромбунсu, 53
A, 10, 531
539 (1970).
6. Sloane N. J. А., Reddy S. М. Chen С. L., Ne\v Binary Codes, /ЕЕЕ Tra1ls.,
IT
18, 503
510 (1972).
7. Kerdock А. М., А Class of Lo,\'
Rate Nonline
r Binarv Co(lcs, /пforт. and
Control, 20, 182
187 (1972); есть русскиЙ перевод: Кердок А. 1\1\., Класс
нелинейных ДВОИЧНЫХ кодов с низкой скоростью перед::\чи, Кибернетиче-
ский сборник, нов ая серия, выв. 1 О, 1973.
8 Peterson W. W., Weldon Е. J., Jr., Error
Correcting Codes, 2nd ed., lV1I'f
Press, Cambridge, Mass., 1972; есть русскиЙ перевод: Пн repcoIl У., УЭ.1-
дон Э., КОДЫ, исправляющие Оlllибки, изд-во «Мир», 1976.
9. Berlekamp Е. R., Algebraic Coding Theory, McGra\\T
Hill, N. У., 1968; есть
русскиЙ перевод: Берлекэмп Э., Алrебраическая теория кодироваНIIЯ,
изд
во «Мир», 1971.
10. Wagner Т. J., А Remark Concerning the Existen
e of Binary Quasi
Per-
fect Codes, /ЕЕЕ Trans., IT
12, 401 (1966).
11. Gorenstein О., Peterson W. W., Zierler N., Т\\'о Error
Correcting Bose
Chandhuri Codes are Quasi Perfect, /пforl1l. iJпd Coп!rol, 3, 291
294
(1960); есть русскиЙ перевод: rоренстеЙн Д., Питерсов У.. ЦИрJlер Н.,
КваЗIlсовершеНlIОСТЬ кодов Боуза
Чоудхури с IIсправлением двух Olllll-
бок, КибернетическиЙ сборник, вып. 6, ИЛ, 1963, стр. 20
24.
12. Reiger S. Н., Codes for the Correction of Clustered Errors, / RE Traпs.,
IT
6, 16
21 (1960).
13. Tokura N., Taniguclli 1(., Kasami Т., А Search Procedure for Finding Opti-
тит Group Codes for the Binary Symrnetric Cllannel, /ЕЕЕ Trans., IT
13,
587
595 (1967).
14. Gilbert Е. N., А Comparison of Signalling AlphaJJets, BST.f, 31, 50
t
522
(1952) .
15. Варшамов Р. Р., Оценка числа сиrналов в кодах с кор реl\Il 11 С i'( ошибок,
ДАН СССР, 117, N2 5, 739
741 (1957).
16. Sacks G. Е., Multiple Error Correction Ьу Means of Parity Cllecks, /RE
Traпs., 11
4, 145
147 (1958).
17. .1V\acWilliams Е. J., А Theorem оп the Distribution оУ \Veights in а Syste-
matic Code, BST J, 42, 79
94 (1963).
18. Assmus Е. F., M
ttson н. F., Turyn R., Cyclic Codrs. Scientific Report,
AFCRL
65
322, Air Force Cambridge Research Labs., Bedford, Mass., 1965.
19. Forney G. О., Jr., Concatenated Codes, !\\IT Press, Canlbridg'c, l\'ass., 1966;
есть русский перевод: Форни r. Д., КаскаДlIые коды, IfЗД
ao «Мир», 1970.
20. Kasami Т., Lin S, Peterson W. W., Some Results оп \\r e igllt Distributions
of ВСН Codes, /ЕЕЕ Trans., IT
12, 274 (1966).
21. Kasami Т., Weight Distribution of вен Cod
s, Ch. 20 in: Combinatorial
Mathematics and its Applications, Bose R. С., Dow1ing Т. А.. eds., The
Univ. of North Carolina Press. Chapel Hill, N. С., 1969.
22. Sloane N. J. А., Berlekamp Е. R., Weight Enumerator for Second
Order
Reed-Muller Codes, /ЕЕЕ Trans., 11
16, 745
751 (1970).
23. Kasami Т., Tokura N., Оп the Weight Structt1re of Reed
Muller Codes,
1 ЕЕЕ Trans., 11-16, 752
759 (1970).
24. Berlekamp Е. R., The Weight Enumerators for Certain Subcodes of the
2nd Order Binary Reed
l\1uller Code, /nforпz. aпd Contral, 17. 485
500
(1970) .
25. Kasami Т., The Weight Enumerators for Several Classes оУ Subcodes of the
2nd Order Binary Reed
Mt111er Codes, /пfOrl1l. aпd C01ltrol, 18, 3G9
394
( 1971 ) .
Литература
559
26. Baumert L. О., МсЕНесе R. J., Weights of Irreducible Cyclic Codes, In
{orm. aпd Coп/rol, 20, 158
175 (1972).
27. Pless У., Powler Moment 1 dentities оп \\Teight Distributions in Error Cor-
recting Codes, Inforт. and Con/rol, 6, 147
152 (1963).
28. Mac'Villiams F. J., Sloane N. J. А., Goethals J. 1\'\., The N\acWilliams
Identities for Nonlinear Codes, 8STJ, 51, 803
819 (1972).
29. Prange Е., СусНс Error-Correcting Codes in Tv/o Symbols, AFCRC- TN-
57-103, Air Force Cambridge Research Center, Cambridge Mass., 1957.
30. Peterson W. W., Encoding and Error-Correction Procedures for the Bose-
Chaudhuri Codes, I RE Trans., 11
6, 459
4 70 (1960).
31. Касами Т., О систематических кодах на основе двоичных последователь-
ностеЙ реrистров сдвиrа, Дзёхо сёрu, 1, 198
205 (1960).
32. Rudolph L. О., Easily Implenlented E.'ror-Correction Ei1coding-Decoding,
G. Е. Tech. Rept., 62 МСО 2, Oklahoma City, Okla., 1962.
33. Prange Е., TJle Use of Information Sets in Decoding СусНс Codes, I RE
Trans., 11
8, S5
S9 (1962).
34. КаsаПli Т., А Decoding Procedure for 1\\ultiple Error-Correcting Cyclic
Codes, /ЕЕЕ Trans., IT
10, 134
139 (1964).
35. Rudolf L. О., Mitchell 1\\. Е., 1 mplementatiol1 оУ Decoclers for Cyclic Codes,
/ЕЕЕ Traпs., IT
10, 259
260 (1964).
36. Lin S., Introduction {о Error to Correctil1g Codes, Prentice-Hall, Engle\\'ood
Cliffs, N. J., 1970.
37. N\acWilliams F. J., Permutation Decoding of Systematic Codes, 8ST J, 43,
485
505 (1964).
38. Kasami Т., Ап Upper Bound оп k/п for Affine-Invariant Codes with Fixed
d/п, IЕЕЕ Trans, IT
15, 174
176 (1969).
39*. Блох Э. Л., Зяблов В. В., Обобlценные каскадные коды, изд-во «Связь»,
1976.
40*. Бассалыrо Л. А., Формализация задачи о сло}кности задааия кода, Про
блеАtbl передачи UНфОр
tацuu, 12, N2 4, I05
106 (1976).
1( rлаве 4
1. Hocquenghem Л., Codes correcteurs d'erreures, Chiffres 2, 147
156 (1959).
2. Bose R. С., Ray
Chandlluri О. К., Оп а Class of Error Correctil1g Codes,
/пfortll. and Con/rol, 3, 68
79 (1960); есть русский перевод: Боуз Р. К.,
РоЙ
Чоудхури Д. К., Об одном классе двоичных rpynnoBbIX кодов с ис-
правлением ошибок, КибернетическиЙ сборник, вып. 2, ИЛ, 1961, стр. 83
94.
3. Berlekanlp Е. R., AIgebraic Coding Theory, N\cGra\V'
Hill, N. У., 1968; есть
русскиЙ перевод: Берлекэмп Э., Алrебраическая теория кодирования,
нзд
во «1\1I1Р», 1971.
4. PetE'rsoll W. \\'., We1don Е. J., Jr., Error
Correcting Codes, 2nd ed., MIT
Prrss, СаIпЬridgе, Mass., 1972; есть русскиЙ перевод: Питерсон У., Уэл-
..1011 Э., Коды, IIспраВЛЯЮIцне ошиБКII, IIЗД-ВО «N\ир», 1976.
5. Коя, 1\'\аТРIIЦЫ и определитеЛlI, IIЗД-ВО «БаЙфукан»), 1957.
6. Bussey W. Н., Galois Field Tables of Orderless than 100, Bull. Aпzer.
Л1аtll. Soc., 16, 188
206 (1909).
7. Prange Е., Cyclic Error
Correcting Codes in t\\.o Symbols, AFCRC- TN -57,
103, Air Force Cambridge Research Center, Cambridge, l\t\ass., 1957.
8. Reed 1. S., Solomon G., Polynomial Codes over Certllin Finite Fields,
SI АМ J. А ppl. Ma/h., 8, 300
304 (1960); есть русский перевод: Рид И. С.,
Соломон 1'., Полиномиальные коды над неКОТОРЫМ1I полями, Кибернетп-
ческиЙ сборник, вып. 7, ИЛ, 1963, стр. 74
79.
g. Kasarni Т., Tokura N., Some Remarks оп вен Bounds :Ind lv\inimunl
Weigllts of Binary Pril11iti\'c BCI
I Codes, IЕЕЕ Traпs., IT
15, 408
413
(1969).
560
tП атература
10. Касами Т., ЛИН С., Питерсон У., О свойствах линейных кодов, инва-
риантных относительно аффинных преобразований:, и минимальное рас-
стояние БЧХ-кодов, Дэнсtl цусин zaKKau ромбунси, 50, 1617 1622 (1972).
11. Chen С. L., Lin 5., Further Resu1ts оп Pol ynoll1ial Codes, [nform. aпd
Control, 15, 38 60 (1969).
12. Lin 5., Weldon Е. J., Jr., Further Results оп Cyclic Product Codes, [ЕЕЕ
Trans., IT 16, 445 451 (1970).
13. Kasami Т., Lin S., Some Resu1ts оп the N\inimum \Veight of Primitive ВСН
Codes, [ЕЕЕ Trans., IT-18, 824 825 (1972).
14. Hartman С. R. Р., Tzeng К. К., Chien R. Т., 50mе Results оп the МiпiПlutn
Distance Structure of Cyclic Codes, [ЕЕЕ Trans., IT 18, 402 408 (1972).
15. Pcterson W. W., Encoding and Error-Correction Procedurcs for the Bose"
Chaudhuri Codes, [RE Trans., 'Т-6, 459 470 (1960).
16. Gorenstein О., Zierler N., А Class of Cyclic Linear Codes iп р1n Symbol,
S[AM J. Appl. Math., 9, 207 214 (1961); есть русскиЙ перевод: rOpeH-
стейн Д., Цирлер Н., Класс кодов из рт символов С исправлением ошп-
бок, КибернетическиЙ сборник, вып. 7, ИЛ, 1963.
17. Messey J. L., Shift Register 5ynthesis and ВСН Decoding, [ЕЕЕ Trans.,
'Т-15, 122 127 (1969).
18. Forney G. О., Jr., Оп Decoding ВСН Codes, / ЕЕЕ Traпs., IT 11, 549 557
(1965).
19. Trench W. F.. Ап Algorithm for tJle Invcrsiol1 оУ Finite Teoplitz l\1atrices,
J. Soc. /ndust. Appl. Л1аfh., 12, 515 5?2 (1964).
20. Ван дер Варден Б. Л., Алrебра, ИЗД-ВО «Наука», 1976 (перевод с немец-
Koro) .
21. Hartmann С. R. Р., Tzeng К. К., GeneraJizatioll of the BCI--I Bound, [п
form. and Control, 20, 489 498 (1972).
22. Massey J. L., Threshold Decoding. /\'\IT PI"ess Research i\10поgrарh 20,
Cambridge, lV\ass., 1963.
23. Lin 5., Introduction to Error Corrccting Codes, Prentice Hall, Inc., Engle
wood Cliffs, N. J., 1970.
24. Weldon Е. J., Jr., 50mе Results оп Majority Logic Decoding, Ch. 8 in:
Error Correcting Codes, Мапп N., ed.. Wiley, 1968.
25. Reed 1. 5., А Class of Л1ultiрlе Еrrоr Соrrесtiпg Codes апd the Decoding
Sheme, [RE Traпs., PGIT 4, 38 49 (1954); ссть русскиii перевод:
Рид И. С., Класс кодов с исправлением ошибок и схема деI<одироваНIIЯ,
Кибернетический сборник, выл. 1, ИЛ. 1960. стр. 189 205.
26. Rudolf L. О., А Class of Majority Logic Decodable Codes, / ЕЕЕ Trans.,
'Т 13, 305 307 (1967).
27. Rudolf L. О., Threshold Decoding of Cyclic Codes, / ЕЕЕ Traпs., IT 15,
414 418 (1969).
28. Gore W. С., Generalized Tllreshold Decoding of Linear Codes, [ЕЕЕ Traпs.,
'Т 15, 590 592 (1969).
29. Chow D., Оп threshold Decoding of Cyclic Codes, [nform. aпd Control, 13,
471 483 (1968).
30. Chen С. L., Оп Majority Logic Decoding of Finite Geometry Codes, 1 ЕЕЕ
Trans., 'T 17, 332 336 (1971).
31. Kasami Т., Lin 5., Оп the Construction of а Class of Majority Logic Оесо-
dable Codes, /ЕЕЕ Trans., IT 17, 600 610 (1971).
32. Mattson Н. F., Solomon Ci, А Ne\v Treatnlent of Bose Chandhttri Codes,
S[AM J. Appl. Math., 9, 654 669 (1961).
33. Митани, О кодах, обнаруживающих и исправляющпх ошибки, Дэнки си-
кэндзё ихо, 15, 5, 18 22 (1951).
34. Muller О. Е., Application of Boolean Algebra to 5\vitching Circuit Design
and to Error Detection, [RE Trans.. EC 3. 6 12 (1954).
35. Kasami Т., Lin 5.. Peterson \V. W., Ne\\' Generalizations of the Reed-Muller
Codes, Part 1: Primitive Codes, [ЕЕЕ Trafls., IT 14, 189 199 (1968).
л итература
561
36. Касами Т., Лин С., Питерсон У., О кодах Рида Малера и их обоб-
U!ении, Дэнси цусин ёаккай ромбунси, 51..С, .g8 105 (1968).
37. Kasami Т., Lin S., Peterson W. W., Polynomial Codes, [ЕЕЕ Traпs., IT 40,
807 814 (1968).
38. Weldon Е. J., Jr., Euclide3n Geometry Cyclic Codes, in: Proc. Symp. СОП1-
binatorial Math., Univ. North Carolina, Chapel Hil1, 1967.
39. Weldon Е. J., Jr., New Generalizations of the Reed......... Muller Codes,
Part 11: NопрriПlitivе Codes, [ЕЕЕ Trans., IT-14, 199 206 (1968).
40. Goethals J. М., Delsarte Р., Оп а Class of Majority-Logic Decodable Сус-
Нс Codes, I ЕЕЕ Trans., IT-14, 182 188 (1968); есть русскнй перевод:
rёталс Д>к. М., Делзарт П., Один класс циклических кодов с мажори
тарным декодированием, Кибернетический сборник, новая серия, вып. 6,
изд-во «Мир», 1969.
41. Lin 5., Оп а Class of Cyclic Codes, in: Error-Correcting Codes, N\ann Н. В.,
ed., 1968, рр. 1.3 1 148.
42. Delsarte Р., Оп Cyclic Codes that are In\'ariant ul1der the General Linear
Group, /ЕЕЕ Trans., IT 16, 760 769 (1970).
43. Kasami Т., Lin 5., Оп Majority-Logic Decoding for Dl1als of Primitive
Polynomial Codes, [ЕЕЕ Trans., 'T 17, 322 331 (1971).
44. Weldon Е. J., Jr., Difference-Set Cyclic Codes, 8STJ, 45, 1045 1055 (1966);
есть русскнй перевод: Велдон И. Д>к., ЦПI<.lIические коды, задаваемые
раЗНОСТНЫМII множествами, в сб. Н екоторые вопросы теории Koдиpoвa
ния, изд-во «Мир», 1970, стр. 9 21.
45. Lin 5., N\ultifold Et1clidean Geometry Codes, [ЕЕЕ Trans., 11 19, 5З7 548
(1973) .
46 Delsarte Р., А Geometric Approach to а Class of СусНс Codes, J. СотЬ.
Th., 6, 340 359 (1969).
47. Lin 5., Оп the Number of Information 5Ynlbols in Polynonlinl Codes, [ЕЕЕ
Trans., 'T 18, 785 794 (1972).
48. Hamada N., The Rank of the Incident Л'\аtJ'iх of Points of d Flats in
Finite Geometries, J. Sci. /firoshiтa Univ., 32, 381 396 (1968).
49. Forney G. О., Jr., COt1catellated Code, MIT Press Research Monograph, 37,
1966; есть русский перевод: Форни r. Д., Каскадные коды, нзд-во «Мир»,
1970.
50. Justesen J., А Class of Constructive Asymptotically Good Algebraic Codes,
/ЕЕЕ Trans., 11-18, 652 656 (1972).
51. Berlckamp Е. R., Justesen J., 50те Long Binary Codes are not so Bad,
[ЕЕЕ Traпs., 11 20, 351 356 (1974).
52. Berlekamp Е. R., Long Primitive Binary ВСН Codes flave Distance
d;oov 2nlnR t/logn, [ЕЕЕ Trans., 'T 18, 415 426 (1972).
53. ronna В. Д., Новый класс линейных корректирующих I{ОДОВ, Проблемы
передачи информации, 6, вып. 3, 24 30 (1970).
54. rоппа В. Д., Рациональное представление кодов и (L, g) -коды, Проблемы
передачи информации, 7, вып. 3, 41 49 (1971).
55. Berlekamp Е. R., Goppa Codes, [ЕЕЕ Trans., IT 19, 590 592 (1973).
56. Berlekamp Е. R., Moreno О., Exten(led Double Error Correcting Binary
Goppa Codes are Cyclic, [ЕЕЕ Trans., 11..19, 817 818 (1973).
57. Reiger 5. N., Codes for the Correction оУ Clustered Errors, I RE Traпs.,
IT 6, 16 21 (1960).
58. Fire Р., Л Class of Мutiрlе Еrrоr-Соrrесtiпg Binary Codes for Noninde-
pent Errors, 5ylvania Report R5L-E-2, 5ylvania Electronic Defense Lab.
Moutain Vicw, CaJifornia, 1959. '
59. Melas С. М., Gorog Е., А Note оп Extending Certain Codes to Correct
Error Bursts in Longer Mcssages, 18"1 J. Res. Develop.; 7, 151 152 (1963).
60. Abralllson N. М., Л Class of 5ystelllatic Codes for Non-Independent Er
rors, /RE Tralls., IT 5, 150 157 (1959).
562
Литература
61. Касами Т., Систематические llиклические КОДЫ, IIсправляющие rруппи-
РУЮIциеся ошибки, Дэнси цусuн ёаккаu ромБУНGU, 45, 9 16 (1962).
62. Elspas В., Short R. А., А Note оп ОрtiП1tlin ВU1'st Еп'оr Соrrесtiп Codes,
/RE Trans., 11 8, 39 42 (1962).
63. Касами Т., Построение с помощью вычислительноЙ маШliilЫ кодов, исправ-
ляющих rРУППИРУЮULиеся ошибки, ДЭНСll цусuн С!аккай РОАlБУflси, 45,
1527 1532 (1962).
64. Kasami Т., Matoba S., Some Efficient Shortened Cyclic Codes for Burst-
Error-Correction, /ЕЕЕ Trans., 11-10, 252 253 (1964).
65. Lucky R. W., Salz J., Weldon Е. J., Jr., Principles of Dat:.1 Communication,
McGraw-Нill, N. У., 1968.
66. Hsu Н. Т., Kasami Т., Chien R. Т., Error Correctillg Codes for а C01l1pound
Channel, /ЕЕЕ Trans., 'T 14, 135 139 (1968).
67. Stone J. J., Multiple Burst Error Correction, /n{01111. aпd COlltrol, 4. 324
331 (1961 ) .
68. Имаи, Двумерные коды, IIспраВЛЯЮЩIIЕ' пачю! ОШIIБОI\, Дэнсu ЦУСllН са,.:-
кай РОJvlбунси, 55 A, 385 Э92 (1972).
69. Kasami Т., Construction and Decomposition of СусНс Codcs of C0111positc
Length, /ЕЕЕ Trans., 'T 20, 680 683 (1974).
70. Суrияма, Такахара, Хирасава, Намекава, О кодах rОIlllЫ, Научное обще
ство электроники 11 СВЯЗII, 1атериа.пы IIсследованнй по раСIIОЗllаванию
образов, PRL 73-77, январь 1974.
71. ronna В. д., Частное сообlцение.
72*. Блох Э. Л., Зяблов В. В., Обобщенные каскадныс коды, НЗД П0 «Связь»,
1976.
к rлаве 5
1. Elias Р., Coding for Noisy Channel, IRE Con\'ention Record, Part 4, 37 46
( 1955).
2. Massey J. Т., Threshold Decoding, MIT Press, Calnbridge Mass., 1963;
есть русский перевод: МеССIl Дж., Пороrовое ДСJ(о:tИРОВ3I1ие, riЗД-ВО «J\\Ир».
1966.
3. Robinson J. Р., Bernstein А. J., А Class of Binary l ecurI'ent Codes \\'ith
Limited Error Propagation, /ЕЕЕ T,'aпs., IT 13, 106 113 (1967).
4. Hagelbarger О. W., Recurrent Codes: Easily Machlnized, Burst Correcting,
Binary Codes, BST J, 38, 969 98-! (1959).
5. Berlekanlp Е. R., Note иП RecLtrrent Codes, /ЕЕЕ Trans., IT IO, 257 258
( 1964) .
6. Wyner А. О., Ash R. В., Al1alysis of Recurrent Codes, / ЕЕЕ Traпs., IT 9,
143 156 (1963).
7. Preparata F. Р., Systematic Constructions of Optilllal Lin{ ar Recurrent
Codes for Burst-Еrrоr Соrrесtjоп, CQlcolo, 2, 1 7 (1964).
8. Massey J. 1....' Inplementation of Bllrst Correctin Con\'olutional Codes,
/ ЕЕЕ Trans., .IT 11, 416 422 (1965).
9. Kohlenburg А., Random and Burst Error Correction, 1st IEEE Annual (0111-
munications Convention, Boulder, Соl0., June 7 9, 1965.
10. Ивадари, Об оптимальных рекуррентных кодах, нспраВЛЯЮЩJIХ паЧI\lI оши
бок. Научное общество электросвязи, материалы I1СС ,]СДОDаНIIi'I по теории
информации, октябрь 1966.
11. Iwadare У., Оп Туре В-l IЗurst Еrrоr Соrrссtillg Сопvоltltiапаl Codes,
/ЕВЕ Trans., IT 14, 577 583 (1968).
12. I\v'adare У., Sirnple and Efficient Procedures of Burst-Error CorrectioI1, Dis-
sertation for the Degree of Dr. of Engineering, Uпiv. оУ Тоl<уо, 1967.
13. Tong S. У., Systematic Construction of Self Orthogonal I1iffl1SC Co(ics, 1 ЕЕ
Traпs., IT 16, 594 -604 (1970).
Литература
563
14. \Vozencraft J. М., Sequcntial Decoding for Reliable Communication, N\IT
Research Са Ь. of Е lесtrоп ics Tech. Report 325, Cambridge, Л1аss., 1957.
15. Perry К. М., Wozencraft J. М., Seco: а S(1lf-Regulating Error Correcting
Coder Decoder, / RE Trans., 'T 8, 128 135 (1962).
16. \Vozencraft J. М., Reiffen В., Sequential Decoding, MIT Press, Cambridge,
i\\ass., 1961; есть PYCCKIlIul перевод: Возенкрафт Дж., РеЙффен Б., После
довательное декоднрование, ИЛ, 1963.
17. Fano R. М., А HeuJ'istric Discussion of Probabilistic Decoding, / ЕЕЕ
Trafls., IT 9, 64 73 (1963); ссть русский перевод: Фано Р., ЭВРИСТlIческое
оБСУ)l(дение веРОЯТlIостноrо декодирования, в сб. TeopnQ кодирования,
lIЗД-БО «Мир», 1964, стр. 166 198.
18. Sa\'age J. Е., The Computation Prob[em with Sequential Decoding, MIT Re-
search Lab. of Elcctronics, Tech. Rep. 439, 1965.
19. Sa\'age J. Е., Progrcss in Sequcntial Decoding, in: Adyances in Communi-
cation Systerns, Balakrishnan А. V., ed., Academic Press, N. У., 1968.
20. Jacobs 1. Е., Berlekamp Е. R., А Lo\\'er Bound to the Distl"ibution of Сот-
putation for Sequential Decoding, /ЕЕЕ Traпs., 'T 13, 167 174 (1967).
21. Jordan К. L., Jr., The Performance of Sequentia 1 Decod ing in Conjunction
\vith Efficient Modulation, /ЕЕЕ Traпs., COM 14, 283 296 (1966).
22. Bussgang J. J., Some Properties of Вiпаrу Con\'olutional Code Generators,
/ ЕЕЕ Traпs., 'Т J 1, 90 99 (1965).
23. Lin S., LYl1c Н., Somc Results of Binary Convolutional Code Generators,
/ ЕЕЕ Trans., IT 13, 134 139 (1967).
24. Costello О. J., Jr., Д Construction ТесhпiЧl1е for Rапdоm-Еrrоr Соrrесtiпg
Convolutional Codes, /ЕЕЕ Traпs., 'T 15, 631 636 (1969).
25. Vitel bi д. J., Error BOUllds for СопvоlutiОП(l1 Codes and ап Asymptotically
Optinlum Decoding Algorithm, /ЕЕЕ Traпs., 'T 13, 260 269 (1967); есть
РУССКIlЙ перевод: Вптерби А., rраНIIЦЫ ОШlIбок для свеРТОЧНblХ кодов 11
аСНМПТОТllчески оптимальный а.лrОРIIТМ деКОДllрОВ3I1ИЯ, в сб. Некоторые
вопросы теории кодирования, 113Д-ПО «l\1ир»), 1970, стр. 142 165.
26. Jelinek F., Fast Sequential Decoding AIgorithm Using а Stack, / BJ1 J. Res.
Develop.. 13, 675 685 (1969).
27. 3нrаНПlрОВ К. Ш., Некоторые пос.ледовате.'Iьные процедуры декодирова
III1Я, П роблеАtbl передачи uнфорл,tQЦИU, 2, 13 25 (1966).
28. Yudkin Н. L., Channel State Testing iп Information Decoding, Sc. О. The-
sis, Dept. оЕ Еlес. Engrg., MIT, Call1bridge, Mass., 1964.
29. Forney G. О., Jr., Convolutional Codcs 1: Algebraic Structure, /ЕЕЕ Traпs.,
IT 16, 720 738 (1970).
30. N\assey J. L., Application оУ Automata Theory in Coding in: Applied Auto-
rnata Tlleory, Топ J. Т., ed., Academic Press, N. У., 1968.
31. HLtffman О. Д., The Synthesis of Linear Seq1Jential Coding Net\vork, in:
1 пfОПllаtiоп Theory, Cherry С., ed., Academic Press, N. У., 1956.
32. MClssey J. L., l..ill R. \V., Application of LyapL1no'J's Direct Method to the
Error Propagation Effect in ConvolutionRl Codes, / ЕЕЕ Trans., 'Т 10, 248
250 (1964).
33. Robinson J. Р., Error Propagation and Definite Decoding of Convolutional
Codes, /ЕЕЕ Trans., 'Т-14, 121 128 (1968).
34. Massey J. L., НеопуБЛИI<ованный меморандум, July 1967.
35. Sullivan О. о., Error Propagation PrOpel"ties of Uniform Codes, /ЕЕЕ
Trans., 'T 15, 152 161 (1969).
36. Robinson J. Р., Punctured Uniform Codes, /ЕЕЕ Trans., IT 15, 149 152
(1969) .
.37. Singer J., А. Theorem in Finite Projective Geometry and Some Applications
to Number Theory, AMS Trans., 43, 377 385 (1938).
38. I alconer о. О., Л Hybrid Coding Sclleme for Discrete l\J\еlпоrуlеss Chan-
nels, BSTJ, 47, 6 .)I .728 (1968).
564
Литература
39. Lucky R. W. et al., Principles of Oata Communication, McGraw-Нill, N. У.,
1968.
40. Townsend R. L., Weldon Е. J., Jr., Self-Orthogonal Quasi Cyclic Codes,
/ЕЕЕ Trans., 'T 13, 183 195 (1967).
41. Gallager R. а., Iпfоrmаtiоп Theory and Reliable Comnlunication, Wiley,
N. У., 1968; есть русский перевод: rаЛ.rIаrер Р., Теория информации 11
надежная связь, изд-во «Советскос радио», 1974.
42. Kohlenburg А., Forney G. О., Jr., Сопvоlutiопзl Coding for Channels \\.ith
Memory, /ЕЕЕ Traпs., IT-14, 618 626 (1968).
43. Hsu Н. Т., Kasami Т., Chien R. Т., Error-Correcting Codes for а COlnpound
Channel, / ЕЕЕ Trans., IT 14, 135 138 (1968).
44. Weldon Е. J., Jr., New Genera1ization of the Reed Muller Codes Part 11:
Non-Primitive Codes, / ЕЕЕ Trans., IT 14, 199 206 (1968).
45. Robinson J. R., Частное сообщение, April 1973.
1( rлаве 6
1. Wozencraft J. М., Sequential Decoding for Reliable Comm:lnication, MIT
Research Lab. оС Electronics, Tech. Report 325, Cambridge, N\ass., 1957.
2. Shannon С. Е., А Mathematical Theory of Communica tions, BST J, 27, 379
423 (Part 1), 623 656 (Part 11), 1948; есть русскиЙ перевод: IlIeHHoH К.,
Математическая теория связи, сб. Работы по теории UНфОРАtаЦllll и Кllбер
нетике, ИЛ, 1963, стр. 242 332.
3. Gallager R. а., А Simple Oerivation of the Coding Theorem and SОПlе
Applications, /ЕЕЕ Trans., 'T 11, 3 18 (1965): есть русскиЙ перевод: I"'ал
лаrер Р., Простой вывод теоремы кодирования и некоторые применеНIfЯ,
Кибернетический сборник, новая серия, вып. 3, изд-во «Мир», 1966,
стр. 50 90.
4. Viterbi А. J., Error Bounds for Convolutional Codes and ап l\5Ynlptotically
Optimum Oecoding Algorithm, I ЕЕЕ Trans., IT..13, 260 269 (1967); есть
русский перевод: Ви:терби А., rраницы ошибок для сверточных кодов 11
асимптотически оптимальныii алrоритм декодирования, сб. Н екоторые вo
просы теории кодирования, изд-во «Мир», 1970. стр. 142 165.
5. Shannon С. Е., Gallager R. а., Berlek;lInp Е. R., Lo\ver Bounds to Error
Probabi1ity for Coding оп Oiscrete Memoryless Chanl1els, /nfof'nz. and
Control, 10, 65 103 (Part 1), 525 552 (Part 11), 1967; eCTh русскиЙ пере-
вод: Шеннон К., rаллаrер Р., Берлекэмп Е.. Нижние rраницы вероятно-
сти ошибки для кодирования в дискретном канале без памяти, 3арубеж
ная радиоэлектроника, 2 и 6, стр. 52 81 И 41 64 (1968).
6. Wozencraft J. М., Reiffen В., Sequential Oecodil1g, MIT Press, Call1bridge,
Mass., 1961; есть русский перевод; Возенкрафт Дж., Рейффен Б., fl0сле-
довательное декодирование, ИЛ, 1963.
7. Jelinek F., Fast Sequential Decoding Algorithm Using а Stack, 18М J. Res.
Develop., 13, 675 685 (1969).
8. Зиrанrиров К. Ш., Некоторые последовательные процедуры декодирова.
ния, Проблемы передачи информации, 2, 13 24 (1966).
9. Savage J. Е., Progress in Sequential Oecoding, in: Аdvяпсеs in Communi-
cation Systems, Balakrisknal1 А. V., ed., АсаdеПliс Press, N. У., 1968.
10. Savage J. Е., The Computation Problem with Sequential Oecoding, MIT
Research Lab. of Electronics, Tech. Report 439, 1965.
11. Gallager R. а., Information Theory and ReliabIe Соmlnt1пicаtiоп, \Viley,
N. У., 1968; есть русский перевод: rаллаrер Р., Теория информации и Ha
дежная связь, изд.во «Советское радио», 1974.
12. Jacobs 1. М., Berlekamp Е. R., А Lower Bound to the DisLriblltion оС Сот-
putation for Sequential Decoding, 1 ЕЕЕ Trans., IT 13, 167 174 (1967).
13. Yudkin Н. L., Channel State Testing in Information Decoding, Ph. D. Dis-
sertation, Dept. оС Elec. Engrg., MIT, CaInbridge, Mass., 1964.
Литература
565
14. Forney а. О., Jr., Convolutional Codes 11: Maximum Likelihood Decoding
and Convolutional Codes 111: Sequential Decoding, Technical Report No.
7004-1, Information Systems. Lab., Stanford Univ., 1972.
15. Gejst J. М., А Comparison of the Fano and Jelinek Sequential Decoding
Algorithm, Technical Report ЕЕ 701, Univ. of Notre Dame, Notre Dame,
Indiana, 1970.
16. Falconer О. О., А Hybrid Sequential and Algebraic Decoding Scheme,
Ph. О. Thesis, Dept. of Elec. Engrg., MIT, Cambridge, Mass., 1966.
17. Massey J. L., Threshold Decoding, MIT Press, Cambridge, Mass., 1963;
есть русский перевод: Месси Дж., Пороrовое декодирование, изд-во «Мир»,
1966.
18. Massey J. L., Some Algebraic and Distance Properties of Conyolutional
Codes, in: Error Correcting Codes, Мапп I--I. В., ed., Wiley, N. У., 1968.
19. Costello D. J., Jr., А Construction Technique for Random-Error-Correcting
Convolutional Codes, /ЕЕЕ Traпs., 'T 15, 631 636 (1969).
20. Park J. Н., Jr., Inductive Proof of ап Ilnportant Inequality, / ЕЕЕ Trans.,
IT 15, 618 (1969).
21. Bussgang J. J., Some Properties of Binary Convolutional Code Generators,
/ ЕЕЕ Trans., IT 11, 90 99 (1965).
22. Lin S., Lyne Н., Some Results of Binal'y Convolutional Code Generators,
/ ЕЕЕ Trans., 11 13, 134 139 (1967).
23. Fano R. М., А Heuristic Discussion of Probabilistic Decoding, I ЕЕЕ Traпs.,
'T 9, 64 73 (1963); есть русский перевод: Фано Р., ЭВР 1стическое обсу-
ждение вероятностноrо декодирования, сб. Теория кодирования, изд-во
«Мир», 1964, стр. 166 198.
24. Wozencraft J. М., Jacobs 1. М., Principles of Communication Engineering,
Wi1ey, N. У., 1968; есть русский перевод: Возенкрафт Дж., Джекобс И.,
Теоретические основы техники связи, изд-во «Мир», 1969.
25. Je1inek F., Probabi1itic Information Theory, McGraw-Нill, N. У., 1968.
26. Falconel' О. О., Niessen С. W., Simulation of Sequ€ntial Decoding for
а Telemetry Channel, Massachusetts Inst. of Technology, Research Lab. of
Electronics, Quart. Progress Rep. 80, 183 193, 1966.
27. Viterbi А. J., Convolutional Codes and Their Performance in Communica-
tion Systems, /ЕЕЕ Trans., CM 19, 751 772 (1971).
28. Massey J. L., Costello D. J., Jr., Justesen J., Ро1упопJiаl Weights and Code
Construction, /ЕЕЕ Trans., 'T 19, 101 110 (1973).
1( rлаве 7
1. Киясу, Mypora, Теория информации, Серия «Современная ПРИI<ладная Ma
тематика», изд-во «Иванами», 1957.
2. Ci1ien R. Т.. Coding for Error Control in а Computer-Manufacturer's Envi-
ronment: а Fore\\!ord, / BJvl J. Res. Develop., 14, 342 (1970).
3. Grosch Н. R. J., High Speed Arithmetic: the Dig'ital Computer a а Re-
search Tool, J. О ptical Soc. о{ America, 43, 306 310 (1953).
4. Кобаяси, Като, О повышении надежности полупроводниковой оперативной
памяти с помощью кодов, испраВ.1JЯЮЩИХ ошибки, Тезисы докладов на-
циональной конференции общества связи, NQ 1215, 1971.
5. Holsinger J. L., Digital Communication over Fixed-Continuous Channels
with Memory-with Special Application to Telephone Channels, MIT Lincoln
Lab. Tech. Report 366, 1964.
6. Ивадари, Общие принципы проектирования систем связи с контролем
ошибок, ДЭНСtl цусин ёаккай ромбунеи, 54 A, 87 95 (1971).
7. Cahn С. R., Performance of Digital Phase Modulation COlllmunication Sys-
tems, /RE Trans., CS 7, З 6 (1959).
566
Литература
8. Имаи, Катаока, .iV\иякава, l\\поrоступенqатое КОДl!рование и ero примене-
ние в системах связи с полифазной модуляцией, ЭНСU цусuн ёаккай РОМ-
бунси, 54 A, 597 604 (1971).
9. Wozencraft J. М., Kennedy R. 5., Modulation and Demodulation for Pro
babilistic Coding, [ЕЕЕ Trans.. 11..12, 291 297 (1966).
10. Jordan К. L., Jr., The Performance of Sequential Decoding in CO!ljunction
with Efficient Modulation, [ЕЕЕ Trans. оп Сотт. Tech., COM 14, 283 297
( 1966) .
11. Levesque А. Н., Recent Development in Error Control Techniques, Signal
Processing Techniques in Digital Communication, 1969 W scon Tech. Papers,
1969.
12. Bennet W. R., Darey J. R., Data Transmission, l\'\cGra\v-Нill, N. У., 1965.
13. Cacciamani Е. R., Jr., The SPADE System as Applied to Data Communica-
tion and Small Earth Station Operation, COMSAT, Tech. J., 1, 171 182
(1971).
14. Сэкимото, Утино, Сабури, Система SP АОЕ дЛЯ спутннковоii связи, Мате-
риалы исследований по система связи научноrо общеСТiЗа элеКТРОНИКII
и связи, CS 71-131, 1972.
15. Кумаrая, Предисловие к специальному выпуску, ПОСВЯlценно).1У современ-
ной технике передачи информации, энси цусuн саккай ромБУflСll, 53, 11,
1466 (1970).
16. [ВМ J. Res. Develop., 14 (1970).
17. Tang D. Т., LUfn У. У., Error Control for Terminals \\,ith HUnlan Sperators,
I ВМ J. Res. Develop., 14, 409 416 (1970).
18. Hsiao М. У., Bossen В. С., Chien R. Т., Orthogot1al Latin Square Codes,
1 ВМ J. Res. Develop., 14, 390 394 (1970).
19. Iwadare У., А Class of High Speed DecodC\ble Bur5t Correcting Codes,
[ЕЕЕ Trans., 11 18, 817 821 (Corresp.) (1972).
20, Chien R. Т., Burst-Correcting Codes \\"ith High Speed Decodil1g, 1 ЕЕЕ
Trans., 11 15, 109 113 (1969).
21. Golomb S. W., ed., Digital COlnnlunications \\'ith Space Applications, Pren-
tice Hall, Inc., Englewood Cliffs, N. J., 1964.
1( rлаве 8
1. Уоп Neumann J., Probabilistic Logics and the Synt11esis of Rcliable Orga-
nisms from Unreliable Components, in: Automata Studies, Princeton Univ.
Press, Princeton, N. J., 1956; есть русский перевод: llеймаll Дж., Вероят-
ностная лоrика и синтез надежных орrанизмов из lIенадежных компонент,
сб. Автоматы, ИЛ, 1956, стр. 68 139.
2. Wir!ograd S., Cowan J. О., Reliable Computation in the Presence of Noise,
MIT Press, Cambridge, Mass., 1963; есть русский перевод: ВИllоrрад С.,
Коуэн Дж., Надежные вычисления при наличии IIIYMOB, изд во «Наука»,
1 968.
3. Elias Р., Computation in the Presence of Noise, 18М J. Res. Develop., 2,
346 353 (1958).
4. Diamond J. М., Checking Codes for Digital Computers, Proc. of I RE, 43,
487 488 (1955).
5. Brown О. Т., Error Detecting and Correcting Binary Codes for Atithmetic
Operations, [RE Traпs., EC 9, 333 337 (1960).
6. Такаrи, Лекции по теории чисел, изд-во «Томотати», 1931.
7. Виноrрадов И. М., Основы теории чисел, изд-во «Наука», 1965.
8. Reitwiesner G. Н., Binary Arithmetic, in: Advances in Computers, Alt F. L.,
ed., Vol. 1, 232 308, Academic Press, N. У., 1969.
9. Peterson W. W., Error-Correcting Codes, MIT Press and Wiley, N. У.,
( 1961 ) .
Литература
567
10. Ерош И. Л., Ерош С. Л., Арифметическне I{ОДЫ с исправлением MHoro-
кратных ошибок, П роблеАtbl передачи и1-lформацuи, т. 3, вып. 4) 72
80
( 1967) .
11. Massey J. L., Survey of R
$idue Coding for Arithmetic Errors, International
Computation Center Bullefln, UNESCO, Rome, Italy, 3, 195
209 (1964).
12. Chiang А. С. L., Reed 1. S., Arithmetic Norms and Bounds of the i\rithmetic
AN Codes, /ЕЕЕ Traпs., IT
16, 470
476 (July 1970).
1( rлаве 9
1. Mandelbaum О., Arithmetic Codes with Large Distance, / ЕЕЕ Trans., IT
13,
237
242 (1967).
2. Tsao
Wu N., Arithmetic Cyclic Codes, Dept. of Electrical Eng., Northeastern
Univ., Boston, Mass., Part 1 of Commt1nication Theory Group Report No. 10,
Fina I Report AFC I
L-68-0512, 19б8.
3. Асано, Теория колец и идеалов, IIЗД-ВО «Томотати», 1959.
4. Goto М., Fukumura Т., The Distance of Arithmetic Codes, A1eтoirs о! the
Faculty о! Engineeriпg, Nagoya Univ., 20, 474
482 (1968).
5. Chien R. Т., Hong S. Т., Preparata F. Р., Some Results in the Theory оУ
At.ithmetic Codes, Coordinated Science Labs., Univ. of lllinois, Urbana, Re-
port R
440, 1969.
6. Mandelbaum О., Aritllmetic Error Detecting Codes for Communication Links
Involving Computers, /ЕЕЕ Trans., COM
13, 165
17 (1965).
7. Атовара, Фукумура, Методы построения AN
KOДOB, исправляющих пачки
ошибок, Дэне и цусин 2аккай ромбунеи, 50, 2101
2107 (1967).
8. Massey J. С., Garcia О. N., Error
Correcting Codes in Computer Arithmetic,
in: Advances in Information Systenls Science, Тои J. Т., ed., Vol. 4, Plenum
Press, N. У., 1971.
9. Avizienis А., Л Study of the Effecti\'eness of Fault-Detecting Codes for
Binary Arithnletic, Jet Propulsion Lab., Pasac1ena, Calif., Technical Report
32
711, 1965.
10. Chiang А. С. L., Reed 1. S., Arithmetic Norms and BoLtnds of the Arithmetic
AN Codes, [ЕЕЕ Traпs., IT
16, 470
476 (July 1970).
11. Rao Т. R. N., Garcia О. N., СусНс and J
\ulti-Residue Code for Arithmetic
Operations, /ЕЕЕ Traпs., IT
17:85
91 (Jan. 1971).
12. Rao Т. R. N., Error Coding for Arithmetic Processors, Academic Press, N. У.
and London. 1964.
13*. КабаТЯНСJ<иli r. А., О rраннцах для ЧIIС.1Jа кодовых слов в двоичных ариф-
метических кодах, П роблеМbl передачи информации, 12, вып. 4, 46
54
(1967) .
Предметный указатель
А.пrоритм
итербп
26
Евк.пида 6U
Зиrанrирова
ДЖlлинека 225
Фано 224
АN-код 466, 479
дополняющий 520
. исправляющий кратные ОIlIиБКlI
499
ошибки веса 1, 493
пачки ошибок 541
методы декодирования 502
обнаруживающиЙ ошибки веса
493
пачки ошибок 541
оптимальный 531
простой 510
сильно циклический 506
совершенный
исправляющий ошиБКII веса 1
493
циклическиЙ
разложение 509
Асимптотически хорошая ПОС
lедова-
тельность кодов 204
Базис 80
дополняющий 122
Вектор кодовый 128
нулевой 78
ошибок 134
Векторы линейно зависимые 79
линейно независимые 79
ортоrональные 80
Вес 20
арифметический 487
минимальный 129
модулярный 518
Хэмминrа 128
Вычет квадратичный 110
rеометрия аффинная 115
......... еВКЛИ.ll.ова 115
проективная 118
rиперплоскость 115
rомоморфизм 57
rраница БЧХ 161
Варшамова
rилбертз 140
верхняя минима
'Iьноrо расстояния
AN
Koдa 527
Плоткина 32
Хэмминrа 30
Элайса 34
СJIучайноrо кодирования 39
I"руппа 54
абелева 55
аддитивная 56
бесконечная 58
изоморфизм 58
коммутативная 5!5
конечная 58
ЦlIк.rIическзя 65
Декодер 24
Декодирование дефинитное 270
мажоритарнос 179
по маКСIIМУМУ правдоподобllЯ 26
noporoBoe 222
последовательное 222
с обратной связью 239
списком 52
Делитель нуля 72
Длина двоичноrо AN -кода 480
кода 23
Дистрибутивность 69
Закон взаимности 476
Идеал 70
rлавный 507
Избыточность 13
АN-кода 481
Изоморфизм 58
Индекс подrруппы 61
п редЛlетный иказатель
569
Информационный шумовой символ
243
Исправление ошибок 13
АN кодом 490
Исправляемая конфиrурация ошибок
532
Канал двоичный симметричныЙ 26
дискретныЙ без памяти 38
Китайская теорема об остатках 542
Код арифметический 466
блоковый 23
Васильева 3)
rолея 31
ronnbl 206
rрупповой 128
двойственный 129
диффузный 223
допускающий полную ортоrонали-
зациlO 188
Ивадари 223
из последовательностей макси
мальной длины 34
IIсправляющиЙ ошибки 24
каскадный 200
квазисовершенныЙ 136
линейныЙ 128
вычетныЙ 466
мноrоостаточный 542
обнару}кивающий ОUlибки 24
ортоrова.лнзирусмый 254
пеРфОРllрованный paBHoMepHbIii
293
по.пИllомнальныlt 196
равновесныЙ 16
равномерныЙ 223
расширенныЙ 21
еВКJlидово rеометрическиЙ 197
рекуррентныЙ 222
Рида Маллера 189
обобщенный 189
расширенный 189
цикличсский укороченный 189
Рида Соломона 166
сверточный 222
самоортоrональный 223
СlIстематический 228
систематический 23
с маl<симально достижимым рас-
стоянием 133
совершенныЙ 30
укороченныЙ 131, 161
ФаЙра 220
Хэмминrа 20
двоичный 158
обобщенный 134
циклический 164
циклический 148
укороченный 161
Шенrейма 31
эквидистантный 34
Юстесена 204
Кодер 23
Кодовое слово 23
АN кода 479
число АN кода 479
Кодов ый вектор 20
Кольцо 69
вычетов 72
коммутативное 69
мноrочленов 70
с единицей 69
цe.ТIЫX чисел по модулю 2 е 1 506
Корень 84
KpyroBoe число 477
k npocTpaHcTBo 115
Линейная комбинация 79
Локатор ошибок 170
Мажоритарная функция 179
Матрица Адамара 111
порождающая 129
проверочная 129
Метод деl<одирования, основанный
на пере боре 537
циклических сдвиrах 534
перемежения 218
Минимальное представление 485
Мноrоуровневая фазовая МОДУ.ПЯЦIlЯ
432
Мноrочлен 82
двойственный 103
круrовой 106
Матеона Соломона 184, 189
минимальный 97
неприводимый 84
нормированный 84
порождающий 150
примитивный 98
проверочный 151
самодвойственный 103
Модуль 469
Наибольшиil общий делитель 468
Наименьшее общее кратное 467
570
п pea.llteTHbltl УКQзtlте ль
l-Iевычет квадратичныЙ 110
Неортоrональная проверка 184
Нормированный делитель 62
Нумератор 143
Область целостности 72
Обнаружение ошиБОI{ АN кодом 490
Обобщенный метод чередования 271
Операция 54
Ортоrональное дополнение 80
Ортоrональность линейных e CYMM 180
Отображение биективное 57
rомоморфное 57
изоморфное 58
инъеКТlIвное 57
сюръективное 57
Ошибка арифмеТlIческая 531
веса t 26, 489
исправ яемая 532
реально возможная 505
Пачка ошибок 28
типа ВI 280
. 82 280
Подrруппа 59
собственная 59
Подкод 128
над подполем 195
четный 131
Подполе 76
Подпространство 80
Показатель 470
Поле 72
изоморфизм 74
конечное 73
простое 107
Полная ортоrона изация 182
Полная система вычетов 469
Порождающее число АN-кода 479
Порядок 58, 64
Последовательность максимальной
длины 159
Правило ортоrонализации 238
Представление 66
в виде степеней 95
векторное 94
минимальноrо веса 482
мноrочленное 94
Приведенная система вычетов 470
ПРИМIIТИВНЫЙ корень степени d 476
ПримитивныЙ Э 1емент 471
Проверочная сумма 180
ПроверОЧНUlii пара:l.lе.l0rрамм 285
Производная мноrОЧ.lена 87
Пространство векторное 78
Путь 301
Разложение МУ..1ЫIlП.1нкаТIIВНОЙ rpyn-
пы 473
на простые сомножнтеJIIl 468
Размерность 79
Разностное множество 121
Распределение весов 143
Распространсние Оlllнбок 239
Расстояние арIlфМСТIIllеское 483
КОНСТРУКТlIвное 164
Ли 22
МННIIмальное 23
АN кода 489
npocToro АN I\ода 517
модулярное 518
свободное 471
столбцевое 371
Хэмминrа 20
Расширение поля 76
I<ода 131
CII МВО/( I1НфОрМ аЦIlОННЫЙ 23
Лежандра 475
проверки на четность 18
проверО4НЫЙ 23
Снндром 134, 229
АN кода 502
усеченный 233
СIIстема алrебраическая 54
Скалярное произведенне 80
Скорость передачи 23
След 122
СмежныЙ класс левыЙ 59
правый 59
Составная проверка 239
Сравнимость по модулю 67
Стек алrоритм 225
Структура циклическоrо АN-кода 509
Структурная избыточность 466
Таблица rруппова 57
декодирования 24
Теорема Лаrранжа 61
Ферма 470
Э'U 1 .r1ера 470
Точка бесконечно удаленная 121
п редметныа указатель
571
Укорачивание 161
Укорочение кода 131
Цена пути 304
Цикл 103
Факторrруппа 62
Функция Кармайкла 472
надежности 44
производящая 91
Эi'I 1ера 69, 468
мулыипликативность 469
Частное 467
Число информационных символов 23
ортоrональных проверок 241
проверочных символов 20, 23
простое 468
составное 468
Характеристика поля 77
Элемент единичный 55, 73
нулевой 73
обратный 56
примитивный 96
ЦентральныЙ интервал 519
Оrлавление
Предисловие редакторов PYCCKoro издаНIIЯ . . .
Предисловие авторов. . . . . . . . . . .
5
7
1. Основные понятия теории кодирования. . . . . . .. ... 13
1.1. Коды, обнаруживающие и испраВЛЯIОiцие ОUJибки . ... 13
1.2. Блоковые коды. Систематические коды . . . . . . . . . . 21
1.3. Двоичный симметричныЙ канал. . . . . . . . . .. . 26
1.4. Верхние rраницы ДЛЯ минимальноrо расстояния кодов . 28
1.4.1. Верхняя rраница Хэмминrа. . . . . . 30
1.4.2. Верхняя rраница Плоткина. . . . . . . . З2
1.4.3. Верхняя rраница Элайса. . . . 34
1.5. Теорема кодирования . . . . . . . .. ... . 38
1.5.1. rраница случайноrо кодирования. . . . . . . . 39
1.5.2. Свойств а функции надежности . 44
1.5.3. rраница сферической упаковки . . . . . . . .. 50
1.5.4. Декодирование списком . . . . . . . 52
2. Конечные ПОJIЯ . . . . . . . . . . . . . . . . .
2.1. rруппы. . . . .
2.2. Кольца и поля . . . .
2.3. Векторные пространства
2.4. Мноrочлены . . . . . . . . .
2.5. Конечные поля. . . . . . . . . . . . . . .
2.6. Дополнительные сведения о конечных полях .
2.6.1. Вычисления в конечных полях . ...
2.6.2. Матрицы Адамара . . . .
2.6.3. Конечные rеометрии. . . ., ...
2.6.4. Разностные множества. . .. ...
2.6.5. ДополняющиЙ базис. . . . . .
2.6.6. Некоторые понятия, необходимые для
ronnbI . . . . . . .
Зада чи . . . . . . . . . . . . . . . .
. 54
54
. . . . . . 69
. 78
. 82
. 90
. . . . . 110
. . . . 110
111
115
. 121
. . . . 122
3. Л инейные и циклические коды . . . . . . .
3.1. Л инейные коды. . . . . . . . . . .
3.2. Методы декодирования линейных кодов
3.3. Нижняя rраница Варшамова
rилберта .
3.4. Распределение весов. . . .
З.5. Циклические коды (1). .
3.6. Циклические коды ( 1 1)
3.7. Укороченные коды. . . . .
определения кодов
. 125
. 125
. 128
128
134
140
142
148
155
161
4. Важнейшие коды . . . . .. ...
4.1. Коды Боуза
Чоудхури
ХокпинrеМа .
4.2. Декодирование БЧХ
кодов
4.2.1. Основные этапы . . . . . .
. . .
. 163
. . 163
. . 169
. 169
Оелавленuе
573
4.2.2. Итеративный алrориrм БерлеК9мпа. . . . .
4.3. Методы мажориrарноrо декодирования . .
4.4. Мноrочлены Матсона
Соломона. . . . . . . .
4.5. Полиномиальные коды. . . . . . . .
4.5.1. Обобщенные коды Рида
Маллера . . . . .
4.5.2. llолиномиальные коды и двоЙственные к ним коды
4.6. Каскадные коды и коды Юстесена . . . .
4.6.1. Каскадные I{ОДЫ . .. . . . . .
4.6.2. Коды Юсrесена . . . . .
4.7. Коды rOnnbI. . . . . . . . . .
4.7.1. Определение. . . . .
4.7.2. Метод декодирования . . . . . . . . . .
4.8. Коды, исправляющие пачки ошибок. . . .
. 174
. . . . 178
. 184
188
. 188
195
. . . 200
.200
. 204
. 206
. . . . . 206
. 214
. . 218
5. Сверrочные коды. 1. Методы nopor080ro декодирования . . . . . . 222
5.1. Общий обзор сверточных кодов . . . . . . . .. .. 222
5.1.1. Метод noporoBoro декодирования. . . . . . . 222
5.1.2. Методы ПОС.ТIедоваrельноrо декодирования . . .. . 223
5.1.3. Методы декодирования по максимуму правдоподобия. . . 225
5.2. Представление сверточных кодов. . . . . . . .. .. 226
5.2.1. Представление с помощью операторов задержки . 226
5.2.2. Представление с помощью матриц. . . . . .. . 230
5.3. Пример noporoBoro декодирования. ... . . 236
5.4. Принцип noporoBoro декодирования . . . . . . 239
5.5. Самоортоrональные коды. . . . . . .. .. 242
5.5.1. Определение самоортоrональноrо кода. . . . .. . 242
5.5.2. Простой пример . . . . .. ...... . 244
5.5.3. Коды, строящиеся с помощью простых совершенных раз
ностных МНО)l{еств. . . . . 248
5.5.4. Примеры кодов. . . . . . . . . . . . . . 251
5.5.5 Оптимальность кодов . . . . . . 251
5.6. OpToroH ализируемые I{ОДЫ. . .. ...... .. 254
5.6.1. Простейшие примеры . . . . . . . . . 254
5.6.2. Способ построения кодов . ... ... . 255
5.6.3. Примеры кодов. . . . . .. .,. . . 256
5.6.4. Связь с блоковыми кодами. . . . . . . . . . 256
5.6.5. Сопоставление с циклическими кодами, построенными на
основе разностных множеств . . . . . . . . . . . . 259
5.7. Распространение ошибок. . . . . . . . . . . . . . . . 260
5.7.1. Анализ rлубины распространения ошибок . . . . . . . 261
5.7.2. Критерий устойчивости пороrовой декодирующей лоrиqеской
схемы . . . . . . . . . . . . . . . . . . . . . 264
5.7.3. Критерий, основанный на использовании функции Ляпунова 266
5.7.4. Дефинитное декодирование. . . . . . . . . . . . . 270
5.8. Сверточные коды, исправляющие пачки ошибок . . . 270
5.8.l. Методы чередования. . . . . . . . . . . . . 271
5.8.2. Принцип построения кодов. . . . . . . . . . . . . 273
5.8.3. Способ построения кодов. . . . . . . . . .. . 274
5.8.4. Конкретные I{ОДЫ. . . . . . . . . .. .... 276
5.8.5. Оценки кодов и сравнение их параметров . .... 277
5.8.6. Друrие коды. . . . . . . . . . . . . . . 279
5.9. Сверточные коды, исправляющие пачки ошиБОI{ инезаВИСИМые
ошибки (диффузные коды) . . . . _ ...... 279
5.9.1. Два типа пачек ОUlибок. . . . . . . . 280
5.9.2. КорреКТИРУlощая спосоБНОСТI> . . . . 280
5.9.3. ПростоЙ при мер . . . .. '" . 281
5.9.4. Самоортоrональные коды . . . . . . . . 282
574
Оzлавленuе
5.10.
Равномерные сверточные коды . . . .
5.10.1. Определение р aBHoMepHoro кода . . . .
5.10.2. Правило ортоrонализации. . . . .
5.10.3. Метод ортоrонализации, обеспечивающий небольшую rлу-
бину распространения ошибок
5.10.4. Перфорированные равномерные коды
Задачи . . . . . . . . . . . .
. 284
. 284
. 285
288
. 290
. . . 293
6. Сверточные коды. 11. Пос..lJедовательное декодирование. . .. . 298
6.1. Древовидные коды и принцип последовательноrо декодирования 299
6.1.1. Древовидные коды . . . . . . . . 299
6.1.2. Принцип последовательноrо декодирования . 301
6.2. Алrоритм Фано. . . . . . 305
6.2.1. Цена пути. . . .. .... _ . 305
6.2.2. Поведение декодера . ... . . . . . . 307
6.3. Среднее число операций при декодировании . . . 311
6.3.1. Среднее число операций . . . . . .. ... . 311
6.3.2. Свойство независимости в древовидном коде . . 315
6.3.3. Верхняя rраниuа для среднеrо числа операций . 317
6.4. Распределение числа операций и вероятность переполнения бу-
фер а . . . . . . . . . . . . . . . . . . . . . 321
· 6.4.1. Структура и функционирование буфера . . 322
6.4.2. Нижняя rраница для р[с
1.] . . . . . 323
6.4.3. Верхняя rраница для р [с
L] . . ., ..... 328
6.4.4. Связь с вероятностью переполнения буфера . 329
6.5. Вероятность необнаружения ошибки ... .... 334
6.6. rраницы Витерби и декодирование по максимуму правдоподобlIЯ 338
6.6.1. Верхняя rраница для вероятности ошибки. : . . . . . 339
6.6.2. Нижняя rраница для вероятности ошибки. . . . . . . 344
6.7. fибридные методы КОДИРОI3ания . . . . 348
6.7.1. Системы rибридноrо кодирования . . 348
6.7.2. Характеристики rибридноrо кодирования .... 353
6.8. Стек-алrоритм , . . . . . . . . . . . . . 358
6.9. Структура расстояний сверточных кодов . . . . . . . 362
6.9.1. Верхняя rраница П.поткина при декодировании с обратной
связью . .. .......... ., 363
6.9.2. Нижняя rраница rилберта для сверточных кодов при деко-
дировании с обратной связью. . . . . . . . . . . . 367
6.9.3. Верхняя и нижняя rраницы МИIl!lмальноrо расстояния при
дефинитном декодировании. . . . . . . . .. . 370
6.10. Коды, используемые при декодирова нии с обраТIIОi'1 связью. . . 371
6.11. Коды, используемые при последоватеJlЬНОМ лскодировании .. 376
Задачи и упражнения " . . . . . . . . .' .. 379
7. Реализация и применение кодов, исправляющих ошибки ..... 383
7.1. Реализация кодов, испраВЛЯЮIЦИХ ошибки. . . . . 383
7.1.1. Стандарные схемы . . '. '" . 385
7.1.2. Кодеры циклических I<ОДОВ . . . . . . . . . . . . . 388
7.1.3. Декодеры циклических кодов . .. . 391
-7.2. Реализация пороrовоrо декодирования . . . . 405
7.2.1. Кодеры. . . . . . . . . . . 405
7.2.2. Декодер. . . . . . . . . . . . . . . . 410
7.2.3. Схема преобразования паралле.1ЬНЫХ слов в послеДОВc:tтеЛh-
ные и обратная схема ....... .... 410
7.2.4. РеаЛИ'3ация сверточных кодов, испраВJlЯЮIЦИХ паЧl{Н ошибок 411
Оzлааленuе
575
7.3.
ОБСУ/!{ДСllIlС СIНIЗIJ TCOplIII I<ОДllроваНllН с pCd..1bIIbl
1l1 теХllllчеСIПI-
:\111 пробле
I
ЫII . ... ... . 412
7.3.1. Задача ТСОрИII кодирования ... . 415
7.3.2. Стонмость и надежность 417
7.3.3. ПрllМСllеllне в ВЫЧИСЛНТС"lLIIЫХ СIlстеызх. . . 418
Различные преДПОЛО)I(СНIIЯ, нспользуе
lые в теории кодирования 420
7.4.1. ДИСI<РСТllые веЛИЧИIIЫ . . . . . . . . 421
7.4.2. Л\етоды принятия решеllll{1 421
7.4.3. РаССТОЯllие Хэмминrа . 424
7.4.4. Положительные стороны теории I<ОДllрова
ия . 425
ПрнмеIlеНIJЯ в СIIСТСМЭХ связи метода повторнои передаЧIl . 426
7.5.1. CllcTe:VlbI с IIОЛНОЙ обратноЙ связью 11 системы с дублирова-
нием IIсреда чи . . . . 426
7.5.2. Обнаружение ошибок . . . . . 427
Примснения в СIlстемах связи КОДОВ, испраВЛЯЮJДИХ ошибки. . 428
7.6.1. J\10ДУЛЯЦИЯ и кодирование . . 428
7.6.2. Вероятность ошибки при ИСПОЛfJзовании алrебранческнх ко-
дов. .,. . . . . . . 430
7.6.3. МноrОУРОВllеная фазовая МОДУЛЯЦIIЯ и ;<одироваНllе. 432
7.6.4. ПРllменения кодов в космических и спутниковых системах
связи . . . . . . . . . . . 437
7.6.5. ОСlIовные понятия о проектироваllИИ систем связи с помехо-
устоЙчивым кодированием. . 448
7.6.6. Проблемы, ВОЗНИl<ающие при проектированни систем связи
с помехоустойчивым кодированием ИНФОРМЗЦilIl . 450
7.6.7. Пример применения noporoBoro декодирования в спутнико-
вой связи . 451
Применеllие в системах обработки информации. . 453
7.7.1. Применение кодов при общении человеI<а с маUIИНОИ. . .454
7.7.2. Коды на основе ортоrональных .1а fПНСIОIХ квадратов . . 457
7.7.Э. Коды, испраПЛS11О1ЦИ
пачки оши601{ JI допускаlОUL!Iе быстрое
декодирование . . . . . 461
3 ада ЧII . . . . . . .. ............. 465
7.4.
7.5.
7.6.
7.7.
8. КОДЫ для арифметических устройств. . .
. .
. 466
8.1. ОСlIовные ПОIlЯТIIЯ теОрИII Чllсел . 467
8.1.1. Делимость целых чисел . .. 467
8.1.2. Наименьшее общее кратное 11 lIаибо.'IЬШИЙ оБЩilЙ делитель 467
8.1.3. Простые числа и разло}кение на простые СОj,IIIожители. . 468
8.1.4. Функция ЭЙлера . . . . . 468
8.1 5. Сравнимость и классы вычетов. . . . 469
8.1.6. Теоремы ЭЙлера н Ферма. . . . . . . . . . 470
8.1.7. Показатели экспоненты и примитивные КОрllИ . 470
8.1.8. Мультипликативные rpYnnbI и их разложение . . 473
8.1.9. Квадратичные вычеты и символ Ле)кандра. . . . . . 475
8.1.10. KpyroBbIe МlIоrочлены и их сомножители . . . 476
8.1.11. Минимальное представление дроби . . . . . 478
8.2. Определение AN
Koдa .' ..... 479
8.3. АрифметичеСКllil вес 11 арифметическое расстояние . . 481
Алrоритм IIRхождеllllЯ представления. удовлеТВОРЯlOlцеrо yc.ryO-
вию М . '" .., .... 481
8.4.
\инимальное раССТОЯllие и корректирующая способность АN
кода 489
8.5. Обllару}кение 11 исправление незаDИСНМЫХ ошибок веса 1 . 493
8.6. АN
коды, испраВЛЯЮIЦllе кратные ошибки . . . . . 499
8.7. Синдромы н методы декодироваllIlЯ АN
кодов. ... 502
576
Оzлавленuе
9. Циклические АN-коды. .
9.1. Структура циклических АN
кодов. . . .
9.1.1. Определение ЦlIклическоrо АN
кода
9.1.2. Кольцо целых чисел по модулю 2 е
1 и ero идеалы .
9.1.3. Задание циклических кодов . .. ....
9.1.4. Разложение и структура циклических АЛ'-кuдон .
9.2. Л1ИIIIIмальное расстояние циклических AN
KOДOB . .
9.2.1. l\'\инимальное расстояние простых кодов . .
9.2.2. Минимальное расстояние АN-кодов, удовлеТDОРЯЮULИХ спе-
циальным условиям . . .. 521
9.2.3. Минимальное расстояние uиклических I1N -кодов (В
про-
стое число) . . 524
9.2.4. Минимальное расстояние пиклических AN
KOД09 (В
со-
ставное число) . . . . . . . . 528
9.3. Декодирование циклических AN -кодов . 531
9.3.1. Вычеты по модулю А и конфиrурации ошибок " . 531
9.3.2. Метод декодирования, основанныil на циклических сдвнrах
вычетов . . 534
9.3.3. Метод декодирования, основанный на переборе 537
9.4. Дополнение . 540
Приложения . . 545
Приложение 1. Разложение чисел вида 2 n
1 на простые МНО}К1IТС.1I1
и таблица неприводимых мноrочлеНОD
11риложеНllе 2. Параметры двоичных БЧХ
кодов В УЗКОМ С\lысле
длины 1023 11 менее .
506
. 506
. 506
. 506
. 508
. 509
. 517
517
. 545
Литература . .
ПредметныЙ указате.1Ь
546
556
. 568
ИВ N2 579
Т. Касами, Н. Токура, Е. Ивадари, Я. Инаrакп
ТЕОРИЯ КОДИРОВАНИЯ
Редактор Л. Якименко Художник А. Быков ХудожественныА редактор В. Бисенrалнев
Технический редактор r. АЛЮЛlIна Корректор В. Соколов
Сдано в набор 07.09.77. По..1.писано к печати 16.02.78. Формат 60X90 1 / 1 6. Бум. тип. N'1 1.
Литературная rарнитура. Высокая печать. 18,00 бум. л., 36,00 печ. л. Уч.-изд. л. 34,25.
Зак. .N'2 761. Цен а 2 р. 70 к.
Издательство СМИР:'.l\\осква, I-A Рижский пер.,
Ордена Трудовоrо KpacHoro Знамени Ленинrрадская типоrрафия Н!! 2
имени Евrении СОКОЛОВОЙ СОЮЗПОJ1иrрафпрома при rосударствеНIIОМ комитете
Совета Министров СССР по делам издательств, ПОJlиrраФIIИ и книжной торrовли.
198052, ЛеНИНI'рад, Л
52, Измайловский проспект, 29.




































































































































































































































































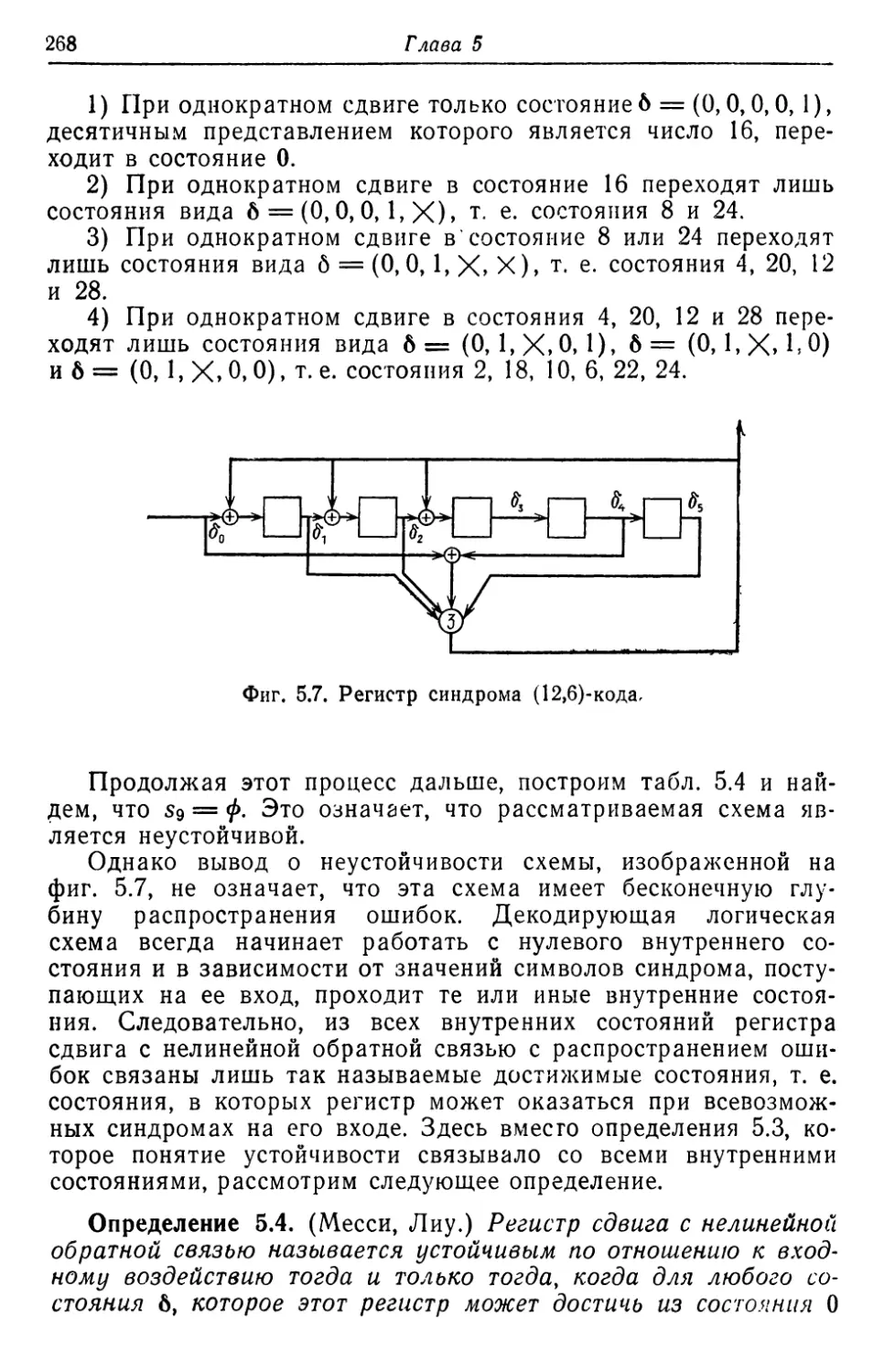














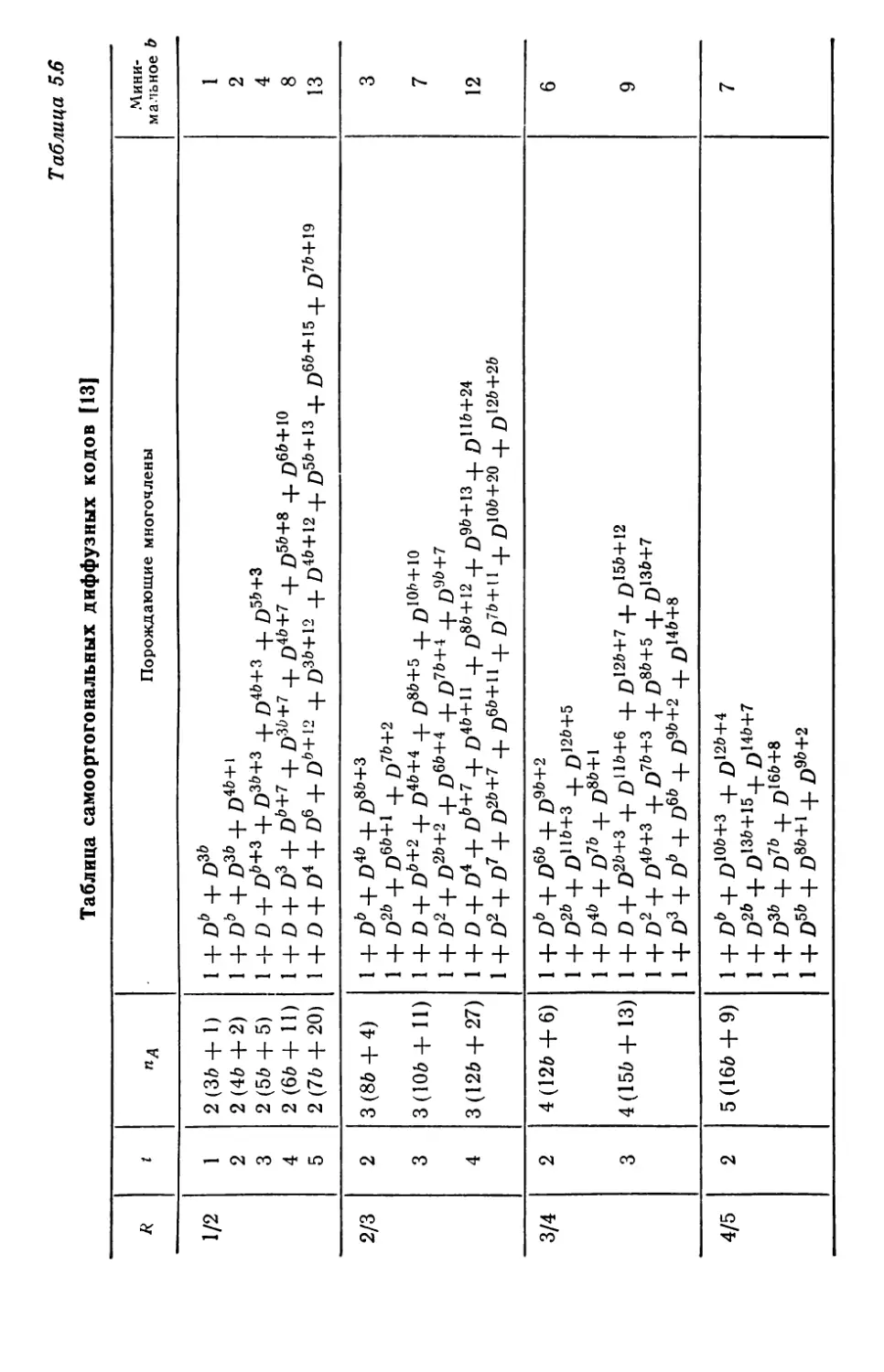



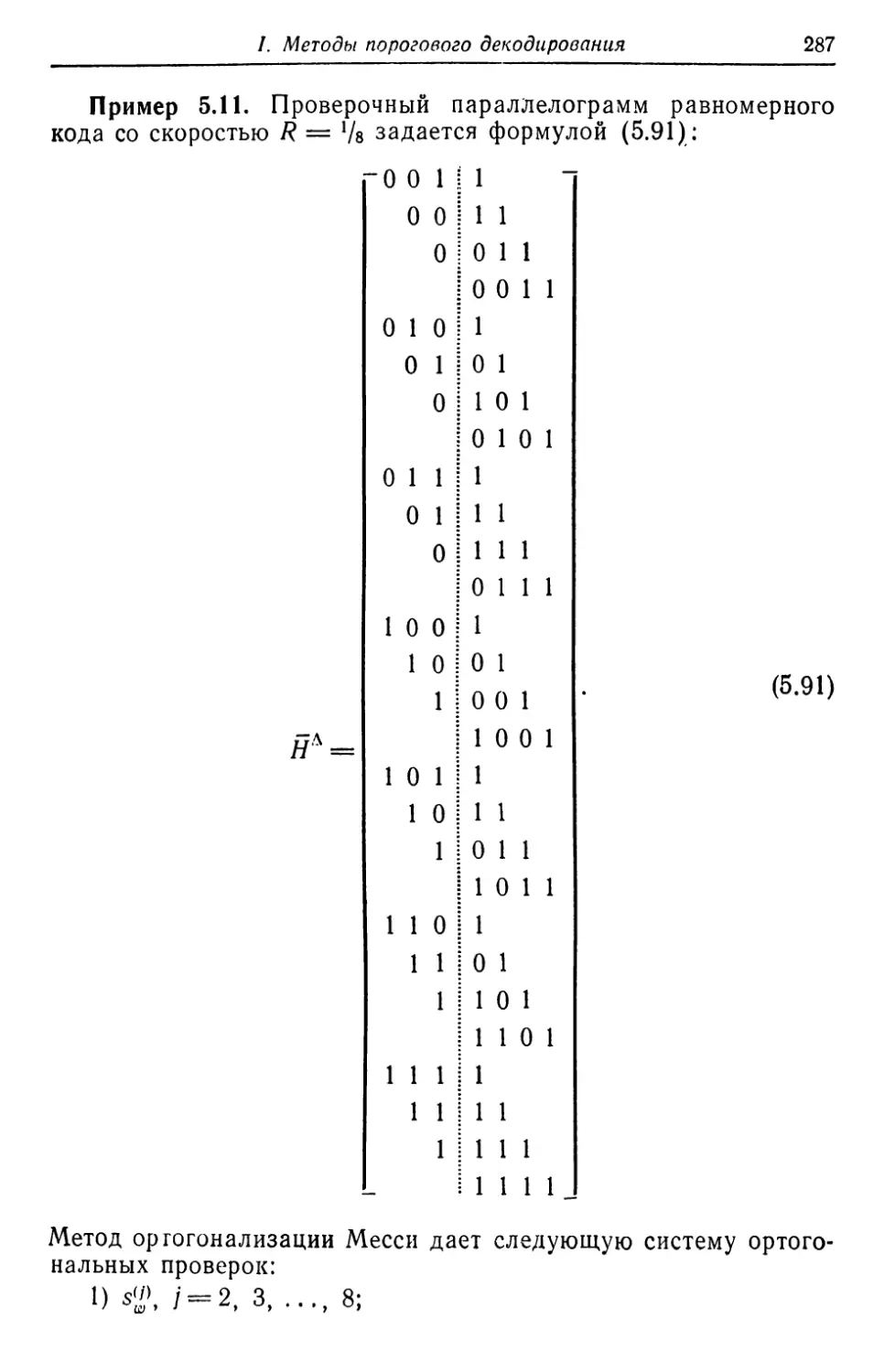




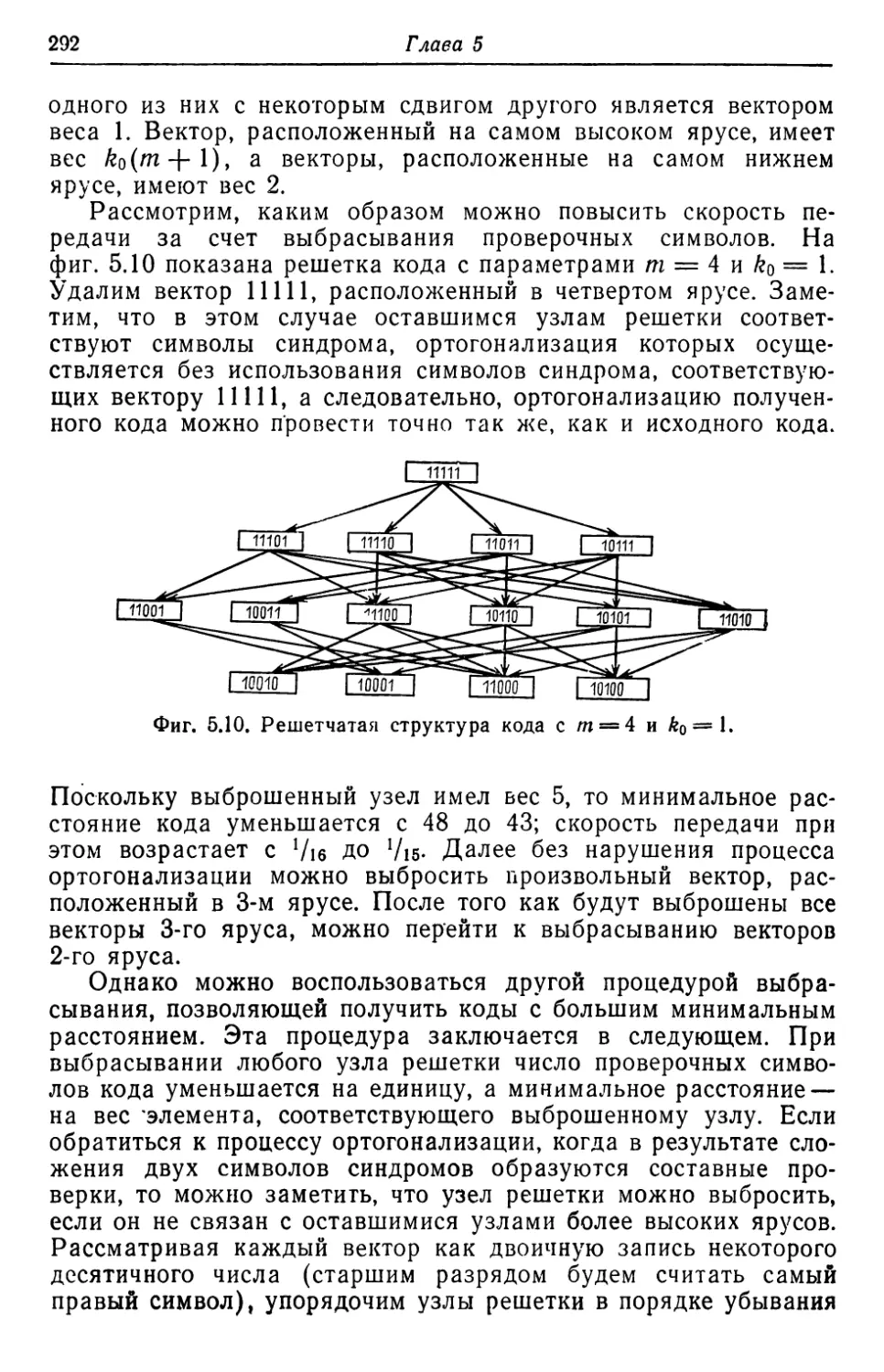



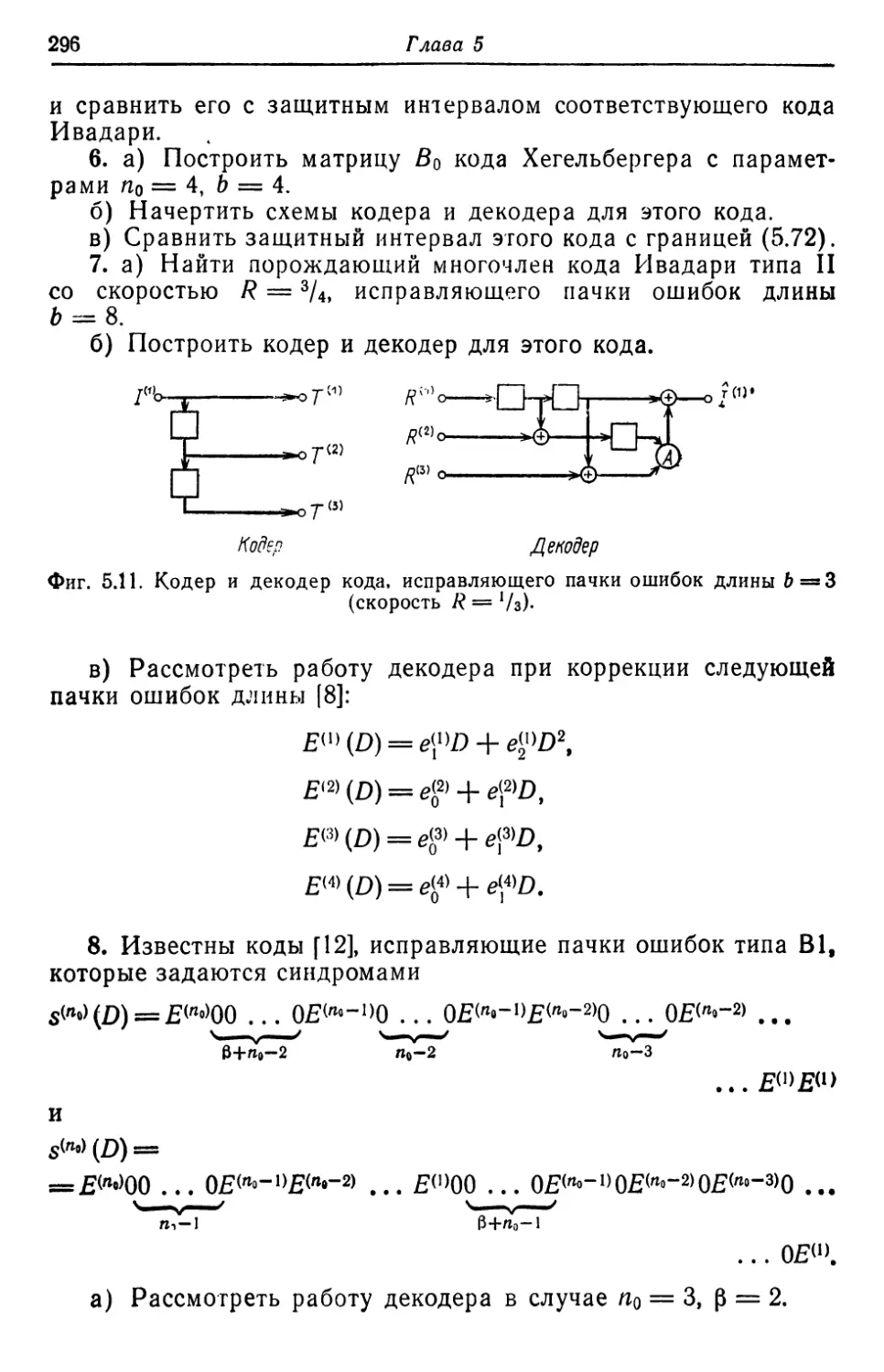






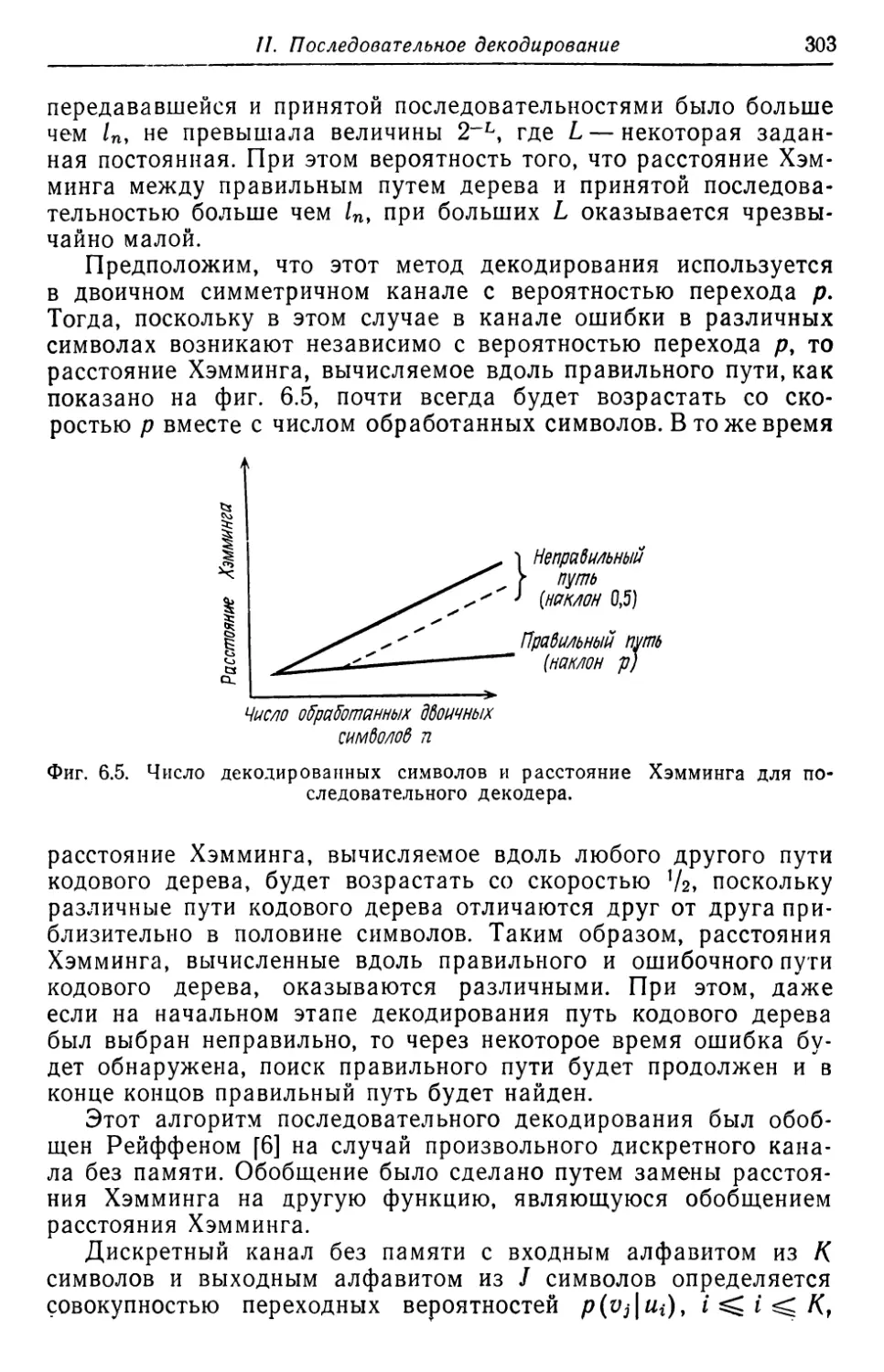





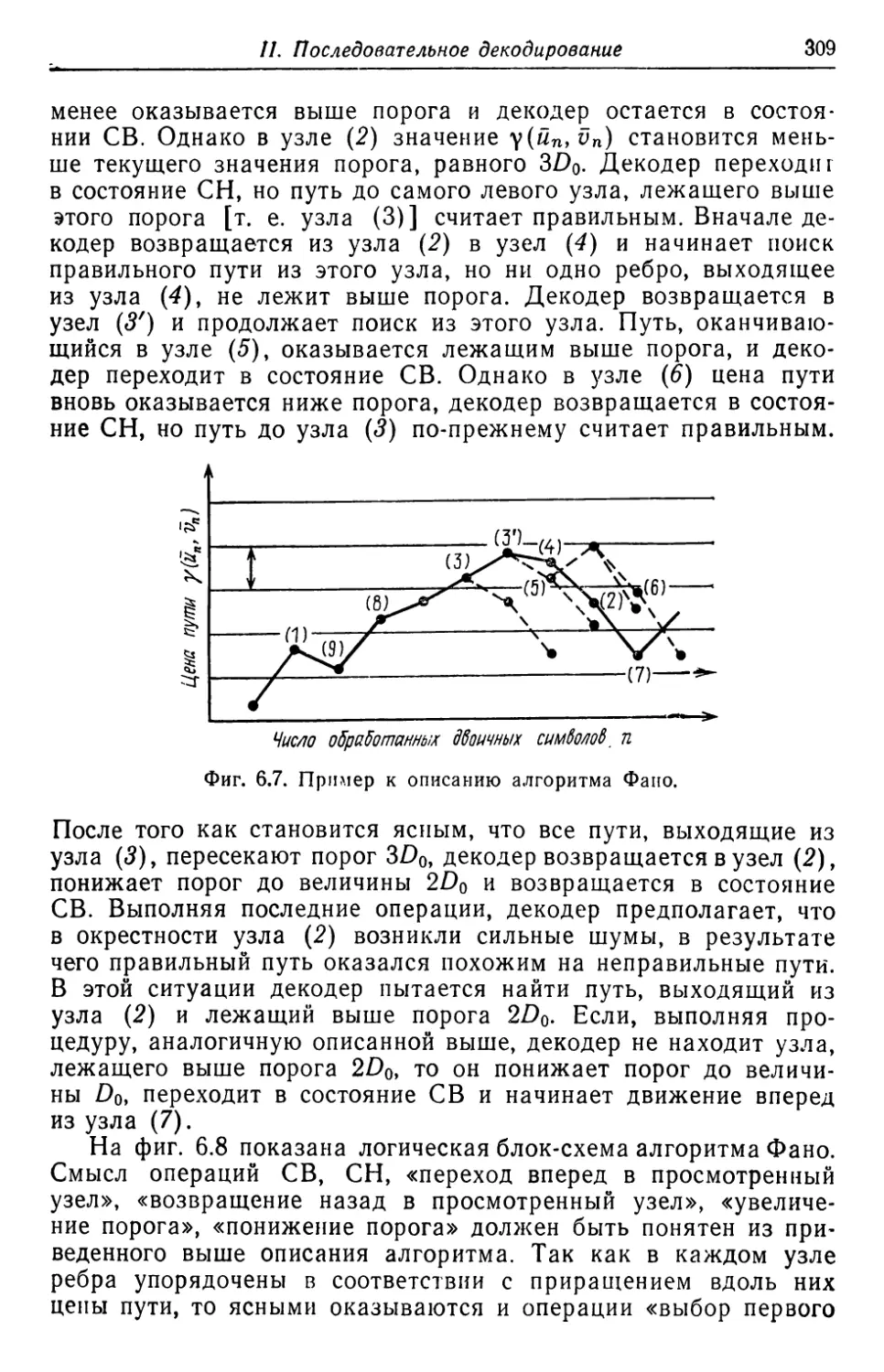
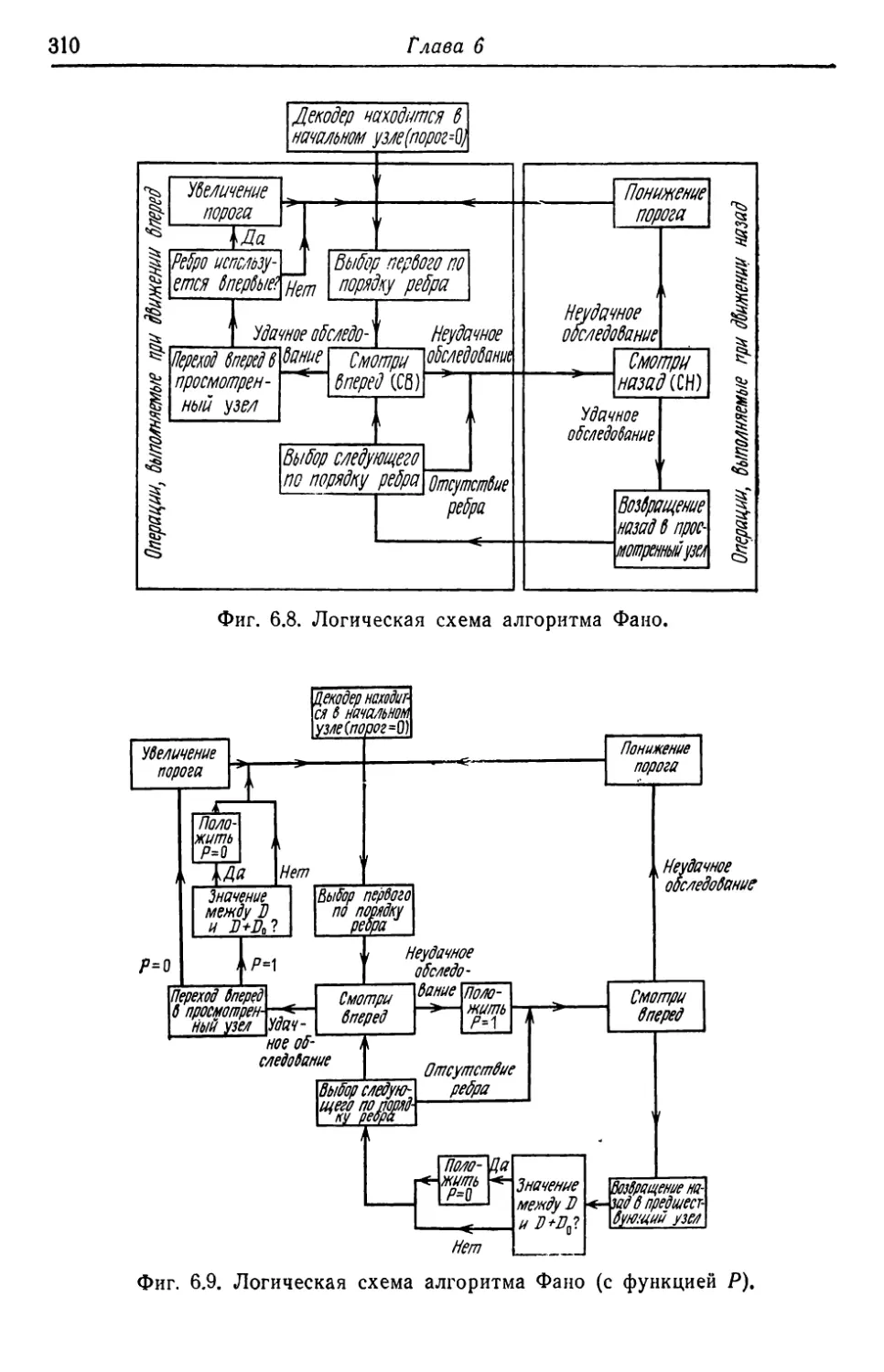












![6.4.2. Нижняя граница для р[с > L]](https://djvu.online/jpg/Y/U/O/YUOdCEXSTIxke/324.webp)




![6.4.3. Верхняя граница для р[с > L]](https://djvu.online/jpg/Y/U/O/YUOdCEXSTIxke/329.webp)