УДК 517.5
ББК 22.161.5
С24
СВЕШНИКОВ А. Г., ТИХОНОВ А. Н. Теория функций ком-
комплексной переменной: Учеб.: Для вузов. — 6-е изд., стереот. — М.:
ФИЗМАТЛИТ, 2005. — 336 с. — (Курс высшей математики и мате-
математической физики). — ISBN 5-9221-0133-1 (Вып. 5).
Один из выпусков «Курса высшей математики и математической физики»
под редакцией А. Н. Тихонова, В. А. Ильина, А. Г. Свешникова. Учебник создан
на базе лекций, читавшихся авторами в течение ряда лет на физическом факуль-
факультете Московского государственного университета. В книге изложена теория функ-
функций комплексной переменной и операционного исчисления. Приведены примеры
применения методов теории функций комплексной переменной. Даны основные
понятия теории функций многих комплексных переменных.
Для студентов высших учебных заведений, обучающихся по специальности
«Физика» и «Прикладная математика».
Ил. 60.
ISBN 5-9221-0133-1 (Вып. 5)
ISBN 5-9221-0134-Х	© физматлит, 2001, 2005

ОГЛАВЛЕНИЕ
От редакторов серии		9
Предисловие к пятому изданию		10
Предисловие к третьему изданию		10
Предисловие к первому изданию		11
Введение		12
Глава 1. Комплексная переменная и функции комплексной
переменной	 13
§ 1. Комплексное число и действия над комплексными числами . . 13
1. Понятие комплексного числа A3). 2. Действия над комплекс-
комплексными числами A3). 3. Геометрическая интерпретация комп-
комплексных чисел A5). 4. Извлечение корня из комплексного числа
A7).
§ 2. Предел последовательности комплексных чисел	 19
1. Определение сходящейся последовательности A9). 2. Крите-
Критерий Коши B1). 3. Бесконечно удаленная точка B1).
§ 3. Понятие функции комплек-ной переменной. Непрерывность . . 23
1. Основные определения B3). 2. Непрерывность B5). 3. При-
Примеры B8).
§ 4. Дифференцирование функции комплексной переменной .... 33
1. Определение. Условия Коши—Римана C3). 2. Свойства ана-
аналитических функций C6). 3. Геометрический смысл производ-
производной функции комплексной переменной C7). 4. Примеры C9).
§ 5. Интеграл по комплек—ной переменной	 41
1. Основные свойства D1). 2. Теорема Коши D4). 3. Неопреде-
Неопределенный интеграл D7).
§ 6. Интеграл Коши	 50
1. Вывод формулы Коши E0). 2. Следствия из формулы Коши
E2). 3. Принцип максимума модуля аналитической функции
E3).
§ 7. Интегралы, зависящие от параметра	 56
1. Аналитическая зависимость от параметра E6). 2. Существо-
Существование производных всех порядков у аналитической функции
E8).

ОГЛАВЛЕНИЕ
Глава 2. Ряды аналитических функций	 61
§ 1. Равномерно сходящиеся ряды функций комплексной переменной 61
1. Числовые ряды F1). 2. Функциональные ряды. Равномер-
Равномерная сходимость F3). 3. Свойства равномерно сходящихся ря-
рядов. Теоремы Вейерштрасса.(бб). 4. Несобственные интегралы,
зависящие от параметра F9).
§ 2. Степенные ряды. Ряд Тейлора	 70
1. Теорема Абеля G0). 2. Ряд Тейлора G5).
§ 3. Единственность определения аналитической функции	 79
1. Нули аналитической функции G9). 2. Теоремы единственно-
единственности G9).
Глава 3. Аналитическое продолжение. Элементарные
функции комплексной переменной	 83
§ 1. Элементарные функции комплексной переменной. Продолже-
Продолжение с действительной оси	 83
1. Продолжение с действительной оси (83). 2. Продолжение со-
соотношений (87). 3. Свойства элементарных функций (91). 4.
Отображения элементарных функций (94).
§ 2. Аналитическое продолжение. Понятие римановой поверхности 99
1.	Основные принципы. Понятие римановой поверхности (99).
2.	Аналитическое продолжение через границу A02). 3. Приме-
Примеры построения аналитического продолжения. Продолжение че-
через границу A03). 4. Примеры построения аналитического про-
продолжения. Продолжение с помощью степенных рядов A08). 5.
Правильные и особые точки аналитической функции A11). 6.
Понятие полной аналитической функции A14).
Глава 4. Ряд Лорана и изолированные особые точки .... 116
§ 1. Ряд Лорана	116
1. Область сходимости ряда Лорана A16). 2. Разложение ана-
аналитической функции в ряд Лорана A18).
§ 2. Классификация изолированных особых точек однозначной ана-
аналитической функции	120
Глава 5. Теория вычетов и их приложения	128
§ 1. Вычет аналитической функции в изолированной особой точке 128
1. Определение формулы вычисления вычета A28). 2. Основная
теорема теории вычетов A30).
§ 2. Вычисление определенных интегралов с помощью вычетов . . 133
2тг
1. Интегралы вида J R(cos 6, sin 6) d6. A34). 2. Интегралы ви-
о
оо	оо
да / f(x)dx A35). 3. Интегралы вида / etaxf(x)dx. Лемма
— оо	—оо
Жордана A38). 4. Случай многозначных функций A44).
§ 3. Логарифмический вычет	150
1. Понятие логарифмического вычета A50). 2. Подсчет числа
нулей аналитической функции A51).

ОГЛАВЛЕНИЕ	7
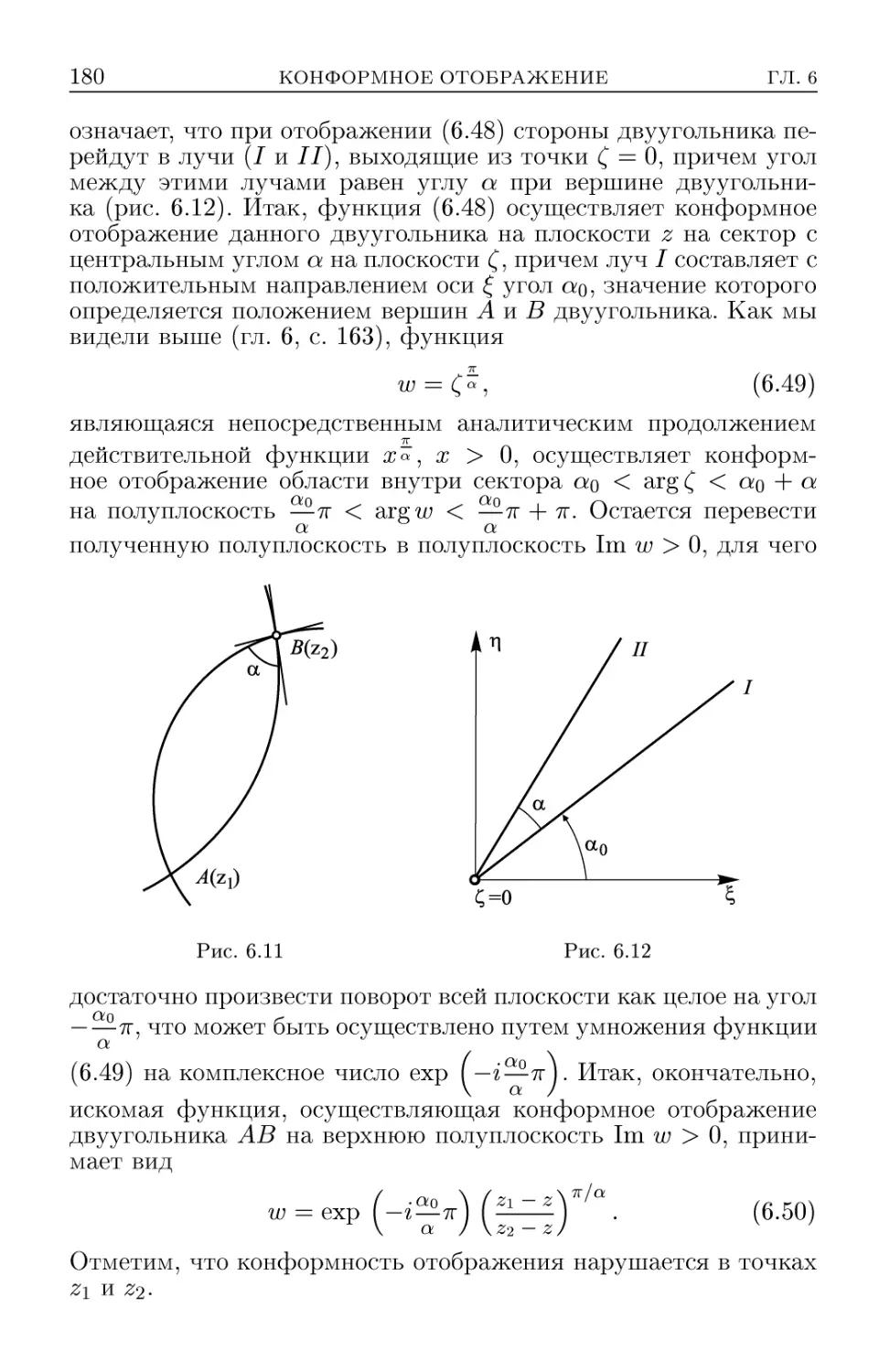
Глава 6. Конформное отображение	155
§ 1. Общие свойства	155
1. Определение конформного отображения A55). 2. Простей-
Простейшие примеры A59). 3. Основные принципы A63). 4. Теорема
Римана A68).
§ 2. Дробно-линейная функция	171
§ 3. Функция Жуковского	181
§ 4. Интеграл Шварца-Кристоффеля. Отображение многоугольни-
многоугольников 	184
Глава 7. Применение аналитических функций к решению
краевых задач	193
§ 1. Общие положения	193
1. Связь аналитических и гармонических функций A93). 2.
Сохранение оператора Лапласа при конформном отображении
A94). 3. Задача Дирихле A96). 4. Построение функции источ-
источника A99).
§ 2. Приложения к задачам механики и физики	201
1. Плоское установившееся движение жидкости B01). 2. Плос-
Плоское электростатическое поле B12).
Глава 8. Основные понятия операционного исчисления . . . 221
§ 1. Определения и основные свойства преобразования Лапласа . . 221
1. Определение преобразования Лапласа B21). 2. Изображение
элементарных функций B26). 3. Свойства изображения B28).
4. Таблица свойств изображений B36). 5. Таблица изображений
B36).
§ 2. Определение оригинала по изображению	238
1. Формула Меллина B38). 2. Условия существования ориги-
оригинала B41). 3. Вычисление интеграла Меллина B44). 4. Случай
регулярной на бесконечности функции B49).
§ 3. Решение задач для линейных дифференциальных уравнений
операционным методом	261
1. Обыкновенные дифференциальные уравнения B61). 2. Урав-
Уравнение теплопроводности B57). 3. Краевая задача для уравне-
уравнения в частных производных B58).
Приложение 1. Метод перевала	261
1. Вводные замечания B61) . 2. Метод Лапласа B64). 3. Метод
перевала B72).
Приложение 2. Метод Винера—Хопфа	281
1. Вводные замечания B81). 2. Аналитические свойства пре-
преобразования Фурье B86). 3. Интегральные уравнения с ядром,
зависящим от разности аргументов B88). 4. Общая схема ме-
метода Винера-Хопфа B93). 5. Задачи, приводящие к интеграль-
интегральным уравнениям с ядром, зависящим от разности аргументов
B98). 5.1. Вывод уравнения Милна B98). 5.2. Исследование
решения уравнения Милна C02). 5.3. Дифракция на плоском

ОГЛАВЛЕНИЕ
экране C06). 6. Решение краевых задач для уравнения в част-
частных производных методом Винера-Хопфа C07).
Приложение 3. Функции многих комплексных переменных 312
1. Основные определения C12). 2. Понятие аналитической
функции многих комплексных переменных C13). 3. Формула
Коши C15). 4. Степенные ряды C16). 5. Ряд Тейлора C18).
Аналитическое продолжение C19).
Приложение 4. Метод Ватсона	323
Литература 	331
Предметный указатель	332

ОТ РЕДАКТОРОВ СЕРИИ
Настоящая книга представляет собой пятый выпуск серии
«Курс высшей математики и математической физики» и посвя-
посвящена изложению основ теории функций комплексной перемен-
переменной и операционного исчисления. В книге также даны примеры
применения методов теории функций комплексной переменной
к задачам гидродинамики и электростатики, разобраны некото-
некоторые вопросы метода перевала и метода Винера-Хопфа.

ПРЕДИСЛОВИЕ К ПЯТОМУ ИЗДАНИЮ
Четвертое издание этой книги, являющейся пятым выпуском
серии «Курс высшей математики и математической физики»,
вышло в свет в 1979 г. Поскольку последние двадцать лет книга
использовалась как основной учебник по курсу теории функ-
функций комплексной переменной не только на физическом факуль-
факультете МГУ, но и во многих других вузах, она стала библиогра-
библиографической редкостью, а имеющиеся в учебных библиотеках эк-
экземпляры пришли в практическую негодность. Поэтому можно
только приветствовать инициативу Издательской фирмы «Нау-
«Наука. Физматлит» РАН, предложившей настоящее, пятое, переиз-
переиздание данного учебника.
Чтя память моего учителя и соавтора этой книги академика
РАН Андрея Николаевича Тихонова, скончавшегося 7 октября
1993 г. , я решил не вносить никаких изменений в текст предыду-
предыдущего издания, вышедшего еще при жизни Андрея Николаевича.
Июнь 1998 г.	А. Г. Свешников
ПРЕДИСЛОВИЕ К ТРЕТЬЕМУ ИЗДАНИЮ
В третьем издании книги устранены замеченные неточности
изложения, добавлен ряд приложений теории функций комп-
комплексной переменной (несобственные интегралы, зависящие от
параметра, преобразование Ватсона и т. д. ), дано представле-
представление об основных понятиях теории функций многих комплексных
переменных.
Мы глубоко благодарны редактору этой книги С. Я. Секерж-
Зеньковичу, работа которого способствовала улучшению ее со-
содержания.
Авторы

ПРЕДИСЛОВИЕ К ПЕРВОМУ ИЗДАНИЮ
Содержание этого выпуска в основном соответствует курсу
лекций по теории функций комплексной переменной, читавше-
читавшемуся авторами в течение ряда лет на физическом факультете
МГУ.
Изложение основного материала достаточно близко к тради-
традиционному. Однако мы не проводим специального рассмотрения
элементарных функций комплексной переменной в самом нача-
начале курса, как это делается в большинстве учебников, а вводим
элементарные функции комплексной переменной как непосред-
непосредственное аналитическое продолжение элементарных функций
действительной переменной. Теоремы об аналитическом продол-
продолжении соотношений позволяют единообразно перенести в ком-
комплексную область известные свойства элементарных функций
действительной переменной.
Естественно, что стремление к цельности изложения заста-
заставило рассмотреть отдельные вопросы несколько подробнее, чем
обычно удается в рамках сжатой лекционной программы. В пер-
первую очередь это относится к общим принципам конформно-
конформного отображения и применения методов теории функций комп-
комплексной переменной к решению краевых задач гидродинами-
гидродинамики и электростатики. Кроме того, в книге имеются два при-
приложения, посвященные изложению метода перевала и метода
Винера-Хопфа, которыми физики весьма широко пользуются.
При работе над книгой мы пользовались советами многих
наших товарищей по кафедре, в первую очередь В. А. Ильина
и Д. П. Костомарова. Большую помощь оказали многочислен-
многочисленные и важные замечания, сделанные Г. Л. Лунцем и М. В. Фе-
дорюком, прочитавшими книгу в рукописи, а также тщатель-
тщательное редактирование текста книги, проведенное С. Я. Секерж-
Зеньковичем. Всем этим лицам мы выражаем самую искреннюю
благодарность.
Авторы

ВВЕДЕНИЕ
В настоящем выпуске излагаются основные понятия теории
функций комплексной переменной. Понятие комплексного чис-
числа возникло в первую очередь в результате потребностей авто-
автоматизации вычислений. Даже простейшие алгебраические опе-
операции над действительными числами выводят за пределы обла-
области действительных чисел. Как известно, не всякое алгебраиче-
алгебраическое уравнение может быть разрешено в действительных чис-
числах. Тем самым надо или отказаться от автоматического приме-
применения установленных методов решения и каждый раз проводить
подробное исследование возможностей их применения, или рас-
расширить область действительных чисел с тем, чтобы основные
алгебраические операции всегда были выполнимы. Таким рас-
расширением области действительных чисел являются комплекс-
комплексные числа. Замечательным свойством комплексных чисел явля-
является тот факт, что основные математические операции над ком-
комплексными числами не выводят из области комплексных чисел.
Введение комплексных чисел и функций комплексной пере-
переменной удобно так же при интегрировании элементарных функ-
функций, при решении дифференциальных уравнений и т. д. , где
часто приходится выходить в область комплексных чисел. Ком-
Комплексная форма записи оказывается удобной и при математиче-
математической формулировке многих физических положений (например,
в электро- и радиотехнике, электродинамике и т. д. ).
Один из основных классов функций комплексной перемен-
переменной — аналитические функции — находится в тесной связи с
решениями уравнения Лапласа, к которому приводятся многие
задачи механики и физики. Поэтому методы теории функций
комплексной переменной нашли весьма широкое и эффективное
применение при решении большого круга задач гидро- и аэро-
аэродинамики, теории упругости, электродинимики и других есте-
естественных наук.

ГЛАВА 1
КОМПЛЕКСНАЯ ПЕРЕМЕННАЯ И ФУНКЦИИ
КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
§ 1. Комплексное число и действия над комплексными
числами
1.	Понятие комплексного числа. Мы считаем, что с по-
понятием комплексного числа и определением арифметических
действий над комплексными числами читатель уже знаком.
Комплексные числа и действия над ними изложены в предыду-
предыдущих выпусках курса1). Однако из соображений цельности изло-
изложения имеет смысл еще раз напомнить основные понятия.
Комплексным числом z называется пара действительных
чисел (а, Ь) с установленным порядком следования чисел а и Ъ.
Это условно записывается в виде z = (а, Ъ). Первое число а пары
(а, Ъ) называется действительной частью комплексного числа
z и обозначается символом а = Re z\ второе число Ъ пары (а, Ъ)
называется мнимой частью комплексного числа z и обознача-
обозначается символом b = Im z.
Два комплексных числа z\ = (ai, Ь\) и ^ = (^2,^2) равны
тогда и только тогда, когда равны их действительные и мнимые
части, т. е. когда а\ = a 2 и Ъ\ = 62.
2.	Действия над комплексными числами. Перейдем к
определению алгебраических операций над комплексными чис-
числами.
Суммой комплексных чисел z\ = {а>\^Ъ\) и Z2 = (^2^2) на-
называется такое комплексное число z = (a, 6), для которого а =
= а\ + а,2, Ь = Ъ\ + 62. Легко видеть, что при таком определении
сохраняются переместительный и сочетательный законы сложе-
сложения, т. е. z\ + Z2 = Z2 + z\ и z\ + B2 + 23) = B1 + 22) + 23 • Так
же, как и в области действительных чисел, нулем называется
:) См. вып. 1.

14	ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ	ГЛ. 1
такое комплексное число 0, сумма которого с любым комплекс-
комплексным числом z равна этому числу z, т. е. z + 0 = z. Очевидно, что
существует единственное комплексное число 0 = @,0), облада-
обладающее этим свойством.
Произведением комплексных чисел z\ = (ai,bi) и Z2 —
— (^2^2) называется такое комплексное число z = (&,fr), для
которого а = а\A2 — bi&25 b = ai62 + a2&i. При таком определении
произведения выполняются переместительный (z\Z2 = ^2^1)?
сочетательный (z\(z2 • z$) = (^i • ^2)^3) и распределительный
((^i + ^)^з = ^1^3 + ^2^з) законы.
Включим действительные числа в множество комплексных
чисел, рассматривая действительное число а как комплексное
число а = (а,0). Тогда, как следует из определения действий
сложения и умножения, для комплексных чисел сохраняют-
сохраняются известные правила действий над действительными числами.
Поэтому множество комплексных чисел рассматривается как
расширение множества действительных чисел1). Заметим, что
умножение на действительную единицу A,0) не меняет комп-
комплексного числа: z • 1 = z.
Комплексное число вида z = @, b) называется чисто мни-
мнимым и символически обозначается как z = ib. Чисто мнимое
число @, b) = ib можно рассматривать как произведение мни-
мнимой единицы @,1) и действительного числа F,0). Мнимую еди-
единицу обычно обозначают символом @,1) = г. В силу определе-
определения произведения комплексных чисел справедливо соотношение
г • г = г2 = — 1. Оно позволяет придать прямой алгебраический
смысл так называемой алгебраической форме записи комплекс-
комплексного числа
z = (a, 6) = a + ib	A.1)
и производить операции сложения и умножения комплексных
чисел по обычным правилам алгебры многочленов.
Комплексное число ~z = а — ib называется комплексно сопря-
сопряженным числу z = а + ib.
Операция вычитания комплексных чисел определяется как
операция, обратная сложению. Комплексное число z = a + ib
называется разностью комплексных чисел z\ = а\ + %Ь\ и Z2 =
= CL2 + г&2, если а = а\ — а,2, b = b\ — 62.
Операция деления комплексных чисел определяется как опе-
операция, обратная умножению. Комплексное число z = а + ib на-
х) Как будет следовать из дальнейших рассмотрений, множество комп-
комплексных чисел, в отличие от множества действительных чисел, не обладает
свойством упорядоченности, так как не существует рациональной системы
сравнения комплексных чисел.

§ 1	КОМПЛЕКСНОЕ ЧИСЛО	15
зывается частным комплексных чисел z\= а\ + гЬ\ и Z2 = п>2 +
+ г&2 Ф 0, если z\ = z- Z2- Отсюда следует, что действительная а
и мнимая b части частного z определяются из линейной системы
алгебраических уравнений
аъа — 626 = ai,
62a + 0,2b = 61
с определителем а^ + Щ, отличным от нуля. Решив эту систему,
получим
	 z\ 	 OL1OL2
a2+&2	a2+62	U4
3. Геометрическая интерпретация комплексных чи-
чисел. При изучении свойств комплексных чисел весьма удобной
является их геометрическая интерпретация. Поскольку комп-
комплексное число определяется как пара действительных чисел, то
естественной геометрической интерпретацией является изобра-
изображение комплексного числа z = а + ib точкой плоскости ху с де-
декартовыми координатами х = а и у = Ь. Число z = 0 ставится в
соответствие началу координат данной плоскости. Такую плос-
плоскость мы в дальнейшем будем называть комплексной плоско-
стъю, ось абсцисс — действительной, а ось ординат — мнимой
осью комплексной плоскости. При этом, очевидно, устанавлива-
устанавливается взаимно однозначное соответствие между множеством всех
комплексных чисел и множеством точек комплексной плоско-
плоскости, а также между множеством всех комплексных чисел z = a-\-
-\-ib и множеством свободных векторов, проекции хну которых
на оси абсцисс и ординат соответственно равны а и Ь.
Весьма важной является также другая форма представления
комплексных чисел. Для определения положения точки на плос-
плоскости можно пользоваться полярными координатами (р, ф), где
р — расстояние точки от начала координат, а (р — угол, кото-
который составляет радиус-вектор данной точки с положительным
направлением оси абсцисс. Положительным направлением из-
изменения угла ср считается направление против часовой стрелки
(—оо < ср < оо). Воспользовавшись связью декартовых и поляр-
полярных координат: х = pcos <р, у = psmcp, получим так называемую
тригонометрическую форму записи комплексного числа:
z = p(cos(p + г sincp).	A.3)
При этом р обычно называют модулем, а ср — аргументом
комплексного числа и обозначают р = \z\,cp = Argz. Предше-
Предшествующие формулы дают выражение действительной и мнимой
частей комплексного числа через его модуль и аргумент. Легко
выразить модуль и аргумент комплексного числа через его дей-

16
ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
ГЛ. 1
ствительную и мнимую части: р = л/а2 + б2, tg (p = - (при выбо-
выборе из решений последнего уравнения значения ср следует учесть
знаки а и Ь). Отметим, что аргумент комплексного числа опре-
определен не однозначно, а с точностью до аддитивного слагаемого,
кратного 2тг. В ряде случаев удобно через argz обозначать зна-
значение аргумента, заключенное в пределах сро ^ argz < 2тг + сро,
где (ро — произвольное фиксированное число (например, щ = О
или (ро = — тг). Тогда Argz = argz + 2ктг (к = О, =Ы, ±2, ...).
Аргумент комплексного числа z = 0 вообще не определен, а его
модуль равен нулю. Два отличных от нуля комплексных числа
равны между собой в том и только в том случае, если равны их
модули, а значения аргументов или равны, или отличаются на
число кратное 2тг. Комплексно сопряженные числа имеют один и
тот же модуль, а значения их аргументов при соответствующем
выборе областей их изменения различаются знаком. Наконец,
получаем так называемую
показательную форму записи
комплексного числа:
z = pei(p.	A.4)
Отмеченное выше соответ-
соответствие между множеством всех
комплексных чисел и плоски-
плоскими векторами позволяет ото-
отождествить операции сложения
и вычитания комплексных чи-
чисел с соответствующими операциями над векторами (рис. 1.1).
При этом легко устанавливаются неравенства треугольника:
р	р
используя известную формулу Эйлера1) ег(р = cos (p
Рис. 1.1
- \Z2\
A.5)
Модуль разности двух комплексных чисел имеет геометриче-
геометрический смысл расстояния между соответствующими точками на
комплексной плоскости. Отметим, кроме того, очевидные нера-
нера\\	\\
венства \z\
a,
\z\ ^ Ь.
Для выполнения операции умножения удобно пользовать-
пользоваться тригонометрической формой представления комплексных чи-
1) Это выражение мы пока будем рассматривать как сокращенную форму
записи комплексного числа z = cos (p + г sin (p. Полный смысл этого обозна-
обозначения будет установлен в дальнейшем.

§ 1	КОМПЛЕКСНОЕ ЧИСЛО	17
сел. Согласно правилам умножения получаем 1)
z = p(cos (р + г sin ер) = zi • Z2 =
= pi(cos(pi + isin(/9i)p2(cos(/92 + isin^) =
(	i sin(f2) +
sin(^2) =
^2)] = Pi • P2 • е1^1+(р2\
Отсюда /9 = pi • /92, <p = ^1 + ^25 т- е- модуль произведения
равен произведению модулей, а аргумент — сумме аргументов
сомножителей. В случае деления комплексных чисел при р2 ф О
имеет место аналогичное соотношение:
?1 = EL e*(<Pi-<P2)ш
^2	Р2
4. Извлечение корня из комплексного числа. Три-
Тригонометрическая и показательная формы записи комплексного
числа удобны при рассмотрении алгебраических операций воз-
возведения комплексного числа в целую положительную степень и
извлечения корня из комплексного числа. Так, если z = z™, то
р = pi и (р = п<рь
Комплексное число z\ = a/J называется корнем п-й степени
из комплексного числа z, если z = z™. Из этого определения сле-
следует, что р\ = yfp в. (fi = —. Как было отмечено выше, аргумент
комплексного числа определен не однозначно, а с точностью до
аддитивного слагаемого, кратного 2тг. Поэтому из выражения
для аргумента комплексного числа z\\
где ср — одно из значений аргумента комплексного числа z, по-
получим, что существуют различные комплексные числа, которые
при возведении в n-ю степень равны одному и тому же комп-
комплексному числу z. Модули этих комплексных чисел одинаковы
и равны ^/р, а аргументы различаются на число, кратное —.
Число различных значений корня n-й степени из комплексного
числа z равно п. Точки на комплексной плоскости, соответству-
соответствующие различным значениям корня n-й степени из комплексно-
комплексного числа z, расположены в вершинах правильного п-угольника,
вписанного в окружность радиуса ^[р с центром в точке z — 0.
Соответствующие значения ср^ получаются при /с, принимающем
значения /с = 0, 1, ..., п — 1.
:) Эта формула показывает, что введенная выше функция ег(р обладает
свойством ei<pi • ei<P2 = ei{(pi+<P2).

18
ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
ГЛ. 1
Классический анализ поставил задачу так расширить мно-
множество действительных чисел, чтобы не только элементарные
алгебраические операции сло-
сложения и умножения, но и опе-
операция извлечения корня не
выводила из этого расширен-
расширенного множества. Как мы ви-
видим, введение комплексных
чисел решает эту задачу.
Примеры: 1. Найти все
значения \Г%. Записав в по-
показательной форме комплекс-
Лтг\
ное число z = % = ехр (% - 1,
V ^ /
получим для значений ква-
квадратного корня из данного
комплексного числа выраже-
ния zk = ехр {г- +2—J,
к = 0,1 (рис. 1.2), откуда
Рис. 1.2
= ехр {г-j = cos - + г sin - = —A + г),
1 = -ехр (г-) = - —A+г).
=ехр
2.	Найти все значения y/l, где р > 0 — целое число. Восполь-
Воспользовавшись представлением 1 = ег0, так же, как и в предыдущем
примере, получим z^ = ехр ii—k\ ,А; = 0, ..., р — 1, откуда
гО 1	Л27Г^	2тг . . . 2тг
zq = е =1, ^i = ехр г— = cos — + г sm —,
V р )	р	р
Л2тт/ 1Ч\	/ .2тг\	2тг . . 2тг
.... 2;w_i = ехр г — (р — 1 = ехр —г— = cos — — zsm —.
у	^ V р	/	V р )	р	р
То есть корень р-й степени из 1 имеет ровно р различных значе-
значений. Эти комплексные числа соответствуют вершинам правиль-
правильного ^-угольника, вписанного в окружность единичного радиу-
радиуса с центром в точке z = 0, причем одна из вершин лежит в
точке z = 1.
3.	Найти все значения у 1 — гуЗ. Так как z = 1 — гуЗ =
= 2е~г7Г/3, то для значений квадратного корня из данного комп-
/?:	/ .тг . .2тг^\
лексного числа получим выражения zj~ = у 2 ехр I —г— + г	),
V о	z /

2 ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ КОМПЛЕКСНЫХ ЧИСЕЛ 19
к = 0,1, откуда
zq = V2 exp у-г-J = v 2 (^cos -
тг	тг\ л/3 — i
- - г sin -J =
/К	( -5тг \	л/3 — г
= л/2ехр («—) = --
6У ^ '
г
л/2 " " ~^°*
Итак, для извлечения корня n-й степени из комплексного
числа надо перейти к показательной форме записи комплексного
числа, извлечь корень п-й степени из модуля данного комплекс-
комплексного числа (берется арифметическое — действительное и поло-
положительное — значение корня), а аргумент данного комплексного
числа разделить на п. (Для получения всех значений корня надо
иметь в виду многозначность аргумента.)
§ 2. Предел последовательности комплексных чисел
1. Определение сходящейся последовательности.
Для построения теории функций комплексной переменной
большое значение имеет перенесение основных идей анализа
в комплексную область. Одним из фундаментальных понятий
анализа является понятие предела и, в частности, понятие
сходящейся числовой последовательности. Аналогичную роль
играют соответствующие понятия и в области комплексных
чисел. При этом многие определения, связанные с предельным
переходом, полностью повторяют соответствующие определения
теории функций действительной переменной.
Последовательностью комплексных чисел называется пе-
перенумерованное бесконечное множество комплексных чисел. В
дальнейшем последовательность комплексных чисел мы будем
обозначать символом {zn}. Комплексные числа zn, образующие
последовательность {^п}, называются ее элементами1).
Число z называется пределом последовательности {zn}, ес-
если для любого положительного числа е можно указать такой
номер N(e), начиная с которого все элементы zn этой после-
последовательности удовлетворяют неравенству
I	I ^	— Л 7" / \	(Л Г*\
>у 	 у <Г f 77 ТI1 Т1 ^ 1\ I f I	in
Последовательность {zn}, имеющая предел z, называется схо-
сходящейся к числу z, что записывается в виде lim zn = z.
п—)>оо
Для геометрической интерпретации предельного перехода в
комплексной области удобным оказывается понятие ?-окрест-
ности точки комплексной плоскости.
) Определение последовательности не исключает возможности повторя-
повторяющихся элементов, и, в частности, все элементы последовательности могут
совпадать между собой.

20	ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ	ГЛ. 1
Множество точек z комплексной плоскости, лежащих вну-
внутри окружности радиуса е с центром в точке z${\z — z$\ < е),
называется е-окрестностью точки zq.
Из этого определения следует, что точка z является пределом
сходящейся последовательности {zn}, если в любой ?-окрест-
ности точки z лежат все элементы этой последовательности, на-
начиная с некоторого номера, зависящего от е.
Поскольку каждое комплексное число zn = ап + %Ъп харак-
характеризуется парой действительных чисел ап и Ьп, то последова-
последовательности комплексных чисел {zn} соответствуют две последо-
последовательности действительных чисел {ап} и {Ьп}, составленные
соответственно из действительных и мнимых частей элементов
zn последовательности {^п}.
Имеет место следующее утверждение.
Теорема 1.1. Необходимым и достаточным условием схо-
сходимости последовательности {zn} является сходимость по-
последовательностей действительных чисел {ап} и {bn} {zn =
= ап + ibn).
Доказательство. В самом деле, если последова-
последовательность {zn} сходится к числу z = а + ib, то для любого е > 0
\ап — а\ ^ \zn — z\ < е и \Ъп — Ъ\ < е при п ^ N{e). Это и до-
доказывает сходимость последовательностей {ап} и {Ьп} к а и b
соответственно. Обратное утверждение следует из соотношения
\%п — А — \/{ап — оJ + {Ьп — ЬJ, где а и b являются пределами
последовательностей {ап} и {Ьп} и z = а + гЬ.
Последовательность {zn} называется ограниченной, если
существует такое положительное число М, что для всех эле-
элементов zn этой последовательности имеет место неравен-
неравенство \zn\ < М. Основное свойство ограниченной последователь-
последовательности характеризует следующая теорема.
Теорема 1.2. Из всякой ограниченной последовательности
можно выделить сходящуюся подпоследовательность.
Доказательство. Поскольку последователь-
последовательность {zn} ограничена, то ясно, что соответствующие ей дей-
действительные последовательности {ап} и {Ьп} также ограниче-
ограничены. Рассмотрим последовательность {ап}. Так как эта последо-
последовательность ограничена, то из нее можно выделить сходящуюся
подпоследовательность г) {ащ}, предел которой обозначим бук-
буквой а. Последовательности {ащ} соответствует последователь-
последовательность {Ьщ}, также являющаяся ограниченной. Поэтому из нее
можно в свою очередь выделить сходящуюся подпоследователь-
подпоследовательность {ЪПк\, предел которой обозначим буквой Ь. При этом со-
:) См. вып. 1.

§ 2 ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ КОМПЛЕКСНЫХ ЧИСЕЛ 21
ответствующая последовательность {аПк} по-прежнему сходит-
сходится к а. Отсюда следует, что последовательность комплексных
чисел {znk} = {аПк + гЬПк} также является сходящейся, причем
lira zn, = z = а + гЬ, что и доказывает теорему.
)ОО
2. Критерий Kolqh. При исследовании сходимости после-
последовательности во многих случаях удобным оказывается необхо-
необходимый и достаточный признак сходимости последовательности,
известный под названием критерия Коши.
Критерий Коши. Последовательность {zn} сходится то-
тогда и только тогда, когда для любого е > 0 можно указать
такое N(e), что
\*п -^n+m| < ^	A-7)
при п ^ N(e) и для любого номера т ^ 0.
Доказательство. Для доказательства критерия Ко-
Коши мы опять воспользуемся эквивалентностью сходимости по-
последовательности {zn} и последовательностей действительных
чисел {ап} и {6П}, а также тем обстоятельством, что критерий
Коши является необходимым и достаточным признаком сходи-
сходимости последовательности действительных чисел1). Начнем с
доказательства необходимости критерия Коши. Так как после-
последовательность {zn} сходится, то сходятся и последовательности
действительных чисел {an} и {Ьп}. Отсюда следует, что для лю-
любого е > 0 и любого номера т > 0 \ап—an+m| < - при п ^ Ni(e)
и \Ьп — Ьп+т\ < - ПРИ ^ ^ -№(?)• Выбирая в качестве N (б) наи-
наибольшее из N\ и iV, в силу неравенства треугольника получаем
\zn ~ Zn+m\ < ? при п > N(e).
Перейдем к доказательству достаточности признака Коши.
Из соотношения A.7) при п ^ N следуют неравенства
\zn zn-\-m\ <c ?, \оп оп-\-т\ ^ \zn zn-\-m\ <c е,
являющиеся достаточными условиями сходимости последова-
последовательностей {ап} и {6П}, т. е. сходимости последовательности
{^п}. Тем самым доказано, что для сходимости последователь-
последовательности {zn} с комплексными элементами необходимым и доста-
достаточным является выполнение критерия Коши.
3. Бесконечно удаленная точка. Введем понятие бес-
бесконечно удаленной точки комплексной плоскости, существенное
для дальнейшего. Пусть дана последовательность комплексных
чисел {zn} такая, что для любого положительного числа R най-
найдется номер 7V, начиная с которого члены последовательности
удовлетворяют условию \zn\ > R при п ^ N. Такую последова-
последовательность назовем неограниченно возрастающей. Согласно вве-
х) См. вып. 1.

22	ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ	ГЛ. 1
денным ранее определениям данная последовательность, так же
как и всякая ее подпоследовательность, предела не имеет. Такое
особое положение неограниченно возрастающей последователь-
последовательности вызывает ряд неудобств. Чтобы избежать этого, введем
комплексное число z = оо и будем считать всякую неограниченно
возрастающую последовательность сходящейся к этому чис-
числу, которому мы поставим в соответствие бесконечно удаленную
точку комплексной плоскости. Введем понятие полной комп-
комплексной плоскости, состоящей из обычной комплексной плос-
плоскости, и единственного бесконечно удаленного элемента — бес-
бесконечно удаленной точки1) z = оо. Если мы будем пользовать-
пользоваться геометрической иллюстрацией, ставя в соответствие элемен-
элементам неограниченно возрастающей последовательности {zn} точ-
точки комплексной плоскости, то обнаружим, что точки рассматри-
рассматриваемой последовательности с возрастанием их номера располага-
располагаются вне концентрических кругов с центром в начале координат,
радиусы которых могут быть сколь угодно большими. Отметим,
что точки данной последовательности стремятся к точке оо неза-
независимо от направления на полной комплексной плоскости.
В связи с введенными понятиями естественно называть
окрестностью бесконечно удаленной точки множество точек
z полной комплексной плоскости, удовлетворяющих условию
\z\ > i?, где R — достаточно большое положительное число.
Определим алгебраические свойства числа z = оо. Из эле-
элементов неограниченно возрастающей последовательности {zn}
составим последовательность \ — >. Эта последовательность
сходится к точке z = 0. Действительно, из предыдущих рас-
рассмотрений следует, что для любого е > 0 можно указать такой
номер 7V, что — < е при п ^ N. Очевидно и обратное утвер-
ждение, т. е. если последовательность {Сп} сходится к нулю и
состоит из отличных от нуля элементов, то последовательность
\ — \ сходится к бесконечно удаленной точке.
С	11
В связи с этим полагают — = 0 и - = оо. Вообще для беско-
оо	0
нечно удаленной точки устанавливаются следующие соотноше-
соотношения: z-oo = оо при 2;^0и ?+оо = оо, — = 0 при z ^ оо, которые
естественны с точки зрения предельного перехода в операциях
сложения и умножения. С этой точки зрения операция —, есте-
оо
ственно, является неопределенной.
г) Заметим, что аргумент комплексного числа оо не определен, так же
как и его действительная и мнимая части.

ПОНЯТИЕ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ.
23
§ 3. Понятие функции комплексной переменной.
Непрерывность
1. Основные определения. Целью настоящего пункта
является введение понятия функции комплексной переменной.
Это понятие вводится так же как и понятие функции действи-
действительной переменной. Будем говорить, что на множестве Е комп-
комплексной плоскости задана функция комплексной переменной, ес-
если задан закон, ставящий в соответствие каждой точке множе-
множества Е некоторое комплексное число. Множество Е будем назы-
называть множеством значений независимой переменной. Структура
этого множества может быть весьма сложной и разнообразной,
однако в теории функций комплексной переменной рассматри-
рассматривают множества специальной структуры. Для дальнейшего нам
потребуется ряд вспомогательных понятий.
Точка z называется внутренней точкой множества Е, если
существует ^-окрестность точки z, все точки которой принадле-
принадлежат множеству Е. Например, точка z множества \z\ ^ 1 являет-
является внутренней, если \z\ < 1; точка z = 1 не является внутренней
точкой данного множества.
Множество Е называется областью, если выполняются
следующие условия: 1) каждая точка множества Е — вну-
внутренняя точка этого множества; 2) любые две точки множе-
множества Е можно соединить ломаной, все точки которой принад-
принадлежат Е.
В данном определении области второе требование являет-
является условием связности области. Например, множество точек
\z\ < 1 образует область. Точ-
Точно также и ^-окрестность точ-
точки zq (\z — zq\ < е) образу-
образует область. Множество точек
\z\ ^ 1 не является областью,
так как не все его точки яв-
являются внутренними. Также
не являются областями мно-
множество точек \z\ т^ 1 и мно-
множество \z\ < 1, \z — 4| < 2
(рис. 1.3), поскольку они не
являются связными.
Для обозначения области обычно применяются буквы Q, G, D.
Точка z называется внешней точкой области Q, если суще-
существует такая ^-окрестность точки z, все точки которой не при-
принадлежат области Q.
Точка z называется граничной точкой области Q, если в
любой ее ^-окрестности содержатся как точки, принадлежащие
области Q, так и точки, не принадлежащие области Q. Например,
Рис. 1.3

24
ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
ГЛ. 1
точка z = 1 является граничной точкой области \z\ < 1. Сово-
Совокупность всех граничных точек образует границу области. В
дальнейшем границу области мы будем обычно обозначать бук-
буквами 75 Г, С. Простейшим примером границы области, очевид-
очевидно, является кривая; однако граница области может состоять и
из дискретного множества точек. Например, множество точек
\z\ т^ 0 образует на комплексной плоскости область, границей
которой является точка z = 0.
Множество, полученное присоединением к области всех ее
граничных точек, называется замкнутой областью. Замкну-
Замкнутую область обычно будем обозначать, ставя черту над симво-
символом области, например: Q, G, D.
В дальнейшем мы будем рассматривать те случаи, когда гра-
граница области представляет собой одну или несколько кусочно
гладких кривых1), которые, в частности, могут вырождаться
в отдельные точки. При этом будут рассматриваться как од-
носвязные, так и многосвязные области2). Например, область
\z — г\ < 2 является односвязной областью, границей которой
является окружность \z — г\ = 2; круговое
кольцо 1 < z\ < 2 (рис. 1.4) представляет
собой двухсвязную область; множество то-
точек z т^ 0 представляет собой односвязную
область и т. д.
Если область Q целиком лежит вну-
внутри некоторого круга конечного радиуса,
то она называется ограниченной. В про-
противном случае — неограниченной.
Мы будем рассматривать в основном
те случаи, когда множество Е значений
комплексной переменной представляет со-
собой область Q или замкнутую область Q
комплексной плоскости. Тогда однозначная функция комплекс-
комплексной переменной z, заданная в области Q', определяется законом,
ставящим каждому значению z из области Q в соответствие
определенное комплексное число w. Символически указанное со-
соответствие будем записывать в виде
w = f(z).	A.8)
Множество комплексных чисел w, соответствующих всем
z Е Q, называется множеством значений функции f(z). По-
Поскольку каждое комплексное число характеризуется парой дей-
действительных чисел, то задание комплексной функции w = и -\-
+ iv комплексной переменной z = х + гу эквивалентно заданию
Рис. 1.4
:) Понятие кусочно гладкой кривой см. вып. 2.
2) Понятие многосвязной области см. вып. 2.

§ 3	ПОНЯТИЕ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ.	25
двух действительных функций двух действительных перемен-
переменных, что может быть записано в виде
w(z) = и(х, у) + iv(x, у).	A.9)
Функции и(х,у) nv(x,y) определены в области Q плоскости дей-
действительных переменных ж, у, соответствующей области Q комп-
комплексной плоскости z. Функция и(х,у) называется действитель-
действительной, а функция v(x,y) — мнимой частью функции w = f(z). В
дальнейшем, если это не оговорено особо, мы всегда будем поль-
пользоваться представлением A.9), обозначая действительную часть
функции f(z) символом и, мнимую — символом v.
Часто рассматривают многозначные функции комплексной
переменной, когда каждому значению z Е Q ставится в соот-
соответствие несколько комплексных чисел. В настоящей главе мы
будем рассматривать только однозначные функции комплекс-
комплексной переменной. Подробное рассмотрение многозначных функ-
функций будет проведено ниже.
Множество значений w функции f(z) на комплексной плос-
плоскости w может иметь самую разнообразную структуру. В част-
частности, это может быть область G или замкнутая область G. В
дальнейшем мы будем рассматривать только такие случаи.
Заданием функции w = f(z) устанавливается соответствие
между точками области Q комплексной плоскости z и точка-
точками области G комплексной плоскости w. Говорят, что при этом
задано отображение области Q на область G. Очевидно, устанав-
устанавливается и обратное соответствие — каждой точке w E G ста-
ставится в соответствие одна или несколько точек z области Q. В
последнем случае можно говорить, что в области G задана мно-
многозначная функция комплексной переменной w. Функция, осу-
осуществляющая отображение области G комплексной плоскости
w на область Q комплексной плоскости z, называется обратной
функции f(z). В этой главе мы в основном будем рассматривать
тот случай, когда обратная функция
z = (p(w)	A.10)
является однозначной в области G. Тогда функция w = f{z)
осуществляет взаимно однозначное отображение области Q на
область G.
Функция f(z) называется однолистной функцией в области
Q, если в различных точках z этой области она принимает
различные значения.
Из этого определения следует, что однолистная функция осу-
осуществляет взаимно однозначное отображение.
2. Непрерывность. Перейдем к понятию непрерывности
функции комплексной переменной. Пусть функция f(z) опреде-
определена на некотором множестве Е. Рассмотрим различные после-

26	ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ	ГЛ. 1
довательности точек этого множества {^п}, сходящиеся к неко-
некоторой точке zq и состоящие из точек zn, отличных 1) от точки z$
(zn / 2;o), и соответствующие им последовательности значений
функции {f(zn)}. Если независимо от выбора последователь-
последовательности {zn} существует единственный предел lira f(zn) = г^о,
то этот предел называется предельным значением, или преде-
пределом, функции f(z) в точке zq, что записывается в виде
lira f(z) =w0.	A.11)
z-tzo
Часто употребляется и другое2) определение понятия пре-
предельного значения (или предела) функции.
Число wq называется предельным значением функции f(z)
в точке zo, если для любого е > 0 можно указать такое
5 > 0; что для всех точек z E E и удовлетворяющих условию
О < \z — zq\ < 5, имеет место равенство \f(z) — wq\ < e.
Докажем эквивалентность этих определений. Пусть функция
f(z) удовлетворяет второму определению. Возьмем произволь-
произвольное положительное число е и выберем для него соответствующее
S(e). Рассмотрим произвольную последовательность {zn} Ч^и
найдем N[5(e)] = i\T(e), начиная с которого 0 < \zn — z§\ < 5. То-
Тогда по условию \f(zn) — wq\ < е для п ^ N(e)\ а так как е > 0 —
любое, то это в силу произвольности выбора последовательно-
последовательности {zn} и означает, что lira f(zn) = u>o, т. е. функция f(z)
Zn^-Zo
удовлетворяет и первому определению. Тем самым из второго
определения следует первое.
Докажем теперь, что из первого определения вытекает вто-
второе. Предположим, что это не имеет места. Тогда можно ука-
указать такое ?о > 0, что для любого 8п > 0 найдется такая точка
zn Е Е, что при 0 < \zn — zq\ < Sn будет выполнено неравенство
\f(zn) ~wo\ > ?o- Выберем стремящуюся к нулю последователь-
последовательность {5п} —)> 0 и соответствующую ей последовательность точек
{^п}, удовлетворяющих приведенным выше неравенствам. Оче-
Очевидно, zn —)> zq, а последовательность {f(zn)} не сходится к чис-
числу г^о, так как все члены этой последовательности отличаются
от г^о больше чем на sq . Но полученный результат противоречит
первому определению. Тем самым сделанное предположение не
имеет места, т. е. из первого определения вытекает второе. Эк-
Эквивалентность обоих определений доказана.
:) При этом предполагается, что точка zq является точкой сгущения мно-
множества Е, т. е. существуют последовательности {zn} точек этого множества,
сходящиеся к точке zq.
2) Заметим, что это определение, в отличие от первого, имеет смысл лишь
для конечных значении zq и wq.

§ 3	ПОНЯТИЕ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ.	27
Так же, как и в случае действительной переменной, важную
роль играет понятие непрерывности функции. Начнем с понятия
непрерывности в точке. При этом будем считать, что точка ^о,
в которой определяется это понятие, обязательно принадлежит
множеству Е задания функции.
Функция f(z), заданная на множестве Е, называется
непрерывной в точке zq E Е, если предельное значение этой
функции в точке zq существует, конечно и совпадает со зна-
значением f(zo) функции f(z) в точке zq, т. е. lira Hz) = Hz§).
Это определение непрерывности распространяется как на
внутренние, так и на граничные точки множества1).
Если функция f(z), заданная на множестве Е, непрерывна во
всех точках этого множества, то говорят, что функция f(z) не-
непрерывна на множестве Е. В частности, мы будем рассматривать
функции, непрерывные в области, в замкнутой области и на кри-
кривой. Подчеркнем еще раз, что в силу данных выше определений
следует рассматривать предельные значения функции f(z) лишь
на последовательностях точек, принадлежащих данному множест-
множеству в последних случаях замкнутой области, кривой и т.д.).
С помощью е — E-определения предельного значения условия
непрерывности функции f(z) в точке zq можно также сформу-
сформулировать следующим образом. Функция f(z) непрерывна в точ-
точке zq, если для любого ?>0 можно указать такое 5 > О, что
для всех точек z^E, удовлетворяющих неравенству \z — zq\<S,
имеет место неравенство \f(z) — f(zo)\ < e. Геометрически это
означает, что функция комплексной переменной, непрерывная
в некоторой точке2) zo, ставит в соответствие каждой точке
из E-окрестности точки zq некоторую точку, принадлежащую
^-окрестности точки wq = f(zo).
Из непрерывности функции комплексной переменной f(z) =
= и(х,у) + iv(x,y) следует непрерывность ее действительной
и(х,у) и мнимой v(x,y) частей по совокупности переменных
ж, у3). Имеет место и обратное утверждение, т. е. если и(х,у) и
:) Если точка zq является изолированной точкой множества Е (т. е. суще-
существует такая ^-окрестность точки zq , в которой нет других точек множества
Е), то функция f(z), по определению, считается непрерывной в точке zq.
2) Заметим, что данные определения понятия непрерывности функции
f(z) в точке zq справедливы не только в случае конечной точки zo, но и
в случае бесконечно удаленной точки zq = oo. При этом под предельным
значением функции f(z) в точке оо, в силу определения на с. 26, надо пони-
понимать предел последовательности {f(zn)}, где {zn} — любая неограниченно
возрастающая последовательность. Во втором определении непрерывности
условие \z — zo\ < S надо заменить на условие \z\ > R.
) Определение непрерывности функции двух действительных перемен-
переменных по совокупности переменных см. вып. 1.

28	ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ	ГЛ. 1
v(x,y) суть непрерывные функции по совокупности переменных
ж, у в некоторой точке (жо,уоM то f{z) — и(х^у)~\~^(х^у) являет-
является функцией комплексной переменной z = ж + iy, непрерывной в
точке zq = xq + iyo- Данные утверждения являются следствием
того, что необходимым и достаточным условием сходимости по-
последовательности комплексных чисел является сходимость по-
последовательностей их действительных и мнимых частей.
Это позволяет перенести на функции комплексной перемен-
переменной основные свойства непрерывных функций двух действи-
действительных переменных1). Так, сумма и произведение двух функ-
функций комплексной переменной fi(z) и /2B), непрерывных в обла-
области Q', также являются непрерывными функциями в этой обла-
области; функция cp(z) = }(Z\ непрерывна в тех точках области ?/,
где /2B) ф 0, функция f(z), непрерывная на замкнутом множе-
множестве Е, ограничена по модулю на ? и т. д.
3. Примеры. Рассмотрим несколько простейших приме-
примеров.
1. В качестве первого примера функции комплексной пере-
переменной рассмотрим линейную функцию
f(z) =w = az + b.	A.12)
Здесь а и b — заданные комплексные постоянные. Будем счи-
считать, что а ф 0, так как в противном случае функция A.12) ста-
ставит в соответствие всем точкам z комплексной плоскости одно и
то же комплексное число Ь. Функция A.12) определена при всех
значениях независимой переменной z. Областью ее задания яв-
является полная 2) комплексная плоскость z. Каждому значению z
соответствует только одно значение w, т. е. f(z) — однозначная
функция z. Очевидно, обратная функция tp(w) = z = -w	=
ex	a
= aiw + bi обладает теми же свойствами, что и f(z). Тем самым
f(z) — однолистная функция z на полной комплексной плоско-
плоскости, устанавливающая взаимно однозначное соответствие между
плоскостями z и w. В силу непрерывности действительной и мни-
мнимой части f(z) по совокупности переменных ж, у эта функция
непрерывна на всей комплексной плоскости при любых конечных
значениях ж, у). Чтобы выяснить геометрический смысл данно-
данного соответствия, рассмотрим вспомогательную функцию ( = az.
*) См. вып. 1.
2) В дальнейшем мы будем говорить, что функция комплексной перемен-
переменной f(z) определена на всей комплексной плоскости, если она определена
для всех значений комплексного аргумента z, ограниченных по модулю,
и будем говорить, что f{z) определена на полной комплексной плоскости,
если она задана и при z = 00. В нашем примере /(оо) = оо.

§ 3	ПОНЯТИЕ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ.	29
На основании правила умножения комплексных чисел имеем
( = \а\ • \z\ • {cos (arga + arg;?) + isin (arga + arg;?)} .
Отсюда следует \(\ = \a\ • \z\, arg? = arg? + arga. To есть функ-
функция ? = az любому комплексному числу z ставит в соответствие
комплексное число ?, модуль которого в \а\ раз больше модуля
z, а аргумент получается из аргумента z прибавлением постоян-
постоянного слагаемого — аргумента комплексного числа а. Геометри-
Геометрический смысл этого преобразования очевиден: подобное растя-
растяжение плоскости z в \а\ раз и поворот этой плоскости как целого
вокруг точки z = 0 на угол arg a.
Возвращаясь к функции A.12), которую теперь можно запи-
записать в виде w = С + 6, видим, что геометрический смысл послед-
последнего преобразования состоит в сдвиге плоскости z, характери-
характеризуемом вектором Ь.
Итак, линейная функция преобразует комплексную плос-
плоскость z в комплексную плоскость w путем подобного растяже-
растяжения, поворота и сдвига.
2. В качестве следующего примера рассмотрим функцию
w = f{z) = \.	A.13)
Эта функция также определена на полной комплексной плос-
плоскости, причем /@) = оо и f(°°) = 0. Как и в первом приме-
примере, устанавливаем, что f(z) является однозначной и однолист-
однолистной функцией z, отображающей полную плоскость z на пол-
полную плоскость w. Легко установить, что функция f(z) является
непрерывной на полной комплексной плоскости, за исключением
точки z = 0. Для геометрической интерпретации данной функ-
функции воспользуемся показательной формой записи комплексных
чисел: w = гег^ = - e~l(p(z = рег(р). Это равенство означает, что
&rgw = —argz , \w\ = |—г. Полученные соотношения позволя-
II
ют рассматривать отображение, осуществляемое данной функ-
функцией, как совокупность двух отображений: ? = C(z)? гДе |С| =
= \z\, arg( = -arg?, и w = w((), где \w\ = —, argw = arg(.
Первое отображение имеет геометрический смысл зеркального
отражения относительно действительной оси, при котором точ-
точка z переходит в точку г", а второе отображение имеет смысл
инверсии1) в единичном круге, переводящей точку ~z в точку
х) Инверсией (или преобразованием обратных радиусов) в круге радиу-
радиуса а называется такое преобразование, при котором каждой точке внутри
(вне) круга ставится в соответствие точка вне (внутри) круга, лежащая на
луче, проведенном из центра круга в данную точку так, что произведение
расстояний от этих точек до центра круга равно квадрату радиуса круга.

30
ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
ГЛ. 1
w = - (рисунки 1.5, 1.6). При этом точки плоскости z, лежа-
лежащие вне единичного круга, переходят в точки, лежащие внутри
единичного круга плоскости w, и наоборот.
z=0
Рис. 1.5
Рис. 1.6
3. Рассмотрим функцию
w = f(z) = z2.	A.14)
Эта функция является однозначной функцией комплексной пе-
переменной z, определенной на полной комплексной плоскости z.
Для изучения ее свойств опять удобно представить комплексные
числа в показательной форме: z = рещ\ w = гег^ = р2ег2(р. От-
Отсюда легко заключить, что точки плоскости z, лежащие на луче,
составляющем угол ср с положительным направлением действи-
действительной оси, переходят в точки плоскости w, лежащие на луче,
составляющем с положительным направлением действительной
оси угол 2ср. Поэтому точкам z и —z, аргументы которых раз-
различаются на тг, а модули одинаковы, соответствует одно и то
же значение w (ег2п = cos2tt + isin2Tr = 1). Тем самым обрат-
обратная функция оказывается многозначной. Рассмотрим подробнее
отображение, осуществляемое функцией w = z2. Верхняя полу-
полуплоскость z вместе с действительной осью переходит в полную
плоскость w. Положим для определенности, что в верхней по-
полуплоскости аргумент z заключен в пределах 0 < (р < тт. Тогда
различным точкам области 0 < (р < тг соответствуют различ-
различные значения w. Такая область изменения независимой перемен-
переменной, различным точкам которой соответствуют различные зна-
значения функции, называется областью однолистности функции.
В предыдущих примерах областью однолистности являлась вся
область задания функции; в данном случае для функции w = z2,
областью задания которой является полная комплексная плос-
плоскость z, областью однолистности служит полуплоскость. Отме-
Отметим, что в рассматриваемом случае границы области однолист-
однолистности — лучи ср = Оиср = тт — переходят в одну и ту же пря-

§ 3	ПОНЯТИЕ ФУНКЦИИ. НЕПРЕРЫВНОСТЬ.	31
мую — положительную часть действительной оси плоскости w.
Продолжая наши рассмотрения, легко показать, что функция
w = z2 производит отображение и нижней полуплоскости z вме-
вместе с действительной осью на полную плоскость w. Тем самым
обратная функция
z = y/w,	A.15)
определенная на полной плоскости w, уже не является одно-
однозначной — одной и той же точке плоскости w соответствуют две
различные точки плоскости z: одна — в верхней, другая — в
нижней полуплоскости.
Чтобы изучить отображение, осуществляемое данной функ-
функцией, воспользуемся опять показательной формой записи комп-
комплексного числа: w = те1^. Тогда, согласно правилу извлечения
корня из комплексного числа, мы получаем два различных зна-
значения функции z(w): г^ = л/тех.р -(ф + 2тгк) (к = 0, 1) (заме-
(заметим, что arg^i — arg^o = тг).Рассмотрим на плоскости w некото-
некоторую замкнутую кривую С, не имеющую самопересечений. Фик-
Фиксируем на ней точку г^о, которой припишем определенное значе-
значение аргумента ^о, найдем zq(wqI zi(wq) при непрерывном дви-
движении точки w по кривой С. Аргумент точки w на кривой С
изменяется непрерывно. Поэтому, как легко видеть, функции
zq(w) и z\(w) являются непрерывными функциями w на кривой
С. При этом возможны два различных случая. В первом случае
кривая С не содержит внутри точку w = 0. Тогда после обхода
кривой С аргумент точки г^о вернется к первоначальному зна-
значению argi^o = фо- Следовательно, и значения функций zq(w) и
z\ (w) в точке w = wq после обхода кривой С будут равны их пер-
первоначальным значениям. Тем самым на кривой С в этом случае
определены две различные однозначные функции комплексной
переменной w: zq = л/тexp f — 1 и z\ = л/техр -(ф + 2тг) (ф из-
изменяется непрерывно на кривой G, начиная от значения ^о в
точке г^о). Очевидно, если область D плоскости w обладает тем
свойством, что любая замкнутая кривая в этой области не со-
содержит точки w = 0, то в D определены две различные одно-
однозначные непрерывные функции zq(w) и z\(w). Функции zq(w) и
zi(w) называются ветвями многозначной функции z(w) = л/w.
Во втором случае кривая С содержит внутри точку w = 0.
Тогда после обхода кривой С в положительном направлении
значение аргумента точки г^о уже не вернется к первоначаль-
первоначальному значению ^о, а изменится на 2тг: argi^o = фо + 2тг. Поэто-
Поэтому и значения функций zq(w) и z\{w) в точке г^о в результате
их непрерывного изменения после обхода кривой С уже не бу-
будут равны их первоначальным значениям. Более точно, получим

32	ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ	ГЛ. 1
^o(wo) = ?о(^о)ег7Г, zi(wq) = zi(wo)em. To есть функция zq(w)
перейдет в функцию zi(w), и наоборот.
Если для точки zq можно указать такую ^-окрестность, что
при однократном обходе точки zq по любому замкнутому кон-
контуру, целиком лежащему в этой ^-окрестности, одна ветвь мно-
многозначной функции переходит в другую, то точка zq называется
точкой разветвления (ветвления) данной многозначной функ-
функции. В окрестности точки разветвления отдельные ветви мно-
многозначной функции уже нельзя рассматривать как различные
однозначные функции, поскольку при обходе точки разветвле-
разветвления их значения меняются. В рассматриваемом примере точкой
разветвления является точка w = 0.
Заметим, что обход окружности \z\ = R сколь угодно боль-
большого радиуса соответствует обходу на плоскости ? = - точки
1
С = 0 по окружности |?| = р = —. Согласно п. 2.3 имеет место
1
соотношение - = оо. Поэтому будем считать, что обход окруж-
окружности бесконечно большого радиуса (R —>• оо) есть обход беско-
бесконечно удаленной точки z = оо. Как легко видеть, в рассматри-
рассматриваемом примере при обходе точки w = оо одна ветвь функции
z = л/w переходит в другую. Таким образом, второй точкой раз-
разветвления функции z = л/w на комплексной плоскости w явля-
является точка w = оо. Областью D, в которой определены однознач-
однозначные ветви функции z = y/w, является любая область плоскости
w, в которой невозможен обход по замкнутому контуру точек
разветвления w = 0 и w = оо. Такой областью является, напри-
например, вся плоскость w с разрезом вдоль положительной части
действительной оси. При этом берега разреза являются грани-
границей данной области, так что при непрерывном движении внутри
области мы не можем пересекать разрез (границу области).
Если считать, что аргумент точек w для первой ветви изме-
изменяется в пределах 0 < axgw < 2тг, а для второй — в пределах
2тг < argiu < 4тг, то первая ветвь функции z = л/w производит
отображение плоскости с разрезом на верхнюю полуплоскость
z, а вторая ветвь данной функции отображает ту же область на
нижнюю полуплоскость z.
Аналогичным образом легко показать, что функция w = zn
(n > 0 — целое число) производит отображение любого секто-
ра 	 < argz < —^	'- [к = 0,1,...,п — 1) плоскости z
на полную плоскость w, разрезанную по положительной части
действительной оси. Тем самым эти секторы представляют со-
собой области однолистности данной функции. Обратная функция
z = y/w является многозначной, и точки w = 0 и w = оо пред-
представляют собой ее точки разветвления.

§ 4	ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИИ	33
§ 4. Дифференцирование функции комплексной
переменной
1. Определение. Условия Коши-Римана. До сих пор
теория функций комплексной переменной строилась в полной
аналогии с теорией функций действительной переменной. Од-
Однако понятие дифференцируемой функции комплексной пере-
переменной, введенное по аналогии с соответствующим понятием
теории функций действительной переменной, приводит к суще-
существенным различиям.
Дадим определение производной функции комплексной пе-
переменной. Пусть в области Q комплексной плоскости z задана
функция f(z). Если для точки zq Е Q существует при Az —>> О
предел (предельное значение) разностного отношения
/(го + Az) - /(го)
Az
то этот предел называется производной функции f(z) no
комплексной переменной z в точке zq и обозначается /'(^о),
т. е.
Функция f(z) в этом случае называется дифференцируемой
в точке zq. Подчеркнем еще раз, что если существует предел
A.16), то он не зависит от способа стремления Az к нулю, т. е.
от способа приближения точки z = zq + Az к точке zq . Требова-
Требование дифференцируемости функции комплексной переменной в
точке zq накладывает весьма важные условия на поведение дей-
действительной и мнимой частей этой функции в окрестности точки
(жо, Уо)- Эти условия известны под названием условий Коши-
Римана, которые могут быть сформулированы в виде следую-
следующих теорем.
Теорема 1.3. Если функция f(z) = и(х, у) + iv(x, у) диф-
дифференцируема в точке zq = xq + гусь то в точке (жо, Уо) су-
существуют частные производные функций и(х,у) и v(x,y) no
переменным ж, у, причем имеют место следующие соотноше-
соотношения1):
ди(хо,уо) _ dv(xo,yo)	ди(хо,уо) _ _ду(хо,уо)	,, ^ч
Зх ~ ду '	ду ~	дх '	[ }
Доказательство. По условию теоремы существует
предел A.16), не зависящий от способа стремления Az к нулю.
:) Соотношения A.17) обычно и называются соотношениями Коши-
Римана.
2 А.Г. Свешников, А.Н. Тихонов

34	ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ	ГЛ. 1
Положим Az = Аж и рассмотрим выражение
rf/ \ у и(хо + Аж,г/о) — и(хо,уо) . -,. v(xo + Аж,г/о) — г;(жо,уо)
/ (^о J= lim 	д-	+г lim 	—	.
Аж^О
Из существования предела комплексного выражения следует су-
существование пределов его действительной и мнимой частей. По-
Поэтому в точке (жо, У о) существуют частные производные по ж
функций и(х,у) и v{x1y) и имеет место формула
f'(z0) = их(х0, уо) + ^ж(ж0, уо).
Полагая А^ = гАу, находим
/'(so) =
ц(жоуо +Ay) -ц(жоуо)
Ay^O	Ay
= -iuy(xo,yo) + ^(ж0, уо).
Сравнивая две последние формулы, убеждаемся в справедливо-
справедливости соотношений A.17).
Теорема 1.4. Если в точке (жо, Уо) функции и(х,у) и v(xyy)
дифференцируемы, а их частные производные связаны соотно-
соотношениями A.17), то функция f(z) = u(x,y) +iv(x,y) является
дифференцируемой функцией комплексной переменной z в точ-
точке zo = хо + гу0-
Доказательство. По определению дифференциру-
емости1), приращения функций и(х,у) и v(x,y) в окрестности
точки (жо, у о) могут быть записаны в виде
и(х0 + Дж, уо + Ау) - и(х0, уо) =
f (ж, у),
^(ж0 + Аж, уо + Ау) - г;(жо, уо) =
= ^ж(ж0, уо) Аж + Vy(xo,yo)Ay + 7/(ж, у), A.18)
где функции ?(ж,у) и г/(ж,у) стремятся к нулю при ж—)>жо,
у —)> уо быстрее, чем Аж и Ау ( lim , д', = 0, lim , д , = О,
\|Дя|-Я) \Az\	\Az\^0 |A^|
\Az\ = л/(АжJ + (AyJ). Составим теперь разностное отноше-
отношение f^Zo + д	, где А^ = Аж + гДу, и используя A.18) и
) См. вып. 1.

§ 4	ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИИ	35
A.17), преобразуем его к виду
f(zo +Az) - f(z0)	(	^Ax
Заметим, что при стремлении А^ к нулю последнее слагаемое
этой формулы стремится к нулю, а первые остаются неизменны-
неизменными. Поэтому существует предел lira ^^	-^—lif^Z —
что и доказывает дифференцируемость функции f(z) в точке zq.
Если функция f(z) дифференцируема во всех точках неко-
некоторой области Q, а ее производная непрерывна в этой обла-
области, то функция f(z) называется аналитической функцией1)
в области Q.
Как известно2), непрерывность частных производных явля-
является достаточным условием существования первого дифферен-
дифференциала (дифференцируемости) функции многих переменных. По-
Поэтому из теорем 1.3 и 1.4 следует, что необходимым и достаточ-
достаточным условием аналитичности функции f(z) = u(x,y) -\-iv(x,y)
в области Q является существование в этой области непре-
непрерывных частных производных функций и(х,у) и г;(ж,у), связан-
связанных соотношениями Коши-Римана A.17).
Понятие аналитической функции является основным поня-
понятием теории функций комплексной переменной в силу особой
роли, которую играет класс аналитических функций как при
решении многочисленных математических проблем, так и при
различных приложениях функций комплексной переменной в
смежных областях естествознания.
Соотношения Коши-Римана часто используются при иссле-
исследовании различных свойств аналитических функций. При этом
равенства A.17) не являются единственно возможной формой
соотношений Коши-Римана. Как может установить сам чита-
1) Приведенное здесь определение аналитической функции отличается от
обычно принятого в литературе дополнительным требованием непрерыв-
непрерывности производной. Это сделано с целью облегчения последующих дока-
доказательств. Кроме того, как это следует из более подробного исследования,
математическое содержание понятия аналитической функции при этом не
меняется. В частности, можно показать, что при дополнительном требова-
требовании непрерывности функции f(z) в области Q выполнение условий Копти—
Римана A.17) всюду в этой области является необходимым и достаточным
для аналитичности f(z) и непрерывности всех ее производных в области Q.
См. подробнее А. И. Маркушевич. Теория аналитических функ-
функций. — М.: Гостехиздат, 1950.
) См. вып. 1.

36	ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ	ГЛ. 1
тель, действительная и мнимая части аналитической функции
f(z) = и(р,ф) +iv(p,(p) комплексной переменной z = рег(р свя-
связаны соотношениями
ди 	 1 dv	1 ди 	 dv	(IIQ}
dp pdip	p dip	dp
где риср — полярные координаты точки (ж, у). Аналогичным об-
образом легко установить, что модуль и аргумент аналитической
функции f(z) = Я(х,у)егФ(х'у^ связаны соотношениями
9R=Rd*	9R = _кдФ	A 20)
ох	ду	ду	дх
Отметим также, что соотношения A.17) позволяют получить
различные выражения для производной функции комплексной
переменной
f'(z) = их(х, у) + ivx(x, у) = vy(x, у) + ivx(x, у) =
= их(х, у) - iuy(x, у) = vy(x, у) - iuy(x, у). A.21)
При этом каждый раз производная f(z) выражается через част-
частные производные функций и(х,у) и v(x,y).
2. Свойства аналитических функций. Определение
производной A.16) позволяет перенести на аналитические функ-
функции комплексной переменной ряд свойств дифференцируемых
функций действительной переменной.
1.	Если функция f(z) является аналитической в области ?/,
то она непрерывна в этой области.
2.	Если fi(z) и /2B) суть аналитические функции в области
5, то их сумма и произведение также являются аналитически-
аналитическими функциями в области ?/, а функция (p(z) = _}. , является
аналитической функцией всюду, где /2B) ^ 0.
3.	Если w = f(z) является аналитической функцией в обла-
области Q плоскости комплексной переменной z, причем в области ее
значений G на плоскости w определена аналитическая функция
( = <p(w), то функция F(z) = <p[f{z)] является аналитической
функцией комплексной переменной z в области Q.
4.	Если w = f(z) является аналитической функцией в обла-
области Q, причем |/7(^)| ф 0 в окрестности некоторой точки zq E G,
то в окрестности точки г^о = f(zo) области G значений функ-
функции f(z) определена обратная функция z = <p(w), являющаяся
аналитической функцией комплексной переменной w. При этом
имеет место соотношение ff(zo) = —-—-.
(p'(w0)
Доказательство. Для существования обратной
функции необходимо, чтобы уравнения и = и(х,у) и v = v(xyy)
можно было разрешить относительно ж, у в окрестности точ-

§ 4	ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИИ	37
ки г^о • Для этого достаточно 1) , чтобы в окрестности точки z$
выполнялось условие
= uxvy - uyvx ^ 0.
Vx
В силу соотношений A.17) эго условие можно переписать в
виде и^ + v^ 7^ 0. Но при условии |/7(^)| "ф 0 последнее имеет
место. Тем самым существование обратной функции z = ip(w)
доказано. Составив разностное отношение —— = -г—, легко до-
доказать существование и непрерывность производной cpf(wo) при
условии \f'(zo)\ ф 0.
5.	Пусть в области Q плоскости ху задана функция и(х^уI
являющаяся действительной частью аналитической функции
f(z). Тогда мнимая часть этой функции определяется с точно-
точностью до аддитивной постоянной. Действительно, в силу условий
Коши-Римана по заданной функции и(х,у) однозначно опреде-
определяется полный дифференциал неизвестной функции v(x,y):
dv = vxdx + Vydy = —Uydx + uxdy,
что и доказывает высказанное утверждение 2).
6.	Пусть функция f(z) является аналитической в области Q.
Рассмотрим в соответствующей области плоскости ху семейства
кривых и(х,у) = С и v(x,y) = G, представляющие собой линии
уровней действительной и мнимой частей функции f(z). С по-
помощью соотношений A.17) легко показать, что во всех точках
данной области grad и • grad v = uxvx + uyvy = —uxuy + uyux = 0.
Так как градиент ортогонален линии уровня, то отсюда следует,
что семейства кривых и(х,у) = С и v(x,y) = С взаимно ортого-
ортогональны.
3. Геометрический смысл производной функции
комплексной переменной. Пусть f(z) является аналитиче-
аналитической функцией в некоторой области Q. Выберем какую-либо
точку zq Е Q и проведем через нее произвольную3) кривую 71?
целиком лежащую в Q. Функция f(z) производит отображение
области Q комплексной плоскости z на некоторую область G
комплексной плоскости w. Пусть точка zq переходит в точку г^о,
а кривая 71 — в проходящую через г^о кривую Pi (рис. 1.7). По
:) Об условиях существования неявных функций см. вып. 1.
2)	Определение функции двух действительных переменных по ее полному
дифференциалу см. вып. 2.
3)	Здесь и в дальнейшем, если это не будет оговорено особо, под произ-
произвольной кривой мы понимаем гладкую кривую.

38
ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
ГЛ. 1
условию существует производная f'{z) функции w = f(z) в точ-
точке zq. Предположим, что ff(zo) ф 0, и представим комплексное
число ff(zo) в показательной форме1) :
g = А;еш.	A.22)
Выберем такой способ стремления Az к нулю, при котором
точки z = zq + Az лежат на кривой 71 • Очевидно, соответству-
соответствующие им точки w = wq-\- Aw лежат на кривой Гх. Комплексные
числа Az и Aw изображаются векторами секущих к кривым 71
и Гх соответственно. Заметим, что argAz и argAiu имеют гео-
геометрический смысл углов соответствующих векторов с положи-
положительными направлениями осей х и и, а | Az\ и | Дги| представляют
собой длины этих векторов. При Az —>> 0 векторы секущих пе-
переходят в векторы касательных к соответствующим кривым. Из
A.22) следует, что
a = arg//(zo)= lim argAiu — lim ашД;? = Фх— <z?i, A.23)
Az^O	Az^O
т. е. аргумент а производной имеет геометрический смысл раз-
разности угла Фх вектора касательной к кривой Гх в точке г^о с
осью и и угла (pi вектора касательной к кривой 71 B точке zq
Vi\
У 1
z=0
—с
1
w=0
Рис. 1.7
с осью х (рис. 1.7). Так как производная ff(zo) не зависит от
способа предельного перехода, то эта разность будет той же и
для любой другой кривой, проходящей через точку zq (хотя зна-
значения самих углов Фх и cpi могут измениться). Отсюда следует,
что при отображении, осуществляемом аналитической функци-
функцией f(z)j удовлетворяющей условию ff(zo) ф 0, угол (р = (f2 — (fi
между любыми кривыми 72, 7ъ пересекающимися в точке zq,
Условие ff(zo) ф 0 необходимо для возможности такого представления.

§ 4	ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИИ	39
равен углу Ф = Ф2 — Фг между их образами (кривыми Г2 и Г]_),
пересекающимися в точке г^о = /(^о)- Заметим, что при этом
сохраняется не только абсолютная величина углов между кри-
кривыми 72, 7i и их образами, но и направление углов. Это свойство
данного отображения носит название свойства сохранения углов.
Аналогично из соотношения A.22) получим
A.24)
Az->o |Дз|
То есть с точностью до величин более высокого порядка малости
имеет место равенство \Aw\ = fc|A^|. Заметим, что и это соотно-
соотношение не зависит от выбора кривой 71 • Геометрический смысл
этого соотношения состоит в том, что при отображении, осуще-
осуществляемом аналитической функцией, удовлетворяющей условию
ff(zo) ф 0, бесконечно малые линейные элементы преобразуют-
преобразуются подобным образом, причем |/7(^о)| определяет коэффициент
преобразования подобия. Эго свойство данного отображения но-
носит название свойства постоянства растяжения.
Отображение окрестности точки zq на окрестность точ-
точки wq, осуществляемое аналитической функцией w = f(z) и
обладающее в точке zq свойством сохранения углов и постоян-
постоянством растяжений, называется конформным отображением.
При конформном отображении окрестности точки zq на окрест-
окрестность точки г^о бесконечно малые треугольники с вершиной в
точке zq преобразуются в подобные им бесконечно малые тре-
треугольники с вершиной в точке г^о- Более подробное изложение
основных понятий теории конформного отображения будет дано
в гл. 6.
4. Примеры. В заключение данного параграфа отметим,
что, как легко проверить, линейная функция и функция w = z2,
введенные в предыдущем параграфе, являются аналитически-
аналитическими функциями на всей комплексной плоскости; функция w = -
является аналитической всюду, за исключением точки z = 0.
Так как определение производной A.16) аналогично определе-
определению производной функции одной действительной переменной,
то для производных данных функций комплексной переменной
имеют место выражения:
"W = -pr-	(L25)
Рассмотрим функцию комплексной переменной w = ez, ши-
широко применяющуюся в приложениях. Определим эту функцию,
задав аналитические выражения ее действительной и мнимой
частей:
и(х,у) = ех cosy, v(x,y) = ex smy.	A.26)

40	ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ	ГЛ. 1
На действительной оси эта функция совпадает с действительной
функцией ех действительного аргумента х и, как будет показа-
показано в дальнейшем, в комплексной области сохраняет основные
свойства экспоненты. Поэтому для нее естественно сохранить
обозначение
ez = ex(cosy + ismy) = ех • eiy.	A.27)
Покажем, что ez является аналитической функцией на всей
комплексной плоскости z. Для этого проверим выполнение усло-
условий Коши-Римана A.17)
ди х	dv	ди	х •	dv
— = е cosy=—, — = -е sin у = - —
дх	ду	ду	дх
и заметим, что все производные в этих равенствах непрерыв-
непрерывны по совокупности аргументов на всей плоскости ху. Проводя
вычисление производной ez по формулам A.21), получаем
(ez)f = их + ivx = ex(cosy + is'my) = ez.
Аналогично
(eaz)' = aeaz,	A.28)
где а — произвольная комплексная постоянная.
Рассмотрим еще две функции fi(z) и /2B), определенные с
помощью соотношений
/i(*) = \(егг + е-% f2(z) = 1(е<* - <Г").	A.29)
Как легко видеть, для действительных значений комплексной
переменной z = x эти функции совпадают с cos ж и sin ж; по-
поэтому для них естественно сохранить прежние обозначения. В
дальнейшем мы подробно изучим свойства этих функций, а сей-
сейчас лишь отметим, что, как сложные функции от аналитической
функции, cos z и sin z являются аналитическими на всей комп-
комплексной плоскости. Непосредственной проверкой легко убедить-
убедиться, что (cos;?:O = — s'mz. Действительно, с помощью A.28) полу-
получим
f[{z)=i-{e^-e-^) = -f2{z).	A.30)
Аналогично прямое вычисление дает
fi(z) + fl(z) = l,	A.31)
так как согласно правилу возведения комплексного числа в це-
целую степень из формулы A.27) получим
(eazJ = e2az.	A.32)

§ 5	ИНТЕГРАЛ ПО КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ	41
§ 5. Интеграл по комплексной переменной
1. Основные свойства. Пусть на комплексной плоскости
z задана кусочно гладкая кривая С конечной длины L. Исполь-
Используя параметрическое представление кривой С, зададим коорди-
координаты ?,7/ каждой ее точки уравнениями ? = ?(?), г/ = r/(t), где
?(?) и rj(t) — кусочно гладкие функции действительного пара-
параметра ?, изменяющегосяв пределах a^t^/3(an/3 могут со-
соответственно принимать значения ±оо), удовлетворяющие усло-
условию [?7(?)]2 + Ь/№]2 7^ 0- Задание координат ?, г/ точек этой кри-
кривой С эквивалентно заданию комплексной функции (*(?) = ?(?) +
+ ir/(t)действительной переменной ?.
Пусть в каждой точке ( кривой С определено значение функ-
функции /(С)- Важным понятием в теории функций комплексной пе-
переменной является понятие интеграла от функции /(С) по кри-
кривой С. Это понятие вводится следующим образом. Разобьем кри-
кривую С на п частичных дуг точками деления С(Ь Съ С2?- • • ? Сп? соот-
соответствующими возрастающим значениям параметра t (?г+1 > ^г)-
Введем обозначение AQ = Ci ~ Сг-i и составим сумму
A.33)
г=1
где Q — произвольная точка i-й частичной дуги.
Если при тах|А^| —>> 0 существует предел сумм A.33), не
зависящий ни от способа разбиения кривой С, ни от выбора
точек ?*, то этот предел называется интегралом от функции
f(() no кривой С и обозначается как
f
f(()d(.	A.34)
с
Вопрос существования интеграла A.34) сводится к вопросу
о существовании некоторых криволинейных интегралов от дей-
действительной и и мнимой v частей функции f(z). В самом деле,
записав /((*) = u(P*)+iv(P*), AQ = А^ + гАгц, где Р*(#,т?) -
точка кривой С на плоскости жу, мы мож:ем представить выра-
выражение A.33) в виде
г=1	г=1
Действительная и мнимая части S(Q,Q) представляют собой
интегральные суммы криволинейных интегралов второго рода
fud^ — vdr] и	\udrj-\-vd^	A.35)
с	с

42
ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
ГЛ. 1
соответственно1), откуда и следует высказанное утверждение.
Подчеркнем, что для существования криволинейных интегралов
A.35), а тем самым и интеграла A.34) по комплексной перемен-
переменной достаточно лишь кусочной непрерывности функций и и v
действительных переменных. Это означает, что интеграл A.34)
существует и в случае неаналитической функции f(z), если эта
функция является кусочно непрерывной.
Итак, интеграл A.34) представим в виде
J/(C)rfC= / ud^-vdrj + i f udrj
A.36)
е
е
с
Это соотношение может само служить определением интегра-
интеграла от функции f(z) по кривой С. Из него следует ряд свойств,
являющихся очевидным следствием соответствующих свойств
криволинейных интегралов:
f f(()d( = - f
AB
BA
2.	/ /(C) d( + / /(C) d( = J /(C) d( .
Ci	C2	d + C2
3.	Если а — комплексная постоянная, то
faf(()d( = aff(()d(.
с
с
4.
5.
с
е
е
ff(()d(
с
A-37)
A.38)
A.39)
A.40)
A.41)
с
где gLs — дифференциал длины дуги кривой С, а интеграл, стоя-
стоящий справа, является криволинейным интегралом первого рода.
Действительно, в силу неравенства треугольника имеем
ff(()d(
С
lim, YJ(Q
lim V|/(C)||AC,| =
:) Определение криволинейных интегралов и теорему существования см.
вып. 2.

ИНТЕГРАЛ ПО КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ	43
Если max |/(С)| = М и L — длина дуги кривой С, то
ff(()d( ^M-L.	A.42)
с
6. Имеет место следующая формула замены переменной ин-
интегрирования:
J f(z) dz= f f[(p(Q](p'(Q d?,	A.43)
с	г
где z = ср(() — аналитическая функция ?, устанавливающая
взаимно-однозначное соответствие между кривыми С и Г. В
частности,
/3
ff(z)dz= ff[z(t)]z'(t)dt,	A.44)
С	а
где z = z(t) есть параметрическое задание кривой С, a z(а) и
z(f3) суть начальная и конечная точки последней.
П р и м е р. В качестве существенного для дальнейшего при-
примера вычисления интеграла по комплексной переменной рассмо-
рассмотрим интеграл
где кривая Ср представляет собой окружность радиуса р с цен-
центром в точке ^о, обходимую против часовой стрелки. Воспользо-
Воспользовавшись параметрической формой задания кривой Ср: С — ^о +
+ рег(р @ ^ ср ^ 2тг), получим
2тг	2тг
(L46)
о	о
Отсюда следует, что интеграл A.45) не зависит ни от р, ни от zq.
Замечание. Формула A.36), в силу которой интеграл по
комплексной переменной представляет собой комплексное чис-
число, действительная и мнимая части которого являются криволи-
криволинейными интегралами второго рода, а также соотношение A.44)
позволяют непосредственно перенести понятие несобственного
интеграла от функции действительной переменной 1) на случай
комплексной переменной. В нашем курсе мы будем главным об-
образом иметь дело с несобственными интегралами первого ро-
рода — интегралами по бесконечной кривой С. Несобственный ин-
:) См. вып. 2.

44	ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ	ГЛ. 1
теграл первого рода по бесконечной кривой С называется схо-
сходящимся, если существует предел последовательности интегра-
интегралов J /(С)^С> по любой последовательности конечных кривых
Сп
Сп, составляющих часть С, при Сп, стремящихся к С, причем
этот предел не зависит от выбора последовательности {Сп}. Ес-
Если лишь при определенном выборе последовательности {Сп} су-
существует предел последовательности интегралов J /(С)^С? т0
сп
несобственный интеграл называется сходящимся в смысле глав-
главного значения.
В дальнейшем мы будем рассматривать интегралы от функ-
функций, аналитических в некоторой ограниченной области, причем
нас в основном будет интересовать тот случай, когда границей
области является кусочно гладкая замкнутая кривая, не име-
имеющая самопересечений. Кусочно гладкую замкнутую кривую,
не имеющую точек самопересечения, будем называть замкну-
замкнутым контуром. Если функция z(t) (a ^ t ^ /3) задает пара-
параметрически замкнутый контур, то она удовлетворяет условию
z(ti) Ф z(tk) при ti ф ?&, за исключением случая t{ = а, ?& =
= /3. Интеграл A.34) по замкнутому контуру часто называется
контурным интегралом.
2. Теорема Коши. Поскольку значение контурного ин-
интеграла зависит от направления интегрирования, условимся в
качестве положительного направления обхода контура прини-
принимать направление, при котором внутренняя область, ограни-
ограниченная данным замкнутым контуром, остается слева от на-
направления движения. Интегрирование в положительном на-
направлении будем обозначать символом f f(z)dz или просто
с+
J f(z) dz, интегрирование в отрицательном направлении — сим-
с
волом J f(z) dz.
с-
Свойства интегралов по замкнутому контуру от функций,
аналитических внутри области, ограниченной данным конту-
контуром, во многом определяются известными свойствами криволи-
криволинейных интегралов второго рода1). Как известно2), для криво-
*) См. вып. 2. Напомним, что по принятому нами определению контуры
интегрирования всегда являются кусочно гладкими кривыми.
2) В вып. 2 эта теорема доказана при дополнительном условии ограничен-
ограниченности частных производных функций Р и Q в области Q, введенном с целью
облегчения доказательства. В случае кусочно гладкой границы это условие
может быть снято с помощью дополнительного предельного перехода. Мы
здесь не будем приводить подробное доказательство, а ограничимся лишь
данным замечанием.

§ 5	ИНТЕГРАЛ ПО КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ	45
линейных интегралов по замкнутому контуру имеет место сле-
следующее утверждение: если функции Р(х,у) и Q(x,y) непрерыв-
непрерывны в замкнутой области Q', ограниченной кусочно гладким кон-
контуром С, а их частные производные первого порядка непрерыв-
непрерывны в Q^ то
J ?JJ{^-^}dxdy.	A.47)
С	G
Перейдем теперь к доказательству основного положения дан-
данного параграфа.
Теорема 1.5 (теорема Коши). Пусть в односвязной
области Q задана однозначная аналитическая функция f(z).
Тогда интеграл от этой функции f(z) no любому замкнуто-
замкнутому контуру Г, целиком лежащему в области Q, равен нулю.
Доказательство. Согласно формуле A.36)
I f (С) d( = I udx — v dy + i ? v dx + udy.
г	г	г
Так как функция f(z) — аналитическая всюду внутри контура
Г, то функции и(х, у) и г;(ж, у) в области, ограниченной этим кон-
контуром, обладают непрерывными частными производными пер-
первого порядка. Поэтому к криволинейным интегралам, стоящим
в правой части последнего равенства, можно применить форму-
формулу A.47). Кроме того, частные производные функций и(х,у) и
v(x,y) связаны соотношениями Коши-Римана. Поэтому
J
udx-vdy =
g
и
vdx + udy = JJ {g-g
что и доказывает утверждение теоремы.
Итак, теорема 1.5 устанавливает факт равенства нулю инте-
интеграла от аналитической функции по любому замкнутому кон-
контуру, целиком лежащему в односвязной области ее аналитич-
аналитичности. При дополнительном условии непрерывности функции
в замкнутой области данное утверждение справедливо и для
замкнутого контура, являющегося границей области аналитич-
аналитичности. Последнее утверждение фактически является несколько
видоизмененной формулировкой теоремы Коши, но ввиду его
важности для практических приложений мы выделим это утвер-
утверждение в отдельную теорему.
Теорема 1.6 (вторая формулировка теоремы Коши).
Если функция f(z) является аналитической функцией в одно-

46
ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
ГЛ. 1
связной области Q, ограниченной кусочно-гладким контуром С,
и непрерывна в замкнутой области Q, то интеграл от функ-
функции f(z) no границе С области Q равен нулю:
A.48)
/ /(С) dC = 0.
с
Теорема Коши устанавливает одно из основных свойств ана-
аналитической функции комплексной переменной. Ее фундамен-
фундаментальное значение будет следовать из дальнейшего изложения,
здесь же мы ограничимся следующим замечанием.
Теорема формулировалась для односвязной области, однако
ее легко обобщить и на случай многосвязной области. В этом
случае полная граница области состоит из нескольких замкну-
замкнутых контуров: внешнего Со и внутренних Ci, C2, ..., Сп. Поло-
Положительным направлением обхода полной границы многосвяз-
многосвязной области будем называть такое направление движения, при
котором область все время остается слева. При этом внешний
контур обходится в положительном, а внутренние — в отрица-
отрицательном направлении.
Теорема 1.7. Пусть f(z) является аналитической функ-
функцией в многосвязной области Q, ограниченной извне контуром
Со, а изнутри контурами Ci, C2,..., Сп, и пусть f(z) непре-
непрерывна в замкнутой области Q. Тогда //(С)^С = 0? г^е С —
полная граница области Q,
состоящая из контуров Со,
Ci,..., Сп, причем обход грани-
границы С происходит в положи-
положительном направлении.
Доказательство.
Проведем гладкие кривые 7ъ • • •
..., 7га ? соединяющие контур Со
с контурами Ci, C2 и т. д. (рис.
1.8). Тогда область, ограничен-
ограниченная кривыми Со, С\, ..., Сп и
кривыми 7i5 725 • • • 5 7га ? прохо-
проходимыми дважды в противопо-
противоположных направлениях, оказы-
оказывается односвязной х). В силу теоремы 1.6 интеграл по грани-
границе этой области равен нулю. Но интегралы по вспомогательным
кривым 7ъ • • • ? 7га проходятся дважды в противоположных на-
направлениях и при суммировании интегралов выпадают. Поэтому
Рис. 1.8
« 1 ^
х) Как нетрудно убедиться, кривые 71? •••5 In всегда можно выбрать
так, чтобы они не пересекались, т. е. получим действительно односвязную
область.

§ 5	ИНТЕГРАЛ ПО КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ	47
имеет место равенство
/ /(С) d( + / /(С) rfC + • • • + / /(С) ^С = о A.49)
Со	C-l	Cn
(верхние индексы у С{ указывают направление обхода).
В заключение отметим, что если функция f(z) является ана-
аналитической в многосвязной области Q и Г — произвольный за-
замкнутый контур, целиком лежащий в Q, то интеграл f f(()d(
г
может, вообще говоря, оказаться отличным от нуля. Например,
пусть область Q представляет собой круговое кольцо 1 < \z\ < 3.
Функция f(z) = 1/z является аналитической в этой области.
В силу примера, рассмотренного на с. 43, / -j- = 2тгг ф 0.
И = 2
Данное обстоятельство связано, в частности, с тем, что контур
\z\ = 2 не образует полную границу области аналитичности рас-
рассматриваемой функции.
3. Неопределенный интеграл. Важным следствием те-
теоремы Коши является следующее положение. Пусть функция
f(z) является аналитической функцией в односвязной области
Q. Фиксируем в этой области некоторую точку zq и обозначим
через f f(C)d>C интеграл по какой-либо кривой, целиком лежа-
лежало
щей в Q и соединяющей точки z и zq. В силу теоремы Коши
этот интеграл не зависит от выбора кривой интегрирования в
области Q и является однозначной функцией z:
<b(z).	A.50)
Теорема 1.8. Пусть функция f(z) определена и непрерывна
в некоторой односвязной области Q^ а интеграл от этой функ-
функции по любому замкнутому контуру Г, целиком лежащему в
данной области, равен нулю. Тогда функция Ф(^) = f f(()d(
zo
(z, zq E Q) является аналитической функцией в области Q и
&(z) = f(z).
Доказательство. Составим разностное отношение
z + Az
\ = ± J f(C)dC.
ZQ	)	Z

48
ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
ГЛ. 1
Последнее равенство имеет место в силу независимости значе-
значения интеграла, определяющего функцию Ф(^), от пути интегри-
интегрирования и A.38). Выберем в качестве пути интегрирования в
последнем интеграле прямую, соединяющую точки z и z + Az.
Такой путь интегрирования является удобным, поскольку имеет
z+Az
место очевидное соотношение J dC, = Az. Оценим выражение
Az
-f(z)
\Az\
: + Az
J {f(C)-f(z)}d(
max
Ce[z,z+Az]
- f(z)\ ¦ \Az\ = max
-м\-
В силу непрерывности функции f(z) в точке z для любого поло-
положительного числа е может быть указано такое значение S > О,
что при \Az < 5 max \f(C)~f(z)\ < 6? т- е- Для любого ? > О
te[+A]
t[,]
можно указать такое S > 0, что
-/(*)
< е при 0 <
<5.
Это и означает, что существует
lim	Л	= ф'(г) = f(z)-
A.51)
Итак функция Ф(^), определенная интегралом A.50), во всех
точках области Q имеет непрерывную производную (функция
f(z) по условию теоремы непрерывна в Q). Тем самым Ф(^) яв-
является аналитической функцией в области Q.
Доказанная теорема позволяет ввести понятие неопределен-
неопределенного интеграла функции комплексной переменной. Аналитиче-
Аналитическая функция Ф(^) называется первообразной функции f(z) в
области Q', если в этой области имеет место соотношение Ф1 (z) =
= f(z). Очевидно, функция f(z) имеет множество различных
первообразных, но, как легко доказать, все первообразные этой
функции различаются между собой лишь постоянными слагае-
слагаемыми1) . Совокупность всех первообразных функции f(z) на-
называется неопределенным интегралом от функции f(z).
:) Действительно, так как Ф'(^) = &i(z) — ФЦг) = 0, где Ф^г) и Фг(^)
суть различные первообразные функции f(z), то из A.21) следует, что все
частные производные действительной и мнимой частей функции Ф(г) то-
тождественно равны нулю, откуда по известной теореме анализа (см. вып. 1,
гл. 8) получим Ф(г) = const.

§ 5	ИНТЕГРАЛ ПО КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ	49
Так же, как и в случае функции действительной переменной,
имеет место формула
z\
где F(z) — любая первообразная функции f(z). Действительно,
интеграл, стоящий слева, не зависит от пути интегрирования.
Поэтому его можно представить в виде
Z2	%2	Z\
f№<K= J/(CR- f№<K,
z\	zq	zq
где zq — произвольная точка области Q. Согласно A.50) каж-
каждый из интегралов в правой части этой формулы представляет
собой значение определенной первообразной в соответствующих
точках, а так как все первообразные различаются лишь на по-
постоянную, то безразлично, какую первообразную мы подставим
в данную формулу.
В качестве существенного для дальнейшего примера рассмо-
рассмотрим функцию
z
ff-	A-52)
Так как подынтегральная функция является аналитической на
всей комплексной плоскости z, за исключением точки z = 0, то
выражение A.52) имеет смысл при условии, что кривая инте-
интегрирования не проходит через точку z = 0. При этом в любой
односвязной области Q комплексной плоскости, не содержащей
точку z = 0, функция f(z) является однозначной аналитиче-
аналитической функцией z, не зависящей от выбора пути интегрирования
в формуле A.52). В качестве такой области будем рассматривать
полную комплексную плоскость z, разрезанную по отрицатель-
отрицательной части действительной оси, т. е. область —тг < axgz < тг. Бу-
Будем считать, что путь интегрирования в формуле A.52) лежит
целиком в области —тг < argz < тг, т. е. не пересекает разре-
разреза и не проходит через точку z = 0. Тогда для действительных
положительных значений z = ж, выбрав в качестве пути инте-
интегрирования в формуле A.52) соответствующий отрезок действи-
действительной оси, получим
f{x) = Г^- = Ых.	A.53)
1
То есть для положительных значений своего аргумента функ-
функция f(z) совпадает с логарифмической функцией действитель-

50	ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ	ГЛ. 1
ной переменной. Поэтому для функции A.52) в рассматривае-
рассматриваемой области (—тг < axgz < тг) сохраним прежнее обозначение,
положив
In *= / —.
Последнее равенство (в котором путь интегрирования выбирает-
выбирается указанным выше способом) можно рассматривать как опреде-
определение логарифмической функции для всех комплексных значе-
значений ее аргумента, за исключением значений, лежащих на отри-
отрицательной части действительной оси z = х ^ 0. В дальнейшем
(гл. 3) мы подробно изучим свойства этой функции, а сейчас
лишь отметим, что в силу формулы A.51) имеет место соотно-
соотношение
(]nz)' = -,	A.55)
z
т. е. в области —тг < argz < тг производная логарифмической
функции имеет то же выражение, что и для действительных
положительных значений аргумента. Ниже будет установлено,
что функция A.54) является обратной к функции w = ez, вве-
введенной в §4 настоящей главы.
§ 6. Интеграл Коши
1. Вывод формулы Коши. В предыдущем параграфе
мы доказали теорему Коши. Эта теорема влечет за собой ряд
важных следствий, в частности, позволяет установить опреде-
определенную связь между значениями аналитической функции во
внутренних точках области ее аналитичности и граничными зна-
значениями этой функции. К установлению данного соотношения
мы сейчас и перейдем.
Пусть функция f(z) является аналитической в односвязной
области Q, ограниченной контуром С. Возьмем произвольную
внутреннюю точку zq и построим замкнутый контур Г, целиком
лежащий в Q и содержащий точку zq внутри себя. Рассмотрим
вспомогательную функцию
ф) = Ш_%	A.56)
Z — Zq
Функция tp(z), очевидно, является аналитической функцией
всюду в области (/, за исключением точки zq. Поэтому, если
мы в области Q возьмем такой замкнутый контур 7, лежащий
внутри Г, чтобы точка zq попала внутрь области, ограниченной
контуром 75 т0 функция (f(z) будет аналитической в двухсвяз-
двухсвязной области Q*, заключенной между контурами Г и 7- Соглас-
Согласно теореме Коши интеграл от функции <p(z) по кривой Г + 7

ИНТЕГРАЛ КОШИ
51
равен нулю:
= 0.
Г+	7~
Изменив направление интегрирования во втором интеграле, это
равенство можно переписать в виде
Г+	7+
Поскольку интеграл, стоящий слева, не
зависит от выбора контура 7? т0 этим
свойством обладает и интеграл, стоя-
стоящий справа. Для дальнейших рассмо-
рассмотрений удобно в качестве контура ин-
интегрирования 7 выбрать окружность jp
некоторого радиуса р с центром в точ-
точке Zq (рИС. 1.9). ПОЛОЖИВ ( = Zq + рвЩ',
имеем
2тг
№d<p.
J ^l
Рис. 1.9
Г+	0
Последний интеграл преобразуем следующим образом:
2тг
2тг
2тг
/ /(С) dV = / [/(С) - /Ы] ^ + /
оо	о
2тг
= / [/(С) - /Ы] ^ + 27г/(*0). A.58)
о
Устремим теперь р к нулю. Так как f(z) — аналитическая, а сле-
следовательно, непрерывная функция в области (/, то для любого
положительного числа е можно указать такое значение р, что
1/@ ~/(^о)| < ? Для |С~^о| < Р- Отсюда следует, что при р —>> 0
существует предел
2тг
Um f [/(С)-
Так как в формуле A.58) последнее слагаемое не зависит от
2тг	г* f(?\
то Г /(С) dip = 2тг/(^о), а следовательно, / n ; d^
п	^ С — ^о

52	ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ	ГЛ. 1
и согласно A.57)
ЬЦ^	(L59)
г
Интеграл, стоящий в правой части A.59), выражает значе-
значение аналитической функции f(z) в некоторой точке zq через ее
значения на любом контуре Г, лежащем в области аналитич-
аналитичности функции f(z) и содержащем точку zq внутри. Этот
интеграл и называется интегралом Коши. Формула A.59) ча-
часто называется формулой Коши.
Замечание 1. В формуле A.59) интегрирование произ-
производится по замкнутому контуру Г, целиком лежащему в области
аналитичности функции f(z) и содержащему внутри точку zq.
При дополнительном условии непрерывности f(z) в замкнутой
области Q аналогичная формула имеет место в силу теоремы 1.6
и при интегрировании по границе С области Q'.
Замечание2. Проведенные рассмотрения остаются
справедливыми и в случае многосвязной области Q. При этом
для вывода основной формулы A.59) следует рассматривать та-
такой замкнутый контур Г, который может быть стянут к точке
2о, все время оставаясь в области Q. Тогда легко показать, что
при условии непрерывности функции f(z) в замкнутой области
Q с кусочно гладкой границей формула A.59) остается спра-
справедливой при интегрировании в положительном направлении по
полной границе С данной многосвязной области.
2. Следствия из формулы Коши. Сделаем ряд заме-
замечаний по поводу формулы A.59).
1. Интеграл вида —- / /^ dC по замкнутому контуру Г,
2тгг J Q — zq
Г
целиком лежащему в области Q аналитичности функции f(z),
имеет смысл для любого положения точки zq на комплексной
плоскости при условии, что эта точка не лежит на контуре Г.
При этом, если точка zq лежит внутри Г, то значение интегра-
интеграла равно /(^о); если точка zq лежит вне Г, значение интеграла
равно нулю, поскольку в этом случае подынтегральная функция
является аналитической всюду внутри Г. Итак,
J_ Г Ж. <% = \{ы> zo ~ внутРи г'	A.60)
2тгг J C-zo s [0,	Zq - вне Г.	V J
Г
При zq Е Г интеграл I{zq) = —- /	d( в обычном смы-
Z7TZ U ц — Zo
Г
еле не существует, однако при дополнительных требованиях на

ИНТЕГРАЛ КОШИ	53
поведение функции /(?) на контуре Г этому интегралу может
быть придан определенный смысл. Так, если функция /(?) удо-
удовлетворяет на контуре Г условию Гёльдера 1)
то существует главное значение по Коти интеграла I(zq)
V.p. I(zQ) = lim —
где Г? представляет собой часть контура Г, лежащую вне круга
\z — ^ol < е. При этом
V. p. I(z0) = \f(z0).
2. Пусть f(z) — аналитическая функция в односвязной обла-
области Q и zq — некоторая внутренняя точка этой области. Опишем
из этой точки как из центра окружность радиуса i?o, целиком
лежащую в области Q. Тогда по формуле Коши получим
Но на окружности Cr0 ( = zq + Ще^, поэтому
2тг
71 о
ИЛИ
2тгЯп J
Эта формула носит название формулы среднего значения и вы-
выражает значение аналитической функции в центре окружности
как среднее из ее граничных значений.
3. Принцип максимума модуля аналитической
функции. Пусть функция f(z) является аналитической в
области Q и непрерывной в замкнутой области Q. Тогда или
\f(z)\ = const, или максимальные значения \f{z)\ достигаются
только на границе области.
Действительная функция двух действительных переменных
\f(z)\ =
По поводу условий Гёльдера см. вып. 2.

54	ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ	ГЛ. 1
по условию является непрерывной в замкнутой области. Поэто-
Поэтому она достигает своего максимального значения М в какой-
либо точке (жо, Уо) данной области. То есть
м = |№»I»I/WI, f6V + *"> A-«з)
Предположим, что точка zq — внутренняя точка области Q. По-
Построим в области Q круг Kq некоторого радиуса R с центром
в точке zq и запишем формулу среднего значения для zq и R.
Учтя A.63), получим
2тгМ =
Следовательно,
2тг
2тг
2тг
A.64)
Из этого соотношения в силу непрерывности функции /(О на
контуре интегрирования и неравенства A.63) следует, что
=М при С = ^о + Дег^.	A.65)
Действительно, по A.63) функция |/@| не может быть больше
М ни в одной точке контура интегрирования. Если мы пред-
пол ожим, что в какой-либо точке (о контура интегрирования
функция |/(Со)| строго меньше М, то из непрерывности |/@|
следует, что |/@| строго меньше Мив некоторой окрестности
точки (о, т- е- можно указать отрезок [^1,^2] интегрирования,
на котором
|/(С)| <М-е, е>0.
Тогда
2тг	(р2	<pi	2тг
f\f(Q\d<p= / |/@| dv+ / 1/@1 <V+ / 1/@1 dv^
0	(fl	0	(f2
^ (M - e)(<p2 - ^1) + М[2тг - ((p2 ~ <Pi)] < 2kM,
что противоречит A.64). Итак, соотношение A.65) действитель-
действительно имеет место. Это означает, что на окружности радиуса R с
центром в точке zq функция \f(z)\ имеет постоянное значение,
равное своему максимальному значению в области Q. То же бу-
будет иметь место и на любой окружности меньшего радиуса с
центром в точке zo, а следовательно, и во всем круге Kq. Те-
Теперь легко показать, что это же значение функция \f(z)\ имеет
и в любой другой внутренней точке z* области Q. Для этого

ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА
55
соединим точки zq и z* кривой С, целиком лежащей в обла-
области Q и отстоящей от ее границы не меньше чем на некоторое
положительное число d. Возьмем точку z\, являющуюся послед-
последней общей точкой кривой С и круга Kq (рис. 1.10). Поскольку
|/(^i)| = М, то, повто-
повторяя проведенные выше
рассуждения, покажем,
что внутри круга К\ С
С Q с центром в точке z\
радиуса R\ ^ d модуль
функции f(z) принима-
принимает постоянное значение,
равное максимальному
значению М. Взяв на
кривой С точку Z2, явля-
являющуюся последней об-
общей точкой кривой С и
круга К\, и продолжая	Рис. 1.10
данный процесс, мы в
результате конечного числа шагов получим, что внутри кру-
круга Кп, которому принадлежит точка ?*, имеет место равенство
\f(z)\ = М, что и доказывает высказанное утверждение.
Итак, мы показали, что если |/(г)| принимает максимальное
значение М в некоторой внутренней точке области, то \f(z)\=M
во всей области г).
Таким образом, если функция \f(z)\ не является постоян-
постоянной величиной в области Q, то она не может достигать своего
максимального значения во внутренних точках Q. Но так как
функция, непрерывная в замкнутой области, достигает своего
максимального значения в какой-либо точке этой области, то в
последнем случае функция \j{z)\ должна достигать своего мак-
максимального значения в граничных точках.
В качестве последнего замечания отметим, что если анали-
аналитическая в области Q функция f(z)_ne равна нулю ни в одной
точке этой области и непрерывна в Q, то имеет место прин-
принцип минимума модуля этой функции. Для доказательства это-
этого утверждения достаточно рассмотреть функцию (f(z) = —г^- и
j\z)
воспользоваться принципом максимума модуля этой функции.
) Как следует из соотношений A.20), в этом случае и аргумент анали-
аналитической функции f(z) также сохраняет постоянное значение в области Q,
откуда следует, что если модуль аналитической функции постоянен в неко-
некоторой области, то эта функция тождественно равна постоянной в данной
области.

56	ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ	ГЛ. 1
§ 7. Интегралы, зависящие от параметра
1. Аналитическая зависимость от параметра. Рас-
Рассматривая интеграл Коши, мы видим, что подынтегральная
функция зависит от двух комплексных переменных: перемен-
переменной интегрирования ? и фиксированного значения переменной
zq. Тем самым интеграл Коши является интегралом, зависящим
от параметра zq. Естественно поставить вопрос об общих свой-
свойствах интегралов по комплексной переменной, зависящих от па-
параметра.
Пусть задана функция двух комплексных переменных1)
tp(z, С), однозначно определенная для значений комплексной пе-
переменной z = x+iy из области Q и для значений комплексной пе-
переменной ? = ? + *?7? принадлежащих некоторой кусочно гладкой
кривой С. Взаимное расположение области Q и кривой С может
быть совершенно произвольно. Пусть функция двух комплекс-
комплексных переменных cp(z^) удовлетворяет следующим условиям:
а)	Функция cp(z, () при любом значении ( Е С является ана-
аналитической функцией z в области Q.
б)	Функция cp(z^) и ее производная -^-(z,?) являются
непрерывными функциями по совокупности переменных z, ?
при произвольном изменении z в области Q и ( на кривой С.
Условие б) означает, что действительная и мнимая части
функции -^(z,() непрерывны по совокупности переменных
я, У, f, V-
Очевидно, что при сделанных предположениях интеграл от
функции <p(z, С) по кривой С существует при любом z E Q и
является функцией комплексной переменной z:
F(z) = J tp(z, С) d( = U(x, у) + iV(x, у).	A.66)
с
Естественно поставить вопрос о свойствах функции F(z). Ока-
Оказывается, что при сделанных предположениях относительно
функции ip(z^) функция F(z) является аналитической функ-
функцией комплексной переменной z в области Q', причем производ-
производную функции F(z) можно вычислять при помощи дифферен-
дифференцирования под знаком интеграла.
х) Функция двух комплексных переменных z, С, определяется законом,
ставящим в соответствие каждой паре значений z, С из области их опре-
определения некоторое комплексное число w. Подробнее о функциях многих
комплексных переменных см. Приложение 3.

§ 7	ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	57
Для того чтобы доказать это утверждение, рассмотрим кри-
криволинейный интеграл
U(x, у) = J и{х, у, f, r/) df - v{x, у, f, г/) dr/.
с
Так как, по предположению, функции wav обладают частными
производными по ж и у, непрерывными по совокупности пере-
переменных, то частные производные функции U(x,y) по перемен-
переменным ж, у существуют и их можно вычислить при помощи диф-
дифференцирования под знаком интеграла1) :
Ux{x, у) = f uxd?- vx dr],
с
Uy(x, у) = J uyd? - vy dr].
с
Сами функции Ux и Uy явл яются непрерывными функциями пе-
переменных ж, у в области Q 2). На основании аналогичных свойств
функции V(x,y) и используя условия Коши-Римана для функ-
функции <p(z,?), получим
Vy(x, у) = f Vyd? + uydri= J ux d^ -vxdr] = Ux,
с	с
Vx(x, у) = f vx dt; + ux dr] = - f uy dt; - Vy dr] = -[/r
с	с
Таким образом, для F(z) выполнены условия Коши-Римана
(частные производные функций U(x,y) и V(x,y) непрерывны
и связаны соотношениями A.67)), что и доказывает аналитич-
аналитичность f(z) в области Q.
Заметим, что
= J ux d^ - vx dr] + i J vx dt; + ux dr\ = J ^f fo 0 ^C- A.68)
с	с	с
Отсюда следует возможность вычисления производной от инте-
интеграла путем дифференцирования подынтегральной функции по
тт	dip
параметру. При этом, если -^- удовлетворяет тем же условиям
1) Об условиях дифференцируемости по параметру интеграла, зависяще-
зависящего от параметра, см. вып. 2, гл. 10.
) См. вып. 2, гл. 10.

58	ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ	ГЛ. 1
а) и б), что и <p(z,?), то F(z) также является аналитической
функцией в области Q.
2. Существование производных всех порядков у ана-
аналитической функции. Рассмотренное свойство интегралов,
зависящих от параметра, позволяет установить важные харак-
характеристики аналитических функций. Как мы видели, значение
функции f(z), аналитической в некоторой области (/, ограни-
ограниченной контуром Г, и непрерывной в замкнутой области Q, во
внутренних точках этой области может быть выражено через
граничные значения с помощью интеграла Коши:
Рассмотрим в области Q некоторую замкнутую подобласть ?/,
расстояние всех точек которой от границы Г области Q больше
некоторого положительного числа d (\z — ?| ^ d > 0). Функция
s — z
является аналитической функцией z в области Q1', причем ее
д(р	/(С)	~ г
частная производная —— = . v \о в этой области является
dz	(С - zJ
непрерывной функцией своих аргументов. Тем самым в силу об-
общих свойств интегралов, зависящих от параметра, во внутрен-
внутренних точках области Q' производная f'{z) может быть представ-
представлена в виде
Ъ1У«-	(L70)
Интеграл A.70) опять является интегралом, зависящим от па-
параметра, причем его подынтегральная функция обладает те-
теми же свойствами, что и подынтегральная функция интеграла
A.69). Следовательно, f'{z) является аналитической функцией
z в области Q1\ причем для ее производной справедлива формула
Г
Так как для любой внутренней точки z области Q может быть
построена соответствующая замкнутая подобласть Q\ то форму-
формулы A.70) и A.71) справедливы в любой точке z. Имеет место и
более общая теорема.
Теорема 1.9. Пусть функция f(z) является аналитиче-
аналитической в области Q и непрерывной в замкнутой области Q. Тогда

§_J7	ИНТЕГРАЛЫ, ЗАВИСЯЩИЕ ОТ ПАРАМЕТРА	59
во внутренних точках области Q существует производная лю-
любого порядка функции f(z), причем для нее имеет место фор-
формула
f(n)
J
)(z\ _ jL f /@ dC
[Z)~ 2m J (C-*)n+1 ^
Для доказательства этой теоремы достаточно повторить пре-
предыдущие рассуждения соответствующее число раз.
Итак, если функция f(z) является аналитической функцией
в области Q1', то в этой области функция f(z) обладает непре-
непрерывными производными всех порядков. Это свойство аналити-
аналитической функции комплексной переменной существенным обра-
образом отличает ее от функции действительной переменной, имею-
имеющей непрерывную первую производную в некоторой области. В
последнем случае из существования первой производной, вооб-
вообще говоря, не следует существование высших производных.
Рассмотрим ряд важных следствий установленного свойства
аналитической функции комплексной переменной.
Теорема 1.10 (Морера). Пусть функция f(z) является
непрерывной в односвязной области Q и интеграл от f(z) no
любому замкнутому контуру, целиком принадлежащему Q, ра-
равен нулю. Тогда f(z) является аналитической функцией в обла-
области Q.
Доказательство. Выше г) было доказано, что при
условиях теоремы функция
F(z)= ff(()d(,
где zq n z — произвольные точки области Q, а интеграл берется
по любому пути, соединяющему эти точки в области Q, является
аналитической в этой области функцией, причем F'(z) = f(z).
Но, как только что было установлено, производная аналитиче-
аналитической функции также является аналитической функцией, т. е.
существует непрерывная производная функции Ff(z), а именно
функция F"(z) = ff(z), что и доказывает теорему.
Отметим, что теорема 1.10 является в определенном смысле
обратной по отношению к теореме Коши. Ее легко обобщить и
на многосвязные области.
Теорема 1.11 (Лиувилля). Пусть на всей комплексной
плоскости функция f(z) является аналитической, а ее модуль
равномерно ограничен. Тогда эта функция f(z) тождественно
равна постоянной.
См. теорему 1.8, с. 47.

60	ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ	ГЛ. 1
Доказательство. Запишем значение производной
f'(z) в произвольной точке z по формуле A.70):
™-ш/№?«-
Cr
причем интегрирование будем вести по окружности некоторого
радиуса R с центром в точке z, т. е. \( — z\ = R. По условию тео-
теоремы существует такая константа М, что |/(С)| ^ М независимо
от R. Поэтому
Cr
Так как радиус R можно выбрать сколь угодно большим, a fr(z)
не зависит от i?, то |/7(^)| = 0. В силу произвольности выбора
точки z заключаем, что |/7(^)| = 0 на всей комплексной плоско-
плоскости. Отсюда следует, что f(z) = const.
В § 4 мы ввели тригонометрические функции комплекс-
комплексной переменной и показали, что они являются аналитически-
аналитическими функциями на всей комплексной плоскости. В силу только
что доказанной теоремы эти функции не могут быть равномерно
ограничены на всей комплексной плоскости. Отсюда, в частно-
частности, следует, что найдутся такие значения комплексной перемен-
переменной z, для которых
|sinz| > 1.	A.73)
Этим тригонометрические функции комплексной переменной
существенно отличаются от соответствующих функций действи-
действительной переменной.

ГЛАВА 2
РЯДЫ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
В настоящей главе будут рассмотрены основные свойства
функциональных рядов, члены которых являются функциями
комплексной переменной. Особую роль в теории функций комп-
комплексной переменной играют ряды аналитических функций и, в
оо
частности, степенные ряды вида J^ cn(z — zq)u, где сп — задан-
п=0
ные комплексные постоянные, zq — фиксированная точка комп-
комплексной плоскости. Изучение этих рядов оказывается весьма су-
существенным как для выяснения ряда общих свойств функций
комплексной переменной, так и для решения различных задач,
связанных с применением методов теории функций комплекс-
комплексной переменной.
§ 1. Равномерно сходящиеся ряды функций
комплексной переменной
1. Числовые ряды. Начнем с рассмотрения некоторых
общих свойств числовых рядов с комплексными членами, т. е.
выражений вида
оо
к=1
где {а^} — заданная числовая последовательность с комплекс-
комплексными членами.
Ряд B.1) называется сходящимся, если сходится последова-
оо
тельность {Sn} его частичных сумм Sn= ^ а^. При этом пре-
к=1
дел S последовательности {Sn} называется суммой ряда B.1).
оо
Ряд Y2 а^ называется п-м остатком ряда B.1). В случае схо-
k=n+l

62	РЯДЫ АНАЛИТИЧЕСКИХ ФУНКЦИЙ	ГЛ. 2
дящегося ряда сумму его n-го остатка обозначают через гп и
обычно также называют остатком ряда B.1). Для сходящегося
ряда S = Sn + тп и для любого е > 0 можно указать такой номер
7V, что \гп\ < е при п ^ N. Из определения сходящегося ряда
следует, что необходимым и достаточным признаком его сходи-
сходимости является критерий Коши1). А именно, ряд B.1) сходится
тогда и только тогда, когда для любого е > 0 можно указать та-
п-\-р
кой номер N, что
при п^ N и любом натуральном р.
к=п
Необходимым условием сходимости ряда B.1) является тре-
требование lira an = 0. Действительно, из сходимости этого ряда,
п—)>оо
в силу критерия Коши, следует, что для любого е > 0 можно
указать такое 7V, что |an+i| = IS^+i — Sn\ < е при п ^ N.
Если сходится ряд
сю
B-2)
с действительными положительными членами, то, очевидно,
сходится и ряд B.1), который в этом случае называется абсо-
абсолютно сходящимся. Одним из наиболее часто употребляемых
способов исследования сходимости ряда с комплексными члена-
членами является рассмотрение ряда с действительными членами, яв-
являющимися модулями членов исходного ряда. Как известно2),
достаточными признаками сходимости ряда с действительны-
действительными положительными членами являются признаки Даламбера и
Коши.
Согласно признаку Даламбера ряд B.2) сходится, если, на-
начиная с некоторого номера 7V, отношение
/ < 1 для всех
п^ N.
Отметим, что если, начиная с некоторого номера 7V, отноше-
отношение n+1 ^ 1, то ряд B.1) с комплексными членами расходится.
Cin
Действительно, в этом случае все члены ряда B.1), начиная с
адг, удовлетворяют соотношению \ап\ ^ |адг| ф 0, т. е. не выпол-
выполнен необходимый признак сходимости ряда.
Согласно признаку Коши ряд B.2) сходится, если
^ q < 1 для всех п ^ N. Если, начиная с некоторого 7V, для
всех п ^ N имеет место соотношение \/|а^| ^ 1, то ряд B.1)
расходится.
1)	Являющийся прямым следствием критерия Коши сходимости числовой
последовательности {Sn}; см. с. 21.
2)	См. вып. 1, гл. 13.

§_L	РАВНОМЕРНО СХОДЯЩИЕСЯ РЯДЫ ФУНКЦИЙ	63
2. Функциональные ряды. Равномерная сходимость.
Перейдем теперь к рассмотрению функциональных рядов, чле-
членами которых являются функции комплексной переменной.
Пусть в области Q определена бесконечная последовательность
однозначных функций комплексной переменной {un(z)}. Выра-
Выражение вида
п(*)	B.3)
п=1
будем называть функциональным рядом. При фиксированном
значении zq Е Q ряд B.3) превращается в числовой ряд вида
B.1).
Функциональный ряд B.3) называется сходящимся в обла-
области Q, если при любом z E Q соответствующий ему числовой
ряд сходится. Если ряд B.3) сходится в области б, то в этой
области можно определить однозначную функцию f{z), значе-
значение которой в каждой точке области Q равно сумме соответству-
соответствующего числового ряда. Эта функция называется суммой ряда
B.3) в области Q. В силу данных определений в этом случае
для любой фиксированной точки z EG и любого заданного по-
положительного числа е можно указать такой номер 7V, что
< е при п ^ N(s,z).
k=i
Заметим, что в общем случае N зависит и от е и от z.
В теории рядов функций комплексной переменной, так же
как и в случае действительной переменной, особую роль играет
понятие равномерной сходимости. Например, как помнит чита-
читатель из курса анализа1), сходящийся ряд непрерывных функ-
функций далеко не всегда сходится к непрерывной функции. В то же
время сумма равномерно сходящегося ряда непрерывных функ-
функций всегда является непрерывной функцией. Равномерно схо-
сходящиеся ряды функций комплексной переменной, так же как
и в случае действительной переменной, обладают рядом весьма
важных свойств, к изучению которых мы и перейдем. Начнем с
определения.
Если для любого положительного числа е можно указать
такой номер N(s,) что при п ^ N(e) неравенство
<е
k=i
выполняется сразу для всех точек z области G-> то ряд B.3)
называется равномерно сходящимся в области Q.
:) См. вып. 2.

64	РЯДЫ АНАЛИТИЧЕСКИХ ФУНКЦИЙ	ГЛ. 2
оо
Обозначив rn(z) = ^ uk(z)i условие равномерной сходи-
к=п+1
мости ряда B.3) можем записать в виде |rn(^)| < е при п ^ N{e).
Ниже будет установлен ряд свойств равномерно сходящихся ря-
рядов.
Укажем важный для приложений достаточный признак рав-
равномерной сходимости.
Признак Вейерштрасса. Если всюду в области Q члены
функционального ряда B.3) могут быть мажорированы члена-
членами абсолютно сходящегося числового ряда, то ряд B.3) сходит-
сходится равномерно в области Q.
Доказательство. По условию имеет место равномерная
оценка
\ 11 ( У I ^ П	У (^- Cj	(^У Л i
\и"п\4>)\ ^ \пп\-) * ^= У-	1^* V
(X)
Так как ряд ^ \ап\ сходится, то для любого е > 0 можно ука-
~~	сю
зать такое 7V, что ^ \а^\ < е при п ^ N. Но в силу B.4) в
к=п+1
области Q имеет место неравенство
(X)
к=п+1	к=п+1	к=п+1
при п ^ N , что и доказывает равномерную сходимость ряда
B.3) в области Q.
Следует иметь в виду, что признак Вейерштрасса является
лишь достаточным признаком равномерной сходимости. Имеет
место следующий необходимый и достаточный признак равно-
равномерной сходимости.
Критерий Коши. Для того чтобы ряд B.3) сходился рав-
равномерно в области Q, необходимо и достаточно, чтобы для лю-
любого е > 0 существовало такое N(s), что одновременно во всех
точках области Q выполняется соотношение
\Sn+m(z) - Sn(z)\ <e	B.5)
при п ^ N и для любого натурального т.
Доказательство. 1) Необходимость.
Из равномерной сходимости ряда B.3) следует, что для любого
е > 0 можно указать такое Л/"(б), что во всех точках z области Q
имеют место неравенства
при п ^ N и для любого натурального га, откуда и следует B.5).
2) Достаточность. Из соотношения B.5) в силу кри-
критерия Коши для числовой последовательности с комплексными

РАВНОМЕРНО СХОДЯЩИЕСЯ РЯДЫ ФУНКЦИЙ
65
членами1) следует, что при любом фиксированном z E Q по-
последовательность {Sn(z)} является сходящейся. Следовательно,
при выполнении B.5) ряд B.3) сходится в области Q к некоторой
функции f(z) = lira Sn{z). Но в силу B.5)
lim \Sn+m{z) - Sn(z)\ = \f(z) - Sn(z)\ <e при п > N(e)
m—^oo
во всех точках области Q одновременно, что и доказывает рав-
равномерную сходимость ряда B.3) в области Q.
3. Свойства равномерно сходящихся рядов. Теоремы
Вейерштрасса. Перейдем теперь к рассмотрению некоторых
общих свойств равномерно сходящихся рядов.
Теорема 2.1. Если функции un(z) непрерывны в области Q,
оо
а ряд ^2 un(z) сходится в этой области равномерно к функции
п=1
f(z), то f(z) таксисе непрерывна в области Q.
Доказательство. Рассмотрим выражение
\f(z + Az) — f(z) |, где точки z и z + Az принадлежат области Q.
оо
В силу равномерной сходимости ряда ^ un(z), для любого
п=1
е > 0 можно указать такое 7V, что одновременно имеют место
неравенства
N
k=i
N
k=i
| B-6)
для любых точек z n z -\- Az, принадлежащих области Q. В силу
непрерывности функций u^z\ в любой точке z E Q для задан-
заданного е и выбранного N можно указать такое S > 0, что
N
N
Az) -
k=i
N
k=l
I w
при \Az\ < S. Из B.6), B.7) и из того, что модуль суммы не пре-
превосходит сумму модулей, следует, что для любого е > 0 можно
указать такое ?, что \f(z + Az) — f(z)\ < е при |А^| < 6. Это и
доказывает непрерывность функции f(z) в области Q.
Теорема 2.2. Если ряд B.3) непрерывных функций un(z)
сходится равномерно в области Q к функции f(z), то интеграл
от этой функции по любой кусочно гладкой кривой С, целиком
лежащей в области Q, можно вычислить путем почленного
:) См. гл. 1, с. 21.
3 А.Г. Свешников, А.Н. Тихонов

66	РЯДЫ АНАЛИТИЧЕСКИХ ФУНКЦИЙ	ГЛ. 2
интегрирования ряда B.3), т. е.
С	71 = 1 С
Доказательство. Так как ряд B.3) сходится рав-
равномерно, то для любого заданного е > 0 можно указать такой
номер 7V, что для всех точек ( Е Q
IMg| < - при п
где L — длина дуги кривой С. Тогда
С	k=l С
с
с
что и доказывает теорему.
Отметим, что свойства равномерно сходящихся рядов с ком-
комплексными членами, сформулированные в теоремах 2.1 и 2.2,
совершенно аналогичны соответствующим свойствам функцио-
функциональных рядов с действительными членами, и проведенные до-
доказательства фактически повторяют доказательства соответ-
соответствующих теорем анализа1).
Перейдем теперь к рассмотрению важнейшего свойства рав-
равномерно сходящихся рядов, характеризующего поведение ряда,
членами которого являются аналитические функции.
Теорема 2.3 (теорема Вейерштрасса). Пусть функции
(X)
un(z) являются аналитическими в области Q^ а ряд ^ un(z)
71 = 1
сходится равномерно в любой замкнутой подобласти Q1 обла-
области Q к функции f(z). Тогда:
1) f(z) является аналитической функцией в области Q;
71 = 1
(X)	/, ч
3) ряд ^2 ип {z) сходится равномерно в любой замкнутой
подобласти Q1 области Q.
Доказательство. Проведем доказательство каждого
из вышеперечисленных утверждений.
1. Рассмотрим произвольную внутреннюю точку zq Е Q и
построим односвязную подобласть Q' области Q, содержащую
ТОЧКу Zq Внутри.
В силу теоремы 2.1 f(z) является непрерывной функцией
в области Q. Рассмотрим интеграл от f(z) по произвольному
:) См. вып. 2, гл. 8.

РАВНОМЕРНО СХОДЯЩИЕСЯ РЯДЫ ФУНКЦИЙ
67
замкнутому контуру С, целиком лежащему в области Q1. По те-
теореме 2.2 этот интеграл можно вычислить путем почленного ин-
интегрирования ряда B.3). Тогда в силу аналитичности функций
un(z) получим
С	71 = 1 С
Тем самым выполнены все условия теоремы Морера. Следова-
Следовательно, f(z) — функция аналитическая в окрестности Q' точ-
точки zq. В силу произвольности выбора точки zq отсюда следует
аналитичность f(z) в области Q. Заметим, что для любого нату-
ОО	П
рального числа п функция rn(z) = ^ uj(z) = f(z) ~ S uj{z)->
j=n+l	j=l
представляющая собой сумму конечного числа аналитических
функций, также является аналитической функцией в области Q.
2. Фиксируем произвольную точку zq Е Q и выберем произ-
произвольный замкнутый контур С, целиком лежащий в построенной
выше подобласти Q' и содержащий точку zq внутри. Минималь-
Минимальное расстояние от точки zq до контура С обозначим через d.
Рассмотрим ряд
(z - zo)
fc+1
Егбп(х
п=1
fc+1'
Так как min|^ — zq\ = d > 0, то этот ряд в силу условий тео-
ремы сходится равномерно на С. Поэтому, проинтегрировав его
почленно по контуру С и воспользовавшись выражением произ-
производной аналитической функции через интеграл Коши, получим
/(/°Ы =
Так как
п=1
zq — произвольная точка области
G, то утверждение 2 доказано.
3. Рассмотрим произвольную
подобласть Q' области Q и по-
построим в области Q замкнутый
контур С, содержащий Q' вну-
внутри, причем так, чтобы рассто-
расстояние от произвольной точки z Е
Е Q' до любой точки ( Е С бы-
было не меньше некоторого поло-
положительного числа rf, \z — (\ ^ d > 0 (рис. 2.1) (очевидно, для
любой подобласти Q' области Q найдутся соответствующие кон-
контур С и число d). Так как rn(z) является аналитической функ-
функцией в ?/, то для любой точки z E Q' имеет место соотноше-

68	РЯДЫ АНАЛИТИЧЕСКИХ ФУНКЦИЙ	ГЛ. 2
ние —: / ——\к+1 dQ = Гп \z). Причем, согласно только что
Z7TZ г) (С — Z) '
(к)
доказанному утверждению, Гп (z) представляет собой остаток
ОО ,, ч
ряда ^2 Un (z). В силу равномерной сходимости исходного ря-
п=1
ОО
да ^2 un(z)i для любого е > 0 можно указать такое 7V, что на
п=1
контуре С при п ^ N имеет место равномерная оценка |?
< е • ——	, где L — длина контура С. Тогда
/с! 1j
_	С
для всех z ? Q' одновременно, что и доказывает утверждение 3.
Приведенное доказательство относится к случаю односвязной
области Q. Случай многосвязной области рассматривается ана-
аналогично. Итак, теорема доказана.
Заметим, что примененный метод доказательства позволяет
доказать равномерную сходимость ряда из производных лишь в
любой замкнутой подобласти Q' области Q', даже если исход-
исходный ряд B.3) сходится равномерно и в замкнутой области. Как
показывают простые примеры, из равномерной сходимости ряда
B.3) в замкнутой области Q не следует равномерная сходимость
в этой области ряда, составленного из производных. Например,
ОО п	ОО п—1
ряд Y2 ~ч СХОДИТСЯ равномерно в круге \z\ ^ 1, а ряд ^ 	,
71 = 1 П	71 = 1 П
составленный из производных членов исходного ряда, не может
сходиться равномерно в круге \z\ ^ 1, так как он расходится
при z = 1. Таким образом, утверждение п. 3 теоремы о равно-
равномерной сходимости ряда, составленного из производных, лишь в
замкнутой подобласти исходной области не может быть, вообще
говоря, расширено.
Сделаем еще одно замечание. При доказательстве теоремы
2.3 мы предполагали равномерную сходимость ряда в любой за-
замкнутой подобласти Q1 области Q. Ясно, что теорема тем более
будет иметь место при условии равномерной сходимости ряда
B.3) в замкнутой области Q1'. Как показывает нижеследующая
теорема, последнее условие может быть заменено условием рав-
равномерной сходимости ряда B.3) на границе Г области Q.
Теорема 2.4 {вторая теорема Вейерштрасса). Пусть
функции un(z) являются аналитическими в области Q, непре-
		ОО
рывными в Q' и ряд ^2 un(z) сходится равномерно на границе Г
п=1

§_L	РАВНОМЕРНО СХОДЯЩИЕСЯ РЯДЫ ФУНКЦИЙ	69
оо
этой области. Тогда ряд ^ un(z) сходится равномерно и в Q.
п=1
Доказательство. Разность частичных сумм данного
ряда, функция Sn+P(z) — Sn(z), как конечная сумма аналитиче-
аналитических функций, является аналитической в Q и непрерывной в Q.
Из равномерной сходимости на Г следует, что
\Sn+p(() - Sn(()\ = \un+p(() + ... + ип+1(()\ < е
при п ^ N для любого натурального р и всех точек ( Е Г одно-
одновременно. Следовательно, по теореме о максимуме модуля ана-
аналитической функции \SnjrP{z) — Sn(z)\ < е при п ^ N для любого
натурального р и для всех z E Q. Тем самым для данного ряда
выполнен критерий Коши, что и доказывает теорему.
Замечание. Очевидно, что все доказанные выше свой-
свойства функциональных рядов справедливы и для функциональ-
функциональных последовательностей.
4. Несобственные интегралы, зависящие от парамет-
параметра. В гл. 1 мы, рассматривая свойства интегралов, зависящих
от параметра, ограничились лишь случаем собственных инте-
интегралов по кривой С конечной длины. Теорема Вейерштрасса
позволяет обобщить полученные результаты на случай несоб-
несобственных интегралов. Будем рассматривать зависящий от пара-
параметра несобственный интеграл первого рода F(z) = / f(z,()d(
с
по неограниченной кривой С. Пусть функция двух комплексных
переменных f(z. С), определенная при z E Q и ( Е С, удовлетво-
удовлетворяет тем же условиям, что и cp(z^) в § 7 гл. 1, а именно:
а)	функция /(^,С) ПРИ любом значении ? Е С является ана-
аналитической функцией z в области Q;
б)	функция f(z, () и ее производная -J-{z, С) являются непре-
непрерывными функциями по совокупности переменных z, ? при
z е g и с е с.
Пусть несобственный интеграл первого рода f f(z,()d( cxo-
с
дится равномерно по параметру z в любой замкнутой подобла-
подобласти Q1 области Q. Это означает, что при любом выборе по-
последовательности конечных кривых Сп, составляющих часть
G, при Сп —>• С функциональная последовательность un(z) =
= f f(z, () d( сходится равномерно в Q1 к функции F(z).
Сп
Легко показать, что при выполнении всех перечисленных
условий функция F(z) является аналитической в Q и
С

70	РЯДЫ АНАЛИТИЧЕСКИХ ФУНКЦИЙ	ГЛ. 2
Действительно, как доказано в §7 гл. 1, собственные инте-
интегралы — функции un(z) J /B, С)^С являются аналитическими
Сп
функциями в Q и u'n{z) = / -J-(z,C) d(. Последовательность
сп	_
{un(z)} сходится к F(z) равномерно в любой Q'. Следовательно,
по теореме Вейерштрасса функция F(z) — аналитическая в Q и
F'{z) = J fz (;
С
§ 2. Степенные ряды. Ряд Тейлора
1. Теорема Абеля. В предыдущем параграфе рассматри-
рассматривались общие функциональные ряды B.3), причем вид функций
un(z) не конкретизировался. Очень важными являются так на-
называемые степенные ряды, для которых un(z) = cn(z — zqO1 ,
где сп — некоторые комплексные числа, a zq — фиксированная
оо
точка комплексной плоскости. Члены ряда ^ cn(z — zq)u явля-
п=0
ются аналитическими функциями на всей комплексной плоско-
плоскости, поэтому для исследования свойств данного ряда могут быть
применены общие теоремы предыдущего параграфа. Как было
установлено, многие важные свойства являются следствием рав-
равномерной сходимости. Тем самым при исследовании степенного
сю
ряда ^2 cn(z — zqO1 важно установить область его равномерной
п=0
сходимости. Сразу заметим, что область сходимости степенно-
степенного ряда определяется видом коэффициентов сп. Например, ряд
оо
Y2 n\(z — zqO1 сходится лишь в одной точке z = zq. Действи-
п=0
тельно, отношение модулей двух последовательных членов ряда
= (n + l)\z — zq\ > 1 при любом фиксированном значении
ип
z ф zq, начиная с некоторого N(z), что, согласно рассмотрениям
на с. 62, свидетельствует о расходимости данного ряда. С дру-
другой стороны, с помощью признака Даламбера легко установить
~ (Z-Zo)n
абсолютную сходимость ряда 2^	^— ПРИ любом z.
Для определения области сходимости степенного ряда суще-
существенной оказывается следующая теорема.

СТЕПЕННЫЕ РЯДЫ. РЯД ТЕЙЛОРА
71
Теорема 2.5 (теорема Абеля). Если степенной ряд
(X
^2 cn(z — zo)n сходится в некоторой точке z\ ^ zo, то он абсо-
лютно сходится и в любой точке z, удовлетворяющей условию
\z — zq\ < \z\— zq\; причем в круге \zi—zq\ ^ p радиуса р, меньше-
меньшего \z\ — zo\, ряд сходится равномерно.
Доказательство. Выберем произвольную точку
z, удовлетворяющую условию \z — zq\ < \z\ — zo\, и рассмотрим
(X
ряд ^2 cn(z — zo)n. Обозначим \z — zq\ = q\z\ — zo\, q < 1. В силу
n=0
(X
необходимого условия сходимости ряда ^ Cn(zi~zo)n ег0 члены
п=0
стремятся к нулю при п —>• оо. Следовательно, существует такая
М. Отсюда для коэффициен-
м
р	у р
константа М, что \сп\ • \z\ — zo\
тов сп данного степенного ряда получим оценку
Тогда
(X
Zp)
п=0
Z - ZQ
mYI
п=0
По условию теоремы число q =
^-^ \z\ - .
(X
< 1. Ряд ^2 Я™? предста-
п=0
вляющий собой сумму бесконечной геометрической прогрессии
со знаменателем, меньшим единицы, сходится. Тогда из B.8)
следует сходимость и рассматриваемого ряда. Чтобы доказать
(X
равномерную сходимость ряда ^ cn(z — zqO1 в круге \z — zq\ ^
п=0
^ р < |^i ~ ^о|5 достаточно, в силу признака Вейерштрасса,
построить сходящийся числовой ряд, мажорирующий данный
функциональный ряд в рассматриваемой области. Очевидно, та-
(X	п
ковым является ряд М ^2 ]—
n=0 "* ~
такж:е представляющий со-
бой сумму бесконечной геометрической прогрессии со знамена-
знаменателем, меньшим единицы. Теорема полностью доказана.
Из теоремы Абеля можно вывести ряд важных следствий.
(X
Следствие 1. Если степенной ряд ^ cn(z — zqO1 расходит-
п=0
ся в некоторой точке zi, то он расходится и во всех точках z,
удовлетворяющих неравенству \z — z$\ > \z\ — zq\.
Предполагая противное, получим, что по теореме Абеля ряд
должен сходиться в любом круге радиуса р < \z—zo\,b частности
и в точке ^i, что противоречит условию.

72	РЯДЫ АНАЛИТИЧЕСКИХ ФУНКЦИЙ	ГЛ. 2
Рассмотрим точную верхнюю грань R расстояний \z — z$\ от
оо
оо
точки zq до точек z, в которых сходится ряд ^2 cn(z — zo)
Если R т^ оо, то во всех точках z*, удовлетворяющих условию
\zf — zq\ > i?, данный степенной ряд расходится. Пусть R строго
больше нуля, тогда наибольшей областью сходимости данного
ряда является круг \z — zq\ < R. Всюду вне этого круга ряд рас-
расходится, в точках границы \z — z$\ = R он может как сходиться,
так и расходиться.
Область \z — zq\ < R (R > 0) называется кругом сходимости
степенного ряда, а число R — его радиусом сходимости.
Итак, мы установили
Следствие 2. Для всякого степенного ряда существует та-
такое число i?, что внутри круга \z — z$\ < R данный степенной
ряд сходится, а вне этого круга расходится.
В круге \z — zq\ ^ р < R любого радиуса р, меньшего, чем ра-
(X)
диус сходимости i?, степенной ряд ^ cn(z — zqO1 сходится рав-
п=0
номерно. Отметим, что радиус сходимости степенного ряда в
зависимости от вида его коэффициентов может иметь любое
значение в пределах от 0 до оо. Первый предельный случай бу-
будет соответствовать ряду, сходящемуся лишь в точке zo, вто-
второй — сходящемуся на всей комплексной плоскости. Примеры
соответствующих рядов уже были приведены. Радиус сходимо-
сходимости степенного ряда может быть определен через его коэффи-
коэффициенты сп.
Следствие 3. Внутри круга сходимости степенной ряд схо-
сходится к аналитической функции. Действительно, члены степен-
степенного ряда un(z) = cn(z — zo)n представляют собой функции, ана-
аналитические на всей комплексной плоскости, ряд сходится рав-
равномерно в любой замкнутой подобласти круга сходимости. Сле-
Следовательно, по первой теореме Вейерштрасса сумма ряда есть
аналитическая функция.
Следствие 4. Степенной ряд внутри круга сходимости
можно почленно интегрировать и дифференцировать любое
число раз, причем радиус сходимости полученных рядов равен
радиусу сходимости исходного ряда. Это свойство также явля-
является прямым следствием теорем Абеля и Вейерштрасса.
Следствие 5. Коэффициенты степенного ряда
Е
n=0
ее производных в центре круга сходимости по формулам
cn(z — zo)n выражаются через значения суммы ряда f(z) и
B-9)

§ 2	СТЕПЕННЫЕ РЯДЫ. РЯД ТЕЙЛОРА	73
Положив z = zq в выражении суммы степенного ряда f(z) =
оо
= S сп(^ — ^о)п5 получим /(^о) = со; продифференцировав
п=0
ряд почленно и положив 2 = zq в выражении для производ-
оо
ной ff(z) = Yl cnn(z — Z())n~1, получим ff(zo) = ci; аналогично,
положив 2 = ?o в выражении для к-й производной
пп(п - 1)... (п - Л + 1)(* - *<,)"-*,
получим
Следствие 6. Радиус сходимости R степенного ряда
^2 cn(z — ^о)п определяется формулой1) R = -, где / =
п=о	 		1
= lim л/lcJ" есть верхний предел 2) последовательности { \/|сп||.
Предположим вначале, что 0 < / < оо. Нам надо показать,
что в любой точке z\, удовлетворяющей условию \z\ — z§\ < у,
ряд сходится, а в любой точке Z2, удовлетворяющей условию
1^2 — ^о| > у 5 — расходится. Так как / — верхний предел последо-
последовательности { >/|сп|}, то для любого е > 0 можно указать номер
7V, начиная с которого \/|сп| < / + е. С другой стороны, для то-
того ж:е е найдется бесконечно много членов последовательности
{ \/1с™1}> больших / — е. Возьмем произвольную точку z\, удо-
удовлетворяющую неравенству l\z\ — z§\ < 1, и выберем в качестве
е число 1~^Zl~z^ > 0. Тогда
оо
Отсюда следует, что ряд ^ Cn(zi~zo)n маж:орируется геометри-
п=0
оо
ческой прогрессией ^ gn со знаменателем, меньшим единицы,
п=0
что и доказывает его сходимость. Взяв теперь некоторую точ-
точку Z2, удовлетворяющую неравенству I\z2 — z$\ > 1, и выбрав в
:) Эта формула часто называется формулой Коши-Адамара.
2)Нап
апомним определение понятия верхнего предела числовой последова-
последовательности. Верхним пределом ж, последовательности {хп} называется наи-
наибольшая предельная точка этой последовательности (см. вып. 1).

74	РЯДЫ АНАЛИТИЧЕСКИХ ФУНКЦИЙ	ГЛ. 2
качестве е число -Ц^	—:— > 0, получим
\Z2 Zq\
z2 -zo\ > (l-e)\z2 - zo\ = 1
для бесконечного множества значений п. Отсюда \cn(z2 — zo)n\ > 1,
что на основании необходимого признака сходимости свидетель-
оо
ствует о расходимости ряда ^ cn(z2 — zqO1.
Замечание. Мы провели доказательство для случая
О < / < оо. Рассмотрим теперь предельные случаи.
ОО
При / = 0 ряд Y2 cn(z — zo)n сходится в любой точке z, т. е.
п=0
R = оо. Действительно, в этом случае для любого е > 0 может
быть указано такое число 7V, начиная с которого \/|сп| < е.
Выбрав в качестве е число -—-—-, где z — произвольная точка
комплексной плоскости и 0 < q < 1, получим \cn(z — z$)n\ < qn,
сю
что и доказывает сходимость ряда ^ cn(z — zqO1 .
n=0
оо
При / = оо ряд Y2 cn(z — zqO1 расходится в любой точке
п=0
z т^ zo, т. е. R = 0. Действительно, в этом случае для любо-
любого числа М найдется бесконечно много коэффициентов сп та-
таких, что >/|сп| > М. Рассмотрим произвольную точку z ^ zq
и выберем М так, чтобы M\z — zq\ = q > 1. Тогда бесконечное
(X)
множество членов ряда ^ cn(z — zqO1 удовлетворяет условию
п=0
\cn(z — zo)n\ > 1, что и доказывает его расходимость.
Итак, формула Коши-Адамара R = -, где / = lira л/|сп|,
/	п^оо
справедлива при любом значении /.
В качестве примера, существенного для дальнейшего, рас-
оо
смотрим степенной ряд ^ (z — zqO1, все коэффициенты сп кото-
п=0
рого равны 1. По признаку Даламбера получим, что данный ряд
сходится в круге \z — zq\ < 1 к некоторой аналитической функ-
функции. Чтобы найти эту функцию, применим прямое определение
суммы ряда как предела частичных сумм:
f(z) = lim Sn(z) = lim 1"G"o)" = I . B.10)
П—>-OO	П—>-OO i- — [Z — ZQ)	1 — \Z — ZQ)
Здесь мы воспользовались, очевидно, справедливой и в области
комплексных чисел формулой суммы геометрической прогрес-
прогрессии с конечным числом членов и возможностью предельного

СТЕПЕННЫЕ РЯДЫ. РЯД ТЕЙЛОРА
75
перехода в числители дроби, знаменатель которой отличен от
нуля. Равенство B.10) означает, что формула для суммы беско-
бесконечно убывающей геометрической прогрессии справедлива и в
комплексной области.
2. Ряд Тейлора. Итак, степенной ряд внутри круга схо-
сходимости определяет некоторую аналитическую функцию. Есте-
Естественно поставить вопрос: можно ли функции, аналитической
внутри некоторого круга, сопоставить степенной ряд, сходящий-
сходящийся в этом круге к данной функции? Ответ на этот вопрос дает
следующая теорема.
Теорема 2.6 (теорема Тейлора). Функция f(z), анали-
аналитическая внутри круга \z — zq\ < R, может быть представ-
представлена в этом круге сходящимся степенным рядом f(z) =
оо
= ^2 cn(z — zo)n, причем этот ряд определен однозначно.
Доказательство. Выберем произвольную точку z
внутри круга \z — zq\ < R и построим окружность Ср с центром в
точке zq радиуса р < i?,
содержащую точку z внутри
(рис. 2.2). Очевидно, для лю-
любой точки z данной области та-
такое построение возможно. Так
как точка z — внутренняя точ-
точка области | ^г — ^г01 < Р-) в ко-
которой функция f(z) является
аналитической, то по формуле
Коши имеем
B.11)
Со
Осуществим в подынтеграль-
подынтегральном выражении преобразова-
преобразование
Рис. 2.2
C-z
С -
п=0
(С -
B.12)
Здесь мы воспользовались формулой B.10) и очевидным соот-
соотношением	 < 1. При ? Е Ср ряд B.12) сходится равномер-
равномерно по С, так как он мажорируется сходящимся числовым рядом
тг+°| (\z — zq\ < р). Подставляя B.12) в B.11) и интегрируя
п=о

76	РЯДЫ АНАЛИТИЧЕСКИХ ФУНКЦИЙ	ГЛ. 2
почленно, получаем
оо
n=0
Введя обозначение
Cn = 1- [ Щп+1 dC,	B.14)
cP
перепишем B.13) в виде сходящегося в выбранной точке z сте-
степенного ряда:
n(z-z0)n.	B.15)
п=0
В формуле B.14) окружность Ср можно заменить, в силу теоре-
теоремы Коши, любым замкнутым контуром С, лежащим в области
\z — zo\ < R и содержащим точку zq внутри. Так как z — произ-
произвольная точка данной области, то отсюда следует, что ряд B.15)
сходится к f(z) всюду внутри круга \z — zq\ < i?, причем в круге
\z — ^о| ^ р < R этот ряд сходится равномерно. Итак, функ-
функция f(z)j аналитическая внутри круга \z — zq\ < i?, разлагается
в этом круге в сходящийся степенной ряд. Коэффициенты раз-
разложения B.14) на основании формулы A.72) для производных
аналитической функции имеют вид
с _ 1 [ №<% _/ыЫ	B16)
С
Остается доказать единственность разложения B.15). Предпо-
Предположим, что имеет место другое разложение:
п=0
где хотя бы один коэффициент с'п ^ сп. Степенной ряд B.157)
сходится в круге \z — zq\ < i?, поэтому на основании форму-
лы B.9), с'п = -—\^-, чт0 совпадает с выражением B.16) для
коэффициентов сп. Тем самым единственность определения ко-
коэффициентов доказана.
Разложение функции, аналитической в круге \z — zq\ < i?, в
сходящийся степенной ряд B.15) часто называется разложением
Тейлора, а сам ряд B.15) — рядом Тейлора.
Доказанная теорема устанавливает взаимно однозначное со-
соответствие между функцией, аналитической в окрестности неко-
некоторой точки zqj и степенным рядом с центром в этой точке. Это

§ 2	СТЕПЕННЫЕ РЯДЫ. РЯД ТЕЙЛОРА	77
означает эквивалентность понятий аналитической функции, как
функции, бесконечное число раз дифференцируемой, и функ-
функции, представимой в виде суммы степенного ряда1). Последнее
имеет не только большое значение для построения теории ана-
аналитических функций, но и находит широкое применение при ре-
решении многочисленных прикладных вопросов.
Заметим, наконец, что если функция f(z) является анали-
аналитической в области Q и zq — внутренняя точка этой области,
то радиус сходимости ряда Тейлора f(z) = ^ -—y-^-(z — zq)u
п=о п-
этой функции не меньше, чем расстояние от точки zq до грани-
границы области Q.
Пример!.. В качестве простейшего примера рассмотрим
разложения в ряд Тейлора функции f(z) =	-. Эта функ-
функция является аналитической на всей комплексной плоскости,
за исключением точек z\^ = =Ьг, в которых знаменатель дро-
дроби обращается в нуль. Поэтому в любом круге на комплексной
плоскости, не содержащем точек z\^ = =Ьг, эта функция в силу
теоремы 2.6 может быть разложена в ряд Тейлора. Начнем с
круга \z\ < 1. При условии \z\ < 1 выражение	 может рас-
рассматриваться как сумма бесконечно убывающей геометрической
прогрессии. Поэтому в силу B.10)
сю
-l)nz2n,	B.17)
п=0
что и дает искомое разложение. Заметим, что радиус сходимо-
сходимости ряда B.17) равен 1, т. е. определяется расстоянием от цен-
центра разложения до границы области аналитичности функции
h
г) Заметим, что аналогичная эквивалентность для функций действитель-
действительной переменной не имеет места. Действительно, из существования на от-
отрезке [а, Ь] всех производных функции f(x) еще не следует возможность
оо
разложения этой функции в степенной ряд вида f(x) = ^ сп(х — жо)п, где
п=0
хо G [а, Ь], сходящийся на всем отрезке [а, Ь]. Например, функция f(x) =
1	.
=	 при люоом действительном х имеет производные всех порядков,
оо
однако при ж о = 0 степенной ряд ^ (—1)пх2п сходится к данной функции
п=0
лишь на интервале —1<ж<1,анена всей действительной оси х. Подроб-
Подробнее о разложении функций действительной переменной в степенные ряды
см. вып. 2, гл. 8.

78	РЯДЫ АНАЛИТИЧЕСКИХ ФУНКЦИЙ	ГЛ. 2
Найдем теперь разложение функции f(z) =	 в ряд Тей-
Тейлора в круге \z — 1| < д/2. Определение коэффициентов сп ря-
оо
да ^2 cn(z — 1)п по формуле B.16) в данном случае связано
п=0
с довольно громоздкими вычислениями. Поэтому, представив
	 = — (	: —	:] и воспользовавшись формулой B.10),
± "т" Z	?% \ Z %	Z ~\ % J
справедливой в данном случае при условии \z —1| < л/2, получим
ОО	г	-|
1 + ^2 /_^\ ) 2г \(l-i)n+i (i + j)n+i V	;
n=0	L	J
С помощью показательной формы записи комплексных чисел
1 — г = л/2 exp f — г j ), 1 + г = л/2 ехр у г j ), легко теперь полу-
получить
n=0
2 2
Как следует из формулы Коши-Адамара, радиус сходимости
ряда B.18) равен л/2, т. е. опять определяется расстоянием от
центра разложения до границы области аналитичности рассма-
рассматриваемой функции.
Пример2.В качестве следующего примера рассмотрим
разложение в ряд Тейлора функции f(z) = \nz = I у, вве-
1
денной в гл. 1 (с. 49). Выше было установлено, что эта функция
является аналитической на всей комплексной плоскости с раз-
разрезом по отрицательной части действительной оси, а следова-
следовательно, и внутри круга \z — 1| < 1. Полагая zq = 1 и вычисляя
коэффициенты сп по формуле B.16), получаем
со = In 1 = 0, с\ = -
с - 1 (
п ~ п! ^
=l
= 1,
z=l
гг~1-, n =
Отсюда
oo
" -l)«-i(izi):.	B.19)
П = 1
Как легко убедиться с помощью признака Даламбера, кругом
сходимости ряда B.19) является круг \z — 1| < 1.

§ 3	ЕДИНСТВЕННОСТЬ ОПРЕДЕЛЕНИЯ ФУНКЦИИ	79
§ 3. Единственность определения аналитической
функции
Уже изученные нами свойства функций комплексной пере-
переменной позволяют заключить, что для определения функции,
аналитической в данной области, можно ограничиться задани-
заданием значений этой функции не во всей области. Например, зада-
задавая значения аналитической функции на границе области, мы
с помощью интеграла Коши можем определить ее значения во
всех внутренних точках области. Тем самым функция, аналити-
аналитическая в данной области, определяется заданием неполной ин-
информации о ее значениях в этой области. Естественно поставить
вопрос: какова та «минимальная» информация, которую надо
иметь, чтобы полностью определить функцию, аналитическую
в данной области?
1. Нули аналитической функции. Предварительно
введем понятие нуля аналитической функции. Пусть f(z) явля-
является аналитической функцией в области Q. Точка zq Е Q назы-
называется нулем f(z), если /(zq) = 0. Из разложения f(z) в окрест-
ОО
ности точки zq в степенной ряд, f(z)= ^ cn(z — ^o)n, следует,
п=0
что в данном случае коэффициент cq = 0. Если не только ко-
коэффициент со, но и коэффициенты ci, C2, ..., Ck-i равны нулю,
а коэффициент с^ отличен от нуля, то точка zq называется ну-
нулем к-го порядка функции f(z). Согласно формуле B.9) в нуле
k-то порядка не только сама функция, но и ее первые к — 1 про-
производных равны нулю, а к-я производная отлична от нуля. В
окрестности нуля порядка к разложение функции f(z) в степен-
степенной ряд имеет вид
п=к
оо
= (z- zo)k J2 cn+k(z - zo)n = (z- zo)k<p(z), B.20)
n=0
где (p(z) является аналитической функцией в окрестности точ-
точки 2о, разложение которой в степенной ряд имеет вид cp(z) =
оо
= Yl cn+k(z — z$)ni причем (f(zo) ф 0. Отметим, что последний
п=0
ряд сходится в том же круге, что и исходный.
2. Теорема единственности. Перейдем теперь к форму-
формулировке основного положения данного параграфа.
Теорема 2.7. Пусть функция f(z) является аналитиче-
аналитической в области Q и обращается в нуль в различных точках
zn E Q, п = 1,2,... Если последовательность {zn} сходится

80	РЯДЫ АНАЛИТИЧЕСКИХ ФУНКЦИЙ	ГЛ. 2
к пределу а, принадлежащему той же области, то функция
f(z) тождественно равна нулю в области Q.
Доказательство. Так как а Е Q, то функцию
f(z) можно разложить в степенной ряд в окрестности данной
оо
точки: f(z)= ^2 cn(z — о)п-> причем радиус Rq сходимости дан-
п=0
ного ряда не меньше расстояния от точки а до границы обла-
области. Из определения непрерывности функции f(z) следует, что
/(а) = 0. Отсюда следует, что cq = 0, и разложение функ-
функции f(z) в окрестности z = а имеет вид
f(z) = (z-a)fi(z), где fi(z) = ^ cn+1(z - а)п.
Будем предполагать, что все точки последовательности {zn} от-
отличны от а. Это не уменьшает общности наших рассмотрений,
так как только одна из этих точек могла быть равна а. В си-
силу последнего условия fi(zn) = 0, и по определению непре-
непрерывной функции /i(a) = 0. Отсюда с\ = 0, и разложение
fi(z) в окрестности а принимает вид : fi(z) = (z — a)/2B), где
(X)
h(z) = S cn+2(z — o)n• Аналогично предыдущему получим, что
п=0
и Л(^) = 0, т. е. С2 = 0. Продолжая неограниченно данный про-
процесс, получим, что все коэффициенты сп в разложении f(z) в
степенной ряд
(X)
/(*) = ?>(*-а)"
п=0
в окрестности точки а равны нулю. Отсюда следует, что f(z) =0
внутри круга |г — a| < Rq.
Обратимся теперь к доказательству 1) тож:дественного ра-
равенства функции f(z) нулю во всей области Q. Достаточно по-
показать, что f{z\) = 0, где z\ — произвольная точка области Q,
лежащая вне круга \z — а\ < Rq. Для этого соединим точки а и
z\ спрямляемой кривой L, целиком лежащей в Q и отстоящей от
ее границы на расстояние d > 0. Поскольку любую точку круга
\z — а\ < i?o, лежащую внутри области Q, можно рассматривать
как предел последовательности нулей функции f{z), то, выбрав
в качестве нового центра разложения последнюю точку z = a\
пересечения кривой L с окруж:ностью \z — a\ = i?o, получим, что
f(z) = 0 внутри круга \z — а\\ < i?i, где R\ ^ d. Продолжая
аналогичным образом, покроем всю кривую L конечным чис-
числом кругов радиусов, не меньших с/, внутри которых f(z) = 0.
Это доказательство проводится аналогично доказательству на с. 55.

§ 3	ЕДИНСТВЕННОСТЬ ОПРЕДЕЛЕНИЯ ФУНКЦИИ	81
При этом точка z = z\ попадает внутрь последнего круга, тем
самым f(z\) = 0. Поскольку z\ — произвольная точка области
(/, отсюда следует, что f(z) = 0 в Q.
Доказанная теорема имеет ряд важных следствий.
Следствие 1. Функция f(z) ^ 0, аналитическая в области
?/, в любой замкнутой ограниченной подобласти Q' области Q
имеет лишь конечное число нулей.
Если множество нулей функции f(z) в области Q1 бесконечно,
то по теореме 1.2 из него можно выделить сходящуюся после-
последовательность {zn} —>• а, причем предел а этой последователь-
последовательности принадлежит Q'. Отсюда f(z) = 0 в ?/, что противоречит
условию.
Следствие 2. Если точка zq Е Q является нулем беско-
бесконечного порядка1) функции f(z) (т. е. в разложении f(z) =
оо
= S cn(z — zo)n в окрестности точки zq все коэффициенты сп = 0),
то f(z) = 0 в области Q.
Следствие 3. Аналитическая функция может иметь беско-
бесконечное число нулей лишь в открытой или неограниченной обла-
области.
Функция комплексной переменной, аналитическая на всей
комплексной плоскости (z ф оо), называется целой функцией.
Из предыдущих рассмотрений следует, что целая функция в
любой ограниченной части комплексной плоскости имеет лишь
конечное число нулей. Следовательно, все нули целой функции
можно перенумеровать в каком-либо порядке, например в по-
порядке возрастания их абсолютных величин. На полной плоско-
плоскости целая функция может иметь лишь счетное множество ну-
нулей, причем предельной точкой этого множества является бес-
бесконечно удаленная точка комплексной плоскости. Целые функ-
функции играют важную роль как в теории функций комплексной
переменной, так и в ее приложениях.
Теорема 2.8. Пусть функции f(z) и cp(z) являются ана-
аналитическими в области Q. Если в Q существует сходящаяся
к некоторой точке а Е Q последовательность различных то-
точек {zn}, в которых значения функций f(z) и tp(z) совпадают,
то f(z) = <p(z) в g.
Для доказательства теоремы достаточно с помощью теоремы
2.7 установить, что функция ^p(z) = f(z) — tp(z) = 0 в Q.
Теорема 2.8 имеет чрезвычайно большое значение, поскольку
она означает, что в данной области Q может существовать лишь
единственная аналитическая функция, принимающая заданные
:) Очевидно, при этом и сама функция f(z) и все ее производные в точке
равны нулю.

82	РЯДЫ АНАЛИТИЧЕСКИХ ФУНКЦИЙ	ГЛ. 2
значения в последовательности точек {zn}, сходящейся к точ-
точке а Е Q. Эту теорему называют теоремой единственности
определения аналитической функции.
Часто применяются следующие следствия теоремы един-
единственности.
Следствие 1. Если функции fi(z) и /2B), аналитические
в области Q', совпадают на некоторой кривой L, принадлежащей
данной области, то они тождественно равны в области Q.
Следствие 2. Если функции fi(z) и /2B), аналитические
соответственно в областях Q\ и ?/25 имеющих общую подобласть
(/, совпадают в (/, то существует единственная аналитическая
функция F(z) такая, что
Теореме единственности и ее следствиям можно придать так-
также следующие формы.
1° Пусть в области Q выбрана сходящаяся к точке а Е Q по-
последовательность различных точек zn G Q. Тогда в этой области
может существовать лишь единственная аналитическая функ-
функция f(z), принимающая в точках zn заданные значения.
2° Пусть в области Q дана некоторая кривая L. Тогда в Q мо-
может существовать лишь единственная аналитическая функция
f(z)j принимающая заданные значения на L.
3° Пусть в области Q дана некоторая подобласть Q1. Тогда
в области Q может существовать лишь единственная аналити-
аналитическая функция f(z), принимающая заданные значения в под-
подобласти Q'.
Если существует функция f(z), определенная в области 0,
о которой говорилось в 1°, 2° и 3°, то она может быть названа
аналитическим продолжением в Q с множества {^п}5 линии L
или подобласти Q1.
Отметим, что задание значений аналитической функции на
соответствующем множестве точек не может быть произведено
произвольно. Однако мы здесь не будем обсуждать требования,
которым должны удовлетворять эти значения, чтобы их можно
было аналитически продолжить в области Q.

ГЛАВА 3
АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ.
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ КОМПЛЕКСНОЙ
ПЕРЕМЕННОЙ
В этой главе мы рассмотрим ряд фундаментальных след-
следствий теоремы о единственности определения аналитической
функции. Как было установлено, аналитическая функция од-
однозначно определяется заданием ее значений на некотором мно-
множестве точек в области ее определения. Это обстоятельство по-
позволяет построить аналитическое продолжение в комплексную
область элементарных функций действительной переменной и
выяснить их свойства в комплексной плоскости. Мы также крат-
кратко рассмотрим общие принципы аналитического продолжения.
§ 1. Элементарные функции комплексной переменной.
Продолжение с действительной оси
1. Продолжение с действительной оси. Теорема о
единственности определения аналитической функции позволяет
автоматически распространить на комплексную область элемен-
элементарные функции действительной переменной. Предварительно
отметим справедливость следующего утверждения: пусть на от-
отрезке [а, Ь] действительной оси х задана непрерывная функция
f(x) действительной переменной; тогда в некоторой области Q
комплексной плоскости, содержащей отрезок [а, Ь] действитель-
действительной оси, может существовать только одна аналитическая функ-
функция f(z) комплексной переменной z, принимающая данные зна-
значения f(x) на отрезке [а, Ь]. Назовем функцию f(z) аналитиче-
аналитическим продолжением функции f(x) действительной переменной
х в комплексную область Q.
Перейдем к рассмотрению примеров построения аналитиче-
аналитических продолжений элементарных функций действительной пере-
переменной. Среди элементарных функций действительной перемен-

84	АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ	ГЛ. 3
ной особую роль играют показательная функция ех и тригоно-
тригонометрические функции sin ж и cos х. Как известно 1), эти функции
могут быть заданы своими разложениями в ряды Тейлора:
п=0
ОО
п=0
_1Г(?_?	C-3)
п=0
причем эти ряды сходятся при всяком значении х.
Рассмотрим на комплексной плоскости следующие степен-
степенные ряды:	^
п=0
п=0
(X)
п=0
При действительных z = х выражения C.4)—C.6) и C.1)—C.3)
соответственно совпадают.
Как следует из теоремы Абеля, областью сходимости рядов
C.4)—C.6) является вся плоскость комплексной переменной, т. е.
эти ряды представляют собой целые функции комплексной пе-
переменной z, являющиеся аналитическим продолжением на всю
комплексную плоскость элементарных функций действительной
переменной еж, sin ж и cos ж. Для введенных функций естествен-
естественно сохранить прежние обозначения. Положим
оо
= Е S'
n=0
"i)n(?ri)!'	C-8)
n=0
= > (-l)n-i_.	C.9)
n=0
1) Определение и основные свойства этих функций действительной пере-
переменной см. вып. 1.

§ 1 ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ 85
С помощью функции ez построим гиперболические функции
комплексной переменной:
ch^= eZ\e~Z	C.10)
C.11)
В силу общих свойств аналогических функций эти функции так-
также являются целыми.
Аналогичным образом с помощью основных тригонометри-
тригонометрических функций sin z и cos z путем формального переноса в ком-
комплексную область соответствующих определений могут быть по-
построены и остальные тригонометрические функции: tgz = 	,
-|	COS Z
msec z = -— и т. д. Эти функции уже не являются целыми, по-
поскольку их аналитичность нарушается в тех точках плоскости
z, где знаменатели определяющих их выражений обращаются в
нуль.
Как будет показано ниже, для всех построенных функций
комплексной переменной сохраняются многие основные свой-
свойства соответствующих элементарных функций действительной
переменной. Это будет установлено на основании некоторых об-
общих положений, а сейчас мы построим продолжение на ком-
комплексную область еще двух элементарных функций. Рассмотрим
следующие степенные ряды:
C.12)
в-
71 = 1
ОО
V 1
•3.
..Bп
_1)п
п
- 1)х2п+1
(з 13)
п=1
Как известно, первый ряд1) сходится в интервале 0 < х < 2, а
второй — в интервале — 1 < х < 1 к функциям действительной
переменной In ж и arcsinx соответственно. Как легко установить,
степенные ряды
-1)п"и* ч	C.12')
п
71 = 1
И
2»-п!Bп
П=1
:) См. вып. 1, где приведено разложение In A + г/), замена г/ = ж — 1 дает
C.12).

86	АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ	ГЛ. 3
сходятся, первый — внутри круга \z — 1| < 1, а второй — внутри
круга |^| < 1 и на соответствующих отрезках действительной
оси совпадают с рядами C.12) и C.13). Поэтому аналитические
функции комплексной переменной z, определенные с помощью
рядов C.12') и C.13') внутри их кругов сходимости, являются
аналитическим продолжением на соответствующую комплекс-
комплексную область элементарных функций In ж и arcsinx действитель-
действительной переменной х. Для этих функций мы также сохраним преж-
прежние обозначения, положив
In г = ^(-l)™-1^-!)^	C.14)
71 = 1
и
. v> 1.3...Bn-l)*2n+1	/q1.n
arcsm^ = z + > —-—y———J-—	.	C.15)
^ 2n • n!Bn +1)	v ;
n=l
Отметим, что функции C.14) и C.15), в отличие от введен-
введенных выше функций C.7)-C.9), уже не являются целыми функ-
функциями, так как определяющие их ряды сходятся не на всей комп-
комплексной плоскости, а лишь внутри кругов единичного радиу-
радиуса. Свойства этих функций также будут рассмотрены несколько
позже. Отметим только, что функция C.14) в круге \z — 1| < 1
совпадает с введенной иным способом в гл. 1, с. 49, функцией
Inz = i -r, так как обе эти аналитические функции определе-
J С
1
ны в указанной области и совпадают на общем интервале дей-
действительной оси 0 < х < 2 с одной и той же функцией In x.
Поэтому для обеих функций мы используем одно и то же обо-
z
значение. Тем самым и функция f(z)= / -г, определенная
1
на комплексной плоскости z, разрезанной по отрицательной ча-
части действительной оси, является аналитическим продолжением
функции In ж на соответствующую область.
В заключение заметим, что если функция f(x) действитель-
действительной переменной х задана своим степенным рядом
п=0
сходящимся на отрезке [а, 6], то существует аналитическая
функция f(z) комплексной переменной z, являющаяся анали-
аналитическим продолжением f(x) в комплексную область Q, содер-
содержащую отрезок [а, Ь] действительной оси. Указанное обстоятель-

§ 1 ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ 87
ство позволяет называть функцию действительной переменной
/(ж), представимую рядом C.16), аналитической функцией. На-
Напомним1), что функция действительной переменной, предста-
вимая на отрезке [а, Ь] степенным рядом C.16), имеет на этом
отрезке производные всех порядков. Очевидно, аналитическим
продолжением производной f^n\x) в область Q является произ-
производная f(n\z).
2. Продолжение соотношений. Перейдем к рассмо-
рассмотрению дальнейших следствий из теоремы о единственности
определения аналитической функции. Эта теорема позволяет
не только строить аналитические продолжения элементарных
функций действительной переменной, но и аналитически про-
продолжать в комплексную область соотношения, имеющие место
между соответствующими функциями действительной перемен-
переменной. В качестве типичных примеров рассмотрим, во-первых, со-
соотношения вида
sin2 х + cos2 x = 1,	C-17)
еЫх = х	C.18)
и, во-вторых, соотношения вида
еХ1 .еХ2 = еЖ1+^	C.19)
cos (xi + X2) = cos^i • cos #2 — sin^i • sina^.	C.20)
Соотношения C.17) и C.18) устанавливают связь между раз-
различными функциями одной действительной переменной; в соот-
соотношения C.19) и C.20) входят функции нескольких перемен-
переменных. Это одни из основных соотношений для элементарных
функций действительных переменных. Естественно поставить
вопрос: останутся ли они справедливыми для аналитических
продолжений элементарных функций в комплексную область?
Установим, что тождество C.17) остается справедливым и в
комплексной области. Для этого рассмотрим функцию
F(z) = sin2 z + cos2 z — 1
комплексной переменной z. Согласно общим свойствам аналити-
аналитических функций (см. гл. 1, с. 36) F(z) является целой функцией
z, причем для действительных значений z = x (в силу C.17))
F(x) =0. Отсюда по теореме единственности мы и получим, что
на всей комплексной плоскости z выполняется соотношение
sin2 z + cos2 z = l.	C.21)
Подобные же рассмотрения могут быть проведены и для дока-
доказательства справедливости в комплексной области выражения
См. вып. 2.

88	АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ	ГЛ. 3
C.18) и других соотношений, связывающих различные аналити-
аналитические функции одной комплексной переменной. Однако нет ну-
нужды каждый раз проводить специальное исследование, а можно
сформулировать общую теорему.
Пусть дана функция F[w\,..., wn] комплексных переменных
wi,..., wn, аналитическая по каждой переменной г) W{ E Din та-
dF
кая, что она сама и ее частые производные -— — непрерывны по
совокупности переменных w\,..., wn. Обладающую указанными
свойствами функцию F\w\,... ,wn] будем называть аналитиче-
аналитической функцией многих комплексных переменных. Пусть даны п
функций fi(z),..., fn(z) комплексной переменной z, определен-
определенные в области Q комплексной плоскости z, причем fi(z) E Di.
Будем говорить, что функции fi(z) удовлетворяют соотно-
соотношению F[fi(z),... , fn(z)] = 0 на множестве М, если это соот-
соотношение удовлетворяется во всех точках z E М. В дальнейшем
будем рассматривать соотношения, задаваемые только аналити-
аналитическими функциями многих комплексных переменных. Имеет
место
Теорема 3.1. Если функции fi(z) являются аналитически-
аналитическими функциями z в области Q, содержащей отрезок [а,Ь] дей-
действительной оси х, то из соотношения F[f\{x), ..., fn(%)] — 0
при а ^ х ^ b следует соотношение F[fi(z), ..., fn(z)] = 0 при
Доказательство. Для доказательства теоремы до-
достаточно показать, что при сформулированных условиях функ-
функция Ф(г) = F[fi(z), ..., fn(z)] является аналитической функ-
функцией комплексной переменной z в области Q. Доказательство
проведем для случая двух переменных W{, т.е. когда Ф(^) =
= F[fi(z),f2(z)]. Фиксируем в области Q произвольную точку
zq Е Q и обозначаем fi(zo) = w\ и /2(^0) = ^2- Составим выра-
ж:ение
Ф(^о + Дя) -Ф(^о) = F[wi + Awi,W2 + Aw2] — F[wi,W2\, C.22)
где Au;i, Дг^2 суть приращения функций fi(z) и /2(^M соответ-
:) Назовем функцию многих комплексных переменных F(zi,..., zn),
определенную для значений z% G Di, аналитической функцией каж:дой из
своих переменных z% (t = 1, 2,..., т\ т ^ п), если при любом г = 1, 2,..., га
соответствующая функция Ф^(^) = ^(^?,..., ^?-i, ^г, ^?+i,..., 2°) одной
комплексной переменной ^г, получающаяся при произвольных фиксирован-
фиксированных значениях остальных переменных Zj = Zj (j ф г), является аналитиче-
аналитической функцией данной переменной. Производные функции Ф^(^) по соот-
соответствующим переменным будем называть частными производными функ-
ции F(zi,..., zn) многих комплексных переменных ФЦ^) =	—' ' п .
oz%
Подробнее см. Приложение 3.

§ 1 ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ 89
ствующие приращению Az независимой переменной z. Так как,
по предположению, существуют частные производные функции
F, непрерывные по совокупности переменных, то C.22) можно
преобразовать к виду
^(w\,wl + Aw2
+ гцAw! + ^L(w°1,w%)Aw2 + m • Aw2, C.23)
где функции гц и щ бесконечно малы при Aw\ и Aw2i стремя-
стремящихся к нулю, а тем самым и при Az -Л 0. Составив теперь
разностное отношение —— и перейдя к пределу при Az —>> 0, в
силу непрерывности частных производных функции F по сово-
совокупности переменных, получим
что и доказывает существование производной Ф7(^о) в точке zq.
В силу сделанных предполож:ений функция Ф' (z) непрерывна в
точке zqj а так как zq — произвольная точка области Q, отсюда
и следует аналитичность функции Ф(г) в области Q. В случае
большего числа переменных Wi доказательство проводится со-
совершенно аналогично.
Теорема 3.1 позволяет аналитически продолжать в комплекс-
комплексную область соотношения вида C.17), C.18) между элементар-
элементарными функциями одной действительной переменной, что суще-
существенно для изучения различных свойств элементарных функ-
функций комплексной переменной. Соответствующие примеры будут
приведены ниже, а здесь ограничимся лишь следующим замеча-
замечанием к теореме 3.1.
Следствие. Если выполнены условия теоремы 3.1 и функ-
функции fi(z) соответственно равны: fi(z) = f{z), /2B) =
= ff(z), ... , fn+i(z) = f(n\z), то из соотношения
F[f(x),...,f№(x)]=0 при a<x<b	C.24)
следует
F{f(z),...,fW(z)]=0, zeQ.	C.25)
Это означает, что если функция действительной переменной
f(x) является решением дифференциального уравнения C.24),
то ее аналитическое продолжение f(z) в область Q удовлетво-
удовлетворяет в этой области дифференциальному уравнению C.25), яв-
являющемуся аналитическим продолжением уравнения C.24) в
область Q.

90	АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ	ГЛ. 3
Перейдем теперь к обоснованию аналитического продолже-
продолжения соотношений вида C.19) и C.20). Мы не будем рассматри-
рассматривать каждое из этих соотношений в отдельности, а сразу сфор-
сформулируем общую теорему.
Теорема 3.2. Пусть функции w\ = f\(z\),..., wn = fn(zn)
являются аналитическими функциями комплексных перемен-
переменных z\, ..., zn в областях Q\, ..., Qn, содержащих отрезки
[a,i,bi] (г = 1, ..., п) действительной оси х. Пусть функция
F[w\, ..., wn] является аналитической функцией по каждой из
переменных w\, ..., wn в области их изменения. Тогда из со-
соотношения F[fi(xi), ..., fn{%n)] — 0 пРи ai ^ х ^ fy следует
соотношение F[/1B:1), ..., fn(zn)] — 0 пРи z% ? Q%-
Доказательство. Для доказательства теоремы
фиксируем значения переменных Х2 = х%, • • • , хп = х^
и рассмотрим функцию комплексной переменной <&i(zi) =
= F[fi(zi), /2^),..., /п(ж°)]. Эта функция, как сложная
функция комплексной переменной z\, в силу утверж:де-
ния гл. 1, с. 36, является аналитической функцией комп-
комплексной переменной z\EQ\. Поэтому по теореме о един-
единственности определения аналитической функции из соотно-
соотношения F[/i(zi), f2(x9,),...Jn(x°n)]=0 при ai^xiOi сле-
следует F[fi(zi),f2{xl), ... Jn(x°n)] = 0 при ziEGi. Заметим,
что отсюда в силу произвольности #2,...,жЛ вытекает, что
[(M /2(^2M • • • ^ /n(#n)] — 0- Фиксируем теперь произволь-
произвольное значение комплексной переменной z\$LQ\ и рассмотрим
функциюФ2(^2)=^[/1(^),/2(^2),/з(жзM '•• ? /пD)] комплекс-
ной переменной ^Gfe- Так же как и <3>i(?i), функция $2(^2)
является аналитической функцией переменной ^Gfe- По-
Поэтому из соотношения F[/i(^), /2(^2), /з(^з)? ••• ^/п(^п)]=°
при а2^ж2^&2 следует F[/i(^),/2 (^2 ),/з(#з)^ ••• ^/п(#п)] = 0
при ^Gfe- В силу произвольности выбора z\ мы по-
получим, что соотношение F[fi(xi), /2(^2), /3(^3),. • •, /n(^)] =0
при ai ^ #i ^ 61, a2 ^ X2 ^ &2 влечет за собой соотношение
F[f1(z1),f2(z2)J3(x03),...,fn(x0n)} = 0 при z1eg1,z2? 02-
Продолжая аналогичным образом, мы и докажем теорему.
Заметим, что доказательство теоремы не зависит от взаимного
расположения областей Qi.
Теорема 3.2 позволяет строить аналитические продолжения
соотношений вида C.19) и C.20). Рассмотрим, например, соот-
соотношение C.19) и введем функции w\, w2l w% комплексных пере-
переменных Z\j Z2 И Z% = Z\ + Z2'.
Wl = ez\ w2 = ez\ w3 = eZ3 = eZl+z\	C.26)

§ 1 ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ 91
Рассмотрим функцию трех комплексных переменных
F[wi,W2,ws] = ws — wi • W2.	C.27)
Поскольку функции C.26), C.27) являются целыми функция-
функциями своих переменных, a F = 0 при z\ = #i, Z2 = #2, zs = ^з
(—оо < а^ < оо), то выполнены все условия теоремы 3.2, что и
доказывает справедливость соотношения C.19) при любых зна-
значениях комплексных переменных z\ и z^-
3. Свойства элементарных функций. Перейдем теперь
к более детальному изучению основных свойств введенных выше
элементарных функций комплексной переменной. В силу теорем
3.1 и 3.2 при всех значениях комплексной переменной z имеют
место соотношения
sin2 z + cos2 z = 1,	C.28)
ch2z-sh2z = l	C.29)
и другие известные тождества для различных тригонометриче-
тригонометрических и гиперболических функций одной комплексной перемен-
переменной. Также имеют место соотношения
eZl+Z2=eZl-eZ2,	C.30)
sin B1 + Z2) = sin^i cos ^2 + cos^i sin22,	C.31)
cos (z\ + Z2) = cos z\ cos Z2 — sinz\ sinZ2	C.32)
и другие тригонометрические формулы, являющиеся аналити-
аналитическим продолжением в комплексную область известных соот-
соотношений для элементарных функций действительной перемен-
переменной.
Установим связь между показательной и тригонометриче-
тригонометрическими функциями комплексной переменной. Для этого вернем-
вернемся к выражению C.7) для функции ez и сделаем в нем замену
переменной, положив z = г?. Тогда
Разбив последний абсолютно сходящийся ряд на сумму двух ря-
рядов, получим
(X)	(X)
2	2 + 1
(у	} Bп + 1)!'
п=0	п=0
т. е.
е< = cosC + isinC.	C.33)
Очевидно, это тож:дество имеет место для всех значений
комплексной переменной ?.

92	АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ	ГЛ. 3
Соотношение C.33), устанавливающее связь между показа-
показательной и тригонометрическими функциями комплексной пере-
переменной, носит название формулы Эйлера. Из него следуют весь-
весьма важные для приложений формулы г)
l-{elz + e~lz)	C.34)
и
sm^ = -(e -e ).	C.35)
С помощью этих формул и формул C.10), C.11) легко уста-
установить следующие соотношения, связывающие тригонометриче-
тригонометрические и гиперболические функции комплексной переменной:
smz = — ishiz, cosz = chiz.	C.36)
В частности,
sin гу = г sh у, cos гу = ch у.	C.37)
Установим еще некоторые важные свойства рассматривае-
рассматриваемых функций. Предварительно заметим, что в силу формулы
C.30) имеет место соотношение
w = ez = ex+iy = ех • eiy.	C.38)
Отсюда следует, что \w\ = ех и arg и? = у.
Z
Рассмотрим теперь функцию w = In z = I -г-, являющуюся
J С
о
аналитическим продолжением In ж на комплексную плоскость,
разрезанную по отрицательной части действительной оси. Так
как для действительных положительных х функция In ж явля-
является обратной экспоненте, то в силу теоремы 3.1 в области — тг <
< arg z < тг сохраняется соотношение
elnz = z,	C.39)
являющееся аналитическим продолжением соотношения е1пж =
= х (х > 0) в комплексную область. Тем самым функция In z
является обратной к функции ew.
Отметим важное следствие формулы C.39). В силу этой фор-
формулы и формулы C.38) из соотношения w = u + iv = \nz следует
Отсюда \z\ = еи, arg z = v, а так как и и \z\ — действительные
переменные, окончательно получим
г^ = 1п|^|, v = a,rgz,	C.41)
:) Напомним, что в гл. 1 мы с помощью этих формул определили функции
cos z и sinz, а также формально ввели соотношение Эйлера.

§ 1 ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ 93
где символ In \z\ означает действительную логарифмическую
функцию действительного положительного аргумента. Тем са-
самым для функции комплексной переменной In z получим алге-
алгебраическую форму записи в виде
\nz = ln|z| + i&rgz.	C.42)
Из C.42) получим значения: lni = г-, 1пA) = 0, 1п(—г) = —г-,
1пA + г) = Inу2 + г— и т. д.
Аналогичным образом на основании теоремы 3.1 нетрудно
показать, что и функция arcsinz, определенная формулой C.15),
является обратной к функции sin z, т. е.
sin (arcsin z) = z.	C.43)
Выше была установлена связь между показательной и три-
тригонометрическими функциями. Очевидно, и функции, обратные
к данным, например Inz и arcsin;?, также связаны между собой
определенными соотношениями.
В силу C.43) из выражения w = arcsin ? следует z = sinu?,
что согласно C.35) можно переписать в виде
z= 1(е^_е-^)	C.44)
или
e2iw - 2izeiw -1 = 0.	C.45)
Разрешив квадратное уравнение C.45) относительно егт, полу-
получим
eiw = iz + \fl-z2.	C.46)
Мы не пишем знак ± перед корнем, потому что функция
л/1 — z2 комплексной переменной z сама является многозначной
функцией (см. гл. 1, с. 30). Выбор ветви многозначной функции
л/l — ~z2 здесь производится из условия, чтобы рассматриваемая
функция w = arcsin ? являлась аналитическим продолжением
соответствующей функции действительной переменной. Из по-
последнего условия следует, что должно быть взято то значение
корня, которое положительно при положительных действитель-
действительных значениях подкоренного выражения. Из C.39) и C.46) сле-
следует
iw = In [iz + у 1 — z2\
откуда окончательно получим
w = arcsin ? = — iln[iz + у 1 — z2].	C.47)
Это выражение на первый взгляд довольно сложно, и невольно
возникает сомнение, дает ли оно, в частности, действительные

94	АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ	ГЛ. 3
значения arcsinx для действительных значений z = х, удовле-
удовлетворяющих условию |ж| ^ 1. Однако сомнение нетрудно рассе-
рассеять. Обозначим ? = iz + л/1 — z2. Для действительных значе-
значений z = ж, удовлетворяющих условию |ж| ^ 1, получим \(\ =
= л/ж2 + 1 — х2 = 1 и arg? = arctg —^=^ = arcsinx. Отсюда в
V1 — ж2
силу формулы C.42) имеем — iln? = —i[lnl +iarg?] = arg? =
= arcsinx.
Так как функция C.42) определена для всех значений своего
аргумента на комплексной плоскости с разрезом по отрицатель-
отрицательной части действительной оси, то формула C.47) дает анали-
аналитическое продолжение функции arcsinz на некоторую область
плоскости z. При этом точки z = =Ы оказываются в определен-
определенном смысле особыми. Действительно, в результате обхода любой
из этих точек на плоскости z по замкнутой кривой, принадлежа-
принадлежащей достаточно малой 6-окрестности этой точки, при непрерыв-
непрерывном изменении функции C.47) она изменит свое значение, так
как при однократном обходе точки z = 1 или z = — 1 функция
л/l — z2 изменяет свое значение1). Поэтому в качестве области
однозначного определения функции C.47) может быть выбра-
выбрана, например, полная плоскость z с разрезами вдоль отрезков
действительной оси [—оо, — 1], [1,оо].
4. Отображения элементарных функций. В заключе-
заключение данного параграфа, посвященного элементарным функци-
функциям комплексной переменной, рассмотрим некоторые геометри-
геометрические свойства отображений, осуществляемых этими функци-
функциями. Начнем с простейших примеров.
П р и м е р 1. В гл. 1 была рассмотрена простейшая степен-
степенная функция w = z2. Рассмотрим теперь отображение, осуще-
осуществляемое функцией
w = zn,	C.48)
где п — произвольное целое число. Эта функция, очевидно, яв-
является целой функцией. Для изучения геометрических свойств
ее отображения удобно воспользоваться показательной формой
записи комплексных чисел: z = рег(р, w = гег^ = рпеШ(р, из
которой следует, что любой сектор2) с центральным углом а =
= — плоскости z данной функцией отображается на полную
п
плоскость w. Различные внутренние точки этого сектора ото-
отображаются на различные точки плоскости w. При этом грани-
границы сектора переходят в один и тот же луч ф = ^о на плоскости
w. Для установления взаимно однозначного соответствия меж-
:) См. с. 31 - 32.
2) Здесь под сектором мы понимаем замкнутую область.

§ 1 ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ 95
ду областью однолистности функции zn и плоскостью w будем
считать, что на плоскости w произведен разрез по лучу ф = фо
и границам данного сектора плоскости z сопоставлены различ-
различные берега разреза. Например, сектор 0 ^ ср ^ — плоскости
z функцией C.48) отображается на полную плоскость w, при-
причем обе границы этого сектора, лучи I и II на рис. 3.1, пере-
переходят в положительную часть действительной оси и плоскости
w. Сектор — ^ (р ^ — также отображается на полную плос-
плоскость w и т. д. Поэтому геометрический образ функции w = zn
представляет собой плоскость w, повторенную п раз. Тем са-
самым отображение полной плоскости z на полную плоскость w,
осуществляемое данной функцией, не является взаимно одно-
однозначным. Однако если в качестве геометрического образа функ-
z=0
II
Рис. 3.1
ции w рассматривать более сложное многообразие, чем обычная
комплексная плоскость, можно сохранить взаимную однознач-
однозначность отображения. Будем считать, что мы имеем п экземпля-
экземпляров (листов) плоскости w, разрезанной по положительной части
действительной оси, на каждом из которых argu? изменяется в
пределах 2тг(к — 1) ^ a,rgw ^ 2тгА;, где к = 1,2,... ,п. Сектору
— (к — 1)
Т1
)
ср ^ —к плоскости z функция C.48) ставит в соот-
Т1
ветствие к-й лист плоскости w\ луч ср = — (к — 1) переходит в
ть
верхний берег разреза к-то листа, а луч ср = — к — в нижний
п
берег разреза этого же листа. Построим из этих листов непре-
непрерывное геометрическое многообразие так, чтобы непрерывному
движению точки на плоскости z соответствовало непрерывное
движение точки w на данном многообразии. Для этого заме-
заметим, что нижний берег разреза к-го листа и верхний берег раз-
разреза (к + 1)-го листа имеют один и тот же аргумент ф^ = 2тг • к.
Когда точка z в своем непрерывном движении по плоскости z пе-

96
АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ
ГЛ. 3
реходит из одного сектора в другой, соответствующая ей точка
w переходит с одного листа плоскости w на соседний лист. Оче-
Очевидно, чтобы сохранить непрерывность отображения, мы долж-
должны соединить соседние листы, склеивая нижний берег разреза
к-то листа с верхним берегом разреза (к + 1)-го листа. При этом
остаются свободными верхний берег разреза 1-го и нижний бе-
берег разреза n-го листов. Пусть точка z совершит на плоскости z
полный оборот вокруг точки z = 0, последовательно пройдя че-
через все п секторов этой плоскости, начиная с первого сектора, и
вернется к своему первоначальному положению. Тогда соответ-
соответствующая ей точка w пройдет п листов, и, чтобы она вернулась
на первый лист, надо склеить остававшиеся свободными берега
разрезов на 1-м и п-м листах. Тем самым полной плоскости z
функция w = zn ставит в соответствие п листов плоскости и?,
склеенных указанным выше образом. Такое геометрическое мно-
многообразие представляет собой частный случай так называемой
римановой поверхности. Функция w = zn является п-листной
функцией.
П р и м е р 2. Рассмотрим отображение, осуществляемое
функцией w = ez. Из представления C.38) следует, что эта
функция каждому комплексному числу z = x + iy ставит в соот-
соответствие комплексное число w, модуль которого есть еж, а аргу-
аргумент у. Это означает, что показательная функция w = ez произ-
производит отображение прямой у = уо плоскости z на луч arg w = уо
плоскости w. Как легко видеть, полоса плоскости z, ограничен-
II
/
^ y=An
y=2n
z=0
у=-2п
м v
Рис. 3.2
ная прямыми у = 0 и у = 2тг, перейдет в полную плоскость w,
причем граничные прямые у = 0 и у = 2тг будут отображаться
на один и тот же луч плоскости w — положительную часть дей-
действительной оси и (рис. 3.2). При этом устанавливается взаимно
однозначное отображение открытой области 0 < у < 2тг на плос-
плоскость w с выброшенной положительной частью действительной

§ 1 ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ 97
оси и. Чтобы установить взаимно однозначное отображение со-
соответствующих замкнутых областей, будем считать, что произ-
произведен разрез по положительной части действительной оси и и
установлено взаимно однозначное соответствие между верхним
берегом разреза и прямой у = 0, а также между нижним бере-
берегом разреза и прямой у = 2тг плоскости z. Итак, показательная
функция ez производит взаимно однозначное отображение по-
полосы 0 ^ у ^ 2тг плоскости z на полную плоскость w, разрезан-
разрезанную по положительной части действительной оси 1). Ана-
Аналогичным образом устанавливается, что показательная функ-
функция производит взаимно однозначное отображение любой по-
полосы 2тгп ^ у ^ 2тг(п + 1) (п = 0, ±1,...) плоскости z на ту
же полную плоскость w с разрезом вдоль положительной части
действительной оси и. При этом точки zq = xq + iyo и z\ = xq +
+ г(уо + 2тгк) (к = ±1, ±2,...) переходят в одну и ту же точку
плоскости w. Это означает, что показательная функция явля-
является бесконечнолистной периодической функцией комплексной
переменной z с мнимым периодом 2тгг. Областью ее однолист-
однолистности является любая полоса уо < у < уо + 2тг, отображающаяся
на полную плоскость w с разрезом, по лучу &rgw = уо- Заме-
Заметим, что аргумент и? на плоскостях, соответствующих различ-
различным полосам 2тгп ^ у ^ 2тг(п + 1) (п = 0, ±1,...) изменяется
соответственно в различных пределах. Тем самым мы получаем
бесконечный набор различных экземпляров плоскости w, разре-
разрезанной по положительной части действительной оси и. Чтобы
непрерывному движению точки z на плоскости z, при котором
она переходит из одной полосы в другую, отвечало непрерывное
движение w, соответствующие экземпляры (листы) плоскости w
должны быть соединены между собой, причем, очевидно, верх-
верхний берег разреза n-го листа должен быть соединен с нижним
берегом разреза (п — 1)-го листа и нижний берег разреза п-го
листа — соединен с верхним берегом разреза (п + 1)-го листа.
Полученное геометрическое многообразие образует бесконечно-
листную риманову поверхность.
Аналогичные рассмотрения могут быть проведены и для
тригонометрических функций комплексной переменной. Сразу
заметим, что в силу формул C.34), C.35) тригонометрические
функции являются бесконечнолистными функциями комплекс-
комплексной переменной z, периодическими с действительным перио-
периодом 2тг. Так же, как и в случае функции е^, нетрудно рас-
рассмотреть геометрические свойства отображений, осуществляе-
осуществляемых тригонометрическими функциями. Мы ограничимся лишь
функцией cos z. С помощью установленных выше свойств три-
) При этом граница полосы у = 0 переходит в верхний, а граница у =
= 2тг — в нижний берег разреза плоскости w.
4 А.Г. Свешников, А.Н. Тихонов

98
АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ
ГЛ. 3
гонометрических функций получаем
cosz = cos (х + гу) = и(х,у) + iv(x,y) = cosx • chy — is'mx • shy.
Отсюда следует, что прямую х = xq плоскости z функция cos z
отображает в ветвь гиперболы
= 1
C.49)
на плоскости w. При 0 < xq < — прямая х = xq переходит в пра-
вую ветвь гиперболы, а прямая х = тг — xq — в ее левую ветвь.
Как легко установить, все гиперболы C.49) являются софокус-
ными, причем их фокусы лежат в точках ±1 действительной
оси и. Прямая xq = — функцией cos z отображается на мнимую
ось v плоскости w, а прямые жо = Оижо=тг — в лучи [1,оо]
и [—оо, — 1] действительной оси и плоскости -ш, причем при дви-
ж:ении точки z по данной прямой (например, по прямой xq = 0)
соответствующий луч проходится дважды. Тем самым функция
Рис. 3.3
cos z осуществляет взаимно однозначное отображение полосы
0 ^ х ^ тг плоскости z на полную плоскость w, разрезанную по
лучам действительной оси [1, оо] и [—оо, — 1]. При этом верхняя
полуполоса 0^ж^тг,у>0 переходит в нижнюю полуплоскость
v < 0, а нижняя полуполоса 0^ж^тг,у<0 — в верхнюю по-
полуплоскость v > 0, что отмечено соответствующей штриховкой
на рис. 3.3. Как легко видеть, следующая полоса тг ^ х ^ 2тг

§J2	ПОНЯТИЕ РИМАНОВОЙ ПОВЕРХНОСТИ	99
функцией cos z отображается на ту же полную плоскость w с
разрезами по лучам действительной оси [1,оо] и [—оо, —1]. Так
как cos (z + тг) = —cosz, то верхняя полуполоса тг ^ х ^ 2тг,
у > 0 переходит в верхнюю полуплоскость v > 0, а нижняя
полуполоса тг^ж^2тг,у<0 — в нижнюю полуплоскость
г; < 0 (рис. 3.3). Аналогичное положение, очевидно, имеет место
и для любой полосы птг ^ х ^ (п + 1)тг. Отсюда следует, что
областью однолистности функции cos z является полоса птг <
< х < (п + 1)тг. Функция cos 2 представляет собой бесконечно-
листную функцию, а ее областью значений является бесконеч-
нолистная риманова поверхность, получающаяся путем склеи-
склеивания плоскостей w, разрезанных по лучам действительной оси
[—оо, — 1] и [1,оо], по соответствующим берегам разрезов.
В заключение наших рассмотрений основных свойств пока-
показательной и тригонометрических функций исследуем вопрос о
нулях этих функций. Показательная функция w = ez не обра-
обращается в нуль ни при каком значении комплексной переменной
z, как это следует из формулы C.38). Все нули тригонометри-
тригонометрических функций лежат на действительной оси. В самом деле,
если sin z = 0, то elz — e~lz = 0, e2lz = 1. Но если комплексные
числа равны, то их аргументы различаются на число, кратное
2тг, откуда z = птг, что и доказывает высказанное утверждение.
§ 2. Аналитическое продолжение. Понятие римановой
поверхности
1. Основные принципы. Понятие римановой поверх-
поверхности. Основной задачей аналитического продолжения явля-
является продолжение значений функции f(z), заданной в некоторой
области Q' на большую область Q.
Пусть на комплексной плоскости даны две области Q\ и Q2
имеющие общую часть 1) Qyi (рис. 3.4). Пусть однозначные ана-
аналитические функции fi(z) и /2B) заданы соответственно в обла-
областях Q\ и ?/2 и тождественно совпадают между собой в пересе-
пересечении Qyi- Тогда функция F{z), определенная соотношениями
\
является аналитической в расширенной области Q = Q\ + Q2 и
совпадает с fi(z) в^ис /2(z) в Q2.
х) При этом могут быть различные случаи. Например: а) область Q\ со-
содержится в области С/2, тогда ?/i2, очевидно, совпадает с областью Q\\ б) пе-
пересечение (/12 является односвязной или многосвязной областью; в) пере-
пересечение (/12 состоит из нескольких (может быть, и бесконечного числа) от-
отдельных связных областей.

100
АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ
ГЛ. 3
Функция F(z) называется аналитическим продолжением
функции fi(z) (/2B))™ область Q = Q\ + Q2- Функцию /2B)
(fi(z)) также называют аналитическим продолжением функции
fi(z) (h(z)) на область Q2 (G\).
Как легко видеть, ана-
аналитическое продолжение F(z)
функции fi(z) на область Q =
= Q\ + G2 определено един-
единственным образом. Действи-
Действительно, предположение о су-
существовании в области Q двух	Рис> з.4
различных функций, тожде-
тождественно совпадающих с fi(z) в области Gi, приводит к противо-
противоречию с теоремой о единственности определения аналитической
функции, доказанной в предыдущей главе.
Данный способ аналитического продолжения функции fi(z)
из области Q\ на более широкую область Q представляет собой
простейшую форму принципа аналитического продолжения.
Обратимся теперь к случаю,
когда функции fi(z) и /2B) то-
тождественно совпадают лишь на
части Q[2 пересечения Gn обла-
областей Q\ и (/2 (рис. 3.5). Рассмо-
Рассмотрим область Q = Q\ + Q2 — Qi2i
где Q = G12 - G'12 — та часть
пересечения Q\2, в которой функ-
функции f(z) и /2B) различны. Со-
Согласно предыдущим рассмотрени-
рассмотрениям в Q определена единственная
аналитическая функция F(z), яв-
являющаяся аналитическим продолжением fi(z), заданной в обла-
области Q\ —G12 на область Q. Эта функция тождественно совпадает
с функцией fi(z) в области Q\ — Q'B и с h(z) в области G2 —
— Q'{2' Функция F(z) может быть аналитически продолжена на
множество Q'l2 двумя способами:
Рис. 3.5
F1(z) =
6 g>{
C.51)
{2
или
) lee»	C-52>
Это нас, естественно, приводит к необходимости рассмотрения

§ 2	ПОНЯТИЕ РИМАНОВОЙ ПОВЕРХНОСТИ	101
многозначной аналитической функции F(z), определенной в
области Q = Q\ + Q2 и принимающей различные значения в од-
одних и тех же точках части Q^2 области Q'. В частности, в данном
случае мы получаем двузначную аналитическую функцию F(zI
принимающую в одной и той же точке zq Е ^ два различных
значения, совпадающие со значениями функций f\{z) или /2B)
в этой точке.
Оперируя с многозначной функцией F(z), имеющей различ-
различные значения в одной и той же точке комплексной плоскости,
приходится встречаться с трудностями выбора ее значений в
данной точке. Для удобства выбора этих значений часто поль-
пользуются понятием ветви аналитической функции 1), являющейся
однозначной и непрерывной функцией в соответствующей части
области определения функции F(z). Однако более удобным ока-
оказывается несколько иное представление, позволяющее рассма-
рассматривать данную функцию как однозначную, но определенную на
более сложном многообразии, чем использовавшаяся до сих пор
обычная плоскость комплексной переменной. Так, возвращаясь
к рассмотренному выше примеру двузначной функции F(z), бу-
будем считать, что области Q\ и Q2 склеены по общей части Q[2j B
которой функции fi(z) и /2B) совпадают, а два экземпляра Ql
принадлежащие областям 5i и й, оставлены свободными.
Тогда на полученном геометрическом многообразии, пред-
представляющем собой объединение областей 5i и й, склеенных по
Q'l2 (так что точки, принадлежащие Q'{2l перекрыты дважды),
функция F(z) является однозначной аналитической функцией.
Построенное таким образом многообразие называется рима-
новой поверхностью аналитической функции F(z), являющей-
являющейся аналитическим продолжением функции fi(z) (/2B)), а от-
отдельные экземпляры повторяющихся областей — различными
листами римановой поверхности.
Таким образом, вместо рассмотрения многозначной функции
на комплексной плоскости z мы можем рассматривать однознач-
однозначную функцию на римановой поверхности. Так же как и в про-
простейшем случае, рассмотренном в начале данного пункта, при-
приведенный способ аналитического продолжения функции Д (z) из
области Q\ на более широкую область, представляющую собой
уже риманову поверхность, является частной формой общего
принципа аналитического продолжения. Очевидно, можно ана-
аналогичным образом строить и аналитическое продолжение одно-
однозначных аналитических функций, заданных на римановой по-
поверхности. При этом мы, естественно, придем к многолистным
г) Например, такое рассмотрение мы проводили в гл. 1 при изучении
функции z = y/w.

102
АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ
ГЛ. 3
римановым поверхностям, представляющим собой геометриче-
геометрическое многообразие, в которое одна и та же область комплексной
плоскости входит уже не в двух, а во многих экземплярах. Со-
Соответствующие примеры будут рассмотрены в п. 3 данного па-
параграфа, а сейчас рассмотрим еще один способ аналитического
продолжения.
2. Аналитическое продолжение через границу. В ря-
ряде случаев для аналитического продолжения функции fi(z),
первоначально заданной в обла-
области Q\, используется также сле-
следующий способ. Пусть области Q\
и ?/2 имеют в качестве общего
участка границы кусочно глад-
гладкую кривую Fi2 (рис. 3.6) и в
этих областях заданы аналитиче-
аналитические функции fi(z) и /2B), непре-
непрерывные соответственно в Q\ + Г12
и ?/2 + Г*12 и совпадающие на Г]_2.
рис. з.б	Рассмотрим множество точек Q —
= Q\ + Q2 + Г12. Так как точки
z E Г12 являются внутренними точками этого множества, то
множество Q является областью. Покажем, что функция F(zI
определенная с помощью соотношений
F(z) _
C.53)
является аналитической в области Q = Q\ + Q2 + Г12. Очевид-
Очевидно, достаточно доказать, что для каждой точки zq области (/,
лежащей на кривой Г12, можно указать такую окрестность, в
которой функция F(z) является аналитической. Возьмем про-
произвольную точку zq E Г12 и построим окружность Со с центром
в этой точке, целиком лежащую в Q. Рассмотрим интеграл типа
интеграла Коши
1(.	C.54)
Со
В силу установленных ранее свойств интегралов, зависящих от
параметра (гл. 1, с. 56), функция Ф(^) является аналитической
функцией z при любом положении точки z, не лежащей на кри-
кривой Со- Покажем, что когда точка z лежит внутри окружности
Со, то Ф(г) =F(z). Действительно, представим интеграл C.54)
в виде
1 [F{QdC_ 1 Г MOdC , 1 [
НО
dC /355)
Ci+712
712+С2

§J2	ПОНЯТИЕ РИМАНОВОЙ ПОВЕРХНОСТИ	103
где С\ и С2 суть части окружности Со, лежащие в G\ и Gi (Со =
= С1 + С2). a 712 — часть кривой Г12, попавшая внутрь окружно-
окружности Со. Если точка 2 принадлежит области G\, то в силу теоремы
Коши1) получим
L I Ш« Ш JL I MO<K 0 C.56)
C1+712	712+С2
откуда Ф(^) = fi(z) = F(^) при z E Gi- Аналогично Ф(^) =
= /2B) = i^(^) при 2: E G2- В точке ^о, принадлежащей 712, в
силу непрерывности функций Ф(^), /i(^), /2B) внутри окруж-
окружности Со, также будем иметь Ф(^о) = /i(^o) = /2(^0) = F{zo),
откуда и следует, что F(z) является аналитической функцией в
области G-
И в этом случае, так же как и в предыдущих, мы будем гово-
говорить, что функция fi(z) (/2B)), заданная в области G\ (?/2)? ана-
аналитически продолжена на область G2 {Gi)- Построенная выше
функция F(z) является аналитическим продолжением функ-
функции fi(z) в область G = G\ + G2 + Г12. Описанная конструкция
представляет собой частную форму общего принципа аналити-
аналитического продолжения — аналитическое продолжение через гра-
границу области. При этом, так же как и в предыдущих случаях,
мы при продолжении через границу можем прийти к необхо-
необходимости рассмотрения однозначной аналитической функции на
римановой поверхности в тех случаях, когда области 5i и fe,
кроме общего участка границы Г]_2, имеют непустое пересече-
пересечение G121 B котором функции fi(z) и /2B) не равны тождественно
ДРУГ Другу.
Рассмотрим теперь ряд примеров применения общих прин-
принципов аналитического продолжения, приводящих как к много-
многозначным, так и однозначным функциям.
3. Примеры построения аналитического продолже-
продолжения. Продолжение через границу. Рассмотрим некоторые
примеры построения аналитического продолжения функции
fi(z), первоначально заданной в области G\ комплексной плос-
плоскости z. При этом, как было отмечено выше, мы в ряде случаев
приходим к необходимости рассмотрения функции, многознач-
многозначной на комплексной плоскости.
В гл. 1 мы уже имели простейший пример многозначной
функции комплексной переменной — функцию w = д/5", явля-
являющуюся2) обратной степенной функции z = w2. Рассмотрим
) Применимость теоремы Коши к интегралам в правой части C.55) оче-
очевидна в силу сделанного предположения о кусочной гладкости кривой Г12
и выбора кривой Со.
2) Мы изменили здесь обозначения зависимой и независимой переменных.

104	АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ	ГЛ. 3
теперь эту и ряд других функций с более общей точки зрения
аналитического продолжения.
Пример 1. Функция w = y/z. Согласно правилу извлече-
извлечения корня п-й степени из комплексного числа одному значению
z соответствует п различных комплексных чисел w, вычислен-
вычисленных по формуле
Ш — / о — л/ fJ сЛ-JJ I I	 I	\hj — U, -L ,...,/1	± I, \O.Oil
где z = рег(р ж if — одно из значений Argz. Функция w = л/z
является многозначной функцией, имеющей п различных вет-
ветвей. Будем считать, что ср изменяется в пределах 0 ^ ср ^ 2тг,
и выберем ту ветвь функции w = yfz^ которая является анали-
аналитическим продолжением действительной функции и = у/х дей-
действительной положительной переменной х > 0. Очевидно, это
будет
exp (i^) @ ^ if ^ 2тг).	C.58)
Областью Q\ определения функции w\ является плоскость z,
разрезанная по положительной части действительной оси х.
Верхний берег разреза соответствует значению axgz = 0, ниж-
нижний — значению argz = 2тг. Очевидно, функция wi, являющаяся
обратной функции z = wn, осуществляет взаимно однозначное
отображение замкнутой области Q\ плоскости z на сектор 0 ^
^ argiu ^ — плоскости w. В силу общих свойств аналитических
тх
функций (см. гл. 1, с. 36) функция w\ в области Q\ является од-
однозначной аналитической функцией, производная которой вы-
числяется по формуле w\ (z) = —zn L = —nn L exp up	 .
n	n		V n J
Рассмотрим теперь замкнутую область Q2 — ту же плоскость
z с разрезом по положительной части действительной оси ж, но
на которой аргумент z изменяется в пределах 2тг ^ argz ^ 4тг.
Верхний берег разреза соответствует значению argz = 2тг, ниж-
нижний — значению arg z = 4тг. Рассмотрим в этой области функцию
W2(z) = Уд ехр (г^^-) @ ^ <р ^ 2тг).	C.59)
Эта функция осуществляет взаимно однозначное отображе-
отображение замкнутой области Q2 на сектор — ^ arg w ^ — плоскости
п	п
w и является однозначной аналитической функцией z в обла-
области @2- Замкнутые области Q\ и Q2 имеют общую часть границы
Г12 — луч arg z = 2тг, — на которой совпадают функции w\ и^,
непрерывные в ?/i+Pi2 и Q2~\~^12 соответственно. Поэтому в силу
принципа аналитического продолжения через границу функция
() является аналитическим продолжением функции w\(z) в

§ 2	ПОНЯТИЕ РИМАНОВОЙ ПОВЕРХНОСТИ	105
область @2- С другой стороны, Q\ и Q2 фактически совпадают на
плоскости z, так как точки комплексной плоскости с равными
модулями и отличающимися на 2тг аргументами совпадают. По-
Поскольку функции C.58) и C.59) в одной и той же точке z имеют
различные значения, то согласно предыдущим рассмотрениям,
для того чтобы функция
2(z), z e ^2 + Ti52,
была однозначной в области определения R\ = Q\ + Q2 + Г 1,2,
мы должны считать, что многообразие R\ является римановой
поверхностью, склеенной из листов 5i и й- Очевидно, что дан-
данное склеивание следует произвести по общей части границы Г^
лучу argz = 2тг, склеив нижний берег разреза области Q\ с верх-
верхним берегом разреза области Q2. Повторив наши рассмотрения,
мы установим, что функция
wk+1{z) = ^~р exp U4±2^\ @ < v < 2тг),	C.61)
Ti
определенная в замкнутой области Qk+i Bтг/с ^ argz ^ 2тг(к -\-
+ 1)), является аналитическим продолжением функции Wh(z),
определенной в Q^. Заметим, что функция wn+i(z) тож:дествен-
но совпадает с функцией ^1B:). Поэтому естественно рассматри-
рассматривать однозначную аналитическую функцию
W2(z), *е02 + г1>2 + г2>3,	C<62)
определенную на римановой поверхности R = Q\ + G2 + ...
• • -~\~Gn~\~Ti2~\~• • - + ГП_15П, склеенной указанным выше способом
из п листов, представляющих собой плоскость z с разрезом по
положительной части действительной оси х. При этом остаются
свободными верхний берег разреза (arg z = 0) на первом листе
Q\ и нижний берег разреза (argz = 2тгп) на п-м листе Qn. Что-
Чтобы сохранить непрерывность функции F(z) во всей области ее
определения, мы произведем склеивание этих берегов разрезов
(рис. 3.7) 1). Функцию C.62) называют полной аналитической
функцией w = yfz^ а построенное указанным выше способом
замкнутое многообразие R — полной римановой поверхностью
) Для большей наглядности можно произвести указанные склеивания на
разрезанных листах бумаги. При этом последнее склеивание оказывается
физически невозможным и может быть произведено лишь мысленно.

106	АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ	ГЛ. 3
этой функции. На каждом листе римановой поверхности опре-
определена отдельная ветвь данной многозначной функции.
Отметим еще следующее обстоятельство. Фиксируем на
плоскости z некоторую точку zq и проведем через нее замкну-
замкнутую кривую С. Тогда,
если arg z при дви-
движении по кривой С
изменяется непрерыв-
непрерывным образом и кривая
С пересекает линию
разреза на плоскости
z, то при полном об-
обходе кривой С априо-
априори возможны два слу-
случая (рис. 3.8) В пер-
первом случае точка z =
= 0 лежит вне кривой
С. Поэтому, выйдя из
Рис з.7	точки z = zo (arg z0 =
= с^о) на к-м листе1),
мы после обхода этой кривой вернемся в исходную точку zq на
том же к-м (arg^o = tpo) листе, хотя в процессе движения мы,
пересекая линию разреза, переходили и на другие листы. Во
втором случае, точка z = 0 лежит внутри кривой С. Поэтому,
(Г)	(л)
(V
-*»
Рис. 3.8
; и:
B1
выйдя из точки z = zq (arg zq = ifo) на к-м листе, мы после об-
обхода кривой С вернемся в точку z = zq уж:е не на исходном fc-м,
а например, на (к + 1)-м листе (arg^o = (ро + 2тг). Точка ^о, при
обходе которой по любой замкнутой кривой в достаточно малой
окрестности этой точки происходит переход с одного листа ри-
римановой поверхности аналитической функции F(z) на другой ее
лист, называется точкой разветвления функции F(z). Как лег-
) Рисунок 3.8 соответствует случаю к = 1.

§ 2	ПОНЯТИЕ РИМАНОВОЙ ПОВЕРХНОСТИ	107
ко видеть, это определение точки разветвления эквивалентно
определению, данному в гл. 1, с. 32. Очевидно, в рассматривае-
рассматриваемом примере функции w = y[z точками разветвления являются
точки 2: = 0и2; = оо.
П р и м е р 2. Функция w = Lnz.
Рассмотрим в замкнутой области Qq, представляющей собой
плоскость z, разрезанную по отрицательной части действитель-
действительной оси — тг ^ arg z ^ тг, функцию In z, о которой шла речь в
предыдущем параграфе:
г^о = In (z) = ln \z\ + iargz ... (—тг ^ arg z ^ тг). C.63)
Как мы знаем, эта однозначная аналитическая функция являет-
является аналитическим продолжением действительной функции и =
= In ж и обратна функции z = ew. Поэтому функция C.63) ото-
отображает область Qо плоскости z на полосу — тг < Im w < тг плос-
плоскости w. Рассмотрим в замкнутой области Q\ (тг ^ arg z ^ Зтг)
функцию
w\ = lni (z) = ln \z\ + г arg z, тг ^ arg z ^ Зтг.	C.64)
Очевидно, функция w\(z) является аналитическим продолж:е-
нием г^о(^) в область Q\. Аналогично функция
w-i = ln_i(^) = In \z\ + i&rgz, —Зтг ^ arg z ^ —тг, C.64')
определенная в замкнутой области Q_\ (—Зтг ^ argz ^ — тг), яв-
является аналитическим продолжением функции г^о(^) в области
Q-\. Также и функция Wk(z):
wk(z) — ln/c(^) — ln \z\ +i&Ygz, ттBк — 1) ^ arg z ^ тгBк + 1),
_	C.65)
определенная в замкнутой области ?/&, тгBк — 1) ^ arg z ^
^ тгBк + 1), является аналитическим продолжением функции
Wk-i(z). Функция Wk(z), однозначно отображающая область Q^
на полосу тгBк — 1) < Im w < тгB/с + 1), такж:е является обратной
функции z = ew. В отличие от предыдущего случая, ни одна из
функций Wk(z) (к т^ 0) не равна тождественно функции wq(z).
Поэтому данный процесс аналитического продолжения следует
вести неограниченно как для к > 0, так и для к < 0. Тем самым
полная аналитическая функция
F(z) = Ln z = ln \z\ = i Arg z = <
C.66)

108	АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ	ГЛ. 3
является бесконечнозначной на обычной плоскости z и одно-
однозначной на бесконечнолистной римановой поверхности R =
оо
= ^2 Qn-> составленной из бесконечного множества листов Qn
п= — оо
путем склеивания верхнего берега разреза каждого (к + 1)-го
листа с нижним берегом разреза предыдущего к-то листа. Как и
в предыдущем случае, точки z = 0 и z = оо являются точками
разветвления функции Lnz.
Отметим еще раз, что функция w = Lnz является обратной
функции z = ew. Это позволяет определить степенную функцию
za для любого комплексного значения а в виде
za = (eLnz)a = eaLnz.	C.67)
4. Примеры построения аналитического продолже-
продолжения. Продолжение с помощью степенных рядов. В рас-
рассмотренных примерах различные ветви аналитической функ-
функции задавались в явном виде на всей комплексной плоскости и
построение аналитического продолжения производилось путем
соответствующего склеивания областей определения этих вет-
ветвей. Рассмотрим теперь еще один метод конкретного построе-
построения аналитического продолжения аналитической функции, пер-
первоначально заданной в некоторой области Q\ комплексной плос-
плоскости Z.
Пусть функция fi(z) является аналитической в области Q\.
Выберем произвольную точку zq Е Q\ и разложим fi(z) в сте-
степенной ряд в окрестности этой точки:
n=0	n=0
Рассмотрим ряд, стоящий в правой части C.68). Априори воз-
возможны два случая (рис. 3.9). В первом случае радиус сходи-
сходимости Rq ряда C.68) не превосходит расстояния от точки zq
до границы Pi области Q\. В этом случае разложение C.68) не
выводит за границы области Q\ первоначального определения
аналитической функции fi(z). Во втором случае радиус сходи-
сходимости Rq ряда C.68) больше расстояния от точки zq до границы
Pi области Q\. В этом случае область ^2, представляющая собой
круг |^г — ^г01 < Roi Уже не является подобластью области Q\,
а лишь имеет с ней общую часть Qyi- В области Q2 сходящийся
степенной ряд C.68) определяет аналитическую функцию /2(^O
совпадающую с fi(z) в Qi2. Эта функция /2^) является анали-
аналитическим продолжением fi(z) в область Яъ- Следовательно, в

ПОНЯТИЕ РИМАНОВОЙ ПОВЕРХНОСТИ
109
области G = G\ + G2 определена аналитическая функция
nz) = \fM Hi1:	C.69)
Итак, в рассматриваемом случае разложение C.68) выводит за
границу Fi области G\ первоначального определения аналити-
аналитической функции fi(z). Проведя аналогичные рассмотрения для
Рис. 3.9
некоторой точки z\ построенной области G2-) затем для точки
Z2 области Gz и т- Д-? мы получим аналитическое продолже-
продолжение функции fi(z) вдоль цепочки областей Gi, G24 • • • iGrn • • •
При этом возможны такие взаимные наложения областей цепоч-
цепочки, которые приводят к необходимости рассматривать функцию
F(z) как однозначную аналитическую функцию, определенную
уже не на обычной комплексной плоскости 2;, ана римановой
поверхности.
Рассмотрим конкретный пример разобранного способа ана-
аналитического продолжения.
П р и м е р 3. Пусть первоначально функция fi(z) задана
своим степенным рядом
оо
C.70)
п=0
Этот ряд сходится внутри круга \z\ < 1 к аналитической функ-
функции fi(z) = 	. Всюду вне круга \z\ < 1 ряд расходится; следо-
следовательно, fi(z) не определена вне круга \z\ < 1. Выберем некото-
некоторую точку zq внутри круга \z\ < 1 и построим разложение fi(z)
00
в степенной ряд ^ cn(z — zo)n с центром в этой точке. Вычислив
п=о 1
коэффициенты сп по формуле B.16), получим сп = —	wTT*
Легко показать, что радиус сходимости данного ряда p(zq) ра-
равен |1 — zq\. Как следует из элементарных геометрических со-

по
АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ
ГЛ. 3
ображений, в том случае, когда точка zq не лежит на отрезке
действительной оси [0,1], круг сходимости данного ряда выйдет
за пределы первоначального круга сходимости \z\ < 1. Следова-
тельно, функция /2B) = ^2
является аналитическим
^2
n=0
продолжением функции fi(z) на область \z — zq\ < \1 — zq
Заметим, что степенной ряд, определяющий функцию
также легко суммируется, причем /2B)
Поэтому взяв
в качестве нового центра разложения точку z\ внутри круга
^ (Z-Zl)n
получим ряд 2^ ^	ч^тг5 сходящийся внутри
п=0 ^ Zl
\z — zq\ < 1 — zq
круга \z — zi\ < |1 — 2i| к функции fs(z) = 	, совпадающий с
/2B) и fi(z) в общих частях круга \z — z\\ < \1 — z\\ и областей
определения соответствующих функций. Тем самым /з(^) явля-
является аналитическим продолжением f\{z) на новую область. От-
Отметим, что при любом выборе точки z\ граница соответствующе-
соответствующего круга сходимости прой-
пройдет через точку z = 1
(рис. 3.10). Поступая анало-
аналогичным образом, можно по-
построить аналитическое про-
продолжение функции fi(z) на
полную плоскость комплекс-
комплексной переменной, за исключе-
исключением точки z = 1. При этом
аналитическим продолжени-
продолжением fi(z), полученным с помо-
помощью степенных рядов, явля-
является функция F(z) = 	,
определенная и аналитиче-
аналитическая всюду, за исключением
точки z = 1.
Итак, нам удалось расши-
расширить область первоначаль-
первоначального задания аналитической
функции F(z) — круг \z\ < 1, в которой была задана функция
Si{z)i — на большую область. Заметим, что, хотя и имеют ме-
место многочисленные взаимные наложения построенной цепочки
областей, полученная аналитическая функция F(z) =
Рис. 3.10
1 -,
яв-
является однозначной во всей области своего определения — на
полной плоскости z с выброшенной точкой z = 1. Дальнейшее
аналитическое продолжение функции F(z) на большую область

§ 2	ПОНЯТИЕ РИМАНОВОЙ ПОВЕРХНОСТИ	111
уже невозможно. Точка z = 1, являющаяся границей области
аналитичности функции F(z), представляет собой в определен-
определенном смысле особую точку этой функции. Поведение аналити-
аналитической функции в окрестности таких точек заслуживает более
подробного изучения, что и будет проведено в дальнейшем.
5. Правильные и особые точки аналитической функ-
функции. Пусть функция f(z) ^задана в области Q, ограниченной
контуром Г. Точка zq Е Q называется правильной точкой
функции f(z), если существует сходящийся степенной ряд
оо
^2 cn(z — zo)n, который в общей части области Q и своего круга
сходимости \z — zq\ < p(zq) сходится к функции f(z). На значе-
значение числа p(zq) накладывается единственное ограничение: p(zq)
строго больше нуля. Точки z E Q, не являющиеся правильными
точками функции f(z), называются ее особыми точками. Ясно,
что если f(z) — аналитическая в области Q, то все внутренние
точки этой области суть правильные точки функции f(z). Точки
границы Г могут быть как правильными, так и особыми точками
аналитической функции f(z). Очевидно, что все точки границы
Г, лежащие внутри круга \z — zq\ < p(zq) с центром в некоторой
правильной точке zq G Q, также являются правильными точка-
точками функции f(z). Так, в рассмотренном выше примере все точки
границы |^| = 1 области первоначального определения функции
оо
fi(z) = S %п-> за исключением точки z = 1, являются правиль-
п=0
ными точками. Единственной особой точкой этой функции мо-
может быть лишь точка z = 1. Она же является и особой точкой
функции F(z) = 	, аналитического продолжения функции
fi(z) на расширенную область. Аналогично точки z = 0, оо яв-
являются особыми точками функций ^fz и Lnz, рассмотренных
в п. 3.
Пусть аналитическая функция f\{z) первоначально задана
в области Qij и пусть все точки связного участка Г7 границы
Г этой области являются правильными точками функции Д (z).
Тогда из проведенных выше рассмотрении следует, что функ-
функция fi(z) может быть аналитически продолжена через Г7 на
большую область. Может оказаться, что все точки границы Г
области Q\ первоначального задания аналитической функции
f(z) являются правильными. В этом случае функцию f(z) бу-
будем называть аналитической в замкнутой области Q\. Из пре-
предыдущих рассмотрений следует, что функцию, аналитическую
в замкнутой области Q\, можно аналитически продолжить
на большую область Q, содержащую область Q\.

112	АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ	ГЛ. 3
Аналитическое продолжение через участок границы, содер-
содержащий лишь особые точки функции /i(^), очевидно, невозможно.
Приведем пример аналитической функции, заданной в
ограниченной области, которую невозможно продолжить на
большую область.
П р и м е р 4. Рассмотрим аналитическую функцию f(z),
заданную степенным рядом
оо
/(*) = ? ^ •	C-71)
п=0
Как легко определить с помощью простейших признаков, ряд
C.71) сходится внутри круга \z\ < 1. При действительном
оо
х —>> 1 сумма ^2 х2П неограниченно возрастает, тем самым точка
п=0
z = 1 является особой точкой f(z). Покажем, что и точки z^^m =
= exp (i-^rm), где т = 1, 2, 3,... , 2к, а к — любое натуральное
число, являются особыми точками функции f(z). Для этого рас-
рассмотрим точку %?m = р exp (г—га) @ < р < 1) и представим
значение функции f(z) в этой точке в виде
к-1	оо
/W = EC + EC	C-72)
п=0	п=/с
Первое слагаемое в C.72), являющееся суммой конечного числа
слагаемых, по абсолютной величине ограничено, а второе, в силу
выбора точки Zk,m-> может быть преобразовано к виду
п=к	п=к
При р —>> 1 сумма выражения, стоящего справа в C.73), неогра-
неограниченно возрастает. Это и доказывает, что точки ^?ш являются
особыми точками функции f(z). Но при А; —>• оо эти точки всюду
плотно1) расположены на окружности \z\ = 1. Отсюда следует,
что функция C.71) действительно непродолжима ни через ка-
какую дугу этой окружности.
Строя аналитическое продолжение функции F(z) =	 с
помощью степенных рядов, мы видели, что граница круга схо-
сходимости каждого ее элемента fk(z) проходит через точку z = 1,
:) То есть в любой ^-окрестности каждой точки окружности \z\ = 1 най-
найдутся точки последовательности {zk,m}-

ПОНЯТИЕ РИМАНОВОЙ ПОВЕРХНОСТИ
113
особую точку этой функции. Тем самым на границе круга схо-
сходимости любого из построенных степенных рядов лежит особая
точка аналитической функции, к которой этот ряд сходится. Это
свойство является общим следствием следующей теоремы.
Теорема 3.3. На границе круга сходимости степенного ря-
ряда лежит хотя бы одна особая точка аналитической функции
F(z), к которой сходится данный ряд.
Доказательство. Предположим, что все точки
оо
окружности Со круга Kq сходимости ряда f(z) = ^2 cn(z — zq)u
являются правильными, т. е. для любой точки z Е Со существу-
существует такое p(z) > 0, что в общей части круга Kq и своего круга
оо
сходимости \z — z\ < p(z) соответствующий ряд ^2 cn(z)(z — z)n
сходится к f(z). Пусть радиус круга Kq есть Rq.
Рассмотрим функцию p{z), определенную на окружности Со-
Покажем, что для любых двух точек z\ и z% на окружности Со
выполнено условие
\p(zi) ~
C.74)
Действительно, предположим, что это условие не выполнено, на-
например, \p(z2) — p{zi)\ = \zi — Z21 + S, где S > 0. Тогда круг
\Z ~
< p(z\) сходимости
ряда Y, Cn(zi)(z - h)n =
n=0
= fi(z) лежит внутри круга
\z — Z2\ < P(Z2) СХОДИМОСТИ ря-
oo
да Y cn{h){z - z2)n = /2B)
n=0
(рис. 3.11). В общей части
этих кругов и круга Kq оба
ряда сходятся к одной и той
же функции f(z). Следова-
Следовательно, функция /2B) явля-	Рис. 3.11
ется аналитическим продол-
продолжением функции fi(z). Это означает, что в круге \z — z\\ <
< p(z\) + 6 определена аналитическая функция /2B), совпада-
совпадающая с fi(z) в круге \z — z\\ < p(z\). В силу теоремы Тейлора
оо
отсюда следует, что радиус сходимости ряда ^ cn(z\)(z — zi)n
n=0
не меньше чем p(z\) + #, что противоречит исходным данным.
Итак, условие C.74) установлено.

114	АНАЛИТИЧЕСКОЕ ПРОДОЛЖЕНИЕ	ГЛ. 3
Из этого условия следует равномерная непрерывность функ-
функции p(z) на кривой Cq. Действительно, соотношение \p(zi) —
~ р{%2)\ < е выполняется для любого наперед заданного е > О,
если только выполнено условие \z\ — z<i\ < s. Так как функция
p(z) > 0, то она ограничена снизу и в силу непрерывности дости-
достигает на Со своей точной нижней грани г) p(z) ^ p{zq) = ро > 0.
Последнее неравенство имеет место, потому что для всех z Е Со
выполняется строгое неравенство p(z) > 0.
В силу единственности аналитического продолжения можно
утверждать, что в круге \z — zq\ < Ro + ро определена одно-
однозначная аналитическая функция F(z), совпадающая с функци-
функцией f(z) в круге \z — zq\ < Ro. Следовательно, радиус сходимости
ОО
исходного степенного ряда ^ cn(z — zo)n должен быть Rq + ро,
п=0
а не Ro. Но это противоречит условию теоремы. Итак, предпо-
предположение, что все точки границы круга сходимости правильные,
приводит к противоречию. Теорема доказана.
Из теоремы 3.3 следует, что радиус круга сходимости сте-
степенного ряда определяется расстоянием от центра сходимо-
сходимости до ближайшей особой точки той аналитической функции,
к которой сходится данный ряд.
6. Понятие полной аналитической функции. Преды-
Предыдущие рассмотрения позволили построить аналитическое про-
продолжение функции fi(z)j заданной в области Gi, на большую
область G = Gi + G2 или соответствующую риманову поверх-
поверхность. Как мы видели, можно рассматривать аналитическое
продолжение вдоль цепочки областей Gi, G2,-• • •> Gn, имеющих
общие части G'a+i, B которых совпадают аналитические функ-
функции fi(z), /2B),..., fn{z), заданные в областях Gi, G2-,- • •, Gn-
При этом мы получим в области Q — Gi + G2 + * * * + Gn или на
соответствующей римановой поверхности R однозначную ана-
аналитическую функцию F(z), являющуюся аналитическим про-
продолжением функции fi(z).
Если аналитическая функция fi(z) первоначально задана в
области Gi-, то, строя различные цепочки областей, выходящие
из области Gi, мы можем получить аналитическое продолжение
функции fi(z) на различные области, содержащие область Gi-
При этом существенным является понятие полной аналитиче-
аналитической функции.
Функция F(z), полученная путем аналитического продол-
продолжения вдоль всевозможных цепочек областей, выходящих из
:) См. вып. 1.

§ 2	ПОНЯТИЕ РИМАНОВОЙ ПОВЕРХНОСТИ	115
области Q\ первоначального задания аналитической функции
/l(^), называется полной аналитической функцией. Ее область
определения R называется естественной областью существо-
существования полной аналитической функции.
Согласно только что проведенным рассмотрениям естествен-
естественная область существования R полной аналитической функции
F(z) может быть римановой поверхностью. Отметим, что ана-
аналитическое продолжение функции F(z) за границу Г ее есте-
естественной области существования R уже невозможно. При этом
все точки этой границы являются особыми точками функции
F(z). Это легко доказать. Предположим, что точка zq Е Г яв-
является правильной точкой функции F(z). В таком случае, по
определению правильной точки, внутри круга \z — zq\ < p(zo)
существует некоторая аналитическая функция Ф(^), совпадаю-
совпадающая с F(z) в общей части данного круга и области Q. Но круг
\z — zo\ < p(zo) заведомо выходит из области Q, поэтому Ф(^)
является аналитическим продолжением полной аналитической
функции через границу ее естественной области существования,
что невозможно.
В рассмотренных в предыдущих пунктах примерах мы по-
построили ряд полных аналитических функций и их естествен-
естественные области существования. Так, естественными областями су-
существования полных аналитических функций yfz и Lnz явля-
являются соответственно n-листная и бесконечнолистная римановы
поверхности; естественной областью существования полной ана-
аналитической функции 	 — полная комплексная плоскость с
выброшенной точкой z = 1; естественной областью существова-
существования функции C.71), рассмотренной в примере 4, — единичный
круг \z\ < 1.
При этом в последнем примере область Q\ первоначального
задания аналитической функции fi(z) такова, что невозмож-
невозможно аналитическое продолжение функции fi(z) за границу Г\
области Q\. Это и означает, что fi(z) — полная аналитическая
функция и Q\ — ее естественная область существования. Ес-
Если же область Q\ такова, что возможно аналитическое продол-
продолжение fi(z) на большую область, то функцию fi(z) называют
элементом полной аналитической функции F(z). Аналитиче-
Аналитическое продолжение /2B) функции /i(^), заданной в области Q\,
на область Qi, имеющую с Q\ общую часть Qyi, будем назы-
называть непосредственным аналитическим продолжением функ-
функции fi(z).

ГЛАВА 4
РЯД ЛОРАНА И ИЗОЛИРОВАННЫЕ ОСОБЫЕ
ТОЧКИ
В этой главе будет изучено поведение однозначной анали-
аналитической функции в окрестности ее изолированных особых то-
точек. Знание этого поведения не только позволяет глубже про-
проникнуть в природу аналитических функций, но и находит пря-
прямое практическое применение в многочисленных приложениях
теории функций комплексной переменной.
В предыдущих главах мы видели, какую большую роль игра-
играют степенные ряды и, в частности, ряд Тейлора в изучении
свойств аналитических функций в области, где отсутствуют осо-
особые точки исследуемых функций. Аналогичную роль при изу-
изучении свойств аналитических функций в окрестности их изоли-
изолированных особых точек играет ряд Лорана.
§ 1. Ряд Лорана
1. Область сходимости ряда Лорана. Рассмотрим ряд
вида
ОО
? Cniz-zoT,	D.1)
п= — оо
где zq — фиксированная точка комплексной плоскости, сп —
некоторые комплексные числа, а суммирование ведется как по
положительным, так и по отрицательным значениям индекса п.
Ряд D.1) носит название ряда Лорана. Установим область схо-
сходимости этого ряда. Для этого представим выражение D.1) в
виде
оо	оо	оо
cn(z - zof = ? cn(z - zof + ? (^r-	D.2)
n=0	n=l

РЯД ЛОРАНА	117
Очевидно, областью сходимости ряда D.1) является общая часть
областей сходимости каждого из слагаемых правой части D.2).
оо
Областью сходимости ряда ^ cn(z — zqO1 является круг с цен-
п=0
тром в точке zq некоторого радиуса R\ (как было установлено
в гл. 2, значение R\ может, в частности, равняться нулю или
бесконечности). Внутри круга сходимости этот ряд сходится к
некоторой аналитической функции комплексной переменной
п=0
Для определения области сходимости ряда }2 т	ILT~ сделаем
х	71 = 1 ^ ~ ZQ>
замену переменной, положив ? = 	. Тогда этот ряд примет
оо	z~z°
вид ^2 с-пСп- То есть он представляет собой обычный степенной
п=1
ряд, сходящийся внутри своего круга сходимости к некоторой
аналитической функции ср(() комплексной переменной (. Обо-
Обозначим радиус сходимости полученного степенного ряда через
—. Тогда
2	оо
п=1
Возвращаясь к старой переменной и полагая (p(?(z)) = /2(^M
получим
оо
с"" , \z-zQ\>R2.	D.5)
ОО
Отсюда следует, что областью сходимости ряда ^ -—~п по
n=i (z ~ z®>
отрицательным степеням разности (z — zq) является область,
внешняя к окружности \z — zq\ = R2 (так же как и i?i, значение
i?2 может, в частности, равняться нулю или бесконечности).
Итак, каждый из степенных рядов правой части D.2) схо-
сходится в своей области сходимости к соответствующей аналити-
аналитической функции. Если i?2 < i?i, то существует общая область
сходимости этих рядов - круговое кольцо i?2 < \z — zq\ < i?i, в
котором ряд D.1) сходится к аналитической функции
f2(z) = Y, c^z ~ ^о)П' R2<\z- zo\ < Rl
n= — 00
D.6)

118
РЯД ЛОРАНА И ИЗОЛИРОВАННЫЕ ОСОБЫЕ ТОЧКИ
ГЛ. 4
Так как ряды D.3) и D.4) являются обычными степенными ря-
рядами, то в указанной области функция f(z) обладает всеми свой-
свойствами суммы степенного ряда. Это означает, что ряд Лорана
D.1) сходится внутри своего кольца сходимости к некоторой
функции f{z)j аналитической в данном кольце.
Если i?2 > R\, то ряды D.3) и D.5) общей области сходи-
сходимости не имеют. Тем самым в этом случае ряд D.1) нигде не
сходится к какой-либо функции.
2. Разложение аналитической функции в ряд Лора-
Лорана. Теперь естественно поставить вопрос: можно ли функции,
аналитической в некотором
круговом кольце, сопоста-
сопоставить ряд Лорана, сходящий-
сходящийся к этой функции в данном
кольце? Ответ на этот вопрос
дает следующая теорема.
Теорема 4.1. Функция
f(z), аналитическая в круго-
круговом кольце i?2 < \z — zq\ <
<	i?i, однозначно предста-
представляется в этом кольце схо-
сходящимся рядом Лорана.
Доказательство.
Фиксируем произвольную
точку z внутри кольца R2 <
<	\z — zq\ < R\ и построим
Рис. 4.1 окружности Cr^ и Сщ с цен-
центрами в 2о, радиусы которых
удовлетворяют условиям R2 < R2 < R[ < R\, R'2 < \z — z$\ < R[
(рис. 4.1). Согласно формуле Коши для многосвязной области
имеет место соотношение
На Cri выполняется неравенство
представив дробь
С-*
в виде
1
С - zo
1
q < 1. Поэтому,
C-
(С - го) - (г - г0) С - го i z ~ z° С, - z0 ^\C, - z0
С - го	и=0
и проведя почленное интегрирование, что возможно в силу рав-
равномерной сходимости ряда по переменной С (подробнее см. гл. 2),

РЯД ЛОРАНА
119
получим
где
- l [ /
n=0
Так как на CR/ выполняется неравенство
логично предыдущему имеем
С-*
п=0
z — zo
D.8)
D.9)
< 1, то ана-
В результате почленного интегрирования этого ряда получим
/ОО
Ж1^с = У-^-,	D.Ю)
C-z	^ (z - zo)n	V }
\
ск
п-\
где
D.11)
Изменив направление интегрирования в D.11), перепишем это
выражение в виде
Ж) At
(С-*<>)-'
> 0.
D.12)
Заметим, что подынтегральные функции в D.9) и D.12) являют-
являют~^о| <
- Поэто-
Поэтося аналитическими в круговом кольце i?2 < ||
му в силу теоремы Коши значения соответствующих интегралов
не изменятся при произвольной деформации контуров интегри-
интегрирования в области аналитичности подынтегральных функций.
Это позволяет объединить формулы D.9) и D.12):
х dC, n = 0,±l,±2,...,	D.13)
(С
с
где С — произвольный замкнутый контур, лежащий в кольце
i?2 < |^ "" 2о| < i?i и содерж:ащий точку ^о внутри. Возвратив-
Возвратившись к формуле D.7), получим
ОО
= E
-zof, D.14)
п=0
п=1

120	РЯД ЛОРАНА И ИЗОЛИРОВАННЫЕ ОСОБЫЕ ТОЧКИ	ГЛ. 4
где коэффициенты сп для всех значений индекса п определяют-
определяются единообразной формулой D.13). Так как z — произвольная
точка внутри кольца i?2 < \z — zq\ < i?i, то отсюда следует, что
ряд D.14) сходится к функции f(z) всюду внутри данного коль-
кольца, причем в замкнутом кольце i?2 < R2 ^ \z — zq\ ^ R\ < R\ ряд
сходится к функции f(z) равномерно. Остается доказать един-
единственность разложения D.14). Предположим, что имеет место
другое разложение:
оо
п= — оо
где хотя бы один коэффициент с'п ф сп. Тогда всюду внутри
кольца i?2 < \z — z$\ < R\ имеет место равенство
cn(z-z0)n= ^ <И*-*о)п.	D.15)
п= — оо	п= — оо
Проведем окружность Cr радиуса i?, R2 < R < i?i, с центром в
точке го- Ряды D.15) сходятся на Ся равномерно. Умножим их
на (z — zo)~m~11 где т — фиксированное целое число, и проин-
проинтегрируем почленно. Рассмотрим J (z — zo)n~m~1 dz. Положив
с*
z — zq = Ret(p, получим	R
f (z- zQ)n-m~l dz = Rn~mi Je^n-m^ d^ = { °' " Ф m'
сл	о	I 27ri' n =m-
D.16)
Учтя D.16), найдем, что после указанного интегрирования вы-
выражения D.15) отличными от нуля окажутся лишь по одному
слагаемому из бесконечных сумм в левой и правой частях этого
выражения. Отсюда получим: ст = с'т. Так как т — произ-
произвольное число, то это и доказывает единственность разложения
D.14). Теорема полностью доказана.
Из полученных результатов следует, что точной областью
сходимости ряда Лорана D.1) является круговое кольцо i?2 <
< \z — zq\ < i?i, на границах которого имеется хотя бы по одной
особой точке аналитической функции f(z), к которой сходится
ряд D.1). Последнее утверждение является следствием теоре-
теоремы 3.3.
§ 2. Классификация изолированных особых точек
однозначной аналитической функции
Точка zq называется изолированной особой точкой функ-
функции f(z), если f(z) — однозначная и аналитическая в круговом

§ 2	КЛАССИФИКАЦИЯ ИЗОЛИРОВАННЫХ ОСОБЫХ ТОЧЕК	121
кольце 0 < \z — zq\ < i?i, а точка zq является особой точ-
точкой функции f(z). В самой точке zq функция f(z) может быть
не определена. Изучим поведение функции f(z) в окрестности
точки zq. Согласно предыдущему параграфу функцию f(z) в
окрестности точки zq можно разложить в ряд Лорана D.14),
сходящийся в кольце 0 < | z — zq | < R\. При этом возможны три
различных случая:
1° Полученный ряд Лорана не содержит членов с отрица-
отрицательными степенями разности (z — zq).
2° Содержит конечное число членов с отрицательными сте-
степенями разности (z — zq).
3° Содержит бесконечное число членов с отрицательными
степенями разности (z — zq).
В зависимости от указанных возможностей и производится
классификация изолированных особых точек. Перейдем к после-
последовательному рассмотрению каждого из указанных выше слу-
случаев.
1° Ряд Лорана функции f(z) в окрестности ее изолирован-
изолированной особой точки zq не содержит членов с отрицательными сте-
оо
пенями разности (z — zq), т.е. f(z) = ^ cn(z — zqO1. Как лег-
п=0
ко видеть, при z —>• zq существует предельное значение функ-
функции f(z), причем это предельное значение равно со- Если функ-
функция f(z) не была определена в точке zq, to доопределим ее, по-
положив /(zq) = со- Если первоначально заданное значение /(zq)
не совпадает с со, то изменим значение функции f(z) в точке
zq, положив f (zq) = Со- Так определенная функция f(z) будет
аналитической всюду внутри круга \z — zq\ < R\. Тем самым мы
устранили разрыв функции f(z) в точке zq. Поэтому изолиро-
изолированная особая точка zq функции f(z), для которой разложение
f(z) в ряд Лорана в окрестности zq не содержит членов с отрица-
отрицательными степенями разности (z — zq), называется устранимой
особой точкой.
Проведенные рассмотрения доказывают следующую теорему.
Теорема 4.2. Если точка zq является устранимой особой
точкой аналитической функции f(z), то существует предель-
предельное значение lira f(z) = со, причем \cq\ < оо.
Заметим, что в окрестности устранимой особой точки функ-
функция f(z) ограничена и может быть представлена в виде
f(z) = (z — zo)m(p(z),	D.17)
где т ^ 0 — целое число, а (p(zq) ф 0. При этом, если lira f(z) = 0,
то в представлении D.17) число т > 0 определяет порядок нуля
функции f(z) в точке zq.

122	РЯД ЛОРАНА И ИЗОЛИРОВАННЫЕ ОСОБЫЕ ТОЧКИ	ГЛ. 4
Имеет место и обратная теорема, которую мы докажем в уси-
усиленной формулировке.
Теорема 4.3. Если функция f(z), аналитическая в круго-
круговом кольце 0 < \z — zq\ < i?i, ограничена (\f(z)\ < М при 0 <
< \z — zq\ < i?i), то точка zq есть устранимая особая точка
функции f(z).
Доказательство. Разложим функцию f(z) в ряд Ло-
Лорана D.14) и рассмотрим выражение D.13) для коэффициентов
этого ряда:
с
В качестве контура интегрирования выберем круг с центром в
точке zq радиуса р. Тогда в силу условия теоремы имеет место
мажорантная оценка
\сп\ <Мр~п.	D.18)
Будем рассматривать коэффициенты с отрицательным индек-
индексом п < 0. Так как значение коэффициентов сп не зависит от р,
то из D.18) получим сп = 0 при п < 0, что и доказывает теорему.
2° Ряд Лорана функции f(z) в окрестности ее изолированной
особой точки zq содержит конечное число т членов с отрицатель-
оо
ными степенями разности (z — zq\ т. е. f(z) = ^ cn(z — zo)n.
п=—т
В этом случае точка zq называется полюсом порядка т функ-
функции f(z). Поведение аналитической функции в окрестности ее
полюса определяется следующей теоремой.
Теорема 4.4. Если точка zq является полюсом аналитиче-
аналитической функции f(z), то при z —>• zq модуль функции f(z) неогра-
неограниченно возрастает независимо от способа стремления точки
Z К Zq.
Доказательство. Представим функцию f(z) в
окрестности точки zq в виде
п=0
)-m{c-m + c-m+i(z -zo) + ... + c-i(z- zo)m~1} +
(X)
n(z - ^T = (z- *оГтф) + Y,cn(z- zo)n. D.19)
n=0	n=0
Функция tp(z), очевидно, является ограниченной аналитической
функцией в окрестности точки zq. Из представления D.19) сле-
следует, что при z —>• zq модуль функции f (z) неограниченно возра-

§ 2	КЛАССИФИКАЦИЯ ИЗОЛИРОВАННЫХ ОСОБЫХ ТОЧЕК	123
стает независимо от способа стремления точки z к точке zo, что
и доказывает теорему. Заметим, что, если доопределить функ-
функцию (p(z) в точке zqj положив (f(zo) = c_m ф 0, формула D.19)
может быть переписана в виде
f(z) = №)	D.20)
J v J (z- zo)m'	v J
где i/j(z) — аналитическая функция и ip(zo) ф 0] число т назы-
называется порядком полюса.
Имеет место и теорема, обратная теореме 4.4.
Теорема 4.5. Если функция f{z), аналитическая в окрест-
окрестности своей изолированной особой точки zq, неограниченно воз-
возрастает по модулю независимо от способа стремления точки
z к точке z$, то точка zq является полюсом функции f(z).
Доказательство. По условию теоремы для любого
числа А > 0 можно указать такую ^-окрестность точки ^о, в ко-
которой |/(;z)| > А. Рассмотрим функцию g(z) = -т^т- В указанной
^-окрестности точки zq эта функция является аналитической и
lira g(z) = 0. Поэтому на основании теоремы 4.3 точка zq явля-
ется устранимой особой точкой функции g(z), и функция g(z) в
силу формулы D.17) в окрестности точки zq может быть пред-
представлена в виде g(z) = (z — z$)m(p(z), где cp(z) — аналитическая
функция, причем <p(zo) Ф 0, а т > 0. Тогда в окрестности точки
zq для исходной функции f (z) имеет место представление f(z) =
= —— =	— = —r^r- Оно в силу условия (f(zo) ф 0 может
быть переписано в виде f(z) =	\ш ? совпадающем с пред-
\Z Zq j
ставлением D.20), где ip(z) — аналитическая функция. Отсюда
и следует, что точка zq является полюсом порядка т функции
f(z). Теорема доказана.
Заметим, что точка ^о, являющаяся нулем порядка т анали-
аналитической функции g(z), является полюсом того же порядка т
функции f(z) = —г^-, и наоборот. Это устанавливает очень про-
простую связь между нулями и полюсами аналитических функций.
3° Ряд Лорана функции f(z) в окрестности ее изолированной
особой точки zq содержит бесконечное число членов с отрица-
/	°°	\
тельными степенями разности (z — zq) lf(z)= ^ cn(z — zo)n\.
^	п= — сю	^
В этом случае точка zq называется существенно особой точкой
функции f(z). Поведение аналитической функции в окрестности
ее существенно особой точки описывается следующей теоремой.

124	РЯД ЛОРАНА И ИЗОЛИРОВАННЫЕ ОСОБЫЕ ТОЧКИ	ГЛ. 4
Теорема 4.6 (теорема Сохоцкого-Вейерштрасса).
Каково бы ни было е > 0, в любой окрестности существенно
особой точки zq функции f(z) найдется хотя бы одна точка z\,
в которой значение функции f(z) отличается от произвольно
заданного комплексного числа В меньше чем на е.
Доказательство. Предположим, что теорема неверна,
т.е. при заданном комплексном числе В и заданном е > 0 най-
найдется такое г/о > 0, что во всех точках z из r/o-окрестности точки
zq значение функции f(z) отличается от заданного В больше
чем на е:
\f(z)-B\>e, \z-zo\<m.	D.21)
Рассмотрим вспомогательную функцию i/j(z) = -7Гт—-. В силу
f(z) - В
D.21) функция i/j(z) определена и ограничена в г/о-окрестности
точки zq. Следовательно, по теореме 4.3 точка zq является устра-
устранимой особой точкой функции ^(z). Это означает, что разложе-
разложение функции i/j(z) в окрестности точки zq имеет вид
ф(г) = (z - zo)m<p(z), ФЫ^О.
Тогда, в силу определения функции ip(z), в данной окрестности
точки zq имеет место следующее разложение функции f(z):
f(z) = (z-zo)-mip(z)+B,	D.22)
где аналитическая функция (f(z) = —— ограничена в г/о-окрест-
(p(z)
ности точки zq. Но разложение D.22) означает, что точка zq яв-
является или полюсом порядка га, или при га = 0 правильной
точкой функции f(z)j и разложение в ряд Лорана последней
должно содержать лишь конечное число членов, что противоре-
противоречит условию теоремы. Полученное противоречие и доказывает
теорему.
Теорема 4.6 дает следующую характеристику поведения ана-
аналитической функции в окрестности \z — zq\ < щ существенно
особой точки: в существенно особой точке zq не существует ко-
конечного или бесконечного предельного значения аналитической
функции. В зависимости от выбора последовательности точек,
сходящейся к точке ^о, мы можем получить последовательно-
последовательности значений функции, сходящиеся к различным пределам. При
этом всегда можно выбрать последовательность, сходящуюся к
любому наперед заданному комплексному числу, включая и оо.
Очевидно, нет необходимости доказывать теорему, обратную
теореме 4.6, так как если при z —>> zq не существует конечного
или бесконечного предела функции f(z), то в силу теорем 4.2 и
4.4 точка zq не может быть ни устранимой, ни полюсом.

§ 2	КЛАССИФИКАЦИЯ ИЗОЛИРОВАННЫХ ОСОБЫХ ТОЧЕК	125
Заметим также, что если точка zq является существенно осо-
особой точкой функции f(z), причем f(z) ^ 0 в некоторой окрест-
окрестности точки zqj то и для функции g(z) = l/f(z) точка zq явля-
является существенно особой точкой.
Рассмотренные три случая исчерпывают возможный вид
разложения аналитической функции в ряд Лорана в окрестно-
окрестности ее изолированной особой точки и имеют решающее значение
для выяснения общего хода изменения аналитической функции
в окрестности ее особых точек.
Из проведенных рассмотрений следует, что возможны две
различные точки зрения на классификацию изолированных осо-
особых точек однозначной аналитической функции, приводящие к
одинаковым результатам. Мы исходили из аналитической точ-
точки зрения, основанной на характере разложения функции в ряд
Лорана, и установили, как ведет себя сама функция при стрем-
стремлении к особой точке. Возможен и другой, геометрический под-
подход, при котором в основу классификации кладется поведение
функции в окрестности ее изолированной особой точки. При
этом, если функция ограничена в окрестности особой точки, то
эта точка называется устранимой и, как следует из теоремы 4.3,
разложение данной функции в ряд Лорана в окрестности этой
особой точки не содержит отрицательных степеней. Если при
стремлении к особой точке функция имеет бесконечный предел,
то эта точка — полюс и разложение в ряд Лорана имеет конеч-
конечное число отрицательных степеней. И наконец, если функция
при стремлении к особой точке не имеет конечного или беско-
бесконечного предела, то это — существенно особая точка, разложе-
разложение в ряд Лорана содержит бесконечное число отрицательных
степеней.
В заключение данного параграфа остановимся на вопросе
о поведении аналитической функции в окрестности бесконеч-
бесконечно удаленной точки. Бесконечно удаленная точка комплексной
плоскости является изолированной особой точкой однозначной
аналитической функции f(z), если можно указать такое значе-
значение i?, что вне круга \z\ > R функция f(z) не имеет особых то-
точек, находящихся на конечном расстоянии от точки z = 0. Так
как f(z) является аналитической функцией в круговом кольце
R < \z\ < oo, то ее можно разложить в ряд Лорана
ОО
f(z) = V cnzn, R<\z\< oo,	D.23)
п= — оо
сходящийся к f(z) в данном кольце. Так же как и для конечной
изолированной особой точки zq здесь возможны три случая:
1° Точка z = оо называется устранимой особой точкой
функции f(z), если разложение D.23) не содержит членов с по-

126	РЯД ЛОРАНА И ИЗОЛИРОВАННЫЕ ОСОБЫЕ ТОЧКИ	ГЛ. 4
оо	оо
ложительными степенями z, т. е. f(z) = ^ -^- = cq + ^ ~~^г>
п=0 ^	п=1 ^
или если при z —>• оо существует конечное предельное значение
функции /(^), не зависящее от способа предельного перехода.
Если со = c_i = ... = c_m+i = 0, с_т т^ 0, то бесконечно уда-
удаленная точка является нулем m-го порядка функции f(z).
2° Точка z = оо называется полюсом порядка т функции
f(z), если разложение D.23) содержит конечное т число членов
т
с положительными степенями z, т.е. f(z) = J^ cn?n (га > 0),
п= — оо
или если эта функция неограниченно возрастает по модулю при
z —>• оо независимо от способа предельного перехода.
3° Точка 2 = оо называется существенно особой точкой
функции f(z), если разложение D.23) содержит бесконечное
число членов с положительными степенями z, т. е. f(z) =
оо
= S cnzn\ или если в зависимости от выбора последователь-
п= — оо
ности {zn} —>> оо можно получить последовательность значений
()}, сходящуюся к любому наперед заданному пределу.
Очевидно, доказательство эквивалентности всех приведен-
приведенных выше определений характера изолированной особой точки
z = оо может быть проведено так же, как и для случая конечной
изолированной особой точки.
Кроме того, как легко видеть, преобразование z = — переводит точку
оо плоскости z в точку С = 0, характер же особой точки при этом преобра-
преобразовании не меняется в силу следующей общей теоремы.
Теорема 4.7. Пусть точка zq является изолированной особой точкой
функции f{z), аналитической в области Q. Пусть аналитическая функция
? = ip(z) устанавливает взаимно однозначное соответствие между обла-
областью Q и областью Q' комплексной плоскости С, в которой определена
обратная функция z = <^(С)- Тогда точка (о = ф(%о) является изолирован-
изолированной особой точкой аналитической функции F{?) = /[^(C)L причем харак-
характер этой особой точки тот же , что и точки zq.
Эта теорема является очевидным следствием свойства аналитических
функций, установленного в гл. 1, в силу которого аналитическая функция
от аналитической функции является аналитической, а также геометриче-
геометрических свойств аналитической функции в окрестности изолированной особой
точки.
Пример. Рассмотрим функцию f(z) = —-^^=. Данная
v 1 + z2
многозначная функция имеет две точки разветвления z = =bi.
Точка z = оо — ее правильная точка. Поэтому в круговом коль-
кольце 1 < \z\ < оо определены две ветви этой функции, являющие-
являющиеся однозначными аналитическими функциями в данном кольце.
Выберем ветвь, являющуюся непосредственным аналитическим

КЛАССИФИКАЦИЯ ИЗОЛИРОВАННЫХ ОСОБЫХ ТОЧЕК
127
1
продолжением действительной функции	действительной
переменной х > 1, и построим ее разложение в ряд Лорана в
окрестности точки z = оо. Для этого, положив ( = -, отобра-
z
зим данное кольцо на круг единичного радиуса на плоскости ?
(при этом точка z = оо переходит в точку ( = 0) и разложим
1 _ С
функцию
в ряд Тейлора в окрестно-
окрестности ее правильной точки ? = 0. Предварительно заметим, что
функция <р(?) является производной функции VKC) = лА + С2-
(При этом наш выбор ветви исходной функции f(z) определяет
выбор той ветви функции VKC)? Для которой ^@) = +1.) Что-
Чтобы разложить функцию ф(() в ряд Тейлора, положим w = B
и рассмотрим функцию х(^) = л/1 + w. Вычисляя производные
функции xiw)i получаем
—п
w=0
г-1 Bп-2)!
= ("IO
Тогда разложение выбранной ветви функции
\w\ < 1 принимает вид
22п-1(п-1)\'
^) в круге
Отсюда для функции ^(С) ПРИ ICI < 1 получим
и для функции
n=l
Bп-_2)!	>2n-l =
п=1	к=0
Наконец, для выбранной ветви функции f(z) в кольце 1 < \z\ <
< оо получаем разложение в ряд Лорана
(X)
,к Bк)\ 1
/(*) =
D.24)

ГЛАВА 5
ТЕОРИЯ ВЫЧЕТОВ И ИХ ПРИЛОЖЕНИЯ
§ 1. Вычет аналитической функции в изолированной
особой точке
1. Определение и формулы вычисления вычета.
Введем важное для приложений понятие вычета однозначной
аналитической функции в изолированной особой точке.
Пусть точка zq является изолированной особой точкой од-
однозначной аналитической функции f(z). Согласно предыдущим
рассмотрениям в окрестности этой точки функция f(z) может
быть единственным образом разложена в ряд Лорана
/(*)= ^ cn(z-zof,	E.1)
п= — оо
где
с
и, в частности,
С-1 = —
с
Вычетом аналитической функции f(z) в изолированной осо-
особой точке zq называется комплексное число, равное значению
интеграла —://(С)^Сэ взятому в положительном направле-
2ш 7
нии по любому лежащему в области аналитичности функции
f(z) замкнутому контуру 7? содержащему единственную осо-
особую точку zq функции f(z). Для обозначения вычета обычно
применяются выражения Выч [f(z), zq] или res [f(z), zq]. Мы в
дальнейшем будем пользоваться первым обозначением. Очевид-
Очевидно, что если точка zq является правильной или устранимой осо-

§ 1	ВЫЧЕТ ФУНКЦИИ В ИЗОЛИРОВАННОЙ ОСОБОЙ ТОЧКЕ 129
бой точкой функции f(z), то вычет f(z) в этой точке равен ну-
нулю. Для вычисления вычета функции f(z) в ее изолированной
особой точке может быть применена формула E.3):
Выч [/(*), *о] = зЬ
с
Однако в ряде случаев может быть указан более простой способ
вычисления вычета, сводящийся к дифференцированию функ-
функции f(z) в окрестности точки zq. Тем самым вычисление контур-
контурного интеграла от аналитической функции может быть заменено
вычислением производных от этой функции в некоторых точках,
лежащих внутри контура интегрирования. Это обстоятельство
определяет одно из основных приложений теории вычетов. Пе-
Перейдем к рассмотрению указанных случаев.
1° Пусть точка zq является полюсом первого порядка функ-
функции f(z). Тогда в окрестности этой точки имеет место разложе-
разложение
f(z) = c-i{z - ^о) + с0 + cx(z - z0) + ...	E.5)
Умножив обе части E.5) на (z — zq) и перейдя к пределу при
z —>• zqj получим
c_i = \im(z - zo)f(z).	E.6)
Заметим, что в данном случае функция f(z) в окрестности точ-
точки zq может быть представлена в виде отношения двух анали-
аналитических функций:
причем (f(zo) ф 0, а точка zq является нулем первого порядка
функции i/j(z), т.е.
^±{z - z0J + ..., ф'(го) ф 0. E.8)
Тогда из E.6)-E.8) получим следующую формулу.
Формула вычисления вычета в полюсе первого порядка:
Пример 1. Пусть f(z) = ——-. Особыми точками функции
f(z) являются точки Zk = \/l= exp [i-^— ) (k = 0,1,... ,n — 1),
V ft J
причем все эти точки представляют собой полюсы первого по-
порядка. Найдем Выч [f(z),Zk]. Согласно формуле E.9) получим
Выч [/(*), zk\ = -^T=1-zl=1- exp (г^) {zl = 1). E.10)
5 А.Г. Свешников, А.Н. Тихонов

130	ТЕОРИЯ ВЫЧЕТОВ И ИХ ПРИЛОЖЕНИЯ	ГЛ. 5
2° Пусть точка zq является полюсом порядка т функции
f(z). Согласно предыдущему в окрестности этой точки имеет
место разложение
f(z) = c-m(z - zo)-m + ... + c-i(z - zq)-1 + c0 + ci(z - zQ) + ...
E.11)
Умножив обе части E.11) на (z — zqI71, получим
(z - zo)mf(z) = c_m + c-m+1(z -zo) + ... + c-1(z- zo)™'1 + ...
E.12)
Взяв производную порядка (га — 1) от обеих частей этого равен-
равенства и перейдя к пределу при z —>• zq, окончательно получим
следующую формулу.
Формула вычисления вычета в полюсе порядка га:
Выч [/(*),«,] = J-L_Jimo?^T[(z-z0rf(z)}. E.13)
Как легко видеть, формула E.6) является частным случаем по-
последней формулы.
Пример 2. Пусть f(z) = —	—. Особыми точками
этой функции являются точки ;?i52 = =Ьг, причем обе эти точки
представляют собой полюсы порядка п. Вычислим Выч [f{z),i].
Согласно E.13) получим
Выч
	^—Л = т	гг lim	 (z — i
L(l + ^2)n4 (n-1)! z^idz™-1 LV
(n-1)!,
= (-1)»-12!
(n-1)!
Z=l
_i Bn-2)! 1 = ¦ Bn-2)!
]2* V
2. Основная теорема теории вычетов. Перейдем те-
теперь к рассмотрению важнейших применений введенных поня-
понятий. Для многих теоретических рассмотрений и практических
применений весьма существенной является следующая
Теорема 5.1 {основная теорема теории вычетов).
Пусть функция f(z) является аналитической всюду в замкну-
замкнутой области Q^ за исключением конечного числа изолированных
особых точек z^ (k = 1,...,7V), лежащих внутри области Q.
Тогда
N
f /(С) d( = 2т Y, Выч [/(*),**],	E.15)
Г+	к=1

ВЫЧЕТ ФУНКЦИИ В ИЗОЛИРОВАННОЙ ОСОБОЙ ТОЧКЕ 131
где Г+ представляет собой полную границу области Q, прохо-
проходимую в положительном направлении.
Доказательство. Напомним, что если функция f(z)
является аналитической в замкнутой области Q, то все точки
границы Г этой области суть правильные точки функции f(z).
Выделим каждую из особых точек z^ функции f(z) замкнутым
контуром 7ь не содержащим внутри других особых точек, кроме
ТОЧКИ Zk.
В замкнутой многосвязной области, ограниченной контуром
Г и всеми контурами 7/с (рис. 5.1) функция f(z) является всюду
аналитической.
Поэтому по второй теореме Коши получим
N
/ /(С)^С = о.
E.16)
Перенеся второе слагаемое в E.16) направо, мы в силу формулы
E.4) и получим утверждение теоремы:
N
Г+	к=1
Большое практическое значение этой формулы заключается
в том, что во многих случаях оказывается гораздо проще вычис-
вычислить вычеты функции f(z)
в особых точках, лежащих
внутри области интегриро-
интегрирования, чем непосредственно
вычислять интеграл, стоя-
стоящий в левой части E.15).
В дальнейшем мы рассмо-
рассмотрим ряд важных приложе-
приложений полученной формулы, а
сейчас введем еще одно по-
понятие — понятие вычета в
бесконечно удаленной точке.
Пусть точка z = oo явля-
является изолированной особой точкой аналитической функции f(z).
Вычетом аналитической функции f(z) в точке z = oo на-
называется комплексное число, равное значению интеграла
Рис. 5.1
С
где контур С — произвольный замкнутый контур, вне кото-

132	ТЕОРИЯ ВЫЧЕТОВ И ИХ ПРИЛОЖЕНИЯ	ГЛ. 5
рого функция f(z) является аналитической и не имеет особых
точек, отличных от оо. Очевидно, в силу определения коэф-
коэффициентов ряда Лорана имеет место формула
Выч [/(*), оо] = -^ / /(С) d( = -c_l	E.17)
Отсюда, в частности, следует, что если точка z = оо является
устранимой особой точкой функции f(z), то Выч [f(z), оо] может
оказаться отличным от нуля, в то время как вычет в конечной
устранимой особой точке всегда равен нулю.
Формулы E.15) и E.17) позволяют доказать следующую
теорему.
Теорема 5.2. Пусть функция f(z) является аналитиче-
аналитической на полной комплексной плоскости, за исключением конеч-
конечного числа изолированных особых точек z^ (k = 1,2, ...,7V),
включая и z = оо (zn = оо). Тогда
N
Выч [f(z), Zk] = 0.	E.18)
k=i
Доказательство. Действительно, рассмотрим
замкнутый контур С, содержащий внутри все (N — 1) особые
точки Zkj расположенные на конечном расстоянии от точки z =
= 0. По теореме 5.1
N-1
1
С+	k=l
Но, в силу E.17), интеграл, стоящий слева, равен вычету функ-
функции f(z) в точке z = оо, взятому с обратным знаком, откуда и
получим утверждение теоремы 5.2.
Доказанная теорема иногда позволяет упростить вычисление
интеграла от функции комплексной переменной по замкнуто-
замкнутому контуру. Пусть функция f(z) является однозначной и ана-
аналитической на полной комплексной плоскости, за исключением
конечного числа изолированных особых точек, и требуется вы-
вычислить интеграл от f(z) по некоторому замкнутому контуру Г.
Если внутри Г содержится много особых точек функции f(z),
то применение формулы E.15) может быть сопряжено с весь-
весьма трудоемкими вычислениями. При этом может оказаться, что
вне Г функция f(z) имеет лишь несколько особых точек z^ (к =
= 1, 2,... ,?77), значение вычетов в которых, а также вычет в
бесконечно удаленной точке определяются достаточно просто.
Тогда удобнее вместо прямого вычисления искомого интеграла

§ 2	ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ	133
по формуле E.15) воспользоваться очевидным следствием фор-
формул E.15) и E.18):
т
/ /(С) d( = -2т Y, Выч [/(*),**] " 2тгг Выч [/(*), оо]. E.19)
Г+	к=1
Формула E.19) позволяет легко получить обобщение форму-
формулы Коши (см. гл. 1, § 6, формулы A.59), A.60)) на случай неогра-
неограниченной области. Рассмотрим функцию f{zI аналитическую
вне замкнутого контура Г, являющегося границей ограничен-
ограниченной области Q. Пусть все точки Г — правильные точки функ-
функции f(z), а точка z = оо — ее устранимая особая точка. Обозна-
f (z)
чим lira f(z) = /(оо). Построим вне Г функцию (p(z) =	,
z^oo	z — Zq
где zq - произвольная точка комплексной плоскости. Очевидно,
что точка z = оо является устранимой особой точкой и функции
(p(z), причем Выч [(f(z), оо] = —/(оо).
Если точка zq леж:ит внутри Г, то функция <p(z) других осо-
особых точек не имеет. Если точка zq — вне Г, то z = zq явля-
является полюсом не выше первого порядка функции tp(z), причем
BbL4[ip(z),Zo] = f(z0).
Рассмотрим интеграл J (p(() d( = J ^ ^ d(, в котором кон-
г+	г+ ^ ~ Zo
тур Г обходится таким образом, что область Q остается слева. В
силу формулы E.19) получим
2т]
JiCLdC=\ /(oo),,o-внутри Г,
С - ^о	I /(оо) _ /(^0) Zo - вне Г.
г+	ч
Формула E.20) и является обобщением интегральной формулы
Коши на случай функции f(z), аналитической в неограниченной
области.
§ 2. Вычисление определенных интегралов с помощью
вычетов
Доказанные в предыдущем параграфе теоремы находят много-
многочисленные применения не только при вычислении интегралов
от функций комплексной переменной, но и при вычислении раз-
различных определенных интегралов от функций действительной
переменной, причем часто удается достаточно просто получить
ответ и в тех случаях, когда применение других методов ана-
анализа оказывается затруднительным. Рассмотрим ряд типичных
случаев.

134	ТЕОРИЯ ВЫЧЕТОВ И ИХ ПРИЛОЖЕНИЯ	ГЛ. 5
2тг
1. Интегралы вида f R(cos63 sin 6) A6. Рассмотрим ин-
о
теграл
2тг
J= Ji2(cos0,sin0)d0,	E.21)
о
где R — рациональная функция своих аргументов. Интегралы
типа E.21) легко могут быть сведены к интегралам от аналити-
аналитической функции комплексной переменной по замкнутому конту-
контуру. Для этого сделаем замену переменной интегрирования, введя
комплексную переменную z, связанную с переменной в соотно-
соотношением z = е . Очевидно,
i(e» + «Г») = i (* + i) , sin* = 1 [z -
При изменении в от 0 до 2тг комплексная переменная 2 пробе-
пробегает замкнутый контур — окружность \z\ = 1 в положительном
направлении. Таким образом, интеграл E.21) переходит в инте-
интеграл по замкнутому контуру от функции комплексной перемен-
переменной:
1=1 Г R\z + l,z-\]^	E.22)
г J	L z	z\ z
В силу общих свойств аналитических функций подынтеграль-
подынтегральная функция в E.22), являющаяся, очевидно, рациональной
функцией
Ъ( \ _ ao+aiz + ...+anzn	,- ?^ч
представляет собой функцию, аналитическую внутри круга
|^| = 1 всюду, за исключением конечного N ^ т числа особых
точек Zk, являющихся нулями знаменателя в E.23). Поэтому в
силу теоремы 5.1
N
I = 2тг Y^ Выч [R(z),zk].	E.24)
к=1
Точки Zk являются полюсами функции R(z). Пусть а^ — по-
/	N	\
рядок полюса z^ (очевидно, ^ а^ ^ ш). Тогда на основании
v	k=i	J
формулы E.13) мож:но переписать E.24) в виде
1 = 2-Е ^Dfft ?^[(- " ЪГШ	E-25)
к=1

ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ	135
Пример 1. Вычислить интеграл
2тг
/ =
О
Положив z = е , получим
Z7T
= Г	^_^, |о|<1.	E.26)
J l + acos<?'	'	v >
E.27)
Особыми точками подынтегральной функции являются нули
1 . ГГ Г ^
знаменателя ^i52 = — -± у — — 1. Это полюсы первого порядка.
Так как z\ • Z2 = 1, то лишь одна из этих точек лежит внутри
круга \z\ = 1. Как легко видеть, это — точка z\ = — - + у — — 1.
Поэтому в силу теоремы 5.1
= 4тгВыч [——^	,^i] =4тг
E.28)
ОО
2. Интегралы вида f f(x)dx. В этом пункте мы рас-
—оо
смотрим применение теории вычетов к вычислению несобствен-
(X)
ных интегралов первого рода х) вида J f(x) dx. Мы будем рас-
— оо
сматривать тот случай, когда функция f(x) задана на всей дей-
действительной оси и может быть аналитически продолжена на
верхнюю полуплоскость так, что ее продолжение удовлетворяет
некоторым дополнительным условиям. Эти условия будут сфор-
сформулированы ниже в теореме 5.3.
Для дальнейших рассмотрений нам потребуются некоторые
вспомогательные положения.
Лемма 1. Пусть функция f(z) является аналитической в
верхней полуплоскости Im2:>0 всюду, за исключением конеч-
конечного числа изолированных особых точек, и существуют такие
положительные числа Rq, M и 8, что для всех точек верх-
верхней полуплоскости, удовлетворяющих условию \z\ > Rq, имеет
место оценка
^	>Ro-	E.29)
:) Определение несобственных интегралов см. вып. 2.

136
ТЕОРИЯ ВЫЧЕТОВ И ИХ ПРИЛОЖЕНИЯ
ГЛ. 5
Тогда
lim
E.30)
где контур интегрирования C'R представляет собой полу-
полуокружность \z\ = R, Im z > 0 в верхней полуплоскости z
(рис. 5.2).
Действительно, в силу A.41) и условий леммы при R > R$
/
МттД тгМ
что и доказывает лемму.
Замечание 1.
каком-либо секторе
Если условия леммы выполнены в
< arg z < if2 плоскости z, то формула
E.30) имеет место при инте-
интегрировании по дуге C'R окруж-
окружности, лежащей в данном сек-
секторе.
Замечание 2.
Условия леммы, очевидно, бу-
будут выполнены, если функция
f(z) является аналитической
в окрестности бесконечно уда-
удаленной точки и точка z = оо
представляет собой нуль не ни-
ниже второго порядка функции
f(z). Действительно, в этом
случае разложение функции f(z) в ряд Лорана в окрестности
z = оо имеет вид
Рис- 5'2
причем 1^(^I < М, откуда и следует оценка E.29) при 5 = 1.
Лемма 1 находит широкое применение при вычислении ряда
оо
несобственных интегралов вида J f(x)dx.
— оо
Теорема 5.3. Пусть функция /(ж), заданная на всей дей-
действительной оси —оо < х < оо, может быть аналитиче-
аналитически продолжена на верхнюю полуплоскость Im z ^ 0, причем
ее аналитическое продолжение, функция f(z), удовлетворяет
условиям леммы 1 и не имеет особых точек на действитель-
оо
ной оси. Тогда несобственный интеграл первого рода f f(x)dx

2	ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ	137
существует и равен
оо	N
Y,Vbi4[f(z),zk],	E.31)
к=1
оо
f
где Zk — особые точки функции f(z) в верхней полуплоскости.
Доказательство. По условию теоремы функция f(z)
в верхней полуплоскости имеет конечное число особых точек #&,
причем все они удовлетворяют условию \zk\ < Rq. Рассмотрим
замкнутый контур, состоящий из отрезка действительной оси —
—R ^ х ^ R (R> Rq) и полуокружности C'Rl \z\ = i?, в верхней
полуплоскости. В силу основной теоремы теории вычетов
R	N
J f(x)dx+ J f(z)dz = 2m^2Bbi4[f(z),zk].	E.32)
-R	C'R	k=l
Так как выполнены условия леммы 1, то предел второго слагае-
слагаемого в левой части E.32) при R —>• оо равен нулю; правая часть
E.32) при R > Rq от R не зависит. Отсюда следует, что пре-
предел первого слагаемого существует и его значение определяется
формулой E.31). Теорема доказана.
Пример 2. Вычислить интеграл
1= -^-.	E.33)
Аналитическое продолжение подынтегральной функции в верх-
верхнюю полуплоскость, функция f(z) = ——-, очевидно, удовле-
удовлетворяет условиям теоремы 5.3. Ее особыми точками в верхней
полуплоскости являются точки год = ехр (г	1 [к = (J, 1J,
причем обе эти точки — полюсы первого порядка. Поэтому
)] +Выч
1
От)]} =
?=ехр(г|)
7Г
л/2
E.34)
Замечание 1. Если функция f(x) является четной
функцией и удовлетворяет условиям теоремы 5.3, то
оо	N
f f(x) dx = m^ Выч [f(z),zk].	E.35)
О	к=1

138
ТЕОРИЯ ВЫЧЕТОВ И ИХ ПРИЛОЖЕНИЯ
ГЛ. 5
Действительно, если f(x) — четная функция, то
оо	оо
J f(x)dx = 2 / f(x)dx,
О	-оо
откуда и следует формула E.35).
Замечание 2. Очевидно, имеет место аналогичная тео-
теорема и в том случае, когда аналитическое продолжение функции
f(x) в нижнюю полуплоскость удовлетворяет условиям леммы,
аналогичной лемме 1.	оо
3. Интегралы вида / emxf(x)dx. Лемма Жордана.
—оо
Вычисление следующего важного класса несобственных инте-
интегралов с помощью теории вычетов основано на применении так
называемой леммы Жордана, к доказательству которой мы сей-
сейчас перейдем.
Лемма 2 (лемма Жордана). Пусть функция f(z) яв-
является аналитической в верхней полуплоскости Im z > 0, за
исключением конечного числа изолированных особых точек, и
равномерно относительно arg z @ ^ arg z ^ тг) стремится к
нулю при \z\	д
E.36)
g (
оо. Тогда при а > О
lim Г eiaCf(()d( = O,
Яюо
где C'R — дуга полуокружности \z\ = R в верхней полуплоско-
полуплоскости z.
Доказательство. Условие равномерного стремления
f(z) к нулю означает, что при \z\ = R имеет место оценка
=R,
E.37)
где цц —>• 0 при R —>• оо. С помощью соотношения E.37) оценим
исследуемый интеграл. Сделаем замену переменной, положив
С = Rel{p', и воспользуемся очевидным соотношением
Тогда получим
simp ^ -if
тг
при
0
2
E.38)
тг/2
R j e-aRsinv dip = 2fjiR • R j e-aRsin^dip<
тг/2
< 2/jlr • R f exp ( — -^—
J	V тг
0
0 E.39)
что и доказывает лемму.

ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
139
[У
Замечание 1. Если а < 0, а функция f(z) удо-
удовлетворяет условиям леммы Жордана в нижней полуплоскости
Im z ^ 0, то формула E.36) имеет место при интегрировании
по дуге полуокружности C'R в нижней
полуплоскости z. Аналогичные утвер-
утверждения имеют место и при а = ±т
(а > 0) при интегрировании соответ-
соответственно в правой (Re z ^ 0, рис. 5.3)
или левой (Re z ^ 0) полуплоскости z.
Доказательства этих утверждений про-
проводятся совершенно аналогично преды-
предыдущему, и мы предоставляем их чи-
читателю. Выпишем только важную для
дальнейших приложений форму леммы
Жордана, относящуюся к интегрирова-
интегрированию в правой полуплоскости:
lim
Г
а>0,
z=0
где C'R - дуга полуокружности
Рис. 5.3
E.40)
z\ = R
в правой полуплоскости Re z ^ 0. Фор-
Формула E.40) и ряд последующих, в част-
частности, будут широко использованы в гл. 8 при вычислении раз-
различных интегралов, играющих важную роль в операционном ис-
исчислении.
Замечание 2. Лемма Жордана остается спра-
справедливой и в том случае, когда функция f(z) удовлетворяет
сформулированным выше условиям в полуплоскости Im z ^ уо
(уо - фиксированное число, которое может быть как положи-
положительным, так и отрицательным), а интегрирование производится
по дуге полуокружности \z — iy$\ = R в полуплоскости Im z ^ уо-
Доказательство проводится аналогично предыдущему, причем
при оценке интеграла следует сделать замену переменной инте-
интегрирования ( = Ret(p + гуо.
Замечание 3. Лемма Жордана остается справедливой
и при ослабленных условиях на функцию f(z). Пусть функция
f(z) в верхней полуплоскости Im z > у о при \z\ > Rq равномерно
относительно аргумента z — iyi стремится к нулю при \z\ —>> оо в
секторах -<р0 ^ arg (z-iyi) ^ <pi, тг-<р2 ^ arg (z-iyi) ^ тг + ^0
и равномерно ограничена в секторе (fi ^ arg (z — iyi) ^ тг — (р2, где
сро, (pi и ср2 - заданные положительные числа 0 ^ <ро? <Ръ ??2 ^ -
и 2/1 > Уо- Тогда интеграл / em^(()d( по дуге Cr окружности
cR
\z — Wi\ = R-) Iй1 % ^ Уо стремится к нулю при а > 0 и R —>• оо.

140	ТЕОРИЯ ВЫЧЕТОВ И ИХ ПРИЛОЖЕНИЯ	ГЛ. 5
Для доказательства разобьем этот интеграл на сумму / =
= Ii +12 + h + h + h интегралов по дугам CR (у\ > Im z > г/о?
arg (z - iyi) < 0), C{R] @ < arg (z - iyi) < c^i), cf fa <
< arg (z - iyi) < тт - <p2), C^ (тт - (p2 < arg B; - iyi) < тг) и C^5)
(yi > Im z > yo, arg B — iyi) > тг) и докажем сходимость к нулю
каждого интеграла в отдельности. Для интеграла 1\ получим
\I\\ ^ I^R^~amLiR\ где LiR* — длина кривой CR . При i? —)> 00
величина L^ остается ограниченной и стремится к значению
yi — уо- Поэтому |Д| ^0 при i? —)> 00. Аналогично /5 —>> 0. Схо-
Сходимость к нулю интегралов 12 и 1^ устанавливается приемом,
использованным в доказательстве леммы Жордана. Для инте-
интеграла /з легко получить оценку |/з| < Ce~aRsm(p RGr — (fi — ^2)?
где |/(С)| < С и (р* = minimi, ^2}, из которой следует, что /з —^ 0
при i? —)> 00.
Итак, лемма Жордана имеет место при значительно более
слабых ограничениях на функцию /(^), чем в случае леммы 1.
Это связано с наличием в подынтегральной функции дополни-
дополнительного множителя eia(^, который при а > 0 обеспечивает доста-
достаточно быстрое убывание подынтегральной функции в секторе
0 < ip\ ^ arg (z — iyi) ^ тг — if2 при \z\ —>> 00.
Лемма Жордана находит многочисленные применения при
вычислении широкого класса несобственных интегралов.
Теорема 5.4. Пусть функция /(ж), заданная на всей дей-
действительной оси —оо < х < оо, может быть аналитически
продолжена на верхнюю полуплоскость Im z ^ 0, а ее анали-
аналитическое продолжение f(z) в верхней полуплоскости удовле-
удовлетворяет условиям леммы Жордана и не имеет особых точек
оо
на действительной оси. Тогда интеграл f emxf(x)dx1 a > 0,
— сю
существует и равен
оо
J emxf(x)dx = 2тгг^Выч[е^/(^),^],	E.41)
-оо	k=l
где Zk — особые точки функции f(z) в верхней полуплоскости z.
Доказательство. По условию теоремы особые точки z^
функции f(z) в верхней полуплоскости удовлетворяют условию
\zk\ < Rq. Рассмотрим в верхней полуплоскости z замкнутый
контур, состоящий из отрезка действительной оси —R^x^
^ Д, Л > До и дуги C'R полуокружности \z\ = R в верхней

§ 2	ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ	141
полуплоскости z. По основной теореме теории вычетов
R	п
J ешх/(х) dx+ f e^f(C) d( = 2m ^ Выч [eiazf(z),zk].
-R	C'R	k=l
E.42)
По лемме Жордана предел второго слагаемого в левой части
E.42) при R —>• оо равен нулю. Отсюда и следует утверждение
теоремы.
Пример 3. Вычислить интеграл
1=1 C9°SQai dx, a > 0, a > 0.	E.43)
— СЮ
Чтобы иметь возможность воспользоваться леммой Жордана,
заметим, что в силу формулы Эйлера
сю
I = Re Д = Re
Г ^— dx.	E.44)
J x2 + а2
— сю
Аналитическое продолжение подынтегральной функции инте-
интеграла 1\ — функция emz —	 — удовлетворяет условиям тео-
ремы 5.4 и имеет в верхней полуплоскости единственную особую
точку z\ = m, являющуюся полюсом первого порядка. Поэтому
h = 2тггВыч [^— ml =
\_z2 + а2 \
= -е~аа.
2га а
Отсюда
/ = Re/1 = -ae~aa.	E.45)
Замечание 1. Если f(x) является четной функцией,
удовлетворяющей условиям теоремы 5.4, то при а > 0
\ f(x) cosaxdx = TrRe г ^^Выч [emz f'(z), z^\ =
о	k=i
n
=-Trim J]Выч [e<flVW^ib]. E.46)
k=i
Замечание 2. Если f(x) является нечетной функцией,
удовлетворяющей условиям теоремы 5.4, то при а > 0
сю	п
f f(x)smaxdx = 7rRe ^Выч[е^/(^),^].	E.47)
о	k=i
Мы доказали леммы 1 и 2, предполагая, что функция f(x)
имеет лишь конечное число особых точек в верхней плоскости.

142	ТЕОРИЯ ВЫЧЕТОВ И ИХ ПРИЛОЖЕНИЯ	ГЛ. 5
Однако, как легко видеть, при незначительном изменении фор-
формулировок этих лемм они остаются справедливыми и в случае
бесконечного числа изолированных особых точек функции f(z).
Потребуем, чтобы существовала такая неограниченно возраста-
возрастающая при п —>> оо последовательность чисел i?n, что на дугах
полуокружностей C'R в верхней полуплоскости выполнялись бы
условия E.29) или E.37) соответственно. Тогда утверждения
E.30) или соответственно E.36) лемм 1 и 2 будут иметь место
при условии, что предельный переход в рассматриваемых инте-
интегралах совершается по последовательности дуг C'R при п —>• оо.
Очевидно также, что в случае существования соответствующих
интегралов мы можем распространить рассматриваемые мето-
методы интегрирования и на случай функций с бесконечным числом
изолированных особых точек. Важным классом таких функций
являются так называемые мероморфные функции.
Функция комплексной переменной f(x) называется меро-
морфной, если она определена на всей комплексной плоскости и
не имеет в конечной части плоскости особых точек, отличных
от полюсов. Как легко видеть, в любой ограниченной области
комплексной плоскости мероморфная функция имеет конечное
число особых точек. Действительно, если бы число особых точек
в ограниченной области было бесконечным, то согласно теореме
1.2 в этой области существовала бы предельная точка данно-
данного множества, которая тем самым не была бы уже изолирован-
изолированной особой точкой, что противоречит условию. Примерами ме-
роморфных функций являются дробно-рациональные функции,
тригонометрические функции tgz, secz.
При доказательстве теорем 5.3 и 5.4 мы предполагали, что
функция f(x) не имеет особых точек на действительной оси.
Однако незначительные дополнительные рассмотрения позволя-
позволяют применять доказанные выше теоремы к вычислению несоб-
несобственных интегралов и в том случае, когда функция f(x) имеет
несколько особых точек на действительной оси.
Проиллюстрируем высказанное утверждение на простом
примере.
Пример 4. Вычислить интеграл
оо
т- / sin ах 7	^ г»	/г /io\
I = 	dx, a > 0.	E.48)
о
Воспользовавшись формулой Эйлера и свойством четности
подынтегральной функции, осуществим формальное преобразо-
преобразование	QQ
1	f eiax	I
7=2Im j —dX=2lmh-	E'49)

ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
143
Заметим, что интеграл 1\ имеет смысл лишь как главное значе-
значение несобственного интеграла второго рода1):
оо	( -р	R	\
/I р	р ¦	I
гах	I / гах	I гах	I
— dx = lim <	/ — dx + / — dx > . E.50)
х	р^о I	J x	J x	I
-OO	R^OO {-R	p	)
Рассмотрим в верхней полуплоскости Im z ^ 0 замкнутый
контур Г, состоящий из
отрезков действительной
оси [—Д, —р], [р-)Щ и
дуг полуокружностей С'р1
= р, и C'Ri
= R
-R
-P I P
R
(рис. 5.4). Функция 	,
являющаяся аналитиче-
аналитическим продолжением в
верхнюю полуплоскость
Im z > 0 функции 	,
положи-
положиРис. 5.4
заданной на
тельной части действительной оси 0 < х < оо, в области,
ограниченной контуром Г, особых точек не имеет. Поэтому на
основании теоремы Коши
-р	R
Г f({\ At — I е1аХ 4- f е1аХ 4- f е^С dC 4- f е^С dC — 0
J	7^ x J ~ x J ~c~ J ~c~
V	-R	p	с1'	C'+
E.51)
Последнее слагаемое правой части E.51) стремится к нулю при
R —)> оо в силу леммы Жордана. Рассмотрим третье слагаемое.
Заметив, что в этом интеграле полуокружность С' проходится
в отрицательном направлении (по часовой стрелке), и сделав
получим
о
замену переменной интегрирования ? = рег(р
е—— d( = г / exp [iap(cos ср + г sin cp)] dip.	E.
=>	J
52)
с
Подынтегральная функция в E.52) является непрерывной
функцией параметра р, и при р —>> 0 ее предел равен 1. Поэтому
lim h = —гтг.	E.53)
:) См. вып. 2.

144	ТЕОРИЯ ВЫЧЕТОВ И ИХ ПРИЛОЖЕНИЯ	ГЛ. 5
Перейдя в E.51) к пределу при р —>> 0 и R —>> оо, согласно E.50)
и E.53) получим
оо
	cfe = гтг, а > 0,	E.54)
— оо
откуда
оо
1	dx = -, а > 0.	E.55)
о
При а < 0 имеет место формула
sinaa;
E.56)
в чем легко убедиться при помощи изменения знака у а в фор-
формуле E.55).
4. Случай многозначных функций. Во всех предыду-
предыдущих рассмотрениях мы фактически основывались на формуле
Коши, справедливой для однозначной аналитической функции.
Следовательно, рассмотренные методы можно применять лишь
тогда, когда аналитическое продолжение f(z) функции f(x) с
действительной оси в область, ограниченную контуром интегри-
интегрирования, является однозначной аналитической функцией. В тех
же случаях, когда полная аналитическая функция F(z) оказы-
оказывается многозначной на полной комплексной плоскости z, надо
так выбирать контур интегрирования, чтобы внутри его не со-
содержалось точек разветвления функции F(z), и рассматривать
лишь однозначную ветвь f(z) полной аналитической функции
F(z), являющуюся непосредственным аналитическим продол-
продолжением функции f(x) в комплексную область. Эти соображения
позволяют распространить рассмотренные выше методы на ряд
несобственных интегралов, часто встречающихся в приложени-
приложениях. Рассмотрим несколько типичных случаев.
1° Интегралы вида
оо
I = J xa-lf(x) dx, 0 < а < 1.	E.57)
о
Пусть функция /(ж), заданная на положительной части дей-
действительной оси, может быть аналитически продолжена на всю
комплексную плоскость. Пусть ее аналитическое продолжение
f(z) является однозначной аналитической функцией, за ис-
исключением конечного числа изолированных особых точек Zf~

ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
145
(к = 1,...,п), не лежащих на положительной части действи-
действительной оси, и z = оо является нулем не ниже первого поряд-
порядка функции f(z), а точка z = 0 — устранимой особой точкой.
Функция
ф) = za-lf{z)	E.58)
в области Q [0 < arg z < 2тг], представляющей собой плоскость
z с разрезом по положитель-
положительной части действительной оси,
очевидно, является аналитиче-
аналитическим продолжением подынте-
подынтегральной функции, совпадаю-
совпадающей с ней на верхнем бере-
берегу разреза (arg z = 0). Функ-
Функция cp(z) является однознач-
однозначной функцией в области Q, и
ее особые точки совпадают с
особыми точками zk функции
f(z). Рассмотрим в области Q
замкнутый контур Г, состав-
составленный из отрезков действи-
действительной оси [р, R] на верхнем
Рис- 5-5	и нижнем берегах разреза и
разомкнутых окружностей Ср,
= р, и Cr, \z\ = R (рис. 5.5). По основной теореме теории
вычетов
R
= f xa~lf(x) dx + f C'1
P	C+
n
+ / Ca"V(C) ^C = 2тгг Y^ Выч
R
l f{z),zk]. E.59)
к=1
Рассмотрим каждое из слагаемых правой части равенства
E.59).
J
MRa
R
0,
E.60)
так как по условию в окрестности точки z = оо для функции
f(z) имеет место оценка \f(z)\ < рг. Третье слагаемое в E.59)
представляет собой интеграл по нижнему берегу разреза, где
arg z = 2тг, т.е. z = х • e
i2n
(х > 0) и za~l = xa~l

146
ТЕОРИЯ ВЫЧЕТОВ И ИХ ПРИЛОЖЕНИЯ
ГЛ. 5
Поэтому
R
R
'1 f@ d( = -е*2^-1) / x*-lf{x) dx.
E.61)
Наконец,
/ C^KQdC <М1ра-1-2тгр -+ 0,	E.62)
так как в окрестности точки z = 0 имеет место оценка |/(^)| < М\
и а > 0.
Перейдя к пределу в E.59) при р —>> 0 и i? —)> оо, на основании
E.60)-E.62) окончательно получим
оо	N
/с=1
Пример 5. Вычислить интеграл
сю
= / f^ rfx,
0 < а < 1.
E.64)
Подынтегральная функция в E.64) удовлетворяет всем пе-
перечисленным выше условиям. Поэтому
2тгг
Выч
1 - ег2па
2° Интегралы вида г)
-Л
1
J
27rzei7r(a-1)	тт
=	— =
J	1 _ ег2тга	Sin
Sin Q7T
1
J
rfx, 0 < а < 1.
E.65)
E.66)
Пусть функция /(ж), заданная на отрезке действительной оси
@,1), может быть аналитически продолжена на всю комплекс-
комплексную плоскость. Пусть ее аналитическое продолжение является
однозначной аналитической функцией, за исключением конеч-
конечного числа изолированных особых точек z^ (k = 1,2,... ,7V),
не лежащих на отрезке 0 ^ х ^ 1, а точка z = оо — устра-
устранимая особая точка функции f(z). Тогда интеграл E.66) легко
может быть вычислен методами, аналогичными разобранным
Как легко видеть, данный интеграл с помощью замены у =
может быть сведен к интегралу типа E.57), однако в ряде случаев проще
произвести непосредственное вычисление интеграла E.66), что и делается
в этом пункте.

ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
147
выше. Заметим, что аналитическое продолжение подынтеграль-
подынтегральной функции Ф(г) = za~1(l — z)~af(z) имеет две точки раз-
разветвления: z = 0 и z = 1. Точка z = оо является устранимой
особой точкой функции Ф(^). Действительно, полный обход по
окружности достаточно большого радиуса, содержащий внутри
обе точки разветвления z = О
и z = 1, не меняет значе-
значения функции Ф(^). Рассмо-
Рассмотрим область Q', представляю-
представляющую собой полную плоскость
z с разрезом по отрезку дей-
действительной оси [0,1]. Ветвь
функции Ф(г), совпадающая
на верхнем берегу разреза
с подынтегральной функцией
E.66) действительной пере-
переменной ж, является однознач-
однозначной аналитической функцией
в Q. Выберем в Q замкнутый
контур Г, состоящий из обоих
берегов разреза [0,1], замы-
замыкающих их окружностей С'р1
Рис. 5.6
\z\ = р, и
\z - 1| = р, до-
достаточно малого радиуса р и окружности С#, \z\ = i?, содер-
содержащей внутри отрезок [0,1] и все особые точки функции f(z)
(рис. 5.6). По основной теореме теории вычетов
Ф(С) dC =
Г	9
a-1
{l-x)-°f{x)dx+
1-р
С'"
= 2т > Выч I
к=1
]. E.67)
Рассмотрим каждое слагаемое в правой части равенства E.67).
По условию z = оо — устранимая особая точка f(z), т.е. в окрест-
окрестности z = оо имеет место разложение
/(*)=ао + ^ + ...,	E.68)
где а0 = Hm f(z).
z^oo

148	ТЕОРИЯ ВЫЧЕТОВ И ИХ ПРИЛОЖЕНИЯ	ГЛ. 5
Рассмотрим функцию
l(^y,	E.69)
являющуюся указанной выше ветвью функции <f>(z)/f(z). Точка
z = оо является правильной точкой выбранной ветви функции
<p(z)] поэтому в окрестности точки z = оо функция <p(z) может
быть представлена в виде
Ф) = ^ + ^А	E-70)
где ipi(z) — ограниченная аналитическая функция в окрестно-
окрестности точки z = оо. Отсюда для разложения функции Ф(г) в ряд
Лорана в окрестности точки z = оо получаем выражение
E.71)
где ip(z) — ограниченная аналитическая функция в окрестности
точки z = оо. Из E.71) находим
Выч [Ф(г), оо] = -aoei7ra.	E.72)
Поэтому по формуле E.17)
J Ф(()^ = 27гт0е^.	E.73)
Так как при обходе точки z = 1 по часовой стрелке аргумент
выражения A — z) меняется на — 2тг, то аргумент функции Ф(#)
на нижнем берегу разреза больше аргумента на верхнем берегу
разреза на 2тга. Поэтому
р	1 - р
J Ф(()^ = -е*2™ J <&(x)dx.	E.74)
1 - р	р
Как легко показать с помощью оценок, аналогичных E.62), при
0 < а < 1 интегралы по малым окружностям С'р и Ср стремятся
к нулю при р —)> 0. Тогда, переходя в E.67) к пределу при р —>> 0,
получаем
N
A - ei2™)I + 27rieinaa0 = 2т ^ Выч [za~lA - z)-af(z),zk],
k=l
откуда
Е Выч I^ A " *Гв/(*),**], E-75)
где clq = lira

§ 2	ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ	149
Пример 6. Вычислить интеграл г)
1
J= fxa~1(l-x)~adx, 0<а<1.	E.76)
о
Так как выполнены все сформулированные выше условия и
CLQ = 1, ТО
E.77)
sinTra
3° Интегралы вида
ОО
1= J f(x)lnxdx.	E.78)
о
Пусть функция f(x) является четной функцией и может быть
аналитически продолжена на верхнюю полуплоскость Im z > 0,
причем ее аналитическое продолжение удовлетворяет услови-
условиям леммы 1. Рассмотрим в верхней полуплоскости замкнутый
контур Г, состоящий из отрезков действительной оси [—Д, —р],
[p,R] и соединяющих их полуокружностей С'р1 \z\ = р, и C'Rl
\z\ = R. Функция Ф(^), являющаяся ветвью полной аналити-
аналитической функции и совпадающая с f(x) In x на положительной
части действительной оси (х > 0), на отрицательной части дей-
действительной оси при z = |^|ег7Г = хеш = —х (х > 0) принимает
значение
ф0?) \z=xe™ = f(x)ln (хеШ) = /(ж)[Inж + гтг].
Поэтому
R	R
Q d( = J f(x)lnxdx+ ? Ф(С) ^С + [ f(x)[lnx + in] dx +
p	c'+	p
N
+ f Ф(С)(К = 2т^2Выя[/(г)]пг,гк]. E.79)
с'-	k=i
:) Заметим, что рассматриваемый интеграл является частным случаем
.В-функции (см. вып. 2):
B(p,q)= J xp~1(l-x)q~1dx.

150	ТЕОРИЯ ВЫЧЕТОВ И ИХ ПРИЛОЖЕНИЯ	ГЛ. 5
Рассмотрим второе слагаемое в правой части E.79)
-V +
0. E.80)
Проведя аналогичные оценки, легко показать, что и последнее
слагаемое в правой части E.79) стремится к нулю при р —>• 0.
оо
Наконец, несобственный интеграл f f(x) dx существует и в силу
E.35) равен	о
оо	N
Y, Выч [f(z),zk].	E.81)
о	k=i
Поэтому, перейдя в E.79) к пределу при р —>> 0 и R —>> оо, полу-
получим
оо	7V
/= //0гIпЖ^ = 7гг^Выч [/(^(ln*-^),**]. E.82)
о	k=i
Пример 7. Вычислить интеграл
оо
J f(x)
Согласно проведенным выше рассуждениям
§ 3. Логарифмический вычет
1. Понятие логарифмического вычета. Пусть в обла-
области Q задана однозначная функция f(z), аналитическая всюду в
Q, за исключением конечного числа изолированных особых то-
точек Zh (к = 1,... ,р), причем все z^ являются полюсами. Пред-
Предположим, что на границе Г области Q нет ни нулей, ни особых
точек функции f(z), и рассмотрим вспомогательную функцию
Ф) = 7^-	E-85)
Функцию (p(z) часто называют логарифмической производной
функции f(z)j а вычеты функции (f(z) в ее особых точках zm
(т = 1,..., М) — логарифмическими вычетами функции f(z).
Определим особые точки функции (f(z) в области Q. В силу об-
общих свойств аналитических функций ясно, что особыми точ-
точками фуНКЦИИ (f(z) будут НуЛИ Zk (k = 1,...,п) И ПОЛЮСЫ Zk
(к = 1,... ,р) функции f(z). Найдем значение вычета функции

§_3	ЛОГАРИФМИЧЕСКИЙ ВЫЧЕТ	151
(p(z) в каждой из ее особых точек. Пусть точка z = % являет-
является нулем порядка п^ функции f(z). Тогда в окрестности этой
точки функция f(z) имеет вид
f(z) = (z- zk)nkh(z), fi(zk) Ф 0,	E.86)
причем точка % является правильной точкой функции fi(z).
Вычисляя функцию tp(z) в окрестности точки z = % по формуле
E.85), получаем
ф) = Qnf(z))' = nk(ln (z - zk))' + (b.
f[(z)
z - Zk /1 (z)'
Отсюда следует, что точка % является полюсом первого порядка
функции <p(z), причем вычет функции cp(z) в этой точке равен
п&. Итак, в нуле порядка п^ функции f(z) ее логарифмический
вычет равен п^, т.е. порядку нуля:
E.87)
Пусть точка zj^ является полюсом порядка pj~ функции / (z).
Тогда в окрестности этой точки функция f(z) имеет вид
причем точка zj^ является правильной точкой функции fi(z).
Поэтому для логарифмической производной функции f(z) в
окрестности точки z = z^ получим выражение
Отсюда следует, что точка zj^ такж:е является полюсом первого
порядка функции tp(z), причем вычет в этой точке равен —pk-
Итак, в полюсе порядка р^ функции f(z) ее логарифмический
вычет равен порядку полюса, взятому со знаком минус:
=-рА.	E.89)
2. Подсчет числа нулей аналитической функции.
Полученные результаты позволяют доказать следующую важ-
важную теорему.
Теорема 5.5. Пусть функция f(z) является аналитиче-
аналитической всюду в замкнутой области Q^ за исключением конечного
числа лежащих внутри Q изолированных особых точек Zk, ко-
которые все являются полюсами, и пусть f(z) не обращается в
нуль ни в одной точке границы Г области Q. Тогда разность
между полным числом нулей и полным числом полюсов функ-
функции f(z) в области Q определяется выражением
j§dC	E-90)
г+

152	ТЕОРИЯ ВЫЧЕТОВ И ИХ ПРИЛОЖЕНИЯ	ГЛ. 5
Под полным числом нулей (полюсов) понимается число нулей
N (полюсов Р) с учетом их кратности:
п	V
к=1	к=1
Доказательство. Для доказательства теоремы
заметим, что интеграл по Г от функции (p(z) = .(! может
быть вычислен с помощью основной теоремы теории вычетов,
причем так как все особые точки функции <p(z) — это нули и
полюсы функции f(z)j а вычеты в этих точках определяются
формулами E.87) и E.89), то
м
J (р(() d( = 2т ^2 Выч Ы^^т] =
Г+	т=1
( п	V Л
1^	Y	- Р),
[к=1	к=1 )
что и доказывает теорему.
Отметим простой геометрический смысл доказанной теоре-
теоремы, для чего преобразуем интеграл, стоящий в правой части
E.90):
г+	г+	г+
г+	г+
Действительная функция 1п|/(?)| является однозначной функ-
функцией, поэтому ее вариация (изменение) при обходе точкой ( за-
замкнутого контура Г равна нулю. Следовательно, первое слага-
слагаемое в правой части E.92) равно нулю. Второе слагаемое пред-
представляет собой полную вариацию аргумента функции f(() при
обходе точкой ? замкнутого контура Г, деленную на 2тг. Итак,
N-P= ^Var [arg f(z)]T+.	E.93)
Будем изображать значения функции w = f(z) точками на
комплексной плоскости w. Так как функция f(z) непрерывна
на контуре Г, то при полном обходе точкой z контура Г на плос-
плоскости z соответствующая ей точка на плоскости w описывает
некоторый замкнутый контур С. При этом точка w = 0 может
оказаться как вне, так и внутри области, ограниченной контуром
С. В первом случае вариация аргумента w при полном обходе

§ 3	ЛОГАРИФМИЧЕСКИЙ ВЫЧЕТ	153
С, очевидно, равна нулю. Во втором случае вариация аргумен-
аргумента w определяется числом полных обходов вокруг точки w = О,
которые совершает точка w при своем движении по контуру С.
При этом точка w может обходить точку w = 0 как против часо-
часовой стрелки (в положительном направлении), так и по часовой
стрелке (в отрицательном направлении). Итак, разность между
полным числом нулей и полюсов функции f(z) в области Q опре-
определяется числом оборотов, которые совершает точка w = f(z)
вокруг точки w = 0 при положительном обходе точкой z конту-
контура Г. Эти соображения часто оказываются существенными при
подсчете полного числа нулей аналитической функции в задан-
заданной области. При этом во многих случаях соответствующие вы-
вычисления можно значительно облегчить благодаря следующей
теореме.
Теорема 5.6 (теорема Руше). Пусть функции f(z) и
ip(z) являются аналитическими в замкнутой области Q^ при-
причем на границе Г области Q имеет, место неравенство
\№\Г>Ш\г.	E-94)
Тогда полное число нулей в области Q функции F(z) = f(z) +
+ (p(z) равно полному числу нулей функции f(z).
Доказательство. Для функций f(z) и F(z) =
= f(z) + <p{z) выполнены все условия теоремы 5.5. Действитель-
Действительно, функция f(z) не имеет особых точек на Г (она аналитиче-
аналитическая в Q) и не обращается в нуль на Г в силу E.94). Эти условия
также выполнены для функции F(z), так как |F(^)|r = \f{z) +
+ (f(z)\ ^ |/(г)|г — |<р(г)|г > 0. Поэтому на основании формулы
E.93) получим
N\f(z) + ф)\ = ^Var [arg (/ + <р)]Г
] = i;Var [arg/(*)]г.
Рассмотрим разность
tp(z)]-N[f(z)] =
= ^Var [arg (/ + у) - arg /]г = ^-Var [arg
(arg (/ + ?>)- arg / = arg f-j
Введем функцию w = 1 + ^^-. Как легко видеть, при обходе точ-
точкой z контура Г соответствующая ей точка w опишет замкнутую
кривую С, которая в силу условия E.94) будет целиком лежать
внутри некоторого круга \w — 1| ^ ро < 1 (рис. 5.7). Тем самым

154
ТЕОРИЯ ВЫЧЕТОВ И ИХ ПРИЛОЖЕНИЯ
ГЛ. 5
точка w = 0 лежит вне кривой С. Следовательно, Var [arg w]~p =
= 0, что и доказывает теорему.
Пример. Найти полное число нулей функции F(z) =
= ?8 — 5^5 — 2z-\-l внутри единичного круга \z\ < 1. Представим
функцию F(z) в виде F(z) = /B:) + <p(;z), положив f(z) = —5^5 +
+ 1 и cp(z) = z8 - 2z. Тогда
откуда |/(^)||^|=1 >
нулей в области \z
нулей функции /
^(^I^1-! > 0. Следовательно, полное число
< 1 функции F(z) равно полному числу
^), но
последняя имеет, очевидно,
ровно пять нулей:
5/Г
Zk = V 5
(А; = 0,1,...,4).
Важным принципиаль-
принципиальным следствием теоремы
Руше является
Основная теорема
высшей алгебры. Поли-
Полином п-й степени имеет
на комплексной плоскости
ровно п нулей (с учетом их
кратности).
w=0
Рис. 5.7
)
Доказательство. Представим полином F(z) =
+aizn~1 + .. .+ап в виде F(z) = f(z)+(p(z), положив f(z) =
= a\zn l + ... + an.
Составим отношение
+ ... + — —. Как легко видеть, при любых заданных значениях
коэффициентов ao, ai,..., ап всегда найдется такое значение i?o,
что для всех значений \z\ = R > Rq имеет место неравенство
0<
< 1.
E.95)
\z\=R
В силу теоремы Руше из E.95) следует, что полное число ну-
нулей функции F(z) в круге \z\ = R равно числу нулей в этом
круге функции f(z) = a$zn. Но функция f(z) = a$zn на всей
комплексной плоскости имеет единственный n-кратный нуль —
точку z = 0. Отсюда в силу произвольности R ^ Rq и следует
утверждение теоремы.

ГЛАВА 6
КОНФОРМНОЕ ОТОБРАЖЕНИЕ
Как при построении общей теории функций комплексной пе-
переменной, так и в ее многочисленных приложениях, в частно-
частности к решению задач механики и физики, большое значение
имеет изучение геометрических свойств конформных отобра-
отображений, осуществляемых аналитическими функциями. В гл. 1
было введено понятие конформного отображения, обладающего
свойствами сохранения углов и постоянства растяжений. Фунда-
Фундаментальной задачей теории конформных отображений является
следующая. Даны две области комплексной плоскости, и требу-
требуется найти функцию, осуществляющую взаимно однозначное и
конформное отображение одной области на другую. При этом,
конечно, возникают вопросы об условиях существования и од-
однозначного определения такой функции.
В этой главе будут кратко изложены основные понятия те-
теории конформного отображения. Мы также рассмотрим неко-
некоторые геометрические свойства отображений, осуществляемых
рядом аналитических функций, находящих наиболее широкое
применение в приложениях.
§ 1. Общие свойства
1. Определение конформного отображения. В гл. 1
при рассмотрении геометрического смысла модуля и аргумен-
аргумента производной было введено понятие конформного отображе-
отображения. Было показано, что если функция w = f(z) является од-
однозначной и аналитической в окрестности некоторой точки zq и
ff(zo) Ф О? т0 отображение, осуществляемое данной функцией,
в точке zq обладает свойствами сохранения углов и постоянства
растяжений. То есть угол между любыми двумя гладкими кри-
кривыми, пересекающимися в точке ^о, равен и по абсолютной ве-
величине и по направлению углу между их образами на плоскости
w в точке г^о = /(^оM а бесконечно малые линейные элементы,

156	КОНФОРМНОЕ ОТОБРАЖЕНИЕ	ГЛ. 6
выходящие из точки ^о, преобразуются подобным образом. Это
означает, что при рассматриваемом отображении любой беско-
бесконечно малый треугольник с вершиной в точке zq преобразуется в
подобный ему бесконечно малый треугольник с вершиной в точ-
точке г^о- Отметим, что в силу общих свойств аналитических функ-
функций х) в окрестности точки wq определена однозначная анали-
аналитическая функция z = (f(w). Тем самым между окрестностями
точек zq и г^о установлено взаимно однозначное соответствие.
Введем следующее фундаментальное определение.
Взаимно однозначное отображение области Q комплексной
плоскости z на область G комплексной плоскости w назы-
называется конформным, если это отображение во всех точках
z Е Q обладает свойствами сохранения углов и постоянства
растяжений. Подчеркнем, что данное определение подразуме-
подразумевает непрерывность рассматриваемого отображения.
Из предыдущего ясно, что при конформном отображении
области Q на область G бесконечно малые плоские фигуры обла-
области Q преобразуются в подобные им бесконечно малые фигуры
области G. Также легко видеть, что при конформном отобра-
отображении сохраняется свойство взаимной ортогональности системы
кривых на плоскости. Действительно, пусть в области Q плоско-
плоскости z (z = х + гу) заданы два взаимно ортогональных однопара-
метрических семейства кривых ср(х,у) = с и ф(х,у) = с, причем
через любую точку области Q проходят по одной кривой каждо-
каждого семейства. Тогда при конформном отображении области Q на
некоторую область G плоскости w (w = и + iv) образы данных
кривых на плоскости w — кривые Ф(и,у) = с и Ф(гл, г;) = с —
на основании свойства сохранения углов также будут взаимно
ортогональны. Это означает, что если в области Q введена неко-
некоторая ортогональная криволинейная система координат, то при
конформном отображении эта система координат перейдет так-
также в ортогональную систему.
Выясним теперь, какими свойствами должна обладать функ-
функция комплексной переменной для того, чтобы отображение, осу-
осуществляемое этой функцией, было конформным.
Имеет место следующая теорема.
Теорема 6.1. Пусть функция f(z) является однозначной
и однолистной аналитической функцией в области Q и ff(z) ф О
при z E Q. Тогда функция f(z) производит конформное ото-
отображение области Q на область G комплексной плоскости wy
представляющую собой область значений функции w = f(z)
при z E Q.
См. гл. 1, с. 36.

ОБЩИЕ СВОЙСТВА	157
Доказательство. Действительно, в силу условия
f'(z) 7^ 0 при z Е Q отображение, осуществляемое функцией
f(z), во всех точках области Q обладает свойствами сохранения
углов и постоянства растяжений, что и доказывает теорему.
Итак, условия аналитичности, однолистности и отличия от
нуля производной функции комплексной переменной являются
достаточными условиями конформности отображения, осуще-
осуществляемого этой функцией. Естественно поставить вопрос, яв-
являются ли эти условия необходимыми. На этот вопрос отвечает
следующая теорема.
Теорема 6.2. Пусть функция f(z) осуществляет кон-
конформное отображение области Q комплексной плоскости z на
область G комплексной плоскости w и ограничена в Q. Тогда
функция f(z) является однолистной и аналитической в обла-
области Q^ причем f'(z) 7^ 0 при z E Q.
Доказательство. Так как отображение, осуще-
осуществляемое функцией f(z), является конформным, то оно явля-
является взаимно однозначным, и в любой точке zq G Q выполняются
свойства сохранения углов и постоянства растяжений. Следова-
Следовательно, для любых точек z\ и ^2, принадлежащих окрестности
точки 2о, с точностью до бесконечно малых величин выполня-
выполняются соотношения
arg Au>2 — arg Awi = arg Az2 — arg Azi	F.1)
и
где Azi = zi—zq и А^2 = Z2—zq суть бесконечно малые линейные
элементы, выходящие из точки zq, a Ai^i и Аг^2 — их образы
Рис. 6.1
(рис. 6.1). Заметим, что в силу F.1) соответствующие углы в
точках zq и г^о равны не только по абсолютной величине, но и
по направлению. Обозначив arg —— через а, из F.1) найдем,
Аил	тт „	Az2
что и arg —— = а. Действительно,

158	КОНФОРМНОЕ ОТОБРАЖЕНИЕ	ГЛ. 6
arg —— = arg Aw2 — arg Az2 = arg Aw\ — arg Az\ = arg —— = a.
/\Z2	lAZi
F.3)
Из F.2) и F.3) получим, что с точностью до бесконечно малых
величин имеет место соотношение
%Ш = ^1 = kei*m	F.4)
Az2 Azi	v J
В силу произвольности выбора точек z\ и Z2 в окрестности точки
zq соотношение F.4) означает, что существует предел разност-
разностного отношения —— при Az —>> 0. Этот предел по определению
/\z
является производной функции f(z) в точке zq. Так как к ф 0,
то эта производная отлична от нуля:
Точка zq - произвольная точка области Q; поэтому из F.5) сле-
следует, что функция f(z) является аналитической1) в области Q
и f'{z) ф 0 при z Е Q. Однолистность f(z) следует из взаимной
однозначности отображения. Теорема доказана.
Итак, конформное отображение области Q комплексной
плоскости z на область G комплексной плоскости w осуще-
осуществляется только однолистными аналитическими функция-
функциями комплексной переменной с производной, отличной от нуля
во всех точках области Q.
Отметим, что условие ff(z) ф 0 всюду в области Q является
необходимым, но недостаточным условием конформности ото-
отображения области Q на область G, осуществляемого функцией
f(z). Очевидно, если функция f(z) является аналитической в
области Q и ff(z) ф 0 всюду в Q, но функция f(z) не является
однолистной в ?/, то отображение, осуществляемое этой функ-
функцией, не будет взаимно однозначным, а тем самым не будет и
конформным. Таким простейшим примером является функция
w = ?4, заданная в полукольце 1 ^ \z\ ^ 2, 0 ^ argz ^ тг. Эта
функция аналитична в данной области, ию' = Az3 ф 0 всюду в
данном полукольце. Однако эта функция отображает данное по-
полукольцо на область 1 ^ |ги| ^ 16, 0^ arg u? ^ 4тт, т.е. область,
дважды покрывающую соответствующее кольцо на плоскости
w, что и нарушает взаимно однозначное соответствие.
Итак, однолистность однозначной аналитической функции в
области Q является важнейшим условием конформного отобра-
отображения. Как будет показано ниже (см. теорему 6.3 — принцип
взаимно однозначного соответствия), это условие является необ-
необходимым и достаточным условием конформности отображения.
См. сноску на с. 35.

ОБЩИЕ СВОЙСТВА	159
Как было отмечено выше, свойство сохранения углов означа-
означает, что сохраняется не только абсолютная величина углов меж-
между кривыми, пересекающимися в точке го, и их образами, но
и их направление. Отображение, при котором сохраняются аб-
абсолютные величины углов между кривыми и их образами, но
направление углов меняется на противоположное, называется
конформным отображением второго рода. Рассмотренное вы-
выше отображение называется конформным отображением пер-
первого рода.
Нетрудно показать, что конформное отображение второго
рода осуществляется функциями комплексной переменной, яв-
являющимися комплексно сопряженными аналитическим функци-
функциям с отличной от нуля производной. Действительно, пусть функ-
функция w = f(z) осуществляет конформное отображение второго
рода некоторой области Q комплексной плоскости z на область
G комплексной плоскости w. Рассмотрим функцию w\ = w, ото-
отображающую область G на область G* комплексной плоскости
w\. Очевидно, геометрический смысл последнего отображения
заключается в зеркальном отражении области G относительно
действительной оси и плоскости w. Но при зеркальном отраже-
отражении направление всех углов меняется на противоположное при
сохранении их абсолютной величины. Это означает, что отобра-
отображение области Q на область G*, осуществляемое функцией
<p(z) =wi =w = f(z), z<EG,	F.6)
является конформным отображением первого рода. Тем самым
функция cp(z) должна быть аналитической в области Q, причем
(p'(z) 7^ 0, z Е G- Но из F.6) следует, что f(z) = ip(z), что и
доказывает высказанное утверждение. До сих пор мы предпо-
предполагали, что производятся конформные отображения ограничен-
ограниченной области Q на ограниченную область G. В некоторых случа-
случаях приходится рассматривать отображение окрестности точки
zq на окрестность точки w = оо (или наоборот). При этом мы
будем называть данное отображение конформным, если окрест-
окрестность точки zq конформно отображается на окрестность точки
( = 0, где ( = —. Аналогично определяется конформное отобра-
отображение окрестности точки z = оо на окрестность точки w = оо.
2. Простейшие примеры. В предыдущих главах мы уже
рассмотрели некоторые геометрические свойства отображений,
осуществляемых рядом элементарных функций. Выясним те-
теперь, являются ли эти отображения конформными, и если да,
то в каких областях.
Как легко видеть, линейная функция w = f(z) = az -\- b
(о / 0 и i - произвольные комплексные постоянные) осуще-
осуществляет конформное отображение полной комплексной плоско-

160	КОНФОРМНОЕ ОТОБРАЖЕНИЕ	ГЛ. 6
сти z на полную плоскость w, поскольку эта функция однолист-
однолистна и ее производная f'{z) = а отлична от нуля во всех точ-
точках плоскости z. Чтобы убедиться в сохранении конформности
отображения окрестности точки z = оо на окрестность точки
w = оо, положим (следуя сделанному выше замечанию) t = - и
1 t	z
( = —. Функция w = az + b перейдет в функцию ( =	—, кото-
(JU	\Х | (JL
рая осуществляет конформное отображение окрестности точки
t = 0 на окрестность точки ( = 0 (точка t = 0 является правиль-
правильной точкой этой функции, и С7(?) к=о = - Ф 0).
а
Выше мы видели, что геометрический смысл отображения,
осуществляемого линейной функцией, заключается в подобном
растяжении и сдвиге плоскости z. Поэтому данная функция мо-
может быть применена для построения конформных отображений
подобных фигур.
Пример 1. Построить функцию, осуществляющую кон-
конформное отображение круга \z — 1 — i| ^ 2 на единичный круг
Н ^ 1.
Так как области Q и G представляют собой подобные фигу-
фигуры, то задача может быть решена при помощи линейной функ-
функции, которая осуществляет подобное растяжение плоскости z и
сдвиг начала координат. Как легко видеть, искомая функция
имеет вид
w = a(z — 1 — г),
где \а\ = -, а аргумент комплексного числа а может иметь любое
значение, определяя поворот плоскости w вокруг точки w = 0.
Рассмотрим степенную функцию w = f(z) = zn', где п > 1 —
целое число. Как следует из рассмотрений, проведенных в гл. 1 и
3, эта функция осуществляет взаимно однозначное отображение
области своей однолистности — сектора ^о < arg z < фо + — —
на полную плоскость w, разрезанную по лучу arg и? = пфо. Ее
производная ff(z) = nzn~1 отлична от нуля и ограничена всюду
внутри данного сектора и в точках его границы, за исключением
точек z = 0 и z = оо. Поэтому данная функция осуществляет
конформное отображение области внутри указанного сектора на
разрезанную плоскость w. Любая бесконечно малая плоская фи-
фигура, лежащая внутри данного сектора, переходит в подобную
ей бесконечно малую фигуру на плоскости w, например парал-
параллелограмм ABCD, сторонами которого являются координатные
линии полярной системы координат (рис. 6.2), перейдет в подоб-
подобный ему бесконечно малый параллелограмм A'B'C'D', сторо-
сторонами которого также являются координатные линии полярной
системы координат на плоскости w. Однако в граничной точке

ОБЩИЕ СВОЙСТВА
161
z = 0 конформность отображения нарушается. Действительно,
рассмотрим кривые 71 и 72> лежащие внутри данного сектора и
пересекающиеся в точке z = 0 под углом щ (рис. 6.3). Как легко
видеть, функцией w = zn эти кривые переводятся в кривые Т\
и Г2, пересекающиеся в точке w = 0 под углом Фо = перо ^ сро.
Тем самым бесконечно малый треугольник с вершиной в точке
- 1С
г
N С
лГ
w=0\
\
X
\
Рис. 6.2
2: = 0 данной функцией отображается на треугольник, который
уже не является подобным исходному. Отметим, что в точке z = О,
где нарушается конформность отображения, производная функ-
функции f(z) = zn равна нулю. Продолжая наши рассмотрения, лег-
легко установить, что функция w = zn осуществляет конформное
Рис. 6.3
отображение области комплексной плоскости z, представляю-
представляющей собой полную плоскость z, кроме точек z = 0 и z = оо, на
n-листную риманову поверхность обратной функции z = y/w.
Причем точкам ? = 0и? = оо,в которых нарушается кон-
6 А.Г. Свешников, А.Н. Тихонов

162	КОНФОРМНОЕ ОТОБРАЖЕНИЕ	ГЛ. 6
формность отображения, соответствуют точки w = 0 и w = оо,
являющиеся точками разветвления обратной функции.
В общем случае степенная функция w = f(z) = za, где а > 0 —
заданное действительное число, осуществляет отображение сек-
сектора —к < argz < —(к + 1) (к = 0, ±1,...) своей римановой
поверхности (бесконечнолистной для иррационального а, конеч-
нолистной для рационального дробного а и обычной плоскости
z для целого а) на полную плоскость w луч argz = —к ото-
V	а
бражается на положительную часть действительной оси 1. Ее
производная ff(z) = azOL~l существует и отлична от нуля всюду
внутри данного сектора, кроме точек z = 0 и z = оо. Тем самым
и эта функция осуществляет конформное отображение данного
сектора на разрезанную плоскость w.
В точках z = 0 и z = оо, так же как и для функции w = z71,
конформность отображения нарушается.
Пример 2. Построить функцию, конформно отобража-
отображающую первый квадрант плоскости z (Re z > 0, Im z > 0) на
верхнюю полуплоскость w (Im u? > 0).
Легко видеть, что функция
w = az2 + 6,
где а > 0 и 6 — произвольные действительные постоянные, дает
решение этой задачи. В точках z = 0 и 2 = оо конформность
отображения нарушается.
В гл. 3 мы рассмотрели отображение, осуществляемое по-
показательной функцией w = f(z) = ez. Было показано, что эта
функция осуществляет взаимно однозначное отображение лю-
любой своей области однолистности — полосы уо < Im z < уо -\-
+ 2тг плоскости z — на полную плоскость w, разрезанную по
лучу &rgw = уо. Так как производная рассматриваемой функ-
функции ff(z) = ez отлична от нуля всюду внутри данной полосы,
то это отображение является конформным. Как легко видеть,
при данном отображении ортогональная сетка декартовых ко-
координат х = Ci, у = С2 внутри рассматриваемой полосы пере-
переходит в ортогональную сетку полярных координат \w\ = eCl,
argiu = С2 на плоскости w. Полная аналитическая функция
F(z) = ez, являющаяся целой функцией на плоскости z, осу-
осуществляет конформное отображение полной плоскости z на
бесконечнолистную риманову поверхность обратной функции1)
z = Lnw. Заметим, что конформность отображения нарушается
в окрестности точек w = 0 и w = 00 плоскости w, являющихся
Построение римановой поверхности функции Ln^, см. гл. 3, с. 107.

ОБЩИЕ СВОЙСТВА	163
точками разветвления функции Ьпи?, где отображение не явля-
является взаимно однозначным.
Пример 3. Построить функцию, конформно отображаю-
отображающую полосу 0 < Re z < а на верхнюю полуплоскость Im w > 0.
Функция z\ = —z отображает исходную полосу на полосу
а
0 < Re z\ < тг. Функция Z2 = iz\ переводит полученную полосу
в полосу 0 < Im Z2 < тт. Наконец, функция w = eZ2 осуществляет
конформное отображение данной полосы на верхнюю полуплос-
полуплоскость Im w > 0. Поэтому функция, осуществляющая заданное
конформное отображение, может быть взята в виде
w = exp I г —
3. Основные принципы. Мы рассмотрели некоторые
простейшие примеры функций, осуществляющих конформные
отображения, и с их помощью решили основную задачу кон-
конформного отображения для ряда простейших областей. Рассмо-
Рассмотрение более сложных примеров требует использования общих
принципов конформного отображения, к изложению которых
мы переходим. При этом в ряде случаев ограничимся лишь фор-
формулировкой соответствующих положений, не проводя их строго-
строгого обоснования, что значительно выходит за рамки настоящего
курса.
а) Взаимно однозначное соответствие. Как
было отмечено, при конформном отображении области Q комп-
комплексной плоскости z на область G плоскости w, осуществляе-
осуществляемом аналитической в Q функцией f(z), устанавливается взаим-
взаимно однозначное соответствие этих областей. Тем самым усло-
условие однолистности функции f(z) в области Q является необхо-
необходимым условием конформности отображения. Оказывается, что
это условие является и достаточным.
Теорема 6.3. Пусть функция f(z) является однозначной
аналитической функцией в области Q^ осуществляющей вза-
взаимно однозначное отображение области Q на область G комп-
комплексной плоскости w. Тогда это отображение является кон-
конформным.
Доказательство. Для доказательства теоремы, оче-
очевидно, достаточно показать, что при выполнении условий теоре-
теоремы производная функции f(z) отлична от нуля всюду в области
Q. Предположим, что это не имеет места, т.е. что в области Q
существует такая точка zo, в которой f'(zo) = 0. Так как f(z)
является аналитической в области Q, то в силу сделанного пред-
предположения ее разложение в степенной ряд в окрестности точки
zq должно иметь вид
f(z) =ao + ak(z- zo)k + ak+1(z - zo)k+1 + ...,	F.7)

164	КОНФОРМНОЕ ОТОБРАЖЕНИЕ	ГЛ. 6
причем к ^ 2 и ак ф 0. Если /7(^)^0, то точка ^о не может
быть предельной точкой нулей функции f'(z). Это означает, что
можно указать такое значение 81, что f'(z) ф 0 во всех точках
z Ф zq внутри круга \z — zq\ < 8'. Кроме того, очевидно, можно
выбрать такое значение 8П, чтобы имело место неравенство
ф(г) = ак + ak+1(z - г0) + ... ф 0
при | ^г — ^г01 < $" -
Выбрав 8 = шт{8',8"}, получим
f'{z) фО	при z ф г0, 1
> при |г — zq\ ^8. F.8)
^(г) = ак + а/ь+1(г - г0) + • • • ф 0 J
Из последнего соотношения следует в силу непрерывности
функции i/j(z), что
г-го)^^)!^-^!^ = т > 0.
Выберем некоторое комплексное число а, удовлетворяющее
условию \а\ < т. Согласно теореме Руше аналитическая функ-
функция
ф) = (z- zo)^(z) -a = f(z) -ao-a	F.9)
имеет внутри круга |г — го| ^ 8 столько же нулей, сколько и
функция (г — го)^^(^)- Последняя в силу условия F.8) имеет
в этом круге к нулей — точка z = zq является ее нулем к-то
порядка. Тогда из F.9) следует, что уравнение
/0?)=ao + a	F.10)
имеет к корней в круге |г — го| ^ S, причем все эти корни про-
простые, так как точка г = zq не является корнем уравнения F.10)
и в силу F.8) f'(z) ^0в остальных точках данного круга. Это
означает, что в к различных точках круга |г — го| ^ 8 функ-
функция /(г) принимает одно и то же значение /(г) = clq + а. Но
последнее противоречит условию взаимной однозначности ото-
отображения области Q на область G, что и доказывает теорему.
Итак, из доказанной теоремы следует, что необходимым и
достаточным условием того, чтобы однозначная функция /(г),
аналитическая в области Q, осуществляла конформное отобра-
отображение этой области на некоторую область G плоскости w, явля-
является условие однолистности /(г) в области Q.
б) Принцип соответствия границ. При ре-
решении конкретных задач конформного отображения заданной
области Q на заданную область G обычно следят лишь за тем,
чтобы искомая функция /(г) производила отображение грани-
границы 7 области Q на границу Г области G, не рассматривая специ-
специально отображения внутренних точек. Это можно делать в силу
так называемого принципа соответствия границ, доказательство

ОБЩИЕ СВОЙСТВА
165
которого будет проведено ниже. Предварительно сделаем следу-
следующее замечание. Пусть в области Q задана однозначная непре-
непрерывная функция w = f(z). Очевидно, эта функция переводит
любую замкнутую кривую 7? целиком лежащую в области Q,
также в замкнутую кривую Г на плоскости w. Мы будем гово-
говорить, что при отображении кривой 7, осуществляемом функци-
функцией f(z), сохраняется направление обхода, если при непрерывном
движении точки в положительном направлении вдоль кривой 7
соответствующая ей точка обходит кривую Г также в положи-
положительном направлении. Перейдем теперь к рассмотрению самого
принципа.
Теорема 6.4. Пусть в конечной области Q, ограниченной
контуром 7, задана однозначная аналитическая функция f(z),
непрерывная в Q и осуществляющая взаимно однозначное ото-
отображение контура 7 на некоторый контур Г комплексной плос-
плоскости w. Тогда, если при данном отображении контуров со-
сохраняется направление обхода, то функция f(z) осуществляет
конформное отображение области Q на внутреннюю область
G, ограниченную контуром Г.
Доказательство. Очевидно, для доказательства
теоремы достаточно показать, что функция f(z) устанавливает
взаимно однозначное соответ-
соответствие между областями Q и G,
т.е. надо показать, что функция
f(z) каждому значению z E Q
ставит в соответствие некото-
некоторую точку w E G и для каждой
точки w\ E G найдется, и при-
притом только одна, точка z\ E Q
такая, что f{z\) = w\. Для это-
этого рассмотрим две произволь-
произвольные ТОЧКИ W\ E G И W2 ? G
(рис. 6.4) и построим в области
Q вспомогательные функции
Рис. 6.4
= f(z)-wu
Подсчитаем число нулей этих функций в области Q, для чего
воспользуемся формулой E.93). Так как в силу условий теоре-
теоремы положительному обходу контура 7 соответствует положи-
положительный обход контура Г, получим
z)} = ^Var [arg (/ - «>i)]7 = 1	F.12)
= ^Var [arg (/ - w2)]1 = 0.
F.13)

166	КОНФОРМНОЕ ОТОБРАЖЕНИЕ	ГЛ. 6
Из F.13) в силу произвольности выбора точки W2 вне области G
следует, что все значения функции f(z) при z Е Q принадлежат
области G. Из F.12) следует, что для любой точки w\ E G в
области Q найдется одна и только одна точка z\, для которой
f(zi) = wii чт0 и доказывает взаимную однозначность данного
отображения. Теорема доказана.
Замечание. Если функция f(z) является аналитиче-
аналитической в области Q, за исключением единственной особой точки
zqj являющейся полюсом первого порядка, и при отображении
границы области Q', контура 7, на контур Г плоскости w направ-
направление обхода меняется на противоположное, то функция f(z)
осуществляет конформное отображение области Q на область
Gr7, внешнюю к контуру Г, на плоскости w (при этом точка z$
соответствует точке w = оо).
Данное утверждение доказывается аналогично предыдущей
теореме, причем вместо F.12) и F.13) получим соотношения
tiz)] - 1 = ^Var [arg (/ - U;1)]7 = -1	F.14)
N[F2(z)} - 1 = ^Var [arg (/ - w2)}1 = 0,	F.15)
из которых и следует справедливость высказанного утвержде-
утверждения.
Приведем без доказательства утверждение, в известном смы-
смысле обратное доказанной теореме.
Теорема 6.5. Если функция f(z) осуществляет конформ-
конформное отображение области Q комплексной плоскости z на огра-
ограниченную область G плоскости w, то функция f(z) непрерывна
на границе области Q и осуществляет непрерывное и взаимно
однозначное соответствие границ j и Г областей Q и G.
в) Принцип симметрии. Этот принцип находит
многочисленные применения при решении задач конформного
отображения областей, границы которых имеют прямолинейные
участки. Пусть граница j области Q имеет прямолинейный уча-
участок 77 (рис. 6.5). Область С/, полученную путем зеркального
отражения области Q относительно прямой, на которой лежит
отрезок 77, будем называть областью, симметричной области Q
относительно j'. Симметрию точек областей Q и Q будем обо-
обозначать символом z <-> z. Принцип симметрии может быть сфор-
сформулирован в виде следующей теоремы.
Теорема 6.6. Пусть в замкнутой области Q, граница 7
которой имеет прямолинейный участок jf', задана непрерыв-
непрерывная функция f(z), осуществляющая конформное отображение
области Q на область G комплексной плоскости w, при кото-
котором участок jf границы 7 переходит также в прямолинейный

ОБЩИЕ СВОЙСТВА	167
участок Г7 границы Г области G. Тогда в области ?/, симмет-
симметричной Q относительно отрезка jf, можно построить функ-
функцию f(z), являющуюся аналитическим продолжением функции
f(z) из области Q в область ?/, осуществляющую конформное
отображение области Q на область G комплексной плоскости
w, симметричную области G относительно отрезка Г7.
Заметим, что полученная таким образом область Q = Q -\- Q
может иметь участок Qyi-, принадлежащий одновременно обла-
областям Q и Q. Тогда полная аналитическая функция F(zI полу-
полученная аналитическим продолжени-
продолжением функции f(z) в область Q, долж-
должна рассматриваться на соответству-
соответствующей римановой поверхности (то же
относится и к областям Си G).
Перейдем теперь к доказатель-
доказательству теоремы.
Доказательство. Со-
Сопоставим каждой точке z Е Q сим-
симметричную ей относительно отрезка
77 точку z Е (?, а точке w E G — сим-
симметричную ей относительно отрезка
Г7 точку w E G:
Z^tZ, W^W.	F.16)
^	Рис. 6.5
Определим в области Q функцию
/(?), задавая ее значения для каждого z E Q по схеме z ^ z\
z —)> w = f(z); w <r> гЬ, f(z) = w. Как легко видеть, постро-
построенная функция f(z) является аналитической в области Q. Дей-
Действительно, в силу соответствий F.16) из существования пре-
предела разностного отношения —— следует существование предела
разностного отношения ¦—. Аналитические функции f(z), zEG,
и /(?), z E G, совпадают и непрерывны на общем участке jf
границ областей Q и Q. Поэтому в силу принципа аналитиче-
аналитического продолжения функция f(z) и является аналитическим
продолжением функции f(z) из области Q в область Q. Первая
часть утверждения теоремы доказана. В силу F.16) отображе-
отображение области Q на область G, осуществляемое функцией /(?),
является взаимно однозначным. Следовательно, на основании
теоремы 6.3 это отображение является конформным. Теорема
полностью доказана.

168	КОНФОРМНОЕ ОТОБРАЖЕНИЕ	ГЛ. 6
Замечание. Доказанная теорема остается справедливой
и в том случае, если в формулировке теоремы прямолинейный
отрезок 77 заменить на отрезок дуги окружности. При этом сим-
симметрию относительно отрезка дуги окружности надо понимать
как зеркальное отражение в данной окружности, осуществляе-
осуществляемое преобразованием инверсии. Как будет показано ниже, все-
всегда можно осуществить конформное отображение области Q на
новую область Q\ так, чтобы отрезок jf дуги окружности, явля-
являющийся частью границы 7 области Q, перешел в прямолинейный
отрезок 71? являющийся частью границы 71 области Q\. Это и
докажет справедливость высказанного утверждения.
4. Теорема Римана. До сих пор мы проводили наши рас-
рассмотрения, предполагая, что существует функция f(z), осуще-
осуществляющая конформное отображение данной области Q комп-
комплексной плоскости z на заданную область G комплексной плос-
плоскости w. Сейчас мы сформулируем условия, гарантирующие
существование и единственность такого отображения. Соот-
Соответствующая теорема, являющаяся фундаментальной теоремой
теории конформных отображений, была доказана Риманом в
1851 г. Доказательство существования конформного отображе-
отображения выходит за рамки нашего курса, поэтому мы ограничимся
лишь формулировкой теоремы 1).
Теорема 6.7 (теорема Римана). Всякую односвязную
область Q комплексной плоскости z, граница которой состо-
состоит более чем из одной точки, можно конформно отобразить
на внутренность единичного круга \w\ < 1 плоскости w.
Очевидно, из данной теоремы следует возможность кон-
конформного отображения данной односвязной области Q плоско-
плоскости z на заданную односвязную область G комплексной плос-
плоскости w, если граница каждой из этих областей состоит более
чем из одной точки. Действительно, отобразив области Q и G
на вспомогательный круг |?| < 1 (что возможно в силу теоремы
Римана), мы и получим требуемое отображение.
Условие односвязности областей Q и G является существен-
существенным, так как предположение о возможности конформного ото-
отображения многосвязной области Q на односвязную область G
приводит к противоречию. Действительно, возьмем в Q замкну-
замкнутый контур 7, внутри которого лежат граничные точки области
Q. Контур 7 отображается на некоторую замкнутую кривую Г,
целиком лежащую в односвязной области G (рис. 6.6). Будем
стягивать Г к некоторой внутренней точке г^о области G] тогда
в силу непрерывности отображения контур 7 также должен стя-
х) Подробное доказательство см., например, А. В. Бицадзе. Основы
теории аналитических функций комплексного переменного. — М.: Наука,
1972.

ОБЩИЕ СВОЙСТВА	169
гиваться к некоторой внутренней точке zq области (/, оставаясь
все время внутри этой области, что, очевидно, невозможно в си-
силу многосвязности области Q и указанного выбора контура 7-
Итак, конформное отображение многосвязной области на одно-
связную невозможно. Однако, как будет показано ниже, в ряде
случаев возможно конформное отображение областей одинако-
одинаковой связности.
Рис. 6.6
Перейдем теперь к определению условий, однозначно опреде-
определяющих функцию, осуществляющую заданное конформное ото-
отображение. Ясно, что такие условия необходимы, поскольку, как
видно из предыдущих примеров, единичный круг с помощью
простейшего линейного преобразования, заключающегося в по-
повороте комплексной плоскости, можно конформно отобразить
сам на себя. Поэтому, если функция f(z) осуществляет кон-
конформное отображение заданной области Q на единичный круг,
то и любая функция, полученная из f(z) с помощью указанно-
указанного линейного преобразования, будет осуществлять конформное
отображение области Q на тот же единичный круг.
Теорема 6.8. Функция f(z), осуществляющая конформное
отображение заданной односвязной области Q( граница кото-
ой состоит более чем из одной точки) на единичный круг
w\<l так, что f(zo) =0 и arg/'^o) = «о( где zqGQ и ао — за-
заданное действительное число ), определена единственным об-
образом.
Доказательство. Предположим, что в области Q
существуют две различные функции w\ = fi(z) и W2 = /2B),
осуществляющие заданное конформное отображение, т. е.
/iB0) = 0, arg/{(^o) = а0, |/i(*)|7 = 1,
/2B0) = 0, arg/^o) = а0, 1/2B) |7 = 1.
Заметим, что в силу теоремы 6.5 функции w\ = fi(z) и W2 =
= /2B) устанавливают взаимно однозначное и непрерывное со-
соответствие между границей 7 области Q и окружностями \w\\ =
= 1 и \w2\ = 1 соответственно.

170
КОНФОРМНОЕ ОТОБРАЖЕНИЕ
ГЛ. 6
Так как при конформном отображении устанавливается вза-
взаимно однозначное соответствие, то тем самым установлено и
взаимно однозначное соответствие между точками единичных
кругов \wi\ ^ 1 и \иJ\ ^ 1. Значит, установленные соответствия
определяют аналитическую функцию W2 = (p(wi), осуществля-
осуществляющую конформное отображение единичного круга \w\\ < 1 на
единичный круг \иJ\ < 1, причем
?>@)=0,
Заметим, что, кроме того, в силу взаимно однозначного соответ-
соответствия областей \wi\ < 1 и \иJ\ < 1 имеет место условие
(p(w\) ф 0 при w\ ф 0.
Вычисляя значение производной —- по правилу определения
производной от сложной функции, получаем
АиJ
dip
dwi wi=0
Az
Отсюда следует, что производная -—^ в точке w\ = 0 является
dwi
положительным действительным числом. Рассмотрим вспомога-
вспомогательную функцию, определенную при \w\\ ^ 1,
= ^ > 0.
hi
F.17)
Очевидно, функция ф(уо\) является однозначной аналитической
функцией в области 0 < \w\\ < 1. Точка w\ = 0 — устранимая
особая точка этой функции. Доопределим i/j(wi) при w\ = 0 по
непрерывности. Разложим (p{w{) в окрестности w\ = 0 в ряд
Тейлора:
wi=0
i
+ . . . =
wi=0
W\ + . . .
Переходя к пределу при w\ —)> 0, получаем
dwi
wi=0
F.18)
Функция i/j(wi) непрерывна в замкнутой области \w\\ ^ 1, при-
причем в этой области ф(гп\) /Ои
\ФЫ\\т\=1 = 1.	F.19)
В силу принципа максимума и минимума модуля аналитической
функции из F.19) следует, что
|^(wi)| = 1 при |w

§ 2	ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИЯ	171
откуда в силу замечания на с. 55 (гл. 1) получим, что
ф{уо\) = const при \vo\\ ^ 1.	F.20)
Чтобы найти эту постоянную, заметим, что в силу F.18) она
равна —, т.е. является положительным действительным числом.
Согласно F.19) модуль этого числа равен единице. Отсюда сле-
следует, что ij)(wi) = 1. Следовательно, W2 = <p(wi) = w\. Это и
доказывает, что не существует двух различных функций, осуще-
осуществляющих заданное конформное отображение данной области
Q на внутренность единичного круга.
Замечание. Сформулированные выше условия однознач-
однозначного определения функции f(z), осуществляющей конформное
отображение заданной односвязной области Q на внутренность
единичного круга \w\ < 1, можно заменить требованием соответ-
соответствия трех граничных точек границы j области Q трем точкам
окружности \w\ = 1.
Мы ограничимся лишь формулировкой данного утвержде-
утверждения, не приводя его доказательства.
Мы рассмотрели ряд основных общих свойств конформного
отображения. Однако проведенные рассмотрения не дают об-
общих рецептов решения основной задачи построения конформно-
конформного отображения данной области Q комплексной плоскости z на
заданную область G плоскости w. В самом общем случае ука-
указать такой рецепт и не представляется возможным, для решения
конкретных задач приходится прибегать к различным специаль-
специальным методам. При этом большую пользу оказывает достаточно
полное представление о геометрических свойствах ряда функ-
функций комплексной переменной, наиболее часто используемых при
решении практических задач.
§ 2. Дробно-линейная функция
Так называется функция комплексной переменной, имеющая
вид
W = /(*) = ±±%,	F.21)
где а, 6, с, d — заданные комплексные постоянные, которые,
очевидно, должны удовлетворять условию
-с ^ I'	^
так как в противном случае функция f(z) тождественно рав-
равна постоянной. Без ограничения общности можно считать, что
b ф 0 и d ф 0, ибо в противном случае w переходит в уже изу-
изученные линейную функцию и функцию w = -. Итак, можно

172	КОНФОРМНОЕ ОТОБРАЖЕНИЕ	ГЛ. 6
записать F.21) в эквивалентной форме:
w = /(*) = A^f' Л = 5' а = V & = 1> а ф Р- F3)
Функция F.21), F.23) является однозначной аналитической
функцией на полной комплексной плоскости z, имеющей един-
единственную особую точку — полюс первого порядка zq = — - = — /3.
Обратная функция
XaJw	( 4)
-\
также является дробно-линейной функцией, определенной на
полной плоскости w. При этом точка zq = — - = — /3 переходит
в точку w = оо, а точка z = оо переходит в точку г^о = А = -.
Найдем производную функции w = f(z):
/'(*) = Л(|т^ ф °-	F-25)
В силу условия F.22) производная дробно-линейной функции
отлична от нуля во всех конечных точках плоскости z. Это озна-
означает, что дробно-линейная функция осуществляет конформное
отображение плоскости z на плоскость w. Конформность ото-
отображения в бесконечно удаленных точках легко проверяется
указанным выше способом.
В выражение дробно-линейной функции входят три произ-
произвольных параметра А, а, /3, тем самым существует бесконечное
множество дробно-линейных функций, осуществляющих кон-
конформное отображение полной плоскости z на полную плоскость
w. Естественно поставить вопрос об условиях, однозначно опре-
определяющих дробно-линейную функцию.
Теорема 6.9. Заданием соответствия трем различным
точкам плоскости z трех различных точек плоскости w
дробно-линейная функция определена однозначно.
Доказательство. Мы должны доказать, что условия
f(zi) = wi, f(z2) = w2, f(z3) = гу3,	F.26)
где ?i, ^2, z% и wi, u>2, г^з — заданные комплексные числа, од-
однозначно определяют значения параметров А, а, /3. Составим
выражения
--»3 = Л||ТМ^,	F.27)

ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИЯ	173
Разделив F.27) на F.28), получим
Wi — W3 _ Z\ — Z2, /3 + Z2
F.29)
W2 — Ws	Z2 — Zs /3 + Z\
Для произвольной точки z можем записать аналогичное соотно-
соотношение:
Wi-W _ Zi - Z j3 + Z2	//, oq\
W2 — W	Z2 — Z /3 + Z\ '
Исключив из соотношений F.29) и F.30) параметр /3, оконча-
окончательно получим
Wi — W I W\ — Ws _ Z\ — Z I Z\ — Zs	/n o-i\
W2 — W I W2 — Ws	Z2 — Z I Z2 — Zs'
Соотношение F.31) и представляет собой неявное выражение
искомой дробно-линейной функции. Очевидно, разрешив F.31)
относительно w, мы получим явное выражение коэффициентов
А, а, /3 дробно-линейной функции через заданные числа z\, #2,
?3, w\j W2-) u?3, что и доказывает теорему.
Заметим, что поскольку дробно-линейная функция осуще-
осуществляет конформное отображение полной плоскости z на полную
плоскость и?, то одна из точек Z{ и одна из точек W{, заданием
которых определяется дробно-линейная функция, могут быть
бесконечно удаленными точками.
Рассмотрим геометрические свойства отображения, осуще-
осуществляемого дробно-линейной функцией. Для этого несколько
преобразуем выражение F.23), представив его в виде
F-32)
и введем вспомогательные функции
Zl=P + z, Z2 = ^ ^ = \(a- p)z2^r\.	F.33)
Из соотношений F.33) следует, что отображение, осуществля-
осуществляемое дробно-линейной функцией, представляет собой совокуп-
совокупность простейших отображений, осуществляемых линейными
функциями z\ и ^з и функцией -, рассмотренными в гл. 1. Тем
Z
самым рассматриваемое отображение слагается из подобных ра-
растяжений, поворотов и сдвигов комплексной плоскости, а также
преобразования инверсии в круге. При этом данное отображение
обладает рядом важных свойств, на которых мы остановимся
подробнее.
Теорема 6.10 (круговое свойство дробно-линейной функ-
функции). Дробно-линейная функция переводит окружности на
плоскости z в окружности на плоскости w. При этом мы вклю-
включаем прямые в семейство окружностей, рассматривая прямые
как окружности бесконечно большого радиуса.

174	КОНФОРМНОЕ ОТОБРАЖЕНИЕ	ГЛ. 6
Доказательство. Очевидно, для доказательства теоре-
теоремы достаточно показать, что преобразование инверсии, осуще-
осуществляемое функцией w = -, обладает круговым свойством, так
как сохранение окружности при линейном преобразовании не
может вызывать сомнений. Рассмотрим произвольную окруж-
окружность, уравнение которой на плоскости z имеет вид
А(х2 + у2) + Вх + Су + D = О,	F.34)
где А, В, С, D - действительные числа, удовлетворяющие усло-
условиям А ^ О, В2 + С2 > AAD. При А = 0 мы, очевидно, получим
прямую; при D = 0 окружность F.34) проходит через начало
координат (точку z = 0). При преобразовании, осуществляемом
функцией w = и + iv = -, координаты ж, у связаны с координа-
координатами и, v соотношениями
х =	2, у = - 2-L 2.	F.35)
Поэтому окружность F.34) в новых координатах примет вид
D(u2 + v2) + Bu-Cv + A = 0,	F.36)
что и доказывает утверждение теоремы.
Заметим, что при D = 0 уравнение F.36) представляет урав-
уравнение прямой, т. е. окружность, проходящая через точку z = 0,
функцией w = - отображается в прямую.
Рассмотренное свойство дробно-линейной функции находит
широкое применение при решении многих конкретных задач
конформных отображений, связанных с отображением обла-
областей с круговыми границами. Действительно, пусть надо осу-
осуществить конформное отображение области (/, ограниченной
окружностью 7? на плоскости z на область G, ограниченную
окружностью Г, на плоскости w. Как известно, положение
окружности на плоскости полностью определяется заданием
трех точек. С другой стороны, в силу теоремы 6.9, задав со-
соответствие трех точек z^ плоскости z, лежащих на окружности
7, трем точкам w^ плоскости w, лежащим на окружности Г, мы
полностью определим дробно-линейную функцию, осуществля-
осуществляющую конформное отображение плоскости z на плоскость w.
При этом согласно теореме 6.10 окружность 7 перейдет в окруж-
окружность Г. Если при этом соответствие точек z^ и w^ выбрано так,
что сохранено направление обхода, то в силу теоремы 6.4 данная
функция осуществляет конформное отображение области Q на
область G. Заметим, что при этом область, внешняя окружности
7 на плоскости z, конформно отображается на область, внеш-
внешнюю окружности Г на плоскости w. Если соответствие точек zj~

ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИЯ
175
и Wk установлено так, что направления обхода окружностей 7
и Г противоположны, то область Q конформно отображается на
область, внешнюю окружности Г на плоскости w.
Пример 1. Найти функцию, конформно отображающую
единичный круг \z\ < 1 на верхнюю полуплоскость Im w > 0.
Для решения поставленной задачи установим следующее со-
соответствие граничных точек данных областей (рис. 6.7):
Zl = 1 _> Wl = 0,	F.37')
z2 = I _> W2 = i,	F.37")
z3 = -1 ^^з = oo,	F.37'")
и найдем коэффициенты А, а, /3 дробно-линейной функции, осу-
осуществляющей искомое отображение. Как легко видеть из усло-
Рис. 6.7
вий F.37') и F.37'"), сразу определяются значения а и /3, после
чего искомая функция принимает вид
л z — 1
Последний коэффициент А определяется из условия F.37"):
откуда А = — г. Тем самым функция, осуществляющая искомое
отображение, имеет вид
1 + Z
Отметим, что функция F.38) осуществляет конформное отобра-
отображение области \z\ > 1 на нижнюю полуплоскость Im w < 0.
Как следует из рассмотренного примера, построение иско-
искомой дробно-линейной функции проводится наиболее просто в
том случае, когда заданными точками плоскости w являются
точки /ш = 0и'ш = оо.В этом случае сразу определяются зна-
значения коэффициентов а и /3.

176
КОНФОРМНОЕ ОТОБРАЖЕНИЕ
ГЛ. 6
Следующее свойство дробно-линейной функции заключает-
заключается в сохранении точек, симметричных относительно окружно-
окружности. Напомним, что точки Р и Р' называются симметричны-
симметричными относительно окружности С, если они лежат на общем лу-
луче, проходящем через центр О окружности С, и произведение
их расстояний от центра равно квадрату радиуса окружности:
ОР • OP' = R2. Имеет место
Теорема 6.11. При отображении, осуществляемом дробно-
линейной функцией, точки, симметричные относительно лю-
любой окружности, переходят в точки, симметричные относи-
относительно образа этой окружности.
Доказательство. Воспользуемся следующими
вспомогательными утверждениями элементарной геометрии.
Утверждение 1. Любая окружность С, проходящая
через точки РиР', ортогональна окружности С.
Действительно, проведя луч ОР1 и радиус О А в точку пе-
пересечения окружностей С ж С (рис. 6.8), мы в силу симметрии
точек Р и Р1 относительно окруж-
окружности С получим
ОР-ОР' = {О AJ = R2.
Но это, согласно известной теореме
элементарной геометрии 1), озна-
означает, что О А является касатель-
касательной к окружности С, проведенной
из точки О, откуда и следует, что
С ±С.
Утверждение 2. Две
взаимно пересекающиеся окружно-
окружности С и С", ортогональные одной
и той же окружности С, пересекаются в точках РиР', симмет-
симметричных относительно окружности С.
Проведем через точку Р пересечения окружностей С и С",
лежащую внутри окружности С, луч ОР. Предположим, что
луч ОР пересекает окружности С' и С" в различных точках,
соответственно Р* и Р** (рис. 6.9). Так как окружности С и
С" ортогональны окружности С, то по указанной выше теореме
элементарной геометрии имеют место соотношения
OP-OP* =R2,	F.39)
OP-OP** =R2.	F.40)
Но, так как точки Р* и Р** лежат на одном луче, равенства
С
Рис. 6.8
:) Произведение отрезков секущей, проведенной из внешней точки
окружности, равно квадрату отрезка касательной, проведенной из той же
точки.

ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИЯ
177
с
F.39) и F.40) возможны только в том случае, когда точки Р*
и Р** совпадают, Р* = Р** = Р7, что и доказывает это утвер-
утверждение.
Перейдем теперь к доказательству теоремы. Пусть точки Р
и Р' симметричны относительно окружности С. Проведем че-
через эти точки две вспомогательные окружности С' и С". В си-
силу утверждения 1 окружности С и С" ортогональны С. При
конформном отображении, осуществляемом какой-либо дробно-
линейной функцией, окружности С, С1 и С11 перейдут соответ-
соответственно в окружности К, К\ и К", причем окружности К7 и К"
будут ортогональны окружности К. Точки Р и Р7 пересечения
окружностей С и С" пе-
перейдут в точки Q и Qf
пересечения их образов —
окружностей К' и К". Но
в силу утверждения 2 точ-
точки Q и Q' должны быть
симметричны относитель-
относительно окружности К, что и
доказывает теорему.
Очевидно, доказанная
теорема остается спра-
справедливой и в том случае,
когда рассматриваются и
окружности бесконечно
большого радиуса, т. е.
прямые.
Доказанная теорема находит многочисленные применения
при решении конкретных задач конформных отображений, и
мы будем в дальнейшем неоднократно к ней прибегать. Здесь
же ограничимся лишь двумя примерами.
Пример 2. Найти функцию, конформно отображаю-
отображающую единичный круг \z\ < 1 сам на себя так, чтобы заданная
внутренняя точка zq перешла в центр круга.
Очевидно, для решения задачи можно воспользоваться дроб-
дробно-линейной функцией. При этом точка zq и точка z\, симмет-
z\ = 1, перейдут в точки,
Рис. 6.9
= 1. Но поскольку
ричная ей относительно окружности
симметричные относительно окружности w
точка, симметричная центру окружности, есть бесконечно уда-
удаленная точка, а точка zq должна перейти в точку w = 0, то точ-
точка z\ должна перейти в точку w = oo. Следовательно, искомая
дробно-линейная функция имеет вид
w = X-
F.41)

178
КОНФОРМНОЕ ОТОБРАЖЕНИЕ
ГЛ. 6
Так как z\ = —, то F.41) можно переписать в виде
w = Xzn
'zzo-1
F.42)
Для того чтобы при отображении F.42) окружность \z\ = 1 пе-
перешла также в окружность \w\ = 1 единичного радиуса, должно
выполняться условие
e^ - zo
ei<PZo — 1
-|Лг0
e1^ - zo
Zq - e*V
Отсюда А^о = еш, где а — произвольное действительное число,
и решение нашей задачи получаем в виде
w = e
z — Zq
ZZq — 1
F.43)
Заметим, что мы получили решение, определенное с точностью
до одного произвольного параметра а, который, очевидно, опре-
опре\\
деляет поворот окружности
w
= 1 вокруг центра. Задание зна-
значения аргумента производной
функции w в точке z = zq
полностью определяет функ-
функцию w.
Пример 3. Найти функ-
функцию, конформно отображаю-
отображающую эксцентрическое кольцо
на концентрическое.
Пусть требуется постро-
построить конформное отображение
области, ограниченной двумя
окружностями с несовпадаю-
несовпадающими центрами (рис. 6.10),
на какое-либо концентрическое
кольцо. Поскольку мы имеем
дело с двухсвязными областя-
областями, то теорема Римана о существовании конформного отобра-
отображения здесь уже не имеет места и, как мы увидим, нельзя про-
произвольно задать отношение радиусов окружностей концентри-
концентрического кольца, на которое требуется конформно отобразить за-
заданное эксцентрическое кольцо. Для удобства дальнейших рас-
рассмотрений положим, что центр большей окружности С находит-
находится в точке z = 0, ее радиус равен i?, а центр меньшей окруж-
окружности С7, радиуса г, лежит в точке z = а на действительной
оси. Найдем точки Р\ и ?25 которые являются симметричными
одновременно относительно обеих окружностей С и С. Очевид-
Очевидно, эти точки лежат на действительной оси (рис. 6.10). Тогда их
Рис. 6.10

§ 2	ДРОБНО-ЛИНЕЙНАЯ ФУНКЦИЯ	179
абсциссы %\ и %2 должны удовлетворять соотношениям
(xi - а)(х2 - а) = г2,	F.44)
Х1 -х2 = ^2.	F.45)
Из F.44) и F.45) следует, что х\ и х% являются корнями ква-
квадратного уравнения
ах2 - (R2 - г2 + а2)х + aR2 = 0.	F.46)
Дискриминант этого уравнения (В2 — г2 + а2J — 4а2R2 положи-
положителен, так как имеет место очевидное соотношение R — г > а.
Построим дробно-линейную функцию
w = A i^i,	F.47)
Z — Х2
где х\ ж Х2 — абсциссы точек Р\ и ?2^ найденные из уравне-
уравнения F.46). При отображении, осуществляемом функцией F.47),
окружности С ж С перейдут в некоторые окружности К и К'
плоскости w, внешняя к окружностям СиС" точка Р2 — в точку
w = оо. Симметричная относительно окружностей С и С' точке
?2 точка Р\ должна при этом перейти в точку, симметричную
точке w = оо относительно окружностей К ж К'. Но точка, сим-
симметричная бесконечно удаленной точке, есть центр окружности.
Следовательно, при отображении F.47) точка Р\ перейдет в об-
общий центр окружностей К и К'. Тем самым искомое отображе-
отображение построено. Заметим, что в выражении F.47) у нас остался
произвол в определении параметра А, однако изменение послед-
последнего приводит лишь к подобному растяжению плоскости w, что
не может изменить отношения радиусов окружностей получен-
полученного концентрического кольца.
В заключение данного параграфа рассмотрим вопрос о при-
применении дробно-линейной функции для построения конформ-
конформного отображения двуугольников. Двуугольником называется
плоская фигура, образованная пересечением дуг двух окружно-
окружностей, вообще говоря, разных радиусов (рис. 6.11). Очевидно,
углы при вершинах двуугольника равны друг другу. Пусть дан
двуугольник с вершинами в точках A(z\) и B(z2) и углом а при
вершине и требуется построить конформное отображение вну-
внутренней области данного двуугольника на верхнюю полуплос-
полуплоскость Im w > 0. Рассмотрим вспомогательную функцию
c = J^f (c = e+^). F.48)
Дробно-линейная функция F.48) производит конформное ото-
отображение полной плоскости z на полную плоскость С, при кото-
котором точка z = z\ переходит в точку ? = 0, а точка z = Z2 — в точ-
точку ? = оо. В силу кругового свойства дробно-линейной функции
при отображении F.48) окружности, образующие двуугольник,
переходят также в окружности. Но окружность, проходящая че-
через точки С = 0 и С = оо, имеет бесконечно большой радиус. Это

180
КОНФОРМНОЕ ОТОБРАЖЕНИЕ
ГЛ. 6
означает, что при отображении F.48) стороны двуугольника пе-
перейдут в лучи (/ и //), выходящие из точки ? = 0, причем угол
между этими лучами равен углу а при вершине двуугольни-
двуугольника (рис. 6.12). Итак, функция F.48) осуществляет конформное
отображение данного двуугольника на плоскости z на сектор с
центральным углом а на плоскости ?, причем луч / составляет с
положительным направлением оси ? угол «о, значение которого
определяется положением вершин А и В двуугольника. Как мы
видели выше (гл. 6, с. 163), функция
w =
F.49)
являющаяся непосредственным аналитическим продолжением
действительной функции ж», х > 0, осуществляет конформ-
конформное отображение области внутри сектора ао < arg ? < ао -\- а
на полуплоскость — тг < a,rgw < — тг + тг. Остается перевести
а	а
полученную полуплоскость в полуплоскость Im w > 0, для чего
B(z2)
II
A(zx)
Рис. 6.11
Рис. 6.12
достаточно произвести поворот всей плоскости как целое на угол
— — тг, что может быть осуществлено путем умножения функции
F.49) на комплексное число ехр (—г—тг). Итак, окончательно,
V a J
искомая функция, осуществляющая конформное отображение
двуугольника АВ на верхнюю полуплоскость Im w > 0, прини-
принимает вид
() (Yla .	F.50)
w = ехр (-г^т
Отметим, что конформность отображения нарушается в точках
Z\ И Z2-

§ 3	ФУНКЦИЯ ЖУКОВСКОГО	181
Пример 4. Построить конформное отображение верхней
половины круга \z\ < 1, Im z > 0, на верхнюю полуплоскость
Im w > 0.
Очевидно, данная область представляет собой двуугольник
с вершинами в точках z\ = — 1 и ^ = 1 и углом а = ^ при
вершине. Вспомогательная функция
С = ?f	F-51)
осуществляет конформное отображение этого двуугольника на
первый квадрант плоскости ?, а функция
(й)	F-52)
и дает искомое отображение.
§ 3. Функция Жуковского
Так называется функция комплексной переменной
F.53)
Эта функция была широко использована Н. Е. Жуковским
при решении многих задач гидро- и аэродинамики.
Функция F.53), очевидно, является аналитической на всей
комплексной плоскости, за исключением точки z = 0, предста-
представляющей собой полюс первого порядка данной функции. Вычис-
Вычисляя производную функции F.53), получаем
= I (l - 1) .	F.54)
Отсюда следует, что производная функции Жуковского отлич-
отлична от нуля во всех точках плоскости z, кроме точек ±1. Тем
самым отображение, осуществляемое этой функцией, является
конформным в окрестности любой точки z, за исключением этих
двух точек. Найдем области однолистности функции Жуковско-
Жуковского. Предположим, что две различные точки комплексной плос-
плоскости z\ Ф Z2 переводятся функцией f(z) в одну и ту же точку
плоскости w, т. е.
z\ + — = z2 + —,
Z\	Z2
ИЛИ
Zl-Z2 = ?L=J1.	F.55)
Так как z\ Ф Z2, то из соотношения F.55) следует
Z\ Z2 = 1.	F.56)

182	КОНФОРМНОЕ ОТОБРАЖЕНИЕ	ГЛ. 6
Полученное соотношение означает, что областями однолистно-
однолистности функции Жуковского являются, в частности, области вну-
внутри (\z\ < 1) и вне (\z\ > 1) единичного круга. Обе эти обла-
области функцией F.53) отображаются конформно на одну и ту же
область плоскости w. Чтобы определить эту область, рассмо-
рассмотрим отображение окружностей \z\ = го, осуществляемое функ-
функцией F.53). Для этого перейдем к показательной форме записи
комплексных чисел: z = гег(р — и найдем выражение действи-
действительной и мнимой частей функции F.53):
и(г, Ч>) = \ у + I) cos <Р> v(ri Ч>) = \ у ~ I) sin Ч>- F-57)
Положив г = го и исключив параметр <р, получим
2
1 ( IV 1 f 1
- го + —	- го
4 V roj	4 V
F.58)
Из соотношения F.58) следует, что функция F.53) отображает
концентрические окружности \z\ = tq в эллипсы. Как легко ви-
видеть, фокусы всех эллипсов F.58) лежат в одних и тех же точках
действительной оси и:
с = ±1.	F.59)
Тем самым функция F.53) производит отображение семейства
концентрических окружностей \z\ = г о плоскости z на семей-
семейство СОфокуСНЫХ ЭЛЛИПСОВ ПЛОСКОСТИ W. При ЭТОМ, еСЛИ 7*1 < 1, ТО
положительному направлению обхода окружности \z\ = r\ соот-
соответствует отрицательное направление обхода эллипса F.58); ес-
ли г2 = — > 1, то положительному направлению обхода окруж-
7*1
ности \z\ = г2 соответствует положительное направление обхода
эллипса F.58). При г\ —>• 1 эллипс F.58) вырождается в от-
отрезок [—1,1] действительной оси и, проходимый дважды. При
г\ —)> 0 эллипс F.58) переходит в окружность бесконечно боль-
большого радиуса. Тем самым функция F.58) производит конформ-
конформное отображение области внутри единичного круга \z\ < 1 на
плоскости z на плоскость w, разрезанную по отрезку [—1,1]
действительной оси. Граница области — окружность \z\ = 1 —
отображается на этот отрезок, причем верхняя полуокружность
отображается на нижний, а нижняя — на верхний берег разреза.
Аналогично область \z\ > 1 вне единичного круга на плоскости z
отображается на второй экземпляр плоскости w, разрезанной по
отрезку [—1,1] действительной оси, причем верхняя полуокруж-
полуокружность \z\ = 1, Im z > 0, отображается на верхний берег, а нижняя
полуокружность |^| = 1, Im z < 0 — на нижний берег разреза.
Тем самым функция Жуковского F.53) осуществляет конформ-

§ 4	ОТОБРАЖЕНИЕ МНОГОУГОЛЬНИКОВ	183
ное отображение полной плоскости z на риманову поверхность
обратной функции
z = (p(w) = w + yw2 — 1.	F.60)
Риманова поверхность функции F.60) представляет собой
двулистную поверхность, составленную из двух экземпляров
плоскости w, разрезанной вдоль отрезка [—1,1] действительной
оси. Нижний берег разреза одного листа склеен с верхним бере-
берегом разреза другого листа, и наоборот. Функция F.60) является
однозначной аналитической функцией на своей римановой по-
поверхности, имеющей две точки разветвления w = =Ы, при обхо-
обходе каждой из которых происходит переход с одного листа этой
римановой поверхности на ее другой лист. Заметим, что при
одновременном обходе обеих точек разветвления w = =Ы по за-
замкнутой кривой, не пересекающей отрезка [—1,1], мы все время
находимся на одном и том же листе.
Итак, функции F.53) и F.60) устанавливают взаимно од-
однозначное соответствие между полной плоскостью z и данной
римановой поверхностью. Отображение, осуществляемое этими
функциями, является всюду конформным, за исключением то-
точек z = =Ы, в которых производная функции F.53) равна нулю.
Заметим, что этим точкам соответствуют точки w = =Ы, яв-
являющиеся точками разветвления функции F.60), обратной по
отношению к функции F.53).
В заключение найдем образ лучей arg z = щ при отобра-
отображении, осуществляемом функцией Жуковского. Для этого ис-
исключим из соотношений F.57) параметр г и положим ср = (р$.
Тогда
2	?
= 1-	F.61)
COS (fo	Sin LpQ
Соотношение F.61) означает, что при отображении F.53) отрез-
отрезки лучей arg z = (ро переходят в ветви гиперболы F.61). Отме-
Отметим, что при любом значении сро фокусы этой гиперболы на-
находятся в точках ±1. Тем самым функция Жуковского осуще-
осуществляет преобразование ортогональной системы полярных ко-
координат на плоскости z в ортогональную криволинейную систе-
систему координат, координатными линиями которой являются со-
фокусные семейства эллипсов F.58) и гипербол F.61).
Как уже отмечалось, функция Жуковского находит весь-
весьма широкое применение при решении многих конкретных задач
конформных отображений, особенно связанных с исследованием
гидродинамических проблем. На этих вопросах мы остановим-
остановимся несколько позже, а сейчас рассмотрим еще одну функцию,
находящую многочисленные приложения.

184	КОНФОРМНОЕ ОТОБРАЖЕНИЕ	ГЛ. 6
§ 4. Интеграл Шварца—Кристоффеля. Отображение
многоугольников
Пусть на комплексной плоскости w задан n-угольник с вер-
вершинами в точках А\, A2, ..., Ап и внутренними углами при этих
(	п
вершинах а^тг, «2тг, ..., аптг соответственно. ( Очевидно, У^ щ =
v
= п — 2, п > 2. ] Пусть требуется построить конформное ото-
отображение верхней полуплоскости z на внутренность такого мно-
многоугольника. Эта задача решается с помощью так называемого
интеграла Шварца-Кристоффеля, изучение некоторых свойств
которого и составляет содержание настоящего параграфа.
Рассмотрим функцию комплексной переменной z, определен-
определенную в верхней полуплоскости z с помощью выражения
z
w = f(z) = С J (С - ах)... (С - onH» d( + d. F.62)
Здесь zqj G, С\ — заданные комплексные постоянные; ai,...
..., ап — действительные числа, расположенные в порядке воз-
возрастания; ai,...,an — положительные постоянные, удовлетво-
удовлетворяющие условиям
<ц = п-2,	F.63)
г=1
О < а{ < 2.	F.64)
В подынтегральном выражении выбраны те ветви функций
(( — ai)ai~l, которые являются непосредственным аналитиче-
аналитическим продолжением в верхнюю полуплоскость действительных
функций (х — ai)ai~l действительной переменной х > щ. В та-
таком случае функция F.62) является однозначной аналитической
функцией в верхней полуплоскости Im z > 0. Точки a^, лежащие
на действительной оси, являются особыми точками этой функ-
функции. Функция F.62) и называется интегралом Шварца-Крис-
Шварца-Кристоффеля. Функция F.62) при соответствующем выборе точек а,{
осуществляет конформное отображение верхней полуплоскости
Im z > 0 на область внутри некоторого n-угольника на плос-
плоскости w. Будем вначале считать, что все числа щ ограничены.
Покажем, что при этом функция F.62) остается ограниченной
всюду при Im z ^ 0. В силу условия F.64) интеграл F.62) оста-
остается ограниченным в окрестности особых точек щ. Убедимся,
что интеграл F.62) остается ограниченным и при z —>• 00. Преоб-

§ 4	ОТОБРАЖЕНИЕ МНОГОУГОЛЬНИКОВ	185
разуем подынтегральную функцию, использовав условие F.63):
= М1"?') ¦¦¦A"т) ¦ F-65)
Из полученного выражения и следует сходимость интеграла при
z —>• оо. Таким образом, интеграл F.62), являющийся однозначной
аналитической функцией 2 в верхней полуплоскости Im z > О,
осуществляет отображение этой полуплоскости на некоторую
ограниченную область Q плоскости w.
Посмотрим, в какую кривую при этом переходит действи-
действительная ось плоскости z. Рассмотрим выражение производной
функции F.62):
/'(*) = C(z - ах)... (z - ап)а"-\	F.66)
Из этого выражения следует, что производная функции f(z) от-
отлична от нуля всюду в верхней полуплоскости Im z ^ 0, за ис-
исключением особых точек а^, в которых она обращается в нуль
или бесконечность. При изменении z на каждом из интервалов
пк < х < а&+1 (к = 1,..., п — 1) действительной оси аргумент
производной не меняется. Действительно, в силу указанного вы-
выше выбора ветвей функций (z — ai)ai~l аргумент этих функций
на данных интервалах действительной оси принимает значения
aig(x-ai)ai = <	F.67)
[	О,	X > CLi,
что и доказывает высказанное утверждение. В силу геометри-
геометрического смысла аргумента производной1) это означает, что от-
отрезки действительной оси а& < х < а&+1 функцией f(z) ото-
отображаются также на прямолинейные отрезки плоскости w. При
этом точки ak действительной оси функцией F.62) переводятся
в точки Ак плоскости w — концы соответствующих прямоли-
прямолинейных отрезков AkAk+i, на которые функция F.62) отобра-
отображает отрезки действительной оси [a^,a^_|_i]. Тем самым функ-
функция F.62), непрерывная и однозначная на действительной оси,
производит отображение действительной оси плоскости z на
некоторую замкнутую ломаную А\А2 ... Ап, звеньями которой
являются прямолинейные отрезки А^Ак+х (рис. 6.13 а). При
этом, когда точка z проходит всю действительную ось в поло-
положительном направлении, соответствующая ей точка w соверша-
:) Аргумент производной функции f(z) в точке zq определяет величину
угла, на который нужно повернуть касательную к любой гладкой кривой
7, проходящей через точку zo, чтобы получить касательную к образу этой
кривой в точке wq = f(zo).

186
КОНФОРМНОЕ ОТОБРАЖЕНИЕ
ГЛ. 6
ет полный обход замкнутой ломаной A\A% ... Ап. Заметим, что,
вообще говоря, ломаная А\А2 ... Ап может иметь точки самопе-
самопересечения (рис. 6.13 б).
Рис. 6.13
Определим теперь величину углов между соседними отрез-
отрезками полученной ломаной. Для этого рассмотрим, как меняется
аргумент производной F.66) при переходе z через точку щ. Из
F.67) следует, что при движении точки z по действительной
оси в положительном направлении, при котором особая точка
di обходится по дуге бесконечно малого радиуса в верхней по-
полуплоскости, аргумент производной изменяет свое значение на
величину — тг(с^ — 1). В силу геометрического смысла аргумента
производной это означает, что величина угла между направле-
направлениями векторов1) А{-\А{ и А{А{+\ равна — тг(с^ — 1). При этом
при oti < 1 переход от направления вектора А{_\А{ к направле-
направлению вектора А{А{+\ происходит в положительном (рис. 6.14 а),
а при ai > 1 в отрицательном (рис. 6.14 б) направлении. Как
легко видеть, в обоих случаях величина угла при переходе в по-
положительном направлении от направления вектора А{А{+\ к на-
направлению вектора A{Ai-\ равна тгс^ (рис. 6.14). Если замкнутая
ломаная А\Аъ ... Ап не имеет самопересечений, то она ограничи-
ограничивает некоторый n-угольник. Если, кроме того, движению точки
z в положительном направлении действительной оси соответ-
соответствует обход ломаной А\Аъ ... Ап в положительном направле-
направлении, то внутренний угол данного n-угольника при вершине А^
на которую отображается точка щ действительной оси плоско-
плоскости z, равен тгс^. В силу условия F.63) при этом сумма всех
внутренних углов данного n-угольника равна (п — 2)тг, как и
1) При этом под углом между направлениями пересекающихся прямых Ъ\,
&2 мы понимаем величину угла наикратчайшего поворота, совмещающего
прямую Ъ\ с прямой &2.

ОТОБРАЖЕНИЕ МНОГОУГОЛЬНИКОВ
187
должно быть.
На основании принципа соответствия границ (теорема 6.4)
можно утверждать, что если ломаная A\A% ... Ап, на которую
функция F.62) отображает действительную ось плоскости z, не
имеет точек самопересечения и сохраняется направление обхо-
обхода, то функция F.62) осуществляет конформное отображение
верхней полуплоскости Im z > 0 на внутренность п-угольника,
ограниченного ломаной А1А2 ... Ап.
-7u(arl)
¦1+1
Рис. 6.14
Как показывает детальное исследование, если на плоскости
w задан произвольный n-угольник (известно положение его вер-
вершин А\, А2, • • •, Ап и углы при этих вершинах), то всегда можно
задать значения постоянных С, С\ и точки ai,..., an действи-
действительной оси так, чтобы соответствующим образом построенная
функция F.62) осуществляла конформное отображение верхней
полуплоскости Im z > 0 на внутренность данного п-угольника.
Мы не будем останавливаться на доказательстве этого положе-
положения 1), а ограничимся лишь некоторыми замечаниями и приме-
Замечание 1. В формулу F.62) входит ряд по-
постоянных. Однако при построении конформного отображения
верхней полуплоскости Im z > 0 на заданный многоугольник
А\ ... Ап плоскости w можно произвольно задавать лишь три
точки сц, aj, dk действительной оси ж, переходящие в какие-
либо три выбранные вершины многоугольника А{, А/, А^. При
этом остальные постоянные в формуле F.62) определяются од-
однозначно. Действительно, F.62) определяет функцию f(z), свя-
z
занную с функцией f(z) = /(( — a\)ai~l...(( — an)an~l d( ли-
:) См., например, И. И. Привалов. Введение в теорию функций
комплексного переменного. — М.: Наука, 1967.

188	КОНФОРМНОЕ ОТОБРАЖЕНИЕ	ГЛ. 6
нейным преобразованием, представляющим собой преобразова-
преобразование подобного растяжения, поворота и параллельного переноса.
Следовательно, если функция f(z) отображает верхнюю полу-
полуплоскость Im z > 0 на заданный многоугольник плоскости к;,
то функция f(z) отображает эту полуплоскость на многоуголь-
многоугольник, подобный данному. При заданных значениях с^ для того,
чтобы n-звенная замкнутая ломаная, на которую отображается
функцией f(z) действительная ось, представляла бы собой мно-
многоугольник, подобный данному, достаточно, чтобы п — 2 звена
этой ломаной были пропорциональны соответствующим сторо-
сторонам многоугольника. (Два крайних звена полностью определя-
определяются заданием их направлений.) Тем самым мы имеем п—3 урав-
уравнения относительно п постоянных щ. Если произвольно задать
три из этих постоянных, то остальные из соответствующих урав-
уравнений определятся однозначно. Данное обстоятельство является
также следствием теоремы Римана об однозначном определении
функции, осуществляющей конформное отображение односвяз-
ных областей, при задании соответствия трех точек границы
одной области трем точкам границы другой области. Заметим,
кроме того, что положение заданного многоугольника (заданы
длины сторон и величина углов при вершинах) на плоскости
однозначно определяется положением трех его вершин.
Замечание 2. Мы предполагали, что все числа с^ в
формуле F.62) являются положительными. При этом интеграл
F.62) сходится при всех значениях Im z ^ 0. Если какое-либо
число oik отрицательно, то при z —>> а& интеграл F.62) расходит-
расходится. Это означает, что соответствующая вершина А^ многоуголь-
многоугольника А\ ... Ап лежит в бесконечно удаленной точке w = oo. При
этом величину угла при вершине А^ мы полагаем равной взятой
со знаком минус величине угла между продолжением отрезков
AfcAk-i и AfcAk+i в конечной точке их пересечения. Как легко
видеть, при таком определении угол при вершине А^ равен а^тт
(аь < 0), ив силу условия F.63) сумма внутренних углов по-
полученного n-угольника с вершиной А^ в бесконечно удаленной
точке по-прежнему равна (п — 2)тг. Данное замечание остается
в силе и в том случае, когда несколько чисел а& отрицательны.
Замечание 3. При исследовании формулы F.62) мы
предполагали, что все точки щ конечны. Легко освободиться от
этого условия. Введем новую комплексную переменную ?, свя-
связанную с z соотношением
z = ап - -.	F.68)
При этом точка z = ап переходит в точку t = oo. Данное преоб-
преобразование означает, что при отображении верхней полуплоско-
полуплоскости Im t > 0 на внутренность многоугольника А\Аъ ... Ап плос-

§ 4	ОТОБРАЖЕНИЕ МНОГОУГОЛЬНИКОВ	189
кости w бесконечно удаленная точка t = оо отображается на
вершину Ап. На комплексной плоскости t функция F.62) имеет
вид
t
Г/	1\а1-1 /	xxan-1-l/ l\an-l dr
w = CJ(an-ai--) ...(an-an-i--J	(--J	— +
to
t
+ Ci = A f(r - а[)а1-г... (r - «d)"»-1 dr + Ci. F.69)
to
Здесь использовано соотношение F.63) и введены обозначения
а- = (ап - ai)~l, t0 = 	,
ап — zo
А = С(ап - ^Г... К - an-^-i-H-l)"»-1.
Соотношение F.69) означает, что в том случае, когда при кон-
конформном отображении верхней полуплоскости на внутренность
многоугольника А1А2 ... Ап бесконечно удаленная точка t = 00
переходит в одну из вершин (Ап), это отображение осуществля-
осуществляется интегралом Шварца-Кристоффеля F.69), в подынтеграль-
подынтегральной функции которого опущен множитель, соответствующий
данной вершине (Ап). Это обстоятельство часто используется на
практике, поскольку, как мы отметили выше (замечание 1), при
решении задач о построении конформного отображения верхней
полуплоскости Im z > 0 на заданный многоугольник плоскости
w приходится, в случае большого числа вершин многоугольника,
определять большое число неизвестных.
Рассмотрим некоторые простейшие примеры.
Пример 1. Найти функцию, конформно отображающую
верхнюю полуплоскость Im z > 0 на сектор 0 < &rgw < атг,
О < а < 2.
Так как данный сектор представляет собой многоугольник
с вершинами A\(w = 0) и A2(w = оо), то для решения задачи
можно применить интеграл Шварца-Кристоффеля. Установим
следующее соответствие точек действительной оси z вершинам
данного многоугольника:
= сю) —>> A<i{w = сю).
Тогда согласно F.69) отображающая функция принимает вид
w =
Положив zq = 0 и использовав F.70), найдем, что постоянная

190
КОНФОРМНОЕ ОТОБРАЖЕНИЕ
ГЛ. '
С\ равна нулю. Отсюда
w =
2-1
d( = -za.
а
F.71)
Функция F.71) определена с точностью до постоянного мно-
множителя, определяющего преобразование подобия. Данный про-
произвол связан с тем, что условия F.70) содержат требование
соответствия лишь двух граничных точек, а, как мы видели
(см. замечание на с. 171), функция, осуществляющая конформ-
конформное отображение, однозначно определяется заданием соответ-
соответствия трех граничных точек. Потребовав, например, чтобы на-
наряду с F.70) имело место дополнительное соответствие гранич-
граничных точек
z = 1 —»> w = 1,
определим значение оставшейся в F.71) произвольной постоян-
постоянной С = а.
Итак, окончательно, функция
w = za	F.72)
осуществляет конформное отображение верхней полуплоскости
Im z > 0 на заданный сектор плоскости w. При этом в силу ука-
указанного выше выбора ветвей в подынтегральной функции инте-
интеграла Шварца-Кристоффеля F.62) должна быть взята та ветвь
многозначной функции F.72), которая является непосредствен-
непосредственным аналитическим продолжением действительной функции ха
действительной положительной переменной х.
Пример 2. Найти функцию, конформно отображающую
верхнюю полуплоскость Im z > 0 на прямоугольник А1А2А3А4
(рис. 6.15).
w
=-a+ib
о'
а3
а4
w=-a
w=a+ib
о .
w=a
А4
Рис. 6.15
Пусть вершины прямоугольника на плоскости w расположены
в точках Ai(w = a), А2(w = а + гЪ), As(w = — а + гЪ), А±(гш = — а).
Положим, что с помощью некоторой функции fi(z) произве-
произведено конформное отображение первого квадранта плоскости z

§ 4	ОТОБРАЖЕНИЕ МНОГОУГОЛЬНИКОВ	191
(Re z > 0,1m z > 0) на правую половину ОА1А2О' прямоуголь-
прямоугольника (рис. 6.15), при котором положительная часть мнимой оси
плоскости z перешла в отрезок 00'. Тогда на основании прин-
принципа симметрии (см. с. 166) функция, являющаяся аналитиче-
аналитическим продолжением f\{z) в область (Re z < 0,1m z > 0), осу-
осуществляет конформное отображение данной области на левую
часть исходного прямоугольника. При этом в вершины А\ и А^
переходят соответственно симметричные точки действительной
оси z. То же имеет место для вершин А2 и А%. Поэтому можем
установить следующее соответствие точек:
ai(z = 1) ->> Ai(w = a),
a^z = —1) —>> A±(w = —а).
Кроме того, очевидно, должно иметь место соответствие
z = 0 -+ w = 0.	F.74)
Соотношения F.73), F.74) устанавливают соответствие трех
граничных точек. Поэтому произвольно задать точку п2 на дей-
действительной оси z, переходящую в вершину А2 прямоугольни-
прямоугольника, уже нельзя. Положим, что в вершину А2 переходит точка п2
действительной оси z, имеющая координату -, значение которой
к
будет определено в дальнейшем. Очевидно, 0 < к < 1.
Итак, функция, осуществляющая конформное отображение
верхней полуплоскости на заданный прямоугольник, может
быть представлена в виде
w =
+ d = C f / dC = + d. F.75)
J V(i-c2)(i-FC2)
Положив zq = 0 и использовав соотношение F.74), получим
Сг = 0. Тогда
W = C f	dC =.	F.76)
J V(i-C2)(i-FC2)
о
Остается определить постоянные С и к из соответствия точек а\
и п2 действительной оси z вершинам А\ и А^. Отметим, что ин-
интеграл F.76) не выражается в элементарных функциях. Это так
называемый эллиптический интеграл г) I рода, который обычно
г) См. вып. 1.

192	КОНФОРМНОЕ ОТОБРАЖЕНИЕ	ГЛ. 6
обозначается
V ' /	/	// -л	>О \ / -1	7 О >О \ *	\ *	/
О
Условия F.73) дают
1
а = С [	dC ^.	F.78)
7 л/A-с2)A-^2с2)
о
Интеграл, стоящий справа, так называемый полный эллиптиче-
эллиптический интеграл I рода
1
= Г	^ = ,	F.79)
7 л/A-с2)A-^2с2)
о
нной и табулированной функцией. Соот-
Соответствие точек п2 B = — ) <<->• ^(и? = а -\- гЪ) позволяет записать
о
является хорошо изученной и табулированной функцией. Соот-
СоотJ
л/A-С2)A-^2С2) J л/A-С2)A-^2С2)
о	1
откуда, учтя F.78), получим
F.80)
Ь = С [	dC = = CF (I A;) ,	F.81)
У л/(С2-1)A-^2С2)	U' /'	V ;
1
где через F[-,k) обозначен интеграл в формуле F.81). Из
F.78) и F.81) при заданных величинах а и b можем, решив
трансцендентное уравнение
aFQ,fc) =ЪК(к),	F.82)
определить значения постоянных к и С. Тем самым функция
F.76), осуществляющая конформное отображение верхней по-
полуплоскости Im z > 0 на заданный прямоугольник плоскости
w, полностью определена. С другой стороны, если в формуле
F.76) заданы величины fc и С, то эта функция осуществляет
конформное отображение верхней полуплоскости Im z > 0 на
прямоугольник плоскости и?, отношение сторон ( — 1 которого
определяется формулой F.82), а абсолютная величина сторон —
постоянной С. Произвольно изменяя значение этих постоянных,
можно получить конформное отображение верхней полуплоско-
полуплоскости Im z > 0 на любой прямоугольник плоскости w.

ГЛАВА 7
ПРИМЕНЕНИЕ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
К РЕШЕНИЮ КРАЕВЫХ ЗАДАЧ
Методы теории функций комплексной переменной весьма
широко и эффективно применяются для решения большого чис-
числа математических задач, возникающих в различных областях
естествознания. В частности, применение аналитических функ-
функций дает во многих случаях достаточно простые способы реше-
решения краевых задач для уравнения Лапласа, к которым приво-
приводятся различные задачи гидро- и аэродинамики, теории упруго-
упругости, электростатики и т.д. Это определяется тесной связью, су-
существующей между аналитическими функциями комплексной
переменной и гармоническими функциями двух действительных
переменных. В настоящей главе мы остановимся на некоторых
общих вопросах применения аналитических функций к реше-
решению краевых задач для уравнения Лапласа и приведем ряд при-
примеров решения физических и механических задач.
§ 1. Общие положения
1. Связь аналитических и гармонических функций.
Пусть в области Q комплексной плоскости z задана аналити-
аналитическая функция f(z) = и(х,у) + iv(x,y). Тогда всюду в этой
области функции и ж v связаны условиями Коши-Римана:
ди 	 dv ди 	 dv	G Л\
дх ду"* ду	дх'
Так как аналитическая функция имеет в области Q производные
всех порядков, то и действительные функции и(х,у) и v(xyy)
имеют в соответствующей области плоскости ху частные произ-
производные любого порядка. Это позволяет дифференцировать вы-
выражения G.1) по переменным ж, у любое число раз. Продиф-
Продифференцировав первое из равенств G.1) по ж, второе — по у и

194 ПРИМЕНЕНИЕ АНАЛИТИЧЕСКИХ ФУНКЦИЙ ГЛ. 7
сложив их, получим
д2и д2и п	п	/7О>,
— + — = 0, х,уед.	G.2)
Аналогично продифференцировав первое из равенств G.1) по у,
второе — по ж и вычтя одно из другого, получим
о2	<л2
— + — = о, х,уед,	G.3)
откуда следует, что функции и(х,у) и v(x,y) являются гармони-
гармоническими в данной области плоскости ху. Итак, действительная
и мнимая части функции f(z), аналитической в области Q, яв-
являются гармоническими функциями в соответствующей области
плоскости ху. При этом данные гармонические функции связа-
связаны условиями G.1). С другой стороны, если в области Q плоско-
плоскости ху заданы две гармонические функции и(х, у) и v(x, у), удов-
удовлетворяющие в этой области условиям G.1), то функция f(z) =
= и(х, у) + iv(x, у) комплексной переменной z = x + iy является
аналитической в соответствующей области плоскости z. Тем са-
самым необходимым и достаточным условием аналитичности
функции f(z) = и(х,у) + iv(x,y) в области Q является тре-
бование, чтобы функции и(х,у) и v(x,y) были гармоническими
и удовлетворяли условиям G.1) в соответствующей области
плоскости ху. В гл. 1 (см. с. 37) было показано, что заданием
лишь одной действительной (или одной мнимой) части анали-
аналитической функции комплексной переменной последняя опреде-
определяется с точностью до постоянного слагаемого. Отсюда следу-
следует, что все аналитические функции комплексной переменной,
для которых заданная гармоническая функция двух действи-
действительных переменных является действительной (или мнимой) ча-
частью, различаются только на аддитивную постоянную.
Установленная связь между аналитическими и гармониче-
гармоническими функциями позволяет использовать для изучения раз-
различных свойств гармонических функций свойства аналитиче-
аналитических функций. Так, например, из формулы среднего значения
аналитической функции (см. гл. 1, с. 52) непосредственно полу-
получается формула среднего значения для гармонической функции
и(хо,уо) = ^- J u(?,ri)ds,	G.4)
Cr0
где точка жо,уо является центром круга Cr0 радиуса i?o, цели-
целиком лежащего в области гармоничности функции и(х,у).
2. Сохранение оператора Лапласа при конформном
отображении. Пусть в области Q плоскости ху задана гармо-
гармоническая функция и{х,у)\ т. е.
= 0> х'уеб- G-5)

ОБЩИЕ ПОЛОЖЕНИЯ	195
С помощью невырожденного преобразования независимых пе-
переменных
f = ?(я,у), r] = ri(x,y),	G.6)
?ЙН°- х'уед-	G-7)
отобразим область Q плоскости ху на новую область Q плоскости
?7/. Заметим, что задание двух действительных функций G.6),
двух действительных переменных ж, у, эквивалентно заданию в
области Q комплексной плоскости z одной функции ? = f(z) =
= ?(ж,у) + irj(x^y) комплексной переменной z = х + гу. При
этом функция f(z) осуществляет отображение области Q комп-
комплексной плоскости z на область Q' комплексной плоскости (. В
силу условия G.7) уравнения G.6) однозначно разрешимы отно-
относительно старых переменных, и тем самым в области Q1', плоско-
плоскости ?г/ определена функция ?/(?, г/) = и[х(^ г/), у(?, г/)]. Выясним,
при каких условиях на преобразование G.6) функция [/(?, г/) бу-
будет гармонической функцией переменных ?, г/. Предполагая, что
функции G.6) дважды непрерывно дифференцируемы в области
Q', выразим частные производные второго порядка от функции
и(х,у) по старым переменным через производные от функции
[/(?, г/) по новым переменным:
д2и д2Ц и Л2 | о d2U c L02U{ \2,dU^	dU
2и д2Ц2 д2Ц	д2Ц2 dU	<№
д2и _ д2Ц(с ^2 | о д2Ц с , д2Ц
ду2 ~ д?2^у) ^Z^^
Подставив эти выраж:ения в G.5), получим следующее уравне-
уравнение для функции ()
Щ	^	0. G.9)
Для того чтобы это уравнение было уравнением Лапласа, долж-
должны выполняться следующие соотношения:
^хх + iyy = 0, rixx + Г]уу = 0,	G.10)
?ж% + €yVy = °	G-п)
^ + ^ = ^ + ^^0.	G.12)
Соотношения G.10) означают, что функции ?(ж,у) и г](х,у)
должны быть гармоническими в области Q. Перепишем G.11)
в виде
^ = -^ = ^(Ж,у),	G.13)

196 ПРИМЕНЕНИЕ АНАЛИТИЧЕСКИХ ФУНКЦИЙ ГЛ. 7
где ц(х,у) — некоторая, пока неизвестная функция. Тогда соот-
соотношение G.12) дает
U + Й = Atfy + vl] = vl + vl Ф о-
Отсюда ц2(х,у) = 1 при х,у ? Q. Таким образом, неизвестная
функция 1л(х,у) определена: /i = =Ы. При \i = 1 соотношения
G.13) дают
т.е. гармонические в области ^ функции (иг| должны удовле-
удовлетворять в этой области условиям Коши-Римана. Это означа-
означает, что функция f(z) = ?(ж,у) +ir](x,y) должна быть аналити-
аналитической функцией в области Q комплексной плоскости z. Заме-
Заметим, что из G.7) и G.12) следует, что отображение области Q на
Q' должно быть взаимно однозначным, а производная функции
f(z) должна удовлетворять условию ff(z) ф 0 всюду в области
Q. Тем самым отображение области Q плоскости z на область
Q' плоскости С, осуществляемое функцией f(z), должно быть
конформным.
При \i = — 1 соотношения G.13) дают
Цж = ~г1у) ^у — %•
Как легко видеть, в этом случае функция f{z)=^{x1 y)—ir](x,у)
должна быть аналитической, а отображение, осуществляемое
функцией f(z) = i{x,y) +гг/(ж,у), должно быть конформным
отображением II рода.
Итак, мы получили окончательный ответ на вопрос, постав-
поставленный в начале этого пункта. При отображении области Q
плоскости z на область Q' плоскости ?, осуществляемом функ-
функцией f(z) = i(x,y) +гг/(ж,у), уравнение Лапласа для функции
и(х,у) перейдет в уравнение Лапласа для функции U(^r]) =
= и[х(?,г)),у(?,г))] лишь в том случае, если данное отображе-
отображение является конформным отображением I или II рода. За-
Заметим, что при данных отображениях оператор Лапласа Аху
переходит в оператор \f'(z)\2A^ =	А^, где z = (р(() —
обратная функция, осуществляющая конформное отображение
области Q1 на область Q. Тем самым даже простейшее уравне-
уравнение эллиптического типа с постоянными коэффициентами Аи +
+ си = 0, с = const ф 0, при конформном отображении перей-
перейдет, вообще говоря, в уравнение с переменным коэффициентом
2
3. Задача Дирихле. Полученные в предыдущем пункте
результаты позволяют применить метод конформных преобра-
преобразований к решению краевых задач для гармонических функций.

ОБЩИЕ ПОЛОЖЕНИЯ	197
Рассмотрим основную идею этого метода на примере решения
задачи Дирихле.
Пусть требуется найти функцию u(x,z), удовлетворяю-
удовлетворяющую уравнению Лапласа
в области (/, непрерывную в замкнутой области Q = Q + Г и
принимающую заданные значения на границе Г:
и(Р) |г = а(Р),	G.14)
где ot(P) - заданная непрерывная функция точки Р контура Г.
Как известно 1), решение этой задачи методом разделения пере-
переменных может быть получено лишь для ограниченного класса
областей Q с достаточно простой границей Г.
Метод конформных преобразований дает достаточно универ-
универсальный алгоритм решения задачи Дирихле для плоских обла-
областей. Начнем с решения задачи Дирихле для круга радиуса а.
Введем полярную систему координат г, ср с началом в центре
круга. Тогда функция ol{P) будет функцией лишь переменной (р.
Постараемся выразить значение неизвестной функции и(г,ф) в
произвольной внутренней точке (го,<^о) круга через ее гранич-
граничные значения ot((p). Для этого построим конформное отображе-
отображение заданного круга на единичный круг \w\ < 1 плоскости ги,
при котором точка го, ^о перейдет в центр w = 0. Решение этой
задачи легко получить с помощью дробно-линейной функции,
рассмотренной в гл. 6 (см. § 2). Отображающая функция имеет
вид
z) = A	ф = A	-^	,	G.15)
z
r0
где постоянная А выбирается из условия, чтобы граничные точ-
точки z = аег(р заданного круга перешли в граничные точки \w\ = 1
единичного круга плоскости w\ при этом |А| = —, a argA, опре-
го
деляющий поворот круга \w\ ^ 1 вокруг его центра w = 0, мо-
может быть выбран произвольным. В результате произведенного
преобразования искомая функция и(г, ф) перейдет в функцию
и(р,ф) = и[г(р,ф),(р(р,ф)], где р, ф — полярные координаты
на плоскости w, связанные с координатами г, ср соотношением
G.15). При этом заданная граничная функция <у.(ф) перейдет в
функцию А(ф) = а[(рA,ф)]. Так как функция Ц~(р,ф) являет-
является гармонической функцией своих переменных, то ее значение в
центре круга может быть найдено по формуле среднего значе-
:) См. А. Н. Тихонов, А. А. Самарский. Уравнения
математической физики. — М.: Наука, 1972.

198	ПРИМЕНЕНИЕ АНАЛИТИЧЕСКИХ ФУНКЦИЙ	ГЛ. 7
ния G.4), откуда
2тг
ti(r0, tpo) = U\w=o = ±f А(ф) йф.	G.16)
о
Из G.16) мы получим явное выражение решения задачи Дирихле
для круга, если выразим функцию А(ф) через первоначально
заданную функцию а(ср). Заметим, что для соответствия гра-
граничных точек круга \z\ ^ а и круга \w\ ^ 1 формула G.15) дает
е# аае«>-roe*'	GЛ7)
е =	GЛ7)
го	а .
аеъ<р	ег^0
ГО
откуда
йф =	2 а" ~ Г°2 ,	 dip.
а2 + г? - 2ar0 cos((p - (ро)
Поэтому, сделав в интеграле G.16) замену переменной интегри-
интегрирования ф = ф((р), где связь переменных ф и ср определяется
формулой G.17), получим
2тг
и(П), <Ро) = f- / 2 ^ 2 f " rg ,	М<р) dip.	G.18)
v	' 2тг у а2 +г5 - 2ar0cos(<? - <^о)
О
Формула G.18) и дает явное аналитическое выражение решения
задачи Дирихле для круга радиуса а через функцию граничных
условий а(ср). Эта формула, носящая название интеграла Пуас-
Пуассона, может быть получена и рядом других способов, например
методом разделения переменных или с помощью функции ис-
источника 1).
Полученные результаты позволяют в принципе решить зада-
задачу Дирихле для любой области Q, которую можно конформно
отобразить на единичный круг \w\ ^1 плоскости w. Действи-
Действительно, при конформном отображении уравнение Лапласа со-
сохраняется, а решение задачи Дирихле для круга нами получе-
получено. Совершив в интеграле G.18) или G.16) замену переменной
интегрирования, исходя из связи граничных точек области Q и
единичной окружности \w\ = 1 при данном конформном отобра-
отображении, мы и получим выражение решения задачи Дирихле во
внутренних точках области через граничную функцию G.14).
Пример 1. Решение задачи Дирихле для полуплоско-
полуплоскости. Пусть требуется определить ограниченную на бесконечно-
бесконечности функцию гл(ж,у), гармоническую в верхней полуплоскости
у > 0, непрерывную при у ^ 0 и принимающую значения:
и(х,0) = а(х) при у = 0.	G.19)
:) См. сноску на с. 197.

ОБЩИЕ ПОЛОЖЕНИЯ	199
Отобразим конформно верхнюю полуплоскость Im z > 0 на
внутренность единичного круга \w\ < 1 так, чтобы заданная
точка zq = xq + iyo (yo > 0) перешла в центр w = 0 этого круга.
Как легко видеть, это преобразование осуществляется дробно-
линейной функцией:
w = f(z) = J^g.	G.20)
При этом граничные точки связаны соотношением
и граничная функция а(х) переходит в функцию А(ф) =
= а[ж(^)], где х(ф) определяется из соотношения G.21). Заме-
Заметим, что соотношение G.21) дает
Лф =	Щ-	, dx.	G.22)
г (х-хоJ + у2о	v }
Значение искомой функции и(х,у) в точке жо, Уо определяется
интегралом G.16). Произведя в нем замену переменной интегри-
интегрирования по формулам G.21), G.22), получим
w^rTvia{x)dx> G-23)
что и дает решение поставленной задачи. Формула G.23), даю-
дающая решение задачи Дирихле для полуплоскости, носит также
название интеграла Пуассона.
4. Построение функции источника. Методы конформ-
конформного отображения позволяют построить функцию источника
первой краевой задачи для уравнения Лапласа в плоской обла-
области Q, которую можно конформно отобразить на единичный
круг \w\ < 1 плоскости w. Как известно, функция источника
G(Mq,M) данной задачи определяется следующими условиями:
1)
AMG(M0,M)=0 при МфМъ\	G.24)
2) в окрестности точки Mq
±ln^— + v(M0,M),	G.25)
Z7T	ГММ
где функция v(Mo, M) является гармонической функцией точки
М всюду в области Q\
3)
С(М0,М)|Мег = 0,	G.26)
где Г — граница области Q. Имеет место следующая теорема.
Теорема 7.1. Если функция w = f(zo,z) осуществляет
конформное отображение заданной области Q плоскости z на
внутренность единичного круга \w\ < 1 так, что точка zq E Q

200 ПРИМЕНЕНИЕ АНАЛИТИЧЕСКИХ ФУНКЦИЙ ГЛ. 7
переходит в центр w = 0 этого круга, то функция
G(M0,M) = ±- In ^L-	G.27)
является функцией источника первой краевой задачи для урав-
уравнения Лапласа в области Q. Здесь координаты точки М Е Q
суть ж, у и z = х + гу.
Доказательство. Для доказательства теоремы
проверим, что функция, определенная формулой G.27), удовле-
удовлетворяет условиям G.24)-G.26). Функция J(z,zq), осуществляю-
осуществляющая данное конформное отображение, является аналитической
функцией, причем /(z,zq) ф 0 при z ф zq. Отсюда следует, что
и функция
\nf(z,z0) = ln\f(z,zo)\ + iaigf(z,z0)
является аналитической функцией всюду в области Q, за исклю-
исключением точки zq. Так как действительная часть аналитической
функции есть функция гармоническая, то условие G.24) выпол-
выполнено. Поскольку /'(z^zq) ф 0 всюду в области Q, включая и
точку z = zq, a /(z,zq) = 0, то точка zq является нулем первого
порядка данной функции, т. е. в окрестности этой точки имеет
место разложение
f(z,z0) = (z-zo)ip(z,zo),
где (p(z,zq) — аналитическая в окрестности точки zq функция,
причем <p(zq,zq) Ф 0. Отсюда следует выполнение условия G.25)
для функции G.27). Наконец, так как \f(z, ^о)|г = 1, то функция
G.27) удовлетворяет и условию G.26). Теорема доказана.
Приведем пример применения доказанной теоремы.
Пример 2. Построить функцию источника первой краевой
задачи для уравнения Лапласа в полосе —оо<ж<оо,0<у<тг.
Согласно только что доказанной теореме для решения задачи
надо построить конформное отображение данной полосы плос-
плоскости z на внутренность единичного круга \w\ < 1, при котором
заданная точка zq переходила бы в центр круга w = 0. Как лег-
легко видеть, функция, осуществляющая требуемое отображение,
имеет вид
) = ?ff?-	G-28)
Поскольку имеет место соотношение
\ez — eZo\ = {(ех cosy — ех° cosyoJ + (ех smy — ех°
= exp (^t??) V2{ch (x - xq) - cos (y - yo)}1/2,
то после элементарных преобразований получим искомую функ-
функцию в виде
G(M0,M) = j-Ь^Д-^ = 1 in'h(»-xo)-cos(y + lto)
2тг |/Bо2)| 4тг ch(x-xo)-cos(y-у0)

§ 2	ПРИЛОЖЕНИЯ К ЗАДАЧАМ МЕХАНИКИ И ФИЗИКИ	201
§ 2. Приложения к задачам механики и физики
1. Плоское установившееся движение жидкости.
Будем рассматривать плоское потенциальное установившееся
течение несжимаемой идеальной жидкости. Как известно, в слу-
случае потенциального движения в области, свободной от источни-
источников, вектор скорости лг(х,у) удовлетворяет уравнениям1)
rotv = 0,	G.30)
divv = 0.	G.31)
Так как движение потенциальное, то существует скалярная
функция и(х^уI называемая потенциалом скоростей, связанная
с вектором скорости v соотношением
v = grad^(x,y),	G.32)
т. е.	я	я
vx = —- и лгу = — .	G.33)
дх	у ду	v ;
При этом вектор скорости v в каждой точке течения направлен
по нормали к линии уровня и(х,у) = const потенциала скоро-
скоростей. Подставив G.32) в уравнение G.31), получим
Й + Й = 0,	G.34)
дх2 ду2	v y
т. е. в рассматриваемом случае потенциал скоростей является
гармонической функцией.
Построим аналитическую функцию комплексной перемен-
переменной f(z) = и(х,у) + гг>(ж,у), для которой потенциал и(х,у) рас-
рассматриваемого течения является действительной частью. Как
было отмечено (см. с. 37), при этом функция f(z) определена
с точностью до постоянного слагаемого. Ранее (см. с. 37) было
показано, что линии уровня и(х,у) = const и v(x, у) = const дей-
действительной и мнимой частей аналитической функции взаимно
ортогональны. Поэтому вектор скорости v в каждой точке те-
течения направлен по касательной к линии уровня v(x,y) = const,
проходящей через данную точку. Функция v(x,y), являющая-
являющаяся мнимой частью построенной таким образом аналитической
функции /(^), называется функцией тока, а сама функция f(z)
комплексным потенциалом течения.
Область течения, ограниченная двумя линиями тока
v(x,y) = С\ и v(x,y) = С2, называется трубкой тока. Так как
скорость жидкости в любой точке направлена по касательной
к линии тока, то в силу несжимаемости жидкости и стационар-
стационарного характера движения количество жидкости, протекающее
за единицу времени через любые два поперечных сечения Si и
См. сноску на с. 197.

202 ПРИМЕНЕНИЕ АНАЛИТИЧЕСКИХ ФУНКЦИЙ ГЛ. 7
$2 трубки тока, остается постоянным. Таким образом, разность
значений постоянных С\ и С<2, определяет расход жидкости в
данной трубке тока.
Из условий Коши-Римана и формул G.33) следует, что ком-
компоненты скорости могут быть выражены через частные произ-
производные от функции тока:
ди dv	ди	dv	/f7Or\
v* = ^ = v Yy = Ty = -d-x- G-35)
Как было отмечено в гл. 1, комплексное число w = vx + ivy
можно интерпретировать как плоский вектор с компонентами
vx ж \у. Имеет место очевидное соотношение
ди .ди ди .dv
+ г	г
. .	ди .ди ди .dv "F77~T	tn оа\
« = v* + »vy = ш + гТу = Тх - г- = f'(z),	G.36)
которое связывает вектор скорости и производную от комплекс-
комплексного потенциала течения.
В гидродинамике существенную роль играют понятия цир-
циркуляции и потока вектора скорости. Дадим выражение этих ве-
величин через комплексный потенциал течения.
Рассмотрим кусочно-гладкую плоскую кривую С (разомкну-
(разомкнутую или замкнутую) и введем на ней векторы дифференциалов
дуги ds и нормали dn с помощью соотношений
ds = \dx +jdy,	G.37)
dn = i dy — j dx.	G.38)
Имеет место очевидное соотношение nds = dn, где п — единич-
единичная нормаль к кривой С, a ds - дифференциал длины дуги этой
кривой.
При положительном обходе замкнутой кривой С формула
G.38) дает направление внешней нормали.
Потоком вектора скорости v через кривую С (разомкнутую
или замкнутую) называется криволинейный интеграл от нор-
нормальной составляющей скорости
Nc = / (v • n) ds.	G.39)
с
Очевидно, этот интеграл определяет количество жидкости, про-
протекающей через кривую С за единицу времени. Интеграл G.39)
запишем в виде
NC = Jvdn= Jvxdy-vydx = J^dy-^dx = J^-dx+^dy.
с	с	с	с
G.40)
При определении подъемной силы, действующей со сторо-
стороны потока жидкости на обтекаемое им тело, большое значение
имеет степень завихренности потока, которая характеризуется
значением циркуляции. Циркуляцией вектора скорости вдоль

§ 2	ПРИЛОЖЕНИЯ К ЗАДАЧАМ МЕХАНИКИ И ФИЗИКИ	203
кривой С называется криволинейный интеграл от касательной
составляющей вектора скорости:
Гс= fvds.	G.41)
с
Выражая скорость v через комплексный потенциал, получим
ее	с	с
G.42)
Рассмотрим на комплексной плоскости интеграл вдоль кривой
С от производной комплексного потенциала:
%<*+%*,. G.43)
С	С	С
Сравнение G.40), G.42) и G.43) приводит к формуле
f ff(z)dz = rc + iNc.	G.44)
с
Эта формула, дающая выражение циркуляции и потока вектора
скорости через производную комплексного потенциала, находит
многочисленные применения в гидродинамике. Заметим, что ес-
если область Q, в которой рассматривается движение, является
односвязной, то интеграл G.44) по любой замкнутой кривой С,
целиком лежащей в Q, равен нулю в силу теоремы Коши. В слу-
случае движения в многосвязной области Q интеграл по замкнутой
кривой С, целиком лежащей в Q, может быть отличен от ну-
нуля. Это будет иметь место, когда внутри кривой С содержится
область Q', не принадлежащая Q, в которой находятся источни-
источники и вихревые точки рассматриваемого течения. В этой обла-
области, очевидно, нарушаются уравнения G.30) и G.31). В частном
случае область Q1 может состоять из отдельных точек, которые
при этом являются изолированными особыми точками аналити-
аналитической функции f(z) — комплексного потенциала течения.
Итак, всякое плоское потенциальное течение в области, в
которой отсутствуют источники и вихревые точки, может
быть описано с помощью комплексного потенциала, являюще-
являющегося аналитической функцией комплексной переменной. Тем са-
самым для изучения данного класса течений может быть исполь-
использован весь аппарат теории аналитических функций.
Рассмотрим ряд примеров простейших
течений, описываемых элементарными
функциями комплексной переменной.
а) Пусть комплексный потенциал течения имеет вид
f(z) = az,	G.45)

204	ПРИМЕНЕНИЕ АНАЛИТИЧЕСКИХ ФУНКЦИЙ	ГЛ. 7
где а = а\ + Ш2 — заданное комплексное число. Тогда
и(х, у) = а\х - а2у, v(x, у) = а2х
и линии тока v(x,y) = С представляют собой прямые, угол на-
наклона которых к оси х определяется выражением tga = — —.
Формула G.36) дает
w = vx + ivy = f'(z) =a = ai— ia2,	G.46)
откуда следует, что скорость течения постоянна и направление
вектора скорости совпадает с прямыми v(x,y) = С. Итак функ-
функция G.45) определяет плоскопараллельное течение.
б)	Пусть комплексный потенциал течения имеет вид
f(z) = a\nz,	G.47)
где а — действительное число. Тогда, перейдя к показательной
форме записи z = тещ\ получим выражение потенциала и функ-
функции тока в полярных координатах:
гл(г, ф) = a In г, г; (г, ф) = сир.
Отсюда следует, что линии тока представляют собой лучи, вы-
выходящие из начала координат, а эквипотенциальные линии —
окружности с центром в начале координат. Абсолютная величи-
величина скорости при этом равна
N = 1/'(*I = jf[ = у-	G-48)
а вектор скорости направлен по лучу (р = const. Из G.48) следу-
следует, что в начале координат скорость обращается в бесконечность.
Точка z = 0, особая точка функции f(z), в этом случае является
источником течения (положительным источником при а > 0, ко-
когда скорость направлена от начала координат, и отрицательным
источником или стоком при а < 0, когда скорость направлена
к началу координат). Взяв произвольный замкнутый контур G,
содержащий точку z = 0 внутри, по формуле G.44) получим
J f'(z) dz= f - dz = i • 2тга = Tc + iNc.
с	с
Отсюда Nc = 2тга. Тем самым в рассматриваемом случае поток
жидкости через любой замкнутый контур, содержащий внутри
источник, постоянен и равен 2тга. Эту величину называют мощ-
мощностью источника.
в)	Пусть комплексный потенциал имеет вид
f(z) =ia]nz,	G.49)
где а - действительное число. В этом случае линии тока предста-
представляют собой концентрические окружности с центром в начале
координат. Из формулы G.44), так же как и в предыдущем слу-
случае, получим Nc = 0, Тс = — 2тга. Точка z = 0 в этом случае
называется вихревой точкой течения.

§ 2	ПРИЛОЖЕНИЯ К ЗАДАЧАМ МЕХАНИКИ И ФИЗИКИ	205
г) Пусть комплексный потенциал течения имеет вид
f(z) = a\n(z + h) -a\n(z-h),	G.50)
где а - положительное действительное число, a h - некоторая
комплексная постоянная. Согласно предыдущему этот потенци-
потенциал определяет течение с положительным источником в точке
z = —h и стоком в точке z = +/i, причем мощность источника и
стока одинакова и равна 2тга. Перепишем G.50) в виде
и перейдем к пределу при h —>> 0, полагая, что мощность источ-
источника и стока при этом возрастает так, что величина т = а • 2h
остается постоянной. В результате получаем
fo(z) = f.	G.51)
Функция G.51) представляет собой комплексный потенциал ди-
диполя мощности га, находящегося в начале координат. Линии то-
тока диполя, очевидно, определяются уравнениями
ту
х2 + у2
или
.2 , 2
= с
С(х2 + у2) + ту = 0,	G.52)
т. е. представляют собой окружности с центрами на оси у, касаю-
касающиеся оси х в начале координат. При этом абсолютная величина
скорости, равная
I | т	т	/^ го\
И = W = ^т^'	G'53)
стремится к нулю на бесконечности.
д) Рассмотрим течение, комплексный потенциал которого
имеет вид
f(z)=vO0z + ^,	G.54)
где Vqo и т — положительные действительные числа. Очевид-
Очевидно, это течение представляет собой суперпозицию плоскопарал-
плоскопараллельного течения со скоростью, параллельной оси х и равной Vqo,
и течения, создаваемого диполем мощности га, находящимся
в начале координат. Линии тока этого течения определяются
уравнениями
-ооУ - ^ = С.	G.55)
Значению G = 0 соответствует линия тока, уравнение которой
имеет вид
Она распадается на прямую у = 0 и окружность х2 + у2 = а
2 = а2

206	ПРИМЕНЕНИЕ АНАЛИТИЧЕСКИХ ФУНКЦИЙ	ГЛ. 7
где а = —. 1ак как
/'(*) = Voo " f = Voo (l " J) ,	G.56)
то на бесконечности скорость течения равна v^ и направлена
вдоль оси х. В точках окружности х2 -\-у2 = а2, являющейся ли-
линией тока, скорость направлена по касательной к этой окружно-
окружности. Для абсолютной величины скорости в точках окружности
z = аещ из формул G.36) и G.56) получим
=а = v°o|l - е2щ\ = 2v°o| sinH- G-57)
И|и=а = 1/'(*
В рассмотренных примерах мы по заданному комплексно-
комплексному потенциалу определяли гидродинамические характеристики
течения. Перейдем теперь к решению в определенном смысле
обратной задачи, задачи об определении комплексного потен-
потенциала течения по его гидродинамическим характеристикам.
Заметим, что поскольку физическая скорость течения выража-
выражается через производную комплексного потенциала (см. форму-
формулу G.36)), то сам комплексный потенциал для заданного тече-
течения определяется неоднозначно. Однако его производная явля-
является однозначной аналитической функцией. Это означает, что в
окрестности любой правильной точки течения имеет место раз-
разложение
оо
f'{z) = Y,an{z-zo)n,	G.58)
71 = 1
а в окрестности изолированной особой точки — разложение
сю
/'(*)= Y, bn(z-zo)n.	G.59)
п= — оо
Из G.59) для комплексного потенциала в окрестности особой
точки zq получим разложение
оо
/(*) = &_! In (*-*o)+ Y, cn(z-z0)n.	G.60)
п= — оо
В частности, если бесконечно удаленная точка ^оо принадлежит
области течения и комплексная скорость
Woo = (V^)oo +i(Vy)oc
течения в этой точке ограничена, то разложение комплексного
потенциала в окрестности точки Zqq имеет вид
^-	G-61)
п=0

ПРИЛОЖЕНИЯ К ЗАДАЧАМ МЕХАНИКИ И ФИЗИКИ	207
Отсюда получаем
J f\z)dz = 2mb-u	G.62)
cR
где Cr — окружность \z\ = R достаточно большого радиуса i?,
вне которой нет особых точек функции f(z), за исключением
точки Zoo. С другой стороны, в силу формулы G.44) интеграл
G.62) определяет поток и циркуляцию вектора скорости через
кривую Cr. Так как скорость в точке Zqq ограничена, то эта
точка не является источником, поэтому поток вектора скорости
через кривую Cr равен нулю, и формула G.62) дает
2тгг6_1 = Гоо.
Выпишем окончательное разложение комплексного потенциала
в окрестности бесконечно удаленной точки, являющейся пра-
правильной точкой течения:
^-	G-63)
п=0
Рассмотрим теперь задачу обтекания замкнутого контура
плоскопараллельным потоком. Пусть поток, имеющий на бес-
бесконечности заданную скорость w^ и циркуляцию Гоо, обтекает
тело S, ограниченное замкнутым контуром С. Требуется опре-
определить скорость в любой точке потока по заданным гидродина-
гидродинамическим характеристикам на бесконечности при условии, что в
точках контура С скорость течения направлена по касательной
к контуру С. Последнее условие означает, что кривая С предста-
представляет собой линию тока рассматриваемого течения, т.е. мнимая
часть комплексного потенциала, описывающего данное течение,
должна сохранять постоянное значение на кривой С
v(x,y) \c = const.	G.64)
Задача сводится к определению вне контура С на комплексной
плоскости аналитической функции f(z), в разложении G.63) ко-
которой заданы значения Wqq и Гоо, а на контуре С выполняет-
выполняется условие G.64). Так как комплексный потенциал определен с
точностью до постоянного слагаемого, то значение постоянной
в условии G.64) можно положить равным нулю.
Начнем с задачи обтекания кругового цилиндра радиуса R с
центром в начале координат. Пусть скорость потока на бесконеч-
бесконечности равна Vqo и направлена параллельно оси ж, а циркуляция
отсутствует, Т^ = 0. Мы должны найти комплексный потенци-
потенциал, разложение которого в окрестности бесконечно удаленной
точки имеет вид
g"	G.65)
п=0

208 ПРИМЕНЕНИЕ АНАЛИТИЧЕСКИХ ФУНКЦИЙ ГЛ. 7
и мнимая часть которого обращается в нуль при \z\ = R. Комп-
Комплексный потенциал такого типа был нами уже рассмотрен выше
в примере д). Поэтому решение данной задачи имеет вид
G.66)
При этом скорость в точках, лежащих на обтекаемом цилиндре,
определяется формулой G.57), откуда следует, что она обраща-
обращается в нуль в двух критических точках: в точке z = — i?, в ко-
которой линия тока у = 0 разветвляется на две линии тока, сов-
совпадающие с верхней и нижней полуокружностями \z\ = i?, и в
точке z = i?, в которой эти линии тока сходятся опять в прямую
у = 0. Эти точки называются точкой разветвления и точкой схо-
схода соответственно. Заметим, что если скорость потока на беско-
бесконечности не параллельна оси ж, а имеет вид Wqq = v^e^0, то с
помощью преобразования ? = ге~г(ро мы приходим к уже рас-
рассмотренной задаче на плоскости (. Тогда для решения исходной
задачи получим выражение
f(z) = wooz + ^!.	G.67)
Z
Пусть теперь циркуляция Г^ не равна нулю. Как мы виде-
видели выше (см. пример в) ), линии тока у течения с комплексным
потенциалом ia \nz (a — действительное число) представляют
собой концентрические окружности с центром в начале коор-
координат. Поэтому комплексный потенциал течения, обтекающего
круговой цилиндр радиуса R с заданной скоростью на бесконеч-
бесконечности Vqo и заданной циркуляцией Гоо, имеет вид
G.68)
Найдем критические точки течения, в которых скорость течения
обращается в нуль. Согласно формуле G.36) имеем
Отсюда
2 ?z -в2 = о	G.69)
Г	/	Г2
7 — д°° 4- а /?2 —	°°	G 70 "I
Р	4tTV	V	1б7Г2У§
4ttvo
Поэтому
подкоренное выражение в G.70) положительно.
FkP|

ПРИЛОЖЕНИЯ К ЗАДАЧАМ МЕХАНИКИ И ФИЗИКИ
209
т. е. обе критические точки находятся на окружности
= R
обтекаемого цилиндра, причем при Г^ > 0 (vqo > 0) обе точки
лежат на верхней, а при Г^ < 0 (vqo > 0) — на нижней полу-
полуокружности. Тем самым наличие циркуляции сближает точки
разветвления и схода линий тока (рис. 7.1). При
4ttvo
критические точки совпадают (с точкой z = iR при
р
точкой z = —iR при Гоо < 0). Наконец, при
4тгуо
= R обе
> 0 или
> R в обла-
сти \z\ > R остается лишь одна критическая точка, лежащая на
мнимой оси у. (Как следует из уравнения G.69), произведение
корней этого уравнения равно — i?2, поэтому вторая критическая
точка лежит внутри окружности \z\ = R.) Через эту точку про-
проходит линия тока, отделяющая замкнутые линии тока течения
от незамкнутых (рис. 7.2).
Рис. 7.1
Рис. 7.2
Полученные результаты позволяют в принципе решить за-
задачу обтекания произвольного замкнутого контура С. Действи-
Действительно, пусть функция С = <p(z) осуществляет конформное ото-
отображение области Q комплексной плоскости z, внешней контуру
С, на область Q' плоскости С, внешнюю единичной окружности
|?| = 1, так что <р(оо) = оо. Тогда, очевидно, рассматриваемая
задача оказывается эквивалентной задаче обтекания кругового
цилиндра единичного радиуса. При этом скорость потока на бес-
бесконечности, которая, вообще говоря, изменится, может быть лег-
легко определена. Комплексный потенциал f(z) исходного течения
при данном конформном преобразовании перейдет в функцию

210
ПРИМЕНЕНИЕ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
ГЛ. 7
F(() = f[z(()]. Поэтому по формуле G.36) найдем
ттт 	 dF		 df	dz
d( (=00 dz z=ocdC C=°o
И
С=оо
= wco-
С=оо
В силу формул G.67) и G.68) решение преобразованной за-
задачи имеет вид
Отсюда для решения исходной задачи получим выражение
Tz
I. G.71)
В качестве примера рассмотрим бесциркуляционное обтека-
обтекание бесконечной пластинки плоским потоком жидкости. Пусть
плоскость ху пересекает пластинку по отрезку — а ^ х ^ a, a
вектор скорости потока лежит в плоскости ху и на бесконечно-
бесконечности имеет заданное значение w^. Как следует из рассмотрения
свойств функции Жуковского (см. гл. 6, с. 181), функция
z = -
G.72)
осуществляет конформное отображение внешности единичного
круга плоскости ? на плоскость z, разрезанную по отрезку —
^ х ^ а. При этом ф(оо) = оо и —
—а
d(
= -. Поэтому рас-
С=оо 2
сматриваемая задача эквивалентна задаче обтекания без цир-
циркуляции кругового цилиндра единичного радиуса на плоскости
( потоком, имеющим на бесконечности комплексную скорость
Жх) = -^оо- Комплексный потенциал последней задачи имеет
вид
Подставим сюда вместо ( и - найденные из G.72) величины
С =
Здесь V'z2 — а2 > 0 при z = х > а. Разобьем
ную и мнимую части:
на действитель-

действитель§ 2	ПРИЛОЖЕНИЯ К ЗАДАЧАМ МЕХАНИКИ И ФИЗИКИ	211
Тогда для комплексного потенциала исходной задачи получим
окончательное выражение
f(z) = (yx)ooz - i(vy)ooVz2-a2.	G.73)
В заключение найдем силу, действующую со стороны потока
на обтекаемое им тело. Сила давления, действующая на элемент
ds дуги контура С, пропорциональна гидродинамическому дав-
давлению р в данной точке потока и направлена по направлению
внутренней нормали —dn = — idy+j dx. Поэтому для компонент
силы, действующей на контур С, получим выражения
Rx = ~ f pdy, Ry = Jpdx.
с	с
Определив гидродинамическое давление р из интеграла Бернулли:
где А — постоянная, ар — плотность жидкости, и введя ком-
комплексную величину R = Ry + iRXi получим
R = -? [v2(dx-idy) = -?- [v2dz.	G.74)
2 J	2 J
С	С
(Интеграл от постоянной А по замкнутому контуру С, очевид-
очевидно, равен нулю.) Преобразуем интеграл G.74). Так как в точках
контура С скорость направлена по касательной к контуру, то
комплексная скорость течения w связана с величиной физиче-
физической скорости v соотношением w = veZ(iP, где ср — угол меж-
между касательной к контуру и осью х. Тогда формула G.36) дает
уе~г(р = f'(z). С другой стороны, dz = dse~t(p. Поэтому v2 dz =
= у2е~г2(р ds ещ = //2 dz, и формула G.74) примет вид
f\z)dz.	G.75)
С
Это так называемая формула Чаплыгина, выражающая силу,
действующую со стороны потока на обтекаемое им тело, через
производную комплексного потенциала. Из выражения G.63)
для комплексного потенциала вне обтекаемого тела получим
п=2
оо
п=2
Следовательно,
с

212 ПРИМЕНЕНИЕ АНАЛИТИЧЕСКИХ ФУНКЦИЙ ГЛ. 7
Подставив это выражение в формулу G.75) и отделив действи-
действительную и мнимую части, найдем
¦Ll'X г\ У) ОО -L ОО5	~^У	г\ X) ОО *- ОО *	\	/
Отсюда
|i?|=Hvoo|-|roo|.	G.77)
Формула G.77) представляет собой теорему Жуковского о подъ-
подъемной силе: сила давления безвихревого потока, имеющего на
бесконечности скорость v^ и обтекающего контур С с цирку-
циркуляцией Г, выражается формулой \R\ = p|voo| • |Г|. Направление
этой силы получается поворотом вектора v^ на прямой угол в
сторону, противоположную циркуляции.
Использование аппарата аналитических функций комплекс-
комплексной переменной позволило Н. Е. Жуковскому и С. А. Чаплыги-
Чаплыгину развить методы решения задач гидро- и аэродинамики, по-
послуживших теоретической основой для практики авиастроения.
Тем самым методы теории функций комплексного переменного
сыграли огромную роль в развитии современной авиации.
2. Плоское электростатическое поле. Методы теории
функций комплексной переменной, использованные в предыду-
предыдущем пункте для изучения плоского потенциального течения иде-
идеальной жидкости, могут быть столь же успешно применены и
при исследовании любого плоского векторного поля иной фи-
физической природы. В этом пункте мы рассмотрим применение
данных методов к решению некоторых задач электростатики.
Задачи электростатики заключаются в определении стаци-
стационарного электрического поля, создаваемого в среде заданным
распределением зарядов. В зависимости от постановки конкрет-
конкретной физической задачи задаются или плотность распределения
зарядов как функция координат, или полный заряд, распреде-
распределенный на поверхности идеального проводника. В последнем
случае основная цель исследования заключается в определении
плотности распределения зарядов на поверхности проводника.
Чтобы получить основные уравнения для вектора напряжен-
напряженности электростатического поля, будем исходить из общей систе-
системы уравнений Максвелла1) в изотропной среде:
, тт 1 <9D . 4тг «ст	in	1 дЪ
rotH= --:?- + —JCT, rotE = ---дг,
с dt с	с dt
divB = 0,
D = 6-Е, В = /iH.
В случае стационарного электромагнитного поля уравнения
Максвелла для вектора Е напряженности электрического поля
См. И. Е. Т а м м. Основы теории электричества. — М.: Наука, 1966.

§ 2	ПРИЛОЖЕНИЯ К ЗАДАЧАМ МЕХАНИКИ И ФИЗИКИ	213
в однородной среде принимают вид
rot E = 0, div E = —р,	G.78)
где е — диэлектрическая постоянная среды, ар — плотность ста-
статических зарядов, создающих данное поле. В дальнейшем будем
считать е = 1 и будем рассматривать плоскую задачу, когда за-
заряды, создающие поле, распределены в пространстве так, что
плотность их распределения не зависит от одной из координат
(например, от координаты z\ а является функцией лишь двух
других координат, т.е. р = р(х,у). Очевидно, при этом вектор Е
имеет лишь две отличные от нуля компоненты, которые также
являются функциями лишь координат х,у:
Е(ж,у) = iEx(x,y) + ]Еу(х,у).	G.79)
В силу первого из уравнений G.78) поле Е является потенци-
потенциальным:
Е(Ж, у) = -grad^y), Ex = -^, Еу = -^, G.80)
причем на основании второго из уравнений G.78) функция
v(x,y) удовлетворяет уравнению
Дг; = -4пр(х,у).	G.81)
Из G.81) следует, что в области, свободной от зарядов, потен-
потенциальная функция v(x,y) является гармонической. Поэтому в
этой области можно построить аналитическую функцию комп-
комплексной переменной
f(z)=u(x,y)+iv(x,y),	G.82)
для которой потенциальная функция v(x,y) данного электро-
электростатического поля является мнимой частью.
Функция G.82) называется комплексным потенциалом элек-
электростатического поля. Линии уровня v(x,y) = С называются
эквипотенциальными линиями данного поля. Из формул G.80)
следует, что вектор напряженности Е в каждой точке эквипо-
эквипотенциальной линии v(x,y) = С направлен по нормали к этой
линии. Так как линии v(x,y) = С и и(х,у) = С взаимно орто-
ортогональны, то направление вектора Е совпадает с касательной к
линии и(х,у) = С в каждой точке этой кривой. Поэтому линии
и(х,у) = С являются силовыми линиями данного поля.
Сопоставим вектору Е комплексное число w = Ех + гЕу. То-
Тогда на основании G.80) и условий Коши-Римана получим
т-, . . т-,	dv .dv	dv .ди
w = Ьх + гЬу = — — — г— = — — — г— =
у	дх ду	дх дх
7-83»

214	ПРИМЕНЕНИЕ АНАЛИТИЧЕСКИХ ФУНКЦИЙ	ГЛ. 7
Отсюда
|Е| = |/'(*)|.	G.84)
Формулы G.83) и G.84) дают выражение компонент вектора
напряженности электростатического поля в области, свободной
от зарядов, через производную комплексного потенциала.
Пусть заряды, создающие данное электростатическое поле,
сосредоточены в некоторой области, ограниченной замкнутой
кривой Со 1). Тогда интеграл по любому замкнутому контуру
С, содержащему Со внутри, от нормальной составляющей на-
напряженности электрического поля, согласно теореме Гаусса2),
равен суммарному заряду (отнесенному к единице длины ци-
цилиндра, в котором распределены заряды в пространстве):
Еп ds = 4тге.	G.85)
с
На основании формул G.80), G.37), G.38), учитывая соотноше-
соотношения Коши-Римана, получим
дх	дх »'
С	С
Так как электростатическое поле всюду потенциально, то цир-
циркуляция этого поля по любому замкнутому контуру равна нулю,
т. е.
с	с
Рассмотрим интеграл по замкнутому контуру С от производной
комплексного потенциала:
ее	с
Сравнение приведенных выше формул дает
J f\z) dz= J Ends = 4тге,	G.87)
с	с
т. е. заряд, заключенный внутри области, ограниченной конту-
контуром С, определяется интегралом по этому контуру от про-
производной комплексного потенциала электростатического поля,
г) Это означает, что в пространстве заряды распределены внутри беско-
бесконечного цилиндра, контуром поперечного сечения которого является кри-
кривая Со, причем плотность распределения зарядов не зависит от координаты
z вдоль образующей цилиндра, а является лишь функцией координат ж, у
в поперечном сечении.
2) См. сноску на с. 212.

§ 2	ПРИЛОЖЕНИЯ К ЗАДАЧАМ МЕХАНИКИ И ФИЗИКИ	215
создаваемого данным распределением заряда. Если Cq предста-
представляет собой контур поперечного сечения идеально проводящего
цилиндра, то весь заряд сосредоточен на его поверхности с по-
поверхностной плотностью cr(s), причем
J a(s)ds = e.	G.88)
Со
Как известно 1), имеет место соотношение
a(s) = -1
1
Со
)n
Со
G.89)
С другой стороны, из G.83) и G.89) получим
±	G.90)
<r(s) ±\f
Знак в формуле G.90) определяется знаком суммарного заряда
е, распределенного на поверхности данного идеально проводя-
проводящего проводника. Формула G.90) находит многочисленные при-
приложения при решении различных задач электростатики.
Заметим, наконец, что, так же как и в задачах гидродина-
гидродинамики, производная комплексного потенциала f'{z) на основа-
основании G.83) является однозначной аналитической функцией z. Ес-
Если напряженность данного электростатического поля ограниче-
ограничена на бесконечности, то разложение ff(z) в окрестности точки
z = оо имеет вид
оо
71 = 1
Отсюда для самого комплексного потенциала получим разложе-
разложение
оо
f(z) = WoQZ + С0 + h In 2 + ^ ^-	G-91)
71 = 1
Так как
Cr
где контур Cr содержит все заряды, создающие данное поле,
внутри, то из G.87) получим окончательное разложение комп-
комплексного потенциала в окрестности точки z = оо в виде
f(z) = w^z - г • 2e\nz + ^ ^.	G.92)
п=0
Как мы видим, комплексный потенциал электростатическо-
электростатического поля имеет чрезвычайно много общего с комплексным гидро-
См. сноску на с. 212.

216	ПРИМЕНЕНИЕ АНАЛИТИЧЕСКИХ ФУНКЦИЙ	ГЛ. 7
динамическим потенциалом1). Поэтому исследование плоского
электростатического поля с помощью комплексного потенциала
может быть проведено теми же методами, что и решение соот-
соответствующих гидродинамических задач. Так, все примеры тече-
течений, рассмотренные на с. 203-205, допускают простую электро-
электростатическую интерпретацию.
Например, рассмотрим электростатическое поле, описывае-
описываемое комплексным потенциалом
f(z) = -i-2elnz, e>0.	G.93)
Введя полярные координаты г, ср и учтя, что z = rel{p', получим
г;(г, (р) = —2е In \z\ = 2е In -, гл(г, ф) = 2е arg z = 2etp.
Отсюда следует, что эквипотенциальными поверхностями дан-
данного поля являются концентрические окружности с центром в
начале координат, а силовыми линиями — лучи ср = const. Век-
Вектор Е в каждой точке z Ф 0 направлен по лучу (р = const, а по
абсолютной величине в силу формулы G.84) равен
|Е| = |/'(*)| = ^.
Так как интеграл по любой окружности \z\ = г от нормальной
составляющей напряженности данного поля имеет постоянное
значение, равное 4тге, то, очевидно, это поле создается точечным
зарядом величины е, находящимся в начале координат (в про-
пространстве заряды, создающие данное поле, распределены с по-
постоянной плотностью е вдоль прямой, перпендикулярной плос-
плоскости ху и проходящей через начало координат).
Рассмотрим некоторые типичные за-
задачи электростатики, которые могут
быть решены с помощью комплексного
потенциала.
а) Определение плотности распределения заряда на идеаль-
идеально проводящем проводнике. Пусть боковая поверхность идеаль-
идеально проводящего проводника представляет собой бесконечный
цилиндр, поперечное сечение которого ограничено контуром С.
Предположим, что плотность распределения заряда постоян-
постоянна вдоль образующих цилиндра и на единицу длины цилин-
цилиндра приходится заряд е. Требуется определить поверхностную
плотность заряда <j(s) на контуре С поперечного сечения. Оче-
Очевидно, решение данной задачи дается формулой G.90) при нор-
1) Очевидно, то, что потенциальная функция в электростатике являет-
является мнимой частью комплексного потенциала, а в гидродинамике потенциал
скорости является действительной частью комплексного потенциала, пред-
представляет собой несущественное различие, которое может быть устранено
введением дополнительного множителя, равного —г. Однако мы придержи-
придерживаемся установившейся терминологии, при которой имеет место указанное
различие.

§ 2	ПРИЛОЖЕНИЯ К ЗАДАЧАМ МЕХАНИКИ И ФИЗИКИ	217
мировочном условии G.88). Тем самым задача сводится к по-
построению комплексного потенциала f{zI являющегося анали-
аналитической функцией вне контура С, при условии, что мнимая
часть f(z) имеет постоянное значение на контуре Сив окрест-
окрестности точки z = оо разложение f(z) дается формулой G.92), где
^оо = 0, а коэффициент е равен заряду, приходящемуся на еди-
единицу длины проводника.
Начнем с простейшего случая, когда проводник представляет
собой круговой цилиндр единичного радиуса. Выше было пока-
показано, что эквипотенциальные линии комплексного потенциала
G.93) представляют собой концентрические окружности с цен-
центром в начале координат. Поэтому, чтобы удовлетворить усло-
условию на границе проводника, естественно искать потенциал дан-
данного поля в виде
f(z) = -iClnz,
где С — постоянная, подлежащая определению. Из условия на
бесконечности G.92) получим С = 2е. Тогда формула G.90) дает
очевидный результат
Если контур поперечного сечения проводника представляет
собой произвольную замкнутую кривую С, то осуществив с по-
помощью функции ( = cp(z) конформное отображение области вне
контура С на внешность единичного круга |?| > 1 так, чтобы
удовлетворялось условие (f(oo) = оо, мы сведем задачу к только
что решенной. Тем самым комплексный потенциал будет иметь
вид
f(z) = -г-2е1пф),	G.94)
а для плотности поверхностных зарядов согласно G.90) получим
выражение
		С 		dz
Tz ~ ^ T ~"^
С
||
G.95)
В качестве примера рассмотрим задачу об определении плот-
плотности заряда на полосе ширины 2а. Пусть данная полоса пере-
пересекает плоскость ху по отрезку —а<х<а. Функция
z = -
производит конформное отображение внешности единичного
круга плоскости ( на плоскость z, разрезанную по отрезку дей-
действительной оси —а < х < а. Поэтому формула G.95) дает
-1
e
2ir
1
|C|=i
G.96)

218
ПРИМЕНЕНИЕ АНАЛИТИЧЕСКИХ ФУНКЦИЙ
ГЛ. 7
Так как
и
с2
то
1 2
формула
/ \ еа
G.96)
1
к.
а2 + 2;а
дает
- х2 х -+
>
- iy/a?
-о?
1
— ж
а
J
2"
—а<ж<а
-а2
е
2тг
G.97)
Заметим, что плотность заряда неограниченно возрастает при
приближении к краю пластины. Этот факт имеет простой фи-
физический смысл. Край пластины имеет бесконечную кривизну,
и для того, чтобы зарядить его до некоторого потенциала, надо
поместить на него бесконечный заряд.
б) Определение поля бесконечного плоского конденсатора.
Пусть требуется найти электростатическое поле между двумя
заряженными до некоторого потенциала идеально проводящи-
проводящими непересекающимися цилиндрическими поверхностями, обра-
образующие которых параллельны между собой, а направляющие
проходят через бесконечно удаленную точку плоскости z (рис.
7.3). В этом случае задача состоит в определении в криволиней-
криволинейной полосе Q комплексного потенциала f{zI представляющего
собой аналитическую функцию, мнимая часть которой прини-
принимает постоянные значения v\ и V2 на кривых С\ и (?2. Очевид-
Очевидно, аналитическая функция w = f(z) осуществляет конформное
отображение данной криволинейной полосы плоскости z на по-
полосу плоскости w, ограниченную прямыми Im w = v\, Im w =
= V2- Тем самым для решения данной задачи достаточно по-
построить указанное конформное отображение.
Рис. 7.3
Рис. 7.4
В качестве примера найдем поле конденсатора, изображен-
изображенного на рис. 7.4, если значения потенциала на кривых С\ и Съ
соответственно равны 0 и 1. Предварительно найдем функцию
z = у?(С), осуществляющую конформное отображение верхней

§ 2	ПРИЛОЖЕНИЯ К ЗАДАЧАМ МЕХАНИКИ И ФИЗИКИ	219
полуплоскости С, Im ? > 0, на данную криволинейную полосу
Q плоскости z. Так как область Q представляет собой треуголь-
треугольник1) А1А2А3, то искомое отображение можно получить при
помощи интеграла Шварца-Кристоффеля (см. гл. 5, § 4). Уста-
Установим следующее соответствие точек действительной оси плос-
плоскости С и вершин треугольника:
Ai -> С = О, А2 -> С = оо, А3 -> С = -I-
Так как углы при вершинах треугольника соответственно
равны тг«1 = 0, тг«2 = — тга и тгаз = тгA + а), то искомый инте-
интеграл должен иметь вид
С
* = С J C\l + СГ ^С + Сь	G.98)
Со
Из соответствия точек A3 (z = ih) и ? = — 1 следует, что при
Со = — 1 получим
С
^-P^dC + ih.	G.99)
-1
Чтобы определить постоянную С, заметим, что обходу точки
С = 0 в верхней полуплоскости по дуге полуокружности беско-
бесконечно малого радиуса р в направлении против часовой стрелки
соответствует переход со стороны А2А1 на сторону А1А3. При
этом приращение z равно
Az = ih.
С другой стороны, из G.99), положив ( = рещ и перейдя к пре-
пределу при /э —)> 0, получим
= iC\im [ A + peitp)a dtp = inC.
G.99) имеет вид
Отсюда С = -, и окончательное выражение для интеграла
7Г
С
z = —
-1
Функция С = eKW осуществляет конформное отображение по-
полосы 0 < Im w < 1 плоскости w на верхнюю полуплоскость (.
Поэтому функция
h f (Л A- t\a
z=— -—-^—dQ + in	G.100)
^ J С
-1
) Заметим, что вершины А\ и у4.2 находятся в бесконечности.

220	ПРИМЕНЕНИЕ АНАЛИТИЧЕСКИХ ФУНКЦИЙ	ГЛ. 7
осуществляет конформное отображение полосы 0 < Im w < 1
плоскости w на данную криволинейную полосу Q плоскости z.
При этом прямая Im w = 0 переходит в нижнюю обкладку кон-
конденсатора А\А2^ а прямая Im w = 1 — в верхнюю обкладку,
представляющую собой ломаную А2А3А1. Из формулы G.100)
при v = Im w = const получим параметрические уравнения по-
потенциальных кривых данного электростатического поля. Напри-
Например, в частном случае при а = 1 интеграл G.100) вычисляется
в элементарных функциях:
z= -(l + TTW + e™).
Тогда параметрические уравнения эквипотенциальной кривой
v = vq = const @ ^ г'о ^ 1) принимают вид
х = -A + тш + cosTryo • е7™),
^	— оо < гл < оо,
у = -(ttvq + sinTr^o • е71'^).
В частности, уравнение средней эквипотенциальной линии
— « )
имеет вид
Эквипотенциальные линии, соответствующие различным значе-
значениям v, приведены на рис. 7.5. При vq > - легко определяется
значение жтах по фор-
vo<2
k / /'
l{ у	w. z у z муле
Полученные резуль-
Jx ,'	таты легко позволяют
" I s	определить то расстоя-
' \	ние от края конденса-
I	тора, изображ:енного на
^=0	z=0 xmax	^ Рис- '-^, на котором поле
конденсатора с заданной
рис ^ 5	степенью точности мож-
можно считать плоским.
Вообще, методы конформных отображений широко исполь-
используются при расчете плоских электростатических и магнито-
статических линз, применяемых для фокусировки электрон-
электронных пучков, что необходимо для работы многих физических
устройств.

ГЛАВА 8
ОСНОВНЫЕ ПОНЯТИЯ ОПЕРАЦИОННОГО
ИСЧИСЛЕНИЯ
Методы операционного исчисления представляют собой свое-
своеобразный способ решения различных математических задач, в
первую очередь дифференциальных уравнений, получивший до-
довольно широкое распространение. В основе этих методов лежит
идея интегральных преобразований, связанная с сопоставлением
решению исходной задачи, функции /(?) действительной пере-
переменной, некоторой функции F(p) комплексной переменной так,
что обыкновенное дифференциальное уравнение для функции
f(t) переходит в алгебраическое уравнение для F(p). Аналогич-
Аналогично уравнению в частных производных для функции двух дей-
действительных переменных может быть сопоставлено обыкновен-
обыкновенное дифференциальное уравнение и т.д. Это позволяет облег-
облегчить технику вычислений. Основную роль в операционном ис-
исчислении играет преобразование Лапласа, с изучения свойств
которого мы и начнем изложение.
§ 1. Определение и основные свойства преобразования
Лапласа
1. Определение преобразования Лапласа. Преобразо-
Преобразование Лапласа ставит в соответствие функции /(?) действитель-
действительной переменной t функцию F(p) комплексной переменной р с
помощью соотношения
F(p)= fe-*f(t)dt.
Естественно, что не для всякой функции /(?) этот интеграл име-
имеет смысл. Поэтому мы начнем с определения класса функций
/(?), для которых данное преобразование заведомо реализуемо.
Будем рассматривать функции /(?), определенные для всех зна-

222 ОСНОВНЫЕ ПОНЯТИЯ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ ГЛ. 8
чений действительной переменной — оо < t < оо и удовлетво-
удовлетворяющие следующим условиям:
1)	при t < 0 функция /(?) = 0;
2)	при t ^ 0 функция /(?) на любом конечном участке оси t
имеет не более чем конечное число точек разрыва первого рода;
3)	при t —>• оо /(?) имеет ограниченную степень роста, т. е.
для каждой функции рассматриваемого класса существуют та-
такие положительные постоянные М и а, что для всех t > 0
|/(i)|^Mea*.	(8.1)
Точная нижняя грань тех значений а, для которых имеет
место неравенство (8.1), называется показателем степени ро-
роста функции /(?). Легко, в частности, видеть, что показатель
степени роста степенной функции /(?) = tn равен нулю.
Отметим, что функция /(?) может быть комплексной функ-
функцией действительной переменной t: f(t) = /i(t) +i/2(t), где /i(t)
и /2^) — действительные функции.
Введем основное определение.
Преобразованием Лапласа заданной функции /(?) действи-
действительной переменной t называется преобразование, ставящее в
соответствие функции f(t) функцию F(p) комплексной пере-
переменной р, определенную с помощью интеграла
F(p)= fe-^f(t)dt.	(8.2)
о
Заметим, что интеграл (8.2) является несобственным инте-
интегралом, зависящим от переменной р как от параметра. Очевид-
Очевидно, интеграл (8.2), вообще говоря, сходится не при всех значе-
значениях параметра р. Действительно, если функция /(?) стремится
при t —>• 00 к отличному от нуля пределу, a Re p < 0, то интеграл
заведомо расходится. Поэтому естественно поставить вопрос об
области сходимости интеграла (8.2), а тем самым об области
определения функции F(p).
Теорема 8.1. Интеграл (8.2) сходится в области Re p > а,
где а — показатель степени роста функции /(t), причем для
любого xq > а интеграл (8.2) при Re p ^ xq > а сходится рав-
равномерно.
Доказательство. Для любого р = х + гу при х > а
можно указать г) такое е > 0, что х > а\ = а + ?, причем \f(t)\ <
< Meait. Тогда, воспользовавшись признаком сравнения сходи-
:) Это позволяет рассматривать и неограниченные функции, показатель
степени роста которых равен нулю.

§ 1	ОСНОВНЫЕ СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА	223
мости несобственных интегралов1), получим
ОО	ОО
= | fe-ptf(t)dt <M fe-xteaitdt= -^-, ж > оь
О
О
(8.3)
что и приводит к выводу о сходимости интеграла (8.2) при х > а.
Если х ^ xq > а, то аналогичная оценка дает
f е-^х°-а1^ dt = —^—,	(8.4)
J	жп — аи
- сы
и
что и доказывает в силу признака Вейерштрасса равномерную
сходимость интеграла (8.2) по параметру р в области Re p ^
^ xq > a.
Приведенное доказательство существенно опиралось на условия 2 и 3
определения рассматриваемого класса функций fit) действительной пе-
переменной t. Однако можно расширить класс функций /(?), допускающих
преобразование Лапласа. Для этого предварительно докажем следующую
лемму.
Лем,м,а. Пусть функция fit) действительной переменной t определе-
определена для всех t ^ 0, и пусть существует такое комплексное число ро, что
сходится интеграл
ОО
J e-potf(t)dt.	(8.5)
о
Тогда для всех р, удовлетворяющих условию Re p > Re po, сходится
интеграл
ОО
/ e~ptf(t)dt.	(8.6)
о
Доказательство. Введем обозначение ip(t) = e~Potf(t) и
ОО
вспомогательную функцию F(t) = — f (p(r)dt. Заметим, что F'(t) = <p(t).
t
Кроме того, в силу сходимости интеграла (8.5), очевидно, для заданного
г' > 0 можно указать такое То, что \F(t)\ < г' при t ^ То.
Рассмотрим теперь интеграл J e~pt fit) dt, где Т\ и Тг — произвольные
действительные числа, удовлетворяющие условию Т2 > Ti, и представим
его в виде
Tq,	Т2	Т2
J e~p*/(*) ^ = / e"(p"Po)V(^) dt = f e-{p-po)tF'(t) dt.
Тг	Тг	Тг
См. вып. 2.

224 ОСНОВНЫЕ ПОНЯТИЯ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ ГЛ. 8
Вычисляя последний интеграл по частям, получаем
т2
+ (р - р0) f e~{p-pQ)tF(t) dt.
Ti
Отсюда при Ti, T2 > To и Re (p — po) > 0 получим
e~ptf(t) dt <: (e" Re {
e" Re (p-
\P~Po\
-Re (р-ро)Тг _ -Re (p-
(Р-Ро)
Re(p-p
Очевидно, всегда можно так выбрать значение То, чтобы полученное вы-
выражение было меньше любого наперед заданного е > 0. Это на основании
признака Коши :) и доказывает сходимость интеграла (8.6).
Можно доказать и равномерную по параметру р сходимость интеграла
(8.6) при Re p ^ Re p\ > Re po-
На основании доказанной леммы можно в качестве основного класса
функций f(t) действительной переменной ?, для которых строится преоб-
преобразование Лапласа (8.2), рассматривать функции, удовлетворяющие усло-
условию (8.5). Функции, удовлетворяющие данному условию, будем называть
принадлежащими классу А(ро).
Итак, с помощью преобразования (8.2) функция F(p) комп-
комплексной переменной р определена в полуплоскости комплексной
плоскости р правее прямой Re p = а, параллельной мнимой оси.
Заметим, что из формулы (8.3) следует, что |-Р(р)| —> 0 при
Re p —)> оо.
Функция F(p), определенная через функцию f(t) с помощью
преобразования (8.2), называется изображением Лапласа функ-
функции /(?). Функция /(?) называется оригиналом функции Р(р).
Связь функций f(t) и F(p) будем символически обозначать сле-
следующим образом2):
№ = F(p) или F(p) = f(t).	(8.7)
Отметим, что в практических приложениях часто пользуют-
пользуются так называемым преобразованием Хевисайда:
оо
t,	(8.8)
:) Признак Коши сходимости несобственных интегралов см. вып. 2.
2) В литературе встречаются и другие символические обозначения, на-
пример: F(p) -> f(t), F(p) .-4 /(*), F(p) \\ /(*) и т.д.

§ 1	ОСНОВНЫЕ СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА	225
отличающимся от преобразования Лапласа дополнительным
множителем р. Очевидно, область определения функции F(p) та
же, что и для функции F(p). В дальнейшем мы будем рассма-
рассматривать только преобразование Лапласа (8.2). Свойства преоб-
преобразования Хевисайда (8.8) легко могут быть получены на осно-
основании рассматриваемых ниже свойств преобразования Лапласа.
Как мы видели, наиболее важным классом функций комп-
комплексной переменной являются аналитические функции. Выяс-
Выясним, является ли функция F(p) аналитической.
Теорема 8.2. Изображение Лапласа (8.2) функции f(t) яв-
является аналитической функцией комплексной переменной р в
области Re р > а, где а — показатель степени роста функ-
функции f(t).
Доказательство. В силу теоремы 8.1 несобственный
интеграл (8.2) сходится в области Re p > а. Разобьем интервал
интегрирования на отрезки [?^, ^г+i] произвольной конечной дли-
длины, причем to = 0, tn —>> оо при п —>> оо. Тогда функция F(p)
при Re p > а представляет собой сумму сходящегося ряда
un(p)- (8-9)
n=0 tn	n=0
Заметим, что поскольку п-й остаток сходящегося ряда (8.9) ра-
оо
вен J e~ptf(t)dt, то согласно теореме 8.1 ряд (8.9) сходится
tn + l
равномерно в области Re p ^ xq > а. Каждая из функций
и
tn +
(р)= f
определена как интеграл, зависящий от параметра р, по отрез-
отрезку конечной длины на комплексной плоскости t. На основании
общих свойств интегралов от функций двух комплексных пере-
переменных, зависящих от параметра1), функции ип(р) являются
целыми функциями р. Из проведенных рассуждений следует,
что ряд (8.9) в области Re p > а удовлетворяет всем услови-
условиям теоремы Вейерштрасса2), а значит, функция F(p) является
аналитической в области Re p > а и ее производные можно вы-
вычислять, дифференцируя подынтегральную функцию в (8.2) по
параметру р.
:) См. гл. 1 с. 56.
2) См. гл. 2 с. 62.
А.Г. Свешников, А.Н. Тихонов

226 ОСНОВНЫЕ ПОНЯТИЯ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ ГЛ. 8
2. Изображение элементарных функций. Пользуясь
определением (8.2), найдем изображение ряда элементарных
функций действительной переменной.
а) Единичная функция Хевисайда. Пусть
(	(8.10)
II, t ^ U.
Тогда
причем функция F(p), очевидно, определена в области Re р > 0.
Итак,
<*(*) = I J' l^l .= ?, Rep>0.	(8.11)
Отметим, что если вместо преобразования Лапласа (8.2) пользо-
пользоваться преобразованием Хевисайда (8.8), то изображением еди-
единичной функции <то(?) будет функция F(p) = l. Этим объясняет-
объясняется достаточно широкое применение преобразования Хевисайда.
Однако в случае преобразования Хевисайда (8.8) усложняется
ряд других формул, в частности формула обратного преобразо-
преобразования, формула изображения свертки (см. ниже с. 232).
Условимся всюду в дальнейшем, если это не оговорено осо-
особо, под функцией /(?) понимать произведение /(?) • ао(?), т. е.
функцию, тождественно равную нулю при t < 0, не отмечая это
специально в соответствующих формулах.
б)	Показательная функция
№ = eat.	(8.12)
Вычисляя интеграл (8.2), получаем
оо
F(p) = [ e-pteat dt = —!—, Re p > Re a;
J	P~a
о
eat = -J—, Re p > Re a.	(8.13)
p — a
в)	Степенная функция
fit) = ?, v> -1.	(8.14)
В этом случае интеграл (8.2) имеет вид
оо	оо
F(p) = J e~ptf(t) dt= J е~рЧи dt, Re p > 0. (8.15)
о	о

§ 1	ОСНОВНЫЕ СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА	227
Заметим, что при v < 0 функция (8.14) уже не удовлетворяет
условию 2 с. 222 (точка t = 0 является точкой разрыва второ-
второго рода этой функции) и тем самым не принадлежит основному
рассматриваемому классу функций действительной переменной,
для которых существует изображение Лапласа. Однако, как лег-
легко видеть, при v > — 1 эта функция принадлежит расширенно-
расширенному классу, введенному на с. 223 (интеграл (8.15) сходится при
Re р > 0 л v > — 1). Поэтому и в случае — 1 < v < 0 изображе-
изображение Лапласа функции (8.14) в области Re р > 0 существует и
определяется формулой (8.15).
Перейдем к вычислению интеграла (8.15). Начнем со случая,
когда переменная р принимает действительное значение р = х > 0.
Сделав в интеграле (8.15) замену переменной интегрирования
xt = «s, получим
оо	оо
F(x) = J e~xtf dt=^$ e-ss» ds =
о	о
где Т(и-\-1) — гамма-функция г) Эйлера. Так как функция F(p),
определенная формулой (8.15), является аналитической в обла-
области Re p > 0, имеющей на положительной части действительной
оси х > 0 значение (8.16), то в силу единственности аналитиче-
аналитического продолжения для функции F(p) в области Re p > 0 полу-
получим выражение
оо
F(p)= /e-^di=E?+±).	(8.17)
о
При этом в случае дробных v следует выбирать ту ветвь мно-
многозначной функции -^-, которая является непосредственным
аналитическим продолжением в область Re p > 0 действитель-
действительной функции	действительной переменной х > 0. Итак,
Г==Щ+Я, и>-1, Rep>0.	(8.18)
Для целых v = n из формулы (8.18) получим
„ .Г(п + 1)= Ы	R	Q	(819)
рп+l	рп+l'	Г	V	/
Вычисляя интеграл (8.2), можно получить изображение еще ря-
ряда функций действительной переменной, однако во многих слу-
случаях для вычисления изображения заданной функции удобнее,
оказывается, пользоваться общими свойствами изображения Ла-
Лапласа, к рассмотрению которых мы и перейдем.
Определение и свойства гамма-функции см. вып. 2.

228 ОСНОВНЫЕ ПОНЯТИЯ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ ГЛ. 8
3. Свойства изображения.
а) Линейность изображения. В силу известных
свойств определенных интегралов, имеет место
Свойство 1. Если Fi(p) = fi(t), Re р > щ (г = 1,... , п),
то
п	п
F(p) = ^ctiFiip) = ^аг/г(?), Rep > тахаг, (8.20)
г=1	г=1
где ol{ — заданные постоянные числа (действительные или ком-
комплексные), о,{ — показатели степени роста функций fi(t).
Данное свойство позволяет по найденным изображениям функций
(8.13), (8.18), (8.19) найти изображения многочлена, тригонометрических
и гиперболических функций.
Например, с помощью (8.13) получим
cosujt = -(е + е ) = -
2	2
Р
2 \p — too p + iuj J p2 + uj2
Rep>|Imcj|.	(8.21)
Аналогично
sincj?=^	о j Re p > I Im cj .	(8.22)
б) Свойство 2. Пусть F(p) = /(t), Re p > а, тогда
= f(at), a > 0, Rep>a.	(8.23)
Действительно,
(X)	(X)
в) Свойство 3 (теорема запаздывания).
Пусть F(p) = /(t), Re p > а и задана функция
[ /(*-г), ? > т.
Тогда
/г(<) = ^r(p) = e-pTF(p), Rep>a.	(8.25)
Действительно,
FT{p) = J e-*fT(t) dt= J e-*f(t - т) dt.

§ 1	ОСНОВНЫЕ СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА	229
Сделаем в последнем интеграле замену переменной, положив
t-т = tf. Тогда
ОО
FT(p) = J e-^'+-)/(t') dtf = e-^F(p),
о
что и доказывает свойство 3.
В качестве первого примера рассмотрим изображение ступенчатой
функции
/(О = ( °' t<T'	(8-26)
[ n/о, пт ^ t < (п + 1)т, п = 1, 2,...
Представим /(?) с помощью единичной функции Хевисайда сто:
f{t) = fo[cro(t - т) + (то(t - 2r) + .. .].
Использовав свойство линейности и теорему запаздывания, получим
/(*) = F(p) = /се"-! + /се-! + ... = ^^^-	(8.27)
Аналогично легко показать, что изображением периодической функции
*<B" + 1К. „ = 0,1,2,..., (8.28)
<B + 2)
-/о, Bп + 1)т^<Bп + 2)
является функция
^^	(8.29)
р 2
Теорема запаздывания позволяет получить и довольно общую формулу
для изображения периодической функции. Предварительно рассмотрим тот
случай, когда функция f{t) действительной переменной t имеет вид
0, r^t.
Обозначим изображения функций cp(t) = Ф(р) и (p(t-\-r) = Фт(р). Пере-
Перепишем (8.30) в виде
Г О,	О ^ t < г,
^(t + r-r), t^r.
Воспользовавшись линейностью изображения и теоремой запаздывания,
получим
/(*) = F(p) = Ф(р) - е-ртФт(р).	(8.31)
Пусть теперь функция <p(t) является периодической функцией t с периодом
т~ т е
p(t + т) = ?>(*).	(8.32)
Тогда Фт(р) = Ф(р), и формула (8.31) позволяет выразить изображение Ф(р)
периодической функции y?(t) через изображение F(p) функции /(?), равной
функции 9?(t) на первом периоде O^t^rn нулю вне его при t ^ г:
Ф(р) = F(p) .	(8.33)

230 ОСНОВНЫЕ ПОНЯТИЯ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ ГЛ. 8
В качестве примера найдем изображение функции
uj > 0.	(8.34)
Эта функция является периодической при t > 0 с периодом —. Предвари-
UJ
тельно найдем изображение функции
(8.35)
С помощью формул (8.31), (8.22) и равенства sincj lt-\	) = — smut
получим
Отсюда по формуле (8.33) получим
/ 7Г \
1 + ехр (	р 1
V oj /
.'-.	(8.36)
г) Изображение производной. Сейчас
будет доказано одно из основных свойств изображения, позво-
позволяющее заменить дифференцирование оригинала умножением
изображения на независимую переменную.
Свойство 4. Если ff(t) удовлетворяет условиям суще-
существования изображения при Re p > а и /(?) = F(p), Re p > а,
то
/'(t) =pF(p) - /@), Re p > а.	(8.37)
Действительно, интегрируя по частям, получаем
оо	оо
/'(?) = J e-ptff(t) dt = e-ptf(t)\™+p f e~ptf(t) dt = pF(p)-f@)
о	о
что и доказывает данное свойство.
Аналогично может быть доказано
Свойство 47. Если f^n\t) удовлетворяет условиям
существования изображения при Re р > а и f(t) = F(p), Re p >
> а, то
р	р2	рп
(8.38)
Формула (8.38) особенно упрощается в том случае, когда
f{n)(t)=pnF(p).	(8.39)

§ 1	ОСНОВНЫЕ СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА	231
Полученный результат находит многочисленные применения.
Рассмотрим, например, решение следующей задачи Коши
для обыкновенного дифференциального уравнения, линейного
с постоянными коэффициентами:
М + ац/*1) + ... + any(t) = /(*),	(8.40)
О,	(8.41)
где f(t) — заданная при t ^ 0 функция t. Положив, что /(?) = О
при t < 0, мы в том случае, если /(?) удовлетворяет услови-
условиям существования изображения, можем построить изображение
F(p) функции /(?). Предположим, что функция у(?), являюща-
являющаяся решением задачи (8.40), (8.41), и все ее производные до п-го
порядка удовлетворяют условиям существования изображения.
Тогда, умножив обе части уравнения (8.40) на e~pt и проинте-
проинтегрировав по t от 0 до оо, в силу линейности изображения и на-
начальных условий (8.40) получим
Y(p){aoPn + alPn~l + ... + an} = F(p),
ОО
где через Y(p) = f e~pty(t) dt обозначено изображение иско-
о
мого решения задачи (8.40), (8.41). Обозначив Рп(р) = аорп +
+ а\рп~1 + ... + ап, получим
= *М.	(8.42)
Формула (8.42) дает достаточно простое выражение изо-
изображения искомого решения y(t) через известные функции-
полином Pn(p)i коэффициенты которого определяются уравне-
уравнением (8.40), и изображение F(p) заданной правой части урав-
уравнения. Тем самым, если мы сможем определить неизвестный
оригинал y(t) по его известному изображению Y(p), то зада-
задача (8.40), (8.41) будет решена. Ниже мы рассмотрим различные
способы определения оригинала по заданному изображению, а
сейчас продолжим рассмотрение еще ряда общих свойств изо-
изображения.
д) Изображение интеграла.
Свойство 5. Пусть /(?) = F(p), Re p > а. Тогда
t
<p(t) = J /(r) dr = -F(p), Rep>a.	(8.43)
о	P
Действительно, легко проверить, что функция cp(t) удовле-
удовлетворяет всем условиям существования изображения, причем
(p(t) имеет тот же показатель степени роста, что и /(?). Вычис-

232 ОСНОВНЫЕ ПОНЯТИЯ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ ГЛ. 8
лив изображение функции cp(t) по формуле (8.2), получим
t	оо	t
ff(r)dr= fe-VdtffWdr.
О	0	0
Меняя в последнем интеграле порядок интегрирования1),
получаем
t	(X)	(X)	ОО
/ /(г) dr = J f(r)dr J e-*dt = - / e-^/(r) dr = l-F{p),
0	Or	P 0	P
что и доказывает формулу (8.43).
Аналогичным образом может быть доказано
Свойство 5'. Пусть /(?) = F(p), Re p > а; тогда
t ti	tn-i
fdhfdt2... J f(tn)dtn = \F{p), Rep>a. (8.44)
ooo	p
Свойства 5 и 5' находят многочисленные применения при вы-
вычислении изображений различных функций.
Например, найдем изображение пилообразной функции /(?), предста-
представляющей собой периодически повторяющийся равнобедренный треугольник
с основанием 2т и высотой /от. Как легко видеть, эта функция представля-
представляет собой интеграл от 0 до t от функции (8.28), изображение которой дается
формулой (8.29). Поэтому
4 th^.	(8.45)
е) Изображение свертки. Сверткой функций fi(i)
и f2{t) называется функция у?(?), определенная соотношением
t	t
t	t
?>(*) = / /i W/2(* " т) dr = J h(t - r)f2(r) dr.	(8.46)
о	о
В справедливости последнего равенства легко убедиться, сделав
в первом интеграле замену переменной интегрирования t — г =
= tf. Имеет место следующее
Свойство 6. Если /i(t) = Fi{p), Re P > «ь /г(*) .=' ^(р),
Re р > а2, то
?>(*) = / h(r)hit ~ г) dr = Fi(p)F2(p), Re p > max {аьа2}.
о
(8.47)
) Возможность изменения порядка интегрирования следует из теоремы
10.9, вып. 2, выполнение условий которой в данном случае легко проверя-
проверяется.

§_L	ОСНОВНЫЕ СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА	233
Свертка функций fi(t) и f2{t) с ограниченной степенью ро-
роста также является функцией с ограниченной степенью роста.
Действительно,
t	t
f /i(r)/2(t ~r)dr ^ M1M2 f еа'теа^-^ dr =
о	о
Аналогичным образом легко проверить, что свертка функций
fi(t) и f2(t) с ограниченной степенью роста и при а\ = а2
также является функцией с ограниченной степенью роста. Сте-
Степень роста свертки, очевидно, равна наибольшей степени роста
функций fi(t) и f2(t). Легко видеть, что (p(t) удовлетворяет и
остальным условиям существования изображения. Для вычис-
вычисления изображения свертки воспользуемся формулой (8.2) и из-
изменим порядок интегрирования1):
оо	t	00	00
Г e~pt dt Г /i(r)/2(t -r)dr= Г .h(t) dr f e-P*/2(t - r) dt.
0	0	От
Сделав замену переменной t — г = t' во внутреннем интеграле,
окончательно получим
t	(X)	(X)
/ /i(r)/2(t-r) dr = J e'^hir) dr J e-^'f2{t') dt' = Fl{p)F2{p)
0	00
что и доказывает свойство 6.
В приложениях формула (8.47) часто используется для опре-
определения оригинала по заданному изображению, когда задан-
заданное изображение удается разбить на сомножители, для которых
оригиналы известны.
Например, пусть требуется найти оригинал функции F(p) = ——	^—¦.
Ранее мы нашли (см. формулы (8.21) и (8.22)), что
р
р2 + uj2	р2 + uj2
Поэтому
t
F(p) = Г sincjr • cosuu(t — r)dr = - sir
о	2
Рассмотрим еще ряд общих свойств изображений.
) О возможности изменения порядка интегрирования см. ссылку на
с. 232.

234 ОСНОВНЫЕ ПОНЯТИЯ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ ГЛ. 8
ж) Дифференцирование изображения.
Свойство 7. Пусть F(p) = /(?), Re р > а. Тогда
F'(p) = -tf(t), Rep>a.	(8.48)
Действительно, выше мы отмечали, что производную аналити-
аналитической функции F(p) в области ее определения Re p > а мож-
можно вычислять, дифференцируя подынтегральную функцию в
несобственном интеграле (8.2) по параметру. Проделав это, по-
получим
что и доказывает свойство 7. Заметив, что умножение функции
f(t) на любую степенную функцию tn не меняет ее степени ро-
роста, получим
Свойство Т. Если F(p) =' /(?), Re p > а, то
F^{p) = (-l)ntnf(t), Rep>a.	(8.49)
Формулы (8.48) и (8.49) могут быть применены для вычис-
вычисления изображения от произведения tn на функцию /(?), для
которой изображение известно. В дальнейшем мы получим об-
общую формулу, выражающую изображение произведения через
изображения сомножителей, а сейчас рассмотрим еще одно свой-
свойство изображений.
з) Интегрирование изображения.
Свойство 8. Если функция ^-^- удовлетворяет условиям
существования изображения и f(t) = F(p), Re p > а, то
(X)	(X)
Ш _• I e-PtM dt= Г F(q) dq, Rep>a.	(8.50)
о	v
Обозначим
оо
I(p)= [e-ptMdt.	(8.51)
о
По теореме 8.2 функция 1(р) является аналитической в области
Re р > а, причем в силу замечания на с. 224 /(оо) = 0. Найдем
производную функции 1(р), дифференцируя интеграл (8.51) по
параметру:

§ 1	ОСНОВНЫЕ СВОЙСТВА ПРЕОБРАЗОВАНИЯ ЛАПЛАСА	235
Отсюда, учитывая условие /(оо) = 0, получаем
р	оо
= /(оо) - j F(q) dq = J F(q) dq,
ОО	p
что и доказывает свойство 8.
В качестве примера найдем изображение функции - smut.
т
Так как sin ut = —	, то
р2 + uj2
оо
sin^ =' / fdp=I arctg ?• (8-52)
С помощью свойства 5 из выражения (8.52) получаем
t
sit= ^-^- dr = - (^ - arctgp) .	(8.53)
J т	р \2	J
о
Функция si t носит название интегрального синуса.
и) Последнее свойство изображений, которое будет рассмо-
рассмотрено в данном параграфе, носит название теоремы
смещения.
Свойство 9. Если /(?) = F(p), Re p > а, то для любого
комплексного числа А
F(p + А) = e~xtf{t), Re p > а - Re A.	(8.54)
Действительно, функция (p(t) = e~xtf(tI очевидно, удовлетво-
удовлетворяет условиям существования изображения, которое по формуле
(8.2) определено в области Re р > а — Re А, но
оо	оо
Г e-pte-Mf(t) dt= Г e-{p+X»f{t) dt = F(p + Л),
и	и
О	О
что и доказывает теорему смещения.
Формула (8.54) может быть применена для определения изображения
произведения функции e~xt на функцию /(?), для которой изображение
известно. Так, с помощью этой формулы и уже полученных изображений
можно найти
teat = l	Rep >Re а,	(8.55)
(р - аJ
fneat _. 	n-	Re p > Re а,	(8.56)
(р - а)гг+1
Re р > | Im u\ - Re а.	(8.57)
и т.д.

236 ОСНОВНЫЕ ПОНЯТИЯ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ ГЛ. 8
В заключение данного параграфа приведем таблицу рассмо-
рассмотренных свойств изображений и таблицу изображений ряда эле-
элементарных и специальных функций, наиболее часто используе-
используемых в приложениях.
4. Таблица свойств изображений. Пусть /(?) = F(p).
Тогда
п	п
1) Е <*ifi(t) = Yl <XiFi(p), oti = const;
г=1	г=1
2) f(at) = ^-F (|V a = const, a > 0;
о	p
6) / /i(r)/2(t -T)dr = }h{t- r)/2(r) dr = F1(p)F2(p);
5. Таблица изображений.
1)	1 = -, Re p > 0;
v
2)	^-"^^ТГ1» ">"!> R
3)	tn = -^-, n — натуральное, Re p > 0;
4)	ea* .= —!—, Re p > Re a;
p — a
5)	sino;i.= ^	5-,	Re p > Im
6)	cos o>^ .= 2 P 2,	Rep>|Imo;|;
7)	sh At = Л	Re p > | Re Л|;
p — Л
8)	ch\t= 2РЛ2,	Rep>|ReA|;
p Л

ОПРЕДЕЛЕНИЕ ОРИГИНАЛА ПО ИЗОБРАЖЕНИЮ
237
9) tneat =
10)
l)
(p - a)^1
__. 2puo
11) t COS UJt =
12)
13)
14)
15)
-, Re p > Re a;
—-, Rep > |Im a;|;
—' —	злг", Re p > | Im a;|;
Re p> (Re A + | Im (
Re p > (Re A + | Im
= - — arctg —, Re p > \ Im o;|;
t	2	LO
-1,
.^-, Rep>0,
A; = 0,1,2,...;
16)
p2 + w2
20)
21)
22) JJt) =
1 w
(
23) si * = i ^| - arctgpj;
24)
25) 1-Ф f-^-) = -e~aVP.
J	\2VtJ p
При действительных значениях параметров, входящих в
функции /(?) в формулах 17)—25), изображения соответствую-
соответствующих функций заведомо определены в области Re p > 0.

238 ОСНОВНЫЕ ПОНЯТИЯ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ ГЛ. 8
§ 2. Определение оригинала по изображению
В этом параграфе мы рассмотрим методы определения ори-
оригинала по заданному изображению, а также приведем неко-
некоторые достаточные условия, при которых заданная функция
F(p) комплексной переменной р является изображением функ-
функции /(?) действительной переменной t.
Во-первых, отметим, что имеются различные таблицы изо-
изображений наиболее часто встречающихся в приложениях функ-
функций, так что при решении конкретных задач часто удается най-
найти в соответствующем справочнике 1) выражение оригинала для
полученного изображения.
Во-вторых, приведенные в предыдущем параграфе свойства
изображений 1)-9) во многих случаях позволяют решить и
обратную задачу построения оригинала по заданному изобра-
изображению. В первую очередь это относится к теореме смещения,
интегрированию и дифференцированию изображения и изобра-
изображению свертки функций. Ряд примеров был уже рассмотрен в
§ 1, некоторые примеры будут приведены в дальнейшем.
Однако все эти методы, по существу, являются методами
подбора. Основной целью данного параграфа является изложе-
изложение общего метода построения оригинала по изображению.
1. Формула Меллина. Начнем с того случая, когда по
условиям задачи известно, что заданная функция F(p) комп-
комплексной переменной р является изображением кусочно гладкой
функции /(?) с ограниченной степенью роста \f(t)\ < Meat,
причем значение постоянной а заданно. Требуется по заданной
функции F(p) построить искомую функцию /(?). Эта задача ре-
решается с помощью следующей теоремы.
Теорема 8.3. Пусть известно, что заданная функция F(p)
в области Re p > а является изображением кусочно гладкой
функции /(?) действительной переменной ?, обладающей сте-
степенью роста а.
Тогда
х>а.	(8.58)
Доказательство. По условию теоремы функция
f(t) существует и нам известна ее степень роста. Рассмотрим
вспомогательную функцию (p(t) = e~xtf(t), x > а. Эта функ-
:) Достаточно подробные таблицы читатель может найти в книге
В. А. Диткина и А. П. Прудникова. Интегральные преобразования и опера-
операционное исчисление. — М. : Физматгиз, 1961. Там же приведен и подробный
список справочной литературы по операционному исчислению.

§ 2	ОПРЕДЕЛЕНИЕ ОРИГИНАЛА ПО ИЗОБРАЖЕНИЮ	239
ция является кусочно гладкой, на любом ограниченном участке
оси t имеет конечное число точек разрыва первого рода и экс-
экспоненциально стремится к нулю при t —^ оо. Она может быть
представлена с помощью интеграла Фурье1)
оо оо
№-ri drj.	(8.59)
Подставляя в (8.59) выражение функции cp(t) через искомую
функцию /(?), получаем
оо оо
— ОО —ОО
ОО	ОО
= h I St di I eiX+zOr>f(v) dr,, (8.60)
так как /(г/) = 0 при г/ < 0.
Обозначим р = х + г^ и заметим, что внутренний интеграл в
(8.60) представляет собой заданное изображение F(p) искомой
функции /(?). Тогда выражение (8.60) принимает вид
2тгг
— оо	х — гоо
что и доказывает теорему. Заметим, что в формуле (8.58) инте-
интегрирование производится на комплексной плоскости р по пря-
прямой, параллельной мнимой оси и проходящей правее прямой
Re p = а. Значение интеграла (8.58), очевидно, не зависит от ве-
величины х при условии, что прямая интегрирования лежит пра-
правее прямой Re p = а.
Формула (8.58) часто называется формулой Меллина, она яв-
является в определенном смысле обратной преобразованию Лапла-
Лапласа (формула (8.2)), так как выражает оригинал через заданное
изображение. Отметим, что поскольку мы в процессе вывода
формулы Меллина от самой неизвестной функции /(?) перешли
к ее интегралу Фурье, сходящемуся к функции /(?) лишь в точ-
точках непрерывности этой функции, то и интеграл (8.58) совпада-
совпадает с функцией /(?) лишь в точках ее непрерывности.
В качестве примера применения доказанной теоремы рассмо-
рассмотрим вопрос об определении изображения произведения по из-
известным изображениям сомножителей.
:) Определение интеграла Фурье и обоснование интегральной формулы
В.59) см. вып. 2.

240 ОСНОВНЫЕ ПОНЯТИЯ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ ГЛ. 8
Теорема 8.4. Пусть fi(t) = F\{p), Re р > а\ и f2(t) = i*2(p)?
p > а,2. Тогда
х + гоо
Теорема 8.4.
Re p > а,2. Тогда
№ = fi(t)f2(t) = F(p) = ±-.
+
= гЬ / F1(p-q)F2(q)dq, (8.61)
ж — гоо
х + гею
причем функция F(p) определена и аналитична в области
Re р > а\ + а,2, а интегрирование производится по любой пря-
прямой^ параллельной мнимой оси, удовлетворяющей в первом слу-
случае условию а\ < Re q < Rep — 0,2, а во втором — условию
а2 < Re q < Re p — а\.
Доказательство. Так как функция f(t) удовлетворяет
всем условиям существования изображения, то для нее имеет
место преобразование Лапласа
оо
/(t) = F(p) = J e-^h{t)f2{t) dt.	(8.62)
о
Представляя в (8.62) функцию /i(t) в виде ее интеграла Мелли-
на (8.58) и меняя порядок интегрирования, что возможно в силу
равномерной сходимости данных несобственных интегралов, за-
зависящих от параметра, получаем
оо	х + гоо
J e<>tF1(q)dq =
х — гоо
х + гоо	оо
0
х + гоо
. (8.63)
Заметим, что в (8.63) Re q = x > ai, а функция F2(p — q) опреде-
определена при Re (p — q) > 0,2, откуда Re p > а\ +п2- Заменив в (8.62)
функцию h{t) по формуле обращения, можно получить второе
равенство в (8.61). Теорема доказана. Отметим, что доказанная
теорема в известном смысле обратна свойству 6.
Пример 1. Пусть h(i) = cosa;t, h(i) = t. Найдем
изображение функции /(?) = t cos cot.

§ 2	ОПРЕДЕЛЕНИЕ ОРИГИНАЛА ПО ИЗОБРАЖЕНИЮ	241
Так как cos cot = -7—-—-, ? = —, то
р2 + и2	р2
ж+гоо
F^ = яг / tf+X-ti-	(8'64)
ж—гею
где Re р > |Imo;|, а интегрирование производится по любой
прямой, параллельной мнимой оси и лежащей правее прямой
Re q = I Im uo\. В качестве такой прямой интегрирования выбе-
выберем прямую, проходящую левее точки q = р, и рассмотрим на
комплексной плоскости q замкнутый контур Г, состоящий из от-
отрезка [х — ii?, х + iR] данной прямой и замыкающей его в правой
полуплоскости дуги полуокружности \q — x\ = R. Внутри данно-
данного контура подынтегральная функция из (8.64) является всюду
аналитической, кроме точки q = р, которая есть полюс второго
порядка данной функции. Точка q = 00 является нулем третьего
порядка этой функции. Поэтому в силу леммы 1 гл. 5 значение
интеграла (8.64) определяется вычетом в особой точке подынте-
подынтегральной функции. Заметив, что обход контура Г совершается
в отрицательном направлении, получим
\1
pip) = -±
УР)	dq
Итак,
t cos uot = ,Р1~Ш*	(8.65)
(р2+и2J
2. Условия существования оригинала. В настоящем
пункте мы рассмотрим некоторые достаточные условия, при ко-
которых заданная функция F(p) комплексной переменной р яв-
является изображением некоторой функции /(?) действительной
переменной ?, и покажем, как найти последнюю.
Теорема 8.5. Пусть функция F(p) комплексной переменной
р = х + гу удовлетворяет следующим условиям:
а)	F(p) — аналитическая функция в области Re p > а;
б)	в области Re p > а функция F(p) стремится к нулю при
\р\ —)> оо равномерно относительно argp;
в)	для всех Re р = х > а сходится интеграл1)
х + гоо
\F(p)\dy<M, x>a.	(8.66)
Тогда функция F(p) при Re p > а является изображением
функции f(t) действительной переменной ?, которая опреде-
:) Интеграл (8.66) представляет собой несобственный интеграл первого
рода по прямой Re р = х от действительной функции |()|

242 ОСНОВНЫЕ ПОНЯТИЯ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ ГЛ. 8
ляется выражением
х + гею
Доказательство. Итак, надо доказать, что инте-
интеграл (8.67) является оригиналом функции F(p). Первым делом
возникает вопрос о существовании этого несобственного инте-
интеграла1). Очевидно, что
х + гоо	х + гоо
х — гоо	х — гоо
w x + гоо
: М-ех\ (8.68)
откуда и следует сходимость интеграла (8.67) при любом х > а.
Отметим для дальнейшего, что из оценки (8.68) следует равно-
равномерная сходимость интеграла (8.67) по параметру t на любом
конечном промежутке 0 ^ t ^ Т.
Для того чтобы доказать, что интеграл (8.67) является ори-
оригиналом заданной функции F(p), следует установить, что:
1° Интеграл (8.67) не зависит от ж и определяет функцию
/(?) лишь одной переменной ?, причем эта функция обладает
ограниченной степенью роста.
2° При ?<0 /(?)=0.
3° Изображением Лапласа функции /(?) является заданная
функция F(p).
Докажем каждое из высказанных утверждений.
1° Рассмотрим в области Re p > а замкнутый контур Г, со-
состоящий из отрезков прямых \х\ — %А^ х\ + г А] и [х2 — iA, Х2 +
+ iA]j параллельных мнимой оси, и соединяющих их отрезков
прямых [х\ — г А, Х2 — г А], [х\ + г А, Х2 + г А], параллельных дей-
действительной оси (рис. 8.1). Здесь А > 0; жх, Х2 — произвольные
числа, большие а. Так как функция F(p) является аналитиче-
аналитической в области Re p > а, то в силу теоремы Коши интеграл от
функции eptF(p) по контуру Г равен нулю. Устремим А к беско-
1) Несобственный интеграл (8.67) вычисляется вдоль прямой Re р = х и
понимается в смысле главного значения, т.е.
х + гоо	х -\-iA
Г eptF(p)dp= lim Г eptF(p)dp.
J	A—)-oo J
х — iA

ОПРЕДЕЛЕНИЕ ОРИГИНАЛА ПО ИЗОБРАЖЕНИЮ
243
нечности, оставляя фиксированными жх, %2- Тогда по условию
б) теоремы интегралы по горизонтальным отрезкам пути инте-
интегрирования дадут в пределе нуль. В то же время интегралы по
вертикальным прямым переходят в интеграл (8.67). Отсюда
х\ + гею
1 + гею	Х2 + гею
J eptF(p)dp= J eptF(p)dp,
х\ — гею
что в силу произвольности х\ и Х2 доказывает утверждение 1°.
Итак, интеграл (8.67) является функцией лишь одной перемен-
переменной t. Отметим, что при этом из оценки (8.68) сразу следует, что
интеграл (8.67) представляет собой функцию ограниченной сте-
степени роста по ?, причем показатель степени роста этой функции
равен а.
2° Рассмотрим значение интеграла (8.67) при t < 0. Для это-
этого в области Re р > а рассмотрим замкнутый контур С, состо-
состоящий из отрезка прямой [х — iR,x + гД], х > а, и замыкающей
его дуги C'R полуокружности \р — х\ = R (рис. 8.2). По теореме
Коши интеграл от функции eptF(p) по данному контуру равен
x+iR
x2+iA
р=0
xi-iA x2-iA
Рис. 8.1
нулю. В силу замечания к лемме Жордана (см. гл. 5, с. 139)
при R —>• оо интеграл по дуге CfR стремится к нулю при t < 0.
Поэтому
х + гею
/(*) = -L Г eptF(p) dp = 0, t < 0, Re p > а,	(8.69)
Z7TZ *J
х — гею
и утверждение 2° доказано.
3° Построим изображение Лапласа функции (8.67) и рас-

244 ОСНОВНЫЕ ПОНЯТИЯ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ ГЛ. 8
смотрим его значение при некотором произвольном ^о, где
Re po > а:
оо	оо	х + гоо
/ e-potf(t) dt=^-f e~pot dt f eptF(p) dp.	(8.70)
0	0	x - гоо
Внутренний интеграл в (8.70) не зависит от х. Выберем значение
ж, удовлетворяющее условию а < х < Re po, и изменим порядок
интегрирования, что возможно в силу равномерной сходимости
соответствующих интегралов; получим
х + гоо	оо
=^- J
х + гоо
= it- f F{p)-^—. (8.71)
2ттг J	po — p
x — гоо
Интеграл (8.71) может быть вычислен с помощью вычетов, так
как в силу условия б) теоремы подынтегральная функция стре-
мится к нулю при |_р| —>> сю быстрее, чем функция -. Поэтому,
учтя, что единственной особой точкой подынтегральной функ-
функции — полюсом первого порядка — является точка р = ро и что
при замыкании (8.71) в правой полуплоскости интегрирование
производится в отрицательном направлении, получим
оо
(8.72)
Поскольку pq — произвольная точка в области Re p > а, теорема
доказана. Естественно, что интеграл (8.67) совпадает с форму-
формулой Меллина (8.58), выведенный в предположении существова-
существования оригинала. Итак, нами установлены некоторые достаточные
условия, при которых заданная функция F(p) комплексной пе-
переменной р является изображением.
3. Вычисление интеграла Меллина. Во многих прак-
практически важных случаях интеграл (8.58), (8.67), дающий выра-
выражение оригинала по заданной функции F(p) комплексной пере-
переменной, может быть вычислен с помощью рассмотренных вы-
выше (см. гл. 5) методов вычисления контурных интегралов от
функции комплексной переменной. Пусть функция F(p), перво-
первоначально заданная в области Re p > а, может быть аналитиче-
аналитически продолжена на всю плоскость р, за исключением конечного
числа особых точек и разрезов. Пусть ее аналитическое продол-
продолжение удовлетворяет при Re p < а условиям леммы Жордана.

§J2	ОПРЕДЕЛЕНИЕ ОРИГИНАЛА ПО ИЗОБРАЖЕНИЮ	245
Тогда при t > О
J eptF(p) dp -+ О, R^oo,	(8.73)
где С^ — дуга полуокружности \р — х\ = R в левой полуплос-
полуплоскости. В этом случае интеграл (8.67) может быть вычислен с
помощью теории вычетов. Рассмотрим ряд примеров.
Пример 2. Найти оригинал функции F(p) = —	-,
pz + uz
Re p > О, о;2 > 0. Так как условия теоремы 8.5 выполнены, то
ж+гоо
Аналитическое продолжение функции F(p) в левую полу-
полуплоскость Re р < 0, функция —	-, удовлетворяет условиям
леммы Жордана и имеет две особые точки — полюсы первого
порядка при pi?2 = ±iw. Поэтому при t ^ 0
2
Условия теоремы 8.5, в частности условие в), являются доста-
достаточными условиями существования оригинала аналитической в
области Re p > а функции F(p). Нетрудно привести примеры,
показывающие, что, если это условие не имеет места, функция
F(p) может все же быть изображением некоторой функции дей-
действительной переменной.
Пример 3. Найти оригинал функции F(p) = 1,
— 1 < а < 0, Re p > 0. Эта функция является многозначной
в рассматриваемой области. Мы будем понимать под функцией
F(p) ту ветвь данной многозначной функции, которая являет-
является непосредственным аналитическим продолжением в область
Re р > 0 действительной функции —^ действительной пере-
переменной х > 0. При этом мы, очевидно, должны считать axgp = 0
при р = ж, х > 0. Функция F(p) не удовлетворяет условию в)
теоремы 8.5. Покажем, однако, что функция
ж-Моо
е^ф' ж>0' <8-74)
является оригиналом заданной функции F(p).
Аналитическое продолжение функции F(p) на левую полу-

246 ОСНОВНЫЕ ПОНЯТИЯ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ ГЛ. 8
плоскость Re р < 0 является многозначной функцией, имею-
имеющей точками разветвления точки р = 0 и р = оо. Будем рас-
рассматривать в области ?/, представляющей собой комплексную
плоскость р с разрезом по отрицательной части действитель-
действительной оси, ту ветвь многозначной
x+iR' функции
р*Л
которая явля-
являx-iR'
ется непосредственным анали-
аналитическим продолжением функ-
функции F(p), первоначально за-
заданной в правой полуплоско-
полуплоскости Re р > 0. В области Q рас-
рассмотрим замкнутый контур Г,
состоящий из отрезка прямой
[х — iR1\х + iR'], х > 0, отрез-
отрезков —R < х < — р на берегах
разреза и замыкающих их ду-
дуги окружности С'р, \р\ = р, и
дуг окружности С^, \р — х\ =
= i?7, соединяющих берега раз-
разреза с вертикальным отрезком
[x-iR',x + iRr] (рис. 8.3). Так
как функция ept—^ в области
Рис. 8.3
Q особых точек не имеет, то
по теореме Коши интеграл от
этой функции по контуру Г ра-
равен нулю. Устремим R' к бес-
бесконечности, а р к нулю. В силу леммы Жордана интегралы по
кривым C'^j дадут в пределе нуль. Оценим интеграл по окруж-
окружности С'р, положив р = рег(р:
2тгг
Г1'
7Г
1 [
2ттра J
if)coa(p
d<p.
Так как — 1 < а < 0, то интеграл по С' также стремится к
нулю при р —>> 0. Тем самым остаются лишь интегралы по пря-
прямолинейным участкам контура интегрирования. Заметим, что
на нижнем берегу разреза argp = —тг, на верхнем argp = тг.
Поэтому получим
ж+гоо
- — f
~ 2ттг J

ОПРЕДЕЛЕНИЕ ОРИГИНАЛА ПО ИЗОБРАЖЕНИЮ	247
dx
(-ж)°Н
с/ж
(-ж)"
2тгг
¦/¦
е — I e-xtx~a-ldx-e^a / e^aT",
ОО
	 sin(—тга) /
e-xtx-a-l
z. (8.75)
Сделав в интеграле (8.75) замену переменной интегрирования
xt = 5, получим
Воспользовавшись равенством1)
Г(-а)ГA + а)
окончательно получим формулу
sin (—тга)'
являющуюся обращением формулы (8.18), что и доказывает на-
наше утверждение.
Пример 4. Найти оригинал функции F(p) = -е~а^
а > 0, Re р > 0. При этом, так же как и в предыдущем при-
примере, мы рассматриваем ту ветвь многозначной функции д/р,
которая является непосредственным аналитическим продолже-
продолжением в область Re p > 0 действительной функции у/х действи-
действительной переменной х > 0. Напомним, что в этом случае мы
должны положить argp = 0 при р = х > 0. Аналитическое
продолжение функции F(p) в левую полуплоскость Re p < 0
опять имеет точками разветвления точки р = 0 и р = оо. Бу-
Будем рассматривать область ?/ — плоскость р с разрезом вдоль
отрицательной части действительной оси. В этой области опре-
определена однозначная аналитическая функция -е~а^\ являюща-
являющаяся непосредственным аналитическим продолжением функции
F(p). Отметим, что функция F(p) при Re p > 0 удовлетворяет
условиям теоремы 8.5, а ее аналитическое продолжение в обла-
области Q в левой полуплоскости Re р < 0 при t > 0 удовлетворяет
условиям леммы Жордана. Поэтому, выбрав тот же контур ин-
интегрирования Г, что и в предыдущем примере, и заметив, что на
См. вып. 2.

248 ОСНОВНЫЕ ПОНЯТИЯ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ ГЛ. 8
верхнем берегу разреза argp = — тг, что дает р = ?ег7Г = — ?, у/р =
= у^ ехР Итг) = ^л/С? а на нижнем берегу разреза argp = — тг,
что дает р = ?е~г7Г = -?, д/р = лД exp (-i|J = -&л/?(? > 0),
получим
ж+гоо
.=• /с*) = гЬ
х—гоо
оо
1
-0
Так как
lim -L
2ттг
TO
оо
= — /
Сделаем в этом интеграле замену переменной, положив л/^ = ж,
учтем, что
= Г cos f3xdf3.
о
и изменим порядок интегрирования. Получим
оо	а	оо
cos
/¦ e_#sinaV| d^ = 2 Г df3 f
(8.77)
0	0 0
Внутренний интеграл в (8.77) легко может быть вычислен г). Он
равен
Отсюда
:) Например, дифференцированием по параметру (см. вып. 2).

ОПРЕДЕЛЕНИЕ ОРИГИНАЛА ПО ИЗОБРАЖЕНИЮ	249
о
Положив -j= = г/, окончательно получим
F(p) = te~*VP = i _ ф ( -2- ) , а > 0, Re р > 0, (8.78)
где функция
z
${z) = 4= Г е"^2 dr?	(8.79)
о
есть так называемая функция ошибок 1).
4. Случай регулярной на бесконечности функции.
Рассмотрим еще один частный случай, когда определение ориги-
оригинала для заданной функции F(p) комплексной переменной про-
производится особенно просто. Пусть аналитическое продолжение
первоначально заданной в области Re p > а функции F(p) явля-
является однозначной функцией на полной плоскости комплексной
переменной р, причем точка р = оо — правильная точка функ-
функции F(p). Это означает, что разложение функции F(p) в ряд
Лорана в окрестности точки р = оо имеет вид
^.	(8.80)
рп	v ;
При рассмотрении свойств изображения было отмечено, что
\F(p)\ —)> 0 при Re p —)> +оо. Поэтому в разложении (8.80) коэф-
коэффициент со равен нулю и
F(p) = ^Г ^.	(8.81)
Легко найти функцию f(t) действительной переменной ?, для
которой функция (8.81) является изображением.
Теорема 8.6. Если точка р = оо является правильной точ-
точкой функции F(p) и F(oo) = 0, то функция F(p) представляет
собой изображение Лапласа функции действительной перемен-
переменной
0,	t < 0,
п=0
г^е сп сушъ коэффициенты разложения функции F(p) в ряд Ло-
Лорана (8.81) в окрестности точки р = оо.
:) Определение и свойства функции Ф(г) см. А. Н. Т и х о н о в,
А. А. Самарский. Уравнения математической физики. — М. :
Наука, 1972.

250 ОСНОВНЫЕ ПОНЯТИЯ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ ГЛ. 8
Доказательство. Выше было показано, что коэф-
коэффициенты разложения (8.81) определяются формулой1)
Cr
где Cr — окружность \р\ = i?, вне которой нет особых точек
функции F(p). Так как точка р = оо является нулем функции
F(p), то |-Р(р)| < — при \z\ > R. Поэтому формула для сп дает
R
\сп\ <MRn~\
Из этой оценки следует сходимость ряда (8.82). Действительно,
Г
п=0
п=0	п=0
Отсюда же следует, что в круге любого конечного радиуса ряд
(8.82) сходится равномерно, тем самым определяя некоторую
целую функцию комплексной переменной t:
п=0
(Заметим, что функцию /(?), определенную формулой (8.82),
мы можем рассматривать как произведение функции f(t) на
единичную функцию Хевисайда ao(t).)
Умножив функцию f(t) на e~pt и проинтегрировав по t рав-
равномерно сходящийся ряд (8.82) почленно, на основании соотно-
соотношения 2)
tn = -nL
получим
n=0	n=0	x	nr = l
что и доказывает теорему.
Пример 5. Пусть
F(p) = -±=	(8.84)
л/Р + 1
Эта функция имеет две особые точки pi^ = =Ьг и является одно-
однозначной аналитической функцией в окрестности точки р = оо,
:) См. с. 119.
2) См. формулу (8.19).

§ 3	РЕШЕНИЕ ЗАДАЧ ОПЕРАЦИОННЫМ МЕТОДОМ	251
причем в окрестности этой точки, как было показано выше1),
функция F{p) может быть разложена в ряд Лорана:
k=0
Поэтому формула (8.83) дает
ОО
лЛк t2k
v^	k=0	k=0
Ряд, стоящий справа в (8.85), представляет собой разложение
весьма важной специальной функции — так называемой функ-
функции Бесселя2) нулевого порядка
ОО
1Ч*(*/2J*
(fc!J '
Итак,
, * = J0(t).	(8.86)
Заметим, что, представив
1 _ 1	1
Р2 + 1 ~ л/р^ТТ л/р^ТТ
и воспользовавшись изображением функции sint (см. формулу
(8.22)), на основании теоремы о свертке получим
t
J Jo(r)Jo(t — r)dr = sin*.
о
Пример 6. Пусть
Эта функция, очевидно, удовлетворяет условиям теоремы 8.6,
причем
(X
ir-1
п=1
Тогда
»"
п=0	/с=0
:) См. пример на с. 126.
2) Определение и свойства функции Бесселя см. А.Н. Тихонов,
А.А. Самарский. Уравнения математической физики. — М. : Наука,
1972.

252 ОСНОВНЫЕ ПОНЯТИЯ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ ГЛ. 8
§ 3. Решение задач для линейных дифференциальных
уравнений операционным методом
В этом параграфе будут рассмотрены применения методов
операционного исчисления к решению ряда задач для линейных
дифференциальных уравнений.
1. Обыкновенные дифференциальные уравнения. В
§ 1 мы уже видели, как с помощью операционных методов мож-
можно свести задачу Коши с нулевыми начальными условиями для
линейного дифференциального уравнения к простейшей алге-
алгебраической задаче для изображения. Рассмотрим более общую
задачу Коши:
аоУ{п)(t) + aiy^-l\t) + ... + any(t) = /(i),	(8.88)
у@) = уо, У'(О) = Уъ - - •, У(п}@) = Уп-ъ	(8.89)
где а0, аь ..., ап, у0, Уъ • • •, Уп-i ~ заданные постоянные, /(?) —
заданная функция независимой переменной ?, которую мы бу-
будем полагать удовлетворяющей всем условиям существования
изображения 1). Поскольку задача (8.88), (8.89) является линей-
линейной, можно отдельно рассматривать решение однородного урав-
уравнения с начальными условиями (8.89) и решение неоднородного
уравнения (8.88) с нулевыми начальными условиями.
Начнем с решения первой задачи. Как известно 2), для ее ре-
решения достаточно построить фундаментальную систему реше-
решений однородного уравнения (8.88). В качестве таковой выберем
решения однородного уравнения
а^)+а1ф^-1){1)+...+апфк{1)=^ к = 0,1,... ,п-1, (8.90)
удовлетворяющие начальным условиям
*«>«» = «„, * = °.|.-.»-i.	(891)
3 =0,1,...,п-1,
где
Очевидно, функции фк{1) образуют фундаментальную систему,
так как их определитель Вронского при t = 0 заведомо отличен
от нуля. Решение задачи (8.88), (8.89) при /(?) =0 через эти
*) Об условиях существования изображения см. с. 222.
2) См. вып. 3.

§ 3	РЕШЕНИЕ ЗАДАЧ ОПЕРАЦИОННЫМ МЕТОДОМ	253
функции выражается наиболее просто:
п-1
к=0
Для определения функций фк{^) применим операционный
метод. Имея в виду, что функция ^(t) и все ее производные
до n-го порядка удовлетворяют условиям существования изо-
изображения1), в силу (8.91) и формулы (8.38) получим
где
0, j < /г,
Умножив обе части уравнения (8.90) на e~pt и проинтегрировав
по ?, получим
Ф*(р)-Рп(р)=^*(р),	(8-92)
где полиномы Рп(р) и Р&(р) соответственно равны
Рп(р) = «o^n + aipn~l + ... + an
и
Pfc(p) = «oJ5n-(fe+1) + aiJ5n-(fe+2) + ... + an_(fc+1).	(8.93)
Из (8.92)
Ф^) = ад' * = 0,1,...,п-1	(8.94)
и, в частности,
Формула (8.95) будет использована в дальнейшем. Оригиналы
функций Ф&(р) могут быть найдены по формуле Меллина:
ж+гоо
где прямая ж = а проходит правее всех особых точек подынте-
подынтегральной функции из (8.96). Так как функция (8.94) представля-
представляет собой отношение двух полиномов, то ее особыми точками мо-
могут быть лишь нули знаменателя Рп (р), причем все они являют-
являются полюсами. Кроме того, при t > 0 подынтегральная функция
:) Действительно, функции ipk(t), как решения уравнения (8.90), явля-
являются гладкими функциями, растущими на бесконечности не быстрее, чем
экспонента с линейным показателем. (Подробнее о свойствах решений ли-
линейных уравнении с постоянными коэффициентами см. вып. 3.)

254 ОСНОВНЫЕ ПОНЯТИЯ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ ГЛ. 8
из (8.96), очевидно, удовлетворяет условиям леммы Жордана в
левой полуплоскости Re р < а. Поэтому
(8-97)
г=1
где pi — нули полинома Рп (р).
Если все нули щ полинома Рп(р) являются простыми, то,
п
представив его в виде произведения Рп (р) = clq Yi (р ~ Pj) ? из
формулы (8.97) получим
п
ЛМ = ЕЙ^.	(8-98)
г=1
где
ао П (Pi -Рз)
Если нули pi полинома Рп(р) являются кратными, то раз-
т
ложение полинома имеет вид Рп{р) — &о Yi (p ~ Pi)ai•> гДе ai —
г=1
т
кратность соответствующего нуля, причем ^ ai = п. В этом
г=1
случае, пользуясь правилом вычисления вычета в полюсе поряд-
порядка к > 1 и вычисляя производную от произведения по формуле
Лейбница, получаем
3.100)
3.101)
г=1
где полиномы qki(t) имеют вид
причем коэффициенты Ьш^^ вычисляются по формуле
П
Р=Рг
Отметим, что нули щ полинома Рп(р) совпадают с нулями
характеристического многочлена для уравнения (8.90). Поэто-
Поэтому формулы (8.98) и (8.100) дают представление каждого из

§ 3	РЕШЕНИЕ ЗАДАЧ ОПЕРАЦИОННЫМ МЕТОДОМ	255
частных решений уравнения (8.90), удовлетворяющих началь-
начальным условиям (8.91), через частные решения уравнения (8.90),
полученные с помощью характеристического уравнения1).
Пример 1. Решить задачу Коши
yAY) + 2у" + у = 0, j,@) = !/'@) = !/"@) = 0, у'"@) = 1.
Очевидно, решением задачи является функция фз^), которая может
быть найдена по формуле (8 96):
р4 + 2р2 + 1
х — гоо
Подынтегральная функция в (8.103) имеет две особые точки
являющиеся полюсами второго порядка. Поэтому
d Г ы 1 1	d Г ы 1 1	1
Перейдем теперь к решению задачи Коши с нулевыми на-
начальными условиями для неоднородного уравнения (8.88):
L[y(t)} = f(t).
В силу нулевых начальных условий, перейдя к изображениям 2)
У{р) .=' 2/(*)> f(p) .=' /(*), получим
откуда
Так как функция Y(p) является изображением, то ее оригинал в
:) О характеристическом уравнении см. вып. 3.
2) Заметим, что для существования изображения F(p) правой части урав-
уравнения (8.88), функции /(?), во многих случаях несущественно поведение
этой функции при t —> оо. Действительно, нас часто интересует решение
уравнения (8.88) лишь на ограниченном отрезке времени 0 ^ t ^ T, ко-
которое полностью определяется заданием функции f(t) на этом отрезке и
не зависит от поведения функции f(t) при t > Т. Поэтому мы можем из-
изменять значения функции f(t) при t > Т как угодно, лишь бы условия
существования изображения F(p) функции f(t) были выполнены. Напри-
Например, можно положить f(t) = O при t > Т. (Подчеркнем, что для определения
изображения F(p) функция f{t) должна быть задана на всем бесконечном
промежутке 0 ^ t < oo.) При этом мы, конечно, будем получать различные
изображения, однако их оригиналы, естественно, совпадают при t ^ Т. Сле-
Следует иметь в виду, что указанное положение относится не только к случаю
уравнения (8.88), но и ко многим другим физическим задачам, в которых
решение ищется на ограниченном промежутке изменения времени.

256 ОСНОВНЫЕ ПОНЯТИЯ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ ГЛ. 8
силу теоремы 8.3 может быть найден с помощью интеграла Мел-
лина. Однако в данном случае можно обойтись без вычисления
этого интеграла. Действительно, согласно (8.95) функция —j—
представляет собой изображение функции ipn-i(t) — решения
задачи Коши для однородного уравнения (8.90) с начальными
условиями специального вида:
Поэтому по теореме о свертке из (8.105) получим
t
Y(p) = y(t) = ±f фп-At - r)/(r) dr.
0
Функция фп-iit) часто называется функцией единичного то-
точечного источника для уравнения (8.90) и обозначается g(t).
Приняв это обозначение, перепишем решение задачи Коши с ну-
нулевыми начальными условиями для уравнения (8.88) в виде
t
y(t) = j-Jg(t-r)f(r)dr.	(8.106)
о
Формула (8.106) носит название интеграла Дюгамеля1).
Пример 2. Решить задачу Коши
y" + y = smt, у@) = у'@) = 0.
Найдем функцию g(t):
g" + g = O, g@)=0, g'@) = l.
Для ее изображения G(p) по формуле (8.95) получим
Отсюда с помощью таблицы изображений находим G(p) = sint
и тем самым
t
y(t) = Г sin(t — т) sin т dr = -(sint — tcost).
J	2
0
2. Уравнение теплопроводности. Рассмотрим приме-
применение операционного метода при решении краевых задач для
уравнения теплопроводности на примере распространения кра-
краевого режима по полу бесконечному стержню.
Пусть требуется найти распределение температуры в полу-
полубесконечном стержне 0 < х < оо, если начиная с момента вре-
времени t = 0 на его левом конце х = 0 поддерживается заданный
) О применении интеграла Дюгамеля в задачах математической физики
см. также А. Н. Тихонов, А. А. Самарский. Уравнения
математической физики. — М. : Наука, 1972.

§ 3	РЕШЕНИЕ ЗАДАЧ ОПЕРАЦИОННЫМ МЕТОДОМ	257
температурный режим. Начальная температура стержня равна
нулю. Математическая задача заключается в определении огра-
ограниченного для 0^ж<оо,?^0 решения u(x,t) уравнения
щ = а?ихх, х > О, t > О,	(8.107)
с дополнительными условиями
и(х, 0) = 0, и@, t) = q(t),	(8.108)
где q(t) — заданная функция времени, которую мы будем пред-
предполагать удовлетворяющей условиям существования преобразо-
преобразования Лапласа. Предположим, что искомое решение u(x,t), a
также его производные, входящие в уравнение (8.107), удовле-
удовлетворяют условиям существования преобразования Лапласа по
?, причем условия ограниченности степени роста по t функции
u(x,t) и ее производных не зависят от х. Тогда получим
u{x,t) =U(x,p),
ut(x,t)=pU(x,p)	(8.109)
uxx(x,t) = Uxx(x,p).
Вторая из формул (8.109) получена с учетом нулевого началь-
начального условия (8.108). Последняя из формул (8.109) имеет место
в силу того, что сделанных предположений достаточно для вы-
вычисления производных несобственных интегралов, зависящих от
параметра, путем дифференцирования по параметру подынте-
подынтегральных функций 1).
Переходя к изображениям, вместо задачи (8.107), (8.108)
для функции u(x,t) получаем краевую задачу для изображения
Щх,р):
Uxx(x,p)-^U(x,p)=0,	(8.110)
U@,p) = Q(p), \U(x,p)\<M.	(8.111)
Это — краевая задача для обыкновенного дифференциального
уравнения, в которой переменная р играет роль параметра. Как
легко видеть, решение задачи (8.110), (8.111) имеет вид
U(x,p) = Q(p)exp (-^ж) .	(8.112)
Решение u(x,t) исходной задачи может быть найдено по его изо-
изображению (8.112) с помощью формулы Меллина, однако в слу-
случае произвольной функции Q(p) вычисление соответствующего
интеграла может привести к значительным трудностям. Поэто-
Поэтому естественно попытаться обойти прямое вычисление интегра-
интеграла Меллина для определения оригинала функции (8.112). Заме-
Заметим, что выше мы нашли оригинал для функции (см. пример 4,
х) См. вып. 2.
А.Г. Свешников, А.Н. Тихонов

258 ОСНОВНЫЕ ПОНЯТИЯ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ ГЛ. 8
с. 247)
Ie-°vf =• 1 - Ф (-2L ) = * [ e-n2dV.	(8.113)
Поэтому, представив U(x,p) = Q(p) • р • exp f — — х 1 • - и учтя,
что согласно (8.113)
)()С(х,*),	(8.114)
на основании теорем об изображении производной и свертки по-
получим
t
U(x,p) =u(x,t) = / —G(x,t-r)q(r)dr.
о
Подставив явное выражение (8.114) функции G(x,t) и про-
произведя дифференцирование, получим выражение решения зада-
задачи1) (8.107), (8.108) в виде
t
о
3. Краевая задача для уравнения в частных произ-
производных. Изложенный в предыдущем пункте метод может быть
формально перенесен и на решение краевой задачи для уравне-
уравнения в частных производных более общего вида.
Рассмотрим уравнение
Pn[u(x,t)] - L2[u{x}t)] = f(x,t),	(8.116)
где Рп[/м] — линейный дифференциальный оператор с постоян-
постоянными коэффициентами вида
р г 1	дпи , д^и ,	,	ди
и] — линейный дифференциальный оператор второго поряд-
) Заметим, что данное выражение получено в предположении существо-
существования решения, тем самым проведенные рассмотрения являются фактиче-
фактически доказательством единственности решения данной задачи в рассматри-
рассматриваемом классе функций. Если заранее не известно существование решения
поставленной задачи, то необходимо показать, что формально полученное
выражение (8.115) действительно представляет собой решение рассматри-
рассматриваемой задачи.

РЕШЕНИЕ ЗАДАЧ ОПЕРАЦИОННЫМ МЕТОДОМ	259
ка1) вида
коэффициенты bi(x) которого являются функциями лишь одной
независимой переменной х] f(x,t) — заданная функция перемен-
переменных ж, ?, достаточно гладкая в области решения задачи. Будем
искать решение u(x,t) уравнения (8.116) в области2) t > О, а <
< х < 6, удовлетворяющее начальным
и(х,0) = (ро(х), ^(ж,0) = (pi(x), ... ,|—^(ж,0) =(pn-i(x)
и граничным условиям
Будем предполагать, что начальные и граничные условия
задачи, а также функция f(x,t) таковы, что существуют изо-
изображения Лапласа по t функции u(x,t) и всех ее производных,
входящих в уравнение (8.116):
оо	оо
и(х, t) = U(x,p) = [ e-ptu(x, t) dt, ^ = Г e-pt^(x, t) dt
J	ox J	ox
о	о
(8.117)
и т.д., причем предположим, что условия ограниченности степе-
степени роста по t функции u(x,t) и ее производных не зависят от х.
Тогда в силу равномерной сходимости по параметру х интеграла
(8.117) получим
дх{ ' > ~ дх{ 'Ph дх*( ' > ~ дх2 { 'р>
и
%?(x,t) =PkU(x,p) -p*-Vo(s) -/"ViW - • • • - 4>k-i{x).
Кроме того, предположим, что существуют изображения по t
ФУНКЦИЙ f(x,t), ^i(t) И 1p2(t)'-
f(x,t) = F(x,p), ^i(t) = Фх(р), ifo(t) = Ф2(р).
Тогда, перейдя в уравнении (8.116) к изображ:ениям, получим
обыкновенное дифференциальное уравнение по независимой пе-
:) Рассматриваемый метод не зависит от порядка дифференциального
оператора L, так же как и Р, однако для большей наглядности изложе-
изложения и ввиду особой важности для приложений мы ограничимся случаем
оператора L второго порядка.
2) Рассматриваемый метод может быть применен и в том случае, когда
а = —оо или Ъ = +оо или одновременно а = —оо, Ъ = +оо.

260 ОСНОВНЫЕ ПОНЯТИЯ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ ГЛ. 8
ременной х для функции U(x,p):
-РпШ(р) + ЫЩЪР)] = -F{x,p) - F0(x,p), (8.118)
где
п-1
F0(x,p) = J]^W^-fc-iW,
k=o
а полиномы Pk(p) определяются формулой (8.93).
Уравнение (8.118) надо решать с граничными условиями
aiUx(a,p) + f3iU(a,p) = Фх(р),
a2Ux(b,p) + /32г/(Ь,р) = Ф2(р).	(8.119)
Краевая задача (8.118), (8.119), в которой р играет роль пара-
параметра, решается обычными методами решения краевых задач
для обыкновенных дифференциальных уравнений х). Обратный
переход от изображения U(x,p) к решению исходной задачи мо-
может быть произведен с помощью формулы обращения (8.67).
См. вып. 3.

ПРИЛОЖЕНИЕ 1
МЕТОД ПЕРЕВАЛА
Метод перевала широко применяется для построения асимп-
асимптотических разложений 1) некоторых контурных2) интегралов
от функций комплексной переменной. Мы будем рассматривать
интегралы вида
F(X) = f ф)ех^ dz,	A)
с
где (p(z) и f(z) — функции комплексной переменной z, аналити-
аналитические в некоторой области Q, содержащей кривую С, которая
может быть и неограниченной; А — большое положительное чис-
число. Будем предполагать, что интеграл A) существует, и поста-
поставим своей целью получить асимптотическое разложение функ-
функции F(X) по обратным степеням параметра А. С интегралами
типа A) часто приходится встречаться при исследовании инте-
интегральных представлений ряда специальных функций, а также
при решении многих задач математической физики и других
разделов математики.
1. Вводные замечания. Начнем с некоторых наводя-
наводящих соображений. Рассмотрим интеграл, определяющий гамма-
функцию Эйлера3)
оо
Г(р + 1) = J xpe~xdx,	B)
о
г) Напомним, что асимптотическим разложением функции /(ж) в окрест-
N
ности точки хо называется представление вида f(x) = ^ ak^fk(x) +
k=i
+ o(ipn(x)), где ак — постоянные коэффициенты, а функции (fk(x) при
х —>- хо удовлетворяют условию <pk+i(x) = о(<рк(х)) (подробнее об асимпто-
асимптотических разложениях см. вып. 2).
) Следуя установившейся терминологии, мы здесь под контуром инте-
интегрирования понимаем не обязательно замкнутую кривую.
3) См. вып. 2.

262	ПРИЛОЖЕНИЕ 1
и попробуем найти для него приближенное выражение при боль-
больших положительных значениях р. Заметим, что, представив
хр _ ер\пх^ мы ПрИведем рассматриваемый интеграл B) к ви-
виду A). Подынтегральная функция в B) стремится к нулю при
х —>• 0 и х —>• оо. Поэтому величина этого интеграла в основном
определяется значением подынтегральной функции в окрестно-
окрестности ее максимума. Преобразуем подынтегральную функцию к
виду
хре-х = ер\пх-х = ef(x)m	C)
Максимальное значение функции f(x) достигается при х = р,
причем
/(р) =р\пр-р, f'(x) \х=р = О, f"(x) \х=р = -1-. D)
Разложив функцию f(x) в E-окрестности точки х = р в ряд Тей-
Тейлора и, ограничившись первыми членами разложения, получим
р + 6
Т(р + 1) ~ I exp mlnp — р — —(х — рJ\ dx =
J	L	2p	J
р — о
р + 8	оо
= ^е"^ / exp [-^^-] rfa:~pPe-P / exp
р - 6	-оо
E)
Приближенные равенства имеют место вследствие того, что
подынтегральная функция при \х — р\ > S мала и быстро стре-
стремится к нулю. Сделаем в интеграле E) замену переменной ин-
интегрирования, положив а —(х — р) = у. Тогда
V р
Г(р + 1) ~ ^рРе-Р f е~У2 dy = v/2^ (^jP .	F)
— ОО
Формула F) и дает приближенное выражение интеграла B)
при больших значениях р. Как будет показано ниже, она пред-
представляет собой первый член асимптотического разложения инте-
интеграла B). Эта формула часто называется формулой Стирлинга.
При выводе этой формулы мы не оценивали точность сделан-
сделанных приближений, поэтому наши рассмотрения носят лишь ил-
иллюстративный характер. В дальнейшем будет проведена оценка
точности формулы F), а сейчас сделаем еще несколько заме-
замечаний, позволяющих легче понять основную идею метода пере-
перевала. Формула F) выражает приближенное значение интегра-

МЕТОД ПЕРЕВАЛА	263
ла B) через значение подынтегральной функции в точке ее мак-
максимума (рре~р) и некоторый дополнительный множитель, соот-
соответствующий длине того отрезка интегрирования, на котором
значение подынтегральной функции достаточно близко к мак-
максимальному.
Обратимся теперь к интегралу A), в котором подынтеграль-
подынтегральная функция является аналитической в области Q комплексной
плоскости z. Этот интеграл также может быть приближенно вы-
вычислен через максимальное значение модуля подынтегральной
функции с поправкой на быстроту ее убывания на контуре инте-
интегрирования. Если путь интегрирования, соединяющий точки z\
и Z2 таков, что на небольшом его участке абсолютная величина
подынтегральной функции достигает наибольшего значения, а
затем быстро спадает, то естественно предположить, что найден-
найденная величина дает хорошее приближение. Так как функция f(z)
является аналитической в области (/, то в силу теоремы Коши
значение интеграла A) определяется лишь заданием начальной
z\ и конечной Z2 точек пути интегрирования, а не видом кривой
С. Отсюда следует, что для заданного интеграла A) возмож-
возможность его приближенного вычисления с помощью рассматрива-
рассматриваемых методов связана с возможностью выбора такого контура
интегрирования, чтобы он удовлетворял указанным выше тре-
требованиям. Нас интересуют значения интеграла A) при больших
положительных значениях параметра А, стоящего в показателе у
экспоненты. Поэтому естественно ожидать, что основной вклад
в значение интеграла дадут те участки пути интегрирования,
на которых функция и(х,у) — действительная часть функции
f(z) = и(х,у) + iv(x,y) — достигает наибольших значений. При
этом следует иметь в виду, что функция и(х,у), являясь гармо-
гармонической в области (/, не может достигать абсолютного макси-
максимума во внутренних точках этой области, т.е. внутри области Q
нет точек, в которых функция и(х,у) возрастала бы или убыва-
убывала по всем направлениям. Поверхность функции и(х,у) может
иметь лишь седловые точки1).
Пусть точка zq = xq + гуо является единственной седловой
точкой поверхности и(х,у) в области Q. Рассмотрим линии по-
постоянных значений и(х,у) = и(хо,уо) = const функции и(х,у),
проходящие через эту точку. В силу принципа максимума для
гармонических функций2) эти линии не могут образовывать
замкнутых кривых (мы не рассматриваем тривиальный случай
г) Определение седловой точки поверхности см. вып. 2.
2) См. А. Н. Тихонов, А. А. Самарский. Уравнения
математической физики. — М. : Наука, 1972.

264	ПРИЛОЖЕНИЕ 1
/=const в Q\ т. е. они либо упираются в границу области (/, либо
уходят на бесконечность в случае неограниченной области. Кри-
Кривые и(х,у) = и(хо,уо) разбивают область Q на секторы, внутри
которых значения функции и(х,у) соответственно или меньше,
или больше значения и(хо,уо). Первые секторы будем называть
отрицательными, вторые — положительными.
Если граничные точки z\ и z% кривой интегрирования лежат
в одном секторе и функция и(х,у) принимает в этих точках раз-
различные значения, то, очевидно, можно так деформировать кон-
контур, чтобы на нем функция и(х,у) изменялась монотонно. При
этом основной вклад в значение интеграла дает окрестность той
граничной точки, в которой значение функции и(х,у) наиболь-
наибольшее.
То же положение имеет место и в том случае, когда точки
z\ и Z2 лежат одна в положительном, а другая в отрицатель-
отрицательном секторах. Метод перевала применяется в том случае, ко-
когда точки z\ и Z2 лежат в различных отрицательных секторах,
что дает возможность выбрать такой контур интегрирования,
проходящий через седловую точку Ж(ьУо5 на котором значение
функции и(х,у) является максимальным в точке xq, у о и быстро
спадает по направлению к граничным точкам. Очевидно, в этом
случае основной вклад в значение интеграла A) будет давать
малый участок в окрестности седловой точки, причем послед-
последний можно выбрать тем меньше, чем быстрее спадают значения
функции и(х,у) вдоль кривой интегрирования. Метод перева-
перевала также иногда называется методом наибыстрейшего спуска.
Эта «альпинистская» терминология, очевидно, связана с топо-
топографией поверхности функции и(х,у) в окрестности ее седловой
точки.
Мы ограничимся здесь этими вводными замечаниями, а сей-
сейчас проведем оценку точности метода, при помощи которого
была получена асимптотическая формула F). При этом будет
установлен ряд положений, лежащих в основе метода перевала.
2. Метод Лапласа. Докажем ряд вспомогательных положе-
положений, лежащих в основе так называемого метода Лапласа асим-
асимптотической оценки интегралов от функций действительной пе-
переменной.
Лемма 1. При р > 0 и А —>> оо имеет место асимптоти-
асимптотическая формула
А
J xp-le~x dx = T(p) + O (e"A/2).	G)

МЕТОД ПЕРЕВАЛА
265
Доказательство. Оценим при р > 1 интеграл г)
оо
е-ххр-г dx = e~A f e-y(y + Af~l dy <
А
< е
-А
f BА)р-1е-У dy+ f Bу)р-1е-У dy
_ о	о
f-\l - e~A) + 2^
• (8)
Отсюда при Ар < еА/2 и следует G).
В дальнейшем большую роль будут играть интегралы вида
а
ф(Л) = J (p(t)e~xt2 dt, 0 < а < оо.
—а
Имеет место следующая лемма.
Лемма 2. Пусть при \t\ ^ S функция cp(t) может быть
представлена в виде
(p(t) = со + c\t + O(t )	(9)
и для некоторого Ао > 0 сходится интеграл
а
f |v?(i)|e-Ao*2 dt < м.	(ю)
—а
Тогда для А > Aq имеет место асимптотическая формула2)
Ф(А) =
dt = со7| + О(А/2).
(и)
Доказательство. Главный член формулы A1)
легко может быть получен из следующих наводящих соображе-
соображений. Если функция ip(t) ограничена при \t\ > а, то естественно
ожидать, что значение интеграла A1) изменится незначитель-
незначительно, если заменить пределы интегрирования —а и а на — оо, со-
соответственно. Тогда первый член разложения (9) дает главный
<р^1 J e~xxp-1dx
А	А
2) Символ O(t2) или, более общо, O(tn) в разложении вида cp(t) =
ckt +O(tn) означает, что при \
fc=0
п-1
- Е Cktk
k=0
J 6 имеет место равномерная оценка
< C\t\n, где С - постоянная.

266	ПРИЛОЖЕНИЕ 1
член формулы A1), интеграл от второго члена в силу нечетно-
нечетности подынтегральной функции равен нулю, и остается оценить
остаточный член. Эта оценка и возможность указанной заме-
замены пределов интегрирования и составляют основное содержание
леммы. Перейдем к ее строгому доказательству.
Разобьем интеграл Ф(А) на три слагаемых:
—6	6	а
Ф(А) = J (p(t)e~xt2 dt+ J (p(t)e~xt2 dt + f (p(t)e~xt2 dt, A2)
-a	-6	6
где 6 > 0 — фиксированное число. Оценим последнее слагаемое:
f (p(t)e-xt2 dt ^ е-(А-А0)?2 J |^(?)|e-Ao*2 dt
.е-л^2=О(е-л^2). A3)
Здесь мы воспользовались условием A0) и очевидным неравен-
неравенством
At2 = XS2 + А(?2 - S2) > XS2 + А0(?2 - S2) = (А - \0M2 + А0?2,
имеющим место при А > Ао, t > S. Аналогично оценивается
и первое слагаемое в A2). Отсюда следует, что при достаточ-
достаточно больших А основной вклад в значение интеграла Ф(А) дает
второе слагаемое, в то время как крайние слагаемые в A2) экс-
экспоненциально стремятся к нулю при А —>> оо.
Перейдем к рассмотрению главного члена в A2). Подставив
вместо функции (p(t) ее разложение (9), получим
Ф2(Л) = J ip(t)e-xt2 dt =
-5
6	6	6
= с0 / e~xt2 dt + d f e~xt2tdt + J O(t2)e~xt2 dt. A4)
-6	-6	-6
Второй интеграл в A4) в силу нечетности подынтегральной
функции равен нулю. Для оценки первого интеграла сделаем в
нем замену переменной интегрирования, положив At = т. По-
Получим
6	6	Х62
f e~xt2 dt = 2f e~xt2 dt=j=f r'^e^ dr.	A5)
-6	о	^X о
Но в силу леммы 1 при А —>> оо имеет место асимптотическая

МЕТОД ПЕРЕВАЛА	267
формула
Аи2
'-^))- A6)
Так как при любом фиксированном 6 функция exp ( — —- j при
А —>• оо стремится к нулю быстрее, чем А~3'2, то можно записать
6
со / e~xt2 dt = c0^/l + O (A/2) .	A7)
-6
Остается оценить последнее слагаемое в A4):
6	6	6
J O(t2)e~xt2 dt <C J t2e~xt2 dt = 2C J t2e~Xf2 dt. A8)
-6	-6	о
В интеграле A8) опять сделаем замену переменной интегриро-
интегрирования, положив At2 = т. Тогда получим
6	Х62
О	О
Интеграл A9) также удовлетворяет условиям леммы 1. Поэтому
окончательно получим
т.	/^-v 1 IO/Z) . s~\ I	I	/\О \ \	/<-\
dt = с^г + ° (ехР {-—)) = °
B0)
Формулы A3), A7) и B0) после подстановки их в A2) и дока-
доказывают лемму.
Сделаем ряд замечаний к доказанной лемме.
Замечание 1. Повторяя проведенные рассуждения,
можно доказать, что если функция (p(t) при \t\ ^ 6 разлагается
в строку Тейлора
п-1
ECfct + O(tn), C& =	,	B1)
к=0

268	ПРИЛОЖЕНИЕ 1
то имеет место асимптотическое разложение
[71—1]
а	[ 2 J
Ф(А) = Г ф)е~хг2 dt V с2т^	Р- + О (\-^) , B2)
-а	т=0	л 2
где символ ^—— означает наибольшее целое число, меньшее
п-1
или равное —-—.
В частности, при п = 1, когда разложение функции <р(?) име-
имеет вид (p(t) = со + O(t), остаточный член в формуле B2) имеет
порядок А, поскольку при оценке остатка главную роль играет
интеграл
6	6	6
J O(t)e-Xt2 dt<C J \t\e~xt2 dt = 2C J te~xt2 dt.
-5	-5	0
Замечание 2. Лемма остается справедливой и в том
случае, когда интегрирование проводится по отрезку [ai, a^ где
а\ < 0, а,2 > 0 и —а\ ф а,2. Следующее замечание настолько
существенно для дальнейшего, что мы сформулируем его в виде
самостоятельной леммы.
Лемма 3. Пусть на отрезке \t\ ^ So функции tp(t) и
представимы в виде
<p(t) =c0 + ci? + O(?2),	(9)
3	4,	B3)
и пусть при А —>> оо функция S(X) ^ Jo удовлетворяет услови-
условиям1)
AJ2(A)^oc, AJ3(A)^0.	B4)
Тогда при А —>• оо имеет место асимптотическая формула
I(X)= / ^)eA^2+Mt)]^ = C0^+O(A-3/2^ B5)
Доказательство. Как легко видеть, при выпол-
выполнении условий (9), B3) и B4) на отрезке \t\ ^ S(X) имеет место
равенство
= с0 + cit + c0c3At3 + O(t2) + O(A2t6) + O(At4). B6)
:) Например, функция S(X) = A 2^5 удовлетворяет условиям B4).

МЕТОД ПЕРЕВАЛА	269
Тогда, повторяя рассуждения, проведенные при доказательстве
леммы 2, получим, что при подстановке разложения B6) в фор-
формулу B5) первое слагаемое в силу условия B4) даст главный
член правой части B5); второй и третий члены полученного вы-
выражения обратятся в нуль в силу нечетности подынтегральных
функций; последние три слагаемых имеют одинаковый порядок
малости О(А~3/2). Лемма доказана.
Доказанные леммы позволяют доказать следующую теорему,
являющуюся основной в методе Лапласа асимптотического раз-
разложения интегралов от функций действительной переменной.
Теорема 1. Пусть функция /(?), заданная на отрезке [а, Ь],
достигает своего абсолютного максимума в некоторой вну-
внутренней точке to, причем f"{t$) < 0, и пусть существует та-
такое Sq > 0, что при \t — to\ < Sq имеет место представление
f(t) = f(t0) + ?&±(t - toJ + M<).	B7)
Тогда, если функции tp(t) и //(?) при \t — to\ ^ #о удовлетворяют
условиям леммы 3, т.е.
<p{t) = с0 + a(t -10) + O[(t -10J},	(9)
^(t) = C3(t-toK + 0[(t-t0L].	B3)
то имеет место асимптотическая формула
Ф(А) = / <р®*™ dt = e^'o) y__^_f(to) + о (
B8)
если выполнены следующие дополнительные условия :
а) для данного Sq одновременно выполняются соотношения
npu\t-to\^So \fi(t)\<^(tt0),
npu\t-to\>8o f()f()hO
б) для некоторого Ао > 0 сходится интеграл
ь
J |v?(t)|eAo/W dt < M.	C0)

270	ПРИЛОЖЕНИЕ 1
Доказательство. Разобьем интеграл в B8) на сумму
следующих слагаемых:
b	to-6o	t0- б(\)
ф(А) = J (p(t)exf^ dt = f (p(t)exf^ dt+ f <p(t)exf® dt+
a	a	to — 5o
to + <*(A)	to + So	b
+ J (p(t)exf® dt + J (p(t)exf® dt + J (p(t)exf® dt,
to - S{\)	to + S(X)	to + *o
C1)
где функция S(X) удовлетворяет условиям B4) леммы 3. Край-
Крайние интегралы в C1) оцениваются так же, как и в лемме 2. Дей-
Действительно, используя очевидное неравенство
А[/(*о) - /(*)] = (А - Ао)[/(*о) - /(*)] + Ao[/(to) - /(<)] >
> h(X - Ао) + Ao/(to) - A0/(t), C2)
имеющее место при а ^ t ^ to — Sq и А > Ао, получаем
°
е(А-Ло)/(*о)-МА-Ао) °J "
). C3)
Так же оценивается и интеграл по отрезку [?о+#(ь Ь]. Для оценки
второго интеграла воспользуемся условиями B7), B9), в силу
которых при to — Sq ^ t ^ to — д(Х) имеет место неравенство
/(to) - lit) > ~^(t - t0J > -tM82(\).	C4)
Поэтому, повторив выкладки, проведенные при выводе форму-
формулы C3), получим
to - 6(\)
f tp(t)exM dt
C5)
Но в силу условия B4) величина в правой части C5) также имеет
экспоненциальный порядок малости1). Аналогичным образом
оценивается и четвертый интеграл.
*) При 6(\) = \~2/ъ получим О (е-сл1/5).

МЕТОД ПЕРЕВАЛА	271
Перейдем к рассмотрению основного интеграла форму-
формулы C1):
to + 6(Х)
Ф3(А)= / if(t)exf^dt.	C6)
to - S(X)
В силу условия B7) этот интеграл можем переписать в виде
to + 6(Х)
Фз(А) = еА**°> / tp(t) exp {a [^M(t - t0J + /i(*)] } <**¦
()
C7)
Приведем интеграл C7) к виду B5), сделав замену перемен-
ной — ° (t — toJ = т2. Как легко видеть, полученный при
этом интеграл удовлетворяет всем условиям леммы 3. Поэтому
окончательно получим
C8)
Поскольку Фз(А) отличается от оцениваемого интеграла на ве-
величину экспоненциального порядка малости, формула C8) и до-
доказывает теорему.
Замечание 1. Теорема остается справедливой и в
том случае, когда один или оба предела интегрирования равны
бесконечности, поскольку оценка интеграла C3) остается спра-
справедливой и при а = — оо.
Замечание 2. Мы получили лишь первый член асим-
асимптотического разложения интеграла B8). Аналогичным образом
можно получить выражение и для последующих членов асим-
асимптотического разложения, однако мы на этом останавливаться
не будем.
Замечание 3. Проведенное доказательство может быть
перенесено и на тот случай, когда максимальное значение функ-
функции /(?) достигается в какой-либо из граничных точек отрезка
[а, Ь]. При этом в формуле B8) появляется дополнительный мно-
множитель -.
Замечание 4. В том случае, когда функция /(?) вну-
внутри отрезка [а, Ь] имеет несколько максимумов, равных по вели-
величине, асимптотическое разложение интеграла B8) по обратным
степеням большого параметра А можно получить, оценивая ин-
интегралы типа C6) по E-окрестности каждой из точек максимума
и суммируя результаты.
Рассмотрим пример применения доказанной теоремы.

272	ПРИЛОЖЕНИЕ 1
Пример 1. Получить асимптотическое разложение гамма-
функции Эйлера
оо
Г(р+1)= fcpe-xdx.	B)
о
Представим подынтегральную функцию в виде хре~х =
_ ер\пх-х и Сделаем замену переменной, положив х = pt. Тогда
интеграл B) преобразуется к виду
оо
Г(р + 1) = pP+1 f <J>O*t-t) dt.	C9)
о
Это интеграл типа B8) с cp(t) = 1 и f(t) = hit — t. Функция f(t)
достигает своего максимального значения при to = I, причем
/A) = -1, /'(t)k=i=O, f"(t) \t=i = -1.	D0)
Поэтому по формуле B8) получаем
D1)
Тем самым мы получили асимптотическую оценку точности по-
полученной ранее из наводящих соображений формулы F). Как
было указано выше, рассмотренные методы позволяют получить
и последующие члены асимптотического разложения. Приведем
без вывода несколько первых членов формулы Стирлинга:
D2)
3. Метод перевала. Перейдем теперь к рассмотрению са-
самого метода перевала получения асимптотических разложений
интегралов вида A):
F(X) = J ip(z)exf^ dz.
с
В силу наводящих рассмотрений п. 1 естественно предположить,
что если контур С таков, что на небольшом его участке зна-
значения действительной части и(х,у) функции f(z) = и(х,у) +
+ iv(x,y) достигают наибольшей величины и затем быстро спа-
спадают, а мнимая часть v(x,y) остается постоянной (чтобы обес-
обеспечить отсутствие нежелательных быстрых осцилляции подын-
подынтегральной функции), то основной вклад в величину интегра-
интеграла A) и дает интегрирование по данному участку контура С.
Поэтому для приближенного вычисления интеграла A) следует
деформировать контур С так, чтобы подынтегральная функция

МЕТОД ПЕРЕВАЛА	273
на нем обладала указанными свойствами. При этом, как было
установлено нашими предыдущими рассмотрениями, необходи-
необходимая деформация контура С определяется в первую очередь то-
топографией поверхности уровня функции и(х,у). В частности,
контур интегрирования должен проходить через седловую точ-
точку поверхности функции и{х,у) в направлении наибыстрейшего
изменения этой функции.
Остановимся подробнее на топографии поверхности гармо-
гармонической функции и{х,у) в окрестности ее седловой точки
Мо(хо,уо). Определим направления наибыстрейшего изменения
этой функции, проходящие через точку Mq. Эти направления,
как известно, определяются направлением вектора gr&du. Пусть
gididu ф 0. Так как для аналитической функции \7и • Vv = 0
(см. с. 37), то направление вектора gr&du определяет кривую
v{x,y) = const. Итак, если на кривой v{x,y) = const, gr&du ф
Ф 0, то функция и{х,у) изменяется вдоль этой кривой наиболее
быстро. Однако в самой седловой точке Мо(жо5Уо) поверхности
функции и(х,у) вектор grad^(Mo) = 0. Рассмотрим подробнее
поведение функций и(х,у) и v{x,y) в окрестности этой точки.
Очевидно, в точке Mq производные функций и{х,у) и v{x,y) по
направлению / касательной к кривой v{x,y) = const, проходя-
проходящей через точку Mq, равны нулю:
^(Жо,Уо)=О, |^о,2/о) = О.	D3)
Так как производная аналитической функции не зависит от на-
направления, то отсюда следует, что
/'Ы = 0.	D4)
Следовательно, разложение функции f(z) в окрестности точки
zq имеет вид
f(z) = /(го) + (z - zof{co + Cl(z-zo) + ...},	D5)
где р ^ 2 и со ф 0. Положив сп = гпегвп, п = 0,1,..., z — zq =
= рег1р, получим
f(z) - /(го) = /{гое^^+0°) + pnJfo+Vv+W + ...}. D6)
Запишем уравнения кривых и(х,у) = const n v(x,y) = const,
проходящих через точку ^о, с помощью введенных обозначений.
Имеем
U(p, ф) = г0 cos {pip + в0) + РП cos [(p + l)ip + 0i] + ... = 0, D7)
V(p, ф) = r0 sin {ptp + во) + рп sin [{р + 1)<р + 0i] + ... = 0. D8)
Здесь
и{х,у) - и{хо,уо) = (PXJ{p, ip),
v{x,у) - v{xo,yo) = (?V{p, (p).

274	ПРИЛОЖЕНИЕ 1
Так как функция cos (jxp + #о) при изменении (р от 0 до 2тг ме-
меняет знак 2р раз, то из формулы D7) следует, что окрестность
точки zq разбивается на 2р криволинейных секторов, внутри ко-
которых функция U(p, ф) сохраняет знак. Границы этих секторов
определяются из решения уравнения D7). Секторы, в которых
и(р,ф) < 0, будем по-прежнему называть отрицательными, а
секторы, в которых U(p,cp) > 0, - положительными. Направле-
Направления наибыстрейшего убывания (наибыстрейшего спуска) функ-
функции и(х,у), очевидно, лежат в отрицательных секторах и опре-
определяются теми значениями угла <р, при которых в окрестности
точки (жо,уо) У^РчФ) = 0 и U(p,(p) < 0, т.е. cos (pip + во) = —1.
Эти значения равны
во . 2т + 1	п л	л	,АсЛ
(рт =	1	тг, т = 0,1,... ,р- 1.	D9)
Отметим, что направления наибыстрейшего спуска совпадают с
биссектрисами отрицательных секторов.
В дальнейшем мы будем рассматривать лишь случай р = 2,
когда f"(zo) Ф 0. При этом cq = -/"(zq) и 6q = arg//7(^o). В этом
случае имеются лишь два отрицательных сектора, внутри ко-
которых проходит линия наибыстрейшего спуска функции и(хуу).
Направление касательной к этой линии в точке zq согласно фор-
формуле D9) определяется углами
— во + 7Г	— во + ЗТГ	.	/гп\
ср0 = —-— и cpi =	= ip0 + тг.	E0)
Очевидно, выбор угла сро или cpi определяется заданием направ-
направления интегрирования вдоль линии наибыстрейшего спуска.
Перейдем теперь к доказательству основной теоремы метода
перевала.
Теорема 2. Пусть функции (p(z) и f(z) = и(х,у) +iv(x,y)
являются аналитическими в области Q и удовлетворяют сле-
следующим условиям:
1)	поверхность функции и(х,у) имеет внутри Q единствен-
единственную седловую точку zq = xq + гуо, причем //7(^о) Ф 0;
2)	существует такое S > 0, что на линии L постоянного
значения функции v(x,y) = v(xo,yo), проходящей через точ-
точку zq, в обоих отрицательных секторах этой точки функция
и(х,у) вне 8-окрестности точки zq удовлетворяет условию
и(хо,уо) - и(х,у) > h > 0;	E1)
3)	при некотором значении Xq > 0 сходится криволинейный
интеграл
J \ф)\еХо<х^ ds < М,	E2)
с

МЕТОД ПЕРЕВАЛА	275
где кривая С целиком лежит в области Q, причем ее начальная
(zi) и конечная (^) точки расположены в различных отрица-
отрицательных секторах точки zq так, что их можно соединить с
кривой L кривыми 7i и 72 конечной длины, на которых функция
и(х,у) удовлетворяет условию E1).
Тогда для всех А ^ Ао имеет место асимптотическая фор-
формула
F(X) =$ф)ех^ dz = ел^о) ^_^_^о)е^ + O(A/2)J ,
E3)
где срт =	 + ттг (га = 0,1) и 6q = arg/'^o). Выбор значе-
значения срт определяет знак в формуле E3) и, естественно, зависит
от направления интегрирования вдоль контура С.
Доказательство. Интеграл E3) не изменит сво-
своего значения, если деформировать кривую интегрирования С в
кривую Г = L + 7i + 72- В силу условия E1) для интегралов по
кривым 7i и 72 имеет место оценка
ip(z)exf^ dz = exf^O(e-Xh).	E4)
71,2
Рассмотрим интеграл
Fi(A) = J cp(z)exf^ dz.	E5)
L
Введем на кривой L натуральный параметр 1) «s, причем будем
считать, что точке zq соответствует значение 5 = 0. Уравнение
кривой L запишем в виде z = z(s). Произведя в интеграле E5)
замену переменной интегрирования, положив z = z(s), получим
J
^-sds,	E6)
где
Ф(з) = <p[z(s)], U(s)=u[x(s),y(s)},
О < а < оо, 0 < 6 < оо.
Интеграл E6) удовлетворяет всем условиям теоремы 1, при-
причем функция U(s) достигает своего максимального значения в
d2U
Oti (_У
ds2
s=0
Понятие натурального параметра см. вып. 1.

276
ПРИЛОЖЕНИЕ 1
Тогда согласно B8)
*i(A) =
О(Л-3/2)] ,	E7)
и остается выразить входящие в E7) величины через значения
функций cp(z) и f(z) в точке zq. Очевидно, Ф@) = ^p(zq). Так
d2V
как
= 0, то
d2U
ds2
_ d2f[z{s)]
ds2
Отсюда в силу D4) получим
т2 г Т
d и
s=0
fe	E8)
E9)
Так как в окрестности точки zq с точностью до величин высше-
высшего порядка малости имеет место соотношение z — zq = se1^, то
as
s=o
= ещ ^ и остается определить направление касательной к
кривой L в точке zq. Но по самому способу построения кривой L
касательная к этой кривой в точке zq совпадает с направлением
наибыстрейшего изменения функции и(х,у). Тогда из E0) для
угла (рт получим формулу
+ ттг, m = 0,1,
F0)
где #о = arg
а значение m определяется направлением
72 ТТ
интегрирования. Заметим, что -—г
ds2 s
формулу E9) можно записать в виде
< 0 и
ds
s=0
=1. Тогда
d2U
ds2
s=0
= -\гы\.
Итак, окончательно получим
F(X) =
2тг
F1)
F2)
где значение угла срт дается формулой F0). Знак главного чле-
члена в правой части F2) определяется выбором значения т и за-
зависит от направления интегрирования вдоль кривой С.
Сделаем ряд замечаний по поводу доказанной теоремы.
Замечание 1. Из доказанной теоремы следует, что если
обе граничные точки z\ и Z2 кривой интегрирования С лежат
в одном и том же отрицательном секторе седловой точки ^о, то
для интеграла A) имеет место оценка E4).
Замечание 2. В приложениях особенно часто при-
приходится рассматривать интегралы типа A) в неограниченной

МЕТОД ПЕРЕВАЛА
277
области с кривой интегрирования С, уходящей в бесконечность.
Из проведенных рассмотрений очевидно, что в этом случае для
сходимости интеграла A) необходимо, чтобы кривая интегриро-
интегрирования уходила в бесконечность в отрицательных секторах сед-
ловой точки zq. При этом теорема 2 и формула E3) сохраняют
силу.
Замечание 3. Теорема 2 была доказана в предпо-
предположении, что точка zq является единственной седловой точкой
поверхности функции и(х,у) в области Q и fff(zo) ф 0. Если
эти предположения не выполнены, то могут быть проведены
аналогичные рассмотрения, которые приводят к асимптотиче-
асимптотическим разложениям интеграла A), подобным формуле E3). Од-
Однако когда в области Q имеется несколько седловых точек, то
выбор контура интегрирования требует специального исследо-
исследования. Если контур интегрирования проходит через несколько
седловых точек, то асимптотическое разложение интеграла A)
может содержать несколько слагаемых типа первого члена E3),
имеющих один и тот же порядок, что может существенно изме-
изменить окончательный результат.
Рассмотрим ряд примеров применения полученных резуль-
результатов.
Пример 2. Асимптотическая формула для функции
Ханкеля.
Как известно х), функция Ханкеля первого рода Щ \х) мо-
может быть представлена с помощью
интеграла
„ixsmz —ivz
dz, F3)
с
где контур интегрирования С на
комплексной плоскости z переходит
из полуполосы — - < Re z < -,
Im z > 0 в полуполосу - < Re z <
< -7Г, Im z < 0 через точку zq = -
(рис. 1). Эта точка является седло-
вой точкой функции f(z) = г sin z
в полосе 0 < Re z < тг, так как
z=0
Рис. 1
f (-) = 0, f" [ — ) = — г ф 0. Указанные выше полуполосы
V ^ /	\ 2, у
представляют собой отрицательные секторы этой седловой точ-
точки, что, в частности, обеспечивает сходимость данного несоб-
:) См. кн. А. Н. Тихонов, А. А. Самарский. Уравнения
математической физики. — М. : Наука, 1972.

278	ПРИЛОЖЕНИЕ 1
ственного интеграла. Найдем асимптотическое значение этого
интеграла при больших положительных значениях х^> \v\. Дан-
Данный интеграл, где f(z) = г sin z, ip(z) = e~lvz, очевидно, удо-
удовлетворяет условиям теоремы 2. Поэтому для его вычисления
может быть применен метод перевала. Так как f'(z) = г cos z, то
в полосе — — < Re z < -тг находится лишь одна седловая точка
z0 = §. При этом f(zo) = г, f(z0) = 0, \f"(zo)\ = 1, в0 = f •
Учитывая направление интегрирования, из E0) получим щ =
= — —. Отметим, что это направление совпадает с биссектрисой
отрицательного сектора седловой точки zq = -. Окончательно
на основании формулы E3) получим
7Г
Формула F4) находит весьма широкое применение при решении
различных задач, в которых приходится использовать асимпто-
асимптотические представления цилиндрических функций.
Пример 3. Асимптотическая формула для полиномов
Леэюандра 1).
Будем исходить из интегрального представления2) полино-
полиномов Лежандра
,ехр i n+- d
Рп(со8 0) = -L= / 	/ v \ ]-d(p, 0 < 0 < тг. F5)
тгу 2 J v cos 9? — cos О
Как легко видеть, подынтегральная функция имеет интегри-
интегрируемую особенность при if = ±0. Нашей целью является по-
получение асимптотического выражения для функции Pn(cos#)
при больших значениях индекса п. Рассмотрим аналитиче-
аналитическое продолжение подынтегральной функции на комплексную
) Определение полиномов Лежандра и их основные свойства см. в кн. :
А. Н. Тихонов, А. А. Самарский. Уравнения математической
физики. — М. : Наука, 1972.
2) См. кн. : Н. Н. Лебедев. Специальные функции и их приложения.
— М. : Гостехиздат, 1953. С. 76.

МЕТОД ПЕРЕВАЛА
279
плоскость z = х + гу:
w(z) =
ехр
F6)
-0+iH
0+Ш
л/cos г — cos в
Функция w является аналитической в верхней полуплоскости
Im z > 0. Поэтому интеграл по любому замкнутому контуру,
целиком лежащему в верхней
полуплоскости, от этой функ-
функции равен нулю. Выберем замк-
замкнутый контур1) Г, состоящий
из отрезка (у = 0, — в ^ х ^ в)
действительной оси, вертикаль-
вертикальных отрезков (х= — 6,0 ^ у ^
<: я), (х = в,о <: у <: я),
параллельных мнимой оси, и
замыкающего горизонтального
отрезка (у = Я, —в ^ х ^ в)
(рис. 2). Как легко видеть, на
последнем отрезке модуль
ехр \-
\w\ =
-в
д/cos (х + Ш) — cos в
F7)
z=0
Рис. 2
экспоненциально стремится к нулю при Я —>• оо. Поэтому, пе-
перейдя к пределу при Я —>• оо, получим
-/
ехр | г ( п + -
д/cos 9? — cos в
= h + h,
F8)
где
=гехр 1-г fп + -) в\ /
J
ОО	1/1
ехр | - ( п + - ] у
д/cos (в — iy) — cos в
F9)
h = -iexp г
ехр | - ( n + - ] у
д/cos @ + гу) — cos 0
dy. G0)
Для приближенного вычисления интегралов 1\ и 1% при больших
значениях п применим метод перевала. Рассмотрим интеграл 1\
) При этом особые точки z = d=# обходим по дугам окружностей беско-
бесконечно малого радиуса, который затем устремляем к нулю.

280
ПРИЛОЖЕНИЕ 1
(/2 вычисляется аналогично). Положим у = t2 и обозначим п -\-
+ - = А. Тогда из F9) получим
ф(А) = -ieiXeh = 2 Г
s~xttdt
д/cos (в — it2) — cos в
G1)
Интеграл G1), очевидно, удовлетворяет всем условиям теоре-
теоремы 1, причем /(?) = — t2 и точка to = 0, в которой функция
f(t) достигает своего максимального значения /@) = 0, совпа-
совпадает с граничной точкой интервала интегрирования. При этом
/"@) = -2, а
= lim
t->0 ^€08A9 -it2) -COS в
ехР {~г4
л/sin^
G2)
Поэтому по формуле B8), в которой надо ввести дополнитель-
дополнительный множитель -, так как точка to совпадает с граничной точ-
точкой интервала интегрирования, получим
G3)
Ф(А) = л/|- -^=ехр (-%) +О(А/2),
V А у sin #	\ 4 /
/1 = гехр [-г (п + 1) в] [Т^^ехр (_ij) +О{п~^ .
откуда
Аналогично
/2 = -iexp
(n + 1/2) sin в
G4)
ехр (г|) + О(п-3/2)| .
G5)
Тогда после простых преобразований, учтя, что
отли-
отлиAT"
чается от л/- на величину порядка О(п~3/2), получим оконча-
V ft
тельную асимптотическую формулу для многочленов Лежан-
дра, справедливую при п^>1 и 0 < в < тг:

ПРИЛОЖЕНИЕ 2
МЕТОД ВИНЕРА-ХОПФА
Данный метод находит широкое применение при решении
некоторых интегральных уравнений и различных краевых за-
задач математической физики с помощью интегральных преоб-
преобразований Лапласа, Фурье и ряда других. Первоначально этот
метод был применен в совместной работе Н. Винера и Э. Хопфа
A931 г.) к решению интегральных уравнений с ядром, завися-
зависящим от разности аргументов, в случае полу бесконечного проме-
промежутка
оо
и{х) = А Г v(x — s)u(s) ds + f(x).
о
В дальнейшем уравнения подобного вида рассматривались
В.А. Фоком 1), внесшим большой вклад в развитие общих мето-
методов их решения.
Общий метод решения функциональных уравнений, полу-
получивший название метода Винера-Хопфа или метода фактори-
факторизации, был с успехом использован при решении многих задач
дифракции и теории упругости, краевых задач для уравнения
теплопроводности, интегральных уравнений теории переноса из-
излучения (так называемая проблема Милна) и многих других за-
задач математической физики2). Не ставя своей целью строгое
математическое обоснование метода Винера-Хопфа, мы изло-
изложим его основную идею на примерах решения ряда практически
важных задач.
1. Вводные замечания. Начнем с наводящих соображений,
иллюстрирующих применение методов интегральных преобра-
г) В. А. Фок. О некоторых интегральных уравнениях математической
физики// Матем. сборник. 1944. Т. 14. С. 1.
) Большое количество примеров применения метода Винера—Хопфа мож-
можно найти в книге Б. Нобла, где приведена достаточно подробная библио-
библиография. (Б. Н о б л. Применение метода Винера-Хопфа для решения
дифференциальных уравнений в частных производных — М. : ИЛ, 1962.)

282	ПРИЛОЖЕНИЕ 2
зований при решении интегральных уравнений. Рассмотрим ин-
интегральное уравнение вида
СЮ
и{х) = А Г v(x — s)u(s) ds + f(x)	A)
— сю
с ядром v(x — s), зависящим от разности аргументов. Мы не
будем здесь исследовать условий разрешимости этого уравнения
и проводить обоснование методов его решения, а лишь укажем,
что для действительных значений А при выполнении условий
оо	оо
/ \f(x)\2dx<A, A J \v(t)\dt<l,	B)
— сю	—сю
где А — произвольное фиксированное число, уравнение A) име-
имеет единственное решение1) и(х), интегрируемое с квадратом в
бесконечном промежутке
сю
J \u(x)\2dx < оо.	C)
— сю
Будем считать, что существуют преобразования Фурье2)
всех функций, входящих в уравнение A):
сю
U(к) = -j= J u(x)eikxdx,	D)
-сю
сю
/ v(t)eiktdt,	E)
— сю
сю
= j= J f(x)eikxdx.	F)
Тогда, умножив A) на ——е и проинтегрировав по бесконеч-
л/2тг
ному промежутку, получим
сю
л
U(к) = F(k) + -4= Г eikx dx Г v(x - s)u(s) ds = F(k) + I(k).
л/2тг J	J
— сю	—сю
G)
:) Подробно этот вопрос изложен, например, в кн.: В. Титчмарш.
Введение в теорию интегралов Фурье. — М. : Гостехиздат, 1948.
2) Определение преобразования Фурье и его основные свойства см. в
вып. 2.

МЕТОД ВИНЕРА-ХОПФА	283
Изменив в последнем слагаемом порядок интегрирования, пред-
представим этот интеграл в виде
(X	(X
= _L Г u(s)ds f eikxv(x-s)dx.	(8)
л/2тг J	J
— (X	—(X
Сделаем замену переменной интегрирования, положив х — s = t.
Тогда в силу D) и E)
(X	(X
= _L Г u(s)eiksds Г v(t)eiktdt = Ху/Ъг U(k)V(к). (9)
л/2тг J	J
— (X	—(X
Формула (9) фактически означает, что в случае преобразова-
преобразования Фурье справедлива формула преобразования свертки, полу-
полученная нами для одностороннего преобразования Лапласа (см.
с. 232).
Теперь формулу G) можно переписать в виде
U {к) = F{k) + \y/2nU{k)V{k).	A0)
Итак, с помощью преобразования Фурье нам удалось свести
решение исходного интегрального уравнения A) к решению ал-
алгебраического уравнения A0) для преобразования Фурье иско-
искомого решения. Решение последнего уравнения не представляет
труда:
U (к) = 	Щ	.	A1)
Тем самым преобразование Фурье A1) решения исходного
интегрального уравнения оказалось выраженным через преоб-
преобразования Фурье заданных функций — ядра и правой части
уравнения. Само решение может быть легко выражено через его
преобразование Фурье с помощью известной формулы обратно-
обратного преобразования 1):
(X	(X	_.к
и(х) = -L Г U{k)e~ikxdk = -L Г F{k)t! X dk. A2)
Формула A2) фактически решает задачу, однако она не всегда
удобна для использования, так как требует вычисления преоб-
преобразования Фурье F(k) для каждой правой части f(x). Во мно-
многих случаях более удобным оказывается представление решения
неоднородного интегрального уравнения через ядро (резольвен-
:) См. вып. 2.

284	ПРИЛОЖЕНИЕ 2
ту) исходного уравнения:
оо
и{х) = f(x) + Л / g(x - s)f(s) ds.	A3)
— ОО
Чтобы получить требуемое представление, заметим, что форму-
формула A0) может быть преобразована к виду
U(к) - F(k) = \V2^F(k)G(k),	A4)
где
G(k) =	Щ	.	A5)
Из соотношения A4) с помощью формулы обратного преоб-
преобразования A2), замечая, что в силу формулы (9) оригиналом
функции л/2тг F(k)G(k) является функция
сю
J g(x-s)f(s)ds,
— сю
где
(X)
g(i) = J= J G(k)e~iktdk,	A6)
— СЮ
получим
сю
и{х) = f(x) + Л / g(x - s)f(s) ds.	A3)
— сю
Таким образом, для определения решения исходного интеграль-
интегрального уравнения A) достаточно найти функцию g(t), определен-
определенную формулой A6).
Функция g(t) представляет собой решение уравнения A) при
специальном виде функции f(x). Действительно, из формул A1)
и A5) следует, что при U(k) = G(k) функция F(k) равна V(k).
Это означает, что решением уравнения A) при f(x) = v(x) яв-
является функция и(х) =g(x), т. е. резольвента уравнения A) удо-
удовлетворяет интегральному уравнению
сю
g(x) = Г v(x — s)g(s) ds + v(x).	A7)
— сю
Пример 1. Решить интегральное уравнение
сю
и(х) = А / v(x — s)u(s) ds + /(ж),	A8)
— сю

МЕТОД ВИНЕРА-ХОПФА	285
где
v(t) = e~CL\t\ a>0.	A9)
Найдем функцию g(t), для чего вычислим
сю
V(k) = -j= Г e~a^eiktdt = L_ 92a,9.	B0)
/О	/	/О /Т/^ —I— к*^
— сю
Тогда по формуле A5)
откуда
^ / - i / ;:: *. B2)
Положим, что А < —. Тогда интеграл B2) имеет смысл и легко
может быть вычислен с помощью теории вычетов путем приме-
применения леммы Жордана. После простых выкладок найдем
= .ехр (ЧуДд)
и, окончательно,
и{х) =
сю
+ a	Г ехр \—\х — s\ у а2 — 2аХ] f(s) ds.
у а2 — 2а\ J	V	/
B4)
Итак, применение рассмотренного метода, сводящего реше-
решение исходного интегрального уравнения A) к решению алгебра-
алгебраического уравнения, было связано с возможностью применения
преобразования Фурье к входящим в это уравнение функциям
и использования формулы свертки. Нашей ближайшей целью
является перенесение рассматриваемых методов на решение ин-
интегральных уравнений с ядром, зависящим от разности аргу-
аргументов, в случае полу бесконечного промежутка
сю
и(х) = A J v(x - s)u(s) ds + f(x).	B5)
о
Однако для этого нам понадобятся некоторые аналитические
свойства преобразования Фурье, в частности определение обла-
областей аналитичности преобразования Фурье функций действи-
действительной переменной, как убывающих, так и возрастающих на
бесконечности.

286	ПРИЛОЖЕНИЕ 2
2. Аналитические свойства преобразования Фурье.
Пусть функция f(x) определена при всех значениях — оо < х <
< оо. Рассмотрим преобразование Фурье этой функции
ОО
J f(
x)eikxdx.	B6)
При этом будем считать, что параметр /с, входящий в преобра-
преобразование B6), вообще говоря, может принимать и комплексные
значения. Поставим вопрос о свойствах функции F(k), рассма-
рассматриваемой как функция комплексной переменной к. Для этого
представим функцию f(x) в виде
f(x) = f+(x) + f-(x),	B7)
где функции /+(ж) и f-(x) соответственно равны
/ 0, х < О,	/ f(x), х < О,
\ f(x), х>0,	\ О, Ж>0.
Преобразование Фурье F(k) функции f(x) при этом, очевид-
очевидно, равно сумме преобразований Фурье F+(fc), F-(k) функций
f+(x) и /_(ж). Мы выясним аналитические свойства функ-
функции F(k)j установив аналитические свойства функций F+(k) и
F-(k). Итак, рассмотрим функцию
[ /(ж), ж > 0.
Ее преобразованием Фурье является функция
оо
F+(k) = ^= J и(х)егкх dx.	B9)
Повторяя рассуждения теорем 8.1 и 8.2, легко показать, что если
функция /+(ж) удовлетворяет условию
\U(x)\ < Мет~х при ж ^ оо,	C0)
то функция F+(fc), определенная формулой B9), является ана-
аналитической функцией комплексной переменной к = а-\-гт в обла-
области Im к > т_, причем в этой области F+(k) —>> 0 при |fc| —>> оо.
С помощью рассуждений, аналогичных проведенным в теоре-
теореме 8.5, можно показать, что функции /+(ж) и F+(k) связаны
обратным соотношением:
оо + гт
1	F+(k)e~ikx dk,	C1)
-1=
— оо + гт

МЕТОД ВИНЕРА-ХОПФА	287
где интегрирование производится по любой прямой Im к = т >
> т_, параллельной действительной оси на комплексной плос-
плоскости к.
При т_ < 0 (т. е. для убывающих на бесконечности функций
f(x)) область аналитичности функции F+(k) содержит действи-
действительную ось и в формуле C1) можно проводить интегрирование
вдоль действительной оси. Если т_ > 0 (т.е. функция /+(ж) ра-
растет на бесконечности, но не быстрее, чем экспонента с линей-
линейным показателем), то область аналитичности функции F+(k)
лежит над действительной осью комплексной плоскости к (при
этом на действительной оси к интеграл B9) может расходиться).
Аналогично, если функция
= I 0 ж О
удовлетворяет условию
/_(ж) <Мет+х приж-)- -оо,	C3)
то ее преобразование Фурье, функция
о
F-(k) = -j= J f-(x)eikxdx,	C4)
— ОО
является аналитической функцией комплексной переменной к в
области Im к < т_|_. Функция f-(x) выражается через функцию
F-(x) с помощью соотношения
оо + гт
F_(k)e~ikx dk,	C5)
/_(s) ==
—	оо + гт
где Im к = т < т_|_.
Если т+ > 0, то область аналитичности функции F-(k) со-
содержит действительную ось.
Очевидно, при т_ < т+ функция F(fc), определенная по фор-
формуле B6), является аналитической функцией комплексной пе-
переменной к в полосе т_ < Im к < т_|_. При этом функции /(ж) и
F(fc) связаны обратным преобразованием Фурье:
оо + гт
/(*) = -!= / F(k)e~^dk,	C6)
—	оо + гт
где интегрирование производится по любой прямой, параллель-
параллельной действительной оси комплексной плоскости /с, лежащей в
полосе т_ < Im к = т < т+. В частности, при т_ < 0 и т+ >0
функция F(k) является аналитической в полосе, содержащей
действительную ось комплексной плоскости к.

288	ПРИЛОЖЕНИЕ 2
Так, функция V(x) = е ах при а > 0 обладает преобразо-
преобразованием Фурье
^^F-	C7)
являющимся аналитической функцией комплексной переменной
к в полосе — а < Im к < а, содержащей действительную ось.
Перейдем теперь к изложению основной идеи метода
Винера-Хопфа. Мы продемонстрируем ее сначала на примере
решения интегрального уравнения специального типа.
3. Интегральные уравнения с ядром, зависящим от
разности аргументов. Начнем с рассмотрения однородного
интегрального уравнения вида
оо
и(х) = А / v(x — s)u(s) ds,	C8)
о
ядро которого, функция v(x — s), зависит от разности ж — s = ?
и определено для всех значений своего аргумента — оо < ? < оо.
Решение этого уравнения, очевидно, находится с точностью до
произвольного множителя; он может быть найден из дополни-
дополнительных условий задачи, например условий нормировки. Будем
считать, что уравнение C8) определяет функцию и(х) для всех
значений переменной ж, как положительных, так и отрицатель-
отрицательных. Введем функции и+ и и-\
( О, ж < 0,	/ и(х), х < О,
и+(х) = <	и-{х) = \	C9)
у и(х), ж > 0,	[ 0, ж > 0.
Очевидно, и(х) = гл+(ж) +гл_(ж), и уравнение C8) можно пере-
переписать в виде
(X)
гл+(ж) = А Г г;(ж — s)?i+(s) ds, ж > 0,	D0)
о
оо
и-(х) = А / г;(ж — s)ia+(s) ds, ж < 0.	D1)
о
То есть функция гл+(ж) определяется из решения интегрального
уравнения D0), а функция и-(х) выражается через функции
и+(х) и v(x) с помощью квадратурной формулы D1). При этом
имеет место соотношение
сю
гл+(ж) + гл_(ж) = А Г г;(ж — s)u+(s) ds,	D2)
о
эквивалентное исходному уравнению C8).

МЕТОД ВИНЕРА-ХОПФА
289
Пусть функция v(^) удовлетворяет условиям
\v(?)\ < Мет-? при f ->> оо,
\v(?)\ < Мет+^ при f->>-оо,
где т_ < 0, т+ > 0. Тогда функция
D3)
D4)
является аналитической в полосе т_ < Im к < т+.
Будем искать решение уравнения C8), удовлетворяющее
условию 1)
|гл+(ж)| < М\е^х при х —>> оо,	D5)
где \i < т_|_. При этом интегралы в правых частях соотношений
D0) и D1), как несложно проверить, являются сходящимися,
причем для функции и-[х) имеет место оценка
\и-{х)\ < М2ет+Х при х ->> -оо.	D6)
Из условий D5) и D6) следует, что преобразование Фурье
U+(k) и U-{к) функций и+(х)
и и-(х) являются аналитическими
функциями комплексной перемен-
переменной к при Im к > \i и Im fc < т+
соответственно (на рис. 1 для опре-
определенности положено /j, > T-).
Перейдем теперь к решению ин-
интегрального уравнения C8) или эк-
эквивалентного ему уравнения D2),
для чего воспользуемся преобразова-
преобразованием Фурье. С помощью формулы
(9) преобразования свертки, в спра-
справедливости которой в рассматрива-
рассматриваемом случае полубесконечного про-
промежутка легко убедиться непосред-
непосредственно, получим из D2)
U+(k),L+(k)
"ImA;=|u
¦ 1т?=т-
U.(k),L.(k)
Рис. 1
U-(k) =
или
где
k) + U-(k) =0,
L(k) = l-y/27r\V(k).
D7)
D8)
:) Мы не останавливаемся на доказательстве существования решения
уравнения D0), обладающего указанным свойством. Подробнее см., напри-
например, цитированную выше статью В.А. Фока.

290	ПРИЛОЖЕНИЕ 2
Итак, с помощью преобразования Фурье мы опять перешли
от исходного интегрального уравнения к алгебраическому урав-
уравнению для преобразований. Однако теперь в уравнение D7) вхо-
входят уже две неизвестные функции. Вообще говоря, из одного
алгебраического уравнения нельзя однозначно определить две
неизвестные функции. Метод Винера-Хопфа позволяет решить
эту задачу для определенного класса функций. Он в первую оче-
очередь связан с изучением областей аналитичности, входящих в
уравнение функций, и специальным представлением этого урав-
уравнения. Основная идея метода Винера-Хопфа заключается в сле-
следующем.
Пусть удалось представить уравнение D7) в виде
L+(k)U+(k) = -L-(k)U-{k),	D9)
где левая часть является аналитической в верхней полуплоско-
полуплоскости Im к > /i, а правая — аналитической в нижней полуплос-
полуплоскости Im к < т+, причем /j, < т+, так что существует общая
полоса аналитичности этих функций \i < Im к < т+. Тогда в си-
силу единственности аналитического продолжения можно утвер-
утверждать, что существует единственная целая функция комплекс-
комплексной переменной, совпадающая с левой частью D9) в верхней
и правой частью D9) в нижней полуплоскости соответственно.
Если при этом известно, что функции, входящие в D9), растут
на бесконечности не быстрее, чем конечная степень А;п, то в си-
силу теоремы Лиувилля данная целая функция определяется с
точностью до постоянных множителей. В частности, в случае
ограниченной на бесконечности функции получим
L+(k)U+(k) = -L-(k)U-(k) = const.	E0)
Отсюда функции U+(k) и U-(k) определяются однозначно.
Итак, применим данную схему к решению уравнения D7).
Из проведенных выше рассмотрений следует, что области анали-
аналитичности функций [/+(&), U-{к) и L(k) = 1 — л/2тг XV(к) соответ-
соответственно представляют собой верхнюю полуплоскость Im к > /i,
нижнюю полуплоскость Im к < т+ и полосу т_ < Im к < т_|_. Тем
самым это уравнение справедливо в полосе г) \i < Im к < т+, яв-
являющейся общей областью аналитичности всех входящих в это
уравнение функций. Для преобразования уравнения D7) к виду
D9) предположим, что возможно разложение функции L(k):
E1)
1) Мы для определенности положим /л > т~. В противном случае общей
областью аналитичности будет полоса т~ < Im к < т+.

МЕТОД ВИНЕРА-ХОПФА	291
где функции Ь+{к) и L_(fc) являются аналитическими при
Im к > /j, и Im к < т+ соответственно. Кроме того, предполо-
предположим, что в областях своей аналитичности эти функции на бес-
бесконечности растут не быстрее, чем А;п, где п — некоторое поло-
положительное целое число. Разбиение E1) аналитической функции
L(k) обычно называется факторизацией. Возможность факто-
факторизации заданной аналитической функции комплексной пере-
переменной будет обоснована ниже (см. леммы 1 и 2 на с. 294, 296).
Итак, в результате факторизации исходное уравнение приве-
приведено к виду
L+(k)U+(k) = -L-(k)U-{k).	D9)
Из предыдущих рассмотрений следует, что оно определяет
некоторую целую функцию комплексной переменной к.
Так как U±(k) —> 0 при |/с| —^ ос, a L±(k) растут на беско-
бесконечности, как конечная степень А;п, то данная целая функция
может быть лишь полиномом Pn_i(k) степени не выше п — 1.
Если функции L±(k) растут на бесконечности, лишь как пер-
первая степень переменной /с, то из соотношений E0) в силу теоре-
теоремы Лиувилля следует, что соответствующая целая функция есть
постоянная С. Тогда для неизвестных U+(k) и U-(k) получим
выражения
определяющие преобразования Фурье искомого решения с точ-
точностью до постоянного множителя, который может быть найден
хотя бы из условий нормировки. В общем случае выражения
и^ = Шу и-{к) = ~Ш)	E3)
определяют преобразования Фурье искомого решения инте-
интегрального уравнения C8) с точностью до неопределенных по-
постоянных, которые можно найти из дополнительных условий
задачи. Само решение определяется с помощью обратного пре-
преобразования Фурье C1) и C5).
Рассмотрим пример применения изложенного метода.
Пример 2. Рассмотрим уравнение
ОО
и(х) = A J e~\x~8\u{s) ds,	E4)
о
ядро которого имеет вид v(^) = e~^L
Найдем преобразование Фурье функции г;(?):
оо
V(k) = -L Г v(Z)eikt(% = -=Л	.	E5)

292	ПРИЛОЖЕНИЕ 2
Функция V(k) E5) является аналитической функцией комплекс-
комплексной переменной к в полосе — 1 < Im к < 1. Представим выраже-
выражение
L(k) = 1-V2irXV(к) = " ~ГД~±;	E6)
в виде E1), где
+ (/с) =	—:	-, L—ук) = к — г.	\р()
Функция L_|_(fc) в E7) является аналитической и отличной от
нуля функцией к в области Im к > Im л/2 А — 1. При 0 < А <
< - эта область определяется условием Im к > \J\ — 2А, причем
\i < 1. При А > - функция Ь+(к) является аналити-
аналитической и отличной от нуля в области Im к > 0. Функция L_(A;),
очевидно, представляет собой отличную от нуля аналитическую
функцию в области Im к < 1. Поэтому при 0 < А < - обе функ-
функции удовлетворяют требуемым условиям в полосе \i < Im к < 1.
При - < А общей областью аналитичности функций L+(k) и
L-(k) является полоса 0 < Im к < 1. Таким образом, необходи-
необходимая факторизация функции E6) произведена.
Рассмотрим выражения U±(k)L±(k). Так как U±(k) —>• 0
при \к\ —>• оо, a L±{kI согласно E7), растут на бесконечности,
как первая степень /с, то целая функция Рп(к), совпадающая с
U+(k)L+(k) при Im к > \i и с U-(k)L-(k) при Im A; < 1, может
быть лишь полиномом нулевой степени. Поэтому
U+(k)L+(k) = C.	E8)
Отсюда
и, согласно C1),
оо+гт
и+(х) = 4= f k._\tx-if~tkXdk>	F°)
— оо+гт
где \i < т < 1.
Для вычисления интеграла F0) можно применить методы
гл. 5. Замкнув контур интегрирования при х > 0 дугой полу-
полуокружности в нижней полуплоскости и оценив интеграл по этой
дуге с помощью леммы Жордана, после элементарных вычисле-

МЕТОД ВИНЕРА-ХОПФА	293
ний получим
/ \ т^ \ /^г\ т . sin л/2Л — 1 х \	(пл \
и+ (х) = D \ cos v 2A — 1х + —]; — ,	F1)
/2Л - 1
где D — новая постоянная. При 0 < А < - это решение экспо-
экспоненциально возрастает с ростом ж, при - < А < оо — ограничено
на бесконечности.
Итак, уже пример решения однородного интегрального урав-
уравнения C8) выявляет основную идею метода Винера-Хопфа, за-
заключающуюся в представлении с помощью факторизации ис-
исходного функционального уравнения D7) в виде целой функ-
функции D9). Дадим теперь обоснование возможности факторизации
аналитической функции комплексной переменной, причем бу-
будем исходить из несколько более общего функционального урав-
уравнения, чем уравнение D7).
4. Общая схема метода Винера—Хопфа. В общем случае
задача, решаемая методом Винера-Хопфа, сводится к следую-
следующей.
Требуется определить функции Ф+(&) и Ф_(/с) комплексной
переменной /с, аналитические соответственно в полуплоскостях
Im к > Г- и Im к < т+ (т_ < т+), стремящиеся к нулю при
\к\ —>> оо в своих областях аналитичности и удовлетворяющие в
полосе (т_ < Im к < т_|_) функциональному уравнению
А(к)Ъ+(к) + B(k)V-(k) + С (к) = 0.	F2)
Здесь А(к), В (к), С (к) — заданные функции комплексной
переменной /с, аналитические в полосе т_ < Im к < т+, причем
А(к) и В (к) отличны от нуля в этой полосе.
Основная идея решения этой задачи основана на возмож-
возможности факторизации выражения А(к)/В(кI т. е. возможности
представить его в виде
А{к) _ Ь+{к)
Щ) - ИЩ
где функции Ь+{к) и L_(fc) являются аналитическими и отлич-
отличными от нуля соответственно в полуплоскостях Im к > т_ и
Im А; < т+, причем полосы т_ < Im к < т+ и т'_ < Im к < т+
имеют общую часть. Тогда с помощью F3) уравнение F2) мож-
можно переписать в виде
L+{k)V+{k) + L-(k)V-(k) + Ь-(к)Щ = 0.	F4)
Если последнее слагаемое в F4) можно представить в виде
F5)

294	ПРИЛОЖЕНИЕ 2
где функции D+(k) и D_(k) являются аналитическими в полу-
полуплоскостях Im к > т"_ и Im к < т^ соответственно, и все три
полосы т_ < Im к < т+, т'_ < Im t < т| и т" < Im к < т+ имеют
общую часть — полосу т°_ < Im fc < т|, то в этой полосе имеет
место функциональное уравнение
?+(?;)*+(?;) + D+(k) = -L_(kL>_(k) - D_(k). F6)
Левая часть F6) представляет собой функцию, аналитическую
в полуплоскости т®_ < Im /с, правая — функцию, аналитиче-
аналитическую в области Im к < т^_. Из равенства этих функций в полосе
т°_ < Im к < т+ следует, что существует единственная целая
функция Р(к), совпадающая соответственно с левой и правой
частями F6) в областях их аналитичности. Если все функции,
входящие в правые части F3) и F5), растут на бесконечности
в своих областях аналитичности не быстрее, чем A;n+1, то из
условия Ф±(/с) —> 0 при \к\ —>> оо следует, что Р(к) является
полиномом Рп(к) степени не выше п. Тем самым равенства
ф (и) = Ык)-В+(к)
определяют искомые функции с точностью до постоянных. По-
Последние могут быть найдены из дополнительных условий задачи.
Итак, применение метода Винера-Хопфа основано на пред-
представлениях F3) и F5). Возможность этих представлений обес-
обеспечивается следующими леммами.
Лемма 1. Пусть функция F(k) является аналитической
в полосе г- < Im k < т+, причем в этой полосе F(k) равно-
равномерно стремится к нулю при \к\ —>> оо. Тогда в данной полосе
возможно представление
F(k)=F+(k)+F-(k),	F9)
где функция F+(k) — аналитическая в полуплоскости Im k >
> т_, а функция F-(k) — в полуплоскости Im k < т+.
Доказательство. Рассмотрим произвольную
точку &о, лежащую в данной полосе, и построим прямоуголь-
прямоугольник abed, содержащий точку &о, внутри и ограниченный отрез-
отрезками прямых Im к = rf_, Im к = т+, Re к = —A, Re к = А,

МЕТОД ВИНЕРА-ХОПФА
295
где т < т'_ < т\ < т+ (рис. 2). По формуле Коши
' +
А+гт'_
A+ir'
-A+irf
A+irf
-A+ir'
J_ f lttLdC + ^ [
2тгг J C-^o	2ттг J
- k0
d(. G0)
-А+гт+/
Перейдем в G0) к пределу при А —>• оо. Так как по условию лем-
леммы F(k) равномерно стремится к нулю при \к\ —>• оо, то предел
второго и четвертого слагаемых в правой части G0) равен нулю,
и мы получим
()()()	G1)
где
2ni J
— oo-\-ir'_
oo-\-ir'+
С-ко
G2)
G3)
Интегралы G2) и G3), как интегралы, зависящие от парамет-
параметра1), определяют аналитические функции комплексной пере-
переменной ко при условии,
что точка ко не лежит
на контуре интегриро-
интегрирования.
В частности F+(fco)
является аналитиче-
аналитической функцией в полу-
полуплоскости Im ко > rf_i a
F-(ko) — в полуплоско-
полуплоскости Im ко < т+. В силу
произвольности выбора
к
точки ко
ко
и прямых
т'_ и т'+ соотношения
G1)—G3) и доказывают
лемму.
d
-А
а
к=0
т;
т_
с
1
Ь
Рис. 2
:) См. с. 69.

296	ПРИЛОЖЕНИЕ 2
Замечание 1. Заметим, что из сходимости интегралов
G2) и G3) следует ограниченность построенных таким образом
функций F+(k) и F-(k) при \к\ —>> оо в данной полосе.
Лемма 2. Пусть функция Ф(к) является аналитической
и отличной от нуля в полосе т_ < Im к < т+, причем Ф(к)
равномерно в этой полосе стремится к единице при \к\ —>• оо.
Тогда в данной полосе имеет место представление
ф(&) = Ф+(к) • Ф_(&),	G4)
где функции Ф+(к) и Ф-(к) являются аналитическими и от-
отличными от нуля соответственно в полуплоскостях Im к > т_
и Im к < т+.
Доказательство. Рассмотрим функцию F(k) =
= 1пФ(/с), которая, очевидно, удовлетворяет всем условиям лем-
леммы 1. Поэтому для функции F(k) возможно представление
G1)-G3). Полагая
Ф+(А;) =exp[F+(A;)], Ф_(&) = exp[F_(A;)],	G5)
где функции F+(k) и F-(k) определены формулами G2), G3),
получаем
1пФ+(*0 = F+(fe), 1пФ_(*0 = F-(fc).	G6)
Тогда формула G1) дает
1пФ(А;) = 1пФ+(*0+1пФ-(*0>	G7)
откуда и следует соотношение G4). Так как функции F+(k) и
F-(k), согласно лемме 1, являются аналитическими в полуплос-
полуплоскостях Im к > Т- и Im к < т+ соответственно, то и функции
Ф+(к) и Ф_(/с), определенные по формулам G5), будут обладать
требуемыми свойствами. Лемма доказана.
Замечание 2. Возможность факторизации G4) сохра-
сохраняется в том случае, когда функция Ф(к) имеет конечное число
нулей к{ в полосе т_ < Im к < т_|_.
Для доказательства леммы 2 в этом случае достаточно ввести
вспомогательную функцию
F(k) = In
где ol{ — кратность нуля ki\ N — полное число нулей с учетом их
кратности; положительная постоянная b > |т_|, |т_|_| выбирается
из условия, чтобы функция, стоящая под знаком логарифма, не
имела дополнительных нулей в полосе т_ < Im к < т+. Послед-
Последняя функция, очевидно, стремится на бесконечности к единице.
Построенная таким образом функция F(k) по-прежнему удовле-
удовлетворяет всем условиям леммы 1.
Доказанные леммы и определяют возможность представле-
представлений F3), F5), составляющих основу метода Винера-Хопфа.

	МЕТОД ВИНЕРА-ХОПФА	297
Мы рассмотрели применение метода Винера-Хопфа для ре-
решения функционального уравнения F2). Легко видеть, что к
этому уравнению сводится и неоднородное инте-
интегральное уравнение на полубесконечном промежутке
с ядром, зависящим от разности аргументов:
оо
и(х) = A J v(x - s)u(s) ds + f(x).	G9)
о
Будем предполагать, что ядро уравнения G9) и функция
f(x) удовлетворяют условиям D3), и будем искать решение
уравнения G9), удовлетворяющее условию1)
|гб+(ж)| <Mie^ при х -+ оо (^<т+).	(80)
Тогда, проводя рассуждения, аналогичные рассуждениям
при выводе функционального уравнения D7) для однородно-
однородного интегрального уравнения, получаем, что в случае уравнения
G9) в полосе \i < Im к < т+ должно удовлетворяться функцио-
функциональное уравнение
U+{k) + U-{к) = \V2^V(k)U+(k) + F+(fc) + F-(k) (81)
или
L(k)U+(k) + U-{к) - F(k) = 0,	(82)
где
L(k) = l-y/2n\V{k).	(83)
Уравнение (82) является частным случаем уравнения F2).
Функция Ь(к) в полосе т_ < Im к < т+ является аналитиче-
аналитической и равномерно стремится к единице при \к\ —>• оо, так как
|F(A;)| —)> 0 при \к\ —)> оо. Если, кроме того, функция Ь(к) име-
имеет конечное число нулей в этой полосе, то все условия леммы 2
выполнены и функцию Ь(к) можно представить в виде
ад = f±|,	(84)
где Ь+(к) является аналитической функцией в верхней полу-
полуплоскости Im к > т_, a L-(k) — в нижней полуплоскости Im к <
< т_|_. Тогда уравнение (82) принимает вид
(k) =0. (85)
Для приведения последнего уравнения к виду F6) достаточно
разложить последнее слагаемое:
F+(k)L_(k) = D+(k) + D-(k),	(86)
) Мы опять не останавливаемся на обосновании существования решения
уравнения G9), удовлетворяющего условию (80).

298	ПРИЛОЖЕНИЕ 2
на сумму функций D+(k) и D_(fc), являющихся аналитическими
в полуплоскостях Im к > \i и Im к < т+ соответственно.
Для обоснования возможности такого представления заме-
заметим, что в силу условия D3) функция F+(k) является аналити-
аналитической в верхней полуплоскости Im к > т_ и равномерно стре-
стремится к нулю при \к\ —>• оо. Функция L-(k) является анали-
аналитической в нижней полуплоскости Im к < т+, и по способу ее
построения в силу леммы 2 и замечания к лемме 1 можно так
провести факторизацию (84), чтобы L-(k) оставалась ограни-
ограниченной в полосе т < Im к < т+ при \к\ —>• оо. Отсюда следует,
что для функции F+(k)L_(k) в полосе т_ < Im к < т+ выпол-
выполнены все условия леммы 1, что и достаточно для обоснования
представления (86).
Проведенные рассмотрения позволяют при дополнительных
условиях, что функции L±(k) растут на бесконечности не бы-
быстрее, чем А;п, представить преобразования Фурье решения неод-
неоднородного интегрального уравнения G9) в виде
(87)
Само решение может быть получено из (87) с помощью формул
C1) и C5) обратного преобразования Фурье.
5. Задачи, приводящие к интегральным уравнениям
с ядром, зависящим от разности аргументов.
5.1. Вывод уравнения Милна. К интегральным уравнениям
с ядром, зависящим от разности аргументов, сводится большое
число физических задач. В качестве первого примера укажем
классическую проблему Милна, описывающую процесс переноса
нейтронов (или излучения) через вещество.
Пусть в полупространстве х > 0, заполненном однородным
веществом, плотность которого определяется числом щ частиц в
единице объема, распространяется поток нейтронов. Будем счи-
считать, что частицы вещества являются тяжелыми атомами, рас-
рассеивающими нейтроны так, что абсолютная величина скорости
нейтронов остается постоянной, а меняется лишь ее направле-
направление. Рассмотрим стационарный процесс и предположим, что все
нейтроны имеют одну и ту же абсолютную величину скорости
^о = 1 и плотность их распределения зависит лишь от одной ко-
координаты х. Введем функцию /(x,/i), характеризующую плот-
плотность нейтронов в сечении ж, скорость которых составляет с по-
положительным направлением оси х угол в, где \i = cos в 1). Чис-
Число нейтронов в единице объема в данном сечении, направление
х) Очевидно, — 1 ^ /х ^ 1 при 0 ^ в ^ тг.

МЕТОД ВИНЕРА-ХОПФА	299
скорости которых лежит в пределах (ц^ц + rf/i), определяется
величиной /(ж, /i) d/j,.
Полная плотность нейтронов р(х) в данном сечении равна
1
р(х)= f f(x,fi)dfi.	(88)
-i
Нашей ближайшей целью является вывод уравнения для функ-
функции распределения /(ж, /i). Для этого составим соотношение пол-
полного баланса числа нейтронов, имеющих направление скорости
в интервале (/i, \i + d\i) и находящихся в слое между сечениями
х и х + dx. В силу стационарности процесса поток нейтронов,
выходящих из данного слоя
fif(x + dx, /i) dfi - fif(x, /i) d/i,	(89)
определяется разностью между числом нейтронов, приобретших
скорость в заданном направлении (/i, /j+d/j,) в результате рассея-
рассеяния на частицах вещества в данном слое, и числом нейтронов,
имевших скорость в заданном направлении и изменивших это
направление после рассеяния. Мы будем считать, что рассеяние
нейтронов на частицах вещества является изотропным, т. е. оно
равновероятно во всех направлениях, и вероятность рассеяния
нейтрона на одной частице характеризуется эффективным се-
сечением рассеяния Q. Тогда число нейтронов, имевших заданное
направление скорости (/i, \i + d\i) и рассеянных в данном слое,
очевидно, равно
f(x,/j)d/j • Qnodx,	(90)
а число нейтронов, приобретших в результате рассеяния ско-
скорость в требуемом направлении, равно
1
-d/jQ-nodx Г /(ж,//) d\i .	(91)
-1
На основании выражений (89) - (91) уравнение баланса запи-
запишется в виде
, /i) d/j, — /i/(x, /i) d/j, =
l
+(^diJidx f /(ж,//)ф/. (92)
2	J
-1
Разделим обе части равенства на d\idx и перейдем к пределу
при dx —>• 0. Учтя (88), получим уравнение для функции рас-
распределения нейтронов в виде
^(x).	(93)

300	ПРИЛОЖЕНИЕ 2
Это уравнение часто называется уравнением переноса или
транспортным уравнением. Оно справедливо не только в случае
рассмотренной конкретной физической задачи, но и для многих
других физических процессов, связанных с переносом вещества
или излучения г).
Для дальнейшего удобно переписать уравнение (93) в
несколько ином виде, введя безразмерную пространственную ко-
координату ?, связанную с х соотношением х = А?, где А= —— —
nQo
средняя длина свободного пробега. Тогда уравнение переноса
примет вид2)
Функция /(?,/i) должна быть подчинена граничным услови-
условиям, вытекающим из физической постановки задачи. Будем счи-
считать, что поток нейтронов из внешнего полупространства ? < О
равен нулю, а при ? —>> оо имеется постоянный поток нейтро-
нейтронов единичной мощности в отрицательном направлении оси ?
(т.е. при ? —>• оо отсутствуют нейтроны, направление скоро-
скорости которых составляет с отрицательным направлением оси ?
острый угол, отличный от нуля). Тогда граничные условия для
функции /(?,/i) запишутся в виде
0 = о, »> о,	(95)
/^oo,/i) = 0, —1 < /i < 0.
Установим важные следствия уравнения (94) и условий (95),
для чего сначала проинтегрируем (94) по /i:
1	1	1
Or	г	1 г
— / /(?,/i)/irf/i = — / f\?->lj)dii + -p{?)) \ d\i =
-1	-1	-1
= -р@ +р@ = 0. (96)
1
Так как интеграл j(?) = J /(?,/i)/irf/i равен потоку нейтронов
-1
через данное сечение, то уравнение (96) дает
-| = 0 или j(?) = const.	(97)
:) Подробный вывод уравнения переноса для более общих случаев см.,
например, в кн. : Морс и Фешбах. Методы теоретической физики.
Т. 1. — М. : ИЛ, 1958.
2) Мы сохранили для функции /(?,//) старое обозначение.

МЕТОД ВИНЕРА-ХОПФА	301
В силу условий нормировки (при ? —>• оо) получим /(?) =
= — 1 (единичный поток при ? —>• +оо направлен в отрицатель-
отрицательном направлении оси ?).
Теперь умножим (94) на /i и снова проинтегрируем от —1
1
до 1. Введя обозначение if(?) = / /(?,/i)/i2 d/i, получим
-l
^ = 1 или #(?) = #(())+?,	(98)
где в силу (95)
о
J2d/i.	(99)
-1
Уравнение (94) является интегро-дифференциальным, так как
неизвестные функции р(^) и /(?,/i) связаны интегральным со-
соотношением (88). Однако легко получить интегральное уравне-
уравнение для функции р(^). Решая обыкновенное дифференциаль-
дифференциальное уравнение (94) относительно функции /(?,/i), в силу (95)
получим
/ exp ( -—- J p(rj) dr], /i > О,
° со	f _	A00)
— Г exp ( -—- ) p(rj) dr), /i < 0.
e v p У
Проинтегрировав A00) no /i от —1 до 1, получим интегральное
уравнение для функции
1 оо
= \ / / PW exp (-Ji^L) d^.	A01)
0 0
0 0
Изменив в A01) порядок интегрирования, получим окончатель-
окончательное уравнение для плотности нейтронов в сечении ?:
сю
Р(О= fv^-fi)p(fi)dri.	A02)
о
Как видим, это есть интегральное уравнение в полубесконечном
промежутке с ядром, зависящим от разности:
()

302	ПРИЛОЖЕНИЕ 2
Уравнение A02) обычно называется уравнением Милна, ко-
который впервые получил это уравнение при исследовании про-
процессов переноса излучения в звездной атмосфере.
Отметим, что во многих случаях удобным оказывается
несколько иное представление ядра, получающееся при замене
в интеграле X(t) = /exp ( — — ) — переменной интегрирования
\i = -. Тогда
ОО
X(t) = Г e~^v—.	A04)
1
Интеграл A04) часто называется функцией Хопфа. Интегри-
Интегрированием по частям легко может быть получено его асимптоти-
асимптотическое разложение при больших положительных значениях t:
5.2. Исследование решения уравнения Милна. Уравнение
A02) принадлежит к типу уравнений, рассмотренных в п. 3, и
для его решения может быть применен общий алгоритм метода
Винера-Хопфа. Мы не будем проводить здесь подробного реше-
решения этого уравнения и исследования его физического смысла1),
а ограничимся лишь рядом замечаний.
Во многих практических задачах основной интерес предста-
представляет определение лишь функции распределения нейтронов, вы-
выходящих из данной среды, т.е. функции /@,/i) при \i < 0. Со-
Согласно A00) эта функция определяется выражением
= щ f e-"/Mp(r)) dr,, /x < 0.
A06)
Как легко видеть, в силу B9) последний интеграл есть не что
иное, как одностороннее преобразование Фурье функции p{rj)
при к = —г. т.е.
И
Тем самым в указанных задачах достаточно найти не само
решение интегрального уравнения A02), а лишь его преобразо-
преобразование Фурье.
:) Подробнее см, например, широко известную работу Хопфа: Н о р f,
Mathematical Problems of Radiative Equilibrium. — Cambridge, 1934.

МЕТОД ВИНЕРА-ХОПФА
303
Согласно общей схеме метода Винера-Хопфа для решения
последней задачи следует найти преобразование Фурье ядра ин-
интегрального уравнения, а затем произвести факторизацию E1)
функции L(k) = 1 — л/2тгXV(к). В нашем случае А = 1 и
оо
v{k) - 7В I
elkxv(x)dx =
о	l
elkx dx
boo	0
оо	1
гкх
Г егкх dx Г ех'^ + Г егкх dx Г e~x'^
elKX dx
о	о
1
_ 1 i 1	djj, _ 1
arctgA; _ 1 1 , 1 + ik
Поэтому
L(k) = 1 - V2^XV(k) =
1 , 1 + ik (-\C)Q)
(Ю9)
Функция L(k), очевидно, является аналитической в полосе
— 1 < Im к < 1, стремящейся к нулю в этой полосе при \к\ —>• оо.
Точка А; = 0 является нулем второго порядка этой функции.
Последнее обстоятельство несколько затрудняет факторизацию
функции Ь(к).
Согласно замечанию 2 (см. с. 296) построим вспомогатель-
вспомогательную функцию ———L(k), удовлетворяющую всем условиям лем-
мы 2, и рассмотрим функцию
= in
= in
J! (i - z
(по)
которую легко представить в виде Ф(к) = Ф_(/с) + Ф+(/с), где
функции Ф_(/с) и Ф+(/с) являются аналитическими соответ-
соответственно в нижней Im к < т+ < 1 и верхней Im А; > т_ > — 1
полуплоскостях. При этом
оо+гт_
(по')
— оо+гт_
а функция L+(fc), являющаяся числителем в формуле фактори-
факторизации E1) функции Ь(к):

304	ПРИЛОЖЕНИЕ 2
может быть выбрана в виде
L+(k) = ?-геФ+(к).	A11)
Функция L+(k) является аналитической в верхней полуплоско-
полуплоскости Im к > т_ и при \к\ —>• оо растет, как первая степень /с, по-
поскольку в силу сходимости интеграла (ПО7) Ф+(&) ограничена
при \к\ —>> оо. Поэтому функция R+(k) определяется по форму-
формуле E2):
я^ лк41
Отсюда следует, что для определения функции распределения
нейтронов, выходящих из полупространства х > 0, необходи-
необходимо найти Ф+(/с). Это может быть сделано с помощью формулы
(ПО7). Для вычисления этого интеграла положим т_ = 0 и при-
приведем его к следующему виду:
О	оо
— оо	l^oo	0
A13)
Воспользовавшись четностью функции Ф(С) и сделав в первом
интеграле замену переменной интегрирования (' = —?, оконча-
окончательно получим
A14)
Последний интеграл может быть легко табулирован, что и
позволяет найти /@,/i) при /i < 0 с точностью до постоянного
множителя А. Для определения последнего воспользуемся усло-
условием нормировки (97) и следующими соображениями. Умножим
уравнение (94), справедливое при ? > 0, на —=егк^ и проинте-
грируем его по ? от 0 до оо. Пусть к — комплексная величина
с малой положительной мнимой частью. Тогда, применив фор-
формулу интегрирования по частям
k,^	A15)
получим
^	) + \R+(k), (П6)

	МЕТОД ВИНЕРА-ХОПФА	305
ИЛИ
Г ..	1 1
A17)
Результат интегрирования A17) по /i от —1 до 1 в силу очевид-
1
ного соотношения i?+(fc) = / F+(k, /i) d/j и условия (95) дает
-1
A18)
-1
Так как
1 / ^M 	 1т 1 Ч- г/с
-1
то окончательно получим
о
arctg A;
— -1 Л arctgAA [ /@,//) 7	/19Пл
" ^ I1 " ^^) J r^Vdl*.	A20)
-1
Разложим правую часть A20) в ряд Лорана в окрестности точки
к = 0. Воспользовавшись равенством х)
о	1
= -l	A21)
и введенным ранее обозначением (99), получим
R+(k) = —т=р{1 + ^@) • А; + ...}•	A22)
С другой стороны, мож:но найти первые члены разложения
в ряд Лорана в окрестности точки к = 0 функции, стоящей в
правой части формулы A12).
Вычислим сначала Ф+@). Обратимся к формуле (ПО7) и вы-
выберем в качестве пути интегрирования действительную ось с
обходом точки С = 0 по дуге полуокружности в нижней по-
полуплоскости. Устремив радиус последней к нулю и учтя, что в
силу нечетности подынтегральной функции интеграл по участ-
участкам действительной оси равен нулю, получим
-mJj. (Ш)
Равенство A21) имеет место в силу (95) и условия нормировки (97).

306	ПРИЛОЖЕНИЕ 2
Используя A23), находим, что разложение функции R+(k) в
окрестности точки к = 0 имеет вид
^-{l + iCk + ...}.	A24)
/с
Сравнив A22) и A24), определим значение постоянной А:
А = ^Li.	A25)
Подставив полученные результаты в формулы A07), A12),
A14), окончательно получим при \i < 0
/@,/*) =
оо
что и дает функцию углового распределения нейтронов, выхо-
выходящих из полупространства х > 0.
5.3. Дифракция на плоском экране. Рассмотренные до сих
пор интегральные уравнения являются уравнениями Фредголь-
ма второго рода. Однако ряд физических задач естественным
образом приводит к интегральным уравнениям первого рода в
полубесконечном промежутке с ядром, зависящим от разности
аргументов. В качестве примера рассмотрим задачу дифрак-
дифракции электромагнитных волн на плоском экране. Пусть в одно-
однородном пространстве помещен плоский идеально проводящий
экран, совпадающий с полуплоскостью ж>0,у = 0,—оо<
< z < оо. Пусть вне экрана расположены локальные источники
электромагнитного поля, создающие периодические электромаг-
электромагнитные колебания частоты о;, поляризованные таким образом,
что вектор Е напряженности электрического поля параллелен
оси ? и не зависит от координаты z. Тогда для амплитуды и(хуу)
вектора Е получим скалярную задачу
Аи + к2и = -/(ж, у),
14(ж,0)=0, х>0.
Кроме того, функция и(х,у) должна удовлетворять усло-
условиям излучения на бесконечности, определяющим отсутствие
волн, приходящих из бесконечности 1). Здесь к = — — волновое
число (с — скорость света в среде вне экрана), /(ж,у) — задан-
заданная функция, определяющая плотность источников. Будем ис-
:) Подробнее постановку задач дифракции см. в кн. : А. Н. Тихонов,
А.А. Самарский. Уравнения математической физики. — М. : Наука,
1972.

МЕТОД ВИНЕРА-ХОПФА	307
кать решение задачи A27) в виде и(х,у) = щ(х,у) + г>(ж,у), где
функция щ(х,у) — поле, создаваемое заданными источниками
в отсутствие экрана, которое через функцию /(ж, у) выражается
в виде волнового потенциала г)
ио(х,у) =l-jJH(?\kr)f{i1r])didr]l	A28)
где Щ \z) — функция Ханкеля первого рода, г = [(х — ^J-\-(у —
— г/J]1/2, а интегрирование ведется по всей области *S, в которой
расположены источники. Для функции v(x,y) получим задачу
v(x,0) = — зд(ж,0), х > 0.
Кроме того, v(x,y) должна удовлетворять условиям излучения
на бесконечности. Решение задачи A29) будем искать в виде
волнового потенциала простого слоя
оо
v(x,y)= fHP(kr'MZ)dZ,	A30)
о
где г1 = [(х — ?J + у2]1/2, a /i(?) — неизвестная плотность, для
определения которой с помощью граничного условия при у = О,
х > 0 получим интегральное уравнение первого рода
оо
= -ио(х,О), х > 0.	A31)
Мы опять получили неоднородное интегральное уравнение в
полу бесконечном промежутке с ядром, зависящим от разности
аргументов. Однако, в отличие от G9), это уже уравнение перво-
первого рода. Данное уравнение также может быть решено с помощью
метода Винера-Хопфа, однако мы не будем останавливаться на
деталях этого исследования.
6. Решение краевых задач для уравнений в частных
производных методом Винера—Хопфа. Метод Винера-Хоп-
Винера-Хопфа может быть с успехом применен не только для решения ин-
интегральных уравнений, но и для решения краевых задач для
уравнений в частных производных. При этом конкретная фор-
форма применения данного метода может несколько отличаться от
:) Определение и свойства волновых потенциалов см. в кн.: А. Н. Т и-
хонов, А. А. Самарский. Уравнения математической физики. —
М. : Наука, 1972.

308	ПРИЛОЖЕНИЕ 2
изложенной выше, хотя общая идея, заключающаяся в факто-
факторизации выражений вида F3), F5), всегда составляет основу
метода. В качестве типичного примера рассмотрим следующую
краевую задачу для уравнения Лапласа.
Пример 3. В верхней полуплоскости у > 0 найти гармо-
гармоническую функцию, удовлетворяющую при у = 0 смешанным
краевым условиям
и(х, 0) = е~ах, а > 0, х > 0,	A32)
^(ж,0)=0, х<0,	A33)
оу
и стремящуюся к нулю при у —>• оо.
Для решения этой задачи мы воспользуемся приемом, часто
употребляемым в математической физике. Решим сначала кра-
краевую задачу A32), A33) для уравнения
Аи - к2и = 0,	A34)
где ус2 = гио^ щ > 0, а затем в полученных формулах перей-
перейдем к пределу при ж —>• 0. С помощью метода разделения пере-
переменных1) легко получить интегральное представление общего
решения уравнения A34), убывающего при у —>> оо, в виде
оо
и(х,у) = Г f(k)e~^yetkxdk,	A35)
где f(k) — произвольная функция параметра /с, a \i = л/к2 + ^г2,
причем взята та ветвь корня, которая является непосредствен-
непосредственным аналитическим продолжением арифметического значения
корня \i = \к\ при ус = 0. Отметим, что при этом Re \i > 0
при — оо < к < оо, что и обеспечивает убывание функции A35)
при у —)> +оо. Функция A35) будет удовлетворять граничным
условиям A32), A33), если функция f(k) удовлетворяет функ-
функциональным уравнениям
оо
f f(k)eikx dk = е~ах, х>0,	A36)
— оо
оо
J f(k)L(k)eikx dk = O, x<0,	A37)
где введено обозначение L(k) = ц{к) = л/А;2 + х2. Решение зада-
задачи A36), A37) легко может быть построено, если функция L(k)
:) См. А. Н. Тихонов, А. А. Самарский. Уравнения
математической физики. — М. : Наука, 1972.

	МЕТОД ВИНЕРА-ХОПФА	309
является аналитической функцией комплексной переменной к в
полосе т_ < Im к < т+ (т_ < 0, т+ > 0) ив этой полосе может
быть представлена в виде
L(k) = (к2 + a2)L+(k) • L_(k),	A38)
где Ь+{к) — функция, отличная от нуля и аналитическая в верх-
верхней полуплоскости Im А; > т, причем при |fc| —>> оо L+(k) стре-
стремится к нулю медленнее, чем А;2, а функция Ь-(к) — аналити-
аналитическая в нижней полуплоскости Im к < т+, равномерно стремя-
стремящаяся к нулю на бесконечности.
При выполнении этих условий непосредственной проверкой
легко убедиться, что уравнениям A36), A37) удовлетворяет
функция
где постоянная С определяется из условия
С = -L+(ia).	A40)
7Г
Действительно, подставляя в интеграл A36) первое из равенств
A39), замыкая контур интегрирования дугой полуокружности
бесконечно большого радиуса в верхней полуплоскости, инте-
интеграл по которой в силу леммы Жордана равен нулю, на осно-
основании A40) получаем, что интеграл A36) равен е~ах при х > 0.
Аналогично с помощью леммы Жордана, примененной к инте-
интегралу по дуге полуокружности бесконечно большого радиуса в
нижней полуплоскости, при х < 0 легко установить справедли-
справедливость A37) для функции /(&), определенной второй формулой
A39). Итак, решение рассматриваемой задачи связано с возмож-
возможностью представления A38). В данном случае функция L(k) =
= л/к2 + к2 в силу указанного выше выбора ветви корня явля-
является однозначной аналитической функцией, отличной от нуля
в полосе Im (гх) < Im к < — 1т(гх) Aт (гх) < 0). Рассмотрим
функцию
Ьк(к) = -7Ш= = ^2 + *\	A41)
Гъ \ /	/79	9	/79	9	^	'
V& + а	л/к2 + а2
Эта функция при а > — Im (гх) также является аналитической
и отличной от нуля в данной полосе, причем L{k) —>• 1 при \к\ —>•
—>> оо. Поэтому в силу леммы 2 требуемая факторизация функ-
функции !/(&), а следовательно, и Ь(к) возможна. Легко видеть, что
функции
Ь+(к) = ^ + ы L-(k) = V7h ~Ы	A42)
+v J к + ia '	v J к-га	v J
удовлетворяют всем поставленным требованиям. Тогда на осно-
основании формул A35), A39), A42) получим интегральное пред-

310
ПРИЛОЖЕНИЕ 2
ставление решения уравнения A34), удовлетворяющего услови-
условиям A32), A33) и убывающего при у —>• +оо, в виде
и(х
CXJ
с
/к + i>c (к — ia)
kx dk,
где постоянная С на основании A40), A42) равна
/га + гх.
с =
2тгг
A43)
A44)
Перейдя в A43), A44) к пределу при н —>> 0, получим интеграль-
интегральное представление решения исходной задачи
оо
у/к (к — га
2тг
ехр (-г^Ч
h'y+ik'x
/^?(kf -га)
-— dk' + ехр
оо
на/
e-ky+ikx
у/к (к — ia)
¦dk
A45)
Сделаем в первом интеграле A45) замену переменной интегри-
интегрирования, положив к' = —к. Так как
О	оо	оо
%/=F(fc'-w)
то A45) принимает вид
e~ky-ikx
у/к(к + га)
dk = е /
-ky-ikx
- га)
A46)
ехр (г^
оо	оо
Г e~ky-ikx	Г
if) / —=	dk + ехр (—г?) /
e~ky+ikx
у/к (к — ia)
dk
ехр (-if)
^-ky+ikx
у/к (к — ia)
Для вычисления интеграла A47) рассмотрим интеграл
J(a,p) =
V? (?
• A47)
A48)

МЕТОД ВИНЕРА-ХОПФА	311
Этот интеграл заменой переменной интегрирования ? + /3 = т\
может быть приведен к виду
J(a,/3)=e^J(a,/3),	A49)
где
ОО
[ ^.	A50)
Qa —	/ /Z	o^'l — ^	Л/ л,'	A51)
Интеграл A50) может быть вычислен с помощью дифференци-
дифференцирования по параметру 1):
оо
di
Так как
/3
то, проинтегрировав A51), получим
^^[(^], (Ш)
о
О	9
где Ф(^) = —= f e~x dx - функция ошибок. Отсюда
v п 0
J(a,C) =тг^[1-ф(^)].	A54)
Возвратившись к A47), получим
м(ж, у) = Re {e-a^ [l - Ф (V^)] } ,	A55)
где z = х -\- гу.
1) Вычисление интегралов с помощью дифференцирования по параметру
см. в вып. 2.

ПРИЛОЖЕНИЕ 3
ФУНКЦИИ МНОГИХ КОМПЛЕКСНЫХ ПЕРЕМЕННЫХ
Теория функций многих комплексных переменных, являю-
являющаяся естественным развитием теории функций одной комп-
комплексной переменной, в последнее время представляет значи-
значительный интерес благодаря эффективным применениям мето-
методов этой теории в различных областях естествознания, в част-
частности в квантовой теории поля. В настоящем приложении да-
дается краткий обзор основ теории функций многих комплексных
переменных.
1. Основные определения.
Будем рассматривать TV-мерное комплексное пространство
CN, точки которого z = B:1, ^2, • • •, zjsf) представляют собой упо-
упорядоченную совокупность комплексных переменных Zk = ж& +
+ гук- Комплексное пространство CN можно интерпретировать
как обычное евклидово пространство действительных перемен-
переменных жь уь ..., xn, yN размерности 2N. Поэтому понятия откры-
открытой и замкнутой области, внутренней, внешней и граничной точ-
точки, E-окрестности и т.д. вводятся так же, как и в теории функ-
функций многих действительных переменных 1). Так, E-окрестностью
точки 2° будем называть множество C(S,z®) точек z Е CN, удо-
удовлетворяющих условию
\zk-z°k\<Sk, k = l,2,...,N.
Под символом S = (#х, • • •, 5n) мы понимаем упорядоченную со-
совокупность действительных чисел дк > 0. Множество точек z E
Е CN, удовлетворяющих условию |^ — 2^| < г к (г к > 0) назы-
называется поликругом К (г, z°) радиуса г = (гх,..., гдг) с центром в
точке z° =
zi,..., z®N).
Функция w = f(z) = /(^x,..., zn) многих комплексных пере-
переменных z = (^х,..., zn), заданная на множестве EdCN, опре-
См. вып. 2.

ФУНКЦИИ МНОГИХ КОМПЛЕКСНЫХ ПЕРЕМЕННЫХ	313
деляется законом, ставящим в соответствие каждому значе-
значению z Е Е определенное комплексное число w E С1. Так как
комплексное число w представляет собой пару действительных
чисел и и v (w = и + iv), то задание функции f(z) на мно-
множестве Е С CN есть одновременное задание на соответствую-
соответствующем множестве 27У-мерного евклидова пространства двух дей-
действительных функций u(xi,yi,...,xN,yN), v(xi,yi,... ,xN,yN)
от 27V действительных переменных #i, yi,..., ждг, удг
f(z) = и(хъ ..., yN) + iv(xu • • •, Vn)-	A)
Функции и(х\,..., удг) и г;(жх,..., y^v) называются соответствен-
соответственно действительной и мнимой частями функции f(z).
Очевидно, что ряд понятий и свойств функций многих дей-
действительных переменных может быть перенесен и на функции
многих комплексных переменных. Так, функция f(z), заданная
на множестве Е С CN, непрерывна в точке z® E Е, по сово-
совокупности переменных z\,..., zjy, если для любого е > 0 можно
указать такое 5 = (?i,... ,?/v)j что для всех 2 E С(?,?°) имеет
место неравенство
|/(*)-/(*°)|<е.	B)
В дальнейшем функцию f(z), непрерывную по совокупности
переменных z\,..., zn, мы будем просто называть непрерывной
функцией.
Если функция f(z) непрерывна в каждой точке z E Е, то она
называется непрерывной на множестве Е. Справедлива
Теорема 1. Необходимым и достаточным условием непре-
непрерывности функции f(z) = u(xi,..., ум) + гг;(жх,..., удг) на
множестве Е С С^ является непрерывность по совокуп-
совокупности переменных действительных функций и(х\,... ,удг) и
v(xi,..., удг) 27V действительных переменных на соответ-
соответствующем множестве евклидова пространства размерно-
размерности 2N.
Свойства непрерывных функций одной комплексной пере-
переменной непосредственно переносятся на случай многих комп-
комплексных переменных. Так, равномерно сходящийся в области
G ряд непрерывных функций многих комплексных переменных
сходится к непрерывной функции.
2. Понятие аналитической функции многих комп-
комплексных переменных. Так же как и в случае одной комп-
комплексной переменной в теории функций многих комплексных пе-
переменных одним из основных понятий является понятие анали-
аналитической функции.
Пусть в области G С CN задана функция w = f(z) многих
комплексных переменных. Если мы фиксируем значения пере-

314	ПРИЛОЖЕНИЕ 3
менных z®,..., ^_l5 ^+15 • • •, ^дг, то получим функцию
fi(zi) — /(^1? • • • ^г-Ъ^Ь^г+Ъ • • • izn)
одной комплексной переменной ^, заданную в некоторой обла-
области Gi комплексной плоскости Z{. Пусть при любых фиксирован-
фиксированных значениях z\,..., ^_l5 ^+1,..., z®N каждая функция fi(zi)
(г = 1, 2,... , N) является аналитической функцией комплексной
переменной ^ ? Gj. В этом случае функцию f(z) будем назы-
называть аналитической по каждой переменной в области G. Про-
Производные fl(zi) функции fi(zi) по переменной Z{ будем называть
частными производными функции f(z) и обозначать через -^-.
UZi
Очевидно, что
dzi Az^O	Azi	У )
Частные производные -^- могут быть выражены через частные
UZi
производные функций u{xi,..., ум) и v{x\,...,
причем для них выполняются условия Коши-Римана
ди _ dv	ди _ dv	,~\
dxi dyi'	dyi	dxi
Введем теперь основное определение:
Функцию f(z) многих комплексных переменных z =
= Bi,...,2/v) будем называть аналитической1) в области G,
если в этой области функция f(z) аналитична по каждой пе-
переменной Zi, а все ее частные производные -^- непрерывны.
UZi
Аналитические функции многих комплексных переменных
обладают рядом замечательных свойств, подобных свойствам
аналитической функции одной комплексной переменной. Ниже
будет дан краткий обзор этих свойств, причем для простоты
изложения будем рассматривать случай двух независимых пе-
переменных. Для большего числа переменных все рассуждения со-
сохраняют силу.
1) Так же как и в случае одной комплексной переменной, мы с целью
облегчения последующих доказательств включили в определение аналити-
аналитической функции многих комплексных переменных лишнее условие непре-
непрерывности частных производных, что, однако, не сужает рассматриваемого
класса функций, как это следует из так называемой теоремы Гартогса (см.,
например, кн. : В. С. Владимиров. Методы теории функций многих
комплексных переменных. — М. : Наука, 1964).

	ФУНКЦИИ МНОГИХ КОМПЛЕКСНЫХ ПЕРЕМЕННЫХ	315
3. Формула Коши. Пусть f(z\,Z2) является аналитической
функцией в области G = G\ x G?2, причем области G\ и G2 явля-
являются односвязными. Возьмем в областях G\ и G% произвольные
замкнутые контуры С\ и С<2, соответственно и рассмотрим по-
повторный интеграл
i= [ль [ , sf?) c)dc2,	F)
J	J (zi -С1Д22 -C2)
Ci	C2
где z\ и Z2 — произвольные точки, лежащие внутри контуров С\
и С/2 соответственно.
Подынтегральная функция в F) непрерывна по совокупности перемен-
переменных, что является достаточным условием для возможности изменения по-
порядка интегрирования в данном повторном интеграле ). Следовательно,
Так как функция /(СъС2) аналитична по каж:дой перемен-
переменной, внутренний интеграл в F) в силу формулы Коши A.59)
равен
f (z ff\fz2)
J yz\ - Qi){Z2 -
Воспользовавшись еще раз формулой Коши, получим оконча-
окончательно
Ci	С2
что можно переписать в виде
Ci	С2
Аналогично в случае 7V переменных имеет место формула
-, (ю)
где точки Zk лежат внутри замкнутых контуров С&, принадле-
принадлежащих односвязным областям G&, и функция f(z) является ана-
:) См. вып. 2.

316	ПРИЛОЖЕНИЕ 3
литичной в области G = G\ х ... х Gjy. Формулы (9) и A0) и
представляют собой обобщения формулы Коши A.59) на случай
многих комплексных переменных.
Из этих формул можно получить ряд важных свойств ана-
аналитической функции многих комплексных переменных. В част-
частности, как и в случае одной комплексной переменной с помощью
формулы (9) можно показать, что аналитическая функция двух
комплексных переменных имеет частные производные всех по-
порядков, для которых справедливы выражения
<9n4
z2) _ п\т\ [„ [
4тГ2 J aU J
J
C2
Аналогично устанавливается справедливость принципа макси-
максимума модуля и т.д.
Соответствующие результаты получаются из формулы A0)
для аналитической функции многих комплексных переменных.
4. Степенные ряды. В случае двух независимых перемен-
переменных степенным рядом назовем выражение
C^m(zi ~ a1)n(z2 - o2)m,	A2)
n=0m=0
где Cn?m, ai, п2 — заданные комплексные числа. Имеет место
утверждение, аналогичное теореме Абеля (теорема 2.5).
Теорема 2. Если ряд A2) сходится абсолютно в точке z° =
= (zi т^ аЪ^2 7^ а2), то он абсолютно сходится внутри поли-
поликруга К(г°,а) радиуса r° = (\z\ — ai|, \z® — а2|), причем в любом
поликруге меньшего радиуса1) с центром в точке а ряд схо-
сходится равномерно.
Доказательство. В силу абсолютной сходимо-
сходимости ряда A2) в точке z® все члены ряда в этой точке равно-
равномерно ограничены. Поэтому имеет место оценка коэффициентов
ряда A2)
\С\ ^	5
с общей константой М для всех коэффициентов. Возьмем произ-
произвольную точку z = B:1, z^) внутри поликруга if(r°, a) и полож:им
где 0<^i<1,0<^2<1- Тогда, пользуясь оценкой A3), для
Будем говорить, что радиус г^ поликруга К^г^^а) меньше радиуса
« < г<,2)
, рду	ру ^
поликруга К{г^\ а), если rf' < г<2),..., г« < г<,2)

ФУНКЦИИ МНОГИХ КОМПЛЕКСНЫХ ПЕРЕМЕННЫХ	317
выбранной
(X (X
У^ У^ сп
п=0 т=0
ТОЧКИ
Z
- с
получим
(X) (X)
^ м У^ У^ g
п=0 т=0
?q^ =
что и доказывает сходимость ряда A2) в точке z.
Так как z — произвольная точка поликруга К(г®,а), то от-
отсюда следует абсолютная сходимость ряда A2) внутри К(г®,а).
Равномерная сходимость ряда A2) в любом поликруге К(г^\а)
меньшего радиуса доказывается с помощью A4) так же, как и в
случае одной комплексной переменной (теорема 2.5).
Доказанная теорема позволяет установить, что областью схо-
сходимости степенного ряда является поликруг K(R,a) радиуса
R = (Ri^R2). Внутри K(R,a) ряд A2) абсолютно сходится, вне
данного поликруга — расходится, в любой замкнутой подобла-
подобласти K(R,a) ряд A2) сходится равномерно. Отметим, что ради-
радиусы R\ и i?2 определяются совместно и не могут быть, вообще
говоря, определены каждый в отдельности.
В качестве примера рассмотрим степенной ряд
/(*) = ? Е {^**>	^
n=0 m=0
коэффициенты которого представляют собой биномиальные коэффициен-
коэффициенты. Так как внутри своего поликруга сходимости ряд сходится абсолютно,
то ряд с положительными членами
п=0 т=0
является сходящимся в поликруге сходимости ряда A5). Сгруппировав чле-
члены ряда A6), у которых сумма степеней п + т = s, получим
ОО
Ed^l + N)*'	A6')
s=0
откуда следует, что радиусы R\ и R2 поликруга сходимости ряда A5) опре-
определяются из условия Ri + R2 = 1, т.е. при уменьшении R\ значение R2
увеличивается и наоборот.
Рассмотрим ряд A2) внутри его поликруга сходимости
K(R,a). Воспользовавшись абсолютной сходимостью ряда,
сгруппируем те его члены, у которых сумма степеней п-\-т = «s,
в(*Ь*2).	A7)
s=0

318	ПРИЛОЖЕНИЕ 3
Выражение A7) дает представление исходного ряда в виде ряда
однородных полиномов относительно переменных z\ = z\ — ai,
h = ^2 — CL2
Ck,s-kZkiZS2-k.	A8)
Так как функции us(zi,Z2) являются аналитическими по
каждой переменной и ряд сходится равномерно внутри поли-
поликруга K(R,a), то в силу теоремы Вейерштрасса (теорема 2.3)
функция f(z) также является аналитической по каждой пере-
переменной внутри K(R,a), причем ее частные производные мож-
можно вычислить путем почленного дифференцирования ряда A7).
Как легко видеть, при этом радиус сходимости полученного ряда
равен радиусу сходимости ряда A2), и частные производные ^~
и —— непрерывны внутри K(R,a). Отсюда следует, что внутри
OZ2
поликруга сходимости степенной ряд A2) сходится к анали-
аналитической функции многих комплексных переменных.
Так же как и в случае одной комплексной переменной, легко
установить, что коэффициенты степенного ряда A2) выража-
выражаются через значения частных производных его суммы в центре
поликруга сходимости — точке а = (ai,a2) — по формулам
5. Ряд Тейлора. Покажем теперь, что функции, аналити-
аналитической в некотором поликруге K(R^aI может быть сопоставлен
степенной ряд, сходящийся к данной функции внутри K(R,a).
Имеет место
Теорема 3. Функция f{z), аналитическая внутри поли-
поликруга K(R,a), единственным образом представляется внутри
K(R,a) в виде суммы абсолютно сходящегося степенного ряда
(X) (X)
= Е Е Cw(zi - «i)n(^2 - a2)
п=0 т=0
Доказательство. Возьмем произвольную точку
z E K(R,a). По формуле (9) имеем
(^i^5)«- B0)
с; с;
где С[ и С2 — окружности с центрами в точках а\ и а2 ради-
радиусов R[ и i?f), удовлетворяющих условиям \z\ — а\\ < R[ < R\

	ФУНКЦИИ МНОГИХ КОМПЛЕКСНЫХ ПЕРЕМЕННЫХ	319
и \z2 — «2! < R*2 < i?2- Из предыдущих рассуждений следует,
что рациональная дробь —	—	 может быть разложе-
(Cl -^l)(C2 - Z2)
на в абсолютно и равномерно сходящийся относительно (д и B
степенной ряд
(Ci - ^i)(C2 - ^2)	(^ 1)(С2 2)
n=0m=0
Подставляя разложение B1) в B0) и повторно производя по-
почленное интегрирование соответствующих равномерно сходя-
сходящихся рядов, получаем
ОО ОО
/(*) = Е Е СпА*1 - «i)n(^2 - «2)m,	B2)
n=0 m=0
где через Cn?m обозначены выражения
что в силу A1) можно переписать в виде
B4)
г dn+mf{z)
!m!
Так как 2: — произвольная точка K(R, а), то из формулы B2)
и следует разложимость функции, аналитической в поликруге
^I в сходящийся степенной ряд.
Сопоставление формул B4) и A9) приводит к заключению
об единственности разложения. Теорема доказана.
По аналогии с результатами, полученными для функции од-
одной комплексной переменной (см. теорему 2.6), разложение B2)
естественно назвать рядом Тейлора функции f(z).
В заключение заметим, что радиус сходимости Д° ряда B2)
может оказаться больше радиуса R поликруга K(R,a). В этом
случае сумма этого ряда будет представлять собой функцию,
аналитическую в поликруге K(R°,a) и совпадающую с исход-
исходной аналитической функцией f(z) в поликруге K(R,a) меньше-
меньшего радиуса.
Проведенные рассмотрения непосредственно переносятся и
на случай многих комплексных переменных.
6. Аналитическое продолжение. Представление анали-
аналитической функции многих комплексных переменных с помо-
помощью степенного ряда позволяет, так же как и в случае одной

320	ПРИЛОЖЕНИЕ 3
комплексной переменной, выяснить вопрос об единственности
определения аналитической функции (см. теорему 2.8). Так, ес-
если в области G заданы две аналитические функции /1(^1,^2)
и /2(^1,^2M совпадающие в подобласти G1 области G, то лег-
легко показать, что /1(^1,^2) = /2(^1^2) при z = (^1,^2) ? G. На
основании этого положения можно в следующей форме ввести
Принцип аналитического продолжения. Пусть в областях
и G^2\ имеющих общую подобласть G^1'2), заданы аналити-
аналитические функции fi(z) и /2B), совпадающие в G^1'2). Тогда эти
функции являются аналитическим продолжением одна другой,
т.е. в области G = G^ + G^ существует единственная ана-
аналитическая функция f(z), совпадающая с fi(z) в G^ и /2B)
Так же как и в случае одной комплексной переменной, можно
строить аналитическое продолжение первоначально заданной в
некоторой области G^ аналитической функции fi(z) вдоль все-
всевозможных выходящих из области G^ цепочек областей, име-
имеющих попарно общие части.
Такое аналитическое продолжение можно, например, получить, разла-
разлагая функцию f(z) в степенной ряд Тейлора B2) в окрестности различных
точек z^%> G G^\ Если радиус поликруга сходимости какого-либо из этих
разложений окажется больше расстояния точки z^%> до границы области
G^x>, то мы и получим аналитическое продолжение f(z) на большую область
G, содержащую G^\
При этом мы приходим к понятию полной аналитической
функции F(z) и ее естественной области существования G, или,
как говорят, области аналитичности (или, как иногда говорят,
области голоморфности). Вообще говоря, аналитическое продол-
продолжение может привести и к многозначной функции, областью
аналитичности которой является некоторое неоднолистное мно-
многообразие, получающееся путем введения так называемых обла-
областей наложения 1).
В приложениях теории функций многих комплексных пере-
переменных, в частности в квантовой теории поля, существенным
оказывается вопрос, является ли заданная область G областью
аналитичности. Другими словами, найдется ли такая функция
f(z)j аналитическая в G, для которой область G является есте-
естественной областью существования. Если область G не является
областью аналитичности, то всякая аналитическая в G функция
:) Подробнее см. : В. С. Владимиров. Методы теории функций
многих комплексных переменных. — М. : Наука, 1964.

ФУНКЦИИ МНОГИХ КОМПЛЕКСНЫХ ПЕРЕМЕННЫХ
321
f(z) может быть аналитически продолжена на большую область
G*, содержащую область G.
Как мы видели (см. пример 4 § 2 гл. 3), в случае одной
комплексной переменной единичный круг \z\ < 1 является обла-
областью аналитичности. Пользуясь теоремой Римана о возможно-
возможности конформного отображения произвольной области на еди-
единичный круг, легко показать, что в случае одной комплексной
переменной всякая область есть область аналитичности.
В случае многих комплексных переменных данное утвержде-
утверждение уже не имеет места.
Чтобы это доказать, покажем, что уже в С область
G:{z = (zu z2): К \z\ = (|^|2 + \z2\2I'2 < 5}
не является областью аналитичности1). Для этого достаточно
доказать, что всякая функция, аналитическая в G, может быть
аналитически продолжена в большую область G*, содержащую
G, например в шар \z\ < 5.
Итак, пусть f(z) — произвольная функция, аналитическая в
G. Рассмотрим функцию
<p(z) =<p(zuz2) = ^- I
B5)
ldl=4
Функция <p(z) представляет собой интеграл, зависящий от пере-
переменных z\ и Z2 как от параметров. Подобласть {|(д| = 4, \z<i\ < 3}
принадлежит G (рис. 1). Поэтому
функция <p(z) является аналити-
аналитической по каждой переменной z\ и
Z2 в поликруге К : \\z\\ < 4, \z2\ < 5
Легко видеть, что частные
производные функции cp(z) при
этом непрерывны. Отсюда следу-
следует, что в поликруге К : {\z\\ <
< 4; 1^21 < 3} функция (f(z) яв-
является аналитической функцией
двух комплексных переменных z\
и Z2- В частности, (f(z) являет-
является аналитической и в замкнутой
4 5
Рис. 1
) Данный пример является незначительной модификацией примера, рас-
рассмотренного в книге С. Бохнера и У.Т. Мартина «Функции многих комп-
комплексных переменных». — М. : ИЛ, 1951. См. также В. С. Владимиров.
Методы теории функций многих комплексных переменных. — М. : Наука,
1964.

322	ПРИЛОЖЕНИЕ 3
области G :{|^i|^4,l^|^2|^3}, принадлежащей одновремен-
одновременно полукругу К и исходной области G. В силу формулы Коши
A.59) в G' имеет место равенство
f{CuZ2)dA=f(z1,z2).	B6)
2тг1 J
Ц1 - 2l
ldl=4
Отсюда следует, что в G1 аналитические функции f(z) и (f(z)
совпадают. Тем самым в расширенной области G* (шаре \z\ <
< 5), содержащей исходную область G, определена аналитиче-
аналитическая функция F(z), равная f(z) в G и (f(z) в К, являющаяся
аналитическим продолжением f(z) в G*. Что и требовалось до-
доказать.
Итак, в случае многих комплексных переменных не всякая
область является областью аналитичности. Этот факт суще-
существенно отличает теорию функций многих комплексных пере-
переменных от теории функций одной комплексной переменной.

ПРИЛОЖЕНИЕ 4
МЕТОД ВАТСОНА
Метод Ватсона применяется главным образом при суммиро-
суммировании и асимптотическом анализе рядов. Первоначально этот
метод был предложен Г.Н. Ватсоном в 1919 г. при исследовании
задачи о дифракции радиоволн на сфере. Методом разделения
переменных легко получить аналитическое представление реше-
решения этой задачи в виде ряда по собственным функциям. Однако
при длине падающей волны, многим меньшей радиуса сферы,
что имеет место, например, в задачах о дифракции радиоволн на
поверхности Земли, полученный ряд сходится чрезвычайно мед-
медленно. Ватсону удалось разработать метод, позволяющий пре-
преобразовать этот медленно сходящийся ряд в другой ряд, сходя-
сходящийся достаточно быстро. Этот метод и получил впоследствии
название метода Ватсона.
Основная идея метода Ватсона необычайно проста и основы-
основывается на том факте, что при вычислении интеграла по комп-
комплексной переменной с помощью теории вычетов можно, различ-
различным образом замыкая контур интегрирования, получать пред-
представление исходного интеграла в виде различных рядов. Однако,
несмотря на простоту основной идеи метода Ватсона, его реали-
реализация во многих конкретных случаях требует большого искус-
искусства.
Проиллюстрируем основные положения метода Ватсона на
достаточно простых примерах1). Пусть требуется просуммиро-
просуммировать ряд
S=
п= — оо
где а — некоторое положительное число.
г) Приведенные ниже примеры применения метода Ватсона были пред-
предложены С. Я. Секерж-Зеньковичем, которому авторы приносят
искреннюю благодарность.

324
ПРИЛОЖЕНИЕ 4
Заметим, что при а ^> 1 численное суммирование ряда A) с
высокой точностью представляет собой не совсем тривиальную
задачу.
Рассмотрим вспомогательный интеграл
7 = 1 f -L-
2г J v2 + а2
B)
где интегрирование производится на комплексной плоскости v
по прямым ?+ и ?~, параллельным действительной оси и от-
отстоящим от нее на расстоянии d в верхней и нижней полуплос-
полуплоскостях, причем d < а (рис. 1). По прямой ?+ интегрирование
Im v
с;
Rev
-ia
Рис. 1
ведется справа налево, а по прямой С~ — в противоположном
направлении. Несобственный интеграл B) является абсолютно
сходящимся. Действительно, имеет место очевидная оценка
C)
SHITTY
\l-e-
Im v=q
Аналогичная оценка имеет место и при Im^ = —d. Итак вто-
второй сомножитель в подынтегральной функции B) ограничен, а
первый стремится к нулю, как l/|z^|2, что и обеспечивает абсо-
абсолютную сходимость интеграла B).
Покажем, что интеграл B) равен сумме исходного ряда A).
Построим вспомогательный интеграл
N ~ 2i J v2 + a2 sin тг
¦ dv
D)

МЕТОД ВАТСОНА
325
по замкнутому контуру Гдг, составленному из отрезков
прямых СЛ и С~ между точками
и C
N
А? =
N
+\,d), A»=(-N-\,d), A»=(-N-\,-d),
соответственно и соединяющих их вертикальных отрезков
Jn(A^А^) и ^^(А^А^) (рис. 1). Внутри области, ограничен-
ограниченной контуром Гдг, подынтегральная функция D) имеет полюсы
первого порядка в точках v^ = к (к = 0, ±1,... , ±N). Поэтому,
вычисляя интеграл D) с помощью теории вычетов, получим
N	.^	N
Выч [i?hfi ?Ь*к]= E
k=-N	k=-N
откуда следует, что сумма S ряда A) равна lira /
N
= Ч Е
С другой стороны, предел интеграла /дг при N —>> оо равен
интегралу B). Действительно, в силу абсолютной сходимости
несобственного интеграла B) имеем
lira
— /
2г J
dv = /,
а интегралы по прямым 7дг и 7tv стремятся к нулю при N
что легко установить на основании оценки
_ — тг Im v
SHITTY
7iv
Итак
sin7r(Re v + zlm
s =
сЬ(тг1т v)
= i,
F)
оо,
G)
(8)
и исходная задача суммирования ряда A) сводится к вычис-
вычислению интеграла B). Последняя задача может быть решена
опять с помощью теории вычетов. Заметим, что подынтеграль-
подынтегральная функция в B), кроме особых точек на действительной оси,
имеет еще два полюса в точках v = zbia. Для вычисления ин-
интеграла по прямой ?+ рассмотрим в верхней полуплоскости за-
замкнутый контур Cjv, состоящий из отрезка С^ и замыкающей
его дуги полуокружности C'N. Легко видеть, что при Im v ^ d
имеет место оценка, аналогичная C)
Im

326
ПРИЛОЖЕНИЕ 4
откуда следует, что интеграл по дуге C'N стремится к нулю при
N —>> оо. Поэтому, вычисляя интеграл по прямой ?+ с помощью
теории вычетов, получим
1
Аналогично
откуда
27гго Г
= -—-Выч
2г	\_
1
ъ>2 + a2 shittz/
1
. 1
,га =
J
тг е
2m sin гтга 2а sh тга'
1_
2г
+ а2 sm7rv
не-
неa2 sin тп/
A1)
A2)
?++?-
что и решает исходную задачу суммирования ряда A).
Рассмотренный пример, несмотря на его простоту, содержит
все основные элементы метода Ватсона. Этот метод асимпто-
асимптотического исследования рядов состоит из ряда этапов. На пер-
первом этапе надо построить интеграл по комплексной переменной,
равный сумме исходного ряда. Подынтегральная функция этого
интеграла должна содержать множителем аналитическое про-
продолжение общего члена ряда в комплексную плоскость его но-
номера. Следующий этап заключается в независимом вычислении
построенного интеграла. Во многих случаях удается получить
выражение искомого интеграла через сумму вычетов подынте-
подынтегральной функции в особых точках аналитического продолже-
продолжения общего члена ряда. Если число таких особых точек конечно,
то мы получаем явное выражение для суммы исходного ряда, ес-
если число этих особых точек бесконечно, то мы преобразуем ис-
исходный ряд в новый, который может оказаться более простым
для асимптотического исследования.
В качестве следующего примера рассмотрим задачу вычис-
вычисления ряда
оо
71 = 1
где 0^#<тг,аа — заданное положительное число, удовлетво-
удовлетворяющее условию a<Cl. Ряд A3) является типичным для многих
задач математической физики, решение которых строится мето-
методом разделения переменных. Как легко видеть, в силу условия
а <^ 1 большое число первых членов ряда имеет один и тот же

МЕТОД ВАТСОНА
327
порядок (например, при а = 10 4 и # = 0 первые 1000 членов ря-
ряда по абсолютной величине изменяются от 1 до 0,995). Поэтому
прямое численное суммирование ряда A3) при а<^1 оказывает-
оказывается весьма затруднительным. Однако, применяя метод Ватсона,
можно преобразовать ряд A3) в новый ряд, для которого легко
получить асимптотическое представление при а <С 1.
Рассмотрим вспомогательный интеграл
A4)
ch av sin vtt
где контур интегрирования П на комплексной плоскости v пред-
представляет собой бесконечную петлю, охватывающую положитель-
положительную часть действительной оси (рис. 2) и пересекающую действи-
Im v
Рис. 2
тельную ось в точке v = 1/2. Интегрирование по контуру П про-
производится в положительном направлении так, что действитель-
действительная ось остается слева от направления движения. Легко видеть,
что интеграл A4) равен исходному ряду A3). Действительно,
рассмотрим интеграл
Ue) = ±
ch аи sin z/тг
dv
A5)

328	ПРИЛОЖЕНИЕ 4
по замкнутому контуру Пп, состоящему из конечного участка
петли П и замыкающего его вертикального отрезка А\Аъ^ пе-
пересекающего действительную ось в точке v = п + -. Подынте-
Подынтегральная функция f(y) в A5) является аналитической функци-
функцией комплексной переменной v внутри контура интегрирования,
за исключением конечного числа изолированных особых точек
V{ = г (г = 1,2, ...,п), представляющих собой полюсы первого
порядка. Поэтому, применяя теорему в вычетах, получим
k=l
Оценим значение функции f(u) в A5) на отрезке А1А2. Так как
на этом отрезке Re v = n + 1/2, то, воспользовавшись соотно-
соотношением
8т^7г|Кег/=п+1/2 = sinBn + 1)|сп(тг1т v) +
+ ish (тг1т v) cos Bn + 1)^ = (—l)n ch (тг1т z/), A7)
получим
| smv7r\A1A2 = сЬ(тг1т v).	A8)
Имеет место очевидная оценка
откуда
рв|1т1"	IT~""- m-	B0)
е
ch (тг Im i/)
С другой стороны, очевидно,
> |l e|e\
В силу B0) и B1) подынтегральная функция в A5) на от-
отрезке А\А2 экспоненциально убывает при п —>• оо. Поэтому, пе-
переходя к пределу при п —)> оо в выражении A5), получим
B2)
fc l
что и доказывает равенство исходного ряда A3) интегралу A4).
Перейдем теперь к вычислению интеграла A4). Для этого
аналитически продолжим подынтегральную функцию A4) на
всю комплексную плоскость v и определим особые точки функ-
Лч cos i/9	п А
V) =	 вне петли 11. Очевидно, таковыми явля-
ch olv sin i/тг
ются точки vn = п (п = 0, —1, —2,...), v^ = г — Bк + 1)- (к = 0,
±1,±2,...), причем все эти точки — полюсы первого порядка.

МЕТОД ВАТСОНА	329
Заметим, кроме того, что подынтегральная функция f{y) явля-
является нечетной функцией комплексной переменной v.
Построим на комплексной плоскости v замкнутый контур
Гп,ш5 состоящий из конечного участка Пп петли П между точ-
точками А\ и ^2 (см. рис. 2), прямолинейных отрезков
f	(	\\	Г	(
A7Ai |Л7 = (п + |' Ш * ) } и контУРа А^А5А6А7, пред-
представляющего собой прямолинейный отрезок А^А7 с обходом точ-
точки v = 0 по дуге полуокружности достаточно малого радиуса р.
Рассмотрим интеграл
! /"	B dv,	B3)
/
2г у chai/sini/тт
где интегрирование производится в отрицательном направле-
направлении. Очевидно,
т	Л
[/(!/), 0] +J]BbI4 [/(!/), 1/Л] .	B4)
/с=0	J
С другой стороны (см. рис. 2),
АА	Аз	А2
+ J f{y) dv + J /A/) rfi/ + J /A/) rfi/ + J /H rfi/j. B5)
C~	M	M	A3
В силу нечетности функции f(u)
Aq	Aa
f f{y)dv+ f f(u)du = 0.	B6)
A7	A5
Кроме того, очевидно,
lim
/COSZ/0	7	•	/от\
	.	dv = -%. B7)
en olv sin z/тг
Оценим оставшиеся интегралы. В силу проведенных выше оценок
(см. формулы B0), B1)) функция f(v) экспоненциально стре-
стремится к нулю при п —)> оо на отрезках А\А7 и А3А2. Для оценки
функции f(v) на отрезке А%А/± заметим, что аналогично A7)
|chai/|Imi/=m7r/a = ch(aRe v) > 1.	B8)

330	ПРИЛОЖЕНИЕ 4
Кроме того, очевидно,
| COS v6\im „=т1г/а ^ ехР i^0) >	B9)
а
I sin^Trlj -	> -II — е-2т7т2/а\еттг2/а > ^gm
~~ '	2	4
Из B9) и C0) получим
COSZ/0
<4ехр \-^(ъ-в)\.	C1)
Im 1У=тп7г/а	la	J
В силу B8) и C1) заключаем, что функция f(u) на отрезке А3А4
экспоненциально стремится к нулю при m —>• 00 и б < тг.
Переходя в B5) к пределу при п, га —)> оо и р —)> 0 и учтя B4)
и A5), получим в силу приведенных оценок
W - \ = -к \ Выч [/И, 0] + f; Выч [/(i/), 1/Л] 1 . C2)
Так как
Выч Г cos^	1 = 1	C3)
L en olv sin i/тг J тг
и
Г6»7Г/Л7
Вш[- ,i,Stl|iUH!!>!q, C4)
[	j
то окончательно получим
1{в) = F{6) = ~\ + l Е(-1)"Ч^	Г C5)
/с=0	sh |^Bfc + l)
Очевидно, члены ряда C5) имеют асимптотический порядок
ехр — — ik + -1 (тг — в)\ при а —)> 0, что и обеспечивает бы-
быструю сходимость ряда C5) при в < тг. При достаточно малом а
для практических расчетов можно ограничиться лишь первыми
членами этого ряда.
Следует подчеркнуть, что конкретные применения метода
Ватсона в каждом отдельном случае могут быть различными —
по-разному можно строить интеграл, эквивалентный исходному
ряду, различными способами можно проводить его вычисление.
Наиболее эффективный путь реализации метода в каждом кон-
конкретном случае должен выбираться, исходя из специфики ис-
исследуемого ряда.

СПИСОК ЛИТЕРАТУРЫ
1.	Бицадзе А. В. Основы теории аналитических функций комп-
комплексного переменного. — М. : Наука, 1972.
2.	Привалов И. И. Введение в теорию функций комплексного
переменного, изд. 11. — М. : Наука, 1967.
3.	Лаврентьев М. А., Шабат Б. В. Методы теории функций
комплексного переменного. — М. : Физматгиз, 1972.
4.	Маркушевич А. И. Теория аналитических функций. — М. :
Гостехиздат, 1950.
5.	Смирнов В. И. Курс высшей математики. Т. 3, ч. 2 (изд. 9). —
М. : Наука, 1967.
6.	Стоилов С. Теория функций комплексного переменного /Перев.
с рум. — М. : ИЛ, 1962.
7.	Голузин Г. М. Геометрическая теория функций комплексного
переменного. — М. : Наука, 1966.
8.	Курант Р. Геометрическая теория функций комплексной перемен-
переменной /Перев. с нем. — М. : ОНТИ, 1934.
9.	Тихонов А. Н., Самарский А. А. Уравнения математической
физики. — М. : Наука, 1972.
10.	Морс Ф. М., Фешбах Г. Методы теоретической физики /Перев.
с англ. - М. : ИЛ, 1958.
11.	Диткин В. А.,Прудников А. П. Интегральные преобразо-
преобразования и операционное исчисление. — М. : Физматгиз, 1961.
12.	Ван-дер-Поль Б., Бремер X. Операционное исчисление на
основе двустороннего преобразования Лапласа /Перев. с англ. — М. :
ИЛ, 1952.

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Алгебраическая форма комплексно-
комплексного числа 14
Алгебры основная теорема 154
Аналитическая функция, существо-
существование производных всех порядков
58
Аналитических функций свойства
36
Аналитическое продолжение 99
	 непосредственное 115
	с действительной оси 83
	соотношений 87
	с помощью степенных рядов 108
	через границу 102, 103
Аналитической функции нули 79
	особые точки 111
	риманова поверхность 96, 101
	теорема единственности 79
Аргумент комплексного числа 15
Асимптотическая формула полино-
полиномов Лежандра 278
	функций Ханкеля 277
Асимптотическое разложение 262
	гамма-функции 272
	функции Хопфа 302
Бесконечнолистная функция 97
Ватсона метод 323
Вейерштрасса признак 64
Ветвления точка 32
Ветвь многозначной функции 31
Винера-Хопфа, метода общая схема
293
Вычет 128
Вычет логарифмический 150
—	— относительно бесконечно уда-
удаленной точки 131
Вычетов сумма на полной комплекс-
комплексной плоскости 127
—	теории, основная теорема 130
Вычисление интегралов с помощью
вычетов 133
Вычисление интегралов от много-
многозначных функций 144
Вычитание комплексных чисел 14
Гамма-функции асимптотическое
разложение 272
Гармонической и аналитической
функций связь 193
Геометрическая	интерпретация
комплексных чисел 15
	функции комплексной перемен-
переменной 25
Геометрический смысл производной
37
Граница области 24
Даламбера признак 62
Двуугольника отображение 179
Действительная ось 15
—	часть комплексного числа 13
Действия над комплексными числа-
числами 13
Деление комплексных чисел 14
Дирихле задача 196
	для круга 197
	полуплоскости 198
Дифракция на плоском экране 306
Дифференцирование изображения
234
Естественная область существова-
существования полной аналитической функ-
функции 115
Жордана лемма 138
Извлечение корня из комплексного
числа 17
Изображение по Лапласу интеграла
231
—	производной 230
—	свертки 232

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
333
Изображение функции 224
Инверсия 29
Интеграл Дюгамеля 256
—	контурный 44, 261
—	Коши 52
—	неопределенный 47
—	несобственный 43
—	по комплексной переменной 41
—	Шварца-Кристофеля 183
—	элиптический 191
Интеграла главное значение 53
—	изображение 231
—	Меллина вычисление 244, 249
—	по комплексной переменной свой-
свойства 42
Интегралы, зависящие от параметра
56
—,	несобственные 69
Интегральные уравнения с ядром,
зависящим от разности аргумен-
аргументов 281, 288, 297
Интегрирование изображения 234
Источник 204
Классификация изолированных осо-
особых точек 120
Комплексная переменная 23
—	плоскость 15
	полная 22, 28
Комплексное число 13
Комплексного числа алгебраическая
форма 14
	аргумент 15
	модуль 15
	показательная форма 16
	тригонометрическая форма 16
Комплексно-сопряженные числа 14
Комплексный потенциал течения
201
	электростатического поля 212
Комплексных чисел вычитание 14
	геометрическая интерпретация
15
	 деление 15
	 последовательность 19
	 равенство 13
	сложение 13
	умножение 14
Контур замкнутый 44, 261
Конформное отображение 39, 155
	в бесконечно удаленной точке
159
	, взаимно однозначное соответ-
соответствие 163
	второго рода 159
	, основные принципы 163
Конформное отображение, принцип
симметрии 166
	, соответствия границ 164
Коши критерий равномерной сходи-
сходимости 64
	сходимости последовательности
21
—	признак 62
Критерий Коши равномерной сходи-
сходимости ряда 64
	сходимости последовательности
21
Круг сходимости 72
Лапласа изображение функции 224
—	метод асимптотических разложе-
разложений 264
Лемма Жордана 138
Линейная функция 28, 159
Линия тока 201
Листы римановой поверхности 101
Логарифмический вычет 150
Лорана ряд 116
Максимума модуля принцип 53
Меллина интеграла вычисление 244,
249
—	формула 238
Метод Винера - Хопфа 281, 293
—	Лапласа 264
—	наибыстрейшего спуска 264
—	перевала 259
Милна уравнение 298, 302
Мнимая единица 14
—	ось 15
—	часть комплексного числа 13
Многих переменных ряд степенной
316
Многих переменных ряд Тейлора
318
	функция аналитическая 314
	непрерывная 313
Множество значений независимой
переменной 23
	функции 24
Модуль комплексного числа 15
Наибыстрейшего спуска метод 264
	 направление 274
Необходимое и достаточное условие
аналитичности функции 35, 194
	аналитичности сходимости
последовательности 21
	числового ряда 62
Непрерывность функции в бесконеч-
бесконечно удаленной точке 27

334
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Непрерывность функции в точке 27
	на множестве 27
Неравенства треугольника 16
Нули аналитической функции 79
Область 23
Область замкнутая 24
—	неограниченная 24
—	ограниченная 24
Обтекание кругового цилиндра 207
—	произвольного замкнутого конту-
контура 208
Обхода полной границы области по-
положительное направление 46
Окрестность точки 20
Операционный метод 252
Оригинал-функция 224
Основная теорема теории вычетов
130
Остаток ряда 61
Отображение конформное 39, 155
	в бесконечно удаленной точке
159
	второго рода 159
Отображение элементарных функ-
функций 94
Отражение зеркальное 29
Первообразная функция 48
Перевала метод 272
Плоское потенциальное течение
жидкости 200
—	электростатическое поле 211
Плотность распределения заряда
215
Поверхность Римана 96
Показательная форма комплексного
числа 16
Поле бесконечного плоского конден-
конденсатора 217
Полная комплексная плоскость 22,
28
Положительное направление обхода
контура 44
	полной границы области 46
Полюс 122
Порядок нуля аналитической функ-
функции 79
Последовательность комплексных
чисел 19
—	неограниченно возрастающая 21
—	ограниченная 20
Постоянства растяжений свойство
39
Потенциал комплексный течения
201
Потенциал комплексный электро-
электростатического поля 212
Поток вектора скорости 202
Предел последовательности 19
—	функции 26
Предельное значение функции в бес-
бесконечно удаленной точке 27
Преобразование Лапласа 221
—	Фурье 282
	, аналитические свойства 286
	обратное 287
—	Хевисайда 224
Признак Вейерштрасса 64
—	Даламбера 62
—	Коши 62
Принцип максимума модуля 53
—	минимума модуля 55
Продолжение аналитическое 99
Производная функция, геометриче-
геометрический смысл 37
	комплексной переменной 33
Производной изображение по Ла-
Лапласу 230
Равенство комплексных чисел 13
Равномерная сходимость ряда 63
Радиус сходимости 72
Резольвента 283
Римана поверхность 96, 101
Ряд Лорана 116
—	равномерно сходящийся 63
—	степенной 70
—	Тейлора 75
—	функциональный 63
—	числовой 61
Свертки изображение по Лапласу
232
Свойства аналитических функций
36
—	изображения 228
—	интеграла по комплексной пере-
переменной 42
—	непрерывных функций 28
—	равномерно сходящихся рядов 65
—	элементарных функций 91
Свойство постоянства растяжений
39
—	сохранения углов 39
Сила воздействия потока на обтека-
обтекаемое тело 210
Система решений фундаментальная
252
Сложение комплексных чисел 13
Сохранения углов свойство 36
Среднего значения формула 53

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
335
Степенная функция 108
Степенные ряды 70
Сток 204
Сумма ряда функционального 63
	 числового 61
Существенно особая точка 123
Существование производных всех
порядков у аналитической функ-
функции 58
Таблица изображений 236
—	свойства изображений 236
Тейлора ряд 75
Теорема Абеля 71
—	Вейерштрасса 66
	 вторая 68
—	Гаусса 213
—	единственности аналитических
функций 79
—	Жуковского 211
—	запаздывания 228
—	Коши 45
	, вторая формулировка 45
	для многосвязных областей 46
—	Лиувилля 59
—	Морера 59
—	основная алгебры 154
	теории вычетов 130
—	Римана 168
—	Руше 153
—	смещения 235
—	Сохоцкого - Вейерштрасса 124
—	Тейлора 75
Точка бесконечно удаленная 21
—	вихревая течения 204
—	внешняя 23
—	внутренняя 23
—	граничная 23
—	особая 111
	бесконечно удаленная 125
	 изолированная 120
	устранимая 121
—	правильная 111
—	разветвления 32
—	существенно особая 123
Точки критические течения 208
—	седловые поверхности 263
Тригонометрическая форма комп-
комплексного числа 15
Тригонометрические функции 40, 84
Трубка тока 201
"Уравнение Милна 298
Условия Коши-Римана 33
—	существования изображения 221
	оригинала 241
Факторизация 291, 293
Формула вычисления вычета 130
	коэффициентов степенного ря-
ряда 72
—	Коши-Адамара 73
—	Меллина 238
—	среднего значения 53
—	Стирлинга 262
—	Чаплыгина 210
—	Эйлера 16, 92
Функции Бесселя 251
—	геометрическая интерпретация 25
—	гиперболические 85
—, множество значений 24
—	предел 26
—	производная 33
—	тригонометрические 40, 84
Функция аналитическая в замкну-
замкнутой области 111
	 области 35
	многих комплексных перемен-
переменных 88, 312
	многозначная 101
	 полная 114
—	бесконечнолистная 97
—	гармоническая (связь с аналити-
аналитической) 193
—	дробно-линейная 171
	, круговое свойство 173
—	единичная Хевисайда 226
—	Жуковского 181
—	источника задачи Дирихле 199
Функция комплексной переменной
23, 25
—	логарифмическая 49, 92, 107
—	мероморфная 142
—	многозначная 25
—	обратная 25, 36
—	однолистная 25
—	степенная 108
—	целая 81
Хевисайда единичная функция 226
—	преобразование 224
Целая функция 81
Циркуляция вектора скорости 202
Число нулей и полюсов аналитиче-
аналитической функции 151
Чисто мнимое число 14
Элемент полной аналитической
функции 115

Учебное издание
СВЕШНИКОВ Алексей Георигиевич
ТИХОНОВ Андрей Николаевич
ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
Серия «Курс высшей математики и математической физики»
Редакторы: С. Я. Секерснс-Зенькович, Д.А. Миртова
Оригинал-макет: О.Б. Широкова
ЛР №071930 от 06.07.99
Подписано в печать 20.04.04. Формат 60x90/16
Бумага офсетная №1. Печать офсетная.
Усл. печ. л. 21. Уч.-изд. л. 19,15. Заказ №
Издательская фирма «Физико-математическая литература»
МАЙК «Наука/Интерпериодика»
117864 Москва, Профсоюзная ул., 90
E-mail: fizmat@maik.ru, fmlsale@maik.ru
http://www.fml.ru
Отпечатано с готовых диапозитивов в ПФ «Полиграфист»
160001, г. Вологда, ул. Челюскинцев, 3
Тел.: (8172) 72-55-31, 72-61-75, факс: (8172) 72-60-72
E-mail: form.pfp@votel.ru http://www.vologda/~pfpv