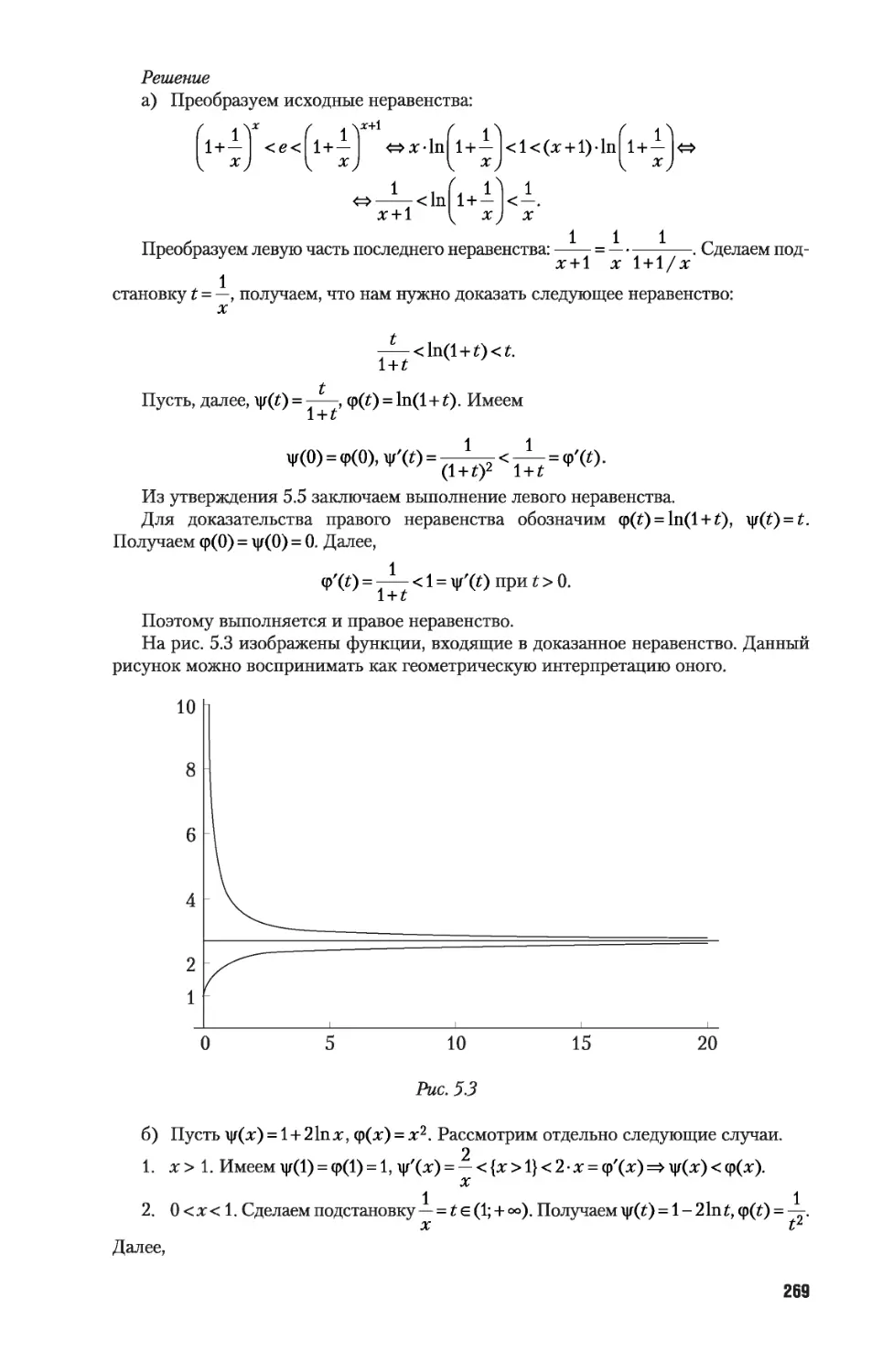
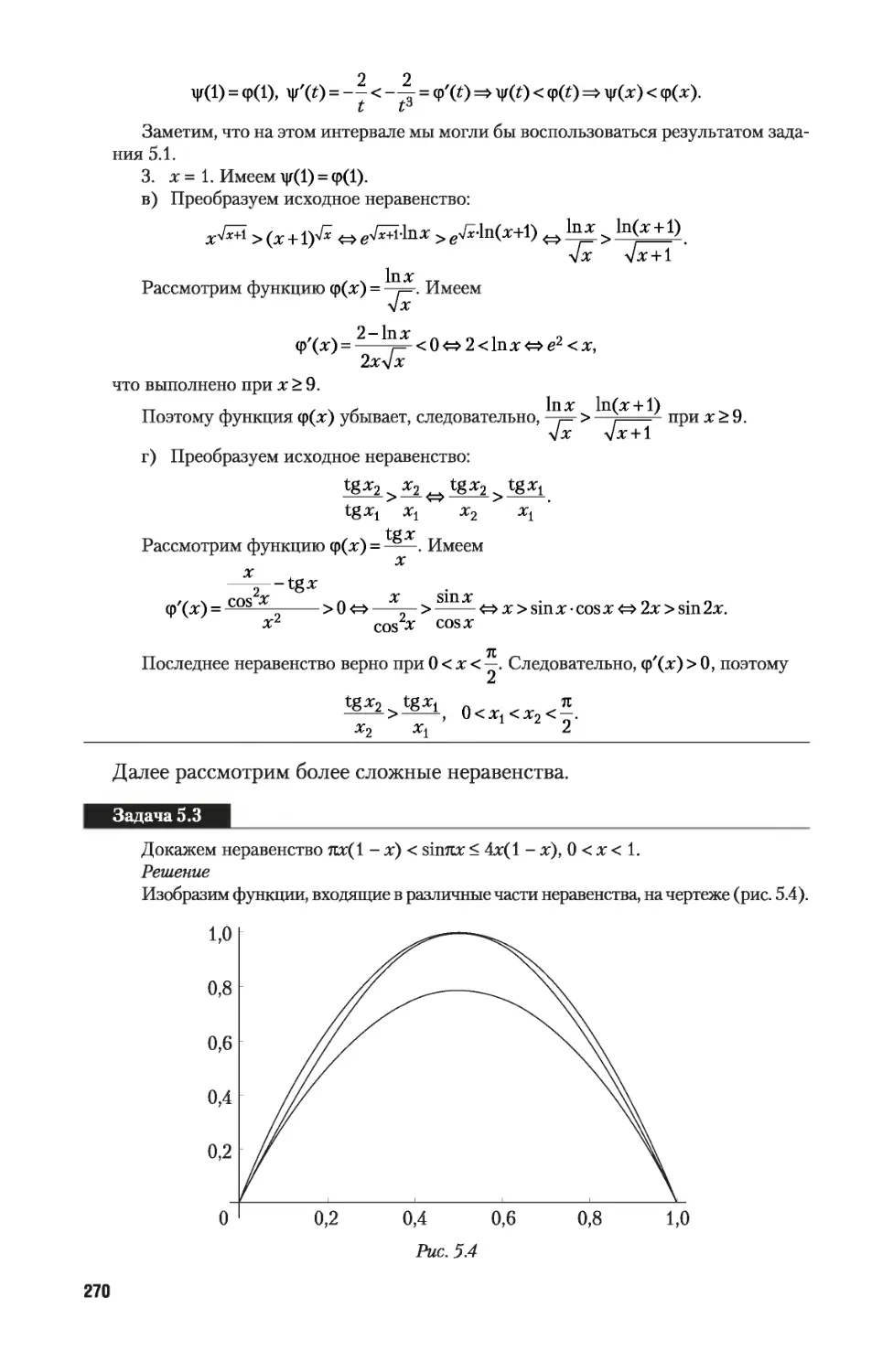
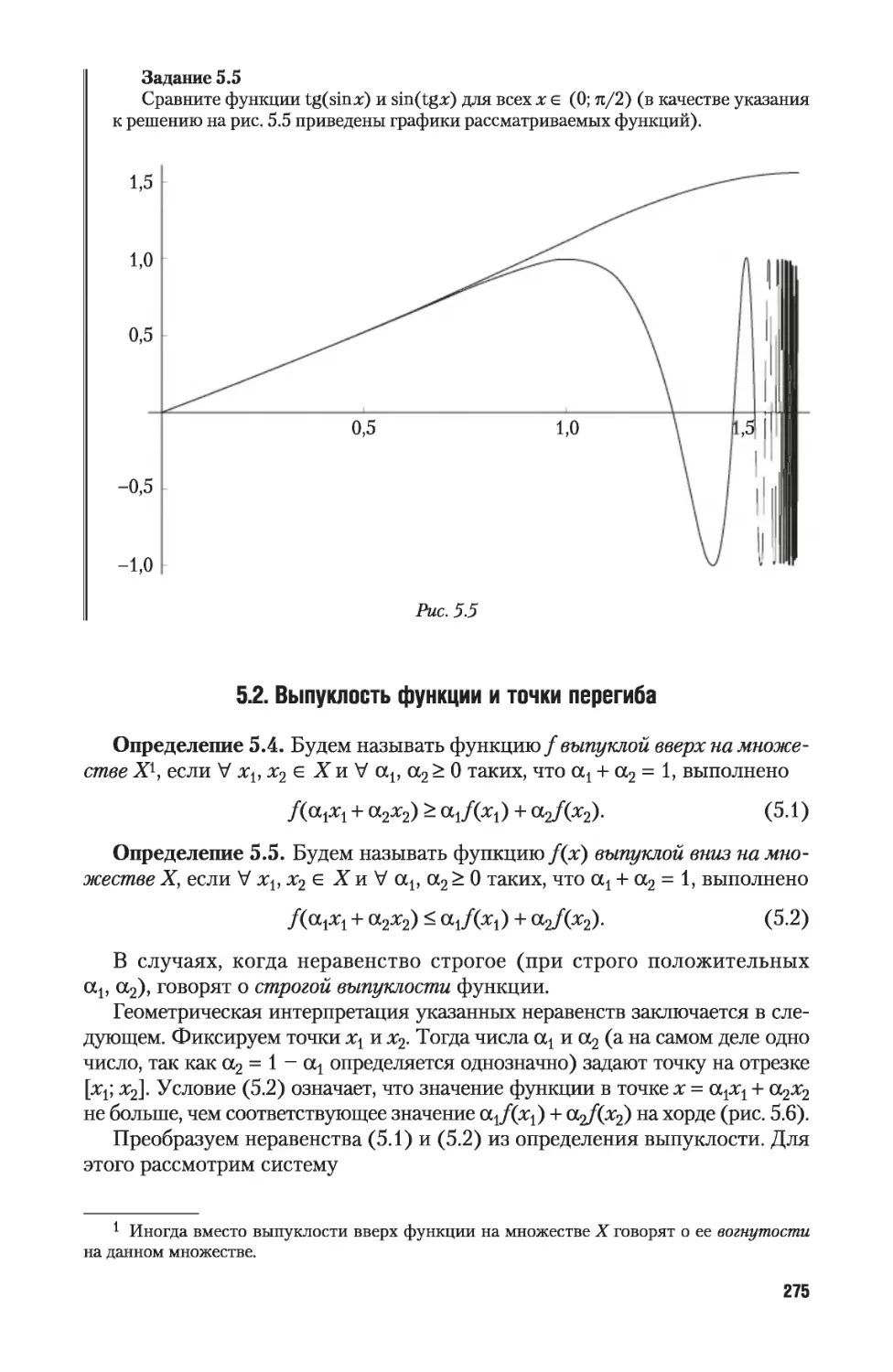
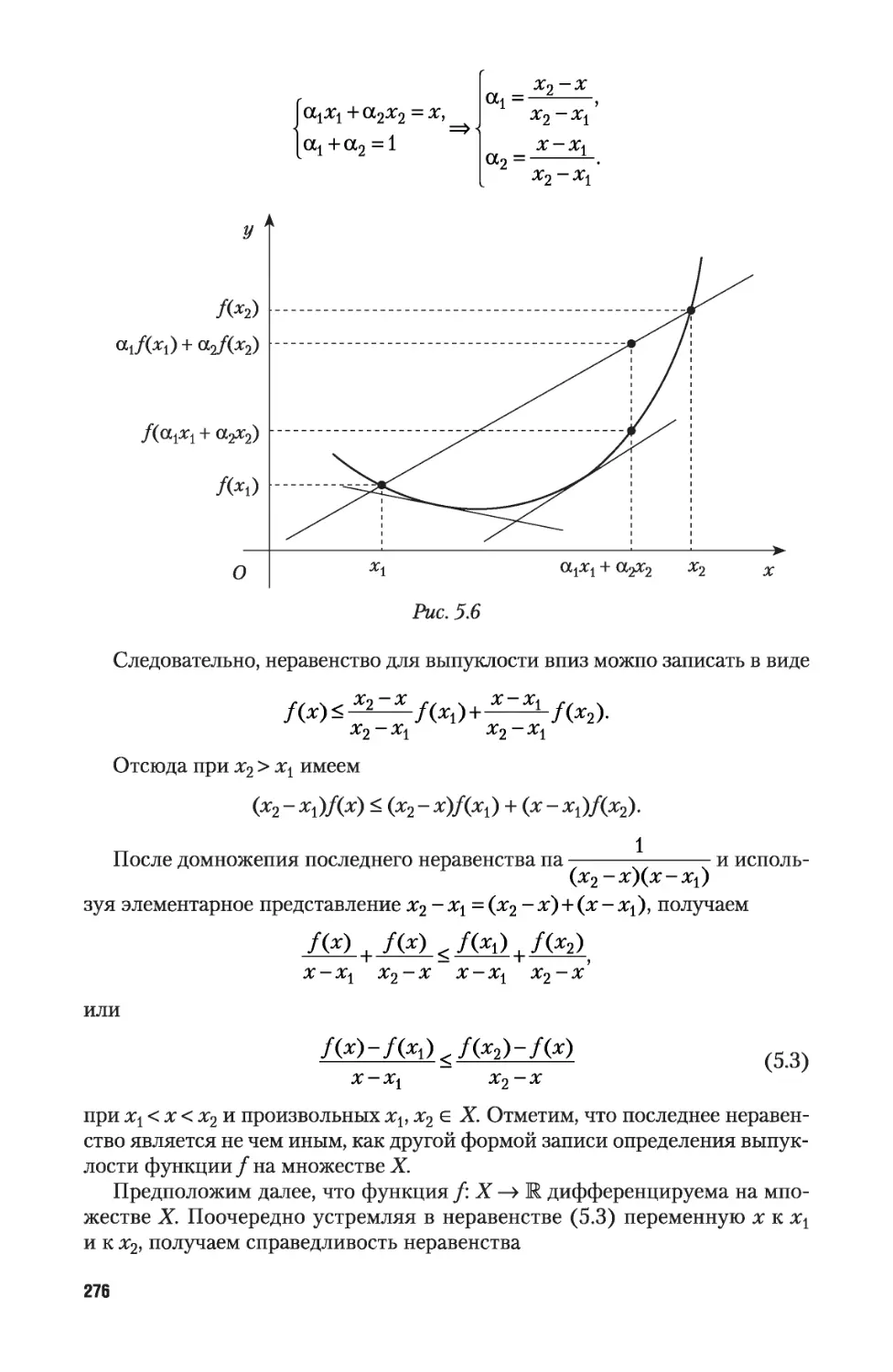
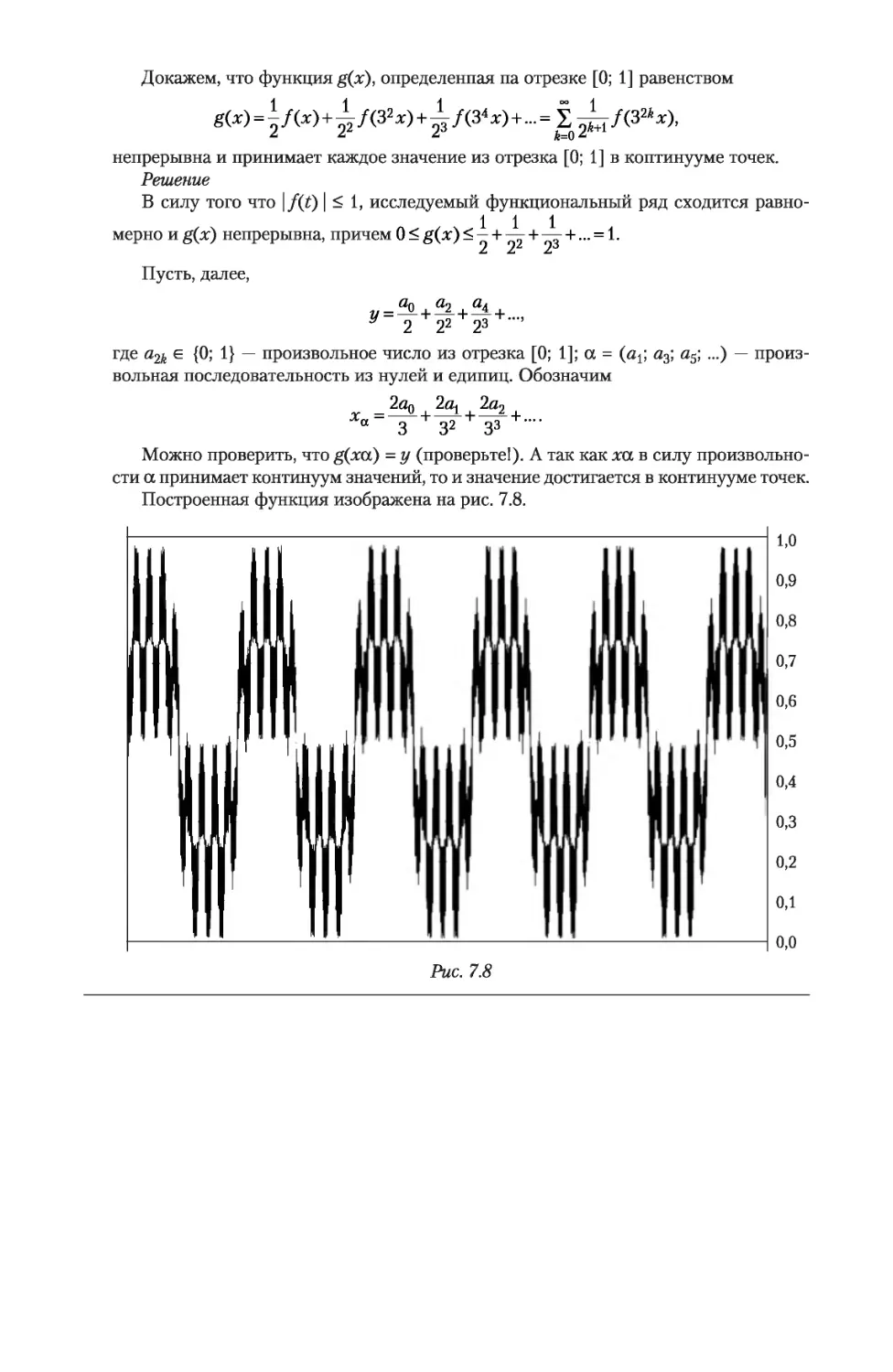
Автор: Никитин А.А. Фомичев В.В.
Теги: анализ математический анализ функциональный анализ высшая математика
ISBN: 978-5-534-00464-9
Год: 2918
Текст
А. А. Никитин, В. В. Фомичев
МАТЕМАТИЧЕСКИЙ
АНАЛИЗ.
УГЛУБЛЕННЫЙ КУРС
УЧЕБНИК И ПРАКТИКУМ
ДЛЯ АКАДЕМИЧЕСКОГО БАКАЛАВРИАТА
2-е издание, исправленное и дополненное
Рекомендовано Учебно-методическим отделом
высшего образования в качестве учебника для студентов
высших учебных заведений, обучающихся по естественнонаучным
направлениям и специальностям
Книга доступна в электронной библиотечной системе
biblio-online.ru
Москва ■ Юрайт ■ 2018
УДК 517(075.8)
ББК 22.161я73
Н62
Авторы:
Никитин Алексей Антонович — кандидат физико-математических наук, доцент
кафедры общей математики факультета вычислительной математики и кибернетики
Московского государственного университета имени М. В. Ломоносова, доцент кафе¬
дры высшей математики департамента математики факультета экономики Нацио¬
нального исследовательского университета «Высшая школа экономики»;
Фомичев Василий Владимирович — доктор физико-математических наук, про¬
фессор, заместитель заведующего кафедрой нелинейных динамических систем и про¬
цессов управления факультета вычислительной математики и кибернетики Москов¬
ского государственного университета имени М. В. Ломоносова.
Рецензенты:
Крищенко А. П. — доктор физико-математических наук, профессор, член-коррес¬
пондент Российской академии наук, заведующий кафедрой математического моделиро¬
вания Московского государственного технического университета имени Н. Э. Баумана,
лауреат Премии Правительства РФ в области науки и техники;
Фоменко Т. Н. — доктор физико-математических наук, профессор кафедры общей
математики факультета вычислительной математики и кибернетики Московского
государственного университета имени М. В. Ломоносова.
Никитин, А. А.
Н62 Математический анализ. Углубленный курс : учебник и практикум для академи¬
ческого бакалавриата / А. А. Никитин, В. В. Фомичев. — 2-е изд., испр. и доп. — М. :
Издательство Юрайт, 2018. — 460 с. — Серия: Бакалавр. Академический курс.
ISBN 978-5-534-00464-9
Данный учебник предназначен для желающих более глубоко освоить материал,
входящий в курс математического анализа: основы теории множеств, числовые после¬
довательности и ряды, непрерывность и дифференцируемость функций, определен¬
ный интеграл и т.д. Учебник содержит в конспективной форме материал, входящий
в классический курс математического анализа для студентов первого курса, а также
многочисленные теоремы, примеры и задачи, выходящие за рамки классического
Kjrpca, но полезные для более глубокого и всестороннего изменил основ современной
математики.
Соответствует актуальным требованиям Федерального государственного образо¬
вательного стандарта высшего образования.
Для студентов, обучающихся по математическим направлениям и специально¬
стям. Учебник может быть рекомендован также преподавателям математического
анализа, ведущим дополнительные занятия, спецсеминары и факультативы, а также
всем интересующимся данной дисциплиной.
УДК 517(075.8)
ББК 22.161я73
Efc
Delphi Law Company
Все права защищены. Никакая часть данной книги не может быть воспроизведена
в какой бы то ни было форме без письменного разрешения владельцев авторских прав.
Правовую поддержку издательства обеспечивает юридическая компания «Дельфи».
ISBN 978-5-534-00464-9
© Никитин А. А., Фомичев В. В., 2015
© ООО «Издательство Юрайт», 2018
Оглавление
Предисловие 7
Глава 1. Теория множеств 11
1.1. Аксиоматика множества действительных чисел 11
1.2. Мощность множества. Кардинальные числа 19
1.3. Метрические пространства 28
1.4. Ограниченные и неограниченные множества на прямой 34
1.5. Принцип вложенных отрезков 38
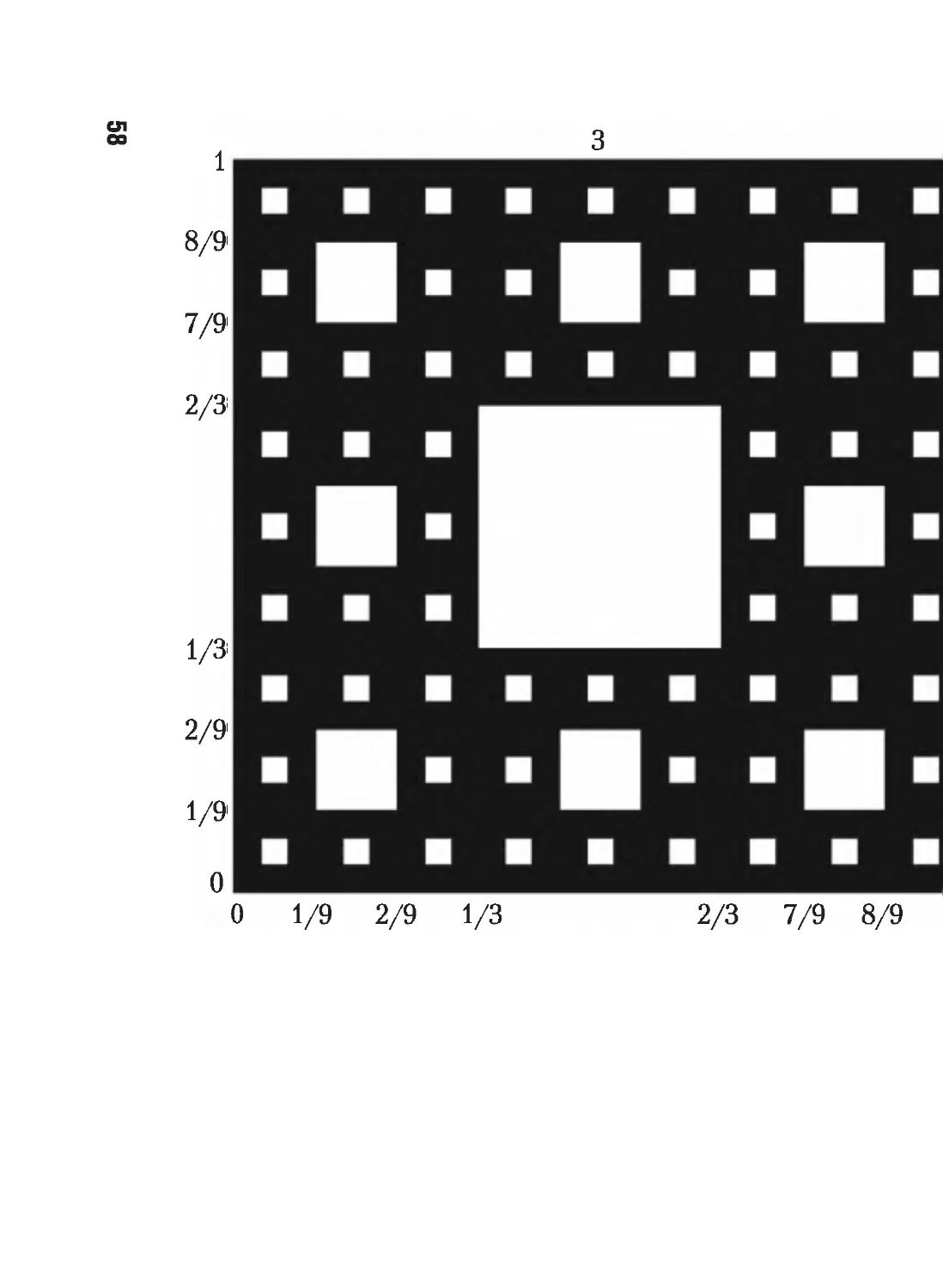
1.6. Множество Кантора 43
1.7. Совершенные нигде не плотные множества на плоскости 57
1.8. Общие теоремы об открытых, замкнутых и совершенных
множествах. Точки конденсации 64
Глава 2. Теория числовых последовательностей 70
2.1. Понятие последовательности и ее предела 70
2.1.1. Понятие последовательности. Ограниченные последовательности... 70
2.1.2. Бесконечно большие и бесконечно малые последовательности 73
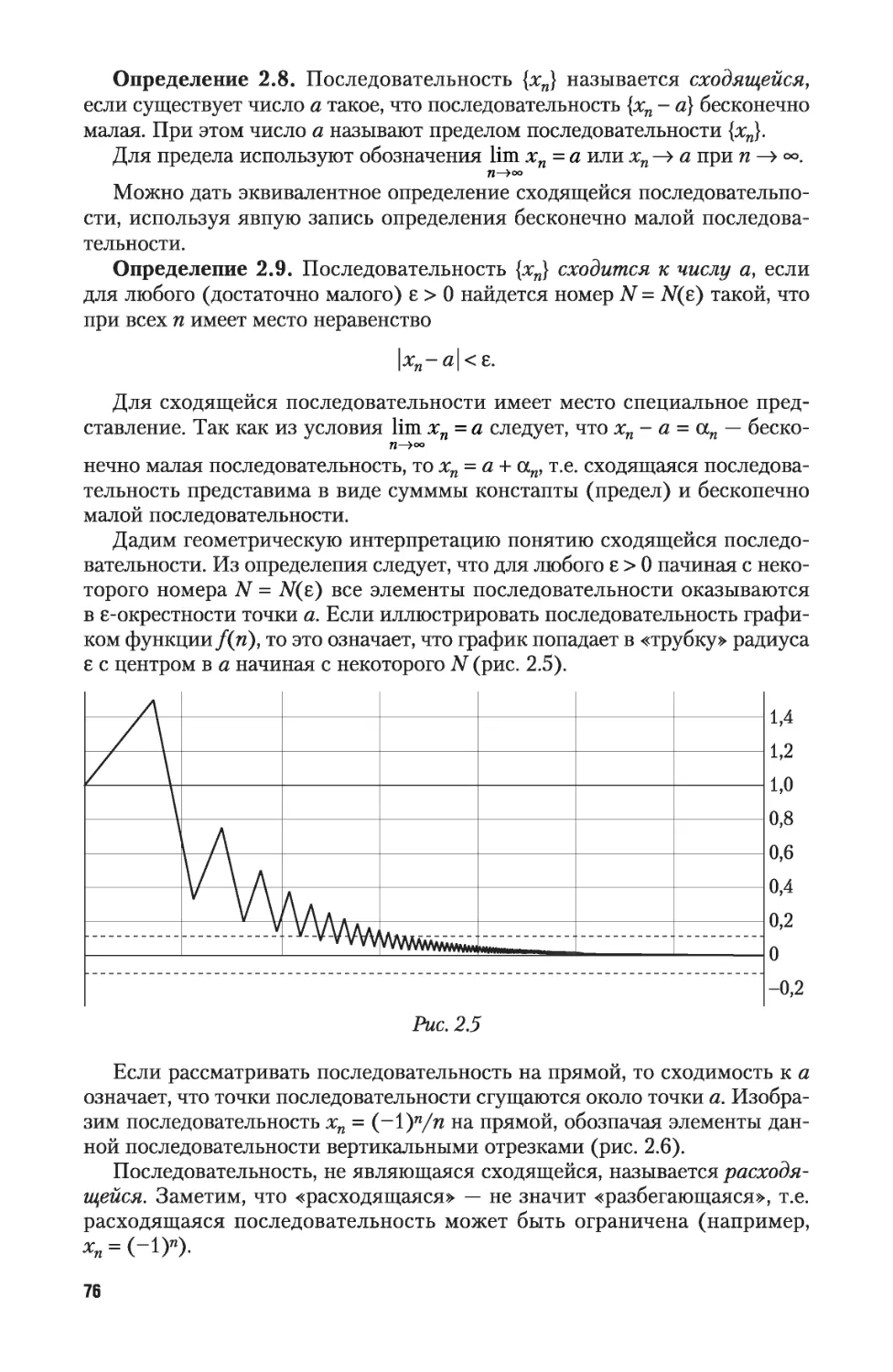
2.1.3. Сходящиеся последовательности 75
2.1.4. Монотонные последовательности 78
2.1.5. Подпоследовательности. Предельные точки 78
2.1.6. Фундаментальные последовательности 84
2.1.7. Определение множества вещественных чисел
через фундаментальные последовательности из множества
рациональных чисел 87
2.2. Примеры задач на числовые последовательности 92
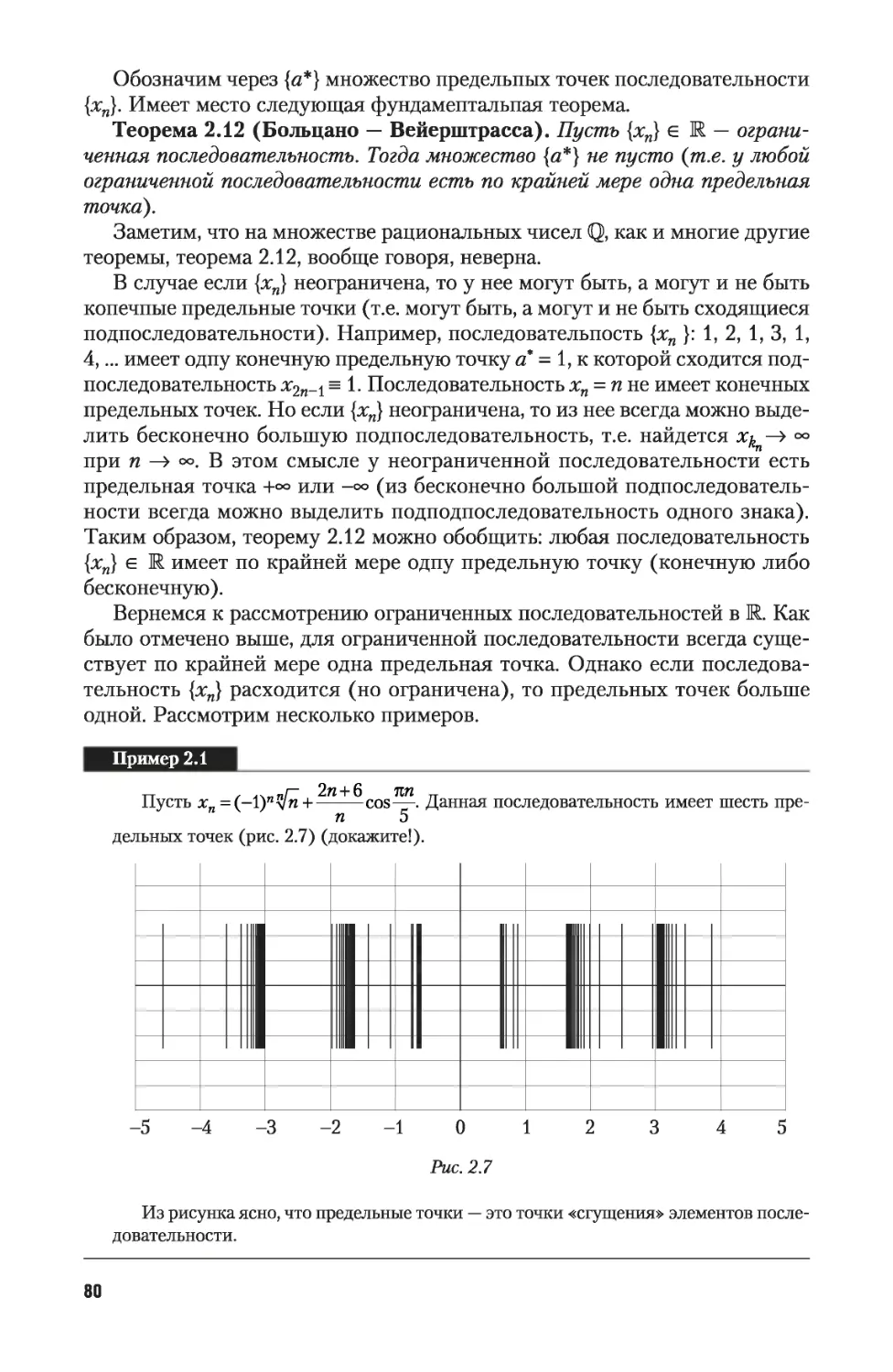
2.3. Монотонные числовые последовательности 98
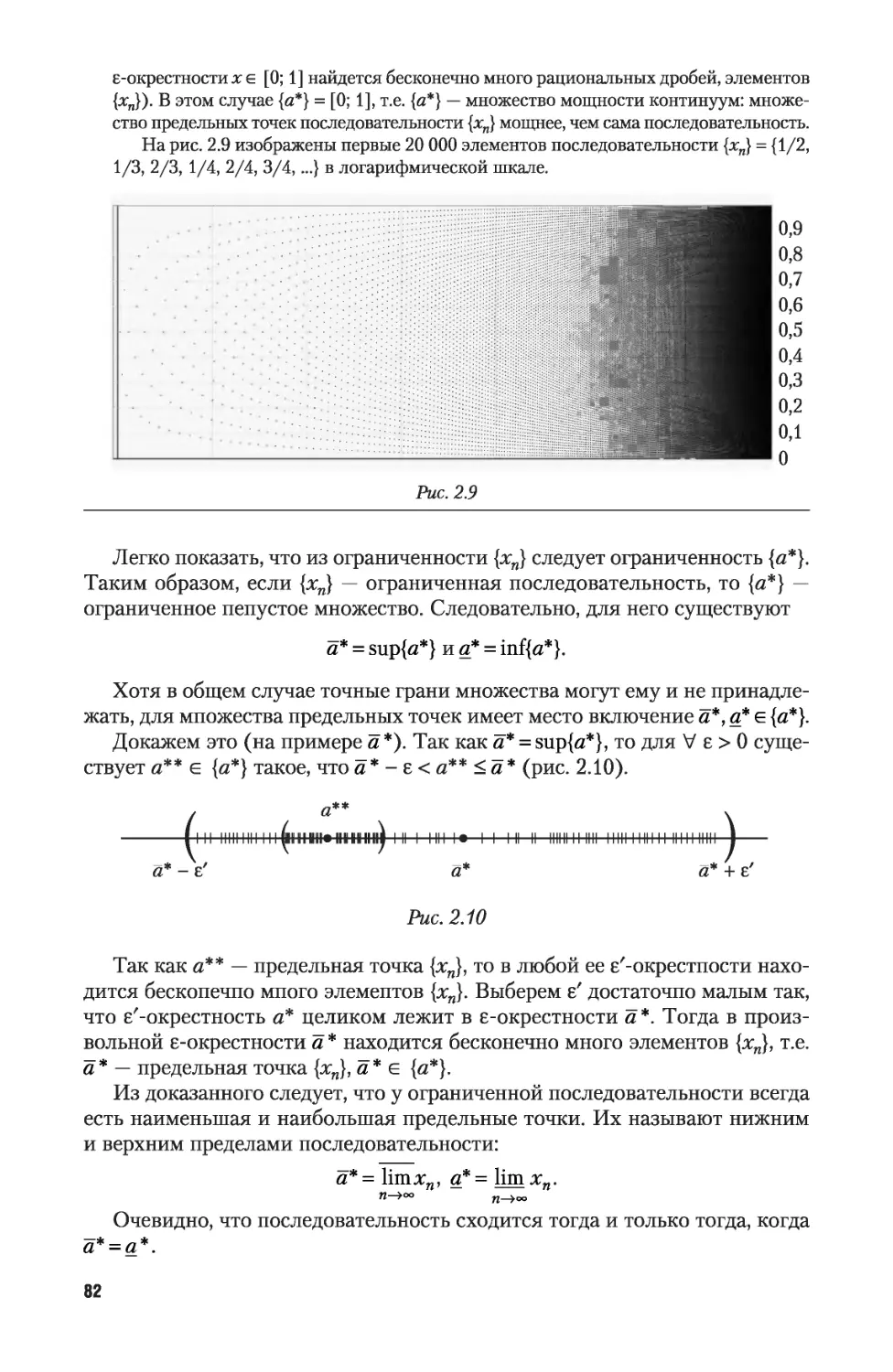
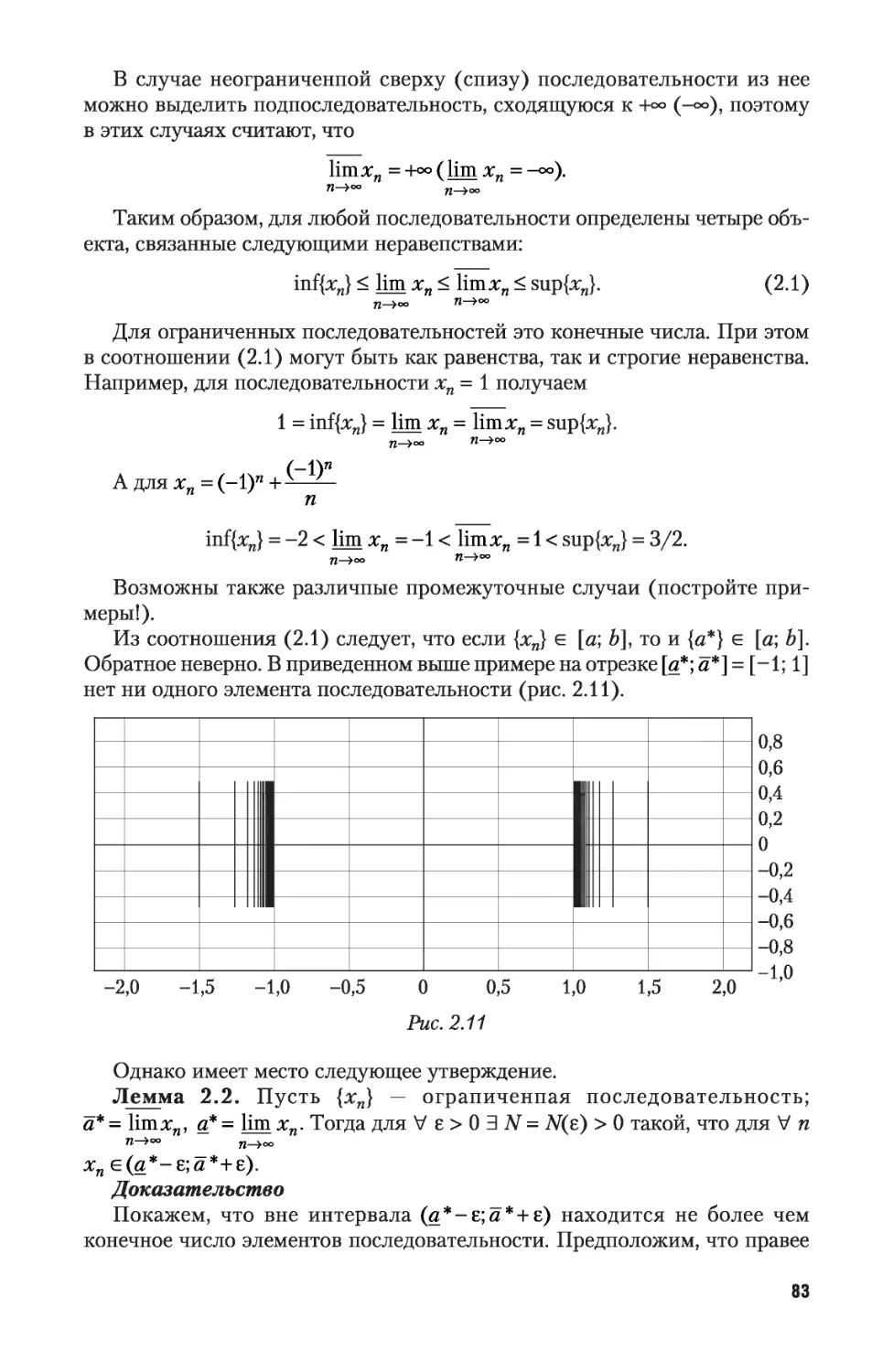
2.4. Предельные точки последовательности и множества 115
2.5. Числовые ряды 121
2.6. Знакопеременные числовые ряды. Абсолютная и условная сходимость... 139
Глава 3. Функции одной переменной. Непрерывность 154
3.1. Различные способы определения предела функции 154
3.2. Асимптотическое сравнение функций. О-символика 159
3.3. Непрерывность функции. Свойства непрерывных функций 165
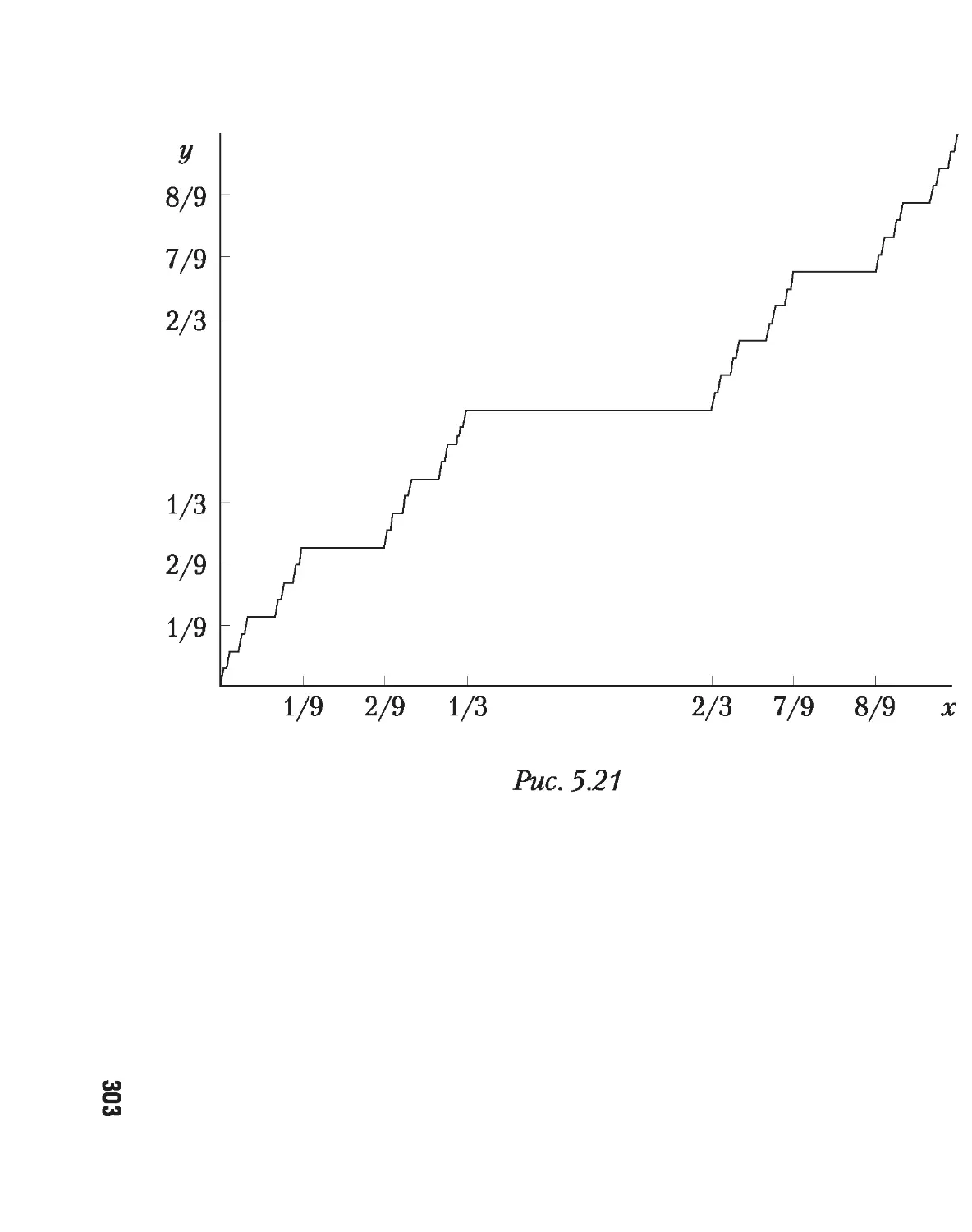
3.4. Функция Кантора 184
3.5. Непрерывные кривые. Кривые Пеано на плоскости и в пространстве 194
Глава 4. Дифференцирование функции одной переменной 206
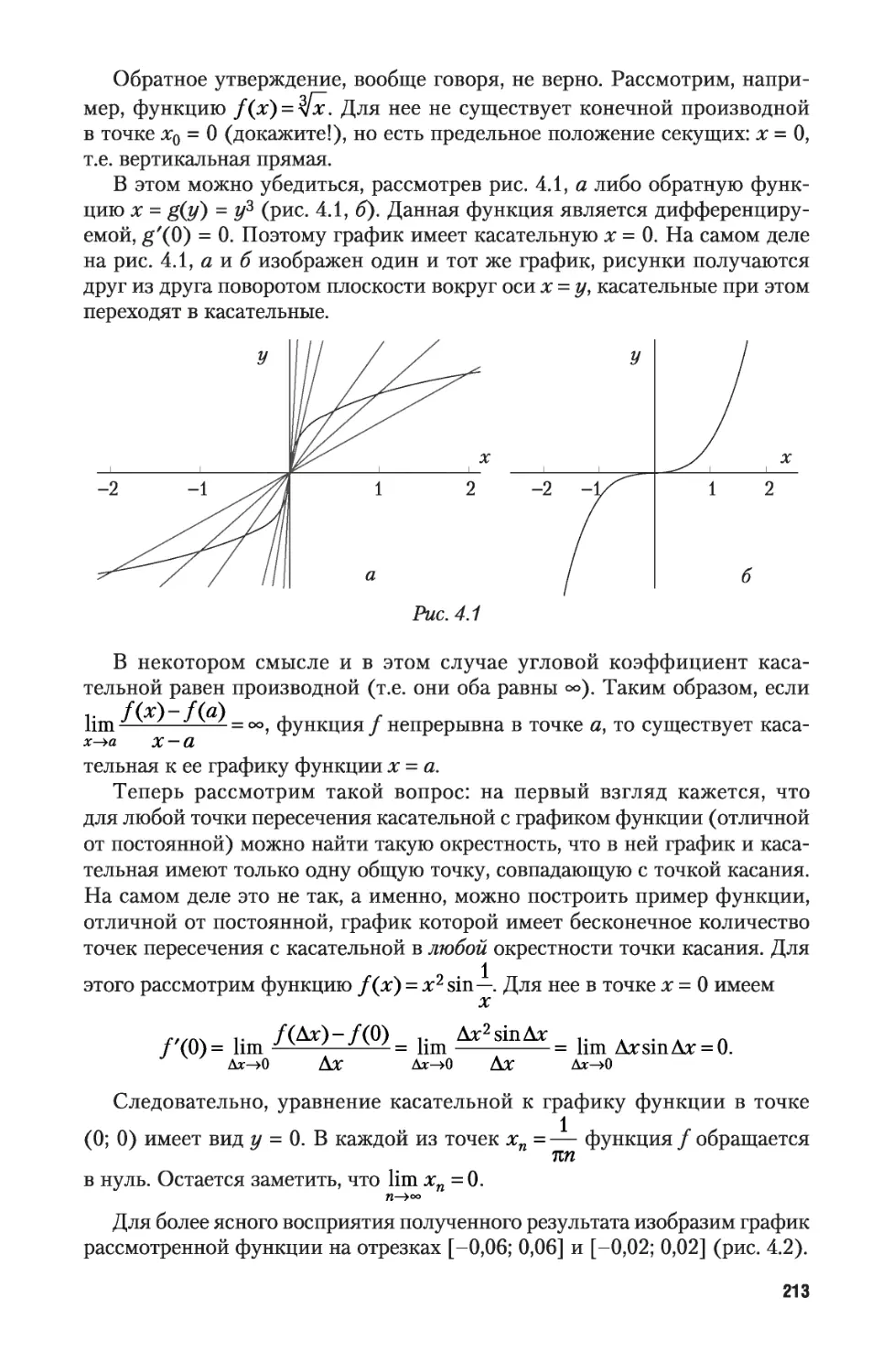
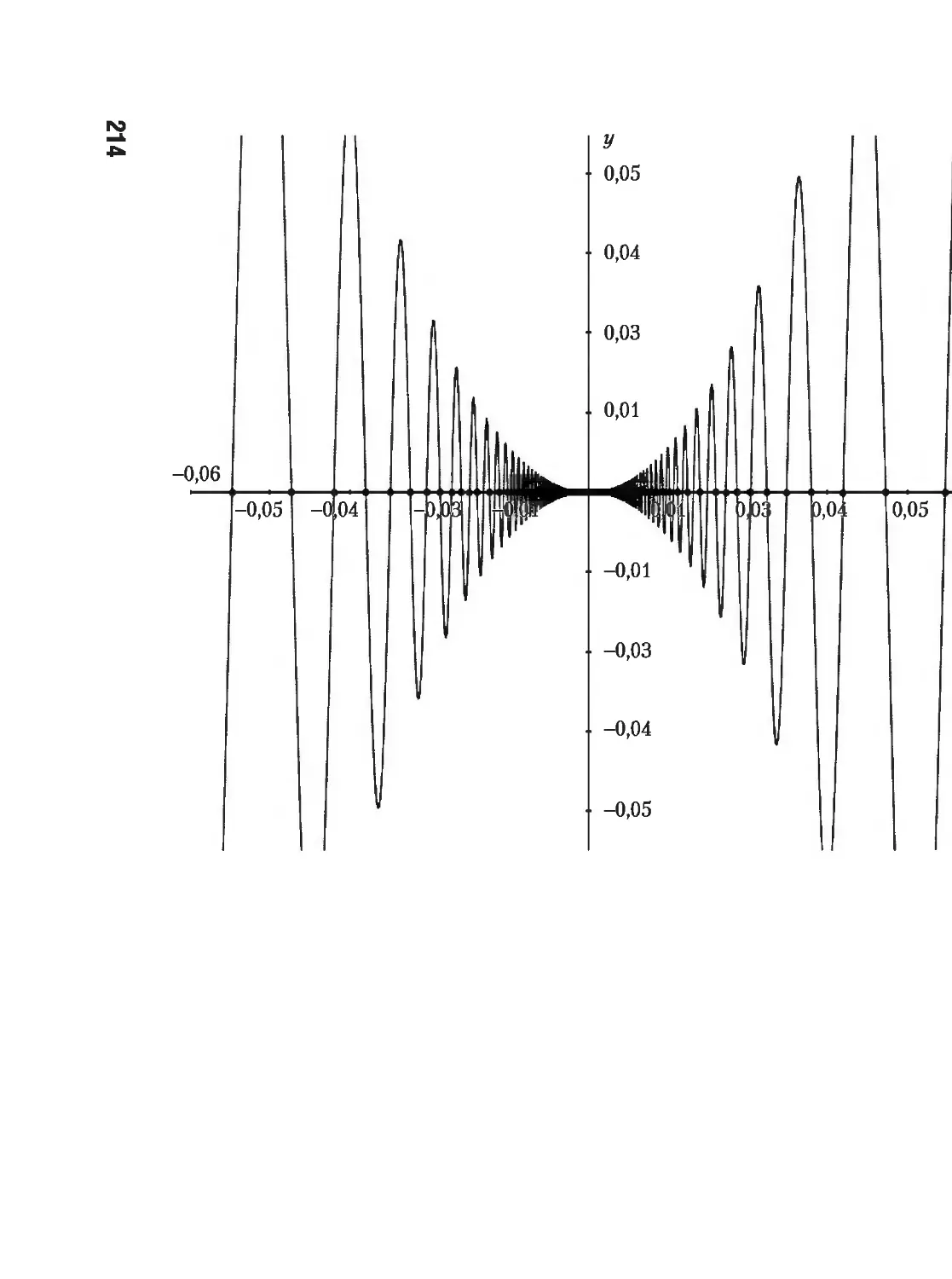
4.1. Основные понятия 206
4.2. Касательная, геометрический смысл производной и дифференциала 212
4.3. Производные и дифференциалы высших порядков 218
3
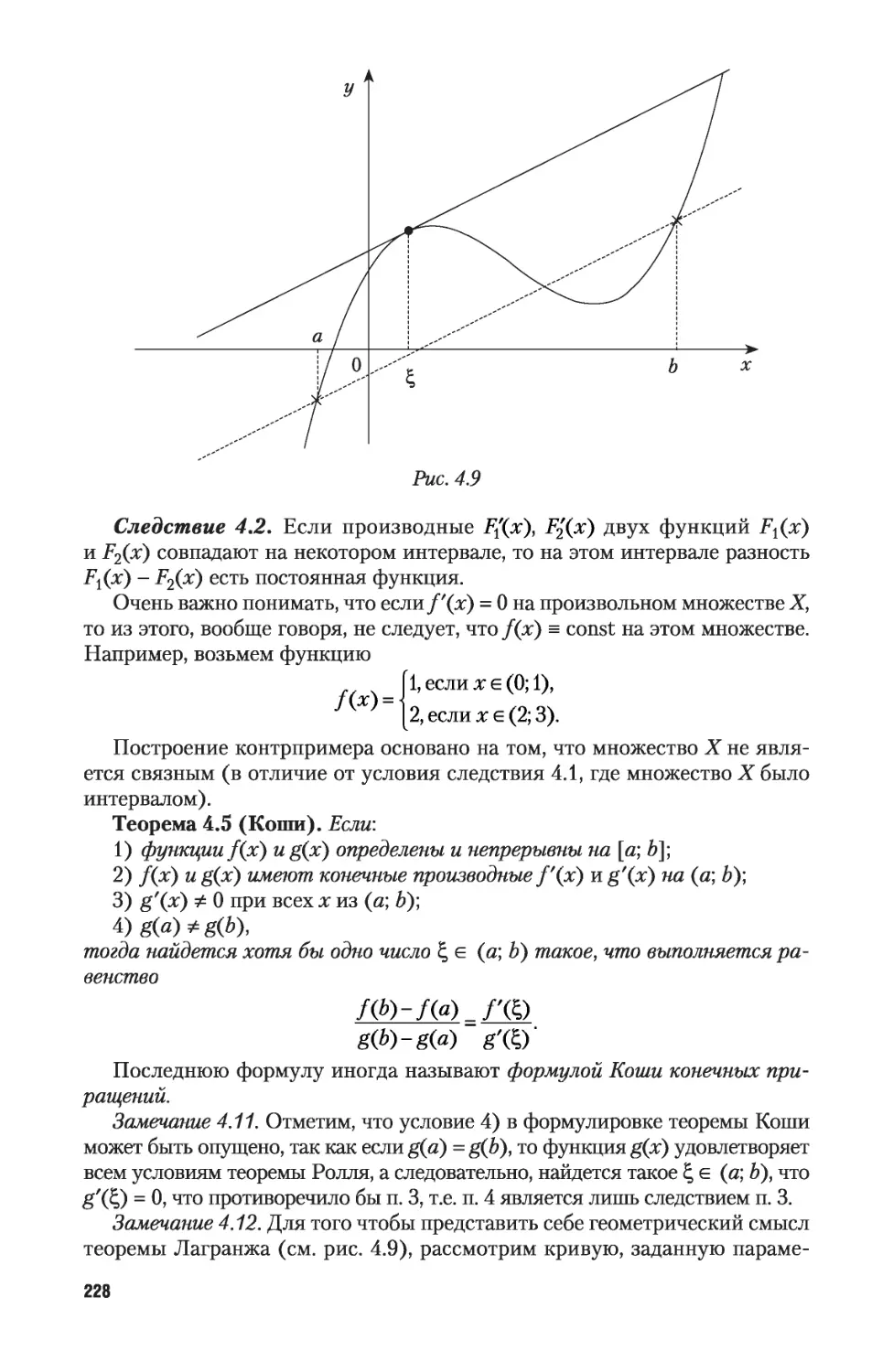
4.4. Основные теоремы дифференцируемых функций 226
4.5. Равномерная непрерывность 237
4.6. Правило Лопиталя 251
4.7. Теорема Тейлора и ее приложения 255
Глава 5. Применение дифференциального исчисления
для исследования функций 264
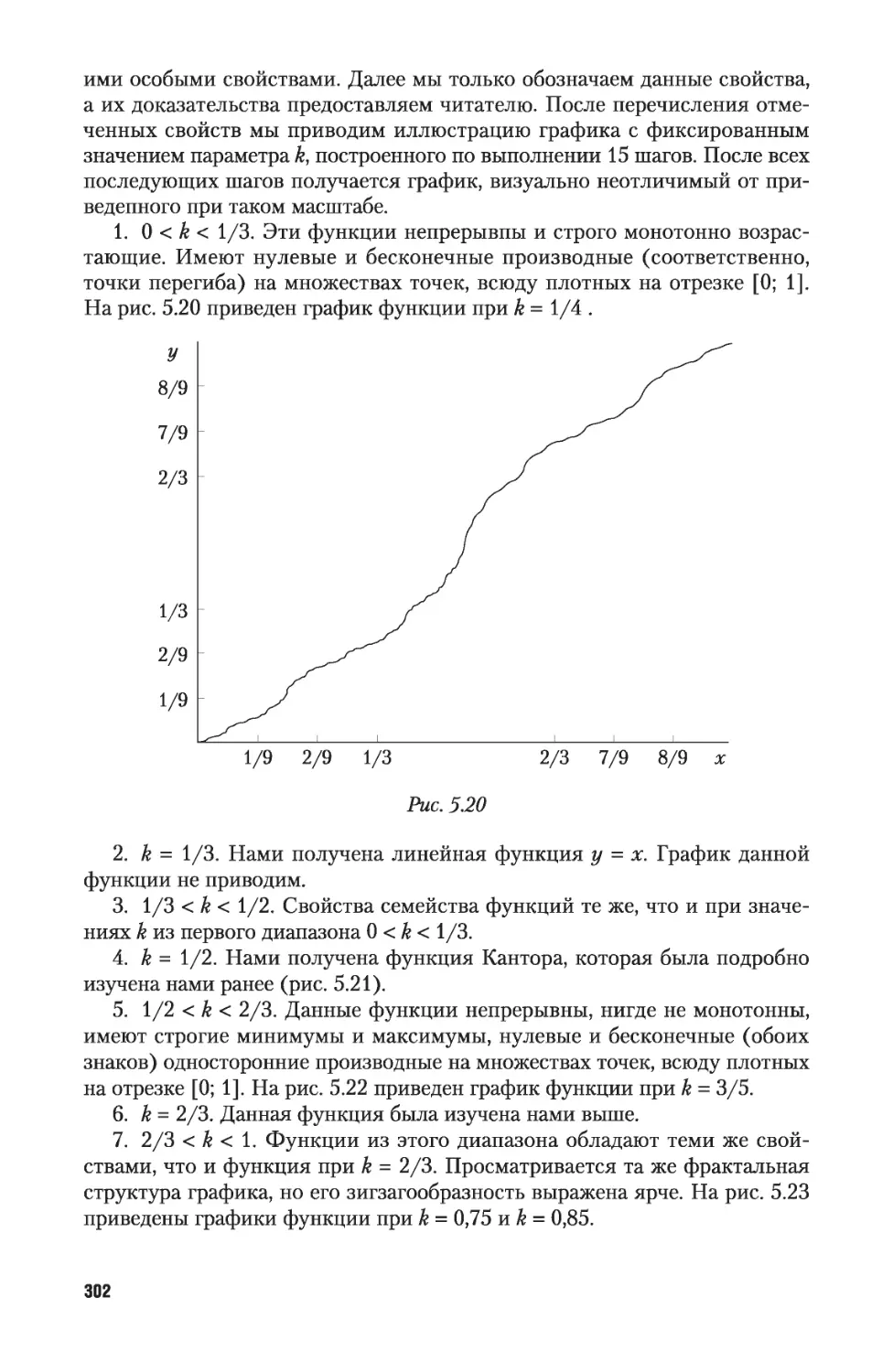
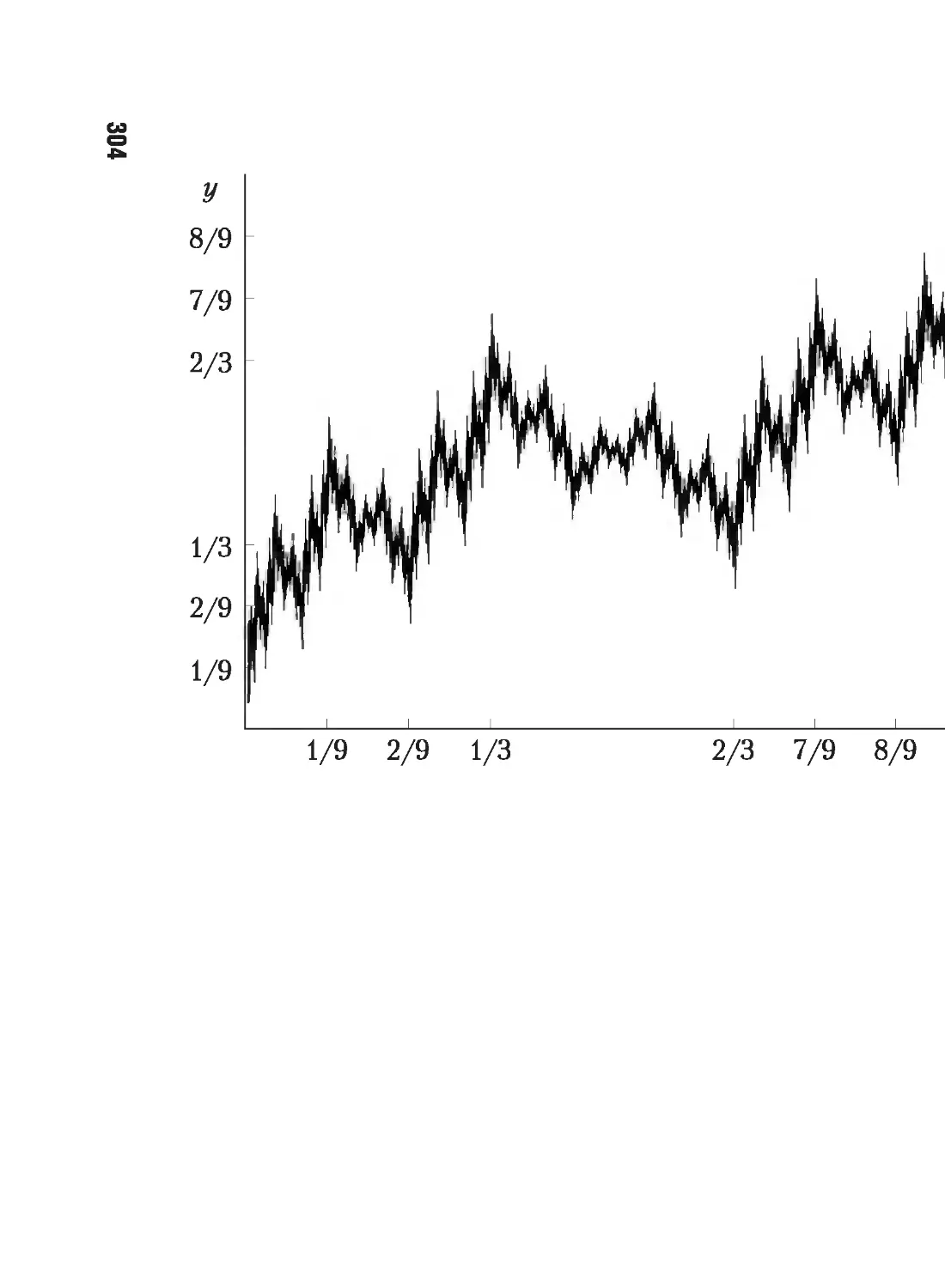
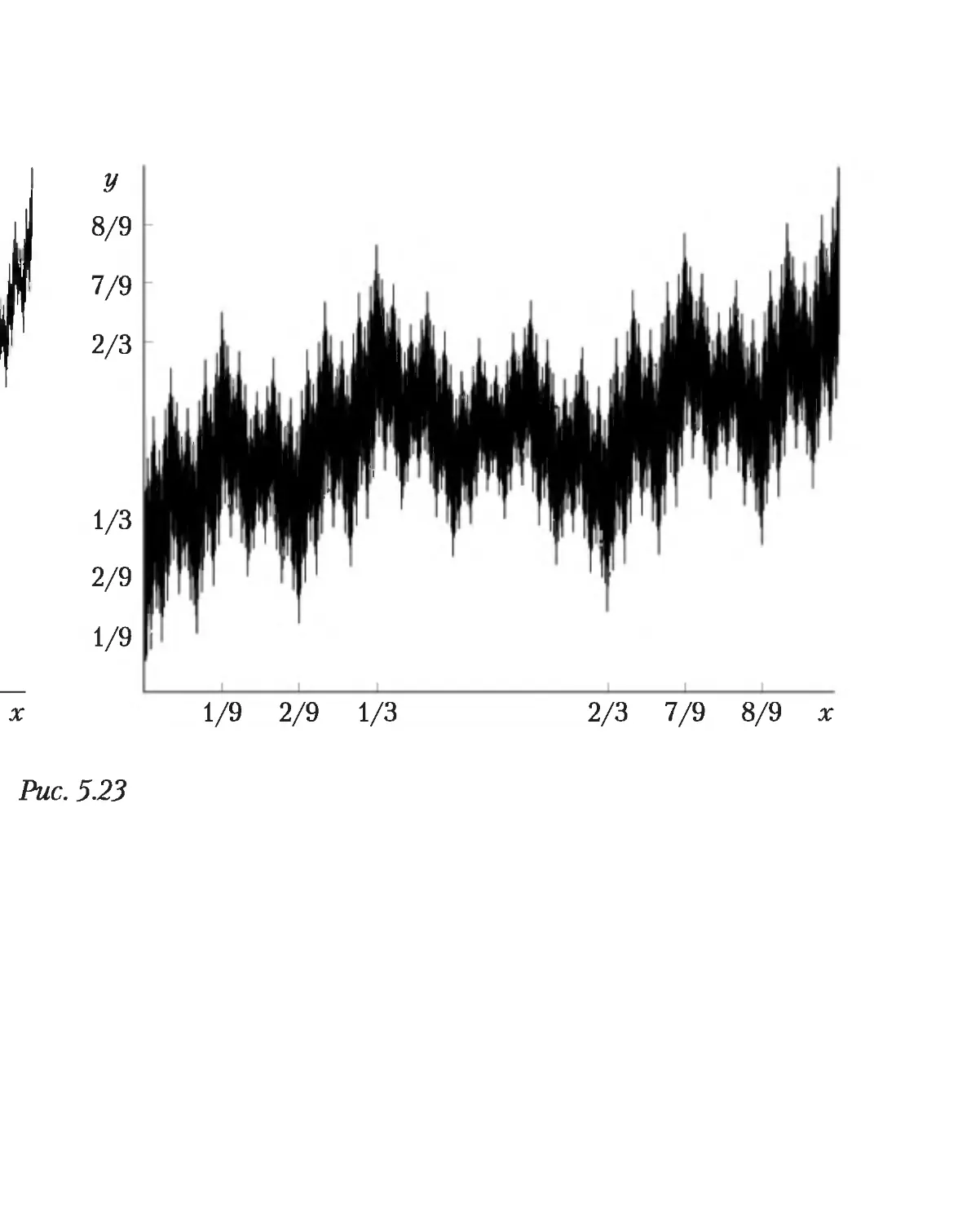
5.1. Возрастание и убывание функции. Монотонность 264
5.2. Выпуклость функции и точки перегиба 275
5.3. Локальные экстремумы 284
5.4. Асимптоты графика функции 291
5.5. Разные задачи 294
Глава 6. Интегрирование 305
6.1. Неопределенный интеграл и его свойства 305
6.2. Основные методы интегрирования 306
6.3. Определенный интеграл Римана 315
6.4. Критерии интегрируемости 316
6.5. Связь между определенным и неопределенным интегралами 325
6.6. Разные задачи на тему интегрального исчисления 335
6.7. Свойства интегрируемых функций 342
6.8. Оценки интегралов. Теоремы о среднем 349
6.9. Несобственные интегралы. Условная и абсолютная сходимости 357
Глава 7. Функциональные последовательности и ряды 377
7.1. Понятие равномерной сходимости 377
7.2. Достаточные признаки равномерной сходимости 384
7.3. Свойства равномерно сходящихся рядов 393
7.4. Степенные ряды 400
7.5. Применение степенных рядов для суммирования числовых рядов 410
7.6. Применение теории функциональных рядов для построения
нетривиальных примеров функций 417
Глава 8. Функции многих переменных 425
8.1. Евклидово пространство 425
8.2. Предел функции многих переменных. Непрерывность функции
многих переменных 428
8.3. Свойства непрерывных функций 433
8.4. Дифференцируемость функций многих переменных 434
8.5. Свойства дифференцируемых функций 435
8.6. Производные высших порядков 438
8.7. Формула Тейлора 440
8.8. Неявные функции 441
8.9. Системы уравнений 446
8.10. Зависимость функций. Функциональные матрицы 449
Список литературы 452
Предметный указатель 457
Посвящается памяти
нашего дорогого учителя
Владимира Александровича
ИЛЬИНА
Предисловие
Предлагаемый читателям учебник «Углубленный курс математического
анализа: учебник и практикум для академического бакалавриата» не похож
на классический учебник по математическому анализу. Хотя он и содер¬
жит основные сведения, необходимые для изучения классического курса
«Математический анализ I», изучаемого студентами математических спе¬
циальностей университетов на первом году обучения, основное внимание
уделяется тем вопросам, которые тесно примыкают к стандартным, базо¬
вым курсам, но ввиду своей сложности не разбираются на лекциях и семи¬
нарах, а выносятся на самостоятельное изучение сильными студентами
либо рассматриваются в рамках дополнительных занятий, факультативов,
спецкурсов по математическому анализу. Представленный учебник как раз
и возник из спецсеминара, который проводился одним из авторов учебника
на протяжении нескольких лет для студентов факультета вычислительной
математики и кибернетики Московского государственного университета
им. М. В. Ломоносова.
По своей структуре учебник в целом совпадает с классическими кур¬
сами, читаемыми в университетах. В основном авторы, конечно, следовали
структуре курса В. А. Ильина, читаемого на факультете вычислительной
математики и кибернетики Московского государственного универси¬
тета им. М. В. Ломоносова, на котором они «выросли». В предлагаемом
учебнике в краткой форме приводятся основные сведения из этого курса
(основные определения, теоремы и т.д.). Однако основной целью авторов
при работе над данным учебником было выйти за рамки того стандарт¬
ного материала, который преподается студентам в обязательном порядке.
Конечно, такой «выход» отражает авторский взгляд на то, какие вопросы
будут интересны и полезны сильным студентам, желающим глубже про¬
никнуть в темы, составляющие курс математического анализа для студен¬
тов младших курсов. В отличие от большинства продвинутых курсов мате¬
матического анализа в настоящей книге авторами предпринята попытка
«углубления» материала без существенного его «расширения», т.е. предла¬
гаемый материал основывается на тех понятиях и утверждениях, которые
рассматриваются в стандартной программе.
Кроме теоретического материала учебник содержит большое количе¬
ство задач (как разобранных, так и предназначенных для самостоятельного
изучения). Основная цель этих задач (многие из которых вполне могли бы
стать основой для самостоятельных утверждений; учебник не содержит
«технических», типовых задач) — помочь более глубокому пониманию раз¬
личных аспектов теории.
7
Авторами была сделана попытка свести в едином учебнике углубленные
задачи и теоремы из всех основных разделов курса математического ана¬
лиза, читаемого на первом году обучения студентам математических спе¬
циальностей. В частности, в данном учебнике подробно рассматриваются
основы теории множеств, изложены три подхода к построению множества
вещественных чисел: аксиоматический подход, метод дедекиндовых сече¬
ний и подход к введению множества вещественных чисел через фундамен¬
тальные последовательности из рациональных чисел, которые редко так
подробно излагаются в учебниках по математическому анализу. Подробно
разбираются элементы теории множеств, которые выходят за рамки стан¬
дартных курсов: множество Кантора, совершенные множества на плоско¬
сти и т.д. При этом материал изложен в доступной для студентов первого
курса форме. Надеемся, что такой материал будет интересен сильным сту¬
дентам для самостоятельного обучения.
В учебнике наряду со стандартной теорией числовых последовательно¬
стей приведены задачи повышенной сложности. В частности, подробно раз¬
бираются теоремы Штольца, Теплица, вопросы их применимости. В книгу
включена также теория числовых рядов, тесно примыкающая к теории
числовых последовательностей. Хотя теория рядов обычно входит в курс
«Математический анализ II», ее использование позволяет глубже раскрыть
свойства числовых последовательностей, построить ряд интересных при¬
меров.
В учебнике подробно рассматриваются свойства непрерывных и диф¬
ференцируемых функций, особое внимание при этом уделяется примерам,
выходящим за рамки стандартного курса. Так, рассматриваются функция
Кантора и ее свойства, теория непрерывных кривых, геометрические при¬
ложения теории дифференцируемости, а именно исследования возраста¬
ния-убывания, выпуклости-вогнутости кривых и т.д.
В учебнике рассматривается классическая для курса «Математический
анализ I» тема — определенный интеграл Римана. Но дается не только
систематическое изложение основных результатов (определение инте¬
грала, леммы Дарбу и т.д.), которые есть во всех классических учебниках.
В данном учебнике строго получены необходимые и достаточные условия
интегрируемости Коши, Дюбуа — Реймона и Лебега, подробно рассматри¬
вается теория несобственных интегралов, приведены различные условия
их сходимости и ряд оригинальных задач и примеров.
Включена в учебник и тема «Функциональные последовательности
и ряды». Хотя обычно этот раздел входит в курс «Математический ана¬
лиз II», авторы приводят многочисленные примеры построения функций
с оригинальными свойствами (например, нигде не дифференцируемые
функции), а эти примеры удобно строить как раз с помощью функцио¬
нальных последовательностей и рядов. В свою очередь, такие примеры
полезны при изучении непрерывности и дифференцируемости функций
одной вещественной переменной.
В последней главе учебника рассматриваются основные понятия теории
функций многих переменных: непрерывность, дифференцируемость, неяв¬
8
ные функции и т.д. Приводится ряд примеров, иллюстрирующих отличие
функций многих переменных от функций одной переменной.
Важной особенностью настоящего учебника является большое число
описанных в нем «патологических» примеров множеств и функций. Доста¬
точно подробно были рассмотрены множество Кантора, совершенные нигде
не плотные множества на плоскости (ковер Серпинского, кладбище Cep-
пинского, гребенка Кантора), функция Кантора, кривая Вада, кривая Пеано,
несколько способов построения всюду непрерывной, но нигде не диффе¬
ренцируемой функции и т.д. При этом авторы преследовали несколько
целей: во-первых, познакомить читателя с различными способами построе¬
ния красивейших и известнейших примеров и контрпримеров, а во-вторых,
попытаться преодолеть многие из формирующихся у людей, изучающих
математический анализ, стереотипов (например, таких: множество меры
нуль — очень маленькое и почти незаметное; функция, производная кото¬
рой равна нулю почти всюду, — константа; непрерывная кривая не может
быть общей границей трех или большего числа множеств на плоскости;
кривая Жор дано — «тонкий штрих, вьющийся на плоскости»; непрерывная
функция дифференцируема почти всюду и т.п.).
Многие задачи, теоремы и утверждения, помещенные в учебник, были
взяты авторами из пособий, книг и интернет-сайтов, указанных в спи¬
ске литературы. При этом в большинстве случаев авторы позволяли себе
не указывать источники рассмотренных тем, поскольку они легко опреде¬
ляются по указанным книгам.
Учебник содержит около сотни оригинальных иллюстраций, кото¬
рые призваны способствовать более полному пониманию предлагаемого
материала. Для их создания использовались программы Matlab, Wolfram
Mathematica, JavaScript и др. Еще больше иллюстраций и анимаций, кото¬
рые, по понятным причинам, не могут попасть в печатное издание, можно
найти на сайте www.visualmath.nl, который поддерживается одним из авто¬
ров учебника.
Для успешного изучения дисциплины «Математический анализ» сту¬
дент должен обладать знаниями по элементарной математике в объеме,
изучаемом в средней школе. Для успешного освоения курса необходимо
параллельное изучение курсов «Алгебра», «Аналитическая геометрия»,
«Линейная алгебра и геометрия».
Для освоения курса «Углубленный курс математического анализа»
предполагается, что читатель знает основные положения теории множеств,
теории пределов, теории непрерывных функций, теории дифференциаль¬
ного и интегрального исчисления, теории числовых и функциональных
рядов, теории несобственных интегралов, теории функций многих пере¬
менных. Студент также должен быть хорошо знаком с основными поня¬
тиями из курса алгебры: линейного пространства, нормированного и гиль¬
бертова пространства и т.д. Читатель должен уметь считать производные
функций нескольких переменных, находить неопределенные интегралы,
исследовать на сходимость и равномерную сходимость ряды и несобствен¬
ные интегралы.
9
В результате освоения курса студенты расширят свои знания по теории
множеств, теории вещественных чисел, теории числовых последовательно¬
стей, теории непрерывных функций, теории дифференциального и инте¬
грального исчисления, теории несобственных интегралов и других разде¬
лов математического анализа.
В результате освоения дисциплины студент должен:
знать
• основные понятия, определения и факты теории множеств, теории
числовых последовательностей и рядов, дифференциального и интеграль¬
ного исчисления;
уметь
• применять на практике основные методы математического анализа;
• уметь решать задачи по основным разделам математического ана¬
лиза: теории множеств, теории числовых последовательностей и рядов,
дифференциального и интегрального исчисления;
• уметь доказывать утверждения, строить примеры и контрпримеры
к различным утверждениям из курса математического анализа;
владеть
• навыками решения практических задач математического анализа;
• методами математического анализа, проблемно-задачной формой
представления математических знаний;
• проблемно-задачной формой представления естественнонаучных
знаний.
Авторы выражают благодарность рецензентам А. П. Крищенко и Т. Н. Фо¬
менко за ряд ценных замечаний, а также П. А. Макарову, чья работа вышла
далеко за рамки простой редактуры. Авторы благодарны многим своим кол¬
легам с факультета вычислительной математики и кибернетики Московского
государственного университета и из других вузов. Из их числа особенно
хотелось бы выделить А. А. Кулешова, А. А. Полосина, И. В. Садовничую,
А. В. Домрину и А. X. Шеня. Также авторы благодарят за помощь при под¬
готовке рукописи аспирантов А. В. Мальцеву, Е. И. Атамася. Некоторые
из приведенных решений принадлежат различным студентам, которые посе¬
щали лекции и семинары авторов. Здесь хотелось бы выделить Антона Саво¬
стьянова. Наконец, очень многие из иллюстраций, которые были помещены
в учебник, были запрограммированы студентами авторов. Особую благодар¬
ность заслуживают Алеся Яковчук и Василий Рубцов.
Глава 1
ТЕОРИЯ МНОЖЕСТВ
1.1. Аксиоматика множества действительных чисел
Для доказательства ряда основных утверждений из курса математиче¬
ского анализа требуется знать «точную структуру» множества действи¬
тельных чисел. Оно очень похоже, например, на множество рациональных
чисел, но обладает и некоторыми отличиями. Эти отличия (например,
свойство полноты) приводят к тому, что ряд утверждений верен для дей¬
ствительных, но не верен для рациональных чисел.
Изучим подробнее множество действительных (вещественных) чисел.
Существует целый ряд конструктивных способов определения этого мно¬
жества: теория бесконечных десятичных дробей, теория сечений в обла¬
сти рациональных чисел, теория фундаментальных последовательностей
из рациональных чисел (последовательности Кантора). Далее рассмотрим
кратко аксиоматический способ введения действительных чисел. Более
подробное освещение данного способа читатель может найти в источниках
из списка литературы.
Определение 1.1. Пусть даны два множества X и Y. Декартово произ¬
ведение множества X и множества Y есть такое множество Z, элементами
которого являются упорядоченные пары (х, у) для всевозможных х G X
и у G Y (обозначение: Z = Xx У).
Определение 1.2. Множество M называется множеством действитель¬
ных (вещественных) чисел, а его элементы — действительными числами,
если выполнены следующие условия {аксиоматика действительных чисел).
1. Аксиомы сложения.
На множестве R определена операция сложения
+ : R х R —> R,
которая сопоставляет каждой упорядоченной паре (х; у) элементов х G R,
у е R некоторый элемент х + у е R, называемый суммой х и у, для которого
выполнены следующие условия:
а) существует такой элемент (обозначаемый в случае сложения нулем, 0),
что для VxgR
х + 0 = 0 + х = х;
б) для любого элемента х G R имеется элемент -х G R, называемый про¬
тивоположным к х, такой что
х + (-х) = (-х) +х=0;
11
в) операция «+» ассоциативна, т.е. для V х, у, z е R выполнено
х + (у + z) = (х + у) + z;
г) операция «+» коммутативна, т.е. для V х, у E R справедливо
х + у = у + х.
Если на множестве X определена операция, удовлетворяющая аксио¬
мам 1а, 16, 1в, то говорят, что X есть аддитивная группа1. Если, кроме того,
выполнена аксиома 1г, то группу называют коммутативной или абелевой.
2. Аксиомы умножения.
На множестве R определена операция умножения
•: R х R ^ R,
которая сопоставляет каждой упорядоченной паре (х; у) элементов х е R,
у E R некоторый элемент х ■ у E R, называемый произведением хиу, для ко¬
торого выполнены следующие условия:
а) существует такой элемент (обозначаемый в случае умножения едини¬
цей, 1), что для VxeR
х-1 = 1-х = х;
б) для любого элемента х е R\{0} имеется элемент х-1, называемый
обратным, такой что
X, /у-—1 — у—1 , 'У' — i •
Jv — ш/V Jv — X. J
в) операция умножения ассоциативна, т.е. для V х, у, z е R выполнено
X • (у ■ Z) = (х • у) • 2;
г) операция умножения коммутативна, т.е. для V х, у е R справедливо
х-у = у-х
(заметим, что по отношению к операции умножения множество R\{0} яв¬
ляется (мультипликативной) группой);
д) совместная аксиома сложения и умножения: умножение дистрибу¬
тивно по отношению к сложению, т.е. V х, у, z E R выполнено
(х + у) • z = х • z + у • 2.
Если на множестве X действуют две операции, удовлетворяющие всем
перечисленным аксиомам, то X называется числовым (алгебраическим)
полем или просто полем.
В качестве самостоятельной работы предлагаем читателю доказать сле¬
дующие свойства аксиом сложения и умножения.
Задание 1.1. Докажите, что:
(а) в множестве действительных чисел R существует лишь единственный нуль;
(б) в множестве R для каждого элементах существует лишь единственный противо¬
положный элемент;
1 Подробнее о понятии группы читатель может узнать, например, в книге [11].
12
(в) в множестве R существует единственная единица;
(г) в множестве R для каждого элемента х Ф О существует лишь единственный
обратный элемент.
3. Аксиомы порядка.
Между любыми двумя элементами R имеется отношение неравенства <,
т.е. для У х, у E R установлено, выполняется ли х < у (х меньше или равно у)
или нет. При этом будем требовать выполнения следующих условий:
а) для каждогоie Rвыполненох<х (рефлексивность);
б) из х<у иу <хследуетх = у (антисимметричность)',
в) из x<yuy<z следует x<z (транзитивность)',
г) для всех х, у E R выполнено или х < у, или у < х.
Множество, между некоторыми элементами которого имеется отно¬
шение неравенства, удовлетворяющее аксиомам За, 36 и Зв, называют
частично упорядоченным, а если кроме того выполнена аксиома Зг, то
линейно упорядоченным',
д) связь сложения и порядка в R: для х, у E R таких, что х < у, и всех
2 G R выполнено
X + Z < у + 2.
е) связь умножения и порядка в R: Для x,y,zE R таких, что х < у и z > О,
выполнено
х-z<y -Z',
Замечание 1.1. Заметим, что всем уже перечисленным аксиомам удов¬
летворяет и множество рациональных чисел Q1. А вот следующей аксиоме
множество Q уже не удовлетворяет.
4. Аксиома непрерывности (аксиома полноты).
Если X и Y- непустые подмножества R, обладающие тем свойством,
что для VxgXh У у е Y выполнено х < у, то 3 с G R такое, что х<с<у
для VxgXhVz/g Y2.
Упорядоченное поле, удовлетворяющее аксиоме непрерывности, называ¬
ется непрерывным упорядоченным полем.
Покажем, что множество Q не удовлетворяет аксиоме непрерывности.
Рассмотрим два подмножества множества Q:
P= {р E Q\p>Q,p2<2}, R = {ге Q|r>0, r2>2}.
Очевидно, что для У р E Р, VrG R выполнено неравенство р < г, но X с G
G Q такого, что с2 = 2 (доказательство элементарно проводится от против¬
ного), а поэтому X с такого, что выполнено неравенство р < с < г для любых
элементов р E Риге R. Таким образом, приведенные аксиомы определяют
«более существенное» множество, чем Q. Покажем, что в некотором смысле
они определяют множество R единственным образом.
1 Строгое определение множества рациональных чисел Q будет дано в дальнейшем.
2 Важным фактом является то, что элемент с ищется не для каждой пары элементов х и у
в отдельности, а он один и тот же для всех элементов из данных множеств.
13
Определение 1.3. Два поля X и Y называются изоморфными, если суще¬
ствует такое взаимно однозначное отображение1 / поля X на поле Y, что
для любых двух элементов х е X и у е Y выполняются два условия:
/(* + у)= Ах) + f(y);Ax• У) = Ах) ■ Ay)-
Отображение / называется в этом случае изоморфизмом или изоморф¬
ным отображением. Другими словами, два поля называются изоморфными,
если существует биекция, сохраняющая операции сложения и умножения.
Если поля X и Y линейно упорядочены и существует изоморфное ото¬
бражение/поля X на поле Y, сохраняющее отношение порядка, т.е. для всех
х, у G X таких, что х<у, имеет место соотношение/(х) <f(y), то поля X и Y
называются изоморфными упорядоченными полями.
Примем без доказательства следующую важнейшую теорему.
Теорема 1.1. Все непрерывные упорядоченные поля изоморфны между
собой.
Таким образом, указанные аксиомы однозначно (с точностью до изо¬
морфизма) определяют множество вещественных чисел.
Множества натуральных чисел N, целых чисел Z и рациональных
чисел Q естественным путем «вкладываются» в множество действитель¬
ных чисел М. Так, под множеством натуральных чисел N будем понимать
множество чисел п е R таких, что я = 1 + 1 + ... + 1, где 1 — особый элемент
' V '
п слагаемых
для операции умножения.
Натуральные числа, противоположные им и нуль называются целыми
числами (обозначение: Z). Частные т/п, где т,п — взаимно простые целые
числа ии#0, называются рациональными числами (обозначение: Q). Все
остальные вещественные числа называются иррациональными.
Рассмотрим далее еще один способ определения множества веществен¬
ных чисел, а именно, способ введения этих чисел с помощью сечений мно¬
жества рациональных чисел (дедекиндовы сечения).
Определение 1.4. Сечением множества рациональных чисел будем назы¬
вать упорядоченную пару непустых множеств {Л; В), где A, Ba Q такие, что:
1) для V a G А, \/ b е В => а<Ь;
2) для V в > 0 3 я е A, 3b е В :Ь - а<е;
3) для V a* E A, V я е Q : я < я* => а E А; для V Ъ* G В, V Ъ е Q :b>b* =>
=> Ь G В)
4) в множестве А нет максимального элемента, в множестве В нет мини¬
мального элемента.
Из определения 1.4 следует, что либо AuB = Q, либо AuB = Q\{p},
р g Q, т.е. объединение АиВ дает либо все множество Q, либо Q без одного
элемента. Действительно, если два рациональных числа р' и р", где р' < р",
не принадлежат объединению А и В, то и V q G Q, р' < q < р", также не при¬
надлежит AuB (иначе в силу условия 3 либо р' G А, либо р" G В). Но тогда
1 Здесь подразумевается, что читатель уже знаком с понятием взаимно однозначного
отображения. Его строгое определение будет дано в дальнейшем.
14
(V a G A=>a<p',Vbe В =>b> р") => V a g А, \/ b е В выполнено b - а>
> р" - р' = е* > 0, что противоречит условию 2.
Сечение {Л; В} соответствует рациональному числу р, если Л u B = Q\{p}.
Сечение {Л; В} в случае Л u В = Q и будем считать новым объектом — веще¬
ственным числом. На самом деле (если множество уже введено), в случае
если AuB = Q, фактически множества Л и В определяются условием а <х,
b > х для некоторого иррационального х.
В литературе обычно отказываются от условий 3, 4 и заменяют их
на условие Л u В = Q, и в случае если в Л есть максимальный элемент
либо в В есть минимальный элемент, сечение ассоциируют с соответству¬
ющим рациональным числом. Но это приводит к некоторым техническим
трудностям при строгом доказательстве аксиоматики вещественных чисел,
поэтому ниже будем опираться на приведенное выше «неклассическое»
определение сечения.
Покажем, что, опираясь на это определение, можно ввести три операции
{сравнения, сложения и произведения) и установить для них свойства, пере¬
численные в аксиоматическом подходе.
Операция сравнения. Пусть заданы два сечения
х' = {А'; В'} их" = {А"; В"}.
Будем говорить, что х' = х", если для V a' G Л', V b' G В', V а" G А",
V b" G В" выполнено а' < Ъ", а" < Ь'.
Покажем, что в этом случае для сечений х' и х" выполнены равенства
А'= A", В' = B".
Пусть a' G Л'. Покажем, что a' G А". Предположим, что это не так, т.е.
a' g Л\ Тогда либо a' G В", но в этом случае в силу п. 4 определения сече¬
ния1 3 b" G В" такое, что Ь" < а', что противоречит условиям из определения
равенства (V а' < Ъ"); либо возможен второй вариант: а' G 0\{Л" и В"), т.е.
А" и В" = Q\{a'}, сечение х" соответствует рациональному числу а'. Но так
как во множестве Л' нет максимального элемента, то 3 я' G Л', а' > а' =>
=> d' G В" и, как было показано выше, 3 b" G В", Ь" < а', что вновь приво¬
дит нас к противоречию. Таким образом, выполнено: V a' G Л' =яг' G А".
В силу симметричности множеств в определении сравнения можно пока¬
зать, что для V a" G А" справедливо a" G Л', т.е. А' = А".
Аналогично (с рассмотрением противоположных неравенств) доказыва¬
ется равенство В' = В".
Если эти условия не выполняются, то для х' = {А'; В'} их" = {А"; В") воз¬
можны следующие ситуации.
1. Для V a' G Л', V b" G В" выполнено а' < Ь", но 3 b' G В', 3 а" е А"
такие, что а" > Ь'. Тогда говорят, что х' < х".
2. Для V a" G А", V b' G В' выполнено а" < Ь', но 3 a' G Л', 3 b" G В"
такие, что а' > Ь". Тогда говорят, что х' > х".
Ситуация, когда 3 а', а", Ь', Ь" такие, что а' > Ь", а" > Ь', невозможна, так
как в этом случае в силу п. 1 для сечения х" выполнено а' > b" > а" > b' =>
1 В силу отсутствия минимального элемента в множестве В".
15
=> o' > b', что противоречит п. 1 для сечения х'. Таким образом, любые два
сечения связаны одним из знаков: =, >, <.
Покажем, что для введенной операции выполнено свойство транзитив¬
ности, т.е.
I) х = х , х =х => х =х ;
о\ . ._// __// ^ Л_/// . ^ __///
OC ^ OC j OC ^ OC У OC ^ OC •
Доказательство
1. Пусть х' = х", х" = х'". Тогда, как было показано выше,
A! = А", В' = В", А" = А'", В" = В'" =>Л' = А'", В' = В'" => х' = х'".
2. Пусть х' < х", х" < х'". Тогда:
• для всех a' е А', Ь" е В" выполнено а' < Ь"; найдутся b' и а" такие, что
а”>Ь'\
• для всех a" G A", b'" G В'" выполнено а" < Ь"'\ найдутся Ь" и а'" такие,
что а'" > Ъ" (рис. 1.1).
А'
\
В'
( .
А"
>
В"
А'"
I
•
А ?
W
/
V b'
а" / 4 Ь"
Рис. 1.1
а'"
в
///
Тогда для всех а' и Ь'" справедливо
a'<b'<a"<b"<a"'<b'".
При этом 3 а'" кЬ'\Ь' < а" < Ь" < а"', откуда х' < х'". ■
Операция сложения. Пусть заданы два сечения х' = {А'; В'} и х" = {А"; В"}.
Суммой х' и х" назовем сечение х = {А; В} такое, что A = {а' + a", a' g А',
a" G A"}, B = (b' + b", b' G В', b" G В"}, т.е. А и В — множества всевозможных
сумм соответствующего вида. Покажем, что х = х' + х" — сечение. Действи¬
тельно:
1) так как для V а', а", Ь', Ь" имеем а' < Ь', а" < Ь", то а' + а" = а < Ь' +
+ b" = b;
2) для V е > 0 3 a', a", b', b": a' -b' < е/2, а" - b" < е/2 => а - b = (a' + а") -
- (b' - b") < в;
3) пусть AG А Рассмотрим У а < a, a g Q. Так как a G А, то а = а' + а",
a', a", d E Q. Тогда а - а = в > 0, в g Q => а = а' + а" - в = {а' - в) + а" =>
=> (а' -г) E Q, (а' - в) < а' => (a' - в) g А' => а е А. _
Аналогично если b E В, то для любого b E Q, b > b => b E В;
4) для У a E А, т.е. а = а' + а" => 3 а' > а', 3 а" > а” => 3 а = а' + а” > а,
CLE А.
Аналогично для У b E ВЗЪ E В.Ъ <Ь.
Таким образом, определенная выше сумма в свою очередь является
сечением.
Установим, что для определенной суммы выполнены соответствующие
свойства.
16
1. x' + x" = x" + x'.
Доказательство
Пусть заданы сечения х' = {Л'; В'} и х" = {Л"; В"). В силу коммутатив¬
ности сложения для рациональных чисел получаем
a'+ a" = a"+ a', b'+ b" = b" + b'^x'+х" = х" + х'.Ш
2. (х' + х" ) + хт = х' + (х" + х'").
Доказательство
Аналогично п. 1. ■
3. Существует сечение 0 такое, что V х выполнено х+0 = 0 + х = х.
Доказательство
В качестве такого сечения рассмотрим сечение {Л*; В*}, где А* = {р: ре Q,
р < 0}; В* = {q: q е Q, q > 0}. Тогда для V х = {Л; В} сумма х + 0 = {Л; В}, где
A = {а+ р е Q, р < 0}; В = {b + q е Q, q > 0}. Тогда, выбирая произвольные
а, Ь, а, Ь, получаем
a = a+p<a<b; b = b + q>b>a.
Следовательно, а < b и Ъ > а, т.е х + 0 = х. ■
4. Для любого х = {Л; В) 3 х' = {Л'; В'}: х + х' = 0.
Доказательство
В качестве х' можно рассмотреть сечение вида А! = {-b, b е В}; В' = {-а,
а е А). Очевидно, что это сечение (так как {Л; В] — сечение), при этом
для суммы х + х' = {Л; В) выполнены условия
Л = {а = а - Ь) => а < 0; В = {Ь = Ъ - а) => Ъ > 0 => {Л; В) = 0,
т.е. х' + х = 0. ■
Операция произведения. Для того чтобы определить произведе¬
ние сечений х' и х", рассмотрим сначала базовый случай: х' > 0, х" > 0.
В силу определения нуля (0) и операции сравнения это означает, что
для х' = {А'; В'} их" = {ЛВ") найдутся а', а" такие, что а' > 0, а" > 0
(и конечно, V b', b" => Ь' > 0, Ь" > 0). Тогда произведением х' и х" назовем
сечение х = {Л; В) такое, что
В = {b'- b"}, А = {р < 0, р е Q} и {а' ■ а", а' > 0, а" > 0},
где а', а", Ь', Ь" — всевозможные элементы из соответствующих множеств.
Как и в случае определения суммы, несложно показать, что {Л; В] действи¬
тельно сечение.
В случае если х = 0 имеем х ■ х =0 для V х.
Если х Ф 0, то можно определить | х \ > 0: | х \ = х при х > 0 и | х \ = х', х' —
противоположный для х (см. свойство 4 операции сложения), если х < 0.
Тогда под произведением х' Ф0 их" будем понимать
I х' I • I х" |, если х' > 0 и х" > 0 или х' < 0, х" < 0,
противоположный элемент к | х' \ • \ х" \, в противном случае.
17
Для операции умножения по аналогии с операцией сложения можно
показать, что выполнены следующие свойства.
1../ ._// ._//
.X-X =X • X .
2. (х'■ х") х'" = х'■ (х" ■ х'").
Свойства легко доказываются сначала для х' > 0, х" > 0 с учетом свойств
рациональных чисел, потом обобщаются на случай произвольных знаков.
3. 3 1 : для Vi^i-I=X
В качестве 1 берем сечение
{А;В}:А = \ре Q,p<\},B = {qe Q,?>1}.
Легко показать, что х ■ 1 = х при х > 0, далее свойство распространяется
на случай х < 0.
4. Для V х Ф 0 3 х': х • х' = 1.
Если х > 0, то в качестве х' возьмем сечение
{А'; В'}: В' = {1/а, а > 0}, А' = {р < 0, р е Q} и {1 /Ь}.
Легко показать, что это действительно сечение, при этом х • х' = 1. Далее,
если х < 0, то в качестве х' берем элемент, противоположный к обратному
ДЛЯ I X |.
Таким образом, для сечений выполнены все свойства умножения. Уста¬
новим теперь совместные свойства операций сравнения, сложения и умно¬
жения.
1 (у' А- у"\ • у'" — у' ■ у"' -I- у" ■ У
-L • \ И/ I «V J V1V1 — «V I тЛ/ тЛ/ •
Доказательство
Свойство следует из определения операций сложения и умножения,
а также из соответствующего свойства для рациональных чисел. ■
2. Для х', х" таких, что х' > х", и для V х'" выполнено: х' + х"' > х" + х"'.
Доказательство
Так как х' > х", то 3 а', Ъа' > Ь". Обозначим е = а' - Ь" > 0. В сечении х"
найдутся а"' и Ьш такие, что Ь"' - а'" < е. Следовательно, а' + аш > Ь" + Ь'", так
как a' - b" > b'" - а'". Но это означает, что х' + х'" > х" + х'". ■
3. Для всех х', х", х"' таких, что х' > х", х'" > 0, выполнено х' • хш > х" х
х хш.
Доказательство
Свойство устанавливается аналогично свойству 2 с учетом определения
операции умножения. ■
Покажем теперь, что для построенного множества сечений выполнено
свойство непрерывной упорядоченности, т.е. пусть X, Y — непустые под¬
множества множества всевозможных сечений, такие что для всех х е X
и у G Y выполнено х < у. Тогда найдется сечение с: х < с < у для VxgX
и V у G Y.
Доказательство
Пусть заданы непустые подмножества X и У. Рассмотрим всевозможные
элементы
х = {А'; В'} G X; у = {А"; В"} G У.
18
Определим A = \J А'. Очевидно, что А не имеет максимального элемента
хеХ
(иначе этот элемент максимальный и для какого-то А'). Зафиксируем про¬
извольное a* е А (значит, а* лежит в некотором А') и выберем произволь¬
ное рациональное а, меньшее а*. Получаем, что а лежит в том же самом А',
а значит, и в Л.
Далее, так как ByeY такой, что у>х для Vxe X, то 3 В": для V Ъ" е В"
Ъ" > а' для V а' из любого А! => Ъ" > а для MaeA. Таким образом, имеем
непустое множество В, состоящее из рациональных элементов Ъ > а
для MaeA. Множество В может содержать, а может и не содержать
минимальный элемент. Рассмотрим B = B, если в В нет минимального эле¬
мента, либо В = В\{Ь*}, где Ь* — минимальный элемент В. Таким образом
построено сечение с = {Л; В) (проверьте, что это действительно сечение!).
Покажем, что для M х е X, M у е Y выполнено х < с <у. Пусть х е X, т.е
х = {Л'; В'}. Для произвольного а' е А' выполнено, что а' е А, а значит, а' <Ь
для MbeB, т.е. х < с.
Пусть у е Y. Предположим, что с> у. Тогда Bae Aub" е В" такие, что
а > b". Но так как ае А, то В А': а е А' => В х е Х\х>у, что противоречит
условию на X и Y, значит, с < у. ■
Таким образом, построенное множество сечений удовлетворяет всем
аксиомам из аксиоматического описания множества R, значит, оно изо¬
морфно множеству R.
1.2. Мощность множества. Кардинальные числа
Как было отмечено выше, множество вещественных чисел R является
существенным расширением множества рациональных чисел Q. В связи
с этим возникает вопрос: а насколько существенно это расширение? И как
вообще сравнивать различные бесконечные множества? Ответ на этот
вопрос дает канторова теория множеств.
Для дальнейшего изложения нам потребуются следующие определения.
Определение 1.5. Взаимно однозначное соответствие (биекция) двух
множеств — соответствие, при котором каждому элементу одного мно¬
жества соответствует один и только один элемент другого множества,
и обратно.
Определение 1.6. Два множества называются эквивалентными, если
между ними возможно установить взаимно однозначное соответствие.
Относительно двух эквивалентных множеств говорят, что они имеют оди¬
наковую мощность (обозначение: А ~ В).
Замечание 1.2. На вопрос, что такое мощность множества, можно отве¬
тить так: мощность — это нечто, что есть общего у всех эквивалентных
между собой множеств {определение через абстракцию). Обозначение мощ¬
ности множества А: А, \А\ или cardA
Определение 1.7. Всякое множество А, эквивалентное множеству нату¬
ральных чисел N, называется исчислимым или счетным (обозначение мощ¬
ности счетного множества: K0 (алеф-нуль)).
19
Фактически последнее определение означает, что элементы бесконеч¬
ного множества А можно пронумеровать.
Определение 1.8. Всякое бесконечное множество, неэквивалентное
множеству натуральных чисел, называется неисчислимым или несчетным.
Изложение теории проведем в форме решения задач.
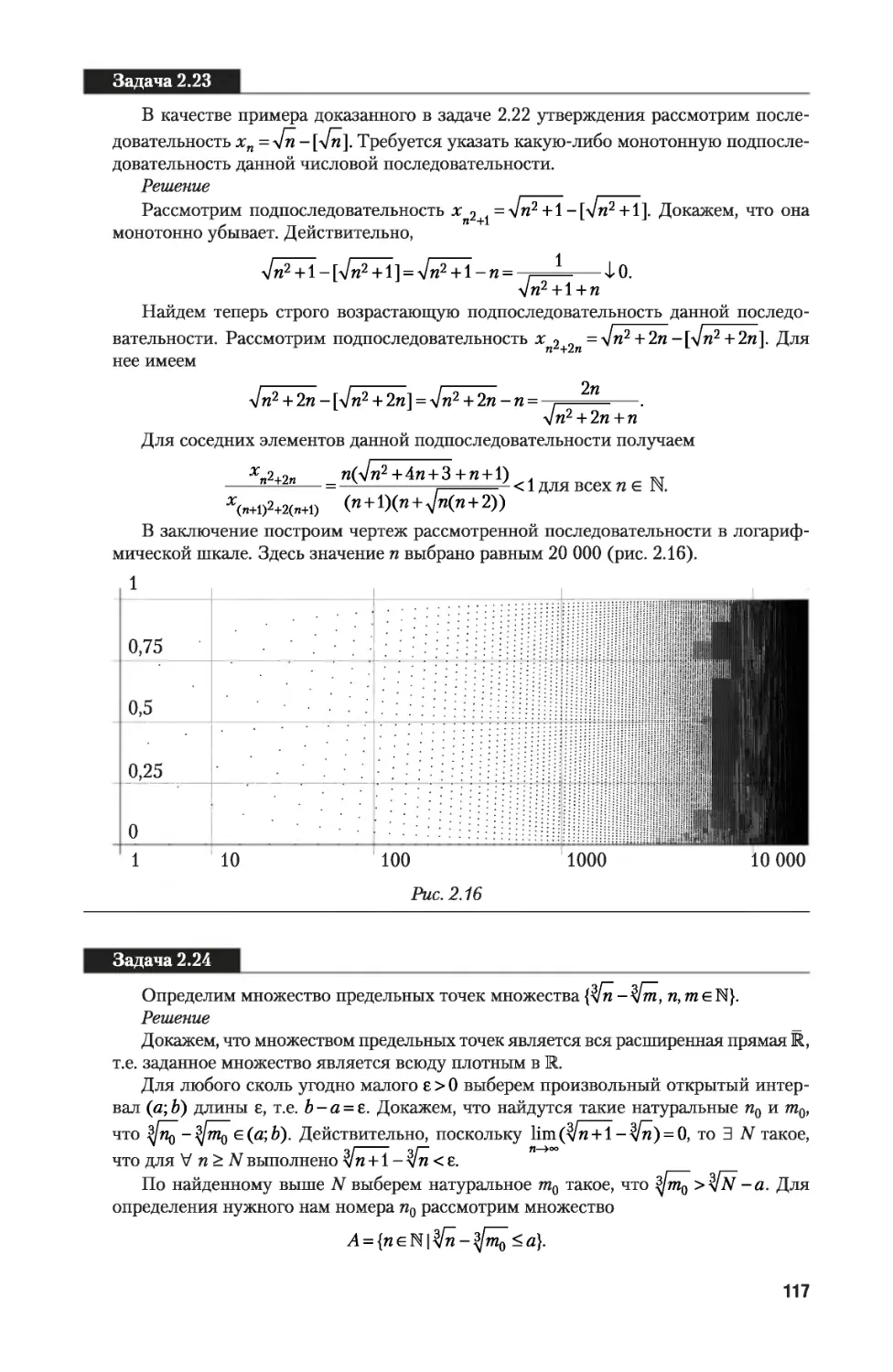
Задача 1.1
Докажем, что из любого бесконечного множества Л можно выделить счетное под¬
множество D.
Решение
Рассмотрим бесконечное множество А. Выделим из данного множества произ¬
вольный элемент ^1. Так как множество А бесконечно, то и множество Л^аД беско¬
нечно, и мы можем выделить элемент а2 из оставшегося множества. По тем же сооб¬
ражениям множество Л\{а1; а2} бесконечно, и мы можем выделить из него элемент а3.
Ввиду бесконечности множества Л данный процесс можно продолжать неограниченно,
в результате чего мы получим последовательность выделенных элементов {аи а2,...,
ап,...}, которая и образует искомое множество D1.
Задача 1.2
Докажем, что всякое бесконечное подмножество счетного множества счетно.
Решение
Ясно, что, для того чтобы множество Л было счетным, необходимо и достаточно,
чтобы его можно было представить в виде последовательности {аь а2,..., ап,...} (дока¬
зывается соотношением элемента ап и его индекса п). Далее, пусть Л — счетное мно¬
жество, а В — его бесконечное подмножество. Так как множество Л счетно, располо¬
жим его в порядке нумерации его элементов и будем перебирать их один за другим
в порядке возрастания их номеров. При этом мы время от времени будем встречать
элементы множества В, и каждый элемент этого множества рано или поздно встре¬
тится нам. Соотнося каждому элементу В номер «встречи» с ним, мы перенумеруем
данное множество, причем в силу его бесконечности нам придется израсходовать
на эту нумерацию «все натуральные числа».
Указанные свойства счетного множества позволяют нам утверждать,
что счетные множества являются наименьшими в некотором смысле (кото¬
рый будет указан далее) бесконечными множествами.
Задание 1.2
Докажите, что: а) объединение конечного и счетного множеств счетно; б) объеди¬
нение двух счетных множеств счетно.
Задача 1.3
Докажем, что объединение счетного множества попарно непересекающихся счет¬
ных множеств есть счетное множество.
1 Вопрос о том, как можно за конечное время проделать некоторую операцию бесконеч¬
ное число раз, мы здесь и далее опускаем. Читатель не согласный с таким подходом, может
обратиться к литературе по аксиоме выбора и попробовать перевести предлагаемые конструк¬
ции на язык, в котором процедура выбора бесконечное число раз за конечное время отсут¬
ствует. Мы же будем заботиться в первую очередь о наглядности проводимых построений.
20
Решение
Пусть счетные множества Ak попарно не пересекаются и счетны. Запишем эти
множества так:
A1
A2 =
Ап = {а\п\а£\...,а%\...},
Заметим, что элементов, у которых сумма индексов равна р е N, конечное число.
Сначала мы выпишем элемент а^, затем элементы afp и у которых сумма верх¬
него и нижнего индексов равна 3, затем те элементы, у которых эта сумма равна 4
(занумерованные в произвольном порядке), и т.д. В результате объединение S = U \
ы
окажется представленным в форме последовательности
откуда и следует ее счетность.
Заметим, что данный способ нумерации множества S не является един¬
ственным. Предлагаем читателю придумать еще несколько.
Задача 1.4
Пусть E — бесконечное множество, D z Е, D — не более чем счетное множество
и E\D бесконечно. Докажем, что множества E\D и E равномощны.
Решение
Выделим помимо подмножества D еще одно счетное множество F в E\D. Это
всегда можно сделать, используя предыдущие результаты, так как множество E\D
бесконечно. Тогда имеем
E = (E\D) u D = (E\D\F) u (Du F)~(E\D\F) u F = E\D.
Здесь мы использовали, что объединение двух счетных множеств счетно, т.е.
DuF^F.
Задача 1.5
Докажем, что если к бесконечному множеству А прибавить конечное или счет¬
ное множество В новых элементов, то это не изменит его мощности, т.е. А и В ~ А.
Решение
Выделим, пользуясь доказанными выше утверждениями, из множества А счет¬
ное подмножество С. И пусть А\С = D, тогда
AuB = Du(CuB)-DuC = A.
Здесь мы использовали, что объединение двух счетных множеств счетно.
Задача 1.6
Пусть А — бесконечное множество. Докажем существование множества В (такого,
что BzA и А\В бесконечно), мощность которого равна мощности А.
21
Решение
Выберем счетное подмножество P = {pk}%= сД и пусть С = А\Р бесконечно.
Положим
Р\ ~ {Pik-\}Г=1 > ^2 ~{Pik)U> В-А\P2-
Отсюда, так как мощности множеств P и P1 совпадают, следует, что
B = AXP2=CuPi-CuP = A.
Кроме того, заметим, что B = CuPi, т.е. множество В бесконечное, что и доказы¬
вает требуемое.
Задача 1.7 (теорема Кантора об алгебраических числах)
Число а € M называется алгебраическим, если оно является корнем некоторого
уравнения вида
bfpc” + Ьп^хп~1 +... + Ь]Х + Ь0 = О,
где bj е Z, т.е. а — корень полинома с целыми коэффициентами. Докажем, что мно¬
жество всех алгебраических чисел А счетно.
Решение
Докажем сначала, что, если {Aj}"=1 — конечный набор счетных множеств, то их
декартово произведение счетно. Воспользуемся методом математической индукции.
Пусть п = 2 и пусть C = AxB, где А = {аь а2,...,ап,...}, B = {bvb2,..., Ъп,...}. Определим
для всех натуральных i множества
Ci= Kai,bj), .7 = 1,2,...}.
OO
Заметим, что каждое множество Ci счетно и C = IJ Ci счетно.
I=1
Предположим, что для (п -1 )-го множества все доказано. Положим 0 = Дх...х Dni.
Тогда по предположению индукции множество D счетно. Отсюда множество
DiX-^xDn = DxDn
тоже счетно. Здесь мы воспользовались тем фактом, что для двух счетных множеств
данное утверждение уже было доказано.
Далее, пусть An — множество всех алгебраических чисел, являющихся корнями
уравнений с целыми коэффициентами, степень которых не превосходит п. Из дока¬
занного выше следует, что множество самих таких уравнений счетно. По основной
теореме алгебры количество различных действительных корней каждого такого урав-
OO
нения не превосходит п. Поэтому An счетно. Так как А = |JAn, то А тоже счетно.
W=I
Замечание 1.3. В частности, мы доказали, что множество Qw (т.е. декар¬
тово произведение конечного числа рациональных чисел) счетно.
Определение 1.9. Всякое множество, эквивалентное множеству точек
отрезка [0; 1], называется множеством мощности континуума (обозначе¬
ние: с).
Задача 1.8
22
Докажем, построив взаимно однозначное соответствие, что:
а) множества [0; 1), (0; 1] и (0; 1) имеют мощность континуума с;
б) множества R, (0; +°°), [0; +°°), (_°°; 0] и (-°°; 0) имеют мощность континуума с.
Решение
а) Определим отображение:
/О) =
х, если х /п, п е N,
1
,еслих = 1/и,иеМ.
п +1
Тогда /(ж) есть взаимно однозначное соответствие между множествами [0; 1]
и [0; 1). Остальные утверждения доказываются аналогично.
б) Согласно предыдущему пункту интервал (0; 1) имеет мощность континуума.
Взаимно однозначное отображение между интервалом (0; 1) и множеством R уста¬
навливается, например, функцией f(x) = tg
г
я
ях —
2
; между R и (0; +°°) — функцией
f(x) = lnx. Равенство остальных мощностей проверяется так же, как в предыдущем
пункте.
Замечание 1.4. Из задачи 1.5 следует, что так как
[0; 1] = (0; I) и {0,1}, (0; 1] = (0; I) u {1}, [0; 1) = (0; 1) и {0},
т.е. три множества получаются из интервала (0; 1) путем добавления ко¬
нечных множеств, то все они эквивалентны интервалу (0; 1), а значит, эк¬
вивалентны между собой.
Замечание 1.5. Используя результаты последних двух задач (счетность
множества алгебраических чисел и несчетность действительных), можно
сделать вывод о том, что существуют трансцендентные (неалгебраические)
числа.
Выше было дано определение эквивалентных (фактически равномощ¬
ных) множеств. Возникает вопрос: если множества не эквивалентны, можно
ли определить, какое из них мощнее? Корректное определение сравнения
мощностей множеств опирается на следующую фундаментальную теорему.
Теорема 1.2 (Кантора — Бернштейна). 1. Если множество А эквива¬
лентно некоторой части В' множества В, а В эквивалентно некоторой
части А' множества А, то А ~ В. 2. Если А с В с С, причем А ~ С, то А ~ В.
Доказательство
Не ограничивая общности, считаем, что множества Л и В не пересека¬
ются. Пусть
/:А—>В'сВи£:В—>А'сА
— две биекции, существующие по условию доказываемой теоремы. Как
обычно, для каждого х е А назовем его прообразом такой элемент у е В,
что g(y) = х. В силу того что g — биекция, если прообраз существует, то он
единственен. Аналогично для у E В определим прообраз х е А такой, что
/(*) = У-
Далее, для каждого элемента из А или В будем брать его самого, его
прообраз, прообраз прообраза и т.д. (пока это возможно). Как уже было
отмечено выше, данное построение однозначно. Назовем длину получа¬
ющейся цепочки рангом начального элемента. Очевидно, что ранг может
быть и бесконечным. Элементы первого ранга — это, очевидно, элементы
из А\А' и В\В'. Для всякого неотрицательного п обозначим через AnCL А
23
множество элементов ранга п, а через A00 — множество элементов бесконеч¬
ного ранга. Аналогичный смысл имеют обозначения Bn и B00.
Отметим, что ранг /(х) на единицу больше ранга элемента х при любом
х E А. Аналогично ранг g(y) на единицу больше ранга у для любого
у E В. Отсюда следует, что / взаимно однозначно отображает элементы
нечетных рангов в А на элементы четных рангов в В. Аналогично для g.
Вместе мы получаем взаимно однозначное соответствие между элементами
конечных рангов в А и В.
Остается установить взаимно однозначное соответствие между эле¬
ментами бесконечного ранга в А и В. Это можно сделать и с помощью /,
и с помощью g.
Окончательно биекцию ср: А —> например, можно определить так:
Ф(х) = -
/(х), если х E ^2k’
£_1(х),еслихе ^2k
/(х), если х E A00.
-и
Доказательство второго пункта оставляем читателю. ■
Введем далее важнейшее определение — операцию сравнения мощно¬
стей двух произвольных множеств.
Определение 1.10. Если множества А и В неэквивалентны, но
3 B1 с В: Bi ~ А и X A1 с А : A1 ~ Bf
то мы считаем, что А < В.
Заметим, что для любых множеств А и В в силу теоремы Кантора —
Бернштейна выполнено одно из определений: A = B, А<В или А>В, т.е.
мощности любых двух множеств можно сравнить.
Задача 1.9
Установим эквивалентность полуинтервала (0; 1] и единичного квадрата (0; 1] х
х (0; 1].
Решение
Представим каждое число из полуинтервала (0; 1] в виде бесконечной двоичной
дроби, т.е. дроби с бесконечным числом единиц1. Такое представление возможно един¬
ственным образом, и, следовательно, этим устранена двузначность, получающаяся
при представлении числа десятичной (или двоичной) дробью. Будем записывать это
представление так: х = {хь X2,...}.
Точке М(х; у) е (0; 1] х (0; 1], где у = {yv у2,...} поставим в соответствие число
Ь = {х1,уьх2,у2,...}Еф\Ц.
И обратно, из числа t = {t{, t2, t3, tA,...} E (0; 1] мы можем получить пару чисел
X — ^з,...}, у — {t2,t^,...}.
Заметим, что при этом соответствии получаются не все точки полуинтервала (0; 1],
а именно, не получится ни одной точки, разложение которой в бесконечную двоич¬
ную дробь содержит нули на всех четных (или нечетных) местах начиная с неко¬
торого номера. Поэтому это не будет взаимно однозначным соответствием между
1 Например, х - {0, I, I, 1,...} вместо х - {1, 0, 0, 0,...}.
24
точками квадрата (0; 1] х (0; 1] и полуинтервала (0; 1]. Однако это соответствие
является взаимно однозначным соответствием между точками квадрата и точками
некоторого подмножества полуинтервала. Далее для установления эквивалентности
(0; 1] ~ (0; 1] х (0; 1] остается воспользоваться вторым пунктом теоремы Кантора —
Бернштейна и заметить, что
(0; 1] ~ C = |(лг; г/) | л: = 0 < г/ < l| с (0; 1] х (0; 1].
Замечание 1.6. Аналогично может быть построено (постройте!) взаимно
однозначное соответствие между отрезком [0; 1] и единичными квадратами
(0; 1] х (0; 1] или [0; 1] х [0; 1], между отрезком [0; 1] и кубом [0; 1] х [0;
1] х [0; 1] и т.д.
Задача 1.10
Установим взаимно однозначное соответствие между множеством иррациональ¬
ных чисел и множеством действительных чисел.
Решение
Обозначим через 3 множество иррациональных чисел, а {гп} — последователь¬
ность всех рациональных чисел, занумерованных так, что T1 = 0 (остальные — про¬
извольно). Построим соответствие между множествами M и 3, положив для любого
натурального п
Q = М\3 э гп <-> 2и72 е 3,
M э пу/2 (2 п +1)>/2 е 3.
Оставшиеся иррациональные числа поставим в соответствие самим себе. Легко
проверить, что данное отображение взаимно однозначно.
Задача 1.11
Докажем, что:
а) объединение счетного числа непересекающихся множеств мощности конти¬
нуума имеет мощность континуума;
б) континуум непересекающихся множеств мощности континуума имеет мощ¬
ность континуума.
Решение
OO
а) Пусть M = Mi, где все множества Mi, i е N, имеют мощность континуума.
I=1
Заметим, что множество M имеет мощность не менее континуума. C другой стороны,
каждому множеству Mi поставим в соответствие полуинтервал [г — 1; г), г = 1,2,.... Тогда
множеству M ставится в соответствие луч [0; + °°), поэтому M — множество мощно¬
сти континуума.
б) Пусть M = [JMa, где Ma = с, I = с. Установив взаимно однозначные соответ-
сс el
СТВИЯ
а<->лге [0;1 ], Moc <->{(*, г/) |г/е(0;1)},
получаем эквивалентность M ~ [0; 1] х [0; 1]. Причем единичный квадрат, как было дока¬
зано ранее, имеет мощность континуума.
Как мы уже заметили, объединение двух счетных множеств является
множеством счетным, объединение двух континуальных множеств конти¬
25
нуально. Возникает следующий вопрос: верно ли, что объединение двух
бесконечных равномощных множеств имеет такую же мощность, как и эти
множества?
Задание 1.3
Докажите, что если объединение двух множеств континуально, то хотя бы одно
из них континуально.
Задача 1.12 (теорема Кантора)
Пусть X — произвольное множество, а 2х — множество всех его подмножеств,
включая 0 и X. Докажем, что мощность множества X меньше, чем мощность мно¬
жества 2х.
Решение
Обозначим через X' множество одноэлементных подмножеств множества X. Так
как X' с 2х и в то же время X ~ X', то неравенство 2х > X выполнено. Докажем, что
данные множества неэквивалентны. От противного, пусть 2х ~ X и пусть ср — вза¬
имно однозначное соответствие между этими множествами, т.е. для VxeXB ф(х) е 2х,
и каждый элемент 2х есть ср(х) для одного и только одного хеХ.
Назовем элемент хеХ правильным, если хеср(х) (т.е. х лежит в том множестве,
которое ему соответствует), и неправильным в противном случае. Заметим, что эле¬
мент, который в соответствии ср отвечает самому множеству X, очевидно, правиль¬
ный, а элемент, отвечающий пустому множеству, очевидно, неправильный, т.е. дан¬
ные два множества непусты, и каждый элемент хеХ лежит в одном и только в одном
из данных множеств.
Обозначим далее через В множество всех неправильных (и только неправильных)
элементов множества X. Так как В с 2х, то в соответствии ср этому множеству отве¬
чает некоторый элемент X0 е X, т.е. В - ср(х0). Каков же этот элемент X0 — правиль¬
ный или неправильный? Допустим, что он правильный. Это значит, что X0 € ср(х0) = В.
Но так как множество В по определению состоит только из неправильных элемен¬
тов, то х0 — элемент неправильный, что противоречит сделанному допущению. Итак,
х0 — неправильный элемент. Но тогда по определению множества В х0 gcp(х0)сД
а это, в свою очередь, означает, что X0 — правильный. Стало быть, элемент X0 ни пра¬
вильный, ни неправильный, что противоречит тому, что всякий элемент — или пра¬
вильный, или неправильный. Данное противоречие и показывает неэквивалентность
множеств 2х и X.
Определение 1.11. Назовем функцию
Xa(х) =
[1, если хе А,
[О, если х € А
характеристической функцией множества А.
Определение 1.12. Назовем мощность множества всех подмножеств
отрезка [0; 1] мощностью гиперконтинуума.
Задача 1.13
Докажем, что множество всех действительных однозначных функций на отрезке
[0; 1] имеет мощность гиперконтинуума.
Решение
C одной стороны, данное множество содержит в себе все характеристические
функции всех подмножеств отрезка [0; 1], поэтому его мощность не меньше гипер¬
26
континуума. C другой стороны, любая функция однозначно задается своим графи¬
ком на плоскости. Следовательно, мощность множества всех вещественнозначных
функций не превосходит мощности множества всех подмножеств [0; 1] х R. Последняя
равна гиперконтинууму, так как [0; 1] х R ~ [0; 1] х [0; 1]. Применяя теорему Кантора —
Бернштейна, получаем требуемое.
Задача 1.14
Докажем, что множество всех двоичных (т.е. состоящих из 0 и 1) последователь¬
ностей имеет мощность континуума.
Решение
Покажем, что множество всех двоичных последовательностей не является счет¬
ным. Предположим противное, пусть множество всех двоичных последовательно¬
стей можно пронумеровать. В этом случае все они могут быть расположены по стро¬
кам бесконечной таблицы. Выделим последовательность из нулей и единиц, стоящих
на диагонали. Далее инвертируем данную последовательность, т.е. на всех местах,
где стоит нуль, поставим единицу, и наоборот. Очевидно, что построенная двоич¬
ная последовательность не лежит в рассматриваемой таблице, так как она отлича¬
ется от первой строки в первом элементе, от второй во втором и т.д. Следовательно,
наше предположение неверно, что доказывает требуемое.
Таким образом, множество двоичных последовательностей — более мощное, чем
счетное. Покажем, что на самом деле оно имеет мощность континуума. Приведем кон¬
структивное доказательство этого факта. Построим соответствие между веществен¬
ными числами отрезка [0; 1] и подмножеством двоичных последовательностей сле¬
дующим образом. Выберем произвольное число х е [0; 1] и разобьем данный отрезок
на две равные части:
Если х лежит в левом отрезке, положим X1 = 0,
если в правом -X1=I (случай х =
1
2
будет рассмотрен ниже). Далее разбиваем отре¬
зок, в котором лежит х, на две равные части; если х лежит в левой, положим х2 = 0,
иначе X2 = 1. И продолжаем данный процесс бесконечное число раз. Если число х
TTl
лежит на границе отрезка, т.е. представляет из себя число вида —, т = 1,...,2”, то
выбираем в качестве хп единицу. Этим мы строим соответствие вещественных чисел
отрезка [0; 1] и двоичных последовательностей, за исключением тех, у которых начи¬
ная с некоторого номера стоят нули, т.е. мощность отрезка [0; 1] не больше, чем мощ¬
ность множества двоичных последовательностей.
Обратно, каждой двоичной последовательности поставим в соответствие двоич¬
ную последовательность, у которой на всех четных местах стоят нули, а на нечет¬
ных — элементы рассматриваемой последовательности, т.е.
{0,1,1, 0,...}<->{0, 0,1,0,1,0, 0, 0,...}.
Очевидно, что каждой двоичной последовательности можно поставить в соответ¬
ствие единственное вещественное число из отрезка [0; 1]. И так как мы избавились
от случая периода из единиц, каждому из поставленных в соответствие веществен¬
ных чисел (безусловно, это будут не все числа отрезка [0; 1]) будет соответствовать
только одна двоичная последовательность, т.е. мощность отрезка [0; 1] не меньше,
чем мощность множества двоичных последовательностей. Остается воспользоваться
теоремой Кантора — Бернштейна.
Данное утверждение позволяет доказать еще один важный факт.
27
Задача 1.15
Докажем, что множество всех подмножеств счетного множества является множе¬
ством мощности континуума, т.е. 2м = с.
Решение
Пусть задано счетное множество X. Занумеруем его элементы: х1,х2,...,хп,... .
Любое его подмножество X можно однозначно описать двоичной последовательно¬
стью {at} так, что если Xi еХ, то а{ =1, иначе а, =0. Таким образом, множество всех
подмножеств множества X эквивалентно множеству всех двоичных последователь¬
ностей, а значит, используя предыдущее утверждение, получаем 2м = с.
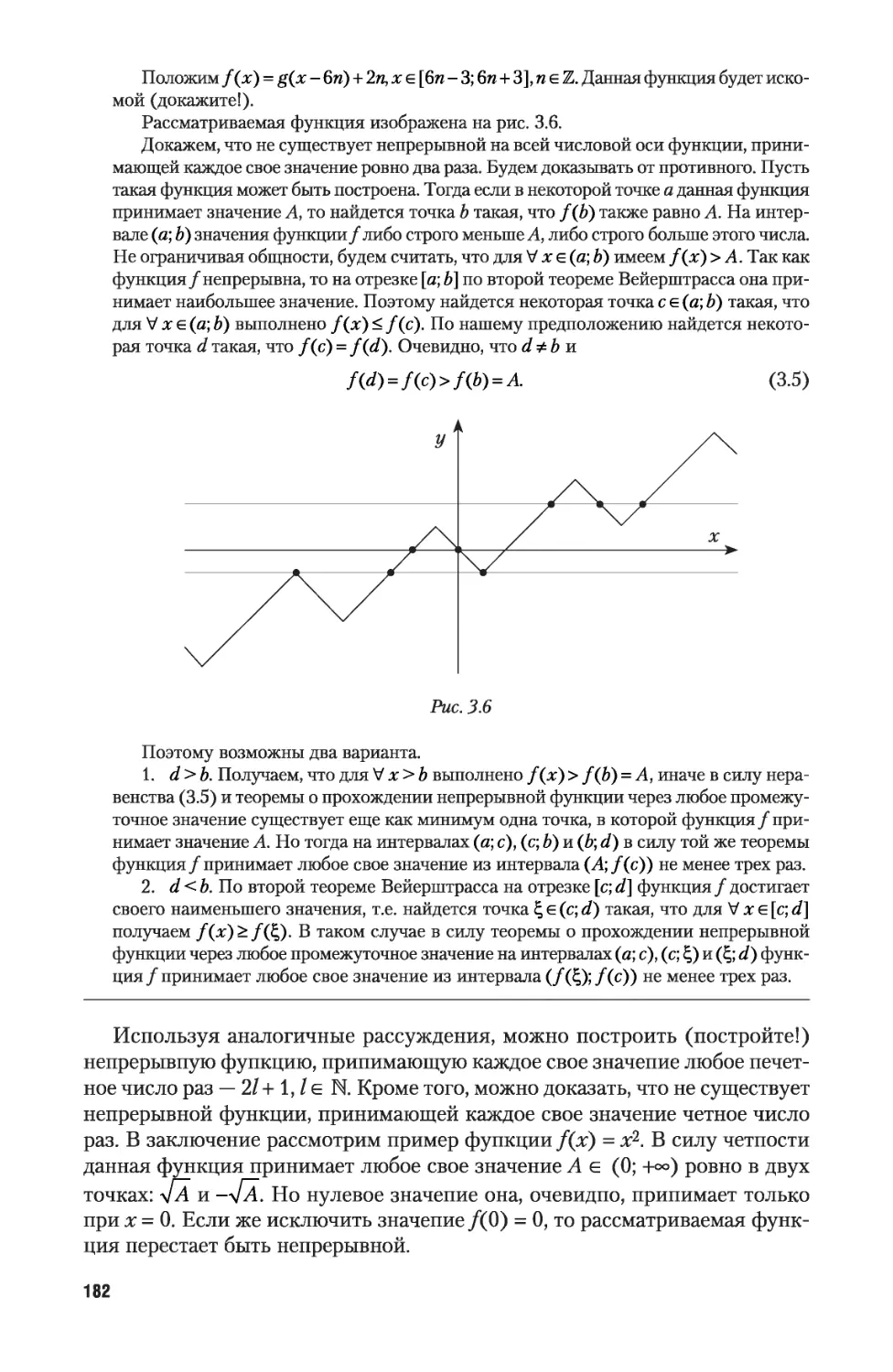
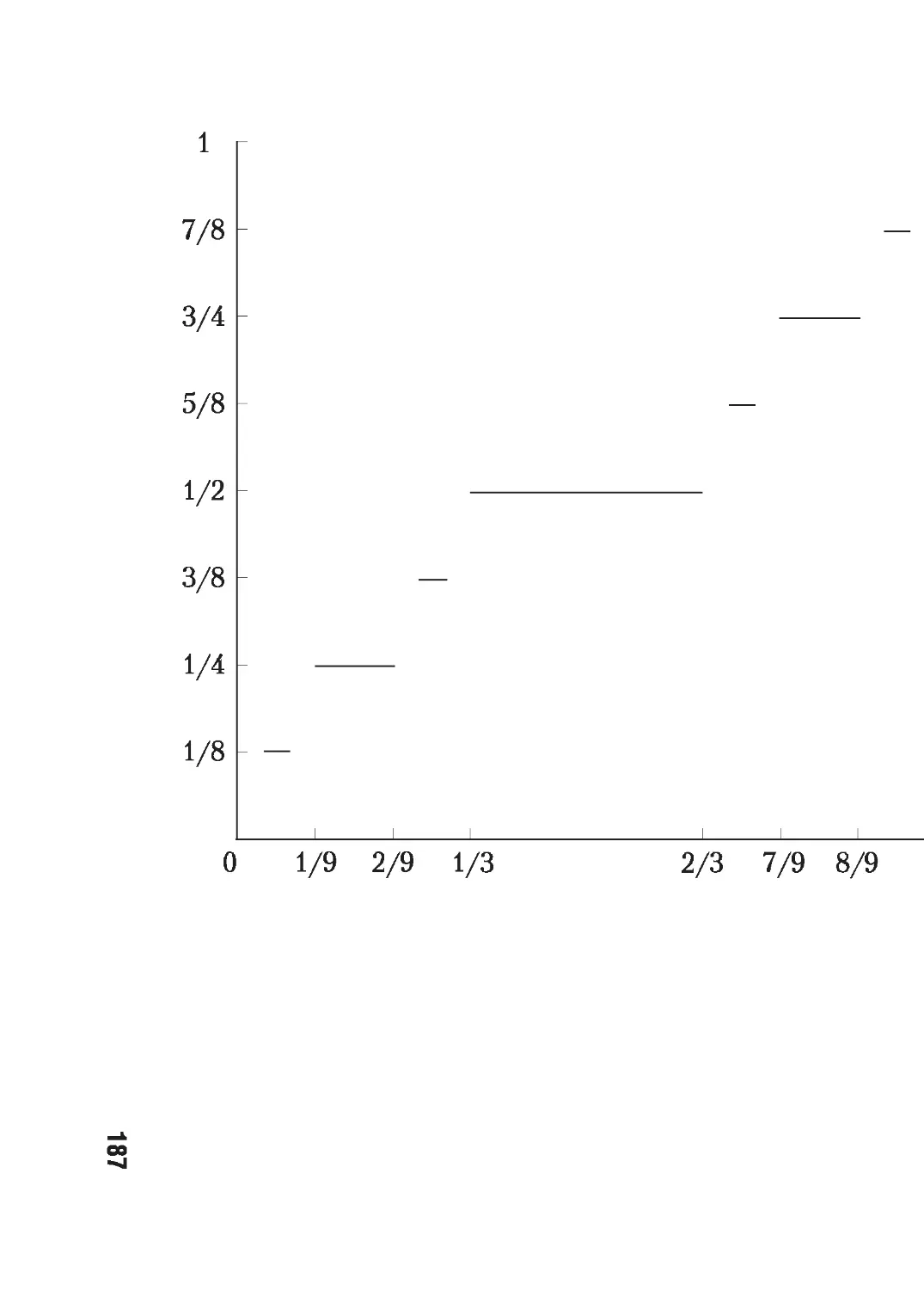
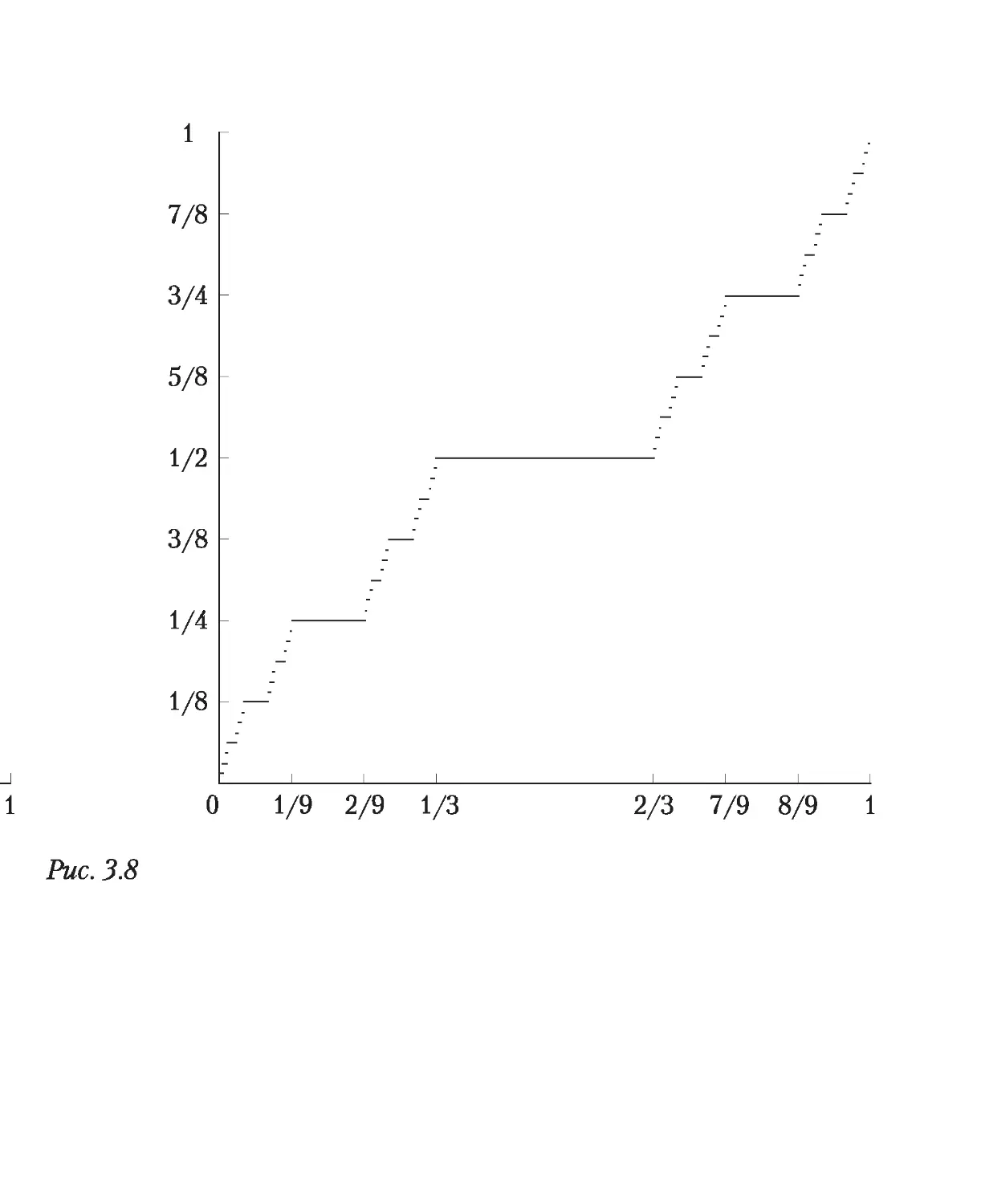
Задание 1.4
Докажите, что множество чисел х е (0; 1), в троичном разложении которых со¬
держится п единиц, имеет мощность континуума.
Задание 1.5
Докажите, что множество чисел х е (0; 1), в троичном разложении которых со¬
держится бесконечно много единиц, имеет мощность континуума.
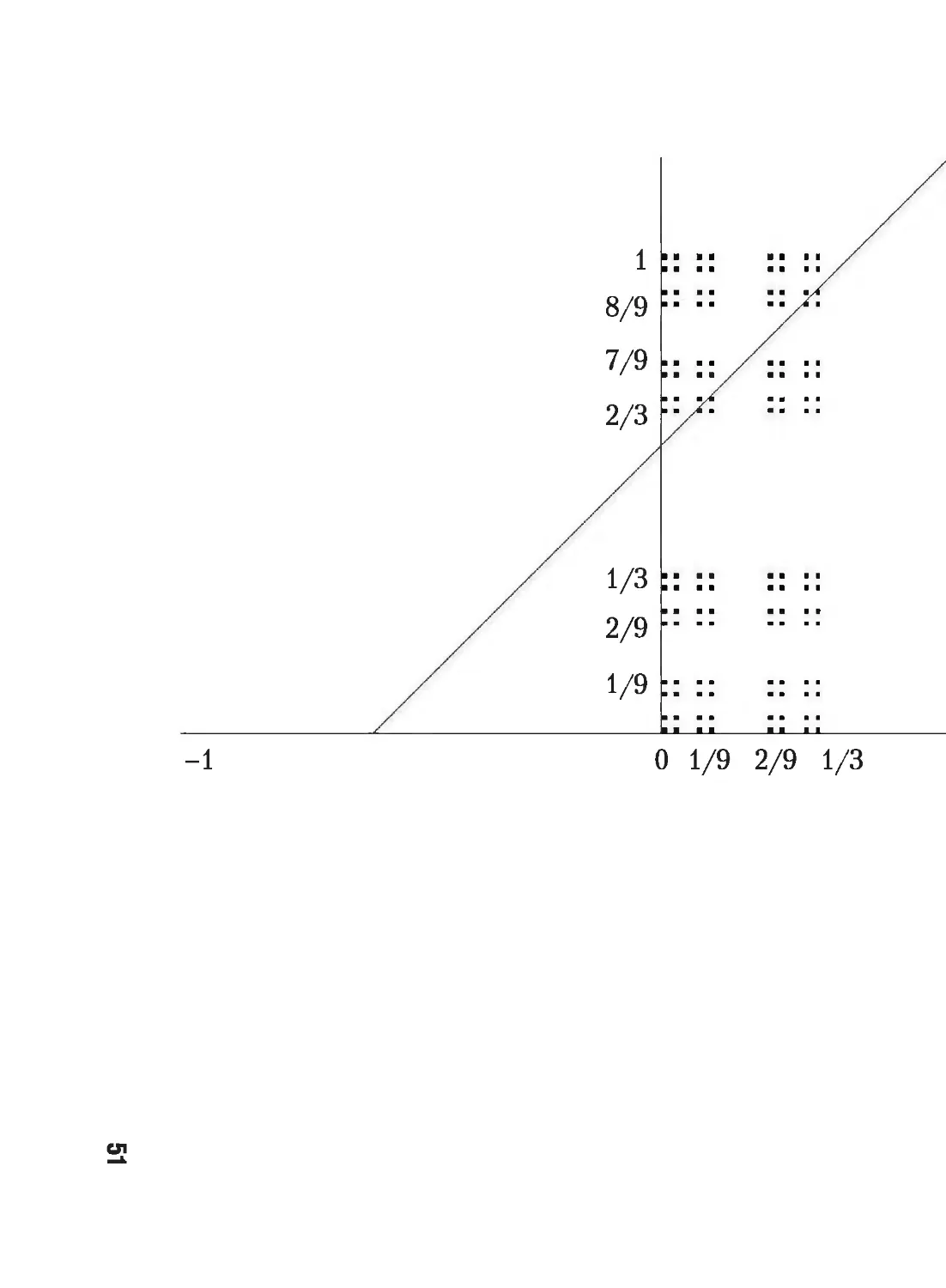
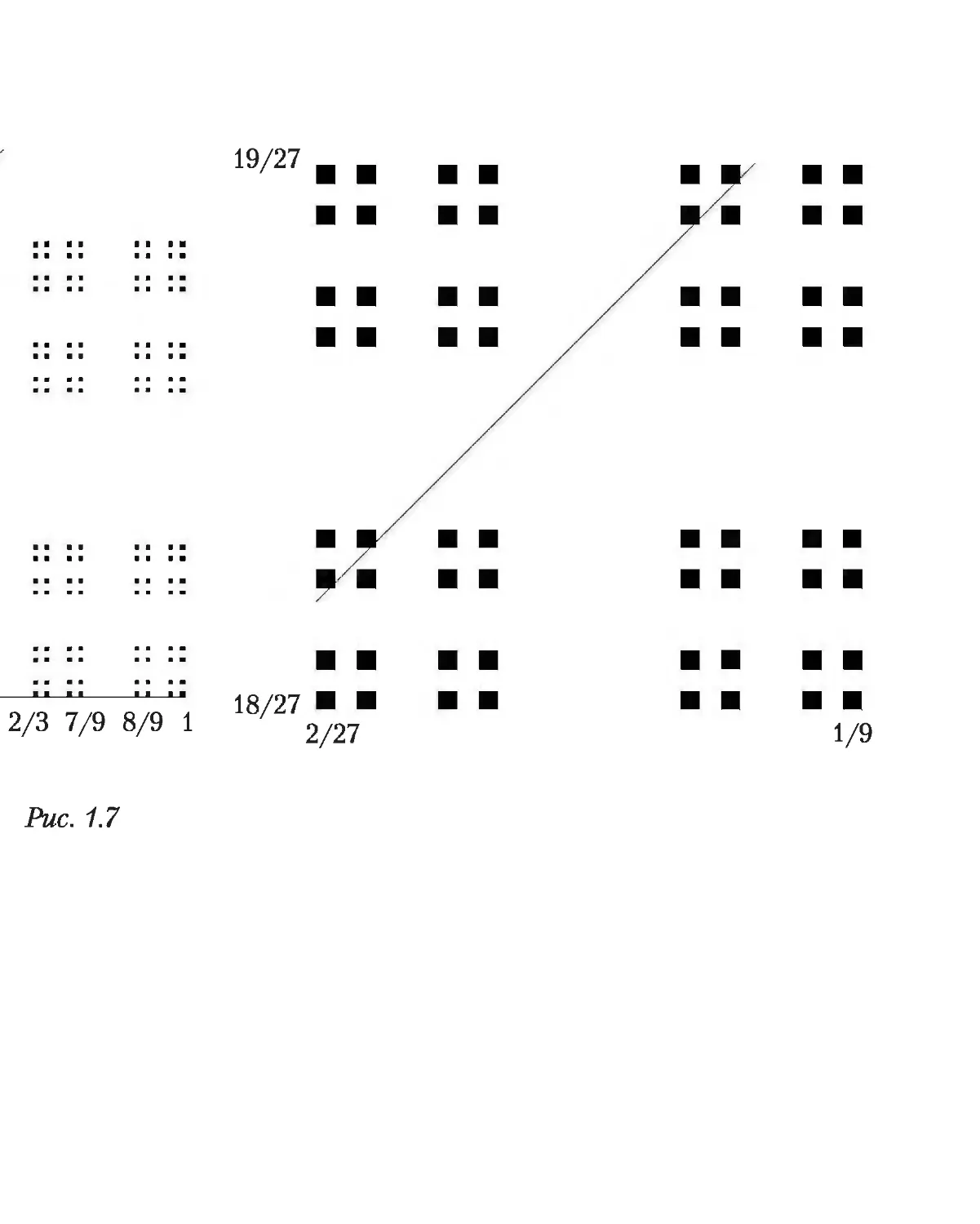
1.3. Метрические пространства
Определение 1.13. Будем говорить, что множество X представляет
из себя метрическое пространство, если любым двум элементам х и у этого
множества соответствует вещественное число р(х; у), называемое рассто¬
янием от х до у, такое что:
1) р(х; у) > 0, если х Фу, и р(х; у) = 0, если х = у (неотрицательность);
2) р(х; у) = р(г/; х) (симметричность);
3) р(х; у) < р(х; z) + р(г; у) при любом z е X {неравенство треугольника).
Обозначение метрического пространства (с указанной метрикой): {X, р).
Замечание 1.7. Элементы метрического пространства обычно называ¬
ются точками.
Докажем элементарные следствия из неравенства треугольника.
Утверждение 1.1. Для любых точек X1, х2,..., хп метрического простран¬
ства {X, р) имеет место неравенство
p(xt; хп) < p(xt; х2) + р(х2; х3) +... + р{хп_{, хп).
Доказательство
Последовательно применяя неравенство треугольника, получим
p(xi; хп) < PCx1; х2) + р(х2; хп) < PCx1; х2) + р(х2; X3) + р(х3; хп) <... <
< PCx1; х2 ) + р(х2; х3 ) +... + PCx^1; хп ). U
Утверждение 1.2. Для каждых четырех точек х, у, z, w метрического
пространства (X, р) имеет место неравенство четырехугольника
|р(х; у) - p(z; w)I < р(х; z) + р{у; w).
28
Доказательство
Дважды применяя неравенство из предыдущего утверждения, получаем
Отсюда имеем
р(х; у) < р(х; г) + р (z; w) + р (щ у),
p(z) w) < р (Z) х) + р(х; у) + р (у; w).
р(х) у) - р (Z) w) < р(х) z) + р (w) у),
P (z) w) - р(х; у) < р (Z) х) + р (у) w).
Воспользовавшись аксиомой симметричности, получаем, что правые
части данных неравенств совпадают, а левые части отличаются знаком.
Следовательно, требуемое неравенство установлено. ■
Пример 1.1
Вещественная прямая R с введенным на ней расстоянием по формуле р(х; у) =
= \х-у \ является метрическим пространством. Выполнение условий метрического
пространства моментально следует из свойств модуля.
Пусть, далее, (X, р) — метрическое пространство (с указанной метри¬
кой), все упоминаемые ниже точки и множества считаются элементами
и подмножествами пространства X.
Определение 1.14. Окрестностью точки х (8-окрестностью) шаром
с центром в точке х) называется множество В8(х), состоящее из всех точек у
таких, что р(х; у) < 8. Число 8 называется радиусом окрестности В5(х).
Отметим, что окрестностями на прямой R являются интервалы, а на пло¬
скости R2 — внутренности окружностей.
Рассмотрим далее подмножество метрического пространства (X, р) —
Лс1.
Определение 1.15. Точках называется предельной точкой множества А,
если каждая окрестность точки х содержит точку у Ф х такую, что у G А.
Определение 1.16. Точка х называется изолированной точкой множе¬
ства А, если х G А и существует такая окрестность точки х, в которой
не содержится других точек множества А, т.е. точка х не является предель¬
ной точкой этого множества.
Совокупность предельных и изолированных точек множества А состав¬
ляет множество точек прикосновения данного множества. Заметим, что
любая точка множества А является его точкой прикосновения. Обратное,
вообще говоря, неверно. Достаточно рассмотреть пример интервала (0; 1)
и точек 0, 1.
Определение 1.17. Точка х называется внутренней точкой множества
А, если она имеет окрестность В8(х), полностью лежащую в множестве А.
Определение 1.18. Множество А будем называть открытым, если каж¬
дая из его точек является внутренней.
Определение 1.19. Множество А называется замкнутым, если оно
содержит все свои предельные точки.
Определение 1.20. Точка х называется внешней для множества А, если
найдется окрестность В8(х), целиком не принадлежащая X (т.е. В8(х) п
пЛ = 0).
29
Определение 1.21. Точка х называется граничной точкой множества А,
если она не внутренняя и не внешняя.
Можно дать и альтернативное определение.
Определение 1.21'. Точка х называется граничной точкой множества А,
если в любой окрестности В5(х) есть точки, как принадлежащие множе¬
ству А, так и не принадлежащие ему.
Задание 1.6
Докажите, что изолированная точка является граничной точкой множества.
Определение 1.22. Совокупность граничных точек множества называют
границей множества А (обозначение: ЭЛ).
Теперь мы можем доказать следующее утверждение.
Утверждение 1.3. Множество А замкнуто тогда и только тогда, когда
оно содержит все свои граничные точки.
Доказательство
Достаточность. Пусть множество А содержит все свои граничные
точки. Следовательно, все точки, которые не входят в данное множество,
являются внешними. Предельные точки, по определению, внешними
не являются. Поэтому все они принадлежат множеству А.
Необходимость. Пусть множество А замкнуто, т.е. содержит все свои
предельные точки. Предположим также, что существует граничная точка х,
не принадлежащая А, т.е. для Vs>0 в Ве(х) есть точки из множества А,
причем отличные от точки х (точка х не принадлежит множеству А). Сле¬
довательно, по определению, точка х — предельная. Получили противоре¬
чие. ■
Пример 1.2
Рассмотрим множество А, состоящее из всех рациональных точек интервала [0; 1],
т.е. А = Q п [0; 1]. Тогда границей данного множества является весь отрезок [0; 1].
При этом А с ЭЛ, т.е. граница мощнее самого множества.
Пример 1.3
Рассмотрим множество А - (0; 1] и {2}. Точки интервала (0; 1) являются предель¬
ными, но не являются граничными. Точка {1} является и предельной, и граничной.
Точка {2} является граничной, но не является предельной.
Определение 1.23. Если множество А незамкнуто, то, добавив к нему
все его предельные точки, получим замкнутое множество, называемое
замыканием множества А (по сути, замыкание — минимальное замкнутое
множество, содержащее А). Обозначение: А.
Проверьте, что замыкание А можно получить, добавив к нему все гра¬
ничные точки.
Теорема 1.3. Всякая Ь-окрестность является открытым множеством.
Доказательство
Для каждой точки рассматриваемой окрестности у&В8(х) обозна¬
чим расстояние р(г/;x) = d<8. Далее рассмотрим шар с центром в точке у
30
радиуса и докажем, что он полностью лежит в B8 (х). Действительно,
для любого z G B8_d (у) по неравенству треугольника имеем
~2~
p(z; х) < p(z; у) + p(z/; х) <- Yd = < 8, так как d< 8. ■
Теорема 1.4. Если х — предельная точка множества А, то любая окрест¬
ность точки х содержит бесконечно много точек множества А.
Доказательство
Предположим, что существует окрестность точки х, содержащая только
конечное число точек множества А, отличных от нее самой: х1,х2,...,хп.
Положим
d = min р(х;хЛ
I <i<n
Ясно, что d > 0. Окрестность Bd{x) не содержит ни одной точки множе¬
ства А, отличной от х. Поэтому х — не предельная точка множества А. Это
противоречие и доказывает теорему. ■
Из теоремы 1.4 вытекает элементарное следствие.
Следствие 1.1. Конечное множество не может иметь предельных точек.
Теорема 1.5. Объединение любой совокупности открытых множеств
и пересечение конечной совокупности открытых множеств снова являются
открытыми множествами.
Доказательство
Рассмотрим множество U Aa, где I — произвольное множество индексов
осе/
и для любого a G / множество Aa открыто. Выберем далее произвольную
точку х0 G U Aa, т.е. найдется индекс а0 g I такой, что X0 g А0» а так как Aa^
ael
открыто, то получим существование 8 > 0 такого, что B8(X0) с Aa с UAx-
ссе/
Рассмотрим далее пересечение конечной совокупности открытых мно-
П
жеств и произвольную точку X0 G ПА- Получаем, что точка X0 принадле-
4=1
жит каждому множеству Ab ...,An и входит в первое из них вместе с окрест¬
ностью ВГ1(х0), во второе — с окрестностью Br^(X0) и т.д. Пусть теперь
r = min{r1,r2,...,rj. Тогда очевидно, что шар Вг(х0) содержится в каждом
из шаров Br,...,Br , а значит, и в каждом из множеств A1, ..., An, следова¬
тельно, содержится в их пересечении. ■
Замечание 1.8. Отметим, что для бесконечной совокупности открытых
множеств рассуждение насчет пересечения множеств может уже не иметь
места, так как точная нижняя грань строго положительных чисел ц может
быть равной нулю. Действительно, пересечение бесконечного числа откры¬
тых множеств
An = {х: р(х, 0) < \/п, п = 1, 2,...}
содержит только точку 0. Поэтому данное пересечение не является откры
Г 1 . 1Л
тым множеством. Еще один пример: An =
—; 1+
п п
, тогда А = UA = [0; 1]
k 1
31
C
замкнутое множество; An =
л
--■л
п
, А = [0; 1) — не открыто и не замкнуто;
An = (0; I), А = (0; 1) — открытое.
Определение 1.24. Дополнением множества А (обозначается символом
Ac или CA) называется множество всех точек х E X таких, что х £ А.
Считается, что пустое множество, как и все пространство X, открыто
и замкнуто.
Теорема 1.6. Множество А открыто тогда и только тогда, когда его
дополнение замкнуто.
Доказательство
Предположим, что множество А открыто. Пусть х — предельная точка
множества Ac. Тогда каждая окрестность данной точки содержит некото¬
рую точку множества Ac, поэтому х не является внутренней точкой мно¬
жества А. Поскольку А открыто, получаем, что х £ А, т.е. х E Ac. Следова¬
тельно, Ac замкнуто.
Пусть теперь Ac замкнуто. Выберем произвольную точку те А. Тогда
х&Ас и х не является предельной точкой для множества Ac. Следова¬
тельно, существует окрестность точки х такая, что ее пересечение с Ac
пусто, т.е. она полностью лежит во множестве А. Таким образом, х — вну¬
тренняя точка множества А иА открыто. ■
Следствие 1.2. Множество А замкнуто тогда и только тогда, когда его
дополнение открыто.
Утверждение 1.4 (правила двойственности). Для любых двух мно¬
жеств А и В справедливы следующие равенства:
(A u В)С = A^n ВС, (A n В)С = A^u BC
Доказательство
Докажем, например, первое равенство (второе рассматривается анало¬
гично — меняя местами символы и и п, а также заменяя «и» на «или»).
Имеем
хG(АиВ)С фф х £ (А и В) <=> х £ А и х £ В <=> х G Ac и х G Bc <=> х G Ac n Bc. ■
Используя теоремы об объединении и пересечении открытых множеств,
а также правила двойственности, можно доказать следующую теорему.
Теорема 1.7. Пересечение любого семейства замкнутых множеств есть
замкнутое множество. Объединение конечного числа замкнутых множеств
есть замкнутое множество.
Задание 1.7
Постройте пример бесконечного объединения замкнутых множеств, не являюще¬
гося замкнутым множеством (открытым, не открытым и не замкнутым).
Определение 1.25. Множество AczX ограничено, если существуют такое
вещественное число M и точка х E X, что р(у; х) < M при всех у E А.
Задание 1.8
Покажите, что если множество AcX ограничено, то для Vjce I найдется чис¬
ло M такое, что р(у; х) < M для VyeA, т.е. точку х е X в определении ограниченного
32
множества можно выбрать произвольной (часто если в X есть нулевой элемент, то
в качестве этого х выбирают именно его).
Рассмотрим далее задачу, в решении которой мы пользуемся понятием
числовой последовательности. Читателям, незнакомым с ним, предлага¬
ется вернуться к данной задаче после изучения второй главы.
Задача 1.16
Определим множество всех предельных в R точек множества X ~{4п -[-s/и], VwgN),
где [4п ] — целая часть числа л/п.
Решение
Заметим, что X с [0; 1], и докажем сначала, что, построив подпоследовательность,
состоящую из элементов множества X, в качестве ее частичных пределов можно полу¬
чить любое число из множества Q п [0; 1 ]. Приведем соображения, которые подскажут
выбор подходящей подпоследовательности. Будем искать ее в виде xk = yjт% + Ik - mk
при условии, что [\Jmk + Ik ] = mk, т.е. 0 < Ik < 2mk. Фиксируем далее произвольные р
и q. Тогда при больших k элементы этой подпоследовательности
X = ^Jm2 +1 -m~ — s(0; 1) <=> m2 + / ~ m2 + ^Pm +1L
q q q2
Следовательно, выбрав mk = kq, получим Ik = 2pk. Докажем, что выбранная под¬
последовательность действительно сходится к требуемому числу. Имеем
Ч = дК2 +Ik-Tnk = Jk2q2 +2pk-kq= I 2Р* =i 1Р
yjk2q2 + 2pk+kq ^jq2 + 2p / k+q 4
В качестве подпоследовательностей, состоящих из элементов рассматриваемого
множества, сходящихся к числам {0} и {1} соответственно, выбираем
хР = 4k2 -k = 0n xf = \lk2 + 2k -k= , ^ > I.
yjk2 + 2k+kn~^°°
Далее, используя то, что для каждого хе[0;1] и любого е>0 в Be(х) найдутся
рациональные числа, делаем вывод о том, что отрезок [0; 1] и является множеством
всех предельных точек изучаемого множества.
Задание 1.9
Докажите, что у любых двух различных точек расширенной числовой прямой (т.е.
числовой прямой, включающей в себя +°°) существуют непересекающиеся окрест¬
ности (в качестве указания предлагаем рассмотреть рис. 1.2).
U
а;
Ъ-а
2 )
а
и
\ Ь-o'
о;
I 2 J
„ -
Ъ
С/(—°о; 8) t/(+°°; 8)
1 «С-
а = —оо О b = -оо
U
V
1 '
|6| + 1,
ЩЬ-, 1)
Ща-, 1)
U
+оо;
1 ^
|а| + 1,
а = -«о
а
Ь = —оо
Рис. 1.2
33
1.4. Ограниченные и неограниченные множества на прямой
В соответствии с приведенным выше определением произвольного огра¬
ниченного множества, используя естественную метрику в R, для множеств
на числовой прямой можно расширить теорию ограниченных и неограни¬
ченных множеств.
Определение 1.26. Будем говорить, что множество XcR ограничено,
если
3 М> 0: V х G X выполнено \ х\ <М.
Фактически речь идет о расстоянии до 0 G R, т.е. р(х, 0) = | х - 0 | < М.
Определение 1.27. Будем говорить, что множество XcR ограничено
сверху (снизу), если BMgR такое, что х < M (соответственно M < х)
для VxgX
Отрицание: X не ограничено сверху тогда и только тогда, когда
для VMg RBxg Х:х>М.
Определение 1.28. Число M в случае ограниченного сверху (снизу)
множества называют верхней (нижней) границей множества X или, также,
мажорантой (.минорантой) множества X.
Замечание 1.9. Множество, ограниченное и сверху, и снизу, является
ограниченным.
Определение 1.29. Элемент а е X называется наибольшим {наимень¬
шим) элементом множества XcR, если для VxgX выполнено х<а{а<х).
Замечание 1.10. Из аксиомы 3б порядка следует, что если в числовом
множестве есть наибольший (наименьший) элемент, то он только один
(покажите!). Однако не во всяком, даже ограниченном, множестве имеется
наибольший (наименьший) элемент. Например, их нет во множестве
{xg R|0<x< 1} = (0; 1).
Определение 1.30. Наименьшее из чисел, ограничивающих множество
XcR сверху, называется точной верхней гранью множества X и обознача¬
ется supX, т.е.
P = SUpX <=> 1)VxgXx<P; 2)VP'<P3xgX: х>Р'.
Альтернативное определение:
P = supX <=>l)VxGXx<P;2)Ve>03xGX:x>P-e.
Определение 1.31. Наибольшее среди всех чисел, ограничивающих
множество XcR снизу, называется точной нижней гранью множества X
и обозначается infX, т.е.
a = infX ^ l)VxGXx>a; 2)Va'>oc3xgX: x<a'.
Альтернативное определение:
a = infX ol)VxGXx>a;2)V£>03xGX:x<a + e.
34
Выше приводился пример того, что не всякое множество обладает мини¬
мальным или максимальным элементом. Выясним вопрос: всегда ли у число¬
вого множества существует его точная верхняя (нижняя) грань? Очевидно,
что если множество не ограничено сверху (снизу), то не существует чисел,
которые бы ограничивали его сверху (снизу). Таким образом, в данном слу¬
чае у числового множества нет верхней (нижней) грани. Если же рассматри¬
ваемое множество ограничено, то ответ дает следующее утверждение.
Утверждение 1.5 (принцип верхней грани). Всякое непустое ограни¬
ченное сверху числовое множество в R имеет, и притом единственную, точ¬
ную верхнюю грань.
Доказательство
Единственность точной верхней грани нами уже была отмечена. Дока¬
жем ее существование.
Обозначим рассматриваемое числовое множество за X, a Y = {у G R | V х G
G X: х < у) — множество чисел, ограничивающих X сверху. Так как, по усло¬
вию, множества X и Y не пустые, то в силу аксиомы непрерывности суще¬
ствует число |3gR такое, что для любых х G X и у G Y выполняется х < P <у.
Число Р, таким образом, является мажорантой X и минорантой Y. Как мажо¬
ранта X число P принадлежит множеству Y, но как миноранта Y число P
является минимальным элементом множества Y. Итак, P = min У = supX. ■
Аналогично доказываются существование и единственность точной
нижней грани у ограниченного снизу числового множества, т.е. верно сле¬
дующее утверждение.
Утверждение 1.6 (принцип нижней грани). Всякое непустое ограни¬
ченное снизу числовое множество имеет, и притом единственную, точную
нижнюю грань.
Заметим, что если числовое множество обладает максимальным эле¬
ментом, то он всегда совпадает с его точной верхней гранью. Между тем
уже приводившееся выше множество X = (0; 1) не имеет максимального
элемента, но 3 supX = 1. Аналогичные рассуждения имеют место и для inf,
и минимума. Читатель может легко убедиться, что точка х = 1 является
предельной для множества X В общем случае это не является случайным,
а именно, верна следующая теорема.
Теорема 1.8. Если верхняя (нижняя) грань supX = ос (infX = Р) множе¬
ства X не содержится в нем, то точка a (P) есть предельная для данного
множества.
Доказательство
Действительно, пусть существует supX = а. По определению точной
верхней грани убеждаемся в том, что в любой окрестности Be (ос) точки а,
когда а не принадлежит X, найдутся точки х > а - в, принадлежащие рас¬
сматриваемому множеству. Это и означает, что точка а в этом случае явля¬
ется предельной для множества X. ■
Доказательство теоремы в случае существования нижней грани предо¬
ставляем читателю.
Замечание 1.11. Если множество X ограничено сверху (снизу), то
supX = ос (infX =P)- точка прикосновения множества X, и притом макси¬
мальная (минимальная) из всех точек прикосновения (докажите!).
35
Для множества рациональных чисел Q, как было отмечено выше,
не выполняется аксиома непрерывности, а потому для Q и принцип точных
граней также не выполняется.
Рассмотрим, например, множество
X = {х G Q, X2 < 2}.
Это множество ограничено и сверху, и снизу, но среди рациональных
чисел нет таких, которые удовлетворяли бы определениям supX и infX.
Однако такие числа найдутся на множестве М:
supX = л/2, infX = -л/2.
Задание 1.10
Пусть X — ограниченное множество, а (-Х) — множество чисел, противоположных
числам xs X. Выразите: a) inf(-X) через supX; б) sup(-X) через infX.
Задание 1.11
Пусть X + Y — множество всех сумм х + у, где х s X, у е Y. Докажите равенства:
a) inf(X + У) = infX + inf У; б) sup(X + Y) = supX + sup У.
Задание 1.12
Пусть XY — множество всех произведений ху, где х s X, у е У, причем х > 0, у > 0.
Докажите равенства: a) infXY = infX • inf У; б) supXF = supX • sup У.
Сформулируем предложение, которое будет нам полезно в дальнейшем.
Принцип Дирихле. Если кролики рассажены в клетки, причем число
кроликов больше числа клеток, то хотя бы в одной из клеток находится
более одного кролика.
Предположим теперь, что существует такое число а е R, что для любого
натурального п выполнено п < а, т.е. множество натуральных чисел N огра¬
ничено сверху. Отсюда из принципа наличия верхней грани у ограничен¬
ного множества моментально следует ее существование у множества N.
Обозначим ее через А. Так как А - 1 < А, то из определения Бирнайдется
такое натуральное п, что п> А - 1. Поэтому п + 1 > А, но п + I G N. Полу¬
ченное противоречие показывает, что верна следующая теорема.
Теорема 1.9 (Архимеда). Каково бы ни было действительное число а,
существует такое натуральное число п, что п> а.
Используя данную теорему, докажем следствие из нее.
Следствие 1.3. Каковы бы ни были числа а и b, 0 < а < Ь, существует
такое натуральное число k, что выполнено неравенство
(k - I )а <b<ka.
Тогда число k - I g N называется целой частью дроби Ь/а и обознача¬
ется [Ь/а\.
Действительно, согласно теореме Архимеда для вещественного числа —
а
найдется такое натуральное п, что п>—. Умножая последнее неравенство
а
на а > 0, получаем b < па. Очевидно, что найденное натуральное число п,
36
вообще говоря, не является искомым (так как неравенство {п -1 )а < Ъ может
не быть выполнено). Поэтому разделим отрезок [0; па] на п подотрезков
длины а:
[0; а], [а; 2а],..., [(и -1 )а, па].
Одному из них согласно принципу Дирихле принадлежит точка b (так
как число точек b больше нуля и в одном из подотрезков будет более нуля
точек). Следовательно, существует натуральное k такое, что (k -1 )а <b<ka
(рис. 1.3).
(k - I )а ka
па
0
а
Рис. 1.3
Изучим далее немного другое доказательство данного факта, основан¬
ное на принципе точных граней.
Зададим множествоXследующим образом: X = jxGN|cr> — |. Согласно
I а]
теореме Архимеда множество X непустое. Кроме того, оно ограничено
снизу. Поэтому 3 п* = inf X. Далее заметим, что если подмножество X нату¬
ральных чисел ограничено снизу, то п* = inf X = ттпл X (докажите!). Следо¬
вательно, п* > —. Кроме того, п* — I g X => п* -1 < —. Отсюда получим требу-
а а
емое неравенство.
Покажем, что для любого a G M и любого и G N найдется целое т такое,
т ^ „ т + 1
что — <а< .
п п
Рассмотрим число с = па, cg 1. Пусть а > 0, тогда с > 0. Если па , то
принимаем т = 0. Если же па > 1, то по следствию из теоремы Архимеда
для с>1>0 найдется натуральное т* такое, что {т* -\)Л<с<т* Л. Взяв
т = т* -1, получим
т<па<т + \
т ^ „ т + 1
— <а< .
п п
Далее, пусть а < 0. Тогда \а \ > 0 и для него найдется т' такое, что
т'\ I
— <|а|<
п
т' +1
п
Возьмем т = -(m' +1), тогда (m + 1) = -т' и
ш Ii ^ т + 1
— <-\а\ = а< .
п п
Наконец, пусть а = 0. Тогда для любого п G N можно взять т = 0 либо
т = -1.
37
Рассмотрим теперь еще одно важнейшее следствие из теоремы Архи¬
меда, к которому мы будем часто возвращаться в дальнейшем. А именно,
докажем, что выполнено следующее утверждение.
Утверждение 1.7. Между двумя любыми действительными числами а
и b найдется рациональная точка.
Доказательство
Действительно, пусть а < Ь, т.е. А = Ь-а>0. Тогда по теореме Архимеда
2 2
найдется такое натуральное п, что выполнено п > —, или — < А. Далее, из только
А п
что доказанного следствия теоремы Архимеда получаем, что существует
т „ т + 2 т + 2 т 2 2 4 ,
такое целое т, что — <а< . При этом а = а + — < — < A = Ь-а.
п п п п п п
Поэтому
т + 2
п
< Ь. Следовательно,
т + 2 ,
а < < о,
п
Остается заметить, что число
т + 2
п
рациональное. ■
Рассмотрим далее интересный пример. Запишем его в виде задачи.
Задача 1.17
Существует ли такой набор / интервалов, лежащих в интервале (0; 1), что каждая
рациональная точка интервала (0; 1) принадлежит конечному числу интервалов из I,
а каждая иррациональная точка этого отрезка — бесконечному числу интервалов из /?
Решение
Ответ на данный вопрос — положительный. Положим:
In-
а
а +1
, a = 0,l,...,n!-lk/ = |J/n.
I Я=1
%и!’ п\
Каждая иррациональная точка принадлежит ровно одному интервалу из каждого
множества In, т.е. бесконечному множеству интервалов из I. Каждая же рациональная
P
точка (например, —) не принадлежит интервалам из множеств In при n>q.
Я
Замечание 1.12. Обратим внимание на то, что набора интервалов /
такого, что каждая рациональная точка интервала (0; 1) принадлежит бес¬
конечному числу интервалов из /, а каждая иррациональная точка этого
отрезка — конечному числу интервалов из /, не существует1.
1.5. Принцип вложенных отрезков
Дадим следующее определение.
Определение 1.32. Система числовых отрезков
[ац bt], [а2; Ь2], ■■■, [ап; Ьп],..., ап е R, bn е R, п е N,
1 Но доказательство этого факта выводит нас за рамки курса, рассматриваемого в данной
книге.
38
называется системой вложенных отрезков, если
а^<а2< ... < ап<... < Ьп<... <Ъ2< Ьь (1.1)
т.е. каждый следующий отрезок [ап+1, Ьп+1] содержится в предыдущем [ап, Ьп\:
^1] z) [а2, b2\ ZD ... з [ап, Ьп] ZD ....
Докажем теперь, что для всякой системы вложенных отрезков суще¬
ствует хотя бы одно число, которое принадлежит всем отрезкам данной
системы (рис. 1.4).
Рис. 1.4
Доказательство
Действительно, пусть {[яи; bn\, п е N} — некоторая система вложенных
отрезков. В силу неравенств (1.1) получаем, что множество {ап} всех левых
концов ограничено сверху, в частности любым Ьп, а множество всех пра¬
вых концов {Ьп} ограничено снизу, в частности любым ап. Следовательно,
по принципам верхней и нижней граней существуют sup{<2w} и inf{bn}, кото¬
рые мы обозначим а и P соответственно. Причем так как число а ограни¬
чивает множество {Ъп} снизу (все Ьп являются верхними гранями для {ап},
поэтому sup{a„} < bn для V и), a P — точная (т.е. наибольшая) нижняя грань
множества {>Ьп}, то для всех натуральных п имеем а < р. Отсюда и из опре¬
деления точных граней вытекает справедливость неравенства
an-a-fi-bn,
т.е. отрезок [а; Р] (который может выродиться в точку, если а = Р) содер¬
жится во всех отрезках системы {[ап, &„]}. ■
Доказанное утверждение называется леммой о вложенных отрезках.
Установим с его помощью несчетность (т.е. неэквивалентность множеству
натуральных чисел N) отрезка [0; 1].
Доказательство
Предположим, что точки отрезка [0; 1] можно занумеровать, т.е. пред¬
ставить их в виде счетной совокупности точек: х1,х2,...,хп>... . Выбираем
на отрезке [0; 1] некоторый отрезок \а{, A1], не содержащий точку X1, далее
внутри \а{, Ьх\ выбираем отрезок \а2, Ь2], не содержащий точку х2. И т.д., вну¬
три отрезка [ап; Ьп], не содержащего точку хп, выбираем (так как Ьп-ап> 0,
это всегда можно сделать) отрезок [ап+\, Ьп+1], не содержащий точку хп+1.
В результате нами получена система вложенных отрезков
[0; 1] з [а{, bt] ^ [а2, b2\ZD... ZD [ап\Ьп\э...,
которая по предыдущему утверждению содержит хотя бы одну общую точ¬
ку \ G [0; 1]. Из построения очевидно, что данная точка не совпадает ни с од¬
ной из точек X1, х2,..., хп,.... Получили противоречие. ■
39
( I ^
п-
CZ
г о
п-
'Л Л
V п + \)
и,
I nJ
Отметим, что для числовых промежутков других типов, нежели отрезки,
утверждение о вложенных отрезках, вообще говоря, может не иметь места.
А именно, найдется, например, система вложенных интервалов, которая
имеет пустое пересечение. Рассмотрим, например, интервалы (0; 1 /п),
п= 1,2,..., каждый последующий интервал содержится в предыдущем, т.е.
OO ^ I
,п = 1,2,.... Но так как $ х G р| 0; — , то эта система имеет
W=Iv
пустое пересечение. Стоит отметить, что существуют и такие системы вло¬
женных интервалов, которые имеют непустое пересечение.
Далее введем следующее определение.
Определение 1.33. Пусть задана система отрезков [аи; bn\, ап G М, bn G М,
п = 1, 2,.... Будем говорить, что длина Ьп- ап отрезков этой системы стре¬
мится к нулю, если для V в > О найдется номер N{в) такой, что для V п> N
выполняется неравенство Ъп - ап< в.
Теперь докажем следующее важное утверждение.
Утверждение 1.8 (лемма Коши — Кантора). Для всякой системы
{[а„; bn\, п G N} вложенных отрезков с длинами, стремящимися к нулю
(такие системы мы будем называть стягивающейся системой отрезков),
существует единственная точка принадлежащая всем отрезкам данной
системы, причем
\ = supK} = inf{bn}.
Доказательство 1
Обозначим а = sup{an}, P = inf{bn}. В доказательстве леммы о вложенных
отрезках было получено неравенство
а.
<а<Р <Ьп
(1.2)
OO
Отсюда получаем, что [а;Р]с [\\ап;bn\. C другой стороны, пусть
П=1
OO
х G Р)[ап‘,Ьп\, т.е. для всех и g N имеем ап< х< Ьп. Так как число х ограни-
W=I
чивает множество левых концов {ап} сверху, а а = sup{a„}, то а < х. Анало-
OO
гично получаем, что х < р. Следовательно, х G [а; Р], или Р) [ап\ Ьп\ с: [а; Р].
71=1
Отсюда и из неравенства (1.2) заключаем, что справедливо соотношение
[а;р]=ПК;6„]. (1-3)
TZ=I
Далее, пусть в > О — произвольное фиксированное число. Так как система
вложенных отрезков [ап]Ьп\ стремится к нулю, то существует номер N(e)
такой, что для всех п > N имеем Ьп-ап< в. Отсюда и из неравенства (1.2)
справедливо О < P - а < в, что в силу произвольности в > О возможно лишь
при а = р. Таким образом, отрезок [а; Р] в рассматриваемом случае перерож¬
дается в точку а = P = ^, которая в силу соотношения (1.3) и является един¬
ственной точкой, принадлежащей всем отрезкам системы {[а„; bn], п g N}. ■
40
Приведем еще одно доказательство этого факта (по сути то же самое),
используя метод доказательства от противного, которое более короткое,
но менее наглядное.
Доказательство 2
Пусть существуют два различных числа < \2, оба принадлежащие
OO
пересечению Р|[аи;Ьп\, т.е. для V п выполнено неравенство ап <^ К-
Я=1
Отсюда bn - ап > > О для V п. Получаем противоречие со стремлением
длины Ьп - ап отрезков этой системы к нулю. ■
Обращаем внимание читателя, что справедливо и обратное утвержде¬
ние к лемме Кантора, т.е. если существует единственная точка принад¬
лежащая всем отрезкам данной системы, то вложенная система отрезков
является стягивающейся. Действительно, рассмотрим систему вложенных
отрезков {[яи; 6И]}. Так как sup{an} и inf{&и} — заведомо общие точки, то
они совпадают. Пусть £, = sup{a„} = inf{bn}. По определению точных граней
для заданного е > О найдутся такие номера щ и п2, что
е е , C8
2’
Не ограничивая общности, считаем, что щ < п2, тогда получаем [ап^ ; /ц ] с:
cK1^rc1] и ап2 откУДа K2 -аП2 <е. Используя то, что рассма¬
триваемая система отрезков — вложенная, получаем требуемое.
В заключение параграфа приведем две важнейшие леммы, доказатель¬
ства которых основываются на принципе вложенных отрезков. Для их
формулировки нам понадобятся следующие определения.
Определение 1.34. Говорят, что система множеств S = {X} покрывает
множество Y, если любой элемент у E Y содержится по крайней мере
в одном из множеств X данной системы, т.е. Fe |J X.
Xe S
Определение 1.35. Подмножество множества S = {X}, являющегося
системой множеств, будем называть подпокрытием системы S (т.е. подпо¬
крытие системы множеств само является системой множеств того же типа).
Лемма 1.1 (Гейне — Бореля). В любой системе интервалов, покрыва¬
ющей отрезок, имеется конечное подпокрытие, также покрывающее этот
отрезок.
Доказательство
Пусть S = {(af; Pi)} — система интервалов (г принадлежит бесконечному,
необязательно счетному множеству), покрывающая исходный отрезок
\а‘,Ь\ = \а{,К\ Если бы интервал [а{, AJ не допускал покрытия конечным
набором интервалов системы, то, поделив данный отрезок пополам, мы
получим, что хотя бы одна из его половинок (обозначим ее [а2;Ь2]) также
не допускает конечного подпокрытия. C отрезком [а2, Ъ2\ проделаем ту же
процедуру деления пополам, получим отрезок [а3; Ь3\ и т.д.
Таким образом, возникает последовательность вложенных отрезков
[аь К ] => [<h> К\ => - => К; К] => •••>
41
не допускающих конечного покрытия интервалами системы S. Далее, так
как длина отрезка, полученного на п-м шаге по произведенному построе¬
нию, может быть найдена по формуле
то Ьп - ап —> 0 при п —» со.
Учитывая вложенность рассматриваемых отрезков, получаем систему
стягивающихся отрезков, которая в силу леммы Кантора имеет единствен¬
ную точку принадлежащую всем отрезкам \ап, bn\, п G N. По условию,
так как S1G [а\ Ь], то найдется интервал (а; |3) g S, содержащий точку х. Сле¬
довательно, а<^<|3. Выберем в как min{£-a, (3-¾ и найдем в построен¬
ной последовательности такой отрезок [ап, Ьп\, что Ьп-ап< в. Поскольку
£ G (ап\ Ьп) и Ъп -ап < в, то заключаем, что [ап; bn\ с (а; (3). Но это противо¬
речит нашему допущению о том, что отрезок [ап; Ьп\ нельзя покрыть конеч¬
ным набором интервалов системы S. ■
Лемма 1.2 (Больцано — Вейерштрасса). Всякое бесконечное ограни¬
ченное числовое множество имеет по крайней мере одну предельную точку.
Доказательство
Пусть XcM- данное бесконечное ограниченное подмножество. Из огра¬
ниченности следует, что существует отрезок [а; b] такой, что X с [а; Ь]. Тре¬
буется показать, что хотя бы одна точка данного отрезка является предель¬
ной для множества X
Предположим, что это не так. Тогда для всех точек х отрезка [а; b]
имеется окрестность В(х), в которой либо вообще нет, либо конечное
число точек множества X. Система {В(х)} таких окрестностей, построен¬
ных для всех точек отрезка [а; Ь], образует его покрытие интервалами.
Из этого покрытия по лемме Гейне — Бореля можно выделить конечное
подпокрытие B(Xi), ..., B(Xn) интервалов, покрывающих отрезок [а; Ь\,
а следовательно, и множество X. Между тем в каждой окрестности B(xk)
находится только конечное число точек множества X, значит, и в их
конечном объединении также содержится конечное число точек. Следо¬
вательно, множество X конечно. Полученное противоречие доказывает
лемму. ■
В завершение данного параграфа выведем аксиому непрерывности
(полноты) из принципа вложенных отрезков и теоремы Архимеда. Тем
самым мы докажем, что все три принципа полноты — аксиома непрерывно¬
сти, принцип точных граней и принцип вложенных отрезков — выводятся
один из другого, а значит, эквивалентны друг другу.
Итак, пусть для всякой системы {[ап, bn\, п G N} стягивающейся системы
сегментов существует единственная точка принадлежащая всем сегмен¬
там данной системы, а также пусть каково бы ни было действительное
число А, существует такое натуральное число п, что п> А. Тогда для любых
двух непустых числовых множеств X и Y, обладающих тем свойством, что
для VjtgXh Vz/g Y выполнено х < у, существует с G R такое, что х<с<у
для любых элементов х G X и у G Y.
42
Доказательство
Выберем произвольные элементы X1 е X и Zz1 е У и поделим отрезок
[X1; z/J пополам. Может так случиться, что середина отрезка уже
разделяет множества X и Y, т.е. правее этой точки нет элементов из множе¬
ства X, а левее ее — элементов множества У, тогда разделяющий элемент с
нами найден. В противном случае хотя бы с одной стороны средней точки
найдутся элементы и из множества X, и и из множества У. Обозначим эту
половину через [х2; Zz2]1- Повторяем описанную процедуру еще раз и т.д.
В результате получаем следующее. Если наше построение заканчи¬
вается за конечное число шагов, то разделяющий элемент был нами
построен. Если же нет, то мы получаем систему стягивающихся сегментов,
в каждом из которых существуют элементы и из множества X, и из мно¬
жества У. По принципу вложенных отрезков существует точка с, принад¬
лежащая каждому отрезку [хи; уп]. Докажем, что данная точка и является
искомым разделяющим элементом. Если существует у е У такой, что у < с,
то по аксиоме Архимеда найдется такой номер п, что у < хп (т.е. уп- хп<
< с - у)2. Но в этом случае на отрезке [хи; zz„] отсутствуют элементы множе¬
ства X, что противоречит нашему предположению.
Если же существует элемент х е X такой, что с < х, то аналогично суще¬
ствует п такой, что уп < х (т.е. уп - хп < х - с). Тогда на отрезке [хи; уп] нет
элементов множества У. ■
1.6. Множество Кантора
Определение 1.36. Множество А будем называть совершенным, если оно
замкнуто и не содержит изолированных точек, т.е. каждая его точка явля¬
ется предельной. Иначе, числовое множество называется совершенным,
если оно содержит все свои предельные точки и состоит только из них.
Пример 1.4
Примером совершенного множества на прямой может служить отрезок.
Определение 1.37. Будем говорить, что множество А всюду плотно в X,
если каждая точка множества X либо является предельной точкой множе¬
ства А, либо принадлежит этому множеству (либо и то и другое), т.е. A = X.
Пример 1.5
Воспользуемся доказанным выше утверждением о том, что между двумя любыми
действительными числами найдется рациональная точка. Можно сделать вывод о том,
что множество рациональных чисел Q является всюду плотным на действительной
прямой R.
1 Безусловно, мы не утверждаем, что X2 е Х,ау2е У, но это в данном случае неважно,
о ^ /
А В силу того что Уп~ Xn = — <с-у = const начиная с некоторого п.
43
Определение 1.38. Будем говорить, что множество А нигде не плотно
{вполне разрывно) в метрическом пространстве М, если любое открытое
множество этого пространства содержит другое открытое множество, цели¬
ком свободное от точек множества А.
Пример 1.6
Множество натуральных чисел является нигде не плотным на числовой оси.
Отметим, что нигде не плотное множество может иметь предельные точки.
Например, множество чисел X = I-,яен[ имеет предельную точку 0, но нигде
не плотно на К.
п
Определение 1.39. Точка a е X, в любой окрестности которой содер¬
жится несчетное множество точек данного множества, называется точкой
конденсации множества X.
Из данного определения следует, что всякая точка конденсации мно¬
жества есть его предельная точка, но, очевидно, не наоборот (т.е. предель¬
ная точка множества может и не быть его точкой конденсации, если в ее
окрестности содержится только счетное множество точек из X).
Задание 1.13
Предлагаем читателю доказать следующее утверждение: пусть а — точка конден¬
сации множества X. Если из этого множества выкинуть любую последовательность,
сходящуюся к а, то данная точка все равно останется точкой конденсации. Более того,
предельная точка а — точка конденсации тогда и только тогда, когда она удовлетворяет
этому условию.
Пример 1.7
Множество точек конденсации для множества точек интервала (0; 1) (или отрезка
[0; 1]) состоит из всех точек отрезка [0; 1]. Множество иррациональных точек неко¬
торого отрезка имеет в качестве множества точек конденсации весь данный отрезок.
Для множества X = {1 /п, п е N} точка 0 является предельной, но не является точ¬
кой конденсации.
Перейдем к построению множества Кантора. Рассмотрим отрезок [0; 1]
и назовем его отрезком нулевого ранга П0. Разделим данный отрезок
на три равные части и выбросим средний интервал (1/3; 2/3). Два остав¬
шихся отрезка [0; 1/3] и [2/3; 1] мы назовем отрезками первого ранга,
а выброшенный интервал — смежным интервалом первого ранга. Обозна¬
чим через Щ объединение отрезков первого ранга: Щ = [0; 1/3] и [2/3; 1].
Далее делим каждый отрезок первого ранга на три равные части и удаляем
из них средние интервалы — (1/9; 2/9) и (7/9; 8/9) (смежные интервалы
второго ранга). Получаем четыре отрезка второго ранга [0; 1/9], [2/9; 3/9],
[6/9; 7/9], [8/9; 1]. Их объединение обозначим через Yl2. Продолжая опи¬
санный процесс счетное число раз, получим на шаге п в качестве Yln объ¬
единение 2я отрезков п-то ранга.
Определение 1.40. Множество Yln называется предканторовым множе¬
ством п-го ранга.
44
Определение 1.41. Счетное пересечение предканторовых множеств
OO
п=Пп„ называется канторовым множеством или канторовым дисконти-
W=O
нуумом (рис. 1.5).
Вычислим суммарную длину выброшенных смежных интервалов:
12 4 1/3
1 1 h... — — 1.
3 9 27 1-2/3
Если сравнить этот результат с тем, что длина исходного отрезка равна
в точности 1, то получается, что нами были выброшены практически все
точки отрезка [0; 1]. Возникает вопрос: принадлежат ли какие-нибудь
точки отрезка [0; 1] множеству П? Очевидно, что все концы смежных
интервалов, т.е. точки вида 1/3, 2/3, 1/9 и т.д., остаются во множестве П.
Назовем их точками множества Кантора первого рода. Эти точки могут
быть упорядочены по возрастанию внутри концов отрезка я-го ранга (слева
направо), а в целом — по возрастанию п, причем точки первого рода обра¬
зуют счетное множество (докажите!). Но есть ли во множестве Кантора
еще какие-нибудь элементы? Легко заметить, что ему принадлежит, напри¬
мер, точка 1/4, так как отрезок любого ранга, которому она принадлежит
([0; 1], [0; 1/3], [2/9; 1/3],...), она делит в соотношении 1 : 3. То же самое
можно сказать о точке 3/4 и многих других.
Докажем, что множество Кантора имеет мощность континуума. Для
этого зафиксируем произвольную точку х из данного множества. Это озна¬
чает, что х не содержится ни в одном из смежных интервалов. Начинаем
составлять бесконечную двоичную последовательность следующим обра¬
зом. Если точка х находится слева от смежного интервала первого рода,
то положим X1 = 0, иначе X1 = 1. Далее, если точка х находится на отрезке
второго ранга, расположенном слева от смежного интервала второго рода,
выброшенного из центра соответствующего отрезка первого ранга, то поло¬
жим х2 = 0, иначе X2 = 1. И т.д., бесконечное число раз.
В результате нами будет получена произвольная двоичная последо¬
вательность, причем любой двоичной последовательности соответствует
45
некоторая точка х из множества Кантора. Собственно говоря, мы состав¬
ляем бинарный код, который описывает положение точки х в системе
отрезков. Используя ранее доказанный факт о том, что множество дво¬
ичных последовательностей имеет мощность континуума, получаем тре¬
буемое. Так как точек множества Кантора первого рода счетное число,
а всего точек континуум, то во множестве Кантора существует несчетное
число точек, не являющихся концами смежных интервалов. Все их будем
называть точками множества Кантора второго рода (к ним, в частно-
1 3
сти, относятся точки —, — и т.д.). Структура этих точек будет объяснена
позже.
Изучим свойства множества Кантора. Начнем, доказав следующее
утверждение.
Утверждение 1.9. Множество Кантора П замкнуто.
Доказательство
Доказываемый факт следует из построения и того, что объедине¬
ние счетного числа открытых множеств (смежных интервалов) открыто,
а дополнение к открытому множеству замкнуто.
Другое доказательство может быть получено от противного. Пусть
некоторая предельная точка множества П не принадлежит этому множе¬
ству. Значит, она должна лежать в некотором смежном интервале, куда,
в силу открытости последних, она входит с некоторой окрестностью точек,
т.е. точек, не лежащих во множестве Кантора. Последнее вступает в про¬
тиворечие с тем, что рассматриваемая точка есть предельная точка множе¬
ства П. ■
Теорема 1.10. Множество Кантора не содержит изолированных точек.
Доказательство
Действительно, пусть а — произвольная точка множества П. Нам тре¬
буется доказать, что для Vе>0 в окрестности Be(а) найдется хотя бы одна
точка из П, отличная от а.
Для этого по произвольному 8 выберем натуральное п такое, что спра- З З1 1
ведливо неравенство — < е. Пусть, далее, [ап, Ьп\ — тот отрезок длины
Зп
Зп
предканторова множества Yln, который содержит точку а (рис. 1.6).
а - е
а„
а + г
)
Рис. 1.6
Из последнего неравенства следует, что [an;bn\(z ВЕ(а). Следовательно,
из построения множества Кантора ап е П и Ьп е П. Хотя бы одна из этих
точек не совпадает с а. ■
Следствие 1.4. Множество Кантора представляет собой пример совер¬
шенного множества на прямой.
46
Определение 1.42. Метрическое пространство X называется сепара¬
бельным, если существует не более чем счетное множество А а X, всюду
плотное в X.
Пример 1.8
Из доказанного свойства рациональных чисел следует, что множество M — сепа¬
рабельное.
Следствие 1.5. Каждую точку множества Кантора можно сколь угодно
точно приблизить точками первого рода, т.е. точки первого рода — счетное
всюду плотное множество в П, а множество Кантора с введенной на пря¬
мой R метрикой — сепарабельное.
Теорема 1.11. Множество Кантора П нигде не плотно на прямой R.
Доказательство
Пусть L — произвольный интервал отрезка [0; 1]. Если LnП = 0, то
построение закончено (интервал, не содержащий точек множества Кантора,
найден). Если Б х е П такой, что х е L, то выберем столь большой номер п,
что xe[an;bn\<zH n[an)bn](zL. Возьмем интервал длины
1
3n+1
с центром
в середине отрезка [аи; Ьп\. Этот интервал выбрасывается на следующем
шаге построения множества Кантора. Следовательно, он не содержит точек
множества П и целиком содержится в L. ■
Пусть построены 2П отрезков n-то ранга Aiii где ik = {0, 1}, причем
каждый индекс ц выбирается в зависимости от того, лежит ли данный
отрезок слева или справа от выбрасываемого на k-м шаге интервала. Обо¬
значим через Jn множество всех точек множества Кантора, лежащих
на отрезке Aij и докажем, что верна следующая теорема.
Теорема 1.12. Каждая точка множества Кантора П является его точ¬
кой конденсации.
Доказательство
Действительно, при преобразовании подобия (с коэффициентом
и соответствующем сдвигом, переводящим отрезок [0; 1] в отрезок Aii
множество Кантора П, очевидно, взаимно однозначно переходит в множе¬
ство откуда следует, что каждое множество имеет мощность
континуума.
Выше нами было показано, что для V а е П и V г > 0 можно выбрать
такой номер п, что отрезок Aii ^ (а следовательно, и множество
будет лежать целиком в ВЕ(а). Поэтому Be(а) содержит часть множества П,
имеющую мощность континуума. ■
Заметим, что последние утверждения показывают, что множество Кан¬
тора представляет собой счетное объединение множеств мощности конти¬
нуума! Этот факт будет очень интересно сравнить с нашим самым первым
наблюдением о «длине» данного множества. Нами было показано, что
в процессе построения множества Кантора мы выкинули из отрезка [0; 1]
47
интервалы, сумма длин которых равна единице. Но на самом деле (учи¬
тывая, что исходный отрезок имел мощность континуума) мы не то что
ничего не выбросили, но и наоборот — «размножили» исходное множество
в счетное число раз (I)1.
Замечание 1.13. Понятие «точка конденсации» было введено Э. Линде-
лефом2.
Далее дадим арифметическую характеристику (установим характери¬
стическое свойство) множеству Кантора. C этой целью привлечем аппарат
троичных дробей. Действительно, любую точку отрезка [0; 1] можно запи¬
сать в виде
00 (о
х = E = {©1. ©2> -Ь> r«e ©n = {°> 1> 2}-
W=I ^
Утверждение 1.10. Канторово множество П может быть представлено
как множество всех точек отрезка [0; 1], имеющих разложение в троичную
дробь, состоящее лишь из цифр 0 и 2.
Доказательство
Точки смежного интервала
_1.2
З’З
характеризуются тем, что их разложе¬
ние в троичную дробь имеет необходимо OD1 = 1. Концы же этого интервала
допускают по два представления:
1.
3
= {1,0,0, ...}3 = {0,2,2,2, ...}3;
= {2,0,0, ...}3 = {1,2,2,2, ...}3,
одно из которых не содержит 1.
Далее, точки, троичное разложение которых при OD1 G {0; 2} имеет OD2 = 1, —
L 2} (7 8Л
это точки интервалов
9’ 9
и
9’ 9
, являющихся смежными, и т.д.
J
Удаляя из отрезка [0; 1] все смежные интервалы рангов < п, мы удалим
все точки, имеющие цифру 1 по крайней мере на одном из первых п мест
троичного разложения. Следовательно, объединение всех смежных интер¬
валов ко множеству П состоит из всех точек отрезка [0; 1], троичное разло¬
жение которых непременно имеет хотя бы одну цифру 1, и только из них,
откуда следует доказываемое утверждение.
В заключение доказательства отметим, что каждая из точек множества
V
Кантора первого рода, будучи точкой вида имеет два троичных разло-
Зп
жения, одно из которых не содержит 1. ■
Замечание 1.14. Последнее утверждение может быть рассмотрено как
еще одно доказательство несчетности множества Кантора, а также доказа¬
тельство счетности точек множества Кантора первого рода.
1 На этом месте один из авторов обычно загадывал студентам на своем спецсеминаре
детскую задачку «Что такое? Входишь в одну дверь, а выходишь из трех. Думаешь, что
вышел, а на самом деле вошел». На что год за годом получал один и тот же ответ — множе¬
ство Кантора.
2 Эрнст Линделеф (Е. Lindelef; 1870—1946) — финский математик.
48
Замечание 1.15. Установленное соответствие между множеством Кан¬
тора и отрезком [0; 1] через троичные дроби, содержащие 0 и 2, однозначно,
но не взаимно однозначно, в силу того что одно и то же число может изо¬
бражаться различными троичными дробями. Поэтому П имеет мощность
не меньше, чем континуум. Но П — часть отрезка [0; 1], следовательно, его
мощность не может быть больше, чем континуум.
Утверждение 1.11. Точки множества Кантора, у которых все коэф¬
фициенты троичного разложения сои, начиная с некоторого, равны между
собой, соответствуют точкам множества Кантора первого рода.
Доказательство
Утверждение следует из того, что каждая точка множества Кантора пер-
P
вого рода имеет вид —, р = 0,1,..., 3”. ■
3й
Таким образом, множество левых точек множества Кантора первого
рода определяется разложением ^ все коэффициенты которого начи-
k=\ 3*
ная с некоторого равны 2: ((Q1, о)2,...,(Ои,2,2,...}3. Множество же правых
точек определяется разложением, в котором все коэффициенты начиная
с некоторого равны между собой и равны 0: ((D1, ш2,..., со„, 0,0, ...}3.
Пример 1.9
Например, троичному разложению t = {0, 2, 0, 2, (0, 2), ...}3 соответствует число
2
~ 2 о 1 “23
2 -Zr = а = —. А разложению t = {2, 0, 2, 0, (2,0)...}3 — число ^ , = —. Эти числа
ыЗ2* 1_1 4 k=i3Ik 1 4
9
являются точками множества Кантора второго рода, так как в приведенных приме¬
рах бесконечное число раз повторяется сочетание двух троичных цифр, а не одной.
После того как основные результаты по структуре множества Кантора
были нами получены, рассмотрим несколько задач.
Задача 1.18
Можно ли представить множество Кантора в виде счетного объединения попарно
непересекающихся непустых замкнутых множеств?
Решение
Да, можно. Например, так: обозначим через C1 середину смежного интервала пер¬
вого ранга
щего справа,
12
v3;3y
1J
9’ 9
щего справа от ck_b т.е
через с2 — середину смежного интервала второго ранга, лежа-
, и вообще, Ck — середина смежного интервала k-vo ранга, лежа-
1
15
Cl 2’ Сз 18'
■>ck =
. 2 , 1
1 г + 1 г
_ 3* 3*
1
2 " 2-3*-1’""
Тогда множество Кантора может быть представлено в виде
П = (Рп [0; C1]) u (Р n [q; C2]) u (Р n [с2; C3]) и... и (Р n [ck_t; ck]) и... и {1}.
49
Замечание 1.16. Интересно отметить, что ни сам отрезок [0; 1], ни пря¬
мая M не представимы в виде счетного объединения попарно непересекаю-
щихся непустых замкнутых множеств (докажите!).
Рассмотрим далее близкую к этой теории теорему.
Теорема 1.13 (Бэра). Отрезок нельзя представить в виде счетного объ¬
единения нигде не плотных множеств.
Доказательство
Докажем данное утверждение от противного. Пусть существует после-
оо
довательность [An) нигде не плотных множеств, таких что [^An = [а; Ь\.
г=1
Построим последовательность отрезков по следующему правилу. Пусть I1 —
какой-нибудь отрезок, вложенный в [а; b] и не пересекающийся с Ai. По опре¬
делению нигде не плотного множества на отрезке Ii найдется какой-нибудь
отрезок, не пересекающийся с A2. Назовем его I2. Далее, на отрезке I2 возьмем
аналогичным образом отрезок I3, не пересекающийся с A3, и т.д. Как было
доказано нами ранее, у последовательности [Ik) вложенных отрезков есть
хотя бы одна общая точка. Эта точка, по построению, не лежит ни в одном
из множеств An, значит, эти множества не покрывают весь отрезок [я; Ь]. U
Вернемся к задачам о множестве Кантора.
Задача 1.19
Опишем множество Ii-Ii = {у - х\х, у е Ii).
Решение
Для ответа на поставленный вопрос заметим, что числа -1 и 1 лежат в множестве
П - П. Далее используем то, что множеству Кантора П принадлежат все возможные
точки, троичное разложение которых содержит 0 и 2. Поэтому любое вещественное
число между -1 и 1 может быть получено в результате вычитания двух таких чисел
(докажите!), т.е. П - П = [-1; 1].
Но в то же время по произвольному числу х из отрезка [-1; 1] может быть не очень
просто подобрать два числа из множества Кантора, разность которых равна х. Поэтому
рассмотрим также геометрическое решение. Проведем для этого предваритель¬
ные построения. Пусть Mn = Iin х П„, где П„, как и выше, — объединение 2я отрез¬
ков п-го ранга. Любое из множеств Mn состоит их 4я квадратов со сторонами длины
JL
Зг
прямую. Данная прямая пересекает единичный квадрат [0; 1] х [0; 1] лишь при | у | < 1.
Далее, равенство у - х = у, где х, у е П, геометрически равносильно тому, что прямая
Ly пересекается с множеством П х П. Покажем, что это выполняется при всех | у | < 1.
Действительно, Ly пересекает квадрат первого ранга [0; 1] х [0; 1]. Из соображения сим¬
метрии она также пересекает и некоторый квадрат второго ранга, далее — третьего
ранга и т.д. Общая точка получаемых таким образом квадратов лежит на Ly и вхо¬
дит в П х П. В силу произвольности у E [-1; 1] получаем, что П - П = [-1; 1]. На рис. 1.7
приведены иллюстрации для п = 4 и п = 6. * 1 * 1OO
Заметим, что f)Mn = ПхП. Обозначим через Ly = {(х,у) \у-х = у} произвольную
Определение 1.43. Производным множеством множества А (обозначе¬
ние: А') называется совокупность всех предельных точек этого множества.
Примеры производных множеств:
1) A = (0; 1), А! = [0; 1] = А" (где А!' = (AJ);
2) A = [I/п, п G N}, А' = {0}, А" = 0;
50
сл
19/27
■ ■ ■ ■
2/3 7/9 8/9 I
18/27 ■
2/27
3) Ai = {1/г + 1/п , п е N}, А = UAi, A' = {t/n, п е N и 0}, А" = {0}, А'" = 0.
г=1
Последний пример может натолкнуть нас на следующие размышления.
Пусть А = {1 /п, п G N и 0}. Тогда А' = {0}, т.е. множество А — замкнутое
(содержит единственную предельную точку), но А Ф А'. Для выполнения
A=A' нужно, чтобы множество А было совершенным.
Задача 1.20
Обозначим через E множество всех середин смежных интервалов множества
Кантора. Что представляют собой производное этого множества (-F)? Второе про¬
изводное множество? Замыкание множества Е?
Решение
Как было показано выше, в любой окрестности каждой точки из множества
Кантора находится бесконечно много смежных интервалов, а следовательно, и их
середин. Поэтому все точки из множества Кантора являются предельными для мно¬
жества Е. Безусловно, точки из смежных интервалов не являются предельными
для множества Е, так как все они отдалены от него на положительное расстояние.
Следовательно, других предельных точек (кроме множества П) у множества E нет.
Второе производное множество (в силу совершенности множества Кантора) совпа¬
дает с первым. Замыканием множества E является объединение £иП.
Задача 1.21
Найдем: а) какую-либо точку множества Кантора первого рода, заключенную
между числами 0,1 и 0,2; б) какую-либо точку множества Кантора второго рода, заклю¬
ченную между числами 0,05 и 0,1. Можно ли выбрать точку в п. б так, чтобы она
была рациональной?
Решение
4 1
а) Например, — или —.
27 9
б) Получаем 0,05 = ^, 0,1 = ^;
111112 12 2 1
->—, —<—, —< — <—, — + — + ...>—.
9 10 27 20 20 27 10 27 81 10
Мы видим, что искомое решение имеет троичное разложение:
_2_
{0,0,2,0,2,0,2, ...)з = Jr+Jr+... = = JL.
9
тт Iiii
Имеем — < — < —, рациональная точка второго рода.
20 12 10 12 Р ним
Задача 1.22
Существует ли интервал, содержащий точки множества Кантора первого рода,
но не содержащий ни одной точки второго рода?
Решение
Нет, не существует. Выше нами было доказано, что любая точка множества
Кантора является точкой конденсации, а так как точек множества Кантора первого
рода только счетное число, то в любом интервале, содержащем точку множества
52
Кантора первого рода, должно еще находиться несчетное число точек второго рода.
Ибо, как было показано выше, в соответствующей задаче раздела про мощность мно¬
жеств, что если к бесконечному множеству прибавить (или отнять из него) счетное
множество новых элементов, то это не изменит его мощности.
Определение 1.44. Два вещественных множества Л и В на прямой назо¬
вем подобными с сохранением порядка следования, если между элементами
этих множеств можно установить взаимно однозначное соответствие,
сохраняющее порядок следования, т.е. если X1, X2 е А; уь у2е В и X1 <-> ух,
х2 <-» у2, то из X1 < X2 следует, что ух < у2х.
Задание 1.14
Покажите, что множества натуральных N и целых чисел Z эквивалентны, но не по¬
добны с сохранением порядка следования.
Задача 1.23
Является ли множество всех рациональных точек отрезка [0; 1] подобным с сохра¬
нением порядка следования множеству всех точек первого рода множества Кантора?
Решение
Можно заметить, что оба этих множества счетны, но они не являются подобными.
Действительно, пусть это не так и между элементами данных множеств существует
взаимно однозначное соответствие, сохраняющее порядок (х е П <-» г е Q).
Возьмем X1 и х2 — два конца одного и того же смежного интервала, и пусть I1Hr1,
X2 г2, где гь г2 е Q[o;i]- Между гх и г2 всегда найдется рациональное число г3, и пусть
х3 нн г3. Но нам известно, что между X1 и X2 не найдется точек множества Кантора.
Следовательно, либо X3 < X1, либо X2 < х3, поэтому выполняется X3 < X1 < X2 или
X1 < X2 < х3, тогда как гх<гъ< г2. Поэтому соответствие х HH г не сохраняет порядок
следования.
Задача 1.24
Пусть множество £с! обладает свойством: между любыми двумя его точками
существует третья из этого множества. Обязательно ли замыкание E содержит непу¬
стой интервал?
Решение
Необязательно. В качестве множества E можно взять, например, множество П \ Qn1 1 2
или множество середин смежных интервалов (C). Действительно,
П\йп = П, C = CuП.
Замечание 1.17. Само множество Кантора П не подходит, так как между
левой и правой граничными точками смежных интервалов не существует тре¬
тьей точки. Следовательно, это множество не удовлетворяет условиям задачи.
Следующие задачи предполагают, что читатель знаком с понятием
непрерывности действительнозначных функций. Желающие могут сейчас
эти задачи пропустить и вернуться к ним после знакомства с гл. 3.
1 Дальнейшее исследование этого определения приводит к таким понятиям, как орди¬
налы (или порядковые типы). Подробнее об этом см., например, в работе [1].
2 Символом Qn обозначены точки множества Кантора первого рода.
53
Задача 1.25
а + |3
а;
и
/+Р;р|
L 2 J
L 2 J
Исследуем на непрерывность функцию, заданную на отрезке [0; 1] следующими
равенствами:
1) /(х) = 0 при х е П;
2) /(х) = Ib середине смежного интервала;
3) для точек смежного интервала a, P (а, P е П, поэтому /(а) = /(P) = 0,
( ос + P^
/ ——= 1) функция / определяется как линейная на
I 2 J
Решение
Интерес в данной задаче имеет тот факт, что на первый взгляд рассматриваемая
функция является непрерывной, кажется, что мы просто «строим линейные крышки»,
затыкая промежутки во множестве Кантора. Левый чертеж на рис. 1.8, построенный
при п - 5, только усиливает эту мысль. Но правый чертеж на рис. 1.8, сделанный
при п = 13, показывает, что точки разрыва скорее всего присутствуют.
Действительно, на смежных интервалах функция / очевидно, является непрерыв¬
ной. Поэтому остается исследовать лишь пределы в точках множества Кантора. Любую
точку множества Кантора можно получить и как предел точек из множества Кантора
(так как в любой окрестности х их несчетное число), и как предел середин смежных
интервалов (так как в любой окрестности х найдется смежный интервал). Далее, так как
предел по точкам из множества Кантора равен нулю, а по серединам смежных интерва¬
лов — единице, получаем, что в точках множества Кантора функция /(х) терпит разрыв.
Отметим однако, что в точках множества Кантора первого рода (за исключением
точек х=0их = 1)со стороны смежного интервала предел функции / существует
и равен нулю. Поэтому мы можем говорить об односторонней непрерывности в дан¬
ных точках.
Безусловно, задачу 1.25 можно обобщить, рассмотрев следующую задачу.
Задача 1.26
Исследуем на непрерывность функцию, заданную на отрезке [0; 1] следующими
равенствами:
1) fix') — 0 при X G П;
2) /(х) = сп E Rb середине смежного интервала;
3) /(х) линейна на участках
ап+К
И
ап+К.и
г» ’ Un
Предполагается, что смежные интервалы множества Кантора (ап, Ьп) перенуме¬
рованы в порядке убывания их длины слева направо:
(A1, bt) = (1/3, 2/3), (а2, b2) = (1/9, 2/9), (а3, b3) = (7/9, 8/9),....
Рассмотрим случаи последовательности сп, для которых выполняется:
a) Hm сп = 0; б) Imcra *0; в) $ Iimcn.
П—о о
Решение
Рассмотрим первый случай. Пусть X0 еП — точка первого рода. Тогда функция/
непрерывна в точке X0 с одной стороны (стороны смежного интервала). C другой сто¬
роны для V е > 0 (достаточно малого) внутри 8-полуокрестности есть только достаточно
малые смежные отрезки. Следовательно, /(х) < е при достаточно малом 8. Аналогично
доказывается и непрерывность построенной функции в точках множества Кантора вто¬
рого рода (докажите!). Отсюда мы получаем непрерывность функции/при Hm Cn= 0.
п—
Совершенно аналогично предыдущей задаче доказываем, что при последователь¬
ности сп из п. б и в функция / разрывна в точках из множества Кантора.
54
5
СЛ
сл
13
Рис. 1.8
Последний результат, очевидно, наталкивает нас на следующий вопрос.
Задача 1.27
Можно ли построить вещественнозначную функцию, непрерывную во всех точ¬
кам множества Кантора и разрывную во всех точках смежных интервалов?
Решение
Да, можно. Положим F(x) = D(x)• f(x), где D(x) — функция Дирихле, a /(х) —
функция из предыдущей задачи при Iim Cn= 0, т.е.
п—
ff(x), если х G О,
О, еслихЕК\(0).
В таком случае функция F(x) разрывна как модификация функции Дирихле во
всех точках, где /(х)^0, т.е. во всех точках множества [0; 1]\П. Если же х' еП, то
Hm /(х) = 0 и Iim F(x) = 0 и прихе Q,h прих е M\Q. Поэтому во всех точках мно-
х—>х' х—>х'
жества Кантора построенная функция является непрерывной.
Задача 1.28
Пусть функция/: [0; 1] —> К. непрерывна. Будем говорить, что данная функция
пересекает ось абсцисс в точке х, если выполнено:
1) /(х) = 0;
2) в любой окрестности точки х найдутся точки у и z такие, что f(y) < 0, f(z) > О* 1 1.
Легко построить пример функции, которая пересекает ось абсцисс бесконечное
число раз, причем в сколь угодно малой окрестности точки х = 0:
. 1
. xsm—,еслиX^О,
/00= х
0, если х = 0.
Гораздо интереснее следующий вопрос: существует ли непрерывная функция,
которая пересекает ось абсцисс несчетное число раз?
Решение
Ответ на поставленный вопрос — положительный. Проведем построение графика
искомой функции /(х) за счетное число шагов. На нулевом шаге положим /(х) = 0
при всех хеП. На первом шаге построим нижнюю полуокружность на смежном
интервале первого ранга
12
З’З
как на диаметре. На втором шаге построим верх¬
ние полуокружности на двух смежных интервалах второго ранга
12
9’ 9
и
7.8
9’ 9
как
на диаметрах. На третьем шаге построим нижние полуокружности на четырех смежных
интервалах третьего ранга и т.д., на (2п - 1)-м шаге строим нижние, а на 2и-м шаге —
верхние полуокружности на смежных интервалах (2п - 1)-го и 2п-го рангов соответ¬
ственно, и так делаем счетное число раз.
Построенная функция/(х) обращается в нуль в континууме точек множества П.
И сколь угодно близко от точки из П найдутся смежные интервалы (2п - 1)-го
и 2п-го рангов, в точках которых функция / принимает отрицательные и положи¬
тельные значения соответственно. Непрерывность функции / доказывается анало¬
гично случаю а из задачи 1.26 (кстати, тот пример, с очевидными изменениями, также
подходит и в этой задаче).
1 Данное условие требуется для того, чтобы избежать наложений на ось абсцисс.
56
На рис. 1.9 изображен график данной функции при п = 7.
7
1.7. Совершенные нигде не плотные множества
на плоскости
Под стандартным открытым множеством (окрестностью) на плоскости
будем понимать круг с центром в точке (х0; г/0) без границы:
Kr = {(х; у) G M2 I (х - х0)2 +(у- г/0)2 < R2), (х0; г/0) G M2.
Определения совершенного и нигде не плотного множества аналогичны
случаю числовой прямой: плоское множество мы будем называть совер¬
шенным, если оно замкнуто и не содержит изолированных точек, т.е. каж¬
дая его точка является предельной.
Будем говорить, что множество на плоскости нигде не плотно в метри¬
ческом пространстве M2, если любой открытый круг этого пространства
содержит другой открытый круг, целиком свободный от точек данного
множества.
Построим на плоскости множество А следующим образом: разделим
единичный квадрат {0 < х < 1, 0 < г/ < 1} прямыми х = 1/3, х = 2/3, у = 1/3,
у = 2/3 на девять равных квадратов и выкинем центральный открытый ква¬
драт (т.е. квадрат {1/3 < х < 2/3, 1/3 < у < 2/3}). Затем каждый из восьми
оставшихся замкнутых квадратов делим на девять равных квадратиков
и выбрасываем все центральные открытые квадратики. Далее продолжаем
процесс неограниченно. Множество, оставшееся после счетного числа
шагов, обозначим А и назовем ковром Серпинского. На рис. 1.10 приведены
иллюстрации построения данного множества для трех и шести шагов.
57
О 1/9 2/9 1/3
2/3 7/9 8/9
6
Рис. 1.10
Вычислим площадь выброшенных квадратов:
1
1 8 64 о
—I 1 ь... — — 1.
З2 З4 З6 ^8
9
Следовательно, нами была выброшена часть исходного квадрата с пло¬
щадью, равной площади исходного. Докажем, что построенное множество
является совершенным и нигде не плотным. Аналогично построению мно¬
жества Кантора П можно ввести понятия замкнутых квадратов гг-го ранга An.
Обозначим через Pn сумму всех замкнутых квадратов гг-го ранга. Ясно, что
OO
А = Р|Pn. Из замкнутости каждого Pn вытекает замкнутость множества А.
п=1
Чтобы доказать нигде не плотность ковра Серпинского, рассмотрим про¬
извольный открытый круг К, и пусть он содержит некоторую точку M мно¬
жества А. Тогда мы можем найти замкнутый квадрат An, содержащий данную
точку, полностью содержащийся в круге К. Для этого нужно выбрать такой
квадрат, чтобы его диагональ была меньше расстояния от точки M до гра¬
ницы рассматриваемого круга (это всегда можно сделать, так как диагонали
квадратов An стремятся к нулю при стремлении их ранга п к бесконечности).
Тогда открытый квадрат (п + 1)-го ранга, лежащий в середине квадрата An,
не содержит точки множества А. Вписав в него круг, мы найдем окрестность,
лежащую внутри круга К, полностью свободную от точек множества А.
Аналогично, учитывая, что границы замкнутого квадрата заведомо вхо¬
дят в множество А, заключаем, что точка M не является изолированной и,
более того, является точкой конденсации этого множества. Поэтому ковер
Серпинского является совершенным множеством.
Выясним арифметическую структуру множества А. На первом шаге мы
исключаем из квадрата такие точки, абсцисса и ордината которых при раз¬
ложении в троичную дробь обязательно содержат единицу на первом месте.
На втором шаге исключаются, кроме того, все точки, у которых абсцисса
и ордината содержат единицу на втором месте, и т.д. Таким образом, в мно¬
жестве А останутся все такие точки М(х; у), у которых абсциссу и ординату
можно разложить в троичные дроби х = (X1, х2, х3, ...}3, у = {уь у2, г/3, ...}3 так,
чтобы ни при каком значении гг е N не выполнялось равенство хп = уп = 1.
Далее построим на плоскости еще одно интересное множество В сле¬
дующим образом: разделим опять квадрат {0<х<1,0<г/<1} прямыми
х = 1/3, X = 2/3, у= 1/3, г/ = 2/3 на девять равных квадратов и выбросим
их них пять открытых, не примыкающих к вершинам исходного квадрата.
Затем каждый из оставшихся квадратов также разделим на девять частей
и выбросим пять из них и т.д. Множество, оставшееся после счетного числа
шагов, обозначим В и назовем кладбище Серпинского. Аналогично случаю
выше вычислим площадь выброшенных квадратов:
5
5 20 80 9 .
— н + 1-...= v =1.
З2 З4 З6
1 9
На рис. 1.11 приведены иллюстрации построения данного множества
для трех и пяти шагов.
59
О)
1I
8/91
7/91
2/31
1/3 и
■
■
■
2/9 Н
■
■
■
1/9 н
■
■
■
■
■
■
■
О
1/9
2/9
1/3
2/3 7/9 8/9 I
Рис. 1.11
I....
8/9-:
7/9::::
2/3::::
1/3;:;; ;;;; ;;;; ;;;;
2/9
1/9=;
О 1/9 2/9 1/3
2/3 7/9 8/9 I
Аналогично предыдущему множеству доказывается, что кладбище Cep-
пинского является совершенным и нигде не плотным множеством. Арифме¬
тическая структура множества В такова: в это множество входят все точки
М(рг, у), у которых как абсцисса, так и ордината могут быть записаны в виде
троичных дробей, не содержащих цифру 1 среди всех своих троичных знаков.
Назовем канторовой гребенкой (гребенкой Кантора) множество D
на плоскости Оху, состоящее из всех точек М(х; у), координаты которых
удовлетворяют следующим условиям:
О <х< 1,у G П,
где П — множество Кантора на оси Oy. Аналогично первому множеству
можно доказать, что канторова гребенка является совершенным нигде
не плотным множеством на плоскости. Множество D состоит из всех точек
М(х; у) исходного единичного квадрата, абсциссы которых произвольны
(О < х <1), а ординаты могут быть записаны в виде троичной дроби, не со¬
держащей единицы среди своих троичных знаков. На рис. 1.12 приведены
иллюстрации третьего и пятого шагов построения гребенки Кантора.
Зададимся вопросом: можно ли множества А (ковер Серпинского), В (клад¬
бище Серпинского) и D (гребенка Кантора) выразить через множество Кан¬
тора П с помощью действий дополнения до отрезка [0; 1] и декартова произ¬
ведения? Очевидно, что множества В и D выражаются элементарно:
5 = П х П, D = [0; 1] х П.
Далее, при построении ковра Серпинского на каждом из счетного числа
шагов из единичного квадрата исключались плоские множества, аналогич¬
ные одномерным смежным интервалам, т.е. множество [0; 1]\П х [0; 1]\П.
Поэтому множество А представимо в виде
А = ([0; 1] х [0; 1])\([0;1]\П х [0; 1]\П).
В заключение параграфа рассмотрим плоское множество С, являющееся
по своим свойствам противоположным к рассмотренным нигде не плотным
множествам, а именно, построим всюду плотное множество в единичном ква¬
драте E = {0 < х < 1, 0 < у < 1}, которое любая прямая, проходящая через дан¬
ный квадрат и параллельная осям координат, пересекает ровно в одной точке1.
Самым простым всюду плотным в единичном квадрате множеством
(не совпадающим со всем квадратом) является, безусловно, множество
Q[0; Ijх[0; 1] всех точек данного квадрата с рациональными координатами.
Но очевидно, что оно нам не подходит, так как любая прямая, параллель¬
ная осям координат, с рациональной координатой пересекает его в счетном
числе точек, а любая прямая с иррациональной координатой не пересекает
его ни в одной точке. Модифицируем это множество. На нулевом шаге
включим в множество C диагональ квадрата (соединяющую точки (0; 0)
и (I; 1)). Этим мы добиваемся того, что любая прямая, параллельная осям
координат, будет иметь с множеством C хотя бы одну общую точку. На пер¬
вом шаге выбираем произвольную точку из множества {0 < х <1, 0 < г/ < 1},
принадлежащую верхней относительно построенной диагонали половине
1 Данная задача является усложнением примера из книги [14].
61
I
8/9
7/9
2/3
1/3
2/9
1/9
О 1/9 2/9 1/3 2/3 7/9 8/9 I
Рис. 1.12
п = 5
I
8/9
7/9
2/3
1/3
2/9
1/9
О 1/9 2/9 1/3
2/3 7/9 8/9 1
квадрата. Обозначим ее (X1; Zz1), добавим в множество C точку из нижней
половины квадрата, симметричную первой относительно проведенной диа¬
гонали (обозначим ее (х(; Zz1')). Далее вычеркиваем из построенной диагона¬
ли точки, полученные пересечением ее с прямыми х = X1 и у = Zz1.
На втором шаге разделим квадрат E на четыре равных квадрата верти¬
кальными и горизонтальными прямыми. Выбираем в одном из них про¬
извольную точку (обозначим ее (х2; у2)) множества Q[0; i]X[o; i]> так, чтобы
х2 Ф X1, х2 Ф X1', х2 Ф X1, х2 Ф х(, zz2 Ф Zz1, zz2 Ф гZ1', у'2 Ф уь гZ2 Ф у[,
где (x2;zz2) — точка, симметричная точке (х2; у2) относительно диагонали
выбранного квадрата, которую также добавляем в множество С. Далее вы¬
черкиваем из диагонали точки, полученные пересечением ее с прямыми
х = X2 и zz = Zz2. После этого проводим аналогичные построения в другом
квадрате, выбирая точку (х3; у3), сравнивая ее координаты со всеми точ¬
ками из множества С. После этого аналогично выбираем точки (х4; zz4)
и (х5; Zz5) в третьем и четвертом квадратах.
На третьем шаге разбиваем единичный квадрат на 16 равных квадрати¬
ков и во всех из них проводим те же самые построения. Продолжая этот
процесс до бесконечности и деля единичный квадрат на п-м шаге на 4я-1
частей, мы получим требуемое множество: так как в любом достаточно
малом «типовом» квадрате есть точки из множества, то оно всюду плотное.
Отметим только, что так как в Q[0; 1]Х[о; i] находится счетное число точек, мы
на счетном числе шагов можем выбрать точку с оригинальными абсциссой
и ординатой. На рис. 1.13 приведена иллюстрация построения описанного
множества для 40 000 точек.
Рис. 1.13
63
1.8. Общие теоремы об открытых, замкнутых
и совершенных множествах. Точки конденсации
В предыдущих параграфах нами были построены очень красивые при¬
меры числовых множеств. Далее станет понятно, что этим были разобраны
не просто примеры, любопытные и интересные сами по себе, но примеры,
которые являются важными и основополагающими при построении более
общей теории совершенных множеств и точек конденсации. Действи¬
тельно, давайте проведем обобщения рассуждений из предыдущих парагра¬
фов. Для этого нам понадобятся вспомогательные понятия и утверждения.
Определение 1.45. Пусть G — открытое множество из R. Если интер¬
вал (а; b) содержится в G, но его граничные точки а и b этому множеству
не принадлежат, то интервал (а; Ь) называется составляющим интервалом
множества G.
Задание 1.15
Докажите, что если G есть непустое ограниченное открытое множество, то каждая
его точка принадлежит некоторому его составляющему интервалу.
Утверждение 1.12. Непустое ограниченное множество G является
открытым тогда и только тогда, когда оно является суммой конечного или
счетного множества попарно непересекающихся интервалов, граничные
точки которых не принадлежат множеству G.
Доказательство
В одну сторону доказательство утверждения следует из того, что каждый
интервал есть открытое множество, а объединение любого числа открытых
множеств есть множество открытое.
Обратно, рассмотрим непустое ограниченное открытое множество G.
Различные составляющие интервалы данного множества не могут иметь
попарно общих точек, так как они целиком состоят из точек множества G,
и один из них отличается от другого по крайней мере не принадлежащей
им граничной точкой так, что граница одного из них не может быть вну¬
тренней точкой другого. Не более чем счетность множества составляющих
интервалов может быть доказана, если выбрать на каждом из них по раз¬
личной рациональной точке. ■
Теорема 1.14. Всякое непустое ограниченное замкнутое множество
А с R или является отрезком, или получается из некоторого отрезка удале¬
нием из него конечного или счетного множества попарно непересекающихся
интервалов, концы которых принадлежат множеству А.
Доказательство
Так как множество А является ограниченным, то существует наимень¬
ший отрезок (который мы обозначим А), включающий в себя множество А.
Если множество А\А пусто, то А представляет собой отрезок. В обрат¬
ном случае, т.е. если А\А не пусто, докажем, что оно является открытым.
Действительно, рассмотрим произвольную точку х е А\А В этом случае
х £ А, а следовательно, так как множество А замкнуто, точка х не является
предельной точкой этого множества. Поэтому существует окрестность
В(х), целиком состоящая из точек множества А\А, т.е. точка х — внутрен¬
няя для этого множества.
64
Ограниченное и открытое множество А\А по предыдущему утвержде¬
нию есть объединение конечного или счетного числа составляющих его
интервалов. Удаление этих интервалов из отрезка А и оставит в нем только
точки замкнутого множества А. ■
Задание 1.16
Докажите, что справедливо и обратное утверждение к теореме 1.14. А именно, если
из некоторого отрезка удалить конечное или счетное множество попарно не пересека¬
ющихся интервалов, то в результате получится замкнутое множество.
Определение 1.46. Пусть [а; Ь] — наименьший отрезок, включающий
в себя замкнутое множество А. Тогда составляющие интервалы множества
[я; Ь]\А и два луча (-°°; а) и (6; -и») называются смежными интервалами
замкнутого множества А.
Докажем следующую лемму, играющую важную роль в теории совер¬
шенных множеств.
Лемма 1.3. Для того чтобы точка х являлась изолированной точкой
ограниченного замкнутого множества А, необходимо и достаточно, чтобы
она была общей границей двух соседних смежных интервалов.
Доказательство
Достаточность. Используя определения изолированной точки и смеж¬
ного интервала, получаем, что точка х, являющаяся общей границей двух
соседних смежных интервалов, удаленных из прямой при построении зам¬
кнутого множества А, принадлежит множеству А и является его изолиро¬
ванной точкой.
Необходимость. Пусть х — изолированная точка множества А. Тогда
существует окрестность Ве(х), полностью свободная от точек этого мно¬
жества. Вся данная окрестность (х - в; х + в) не может целиком принадле¬
жать смежному интервалу, так как в смежном интервале не может лежать
точки XE А. Следовательно, ее левая часть (х-в;лг) принадлежит одному
из смежных интервалов множества А, а правая часть (х; х + в) — другому.
Причем точка х является их правой и левой границей соответственно. ■
Так как всякое ограниченное совершенное множество есть множество
замкнутое и не содержащее изолированных точек, то на основании леммы
мы можем сформулировать два важных следствия, являющихся взаимно
обратными.
Следствие 1.6. Всякое ограниченное совершенное множество либо есть
отрезок, либо получается из некоторого отрезка удалением конечного или
счетного множества попарно непересекающихся интервалов, не имеющих
общих границ ни друг с другом, ни с исходным отрезком.
Следствие 1.7. Если из некоторого отрезка удалить конечное или счет¬
ное множество попарно непересекающихся интервалов, не имеющих общих
границ ни друг с другом, ни с исходным отрезком, то оставшееся множе¬
ство точек отрезка есть совершенное.
Выше нами было доказано, что совершенное множество Кантора имеет
мощность континуума с. Установим, что эту мощность имеет каждое непу¬
стое совершенное множество. А именно, верна следующая теорема.
65
Теорема 1.15. Всякое непустое совершенное множество имеет мощ¬
ность континуума с.
Доказательство
Очевидно, что мощность любого числового множества не может быть
больше с. Кроме того, понятно, что совершенное множество, включающее
в себя некоторый отрезок, имеет искомую мощность. Поэтому интересным
является исключительно доказательство того, что любое совершенное нигде
не плотное на числовой прямой множество имеет мощность континуума.
В самом деле, пусть дано некоторое совершенное нигде не плотное
на числовой прямой множество А. На основании следствия 1.6 из леммы
оно получается из некоторого отрезка [я; b] удалением из него счетного
(не конечного, так как множество А нигде не плотно) множества попарно
непересекающихся интервалов, не имеющих общих концов ни друг с дру¬
гом, ни с исходным отрезком.
Для доказательства сформулированного утверждения покажем, что
элементы множества А можно поставить во взаимно однозначное соответ¬
ствие элементам множества Кантора П. Действительно, обозначим отрезок
(\
[0; 1] через А, а [я; Ь\ — через А'. Далее, обозначим смежный интервал —; —
13 3
удаленный из А на первом шаге построения множества Кантора, через 6,
а наибольший из интервалов, удаленных из А' (или самый левый из наи¬
больших, если их было несколько), — через 5' (заметим, что в силу ограни¬
ченности А' такой интервал найдется).
Затем отрезки, оставшиеся после удаления 5 и 6' из А и А', обозначим слева
направо соответственно A0, A2 и Ag, Ar2, а наибольшие интервалы, удаляе¬
мые из каждого из них, — соответственно S0, S2 и 8'0,S2. Продолжим процесс
неограниченно, нумеруя далее отрезки, оставшиеся после удаления интер¬
вала Sai ak из отрезка Aai^ , слева направо соответственно через Aflij
и Aa1 ak 2 >а отрезки, оставшиеся после удаления интервала Sfli ^ из отрезка
A^,слева направо соответственно через A^ и A^ ^2.
Возьмем теперь некоторую точку хеП. Она обязательно входит в А,
затем только в один из отрезков Aai (= 0 или A1 = 2), только в один
из отрезков Aaja2 (я2 =0 или я2 =2) и т.д. Таким образом, каждая точка
{а±,а2,...,Я£,...}3 из множества П в принятых обозначениях определится
единственной стягивающейся к ней последовательностью отрезков
Afl1 zjAfl1O2 z^
■ 3 AOia2-Mk 3 •
Поставим в соответствие данной точке из множества Кантора ту точку
из множества А, которая определяется последовательностью стягиваю¬
щихся отрезков:
Afl1O2
z>...z> А' „
Olfl2.
ak
Z)...
Очевидно, что такое соответствие определяется последовательностью
индексов я1; я2,..., ak,.... Оно взаимно однозначно, что и доказывает теорему. ■
Рассмотренная теорема легко переносится на случай неограниченного
совершенного множества, ибо такое множество содержит в себе целиком
некоторый отрезок или, если оно нигде не плотно на прямой, содержит
66
в себе ограниченную нигде не плотную совершенную часть и, следова¬
тельно, также обладает мощностью континуума с. Между прочим, все
в обе стороны неограниченные совершенные нигде не плотные множества
подобны между собой и подобны, например, множеству Кантора, из кото¬
рого удалены две его крайние (самая левая и самая правая) точки. Ана¬
логично совершенное нигде не плотное множество, ограниченное только
снизу (только сверху), подобно множеству Кантора без его самой правой
(самой левой) точки.
Для формулировки дальнейших результатов напомним читателю, что
под точкой конденсации множества E мы понимали точку, в любой сколь
угодно малой окрестности которой имеется несчетное множество точек
из Е.
Докажем следующие элементарные вспомогательные утверждения.
Утверждение 1.13. Множество всех рациональных окрестностей (т.е.
окрестностей с центром в рациональных точках и с рациональными ради¬
усами) счетно.
Доказательство
Утверждение немедленно следует из счетности рациональных чисел. ■
Утверждение 1.14. Для любой точки х действительной прямой M
и любой ее окрестности 5§(х) существует окрестность Вг(г) с центром
в некоторой рациональной точке г и рациональным радиусом в, содержа¬
щая данную точку х и целиком содержащаяся в окрестности В8(х).
Доказательство
Достаточно взять рациональную точку г на расстоянии меньшем, чем —
от точки х, с радиусом в, удовлетворяющим неравенству
5 25
- < в < —.
3 3
Из этих утверждений следует, что всякая окрестность В(х) точки х
содержит в себе хотя бы одну, а значит, и бесконечно много рациональных
окрестностей, включающих в себя ту же точку. Теперь мы готовы доказать
справедливость следующих теорем.
Теорема 1.16. Если множество А не имеет точек конденсации, то оно
счетно или конечно.
Доказательство
Рассмотрим произвольную точку х множества А и построим некоторую
окрестность В(х) данной точки. По условию теоремы, так как рассматрива¬
емое множество не имеет точек конденсации, данная окрестность содержит
не более чем счетное число точек множества А. Построим внутри окрестно¬
сти В{х) рациональную окрестность В (г), содержащую точку х. Аналогично
каждую точку множества А заключим внутрь некоторой рациональной
окрестности. Данных окрестностей, как было сказано выше, существует
лишь счетное множество. Некоторая часть этого счетного множества,
конечная или счетная, будет включать в себя все точки множества А. А так
как в каждой окрестности В(г) имеется лишь конечное или счетное под¬
множество точек множества А, то данное множество как сумма конечного
или счетного числа конечных или счетных множеств будет множеством
конечным или счетным. ■
67
Теорема 1.17. Если множество А несчетно, то существует несчетное
множество точек конденсации множества А, принадлежащих ему.
Доказательство
Пусть точка х множества А не является его точкой конденсации.
Построим для каждой такой точки рациональную окрестность, содержа¬
щую данную точку х и конечное или счетное множество точек множества А.
Таких окрестностей на основании рассуждений предыдущей теоремы ока¬
жется не более счетного числа, а значит, и точек множества, принадлежа¬
щих всем этим окрестностям, окажется не более чем счетное множество.
Все же остальные точки несчетного множества А являются его точками
конденсации. Так как рассматриваемое множество несчетно, то и множе¬
ство точек конденсации окажется несчетным. ■
Теорема 1.18. Множество точек конденсации любого множества есть
совершенное множество.
Доказательство
Рассмотрим некоторое множество А. Если оно не более чем счетное,
то утверждение теоремы становится тривиальным, так как в данном слу¬
чае множество точек конденсации представляет из себя пустое множе¬
ство, которое является совершенным. Предположим далее, что множе¬
ство А несчетно и К есть множество его точек конденсации. Докажем, что
оно содержит в себе все свои предельные точки и состоит только из них.
Для этого обозначим через К', как обычно, замыкание данного множества
и докажем, что K = K'. Для этого нам потребуется доказать два вложения:
I) KqK' и 2) Kq К'.
1. Рассмотрим произвольную точку ieK', т.е. пусть х — предельная
точка множества К. Тогда в любой окрестности точки х имеются точки мно¬
жества К, отличные от нее самой, т.е. точки конденсации множества А. Сле¬
довательно, в любой окрестности точки х вместе с точками множества К,
отличными от х, имеется несчетное множество точек множества А. Таким
образом, х есть точка конденсации множества А, а значит, х е К и выпол¬
нено К Q К'.
2. Для доказательства обратного вложения KqK' нам достаточно
доказать, что в множестве К все точки предельные, т.е. нет изолированных
точек. Пусть х — произвольная точка из множества К, т.е. некоторая точка
конденсации множества А. Так как всякая окрестность точки х содержит
в себе несчетное множество точек множества А, то, следовательно, у этого
несчетного множества на основании предыдущей теоремы имеется несчет¬
ное множество точек конденсации множества А, т.е. точек множества К.
Таким образом, всякая точка множества К заведомо есть предельная точка
этого множества и выполнено К Q К'. ■
Следствие 1.8. Всякое несчетное замкнутое множество есть сумма
совершенного множества своих точек конденсации и не более чем счетного
множества остальных точек.
Доказательство
Рассмотрим произвольное несчетное замкнутое множество А, и пусть
К — множество его точек конденсации. По теореме 1.18 множество К —
совершенное. KqA, так как всякая точка конденсации есть предельная,
68
а множество А замкнуто. Обозначим D = А\К. Множество D не может быть
несчетным, так как в противном случае по теореме 1.17 следовало бы, что
существует несчетное множество точек конденсации множества D (а зна¬
чит, и множества А), принадлежащих ему. Получаем противоречие с опре¬
делением множества D как множества, не содержащего точек конденсации
множества А. Отсюда A = DkjK, где К — совершенное несчетное множе¬
ство, a D не более чем счетно. ■
Замечание 1.18. В этом параграфе мы рассматривали, вообще говоря,
одномерные множества, лежащие на числовой прямой. Понятно, что ана¬
логичными рассуждениями все данные результаты могут быть распростра¬
нены на множества более высоких размерностей, являющиеся подмноже¬
ствами пространства R”.
Глава 2
ТЕОРИЯ ЧИСЛОВЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
2.1. Понятие последовательности и ее предела
2.1.1. Понятие последовательности.
Ограниченные последовательности
Понятие числовой последовательности хорошо знакомо любому, кто
знает математику даже на базовом уровне. В частности, в рамках школь¬
ной программы изучаются свойства арифметических и геометрических
прогрессий, которые являются частными случаями числовых последова¬
тельностей. В то же время такой простой объект, как числовая последо¬
вательность, является мощным инструментом для изучения значительно
более сложных понятий.
Формально определение последовательности можно дать разными спо¬
собами. Простейший, интуитивно понятный, способ: пусть каждому нату¬
ральному числу п по некоторому закону ставится в соответствие некото¬
рое число хп, тогда говорят, что задана числовая последовательность X1, х2,
Xg, ..., Xn, ... .
Числа хп называют элементами последовательности или членами после¬
довательности. Для сокращенной записи последовательности используют
обозначение {хи}.
Числа хп могут принадлежать различным множествам: множеству
натуральных, целых, рациональных, вещественных чисел. В зависимости
от этого для последовательности могут выполняться либо не выполняться
некоторые утверждения. Далее, если это не оговаривается особо, считаем,
ЧТО Xn G М.
Для последовательностей, как правило, важны свойства элементов
при больших номерах п, поэтому иногда последовательность бывает опре¬
делена при п > N*, где N* — некоторое натуральное число (обычно N* = 1).
Последовательность {хи} можно рассматривать и как функцию, опреде¬
ленную на множестве натуральных чисел N: хп =f{n). При этом для нагляд¬
ного представления последовательности можно рассматривать график
такой функции. Например, для последовательности {(п + 1 )/п} элементы
равны Xn = (п+ 1 )/п, функция/(х) = (х + 1)/х, график последовательности
представлен на рис. 2.1.
Для иллюстрации свойств последовательности удобно изображать ее
элементы на одной числовой прямой (каждому значению хп соответствует
тонкая вертикальная прямая). Например, последовательность хп = (-1)” +
+ 1 /п изображена на рис. 2.2.
70
Рис. 2.2
Для числовых последовательностей определены такие понятия, как
сумма, разность, произведение и частное двух последовательностей.
Пусть заданы две последовательности {л:и} и {z/Д. Тогда суммой, раз¬
ностью, произведением и частным этих последовательностей называют
последовательности {хп + уп), {хп - г/„}, {хп ■ уп} и {хи/г/и} соответственно
(последняя, естественно, определяется в предположении, что элементы {г/и}
отличны от нуля начиная с некоторого номера; с этого номера и определя¬
ется частное).
Совокупность элементов числовой последовательности {хп} обра¬
зует некоторое (не пустое) множество X. Это множество может состоять
71
как из конечного числа элементов (например, для последовательности
хп = (-1)” множество X = {-1, 1}, т.е. состоит из двух чисел), так и из бес¬
конечного числа элементов (например хп = I/п). Во втором случае, есте¬
ственно, множество X является счетным.
Так как для произвольного числового множества определены понятия
ограниченности, точных граней, то такие понятия определены и для мно¬
жества X значений, которые принимают элементы последовательности.
Для дальнейших рассуждений удобно сформулировать эти определения
в явном виде в терминах элементов последовательности.
Определение 2.1. Последовательность {хп} ограничена сверху (снизу),
если существует число M (т) такое, что для всех номеров п (т.е. для всех
элементов последовательности) имеет место неравенство хп< M (хп > т).
Определение 2.2. Последовательность {х„} ограничена, если она ограни¬
чена сверху и снизу.
Для ограниченной последовательности можно дать альтернативное
определение.
Определение 2.2'. Последовательность {хп} ограничена, если найдется
такое число M > 0, что для всех п имеет место неравенство \хп \ <М.
Определение 2.3. Последовательность {хи} не ограничена, если для
любого положительного M найдется номер п (т.е. найдется элемент после¬
довательности) такой, что \хп\> М.
Заметим, что в данных определениях не оговаривается, из какого множе¬
ства берутся числа тиМ. Как правило, они берутся из того же множества,
что и элементы последовательности, т.е. если речь идет о последовательно¬
стях из рациональных чисел, то т и M — рациональные, если же речь идет
о последовательностях из вещественных чисел, тошиМ - вещественные.
Это нужно для того, чтобы операции сравнения в этих определениях были
корректны. Аналогичные замечания можно сделать и для ряда дальнейших
определений.
Также заметим, что в приведенных выше неравенствах знаки могут быть
как строгие, так и нестрогие. Легко показать, что это эквивалентные формы
определений.
Как и для ограниченных множеств, для числовых последовательностей
можно ввести понятие точных граней.
Определение 2.4. Пусть последовательность {хп} ограничена сверху.
Число М* называют точной верхней гранью последовательности {хп}, если:
1) хп < М* для всех п;
2) для любого M < М* найдется номер п такой, что хп > М.
Определение 2.5. Пусть последовательность {хп} ограничена снизу.
Число т* называют точной нижней гранью последовательности {хп}, если:
1) хп>т* для всех п;
2) для любого т>т* найдется номер п такой, что хп< т.
Точные грани обозначают М* = sup{xn}, т* = inf{x„}.
В случае неограниченной сверху последовательности {хп} считают, что
sup{x„} = +°о. В случае неограниченной снизу последовательности {хи} счи¬
тают, что inf{xn} = -оо.
72
Если последовательность {хп} состоит из вещественных чисел, то и мно¬
жество ее значений JcRB этом случае из ограниченности сверху (снизу)
последовательности {хп} (и, соответственно, множества X) следует суще¬
ствование sup{.xw} (inf{xw)) среди вещественных чисел. Для последователь¬
ностей из рациональных чисел это не так. Например, последовательность
X1 = I, х2 = 1,4, х3 = 1,41, х4 = 1,414, х5 = 1,4142,...,
т.е. последовательность из приближений числа л/2 с точностью до п-то зна¬
ка, очевидно, ограничена сверху (например рациональным числом 2), одна¬
ко среди рациональных чисел не существует числа M*, удовлетворяющего
определению точной верхней грани. Если же рассматривать эту последова¬
тельность как последовательность вещественных чисел, то вещественное
число л/2 и будет точной верхней гранью последовательности.
Так же как и для произвольных числовых множеств, точные грани (если
они существуют) могут как достигаться на элементах последовательности,
так и не достигаться. Так, для последовательности Xn = (-1)” точные грани
sup{xw) = 1 и inf{x„) = -1 достигаются на элементах последовательности,
Tl
а для хп = (-1)и , которая имеет такие же точные грани, они не дости-
п +1
гаются (рис. 2.3).
2.1.2. Бесконечно большие
и бесконечно малые последовательности
Перейдем теперь к рассмотрению понятий, определенных для последо¬
вательностей, но не для множеств. Введем понятия бесконечно большой
и бесконечно малой последовательностей.
Определение 2.6. Последовательность {х„} называется бесконечно боль¬
шой, если для любого M > О найдется номер N = N(M) (т.е. номер N зависит
от М) такой, что начиная с этого номера, т.е. при всех п> N, имеют место
неравенства \хп\>М.
Очевидно, что любая бесконечно большая последовательность неогра-
ничена. Обратное утверждение неверно. Отличие бесконечно большой
последовательности от неограниченной в том, что у первой все элементы,
начиная с некоторого, достаточно большие (т.е. по модулю больше M),
а у неограниченной — только некоторые. Например, последовательность
{х„}: 1, 2, 1,3, 1, 4, ... неограниченная, но не бесконечно большая, так как
для M= 2 не существует номера N такого, что все элементы при п удовлет¬
воряют неравенству \хп \ > 2.
Бесконечно большие последовательности — неограниченные «в целом»,
но могут быть ограничены с одной стороны (сверху либо снизу). Так, после¬
довательность хп = п бесконечно большая и ограничена снизу, а последова¬
тельность хп = -п — бесконечно большая и ограничена сверху. В то же время
последовательность хп = п(-1)” — бесконечно большая, не ограниченная ни
снизу, ни сверху. А последовательность [(-1)ии](_1)я(”+1)/2 — не бесконечно
большая, не ограничена сверху и неограничена снизу (рис. 2.4).
Введем теперь понятие бесконечно малой последовательности.
73
1,0
200
100
0_
-А
-100
-200
Рис. 2.4
Определение 2.7. Последовательность {хп} называется бесконечно малой,
если для любого (достаточно малого) 8 > 0 найдется номер N = N(e) такой,
что при всех п имеет место неравенство \хп \ < е.
Примерами бесконечно малых последовательностей, например, явля¬
ются хп = I/п, хп = (-1 )п/п, хп = qn при I <71 < 1 и т.д.
Для бесконечно малых последовательностей имеют место простые
утверждения, доказательства которых можно найти в любом учебнике
математического анализа. Коротко перечислим основные свойства беско¬
нечно малых последовательностей (без доказательства).
Теорема 2.1. Сумма, разность двух бесконечно малых последовательно¬
стей — также бесконечно малая последовательность.
Теорема 2.2. Бесконечно малая последовательность ограничена.
Заметим, что не всякая ограниченная последовательность является
бесконечно малой. Например, хп = (-1)” ограничена (\хп \ < 1 при всех п),
но для в = 1/2 не существует номера Nтакого, что \хп \ меньше е (при n>N).
Теорема 2.3. Произведение бесконечно малой и ограниченной последова¬
тельностей — бесконечно малая последовательность.
Следствие 2.1. Произведение двух бесконечно малых последователь¬
ностей — бесконечно малая последовательность.
Таким образом, сумма, разность и произведение бесконечно малых
последовательностей (любого конечного их числа) дают бесконечно малую
последовательность. C частным ситуация сложнее. Рассмотрим несколько
примеров, где {хп} и {уп} — бесконечно малые.
1. Xn = а/п, а Ф 0, уп = i/n=> XrJyn = а — ограничена, но не бесконечно
малая.
2. хп = 1 /п2, уп = 1/и => хJyn = 1 /п — бесконечно малая.
3. хп = I/п, уп = 1 /п2 => хJyn = п — бесконечно большая.
4. Пусть zn = {1, 2, 1, 3, 1, 4,...}. Тогда хп = zjn2, уп = I/п2 => xjyn = Zn-
неограничена, но не бесконечно большая.
Таким образом, частное бесконечно малых может быть чем угодно. Тем
не менее для частного имеет место следующий результат.
Теорема 2.4. Пусть {xj — бесконечно малая последовательность и ее
элементы начиная с некоторого номера п * отличны от нуля. Тогда начи¬
ная сп* определена последовательность {1/хи}, которая является беско¬
нечно большой. Если {xj — бесконечно большая последовательность, то
существует номер п* такой, что начиная с этого номера все элементы {хп}
отличны от нуля. Тогда начиная сп* определена последовательность {1/хп},
которая является бесконечно малой.
(Короткая, «жаргонная» формулировка этой теоремы: единица на бес¬
конечно малую — бесконечно большая, единица на бесконечно большую —
бесконечно малая.)
2.1.3. Сходящиеся последовательности
Обобщим понятие бесконечно малой последовательности и введем важ¬
ное понятие сходящейся последовательности. Это можно сделать, исполь¬
зуя понятие бесконечно малой последовательности.
75
Определение 2.8. Последовательность {хп} называется сходящейся,
если существует число а такое, что последовательность {хп - а} бесконечно
малая. При этом число а называют пределом последовательности {хп}.
Для предела используют обозначения Hm Xn= а или хп —> а при п —>
П—¥°°
Можно дать эквивалентное определение сходящейся последовательно¬
сти, используя явную запись определения бесконечно малой последова¬
тельности.
Определение 2.9. Последовательность {х„} сходится к числу а, если
для любого (достаточно малого) е > 0 найдется номер N = ЛГ(в) такой, что
при всех п имеет место неравенство
\хп-а\<г.
Для сходящейся последовательности имеет место специальное пред¬
ставление. Так как из условия Hm Xn= а следует, что хп - а = ап — беско-
п—>°°
нечно малая последовательность, то Xn = а + аи, т.е. сходящаяся последова¬
тельность представима в виде сумммы константы (предел) и бесконечно
малой последовательности.
Дадим геометрическую интерпретацию понятию сходящейся последо¬
вательности. Из определения следует, что для любого в > 0 начиная с неко¬
торого номера N = N{в) все элементы последовательности оказываются
в в-окрестности точки а. Если иллюстрировать последовательность графи¬
ком функции f(n), то это означает, что график попадает в «трубку» радиуса
в с центром в а начиная с некоторого N (рис. 2.5).
1,4
1,2
1,0
0,8
0,6
0,4
0,2
0
-0,2
Если рассматривать последовательность на прямой, то сходимость к а
означает, что точки последовательности сгущаются около точки а. Изобра¬
зим последовательность хп = (-1 )п/п на прямой, обозначая элементы дан¬
ной последовательности вертикальными отрезками (рис. 2.6).
Последовательность, не являющаяся сходящейся, называется расходя¬
щейся. Заметим, что «расходящаяся» — не значит «разбегающаяся», т.е.
расходящаяся последовательность может быть ограничена (например,
76
0,8
0,6
0,4
0,2
J—0
-0,2
-0,4
-0,6
-0,8
-1,0
-1,0 -0,8 -0,6 -0,4 -0,2 0 0,2 0,4 0,6 0,8 1,0
Рис. 2.6
I I I
Обобщая понятие сходящейся последовательности, для бесконечно
больших последовательностей также используют понятие предела следу¬
ющим образом. Если последовательность {хп} — бесконечно большая, то
используют запись Iim Xn= °° (или хп —> °° при п —> °°). Если, кроме того,
га—>°°
все элементы {х„} начиная с некоторого номера положительны (отрица¬
тельны), то говорят, что Iim хп = +°° (-°°) (или хп —> +°° (-°°) при п —> °°).
га—>°°
Заметим, что еслихп—> +°° (-оо), то заведомо хп—>°° (обратное неверно).
Например, хп = (-1)” • п —» °°, но хп ^4 +°° (-°°) при п —>
Для сходящихся последовательностей имеют место простые утвержде¬
ния (приведем их без доказательства и советуем читателю обосновать их
самостоятельно).
Теорема 2.5. Сходящаяся последовательность имеет только один пре¬
дел.
Теорема 2.6. Сходящаяся последовательность ограничена.
Обратное утверждение (как уже было показано выше), вообще говоря,
неверно (например, хп = 1 + (-1)” ограничена, но не является сходящейся).
Теорема 2.7. Если Hm хп = a, Hm уп = Ь, то существуют Hm(хп ±уп) =
га—»°° га—>°° и—»°°
Лп
Ura
а
= — (последнее равенство при условии
о
= а ± b, Hm(хи ■yn) = a-b, Hm
п—>°° и—
Уп*0,Ьф 0).
Теорема 2.8. Если Hm хп=аихп<Ь (начиная с некоторого номера), то
а<Ъ.
п—>°°
Отметим, что из условий хп < b и Hm Xn= а не следует, что а < Ь. Напри-
-J^ га—
мер, для хп = 1— справедлива оценкахп< 1, но Hm хп = 1.
П га-»°°
Из теоремы 2.8 следует, что если хп E [а; Ъ] (начиная с некоторого
номера) и Hm хп = с, то с E [я; Ь\.
и—
Теорема 2.9. Если хп < уп {начиная с некоторого номера) и хп —> а, уп —> b
при п^>°°,то а<Ъ.
Теорема 2.10. Если хп< у п< Zn {начиная с некоторого номера) и хп —> а,
Zn —> а при п —> °°, то уп —> а при п —> °°.
77
2.1.4. Монотонные последовательности
Рассмотрим важный частный случай последовательностей — монотон¬
ные последовательности.
Определение 2.10. Последовательность {хп} называется возрастающей
(убывающей), если хи+1 > хп (xn+1 < Xn) при всех п е N. Обозначение: хиТ
(хи1).
Определение 2.11. Последовательность {хп} называется неубывающей
(;невозрастающей), если хи+1 > хп (хи+1 < Xn) при всех и G N. Обозначение:
Xw/1 (хи\).
Определение 2.12. Последовательность {хп} называется монотонной,
если она невозрастающая или неубывающая. Последовательность строго
монотонная, если она возрастает или убывает.
Для монотонных последовательностей из вещественных чисел имеет
место следующая теорема о сходимости.
Теорема 2.11 (Вейерштрасса о монотонной последовательности).
Пусть {хи} G R монотонна и ограничена. Тогда она сходится.
Фактически ограниченность является необходимым и достаточным
условием сходимости монотонной последовательности в R. Если последо¬
вательность монотонна, то она всегда ограничена с одной стороны своим
первым элементом (неубывающая — снизу, невозрастающая — сверху).
Поэтому при изучении ограниченности монотонной последовательности
речь идет об ограниченности «с другой стороны», т.е. об ограниченности
сверху для неубывающих или снизу для невозрастающих последовательно¬
стей. При этом оказывается, что монотонные последовательности сходятся
к своим точным граням, т.е.
хп+\ Hm хп = sup{x„};
Я—о
хп+1 ^ хп => Hm хп = inf{x„}.
TZ-
Это утверждение верно и для неограниченных последовательностей
в том смысле, что для них
хи+1 >хи=> Hm хп = sup{x„} = +°о;
и—»°°
хп+1 ^ хп => Hm хп = inf{x„ } = -оо.
и—
Заметим, что если {хи} G Q монотонна и ограничена, то она может
не иметь предела в Q (если она не имеет соответствующей точной грани
в Q).
2.1.5. Подпоследовательности. Предельные точки
Пусть задана последовательность {хп} и некоторая строго возрастающая
последовательность {kn} G N. Тогда каждому натуральному п можно поста¬
вить в соответствие элемент исходной последовательности с номером kn,
т.е. Xkn. Так как каждому номеру ставится в соответствие число, то задана
новая последовательность {xk }. Такую последовательность называют под¬
последовательностью исходной последовательности {хп}. В частности,
при kn = n получим саму последовательность {хи} (т.е. любая последователь-
78
ность является своей подпоследовательностью). Фактически подпоследо¬
вательность — это часть последовательности, если из нее удалить некото¬
рые элементы так, чтобы осталось бесконечно много элементов. При этом
для подпоследовательности [XkJ в свою очередь можно построить подпо¬
следовательность (подподпоследовательность исходной), которая, оче¬
видно, будет подпоследовательностью для исходной последовательности
W-
Подпоследовательности, так же как и последовательности, могут быть
ограниченными и неограниченными, сходящимися, расходящимися, беско¬
нечно большими и т.д. Подпоследовательности наследуют свойства исход¬
ной последовательности, т.е. если исходная последовательность обладает
одним из свойств: ограничена, монотонна, бесконечно большая, бесконечно
малая, сходится (к числу а), то таким же свойством обладает и любая под¬
последовательность.
Верно и обратное утверждение: если любая подпоследовательность
исходной последовательности обладает одним из перечисленных выше
свойств, то таким же свойством обладает и вся последовательность. Но это
утверждение тривиально и не имеет большого смысла, так как в число всех
подпоследовательностей входит и сама последовательность.
А вот из того, что отдельные подпоследовательности обладают некото¬
рыми свойствами, в основном нельзя сделать выводы о свойствах последо¬
вательностей в целом.
Задание 2.1
Покажите, что если у последовательности {хп} найдется ограниченная подпосле¬
довательность [XkJ, то эта последовательность не может быть бесконечно большой.
Если же найдется неограниченная подпоследовательность [XkJ, то последовательность
[хп} не может быть сходящейся.
Рассмотрим понятие предельной точки последовательности [хп]. Можно
дать два эквивалентных определения.
Определение 2.13. Точка а* называется предельной для последователь¬
ности [хп}, если существует подпоследовательность [XkJ —> а* при w —>
Определение 2.13'. Точка а* называется предельной для последователь¬
ности [хп}, если для любого в > 0 в е-окрестности точки а* находится бес¬
конечно много элементов последовательности [xj.
Эквивалентность этих определений легко доказывается (докажите!).
Первое из определений опирается на понятие подпоследовательности
(предельная точка, или иначе частичный предел — предел некоторой под¬
последовательности) и подходит только для последовательностей. Второе
определение — более общее. В случае замены термина «последователь¬
ность {хи}» на «произвольное множество {х}» мы получим определение
предельной точки множества.
Из приведенных выше свойств подпоследовательностей следует, что
последовательность сходится тогда и только тогда, когда у нее есть только
одна предельная точка. Однако предельных точек может быть больше
одной, причем как любое конечное число, так и бесконечно много.
79
Обозначим через {а*} множество предельных точек последовательности
{хи}. Имеет место следующая фундаментальная теорема.
Теорема 2.12 (Больцано — Вейерштрасса). Пусть {хп} е R - ограни¬
ченная последовательность. Тогда множество {а*} не пусто (т.е. у любой
ограниченной последовательности есть по крайней мере одна предельная
точка).
Заметим, что на множестве рациональных чисел Q, как и многие другие
теоремы, теорема 2.12, вообще говоря, неверна.
В случае если {хп} неограничена, то у нее могут быть, а могут и не быть
конечные предельные точки (т.е. могут быть, а могут и не быть сходящиеся
подпоследовательности). Например, последовательность {хп }: 1, 2, 1,3, 1,
4,... имеет одну конечную предельную точку а* = 1, к которой сходится под¬
последовательность х2п-1 = 1. Последовательность Xn = п не имеет конечных
предельных точек. Но если (¾} неограничена, то из нее всегда можно выде¬
лить бесконечно большую подпоследовательность, т.е. найдется Xk —> °°
при п —> °°. В этом смысле у неограниченной последовательности есть
предельная точка
ности всегда моя
Таким образом, т
{х„} е IR имеет пс
бесконечную).
Вернемся к ра<
было отмечено вь
ствует по крайне
тельность {хп} ра<
одной. Рассмотри
+оо или -оо (из бесконечно большой подпоследователь-
;но выделить подподпоследовательность одного знака),
еорему 2.12 можно обобщить: любая последовательность
крайней мере одну предельную точку (конечную либо
смотрению ограниченных последовательностей в IR. Как
пне, для ограниченной последовательности всегда суще-
й мере одна предельная точка. Однако если последова-
"ходится (но ограничена), то предельных точек больше
м несколько примеров.
де;
Пусть :
IbHbIX Т(
*п = (-
зчек (р
I y^fn+-
ис. 2.7) О
1 + 6
COS
п
докажи'
ЛИ JJ
—. Дан]
5
ге!).
ная П0(
следоват<
зльность
имеет
шесть п
ре-
ЩИ
111
Г
г
ш.
1:
I
г
Ат
И
-5 -4 -3 -2 -1 0 1 2 3 4 5
Рис. 2.7
Из рисунка ясно, что предельные точки — это точки «сгущения» элементов после¬
довательности.
80
Пример 2.2
Рассмотрим последовательность из бесконечного числа повторяющихся элементов
{%п} ~ {®1 > ®2> •••> ®1> ®2> •••> •" }•
Для нее {а*} = {аь а2,..., (¾} — предельных точек k шт., т.е. заданное конечное число.
Пример 2.3
Рассмотрим последовательность
{^1> ®1» ®2» ®1» ®2> «3> ®1> @k’ ^k+\’
Для нее {а*} = Ja1, я2> •••> аь ak+b •••} — множество предельных точек включает
в себя заданное счетное множество. При этом {а*} не менее чем счетное. Заметим,
что в этом случае имеет место включение, но не обязательно равенство. Множество
{а*} содержит также все предельные точки последовательности {хп}, которые могут
и не принадлежать самой последовательности {хп}.
Вообще говоря имеет место следующее утверждение.
Лемма 2.1. Пусть {а*} — множество предельных точек последователь¬
ности {хп}, а** — предельная точка множества {а*}. Тогда а** е {а*}.
Доказательство
Рассмотрим произвольное е > 0. Покажем, что в е-окрестности точки а**
находится бесконечно много элементов {хп} (тогда а** — предельная точка
{хп}, т.е. a** G {а*}).
Так как а** — предельная точка {а*}, то в е-окрестности а** находится
по крайней мере одна точка a* G {а*}, а Ф а* (рис. 2.8).
cl* - е'
* / * * /
(а - г а а + е
Il III INI III Ill^lllllllllllltelllllllllllllllllllllll
I
I I I liiiiiiiiii ill 111 mm mi mini» ini min mill i n i him» i i mi ii iiiiiiiiiiii him him ii him him i i| 111
a**
Puc. 2.8
a**+ e'
Выберем в' > 0 достаточно малым так, что е'-окрестность точки а* цели¬
ком лежит в е-окрестности а**. Так как а* — предельная точка {хп}, то
в е'-окрестности а* находится бесконечно много элементов {хп}. Но все они
находятся и в е-окрестности а**. Лемма доказана. ■
Рассмотрим частные случаи предыдущего примера.
Пример 2.4
Пусть ап = 1 /п, тогда
{e*} = {0,1,1/2,..., 1/и, ...} = {*„} U {0},
т.е. к {хп} добавилась единственная предельная точка — нуль. Множество {а*} — счетное.
Пример 2.5
Пусть {:хп)\ = {1/2, 1/3, 2/3, 1/4, 2/4, 3/4, 1/5, 2/5, 3/5, 4/5, ...}. В этом случае,
очевидно, предельными точками {хп} будут все точки из отрезка [0; 1] (в любой
81
е-окрестности х s [0; 1] найдется бесконечно много рациональных дробей, элементов
{xn}). В этом случае {а*} = [0; 1], т.е. {а*} — множество мощности континуум: множе¬
ство предельных точек последовательности {хп} мощнее, чем сама последовательность.
На рис. 2.9 изображены первые 20 000 элементов последовательности {хп} = {1/2,
1/3, 2/3, 1/4, 2/4, 3/4,...} в логарифмической шкале.
Легко показать, что из ограниченности {хп} следует ограниченность {а*}.
Таким образом, если {хп} — ограниченная последовательность, то {а*} —
ограниченное непустое множество. Следовательно, для него существуют
а* = sup{/z*} и a* = inf{a*}.
Хотя в общем случае точные грани множества могут ему и не принадле¬
жать, для множества предельных точек имеет место включение а*, а* е {а*}.
Докажем это (на примере а *). Так как а* = sup{a*}, то для V е > 0 суще¬
ствует а** е {а*} такое, что а* - в < а** <а* (рис. 2.10).
а**
^lll Illll MN 111 Ijllllllllll* INI Illl Il Il^ I Il I Mill» I I III Il llllllllllll llllllllllll llllllllll ^
а* - e' а* а* + г'
Рис. 2.10
Так как а** — предельная точка {хп}, то в любой ее е'-окрестности нахо¬
дится бесконечно много элементов {хи}. Выберем в' достаточно малым так,
что в'-окрестность а* целиком лежит в е-окрестности а*. Тогда в произ¬
вольной е-окрестности а * находится бесконечно много элементов (¾}, т.е.
а* — предельная точка {хп}, а* е {а*}.
Из доказанного следует, что у ограниченной последовательности всегда
есть наименьшая и наибольшая предельные точки. Их называют нижним
и верхним пределами последовательности:
a* = Hmxn, a* = Hm хп.
П—¥°° п—>оо
Очевидно, что последовательность сходится тогда и только тогда, когда
а* = а*.
82
В случае неограниченной сверху (снизу) последовательности из нее
можно выделить подпоследовательность, сходящуюся к +°° (-°°), поэтому
в этих случаях считают, что
Iimxn = +оо (Ит хп = -оо).
и—»°° П—¥°°
Таким образом, для любой последовательности определены четыре объ¬
екта, связанные следующими неравенствами:
inf{xn} < Iim хп < Hmxn < sup{xn}. (2.1)
П—¥ °° П—>°°
Для ограниченных последовательностей это конечные числа. При этом
в соотношении (2.1) могут быть как равенства, так и строгие неравенства.
Например, для последовательности xn = 1 получаем
I = inf{xn} = Hm xn = Hmxn = sup{xn}.
И->оо П~>°°
Г-1 Y
А для хп = (-1)” + -——
п
inf{xn} = -2 < Hm xn = -I < Hmxn = I < sup{xn} = 3/2.
я—¥°° П—¥°°
Возможны также различные промежуточные случаи (постройте при¬
меры!).
Из соотношения (2.1) следует, что если {xn} G [я; Ь\, то и {я*} G [я; Ъ\.
Обратное неверно. В приведенном выше примере на отрезке [я*; я*] = [-1; 1]
нет ни одного элемента последовательности (рис. 2.11).
0,8
0,6
0,4
0,2
О
-0,2
-0,4
-0,6
-0,8
-1,0
-2,0 -1,5 -1,0 -0,5 0 0,5 1,0 1,5 2,0
Рис. 2.11
Однако имеет место следующее утверждение.
Лемма 2.2. Пусть {хп} — ограниченная последовательность;
a* = Hmxn, а* = Hm хп. Тогда для V е > 0 3 N = N(e) > 0 такой, что для V п
И->°° я—>°°
хп е(а*-£,а*+в).
Доказательство
Покажем, что вне интервала (я*-е;я* + в) находится не более чем
конечное число элементов последовательности. Предположим, что правее
83
а * + 8 находится бесконечно много элементов {хп}. Тогда они образуют под¬
последовательность {.Xk }, которая ограничена (как и исходная последова¬
тельность fxj). Тогда из {.Xk } можно выделить сходящуюся подпоследова¬
тельность {х }. Так как Xk > а *+в, то
kn п
a* =Hmхт, >а*+Е>а*,
И—>°°
тк
т.е. у последовательности {хп} есть предельная точка, большая наибольшей.
Получили противоречие, следовательно, правее а*+в находится не более
чем конечное число элементов {хп}. Аналогично, можно показать, что левее
a*-E также лежит лишь конечное число элементов {хп}. Лемма доказана. ■
Замечание 2.1. Утверждение последней леммы в некотором смысле
обобщает определение сходящейся последовательности: оно совпадает
с определением сходящейся последовательности в случае а* = а*,ав случае
а* < а * из леммы 2.2 следует, что последовательность начиная с некоторого
номера попадает в е-окрестность отрезка [а*; а*].
Приведенные выше рассуждения легко обобщаются на случай про¬
извольного ограниченного множества вещественных чисел. А именно,
у любого ограниченного XcR (естественно, X содержит бесконечно много
элементов) есть по крайней мере одна предельная точка; множество пре¬
дельных точек {а*} ограничено; среди предельных точек есть наименьшая
и наибольшая (а*иа* соответственно), при этом
inf{x„} < а* < а * < sup{x„}
и для V е > О вне интервала (я *- е; а *+ е) находится конечное число элемен¬
тов множества.
Рассмотрим следующий вопрос. Выше нами был построен пример
(-1 Yn
(и построен чертеж) расходящейся числовой последовательности -—-—,
п +1
которая не имеет ни наибольшего, ни наименьшего члена. Возникает вопрос:
а можно ли построить пример сходящейся последовательности, удовлетво¬
ряющей данному свойству? Ответ на данный вопрос — отрицательный. Дей¬
ствительно, пусть это возможно и такая последовательность хп найдется.
Следовательно (в силу сходимости), она является ограниченной. Поэтому
у нее существуют точные верхняя и нижняя грани, которые по нашему пред¬
положению не достигаются. В этом случае можно доказать (докажите!), что
supfxj и inffxj — предельные точки последовательности {хп}. Тогда либо
inffxj < supfxj и последовательность {хп} расходится, либо inffxj = supfxj
и последовательность fxj постоянна.
2.1.6. Фундаментальные последовательности
Перейдем теперь к рассмотрению такого основополагающего понятия,
как фундаментальная последовательность.
В определении сходящейся последовательности в явном виде фигури¬
рует значение предела, т.е. для исследования последовательности на схо¬
димость, используя определение предела, требуется угадать его значе¬
ние, а потом доказать, что именно к нему последовательность и сходится.
84
В связи с этим возникает вопрос: можно ли установить сходимость (рас¬
ходимость) последовательности, не зная значения предела? Ответ на этот
вопрос дают критерий Коши и понятие фундаментальной последователь¬
ности.
Определение 2.14. Последовательность {хп} называется фундаменталь¬
ной, если для любого е > 0 найдется номер N = N(E) > 0 такой, что при всех
п> Nnm> N имеет место неравенство \хп- хт\< г.
Фактически определение говорит, что элементы последовательности
становятся «близкими» друг к другу с ростом номеров. Дадим эквива¬
лентную формулировку определения, которую часто удобно использовать
при решении задач.
Определение 2.14'. Последовательность {хп} называется фундаменталь¬
ной, если для любого е > 0 найдется номер N = N(e) такой, что при всех
п > Nи всех p>0,n,pe N, имеет место неравенство \хп+р - хп\ < е.
Для последовательностей из вещественных чисел имеет место следую¬
щая теорема.
Теорема 2.13 (Коши). Последовательность {хп} е R сходится тогда
и только тогда, когда она фундаментальная.
Доказательство
Необходимость. Пусть хп —» а при п —> °°. Тогда для любого в > 0 суще¬
ствует номер N = N(в) такой, что для Vn>N,Vm>N выполнено
^ в
зсп-а
“2’
Xwi — а
TJl
Тогда в силу неравенства треугольника
\хп -л:т < ргя - а\ + \хт + а\ < в,
т.е. {л:„} — фундаментальная.
Достаточность. Пусть {хп} — фундаментальная. Тогда для любого в > О
существует номер N = N(e) такой, что для \/n>N,\/m>N
Возьмем в качестве т сам номер N (т.е. т = N). Тогда
Хп Хт
<Е.
\Х п - xN < В => хп G [хлг - е; xN + е]
при всех n>N. Отсюда следует, что вне отрезка находится лишь конечное
число элементов последовательности. Выберем произвольное в > 0 и выберем
а ппп{хд^£^ в, х^, Х2,..., -^jv(e) }»б П1ах{хд^£^ -ь в, хХ2,..., } ■
Тогда {хп} е [а; Ь] при всех п е N, т.е. фундаментальная последователь¬
ность ограничена. Из этого следует, что множество ее предельных точек
не пусто и ограничено. Покажем, что оно состоит из одной точки.
Обозначим, как и ранее, через а* и а* наименьшую и наибольшую
предельные точки. Пусть а*<а*. Рассмотрим в<
а*-а*
т.е. такое, что
в-окрестности а * и а * не пересекаются и расстояние между элементами
этих окрестностей не меньше в (рис. 2.12).
85
х„
х„
сг
СГ
Рис. 2.12
Если {х„} — фундаментальная последовательность, то для в > 0 суще¬
ствует ЛГ(е) такой, что при всех n,m>N хп-хт < в. Но так как а * и а * —
предельные точки, то в е-окрестностях этих точек находится бесконечно
много элементов {хи} (в том числе с номерами больше ЛДе)), а значит,
существуют х• E е-окрестности а * и х E в-окрестности а*, где п*, т* > N.
Но тогда х * - х * > в. Получили противоречие, а значит, а* = а*, т.е. мно¬
жество предельных точек последовательности {хп} состоит из единствен¬
ного числа а* = а* = а, т.е. существует Iim хп = а. Теорема доказана.
п—»°°
Таким образом, для последовательностей {хп} е M фундаментальность
эквивалентна сходимости. Но в общем случае (т.е. в случае {хп} из какого-то
другого множества) это не всегда так. Например, если {хп} E Q и {хи} фун¬
даментальная, то из этого не следует, что для {хп} найдется а е Q такое,
что хп —> а при п —> °°. Заметим, что из сходимости {хп} в произвольном
множестве, в том числе в Q, следует фундаментальность (доказательство
необходимости в теореме 2.13 опиралось лишь на определения сходимости
и фундаментальности, но не на свойства R).
Таким образом, фундаментальность слабее сходимости.
Для иллюстрации неэквивалентности сходимости и фундаментально¬
сти в Q рассмотрим простой пример. Возьмем последовательность {хп} вида
Хп+1 о
хп+-
X.
, X1 = 2.
п J
Очевидно, что {хп} E Q. Покажем, что {хп} убывает и ограничена снизу.
Второй факт тривиален, так как хп > 0.
Первый факт докажем методом математической индукции.
Покажем, что если х2>2 (а х^=4>2), то 2<х^+1<х^, т.е. х^+1>2
и при этом хи+1 < Xw т.е. {хп} строго убывает. Действительно, так как хп > 2,
то
у2
•^w+l _
у2
лп
"l
(л 2^
2
"1
(а 2 ^
I2
1 + —
<
2
-у 2
iV лп)
2
I 2 J
= 1.
Кроме того,
у-2 _
лп+1
Л2
хп +-
X.
п
2 А 4
*„2+4+-^
V
х
= 1 + -
=i+‘
2
(X2 2
— + —
V
X.
п
п J
>1 +—2 = 2.
2
X2 +
An ^
4
х-
п У
Здесь учли, что сумма двух взаимно обратных величин больше двух,
если они не равны единице.
86
Таким образом, {хп} монотонна и ограничена, а следовательно, если
рассматривать {хп} как последовательность из R, то она сходится, т.е. 3 а:
хп —> а при п —> Из определения последовательности в пределе получаем
Г оЛ
CL =
1
CL + ■
а
а
2
J.
а
а2 = 2,
т.е. а£ Q (я = V2). Таким образом, для {хге} не существует предела среди
рациональных чисел.
Но в то же время, так как {хп} в R сходится, то она и фундаментальна
в R. Но тогда, очевидно, она фундаментальна и в Q. Таким образом, {хп}
является примером фундаментальной, но не сходящейся в Q последова¬
тельности.
Множества, в которых фундаментальность влечет за собой сходимость
последовательности, называются полными. Из приведенных выше рассуж¬
дений следует, что множество вещественных чисел R — полное, а множе¬
ство рациональных чисел Q — нет.
2.1.7. Определение множества вещественных чисел
через фундаментальные последовательности
из множества рациональных чисел
Выше было показано, что множество вещественных чисел обладает
свойством полноты, а множество рациональных чисел таковым свойством
не обладает. Но можно пойти и обратным путем, а именно, пополнить
множество Q, и получившееся полное множество считать множеством
вещественных чисел. Таким образом, мы приходим к еще одному способу
введения множества вещественных чисел, основанному на использовании
фундаментальных последовательностей из Q1. Конспективно изложим
основные идеи этого построения.
Рассмотрим множество фундаментальных последовательностей из Q,
т.е. {otre} с Q. Заметим, что имеют место простые леммы.
Лемма 2.3. Пусть последовательности {ссге}, {|Зге} с Q — фундамен¬
тальные последовательности. Тогда последовательности {уосге}, где у е Q,
и {ап ± Р„} — фундаментальные.
Доказательство
Так как {осге} — фундаментальная, то для V в > 0 найдется номер N(e) > О
такой, что при V п,т> N
I £
(считаем, что у Ф 0: если у = 0, то ап • у = 0 — фундаментальная последова¬
тельность). Тогда при всех п, т> N имеет место оценка Iyot7re -усси| < в, т.е.
{уаге} — фундаментальная.
Если {аи} и {Рге} фундаментальные, то для V в > 0 найдется N(e) > 0
такой, что для V п,т> N
1 При этом число е из определения фундаментальной последовательности мы также
будем брать из Q.
87
-a J<-
|Ри.-Рп|<2> r«
Тогда при V п,т> N имеет место оценка
|(an±Pn)-(aWJ±Pm)|<e>
т.е. последовательности {ап ± Pn} фундаментальные.
Лемма доказана. ■
Заметим, что лемма справедлива для фундаментальных последователь¬
ностей не только из Q.
Таким образом, линейные операции для фундаментальных последова¬
тельностей не выводят нас из этого класса. Покажем теперь, что и произ¬
ведение фундаментальных последовательностей принадлежит этому же
множеству.
Лемма 2.4. Пусть {an}, {Pn} с Q — фундаментальные последовательно¬
сти. Тогда {ап ■ Рп} — фундаментальная последовательность.
Доказательство
Прежде всего заметим, что из фундаментальности {ап} и {Рп} следует их
ограниченность (докажите!).
Пусть А, В G Q, А, В > 0, ап < А, |РЯ|< Л при всех п е N. Так как {осп}
и {Рп} — фундаментальные последовательности, то для V в > 0 существует
N(z) > 0 такой, что для V п,т> N
ctlTTi
<|. |Р»-Р:
т
Тогда для V п,т> N выполняется
I^nPn — ctTrftm I — I^nPn — ctIftm ctTftm ~ ctTtftm I —
“иНРи-РягНРя
ctU
. 8 D 8
<А- — + В = 8,
А В
т.е. последовательность {ап • Рп} фундаментальная.
Лемма доказана. ■
Таким образом, на множестве фундаментальных последовательностей
определены операции сложения и умножения фундаментальных последо¬
вательностей.
C фундаментальными последовательностями можно ассоциировать
вещественные числа (которые, по сути, являются пределами фундамен¬
тальных последовательностей). Однако разные фундаментальные после¬
довательности могут сходиться к одному пределу. Логично их ассоцииро¬
вать с одним и тем же числом из М. Для этого напомним читателю понятие
класса эквивалентности.
Определение 2.15. Отношение эквивалентности (обозначается обычно ~)
на множестве А — это бинарное отношение, для которого выполнены следу¬
ющие условия:
1) рефлексивность: а ~ а для VaeA;
2) симметричность: а~Ь <^>Ь ~ а;
3) транзитивность: а ~ b,b ~ с =$ а ~ с.
88
Классом эквивалентности С(а) элемента а е А называется подмноже¬
ство элементов из А, эквивалентных а.
Из определения отношения эквивалентности следует, что если b е С(а),
то С(Ь) = С(а), т.е. каждый класс эквивалентности порождается любым
своим элементом.
Введем на множестве фундаментальных последовательностей следую¬
щее отношение эквивалентности.
Определение 2.16. Две фундаментальные последовательности {ая}
и {Рга} эквивалентны, если последовательность {ап - P7J бесконечно мала.
Это определение может применяться к последовательностям как из R,
так и из Q. То, что для так введенного отношения эквивалентности выпол¬
няются все три свойства из определения эквивалентности, легко проверя¬
ется:
1) {ая- ага} = {0} — бесконечно малая (т.е. {ая} ~ {ага});
2) {ага- P7J — бесконечно малая <=> {Ря- ап} = {(-1) • (ага- Ря)} — беско¬
нечно малая;
3) {(оси - P7J — бесконечно малая; {Р„- Y7J — бесконечно малая => {ап - уп} =
= {ап - P7J + {Ря - Y7J — бесконечно малая.
Таким образом, все множество фундаментальных последовательностей
из Q может быть разбито на непересекающиеся классы эквивалентности.
Тогда эти классы эквивалентности можно принять за определение веще¬
ственных чисел. При этом на таком множестве можно ввести три операции:
сравнения, сложения и умножения.
Операцию сравнения вводят следующим образом. Пусть заданы два
класса эквивалентности х и у. Если это один и тот же класс, то х = у. Если
х Фу, то возьмем из каждого класса по одному представителю: {ага} и {Ря}.
Покажем, что из фундаментальности {ага} и {Ря} и того факта, что {ап - Ря}
не является бесконечно малой, следует, что существуют у > 0, у е Q,
и п* е N, такие что (ая - Ря) > у либо (ая - Ря) < -у при п>п.
Действительно, так как {ап} и {Ря} — фундаментальные, то {ая - Ря} —
фундаментальная. Так как {ап - Ря} не является бесконечно малой, то най¬
дется 2у > 0: для любого n' е N существует т>п' такое, что
K-Pj>2y. (2.2)
Из определения фундаментальной последовательности следует, что
для е = у > 0 найдется п* > 0 такое, что для V п,т>п выполнено
I (ап - Ря) - (ат - Ря,)1 - Y-
Фиксируем т > п, при этом т выберем из условия (2.2). Тогда для V п > п
выполнено
I (сся - ря) - (CC7ra - pm)| < у; Ia7ra - P7raI > 2у.
Во втором неравенстве возможны два случая: а) ат - P7ra > 2у; б) ат - P7ra <
< -2у.
Рассмотрим случай а). Имеем
-Y + OC7ra-Рт< ая-ря< у + CLm-Pm => У< ая-Ря.
89
Во втором случае также легко показать, что ап - (Зи < -у.
Таким образом, если х Фу, то, выбрав представителей из этих классов
эквивалентности, получим, что элементы либо (ап - Ри), либо (Р„ - ап)
начиная с некоторого номера положительны и отделены от нуля некоторой
константой. В первом случае будем считать, что х > у, во втором — у > х.
Непосредственной проверкой нетрудно убедиться, что введенная опера¬
ция сравнения обладает свойством транзитивности:
X = у, у = z=$ X = Z.
х > у, у > Z =$ Х> Z.
Операции сложения и умножения вводятся естественным образом.
Пусть х и у — два класса эквивалентности на множестве фундаментальных
последовательностей из Q; {ап} и {Ри} — представители этих классов.
Суммой х и у будем считать класс эквивалентности z, порожденный
фундаментальной последовательностью {осп+ Ри}, а произведением — класс
эквивалентности, порожденный фундаментальной последовательностью
{ап ■ Ри}. Покажем, что это определение корректно. Для этого надо показать,
что оно не зависит от выбора представителей {аи} и {Ри} из соответствую¬
щих классов эквивалентности.
Пусть из классов х и у выбраны другие представители: {ос'} и {Р„}. Им
соответствуют последовательности {а„+Р^} и {ос' -$'п}. Покажем, что эти
последовательности эквивалентны {оси + Р„} и {оси • Ри} соответственно (т.е.
порождают те же классы эквивалентности).
Действительно, так как {ап} и {ая} принадлежат одному классу экви¬
валентности, то {оси - ос'} — бесконечно малая последовательность. Анало¬
гично {Ри -Ря} — бесконечно малая. Но тогда и
{(аи + ри > - («;+р;)} = {(ося - о+(ря - р;)}
— бесконечно малая, т.е. {ося+ Р„} ~ {сся +Ря}.
Для произведения
КPk - } = KPn - <Ря + <Рп - <Рп } =
= {К-<)Ри+<(Рп-Рп)}
— бесконечно малая, т.е. {ос„ • Р„} ~ {а'п -P'}, что завершает доказательство
корректности определений сложения и умножения.
Отметим, что рациональные числа естественным образом «вкладыва¬
ются» в построенное множество вещественных чисел. Для этого с рацио¬
нальным числом а связывается класс эквивалентности, порождаемый
последовательностью хп = а.
Пользуясь свойствами арифметических операций для рациональных
чисел, несложно показать, что для определенных выше операций сравне¬
ния, сложения и умножения также выполнены основные свойства.
1. X = у, у = z=> x = z, х<у, у <z=> x<z (транзитивность; было рас¬
смотрено ранее).
2. х + у = у + х (коммутативность).
90
Действительно, выберем из классов х и у представителей {ап} и {Ря}.
Тогда (х+ у) — класс, порожденный последовательностью {ап + Ря}.
Но так как для рациональных чисел выполнено (ап + РЯ) = (РЯ + ая), то
{(OLn +РИ}~{Р„ +¾}1. Следовательно, (х + у) и (у + х) — один и тот же класс
эквивалентности.
3. (х + у) + z = х + (у + z) (ассоциативность).
Это свойство доказывается, как и предыдущее, на основании определе¬
ния и ассоциативности операции сложения для рациональных чисел.
4. Существует 0:х + 0 = 0 + х = х для любого х.
В качестве OgR возьмем класс эквивалентности, порождаемый после¬
довательностью OLn= 0. В этот класс, очевидно, входят бесконечно малые
последовательности. Но тогда (х + 0) порождается последовательностью
(Ри+о>=ри, где Ри порождает х. Отсюда следует, что (х + 0) и х — один и тот
же класс эквивалентности, т.е. х + 0 = х.
5. Для V х существует х': х + х' = 0.
Пусть х порождается последовательностью {ая}. Рассмотрим класс х',
порожденный последовательностью {-ая}. Тогда сумма (х + х') порожда¬
ется последовательностью On-On= 0, т.е. х + х' = 0.
Аналогичные свойства имеют место и для произведения.
6. х • у = у • х.
7. (х- у) -Z = х- {у -z).
8. Существует 1:х ■ I = 1 ■ х = хдля любогох.
В качестве IgR можно взять класс эквивалентности, порождаемый
последовательностью On = 1.
9. Для Vi^O существует х'\ х ■ х' = х' • х = 1.
Пусть последовательность {оп} порождает класс хФ0. Тогда {ая}
не является бесконечно малой. Выше было показано, что в этом случае най¬
дутся номер N и у > 0 такие, что при всех п > N либо On > у, либо On < -у,
т.е. IaJ > у, оп Ф 0. Рассмотрим последовательность {Ри}, где Ри = 1 при п = 1,
1
2, ..., N, а при п > N определим Ри = —. Тогда элементы последовательно¬
сти
сти оп ■ Ри = 1 при n>N. Отсюда следует, что (а„ • Ря - 1) при n>N, т.е.
(ая • Р„ - уп) — бесконечно малая, где уи = 1 — последовательность, порож¬
дающая число 1. Таким образом, последовательность оп • (3„ принадлежит
классу эквивалентности 1, значит, для х', порождаемого последовательно¬
стью {Ря}, имеет место равенство х-х' = 1.
10. (х + у) • Z = х ■ z + у • z (дистрибутивность).
Доказательство легко получить исходя из определения операций сло¬
жения и умножения, а также дистрибутивности для рациональных чисел.
11. Если х> у, то x + z>y + z для V z.
Пустьх>у. Это означает, что для произвольных представителей классов
х и у последовательности {ая} и {|3И}, начиная с некоторого номера N выпол¬
нено ая ~РЯ > у > 0 при некоторой константе у > 0. Выберем {т!я} — после¬
довательность, порождающую z. Tогда (ая + Zn ) - фя + Zn ) = (оп - Ря ) > у при
n>N. По определению это означает, что выполнено x + z>y + z.
1 {(a„ + Р„) - (P„ + ос„ )} = {0} — бесконечно малая.
91
12. Если х > у, z > 0, то х • z > у • z.
Доказательство аналогично предыдущим. Выберем представителей
классов х и у, последовательности {ая} и {|3И}. Тогда найдется номер Ni,
начиная с которого ап - Ря > у* > 0. Так как z > 0, то для последовательности
{уи}, представителя класса z найдется номер N2 такой, что при п> N2 имеет
место неравенство уп > у** > 0. Тогда при п> N = тах{Л^,Л^2} будут выпол¬
нены неравенства
Yn («и - Pn ) = Упап ~ YnPn > Y* • Y** = Y > 0.
Но это и означает, что х • z > у -г.
13. Аксиома Архимеда. Для любого х можно повторить число 1 слагае¬
мым столько раз, что сумма превзойдет х.
Здесь 1 — особый элемент относительно операции умножения. Поэтому
выберем в качестве представителя этого класса последовательность уи = 1.
Тогда для суммы из конечного числа 1 (в частности, из k таких слагаемых)
в качестве представителя можно взять у\ = к. Покажем, что для VxgM най¬
дется & G N такой, что k > х, т.е. у\ - ап > у > 0 начиная с некоторого номера
(здесь {ап} — представитель класса х). Действительно, если xgM, {ос„} —
представитель х, то {а„} — фундаментальная последовательность, но тогда
{ап} ограничена, т.е. 3 C > 0, C G Q такое, что |а„ | < C при всех п G N.
Выберем k = [С\ + 2, где [.] — целая часть числа. Тогда, очевидно,
при всех и G N
Yn -оси =^~ап -1>0-
Таким образом, для введенного указанным выше образом множества M
выполнены все основные свойства.
2.2. Примеры задач на числовые последовательности
После того как нами были определены основные понятия и сформули¬
рованы основные теоремы из теории числовых последовательностей, рас¬
смотрим несколько интересных и важных задач по этой теме.
Задача 2.1
Определим последовательность {ап} (.модификация последовательности Фарея)
следующим образом:
«о 1> ^2n+l ^2п+2 ®я+1, ^ ^ ^ — 0.
Докажем, что множество {an_Jan, п е N} содержит все положительные рацио¬
нальные числа.
Решение
Рассмотрим, что из себя представляет заданное отношение:
а,
п-1
,neN
[1 1 2 1 3 2 3 ]
[Т 2’ 1 ’ 3’ 2’ 3’ I ’ J
Для решения поставленной задачи требуется доказать, что для любых двух вза¬
имно простых положительных целых чисел г и 5 существует натуральное число п
такое, что ап = г, an+i = s. Воспользуемся индукцией по г+5. Для г+ s = 2 имеем а0= 1,
A1 = 1. Пусть далее г и 5 взаимно просты и г + s > 2 (поэтому г ^ s). Имеем два случая.
92
1. г > s. Tогда, так как г < г + s, то по предположению индукции найдется номер п
такой, что ап = г - s > 0, an+l = s. Тогда ап + ап+1 = г и, следовательно, а2п+2 = ап + ап+\= г>
а2п+ъ = ап+1 = 5 и, соответственно, а2п+2 + а2п+3 =r + s.
2. s > г. В этом случае предыдущие выкладки не проходят, так как г - s < 0.
Действуем аналогично: так как 5 < г + s, то по предположению индукции существует
такой номер п, что ап = г, ая+1 = s - г > 0. Тогда ап + ап+1 = s. В этом случае а2п+1 = ап=г,
а2п+2 ~ On + ®л+1 — И ПОЭТОМУ &2n+i ^2п+2 ~ ^ S.
Рассмотрим еще одно понятие для произвольной числовой последова¬
тельности.
Определение 2.17. Последовательность {хи} называется выпуклой, если
^ хп-\ хп+1 о о
хп < 2 ПРИ и = 3,....
Задача 2.2
Докажем, что для любой положительной строго убывающей к нулю последова¬
тельности {ап} можно построить мажорирующую ее выпуклую последовательность,
стремящуюся к нулю.
Решение
Действительно, для произвольной положительной строго убывающей к нулю
последовательности {ап} построим последовательность {Ьп}, определенную следую¬
щим образом:
К = «ц Ъ2 = а2, bn+l = тах{а„+1, 2 Ьп - ЬпЛ) при п> 2.
Тогда имеем ап<Ъп и Ьп+Х > 2 Ьп - Ьп_ь откуда
b < К-\ + K+i для п > 2.
" 2
Докажем, используя метод математической индукции, что построенная последо¬
вательность {Ьп} убывает к нулю. Действительно, в силу строгого убывания последо¬
вательности {ая} выполнено = Ci1 < а2 = Ъ2. Далее, пусть выполнено Ьп_х > Ьп. Для
члена последовательности bn+i возможны две альтернативы:
К+\ = 2K ~ K-I = К~ (K-I ~К)<К или Ъп+1 = ««+1 ^по¬
следовательно, последовательность {Ьп} строго убывает. Для элементов после¬
довательности {Ьп} в силу строгой положительности всех ап выполнено неравенство
Ьп >ап >0. Поэтому по теореме Вейерштрасса 2.11 построенная последовательность
является сходящейся.
Докажем, что справедливо равенство Mmbn = 0. Если для всех п е N выполнено
П—^00
Ьп = ап, то последовательность {Ьп} убывает к нулю по условию задачи. Если же най¬
дется номер щ такой, что справедливо Ьп > anf, то обязательно найдется номер щ + /,
для которого будет выполняться Kk+! = ank+i- Действительно, в противном случае
имеем
Kjl+! 2Kfl+!-I Kfi+!-2 Kfi+!-1
" (.Kk+l-2 — Kk+l-i)'
(2.3)
Отсюда
Kfi+! Kfi +1-2 Kjl+!-Г Аналогично получим Kk+l_2 - 2ц+м - Ьщ+1_3
- Kk+l-2 и Т-Д- Поэтому, продолжая равенство (2.3), имеем
Jnu+l-1 — (Kl+1-2 — Kl+1-l) — Kl+1-2 — (.Kl+1-3 — Кь+l-2) — (.Ku+l-2 — Kf,+l-i) ~
FC FC FC FC FC FC FC FC
-Kjl+!-2 2(Kk+l-3 Kk+!-2) — ••• — Kfl KKfi-I Kf1 )■
Kk+! =K
93
Следовательно, так как Ь„ _л-Ь„ >0, a I — произвольное натуральное число, то
nk 1 nk
найдется такое /, что Ъп^ < 0, что неверно.
Из этого получаем, что найдется бесконечно много номеров (обозначим их пт)
таких, что выполнено а - Ъ ■ Отсюда и из того, что а„ и Ь„ — подпоследователь-
пт пт пт пт
ности сходящихся последовательностей ап и Ъп, получаем
Hm b„ - Hm b„ - Hm а„ - Hm а„ - 0.
П—>°° П—т П >°° 771 П—
Замечание 2.2. Отметим, что для нестрого убывающей последователь¬
ности {ап} построенная последовательность {Ьп}, вообще говоря, может
не убывать к нулю. Рассмотрим пример: A1 = I, а2 = I, A3 = A4 = ... = 0.
В этом случае получим bi-b2-b3- ... = 1.
Но между тем для построенной последовательности {аи} в качестве
искомой выпуклой бесконечно малой мажорирующей последовательности
можно взять, например, последовательность Ьп = 22-и, для которой выпол¬
нено
b = 22~п < 22~п + 22~п~2 =
22-Я+1+ 22-Я-1
К+\+Ьп-\
Пусть, далее, про последовательность {аи} известно лишь то, что она
сходится к нулю. Построим мажорирующую ее строго убывающую к нулю
последовательность. В самом деле, пусть {A„} = sup{|Aj|}. Тогда последова¬
ли
тельность {ап} неотрицательна, стремится к нулю и не возрастает. Далее,
_ _ 1 _
построим {ап} = апл— > аи > ап. Эта последовательность и будет искомой.
п
Подводя итог вышесказанному, получаем, что нами было доказано сле¬
дующее утверждение.
Утверждение 2.1. Для любой стремящейся к нулю последовательности
{ап} можно построить мажорирующую ее выпуклую последовательность,
также сходящуюся к нулю.
Построим графики произвольной сходящейся к нулю последовательно¬
сти {ап} и, далее, последовательностей {ап},{ап}, {йи} (рис. 2.13).
5
о\ 5
> • Д * «1
J W 'Vй 1 -ч
/ Y 10
15
20 ';
25
30
35
40
45
50
55
60
65
-5
Рис. 2.13
Предлагаем читателю построить выпуклые последовательности, сходя¬
щиеся к строго положительному пределу и к
94
Задача 2.3 (вавилонский алгоритм вычисления л/2)
Последовательность {х„} задана условиями
-1
xI хп+\ 2
/
Л
Хп + г
V jlTiJ
, п> 1.
Докажем, что Iim Xn = 42. К чему будет стремиться данная последовательность,
п—>°°
если в качестве начального условия выбрать X1 = -1?
Решение
Выше, во время разговора о фундаментальных последовательностях, нами уже
была решена первая их этих задач. Приведем здесь немного другое доказательство
данного факта. Введем обозначение гп-хп-42 при п > 2. Тогда последовательность
{г„} при таких п будет удовлетворять рекуррентному соотношению гп+1 =
2(Л+г„)’
так как
гп+\ Хп+1
-72=4
X +-
_^=х1 + 2-2хпЛ _(х„-л/2)2
= {хп=гп++2} =
X,
я У
2х„
2х„
2(Л + г„)'
Начиная с п = 2 выполнено неравенство г2 = — - 42 > 0. Имеем
°<r„+i =
г г г
_ 1И iTi ^
2(V2 + r„) 2 г„+Л 2
Далее по индукции имеем
2 4
0 < rn+i <-< <... <
1,5-42
)п-1
)я-1
->0 + 0
при п —^ °°.
Следовательно, Iim ги = 0 + 0, откуда Iim хп = 42.
Я—»00 Я^°°
При X1 = -1 проведем аналогичные рассуждения. Пусть rn = хп +42. Тогда rn< 0
начиная с п - 2. Поэтому
гя+1 =
_rn ^ >гп>гп-1>"> г2
2(rn-+2) 2 r„S 24 - 2”-i'
ОтсюдаО > rn+1 > —+ —> 0—0. Следовательно, Iim 0-0. Поэтому Iim Xn = -+2.
4 fi—^oo »1—^oo
Я—>°°
Замечание 2.3. Вычисления показывают, что последовательность {хп}
сходится к ±42 очень быстро. Так, например, при X1 = 1 получаем X4 - S=
= 2,124 • 10 6.
Задание 2.2
Покажите, что указанная последовательность будет сходиться к 42 при любом
начальном X1 > 0 и к числу -42 при любом X1 < 0.
95
Задача 2.4 (итерационная формула Герона)
Докажем, что последовательность чисел {хп}, заданная условиями
_1
Х\ I, хп+^
X + -
An T
а
х.
, п > 1, а > О,
и у
сходится. Найдем предел этой последовательности.
Решение
Обозначим при п > 2 через гп разность гп = хп -\[а. Тогда
Vi х„+1
_ Г _х1+а~2хп4а _ (хп -4а)2 _
а~ Ъс„ " 2х„ "
т
_ п
T
2(гп+4а) 2 гп+4а 2
Используя неравенство Коши между средними арифметическим и геометриче¬
ским, имеем
X9 = > 4аЛ => г?= Xn- 4а > 0.
Начиная с п = 2 выполнено неравенство Vi =
2 (Гп+4а)
> 0. Следовательно,
0 < г'.л < — < 1A <... < —> 0 + 0 => Iim хп - 4а.
”+1 2 4 9«-i п
П—>°°
Задача 2.5
Пусть a>0nft>0— произвольные действительные числа. Определим последо¬
вательность {а„} равенствами
_ 1
ао — а> ап+1 ~ 2
Л
ап+ —
V anj
,п> 0.
Докажем, что при VneN выполняется равенство
(а-4~кл2’
Clvi
an+4k
ya + 4k j
Решение
Воспользуемся методом математической индукции. При п = 0 имеем
a-4k a -4k
Пусть выполнено —
ra-4k^
a + 4k
an+4k
^a + 4k j
O0-4k
On+4k
ап+!~4k _ 2
ап+ —
1V ап)
Аап~<
^)2
ап+\ ^k 1
2
( к)
ап+—
V ап)
+4к <а»+Л>2
для некоторого n e N. Тогда
( 47 ^
а +
4k
Задание 2.3
Пусть а > 4k > 0. Покажите, что из доказанного в задаче 2.5 равенства следует,
чтояя —> 4k.
96
Задача 2.6
I п~^ 2 — /i—г 1
Пусть A1 = I, ап = — akan_k при п > 2. Докажем, что — < Hm я а < —/=.
Tlk=I 4 In
л/2'
Решение
1
Заметим, что 0,7 < -^=. Поэтому для доказательства правого неравенства доста¬
точно показать, что для всех достаточно больших п выполнено неравенство ап < (0,7)”.
Доказательство проведем методом математической индукции. Для малых значений
п имеем
. I I 1
а\ — И а2 ~ 2 — 2 ’ ~ 3
1 1
1
2 2
1
1
3 4 4
I I 1
—I—I—
3 4 3
11
= — <(0,7)4.
48 4 7
Далее, пусть для п -1 > 3, т.е. для п > 4, указанное неравенство выполняется. Тогда
имеем
1 w-i о 1 1 п-з 2 1 и-1!
а.=- Ъчап-к = -«„-1 +-«„-2 + - 2¾¾., £-(0,7)»-‘ + -(0.7)»-2 +—(0,7)” =
Tlk=I TlTlTlk=3 W W W
= (0,7)” +
(0,7)”
и
2 1 е
1 5
0,7 0,49
<(0,7)”.
Докажем левое неравенство, фигурирующее в условии задачи. Для этого доста-
(2^п
точно установить выполнение неравенства ап >
для всех достаточно больших п.
Снова воспользуемся методом математической индукции. Действительно, имеем
1
2
а2=->
Z2V2
. Пусть для п — I > 1, т.е. для п> 2, указанное неравенство выполняется.
Тогда получаем
•[ я-1
^ я-2
ап ^j^kPri-k ®n-i —
Tlk=I W Tl k=2 П
v3 у
+ -
и-ЗГ 2
Л”
и
^ 2 Y Г2 3 , 3^1 (2Л”
+ 1 —
v3y
п 2
п
v3y
Задача 2.7
Докажем, что Iim
Я—
А Л”
хп+\
\ хп J
> е для любой положительной последовательно¬
сти {хя}.
Решение
Докажем данное утверждение от противного. Пусть выполнено
Iim
Я—
/ \п
xI хп+\
V Хп J
<е.
Тогда 3е>0 такое, что Iim
я—
( , Л”
Xi + ^„+1
\ Хп J
= е — Е, и начиная с некоторого ЛГ для
V п> N выполнено
C , Y
х\+хп+\
\ хп J
<е — —. Далее, так как
и + 1
Y
V п J
-jTe, то найдется
номер N* > N такой, что для V п> N * выполнено
xI Хп+1
'»+О"
V Хп J
\ Tl J
97
Отсюда, не ограничивая общности, можем считать, что начиная с некоторого k*
при V k > k* выполняется
xI ^ xk xk+\
k +1 k k +1
Суммируя последнее неравенство по k от k * до достаточно большого п, получим
и л
xI ■ E ~ГГ7 - £
k=k'
п ( -у. V. Л -V. .. V X,*
k=k* k + i
xk xk+l
k k + 1
_ xk* Xn+1 ^ "k'
k* n +1 k* ’
I
что невозможно, так как левая часть, в силу того что сумма Y1” * может быть сде-
к=к k + i
лана сколь угодно большой при большом п, неограничена, а правая часть ограничена.
Задача 2.8
Построим примеры положительных последовательностей хп, для которой рассмо¬
тренный в задаче 2.7 верхний предел равен е и строго больше е.
Решение
Выберем в качестве X^ = и1п(и +1). Тогда имеем
( .v(l) . .v(l) Y
Iim
П—>°°
xI Хи+1
г<1)
V лп
= Iim
П—>°°
In 2 + (п + 1)1п(и + 2)
\п
V
п!п(и + 1)
= Hm
П—»°о
In 2 + 1п(и + 2) + win П + ^
1 + —
п +1
V
Следовательно, так как Iim
И—>°°
и1п(и + 1)
1п2 + 1п(и + 2) + и1п
и + 2
w + ^ = 1, то исходный предел равен
1п(п +1)
числу е. Отметим, что нами было получено, что оценка, фигурирующая в данной
задаче, неулучшаема.
Далее, пусть x*jp = п2. Получаем
Iim
^ r(2) , у(2)
xI +хп+1
г(2)
Y п
= Hm
Г 2 + 2 п^п
1 + (п + 1)2
п*
1+:
п2 J
= е2>е.
Произвольное число а > е можно получить в качестве искомого предела, взяв
в качестве последовательности хп X^ = п1па, где а>е (проверьте!).
2.3. Монотонные числовые последовательности
еп =
Напомним, что числом е называется предел последовательности
. Можно доказать, что к данному пределу сходится и последо-
Г 1 Ли
1 + -
п
\ 'V
вательность
о 1 1 1
S11 — 2 H 1 ь... и—.
" 2! 3! п\
98
Действительно, воспользовавшись биномом Ньютона, получаем
еп =
1 +
1
Y
п
= Il п 1 , П(П-1) 1 | | П(П-1)...[П-(П~1)] 1
п 2! п2 /г! и”
г о
1
Г Л
(4 ^
Г n-i')
1—
I
+
1
1
...
1
I nJ
Yll
I nJ
I nJ
I nJ
= 2+—
2!
Учитывая, что каждое выражение, стоящее в скобках, меньше единицы,
11 1
получим е„ <2 + — н 1-... + — =
и 2! 3! п\
Зафиксируем теперь произвольное k и будем рассматривать n>k. Имеем
2 +
1_
2!
1-
1
п
\(
<2 + —
2П,
1--Л
Tlj
1
+ ... + —
k\
г
+ ...+
1
1--
. п)
1-
1-
1
п
1-
6-1
V
k-\
п
1
+ ...+—
п\
п
(
1--
п
1-
Yl- 1
И
Заметим теперь, что левая часть данного неравенства при п —» °°
и фиксированном k стремится к а правая — к числу е. Следовательно,
при любом натуральном k выполнено неравенство Sk < е. Объединяя данное
неравенство с предыдущим, получаем важный результат:
ek<sk<e для всехk N,
откуда и из теоремы Вейерштрасса о монотонных последовательностях вы¬
текает требуемое.
Замечание 2.4. Отметим, что последовательность {sn} сходится к числу е
существенно быстрее последовательности {еп} и поэтому применима
к вычислениям числа е значительно лучше. Например, е - е5 ® 0,2299;
е - S5- 0,0016. Более подробно скорости сходимости данных последова¬
тельностей можно изучить по рис. 2.14.
Исследуем теперь связь сходящейся последовательности и последова¬
тельности, составленной из средних арифметических (геометрических, гар¬
монических) ее первых п членов.
Утверждение 2.2. Пусть числовая последовательность {яи} моно¬
тонно не убывает. Тогда и последовательность ее средних арифметических
ал + а<) +... + а„ ^
— — также монотонно не убывает.
Yl
Доказательство
В силу неубывания последовательности {аи} очевидно выполнение нера¬
венства
Ai =
_ ai+a2+... + an ^ Yian+i _
^ S „ “ ап+1-
Yl Yl
Отсюда моментально получается неравенство
д^ _ ^Ai flWi > ^Ai Ai _ I
Yl +1 Yl +1
99
е
е
Рис. 2.14
{sw}-2 + ^j + - +
Jl
п\
Замечание 2.5. Очевидно, что если последовательность {ая} строго воз¬
растает, то и {Ап} также строго возрастает. Аналогичные утверждения
имеют место для невозрастающих (убывающих) последовательностей.
Отметим, что обратное утверждение к данному, вообще говоря, может быть
неверно. В качестве примера можно взять следующую последовательность:
ах = 0, а2 = 2, ап+1 = An+Dn, где Dn = йп .
Действительно, имеем
A1 - О, A2- 1, Дз+1 -
_п1Ап±
^и+1 _ (п + 1 )А +Dn _ л , Ц
п + 1
п + 1
= A +
п +1
Далее заметим, что
2Дг+1 =an+i~A+i = A+Dn-А ~7 = Аг '~Гл' ^D2 = 1/2 > 0.
п+1 п+1
Отсюда при V п > 2 получаем, что Dn > 0, поэтому Ап+1 > An, и после¬
довательность {Ая} возрастает. Остается заметить, что начиная с третьего
номера последовательность {<яп} убывает, так как в силу положительности
ап - An для всех п > 2
ап+X=A + aH <А+ап~А=ап•
Совершенно аналогично может быть рассмотрено следующее утвержде¬
ние, доказательство которого предлагаем читателю в качестве упражнения.
Задание 2.4
Докажите, что, если числовая последовательность {ап}, ап > 0, монотонно не убы¬
вает, тогда и последовательность ее средних геометрических Gn = ^Ja1 -а2 ■...■ап также
монотонно не убывает.
Его доказательство предоставляем читателю.
Утверждение 2.3. Если последовательность {ап} сходится к конеч¬
ному пределу а, то и последовательность ее средних арифметических
. а* + а2 +... + а„
An = — также сходится к числу а.
п
Доказательство
В силу сходимости последовательности {ап} для произвольного е>0
найдется номер iV(e) такой, что при всех номерах п, больших данного,
выполняется неравенство
а„ - а <—.
Распишем для V п > N(e) разность:
„ _ (а1-а) + (а2-а) + ... + (ап-а) _
Лп~а~ “ -
п
= a1+a2+... + aN-N-a | (aN+l-a) + (aN+2-а) + ... + (ап-а)
п
п
101
Учитывая, что числитель первой дроби представляет собой фиксиро¬
ванное число, при увеличении п можно сделать первую дробь меньше
Поэтому получим
е е n-N
<- +
2 2 п
е е
<- + - =
2 2
в. ■
Докажем аналог данного утверждения для а = +°°.
Утверждение 2.4. Если последовательность {ап} стремится к +°°, то
и последовательность ее средних арифметических An также стремится к +°°.
Доказательство
Действительно, пусть Iim ап = +°°. Это означает, что для V E > О BN(E)
п—>°°
такое, что для V п > N(E) выполнено ап > 2Е. Отсюда
CL\ + G9 +... + Qn CL^ + (Io +... + С1\г С1\т±.\ +... + CL.
■N I uN+1
П
П
п
ai+a2+... + aN (n-N)2E ai+a2+... + aN 2 EN
1 = h IE .
п
п
п
п
Далее, увеличивая п, можно сделать разность дробей
CL^ + CL2 +... + CLу
2 EN
п п
по модулю меньше Е. Следовательно, найдется такой номер N(E), начиная
с которого заведомо выполняется требуемое неравенство An > E. ■
Совершенно аналогично доказывается следующее утверждение (дока¬
жите!).
Утверждение 2.5. Если последовательность {ап} стремится к -°°, то
и последовательность ее средних арифметических An также стремится к
Отметим, что данное утверждение в случае Hm ап = вообще говоря,
я—
не имеет места. Рассмотрим, например, последовательность ап = {1, -1, 3,
-3, 5, -5,...}. Очевидно, что Hm ап = °°, но последовательность An = {1, 0, 1,
я—»°°
О,...} расходится.
Далее усилим последние утверждения, доказав, что
Hmап < HmAn < HmAn < Hman.
П—¥°° Я—>°°
Я—
Я—>°°
Доказательство
Обозначим Hman =L. Так как для произвольного е> лишь конечное
ЯН>°° g
число членов последовательности ап будет превышать L + —, то для такого
2
е найдется номер N(e) такой, что для всех n>N(e) будет выполнено
£
а„< L + -. Имеем
я 2
_ а1 +а2 +... + ап _ щ +а2 +... + aN | aN+l + а2 +... + an ^
п п п
const
< +
п
L +
(n-N)
п
<ап +l + 2>
102
где ап — бесконечно малая последовательность. В силу того что ап — бес¬
конечно малая, начиная с некоторого номера \ап \ < —, а значит, An < L + в.
Аналогично, обозначив Iimап = I, можно показать, что начиная с неко-
га—
торого номера выполнено An >/-е. Таким образом, для любого е>0 вне
отрезка [l-e, L+ г] находится лишь конечное число элементов последова¬
тельности An. Но тогда все предельные точки данной последовательности
лежат на отрезке [/; L], поэтому HmAn, HmAn е [/; L]. ■
га—>°°
га—
Замечание 2.6. Обратное утверждение к только что доказанным, вообще
говоря, неверно, т.е. если An —> а, то из этого не всегда следует, что ап —» а.
Рассмотрим следующий пример. Пусть ап = (-1)и+1. Тогда
A =
0 при п = 2k,
1
— при п = 2k+ 1
.п
A^ о,
хотя сама последовательность сходящейся не является.
Из приведенных выше рассуждений следует, что если An —> а, то после¬
довательность {ап} либо сходится к а, либо расходится. Если An —> а, но {ап}
расходится, то говорят, что она сходится к числу а в среднем.
Утверждение 2.6. Если последовательность строго положительных
чисел {ап} сходится к конечному пределу а, то и последовательность их
средних геометрических Gn = ' — 'ап также сходится к пределу а.
Доказательство
Рассмотрим вместе с последовательностью {яи} последовательность
средних гармонических Гя =
п
1
1
1
—
+ —
.. +
«1
а2
ап
Используя метод математи¬
ческой индукции, можно доказать (докажите!), что для любой последова¬
тельности строго положительных чисел {ап} имеет место неравенство Коши
Г <G <А..
п — п --ixTT
I 1
Рассмотрим случай, когда ап —» а > 0. Тогда > —, а средние арифме-
а„
а
тические для
1
I 1
f, т.е. —, сходятся к —. Но тогда Ги —» а, и по известной
Гга а
теореме о двух милиционерах1 (так как и An —» а) следует, что Gn —» а.
Пусть теперь а = 0. Найдем по произвольному в>0 номер N(e) такой,
что при всех n>N(e) выполнено ап < е. Далее имеем
n-N
' a^---aN^
a{---aN ■ \JaN+i■ ■ -ап <Ц
^ai • • -aN • 8 п =
P N
\ 8 )
\1/га
•8.
1 См., например, книгу [28].
103
Так как
чаем, что
/ л1/и
' Oi-Qlf '
V
?N
—» 1, при и —» Ooj то в силу произвольности 8 заклю-
Iim Gn = O = а.
п—>°°
Замечание 2.7. В случае предела а, равного -н», имеем 1/Гя —> 0. Поэтому
Ги —> +°°. Отсюда и из неравенства Г„ < Gn имеем Hm Gn = +°°.
п—>°°
Следствие 2.2. Hm tfn\ = Hm ^/l-...-п = Hm п = -н», так как для ап = п
П—^00 П^>°°
выполнено, что Gn = tfn\.
Утверждение 2.7. Пусть рп> О для всех натуральных п и существует
предел Hm = L. Тогда существует предел Hm ^fpn, также равный L.
И-»°° Рп_1 п->°°
Доказательство
P
Пусть 3 Hm —— = L. Рассмотрим последовательность
n^aoPn-X
а -п a а - Рп
Ui -Pi, а2- ,...,ип —
Px Pn-X
Заметим, что Hm ап = Hm =L, а также то, что выполнено тождество
П—>°° П—¥°° Рп_1
^Jai--On =%[р^. Отсюда, используя предыдущее утверждение, получаем
требуемое. ■
Замечание 2.8. Позже нами будет доказано, что для любой последова¬
тельности с положительными членами ап в случае существования пределов
Hm
^ и Hm ^
п—>са ап п—>°° ап
справедливо неравенство
Hm < Hm < Hm < Hm
П—>°° И—■- ■ " ' "и
Используя доказанные утверждения, можно решить ряд красивых задач.
п—>°°
п—а
Задача 2.9
п
Докажем, что последовательность \ —/=, п>\\строго возрастает и сходится к чис¬
лу е, а последовательность
Решение
п
Ы) 2
,п>2> строго убывает и сходится к нулю.
Tl I—
Положим х„ = —. Тогда -т= = . Остается заметить, что хп>0 для Vn и
и! Щп\
limi=lim^._fcj)! = Um
п~*°°хп^ п\ (п — 1)” 1 я-»~
(< 1
1 +
^ п — 1
\я-1
= е.
Второй предел вытекает из первого, если использовать полученное ранее тож¬
дество Hm л[гг\ - оо.
104
Теперь будет просто получить следующий результат.
Задача 2.10
1 / ^
Докажем, что Hm-«и! + Яи! + ... + \/й1 =-.
и—»<*> п У V е>
п—>°о Tl >
я факториалов
Решение
Действительно, оценивая данную последовательность тривиальным образом, заме¬
чаем, что
yfni 1
< —
п п
^nl + фг
\ + ... + Щп\ <
yjn-n\
п
п факториалов
Остается воспользоваться предыдущим результатом, теоремой о двух милицио¬
нерах и равенством Iim \fn = 1. * I 2 * I 2Рассмотрим теперь ряд признаков сходимости последовательности {яи}.
Теорема 2.14 (Коши о прореживании, или телескопический признак
сходимости). Пусть для элементов последовательности {ап} выполнено
соотношение ai>a2>a3>... > 0. Последовательность хп = A1 + а2 + ... + ап
сходится тогда и только тогда, когда сходится последовательность уп = A1 +
+ Ia2 + Aa4 + ... + 2¾^-
Доказательство
Так как последовательности {хп} и {уп} монотонно не убывают, то в силу
теоремы Вейерштрасса о монотонных последовательностях их сходимость
эквивалентна ограниченности сверху. Далее, в силу неравенства 2И+1 -1 > п
имеем
хп =ai +а2+... + ап <ах+а2 +... + а2П +... + а^^=
= ai+(a2+a3) +... + (а2П +... + а2П+^1) < A1 + Ia2 +... + 2 па2П = уп.
Обратно ползаем
I 1
x2k = а1+а2+(а3+а4) +... + (я2ы+1 + - + ) > -^1 + а2 + 2 а4 +... + 2*_1 alk = —yk.
Отсюда из-за ограниченности последовательности {х^} получаем огра¬
ниченность последовательности {yk}.
Аналогичное доказательство можно было получить, складывая неравенства
а2 — а2 — а^,
2 а4 — а3 + а4 — 2 а2,
4а8<а5 + а6+а7+а8< Aa4,
2 ^2я+1 — ®2”+1 ^2п+^ ~ ^
и установив соотношение ^w+1^ < х2П+1 -а1< уп, откуда вытекает требуемое.
Доказанная теорема имеет некоторые весьма важные приложения.
Например, она может быть использована при исследовании сходимости
105
п \
последовательности х„ = Y -— при любом значении р. C помощью крите-
bi kP
рия Коши легко можно доказать (докажите!), что данная последователь¬
ность расходится при р < 1 и сходится при р > 2. Вопрос о ее сходимости
(или расходимости) при р G (1; 2) оставался открытым.
Задача 2.11
Докажем, что последовательность хп = 1 + — + — сходится тогда и только
тогда, когда р > 1.
Решение
По теореме Коши о прореживании сходимость рассматриваемой числовой после¬
довательности эквивалентна сходимости следующей последовательности:
О A On п
у = 1 + —+ = У 2*<н»>.
п 2 P 2 2P 2 nP ы>
П
Последовательность уп = ^ 2является при 21-р < 1 последовательностью
Ы)
конечных сумм бесконечно убывающей геометрической прогрессии, поэтому она
сходится тогда и только тогда, когда 2 1-р < 1, т.е. при р> 1.
Задача 2.12
Докажем, что последовательность х„ =— 1 + ...H сходится
” 2(1п2 )р 3(1пЗ)р п(\пп)Р
тогда и только тогда, когда р > 1.
Решение
В самом деле, по теореме Коши о прореживании сходимость данной числовой
последовательности эквивалентна сходимости следующей последовательности:
2 4 2”
Уп ~ 2(1п2у + 4(1п4)^ +‘"+ 2”(1п2”)^ “
= I I I = I f1 + J_+ +J_"
~(1п2)р (1п4)р "■ (1п2”)р ~(1п2)р [ 2р пР
Используя предыдущий результат, получаем требуемое.
Замечание 2.9. Для исследования сходимости данных числовых после¬
довательностей более удобен интегральный признак Коши — Маклорена,
использование которого будет обосновано далее в главе о несобственных
интегралах.
Рассмотрим еще одно понятие.
Определение 2.18. Будем говорить, что последовательность {хи} имеет
ограниченное изменение (или ограниченную вариацию), если 3 C > 0:
Ix2-XiI +1лс3 — л:21 +... + |хи-хи_!|< С,п = 2,3,....
Задача 2.13
Докажем, что последовательность с ограниченным изменением сходится.
Решение
Пусть последовательность {хп} имеет ограниченное изменение. Запишем для нее
условие Коши: для V в > 0 3 N(г): для V п > N(г), VpeN выполнено \хп+р - х„| < е.
106
Заметим далее, что
l^n+p — ХП I — l^n+p
^k+i-^l+k+2
-X.
n+p-i
+ X
X.
я+1
+ ...+
n+p-i хп+р-2 хп+2 *я+1 хп+1 хп I —
|^i+jj-1 — ^п+р-21 + |-^я+р — х n+p-i I — |^/я+р — Уп\>
где уп = X1 -х21 +1¾ -хзI+ — + |хя-1 -*„• Последовательность {г/„} монотонно не убы¬
вает, а также ограничена сверху, в силу того что последовательность {хп} имеет огра¬
ниченное изменение. Следовательно, данная последовательность сходится, а значит,
удовлетворяет условию Коши. Поэтому модуль разности |уп+р -уп |, а с ним и \хп+р - хп |
может быть сделан сколь угодно малым при V п > N(e), VpGN. Поэтому для после¬
довательности {хп} условие Коши выполнено.
Замечание 2.10. Предел последовательности уп = Ix1 - х2 \ + |х2 - X31 + ... +
+ |хи_1 - хи| (он же — ее точная верхняя грань) называют вариацией после¬
довательности хп, т.е.
Varxw =supz/w = Iim уп.
n—+°°
Отметим, что утверждение, обратное к вышеприведенному, вообще
говоря, неверно, т.е. не всякая сходящаяся числовая последовательность
имеет ограниченное изменение. Например, такой является последователь¬
ность xw = (1 - (-1)”)/2п.
1
Действительно, Iim Xw = 0. Однако, используя неравенство — > In
п—>°° k
получаем
1 +
1
X9 — Xi I + |хч - X91-I-... + Ix2w - X1
,22 2
= 1 + —+ - + ... +
3 5 2/z-l
l2n-1
,11 1
>1 + - + —+ ... + —>
2 3 п
> ln(l +1) + In
при п > [ем].
(Л * * 1I
1+-
(Л ^
^ I
+
т-Н
+ In
+ ... + In
I 2J
I 3J
I nJ
= 1п(/г +1) > M
Задача 2.14
Докажем, что для всякой последовательности {хп} с ограниченным изменением
существуют возрастающие ограниченные последовательности {ап} и {Ьп} такие, что
хп = ап~ К nsN.
Решение
Рассмотрим последовательность An = хп-хп_ь п= 1,2,... (х0 =0). Так как {хп} —
последовательность с ограниченным изменением, то
£|Д„|<С для V N.
W=I
Рассмотрим две последовательности:
_ [О, еслиДя<0, - [О, еслиДя>0,
” [Д„,если An >0; " |-Д„,если Дп <0.
Получаем, что ап > 0, Ъп > 0 и ап - bn - An для V п.
Рассмотрим далее
W П _
«я-5Х K-^bi.
г=I i=i
107
Тогда
On ~ К = 2(¾ -k) = ^A1 = (X1 -х0) + (х2 - X1) +... + (х„ -X^1) = xn.
z=I
Z=I
Последовательности яп и Ьп, очевидно, не убывают. Кроме того, ап, bn < ^ | Ai | < С,
Z=I
т.е. ап и Ьп ограничены. Следовательно, они сходятся.
Можно сделать последовательности ап и Ьп строго возрастающими, положив
I ~ 1
CLn = Cl + ——, Ьп = b +7”.
ZZ п Qn ”2”
Задача 2.15
Определим, существует ли предел последовательности xn = sin п.
Решение
Если предположить, что данный предел существует, то рассматриваемая после¬
довательность хп — фундаментальная. Положив, например, в условии Коши р = 2,
получаем, что для Vе>03iV(e) такой, что для Vп>N(е) выполнено
I sin(n + 2) - sin n| < е,
т.е. Hm (sin(w + 2) - sin п) = 0. Отсюда, используя тождество
П—^tso
sin(n + 2) - sin п = 2 sin I • cos(n +1),
получаем, что Iim cosn = 0. Далее, вычисляя предел последовательности sin2n, полу-
П—>°о
чаем
Iim sin 2п = 2 Iim sin п ■ Hm cos п = 0,
И—>°° П—П—»°о
так как по предположению limsinra<°o. Поэтому Hmsinra = O. Вспоминая, что
П-^> OO я—
Hm cos га = 0, получаем противоречие с основным тригонометрическим тождеством.
Я—о
Отметим, что множество частичных пределов последовательности
хп = sinw представляет из себя весь отрезок [-1; 1]. Оставляем доказать
данный факт читателю и приведем чертеж данной последовательности
в логарифмической шкале для п = 50 000 (рис. 2.15).
Рис. 2.15
Рассмотрим еще ряд признаков, помогающих исследовать последова¬
тельность на сходимость.
108
Во многих учебниках рассматривается следующая теорема.
Теорема 2.15 (Штольца). Пусть хпиуп — две последовательности веще¬
ственных чисел, удовлетворяющие следующим условиям:
1) для всех п G N выполнено неравенство уп < уп+1;
2) Hm уп = +°о;
я—
хп Хп-1
3) существует предел Hm
ч Уп ~ Уп-i
знака).
{конечный или бесконечный одного
Xr
Тогда существует предел Hm —, причем справедливо равенство
n^00Vn
Hm — = Hm Хп Хп~1.
п^°° Уп п^°° Уп - Уп-1
Доказательство
Сначала рассмотрим случай конечного предела, т.е. пусть
3 Hm Хп x^1-
= а <
и_>°° Уп ~ Уп-i
Тогда для V е > 0 3 N(г) такое, что для V п> N выполнено
хп хп-1
-а
Уп Уя—1
е
2
Отсюда имеем а - — < ——3^lA. <a + !L Запишем данное неравенство для
2 Уп-Уп-t 2
номеров N +1, N + 2,..., п:
а — — < XN+l XN XN+2 XN+l
Хп Хп-1
0 , — <«+о-
2 Ун+\ Ун Уы+2 Ун+\ Уп Уп-i 2
Домножим каждое из данных неравенств на знаменатель стоящей в нем
дроби и просуммируем их. Пользуясь верным для всех п неравенством
Уп < Уп+ь получаем
f 8Л
а —
2
КУп ~Уп-i) + (Уп-i ~Уп-2) + ••• + (Ун+1 ~Ун)\<
< (Хп - Хп-1) + (Хп-1 - Хп-2) + ••• + (½+! - xN) <
а+-
Kyп - Уп-i) + (Уп-i - Уп-2) + - + (yN+i - Уn)1
8 /у __ /у
=>а — <— — <а + —<=>
Уп~Уы
8
2
Хп XN
-а
Уп~Уы
8
2
х.
П_
Уп
Далее, так как — - а = — +
Xr
-а
_ xN аУн
Уп
XN ~ aVN
\
1-
Уп
Уп
Ун
Уп)
г
Хп xN
Уп~Ун
\
-а
, то
Хп xN
Уп-Ун
-а
1-
Ун_
Уп
109
Слагаемое
—; слагаемое
2
Xn Xn
-а
У п-Уы
xN ~ аУы
, как мы установили, при n>N становится меньше
Уп
< — при достаточно больших п > N(г), так как вели¬
чина (xN - ayN) фиксирована, а г/и —> +°° Наконец, множитель
\_Mjl
Уп
в силу
монотонности последовательности уп строго меньше единицы при п> N(в).
Поэтому
х„
-а
Уп
8 8
<- + - = 8,
2 2
для \/е>0и V n > max{JV(e); iV(e)}
Случай бесконечного предела легко приводится к рассмотренному слу¬
чаю. Пусть, например, выполнено
Hm Хп ХпЛ=+оо.
п^°°Уп~Уп-1
Следовательно, для достаточно большихп выполненохп-хп_^ >уп-уп_\ >
> 0. Отсюда вытекает, что Hm хп = +°°. Остается применить уже доказанную
п—»<*>
теорему Штольца к перевернутой дроби. Действительно,
Iim Мл—Уг}гА_ _ о + о = Hm — => Hm — = +°°. ■
Xn - Хп-\ п^°°Хп п^~Уп
Замечание 2.11. Отметим, что если предел Hm ——равен бесконеч-
и_>°° Уп ~ Уп-\
ности без знака, то предел Hm — может не существовать. Действительно,
п^°°Уп
рассмотрим следующий пример: хп = {1, 0, 3, 0, 5, 0, 7, 0, ...}, уп = п. Тогда
уп - уп-\ = 1 > 0; ——= хп- хп_х = {-1,3, - 3,5, - 5,...} —> °°. Однако — =
Уп~Уп-1 Уп
= {1, 0, 1, 0,...}. Поэтому $ Hm —.
п^°°Уп
Если же хп = {1,0, л/з, 0, л/5,0, л/7,0,...}, уп = п, то Hm — = 0.
п^°°Уп
Замечание 2.12. Очевидно, что неравенство уп<уп+1 может быть выпол¬
нено не для всех п е N, а только начиная с некоторого номера.
Замечание 2.13. Если в формулировке теоремы Штольца допустить,
что положительная последовательность {г/и} монотонно убывает к нулю, то
если Hm хп = 0, справедлив тот же результат.
п—>°°
Действительно, в силу условия теоремы выполняется равенство
Хп Хп-1
Уп ~ Уп-\
а + оси,
110
где ап — бесконечно малая последовательность. Зафиксируем произволь¬
ный в > 0. Тогда найдется такой номер N0, что для всех k > N0 справедливо
неравенство \ak \ < в.
Зафиксируем далее произвольный номер N > N0 и рассмотрим (как
и в доказательстве предыдущей теоремы) цепочку равенств
XN+1 ~ XN = а(Уы+1 ~ Уn) + aN+1 (З/лГ+1 — УN)’
XN+2 ~ XN+1 = а(.Уы+2 ~ УN+1) + аы+2(.Уи+2 ~ УN+l)’
-■xn-i = а(Уп ~Уп-д + (Уп ~Уп-\У
Складывая, получаем
хп XN = ^(.Уп ~ ^jv) ^JV+l(^AT+l — Vn ) + ••• + &П (.Уп ~Уп-\)•
Отсюда в силу монотонности последовательности {уп} находим
\хп~ xN- а(Уп ~Ум) ,max \ak | • (| yN+i - yN \ +... +1 уп - yn_Y |) < г(ук -уп).
N+l<k<n
Переходя в последнем неравенстве к пределу при w —> и используя то,
что Iim хп = 0 и Iim уп = 0, получим оценку
п—>°° п—>°°
\xN Щ!N — ЕУм > или
X
N
-а
Ум
< е < 2е,
для произвольного N > N0, что и доказывает требуемое.
Задание 2.5
Можно ли в формулировке последнего утверждения отказаться от требования
монотонного стремления к нулю последовательности {уп} (если можно — докажите,
если нет — постройте контрпример)?
Замечание 2.14. Легко видеть, что утверждение о пределе среднего ариф¬
метического элементов числовой последовательности является прямым
следствием теоремы Штольца.
Действительно, пусть хп =ai+a2 +... + ап,уп = п. Тогда
Hm flI+д2 +- + дя = Hm bL = Iim хп Хп-1
п Уп п^°° Уп - Уп-\
= Hm ап.
п—>°°
Замечание 2.15. Доказанные утверждения позволяют рассматривать тео¬
рему Штольца как дискретный аналог правила Лопиталя1.
Приведем несколько примеров использования теоремы Штольца.
Задача 2.16
Найдем следующие пределы:
( Л * \
а)
Iim —^
я->°° уп
, 1 1
1 + -^= + ... + -^=
. v2 Vw.
1 Читателям, не знакомым с правилом Лопиталя, мы советуем обратиться к гл. 4.
111
6) Iim
I*+2 k + ... + nk
п
nR
k + 1
, где & e N;
в) Hm -К • (-\[с% + \jc%+i +... + sjc^n ), где C2 - п(п^ ^ _ биномиальные коэффици-
п—>°° П
енты.
Решение
I 1
а) Взяв в качестве хп =1 + —== + ... + —==, уп = Vn, по теореме Штольца получим
V 2 Vn
Hm —j=
л 1 1
1 Ч ;= + ... Ч ;=
п->°° Vn I4 V2 Vn
\/4п
= Hm — = Hm %п %п~х =
моог/л n^yn-Vn-1
= Hm
= Iim =2.
«->“ Vn - Vn-I я-»“ Vn • (п-п +1)
б) Для выражения, стоящего в скобках, получаем
1* + 2*+... + и* п (& + 1)(1* + 2*+... + и*)-и*+1
пК
k + i
(k + l)nh
Взяв в качестве xn = (k +1)(1* + 2* +... + n*) - n*+1, yn = (k +1)nk, по теореме Штольца
находим
(k + \)k
Iim^= Iim jVl^zi = Iim (*+!>■* 0*4 _ lim^JL
n*_1 +...
I
п->°°У„ п~>°°Уп~Уп-1 n_>“ + l)[n* — (n — I)*] (& + l)&-n* 1 +... 2
в) Пусть xn- +VCi +... + Vc|„, = n2. Тогда по теореме Штольца получаем
Iim -i • (Vq + +... + slci,) = Iim ^ =
и->°° П
= Hm^ xn-i = JcEl =
п~>°° Уп ~ Уп-i 2n -1 V
2и(2п -1) I = 1
2 2n-l V2'
Для самостоятельного решения мы предлагаем читателю рассмотреть
следующее упражнение.
Задание 2.6
Вычислите с помощью теоремы Штольца следующие пределы:
Ek2(k+i)
a) Hm——
' п
E Hh+3)(26+1)
A=I
г) Hm—K= E k\[k;
n2Vn A=I
б) Hm—E ;
Я_>0° Я &=1 « + 1
Tl п /2^-^
Д) Hm^EV’G>1;
я-*» a™ я
,. 1 ”(пг + &)!
в) lim ^ щ ;
nm+1 k=l «!
I ”
е) Hm E ^ak, а > 1.
я->~ пап k=i
Рассмотрим далее несколько менее элементарных применений теоремы
Штольца.
Задача 2.17
2
Найдем предел последовательности ап = (Cn ■ Cn ■ C2 •... • Cn )"(”+1).
Решение
Рассмотрим логарифм данной последовательности:
Inan =— (1пС° + InC* + ... + In С”).
” и(и +1) v ”
112
Применяя теорему Штольца, получаем
HmIn ап = 2Hm = ; _0)_
п^°° n n-*~ я(я +1) — (/Z — 1)я * * 1 ”
= 2 Hm
П—>°о
/°0 /°я-1
In °и I I |п
С°_! Qr11 _ [ С* _ n\k\{n-i-k)\ _ я 1 _
2я
= Iim
Я—»°°
[C^1 k\(n-k)l(n-i)l n-k J
, я , я ,я
In +In + ... + In
W Я — 1 ф
я
Снова применяя теорему Штольца, имеем
Iim lna„ = Hm
, я , я ,я
In—+ In—+ ... + In—
1 2
я
= Iim (я-I)-In = Iim In
я—Я — 1 я—
Г, 1
1+
^ я — 1
\ я—1
я — 1 , я — 1
я — 1
In—+ In—+ ... + In
I 2 я — I
(
= 1, так как Iim
Я—
1+-
1
\ я—1
Я — 1
= е.
Отсюда получаем, что Iim ап = е.
Задача 2.18
Пусть Hm an = а, а е R, а € M — фиксированное число, такое что | а | < 1, и Ьп = ап+
Я—>°°
+ Ocan-! + а2ая_2 + ... + ап~1аь я € N. Вычислим предел Hm Ъп.
И—>оо
Решение
1
Пусть q = —. Представим последовательность Ьп в виде
ос
Ьп=-^-1,ЩкЛ-
Qn 1 k=i
Применяя теорему Штольца, получим
Hm Ьп
П—>°о
= Hm
П—>°°
«я?”-1
qn~i _ qri-2
= Hm an
я—
q
q-1
a
l^oc
Задача 2.19
Пусть O1 = I и an+1 = an(l + |sin an|) 1, я > I. Вычислим предел Нт(я-ап).
Я—>°°
Решение
Так как (I +1 sin an|)_1 < 1 то 0 < an+1 < ап, я > 1, и по теореме Вейерштрасса о моно¬
тонных последовательностях получаем, что существует Hm ап > 0, который мы обо-
Я—о
значим через а. Для данного предела с использованием непрерывности имеем равен¬
ство а - a(l + I sin an|)_1.
Следовательно, либо а = 0, либо
I +1 sin а\ = 1 <=> I sin а\ = 0 <=> а = n + пп.
Но так как 0 < an < 1, то остается только а - 0.
Далее запишем
I 1 1 +Isinan-J I |sinan_J
= —1 1 = J L—>1 при я —^ °°.
ап ап-\ «л-1 ая-1 ая-1
113
Далее по теореме Штольца получим
Однако Yi
k=2
Iim
п-
1
п
1
k=2
Г1 п
V ®Я-1 /
Г1 п
П
V ап ап-\ J
\ап ап-\ J
=1.
I 1
= . Следовательно, имеем
ап U1
JL_Jl
——— —»1 => — »I => Hm п ■ а = 1, или а ~ —.
п пап Tia1 я->°° п
Задача 2.20
Числовая последовательность {хп} задана рекуррентным соотношением X1 = 1,
1
хп+1 = *„+—, и > 1. Докажем, что:
OCrt
1) последовательность {хп} неограничена;
X
2) существует предел Hm —Л (и найдите его).
п->°° Щп
Решение
1
Так как хп+1 = хп+ — >хп, то последовательность {хп} строго возрастает и хп > 1
хп
при п > 1. Если предположить ограниченность рассматриваемой последовательно¬
сти, то из теоремы Вейерштрасса будет вытекать ее сходимость. Пусть Hm Xn=C,
Я—о
где C = const > 0. Тогда если перейти к пределу при п->«>в заданном рекуррентном
1
соотношении, то мы получим C = C + —-, что невозможно. Следовательно, последо-
C1
вательность {хп} неограничена. Более того, в силу монотонности этой последователь¬
ности заключаем, что Hm хп = +°°.
X
Исследуем предел Hm —Л. Рассмотрим последовательность ап = х%. Для нее,
«->“ yjn
используя заданное соотношение, получаем следующее рекуррентное соотношение:
(
«п+1 хп+1
1
\
Х" + X2
V лп J
о „ 3 1 _ уп
= х*+Ъ + — + — = аи+3 + — при п —>°о,
а*
где у„ — бесконечно малая последовательность.
Так как Hm хп = +°°, то Нт(ос„+1 -а„) = 3. Применим теперь к вычислению пре-
П—>°° TL—
ос
дела Hm теорему Штольца, так как все условия данной теоремы выполнены (про-
п—П
верьте!). Получаем
Hm = Hm а”+1 а” = Hm (аи+1 - а.) = 3.
я—П я—(и + 1)-и П—¥ оо
Таким образом, Hm ? — = Hm ;
я—\ Tl
Замечание 2.16. Отметим, что в процессе доказательства не было исполь¬
зовано условие X1 = 1. Для решения важно лишь то, чтобы X1 было таким,
114
что начиная с некоторого номера п элементы последовательности {хи} ста¬
нут положительными. Например, значение X1 можно подчинить условию,
чтобы было выполнено неравенство
1 А
Xn = Xa + -Г- > 0.
1 /у Jl
2.4. Предельные точки последовательности
и множества
Напомним, что множество А с M1 называется замкнутым, если оно
содержит все свои предельные точки, т.е. для любой последовательности
{ап}, состоящей из элементов множества А, сходящейся к числу eel,
предел а также принадлежит множеству А. Зададимся вопросом: можно
ли построить числовую последовательность, имеющую множеством своих
частичных пределов произвольное замкнутое множество А с R, и только
его?
Сначала рассмотрим случай А — ограниченное множество. Для любого
целого т>0 рассмотрим представление числовой прямой R в следующем
виде:
■= и
k k + V
2 т ’ 2 т
и определим по заданному множеству А множество рациональных дробей
Cm = \слАф0 дляVkeN
f*
1
Л*
k + l\
[2т
I
ю
2т J
Очевидно, что множества Cm для любого индекса т являются непу¬
стыми и ограниченными. Если множество А ограничено (как предполага¬
ется выше), то все множества Cm конечны. Построим следующую числовую
последовательность:
{ап} iXl’ —> Xq^ Xq^+1’ Xq\+q2> Xq\+q2+1’ +-+?„’
где {xv..., Xq^} = C1, {x^+1,..., xqi+q2} = C2 и т.д. При этом сами множества мо¬
гут пересекаться.
Убедимся в том, что множество всех предельных точек построенной
последовательности суть множество А, и только оно. Действительно, пусть
а — предельная точка множества А, тогда, очевидно, в любой ее окрест¬
ности находится бесконечное число точек вида
входящих в последо¬
вательность {яи}. Обратно, предположим, что существует с — предельная
точка последовательности {яД, не входящая в множество А. Тогда рассто¬
яние d от точки с до ближайшей граничной точки множества А (в силу его
замкнутости) строго больше нуля. Очевидно, что в окрестность размера
1 Под множеством R мы понимаем числовую ось с добавленными в нее ±°°.
115
меньше, чем входит не более чем конечное число элементов последо¬
вательности {ап} (в силу построения). Поэтому с не есть предельная точка
этой последовательности.
Если же +оо принадлежит множеству Л, то в построенную последова¬
тельность можно добавить все целые числа1, чтобы в ней заведомо нашлись
подпоследовательности, сходящиеся к +°°. При этом множества Cm явля¬
ются счетными, и мы строим счетное объединение счетных множеств, кото¬
рое порождает искомую последовательность2.
Задача 2.21
Опишем множество А всех частичных пределов монотонной последовательности.
Решение
Если последовательность ограничена, то она сходится к некоторому числу se R,
В этом случае А = {а}. Если она не является ограниченной, то A = {-°°}, если рассма¬
триваемая последовательность монотонно убывает, и A = {+°°}, если она монотонно
возрастает.
Задача 2.22
Докажем, что любая последовательность действительных чисел содержит моно¬
тонную подпоследовательность.
Решение
Это следует из теоремы Больцано — Вейерштрасса и из того, что сходящаяся
последовательность содержит монотонную подпоследовательность (докажите!).
Но полезно будет провести независимое доказательство.
Для этого рассмотрим множество индексов, заданное следующим образом:
M - {п е N I V т > п: ат > ап} и {О}3.
Если множество M бесконечно и M = {щ, п2,..., nk,...}, при этом щ<п2<п3<..., то
согласно определению множества M имеем
ап^ ^ aTI2 ^ ••• ^ aTifl ^ •••>
т.е. подпоследовательность {a„k} возрастает.
Если же множество M конечно, тогда найдется наименьший индекс (обозначим
его через щ, щ =шах{М} + 1), такой что для всех натуральных т>щ выполняется
теМ. Так как щеМ, то найдется номер п2 > щ, такой что > а„2. Аналогично, так
как п2 е М, то найдется номер щ > п2, такой что а„2 -ап3’ и Т-Д- Таким образом, мы
получили невозрастающую подпоследовательность {ап^}.
Замечание 2.17. Если множество M конечно, то это не значит, что из {ап}
нельзя выделить возрастающую подпоследовательность (постройте при¬
мер!).
1 При этом полученное множество останется счетным, так как множество Z счетное.
2 Здесь нужно сделать замечание о том, что, вообще говоря, мы строим не совсем объеди¬
нение Cm. Каждое Cm превращаем в последовательность с1,, с2,..., с£,.... Потом строим резуль¬
тирующую последовательность с|; с\; C12; d>; с}; C12; C13; с\; с|; djj.... При объединении множеств
общие элементы сливаются.
3 Этим мы добиваемся, чтобы множество M было не пусто.
116
Задача 2.23
В качестве примера доказанного в задаче 2.22 утверждения рассмотрим после¬
довательность хп = Vn-[Vn]. Требуется указать какую-либо монотонную подпосле¬
довательность данной числовой последовательности.
Решение
Рассмотрим подпоследовательность xn2+l = \Jn2 + 1 -[Jn2 +1]. Докажем, что она
монотонно убывает. Действительно,
Vw2+ !-[Vrc2+ IJ = Vn2+ 1 — и= . 1 ^0.
Vn2 +1 + W
Найдем теперь строго возрастающую подпоследовательность данной последо¬
вательности. Рассмотрим подпоследовательность %п2+2п = Vw2 + 2n -[Vn2 + 2п]. Для
нее имеем
Vn2 + 2n - [Vn2 + 2и] = Vn2 + 2и -п =
2 п
Vn2 + 2п + п
Для соседних элементов данной подпоследовательности получаем
хп2 * *+2п n(Vn2 * *+4n + 3+n + l) ш
— = — , 7 < 1 для всех п е N.
^(п+1)2+2(п+1) (и + 1)(и + Mn + 2) )
В заключение построим чертеж рассмотренной последовательности в логариф¬
мической шкале. Здесь значение и выбрано равным 20 000 (рис. 2.16).
1
0,75
0,5
0,25
0
IiiijiH!
ill
!'SitrlttjJjJjJjl
10
100
1000
10 000
Рис. 2.16
Задача 2.24
Определим множество предельных точек множества {Vn - Vnz, и, т е N}.
Решение
Докажем, что множеством предельных точек является вся расширенная прямая R,
т.е. заданное множество является всюду плотным в R.
Для любого сколь угодно малого е > 0 выберем произвольный открытый интер¬
вал (а; Ь) длины е, т.е. Ь-а = г. Докажем, что найдутся такие натуральные п0 и т0,
что V^o - V^o е (.а; Ъ). Действительно, поскольку Hm(VnTl-Vn) = O, то 3 N такое,
о/ о I Tl—^co
что для V и > JV выполнено vn + l- vn<e.
По найденному выше N выберем натуральное т0 такое, что > ViV - а. Для
определения нужного нам номера и0 рассмотрим множество
А = (n G NI Vn - < а).
117
Это множество непустое, так как N е А и ограничено, так как а — фиксирован¬
ное действительное число. Следовательно, существует щ = sup А Положим U0 = щ +1.
Тогда
> а, так как щ г А => >а + > %[n => щ > N.
Поэтому из задания числа N и множества А имеем
- = \1п1 + 1- < г =* tfh < + е < а + + е,
откуда
^-^<й + е=>^-^е(а; i).
В силу произвольности числа е и произвольности интервала (а; b) делаем вывод
о том, что искомое множество предельных точек представляет собой расширенную
числовую ось R.
Аналогично можно доказать следующее, более общее утверждение.
Утверждение 2.8. Пусть последовательность вещественных чисел {х„}
такова, что выполнено Нт(хи+1-хи) = 0. Тогда промежуток с концами
п—¥°°
Ximx„ и Hmxn является множеством ее частичных пределов.
„_>оо Я->°°
Доказательство
Обозначим Hmxn = /, Hmxn = L. Покажем, что любая точка с G (/; L) явля-
И->°о
ется предельной для последовательности {хп}. Рассмотрим произвольную
достаточно малую в-окрестность точки с. Не ограничивая общности, будем
считать, что (с - в; с + в) с (/; L). Рассмотрим в'- и в"-окрестности точек I и L
такие, что они не пересекаются с в-окрестностью точки с (рис. 2.17).
Рис. 2.17
Так как Нт(хи+1 -хп) = 0, то для выбранного выше в найдется такой
п—»<*>
номер N, что для всех п > N выполнено |хи+1 - х„ | = |Лхп | < в.
В силу того что точка I — предельная точка последовательности {хп}, то
3 п' > N такой, что хп> лежит в в'-окрестности точки /. Аналогично в силу
предельности точки L Зп">п' такой, что хп» лежит в е"-окрестности
точки L. Но так как |Дх„| < в, то между номерами п' и п" найдется щ такой,
что Xn^ лежит в в-окрестности точки с. Покажем, что для любого щ > N
такого, что хп. лежит в в-окрестности точки с, найдется номер ni+1 > щ такой,
что хп также лежит в данной окрестности. Действительно, так как IylL-
предельные точки последовательности {хп}, то найдутся щ >щ и щ» >щ>
такие, что хп„ лежит в в'-окрестности точки /, а хи.„ — в в"-окрестности
точки L. Но тогда между ними найдется номер ni+1 такой, что хи.+1 лежит
в в-окрестности точки с, при этом пм > > щ. Таким образом, построена
подпоследовательность {хп^}, все члены которой лежат в в-окрестности
118
точки с. Следовательно, в силу произвольности е > 0 мы заключаем, что
с — предельная точка1. ■
Рассмотрим еще одну, близкую к предыдущей, задачу.
Задача 2.25
х,
Пусть Iim Xn= а. Что можно сказать о пределе Hm —— ?
га—»°° п—Xn
Решение
Если предел а Ф 0, то из теоремы об арифметических операциях над пределами
следует, что
х , Hm хп+1
Hm = = - = 1.
и->°° хп Hmxn а
п—
Случай а = 0 гораздо интереснее. В этом случае для искомого предела мы имеем
неопределенность вида —. Рассмотрим несколько примеров.
1. х<4> = дп, 0 < \q\ < 1. Получаем Hm Xn11 = 0, однако Hm = ^e (-1; 0) и (0; 1).
(1)
П—>°° JQ
(1)
1 г(2)
2. х<2> = —. Получаем Hm хп21 = 0, a Hm —уу = 1.
П—^°° JQ
(2)
п
3. х<3> = ^ ^ . Получаем Hm хп31 = 0, a Hm уу = -1.
Yl и—и—-vW
_(4)
4. х<4> = —. Тогда Hm хп41 = 0, a Hm -¾1- = Hm = 0.
Yl! п—п—/2 + 1
5. х® = (¾, q2, ql, q%,..., qf, gj,...}, 0 < U < 1,0 < LI < I. Тогда Hm x<5) = 0, но Hm -¾--
Л2я-1
= Hm —, Hm —= Hm ——, т.е. предела Hm "+1 не существует.
.(S)
п—>°° д" n-»°° х*2п п->°° д"
П—>°°
(S)
Докажем далее, что не существует последовательности {хга}, для которой выпол¬
нено
Хп+1 ^ /1;_ хп+1
Hm хп = 0, но Hm —^ > I (Hm —^ < -1).
я-»“ Xn Xn
Действительно, если предел Hm oc^- = L > 1, то и предел для модулей больше еди-
ницы. Поэтому, не ограничивая общности, считаем {хп} последовательностью из поло¬
жительных элементов. По определению предела получаем: для Ve>0 3N(e) такой,
что Vп>N(E) выполнено
X.
га+1
-L
х„
< E <=> L - E < < L + Е.
Х„
L-1
^^
Выбирая е = > 0, заключаем, что начиная с номера N(E) отношение —— больше
х„
единицы, т.е. последовательность из положительных элементов начиная с данного
номера монотонно возрастает. Получено противоречие с условием Hm хп = 0.
1 Данное утверждение можно проиллюстрировать задачей о лягушке, прыгающей в пруду
по кувшинкам, длина прыжка которой с течением времени стремится к нулю. В этом случае
лягушка должна бесконечно часто перепрыгивать с левой кувшинки на правую и наоборот, а так
как длина прыжка мала, то она бесконечно часто будет запрыгивать и на центральную кувшинку.
119
Рассмотрим далее теорему, с помощью которой можно значительно
упростить решения задач, касающихся пределов средних арифметических,
геометрических и гармонических, которые были рассмотрены нами выше.
Теорема 2.16 (Теплица, о регулярном преобразовании последователь¬
ности). Рассмотрим последовательность Anm, зависящую от двух индексов,
удовлетворяющую условиям:
1) Anm > 0 для всех п,те N;
2) Anl + ... + Ann=I для V п;
3) Hm Anm = 0 для любого фиксированного me N,
п—>°°
а также числовую последовательность {хп}, такую что
А) 3 Hm хп=а<°°.
Я—
я
Тогда последовательность Sn = ^jAnmXm сходится и Hm Sn= а.
IB=1 я->°°
Доказательство
Для V е > 0 рассмотрим при достаточно больших п модуль разности
тХт а
т=1
= EAm = U=
[т=1
^Kim (Хт я)
т=1
S EAi
т=1
т А'т «
(2.4)
Получение оценок из условий 3 и 4. Так как 3 Hm Xn= а, то для V в > 0,
я—
которое было выбрано выше, 3 Nx(E) такой, что для V п > Nx(E) выполнено
(2.5)
Далее, так как 3 Hm хп = а < °°, то {хп} ограничена, т.е. 3 M > \а\ > 0 такое,
п—¥°°
что \хп I < М, а
\хп -я|<|хи| + |а|<2М. (2.6)
для V п > N.
Так как Hm Anm = 0 и Anm > 0, то для фиксированного нами в > 0 3 NA(в) >
П >°°
> Nx(E) такое, что
0 ^Anm
в
КШХМ
(2.7)
для V т = 1,..., Nx и V п > Na.
Продолжаем оценивать выражение (2.4), используя неравенства (2.5)—
(2.7).
Пусть п > Nа(е), тогда
^j-\im\xm а\ ^nX I х\ я| + ... + Д^
т=\
хм —а
ух
+At
<Мх+1
XNx+1 a
+ ... + AnnIx-UW
<NX— 2М + -(Anw +1+... + А_)<- + - = е.
xANM 2V nN*+i w 2 2
Отсюда и из выражения (2.4) следует искомый результат.
120
Задание 2.7
Пусть второе условие из теоремы Теплица заменено на:
а) Anl +... + Ann = с для V п;
б) Anl + ... + Ann = сп, сп < с для V и;
в) + ... + Ann = сп, сп — неограниченны для V п;
Изменится ли значение предела Hm Sn?
П—> «>
Задание 2.8
Докажите, используя теорему Теплица, что если последовательность {хп} сходится
к пределу L, то и последовательности средних арифметических, средних геометриче¬
ских (если хп > 0) и средних гармонических (если хп > 0) сходятся, причем сходятся
к тому же числу L.
Задание 2.9
Докажите, используя теорему Теплица, что если Hm уп - +°°, то последовательности
П—
средних арифметических и средних гармонических стремятся к +°°. Будет ли в этом
случае стремиться к -н» последовательность средних геометрических?
2.5. Числовые ряды
В заключение этой главы мы уделим больше внимания очень важному
классу числовых последовательностей, а именно — числовым рядам. Оста¬
новимся немного подробнее на важнейших определениях и утверждениях.
Определение 2.19. Числовой ряд
OO
а\ + а2 + - + ап + - = Yjan
77=1
называется сходящимся, если существует конечный предел
Hm Sn = S,
П—
Где Sn = CL^ + #2 "I" ••• "I"
При этом число S называется суммой ряда, а элементы последователь¬
ности Sn — частичными суммами ряда. В противном случае данный ряд
называется расходящимся.
OO
Обозначения сходимости и расходимости соответственно ^ап—»
77=1
°° /
И Ъап^ •
я=1
Определение 2.20. Числовой ряд называется знакопостоянным, если
все члены этого ряда имеют один и тот же знак, в противном случае он
называется знакопеременным.
OO
Теорема 2.17 (критерий Коши). Числовой ряд ^an сходится тогда
W=I
и только тогда, когда для V е > О 3 N(e) такое, что для V п > ЛГ(е) и V р g N
выполнено
I? -Vl =
I ‘-’п+р I
flw+1 "I" ^n+2
+ а.
п+р
<6.
121
Следствие 2.3 (необходимое условие сходимости ряда). Если ряд ^an
W=I
сходится, то Hm ап = 0.
TZ->°о
Теорема 2.18 (признаки сравнения). Если для п>п0 выполнено 0 < ап <
< Ьп, то
OO OO
1) из сходимости ряда ^bn следует сходимость ряда ^an;
W=I W=1
OO со
2) из расходимости ряда ^an следует расходимость ряда ^bn.
TZ=I TZ=I
d OO OO
В частности, если ап ~ Ъп при п —> °° (т.е. Iim -Jl = 1), то ряды ^an и ^bn
W=I W=I
и—I
сходятся и расходятся одновременно.
Теорема 2.19 (частный признак сравнения). Если ап = О*
Г л \
\ПР
при п —» оо
(т.е. 3 Hm ап-пР =k<oo}k*0), то прир > 1 ряд ^an сходится, а прир < 1
я->°° W=1
данный ряд расходится.
Рассмотрим далее несколько утверждений о сходящихся числовых
рядах.
OO
Утверждение 2.9. Предположим, что ряд ^an сходится. Тогда ряд
W=I
оо Pn+l 1
^lAn, где An= ai (I= Pi < Р2 < Рз < •••)> полученный в результате груп-
W=I j=p„
пировки членов данного ряда без нарушения порядка их следования, также
сходится и имеет ту же сумму.
Доказательство
OO
Пусть ^an = S. Составим следующую подпоследовательность частич-
W=I
ных сумм исследуемого ряда:
B1=O1= {Pi = 1} = OpitB2 = Oi +-. + ар2Л = A1,
B3 =O1+... + а^ =А1+А2,...,Вп+1 =a1+... + aPn+i_i =А1+... + Ап,....
Так как из сходимости числовой последовательности вытекает схо¬
димость (причем к тому же числу) и любой ее подпоследовательности,
OO
то из сходимости ряда ^an следует существование предела последо-
W=I
вательности {Вп}, причем НтВя+1=5, а так как A1+... + An= Вп+1, то и
W->°°
Hm (A1 + A2 +... + An ) = S. И
W—>°°
Зададимся теперь следующим вопросом: будет ли верно обратное
утверждение? Ответ на этот вопрос — отрицательный. Рассмотрим следу¬
ющий пример:
On = (-!)И+1>Р1 = Up2 = 3’Рз = 5> - •
122
OO
OO
Pn+l ^
Тогда An= Y Aj=I-I = On^O = O. Однако ряд Y (-1)и+1 расходится.
i=Pn W=I W=I
Заметим, что в построенном нами контрпримере фигурирует ряд со зна¬
копеременными элементами. Это неслучайно. Рассмотрим следующее
утверждение.
OO OO
Утверждение 2.10. Пусть члены ряда Y ап положительны и ряд ^An,
W=I W=I
полученный в результате группировки членов данного ряда, сходится. Тогда
данный ряд также сходится, причем сходится к той же сумме, что и ряд
ЕЛ,-
Tl= 1
Доказательство
Здесь и далее мы будем обозначать п-ю частичную сумму ряда с элемен¬
тами ап (An) символамиSn (Sn).
В силу строгой положительности членов ряда ап справедливо неравен¬
ство Sn < Sn. Далее, так как ряд с положительными членами сходится тогда
и только тогда, когда последовательность его частичных сумм ограничена,
то последовательность {5^} ограничена, а значит, ограничена и последова¬
тельность {Sn}, т.е. ряд Yjan сходится.
W=I
Далее, так как {S£} — подпоследовательность последовательности {51®},
то Hm S% - Hm Sfi. ■
w—п—
Замечание 2.18. Собственно говоря, в последнем утверждении нами
было использовано, что монотонная последовательность будет сходящейся,
если сходится некоторая ее подпоследовательность.
OO OO
Утверждение 2.11. Предположим, что ряды Yan и YjK СХОДЯТСЯ
W=I W=I
и для некоторого NeN выполнено неравенство ап<сп<Ьп для Vп>N.
OO
Тогда ряд Ycn также сходится.
Yl=1
Доказательство
OO OO
В силу сходимости рядов Yan и YK из критерия Коши получаем:
W=I W=I
для V в > О 3 N(в) такой, что V п > N(г), Vpe N выполнено
и S%+p -S% <в. Отсюда
C а _ C а
п+п tjTl
<8
-е < S«+p ~ Si < S^p-ScnK- Stp Sb„<t
Ce _ Ce
ип+р ип
<8.
По критерию Коши получаем требуемое. ■
Зададимся следующим вопросом: что можно сказать о сходимости ряда
OO OO OO
Ycn, если оба ряда YanllYK расходятся? На данный вопрос ничего опре-
W=I W=I W=I
деленного сказать нельзя, так как в этом случае ряд Ycn может сходиться,
я=1
а может расходиться. Действительно:
123
I I "
• ak = —-, ck = 0, bk = -; Ycn сходится;
К К п=\
I I 1 “
* ak=W °k = 2k’ bk = k’ ?1C” расходится1-
Утверждение 2.12. Предположим, что ряд с положительными членами
OO OO
Yan сходится и в > О — произвольное число. Тогда ряд Y Яи+Е также сходится.
п=1 W=I
Доказательство
OO
Так как ряд Y ап сходится, по необходимому условию сходимости полу-
W=1
чаем, что ап —» 0. Следовательно, 3 N такое, что для V п > N ап < 1.
W-
Поэтому для всех таких п выполняется неравенство я*+Е <ап, и ряд
OO
Y aIfe сходится по признаку сравнения. ■
TZ=I
Зададимся следующим вопросом: будет ли верно обратное утвержде¬
ние? Ответ на этот вопрос — отрицательный. Пусть ап = 1 /п. Тогда ряд
оо
Yan, очевидно, расходится, несмотря на то, что для произвольного в > О
TZ=I
OO OO ^
ряд Y ali+e = E 77Т СХОДИТСЯ1 1 2.
W=I W=I^
оо оо
Утверждение 2.13. Пусть ряды YaI и E^w сходятся, тогда сходятся
W=I W=I
OO OO OO ££
также ряды Y\antf[ Ek + U2- Е—•
W=I W=I W=I ^
Доказательство
Для доказательства сходимости первых двух рядов воспользуемся при¬
знаком сравнения и неравенствами:
\п h <—- — (п -|- А "\2 <; q2 _|_ 2\п h
ImWwW I — 2 ’ Т Un ' ~ MW Т ^ ImWmW I Х mW •
Для доказательства сходимости третьего ряда положим Ьп = —. Тогда ряд
п
OO OO ^ OO OO
Y4 = E^r сходится и сходимость ряда ^ = ^ |яий„I вытекает из дока-
W=I W=I^ W=I W W=I
занного выше. ■
OO
Утверждение 2.14. Пусть предел Iim w • ап Ф 0. Тогда ряд Yan расходится.
TZ—>°°
TZ=I
Доказательство
По определению сходимости имеем Hm ши = я Ф О <=> для Vb > О 3 N(г)
п—
такой, что для V п> N выполнено \пап - я| < в.
124
1 Если ап > 0, то из признака сравнения следует расходимость сп.
2 См. телескопический признак сходимости.
Не ограничивая общности, считаем, что а > 0. Выберем е > 0 такое, что
CL Cl °° CL
а-г>0 (например, в = —), откуда получаем ап >—. Однако ряд ^— рас-
2 2 п п=i2n
ходится, поэтому и ряд ^ ап расходится. ■
П=1
OO OO
Утверждение 2.15. Пусть йя>Ои ^an сходится. Тогда ряд , где
Yl=1 п=1 M
Tl
Sn = 2«А> расходится.
A=I
Доказательство
Пусть Hm1Sn =а. Так как ап>О и последовательность Sn возрастает,
п—>°°
S “ S
то а>0. Тогда Iimп—-= HmSn #0 и расходимость ряда вытекает
«-><*> и n->°° n=i гг
из утверждения 2.13. ■
Важное место в теории числовых рядов занимает равенство, связываю¬
щее конечные суммы произведений чисел.
П
Утверждение 2.16 {преобразование Абеля). Обозначим через An = ^ak.
A=I
Тогда справедливо следующее тождество:
П
п-1
2¾¾ 4¾ 24(¾ ^*+l)'
*=1 *=1
(2.8)
Доказательство
Воспользовавшись равенством ak=Ak- Ak_b получаем
2¾¾ - E (4-4-0¾ - 24 h ~ E4-i h-
k=\ k=i k=\ k=\
Сделаем замену k -1 —» k во второй сумме и используя, что A0 = 0, заклю¬
чаем
2¾¾ -4 K + 24¾ - 24 4и - 4¾ + 24(¾ ~4и)-■
*=1 *=1 *=1 A=I
Отметим, что преобразование Абеля можно назвать дискретным ана¬
логом формулы интегрирования по частям. Этим преобразованием удобно
пользоваться, когда поведение при гг —» °° суммы A1 + ... + ап известно,
а 4 = K^) — непрерывно дифференцируемая функция. Действительно,
пусть А{х) — ступенчатая функция:
[О, если х <1,
A(X) = I ’ . , Ia
[Ak, если k < х < k +1.
Тогда формулу (2.8) можно переписать в виде
Iatbl= A(n)b(n)- ZA(k) Ki+^ ~ W • Ak.
A=I A=I Ar
125
Задание 2.10
OO
Пусть ряд Y ап сходится и 3 Hm Ъп- ап> где ап=ап+ ап+1 +.... Докажите, что ряды
я=1 «-»00
OO OO
YjaJjn и YjJju -bn+l)-an сходятся и расходятся одновременно.
п=1 Я=1
OO OO
Пусть два ряда Y и^Аяс положительными элементами расходятся
W=I
к +°°. Всегда ли расходится ряд Y min{«n, bn}7 Ответ на данный вопрос —
Я=1
отрицательный. Контрпример строится элементарно. Например,
I 1
ая = 11 2, —, 4, —,.
11 J- 3 J- 5
\ ’ 22’ ’ 42 ’ ’'
Тогда ряд Y т^П{ап’К) = Y СХОДИТСЯ, НО каждый ИЗ рядов YaTi
я=1 Я=I ^ Я=1
И IA расходится к +°°.
я=1
Данный вопрос становится гораздо менее тривиальным, если потребовать
строгую монотонность последовательностей {ап} и {bn}. То есть пусть {a J -I О,
OO OO OO
{&„} i О и Yan =+00> Х^я =+°°- Всегда ли расходится ряд ^тш{ап,^и}?
Я=1 Я=1 Я=1
Ответ на данный вопрос — также отрицательный.
OO OO
Построим сначала два нестрого убывающих ряда Y ап и X К’ расходя-
Я=1 Я=1
OO
щихся к +оо, таких что ряд Y min{an,bn} сходится. Положим
W=I
а
W
1111
22 ’ 22 ’ 22 ’ 22 ’
1111
З2 ’ 42 ’ 52 ’ 62 ’
1111 I Illll.
72’ 82’ 92’ IO2’ 422 ’ 422 ’ 422? 422 ’ 422
1111 I I I I I 1
62’62’62’62’-> 62’ 432 ’ 442 ’ 452 ’ 462
Подчеркнутые серии соответствуют друг другу. В элементах серии
одного из построенных рядов стоит min{a„, bn} равный элементу некото¬
рого сходящегося ряда1. В соответствующей серии другого ряда все члены
равны друг другу и совпадают с последним членом предыдущей серии того
же ряда. Причем сумма всех членов данной серии равна единице. Серии
этих двух типов чередуются в каждом из рядов.
OO OO ^
Очевидно, что ряд Y т1П{ая>^я}= X-T сходится. В то же время ряды
Я=1 Я=1^
OO OO
Yan и YjK расходятся к +°°, так как в каждом из них есть сколь угодно
Я=1 Я=1
далекие от начала (длинные) отрезки членов ряда, в сумме дающие еди¬
1 В нашем примере это 1/п2.
126
ницу, поэтому для сколь угодно большого числа M > О найдется номер п
такой, что S . >М.
Для того чтобы построить пример строго монотонных рядов, можно
добавить к каждому элементу последовательностей {ап} и {Ьп} некоторый
OO ^ OO ^
сходящийся числовой ряд, например 5} — или S—• Строгая монотон-
п^п* * 1 п=\2п
ность и сходимость результирующего ряда достигается в силу того, что
сумма нестрого монотонной и строго монотонной числовых последователь¬
ностей есть строго монотонная последовательность, а сумма двух сходя¬
щихся рядов есть ряд сходящийся.
Задача 2.26
оо I
Исследуем на сходимость ряд , где хп — положительные корни уравнения
я=1*я
tgx = х, занумерованные в порядке возрастания.
Решение
Обратимся к графикам функций х и tgx (рис. 2.18).
Получаем хп е
f п^
7ш; кп н—
V
,пеN. Следовательно, справедлива оценкахп>пп>п.
I 1
Отсюда вытекает неравенство — < —. Используя признак сравнения, делаем заклю-
х2 п2
чение о сходимости исследуемого ряда.
OO I
Аналогично может быть доказана расходимость ряда ^— (докажите!).
n=txn
Задача 2.27
1
Определим, сходится ли ряд —, где X1 = I, X2 = I, хп = хя_2 + ^n-i ПРИ п - 3
п=1%п
(последовательность Фибоначчи).
Решение
1 (4)”
Докажем, что 4"хп >5” при п > 3 (или — < — ). Воспользуемся для этого мето-
Хп
дом математической индукции. При п = 3 получаем
127
I (4
24 5
у
64
125
. Верно.
Предположим далее, что неравенство верно для n-k. Проверим его для n-k + i.
Получаем
4k+1xk+l > 5A+1 о 4k+1(xk_l + хk)> 5*+1;
4k+ixk_i + 4k+lxk = 42 • 4k~ixk_1 + 4 ■ 4k xk > 42 • 5A_1 + 4 • 5* > 5A+1 <=>
фф 42 + 4 • 5 > 52. Верно.
Следовательно,
I
Гл\п
E-^E -
я=1 %n n=l V ^ у
= 4.
I
Поэтому ряд X сходится.
n=iXn
Замечание 2.19. Для доказательства сходимости исследуемого ряда
можно было воспользоваться формулой общего члена последовательности
Фибоначчи при п > 3
*,»=■
T
fi-VsY
J
2 J
Vs
получающегося из разностного уравнения для данного рекуррентного со¬
отношения.
Задача 2.28
Пусть ап> 0 и последовательность {ап} строго возрастает. Докажем, что огра
OO ( ^
ап
\ ап+1 )
ниченность последовательности {а„} равносильна сходимости ряда Y arccos2
я=1
Решение
Если отношение не стремится к единице при и—» °°, то не выполнено необ-
ая+1
OO
ходимое условие сходимости ряда Xarccos'
П=1
a” -> 1-01,т.е.-^-<1.
ап
VflWi J
. Поэтому пусть выполнено
Яя+1
а
я+1
^ ,. arccos х
Далее, так как Iim —,
^i-O Vl-*
= S , то arccos х ~ ^/2(1-дг) при д:—> 1-0 и сходимость
ряда X arccos2
я=1
V an+t J
эквивалентна сходимости ряда X
я=1
C \
^ ап
V
а.
я+1
\ In 11 °°
Аналогично из предела Hm = 1 + 0 вытекает, что сходимость ряда X
t-»i-o I-1 n=i
( \
I ап
эквивалентна сходимости ряда X
П=1
In^-
а
•я+1
V
а,
я+1 у
1
Так как ап < ап+1.
128
Изучим сходимость последнего ряда:
OO
E
п=1
In я”
N
= Hm Y
In Я"
ап+1
N^n=1
ап+1
= - Hm Y In-^- = - Hm In——^—.
n^00U=I ап+\ N~>°° o-N+1
Последний предел конечен при ограниченности aN, так как ап> 0.
Предположим далее, что последовательность {аи} монотонно убывает
к нулю. Рассмотрим свойства рядов, связанные с монотонностью.
OO
Утверждение 2.17. Пусть ряд Yxn сходится. Тогда
П=1
OO
Rn = E «Л = Фп) ПРИ ^
k=n
Доказательство
OO
Обозначим Tk = YlXf и рассмотрим частичную сумму:
i=k
JV JV N JV-I
E akxk = E -^_i) = E 0*¾ - E ak+irk =
k=n k=n k=n k=n-l
JV-I
= E (¾ ~ak+i)rk ^aNrN ~anrn-l‘
k=n
OO
В силу сходимости ряда Y xn и монотонного стремления к нулю при
Я=1
N получаем
Rn E E (¾ ^k+\)^k ^n^n-i‘
k=n k=n
Поэтому
I^l< E 1¾ -I':suP|r*I + \an\• Iv11<
k=n k>n
f со Л
<sup|^| Xk-^+il + kl * sup |r*|-2-k|.
k>n-I уй=я у k>n-i
Отсюда вытекает выполнение неравенства
Я,
а„
<2 sup |/-А| >0
£>П-1
в силу сходимости ряда а это и означает, что Rn = о(апу. ■
72=1
оо
Утверждение 2.18. Пусть р>0. Тогда из сходимости рядов YnPan
22=1
и X (аи -<2w+i)wP+1 следует, что ап = о
п=1 1 1' I ^
при П—>°о,
1 Подробнее о работе с о-символикой читатель может узнать из гл. 3 книги.
129
Доказательство
OO
Если ряд Y пРап сходится, то
TZ=I
(Z~
Г ~|Р+1
п
-{{ая}^0}< Y kpak —> О,
п—>°°
т.е. а
п
P+1
= о(1) и аи =о
' I ^
При п —> °°.
V" У
OO
Далее, если ряд X(an -an+i)wP+1 сходится, то
TZ=I
пр+1 • аи = «р+1 • E (¾ -«A+i) ^ Е^р+1(«а -ak+i) 0.
k=n k=n
TZ—>°°
Отсюда а„ = о
f 1 Л
при
Следствие 2.4. Если последовательность {яи} монотонно сходится
У1Л
к нулю и ряд Y сходится, то аи = о
при 72 —^ °°.
Оставляем читателю возможность ответить на вопрос, заданный в сле¬
дующем упражнении.
Задание 2.11
Определите, одновременно ли сходятся ли в условиях последнего утверждения
OO OO
ряды YnPan и Yjian ~an+i)nP+i (т.е. сходятся ли они при одних и тех же значениях
п=1 Я=1
параметра р).
P-1
OO
Утверждение2.19. Пусть дополнительно/? > 1 и ряд YlaJp
TZ=I
OO
дится. Тогда ряд сходится.
TZ=I
ГI Y/p
V72y
CXO-
Доказательство
Так как {ап} i 0, — -I О и р > 1, то последовательность ■
п
P=1 Г\\уР
Ori
KnJ
моно¬
тонно убывает к нулю. Тогда из сходимости ряда Yan
TZ=I
ствия 2.4 вытекает, что
PA
KnJ
и след-
а
PA Ip
р
KnJ
= O
KnJ
р-А
<^апр =о
п
\-Ур
= O
( \
1
рА
Kn р )
при п —> °°.
130
/ < л
PZI
P
уПУР j
Следовательно, а„р = о —— при п —» Умножая обе части последнего
равенства на а„ , получаем, что
( р-1
ап=о
\
пУр
при W —> °о.
Тогда из сходимости ряда Y а
PA /W/р
Tl=1
требуемое.
и признака сравнения вытекает
AL
Утверждение 2.20. Пусть дополнительно ряд Y~ сходится. Тогда
W=I ^
выполнено, что ап = о
Доказательство
( I ^
J
при п—И СХОДИТСЯ ряд Yjian ~ап+\)' Inw.
W=I
я.
Докажем первое утверждение. Пусть сходится ряд ^ —. В силу телеско-
W=I ^
пического признака сходимости и критерия Коши сходимости числовых
рядов для любого в>0 получаем неравенство —<е при п>щ.
2п 2Ап
Отсюда, используя монотонность последовательности ап и формулу Эйлера
для п-й частичной суммы гармонического ряда (см. ниже), заключаем:
ап
'")п @“)2п
8 > — V ... Л =Z— > Я09„
2w 22и 2
I 1
—1-... н——
2й 22и
-а
21п
а22п ~а2п +^П
C 22w ^
On
\А J
a22niS^“22n ^2”
Так как {ап} монотонно убывает к нулю, то Hm а22„(а22я -а2„) = 0. По
W-»°°
OO
этому ^Я22„И = 0.
W=I
Теперь пусть 22(”-1) <k<22n. Тогда
(п -1) In 2 < In k < п In 2, я22„ < ak < «22(n-i> •
Поэтому я22„(и-1)1п2<я^1п^<я22(„_1)и1п2, откуда Iimfl4InA = O1.
Далее, так как
гг гг
E Oft - flft+i) ink = Y ч [Ink ~ InO -d\~an+i In п>
ft=l ft=2
то второй ряд сходится тогда и только тогда, когда сходится ряд
Y CijlWnk-InO-I)].
k=2
1 Очевидно, что при п —» °° получаем k
131
Так как1п&-1п(&-1) = у + 0
k
Г 1 л
V*2 У
и У—сходится, то сходимость послед¬
ят
него ряда эквивалентна сходимости первого.
CL.
P-1
Утверждение 2.21. Пусть р > 1. Тогда из сходимости ряда У ” выте-
п=\ПУР
OO
кает сходимость ряда Хап-
га=1
Доказательство
Из утверждения 2.18 вытекает, что =о
7P-1
YIl1iP
Отсюда и из сходимо-
сти ряда У * вытекает требуемое. ■
га=1 ПУр
Существенна ли монотонность в утверждении 2.21? Ответ — да. Pac-
\\,eamn = 2k,
смотрите контрпример с ап = \ , (или см. далее).
О, если п Ф 2*
Задача 2.29
Пусть гп= XaA- Построим примеры:
k=n
OO OO
а) сходящегося ряда X ап с положительными членами, для которого ряд X rn Pac'
я=1 п-1
ходится;
б) бесконечной последовательности расходящихся рядов Xaji*\ k-i,2,..., таких,
что = — и a(nk+i) = о(аJ^) при п —> °о;
Yl
аГ
в) немонотонной последовательности {ап}, для которой ряд X *?, >Р>% схо-
я=1 ПУР
OO
дится, но ряд X ап расходится (ср. с предыдущими утверждениями).
72=1
Решение
1
а) Положим а = —. Тогда
Yl*
dx 1
rn* -T = -
X1 Yl
поэтому ряд X гп расходится.
72=1
б) Первым рядом из нашей последовательности расходящихся рядов возь-
OO ^ OO ^ OO
мем гармонический ряд, т.е. ряд X-. Два следующих1: X —,— и X —, ;—. ,
п=\п п=2 п-тп п=з и • пш • In(Inn)
k-й ряд:
OO
S
n=nk
Yl- In Yl -In(Inn)
ln(ln(...lnn))’
А
1 Расходимость каждого из них следует из телескопического признака сходимости.
132
где щ — минимальный номер, для которого ln(ln(l/4In /¾)) > 0, k>2. Видим, что
A-I
для общих членов любых двух следующих друг за другом рядов выполняется
а^+г> = о(а® ) при п —»
fl, если п = 2к, ~
в) Положим а Тогда ряд X расходится, так как не существует
[О, если п Ф 2\ „=1
°° дД-1 ~ 1
предела: Hm ag, однако ряд X —= X —гг- сходится.
и->°° я=1 « A=I 2 р
Задание 2.12
OO
Пусть гп = 2 aA- Постройте примеры:
k~TL оо оо
а) сходящегося ряда Хая с положительными членами, для которого ряд Хгп
сходится; n=1 ”=1
OO ^ ^ ^
б) расходящегося ряда X ая с положительными членами, для которого ап-о — .
п=I
Перечислим далее несколько признаков сходимости знакопостоянных
рядов.
Теорема 2.20 (признак Даламбера). Пусть ап>О для VweN
м 3 = <7. Тогда
И->оо
OO
при q < 1 ряд X аи сходится,
72=1
при q > 1 ряд X расходится,
77=1
при д = 1 требуется дополнительный анализ.
Теорема 2.21 (признак Коши). Пусть ап>0 для VweNaB Iim Wan = q.
и->°°
Тогда
OO
при q < 1 ряд X сходится,
72=1
при q > 1 ряд X ап расходится,
72=1
при <7 = 1 требуется дополнительный анализ.
Утверждение2.22. Пусть ап> 0. Тогда если 3 Hm^л+L = qt то 3 Ximdan = q.
Tl—>°° <7 "
и—>°°
В случае выполнение равенства Iim Д”+1 = 1 иногда бывают полезны
и—>°° а,
более тонкие признаки сходимости.
72
Теорема 2.22 (признак Раабе). Пусть ап> О для VweN и
(
3 Hm w
и—>■»
а
д__1
= р. Тогда
133
при р < 1 ряд ^ ап сходится,
Yl=1
оо
при р > 1 ряд ^ ап расходится,
Yl=1
при р = 1 требуется дополнительный анализ.
Замечание 2.20. Из условий признака Раабе следует, что выполняется
'1'
соотношение
ап л P
—— = 1 + — + о
а
и+1
П
KnJ
Задача 2.30
Построим пример ряда, к которому не применимы признаки Коши и Даламбера,
но применим признак Раабе.
Решение
1
«=1 п
а
Рассмотрим ряд —. Для его общего члена получаем
я+1 (и + 1)2 , I— Il .
у > ^ ~\ ~2
ап я-»~ V и-4
Следовательно, признаки Даламбера и Коши не применимы. Однако имеем
-> 2, * 1 2т.е. исследуемый ряд сходится по признаку Раабе.
п■
а. ,1
= П■
(in+1)2 и
V an+l у
[ п2 J
Задача 2.31
Построим пример ряда, сходимость которого не устанавливается признаком Раабе,
но устанавливается признаком Коши.
Решение
Положим ап =
1
—,если и = 2k + \,
2п
—,если и -2k.
An
^ I
Тогда Иш^ап = — < 1. Следовательно, рассматриваемый ряд сходится по признаку
оо 2
Коши. Однако признак Раабе к данному ряду не применим, так как
[ п • (2Я+2 -1), если п = 2k +1,
п • (21_” -1), если п = 2k,
п •
( „ \
-
\ип+\ J
т.е. предела Iim п ■
а.
\
д__1
V ап+\ )
не существует.
Отметим, что признаки Даламбера и Коши основаны на сравнении изу¬
чаемого ряда с рядом бесконечно убывающей геометрической прогрессии,
а признак Раабе — на сравнении с рядом
“1,1 1
У, — IH 1 Y...,
па 2“ 3«
a G R.
134
Возникает вопрос: существует ли такой универсальный («предельно мед¬
ленно» сходящийся или расходящийся) ряд, сравнение с которым позволило
бы сделать вывод о сходимости (или расходимости) любого наперед взятого
ряда с неотрицательными членами? Ответ на этот вопрос — отрицательный.
Для того чтобы сформулировать уместный здесь результат, введем сле¬
дующее определение.
Определение 2.21. Пусть даны два сходящихся ряда: Ya k и Yjak- Обо-
k=i k=\
значим символами гп, г'п соответственно их w-e остатки. Будем говорить, что
OO OO у,
ряд Yak сходится медленнее, чем ряд Yak> если Hm -у = 0.
A=I
k=i
гс—Г*
п
Утверждение 2.23. Для каждого сходящегося ряда существует ряд,
сходящийся медленнее этого ряда.
Доказательство данного утверждения мы оставляем читателю или пред¬
лагаем обратиться к учебнику [26].
Сформулируем еще несколько специальных признаков сходимости
рядов с неотрицательными членами.
Теорема 2.23 (признак Гаусса). Пусть ап> О для VweN, в > О — неко-
( ! л
торая постоянная и
-^- = А, + —+ 0
а
и+1
П
п
1+Е
. Тогда:
1) ряд Yan сходится при X > 1 и расходится при X < 1;
W=I
2) если X = 1, то ряд сходится при р > 1 и расходится при р < 1.
Теорема 2.24 (логарифмический признак). Ряд Yan> ап> О, сходится,
W=I
Л Inl/ап Inl/ап Л
если 3 ос > О такое, что — > 1 + а при п>щ,и расходится, если — < 1
In
при п > щ.
п
In
п
Теорема 2.25 (признак Куммера). Даны ряд Yan> > 0, w произвольная
ГС=1
оо I
последовательность неотрицательных чисел {ся} такая, что ряд Y — Рас~
n=icn
Г
ходится. Пусть существует предел Hm
я—
-Crt
\ ап+1
= q, тогда при q > О
ряд Y ап сходится, а при q < О расходится.
Я=1
Теорема 2.26 (признак Бертрана). Если существует предел Hmlnwx
х
w
Clvi
-1
V ап\\ )
-1
п—¥°°
= q, то при q > 1 ряд Yan>an>®’ сходится, а при q < 1
п=1
данный ряд расходится.
Теорема 2.27 (признак Ермакова). Если функция f(x) > О и монотонно
ех f SeX \ °°
убывает при х > 1 и существует предел Hm —^—- = q, то ряд Y f(n)
п^°° f(x)
дится при q < 1 и расходится при q > 1.
схо-
ГС=1
135
Доказательство этих признаков мы также оставляем читателю, но при
желании с ними можно ознакомиться, например, в учебниках [18, 70].
Задача 2.32
Пусть ап > 0 для VneNn ряд ^ ап расходится. Исследуем сходимость следу-
TZ=1
ющих рядов:
a) S7^-; б)
n=\i + a п=\\ + п-а
Решение
Clvi
а) Если апт40 при п —>то —-— т^О и исследуемый ряд расходится. Если
\ + ап
ап —> 0, то °” >—. Поэтому исследуемый ряд расходится в любом случае,
я—>°° 1 + ап 2
°° а °° 1
б) Пусть а -1. Тогда ряд ^ -— = Z расходится. Далее, возьмем
п=11 + п-ап n=in + l
Jo, если п Ф 2к,
” jl, если п - 2k.
OO -J^
Тогда ряд X г сходится. В заключение отметим, что оба из взятых рядов
A=I 1 + 2*
OO
X ап расходятся.
It=1
В качестве самостоятельной работы предлагаем читателю решить сле¬
дующее задание.
Задание 2.13
Clt7
В условиях задачи 2.32 исследуйте сходимость следующих рядов: a) 0,
n=il + a„
б) Z
а„
Й1 + п2-ап
Задача 2.33
Пусть ап> О для VneNn ряд ^ ап сходится. Докажем сходимость ряда ^ dnan
TZ=1
TZ=I
для любой ограниченной последовательности {</„}.
Решение
OO
Пусть 3 > такое, что для VneN выполнено \dn | < M. Тогда, так как ряд ^
Я=1
сходится, по критерию Коши получаем, что для V е > О 3N(e) такое, что для V п> N
HVpeN выполнено
е
\ап+\+- + ап+р\<
M
Отсюда
т.е. ряд ^ dnan сходится.
TZ=I
п+р
п+р
Z ^kak
<м
Z «А
А=я+1
А=я+1
<8,
136
Задача 2.34
Докажем, что для любой последовательности положительных чисел {</„} такой, что
OO
Hm dn = +о®, существует сходящийся ряд с неотрицательными членами Y аю Для кото-
W=I
OO
рого ряд Y d-rfln расходится.
TZ=I
Решение
Так как Hm dn = +°°, то найдутся такие номера ц < V2 <... <in<.... что выполнено
П—>°°
fi^i1 ^1Ai2 ^Z-Ain
Построим последовательность {ап} такую, что
О, еслипФ
и„
1
d; -т
, если п = гт.
Тогда выполнено ak >0, dk >0,
w nI 1 nI 1
A=I m=l df • TH m=i TH
т.е. ряд Y ап сходится. Однако
W=I
df
п «1
fjdk-ak=Jj~r— ^
A=I m=l ^ Wi=I ^
«1 I
= £-->4~
при п и W1 (я) —> оо, так как гармонический ряд расходится.
В заключение параграфа докажем тождество, имеющее множество при¬
ложений в теории числовых рядов.
Утверждение 2.24 (формула Эйлера). Обозначим через Hn п-ю ча-
п I
стичную сумму гармонического ряда, т.е. Hn = Yv- Тогда справедлива сле-
ы k
дующая формула:
Hn = Inn+ C3-Ho(I)1,
где C3 — постоянная Эйлера2.
Доказательство
Воспользовавшись неравенством из доказательства существования
числа е
C 1 Лп
1 + -
V
п
элементарно получаем неравенство
<е<
1
\ 1
1 + -
\И+1
V
П
\
п +1
<1п
1+-
п
<—. Поэтому
п
л 1 , п + 1 1 1 1 1
О < — In < = <—.
п п п п +1 п{п +1) п2
1 Подробнее о работе с О-символикой читатель может узнать из гл. 3 учебника.
2 Сэ = 0,5772156649...
137
Отсюда по признаку сравнения заключаем сходимость ряда ^
Следовательно, его частичная сумма
n=i\n
--In
п + 1
п
E
Jfc=I
(
I , k + 1
VlnIT
= Hn- In(п + 1) —> C = const.
П—¥°°
Остается заметить, что, так как
1п(я + 1)-1пи = In
1 + -
Yl
—ъ о»
П—¥°°
то в последнем равенстве можно заменить 1п(и + 1) на In и и записать ис¬
комое равенство.
Задание 2.14
Докажите непосредственно сходимость следующих рядов и найдите их суммы:
1 “ 1
- + ...= 5) ——— (телескопический ряд);
ч 1 1
а) — + ^r + ...+
б)
1-2 2-3
1
п(п +1)
1
1 • (1 + т) 2 • (2 + т)
Задание 2.15
- + ... + -
я=1 Yl(tl +1)
Л оо
+-=E
1
п(п + т) „=1 п(п + т)
,ms N.
1
Исследуйте на сходимость следующий ряд, используя критерий Коши: ^ = 1 н
1111 2Ч
— + — + — h... (два члена гармонического ряда со знаком «+», один — со знаком «-»).
3 4 5 6
Задание 2.16
Исследуйте сходимость ряда ^sinna, a е R.
W=1
Задание 2.17
Пользуясь признаками Даламбера или Коши, исследуйте сходимость рядов:
а) S'
W=1
П
п-1
п+1
(2п2 + я + 1) 2
V V Г Зи
в) E
я=1\
Л"
п + 5
п + 2
^я + 3 j
\п
б) E
f 2 + (-1)" л”
„tii,5 + (-l)"+V
г) E
/ . \2я-1пя
1 + C0SW
„=i(2 + cosn
Задание 2.18
Пользуясь признаками Раабе и Гаусса, исследуйте сходимость, в зависимости от па¬
раметров, следующих рядов:
а)
а а(а + d) а(а + d)(a + 2d)
b b(b + d) b(b + d)(b + 2d)
а > О, b > 0, d > 0;
б)
в)
г)
п\ ГГP
-, q> 0;
п=\Я(д + ^)-"(д + п)
(2-4а) + (2-Va)(2-л[а) +... + (2-4а)(2-%[а)■...■ (2-\/я) +..., а>0;
°° п I я"
Et — V , 7,а>0, яя > 0, я = 1,2,...,яя —> яприя —>
Я=1(я + я1)(2я + я2)-"(яя + яя)
138
Задание 2.19
00 ln?2
Исследуйте на сходимость ряд ,
и=1 Па
а>0.
Задание 2.20
Определив порядок убывания общего члена ап, исследуйте сходимость ряда ^ ап,
Yl=1
если:
ч • 1 . 1
а) ап =Sin--Ig-=-;
па ну
б) ап=па • (\/з - \/2);
и + 1
и
Замечание 2.21. Поскольку и частный признак сравнения, и признак
Раабе, и признак Гаусса основаны на сравнении членов исследуемого
ряда с последовательностью вида {1 /па}, то ни один из них не дает ответа
на вопрос о поведении ряда, члены которого стремятся к нулю быстрее, чем
I 1
1/п, но медленнее, чем —— для V в > 0. Так, например, для —-—— имеем
п1+е H-(Inn)P
1
H-(Xnn)P
= о
ГХ\
, р > 0, но
г
= O
Задание 2.21
Пусть {Ьп} — последовательность, заданная рекуррентным соотношением bi- 1;
bn = 2 + - 2yji + ^Jb^, п> 2. Найдите сумму ряда Ъп 2п.
п=1
2.6. Знакопеременные числовые ряды.
Абсолютная и условная сходимость
OO
Определение 2.22. Будем говорить, что ряд ^an сходится абсолютно,
TZ=I
оо
если сходится ряд ^ \ап\ (обозначение: ^an —абс >)•
и=1 п=1
Приведем формулировки некоторых известных утверждений и теорем.
OO OO
Утверждение2.25. Если ряд ^ \ап\ сходится, то сходится и ряд ^an.
п=1 п=1
OO
Определение 2.23. Будем говорить, что ряд ^an сходится условно, если
И=1
OO OO OO
ряд ^ ап сходится, а ряд ^ \ап | расходится (обозначение: X ап —усл >)•
И=1 Я=1 И=1
Теорема 2.28 (признак Лейбница). Пусть qn >0, qn+i <#„, Ximqn =0.
П—
OO
Тогда ряд ^(~T)nqn сходится. Кроме того, верна оценка \Sn -S\<qn+1, где
TZ=I
S„ = YJ(-T)kqk, S=XimSn.
k=i п^>°°
139
Определение 2.24. Ряд £ (-1)”qn называется рядом Лейбница.
И=1
Замечание 2.22. C учетом того, что отбрасывание конечного числа чле¬
нов не влияет на сходимость, признак Лейбница распространяется на слу¬
чай, когда условия теоремы 2.28 выполнены начиная с некоторого номера
(т.е. для V n>N, Ne N).
OO
Теорема 2.29 (Коши). Если ряд ^an сходится абсолютно, то любой
TZ=1
ряд, полученный из данного путем перестановки членов, также сходится
абсолютно и имеет ту же сумму, что и данный ряд.
OO
Теорема 2.30 (Римана). Если ряд ^an сходится условно, то каково бы
TZ=I
ни было число L, можно так переставить члены этого ряда, чтобы преоб¬
разованный ряд сходился к L.
OO Я
Когда в основе сходимости ряда ^ ап или ограниченности ^ak лежит
я=1 k=i
взаимное наложение положительных и отрицательных членов последова¬
тельности {ап}, то наиболее эффективными являются следующие достаточ¬
ные признаки сходимости числовых рядов.
Теорема 2.31 (признак Абеля). Пусть выполнены следующие условия:
OO
1) ряд ^an сходится,
п=\
2) последовательность {Ьп} является монотонной и ограниченной.
OO
Тогда ряд ^ апЬп сходится.
п=1
Теорема 2.32 (признак Дирихле). Пусть выполнены следующие условия:
П
1) последовательность частичных сумм Sn = ограничена, т.е. 3 М> 0:
*=1
П
IX
jfc=i
< M для VweN;
2) последовательность {Ьп} монотонно стремится к нулю при w —>
Тогда ряд ^ апЬп сходится.
TZ=I
Замечание 2.23. Признак Лейбница является следствием признака
оо
Дирихле в силу ограниченности частичных сумм ряда X (“!)”•
TZ=I
оо
Обсудим сначала следующий вопрос. Пусть ряд ^an сходится
Я=1
b “
и 3 Hm — = 1. Можно ли утверждать о сходимости ряда ^bn?
а
TZ
TZ=I
Ответ на поставленный вопрос — отрицательный. Выберем в качестве
сходящегося ряда ряд Лейбница, а в качестве второго — сумму данного
ряда и расходящегося. Действительно, возьмем
140
а„
(-1)” . _ (-Ow , I
4п п 4п п
(-1)%1 1+(-1)"
п
4Е- ->1.
1 W-»°°
vv (-1 2)" К 4п
Тогда ряд Zjan = L сходится и -5- = v
w=l w=l V W «и C V
4п
°° (-1)и 1
Однако ряд ^ v у— + — расходится как сумма сходящегося и расходя-
w=l yjn п
щегося рядов.
Замечание 2.24. Сравните данное утверждение с аналогичным утвержде¬
нием для знакопостоянных рядов.
Утверждение 2.26. Пусть выполнены следующие условия:
1) общий член ряда ап стремится к нулю при п —»
сю
2) ряд Yj An, полученный в результате группировки членов данного ряда
W=I
без нарушения их порядка следования, сходится;
Pn+I-1
3) число слагаемых а{, входящих в член = £ ai,pi<p2< ...» ограни-
, k=p„
чено1.
OO
Тогда ряд Yjan является сходящимся,
п=1
Доказательство
Пусть
sn = fjab sf = E4=fli+fl2+-+v-i-
jt=i k=\ 1+1
Выберем достаточно большой номер п такой, что
Sn =а 1 + - + aPi+i-1+ aPi+1 + - + ап= sf + арМ + - + aW2 • (2-9)
Пусть Нш Sf = 5'. Для достаточно больших п (индекс / также выбира-
/-H-OO
ется достаточно большим для того, чтобы удовлетворялось неравенство
п~ Pl+1 < Sf) рассмотрим модуль разности
S--S <
Sf-S
+
а
pi+1
+ — +о*
в 6
< 1
2 2 AT
ЛГ<в3.
Следовательно, Нш Sn = S. ■
И-Н-оо
Предлагаем читателю построить контрпример и показать, что условие
ограниченности числа слагаемых в каждом выражении Ak необходимо
для выполнения условий последнего утверждения. 1 2 31 То есть pi+i ~Pi< N= const.
2 При этом считаем, что выполнено п ~Pi+\ < N.
3 Здесь мы использовали условие, что общий член ряда ап стремится к нулю при п —> °°.
141
Утверждение 2.27. Ряд al -Ya2 + ... + ~ар2 ~ -~api-\ + api +- схо
P3-1 ^p3
(Рп+1-1 ')
E щ
К i=Pn )
, Cl; > О,
дится или расходится одновременно с рядом X (“О”-1
я=1
I =Pl < Р2 < Рз < ••• •
Доказательство
В прямую сторону. Пусть сходится первый ряд. Следовательно, сходится
и любая подпоследовательность его частичных сумм, в том числе и такая:
N
2(-1)"-1
и=1
fPn+I-1 ^
Z ai
V i=Pn
= S
N-
В обратную сторону. Пусть сходится второй ряд. Тогда необходимо
Pn+I-1
получаем ^ а. Q- Тогда
г=р„
И—
^ = 2^=2(-1)""1
г=1 »г=1
^ ^яг+1-1 ^
2 а,
V >=Р|и /
+ apq+1 + - + йя - ^p + Лр(п)>
где р(п) —» оо, —> 0, —Y 5. Поэтому Sn —» S.
п >°° ^ ^ оо гг >°°
Задача 2.35
Применим результат предыдущих утверждений для исследования сходимости
(абсолютной и условной) следующего ряда:
1 + 1/2+ 1/3-1/4-1/5-1/6+1/7+1/8+1/9-....
Решение
Так как знаки трех подряд идущих членов совпадают, сгруппируем их и восполь¬
зуемся доказанными утверждениями. Составим ряд
ЕЛ = E(-i)”"1
п=1 я=1
1
Зп — 2
Зп -1 Зп
- у/ |\я-1 ^7w2 + 2
^iv ' 3га(3и - 2)(3га -1)
Полученный ряд сходится по признаку Лейбница1. По утверждению 2.27 заклю¬
чаем, что исследуемый ряд сходится.
Далее заметим, что ряд, составленный из модулей, расходится как гармонический.
Поэтому данный ряд сходится условно.
Заметим также, что сходимость данного ряда также следует из признака Дирихле:
Ьп > О монотонно, а для последовательности ап -1,1,1, -1, -1, -1,1,1,1,... выпол¬
нено
<3.
Докажем еще одно полезное при исследовании на сходимость знакопе¬
ременных рядов утверждение.
1
Так как
27п2-18п + 2
3п(3п - 2)(3 п -1) п-> о»
142
Утверждение2.28. Знакопеременный ряд £(-1)”-1 •Ъп, Ьп> 0, сходится,
И=1
если
К =
Ьп+\
1 + ^ + 0
п
ГГ|
при П —» °°, р > 0.
Доказательство
Запишем данное нам условие в эквивалентном виде:
C
Iim гг-
И—
h
п у
= P-
V ип-Hl у
Из определения предела заключаем, что для Ve>0 З Af = iV(e) такой, что
для V гг > ЛДе) выполнено
гг
h
V^w+1 у
P
<8.
Переписав последнее неравенство в виде
1 +
р-Е
гг
Ь,
<1 +
га+1
J9 + 8
гг
и выбирая произвольное в из интервала (0; р), получим, что начиная с не¬
которого номера (пусть это будет AT1) справедливо неравенство, гарантиру¬
ющее монотонность последовательности {Ьп}:
-р->1+-^—^>1 <=>6„
К+1 п
>Ъ,
И+1-
Кроме того, для всех гг > N1 выполнено
jNi
Ь1V1 Ъ
AT1H-I
L
я+1 AT1+! AT1+2
Jn+l
1 +
р-Е
N
1 у
1+
р-Е
N^lj
1 +
р-Е
гг
Отсюда, воспользовавшись неравенством Бернулли1, получаем
0 <Ъ,
yAT1
ъ
Ni
n+1 ^ /
-> 0.
1+
р-Е
N
1 у
1 +
JO-B
гг
1 + (^-8)
+ ...+
гг
п—>°°
Подводя итог под вышесказанным, заключаем, что ряд ^(-1)” 1 -Ьп схо-
п=1
дится по признаку Лейбница. ■
Замечание 2.25. Данное утверждение полезно сравнить с признаком
Раабе для знакопостоянных рядов. Рекомендуем также читателю подумать
о том, будет ли это условие необходимым для сходимости знакоперемен¬
ного ряда.
1 Если XiXj >0, *,•>-! для всех г,у = 1,...,и, то (1 + ^)-(1 + ^2)-...-(1 + :^,,)-1 + ^1 + -+ хи-
143
Рассмотрим теперь несколько задач и утверждений, имеющих отноше¬
ние к замечательным теоремам Коши и Римана о перестановке членов чис¬
лового ряда.
Утверждение 2.29. Члены условно сходящего ряда можно без пере¬
становки сгруппировать так, что полученный новый ряд будет абсолютно
сходящимся.
Доказательство
Пусть ряд ^ak сходится условно. Далее, так как ряд ^ak сходится, то для
ы ы
El =
1
2
3 AT1(B1) такой, что для V п > AT1 (выберем п = N1) иУ pt eN выполняется
N1 +P1
E щ
I=AT1+!
1
Далее, для B2 = — 3 AT2(B2) > AT1 такой, что для V п > AT2 (выберем п = AT2)
и V р2 G N выполняется
AT2+р2
E аг
I=AT2+!
1
1
и т.д. На k-м шаге имеем, что для Ek = —гЗ Nk(Ek) > Nk_x такой, что для V п> Nk
2k
и V pk G N выполняется
1
Nk+Pk
E щ
I=ATjfe+!
2*
Используя то, что Pj G N произвольны, выбираем их так, чтобы
AT1 + P1 = AT2, AT2 + р2 = AT3, ...,ATjfe + pk = Nk+1,....
Теперь обозначим
A0 = O1 + а2 +... + aNi, A1 = aNi+1 + aN^+2 +... + aNi2,...,
= aNk+\ + aATjfe+2 + — + aNk+1 ’ ••• •
Il 1 °° 1
Для каждого Ak (k > 1) получаем А, < Ejfe = —г, а ряд ^ —г сходится. Сле-
Ok ,, 2*
довательно, ряд ^ Ak сходится абсолютно. ■
A=I
“ (-1)”
Найдем указанную группировку в ряде Лейбница ^ -——
H=I
Замечая, что
J I _ 1
2п 2n + i 2n(2n + V)’
получаем ряд
E
п=1
(-1)"
и
=-i+E
^12п(2п + 1)’
который сходится абсолютно.
144
Вспоминая доказательство теоремы Римана, предлагаем читателю
решить следующее упражнение.
Задание 2.22
Докажите, что члены условно сходящегося ряда можно переставить так, чтобы он
стал расходиться к +°° (~°°).
Утверждение 2.30. Члены условно сходящегося ряда можно предста¬
вить таким образом, чтобы одновременно выполнялись условия:
1) полученный после перестановки ряд расходится;
2) последовательность частичных сумм ряда ограничена.
Доказательство
OO
Предположим, что ряд J4 ап сходится условно и
W=1
ип = max{0; ап}, vn = min{0; ап}.
Тогда
an = un+vn> Jun = +°°, 5Х=-°°-
W=I W=1
В силу сходимости ряда получаем ап —> 0. Поэтому существует такой
п—>°°
номер N, что |«иI< 1 при п>N. Пусть теперь Af1 — такое число, что
ATh-JV1
Si= Un <2,
я=ЛТ+1
a M1 — такое наибольшее число, что
JH1H-JV
S2 = ^1+ J4 vn>0.
w=JV+l
Пусть, далее, N2 — такое наибольшее число, что
ATh-AT1H-AT2
^3=^2+ J ип—2>
W=ATh-AT1H-I
a M2 — такое наибольшее число, что
+ Af2
S4=S3+ jJ vn>0,
W=ATh-JH1H-I
и т.д. Тогда искомая перестановка получается из ряда
со ДГ Wh-AT1 JVh-JH1 ATh-AT1H-JV2 JVh-JH1H-JH2
Jan = Jan+ J ип+ J Vn+ J ип+ J vn+-
w=l w=l w=JV+l w=JV+1 W=JVh-JV1H-I W=JVh-JH1H-I
естественным удалением нулей (докажите!). ■
Из доказанных выше утвержднний вытекает следующее утверждение.
OO
Утверждение 2.31. Пусть ряд ^«„обладает следующим свойством:
W=I
при любой перестановке своих элементов он сходится. Тогда данный ряд
сходится абсолютно.
145
Задача 2.36
оо /_j\7Z+l
Найдем сумму ряда Лейбница —-—.
п=\ п
Решение
Используя доказанную в параграфе 2.5 формулу Эйлера
яя = Ет = Ья + Сэ + о(1),
k=\R
получаем
2« (-1)*+* * 1 „11 1 1,1 1
2п к 2 3 2п-1 2 п 2 2 п
' 1 1Л
1 + - + ... + —
V 2 Яу
= (1п2п + Сэ + о(1))-(1пя + Сэ +о(1)) = 1п2 + о(1) —» 1п2.
Далее, так как ряд Лейбница сходится, то Э Hm Sn, и Hm = Hm S2n - In 2.
Задача 2.37
°° 1
Переставим члены условно сходящегося ряда ^ т=— так, чтобы он стал рае-
га=! Jn
ходящимся.
Решение
Переставим члены исследуемого ряда, например, так, чтобы за тремя положи¬
тельными членами шел один отрицательный, т.е. пусть
1Lcn =
(
п=1
I 1
1
IH—J= H—1= J=
f
+
I I 1
+ -j= + -
1
V3 V5 л/2 J LV7 V9 VTT л/4
+ ...=
= E
I I 1
ra=ll"v/6n-5 л/вп-З JLJ-1 JLJ
Далее ползаем
I 1
г +
1 2
>
JLJ-3 -у/би-1 JLn V 6?2 — I JLn
1 Ш 1
^ > О1, откуда сп >
JLn-5
Следовательно, ряд ^cra расходится.
П=\
Задача 2.38
00 f—^\7l+1
Докажем, что если члены ряда ^ -—-— переставить так, чтобы группу изр после-
я=1
довательных положительных членов сменяла группа из q последовательных отрица-
1 Т)
тельных членов, то суммой нового ряда станет In2 + — -In—.
2 q
Решение
Покажем, что подпоследовательность частичных сумм переставленного ряда
1 1 „Р
5я(р+?) сходится к In2 H—In-. Имеем
2 q
s =1 1 _1 1_1_
n{p+q) 1+з+-+2р-1 2 А ‘ 2q 2р + ХAp-X
I I 1
- + + ... + -
I 1
--... + -
1
1
2q + 2 Aq
2 пр -1 2 щ
2
1 Так как . >-J= о 2jLn > JeJ-X о 8га> 6п-1 о 2п > -1.
v6ra-l V 2га
146
Далее все отрицательные слагаемые оставляем без изменений, а к положитель-
. 111
ным прибавляем и вычитаем из них числа —, —, :
2 4 2пр
Vp+?)
^ll 1
1 + - + - + ... + -
V
2 3
2 пр
Wll
+
1
V
2 4
+
(,11 1
1 + - + - + ... +
ч 2 3 2пр
л tf
, I 1
1 + - + ... + —
2 пр J
2 пр
'2 4
1
2 щ
л 1 1
1+-+...+—
2 nq J
= C3+ 1п(2 пр) + о(1) ~(СЭ + Ь (пр) + о(1)) - |(СЭ + In (nq) + о(1>) =
= \и(2пр)~—Xnnp-- 1пи^ + о(1) = 1п2 +—In— + о(1) —> 1п2 +—In-.
2 2 2 q я-»~ 2 #
Докажем далее, что частичная сумма переставленного ряда Sm сходится к тому
тп
же самому числу. Действительно, пусть Sm = ^ai. При достаточно больших k(k>K)
i=l
получаем, что \ak\ < е для любого е > 0. Далее для произвольного достаточно большого
т можно найти такое натуральное п, что
т е [п(р + q) +1; (и +1 )(р + q) -1].
Следовательно,
I~ ^n(p+q)I — \^n(p+q)+2 ^n(p+q)+1 | —
^ \^n(p+q)+\ I + \®n(p+q)+2 \ + - + |«m | < (Р + Ч)г = е'>
если п(р + q) + l>K.
Замечание 2.26. Если у членов гармонического ряда заменить знаки нар
положительных, q отрицательных (р Ф q), не переставляя их, то он оста¬
нется расходящимся (докажите!).
Задача 2.39
Проверим, что сумма ряда
,11,11
1 + - + --1 + - + --
2 2 4 4
(группа членов
1
2n+i
■+
1111111111111111
- + - + + - + + - + + - + + - + + ...
2 4 4
J. 1_
2«+i 2”
2884884884884
повторяется 2п раз) равна единице. Найдем переста¬
новку, после которой сумма ряда станет равной -1.
Решение
Перепишем исследуемый ряд, отметив важные моменты:
11111111111111111111
1н—I 1н—I 1—I 1—I 1—I 1—I 1—I н....
2 2 4 4 2 4 4 2 8 8 4 8 8 4 8 8 4 8 8 4
111 I
Имеем An = + - — = 0. Заметим, что каждая дробь вида —, и = 0,1,2,...,
встречается в этом ряде 2” раз со знаком «+» и 2” раз со знаком «-». Поэтому дан¬
ный ряд представим в виде
Ih-H0-I-H1-I-H1-I-H2-I-H2-I-H2-I-H2-I-... = !,
147
так как Ak = 0. Сходимость данного ряда вытекает из утверждения 2.26.
Искомую перестановку получим, переставив члены ряда следующим образом:
11111111111111111111
—1 1-1 1 1 1 1 1 1 ....
2 2 4 4 2 4 4 2 8 8 4 8 8 4 8 8 4 8 8 4
Получаем -I - A0 - A1 - A1 - A2 - A2 - A2 - A2 -... = -1. Обоснование аналогично.
Задача 2.40
Пусть ряд У ап сходится. Обязательно ли сходятся следующие ряды:
Tl=1
а) U1 + Cl2 + Яд + CL0 + Gs + G7 + Gg + Gg + Gjg + Gjg +... + Gg + G32 +...',
б) Gj + G2 + (G3 + G^) + (Gg + Qq + Gg + Gg ) + (Gg + Gj j + Gjg + Gjg + Gjq + Gjg + Gj 4 + Gjg) +
+ (G17 +G19 +...) + ... (числовой ряд разбивается на группы длиной 2к элементов, вну¬
три которой сначала идут 2*-1 элементов с нечетными номерами, а потом 2k~l с чет¬
ными)?
Решение
OO п
а) Введем обозначения 5= У a„, Sn = У G4. Обозначим далее частичную сумму
я=1 A=I
переставленного ряда через Lm и заметим, что выполняется равенство (проверьте!):
Vm=Vi +i2»-Vr (2.10)
Из сходимости исходного ряда Уая вытекает, что Ve>0 3N(e) такой, что для
П-1
V п > N(e) выполнено \Sn - 5 <
е
3
. Следовательно, из равенства (2.10) следует, что
"2'*-1+¾ '
’ V - Г2”"1 +
- 9
'2" 2Я-А
S\ < |52„_j - S\ + |5ои -SI +1S,
2”
2”-A
c\ e e e
d <- + - + - = £,
1 3 3 3
если только n выбрано таким, что 2”-1 > N(г).
б) Данный ряд может и расходиться. Возьмем в качестве сходящегося ряда ряд
Лейбница У -—4=—. Тогда, в обозначениях п. а), для подпоследовательности [L 2)
я=I V п
выполняется следующее равенство (проверьте!):
2”-1-1 Л
^,„-2=v+4J_2v3tt'в=яз
откуда
1
T _ C > 9»-2 •
L3-2"-2 ^
—> + оо.
Поэтому из сходимости последовательности {5 n_j} следует, что [L п_2} —> + °°
Z o'Z у,—V00
В качестве самостоятельной работы предлагаем читателю решить сле¬
дующие задачи.
Задание 2.23
00 {—^ХП+1
Докажите, что сумма ряда У -—-— для V р > 0 лежит между — и 1.
я=1 пР 2
Задание 2.24
OO
Пусть У ап — расходящийся ряд с положительными членами, такими что ап —> 0.
я=1
148
Докажите, что для любого AsR существует последовательность чисел (знаков) {у„},
OO
состоящая из -1 и 1, такая что выполнено Yупа„ = А.
TZ=I
Задача 2.41
Рассмотрим некоторый условно сходящийся ряд Yan- Разобьем п-ю частичную
TZ=I
сумму этого ряда на два слагаемых Sn = Yak = Sn + Sn, где Sn и Sn — суммы соответ-
ы
S~
ственно положительных и отрицательных членов. Докажем, что существует Iim —-,
и найдем его.
Решение
OO
Действительно, так как ряд Yak сходится условно, то (см. доказательство теоремы
k=i
Римана) выполняется, что сумма Sn + Sn — ограничена для V п s N, а Sn - Sn —» + °°.
П—>оо
Отсюда 5+ —» + оо, поэтому
Sn , Sn +Sn _ ,. Sn .
—— +1 = — - —> 0=>1пн —= -1. * 1 2 * 1 2St
S+n ?z—>оо TZ—>°°
Задача 2.42
о® TZ—1 ^
Исследуем сходимость ряда ^а~нп-1,а > 0, где Нп_\ = ^ — частичная сумма гар-
я=2 A=I k
монического ряда.
Решение
По формуле Эйлера получим Hn_t = In(п -1) + C3 + о(1) и рассмотрим два случая.
1. Пусть а < е. Тогда Ya н«-1 > Ye i — расходится, так как е = О
я=2 я=2
2. Пусть а > е. Тогда 3 а > О такое, что а = е + а, откуда
' 1 Л
X (е + а) = Ye iVi
я=2 я=2
' OCЛ
1 + —
V eJ
-Н,
TZ-I
\П-Iy
Последний ряд сходится, так как
е яя-1 = О
( I ^ (.
, а 1 + —
Kn-\j
\ eJ
= 0(rln(n_1)),
^ . ос .
где q > 1, так как I + — > 1.
е
При изучении знакопостоянных рядов нами был доказано следую-
OO
щее утверждение: если ряд Y ап сходится и е > О — произвольное число,
TZ=I
оо
тогда ряд Y аи+е также сходится. Возникает следующий вопрос: будет ли
п=1
этот факт справедлив в случае условно сходящегося ряда? Ответ на этот
вопрос — отрицательный. Действительно, если в = 1, то контрпример стро-
149
V V (_1)и
ится очень просто: ряд Zian = У A
w=l n=l VW
OO OO I
X аи = X — расходится как гармонический.
w=l w=lW
Для 8 = 2 данный пример строится тоже несложно.
сходится как ряд Лейбница, а ряд
Задача 2.43
OO OO
Найдем сходящийся ряд У ип, для которого ряд У расходится.
W=I W=I
Решение
Например, положим
м =
W
2
если n = 3k-2,
1
-Ti=, если n = 3k-i,n = 3k,
vn
k>l.
В качестве последовательности {ап} с ограниченной последовательностью частич¬
ных сумм выберем последовательность
{ап} = {2,-1,-1, 2,-1,-1, 2,-1,-1,...}.
1
В качестве монотонно убывающей к нулю последовательности {Ьп} берем bn = —j=.
Уп
OO OO
Следовательно, ряд У w„ = ^arJbn сходится по признаку Дирихле.
п—\ п—\
DO
Далее, для ряда У и% получаем
W=I
8 118
“ о 8 I 1 8 8 I 1 “ 6
У = + —... + + ...> У
1 2 3 4 Зга-2 Зга-1 3 п ^Зп-2
т.е. ряд У и% расходится.
W=I * 1 2 3 * 1 2 3Предлагаем читателю построить соответствующие примеры для любого
натурального 8.
Более интересен следующий вопрос. Пусть г = p/q - 1, где q — нату¬
ральное нечетное число, аре Nh р> q. Всегда ли можно построить пример
OO OO
сходящегося ряда У ап такого, что ряд У а*+Е расходится (все члены ряда ап
W=I W=I
мы считаем действительными)?
Задача 2.44
Пусть {ап} — числовая последовательность, такая что ап —> 0. Докажите суще-
W-
ствование последовательности {&„}, для которой:
1) Ьх >Ь2 >...>Ьп >...>0 для я>1;
OO
2) ряд уб„ расходится;
W=I
OO
3) ряд У апЬп сходится абсолютно.
W=I
Решение
150
Найдем номер щ > 1 такой, что для V п>щ выполнено |ап| < —. Далее, найдем номер
I I 1
Ti2 > 2щ такой, что для V п > п2 выполнено IaJ < —, и т.д., находим номер пт > 2пт_1
21
такой, что для V п > пт выполнено \а„ < —.
т I »1 2т
Положим теперь bn= 1 при 1 < п < щ Ьп =-
ат ат-1
при пт_1<п<пт,п>2.
Так как мы проверяем абсолютную сходимость, то, не ограничивая общности,
считаем, что все ап>0 (иначе рассматриваем модули). Рассмотрим подпоследова¬
тельность частичных сумм Sn и Sn при щ, п2,..., где
Sn = ZakK Sn = ^bk.
k=i k=i
Обозначив!= sup \а{Ьх\, ползаем
”1 ”2 11 11
snk = Zakh + Z akh+--L'rh+ Z o' +-+ Z —
k=l k-щ+1 ”2_”l 2 Tl2 Tl1 nk~nk-\ ^ ak-\
слагаемых слагаемых
11 I
= L-Tii+-^ + -+ ... + -^<Ь-1ц + 1.
Отсюда, так как последовательность Sn не убывает, а подпоследовательность Sn^
ограничена, получаем, что Sn сходится.
Далее находим
— Tlx + ^ H...+ ^ ^ П\ +1 + 1 +... + I — (г1\ — I) + k,
H2-H1 Щ-Щ nk~nk-\ nk ~ nk-l kPl
слагаемых слагаемых
т.е. подпоследовательность Sn^ неограничена, поэтому и Sn неограничена.
Задача 2.45
Пусть ряд Yj ап сходится условно. Докажем, что существует числовая последова-
П=1
OO
тельность {Ьп} такая, что bn —» О и ряд Zanh расходится.
п-*°° п=1
Решение
Пусть Sn = Щ + а2 +... + \ап . Согласно условию Sn —> + °°. Положим Ьп = . п
Jl +Sn
OO OO \(Х
п = 1,2,.... Тогда —» 0. Докажем, что ряд Zianh = S / ” расходится. Действительно,
я=1 "=1V1 + ^
пусть Sn = 5^-iJsJ=. Тогда
^V1 + 5*
а0
А А
5.=-/24-; s2^^L+1a^>ts2>s^
-^! + S1 yl + S1 Jl + S2
Продолжая так же далее, получаем Sn
fl-j
+
а2\
1 + 52
Ifl1 I
+ ...+
ап\
Sn
м„
lI+Sn
—> + °°.
П—>°°
151
Зададимся далее следующим вопросом: может ли найтись такая число-
OO
вая последовательность в случае абсолютно сходящегося ряда Yarr Ответ
72—1
оо
на данный вопрос — отрицательный. Действительно, пусть ряд Y ап схо-
П=1
дится абсолютно и Iim Ьп =0. Тогда найдется номер N такой, что для всех
п—*°°
п> N выполнено \ bn \ < 1. Тогда
OO OO
O^X Ы-\ЬЯ\* X |аи|<const,
n=N n=N
OO OO
так как ряд Y ап сходится абсолютно. Следовательно, и ряд Y |апЬп | схо-
Tl=1 И=1
OO
дится, а поэтому сходится и ряд Y апЬп. Следовательно, такой последова-
Я=1
тельности не существует.
Задача 2.46
Установим на числовую последовательность {dn} необходимое и достаточное усло¬
вие того, чтобы для любой последовательности неотрицательных чисел {ап} из схо-
OO OO
димости ряда Y ап следовала бы сходимость ряда ^ ап ■ dn.
п=1 п=1
Решение
Докажем, что искомым условием, накладываемым на последовательность {dn},
является ее ограниченность.
Достаточность. Пусть 3 M > О такое, что для VneN выполняется \dn | < M. Тогда,
воспользовавшись критерием Коши сходимости числового ряда, получаем, что
для V е > О 3 N(e) такой, что для V п> NnV р е N выполнено
е
п+р
X
k=n+1
M'
Осталось воспользоваться неотрицательностью чисел {ап} и оценкой
п+р
п+р
X dnan
<М
X ап
k=n+1
k=Tl+l
Необходимость. Пусть последовательность {dn} неограничена. Тогда из данной
последовательности можно выделить бесконечно большую подпоследовательность.
Например, для любого AeN найдется номер щ, такой, что dn^ > k2. В качестве после¬
довательности {(ап} выбираем следующую:
О, если пФщ,
1
ап
k2’
если п = щ.
Тогда ряд Yjan безусловно сходится, но для ряда Yan^n не выполняется необхо-
Tl=I Tl=1
димое условие сходимости, и он расходится.
Зададимся следующим вопросом: какие необходимые и достаточные
условия нужно наложить на последовательность {dn} для того, чтобы
сю
для любой числовой последовательности {ап} из сходимости ряда Yan
и=1
152
OO
следовала бы сходимость ряда Eandn? Используя, например, тождество
W=I
Абеля, можно установить, что данным условием является требование огра-
OO
ниченности ее изменения, т.е. сходимость ряда E |dn - dn+i| (докажите!).
В качестве задач для самостоятельного рен/ёйия мы предлагаем чита¬
телю рассмотреть следующие упражнения.
Задание 2.25
Исследуйте на абсолютную и условную сходимость следующие знакопеременные
ряды:
a) Eb
TZ=I
' 1 Л
1+5Г
V <!П)
^ sinn . “(-l)”+1-n"+1/« “ (-1)1^]
arctg—; б) ExT^ —. Q > 0; в) E-
и
п~\
f
q-n +
1
п)
я=1 П
Задание 2.26
Докажите, что если последовательность {ап} монотонно стремится к нулю, то ряд
OO OO
EапsInnX сходится при всеххеМ,аряд EапcosnX сходится при всеххФ2тп,теZ.
п=\ п=1
Задание 2.27
Исследуйте на абсолютную и условную сходимость, в зависимости от параметров,
следующие ряды:
a) 2(-1)"-1
TZ=I
/1-3-5-...-(2п-1)ЛР
2-4-6-...-(2п)
; б) E tg
TZ=I
(—1)"+171
4n?
smnr-cos
;«) E-
п
„=1 1п1п(и + 1)
,г <
Задание 2.28
апг^ + а,хР~х +... + ап
пусть ад= v,+^,_1+ _ +4J
рациональная функция, где а0 ^ 0,60 ^ О
и 1й0г9 + ^r9-1 +... + bJ > О при г > и0. Исследуйте на абсолютную и условную сходи¬
мость ряд E (+1 )п R(ri).
п=по
Глава 3
ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ.
НЕПРЕРЫВНОСТЬ
3.1. Различные способы определения предела функции
Пусть E с R — некоторое числовое множество и а — предельная точка
множества Е. Пусть также на этом множестве определена действительно¬
значная функция /: E —» М. Мы хотели бы определить следующее базовое
понятие математического анализа: что означает, что при приближении
точки IG^Kfl значения /(х) приближаются к некоторому числу Ь, кото¬
рое мы будем называть пределом функции / при х, стремящемся к а. Обо¬
значение: Hm f(x) = b.
х^а
о
Будем обозначать символом BJa) проколотую (кружок означает «про-
колотость») дельта-окрестность точки а, т.е. объединение двух интервалов:
(а - 5; а) и (а; а + 5), а символом VJJb) = (Jb - s; b + в) — в-окрестность
точки Ь.
Определение 3.1 (предел функции по Коши). Hm /(х) = 6 <=> для любого
Еъх^а
в > 0 существует число 8(b) > 0 такое, что для всех х е E,0<\x-a\< 8(b),
выполнено неравенство |/(х) - b | < в.
о
То же самое коротко: V в > 0 3 8(в) > 0 : V х е EnBJa) имеем |/(х) -b\<
< в.
В дальнейшем, если будет понятно, по какому множеству E берется пре¬
дел, будем просто писать Hm f(x), опуская при этом значок е Е.
х—¥а
Перепишем последнее определение в терминах окрестностей:
Hm f{x) = b фф V Vz(b) 3 BJa) :f(BJa)) с Ve(Jb),
X—
о
т.е. для Vxg BJa) имеем/(х) G VJb).
Другими словами, число b является пределом функции /: E —» R при х,
стремящимся к точке а, если для произвольной е-окрестности VJb) точки b
о о
найдется проколотая 8-окрестность BJa) точки а, образ которой /(B8 (а))
при отображении / полностью содержится в окрестности VJb). Это доста¬
точно универсальная форма определения предела, которая может быть
использована для более сложных случаев топологических пространств1,
с более сложными понятиями окрестностей и отображений.
1 Подробнее о топологических пространствах читатель может узнать из книги [1].
154
Напомним, что окрестностью произвольной точки числовой оси называ¬
ется любой интервал, содержащий эту точку. Учитывая, что в любой окрест¬
ности точки содержится также некоторая симметричная 8-окрестность этой
же точки, мы приходим к следующей форме записи определения предела:
Hm /(х) = b^VV(b)3 В(а) : f(B(a)) с V(Jb)
х—>а
(символом В(а) обозначается произвольная (не обязательно симметрич¬
ная) проколотая оерестность точки а). Из последнего определения получа¬
ем, что для определения понятия предела функции/: X—» Унам достаточно
знания, что такое окрестность точки во множествах X и Y, или, как говорят,
если в данных множествах будет задана топология.
Определение 3.2 (предел функции по Гейне). Iim /(х) = Ь <=> для любой
Еэх^а
последовательности значений аргумента {х„} точек хп е Е\{а}, сходящейся
при п —> оо к точке а, соответствующая последовательность значений функ¬
ции [f(xn)} сходится при и —> оо к числу Ь.
Замечание 3.1. Отметим, что множество Е, на котором задана функция/,
не должно полностью покрывать окрестность B8 (а). Требуется только, чтобы
оно имело хотя бы один элемент в любой проколотой 8-окрестности точки а.
Для развития дальнейшей теории важным является следующее утверж¬
дение.
Утверждение 3.1. Определения предела функции по Коши и по Гейне
являются эквивалентными.
Введем понятие одностороннего предела функции /: E —> M в данной
точке а. Для этого потребуем, чтобы множество E для всех 8 > О имело хотя
бы один элемент, принадлежащий интервалу (а; а + 8) (интервалу (а - 8; а)).
Определение 3.3. Число b называется правым {левым) пределом функ¬
ции / по Коши, если V г > О 3 8(e) > 0, такое что V х,а<х<а + 8 (а- 8<
< х < а), выполнено |/(х) - b | < е.
Обозначение: /(а + 0) = Iim f(x) = Ъ (f(a - 0) = Iim f(x) = b).
х—мг+О
х->а-0
Определение 3.4. Число b называется правым (левым) пределом функции/
по Гейне, если для любой последовательности {хп} и хп> а (хп< а), хп —> °°,
соответствующая последовательность функций {/(хи)} сходится к числу Ь.
Оставляем читателю возможность доказать следующие взаимно обрат¬
ные утверждения.
Утверждение 3.2. Если функция / имеет в точке а как правый, так
и левый пределы, и если эти односторонние пределы равны одному и тому
же числу Ь, то эта функция имеет в точке а предел, равный Ь.
Утверждение 3.3. Если функция / имеет во внутренней точке своей
области определения1 а равный числу b предел, то как правый, так и левый
пределы2 функции / в точке а существуют и оба равны Ь.
1 То есть существует окрестность точки а, полностью лежащая в области определения
функции /.
2 Если область определения представляет из себя интервал (а; а + 8) или (я - 8; а), дела¬
ются соответствующие замечания.
155
Далее мы будем считать, что читатель знаком с понятиями бесконечно
малой и бесконечно большой функции, а также с их свойствами. Выраже¬
ние [а] обозначает ближайшее к а целое число, не превосходящее а, а {а} —
дробную часть числа а.
Приведем аналоги понятий точных граней числовых множеств для чис¬
ловых функций. Пусть XcR, дадим следующие определения.
Определение 3.5 (верхняя и нижняя грани функции). А) М* = supf(x) <=>
х
** I) V X G Xfix) < M*; 2) V в > 0 3 х' е X: f(x') >М*-е; Б) М* = inf/(x) ^
о I) V X G Xfiх) > M*; 2) V в > 0 3 х" G X: fix") < < М* + в.
Определение 3.6. Будем называть функцию / ограниченной на множе¬
стве X, если 3 M > 0 такое, что для VxgX выполнено |/(х)| < M (ограни¬
чена сверху и снизу).
Утверждение 3.4 (о локальной ограниченности функции, имеющей
конечный предел). Пусть/: E —> R и 3 Hm fix) G R. Тогда существует 8 > О,
х—>я
такое, что функция / ограничена на множестве В8{а) n Е.
Далее рассмотрим несколько задач.
Задача 3.1 (модифицированная функция Римана)
Покажем, что функция, определяемая условиями
ш
п, если X = —, НОД(»г, п) = 1,т,пе N,
п
О, если х — иррациональное,
конечна, но неограничена в любой окрестности любой положительной точки х.
На рис. 3.1 изображена рассматриваемая функция на отрезке [0; 1] для всех рацио¬
нальных точек со знаменателем, меньшим 500.
fix) = -
450
400
350
300
250
200
150
Рис. 3.1
Решение
Конечность рассматриваемой функции следует из ее задания, так как в каждой
точки она принимает конечное значение.
156
Докажем ее неограниченность в любой окрестности любой положительной
точки х. Используя определение ограниченности функции, напишем, что означает
неограниченность функции / в окрестности произвольной положительной точки х.
дляУб>0, Ух>0, VM>0 3 — ЕВг(х):щ >М.
щ
Таким образом, по произвольным 5,ти M нужно построить пару Tra1 и щ, удов¬
летворяющую указанным условиям.
Будем рассматривать щ >[М] +1, в этом случае условие щ>M заведомо выпол¬
нено. Кроме того, выберем данное число так, чтобы выполнялось условие -5щ < -1
(это всегда можно сделать, так как 8 > 0). Далее, по положительному числу Xn1 по тео¬
реме Архимеда (см. гл. 1) находим такое число Tra1 е N, что
Vn1-1 < Xn1 < Tn1, или -I < Xnl - Tra1 < 0.
(3.1)
Числа W1 и Tra1 выбираем так, чтобы они были взаимно простыми.
Вернемся к задаче о нахождении для произвольного положительного х такой
дроби —, что выполняется неравенство
щ
х-
тл
щ
<8, или -Sra1 <Xn1 -Tra1 <Sra1.
(3.2)
Сравнивая неравенства (3.1) и (3.2), получаем, что для выбранных Tra1 и TT1 пра¬
вое неравенство из (3.2) выполняется при любых 8 > 0 и щ е N.
Левое неравенство выполнено, так как -Sra1 < -1.
Неограниченность рассматриваемой функции в принципе можно
было доказать от противного. Пусть 8 > 0, х > 0 и функция / ограничена
в 8-окрестности точки х. Следовательно, З 8 > 0, х > 0, M > 0 такие, что
|/(х)| < M для всех XG (х - 8, х + 8).
Отсюда для всех т/п = х g (х - 8, х + 8) n Q выполняется п<М, при этом
х-8<х = — <x + 8=>m<(x + 8)-n.
п
Но тогда, так как п < [М\ + I, т < [(х + 8)М] + 1, то на выбранном интер¬
вале может находиться только конечное число рациональных чисел, что
неверно.
Задача 3.2
Найдем (если они существуют) следующие пределы:
a) Hm х
>о
; б) Hm —
>о а
, а>0,Ь>0; в) Hm
я—>0 X
Решение
а) Представим выражение
'Г
в виде
'Г
fiI
X
X
X
[х]
х
т1-х\х\-
Второе слагаемое в последнем выражении представляет собой произведение бес¬
конечно малой при х —» 0 функции на ограниченную. Следовательно, искомый пре¬
дел равен единице.
157
б) Аналогично п. а получим
X
~Ъ
X
/-J
(»11
Il
I
I
IH
А
(6)
а
X
а
I4X
.*и
а а
xj
Отсюда получаем, что искомый предел равен —.
Ы ®
в) Так как [х] = 0 при 0 < х < 1, то Hm — = 0. Далее, при -1<х<0 имеем [х] =
.г—>0+0 X
\х] [х|
поэтому Hm Следовательно, искомый предел Hm — не существует.
х->0-0 X х—>0 X
-1,
Задание 3.1
( /
Г11
Г ? 1
Г *]Y|
Вычислите предел Hm
X2
+
+ ...+
х->0
I V
-X-
-X-
-x^ AjJ
Определение 3.7. Будем говорить, что число b является пределом функ¬
ции / при х —> +оо (предел при х —> -°° определяется аналогично), если
V е > 0 3 Л(е) > 0 такой, что Vi> Л(е) выполнено \f(x) -Ъ | < е.
Иногда бывает полезно использовать эквивалентное определение.
Определение 3.8 (по Гейне). Будем говорить, что Hm f(x) = b, если
для любой последовательности {хп}, сходящейся к соответствующая
последовательность значений функции {f(xn)} стремится к числу Ь.
Задача 3.3
Пусть/: IR —»M — функция, периодическая с периодом Т> 0 и отличная от посто¬
янной. Докажем, что /(х) не может иметь предела при х —» +°° (х —> -°о).
Решение
Так как функция /(х) не постоянная, то найдутся такие X1, X2 E [Г; 2Г], что выпол¬
нено /(X1) = ухФу2= /(х2 ).
Построим две последовательности: х' = X1 + пТ и х" = X2 + пТ. Заметим, что обе
эти последовательности стремятся к +°° при п —> °°. Ясно, что
Hm f(x'n) = ухФу2 = Hm /(х").
Отсюда делаем вывод, что предела Hm /(х) не существует.
Х-Н-оо
Задание 3.2
Докажите, что не существовуют пределы Hm sinx и Hm cosx, не используя ре-
X—>оо X—>оо
зультат задачи 3.3.
Задача 3.4
Определим, существует ли предел Hm /(х) функции/: [0; +°°) —»М, если для V а > О
Х^+оо
f(a + п) —> О при п —> °°.
Решение
Покажем, что предел не обязательно существует. Пусть, например,
/(*)=■
1, если х = пЛ, nsN,
О, если х E M\{W2}.
158
Рассмотрим две последовательности х'п = {п42} и х" = {п}. Получим, что
Hm f(x'n) = I; Hm fix") = 0.
П—> оо п—> оо
Следовательно, предел Hm /(х) не существует. Однако Hm /(я + п) - О для любого
X—>+°° п—>°°
я е R. Действительно, рассмотрим хп = а + п (для простоты при я>0). Выясним,
сколько элементов этой последовательности могут иметь вид 42т. Рассмотрим
уравнение 42т = а + п при различных я, яг € N. Пусть оно выполнено при каких-то
т и п, т.е. а = \[2т* -п. Если существуют другие тип, которые удовлетворяют
уравнению, то
42т = (42т* -п) + п, или 42(т-т*) = п-п .
Так как 42 — иррациональное число, то последнее равенство возможно лишь при
п - п = О и т - т = 0, т.е. уравнение 42т = а + п если и имеет, то единственное реше¬
ние п, т G N. Следовательно, последовательность Xn = а +п может иметь с множеством
{42т} не более одной общей точки.
Задание 3.3
Определите, существует ли предел Iim f(x) функции/: [0; +°°) —> R, если для V я > О
f(an) —> О при п—> °о.
Задание 3.4
Пусть функция f(pc) определена на бесконечном интервале (*0; +00X ограниче¬
на в каждом интервале (х0; Xi) и существует конечный или бесконечный предел
f(x + 1) — fix)
Iim — \ J 4 ', я = 0,1,2,... . Докажите или опровергните контрпримером следу-
Xn
,. fix) I ,. fix + \)-fix)
ющеетождество: Iim = Iim — .
п +1
х=>°° X
п+1
Xn
3.2. Асимптотическое сравнение функций. О-символика
Рассмотрим задачу об описании поведения функции вблизи некоторой
точки (конечной или бесконечно удаленной), в которой, например, сама
функция не определена. В этом случае говорят, что интересуются асимпто¬
тикой или асимптотическим поведением функции в окрестности данной
точки. Асимптотическое поведение функции, как правило, характеризуется
с помощью другой, более простой для вычислений функции (обычно сте¬
пенной), которая в окрестности исследуемой точки с малой относительной
погрешностью воспроизводит значения изучаемой функции.
Определение 3.9. Если для функций / и g существуют некоторая про-
о о
колотая окрестность Bix0) и постоянная C > О такие, что для Vie Bix0)
выполняется неравенство |/(х)| < C • |g(x)|, то функция / называется огра-
о
ниченной по сравнению с функцией g на Bix0) и это записывается как
fix) = Oigix)), х -> х0.
Замечание 3.2. Иногда удобно представлять функцию /(х) = 0(g(x)),
о
х —> х0, в виде/(х) = cp(x)g(x), где ср(х) ограничена на Bix0).
159
Определение 3.10. Если функции / и g такие, что f{x) = 0(g(x))
и g(x) = 0(f(x)) при х —» х0, то они называются функциями одного порядка
при х —» х0. Обозначение: /(х) — g(x), х —> X0.
Определение 3.11. Функции/и g называются эквивалентными при х —> X0,
о
если в некоторой окрестности В(х0) определена функция ф, такая что
/(х) = ф(х)£(х) и Hm ф(х) = 1. (3.3)
X—>Xq
Замечание 33. Из выполнения условий (3.3) следует, что в некоторой
окрестности точки X0 выполнено равенство g(x) = \|/(х)/(х) и Hm \|/(х) = 1.
X—>Xq
В качестве функции \|/(х) можно взять 1/ф(х). Таким образом, определение
эквивалентности симметрично.
Определение 3.12. Функции / и g, эквивалентные при х —> х0, называ¬
ются также асимптотически равными при х —» х0. Обозначение: /(х) ~ g(x),
х—>х0.
о
Замечание ЗА. Если в некоторой окрестности В(х0) справедливы нера¬
венства /(х) Ф 0, g(x) Ф 0, то условия (3.3) тождественны соотношению
НтЛ£) = 1(или цтЖ£) = 1).
x^x0 g(x) X^x0 /(х)
О
Определение 3.13. Если в некоторой окрестности В(х0) выполнено
/(х) = a(x)g(x), где Iim а(х) = 0, то функция /(х) называется бесконечно
X—>Xq
малой по сравнению с функцией g(x) при х —> х0. Обозначение: /(х) = o(g(x))
при х —> х0.
Замечание 3.5. Если g(x) Ф 0 при х Ф х0, то условие /(х) = oc(x)g(x),
f(x)
Iim a(x) = 0 можно переписать в виде Iim J v ' = 0.
X—>Xq X—>Xq g(x)
При этом надо понимать, что под символами о(/(х)) и 0(/(х)) понима¬
ются не конкретные функции, а множества функций, обладающих соответ¬
ствующими свойствами.
Рассмотрим некоторые утверждения, помогающие исследованию асим¬
птотического поведения функции.
Утверждение 3.5. Если /(х) = o(g(x)) при х —» х0, то /(х) = 0(g(x))
при X —» х0.
Доказательство
Из равенства/(х) = o(g(x)) при х —» X0 следует, что /(х) = a(x)-g(x), где
а(х) есть бесконечно малая функция при х—»х0. Тогда ос(х) ограничена
о
в некоторой окрестности В(х0), поэтому 3 C > 0 такая, что справедливо
|/(х)| = |a(x)g(x)| < c|g(x)|
о
при Vxg В(х0). Это и доказывает требуемое. ■
Замечание 3.6. Обратное, вообще говоря, может не выполняться. Напри¬
мер, выполнено, что xcosx = О(х) при х —» 0, но данная функция не есть
о(х) при х —> 0.
160
Утверждение 3.6. Если /(х) = (p(x)g(x) и 3 Hm ф(х) = k < °°, k Ф 0, то
X—>Xq
Ах) = 0(g(x)), х -» х0.
Доказательство
Доказательство аналогично доказательству утверждения 3.5, использу¬
ется тот факт, что функция, имеющая конечный предел в точке х0, является
ограниченной в данной точке. ■
Замечание 3.7. Условие из утверждения 3.6 берется за определение мно¬
жества 0*(g(x)), т.е. нами было доказано, что 0*(g(x)) с 0(g(x)).
fix)
Утверждение3.7. Если 3 Hm =k<
°°? кф 0, g(x) Ф 0, то /(х) - g(x),
X^x0 g(x)
X —> X0.
Доказательство
Обозначим ф(х) =
f (х)
. Тогда /(х) = (p(x)g(x) и Hm ф(х) = &<°°.
g(x) X^x0
Используя утверждение 3.6, получаем, что /(х) = 0(g(x)), х —> х0. Анало-
ZW
^O, то 3 В(х0) такая, что для VxeB(X0)
гично имеем: так как Hm
х->х0 g(x)
f (х)
справедливо Ф0, а значит, /(х)ф0. Для х из этой окрестности поло¬
жим
g(x)
g(x) I
\|/(х) = ~.v 7 => g(x) = \|/(х)/(х) и Hm \|/(х) = —. Используя утвержде-
/ (х) x->xQ k
ние 3.6, получаем g(x) = 0(/(х)), х —> х0, или /(х) ~ g(x), х —> х0. ■
Утверждение 3.8. Для того чтобы функции / и g были эквивалентными
при х —» х0, необходимо и достаточно, чтобы при х —» х0 выполнялось условие
/(х) = g(x) + o(g(x)) или g(x) =/(х) + o(f(x)).
Доказательство
Необходимость. Пусть /(х) g(x), х > xQ, т.е. /(х) = Ф(х^(х), где
Hm ф(х) = I. В этом случае
X—>Xq
fix) - g(x) = ф(x)g(x) - g(x) = (ф(х) - l)g(x) = a(x)g(x),
где Hm oc(x) = Hm (ф(х) -1) = 0, откуда получаем выполнение асимптоти-
X—^Xq X—^Xq
ческого равенства /(х) = g(x) + a(x)g(x) = g(x) + o(g(x)). Равенство g(x) =
= f(x) + o(f(x)) доказывается аналогично (докажите!).
Достаточность. Пусть выполнено равенство /(х) = g(x) + a(x)g(x),
где Hm a(x) = 0. Тогда /(х) = (I + a(x))g(x) = Ф(х^(х), где Hm ф(х) =
X—>Xq X—>Xq
= Hm (I + ос(х)) = 1, т.е. /(х) g(x), х->х0. ■
X—^Xq
Следующее утверждение бывает исключительно полезно при вычисле¬
нии пределов функций.
Утверждение 3.9. Пусть /(х) Z1(X) и g(x) g^x) при х —» х0. Тогда
.. Z1(X) ,. ZW I. ZW I. ZiW
если 3 Hm , то 3 Hm , причем Iim = Hm .
*->*o£lW х^хо g(x) X^x0 g(x) X^XQg1(X)
161
Доказательство
Предположим, что выполняются равенства
fix) = (${x)f{x), X -> х0, g{x) = \|/(x)g1(x), X -> x0,
■f
где Iim ф(х) = Hm \|/(x) = I. Далее, так как 3 Hm , то gt(x) Ф О
X^>Xq X—>Xq X^>Xq §i\X)
торой проколотой окрестности точки х0. Так как 3 Hm \|/(х) = 1, то \|/(х) Ф О
в неко-
X—>Хл
в некоторой, возможно другой, проколотой окрестности точки X0. Поэтому,
так как g(x) = \|/(x)g1(x), то и функция g(x) должна быть отлична от нуля
в некоторой окрестности точки х0. Следовательно, по крайней мере там же
/(х)
определена дробь J 4 7. Окончательно получим
gfe)
fjx) = Cp(X)Z1(X) _ lim /(х)= lim Ф(х) Ит /Дх) = Ит /Дх) и
g(x) \|/(x)g1(x) X—>Xq ё(х) X—>Xq \|/(x) X—>Xq gl(x) X—>Xq gl(x)'
Утверждение 3.10. Если выполняются асимптотические равенства Zi (х) =
= Ofe1(X)), f2(x) = 0(g2ix)) при х —> х0, то тогда выполнено и f\(x) • f2(x) =
= Ofe1(X) • g2(x)), х —> х0.
Доказательство
Следует из определения символа 0(g) и использования того факта, что про¬
изведение двух ограниченных функций является функцией ограниченной. ■
Рассмотрим далее задачи.
Задача 3.5
Пусть х —> 0 + 0. Покажем, что бесконечно малые Zife) =,—, Z>fe) = е~^х не срав-
Inx
нимы со степенной функцией Xk, каково бы ни было k, т.е. ни при каком k не может
иметь место равенство
Hm = M = const, 0<|м|<°°,г = 1,2.
х^0+0 Xk
Решение
1
Найдем значение предела Iim в зависимости от значения параметра k
х—>0+0 Xkgl/x2
(k Ф 0, так как при k = 0 результат очевиден).
1. При & < 0 имеем lim е1/*2 = +°°, lim Xk =°°. Поэтому искомый предел равен нулю.
х—>0+0 х-»0+0
2. При k > 0, делая подстановку в изучаемом выражении, получаем
1
XkelZx2
tk
при 0 < х < 1 выполнено t> 1.
Используя теорему о двух милиционерах и то, что предел числовой последователь-
72^
ности Iim — = 0 при всех ke R, получаем
ге->°° еп
п tk tk (И+1)* (И+1)* М* л +
0< — < — <VLJr,fe = _J,, у £->+°°.
еМ
Поэтому и в этом случае Hm
1
х—>0+0 х k е ^
[tf
= 0.
еМ
162
Для второго предела рассуждения аналогичные.
1. При k < О неопределенности нет, искомый предел равен нулю.
2. При k > 0 получаем
1
Xk In*
tk
Ini
gklnt
Ini
= {ini = г/} = ~~~ < “
№1
+ —ОО.
Следовательно, при k > О получаем, что Hm —т-
*->0+0 Xk In* *
Задача 3.6
Пусть для я G N число хп — корень уравнения * = tg * из интервала (тш; п(п + 1)).
Докажем, что
Ti 1 „
* = тш + + О
2 тш
Г 1 Л
я2,
Решение
Изобразим графики функций tg * и * (рис. 3.2).
Рис. 3.2
Будем рассматривать положительные корни уравнения * = tg *. Изучение отри¬
цательных корней производится аналогичным образом. Из графиков функций оче¬
видно, что каждый положительный корень хп лежит в интервале
C _л
тг
тш; тш + —
V aJ
,яеК.
Кроме ТОГО, хп —> +OO при Я —> +оо. Поэтому tg*n = *„ —» +OO при Я —> +OO.
Tl
Обозначим уп=хп-т- —. Из приведенных выше рассуждений получаем, что
уп < 0. Далее, используя формулу приведения, получаем
Tl
Уп+пп+2 =xTi=tZxn=tS
Уп + пп + -
Tl
=-Ctg У я
Поэтому ctg уп = -tg хп, откуда уп = arcctg(-tg *„) —> О при я —» +°° в силу непре¬
рывности функции arcctg i и стремления -tg хп к -°° при я —> оо.
Учитывая этот факт, разложим ctgz/ra в ряд по степеням уп.
163
Ctg yn =
ЩУп y„ + 'J."+o(i,l) у- 3
Следовательно,
Уп + ™ + ? = -— + % + °(Уп)» или У1 + Уп
2 Уп 3
( ял
JW + -
V 2У
= -1 + Й + 0(у2).
Замечая, что —у2 + о(у2) = 0(у2), имеем
3
Уп=~
Используем соотношения
1
I 1
+ 0(и2).
пп + п/2 пп + п/2 "
1
JW + Jl/2 7Ш
1 —
П/2
\
пп + п/2
(Ky2n)=O
-— + О
пп
г х\
\П-
1
+ ~0(у2)
V "'- ■ "I “ J
Vl f
= O
1 (1л
= -—+ 0
пп
\.n-j
п
1
(
nz
\
К
-- + О
п
(О
уП;
V
+ Q(y2)
= O
(1 ^
Kn )
О
+
Г П
п
, откуда хп = пп н
I
+
О
гп
JW
W)
2
JW
(n2J
Задание 3.5
Пустьхп=CtgJfre, причемJfre е (пп; п+пп). Докажите, чтоJfre
1
JW + —
пп
Г л \
+ 0
\nL J
п—» +
Задание 3.6
Пусть Jf —» 0 и п > 0. Покажите, что:
а) M ■ O(Xn) = O(Xn)jM^ 0 — постоянная;
б) O(Xn) + O(Xm) = O(Xn), п<т;
в) O(Jfw) • O(Xm) = 0(хп+т).
Замечание 3.8. При х —» °° в задании 3.6 все остается так же, кроме п. б,
в котором уже выполняется O(Xn) + O(Xn) = O(Xm), п<т, так как при х > 1
имеем |х”| < \х?п\.
Задание 3.7
Предположим, что f(x) = o(g(jf)), g(x) —> +°°, jf —> +°°. Докажите или опровергните,
что = o(es(x)), х —» +°°.
Обратимся далее к методу выделения главной части функции, кото¬
рый может быть исключительно полезен при решении различных задач
из курса математического анализа.
Определение 3.14. Пусть функции а(х) и Р(х) определены в некоторой
о
проколотой окрестности В(х0). Если функция ос(х) представима в виде
а(х) = Р(х) + о(Р(х)), х —> х0, то Р(х) называется главной частью функции
а(х) при х —> х0. 1 11 Как было отмечено выше, Iim уп = 0.
П—>°°
164
Отметим, что главная часть функции ос(х) при х —> X0 может быть опре¬
делена неоднозначно. Так, например, справедливы представления
а(х) = 2х- Зх3 + X5 = 2х + о(х); а(х) = 2х- Зх3 + х5 = 2х- Зх3 + о(2х - Зх3)
при х —> 0.
Вообще, в общем случае в качестве главной части можно выбрать произ¬
вольную функцию, эквивалентную а(х). Поэтому возникает правомерный
вопрос о выборе такого вида главной части, чтобы она задавалась един¬
ственным образом. Ответ на это дает следующее утверждение.
Утверждение 3.11. Если функция ос(х) обладает при х —> X0 главной
частью вида А{х - х0)к, Аф 0, то среди всех главных частей такого вида она
определяется единственным образом.
Доказательство
От противного. Пусть при х —> X0 выполнены два тождества:
а(х) = A1 (х - х0 )^ + о((х - х0 )^1) и а(х) = A2 (х - X0 )¾ + о((х - X0 )*2 ),
в которых обе константы, A1 и A2, отличны от нуля. В силу эквивалентностей
A1 (х-X0)^ ~ а(х), A2(х-х0)k2 ~ а(х)
и транзитивности этого отношения получаем, что Д(х -X0)^1 ~ А2(х - X0)^2,
Последнее равенство справедливо только при A1 = A2 и k1 = k2. ■
Замечание 3.9. Пример из задачи 3.5 показывает, что главной части
относительно заданного набора (шкалы) функций может не существовать.
Задание 3.8
Пусть л:—» 0. Выделите главный член вида Caf1, (C=const, п — порядок малости от¬
носительно переменной х) следующих функций: Z1 (х) = Vl-Kr - Vl-х; /2 (х) = х - sin х.
Задание 3.9
Пустьх—»1. Выделите главный член вида С(х-1)” следующих функций: Z(x) = Inx;
Z>(x) = Xх -1; Zj(x) = 4^х - 5Vx +1.
Задание 3.10
3.3. Непрерывность функции. Свойства непрерывных функций
Рассмотрим действительнозначную функцию /: E —» К, определенную
в некоторой окрестности точки а е Ea R.
откуда
Cr-xO^2
Пусть х —> 1 + 0. Выделите главный член вида C следующих функций:
U-I)
165
Определение 3.15. Будем называть функцию / непрерывной в точке
a E Е, если для любой окрестности V(Jia)) значения f(a) функции, прини¬
маемого ею в точке а, найдется такая окрестность В(а) точки а в множестве
E (т.е. В(а) n E), образ которой/(5(a)) содержится в V(f(a)). Обозначение:
f(x) E С(а).
Эквивалентные формулировки:
f(x) — непрерывна в точке а о V Vif (а)) 3 В(а), такая что f(B(a) пЕ) с
с V(f(a)).
f(x) — непрерывна в точке а <=> V в > 0 3 5(в) > 0: для VxeE, такого
что \х - а \ < 8, выполнено |/(х) - f(а)\ < е.
Заметим, что определение функции в точке а (не обязательно предель¬
ной точки множества Е) является необходимым условием непрерывности
функции f т.е. должно существовать значение f(a).
Пример 3.1
Пусть а — изолированная точка множества Е. Следовательно, найдется такая
окрестность В(а), в которой нет других точек множества Е, кроме самой точки а.
В этом случае выполняется В(а) п E = {а}, и поэтому f(B(a) n Е) = f(a) с V(f(a)),
какова бы ни была окрестность V(f(a)). Таким образом, в любой изолированной
точке области определения функция, очевидно, непрерывна.
Замечание 3.10. Обратим внимание читателя на то, что понятие предела
в изолированной точке не определено.
Пусть далее а — предельная точка множества Е. Докажем, что функция
/: £ —» R непрерывна в данной точке тогда и только тогда, когда выполнено
тождество Hm f(x) = f(a).
Еъх^а
Доказательство
Если функция / непрерывна в точке а, то согласно определению
для произвольной окрестности ViJ(а)) найдется окрестность В(а) точки а
о
такая, что f(B(a)r\E)czV(f(a)). Одновременно будем иметь, что f(B(a) п
r\E)a V(J(a)). Поэтому в силу определения предела получаем, что выпол¬
нено Hm f(x) = f(a).
Еэх^а
Обратно, пусть Hm f(x) = J(а). Тогда по окрестности V(J(a)) найдем
Еъх^а
О О
проколотую окрестность В(а), для которой выполнено f(B(a) глЕ) с E(f(a)).
Поскольку f(a) E V(f(a)), то и f(B(a) n Е) с V(f(a)), что и означает непре¬
рывность функции /в точке a E E. ■
Опуская символ Eэх, перепишем условие непрерывности в виде
Hm f(x) = /(Hm х),
х—>а х—>а
т.е. функция / непрерывна в точке а тогда и только тогда, когда она пере¬
становочна с операцией предельного перехода.
Определение 3.16. Будем называть функцию / непрерывной на множе¬
стве Icf, если она непрерывна в каждой точке множества X Обозначе¬
ние: / E C(X).
166
Определение 3.17. Функция/называется непрерывной в точке а справа
{слева), если правый (левый) предел этой функции в точке а существует
и равен частному значению f(a) функции / в точке а.
Договоримся называть функцию / непрерывной на отрезке [а; Ь\, если
она непрерывна в каждой внутренней точке этого отрезка (т.е. на интер¬
вале (а; Ь)) и, кроме того, непрерывна справа в точке а и непрерывна слева
в точке Ь.
Сформулируем несколько важных свойств непрерывных функций,
которые понадобятся нам в дальнейшем. Доказательства этих утвержде¬
ний читатель может найти в любом учебнике по математическому анализу.
Утверждение 3.12 {арифметические операции над непрерывными
функциями). Пусть на одном и том же множестве заданы функции / и g,
непрерывные в точке а. Тогда функции f±g,f-g и f/g также непрерывны
в точке а (в случае частного нужно дополнительно потребовать g{a) Ф 0).
Утверждение 3.13 (о локальной ограниченности функции). Пусть
/: £ -> R и существует конечный предел Hm f{x). Тогда существует 8 > 0,
х—>а
такое что функция / ограничена на множестве E п В8{а).
Утверждение 3.14 {об устойчивости знака непрерывной в точке
функции). Пусть /: E —» R, / непрерывна в точке а этого множества и ее
значение f{a) положительно (отрицательно). Тогда 3 8 > 0 такое, что
f{x) > 0 (/(х) < 0) для Vxg В8{а) n Е.
Замечание 3.11. Иногда удобно пользоваться аналогом этого утверждения
с добавлением отделимости от нуля: пусть функция/непрерывна в точке а
и f{a) > 0 {/{а) < 0). Тогда 38>0иу>0 такие, что для Vxg В${а) n E
/(х) > у > 0 </(х) < -у < 0).
Замечание 3.12. Аналогичную теорему можно сформулировать для функ¬
ции/, непрерывной в точке а справа (слева). В этом случае найдется правая
(левая) 8-полуокрестность, удовлетворяющая тем же свойствам.
Утверждение 3.15 (о прохождении непрерывной функции через
нуль при смене знаков). Пусть функция / непрерывна на отрезке [а; b]
и f{a) ■ f{b) < 0 (т.е. ее значения на концах данного отрезка есть числа раз¬
ных знаков). Тогда внутри отрезка [а; Ь\ найдется точка £, такая что/(£) = 0.
Утверждение 3.16 {о прохождении непрерывной функции через любое
промежуточное значение). Пусть функция /непрерывна на отрезке [я; Ь\,
причем f{a) = a, f{b) = Р, а у — произвольное число, заключенное между а
и р. Тогда найдется точка £, е [а\ Ь], такая что f{t) = у.
Утверждение 3.17 {первая теорема Вейерштрасса). Если функция/
непрерывна на отрезке [а; Ь], то она ограничена на этом отрезке.
Замечание 3.13. Для интервала данное утверждение не имеет места.
Например, функция/(х) = 1/х непрерывна на интервале (0; 1), но она
не ограничена на нем.
Утверждение 3.18 {вторая теорема Вейерштрасса). Если функция/
непрерывна на отрезке [а; Ь], то она достигает на нем своих точных верхней
и нижней граней, т.е. найдутся точки X1, X2 G [а; b] такие, что выполнено
/(X1) = SupZ(X), /(х2)= inf/(*).
[a;b] [а\Ь]
167
Замечание 3.14. В силу последнего результата благодаря достижимости
sup/(x) и inf f(x) мы можем называть точную верхнюю грань максималь-
[сг,Ь] [а-,Ь]
ным значением, а точную нижнюю грань — минимальным значением функ¬
ции /на [й; Ь\.
Замечание 3.15. Обобщая утверждение о прохождении любого проме¬
жуточного значения, можно утверждать, что для каждого у, содержащегося
между sup/(x) и inf/(^)> найдется \ е [а; Ъ\, что такое/(£) = у.
[а;Ь] [а;Ь]
Определение 3.18. Если функция/: E —> R не является непрерывной
в некоторой точке множества Е, то эта точка называется точкой разрыва
функции /
Эквивалентные записи определения: точка ае E — точка разрыва функ¬
ции / о 3 V(f(a)), такая что для V В(а) 3 х е В(а) n E : f(x) € V(f(a)),
т.е. глЕ)<хУ)ффЗе> 0 такое, что для V 5>0 Big E : \х - а \ < Ь,
но I f(x) -f(a) I > в.
Рассмотрим далее несколько общеизвестных примеров разрывных
функций.
I. f(x) = |sgm:|. Имеем Blim = 1, но/(0) = 0.
х-»0
2. f(x) = sgnx В этом случае Hm = -I, Hm = 1. Оба односторонних
х—»0-0 х—>0+0
предела существуют, но они не совпадают между собой и не совпадают со
значением функции /(0) = 0.
3.
/(*)='
sin(l/x), если х Ф 0,
0, если х = 0.
Легко можно доказать, что $ limsin(l/x) (докажите!), хотя функция
х—»0
sin( 1 /х) ограничена.
Данные примеры объясняют следующую терминологию.
Определение 3.19. Точка а называется точкой устранимого разрыва
функции / если предел функции / в данной точке существует, но в точке а
функция /либо не определена, либо имеет частное значение /(а) Ф Hm fix).
х—>я
Определение 3.20. Точка а называется точкой разрыва первого рода
для функции / если существуют не равные между собой односторонние
пределы/(а - 0) Ф f {а + 0). Если все точки области определения функции /
лежат по одну сторону от точки а, рассматривается только один из одно¬
сторонних пределов.
Определение 3.21. Точка а называется точкой разрыва второго рода
для функции/, если в этой точке функция/не имеет по крайней мере хотя
бы одного из односторонних пределов или если хотя бы один из данных
пределов бесконечен.
Зададимся теперь вопросом о непрерывности и точках разрыва моно¬
тонной функции. Напомним следующее определение.
Определение 3.22. Функция /: E —> M называется невозрастающей
{неубывающей) на множестве X, если для любых точек хь X2 G X таких, что
168
X1 < х2, выполняется неравенство /(X1) >f(x2) (соответственно неравенство
/(* i) </(*2))-
Определение 3.23. Функция /: E —> R называется возрастающей (убы¬
вающей) на множестве X, если для любых точек X1, X2 G X таких, что X1 < X1,
выполняется неравенство/^) <f(x2) (соответственно/(X1) >/(х2)).
Утверждение 3.19. Если функция / является монотонной на отрезке
[я; Ь], то у нее существуют левый и правый пределы в любой внутренней
точке данного отрезка и, кроме того, существуют односторонние пределы:
f(a + 0) и/(6-0).
Доказательство
Без ограничения общности будем считать, что функция / монотонно
не убывает и X0 G (я; Ъ). Докажем, что существует предел
Hm /(*)= sup{/(x)}.
x^>xq-0 [a; xq)
Действительно, пусть М* = sup /(х). Из определения точной верхней
[а; х0)
грани числовой функции вытекают два условия:
1) для Vxe[я;х0) /(х)<ЛГ;
2) для V в > 0 3 х' е [я; х0): /(х') > М* - в.
Следовательно, справедливо неравенство в > М* - f(x') > 0 > -в. Далее,
в силу неубывания функции / получаем, что для всех х е [х'; X0) справед¬
ливо /(х) > /(х'). Поэтому для всех х' < х < X0 тем более справедливо нера¬
венство в > М* -/(х) > -в, что и гарантирует выполнимость требуемого. ■
Теорема 3.1. Если функция / определена на отрезке [я; Ь] и является
на нем монотонной, то она может иметь на данном отрезке только точки
разрыва первого рода.
Доказательство
Не ограничивая общности, будем считать, что функция / не убывает
и х0 G (я; Ь\. Тогда для V х G [я; X0) выполнено неравенство
/(*)</(*<,). (3.4)
Согласно доказанному выше утверждению в указанной точке X0 суще¬
ствует левый предел /(х0 -0). Из неравенства (3.4) следует, что/(х0 - 0) <
< /(х0). Аналогично для Vxg (х0; Ь\ выполнено неравенство /(х) > /(х0),
поэтому /(х0 + 0) > /(х0 ).
Если данные пределы совпадают с /(х0), то функция / непрерывна
в точке х0, иначе имеем в данной точке разрыв первого рода. ■
Следствие 3.1. Монотонная функция непрерывна тогда и только тогда,
когда она принимает все свои промежуточные значения.
Следствие 3.2. Множество всех точек разрыва монотонной на отрезке
[я; Ъ] функции не более чем счетно.
Доказательство
Опять предположим, что функция /не убывает на отрезке [я; Ь]. Тогда
в каждой внутренней точке разрыва х выполняется неравенство для левого
и правого пределов: /(х - 0) < /(х + 0).
169
Вспомним результат из гл. 1, гласящий, что каковы бы ни были два
вещественных числа, не равных друг другу, всегда найдется рациональное
число, заключенное между ними. Тогда каждой точке разрыва х можно
поставить в соответствие некоторое рациональное число ot(x) такое, что
f(x - 0) < ct(x) < fix + 0). Остается доказать, что разным точкам разрыва
X1 и х2 будут сопоставлены различные рациональные числа Ct(X1) и ос(х2).
Но это вытекает из монотонности функции /, так как если X1 < х2, то
/(X1 + 0) < /(х2 - О)1, откуда Ot(X1) < ct(x2).
Следовательно, множество точек разрыва функции/на интервале (а; Ь),
а значит, и на отрезке [а; b] эквивалентно некоторому подмножеству мно¬
жества рациональных чисел, которое, как известно, является не более чем
счетным. ■
Забегая вперед, отметим, что множество точек разрыва первого рода произ¬
вольной действительнозначной функции не более чем счетно. Данный резуль¬
тат, являющийся обобщением только что доказанного, мы рассмотрим далее.
Замечание 3.16. Важно понимать, однако, что точки разрыва монотон¬
ной функции могут быть и неизолированными. Для построения примера
такого рода фиксируем произвольное всюду плотное счетное множество
А с (а; b) и построим функцию /, монотонную на интервале (а; b), имею¬
щую разрывы в каждой точке данного множества А и непрерывную во всех
остальных точках интервала (а; Ь).
Для этого расположим точки множества А в виде последовательности
OO
{хп} и рассмотрим произвольный сходящийся ряд ^cn, состоящий из строго
я=1
положительных чисел сп. Зададим функцию / следующим образом:
f{x)= S сп, а<х<b,
п:х>хп
т.е. для вычисления значения данной функции требуется сложить все эле¬
менты сп, индексы п которых таковы, что х > хп. Если слева от х нет точек хп,
OO
то функция / полагается равной нулю. Поскольку ряд ^cn сходится абсо-
Yl=1
лютно, то порядок, в котором производится суммирование, не существенен.
В силу того что сп > О для VweN, функция / монотонно не убывает
на (а; Ъ). Далее, в силу определения функции / выполняется равенство
/(х„ + 0) -/(хп- 0) = сп > 0.
Поэтому каждая точка множества А является точкой разрыва первого
рода. Во всех остальных точках интервала (а; b) функция / представляет
из себя константу, а потому является непрерывной. Заметим также, что
построенная функция является непрерывной на интервале (я; b) слева.
Замечание 3.17. Можно было рассмотреть функцию fix)= ^ сп,
п:х>хп
а < х <Ь, которая также имеет точки разрыва в хп, но непрерывна на (а; Ъ)
1 Так как /(X1 + 0) = inf fix') < fix') < sup fix') = fix2 - 0) для любого X1 < x' < x2.
x >X\ x’<%2
170
справа. Функция же f(x) + fix) разрывна в каждом хп и слева, и справа
(докажите!).
Для формулировки дальнейших результатов напомним, что под откры¬
тым множеством мы понимали множество, состоящее только из своих
внутренних точек, т.е. множество X открыто, если для MxeX найдется
некоторая окрестность этой точки В(х), целиком лежащая в множестве X.
Множество F называется замкнутым, если оно содержит все свои предель¬
ные точки. Пустое множество 0 и всю действительную прямую R мы будем
считать открытыми и замкнутыми одновременно.
Докажем далее критерий непрерывности действительнозначной функ¬
ции / в терминах открытых множеств.
Утверждение 3.20. Функция /: X —» F, где XcR, FcR, непрерывна
на X тогда и только тогда, когда множество /_1(^о) = {% е X | f(pc) E G0}
открыто для любого открытого множества G0 е X, т.е. функция / непре¬
рывна тогда и только тогда, когда прообраз любого открытого множества
во множестве Y открыт в X.
Доказательство
Необходимость. Пусть функция / непрерывна, G0 с F — произволь¬
ное открытое множество, и X z> G = /-1 (G0). Требуется доказать, что мно¬
жество G открыто. Если G — пустое множество, то все доказано. В слу¬
чае, когда G не пусто, выберем произвольную точку <zgG = /_1(G0), т.е.
f{a) E G0. Следовательно, множество G0 можно рассматривать как некото¬
рую окрестность точки/(а), т.е. Vifia)). Так как функция / непрерывна
на множестве X (а значит, и в точке а), то для множества V(Jia)) найдется
окрестность Bid) такая, что /(5(a)) с Vifia)) = G0, т.е. В{а) с /_1(G0). Итак,
для произвольной точки a E /"!(G0) найдется ее окрестность В{а), целиком
лежащая в /_1(^о) = G.
Достаточность. Предположим, что при отображении / прообраз любого
открытого множества открыт. Возьмем произвольную точку a G X и произволь¬
ную окрестность Vifia)) ее образа в F Тогда окрестность Bid) = /_1(И(/(«))),
по предположению теоремы, — открытое множество в X, т.е. является окрест¬
ностью точки а. Причем образ Bid) при отображении /равен
f(B(a)) = = V(f(a)) с V(f(a)).
Следовательно, функция / непрерывна в точке а. В силу произвольно¬
сти точки а заключаем, что / непрерывна на множестве X. ■
Замечание 3.18. Иногда формулировка из утверждения 3.20 берется
за определение непрерывной на множестве функции.
Предположим далее, что функция Дх) отображает всякое открытое мно¬
жество в открытое. Верно ли, что она непрерывна? Ответ на этот вопрос —
отрицательный.
Пример 3.2
Рассмотрим множество Кантора Пс[0;1]. Определим функцию /: [0; 1] —> i?
так, чтобы она была равна нулю на П. В точках смежных интервалов зададим функ¬
цию / как преобразованный тангенс с центром в середине смежного интервала, при-
171
нимающий значения от + до на каждом из этих интервалов. Очевидно, что постро¬
енная функция / терпит разрывы во всех точках множества Кантора.
Однако для всякого интервала (а; b) с [0; 1] имеем следующее. Если (а\ Ь) гл П = 0,
тогда он непрерывно и взаимно однозначно отображается на интервал. Если же
(a; b) п П Ф 0, то, как это было доказано в гл. 1, этот интервал полностью содержит
некоторый смежный интервал, следовательно, отображается навею прямую R. Остается
заметить, что интервал и числовая прямая представляют собой открытые множества,
а любое открытое множество на отрезке [0; 1] представляет из себя объединение интер¬
валов.
На рис. 3.3 изображена рассматриваемая в примере функция, построенная
для нескольких первых шагов построения множества Кантора.
Замечание 3.19. Отметим, что в предыдущем примере вместо множества
Кантора можно было взять любое совершенное нигде не плотное множество.
Предоставляем читателю возможность доказать следующее утверждение.
Утверждение 3.21. Функция /: X —> Y, где XcR, FcR, непрерывна
на X тогда и только тогда, когда прообраз любого замкнутого множества
замкнут.
Рассмотрим далее две очень важные задачи.
Задача 3.7 (функция Дирихле)
Исследуем на непрерывность функцию
Jl, если л: е Q,
[О, если х е R\Q.
Решение
В любой окрестности произвольной точки X0 е R найдутся иррациональные
и рациональные точки. Следовательно существуют два предела
Iim D(x) = 0*1= Iim D(x).
R\Q3X->X0 Q3X—>Xg
Отсюда мы делаем вывод о том, что рассматриваемая функция терпит разрыв
второго рода в каждой точке действительной прямой.
Используя последний результат, можно легко сконструировать пример функции,
непрерывной только в точке 0. Это будет /(х) = х ■ D(x). Действительно,
172
Iim х • D(x) = O = /(0)
X—»0
как произведение бесконечно малой функции на ограниченную. Для доказательства
разрыва функции / во всех точках х0 Ф 0 докажем более общее утверждение: пусть
функция / разрывна в точке х0, а функция g непрерывна в данной точке, причем
g(x0) Ф 0. Тогда функция /(х) • g(x) разрывна в х0. Действительно, пусть функция
h(x) - fix) • g(x) непрерывна в точке х0. Тогда h(x)/g(x) также непрерывна в точке
х0, но h(x)/g(x) = f(x), которая в точке X0 терпит разрыв.
Имеем g(x) = х Ф 0 во всех точках X0 Ф 0. Следовательно, функция х ■ £)(х) тер¬
пит разрыв во всех точках X0 Ф 0.
Аналогично строятся примеры функции
/О(х) = (X-X1) • (х-х2) •... • (х-хга) • Dix),
непрерывной только на конечном множестве точек X1, х2,..., хга, и функции
/(2)(х) = sinx • Dix),
непрерывной только на счетном множестве точек xk - nk, k G Z.
Кроме того, легко строится всюду непрерывная суперпозиция всюду разрывных
функций
/(х) = Dix), g(x) = D(x). Тогда g(/(x)) = D(D(x)) = I.
В последнем равенстве было использовано то, что все значения функции Дирихле
(а именно, числа 0 и 1) рациональны. * б) * б)Задание 3.11
Постройте пример суперпозиции функций /и g, для которых:
а) / непрерывна, g разрывна, а суперпозиция /(g(x)) непрерывна;
б) /непрерывна, g разрывна, а суперпозиция/(g(x)) разрывна;
в) /разрывна, g непрерывна, а суперпозиция/(g(x)) непрерывна;
г) / разрывна, g непрерывна, а суперпозиция /(g(x)) разрывна.
Задание 3.12
Исследуйте на непрерывность и установите характер точек разрыва следующих
функций:
a) fix) =
tgx, если х G (
л/3,
если х е
б) fix) =
smx, если х <
1
—,если х G
2
Задача 3.8 (функция Римана)
Исследуем на непрерывность функцию
Rix) - ■
I 771
—, если X = —, НОД(ш, п) = I, т G Z, п G N,
п п
0, если х — иррациональное.
Функция Римана на интервале (0; 1) представлена на рис. 3.4.
Решение
Если точка X0 рациональная, то i?(x0) > 0, но в любой сколь угодно малой
окрестности данной точки находятся иррациональные точки х, в которых Rix) = 0.
Следовательно, в точке X0 функция R имеет разрыв (как мы докажем далее — устра¬
нимый).
173
0,5
0,4
0,3
0,2
0,1
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0
Рис. ЗА
Далее докажем, что функция R непрерывна в любой иррациональной точке.
Действительно, пусть X1 иррациональная. Выберем произвольное число е > 0.
Существует лишь конечное число натуральных чисел п, не превосходящих выраже-
1 т
ние -, а значит, вблизи точки X1 найдется лишь конечное число рациональных точек —,
е п
для которых
R
'тЛ
KnJ
— > Е. Следовательно, точку X1 можно окружить такой окрестно-
п
стью B(X1), чтобы в нее не попала ни одна из этих точек. Тогда при х е B(X1), будет
ли точка х рациональная или иррациональная, выполняется неравенство \R(x)\ < £.
Поэтому для любой иррациональной точки X1 существуют пределы
^(X1 -0) = R^x1 +0) = 0 = R(X1),
т.е. функция R(x) непрерывна в точке X1.
Отметим, что в любом интервале действительной прямой находится счет¬
ное число рациональных точек и несчетное число иррациональных. Следова¬
тельно, в любом интервале существует счетное число точек разрыва и несчет¬
ное число точек непрерывности. Возникает вопрос: можно ли построить
пример действительнозначной функции, имеющей континуум точек разрыва
и континуум точек непрерывности в любом не пустом интервале действи¬
тельной прямой? Примером такой функции является следующая:
1
, если в троичном разложении числа х E (0; 1)
п +1
содержится п единиц, п = 0,1,...,
0, если в данном разложении единиц бесконечно много.
Действительно, рассмотрим точку х*, в троичном разложении кото¬
рой нет ни одной единицы. Очевидно, что таких точек континуум1. Для
1 См. соответствующую задачу из гл. 1.
Т(х)=\
174
таких точек имеем f(x*) = I. В то же время для любого х = О, X1, х2, X3,где
Xi G {0,2}, можно построить последовательность уп = 0, Xi, х2,..., хи+1,...,
1
Iim уп = х, f(yn) = —. Следовательно, функция/разрывна в точке х*.
п—>°° 2
1 еперь рассмотрим точку х , в троичном разложении которой беско¬
нечно много единиц. Очевидно, что множество таких точек также имеет
мощность континуума. Пусть
** Л
X — U, X^y X 2ч м., ....
1
Рассмотрим е = -. Так как среди Xi бесконечно много единиц, то 3 Xk
такое, что Xk — п-я единица в разложении числа х**. Выберем далее 5 =
1
3k+2
гт-ч ^ **
1 огда каждое х, принадлежащее о-окрестности точки х , уже содержит в раз¬
ложении п единиц. Следовательно, для всех таких х выполнено неравенство
|/(х)| < , т.е. функция / непрерывна
п +1
в точке х
Вернемся к вопросу о мощности множества точек разрыва первого рода
произвольной действительнозначной функции. Трудность данной задачи
заключается в том, что можно построить пример функции, имеющей всюду
плотное множество точек разрыва первого рода в окрестностях некоторой
точки. Действительно, для функции
/(*) =
1
, если х < О,
О, если х = 0,
xsgn
( . 1Л
sin—
V XJ
, если х > 0,
получаем, что 0 — точка разрыва первого рода со скачком1, равным 1/2, в лю¬
бой правой окрестности которой есть бесконечно много других точек разрыва
первого рода (докажите!). Следовательно, стандартная техника доказатель¬
ства не более чем счетности рассматриваемого множества здесь не подходит.
На рис. 3.5 изображена рассматриваемая функция.
1 Под скачком функции / в точке разрыва X0 называется разность ее односторонних
пределов, если они различны.
175
Ответ на поставленный вопрос о мощности множества точек разрыва
первого рода дает следующее утверждение.
Утверждение 3.22. Действительнозначная функция / может иметь
не более чем счетное число точек разрыва первого рода.
Доказательство
Пусть х — точка разрыва первого рода, а Д(х) — скачок функции /,
соответствующий данной точке. Следовательно, для любого в>0 най¬
дется такое 8 > 0, что для V хе(х-8;х) выполнено |/(х) - f(x - 0)| < е, а для
V х E (х; х + 8) выполнено |/(х) - f(x + 0)| < в.
Поэтому для любого х найдется проколотая 8-окрестность, в которой
нет других точек разрыва первого рода со скачком больше 2в.
Разобьем луч (0; + °°) на объединение непересекающихся полуинтервалов:
Г1 Л
X г
I
Mje
^ I-J
U
3’ 2У
и... u [1; 2) и [2; 3) и... =
I 1
U .г
^И=1|_га + 1 п
W (ос Л
U Ut П\П + \)
JJ V«=l
Рассмотрим далее все точки разрыва первого рода х со скачками
из множества [а; Ь). Выберем 2в > а, например в = —, тогда для любой такой
3
точки х найдется число 8(х, в) > 0 такое, что в 8-окрестности х находятся
только точки разрыва первого рода со скачками меньше а (кроме, конечно,
самой ос). Покажем, что такие |-окрестности точек х не пересекаются.
Рассмотрим точки х' и х” такие, что А(х'), Д(х") е [а\ Ь). Пусть далее
8'= 8
г аЛ
х
V Зу
, 8" = 8
и предположим, что окрестности
f аЛ
х
8'
х \х +-
и
§" §
X , X -Y-
2 2
//Л
2 2^
пересекаются. Не ограничивая общности, считаем 8'>8". Но тогда
х" E (х' - 8'; х' + 8'), что противоречит определению числа 8(х, в).
Таким образом, всем точкам х со скачками из [а,Ь) можно поставить
в соответствие попарно непересекающиеся интервалы, т.е. множество точек
разрыва первого рода со скачками из [а; Ъ) счетно. Отсюда множество точек
разрыва первого рода — не более чем счетное объединение счетных мно¬
жеств, т.е. не более чем счетное множество. ■
Отметим, что рассмотренные выше примеры функций Дирихле D
и функции Tдемонстрируют, что множество точек разрыва второго рода
может иметь мощность континуума. Примером функции, имеющей счетное
число точек устранимого разрыва, является функция Римана R. Рассмотре¬
ние вопроса о мощности точек устранимого разрыва оставляем читателю.
Рассмотрим несколько вопросов, связанных с функцией Дирихле.
Задача 3.9
Докажем, что функция Дирихле представима в виде
D(x) = Iim (Iim cos” (шп! х)).
т—>°° п—>°°
176
Решение
Действительно, обозначим сомножитель гс в аргументе косинуса через t = m\x.
Нас интересует вопрос: когда это есть целое число? Очевидно, что при т —> °° число
t целое тогда и только тогда, когда х — рациональное. В этом случае 3 т0 такое, что
t0 = (jnQ\x)еZ и при т>1щ т\хеZ.
Заметим также, что число t в этом случае является четным, так как в число т\
при /га—»«а входят все степени двойки. А значит, cos(£ti;) = 1. Если же х eM\Q, то
такого номера т0 не найдется. Поэтому для V т имеем т\х € Z и |cos(Yrc)| < 1 для V L
Следовательно, выполняется
Iini (lim cos”(rcwz!x)) =
m—>°о п—>оо
[l, если х E (Q),
[О, если х E M \ Q
= D(x).
Введем важное определение.
Определение 3.24. Будем говорить, что последовательность функций
[fn(x)) сходится на множестве X, если числовая последовательность {/и(х0)}
сходится при каждом фиксированном X0 G X. При этом также говорят, что
последовательность [fn(x)) сходится на X поточечно, а данное множество
называется областью сходимости последовательности [fn(x)).
Предположим, что последовательность функций [fn(x)) имеет в каче¬
стве области сходимости некоторое множество X Совокупность пределов,
взятых для всех точек х из множества X, порождает множество значений
некоторой функции /(х), определенной на X. Эту функцию называют пре¬
дельной функцией последовательности {/„(х)}.
Более подробное изучение последовательностей функций (функцио¬
нальных последовательностей) будет проведено в дальнейшем, а сейчас
изучим следующий вопрос. Очевидно, что в предыдущей задаче функция
Дирихле являлась пределом (при т —> °°) функций, последовательность
значений которых имеет вид
{Dm (х)} = {Um cos П(пт! х)} = -
п—>°°
{0,0,
{0,0,
0,1,1,...}, если х G Q,
0,0,0,...}, если х G R \ Q
и которые являются всюду разрывными начиная с некоторого т.
Зададимся вопросом: существует ли последовательность непрерывных
на числовой прямой M функций {Dm(x)} такая, что D(x) = Hm Dm(x)? Ответ
т—>°°
на этот вопрос — отрицательный.
Доказательство
Докажем несуществование последовательности от противного. Предпо¬
ложим, что последовательность {Dm(x)} с указанными свойствами суще¬
ствует. Найдем на числовой прямой M точку в которой последователь¬
ность [Dm(Q) расходится, и тем самым придем к противоречию.
Пусть [а0‘,Ь0] — произвольный отрезок числовой прямой R. Выберем
точку X1 G (а0; &Q ) n Q — произвольное рациональное число, принадлежащее
интервалу (я0; bQ). Так как, по нашему предположению, D(X1) = Hm Dm(X1),
т—>°°
то 3 Tn1 такое, что D(X1)-Dm^(X1)
т.е., так как X1 рационально,
177
12 4
1 -Dmi(Xi) < или - < Dmi(X1) < -.
Так как функция D (х) непрерывна, зафиксируем такой отрезок \щJft1]
4 2 4
с центром в точке Xi, что \а{, ftj с (а0; Ь0) и — < DrrAx) < — для всех х е [щ , ftj.
3 3
Пусть, далее, X2 E(^1Jft1)Pi(RXQ) — произвольное иррациональное число
из интервала (а{, Ь{). Найдем такой номер т2 > ть что
D(X2)-Dm2(X2)
1
< — <=>
3
I I 1
Dm2(xI) < з <=> - з < Dm2(X2) <-.
Далее зафиксируем отрезок [а2,Ь2] с центром в точке X2 так, чтобы
1
[а2, Ь2] с (A1; ft^ и неравенство Dm (х) < — выполнялось для всех хе[а2;Ь2].
^ 3
Возьмем произвольное рациональное число X3 е (а2, Ь2) и повторим проде¬
ланные построения, заменяя (a0;fto) на (¾;¾)* а xI на хз> и Т-Д- По индук¬
ции мы построим такую последовательность номеров Mji и последователь-
1
ность вложенных отрезков {[ak;bk]}, что I-Dm (х) <—, хе[O2M^mL
21—1 3
1
и Dm (х) < —, х G [<я2/; ft2/]. По теореме о системе вложенных отрезков суще-
21 3
ствует хотя бы одно число Zs, принадлежащее всем построенным отрезкам.
2 1
Для такого Zs будет выполнено D2/_1(^)>—; D2i(Zt)K-. Отсюда может быть
3 3
получено неравенство \D2i_i(^)-D2i(^)\>—. Следовательно, по критерию
3
Коши последовательность {Dm (£)} не имеет предела. ■
Задача 3.10
Докажем, используя определение, что функция/(х) = х2 непрерывна в точке х = 1.
Решение
Запишем, что означает Hmx2 = 1 = /(1): для V е > 0 3 5(e) > 0 такое, что для
х->1
V х, |х -1| < 5(e), выполнено Ix2 —1| < е. Преобразуем выражение, стоящее под знаком
модуля:
Ix2 -1| = |(х -1)2 + 2(х -1)| < |х - Il2 + 2 |х -1| < 52 + 25 = е,
например, при 5 = -1 + VlTe.
Отметим, что при решении этой задачи числовая функция 8(e) полу¬
чилась непрерывной функцией от е. Это может натолкнуть нас на форму¬
лировку следующей задачи.
Задание 3.13
Докажите, что в условии непрерывности функции /(х) в точке х = а — для V е >
О 3 5(e) > 0: V х, |х - а \ < 5(e), выполнено |/(х) - f(a)\ < е — функцию 5 = 5(e) всегда
можно подобрать так, чтобы она была непрерывной.
Предлагаем читателю сейчас подумать над этой задачей самостоятельно,
а мы вернемся к ней в главе про интегралы.
178
Задача 3.11
Определим, существует ли непрерывная функция/: R —» R, принимающая рацио¬
нальные значения в иррациональных точках и иррациональные значения в рацио¬
нальных точках.
Решение
Предположим, что данная функция существует. Установим мощность множе¬
ства ее значений. По условию задачи имеем /(R\Q) с Q, т.е. образ множества ирра¬
циональных чисел не более чем счетный. Далее заметим, что в силу однозначно¬
сти функции / образ множества рациональных чисел /(Q) также не более чем счет¬
ный. Следовательно, множество значений исследуемой функции не более чем счетно
и содержит по крайней мере две различные точки (рациональную и иррациональную).
Приведенные построения вступают в противоречие с утверждением о прохожде¬
нии непрерывной функции через любое промежуточное значение. Ибо если непре¬
рывная функция принимает два различных значения, то она принимает и любое зна¬
чение, заключенное между ними, а их несчетное число.
Задача 3.12
Пусть у действительнозначной функции /: R —> R в каждой точке X0 E R суще¬
ствует конечный предел Iim /(х) = g(x0). Верно ли, что функция g(x) непрерывна?
х~*хо
Решение
Выпишем, что означает существование предела Hm /(х) = g(x0): для V е > 0 3 5(e)
о X->Xq
такое, что для V х G B5(X0) выполнено |/(х) - g(x0)| < е.
о
Для фиксированного е выберем произвольное X1 е В8(х0) и перейдем в послед¬
нем неравенстве к пределу при х —> X1. Получим выражение:
о
для V е > 0 3 5(e) такое, что для Vx1 е B5(X0) выполнено Ig(X1) - g(x0)| < е,
что и представляет из себя определение непрерывности функции g(x) в точке х0.
Задача 3.13
Определим, могут ли непрерывные на отрезке [0; 1] функции/(х) и g(x) быть
различными: а) только в конечном числе точек отрезка [0; 1]; б) только на счетном
множестве точек отрезка [0; 1].
Решение
Рассмотрим разность данных функций: h(x) = /(x)-g(x). По теореме об ариф¬
метических операциях над непрерывными функциями получаем, что функция
h(x) непрерывна на отрезке [0; 1]. Предположим, что найдется точка а такая, что
/(а) Ф g(a). Не ограничивая общности, будем считать, что /(а) > g(a). Следовательно,
в данной точке получим h(a)> 0. По теореме об устойчивости знака непрерывной
в точке функции делаем вывод о том, что существует окрестность В(а), в которой
функция h(x) принимает строго положительные значения. В силу того что множе¬
ство точек в этой окрестности имеет мощность континуума, отвечаем на оба постав¬
ленных в задаче вопроса отрицательно.
Рассмотрим далее вопрос о том, как соотносятся непрерывность функ¬
ции и непрерывность ее модуля.
Утверждение 3.23. Если функция / непрерывна, то и F = |/| — также
непрерывная функция.
179
Доказательство
Очевидно, что f(x) = F(x) или -F(x) в окрестности точек х, в кото¬
рых /(х)фО, в силу непрерывности функции/. Поэтому у функции F
может быть разрыв только в точках а, для которых Нш/(х) = 0. Можно
х—>а
доказать, используя определение предела, что и в этом случае получаем
Hm F{x) = 0 = F(O) (докажите!). ■
х—>а
Также для доказательства данного утверждения можно было восполь¬
зоваться определением предела функции по Гейне или тем фактом, что
модуль — непрерывная функция, а суперпозиция непрерывных функций
непрерывна.
Зададимся следующим вопросом: будет ли верно обратное утвержде¬
ние? Ответ на данный вопрос — отрицательный. Предлагаем читателю
самостоятельно построить контрпример всюду разрывной модификации
функции Дирихле, модуль которой есть константа.
Задача 3.14
Пусть функции fug непрерывны на отрезке [я; Ь\. Положим
h(x) - min{/(x); g(x)}, k(x) - max{/(x); g(x)}.
Докажем, что функции h(x), k(x) также являются непрерывными на [я; Ь\.
Решение
Справедливость сформулированного утверждения моментально устанавливается
из следующих неравенств (доказательство которых мы оставляем читателю):
min{/(*); g(x)} =
max{/(x); g(x)} =
f(x) + g(x) - |/(;r) - g(x)|.
/(x) + g(x) + |/(x)-g(x)|
и свойств непрерывных функций, отмеченных выше. * 3 * 3Задание 3.14
Докажите, что если функция/непрерывна на [я; Ь\, то и функции т(х) = inf /(£),
а<Ъ<х
М(х) = sup /(£) также непрерывны на [я; Ь\.
а<\<х
Задача 3.15
Пусть/— непрерывная и ограниченная функция на (х0; +°°). Докажем, что для V T
3 {*„} —» +оо такая, что Hm(/(*„ +Т)-/(*„)) = 0.
П—>°°
Решение
Без ограничения общности мы можем считать, что Т>0, иначе делаем замену
переменной.
Обозначим через ф(х) разность /(х + T)- /(х) и рассмотрим два случая.
1. Найдется число хе[х0; + °о) такое, что для всех х>х функция ср(х) прини¬
мает значения одного знака, предположим, что строго положительные. Рассмотрим
последовательность уп = /(х + пГ), которая в силу неравенства
yn+i- Уп = f(x + (п + 1)Т)~ f(x + пТ) = {х = х + пТ} = f(x + T)-f(x)>0
180
является возрастающей. Так как функция /(х) является ограниченной, то по теореме
Вейерштрасса о сходимости ограниченной монотонной последовательности суще¬
ствует предел Iim уп = Ь<°о. Из критерия Коши делаем заключение о фундаменталь-
ности последовательности {уп}. Отсюда, если выбрать Xn= х л-пТ, получаем, что
Iim (f(xn +T) - f(xn)) = Iim (уп+1 -уп) = 0.
/2^.00
2. Не существует числа , удовлетворяющего условию п. I. В таком случае най¬
дется бесконечно много таких точек хп, что выполняется равенство fixn + T) - f(xn ) = 0,
причем хп —» +оо (так как, если бы бесконечно много таких хп не нашлось, выполнялся
бы случай п. 1).
Задача 3.16
Пусть / — непрерывная на отрезке [я; Ъ\ функция и X1, X2,..., хп — произвольные
числа из этого интервала. Докажем, что на интервале (я; b) найдется число tj такое,
fixl) + fix2) + - + f(xn)
что выполнено /(%*)= — ” .
п
Решение
Обозначим m = min/(х), M = шах/(х). Тогда для любых точек X1, Хо, ..., х„, оче-
[а;6] [а;Ьу
видно, получим пг <
fixl) + fix2) + - + f(xn)
у < М, так как все числа/(X1)1Z(X2),...,
п
Jipcn) лежат между числами m и Ми их среднее арифметическое лежит на этом отрезке.
Далее, в силу того что функция /непрерывна на [я; 6], то по теореме о промежуточных
значениях непрерывной функции на интервале (а; b) найдется точка \ такая, что у = /(£).
Задача 3.17
Докажем, что для любой непрерывной функции / переводящей отрезок [0; 1]
в отрезок [0; 1], существует точка X0 е [0; 1], в которой /(х0) = X0 (неподвижная
точка отображения f). Построим пример непрерывного отображения /: (0; 1) —>
(0; 1), у которого не существует неподвижной точки.
Решение
Если имеем /(O) = O или /(1) = 1, то все доказано. Иначе, если /(O) > О, /(I) < 1,
рассмотрим функцию g(x) = /(х)-х. Тогда имеем g(0) = /(O) > 0, g(l) = /(1) — 1 < 0.
Следовательно, существует точка £ £ (0; 1), в которой функция g принимает нулевое
значение. Данная точка, очевидно, и будет искомой.
На интервале (0;1) искомая точка может не найтись, например для функции
f(x) = х3. При всех х € (0; 1) имеем /(х) < х.
Задача 3.18
Приведем пример непрерывной на всей числовой прямой R функции, которая
принимает каждое свое значение три раза. Существует ли непрерывная функция,
принимающая каждое свое значение ровно два раза?
Решение
Построим вспомогательную функцию, определенную на отрезке [-3; 3]:
g(*) =
х + 2, если х € [-3; -1],
-х, если х е [-1; 1],
х - 2, если х е [1;3].
181
Положим f(x) = g(x - 6 n) + 2n,xs [6n - 3; 6 n + 3], n G Z. Данная функция будет иско¬
мой (докажите!).
Рассматриваемая функция изображена на рис. 3.6.
Докажем, что не существует непрерывной на всей числовой оси функции, прини¬
мающей каждое свое значение ровно два раза. Будем доказывать от противного. Пусть
такая функция может быть построена. Тогда если в некоторой точке а данная функция
принимает значение Л, то найдется точка Ъ такая, что f(b) также равно А. На интер¬
вале (а; Ь) значения функции/либо строго меньше Л, либо строго больше этого числа.
Не ограничивая общности, будем считать, что для V х s (а; b) имеем f(x) > А. Так как
функция/непрерывна, то на отрезке [а; Ь\ по второй теореме Вейерштрасса она при¬
нимает наибольшее значение. Поэтому найдется некоторая точка с s (а; Ь) такая, что
для V х s (а; b) выполнено f(x) < /(с). По нашему предположению найдется некото¬
рая точка dтакая, что /(с) = f(d). Очевидно, что d^b и
т=дс)>т=А. (3.5)
Поэтому возможны два варианта.
1. d > Ь. Получаем, что для V х > b выполнено f(x) > f(b) = А, иначе в силу нера¬
венства (3.5) и теоремы о прохождении непрерывной функции через любое промежу¬
точное значение существует еще как минимум одна точка, в которой функция / при¬
нимает значение А. Но тогда на интервалах (а; с), (с; Ъ) и (6; d) в силу той же теоремы
функция /принимает любое свое значение из интервала (Л; /(c)) не менее трех раз.
2. d<b. По второй теореме Вейерштрасса на отрезке [с; d] функция / достигает
своего наименьшего значения, т.е. найдется точка E1 е (с; d) такая, что для V х s [с; d]
получаем f(x)> /(£). В таком случае в силу теоремы о прохождении непрерывной
функции через любое промежуточное значение на интервалах (а; с), (с; |) и (£; d) функ¬
ция / принимает любое свое значение из интервала (/(¾; /(c)) не менее трех раз.
Используя аналогичные рассуждения, можно построить (постройте!)
непрерывную функцию, принимающую каждое свое значение любое нечет¬
ное число раз — 21+ I, / G N. Кроме того, можно доказать, что не существует
непрерывной функции, принимающей каждое свое значение четное число
раз. В заключение рассмотрим пример функции f(x) = х2. В силу четности
данная функция принимает любое свое значение A G (0; +°°) ровно в двух
точках: у[л и -у/~А. Но нулевое значение она, очевидно, принимает только
при х=0. Если же исключить значение /(0) = 0, то рассматриваемая функ¬
ция перестает быть непрерывной.
182
Определение 3.25. Будем говорить, что функция/: R —> R непрерывна
по Чезаро в точке X0 е R, если для любой последовательности {хп} при
Iim
Хл + ... + X,
п
- = X0 выполнено
Iim /(*<) + ~ + /(*"> = /(*„).
n—>°° П
Задача 3.19
Опишем все функции, непрерывные по Чезаро хотя бы в одной точке.
Решение
Установим, что линейная функция f(x)-ax + b непрерывна по Чезаро на всей
OC “I- OC
числовой прямой R. Действительно, пусть Iim ——— = X0. Тогда
Я—» OO Tl
/(х,) + ...+ f(x„) ,. Ox1 +b + ... + ax„ + Ь а(хл+... + х„) + пЬ ,
Iim J v п/ = Iim—1 п _ Iim ш. = ах +Ь.
п
п
п
Здесь интересен тот факт, что справедливо и обратное утверждение, т.е. если
функция /(х) непрерывна по Чезаро хотя бы в одной точке, то она представляет
из себя линейную функцию.
Действительно, пусть функция / непрерывна по Чезаро в точке х0. Не ограни¬
чивая общности, можем считать, что X2 = 0. Перейдем от функции /(х) к функции
g(x) = /(х + х0)-/(х0), откуда g(x0) = g(0) = 0.
Далее возьмем {хя} = {(-1)"х, х > 0}. Для данной последовательности имеем
.т X1 +... + хя _ j -х + х +... + (—1)"х j.
1-(-1)"
X
Hm
Iim
п
п
п
= 0;
lim g(-*)+g(*)+...+g((-i)-*)=Иш
я-»°° П п->°° П
Отсюда непрерывность по Чезаро функции g в нуле выполняется тогда и только
тогда, когда данная функция нечетная.
Рассмотрим числовую последовательность {хя}, состоящую из -1 и х, х > 0.
Обозначим через уп количество элементов последовательности {хя}, равных х, среди
первых п. Если у —, то
I + X
п
im *1 +••• + ** = Ит Уп-Х-Нп-У„) _ 1 + х
•х- п-
Iim
Tl
= Iim
и
1 + х
Z-
= 0.
Далее, используя доказанное выше равенство g(-l) = -g(l), получим
О = g(0) = Hm g(*i) + - + g(*«) = lim Y„-g(^) + (^-Yw)g(-l) =
п п-^>°о П
^g(x) x-g(l)^g(x)-x-g(l)
I + X I + X I + X
Отсюда g(x) = х • g(l), или, вспоминая «сдвиг» по х0, получаем, что /(х) =
= х •/( 1) -/(0), т.е. функция /представляет из себя линейную.
Другое доказательство данного факта можно было получить, приведя задачу
нахождения функции / к решению функционального уравнения Коши.
В заключение параграфа рассмотрим следующий вопрос. График
хорошо изученной в этом параграфе функции Дирихле состоит из всех
точек прямой у = 0 (оси абсцисс) с иррациональными абсциссами и из всех
183
точек прямой у = Ic рациональными абсциссами и, следовательно, всюду
плотен на прямых у = 0 и у = I1. Возникает следующий вопрос: можно ли
построить (безусловно разрывную) функцию/с графиком, всюду плотным
на плоскости (т.е. каждая точка (х0; у0) Е является предельной для точек
вида (х; /(х))). Ответ на данный вопрос — положительный, и дает его так
называемая функция Серпинского2, которая определяется так:
b + а42, если X = а + b42, где а и b рациональны,
х, если х Фа + b42 ни при каких рациональных аиЬ.
Докажем, что каждому значению х сопоставляется единственное зна¬
чение у = /(х). Действительно, если число х можно представить в виде
а + b42, где аиЬ — рациональные, то такое представление единственно, так
как из равенства a + b42 = а' + vS , где a, b, a', b' — рациональные и аФ а',
Ъ Ф Ь', вытекала бы рациональность числа 42.
Докажем всюду плотность графика функции/на плоскости. Для этого рас¬
смотрим три последовательности ип, Vn и Wn рациональных чисел такие, что
Hm ип = х0, Hm vn = у0, Hm Wn = 42.
га—га—о и—
Образуем последовательность (X1; у^), (х2; у2), ..., (хи; г/„), ... точек гра¬
фика функции Серпинского, где
Хп = (VnWn ~Un) + (UnWn ~ Vn)л/2, У„ = /(Х„) = (UnWn -Vn) + (VnWn - Un)^2.
В этом случае, как легко видеть,
Hm хп = (г/0 42 - X0 ) + (х0 42 - у0 )42 = х0,
га—>°°
Hm уп = (х0 42- г/0) + (у042- х0)42 = у0,
п—>°°
т.е. точка (х0; у0) является предельной для точек (хи; уп) графика функции
У =AxY
Задание 3.15
Докажите, что функция Серпинского f(x) совпадает со своей обратной, т.е. вы¬
полнено условие: если f(x) = у, то f(y) = х.
3.4. Функция Кантора
Зададимся вопросом: можно ли отобразить непрерывно некоторое нигде
не плотное на отрезке [0; 1] множество на сам этот отрезок?
Ответ на этот вопрос — положительный. Действительно, возьмем
в качестве нигде не плотного множества хорошо знакомое нам множество
Кантора П. Нами было доказано, что каждая точка х из данного множества
может быть записана в виде троичного разложения, содержащего только
0 и 2. Пусть
1 Но, безусловно, не покрывающий ни одного отрезка на этих прямых.
2 Sierpinski W. О funkcji odwracalnej, ktorej obrax wsxgdxie ggsto pokrywa ptasxcxyxng (Sur
une fonction inversible, dont !’image est dense dans Ie plan) // Wector. 1914. Xq 7. P. 289—291.
184
x G П и х = (CO1, со2, •••> юи> -Ь> гДе шг= {0. 2}.
Определим на точках данного множества функцию ф, положив
ф(х) = {cot/2, со2/2, ..., со„/2, ...}2,
где правая часть равенства рассматривается как двоичное разложение чис¬
ла из отрезка [0; 1].
Посчитаем некоторые значения функции ф:
Ф(1/3) = ф({0, 2, 2,2, ...}3) = {0,I,1,1, ...}2 = 1/2;
ф(2/3) = ф({2, 0, 0,0, ...}3) = {1, 0, 0,..., 0, ...}2 = 1/2;
Ф(1/9) = {0, 0,1,1, ...}2 = 1/4; Ф(2/9) = 1/4; ф(7/9) = 3/4; ф(0) = 0; ф(1) = 1.
В результате мы получили функцию, определенную на множестве Кан¬
тора П.
Определим, что из себя представляет образ функции ф, т.е. ф(П).
Очевидно, что образом множества Кантора П является некоторое под¬
множество отрезка [0; 1]. Покажем, что [0; 1] с ф(П). Для этого возьмем
произвольную точку у G [0; 1] и рассмотрим его двоичное разложение:
у = {У\> У2’ — Ь- Если число у допускает два различных двоичных разложе¬
ния, то можно рассмотреть их оба.
Положим х = {2у1,2у2,...,2уп,...}3. Тогда х, используя арифметическую
характеристику множества Кантора, принадлежит множеству П, причем
ф(х) = у. Следовательно, [0; 1] с ф(П). Обратное включение Л(П) с [0; 1]
моментально вытекает из задания функции ф. Таким образом, мы устано¬
вили, что ф(П) = [0; 1].
Замечание 3.20. Отметим, что указанное отображение ф не является вза¬
имно однозначным, т.е. можно указать разные точки из множества Кантора,
образом которых является одна и та же точка отрезка [0; 1]. Примерами
таких точек могут служить (как это было ясно выше) 1/3 и 2/3 .
Вообще, две точки X1, X2 G П имеют один и тот же образ при отображе¬
нии ф в том и только в том случае, когда они имеют вид
X1 = (CB1, со2,..., (оп, 0, 2, 2, ...}3, х2 = (Co1, со2,..., со„, 2, 0, 0, ...}3.
Другими словами, равенство ф(хА) = ф(х2) возможно тогда и только
тогда, когда X1 и X2 являются граничными точками одного и того же смеж¬
ного интервала. Вычисляя образ функции ф в данных точках, получаем
Ф(ДГ.) = V(X2) = IJfr+^-.
R—1
Продолжим далее функцию ф на весь единичный отрезок [0; 1] следу¬
ющим образом. Если х G [0; 1] \П, то х принадлежит одному из смежных
интервалов (а; Ъ), удаленному из отрезка [0; 1] при построении множества
Кантора, и поэтому ф(а) = ф(6). Положим по определению
ср(х) = ф(я) = ф(6) для Vxg (а; Ъ).
Другими словами, определенная функция ф постоянна на замыкании
каждого смежного интервала. В точках множества Кантора П функции ф
и ф мы отождествим.
185
В результате мы получили неубывающую функцию (докажите это!),
определенную на отрезке [0; 1] и постоянную в некоторой окрестности
каждой точки из множества [0; 1]\П. Построенная функция ср(д;) называ¬
ется функцией Кантора (канторовой функцией), а ее график, приведенный
на рис. 3.7, — «чертовой лестницей».
Задание 3.16
Установите, что описанную функцию Кантора можно задать следующей формулой:
ф(*) = sup
Ч
£3*
<*,
гк = 0 ИЛИ 1
Докажем, что функция Кантора является непрерывной на отрезке [0; 1].
Действительно, функция ср не убывает на [0; 1] и множество ее значений
составляет весь отрезок [0; 1]. Поэтому функция ф не имеет скачков. А так
как монотонная функция не может иметь других точек разрыва, кроме
скачков (см. критерий непрерывности монотонных функций), то она явля¬
ется непрерывной.
Вспоминая правила построения множества Кантора, делаем вывод о тех¬
нике построения функции Кантора по шагам. На первом шаге на месте пер¬
вого смежного интервала мы строим отрезок, соединяющий точки (1/3; 1/2)
и (2/3; 1 /2). На втором шаге на месте вторых смежных интервалов мы строим
два отрезка, соединяющих точки (1/9; 1/4), (2/9; 1/4) и (7/9; 3/4), (8/9; 3/4),
и т.д. В результате после счетного числа таких шагов мы построим искомую
функцию Кантора. На рис. 3.8 приведены иллюстрации трех и шести шагов
построения этой функции.
186
I
7/8
3/4
5/8
1/2
3/8
1/4
1/8
О 1/9 2/9 1/3
2/3 7/9 8/9
I
7/8
3/4
5/8
1/2
3/8
1/4
1/8
О 1/9 2/9 1/3
2/3 7/9 8/9 I
Рис. 3.8
Любопытным является наблюдение, что график непрерывной функции
Кантора невозможно нарисовать, не отрывая карандаша от бумаги.
Забегая несколько вперед, вспомним, что производная постоянной
функции равна нулю. Отсюда вытекает еще один интересный факт: произ¬
водная функции Кантора, возрастающей на отрезке [0; 1] от нуля до еди¬
ницы, равна нулю всюду, за исключением множества меры нуль (т.е.
за исключением точек множества Кантора). Такие функции, т.е. функции,
непрерывные на некотором отрезке, отличные от постоянной, производная
которых равна нулю за исключением множества меры нуль, называются
сингулярными (т.е. функция Кантора представляет собой пример сингуляр¬
ной на отрезке [0; 1] функции).
Изучим некоторые свойства функции Кантора.
Задача 3.20
Докажем, что выполняется тождество
ср(х)
Ф
при х е [0; 1].
K0J
Решение
В том случае, если хе[0;1]\П, функция Кантора равна постоянной, и ее значе¬
ние совпадает со значением в ближайшей точке множества Кантора. Поэтому нам
достаточно доказать предложенное тождество лишь для точек из данного множе¬
ства. Для них имеем:
х
х — ((O1, со2, ...}з => g - (0, CO1, со2, ...}3;
Ф
f X^
K0J
*Нт-т-
ф(х)
I n ®2 I
4°, п , о ,-Г =(Р
2 2
U/
Задача 3.21
Докажем, что выполняется тождество ф(х) + ф(1 - х) = 1 при х E [0; 1].
Решение
Аналогично предыдущей задаче докажем приведенное тождество для точек
из множества Кантора. Пусть х E П. В этом случае
х = (O)1, (о2, ...}3 => 1 - х = (Q)1, (о2, ...}3, где со, =
(0, если COi = 2,
2, если Coi = 0.
Отсюда ф(х) + ф(1 - х) =
К
®2 ]
ы
SI
А 1
[2'
' 2 ’-j
I2 I
[ 2
2 ’"j
= (1,1Д, ...}2 = 1-
Задание 3.17
Докажите, что выполняется тождество ф
х + —
3"
I 1
= ф(х) + — при 0 < х < —.
't-ч / 2” ^ 3”
Интересным является вопрос о том, при каких х, кроме указанных выше,
выполняется приведенное тождество.
188
Задание 3.18
Докажите, что выполняется тождество ср
х 2
1
3 3
= 2^)+2'
Задача 3.22
Докажем неравенство
( х^0¾2
V z У
< ф(х) < xlog32 при 0 < х < 1.
Решение
Изобразим функции Кантора,
у ^V083 2
и xlog32 на одном чертеже (рис. 3.9, а).
Далее рассмотрим выделенный слева прямоугольник и растянем его до всего ква¬
драта. Получаем следующие изображения (рис. 3.9, б).
X
и фрактальность построения функции
Эти чертежи, неравенство ф
V0J
Кантора приводят нас к пониманию того, что доказываемые неравенства можно дока-
( О
0;-
3
V 0J
зать на любом отрезке вида [а; За], а €
Докажем неравенство ф(х) < xlog32 на отрезке
, а х > ф(х) на этом отрезке. На отрезке
X E
5:1
1-1
3’2
. Действительно, xlog32 > х при
неравенство очевидно (так как
ф(х) = —). В силу вышесказанного получаем ф(х) < xlog32 на отрезке [0; 1].
Докажем левое неравенство
г х V083^2
v2y
1.
< ф(х) на отрезке
2 2
9’ 3
. На отрезке
1.2
З’З
(где
функция Кантора постоянна и равна —) данное неравенство элементарно. На отрезке
2.1
9’ 3
для этого будет достаточно установить неравенство
I 1
г 2 \ V0g3 2
9 + 3"
V 2
<- +
4 2"+1
для V п = 2,3,...,
1
что и будет равносильно требуемому (докажите!). Сокращая на — левую и правую
части данного неравенства, получаем
I 1
1 л -
2 • З”-2
\ 1о8Э 2
что верно, так как
1 +
1
\1°8Э 2
2 • З"-2
<1 +
<1 +
1
2”-1 ’
<1 +
1
2 • З"-2 2”-1
Учитывая вышесказанное, заключаем, что
^ х ^1og3 2
v2y
< ф(х) на отрезке [0; 1].
189
а
Рис. 3.9
Задача 3.23
Найдем длину графика функции Кантора1.
Решение
1
Обозначим через Li длину участка «чертовой лестницы» от 0 до —, через L2 —
3
I 1
длину участка от 0 до —, через L3 — длину участка от 0 до — и т.д. В этом случае
9 27
для длины графика функции Кантора L0 и введенных величин Lk справедливы сле¬
дующие равенства:
L0= — + 2Lit Li= — + 2L2,..., Ln = + 2 Ln+i,....
Отсюда имеем L0 = Hm
п Ok-I
Y-—
Ow 3*
\
+ 2 nLr
. Но длина Ln не меньше диагонали прямо¬
угольника, содержащего соответствующий участок графика, и не превосходит сумму
двух его сторон:
I IrI 1
■ + —тг- ^L„< —— +
Следовательно,
1 +
' 2
22” 32я
<2n-L„ <1 +
2” 3й
(пЛп
Iim 2"-L„ =1.
я 2^-1
Учитывая, что Hm ^ —т~ = 1, делаем вывод, что L0= 1 + 1 = 2.
Я-»оо£_1 3*
Для формулировки следующего вопроса нам потребуется ввести следу¬
ющее определение.
Определение 3.26. Будем говорить, что функция / удовлетворяет
на отрезке [а; Ь] условию Гелъдера — Липшица порядка а, 0 < а < 1, если
3 M > 0, такое что для V х, у е [а; Ъ] выполнено
\f(x)-f(y)\<M- \х-у\а. (3.6)
Обозначение:/(х) G Lipa([a; Ъ]).
Рассмотрим сначала вопрос, что происходит с функциями, удовлетворя¬
ющими условию Гельдера — Липшица порядка ос вне диапазона 0 < ос < 1.
1. Пусть/(х) G Ыра(\а\ Ь]) и а > 1. Тогда, выбирая произвольные х и у
из [я; Ь\, преобразуем неравенство (3.6):
I х — г/1
< M-1 х - у
Переходя к пределу при х —» у, получаем f'(y) = 0. В силу произволь¬
ности точки у G [я; b] заключаем, что функция/представляет из себя кон¬
станту на отрезке [я; Ь\.
1 Строгое понятие длины кривой и ее спрямляемости в данной книге не рассматрива¬
ется. Поэтому проведем вычисления длины графика функции Кантора в предположении,
что такая длина существует.
191
2. Пусть/(x) G LipJ[a\ b]) и а = 0. В этом случае получаем
l/W-/0/)1 SM,
т.е. функция / ограничена.
3. Пусть/(х) G Lip J[a; b]) и а < 0. Записав неравенство (3.6) в виде
M
\х-у\
не получаем даже ограниченности.
Утверждение 3.24. Пусть/(х) G LipJXa', &]) и 0 < (3 < а. Тогда/(х) G
G LipJXa-, b]).
Доказательство
Действительно, пусть |/(х) - f(y)\ < M • |х - у\а для всех х, у G [а; Ь] и 0 < P <
< а. Получаем
\f(x)-f(y)\<M-\x-y\a=M-\x-y\a~^ ~|Р
M-\х - yf, если |х - у\< 1,
\х-у\ <
<\
M • \b - яГ Р • |х - yf, если |х - у\ > 1,
откуда и заключаем требуемое с некоторой константой M. ■
Рассмотрим следующий вопрос: при каких а, 0 < а < 1, функция Кан¬
тора ср(х) будет удовлетворять условию Гельдера — Липшица с показате¬
лем а? Ответ на данный вопрос дает следующая теорема.
Теорема 3.2. Функция Кантора ср(х) принадлежит классу функций
LipJ[0] 1]) при а < log32.
Доказательство
В дальнейших рассуждениях мы будем пользоваться следующей важ¬
ной леммой.
Лемма 3.1. Функция Кантора на отрезках
0;-
и
tell
L з]
|_з’ J
эквивалентна
функции Кантора, построенной на отрезке [0; 1] и сжатой по оси абсцисс
и оси ординат в два и три раза соответственно. Иными словами, на каж¬
дом шаге построение функции Кантора сводится к ее масштабированному
построению на каждом из несмежных отрезков1.
Исходя из этого утверждения все дальнейшие рассуждения будем про¬
водить на основе первого шага построения: смежным отрезком будем назы-
Г1 21
Г. Il
2 ~
вать
Wji
w|
I
, а несмежными —
I
C
Wl
I
и
_3’_
Заметим, что на смежном отрезке, где функция эквивалентна константе,
она удовлетворяет любому условию Гельдера — Липшица с любым показа¬
телем — для любой парыхму со смежного отрезка верно
ср(х) = ф (у) ^O = |ф(х) - ф(г/)| < М\х - yf,
так как модуль всегда неотрицателен, а константа M положительна по опре¬
делению.
1 Имеется в виду несмежный отрезок к множеству Кантора.
192
Исходя из леммы 3.1 получаем, что если на данном шаге построения
функция Кантора на левом несмежном отрезке удовлетворяет условию
Гельдера — Липшица с показателем а и константой М, то функция Кантора
на правом отрезке удовлетворяет условию с теми же показателем и кон¬
стантой.
При выборе пары точек на смежном и несмежном отрезках, как несложно
заметить, критерий и константа для несмежного отрезка все еще нам под¬
ходят. Действительно, значение функции в точке со смежного отрезка
равно значению функции в одной из крайних точек несмежного отрезка,
а расстояние между аргументами по сравнению с критерием для несмеж¬
ного отрезка только увеличилось.
Осталось рассмотреть случай, когда пара точек берется с разных несмеж¬
ных отрезков одного шага. Если для каждого из этих отрезков выполняется
критерий с показателем ос и константой М, то покажем, что для выбранной
пары сработает тот же показатель а и константа, равная
2 M
За ‘
Заметим, что
для выбранной пары точек хиу выполняется неравенство
|ср(х)-ф(г/)|<—М|х-^
а
Оно равносильно неравенству
ф(х)
Ф {у)
<М
х у
2
2
3 3
По лемме 3.1 деление аргумента функции Кантора на 3, а самой функ¬
ции — на 2 как раз соответствует «сжатию» функции Кантора на левый
несмежный отрезок, на котором работает именно этот критерий с показа¬
телем ос и константой М. Поэтому приведенное неравенство верно.
Таким образом, мы установили следующий факт: если для функции
Кантора на левом несмежном отрезке верен показатель ос с константой М,
то он верен и для функции на всем отрезке с увеличением константы в
2_
3«
раз. Аналогичными рассуждениями можно показать и обратное: если
функция на всем отрезке удовлетворяет показателю ос с константой М, то
на каждом из несмежных отрезков она будет удовлетворять показателю ос
3“
с константой —M. В результате получили следующий критерий.
2
Утверждение 3.25 (критерий принадлежности классу Гельдера —
Липшица). Функция Кантора удовлетворяет условию Гельдера — Лип¬
шица с показателем а на области своего определения тогда и только тогда,
когда она удовлетворяет этому условию на отрезке
при VweN,
причем константы для каждого из отрезков вида
вать медленнее, чем в
v2y
0;
3k
не должны убы-
раз.
193
Тогда, поскольку п —»нам осталось рассмотреть концы этого отрезка:
( I
Ф(°) = °> Ф ^
V6 /
Отсюда, если ф(х) е Lip а[0; 1], то
_1_
2й
(докажите!).
ф(0)-ср
ИЛ
V3 nJ
<м
0-
3й
I 1
ф=>— < M—ф=>
2п Зп
V2;
<М.
Исходя из того, что п —> оо, и свойств степенной функции ап получаем,
—> А из этого уже следует, что а < Iog3 2. ■
За
что — < 1, иначе
2
( 3а Y1
v2y
Заметим, что в этом случае необходимое условие на рост константы,
заложенное в критерии, в точности выполняется.
3.5. Непрерывные кривые.
Кривые Пеано на плоскости и в пространстве
Начиная разговор о таком простом с точки зрения интуиции объекте,
как непрерывная кривая на плоскости (или в пространстве), нужно отме¬
тить, что, вообще говоря, четкое определение понятия кривой — очень
и очень сложное. Так как данный вопрос выходит за рамки нашего курса,
мы порекомендуем интересующемуся читателю обратиться к трудам Кан¬
тора, Жордана, Урысона и др. Мы же сейчас рассмотрим самое простое
определение кривой — по Жордану.
Определение 3.27 (Жордана). Кривая — совокупность точек плоскости,
координаты х и у которых даны двумя уравнениями: х = ср(£), у = \|/(£)> где
ср и \|/ — две непрерывные функции переменной t, определенные, например,
на отрезке 0 < t < 1.
Определение 3.28. Если для всех различных значений tut? кривой
Жордана, заданной уравнениями х = ф(£), у = \|/(t), соответствующие точки
плоскости М((ф(^); \|f(t))) и М'((ф(0; V(O)) также различны, то кривая
Жордана называется кривой без кратных точек или простой дугой.
Определение 3.29. Если начальная точка М0(ф(0); V(O)) и конечная
точка М1(ф(1); \р( 1)) кривой Жордана совпадают, т.е. если ф(0) = ф(1)
и \|/(0) = \j/( 1), то кривая Жордана называется замкнутой.
Сформулируем теперь теорему Жордана, которая имеет очень простую
формулировку, но исключительно тяжелое доказательство1.
Теорема 3.3 (Жордана). Всякая замкнутая кривая Жордана без крат¬
ных точек делит плоскость на две области, из которых одна есть внутрен¬
няя по отношению к этой кривой, а другая — внешняя.
Заметим далее, что, например, окружность разделяет плоскость на две
части (внутреннюю и внешнюю) и каждая из этих областей имеет своей
1 Краткое доказательство данной теоремы читатель может найти, например, в статье
Tverberg Н. «А proof of the Jordan curve theorem» // Bull London Mathematical Society. 1980.
Vol. 12. P. 34-38.
194
границей окружность. Говорят, что окружность является совместной гра¬
ницей этих двух областей. Определим далее понятие совместной границы
более строго.
Определение 3.30. Будем говорить, что кривая (линия) L является
совместной границей двух открытых множеств A1 и A2, если выполнены
следующие два условия.
1. Кривая L отделяет области A1HA2 друг от друга, т.е. от точки области
A1 к точке области A2 нельзя провести соединяющую ломаную, не пересе¬
кающую кривой L.
2. Обе области A1 и A2 примыкают к кривой L на всем ее протяжении;
это означает, что как угодно близко к любой точке х е L имеются и точки
области A1, и точки области A21.
Исходя из теоремы Жордана делаем вывод, что всякая замкнутая кри¬
вая Жордана без кратных точек является совместной границей исключи¬
тельно двух областей. Кажется «наглядно очевидным», что никакая кривая
не может быть совместной границей более чем двух областей на плоскости.
Но это предположение неверно\
Приведем далее описание примера Bada2, которое, как нам известно,
принадлежит другому японскому математику К. Йонеяма3.
Предположим, что имеется окруженная морем земля, и на этой земле
три озера: теплое, холодное и пресное. Будем строить сеть каналов от озер
и моря по следующей схеме. В первый день канал отводится от теплого
озера так, чтобы он не сообщался с морской водой и водой двух других
озер и чтобы не далее чем на расстоянии 1 (единицы длины) от каждой
точки суши была вода теплого озера. Конечную точку этого канала обо¬
значим через A ^ Во второй день канал отводится от холодного озера, нигде
не сообщаясь с морем, с другими двумя озерами и уже построенным кана¬
лом. Причем работа ведется до тех пор, пока от каждой точки оставшейся
суши не далее чем на расстояние 1 будет вода холодного озера. Конеч¬
ную точку этого канала обозначим через B1-B третий день канал таким
же образом строится от озера с пресной водой. Конечную точку обозначим
через C1. В четвертый день канал строится от моря. Конечная точка обо¬
значается через D1.
В следующие четыре дня каналы продолжаются далее, начиная от точек
A1, B1, C1 и D1, сеть каналов делается гуще, причем так, чтобы на расстоя¬
нии, меньшем 1/2 от каждой точки оставшейся суши, была морская вода
и вода всех трех озер. Далее густота сети каналов увеличивается так, что
любая вода будет удалена не далее чем на 1 /4 от каждой точки оставшейся
суши, и т.д. Мы можем счетное число раз продолжать работу указанным
путем, продолжая этот процесс. В конце концов (в пределе) нами будет
получена всюду плотная сеть теплой, холодной, пресной и морской воды,
1 Очевидно, имеется в виду, что в любой окрестности любой точки кривой L найдутся
точки, принадлежащие и множеству Ab и множеству A2.
2 Takeo Wada (1882—1944) — японский математик.
3 Yoneyama К. Theory of continuous set of points // Tohoku Mathematical Journal. 1917.
Vol. 12. P. 43-158.
195
которые нигде не пересекаются (не сливаются). То, что в результате всего
этого останется от суши, уже будет «линией», причем как угодно близко
от любой точки этой линии будет любая из вод, т.е. она и будет «совместной
границей» этих четырех непересекающихся множеств!
Иллюстрация построенных множеств1 приведена на рис. 3.10.
Рис. 3.10
Далее мы приступаем к построению еще одной исключительно интерес¬
ной кривой — кривой, имеющей площадь. Рассмотрим вначале несколько
наводящих вопросов.
Вопрос 1. Существует ли непрерывная действительная функция /,
определенная на отрезке [0; 1], принимающая каждое значение из [0; 1]
в континууме точек? Ответ на поставленный вопрос — положительный.
Красивый пример такой функции будет построен в дальнейшем с помо¬
щью функциональных рядов. Еще одному примеру будут посвящены наши
дальнейшие рассуждения.
Вопрос 2. Можно ли отобразить отрезок [0; 1] на квадрат [0; 1] х [0; 1]
непрерывно?
Рассмотрим простейшее отображение, которое у нас было рассмотрено
в гл. 1. Пусть t G [0; 1) и пусть , t2, t3, ...}2 — двоичное разложение числа t.
Для того чтобы разложение было однозначным, мы будем рассматривать
лишь разложения, содержащие бесконечно много нулей (т.е. вместо (B1,
B2, ..., Eb-!, 0, I, 1, ...}2 рассмотрим (E1, E2, ..., Е„_!, 1, 0, 0, ...}2).
Отображение / определим так: если t G [0; 1), то ее образом является
точка (х; у) единичного квадрата Q = [0; 1] х [0; 1], где х = {tb t3, t5, ...}2,
У = ih* ^б> -Ь; если же t = 1, положим/(0 = (I; 1).
1 Иллюстрация взята из работы: Coudene Y. Pictures of hyperbolic dynamical systems //
Notices of the American Mathematical Society. 2006. Vol. 53 (I). P. 8—13.
196
Нетрудно видеть, что / отображает отрезок [0; 1] на Q однозначно (т.е.
каждой точке t е [0; 1] сопоставляется единственная точка из Q), но не вза¬
имно однозначно. Действительно, точка ({1}2 ; {1)2)1 = (1/2; 1/2) является
образом трех различных точек:
{1,1}2, {0,1,1, 0,1, 0,1, 0, ...}2 и {1, 0, 0,1, 0,1, 0,1, ...}2,
и только этих точек.
Отображение / не является и непрерывным. Например, пусть {£„} —
последовательность точек
{0, 0,1,1}2, {0, 0,1,1,1,1}2, {0, 0,1,1,1,1,1,1}2, {0, 0,1,1,1,1,1,1,1,1}2,...
и (хп; г/и) =Zitn). Тогда последовательности {хп} и {уп} совпадают с последо¬
вательностью
{0,1}2, {0,1,1}2, {0,1,1,1}2, {0,1,1,1,1}2,....
В этом случае получим
~{о> ih> ixw Уп) -> ({ih; Uh)-
В то же время
/«о. 1}2) = «0}2; {1}2) Ф ({1}2; {1>2).
Таким образом, Hm /Цп)Ф /(Hm tn), и ответ на заданный вопрос не дан.
«—>°° п—>°°
Формализуем поставленную задачу. Требуется поставить в соответ¬
ствие каждой точке отрезка [0; 1] некоторую точку квадрата [0; 1] х [0; 1],
и притом так, чтобы каждая точка квадрата соответствовала некоторой
точке отрезка. Кроме того, построенное отображение должно быть непре¬
рывным, т.е. удовлетворять тому условию, чтобы достаточным сближением
точек отрезка можно было бы добиться того, чтобы соответствующие им
точки квадрата также были бы сколь угодно близки.
Решение этого непростого вопроса было дано в конце XIX в. Джузеппе
Пеано. Дадим следующее определение.
Определение 3.31. Кривой Пеано мы будем называть кривую Жордана,
лежащую в евклидовом пространстве, размерность которого больше еди¬
ницы, не являющуюся нигде не плотной в этом пространстве.
Далее мы рассмотрим построение одной из разновидностей кривой
Пеано — кривую Пеано — Гильберта2.
Введем следующие обозначения: E= [0; 1], Q= [0; 1] х [0; 1]. Главная
идея построения состоит в том, чтобы разбить E и Q на 9П равных отрезков
и замкнутых квадратов соответственно и установить соответствие между
ними так, чтобы сохранялось отношение включения (т.е. на каждой стадии
разбиения если некоторый квадрат соответствует некоторому отрезку, то
его подквадраты соответствуют подотрезкам указанного отрезка).
1 Нули, стоящие в конце, не пишем.
2 Дж. Пеано, 1890 г. Д. Гильберт, 1891 г.
197
Разделим E на девять равных отрезков первого ранга, a Q — на девять
равных замкнутых квадратов первого ранга. Занумеруем отрезки слева
направо, а квадраты — так, как это показано на рис. 3.11.
Рис. 3.11
Далее каждый отрезок первого ранга разбиваем на девять равных отрез¬
ков второго ранга, а каждый квадрат первого ранга — на девять равных
замкнутых квадратов второго ранга. Получившийся в результате 81 отре¬
зок второго ранга нумеруем слева направо, а квадраты второго ранга нуме¬
руем так, чтобы два квадрата с соседними номерами имели общую сторону
(рис. 3.12). Продолжаем этот процесс счетное число раз.
Рис. 3.12
Далее поставим в соответствие каждому отрезку п-то ранга с номером i
квадрат того же ранга п с тем же номером i. Так мы установим взаимно
однозначное соответствие между отрезками и квадратами одного и того
же ранга. Заметим, что это соответствие обладает следующим свойством:
198
если отрезок п-го ранга Af соответствует квадрату п-то ранга Vf1, а отрезок
(п + 1)-го ранга Af+1 — квадрату (п + 1)-го ранга VJ1+1 и если выполнено
Af Z) Af+1, то и Vf1 =) Vp+K
Установим искомое отображение отрезка E на квадрат Q следующим
образом. Пусть t0 е [0; 1] — произвольная точка отрезка. Построим после¬
довательность отрезков A1 (первого ранга), A2 (второго ранга), ..., An (п-то
ранга), содержащих точку t0 на каждой стадии разбиения (если t0 принад¬
лежит двум отрезкам, выбираем среди них любой).
Этой последовательности отрезков А1, А2,... соответствует последователь¬
ность квадратов У1, V2,.... При этом, так как A1Z) A2 D ..., то и V1 z> V2 z> ...1.
Далее (как уже было сказано ранее), так как диагональ п-го квадрата стре¬
мится к нулю при п —» °°, то существует единственная точка M0, принадле¬
жащая всем Vn. Ее мы и поставим в соответствие точке t0. Следовательно,
мы показали, что каждой точке отрезка соответствует единственная вполне
определенная точка М(х] у) квадрата Q, т.е. мы имеем систему уравнений
х = ср(0>
у = W),
0<£<1.
Следовательно, для того чтобы установить, что построенное нами ото¬
бражение есть кривая Жордана, требуется доказать непрерывность функ¬
ций ср и \|/. Это будет сделано нами далее.
Как было установлено выше, каждая точка отрезка соответствует един¬
ственной точке квадрата, но отметим, что одна и та же точка квадрата может
соответствовать нескольким различным точкам отрезка, т.е. построенное
отображение является однозначным, но не взаимно однозначным. Далее
мы покажем2, что вершины квадратов разбиений всех рангов соответствуют
четырем различным точкам отрезка Е. Аналогичным свойством — соответ¬
ствовать нескольким точкам отрезка — обладает каждая точка стороны ква¬
драта разбиения любого ранга. И только те точки, которые являются вну¬
тренними для квадратов всех рангов (такие точки, безусловно, найдутся,
так как сторон квадратов лишь счетное число), соответствуют лишь одной
точке отрезка Е.
Факт отсутствия взаимной однозначности построенного нами отобра¬
жения не является случайным. Вообще, можно доказать следующую важ¬
нейшую теорему.
Теорема 3.4. Всякая кривая Пеано имеет кратные точки.
Предлагаем читателю самостоятельно доказать эту теорему (от против¬
ного) или обратиться к книге [42].
1 Может, однако, так случится, что некоторой точке f е [0; 1] соответствуют две раз¬
личные последовательности отрезков, содержащих эту точку (f — граничная точка отрезка):
A1 з A2 з ... и A1 з A2 з.... Им отвечают две различные последовательности вложенных ква¬
дратов: У1 з У2 з ... и У1 зУ2 з.... Для того чтобы установить, что точке f соответствует
единственная точка M, требуется доказать выполнимость равенства f\Vn —f\Vn. Это выте-
П П
кает из того, что, так как данная ситуация соответствует исключительно граничным точкам
отрезка, то и квадраты Vi и всегда имеют общую сторону. В силу того что при п —» °°
диагонали (и стороны) квадратов стремятся к нулю, отсюда и вытекает требуемое равенство.
2 См. арифметический способ задания кривой Пеано.
199
Данная теорема показывает принципиальное различие числа измерений
двумерного образа — плоскости и одномерного — прямой. Более общее
утверждение звучит так: взаимно однозначное соответствие между точками
областей различного числа измерений не может быть непрерывным.
Возвращаясь к построенному отображению, докажем, что каждая точка
квадрата соответствует по крайней мере одной точке отрезка. Действи¬
тельно, пусть M0 — произвольная точка квадрата Q. Она принадлежит
по крайней мере одному квадрату Qj первого ранга, по крайней мере одному
квадрату Qj второго ранга (Qj с Qj), по крайней мере одному квадрату Qf
третьего ранга (Qf <z Qj) и т.д.
Рассмотрим отрезки, соответствующие этим квадратам. Пусть это будут
отрезки А\, Aj, Af и т.д. Для них выполнено A) z> Aj z> Af z>....
Причем длина отрезка с ростом номера ранга разбиения стремится
к нулю. Следовательно, все эти отрезки имеют лишь одну общую точку t0.
Этой точке t0 из отрезка [0; 1] и соответствует точка M0 из квадрата Q.
Аргументируем далее, что отображение M = /(£) = (ср(£); \|/(£)} непре¬
рывно во всех точках отрезка [0; 1]. В самом деле, выберем произвольную
точку t0 G [0; 1]. При любом п всякая точка t этого отрезка, достаточно близ¬
кая к точке t0, будет лежать с ней на одном и том же отрезке ранга п или
на соседнем отрезке того же ранга. Но тогда и точки квадрата Q, соответ¬
ствующие значениям параметров t0 и t, окажутся принадлежащими одному
или соседним замкнутым квадратам того же ранга. Следовательно, если
взять точку t достаточно близкой к точке t0 на отрезке Е, то соответству¬
ющие им точки квадрата (х0; у0) и (х; у) также будут лежать достаточно
близко друг к другу:
для V е > 0 3 8 = 5(в) > 0,
такое что для V t, t0 из 11 — £0| < 8 следует
J(X-X0)2+(у-у0)2 <е.
Резюмируя вышесказанное, отметим, что нами было построено непре¬
рывное однозначное отображение отрезка на квадрат, подходящее под
определение кривой Жордана. Следовательно, мы видим, что данное опре¬
деление не подходит под характеризацию понятия кривой в интуитивном
для нас понимании как «тонкого штриха, вьющегося по плоскости»1!
Рассмотрим далее несколько задач, позволяющих лучше понять сущ¬
ность построенного нами объекта.
Задача 3.24
Докажем, что при отображении M=f(t),f: E^Q, прообразом любого вертикаль¬
ного отрезка I = {х = лг0;0 < у <1} с Q является совершенное множество на отрезке
[0; 1] оси Ot
Решение
Как было доказано выше (см. аналог утверждения 3.20 для замкнутых множеств
в параграфе 3.3), прообраз любого замкнутого множества при непрерывном отобра¬
жении замкнут.
1 Или, как давал определение Евклид, «длина без ширины».
200
Далее выберем произвольную точку t0 <е [0; 1], принадлежащую прообразу /-1(7).
Опишем около tQ произвольную Е-окрестность на оси Ot (t0 -е;70 + е).
Докажем, что в ней найдутся точки из /_1(7), отличные от £0. Выделим внутри
этой окрестности отрезок вида
k + i
9”
. Такой отрезок, безусловно, найдется всегда
при некотором достаточно большом п и каком-либо k, 0<k<9”. Согласно построе¬
нию кривой Пеано данный отрезок отображается на некоторый квадрат Qo со сто-
1
ронами длины —,
3”
параллельными осям координат.
Пусть M0 = f(t0 ), тогда M0 е Q0 (и по предположению M0 е 7). Вместе с данной точ¬
кой в квадрат Q0 входит вертикальный отрезок M1M2, являющийся частью отрезка 7
Г k k + l~
(рис. 3.13). Так как прообразы всех точек квадрата Q0 лежат на отрезке —;
9 9
оси Ot (этот отрезок отображается на весь квадрат Q0. При этом не утверждается, что
других прообразов у квадрата Q0 нет!), то на этом отрезке
кроме отрезка
k k + i
9”’ 9”
лежат и все прообразы отрезка M1M2. Значит, в окрестности (tQ - е; tQ + е) найдется
бесконечно много точек из множеств /_1(7). В силу произвольности указанной
Е-окрестности и произвольности точки £0 е /-1(7) заключаем, что прообраз отрезка 7
не имеет изолированных точек, т.е. /_1(7) — совершенное множество.
0 t0 - E t0 t0 + £ I
Ь-ь-—В
_k k + I
9 п 9 п
Замечание 3.21. Более того, по сути, нами было доказано, что каждая
точка прообраза/-^7) является точкой конденсации.
Воспользовавшись результатом рассмотренной задачи, можно получить
доказательство следующего положения.
Следствие 3.3. Отрезок [0; 1] можно представить в виде суммы конти¬
нуума совершенных множеств попарно без общих точек.
201
Доказательство
Отобразим отрезок [0; 1] с помощью кривой Пеано на квадрат [0; 1] х
х [0; 1]. Затем разобьем этот квадрат на континуум непересекающихся
отрезков I = {х = const; 0 < у < 1}.
Прообразы этих отрезков не пересекаются (так как сами отрезки
не пересекаются, и образом точки отрезка [0; 1] оси Ot является единствен¬
ная точка из квадрата [0; 1] х [0; 1] и в сумме представляют весь отрезок
[0; 1]). Согласно результату предыдущей задачи все множества /_1(/) явля¬
ются совершенными.
Итак, отрезок [0; 1] разбивается на континуум непересекающихся
совершенных множеств вида /_1(7), где I — произвольный вертикальный
отрезок квадрата [0; 1] х [0; 1]. Так как /_1(1) — непустое совершенное
множество, значит, оно имеет мощность континуум (см. соответствующую
теорему из гл. 1), а поэтому мы разбили отрезок [0; 1] на сумму континуума
непересекающихся множеств мощности континуум. ■
Задача 3.25
Определим, является ли построенная нами кривая Пеано замкнутой кривой (т.е.
имеет ли место равенство /(0) = /(1)).
Решение
Данная кривая незамкнута. Образом точки £ = 0 является точка (0; 0), а образом
точки t = 1 — точка (I; 1).
Задача 3.26
Построим трехмерную кривую Пеано (т.е. найдем непрерывное отображение
отрезка [0; 1] на замкнутый куб [0; 1] х [0; 1] х [0;1]).
Решение
Данное построение совершенно аналогично двумерному. Для этого надо разделить
отрезок [0; 1] оси Ot на 27 равных частей, затем на 272, 273,... частей. Соответственно
этому, заданный куб делится сначала на 27 одинаковых кубов, затем на 272,273 кубов.
На каждом этапе отрезки нумеруются слева направо, а порядок нумерации кубов
выбирается так, чтобы кубы с соседними номерами имели одну общую грань.
Каждой точке £0 е [0; 1], являющейся пересечением последовательности вло¬
женных отрезков
A1 ID Д2 ID A3 ID ...,
ставится в соответствие точка куба M0, принадлежащая одновременно всем кубам
RiZ) R2z> Д3 з ...,
которые отвечают отрезкам A1, A2, A3, ....
Непрерывность данного отображения в любой точке £0 доказывается аналогично
плоскому случаю (докажите!). Также можно показать, что при построенном отобра¬
жении образы точек отрезка [0; 1] заполняют весь куб [0; 1] х [0; 1] х [0;1].
Замечание 3.22. Собственно говоря, таким образом можно построить
непрерывное отображение отрезка [0; 1] на куб любой размерности п. Для
202
этого будет нужно делить исходный отрезок на все более мелкие и мелкие
части (проверьте!).
Рассмотрим далее другой (арифметический) способ задания кривой
Пеано. Для этого определим на отрезке [0; 1] две функции ср и \|/ следу¬
ющим образом. Пусть t е [0; 1] и t = {tb t2, t3, ...}3 — троичное разложение
данной точки. Положим
ф(0 = {фц Ф2> —}з> V(0 = {Vi> V2- -Ь>
Ф1 - ^1> Ф2 ~
Ф п =
где
t3, если t2 — четное,
2 -t3, если t2 — нечетное;’
I Чп-1>если t2 + - + Чп-2 ~ четное,
[ 2 - t2n_1} если t2 +... + t2n_ 2 — нечетное;
t2, если tx — четное,
2 -12, если — нечетное; ’
I t2n, если t2 +... + £2и_1 — четное,
12- t2n, если t2 +... + £2и_1 — нечетное;
Эквивалентность данного отображения изученному проверяется, напри¬
мер, следующим образом.
Vi =
Vn =
1. Пусть t G
45
9’ 9
еЛ5, ^ - {!»1» Ч, Ч> -h-
Тогда ф(0 = {1, 2 - t3, ...}3, \|/(0 = {1,2- tA, ...}3.
Следовательно, (ф(£);\|/(£))е Q£.
§;ff е Als-«={1.0, о, 0, ¢5,...)3.
Тогда ф(0 = {1,0,t5,...}3, \|/(0 = {2,2,t6,...}3.
Следовательно, (ф(£); V(O) G Qls-
Изобразим приведенные размышления на чертежах (рис. 3.14).
2. Пусть t G
Рис. 3.14
Далее, корректность определения (т.е. выполнение того, что каждой
точке отрезка соотносится единственная точка квадрата) проверяется
203
непосредственным вычислением значений функций ср и \|/ в троично¬
рациональных точках. Докажем, что каждой точке квадрата соответствует
хотя бы одна точка отрезка.
Действительно, если £, r\ е [0; 1], £ = (Cp1, Cp2, ...}3, ц = (Xp1, Mf2, ...}3, то £ = ср(£),
Л = Х|/(£), где t = {tb t2, t3, ...}3, а цифры Ц определяются последовательно, друг
за другом, из следующих формул:
Фц t2
Xp1, если — четное,
...
2 - Xp1, если — нечетное;
= |фя»если t2+...+t2n_2 - четное,
2п-\ 12 - сри, если t2 +...+t2n_ 2 — нечетное;
Mfn, если t2 + ...+£2w_i — четное,
U = (
12-\|/и,еслн£2 +...+t2n_{ — нечетное.
Непрерывность функций ср и хр вытекает из совпадения любого наперед
заданного числа первых цифр, полученных при представлении достаточно
близких точек t0 и t из отрезка [0; 1], в виде троичных дробей (без цифры 2
в периоде).
Отметим, что система уравнений
ф(0 = ¥(0 = Л
(3.7)
имеет не более четырех решений при любых ц е [0; 1]. Это происходит
вследствие того, что различные решения системы (3.7) могут получаться
исключительно в силу неединственности представления чисел E1 и ц в виде
троичных дробей. Например, при
£ = 2/9 = (0,2,0,0, ...}3 = {0,1,2,2, ...}3
ил = 1/3 = (1,0, 0, 0, -}3 = (0, 2, 2, 2, ...}3
система (3.7) имеет четыре решения:
5/108 = (0, 0,1, 0, 2, 0, 2, ...}3; 13/108 = (0,1, 0, 0, 2, 0, 2, ...}3;
11/108 = (0, 0, 2, 2, 0, 2, 0, 2, ...}3; 19/108 = (0,1,1, 2, 0, 2, 0, ...}3.
Задание 3.19
Найдите прообраз точки (1/2; 1/2) при отображении построенной кривой Пеано.
Задание 3.20
Пусть (и; v) — координаты функции кривой Пеано, заданной на отрезке [0; 1].
Покажите, что если и, vs Ыра[ 0; 1], то а < 1/2 .
Задание 3.21
Найдите образ множества Кантора, заданного на отрезке [0; 1], при отображении
кривой Пеано.
Задание 3.22
Определим, какое подмножество отрезка [0; 1] является прообразом ковра Cep-
пинского при отображении кривой Пеано.
204
В заключение отметим, что кривая Пеано не является фракталом
в обычном его понимании (т.е. геометрической фигурой, обладающей свой¬
ством самоподобия, — фигурой, составленной из нескольких частей, каж¬
дая из которых подобна всей фигуре целиком), но тем не менее интересна
как пример патологической фигуры, отображающей множество заданной
размерности на множество большей размерности. Это и другие подобные
открытия примерно того же времени (множество Кантора, пример Вейер-
штрасса и т.п.), оказали существенное влияние на дальнейшее развитие
математического анализа. Стало понятно, что опоры на одну только интуи¬
цию уже недостаточно. Понятие кривой Пеано, безусловно, не является
интуитивным, а изначально появилось из чисто аналитических рассужде¬
ний.
Глава 4
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИИ
ОДНОЙ ПЕРЕМЕННОЙ
4.1. Основные понятия
Определение 4.1. Мы будем говорить, что функция/: E —> R диффе¬
ренцируема в точке г G Е, если ее приращение, отвечающее приращению
аргумента Ar, т.е. A/ = /(г + Ar) - /(г), представимо в виде
Ay = A-Ax + о( Ar), (4.1)
где А = const не зависит от Ar.
Замечание 4.1. При A^O данное тождество показывает, что беско¬
нечно малая AAr эквивалентна бесконечно малой Ay и, значит, служит
для последней ее главной частью. Выражение AAr называется дифферен¬
циалом функции / в точке х.
Дифференциал функции определен однозначно, так как из формулы
(4А) следует, что
Iim /(* + *»)-/(*) = Um
Дг->0 Ar Дг-»0
А +
о(Аг)
Ar
= A,
и в силу единственности предела число А определено однозначно.
Определение 4.2. Предел /'(г)= Hm /(х + ^x)—fix)
Ar->0 Ar
если он суще¬
ствует, называется производной функции / в точке х.
В дальнейшем нам будут полезны следующие утверждения, доказатель¬
ства которых могут быть найдены в любом учебнике по математическому
анализу.
Утверждение 4.1 (необходимое условие дифференцируемости).
Если функция/дифференцируема в точке г, то она непрерывна в ней.
Замечание 4.2. Обратное утверждение, вообще говоря, неверно (см. при¬
меры ниже).
Утверждение 4.2 (критерий дифференцируемости). Функция /
дифференцируема в точке г тогда и только тогда, когда в данной точке
существует конечная производная /'(г). Причем в этом случае А =/'(г).
Утверждение 4.3. Операция дифференцирования обладает следую¬
щими свойствами:
1) (а/(г) + Pg(r))' = а/'(г) + Pgy(г) (линейность);
2) (Jipc) • ё(х)У = f'(x) g(x) + J(x)f(x) (производная произведения);
3) (Jix)Zgix))' = if'ix)g(x) - J(r)/(r))/g2(r) (производная частного);
4) if(g(x))Y =f'(g(x)) •g'(r) (производная суперпозиции).
206
Определение 4.3. Выражениями f'(x) = Iim —, ff(x) = Iim —
у ' Ar->0-0 Ar + Ar->0+0 Ar
определяются соответственно левая и правая производные.
Вспоминая определение предела функции по Гейне, перепишем выра¬
жение для производной функции / в точке х в виде
я—>°° хп
где 0 Ф Xn —^ 0 при га—»°°.
Из последнего равенства вытекает, что если функция / дифференциру¬
ема в точке х, то
Hm n(I(x + 1/га) - f(x)) = /'(*)•
я—>°°
Будет ли верно обратное утверждение? То есть достаточно ли существо¬
вания предела
Iim f(x + xn)~f(x)
п—>°°
Xk
для фиксированной последовательности {хп}, убывающей к нулю, для су¬
ществования производной f'(x)7 Ответ на этот вопрос — безусловно, от¬
рицательный. Рассмотрим функцию
fl/ra, если X = 1/га,
10, если х Ф 1/га.
/00 =
В этом случае
1/га
Hm га(/(1/га)-/(0)) = = 1 для VraeN.
я—>°°
1/га
Пусть, далее, {хп} —> 0, га —> «>, хп Ф 1 /га, тогда
Hm
я—>°°
/(*,)-/(<>) 0 о
Хп Хп
Отсюда мы делаем вывод о том, что производная функции / в точке
х = 0 не существует.
Изучим теперь более сложную задачу.
Задача 4.1
Предположим, что функция / имеет производную в точке а, а последовательно¬
сти {хп} и {zn} таковы, что при каждом п е N выполняется
хп Ф a, Zn Ф а, хп Ф zn, хп —> я, Zn —> а при п —»°°.
Покажем, что:
ч I- f (Xn)-I(Zn)
а) Iim — может существовать, а может и нет;
б) если дополнительно при каждом п > 1 выполнено условие хп< а < Zn, то
Iim Кхп)~ Kzn) = yv(a)
я->°° Г - 2L
я я
207
Решение
а) Для функции / (х) = хт, т е N, получим
Iim Mx"AMzn) = Hm *” ~Z” = Hm(х™"1 + *™-2z„ +... + z™^) = rnam~K
xn~zn
П—> oo
Далее рассмотрим функцию
n^ooXn-Zn n-^oo
Выбрав x*p -
n(4n +1)
Iiix) =
2(i) =
I
X2 -sin—, если x^O,
x
О, если х = 0.
2
получаем
тг(4и + 3)’
/
Цщ ШлЫШ = Цш
тг(4и +1)
Л2 /
+
л(4и + 3)
У___
я-»°° 2 2
я(4и +1) л(4 п + 3)
71
Если же выбрать х^ =
- z(2) =
1
л(2и +1) 2тш
Hm
, получаем
MblzMbl-i
- 0.
хп zn
б) Рассмотрим тождество
/(*я) - Azn) = /(*я) ~ /(«) Хп - а , /Ow) ~ Яа) а
^я zn
х„-а
xn~zn
Zn ®
хп zn
Обозначая ——— = а, ——— = (3, ползаем 0 < a, P < I, а также а + P = 1. Отсюда
*« -Zn
хп zn
и из введенного тождества следует, что при любом п е N величина J к п/—J у п/ лежит
f (xJ-Aa) f(zn ) “ Aa)
между минимумом и максимумом величин —— и — , которые при
Хп~а
Zn~a
w —> оо сходятся к /'(а).
Рассмотрим далее несколько показательных примеров.
Пример 4.1
Пример функции, являющейся дифференцируемой
только в одной точке
Рассмотрим функцию f(pc) = X2 ■ D(x), где D(x) — функция Дирихле. Для нее имеем
/'(О)= Hm /(° + Ах)-/(O) = (Ax)2D(Ax)-Q^q
дж->о Ax Ax
Во всех остальных точках числовой оси функция / не является непрерывной,
а следовательно, по необходимому условию дифференцируемости не является диф¬
ференцируемой в них.
Пример 4.2
Пример функции, являющейся дифференцируемой
только в точках X1, ..., хп
Рассмотрим функцию f(x) = (х - X1)2 • (х - X2)2 •... • (х - Xn)2 • D(x). Доказательство
аналогично предыдущему.
208
Пример 4.3
Пример функции, являющейся дифференцируемой
только в счетном числе точек числовой прямой
Рассмотрим функцию /(г) = sin2 х ■ D(x). Для нее имеем
f'(kti) = Hm Sin2Crcrc + Ах) • Р(кп + Ах) = lim Sin2(Ar) • D(nn + Ar) _ Q
дх->о Лг дх->о Да:
Во всех остальных точках хФкп функция / не является непрерывной, а значит,
и дифференцируемой.
Пример 4.4
Пример функции, являющейся непрерывной,
но не дифференцируемой в точках Jtr1, ..., хп
Рассмотрим функцию /(x) = |r-r1| + |x-r2| + ... + |r-x„|. В каждой из точек
Xjfi = I,..., гс, имеем
lim f(xi + Ar) - f (Xi) ^ Ит f(xi + Ax)-f(xi)
Дх->0-0 Дг Ax —>0+0 Ax
Пример 4.5
Пример функции, являющейся непрерывной,
но не дифференцируемой в бесконечном числе точек
Примером такой функции является f(x) = I sin Tir |. Она не имеет производной во
всех целых числах, где функция f(x) обращается в нуль.
Замечание 43. Забегая вперед, отметим, что в дальнейшем нами будет
построено несколько примеров непрерывных на всей своей области зада¬
ния функций, но не дифференцируемых ни в одной точке числовой пря¬
мой. Более того, множество дифференцируемых хотя бы в одной точке
функций составляет множество меры нуль во множестве всюду непрерыв¬
ных функций!
Примеры 4.4 и 4.5 наводят нас на следующий вопрос.
Задача 4.2
Пусть функция / определена и имеет производную на R. В каких точках функ¬
ция |/| имеет производную?
Решение
Производная функции |/| заведомо существует в тех точках г0, в которых /(X0) Ф 0,
причем тогда | /1' (r0 ) = f'(x0 ) ■ sgn(/(r0 )). Пример функции f(x) = х показывает, что
производная функции |/| может не существовать в тех точках г, в которых /(г) = 0.
Пусть в точке 5с выполнено /(г) = 0 и f'(x) = 0, тогда
гт= пт /(*+а*)-/(*)= lim /ог+дц
Дх—>0 Ax Дх—>0 Ax
Отсюда получим, что /(г + Ar) = а(х) ■ Ar, где ос — бесконечно малая функция.
Следовательно,
Hm
Дг—>0
I/(г + Дг)|
Ar
= Hm |а(г)|--^ = 0.
Дх->о Ax
209
Если же /(х) = 0, но /'(х) = C Ф О, то Iim +
Лх->0 Дх
Iim
Лх—>0+0
|/(х + Ах)|
Ax
/(х + Дх)
Дх
Ax
Дх
= C, поэтому
= ± \с\.
Получаем, что | /' |+^| /' |_, т.е. производной функции/в точке х не существует.
Рассмотрим пример:/(х) = х3. Получаем/(0) = 0,/'(0) = 0 и (|х3|)' = 0.
Задание 4.1
Являются ли дифференцируемыми в точке х = 0 следующие функции:
а) у - х • I sin х |; б) у - х ■ | х3 |?
При исследовании на дифференцируемость функции, которая задана
системой, т.е.
fix) =
ГА(х), если х < X0,
[g(x), если х > х0,
важно ответить на следующий вопрос: каким условиям должны удовлетво¬
рять непрерывные функции hug для того, чтобы функция / была диффе¬
ренцируемой на всей числовой прямой?
На множествах х < X0 и х > X0 для дифференцируемости функции/необ¬
ходимо и достаточно, чтобы на них были дифференцируемы функции hug
соответственно.
В силу непрерывности функций h и g получаем
Hm /(х) = Hm А(х) = А(х0), Hm /(х) = Hm g(x) = g(x0).
X—>Xq-0 х—>Xq-0 X—>Х0+О X—>Xq +0
Отсюда следует, что для дифференцируемости функции / в точке X0
необходимо должно выполняться A(x0) = g(x0).
Далее, используя это равенство и равенство
А(х0 +Дх)-А(х0)
/(х0+Ах)-/(х0)
Ax
Ax
g(x0 + Ах) - g(xQ )
Ax
при Ax < 0,
при Ax > 0,
получаем
А(х0) = Jjm
Дх->0-0 Ax
A-(X0) = lim SOblMzSM = g>fa).
Дх—>0+0 Дх
Следовательно, для дифференцируемости функции /(х) в точке X0
необходимо и достаточно, чтобы выполнялись два условия:
Kx0 ) = g(x0 ), h!_ (х0 ) = g'+ (х0 ).
Задача 4.3
Пусть функция /(х) дифференцируема на интервале (а; Ъ) и Iim /(х) = °°.
х—>а+0
Обязательно ли выполняется: a) Iim f'(x) = °о; б) Iim |/'(х)| - «>?
х->а+0 х->а+0
210
Решение
Ответ на вопрос из п. а — отрицательный. Действительно, рассмотрим на интер¬
вале (0; 1) функцию
fix) = — + cos—.
X X
Для нее имеем Hm f(x) = Однако из выражения для ее производной
X—>0+0
1
. I 1
( ■ 1
—
•sin— = —
Sin-
X2
X X2
I X
.(1)
- 1 г(2) -
1
п
71П П
71/2 +
делаем вывод о том, что
$ Hm
ж—»о+о
Заметим в то же время, что для приведенной функции выполняется Iim /'(х) = °°.
х-»0+0
Докажем от противного1, что это выполняется для всех таких функций /. Пусть функ¬
ция /' ограничена в правой окрестности точки а, т.е. 3 C > 0 такое, что |/'(х)| < C при
хе(а;а + 8). Фиксируем произвольные х* G(а;а+ 8) и хе(а;х*). Ha отрезке [х;ж*]
для функции /выполнены все условия теоремы Лагранжа (докажите!). Используя
эту теорему, получаем
/(*) - /(**) = f'iZXx - X*), или fix) = fix*) + f'i%)ix - X*),
откуда
|/(*)| ^ I fix* )| +1/4¾! • \a ~ X* I < \f(x*)\ + C\b - a\,
т.е. функция /ограничена в правой окрестности точки а, что противоречит условию,
так как выполнено Iim f(x) = °°.
х—>а+0
Задача 4.4
Пусть функция fix) дифференцируема на интервале (а; Ь) и Iim /'(х) = °°.
Обязательно ли Iim fix) = оо? х~*а+0
*->а+0
Решение
Рассмотрим пример: fix) = л[х на интервале (0; 1). Для этой функции
I
Hm f'ix) = Iim —— = °°, однако Hm fix) = Hm \[х = 0.
х->0+0 л:—»0+0 Зх2/3 х->0+0 х—»0+0
Заметим, что то же самое выполняется и для верхнего предела, поэтому данный
вопрос даже не ставится.
Обратимся к вопросу о применении понятия производной при нахождении
предельного значения функции. Для этого рассмотрим следующую задачу.
Задача 4.5
Функция fix) имеет производную при х = а. Вычислим пределы:
,. ап fix)-хп fid)
a) Hm— ^-^-,weN;
х-а
( Л
Г 2)
( ^
Hm п
/
а + —
+ /
а + —
+
+
а + —
~k-fid)
П—>°°
I п)
К nJ
V nJ
,^eN фиксировано.
1 Доказательство этого факта использует теорему Лагранжа (см. теорему 4.4). Читатели,
не знакомые с ней, могут вернуться к данной задаче после прочтения этой главы.
211
Решение
а) Прибавляя и вычитая в числителе данной дроби ап ■ f(a) и используя элемен-
qTI _ jqTI
тарный предел Iim = -па"-1, получаем
ж->а х-а
lim »»/(*)-*■/(<.)=Иш ант-т + lim =
х-а
х-а
х-а
= anf'(a) - па"-1/(а).
б) Представляя изучаемое выражение в виде
и
г л
( 2^
( k)
/
а + —
+ /
а + —
+ - + /
а + —
- k • /(а)
I nJ
I nJ
I nJ
= /(g + l/n)-/(g) f(a + 2/n)-f(a) , f(a + k/n)-f(a)
l/п 2/n k/n
и переходя в нем к пределу при п —» получаем
Hm п
( Л
,( ЬЛ
/
а + —
+ ... + / а + —
~k-f(a)
I п)
У п)
=AeXI+2+...+Л)=Afl)
*(£+1)
Отметим, что мы воспользовались фактом, установленным в начале данной главы.
Задание 4.2
Пусть функция дифференцируема в точке а. Вычислите следующие пределы:
_ К*)ех-т t
*-»о /(*)cosx-/(0)’
a) Iim
а = 0, /'(0) * 0; б) Hm п
/
ал—
п
-/
д- —
п
4.2. Касательная, геометрический смысл производной
и дифференциала
Пусть функция у = /(х) непрерывна в точке а и определена в некоторой
окрестности данной точки. Рассмотрим понятие касательной прямой к гра¬
фику в точке а. Для этого рассмотрим всевозможные секущие, т.е. прямые,
проходящие через точку (а; /(а)) и точки (х; /(х)) при х из окрестности
точки а. Такие прямые образуют пучок прямых
Y - k{x- а) + /(а).
Прямые из этого пучка различаются только угловым коэффициентом k
для точки х*. Для него имеем k = k(x*) =
. Если существует пре-
х -а
дельное положение секущих, то эту предельную прямую называют каса¬
тельной к графику функции / в точке а.
Очевидно, что если существует предел lim k(x*) = k', то существует и пре-
X —
дельное положение секущих, и предельная прямая описывается уравнением
Y = k\x - а) + /(я).
При этом Hm k{x*) = /'(«), т.е. из дифференцируемости функции
х* —>а
в точке а следует существование касательной в этой точке.
212
Обратное утверждение, вообще говоря, не верно. Рассмотрим, напри¬
мер, функцию f(x) = y[x. Для нее не существует конечной производной
в точке = 0 (докажите!), но есть предельное положение секущих: х = О,
т.е. вертикальная прямая.
В этом можно убедиться, рассмотрев рис. 4.1 ,а либо обратную функ¬
цию х = g(y) = у3 (рис. 4.1, б). Данная функция является дифференциру¬
емой, g'(0) = 0. Поэтому график имеет касательную х = 0. На самом деле
на рис. 4.1, а и б изображен один и тот же график, рисунки получаются
друг из друга поворотом плоскости вокруг оси X = у, касательные при этом
переходят в касательные.
В некотором смысле и в этом случае угловой коэффициент каса¬
тельной равен производной (т.е. они оба равны °°). Таким образом, если
I- f{X)~fia) 1 г
Iim — = оо, функция J непрерывна в точке а, то существует каса-
х->а х — а
тельная к ее графику функции х = а.
Теперь рассмотрим такой вопрос: на первый взгляд кажется, что
для любой точки пересечения касательной с графиком функции (отличной
от постоянной) можно найти такую окрестность, что в ней график и каса¬
тельная имеют только одну общую точку, совпадающую с точкой касания.
На самом деле это не так, а именно, можно построить пример функции,
отличной от постоянной, график которой имеет бесконечное количество
точек пересечения с касательной в любой окрестности точки касания. Для
1
этого рассмотрим функцию f(x) = х2 sin— Для нее в точке х = О имеем
х
= Um /(А*>-/(°>= Iim = Iim д*5тдж = 0.
Ax—/\у Ax—/\д7 Ax—
/'(0)
Следовательно, уравнение касательной к графику функции в точке
1
(0; 0) имеет вид у = 0. В каждой из точек х = — функция / обращается
пп
в нуль. Остается заметить, что Hm хп = 0.
П—¥°°
Для более ясного восприятия полученного результата изобразим график
рассмотренной функции на отрезках [-0,06; 0,06] и [-0,02; 0,02] (рис. 4.2).
213
Рис. 4.2
Рассмотрим далее еще несколько задач, описывающих различные инте¬
ресные факты об отрезках касательных и нормалей в классических кривых.
Задача 4.6
X2
Проверим, что любая касательная к гиперболе —
а2
тами треугольник постоянной площади (рис. 4.3).
J/2
Ъ2
= 1 образует с ее асимпто-
Рис. 4.3
Решение
а) Уравнение асимптот гиперболы, заданной каноническим уравнением, имеет вид
-±f=o,
а о
уравнение касательной в точке с координатами (X0Szz0)1 = \ (докажите!).
а1 о1
Вычисляя точки пересечения асимптот и касательной, получаем
(Wi) =
^ a2b ab2
. (¾;½)=
( <>2Ь
ab2
S
I
J
о
I
#
^
^bx0-Vay0 ’
bx0+ayQj
Синус угла ф между векторами (X1;Zz1) и (.X2',у2) Равен
мого треугольника находится по формуле
2 ab
а2+Ь2
. Площадь изучае¬
те • sinф• Jxfvtfi ■ Jxfvy% =
ab
ab
IaAb2 +a2b4 IaAb2 + a2bA
cP--vb2 ]] bx0 - ayо у bx0 + ay0
a4b2+a2bA аъЬъ ab ,
= ab.
°2+b2 Jb2x$- a2yjj ^b2xl-a2yl [xffy[
72 Jj 2
a‘
Задача 4.7
2 2 2
Проверим, что у астроиды хз+г/3=аз для любой касательной длина ее отрезка,
заключенного между осями координат, постоянна (рис. 4.4).
Решение
Введем параметризацию астроиды:
1 Здесь и далее X0 = x(t0), у0 - y(t0).
215
x = acos3t, y = asin3t, £e[0; 2n],
3asin2t cost
и вычислим производную: y'x(t0) = —^ = -tgt0. Отсюда для уравнения
За cos2 t0 sin t0
касательной в точке (^0; у0 ) получаем ^icac = у0 - (х - X0 ) • tg t0.
Точки пересечения данной касательной и осей координат имеют вид
*1 = 0, У1=У0 + x0tgt0VLX2=x0+^-, ^2=O.
tg£0
Длина отрезка касательной между осями координат равна
f „ Л2
^Iix2-xO2+(у2-У1)2
*о+
I Wo)
+ (.-Vo-Xotgt0)2 =1.
Замечание 4.4. Астроида — плоская кривая, описываемая точкой окружно¬
сти радиуса г, катящейся по внутренней стороне окружности радиуса R = 4г.
Задача 4.8
Проверим, что у трактрисы x(t) = a Intg— + cos t , y(t) = a sin t, 0 < t < п, для любой
V 2 )
касательной длина ее отрезка от точки касания до оси Ox постоянна (рис. 4.5).
Решение
Уравнение касательной к трактрисе в точке (*0; у0) имеет вид
У = Уо + Ух(Ч)(х ~ хо) = asin^o + tStO-
х-а
htg+ COSt0
\
)
216
Найдем точку пересечения касательной и оси абсцисс:
( + \
, У = 0.
a sin tn
х- - + а
Wo
In tg + cos t0
Длина отрезка, соединяющего точки (лг0; г/о) и (Х>У)’ имеет вид
\1(х-хо)2+(У-Уо)2 =
Задача 4.9
Проверим, что расстояние от начала координат до любой нормали к кривой, задан¬
ной уравнениями x(t) = «(cost + tsint), y(t) = a(sin£ - tcost), постоянно (рис. 4.6).
Рис. 4.6
Решение
Уравнение нормали в точке (лг0; у0) имеет вид
I 1
У = Уо—77-(*-½) = * +
У о
1
Wo
Xn
Ух(Ч) Wo
Следовательно, расстояние от начала координат до данной нормали равно
Cost0 + f0 Sint0
tg*o
+ Sint0 -t0 COSt0
V1+ Ctg2
-=1.
Для самостоятельной работы предлагаем читателю решить следующую
задачу.
Задание 4.3
Покажите, что касательные к кривой, заданной уравнениями x(t) = a(t - sin t),
y(t) = g(1 - cost), проведенные в точках, соответствующих значениям t0 и t0 + п, пер¬
пендикулярны при любом t0^kii,ke Z.
217
4.3. Производные и дифференциалы высших порядков
Предположим, что функция /: E —> R является дифференцируемой
на множестве Е. В этом случае на данном множестве возникает новая функ¬
ция /': E —» М. Если, в свою очередь, /' имеет производную, то эта произ¬
водная называется второй производной для функции / и обозначается /"
и т.д. В общем случае приходим к следующему определению.
Определение 4.4. Производная порядка п определяется следующим
индукционным соотношением:
/(0) (*) = /(*), /(”>(*) =
^-Г/(и_1)(^)1(иеМ).
OXl J
Замечание 4.5. Если функция /(х) имеет непрерывную производную
/(”)(х) на интервале (я; Ъ), то пишут/(х) G №)(я; Ь). В частности, если/(х)
имеет непрерывные производные всех порядков на (я; Ъ), это обозначают
как /(х) G С(°°)(я; Ъ).
Определение 4.5. Дифференциалы порядка п определяются формулами
dny = d{dn~ly) (п = 2, 3,...), где принято d{y = dy = y'dx.
Замечание 4.6. Если х — независимая переменная, то полагают d2x =
= d3x = ... = 0. В этом случае справедливо
dny = y^dx11 о у(п) =
если у = /(х), ах= ср(£), то dy = y'xdx, dx = x[dt =>dy = y'x • x'tdt = y'tdt — инва¬
риантность формы первого дифференциала;
d2y = d(yxdx) = dyx dx + yxd{dx) = {dyx = yxxdx} = yxxdx2 + yxd2x — отсутствие
инвариантности формы дифференциала второго (и более высокого) порядка.
Пример 4.6
Нарушение инвариантности формы
для дифференциалов высших порядков
Пусть у = хъ. Найдем d2y в случае, когда а) х — независимая переменная; б) х =
= x(t) = t3.
а) Последовательно беря дифференциалы функции у(х), получаем
dy = 3x2dx (I); d2y = Gxdx2 (2).
б) Подставляя выражение x(t) в формулу для у(х), получаем y(t) = t9, откуда
dy = 9t8dt (3); d2y = IZfldt2 (4).
Делаем вывод о том, что если подставить х = £3 и dx = 3t2 в формулу (1), нами
будет получено выражение (3), а если подставить их в формулу (2), мы правильного
выражения (4) не получим. Дело в том, что вместо выражения d2y = Gxdx2 нужно
было использовать тождество
d2y = d(3x2dx) = Gxdx2 +3 x2d2x.
Последнее слагаемое не исчезает, так как в случае, когда переменная х сама
является функцией от t, и d2x Ф 0. Подставляя в данное тождество х = t3, dx = 3t2dt
и dP-x = Gtdt2, получаем dy2 = 54t7dt2 +18t7dt2 = (4).
218
При вычислении производных высших порядков бывает очень полезна
следующая теорема.
Теорема 4.1 (формула Лейбница). Пусть и{х) и v(x) — функции, име¬
ющие на некотором множестве E производные до порядка п включительно.
Тогда для п-й производной и п-го дифференциала от их произведения спра¬
ведливы следующие формулы.
(u-v)Cd = ^CfoPdxp-Ci и<°> = и;
k=o
dn(u-v) = ^CfokU-dC-kfo d°u = u.
k=o
Гораздо менее известной и более сложной является формула для п-й про¬
изводной частного двух функций. А именно, пусть и(х), v{x) имеют на неко¬
тором множестве E производные до порядка п включительно и v(x) Ф О
на Е. Пусть требуется найти п-ю производную от их частного1 *.
Обозначим h(x) = и(х\ Тогда справедливо равенство v(x)-h(x) = u(x).
v(x)
Для удобства опустим далее аргументы функций и последовательно про¬
дифференцируем полученное тождество п раз. Используя формулу Лейб¬
ница, будем иметь
Cfo'h + Cfoh' = и' <ф> Cfoh' = и' - v'h,
Cfo"h + Cfo'h' + Cfoh" = и" о Cfo'h' + Cfoh" = и" - v"h,
• Cfo"'h + C\v"h' + Cfo'h" + Cfoh'" = и'" о C\v"h' + Cfo'h" + Cfoh"' = и'" - v'"h,
Cfopdh + Cfop-dh' +... + CfohCd = ip) о CfoC-Щ' +... + CfohCd = uCd - p)h.
Нами была получена система из п уравнений и п неизвестных: h', h", ...,
ЬР). Рассмотрим матрицу данной системы. Она будет иметь следующий
вид:
C\v
0
0
0
.. 0 "
Ci *2V
Cfo
0
0
.. 0
C13V
Cfo'
Cfo
0
.. 0
CfoC-V
Cfo(n~3d
CfoC-C .
.. Cfoj
Заметим, что ее определитель A = Vn ФО. Следовательно, составленная
система (линейных алгебраических уравнений) разрешима относительно
переменных h', h", ..., hP). В частности, используя формулы Крамера,
для искомой производной находим
h,Cd(x)
Kix)
Vn (х) ’
1 Данный результат взят из книги: Кужелъ А. В. Методы обобщений в математике : учеб,
пособие. Симферополь, 1983.
219
где
V
0
0
u'-v'h
2vf
V
0
.. Uff-Xfh
К(х) =
3v"
3vf
V
.. Ufff-Xfh
и(«-1) („-2)
2
п(п-1)(п-2)^п_я,
6
Разлагая полученный определитель по элементам последнего столбца
(и вспоминая формулу h = —), заключаем, что
V
_ Dn(u)v-uDn(v)
V
где
Dn(T) =
V
2vf
3v"
О
V
3vf
О
О
V
nv(n-1) !) (я-2) 1X7* 2)р(и-3) Х(Я)
2 6
(4.2)
Отсюда искомая формула имеет вид
Сл.\(п)
и
KvJ
Dn(u)v-uDn(v)
V
72+1
(4.3)
где функция Dn(T) определяется через функциональный определитель
по формуле (4.2).
Для первых Di получаем
D2(T) =
Di(T) = Tf,
V T
2vf т‘
= VTff-2vf т'.
Отсюда получаются известные формулы
(vuff - 2 v'u')v - [vvff - 2 (Vf)2Ju
(иЛ
UfV - VfU
CM
I
UJ
Заметим, что дальнейшее применение полученной формулы достаточно
громоздко. Применим ее для вычисления п-й производной от линейной
„ ^ CLX л-Ъ
рациональной дроби -.
сх+ а
Для данной функции получаем
= (ах + й)(”) = 0 = (сх + d)(n) = ц("), п > 1.
220
Следовательно, получим
Dn (т) =
CX+ б/
0
0
0
т'
2с
сх + d
0
0
0
0
3 с
сх+ d ...
0
0
0
0
0
сх-yd
0
0
0
0
пс
0
2с
сх л-d
0
. 0
0
3 с
сх-yd .
. 0
0
0
4с
. 0
= (-1)и-1т 'п\сп~1
0
0
0
. пс
По формуле (4.3) для искомой производной получаем выражение
^ ах + b Y^ _ (-1)”-1 п! си_1 {ad - be)
Kcx + d J (cx + d)n+1
Советуем читателю вычислить данную производную без использования
формулы (4.3).
Рассмотрим далее несколько задач на многократное дифференцирова¬
ние.
Задача 4.10
Вычислим производную порядка п следующих функций:
а) /(х) - sin2x, XG М;
б) f{x) = 1/(х2 - 4), х G К;
в) /(х) = sinax • sin6x, а и b — постоянные;
г) /(х) = 6х • sinx;
д) /(х) = х”-1 • е1/*, х Ф 0, п > 1;
е) /(х) = X1 • Inx, х > 0 , n G N.
Решение
I cos 2х
а) Понижая степень у sin2x, получаем /(х) = — —, откуда, используя фор¬
мулу для n-и производной косинуса, находим
/00 (х) = -2”-1 cos
б) Раскладывая предложенную дробь на простейшие, имеем
f ттл
2х + —
2
( 1 )
(и) J
Г 1 1 ]
(я)_(-1 )п-п\
Г 1
Lx2 — 4 J
~ 4
^х-2 х + 2,
4
ч(х-2)я+1 (х + 2)я+1 J
в) Раскладывая произведение синусов в разность косинусов, получаем
./W(X) = I
/(х) = — [cos х(а - Ь) - cos х(а + Ь)] =>
' , пп) . пп) .
cos х(а-о) + — -{a-by1-cos х(а + о) + — -(а+ о)”
V 2 У V 2 У
221
г) Вычислим первую и вторую производные:
/'(х) = ех sin х + ех cos х-еху[2 sin
/"(X) = Sex
х + —
4
• ( пN
( -Y
п
= 2ех sin
71^
sin х + —
+ COS
х + —
х + —
L I 4J
I 4J.
I 2J
Докажем, используя метод математической индукции, что/С”) = 2”/2ех sin
Действительно,
f 7
х + —
V 4/
/("+1)(*) =
2п/2ех sin
х + -
Tltl
T
sin
nn'
хп
+ COS
Ttns
XH
п+1
= 2 2 exsin
I 4J
I 4J
I 4 J
= 2"/2ех
д) Отметим, что применение формулы Лейбница в этом примере весьма трудо¬
емко. Постараемся угадать ответ. Ситуацию усложняет то, что параметр п, порядка
которого нужно найти производную, входит в саму функцию (т.е. производная каж¬
дого из порядков берется, вообще говоря, от различной функции). Для производных
первых порядков получим
рУ/х
f'(x) = {n = i) = (eV’)’ = -—-,
X1
/"(х) = {п = 2} = (XeiZx )" = ei/x
I + 2х 2ех еУх
Xй
X2 X3
Докажем, используя метод математической индукции, что /С”)(х) = (x”_1 • eV*)(«) =
ех/х
= (-1)" Имеем
п+1
(хп -еУх)(”+1) =[x-(xn~xeVx)fn+x:) = ZcLi'х(к) ■ (Xn^e1/* )(”_A!+1) =
k=o
= x • (Xn^e1Zx )(n+1) + (n +1) • (Xn^e1Zx)O) =
= X'
(-1)"
еУх
V
x
п+1
+ (w + 1)
(-1)"
е1/*
х
п+1
= (-1)"+1-х-е1/*-
X
1 я + 1^ , (-l)"eVx
+ (и + 1)- '
п+З хп+2
X
п+1
= (-1)"+1-
еУх
х
п+2
е) Как и в предыдущем пункте, параметр п входит в значение исследуемой функ¬
ции. Постараемся вычислить первые производные и понять закономерность:
/'(х) = (х■ Inх)' = Inх +1; /"(х) = (х2 • Inх)" = 2lnx + 3 = 2!lnx + 2!
' О
1+-
V 2 У
/С3)(х) = (х3 -1пх)С3) = 6lnx + ll = 6lnx + 6-—= 3!1пх + 3!
6
60
/С4) (х) = (х4 • In х)(4) = 24 In х + 50 = 24 In х + 24 •— = 4! In х + 4!
Докажем, используя метод математической индукции, что
и \
/(")(х) = (х"-1пх)С") = и!1пх + и!- Zt-
k=ik
, I 1
1 + - + -
2 3
,111
1+ - + - + -
2 3 4
222
База была проверена выше, докажем индукционный переход. Предположим, что
выполнено
/(га_1)(л;) = (и-1)!-1пд; + (п-1)!- Ет-
н*
Тогда
/(">(#) = (хп ■ In x)W = (nxn~l Inx + х”-1 )(га_1) = п • (Z^1)(X)) + (х”-1 )(я-1) =
= п!1пх + я!- 2у + (и-1)! = |(п-1)!
a=i« [
п I
я!1пх + п!-Ет-
A=I я
Задание 4.4
Вычислите производную порядка п у функций:
а) /(х) = х2е* х е R; б) /(х) = е М\{1};
1-х
в) /(*) = Л^7> xeR\{-2;2}.
X2 -4
г) /(х) = sin ах ■ cos Ьх, а и b — постоянные;
д) /(х) = COS3Ox, а — постоянная.
Задача 4.11
Докажем следующие тождества, используя многократное дифференцирование:
Tl { Trh ^ f тту] ^
а) ЕС*sin х + — =2”/2sin хн ,хеМ, и>1;
Jfe=O V 2 ) V4J
п Л Л
б) С*=1 + - + ... + -,яе N.
^=I Я 2 Tl
Решение
а) Используя результат из задачи 4.9 (п. г), получаем
е~х(ех sinx)W = 2”/2 • sin
х + -
7Ш
C другой стороны, используя формулу Лейбница, имеем
е~х(ех sinx)W -е~х ■ YC„ -(sinx)W -(ех)(”“*) = ЕС* sin
A=O A=O
б) Используя результат из задачи 4.9 (п. е)), получаем
( 4 4 \
(x"lnx)W =п\
( Tlk^
XH
1 1
Inx +1H 1-... H—
2 п
Если же применить к вычислению данной производной формулу Лейбница, имеем
для той же производной следующее выражение:
(x”lnx)W = ЕС* -(Inx)W -(XnZn-*) = n! In х+ ЕС*
A=O A=I
„i t
A=I Xk k\
f 1 л(*-1)
VXy
= n!lnx+ ЕС* —у——-'yxk = и!1п х + п!- ЕС*
(х”)(”-А) =
(-!)*-<
fc.1 *
Сопоставляя полученные равенства и сокращая на и!, приходим к искомому
результату.
Замечание 4.7. Заметим, что доказательство равенств задачи 4.10 мето¬
дом математической индукции — весьма трудоемкое.
223
Задача 4.12
Зафиксируем удобное нам произвольное конечное или бесконечное положитель¬
ное число а. Построим пример функции/(х) G а), для которой:
a) 6) lim«U
п—>°° п\
Решение
п->°° п
а) Рассмотрим функцию /(х) = , х е (-1; 1). Для нее имеем
1-х
/<">(*) = [(1 -х)-1 ](»>=-
п\
-/W(O) = и!.
(1-х)”+1
б) Выбирая в качестве /(х) = х-ех, xel, получаем
/W(x) = (x-e*)W = п-ех + х-ех =>/(”)(0) = п.
Задание 4.5
Постройте примеры функций /(х), для которых:
а)
п\
Задача 4.13
Построим примеры бесконечно дифференцируемых функций:
а) строго положительной при положительных х и равной нулю при отрицатель¬
ных х;
б) положительной в единичном интервале (0; 1) и равной нулю вне его;
в) равной нулю на (-«>; 0], равной единице на [1; -н») и строго монотонной
на отрезке [0; 1].
Решение
а) Примером такой функции служит
/W =
Je-Vx2j если х > 0,
[О, если х < 0.
Ранее эта функция уже была нами изучена в связи с ее несравнимостью со сте¬
пенной функцией х* при х —> 0 + 0 (см. задачу 3.5). Так как Iim е-1/*2 = 0, то /(х) не-
х—>0+0
прерывна на всей числовой прямой R. Далее, для х > 0 получим
/'(х) = е-1/*2, /"(х) = —е-1/*2 + ^e-1A2,
■уО -у4 уО
лЛ/ лЛ/ шЛ/
/'"(х) = ^e-1/*2 -^e-1/*2 +-^-е-1/*2, и т.д.
уD у/ уУ
•Л/ %Л/ тЛ/
Получим, что /W (х), х > 0, п е N, есть сумма выражений вида е-1/*2, т G N. Так
Xm
как в упоминавшейся выше задаче было доказано, что для всех п G N выполняется
Q
Iim —е~у/х =0, то мы делаем вывод о том, что функция /(х) имеет на R непре-
х—>0+0 Xm
рывные производные всех порядков. Отсюда заключаем, что построенная функция
является бесконечно дифференцируемой,
б) Примером такой функции является
1
/W=-
е X2(I-X)2
если 0 < х < 1,
0, в противном случае.
224
Доказательство аналогично приведенному в п. а),
в) Примером такой функции является
О, если х < О,
1
/(*) =
е (I-*)2
е х
, если 0 < х < 1,
1,если х>1.
Доказательство аналогично приведенному в п. а), оставляем его читателю.
Построим графики функций, указанных в п. б) и в) (рис. 4.7).
1 • IO-7
8 ■ 10-8
6 • 10-8
4 • 10-8
2 • 10-8
Рис. 4.7
Задача 4.14
Предположим, что /(х) — дважды дифференцируемая функция, удовлетворяю¬
щая условиям /(0) = 1,/'(0) = 0 и такая, что для Vxe [0; +°°) выполнено неравен¬
ство /" (х) - 5/'(х) + 6/(х) > 0. Докажем, что для Vxe [0; +°°) справедливо неравен¬
ство /(х) > Зе2* - 2е3х.
Решение
Преобразуем данное нам неравенство:
0 < /"(х) - 5/'(х) + 6/(х) = /"(х) - 2/'(х) - 3 (/'(х) - 2/(х)) =
= {«(*) = /'(*) - 2/(*)> = g\x) - 3g(x).
Отсюда следует, что для всех неотрицательных х справедливо неравенство
g'(x) - 3g(x) > 0, или (g(x) • е~3х)' > 0. Следовательно, функция g(x) ■ е~3х монотонно
не убывает и
g(x) • е-з- > g(0) = /'(0) - 2/(0) = -2 => /'(х) - 2/(х) > -2ез*.
Далее получаем
(/(х) • е_2д: У = /'(х) • е_2лг - 2/(х) • е_2лг =
= (JXx) - 2/(х)) • е-2* > -2е3^ • в”2* = -Iex,
или(/(х) • е-2*)' + 2ех > 0, т.е. (fix) • е_2х + 2ех)' > 0. Таким образом, функция /(х) • е~<1х+
+ 26х возрастает на луче [0; + °о) и принимает свое наименьшее значение в нуле:
f(x) ■ е~2х + 2ех > /(0) + 2 = 3, или /(х) > Зе2х - 2е3х.
В заключение параграфа мы приведем редко встречающуюся (из-за
своей громоздкости) формулу для п-й производной сложной функции. Для
начала рассмотрим несколько частных случаев:
Kg(X)Y0) =Kg(X)); f(g(x))(=K(g(x))g'(x);
225
/(g(x))(2) = (/'(s(*))g w =PK<x))g'(*)2 +/'(g(*))g<2>(*);
f(g(x))<:<> =pKg(x))gKxf + gPKg(x))g'(x)p4x) + f'(g(x))p4x).
Здесь стоит отметить, что подобные равенства выглядят сколько-нибудь
симметрично лишь только для этих конкретных значений п. Например,
четвертая производная будет иметь куда менее красивый вид:
/(g(*))(4) =/(4)(g(*»g'(*)4 +6/(3)(g(*))g(2) (x)g\x)2 +
+4/(2) (g(*))g(3) (x)g'(*) + 3/(¾ (g(x))g(2) (x)2 + f\g(x))g(4) (x).
Сформулируем теперь общее утверждение.
Теорема 4.2 (формула Фаа-ди-Бруно)1. Производная п-го порядка
сложной функции f(g(x)) (при условии ее существования) может быть
вычислена по формуле
/№))« = E/®(g<*))A,/g4x) s<2)(x)
k=0
где Bm
g^(x) gC)(x) g(n~k+i\x)
I!
2!
no формуле
= E
(n-k +1)!
Bn,k(X1’ -½* “^и-A+l) —
I! ’ 2! (гг-^ + l)! ^
— полином Белла, вычисляемый
п\
щ\щ\...тп_к^\
r Xi ^
Tn1
(xA
т2
( х \
•*"n-k+1
-£+!•
In;
12! J
{(n-k + iy.)
\mn-k+\
в которой суммирование ведется по всем таким наборам неотрицательных
чисел mt, что т{ + т2 + ... + mn_k+i = k и Im1 + 2 т2 +... + (n-k + I )mn_k+l = п.
Чаще в литературе можно найти вид этой формулы без полиномов
Белла с изначально записанным суммированием по кортежам.
4.4. Основные теоремы дифференцируемых функций
Теорема 4.3 (Ролля). Если имеют место следующие условия:
1) функция j(х) определена и непрерывна на [я; Ъ]\
2) f(x) имеет конечную производную f\x) на (а; Ъ)\
3) /(о)=/(6),
тогда найдется хотя бы одна точка £, G (я; Ъ) такая, что для нее выпол¬
нено /'(£) = 0.
Замечание 4.8. Геометрический смысл теоремы Ролля заключается в сле¬
дующем: если ординаты обоих концов кривой, удовлетворяющей условиям
этой теоремы, совпадают, то на кривой найдется точка, в которой касатель¬
ная к кривой параллельна оси абсцисс (рис. 4.8).
1 Доказательство формулы Фаа-ди-Бруно, использующее производящие функции, чита¬
тель может найти в книге [79] или в статье: Roman S. The formula of Faa Di Bruno // Amer.
Math. Monthly. 1980. Vol. 87. № 10. P. 805—809, где перечислено большое количество мето¬
дов доказательства с источниками.
226
Замечание 4.9. Кроме того, подчеркнем, что в теореме требуется наличие
конечной производной на интервале (я; Ъ), но не требуется существования
пределов/'(я + 0) и f'(b - 0).
Пример 4.7
Пусть дана функция f(x) = \J1-х2 на отрезке [-1; 1]. Для нее получаем
f\x) = -7=^=, /'(0) = 0, но $ /'(-1 + 0) и $ /'(1 - 0).
Vl-X2
Теорема 4.4 (Лагранжа). Если:
1) функция f(x) определена и непрерывна на [а; Ь];
2) /(х) имеет конечную производную /'(х) на (а; Ъ),
тогда найдется хотя бы одно число £, G (я; Ь), такое, что выполняется
равенство
f(b) -/(я) = /'(£) -(Jb- я) (формула конечных приращений).
Замечание 4.10. Для того чтобы изучить геометрический смысл теоремы
Лагранжа, представим формулу конечных приращений в виде
т-т
Ъ-а
=/'©■
„ Д*)-/(в) „ ,,
Число — есть угловой коэффициент прямой, проходящей через
Ъ-а
концы графика функции/(х) — точки (а; /(я)) и (b\f(b)), а/'(£) — угловой
коэффициент касательной к этому графику в точке (£; /(£)). Из формулы
конечных приращений следует, что существует точка \ G (я; Ь), в которой
касательная к графику функции /(х) параллельна прямой, проходящей
через концы графика (или совпадает с ней) (рис. 4.9).
У теоремы Лагранжа есть несколько важных следствий. Приведем их
без доказательств.
Следствие 4.1 {критерий постоянства функции). Непрерывная на ин¬
тервале (я; Ь) (где аиЬ могут быть бесконечными) функция постоянна на нем
тогда и только тогда, когда ее производная равна нулю в любой точке интер¬
вала (я; Ь).
227
Следствие 4.2. Если производные FiXx), E2 (х) двух функций E1(X)
и Е2(х) совпадают на некотором интервале, то на этом интервале разность
E1(X) - F2(x) есть постоянная функция.
Очень важно понимать, что если /'(х) = 0 на произвольном множестве X,
то из этого, вообще говоря, не следует, что /(х) = const на этом множестве.
Например, возьмем функцию
/(*)=-
1, если х G (0; 1),
2, если х G (2; 3).
Построение контрпримера основано на том, что множество X не явля¬
ется связным (в отличие от условия следствия 4.1, где множество X было
интервалом).
Теорема 4.5 (Коши). Если:
1) функции/(х) ug(x) определены и непрерывны на [я; Ъ]\
2) /(х) и g(x) имеют конечные производные f'(x) и g'(x) на (я; Ь)\
3) g'(x) Ф 0 при всех х из (я; Ъ)\
4) g(а) Фе(Ь),
тогда найдется хотя бы одно число £ G (я; Ь) такое, что выполняется ра¬
венство
№-№ = ПЮ
g(b)-g(a) g'&y
Последнюю формулу иногда называют формулой Коши конечных при¬
ращений.
Замечание 4.11. Отметим, что условие 4) в формулировке теоремы Коши
может быть опущено, так как если g(a) = g(b), то функция g(x) удовлетворяет
всем условиям теоремы Ролля, а следовательно, найдется такое \ е (я; Ь), что
g'(= 0, что противоречило бы п. 3, т.е. п. 4 является лишь следствием п. 3.
Замечание 4.12. Для того чтобы представить себе геометрический смысл
теоремы Лагранжа (см. рис. 4.9), рассмотрим кривую, заданную параме¬
228
трически: u(t) = (Jit), git)). Пусть A = (/(я), g(a)), B = Jib), g{b)). В силу
указанного выше g(a) Ф gib), и значит, точки А и В различны. Теорема
утверждает, что найдется значение £ G (я; Ь) такое, что касательная пара¬
метризованной кривой u(t) в точке я(£) параллельна прямой AB.
Рассмотрим полезное обобщение теоремы Ролля на случай бесконеч¬
ного интервала или бесконечного значения функции на концах интервала.
Утверждение 4.4. Пусть/имеет конечную производную в каждой точке
конечного или бесконечного интервала (я; b) и пусть Hm /(х) = Hm /(х).
х—>а+0 х—>6-0
Тогда Все (я; Ъ), такое что /'(с) = 0.
Доказательство
Для доказательства данного утверждения требуется рассмотреть три
случая.
1. Пусть интервал (я; b) конечен, Hm /(х) = Hm /(х) = А = const.
х—»я+0 х—>6-0
|/(х), если х G (я; 6),
. Имеем: F(x) непрерывна
Построим функцию .F(x) =
А, если х = я или Ь.
на [я; А], существует F'(x) на (я; &), Дя) = F(F). Следовательно, по теореме
Ролля найдется число £ G (я; Ъ) такое, что выполнено F'(£) = 0, а значит,
и /'($) = 0.
2. Пусть интервал (я; &) бесконечен, Hm fix)= Hm fix) = A = const,
х—>а+0 x->b-0
f(x) Ф А. Используя равенство пределов, получаем существование такого
е > 0, что прямая у = А + е (или у = А - в) пересечет кривую у = fix) как
минимум в двух точках A1 и ^1. Для функции/(х) на отрезке \а{, ^1] выпол¬
нены все условия теоремы Ролля, поэтому найдется £ G (A1; bf) с (я; Ь) такое,
что /'(£) = 0.
3. Наконец, пусть Hm fix)= Hm /(х) = +°°. Тогда и в случае конеч-
х—т+0 х—>6-0
ного, и в случае бесконечного интервала (я; Ь) найдется число А > 0 такое,
что уравнение /(х) = А имеет хотя бы два различных корня. Обозначим их
за A1 и Ь{. Для функции/(х) на [а{, ^1] выполняются все условия теоремы
Ролля, поэтому найдется такое £ g (A1; ^1) с (я; Ь), что /'(£) = 0.
Проиллюстрируем случай бесконечного интервала на чертежах (рис. 4.10).
Рис. 4.10 ■
229
Задание 4.6
Предположим, что функция / непрерывна на всей числовой оси R и выполнено
Hm /(х) = Hm f(x) = +°°. Докажите, что функция /ограничена снизу.
х—»-оо X—»+“
Утверждение 4.5. Пусть выполнены условия:
1) функция f(x) (гг - 1) раз непрерывно дифференцируема1 2 на отрезке
[Xq, xw],
2) существует производная/(”)(х) на интервале (х0; xw);
3) /(X0) = /(X1) = ... = /(х„) для х0 < X1 < ... < х„.
Тогда найдется число £ g (х0; х„) такое, что/(”)(£) = 0.
Доказательство
По условию задачи на любом из отрезков [X^1Jxa], k = l,...,n, выпол¬
нены условия теоремы Ролля, следовательно, существует по крайней мере
п точек щ E (х0; хи) таких, что /'(а{) = 0.
Для функции /'(х) на любом из отрезков at\,i = 2,..., п, выполнены
все условия теоремы Ролля, поэтому существует по крайней мере (гг - 1)
точка bj E (х0; хи ) такая, что f"(b-) = 0, j = I,..., гг -1.
Продолжая рассуждения таким же образом, приходим к выводу о том,
что в гг - (гг - 2) = 2 точках из интервала (х0; xw) /(n_1)(q) = 0, I = 1,2. Приме¬
няя теорему Ролля к функции /(и_1)(х) на [C1; с2], получаем, что найдется
£ G (q; с2) с (х0; хя ), в которой /<”>(£) = 0. ■
Утверждение 4.6. Пусть для некоторых натуральных чисел Pnq
выполнено:
1) /(х) G С(РЧ)[а; Ь];
2) 3 /(р+?+1)(х) на (а; Ъ);
3) Ra) =SXa) = ... =JWXa) = 0,/(6) =/'(6) = ... =/*>(6) = 0.
Тогда Bcg (я; Ъ) такое, что /(р+<7+1)(с) = 0.
Доказательство
При доказательстве будем считать, что р < q (рассмотрение слу¬
чая р = q оставляем читателю). В силу теоремы Ролля и равенства
/(я) = f(b) = 0 получим, что на интервале (я; Ъ) найдется такая точка (обо¬
значим ее £{), что /'(£]) = 0. Исходя из того, что справедливо равенство
/'(я) = /'(¾) = f'(b) = 0, делаем вывод о том, что найдется по крайней мере
две точки2 на интервале (я; Ь), в которых вторая производная /"
обращается в нуль. В результате р применений теоремы Ролля мы докажем,
что на интервале (я; Ь) существует по крайней мере р + 1 точек ^f+1,...,
в которых производная /(р+1 2) обращается в нуль.
Используя далее, что все производные функции / до порядка q вклю¬
чительно в точке b равны нулю, делаем вывод о том, что по крайней мере
в р + 1 точке интервала (я; b) производная /(¢+1) обращается в нуль. Обо¬
значим их через £%+1,..., ^11. Применяя теорему Ролля на каждом из отрез¬
ков £f+1;L i = i,...,p, заключаем, что на интервале (я; Ь) существует
1 Выражение «функция k раз непрерывно дифференцируема» означает, что k-я произво¬
дная функции непрерывна на отрезке.
2 При условии, что р > 1.
230
не менее р точек, в которых производная /(?+2) обращается в нуль, и т.д.
Мы находим по крайней мере две точки B£+q и BJj^q', в которых произво¬
дная f(p+Q) обращается в нуль. Отсюда по теореме Ролля (условия которой
выполнены) найдется по крайней мере одна точка ce(B,f+q;B$+q)<^(a;b),
в которой выполнено /(р+?+1)(с) = 0. ■
Рассмотрим несколько простых, но поучительных примеров. А именно,
постараемся ослабить требования теоремы Ролля.
Задача 4.15
а) Рассмотрим функцию f(x) = ■
Получаем, что f(x) имеет раз-
Определим, будет ли справедлива теорема Ролля для функции/на отрезке [а; Ь\,
если:
а) функция/имеет разрыв в одной точке отрезка, пусть даже в граничной;
б) функция / не имеет производной в одной точке интервала;
в) функция / имеет различные значения на концах отрезка.
Решение
[х, если 0 < х < 1,
[0, если X = 1.
рыв только в точке X= I, существует конечная производная на всем интервале (0; 1)
и /(0) =/(1) = 0. Однако 0 ^e(Ojl) такого, что /'(B1) = O.
б) Рассмотрим функцию f(x) = \x\ на отрезке [-1; 1]. Она определена и непре¬
рывна на всем отрезке [-1; 1], существует конечная производная /'(х) всюду, кроме
точки х = 0, и /(-I) =/(1) = 1. Однако 0%е (-1; 1) такого, что выполняется /'(B1) = 0.
в) Рассмотрим функцию f(x) =хна отрезке [-1; 1]. Она удовлетворяет всем усло¬
виям теоремы Ролля, кроме /(-1) =/(1). Для нее /'(х) = 1^0 на (-1; 1).
Отметим, что можно легко построить примеры функций, для кото¬
рых на некотором отрезке нарушаются условия теоремы Ролля, но точка,
в которой производная функции обращается в нуль, найдется (т.е. усло¬
вия теоремы Ролля не являются необходимыми, а только достаточными).
Оставляем работу над данными примерами читателю.
Далее переходим к изучению теоремы Лагранжа. Для начала рассмо¬
трим следующую задачу.
Задача 4.16
Пусть a, b е К, ab < 0. Определим, верна ли формула Лагранжа для функции
Я*)=-
—,если х Ф 0,
х
0, если х = 0
на отрезке [а; Ь\.
Решение
Записываем формулу конечных приращений для функции /на отрезке [а; Ь\.
l/b-l/a__ 1
b-a B2 а-Ъ
1 =±~а-Ь = ?,
что невозможно, так как ab < 0, a B2 > 0.
Отметим, что невыполнимость формулы конечных приращений Лагранжа слу¬
чилась из-за того, что так как ab < 0, то 0 е (а; Ь), а при х = 0 функция / является
неограниченной, т.е. в точке х = 0 нарушаются условия непрерывности и диффе¬
ренцируемости.
231
Зададимся далее вопросом: верна ли теорема, обратная теореме Лагранжа?
А именно, пусть функция/непрерывно дифференцируема на отрезке [а; Ъ\.
Можно ли для V^e (а; Ь) указать такие точки X1, X2 е (а; Ъ), что
/(A2)-Z(Ai) =y,^?
OC 2 OC
Ответ на этот вопрос — отрицательный. Для того чтобы это показать,
достаточно рассмотреть строго монотонную на некотором отрезке функ¬
цию, производная которой обращается в нуль в некоторой точке. Касатель¬
ная в данной точке параллельна оси абсцисс, но на данной кривой не най¬
дется двух точек, секущая в которых параллельна Ох.
Для примера рассмотрим функцию/(х) = х3 на отрезке [-1; 1] и выбе¬
рем на нем точку £ = 0. Пусть X1, X2 G [-1; 1], X1 < х2. В этом случае, так как
X1 + х2 Ф 0, получаем
/(X2)-Z(Xi) X3-X3 о 2_
Л2 ’ Л}Л2 I
OC2 OC^
OC 2 OCI
х.
1
+ п*2
Л* 1 2 3У
+ ±х* 1 2 3>0 = /'(0).
Вспоминая задачу 4.3, приведем еще один способ (не основанный на дока¬
зательстве от противного) установления следующего факта.
Задача 4.17
Пусть функция /(х) дифференцируема, но неограничена на конечном интервале
(а; Ь). Докажем, что ее производная/'(х) также неограничена на (а; b). Будет ли спра¬
ведливо обратное утверждение?
Решение
Предположим, что функция /неограничена при х —> X0 - О, X0 G (а; Ь). Рассмотрим
произвольное (достаточно малое) е > О и функцию/на интервале (х0 - е; X0 ). Фиксируем
произвольное х* G (х0 - е; X0 ). Так как/неограничена на этом интервале, то для любого
M > О найдется точка х g (х0 - е; X0 ) такая, что выполнено /(х) > M ■ е+1 /(х*) |. Тогда,
применяя теорему Лагранжа на отрезке [х;х*] (или [х*;х]), получаем, что найдется
такая точка £ G [х; х*] с (х0 - е; X0 ), для которой выполняется
|у/ф| = |/(х) ~/(х*)| > |/(х)|-|/(х*)|
>м,
IX-X
т.е. в произвольной е-окрестности точки X0 найдется такая точка что |/'(£)| > M.
Обратное утверждение, вообще говоря, неверно: из неограниченности производ¬
ной не следует неограниченность функции на данном интервале. Пример:
fix) = X1/3, f\x) = на [0; 1].
Утверждение 4.7. Если:
1) функция/(х) определена и непрерывна на отрезке [х0; X];
2) /(х) имеет конечную производную/'(х) в интервале (х0; А);
3) существует конечный или бесконечный предел Hm /'(х) = /'(х0 + 0),
х—>Xq +0
то существует, соответственно, конечная или бесконечная односторонняя
производная /+(х0) и /+(х0) = /'(х0 +0).
Доказательство
Выберем произвольную последовательность {хи}, сходящуюся к точке X0
справа, т.е. пусть хп —> х0, хп > X0.
п—>°°
232
По теореме Лагранжа справедливо равенство
/(*»)-/(*<,)=/Ч5п)> ^ е { у
Xn Xq
(4.4)
По определению односторонней производной (по Гейне) получаем, что
Hm f(xn)—/(xO) = /Дх0). Так как Iim = х0 + 0, то Iim /'(£„) = /'(х0 + 0).
и-»°° Xn — X0 П—¥°° Я->°°
Но тогда из тождества (4.4) получаем требуемое, так как у сходящейся
последовательности существует только один предел. ■
Замечание 4.13. Аналогично доказывается утверждение насчет левой
производной.
У утверждения 4.7 есть важнейшее следствие.
Следствие 4.3. Если функция дифференцируема в точке и в окрестности,
то производная функции может иметь только точки разрыва второго рода.
Действительно, так как если функция / дифференцируема в точке х0,
3 /'(х0 + 0) и/'(х0 - 0), то /'(х0) = /Дх0) = f 1(х0).
При этом из наличия производной /'(х0) (а также fI(X0) и /_'(х0))
не следует существования/'(х0 + 0) и/'(х0 - 0).
Пример 4.8
Рассмотрим функцию
/(*) =
Г л \
Xjl -Sin
KxJ
0, если х = 0.
, если х Ф 0,
При 1 < а < 2 существует /'(0) = 0 = /ДО) = /ДО). При этом ^ /'(0 — 0) и/'(0 + 0)
(докажите!). При а > 2 получаем /'(0) = /ДО) = /'(0 + 0) = /ДО) = /'(0 - 0) = 0.
В данном случае при 1 < а < 2 производная /' претерпевает разрыв второго рода,
при а > 2 функция /' непрерывна в точке х = 0.
Пример 4.9
Рассмотрим в нуле функцию f(x) - \ х |. В этом случае
по - 0) = /ДО) = -1; /'(0 + 0) = /ДО) = 1.
В этом примере функция/' претерпевает в нуле скачок, похожий на разрыв пер¬
вого рода, но в данном случае ^ /'(0). Вообще, если существуют конечные пределы
/'(х0 - 0) и /'(х0 + 0), при этом /'(х0 - 0) Ф /'(х0 + 0), то / /'(х0).
Задача 4.18
Определим, существует ли непрерывно дифференцируемая функция /, действу¬
ющая из IR в М, такая что для VxeR выполнено /(х) > 0 и /'(х) = f(f(x))7
Решение
Предположим, что такая функция существует. Тогда для всех действительных х
выполнено неравенство /'(х) = /(/(х)) > 0. Следовательно, функция/монотонно воз¬
растает. Отсюда мы делаем вывод о том, что, так как /(х) > 0, то /'(х) = /(/(х)) > /(0)
для всех действительных х.
233
Пусть х < 0. Записывая теорему Лагранжа для функции /на отрезке [х; 0], получим
^^=т)>/(о)^ях)<т^х-т=(1+х)-т-
-х
Значит, при х < -1 получим /(лг) < 0, что противоречит строгой положительно¬
сти функции /.
Задача 4.19
Функция/дифференцируема на [0; 1],/(0) = 0 и для некоторого M > 0 справед¬
ливо неравенство | /'(х) \ < М\ /(х) |. Докажем, что f(x) = 0 при х е [0; 1 ].
Решение
Для того чтобы было проще провести оценку, рассмотрим данную функцию
на отрезке
0;
2 M
т.е. пусть xs
0;
2 M
п[0;1]. Тогда, используя п раз теорему
Лагранжа и неравенство х • M < —, имеем
|/<Ж)| = I/O) - /(0)1 = |/4*i)|* ^ M\f{xd\x < ||/Oi)|=||/'02)|^i ^ ^-|/02)| ^ ^
В силу доказанной ограниченности функции /(х) и произвольности п s N полу-
1 п[0;1].
чим, что f(x) = 0 при X S
0;
2 M
1
Если Mто
2
0;
1
2 M
Если же M > —, то
2
0;
п [0; 1] = [0; 1], и этим все доказано.
1
с[0; 1]. Тогда проводим аналогичные рассуждения
2 M
дополнительно на каждом из отрезков
1 . 1
1 . 3
[2М] -1 [2М]
[2М]
2 М’М
М’2М
2 M ’ 2 M
2 M ’
Задача 4.20
Функция/: [a; b\ —> M имеет производную во всех точках отрезка [я; Ь] и b - а > 4.
Докажем, что на отрезке [я; Ь\ найдется точка £, такая, что /'(¾) < 1 +/2(£).
Решение
Рассмотрим функцию ф = arctg(/(x)), где хе[а;Ь]. Применим к ней теорему
Лагранжа, получим
afCtg /(6) - arCtg /(я) /'(О
4-о I+/2©
для некоторого Е, е (я; b). Отсюда
2
I + /2½)
f пл
V X
и
4
<1.
Задача 4.21
Пусть аь я2, ..., ап — отличные от нуля действительные числа; Ot1, сс2, ..., ос„ —
попарно различные действительные числа. Докажем, что функция f(x) = A1XotI +
234
+ Ci2XaZ + ... + апхап, определенная при х > 0, может иметь не более (п - 1)-го нуля
на бесконечном интервале (0; +«>).
Решение
Для доказательства данного утверждения воспользуемся теоремой Ролля и мето¬
дом математической индукции. Будем проводить индукцию по п. Пусть сначала п = 2:
f(x) = A1XtxI + Ci2Xa 2.
Предположим, что функция /имеет по крайней мере два положительных корня X1
и х2, т.е /(X1) = /(х2) = 0. Тогда функция ф(х) = A1-I- а2ха2-0li, определенная при х > 0,
также равняется нулю в точках X1 и х2, так как ф(х) = . Как следствие, полу¬
чаем, что функция ф(х) имеет производную при всех положительных значения х.
По теореме Ролля получаем, что существует число с е (X1; X2) такое, что ф'(с) = 0. Но
ф'(с) = А2(а2 -(X1)CtxS-txI-1 и ф'(с)^0 ни при каком значении с. Таким образом, пред¬
положение о том, что функция / имеет два корня или более, приводит к противоре¬
чию. Поэтому функция /(х) = A1XtxI + Cl2XaZ при любых A1, A2 (A1 • A2 Ф 0)| OC1, (X2 (OC1 * (X2)
имеет не более одного положительного корня.
Предположим, что утверждение верно для п, т.е. для любых чисел A1,а2,...,ая,
отличных от нуля, и попарно различных действительных чисел ос1,ос2,...,осп функ¬
ция вида
A1XtxI + A2XtxS +... + А„х“« (4.5)
имеет не больше п — 1 положительных корней. Покажем, что для любых действи¬
тельных чисел A1, A2,..., ая+1, отличных от нуля, и попарно различных действительных
чисел щ,а2,...,ап+х функция
/(х) = A1X01I + Cl2XaZ +... + Ая+1х“я+1
имеет не больше, чем п положительных корней. Предположим, что это не так и /
имеет п +1 положительных корней X1, х2,..., хя+1, т.е.
/(*i)=/(¾)=-=/Ow)=о.
Пусть X1 < х2 <... < хя+1. Значения X1, X2,..., хя+1 будут нулями функции
ф(х) = A1+A2X0t2 а1+А3Хаз 011+... + Ая+1х“и+1 а\
потому ЧТО ф(х) =
fjx)
XotI
Применяя теорему Ролля для функции ф на каждом из отрез¬
ков [X1; х2], [х2; х3],..., [хя; хя+1], получим, что производная ф'(х) имеет по крайней мере
п положительных корней. Производная функции ф(х) равна
ф'(х) = A2 (сс2 - (X1)Xtx2 1 + A3 (сс3 - (X1)X0t3 “! 1 +... + a„+i(0C„+1 - (X1)Xtx"+! aI 1
и имеет вид (4.5) при щ = Ai+1(ai+1 - OC1), ос, = ai+1 -OC1, i = 1,2,..., k.
По предположению индукции функция вида (4.5) не может иметь более п -1 поло¬
жительного корня. Приходим к противоречию и получаем, что /(х) имеет не более
п положительных корней.
Задача 4.22
Пусть функции/, g, h непрерывны на [а; 6], существуют/', g', h' на (а; Ь) и
fix) g(*) h(x)
Fix)= fia) gia) h(a) , xe[a;b\.
fib) g(b) h(b)
Докажем, что 3 £ e (a; b) такое, что Ff(E1) = 0. Выведем из этого утверждения тео¬
ремы Лагранжа и Коши.
235
Решение
Заметим, что по свойствам определителя выполнено
Ra)
g(a)
h(a)
Rb)
g{b)
h(b)
F(d) =
Ra)
g(a)
h(a)
= 0, F(b) =
Ra)
g(a)
h(a)
Rb)
g{b)
h(b)
Rb)
g(b)
h(b)
Представляя функцию Fb виде
g(a) h(a)
F(x) = f(x)'
g(b) h(b)
~g(x)
+ h(x) ■
Ra)
m
g(a)
g(b)
(4.6)
Ra) h(a)
Rb) h(b)
получаем, что она является линейной комбинацией непрерывных на [я; Ь\ и диффе¬
ренцируемых на (я; b) функций. Поэтому по теореме Ролля получаем существова¬
ние £ е (я; Ъ) такого, что Fr(F) = 0.
Положив h(x) = 1 и используя формулу (4.6), для F'(?) получаем
0 = Fr(H) = /'(£) •
g(a) 1
g(b) I
-g'ay
т I
т 1
= №) - g(b))f'(l) - (.Ra) - Rb))gr(Z),
откуда
(g(a) - g(b))fra) = (f(a) - f(b))g'(t) , или
f(b)-f(a) Ag)
g(b)-g(a) gr(%)’
для найденного £. Теорема Коши доказана.
Заметим, что утверждение доказано без предположения g(a) Ф g(b), как доказы¬
вается обычно теорема Коши, т.е. при снятии этого условия можно утверждать, что
выполнено равенство
g\W(b) - Ra)) = тшь) - g(a)),
но не обязательно имеет место разностное отношение; в этом случае, возможно, обе
части нулевые.
Теорема Лагранжа доказывается аналогично, если положить h(x) - I, g(x) = х.
Оставляем ее доказательство читателю.
Задача 4.23
Докажем, что если:
1) функция /имеет вторую производную /" на отрезке [я; Ь\,
2) Па) =/'(4) = 0.
то на интервале (я; Ъ) существует по меньшей мере одна точка с такая, что
|/"(ф-
4
\m-f(a)\.
(b - я)* 1 * 1 2
Решение
Если f(x) = const, то утверждение очевидно.
Так как /'(я) = /'(b) = 0, то функция / отлична от линейной. Применяя формулу
(X _
Коши конечных приращений к функциям / и ср: л: —> — на отрезке
(Ь — хУ
и к функциям / и \|/: х —> - — на отрезке
а + Ь
;Ъ
а;
а + Ь
получаем
( (
/
а + Ь
~/(а)
(b-af
f(£>i) е а + Ь
= я<^<—;
-я 2
236
8
m-f
a + b
W
))
_ Z(S2) a + b ,
-~b^’-T^b-
(b - a)2
Складывая полученные равенства, находим
8(/(0-/0)) _//Si), Z(S2)
(b-af Zi -a b-Z 2'
Поскольку f\a) = fib) = 0, то правую часть равенства (4.7) можно записать в виде
Z(Si) ^ Z(S2) _ Z(Si)-ZO) ZObZ(S2)
(4.7)
- + -
-=ZXnibZX TI2X
(4.8)
Si-a b-z 2 Si-fl *-S2
где a < TJ1 < Zi, S2 < tI2 < Оценивая по абсолютной величине левую часть равенства
(4.7), с учетом формулы (4.8) имеем
Предположим, что f(b) Ф f(a) (в противном случае доказательство тривиально:
точкой с может служить любая точка из интервала (a; b)). В силу нашего предполо¬
жения хотя бы одно из чисел !/rX1Ii)! или !/ XtI2)! отлично от нуля. Обозначим
!/"(с)! = Inax(IZX1Ii)I. !/"(1I2)I)-
Тогда имеем
откуда
8|/№-/(д)|
(Ъ - а)2
I п4>
^ 2 |ZXc)|,
|/(0-/(«)|
(Ъ - а)2
(знак равенства не исключаем, так как возможен случай, когда IZr(Ti1)I = !/"(rI2)I)-
4.5. Равномерная непрерывность
Предположим, что функция/задана на множестве Ed R, и введем важ¬
нейшее определение этого параграфа.
Определение 4.6. Будем говорить, что функция f равномерно непре¬
рывна на множестве Е, если V в > О 3 8(e) такое, что V X1, X2 е E из неравен¬
ства IX1 - х2 I < 8(e) следует, что !/(X1) -/(х2) | < е.
Если мы зафиксируем в определении равномерной непрерывности
точку X1, то получаем определение непрерывности функции /: E —+ M в дан¬
ной точке X1 G Е. Таким образом, справедливо следующее утверждение.
Утверждение 4.8. Если функция / равномерно непрерывна на множе¬
стве Е, то она непрерывна во всех точках этого множества.
Далее будет показано, что непрерывность функции/на некотором мно¬
жестве Е, вообще говоря, не влечет за собой равномерной непрерывности
на этом множестве. Однако очень важную роль в теории равномерной
непрерывности играет следующая теорема. Докажем ее, используя лемму
Гейне — Бореля (см. гл. 1).
Теорема 4.6 (Кантора). Если функция / непрерывна на замкнутом
и ограниченном множестве Ed R, тогда она равномерно непрерывна на этом
множестве.
237
Доказательство
Если функция/определена только на множестве Е, то ее можно продол¬
жить на всю числовую прямую по непрерывности1 * (докажите!). Далее, так
как рассматриваемая функция непрерывна на множестве Е, то для любой
точки х этого множества и произвольного числа е > 0 можно указать такое
Г 8 8Л
8(e) > 0, зависящее, вообще говоря, и от х, что для всех х' E х—;х + —
. 2 2
выполняется неравенство |/(х)-/(х')|< —. Таким образом, множество E
, , „ „ v 8 8Л
может быть покрыто бесконечной системой 2 интервалов
х—;х +
2 2
J
из которой, по лемме Гейне — Бореля, можно выделить конечную подси¬
стему 2 интервалов, также покрывающую множество Е. Обозначим через
g
8' минимальное значение — для этой конечной подсистемы.
2
Пусть теперь X1 и X2 — произвольные точки множества Е, удовлетвори-
Iis- Г 5 5sU-^8
ющие условию P1 - X2 \ < о , и х — центр того интервала х -—; х+— ,8 < —,
системы 2, который покрывает точку X1-TaK как P1 - х| < — < 8 и |х2 - х| < 8, то
2
|/(*1) - /(*)I < | И |/(*2 ) - /(*)I
2’
и поэтому
|/(*i) - f(x2 )| ^ |/0ч ) - /0)1 + I/O) - /O2 )| < ~+1 = е.
Следовательно, для любого е > О мы указали такое 8' > 0, что для любых
точек Xl7X2 G Е, связанных неравенством Ix1 -х2| < 8', выполняется неравен¬
ство f(x2)\<£. Это доказывает равномерную непрерывность функ¬
ции / на множестве [а; Ь\. ■
Отметим, что существенную роль в данной теореме играют замкнутость
и ограниченность множества Е. Это будет показано далее на примерах.
Для того чтобы лучше понять различие между непрерывностью на мно¬
жестве E и равномерной непрерывностью на нем, приведем два формали¬
зованных определения этих понятий рядом.
Функция / непрерывна на множестве E <=>
У у E E V в > 0 3 8(в, у) > 0, Vxg £|х-г/|<8=>| /(х) -f(y) \ < в.
Функция / равномерно непрерывна на множестве E <=>
V в>О 3 8(e) >О Vх,у E Е\х-у\<д=> |/(х) -/(г/)|<в.
Заметим, что в определении непрерывности функции / на множестве
число 8 > О выбирается по точке у E E и числу в > 0. Поэтому оно, вообще 11 То есть можно построить функцию, непрерывную на всей числовой прямой и совпада¬
ющую с исходной на множестве Е.
238
говоря, может меняться от точки к точке. В случае же равномерной непре¬
рывности число 8 > 0 выбирается исключительно по числу е > 0 так, что
сразу для всех точек у е E из соотношения | х - у \ < 8 при х е E выполня¬
ется неравенство | f(x) - f(y) \ < в.
Полезным будет сформулировать отрицание свойства функции быть
равномерно непрерывной.
Функция /не является равномерно непрерывной на множестве E <=>
3 в > 0 такое, что V 8 > 0 3 X1, X2 е Е, I^1 - X21 < 8 => | /(X1) -/(х2) | > в.
Рассмотрим несколько примеров, иллюстрирующих вышесказанное.
Пример 4.10
I f
Рассмотрим функцию /(x) = sin— на конечном полуинтервале
X ^
О;*
П
. Отметим,
что на этом множестве функция/является непрерывной. Рассмотрим две последо¬
вательности точек, сходящиеся к нулю:
х)/ = И х£2) = —, п G N.
” (4п + 1)л ” пп
Для этих точек получаем /(xj/) = I, f(x^) = 0, откуда I/(41}) — /(42))| = 1, несмо-
->0 при Следовательно, при е < 1 нельзя
тря на то что \х.
(0-(2) _
2п + 1
Ann2 + пп
найти такое 8 > 0, которое подходило бы одновременно для всех х, у €
0;-
п
. Хотя
для любого фиксированного у такое 5 найдется в силу непрерывности функции /.
Пример 4.11
Рассмотрим функцию/(х) = х2 на луче [0; +°о). На данном множестве функция/
является непрерывной. Выбрав произвольное 8 > 0, возьмем две точки х и у, для кото¬
рых выполнено Ocy-X = S0 <8. Получим
I Ау) ~ Ах)\=у2-х2 = (у-х)(у + х)> 280х.
Следовательно, для выполнения неравенства |/(у) -/(х) | > е = 1 достаточно, чтобы
1
при любом S0 (80 < 8) выполнялось S0 • 2х > 1, или х > —— (такое х всегда можно найти,
так как луч [0; +°°) не ограничен). 0
Таким образом, при е = 1 и произвольном 8 > 0 мы не получим неравенства | /(х) -
1
-/(у) I < е = 1 при условии |х — у| = S0< 8, т.е. если х>——.
28п
Отметим, что два приведенные примера демонстрируют необходимость
требований замкнутости и ограниченности множества E в теореме Кантора.
Понятие равномерной непрерывности естественно обобщается на ото¬
бражения метрических пространств. А именно, пусть Ei и E2 — два метриче¬
ских пространства с расстояниями P1 и р2. Отображение /: Ei —» E2 называ¬
ется равномерно непрерывным, если V е > 0 3 8(e) > 0 такое, что V X1, х2 g E
таких, что P^x1, х2) < 8, выполнено P2(/(^1//(^2)) < £-
239
Задача 4.24
Исследуем на равномерную непрерывность следующие функции, используя опре¬
деление данного свойства:
а) /(х) - sin х на R;
б) /(х) = arctgx на R;
в) f(x) = 1/хна: 1) [я; +°°), я > 0; 2) (0; я], я > 0;
г) fix) - Vx на [0; -н»);
д) fix) = Inx на (0; 1);
е) fix) = sin(xsinx) на (0; +°°);
Решение
а) Выберем произвольные х, у е R и оценим модуль разности:
|sinx — sin г/|
2 sin
х-у
2
х + и
•cos —
2
<
sin
х-у
\х-у\
COS
х + у
< I f < Ix - г/| < 5.
Поэтому V е > 0 3 5(e) = е > 0: Vx, г/ еМ, таких что |х — г/| < 5, выполнено
|sinx — sin г/| < е. Следовательно, функция /(х) = sin х равномерно непрерывна на R.
б) Рассмотрим произвольные х, у е R такие, что | х - у \ < 5. Возможны два случая:
1) осу > 0. В этом случае
(arctg х-arctg г/1
arctg
х-у
1 + осу
<
Х-у
1 + осу
<\Х-у\<£
при 5 = е.
2) осу < 0, т.е. х и у выбраны из различных окрестностей нуля. В этом случае полу¬
чаем
arctgх - arctg у\ = |arctgx| + |arctgу\ < |х| + \у\ < 25 = е
при 5 = -.
в!) Выберем х,уе [я; + <»), |х -у\< 5, тогда
1_1
х у
\х~у I
осу
\х — у\
< {осу >а2}<1< е при 5 < Ей2.
я^
1
Отсюда делаем вывод о том, что функция /(х) = — равномерно непрерывна на луче
[«;+“)• : : *
Х-у
в2) Заметим, что
1_1
х у
осу
+°°, если при сколь угодно малой, но фиксиро¬
ванной разнице \х - у\ приближать меньшее из х или у к нулю. Докажем неравномер¬
ную непрерывность функции / более строго.
х I I % 8
Возьмем 0 < х < 5, у - —, тогда х - у = — < — < 5. В то же время
1_А
х у
2 2
1 ^ 1
= — > —, так как х < я.
X я
Итак, возьмем х = < а (заметим, что х < 5), у = —^— < я при 5 > 0, E = —.
5 + я 2(5 + я) я
Тогда
\х-у =:
5я
< 5, но
А_А
х у
>-=t.
а
2(5+ я)
г) Представим луч [0; + °°) в виде объединения [0; 2] и [1; + °°).
240
Функция/является непрерывной на всей числовой оси, отрезок [0; 2] замкнутый
и ограниченный. Следовательно, / равномерно непрерывна на [0; 2].
Пусть, далее, х,у E [I; + °°). В этом случае
| Vx -4у\ = —I= ^ {Vx +4у~ 2} - ~—— < E при 5 = 2е.
Ых+^у 2
Отсюда делаем вывод о том, что функция / равномерно непрерывна на [ 1; + °°).
Подводя итог вышесказанному, мы утверждаем, что V е > 0:
3 S1(E) > 0 такое, что V х, у е [0;2], \х -у\< S1, выполнено |Vx - ^fy | < е;
382(е) >0 такое, что V х, у е [I; + °°), \х-у\< S2, выполнено | Vx --Jy\ < е.
Пусть 8 = min|si,82,^|. Тогда Vх, г/E [0; + °°) таких, что \х-у\<5, будет выпол¬
нено, что обе точки х и у принадлежат либо отрезку [0; 2], либо лучу [1; + °°), поэтому
выполняется неравенство
л[х-у[у
<£.
Следовательно, функция /(х) = Vx равномерно непрерывна на множестве [0; + °°).
Замечание 4.14. Если функция/равномерно непрерывна на множествах
Xi и X2, то из этого, вообще говоря, не следует, что она равномерно непре¬
рывна на их объединении. Предлагаем читателям привести пример само¬
стоятельно или посмотреть на пример ниже.
Продолжение задачи 4.24
д) Рассмотрим две последовательности точек: х^ = е~п, х^ = е~пЛ. Получаем
е-1
^.(1) _ „(2)
I 1
Jbn
еп еп+\
„я+1
<8
для достаточно больших п е N.
Однако
/(4'>)-/(*<2))=i> е для ее(0;1). Следовательно, функция /(х) = 1пх
не является равномерно непрерывной на множестве (0; 1).
е) Рассмотрим на отрезке
2тш; 2тш + —
2
функцию g(x) = х sin х. Она на данном
л
множестве непрерывна и монотонно возрастает от 0 до 2лп + —. Следовательно, она
принимает на этом отрезке все свои промежуточные значения. Поэтому найдутся
такие точки
2лп <х1<у1<х2<у2< - < хп<уп= 2лп +
л
2’
71
что выполнено g(xk) = 2 лк, g(yk) = 2лк + —, ksZ, 0 <k<n+ 1. Тогда /(у*) - f(xk) = I,
2
а длина хотя бы одного из отрезков [xk\ yk \ будет меньше, чем —. Отсюда при доста-
An
точно больших п E N получается противоречие с определением равномерной непре¬
рывности.
Задание 4.7
Исследуйте на равномерную непрерывность, используя определение данного
свойства, следующие функции:
а) /(х) = х sinx на [0; +°°); б) /(х) = Inx на (1; +°°); в)/(х) = sin(x2) на [0; +°°).
241
Из предыдущих задач мы видим, что исследование функций на равно¬
мерную непрерывность, даже при наличии замечательной теоремы Кан¬
тора, может представлять из себя достаточно непростую с технической
стороны задачу. Сформулируем и докажем ряд утверждений, облегчающих
данный процесс.
Утверждение 4.9. Пусть интервал (я; Ъ) конечен. Функция / равно¬
мерно непрерывна на (я; b) тогда и только тогда, когда она непрерывна
на (я; Ъ) и существуют пределы Hm /(х), Hm /(х)/(х).
x-Hz+O x->b-О
Доказательство
Достаточность. Пусть функция / непрерывна на (я; b) и существуют
пределы Hm /(х) = Л, Hm /(х) = В. Рассмотрим функцию
х->а+0 х->Ь-0
F(x) =
A, если X = а,
/(х), если х G (я; Ь),
B, если х = Ь.
Данная функция является непрерывной на отрезке [я; Ь\. Следова¬
тельно, по теореме Кантора она равномерно непрерывна на этом отрезке.
Отсюда функция/, совпадающая с Fua интервале (я; Ь), равномерно непре¬
рывна на данном интервале.
Необходимость. Пусть функция /равномерно непрерывна на интервале
(я; Ъ). Тогда она непрерывна на этом интервале. Докажем существование
односторонних пределов. По определению равномерной непрерывности
функции/имеем: для V в > 0 3 8(e) > 0 такое, что для V X1, X2 G (я; min{£, я + 8})
выполнено !/(X1) - /(х2)| < е, что совпадает с условием Коши существования
правого предела в точке я. По критерию Коши получаем, что существует
конечный предел Hm /(х). Существование левого предела Hm /(х)
х—>а+0 *—»6-О
доказывается аналогично. ■
Следствие 4.4. Если функция неограничена на ограниченном интер¬
вале, то она не является равномерно непрерывной на этом интервале.
Утверждение 4.10. Если функция /определена и непрерывна в обла¬
сти [я; +°°) и 3 Hm /(х) < °о, тогда она равномерно непрерывна на [я; -н»).
X-H-OO
Доказательство
Предел Hm /(х) < °° существует тогда и только тогда, когда функция /
Х-Н-оо
удовлетворяет условию Коши при х —» +°°, т.е. для V в > О 3 А(г) > О такое,
что при V X1, х2 > А выполнено |/(ха) — /(х2 )| < в.
Если Л(е) < я, то возьмем произвольное 8. Тогда для всех X1, X2 G [я; + °°)
таких, что Ix1 -х21 < 8 (при этом X1, X2 > А(е)), выполнено !/(X1 )-/(х2)|<8.
Если же для фиксированного е > О имеем Л(е)>я, то разобьем луч
[я; + °°) на две части: [я; А +1] и [Л; + °°).
На отрезке [я; Л + 1] функция/равномерно непрерывна по теореме Кан¬
тора. Поэтому для любого фиксированного в > О найдется такое 8 = 8(e) > О,
что для всех X1, X2 G [я; Л +1], Jx1 - X21 < 8, выполнено !/(X1) - /(х2)| < в.
242
Рассмотрим S1 = min
. Тогда для всех X1, X2 G [а; + °°) и таких,
что Ix1-JT2 <5^ выполнено, что либо X1, X2 е [а; А +1] и P1-JT2PS, либо
X1, JT2 > Л (в) (могут реализовываться и оба варианта). Но в обоих случаях
!/(JT1)-Z(JT2)I < в, т.е. для заданного в > 0 найдется S1(B) из определения
равномерной сходимости. ■
Замечание 4.15. Условие утверждения 4.10 не является необходи¬
мым для равномерной непрерывности функции на неограниченном луче
[а; +со). Рассмотрим, например, функцию /(х) = х. Данная функция, оче¬
видно, является равномерно непрерывной (для произвольного в > 0 можно
выбрать 8(e) = в), но J Hm /(х).
х—>+°°
Утверждение 4.11. Пусть функция / непрерывна на интервале (а; b)
(конечном или бесконечном), монотонна и ограничена на нем. Тогда эта
функция равномерно непрерывна на этом интервале.
Доказательство
Из монотонности и ограниченности функции / на интервале (а; b)
вытекает существование конечных пределов Iim /(х), Iim /(х). Сле-
х—>а+0 х->Ь-0
довательно, если интервал (а; Ь) конечен, то равномерная непрерывность
функции / на нем вытекает из утверждения 4.9, а если бесконечен, то
из утверждения 4.10. ■
Замечание 4.16. Очевидно, что условие утверждения 4.11 также не явля¬
ется необходимым для равномерной непрерывности функции на интервале
(а\ Ъ). Контрпримером, например, является функция /(х) = sinx на число¬
вой прямой R.
Утверждение 4.12. Сумма (или разность) и произведение конечного
числа равномерно непрерывных на ограниченном интервале (а; Ъ) функ¬
ций равномерно непрерывна на этом интервале.
Доказательство
Не ограничивая общности, докажем данное утверждение для двух функ¬
ций. Действительно, пусть fug равномерно непрерывны на интервале
(а; Ь). Для суммы данных функций получаем
|(/(xi) ± g(x1)) - (/(х2 ) ± g(x2 ))| < !/(X1) - /(х2 )| + |g(xt) - g(x2 )| < J+| = е.
Для произведения, учитывая, что равномерно непрерывные на интервале
функции являются на нем ограниченными (F=Sup /(х)|, G = sup|g(x)|),
(а; Ь) (а;Ь)
имеем
|/(Xi) • g(xt) - /(X2 ) • g(x2 )| = (!/(X1) • g(x2 )} =
= |/(*l) • №l) -g(*2>) + ё{*2) ■ (M) - /(*2»| ^
^ |/(*1 )| • |g(*i) - g(pc 2 )| + |g(x2 )| • !/(X1) - /(x2 )|<F~ + G~<e
при Ix1 - X21 < 8, X1, X2 G (a; b). ■
Замечание 4.17. Отметим, что если функция / равномерно непрерывна
на интервале (а; Ь), а функция g не является равномерно непрерывной, то
243
их сумма не является равномерно непрерывной функцией. Действительно,
обозначим Ii= f+g и предположим, что данная функция равномерно непре¬
рывна. Тогда по утверждению 4.12 получаем, что и функция g = h - /равно¬
мерно непрерывна, что не так.
Замечание 4.18. Утверждение 4.12 для бесконечного интервала верно
для суммы (разности), но неверно для произведения. Например, функции
/(х) = g(x) = х равномерно непрерывны на числовой прямой R, но функция
/ • g таковой уже не является.
Утверждение 4.13. Если функция / определена и имеет ограниченную
производную на некотором интервале (а; Ь) (конечном или бесконечном),
то она равномерно непрерывна на нем.
Доказательство
Пусть существует M > 0 такое, что для всех хе(а;Ь) выполнено
|/'(х)| < М. Выберем произвольные точки X1, X2 е (а; Ъ), связанные неравен¬
ством Ix1 -X21 < 8 для некоторого 8 > 0. По формуле Лагранжа получим
|/(*1) - /(*2 )| = 1/4¾! • К - X21 < M • Ix1 - X21 < M • 5,
где £ G (X1; х2) или \ G (х2; X1). Поэтому для произвольного е > 0 достаточно
взять 8(e) = Тогда если Ix1 -х2| < 8(e), то выполняется [/(X1)-Z(X2)I < е,
что доказывает требуемое. ■
C помощью утверждения 4.13 можно легко решить ряд задач, предло¬
женных выше.
Замечание 4.19. Если функция / дифференцируема на множестве X и ее
производная на этом множестве ограничена, т.е. ЗМ> 0 такое, что |/'(х) | < М,
то из этого не следует равномерная непрерывность. Действительно, рассмот¬
рим функцию
/00 =
f 1, если х G (0; 1),
[2, если х G (1;2).
Имеем Х = (0;1)и(1;2). Очевидно, что функция /дифференцируема
на X и /'(х) = 0 для всех х G X. Но данная функция не является равно¬
мерно непрерывной, так как 3e0=l:V8>03x'=l- 8/4 и х" = 1 + 8/41,
для которых |х' - х"| < 8, |/(х') - /(х")| = 1 = е0.
Здесь множество X не связно, т.е. утверждение заведомо верно лишь
для интервала (а; Ъ).
Этот же пример, кстати, показывает, что если функция / равномерно
непрерывна на множествах X1 и X2, то из этого, вообще говоря, не сле¬
дует, что данная функция равномерно непрерывна на всем множестве
Z = X1UX2.
Замечание 4.20. Условие утверждения 4.13 также не является необходи¬
мым для равномерной непрерывности функции на интервале (а; b). Напри¬
мер, функция /(х) = л/х является равномерно непрерывной на интервале
1 Строго говоря, требуется выбрать 5 достаточно малым, чтобы х' и х" не вылезли за гра¬
ницы множества X.
244
(0; 1), но предел ее производной /'(х) = —т= в точке 0 не существует. Отме-
2 Vx
тим, однако, что если Hm /'(х) = °°, то данная функция не является равно-
х—»+°°
мерно непрерывной на луче [а; +°°).
Действительно, предположим, что / равномерно непрерывна на луче
[а; +°°). В этом случае Ve>038>0 такое, что V X1, X2 е [a; +°°), Ix1 - X21 < 5,
выполнено !/(X1) -/(х2)| < в.
Из условия Hm /'(х) = °° получаем: 3 А такое, что V х выполнено
х—»+°°
I /'(х) I > 2/8, где 8 взято из определения равномерной непрерывности. Поло¬
жим далее X1 = А, х2 = А + 8/2 и применим теорему Лагранжа для отрезка
[X1; х2]. Получаем
I /(X1) -/(X2) I = I/'© Их, - X21 > {§ > А) > 2/8 • 5/2 = I = E0.
В силу того что Ix1 - X21 = 8/2 < 8, получаем противоречие с равномерной
непрерывностью функции/на [а; +°°).
Замечание 4.21. Вообще, если на интервале (а; Ъ) существует ограни¬
ченная производная /W(x), k = 2, 3, ..., то функция / равномерно непре¬
рывна на (а; 6). В самом деле, из ограниченности производной /(*)(х), как
было показано выше, следует ограниченность производной /^-1 Дх), далее
ограниченность/(*_2)(х) и т.д. ограниченность производной/'(х). Но выше
было доказано, что из ограниченности /'(х) следует равномерная непре¬
рывность.
Мы, однако, рекомендуем читателю доказать (с помощью теоремы
Лагранжа) следующее утверждение независимо от обозначенного факта.
Утверждение 4.14. Пусть функция / имеет вторую производную
на интервале (а; b), причем sup |/"(х)| = C < +°°. Тогда функция /(х) равно-
Cа;Ь)
мерно непрерывна на (а; Ь).
Далее в свете утверждения 4.13 и замечаний из него рассмотрим сле¬
дующий интересный вопрос: существует ли равномерно непрерывная
и дифференцируемая функция /: [а; +°°) —> R такая, что Hm /(х) = +°°
X—>+°°
и для любого b ее производная /' неограничена на [b; +°°)?
Как это ни странно, ответ на этот вопрос — положительный. Действи¬
тельно, положим в качестве /(х) = х + s^n(x ) для нее имеем Hm /(х) = +°°,
X X—>+<»
/Дх) = 3х COs(X3)-s^f ^+1. Мы ВИДИМ, ЧТО /'(V27Ш ) = 3V27Ш +1
X1
—> +°°,
Л^/2 + 2та) = -(п/2 + 2пи)2/3 ^ “•
Отсюда делаем вывод о том, что производная функции / неограничена,
однако не является бесконечно большой.
Далее заметим, что, как уже было отмечено выше, функция х равно-
sin X^
мерно непрерывна, а функция имеет конечный предел при х —> +°о,
х
и следовательно, равномерно непрерывна по утверждению 4.10. Остается
245
воспользоваться тем фактом, что сумма двух равномерно непрерывных
функций есть функция равномерно непрерывная.
Для понимания следующей теории дадим два определения.
Определение 4.7. Пусть функция /(х) задана на отрезке [я; Ъ\. Тогда
величина
Ю(/» [я; b\) = sup Ifipcf) - fix) I
х,х'е[а; Ъ\
называется колебанием функции/на отрезке [я; Ъ\.
Определение 4.8. Модулем непрерывности а>(8, J) функции / опреде¬
ленной на отрезке [я; Ь\, называется функция
со(8,/,[я;6]) = sup |/(х")-/(х')|, х',х" е[а)Ь].
\х'-х"\<Ь
Утверждение 4.15. Для того чтобы функция /(х) была равномерно
непрерывна на отрезке [я; Ъ\, необходимо и достаточно, чтобы V в > О
3 5 > 0 такое, что при 0 < X2 - X1 < 8, [X1; х2] с [я; Ъ\, выполнялось неравен¬
ство со(f, [X1; х2]) < в.
Доказательство
Необходимость. Пусть для произвольного в > 0 найдется 8 > 0 такое, что
для всех X1, х2 G [я; й], Ix1 - х21 < 8, выполняется неравенство !/(X1) - /(х2 )| <
В таком случае для произвольных точек £, r\ е [X1; X2 ] получаем
в
2'
О < - ri| ^ х2 - X1 < 8 => 1/(¾ - /(ri)| <
В силу произвольности ц из [X1; X2 ] имеем
с°(/, [X1Jx2])= sup |/(£)-/(ri)|<!<e.
^Tiefx1Jx2] 2
Достаточность. Пусть V е>038>0 такое, что при 0 < X1 - X2 < 8, [X1; х2] с
с [я; Ь\, выполняется неравенство юif, [X1; X2]) < в. В этом случае для отме¬
ченных выше точек X1 и х2, связанных лишь соотношением 0 < X1 - X2 < 8,
выполняется
|/(*l)-/(*2>| ^ “(Л [*1> ^2]) < е>
что гарантирует равномерную непрерывность функции/на отрезке [я; Ь\. ■
Утверждение 4.16. Для того чтобы определенная на множестве E
функция Дх) была равномерно непрерывна на нем, необходимо и доста¬
точно, чтобы для ее модуля непрерывности выполнялось равенство
Iim ю(8,/, £) = 0.
5->0+0
Доказательство
Необходимость. Пусть функция / равномерно непрерывна на мно¬
жестве Е: V в > 0 3 8(e) > 0 такое, что Vx1;x2 еЕ, Ix1-X2^S, выполнено
|/(*i)-/(*2)|<|-
246
Используя то, что при расширении числового множества его точная
верхняя грань может только не убывать, получаем, что если 0 < 8' < 8, то
sup !/(X1)-Z(X2)I^ sup !/(X1)-Z(X2)Isf,
Ix1-X2^S' Ix1-X2^S ^
т.е. если 0 < 8' < 8(e), то со(8', /, Е)<е, а это и означает, что Hm со(8', f,E) = 0.
8-»0+0
Достаточность. Пусть Iim со(8, /, Е) = 0. Это означает, что для V в > 0
5—»0+0
3 8(в) > 0 такое, что если 0 < 8' < 8(b), то со(8', /, E) < в.
Выберем какое-нибудь из указанных 8'. Тогда при X1, X2 G Е, Ix1 - х21 < 8',
будем иметь
|/Оч)-/(*2)|^ suP \f(xi) - /(х2 )| = w(8', /, Е) < в,
|xi-x2|<5'
т.е. функция / равномерно непрерывна на множестве Е. ■
Напомним изучавшееся нами в гл. 3 понятие условия Гельдера — Липшица.
Определение 4.9. Будем говорить, что функция / удовлетворяет
(на множестве Е) условию Гельдера — Липшица с показателем а > 0, если
3 k > 0, а > 0 такие, что V X1, X2 G E выполнено | /(X1) - /(х2) | < k Ix1 - X2 |а.
При а = 1 это условие принято называть условием Липшица.
Утверждение 4.17. Пусть функция / удовлетворяет на множестве E
условию Гельдера — Липшица с показателем а > 0. Тогда / равномерно
непрерывна на этом множестве.
Доказательство
Для V в > 0 в определении равномерной непрерывности достаточно
выбрать 8(b) > 0 из условия k8a < в. ■
Утверждение 4.18. Любая непрерывная периодическая функция/ R —> R
является равномерно непрерывной.
Доказательство
Пусть T> 0 — период функции/. Для любых X1, X2 G R таких, что выпол¬
нено соотношение Ix1-X2 < 8 < Т, найдется п G Z, для которого числа X1 + пТ
п х2+пТ лежат на отрезке [0; 2Т]. Поэтому равномерная непрерывность /
получается из того, что на отрезке [0; 2Г] она является равномерно непре¬
рывной по теореме Кантора. Подробнее:
!(X1 + пТ) - (х2 + пТ) I = Ix1 - х21 < 8,
откуда, учитывая равномерную непрерывность на [0; 2Т\, получаем
|/(*1) - /(*2 )| = I/Oi +пТ)- /(X2 + пТ)\ < в.
Утверждение 4.19. Пусть функции /: E —> R и g: R —> R равномерно
непрерывны. Тогда их композиция g(f(x)) равномерно непрерывна на мно¬
жестве Е.
Доказательство
В силу равномерной непрерывности функции g получаем, что для про¬
извольного в > 0 найдется 8 > 0 такое, что для V yiy у2 gR, удовлетворя¬
ющих неравенству IlZ1- у ^ <8, выполнено \g(y\)~ g(y2)\<t- В силу равно-
247
мерной непрерывности функции / для найденного S > О найдется 8' > О
такое, что для всех XllX2EE, удовлетворяющих условию J^c1 — jc2| < S',
выполнено !/(X1)-Z(X2)^S. Следовательно, для всех таких X1, X2 выпол¬
нено |g(/(xt))-g(/(x2)) < в. ■
Задание 4.8
Пусть функция/: [я; +°°) —» К непрерывна, причем для некоторого b > а функция/
дифференцируема на [Ь; +°°), и производная/' ограничена на [Ъ; +°°). Докажите, что
/равномерно непрерывна.
Обратимся далее к вопросу о сравнении роста равномерно непрерывной
и линейной функции. Для этого рассмотрим важное утверждение.
Утверждение 4.20. Пусть функция /: [а; +°°) —> M равномерно непре¬
рывна. Тогда существуют такие фиксированные числа k и Ь, что для всехх,
у е [а; +°°) выполнено неравенство | /(х) - f(y) \ < k • | х - у | + Ь.
Доказательство
В силу того что функция / равномерно непрерывна, имеем: для V в > О
3 8 > 0 такое, что для V х', х", |х' - х"| < 8, выполнено |/(х') - /(х")| < в.
Зафиксируем точки х, у е [а; + °°). Не ограничивая общности, мы можем
считать, что у > х (так как при у = х получаем |/(х) - f(y)\ = 0, и в каче¬
стве чисел k и b подходят любое k и любое b > 0). Разобьем отрезок [х; у\
на п =
У~х
8
+1 равных отрезков: х = X0 < X1 <... < хп = у.
Так как п >
у-х
,то Xi-хм =
У~х
п
< 8 для i = 1,..., п. Тогда получаем
\f(y) ~ f(x)\ = I f(xn ) - /(х0 )| < X |/(xf) - Дхм )| < п • в,
A=I
откуда
\f(y)~f(x)\<n-e<
у-х
+ 1
е=|к-2/|+е>
т.е. в условии утверждения достаточно положить k = —, b = в, где 8 > 0 взято
из условия равномерной непрерывности. ■ 0
Из утверждения 4.20 можно получить важные следствия.
Следствие 4.5. Пусть функция /: [а; +°°) —> R равномерно непрерывна.
Тогда существуют фиксированные числа k и b такие, что для Vxe [а; +°°)
выполнено I /(х) | < kx + Ъ.
Доказательство
Для произвольной точки х е [а; +°°) по утверждению 4.20 найдутся
такие числа k и Ь', что выполнено |/(х) - f(a)\ <kx + b', откуда получаем
|/(х)| < kx + b' + \f(a)\ = kx + b, где b = b' + \f(a)\. ■
Из данного следствия моментально вытекает другое.
Следствие 4.6. Пусть функция /: [а; +°°) —» R равномерно непрерывна,
fix')
тогда функция ограничена,
х
Советуем читателю, однако, провести доказательство данного следствия
без использования утверждения 4.20.
248
Зададимся вопросом: для всех ли равномерно непрерывных функций
f(x)
f(x) существует Iim J у ' 1
X—>+°° х
Ответ на этот вопрос — отрицательный. Рассмотрим функцию f(x) =
= х ■ sin(lnx). Для нее имеем
f'(x) = sin(lnx) + Cos(Inx) < 2.
Следовательно, функция/равномерно непрерывна, однако J к ' = sin(lnx)
X
„Jton Л*>.
X—H-OO X
Утверждение 4.21. Функция /: [я; +°°) —> M является равномерно
непрерывной тогда и только тогда, когда У b>03k>0 такое, что V х,
у G [а; +°°) выполнено |/(х) -f(y) \ < k • \х - у\ + Ь.
Доказательство
Необходимость. Пусть функция / равномерно непрерывна на множе¬
стве [я; +°°). Тогда V Ь>03 8 >0 такое, что V х', х", \х' - х"\ < 8, выполнено
\f{x')~f{x")\<b.
Далее, повторяя все рассуждения из доказательства утверждения 4.20,
получаем
I f(x)~f(y)\<n-b<
[у^ЛЪЛ\х.у\+ъ.
I 5 J 5' '
Таким образом, в условии утверждения достаточно положить k = —, где
8
8 > О взято из условия равномерной непрерывности.
Достаточность. Пусть У b > О 3 k> О такое, что V х, у G [я; +°°) выпол¬
нено
\f(x)-f(y)\<k-\x-y\ + b. (4.9)
Тогда, выбирая для произвольного е > О величину b из формулы (4.9)
” е I I S/ \ е
равной —, а \х - у\< 6(e) = —, из предположенного неравенства получаем
2 2k
\f(x)-f(y)\<k-\x-y\ + b<^ + ^ = e,
что гарантирует нам равномерную непрерывность функции / на луче
[я; + °°). ■
Рассмотрим далее несколько задач.
Задача 4.25
Исследуем следующие функции на равномерную непрерывность на заданном
множестве E:
а) f(x) = yjIn-cos—, E = [2; + °°);
X
б) f(x) - X2 • arctgx, E - [0; +°°);
249
в) /(*)=ln(1+*2), £=[0;+°°);
X
г) f(x) = y[x-\n(! + x2), £ = [0; + °°).
Решение
а) Для производной данной функции имеем
/' 00
XCOS
f-1
+ 2lnx-sin
f-1
UJ
U J
2x2Vlnx
При XS [2; + оо ). Следовательно, функция / равномерно непрерывна на множестве Е.
б) Для производной функции / получаем
г2
/ '(*) =
Xi
х2+1
+ 2х arctg х —> +00 при п —> °°.
Следовательно, функция / не может быть равномерно непрерывной по замеча¬
нию 4.20 из утверждения 4.13.
в) Так как Hm /(х) = 0, то функция /равномерно непрерывна на множестве Е.
2л:3/2 1п(1 + х2)
г) Имеем /'(х) =
-. Получаем: Hm /'(х) = 0, откуда для V е > О
! + X2 2л[х
найдется А > О такое, что для всех х>А выполнено |/'(х)| < £. Используя утверждение
об ограниченности производной, делаем вывод о том, что функция/равномерно непре¬
рывна на луче [А; + °°). На отрезке [0; А +1] функция /является равномерно непрерыв¬
ной по теореме Кантора. Далее остается воспользоваться техникой из задачи 4.24, п. г).
Задание 4.9
Исследуйте на равномерную непрерывность следующие функции:
а) f(x) = X2 sin(lnх), E-(!; +°о);
б) f(x) = х-cos^jx,E= (0; +°°);
в) f(x) = *Jx -COSXtE= (0; +°°);
г) /(л:) = л:-8т—,E= (0; 1).
х
Задача 4.26
Исследуем следующие функции на равномерную непрерывность, в зависимости
от параметров, на заданном множестве Е:
а) fix) =ха, E= (0; +°°);
б) f(x) = ха ■ sin х$, где a, P > 0 на (0; +°°).
Решение
а) Сразу заметим, что при а < 0 функция / не является равномерно непрерыв¬
ной, так как не существует предела Hm f(x).
х—>0+0
При 0 < а < 1 получим, что Iim f(x) = 0 и f'(x) = а ха_1 < 1 при х > 1. Следовательно,
х-Ю+О
функция / при данных значениях параметра а является равномерно непрерывной.
При а > 1 заметим, что Iim f'(x) = Hm а ха_1 = +°°. Следовательно, функция /
X—>+°° X—>+°°
не является равномерно непрерывной на (0; +°°).
б) Рассмотрим два случая.
1. 0<а + Р<1. Для таких значений параметров (a, P > 0) функция/непрерывна
в нуле. Кроме того, производная
f'(x) = Otxct-1 sin(xP) + рх“+Р-1 cos(xP)
250
является ограниченной на луче [0; +°°). Следовательно, используя стандартную тех¬
нику, можно доказать, что функция /является равномерно непрерывной на (0; +°°).
2. а + P > 1. Для доказательства неравномерной непрерывности воспользуемся
необходимым условием равномерной непрерывности из утверждения 4.20, подберем
соответствующие последовательности точек хп, уп и покажем, что неравенство
\f{xn)-f{yn)\<k\x-y\ + b (4.10)
не выполняется ни при каких b и k. Действительно, выберем в качестве хп = (2т
Уп
(
27in + —
2у
. Для данных точек имеем:
|Уя-*я| = (2яя)1/Р
(. 1
1+—
I 4п
\i/P
-1
V ' 4nP 4Р
\f(x„)-f(y„)\ = 0 +
27in + —
2
-(
= (271) P
V
I
n + —
4
~(27i)P«P.
Следовательно, так как ^ +1 = ——“ > 0, то при достаточно больших п нера-
г г H
венство (4.10) не имеет места ни при каких Ъ и к.
Обратим внимание читателя на следующий вопрос (уже рассмотренный
нами выше). Пусть функция / является равномерно непрерывной на мно¬
жествах E1 и E2. Можно ли утверждать, что данная функция является рав¬
номерно непрерывной на объединении данных множеств — E1 u E2? Ответ
на данный вопрос — отрицательный.
sinx
Действительно, рассмотрим пример функции f(x) =J1 на множе-
х
ствах, явлюящихся интервалами, E1 = (-1; 0) и E2 = (0; 1). Для данной
функции получим
Hm fix') = ± sin I, Iim fix) = ±1,
х->±1 х—»0+0
т.е. функция / является равномерно непрерывной на множествах E1 и E2.
Однако равномерная непрерывность на множестве E1 u E2 нарушается, так
* (-1)”
как, выбрав сходящуюся к нулю последовательность хп = -——, имеем
п
Iim f(x2n) = I, HmZ(X2^1) = -I,
п—»°° п—»°°
но х2п и x2„_! лежат в объединении множеств E1 u E2 и расстояние между
ними в силу их одинакового предела можно сделать сколь угодно малым.
4.6. Правило Лопиталя
Предположим, что в задаче о нахождении предела отношения функций
fiX) (L
при х —» а и числитель, и знаменатель стремятся к нулю или оба стре-
g(x)
мятся к бесконечности. В этих случаях говорят, что мы имеем дело с неоп-
251
о °°
ределенностью вида — или —. Нахождение этого предела (если он суще-
0 °°
ствует) называют раскрытием неопределенности. При отыскании таких
пределов часто бывает полезным прием, называемый правилом Лопиталя.
Рассмотрим точку а на вещественной прямой R, возможно, равную
Теорема 4.7 (первое правило Лопиталя). Пусть найдется 5 > 0 такое,
что выполнено:
о
1) функции f(pc), g(x) непрерывны в Bb (a), Hm /(х) = Iim g(x) = 0;
X-Hl
X—Hl
2) производные f'(x) и g'(x) существуют в Вь(а), причем g'(x) Ф 0,
о
х G Вь{а);
3) существует конечный или бесконечный предел Iim ^ ^х\
X^a g (х)
Тогда существует предел Hm ^%^ и выполняется равенство
X-Hl
g(x)
Iim^ =Iim^M
X—ё(х) х->я g (х)
Теорема 4.8 (второе правило Лопиталя). Пусть найдется 8 > 0 такое,
что выполнено:
о
1) функции/(х), g(x) непрерывны в Bb(a), Hm /(х) = Hm g(x) =
х—»я
х—>а
2) производные f'(x) и g'(x) существуют в Вь(а), причем g'(x) Ф 0,
о
х G Вь{а);
3) существует конечный или бесконечный предел Hm ^ ^х\
х^а g (х)
Тогда существует предел Hm ^%^ и выполняется равенство
X-Hl ё(х)
Iim^= Iim /'<*>
X—Hl
ё(х)
х—>я
#'(*)
Замечание 4.22. Раскрытие неопределенностей видов 0 • °° - °°, 1°°, O0
путем алгебраических преобразований и логарифмирования приводится
0 °°
к раскрытию неопределенностей двух первых типов: — или —.
0 °°
Пример 4.12
Рассмотрим функции
/(*) =
1
x2sin—,еслихФ0, , ч
х g(x)=x.
0, если х = 0,
В этом случае 3 Iim J v ' =0. Однако предела отношения производных:
x^0g(x)
252
/'(*)=
I I
2;csin—cos—,еслихФ0, ч .
X X g(x) = I
О (докажите!), если х = О,
не существует. Таким образом, правило Лопиталя дает достаточное, но не необхо¬
димое условие существования предела отношения f^x\ Его можно модифицировать
g(x)
так, что приведенный пример подпадает под модифицированное правило.
Теорема 4.9. Пусть функции fug определены в окрестности В8(а),
Hm f(x) = Hmg(x) = 0, существуют производные f'(а) и g'{a). Тогда
х—»я х—>а
Б Hm = J-Jf*!. (при g'(a) ф 0).
™g(x) g'(«0
fix)
Замечание 4.23. Если f'(a) Ф 0, g'(a) = 0, то Hm J v 7 = <».
х—>а g(x)
Остановимся далее на следующем обобщении правила Лопиталя, спра¬
ведливого при более слабых ограничениях.
Теорема 4.10 (обощение правила Лопиталя). Пусть найдется 8 > 0
такое, что выполнено:
о
1) функции fix), g(x) непрерывны в В8(а), Hm g(x) =
х—>а
2) производные f'(x) и g'(x) существуют в В8(а), причем g'(x) Ф 0, х е
е B8(O)]
3) существует конечный или бесконечный предел Hm JJf),
X^a g (х)
Тогда существует предел Hm JJfJ) и выполняется равенство
х—>я g(x)
IimZW = IimZM.
х—>а g(x) х—>я g(x)
Доказательство
f'(x)
Предположим, что Hm J v ' = b. Выберем произвольные х и у из B8 (а)
х—g'(x)
так, чтобы выполнялось а<х<у. Применяя теорему Коши о конечном при¬
ращении, получаем, что найдется \ е (х\ у) такое, что справедливо равенство
Я*)-/(у) Г(%)
g(x)-g(y) g'©’
откуда
4 ё(У)
I f(x)-m_n\) I _т) g(x) ^
g(x) ±_gjy) gW g(x) g’(%)f(x)-f(y)
g(x)
253
/(*) _ m . /'($)
+-
g(x) g(x) g'(£)
1-
g(y)
g(x).
ff(x)
Зафиксируем у и устремим х к а. В силу условий HmJ v 7 = b
*->a g'(x)
и Hm g(x) - °° можем записать:
х—>а
1) фиксируем у такое, что \х - а \ < \у - а \ и
/Шх, у))
-Ъ
у))
2) фиксируем S1 такое, чтобы при \х - а \ < S1 выполнялось
4’
f{y)
3) фиксируем S2 такое, чтобы при | х - а \ < S2 выполнялось
Таким образом, для \х - а \ < min{|г/ - я|; S1; 82} получаем
g(y)
g(x)
g(x)
<
E
< 2’
е/4
\b\+ е/4’
fix)
g(x)
-b
f(y)
g(x)
+
m)
g'i®
-b
+
Ш) g(y)
g'(Z) g(x)
EE £
< 1 1 = £.
2 4 4
Замечание 4.24. В силу условия g'(x) Ф 0 для Vxg B8 (а) мы получаем,
что в данной окрестности точки а функция g, стоящая в знаменателе, явля¬
ется монотонной. Действительно, в противном случае производная данной
функции меняет свой знак, поэтому (так как производная не может иметь
точек разрыва первого рода) должна перейти через нуль.
Для самостоятельной работы мы предлагаем читателю разобрать следу¬
ющие задачи.
Задание 4.10
Пусть функция / дважды непрерывно дифференцируема, найдите предел
Iim + ^ + ~ ^ ~
А-» 0 A2
Задание 4.11
Пусть функция / трижды непрерывно дифференцируема, найдите предел
.. f(a + 3h)-3f(a + 2h) + 3f(a + h)-f(a)
Й /г3
Задание 4.12
Исследуйте возможность применения правила Лопиталя и вычислите следующие
пределы:
1 + x + sinxcosx
ч .. x-smx ... ..
a) Iim ; б) Iim
x->-H*>x + sinx *->-H»(x + sinxcosx)es
в) Iim
х-А
X3 sin(l/x)
sin2x
Задание 4.13
Постройте примеры:
а) разрывных функций fug таких, что Iim /(х) = Iim g(x) = 0 и выполнено
f(x) f'(x)
lim ZW = Jim/W;
х-ьа g(x) х->а g'(x)
f'(x)
б) непрерывных функций /и g таких, что Hm /(х) = Hm g(x) = 0, но $ Hm J f ' и
-и- Kx)
3 Hm < оо;
х^а g(x)
g'ix)
254
в) бесконечно дифференцируемых функций / и g, для которых существуют
пределы Hm f(x) = Hm g(x) = 0 и Hm 7 v ' < однако Hm f^(x) = 0, Hm g(k)(x) = 0
х—>а х—>а х—>а g(x) х—>а х—
ДЛЯ V k E N.
4.7. Теорема Тейлора и ее приложения
Теорема 4.11. Пусть функция / определена в окрестности В(х0) точки
х0, имеет в этой окрестности производные до (п - 1 )-го порядка включи¬
тельно и пусть существует ftjlKx0). Тогда
/(х) = E ^ ^Х°\х-x0)k + о((х-х0)п) прих —>х0. (4.11)
ы>
Определение 4.10. Многочлен Рп(х) =
Ы) Л!
(x-x0)k называется
многочленом Тейлора функции / в точке х0.
Определение 4.11. Функция rn(x) =/00 - T5nOO называется остаточ¬
ным членом п-то порядка формулы Тейлора.
Определение 4.12. Формула (4.11) называется формулой Тейлора п-то
порядка для функции / в окрестности точки X0 с остаточным членом
в форме Пеано (или локальной формулой Тейлора).
Определение 4.13. Если X0 = 0, то формула (4.11) принимает вид
/00= E
k=o
/(*>( 0)
k\
xk + о(хп) при х —> 0
и называется формулой Маклорена.
Теорема 4.12 (Тейлора). Функция / имеющая в точке X0 производные
до п-го порядка включительно, единственным образом представляется
в виде
/00 = E ak(x~xo)k + °((х~хо)п) ПРИ ххо>
k=o
где коэффициенты разложения определяются формулами
ak
= /¾¾ = 0,1,
k\
П.
Следствие 4.7. Пусть 3 /(и)(х0) и
/00 = а0 + а^рс - х0) +... + ап(х - х0)п + о(х - х0)и при х —> х0. (4.12)
Тогда (4.12) является разложением функции /по формуле Тейлора
с остаточным членом в форме Пеано.
Теорема 4.13. Если функция /(х) имеет в некоторой окрестности В(х0)
точки х0 производные до (п + 1 )-го порядка включительно, то для любой
точки х G В(х0) найдется точка лежащая между х и х0, такая что
/(*) = S ~+ (х ~ xOy"1- (4ЛЗ)
*=о «I (я + 1)!
255
Определение 4.14. Формула (4.13) называется формулой Тейлора
с остаточным членом
г„(х) =
/(и+1)(£)
(я + 1)!
(x-x0)n+i
в форме Лагранжа.
Пусть функция /бесконечно дифференцируема в нуле. Зададимся далее
вопросом: как выглядят разложения по формуле Маклорена данной функ¬
ции в случае четности/нечетности функции /? А именно, докажем следу¬
ющее утверждение.
Утверждение 4.22. Если бесконечно дифференцируемая1 функция/ —
четная, то ее разложение по формуле Маклорена содержит только четные
степени х.
Доказательство
Если функция / является четной, то ее производная — нечетная функ¬
ция, и наоборот, производная нечетной функции — четная функция (дока¬
жите!). Отсюда следует, что для четной функции / выполнено условие
/(2^-1)(0) = 0, для всех k E N, так как любая непрерывная нечетная функ¬
ция принимает при х = 0 нулевое значение. Поэтому формулу Маклорена
для бесконечно дифференцируемой четной функции / можно записать
в виде
f(x) = S ~—J^-X2k + o(x2n+i), х —» 0. ■
*=о (2«)!
Предлагаем читателю самостоятельно доказать аналогичное утверждение.
Задание 4.14
Пусть/— бесконечно дифференцируемая в нуле функция. Докажите, что если/не-
четная, то ее разложение по формуле Маклорена содержит только нечетные степени х.
Остановимся на применении метода неопределенных коэффициентов
для разложения функций по формуле Маклорена. Для начала сформули¬
руем суть данного метода.
Определение 4.15. Метод неопределенных коэффициентов — метод,
используемый для нахождения искомой функции в виде точной или при¬
ближенной линейной комбинации конечного или бесконечного набора
базовых функций (как правило, многочленов). Указанная линейная ком¬
бинация берется с неизвестными коэффициентами, которые определя¬
ются различными способами из условий рассматриваемой задачи. Обычно
для них получается система алгебраических уравнений.
Далее мы считаем, что получены стандартные разложения по формуле
Маклорена:
е*=1 + х + —+ ... + — ■+о(хп);
2! п\
/уЗ 1
sin х = х +... + (-1)и-1 + о(х2п );
3! v ' (2/2-1)! v '
1 Или хотя бы дифференцируемая до какого-нибудь порядка.
256
COSX = I - +... + (-1)” + о(х2и+1);
2! (2 п)\
2 п
1п(1 + х) = х - — +... + (-1)”-1 — + о(хя);
2 п
(l+x)-=l+my+^^>xH...+ m(m~1)-(m~” + 1)x" +0(Х”).
2! /г!
Задача 4.27
Применяя метод неопределенных коэффициентов, получим формулу Маклорена
с о(х5) функции f(x), если: а) /(х) = tgx; б) f(x) = thx.
Решение
а) Используя то, что tgx — нечетная функция и tgx ~ х при х —» 0, ползаем, что
представление функции/по формуле Маклорена ищется в виде
/(х) = tg х = х + а3х3 + и5х5 + о(х5 ).
sinx
Используя данное выражение, формулу tgx = и стандартные разложения,
получаем
C у2 y4
1- —+ —+ о(х5)
2 24 w
COSX
cosx-tgx = sinx<=>
(х + а3х3 + а5х5 + о(х5)) =
5
= X- ——Y — h о(х5 ).
6 120 47
Раскрывая скобки и приравнивая коэффициенты при одинаковых степенях, полу¬
чаем систему уравнений
1
1
H Qq = ,
2 3 6
1
I Uo
Ь Uk =
24 2 5 120
1
аз~3>
«5 =
15'
Следовательно, tgx = x + — + j^x5 + о(х5), х —» 0.
3 15
б) Аналогично предыдущему решению ищем разложение thx в виде
thx = x + a3x3 -Ha5X5 +о(х5),
откуда
(ех +e~x)thx-ex -е~х <=>
<=>
2+ X* 2 + — + о(х5)
12 ^ '
(х + U3X3 + U5X5 + о(х5)) =
X3 X5
= 2х + — + — + о(х5).
3 60 W
Получаем следующую систему уравнений:
1 + 2а3 =-,
d <=>
I 1
—h ао + Iuk = —
12 3 5 60
аз 3>
аз
15'
Следовательно, thx = х- — + — х5 + о(х5), х —» 0.
257
Задание 4.15
Применяя метод неопределенных коэффициентов, получите формулу Маклорена
с о(г5) функции /(г), если:
a) f(,x)=2% +* + 1;б)/(Х)= 2* _;в)/(г) = Х
X2 + Зх +1
-1'
1-sinr
Рассмотрим внимательнее первую задачу из задания 4.16. Вообще
говоря, существует несколько альтернативных способов для вычисления
таких разложений:
1) метод неопределенных коэффициентов, т.е. представление данной
рациональной дроби в виде
2х3 - Ax2 + х + 1 = (х2 + Зх + 1)(1 + A1X + а^с2 +... + A5X5 + о(х5));
2) представление знаменателя в виде:
(2х3 - 4х2 + х + 1)[ 1 + (Зх + х2)]-1 =
= (2х3 - 4х2 + х + 1)[1 - (Зх + х2) +... + (Зх + х2)5 + о(х5)];
3) деление столбиком многочлена на многочлен.
Далее мы остановимся на весьма полезном способе разложения по фор¬
муле Тейлора, а именно, на методе восстановления разложения функции
по разложению его производной. Пусть известно представление формулой
Тейлора в окрестности точки X0 до о((х -х0)и) производной функции/, т.е.
известна формула
/'(х) = Z k(х-х0)k + о((х-х0)п), bk = }(Х°\
k=0 Я!
Тогда существует производная/^+1Hx0), и поэтому функцию/(х) можно
представить в виде
п+1
/(х)= X O^(X-X0)*+о((х-х0)и+1) =
k=0
п
= а0 + E <*k+1(x-xQ)k+i + о((х-х0)я+1),
к=й
,, ч /(4+1)<Л) I k
где O0 =/(¾), а,+1=_^__ = _.
Отсюда
/(х) = /(х0)+ S T^(X-X0)*+1+ о((х-х0)и+1) (4.14)
Ы)/г + 1
где bk — коэффициенты формулы Тейлора функции/'.
Отметим, что приведенный метод фактически является почленным
интегрированием многочлена Тейлора от производной/'.
Задача 4.28
258
Представим формулой Маклорена функцию /(г) до членов указанного порядка:
a) f{x) = arcsinx до о(х2п+2); б) f(x) = r2-ln(r + Vi-Kr2 ) до о(г2п+2);
Решение
а) Имеем
(arcsine)' =
Vi
= (I-^r2)-V2 =
= 1+1(-1)*
A=I
Г 1Л
V
4-‘
X^
\ г
=1+Е
6!
^ Р" X2k + о(л:2я+1).
A=I 2*6! v '
х2* + о(х2”+1) =
Используя формулу (4.14) и равенство arcsinO = 0, получим
” (26-1)!! „2А+1 . Л/^-2п+2>
arcsinx = х+ У —f- —Xz
£2*61(26 + 1)
+ о(х2п+2), х—>0.
б) Отметим, что разложение в формулу Маклорена всего произведения одно¬
временно существенно осложнит задачу. Представим функцию/в виде/(х) = x2F(x)
и разложим по Маклорену функцию F(x) = ln(x + Vl + х2 ). Имеем
F(x) =
Vi
+ X2
= {аналогично п. а)} = I + ^
'£4-1)426-1)!!
х24 + о(х2”), х —» 0.
A=I
2kk\
Воспользовавшись формулой (4.14) и равенством ДО) = Inl = 0, получаем
Пх)=х+%ЧЩ;
или
/(х) = X2ln(x + Vl + x2) = X3 + X i) 'X2^+3 + о(х2п+2).
В качестве самостоятельной работы предлагаем читателям следующую
задачу.
Задание 4.16
Представьте формулой Маклорена функцию/(х) до членов указанного порядка:
а) /(х) = arctgx до о(х2и+2);
f 1)
ДО O(Xs).
б) /(x) = arcsin
* 3
Задача 4.29
Представим формулой Маклорена функцию fix) = 1п(1 + х) + х2|х| до O(Xn).
Определим, какие значения может принимать п.
Решение
Отметим, что точность представления формулой Маклорена не может быть выше
наибольшего порядка производной, существующей в этой точке. Обозначим через g
функцию х2|х|. Torflag(O) = 0, g'(0) = 0, g"(0) = 0, но не существует g(3)(0), так как
g(3)(0) = -6*6 = gf>(0).
Следовательно, представления Маклорена имеют вид
X2
/(х) = х + о(х) при п = 1; /(х) = х- — + о(х2) при п = 2
и не существует разложения функции / при п> 3.
Рассмотрим применение формулы Тейлора к доказательству неравенств. А именно,
решим следующую задачу.
259
Задача 4.30
Покажем, что для всех натуральных п > 1 справедливо неравенство
I 1
<--
2 пе е
1-
1
\п
п
1
<—.
пе
Решение
Преобразовывая предложенное неравенство, получаем неравенство
I I (. 1Л”
< —
2пе е
1--
V я.
1
1
< — фф1 — <е
пе п
rain 1— +1
<1-—,
2 п
домножая на -1 и логарифмируя которое, устанавливаем неравенство
In
Is
I
I
V
Ml
< — In
Ml
I 2nJ
I nJ
I nJ
Раскладывая части данного неравенства по формуле Маклорена, получаем не¬
равенство
CO I DO I CO I
bi k2k nk < bi (k +1)пк < knk ’
справедливое для всех и > 1.
Задача 4.31
Пусть функция / дважды непрерывно дифференцируема на [0; 1] и выполня¬
ются равенства/(O) =/(1) = 0. Пусть также выполнено min f(x) = ~ 1. Докажем, что
[0; 1]
max f"(x) > 8.
[0; l] J
Решение
Пусть функция/достигает минимума в точке X0 е (0; 1). Тогда получаем/(х0) = -1,
/'(Xtt) = 0. '
Запишем для функции/в точке X0 формулу Тейлора с остаточным членом в форме
Лагранжа:
= € (0; 1).
Положив в этой формуле попеременно х = 0 и х = 1, имеем
0 = 0 = -1+£^1>(1-хо)2
=>/" (Qtf)=A,/"(Qd= 2
Xa
(I-X0)2
I 1
Отсюда если 0 < х0 < —, то/'(G0) > 8, а если — < X0 < I, ToZr(G1) > 8. Следовательно,
заведомо получаем, что max f"(x) > 8.
[0; 1]
Задача 4.32
Пусть функция/трижды непрерывно дифференцируема на числовой прямой М,
функции/(х),/'(х),/"(х),/'"(х) всюду положительны. Докажем, что найдется такое
число а > 0, что /(х) > ах2 при V х > 0.
260
Решение
Запишем для функции / формулу Маклорена с остаточным членом в форме
Лагранжа в точке х > 0:
/(X) = /(0) + /'(0)х + X2+1—Ip-х3, где0 G (0; х).
2. о
Отсюда получаем
,, ч /"(0) , 2 /"(0)
fix) > ^ X* * 1 = ах1, где а - ^ .
Задача 4.33
Пусть функция / дважды непрерывно дифференцируема на интервале (0; 1),
и/'(O) Ф 0. Для Vxg (0; 1) величина 0(х) определяется как одно из чисел 0, для кото-
рых f{x) -/(0) = /'(0)х, 0 G (0; 1). Вычислим предел Hm ^ .
лг—»0+0 X
Решение
Разложим данное в условии задачи равенство по формуле Маклорена с остаточ¬
ным членом в форме Лагранжа, получаем
( f"( rrt ")
/(0) + /'(0)х + J-^x1 -/(0) =(/'(О) + /"(0)0)х, (4.15)
V _ z У
где r\ G (0; х), 0 G (0; х), 0 G (0, 0). При х —» 0 + 0 получаем 0 —> 0, 0 —> 0, т| —> 0.
Равенство (4.15) переписывается в виде
= /"(6)хв « = /"(9)6,
0 I /"(л) 1 /"(0) 1
откуда — = — / _ —» — , =—.
J х 2/"(0)^о+о 2/"(0) 2
Задача 4.34
Пусть k — фиксированное положительное число и и-я производная функции
I P (х)
—т— имеет вид —, где Рп(х) — некоторый полином. Найдем величину Pn(I).
хк-\ (хк - l)n+1
Решение
Раскладывая функцию
получаем
1
хк -1
по формуле Тейлора в окрестности точки х = 1,
откуда
и
1
xk-\ k(x -1) + о(х -1) k
= — (х -1)-1 + о(х -1),
dn
dxn
хА-1
(~l)”n!
&(х - X)n+1
+ о(х -1)
Рп(х) = (хк -1)”+1-
dxn
k-\
X
- \k(x -1) + о(х -1)]”+1
+0<<* “ 1^J = <_i)’"!+ °Ф - +
Следовательно, Pn(X) = (-k)nn\, n > 0.
261
Предлагаем читателю самостоятельно получить другое решение зада-
р (х)
чи 4.34, подставив I = 1 в числитель производной выражения ”
(xk-Y)n+i
и воспользовавшись методом математической индукции.
Задача 4.35
Разложим в бесконечную сумму по Маклорену функцию
/(х) = ех cos a sin(x sin а),
где а — произвольное действительное число.
Решение
Вычислим производные функции /:
f'(x) = excosot sinacos(xsina) + excosa cosasin(xsina) = excosa sin(a + xsin a),
f"(x) - excosa sin(2a + xsina), ...,f(n\x) - excosa sin(raa + xsina).
Устанавливаем равенство/M(O) = sin(na). Из формулы Тейлора получаем
k=0 «! k=0
k = у sinW^
ь k\
Другое решение получается, если воспользоваться формулой Эйлера и записать
предложенную функцию /в виде /(х) = Im(excosa+“sintx).
Предлагаем читателю довести данное решение до конца самостоятельно.
Рассмотрим далее задачу, которая иногда называется задачей В. И. Ар¬
нольда.
Задача 4.36 (В. И. Арнольд)
Найдем предел:
,. tg(sin х) - sm(tgx)
Iim .
*->o arctg(arcsin х) - arcsin(arctg х)
(4.16)
Решение
Сложность данной задачи заключается в том, что разложения по Маклорену чис¬
лителя и знаменателя совпадают до 8-го порядка включительно! Поэтому обратимся
к более общей задаче. Рассмотрим вместо функций sinx и tgx две нечетные эквива¬
лентные при х —> О функции:
fix') =X+ (T1X3 * + A1X5 * + C1X7 + O(Xs), g(x) =X+ (T2X3 + A2X5 + C2X7 + O(Xs).
Тогда, раскладывая функции f(g(x)) и g(f(x)) по Маклорену и собирая коэффи¬
циенты при равных степенях х, имеем
f(g(x)) = х + ((T1 + (T2)X3 + (A1 + A2 + 3aia2)x5 + (C1 + с2 + 3 a^f + Sa2A1 + 3aib2)x7 + O(Xs);
g(f(x)) = х + ((T1 + (Т2)х3 + (A1 + A2 + Sa1(T2)X5 + (C1 + C2 + За(а2 + Sa1A2 + 3a2bf)x7 + O(Xs).
Отсюда
f(g(x)) ~ g(f(x)) = (Заш2 + Sa2A1 + Sa1A2 - 3а\а2 - Safb2 - 3a2bf)x7 + O(Xs) =
= [2(a2bi - afbf) + За1а2(а2 - af)\x7 + O(Xs).
Пусть, далее,
/_1(х) = х + O1X3 + А(х5 + с[х7 + o(xs); g_1(x) = х + a2x3 + A2X5 + с2х7 + о(х8).
262
Для того чтобы выразить коэффициенты разложения Маклорена функций /-1
и g-1 через аналогичные коэффициенты функций / и g, воспользуемся равенствами
/(Z1(X)) = х, gigrKx)) = ос.
/(Z-1Or)) = х + (O1 + а[)х3 + (A1 + A1 + 3 OiO^xs + (q + с[ + 3 а^2 + Sa1A1 + 3 аф[)х7 + о(х8).
Аналогично действуем для яОгЧ*)) = х. Следовательно, получаем системы
равенств
Cl1 — Cl1,
■ b[ = 3al~bb
C1 = Sa1A1 - 12а2 - C1;
Проведя алгебраические преобразования, находим
f-\g~\x))- g-\f-\x)) = [2(а'2Ъ[ -a[b'2) + За[а'2(а'2 -а[)]х7 + о(х8) =
= {2[-a2(3af - A1) + а1(3а| - A2)] + За1а2(а1 - а2)}х7 + о(х8) =
= ХКаФ\ -(hb2) + - ai)]*7 + °(^8) = f(g(x))-g(f(x)) + о(х8).
Поэтому, возвращаясь к вычислению предела (4.16), получаем
tg(sin х) - sin(tgx)
а2 ~а2’
b'2=3al~b2,
с2 — 8а2А2 12а2 с2.
Iim-
»0 arctg(arcsin х) - arcsin(arctg х)
= 1.
Задача 4.37
Пусть f{pc) = I + Ci1X + Ci2X2 + ... и пусть все коэффициенты в разложении отноше¬
ния f ^ = A0 + A1X + A2X2 +... по степеням х по модулю не превосходят двух. Докажем,
f(x)
что I а„ I < п + 1.
Решение
Представим производную в следующем виде:
/'(*) =
fix)
f(x)
fix) = (A0 + A1X + A2X2 +...) • (I + а1х + а2х2 +...).
Раскрывая скобки и приводя подобные слагаемые, получаем, что коэффициент
т
при х“ в разложении /'(х) равен ^ akbm_k. В то же время
A=O
/'(х) = at + 2а2х + За3х2 +... = £ (то + l)am+1xm.
т=0
Приравнивая коэффициенты при одинаковых степенях, получим
т
(™ + 1)ат+1=ЪакЬт_к.
A=O
Теперь требуемое неравенство легко доказать методом математической индукции.
Имеем Ia1) = \а0Ь0\ = |А0
Пусть выполнено | ак
ап+11
<2.
< k + 1 для k = 1,..., п. Тогда
I ” , 1
и + 1
2 п
X ((фп-k
A=O
„..Xkli^N-frXkN
П +1 A=O (I +1 A=O
Х(А + 1)= 2 (п + 1)(п + 2) = п + 2.
и + ЬТо и + 1 2
Глава 5
ПРИМЕНЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
ДЛЯ ИССЛЕДОВАНИЯ ФУНКЦИЙ
5.1. Возрастание и убывание функции. Монотонность
Для начала мы напомним читателю важные определения, а также
утверждение, связывающее знак производной и характер монотонности.
Определение 5.1. Функция /возрастает {не убывает) в точке х = X0,
если 3 8 = 8(х0) > 0 такое, что
/(х) </(х0) (Дх) </(х0))
при х0 - 8 < х < X0 и
/(х) >/(х0) (/(х) >/(х0»
при х0 < х < х0 + 8. Обозначение: /(х)T (Дх)/).
Определение 5.2. Функция /убывает {не возрастает) в точке х = х0,
если 3 8 = 8(х0) > 0 такое, что
/(х) >/(х0) (Дх) >/(х0))
при х0 - 8 < х < х0, и
/(х) </(х0) (Дх) </(х0))
при х0 < х < х0 + 8. Обозначение: /(х)^ (Дх)\).
Определение 5.3. Будем говорить, что функция возрастает на интер¬
вале {а; 6), если для любых точек X1 и X2 из данного интервала из неравен¬
ства X1 < X2 следует/(X1) </(х2). Аналогично вводятся определения убыва¬
ния, невозрастания и неубывания функции на интервале.
Утверждение 5.1. Пусть функция /дифференцируема на интервале
{а; Ь). Между характером монотонности данной функции и знаком ее про¬
изводной на этом интервале имеется следующая взаимосвязь:
г (X) > 0 ^f(X)T =» Г (X)> 0 >0 о/(*)/;
/'(х) = 0 <=> /(х) = const;
/'W < о ^/(х)1 =>/'(*) < 0;/'(х) < 0 «/(х)\.
Замечание 5.1. Отметим, что строгая положительность (отрицатель¬
ность) производной не является необходимым условием возрастания (убы¬
вания) функции.
Например, функция /(х) = х3 в точке х = 0 возрастает, но /'(х) = 0.
264
Рассмотрим следующие вопросы. Пусть /: (-1; 1) —» R — функция,
имеющая производную на (-1; 1) и/'(О) > 0. Существует ли окрестность
точки х = 0, в которой функция / возрастает? Существует ли такая окрест¬
ность, если функция /' непрерывна в точке х = 0?
Ответ на первый вопрос — отрицательный. Действительно, рассмотрим
пример следующей функции:
2
г, . х + х2sin—,еслихФ0,
/(Х)Ч х
0, если х = 0.
Имеем
Ax +Ax2 - sin—
/'(0) = Hm = 1 > 0.
Лх->о Ax
При хФО получаем
/'(х) = I + 2х sin 2 cos—.
X X
Выберем далее две последовательности, сходящиеся при п —> °° к нулю:
r(D=J_ г(2) = 1
у% « *А/ у) ■
7Ш ПП + 71/2
Однако /(х^) = -1<0,/(х^) = 3>0. Следовательно, данная функция
не является возрастающей ни на одном интервале, содержащем точку х = 0.
На второй же вопрос ответ — утвердительный. Предлагаем установить
это читателю самостоятельно, используя теорему о возрастании функции
в точке и теорему о локальных свойствах непрерывной функции.
Изобразим функцию /(х) =
х + X2 sin—, если х Ф 0,
Xz
обладающую теми
0, если х = 0,
же (но более ярко выраженными) свойствами, что и изученный при¬
мер (рис. 5.1), и предлагаем читателю изучить ее характер монотонности
в сколь угодно малой окрестности точки х = 0.
Пусть, далее, /: R —» R, g: R —> R — произвольные монотонно возрастаю¬
щие на множестве R функции. Какие из функций вида / + g, / - g, / • g, f(g)
необходимо монотонно возрастают на R?
Для всех х' и х" таких, что х' < х", выполнено:
/(*') < /СО» £(х') < #(0 =* /(xO+б(х') < /(О+SCO;
у' = /(xO < fix") = у" => g(/(x')) = g(y') < g(y") = gif (*'))■
Следовательно, функции f + g и /(g) необходимо монотонно возрастают.
Для двух других комбинаций рассмотрим следующий контрпример.
Пусть /(х) = х, g(x) = 2х. Тогда
/ - g = -х -I на R, / • g = 2х2 на (-°°; 0).
265
Рис. 5.1
Поэтому мы делаем вывод о том, что данные функции не обязательно
возрастают.
Обратим внимание на то, что для произведения можно доказать следу¬
ющее утверждение.
Утверждение5.2. Пусть функции/ng монотонно возрастают и строго
положительны. Тогда их произведение / • g строго возрастает.
Доказательство
Выберем произвольные х', х" такие, что х' <х". Тогда выполнено
О < f(x') < f(x") и 0 < g(x') < g(x").
Поэтому /(*') • g(x') < f(x") ■ g(x') < f(x") ■ g(x"). U
Рассмотрим несколько вопросов, наглядно демонстрирующих различие
случаев монотонного возрастания и убывания.
Задача 5.1
Пусть функция /определена на всем отрезке [0; 1] и отображает его на некото¬
рое подмножество [0; 1]. Верно ли, что найдется такое х е [0; 1], что fix) = х, если
данная функция: а) монотонно возрастает; б) монотонно убывает?
Решение
а) Докажем, что в этом случае такая точка найдется. Если f(x) = 0, то все
доказано. Иначе (для всех х е [0; 1] выполнено f{pc) > 0) рассмотрим множество
А = {х € [0; 1] I f{x) > х), которое ограничено и в силу нашего предположения не явля¬
ется пустым (так как 0 е А). Следовательно, существует sup А, который мы обозна¬
чим через а.
Возможны два случая.
I. Ot < /(Ot) = Y- Тогда, используя монотонное возрастание функции fix) и опре¬
деление sup множества А, получим
Y = /(0O ^ /
а + у
что противоречит предположенному неравенству.
2. а > /(а) = у. Обозначим а - Y = е > 0. Для этого е (по определению sup) суще¬
ствует х' G (а - е; а) такое, что fix') > х'.
В этом случае получаем
Y = /(a)>/«)>:r'>ct-e = Y,
что также неверно. Следовательно, может выполняться только случай /(а) = а.
266
б) Построим пример убывающей функции /, для которой равенство f(x) > х
не выполнено ни для какого х G [0; 1]. Достаточно рассмотреть функцию
л х 1
1 , еслил;< —,
2 2
1 х 1
,если х>—.
2 2 2
Данная функция определена на всем отрезке [0; 1], но равенство f(x) = х не выпол¬
нено нигде. В заключение изобразим чертеж данной функции (рис. 5.2).
/(*) = •
Докажем следующее утверждение.
Утверждение 5.3. Пусть функция / возрастает в каждой точке интер¬
вала (а; Ъ). Тогда данная функция возрастает на этом интервале1.
Доказательство
Выберем произвольные точки х',х" е (а; Ь), х' <х". Далее, для каждой
точки х* E [х'; х"] выбираем правую (5 + 0)-окрестность (каждое 5, вообще
говоря, зависит от точки х*) из определения возрастания функции в точке.
Воспользовавшись леммой Гейне — Бореля, выберем из этого бесконечного
покрытия конечное подпокрытие полуинтервалами, в которых выполнены
условия определения возрастания в точке х*. Добавим к этому конечному
подпокрытию 8-полуокрестности выбранных нами точек х', х". Выбираем
х' = X1 и ее полуокрестность. Внутри этого полуинтервала выбираем точку
х2 — границу одного из полуинтервалов покрытия. В 8-полуокрестности
точки х2 выбираем точку X3 и т.д. В результате мы получаем набор точек
х'= X1KX2K ... KXk= х", для которых выполнено
fix') = /(X1) < /(х2) <... < f(xk) = /(х").
В силу произвольности выбранных точек х' и х" заключаем возрастание
функции/на интервале (а; Ъ).
Рассмотрим далее следующее утверждение.
Утверждение 5.4. Пусть ср — монотонно возрастающая дифференциру¬
емая на R функция и |/'(х) | < ф'(х) при х > х0. Тогда
I fix) -/(X0) I < < ср(х) - ф(х0)
при X > х0.
1 Определения возрастания функции в точке и возрастания на интервале, см. в начале
данной главы.
267
Доказательство
Справедливость данного утверждения моментально следует из теоремы
Коши о конечных приращениях. Предлагаем читателю провести его само¬
стоятельно. ■
Докажем утверждение, которое бывает исключительно полезно
при определении верности различных неравенств.
Утверждение 5.5. Пусть выполнены следующие условия:
1) f(x), g(x) п раз дифференцируемы при х > х0;
2) /Щх0) = ^kKx0), k = 0,..., п - 1;
3) /(”)(х) < g<w)(x) при х > х0.
Тогда/(х) < g(x) при х > х0.
Доказательство
Предварительно докажем вспомогательное утверждение. А именно:
пусть функции fug дифференцируемы при х > X0 и выполнены условия
/(*о) = g(*o)’ /'(*) < &'(*)> X > х0; тогда /(х) < g(x) при х > х0.
Рассмотрим дополнительную функцию F(x) = g(x) - /(х). Для нее
получаем F'(x) > 0 при х > х0. Поэтому F(x) возрастает на этом множестве
и выполнено неравенство F(x)> F(X0) = O. Откуда незамедлительно сле¬
дует доказываемое неравенство.
Далее, так как (/^п~^(х))' < (g(n~0(x)) и /(n_1)(x0) = g(”_1)(x0), т0 п0 Д°-
казанному выше справедливо /(”_1)(x)<g(”_1)(x). Аналогично последова¬
тельно устанавливаем, что
/(п-2)(х) < g(»~2)(x),..., /'(х) < g'(x).
Откуда, так как /(x0) = g(x0), вытекает требуемое, т.е. /(x)<g(x) при
х > х0. ■
Отметим, что данное утверждение можно было доказать, используя
формулу Тейлора с остаточным членом в форме Лагранжа. Предлагаем
читателю провести данное доказательство самостоятельно. В качестве
самостоятельного упражнения предлагаем читателю, кроме того, доказать
следующее утверждение.
Задание 5.1
Пусть функции/ngдифференцируемы на (а; Ь\, атакже/(6) =g(b),f'(x) <g'(x).
Докажите, что тогда f(x) >g(x) на интервале (а; Ь).
В качестве применения приведенных утверждений рассмотрим анализ
некоторых неравенств.
Задача 5.2
Докажем следующие неравенства:
а)
i+i
У
<е<
и1-
\х+1
при х > 0;
V xJ V xJ
б) 1 + 21пх<х2 прих> 0;
в) х^>(х + 1)^ при х >9;
. tg*2 Xn л п
tgXj X1 2
268
Решение
а) Преобразуем исходные неравенства:
(л 1
1 + —
I xJ
\х
(
<е<
1
\х+1
1+—
X J
<=>
<=>Х-1п
1 - < In
1+-
X
X +1
1+—
X
\ (
<1<(х + 1)-1п
)
l"l 1
1+-
X
X
Преобразуем левую часть последнего неравенства:
1
I 1
1
Х + 1 X 1 + 1/х
. Сделаем под¬
становку t = —, получаем, что нам нужно доказать следующее неравенство:
х
—— < ln(l + £) < t.
I + t V '
Пусть, далее, \|/(£) =
t
1+7’
ф(0 = 1п(1 + 0- Имеем
V(O) = Ф(0), \|/'(0 = < ^rt = ф'(0-
Из утверждения 5.5 заключаем выполнение левого неравенства.
Для доказательства правого неравенства обозначим ф(£) = 1п(1 + £), \|/(£) = £.
Получаем ф(0) = \|/(0) = 0. Далее,
1
ф'(£) = < I = v'(0 ПРИ t > о.
Поэтому выполняется и правое неравенство.
На рис. 5.3 изображены функции, входящие в доказанное неравенство. Данный
рисунок можно воспринимать как геометрическую интерпретацию оного.
Рис. 53
б) Пусть \|/(х) = I + 2 Inx, ф(х) = х2. Рассмотрим отдельно следующие случаи.
2
1. х> 1. Имеем \|/(1) = ф(1) = 1, \|/'(х) = — <{х>1}<2-х = ф'(х) =>\|/(х)<ф(х).
х
I 1
2. 0 < х < 1. Сделаем подстановку — = t е (1; + «>). Получаем \|/(£) = 1-2 In t, ф(£) = —.
х t2
Далее,
269
2 2
\|/(1) = ср(1), Y(t) = ~~t<~~t3= Ф'(0 => v(0 < Ф(0 => < Ф(*)-
Заметим, что на этом интервале мы могли бы воспользоваться результатом зада¬
ния 5.1.
3. X= 1. Имеем \|/(1) = ф(1).
в) Преобразуем исходное неравенство:
> (х + 1)Л « «Лй-ln* > eJiln<*+l) „ > Ь(£+1)
VJf VJf + 1
1д х
Рассмотрим функцию ф(х) = —j=. Имеем
VJf
2 — Iti х
ф'(х) = J=- < 0 фф 2 < Injf фф е2 < х,
2хых
что выполнено при х > 9.
Поэтому функция ф(х) убывает, следовательно, + ^ ПрИ х>9.
\]х vx + 1
г) Преобразуем исходное неравенство:
tg X^ Xj X‘2 Xj
ts*x
Рассмотрим функцию ф(х) = ——. Имеем
х
X
2 tS*
л>{- cos х „ > О ФФ —^r- > Sm:t: ФФ х > sinx• cosjf ФФ 2jf > sin2jf.
ф'(*) =
X*
COS х COSJf
я
Последнее неравенство верно при О < Jf < —. Следовательно, ф'(^) > О, поэтому
tgjfo tg Jf1 я
0<дг1<Хп<—.
Xn Xj 2
Далее рассмотрим более сложные неравенства.
Задача 5.3
Докажем неравенство ях(1 - х) < sinraf < 4jf(l - х), О < х < 1.
Решение
Изобразим функции, входящие в различные части неравенства, на чертеже (рис. 5.4).
270
В силу симметричности функций предложенное неравенство достаточно дока-
f п
. Для таких значений х имеем
зать при х е
0;-
V 2;
sin их > их -
Tl3X3
~зГ
K3X3
,Z- 661 2
- > -I Tixz > при х < —, а — > — I > Tix - Tixz,
6 Tiz я2 2
что устанавливает левое неравенство.
Для доказательства правого неравенства рассмотрим функцию f(x) = 4х - 4х2 -
- sin лх. Для нее получаем
f'(x) = 4-8x-ncosnx; f"(x) = -8 + n2sinnx;
/(0) = 0; /ITl = O; /'(О) = 4-я; /'
v2y
'О
v2y
= 0;
/"(0) = -8<0; f'
= л2-8>0.
Следовательно, на интервале
' О
°’2 ,
V zJ
найдется точка х0, в которой вторая произ-
1
. 8
водная функции /обращается в нуль. Обозначим ее через лс0, л;0 = —arcsin—е
л
Kz
( л
°;2 •
V zJ
Г О
0;-
I 2
заключаем, что f"(x) < 0 при х < X0 и f"(x) > 0 при х > х0. Поэтому функция f'(x)
( I-
строго убывает на полуинтервале [0; ^0) и стРого возрастает на полуинтервале
В силу монотонности функции f"(x) (так как f(3\x) = n3 cos яг >0) при хе
х0’2
Имеем
/•// ч < 8 .8 ^
J (хо) = 4—arcsin--л cos
Tl
Tlz
. 8
arcsin—
Tlz
<0:
для некоторой точки л;*е(0;л;0) получаем f'(x*) = 0 и f'(x)> 0 при л:е[0;л:*),
C ф 1]
х*)— . Окончательно получаем, что функция /возрастает на[0;х*)
f\x) < 0 при х е
и убывает на
. 1
х ; —
. Вспоминая, что функция/принимает нулевые значения на кон-
( л \
откуда следует пра-
цах изучаемого отрезка, заключаем, что f(x) > 0 при х
вое неравенство.
0;-
2
V zJ
Задача 5.4
Докажем, что для любого х>0и любого п е N справедливо неравенство
Tl /V*
0<е*-Х4-<-(е*-1).
k=0 k\ п
Решение
Левая часть данного неравенства следует, например, из разложения Маклорена
функции ех.
Для доказательства правой части введем функцию
у Tl yk
Кх) = -ех-ех + ^—.
п а=о й!
271
X
Требуется доказать, что выполнено неравенство f(x) > — при х > 0. Для функ-
п
ции / получаем
у -L 1 Tl I yk
f\x) = ех-ех + Jj-, х>0;
п ьо k\
у _i_ О Ti 2 yk
/"(*) = - e% + E -TT, * > 0.
п k=o k\
C помощью метода математической индукции можно показать, что
;) - х + п ех - ех +1 = —е* +1 > 1, х > 0,
п п
откуда следует, что
/(0) = 0, /'(0) = -, /"(0) = -,...,/(-0(0) = -.
п п п
Поэтому согласно теореме Лагранжа
/(”-0 (х) - /(”-1) (0) = /<я) (¾ • х > {/(”) (л:) > 1} > х, 0 < £ < .
Tl — I Tl — 1
Следовательно, /(и_1)(х) > + х > . Аналогично имеем
п п
,/■„ . . и-2 n —1 _
/('1_2)(х)> 1 л:, х>0.
п п
Таким образом, получим неравенства
/'(х) = — +—х> —, дг>0, и /(х)>—.
п п п п
Задача 5.5
Пусть/: [0; 1] —» R — непрерывная функция. Докажем, что найдется подмноже¬
ство Xc [0; 1] мощности континуум, на котором функция / монотонна.
Решение
Выберем на отрезке [0; 1] произвольные точки а и b такие, что а<Ь и /(я) < f(Jb).
Если такие точки не найдутся, то это означает, что для всех а < b выполнено нера¬
венство f(a)>f(b), т.е. функция /не возрастает на [0; 1] и все доказано.
Далее, для любого у е [/(a); f(b)] определим ху как ху - sup{x е [я; Ь\ |/(х) = у}.
В силу непрерывности функции /получаем, что Jipcy) = у, т.е. ху — самое большое
число из отрезка [я; b] такое, что f(xy) = у. Поэтому для Yi> Y2 G[/(fl)l/(b)] из нера¬
венства Y1 < Y2 следует ху < Xy^, и выполнено f(xу ) = Yi < У2 = f(xy2)■ Таким образом,
отображение у—>ху взаимно однозначно, и так как множество {у} = [/(я); f(b)] имеет
мощность континуум, то и {ху} континуальное.
Построенное множество [ху \ у е [/(я); /(6)]} и есть искомое подмножество отрезка
[0; 1] мощности континуум, на котором функция / монотонна, так как для всех
Xyi < ху2 выполнено /(ху ) < /(х?2).
Вспомним далее задачу о существовании такой непрерывной функции /,
что для каждого у е [0; 1] уравнение/(х) = у имеет континуальное мно¬
жество решений. В гл. 3 нами была построена непрерывная кривая Пеано,
заданная на отрезке [0; 1] и обладающая этим свойством. Зададимся вопро¬
сом: существует ли такая монотонная функция? Сформулируем данный
вопрос в виде задачи.
272
Задача 5.6
Существует ли монотонная функция /: [0; 1] —» [0; 1] такая, что для каждого
у е [0; 1] уравнение /(х) = у имеет несчетное множество решений х?
Решение
Пусть функция/монотонна на отрезке [0; 1]. Для каждой точки у е [0; 1] множе¬
ство Ay = {х G [0; 1] I у = f(x)} представляет из себя (в зависимости от характера моно¬
тонности функции /) либо пустое множество, либо множество, состоящее из одной
точки, либо отрезок. В силу монотонности функции / множества Ay попарно не пере¬
секаются. Следовательно, множеств Ay, представляющих из себя отрезок, не более
чем счетное число (это может быть доказано выбором рациональной точки в каждом
из таких сегментов монотонности). Отсюда можно сделать вывод о том, что ответ
на поставленный вопрос — отрицательный. * 1 2 * 1 2Задача 5.7
Пусть для дважды дифференцируемой функции / выполнено Iim /(х) = 0,
X—»Хд +0
Hm /(х) = 0. Докажем, что на бесконечном интервале (лс0; + °°) имеется по меньшей
.Г—Н-оо
мере одна точка Ъ, такая, что /"(£) = 0.
Решение
Рассмотрим два случая.
1. Функция/принимает и положительные, и отрицательные значения. Так как
функция/непрерывна, то найдется точка q е (х0; + °о), для которой f(q) - 0. Используя
обобщение теоремы Ролля (для бесконечных интервалов, см. гл. 4), получим, что
3%le(x0;q) и е(<?; + °°) такие, что /'(Sll) = 0, /'(£2) = 0, откуда по теореме Ролля
получаем, что 3 £ е (^1; ^2), в которой /"(£) = 0.
2. Функция/знакопостоянна. Не ограничивая общности, считаем, что /(х)> 0
для х > х0. Так как Hm f(x) = Hm /(х) = 0, то по теореме Ролля получаем, что
X—^Xfl+0 X—»+оо
Bbe(х0; + °°), для которой f'(b) = 0.
Далее, так как f(b) > 0, то при х е (Ь; + °°) производная f'(x) не может быть всюду
неотрицательной, т.е. существует бесконечно много точек, в которых выполняется
/'(х) < 0. Ибо, если Bb* >Ь такое, что f'(b*)> 0, то на интервале (6*; + °°) найдется
точка Ъ** > Ь* такая, что f'(b**) < 0. Следовательно, в силу непрерывности f'(x) по тео¬
реме о прохождении непрерывной функции через любое промежуточное значение
найдется точка Ti е (Jb*\ Ь**), для которой /'(ц) = 0 (и все доказано).
Если же f'(x) < 0 при всех хе(Ь; + °°), тогда существует верхний предел
Hm f'(x) = у. Если у < 0, то f'(x) < — при 1>1*,ипо теореме Лагранжа получаем
х->+°° 2
/(*) - fix* ) = /'(£* )(*-**) => fix) < I (х - X* ) + f(x*).
Следовательно, функция / ограничена убывающей (так как Y < 0) при росте х
линейной функцией. Поэтому Hm f(x) = -со, что неверно.
Если же Hm f'(x) = 0, то возможны два случая: либо 3 Hm f'(x) = 0 и все дока-
зано в силу обобщенной теоремы Ролля, либо $ Hm /'(х) = 0. Тогда
X—>+°о
3 Hm /'(х)< Hm f'(x).
Х-М-оо Х->+о°
В этом случае для любого Д е [ Hm f'(x); Hm /'(х)] найдутся последовательно-
х—»+о° Х->+оо
сти Xrf и хп„, в которых f'(хп,) = f'(xn„) = А (докажите!). Остается воспользоваться
теоремой Ролля.
273
Замечание 5.2. Отметим, что было бы неверно утверждать, что для функ¬
ции /, удовлетворяющей условиям последней задачи, существует предел
sinx2
Iim Действительно, рассмотрим следующий пример: /(х) = .
х—>+°° X
Для этой функции выполнено Hm /(х) = 0, Hm /(х) = 0. Однако
х—>*о+о х~>+°°
/'(х) = 2 cos X2 =>^| Hm /'(х).
X2 X—>4-°°
Задача 5.8
Пусть функция/дважды дифференцируема на луче [я; +°°), причем /(я) = А > 0;
/'(а) < 0; f'ipc) < 0 при х > а. Докажем, что уравнение f(x) = 0 имеет единственный
корень на интервале (я; +«>).
Решение
По теореме Лагранжа найдется точка E1 е (а; х), для которой выполнено
А*) - /'(«) = /"(IX* - «) => А*) = А«) + /"(IX* - «)•
Отсюда, так как /'(а) < О, /"(О ^ 0, х - а > 0, получим, что /'(х) < /'(а) < 0 при всех
х > а.
Далее, по теореме Лагранжа найдется точка Ell е (а; х) такая, что
/(*) - /(«)=AIiX* - в) => /(*)=/(«)+AIiX* - «)■
Так как f(a)>0, /'(^1)</'(а)<0, х-я>0, то при
х0 >
/(а)
I/'(a) I
+ я выполнено
/(*о)<°-
Исходя из вышесказанного получаем, что для непрерывной на луче [я; + °°) функ¬
ции / выполнено /(я)>0 и найдется X0 > я такое, что /(х0)<0. Стало быть, суще¬
ствует точка се (я;х0), для которой /(с) = 0. Данный корень единственный в силу
того, что /'(х) < 0 при х > я и функция / монотонно убывает.
Задание 5.2
Пусть /(х) — действительнозначная функция. Обозначим через Im[/] множество
значений данной функции. Докажите или опровергните следующие утверждения:
а) если /(х) непрерывна и Im[/] = М, тогда /(х) монотонна;
б) если /(х) монотонна и Im[/] = R, тогда /(х) непрерывна;
в) если/(х) монотонна и непрерывна, тогда Im[/] = R.
Задание 5.3
Докажите, что функция:
а) /(х) = 1 - — + — - (1-1-х) -е~х строго положительна прих> 0;
( Л
- In 1 + — строго отрицательна при х > 0;
б) /(х) =
2х +1
в) /(х) = Infl + -
X
1+—
Xy
1
V
Vx2 +X
строго отрицательна при х > 0.
Задание 5.4
Докажите, что функция/(х) = logx(x+ 1),х> 1, строго убывает на интервале (1; +°°).
Проверьте, что выполнено неравенство log23 > Iog4S.
274
Задание 5.5
Сравните функции tg(sinx) и sin(tg^) для всех х е (0; п/2) (в качестве указания
к решению на рис. 5.5 приведены графики рассматриваемых функций).
5.2. Выпуклость функции и точки перегиба
Определение 5.4. Будем называть функцию /выпуклой вверх на множе¬
стве X1, если V хь х2 е XhV Oc1, ос2 > 0 таких, что Oc1 + ос2 = 1, выполнено
/(CC1X1 + CC2X2) > OC1Z(X1) + ос2/(х2). (5.1)
Определение 5.5. Будем называть функцию /(х) выпуклой вниз на мно¬
жестве X, если V X1, х2 G XhV Oc1, ос2 > 0 таких, что Oc1 + ос2 = 1, выполнено
/(Ot1X1 + Oc2X2) < Cc1Z(X1) + Oc2Z(X2)- (5.2)
В случаях, когда неравенство строгое (при строго положительных
OC1, ос2), говорят о строгой выпуклости функции.
Геометрическая интерпретация указанных неравенств заключается в сле¬
дующем. Фиксируем точки X1 и х2. Тогда числа OC1 и сс2 (а на самом деле одно
число, так как сс2 = I - CC1 определяется однозначно) задают точку на отрезке
[X1; х2]. Условие (5.2) означает, что значение функции в точке х = OC1X1 + сс2х2
не больше, чем соответствующее значение Oc1Z(X1) + Oc2Z(X2) на хорде (рис. 5.6).
Преобразуем неравенства (5.1) и (5.2) из определения выпуклости. Для
этого рассмотрим систему
1 Иногда вместо выпуклости вверх функции на множестве X говорят о ее вогнутости
на данном множестве.
275
X2 ЭС
[ (X1X1 + CL2X2
Ia1+а2 = 1
х,
а1 =
а2 =
X2-X1
X-X1
X^2 эс 1
Следовательно, неравенство для выпуклости вниз можно записать в виде
<у* /у /у*
/(X) < i^/(x,) + ^!-/(x2).
у — 'у* 'V' — 'V'
Л2 Л2
Отсюда при х2 > X1 имеем
(X2 - Xi)f(x) £ (X2 - х)Ахд + (X- Xjf(X2).
После домножения последнего неравенства на
1
(х2 — х)(х — X1)
зуя элементарное представление X2 - X1 = (х2 - х) + (х - X1), получаем
и исполь-
/(х) | /(х) ^ /(X1) [ /(х2)
Х__ /у* у __ у /у» __ у у __ /у*
Л,2 И/ «+ И/1) «/V
4
ИЛИ
/(х) - /(X1) ^ /(х2 ) - /(х) (53)
Х__ /у* /у. __ /у*
Д»| Jl2 «Д/
при X1 < х < X2 и произвольных X1, X2 G X. Отметим, что последнее неравен¬
ство является не чем иным, как другой формой записи определения выпук¬
лости функции / на множестве X
Предположим далее, что функция /: X —» M дифференцируема на мно¬
жестве X Поочередно устремляя в неравенстве (5.3) переменную х к X1
и к х2, получаем справедливость неравенства
276
/4%)</(X2)_/(Xl)</'(*2).
•)C 2
что устанавливает монотонность производной функции /.
Пользуясь теоремой Лагранжа, и учитывая, что для строго выпуклой
функции неравенство (5.3) строгое, заключаем, что
/'(X1) < /'(¾) = /(x)~/(Xl) < /(Ж2)~/(Х) = /'(¾) S /'(¾)
X-Xi X2-X
при Jr1 < ^1 < х < El2, т.е. строгая выпуклость влечет за собой строгую моно¬
тонность производной.
Подводя итог под вышесказанным, заключаем, что если дифференциру¬
емая функция /выпукла вниз на множестве X, то ее производная /' не убы¬
вает на данном множестве, а в случае строгой выпуклости вниз производ¬
ная /' возрастает на X.
Докажем, что это не только необходимое, но и достаточное условие
выпуклости дифференцируемой функции. В самом деле, для Xi < х < X2
по теореме Лагранжа получаем
/(X)-Z(Xi)
X-X1
/(*2 )-/(*)
X2-X
П% 2>>
где X1 < < х < ^2 < х2> и в случае /'(^)^/4¾) выполняется определе¬
ние выпуклости (5.3) (или определение строгой выпуклости, если /'(^1) <
<пш
Тем самым мы доказали следующую теорему.
Теорема 5.1 (критерий выпуклости). Пусть функция / дифференци¬
руема на множестве X. Тогда она выпукла вниз на этом множестве тогда
и только тогда, когда ее производная f' не убывает на этом множестве.
При этом строгое возрастание производной влечет строгую выпуклость
вниз функции /.
Следствие 5.1. Для того чтобы дважды дифференцируемая функция/:
X —> R была выпукла вниз, необходимо и достаточно, чтобы выполнялось
неравенство f'(x) > 0 на X. Если же справедливо /'(х) > 0, то функция /
строго выпукла вниз.
Проверку данного следствия оставляем читателю.
Далее мы снова обратимся к геометрической интерпретации поня¬
тия выпуклости. Условие выпуклости (5.3) геометрически означает, что
угловой коэффициент хорды, соединяющей точки (X1; /(X1)) и (х; /(х)),
не больше углового коэффициента, соединяющего точки (х; /(х)) и (х2;
/(X2)). Далее вспомним, что z/Kac = /(х0) + /'(х0)(х - х0) — уравнение каса¬
тельной в точке х0.
Теорема 5.2 (геометрическая интерпретация выпуклости). Если функ¬
ция / дифференцируема на множестве X, то для ее выпуклости вниз на этом
множестве необходимо и достаточно, чтобы все точки ее графика лежали
не ниже любой касательной в любой точке множества X. Если функция /
строго выпукла вниз, то все точки графика {за исключением точки касания)
лежат строго выше любой касательной.
277
Доказательство
Необходимость. Пусть функция/строго выпукла вниз. Рассмотрим раз¬
ность
/(*) - укас = fix) ~ /(X0 ) - /'(X0 )(х - X0 ).
По теореме Лагранжа /(х)-/(х0) = //£)(х-х0), где \ лежит между х
и х0. Тогда получаем //£)(х - X0 )-/'(х0 )(х-X0 ) = (//£)-//х0))(х-X0 ).
Теперь если х > х0, то и £ > х0, а ввиду выпуклости вниз //O-Zr(X0) > 0.
Если же х < х0, то и \ < х0, а значит, /'(O-ZZx0) < 0. В любом случае знак
/40-//½) совпадает со знаком х - х0, а значит, произведение неотрица¬
тельно, т.е. fix) - ушс > 0, что и требовалось доказать.
Достаточность. Снова рассмотрим неравенство
fix) ~ Укас = fix) - /(х0 ) - //х0 )(х - х0 ) > 0. (5.4)
Тогда получаем, что
/(х)-/(х0) ,,
— > / (х0),еели х > х0,
х-х0
fix)-fix0) г,, .
— u < / (х0), если х < х0
^ fixQ-fjxo) с /(X2)-Z(X0)
для V X1 < X0 < х2, причем строгое неравенство в формуле (5.4) влечет стро¬
гое неравенство в последнем соотношении, которое является не чем иным,
как определением выпуклости (5.3). ■
Замечание 53. Следует отметить, что функция /(х) = | х | выпукла вниз
на Ж. Однако все точки ее графика (кроме (0; 0)) лежат на касательной,
а в точке (0; 0) касательной не существует. Поэтому условие дифференци¬
руемости функции/является существенным.
Определение 5.6. Пусть функция/дифференцируема в некоторой про¬
колотой окрестности В'(х0). Если на множестве В'_(х0) = {х G В(х0) | х < X0}
данная функция выпукла вниз (или вверх), а на множестве В+(х0) =
= {х£ В(х0) I х > X0} выпукла вверх (или вниз), то точка (х0; /(х0)) графика
функции называется его точкой перегиба.
Например, функция /(х) = х3 имеет точку перегиба X0 = 0.
Замечание 5.4. Отметим, что дифференцируемость в точке X0 может
отсутствовать. Например, функция /(х) = у[х имеет в точке х = 0 точку
перегиба, но $ //0).
Теорема 5.3 (необходимое условие точки перегиба). Пусть функция
/ имеет точку перегиба в точке х0, a f' непрерывна в некоторой точке х0.
Тогда //х0) = 0.
Доказательство
Предположим, что /"(х0) > 0. Тогда из локального свойства сохранения
знака непрерывной в точке функции 3 В(х0 ) такая, что для Vxg В(х0 ) выпол¬
нено /"(х) > 0. Следовательно, точка X0 находится внутри интервала строгой
выпуклости и не является точкой перегиба, что противоречит условию. ■
278
Замечание 5.5. Отметим, что от условия непрерывности второй произ¬
водной в точке X0 можно отказаться, заменив его на существование второй
производной в данной точке. Доказательство при этом заметно усложня¬
ется, читатель может ознакомиться с ним в книге [27].
Теорема 5.4 (достаточное условие точки перегиба). Пусть функция
о
/ дифференцируема в точке х0, дважды дифференцируема в В8(х0). Тогда
если $ /"(X0) или /"(X0) = Ou, кроме того, /" меняет свой знак при переходе
через х0, то х0 — точка перегиба функции /.
Доказательство
о
Предположим, не теряя общности, что /"(х) > 0 при х G В_(х0) и/"(х) <
о
< 0 при х G 5+(х0). Этого достаточно для того, чтобы производная /' в дан¬
ных полуокрестностях была монотонная, но имела разный характер моно¬
тонности. Тогда в силу критерия выпуклости в точке (х0;/(х0)) произой¬
дет изменение направления выпуклости графика, т.е. данная точка будет
его точкой перегиба. ■
Следствие 5.2. Пусть/"(х0) = 0, а/'"(х0) Ф 0. Тогда (х0;/(х0)) — точка
перегиба.
Рассмотрим далее простую задачу, которая интересна тем, что исполь¬
зует результат из курса аналитической геометрии.
Задача 5.9
Покажем, что кривая у(х) =
х + 1
имеет три точки перегиба, лежащие на одной
X2 +1
прямой.
Решение
Вычислим производные данной функции:
. -X2 -2х + 1 ... . пх3+Зх2-Зх-1
У(Х)= (^ + 1)2 ■ У W = 2 (Х2 + 1)3 •
Решая уравнение у"(х) = 0, получаем
X3 + Зх2 -Зх-1 = (х- 1)(х + 2 + \1з)(х + 2-л/3) = 0.
Отсюда получаем три точки:
Jx1=I,
X2 =-2 + л/з,
-1+7з ■
\у1 — 1’
У2~ A(2-s[3)
Уз
-1-л/з
4(2+ -s/З)
Условие, при котором три точки плоскости лежат на одной прямой:
X2-X1 _ У2~У1
X2 X1 у2 у1
X3-X1 Уз~Ух
= 0, или
X3 -X1 Уз - у1
Имеем
х-
q /о” q /о” л/З-З -7з-з
-X1 = -3 + v3; х3 -X1 = -3-л/З; у2-у1=—-—; у3-у1 = .
Следовательно, условие (5.5) выполнено.
Изобразим график изученной кривой (рис. 5.7).
(5.5)
279
Рис. 5.7
-4
Утверждение 5.6 (неравенство Йенсена). Пусть/(х) — выпуклая вниз
на интервале (я; Ъ) функция. Для Vwg N, п > 2, V X1, х2,..., хп G (я; Ъ) и V Gi1,
П
OL2,..., On G [0; 1], 5}осА = 1, выполнено следующее неравенство:
A=I
S
VA=I у A=I
(5.6)
Для строго выпуклой вниз функции неравенство (5.6) является стро¬
гим, если числа X1, ..., хп не все одинаковы, а числа Oi1,..., On положительны.
Доказательство
Для W = 2 неравенство (5.6) совпадает с неравенством из определения
выпуклой вниз функции. База индукции доказана.
Предположим, что данное неравенство справедливо для любого набора
из w > 3 точек. Рассмотрим числа
[Xi,
хп, xn+i} с (я, b), (Oc1,..., оп, on+i) cz [0,1],
п+1
Soca=I.
A=I
Не ограничивая общности, будем считать, что оси+1 < 1.
гр £ OCaXa Д OCtW тт Д OCaXa ,
Тогда 2j———>2j ~— = я. Неравенство 2j— < о доказыва-
A=I 1— 0Си+1 А=11 — On+i А=11 — On+i
ется аналогично. Далее, по предположению индукции,
/
^я+1 N
у
!,Vk
= /
Va=i J
V
“и+А+1 + (1 - оси+1) S
A=I 1 — 0Си+1
Гп Vk Л
<an+1/(xn+1) + (l-an+1)/
Va=H-Oc ,
и Oti я+1
<aw+1/(xw+1) + (l-aw+1)X * /(¾)= SocA/(xA).
A=I 1 — 0Си+1 А=1
tW+! у
и+1
Согласно принципу математической индукции неравенство Йенсена
доказано. ■
Следствие 5.3. Функция /(х) = | х | выпукла вниз на M (докажите!).
Если положить в неравенстве Йенсена Oi = ... = On = 1/w, то мы момен¬
тально получим известное неравенство
П
1>А
A=I
^EkA
A=I
280
Следствие 5.4. Функция /(х) = Inx строго выпукла вверх на луче
(0; +°°) (докажите!). Поэтому из неравенства Йенсена для функции -/,
чисел Oc1 = Oc2 = ... = оси= 1/ии произвольных X1,..., хп E (0; +°°) получаем
^ п In
> - X Inxi ФФ - 2¾ > ГШ*А .
я *=1 я*=1 Va=I
Нами получено неравенство Коши между средними арифметическим
и геометрическим.
In
1 п
Задание 5.6
Докажите, что для V п > 2, V (X1,..., х„} с (0; +°°) и для V (OC1,
выполнено неравенство
f,akxk>f[xakk.
k=i Jfe=I
П
a»}<=[0;l],Z<x*=l,
k=\
Задание 5.7
Пусть p>l,q>\n\/p +1/^=1. Докажите, что для любых x,z/e (0; +°о) выполнено
неравенство Юнга
ху<
хР уЧ
р q'
Задание 5.8
Найдите интервалы выпуклости и точки перегиба функции:
2 I Л X = I +Ctgt,
а) /(*) = —^^ ;б)/(х) = ^-Д в)у = /(х), I cos2t 0<£<я.
(^-I)3 х/х у = ^-,
smt
Задание 5.9
Покажите, что:
а) функции х” (и > I), е* xlnx выпуклы вниз на (0; +«>);
б) функции хп (0 < п < I), Inx выпуклы вверх на (0; +°°).
Задание 5.10
Пусть функция/дважды непрерывно дифференцируема на отрезке [0; 1]. Докажите,
что ее можно представить в виде разности двух выпуклых вниз функций.
Утверждение 5.7. Пусть функция/ограничена и выпукла на интервале
(а; Ъ). Тогда данная функция всюду на этом отрезке непрерывна и имеет
производные слева и справа.
Доказательство
Не ограничивая общности, будем считать, что функция / выпукла вниз
на интервале (а; Ь), причем выполнено неравенство |/(x)|<Z, для всех
х е (а; Ь). Положим в неравенстве
/
Xi +... + х„
п
/(X1)+ ... + /(Xw)
п
xI = X2 =... = хт = х + пЬ, хт+ -... = хп=х, где х — произвольная точка из ин¬
тервала (а; Ь), т < п, а 181 настолько мало, что х + п8 E (а; Ь). Получаем
281
/
nx + mnb
V
п
= f(x + mb) <
mf(x + nb) + (n- m)f(x)
n
mf(x + nb) - mf{x)
n
+ fix),
или
fix + mb) ~ fjx) < f{pc + nb) - f{x)
m n
Из выпуклости вниз рассматриваемой функции получаем
/(x + mS) + /(x mb) > д ^ или/(х + mb) - f{x) > f{x) - fix - mb).
(5.7)
Домножая неравенство (5.7) на -1 и делая замену 5 на -5, устанавли¬
ваем справедливость соотношения
fix) - fjx -mb) > fix) - fix - nb)
m n
Суммируя вышесказанное, будем иметь
fix + nb) - fjx) > fjx + mb) - fjx) > fjx) - fjx - mb) > fjx) - fjx - nb)
n m m n
Положив, в частности, m = I, получим
> f{x + 8) - fix) > fix) - fix- 8) > M=L.
n n
Приближая 8 к нулю и увеличивая п с тем, однако, чтобы х ± nb лежало
на интервале (я; Ъ), получаем, что функция / непрерывна.
Рассмотрим, далее, 8 > 0 при фиксированном х. Получаем
fjx + 8) - fix) fix + S') - fix) s>5,>0
8 8' H
в силу выпуклости вниз. Следовательно, функция gib) =
fix+ S)-fix)
b
монотонно не убывает на промежутке 8е(0;8*) (8* достаточно мало). По¬
этому по теореме об односторонних пределах 3 Hm g(S) = inf g(8). Вы-
5-»0+0 (0;5*)
брав 8** > 0 (достаточно малое), заметим, что 3 gib**), при этом g(8) > gib**)
для всех 8 > 0. Поэтому функция g(8) ограничена снизу на интервале
(0; 8*), a inf g(8) конечен. Отсюда заключаем, что существует предел g(8)
(0; 8*)
при 8 —» 0 + 0, но это и есть /'(х + 0).
Существование левой производной f\x - 0) доказывается аналогично. ■
Задача 5.10
Пусть / — трижды непрерывно дифференцируемая на числовой прямой функ¬
ция. Докажем, что найдется такая точка что
т-туп^-гх^ о.
282
Решение
Если найдется точка а е R такая, что хотя бы одна из функций /, /', /" или /'"
обращается в нуль, то все доказано. Предположим противное. Пусть данные функ¬
ции сохраняют постоянный знак на всей числовой прямой. Пусть функция / зна¬
коопределенная, монотонная и сохраняет на R характер выпуклости. В этом случае
выполняется один из четырех случаев, изображенных на рис. 5.8.
Рис. 5.8
Таким образом, возможны четыре варианта соотношения знаков функции /и ее
производных:
1) /(х) > 0, /'(х) < 0, /"(х) > 0;
2) /(х) > 0, /'(х) > 0, /"(х) >0;
3) /(х)<0, /'(х) > 0, /"(х) <0;
4) /(х) < 0, /'(х) < 0, /"(х) <0.
Отметим, что соотношение знаков функции и ее производной однозначно опре¬
деляет знак второй производной.
Для того чтобы установить знак третьей производной, рассмотрим ту же задачу
для первой производной функции /. Для нее будут справедливы все те же самые усло¬
вия: функции /', (/')', (/')" знакоопределены и не обращаются в нуль, т.е. для них
выполняются те же самые варианты соотношения знаков, что и на рис. 5.8. Используя
это и однозначность определения знака второй производной, найдем знаки второй
производной функции /', т.е. третьей производной функции/. Имеем:
• /'(х)<0,(/'(х))'>0=»3)=»(/'(х))"<0;
• /'(х) > 0, (/'(X))' > 0 => 2) => (/'(X))" > 0;
• /'(х) > 0, (/'(х))' < 0 => 1) => (/'(х))" > 0;
• /'(х) < 0, (/'(X))' < 0 => 4) => (/'(X))" < 0.
Следовательно, каждому из данных четырех вариантов соответствует четное коли¬
чество положительных и отрицательных знаков, откуда исследуемое произведение
имеет знак больше нуля, что и требовалось показать.
Замечание 5.6. Можно было показать (покажите!), что, если функция/
трижды непрерывно дифференцируемая на числовой прямой, причем ни
она сама и ни одна из ее производных /', /", /'" не обращаются в нуль,
то реализуется только случай строгой положительности всех этих четырех
функций.
283
Задание 5.11
Пусть функция / выпукла вниз на отрезке [я; Ь\. Докажите, что односторонняя
производная /'(х+ 0), если рассматривать ее как функцию, заданную на (я; Ъ), непре¬
рывна слева, a f'(x - 0) непрерывна справа при всех х е (я; Ъ).
Задание 5.12
Пусть функция/выпукла вниз на отрезке [я; Ь\. Докажите, что f'(v - 0) < f'(v + 0) <
< f'(u - 0) < f'(u + 0) при всех v,u(a<v<u<b). Пользуясь этими неравенствами, по¬
кажите, что функция /дифференцируема в точке v (я <v <b) тогда и только тогда,
когда одна из функций f'(x + 0) или /'(х - 0) непрерывна в точке V.
Задание 5.13
Пусть функция /выпукла вниз на отрезке [я; Ь\. Докажите, что множества точек
непрерывности функций/'(.г - 0) и/'(х+0) совпадают. Выведите отсюда, что множе¬
ство точек, в которых функция/недифференцируема, не более чем счетно1.
Задание 5.14
Пусть функция / выпукла вниз и дважды дифференцируема при х > 0, причем
f(x)
Hm (х/'(х) - /(х)) < 0. Докажите, что тогда ф(х) = монотонно убывает при х > 0.
/(*)
X
Указание: Вычислите производные функций J 4 ' и х/'(х) - /(х).
х
5.3. Локальные экстремумы
Определение 5.7. Будем говорить, что функция у = f(x) имеет в точке X0
строгий локальный максимум (строгий локальный минимум), если найдется
такая окрестность точки х0, в пределах которой значение /(х0) является
наибольшим (наименьшим) среди всех значений /(х) этой функции, т.е.
о о
3 В(х0): для V х G В(х0) f(x) < f(x0)(f(x) > f(x0)).
Замечание 5.7. Аналогично вводятся понятия нестрогого локального
максимума и минимума. Для этого значение /(х0) является не меньшим
(не большим) среди всех значений /(х) этой функции в указанной окрест¬
ности.
Определение 5.8. Будем говорить, что функция у = /(х) имеет в точке
х0 локальный экстремум, если она имеет в указанной точке либо локальный
максимум, либо локальный минимум.
Приведем ряд теорем.
Теорема 5.5 (необходимое условие экстремума). Пусть х0 — точка
локального экстремума функции / и 3 /'(х0), тогда f'(xQ) = 0.
Теорема 5.6 (достаточное условие экстремума). Пусть 3 8 > 0 такое,
что f(x) непрерывна в B8(X0), 3 f'(x) при 0<|х-х0|<5, а в самой точке X0
производная f'(х0) равна нулю либо не существует. Тогда если /'(X1) /'(X2) <
< 0 для V X1, х2: х0 - 5 < X1 < х0 < х2 < х0 + 8, mo х0 — точка локального экс¬
тремума.
Теорема 5.7. Пусть 3 f'(x) при | х - х0 | < 8, /'(х0) = 0, f'(x0) < 0 (> 0),
тогда точка X0 — локальный максимум (минимум).
1 Пример функции с несчетным множеством точек недифференцируемости приведен
в конце данной главы.
284
Теорема 5.8 (достаточные условия локального экстремума в терминах
старших производных). Пусть 3 f'(x), /"(х), ..., /(и_1)(х) при | х - X0 | < 8
и выполнено f'(xQ) =f'(x0) = ... = /(и_1Дх0) = 0, /(”)(х0) Ф 0. Тогда:
• если п = 2k, то X0 является точкой локального экстремума;
• если п = 2k + 1, то х0 не является точкой локального экстремума
(точка перегиба).
Замечание 5.8. В случае нечетного п равенство нулю первой произво¬
дной /'(х0) не требуется для наличия перегиба.
Рассмотрим внимательнее теорему о достаточных условиях локаль¬
ного экстремума. Для начала зададимся вопросом: можно ли утверждать,
что если всюду дифференцируемая функция / в точке х = X0 имеет стро¬
гий максимум, то в некоторой достаточно малой окрестности этой точки
слева от точки X0 функция / возрастает, а справа от нее — убывает? Ответ
на этот вопрос — отрицательный. Действительно, рассмотрим следующий
пример:
/00 =
г
I-X2
2+ sin
. 1
V
х
, если х Ф 0,
1, если х = 0.
Так как 2 + sin — > 0, то /(0) = /тах = 1. Однако
х
/'00 = -2х
(
V
о • 1
2+ sin—
х
-X2 cos —
X^
X
О 1
= COS- + О(х).
X
2
Следовательно, для V 5 > 0
3 X1, х2: -8 < X1 < х2 < 0 и /'(X1) • /'(х2) < 0,
т.е. функция / не возрастает и не убывает в любой сколь угодно малой
окрестности точки х = 0 слева. Аналогично для правой окрестности точки
х=0. Рассмотренная функция приведена на рис. 5.9.
Замечание 5.9. Рассмотренный пример показывает, что достаточное
условие локального экстремума не является необходимым.
Далее изучим внимательнее теорему о достаточных условиях локаль¬
ного экстремума в терминах старших производных. Являются ли ее усло¬
вия необходимыми? Ответ на этот вопрос — также отрицательный. Рас¬
смотрим следующую функцию:
е-1/х2; если хф 0,
-
О, если х = 0.
Так как выполнено неравенство е-1/* > 0 = /(0), то точка х = 0 — стро¬
гий локальный минимум рассматриваемой функции. Посчитаем производ¬
ные функции / в нуле по определению. Мы уже изучали данную функцию
в гл. 3 и 4. Там было показано, что ее производные любого порядка пред¬
ставляют собой произведение функции е~х/х и различных рациональных
дробей. Поэтому мы сделали вывод о том, что производные данной функ-
285
ции в нуле равны нулю. Достаточные условия локального экстремума
для данной функции не выполнены. Функция -2 обладает тем же
свойством, но имеет в нуле строгий максимум.
В связи с этим примером интересно рассмотреть пример функции,
не имеющей в нуле локального экстремума, все производные которой
в нуле обращаются в нуль. Для этого модифицируем только что изучен¬
ную функцию. Пусть
, ч Xe-iZx2 если х Ф О,
&(*) = 1
О, если х = 0.
Для данной функции получаем g(x) < 0 = g(0) при всех х < 0, g(x) > 0 =
= g(0) при всех х > 0. Поэтому в точке х = 0 локального экстремума у дан¬
ной функции нет. Равенство нулю всех ее производных в нуле доказыва¬
ется аналогично функции /.
Далее рассмотрим вопрос о числе локальных экстремумов у действи¬
тельнозначной функции. Легко можно построить пример функции, имею¬
щей счетное число точек строгого локального экстремума, например
. 1
sin—, если х
х
*■ о,
0, если х = 0.
Зададимся вопросом: может ли функция /: R —» R иметь более чем
счетное число точек строгого локального экстремума? Ответ на этот
вопрос — отрицательный. Покажем, например, что количество точек стро¬
гого локального минимума не более чем счетно (доказательство не более
чем счетности числа точек строгого локального максимума аналогично).
286
Действительно, для любой точки строгого локального минимума найдется
такое число 8 > 0, что /(х0) — минимальное значение функции / на интер-
1
вале (х0 - 8, х0 + 8). Рассмотрим последовательность Sn = —. Для задан-
п
ного п рассмотрим те точки строгого локального экстремума, для которых
S(X)1 > 8П. Обозначим множество таких точек локального минимума через
1
Sn. Если х' E Sw то в —окрестности точки х' нет других точек из Sw Каждой
п
, с 1
точке х из Sn ставим в соответствии рациональное число из окрест-
2 п
ности. Следовательно, Sn — не более чем счетное множество. Множество
оо
локальных минимумов S= IJi1n не более чем счетно.
я=1
Далее в этой главе нами будет построен пример всюду непрерывной,
но нигде не дифференцируемой функции, множество точек строгого
локального экстремума которой плотно на области определения данной
функции. Для такой функции, очевидно, нельзя построить окрестность,
содержащую только один ее экстремум.
Задача 5.11
Докажем, что при х е (0; -н») выполняется ех > хе.
Решение
Заметим, что требуемое неравенство эквивалентно неравенству е^е > X1Zx для
V х>0.
Рассмотрим вспомогательную функцию у = XiZx. Для нее имеем
у'(х) = X1Zx
f
V
I-Inx
\
)
= О <=> х = е.
Отсюда получаем, что утах = у(е) = exZe, что и доказывает требуемое неравенство.
Замечание 5.10. Положив в доказанном неравенстве х = п, получаем
известное неравенство ел > пе (знак строгий, так как п Ф е).
Задача 5.12
Пусть п E Nna1, а2, ..., ап — положительные действительные числа. Докажем,
что выполнено неравенство
1 и \
-%ake ak <-.
я A=I е
Решение
Рассмотрим вспомогательную функцию у(х) - х ■ е~х, х E [0; + °°). Получаем
у'(х) = е~х (1-х) = О,
или х = 1, откуда г/тах = е~\ Следовательно,
п « 1 п л
Y,ake ak < или — 5^аке ak <
A=i е пк=1 е
1 Через 5(х) обозначено 5, найденное для данной точки х.
287
Задание 5.15
Для ие М,и аь а2,..., ап е (0; -н») докажите, что выполняются неравенства:
1 я д п (Q
а) -IjaIe 4 ^-г;б)ГК -
я*=1
ы
Л”
ехр
Vе/
^ -I п \
\jjak
Jk=I
Указание. Рассмотрите функции: для а) у(х) - х2е х; для б) у(х) - хе х/з.
Задача 5.13
Для каждого действительного а определим число действительных корней урав¬
нения ах = Inx.
Решение
\-Q_X
Рассмотрим функцию у(х) = . Для нее получим
У\х)
I-Inx
= 0,
что эквивалентно X = е.
Поэтому Vttihy = у(е) = е~\ Далее имеем Hm у(х) = Hm у(х) = 0. Следовательно,
х—>0+0 х—>+<*>
ггриае(-оо;0]и
у рассматриваемого уравнения только один корень, при а
г
0;
V
Г
1
два корня, при а > — корней нет.
е
Задание 5.16
Для каждого действительного а определите число действительных корней урав¬
нений: a)X3 + Зх2-ах+ 5 = 0; б)х3Inx-х + а = 0.
Задача 5.14 * 1 * 1Построим функцию, точки строгих максимумов и минимумов которой находятся
в любом интервале числовой оси.
Решение
Рассмотрим функцию Римана
R(x) =
1 Tfl
—, если X = —, НОД(т, п) = I, т е Z, п е N,
п п
0, если х — иррациональное число,
изучение непрерывности которой было проведено нами в гл. 3. Покажем, что она
имеет строгие максимумы в любой рациональной точке. Действительно, пусть
Wn „ Mo ^ т,
X0 = —^- е К, где —- — несократимая дробь. В достаточно малой окрестности данной
Щ W0
точки радиуса — могут находиться (за исключением х0) только рациональные числа,
H0
представимые в виде несократимых дробей вида —, где п > % Поэтому — > —. В ирра-
п H0 п
циональных точках функция R(x) обращается в нуль. Получаем, что в данной окрест¬
ности для всех х#0 выполняется R(x0)>R(x). Остается заметить, что рациональ¬
ные числа находятся в любой окрестности любого числа действительной прямой.
Для того чтобы получить функцию, имеющую строгие максимумы и минимумы
в каждом интервале числовой оси, достаточно модифицировать функцию Римана
следующим образом:
288
R(x) =
(-1)” m
-——, если X = —, НОД(пг, п) = I, т е Z, п е N,
п п
О, если х — иррациональное число.
Изобразим изученную функцию на отрезке [0; 1] (рис. 5.10).
Задача 5.15
Предположим, что функция / непрерывна на числовой прямой M и ни на одном
интервале не является монотонной. Докажем, что на любом интервале имеются точки
минимума и максимума функции /.
Решение
Рассмотрим произвольный интервал (х0 - а; X0 + а) с К, содержащий точку х0.
По условию задачи функция /не является монотонно возрастающей на (х0 -а;х0)
и монотонно убывающей на (х0; X0 + а). Поэтому найдутся числа X0- a <p<q< X0
nx0<r<s<x0+a такие, что выполнены неравенства
(5.8)
По теореме Вейерштрасса на отрезке [р; s] функция / достигает своей нижней
грани, и этой точкой локального минимума в связи с неравенствами (5.8) не могут
быть точки р и s. Следовательно, на интервале (р; s) с (х0 - а; X0 + а) имеется точка
минимума функции /.
Аналогично доказывается существование на произвольном интервале точек
локального максимума.
Замечание 5.11. Примеры функций, удовлетворяющих условиям рас¬
смотренной задачи, будут рассмотрены нами далее.
Задача 5.16
Найдем наименьшее значение функции
I 1
Sinx+ COSX+ X+ х + H ,
Cosx sin х
xeR.
Решение
I 1
Преобразуем функцию /(х) = sin х + cos x + x + x-i 1 в вид
cosx sinx
289
f(x) = sin x + cos x + -
SHlX + COS X
=л
cos
Sin X COS X Sin X COS X
fjL '
— X
4
1+V2
cos
+ 2--
71
-X
у _
cos
71
-2x
=Ji
cos
r„ л
Tl
— X
4
1+V2
cos
+ 2-
71
-X
У
Далее, обозначая Л cos
2cos'
V
TI
Л
cos
-x
C- ^
Tl
— X
4
V2c
71
Л
-X
-I
У
-I ' cos
V4 У
Л
через и, приводим задачу нахождения мини-
71
— X
4
мума модуля исходной функции к задаче нахождения минимума модуля функции
2
F (и) = и + на отрезке [~Л\ J]:
и-1
F'(и) = 0 <=> и = I ± J;
Р(±Л) = 2±зЛ, Р(1±Л) = 1±2Л,
откуда
min |/(х)| = min \F(u)\ = 2Л -I.
R R
Иногда найти минимальное и максимальное значения даже не очень
простых функций удается при помощи элементарных алгебраических пре¬
образований. В качестве примера этого рассмотрим следующую задачу.
Задача 5.17
Найдем на луче х > 0 минимальное значение функции
(х + 1/х)6-(х6 + 1/х6)-2
(х +1 /х)3 + (х3 * + 1/х3 * )
Решение
Производя требуемые преобразования, получаем
(х + 1/х)6 -(х6 + 1/х6)-2 _ [(х + 1/х)3]2 -(х3 - 1/х3)2
(х + 1/х)3 +(х3 +1/х3) (х + 1/х)3 +(х3 +1/х3)
= (х + 1/х)3 -(х3 + 1/х3) = 3(х + 1/х)>6.
Задача 5.18
Пусть а1; а2, ..., ап — различные действительные числа. Определим наименьшее
на M значение функции
П
/(х)=£|х-аА|.
ы
Решение
Не ограничивая общности, будем считать, что выполнены неравенства
^ #2 ^ ••• ^ ^п‘
Вычисляя производную функции /на множестве !£/{(¾,¾,-,¾} и приравнивая
ее к нулю, получаем, что
290
п п
Задание 5.17
Пусть PJx) =х2 + q. Найдите min sup | PJx) |, т.е. при каком выборе параметра q
<? —1<дг<1
многочлен Pq(J) наименее отклоняется от нуля на отрезке [—1; 1]. В качестве указания
предлагаем рассмотреть чертежи, представленные на рис. 5.11.
Задание 5.18
Найдите нижнюю (inf) и верхнюю (sup) грани следующих функций:
а) /(*) =
C -2 хп\
X
I + X H Ь... H
2!
и!
е х на интервале (0; + °°);
б) f(x) = е~х2 cos X2 на интервале (-°°; + °°).
5.4. Асимптоты графика функции
Определение 5.9. Прямая х = х0 называется вертикальной асимпто¬
той графика функции у = f(x), если выполнено хотя бы одно из условий:
Hm f(x) = ±°° или Hm f(x) = ±°°.
х——0 ж—>*q+0
Определение 5.10. Прямая у = kx+b называется наклонной асимптотой
графика функции у = fix) при х —> ±°°, если Hm (/(х) - {he + b)) = 0.
х—>±°°
Замечание 5.12. Из определения наклонной асимптоты при х —> ±°° сле¬
дует, что
k = Hm f(x\ Ъ = Hm (f{x)-kx).
X—>±оо X X—^±°°
Определение 5.11. Если k = 0, то асимптота у = b называется горизон¬
тальной.
Рассмотрим несколько примеров нахождения асимптот графиков функций.
291
Задача 5.19
Найдем наклонные асимптоты графика функции /(х) при х —> +°°, если
,, . л/2лг4 +х-1
Kx) = : •
х-1
Решение
Для выделения главной части иррациональной функции воспользуемся форму¬
лой Тейлора при х —> °°:
-у/2лг4 + х-1 rz [. 1 1
= iV2Jl+—+—•
х-1
= W2
1 + 0
г
Kx JJ
1 + —+ 0
X
2х3 2х4
О ^
fi-i
^ X
-1
/
Kx JyI
— х42 + 42 + о(1)
при х —> +°°. Отсюда заключаем, что хл[2 + 42 — наклонная асимптота графика функ¬
ции / при х —> -н».
Задание 5.19
Найдите наклонные асимптоты графика функции fix) при х —> +°°:
. г, ч 2х2 + Зх-2 r, . 4Xi + Зх-1
a) f(x) = ;б)/(х) =
х-1
х-4
При исследовании асимптот иррациональных, трансцендентных функ¬
ций, а также функций, аналитическое выражение которых содержит
модуль, необходимо рассматривать два случая: х —» +°° и х —> -°°. Рассмо¬
трим это на примере.
Задача 5.20
Найдем наклонные асимптоты графика функции /(х) = х + 44х2 + х при х —» +°°
их—> -°°.
Решение
Преобразуем исследуемую функцию:
fix) = х + 4^x2 +х = х + 21 х L /1 + — = х + 2
V 4х
х
1 + - + 0(1)
8х
Отсюда при х —» +оо получаем асимптоту Зх +
J.
4’
1
а при х —» -оо имеем -х —.
4
Задание 5.20
Найдите наклонные асимптоты графика функции/(х) прих —» +°° их—> -°°:
a) /(x) = Vx2 -6х + 14; б) /(х) = л/4х2 - х + 2.
Изучим далее вопросы, связанные со взаимным расположением графика
функции и его асимптоты. Сначала рассмотрим следующее утверждение.
Утверждение 5.8. Предположим, что функция у = /(х) имеет наклон¬
ную асимптоту (при х —> ±°°) и /"(х) > О для всех х. Тогда график данной
функции приближается к этой асимптоте сверху.
292
Доказательство
Предположим, что уравнение асимптоты при х—»+°° (асимптота при
х —> -о=» рассматривается аналогично) имеет вид у = kx + b, тогда из условия
наличия наклонной асимптоты следует существование следующих пределов:
Iim = k, Iim (/(х) - kx) = b.
х—>+°° X х—>+°°
Рассмотрим функцию g(x) = f(x) -kx-b. Тогда Hm g(x) = О и g"(x) =
х->+°°
= f"(x)>0.
Докажем, что функция g не возрастает. Предположим обратное, т.е. пусть
найдется точка X0 такая, что g'(x0) = с > 0. Так как g"(x) > 0, то при х > х0
выполнено неравенство g'(x)>g'(x0) = c. Применяя теорему Лагранжа
на отрезке [х0; х], получаем g(x) > g(xQ) + с(х - х0) при х > х0, что, очевидно,
противоречит условию Iim g(x) = 0. Следовательно, g'(x) < О и функция g
ЗГ—»+°°
не возрастает.
Остается доказать, что для всех х выполняется g(x) > 0. Опять пред¬
положим обратное, т.е. пусть найдется X1 такое, что g(xi) = d< 0. Так как
g'(x) < 0, то при х > X1 выполнено g(x) < g(x^ = d< 0, что невозможно, так
как Hm g(x) = 0.
X—»+°°
Если же найдется точка X2 такая, что g(x2) = 0, то выполнено g(x) = 0
при х > х2, откуда /(х) = kx + b и /"(х) = 0, что противоречит условию. Сле¬
довательно, для всех х получаем g(x) > 0, т.е. /(х) >kx + b, что доказывает:
график данной функции приближается к этой асимптоте сверху. ■
Замечание 5.13. Аналогично можно доказать, что если f'(x) < 0, то гра¬
фик функции приближается к этой асимптоте снизу.
Следствие 5.5. Между расположением графика функции относительно
его асимптоты и характером его выпуклости имеется следующая взаимо¬
связь (рис. 5.12):
1) если функция у = /(х) имеет асимптоту при х —> +°°, дифференциру¬
ема и строго выпукла вниз на луче х > х0, то график функции лежит выше
асимптоты;
2) если функция у = /(х) имеет асимптоту при х —> +°°, дифференциру¬
ема и строго выпукла вверх на луче х > х0, то график функции лежит ниже
асимптоты;
3) могут быть другие случаи поведения графика функции при стремле¬
нии к асимптоте. Например, возможно, что график функции бесконечное
число раз пересекает асимптоту.
Задача 5.21
Определим взаимное расположение графика функции f(x) = ^Jx3 + 6х2 -2х + 14
и его асимптот.
Решение
Выделяя под корнем кубическим полный куб, получаем
X3 + 6х2 - 2х +14 = (х + 2)3 - 14х + 6.
293
Отсюда заключаем, что асимптотой графика функции/является прямая у = * + 2.
Рассматривая разность функции / и ее асимптоты, получаем
fix)-(ос + 2) = -14* + 6
^(* + 2)3-14* + 6 + (* + 2)¾*+ 2)3-14*+ 6 + (* + 2)2 ’
3 3
что больше нуля при * < — и меньше нуля при * > у. Поэтому при * —» +°° график
функции лежит ниже асимптоты, а при * —»-°° — выше нее.
Pz/c. 5.72
Задание 5.21
Определите взаимное расположение графика функции /и его асимптот:
а) f(x) = б) /(*) = V*2 — 6* + 14.
*-1
5.5. Разные задачи
Рассмотрим еще несколько задач на исследование функций.
Задача 5.22
Может ли график непрерывной функции/: M —> M пересекать каждую вертикаль¬
ную (не вертикальную) прямую бесконечное число раз?
294
Решение
Вертикальную прямую бесконечное число раз действительнозначная функция,
безусловно, пересекать не может, так как это противоречило бы определению одно¬
значной функции у = f(x). Каждую не вертикальную прямую бесконечное число раз
пересекает, например, функция f(x) = х2 sin х.
Задача 5.23
Построим график функции у - ln(x + ln(x + 1п(.г + ...))), х > 1.
Решение
При любом фиксированном х > 1 рассмотрим последовательность1:
хп = 1п(л; + 1п(х + 1п(* +...))).
п раз
Заметим, что данная последовательность не убывает. Докажем, что хп < х. Имеем
X1 <х. Пусть хп < X1 тогда
хп+1 = 1п(* + хп) <\п2х<\пх + 1<х.
Следовательно, для любого х > 1 последовательность хп имеет конечный предел
Hm Xn = у{х). Функция у = у(х) удовлетворяет уравнению у = \п(у + х). Решая это
уравнение относительно х, получаем
х = еУ -у, у >0.
Замечаем, что искомая функция у(х) является обратной для функции у_1(х) = ех - х.
Поэтому для построения требуемого графика нужно изобразить график этой функ¬
ции и отразить его относительно прямой у = х (рис. 5.13).
Задание 5.22
Проведите исследование и постройте график функции
X
f(x) = \smt2dt,
о
1 Вообще говоря, хп - хп(рс).
295
Задание 5.23
Нарисуйте график функции y(t), удовлетворяющей дифференциальному тожде¬
ству у '(0 = I + sin2(г/(0). t > 0, и начальному условию у(0) = 0.
Построим пример всюду непрерывной, но нигде не дифференцируемой
функции1.
Построим вспомогательную функцию у = f(x) на отрезке [0; 1] по шагам.
На нулевом шаге зададим две точки: (X1, /(X1)) = (0; 0) и (х2, /(х2)) = (I; 1).
Далее зафиксируем параметр (коэффициент) k = 2/3. На первом и после¬
дующем шагах будем задавать точки по следующему правилу: для каждых
двух соседних по оси абсцисс ранее построенных точек A1 и A2 мы будем
строить две новые точки S1H^2 центрально-симметрично относительно
центра прямоугольника, задаваемого точками A1 и A2 с коэффициентом k.
Таким образом, на первом шаге задаются две новые точки (рис. 5.14):
(х3,7(х3))= и(х4,Дх4))= и т.д.
J 2"
rI г
J5 з,
и(х4,/(х4)) =
J;3,
1
8/9
7/9
2/3
1/3
2/9
1/9
0 1/9 2/9 1/3 2/3 7/9 8/9 1
Рис. 5.14
На (т + 1)-м шаге в дополнение к ранее построенным точкам с абсциссами
х = —,1=0,..., Зт,
3 т’ ’ ’ ’
строятся по две точки во всех промежутках по оси абсцисс между сосед¬
ними уже построенными точками. Это построение выполняется так: про¬
1 Данный пример позаимствован авторами из статьи: Шибинский В. М. Фрактал и построе¬
ние всюду непрерывной, но нигде не дифференцируемой функции // XVI международные
Ломоносовские чтения : сб. научных трудов. Архангельск : Поморский госуниверситет, 2004.
С. 266-273.
296
межутки по оси абсцисс между соседними точками (прямоугольники со
сторонами а и Ь) делятся на три равные части каждый. Затем две новые
точки строятся по одной из схем, приведенных на рис. 5.15.
A2 A1
A1 а/3 2а/3 а а/ 3 2а/3 а
Рис. 5.15
В зависимости от того, какая из соседних точек — A1 или A2 выше,
используем левую или правую схему. На первом шаге, как это было пока¬
зано выше, принимаем а = b = 1.
Повторяем построение счетное число раз при т= 1, 2,3,.... В результате
нами будет получен фрактал, который подобен с точностью до некоторого
аффинного преобразования (растяжение, сжатие, поворот) любой своей
части, заключенной в каждой полосе:
— <х<—, т = 0,1,2,...; / = 0,1,...,3^-1.
3т 3?и ’ ’ ’ ’ ’ ’ ’ ’
Построим иллюстрации точек фрактала на шагах 2 и 3 (рис. 5.16).
В результате построения фрактала получим функцию /(х), определен¬
ную на множестве точек
х = т = 0,1,2, 0,1,..., Зт,
(5.9)
которое всюду плотно на отрезке [0; 1].
297
Данная функция имеет в каждой точке вида (5.9) либо строгий максимум,
либо строгий минимум (докажите!), т.е. функция /(х) нигде не монотонна
и имеет плотные на отрезке [0; 1] множества точек строгих экстремумов.
Докажем, что построенная функция /(х) непрерывна на множестве
точек (5.9). Действительно, расстояния по оси абсцисс между соседними
точками, построенными на шаге т, равны между собой и составляют 1 /Зт.
По оси ординат расстояния между соседними точками разные, но макси¬
мальное из них представляет собой число km, ибо на каждом шаге, начиная
с первого, расстояния по оси ординат между полученными по приведен¬
ной схеме соседними точками (между новыми и между старыми и новыми)
меньше или равно kb (между новыми меньше, между старыми и новыми
равно), где Ь — расстояние по оси ординат между соседними точками,
построенными на предыдущем шаге (см. схему построения). При этом
на первом шаге b = 1.
Таким образом, при стремлении расстояния между точками на оси
абсцисс к нулю (при т —> °°) расстояние между ними по оси ординат
также стремится к нулю. Поэтому функция у = /(х) является непрерыв¬
ной и даже равномерно непрерывной на множестве точек (5.9) (докажите!).
Так как множество точек (5.9) всюду плотно на отрезке [0; 1], то опреде¬
ленная и непрерывная на нем функция /(х) доопределяется по непрерывно¬
сти (предельным переходом) до непрерывной на всем отрезке [0,1] функции.
Обозначим ее через у =/(х). Можно показать (например, от противного), что
и доопределенная функция имеет в каждой точке вида (5.9) строгий макси¬
мум или минимум, она нигде не монотонна и ее множества точек строгих
минимумов и максимумов плотны на отрезке [0; I]1 (докажите!).
Докажем далее, что построенная непрерывная на отрезке [0; 1] функция
у = /(х) не имеет ни в одной точке данного отрезка даже односторонних
производных.
Пусть точка х0 лежит на отрезке [0; 1]. Сначала рассмотрим случай, когда
х0 представляет из себя точку вида (5.9). Не ограничивая общности, счи¬
таем, что в данной точке достигается строгий локальный минимум функции
/. Зафиксируем произвольное в > 0 и рассмотрим правую е-полуокрестность
(х0; х0 + в) точки х0. Так как процесс построения фрактала производится
за неограниченное число шагов, то для выбранного в существует такое
достаточно большое п, что в [х0; X0 + в) попадут четыре подряд идущие точки
вида —, / = 0, 1,..., 3й, включая саму точку х0. Обозначим их абсциссы через
3й
X1, х2, х3. На рис. 5.17 изображена иллюстрация рассматриваемой полу¬
окрестности (система координат смещена вдоль оси ординат).
Отношение приращения функции к приращению аргумента — для
Дх
точек X1 = х0 + 1/3” и х2 = х0 + 2/3” будет равно соответственно
г _ /(*1) - Д*о) г _ /(*2 ) - Д*о)
rI - > '2 -
/у _ /у /у _ /у
1 Здесь читателю полезно вспомнить задачу о количестве точек строгих экстремумов.
298
По построению функции / имеем
/(*i
п=-
1/3*
1/3”
( I л”-1
уЗу
1/3”
= 2,
= 2-
f (X2)-I(X0) b'{ 1-k)
= 4,
где Ь' — высота изучаемого прямоугольника, откуда получаем, что r2 =-4-,
3 3
следовательно, ri-r2>—rl>—.
Так как в любой правой е-полуокрестности точки х0 мы получаем два
отличающиеся не менее чем на 1,5 значения для разностного отношения
—, то предела Hm — в точке X0 не существует. Рассмотрение слу-
Ax Ах—>0+0 Ax
чая левой полуокрестности и доказательство несуществования предела
Iim мы оставляем читателю (для граничных точек отрезка [0; 1]
Ах—>0-0 Ax
рассматривается только одна из двух полуокрестностей). Таким образом,
функция / не имеет ни в одной точке вида (5.9) даже односторонних про¬
изводных.
Пусть теперь х0 — произвольная точка отрезка [0; 1] кроме точек вида
(5.9). Рассмотрим произвольную окрестность (х0 - е; X0 + е) данной точки.
По выбранному е > 0 найдем номер п такой, что в эту окрестность попадут
не менее 10 подряд следующих точек вида —, / = 0, 1,..., 3”.
3”
Изобразим рассматриваемую в-окрестность на рис. 5.18. Обозначим
через X1 и X2 абсциссы второй и пятой точек (точки 4 и 2 на рисунке) из иду-
299
щих от точки X0 слева направо. Не ограничивая общности, будем считать,
что самая левая точка из рассматриваемой окрестности является точкой
максимума. Точка графика (х0; /(х0)) может располагаться только в откры¬
том прямоугольнике, заданном точками 5 и 6 (на рис. 5.18 закрашен).
Используя то, что шаг разбиения на п-ш шаге равен , получаем
1 2
при переходе от точки х0 к X1 приращение аргумента — < Ax1 < —. Учи-
3й 3й
тывая расположение точек в рассматриваемой окрестности и точки 4,
заключаем, что приращение Azz1 > т.е. —^">0. Аналогично получаем,
Ax1
4 Л 5
при переходе от точки X0 к точке X2 приращение аргумента — < Ax2 < —,
3й 3й
а приращение функции Ay2 > 0, т.е. < 0.
Ax2
Учитывая предложенную схему построения точек фрактала (см. рис. 5.15),
g
делаем вывод о том, что справедливо равенство IAgz1 | + |Ду2| = 2 * |^2 I •
3”
Рассмотрим разность
AjZ1 Agz2.
Ax1 Ax2
Azz1
Azz2 _
[Ай >o> <о1-
AzZi
+
Azz2
Ax1
Ax2
[Ax1 Ax1 J
Ax1
Ax2
>{ДГ2>ДГ1>о}>Ы^1>4=|.
з«
300
Так как в произвольной правой полуокрестности точки х0 для разностного
отношения — были найдены два отличающихся более чем на ^ значения, то
Ax 5
делаем вывод о том, что предела Iim — в точке X0 не существует. Анало-
Ax->0+0 Ar
гичные рассуждения справедливы и для левой полуокрестности точки х0.
Таким образом, построенная непрерывная функция у = fix) не имеет ни
в одной точке отрезка [0; 1] даже односторонних производных.
Подводя итог под вышесказанным, можно сделать следующие выводы.
Закладывая на начальных шагах построения фрактала (макроуровне)
некоторые свойства, мы получаем благодаря самоподобию фрактала их
выполнение в любой сколь угодно малой окрестности при предельном
переходе (микроуровне). В последнем примере в схеме построения двух
новых точек графика функции по двум соседним, ранее построенным,
на микроуровне закладываются пропорциональное уменьшение при¬
ращения функции при уменьшении приращения ее аргумента и зигза¬
гообразное изменение функции в пределах любой окрестности, любой
точки отрезка [0; 1]. Эти свойства выражаются на микроуровне во всюду
непрерывности и нигде не дифференцируемости функции / соответ¬
ственно.
В заключение приведем изображение изученного фрактала (рис. 5.19).
При его построении было проведено 15 шагов.
В дальнейшем нами будут изучены другие примеры функций, обладаю¬
щих теми же свойствами, что и эта, но использующие другой математиче¬
ский аппарат — равномерно сходящиеся функциональные ряды.
В рассмотренном примере мы полагали параметр k равным 2/3. Изменяя
значение данного параметра, можно получить семейства функций со сво¬
301
ими особыми свойствами. Далее мы только обозначаем данные свойства,
а их доказательства предоставляем читателю. После перечисления отме¬
ченных свойств мы приводим иллюстрацию графика с фиксированным
значением параметра k, построенного по выполнении 15 шагов. После всех
последующих шагов получается график, визуально неотличимый от при¬
веденного при таком масштабе.
I. О < k < 1/3. Эти функции непрерывны и строго монотонно возрас¬
тающие. Имеют нулевые и бесконечные производные (соответственно,
точки перегиба) на множествах точек, всюду плотных на отрезке [0; 1].
На рис. 5.20 приведен график функции при k= 1/4 . 2 3 4 5 6 7 2 3 4 5 6 72. k = 1/3. Нами получена линейная функция у = х. График данной
функции не приводим.
3. 1/3 < k < 1/2. Свойства семейства функций те же, что и при значе¬
ниях k из первого диапазона 0 < k < 1/3.
4. k = 1/2. Нами получена функция Кантора, которая была подробно
изучена нами ранее (рис. 5.21).
5. 1/2 < k < 2/3. Данные функции непрерывны, нигде не монотонны,
имеют строгие минимумы и максимумы, нулевые и бесконечные (обоих
знаков) односторонние производные на множествах точек, всюду плотных
на отрезке [0; 1]. На рис. 5.22 приведен график функции при k = 3/5.
6. k = 2/3. Данная функция была изучена нами выше.
7. 2/3 < k < 1. Функции из этого диапазона обладают теми же свой¬
ствами, что и функция при k = 2/3. Просматривается та же фрактальная
структура графика, но его зигзагообразность выражена ярче. На рис. 5.23
приведены графики функции при k = 0,75 и k = 0,85.
302
CO
о
Cd
Рис. 5.22
Рис. 5.23
Глава 6
ИНТЕГРИРОВАНИЕ
6.1. Неопределенный интеграл и его свойства
Определение 6.1. Дифференцируемая функция F называется первооб¬
разной функции / на множестве X, если для любого х G X выполнено:
F'(x) = fix), или dF(x) =f(x)cbc.
Пусть F — первообразная функции / на множестве X. Тогда F(x) + С,
где C — const, также является первообразной для / на X, так как (F(x) +
+ Cf = F'(x) = f{x). Верно и обратное утверждение: если F и Ф — две перво¬
образные функции / на множестве X, то Ф(х) = Fix) + С, где C — const.
Замечание 6.1. Под множеством X мы понимаем интервал — конечный
или бесконечный (луч или прямую). Важно понимать, что если X — произ¬
вольное множество, то разность первообразных Ф(х) - Fix) может не быть
константой на X. Например, пусть/(х) = 0 на множестве X= (0; I) и (2; 3).
Тогда функции Ф(х) = 1 на X и
J2, если х G (0; 1),
Х [3, если х G (2,3)
удовлетворяют определению первообразной, но Ф(х) - Т(х) Ф const на всем
множестве X
Определение 6.2. Операция перехода от данной функции к ее первооб¬
разной называется неопределенным интегрированием. При этом функции /
ставится в соответствие некоторая произвольно выбранная первообразная.
Совокупность всех первообразных функции/, определенной на множестве
X, называется неопределенным интегралом от этой функции на X. Обозна¬
чение: J fix)dx.
Общий вид неопределенного интеграла для функции / на множестве X:
I fix)dx = Fix) + С,
где C = const.
Рассмотрим основные свойства неопределенного интеграла.
1. i\fix)dx)' = fix), или dijfix)cbc) = fix)dx.
2. J F\x)dx = J dFix) = Fix) + C.
3 (линейность неопределенного интеграла). Пусть существуют J/ix)dx
и \f2ix)dx. Тогда существует и J(a/1(x)±P/2(x))<^r, в котором а, |3 — про¬
извольные действительные числа, причем J(а/(х) ±Pf2ix))dx = aJ fix)dx ±
±Pj/2(x)<ir, где равенство правой и левой частей следует понимать как
равенство с точностью до константы.
305
Свойства 1 и 2 показывают, что операции дифференцирования
и (неопределенного) интегрирования обратны друг другу. Каждую фор¬
мулу из таблицы производных вида Ft (х) = f(x) можно истолковать как
утверждение, что на соответствующем множестве функция F является
первообразной для /, и значит, в силу второго свойства можно записать
I f(x)dx = F(x) + С. Поэтому, переписывая таблицу производных, получаем
таблицу неопределенных интегралов. Важно понимать, что каждая из фор¬
мул этой таблицы рассматривается на тех множествах, на которых опре¬
делена соответствующая подынтегральная функция. Например, формулу
f—cbc = 1пЫ + С
X
следует рассматривать отдельно на каждом из промежутков (-°°; 0)
и (0; +°°). Здесь мы пишем In \х\ вместо Inx, так как логарифм определен
только при х > 0, а дробь 1/х — при всех х Ф 0.
6.2. Основные методы интегрирования
Теорема 6.1 (интегрирование по частям). Пусть функции и и v диф¬
ференцируемы на множестве X и, кроме этого, существует первообразная
функции V • и'. Тогда на множестве X существует первообразная функции
v'-u, причем справедлива формула
IutVdx = UV-IiivtClx, или Ivdu = uv-Iudv.
Теорема 6.2 (интегрирование заменой переменной). Пусть функция/
имеет на множестве X первообразную F, функция ф: T —> X дифференциру¬
ема на множестве Т. Тогда на T справедлива формула
!fmwm=j Hxydx иФ<0= Fmwc. (ai>
Если в условиях теоремы 6.2 дополнительно предположить, что функ¬
ция ф строго монотонна, то на Y= ф(Г) существует обратная функция ф-1.
Тогда из формулы (6.1) следует, что на множестве Y справедлива формула
замены переменной в неопределенном интеграле
I f(y)dy = I/(Ф(О)-Ф'(О^ 1=ф-1(у) •
Рассмотрим несколько примеров.
Пример 6.1
Пример функции с разрывом первого рода,
не имеющей первообразную
Ранее нам стало известно, что производная действительнозначной функции может
иметь разрыв только второго рода. Поэтому в качестве данного примера можно взять
любую такую функцию. Действительно, рассмотрим, например, на отрезке [-1; 1]
функцию
_ J-1, если х s [-1; 0),
jl, если х е [0; 1].
306
Она имеет первообразную на каждом из полуинтервалов [-1; 0) и (0; 1]:
Г-х + C1, если х е [-1; 0),
[х + C2, если х E (0; 1].
При любых значениях констант C1 и C2 функция F не будет иметь производной
в точке х = 0, так как это будет точка разрыва для функции F (при C1 Ф C2) или точка
несуществования производной (точка излома) (при C1 = C2). Следовательно, первооб¬
разной для функции/не существует ни на одном интервале, содержащем точку х = 0.
Пример 6.2
Пример функции с разрывом второго рода,
не имеющей первообразную
Рассмотрим на отрезке [-1; 1] функцию
/(*)=■
—,если хФ 0,
х
0, если х = 0.
Во всех точках отрезка [-1; 1], кроме х = 0, выполняется (ln|x| + C)' = —. В точке
х
же х = 0 функция 1п| х| не определена, и производной в нуле у нее нет. Доопределить
функцию в точке х = 0 так, чтобы существовала производная доопределенной функции
F(X) =
J In |х| +C1, если х G [-1; о),
[1пх + С2,еслихе (0; 1],
нельзя, так как при любых C1 и C2 функция доказывается разрывной в нуле и не имеет
первообразной.
Возникает вопрос: можно ли построить пример функции с разрывом
второго рода, имеющей первообразную? Ответ на данный вопрос — поло¬
жительный. Рассмотрим функцию
/(,X) =
I 1
2х sin cos—, если х Ф 0,
0, если х = 0,
имеющую в нуле разрыв второго рода (докажите!). Для нее первообразной
будет функция
F(x) =
1
X2 sin— + С, если х Ф 0,
х
С, если х = 0,
где C = const.
Пример 6.3
Пример функции, имеющей бесконечную производную, при которой формаль¬
ная замена переменной в интеграле некорректна
Рассмотрим функции
fix) =
1
1
Зх2 sin——cos—, если х Ф 0,
Xj
X
Х°
И
ф(£) = \/с
0, если х = 0,
307
Первообразной функции /является функция
F(x) = \
X3 sin— + С, если х Ф О,
X3
С, если х - 0.
Используем подстановку x = (p(t) = yft. В данном случае функция /(ф(£))ф'(£)
не имеет первообразной Дф(£)). Действительно, выполнив указанную подстановку,
получаем
%(0)Н
t sin -,если t
* 0,
0, если £ = 0,
т.е. функцию, не имеющую производной при t = 0. Заметим, что функция ф'(.г)
не определена в нуле, что и привело к разрыву F(<p(t)).
Таким образом, формальном замена переменной в неопределенном инте¬
грале, вообще говоря, может быть некорректной.
Зададимся вопросом: можно ли построить пример функции, имеющей
бесконечную производную, при которой формальная замена переменной
в интеграле справедлива? Ответ на данный вопрос — положительный. Дей¬
ствительно, рассмотрим функции f(x) = Зх2, ф(£) = yft. Они обе определены
на всей числовой прямой М, но ф'(£) =
1
3¾2
обращается в бесконечность
при t = 0. При этом
|3x2dx = X3 +С;
j3x2dx = {x = $ft} = j3(\ft)2 —-^j=dt = \dt = t + C'
= X3 +С.
Задача 6.1
Докажем, что любая первообразная нечетной функции является четной, а среди
первообразных четной функции есть одна нечетная.
Решение
Пусть функция / — нечетная, a F - ее произвольная первообразная. Рассмотрим
вспомогательную функцию G(x) = F(x) - F(-x). Для нее в силу нечетности функции
/получаем G'(x) = f(pc) + f(-x) = 0.
Отсюда заключаем, что G(x) = const = G(O) = F(O) - F(O) = 0. Следовательно,
F(x) = F(-x).
Далее, пусть F — произвольная первообразная четной функции /. Функция
G(x) = F(x) - F(O) тоже будет первообразной, при этом G(O) = 0. Рассмотрим функ¬
цию Н(х) - G(x) + G(-x). Для нее в силу четности функции /получаем Н'(х) - f(x) -
- /(-*)= о.
Поэтому Н(х) = const. Ho H(O) = 0, поэтому Н(х) = 0, или G(x) = -G(-x).
В силу того что все первообразные функции / отличаются друг от друга на кон¬
станту, делаем вывод о том, что среди первообразных четной функции есть только
одна нечетная.
Рассмотрим следующее утверждение, которое будет очень полезно
в дальнейшем.
308
Утверждение 6.1. Пусть функция Дх) непрерывна на интервале (я; Ь),
исе (а; Ъ), а функция /: (я; b) —> R непрерывна в точке с. Предположим
также, что функция Дх) есть первообразная функции /(х) на каждом
из интервалов (я; с) и (с; 6). Тогда F{x) есть первообразная функции/(х)
на всем интервале (а; Ъ).
Доказательство
По условию имеем, что F'(x) = /(х) при х G (а; с) и (с; 6). Следова¬
тельно, остается доказать, что функция F дифференцируема в точке с и что
F(C) = /(с).
Рассмотрим последовательность {хп}, сходящуюся к точке с слева.
На отрезке [хи; с] выполнены все условия теоремы Лагранжа о конечных
приращениях. Согласно данной теореме получаем существование точки
G (хя; с) такой, что
F(xn)-F(c) =
Xn-C
Так как точка зажата между хп и с, то, устремляя хпк с слева, полу¬
чаем, что Iin также устремляется к с. Следовательно, в силу непрерывности
функции/в точке с имеем F'(с - 0) =/(с). Аналогично, беря последователь¬
ность {хя}, сходящуюся к точке с справа, заключаем, что F'{c + 0) = /(с).
Отсюда получаем выполнение равенства F'(с) = /(с), а значит, функция F
является первообразной для / на всем интервале (а; Ь). ■
Замечание 6.2. Доказанное утверждение, безусловно, элементарно обоб¬
щается на множества, состоящие из объединения нескольких интервалов.
В качестве применения полученного утверждения рассмотрим несколько
задач.
Задача 6.2
Найдем следующие интегралы:
a) Jlxldx; б) \e\%\dx.
Решение
а) Получаем
I , Г-[хйЬ:,еслих<0,
JIxIar = Cj =
IJ хах, если х > 0
Xi
—— + C1, если х < 0,
х
= ^(х).
— + Су,е слих>0
2 2
Из условий непрерывности функции F получаем
ДО - 0) = ДО) => C1 = С; ДО) = ДО + 0) => C= C2.
Отсюда получаем, что
\\x\cbc = ^М + с.
б) При х > 0 получаем jexdx = ex +С. При х < 0 получаем je~xdx = -е~х +C1.
Из условия непрерывности в точке х = 0 получим
ДО - 0) = ДО + 0) => Iim (-е~х +C1)= Hm (ех + С) => C1 = 2 + С.
*-»0-0 *-»0+0
309
Следовательно, искомая первообразная имеет вид
F(x) =
\-е~х + C + 2, если х < О,
\ех + С, если х > 0.
Нетрудно видеть, что F'(Q) = I = F'(0). Таким образом, функция F дифференциру¬
ема всюду, включая точку X = O.
Задание 6.1
Пусть функция/— монотонная и непрерывная и/-1 — ее обратная. Пусть также
J f(x)cbc = F(x) + С. Докажите формулу
J f~\x)dx = xf~^(x) - F(f~\x) + С.
Задание 6.2
Вычислите интеграл J(|l + x|-|l-x\)dx.
Рассмотрим далее несколько более сложных примеров.
Задача 6.3
Вычислим интеграл Jmin{5 - х2; I; x2}dx.
Решение
Сначала изобразим входящие в подынтегральное выражение функции (рис. 6.1).
Жирной линией выделена подынтегральная функция.
Следовательно,
5-х2, х<-2,
1, -2<х<-1,
min{5-x2; 1; х2} = -
х2, -1 < х < 1, =>
1, 1<х<2,
5-х2, х>2
310
Jmin{5-x2; I; x2}dx =
5x-- + C1, x<-2,
3 1
x+ C2, -2< x <-!,
— + C, -l<x<!,
3
x+ C3, \<x<2,
X3
5x + C4, x >2.
3 4
Для непрерывности первообразной в точках -2, -1,1,2 должны выполняться сле¬
дующие равенства:
Д-2 - 0) = Д-2 + 0) => -10 + 8/3 + C1 = -2 + C2 => C1 = 16/3 + C2;
Д-1 - 0) = Д-1 + 0) => -I + C2 = -1/3 + С=> C2 = 2/3 + С=> C1 = 6 + С;
Д1 - 0) = Д1 + 0) => I + C3 = 1/3 + C => C3 = -2/3 + С;
Д2 - 0) = Д2 + 0) => 2 + C3 = 10 - 8/3 + C4 => C4 = -6 + С.
Поэтому окончательно
з
5х - — + 6 + С, х<-2,
3
I min{5 -х2;1; X2 }dx =
х + — + С, -2<x<-i,
3
r3
— + С, -1 < л: < I,
3
2
х — + С, !<х<2,
3
5л;-——6 + С, х >2.
3
Изобразим окончательный график первообразной при C=O (рис. 6.2).
Рис. 6.2
Замечание 6.3. Константы Ci были подобраны из условия непрерыв¬
ности первообразной F, однако она получается не только непрерывной,
но и гладкой1 (докажите!).
1 То есть непрерывно дифференцируемой.
311
Задача 6.4
Вычислим интеграл J ф(x)dx, где ф(х) — расстояние от числа х до ближайшего
целого.
Решение
Изобразим график функции ф(х) (рис. 6.3).
Представим данную функцию в более удобном для работы виде:
,,I 1
ф(х) = |х-п|, и- — ^%<п + —, пeZ.
Используя задачу 6.2, имеем
F{x) = \(^{x')dx = \\x-n\dx=[———~ + Сп> п~\ ~х<п +
Для непрерывности первообразной функции F в точках х - п + 1/2 получаем
F
о
I
-^h I
+
и
О
+
-^h I
+
CN
CN
( I 1
1
пл п
I 2 J
2
- + C
п + — - (п +1)
п + — - (п +1)
+ C
п+1
^ g + Сп - - g + Сп+1 *=> Сп+1 - ^ + Сп-
Отсюда получаем
сп-\+сп_^...^+с0.
Постоянную п определим из соотношения
1^1.
п — < X <п + — => п < х + — < n +1,
2 2 2
т.е. п -
1
х + —
2
. Окончательно получаем
|ф (x)dx = ~
г
г
\
г
1
г
х-
х + —
х-
х + —
+ -
х + —
V
L 2J
/
L 2J
4
L 2J
+ C0.
Задача 6.5
Вычислим интеграл J(-1)МДх, где [х] — целая часть числах.
Решение
Переопределим подынтегральную функцию нулем в целых точках. Значение инте¬
грала в результате этого не изменится, но это даст нам возможность записать подын¬
тегральную функцию в виде
(-l)M = sgn(sin тег) = •
sin(Tix)
I sin(Tix) I ’
xeR\Z,
О, х е Z.
312
sinfra:) sin(Tir)
Запишем далее -.—-—= , v -—, откуда моментально получаем, что
Ism(Jtr)I д/l-Cos2(Tix)
J (-l)Mdtc = J sin(jix) + С.
у] i-cos2 (юс) п
Для самостоятельной работы мы предлагаем читателю вычислить инте¬
гралы от разрывных функций.
Задание 6.3
Вычислите следующие интегралы:
a) J[г]-1 sin(Tix) I dx, где [х] — целая часть числах, х > 0; б) J[ex]dx.
Задачи на «склеивание констант» часто встречаются при вычисле¬
нии неопределенных тригонометрических интегралов, если используется
замена, включающая в себя тангенс. Рассмотрим в заключение параграфа
несколько таких примеров.
Задача 6.6
doc
Найдем интеграл Г — г.
Решение <sm х+2cos2 xf
Преобразуем подынтегральное выражение:
1
dx
=J
COS4X
(sin2 х + 2 cos2 х)2 1 (tg2 х + 2)2 J (tg2 х + 2)2
dx = \ tg9 ^+J40 d(tgx) =
71
= j t = tgx, x Ф — + nn, n e I
_ f t2+1 . lft2 + 2 + t2
“•* (£2 + 2)2 dt~2> (t2 + 2)2 d ~
Ifdt I, t2 - I f dt Iej
“oJ+ 2 , 0 + oJ/*2 , 0\2^-oJ*2 , O-TJirf
¢2
dt
Vt2 + 2 23 (^2 + 2)2
_3, A t _ 3
~ 4 £2 + 2 _ 4(£2 + 2) ~ 4^/2
3
2J £2 + 2 4
arctg
' I Л
¢2 + 2
WJarctgIVJ
^ tgx ^
"a"
0/2.
tgx
4(tg2 x + 2)
A(t2 + 2)
+ C.
+ C =
Изобразим график полученной первообразной при C = O (рис. 6.4).
У У У
У У У У
-5^ ^
0 ^
^5 /
^ 10 ^
Рис. 6.4
Очевидно, что данный ответ не является верным. Во-первых, это график раз¬
рывной функции, а во-вторых, периодической. Первообразная же для функции
1
/(х) = —- необходимо должна быть непрерывной и возрастать (так
(sin2x + 2cos2 х)2
как F'(x) = /(х) > 0). Все это происходит в силу того, что подстановка t = tgx спра-
313
ведлива только при х Ф п/2 + пп, п е Z. Постараемся исправить полученное несоот¬
ветствие.
Запишем полученную первообразную F в виде
F(x) - —j=arctg
4V2
V V2 j
tgx „Л 71
^ + Crn — + тш < х < — + пп,
4(tg2* + 2) " 2 2
TI
и «склеим» константы Cn в точках — + тш, n е Z. Для этого, как обычно, приравняем
левый и правый пределы первообразной в этих точках:
Л л
— + тш - О
2
= F
— + пп +О
2
— + С ~-— + С
8л/2 8V2 "+1‘
Отсюда получаем
C - I г —ч г1 _ I
•+1_4л/2 ” *“W2
_ 71 Tt 2х + Tt .
Далее, так как — + Ttn < х < — + пп, то п < < п +1.
2 2 2Tt
Следовательно, и =
2^ +Tt
2 Tt
и окончательный ответ имеет вид
cbc
(sin2 х + 2 cos2 х)2
Г
tgx
3ti
2х + п
ч V2 ,
4(tg2 х + 2)
+4=-,/2
2л;
+ C0.
Изобразим график полученной первообразной при C0 = О (рис. 6.5).
Последний график полезно сравнить с предыдущим.
Задача 6.7
Предположим, что функции /: (a; b) —» R, g. (а; 6) —> M имеют производные вто¬
рого порядка/' и g" на (а; Ъ), причем f\x) = afix'), g"(*) = (3g(jr), х е (а; b), с некото¬
рыми числами а и Р, а Ф |3. Найдем первообразную функции fg на (а; Ъ).
Решение
Рассмотрим неопределенный интеграл J fgdx. Интегрируя по частям два раза,
получаем:
314
J fgdx = -J f" gdx = -fg - -J f'g'dx = -(fg - fg')+—\fg"dx = -(fg - fg')+-J fgdx.
a a a a a a a
Отсюда находим
jfgdx =
f'g-fg'
a-(3
В качестве заданий для самостоятельной работы предлагаем читателю
решить следующие задачи.
Задание 6.4
Вычислите интегралы:
а> J
dx
б) J
2sinx + 3cosx
3sinx + 4cosx + 5 J sin2xcosx + 9cos3x
dx; в) J
dx
2sin x-cosx+ 5’
\ r 3
г) ь
Sin2 X • COS2 X
sin8 x + cos8 x
dx; д) jVl-sin2xdx.
6.3. Определенный интеграл Римана
Определение 6.3. Назовем разбиением T = JxiJJL0 отрезка [а; Ъ] множе¬
ство точек Jx0; X1; х2; х3;хп} таких, что а = X0 < X1 < ... < хп = Ь.
Каждый из отрезков [xf-1; Xi], i = 1, ..., п, называется отрезком (частич¬
ным сегментом) разбиения T = {Xj}”=0.
Определение 6.4. Назовем диаметром разбиения длину наибольшего
отрезка разбиения, т.е. dT = шахAxi, где Axi = Xi-X^1, i = 1,..., п.
i
Определение 6.5. Будем говорить, что разбиение T' является измельче¬
нием разбиения Т, и писать Tf >- Т, если каждая точка разбиения T является
и точкой разбиения T'.
Предположим, что на отрезке [a; Ъ] определена числовая функция /
и T = {Xj}f=0 — разбиение этого отрезка. Выберем в каждом отрезке разбие¬
ния точку ^i и составим сумму
sT(J; S1;-; ln) = EZ(^)Axi,
I=1
называемую интегральной суммой Римана функции /.
Замечание 6.4. Если функция / неотрицательна, слагаемое Axi суммы
Римана равно площади прямоугольника с основанием [xi—1; Xi] и высотой
/(¾), а вся сумма — площади ступенчатой фигуры, образованной объеди¬
нением всех таких прямоугольников.
Определение 6.6. Число 7 называется определенным интегралом Римана
ъ
функции / на отрезке [а; b] и обозначается символом J f(x)dx, если для про-
а
извольного в > О найдется 6 = 8(e) > О такое, что для любого разбиения
T = JxiJiL0 этого отрезка с диаметром dT< 8(e) и любого набора отмеченных
точек ^1,..., выполнено
1=1
<8.
315
Функцию / при этом называют интегрируемой по Риману на отрезке
[а; Ь]. Кратко можно записать:
J f(x)dx = JimST(f; S1;\п),
a dT^ о
т.е. определенным интегралом от функции / на [а; 6] называется предел ее
интегральных сумм при диаметре разбиения, стремящемся к нулю.
Теорема 6.3 (необходимое условие интегрируемости). Если функция
интегрируема на отрезке, то она ограничена на нем.
Условие ограниченности функции не является достаточным для ее
интегрируемости. Рассмотрим, например, функцию Дирихле
f 1, если х е Q,
^ ^ |0, еслихеМ\(0)
на отрезке [0; 1]. Для этой функции и произвольного разбиения Tполуча¬
ем St(D) = 1, если все отмеченные точки рациональные, и St(D) = 0, если
все отмеченные точки иррациональные. Следовательно, рассматриваемая
функция не является интегрируемой на отрезке [0; 1].
Более того, можно доказать следующее утверждение, которое мы офор¬
мим в качестве задачи.
Задача 6.8
Докажем, что для всякого действительного числа у, 0 < у < 1, существует после¬
довательность интегральных сумм функции Дирихле, рассматриваемой на отрезке
[0; 1], такая что ее предел равен у.
Решение
Выберем произвольное разбиение {xk)l=0 отрезка [0; 1] такое, чтобы одна из его
точек (для определенности X1, 0 < / < и) совпала с числом у. Далее, на всех отрезках
разбиения до точки Xi выбираем в качестве отмеченных точек рациональные, а после
Xi — иррациональные. В таком случае интегральная сумма S1(D) имеет вид
St(D) =1 • Ax1 +... + 1 • AXi+ 0 • Ах/+1 +... + 0 • Axn = у.
Поэтому Iim St(D) = у.
dp—>0
6.4. Критерии интегрируемости
Пусть функция/определена на отрезке [а; Ь\. Напомним, что ее колеба¬
нием на этом отрезке называют число
т(/, [a; b])= sup |/(х')- f(x")\ = sup f(x)- inf f(x).
x’,x"£.[a\b\ [a;b] [a',b]
Для функции/, определенной на отрезке [а; b], и разбиения T = {xjf=0
ПОЛОЖИМ C0j(/) = ©(/; [Xj_iJ Xi]).
Теорема 6.4 (критерий интегрируемости). Для интегрируемости огра¬
ниченной функции / на отрезке [а; Ъ] необходимо и достаточно, чтобы
316
для любого 6 > 0 3 8(e) > 0 такое, что для любого разбиения T = {х{}?=0,
П
такого что dT< 8(e), выполнялось Xtoi(Z)Axf < е.
Z=
Yl
Данное условие равносильно равенству Iim X t0I (Z)Axi = 0.
dT —>0 i=i
Доказательство
Необходимость. Пусть функция / интегрируема на отрезке [а; b] и
ъ
J f(x)dx=I. Тогда для любого е > 0 3 8(e) > 0 такое, что для любого T = {хг }^=0,
а
dT< 8(e), и для любых ^1,..., выполнено \ST(f; ^1;...; Zn) - /| < е.
Зафиксируем данные е, 8(e) и разбиение Т. Пусть точки ^i, из отрезка
[xi t', Xi] такие, что выполнено COi(/) < 2(/(^)-/(¾')). Тогда
Xcoi(Z)Axi
i=i
<2
E(Z®)"Z®))‘AXi
г=1
<21-Srif]^;...;+2 St(f;ад£)-/ <4е.
П
Отсюда следует, что Hm Xcoi(Z)Axi = 0.
dT -»oi=i
Достаточность. Пусть разбиение Г* ={х*}^=0 является измельчением
разбиения T = {х; }^=0. Покажем, что при этом выполнено
SAf; адW-J7- (Z; S; •••; К-) < Ecoi(Z)Axi.
г=1
(6.2)
Пусть Xi = х* для всех г = 1,
(рис. 6.6).
k, т.е. хм = х*м < х*._1+1 <... < х*._! < Xj. = Xi
X
Л-1+1
X
*
^i-I =X^1
#
X,-. = X1-
J г 1
Рис. 6.6
Тогда, выбирая на каждом отрезке [X^1; Xi] произвольные точки {£*•},
получаем
Ji
Ji
Ji
Z(Si)Axi- _ X Z(SJ)-Ах*
=
J(Si)’ E Ax - X f(Sj)-SXj
J-Ji-1+1
J-Ji-1+1
^ E t0I-(Z)Ax* = COi(Z)Axi.
J=Ji-1+1
Производя суммирование по всем отрезкам разбиения Т, получаем
выполнимость условия (6.2).
Пусть, далее, T' = {х'}^ и Т" = (Xi)^1 — произвольные разбиения отрезка
[а] Ь]. Возьмем разбиение T*, являющееся объединением данных разбиений.
Очевидно, что Т* > T' иТ* > Т". Тогда в силу неравенства (6.2) получаем
317
(6.3)
\Sr(f)-ST4f)\<\Sr(f)-Sr(f) + Sr(J)-Sr(J) <{(6.2)}<
^ E “K/>Ar' + X Mf(Z)Ar'
i=l i=l
Из последнего неравенства и неравенства из условия теоремы вытекает,
что для любого в > 0 3 6(e) > 0 такое, что при dT, dT, < 6 выполнено
IV(Z)-Sr(Z)I < E
(6.4)
(сравните данное утверждение с определением фундаментальности число¬
вых функций и последовательностей).
Далее, возьмем произвольную последовательность разбиений Tn = {xjn^
со стремящимися к нулю диаметрами dj . Для каждого такого разбиения
Tn, отметив произвольно точки <^[п\, составим сумму Римана STJf)
и рассмотрим числовую последовательность (,Sr (/)}“=1. Она является
фундаментальной, так как в силу неравенства (6.4) для любого в > 0 3 пг:
для V п,т>пг выполнено Sr (/) - St (/) < в.
Следовательно, по критерию Коши она сходится.
Пусть I= Iini1Sr (/;£Выбираем разбиение T с диаметром
dT< 8. В силу соотношения (6.3) имеем
Srn(J)-Mf) SEco^(Z)
г=1 г=1
Переходя в последнем неравенстве к пределу при п —» получаем, что
|4-VZ)N i»i(Z)A*i <e=>limnS7-(Z) = /. ■
г=1 яг—»0
Определение 6.7. sT(f) = ^miAxi, где т{ = inf /(х), — нижняя сумма
г=1 *i+ ]
_ п
Дарбу функции/, соответствующая разбиению Т. Sr(/) = ^MiAxi, где
г=1
Mi = sup /(х), — верхняя сумма Дарбу функции / соответствующая раз-
I xI I xi+i ]
биению Т. I* = sup{sr(/)} = Hm sr(/) — нижний интеграл Дарбу функции/.
{Г} d->0
Г = inf {Sr (/)} = Iim Sr(/) — верхний интеграл Дарбу функции /.
{Г} d—>0
Задание 6.5
Выясните геометрический смысл интегральных сумм Дарбу для неотрицательных
функций.
Ясно, что для любой интегральной суммы Римана St(J) выполнено
Sr(Z) <ST(f)<St(J).
Кроме этого, отметим, что
sT(f)~ Mf)=1Х(/)Дхг..
г=1
318
Отсюда мы моментально получаем следствие из критерия интегрируе¬
мости.
Следствие 6.1. Для интегрируемости ограниченной функции /
на отрезке [я; b] необходимо и достаточно, чтобы для V е > 0 3 8(e) > О
такое, что для любого разбиения Т, такого что dT< 8(e), выполнено
Замечание 6.5. Можно доказать, что, для того чтобы ограниченная
на отрезке [я; b] функция / была интегрируемой на этом отрезке, необхо¬
димо и достаточно, чтобы для любого е > 0 нашлось такое разбиение T этого
отрезка, для которого ST(f)~ s_T(f) < в.
В дальнейшем мы изучим другие критерии интегрируемости, а сейчас
рассмотрим несколько утверждений и задач.
Утверждение 6.2. Функция, монотонная на отрезке, интегрируема на нем.
Утверждение 6.3. Функция, непрерывная на отрезке, интегрируема
на нем.
Утверждение 6.4. Пусть функция / ограничена на отрезке [я; b]
и для любого в > 0 существует конечный набор интервалов, сумма длин
которых меньше в, содержащий все точки разрыва функции /. Тогда эта
функция интегрируема на [я; Ь\.
Следствие 6.2. Если функция / ограничена на отрезке [я; Ь\ и имеет
конечное число разрывов, то она интегрируема на нем.
Возникает вопрос: может ли быть интегрируемой функция, содержащая
бесконечное число точек разрыва? Ответ на данный вопрос — положитель¬
ный. Рассмотрим следующую задачу.
Задача 6.9
Исследуем интегрируемость функции Римана
R(x) =
I Ttl
—, если X = —, НОД(яг, ri) = I, т е Z, п е N,
п п
О, если х — иррациональное число.
Решение
Не ограничивая общности, изучим интегрируемость на отрезке [0; 1]. Фиксируем
произвольное е > 0. Для этого е существует только конечное число п(г) точек Tii
£
таких, что /(Tji) > —. Кроме того, для функции Римана, очевидно, справедлива оценка
I R(x) I < 1 (рис. 6.7).
C
Рассмотрим разбиение T с диаметром d < 8(в) =
тральную сумму:
St(R) =
1=1
4 п(е)
^ |Ei R&i )A*i I+1 E2-rC^ )Д*.-1 >
. Составим для него инте-
где первая сумма соответствует сегментам разбиения, в которых присутствуют точки
Tii, а вторая лишена их. Ясно, что в первой сумме не более 2п(г) слагаемых1. Поэтому
для первой суммы справедлива оценка
1 Случай, когда все точки Tii являются точками разбиения попарно непересекающихся
отрезков.
319
IS1 )Д^, I^l- 2п(е)5(Е) = |.
Во второй сумме воспользуемся тем, что значения функции R(x) не превосхо¬
дят а сумма всех отрезков разбиения заведомо не превосходит единицу. Отсюда
получаем оценку
I E £ ^
Следовательно, при d < 5(e) справедливо |5г(/?)| < — + — = е, т.е. jR(x)dx = 0.
2 2 о
•
•
•
•
•
#
•
#
. •
, '
• \
« ,
* ,
. / •
• .
’\
;>л\ iir-Лй-Л
0,5
ОД
0,3
0,2
е/2
ОД
0,0
0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0
Рис. 6.7
Утверждение 6.5 (критерий Коши интегрируемости функции
на отрезке). Функция / интегрируема по Риману на отрезке [я; b] тогда
и только тогда, когда для V е > 0 3 8 > 0 такое, что для любых разбие¬
ний Tb T2 отрезка [я; b] с диаметрами < 5, d2 < 5 выполняется неравен¬
ство STi (/) - St (/) < 8, где St. (/) — интегральная сумма функции f(x)
на отрезке [я; Ь], отвечающая разбиению Ti.
Доказательство
ъ
Необходимость. Пусть функция /интегрируема на [я; b] и I = \f(x)dx.
Тогда для любого е > 0 3 8(e) > 0 такое, что для любого разбиения T с диа-
метром, меньшим 5, выполняется неравенство |ST(f)-I\<—. Поэтому если
2
d^ ^ 8, d2 ^ 8, то
Sri(J)-sT2(J) * Stx(J)-I + I-Sj2(J)
< —+ —= E.
2 2
Достаточность. Если считать St(J) функцией, зависящей от разбие¬
ния T (вернее, даже от величины его диаметра), то данное утверждение
является переформулировкой условия Коши существования предела
320
функции в точке d = 0. Поэтому 3 Hm 5^(/), а следовательно, функция /
<f—>о
интегрируема на отрезке [а\ b\. U
Зададимся теперь вопросом о необходимости различных требований
в определении интегрируемости функций. Например, попробуем отказаться
от произвольности разбиения отрезка интегрирования. Достаточно ли
в определении интеграла рассматривать разбиения отрезка [я; b] на п рав¬
ных отрезков, а значения функций брать в серединах отрезков разбиения?
Ответ на данный вопрос — отрицательный. Рассмотрим следующий пример1.
Пример 6.4
Как мы уже раньше видели, интеграл от функции Дирихле J D(x)dx не существует.
о
Разобьем отрезок [0; 1] на п равных частей. Точки в серединах полученных отрез¬
ков разбиения являются рациональными. Следовательно, D(J^i) = 1 для всех i, откуда
п 1
Iim £ D(%i) Axi = I = D(x)dx.
n->°°z=l 0
Интересно заметить, что по приведенному модифицированному определению
л/2
получаем * J D(x)dx = 0, так как если разбить отрезок [0; V 2] на п равных частей, то
о
середины всех отрезков разбиения будут иррациональными точками. Отметим, что
тем самым нами было получено еще одно доказательство неинтегрируемости функ-
1 л/2
ции Дирихле, ибо [0; 1] с [0; V2], D(x) > 0, но *JD(x)dx = 1 > 0 = * J D(x)dx.
о о
Зададимся вопросом о необходимости требования стремления макси¬
мума длин отрезков разбиения к нулю.
Пример 6.5
Пусть при каждом разбиении отрезка [я; Ь\ длина хотя бы одного отрезка разби¬
ения будет больше некоторого числа а > 0. Рассмотрим произвольную интегрируе¬
мую на [я; Ь\ функцию /, не являющуюся константой ни на одном из отрезков раз¬
биения. Для нее на любом из отрезков разбиения длиной больше а разность макси¬
мального и минимального значений функции будет не меньше числа
P= min (max f{x)~ min f(x)),
Дс[а; 6] хеА хеА
где минимум берется по всем отрезкам разбиения А с длиной больше а, лежащим
в [я; b]. Отметим, что число P строго больше нуля, так как P — наименьшее из неот¬
рицательных чисел, а равенство P = O означало бы, что на отрезке [я; Ь\ существует
отрезок длины а, на котором подынтегральная функция — константа, что противо¬
речит нашему предположению. При этом две интегральные суммы, различающиеся
лишь выбором двух различных точек в отрезке разбиения длиной больше а, будут
(при подходящем выборе этих точек) отличаться не менее чем на ар. Следовательно,
предела интегральных сумм мы не получим.
Далее мы рассмотрим критерии интегрируемости Дюбуа — Реймона
и Лебега.
1 «Интеграл», полученный по новому определению, мы будем обозначать *J.
321
Напомним, что колебанием функции/на множестве X называется вели¬
чина, определяемая равенством co(/; X) = sup | /(X1) - /(х2 ) |.
х^,Х2^Х
Из свойств точной верхней грани вытекает неравенство
ю(/; X1) < со(/; X2), если X1 с X2,
так как при переходе от множества к его подмножеству верхняя грань
не возрастает. А также, если X1 n X2 Ф 0, то со(/; X1 u X2) < со(/; X1) + со(/; X2).
Введем важное определение.
Определение 6.8. Колебанием со(/; х0) функции / в точке X0 G X назы¬
вается нижняя грань колебаний функции на пересечениях всевозможных
окрестностей В(х0) этой точки с множеством X:
“(/; *о ) = jnf '“(/: в(хо ) n ХУ
B(X0)
Введем в рассмотрение множество Xe = {х G X | со(/; х) > е}, где в > 0 про¬
извольно.
Легко видеть, что если ц < в, то Xe с Xti (докажите!).
Утверждение 6.6. Функция / непрерывна в точке х G X тогда и только
тогда, когда со(/; х) = 0.
Доказательство
Необходимость. Если функция/непрерывна в точке X0 G X, то для любого
в > 0 существует такая окрестность В5(х0), что для всех х G -B5(X0) выпол¬
нено |/(х) - /(х0)| < —. Поэтому для любых X1, х2 G В5(х0) n X имеем
|/(*1) - Кх2 )| ^ |/(*1) - KxО )| +1 f(x0 ) - Kx2 )| < J+1 = Е.
Следовательно,
®(/; *о ) = inf ч 1“(/; В(х0 ) n X) < co(/; B5 (х0 ) n X) =
B(X0)
= sup !/(X1)-Z(X2)I^e.
^,Х2еВд(д:0)пХ
Отсюда в силу произвольности в > 0 получаем, что со(/; х0) = 0.
Достаточность. Пусть со(/; х0) = 0. Тогда для любого в > 0 суще¬
ствует такая окрестность В(х0), что со(/; В(х0) n X) < в. Тогда для любого
х G В(х0) n X в силу определения колебания функции / в точке будем
иметь I /(х) - /(х0) I < со(/; В(х0) n X) < в, что совпадает с определением
непрерывности функции / в точке х0. ■
Следствие 6.3. Если X — множество точек разрыва функции / то
OO
X=UXi/,. (6.5)
Tl=1
Доказательство
Если х0 G X — точка разрыва функции /, то в силу утверждения 6.6
имеем со(/; х0) = в > 0, и поэтому X0 G Xe. Следовательно, множество X
точек разрыва функции / представимо в виде
X=UXe.
е>0
322
Далее, используя включение Xe с Xn при ц < е, можно доказать (дока¬
жите!), что
U-Xe= 0 *!/„•■
Е>0 И=1
Докажем далее очень важное утверждение.
Теорема 6.5 (критерий интегрируемости Дюбуа — Реймона). Для суще¬
ствования определенного интеграла функции /на интервале (я; b) необхо¬
димо и достаточно, чтобы по заданным числам в > 0, о > 0 можно было
найти такое 8(в, ст) > 0, что при диаметре разбиения d < 5 сумма ^Axjfe/
V
длин тех интервалов, которым отвечают колебания функции CDjfe/(/)> в,
сама была меньше а.
Доказательство
Необходимость. Пусть функция/интегрируема на интервале (а; Ъ). Тогда
П
= 0.
Далее из неравенства
E Wjfe(Z)AЧ ^ E®4'(Z)axV *
4=1 4' 4'
за счет выбора 8 можно сделать сумму ^cojfe(Z)Axjfe меньше ва. Следователь-
k
HO, ^Axjfe/ <а-
4'
Достаточность. Обозначив значком k" отрезки, на которых колебание
функции со£"(/)<е, получаем
Е®4(/)А^4 =Е®4'(/)А^4' +E®4*(/)^4* <
4 4' 4"
<со(/;[а;&])£Axjfe/ + в^Axjfe// <ю(/;[а;£])а + в(Ь-а) = в'.
4' 4"
Следовательно, функция / интегрируема на отрезке (а; Ъ). ■
Определение 6.9. Множество XcR называется множеством меры нуль
по Лебегу (на прямой), если для любого в > 0 существует покрытие этого
множества конечной или счетной системой интервалов, сумма длин кото¬
рых меньше в.
Рассмотрим далее теорему Лебега, которая вытекает из доказанного
выше критерия Дюбуа — Реймона. Данный критерий интегрируемости
имеет достаточно простую формулировку, благодаря чему становится
исключительно полезным в использовании.
Теорема 6.6 (критерий интегрируемости Лебега). Для того чтобы
ограниченная на отрезке функция была на нем интегрируема, необходимо
и достаточно, чтобы множество ее точек разрыва было множеством меры
нуль по Лебегу.
Доказательство
Необходимость. Пусть функция / интегрируема на отрезке [я; Ь] и X —
множество ее точек разрыва. Зададим произвольное в > 0. Согласно кри¬
Hm X Wjfe(Z)AXjfe
4=1
323
терию Дюбуа — Реймона для каждого натурального п существует такая
конечная система интервалов, покрывающая множество X1^n1, сумма длин
£
которых меньше —. Объединение таких систем состоит из не более чем
счетного числа интервалов, покрывающих в силу равенства (6.5) все мно¬
жество точек разрыва функции /. При этом сумма длин этих интервалов
00 8 ~
меньше, чем ^ — = е, т.е. X — множество меры нуль по Лебегу.
я=12”
Достаточность. Пусть функция /ограничена на отрезке [a; b\, а мно¬
жество ее точек разрыва X имеет меру нуль по Лебегу. Зафиксируем про¬
извольные в > 0 и с > 0. Выберем исходя из условий теоремы не более
чем счетную систему интервалов2, сумма длин которых была бы менее
а, покрывающую все точки разрыва функции /. Выберем натуральное п,
удовлетворяющее неравенству — < в. Указанная выше система интервалов
п
°°
покрывает в силу формулы X= (J Xyn и каждое из множеств Xyw а зна-
Я=1
чит, и Xs, в силу того что Xs с Xyw Множество Xe является ограниченным
(как подмножество отрезка [а; b]) и, в силу своего задания, замкнутым
(докажите!), следовательно, по лемме Гейне — Бореля из рассматриваемой
системы интервалов, покрывающих Xs, можно выделить конечное подпо¬
крытие, причем сумма длин входящих в него интервалов не превосходит
сумму длин исходного покрытия, т.е. о. Отсюда в силу критерия Дюбуа —
Реймона следует интегрируемость функции/на отрезке [а; Ь\. ■
В свете доказанной теоремы особую важность представляет следующее
утверждение.
Утверждение 6.7. Всякое конечное или счетное множество на прямой
R является множеством меры нуль по Лебегу.
Доказательство
Докажем утверждение 6.7 для счетного множества Х = {хи}“=1 (дока¬
зательство для конечного множества оставляем читателю). Зафиксируем
произвольное в > 0. Система интервалов
( „ л
х„ -
п 2я+2
, хп +
2п+2
, п = 1,2,.
покрывает множество X, причем сумма их длин меньше в, так как
” в в 1 в.
У —г = - < в. ■
2И+1 4 1-1/2 2
Следствие 6.4. Всякая ограниченная на отрезке функция, имеющая
конечное или счетное множество точек разрыва, является интегрируемой.
1 Напомним, что X1^n = J х е X \ со(/; х) > — I.
2 Исходя из критерия Дюбуа — Реймона фиксированное выше множество Xe требуется
покрыть конечной системой интервалов, сумма длин которых была бы менее а.
324
Используя тот факт, что множество рациональных чисел счетно, из кри¬
терия Лебега моментально получаем интегрируемость функции Римана.
Более того, теперь мы можем построить пример функции, имеющей несчет¬
ное^) множество точек разрыва на отрезке [0; 1], являющейся интегриру¬
емой на нем. Действительно, рассмотрим характеристическую функцию
множества Кантора П:
fl, если XE П,
хп(*)=п
[0, если xgn.
Очевидно, что данная функция имеет разрывы во всех точках множе¬
ства Кантора, но непрерывна вне его1. Вспоминая, что множество П явля¬
ется несчетным множеством меры нуль по Лебегу, заключаем требуемое.
6.5. Связь между определенным
и неопределенным интегралами
Определение 6.10. Пусть функция / интегрируема на отрезке [я; Ь\.
X
Тогда на этом отрезке определена функция F{x) = J f{t)dt, a<x<b, назы-
а
ваемая интегралом с переменным верхним пределом.
ь
Аналогично можно ввести функцию G(x) = jf(t)dt — интеграл с пере-
X
менным нижним пределом.
Утверждение 6.8. Пусть функция / интегрируема на отрезке [я; Ъ\.
Тогда функция F непрерывна на [я; Ь].
Утверждение 6.9. Пусть функция / интегрируема на [я; b] и непре¬
рывна в точке X0 е [я; b]. Тогда функция F имеет производную в точке X0
и F(X0) =f(x0).
Замечание 6.6. Если X0 = а или х0 = Ь, то под F'(x0) подразумевается
односторонняя производная.
Замечание 6.7. Аналогично имеем G'(x0) = -/(х0).
Утверждение 6.10 (о существовании первообразной). Пусть функ¬
ция/непрерывна на отрезке [я; Ъ]. Тогда она имеет на [я; b] первообразную
F{x) = J f(t)dt, где х0 е [я; Ь\.
Xq
Теорема 6.7 (основная теорема интегрального исчисления). Пусть
функция / непрерывна на отрезке [я; Ь] и F(x) — ее некоторая первообраз¬
ная на этом отрезке. Тогда справедлива формула Ньютона — Лейбница
]f(x)dx = F(b)-F(a) = F(x)l.
а
1 Так как в любой окрестности любой точки из множества Кантора найдется бесконечно
много точек не из множества Кантора, в которых рассматриваемая функция равна нулю,
и для любой точки не из этого множества в силу замкнутости множества Кантора найдется
окрестность, полностью не содержащая точки из множества П.
325
Если подынтегральная функция не является непрерывной, используют
следующее утверждение.
Утверждение 6.11 (обобщение формулы Ньютона — Лейбница).
Пусть функция / интегрируема на отрезке [а; Ь\, терпит разрывы первого
рода во внутренних точках Ci G (a; Ъ), i = 1, п, и, может быть, в точках а
и Ь. Кроме того, пусть F'(x) = f(x) за исключением точек разрыва. Тогда
справедлива формула
J f(x)dx = F(b - 0) - Е(я + 0) + £ [F(Ci - 0) - F(Ci + 0)].
Теорема 6.8 (формула замены переменной). Предположим, что функ¬
ция ср : [а; Р] —» [с; d\ z> [я; А], а = ср(а), b = ср(Р), непрерывно дифференци¬
руема на отрезке [а; Р], а / непрерывна на отрезке [с; <Д. Тогда справедлива
формула
\f(x)dx
а
х = ф(£)
dx = ф '(t)dt
//(Ф(О)Ф'(О^-
а
Теорема 6.9 (интегрирование по частям). Пусть функции uuv непре¬
рывно дифференцируемы на [а; Ь]. Тогда справедлива формула
и
J u(x)v'(x)dx = u(x)v(x) -1 u'(x)v(x)dx.
Рассмотрим вопрос о соотношении интегрируемости функции на неко¬
тором отрезке и существовании ее первообразной на этом же отрезке. Ранее
мы рассматривали пример функции
ч I-1, если х G [-1; 0),
1, если х G [0; 1],
которая, безусловно, интегрируема на отрезке [-1; 1], но не имеет перво¬
образной на нем. Можно построить пример функции, интегрируемой
на отрезке, но не имеющей первообразной ни на каком интервале. Дей¬
ствительно, рассмотрим множество рациональных чисел на отрезке [0; 1]:
Q[0;i] = [q^i и числовой ряд, состоящий из строго положительных чисел
Yj pk, сходящийся к числу Р. Определим функцию/на отрезке [0; 1], по-
k=\
ложив f(x)= Yj Pb т-е- значение / в точке х равно сумме всех членов
k:qk<x
DO
Pk ряда Y Pk таких, что qk<x. Тогда /возрастает на отрезке [0; 1], непре-
ы
рывна в каждой иррациональной точке х и имеет разрыв первого рода (со
скачком, равным pk) во всякой точке qk (т.е. Iim f(x)~ Hm f(x) = pk).
X—.>qk+0 х—»%-0
Функция / будет интегрируемой на отрезке [0; 1], так как она монотонная
(или так как она имеет множество точек разрыва меры нуль). Однако эта
функция не имеет первообразной ни ни каком подынтервале отрезка [0; 1],
поскольку множество точек ее разрывов первого рода всюду плотно на от¬
резке [0; 1].
326
Зададимся другим вопросом: можно ли утверждать, что всякая функ¬
ция, имеющая первообразную на некотором отрезке, обязательна должна
быть интегрируема на нем? Ответ на этот вопрос — отрицательный. Рас¬
смотрим следующий пример.
Пример 6.6
Выберем в качестве первообразной функцию
F(X) =
1
X2 sin—, если х Ф О,
X1
О, если х = 0.
Дифференцируемость функции F очевидна, и ее производная равна
FXx) =
12 1
2xsin— cos—, если хф 0,
у у 2
Л *Л/ *Л/
,. F(Ax) - F(O) Ta-Ia
Iim —-— — = Iim Axsm—- = 0, если х = 0.
Дж-»0 Ax Ax->0 Ax1
Поэтому F может рассматриваться первообразной для своей производной (обо¬
значим ее f) на каком-нибудь отрезке, содержащем точку 0 (например, [-1; 1]).
Полученная на [-1; 1] производная F'(x) = f(x) имеет разрыв в нуле и (из-за вто¬
рого слагаемого) неограничена в любой окрестности точки 0. Следовательно, она
неинтегрируема на [-1; 1].
Рассмотрим еще несколько важных примеров.
Пример 6.7
Функция Римана R является интегрируемой на любом конечном отрезке.
X
Рассмотрим функцию Ф(x) = \R(t)dt, где х — любая точка отрезка [a; b\. В силу
а
отмеченной выше интегрируемости функции R заключаем, что функция Ф опре-
X
делена на [а; b] и так как на любом отрезке [а; х\ имеем J R(x)dx = 0, то Ф(х) = 0
а
на [а; Ъ\. Далее, так как функция R непрерывна во всех иррациональных точках, то
функция Ф в этих точках имеет производную, причем Ф'(х) = R(x) = 0. Однако, так
как Ф(х) = 0 на всем отрезке [а; Ь\, то Ф'(х) = 0 и в рациональных точках, в которых
R(x) Ф 0. Следовательно, построенная функция Ф не есть первообразная для функ¬
ции R на [а; Ь\. Это объясняется тем, что функция Римана не является непрерыв¬
ной функцией на [а; Ь\.
Пример 6.8
Уже рассмотренная нами выше характеристическая функция множества Кантора П
Tl, если х еП,
10, если х <t П.
XnW = -
представляет из себя пример интегрируемой по Риману функции, производная неоп¬
ределенного интеграла которой не совпадает с подынтегральной функцией на мно¬
жестве мощности континуум, т.е. во всех точках множества Кантора1.
1 То есть (\xn(x)dx)' Ф %п(х).
327
Пример 6.9
Функция Кантора ф(х) непрерывна, почти всюду имеет производную, которая
(при соответствующем доопределении) интегрируема по Риману, но неопределен¬
ный интеграл от ее производной Jcp\x)dhc не равен ф(х) + const, так как ф'(х) = О
почти всюду.
При вычислении определенных интегралов, используя формулу Нью¬
тона — Лейбница, важно помнить про возможные точки разрыва пер¬
вообразной. Продемонстрируем это на примере решения следующей за¬
дачи.
Задача 6.10
Вычислим
1 + х* 2
интеграл J
1+ X
dx.
Решение
ПрихФ 0 найдем первообразную подынтегральной функции:
1
+ 1
\^ + Х dx=\ dx-\-
Jl + x4 jI9 j
f I
x
4 X
+ Xj
f
Xz
2 +
X--
1
У I . X2-I _
— = -i=arctg—^ + С.
f “V2‘
х
X
4~2
Разобьем, далее, искомый интеграл на сумму двух:
2 1 + Х2 , ? 1 + Х2 , ?1 + Х2 J
ах =
Г dr- f dr I Г
I CLJC — I CUC T I , I
_Д + Х4 .Д + Х4 q I + ХА
I X2-I
iVJarctgWT
0-0
-I
I X2-I
+ -/=arctg—
V2 xV2
o+o
I 3>/2 TI
!VJarctg~+VT
I X2-I
Предлагаем читателю вычислить величину -^arctg—-j=-
бочности полученного ответа. * I 2и убедиться в оши-
-1
Задача 6.11
Вычислим определенные интегралы от ограниченных разрывных функций:
a) J |cosx |-Vsinx dx, где {£} — множество тех значений отрезка [0; 4п], для которых
{Г}
SlH TlX
подынтегральная функция имеет смысл; б) J dx, и G N.
I M
Решение
а) Для исходного интеграла, используя симметричность подынтегральной функ¬
ции, получаем
Г. п Г~. Зп Г~.
J Icosxl-Vsinx dx = JIcosxI-vsinx dx+ J Icosxl-Vsinx dx =
{E} 0 2п
2 2 g и
■ 4jcosx-v/sinx dx = 4j Vsinx V(sinx) = —sin3/2xb
OO^
8
3'
328
б) Имеем
nI4Sinjix , ^sinjix , ?sinjix , nI1Sinjix ,
ах = ах+\ ах + ...+ ах =
I M { 1 { 2 in
2 п
=~ъ
я k=i
1
^ I |2N
1
со
т-Н
1
( 1 |Я+Л
= —
—cos лх L
H—
COS JlXL
I
+
+
1
I Я llJ
2
п 1L
п
I я 1п J
(~i)*+i
k
Задание 6.6
Вычислите определенные интегралы от ограниченных разрывных функций:
4л 6 ш
a) J хsgn(sinx)d!x; б) J[x]sin—dx.
о
Задача 6.12
Докажем, что если функция /непрерывна на (0; 1), то
я/2 Tt/2 П ^ 71
a) J f(sinx)dx = J f(cosx)dx; б) \xf(sinx)dx = — j f(sinx)dx.
oo о 20
Решение
а) Получаем верность равенства, делая замену переменной:
71/2
I f(sinx)dx =
о
, Tt
t = X
2
dt = -dx
б) Делая замену переменной, получаем
, я'
t = x —
2
dt = dx
ял
х —
2
V
f(sinx)dx =
п/2
= J f(cost)dt.
о
71/2
= J tf(-cost)dt = 0,
-п/2
так как в последнем интеграле стоит нечетная функция. Следовательно,
7Т '
J х f(sinx)dx = — I f (sin x)dx.
о 2 о
Воспользуемся техникой из задачи 6.12 для того, чтобы вычислить
интегралы, не берущиеся в элементарных функциях.
Задача 6.13
Вычислим следующие интегралы:
п, г sin г К/-2
а) jT
о1
+ COS2 X
dx; б) J ln(sinx)fiix.
о
Решение
а) Преобразуем подынтегральное выражение:
xsmx
Sinx
= X-
I + Cos2 х 2 - sin2 х
Используя предыдущую задачу, получаем
= x-/(sinx).
J7
П
XSinx , п пг
ах = —
о J
sinx
+ COSz х
2 о 2 - sin2 х
dx =
я P d(cosx) _ л
Jl Г L
= ~2il
п Tlz
о— = -^arctg(cos^) о = ~т-
+ Cos2 х 2 '0 4
TI
б) Делая в интеграле замену t = — - х, получаем
Ti/2 п/2
J ln(sinx)d!x = J ln(cosx)dx,
о о
329
откуда
я/2
я/2
я/2
я/2
2 J ln(sinx)<fr = J ln(sinx)d!x + J ln(cosx)dk = J In
оооо
sin 2л;
л
dx-
lnr, (sin£A
= olln
I Tl
dt = --2 J ln(sin£)<fe—ln2.
71/2 n
Следовательно, J ln(sinx)d[x = —ln2.
о 2
J t=2x I
I dt = 2dx J
Задача 6.14
я/2
Вычислим интеграл /я = J sinnxdx^ для п е N и {0} и докажем формулу Валлиса1 1 2
о
Hm
И—>оо
(2я)П
(2я-1)П
1 _ 71
2п 2
Решение
Преобразуя исходный интеграл, получаем
я/2 я/2 я/2
In = I ?лъпхс1х = - J sin”-1xfi?(cosx) = -sin”-1xcosx|0 +(и-1) J Cos2Xsmn-2Xdx =
я/2
П-1
= (и -1) J (I - sin2 x)sin”-2 xdx = (n-1)/„_2 - (и -1)/„ /и = ^гЛ„-2-
п
Отсюда, взяв во внимание, что
я/2
I0= J dx = —, Ii= j sinxd!x = l,
O^0
делаем окончательный вывод о значении интеграла In:
я/2
Ilk ~
(2&-1)!! Tt (2*)П Jbc HufOI
(2Л)П 2’ ^24+1 (2^ + 1)!!’ ^ ' ''
(6.6)
Далее из элементарного неравенства sin2”+1X < Sin2nX < sin2”-1X заключаем, что
имеет место соотношение /2я+1 < I2n < Im-V Поэтому из формул (6.6) имеем
(2я)П (2я-1)И Tt (2я-2)П
■ < < <=>
(2я)П
(2я-1)Н
I Tt
< —<
2я + 1 2
(2я)П
(2я-1)Н
Л2
(2я + 1)П (2я)Н 2 (2я-1)Н
Докажем, что разность левой и правой частей стремится к нулю:
2 п
0<
(2я)Н
(2я-1)П
2п
2я
(2я)Н
(2я-1)П
(2я)П
1
(2я-1)П
2и + 1
1
(2я)П
(2я-1)Н
I Tt _
<-—— -> 0.
л2 /
1
1
2 п 2п +1
2я + 1 2п 2 п >°°
Покажем далее, что если
а„<Ь<сп
1 Аналогичный результат может быть получен после вычисления интеграла
я/2
Jn= I cosnxdx. Докажите равенство интегралов In и Jn.
о
2 Напомним, что (2и)!! = 2-4-...-2и, (2я-1)!1 = 1-3-...-(2я-1).
330
где b = const, и ап- сп —> 0, то Iim ап = Hm сп = Ь. Обозначим сп- ап = En, тогда En> О
П—^oo
и En —> 0. Тогда получаем
ап<Ь<сп + гп^О<Ь-ап<Еп.
По теореме о двух милиционерах получаем Hm ап = Ь, откуда и из условия ап -
TZ-» оо
- сп —> О получаем Hm Cn = Ь.
я—п—>°°
Следовательно,
Hm
TZ-
1 Г (2п)П ? 1
(2 п)\\
(2п-1)П
2 п
(2п)П
(2п-1)П
Tt
2п + 1 2
Рассмотрим пример интересного интеграла, подынтегральная функция
которого зависит от натурального параметра п, а его значение от п не зависит.
Задача 6.15
Вычислим интеграл Дирихле J dx, neN.
Решение
smx
TZ-I
Из элементарной формулы sin х + 2 sin х X cos 2kx = sin(2п - 1)х получаем тождество
k=i
1 sin(2n-l)x
— + Vcos Zkx = — —.
2 k=i 2 sin x
TI
Беря интеграл от О до — от левой и правой частей тождества, получаем
я/2
О
я/2 (л
V4 2 k=l
О
E//sin(2n-l)x , л//( I , I'V , п и I Tt
— —ах= — + У cos Ikx dx = \ cos2nxox = 0 для VneNi = -.
1 2sinx jo- ij I /
я/2
J
О
Искомый интеграл равен
42sm(2n-\)x , Tt
J —^ —ах = — для VneN.
sinx
Задача 6.16
Найдем следующие интегралы:
1 dx п/2
a) J ; б) J cosax(cosx)a~2dx, я>1;
i(e* + lK*2 + l) i
Я
в) Ь
xsin2" х
dx, neN; г) J ^ —dx, neN.
qsin2”х + cos2"х ’ ' ' ^n(i + 2x)sinx
Решение
а) Разложим исходный интеграл на два:
dx Я dx
J
(ox .
= I
+i
dx
Д (ех + 1)(х2 +1) Д (ех + 1)(х2 +1) о (еж + 1)(х2 +1)
Делая подстановку х = -х в первом интеграле, получаем
\ dx dx _
{ (<r* + 1)(х2 +1)+J0 (ех + 1)(х2 +1) "
-J
1
1
че-* + 1 + в* + 1,
dx
I + X2 Il
dx
+ х
_ Tt
2~Т
331
б) Вычисляем:
jc/2 п/2
J cosax(cosx)a~2dx = J cos [х(а -1) + x](cos x)a~2dx =
0 о
71/2
= I [cos(ra - 1)х cos x - sin(a - l)x sin x] (cos x)a~2 dx -
о
л/2 <2лт\( si IW
= J cos(a-l)x(cosx)e_1<ix + J — — d(cosa~lx) =
Q n Cl — I
0
Sin(a°_-1)x (COS^)--If = °.
в) Обозначим /(x) = —
sin2" x
sin2" x + cos2” x
. Заметим, что выполнено f(x) = f(n - x).
Разбивая исходный интеграл на два и делая в первом подстановку х = л - х, полу¬
чаем
л jc/2 тс тс Jc
fxf(x)dx = J xf(x)dx + J xf(x)dx = J [(л - х) + x\f(x)dx = л J f(x)dx.
О О п/2 п/2 п/2
Разбивая полученный интеграл на два и делая в первом подстановку х = ^ - х,
получаем
П
Зтс/4 л п (
п J f(x)dx = л j f(x)cbc + п j f(x)cbc = я J
п/2 п/2 Зтс/4 Зтс/4
Остается заметить, что
/I “*] + /(*)
dx.
/
Зя
-х
+/OO=
cos2" х
sin2" х
cos2" х + sin2" х sin2" х + cos2" х
л/
= 1.
Следовательно, искомый интеграл равен —.
г) Выполним преобразования:
W
sinrax
, г Sin TlX , f am л
ах = ах+
J7l(I-^x)Sinx o(l + 2*)
sinrax
-dx =
smx
_и(1 + 2х) sin х
г sinrax j f sinrax , nt(l + 2x)sinrax , ? sinrax ,
= dx+ dx= - dx= dx.
o(l + 2_x)sinx o(l + 2x)sinx J0 (l + 2x)sinx J0 sinx
Для га > 2 получаем
I. - 4-2 = = 2 J cos(n - = O = » I. = J„_2.
smx
Остается заметить, что J0 = 0, J1 = к. Поэтому окончательно имеем
ГО, если га = 26,
In=-
п, если n = 2k + l,
6 = 0,1,2
Оставляем читателю доказать более общее утверждение, чем в п. а) за¬
дачи 6.16, рассмотрение которого аналогично приведенному.
Задание 6.7
Пусть функция / непрерывна на отрезке [-а; а] и четна. Докажите, что
J {^/dx=Jf(x)dx.
-а1 + е О
332
Задача 6.17
].ln(l + дг) J Tl2 Un(I-Xft) J ,
Зная, что I — -ах = —, вычислим интеграл Ik = I — -ах, k E N.
п х 12 п х
Решение
Имеем
n х
t = Xk
, , L , , A? , dx
Ot = RXk 1Clx = —ах, или — = —
х kt х
4}Mz£)*4.
kJQ t k
Далее:
#=|jnOM 1
12 о х J0 х 2 1 2 1
_ 7I2 7l2
откуда Z1 = —,/* = —.
Задача 6.18
TT - Пп(1 + х) ,
Найдем интеграл I — ах.
Л 1 + х2
Решение
Сделаем в предложенном интеграле замену х = tg£. Получаем
1Inn+ г'» 71/4 71/4 ^
f ^ :;&= г in(i+tgo^= г in
п 1 + Х2 n п
я/4
= I In
о
cos
TI
\Л
V
cos?
dt = —ln2+ f In
8 {
я/4
COS
Ia
I
I
И Jj
sin?+ cos?
cost
я/4
fife =
dt- I ln(cos?)6/? = —In2.
о 8
Здесь мы использовали то, что два последних интеграла совпадают (докажите это!).
Задача 6.19
Пусть А(х) ё С[а\ A], h(x) > 0 и hn=jxnh(x)dx. Докажем, что при любом нату-
а
ральном т
det
К
^i
— V2
Vl
к
^2
- Vi
А*
V2
V1
— V-4
V-3
Vi
- ^2т-3
V-2
*0.
Решение
Рассмотрим систему уравнений относительно переменных с0, C1,..., ст4:
ь
0 = C(A) + <А +... + Cm4V1 = J h(x)(cQ + C1X +... + Cm4Xm-1 )<&,
а
ъ
0 = C0A1 + C1A2 +... + Cm4Am = J А(х)х(с0 + C1X +... + ст4хт-1)Дх,
0 = cO Vl + cV + - + Сп-Ат-2 = J A(x)xm-1(c0 + C1X +... + Cm4Xm"1 )Дх.
333
Далее домножим первое уравнение на с0, второе — на C1,последнее — на ст_{
ь
и сложим их. Получаем Jh(x)(c0 + C1X +... + ст_1хт~^)1 dx = 0, откуда в силу положитель-
а
ности функции h(x) получаем условие C0 = C1 = ... = ст-1 = 0, и поскольку однород¬
ная система имеет только тривиальное решение, то ее определитель отличен от нуля.
Задача 6.20
Докажем, что существует многочлен P такой, что для любого натурального числа п
П
выполнено J P(x)dx = nA.
п-1
Решение
Будем искать многочлен P в виде многочлена четвертой степени:
Р(х) = Oxi + Ьх3 + сх2 + dx + e.
После интегрирования получаем
I (от4 + Ьх3 + сх2 +dx + e)dx=
axJ
Ьх4
CXc
- + -
dx2
- + ex
n-1
7Z+1
= anA + 2an3 + 2an2 + an + — + bn3 +^^ + bn + — + cn2 + cn + — + dn+— + e.
5 2 4 3 2
Применяя метод неопределенных коэффициентов, получаем систему
а-1,
-2а + Ь = 0,
2а-—b + с = 0,
2
-a + b-c + d = 0,
1I1Il,
—а—Ь +—с—а+е- 0.
15 4 3 2
1
Решая систему, находим многочлен: Р(х) = X4 + 2х3 + X2 - —.
Замечание 6.8. После нахождения явного вида данного многочлена про-
П
сто получить формулу для суммы Yj Действительно,
Ь1
Y k4 = Y j P(x)dx = J P(x)dx
k=\ k=\k-I о
Hp п4 п3
п
30'
Задание 6.8
Найдите многочлен Р(х) такой, что для любого натурального числа п выполнено
п п
J P(x)dx = п5, и найдите сумму Y к5-
га-1 k~i
Задача 6.21
Определим все непрерывные на [0; +°°) и положительные на (0; +°°) функции,
удовлетворяющие для любого х > 0 условию:
X
a) 2xj f(t)dt = f(x)] б) sin J f(t)dt
о U
I + X
334
Решение
а) Переносим х в правую часть тождества и дифференцируем обе части:
(
_J \л)л
г2
V(X)-I - К**-/(х) «* 2 XV(X)- Пх)х- /(*)«♦ . «
V
У
1= ДгInZ(x)-x2-Inx = C ^ZW = ^re*2; х>0,С>0.
Z(*) х
б) Дифференцируя обе части предложенного тождества по х, имеем
/W~J/<0*-^«c»!/(0*( )-(1+xyf(xy
о
Обозначим I f(t)dt через а. Тогда получим
о
г2
I = sin2 а + cos2 а =
х*
(I + х)2 (I + XyiP(X)'
Решая алгебраическое уравнение, находим fix) =
(I + х)ТТ+2х
Задание 6.9
Определите все непрерывные функции, удовлетворяющие условию J etf(x - t)dt =
о
= sinx для VxeM.
Задача 6.22
Определим дважды непрерывно дифференцируемую на отрезке [0; 1] функцию,
удовлетворяющую условиям
JZCx^r = |, Z(0) = Z'(0) = 1, f"i* * x) ^ 0, х е (0; 1).
о ^
Решение
Рассмотрим на отрезке [0; 1] функцию g(x) = f(pc) - х - 1. Имеем
g(0) = О, g'(0) = О, g»W =Пх) > О, а: > 0.
Следовательно, g(x) > 0 на [0; 1]. Кроме того, получаем
Jg(x)& = J(Z(x)-l-x)& = |-| = 0.
0 0 11
Отсюда g(x) = 0 на [0; 1], a fix) = 1 + х.
6.6. Разные задачи на тему интегрального исчисления
Задача 6.23
Объясним интегрируемость функции f и найдем интеграл J fix)dx с помощью
х
интегральных сумм, если:
а) fix) =х2, X= [-1; 2];
б) fix) = lnx, X = [I; 2];
в) fix) = ln(l - 2acosx + я2), X = [0; 7t] при | а \ < 1 и | а \ > 1.
335
Решение
а) Интегрируемость функции/вытекает из ее непрерывности на отрезке [-1; 2].
Следовательно, для вычисления предела интегральных сумм можно выбрать любую
последовательность разбиений с диаметром, стремящимся к нулю, и любые отмечен¬
ные точки Ъ,к. Будем делить отрезок [-1; 2] на п равных частей, а в качестве точек ^
выбирать правые точки разбиения. Имеем1
3k
\x2dx = Iim Y^l^k H ^xk =—'Xk =xk =-1 +—,k = \,...,n\ =
dT^0 k=i
П
= Hm Y
n~^°°k=i
f
= Iim
n—^
f
\
-1+—
П
\2
Q Tl
— - Hm Y
n я->°° ^=1
n
f. 6k 9k2^
I + ^r-
V
n nr
Q 18 (n + l)n i 27 n(n + l)(2n + l)
O n I ~
n*
n?
= 3.
На рис. 6.8 изображена исследованная интегральная сумма для п = 15.
б) Обоснование интегрируемости — аналогично п. а), но точки разбиения выби¬
раем, как степени показательной функции, чтобы вычисления были более удобными.
Получаем
п
k-1
2 п k k-A k
[Ynxchc = Hm =iAr4 =2« -2 я -^k = 2n;k = i,...,n\ = Hm ^1п2и(2я -2 я ) =
I dT^ok=1 ~ "
i n „ k k-л | 2
= Hm-S^(2«-2 я )=Нт —
я—>°° п к=\ я->°° п
j n~^°°k=l
” -Сц„М.^-0-1 = 2Ь2-1.
2n~YS "
k=\
п—>°° п
I
2« -1
Рис. 6.8
в) Представим I - 2acosx +а2 в виде (а - cosx - ism х)(а - cosx + zsinx) и, исполь¬
зуя формулу Эйлера2, окончательно получаем
ln(l - 2 a cos х + а2) = In [(а - efe)(a - e_fe)].
1 После проведения этих трудоемких вычислений один из авторов предлагал своим
студентам посчитать предложенный интеграл с помощью формулы Ньютона — Лейбница
и убедиться в ее ценности.
2 е“ = cosx + zsinx, см, например, книгу [70, т. 2].
336
Вычислим предложенный нам интеграл:
1 Г /гг jr и 1
Jln((a - е“)(а - е-“))Дг = Jim J f(t,k)Axk = \ Axk = -, [ =
О dT^O A=O [ П П J
__ Yl—I .TZk .TZk __ л—^ .Tzk .Tlk
= Iim — J11п((а -е «)(а-е * ” )) = Hm — In П (а - е * )(а -е '« ).
и j=0 и A=O
Для вычисления получившегося произведения представим многочлен а2п - 1
в виде
2п-1
A2n-I= П («“«у),
j=0
где CLj — корни уравнения а2п- 1, т.е. числа на единичной окружности:
. Tzk . Tzk
е п , k = Q,i,...,n; е п , k-i,...,n-i.
Следовательно, справедливо равенство
2я-1
j^k Yi—\
а2п -1= П (а-ос ) = П(а-е « ) П(а-е ” )•
7=0 A=O A=I
Поэтому искомое произведение равно
Hm — • In <а ~ IXg2n -1),
га а +1
Отсюда ползаем, что при | а \ < 1 искомый предел равен нулю. При | а \ > 1 пре¬
образуем получившееся выражение:
я1п(а-1)(^ —:I), ^fnlna2+1п(«-1Х1-^)^
а + 1 ral а + 1
га
Следовательно, искомый предел равен л In а2. Окончательно получаем
0,если|А|<1
J ln(l - 2а cos х + A2 ) dx = •
л!пА2,если|А|>1.
Задача 6.24
Докажем, что Hm J П = Hm — J Vn2 -k2 =
п-=>°° j_j п2 + к2 и—><*> и2 J=J 4
Решение
Преобразуем первую предложенную сумму:
п _ 1 ” п2 _ I п 1
0.10 ^
jti H2-Vk2 H^iH2-Vk2 Ajti (k
1-1-
га
Это интегральная сумма интеграла: J —г- dx - arctgxl* = —.
01 + х2 '04
Аналогично получаем для второй суммы
Hm Дг J1 /п2 -k2 = Hm- J1 Jl- —1 = f/l-x2dx = —(x/l-x2 + arcsine)]* = —.
п—>°°га j=i гаj=i V ^ra,
Отсюда получаем предлагаемое равенство.
о 4
337
Задание 6.10
Найдите интеграл J f(x)dx с помощью интегральных сумм, если:
х
a)f(x) = i+x,X=[-U2];6)f(x)=x?,X=[U5]-,B)f(x) = -,X=[a-,b] (0<а<Ь);
X
г) f(x) = ах,а>0,Х= [0; 2].
Задача 6.25
C помощью определенных интегралов найдем пределы следующих сумм:
А п Оk/n
а) Нщ-Х
Zu л >
I1 ,JL
кп
б) limit/
П k=i
в) Hm
П—
a + k
2"-I
( k \\
I
1+—
On
\ Z) J
Ъ-а
п
2й
, / — интегрируемая на отрезке [я; 6] функция;
Решение
а) Преобразуем выражение, стоящее под знаком суммы:
I 2*/" = 1 ”, kn2k/n = I 2t/я 1 2*/
1 яЙ 1 + Ап яЙ я*Й1
kn
Оценим второе из получившихся выражений:
1 п nk/n \ п о 2(п-Х\
— = А } -» 0.
w fci 1 + кп п k=\ I + п п(п +1) п->°°
Предел первого выражения найдем с помощью определенного интеграла:
Iim - E 2*/” = Ibxk = /(л:) = 2*1 = j2xdx = Z-.
и^оо»7, . \ П П п 1п2
»-»“ п k=i
Следовательно, для искомого предела получаем
1
1 п 2к/
Hm-E
я-»~ П k=i
1 +
1 1п2
k-n
б) Представим
1 п
1E/
Wfcl
я + &
Ъ-а
п
1 6-я » ,
I Zu J
b-a п k=i
a + k
b-a
п )
откуда
1 "
Hm-E/
w A=i
^ ,6~ЯЛ
Я + й
V
п
в) Рассмотрим рп =
~2я-1
Г k л\
п
_ A=I
1+—
I 2” J
2п
. Имеем далее
1
рп = еыРп=ехр -In
2«-1 (
п
A=I
IH
2”
- = ехр
1 2”-1 / ге
— ЕЬ 1+—
2Я " I Чи
A=I
2”
откуда
Hm рп = ехр
Л
Jln(l + x)dx
Vo
_ g-l+ln4 _ _
338
Задание 6.11
Найдите пределы следующих сумм:
П—1 /э А П—I TT1?
a) Hm S 4; б) Iim-Esin-;
Я->°°А=1
я->°° И A=I
П
в) Hm £ kP, р >0; г) Hm ^ k2$k3 + га3;
я—*» A=I
д) Hm £
га
я->°° И4 A=I
; е) Hm £ ka~lf
(кЛ
n^ea A=I (га + Vra2 + &2 ’ я->°° w“ A=I
,/интегрируема на [0; 1], а > 1;
ж) Hm
п
П
Г. FY
1+-^
п
У
з) Iim
TZ-I
п/
-T
п—^00
A=I
I W2J.
TZ-
.A=I
,WyI.
,/непрерывна на [0; 1],/(х) > 0.
Задача 6.26
Пусть функции/и ф непрерывны на отрезке [я; b]. Докажем, что
п-1 6
lim. n S /(5 а M0A )Д*а = J f(x)<p(x)dx,
тах|Лх4Н04=0 а
где X4 < ^4, G4 < х4+1, Axk = х4+1 -xk,i = 0, I,..., га - I.
Решение
Для интеграла справа получаем
|/(х)ф(х)<& = Hm 5/(£4)ф(£4)Дх4.
тах|Дх4|—>0 4_0
Введем обозначения
Sn = 2 /&Ж5*)Д**. Sn = 2 /((цжадд**.
A=O A=O
Требуется доказать, что |5Я - JU —> 0 при max | Дх4| —> 0. Запишем
E f (^MWaxk - E f (ZkMQk)AXk
k=0 k=0
п-1,
^ E /(5а) • Ф(5а) - ф(0А>| • axIt
A=O
Из непрерывности функции / и теоремы Вейерштрасса вытекает, что 3 M > 0
такое, что для Vxe [я; Ь\ выполнено | /(х) | < М. Используя равномерную непрерыв¬
ность функции Ф(х) (по теореме Кантора), заключаем, что
|ф(5а)“Ф(0а)|^ suP |ф(*1)-ф(^)| = ю4(ф)<——|—г
XllX2Glx4; X4fl] ZM{b~a)
при достаточно малом тах|Дх4|. Окончательно находим
E |/(5а)|- I Ф(5а) - Ф(0а) I шАхк < м——-E \< е.
А=о 2М(о-я)а=о 2
что и доказывает наше утверждение.
Предлагаем читателю подумать над вопросом: будет ли данное утверж¬
дение иметь место, если функция ф лишь интегрируема?
Задача 6.27
Пусть функция /ограничена и монотонна на отрезке [0; 1]. Докажем, что
J/(x)<k--E/
о ^4=I
(к)
= O
'Г
,Wy
,Wy
при га—
339
Решение
1 д ^ ^
можно рассматривать как некоторую интегральную сумму
функции /на отрезке [0; 1]. Следовательно, для него выполнено:
<5.
1 п (
Выражение — ^/ —
«н
1 п .
(к]
H
ч
Vl
‘'з!
Пк=1
Используя то, что для рассматриваемого интеграла выполнено то же самое нера¬
венство
1 _
5 < J f(x)dx < S,
получаем
о
jf(x)dx--fif
о Я A=I
f
\Hj
<S-s.
Не ограничивая общности, будем считать, что функция/монотонно не убывает.
Тогда
- 1 ”
Пк=1
((кЛ
-/
(it-iY
\ 1
( п-1
72-1
1
/со+!;/
-/(0)-2/
=-(/(1)-/(0))=0
IUJ
I я ).
J п
L A=I
UJ
ы
UJ,
п
UJ
Задача 6.28
Докажем, что дважды непрерывно дифференцируемую функцию / можно пред¬
ставить в виде разности двух выпуклых вниз функций.
Решение
Введем в рассмотрение две неотрицательные функции
р(х) = тах{/"(х), 0}, п(х) = тах{-/"(.г), 0}.
t t
Обозначим их первообразные как P(t) = j p(^)d^, N(t) = f n(%)d%.
о о
Получаем f\x) =p(x) - n(x), откуда
X X
f(x) = j P(t)dt - J N (t)dt + ax+ b = u(x) - v(x),
о о
X X
где u(x) = J P(t)dt + ax + b, v(x) = jN(t)dt. Далее, так как u"(x) = p(x) > 0, v"(x) =
0 0
= n(x) > 0, то, используя следствие из критерия выпуклости, заключаем, что обе дан¬
ные функции выпуклы вниз.
Задача 6.29
Пусть функция / имеет производную /' в некоторой окрестности точки х, при¬
чем /' непрерывна в точке х. Докажем, что
( f и \ Л
Hm X
/
V
х +
k2 + n2
-/(*)
=f'(x) ’In л/2.
Решение
Используя теорему Лагранжа, ползаем
/
х +
к2 + п2
-т=п\)
k2 + п2 ’
340
где ^kn
(
х;х +
V
k2 + n2
, I < k < п. Далее, так как для всех k = 1, п выполнено
У
- х| < —, то в силу непрерывности функции/' в точке х получаем, что для V е > О
3 N(e) такое, что для V п > N(e) выполнено | /'(¾^) - /'(х) \ < е.
Следовательно,
EР&Огл*. 2 ~Ъ2к. 2 0ПРИ
A=I Rz+Hz A=I + И2
Далее получаем
k
=^A4[ln(1+*2)It=lnVi
п h \ п hn 1 п м
lim S = Hm - S = Hm - E ^
n->°° A=I R1 + Hz п->°° П A=I Rz + я-»~ П A=I У £ V
J1J
+ 1
Задача 6.30
Определим все интегрируемые на отрезке [0; 1] функции / удовлетворяющие
условиям
/(*Ч
Решение
Последовательно получаем
/
/
f-l
+ /
Гх+п
+/
(х+2Л
\
, [0,1];/
"Г
V
13 J
I з J
I 3 J
/
VjV
= 1.
/(*4
у
/ f +/
V Vd/
^х + Л ,fх + 2Т) 1 Д ,Гх + &Л
V
+ /
У/
=дЕ/|
У A=O
1 Зт-1
= ... = — V f
3- A=O
Х + &
Qffl
V0 У
, т>2.
Таким образом, правая часть есть интегральная сумма для функции / разбие-
1 2
х 1 + х Зт -1 + х
ния {хА} = ^0,—,—,...,П и точек
v KJ Qm Qm к Qm Qm
при т —> оо, получаем
■. Переходя к пределу
/(*) = J f(t)dt => /(х) = const => I f
о I
A-i'
It у
Задача 6.31
Функция/(x): [а; 6] —» R дифференцируема и /'(х)| < 1 всюду на отрезке [а; 6].
1
Докажем, что если а = X0 < X1 < ... < х„ = b, max(Xy5, - Xy5^1) < , Lli е [xk_{, xk), то
b-a
1<А<я
I f(x)dx - X f &к)(хк -X^1)
a A=I
4'
и покажем, что приведенная оценка неулучшаема, т.е. найдется функция, удовлетво¬
ряющая всем условиям задачи, на которой достигается равенство.
Решение
Преобразуем исследуемый интеграл в сумму интегралов по отрезкам \xk_{, xk\\
(6.7)
Ь п
га -rA
J f(x)dx - £ f(lk)(xk - xk_x)
=
E J (f(x)-f(lk))dx
a A=I
k=ixk-\
Имеем, далее, согласно теореме Лагранжа
!/(*) - /&) I=|/'<Ci)|-MJs У Xxi s 1} < |* ■- 5» I.
341
Подставляя последнее неравенство в тождество (6.7), получаем
J f{x)dx - £ /(£*)(** - хм)
k=i
Tl
I \x-%k\dx.
k=\
4-\
Вычислим результирующие интегралы непосредственно:
J \x-%k\dx= J <Xk-x)dx + X\(x-%k)dx=^k + <**£*> =
ч-1 U гг
-\ы + Xlt +251 - 25,(¾., + <йг|ы>!
(так как Ztk < хк, то равенство достигается лишь при ^ = xk_^). Следовательно,
Jf(x)dx- S f(W(xk ~xk-\)
k=i
< Y (xk xk-if <
~b 2
< < --M < i 4 *k~i =
[i<A<n o-aj O-Cik=i 2 2
так как (¾ - Xm) = b-a.
i
/(*) = XtXk- Xk_t = , ^ = Xm
b — a
все написанные неравенства превращаются в равенства.
6.7. Свойства интегрируемых функций
1. Пусть функция / интегрируема на отрезке [а; b] и [а*; й*] с [а; 6].
Тогда функция /интегрируема и на [а*; й*].
2. Пусть а < с < Ь, функция /интегрируема на отрезках [а; с] и [с; b].
Тогда/интегрируема на [а; &], причем
Ь с Ь
J f(x)dx = J f{x)cbc + J f(x)dx (6.8)
а а с
(аддитивность интеграла относительно отрезков интегрирования).
а а Ъ
Замечание 6.9. Положив J f{x)dx = 0, a j f{x)cbc = -J f{x)dx при а < b,
а Ъ а
убеждаемся в том, что равенство (6.8) справедливо при любом располо¬
жении точек а, Ь, с для функции / интегрируемой на отрезке, содержащем
эти точки.
3. Если функции /ng интегрируемы на отрезке [a; b\, a a, P е R, то
функции а/± Pg также интегрируемы на [а; Ь], причем
ь ъ ь
J (af(x) ± Pg(x))dx = а| f{x)dx ± Pj g{x)chc
а а а
{линейность интеграла).
4. Если функции fug интегрируемы на [а; Ь\, то их произведение / • g
также интегрируемо на [а; Ь\.
342
5. Пусть функции fug интегрируемы на [а; Ь] и f<g на [а; Ь\. Тогда
ъ ъ
I f(x)dx < J g(x)dx.
а а
Следствие 6.5. Если для всех х G [а; Ь] выполнено /(х) > 0, то и
Ъ
J f(x)dx > 0.
а
6. Если функция/интегрируема на [а; Ь\, то и | /1 интегрируема на [а; Ъ],
причем справедливо неравенство
jf(x)dx
а
<\\f(x)\dx.
а
Возникает вопрос: следует ли из интегрируемости функции | /1 инте¬
грируемость функции /? Ответ на этот вопрос — отрицательный. Действи¬
тельно, пусть
Jl, если х G Q,
Х |-1, если х 6 R\Q.
Тогда функция |/| тождественно равна единице и интегрируема
по любому конечному отрезку, однако сама функция/неинтегрируема как
модификация функции Дирихле.
7. Пусть функция / интегрируема на отрезке [а; b] и /* отличается от /
лишь в конечном числе точек. Тогда/* также интегрируема на [а; Ь\, при¬
чем
b ь
J f(x)cbc = J f*(x)dx.
а а
Возникает вопрос: можно ли утверждать аналогичное, если функция /*
отличается от/в счетном числе точек? Ответ на этот вопрос — отрицатель¬
ный. Действительно, неинтегрируемая функция Дирихле отлична от тож¬
дественного нуля (понятное дело, интегрируемого) лишь в счетном числе
рациональных точек.
Рассмотрим вопрос об интегрируемости суперпозиции функций. Для
начала поставим следующий вопрос. Пусть функции fug интегрируемы.
Обязательно ли будет интегрируема их суперпозиция g(f)? Ответ на дан¬
ный вопрос — отрицательный. Действительно, пусть
1, если X = 0,
£(*) =
[1, если х Ф 0,
[О, если х = 0;
/(*) = -
—, если X = — gQ,
п п
0, еслихеМ\(0).
Выше было доказано, что обе эти функции интегрируемы на отрезке
[0; 1]. Тогда
g(/(х)) = D(X) =
[l, если х G Q,
[0, e^HXGR\Q.
343
Нами получена неинтегрируемая функция, являющаяся суперпози¬
цией двух интегрируемых функций. Следовательно, появляется такой
вопрос: какие дополнительные требования нужно наложить на функции /
и g для того, чтобы их суперпозиция была бы интегрируемой? Напомним
читателю следующее определение.
Определение 6.11. Говорят, что функция / удовлетворяет условию Лип¬
шица на отрезке [я; Ь]1, если 3 С> 0 такая, что для V X1, X2 е [я; Ь] выполнено
I/(Xi) -/(х2) I < Cjx1 - х2|, при этом C называется константой Липшица.
Теорема 6.10. Пусть функция / интегрируема на отрезке [я; Ъ],
M = sup /(х), т = inf fix), и пусть функция g удовлетворяет условию Лип-
[а\Ъ\ [«;*]
шица на отрезке [т; М\ с константой C > 0. Тогда сложная функция gif)
интегрируема на отрезке [я; Ъ].
Доказательство
Зафиксируем произвольное е > 0. В силу интегрируемости функции /
на [я; Ь] существует разбиение T = [Xi) отрезка [я; Ь] такое, что для верхней
и нижней сумм Дарбу выполнено
ST(/)-lr(/)<j-
Пусть, далее, Mk, mk, M*k, mk — точные верхние и нижние грани на отрезке
\xk_{, xk] функций / и gif) соответственно. Тогда для всех ^1, ^2 G \xk_{, xk]
справедливо
g(/(li))-g(/(l2))£|g(/(li))-«(/(l2))|^C|/(li)-/&)NC(Ms-mj).
Поскольку точки и \2 выбираются произвольно, то полученное нера¬
венство гарантирует выполнимость неравенства M*k -m*k< CiMk - mk). Сле¬
довательно,
Srigif))-srigif)) =IiMl-m*k)Axk <C^iMk-mk)Axk <C- = в.
k=\ k=\ C
Очевидно, что функция, удовлетворяющая условию Липшица на неко¬
тором отрезке, является равномерно непрерывной. Обратное, вообще
говоря, неверно. Рассмотрим пример непрерывной на [0; 1] функции
fix) = л/х. Предположим, что она удовлетворяет условию Липшица. Пусть
3 C > 0 такое, что для всех X1, X2 G [0; 1] выполняется
-X2
Положим х2 = 0, X1 > 0. Получаем
< C^x1I <=>-
1
зГуЛ
Устремляя X1 к нулю, получаем противоречие.
1 Напомним, что условие Липшица является частным случаем условия Гельдера — Лип¬
шица при показателе а = 1.
344
Возникает вопрос: можно ли ослабить формулировку последней тео¬
ремы и заменить удовлетворение условию Липшица на непрерывность?
Ответ на этот вопрос — положительный.
Теорема 6.11. Пусть функция / интегрируема на отрезке [я; b] и
M = sup/(x), ти= inf/(х). Пусть, кроме того, функция g непрерывна
[аМ
на отрезке [т; М]. Тогда их суперпозиция g(f) интегрируема на [а; Ь].
Доказательство
Выберем произвольные числа в > 0 и о > 0. Так как функция g непре¬
рывна на отрезке [7тг; М\, то она равномерно непрерывна на [77г; М]. Тогда
по выбранному выше числу в найдется число ц(е) > 0 такое, что в любом
интервале значений функции / с длиной меньше Г| колебание функции g
co(g) меньше в. Отметим знаком k' интервалы с колебаниями, большими
либо равными ц, a k" — интервалы с колебаниями, меньшими ц.
Далее, так как функция / интегрируема на [я; Ъ\, то по числам г\ и ст
найдется число 8(г|, о) такое, что при диаметре разбиения, меньшем 8,
сумма длин тех из интервалов, для которых колебания функции (%(/) > Г|,
сама меньше о. Для прочих интервалов имеем (%, (/) < г\, а следовательно,
по найденному числу ц (см. начало), со(g(f)) < в. Таким образом, для функ¬
ции g(f) колебания могут оказаться больше либо равны в лишь в некоторых
из интервалов первой группы, сумма длин которых меньше о. По критерию
Дюбуа — Реймона заключаем, что функция g(f) интегрируема на отрезке
[я; b\. U
Отметим, однако, что требование непрерывности функции g не явля¬
ется необходимым для интегрируемости сложной функции g(f). Рассмо¬
трим следующий пример. Пусть /(х) = х, g(y) = R(y), где R — функция
Римана. Тогда g(f(x)) = R(x) интегрируема на любом отрезке, несмотря
на то что функция g имеет точки разрыва всюду плотно. Обратим внима¬
ние и на то, что композиция g(f), где g — интегрируема, а / — непрерывна,
может и не быть интегрируемой1.
Рассмотрим далее интересный вопрос, который поднимался нами ранее.
Задача 6.32
Пусть функция / непрерывна в точке X0 е М, т.е. для V е > 0 3 8(e) > 0 такое,
что для V х е -B5(X0) выполнено |/(х) -/(х0) | < е. Докажем, что в данном условии
для V е > 0 всегда можно так подобрать 8(e), чтобы функция 8(e) будет непрерыв¬
ной при е > 0.
Решение
Рассмотрим вспомогательную функцию
Д(е) := sup{8 > 01V х ё -B5(X0) => |/(х) - /(х0)| < е}.
Для нее получаем Д(е) > 0, причем Д(е) может принимать значение +°°. Однако
если для V е > 0 имеем Д(е) = +°°, то /(х) = /(х0) и в качестве 8(e) (из определе¬
ния непрерывности) может быть выбрана, например, любая постоянная функция.
Заметим также, что если 0 < B1 < е2, то Д(еД < Д(е2), т.е. функция Д(е) монотонна,
а значит, интегрируема. 1 11 Предлагаем читателю обратиться за примером к ресурсу www.mathoverflow.net.
345
Пусть, далее, е = sup{e > 018(e) < +°°}. Составим функцию
5(e) =
1
-J A (t)dt, если 0 < е < е0,
eO
I Ео
— J A(t)dt, если е0 < е.
ео о
Так как интеграл с верхним пределом и 1/е — непрерывные функции, то и их
произведение — непрерывная функция. Кроме того, легко показать, что для моно-
1е
тонной функции Д(е) выполнено -J A(t)dt < Л(е), т.е. указанная функция удовлет¬
воряет условиям задачи. * 1 * 1В заключение данного параграфа рассмотрим несколько задач на инте¬
грирование функции Кантора (см. гл. 3). Для начала проведем следующие
выкладки. Так как функция Кантора ср непрерывна на отрезке [0; 1], то она
интегрируема на нем. Вычислим интеграл J(p(j<c)dx\
I I
J ф (x)dx = {ф(х) + ф(1 — х) = l} = J (1 — ф(1 - x))dx =
о о
I 1
= I-J ф(1 - x)dx = I-J ф (x)dx.
0 о
1 1 1
Отсюда заключаем, что 2J ф(x)dx = IhJ ф(x)cbc = —. Отметим также, что
о
нами была вычислена площадь под графиком функции Кантора (рис. 6.9),
которая, однако, могла быть найдена при использовании симметрии гра¬
фика данной функции относительно прямой у = х.
346
Рассмотрим далее более сложную задачу, а именно, попробуем вычис¬
лить интеграл
1
J х2ср {x)dx.
о
Для начала покажем поучительное неправильное решение предлагаемой
задачи.
А именно, интегрируя данный интеграл по частям и используя то, что
производная функции Кантора равна нулю почти всюду, получаем
J х2ф (x)dx = — фОО|р - J—ф '(x)cbc = — = \x2cbc.
о 3 о 3 3 о
Но в силу того что ф(х) < 1 при х G [0; 1), должно выполняться строгое
I 1
неравенство: J x2(p(x)cbc < J x2dx. Это хорошо видно и на рис. 6.10, где рядом
о о
изображены функции у = х2,у = х2ц>(х) и отмечена разность между их пло¬
щадями. Предлагаем читателю самостоятельно разобраться в возникнове¬
нии полученной ошибки и приведем правильное решение.
Воспользуемся формулами, которые приводились в гл. 3:
Ф
=|ф(*);
ф
2 х
1
3 3
л 1 j
= — + -ф(х).
2 2
Кроме того, вспомним, что на отрезке [1/3; 2/3] функция Кантора пред¬
ставляет из себя константу 1/2. Вычислим сначала вспомогательный инте¬
грал:
347
J = j хф {x)dx = J хф (x)dx + — + J хф(х)й6с = J-Ф
+J
о
Г 2 О
(2 О
Ф
1з 3J
1з 3J
dt J 11
— = 1 1—
3 18 12 18
2
3
Sr- 1
v3 у
dt 1
—I 1-
3 12
л
- + l(2 + t)q>(t)dt
о
J
т 2 1
= —+ - +—(1 + /)•
18 9 18v
1 5
Отсюда J = |хф(х)г&: = —. Выше мы воспользовались формулой
о 16
1 1
Jcp(x) = —. Далее получаем
о ^
1
1 з у I 1
I = I х2ф (x)dx = J x2q>(x)dx H + J х2ф (x)dx = J
о о 132 2 о
v3y
I dt 7
-ф(0— + +
2yw3 162
Itn + Л2 (I I
2 t
1
3 3
+ -ф(0
2 2yw
26 1
dt
I
4_
26
1
3 “
54
162
54
(
54 +162 ' 54
л
2 + - + /
4
= — +
о
143
И
27 168 48
Отметим, что, используя аналогичную технику, можно вывести итера-
1
ционную формулу для вычисления интеграла J xk(p(x)dx, k E N. Оставляем
о
эти рассуждения читателю.
Для самостоятельной работы предлагаем читателю следующие задачи.
Задание 6.12
Вычислите интегралы:
I 1
a) L(a) = Ieax ф(x)dx; б) J sin(7ix)9(x)d!r.
о о
Указание: Для вычисления первого интеграла выведите рекуррентную формулу,
1
далее перейдите в ней к пределу, используя тот факт, что Iim Да) = —. Второй инте-
а—> 0 2
piwc _ 0-im
грал выводится из первого при использовании формулы Эйлера Sin(Tix) =
I
Отсюда данный интеграл равен - L(-iri)).
2i4 '
Задание 6.13
Докажите равенство J arct§ х dx=— J dt.
2 i
х
2 о sin^
Задание 6.14
Пусть функция / дважды непрерывно дифференцируема. Найдите интеграл
ь
I xf"(x)dx.
348
Задание 6.15
Пусть функция /непрерывна и строго положительна на отрезке [0; 1]. Найдите
интеграл J
/(*)
о/0) + /(1-*)
cbc.
Задание 6.16
Пусть функция f(x) интегрируема на отрезке [а; Ь\. Докажите, что
6-е Ъ
Hm J f(x)dx = ff(x)dx, 0<e<b-a.
е->0+0 * „
а+е а
Задание 6.17
Пусть функция / удовлетворяет на отрезке [0; 1] условию Липшица порядка 1
1
с постоянной L и такова, что J f(x)dx = 0. Докажите, что для всех натуральных п вы-
о
полняется неравенство
п-1
(кЛ
If
k=0
6.8. Оценки интегралов. Теоремы о среднем
Определение 6.12. Пусть функция / интегрируема на отрезке [я; Ь\,
тогда выражение
М[/] =
называется средним значением функции/на [я; Ь].
Утверждение 6.12. Если функция / непрерывна на отрезке [я; Ь\, то
3 £ е (а; Ъ) такое, что M[f] = /(£).
Теорема 6.12 (первая теорема о среднем). Пусть выполнено:
1) f и ср интегрируемы на [а; Ь];
2) ср > 0(или < 0) на [я; Ь\.
ъ ъ
Тогда 3 р g [ inf f(x); sup f(x)\ такое, что J f(x)q>(x)cbc = pj ф(x)dx. Если,
[a;b] a a
дополнительно, f(x) непрерывна на [я; b], тоЗ^е [я; b] такое, что р = /(£).
Теорема 6.13 (вторая теорема о среднем). Пусть выполнено:
1) / и ф интегрируемы на [а; Ь\,
2) ф монотонна на [я; Ь\.
ъ % ь
Тогда 3 £ е [я; b] такое, что J f(x)<p(x)dx = ф(я)| f(x)dx + ф(й)| f(x)dx.
а а Ъ,
b
Если ф(х) > 0, ф(х)\, то 3 е [я; Ь\ такое, что J f(x)q>(x)dx = ф(я) J f{x)dx.
а а
b b
Если ф(х) > 0, ф(х)/, то 3 е [я; Ь] такое, что { f{x)($(x)cbc = ф(b) J f(x)dx.
а &
Замечание 6.10. Последние две формулы иногда называют формулами
Бонне.
~г~ j f(x)dx
b-at
349
Рассмотрим далее несколько теоретических задач.
Задача 6.33
1?
Пусть функция/интегрируема на [0;+оо) и Hm /(х) = А. Найдем Hm —jf(t)dt.
х->+“ X ,
Решение
По определению предела Hm f(x) = Л<=>Уе>03б>0:Ух>й выполнено
|/(х)-Л|<—.
Выберем х > Ъ, тогда имеем
-1 f(t)dt = -\f(t)dt + -\f(t)dt.
х
X1
X
b
В силу интегрируемости функции / получаем J f(t)dt = C = const. Используя это
о
и применяя ко второму интегралу первую теорему о среднем, получаем
rSfm=£+№’Sdt=£
ЛУ* * yV/. АЛ * /у4
•Д/ п A A I1 «А
I-A
х
, Tl(X) E (inffit), sup fit)).
[b;x] [b;x]
Следовательно,
-\f(t)dt-A
C / 4
— + Tl(X)
X
1--
X
-A
JC-ri(x)6| I . . .I
<J + m(x) - A < e
x
при достаточно большом x > feH Отсюда заключаем, что
А X
Hm —\f(t)dt = A.
ж->+“ X п
Замечание 6.11. Если предполагать, что функция / непрерывна, то ее
X
первообразная F(x)=jf(t)dt дифференцируема. Тогда доказанное утверж-
о
дение вытекает из правила Лопиталя.
Можно ввести понятие сходимости интеграла в среднем.
+OO
Определение 6.13. Будем говорить, что интеграл J f(t)dt сходится
в среднем к числу А, если
]f{t)dt
3 Iim
х—>+°° X
■= Hm M[f] = А.
х—>+°°
Выше было фактически показано, что если Hm f(x) = A, то и в сред-
X—»+°°
нем интеграл сходится к числу А. Возникает следующий вопрос: будет ли
справедлива обратная теорема (т.е. верно ли, что если 3 Hm M[f] = А, то
X—>+°°
и Hm f(x) = А)? Ответ на этот вопрос будет дан ниже.
X—>+°° 1 11 Так как/(х) —> А при х —> +°°, то и ri(x) —> А.
350
Задание 6.18
Пусть функция / непрерывна на луче [0; +°°) и Iim /(х) = А. Вычислите предел
Х-Н-оо
1
Hm J f(nx)dx.
И—H-оо q
Задача 6.34
Пусть / и g непрерывны на луче [0; +«>), причем Hm /(х) = a, Hm xg(x) - b.
л:—>+°° х—>+°°
(
х
\
Вычислим предел Hm
X—И-00
g(x)\f(t)dt .
V о
Решение
Преобразовывая исходное выражение, получаем
g(x) J f(t)dt = g(x) -X--J f(t)dt.
O "rO
Тогда из предыдущей задачи получаем, что искомый предел равен
( х \
Iim
х—
g(x)jf(t)dt
= Ъа.
Отметим, что требование существования предела на бесконечности
подынтегральной функции не является необходимым для существова¬
ния предела данного выражения. Действительно, рассмотрим следующий
вопрос.
Задача 6.35
Приведем пример непрерывной на [0; +°°) функции /, для которой существует
конечный предел Hm
X—>+°°
Г AX Л
-\f(t)dt
vx0
, но не существует Hm /(х).
Решение
Выберем какую-либо периодическую функцию. Например, пусть /(х) = sinx.
Предела Hm sinx не существует (докажите!). Однако
X—>+■»
\х I IX
-Isintdt = —cos Д
'у * у IO
шЛ/ 0 яЛ/
I-COSX
X
= 0.
Задача 6.36
Пусть функции/ngнепрерывны на полуотрезке [0; 1), причем: 1) для Vxe [0; 1)
/ N-1
X X
х f(x) х
g(x)> 0;2) Hm \g(t)dt = +°°; 3) Hm J ' = а. Докажем, что Hm J f(t)dt ■ J g(t)dt
4. V 4 Л* я- Л rf Я Л/* \ ля V-I Ae- *
л;—>1-0
О
*->l-Og(;t:)
ж->1-0
О
VO
= а.
Решение
fix)
Пусть J v ' = а + а(х), где а(х) —» 0. Тогда
g(x) х->1-0
fix) - g(x)(a + а(х)) <=> J fix)dx - J g(x)(a + aix))dx.
о о
Далее, для любого E > О (выберем его равным —) можно найти такое 5(e), что
а
для всех х из интервала (1 - 5; 1) будет выполнено а + а(х)>—. Следовательно,
351
для всех таких х получаем \f(t)dt >—jg(t)dt
о ^ о
непрерывности функций / и g на [0; 1) получаем дифференцируемость функций
X X
F(x) = $ f(t)dt и G(x) = I g(t)dt. Применяя правило Лопиталя к искомому пределу,
о о
получаем требуемое.
Поэтому Hm \f(t)dt = +°°. В силу
л:—>1—0 q
Для решения следующей задачи нам потребуется предварительно дока¬
зать утверждение.
Утверждение 6.13 (интегральное неравенство Коши — Буняков-
ского). Если функции /и g интегрируемы на отрезке [а; Ь\, то выполнено
неравенство
(ъ
\а
\f(t)g{t)dt <\f2(t)dt-\g2(t)dt.
Доказательство
Для произвольного XgR имеем
J</(f)+Ag(O)2A >0^
а
ъ ъ ъ
=^>X2jg2 (t)dt + 2Xf f(t)g(t)dt + \f2 (t)dt = AX2 +2BX + C>0,
a a a
где А, В, C — постоянные. В левой части неравенства стоит квадратный
трехчлен относительно X. Его неотрицательность свидетельствует о том,
что он не имеет различных действительных корней, т.е. его дискриминант
B2-AC < 0, или
(ъ
\2
\а
/ f(f)g(f)dt < J f2 (t)dt ■ J g2 (t)dt.
Задача 6.37
Пусть / — непрерывно дифференцируемая на отрезке [а; Ь\ функция, /(а) = 0,
M=sup I f(x) |. Докажем, что
[о; Ь]
ъ
M2 <(b- a)j {f'{xpdx.
а
Решение
Из интегрального неравенства Коши — Буняковского, примененного к функциям
/'и 1, получаем, что для Vxe (а; b) выполнено
а
Поэтому, используя условие /(а) = 0, получаем
|/(х)| < Jj (/Xtjfdt ■ fx-a < j (JXtpdt ■ fb-a.
352
Отсюда, возводя левую и правую части неравенства в квадрат (обе они неотри¬
цательны), получаем требуемое.
Задача 6.38
Пусть функция / непрерывна на отрезке [я; Ъ
что для любых а, (3 (я < а < (3 < Ъ) выполнено
и найдутся такие числа М, 5 > О,
J f(x)dx
<М I (3 - а |1+5 . Докажем,
что f(x) = 0 на отрезке [я; Ь\.
Решение
Для произвольного а е [я; Ь] выберем строго положительные числа Ek такие, что
Ek —> 0 и а + Ek < Ъ. Тогда по условию задачи получаем
£->°°
(Х+Е*
J f(x)dx
<Ме|+5.
а
Далее по теореме о среднем получаем
«+е*
I fix)dx = filk)Ek,
а
где Sa 6 (а; а + Ek).
Следовательно, \fi%k)\Ek <Me|+1, или |/(^)|<MEk. Отсюда заключаем, что
|/(£а)| 0. Так как функция /непрерывна и Stk —> а, имеем/(а) = 0. В силу произ-
k—> OO OO
вольности выбора а получаем, что fix) = О на [я; Ь), а в силу непрерывности функ¬
ции / на отрезке [я; b] получаем, что и fib) = 0.
Задача 6.39
Пусть функция /непрерывна на луче [0; -н») и для любых я, Ь, таких что О < я < Ъ,
и 8 > О выполнено неравенство
Ъ 6+5
\fix)dx< J fix)dx.
а а+5
Докажем, что функция/не убывает на [0; +°°).
Решение
Пусть произвольные числа X1 и X2 такие, что О < X1 < X2. Возьмем в неравенстве
из условия задачи а = X1, b = X1 + х, х > 0, 8 = X2 - X1.
х^+х Х2+х
Тогда получаем J fit)dt< J fit)dt. По теореме о среднем имеем
х\ х2
fi&iix))x < fi&2ix))x <=> /(едх)) < Де2(х)),
где X1 < 0/х) <х1 + х,х2< 02(х) <х2 + х. Переходя к пределу прих —> 0, с учетом непре¬
рывности функции/получаем требуемое неравенство:/^) </(х2).
Замечание 6.12. Условие из последней задачи можно записать в виде
л Ъ л Ь+Ъ
-—\fix)dx<-— I f(x)dx,
b~aa b~aa+b
т.е. М[а;А][/]<М[а+5;й+5][/], функция f в среднем не возрастает. Покажите,
что если функция/интегрируема на [0; х] для любого хине возрастает, то
353
она не возрастает и в среднем. Обратное, как показано выше, верно для не¬
прерывных функций. Однако для только лишь интегрируемых функций
обратное утверждение, вообще говоря, не верно. Например, рассмотрим
функцию
/(*)=•
п, если х = п е N,
О, если i^weN.
Ь Ь+8
Тогда, для любых а, Ь, 8 получаем J f{x)dx = 0 < J f(x)dx = 0, но функ-
а а+5
ция / не монотонна.
Для функции
[ п, если i = wgN,
I -х, если х 5* я е N
/(*) = ■
неравенство строгое, но вывод тот же* 1 *.
Задача 6.40
Пусть функция /непрерывно дифференцируема на отрезке [0; 1]. Докажем, что
3 £ € (0; 1) такое, что
jf(x)dx = f( 0) + ^¾
о z
Решение
Имеем
J f(x)dx = { f(x)d(x -1) = (х -1) /(х)| J - J(x -1 )f'(x)dx.
оо о
Применив к последнему интегралу теорему о среднем, получаем
}/(*)*=/(0)-/'(OJ(*-l)*=/(0)+^S), £.е(0;1).
0 Oz
Предлагаем читателю самостоятельно рассмотреть следующую задачу.
Задание 6.19
Пусть функция /дважды непрерывно дифференцируема на отрезке [0; 1]. Дока-
1 f'(0) f"(£)
жите, что 3 £ е (0; 1) такое, что f f(x)dx = /(0) + —— + J .
о 2 6
Задача 6.41
Вычислим пределы:
п/2
а) Hm f sin nxdx;
о
f(x)
б) Iim J J v ' dx, где a > 0, b > 0 и f(x) непрерывна на [0; I];
e^0+0 aE x
в) Hm
f n+1
П4 J -
J I
V я
X
+ X3
dx
1 Вообще, можно для многих утверждений показать, что они верны для непрерывных
функций, но не для интегрируемых.
354
Решение
а) Зафиксируем произвольное е, удовлетворяющее неравенству 0 < E < л, и разо¬
бьем исходный интеграл на сумму двух:
я/2 я/2-е/2 л/2
In = J sinnxdx= I smnxcbc+ J smnxdx = +1^2\
О 0 я/2-б/2
Ь
Применяя теорему о среднем (если 0 < /(х) < С, то J f(x)dx < C(b - а)) и исполь-
а
зуя неравенство sin" х < 1, получаем
IiiKiPz
^JI EN
^TI E^j
I
I
1<М
sin
\2~2)_
где у = sin
Г П E^
2~2
E 71 „ E
+ -< — -Y +-,
2 2' 2
< 1. Поэтому 3 N(е) : для V п > Nвыполнено уп <—.
л
E E
Следовательно, для таких и выполнено 0<1п < — + — = £, т.е. Hm In = 0.
2 2 я—>°°
б) Применяя первую теорему о среднем, получаем
^ /Y -»Л ^ //у А
= — =/©1п-,
^ f {\ Jj
где ае<Е< be. Поэтому Hm £ = 0, a Hm f 7 v J chc = /(O)In-.
Е->0+0 е->о+о 4 X а
в) Вычисление предложенного интеграла весьма трудоемко, поэтому восполь-
1 х 1
зуемся неравенством — < - < —, откуда
Я+1 4 П+1 „ Я+1 4
I jdx< [ edx < f —rdx.
я О + 1)4 п 1 + Х п Х
Вычисляя интегралы, стоящие слева и справа (домноженные на п4), получаем
я+1
я+1
Hq
Hq
я+1
3(п +1)3 3(n + 2)3
< п
р X 1 и~
-ах<—--
I 1 + х5 Зп3 3(п +1)3
nq
Пределы левой и правой частей равны единице. Следовательно, и
я+1
Hm
П-^оо
A C Х
п S
1 1 + Х5
-dx
= 1.
Для самостоятельной работы предлагаем читателю следующие задания.
Задание 6.20
Докажите справедливость тождества
£+1 X
Hm t4 f -dx = 1, где t е К.
t 1 + х5
Задание 6.21
п+Р sin X 2” X
Вычислите пределы: a) Hm [ dx, р> 0; б) Hmw3 [ -dx.
п=>°° п X п=>°° ^ 1 + Х5
Задача 6.42
Пусть /(х) =
cos^,еслих>0,и = Jх>0 Вычислим F(O).
0, если х = 0 0
355
Решение
Имеем F(O) = 0. Для х > 0 по определению несобственного интеграла второго
X
рода1 выполнено F(x) = Hm J f(t)dt. Далее получаем
5->0+0 g
X ^ X
Jcos -dt = -\t2d
St 8
=> F(x) = Hm
8->0+0
(. 0
Sin-
■ 2 • 1
= -tl sm-
I tJ
t
X ^
+ 2\tsm-dt-
\
-X2 sin— + 82 sin— + 2 f £ sin-fife
x Si t
1*1
=-X2 sin— + 2j£sin-dt, x>0.
x
Следовательно,
,. F(x)-F(O) . I , 2xt . 1A
-F (0) = Hm — = -xsin— + —I tsm-dt.
*->0 X XXnt
Используя результат задачи 6.36, получаем
О X л (
откуда F'(0) = 0.
А " 1
Hm-J £ sin-fife = 2 Hm
X—>0 X Q t %—
. I
xsm—
X
V
= 0,
Задача 6.43
Пусть 0 < а < Ь. Докажем, что J(x2 + i)e~x2dx>e~al -e~bl.
Решение a
X
Обозначим f(x) = J (t2 + V)e~t2, g(x) = -e~x'2. Используя теорему Коши о конечных
о
приращениях и неравенство Коши (между обыкновенными средними), получаем
т-т /'® п
S'® 2&-i2 2
I
I
Поэтому
t+i№-L
J (х2 +1) e~%2dx = f(b) - f (а) > g(b) - g(a) = e~a2 - e~b2
Другое решение задачи 6.43 можно получить, используя неравенство (х2 + \)е~х2 >
> 2хе~х2. Оставляем его читателю.
Задача 6.44
Пусть/— непрерывная функция, действующая из [0; 1] в R, такая что для Ух, у E [0; 1]
TL
выполняется неравенство xf(y) + yf(x) < 1. Докажем, что J f(x)dx < —, и найдем функ-
о 4
цию, которая данное неравенство обращает в тождество.
Решение
Делая в исследуемом интеграле замены х = sin а и у = cos а, получаем
1 я/2 п/2
\f(x)dx= J /(sina)cosafi?a= J /(cos a) sin a a.
oo о
1 Читатель, незнакомый с несобственными интегралами, может вернуться к данной
задаче после прочтения главы до конца.
356
Используя неравенство из условия задачи, получаем
п/2
к/2
TL
2 J f(x)dx = J (/(sin a)cos а + /(cos а)sin a)da < J da. = —,
oo о 2
TL
или J f(x)dx < —, что и требовалось доказать,
о 4
Равенство достигается, например, на функции f(x) = \Ji-x2. Данная функция
является непрерывной, для нее получаем j^li-x2dx = — и при х = sin а, у = sin|3,
о 4
а,Pg
V 2у
, имеем
xf(y) + у fix) = sin а cos P + sin P cos а = sin(a + Р) < I.
6.9. Несобственные интегралы.
Условная и абсолютная сходимости
Определение 6.14. Пусть для любого be R функция / интегрируема
на отрезке [а; Ь]. Несобственным интегралом первого рода называется выра¬
жение
+OO Ъ
f(x)dx = Hm
Если данный предел существует, то несобственный интеграл сходится
(обозначение —>), иначе — расходится (обозначение /4).
Интеграл от функции / по бесконечному интервалу (-°°; +°°) определя¬
ется как
А"
Hm J f{x)dx
А —OO Л,
при независимом стремлении А' —» А" —» +°о.
Определение 6.15. Пусть для любого е > О функция / интегрируема
на [а; b - е] и Hm , или функция/не ограничена в окрестности
х->6-О
точки Ъ. Несобственным интегралом второго рода называется выражение
ь
Ь-е
[ f(x)dx - Hm
■ Е->0+0
а
J f{x)dx.
Сходимость/расходимость определяются аналогично предыдущему
случаю.
1
Замечание 6.13. Заменой11 = несобственный интеграл второго рода
х-Ъ
преобразуется в несобственный интеграл первого рода. При этом особен¬
ность второго рода преобразуется в особенность первого рода (докажите!).
1 Теорема о замене переменных в несобственном интеграле приведена ниже.
357
Утверждение 6.14 (формула интегрирования по частям для несоб¬
ственного интеграла). Пусть/и g — непрерывно дифференцируемые
4-00 4-00
на луче [<а; +°°) функции, один из интегралов J f{x)g'{x)dx, J f'{x)g{x)cbc
а а
сходится и существует предел Iim (f(A)g(A)). Тогда второй из интегралов
л—»+°°
тоже сходится и справедлива формула
J f(x)g'(x)dx = Hm (f(A)g(A))-f(a)g(a)~ j f'(x)g(x)dx.
Доказательство
He ограничивая общности, будем считать, что сходится интеграл
+OO А
I f'(x)g(x)cbc. Это означает, что существует предел Hm J f'(x)g(x)dx.
„ Л—»+оо
а а
Для собственных интегралов получаем
j f(x)g'(x)dx = f(x)g(x)\* - J f'(x)g(x)dx.
а а
Переходя к пределу при А —» +°° в последнем равенстве и учитывая
л
существование пределов Hm J f'(x)g(x)dx и Hm {f{A)g{A)), получаем
а
требуемое. ■
Утверждение 6.15 (замена переменных в несобственных интегралах
первого и второго родов). Предположим, что выполнены условия:
1) функция / определена и непрерывна в конечном или бесконечном
промежутке [а; Ъ), где Ъ — единственная особая точка первого или второго
рода1;
2) функция ср = ф(£) определена, непрерывно дифференцируема и моно¬
тонно возрастает на промежутке [а; (3) (где P может быть и -и»).
Допустим, что ср(а) = а и Нтф(£) = Ь2. Тогда выполняется равенство
г-»р
ъ P
\f(x)dx = \f(t)dt, (6.9)
а а
в предположении, что существует один из этих интегралов3.
Доказательство
По теореме об обратной функции получаем, что у функции ф = ф(£)
существует обратная функция t = t(x), которая является непрерывной
и монотонно возрастающей функцией от х на [а; Ь), причем Hm t(x) = (3.
Будем действовать так же, как и в предыдущем доказательстве. А именно,
пусть далее X0 и £0 — произвольные, но соответствующие одно другому зна¬
1 Заметим, что при этих условиях функция/интегрируема в собственном смысле в каж¬
дой части данного промежутка, не содержащей точки Ь.
2 При этом выполняется, что множеством значений функции ср является промежуток [я; Ь).
3 Существование второго отсюда уже вытекает.
358
чения переменных х и t из промежутков (а; b) и (а; Р). Тогда, применяя
к этим промежуткам теорему о замене переменных в определенном (соб¬
ственном) интеграле Римана, получим
*0 tO
I f(x)dx = J /(ср(О)ф'(О^-
а а
Не ограничивая общности, будем считать, что существует интеграл
из правой части доказываемого равенства. Тогда мы станем приближать
произвольным образом X0 к Ь. При этом £0 = £(х0) устремится к (3, что дока¬
зывает существование интеграла в левой части равенства (6.9) и одновре¬
менно справедливость данного равенства. ■
Замечание 6.14. В результате замены переменной второй интеграл
в равенстве (6.9) будет либо собственным, либо несобственным — с един¬
ственной особой точкой р.
В качестве примера преобразования в результате замены переменной
(несобственного интеграла к собственному) рассмотрим следующий интеграл:
+OO
J
dx
1 xVx2 + х + 1
1
X = -
t
clx = -
dt
=I-
dt
л2
.t+2,
V aJ
+ -
4
(
= In
V
f. I
t-\—
v 2,
л2
-л
3
+ —
4
у
= In
l+f
Замечание 6.15. Аналогично доказываются случаи монотонно убываю¬
щей функции ф, когда а > Р, и рассматриваются другие возможные случаи
распределения особых точек. При расстановке пределов в преобразован¬
ном интеграле всегда следует помнить, что нижний предел а должен соот¬
ветствовать нижнему пределу а, а верхний предел P — верхнему пределу b
вне зависимости от того, будет ли а меньше или больше р.
Сформулируем ряд утверждений, которые понадобятся нам в дальнейшем.
Теорема 6.14 (критерий Коши). Интеграл \f(x)cbc сходится тогда
а
и только тогда, когда для V е > О 3 Ь(е) > а : для M Ь', Ь" > Ь(е) выполнено
J f(x)dx
Ь'
<8.
Теорема 6.15. Пусть функция fix) определена и неотрицательна на луче
[а; -и») и собственно интегрируема на любом отрезке [а; А], где А>а. Тогда
+оо
для сходимости интеграла J f{x)dx необходимо и достаточно, чтобы
а
А
нашлось такое L > 0, что
J f(x)dx
< L для всех А.
359
Теорема 6.16 (первый признак сравнения). Пусть |/(х)| < F(x)
OO OO OO
для V х > а и J F(x)dx сходится, тогда и J f(x)cbc сходится. Если же J f(x)chc
а а а
OO
расходится, той jF{x)dxрасходится.
а
Замечание 6.16. Первый признак сравнения относится к достаточным
признакам и поэтому не дает ответа на вопрос о сходимости (расходимо¬
сти), если его условия не выполняются.
К достаточным можно отнести и следующий признак.
Теорема 6.17 (второй признак сравнения). Пусть функции f(x) и F(x) > О
f(x)
при х G [а; +°°) и существует предел Hm =k. Тогда справедливы следу-
X—>°°
F(x)
ющие утверждения:
OO OO
1) если О < k < +оо, то интегралы \f(x)dx и jF(x)dx сходятся и расхо-
а а
дятся одновременно',
OO
2) если k = 0, то из сходимости интеграла \F(x)dx следует сходи-
а
OO
мость интеграла J f(x)dx;
а
OO
3) если k = +°°, то из расходимости интеграла \F(x)dx следует расхода-
а
OO
мость интеграла jf(x)dx.
а
Теорема 6.18 (частный признак сравнения). Для f(x) > О выполняется
следующее.
f 1 л °°
1. Пусть f(x) = О* — при х —» +°°, тогда J f(x)dx сходится при р> 1
\*PJ
и расходится при р < 1.
2. Пусть f(x) = О*
1
Л ъ
при х^Ъ- 0, тогда jf(x)dx сходится
(Ь-х)р
при р < 1 и расходится прир > 1.
Замечание 6.17. Отметим, что последний признак может быть использо¬
ван и для доказательства сходимости, и для доказательства расходимости
несобственного интеграла. Этим он выгодно отличается от достаточных
признаков сходимости.
Продолжая тему вычисления пределов различных интегралов, подня¬
тую в предыдущем параграфе, рассмотрим следующие примеры.
Задача 6.45
I А ( 1
Вычислим предел Hm Jln I + —j=
1 ^ Jx
dx.
360
Решение
А (
Вычислим интеграл J In
1
1 +
1
А (
Jln
1 +
1
4%
4%
dx = x In
dx. Интегрируя по частям, находим:
А
' 1 '
+ 1
у[х
\[x+xln
Vv-I
\
[ Аг 1
1 +J1 2(1 + 7^)
dx =
T+1
.sx
- \п(\[х +1)
Следовательно, искомый предел будет равен
Hm -L=
уд
4а+а\п
1 +
1
■1п(1+7л)
= 2.
Безусловно, предел в задаче 6.45 мог быть найден с помощью правила
Лопиталя. Предлагаем читателю провести эти обоснования и вычисления
самостоятельно.
Задача 6.46
1
Найдем предел Hm f ta~x In tdt для положительного я.
e->0+0g
Решение
Делаем замену Int = у и, интегрируя по частям, получаем
1 о г ■
J ta~x In tdt = J yeaydy =
InE
У _. 1
^-еау еау
а а2
Ine
а
I EaIne Ea
~2
+ ~2'
a a1
Отсюда искомый предел равен —\г.
а1
Задача 6.47
§4П^ £
Найдем предел Hm f dt (т, п s N).
х^0+0 3xtn
Решение
Так как функция ~~ убывает на (0; п) и < 1, то получаем неравенство
sin 2х sin t .
< < 1 при х е
2
,t е[х; 2х].
V
2х t
Возведем все части данного неравенства в степень т, домножим его на tm~n и про¬
интегрируем по t от х до 2х, получаем
sin 2л:
^ 2х
Лт 2х 2х
■ J tm~ndt < J
Jx X
sinm £
tn
2х
dt<\ tm~ndt.
X
2х
Вычисляем J tm~ndt:
X
2х
I tm~ndt = ■
y-i+m-n
2п _ 2m+i
, если т - п +1Ф 0,
2”(п-»г-1)
In 2, если т - п +1 = 0.
361
Используя то, что
Hm
>0+0
^sin2x
„ 2х
\т
/
= 1 для любого т е N, и теорему о двух мили¬
ционерах, получаем ответ
2*
Hm f
*->о+о".
sinm £
tn
dt - ■
0,
In 2,
если т - п +1 > 0,
если т-п +1 = 0,
если т-п +1 <0.
Замечание 6.18. Отметим, что для натуральных чисел тип условие т >
> п - 1 равносильно условию т>п.
Другое решение получается из следующих рассуждений. Обозначая
подынтегральную функцию через /(£), заключаем, что если т > п, то суще-
X
ствует предел lim/(£). Поэтому существует обычный интеграл jf(t)dt.
£->° Q
Отсюда
2х 2х х
J /(t)dt = j f(t)dt-\f(t)dt-
х 0 0
2х
х—>0+0
->0.
^ ZX ^
При т = п - 1 имеем f(t)— и J -dt = In2. А при т < п - 1 получаем
t X t
1
fit) , а > 1, и интеграл расходится.
ta
Задание 6.22
Найдите следующие пределы:
а)
Hm л: f
*—>о+о х
cos t
dt,
J
б) Hm 4
X6
J e~4~ldt
в) Hm
*->о+о
1п(1/х)
Задача 6.48
+OO
Докажем, что интеграл J
dx
не зависит от величины а.
J0 (1 + х2)(1 + ха)
Решение
Разобьем исследуемый интеграл на сумму двух и сделаем в первом подстановку
1
х = -, получаем
+°°
I
dx
1
11
dx
+°°
dx
J0 (I + X2Kl + Х“) Jo (I + X2Kl + Х“) + I (I + X2Kl + Х“)
« ^ dx т dx л
= I
Xv
-dx+ I
i (1 + х2)(1 + х“) - ' { (1 + х2)(1 + х“) I 1 + х2 4’
что, безусловно, от а не зависит.
362
Задача 6.49
Пусть при х > О функция / монотонна и несобственный интеграл j f(x)ebc суще-
о
ствует. Докажем, что тогда
Iim h • (/(A) + f(2h) + /(36) +...) = J f(x)cbc.
А-» 0+0 Q
Решение
В силу монотонности функции / заключаем, что Hm f(x) = 0 и данная функция
х—>0
сохраняет свой знак при х > 0.
Не ограничивая общности, будем считать, что функция / монотонно не возрас¬
тает и положительна, откуда получаем
(m+V)h mh
{ f(x)dx<h-(f(h) + f(2h) + ... + f(mh))< J f(x)dx.
h
0
Переходя к пределу при т —> +°°, имеем
j f(x)dx<hj£f(nh)< { f(x)dx,
h п=I 0
причем бесконечная сумма существует, так как это предел неубывающей, ограничен-
т
ной сверху последовательности ym=h^ f(nh) (ут зависит, конечно, от К). Отсюда
Yl-1
по теореме о двух милиционерах
Hm h ^ f(nh) = f f(x)dx.
А—»0+0 И=1 0
Задача 6.50 (формула Фруллани)
f(x)
Пусть/— непрерывная на луче [0; +°°) функция и интеграл J -dx
8 х
для всех 8 > 0. Докажем справедливость следующего тождества:
f(ax)-f(bx) , , , b
j J_y. LfJx = /(O)In-, Я>0,О>0.
о
Решение
Рассмотрим интеграл
имеет смысл
х
а
Jfm-Zmdx. г Дох) ь _ Jfmdx.
» /у J /у J--
с Л £ Л £ Л
X
=Jmdt-JMdt=Jmd,
Lt Lt Lt
Далее, применяя первую теорему о среднем, получаем
+“ ff _ ffu„\ Sb ,
J0^bx)dx = /($)J — = /($)In-,
s х Lt а
где 5а<Ъ,< 86. Отсюда заключаем, что £ —> 0 + 0 при 8 —> 0 + 0. Следовательно, так
как функция / непрерывна, то
Hm /(¾= Hm /(0 = /(°)
8-»0+0 i;—»0+0
363
и
Hm T 1^ЫМA = T/(aa:)~/(fa)& = /(0)ln^.
5->о+о i х г, х а
Задача 6.51 (вычисление интеграла Фруллани)
Пусть / — непрерывная функция. Вычислим интеграл
+OO
J
О
fjax)-f(bx)
х
dx,a>0,b>0,
в следующих случаях:
а) при некотором T > О для всех х > О справедливо равенство f(x + Т) - f(x);
б) существует конечный предел / = Hm fix).
X—>+°°
Решение
а) Если выполняется условие J f(t)dt = 0, то в силу периодичности функции /
о
+“ fix)
выполняется условие из предыдущей задачи (интеграл f J v ' dx сходится по при-
5 X
знаку Дирихле1), и по формуле Фруллани получаем ответ
f Да*)-/<fa)
п х а
1 т
В противном случае рассмотрим функцию g(x) = fix)—J f(t)dt. Для нее усло-
^ о
т
вие J g(x)dx = О заведомо выполняется, поэтому получаем
о
J-Ao*)-AbxidxX
п X л
1 T Л ( 1 T
f{ax)~IrIfi^dt - f(bx)--jf(t)dt
dx =
х
=7 S^LjfMdx = g(0)i+=I m-(]/№
1 п
X
а
In*.
б) Преобразуем интеграл:
IJTKox)-f(bx)dx= ит U(OX)-Kbx)= ,Jm Г?МА_TMrft
J ПЛ SvH1Hj^-
5—>0+0 *
Л->-к~'
5—>0+0 г t
Aa
Применяя первую теорему о среднем в обоих интегралах, получаем
f
I= Hm
5—>0-1-0
Sъ Jt Ab Jt)
5a ^ Aa ^ ;
где а е [5а; 56], P е [Ла; АЬ\.
Используя непрерывность функции/и существование предела данной функции
на бесконечности, из полученного соотношения имеем
/=7 Jx=Intim.,).
о
X
а
1 См.
далее.
364
Воспользуемся доказанной выше формулой для решения следующей
задачи.
Задача 6.52
TT и л л тэ T arctg(flx")-arctg(6x”) ,
Пусть а, о > 0, п > 0. Вычислим интеграл I — — -ах.
о *
Решение
Отметим, что принимать за функцию /(£) из формулы Фруллани arctg t нельзя,
так как интеграл J arct^ dt расходится при любом 5 > 0. Преобразуем интеграл,
5 t
делая замену хп = t:
j _ у arctg(ахп)~ Mctg(Jbxn) _ I "1J arctg(at) - arctg(bt) ^ _
о
X
п
о
4Т
Г J1W яЛ
arctg(at) - — - MCtg(H) - „
1J V 1
п
4.17 мсшл,
п n t
71
где f(t) = arctg t - —. По формуле Фруллани получаем1
/=ZWjnA=W.
п а 2п а
Задача 6.53
Пусть функция и удовлетворяет следующим условиям:
1) она непрерывно дифференцируема на бесконечном интервале (0; +°°);
2) и(х) > 0, и'(х) > 0;
3) I
dx
и(х) + и'(х)
сходится.
Докажем, что
+°°
интеграл J
1
dx
и(х)
сходится.
Решение
Рассмотрим разность исследуемого интеграла и интеграла, сходящегося по усло¬
вию:
+°° ( А
Г
1
и(х) и(х) + и'(х)
dx.
Далее имеем
I 1
г л V
0<
и'(х) \ Al ^ и'(х) 1
= < \и(х) > 0} < . =
и(х) и(х) + и(х) и(х)(и(х) + и (х)) U1(X)
V “(4;
Поэтому,
1
1
и(х) и(х) + и'(х)
+°° f А
dx< J d
\ и(х) j
1 Iim 1
к(1) ж->°° и(х)
1 Отметим, что в силу разложения arctg t
сходится для любого 5 > 0.
п
2
I
'0
- + 0
t
jj
-K»arctgZ- —
приt—>+ооинтеграл J —dt
s t
365
Так как и'(х) > 0, то функция и монотонно возрастает. Следовательно,
м(1)
-Iim-
х->°° и(х)
<оо и интеграл J
1
1
dx сходится. Из свойств предела
и(х) и(х) + и'(х)
числовых функций вытекает, что сходимость данного интеграла эквивалентна схо¬
димости исследуемого.
Задача 6.54
Исследуем сходимость интеграла J x|sinx|* dx.
71
Решение
Докажем, что интеграл расходится. Для достаточно малых 5 > 0 получаем
+OO 2 OO Я(я+1) 2 OO JI/2+JIJI+8 2
Jxlsinxl dx=Yj J x|sinx| dx>^ J x|sinx| dx.
я JJ=I лn JJ=1ji/2+jijj-8
Сходимость данной суммы эквивалентна сходимости суммы
OO JI/2+8 2 оо 5 2 оо 5
У п f |cosx|” dx - У п f |cosx|” dx - У п f e«2Mcos*|dx,
JJ=1 тш-8 Я=1 -8 Я=1 -8
что эквивалентно сходимости суммы
оо S оо Tl5
У м J e~n2jc2dx = У J e~t2dt,
«=I -8 JJ=I-JjS
а она заведомо расходится, так как не выполняется необходимое условие сходимо¬
сти числового ряда (см. гл. 2).
Обратим внимание читателя на то, что в отличие от числовых рядов,
у которых необходимым условием сходимости ряда является стремление
к нулю общего члена, для несобственных интегралов стремление к нулю
подынтегральной функции не необходимо для его сходимости. Действи-
°° I TL
тельно, известный интеграл Френеля J sinx2dx сходится и равен J-.
-оо V 2
Однако предела Hm sinx2 не существует. Более того, для функции
п, если х = п G N,
О, если хФп
/(*) =
+OO
несобственный интеграл J f{x)cbc = O* * 1, но функция/не ограничена на (-°°;+°°).
Можно построить пример непрерывной неограниченной при стремлении к ±°°
функции, интеграл от которой сходится.
Установим условие, которое нужно добавить к сходимости несобствен¬
ного интеграла для того, чтобы необходимо выполнялось Hm /(х) = 0. Для
х—»+°°
этого рассмотрим следующую задачу.
А2
1 Рассмотрите собственный интеграл J f(x)dx, который равен нулю для любых A1 и A2
~Л1
(докажите!), и воспользуйтесь тем, что предел тождественного нуля есть нуль.
366
Задача 6.55
Пусть /: [0; +°°) —» M — равномерно непрерывная функция. Известно, что несоб-
+OO
ственный интеграл J f(x)cbc сходится. Докажем, что Hm fix) = 0.
о
Решение
Предположим, что предел Hm f(x) не существует или не равен нулю. Тогда най-
х—>+°°
дется такое е > 0, что для всех Ъ > О существует число х* > Ь, для которого | f(pc*) \ > е.
Из условия равномерной непрерывности для найденного выше е существует такое
8 > 0, зависящее только от е и не зависящее от х*, что для Ухе В8(х*) выполнено
неравенство |/(л:)| >
е
2'
Следовательно, в силу равномерной непрерывности мы получаем знакоопреде¬
ленность функции / в В§(х*) и выполнимость неравенства
х+8
J f(x)dx
дг*-8
ж*+5
J \f(x)\dx>eS,
ж*-8
+оо
что противоречит критерию Коши для сходимости интеграла J f(x)dx.
о * 1 2 * 1 2В дальнейшем нами будет установлено еще одно достаточное условие
для стремления к нулю подынтегральной функции.
Рассмотрим далее несколько более тонких признаков сходимости несоб¬
ственного интеграла, а также понятия условной и абсолютной сходимости.
Для начала изучим следующие формулировки.
+OO
Теорема 6.19 (признак Дирихле). Рассмотрим интеграл J f(x)g{x)cbc.
а
Пусть выполнено следующее:
1) функция g монотонно стремится к нулю при х —> +°°;
2) функция / интегрируема на любом конечном отрезке
3 M > О такое, что для любого х>а |^(х)|
<М.
[iя; х], причем
а
+OO
Тогда интеграл j f(x)g(x)dx сходится.
а
Отметим, что условие на функцию/может формулироваться в несколь¬
ких видах:
2а) функция / непрерывна на луче [а; +°°) и первообразная функции /
ограничена;
26) функция / интегрируема на любом отрезке [а; х] и функция F(x) =
X
= J f(t)dt ограничена.
а
Заметим, что если функция / непрерывна на [а; +°°), то эти условия
эквивалентны, так как функция F из второго условия — одна из первооб¬
разных. Но в случае если / только интегрируема, условие 26 более общее.
Ему эквивалентно следующее условие:
367
2в) Функция / интегрируема на любом отрезке [с; d\ с [а; х] и 3 M > О
d
такое, что для V с, d выполнено
\f(t)dt
<М.
Теорема 6.20 (признак Абеля). Пусть функции fug определены на [<а; +°°),
+OO
причем интеграл J f(x)dx сходится, а функция g монотонна и ограничена.
+оо
Тогда интеграл J f(x)g(x)cbc сходится.
а
+OO
Определение 6.16. Интеграл J f(x)dx сходится абсолютно, если схо-
а
-и» -и» абс
дится интеграл J \f(x)\dx. Обозначение: J f(x)ehc^>.
а а
+OO
Определение 6.17. Интеграл J f(x)dx сходится условно, если схо-
а
+OO +OO
дится интеграл J f(x)dx, но интеграл J \f(x) \dx расходится. Обозначение:
а а
+оо уел
J f(x)cbc —».
а
+OO
Утверждение 6.16. Если сходится интеграл J \f{x)\dx, то сходится
а
+OO
и интеграл J f{x)dx.
а
Задача исследования на абсолютную и условную сходимость интеграла
+оо
I f(x, a)dx, где ае А — параметр, означает определение трех множеств:
а
Ai^A2UA3= A, Ai n Aj = {0},
где при a G A1 изучаемый интеграл сходится абсолютно, при a G A2 схо¬
дится условно и при а G A3 расходится.
Определение 6.18. Если функция /такова, что при любом в > О суще-
C-E Ъ
ствуют собственные интегралы J f(x)dx и J f(x)dx(a<c<b), то под
а с+е
главным значением в смысле Коши (р.р.) понимается число
Ъ fс-г Ъ ^
v.p.jf(x)dx= Hm J f(x)dx+ J f(x)dx .
а £—>0+0^ а с+£ ^
Аналогично
+OO А
v-P-l f(x)dx= Hm J f(x)dx.
А—> оо .
—OO -А
368
Докажем очень полезное следствие из признака Абеля.
Утверждение 6.17. Пусть для некоторого a е R функции /и g непре-
+OO
рывны на луче [а; +°°), а несобственные интегралы Ii = J f(x)g(x)dx
+00
и I2= j f(x)dx имеют единственную особенность +°°. Если, кроме того,
а
функция g монотонна на [а; +°°) и существует конечный и не равный нулю
предел Hm g(x) = 1гФ 0, то интегралы Ii и I2 либо оба сходятся абсолютно,
х—>+°°
либо оба сходятся условно, либо оба расходятся.
Доказательство
В силу того что k Ф 0, в некоторой окрестности +°° справедливо нера¬
венство
0<^\k\<\g(x)\<^\k\.
Следовательно, в этой окрестности функции
1
g(x), |g(*)|, —Г
и
g(x) |g(x)|
ограничены, непрерывны и монотонны. Воспользовавшись элементарным
равенством
f(x) = (f(x)g(x))-j—,
gipc)
по признаку Абеля получаем выполнимость утверждения. ■
Для демонстрации применения доказанного признака рассмотрим сле¬
дующую задачу.
Задача 6.56
Исследуем на абсолютную и условную сходимость интеграл J aTC^(^x)
* -V-CX
^ Л
Решение
Функция g(x) = arctg(2x) монотонна на [1; -н») и существует конечный, не рав¬
ный нулю предел Hm g(x) = Следовательно, по утверждению 6.17 заключаем, что
х->+°° 2
+00 ^
сходимость исследуемого интеграла эквивалентна сходимости интеграла [ —, кото-
* 'V CC
-j и>
рый сходится абсолютно при а > 1 и расходится при а < 1 (проверьте!).
Предлагаем читателю самостоятельно изучить сходимость интеграла
Tarctg(Zr)tfa
J -у-а
О л
Установим далее еще два достаточных условия для стремления к нулю
подынтегральной функции.
+OO
Утверждение 6.18. Пусть несобственный интеграл J f(x)dx сходится
а
и существует конечный предел Hm f(x). Тогда данный предел равен нулю.
л:—»+°°
369
Доказательство
Доказываем от противного. Пусть Hm /{х) = Ьф 0 (не ограничивая
X—H-OO
общности, можем считать, что L > 0). Это означает, что для V е > О 3 5(e)
такое, что для Vi>5(e) выполнено | /(х) -L | < е.
Последнее неравенство равносильно неравенству: f(x)> L-Z = - при
в = ^ > 0. Далее заключаем, что для V b > 5(e) 3 Ъ', Ъ" > Ъ такие, что
J f(x)dx
Ъ'
>±\b"-b'\ = z0.
Мы получили противоречие с критерием Коши сходимости интеграла
j f(x)dx. U
а
Утверждение 6.19. Пусть функция / непрерывно дифференцируема
+°°
на луче [а; +°°), |/'(х) | < C при х е [а; +°°) и интеграл J |/(x)|<fr сходится.
Тогда Hm /(х) = 0.
X—>+°°
Доказательство
Применим теорему о среднем к следующему интегралу:
+OO
+OO
+OO
J \f'(x)f(x)\dx = |/'(£)|• J [/(х)\dx < C J [/(х) Idx.
а а а
+OO
Из признака сравнения вытекает сходимость интеграла J \ f'(x)f(x)\cbc,
а
+OO
а поэтому и интеграла J f'{x)f{x)cbc. Имеем
а
J f'(x)f(x)dx = /2(х)£ - J f'(x)f(x)dx =>
2j f'(x)f(x)dx = /2(х) = f2(A)~ f2(a).
Далее, так как было доказано, что предел левой части при А —> +°° суще¬
ствует, поэтому существует и предел правой части, т.е. Hm /2(Л). Сле-
А->+OO
довательно, существует предел Hm /(Л). Из предыдущего утверждения
А—¥+°°
заключаем, что Hm /(Л) = 0. ■
А ^+OO
Рассмотрим далее ряд задач.
Задача 6.57
Пусть а е R, для V А > а функции /, g интегрируемы на [а; А] и интегралы
+OO +OO +OO
I f2(x)dx, I g2(x)dx сходятся. Докажем, что интеграл J f(x)g(x)cbc сходится.
а а а
370
Решение
Воспользуемся интегральным неравенством Коши — Буняковского:
I f{x)g{x)dx < I f2(x)dx■ J g2(x)dx.
V a Ja а
Из него моментально вытекает требуемое.
Задача 6.58
Пусть функция/непрерывно дифференцируема на всей числовой прямой и несоб-
+OO
ственный интеграл J f'(x)dx сходится. Докажем, что 3 Iim f(x).
—OO
Решение
+OO +OO
Из сходимости интеграла J f'(x)cbc вытекает сходимость интеграла J f'(x)dx.
—оо о
Поэтому существует предел
Iim jf'(x)dx = Hm (/(Л) -/(О)) => 3 Iim /(Л),
А—>+°° q Л—>+°° А—>+°°
так как /(O) = const. Исследование предела на производится аналогично.
Задача 6.59
Пусть функция/дважды непрерывно дифференцируема на всей числовой прямой
+OO +OO +OO
M и сходятся интегралы J f2(x)dx, J (f'(x))2dx, J (f"(x))2dx. Докажем равенство
—OO —OO —OO
J (f'(,x))2dx=-\ f"(x)f(x)dx.
—OO -OO
Решение
Используя неравенство Коши — Буняковского, получаем
A (A V72 (А V72
J\f"(x)f(x)\dx< f(f"(x))2dx j(f(x))2dx <С
о Vo у Vo у
+OO
для V Л > 0. Поэтому интеграл J f"(x) f(x)chc сходится абсолютно. Аналогично
о
А (А Л172 (А V72
J\f'(x)f(x)\dx< J(f'(x))2dx l(f(x))2dx <С
О VO У VO у
+OO
для V Л > 0. Поэтому интеграл J f'(x)f(x)cbc также сходится абсолютно.
о
Далее находим
+~
А ( А \
j(f'(x))2dx= Iim \(J\x))2dx= Hm /'(Л)/(Л) - /'(0)/(0) - J f"(x)f(x)dx
/1—> t OO •
Л—»+оо
А А
Так как 3 Hm j (f'(x))2dx и 3 Hm J f"(x)f(x)dx, то из последнего равенства
А-^+оо
А ^+°° (
заключаем, что 3 Hm /'(Л)/(Л). Отсюда и из сходимости интеграла f f\x)f(x)chc
Л—>+00 Q
вытекает, что Hm ПАЖА) = 0.
Л->+оо
371
Следовательно,
T C/W*=-7 /"W/W*-/'(0)/(0).
о о
О -И»
Аналогично имеем J (JXx)Ydx = - J f"(x)f(x)dx + /'(0)/(0)- Поэтому
—оо О
J (/'(*))2^=-J f"(x)f(x)dx.
—оо —оо
Задача 6.60
Пусть функция/дважды непрерывно дифференцируема на луче [а; +°°), сходятся
+OO +OO
интегралы J f2(x)dx и J (J"(x))2dx и существует IgR такое, что для всехх> а
а а
+OO
выполнено \f(x)f'(pc) \ < L. Докажем сходимость интеграла J (JXx))2 dx.
а
Решение
Аналогично предыдущей задаче получаем
J (J'(x))2dx
J fXx)d(f(x))
f\A)f(A) - fXa)f(d) - J f(x)f"(x)dx
(A
Y/2 (A
<21 + j\f(x)f"(x)\dx<2L + I f2(x)dx ■ j(f"(x))2dx
\a
\l/2
\a
<M.
Следовательно, интеграл J (JXx)Ydx сходится.
Задача 6.61
Пусть интеграл J f(x)dx сходится и равен I Докажем, что интеграл J /
1
х —
X
dx
также сходится и равен I.
Решение
1
Для того чтобы сделать замену t = х , разобьем предложенный интеграл
х
на сумму двух:
( 1 ^ ° ( лЛ ( 1^
'dx= J / х ' ' г '
х —
X
V
X =
J=H
—OO
гаем вы
L, а при х > О — х =
V
х
dx+ J /
о
х —
х
V
dx.
Далее сделаем вышеуказанную замену, замечая, что при х < О получаем
t -Jt2 +4 n t + Jt2 +4
Л +OO
jJ\m
(
^ . Отсюда
Л ., +« (
1-
Jt2 + 4
dt + \\ /(*)
1 +
JtH-4
dt-Jl+J2.
В силу сходимости интеграла j f(t)dt, монотонности и ограниченности функции
—OO
t +“ t
I и признака Абеля делаем заключение о сходимости интеграла J f(t) ,—=dt,
Jt2+ 4 Jt2+А
а с ней и о сходимости интегралов Ji и J2, причем
4 +оо
-Jm
1-
Jt2+4
dt+\\ /(О
1+
Jt2+ 4
<& = { f(t)dt = I.
372
Обратимся далее к утверждению о соотношении абсолютной и услов¬
ной сходимостей. Рассмотрим следующий пример:
1
—,если XE Q,
X1
1
—-, если х G R\Q.
X1
+°° ^
Заметим, что интеграл J |zj(x)|<fr сходится по частному признаку срав-
1
+°° ^
нения, однако интеграл J D(x) dx расходится как модификация функции
1
Дирихле. Следовательно, можно заключить, что из сходимости несобствен¬
ного интеграла от модуля, вообще говоря, не следует сходимость самого
интеграла. Верно ли это?
Ошибка в приведенных рассуждениях кроется в том, что для пред¬
ложенной функции D не выполняется основное требование, накладыва¬
емое на несобственный интеграл. А именно, на подынтегральную функ¬
цию накладывается условие о том, что она должна быть интегрируема
по любому конечному отрезку. Следовательно, ни о какой абсолютной схо¬
димости здесь говорить не приходится. Поэтому утверждение, к которому
был построен данный «контрпример», к этой функции не применимо.
Продолжим рассмотрение задач.
D(x)=-
Задача 6.62
Пусть функция/непрерывна на отрезке [0; 1]. Докажем справедливость тождества
Hm
р—H-OO
\\f(x)\Pdx
Vo
= max \f(x).
лге[0;1]'
Решение
Пусть max |/(л:)| -M- const и, заменяя I f(x)I, стоящий в подынтегральной функ-
хе[0; 1]
ции, на его максимум, получаем неравенство
f\ fi д/р
Vo
JV(A) \рdx < I(M)Pdx
/
Vo
= M.
(6.10)
У
Далее, для любого E > 0 найдем на отрезке [0; 1] интервал (а; Ь) такой, что для всех
I I
х G (а; Ь) выполняется неравенство \f(x)\ > M - — . Тогда получаем
(1
Л1/р (ь
Vo
\\f(x)\Pdx > \\f(x)\Pcbc
\Vp (
Ь( Р \Р
M--
2
\1/р
а \
dx
•)
( 8Л
M--
V 2У
(Ь-ау/р.
Так как Ъ - а < 1, то Hm (Ъ - а)1/р =1-0. Следовательно, для достаточно боль-
р—»+<*>
Л
ших р получаем неравенство | M - —
и неравенства (6.10) получаем
(b - of/ P > M - е. В силу произвольности е > О
1 Это можно сделать в силу непрерывности функции /.
373
(I
Iim Wf(X)^dx
P-hHo
Y/p
= M= max f(x)\
хфЛУ 1
Задача 6.63
I
Пусть функция/непрерывна на отрезке [0; 1 ]. Найдем предел Iim -In
(У
J ch(tf(x))dx
VO
Решение
Принимая во внимание четность функции ch, при t е [0; 1] получаем
-In
t
(У ^ ] А
Jch(tf(x))dx — —In Jch(£ I f(x) \)dx
Vo
Vo
Обозначим снова max I f(x) I= M. Тогда получаем оценку
xe[0; 1]
-In
t
(у ^ I А
Jch(£ I f(x) \)dx <-ln fcb.(tM)dx
Vo
/
Vo
ln(ch(£M))
Используя непрерывность функции /, найдем на отрезке [0; 1] интервал (а; Ь)
такой, что для всех х е (a; Ь) и для произвольного е > 0 выполняется неравенство
I I в
|/(х)| > M - —. Вспоминаем, что функция ch неотрицательна, имеем
-In
t
1 (ъ
Jch(£ I f(x) \)dx >-ln Jch(£ | f(x) \)dx
Vo
I
ка
(ь
{
f
P Y
\ у
=—In
f
( рЛ
\ V
Jch
t
M-
с
о
dx
ch
t
M--
9
(Ь-а)
Va
L
V
1Л
Z )
L
V
V
V
Z )
>-1п
t
В результате этих рассуждений мы приходим к неравенству
г
г
( РЛ
\ \
In
ch
t
m-у
(Ь-а)
V
V
L 2J
Z У
<-1п
t
(I V
\dn(t\f(x)\)dx
< ln(ch(£M))
t
Вычисляя пределы левой и правой частей полученного неравенства, находим
Iim
(
f
( р\
\ Л
In
ch
t
M-У
(Ь-а)
L
V
I 2J
Z У
= M-V HmMchCM))
2 t—»+°° t
Следовательно, для произвольных E1 > 0 и е > 0 найдется такое В(е, E1), что для всех
t > В получаем
M ---E1 <-1п
2 1 t
(1
\ch(t\f (x)\)dx
Vo
<М + E1.
Таким образом,
Hm -In
£-»+<*>£
(\
\
J ch(tf(x))dx
Vo
= Hm -In
(У
\c\i(t\f(x)\)dx
Vo
-M- max /"(^).
xe[0; 1] 1
374
Задача 6.64
Исследуем сходимость интеграла J sinx-sinx2d!x.
Решение 0
1
Так как интеграл J sinx -sinx2d!r является собственным, то сходимость изучаемого
о
+OO
интеграла эквивалента сходимости интеграла J sinx -sinx2 Дг. Для изучения его схо-
1
димости рассмотрим интеграл
вг . . -J ^sinx ,, sinxcosx2
I sinx-sinx2ax = -| a (cos х2) =
2х
о
2х
+J
B/^cosx sinx^
cos x2dx.
400Sinxcosx2
„ ,. sinBcosB2 n f
Заметим, что Iim = 0, а интеграл
л-н- 2 В F { 2х2
2х 2х2
dx сходится абсолютно.
Имеем далее
scosxcosx2 , cos х sinx2
ах =
J
2х
4х2
b^ cosx sinx^
-J
1 1
2х3 4х2
sin x2dx,
т.е. все получившиеся интегралы сходятся абсолютно. Следовательно, исследуемый
интеграл также абсолютно сходится.
Задача 6.65 * 1 * 1Исследуем на сходимость несобственный интеграл
+°° /,COS* ci г
eC0SX sin(sinx) ^
х
Решение
Воспользуемся признаком Дирихле сходимости несобственного интеграла.
1
Функция g(x) = — монотонно стремится к нулю при х —> -и». Докажем ограничен-
х
ность первообразной функции /(х) = eC0SXsin(sinx). Для произвольного достаточно
большого А > 1 выберем N е N такое, что 2лN <А< 2л (N +1). Получаем
J ecosxsin(sinx)d!r
2тс 2 TtN А
J + J gcosx sin(sinx)<ir + I ecosx sin(sinx)<ir
1 2n 2kN
2 n A
Jecosx sin(sinx)d!x+ J eC0SXsin(sinx)d!x
1 2%N
2к A
< J |ecosxsin(Sinx)|(ir+ J |ecosxsin(sinx)|<fr<2 J |ecosx|<ir
2kn о
<
2k
1
2k
<2 J \eC0SX\dx +(N-I)
о
2 71
I eC0SXsin(sinx)dx
< 2 • 27ie + O = 4ле,
так как ecosx < e и
271 71 2тс
J eC0SXsin(sinx)<& = Jecosx sin(sinx)<£t+ J ecosx sin(sin x)dx = ^ = 2л-х} =
O O Tt
Ti O
= J ecosx sin(sin x)dx + J ecost(- sin(sin t)d(-t) = 0.
О тс
375
Докажем далее абсолютную расходимость. Действительно,
+2яи ecosx sin(sjn х) ^ > 1 Я+27СТ
2пп
X
п + 2кп
+2тт ^ я
Г gcosx sin(sin %)dx = f ecosx sin(sin x)dx,
и + 2 nn
2im
0
причем A = jecosx sin(sinx)dx > 0, откуда
о
+°°gcosx |sin(sin x)l
I
2n
dx>Y,
- = -|-oo>
x ra=i n + 2тш
Следовательно, исследуемый интеграл сходится условно.
Задание 6.23
_ ^ . 4TVinxSin(Sinx) ,
Докажите, что несобственный интеграл I = J -ах расходится.
Задание 6.24
Исследуйте на абсолютную и условную сходимости интегралы в зависимости
от действительнозначных параметров:
sm(3*-6) .Л;б)}£2£а^)Л.
а) J
[х - 1п(х -1) - 2]°
XP
+“ P (х\
в) I jSiuxdx, где PJx) и PJx)
а Рп(х)
целые многочлены и PJx) > 0, если х > 0.
Глава 7
ФУНКЦИОНАЛЬНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И РЯДЫ
7.1. Понятие равномерной сходимости
Дадим ряд определений, которые понадобятся нам в дальнейшем.
Определение 7.1. Предположим, что функциональная последователь-
OO
ность {fn{x)} или ряд Yun (х) определены на множестве X. Фиксируем про-
я=1
извольную точку X0E X и рассмотрим все члены этой последовательности
(или ряда) в точке х0. При этом получим числовую последовательность
(или ряд). Если указанная числовая последовательность (или ряд) схо¬
дится, то говорят, что функциональном последовательность {или ряд) схо¬
дится (;поточечно) в точке х0. Множество точек х0, для которых сходится
последовательность (или ряд), называют областью сходимости.
Определение 7.2. Предположим, что функциональная последователь¬
ность \fn{x)} имеет в качестве области сходимости множество X0. Совокуп¬
ность пределов, взятых для всех значений х из данного множества, образует
некоторую функцию f(x), называемую предельной функцией последователь¬
ности {fn{x)}.
OO
Определение 7.3. Аналогично если функциональный ряд Yun(x) сх0_
Я=1
дится на множестве X0, то на этом множестве определена функция S(x),
являющаяся предельной функцией последовательности его частичных
OO
сумм и называемая суммой ряда Yun(x)-
я=1
Определение 7.4. Функциональная последовательность {fn(x)} называется
х
равномерно сходящейся на множестве X (обозначение: {/„(x)}=t/(x)), если:
1) существует предельная функция f{x)= Iim fn(x), хеХ;
Я—»<*>
2) для V в > О 3 N(e) : для V п(е) > N(e) и Vie I выполнено | fn(x) -
-/(х)|<8.
Замечание 7.1. В этом определении существенно, что число N зависит
только от е и не зависит от х.
OO
Определение 7.5. Функциональный ряд Yiun(x) называется равномерно
Jl=1
сходящимся на множестве X, если последовательность его частичных сумм
(5и(л:)} сходится к своей предельной функции ^(х) равномерно на X. Обо-
оо х
значение: ^мя(х)=^5'(х).
Jl=1
377
Критерий Коши равномерной сходимости функциональных последо-
х
вательностей и рядов. 1. {fnix)}=Xfix) <=> для V е > 0 3 М(е) такой, что
для V п(в) > N(e), VpeNuVxeX выполнено \ fn+p(x) - fn(x) \ < е.
OO X
2. ^ для V е > О 3 Х(е) такой, что для V п(г) > М(е),
72=1
VpeNwVxeX выполнено
п+р
E «*(*)
k=n+i
<е.
Попытаемся далее сформулировать на языке «е — 8» следующие утверж¬
дения.
1. Функциональная последовательность {/я(х)}~=1 сходится на множе¬
стве X к функции /:
для VxgX и V е > О 3 Me: х) : для V п> N выполнено | /я(х) -f(pc) \ < в.
2. Функциональная последовательность {/я(х)}я=1 сходится равномерно
на множестве X к функции /:
для V в > О 3 Мв) : для V п > N и VxgX выполнено | /я(х) - /(х) | < в.
3. Функциональная последовательность {/я(х)}я=1 сходится к своей
предельной функции / на множестве X неравномерно:
для Vxg XhVb>03 Me: х) : V п> N выполнено | /я(х) - /(х) | < в, но
3 B0 > О : для VkE N3w>£h3x'g X такие, что |/я(х') - fix') \ > е0.
4. Функциональная последовательность {/я(х)}”=1 не удовлетворяет
на множестве X условию Копти:
3 E0 > О : для VkE N3w>£n3pG Nh3x'g X такие, что \fn+pix') -
-fnix') I > е0.
5. Функциональная последовательность {/я(х)}я=1 сходится равномерно
на каждом конечном интервале (а; Ь) с (х0; +°°) к функции /:
для V a, b E (х0; +°°), а<Ъ, Ve>03 Me: a: b): для V п > N и V х G (а; £)
выполнено I fnix) - fix) \ < в.
Обращаем внимание читателя на выделенные фрагменты в написанных
утверждениях. Особый интерес в данных формулировках представляет то,
от чего зависит номер N. Например, в определении поточечной сходимо¬
сти данный номер зависит от точки х. Если взять другое значение х, то
получится другая числовая последовательность, и найденный Х(е) может
оказаться непригодным.
Одной из важнейших задач из этой темы, безусловно, является опре¬
деление характера сходимости функциональных последовательностей
и рядов. При этом очень важно иметь критерий равномерной сходимо¬
сти, который был бы легко применим (ибо критерий Коши, как обычно,
носит скорее теоретический характер и для практических вычислений
применим слабо). C этой ролью вполне справляется следующее утверж¬
дение.
Утверждение 7.1 (критерий равномерной сходимости функцио¬
нальных последовательностей). Функциональная последовательность
(/и(х)} сходится равномерно на множестве X к предельной функции /(х)
тогда и только тогда, когда Hm (sup ги(х)) = 0, где ги(х) = |/и(х) - fix) |.
га—х
378
Доказательство
Необходимость. Предположим, что функциональная последователь¬
ность {/„(х)} сходится равномерно на множестве X к предельной функ¬
ции fix'). В этом случае выполняется условие: для V е > 0 3 iV(e): V п> N,
У XE Xвыполнено | /и(х) -/(х) | < в.
Поэтому для \/в>0и Vie I для достаточно больших п выполнено
неравенство гп(х) < в. Следовательно, для таких п выполнено suprw(x)<E,
х
т.е. Hm(sup ги(х)) = 0 по определению предела.
п—>°° х
Достаточность. Пусть выполняется, что lim(suprw(x)) = 0. Запишем
П—¥°° ]£
определение предела числовой последовательности: для V в > 0 3 ЛГ(в) :
для V п> N выполнено sup гп(х) < в.
х
Но так как rn(x) < sup гп(х), то и rn(x) = \ fn(x) -/(х) \ < в для VxgX По-
х
Jf
этому по определению равномерной сходимости получаем, что {/я (х)} =4/(х)
ПрИ П —> оо. ■
Аналогично может быть рассмотрено следующее утверждение.
Утверждение 7.2 {критерийравномерной сходимости функциональ¬
ных рядов). Функциональный ряд ^z/„(x) сходится равномерно на мно-
и=1
жестве X к предельной функции S(x) тогда и только тогда, когда для V в > О
3 N{в): для V п{в) > N, V х G Xвыполнено rn (х) = \Sn (х) - S(x)\ =
E щ(х)
k=n+i
< Б.
Оставляем читателям возможность доказать данное утверждение само¬
стоятельно.
Рассмотрим далее несколько теоретических задач.
Задача 7.1
Пусть {/„(х)}=4 /(х) при п —> +оо. Пусть дополнительно предельная функция f(x)
ограничена на множестве X. Докажем, что 3 L > 0, щ е N такие, что для V п> п0,
V х € X выполнено | /и(х) | < L.
Решение
Из равномерной сходимости {/„(х)} к /(х) вытекает, что для V е > 0 3 N(e) такой,
что для V п(е) > N, V х е X выполнено | /„(х) — /(х) | < е.
Последнее неравенство равносильно выражению /(х) - е </„(х) < /(х) + е. Из огра¬
ниченности функции / следует, что 3 M > 0 такое, что | /(х) | < M для VxeX
Следовательно, для V х е X, V n(e) > N выполнено
I /„(х) I < тах{|/(х) - е |, |/(х) + e\}<M+e = L.
Задача 7.2
X X X
Пусть {/и(х)}=г/(х), {g„(x)} =Tg(X) при п -+ +оо. Докажем, что {/n(x)±g„(x)}=T
5/(x)±g(x).
379
Решение
Используя критерий равномерной сходимости, получаем
lim(sup|/„(x) - /(х)|) = lim(sup|g„(x) -g(x)|) = 0.
п—> °° х п—>°о х
Далее имеем
I (Inix) ± ёп(х)) - (Iix) ± ё(х)) I ^ I In(X) -1(х) I + ISn(X) - g(x) |,
следовательно,
sup\Цп(х) ± g„(x)) - (/(х) ± g(x))| < sup I fn(x) - f(x)I + sup|g„(x) - g(x)|,
X XX
откуда вытекает требуемое.
Возникает вопрос: можно ли утверждать, что при таких же условиях
на множестве X равномерно сходится последовательность [fn(x) • gn(x)}7
Ответ на этот вопрос — отрицательный. Действительно, пусть, например,
1
In(x) = g„(x) = x + ~, Х = [0; + °°).
п
Тогда/(х) = g(x) = х, причем сходимость к предельным функциям рав¬
номерная. Однако
In (■х)ёп (х)=X2++; In (х)ёп (х) ~ f(x)g(x)=^+;
п пг
sup
[0; +°°)
П П*
2х 1
— + _2
п п1
т.е. функция
2х 1
—+—
неограничена.
п п£
Выясним, какие дополнительные условия нужно наложить на последо¬
вательности [fn(x)} и {g„(x)} для того, чтобы можно было утверждать о рав¬
номерной сходимости их произведения. Ответ на данный вопрос дается
следующим утверждением.
Утверждение 7.3. Пусть 3 L > 0 такое, что для VxgX выполнено
х
\f(x) I < < L и I g(x) I < L Тогда [fn(x)-gn(x)}=tf(x)-g(x) при п -> «>, в част-
х
ности {/„ (х) • g(x)} =Г/(х) • g(x) (при gn(x) = g(x)).
Доказательство
Имеем при достаточно больших п
\1п(х)ёп(х) ~ I(x)g(x)I = {±/„(x)g(x)} =
= I (In (X)gn (X) ~ In (X)g(x)) + Цп (X)g(x) ~ /(x)g(x)| <
^ IL (*)| • I ёп (*) - &(*)|+\ё(х)\ • I In (*) - /0)1 <L'^i+L'^i=E
для Vxg XhV п(г) > АД, что и доказывает выполнение сходимости
х
{In(x)-g(x)}^I(x)-g(x) при п -> °°. ■
1 Здесь были использованы условия равномерной сходимости и ограниченности функ¬
ций^ Hg.
380
Задание 7.1
Постройте пример, когда{/„(х)} =4 /(х), {gn(x)} =4 g(x), функция/ограничена, но
{/„(х) • g„(x)} ;zf /(х) • g(x) (т.е. ограниченности только одной функции недостаточно).
Рассмотрим далее задачу, которая связывает два важнейших понятия:
равномерную сходимость и равномерную непрерывность.
Задача 7.3
Пусть при VneN функции/и(х) равномерно непрерывны на R и {/„(x)}=t/(x).
Докажем, что функция /(х) равномерно непрерывна на R.
Решение
В силу равномерной сходимости последовательности {/„(х)} к /(х) на действи¬
тельной прямой R имеем, что V е > 0 3 N(z) такое, что для V х', х" е RhV п(г) > N
выполнены неравенства
|/„(0-/(0|<|, |/„(*")-/(*")|<§.
Далее, так как для N(e) функция/^(х) равномерно непрерывна на R, то V е > 0 3 8(e) =
= 8(е, N) такое, что V х', х" е R таких, что | х' - х"\ < 8, выполнено |/дг(х') - fN(x")\ < —.
3
Поэтому для выбранных х' и х" выполнено
Il (х') - /(х")| < |/(х') - Zjv(X7)I + IZv(x') - Zjv(X77)I +1 fN(x") - Z(X77)I <f + f + f = E>
откуда вытекает требуемое.
Замечание 7.2. Доказанное в задаче 7.3 утверждение верно для любого
множества X с R, а не только для всей прямой R.
Задача 7.4
Пусть ряд YjUnix) сходится на множестве X к ограниченной функции и(х).
W=1
OO
Докажем, что из сходимости ряда Yan следует равномерная сходимость на X ряда
W=1
OO
E k-Hb(X)I-
W=I
Решение
оо
В силу условия Коши сходимости ряда YaI заключаем: для V е > О 3 iV(e) такое,
W=I
п+р
что для V п> N и У р е N выполнено Y aI < Е-
k=n+\
п
Заметим далее, что так как для VxeX последовательность Yuk(x) является
ы
монотонно неубывающей и ограниченной сверху (в силу ограниченности предель-
п+р
ной функции), то 3 L > О : для Vn, ре NnVxeX выполнено О < Y и%(х) <^-
к=п+1
Остается воспользоваться неравенством Коши — Буняковского и записать
<4г-4ь=г'
W+P
7 п+р л
1/2
7 n+p N
Y \ап-ип(х)\<
E «I
E «К*)
k=n+1
^А=п+1 )
^£=П+1 у
381
для V e' > О, V п(е')1 и V р е N. Следовательно, по критерию Коши ряд Y \ап -ип(х)|
It=1
сходится равномерно на множестве X.
Обращаем внимание читателя на то, что требование ограниченности
оо
предельной функции ряда Yun(x) существенно, так как в процессе ДОКИ¬
ПИ
зательства (при применении критерия Коши) существенной была ограни-
п+р
ченность суммы Y uIix) одной константой сразу при всех п,р их. Пред-
k=n+i
лагаем читателю самостоятельно придумать пример последовательностей
ип(х), ап и множества X, удовлетворяющих всем условиям предыдущей
задачи, кроме ограниченности предельной функции и(х), для которых схо-
OO
димость ряда Y \ап 'ип(х)\ на множестве X не равномерная.
Я=1
Пусть, далее, функциональный ряд Yun(x) сходится равномерно на не-
W=I
котором множестве X. Зададимся вопросом: обязательно ли будет равно¬
мерно сходиться ряд Y |ия(х)|? Ответ на данный вопрос — отрицательный.
U=1
Рассмотрим следующий пример:
£(хи-хи+1) -(-1)и, X= [0; 1].
W=I
Получаем, что для всехie [0; 1] данный числовой ряд удовлетворяет
всем условиям признака Лейбница сходимости числового ряда. Следова¬
тельно, так как Xmax = П + п (докажите!), для его остатка справедлива оценка
п + 2
гп(х) < хп+х -хп+2 <
п + 1
п + 2
\я+1
1-
П +1
\^п + 2 j
и + 1^
У
NW+1
П + 1
\п+2
п + 2
п + 2
(п +1)
,п+1
(п + 2)
п+2
-+ 0.
П—¥°°
Отсюда делаем заключение о равномерной сходимости данного ряда.
OO
В то же время ряд ^(х”-хи+1) сходится на отрезке [0; 1] не равно¬
мерно, так как
W=I
Sn(x)=Y(xk-Xk+i) = X-Xn+1 —»
k=i
п—>°°
О, если х = 0 или 1,
х, если XG (0; 1).
Оставшиеся обоснования предлагаем читателям провести самостоя¬
тельно.
1 Число N(e') берется из условия Коши сходимости числового ряда YaI-
п=1
382
Задача 7.5
Пусть для функции /: M —> M существует /' на R и /'(х) равномерно непрерывна
на R. Докажем, что
(
г 0
х + —
\
п■
/
-Rx)
I nJ
У
=I f'(x) при п —»
Решение
В гл. 4 было показано, что Iim п
г
/
1
+
\
-Rx)
I
( nJ
У
- f(x) = /'(х). В силу того что для функ-
у
ции/на числовой прямой R выполнены все условия теоремы Лагранжа о конечном
приращении, получаем, что 3 е
1
х; х + —
п
(
Г о
х + —
\
п
/
-Rx)
I nJ
У
такое, что
= /'&,)■
Далее, из условия равномерной непрерывности функции /' на R вытекает, что
для V е > 0 3 5 = 5(e) : для V X1, X2 е R таких, что | X1 - X2 | < 5, выполнено
Зафиксируем произвольное е > 0, по нему выбираем 5 = 5(e) так, чтобы выполня¬
лось условие равномерной непрерывности. Теперь можно выбрать такое N = JV(S)* б) 1,
1
чтобы для V п> N выполнялось — < 5, например N =
п
1
5(e).
+ 1.
Получаем, что для всех хе R и V ?z > JV выполняется
(
( О
х + —
л
п
/
-Rx)
I nJ
что и доказывает требуемое.
В завершение данного параграфа приведем несколько задач для само¬
стоятельного изучения.
Задание 7.2
Изучите чертежи на рис. 7.1 и исследуйте следующие функциональные последо¬
вательности на равномерную сходимость в указанных промежутках:
а) /и(х) =Xn-Xn+1, 0 <х< 1;
б) /п(х) -Xn-X2", 0 <х< 1.
1 В силу того что 5 само зависит от е, номер N также зависит от е.
383
Задание 7.3
Исследуйте следующие функциональные последовательности на равномерную
сходимость в указанных промежутках:
Xn
а) f„(x) = , 0 < х < 1 - е, 1-е<х<1 + е, 1 + е<х<+°о,гдее>0;
1 + х”
б) fn(x) = Jx2+-^, -оо<х < +оо;
в) fn(x) = arctg(nx),-°о<х<+°о;
г) /re(x) = x-arctg(nx), -°°<х<+°°;
1
Д) fn(x) = n‘sin—> 1<х<+°°;
пх
е) /„(*) = h
( 2 г Л
2 /г •
п4 + е2*
, 0<х<-И»,0<x<fl,ae R;
f пх ^
ж) /„(*) = I -COS
V* +2
з) /й(,) = 2^^, -оо < х < +оо.
, 0<х<1, 1<х<+°°;
Vi-i-e у
Задание 7.4
Исследуйте характер сходимости следующих рядов:
х
a) E
б) E
П=1 [(и -1)* +1] (пх +1)
1
, 0<Х<+°°;
:=1 (х + п)(х + п +1)
пх
в) E
nTi (I + х)(1 + 2х) •• (1 + пх)
г) E-W=T. О < х < 1;
я=1 Vn2 +х2
д) E^-, 1 < ЛГ < 2;
я=1 ^
OO
е) ^их2е_шг, 0<х<+°°;
«=1
, 0<Х<+°°;
, О < х < е, е < х < +°о,гдее>0;
ж) £
л:
1 + п2 X2
1
, О < х < 1;
з) О < х < +оо;
п~\ Yl
Г ! Л
и) Y2" sin
«=1
v3”x.
, 0<х<+°°.
Задание 7.5
OO
При каких значениях х сходится ряд E In
?г=1
' (-1)иЛ
1+———
V
/
7.2. Достаточные признаки равномерной сходимости
Для установления на практике равномерной сходимости конкретных
функциональных последовательностей или рядов указанные в предыду¬
щем параграфе условия малопригодны (так как вычисление предельных
384
функций — трудоемкая задача). Как правило, при решении данных задач
используют на них же основанные, но более удобные в применении доста¬
точные признаки, которые мы сформулируем применительно к рядам.
Начнем мы с самого простого, но обычно наиболее эффективного признака.
Теорема 7.1 (признак Вейерштрасса). Функциональный ряд ^un(X)
и=1
сходится абсолютно и равномерно на множестве X, если существует мажо-
OO
рирующий его сходящийся числовой ряд ^an, т.е. выполнено \ ип(х) \ < ап
Я=1
для VxeXuVne N.
OO
Замечание 7.3. В данном случае сходящийся числовой ряд ^an называ-
Я=1
ется мажорантным рядом (мажорантой) для исходного ряда ^ип(х).
П=1
Обсудим несколько интересных примеров.
Задача 7.6
Рассмотрим на луче [0; +°°) функциональный ряд ^ип(х), где
TZ=I
и„{х) =
—,если X =
п
. 1 1
1+ - + ...+ -
2 п
О, для всех других х
(здесь [а] — целая часть числа а). Докажем, что для данного ряда не существует схо¬
дящейся мажоранты и сам он сходится неравномерно.
Решение
Действительно, каждая функция ип(х) принимает свое единственное ненулевое
1 Г. 1 Г
значение — при натуральном х, х- 1 + — + :
п 2 п
Mi(I) = I, M2(I) = |, M3(I) = -|, м4(2) = |, м5(2) = ..., M11(S) = и т.д.
При всех других х € [0; +°°) эти функции равны нулю.
” 1
Так как —> + °°, то для любого (сколь угодно большого) натурального N
h=l k п—>°°
1
найдется функция ип(х), принимающая свое единственное ненулевое значение —
при X = N.
I I I “1
Для любого х е [0; -н») можно гарантировать лишь оценку \ип(х)\ < —, но ряд £ —
п „=1 п
расходится. Следовательно, данный функциональный ряд нельзя мажорировать схо¬
дящимся числовым, и признак Вейерштрасса к нему не применим.
OO
Покажем, что ряд ^ип(х) сходится не равномерно. Рассмотрим частичную сумму
ZZ=I
П
данного ряда Sn(x) = (*)1- Любая частичная сумма Sn(x) не равна нулю только
k=\
1 Имеем S1(I) = I, S2(I) = 3/2, S3(I) = 11/6 = S4(I) = S5(I) = ...; S4(2) = S2(2) = S3(2) = О,
S4(2) = 1/4, S5(2) = 9/20,..., S10(2) = 2761/2520 = Slt(2) = S12(2) = ...; S4(3) = ... = S10(3) = 0,
S41(3) = 1/11, S12(3) = 23/132 и т.д.
385
при конечном числе натуральных значений аргумента х, х = 1, 2,h(n), где h(n) < п
(в силу асимптотики гармонического ряда (см. гл. 2) и неравенства Inn < n, n G N).
При всехх > h(n) имеем Sn(x) = 0. Сумма ряда S(x) - Hm Sn(x) имеет положительные
Я—»
значения при всех натуральных х. Далее рассмотрим значение предельной функции
S(oc) в точке х = те N. Пусть 1(т) — номер, при котором выполняются неравенства
. I 1
1 + - + ... + -
2 1(т)
Тогда S(m) =
1
- + ... + -
<т,
1
1(т) +1 l(m +1)
„ I I 1
1н—ь... + ь
2 l(m) l(m) +1
. При этом
> т.
л I 1 ,1 I 1
1 + - + ... + - <т, 1 + - + ... + - + -
2 l(m) 2 l(m) l(m) +1
>т,
1
1 + - + ...+ ,
2 1(тп +1)
1
I 11
<пг + 1, 1 + - + ... + - + -
2 /(in + l) /(пг+ 1) + 1
>пг + 1,
откуда
1
- + ...+
1
<1 и
1
+ ... + -
1
/(иг)+ 2 /(иг + 1) /(ги) + 1 /(иг+ 1) + 1
>1. Поэтому
1
/(иг + 1) + 1
<5(иг)<1 +
1
/(иг) +1
Следовательно, так как /(иг) —> +°° при иг —» +°°, то 5(ги) —» 1. Кроме того, 5(х) = О
при xgN. Данный ряд сходится в каждой точке х к своей сумме S(x), но его сходи¬
мость неравномерная, так как для всех п и всех х G N, х > h(n), выполнено неравенство
|5„(х)-5(х)| = 5(х) >|.
Замечание 7.4. Рассмотренный ряд интересен еще и тем, что для любого
n+PQ
фиксированного р0 G N и для всех х G [0; +°°) выполнено ^ uk(x) “^ 0.
k=n+1 и->°°
По определению функций ип(х) при любом х G [0; +°°) выполняется
и
:я+1 (x) + Un+2(x) + ... + un+Po
I 1
- + -
- + ... + -
1
^ Po )
ц + 1 /г + 2 и + P0 я +1 ’
что может быть сделано сколь угодно малым при достаточно больших п.
Предлагаем читателю сравнить данный результат с условием Коши рав¬
номерной сходимости функционального ряда.
Попробуем модифицировать функциональный ряд из разобранной
задачи для того, чтобы получить равномерно сходящийся ряд.
Пусть для всех х G [0; +°°)
ип(х) = -
—, если х = w G N,
п
О, для всех других х.
Частичная сумма ряда имеет вид
*?„(*) = •
—, если х G N, х < п,
х
О, для всех других х.
386
В этом случае получим
S(x) = <
—, если х G N,
X
О, для всех других х.
Сходимость ряда будет равномерной, так как для V в > 0 3 N(e) = [1/в] + 1
такое, что для V п > N и для всех х E [0; +°°) выполнено
&(*)-£(*)| = £(*)<-^ <-^т<е.
п + 1 N
Однако для любого п E N выполнено sup \ип
[0; +°°)
Таким образом,
в этом случае не существует сходящегося числового ряда, который мажори¬
рует члены данного функционального ряда. Поэтому данный пример пока¬
зывает, что условия признака Вейерштрасса лишь достаточны, но не необ¬
ходимы для равномерной сходимости функционального ряда.
Рассмотрим следующую теоретическую задачу.
Задача 7.7
Пусть {фп(л;)}“=1 — монотонные на отрезке [а; b] функции, и ряд Хфи(*) сходится
п=1
OO
абсолютно при х = а и х = Ь. Докажем, что в этом случае ряд XcPnC*) сходится рав-
Jl=I
номерно и абсолютно на всем отрезке [а; Ь\.
Решение
В силу монотонности функции ф, используя элементарные неравенства, получаем
K(X)I =
Еф*(*)^ E |<Р*(лф E тах{|фДа)|,|ф*(6)|}<
k-n+1 k-n+1 k-n+1
^ E (|ф*(в)|+|ф*(*)|)-
k=n+1
(7.1)
Далее, так как числовые ряды X |ф*(а)| и E |ф*(Ь)| сходятся, то для V е > О
k=n+1 k=n+1
3 N(e) : для V n(e) > N выполнено
I Ы*)|<| и 2 |ф*(»)|<|.
k=n+1 ^ k=n+1 ^
Отсюда, используя формулу (7.1), получаем требуемое.
Выше мы уже видели, что признак Вейерштрасса применим не ко всем
функциональным рядам, причем и к равномерно сходящимся, и к сходя¬
щимся не равномерно. Далее мы рассмотрим данный вопрос немного под¬
робнее, но предварительно докажем следующие утверждения.
OO
Утверждение 7.4. Если ряд Хми(х) сходится на отрезке [я; Ь] равно-
Tl=1
мерно, то путем расстановки скобок он может быть преобразован в ряд,
к которому применим признак Вейерштрасса.
387
Доказательство
OO
Запишем условие Коши для равномерно сходящегося ряда Jми(х):
для V в > О 3 N(e): для V п( в) > N, V ре NhVxg X выполнено
TZ=I
п+р
E щ(х)
k=n+\
<8.
Далее возьмем произвольный сходящийся числовой ряд Jan с поло¬
га=!
жительными членами ап. По первому слагаемому ах в силу условия Коши
найдется такой номер ть что
um1+i(x) + - + um1+p(x) р е NhVxg [а;Ь\.
По числу а2 можем найти номер т2 > тх такой, что
\и.
m2+l(X) + - + Um2+p(X) < аЪ И Т-Д-
Положим поочередно р = т2 - WZ11, р = тъ - т2 и т.д. Группируя члены
исходного ряда следующим образом:
(M1(X) +... + Umx (х)) + (m^+1(x) +... + Umi (х)) +
+ Om2+l(*) + - + Um3 (X)) +...,
получим ряд, члены которого, начиная со второго2, по модулю не превос¬
ходят на отрезке [а; Ъ] последовательных членов сходящегося числового
OO
ряда, 2Х.
TZ=I
оо
Утверждение 7.5. Пусть ряд £ |ия(д;)| сходится на отрезке [а; b] равно-
TZ=I
мерно. Тогда и ряд ^u1г(х) сходится на том же отрезке равномерно.
TZ=I
Доказательство
OO
Так как ряд J |ми(х)| сходится на отрезке [я; Ь] равномерно, то по кри-
га=1
терию Коши получаем: для V е > О 3 N(e): V п > N, V р g NhVxg [я; Ь]
выполнено
п+р
E «*(*)
k=n+l
п+р
< J \щ(х)|<е.
k=n+i
Возникает вопрос: будет ли верно обратное утверждение? Пусть ряд
оо
JjUn(X) сходится равномерно. Будет ли равномерно сходиться ряд, состав-
я=1
ленный из его модулей? Ответ на этот вопрос — отрицательный. Рассмо¬
трим следующие примеры.
388
1 Так как номер р произволен.
2 Отбрасывание конечного числа членов не влияет на сходимость.
Пример 7.1
Ряд У
(-1)”
_ сходится на +°°) равномерно, но не сходится на этом множе-
Я=1 X2 + п
стве абсолютно.
К данному ряду при любом х0 е IR применим признак Лейбница (докажите!).
Следовательно, остаток ряда оценивается по модулю своим первым членом, т.е.
Vx0E М|г (х0)|<—-> 0.
и ”V Xq + И +1 И +1 я—»°°
Далее имеем, что для любого х е M выполнено
1
ряд У
72=1
(-1)"
X2 +п
X2 +п
= 0’
Г л \
. Следовательно,
расходится.
Возможно даже такое, что функциональный ряд ^ип(х) сходится абсо-
п-
OO
лютно и равномерно, однако ряд из его модулей У |м„(х)| сходится не рав-
П=\
номерно.
Пример 7.2
S
72=1
- (-1)71-1.^2
Ряд У -—-—-— сходится на (-°°; +°°) равномерно и абсолютно, но ряд
п=1 (Х + Х2)п
сходится на этом множестве не равномерно.
(\ + х2)п
При любом :r0 е R для этого ряда также выполнены все условия признака
Лейбница, откуда, делая ту же оценку и используя бином Ньютона, получаем
к.(*о)|<-
Xk
Xn
Xn
1
-> 0.
(х§+1)"+1 1 + (и + 1)^q +... (n + i)x§ п + 1п->=°
°° (-Х)п~1-X2
Отсюда вытекает, что ряд У сходится на +°°) равномерно.
„ti (1+х2у
OO
Ряд, составленный из его модулей, У
Xi
й(1+X2Y
сходится как геометрическая про¬
грессия, но для Vt0^O выполнено
Xi
оо •'у2 / yI /у-2472+1 yI
гпЫ= I TT^- I =7rrW^lnpH^^0±0-
&=Я+1 (I + -Tq ) ^ ^ (I + ATq )
1 + х2
Следовательно, ряд, составленный из модулей, сходится на M не равномерно.
Возвращаясь к признаку Вейерштрасса, обратим внимание на следую-
оо
щее. Если к ряду У«и(х) признак Вейерштрасса оказался применим, то
п=1
данный ряд необходимо абсолютно сходится. Более того, одновременно
OO
с ним будет равномерно сходиться и ряд У |г/и(х)|, состоящий из модулей
п=1
(докажите!). Между тем в последних примерах было показано, что воз-
389
можны случаи, когда ряд Yiunix) сходится равномерно, будучи не абсо-
и=1
лютно сходящимся. Подобные случаи заведомо не охватываются призна¬
ком Вейерштрасса, для их исследования нужны более тонкие признаки,
на которых мы сейчас вкратце остановимся.
Введем вначале нужное нам определение.
Определение 7.6. Функциональная последовательность {/„(х)} назы¬
вается равномерно ограниченной (ограниченной в совокупности) на множе¬
стве X, если 3 А > 0 такое, что Vig XnVwe N выполнено | /и(х) | < А.
Теперь сформулируем признаки.
Теорема 7.2 (признак Дирихле). Пусть выполнены следующие условия:
П
1) частичные суммы ^ak(x) равномерно ограничены на множестве X;
ы
х
2) У х0 е Xпоследовательность {Ьп{х0)} монотонна, и {Ьп(х)} =40 при п —> °°.
OO
Тогда ряд Y,ап(х)Ьп(х) сходится на множестве Xравномерно.
п=1
Теорема 7.3 (признак Абеля). Пусть выполнены следующие условия:
OO
1) ряд Yjanix) сходится на множестве Xравномерно)
п=1
2) V х G X последовательность {Ьп(х)} монотонна и равномерно ограни¬
чена на X.
OO
Тогда ряд Yian(x)K(x) сходится на множестве Xравномерно.
77=1
Приведем примеры, наглядно демонстрирующие, что сформулирован¬
ные признаки являются только лишь достаточными.
Пример 7.3
Пусть
Получаем
ап(х) = пп+1хп+1, 6„=^Дг, п = 1,2,..., х € (0; 1).
ХПп+Л
Y<*n(x)bn(x)= Е(-1)Я-2--
п=I п=I H
Данный ряд сходится равномерно (достаточно применить признак Вейерштрасса).
п п
В то же время частичные суммы Yak(x) = Xn”+1*"+1 ПРИ любых х е (0; 1) не явля-
k=i k=i
ются ограниченными, так как общий член ряда (nx)n+i —> +°° при п —> +°°.
Далее, Vi0G X последовательность {&„(х0)} =
(-1)”
хп
п+3
не монотонна, а также схо¬
дится к нулю неравномерно в интервале (0; 1). Действительно, для любого сколь
1
угодно большого п возьмем величину х из интервала О < х < _iQ. Тогда
п
п+З
1
Ых) - К*)\ = >1 = е(Л
хп
1 Под Ь(х) мы понимаем предельную функцию последовательности Ьп(х), т.е. тожде¬
ственный нуль.
390
т.е. все условия из признака Дирихле (кроме сходимости последовательности Ъп
к нулю) оказались невыполненными, но это не помешало равномерной сходимости
OO
функционального ряда ^ап(х)Ьп(х).
W=I
Пример 7.4
Пустьап(х) = (-1)”х"+1, Ьп=^Ц~, п = 1,2,..., хе(0;1).
хп*
OO OO
Получаем ^ип(х)Ьп(х)=^—.
я=1 Я=1 U
Данный ряд сходится равномерно (докажите!).
OO OO
В то же время функциональный ряд ип(х) = ^(-1)пхп+1 сходится на интервале
71= 1 71=1
(0; 1) неравномерно. Действительно,
хп+2 1
>
1 + х 4
при х, достаточно близких к единице. Такие х всегда могут быть найдены, так как
\гп(х)\ =
J1 (-l)kxk+i
—
%п+2
k=n+1
1 + х
х
п+2
(-1)”
= 1. Далее, функции Ьп = -—т— не образуют монотонную последовательность
хп1
Iim
х—>1-0 X +1
ни при каком х е (0; 1). Кроме того, данные функции не являются ограниченными,
так как при VneN дробь
(-1Г
XHz
стремится к бесконечности при х —> О + 0.
Таким образом, все условия, накладываемые на функции ап(х) и Ьп(х) из при-
OO
знака Абеля, оказались не выполнены, но функциональный ряд ^а„(х)Ьп(х) явля-
W=I
ется равномерно сходящимся на интервале (0; 1).
Задача 7.8
Пусть ап —> +оо так, что ряд X
п=1
I °° 1
— сходится. Докажем, что ряд ^ сходится
®я п=IX Un
абсолютно и равномерно на любом ограниченном замкнутом множестве X, не содер¬
жащем точек ап, п- 1,2,....
Решение
Обозначим M = max{|inf Х\, |supA|}. Так как «„—> +°°, то 3 N(M) такое, что \ап\> 2M
для V и > N. х
Далее получаем
\х-ап >\ап\-\х\>
|а \ип\
х\<'—^ при Vn> -Wj >-2_'
Следовательно,
1^1 2
Г<Т i i T < 1 i
х-ап\ \ап\-\х\ \а,
'W
И
-н*> л -и» 9
°< £^Ц< S Л
n=N \Х Un n=N \(1п
1
т.е. ряд ^ сходится абсолютно. Кроме того,
п=1 X Un
391
п+р Л
Y
п+р Л
72+р О
Ie е -
IA
M
t
jjTZ+^ ^72
~2 ^ I
A=w+1 % — ^w
£=w+l +- — f^w
6=72+1
OO
По критерию Коши получаем равномерную сходимость ряда E .
W=I % ~ &п
Для самостоятельной работы предлагаем читателю рассмотреть следу¬
ющие задачи.
Задание 7.6
Пусть при х E [0; 1]
Л<Ж) =
О, если О < х <
2 w+i’
I 11
—sin2(2”+1nx), если —-- < х < —,
я 2”+1 2”
1
О, если — <х<1.
2 »
Докажите, что ряд EZwOr) сходится на отрезке [0; 1] равномерно и абсолютно, но его
72=1
нельзя мажорировать сходящимся числовым рядом с неотрицательными членами.
Задание 7.7
Пользуясь признаком Вейерштрасса, докажите равномерную сходимость в ука¬
занных промежутках следующих функциональных рядов:
OO ( \
a) Eb
W=I
1+
X
V
и1п2(и + 1)
на [0; 3];
б) Ee~<x2+shix> на [1; +°°);
72=1
в) E
8 юс
Ii 1 + пах2
, а > 4, на (-оо; +°о);
г) E
Xn
w=i [и/2]!
на (-а; а), где а > О и [у] — целая часть числа у;
х-
Д) X — на[0;+°°);
W=I в”
“ sin(x/n2)
е) E / на (-оо; +оо).
w=l Vn2
+ Xz
Задание 7.8
Исследуйте на равномерную сходимость в указанных промежутках следующие
функциональные ряды:
2пп
а) Е\Л, на (-10; 10); б) E 3
и=0 ^
+ еЛ
W=I л/и2 +X2
на (-оо; +оо);
ч Д sinx-smnx г_ . ч Д cosnx-Sinx-пх
в) E , на [0; +°°); г) E , „ „ на(-оо;+оо);
w=l Z
П + Х
д) E / ; на [0; +°°); е) E
W=I Vn2 +X2
(-1)”
w=l yjn(n + x)
;=1 y/n + л/х
' X
1 + —
V
п
на [0; 1].
1 Как конечное число бесконечно малых членов.
392
7.3. Свойства равномерно сходящихся рядов
В предыдущем параграфе мы ввели исключительно важное определе¬
ние — равномерной сходимости функциональных последовательностей.
Далее мы продолжим разговор об этом понятии, начав с формулировки
основных теорем из этой темы.
OO
Теорема 7Л (почленный переход к пределу). Пусть ряд ^ми(х) схо~
П=1
дится на множестве X равномерно и 3 Iim ип(х) = сп<°°. Тогда ряд ^ сп схо-
W=I
х—>я
Г
дится и Hm
х—>я
Л
jLun(X) = X (HiHttn(X)).
Vw=I J W=I х~>а
Теорема 7.5 (непрерывность суммы ряда). Пусть L,un(x) = S(x). Если
W=I
данный ряд сходится на множестве X равномерно и для VweN функции
ип(х) непрерывны в точке xQ е Х,тои S(x) непрерывна в точке х0.
Замечание 7.5. Иногда бывает полезно пользоваться следующим фактом:
если каждая из функций ип(х) непрерывна в точке X0 е X, а предельная
функция S(x) — разрывная, то сходимость функционального ряда LunCx)
Tl=1
к S(x) неравномерная.
Теорема 7.6 (о почленном дифференцировании ряда). Пусть
для VweN функция ип(х) — непрерывно дифференцируемая на [я; Ь\, ряд
LunCx) сходится в точке с е [а; Ь], а ряд LKCx) сходится на [а; Ь] равно-
W=I W=I
мерно. Тогда:
1) ряд LunCx) сходится на [я; Ь\ равномерно;
Tl=1
оо
2) сумма ряда S{x) = LunCx) непрерывно дифференцируема на [я; Ъ]\
/7=1
f OO Y °°
3) L Mw (*) =LK (х) на Iй; ь\.
^W=I у W=I
Теорема 7.7 (о почленном интегрировании ряда). Пусть для VweN
функция ип{х) интегрируема на [я; й] и ряд L г/и(х) сходится на [я; 6] равно-
/7=1
мерно. Тогда и сумма ряда S(x) = L ми(х) интегрируема на [я; 6], причем ука-
/7=1
Ь OO OO Ь
занный ряд можно интегрировать почленно, т.е. J2X {х)сЬс = n{x)dx.
an=l W=Ia
Замечание 7.6. Данные теоремы переписываются в терминах функцио¬
нальных последовательностей простой заменой LunCx) на l/w(x)} и ^(х)
/7=1
на/(х).
393
Теорема 7.8 (Дини). Пусть для VraeN функция ип(х) непрерывна
OO
на некотором отрезке К и ип(х) > О для V хе К. Пусть также ряд ^ ип(х)
И=1
OO
сходится к непрерывной функции S(x). Тогда сходимость ^ип(х) к S(x) —
И=1
равномерная на К.
Поставим далее несколько вопросов.
1. Может ли последовательность разрывных функций {fn(x)} равно¬
мерно сходиться на отрезке [а; b] к функции fix), непрерывной на [а; Ь]?1
Ответ на данный вопрос — положительный. Рассмотрим /Ах) = где
га
Z)(x) — функция Дирихле. Каждая из данных функций разрывна в любой
точке отрезка [а; b], но
sup|/„(x)-/(x)| = {/(x) = 0} = - ^ 0.
[а; Ъ\ гаи->°°
[а-,Ъ]
Поэтому {/„(х)} =4 О при га —> оо.
2. Может ли последовательность непрерывных на отрезке [а; b] функ¬
ций {fn(x)} равномерно сходиться к разрывной предельной функции/(х)?
Ответ на данный вопрос — отрицательный. Ибо это противоречило бы
теореме о непрерывности предельной функции.
3. Может ли последовательность непрерывных функций {fn(x)} схо¬
диться к разрывной предельной функции?
Ответ на данный вопрос — положительный. Пусть /и(х) = sin”x,
х G [0; я]. Для каждого га g N функция fn(x) непрерывна на [0; я]. Однако
предельная функция
f{x)= Hm fn(x) =
п—>°°
О, если х G [0; я] \
я
1, если X =
я
я
терпит разрыв в точке х = —. Объяснение произошедшего кроется в нерав¬
номерной сходимости функциональной последовательности /п(х) = sin”^
к своему пределу. Предлагаем читателю доказать это непосредственно.
А в заключение продемонстрируем чертежи данной последовательности
при га = 1, 2, 3, 4, 5, 6, 10, 15, 20, 30, 50, 100,..., 3000 (рис. 7.2)2.
Постараемся в следующей задаче избавиться от некоторых условий тео¬
ремы Дини, рассматривая контрпримеры.
1 Если задается такой вопрос, то подразумевается, что либо будет приведен такой при¬
мер, либо будет доказана невозможность его построения.
2 Как очевидно, данная иллюстрация демонстрирует неравномерную сходимость функ¬
циональной последовательности fn(pc) к своему пределу.
394
о
п
п
2
fn(x) = sinnx
Рис. 7.2
Рассмотрим следующие контрпримеры к теореме Дини и докажем утверждения:
составленный из неотрицательных функций, имеет непрерывную сумму, но сходится
к ней неравномерно;
ных неотрицательных функций, имеет непрерывную сумму и сходится к ней равно¬
мерно;
00 Xn
в) ряд Y— на отрезке [-1; 1], каждый нечетный член которого — меняющая
п=\ п\
знак (при переходе через нуль) функция, имеет непрерывную сумму и сходится к ней
равномерно;
рицательных функций, имеет разрывную сумму и сходится к ней неравномерно;
а) ряд Yun(x)> гДе
у —- — —
O')- " Ca а ~ U — 2,3,...,
О, если х G [0; 1] \ —; ,
\п п-1
б) ряд Yun(x)’ где ип(х) =
1/2”, если х eQ,
2/3", если х € R\Q,
составленный из всюду разрыв-
395
д) ряд 5Х(*)> где Kb(X) =
п=1
’ . 1
sin—
, если х G
( I 1 '
47t(w + l)’ ПП
X
0, при всех других х,
составленный из непре-
рывных неотрицательных функций, имеет непрерывную сумму и сходится к ней
f Г
неравномерно на полуинтервале
0;-
п
Решение
а) Суммой рассматриваемого ряда на отрезке [0; 1] является функция S(x) = 1,
так как для всех точек X0 E [0; 1] есть один и только один член ряда, равный в точке
(о- 1 ]
такой, что
OO
E ип(х)
V ’ w +1J
k=n+1
= 1>е0.
1
б) Сумма 5(х) ряда в рациональных точках х будет равна ^ — = 1, в иррацио-
OO 2 TZ=I 2”
нальных — 5) — = 1. Отсюда S(x) = 1 на [0; 1]. Равномерная сходимость рассматри-
п=i3”
ваемого ряда к своей сумме следует из существования сходящегося мажорантного
ряда:
Г 1 2 I
О < и„(х) < max^ } для V и G N.
[2я 3”J
в) Каждый член ряда с нечетным номером является нечетной функцией и при¬
нимает значения разных знаков при переходе через нуль. Равномерную сходимость
°° Yn [0; 1]
п=\П\
I I 1
к непрерывной функции мы получаем в силу мажорирующей оценки \ип(х)\ <—.
п\
г) При х <
'о;-'
V 2у
получаем
ч Д . „ (l-sinx)sinx
(1 - smx) • 2j smn х = -—;—— = smx.
я=1
1-sinx
я
При х = 0 и х = — все члены ряда и, соответственно, его сумма равны нулю.
2 CO
Следовательно, сумма S(x)= Xsin^'Cl-8!11-^) разрывна в точке х = —.
п=1 2
Сходимость неравномерная в силу, например, теоремы о непрерывности предель¬
ной функции и непрерывности для VwgN членов ряда sin”x • (I - sinx).
Для VwgN функции ип(х) непрерывны и неотрицательны на полуинтервале
г Г
0;-
п
Ю
' Г
0;-
п
. Воспользуемся тем, что для любого х <
V
нулю. При X G
1
1
получаем м„(х) =
. 1
Sin-
X
только один член ряда не равен
. В то
. Поэтому JjUn(X) =
П=1
. 1
Sin-
X
7l(w + l)’ 7Ш
же время для любого сколь угодно большого п существует такое достаточно близ-
(п I 1
кое к нулю XE 0; —
, что остаток ряда |гя(х)| =
E
будет больше, скажем, -.
I4 тг)
k=n+1
2
B качестве полезного упражения укажите, какие условия теоремы Дини
были нарушены в каждом из пунктов задачи 7.8.
Рассмотрим далее несколько задач.
396
Задача 7.10
Докажем, что У—-tg—= Ctex--, 0<х<—.
2я 6 2я 6 х 2
Решение
Сначала докажем следующее равенство:
” х smx _ п
cos— = , 0 < х < —.
2я х 2
Действительно,
. х
я г я у Sin
ncosi = n«>s|- £
A=I 2к A=I 2к . X
sinj:
X
2п sin х
smx
Ctrt-X .X X п->~ х
sin— 2я sin— sin—
2я 2я 2я
Далее, логарифмируя доказанное равенство, получаем
Eln
я=1
COS-
V
X
'2я
= In
^sinx^
V X у
(7.2)
сходится, например, при х = 0;
Проверим выполнение условий из теоремы о почленном дифференцировании:
I х ^
COS —
9 TZ
V z У
' хЛ
дифференцируема на интервале I 0; —
V 2
ряд Eln
TZ=1
функция In
Л
ряд Eln
TZ=I
cos-
V 2я У
\
Tt
‘ J
X
COS-
X
2я
_ у tg 2я
1 2я
я=1
сходится равномерно на
^O; —^
V 2у
Следовательно, почленное дифференцирование ряда Eln
TZ=I
(докажите!).
л
COS-
V
X
'2я
возможно.
Дифференцируя левое и правое выражения в формуле (7.2), получаем требуемое.
Задача 7.11 * 1 * 3Докажем равенство \x~xdx = Еи_”-
о я=1
Решение
Доопределим хгх в нуле по непрерывности числом 1. Далее получаем
X-* =е-*1"* =l-*ln* + fc2^+...+.
2! п\
Данный ряд сходится равномерно на [0; 1] (докажите!), каждый из его членов инте¬
грируем. Поэтому на данном отрезке справедливо почленное интегрирование, откуда
]x~xdx = E } (~х ln dx= E ^-\хп\п nxdx.
О я=Оо я! я=0 я! q
Интегрируя по частям, получаем
1 п
Kn = KnInnXdx = —1п,п-1 при п > 1.
О И + 1
I I 1 (-1)яп!
Используя то, что Irt n = fxnfi?x = , заключаем, что fxn1nnxdx = ——-—V- Следо-
3 ”’° Jn и + 1 I (и + 1)я+1
вательно,
\ _rJ ^ (-1)" (-1)"я! ^
Jx xdx=^^K~-, . Krt^ = S-
о
1
= Еи_”-
я=0 я! (и + 1)я+1 „=0(п + 1)я+1 я—1
397
Задача 7.12
nz
Найдем сумму ряда E—.
п=l3"
Решение
Имеем:
°° п2 1
5=£— = -
ЙЗ» 3
(а 4
9
16
_ 1
г
1 м
'1I
2 ^
+ - +
—Ь .
1 + 4
- + 9-
+ ...
I з
9
27
_3
V
3
UJ
)
1
Введем в рассмотрение функцию f(x) = — (1 + 4х + 9Jf2 +16л;3 +...). Заметим, что
3
S = / — .Не вдаваясь в подробности обоснования почленного дифференцирования
v3y
и интегрирования (оставляем это читателю), постараемся вычислить функцию /.
Получаем
\f(x)cbc = — (х + 2х2 +З^3 +...) +C = —^jGn + С,
3 3„=1
где Gn — сумма бесконечной геометрической прогрессии, начинающейся с члена Xn,
-YwTl
T.e.G„= —
. Поэтому
\f(x)dx = ~YGn+C = -- — - + C = - ^г + С.
J Зы " 3 1-х 1-х 3 (1 -х)2
1 1 + X
Продифференцировав обе части этого равенства, получим f(x) = — ■ — —. Следо-
3 (I-*)3'
вательно,
5= Sfr=/
TJ=Ij
(а \
v3 У
Задача 7.13
Найдем следующие пределы:
“ 0~пЧ
а) Iim п~\ п ; б) IimCl-OE-.
*->0+0 In г ^l-O n=il + tn
Решение
е~п
а) Обозначим через /(и) = . Учитывая монотонное убывание данной функ-
п
ции, получаем для Ухе [k;k + l] выполнение f(k) < f(x) < f(k + 1). Интегрируя дан¬
ное неравенство по х от k до k + 1 и суммируя полученное по k от 1 до и, получаем
TJ Я+1 TZ+1
ILf (Ь)> J /(x)dx> LfOO-
k=l I k=2
Отсюда следует, что последовательность
TJ Я+1
LfOO- J f OOdxt neN,
k=i 1
монотонно возрастает и ограничена сверху. Следовательно, существует конечный предел
tn
Hm
И—о
( TJ я+1 ^
Lfoo-1 foodx
Kk=I 1 ,
Я Я+1
т.е. частичные суммы YjfOO и интеграл J f(x)dx асимптотически равны при
k=i 1
398
Вычисляя полученный интеграл, находим
, „ - - +“ р-уг 1 р-у1 +°° р-у1
I dx = J dy = J dy + I dy =
1
х
Ji У
Ji У
У
\ dy } е~У2 -1 , 4T е~У2 ,
= J —+ J dy+ J dy.
)i у Ji у 1 у
Второй и третий интегралы при t—> 0 + 0 имеют постоянные пределы (докажите!),
а следовательно, постоянны и при делении на Int при ^ —+ 0 + 0 дают нули. Вычисляя
предел первого интеграла, получаем
1
г dy
Ji У
1
Отсюда искомый предел равен .
б) Имеем
Int
'~2‘
00 ftl 1 _ f 00 +71
Hm (l-t)У = Iim — (-Int)- У .
i-»l-0 1 + t” ^l-O-Int ^1I + t"
l-t
Используя то, что 3 Hm —— = 1, найдем предел
*-»i-o-lnt
Hm (-Int)-£-^- = Iim (-Int)-У—р
*-»i-ov „tll + t” *-»i-o ^е~пЫ+\
= L
Сделаем подстановку -Int = А и представим искомый предел в виде предела инте-
тральных сумм:
0° Л +°° Л/у-
L = Hm А-У - = f = [x-ln(l + e*)]l =In2.
д—»о+о l + e^ l+e1 lo
В качестве самостоятельной работы предлагаем решить следующие задачи.
Задание 7.9
OO
Докажите, что ряд У [яге-"*-(я-1)^6^"-1)*] сходится неравномерно на [0; 1],
Tl=1
но его сумма есть функция, непрерывная на этом отрезке.
Задание 7.10
Докажите, что тэта-функция 0(д:) = У е~т х определена и бесконечно диффе-
Yl=-OO
ренцируема при х > 0.
Задание 7.11
OO I
Докажите, что дзета-функция Римана ^(х)= У— непрерывна в области х > 1
п=\Пх
и имеет в этой области непрерывные производные всех порядков.
Задание 7.12
Найдите следующие пределы:
a) Hm У
(-1)
Я+1 д-Я
,, б) Hm У (хп-хп+1);
х »1—0 п Xn +1 ж—»1-0 n=i
В) Iim i—;г) Iim У
*-»0+0 п=12" пх ’ ж-»+~ п=\ I + H2X2
399
Задание 7.13
Определите области существования функции/и исследуйте ее на дифференци-
°° (-Vy1X
руемость, если f(x) = —-—.
п=\ П + Х
Задание 7.14
OO
Докажите, что функциональный ряд ^ (R(x))n, где R — функция Римана, сходится
на отрезке
_1.3
4’ 4
П-1
равномерно, несмотря на то что его члены и сумма имеют всюду плот-
ное множество точек разрыва на данном отрезке. Будет ли в этом случае справедливо
почленное интегрирование?
Задание 7.15
^ YUq ^ YVX
Найдите пределы Hm f —-сЬси f Iim —7dx и определите, законен ли пере-
я->°° J01 +Yl2X4 q n—»°° I + Yl^ X^
ход к пределу под знаком интеграла.
7.4. Степенные ряды
Определение 7.7. Ряд Y ап(х-х0)п называется степенным рядом с цен-
и=0
тром в точке х0.
Замечание 7.7. Линейная замена £ = х - X0 переводит степенной ряд с цен-
OO
тром в точке х0 в степенной ряд Yantn с центром в нуле.
п=0
Определение 7.8. Говорят, что функция/: X —> Rраскладывается в сте¬
пенной ряд на интервале (х0 - R; X0 + R) с X, если найдутся такие действи¬
тельные числа ап, п = 0,1, 2,..., что для всех х е (х0 - R; X0 + R) справедливо
равенство /(х)= ^ап(х-х0)п.
W=O
OO
Утверждение 7.6. Для каждого степенного ряда ^an(х-а)п суще-
W=O
ствует интервал сходимости: {х G R \ \ х - X0 | < R}. Множество сходимо¬
сти данного ряда или совпадает с интервалом сходимости, или получается
добавлением к нему одной или обеих концевых точек. Радиус сходимости
R может быть вычислен по формуле Коши — Адамара i?-1 = Hm или
также по формуле Даламбера R = Iim
W-
<2*
а
W+1
W-
если этот предел существует.
Замечание 7.8. Так как \an(-R)n \ = \anRn\, то абсолютная сходимость ряда
YjaTiix-х0)и одном конце интервала сходимости влечет за собой его
W=O
абсолютную же сходимость на другом конце интервала, поэтому множе¬
ство сходимости степенного ряда может быть полуинервалом только тогда,
когда в соответствующем конце этот ряд сходится условно.
400
Теорема 7.9 (Тейлора). Для того чтобы функция f(x) = Yan(x~xo)n
W=O
могла быть разложена в ряд Тейлора на интервале (х0 - R, X0 + R), R > 0,
необходимо и достаточно, чтобы она была бесконечно дифференцируема
и остаточный член в формуле Тейлора для этой функции стремился к нулю
при п —> °° на указанном интервале. Разложение имеет вид
/(х)=Y~—7“^(х-хо)и> xe(x0-R,x0+R). (7.3)
Функция/, разлагающаяся в ряд Тейлора, называется аналитической,
и ее разложение в ряд (7.3) единственно.
Утверждение 7.7 (арифметические действия над степенными ряда¬
ми). Внутри общего интервала сходимости | х - X0 | < R имеем:
OO OO OO
a) аДх - X^n ±^Ъп{х-XqY1 = £ К ±6иМх-х0)и;
n=0 n=0 п=0
б) Y^nix~Ч)п-Ybnix-xQT = Хси-(х-х0^гдеси = аЛ+аА,_1 + - +
п=0 п=0 п=0
OO OO
+ апЬ0 — произведение рядов Yan(x~ хо)п и YKix ~ хо)п п0 Коши;
w=0 W=O
в)
Y
Yan(x~xo)n = Y (п+iX+i(* - хо)”;
Vw=O
w=0
OO OO Q
г) J Yan(x~xo)n dx=Y—— (х-X0)и+1 + С, где C = const.
Vn=O я=пИ + 1
w=0 ^
Теорема 7.10 (первая теорема Абеля). Если степенной ряд S(x) = Y апхП
W=O
сходится в некоторой точке X0 Ф 0, то он сходится абсолютно на множе¬
стве {хе RI |х| < |х0|}.
Утверждение 7.8. Для любого r,0<r<R, степенной ряд Yan(x~xо)”
W=O
сходится равномерно на отрезке {хе R 11х-X0 | < г).
Теорема 7.11 (вторая теорема Абеля). Пусть R — радиус сходимости
степенного ряда Y апхП и $(х) — его сумма для х е (-R, R). Тогда если ряд
W=O
сходится в точке х = R (х = -R), то его сумма является непрерывной функ¬
цией в этой тачке, т.е.
Hm
x->R-О
Yvn
W=O
= Y anRn ( lilB Y Vn = E an(-R)n).
п=О х~^ °+^п=0 п=О
Задача 7.14
„ (-1)"
Рассмотрим сходящийся ряд Лейбница ^ -—— и составим по нему степенной
п-0 2п + 1
+оо /y2n~hl
ряд S(x)=Z{ J .
п-0 2.П + 1
401
Решение
+OO
Для вычисления суммы исходного ряда рассмотрим ряд Y (-1)”х ”. Он сходится
п=
1
при х G (-1; 1), и его сумма равна -. Интегрируя этот ряд почленно на отрезке
1 + Х2
[0; х], где х G (0; 1), получаем
? dt
£ (-1)" Jt2-A = J—j
п=0 О
-и» (-1)”х2”+1
= arctgx + C1.
о о1"1"1- п=о 2и + 1
Используя далее первую теорему Абеля, заключаем, что
Шп5(х) = 1 = 5=Х^.
ж—»1-0 4 „=0 2п + 1
В качестве самостоятельной работы предлагаем следующую задачу.
Задание 7.16
°» (—jy*+i
Вычислите сумму ряда Y ~—— с помощью теоремы Абеля.
п=1 И
Рассмотрим далее несколько теоретических задач.
Задача 7.15
Докажем, что если |х| < 1, то из сходимости на некотором интервале (-R; R)
OQ OO
ряда Yun(x) слеДУет абсолютная сходимость ряда Yun(x)xTt на интервале (-R;R),
п=1 П=1
где i? = min {i?, 1}.
Решение
OO
Функциональный ряд Yun(x) сходится в любой точке интервала (-R; i?).
П=1
Поэтому для каждого х последовательность м„(х) стремится к нулю при п —»
Отсюда для всех х существует sup|wra(x)|. Далее, мажорируя общий член исследуе¬
мого ряда, получаем п
ill л I Iii л
ия(х)х" <|х| sup мя(х) =|х| q(x).
При любом х G (-R; R) ряд Y W Qix) сходится, так как
я=1
Ym q(x) = q(x)Ym =q(x)
я=1 п=1
X
1-
X
Замечание 7.9. Если степенной ряд Y апхП расходится в точке X0 > О,
Я=1
то он расходится и в любой точке х > х0. Действительно, будем рассуждать
от противного: если ряд сходится в некоторой точке х* > х0, то он сходится
во всех точках О < х < х*, а значит, и в точке х0, что неверно.
1 Где C=O (докажите!).
402
Задача 7.16
Пусть ряды ^anXn, ^bnXn имеют радиусы сходимости гх и T2 соответственно.
п=1 п=1
OO
Предположим также, что гх Ф г2. Докажем, что ряд ^(ая +Ьп)хп имеет радиус сходи-
W=I
мости г = Hiinlr1; г2}.
Решение
Заметим, что рассматриваемый ряд сходится для У х \ \х \ к г. Пусть, далее,
T=TxKr2ViriKXKr2. Тогда ряд
E («* + К)х" = E апхП + E Kx"
я=1 я=1 п=1
расходится, так как первый ряд расходится, а второй сходится. При х > Hiaxlr1; г2}
ряд, очевидно, также расходится (см. замечание 7.9).
Зададимся вопросом: что можно утверждать о радиусе сходимости гряда
OO
ЕХйя +ЮхП в условиях задачи 7.16 при тх = г2? Например, при an = bn= 1
Я=1
получаем rx = r2 = г = I. А при ап = I, bn = -1 имеем rx = T2 = 1, однако
оо оо
^ (яи + Ъп )хп = ^O-Xn, т.е. радиус сходимости получившегося ряда равен +°°.
я=1 п=1
Предлагаем читателю самостоятельно ответить на вопрос: можно ли
построить пример ряда, у которого +оо > г > тх = т2?
Задача 7.17
Пусть ряды ^anXn, ^bnXn имеют радиусы сходимости гх и г2 соответственно.
П=1 П=1
OO
Докажем, что ряд £ апЬпхп имеет радиус сходимости гх ■ г2.
W=1
Решение
Получаем
limW| anbn I = Iim(WjaJ • Л]) < • IimW^ (докажите!).
И—>оо W-W—Я—о
Отсюда имеем г > T1 • г2.
Рассмотрим случай an = bn= 1. Получаем г = T1 = r2 = 1. Зададимся вопро¬
сом: может ли неравенство из задачи 7.17 быть строгим? Ответ на этот
вопрос — положительный. Например:
а
П
О, если п = 3k,
■ 1, если п = 3k +1, Ъп
1/2”, если п = 3k + 2;
1, если п = 3k,
■ 0, если п = 3k +1,
1/2”, если n = 3k + 2.
Тогда T1=T2 = 1, а г = 4. Далее, пусть
[О, если п = Ik,
ап ~
1, если n = 2k + l;^n
[ 1, если п = 2k,
[О, если п = 2k + \.
В этом случае Tx = T2 = 1, а г = +оо.
403
Задача 7.18
Определим радиус сходимости ряда ^dnXn, если:
га=О
а) 3 L > О, 3 a G R: Iim \аппа\-L;
б) 3 L > 0, 3 а > 0: Hm \anan\ = L.
П—>°°
Решение
а) Имеем
Следовательно, R = 1.
б) Имеем
Jl
а
Следовательно, R = а.
Задание 7.17
OO
Определите радиус сходимости ряда апхп, если:
га=О
а) 31,>0,3 а >0: lim|a„a^”| = Z,;
П—>°°
б) 3 L > 0: Iim \апп\ = L.
Задача 7.19
Рассмотрим разложение функции f(x) = ех по формуле Тейлора с остаточным
членом в форме Лагранжа:
ех = 1 + х +— + ...+
2!
(п-1)! п\
1 п +1
где О < 0 < 1. Докажем, что если О<*<п+1,то0< — • In .
X п+1-х
Решение
Выпишем разложение функции f(x) = ехъ бесконечный ряд:
■■у 2 уП
„ i Jv Jv
ех =1 +х + — + ... + — + ...=
2!
/^2 ^
= 1 + х + — + ...+
2!
Xh
(п-1)! п!
п!
, х
1 + + -
Xi
п +1 (п + 1)(п + 2)
+ ...
<1 + х + — + ...+
2!
Xn
(п-1)! пМ,
= I + X л ь... +
2!
. X X
1+ +
п + 1 (п + 1)2
Xn 1
+ ...
(п-1)! п! ^ х
п + 1
%2 JC^~ 1
= I + X H Ь... + -
2!
„ Г 1, п+1
уЯ ж- -In
. 0 Iv* п+1—лг
(и — 1)! и!
Отсюда и из формулы (7.4) вытекает требуемое.
(7.4)
404
Задача 7.20
Пусть степенной ряд E ап%п имеет периодические с некоторого места коэффи-
я=0
циенты, т.е. ап = ап+т при п> N. Докажем, что на некотором невырожденном интер-
O (х)
вале (а; Ь) с (-1; 1) он совпадает с рациональной функцией , где QiXx), RnXx) —
Rn(x)
некоторые многочлены.
Решение
Так как коэффициенты данного степенного ряда периодичны начиная с номера
JV+ 1, запишем
OO +оо
E апхп -а0+ O1X +... + aNxN + E(C1X + C1X2 +... + cmxm)-xN+km. (7.5)
п=О A=O
Воспользовавшись формулой для бесконечно убывающей геометрической про¬
грессии1, находим
+OO
E (C1X + C2X2 +... + CmXm)- xN+km =
A=O
(|C1X + C2X2 +... + cmxm)xN
I-Xm
откуда
E апхП =
п=О
(а0 + OiX+ ...+ aNxN)(i-xm)+ (C1X+ C2X2+ ... + CmXm)-xN+km
i-xm
= Qkix)
RmixY
Замечание 7.10. Если (а; Ъ) <Х (-1; 1), то ряд (7.5) расходится и иссле¬
дуемый степенной ряд представляет собой рациональную функцию тогда
и только тогда, когда он является конечным многочленом а0 + a ^x +... + axN.
Зададимся далее вопросом: верно ли обратное утверждение (т.е. всякая
ли рациональная функция может быть представлена в виде степенного ряда
с периодическими коэффициентами)? Ответ на поставленный вопрос —
1
отрицательный. Действительно, рассмотрим функцию fix) = j=^. Тогда
1-V2.
х
получаем
—^j=- = (I - SxYi = 1 + фх) + ф)2х2 +....
1-V2x
Период начиная с некоторого номера получен быть не может.
Постараемся вывести необходимое и достаточное условие того, чтобы
степенной ряд представлял собой рациональную функцию.
Пусть /(,>_£(*>. . £v„.Toraa
Q(x) с0 + C1X +... + Cno XnO и=о
OO
P(x) = Q(x)-^ZanXn ^р0+PiX+ ... + PmoXmO =
и=0
= (с0+CiX+ ... + с Xn^)- Zvn= LQnxn-
и п=0 п=0
Отсюда, используя метод неопределенных коэффициентов, получаем,
что все qn при п>т0 обращаются в нуль. Поэтому справедливы равенства
1 При I х I < 1 получаем (C1X + C2X2 + ... + cmXm)xN+km —> О при k
при k —> +°о.
405
Qn с0ап Cian-I + ••• + Cq &п_щ 0, п > т0.
В обратную сторону. Пусть выполнены равенства (7.6). Тогда
{ OO Л
E Vn • (с0 + - + CnnXnO) = P0+... + PmoXmО.
(7.6)
Vw=O
Все старшие степени «обнулились», поэтому f(x) =
Нами было доказано следующее утверждение.
Pjx)
Q(X)'
Утверждение 7.9. Функция f(x) = Y апхп рациональна, т.е. предста-
W=O
вима в виде
= Р(х) = Po + Pix + - + РщхЩ
Qix) Cq+C1X+ ... + CnoXnО
тогда и только тогда, когда существуют постоянные C0,C1,...,Cnfl такие, что
для всех т, больших некоторого т0, выполнено тождество с0ат+с1ат_1+...+
+ cUQaTn-UQ =0-
Задача 7.21
Рассмотрим разложение в степенной ряд функции
1
= YjanXn- Докажем,
1-2х-х2 п=о
что для любого целого числа п > О найдется целое число т такое, что ап + а2+1 = ат.
Решение
Получаем
I I 1
1-2*-*2 2-(1 + *)2 (V2+1 + *)(V2-1-*)
1
1
Jl
2V2 V. V2 + I + X V2 — 1 — * у 2V2
1
V2-1
V2+1
1 — (1 — л/2)лг 1-(1 + >/2)*у
= £ ^=[(1 + V2)”+1 - (I - V2)”+1]*”.
n=o 2 V 2
Вычисляя выражение а2 + а2+1, находим
+ °п+‘= • [(1+V2)2n+3 - (1 - V2)2n+3] = а2п+2 =>т = 2п + 2.
Задача 7.22
оо %3п
Докажем, что степенной ряд /(*) = Y сходится на М. Покажем справедли¬
во (Зя)!
вость тождества /"(*) +fix) + fix) = 6х, х е R. C учетом равенств /(O) = 1,/'(0) = О
докажем, что
/<хЧ
Решение
Сходимость исследуемого степенного ряда на всей числовой прямой и возмож¬
ность почленного дифференцирования доказываются стандартными методами (дока¬
жите!).
(S 1
ех +2е~х/2 • cos
—X
to
, X E ]
(7.7)
406
00 X^n
Дифференцируя равенство f(x) = £ почленно, получаем
и=о(Зп)!
/'(*)= S
X
Зя-1
п=о (Зп-1)!
. /"(*)= E
X
Зп-2
п=0(Зп-2)\
Следовательно,
/"(*) + /'(*) + f(x) = £ = е*.
я=0 П1
(7.8)
Для того чтобы доказать тождество (7.7), можно решить линейное дифференци¬
альное уравнение (7.8) с граничными условиями /(0) = 1 и f(0) = 0 стандартными
методами. Оставляем это читателю. Можно также воспользоваться формулой Эйлера
и переписать тождество (7.7) в виде
г
/(*>=з
1+iS iJ3—1 ')
ех + е 2 +е 2
V
Далее требуется разложить каждую из экспонент в ряд Тейлора и привести подоб¬
ные слагаемые.
Напомним результат из теории числовых последовательностей. Пред¬
положим, что задана некоторая последовательность {ап} со строго поло¬
жительными членами. И пусть существует предел Hm Q”+1 = q. Тогда
и->°°
существует предел Iim = q. Обратное, вообще говоря, неверно. Мы
Я—о
рекомендуем читателю построить контрпример.
Но между тем справедлив и более сильный результат. А именно, пусть
I = Hm L = Hm Что в этом случае можно сказать о пределе Hm
я->°° CLn я-»” CLn я->°°
Из определения нижнего и верхнего пределов имеем
CL.
для V е > 0 3 N(e) : V п{в) > Nвыполнено / - е < < L + в.
Перемножая данные неравенства для N,N+1,..., п, получаем
(/-в)”
-N
а„ а
я-1
ап-1 ап-2
Следовательно,
fljv+1 <(1 + 8)”-^^ (/
п
а
'N
(I-E)
N CLn < CLn <
(L + еУ
(L + в)
Ял
N “W
(I-Z)-^2 <fn<(L + z)-^^
При достаточно больших п выполнено
/ - 2в < фг^ <L + 2e,
откуда получаем следующее важное неравенство:
HmHm^< Hm< Hm
п—^°° CLn ^00 п—>°° п—¥°° ап
407
В частности, отсюда следуют упомянутый выше результат из теории
числовых последовательностей, а также следующее утверждение.
OO
Утверждение 7.10. Радиус сходимости степенного ряда £ CinXn улов¬
ив
летворяет неравенству О<1<R<L, где I = Hm
п—
ап
, L = Hm
п—>°°
Яи+1
an+i
Задача 7.23
Докажем, что если fix) = ^anXn, причем | п\ ■ ап \ < M (п = 1, 2,...), где M = const,
П=1
то функция f(x) бесконечно дифференцируема в любой точке а E M и справедливо
г/ ч ^/(n)(«)/ ч„ I I
разложение /(#)= 2,-—{х -а)п, |jc| <«».
п=0 П\
Решение
I I “ M \П I
Справедлива оценка /(х) < X — \х\ = Me x'. Формально дифференцируя для про-
п=0 П\
извольного натурального т, получаем
оо
f (т\х) = апп{п -1) •... • in - т + 1)хп~т =>
I \| ^ M п\ I Iп-т
If(mXx)< S — -W
„=тП\ in-m)\
= М^^ = Ме'х'.
k=0 к\
(7.9)
Для VmeN полученные степенные ряды сходятся равномерно на всей числовой
прямой, откуда заключаем бесконечную дифференцируемость в любой точке а е М.
Далее имеем
Rnu(X) = fix)- £ -a)k = ^(*-а)п+\
k=o я! (и + 1)!
где % е (а; х). Поэтому в силу соотношения (7.9)
I I Me 1¾
KMi~а) -*■ *•
(и + 1)! п-»°°
т.е. выполнен и второй пункт данной задачи.
Задача 7.24
оо г^2я+1
Определим радиус R сходимости ряда ^
„=о(2и + 1)П
следующие соотношения:
а) fix) = I + xfix), х G i~R; R);
б) fix) = exl/l Je-u2Z2 du, x e (-Д; R).
о
Решение
а) Имеем
и для его суммы fix) докажем
R~l = Iim 2я+11
1
1 (2п + 1)Н
= О* => R = +о=».
1
1 Здесь мы воспользовались равенством Iim -^= = О (докажите!).
yjnl
408
Далее получаем
OO г2 п OO г2п+2
/'(х) = J-——, 1 + х/(х) = 1 + J
-=1+S
X
2 п
= X-
х
2п
~0(2п-1)!Г “ “ „t0(2n-l)!! „ti(2n-l)H nt0(2n-l)!!’
что доказывает п. а).
б) Рассмотрим производную:
(e~x2/2f(x))' = -xe~x2/2f(x) + e~x2/2f'(x) =
= e~x2/2(f'{x) - xf(x)) = {(a)} = e~x2/2.
Интегрируя последнее равенство по и от О до х и используя равенство /(O) = О,
получаем
e~x2/2f(x) = \e~u2/2du о /(х) = ex2/2fe~u2/2du, iel.
о о
Задача 7.25
1
Представим в виде суммы ряда значение интеграла Jex2 dx.
о
Решение
Раскладывая подынтегральную функцию f(x) = ех в степенной ряд и производя
почленное интегрирование, получаем
1 00 1
\ex2dx= J .
jO „Г0(2п + 1)п!
Задание 7.18
г з °° ап
Докажите соотношение Ieax dx = У , а е К.
jO „=0(Зп + 1)-п!’
Задача 7.26
Предположим, что ап> О для VneN, ряд f(x) = Jапхп сходится на Пятер¬
ик
OO
вале (-R; R), R > 0, и существует предел Hm /(х). Докажем сходимость ряда J anRn.
x^R-0 п=0
Решение
Для любого натурального п получаем
JakRk= Hm JakXk <{ak>0}< Iim /(*).
Ы) X^R-Ok=O x^R-0
Предлагаем читателю сравнить утверждение задачи 7.26 со второй тео¬
ремой Абеля.
Задача 7.27
X
Пусть а0(х) интегрируема на отрезке [0; 1] и an{x) = \an_i(u)du, х е [0; 1], п > 1.
о
OO
Докажем, что ряд J ап(х) = а(х), х е [0; 1], сходится на [0; 1] и его сумма а(х) удоб¬
но
летворяет неравенству |a(x)| < Lex, х е [0; 1], L = sup|a0(x)|.
[0; 1]
409
Решение
Получаем
|«i (х)|
X
\aQ(u)du
о
X X
< JIO0 (и)| du < sup\а0 (х)| \du = Lx
О [0;1] О
х х2
для Vxe [0; 1], откуда\a2(x)\<L\udu = L—,хе [0; 1].
о 2!
Далее методом математической индукции можно доказать (докажите!), что для про-
— , х е [0; 1]. Следовательно,
п\
справедливо неравенство
извольного п е N выполнено неравенство \un(x)\<L
OO
E ап(х)
п= 0
=0 п=О
= Lex, х е [0; 1].
Задание 7.19
Напишите пять членов разложения функции в степенной ряд в окрестности точки
х0 = 0: а) у(х) = еагсс<«х; б) у(х) = e^TCt&x.
Задание 7.20
Применяя различные методы, найдите разложение в степенной ряд с центром
в точке х0 = 0 следующих функций:
а) /(х) = \e~t2dt (распределение Гаусса)', б) /(х) = J arct^^ dt.
n n t
Задание 7.21
Применяя различные методы, вычислите суммы следующих рядов:
a) E
(2п-1)П
пГо (2п)П
t\ и(2и-1)
Задание 7.22
Разложите функцию у = arctgx в степенной ряд с центром в точке X0 = 0. Далее,
используя это разложение, получите разложение в степенной ряд функции х = tgу.
7.5. Применение степенных рядов
для суммирования числовых рядов
Рассмотрим далее вопрос о применении степенных рядов в теории обоб¬
щенных методов суммирования числовых рядов. Вкратце напомним чита¬
телю суть данной проблемы.
OO
До сих пор для заданного числового ряда ^dn в качестве его суммы
TZ=I
определялся предел частичных сумм S = Hm Sn в случае его существования
п—
и конечности. Если данный предел не существовал (или был равен беско¬
нечности), мы считали числовой ряд лишенным суммы (расходящимся).
Для определения сумм расходящихся рядов математики искали способы
суммирования этих рядов, позволяющие получить аналогичный результат,
410
который даст функция/, разложением которой этот ряд получен. За истин¬
ное значение принималось выражение, полученное из непосредственного
вычисления значения функции/, а для расходящегося ряда, полученного ее
разложением, придумывалась (обобщенная) методика вычисления суммы,
дающая такой же самый результат.
Такое искусственное согласование (назовем его метод P) должно удов¬
летворять ряду требований, которые позволяют назвать методику обобщен¬
ной. Первое требование к обобщенной сумме (называемое линейностью)
состоит в том, что если
JtOn = A(P), Jbn = B(P),
и=1 п=1
OO
то для V a, P G R выполнено^(аяи ±Рbn) = оЛ ±(1В (P).
Я=1
Второе требование (называемое регулярностью) заключается в том,
чтобы обобщенное понятие суммы включало в себя обычное понятие
суммы. Это означает, что ряд, сходящийся в классическом смысле и имею¬
щий обычную сумму S, должен иметь «обобщенную сумму», и притом тоже
OO YI со
равную S (т.е. из ^an = Hm Yjak=S должно следовать ^an=A (P) = S).
п=1 п=1
Остановимся в нашем изложении на одном из самых эффективных
методов обобщенного суммирования, а именно, на методе Пуассона —
Абеля, или методе степенных рядов суммирования числовых рядов. Он
состоит в следующем.
OO OO
По данному числовому ряду ^an строится степенной ряд ^апхп~х. Если
п=\ п=\
этот ряд для всех О < х < 1 сходится и его сумма S(x) при х —> I - О имеет
предел S, то это число S и называют обобщенной (в смысле Пуассона —
Абеля) суммой данного ряда.
OO
Обозначение: ^an = S (Л).
п=1
Докажем, что изложенный метод удовлетворяет двум обозначенным
выше свойствам. Линейность метода Пуассона — Абеля вытекает из линей¬
ности степенных рядов. Докажем его регулярность.
Доказательство
OO
Рассмотрим произвольный числовой ряд который имеет сумму S
W=I
в классическом смысле. Требуется доказать, что этот ряд суммируем мето¬
дом Пуассона — Абеля и его обобщенная в смысле данного метода сумма
также равна S.
оо
Докажем сначала сходимость степенного ряда Хаях”-1- ^aic как иссле-
W=I
дуемый числовой ряд сходится, то последовательность его членов явля-
ется бесконечно малой, а поэтому и ограниченной, т.е. 3 M > О такое, что
для VieN выполнено \ak\<M.
411
Следовательно, \ak xk~i \ < M\x\k~! для Ухе (0; 1). Поскольку \х\ < 1,
°° I IW-I 00
то ряд Z\х\ сходится. Поэтому ряд Z апх"~! мажорируем сходящимся
W=I и=1
OO Л
El |и—1
|х| , а значит, он сходится.
W=I
Далее требуется доказать, что 3 Iim S(x) = S. Докажем при Ixl < 1 сле-
*->1-0
дующее тождество:
=(!-*) Zsnxn'x,
(7.10)
где Sn = Zabk>2. Так как ak = Sk-Sk_i при k > 2, a S0 = 0, то
k=\
ZaUxk'1 = ^ZSkXk-1 - ZsH-Ixk^ = JsSkXk'1 + SnXn-1 + ZSkXk =
k=i k=i k=\ k=i k=i
W-I
= (I - x) ZSkXk'1 + Snxn~x.
k=i
Переходя к пределу в последнем равенстве и учитывая, что Iim Snxn~{ =
П—¥°°
= S-0 = 0, получаем выполнимость тождества (7.10).
Далее получаем тождество
Л CO со оо
—— = Zxk'1 => I = (1 ■-х)Zxk^ & S = (\-x)ZSxk-1. (7.11)
1— X k=\ k=\ k=\
Вычитая из тождества (7.10) тождество (7.11), получаем
W=I
|S(x)-S|<(l-x)
= (I-X)
Z(Sn-S)X"-'
W=I
nO
W=I
+ (1-т)
W=Wq+!
1
Так как LS1n -S <— при п > щ! и Zxn'1 = , т.е. Z х"~! < ,
2 w=l I-X w=wn+l I-X
-, ТО
(1-х) S (Sn-S)X"-!
W=Wq+!
Wq+1
^f(l-*) J Х"~!<
^ W=Wq+! ^
nO
Кроме того, так как сумма Z\Sn~S\x" 1 ограничена, то при х, доста-
W=I
точно близких к единице (т.е. при х g (I - 5(e); 1)), получаем неравенство
«о
-s)
72=1
£ £
Из последних трех соотношений следует, что |^(х) — ^|< — + — = е при х,
достаточно близких к единице (т.е. при х G (1-8(е);1)). ■
! Такой номер и0(е) найдется в силу сходимости Sn к S.
412
Задача 7.28
Попробуем просуммировать методом Пуассона — Абеля расходящийся ряд 1 - 1 +
+1 -1 +... + (-1)”-1 + ...= £ (-1)"-1.
It= 1
Решение
Составим по изучаемому ряду степенной ряд и просуммируем его:
п=I 1 + х
11 “ 1
Имеем Hm = —. Следовательно, 5Х-1)”-1 = — (А).
дс—»1—01 + х 2 п=\ 2
Задание 7.23
Просуммируйте по методу Пуассона — Абеля следующие ряды:
00 °° п Чтт
а) ЕС-!)"-1”; б) X COSW0, О < 0< 271, 0 Ф- —, —;
п=1 п=1 ^ *
OO
в) £sinn0, (О<0<2л, в*л).
П=1
Зададимся следующим вопросом: какие нужно добавить условия
на члены числового ряда, суммируемого методом степенных рядов, для того
чтобы он суммировался в классическом смысле? Ответ на этот вопрос дает
следующая теорема.
OO
Теорема7.12 (Таубера). Предположим,что Hm пап = 0,ряд Y апхп = а(х)
и->°° W=O
сходится на интервале (-1; 1) и существует предел Iim a(x) = S. Тогда
х->1-0
OO
выполняется Y ап = S.
W=O
Доказательство
Для любого натурального N и произвольного х E (0; 1) получаем
(7.12)
N
N
OO
OO
M
а
S
I
=
E«w( 1-
хи)- ^ аихи
+ JjanXn-S
W=О
W=O
w=AT+l
п=0
Далее воспользуемся неравенствами
1 — хп = (1-х)(1 + х + х2 + ... + хя_1)<{хе(0; 1)}<я(1-х),
х
N+1
1
Yj ХП = < '
n=N+1 I ^ 1
Из равенства (7.12) имеем
N
N
OO
OO
Yan-S
п=0
<
й
я
Si
+
E v”
n=N+i
+
х v” -S
n=0
N
W=О
< Х(|и«и|-|1-*1)+ E
OO
OO
E k x”+
Y апхп -S
=JV+1
w=0
Inar
■х'
W=O
n=N+1
N + 1
■ +
YanXn-S
W=О
413
< {так как Hm пап = 0, то 8п = таxkak —> 0} <
k>n
w—»°°
< Е50(1-х) + ^-
w=0 iV + I n=N+1
< Nb0(I-X) +
tN+1
(ЛГ+ 1)(1-*)
■ +
и—>°°
OO
ZanXn-S
W=О
OO
ZanxTl -S
W=O
(7.13)
8 S
Выберем далее для е > О величину х = 1 » 1, откуда 1-х = —. По-
N «->“ N
этому по выбранному выше в > О находим такое N0(в), что для V N > N0
выполнено1 bN+i < в2, а х за счет выбора номера N настолько близок к еди¬
нице, что
yZanXn-S
и=0
<в. Следовательно, из соотношения (7.13) получаем
N
Zan-S
W=O
в Ne2
< Nb0 —I И E < SqB + В + E = £/,
N е(Л/Ч 1)
что и заключает требуемое. ■
Замечание 7.11. Другое доказательство получается, если установить пре-
1Л
C
дел разности а
1-
V
т
N
(7.14)
- Za w> гДе а(х) = Sfl пхП’ ПРИ 171 °°> равным нулю.
w=0 W=O
Оставляем проведение данных оценок читателю.
В заключение данного параграфа рассмотрим другой широко распростра¬
ненный метод суммирования расходящихся рядов — метод средних ариф¬
метических, или метод Чезаро, и сравним его с методом степенных рядов.
CXD
Определение 7.9. Говорят, что ряд Zan суммируем методом Чезаро,
W=O
если существует предел средних арифметических частичных сумм (An)
этого ряда:
1ш1а„ = 1ипЛ + Л1+-+Л’-.
При этом предел (7.14) называется обобщенной в смысле Чезаро суммой
данного ряда.
Докажем следующую ключевую теорему.
OO
Теорема 7.13 (Фробениуса). Если ряд Z ап суммируем методом Чезаро
W=O
к конечной сумме А, то одновременно он суммируем также методом Пуас¬
сона — Абеля, и притом к той же сумме.
Доказательству теоремы Фробениуса предпошлем две леммы.
Лемма 7.1 (необходимое условие суммируемости по Чезаро). Если
OO
числовой ряд Z суммируем методом Чезаро к некоторой сумме А, то
необходимо должно выполняться ап = о(п) при
1 Так как bN —> 0.
jV—>°°
414
Доказательство
Пусть выполнено Hm QLn= А. Последовательно находим:
п—
Л Aq + A1 OCq + Af л п
aO = А)»а1 = 2 = 2 =>А=2а1~а0>
а-
qLq + 2ql<-qlq+A2 _
= -9 1 => A2 = За2 - 2щ.
Используя метод математической индукции, получаем тождество
An = (п + 1)а„- покп_х (докажите!),
откуда ап = An- Ап_х = (п + 1)аи- похп_х - пап_х + (л - 1)аи_2.
Поэтому
ап п +1 п и —1 . п , . Л _
— = QLn - 2 аи_1 + а„_2 -^Л-2Л + Л = 0 при п —» ■
п п п
Предлагаем читателю доказать следующее следствие из доказанной
леммы.
оо
Следствие 7.1. Если ряд Y ап суммируем по Чезаро, то степенной ряд
и=0
Y апхп сходится для всех х е (0; 1).
п=0
OO
Лемма 7.2. Пусть ряд Y ап суммируем по Чезаро1 ихе (0; 1). Тогда
W=O
выполняется тождество
OO OO
^(х)= YaTixn =(Х~х)2 X(w + l)awx”- (7-15)
w=0 w=0
Доказательство
OO
Рассмотрим и преобразуем выражение (I - х)2 Y (п +1)&пхп'■
W=O
OO OO OO
(I - 2х + X2 ) ^ (и + 1)осих” = X (и + l)awx” - S (га + 1)2аихи+1 +
w=0 w=0 W=O
OO
+ 5> + 1)сси*-2.
W=O
Заменяя индексы суммирования во второй и третьей суммах2, получаем, что
Y [(га + l)awx” - 2(га + 1)осихи+1 + {п + 1)ссихи+2] =
W=O
OO OO
= E [(га + 1)ая -2тхп_1 + (га - 1)ап_2]хп = Y {[(га + 1)ая -raaw_J-
w=0 w=0
OO OO
-[rian_i-(ii-i)an_2]}xn = Y(Ai-A-i)xn=Yanxn-u
w=0 w=0
1 Данное условие требуется для сходимости ряда Y апхп-
п=О
2 При этом используем то, что при отрицательных п выполнено ап — 0.
415
Доказательство теоремы Фробениуса
OO
Итак, пусть Hm ап = А и ряд ^ апхп при х G (0; 1) сходится. Получаем
я=0
^ (и + 1)х” = 1 + 2х + Зх1 1 2 +... = 1 + х + X2 +... + х + X2 +... + X2 +... =
я=О
I X X2
- + + -
1-х 1-х 1-х
- + ... = —!—(1 + X + X2 +...)= *
1-х
_-уЛ2’
(I-X)
откуда справедливо
I = (I-X)2 £(я + 1)*я.
я=0
Умножаем последнее равенство на Л и вычтем из него почленно равен¬
ство (7.15), получаем
|Л-S(X)I =
(1-х)2£(я + 1)(Л-аи)хи
N-1
(I - х)2 X (и +1)(Л - ая )хи
я=О
я=0
+
(1-х)2 ^ (п + 1)(А-ап)хп
Ti=N
Далее выбираем номер N таким, чтобы при n>N выполнялось Л - ап
Воспользовавшись формулой
(1-х)2 5 (п + 1)х" = (1 -х)2 xNV+ N + Nx) = Xn(\ + N + Nx),
n=N (1-Х)2
показываем, что для достаточно больших N вторая сумма может быть сде¬
лана меньше в/21 независимо от значения х G (0; I)2. Первую же сумму
можно сделать меньше е/2 за счет стремления х к 1 - 0. Следовательно,
Hm S(x) = Л. ■
дг—»1-0
Отметим, что обратная теорема, вообще говоря, не верна. Действительно,
OO OO
рассмотрим, например, ряд £(-1)я(и + 1). Интегрируя ряд ^(-1)и(гг + 1)хи
я=О я=О
почленно и меняя интегрирование с суммой, получаем
J
оо OO /у*Я+1
2(-1 )n(n + l)xndx= £(-1)и(п + 1)-— =
я=О я=О И +1
£(-1)иХи+1 =
я=0
X
X +1
Дифференцируя полученную дробь и переходя к пределу при х —» 1 - О,
имеем
Hm S(x) = Hm
х-»1-0 дг—»1—0 (1 + х)
2
1
4'
1 Так как Iimxiv(I-I-Ar-I-Arx) = OnpHXG (0; 1).
N—> о®
2 Хотя, конечно, для каждого х надо выбирать свое AT.
416
По методу же Чезаро данный числовой ряд не суммируем, так как
для него не выполнено необходимое условие суммируемости по этому
методу:
Hm(-1)" П + 1*0.
я-»°° п
7.6. Применение теории функциональных рядов
для построения нетривиальных примеров функций
Аппарат равномерно сходящихся функциональных рядов является
чрезвычайно эффективным при построении различных примеров функций
с интересными свойствами. В данном параграфе мы рассмотрим несколько
таких конструкций.
Задача 7.29 (Пример Вейерштрасса)
Определим функцию /посредством функционального ряда: f(x)= ^bn cos(annx),
п=О
где Ь £ (0; 1), а — нечетное натуральное число. Докажем, что данная функция непре¬
рывна на R, но является нигде не дифференцируемой (при дополнительных усло¬
виях, накладываемых на параметры а и Ь).
Решение
В силу оценки | Ъп cos(a”7tr) | < Ьп и при условии сходимости числового ряда
OO
Y Ьп заключаем по признаку Вейерштрасса равномерную сходимость ряда
п~0
OO
Yjbn cos(a”7Lt). Остается заметить, что каждый член рассматриваемого ряда, а именно,
п=О
функция bn CosianTix) является непрерывной на прямой R, и сослаться на теорему
о непрерывности суммы функционального ряда. Непрерывность функции /доказана.
В то же время при ab> 1 ряд, полученный при почленном дифференцировании,
- Y Cab)nnsm(annx)
п=0
расходится (докажите!). Понятно, что само по себе это не доказывает недифферен¬
цируемость функции / (так как условия теоремы о почленном дифференцировании
лишь достаточны), однако указывает на такую возможность.
3
Покажем, что при условии ab > 1 +—п функция /не имеет конечной производной
ни при каком значении х. Действительно, рассмотрим отношение
f(x + h)- f(x) _ , п cos(ann(x + h)) - соъ(апш) _
h “„to h “
- 1Yjbn COS^an^X + ^)) - cosCa1lnx) + cosCatlnCx + Ь)) - COs(a”7Lr) _ ^,(1) + ^(2)
п=о Ь
Для начала заметим, что
h
fCx + h)-fCx)
h
(7.16)
Воспользовавшись формулой Лагранжа на интервале {х\ х + h), получаем
Icos(a”7i(x + h)) - cosCaPnx)\ = \annh sin(a”7i(x + Qh))| OnU \h|,
417
m-1 ambm — I ambm
откуда следует оценка Sm ^ X тшпЬп = и— < и——. Далее мы придадим прира-
„=о ab -1 ab -1
щению h специальное значение, а именно, если amx = ат+ Em, где ат е Z, Е;
I-E
3/2,
то положим Jt = — (ясно, что 0 < h < ——). Оценим теперь величину
Действительно:
а"
а"
_i. i
2’2
снизу.
апп(х + h)- ап-татп(х + h) = On-mTiiamX + amh) -
= On-mTiiam+^+ I - = On-mUiam+ 1),
откуда
соsianuix + h)) = cos(a”_m(am + 1)д) = {an~miam +1) е Z} = (-1)“” т(ат+1\
Так как из нечетности числа а вытекает нечетность числа ап~т, то (-1)“” =
= (—l)am+1. Далее получаем
cos ianux) = cos ian~muamx) = cos(an_m7i(am + Em)) =
= cos(an_m7iam ) • cos(a"_mTtEm ) - sin(a”_m7iam ) • sin(a”_m7iEm ) =
- {так как ап~тат e Z, то sin(a”-m7iam) = 0} = cos(a”_m7iam) • cos(an_m7tEm) -
= {так как an~m нечетно, то cos(a”_ramxOT) = (-1 )am} = (-l)“m . cos(a”-mTtEm)-
Следовательно,
\am+l
S2>= £i»(l+cos(a«-^„)).
Ti=TU ft ft n=m
Так как величина On-m^mU лежит в четвертой или первой четвертях, то величина
I + cos(a”-m и Em) строго положительна. Поэтому все члены последнего ряда положи-
I (2)\ Ът 2
тельны. Отбрасывая все члены, кроме первого, получаем оценку ISm ’ > — > —атЬт.
п 3
Продолжая оценивать выражение (7.16), заключаем
fix+ h)-fix)
h
с(2) _ C(I)
tjTTt tjTTt
>атЪп
и
3 аЬ-1
= атЬг
и i 371
г, ab-1
1 2_
3 ab-i
В силу того что ab > 1 + — те при т —> °° (А —> 0 + 0), получаем, что выполнено
fix+ h)-fix)
—» оо. Поэтому конечной (правой) производной /+(#) в произволь-
А—>0+0
ной точке хне существует. Аналогично может быть доказано (докажите!), что и конеч¬
ной левой производной в точке х не существует. Следовательно, у построенной функ¬
ции не существует даже односторонней производной в любой точкеie 1!
График функции, рассмотренной в задаче 7.29, можно описать как
состоящий из бесконечного числа бесконечно малых извилин, но почти
невозможно дать о нем наглядное представление, не исказив его суще¬
ственных черт. Приведем изображения описанной функции при b = 0,5,
а = 12ия = 10 (рис. 7.3), а также при b = 0,7, а = 50 и п = 100 (рис. 7.4).
Замечание 7.12. Позже Г. Харди1 построил такой же пример, но уже
при ab > 1.
1 Hardy G. Н. Weierstrass’s non-differentiable function // Transactions of the American
Mathematical Society. 1916. July. Vol. 17. № 3. P. 301—325.
418
Рис. 7.4
Далее мы приведем пример функции с аналогичными свойствами,
но имеющей совсем другой принцип построения. В его основу положена
недифференцируемость непрерывной функции f(x) = | х | в нуле. C помо¬
щью сдвига этой функции можно определить всюду непрерывную функ¬
цию, которая была бы недифференцируема во всех точках заданного конеч¬
ного множества O1, а2,..., ап, например
f(pc) = I х - A11 +1 х - а2 I +... +1 х - ап \.
419
Аналогично методом «сгущения особенностей» можно построить при¬
мер непрерывной функции, недифференцируемой в счетном числе (даже
всюду плотном множестве) точек. Действительно, пусть {ги}“=1 — после¬
довательность, состоящая из всех рациональных точек отрезка [0; 1].
Положим
CXJ I у Y I
(7.17)
n=0 2”
Функция /непрерывна на отрезке [0; 1] в силу равномерной сходимости
ряда (7.17) и непрерывности каждого из членов суммы. Однако/недиффе¬
ренцируема ни в какой рациональной точке, так как для произвольного h
получаем
f(rk+h)-f(rk)J-l\rk+h-rn\-\rk-rn\ \h\
h h-2n h-2k
у \rk+h-rn\-\rk-rn\
Первая сумма при A —» 0 стремится к некоторому конечному числу А
(так как в ней нет особенностей). Третья сумма сходится, так как может
OO I
быть ограничена сходящимся числовым рядом ^ —. А второе слагаемое
n=k+12й
I 1
стремится к —г при /г—>0 + 0ик-
2*
2k
при /г —> 0-0. Следовательно, произ¬
водной f'iXb) не существует.
Приведем пример функции, использующей бесконечное множество бес¬
конечно малых сдвигов функции | х |, недифференцируемой ни в одной
точке действительной прямой Ш.
Пример 7.5 (Ван-дер-Варден)
Определим функцию/(г) следующими условиями:
Jx, еслихе [0; 1/2],
1 jl-x, если х G (1/2; 1).
Функция Z1 (х) периодически продолжена с периодом 1 на всю прямую М.
На рис. 7.5 изображен график функции Z1 (х) на отрезке [-3; 3].
Далее положим /я(х) =
Zi(^n-1X)
4n-i
и определим функцию /(х) = Xfn(x)•
П=1
Докажем, что построенная функция / непрерывна на всей прямой М,
но не имеет производной ни в одной точкеi£ 1.
420
Доказательство
1 I
Так как О<ZiP)< —, то О < fn(x)< — для всехig Е. Отсюда по при-
2 2-4” 1
оо
знаку Вейерштрасса следуют равномерная сходимость ряда XZn(Z) и всюду
и=1
непрерывность предельной функции fix).
Докажем, что построенная функция является нигде не монотонной.
k
Пусть точка а имеет вид а = , где k е Z, т е N.
Тогда получаем Znp) = О для всех п>т (докажите!) и f(a) =Zi (а) + /2(0) +
1
+... +ZmP)- Немного изменим (пошевелим) точку а, выберем hm = ^2m+i, где
т G N. Тогда fn(a + hm) = О для всех п > 2т + 1 и, следовательно,
ZP + hm)~ f(a) = (Zi P + hm)~ ZiP)) +... + (fm (a + Itm)- fm(a)) +
+Zn+iO + Ki) + ... + f2m+1 (a + ^m) ^ -hmm + hm(m + X) = hm > 0.
Аналогично получаем
f(a - hm) -f(a) > -mhm +(rn+l)hm = hm> 0.
Следовательно, функция Z немонотонна во всех точках вида а = —, а так
как множества таких точек всюду плотны на прямой R, то отсюда следует,
что не существует открытого интервала, на котором функция f была бы
монотонной.
Докажем недифференцируемость функции Z в произвольной точке a G R.
или , так, чтобы
4 п ’ ’
1
Выберем для любого натурального п число hn, равное —
ATl
(в силу линейности функции fn)
I ZnO + К) - Zn(«) I = I ZnOn) \ = \к
Тогда выполняется равенство
|ZnO+^„)-ZnO)|
\hn |, если т < п,
О, если т > п.
Отсюда
ZP+ ^п)~ZP) _ у fm(a + K)-fm(a) _
I1
пп т=1 пп
[целое число, которое четно при четном п,
[целое число, которое нечетно при нечетном п.
Поэтому предел Hm
И—¥°°
не существует и производной ZP)- ®
Замечание 7.13. Отметим, что доказательства нигде не монотонности
недостаточно для доказательства нигде недифференцируемости. Можно
построить пример всюду дифференцируемой, но нигде не монотонной
f(a + h)-f{a)
— -Tl— не существует, а следовательно,
К
421
функции. Конструкция этого примера весьма сложна и приводит к функ¬
ции, которая всюду дифференцируема и имеет плотное множество локаль¬
ных максимумов и плотное множество локальных минимумов1.
В заключение рассмотрения функции Ван-дер-Вардена схематично изо¬
бразим ее график (рис. 7.6).
0,8
0,6
0,4
0,2
0
Задача 7.30
Докажем, что последовательность функций
1 Г I "I
ср„ (х) = —arccos cos 2ш — sgn(cos 2ш)
2п \ п ,
равномерно сходится на К к функции Zi из примера Ван-дер-Вардена.
Решение
Предлагаем читателю доказать следующее равенство:
1
f\(x) = — arccos(cos 2ш).
В силу непрерывности arccos а получаем, что последовательность {(р„(х)} схо-
1
дится к функции /Кх) поточечно. Отметим, что множитель — не влияет на сходи-
2 л
мость, равно кате и замена переменной 2кх на у.
Чтобы доказать равномерную сходимость, нужно показать, что Hm sup Itpn (х) - Z1 (л;)| =
= 0. Покажем, что Hm cos(|(pn(.r) - Zi(x)l) = 1. Очевидно, эти утверждения будут рав-
носильны, поскольку
arccos х е [0; л] => |сря(^) - Zi(x)| ^ п =>
Hm cos[cp„(x) - Z1(X)] = 1 фф Hm Icpn (х) - Z1(X)I = 0.
n—> OO П—>°о
Опуская несущественный множитель и делая указанную выше замену, получаем
f I ^
COS
= COS
arccos
cos у — sgn(cos г/) - arccos(cos у)
V
п
У
+ Sin
arccos
(
V
arccos
1 )
COS у—sgn(cosy)
V п )
I ^
COS у—sgn(cosz/)
п
J
cos(arccos(cos у)) +
sin(arccos(cos у)) = (А).
1 Подробности см. в работе: Hobson Е. W. The theory of functions of a real variable and the
theory of Fourier’s series. Washington, 1950. Vol. 2.
422
Заметим, что cosу е [-1; 1] и cos у—sgn(cosz/)e[-l; 1]. C учетом формулы
п
sin(arccos а) = Vl-Ot2,
где а е [-1; 1], заключаем:
(А) =
cos у—sgn(cos у)
п
COS у +
+ Vl--Cos2X - ./l-cos2 у +—sgn(cosz/)cos у- =
V п п1
- COSz у -
|cos г/|
= COS2 у -
п
|cosy I
п
+ sin2 у -Jl + -
Yin2
2
COS у
1
Sf ' о
п п1
L2
COS у
1
„ „ COSM . „
< COSz у - 1 + Sinz у ■
M-SinzI/ Mz-Sinz у
f Г л\\ ,zJ Л
п
1 + 0
г
KnJJ
<1 + 0
KnJ
из чего следует требуемое.
Замечание 7.14. Получаем, что непрерывная, нигде недифференцируе¬
мая функция Ван-дер-Вардена/может быть представлена как предел рав¬
номерно сходящейся последовательности бесконечно дифференцируемых
функций.
Иллюстрация функциональной последовательности сри(х) при п = 1, ...,
1000 приведена на рис. 7.7.
-3-2-1 О 1 2 3
Рис. 7.7
Далее зададимся следующим вопросом: можно ли посредством функ¬
циональных рядов построить непрерывную действительную функцию,
определенную на отрезке [0; 1], принимающую каждое значение из отрезка
[0; 1] в континууме точек? Ответ на данный вопрос — положительный.
Действительно, рассмотрим следующую задачу.
Задача 7.31
Пусть /— четная, 2-периодичная функция, заданная на отрезке [0; 1] в виде
/(O=
0, если£ е[0;1/3],
3t — 1, если t G [1/3; 2/3],
1, если te [2/3; 1].
423
Докажем, что функция g(x), определенная на отрезке [0; 1] равенством
g(x)=\кх)+^/(з2х)+^-/(3½)+... = £ f (32kx^
непрерывна и принимает каждое значение из отрезка [0; 1] в континууме точек.
Решение
В силу того что I f(t) I < 1, исследуемый функциональный ряд сходится равно-
111
мерно и g(x) непрерывна, причем 0 < g(x) < — + — + — +... = 1.
2 22 23
Пусть, далее,
, _ aO
а,
У 2+* + *+“’
где a2k е {0; 1} — произвольное число из отрезка [0; I]; а = (а{, а3; а5; ...)
вольная последовательность из нулей и единиц. Обозначим
2ап 2^ 2а,
-—^ + —lH *- +
3 з2 з3
произ-
Можно проверить, что g(xa) = у (проверьте!). А так как ха в силу произвольно¬
сти а принимает континуум значений, то и значение достигается в континууме точек.
Построенная функция изображена на рис. 7.8.
Рис. 7.8
Глава 8
ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ
8.1. Евклидово пространство
В данной главе рассматриваются функции вида у = /(X1,Xm) =/(х), где
х G Mm — точка m-мерного евклидова пространства, у е R- вещественное
число.
Напомним ряд основных понятий.
В евклидовом пространстве Rm определено скалярное произведение
т
<х, у) =
Z=1
удовлетворяющее аксиомам скалярного произведения:
1) (х, у) = {у, х>;
2) (х, х) > 0, (х, х) = 0 о х = 0;
3) (ах + Pу, 2) = а(х, z> + |3(г/, z> для V х, г/, г g Rm, а, P g R.
В R7w определена также норма вектора
х|| = р(х,0) =
т
Vz=I
где х = (X1,..., хт), удовлетворяющая аксиомам нормы:
1) ||х I > 0, ||х|| = 0 <=> х = 0;
2) ||Ах|| = |А,| • ||х|| для Vxg Rm и X е R;
3) ||х + у\\ < ||х|| + \\у\\,
т.е. Rm — нормированное пространство.
В пространстве R7w определено расстояние (метрика)
р Ху) = ^IXxi-уХ,
где х = (X1,..., хт), у = (у{,..., ут), удовлетворяющее аксиомам расстояния:
1) р(х, у) > 0, р(х, у) = 0 <=> X = у;
2) р(х, у) = р(у, х);
3) р(х, z) < р(х, у) + р{у, z) для V х, у, z.
Все эти понятия согласованы, т.е.
Р(х, у) = ||х - у\\ = у1(х-у,х-у).
В дальнейшем будем использовать либо запись р(х, у), либо ||х - у\\,
либо, если это понятно из контекста, |х - у\.
Определим е-окрестность точки х*: это множество {х G R777: |х - х*| < е}.
Прямоугольный параллелепипед B1, ..., гт > 0 с центром в х* (прямо¬
угольная B1,..., Ет-окрестность х*): {х g R777 : Ix1 - X11 < B1,..., |хш - | < вт}.
425
Несложно доказать следующее утверждение.
Утверждение 8.1. Для любой точки х* и для V в > 0 найдутся такие
B1, Bm > 0, что прямоугольная B1, ..., вт-окрестность х* содержится
в в-окрестности. И наоборот, для V B1, ..., Bm > 0 найдется такое в > 0, что
в-окрестность точки х* содержится в прямоугольной B1,..., вш-окрестности.
Таким образом, большинство утверждений, которые формулируются
в терминах в-окрестностей, могут быть переформулированы в терминах
прямоугольных окрестностей (и наоборот). Заметим, что в M1 эти два поня¬
тия просто совпадают.
Используя приведенные выше понятия окрестностей, можно опре¬
делить, как в гл. 1, такие понятия, как внутренние, внешние, граничные
и предельные точки множества, ввести понятия ограниченного, замкнутого
и открытого множеств, понятие границы множества и т.д.
На множестве Rm можно, как и в R, ввести понятие последовательно¬
сти точек {X12}, где хп = (xf, х%,..., Xfl). Для последовательности точек в Rm
можно ввести понятие предела (предельной точки): точка a G Rm — пре¬
дел последовательности {х11} G Rm, если для V в > О BN= N(e) такое, что
для V п> N выполнено \хР - а\ < в.
Это определение практически дословно совпадает с понятием предела
в R за исключением того, что под \х^~ а \ теперь понимается расстояние
между точками в R7n (модуль в R имеет тот же смысл).
Для конечномерного пространства Rm имеет место следующая теорема.
Теорема 8.1. Последовательность {X11} —» а (Hm хп = а) тогда и только
П—¥°°
тогда, когда каждая координатная последовательность сходится к соот¬
ветствующей координате точки а, т.е. xf —> а{.
Доказательство
Необходимость. Пусть {х21} —> а. Тогда для V в > 0 3 N: для V п> N выпол-
т
нено “ ai)2 - z2- Тогда для V п> N
i=i
чает, что xf —> а{, i = 1,..., т.
Xf-Ui
< в, i = 1,..., т. Но это и озна-
Достаточность. Пусть xf —> а{ при всех i Это значит, что для V в > 0 3 Ni(E)
такой, что для V п>Ni выполнено
X.
П _
а.
4т
. Выберем N(e) = max{A^(e),...,
т
т 82
AL(b)}. Тогда для V п> N выполнено . Y(xf -аЛ2 < ./У— = в, т.е. > а. ■
Ii=I Vi=I7w
Заметим, что сходимость последовательности точек пространства к а
эквивалентна покоординатной сходимости только в конечномерных про¬
странствах.
Рассмотрим, например, пространство полиномов от х:
Р{х) =Po+PiX+...+ +PrPCn.
Каждому такому полиному можно поставить в соответствие «бесконеч¬
ный вектор»:
P = (P0>Pl’-’Pn>°>
о,...),
где только конечное количество «координат» отлично от нуля. В простран¬
стве полиномов можно ввести метрику
426
P (p, ¢) = J Il(Pi-Vi)2 ■
Vi=O
Заметим, что хотя формально под корнем стоит бесконечная сумма,
но фактически для любых р, q отлично от нуля конечное число слагаемых.
Несложно убедиться в том, что приведенная метрика удовлетворяет
всем аксиомам метрического пространства.
Рассмотрим теперь в пространстве полиномов последовательность
Pnix) = Xn- Им соответствуют векторы рп = (0,..., 0,1,0,..., 0,...) Любая коор-
П
динатная последовательность pf имеет конечное число элементов, отлич¬
ных от нуля (точнее, ровно один), поэтому pf —>0 при i = 1, 2, ..., п, .... Но
рп/40, так как р(|>й,0) = 1 для любого п. Таким образом, в бесконечномер¬
ных пространствах из покоординатной сходимости не следует сходимость
последовательности точек (однако из рп —> а следует, что pf —» щ, i = 1,...,
п,...). При доказательстве теоремы мы существенно использовали т — раз¬
мерность пространства.
В R помимо понятия сходящихся к конечному пределу последователь¬
ностей было введено также понятие бесконечно больших последовательно¬
стей, т.е. сходящихся к бесконечности. По аналогии с одномерным случаем
можно дать следующее определение.
Определение 8.1. Последовательность {хп} —> °° (Hmxw=Oo)j если
п—>°°
для V M > 0 3 N(M) : для V п> N выполнено р(х”, 0) > М, т.е расстояние
от точек Xn до начала координат стремится к бесконечности.
Следует ли из этого, что координатные последовательности xf — бес¬
конечно большие? Ответ на этот вопрос — отрицательный. Например,
для Xn G R2 : Xn = (п, 0) первая координатная последовательность xf —»
а вот xf = 0 — бесконечно малая.
Следует ли из Xn —> °°, что хотя бы одна из координатных последова¬
тельностей xf —» °°? И здесь ответ — отрицательный. Рассмотрим после¬
довательность Xn е R2: (1, 0), (0, 1), (2, 0), (0, 2), (3, 0), (0, 3), ..., (п, 0),
(0, п),.... Очевидно, что Xw-> °°, однако ни xf, ни xf не являются бесконечно
большими (они лишь неограничены). Поэтому если требуется подчеркнуть
покоординатную сходимость к бесконечности, это оговаривается особо.
Очевидно, что если xf —> °° при всех i = 1,..., т (даже при одном г), то Xw —>
Вернемся к рассмотрению сходящихся последовательностей в Жт.
В полной аналогии со скалярным случаем (т.е. R1) для {хи} G Rwz можно
дать определение фундаментальной последовательности: {х”} G Rm фунда¬
ментальная, если и только если для V в > 0 3 N(e): для У п> N, У р > О
выполнено I хР+р - Xй | < в.
Как и в случае т = 1, имеет место следующий критерий.
Критерий Коши. Последовательность {Xй} G Rm сходится тогда и только
тогда, когда она фундаментальна.
Имеет место также важная теорема.
Теорема 8.2 (Больцано — Вейерштрасса). Если последовательность
{х«} ограничена, то из нее можно выделить сходящуюся подпоследователь¬
ность.
427
Заметим, что в бесконечномерных пространствах это утверждение
может быть неверным. Вновь рассмотрим пространство полиномов р(х),
которым соответствуют бесконечные векторы р = (р0,..., рп, 0,О,...). Тогда
последовательность рп(х) = Xn (т.е. рп =(0,...,0,1,0,0,...)) ограничена.
Однако любая ее подпоследовательность не является сходящейся (в част¬
ности, она не является фундаментальной, так как \рп -рт\ = V2 при п Ф т).
8.2. Предел функции многих переменных.
Непрерывность функции многих переменных
Перейдем к рассмотрению понятия предела функции у = /(X1, ..., хт) =
= /(х), х е Rm. Далее считаем, что функция у = f(x) определена в окрест¬
ности точки х* (возможно, проколотой окрестности), хотя для определе¬
ния предела достаточно, чтобы функция была определена на множестве {х},
для которого точка х* является предельной.
Как и в одномерном случае, имеют место два эквивалентных определе¬
ния предела.
Определение 8.2 (предел по Коши). Iim/(х) = Iim = Ь, если
х^а X1-M1,. ..,Xm->ят
для V е > 0 3 8(e) > 0 : для V х, такого что 0 < |х - а \ < 8, выполнено
|/(х) -Ъ\<£.
Отличие от одномерного случая только в интерпретации выражения
Iх- а\, которое теперь понимается как расстояние между точками в Mm.
Определение 8.3 {предел по Гейне). Hm /(х) = Ь, если для V [Xn) g Rra:
х—Уа
Xn —> a, Xn Ф а, выполнено /(Xя) —» Ь. Здесь Xn —» а рассматривается как
последовательность в Rm, а /(Xn) —> b — как последовательность в R.
Для функций, имеющих предел в точке, имеют место простые утверж¬
дения, аналогичные скалярному случаю.
Теорема 8.3 (критерий Коши). Функция у =/(х) имеет в тачке a G Rm
предел тогда и только тогда, когда она удовлетворяет условиям Коши,
т.е. для V в > 0 3 8(e) > 0 : для V х', х" е Rm, таких что 0 < |х' - а\ < в,
0 < \х" - а \ < е, выполнено |/(х') -f(x") \ < е.
Теорема 8.4. Пусть Hm f(x) = b, limg(x) = c. Тогда 3 lim(/(x)±g(x)) =
х—>а х—>а х—>а
= Ь ± с, 3 Hm/(x)-g(x) = be, 3 Hm =- (сх0).
х—х—¥а g(x) C
Однако для функции нескольких переменных можно определить и дру¬
гие понятия предела в точке а. В частности, можно ввести понятие повтор¬
ного предела. Рассмотрим его подробнее на примере функции двух пере¬
менных z = /(х, у), где х,у G R.
Пусть функция z = /(х, у) определена в окрестности (возможно, про¬
колотой) точки (х°, у0). Фиксируем произвольное значение х из окрест¬
ности х° и рассмотрим функцию h(y) = f(x, у) как функцию от у (точнее,
рассматриваем параметрическое семейство функций, зависящих от параме¬
тра х). Пусть у каждой функции из семейства существует предел при у —> г/°
(естественно, предел зависит от параметра х). Тогда определена функция
428
ф(х) = Iim /(х, у). Если, в свою очередь, существует предел Iim ф(х) = Ь,
у—>2/^ х—
то это значение и называют повторным пределом сначала по у, потом по х
функции/(х, у) в точке (х°, у0):
Iim Hm f(x,y) = b.
х—>х® г/—
Аналогично можно определить повторный предел сначала по х, потом
по у:
Iim Hm f(x,y) = c.
г/—»z/° x—>xV
Возникает вопрос: равны ли значения бис, как они соотносятся
с Hm /(х, у) = а — пределом функции/(х, у) по Коши (либо по Гейне)?
х—>х®
У~>У°
Рассмотрим примеры.
Пример 8.1
Функция f(x,y) =
Имеем
——если х2+у2Ф О,
X2 + у2
О, если X2 + у2 = 0.
Hm Iim fix, у) = Hm jAr = 1;
ж—>0г,—>0 лг-Я) X2
Hm Hm fix, у) = Hm = -1,
г/—>0 я—»0 J г/—>0 у2
т.е. повторные пределы не совпадают, они зависят от порядка вычисления. Заметим,
что для указанной функции не существует предела Hm /(х,г/). Действительно, если
х-^а
у^>а
бы такой предел существовал, то из определения по Гейне для любой последователь¬
ности (хп, г/„) —» (0, 0) должен существовать один и тот же Hm f(xn, уп) - а. Но для
П-^>°о
'1 Г
У пу
->(0,0)=>/
у А"
У 11;
= 0 —> 0, для
'2 У
У ПУ
->(0,0)=>/
'2 У
У ПУ
Вообще говоря, если повторные пределы не совпадают, то предел по сово¬
купности переменных не существует.
Пример 8.2
Функция /(х, у) =
Имеем
ху
X2+у2
, если X2 + у2 Ф 0,
0, если X2+ у2 = 0.
Hm Hm fix, у) = Hm 0 = 0;
*—>0у—>0 ж->0
Iim Iim fix, и) - Hm 0 = 0.
у—>0 х—>0 г/—>0
Таким образом, повторные пределы совпадают. Однако и в этом случае предел по со¬
вокупности переменных не существует. Рассмотрим
I I) f
->(0,0 )=>/
п п
1 О 1 1
— ) —.
2 2
п п
429
Для
Г1 )
—,0 —>(0,0) или
( Л
о,-
->(0,0 )=>/
(1 )
-,0
= /
( Л
о,-
Iп J
I nJ
Iп J
I п)
= 0—»0, т.е. не выполнено
определение по Гейне.
Следовательно, из совпадения повторных пределов не следует суще¬
ствование предела по совокупности аргументов.
Пример 8.3
Функция f(x,y) =
I 1
(х + у) sin—-sin—, если осуф 0,
х у
0, если осу = 0.
I 1
Очевидно, что если (хп, уп) —> 0, то (хп + уп) —> 0, sin— и sin— ограничены =>
хп Уп
=>/(хя, у„) —> 0. Таким образом, Iim f(x, у) = 0. Но у этой функции отсутствуют повтор-
х—>0
0
I 1
ные пределы. Действительно, если хп —> 0, то f(x„,y) = (xn + y)sin sin—, где (хп +
хп У
I 1
+ у) —> у, sin — = const, a sin — не имеет предела при хи—> 0. Следовательно при всех у
У
. 1
х„
таких, что sin — х 0, не определен внутренний предел Hm f(x,y), а значит, не опреде-
у х->0
лен и повторный предел. Ситуация со вторым повторным пределом такая же.
Таким образом, существование предела по совокупности переменных
не гарантирует существование повторных пределов.
Тем не менее справедлива следующая теорема.
Теорема 8.5. Пусть функция z =/(х, у) определена в окрестности (х°,у°),
3 Iim /(х, у) = а. Пусть для всех х из окрестности х° (возможно, проко-
х—>х®
лотой) 3 Hm f(x,y) = ср(х). Тогда 3 Hm cp(x)= Hm Hm f{x,y) = a. Пусть
у—>у° х—х—>х° г/—>г/°
для всех у из окрестности у0 {возможно, проколотой) 3 Hm /(х, у) = \|/(г/).
X—>х°
Тогда 3 Hm у (у) = Hm Hm /(х, у) = а.
г/—»г/0 г/—>г/0 х—>х®
Фактически теорема утверждает, что если у /(х, г/) есть предел по сово¬
купности переменных, а повторные пределы можно посчитать, то все они
совпадают.
Указанные результаты легко обобщаются на случай функций произ¬
вольного числа переменных (для функций т переменных возможно опре¬
делить т\ повторных пределов).
Задание 8.1
Покажите, что для функции f(x,y) =
х2у2
х2у2 + (х - у)2
0, если X2 + у2 = 0
, если X2 л-у2 Ф 0,
имеем
Iim Hm f(x, у) = Hm Hm f{x, у) = 0, тем не менее $ Hm f(x, у).
х—»0 у—>0 у—>0 х—>0 х—>0
У-» 0
430
Задание 8.2
Найдите следующие пределы:
.2
a) Hm (х2 +у2)е<х+У>, б) Hm
;в) Hm(х2 + у2)х2У2.
у->+°°
х—>0
у—>0
Перейдем теперь к рассмотрению непрерывных функций многих пере¬
менных.
Пусть функция у = /(X1, ..., хт) определена в окрестности точки
х* = (X1,..., х*т) (в том числе и в самой точке). Функция у =f(x) непрерывна
в точке х*, если 3 Iim /(х) = /(х*). Можно дать определения непрерывно¬
сти по Коши и по Гейне.
По Коши: функция у = fix) непрерывна в точке х*, если для V в > 0 3 8(e) > 0:
для V х, такого что \х - х*\ < 8, выполнено |/(х) -f(x*) \ < в.
По Гейне: функция у = f(x) непрерывна в точке х*, если для Vjcb^x*
выполнено J(Xn) —» f(x*).
Внешне эти определения не отличаются от скалярного случая. Отличие
состоит в смысле, который вкладывается в \х - х*\ и стремление Xn —» х*,
теперь это многомерные понятия.
В скалярном случае наряду с понятием непрерывности вводятся поня¬
тия непрерывности слева и справа. В многомерном случае эти понятия
можно обобщить, введя непрерывность по направлению.
Пусть функция у = f(x) определена в окрестности точки х*. Зададим
прямую, проходящую через точку х*, определяемую вектором е = (е1}..., ет),
задающим направление:
где R - параметр. Рассмотрим функцию у = f(x) только на точках этой
прямой (из окрестности х*, т.е. при значениях параметра ¢ из некоторой
8-окрестности нуля), т.е. на точках «направления е». В результате получим
функцию одной переменной ¢:
Определение 8.4. Функция у = f(x) непрерывна в точке х* по направле¬
нию е, если функция F(t) = f(x* + te) непрерывна в точке ¢=0.
Если рассматривается направление е{, где е{ — базисный единичный
вектор, то непрерывность по направлению ^ называют непрерывностью
по i-й переменной. Фактически непрерывность по г-й переменной озна¬
чает, что функция Fi(Xi) = f(x\,..., х*_1гXi,x*+i,...,хт) от одной переменной
Xi непрерывна в точке Xi = х*.
Возникает вопрос: как связаны между собой понятия непрерывности
(по совокупности переменных) и непрерывности по отдельным перемен¬
ным? Очевидно, из непрерывности у = f(x) по совокупности переменных
(из определения по Гейне) следует непрерывность по любому направле¬
нию, а значит, и по любой переменной. Обратное неверно.
х = х* + te,
F(t) =f(x* + te), t G (-8,8).
431
Пример 8.4
осу
X2 +у2
, если X2 + у2 Ф О,
Рассмотрим функцию из примера 8.2: fix,у) = <
О, если X2+у2= 0.
Для исследования непрерывности /(х, у) в точке (0; 0) по отдельным перемен¬
ным рассмотрим /(х, 0) = 0 и /(0, у) = 0. Так как эти функции непрерывны в точках
х = 0иу = 0 соответственно, то f(x, у) непрерывна в точке (0; 0) по каждой из пере¬
менных. Однако, рассмотрев другие направления, т.е. прямые у = kx, k Ф 0, проходя¬
щие через точку (0; 0), убедимся в том, что
Ьу-2 Ь
f(x,kx)= ”ц I=TVTix0-/№°)=°.
X1 jTR1X1 l + k1
т.е. функция не является непрерывной по всем таким направлениям, а значит,
и не является непрерывной по совокупности переменных.
Таким образом, из непрерывности по каждой переменной не следует
непрерывность функции в точке. А если функция непрерывна по каждому
направлению, то следует ли из этого непрерывность в точке? И на этот
вопрос ответ — отрицательный. Рассмотрим пример.
Пример 8.5
Функция f(x,y) =
, если X2 + уА Ф 0,
X1 + г/4
0, если X2 + г/4 = 0.
На любом направлении у = kx (т.е. на любой прямой, проходящей через точку
(0; 0), кроме прямой х = 0),
/(х, kx) = = ——» 0 при л: —> 0.
’ x2+kAxA i + kAx2 F
На прямой х=0 имеем /(0, г/) = 0 —> 0 при х —» 0. Таким образом, функция непре¬
рывна на любом направлении.
у4 ^
Но для точек кривой х = у2 имеем /{у2,у) = ~г—т = ~■ Значит, не выполнено
yi + Vd 2
определение непрерывности по Гейне (и Д Iim/(х, у)).
х—>0
у-*о
Задание 8.3
Найдите точки разрыва следующих функций:
. х + у 1
а) и = — -;б)и = ~ ; .
X6 + уй smxsinz/
Задание 8.4
Исследуйте на непрерывность следующие функции:
a) fix,у) =
в) Rx,у) =
■ 1
xsin—,если уФО,
х * б) f(x,y) =
0, если у = 0;
а
(х + у) ^ х2 + у2Ф 0,
arete х - arete у
ос - если х Фу,
х-у
0, если X = у,
(х + у)2
X2+ у2
Г) Rx, у) =
1, если X2 + у2 = 0;
осу
X2+у2
, если х е Q, у е <
0, если XgQ или у g <
432
8.3. Свойства непрерывных функций
Для непрерывных функций в R7w справедлив ряд теорем, аналогичных
теоремам о непрерывных функциях в R1, но ряд формулировок требует
уточнения. Свойства непрерывных функций можно разделить условно
на две группы: локальные (свойства функций, непрерывных в точке) и гло¬
бальные (свойства функций, непрерывных на некотором множестве, т.е.
в каждой точке некоторого множества).
Сначала рассмотрим локальные свойства.
Теорема 8.6 (о локальной ограниченности). Пусть функция у = /(х)
непрерывна в точке х*. Тогда существует Ъ-окрестность х* такая, что /(х)
ограничена в этой окрестности.
Теорема 8.7 (о сохранении знака). Пусть/(х) непрерывна вх* и fix) > О
(Jipcs) < 0). Тогда существует Ъ-окрестность х* такая, что/(х) > 0 (J(pc) < 0)
во всех точках этой окрестности.
Речь в этих теоремах идет об окрестностях в Rm, вместо 8-окрестностей
могут использоваться прямоугольные окрестности.
Теорема 8.8 (об арифметических операциях над непрерывными функ¬
циями). Пусть у = fix) иу= gix) непрерывны в х*. Тогда fix) ± g(x), f(x)g(x)
и fix)/gix) (при gix*) Ф 0) непрерывны в х*.
Теорема 8.9 (о непрерывной суперпозиции непрерывных функции).
Пусть у = /(X1, х2, ..., хт) непрерывна в х*, а функции xft) = X1 (^, ..., tk), ...,
xm(t) = XrrJti, ..., tk) непрерывны в точке t* е R*, причем XiJ*) = х*. Тогда
сложная функция е = fix ft),..., xmJ)) = FJ) непрерывна в точке t*.
Теперь перейдем к глобальным свойствам.
Теорема 8.10 (о прохождении через промежуточное значение). Пусть
функция у =/(х) непрерывна на связном множестве X G R”, a, be х, L- пара¬
метрически заданная кривая, содержащая точки аиЬ (т.е. L: X1 = Cp1(O) •••)
хт = Фт(0) t G [а; Р], xfa) = а{, xf(P) = b), LeX. Тогда для любого значения с
между f(a) и fjb) найдется точка х* на кривой такая, что /(х*) = с.
Фактически теорема 8.10 говорит о том, что найдется значение параме¬
тра f, которому соответствует точка х* = (срДС),..., <pmJ*)): fix*) = с.
Теорема 8.11 (первая теорема Вейерштрасса). Пусть у = fix) непре¬
рывна на ограниченном и замкнутом множестве X. Тогда fix) ограничена
на X.
Теорема 8.12 (вторая теорема Вейерштрасса). Пусть у = fix) непре¬
рывна на ограниченном и замкнутом множестве X. Тогда на X найдутся х'
и х" такие, что
fix) = sup fix), fix") = inf fix).
{*} M
Как и в R, в многомерном случае можно дать определение равномерной
непрерывности. Функция у =/(х) равномерно непрерывна на X, если для V в > 0
3 8 = 8(в) > 0 такое, что для V х', х" е X, таких что \х' - х"| < 8, [fix') -fix') \ < в.
Теорема 8.13 (Кантора). Пусть у = /(х) непрерывна на ограниченном
и замкнутом множестве X. Тогда /(х) равномерно непрерывна на X.
433
8.4. Дифференцируемость функций многих переменных
Перейдем теперь к рассмотрению понятия дифференцируемости функ¬
ций в Rm. Пусть, как и ранее, у = /(х) = /(.X1,..., Xm) определена в окрестно¬
сти точки х°. Тогда можно определить следующие понятия.
1. Полное приращение функции, соответствующее приращению аргу¬
мента Ax = (Ax1,..., Axm): А/ = /(х0+ Ах) -/(х°).
2. Частное приращение функции, соответствующее приращению от¬
дельной переменной Axi: Ax.f = fA^AAA^d^ +Axi хР+1 х° -/х°
Фактически A XJ — приращение А/при условии Ax7- = О ,j Ф i. В терми-
нах приращений можно сформулировать условия непрерывности:
/(х) непрерывна в х°, если А/ —> 0 при Ax —> 0;
/(х) непрерывна в х° по переменной Xi, если А*./—> 0 при Axi-> 0.
А %J
Рассмотрим понятие частной производной fx. = Hm
Axi—>0 Axi
Если существует /^, то то Ax f —>0 при Axi-* 0, т.е. /(х) непрерывна
в X0 по Xi.
Дадим определение дифференцируемости: у = /(х) дифференцируема
в точке х° тогда и только тогда, когда
т т
А/ = IAAxi + IX (Ax)Axi, (8.1)
Z=I Z=1
где Ai = const не зависят от Ax (но зависят от х°), OLi(Ax) —> 0 при Ax —» 0.
В определении (8.1) константы Ai — на самом деле частные произво¬
дные по Xi, т.е. //(X0) = Ai. Последняя группа слагаемых в формуле (8.1)
может быть представлена в виде о(|Дх|), таким образом, у =/(х) диффе¬
ренцируема в х° тогда и только тогда, когда
aZ=EZZa^z+O(M)-
Z=1 1
Первая группа слагаемых (линейная часть приращения) называется
т
дифференциалом /(х) в точке x°:df = X/ZAxr
z=I *
Дифференциалы независимых переменных по определению считаются
равными Axi (т.е. Ctxi = Axi). Частные производные обозначаются также:
df
X- = /'. Поэтому первый дифференциал может быть записан в виде
Эх,- 1
т
df = Z^fdxi.
г=1 Эх7
По сути определение дифференцируемости означает, что в окрестности
точки х° функция у =/(х) «подобна» линейной функции z(x):
т т
z - /(х° ) = £/' Axi = YiAi (хг- - X1P ). (8.2)
Z=1 1 Z=I
Если функция у = /(х) дифференцируема, то формула (8.2) представ¬
ляет собой уравнение касательной к графику в точке х°.
434
В одномерном случае наличие производной и дифференцируемость
были эквивалентны. В многомерном случае это не так. Точнее, из диф¬
ференцируемости следует наличие всех частных производных, обратное
утверждение неверно. Рассмотрим пример.
Пример 8.6
Опять рассмотрим функцию fix, у) =
Ее частные производные:
ху
X2+у2
, если X2 + у2 Ф О,
О, если X2 + у2 = 0.
£(0,0) = Iim /(Д*-0)-/(0-0)=0.
Дг—»0 Ax
/'(0,0)= Iim
/(0, Ау) -/(0,0)
= 0.
&у—>о Ау
Однако, как было показано выше, для f(x, у) не существует предела в точке (0; 0),
следовательно, f(x, у) разрывна в точке (0; 0) и не дифференцируема в этой точке.
Задание 8.5
Найдите /Д0;0) и /ДО; 0), если f(x;y) = %[xy. Является ли эта функция диффе¬
ренцируемой в точке (0; 0)?
Задание 8.6
Исследуйте на дифференцируемость в точке (0; 0) функцию
1
fix, У) = -
X2-Vy2
, если X2 + у2 > 0,
0, если х2л-у2= 0.
Задание 8.7
Исследуйте на дифференцируемость в точке (0; 0) функцию /(х, у), если:
а) /(х, у) = ^x3 + у4; б) /(х, у) = sin(e*+y -V^x3-Vy3);
в) /(*> У) = cos %[ху; г) /(х, у) = хД + г/2/3;
д) /(х, у) = |х| • \у\ , где а > 0, (3 > 0.
Задание 8.8
Найдите все точки дифференцируемости функции f(x, у) =х\у\ +у\х\.
8.5. Свойства дифференцируемых функций
Для дифференцируемых функций в Rm справедлив ряд утверждений,
аналогичных одномерному случаю.
Теорема 8.14. Пусть функции у = fix) и у = g(x) дифференцируемы
в точке х°. Тогда f(x) ± g(x), f(x) ■ g(x), f{x)/g(pc) (gipft) Ф 0) дифференци¬
руемы в x°.
Теорема 8.15. Пусть функция у =/(х1;..., хт) дифференцируема в точке
х° = (X10,..., х° ), а функции Xi = gft) = gft^..., tk) дифференцируемы в точке £°,
435
причем gi(t°) = xf. Тогда сложная функция у = f(g\(t), gm(t)) = Е(£) диффе-
о dF ™ Bf Bxi
ренцируема в точке tu, причем — = Z
Btj г=1 Bxi Btj
Для многомерной функции, как и в случае непрерывности, можно опре¬
делить понятие дифференцируемости по отдельному направлению.
Пусть заданы точка х° и единичный вектор е = (еь ..., ет) = (Cosa1, ...,
cosam), задающий направление. Производной в точке у = /(х) по направле¬
нию е называют
= limf(x°+te)-f(x°)
Be t-* о е
Заметим, что частные производные — это производные по направле-
Bxi
ниям, задаваемым базисными векторами
Если у функции у = /(х) в точке х° существуют все частные произво¬
дные, то можно определить вектор из этих производных, который называ¬
ется градиентом функции в точке:
grad/(x) = V/ =
'bf_ df_"
VuxI ujiTn J
Если функция у = f(x) дифференцируема в точке, то производная
по направлению е имеет вид
Bf = у Bf Bxi
Be г=1 Bxi Bt
Cosai = (V/, е).
(8.3)
Отсюда следует, что для дифференцируемой функции из всех произ¬
водных по направлению в заданной точке максимальна та, что определя-
V/
ется вектором е = |^| — единичным вектором, коллинеарным градиенту
(иными словами, градиент задает направление наибольшего возрастания
функции, а вектор (-V/) — наибольшего убывания функции).
Если же функция /(х) не является дифференцируемой в точке х°, то
формула (8.3) может быть неверна. Рассмотрим несколько примеров.
Пример 8.7
Опять рассмотрим функцию f(x,y) =
ху
X1-sCy1
, если X2 + у1 Ф О,
Как было пока-
0, если X2+у2= 0.
зано выше, f(x, у) не является непрерывной и тем более дифференцируемой в точке
(0; 0). Тем не менее у нее существуют частные производные
У
Эх
(0,0)= Iim
Ax->0
/(Ах, 0)-/(0,0)
Ax
= 0и^(0,0) = 0,
оУ
т.е. grad/ = (0, 0). А вот производные по остальным направлениям не существуют,
так как для любого направления, определяемого прямой у - kx, функция
436
/(x, Ax) = j A2 +T
О, если X1-Vy1= 0
разрывна в точке 0, а значит, недифференцируема.
-,еслиX2-Vy2 ФО,
Пример 8.8
Рассмотрим функцию /(х, у) = ^xy2. Она, очевидно, непрерывна в точке (0; 0).
Покажем, что она недифференцируема в этой точке. Найдем ее частные производные:
/(о.о)= Um /(0,0)=0.
OX Дг—>0 Ax ду
Для дифференцируемости требуется, чтобы приращение функции имело вид
Af = /(Дх, Ау) - /(0,0)=д^АхЛАу + 0( V(Ax)2 +(Ay)2).
Bx дх
C учетом найденных значений это означает, что должно выполняться равенство
I f (Ах, Az/)
/(Ах, Ay) = 0(J(Ax)2 +(Ay)2). Но Д Iim , ’ , так как на направлении
^00 f (Ax)2+ (Ay)2
Дг/ = АДх=> Iim
/(Ах, kAx) VA2Ax ^ Va2 л
= Iim , = + , при Ax ^ ±0.
ax^0 V(Ax)2 +A2(Ax)2 a^0 | Ax | Vl +A2 Vl +A2
Найдем производную по направлению у = Ах, т.е. по направлению, определяемому
rI k л
единичным вектором е =
Vl + A2 ’ Vl + A2
dI
Bl
/
= Hm-
t—>0
t tk
^ Vl + A2 ’ Vl + A2
-/(0,0)
= IimJiii
t—if
Va2
VT+А2'
Таким образом, у функции у = f(x) существуют производные по всем направле¬
ниям, но это не гарантирует дифференцируемость функции. И конечно, в этом слу¬
чае не выполняется формула (8.3).
Для дифференцируемости у = f(x) помимо наличия частных производ¬
ных на функцию необходимо накладывать дополнительные ограничения.
В частности, наиболее простым и часто используемым достаточным усло¬
вием дифференцируемости является следующая теорема.
Теорема 8.16. Пусть функция у = f(x) имеет все частные производные
в окрестности точки х°, эти частные производные непрерывны в х°. Тогда
у = f(x) дифференцируема в х°.
Укажем еще одно важное геометрическое свойство вектора градиента.
Пусть функция у = /(Xi, ..., хт) дифференцируема в точке х°. Тогда, как
было указано выше (см. формулу (8.2)), график функции в (т + 1)-мерном
пространстве имеет касательную плоскость в точке (х°, у0), где г/° = /(х°),
уравнение касательной имеет вид
т
У-У0 = ЁтЧ*°)(*г ~х?)’
i=l VXi
437
откуда следует, что вектор нормали к графику функции в точке X0 имеет
вид (grad/, -1). Более того, можно рассмотреть в пространстве R7ra поверх¬
ность уровня, т.е. множество точек х е Rm таких, что fix) = /(х0). Тогда
вектор grad/ ортогонален к этой поверхности уровня в точке х°, уравнение
касательной плоскости в Rm к поверхности уровня в точке х° имеет вид
у Э/(х° )
h дх{
(Xz-X1P) = O.
8.6. Производные высших порядков
Перейдем теперь к рассмотрению производных высших порядков
для функций многих переменных.
Пусть функция у =/(х) =Jixi,..., хт) определена в окрестности точки х°,
имеет в этой окрестности частную производную ff = g(x). Если функция
g(x) в свою очередь имеет частную производную по переменной Xp то эту
производную называют второй производной функции /(х) по переменным
Э 2/
Xi и Xj и обозначают f"x. = -—^—. Аналогично по индукции определяются
^ OX zCjOC~
производные и более высокого порядка.
Пусть в окрестностях0 определена частная производная
э»-1/
Эх- ... Эх.
tW-I tI
= g(x)
по переменным х^,...,Xi . Если функция g(x) в свою очередь имеет част¬
ную производную по переменной Xin, то эту производную называют произ¬
водной порядка п для /(х) по переменным х^,..., Xi :
dg _ Э
Эх,- Эх,-
э-</
Эх,- ... Эх,-
7W-I Ч J
Э»/
f(n) = у
Эх,- ...Эх,- J xIf-xIn j xif-xIn-I 'Х*п
Возникает вопрос: зависит ли результат вычисления производной от по¬
рядка дифференцирования, т.е. справедливо ли равенство
Рассмотрим классический пример.
Э2/ _ эу ?
BxiBxj BxjBxi
Пример 8.9
Функция fix,у) =
осу 2
Xz +У“
0, если X2+ у2 = 0.
Э2/ Э2/
Вычислим производные _ _ и •
Х0 У0, если х2+у2Ф 0,
дхду дудх
|^(о.о)= иш
дх Ах—>0 Ar
к
дх
i3x2y- z/3)(x2 +y2)-2xix3y-y3x)
(г2 + у2)2
0, если X2 + у2 = 0
, если X2 + у2 -ф 0,
438
=-1.
дудх Ау—>о Ay д^->о Ay
Вычислим другую смешанную (т.е. по разным переменным) производную:
ау д?/—>о дг/
(х3 -3у2х)(х2 +у2)-2у(хъу-уъх)
Э/
^ Эг/
О, если X2 + у2 - О
ЭхЭг/ д*->о Ar
= Hm = 1.
Ax3Ax2 - О
Дг—»о Ax
Получили
ЭхЭу дудх
Э2/ Э2/
Таким образом, в общем случае значение смешанной производной зави¬
сит от порядка дифференцирования. Но для достаточно гладкой функции
порядок дифференцирования при вычислении производной оказывается
не важен. Поясним это точнее.
Определение 8.5. Функция у = /(х) п раз дифференцируема в точке х°,
если все ее производные порядка (п - 1) дифференцируемы в точке х°.
В частности, функция дважды дифференцируема, если ее первые част¬
ные производные дифференцируемы. Для этого достаточно, чтобы все
вторые частные производные были непрерывны в точке х° (для я-кратной
дифференцируемости достаточно, чтобы были непрерывны производные
порядка п).
Имеет место следующая теорема.
Теорема 8.17. Пусть функция z = f{x, у) дважды дифференцируема
Как следствие получается следующая теорема.
Теорема 8.18. Пусть функция у = /(X1, ..., хт) п раз дифференцируема
в точке х°. Тогда для любого набора OC1, сс2,..., ocm: CC1 + а2 + ... + ат = п, значе¬
ние производной п-го порядка CLi раз по Xi, i = 1,..., т, не зависит от порядка
вычисления этой производной.
Рассмотрим теперь понятие дифференциала от функции у = f(x) более
высокого порядка, чем первый. Дифференциалом функции у = f(x) порядка
п (и = 2, 3, ...) называется дифференциал от дифференциала (п - 1)-го
порядка (при Sxi = Cbci, где Sxi — приращение на новом этапе дифференци¬
рования, a Cbci — на предыдущих).
Дифференциал второго порядка (и более высоких порядков), как
и в скалярном случае, не обладает свойством инвариантности, т.е. его вид
зависит от того, являются ли требуемые переменные независимыми.
в точке (х°, у0). Тогда
d2z d2z
в точке (х°, г/°).
BxBy ByBx
439
Пример 8.10
Дифференциал второго порядка
d2f = P(dx)2 + ^-dxdy + ^\(dyY + P~dxdy.
дх2 4 ' дхду
Если же х = x(t), у = y(t), то
ду2
дудх
d2f = P^dx2+2
дх2
э2/
дхду
dxdy
+Ir^2+I-рх+Ч-ру'
ду1 дх ду
где d2x, d2y — дифференциалы функций x(t) и y(t) (здесь учтено также равенство сме¬
шанных производных). Однако если x(t) и y(t) — линейные функции от t - (Ц,tk),
то d2x = 0, d2y = 0, а в этом случае имеет место инвариантность дифференциала вто¬
рого (и более высоких) порядка.
Пусть у = /(X1, ..., хт) — функция т независимых переменных. Тогда
из определения следует, что
Э»/
<*"/=ХХ~Хя
*l=li2=1 lTi=i0xH'
.Эх,-
= <Ьсх.... dxx
т
т.е. дифференциал порядка п — сумма всевозможных производных поряд¬
ка п, умноженных на соответствующие дифференциалы независимых пере¬
менных. Однако в этой сумме есть много одинаковых слагаемых (с учетом
равенства соответствующих смешанных производных).
Тогда можно использовать оператор взятия дифференциала:
d = -^—dxx + ... + ^—dxmdnf = (d)n f = -^dx1 +...+
Эх1 OXm I Эх1
—<ь
дх. т
\П
/•
Используя полином Ньютона
(ai + а2
+ ... + ат)п- X
«1+-+« т=п
ПП
^1,
,a.
m
щ осп a.
Q<2 ••• CL.
m
m
где С" „ = : , запишем дифференциал порядка п (с учетом равен-
aI ’-’“яг OC1I--CXm!
ства соответствующих частных производных) в следующем виде:
dnf= S
(¾!+...+(Xm-1
Cn
, aI атп
э nS
Эх011
ч
a
■Эх,
-(Ck1)aI — (dxm)a
пг
тп
8.7. Формула Тейлора
Как и в случае функции одной переменной, в M7ra достаточно гладкую
(п раз дифференцируемую) функцию можно в окрестности точки х° при¬
близить полиномом порядка п. Точнее, имеет место следующая теорема.
Теорема 8.19 (теорема Тейлора с остаточным членом в форме
Лагранжа). Пусть функция у = /(X1, ..., хт) п + 1 раз дифференцируема
в окрестности точки х°. Тогда для любого х из этой окрестности найдется
точка х = х° + 0(х-х°), где 0 G [0; 1], такая, что
440
/(*)=/(*°)+^/U +^2 /U +-+^я/и+(^rf<"+,) Л
n\
11 I
Здесьр(х) = /(х°) + -й[/^0 +—^2/|^0 +" + —{dnAxQ - полином Тейлора
от х степени п (полином т переменных, где (Ixi = Xi - xf, а d^n+v> /I _ —
(п + 1)\ 1х
остаточный член).
Можно дать альтернативную формулировку.
Теорема 8.20 (теорема Тейлора с остаточным членом в форме Пеано).
Пусть функция у = f(x) п раз дифференцируема в точке х°. Тогда для х
из окрестности х° выполнено равенство
/(х) = /(х°) + -^/|хо + ^2/|хо +- + hdnAxb +о(|х-х°Г).
Задание 8.9
Разложите функцию/(г, у) по формуле Маклорена (т.е. в окрестности точки X0 - 0)
до членов указанного порядка малости, если:
а) f(x,y) = \n(i +х2)1п(1 +г/2),п = 6;
б) Rx,y) = avctgX +У ,W = 6;
i + xy
в) f(x, у) = y]cos(x3 +у2), я = 6;
г) f(x, у) = ех2+У2 arctg(^2 - у2), п = 6;
Д) Rx, у) =
1
(1-*)(1-у)
,П = 4;
е) f(x, у) - arctg(ху -Vx2-у3),п- 6.
8.8. Неявные функции
Существуют различные способы задания функции. Чаще всего функции
задаются явно, т.е. в явном виде задается закон, по которому аргументу х
(х E M или х E Rm) ставится в соответствие значение функции у = Rx).
Но есть и неявный способ задания функции. Пусть задана функция
z = F(xb ..., хт, у). Рассмотрим уравнение ^x1, ..., хт, у) = 0. Пусть при раз¬
личных наборах х E X а Rm это уравнение имеет решение у, которое, есте¬
ственно, зависит от выбора х. Тогда фактически каждому х из X ставится
в соответствие у E R (решение соответствующего уравнения), а значит,
задается некоторая функция у =Rx). Она задается неявно, опосредованно,
через функцию z = F(x, у).
Рассмотрим некоторые аспекты такого задания функций. Пусть на мно¬
жестве {х, у} E Rm+1 определена функция z = F(x, у), х е Rm, ye R1 Пусть
для каждого х G {х} уравнение имеет решение. Неявная функция у =Rx) —
это такая функция, что F{x, Rx)) = 0 для VxgX Но при таком опре¬
делении возникает вопрос: а если при некотором х G X решение не един¬
ственно? Какое из решений выбрать?
441
Рассмотрим следующий пример.
Пример 8.11
Пусть функция задана уравнением F(x, у) = х2 - у2 = 0.
При всех х Ф 0 уравнение имеет два решения: у - -х и у - х. Сколько неявных
функций задает это уравнение? Ответ — бесконечно много. Действительно, условию
F{x, у) =OC2-- (у(х))2 = 0 удовлетворяют, например, следующие функции:
1)у = х; 2) у =-ос,
3 )У =
[х, еслих>0,
[-х, если х < 0
\х\;
А) у =
х, если х е Q
I -х, если х <£ (
5) у =
|х, если хе [1;2],
I -х, если х € [i;2]
и т.д., таких функций действительно можно выписать бесконечно много. Среди них
есть непрерывные (первые три), дифференцируемые (первые две), разрывные везде
(четвертая), разрывные только в отдельных точках (пятая) и т.д.
Возникает вопрос: как (в случае неединственности решения уравнения)
выбрать неявную функцию достаточно «хорошей» (непрерывной, гладкой)?
Для того чтобы продемонстрировать основную идею, рассмотрим еще
один пример.
Пример 8.12
Функция Fixl,х2,у) = X1 + X2 + г/2 -1 = 0. Это уравнение в трехмерном простран¬
стве (х1; х2, у) определяет сферу. Если попытаться решить это уравнение явно, то
для всех точек (х1; х2): х2 + х2 < 1 мы сталкиваемся с указанной выше проблемой
неединственности решения: у = 1-х^ -х| или у = -^Jl - X12 -х| ? Очевидно, что
только две указанные функции являются гладкими неявными функциями. Как
выбрать их из всего многообразия возможных решений?
Для этого используем следующую идею. Фиксируем некоторую точку
(х^,х^,г/°):Е(х^,х^,г/°) = 0 (т.е. находим одно решение уравнения в одной интересу¬
ющей нас точке, в случае неединственности решения в заданной точке (X1, X2) выби¬
раем его по каким-то соображениям, связанным с решением общей задачи). В данном
примере указанная процедура означает выбор точки на сфере (причем паре (X10, xj?)
соответствуют две точки (xf, X2, у0): на верхней полусфере при у0 = ^!-(х®)2 -(х2)2
и на нижней полусфере при у0 = -^Ji - X12 - х|).
Выберем для определенности точку на верхней полусфере (рис. 8.1) и рассмо¬
трим малую е-окрестность точки (X1, X2, у0). Если посмотреть на рисунок, то можно
заметить, что при достаточно малом е указанная е-окрестность вырезает из сферы
часть поверхности (с точкой (X1, х2, у0)), которая является графиком гладкой неяв¬
ной функции. В данном конкретном примере е > 0 должно быть таким малым, чтобы
не зацепить точки экватора; в противном случае вырезанная часть сферы не прое¬
цируется однозначно на плоскость (x{\xf), т.е. не является частью графика некото¬
рой функции.
Эту идею можно обобщить на произвольное уравнение Fixi, ..., хт, у) = 0.
Фиксируем (х{\...,х®), найдем соответствующее значение у0 (при этом
выбор у0 может быть неоднозначен). Далее будем искать неявную функцию
У = Kxь хт): F(x> У(х)) = 0,/(х°) = у0, у =f(x) лежит в малой е-окрестности
у0 (т.е. I f(x) - у01 < е). Оказывается, при определенных условиях на Fix, у)
442
и достаточно малом 8 > 0 такая функция существует, единственна и доста¬
точно гладкая. Точнее, имеет место следующая теорема.
Теорема 8.21. Пусть функция F(xt, ..., хт, у) определена в г'-окрестно¬
сти точки (X10,..., х°, у0) = (х°, у0), дифференцируема в этой окрестности,
Э F BF
_F(x°, у0) = 0. Пусть также —— (х°, у0) Ф 0, — непрерывна в г'-окрестности
By By
(х°, г/°). Тогда для любого достаточно малого е (г < е" < е' при некотором г" >
> 0) 3 8 = 8(e): для всех х из 8-окрестности х° в R7ra существует и единственна
неявная функция у - /(х) такая, что |/(х) - у01 < е; при этом неявная функ¬
ция непрерывна и дифференцируема в указанной 8-окрестности точки х°.
Обсудим чуть подробнее условия теоремы 8.21. Для этого рассмотрим
простой (плоский) пример: F(x, у) = х - у2 = 0 (рис. 8.2).
Рис. 8.2
443
Если решать это уравнение относительно у, то для любого х > 0 существует
два решения: у = Vx и у = -Vx; неявных функция таких, что х - (г/(х))2 = О,
бесконечно много. Но только две «хорошие»: у = Vx и у = -Vx. Для выделе¬
ния одной из них (локально, в окрестности интересующей точки) выберем
х° и у0: х° - (у°)2 = 0 (рис. 8.3).
Тогда, выбрав достаточно малую е-окрестность точки, можем заметить,
что внутрь нее попадает часть только одной неявной функции. При этом
величина е зависит от выбора точки (х°, у0). При (х°, у0), близких к точке
(0; 0), е надо выбирать маленьким (и, соответственно, мала 8-окрестность
х°, на которой определена функция). При (х°, у0), далеких от точки (0; 0),
е и 8 могут быть достаточно большими.
Отметим ключевую роль условия отличия от нуля частной производной
Э F
—, частной производной F по той переменной, по которой мы пытаемся
оу
Э F
разрешить уравнение. В той точке, где —— = 0 (в примере это точка (0; 0)),
оУ
условие однозначной локальной разрешимости уравнения может теряться.
В примере не существует такой окрестности точки (0; 0), что она содержит
одну неявную функцию (т.е. часть кривой F(pc, z/) = 0 не может быть спрое¬
цирована на прямую у = 0).
Э F
Смысл условия — Ф 0 логично пояснить также следующим образом. Так
ду
как функция z = F(x, у) дифференцируема в окрестности (х°, у0), то к ней
можно применить теорему Тейлора (с остаточным членом в форме Пеано):
т dF ?IF
z = F(x°, у0)+ X(Xi ~ х?) +—(у - у0)■+ о(р),
J=I OXi ду
где р = I (х, у) |. C учетом того, что Е(х°, у0) = 0, уравнение F(x, у) = 0 при¬
обретает вид
444
c)F m dF
~^-(y -У0) = Ё(*i -*°) + o(p).
oy i=i OXj
Это уравнение в малой окрестности (х°, г/°) близко к линейному относи¬
тельно у (нелинейность в виде о(р) = о
т
Ё(*1-*?)2+(и-у?)2
Л
, конечно,
зависит от у, но мала по сравнению с главной линейной частью), а для раз¬
решимости линейного уравнения требуется, чтобы коэффициент при у
(т.е. —) был отличен от нуля.
ду
Заметим, что это условие является достаточным для локальной одно¬
значной разрешимости уравнения, но отнюдь не необходимым.
Пример 8.13
Рассмотрим функцию F(x, у) =х-у3 = 0. В точке (0; 0) — = Ъу2 = 0. Это уравне-
оу
ние везде однозначно разрешимо, существует лишь одна неявная функция у = у[х.
При выполнении условий теоремы 8.21 неявная функция локально
существует, единственна, непрерывна и дифференцируема. Укажем способ
вычисления частных производных этой функции.
По определению неявная функция у = /(х) такова, что
Р(хь..., xm,/(X1,..., хт» = Ф(хь ..., хт) = 0.
Учитывая, что Ей/ дифференцируемы, а значит, и Ф дифференцируема,
из последнего тождества получаем
dF
ЭФ dF dF dy _ Эу
— = — + — = 0=>^-
Sxi Эхг- dy Эхг- Sxi
dF '
dy
Последняя дробь определена в силу условия — х 0.
dy
Если функция Е(х, у) дважды дифференцируема, то можно найти
и более высокие производные неявной функции. Для этого заметим, что
dy _
3Xj ЭЕ
dy
Эх Эх ^1’У(^1> •Х'тУ)
ЭF
dy
(Xi,...Xm, /(Xi,...,Xm))
д 2У
dxjdxi
Э 2F Э 2F dy
^dXjdxi dydx{ Эх
J J
ЭF
dy
Э 2F Э 2F dy
dx:dy (dy)2 Эх-
K J
JJ
dF
Эх.-
\ЪУ;
445
Подставив в это выражение значение —, получим явный вид второй
оу
производной неявной функции у = /(X1, хт). При достаточной степени
дифференцируемости F(x, у), продолжая аналогичные рассуждения, можно
получить производные функции у = /(х) и более высоких порядков.
Задание 8.10
Приведите пример уравнения F(x, у) = 0:
а) не определяющего функцию у = f(x);
б) определяющего две различные функции;
в) определяющего п различных функций;
г) определяющего несчетное множество различных функций.
Задание 8.11
Пусть а - а(х, у) — переменный параметр. Покажите, что функция z - z(x, у), за¬
данная системой уравнений
Z = Otx + - + /(а),
а
O = X-^y + /' (а),
а2
удовлетворяет дифференциальному тождеству ■ ^=I.
ох оу
Задание 8.12
Пусть X1 = X1(X2) х3,..., хп), X2 = X2(X1) х3,..., хп),..., хп = Xn(X1) х2,..., хп-1) - функ¬
ции, определяемые уравнением F(xb х2, ..., хп) = 0. Вычислите произведение
Sx1 Sx2 Sxn
Sx2 Sx3 Sx1
Задание 8.13
Пусть из уравнения у=xcp(z) + \|/(z) переменная z определяется как неявная функ¬
ция от х и у. Предполагая xcp '(z) + \|/ '(г) Ф 0, установите, что производные этой функции
удовлетворяют следующему тождеству:
S2Z
Sx2
Sz 2 2&z Sz S2z S2Z
кдуу Эх ду SxSz/ Sz/2
\дх j
= 0.
8.9. Системы уравнений
Обобщим понятие неявной функции на случай системы таких функ¬
ций. Пусть в окрестности точки (х{\..., X^1, у\,..., у®) = (х°, у0), где X0 G Rm,
z/° G Rw, заданы п уравнений:
Fi(xi,...,xm,y1,...,yn) = 0,
F2(xv...,xm,yv...,yn) = 0,
(8.4)
/»(*1’Fv •••’ Уп) ~ 0*
Решая при различных х = (X1,..., хт) эту систему относительно у = (уь ...,
уп) (если это возможно), мы получим систему из п неявных функций
У\ =/i(x),..., уп = fn(x). Как и в случае одного уравнения, возникает вопрос:
446
при каких условиях на функции F{{x, y),i=\,..., п, система уравнений (8.4)
разрешима, когда решение единственно, непрерывно, гладкое?
Пусть функции Ft(x, у) дифференцируемы в окрестности точки (х°, у0),
причем
Fi(X0lU0) = OJ= 1, ...,я.
Тогда функции Ft(x, у) могут быть разложены по формуле Тейлора
с остаточным членом в форме Пеано в окрестности (х°, у°), а уравнения
(8.4) с учетом того, что F{(x°, у0) = 0, приобретают вид
п DF т
X - У?) = “ xj) + °(Р)>
г=1 ]=\ OXj
+ (8.5)
п DP т DF
X (Vi ~уЬ = ~~x<j) + °(Р)>
I=I tyi
I п т
где р = jXG/j ~yf)2 + Х(х/ ~ xI )2 • Система (8.5) при малых р близка к ли-
\г=1 j=1
нейной, а для разрешимости линейной системы из п уравнений относи¬
тельно п неизвестных уь ..., уп требуется, чтобы была невырождена матри¬
ца из коэффициентов при указанных переменных. Для системы (8.5) это
матрица
BF1
щ)
Эг/i
дУп
Э Fn
BFn
Эг/i
дуп J
которую называют матрицей Якоби. Определитель этой матрицы называют
якобианом и обозначают
DjF1,..., Fn)
D(y^,..., уп)
Таким образом, для однозначной разрешимости системы уравнений
D(F, , F )
(8.4) в окрестности точки (х°, у0) требуется, чтобы якобиан п
П(У^-,Уп)
был отличен от нуля. Точнее, имеет место следующая теорема.
Теорема 8.22. Пусть функции F{{x, у), i = 1, ..., п, определены в окрест¬
ности тачки (х°, у0), дифференцируемы в этой окрестности; Ft(x°, у°) = О
DF
для всех L Пусть также частные производные -S где i = 1,..., n,j = 1,..., п,
дУ)
447
D(F F)
непрерывны в окрестности точки (х°, у0), а якобиан 1^"* п) Ф 0. Тогда
1,..., У п)
для любого (достаточно малого) 8 > 0 найдется Ъ-окрестность точки х°
такая, что в этой окрестности существует единственная система неяв¬
ных функций у I = fi{x), i = 1,п, таких, что у{ - yf < е, у{ =Aiix) непрерывны
и дифференцируемы в окрестности точки х°.
Как и в случае одного уравнения, величина е (и 8-окрестности, соответ¬
ственно) зависит от конкретной функции и точки (х°, у0); условие отличия
от нуля якобиана — достаточное, но не необходимое условие локальной
однозначной разрешимости системы уравнений.
Как и в случае одного уравнения, можно указать способ вычисления
производных неявных функций в том случае, когда F{{x, у) дифференци¬
руемы. Запишем систему с учетом неявных функций:
Fxix1,..
; Xm, Aiixlt ••
, Xm),-
•> Anix1I ••
•> хт))
= OiO1,--
S
III
о
hi*»-
•> Xm, AiXlt..
-, Xm),..
-Jnix1,-
Xm)) -
= Ф2О1, ••
'-—'
III
о
Fnix1,.
Xjn, AiX 1,..
•> хт)> •
-, Anix1, •
-, хт)) -
= ObOi,-
о
III
✓"s
Продифференцируем эту систему по X1:
дх1 i=1 Byi Bx1 Bx1
Эф2 = BF2 Byi | BF2
Bx1 i=i Byi Bx1 Bx1
ЭФ п BF Bu- BF
и JL = ^ и п . u^1 _|_ и п = Q
Bx1 j=i Byi Bx1 Bx1
Получим систему из п линейных уравнений относительно п неизвест¬
ных -^l, причем матрица коэффициентов при этих неизвестных — матрица
Bx1
Якоби, а значит, в силу невырожденности якобиана эта система однозначно
разрешима, те. из нее можно найти все частные производные ^l. Посту-
иOC ^
пая аналогичным образом, получим системы уравнений относительно ——,
Bxj
которые также будут однозначно разрешимы. Для решений можно исполь¬
зовать формулу Крамера решения системы линейных уравнений. C учетом
явного вида этой системы
D(Fy^Fn)
Byi Diy1,..., г/г-_!, Xj, yi+1,..., уп)
Bxi
DjF,,..., Fn)
Diy1I •••, Уп)
448
Задание 8.14
Найдите в точке (1; 0; 1; -2) частные производные функций и - и(х, у), v - v(x, у),
\xu + yv-u3 — 0,
заданных неявно системой уравнений -I
[x + y + u + v = 0.
8.10. Зависимость функций. Функциональные матрицы
Рассмотрим еще одно понятие, связанное с системами функций многих
переменных, а именно, зависимость (независимость) таких систем.
Пусть в окрестности точки х° E Rm определены функции у 1 =Z1(X), ...,
Уп = Srkx)• Далее считаем, что все функции yt = /г-(х) дифференцируемы
в указанной окрестности. Говорят, что функция у{ =Skx) выражается через
остальные (гладко выражается), если существует гладкая функция (п - 1)-й
переменной Ф такая, что O(Z1^x), ..., /f_i(x), Si+i(x), -, Srkx)) = ф(*) = Skx)
в указанной окрестности х°.
Система функций Zi (х), ...,fn{x) — независимая, если ни одна из функ¬
ций этой системы не выражается через оставшиеся.
Рассмотрим простой пример. Пусть на R2 заданы две функции
Zi (х, у)=х-у, /2(х, у)=х + у.
Покажем, что они независимы. Действительно, предположим, что Zi
выражается через f2, т.е. существует функция Ф такая, что Ф(/2(х, у)) =
= Ф(х + у) = х - у = Zi(x, у). Но тогда на прямой х + у = const функция
Ф(х + у) = Ф(соп8^ = const, в то время как Zi(х, у) = х - у = 2х Ф const — т.е.
функция Zi (х, у) на прямой меняет свое значение. Получили противоречие.
Аналогично можно показать, что f2(x, у) не выражается через Zi(х, у).
Рассмотрим теперь систему из трех функций:
Zi(х,у) =х-у, f2(x,у) =х +у,Z3(x,у) = ху.
В этом случае
S, ч ft(x>y) + Siix’ У) /2(^^)-/1(^.^)
/з(*. У) = ~2 ,
т.е. одна из функций выражается через оставшиеся.
Можно также ввести понятие линейной зависимости. Система из п функ¬
ций линейно зависима, если найдутся константы Ci1, ..., ап такие, что
П
а$ + ... + ос2 ФО и ^CLiSi(X) = O в окрестности х°. Из указанных условий сле-
i=1
дует, что в случае линейной зависимости одна из функций является линей¬
ной комбинацией оставшихся, т.е. найдется линейная функция Ф такая, что
Si = ¢(/1, —,Si-i>Si+и -,Sn)- Таким образом, линейная зависимость — частный
случай зависимости функций.
Возвращаясь к последнему примеру, покажем, что данные три функ¬
ции линейно независимы (хотя и просто зависимы). Предположим, что
они линейно зависимы. Тогда найдутся константы Oi1, а2, а3: аДх + у) +
+ а2(х-у) + CL3(xy) = 0 для всех (х, у) е R2. Возьмем три точки (х, у) E R2,
в них должно выполняться указанное тождество. Тогда получим систему
449
из трех уравнений относительно Gi1, ос2, ос3. В качестве таких точек можно
выбрать, например, (1; 0), (0; 1) и (I; 1). Тогда получим систему
'
Cl1 + Cl2 = 0,
oil — CX2 = О,
2at + a3 = 0.
Отсюда следует, что Oi1 = Oi2 = а3 = 0, что противоречит определению
линейной зависимости. Таким образом, зависимые функции могут быть
линейно независимыми. Укажем теперь достаточные условия независимо¬
сти функций.
Теорема 8.23. Пусть функции /\(рс), i = 1, ..., п, определены и дифферен¬
цируемы в окрестности точки х° е Mm, п<т, существует набор перемен-
4 DWl,-,/,)
ных с номерами гь ..., гп такой, что якобиан отличен от нуля
D(xi^ ’ •••> Xin )
в точке х°. Тогда система функций /f(x), i = 1, ..., п, независима в окрест¬
ности точки х°.
Для анализа независимости функций удобно рассматривать функцио¬
нальную матрицу
э/i
э/И
X1
хт
ЭЛ
Vn
X1
Хт у)
Теорема 8.23 гарантирует независимость системы функций, если в этой
матрице найдется минор максимального порядка п (с учетом того, что
п < т), отличный от нуля в точке х°. Заметим, что это условие является
всего лишь достаточным. Рассмотрим в окрестности точки (0; 0) функции
Z1 (х, у) =X2- у2, /2(х, у) =х2 + у2.
Проводя рассуждения по предложенной выше схеме для системы
из двух функций, легко показать, что эти функции независимы в R2. В то
же время
2х -2у
0
0Л
О
A= ~ ,А(0,0) =
2х 2у J \0 у
т.е. матрица А вырождена в точке (0; 0).
Более тонкий результат дает следующая теорема.
Теорема 8.24. Пусть в окрестности х° е Rт задана система из п диф¬
ференцируемых функций у I = fi(x). Пусть в функциональной матрице этой
системы существует минор порядка 1<п, находящийся в строках ib ..., ц,
отличный от нуля в точке х°. Тогда функции Д,...,Д независимы. Пусть
все миноры порядка больше I равны нулю в окрестности х°. Тогда функции
fi(x), где i£ц,...,ц, выражаются через базисные функции}в указан¬
ной окрестности.
450
Таким образом, для независимости достаточно невырожденности
минора в одной точке, а вот для зависимости требуется вырожденность
соответствующих миноров на целом множестве. Последний пример пока¬
зывает, что вырожденности минора в точке мало для зависимости функций.
Список литературы
1. Александров, П. С. Введение в теорию множеств и общую тополо¬
гию / П. С. Александров. — СПб.: Лань, 2010.
2. Алексеев, В. М. Избранные задачи из журнала American Mathematical
Monthly / В. М. Алексеев. — М.: Мир, 1977.
3. Алфутова, Н. Б. Алгебра и теория чисел для математических школ /
Н. Б. Алфутова, А. В. Устинов. — М.: МЦНМО, 2002.
4. Аржанцев, И. В. Студенческие олимпиады по алгебре на мехмате
МГУ / И. В. Аржанцев [и др.]. - М.: МЦНМО, 2012.
5. Арнольд, В. И. О первой всесоюзной математической олимпиаде
студентов / В. И. Арнольд [и др.] // УМН. — 1975. — Т. XXX. — Вып. 4
(184). - С. 281-288.
6. Берман, Г. Н. Сборник задач по курсу математического анализа /
Г. Н. Берман. — М.: Книга по Требованию, 2013.
7. Бесов, О. В. Лекции по математическому анализу: в 2 ч. / О. В. Бесов. —
М.: Физматлит, 2014.
8. Бурцев, А. А. Методы решения экзаменационных задач по математи¬
ческому анализу / А. А. Бурцев. — М.: МФТИ, 2011.
9. Валле-Пуссен, Ш.-Ж. Курс анализа бесконечно малых : в 2 т. /
Ш.-Ж. Валле-Пуссен. — М.; Л.: ГИТТЛ, 1933.
10. Васильев, Ф. П. Методы оптимизации / Ф. П. Васильев. — М.: Фак¬
ториал Пресс, 2002.
11. Винберг, Э. Б. Курс алгебры / Э. Б. Винберг. — М.: URSS, 2013.
12. Виноградова, И. А. Задачи и упражнения по математическому ана¬
лизу : в 2 т. / И. А. Виноградова, С. Н. Олехник, В. А. Садовничий. — М. :
Дрофа, 2004.
13. Водопьянов, С. К. Интегрирование по Риману / С. К. Водопьянов. —
Новосибирск : Новосибирский государственный университет, 2006.
14. Гелбаум, Б. Контрпримеры в анализе / Б. Гелбаум, Дж. Олмстед. —
М.: URSS, 2010.
15. Грехем, Р. Конкретная математика. Основания информатики /
Р. Грехем, Д. Кнут, О. Поташник. — М.: Вильямс, 2009.
16. Грешнов, А. В. Сборник задач и упражнений по математическому
анализу : в 2 ч. / А. В. Грешнов, С. А. Малюгин, В. Н. Потапов. — Новоси¬
бирск : Новосибирский государственный университет, 2012.
17. Гумеров, Р. Н. Элементы общей топологии : учеб.-метод. пособие /
Р. Н. Гумеров. — Казань : Изд-во КГУ, 2007.
18. Гурса, Э. Курс математического анализа: в 3 т. / Э. Гурса. — М.: Гос.
техн.-теор. изд-во, 1933.
452
19. Данцер, Л. Теорема Хелли и ее применения / Л. Данцер, Б. Грюн-
баум, В. Кли. — М.: Мир, 1968.
20. Дедекинд, Р. Непрерывность и иррациональные числа / Р. Деде-
кинд. — М.: URSS, 2009.
21. Демидович, Б. П. Сборник задач и упражнений по математическому
анализу / Б. П. Демидович. — М.: Астрель, 2003.
22. Домрина, А. В. Задачи по теории функций и функциональному ана¬
лизу / А. В. Домрина, Т. А. Леонтьева. — М.: ИНФРА-М, 2013.
23. Дороговцев, А. Я. Математический анализ. Краткий курс в современ¬
ном изложении / А. Я. Дороговцев. — Киев : Факт, 2004.
24. Дороговцев, А. Я. Математический анализ. Сборник задач /
А. Я. Дороговцев. — Киев : Вища школа, 1987.
25. Зверович, Э. И. Вещественный и комплексный анализ : в 6 ч. /
Э. И. Зверович. — Минск : Вышэйшая школа, 2008.
26. Зорич, В. А. Математический анализ : в 2 ч. / В. А. Зорич. — М. :
МЦНМО, 2007.
27. Иванова, С. В. Формула Тейлора и ее применение / С. В. Иванова. —
М.: МФТИ, 2011.
28. Ильин, В. А. Математический анализ: в 2 т. / В. А. Ильин, В. А. Садов¬
ничий, Бл. X. Сендов. — М.: Юрайт, 2015.
29. Ильин, В. А. Основы математического анализа : в 2 т. / В. А. Ильин,
Э. Г. Позняк. — М.: Физматлит, 2014.
30. Коваленко, Л. И. Методическое пособие по решению задач госу¬
дарственного квалификационного экзамена по математике в МФТИ /
Л. И. Коваленко. — М.: МФТИ, 2007.
31. Коваленко, Л. И. Рациональные методы решения задач по математи¬
ческому анализу / Л. И. Коваленко. — М.: МФТИ, 2006.
32. Кожевников, П. А. Исследование сходимости несобственных инте¬
гралов / П. А. Кожевников. — М.: МФТИ, 2007.
33. Кожевников, П. А. О равномерной непрерывности функций /
П. А. Кожевников. — М.: МФТИ, 2012.
34. Колмогоров, А. Н. Элементы теории функций и функционального
анализа / А. Н. Колмогоров, С. В. Фомин. — М.: Физматлит, 2004.
35. Коновалов, Б. П. Методическое пособие по решению задач мате¬
матической студенческой Олимпиады (1993—2007) / Б. П. Коновалов,
М. В. Балашов. — М.: МФТИ, 2007.
36. Кудрявцев, Л. Д. Курс математического анализа: в 3 т. / Л. Д. Кудряв¬
цев. — М.: Юрайт, 2014.
37. Кудрявцев, Л. Д. Сборник задач по математическому анализу: в 3 т. /
Л. Д. Кудрявцев [и др.]. — М.: Физматлит, 2003.
38. Кужель, А. В. Методы обобщений в математике : учеб, пособие /
А. В. Кужель. — Симферополь, 1983.
39. Курант, Р. Что такое математика / Р. Курант, Г. Робинс. — М. :
URSS, 2013.
40. Ландау, Э. Основы анализа / Э. Ландау. — М.: URSS, 2010.
41. Ландау, Э. Введение в дифференциальное и интегральное исчисле¬
ние / Э. Ландау. — М.: URSS, 2005.
453
42. Лузин, Н. Н. Теория функций действительного переменного: Общая
часть / Н. Н. Лузин. — М.: Учпедгиз, 1948.
43. Львовский, С. М. Лекции по математическому анализу / С. М. Львов¬
ский. - М.: МЦНМО, 2013.
44. Ляшко, И. И. Справочное пособие по высшей математике : в 5 т. /
И. И. Ляшко [и др.]. - М.: URSS, 2006.
45. Макаров, Б. М. Избранные задачи по вещественному анализу /
Б. М. Макаров [и др.]. — СПб.: Невский диалект, 2004.
46. Макаров, И. П. Дополнительные главы математического анализа /
И. П. Макаров. — М.: Просвещение, 1968.
47. Маркушевич, Б. М. Теория аналитических функций : в 2 т. /
Б. М. Маркушевич. — СПб.: Лань, 2009.
48. Математика сегодня: науч.-метод. сб. / под ред. А. Я. Дороговцева. —
Киев : Науч. издат.; TBiMC, 1983—2007.
49. Натансон, И. П. Теория функций вещественной переменной /
И. П. Натансон. — СПб.: Лань, 1999.
50. Очан, Ю. С. Сборник задач и теорем по теории функций действи¬
тельного переменного / Ю. С. Очан. — М.: Просвещение, 1963.
51. Очан, Ю. С. Сборник задач по математическому анализу. Общая тео¬
рия множеств и функций / Ю. С. Очан. — М.: Просвещение, 1981.
52. Пархоменко, А. С. Что такое линия / А. С. Пархоменко. — М. :
ГИТТЛ, 1954.
53. Петрович, А. Ю. Предел, непрерывность и дифференцируемость
функций нескольких переменных / А. Ю. Петрович. — М.: МФТИ, 2007.
54. Полиа, Г. Задачи и теоремы из анализа : в 2 ч. / Г. Полна, Г. Сеге. —
М.: Наука, 1978.
55. Ривкинд, Я. И. 300 задач по математическому анализу / Я. И. Рив-
кинд. — Минск, 1962.
56. Рудин, У. Основы математического анализа / У. Рудин. — СПб. :
Лань, 2004.
57. Садовничая, И. В. Математический анализ. Вещественные числа
и последовательности: Теория и задачи / И. В. Садовничая, Т. Н. Фоменко,
Е. В. Хорошилова — М.: Издательский отдел факультета BMK МГУ, 2011.
58. Садовничая, И. В. Математический анализ. Функции многих пере¬
менных / И. В. Садовничая, Т. Н. Фоменко. — М.: МАКС Пресс, 2008.
59. Садовничая, И. В. Определенный интеграл. Теория и практика
вычислений / И. В. Садовничая, Е. В. Хорошилова. — М. : МАКС Пресс,
2008.
60. Садовничий, В. А. Теория операторов / В. А. Садовничий. — М. :
Дрофа, 2004.
61. Садовничий, В. А. Задачи студенческих математических олимпиад /
В. А. Садовничий, А. А. Григорян, С. В. Конягин. — М.: Изд-во МГУ, 1987.
62. Садовничий, В. А. Задачи студенческих олимпиад по математике /
В. А. Садовничий, А. С. Подколзин. — М.: Наука, 1978.
63. Свиридюк, Г. А. Математический анализ : в 2 ч. / Г. А. Свиридюк,
В. Е. Федоров. — Челябинск : Челябинский государственный университет,
1999.
454
64. Сергеев, П. В. Математика в спецклассах 57-й школы / П. В. Сер¬
геев. - М.: МЦНМО, 2008.
65. Суетин, П. К. Классические ортогональные многочлены / П. К. Cye-
тин. — М.: Физматлит, 2007.
66. Теляковский, С. А. Сборник задач по теории функций действитель¬
ного переменного / С. А. Теляковский. — М.: Наука, 1980.
67. Тер-Крикоров, А. М. Основы математического анализа / А. М. Tep-
Крикоров, М. И. Шабунин. — М.: Физматлит, 2001.
68. Уиттекер, Э. Т. Курс современного анализа / Э. Т. Уиттекер,
Дж. Н. Ватсон. — М.: URSS, 2007.
69. Ульянов, П. Л. Действительный анализ в задачах / П. Л. Ульянов [и
др.]. — М.: Физматлит, 2005.
70. Фихтенгольц, Г. М. Курс дифференциального и интегрального
исчисления : в 3 т. / Г. М. Фихтенгольц. — СПб.: Лань, 2009.
71. Харди, Г. Неравенства / Г. Харди, Дж. Литльвуд, Г. Полна. — М. :
URSS, 2008.
72. Харди, Г. Расходящиеся ряды / Г. Харди. — М.: URSS, 2010.
73. Хаусдорф, Ф. Теория множеств / Ф. Хаусдорф. — М.: URSS, 2010.
74. Хорошилова, Е. В. Неопределенный интеграл / Е. В. Хорошилова. —
М.: МАКС Пресс, 2007.
75. Шибинский, В. М. Примеры и контрпримеры в курсе математиче¬
ского анализа / В. М. Шибинский. — М.: Высшая школа, 2007.
76. Шилов, Г. Е. Математический анализ. Специальный курс /
Г. Е. Шилов. — М.: Физматгиз, 1961.
77. Шилов, Г. Е. Математический анализ. Функции одного переменного :
в 3 ч. / Г. Е. Шилов. — СПб.: Лань, 2002.
78. Яковлев, Г. Н. Функциональные пространства / Г. Н. Яковлев. — М.:
МФТИ, 2000.
79. Comtet, L. Advanced combinatorics / L. Comtet. — D. Reidel Publishing
Company, 1974.
80. Erdman,J. M. A problem text in advanced calculus / J. M. Erdman. —
Portland State University, 2005.
81. Mattuck, A. P. Introduction to analysis / A. P. Mattuck. — Prentice Hall,
Upper Saddle River, NJ, 1999.
82. Trench, W. F. Introduction to real analysis / W. F. Trench. — Prentice
Hall, 2003.
Интернет-сайты
1. http://ahiin.livejournal.com — популярно о науке.
2. http://amc.maa.org/a-activities/a7-problems/putnamindex.shtml —
страница Путмановской олимпиады — главного математического конкурса
США.
3. http://dxdy.ru — научный форум dxdy.
4. http://dmvn.mehmat.net — учебные материалы для студентов мех¬
мата МГУ.
5. http://math.mit.edu/~apm/index.html — домашняя страница Артура
Маттука, профессора математики Массачусетского технологического инсти¬
тута.
455
6. http://mathoverflow.net — страница вопросов и ответов для матема¬
тиков.
7. http://mipt.ru/education/chair/mathematics/olymp — студенческая
олимпиада по математике МФТИ.
8. http://putnam.ho.ua — украинские математические олимпиады
для студентов.
9. http://vyshka.math.ru — материалы курсов факультета математики
НИУ ВШЭ.
10. http://www.imc-math.org — страница международных математиче¬
ских олимпиад студентов университетов.
11. http://www.mccme.ru/circles/oim/stolym.htm — студенческие олим¬
пиады и конкурсы на мехмате МГУ им. М. В. Ломоносова.
12. http://www.mccme.ru/ium/courses.php — учебные материалы
МЦНМО-НМУ.
Предметный указатель
Абелева группа 12
Аддитивная группа 12
Аксиома непрерывности (полноты)
13
Алгебраическое число 22
Аналитическая функция 401
Арифметический способ задания
кривой Пеано 203
Асимптота графика функции 291
Асимптотически равные функции
160
Асимптотическое поведение функ¬
ции 159
Астроида 215
Вариация числовой последователь¬
ности 107
Взаимно-однозначное соответствие
множеств 19
Внешняя точка множества 29
Внутренняя точка множества 29
Возрастание функции на интервале
264
Всюду плотное множество 43
Выпуклая вверх (вниз) функция
275
Выпуклая последовательность 93
Геометрическая интерпретация вы¬
пуклости 277
Главная часть функции 164
Градиент функции в точке 436
Граница множества 30
Граничная точка множества 30
Дедекиндовы сечения 14
Декартово произведение множеств
И
Дзета-функция Римана 399
Дифференциал функции 206
Дифференцируемость функции 206,
434
Дополнение множества 32
Евклидово пространство 425
Задача Арнольда 262
Замкнутое множество 29
Изолированная точка множества 29
Изоморфизм 14
Изоморфные поля 14
Изоморфные упорядоченные поля
14
Интеграл с переменным пределом
325
Интеграл Френеля 366
Интеграл Фруллани 364
Интегралы Дарбу 318
Интегральная сумма Римана 315
Интегральное неравенство Коши —
Буняковского 352
Интегрирование заменой перемен¬
ных 306
Интегрирование по частям 306
Итерационная формула Герона 96
Канторова гребенка 61
Канторово множество (канторов
дисконтинуум) 45
Касательная к графику функции
212
Кладбище Серпинского 59
Класс эквивалентности 89
Классификация точек разрыва 168
Ковер Серпинского 57
Колебание функции на отрезке 246
Кривая Жордана 194
Кривая Пеано — Гильберта 197
Критерий выпуклости 277
Критерий дифференцируемости 206
Критерий интегрируемости в тер¬
минах колебания функции 316
Критерий интегрируемости Дюбуа —
Реймона 323
457
Критерий интегрируемости Коши
320, 359
Критерий интегрируемости Лебега
323
Критерий Коши равномерной схо¬
димости функциональной последо¬
вательности 378
Критерий Коши существования
предела функции многих перемен¬
ных 428
Критерий Коши сходимости несоб¬
ственного интеграла 359
Критерий Коши сходимости после¬
довательности 85
Критерий Коши сходимости число¬
вого ряда 121
Критерий непрерывности в терми¬
нах открытых множеств 171
Критерий постоянства функции 227
Критерий равномерной сходимости
через остаточный член 378
Лемма Больцано — Вейерштрасса
42
Лемма в вложенных отрезках 39
Лемма Гейне — Бореля 41
Лемма Кантора 40
Линейно упорядоченное множество
13
Локальный экстремум функции 284
Мажоранта (миноранта) множества
34
Матрица Якоби 447
Метод неопределенных коэффици¬
ентов 256
Метод степенных рядов суммирова¬
ния числовых рядов 411
Метод Чезаро суммирования число¬
вых рядов 414
Метрическое пространство 28
Многочлен Тейлора 255
Множество действительных чисел
И
Множество мощности гиперконти¬
нуум 26
Множество мощности континуум 22
Модуль непрерывности функции
246
Мощность множества 19
Мультипликативная группа 12
Необходимое и достаточное условия
локального экстремума 284, 285
Необходимое и достаточное условия
точки перегиба 278, 279
Необходимое условие дифференци¬
руемости функции одного перемен¬
ного 206
Необходимое условие интегрируе¬
мости 316
Необходимое условие суммируемо¬
сти по Чезаро 414
Неопределенное интегрирование
305
Неподвижная точка отображения
181
Непрерывное упорядоченное поле
13
Непрерывность по Чезаро 183
Непрерывность функции 166
Неравенство Бернулли 143
Неравенство Йенсена 280
Неравенство треугольника 28
Неравенство четырехугольника 28
Неравенство Юнга 281
Несобственный интеграл первого
и второго родов 357
Неявная функция 441
Нигде не плотное множество 44
Обобщение правила Лопиталя 253
Односторонние производные 207
Окрестность точки 29
Определенный интеграл Римана 315
Открытое множество 29
Отношение эквивалентности 88
Первообразная функции 305
Подобные с сохранением порядка
следования множества 53
Подпокрытие системы множеств 41
Полином Ньютона 440
Полное множество 87
Последовательность Фарея 92
Последовательность Фибоначчи 127
Постоянная Эйлера 137
Правила двойственности 32
Правило Лопиталя второе 252
458
Правило Лопиталя первое 252
Предельная точка множества 29
Предельная точка последователь¬
ности 79
Преобразование Абеля 125
Признак Абеля равномерной сходи¬
мости функционального ряда 390
Признак Абеля сходимости несоб¬
ственного интеграла 368
Признак Абеля сходимости число¬
вого ряда 140
Признак Бертрана сходимости ряда
135
Признак Вейерштрасса равномер¬
ной сходимости функционального
ряда 385
Признак Гаусса сходимости ряда
135
Признак Даламбера сходимости
Ряда 133
Признак Дини равномерной сходи¬
мости функционального ряда 394
Признак Дирихле равномерной
сходимости функционального ряда
390
Признак Дирихле сходимости не¬
собственного интеграла 367
Признак Дирихле сходимости чис¬
лового ряда 140
Признак Ермакова сходимости ряда
135
Признак Коши сходимости ряда 133
Признак Куммера сходимости ряда
135
Признак Лейбница сходимости ряда
139
Признак Раабе сходимости ряда 133
Признаки сравнения числовых ря¬
дов 122, 237
Равномерная сходимость функцио¬
нальной последовательности 377
Разложение в степенной ряд 400
Распределение Гаусса 410
Рациональная функция 153, 405
Ряд Лейбница 140
Сепарабельное метрическое про¬
странство 47
Сингулярная функция 188
Система вложенных отрезков 38
Система неявных функций 446
Смежный интервал множества 44,65
Совершенное множество 43
Совместная граница двух множеств
195
Составляющий интервал множества
64
Степенной ряд 400
Суммы Дарбу 318
Сходимость последовательности
в среднем 103
Сходимость интеграла в среднем
350
Сходимость функциональной по¬
следовательности 377
Счетное множество 19
Телескопический признак сходимо¬
сти 105
Теорема Абеля вторая 401
Теорема Абеля первая 401
Теорема Архимеда 36
Теорема Больцано — Вейерштрасса
80
Теорема Бэра 50
Теорема Вейерштрасса вторая 167,
433
Теорема Вейерштрасса о монотон¬
ных последовательностях 78
Теорема Вейерштрасса первая 167,
433
Теорема Кантора — Бернштейна 23
Теорема Кантора о неэквивалентно¬
сти множеств 26
Теорема Кантора о равномерной не¬
прерывности 237
Теорема Кантора об алгебраических
числах 22
Теорема Коши о перестановке чле¬
нов ряда 140
Теорема Лагранжа о конечных при¬
ращениях 227
Теорема о локальной ограниченно¬
сти функции 167, 433
Теорема о непрерывности суммы
ряда 393
459
Теорема о неявной функции 443
Теорема о почленном дифференци¬
ровании ряда 393
Теорема о почленном интегрирова¬
нии ряда 393
Теорема о почленном переходе
к пределу 393
Теорема о прохождении непрерыв¬
ной функции через любое промежу¬
точное значение 167, 433
Теорема о среднем вторая 349
Теорема о среднем первая 349
Теорема об устойчивости знака
непрерывной в точке функции 167,
433
Теорема Римана о перестановке
членов ряда 140
Теорема Ролля 226
Теорема Таубера 413
Теорема Теплица о регулярном пре¬
образовании последовательности
120
Теорема Фробениуса 414
Теорема Штольца 109
Точка конденсации множества 44
Точка перегиба 278
Точка прикосновения 29
Трактриса 216
Трансцендентные числа 23
Тэта-функция Римана 399
Условие Гельдера — Липшица по¬
рядка а 191, 247
Условие Липшица 247, 344
Формула Бонне 349
Формула замены переменной
в определенном интеграле 326
Формула замены переменной
в определенном интеграле 358
Формула интегрирования по частям
в несобственных интегралах 358
Формула интегрирования по частям
в определенном интеграле 326
Формула Коши — Адамара 400
Формула Коши конечных прираще¬
ний 228
Формула Лейбница для произво¬
дных высших порядков 219
Формула Ньютона — Лейбница 325
Формула Тейлора 255
Формула Тейлора с остаточным
членом в форме Лагранжа 256, 440
Формула Тейлора с остаточным
членом в форме Пеано 255, 441
Формула Фаа-ди-Бруно 226
Формула Фруллани 363
Формула Эйлера для гармоническо¬
го ряда 137
Фрактальный пример всюду непре¬
рывной, но нигде не дифференциру¬
емой функции 296
Фундаментальная последователь¬
ность 85
Функции одного порядка 160
Функциональная зависимость 449
функция Дирихле 172
Функция Кантора 186
Функция Римана 173
Функция Римана модифицирован¬
ная 156, 289
Функция Серпинского 184
Функция, ограниченная по сравне¬
нию с данной 159
Характеристическая функция мно¬
жества 26
Частично упорядоченное множество
13
Частный признак сравнения 122,
360
Числовая последовательность 70
Числовое поле 12
Эквивалентные функции 160
Якобиан 447
Наши книги можно приобрести:
Учебным заведениям и библиотекам:
в отделе по работе с вузами
тел.: (495) 744-00-12, e-mail: vuz@urait.ru
Частным лицам:
список магазинов смотрите на сайте urait.ru
в разделе «Частным лицам»
Магазинам и корпоративным клиентам:
в отделе продаж
тел.: (495) 744-00-12, e-mail: sales@urait.ru
Отзывы об издании присылайте в редакцию
e-mail: red@urait.ru
Новые издания и дополнительные материалы доступны
в электронной библиотечной системе «Юрайт»
biblio-online.ru
Учебное издание
Никитин Алексей Антонович,
Фомичев Василий Владимирович
МАТЕМАТИЧЕСКИЙ АНАЛИЗ.
УГЛУБЛЕННЫЙ КУРС
Учебник и практикум для академического бакалавриата
Формат 70x100 Vi6.
Гарнитура «Petersburg». Печать цифровая.
Уел. печ. л. 35,65.
ООО «Издательство Юрайт»
111123, г. Москва, ул. Плеханова, д. 4а.
Тел.: (495) 744-00-12. E-mail: izdat@urait.ru, www.urait.ru