Автор: Башмаков М.И.
Теги: алгебра математика математический анализ учебник издательство просвещение начало анализа
ISBN: 5-09-003877-5
Год: 1992
Текст
БИОНИЧЕСКИХ КОЛЕБАНИИ
М.И. БАШ МАКОВ
швм
и начала анализа
МОСКВА «ПРОСВЕЩЕНИЕ» 1992
ББК 22.14я72
БЗЗ
Учебник занял первое место на Всесоюзном конкурсе
учебников для средней общеобразовательной школы
Башмаков М. И.
БЗЗ Алгебра и начала анализа: Учеб, для 10-11 кл.
сред. шк. - 2-е изд. - М.: Просвещение, 1992. - 351 с.: ил. -
ISBN 5-09-003877-5.
4306020500-146 ,
Б —юЗ(ОЗ)-91— письм0 “ ^2, доп. № 1 ББК 22.14я72+22.161я72
ISBN 5-09-003877-5
(с) Башмаков М. И., 1991
ПРЕДИСЛОВИЕ
Перед вами учебник по математике.
Математика за 2500 лет своего существования накопила
богатейший инструмент для исследования окружающего нас мира.
Однако, как заметил выдающийся русский математик и корабле-
строитель академик А. Н. Крылов, человек обращается к мате-
матике «не затем, чтобы любоваться неисчислимыми сокровищами.
Ему прежде всего нужно ознакомиться со столетиями испытан-
ными инструментами и научиться ими правильно и искусно вла-
деть».
Учебник научит вас обращаться с такими математическими
инструментами, как функции и их графики, производная и интег-
рал, уравнения и неравенства. Хотя первое ознакомление с боль-
шинством из этих понятий состоялось у вас раньше, книга пред-
ставляет их вам заново. Это удобно для тех, кто забыл из-
учавшийся ранее материал, и полезно всем, так как даже в зна-
комых вещах обнаруживаются новые стороны и явления.
Аналогия математических понятий и результатов с рабочими
инструментами не будет полной, если мы ничего не скажем о мате-
матических рассуждениях и доказательствах, которые играют
роль инструкций и описаний. Не стоило бы так много усилий тра-
тить на изучение математики, если бы ее применение сводилось бы
к использованию справочника. Главная сила математики состоит
в том, что вместе с решением одной конкретной задачи она создает
общие приемы и способы, применимые во многих ситуациях, ко-
торые даже не всегда можно предвидеть.
Так же как кисть художника, его краски и правила пользования
ими еще далеко не определяют то многообразие живописных поло-
тен, которые он может создать, так и математические формулы и
теоремы вместе с их доказательствами не дают представления о
множестве задач, которые можно с их помощью решить. Боль-
шинство задач, решаемых при изучении математики, носят тре-
нировочный характер. Без тренировки в проведении простых
операций невозможно совершенствование ни в каком серьезном
деле. Тем большую радость доставит вам решение интересных и
трудных задач, которые вы найдете в предлагаемом учебнике.
Учебник разбит на шесть глав. Главы разделены на пара-
графы, а параграфы — на пункты. Каждая глава открывает-
ся вводной беседой, подготавливающей появление новых основ-
з
ных понятий. В конце каждой главы помещена заключительная
беседа, которая включает в себя сведения, необязательные для
изучения, но которые могут помочь пытливому человеку.
В конце каждого параграфа помещены контрольные вопросы.
Как правило, они начинаются с напоминания об основных по-
нятиях и обозначениях, появившихся в этом параграфе.
Каждая глава заканчивается задачами, которые расположены
следующим образом. Сначала дается заголовок — новое понятие
или новый алгоритм. Например, «Линейная функция» или «Иссле-
дование функции». К одному заголовку может относиться не-
сколько задач. Для каждой главы задачи пронумерованы от-
дельно. Легкие стандартные задачи отмечены кружком, а труд-
ные — звездочкой. К каждой главе предложено контрольное за-
дание. Оно дается в трех вариантах: первый показывает обя-
зательный уровень требований, второй ориентирован на хорошее
усвоение материала в полном объеме, третий — на повышенный
уровень, соответствующий примерно классам с математическим
уклоном. Объем задания, как правило, велик и не рассчитан
на какое-то определенное время.
В конце книги помещены лабораторные работы (по две на
каждую главу), часто предполагающие вычисления на микро-
калькуляторе.
Большую роль в книге играют иллюстрации. Кроме привычных
чертежей и рисунков, каждая глава снабжена информационны-
ми схемами, которые наглядно изображают основное содер-
жание главы. Они помещены в конце книги.
Сведения по истории математики, как правило, включены в
заключительную беседу. Кроме того, в книге приведены высказы-
вания знаменитых математиков и краткие справки об их жизни.
А для низкой жизни были числа,
Как домашний подъяремный скот,
Потому что все оттенки смысла
Умное число передает.
Н. Гумилев
Глава I
ФУНКЦИИ И ГРАФИКИ
ВВОДНАЯ БЕСЕДА
1. Переменные
«Поворотным пунктом в математике была Декартова перемен-
ная величина. Благодаря этому в математику вошли движение
и тем самым диалектика, и благодаря этому же стало немед-
ленно необходимым дифференциальное и интегральное исчисление,
которое тотчас и возникает и которое было в общем и целом
завершено, а не изобретено Ньютоном и Лейбницем».
Эти слова, принадлежащие Ф. Энгельсу, ярко характеризуют
новый этап в развитии математики, который связан с имена-
ми великих ученых XVII в.: Декарта, Ньютона и Лейбница.
На основе их работ сформировалось понятие функции, были раз-
работаны методы исследования функций, которые в течение
трехсот лет остаются основным инструментом изучения окружаю-
щего мира с помощью математики.
Математика всегда была связана с вычислениями и фор-
мулами. Особенно много формул было получено при решении за-
дач измерения — тысячелетия назад люди овладели формулами
вычисления длин, площадей и объемов простейших фигур.
С помощью формул выражаются соотношения между раз-
личными величинами. Приведем примеры некоторых известных
формул:
1. V=^-nR3 □ — формула объема шара.
2. s=‘-f — формула длины пути при сво- бодном падении.
3. Е=-^~ — формула кинетической энергии.
4. S = ^/p (р — а) (р — Ь) (р — с) — формула Герона для вычисле-
ния площади треугольника.
е —Ь±^Ь2—4ас — формула корней квадратного
2а уравнения.
5
Декарт Рене
(1596—1650) —
французский философ и математик. Одно-
временно с П. Ферма заложил основы анали-
тической геометрии и разработал теорию
алгебраических уравнений. Историк матема-
тики Д. Я. Стройк написал о нем: «Заслуги
Декарта прежде всего в том, что он приме-
нил хорошо развитую алгебру начала сем-
надцатого века к геометрическому анализу
древних».
«И чем труднее доказательство, тем боль-
ше будет удовольствия тому, кто доказатель-
ство найдет».
Р. Декарт
При работе с формулами и при вычислениях по ним приходит-
ся совершать преобразования выражений. Эта сторона математи-
ки вам уже хорошо знакома. Она будет продолжена и в на-
шем курсе. В названии курса слово «алгебра» как раз и отражает
выполнение различных преобразований, или, как говорят, опера-
ционную сторону математики.
Математический анализ, начала которого мы будем изучать
в этом курсе, рассматривает формулу как соотношение между
меняющимися, переменными величинами. Как изменится точность
вычисления объема шара, если точность измерения его радиуса
изменить на одну сотую? Это типичный вопрос математическо-
го анализа. Ответ на него можно получить с помощью пре-
образований, так как формула объема шара не слишком слож-
на. Однако ответ на аналогичный вопрос, связанный с форму-
лой Герона, получить алгебраическими средствами трудно. Ма-
тематический анализ создал методы, с помощью которых мож-
но следить за характером изменения связанных между собой ве-
личин.
В первой из приведенных выше формул участвуют буквы V, R,
л, где V — это объем шара, R — его радиус, л — отношение
длины окружности к диаметру. Ясно, что величины V и R мо-
гут меняться, а л является постоянной. Приближенное значение
константы л равно 3,14159 (с точностью до 0,00001). Во
второй формуле встречаются буквы s, /, g, где s — это длина
пути, t — время движения, a g — ускорение свободного падения.
Величины s и t могут меняться, а величина g в этой формуле
считается постоянной.
Переменная — это общий термин для обозначения различных
меняющихся величин.
6
Например, рассматривая поведение газа в замкнутом объеме,
можно измерить его температуру Г, его объем V, оказываемое
им давление р.
Наблюдая за свободно падающим телом, можно измерить дли-
ну пути s, пройденного телом за время /, его скорость v в
момент времени /, его кинетическую энергию Е в момент вре-
мени t и т. д.
В этих примерах участвуют различные переменные величины,
или просто переменные.
2. Зависимость между переменными
Переменные, появляющиеся при описании какого-либо процес-
са, обычно бывают связаны между собой. Одной из основных
задач экспериментальных наук является изучение этих связей. На-
пример, закон Клапейрона — Менделеева утверждает, что давле-
ние р, объем V и температура Т идеального газа связаны соотноше-
нием
pV 1
±L-_=const.
Реальные процессы обычно связаны с большим количеством пе-
ременных и зависимостей между ними. В то же время можно от-
влечься от каких-то частных деталей, сосредоточив свое внимание
лишь на некоторых сторонах процесса, идеализировав условия, в
которых он протекает. Тогда удается построить математическую
модель процесса, состоящую в перечислении основных характерис-
тик и тех связей, которые между ними имеются.
Например, физики, вводя понятие идеального газа, пренебре-
гают взаимодействием между молекулами газа и их размером и по-
лучают газовые законы в виде соотношений между перемен-
ными р, V и Г.
При изучении падения материального тела можно пренебречь
сопротивлением воздуха, изменением силы тяжести и т. п. и счи-
тать, что движение происходит по прямой с постоянным ускоре-
нием g. Тогда положение тела в любой момент времени t можно
найти, зная его начальное положение и начальную скорость.
Какие значения могут принимать переменные? Во всех при-
веденных выше примерах переменные величины были скаляр-
ными, т. е. их значения задаются числами. И в дальнейшем
мы будем изучать в основном переменные, принимающие число-
вые значения.
Границы, в которых могут меняться числовые значения пе-
ременных, обычно определяются физическими условиями. Так, за-
кон Клапейрона — Менделеева верен лишь при значениях р, V и Г,
лежащих в определенных промежутках.
Изучение различных зависимостей между переменными являет-
ся нашей главной задачей. Хотя величин очень много, но давно
7
было замечено, что разные величины, появляющиеся при описании
далеких друг от друга процессов, могут быть связаны между
собой одной и той же зависимостью. Поэтому для изучения зави-
симостей полезно отвлечься от конкретного физического смысла
рассматриваемых переменных.
Для нас в дальнейшем термин переменная будет означать
просто букву, причем будет указано множество значений,
которое она может принимать.
Например, мы будем говорить: рассмотрим переменную х, при-
нимающую положительные значения.
Так как мы будем встречать в основном переменные, прини-
мающие числовые значения, то полезно вспомнить некоторые
числовые множества.
3. Числовые промежутки
Вам известно, что каждое число можно изобразить точкой чис-
ловой оси и, наоборот, каждая точка оси изображает некоторое
число. Это соответствие между числами и точками числовой оси
настолько естественно, что часто не различают число и изображаю-
щую его точку. Говорят, например, «точка 2», «точка —0,5», «нуле-
вая точка».
Числовые множества удобно изображать на числовой оси. Нам
чаще всего будут встречаться числовые промежутки. Конечные
числовые промежутки, т. е. множества чисел, лежащих между
двумя заданными числами, изображаются отрезками числовой оси.
Бесконечные числовые промежутки, т. е. множества чисел, боль-
ших или меньших заданного числа, изображаются лучами, ле-
жащими на числовой оси. Множество всех чисел заполняет всю
числовую ось и обозначается буквой R. Примеры числовых про-
[о ; 6] и < X ь
а1- Л
(а ; 6] а < X b
и х
[а ; *) а < X ь \//////////////\
'ь X
(а ; ь) а < X ь (//////////////А
О' ‘ь х
(-ОО ;а] X а ////////^
а X
(-ОО ; а) X а ///////X
а X
Га; + оо) X а fzzzzzzzzzzzzzzzz/zzzzzzzT
(а; +оо) X > а ^zzzzzzzzzzzzzzzzzzzzzzzz, а х
(—ОС ; + оо) =/R -оо<х<+оо /////////////////////////////////^ У
Рис. 1
8
межутков, их запись с помощью скобок и неравенств, их изоб-
ражение на числовой оси приведены на рисунке 1.
Если значение одной переменной мы изображаем на координат-
ной прямой (числовой оси), то зависимости между двумя пере-
менными можно изображать на координатной плоскости. Пусть на
плоскости введена прямоугольная система координат с помощью
двух числовых осей. Значения одной переменной (скажем., х) от-
кладываются на одной оси (оси х), значения другой переменной
(скажем, у) — на другой оси (оси у).
Как графически изображается зависимость между перемен-
ными х и у? Возьмем два значения переменных х и у, связанных
данной зависимостью, и построим точку Р с координатами (х; у).
Множество всех таких точек составит некоторую кривую, ко-
торая и является изображением изучаемой зависимости. Эту
кривую называют графиком зависимости и, наоборот, саму за-
висимость называют уравнением кривой.
4. Простейшие зависимости
В огромном море зависимостей между переменными можно вы-
делить три типа простейших зависимостей, которые встречаются
чаще всего,— это прямая и обратная пропорциональность и квад-
ратичная зависимость.
Пусть хну — две переменные.
1) Говорят, что переменные х и у связаны прямой пропорцио-
нальной зависимостью, если их отношение постоянно. С помощью
формул эту зависимость можно записать так: или y = kx,
где k — постоянное число, fe=/=0.
2) Говорят, что переменные х и у связаны обратной про-
порциональной зависимостью, если их произведение постоянно.
Запишем эту зависимость с помощью формул ху — с или у = -£-у
где с — постоянное число, с=/=0.
3) Говорят, что переменная у квадратично зависит от пере-
менной х, если ее значения можно вычислить по формуле у=ах2,
где а — постоянное число, а=/=0.
Заметим, что зависимость первых двух типов имеет симмет-
ричный характер: если переменная у прямо (или обратно) про-
порциональна переменной х, то и, наоборот, переменная х прямо
(или обратно) пропорциональна переменной у.
тт 3 2 5 5
Например, если у=—х, то х=— у или если У=~, то х = ~-
Квадратичная зависимость не является симметричной, в нее
переменные входят неравноправно: если у зависит от х по квад-
ратичному закону, то зависимость х от у не является квадра-
тичной.
9
Ферма Пьер
(1601—1665) —
французский математик, один из создате-
лей аналитической геометриии и дифферен-
циального исчисления. Открыл правило на-
хождения экстремума с помощью производ-
ной. Автор многих теорем теории чисел. Зна-
менитая теорема Ферма из теории чисел, ко-
торую Ферма сформулировал без доказа-
тельства, не доказана и до сих пор.
Графики простейших зависимостей приведены на схеме I. Гра-
фиком прямой пропорциональной зависимости является прямая.
График обратно пропорциональной зависимости называется ги-
перболой. График квадратичной зависимости — парабола.
Большинство известных вам зависимостей между физическими
величинами принадлежит к одному из указанных нами простей-
ших типов.
Приведем примеры.
1. U = RI — закон Ома, где U — напряжение, I — сила тока,
R — сопротивление. Если одна из этих трех переменных по-
стоянна, то две другие по закону Ома связаны прямой или обрат-
ной пропорциональной зависимостью.
2. pV = RT — закон Клапейрона — Менделеева, где р — дав-
ление, V — объем, Т — температура, R — константа (газовая по-
стоянная). При постоянной температуре давление и объем газа
обратно пропорциональны.
3. s = vt — закон равномерного движения, где s — путь, t —
время, v — скорость (постоянная).
л £t2
4. -----закон свободного падения, где $ — путь, t — вре-
мя, g — константа.
5. q = CU— уравнение конденсатора, где U — напряжение,
q — заряд, С — электроемкость.
с С mv2
о. L =—-----кинетическая энергия материальной точки, где
и — скорость, m — масса.
7. Г = у- n,R2H — объем кругового конуса, где R — радиус ос-
нования, Н — высота.
ю
8. [4В]=Л[4]-[В]— соотношение между концентрациями в ра-
створе веществ А, В и их соединения АВ в условиях равновесия,
где k — постоянная.
9. /?=Л"—формула для вычисления расстояния до звезды,
где л" — ее параллакс, вычисленный в угловых секундах.
Ю. т'=-^— формула для нормы прибавочной стоимости, где
т — прибавочный труд, v — необходимый труд.
Контрольные вопросы
1. Обратите внимание на встретившиеся в тексте следующие
ключевые слова и обозначения: переменная, числовая ось, число-
вой промежуток, [a; ft], (а; ft), (—оо; а], (а; +оо), R. Приведите
примеры их использования.
2. Что такое график зависимости?
3. Что такое прямая пропорциональная зависимость между
переменными?
4. Что такое обратная пропорциональная зависимость между
переменными?
5. Какой формулой записывается квадратичная зависимость
одной переменной от другой?
6. Как называются кривые — графики простейших зависи-
мостей?
7. Приведите несколько примеров прямо пропорциональных
величин.
8. Приведите несколько примеров обратно пропорциональных
величин.
9. Приведите примеры квадратичной зависимости.
10. Можете ли вы привести примеры величин, зависимость
между которыми более сложная, чем одна из рассмотренных
простейших зависимостей?
§ 1. ПОНЯТИЕ ФУНКЦИИ
1. Определения и примеры
Пусть даны две переменные х и у. Говорят, что переменная
у является функцией от переменной х, если задана такая зави-
симость между этими переменными, которая позволяет для каж-
дого, значения х однозначно определить значение у.
Примеры функций:
y = kx + b. 4 у=' х>0
2. у=\х\. У *
3. у = х2. 5. у=^[х.
11
В каждом из этих примеров указана формула, позволяющая
для каждого значения переменной х однозначно вычислить зна-
чение переменной у.
Для того чтобы задать функцию, нужно:
1) указать множество всех возможных значений переменной х.
Это множество, которое мы будем обозначать D, называют об-
ластью определения функции;
2) указать правило, по которому каждому числу х из мно-
жества D сопоставляется число у, определяемое числом х. Это
число у называется значением функции в точке х. Переменную х
называют аргументом.
Функция обычно обозначается одной буквой, например f. Зна-
чение функции f в точке х обозначается f (х).
Итак, если задана функция /, то задано множество чисел
D и каждому числу x£D сопоставлено число y = f(x).
Пусть задана функция f с областью определения D. Рас-
смотрим координатную плоскость. По оси абсцисс будем отклады-
вать значение аргумента, а по оси ординат — значение функции.
Для каждого числа x£D можно вычислить y = f(x) и построить
точку М (х; f (х)). Множество всех таких точек образует кривую,
называемую графиком функции f в заданной системе координат.
Итак, графиком функции f называется множество точек пло-
скости с координатами (х; f (х)), где х пробегает область опре-
деления функции f.
На рисунке 2 изображены графики функций, которые были
приведены в качестве примера в начале параграфа.
Рассмотренные нами ранее простейшие зависимости определя-
ют три важнейшие функции:
1) y = kx; 2) У=-^; 3) у = ах2.
Эти функции являются стандартными примерами функций из
трех классов, с которыми мы будем часто сталкиваться в даль-
нейшем: линейных, дробно-линейных и квадратичных.
Рис. 2
12
2. Способы задания функций
Для того чтобы определить переменную у как функцию от
переменной х, нужно задать множество значений аргумента х и
указать правило вычисления значений у в зависимости от х. Сна-
чала обсудим, как задается правило вычисления значений.
Во всех приведенных ранее примерах правило вычисления зада-
валось формулой, содержащей определенные операции.
Обучаясь математике, мы знакомились с различными дейст-
виями, операциями над числами. Например, используя только сло-
жение и умножение, мы можем из числа х получить новые
числа, скажем Зх, 3x4-5, х3 4-3x4-5 и т. п. Уже такого рода выра-
жения, многочлены, могут служить для построения довольно бога-
того запаса функций.
Использование деления сильно расширяет этот запас, позволя-
1 х I 1 2х
ет образовать выражения вида —, , -р—р и т. п. Функ-
ции, которые строятся как отношения многочленов, называют
рациональными.
Операция деления отличается от сложения и умножения тем,
что она не всегда определена — в знаменателе дроби нельзя ста-
вить нуль. Поэтому, например, в выражение можно под-
ставить любые числа, кроме х = 1 и х = — 1, при которых знаме-
натель равен нулю.
Появление новых операций и введение специальных знаков для
их обозначения приводят к дальнейшему обогащению наших
возможностей — извлечение корня, переход к модулю числа
и т. п.
Например, пусть f (х) равно числу —1, если х<0, равно
нулю, если х = 0, и равно 1, если х>0. Этими словами мы опи-
сали некоторое правило вычисления, применимое к любому числу.
Обозначим число f (х), найденное по этому правилу, через sgn х (от
латинского слова signum, что означает «знак»). Теперь мы с
помощью символа для обозначения новой операции можем строить
новые формулы, например g(x)=^—(-sgn(x—1).
Если функция задана формулой и не указано никаких ограни-
чений, ее областью определения считается множество всех зна-
чений аргумента, при которых выполнимы все операции, участ-
вующие в этой формуле. Это множество называют естествен-
ной областью определения данной функции.
Так, естественной областью определения функции у=-у/1—х2
является множество чисел х, для которых 1—х2^0, т. е. про-
межуток [— 1; 1].
Еще раз обратим внимание на то, что две важные операции —
деление и извлечение корня четной степени — выполнимы не всег-
13
да (нельзя разделить на нуль, нельзя извлечь корень четной
степени из отрицательного числа). Это ограничение надо помнить
и учитывать при нахождении области определения функции, в за-
дании которой участвуют указанные операции.
Значения функции у = ^х2-\-1 вычисляются путем последова-
тельного выполнения операций: возведение в квадрат, прибавле-
ние единицы, извлечение квадратного корня. Можно сказать, что
функция г/ = д/х2+ 1 является «сложной функцией», составленной
из более простых: u=x2, и = и+1, Подробнее о по-
нятии сложной функции можно узнать из заключительной беседы
в первой главе.
Итак, правила вычисления значений функции могут задаваться
формулами, полученными с помощью известных нам ранее
действий над числами.
Другой важный способ задания функции — табличный. В таб-
лице можно непосредственно указать значения функции, однако
лишь для конечного набора значений аргумента.
Вычисление значений функции может быть запрограммировано
в калькуляторе. Вычислительное устройство может служить для
вас способом задания новой функции. Современные вычисли-
тельные машины снабжены клавишами, позволяющими немедлен-
но вычислить значения многих полезных функций.
Наконец, часто функцию задают с помощью графика. Гра-
фический способ задания функции очень удобен: он дает воз-
можность наглядно представить свойства функции. Приведем
примеры.
На рисунке 3 изображены вольт-амперные характеристики
некоторых электрических элементов, т. е. графически заданные
зависимости напряжения от силы тока. Они получены не по го-
товой формуле, а экспериментально.
На рисунке 4 изображена кардиограмма работы человеческого
сердца. Ее можно считать графиком изменения электрического
потенциала на волокнах сердечной мышцы во время сердечного
цикла.
Рис. 4
14
Контрольные вопросы
1. Обратите внимание на встретившиеся в тексте следующие
ключевые слова и обозначения: функция, область определения
функции, график функции, y = f (х). Приведите примеры их исполь-
зования.
2. Что нужно указать для задания функции?
3. Что такое график функции?
4. Какие способы задания функции вы знаете?
5. Что понимают под областью определения функции, заданной
формулой?
6. Приведите пример линейной функции.
7. Приведите пример рациональной функции.
8. Приведите пример квадратичной функции.
9. Приведите пример функции, естественная область опреде-
ления которой меньше, чем вся числовая ось R.
10. Приведите пример графического задания функции.
§ 2. ЧТЕНИЕ ГРАФИКА
1. Исследование функции по графику
Рассмотрим функцию y = f(x\ график которой изображен на
схеме II. Что можно сказать о свойствах функции /, глядя
на график?
1) Спроектируем точки графика на ось х. Мы получим отре-
зок [а; Ь]. Этот промежуток является областью определения функ-
ции. Действительно, каждая прямая, параллельная оси у, про-
ходящая через точку этого отрезка, пересекает график ровно в
одной точке; вертикальные прямые, проходящие через точки х вне
отрезка [a; ft], график не пересекают.
2) Рассмотрим точки пересечения графика с осью х. На чер-
теже это %1, х2, *з, х4. В этих точках функция обращается
в нуль. Числа хь х2, *з, *4 являются решениями уравнения
f (х) = 0 и называются корнями функции (или ее нулями).
3) Корни функции f разбивают область определения на
промежутки, в каждом из которых функция сохраняет постоянный
знак. Функция положительна на промежутках [a; Xi), (х2; х3), (х4; ft]
и отрицательна на промежутках (хг, х2), (х3, х4).
Объединение промежутков [а; Х|), (х2; х3) и (х4; ft]
представляет собой решение неравенства f (х)>0, а объединение
промежутков (хи х2) и (х3; х4) — решение неравенства f(x)<0.
4) График функции можно сравнить с профилем дороги,
которая то поднимается в гору, то опускается в ложбину. Самые
верхние и самые нижние точки этой дороги («вершины») играют
важную роль при описании графика. Они соответствуют значениям
аргумента, обозначенным на графике m\, m2, т3.
15
Точка т\ замечательна тем, что если мы рассмотрим, как
меняется функция f вблизи нее, то увидим, что значение f в
этой точке будет наименьшим. Подчеркнем еще раз: f (т\) не
является самым маленьким значением функции f (на чертеже легко
найти далекие от т\ точки, в которых значение f меньше, чем
f (mi)). Оно является наименьшим среди значений f в точках,
близких к т\. Точно так же в точке т2 функция принимает
значение, наибольшее среди ее значений в точках, близких к т2.
Точку т\ называют точкой локального минимума, а точку
т2 — точкой локального максимума. Слово «локальный» означает
«местный» и подчеркивает, что, скажем, f (пц) — наименьшее зна-
чение в некоторой окрестности точки mi.
Итак, в точках т\ и m3 функция f имеет локальный мини-
мум, а в точке т2 — локальный максимум.
Часто употребляют термин экстремум, который объединяет
оба понятия максимум и минимум. Точки т\, т2, т3 — это точки
экстремума функции.
5) Наибольшее значение функция f принимает в точке Ь,
а наименьшее — в точке т3. На этот раз речь идет о самом боль-
шом и самом маленьком значениях функции на всей области опре-
деления. Наибольшее значение функции f равно M = f(b), а наи-
меньшее равно m = f (тз).
Обратите еще раз внимание на возможные различия между
точками экстремума и точками, где функция принимает наиболь-
шее или наименьшее значения.
6) Что можно сказать о поведении функции f между точками
экстремумов?
Из графика ясно, что на отрезке [а; т\] функция f убыва-
ет, затем на отрезке [гиг, т2] она возрастает, далее на отрезке
[т2; тз] функция f убывает и, наконец, на отрезке [т3\ Ь] снова
возрастает.
Часто употребляют термин «монотонность», который объединя-
ет оба понятия «возрастание» и «убывание».
7) Спроектируем точки графика на ось у. Мы получим отре-
зок [m; AI], являющийся областью значений функции f. Он
состоит из всех точек у, являющихся значениями функции f
при каком-либо (необязательно при одном) значении аргумента х.
2. Схема исследования функции
Мы провели исследование функции, изображенной на схеме II,
следуя некоторому плану. Перечислим еще раз его основные мо-
менты для исследования любой функции y = f (х). Этот план, кото-
рый называют схемой исследования функции, включает в себя на-
хождение определенных характеристик функции, словесное опре-
деление которых дано в левой колонке схемы, а графическое —
в правой.
16
1. Область определения, т. е. множест-
во значений аргумента, при которых
задана функция.
2. Корни, т. е. точки, в которых функ-
ция обращается в нуль, или иначе
решения уравнения /(х) = 0.
3. Промежутки постоянного знака, т. е.
промежутки, на которых функция
положительна (отрицательна), или
иначе решения неравенства f(x)>0
(fW<o).
4. Точки экстремума, т. е. точки,
лежащие внутри области определе-
ния, в которых функция принимает
самое большое (максимум) или са-
мое маленькое (минимум) значе-
ние по сравнению со значениями
в близких точках.
5. Промежутки монотонности, т. е. про-
межутки, на которых функция или
возрастает, или убывает.
6. Наибольшее и наименьшее значе-
ния функции (по сравнению со все-
ми возможными в отличие от экст-
ремумов, где сравнение ведется
только с близкими точками).
7. Область значений функции, т. е.
множество чисел, состоящее из
всех значений функции.
1. Проекция графика на
ось х.
2. Точки пересечения
графика с осью х.
3. Участки оси х, со-
ответствующие точ-
кам графика, лежа-
щим выше (ниже)
оси х.
4. «Вершины» на гра-
фике функции.
5. Участки оси х, где
график идет вверх
или вниз.
6. Ординаты самой вы-
сокой и самой низ-
кой точек графика.
7. Проекция графика
на ось у.
Часто график функции является симметричным. На рисунке 5
представлены различные виды симметрии графика: осевая симмет-
рия (относительно оси у; рис. 5, а) ; симметрия относительно на-
чала координат (рис. 5,6). На рисунке 5, в график перио-
дически повторяется. Первым из этих свойств графика обладают
17
четные, вторым — нечетные, третьим — периодические функции.
Определения четной и нечетной функций дадим сейчас, а периоди-
ческие будем изучать в главе III.
Функция y=f (х) называется четной, если при всех значе-
ниях аргумента f (— x)=f (х). При этом имеется в виду, что
если х входит в область определения, то и — х также входит
в нее, т. е. что область определения функции f симметрична
относительно начала координат.
Так как точки (х; у) и ( — х; у) одновременно принадле-
жат или не принадлежат графику четной функции, то этот
график симметричен относительно оси у.
Аналогично функция y=f (х) (с областью определения, сим-
метричной относительно начала координат) называется нечетной,
если при всех значениях аргумента f (— х) — —f (х).
Так как точки (х; у) и ( — х; — у) одновременно принад-
лежат или не принадлежат графику нечетной функции, то этот гра-
фик симметричен относительно начала координат.
Примеры четных функций:
1) у=2; 2) у=х2-, 3) у=4х4—х2+1; 4) у=— -р-.
Примеры нечетных функций:
1) У = х; 2) у = х3 + 2х; 3) У=^\ 4) У=*г^-
Примеры функций, не являющихся ни четными, ни нечет-
ными:
1) у=х2+х; 2) у = угх-, 3) У=-^, х>0; 4) у=-^.
График функции на схеме II представляет собой гладкую кри-
вую. Встречаются графики (рис. 6) с различными нарушениями
18
гладкости — изломами (точка Xi), остриями (точка х2), разры-
вами (точка х3). С изломами и остриями на графике мы встретимся
в главе II.
Если график функции можно начертить, не отрывая карандаша
от бумаги, то такую функцию называют непрерывной. Понятие
непрерывности мы более подробно обсудим в заключительной
беседе.
3. Решение уравнений и неравенств с помощью графика
Если уравнение записано в виде f (х) = 0, то его решения —
это корни функции f. Начертив график функции f и отметив
его точки пересечения с осью абсцисс, можно приближенно
найти решения уравнения f (х) = 0, ответить на некоторые качест-
венные вопросы о них, например: сколько корней имеет уравнение
на заданном промежутке?
Корни уравнения f(x) = a мы найдем, определив точки пере-
сечения прямой у = а, параллельной оси абсцисс, и графика функ-
ции /. Это позволяет определить количество корней уравнения
/(х) = а при различных значениях а. Так, из рисунка 7 видно,
что уравнение f (х)=1 имеет пять корней, f (х) = 3— два корня,
а уравнение f (х) = — 1 — ни одного.
Корни уравнения f (x) = g(x) находятся как абсциссы точек пе-
ресечения графиков функций fug. Например, решая уравнение
х3 + 2х — 3 = 0, переходим к уравнению х3 = — 2х 4- 3. Строя графи-
ки функций у=х3 и у=—2x4-3, мы убеждаемся (рис. 8, а),
что эти графики пересекаются в одной точке (1; 1), т. е.
х=1 — корень уравнения.
Решения неравенства f(x)>0 заполняют те промежутки оси
абсцисс, где точки графика функции f лежат выше этой оси.
Аналогично решения неравенства f(x)>g(x) заполняют про-
межутки, где график функции f лежит выше графика фун-
кции g.
19
Рис. 8
Пример. Решить неравенство х44-х2—-2^0.
Переходим к неравенству х4^— х24-2. Строим графики
функций у=х4 и у= — х24-2 (рис. 8,6). Эти графики пере-
секаются в точках Л (—1; 1) и Рг(1; 1). Решение исходного нера-
венства х^ —-1 их>1,т.е. объединение промежутков (— оо; — 1]
и [1; 4- оо).
Контрольные вопросы
1. Обратите внимание на встретившиеся в тексте следующие
ключевые слова: экстремум, максимум, минимум, монотонность,
четность, нечетность, непрерывность функции. Приведите приме-
ры их использования.
2. Как с помощью графика найти область определения функ-
ции?
3. Как с помощью графика функции определить ее корни
(нули)?
4. Как по графику функции найти промежутки, на которых
функция сохраняет постоянный знак?
5. Что такое точка локального максимума (минимума) функ-
ции?
6. Чем отличается наибольшее значение функции от ее ло-
кального максимума?
7. Как по графику найти область значений функции?
8. Как графически решается уравнение вида f (x) = g (х)?
9. Как графически решается неравенство вида f(x)>g(x)?
10. Перечислите, какие характеристики функции включаются
в схему ее исследования.
20
§ 3. ЛИНЕЙНАЯ ФУНКЦИЯ
1. Свойства линейной функции
Определение. Линейной функцией называется функция
вида у=кх-\-Ь.
Здесь х — независимая переменная, принимающая произволь-
ные значения (аргумент), у — функция, k и b — параметры. Ес-
ли параметр k равен нулю, то линейная функция становит-
ся постоянной: у = Ь. В дальнейшем мы часто будем считать, что
Прямая пропорциональная зависимость между пе-
ременными х и у приводит к простейшей линейной функции y=kx.
Перечислим свойства этой функции, считая, что fe^O.
1) Область определения — множество всех вещественных чи-
сел R.
2) Корни — единственный корень х = 0.
3) Промежутки постоянного знака (они зависят от знака па-
раметра k):
а) если fe>0, то у>0 при х>0, у<.0 при х<0;
б) если /г<0, то у>0 при х<0, у<0 при х>0.
4) Экстремумов нет.
5) Промежутки монотонности:
а) если /г>0, то у возрастает на всей числовой оси;
б) если Л<0, то у убывает на всей числовой оси.
6) Наибольших и наименьших значений нет.
7) Область значений — множество R. (Действительно, урав-
нение kx=a имеет решение при любом а, следовательно, вы-
ражение fcx, где /г=/=0, принимает любое значение.)
8) Функция y=kx нечетная.
Свойства функции y = kx-±b (&=#0) могут быть выве-
дены из свойств простейшей линейной функции y = kx с помощью
следующего преобразования: kx-\-b = k(x-\--j-^ — k (х — Х|), где
Х| = —Точки х и х—Х| на числовой оси получаются друг
из друга сдвигом на Х| (схема III), поэтому графики функций
y = kx и y = k(x — Х|) получаются друг из друга таким же сдвигом
вдоль оси абсцисс. Корень функции «переедет» из точки х = 0
в точку х=Х| = —Аналогичный сдвиг произойдет с промежут-
ками постоянного знака и монотонности. Явление нечетности
пропадет, хотя симметрия графика сохранится (теперь центром
симметрии будет не точка х = 0, а х=Х|).
21
2. График линейной функции
Графиком линейной функции y = kx (прямой пропорциональной
зависимости между переменными х и у) является прямая,
проходящая через начало координат. Коэффициент k называет-
ся угловым коэффициентом этой прямой. Он равен тангенсу
угла наклона этой прямой к оси х, т. е. fe = tg а. При положи-
тельных k этот угол острый, при отрицательных — тупой. Это
соответствует характеру монотонности линейной функции: при
/г>0 она возрастает, при /г<0 убывает.
Графиком функции y = kx-\-b является прямая, параллельная
прямой y — kx, сдвинутая вдоль оси х на Х\ — — при
fe=/=0 (схема III).
Для построения графика линейной функции y = kx-\-b доста-
точно знать угловой коэффициент k и одну точку, лежащую на
графике, т. е. знать значение функции при одном значении аргу-
мента, скажем, у=уо при х=хо- При необходимости из этих
данных коэффициент b находят так: yo = kxo + b, откуда Ь=уо —
— kx0.
Итак, прямая, имеющая угловой коэффициент k и проходящая
через точку (х0; Уо), является графиком линейной функции
у = kx-\-b — kx-\-(yo — kxo). Зависимость у = kx + у0 — kx0 можно
переписать в виде y—y0=kx—kx0 или y — y0 — k (х—х0). Послед-
нюю запись называют уравнением прямой с угловым коэффициен-
том k и проходящей через точку (х0; Уо)-
Часто прямая задается двумя ее точками Pi (xt; yi) и Р2 (х2; у2).
Угловой коэффициент такой прямой вычисляется по формуле
k=y2~V' . Необходимое для применимости этой формулы ус-
%2 — Х\
ловие Х|У=х2 геометрически означает, что прямая Р,Р2 не парал-
лельна оси у.
3. Модуль
Определение. Модулем числа х (обозначается |х|) назы-
вается расстояние от начала отсчета до точки, изображающей чис-
ло х (схема IV).
Модуль числа х можно записать формулой
। । _( х, если х^О,
|х' | —х, если х<0.
Действительно, возьмем число х и изобразим его точкой М
числовой оси. Если х>0, то расстояние | ОМ | между точка-
ми О и М равно х, т. е. |х| =х. Если же х<0, то |ОЛ1| = —х,
т. е. |х| = — х. Если х = 0, то М совпадает с О и верны обе формулы
|х| =х и |х| = — х. Поэтому случай х = 0 можно присоединять к
любому из двух: х>0 или х<0.
22
Теорема. Модуль разности двух чисел равен расстоянию
между точками, изображающими эти числа.
Доказательство. Возьмем числа х и х\. Обозначим
на числовой оси точки, изображающие числа х, Х\ и х—х\ через
М, Mi и М' (схема IV). При сдвиге вдоль оси х на Xi точка О
перейдет в Л4|, а точка М' — в Л4, т. е. |ОЛГ| = |Л41Л1|. Так как
по определению модуля |ОЛГ| = |х — Xi |, то |х —Х| | = |М|Л1|, что
и требовалось доказать. (Обратите внимание на то, что доказа-
тельство не зависит от взаимного расположения точек М и Alj.)
Заметим, что так как |Af|Af| == |ЛШ11, то |х—Х|| = |xi —х|.
В частности, | — х| = |х|. Легко доказать еще одну полезную фор-
мулу:
\k-x\ = \k\-\x\.
Модуль разности можно «раскрыть» аналитически:
। । (х —Xi, если х>хь
если 1<Х1.
Простые уравнения и неравенства с модулем удобно решать,
используя его геометрический смысл. Приведем примеры реше-
ния уравнений и неравенств.
1. |х| =3. Это соотношение геометрически означает, что рас-
стояние от точки х до начала координат равно 3, т. е. х = 3 или
х—— 3. Ответ: х= ±3 (возможна другая форма записи от-
вета: Х| = —3, Х2 = 3).
2. |х+5|=2. Рассматривая |х + 5| как |х — ( — 5)|, прочтем
исходное соотношение так: расстояние от точки х до точки
— 5 равно 2. Откладывая на числовой оси от точки —5 отрезок
длиной 2 (в обе стороны), получим ответ: х\ = —-7, х2 = — 3.
3. |3 — 2х| = 1. Сначала делаем преобразования: |3 —2х| =
= |2х — 3| = |2^х—|-^ | =2 | х—, откуда 2 |х—1-|==1.
Разделив обе части уравнения на 2, получаем | х—2-| =-|-. Ис-
пользуя числовую ось, получаем ответ: Xi = l, х2 = 2.
4. |х|^2. Задачу решения этого неравенства геометрически
можно сформулировать так: найти точки х, расстояния от ко-
торых до начала координат меньше или равны 2. Ответ: — 2^
^х^2, или иначе [ — 2; 2].
5. | —1—2х ^3. Делаем преобразования: | —1—2х|^3,
|2х4-1|>3, 2 *+у-| ^3, | x+-j-| Ответом явля-
ется объединение двух бесконечных промежутков х^С — 2, xj>l
или другая форма записи: (— оо; — 2]U[1; +°°)-
На рисунке 9 изображены график функции у=\х\ и график
функции £/==|х —Xil, который получается из предыдущего гра-
фика сдвигом вдоль оси абсцисс.
23
Рис. 10
Рис. 9
Приведем пример построения более сложного графика.
6. Построить график функции £/=|х + 2| + 1х —2|.
Наносим на ось х корни линейных функций, стоящих под зна-
ком модуля: Х| = —2, х2 = 2. На каждом из трех получившихся
промежутков числовой оси знаки этих линейных функций постоян-
ны, и мы можем избавиться от знака модуля:
если х<—2, то у= — (х + 2) — (х — 2) = — 2х;
если — 2<х<2, то у= +(х + 2) — (х — 2) = 4;
если х>2, то +(х + 2) + (х —2) = 2х.
При построении графика надо провести вертикальные прямые
х = — 2 и х = 2, которые разобьют плоскость на три части. В ле-
вой части надо провести прямую £/=-— 2х, в центральной по-
лосе у = 4 и в правой у = 2х (рис. 10). (Для контроля на-
до следить, чтобы ломаная была непрерывной, т. е. чтобы значе-
ния в разделяющих точках излома, вычисленные по соседним фор-
мулам, совпадали.) В нашем случае при х= — 2 значение функ-
ции у= — 2х совпадает со значением у = 4 и точно так же при х = 2
совпадают значения функций г/= 4 и у = 2х.
4. Метод интервалов
Неравенства вида f (х)>0, когда функцию y = f (х) можно пред-
ставить как произведение линейных множителей, можно решать
методом интервалов, который состоит в следующем:
24
1) разложить f (х) на линейные множители;
2) найти корень каждого множителя и нанести все корни на
числовую ось;
3) исследовать знак произведения на каждом из получившихся
отрезков числовой оси (схема III).
При этом полезно использовать следующее правило: если все
линейные множители различны (имеют разные корни), то произве-
дение будет менять знак при переходе от одного интервала число-
вой оси к соседнему (знаки будут чередоваться). Поэтому доста-
точно определить знак на одном каком-нибудь интервале (обыч-
но это будет крайний правый интервал).
Как применяется это правило, видно из следующих приме-
ров.
1. Решить неравенство (х—1) (х —3)>0.
Нанесем на числовую ось точки Х| = 1 и хг = 3 (корни ли-
нейных функций у=х— 1 и у=х —3). Эти точки разбивают
числовую ось на три интервала: (— оо; 1), (1; 3), (3; +<»). На
каждом из этих интервалов каждый множитель сохраняет
постоянный знак, а при переходе через корень меняет знак
один множитель. Начнем с крайнего правого интервала (3; + оо).
На нем оба множителя положительны. При переходе (справа
налево) через точку хг=3 множитель х —3 стал отрицательным и
все произведение поменяло знак, т. е. стало отрицательным. При
переходе через точку Xi = 1 поменял знак первый множитель
и все произведение стало положительным. Результат исследования
знаков отражен на рисунке II. Ответом будут промежутки
(—оо; 1), (3; +оо). Иначе можно записать: х<1, х>3.
2. Решить неравенство
Нанесем на числовую ось корни соответствующих линейных
функций, т. е. точки — 1; 0; 1; 5, которые разбили числовую ось
на пять интервалов. Распределение знаков дроби на
X (X 1)
этих интервалах изображено на рисунке 12. Ответ можно за-
писать так: (—1; 0), (1; 5), или — 1<х<0, 1<х<5.
0 1 3 х
Рис. 11
-10 1 5 X
Рис. 12
25
Иногда для применения метода интервалов приходится раскла-
дывать на множители левую часть неравенства, с тем чтобы запи-
сать ее в виде произведения или частного двучленов вида х — а.
I X " 2
3. Решить неравенство — > 0.
Преобразовав левую часть: ---0—, по.
\ 2 /
лучим *)<(). Корни линейных функций: Х| = —2, *2=1.
х-т
х3=-|- Ответ: (—оо; —2), (1;.
При решении нестрогих неравенств вида f (х)^0 или f (х)<0
надо включать в множество решений точки, являющиеся корня-
ми линейных функций, стоящих в числителе.
(2—х)х
(2х+5)(2х+3)
4. Решить неравенство
>0.
Перепишем неравенство в виде
_____ili__S______<0
Нанесем на числовую ось точки ——|-; 0; 2. Ответ:
(-f;
Существенной чертой метода интервалов является разбиение
числовой оси на участки и рассмотрение данной функции отдельно
на каждом участке. Это же обычно приходится делать, когда нуж-
но «раскрыть модули».
5. Построить график функции у=|х2 — 4|+х2.
Выясним сначала, при каких х выполняется неравенство
х2 — 4>0. Решая это неравенство с помощью метода интервалов,
получим два луча х>2 и х< — 2.
При этих х выражение под знаком модуля неотрицатель-
но, поэтому, раскрывая модуль, получим, что при этих х
у=х2 — 4 + х2 = 2х2 — 4.
При остальных х, т. е. при —2<х<2, выражение под знаком
модуля отрицательно. Поэтому здесь у=—(х2 — 4) + х2 = 4. Итак,
на интервале ( — 2; 2) данная функция совпадает с функцией
у=4, а на промежутках (— оо; —2] и [2; Ц-оо)— с функцией
у=2х2—4 (рис. 13).
При разложении левой части неравенства могут встретиться
одинаковые множители. Если этих множителей четное число, при
26
Рис. 13
Рис. 14
переходе через их общий корень произведение не будет менять
знак. Если же число одинаковых множителей нечетно, то знак бу-
дет меняться. Множители в четной степени, хотя они и не влияют
на знак всего выражения, отбрасывать нельзя, так как при этом
потеряется точка, в которой этот множитель обращается в нуль.
Приведем пример.
6. Решить неравенство ^>0-
Нанесем на числовую ось х\ = — 1, хг=1, х3 = 2 и определим
знаки дроби на каждом промежутке (рис. 14). Ответ: [—1; 1),
(1; +«> )•
Контрольные вопросы
1. Обратите внимание на встретившиеся в тексте следующие
ключевые слова и обозначения: линейная функция, модуль числа,
уравнение прямой, угловой коэффициент прямой, |х|, |ДВ|, ме-
тод интервалов. Приведите примеры их использования.
2. Перечислите свойства линейной функции.
27
3. Можно ли сказать, что линейная функция является моно-
тонной на всей числовой оси? От чего зависит характер монотон-
ности линейной функции?
4. Сколько раз меняет знак линейная функция? Как опреде-
лить точку, в которой линейная функция меняет знак?
5. Какие значения может принимать линейная функция?
6. Сколько раз принимает каждое свое значение линейная
функция?
7. Каких данных достаточно для того, чтобы построить гра-
фик линейной функции?
8. Как вычислить угловой коэффициент прямой, если извест-
ны две ее точки?
9. Каков геометрический смысл модуля разности двух чисел?
10. Как решаются неравенства методом интервалов?
§ 4. ПРЕОБРАЗОВАНИЕ ГРАФИКОВ
1. Параллельный перенос
Зависимости между переменными величинами описываются с
помощью функций. Основные свойства этих функций не должны
существенно меняться при изменении способа измерения перемен-
ных величин, т. е. при изменении их масштаба и начала отсчета.
С другой стороны, за счет более рационального выбора способа
измерения переменных величин обычно удается упростить запись
зависимости между ними, привести эту запись к некоторому
стандартному виду. На геометрическом языке изменение способа
измерения величин означает некоторые простые преобразования
графиков, к изучению которых мы и переходим.
Изменение начала отсчета переменных приводит к параллель-
ному переносу. Возьмем переменную х и перенесем начало ее от-
счета в точку х0. Новую переменную обозначим через х'. Связь
между переменными х и х' записывается формулой х' —х —х0, или
х = х' + хо. Чтобы не ошибиться в знаке, полезно убедиться
в том, что значению исходной переменной х = х0 соответствует
нулевое значение переменной х'. Аналогично, сдвигая на у0 значе-
ния переменной у, получим переменную у', связанную с у форму-
лой у'=у — уо, или у = у' +уо. Геометрически точки М (х; у),
М' (х'; у') и Мо (х0; уо) связаны векторным соотношением ОМ' =
= 0М + ММ', или ОМ = ОМ' — ММ' (рис. 15).
Установим связь между графиками функций y = f(x) и у =
= f(x — a). Если мы обозначим х — а через х' (т. е. если мы
сдвинем начало отсчета аргумента в точку а), то получим со-
отношение y = f(x'). Это означает, что для построения графика
функции y = f (х — а) надо изобразить график исходной функции
28
в системе координат (%'; у\ т. е. сдвинуть график функции
y=f(x) на вектор ОЛГ(а;0). Так как переменная у не ме-
няется, то сдвиг происходит вдоль оси х (рис. 16, а).
Этим способом мы уже пользовались при сравнении графиков
функций y = kx и y = kx-\-b.
Аналогично график функции y = f(x)-\-b связан с графиком
функции t/=f(x). Обозначив у—b через у', получим y'=f(x). Это
означает, что для построения графика функции y = f(x)-\-b надо
изобразить график исходной функции f в системе координат (х; у'),
т. е. сдвинуть график функции y=f (х) на вектор ОМ' (0; Ь). При
этом происходит параллельный перенос вдоль оси у (рис. 16,6).
Иногда приходится менять начало отсчета одновременно и у
аргумента х и у функции у, т. е. рассматривать зависимость вида
29
y — f(^x — d) + b (или у — b — f (х — а)). При построении графика
функции y = f (х — а) + Ь надо сделать два параллельных переноса
на векторы ОА и ОВ, что можно заменить одним параллельным
переносом на вектор ОС (рис. 16, в). При этом точка (х0; Уо) гра-
фика функции f (х) переходит в точку (%о + а; Уо + b) графика
функции y — f(x — a) + b.
Примеры построения графика с помощью параллельного пере-
носа приведены на рисунке 17.
2. Изменение масштаба
Изменим масштаб измерения величины х. Результат измере-
ния в новом масштабе обозначим через х'. Чтобы найти связь
между значениями х и х', достаточно знать, какое значение пе-
ременной х' соответствует единице масштаба переменной х.
Пусть это значение равно k. Тогда все другие значения перемен-
ной изменятся пропорционально, т. е. -у- = &, или x' = kx (про-
верим, что при х=1 значение х' равно k).
Отсюда следует связь между графиками функций y = f(x) и
= f (fex) = f (х'\ где x' = fex: график функции y = f(kx) получается
30
из графика функции y = f (х) некоторым растяжением или сжатием
вдоль оси х. При k > 1 происходит сжатие графика, так как
х' — 1 получается при x=-i-<l и точка на исходном графике,
соответствующая аргументу, равному 1, соответствует точке ново-
го графика при х=--р Аналогично при 0<fe< 1 происходит растя-
жение графика.
Связь между графиками функций y = f(x) и y=kf(x) ус-
танавливается аналогично. Только теперь надо менять масштаб
измерения у.
У'=-^-У> У=ку’.
Ситуация стала противоположной — при k > 1 происходит ра-
стяжение графика вдоль оси у, а при 0<£<1—его сжатие.
Поведение графика при изменении масштаба изображено на
рисунке 18.
В преобразованиях y = f(kx) и y = kf(x) мы считали, что
k>0. Чтобы включить и случай fe<0, рассмотрим сначала
k= — 1. Так как точки (х; у) и ( —х; у) симметричны отно-
сительно оси у, то и графики функций y=f(x) и y = f(—х) сим-
метричны этой оси. Аналогично графики функций y=f(x) и
t/=—f(x) симметричны относительно оси х (рис. 19).
Пользуясь тремя типами преобразований графиков — парал-
лельным переносом, растяжением (сжатием) и симметрией, мож-
но, исходя из графика функции y=f (х), построить график функции
y=Af (kx-\-b)-\-B при любых значениях параметров А, В, k, b.
Рассмотрим примеры.
1. Построить график функции «/=——.
X-f- Z
у у
Преобразуем правую часть: 777= -77—=1—т.
е.
_2 __2
у= + 1, или у—1= . Отсюда ясно, какие преобразова-
X -f- £, X -f- Л
ния надо сделать со знакомым графиком У=^ чтобы построить
Рис. 18
31
требуемый график. Сначала сделаем отражение относительно оси х,
получим график функции у=—Затем растянем график по
2
оси у, получим график функции у=—Наконец, сделаем
параллельный перенос с помощью вектора с координатами ( — 2; 1),
2
получим график функции у=-------т^-4-1 (рис. 20).
Аналогично можно построить график любой дробно-линейной
ах-\-Ь
cx+d
функции, т. е. функции вида у =
Сначала ее преобразу-
k
ют к виду у—уо=—— , затем строят «крест» — прямые х=х0 и
£/=уо, а потом гиперболу располагают в первом—третьем или
втором — четвертом квадрантах в зависимости от знака k. Зна-
чение k учитывают при нанесении на график двух-трех кон-
трольных точек.
2. Построить график функции у=\х2+х\ — 2.
Сначала строим параболу — график функции у = х2-\-х. Абс-
цисса вершины этой параболы х0 =—ордината Уо=-^-~-=
= —корни Х| = — 1, х2 = 0. Далее строим график у= |х2 + х|,
для чего точки графика функции у=х2+х, лежащие ниже оси
абсцисс (у них у<0\ симметрично отражаем относительно этой
оси (так как |у| = — у при у<0). Затем сдвинем на две едини-
цы вниз (уо= —2) весь график (вдоль оси у) и получим искомую
кривую (рис. 21).
32
3. квадратичная функция
В качестве примера использования техники преобразования
графиков получим свойства произвольной квадратичной функции,
исходя из свойств простейшей функции у=х2.
Пусть у = ах2 + Ьх-\-с, аУ=0. Выполним преобразование квад-
ратного трехчлена, которое называется выделением полного
квадрата:
ах2 + Ьх + с = а + — ) =
=««'!+^'+(£)!Н£)Ч)=
// I Ь \2 b2 — 4ас \ / । b \2 Ь2 —4ас
= а((х+—)--------—2—)==а(х+—)---------.
\\ 2а / 4а2 / \ 2а / 4а
Парабола получается из параболы
£/ = х2 параллельным переносом на вектор с координатами
( Ь Ь2 — 4ас \ г*
( — —;----——) и последующим растяжением вдоль оси у. Гра-
фики квадратичных функций при различных знаках старшего
коэффициента а и дискриминанта D — b2 — 4ас изображены на схе-
ме V.
Сопоставим основные характеристики функций у — х2 и
у = ах2 + Ьх + с.
Функция У = х2 у = ах2 +Ьх-\-с
Вершина Корни Экстремумы Область значений (0; 0) х = 0 Вершина — точка минимума [0; +оо) / b Ь2 — 4ас \ \ 2а' 4а / b -y/b2 — 4ас Х'2~ 2а± 2а при Ь2 — 4ас>0; нет корней при Ь2 — 4ас<0 Вершина — точка минимума, если а>0, и точка максимума, если а<0 Г Ь2 — 4ас \ L 4а ;+°°Л если а>0; если а<0
2 Заказ 836
33
Промежутки постоянного знака и промежутки монотонности
квадратичной функции зависят от знака чисел а и D — b2— 4ас
(схема V).
4. Температурная шкала
Ярким примером использования преобразований координат
служат температурные шкалы и графики зависимостей различных
физических величин от температуры. В практической жизни мы из-
меряем температуру по шкале Цельсия, в которой за начало от-
счета принята точка плавления льда, а масштаб (1°С) выбран
так, чтобы вода кипела в точке 100°. В некоторых странах
температуру измеряют с помощью других шкал. Например, в наз-
вании книги американского писателя Р. Бредбери «451° по Фарен-
гейту» нам не сразу ясно, о какой температуре идет речь.
Для' этого надо суметь перевести градусы по Фаренгейту
в градусы по Цельсию. Как записать этот перевод на язык
формул? Достаточно знать, что по шкале Фаренгейта точка
плавления льда равна 32°, а точка кипения воды 212°. Как
видите, при переходе от шкалы Цельсия к шкале Фарен-
гейта не только сдвигается начало отсчета, но и меняется масш-
таб— на 100° по Цельсию приходится 212° — 32°= 180° по
Фаренгейту. Можно сказать, что шкала измерения температуры по
Фаренгейту растянута по сравнению со шкалой Цельсия в 1,8 раза,
а начало отсчета сдвинуто на 32°. Поэтому связь между темпера-
турой tF по Фаренгейту и температурой /с по Цельсию выразится
формулой tF = 1,8-/с + 32. (Для проверки подставьте точки плав-
ления льда и кипения воды.)
Ясно, что, изучая другие переменные, связанные с температу-
рой (например, давление тела), надо уметь строить графики неза-
висимо от того, в какой шкале измеряется температура. Напри-
мер, если нам известна зависимость p = f (/F) давления р от темпе-
ратуры по Фаренгейту tF, то эта же зависимость р как функция
температуры tc, измеряемая по Цельсию, будет иметь вид
р=Н1,8/с+32).
Кроме рассмотренных температурных шкал Цельсия и Фарен-
гейта, используются шкалы Кельвина (абсолютная шкала) и Рео-
мюра. Ниже в таблице приведены различные температуры в че-
тырех шкалах, обозначенных первыми буквами С, F, К, R (изме-
рения произведены с точностью до единицы). Используя таблицу,
решите следующие задачи:
а) Выразите единицу температуры в шкалах F, К и R через
градус Цельсия (с точностью до 0,1).
б) Считая, что температура человеческого тела в градусах
Цельсия равна 37, вычислите ее в других шкалах.
в) Составьте формулы, выражающие температуру в шкалах
Кельвина и Реомюра через температуру по Цельсию.
г) Зная формулы перехода от температуры по Цельсию к
34
температуре по Фаренгейту и Реомюру, составьте формулу перехо-
да от шкалы Фаренгейта к шкале Реомюра (не используя
больше таблицу).
д) Сколько чисел в таблице (и каких) достаточно оставить,
чтобы можно было восстановить все остальные?
Температуры С F К R
Поверхности Солнца 5727 10 341 6000 45'2
Кипения воды 100 212 373 80
Плавления льда 0 32 273 0
Плавления ртути -39 -38 234 -31
Кипения гелия -269 -452 4 — 215
Контрольные вопросы
1. Обратите внимание на встретившиеся в тексте следующие
ключевые слова и обозначения: изменение начала отсчета, измене-
ние масштаба, f(x — a), f (fex), вершина параболы. Приведите
примеры их использования.
2. Как будет перемещаться график функции y = f(x — а)
при изменении параметра а?
3. Как будет перемещаться график функции y = f(x) + b при
изменении параметра ft?
4. Как связаны между собой графики функций y = f(x),
y = f( — x) и у= — f (х)?
5. Как связаны между собой области определения функций
y = f(x), y=f(x—a), y=f(x+b), y = f( — x) и y=— f(x)?
6. Как будет меняться график функции y = f(kx) при изме-
нении параметра /г? Тот же вопрос для функции y = kf(x).
7. Как построить график произвольной дробно-линейной функ-
ции у==а*^-~ с помощью преобразований графика функции У—~?
8. Как вычислить координаты вершины параболы у = ах2 +
-J- bx -р с?
9. От чего зависит, будут ли ветви параболы у = ах2Ьх-\-с
направлены вверх или вниз?
10. Какие вы знаете шкалы для измерения температуры?
ЗАКЛЮЧИТЕЛЬНАЯ БЕСЕДА
1. Измерение величин
Важнейшее назначение числа — измерять величины, служить
мерой сравнения их значений. Приведем примеры различных
величин, которые можно измерять с помощью чисел: длина,
35
е
I-------------1
e e e
Ь | I. | HI II
a
a)
b b b b t b
a
H = f
6)
Рис. 22
масса, объем, скорость прямолинейного движения, температура,
энергия, электрический заряд, производительность труда, стои-
мость продукции, национальный доход.
Выберем одну из этих величин, например длину, и попробуем
более подробно описать процесс ее измерения. Измерение начина-
ется с выбора масштаба, единицы измерения. Будем измерять
длины отрезков, расположенных на заданной прямой. За единицу
длины примем длину некоторого фиксированного отрезка е.
Рассмотрим произвольный отрезок а. Возможны следующие
случаи:
1) Отрезок е укладывается в отрезке а ровно п раз,
где п — натуральное число (рис. 22, а). В этом случае отрезку
а приписывают длину, равную п (в масштабе е).
2) Отрезок е не укладывается целое число раз, однако су-
ществует такой отрезок ft, который укладывается целое число
как в отрезке е, так и в отрезке а (рис. 22,6). Если ft укла-
дывается в е ровно п раз, а в отрезке а ровно т раз, то
т
отрезку а приписывают длину, равную рациональному числу —
(в масштабе е). В этом случае говорят, что отрезок а соизме-
рим с единичным отрезком е, а отрезок ft называют общей
мерой отрезков а и е. Заметим, что выбор общей меры соизмери-
мых отрезков неоднозначен, например, половина или треть отрезка
ft также является общей мерой отрезков а и е. Эта неоднознач-
ность сказывается на неоднозначности записи рационального чис-
ла в виде —. Так, записи и т. д. являются
it о о У 12 15
разными записями одного и того же рационального числа.
3) Отрезки а и е не имеют общей меры, несоизмеримы. От-
крытие древнегреческими математиками существования несоизме-
римых отрезков (диагональ квадрата несоизмерима с его сторо-
ной) является одним из самых замечательных открытий мате-
матики. Можно предложить различные бесконечные процедуры
измерения отрезка а в масштабе е. Наиболее известная про-
цедура, связанная с десятичной системой счисления, состоит в
следующем. Сначала находится, сколько раз масштаб укладывает -
36
ся в измеряемом отрезке, скажем ао (число а0 может равняться
нулю, если отрезок а меньше, короче, отрезка е). Затем берется
одна десятая отрезка е и откладывается в том остатке, который
получился после откладывания отрезка е в исходном отрезке ао
раз. Пусть а\ — максимальное число раз, которое одна десятая е
откладывается в этом остатке (ai равно 0, 1, 2, ..., 9). За-
тем берется одна сотая отрезка е и откладывается в новом
остатке и т. д. Так получается последовательность ао, аь аг, ..., в
которой ао — целое число, а числа ai, аг, ... могут принимать
значения 0, 1, 2, ..., 9. Эта последовательность, называемая
бесконечной десятичной дробью (и записываемая ao, aia2...),
представляет собой запись процесса измерения длины отрезка а
(в масштабе е) с помощью десятичных дробей.
Считая, что результатом измерения длины является веществен-
ное (или действительное) число, получаем, что это число мы
можем записать в виде бесконечной десятичной дроби (а можем
записать и иначе). Длины отрезков, соизмеримых с масштабом,
т. е. рациональные числа, тоже имеют запись в виде беско-
нечных десятичных дробей. Оказывается, что рациональные чис-
ла — это такие вещественные числа, которые записываются перио-
дическими десятичными дробями.
Диагональ квадрата (если за единицу масштаба принята его
сторона) можно записать непериодической бесконечной десятич-
ной дробью, начало которой таково: 1,414213... . Непериодические
десятичные дроби являются записью чисел, называемых иррацио-
нальными.
Величины, которые можно измерить аналогично измерению
длин отрезков, называют положительными скалярными величина-
ми. Полученное в результате измерения вещественное число на-
зывают значением (или мерой) этой скалярной величины (в
выбранном масштабе). Приписывание знака « + » или « —» поз-
воляет измерять относительные скалярные величины (например,
температуру, скорость прямолинейного движения, рост производи-
тельности труда и т. п.).
2. Развитие понятия функции
Хотя конкретные функции использовались в математике еще
в глубокой древности, потребность в общем понятии возникла
лишь в XVII в. в связи с развитием методов математического
анализа. Сам термин «функция» впервые применил Лейбниц,
а его ученик И. Бернулли в 1718 г. дал определение, близкое
тому, которым мы сейчас пользуемся: «Функцией переменной вели-
чины называется количество, составленное каким угодно способом
из переменной величины и постоянных».
Хотя в определении И. Бернулли и содержатся слова «каким
угодно способом...», математика XVII в. еще не была готова к то-
37
му смыслу этих слов, который сейчас мы в них вкладываем.
В 1748 г. Л. Эйлер пишет о способе задания функции уже более
определенно: «Функция переменной величины есть аналитическое
выражение, составленное каким-либо образом из этой переменной
величины и чисел или постоянных величин».
Мысль о том, что функция однозначно связывается с аналити-
ческой формулой, задающей способ вычисления ее значений,
привела уже в середине XVII в. к знаменитому спору ряда круп-
ных математиков (среди которых был и Л. Эйлер) о том, что можно
считать функцией, а что нельзя. Этот спор не был схоластическим.
Он возник из различных решений важной практической задачи о
форме колебаний струны и в конце концов значительно расширил
понятие функции, привел к открытию новых важных способов ее
задания (например, в виде наложения бесконечного количества
колебаний).
Дальнейшее развитие математики показало, что нельзя огра-
ничиться лишь какими-то «просто» описываемыми способами
задания функций, гораздо полезнее допустить любой мыслимый
способ соответствия между переменными. Это привело в начале
XX в. к отчетливым формулировкам понятия функции как отобра-
жения, которое позволяет каждому элементу данного числового
множества однозначно поставить в соответствие некоторое другое
число.
Такое понимание функции, распространенное к тому же не
только на числа, но и на множества произвольных объектов,
сильно обогатило возможности математики. Одновременно было
придумано много функций, настолько непохожих по свойствам на
те функции, которые встречались раньше, что к ним оказались
неприменимы классические методы математического анализа. Поэ-
тому стало важным выделять функции, «достаточно хорошие»
с той или иной точки зрения. Примером являются непрерывные
функции, о которых мы скажем немного ниже.
Развитие вычислительной техники и ее математического обеспе-
чения привело к изменению взгляда на функцию в другом на-
правлении. Машина может иметь дело с функцией лишь тогда,
когда способ вычисления ее значений задан точным предписанием,
алгоритмом.
3. Сложная функция
Чаще всего мы будем встречать функции, заданные фор-
мулой. Как мы уже объясняли в основном тексте, формула строит-
ся путем последовательного выполнения различных известных
операций над аргументом и постоянными числами. Эта процедура
может быть уточнена с помощью понятия сложной функции.
Пусть даны две функции z=f (у) и y = g(x). Сложной функци-
ей (или композицией функций f и g) называется функция
z — h (х), значения которой вычисляются по правилу A (x) = f (g (х))
38
(т. е. сначала вычисляется g (х), при этом получается некоторое
число у, а затем вычисляется значение f в точке у).
Со сложными функциями мы, разумеется, встречались и рань-
ше. Так, функцию z=^Jl —х^ можно рассматривать как компози-
цию функций у=\ — х2 и г=д[у.
Для вычисления значений сложной функции надо суметь разоб-
раться в последовательности производимых операций, т. е. пред-
ставить сложную функцию как композицию более простых. При
этом встречается несколько трудностей. Первая из них связана
с обозначениями. В приведенном выше определении использованы
три переменные: х, у и г. Ясно, что если у есть функция от
х, a z есть функция от у, то г можно рассматривать как функ-
цию от х. Однако часто приходится составлять сложную функ-
цию из двух функций, обозначенных одной и той же переменной.
Скажем, как составить композицию функций г/=х2 и г/=^-у,
или в общем виде y = f(x) и y = g(x)? Для этого надо уточ-
нить порядок, в котором вычисляются значения данных функций:
например, сначала g, а затем f или, наоборот, сначала f, а1
затем g. Для приведенного примера мы получим две различные
, а в общем виде i/ = f(g(x)) и
/ х \2 х2
функции: {/=(7+1-) и
y=g(f (*))•
Для записи композиции функций употребляется значок °. На-
пример, запись h — f ° g означает, что функция h получена как
композиция функций f и g (сначала применяется g, а затем
f, т. е. (f ° g) (x)=f (g (x))). Как показывает приведенный выше
пример, операция образования сложной функции (или композиция
функций) не обладает переместительным свойством: f о g^g о f.
Другая трудность в обращении со сложными функциями состо-
ит в том, что при этом необходимо следить за областями определе-
ния. Чтобы можно было вычислить сложную функцию h=f (g (х)),
надо, чтобы число g (х), т. е. значение функции g, попадало в
область определения функции f. Так, вычисляя значения функции
£/=Vl “А мы должны брать только те числа х, для
которых 1—х2^0, т. е. те, для которых число 1—х2 попа-
дает в область определения функции у = ^/х.
4. Неявное задание функции
Исторически одним из основных источников появления новых
функций было решение геометрических задач. Исходным объектом
в этих задачах была кривая. Первое употребление Лейбницем
слова «функция» было связано с тем, что он хотел в общем виде
рассматривать различные геометрические объекты, связанные с
кривой (абсцисса и ордината точки, различные отрезки каса-
тельных и т. д.), как переменные, зависящие друг от друга.
39
Рис. 23
Кривая, построенная на координатной плоскости (х; у), мо-
жет быть задана уравнением, связывающим координаты точек
кривой. Уравнения некоторых кривых вам уже известны:
y — kx-\-b — уравнение прямой,
ху = с — уравнение гиперболы.
у = ах2 — уравнение параболы.
На рисунке 23 изображено еще несколько кривых, заданных
своими уравнениями:
х2 + г/2= 1 —уравнение окружности (рис. 23, а),
|xl + l£/|==l —уравнение квадрата (рис. 23,6),
I х |3 + |у |3 = 1 — уравнение астроиды (рис. 23, в).
(Астроида — это траектория движения точки колеса радиуса
которое катится внутри обода радиуса 1.)
Как известно, уравнение кривой определяет зависимость между
координатами ее точек. При таком подходе обе координаты
рассматриваются как равноправные. Однако часто нужно рассмат-
ривать одну координату как функцию другой. Тогда говорят, что
уравнение кривой задает эту функцию неявно. Чтобы сделать зада-
ние функции явным, надо из уравнения кривой выразить одну коор-
динату через другую. В приведенных нами уравнениях прямой и
параболы переменная у с самого начала выражена явно как
функция от переменной х. Из уравнения гиперболы каждая из
переменных легко выражается как функция другой: У=~
и х =—. Из уравнения прямой (если fe=/=0) также легко выразить
у
и — b
х через у, получив х=^-у-.
Рассмотрим другие случаи. Что препятствует тому, чтобы, ска-
жем, выразить из уравнения окружности у как функцию от х?
Поставим этот же вопрос геометрически: почему окружность нель-
40
зя рассматривать как график некоторой функции? Вспомним, как
строится график функции. Для каждого числа х из области опре-
деления строится одна точка с координатами (х; f (х)), т. е. пря-
мая, проведенная через каждую точку х на оси абсцисс параллель-
но оси ординат, пересекает график ровно в одной точке. Это усло-
вие не выполняется для окружности, квадрата, астроиды.
Из затруднения можно выйти следующим образом: рассматри-
вать не всю кривую, а только ее часть. Например, можно взять не
всю окружность, а только ее половину, лежащую в верхней
полуплоскости. Аналитически это означает, что г/^0, и теперь
можно (однозначно) выразить у как функцию от х так: у = ^/\ — х2.
Задача выражения одной переменной из уравнения кривой как
функции от другой не всегда может быть решена элементарны-
ми средствами.
Часто возникает задача выразить из соотношения y = f(x)
переменную х как функцию от у, т. е. для функции f построить
обратную функцию. С этой задачей мы столкнемся в следующих
главах.
5. Монотонность функции
Уточним понятие монотонности функции. При грамотном ис-
пользовании терминов «возрастание» и «убывание» функции надо
обязательно указывать, на каком участке изменения аргумента
рассматривается монотонность функции.
Рассмотрим функцию f и некоторый промежуток, целиком вхо-
дящий в область определения функции f. Обозначим выбранный
промежуток одной буквой, например А. Напомним определение мо-
нотонной функции.
Определение. Функция f называется возрастающей
(убывающей) на промежутке А, если для любых двух чисел Х| и х2
из этого промежутка, таких, что xi<x2, выполняется условие
f (*i)<f (х2) (соответственно f (xi)>f (х2)).
Символически определение возрастания функции может быть
записано так: xj <х2 => f (xi)<f (х2). Символ => мы будем исполь-
зовать для обозначения условного утверждения: если..., то... .
Пользуясь определением монотонности и свойствами нера-
венств, докажите самостоятельно следующие утверждения:
1. Функция у — 2х является возрастающей на всей числовой
оси (и, разумеется, на каждом ее промежутке).
2. Функция £/ = Зх2 является убывающей на промежутке
(— оо; 0] и возрастающей на промежутке [0; + оо).
3. Функция у = ~~~ является убывающей как на промежут-
ке (— оо; 0), так и на промежутке (0; + оо).
Подчеркнем еще раз, что мы будем говорить о монотонности
функции только на промежутке, целиком входящем в ее область
41
Рис. 25
определения. Поэтому нельзя сказать в целом о функции £/=--,
что она монотонна, хотя она убывает на каждом промежутке,
где она определена.
Все функции, с которыми мы будем в дальнейшем встречать-
ся, «склеены» из функций, монотонных на промежутках. Иначе
говоря, мы будем изучать такие функции, область определения
которых можно разбить на промежутки, на каждом из которых
функция монотонна.
Разберемся в том, что может происходить при «склеивании»
функций, монотонных на двух стыкующихся между собой проме-
жутках А и В.
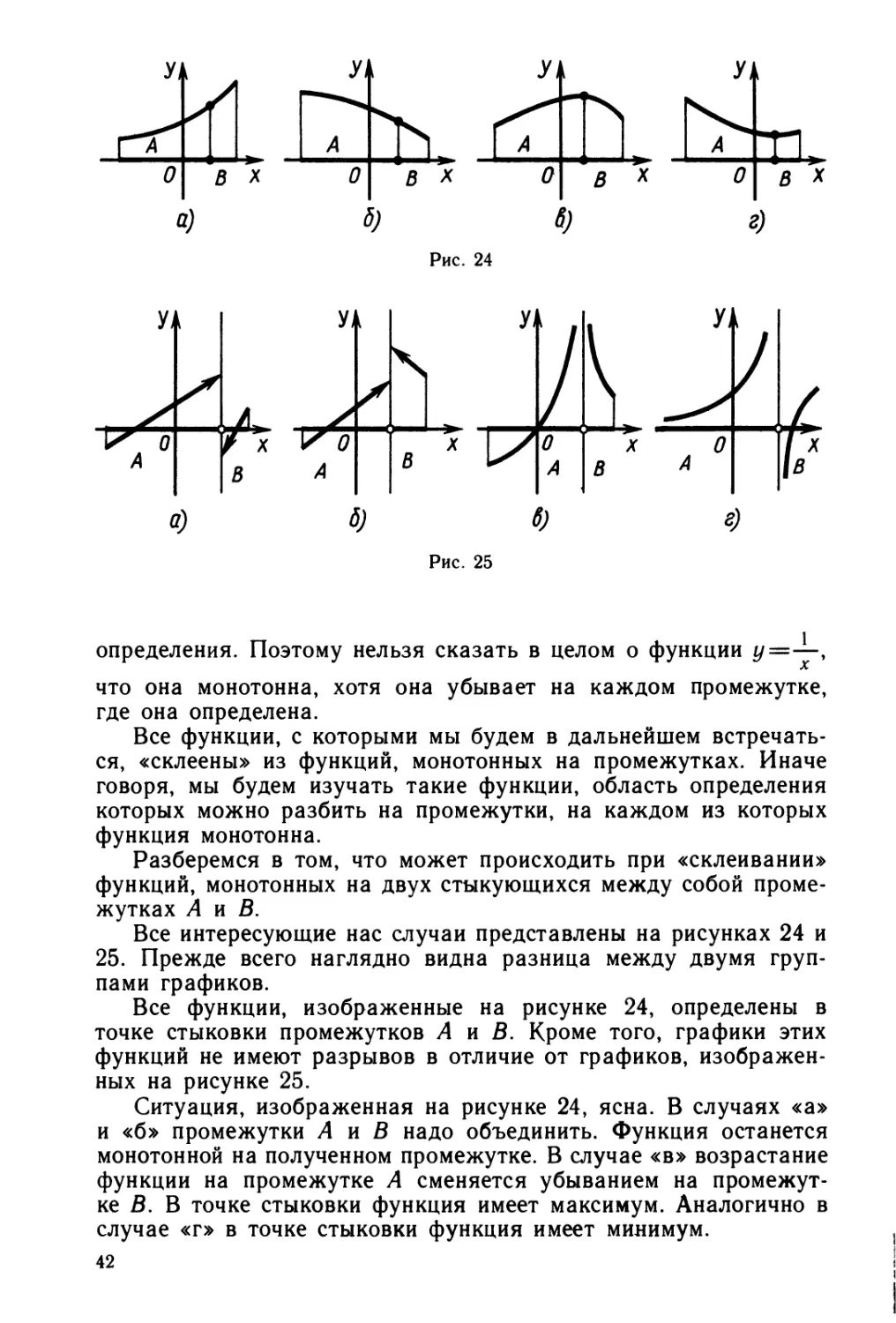
Все интересующие нас случаи представлены на рисунках 24 и
25. Прежде всего наглядно видна разница между двумя груп-
пами графиков.
Все функции, изображенные на рисунке 24, определены в
точке стыковки промежутков А и В. Кроме того, графики этих
функций не имеют разрывов в отличие от графиков, изображен-
ных на рисунке 25.
Ситуация, изображенная на рисунке 24, ясна. В случаях «а»
и «б» промежутки А и В надо объединить. Функция останется
монотонной на полученном промежутке. В случае «в» возрастание
функции на промежутке А сменяется убыванием на промежут-
ке В. В точке стыковки функция имеет максимум. Аналогично в
случае «г» в точке стыковки функция имеет минимум.
42
Во всех случаях, изображенных на рисунке 25, функция име-
ет разрыв в точке стыковки промежутков монотонности. Такая точ-
ка является исключительной, или, как говорят, особой точкой. По-
ведение функции вблизи особой точки может быть различным, как
это видно из рисунка. При построении графиков функций особые
точки придется исследовать отдельно.
6. Непрерывность функции
Вернемся к рисунку 25. На нем были изображены графики
функций, которые мы назвали разрывными. Попробуем более точ-
но описать, что такое непрерывная функция.
Если в данной точке у функции разрыв, то это означает, что
при маленьком изменении аргумента значение функции совершит
скачок. Наоборот, функция непрерывна в данной точке, если при
маленьком изменении аргумента мало будут меняться ее значе-
ния.
Как сопоставить приведенное определение непрерывности с
интуитивным представлением о непрерывной функции как о
функции, график которой можно начертить, не отрывая карандаша
от бумаги? Прежде всего это легко сделать для монотонной функ-
ции.
Пусть функция f монотонна (например, возрастает) на ко-
нечном промежутке [а; Ь]. Пусть f(a) = c и f(b) = d. Непре-
рывность функции f означает, что при изменении аргумен-
та от а до ft она принимает без пропусков все промежу-
точные значения от с до d. Разрывность монотонной функции оз-
начает наличие скачков, пробелов, пропусков среди ее значе-
ний (рис. 26).
Это означает, что для монотонной функции за определение
непрерывности может быть взято следующее ее свойство: монотон-
ная функция непрерывна, если она принимает все промежуточные
значения.
Сложнее обстоит дело с точками стыковки. Прежде всего в
точке стыковки двух промежутков монотонная функция может
быть не определена. Разумеется, го-
ворить о непрерывности в такой точ- ке нельзя. При этом может быть так, что функцию можно «доопределить» в этой точке, после чего она станет непрерыв- ной. Типичным примером такой ситуа- х2—1 ции может служить функция у = . Она не определена при х=1, но если х2— 1 дробь -—р сократить, то получится х4~1. Поэтому если положить значе- ние у при х= 1 равным 2, то определен- ^0 * Рис. 26
43
ная таким образом функция будет не-
прерывной в каждой точке числовой
оси.
Функция У=-“- не определена
при х=0. Однако, как бы мы ни
определяли ее значение в этой точке,
она не может быть непрерывной. То
же самое можно сказать и о функ-
ции y=f(x), где f (х)= —1 при
х<0 и f(x)=l при х>0. Однако
по рисунку ясно, что эта функция и
функция ведут себя вблизи
нуля по-разному. Чтобы различить эти случаи, говорят о «конеч-
ном» и «бесконечном» разрывах.
Мы не даем точного определения этих терминов, считая, что
смысл слов «конечный разрыв» и «бесконечный разрыв» ясен из
приведенных примеров.
Пусть функция f монотонна и непрерывна на отрезке [а; Ь]. Как
мы уже сказали, это означает, что она принимает все проме-
жуточные значения. Отсюда следует, что если на концах отрезка
функция f принимает значения разных знаков, то в некоторой
точке с она обращается в нуль (рис. 27). Это свойство непре-
рывной функции часто будет использоваться при решении
уравнений с помощью графика.
Контрольные вопросы
1. Обратите внимание на встретившиеся в тексте следующие
ключевые слова: сложная функция, неявная функция, непрерыв-
ная функция. Приведите примеры их использования.
2. Какие отрезки называются соизмеримыми?
3. Приведите примеры несоизмеримых отрезков.
4. Как определяется сложная функция?
5. Как найти естественную область определения сложной
функции?
6. Приведите примеры неявного задания функции.
7. Что такое непрерывная функция?
8. Приведите примеры разрывных функций.
9. Как можно определить непрерывность монотонной функции?
10. Какое свойство непрерывных функций используется для
графического решения уравнений?
11. Будет ли композиция двух возрастающих функций снова
возрастающей функцией?
12. Приведите пример функции, возрастающей на каждом
промежутке, входящем в ее область определения, но не являющей-
ся возрастающей на всей этой области.
44
ЗАДАЧИ К ГЛАВЕ I
Числовая ось
Изображение числа точкой числовой оси
1. Изобразите на числовой оси следующие числа:
-1; 0,5; -Ь -2L; 2; -5;
2 4 2
2°. Изобразите на числовой оси следующие числовые множества:
1) х>1;
4) 0<х<5;
7) [2; 4);
2) х<3;
5) 1<х<2;
8) (-оо; 2];
3) - 1<х<1;
6) [-2; 3];
9) (-3; +оо).
Нахождение координаты точки числовой оси
3°. На числовой оси указаны точки и числовые множества
(рис. 28).
1) Найдите (приближенно) координаты указанных точек.
2) Запишите в виде числовых промежутков указанные
множества.
Числовые неравенства
4°. Выясните, какое из чисел больше:
1) 0,429 или 0,432; 2) —12,0027 или —12,003;
3) л или 3,14; 4) -у- или ур
5) —или —6) 0,54 или
5 8 15
5. Укажите какое-либо число, заключенное между числами:
1) 0,373 и 0,374; 2) -0,1 и 0,01;
3) у- и 4) л и 3,14.
Преобразования на числовой оси
6. На числовой оси нанесены точки А и В, изображающие
числа а и Ь. Постройте точки, изображающие следующие
числа:
1) — а; 2) 3) ; 4)
Z 2 и
р3 р, рг р<
-5 -4L -3 -2 -1 0 1234 5 *
Рис. 28
45
7. Даны точки А (а) и В (Ь). Найдите координаты следующих'
точек:
1) середины отрезка АВ\
2) точки, симметричной точке А относительно точки В;
3) точки, симметричной середине отрезка АВ относительно
точки В;
4) точек, расстояния от которых до точки В вдвое мень-
ше их расстояния до точки А.
Десятичная запись чисел
8°. Запишите следующие числа в виде периодических десятичных
дробей:
D 2) 4-; 3) 4) f; 5) А; 6)
9*. Докажите иррациональность следующих чисел:
1) 0,101001000100001...;
2) 0,12345678910111213...;
3) 0,149162536496481100... .
10*. Найдите первые 20 цифр после запятой в десятичной запи-
си следующих чисел:
1) л/1 -(0.1)20; 2) (5-V26)20;
3) (5+л/26)20; 4) (УГбоТ--УТбОО)12.
Вычисления на калькуляторе
11. Вычислите с помощью калькулятора значения следующих
числовых выражений:
1) число «счастливых» автобусных билетов:
32 31 30 29 28 22 21 20 19 18 . 6-5 12 11 10 9 _8_.
5*4*3 *2*1 ^* 5*4*3*21 ""^2 *5*4*3*21’
2) вероятность того, что в классе из 30 человек есть
совпадающие дни рождения:
/! 365 364 363 336 \ 1ппо/
V 365 * 365 * 365 ’” *365 /’1UU/o‘
Переменные и зависимости между ними
Графическое изображение зависимости
12. На рисунке 29 изображены графики шести зависимостей.
Найдите уравнение каждой из них в следующем списке:
£/ = 6х; £/=—-х; ху = 2\ ху——3\ у=2х2\ х = 3у2.
46
13. На рисунке 30 изображены четыре окружности. Найдите
уравнение каждой из них в следующем списке: х2 + у2 = 9;
(х-2)2+у2=9; х2 + (у+2)2=9; (% + 1)2 + (у-1)2= 1.
14. На рисунке 31 изображены пять кривых. Найдите их уравне-
ния в следующем списке: х+у=1; x2-j-y2=l; ху =— 1;
ху—2; х2 + 2х+у2=0.
15°. Постройте графики следующих зависимостей:
1) —=2;
2) —=-3;
У
3) х+2у=1;
4) ху=2\
5) х=——;
У
6) y+v=°;
7)
8) х=3у2.
47
Параметры простейших зависимостей
16. Известно, что зависимость между х и у имеет вид ax + by = 1.
Найдите значения параметров ан Ь, если известно, что точки
(2; —1) и ( — 4; 3) лежат на графике этой зависимости.
17. Зависимость между х и у имеет вид (х — а) (у — b) = 1. Най-
дите значения параметров а и ft, если известно, что начало
координат и точка (3; лежат на графике этой зависи-
мости.
18. Известно, что зависимость y = f(x) имеет вид либо £/ = fex,
либо £/==у, либо у = ах2. Найдите вид зависимости и пост-
ройте ее график, если известно, что f (2) = 2 и f(4)=l.
Области значений переменных
19°. На рисунке 32 изображены зависимости между перемен-
ными х и у. Укажите, какие значения может принимать каж-
дая из этих переменных.
Зависимости между геометрическими величинами
20°. Выразите площадь равностороннего треугольника через дли-
ну х его стороны. Выразите эту же площадь через ра-
диус г вписанной окружности.
21°. Выразите площадь прямоугольника, вписанного в круг ради-
уса 1, через основание прямоугольника х.
22°. Найдите область определения и область значений функции,
описывающей зависимость площади квадрата от длины его
стороны.
48
23. В окружность радиуса R вписан прямоугольник, длины сто-
рон которого равны х и у.
1) Выразите у как функцию от х. При каких значениях
х определено это выражение?
2) Во что превратится прямоугольник, если х = 2/??
3) Выразите площадь прямоугольника как функцию от х.
Выражение переменных из формул
24. Из формулы v = vo(l+kt) выразите t через v. Какой харак-
тер имеет эта зависимость?
25. Зависимость между четырьмя переменными имеет вид F=^-.
Определите характер зависимостей для каждой пары пере-
менных, считая две другие постоянными.
26. Из формулы Ван-дер-Ваальса
(P+-fc)(v-b)=kT
выразите параметр а через остальные буквы.
Физические примеры зависимостей
27. Представим себе полет космической ракеты. Рассмотрим
такие переменные, связанные с этим полетом:
t — время, прошедшее от старта; а — ускорение;
s — расстояние ракеты от Земли; m — масса ракеты;
v — скорость ракеты.
Рис. 32
49
Выделите какие-либо пары переменных и придумайте, какие
могут быть зависимости между ними. Ответ предложите в
виде формулы или с помощью графика.
28°. При свободном падении с нулевой начальной скоростью
зависимости между расстоянием s, скоростью v и временем t
таковы: v = gt. Найдите зависимость между расстоя-
нием и скоростью. Какой характер имеет эта зависимость?
Понятие функции
Вычисление значения функции
В упражнениях 29—36 заданы функции вида y = f(x).
29°. Цх) = х+1. 30°. f(x)=|x|. 31. f(x)=^-.
32. fW = «2- 33. )W«+±. 34-fW={?"^j5o.
3s. fw=(° п₽" 36. f«=( "P"
' ' |x при x>0. v ' |x при x>0.
Для функций, заданных в упражнениях 29—36, вычисли-
те следующие значения:
1)° НО; 2)° И-2); 3)’ f(v)+f(f
4)° НО; 5) Н20; 6) f(i-);
7) Н*+1); 8) Нх-1); 9) Н2х-1);
Ю) 5f(f) ; Н) FU2); 12) (fW)2.
Принадлежность точки графику функции
37°. Даны точки Р,(1; 1), Р2(-1; 1), Рз(1; -1), Л(-1; -1).
Какие из них лежат на графиках функций, указанных в за-
дачах 29—36?
38. При каких значениях а точка Р (4; 4) лежит на графике
функции у = а^/х?
39. Докажите, что точка Л(/2+1; /3~Н) при любом положи-
тельном t лежит на графике функции у = х^х — 1.
Область определения функции
40. Найдите естественные области определения следующих функ-
ций:
1) 2)
50
3) У—х2 Л , . ; 4) у=-—|—Ц-;
х Н-хН-1 ’ v х 1 х—1 ’
5) У=—р—; 6) у=^х2—х+\\
^х— 1
7) У=-^-, 8) у = ^/х; 9) у=л/1—х.
41. Приведите пример функции, естественной областью опреде-
ления которой было бы следующее числовое множество:
1) Я; 2) х=/=2; 3) х=/=±1; 4) [1; +«>); 5) [-2; 2];
6) (-оо; 1); 7) (-оо; - 1)U(I; +оо); 8) [-1; O]U[1; 2}
Построение графика функции
Постройте графики функций y = f(x') (42—45).
42.
43.
44.
{1 при х< — 1,
—х при — 1 <х< 1,
— 1 при Х> 1.
' 0 при х< — 1,
х+! при —
' ' ' 1—х при 0<х^1,
О при х> 1.
f (*)={
— х при х<0,
х2 при х^О.
45.
/(*)=
у- при х<0,
х при х>0.
Переход от графика к формуле
46. Запишите формулами функции, графики которых изображе-
ны на рисунке 33.
Сложная функция
47. Даны две функции f и g. Постройте сложные функции
u=f о g и v — gof, если:
О g(x) = x2+l; 2) f (x)=Vx, g(x)=x2 + x;
3) f(x) = 3x, g(x)=x2; 4) f (x) = x2 + 1, g(x)=x2— 1;
Рис. 33
51
5)* f(x)=|? при x$n’ g(x) = x2+l;
7 1 v 7 | 1 при x>0, 6 v 7 1
(П* f zx)== a(x}=f -x+1 ПрИ x^0’
p’ ' ' ' | 2x4-1 при x>0.
48. Докажите равенство f ° (g ° h.) = (f ° g) ° h.
Неявное задание функции
49. Даны зависимости между переменными. Выразите (если
можно) каждую из них как функцию другой:
1)° 3x + 5t/ = 2; 2)° 2х-7у + 3 = 0;
3) 2у + 3|х| =0; 4) |уЦ-4х=1;
5) s2 = u3 * *; 6) 10s — 1 = /3;
7) 7+г=т: 8) НОМН;
9) (2u + v) (u + v) = v2.
50. Выясните, какие из следующих зависимостей определяют у
как функцию от х:
1) xz/ + x + i/ = 0; 2) х+Л/ху=1;
3) у2 + у=х; 4) у+^/х=х.
Исследование функции
Чтение графика
51°. Проведите исследование функций, графики которых изобра-
жены на рисунке 34.
Исследование функции по ее графику
52. Постройте графики
исследование:
1) У=— 2х;
3) у = х2-4;
5) у= —х2—1;
следующих функций и проведите их
2) У=~±-,
4) у = 9 — х2;
гх24-х, если х^О,
' |х2 —х, если х>0.
График функции с заданными свойствами
53. Нарисуйте график функции, областью определения которой
был бы отрезок [0; 5], а областью значений — отрезок
[-1; 2].
54. К условию предыдущей задачи добавьте условие, чтобы
функция возрастала на отрезке [0; 3] и убывала на отрезке
[3; 5]; была отрицательной на промежутке (0; 2) и положи-
тельной на промежутке (2; 5).
52
Четность функции
55. Докажите, что сумма, произведение, частное четных функций
будут четными функциями.
56. Что можно сказать о четности произведения и частного
двух нечетных функций? четной и нечетной функций?
57. Докажите, что для любой функции f функция g(x) = f(x) +
+ /( —х) будет четной, а функция h (x) = f (х) — f ( — к) — не-
четной.
58. Докажите, что всякая функция является суммой четной и
нечетной функций.
Какие допущения об областях определения функций надо
сделать в задачах 55—58?
Непрерывность функции
59*. Приведите пример графика функции, которая принимает все
промежуточные значения, но которая не является непрерыв-
ной.
53
60. Пусть f и g — непрерывные функции, причем f возрастает
на отрезке [a; ft], a g убывает на этом отрезке. Пусть f (а)<
<g(a) и f(b)>g(b\ Докажите, что уравнение f(x) = g(x)
имеет на отрезке [a; ft] один корень.
Монотонность функции
61. Докажите следующие свойства монотонности функций:
1) если функция f возрастает на отрезках [a; ft] и [ft; с],
то она возрастает на отрезке [а; с];
2) если две функции fug возрастают на одном и том же
промежутке, то и их сумма f + g возрастает на этом проме-
жутке;
3) если функция y = f(x) возрастает на некотором про-
межутке, то функция у= — f (х) убывает на этом промежутке;
4) если функция y = f(x) возрастает на некотором проме-
жутке и f (х)>0 при всех х из этого промежутка, то функция
£/=— убывает на этом промежутке.
62. Если функция f на отрезке [a; ft] возрастает, а на отрезке
[ft; с] убывает, то в точке ft функция имеет максимум, при-
чем f (Ь) — наибольшее значение f на отрезке [а; с]. Докажите.
63. Сформулируйте и докажите аналогичное свойство минимума.
64. Докажите, что композиция двух возрастающих функций есть
возрастающая функция.
Графическое решение уравнений и неравенств
65. С помощью графика функции y = f(x), изображенного на
рисунке 35, а, решите неравенства:
1) f(x)>0; 2) 3) f(x)>l.
66. По графику функции y = f(x) (рис. 35,6) ответьте на сле-
дующие вопросы: Л
1) Сколько корней имеет уравнение f (х) = 0?
2) Каковы (приближенно) корни уравнения f (х)= — 1?
3) При каких а уравнение f(x) = a имеет хотя бы один ко-
рень?
4) При каких а уравнение f (х) = а имеет ровно один корень?
5)* Сколько корней имеет уравнение f(x)=x2?
67. По графику функции y = f (х) (рис. 35, в) выполните задания:
1) Решите уравнения f(x) = O, f(x)=l, f(x)=—2.
2) При каждом значении а определите, сколько корней
имеет уравнение f(x)=a.
3) Решите неравенства f(x)>0, f(x)<l, f (х)^ — 2.
4) Подберите такое значение а, чтобы неравенство f (x)^a:
а) не имело решений; б) было бы верно при любом значе-
нии х.
54
5) Определите, сколько корней имеет уравнение f(x) = x.
6)* При каждом значении k определите, сколько кор-
ней имеет уравнение f(x) = fex.
68. Решите уравнения, используя графики:
1) х2-у-+5 = 0; 2) х34-3х —4 = 0.
Линейная функция
Линейные уравнения и неравенства
69°. Найдите корни линейных функций:
1) у=% + 5; 2) у=\— х; 3) у = Зх + 4;
4) у=3—i-x; 5) 0 = 6(х—1)4-2; 6) у= -3 (2-х)+ 1;
7) 0=-|-(х-1)4-1; 8) у = 0,5x4-4,5; 9) 0 = 0,01x4-1.
70°. Решите уравнения:
1) 2х4-3 = 5х—1; 2) -1-х4-1=0;
55
3) — 2 (1 —х —3 (х + 2))=х; 4) \+ax = b;
5) ГТ=2; 6)
уч % + 2 _2х— 1
’ х —3 “ 2x4-1 *
71°. Найдите промежутки постоянного знака линейных функций
из задачи 69.
72°. Решите неравенства:
1) 2х + 7>0; 2) 2 + 5х<0; 3) -3 + 2х<0;
4) 7х + 3>х-2; 5) -3(2-х)>х; 6) -^у>0;
7> 8> wr>°= 9> ^7<°-
Наибольшее и наименьшее значения линейной функции
на промежутке
73. Найдите наименьшее и наибольшее значения следующих
функций на указанных промежутках:
1) £/ = 2*4-1 на [—1; 1]; 2) у = 2 — х на [0; 5];
3) у = 2 — Зх на (— оо; 2]; 4) у = х-\--^- на [ — 1; 4~ °°)-
Опознание линейной функции по графику
74. На рисунке 36, а изображены графики линейных функций
y = kx при различных значениях k. Для каждого графика
найдите соответствующее значение k из чисел: 1, 2,
-1. -2. -Ь
a) S)
Рис. 36
56
75. На рисунке 36, б изображено пять прямых. Найдите уравне-
ние каждой из них среди уравнений: у=2х, у=—х,
у=— 2х+1, у = 2х — 2, у=— x-j-2.
Задание линейной функции
76. Найдите линейную функцию с угловым коэффициентом k и
проходящую через точку Р, если:
1) Л = 2, Р(1; -1); 2) fe=-l, Р(0; 3);
3) fe=4-, Р( —2; 0); 4) k=2-, Р(3; 6).
Z о
77. Найдите угловой коэффициент прямой, проходящей через
точки Р\ и Р2:
1) Pi (1; 1), Р2 (-1; 3); 2) Р, (0; 1), Р2(1; 0);
3) Pi(3; 1); Р2(5; 1); 4) ?,(-!; -2), Р2 (-2; -5).
78. Даны координаты вершин треугольника АВС:
А (-1; 2), В (2, 3), С(0, -1).
1) Найдите уравнения сторон треугольника (т. е. линейные
функции, графиками которых будут прямые АВ, ВС, АС).
2) Найдите координаты середин сторон треугольника.
3) Найдите уравнения медиан треугольника.
4) Найдите уравнения средних линий треугольника.
79. При подсчете баллов в соревнованиях по скалолазанию
участнику, показавшему лучшее время, присуждается
60 баллов, а участнику, показавшему удвоенное время по-
бедителя, дается 0 баллов. Выведите формулу для определе-
ния баллов в зависимости от показанного времени, зная,
что эта зависимость линейна.
Модуль
Геометрический смысл модуля
80°. Нанесите на числовую ось числа, модуль которых равен 3.
81°. Нанесите на числовую ось точки, расстояние от которых до
точки 1 равно трем.
82°. Запишите с помощью модуля утверждение: «Расстояние от
точки х до точки 5 равно 2». Найдите все такие точки х.
83. Докажите, что |х| = | — х|.
Линейные уравнения и неравенства с модулем
84. Решите уравнения:
1)° \х — 1| =2; 2)° |х + 3| = 1;
3)° |2х-|-1|=4; 4)° |3х —2|=6;
57
5)° 15хН-21 = —2;
7) |xl + |x-3|=5;
9) к+Н + к + 2| = 1;
11) |х+3|-|х-2|=5;
13) |х+ 11 = |х-5|;
15) ||х|-4| = 1;
6) ||х|-1|=2;
8) |х—11 + |х—5| =3;
10) |х —5|— |х—1|=2;
12) |х—11 =2 |х-4|;
14) |х| = |4—х|;
16) ||х—1| —1|=2.
85. Решите неравенства:
1)° к1>1;
3)° |х + 2|>2;
5)° |2-х|>3;
7)° |2х— 3| <5;
9) |х| + |х—11 < 1;
11) |х+ 11< |х—3|;
13) |х| >2 |х —2|;
15) ||х|-5|<2;
2)° |х—11<5;
4)° |х4-5| <1;
6)° |3 + х|<1;
8)° П+2х|>1;
10) ||х|— 2| <1;
12) |х| - |х—11<2;
14) |х-1|<|х+5|;
16) ||х+н + н<з.
Запись выражений без знака модуля
86. Раскройте модули в следующих выражениях:
1)° 1-3,11; 2)° 13—Viol; 3)° |лг— 101;
4)° |23 —32|; 5)° 12—V5|; 6)° lf+f
7)° |х —3|; 8)° 1x4-41; 9)° 15-х|;
10)° |2х—11; 11) |х| 4- |х- 11; 12) 11х|4-П.
Построение графиков
87. Постройте графики следующих функций:
1)° у= |х4-2|; 2)° У=|1-2х|;
3) 0 = 3 |х —2|; 4) 0= |х| + |х — 3|;
5)0=|х-2|-х; 6) 0=2 |х-1| + |х+1|;
7) 0=|х-1|-|х + 3|; 8) 0=||х|-Ц;
9) 0= |х2 —9| +х2.
Доказательство неравенств с модулем
88. Докажите неравенства:
1) |х + 01 < |х| + |0|;
2) |х4-0| > |х| - |0|;
3) |х-|-04-z|< |х| 4-|0| 4-| z|;
4) |x4-04-z| >|х| — |0| —|z|.
Множества на плоскости, задаваемые с помощью модуля
89. Изобразите на плоскости (х; у) множества точек, координаты
которых удовлетворяют следующим условиям:
58
1) Ix| = l;
2) |х|<1;
3) |х + 3|<2;
4) |3х—2| >6;
5) |у|=2;
6) |у|<1;
7) Ii/ + 2|<1;
8) |3 —2х|>4;
9) ( |х + 2|<2,
I \У- 11 <3;
10) ( |х-2|<1,
I 11/1 >2.
Решение уравнений и неравенств с модулем по графику
90. По графику функции y — f(x) (рис. 37) решите уравнения
и неравенства:
1) 1/(х)| = 1; 2) |f(x)-2| = l;
3) |f(x)|<l; 4) |f (х)-2| <2.
91. Используя графики, решите неравенства:
1) ||х|-3|<1; 2) |х1 2 — 5|<4;
3) ||х-1|-2|>3; 4) |х2 + 2х|<^-.
Построение уравнения или неравенства
по множеству его решений
92. Придумайте уравнение или неравенство с модулем, множест-
вом решения которого было бы следующее числовое мно-
жество:
1) Xi = — 2, х2 = 0;
3) -1<х<5;
2) Х|=2, х2 = 3;
4) х<_ —2, х>2.
Метод интервалов
93. Решите неравенства:
1) (х- 1)(х+ 1)<0;
3) (х —2) (3—х)>0;
5) (х+2)(х-3) 0
' (x+3)(x-2)^U’
7) --------->0;
’ (l-x)(2-x)^U>
9) ______—_______<;()•
' (x-l)(x-2)(3-x)^U>
2) х(х+7)<0;
4) х(х+1)(х + 2)(х + 3)>0;
6) (5~2Х)(Х+3)
’ (2х-7)(6-5х)^ ’
8)
Ю)
-----------<0;
(Зх+ 1) (Зх— 1) ’
(х+1)(х2+1)
(2х-1)(х2+х+1)-^и-
59
94. Решите неравенства:
1) х2 + 2х<0;
3) 2х2 + х-3<0;
5>
7>
9) ^-<2;
’ х+1
95. Решите неравенства:
U (х+1)2 >и’
3>
5) ^±^<9(х + 2);
(2х+1)2(х-2)^
' X5 (х+ I)4
4) х3<х2;
х3 —8 х —2
х3 — 1 х — 1
Преобразование графиков
96. На рисунке 38, а изображен график функции f. Постройте
графики следующих функций:
1) i/=fW+l; 2) y = f(x)-l; 3) y = 2f (х);
4) */=4-Ж; 5) y=—f(x); 6) y=\f(x)\;
7)y=2f(x); 8) y=l—f(x); 9) f/=|f(x)|-l;
10) y=\f (x) —1|; 11) y = f(x+l); 12) y=f(x-2\,
13) y = f(-x)- 14) y=f(2x); 15) =
16)!/ = f(-f); 17) y = f(l-x); 18) y=2f(x-l).
97. Дан график функции y = f(x) (рис. 38,6). Постройте гра-
фики функций:
о) 5)
Рис. 38
60
1) y = f(x-2);
4) f/=f(x+l);
7) y--f(-x);
10) y = If (|x|)|;
2) y = f(x + 2);
5) y — f(~x);
8) y=|f(x)|;
11) z/=f(l—x);
3) y=f(x-l);
6) f/=—f(x);
9) y = f(|x|);
12) y = f(-l-x).
Дробно-линейные функции
98. Постройте графики функций:
1) У=-т-г; 2) у=---3) <7=-^;
7 х-Н 7 х—1 х —2
1 2 сч 2х — 3 Зх-Н
4»»-1-7Т2; 6) »=з7ГТ-
99. Найдите область значений каждой из дробно-линейных функ-
ций из задачи 98.
100*. Докажите, что композицией двух дробно-линейных функций
будет снова дробно-линейная функция.
Уравнение окружности
101. Найдите координаты центра и радиус окружностей:
1) х2 + 2х+у2 — 4у+ 1 =0; 2) х2 + у2 + х+у=0;
3) 2х2 —х + 2у2 — у—1; 4) (х+у)2 + (х — у)2 = 4х.
Подобие графиков
102. Докажите, что графики функций y = f(x) и y=kf(^-^
подобны с центром подобия в начале координат.
Различные шкалы
103. Путешествие совершается на двух автомобилях — советском
и британском. Счетчик километража первого из них показы-
вает расстояние в километрах, второго — в милях. В начале
путешествия первый показывал 28 300, а второй — 5615. В
конце путешествия первый— 31 205, второй — 7420.
1) Вычислите длину мили в километрах.
2) Выведите формулы пересчета показаний счетчика одного
автомобиля через показания другого.
Квадратичная функция
Построение графика
104. Найдите координаты вершин, точек пересечения с коорди-
натными осями и постройте параболы:
1) у — х2-\-х — 2; 2) у = х2 — х;
3) у = х2 + 4х— 1; 4) у — 2х2— 1;
61
5) t/ = 3x2 + 6x+1; 6) t/=l—x —x2;
7) t/=2x2-3x + 3; 8) t/ = x-4x2;
9) i/=(2x4-l)(x-l).
Исследование квадратичной функции
105. Даны следующие квадратичные функции:
1) у = 4х2— 1; 2) у=х2Н-х —6; 3) t/ = 2x2 + 3x-5;
4) у = 6х —х2; 5) у — — 2х2 + 3х— 1; 6) у=— х2 — 2х—1;
7) i/=x2-x+l;8) у=— 5 + 2х — х2; 9) у=(х — 1)(2х-3).
Для каждой из них найдите: а) ее корни; б) участки постоян-
ного знака; в) наибольшее и наименьшее значения; г) об-
ласть значений.
Квадратные неравенства
106. Решите неравенства:
1) х2 + 5х + 6<0; 2) х2 + Зх + 5>0; 3) 2х2+х + 2<0;
4) 2 —х —х2>0; 5) -х2 + 3х+ 18>0; 6) х2+х-1<0;
7) х4 —2х2 —8<0; 8) х4-5х2 + 4>0; 9) х6+х3+1>0.
Исследование квадратичной функции на промежутке
107. Найдите область значений каждой из функций:
1) у=х2 + 2х, х£[—2; 1];
2) у = х2 — х, х^ 1;
3) у = х4 + 2х2-3;
4) у=(х2—х)2+х2—х—2.
108. Найдите наибольшее и наименьшее значения функций:
1) t/=x2+x, х£[— 1; 1]; 2) у=2х—х2, xg[— 1; 3];
3) у=х2 —х, х£[1; 2]; 4) у=-у/2—х—х?
Квадратичная функция под знаком модуля
109. Раскройте модули:
1) у=|х2 —4| + Ix|;
2) у=|6—х — х21+х2.
ПО. Постройте графики функций:
1) у=|х2— 1|; 2) у=х2 — | х | — 2;
3) у= |х2 — х — 6| +х; 4) у— |х2—х| + |х2 + х
111. Решите уравнения:
1) |х2 —91 =5; 2) |2х2+х — 3|+х=1;
3) х24-3|х| — 18 = 0; 4) |х2-1| = |х2-х+1
62
Задание квадратичной функции
112. Найдите квадратичную функцию вида y = x2 + px-\-q, для
которой выполнено следующее условие:
1) график проходит через точки Pt (0; —5), Р2 (1; —3);
2) наименьшее значение равно 2 й достигается при х=1;
3) корни равны —2 и 3;
4) один корень вдвое больше другого и точка (—1; 6),ле-
жит на графике;
5) наибольшее значение модуля функции на отрезке [—1; 1]
равно у-.
КОНТРОЛЬНОЕ ЗАДАНИЕ К ГЛАВЕ I
Вариант 1
1. Проведите исследование функции по графику (рис. 39, а).
2. Дана функция У = х±4
63
а) Постройте ее график.
б) Решите неравенство у<0.
в) Решите уравнение \у— 111 = 1.
3. Дана функция y — f(x), где f (х) = — x2 + * + 2.
а) Постройте ее график.
б) Найдите ее область значений.
в) Решите неравенство f(x)^2x.
г) Найдите точки экстремума функции.
Вариант 2
1. Дан график функции y=f(x) (рис. 39,6).
а) Найдите промежутки монотонности функции.
б) Определите число корней уравнения f(x)=a в зависи-
мости от значения параметра а.
в) Найдите область значений функции.
г) Решите неравенство |f(x) — 2|^1.
2. Дана функция y — f(x), где f (х)=^|-.
а) Постройте ее график.
б) Найдите область значений функции.
в) Решите неравенство f(x2)^0.
3. Дана функция y = f(x), где f (х) = 2х2+х — 3.
а) Найдите ее наибольшее и наименьшее значения на отрез-
ке [—1; 2].
б) Постройте график функции у= If (х)|.
в) При каких значениях а уравнение |f(x)|=a имеет че-
тыре корня?
Вариант 3
1. Дан график функции y=f(x) (рис. 39,в).
а) Постройте график функции t/ = f(|x|).
б) Сколько решений имеет уравнение f(x)=fex в зависи-
мости от значений параметра k?
в) Решите неравенство |f(x)|^x.
2. Дана функция z/=f(x), где f(x)=3‘x~^ .
а) Постройте ее график.
б) Решите неравенство f (f (х))<0.
в) Найдите область значений функции y — f(x2').
3. Дана функция у = (а +1) х2 — (2а — 3) х + а.
а) При каких значениях а функция у имеет экстремум при
х = 2?
б) При каких значениях а функция у не имеет корней?
в) Найдите наибольшее значение функции у на отрезке [0; 1)
в зависимости от значений параметра а.
Был этот мир глубокой тьмой окутан.
Да будет свет! И вот явился Ньютон.
А. Поуп
Глава II
ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЕ
ВВОДНАЯ БЕСЕДА
1. Механический смысл производной
Представим себе, что мы отправляемся в автомобильную
поездку. Садясь в машину, посмотрим на счетчик километража.
Теперь в любой момент времени мы сможем определить
путь, пройденный машиной. Скорость движения мы узнаем по
спидометру. Таким образом, с нашим движением (как и с движе-
нием любой материальной точки) связаны две величины — путь s и
скорость и, которые являются функциями времени t.
Ясно, что путь и скорость связаны между собой. В конце
XVII в. великий английский ученый Исаак Ньютон открыл
общий способ описания этой связи. Открытие Ньютона стало
поворотным пунктом в истории естествознания. Оказалось, что
связь между количественными характеристиками самых различ-
ных процессов, исследуемых физикой, химией, биологией, техни-
ческими науками, аналогична связи между путем и скоростью.
Основными математическими понятиями, выражающими эту
связь, являются производная и интеграл. Как вы убедитесь в
дальнейшем, скорость — это производная пути, а путь — это ин-
теграл от скорости.
Построенная Ньютоном модель механического движения
остается самым важным и простым источником математического
анализа, изучающего производную и ее свойства. Вот почему на
вопрос, что такое производная, короче всего ответить так:
производная — это скорость.
А что такое скорость? Оказывается, объяснить это не так
просто. Прочтите диалог между водителем-женщиной и поли-
цейским, взятый из знаменитых «Фейнмановских лекций по
физике»:
— Мадам, Вы нарушили правила уличного движения. Вы еха-
ли со скоростью 90 километров в час.
— Простите, это невозможно. Как я могла проехать 90 кило-
метров за час, если я еду всего лишь 7 минут!
3 Заказ 836 65
— Я имею в виду, мадам, что если бы Вы продолжали
ехать таким же образом, то через час Вы бы проехали 90 кило-
метров.
— Если бы я продолжала ехать, как ехала, еще час, то на-
летела бы на стенку в конце улицы!
— Ваш спидометр показывал 90 километров в час.
— Мой спидометр сломан и давно не работает.
Как видите, полицейский не смог объяснить, что такое скорость
90 км/ч. А вы смогли бы?
Попробуйте объяснить, что такое скорость равномерного дви-
жения и как ее можно измерить.
Разберемся в том, что же такое скорость произвольного
движения. Пусть точка движется по прямой. Мы считаем, что нам
задан закон, по которому можно вычислить путь $ как функцию
времени t.
Например, если точка движется под действием силы тяжести
с нулевой начальной скоростью, то s=^-. (Мы считаем, что
g — ускорение силы тяжести — постоянно.) Возможны и другие
законы движения. Так, ракета, стартовавшая с поверхности Зем-
ли вертикально вверх с начальной скоростью, позволяющей пол-
ностью преодолеть земное притяжение (так называемой второй
космической скоростью), удаляется от центра Земли по закону
2
s=A (/ + С)3, где Л и С — некоторые константы.
Рассмотрим отрезок времени [Л; /2]. Определим среднюю ско-
рость точки на отрезке /2] как отношение пройденного пути к
продолжительности движения:
sftij—sjt,)
с₽ G—Л ’
Для определения скорости точки в момент времени t (ее
в механике часто называют мгновенной скоростью) поступим
так: возьмем отрезок времени [/; Л} вычислим среднюю ско-
рость на этом отрезке и начнем уменьшать отрезок [/; Л], при-
ближая Л к t. Мы заметим, что значение средней скорости при
приближении ti к t будет приближаться к некоторому числу, ко-
торое и считается значением скорости в момент времени t.
В качестве примера рассмотрим свободное падение тела. Счи-
таем известным, что зависимость пути от времени задается функ-
цией $=^-. Зафиксируем произвольный момент времени [/; /|]
и вычислим среднюю скорость на отрезке:
gt2 gt2
Uc₽ h — t h-t 2 h-t 2
Если теперь будем стягивать отрезок [/; к точке t, т. е. будем
брать значения Л все ближе и ближе к t, то сумма Л-И будет
66
g t2,-t2
Лейбниц Готфрид Вильгельм
(1646—1716) —
немецкий математик, физик, философ,
создатель Берлинской академии наук. Осно-
воположник дифференциального и интег-
рального исчисления, ввел большую часть
современной символики математического
анализа. В работах Лейбница впервые появи-
лись идеи теории алгоритмов.
«Предупреждаю, чтобы остерегались от-
брасывать dx,— ошибка, которую часто до-
пускают и которая препятствует продвиже-
нию вперед».
Г. В. Лейбниц
приближаться к t+t=2t, а выражение -—-(fi + О будет прибли-
жаться к-~2/ = £/. Последнее число и является значением мгно-
венной скорости в точке t. Мы получим хорошо известную фор-
мулу скорости v — gt. Процедура, подобная переходу от средней
скорости на отрезке [/; Л] к мгновенной скорости в точке t при
стягивании отрезка в точку /, носит название предельного
перехода. Обычно говорят, что при стремлении t\ к t выражение
+ 0 стремится к gt, и записывают это следующим образом:
+ или +
Используя слово «предел», можно сказать, что мгновенная
скорость в точке t — это предел средней скорости при стягивании
отрезка, на котором она измеряется, в точку t или в символи-
ческой записи
4 tl^t — t
2. Геометрический смысл производной
Честь открытия основных законов математического анализа
наравне с Ньютоном принадлежит немецкому математику Г. Лейб-
ницу. К этим законам Лейбниц пришел, решая задачу проведе-
ния касательной к произвольной кривой.
Чтобы составить наглядное представление о том, как провести
касательную, нужно вообразить себе, что к кривой, изготовленной
из жесткого материала (например, из проволоки), вы приставляете
67
линейку так, чтобы она коснулась этой кривой в выбранной точ-
ке (рис. 40, а).
Если вы вырезаете из бумаги криволинейную фигуру, то нож-
ницы направлены по касательной к ее границе.
Постараемся перевести наглядное представление о касатель-
ной на более точный язык. Будем считать, что кривая — это
ломаная с очень большим числом маленьких звеньев. Именно та-
кая точка зрения была у создателей дифференциального исчисле-
ния. В первом учебнике по анализу, написанном 300 лет назад по-
следователем Лейбница маркизом Лопиталем, дано следующее оп-
ределение касательной: «Если продолжить одно из маленьких
звеньев ломаной, составляющей кривую линию, то эта продолжен-
ная таким образом сторона будет называться касательной к
кривой» (рис. 40, б).
Хорошее представление о касательной дает следующее опи-
сание. Посмотрим в микроскоп на маленький участок кривой. На
рисунке 41 в разных масштабах изображены участки одной и той
68
же параболы вблизи точки М. На первом графике ясно видно,
что парабола искривлена, на втором это искривление уже менее
заметно, а на третьем участок кривой почти неотличим от от-
резка прямой линии, которая и является касательной к параболе
в точке М.
Более точно объяснить, что такое касательная, так же не-
просто, как и дать точное определение скорости. Для этого по-
надобится предельный переход, аналогичный тому, который мы
совершили при вычислении скорости.
Пусть дана некоторая кривая и точка Р на ней (рис. 42).
Возьмем на этой кривой другую точку Р\ и проведем прямую че-
рез точки Р и Р\. Эту прямую обычно называют секущей. Ста-
нем приближать точку Р\ к Р. Положение секущей РР\ будет ме-
няться, но с приближением Р\ к Р начнет стабилизироваться.
Предельное положение секущей РР\ при стремлении точки Р\ к
точке Р и будет касательной к кривой в точке Р.
Как перевести описанное построение на язык формул? Пусть
кривая является графиком функции y = f(x)9 а точка Р, лежа-*
щая на графике, задана своими координатами (х; у). Касатель-
ная является некоторой прямой, проходящей через точку Р. Что-
бы построить эту прямую, достаточно найти ее угловой коэффици-
ент. Обозначим угловой коэффициент касательной k. Сначала най-
дем угловой коэффициент k\ секущей РР\. Пусть абсцисса точки
Р\ равна Х|. Из рисунка 43 ясно, что
Х1 —х
Для нахождения k надо устремить Х| к х. Тогда точка Р\ нач-
нет приближаться к точке Р, а секущая РР\ — к касательной
в точке Р. Таким образом, угловой коэффициент касательной
можно найти как предел выражения ~— при стремлении Х| к
х, или в символической записи:
4 7 х,_^х Х[—Х
69
Мы пришли к той же задаче, которая встретилась при нахож-
дении скорости: осуществить предельный переход в выражении
вида при стремлении Х| к х. Этот предельный переход
носит название дифференцирования функции f.
Дифференцирование, или нахождение производной,— это но-
вая математическая операция, имеющая тот же смысл, что в
механике нахождение скорости, а в геометрии вычисление углово-
го коэффициента касательной.
Для нахождения значения производной в данной точке надо
рассмотреть маленький участок изменения аргумента вблизи этой
точки. Производная будет приближенно равна средней скорости
на этом участке (на языке механики) или угловому коэффи-
циенту секущей (на языке геометрии). Для точного вычисления
производной надо совершить предельный переход — стянуть отре-
зок изменения аргумента в точку. Тогда средняя скорость пре-
вратится в мгновенную, а секущая — в касательную, и мы вычис-
лим производную.
3. Определение производной
Математический анализ, созданный Ньютоном и Лейбницем,
долго развивался на основе интуитивного понятия производной
как «скорости изменения функции». Современное определение про-
изводной появилось лишь в XIX в. после того, как были уточнены
основные понятия математического анализа: вещественное число,
функция, предел. С их помощью можно дать следующее опреде-
ление:
Производной функции y=f (х) называется предел отношения
f (*Z ПрИ стремлении х\ к х.
Х\ —X
Исторически сложилась символика для обозначения участвую-
щих в этом определении выражений. Разность значений аргу-
мента обозначают Дх (дельта икс) и называют приращением
аргумента, а разность значений функций обозначают \у и назы-
вают приращением функции. Иначе говоря, Х|—х = Дх, а
f (х +Дх) —f (х) = Ду. Средняя скорость изменения функции запи-
сывается как . Стягивание отрезка в точку означает стремле-
ние Дх к нулю. Производную функции y=f(x) обозначают с по-
мощью штриха: у' или f'. Получается новый вариант определе-
ния производной:
Производной функции называется предел отношения прираще-
ния функции к приращению аргумента, когда приращение аргу-
мента стремится к нулю.
Символически определение производной можно записать так:
£/'= lim или —>у'.
Дх+о Ах \х дх_>0
70
Ньютон Исаак
(1643—1727) —
английский физик и математик. Создал
современную механику (законы Ньютона) и
открыл закон всемирного тяготения. В его
главном сочинении «Математические начала
натуральной философии» дан математичес-
кий вывод основных фактов о движении не-
бесных тел. Один из создателей дифферен-,
циального и интегрального исчисления.
«Когда величина является максимальной
или минимальной, в этот момент она не течет
ни вперед, ни назад».
И. Ньютон
Как вычисляют производную?
Первый шаг: вычисляют Ду — приращение функции на
отрезке [х; х + Дх] и составляют отношение
Второй шаг: представляют себе, что Дх приближается к
нулю, и переходят к пределу, т. е. находят, к какому значению
приближается отношение при Дх->-0.
4. Предельные переходы
При определении скорости, при нахождении углового коэффи-
циента касательной, при вычислении производной мы совершаем
предельные переходы. Попробуем более точно описать их суть.
Мы имеем дело с переменными величинами. Пусть, например,
переменная у является функцией переменной х. Нас интересует по-
ведение у при приближении аргумента х к некоторому значению а.
Отметим сразу, что это значение а может входить в область опре-
деления функции, а может и не входить. Так, исследуя функции
yi = 34-x2, у2=1^-,
Уз=^Ег- ^=7ТГ
вблизи значения х=1, мы заметим, что его можно подставить
в формулы для у\ и у4 и нельзя — в формулы для у2 и уз. Предель-
ный переход для функций у\ и при приближении х к 1 (при
х—И) совершить просто — надо вычислить значения этих функций
при х = 1:
lim у\ =lim (3 + х2) = 3+ 1 =4; Пт у4 = Пт
71
Так обычно ведут себя функции, заданные известными нам форму-
лами: предел функции при стремлении аргумента к а, входя-
щему в область определения, равен значению функции в точке а,
т. е.
lim / (х)=/(а),
х->-а
если а входит в область определения функции f. Этот принцип, ко-
торый отражает непрерывность элементарных функций во всех
точках, где они определены, позволяет осуществить большое коли-
чество важных предельных переходов. Мы так и будем называть
его: принцип непрерывности. Этот принцип удобно формулируется
на языке приращений:
если Дх->0, то Дг/->0.
Предельные переходы для функций у2 и при х-И так просто
осуществить нельзя: у2 и у$ не определены при х=1. Предельный
переход, который мы хотим осуществить, поясним на примере более
простой функции £/5==-^-. Ясно, что при всех х=/=0 значения этой
функции равны 1. При х = 0 эта функция не определена, но очевид-
но, что ее предельным значением при х->0 надо считать у= 1. Это
значение получается при сокращении числителя и знаменателя
дроби -у на Аналогичное сокращение можно произвести и для
функций у2 и у$:
l-x^i-xHl+x)^ 1 ,
1-х (1-х) ’
У% — 1 _ Ух— 1 ________Ух— 1_____________1________
*2-1 -(х-1)(х+1) —(^_1)(^+I)(x+1)_(^+I)(x+1) •
Полученные после сокращения выражения уже определены при
х=1, и поэтому предельные значения можно получить, под-
ставляя в них число 1 вместо х:
lim t/2 = lim (1 +%)= 1 +1 =2;
х—► I х—► 1
lim уз = Нт ——!------—1——
x-l x-l (з/х+1)(х+1) (1 + 1) (1 + 1) 4
Приведенные примеры не исчерпывают всего разнообразия
встречающихся случаев — в дальнейшем мы встретимся с более
сложными предельными переходами.
Контрольные вопросы
1. Обратите внимание на встретившиеся в тексте следующие
ключевые слова: средняя скорость, мгновенная скорость, секущая,
касательная, приращение аргумента, приращение функции, произ-
водная. Приведите примеры их использования.
72
2. Какое движение называется равномерным?
3. Как вычислить скорость равномерного движения?
4. Что такое средняя скорость неравномерного движения?
5. Как вычислить мгновенную скорость точки?
6. Чем отличается мгновенная скорость от средней скорости?
7. Что можно сказать о движении, если его средняя ско-
рость одна и та же на любом отрезке времени?
8. Что такое касательная к графику функции?
9. Как вычислить угловой коэффициент секущей, проходящей
через две точки графика некоторой функции?
10. Как найти угловой коэффициент касательной к графику
функции?
11. Для какой функции касательная к ее графику совпадает
с самим графиком?
12. Что такое производная?
13. Как вычислить производную?
14. Что такое производная с механической точки зрения?
15. Что такое производная с геометрической точки зрения?
§ 1. ВЫЧИСЛЕНИЕ ПРОИЗВОДНОЙ
1. Схема вычисления производной
Вычисление производной функции y = f(x) производится по
следующей схеме:
1) Находим приращение функции на отрезке [х; х+Дх]:
= f (х + Дх) — f (х).
2) Делим приращение функции на приращение аргумента:
&У = f (* + &*)-/(*)
Дх Дх
3) Находим предел , устремляя Дх к нулю.
Переход к пределу мы будем записывать либо с помощью зна-
ка lim, либо с помощью стрелки
Примеры.
1. Производная линейной функции.
а) у = С — постоянная функция.
Ьу = С — С = 0; ^-=0.
Дх
Так как отношение постоянно и равно нулю, то производная
у тоже равна нулю: у'=0. Итак, производная постоянной равна
нулю:
С' = 0.
73
6) y = ax-\-b— линейная функция.
At/=a (х+Ах) + Ь — (ах + Ь)=аАх;
Ду _ аДх ___
Дх Дх
Как и в первом примере, отношение является постоянным.
Поэтому в качестве производной надо взять функцию, прини-
мающую это постоянное значение а, т. е. у' = а. Итак, производная
линейной функции равна коэффициенту при переменной:
(ах-\-Ь)' = а.
2. Производная функции у=ах2.
А у=а (х+Ах)2 — ах2 = ах2 + 2ах Ах+а (Ах)2 — ах2 =
=2ахАх + а (Ах)2;
^=2ах + аАх;
lim^— Ит(2ах+аЛх)=2ах;
(ах2)' = 2ах.
3. Производная функции у = х3.
Ау=(х + Ах)3 — х3—х3 + Зх2 Ах + Зх (Ах)2 + (Ах)3 — х3 =
= Зх2Ах+Зх (Ах)2+(Ах)3;
|£=Зх2 + ЗхАх + (Ах)2;
Нт ^=3х2;
Дх-0 Дх
(х3)' = Зх2.
4. Производная функции У=±--
д 1________1 х—х —Дх ______Дх .
х-ЬДх х ~~ (х+Дх)х (х + Дх)х ’
Д# ___1 .
Дх (х+Дх)х
Нт ^=—Ь
Дх-о Дх X2
(i)'=-^.
Во всех рассмотренных примерах находится производная
рациональной функции. При этом дробь всегда можно сокра-
74
тить на Дх. Переход к пределу сводится к тому, что можно по-
ложить (после сокращения) Дх = 0.
Рассмотрим более сложный пример.
5. Производная функции у — д[х.
\у=д/х + Дх — д/х;
&у-\jx-\- \х—д[х
\х \х
Для того чтобы сократить на Дх, умножим числитель и зна-
менатель на сумму радикалов:
&у (7х + Дх—7х) (7ХН~ДХ+ТХ)
\х (-yjx + Дх + -у/х)
__ х-}-Дх —х ________1_____
Дх (7*+Дх + х/х) 7Х+^х+7х
При маленьких Дх значение корня 7х+ Д* близко к д/х. Поэ-
тому при переходе к пределу надо заменить в знаменателе д/х +Дх
на д/х. Получим:
У 7*+ 7* 27х
Производные, вычисленные в этих примерах, нужно запом-
нить:
С'=0;
(ах+ Ь)' = а; (х3)' =3х2;
(ах2)' = 2ах;
2. Правила дифференцирования
Теорема. Производные суммы и произведения вычисляются
по следующим формулам:
(a + v)' = u'+v'; (1)
(Си)' = Си'\ (2)
(uv)' — u'v-\-uv'. (3)
Доказательство. Первый шаг в вычислении производ-
ной — это нахождение приращения функции. Обозначим аргумент
функции буквой х, значение функции буквой у и вычислим Дг/,
т. е. приращение функции у на отрезке [х; х + Дх].
1) у = и + v — функция у есть сумма двух функций и и v. Зна-
чение функции у в любой точке является суммой значений
функций и и v в этой точке:
f/(x)=u (x) + v (х).
75
Вычисляем Ay:
\у = у (x+Ax)—У (x) = u (х+Ах)+и (х +Ах) —
— (и (х) + V (х))=(и (х+Ах) — и (х)) + (у (х + Ах) — v (х)).
Первая скобка — это Ди, вторая — Ди.
Запишем кратко результат вычисления:
\у — Ди + Ди,
т. е. приращение суммы функций равно сумме приращений слагае-
мых.
2) у = Си — функция у представлена как произведение посто-
янной С на функцию и. Значение функции у в любой точке являет-
ся произведением постоянной С на значение функции и в этой
точке: у (х) = Си (х).
Вычисляем Дг/:
\у = Си (% + Дх)— Си (х) = С (ц (%4-Дх) — и (х)) = С&и,
т. е. при умножении функции на постоянное число приращение
функции умножается на это число.
3) y = uv — функция у есть произведение функций ини. Зна-
чение функции у в любой точке является произведением значений
функций и и v в этой точке:
у (х)=и(х) V (х).
Вычисляем Дг/:
\у = у (* + Д*) — У (х) = и (х +Дх) v (% + Дх) — и (х) v (х).
Для того чтобы выделить приращения сомножителей Ди и Ди,
заменим и (х + Дх) и v (x-j-Дх) на равные им выражения и (х) +Ди
и v (х) + Ди:
\у = (и (х) + Ди) (V (х) + Ди) — и (х) V (х) =
= и (х) v (х) + Ди • v (х) + и (х) Дv + Ди • Ди — и (х) v (х) =
= Ди • v (х) + и (х) Ди + Ди • Дv.
Окончательно
\y = \u-v (х) + и (х)-Ди + Ди-Ди,
ИЛИ
\у — • v + и • \v + Ди • Ди.
Объединим второй и третий шаги в вычислении производной,
т. е. составим отношение и перейдем к пределу при Дх->0.
1) y = u-\-v,
Дг/ = Ди +Ди,
\у___ Аи
Ах Ах ' Ах
76
Пусть Дх-*О. По определению производной будет прибли-
жаться к и', — к и', а их сумма будет приближаться к сумме
и' + и', т. е.
y'=u' + v'.
2) у —Си,
\у = С\и,
Дх Дх
Пусть Дх->-0. При этом будет приближаться к и', а тогда
и С” будет приближаться к Си', т. е.
у' = Си'.
3) y = uv,
Ду = Д и • и + и • Ди + А и • Д и,
^.=^..и + ы.^+^..ди,
Дх Дх Дх Дх
Пусть Дх->0. Тогда Перейдем к пределу в
каждом слагаемом.
Ди , Ди ,
Если -—► и , то -v-+uv.
Ах Ах
т? Ди / Ди /
Если ---► v . то и--► uv .
Ах Ах
Третье слагаемое является произведением двух переменных мно-
жителей, ведущих себя по-разному при Дх->0. Мы уже знаем, что
Если Дх->0, то по принципу непрерывности Ди->0. Сле-
довательно, u'v + iw', что и требовалось доказать.
Замечание. Формула (Си)' = Си' является следствием
формулы производной произведения: y = uv, v = C, y = u'v + uv' =
= и'С + и-0 = Си'. Однако формула (Cu)' = Cuz настолько важна,
что мы дали ее отдельный вывод.
Теорема. Производная частного вычисляется по формуле
(f <4>
Доказательство. Формулу производной частного мож-
но получить, следуя обычной схеме вычисления производной. Мож-
но поступить проще. Обозначим функцию -у- через h. Получим
u = hv. Найдем производную функции и по правилу диффе-
ренцирования произведения:
и' = h'v + /iu'.
77
Выразим из этой формулы Л', а вместо h подставим его зна-
чение Получим:
, и ,
и-----------------------------------V
£./ и' — hv' v u'v — uvf
fl — -- ----------- $ •— .
V V V
Окончательно
Замечание. Производную функции найденную ра-
нее, можно заново получить, пользуясь формулой производной
частного. Представим у = — как частное функций и=1 и v = x.
Получим: х
/ 1 V Г-х- Ьх' 0-1 1
\ х / х2 х2 х2 '
3. Производная степени
Производную любой степени с натуральным показателем мож-
но получить, пользуясь правилом дифференцирования произведе-
ния. Например, для нахождения производной функции г/ = х4
представим х4 как х3-х. Зная производные функций г/ = х3 и
у = х, вычислим производную произведения:
(х4)' = (х3)'-х + х3-х'=Зх2-х4-х3-1 = 4х3.
Выпишем формулы:
х'=1, (х2)'==2х, (х3)' = Зх2, (х4)' = 4х3.
Легко заметить общую закономерность:
(xrt)'==nxn”1.
Теперь найдем производную функции у=~^г-
, 0 — пхп~' пхп~1 п
У ~ (хп)2 ~ х2п ~~ хп+' '
Заметим следующее: если дробь У=^г записать как у=хк,
где k= — п (т. е. как степень с отрицательным показателем), то
у'=( —га) х_(п+,). Если заменим ( — га) на k, то получим у' = kxk~\
т. е. формула дифференцирования степени, полученная нами для
натуральных показателей, остается верной и для целых отрица-
тельных показателей:
(хк\ = kxk~',
где k — любое целое число, кроме нуля.
78
Выведенная формула остается верной и для дробных показа-
телей. Возьмем известный уже нам случай Это функция
у=^/х=х2. По формуле получится:
4. Линейная замена аргумента
Как меняется производная функции y=f (х), если вместо аргу-
мента х подставить новую функцию? Ответ на этот вопрос мы да-
дим в заключительной беседе, а сейчас разберем важный част-
ный случай линейной замены аргумента.
Теорема. Производная функции y=f (kx-\-b) вычисляется
по формуле
(f(kx + b))'=kf'(k*+b).
Словами теорему можно сформулировать так: при линейной за-
мене аргумента производная умножается на коэффициент при ар-
гументе.
Доказательство. Вычислим производную функции
y = f (kx + b), следуя общей схеме вычисления производной. Пред-
варительно введем обозначения. Функцию y = f (kx-\-b) как функ-
цию от х обозначим через g, т. е. g (x) — f (fex + b). Выражение
kx-}-b обозначим через z, т. е. z=kx-\-b, откуда g(x)=f(z).
Найдем зависимость между Дх и Дг:
Дз=& (х+Дх) + Ь —(fex-\-b) = kДх,
т. е. Дг = /гДх.
Вычислим 7^.;
Дх
Ag _ g(x-t-Ax) —g(x) _ f (k(x + &x) + b)—f (kx + b) _
Дх Дх Дх
__f (kx+b + k&x)—f (kx-\-b)_f (z-t-Az)—f (z)_
Дх Дх
(z+Az)—f (z) Az f(z+Az)—f (z) _,
&z Дх Дг
Перейдем к пределу. Пусть Дх-И). Тогда по принципу не-
прерывности Д?->0.
f' (z\- k -+k-f (z)
Итак, k-f' (z) = k-f' (kx + b), что и требовалось доказать.
79
Физический смысл выведенной формулы очень простой. Пере-
ход от функции y = f(x) к функции y — f (kx + b) означает измене-
ние начала отсчета и масштаба переменной х. Изменение на-
чала отсчета не может повлиять на вычисление скорости: пока-
зания спидометра не зависят от начального показания счетчика
километража. Изменение масштаба измерения аргумента (време-
ни) в k раз повлечет за собой такое же изменение величины
скорости. Так, скорость, измеренная в километрах в час в 60 раз
больше скорости, измеренной в километрах в минуту.
Примеры.
1. f/=(x+l)5, у' = 5(х+1)4.
2. у=(5х—I)4, у' = 5-4-(5х—1)3 = 20 (5х—I)3.
1 12
3‘ ^ = 2х + 3 ’ У = ^~ ^’2*(2х+3)2== “(2х+3)2 *
4. z/== л/6х+ 1, у'=6--—=
v 2 л/бТ+Т
з
л/6х+Т ’
При дифференцировании функций вида y — (kx)n выведенной
формулой пользоваться нерационально. Лучше вынести константу
за знак производной:
((fex)n)' = (Г • xnY = kn • (xn)' = kn • n • xn~1.
Пример. £/ = (Зх)3. Сделав преобразование (Зх)3 = 33х3 = 27х3,
вычисляем производную £/' = 27-Зх2 = 81х2.
Контрольные вопросы
1. Какова схема вычисления производной?
2. Чему равна производная суммы, производная произве-
дения, производная частного двух функций?
3. Что происходит с производной при умножении функции на
некоторую постоянную?
4. Чему равна производная степенной функции?
5. Как меняется производная при линейной замене аргумента?
§ 2. ИССЛЕДОВАНИЕ ФУНКЦИИ
С ПОМОЩЬЮ ПРОИЗВОДНОЙ
1. Связь свойств функции и ее производной
В первой главе мы научились читать график, т. е. находить
свойства функции по ее графику. Сейчас перед нами стоит обрат-
ная задача — научиться строить график функции, зная необходи-
мые для этого ее свойства.
80
Два важнейших свойства функции, необходимые для построе-
ния ее графика,— промежутки монотонности и точки экстрему-
ма — определяются с помощью производной.
Связь между свойствами функции и свойствами ее производ-
ной мы установим с помощью механического истолкования произ-
водной как скорости движения материальной точки.
Пусть материальная точка движется по координатной прямой.
Положение точки определяется значением одной переменной — ее
координатой. Эта переменная зависит от другой переменной —
времени. В механике мы обычно обозначаем время буквой f, ко-
ординату точки, движущейся по прямой, буквой х. Движение
точки по прямой определяется заданием х как функции времени t.
Разумеется, обозначения для переменных можно выбирать по-раз-
ному. Если мы хотим произвольную функцию y = f(x) рассмат-
ривать как закон движения материальной точки, то независи-
мую переменную, аргумент х, мы должны считать временем, а
зависимую переменную у считать координатой движущейся точки.
Итак, пусть дана функция y = f(x). Рассмотрим ее как закон
прямолинейного движения некоторой материальной точки Р. Это
означает, что точка Р движется по оси, причем ее положение
зависит от времени, которое обозначено через х. Для более от-
четливого механического истолкования функции и ее свойств,
составим таблицу, с помощью которой легко найдем связь между
поведением функции и ее производной.
№ Обозначение Понятие или свойство Механическая интерпретация
1 X Независимая перемен- ная, аргумент Время
2 У Зависимая переменная Положение материальной точ- ки, ее координата
3 Зависимость между пе- ременными, функция Закон движения материаль- ной точки Р, зависимость коор- динаты точки Р от времени
4 У ~~ const Функция является по- стоянной Точка Р стоит на месте, ее ко- ордината постоянна
5 у'—f' W Производная Скорость (мгновенная)
6 У Функция возрастает Точка Р движется по оси у в положительном направлении
7 У Функция убывает Точка Р движется по оси у в отрицательном направлении
81
Продолжение
№ Обозначение Понятие или свойство Механическая интерпретация
8 max у (min у) при Х = Х0 Функция приняла мак- симальное (минималь- ное) значение при х = х0 Точка Р заняла самое высокое (низкое) положение (по срав- нению с положением в близ- кие к х0 моменты времени)
9 у'=0 Производная обратилась в нуль Точка Р остановилась (ее ско- рость обратилась в нуль)
10 у’>0 Производная положи- тельна Скорость точки Р положитель- на (точка Р движется в поло- жительном направлении)
11 у’<0 Производная отрица- тельна Скорость точки Р отрицатель- на (точка Р движется в отри- цательном направлении)
Теорема. (Признак постоянства функции.) Если на некото-
ром промежутке производная тождественно равна нулю, то функ-
ция на этом промежутке постоянна.
Доказательство. Будем понимать заданную функцию
y = f(x) как закон движения материальной точки Р (строка 3
таблицы) по оси у. Если производная обратилась в нуль, то точка
Р остановилась (строка 9 таблицы). Если производная все время
равна нулю, то точка Р все время стоит на месте, а тогда
функция у является постоянной (строка 4), что и требовалось
доказать.
Заметим, что верна и обратная теорема: если функция
постоянна, то ее производная равна нулю. Производную постоян-
ной функции мы вычислили ранее, это же следует и из строк 4 и 9.
Таким образом,
f = const о f' = 0.
Теорема. (Признак монотонности функции.) Промежутки
монотонности функции совпадают с промежутками постоянного
знака ее производной.
Доказательство. Будем понимать заданную функцию
y — f (х) как закон движения материальной точки Р по оси у в зави-
симости от времени х (строка 3). Пусть на некотором промежутке
функция f возрастает. На языке механики это означает, что
материальная точка Р движется по оси у в положительном на-
правлении (строка 6). Так как знак скорости совпадает с направ-
лением движения (строка 10), то скорость точки, т. е. произ-
водная функции f, положительна.
82
Обратно: если производная, т. е. скорость точки, положи-
тельна, то точка движется по оси у в положительном нап-
равлении (строка 10), следовательно, функция возрастает
(строка 6).
Аналогично рассматривается случай убывания функции.
Замечание. Если точка движется в одном направлении, то
ее скорость сохраняет постоянный знак, однако в отдельные мо-
менты времени точка может остановиться (ее скорость обратится в
нуль), а затем продолжать двигаться в том же направлении.
Функция, описывающая такое движение точки, будет монотонной.
Значит, если , то f' (х)>0. Верно и обратное. Однако если
f' (х) обращается в нуль не в отдельных точках, а на целом проме-
жутке, то на этом промежутке функция будет постоянной.
Если включить промежутки постоянства функции в промежутки
ее монотонности (как иногда говорят, не требовать строгой моно-
тонности функции), то можно коротко результат исследования
записать так:
Теорема. (Необходимое условие экстремума функции.) В
точке экстремума производная обращается в нуль.
Доказательство. Рассмотрим заданную функцию
y = f(x) как закон движения материальной точки Р (строка 3).
Пусть при х = хо функция у имеет экстремум. Тогда в момент
времени х = х0 точка Р занимает на оси у самое высокое (или
самое низкое) положение (строка 8). В этот момент времени
точка останавливается, т. е. ее скорость обращается в нуль, а зна-
чит, f'(xo) = O (строка 9), что требовалось доказать.
Обратное утверждение неверно. Нельзя утверждать, что если
в некоторой точке производная обратилась в нуль, то в этой
точке у функции экстремум. Кроме обращения производной
в нуль, мы наложим на функцию еще дополнительное ус-
ловие.
Теорема. (Достаточное условие экстремума функции.) Ес-
ли в некоторой точке производная обращается в нуль и, кроме
того, производная, проходя через нее, меняет свой знак, то в этой
точке функция достигает экстремума.
Доказательство. Рассмотрим заданную функцию
y — f (х) как закон движения материальной точки Р по оси у в зави-
симости от времени х (строка 3). Пусть f' (хо) = О. Если перед точ-
кой х0 имеем f' (х)>0, то до момента остановки скорость точки
Р была положительна (строка 10) и точка Р двигалась по оси у
вверх. Так как по условию производная, проходя через точку х0, ме-
83
няет свой знак, то после х0 имеем fz(x)<0, т. е. после момента
остановки скорость точки Р становится отрицательной (строка 11)
и точка Р движется вниз. Тогда в момент времени хо точка Р дости-
гает самого высокого положения на оси у и функция f принимает
максимальное значение (строка 8). Теорема доказана.
Вернемся еще раз к различию между необходимыми и доста-
точными условиями экстремума функции. Пусть производная
функции обратилась в нуль в некоторой точке х0 (необходимое
условие). С механической точки зрения это означает, что матери-
альная точка Р, закон прямолинейного движения которой зада-
ется исходной функцией, в момент времени х0 остановилась.
Ясно, что после мгновенной остановки точка Р могла начать
двигаться в обратном направлении, а могла продолжать двигать-
ся в том же направлении, что и раньше. В первом случае скорость
точки Р поменяла свой знак, а во втором нет. Соответственно
в первом случае положение точки Р на числовой оси достигло
экстремального значения, а во втором нет.
Мы выделили необходимое условие экстремума (обращение
производной в нуль) потому, что оно легко проверяется. Точки
экстремума надо искать прежде всего среди корней производной.
Этих корней, как правило, мало (или вообще нет), поэтому вы-
годно сначала ограничить число точек, «подозрительных на экст-
ремум», а потом уже проверять для них выполнение дополнитель-
ных, достаточных условий. Следует, кроме того, сказать, что
необходимое условие экстремума легко обобщается на более широ-
кий класс функций, чем тот, который мы изучаем в школе,
в то время как достаточные условия обобщаются не так
просто.
Поведение функции f вблизи точки х0, в которой производная
обратилась в нуль, представлено в таблице и на схеме VII.
Знак f' Поведение f в точке х0
перед хо после хо
+ — Максимум
— + Минимум
+ + Экстремума нет (перегиб)
— — Экстремума нет (перегиб)
Простейшими примерами, для которых реализуются случаи,
изображенные на схеме VII, являются функции у — ±х2 и у= ±х3
(точка х = 0).
84
2. Особые точки
Все доказанные нами теоремы
о связи свойств функции и ее про-
изводной опирались на предположе-
ние о том, что рассматриваемая функ-
ция дифференцируема, т. е. имеет
производную в каждой точке облас-
ти определения. На механическом
языке это означает, что материаль-
ная точка Р движется плавно, без уда-
ров и рывков, что позволяет в каж-
дый момент вычислить ее скорость.
Однако, как мы уже знаем, функ-
ция может иметь разнообразные
особые точки. В механической интер-
претации они будут соответствовать
моментам времени, когда нарушает-
ся плавность движения.
Нетрудно привести пример не-
плавного, скачкообразного движения.
Простейшим из них является движе-
ние мяча, падающего на пол и упру-
го отскакивающего от него. На рисун-
ке 44, а изображен закон движения
мяча — график зависимости высоты
h положения мяча над столом от
времени /. При отскоках от пола
(при й = 0) направление движения
мяча меняется (и функция достигает
минимума), однако в эти моменты
скорость мяча не равна нулю, каса-
тельной к графику h провести нельзя.
На рисунке 44, б изображен гра-
фик скорости мяча. В моменты от-
скока скорость мяча однозначно най-
ти нельзя — график скорости в эти
моменты имеет разрывы. Точки, в
которых производная не существует,
являются особыми точками функции. Приведем типичные примеры
функций, имеющих подобные особые точки.
1) у=\х\ (рис. 45). В точке х = 0 функция непрерывна,
однако производная в нуле не существует (при х<0 имеем
у — — х, у'= — 1; при х>0 имеем у = х, у'= + 1). На графике в
этой точке излом.
Аналогично при построении графиков функций типа y=\f(x)\
будут появляться изломы в точках, где f (х) = 0.
85
2) у=\[х. Так как у' =
то при х = 0 произ-
водная не существует (обращается в оо), касательная становит-
ся вертикальной (рис. 46). х = 0 является особой точкой.
К числу особых точек относят также точки разрыва самой
функции.
Наличие особых точек затрудняет исследование функции. Так,
производная функции У — ~ везДе отрицательна (у' == —-~<0 ) ,
однако к функции У = ~^~ нельзя применить признак монотонности
и сказать, что она везде убывает. Особая точка х = 0 «разрыва-
ет» область определения на два промежутка, на каждом из кото-
рых можно применять указанный признак, а на всей области
определения его применять нельзя.
Аналогично производная функции у=\х\ там, где она опреде-
лена, нигде не обращается в нуль, однако к функции нель-
зя применить необходимое условие экстремума и сказать, что она
не имеет экстремумов. Особая точка х = 0 является точкой мини-
мума этой функции.
3. Решение задач
Рассмотрим решение задач на применение производной к ис-
следованию функций. Основную роль в этом исследовании будут
играть корни производной — они нужны для нахождения проме-
жутков монотонности и точек экстремума. В то же время мы
заметили выше, что нужно также обратить внимание на особые
точки функции, так как они могут существенно повлиять на описа-
ние ее свойств. Для удобства мы введем вспомогательное по-
нятие «критическая точка», чтобы объединить с его помощью все
нужные нам точки — корни производной и особые точки.
Назовем критическими точками функции корни ее произ-
водной, точки, где производная не существует, а также точки,
где нарушается непрерывность функции.
86
Приведем алгоритм нахождения критических точек функции:
1) Найти точки разрыва функции у.
2) Найти производную у'.
3) Решить уравнение у' = 0.
4) Найти точки, в которых у' не существует.
Этот алгоритм можно уточнить и упростить для наиболее
часто встречающихся классов функций. Рассмотрим примеры.
1. у = х3 — Зх.
Эта функция является многочленом. Ее производная также
будет многочленом. Многочлен определен при всех значениях
аргумента. Поэтому алгоритм нахождения критических точек мно-
гочлена сводится к двум пунктам.
1) Вычисляем производную: г/' = 3х2 —3.
2) Решаем уравнение у' — О. Получим Зх2 — 3 = 0, х2=1,
X = ~ь~ 1.
Ответ: критические точки х\ = — 1, х2 = 1.
2. У=^-
V х— 1
Эта функция является рациональной, т. е. отношением двух
многочленов. Ее производная также будет рациональной функ-
цией, причем знаменатель производной — это квадрат знаменате-
ля исходной дроби. Поэтому точки, в которых знаменатель об-
ращается в нуль (в них функция не определена, имеет разрыв),
одни и те же — у функции и ее производной. Алгоритм
выглядит следующим образом:
1) Находим корни знаменателя:
х— 1 =0 о Xi = 1.
2) Вычисляем производную:
, _2х (х—1) —(х2-|-3) __х2 —2х —3
У (х—I)2 (х—I)2
3) Решаем уравнение у' = 0. Получим х2 — 2х — 3 = 0, х2 = — 1,
х3 = 3.
Ответ: критические точки х\ = 1, х2 = — 1, х3 = 3.
Теперь мы можем приступить к решению задач на нахождение
промежутков монотонности и точек экстремума (эти две задачи
тесно связаны между собой). Приведем соответствующий алго-
ритм:
1) Найти критические точки функции y = f(x) и нанести
их на числовую ось, выделив точки разрыва функции у.
2) Найти знак производной на каждом из получившихся про-
межутков.
3) Определить по знаку производной характер монотонности
у на каждом промежутке.
4) Выяснить наличие экстремума в каждой критической точке,
отличной от точек разрыва функции у.
87
Рис. 47 Рис. 48
Вернемся к приведенным ранее примерам.
1. у = х3 — Зх.
Наносим на числовую ось критические точки Х\ = — 1, х2=1.
Методом интервалов определяем знак у' на каждом промежутке.
Указываем характер монотонности у. Определяем наличие
экстремума (рис. 47).
Ответ: у возрастает на промежутках (— оо ; — 1 ] и [1; + оо) и
убывает на промежутке [—1; 1], при Х| = — 1 функция имеет
максимум, при х2=1 —минимум.
2. У=^.
х — 1
Наносим на числовую ось критические точки —1, 1,3, выде-
лив корень знаменателя Х| = 1. Методом интервалов определяем
знаки производной. Указываем характер монотонности и наличие
точек экстремума (рис. 48).
Приведем пример символической записи ответа.
Ответ:
У^
У—U
max у
min у
( — оо; — 1 ], [3; + оо);
[-1; 1). (1; 3];
при х= — 1;
при х = 3.
Часто требуется найти не только точки экстремума, т. е.
значения аргумента, при которых функция достигает максимума
или минимума, но и сами экстремальные значения, т. е. зна-
чения функции в точках экстремума. В последнем примере
Утах //min 6.
4. Построение графика функции
1) При построении графика функции прежде всего нужно уточ-
нить и записать ее область определения. Если не сделано спе-
циальных оговорок, то считается, что функция задана в своей
«естественной области определения». Для многочленов это вся
числовая ось /?, для рациональных функций это вся число-
вая ось за исключением тех точек, в которых знаменатель
обращается в нуль.
Найдя область определения, надо отметить ее на оси абсцисс.
Если эта область — вся числовая ось, то никаких отметок мож-
но не делать. Если эта область — промежуток числовой оси, то
полезно провести вертикальные прямые через его концы. Эти пря-
88
мне ограничат полосу, в которой будет лежать график функции.
Если отдельные точки не входят в область определения функ-
ции (например, корни знаменателя), надо отметить их на оси абс-
цисс и провести через них вертикальные прямые.
2) Для отыскания корней функции приравниваем ее к нулю,
решаем уравнение и наносим корни на ось абсцисс. Это первые
найденные нами точки будущего графика функции.
3) Находим промежутки монотонности и точки экстремума,
следуя алгоритму, описанному в предыдущем пункте.
4) Вычисляем значения функции в точках экстремума, а так-
же в других критических точках, где функция определена. Строим
эти точки на плоскости. При этом полезно сразу обозначить по-
ведение функции вблизи этих точек, используя стандартное изоб-
ражение точек экстремума, перегиба, излома (рис. 49).
5) Граничные точки. Если область определения состоит из
одного или нескольких промежутков, надо исследовать поведение
функции вблизи границ этих промежутков. При этом может пред-
ставиться несколько различных случаев:
а) В точке х0 функция «обращается в бесконечность». Ти-
пичный случай — корень знаменателя рациональной функции. Че-
рез точку х0 У нас уже проведена вертикальная прямая.
Около точки х0 график функции будет уходить вверх или вниз,
приближаясь к этой прямой. Для того чтобы узнать, вверх или
вниз уходит график, надо определить знак функции слева и спра-
ва от точки хо. Характерные случаи изображены на рисунке 50.
89
б) Граничная точка х0 входит в область определения функции
(типичный пример — точки х = ±1 для функции //=д/1 —х2) • На-
до вычислить значение функции в точке х0 и построить полу-
ченную точку.
в) В область определения функции входит бесконечный про-
межуток (вся числовая ось или промежуток вида (— оо; а],
[а; 4-оо)). В этом случае полезно представить себе поведение
функции при больших по модулю значениях аргумента или,
как говорят, «на бесконечности», т. е. при х^ — оо или х->4- оо.
На рисунке 51 изображены типичные случаи.
Найденной информации достаточно для того, чтобы, соединив
плавной кривой построенные точки, получить эскиз графика.
Пример 1. Построить график функции у — х3 — Зх.
Решение. Область определения — вся числовая ось R.
Находим корни функции: х3 —Зх = 0, х(х2 — 3) = 0, xi=0,
х2,з= ±д/3- Наносим корни на ось абсцисс. Находим и исследуем
критические точки (эта задача решена нами в предыдущем
пункте): в точке х= — 1 максимум, у (— 1) = 2; в точке х= 1 мини-
мум, у (1) = — 2. На бесконечности функция у ведет себя как куби-
ческая функция у = х3. Строим график (рис. 52).
Пример 2. Построить график функции у=х .
Решение. Область определения — вся числовая ось, кроме
точки х=1. (Можно записать так: х=/=1.) Строим прямую х=1.
Находим корни функции: г/ = 0, х2 4-3 = 0 — корней нет. Критичес-
кие точки (воспользуемся результатом вычислений предыдущего
пункта): х= —1—точка максимума; х = 3 — точка минимума.
Вычислив значения функции в этих точках, строим точки (3; 6) и
( — 1; —2). Находим знаки у слева и справа от точки х = 1. Так как
числитель дроби *положителен при всех х, то ее знак опре-
деляется знаком знаменателя: при х<1 функция отрицатель-
на, при х>1 положительна. Рисуем «хвосты» около прямой
90
Рис. 52
х2 -4-3
х=1. «На бесконечности» дробь ведет себя примерно так
х2
же, как дробь — = х, т. е. как линейная функция. Строим график
(рис. 53). Полезно дополнительно построить точку пересечения
графика с осью у:
х = 0, £/(0)=-3.
Контрольные вопросы
1. Обратите внимание на встретившиеся в тексте следующие
ключевые слова: критическая точка, экстремальное значение. При-
ведите примеры их использования.
2. Дайте интерпретацию на языке механики основных поня-
тий: х, у, y = f(x\ у'. Какая связь между направлением движе-
ния точки и ее скоростью?
3. Сформулируйте признак постоянства функции.
4. Сформулируйте признак монотонности функции.
5. Сформулируйте необходимое условие экстремума.
6. Сформулируйте достаточное условие экстремума.
7. Совпадают ли необходимое и достаточное условия экстре-
мума? В чем разница между ними?
8. Приведите пример функции, имеющей точку, для которой
выполняется необходимое условие экстремума, а экстремума в
ней нет.
9. Каков алгоритм нахождения критических точек функции?
10. Каков алгоритм нахождения промежутков монотонности и
точек экстремума?
91
§ 3. ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ
1. Скорость и ускорение
Понятие производной возникло как математическое описание
скорости движения. Поэтому важнейшим приложением произ-
водной является вычисление скорости. Скорость произвольно дви-
жущейся точки является векторной величиной, так как она опреде-
ляется с помощью вектора — перемещения точки за промежуток
времени. Рассмотрим сначала простейший случай — движение
точки по прямой. При прямолинейном движении точки ее по-
ложение, перемещение, скорость, ускорение и другие характерис-
тики, которые, вообще говоря, имеют векторный смысл, можно
задать одним числом, т. е. считать скалярными величинами.
Как и в предыдущем параграфе, составим таблицу перевода
понятий механики на язык математики, применяя более при-
вычные для физики обозначения.
Понятие на языке механики Обозначения и формулы Понятие на языке математики
Время t Независимая переменная, аргумент
Положение материаль- ной точки, ее координата X Зависимая переменная
Закон движения Функция
Приращение времени, интервал времени \t=t2—tl Приращение аргумента
Перемещение Дх = х(/2) —х(6) Приращение функции
Средняя скорость Ax Ucp“a7 Отношение приращения функ- ции к приращению аргу- мента
Скорость (мгновенная) V (/)=lim vcp V (/)=*' (/) Производная
Закон, описывающий равномерное движение Ax — = v = const А/ x —x0 = u (/ —/о) Линейная функция
Скорость равномерного движения v=x' = k Коэффициент при /, угло- вой коэффициент прямой
92
П родолжение
Понятие на языке механики Обозначения и формулы Понятие на языке математики
Закон, описывающий равноускоренное движе- ние Ли — = а = const Л/ at2 х—~2~ +Уо/4-Хо Квадратичная функция
Скорость равноускорен- ного движения v = x' = at-\-v0 Линейная функция
Ускорение равноускорен- ного движения a = v' Удвоенный коэффициент при /2
Обратим внимание на обозначения. В физике производная
по времени обычно обозначается не штрихом, а точкой. Более рас-
пространена запись и = х (читается: «Икс с точкой»).
Ускорение произвольного движения определяется как скорость
изменения скорости, т. е. как производная скорости по времени:
a = v' = v. Так как скорость есть производная координаты, а уско-
рение есть производная скорости, то ускорение называют второй
производной координаты и обозначают так: а = х" = х.
Через координату точки х = х (/) и ее производные можно выра-
зить другие механические величины:
сила F — т-а = т-х (т — масса),
импульс P = mv = тх,
кинетическая энергия £ =
2. Скорость криволинейного движения
Пусть точка А движется по криволинейной траектории.
Обозначим координаты точки А в момент времени t через
х (/) и у (/). Эти координаты зависят от времени t и являются тем
самым функциями от t. Рассмотрим мгновенную скорость движу-
щейся точки А в момент времени /. Вектор мгновенной скорости
v направлен по касательной к траектории в точке А (рис. 54). Ко-
ординаты вектора и тоже зависят от
времени t и меняются, вообще говоря,
при переходе от одной точки траек-
тории к другой. Покажем, что коор-
динаты вектора скорости v точки А
равны х' (/) и у' (/), где х' и у' — произ-
водные функций х и у в точке /.
Рис. 54
93
За время kt точка А переместится в точку В с координатами
—
+ и + Рассмотрим вектор перемещения АВ. Вектор
—> —>• —>•
АВ является разностью векторов О В и ОД, и его координаты поэ-
тому будут разностями координат этих векторов. Следовательно,
—>•
координаты вектора АВ равны х (/Д- Д/) — х (/) и у (/ Д-Д/) — у (/).
Напомним, что средней скоростью называется отношение пере-
мещения ко времени. Таким образом, вектор средней скорости
Гв
равен —, и поэтому его координаты равны
СР \ д/ ’ д/ ) ’
Вектор средней скорости при уменьшении Д/ приближается
к вектору мгновенной скорости в момент времени t. (Это значит,
что векторная разность между мгновенной скоростью и средней
скоростью может быть сделана сколь угодно малой за счет вы-
бора Д/.)
По определению производной при уменьшении Д/ величина
x(z+^)~x(z) приближается к х' (/), а приближается
к у' (t). Таким образом, координаты вектора мгновенной ско-
рости в момент времени t равны х' (/) и у' (/).
Пример. Рассмотрим движение снаряда, выпущенного под
углом а к горизонту с начальной скоростью vq. Снаряд, если пре-
небречь сопротивлением воздуха, будет двигаться по параболе.
Вектор скорости v направлен по касательной к параболе. Можно
вычислить координаты скорости, зная координаты снаряда:
х (/) = (и0 cos а) /,
z/(/) = (u0 sin а) t—
Мы знаем, что вектор скорости v имеет координаты
(х' (/); у' (/)). Вычисляем производные:
x' = uocosa; y' = vo sin a — gt.
Эти же равенства можно получить из известной векторной фор-
мулы
V = Vo + gt.
При движении точки по окружности радиуса R с постоянной
угловой скоростью со величина скорости и = (о/? остается по-
стоянной, однако направление ее меняется. Зная, что вектор v на-
правлен по касательной, мы сможем выразить координаты и,
а тем самым подсчитать производную синуса и косинуса.
94
3. Дифференциал
Основой разнообразных физических приложений производной
является понятие дифференциала. Дифференциалом функции на-
зывают произведение ее производной на приращение аргумента.
Пусть нам задана функция y = f(x). Ее дифференциал обоз-
начают через dy (или можно писать df). По определению
dy = f' (х) Дх.
Рассмотрим функцию у = х. Так как производная этой функ-
ции постоянна и равна единице, то дифференциал этой функции
равен Дх, т. е. для независимой переменной верно равенство
dx = kx. Поэтому дифференциал функции записывают обычно
в виде
dy = f' (х) dx,
из этой записи происходит одно из обозначений производной:
г
которое можно понимать как отношение дифференциалов.
Какими свойствами обладает введенное нами понятие диффе-
ренциала функции?
1) Дифференциал функции — это главная часть ее прира-
щения.
Сравним приращение функции Дг/ и ее дифференциал dy.
На рисунке 55 видно, что, чем меньше Дх, тем ближе \у к dy.
Действительно, разность \y-dy преобразуется так:
\y — dy = \y — f’ (х) \х = \х Q—f' (*)) •
По определению производной при стремлении Дх к нулю разность
(х) тоже стремится к нулю. При умножении на Дх мы по-
лучим выражение, еще быстрее при-
ближающееся к нулю. Таким обра-
зом, приращение функции отличается
от ее дифференциала на такую функ-
цию, которая стремится к нулю еще
быстрее, чем Дх. Поэтому и говорят,
что дифференциал есть главная часть
приращения функции.
2) Дифференциал функции — это
линейная функция приращения ар-
гумента.
Если мы зафиксируем точку
А (х0; уо) на графике функции
y = f (х) и обозначим f' (х0) через fe, то
на равенство dy = kdx можно смот-
95
реть как на линейную зависимость
между dy и dx. Если через точку А мы
проведем новые оси координат (их
можно обозначить через dx и dy),
то график этой зависимости будет
касательной к графику функции
f в точке А (х0; уо) (рис. 56). Можно
сказать, что дифференциал функции
f — это линейная функция, графи-
ком которой является касательная
к графику f. Геометрически на соот-
ношение dy = f'(xo)dx можно смот-
реть как на уравнение касательной
к графику функции /, записанное в сис-
теме координат (dx; dy). Эта система координат получается из
исходной параллельным переносом начала координат в точку
А (х0; f/о). Это позволяет получить уравнение касательной в исход-
ных координатах в следующем виде:
у — yo=f' (Хо) (х — Хо).
Вывод уравнения касательной легко запомнить следующим об-
разом. Прежде всего касательная проходит через заданную точку
(х0; уо) на графике функции y = f(x). Поэтому ее уравнение мож-
но записать в виде у — yo = k (х —х0). Угловой коэффициент k равен
значению производной в заданной точке: fe = f'(x0).
4. Дифференциал в физике
Для вычисления дифференциала в физике достаточно знать,
что дифференциал — это главная часть приращения функции, ли-
нейно зависящая от приращения аргумента. В примерах мы из фи-
зических соображений будем получать равенства вида dy = kdx и
делать вывод о том, что k — это производная у по х.
1) Работа. Рассмотрим работу, которую совершает заданная
сила F при перемещении по отрезку оси х. Если сила F
постоянна, то работа А равна произведению F на длину пути.
Если сила меняется, то ее можно рассматривать как функцию от
х, т. е. F = F (х). Приращение работы АД на отрезке [х; х Д- dx] нель-
зя точно вычислить как произведение F (х) dx; так как сила меняет-
ся на этом отрезке. Однако при маленьких dx можно считать,
что сила меняется незначительно и произведение представляет
собой главную часть АД, т. е. является дифференциалом ра-
боты: dA=F (х) dx. Таким образом, силу можно считать произ-
водной работы по перемещению.
2) Заряд. Пусть q — заряд, переносимый электрическим током
через поперечное сечение проводника за время t. Если сила тока
I постоянна, то за время dt ток перенесет заряд, равный Idt.
96
При силе тока, изменяющейся со временем по некоторому закону
1 = 1 (/), произведение / (/) dt дает главную часть приращения заря-
да на маленьком отрезке времени [/; /-+-Д/], т. е. является диф-
ференциалом заряда: dq = I (/) dt. Тем самым сила тока является
производной заряда по времени.
3) Масса тонкого стержня. Пусть есть неоднородный тонкий
стержень. Если ввести координаты так, как показано на рисунке
57, то можно рассмотреть функцию m = m (/) — массу куска стерж-
ня от точки О до точки I. Неоднородность стержня означает,
что его линейная плотность не является постоянной, а зависит от
положения точки I по некоторому закону р = р(/). Если на ма-
леньком отрезке стержня [/; l-\-dl] мы будем считать плотность
постоянной и равной р (/), то произведение р (/) dl дает нам диф-
ференциал массы — dm. Это значит, что линейная плотность —
это производная массы по длине.
4) Теплота. Рассмотрим процесс нагревания какого-нибудь
вещества и будем вычислять количество теплоты Q (Г), которое
необходимо, чтобы нагреть 1 кг этого вещества от 0° до Г° (по
Цельсию). Зависимость Q = Q(7) очень сложна и определяется
из опыта. Если бы удельная теплоемкость с данного вещества
не зависела от температуры, то произведение cdT дало бы нам
изменение количества теплоты. Считая на малом отрезке
[Г; 7 + dT] удельную теплоемкость постоянной, мы получим диф-
ференциал теплоты dQ как c(T)dT. Поэтому теплоемкость —
это производная теплоты по температуре.
5) Работа как функция времени. Нам известна характеристика
работы, определяющая ее скорость по времени,— это мощность.
При работе с постоянной мощностью N работа за время dt рав-
на Ndt. Это выражение представляет собой дифференциал ра-
боты, т. е. dA=N (/) dt и мощность выступает как производ-
ная работы по времени.
Все приведенные нами примеры были построены по одному и
тому же образцу. В каждом примере шла речь о связи между
тремя величинами, уже знакомыми нам из курса физики: работа,
перемещение, сила; заряд, время, сила тока; масса, длина, линей-
ная плотность и т. д. Во всех примерах одна из этих величин высту-
пала как коэффициент пропорциональности между дифференциа-
лами двух других, т. е. каждый раз появлялось соотношение
вида dy = k(x)dx. На такое соотношение можно смотреть как на
способ определения величины k (х) — тогда k (х) находится (или
определяется) как производная у по х. Этот вывод мы и зафикси-
ровали в каждом примере. Возможна и обратная постановка
вопроса: как найти зависимость и от
х из заданного соотношения между 1
их дифференциалами? Эту задачу
мы рассмотрим в главе, посвященной О L х
интегрированию. Рис. 57
4 Заказ 836 97
5. Задачи на максимум и минимум
Большую часть своих усилий человек тратит на поиск наилуч-
шего, или, как часто говорят, оптимального, решения поставлен-
ной задачи. Как, располагая определенными ресурсами, добиться
наиболее высокого жизненного уровня, наивысшей производитель-
ности труда, наименьших потерь, максимальной прибыли, ми-
нимальной затраты времени — так ставятся вопросы, над которы-
ми приходится думать каждому члену общества. Не все такие
задачи поддаются точному математическому описанию, не для всех
из них найдены короткие пути решения. Однако часть таких задач
поддается исследованию с помощью методов математического
анализа — это задачи, которые можно свести к нахождению
наибольшего или наименьшего значения функции.
Наиболее важной для приложений ситуацией является следую-
щая: функция f задана на отрезке [а; Ь] и имеет производную во
всех точках этого отрезка. Тогда для нахождения наибольшего
и наименьшего значений этой функции надо поступить так:
найти критические точки (в данном случае корни производ-
ной), вычислить значения функции во всех критических точках и
на концах отрезка, из найденных значений найти наибольшее
и наименьшее.
Функция, график которой изо-
бражен на рисунке 58, задана на
отрезке [а; Ь] и принимает наимень-
у шее значение в точке с (одной из то-
чек локального минимума), а наи-
/ большее значение в точке b (край-
а. / ней точке области определения).
|\ с / \ /_____Встречаются и другие случаи,
д £ х которые можно представить себе по
рисунку 59. Предлагаем вам само-
стоятельно подумать над тем, что
происходит с наибольшим и наимень-
Рис. 58 шим значениями этих функций.
Рис. 59
98
Примеры.
1. Найти наибольшее и наименьшее значения функции
у= 1 — 2х — х2,
заданной на [ — 2; 2].
Находим производную: £/'=—2 — 2%, ее корни (у' = 0 при
х= — 1). Вычисляем значения у в точках —2, —1, 2:
X — 2 -1 2
У 1 2 — 7
Получаем £/Наиб = 2, ^Наим = —7. При этом наибольшее значение
функция принимает в точке локального максимума, а наимень-
шее — на правом конце отрезка.
2. Найти наибольшее и наименьшее значения функции
r/ = sin2 x-j-4 sin %4-2.
Для решения этой задачи не надо знать никаких свойств
функции £/ = sinx, которую мы будем изучать позже, кроме того,
что |sinx|^l. Сделаем замену z = sinx и рассмотрим функцию
£/ = z24-4z4-2. Ее область определения — отрезок [—1; 1], совпа-
дающий с множеством значений функции z = sin х. Находим про-
изводную у как функции от z:
у' = 2z + 4 = 0 о z = — 2.
Заметим, что критическая точка не принадлежит отрезку [—1; 1],
поэтому нам надо сравнить значения у только на концах
отрезка:
Z -1 1
У -1 7
Итак, £/наИб 7, £/наим 1 •
Многие прикладные задачи сводятся к нахождению наиболь-
ших и наименьших значений функций, заданных на отрезке. Та-
кие задачи часто называют задачами на максимум-минимум.
Приведем примеры.
Задача 1. Из прямоугольного листа жести размером 5X8
надо изготовить открытую коробку наибольшего объема, вырезая
квадратные уголки так, как показано на рисунке 60.
99
Рис. 60
Обозначим через х длину стороны вырезаемого квадрата.
Тогда длины сторон прямоугольника уменьшатся на 2х и объем
коробки будет равен:
V = х (8 - 2х) (5 - 2х)= 4х3 - 26х2 + 40х.
При этом х может меняться в следующих пределах:
0^х^2,5. Заметим сразу, что в крайних точках отрезка [0; 2,5]
объем равен нулю. Находим критические точки:
V' = 12x2 —52х + 40, V' = 0 при х1 = 1, х2=^-.
О
Отметим, что значение х2 не принадлежит области определе-
ния. При х=1 объем максимален: Vmax=18.
Задача 2. В данный шар вписать цилиндр наибольшего
объема.
Обозначим через R радиус шара, а через г и h соответствен-
но радиус основания и высоту вписанного цилиндра. Как видно
из рисунка 61, выполняется соотношение —\-r2=R2.
Будем считать h переменной. Тогда
V = nr2/i = n (jR2 -у-) /z —n/?2/z — ——.
Заметим, что h меняется в пределах от 0 до 2/?, причем на
концах отрезка цилиндр вырождается, объем его равен нулю.
Находим критические точки:
V'=0, л/?2—4~лЛ2 = 0, h=A.
4 д/З
При этом значении h объем будет максимальным:
]/ _тт/?3. 4л рЗ
Замечания.
1. Если бы мы стали считать переменной не Л, а г, то получили
бы /г = 2 д//?2 — г2 и V = 2nr2 д//?2 —г2. Находить производную V
(как функции от г) стало бы труднее. Но в этом случае можно
воспользоваться следующим очевидным соображением: функции V
100
и V2 принимают наибольшее значение одновременно. Тогда мы
рассмотрели бы новую функцию W= V2 = 4n2r4 (/?2 —г2) и без тру-
да нашли бы ее критические точки.
2. Функции V, kV (fe>0), V + c, V2 (V>0) принимают наиболь-
шее значение одновременно. Это замечание позволяет при вычис-
лении производных убирать постоянные множители, слагаемые и
радикалы.
Задача 3. Над центром круглого стола радиуса г висит лам-
па (рис. 62). На какой высоте следует подвесить эту лампу,
чтобы на краях стола получить наибольшую освещенность?
Из физики известно, что освещенность обратно пропорциональ-
на квадрату расстояния до источника света и пропорциональна
синусу угла наклона луча света к освещаемой маленькой пло-
щадке. Иными словами,
л /
= , h — расстоя-
где Е — освещенность на краю стола, sin ср
ние от лампы до стола.
Вместо функции E = fe--------—- рассмотрим функцию Г=
(Л2 + '2)У
= -^- . При этом вместо h можно взять переменную
2 = h2 и найти критические точки Т как функции от z:
Т z (z + r2)3 — z-3-(z + r2)2 z + r2 — 3z .
“(7+77’ (z+r2)6 “ (^+r2)4 ’
T' = 0, r2 —2z = 0, z=4-> t. e. h.2=^- и h=-!— .
2 2 V2
Итак, освещенность максимальна, если й=-“, т. е. если tg <р =
r V2 ’
101
6. Приближенные формулы
Одним из важнейших приложений производной является воз-
можность приближенно вычислять значения функций. Пусть нам
дана функция y = f(x) и точка хо, значение функции в которой из-
вестно: yo=f(xo). Мы хотим вычислить приближенно значение
функции в точке х, близкой к х0.
Если мы знаем приращение функции Ду на отрезке [х0; х], то
точное значение f (х) получается из уо прибавлением Ду, равного
f (х) — уо. Приближенные формулы основаны на замене Ду другим
выражением, которое вычисляется более просто. Замена Ду на ли-
нейную функцию dy, т. е. замена приращения функции ее диффе-
ренциалом дает наиболее простые приближенные формулы. При
замене выражения его приближенным значением используется
знак приближенного равенства
Таким образом, основная, наиболее простая формула для при-
ближенных вычислений значения функции может быть записана
так: ky^dy, или раскрывая более подробно: f (х) — yo~f' (х0) Дх.
Приведем другие виды записи приближенной формулы:
y»yo + dy,
У~Цо + [' (х0)(х—х0).
Геометрически замена Ду на dy означает, что вблизи точки х,
мы вместо функции y = f (х) берем линейную функцию, т. е. малень-
кий отрезок графика заменяем касательной. Рассмотрим при-
меры.
1. Дана степенная функция у=хп. Зафиксируем точку х« и
применим полученную выше формулу:
(хо+Дх)" « хо + nxS ~1 Дх.
Например,
(1,0003)5=(1 + О,0003)5 № 1 + 5 • 0,0003 = 1,0015;
(2,0001 )7 = (2 + 0,0001 )7» 27 + 7 • 26 - 0,0001«
«128 + 0,0448 = 128,0448 = 128,05 ± 0,01.
Ту же формулу можно применить и для приближенного вы-
1
числения корней, учитывая что д/х = хл . Получим
11 1_!
д/х0 + Дх=(х 4- Дх)п ~ хоп хоп • Дх
Например,
।
Л/0Д99=(1 —0,001)2 « 1 --у-0,001 =0,9995;
1 _L .
^/27,0003 =(27+0,0003)3 «273 +у--27 3 -0,0003 =
=3 + ‘ ‘ 0,0003 = 3,00001 ± 0,00001.
о У
102
Полезно запомнить формулы при хо=1:
(1 + Ах)п« 1 +«Ах;
VT+Ax«l+-i-Ax
2. Дана функция у=-^~. Получаем приближенную формулу:
1 1 I А
------------ТГ-
ХО 4- Дх Хо-Хо
3. Вычислить приближенно значение функции в точке
х=3,02.
Находим дифференциал функции у:
_____/ х ____х-Н—х^ч___dx
ау\х-{-\ ) ~ (х+1)2 аХ““(х+1)2
Выбираем начальную точку х0==3 и подставляем ее в производ-
ную:
dy=(3+i)2=76’dx
Подставляем значение dx:
Ay«dy=-^ -0,02 «0,001,
f (х)« f (хо) + dy « 0,750 + 0,001 = 0,751.
Контрольные вопросы
1. Обратите внимание на встретившиеся в тексте следующие
ключевые слова и обозначения ^вторая производная, дифференци-
ал, уравнение касательной, х, х, dy, Ny^dy. Приведите примеры
их использования.
2. С помощью какой функции описывается закон равномерного
движения?
3. С помощью какой функции описывается закон равноуско-
ренного движения?
4. Какой физический смысл имеет коэффициент при квадрате
аргумента в записи квадратичной функции?
5. Как вычислить силу, приложенную к материальной точке,
если известен закон ее движения?
6. Как вычислить энергию материальной точки, если известен
закон ее движения?
7. Как вычисляются координаты вектора скорости криволиней-
ного движения?
8. Что такое дифференциал?
9. Какие свойства приращения функции отражены в понятии
дифференциала?
юз
10. Запишите уравнение касательной, проходящей через задан-
ную точку графика функции?
11. Приведите примеры записи связи между физическими вели-
чинами в дифференциалах.
12. С помощью какой замены можно получать приближенные
формулы?
13. Каков геометрический смысл замены приращения функции
ее дифференциалом?
14. Приведите приближенную формулу для вычисления (1 +*)п
при маленьких значениях х.
15. Как будет выглядеть предыдущая формула при конкретных
часто употребляемых значениях п? Приведите примеры.
16. Каков алгоритм нахождения наибольшего и наименьшего
значений функции, заданной на отрезке?
17. Какие преобразования функции могут облегчить нахожде-
ние ее наибольшего и наименьшего значений?
18. Приведите примеры постановок задач на максимум-мини-
мум, связанных с экономикой.
ЗАКЛЮЧИТЕЛЬНАЯ БЕСЕДА
1. Линеаризация
Основная идея Ньютона состояла в следующем. Равномерное
движение хорошо известно — его скорость постоянна и легко вы-
числяется. Пусть движение неравномерно. На коротком отрезке
времени оно приблизительно может считаться равномерным. Так,
стрелка спидометра автомашины не стоит на месте, однако мы
можем пренебречь ее колебанием, если возьмем достаточно малый
промежуток времени.
Примерно так же рассуждал Лейбниц. На малом участке кри-
вая неотличима от Прямой. Так, секущая, проведенная через две
точки кривой, меняет свой наклон, однако при сближении этих
точек изменением наклона секущей можно пренебречь.
Язык функций позволяет максимально сблизить механическую
и геометрическую точки зрения. Начертим график зависимости пу-
ти s от времени t. На маленьком участке этот график очень
близок к отрезку прямой. Замена криволинейного участка графика
на прямолинейный означает замену неравномерного движения
равномерным и одновременно замену участка кривой отрезком
касательной. Можно сказать, что вблизи выбранной точки (или,
как говорят математики, локально) мы заменяем изучаемую функ-
цию линейной. Производная помогает среди всех линейных функ-
ций выбрать ту, которая дает наилучшее локальное приближе-
ние к исходной функции.
Процесс «выпрямления» функции, который хорошо виден, ког-
да мы смотрим как бы в микроскоп на маленький участок ее
104
графика, математики называют линеаризацией. Линеаризация
позволяет приближенно описывать сложные зависимости с по-
мощью линейных.
Линеаризация зависимостей основана на следующем правиле,
которое мы назовем принципом дифференцируемости: малое из-
менение одной величины влечет за собой пропорциональное
изменение другой.
Заметим, что если некоторая функция удовлетворяет принципу
дифференцируемости, то она удовлетворяет и упоминавшемуся
ранее принципу непрерывности. Действительно, если Az//г Ах, то
при Дх->0 имеем и Az/^-O, т. е. малому изменению аргумен-
та отвечает малое изменение функции.
Как следует понимать приближенное равенство Az/^Mx?
Этот вопрос можно поставить более точно: как оценить степень
близости Az/ и линейной функции &Дх? Это важно для практики:
опасно производить все вычисления на глазок — надо суметь оце-
нить погрешность, взвесить ошибку, получаемую при пользова-
нии приближенными формулами. Научиться делать такие оценки
важно и в теоретическом отношении: с их помощью легко обос-
новать правила предельных переходов, которые мы используем
при вычислении производной.
Возьмем функцию у = ахI 2. Вычислим приращение функции:
&у = а (% + Дх) — ах2 = 2ахДх + а (Дх)2. Перепишем это равенство
так: Az/ —2ахДх = а (Дх)2. Так как 2axAx = dz/, то получается
\у — dy = а (Дх)2 или, переходя к модулям, |Ду — dy\ = |а| • | Дх|2.
Мы получили не просто оценку погрешности, а равенство, позволя-
ющее узнать, насколько приращение функции отличается от диф-
ференциала. При оценке погрешности полезно пользоваться сле-
дующими правилами, доказать которые нетрудно:
I +{/г)К I Д1/1 I +1 Д^/21;
|Д (су)\< |с| • |Ду|;
I Д (f/lf/2)l < lyil • I Д£/г1 +lf/2l -1Д//11.
Заменяя Дг/ на dy, мы допускаем определенную погреш-
ность. Нельзя ли ее уменьшить? Иными словами, если нас не
устраивает точность вычислений, получаемая при замене Az/ на dy,
то как увеличить эту точность?
Пусть, например, мы хотим вычислить А/ГО. Возьмем за на-
чальное приближенное число 2 = ^/8. Сделаем простые преобразо-
вания:
V10 = V8 + 2 = V8 (1+0,25) = 2 V1 +0,25.
Первое приближение корня по известной нам формуле дает:
V10«2 (1 +-Z--0,25 ) «2,17.
Как получить лучшее приближение? Проведем рассуждение в об-
щем виде. Нужно вычислить y = ^j\-\-h. (Для удобства мы пишем h
105
вместо Дх. В нашем примере й = 0,25.) Увеличения точности
можно достичь, прибавляя последовательно к начальному значе-
нию у= 1 слагаемые, пропорциональные й, й2, h3 и т. д., т. е. пред-
ставляя УГ+й в виде УТ+Л= 1+Й|Л4-Й2Й2 + й3Л3... . Как из
этого равенства найти коэффициенты йь £2, йз, .? Для этого есть
замечательный способ, открытый сразу вслед за созданием в
XVII в. дифференциального исчисления. Продифференцируем обе
части (по переменной й):
_2_
2_(1 4-й) 3 =*) 4-2M + 3fe3/i2+4M3 + ... •
□
Положив в этом равенстве й = 0, получим известный нам ранее
коэффициент й|=у-.
Но точно так же можно найти и следующие коэффициенты.
Продифференцируем еще раз:
__5_
Т'(—г)(1+/г) 3 =2^ + 3-2-Ы + 4-3-М2 + ... •
Положив /i = 0, получим —|"=2/г2, откуда k2 =—Мы полу-
чили гораздо более точную формулу:
U2.
Возвращаясь к вычислению УШ, получим:
V10 « 2 (1 +-|~ 0,25 - 1 0,06 ) а* 2,167 - 0,007 = 2,160,
где уже имеем точность порядка 0,01. Замечательно, что точность
можно повышать при помощи описанного приема столько раз,
сколько мы захотим. Еще раз продифференцируем:
__8
Т'(-т)(_т)(1+А) 3==6йз + 24М + -...
к
Подставляя й = 0, получаем й3«—«0,0617, и новая добавка
равна «0,0617 й3. При й = 0,25 это слагаемое имеет уже порядок
0,001.
Получаемые описанным методом формулы носят имя Б. Тейло-
ра (1685—1731) —английского математика, ученика Ньютона.
Приведем несколько формул Тейлора:
^Г+7,= 1+ХА-Х„-+Аа>_
106
К ним можно добавить полезную простую формулу суммы беско-
нечной геометрической прогрессии:
2. Производная сложной функции
В § 1 мы вывели правило вычисления производной при линей-
ной замене аргумента. Нетрудно вывести правило вычисления про-
изводной при произвольной замене аргумента.ДЛусть функция h
представлена как композиция функций f и g, т. е. h(x)=f (g(x)).
Можно обозначить g (х) через у, a f (у) через г. Для вычисления
производной переменной z составим отношение —. Домножив и
разделив его на Дг/, получим • При стремлении Дх к ну-
лю Дг/ тоже будет стремиться к нулю (принцип непрерывности).
Первая дробь будет стремиться к производной функции z (у), т. е.
к f' (у). Вторая дробь будет стремиться к производной функции
у(х), т. е. к g'(х). Совершая предельный переход, получаем:
Л' (x)=f' (g)'g' (*)=[' (g (*))•£' (4
Пример. Вычислить производную функции z = (x2-H)5-
Представим z как сложную функцию: z = z/5, где у = х24-1.
Применяя формулу производной сложной функции, получаем:
z' = 5t/4-t/' = 5 (х2 + 1)4-2х= 10х (х2 +1)4-
Правило дифференцирования сложной функции можно при-
менить для вычисления углового коэффициента касательной к
кривой, заданной уравнением. Например, рассмотрим касатель-
ную, проходящую через точку -|-) окружности х2+у2=1
(рис. 63). Конечно, можно выразить у через х и найти произ-
водную. Гораздо проще продифференцировать уравнение окруж-
107
ности по переменной х, считая уравнение тождеством, получаю-
щимся после подстановки в него вместо у его выражения через
х:
х2 + (у(х))2=1.
Получаем 2х-\-2уу' = 0, откуда */'= — у-. Подставляя коорди-
наты точки Р, получаем угловой коэффициент касательной:
3. Гладкость функции
Посмотрим на рисунок 64. Приведенные на нем графики
функций разбиваются на отдельные части, каждая из которых
является гладкой кривой, т. е. кривой, в каждой точке которой
можно провести касательную. Точки стыковки отдельных гладких
частей являются, как говорят, особыми точками. Поведение
функций вблизи особых точек изучают отдельно. В первой
главе мы уже обращали внимание на возможные особенности, свя-
занные с нарушением в точках стыковки принципа непрерыв-
ности. Функции, имеющие конечные разрывы (рис. 64, а, б), встре-
чаются при описании процессов, при которых происходит вклю-
чение и выключение сигнала (работа электрической сети, прием ра-
диопередач и т. п.). Бесконечные разрывы (рис. 64, в) встреча-
ются в приложениях реже, однако они появляются при идеализиро-
ванных, предельных описаниях некоторых процессов (например,
взрывов).
Нарушение гладкости в случае функций, изображенных на
рисунке 64, г, д, имеет другую природу. Здесь сама функция не-
прерывна, но отдельные части ее графика соединены между собой
негладко: если вы попробуете построить графики производных этих
функций, то увидите, что в выделенных точках производная не
определена.
Изучение свойств функции и построение ее графика яв-
ляются одним из самых замечательных приложений производ-
ной. Этот способ исследования функции, открытый более 300 лет
назад, неоднократно подвергался тщательному анализу. Основ-
ная причина, заставляющая вновь и вновь возвращаться к прос-
тому, казалось бы, вопросу о связи свойств функции и ее произ-
водной, состоит в том, что в приложениях математики приходилось
иметь дело со все более и более сложными функциями, появляю-
щимися при изучении новых явлений. Появились исключения из
разработанных математикой правил, появились случаи, когда
вообще созданные правила не годились. Скажем, появились функ-
ции, не имеющие ни в одной точке производной. Трудно пред-
ставить себе движение, при котором ни в один момент времени
нельзя вычислить скорость. Однако, отправляясь от броуновско-
108
Рис. 64
го движения мельчайших частиц, такую математическую модель
построить можно. Рассмотренные нами методы доказательства
правил исследования функций, основанные на простых механичес-
ких и геометрических соображениях, близки к тем, которые были
созданы еще Ньютоном и Лейбницем. Они уже непригодны в более
сложных ситуациях и требуют уточнений.
Новые теоремы в математике доказывают путем логического
рассуждения (вывода) с использованием ранее доказанных
теорем или некоторых исходных простых утверждений (аксиом),
которые мы принимаем без доказательства. В наших рассужде-
ниях о связи свойств функции и ее производной роль таких исход-
ных утверждений играли простые соображения механики, которые
мы приняли без доказательства. Например, мы посчитали за оче-
видное то, что при прямолинейном движении направление ско-
рости совпадает с направлением перемещения.
Использование модели (интерпретации) для проведения мате-
матического доказательства требует умения переводить мате-
матические понятия на язык этой модели (или знать правила
перевода). Так, при использовании механической модели мы
составили таблицу такого перевода.
Преимущество проведенных нами доказательств о связи
свойств функции и ее производной состоит в том, что они позво-
лили нам получить новые содержательные утверждения (напри-
мер, о связи монотонности функции и ее производной), исходя из
более простых и более очевидных утверждений механики.
Недостатком их является то, что перевод теоремы на язык
механической модели сделан описательно, без формулировки точ-
109
них определений и аксиом, опираясь на наши индивидуальные
представления о механическом движении и его характеристиках.
То же самое относится и к пояснениям теорем с помощью
геометрической модели. При таких пояснениях мы опираемся на
геометрические представления о расположении касательной.
Однако в приложениях математики стремятся как раз к об-
ратному. Для исследования какого-либо реального процесса или
явления (например, механического движения) переводят основные
понятия и свойства этого явления на язык математики. Затем
проводятся математические рассуждения — выводят новые фор-
мулы, связывающие введенные величины, доказывают их новые
свойства и т. п. Наконец, возвращаются к исходному явлению и
смотрят на то, что дают для его изучения полученные математи-
ческие теоремы. Усилиями великих математиков XIX в. О. Коши
(1789—1857) и К. Вейерштрасса (1815—1897) была построена
строгая теория математического анализа, основанная на понятии
предела. Ознакомиться с этой теорией можно с помощью любого
учебника по математике, предназначенного для высших учебных
заведений.
Контрольные вопросы
1. В чем состоит идея линеаризации функции?
2. В чем состоит принцип дифференцируемости функции?
3. Какова связь между дифференцируемостью и непрерыв-
ностью функции?
4. Как можно добиться улучшения приближения функции?
5. Приведите правило дифференцирования сложной функции.
ЗАДАЧИ К ГЛАВЕ II
Определение производной и ее вычисление
Механический смысл производной
1°. Для заданного закона движения точки $ = $(/) вычислите
среднюю скорость иср на указанных отрезках времени:
1) s(/) = 3f-l, [0; 1], [0; 5], [-3; 3], [fi; /2];
2) s(/) = /2 + 3f, [0; 1], [-1; 1], [2; 5]; [6; t2]\
3) s(0=77T’ [0; 1]’ [0; 31 [1; 91 M
2°. Зависимость пути s от времени t задана графиком (рис. 65).
Найдите среднюю скорость движения на следующих отрезках
времени: [0; 1], [1; 2], [2; 3], [3; 4], [0; 2], [2; 4], [0; 4].
3°. Точка движется прямолинейно по закону s = 3/4-2. Найдите:
1) среднюю скорость на отрезках [2; 2,2], [2; 2,02], [3; 4], [3; 3,3];
2) мгновенную скорость при / = 2, / = 3.
по
4°. Точка движется прямолинейно по закону s = t2. Найдите:
1) среднюю скорость на отрезках [1; 2], [1; 1,2], [1; 1,02],
[2; 2,02];
2) мгновенную скорость при /=1, t = 2.
5°. Зависимость пути от времени s = s(/) задана графиком
(рис. 66). Найдите среднюю скорость движения тела для
отрезков времени: [0; 4], [2; 4], [3; 4], [3,5; 4]. Чему
равна мгновенная скорость в момент времени / = 4?
6. На рисунке 67 изображен график зависимости перемещения х
от времени /.
1) На каких отрезках средняя скорость движения была
наибольшей?
2) В какой точке мгновенная скорость движения была
наибольшей?
3) Приведите примеры отрезков времени, на которых сред-
ние скорости одинаковы.
4) Приведите примеры моментов времени, в которые мгно-
венные скорости одинаковы.
7°. По графику зависимости пути s от времени t (рис. 68)
вычислите скорость в моменты времени / = 0, t — 1, / = 2, / = 3.
Постройте график скорости.
111
8. На рисунке 69 изображена зависимость перемещения х тела от
времени t в случае упругого удара. Постройте график зави-
симости скорости от времени.
Геометрический смысл производной
9°. Дана функция у = х2. Постройте на графике этой функции
точки Р|, Р2, Рз, Ра с абсциссами Х| = — 1, х2 = 0, х3=1,
*4 = 3. Найдите угловые коэффициенты секущих, проходящих
через каждые две из указанных точек.
10. По графику функции (рис. 70) вычислите угловые коэффици-
енты секущих РР|, РР2 и РР3, проходящих через точки,
указанные на графике.
11. На рисунке 71 изображено 6 графиков. Объедините их в пары
«функция — ее производная».
12. По заданному графику функции (рис. 72) постройте график
ее производной.
Рис. 71
112
Рис. 73
13*. Рисунок 73 изображает алгоритм построения графика ско-
рости по графику пути. Разберите этот алгоритм по рисунку
и примените его для построения графиков производной для
функций, изображенных на рисунке 74. Попробуйте дать обос-
нование алгоритма.
из
14. По заданному графику производной (рис. 75, а, б) восста-
новите примерный график функции.
Приращение аргумента и приращение функции
15°. Для функции у=х2—х найдите Ду, если:
1) х= 1,5 и Ах=2,5;
2) х= 1,5 и Ах = 3,5;
3) х=4 и Ах = 3.
16°. Найдите , если:
1) у=ах2 + Ьх; 2) у=ах3; 3) у=х+±-.
17°. Найдите среднюю скорость роста функции у=х2 — 4х на
отрезках [0; 1], [0; 0,5], [0; 0,1], [0; 0,01]. Чему равна производ-
ная этой функции в точке х=0?
18°. Для функции У=-^- найдите Ау и если:
1) х = 9, Дх=0,06; 2) х=4,02, Ах = 0,02;
3) х = 5,06, Ах=—0,03; 4) х=6, Дх=—0,02.
19. На каждом из рисунков (рис. 76) изображены графики двух
функций на одном и том же отрезке. У какой из этих функ-
ций средняя скорость роста на этом отрезке больше?
20. На каждом из рисунков (рис. 77) изображен график функции.
Выясните, что больше: средняя скорость роста этой функции на
отрезке [а; б] или на отрезке [б; с].
Рис. 76
114
Рис. 77
Вычисление производной по определению
21°. Используя схему вычисления
водные следующих функций:
производной, найдите произ-
1) у = 2х2 + 3х; 2) у=2х3; 3) у — х3+х; 4)
5>« = 7; б*у = Г+Т; 8)S=-A,;
9) y = 10) 1/-V7+T; 11) y=-L; 12) J-V?.
-yjx
Вычисление производной
22°. Вычислите производные:
1) у = 3х2; 2) z/ = 4x4; 3) у=^-, 4) у=^-,
5) У—~\ y=h 7)f/ = 3^; 8) у=^;
9) У=^/^ Ю) у=^/2х- 11) у=-^с, 12) У = х+-^;
13) у=х-^-; 14) У=^ 15) z/ = 2x2-3x + 5;
16) у=^-Зх2 + 6х-1; 17) у = 2--^—х2; 18) у=3х4;
О Z
19) t/ = 4 —х4; 20) у = х4-х2; 21) у=^-, 22) у=^-,
23) у=5х4 —7х2 —х; 24) t/=x5 + 2x3-^-;
25) i/=x4 + 4x3-x2 + 2x-5; 26) t/=х5+2х3~2х+5 ;
115
27) У=^-; 28) у = х7—-^-; 29) х л Ух
30) У=Ух\ 31) у = х-\/х; 32) У = у/х 5-; V*
33) у = М^- 34) У=-^’ 35) у=±-,
X \Х ух
36) у=х2+д/?; 37) У= ; 38) у = (х + у/х?; ух — 1
39) У — (х2 — 1)(х2+1); 40) i/=(x+-L)(x2-3x-8);
41) У=(х+т+р-)(х< 4-x+l); 42) y=(x4--L)(x3 + ^) ;
43) * 1 w NO ^ттг= 45> у-^т-’
46) х — 2 У 2х2—1 ’ 47) у-^ТГ' 48> У=^Т’
49) __ х2 —Зх-|- 1 . 5Q \ У х24-х-Н ’ * + д/х . к I \ и Юх4 —Зх2 . У - 51' У (Зх2-1)2 ’
//— 1 V2 1 и— х _ • 54) // — ! •
У f~ , 9 м’ У 1 > / У 1 ’
д/х (х2 — 1) 1 1 । 1 х Н X х
55) у = 3 V?+2x -?) 56)s = Vx+^;
57) у=— 1—-—; у ^+i 1 -fi_{ 58) i);
59) у=Мх* (V?—V*); 60) у = (х-2)2+7^.
23. Вычислите производные:
1) у=(х—З)7; 2) z/ = (l — х)^;
3) у = (Зх-4)9; 4) у = (х+1)2-Зх;
5) f/=(l -2х)4; 6) У (Зх+ I)3 ’
7) 2 У (Зх + 2)3 ’ 8) у—УБх2-,
9) У=Ч~х\ 10) у=Л/5х-1;
И) t/ = V(x+2)5; 12) t/=V2Jt —7;
13) f/=V(3x+l)2; 14) л/1 —X
15) у=у/х+2—-у/х — 2; 16) у = (х-I)4 (х+ I)3;
17) у=(2х+ 1)3 + 5 (Зх— 18> ^-х+1)2 + 1’
19) у=(х~1У • У (х+З)3 ’ 20) у=а-^. 7 сх + d
И6
24*. Выведите формулу (f2 (х))' = 2f' (x)-f (x) и вычислите с ее по-
мощью производные:
1) f/=(V*+i)2;
3) y = (x + -t-V*)2;
2) z/ = (x3 + 2x2 + x-l)2;
25°. Вычислите значения производных в данных точках:
1) f(x)=x3-x + 2, х=—2; -1; 0;
2) *=°; —2; и
з) х=~1’ °;
4) /«=^7-, х=—5; 0; 2.
26°. В какой из двух точек Xi и хг функция у = 3х2 растет
быстрее, если:
1) Xi = 1, Х2 = — 1; 2) Xi = 1, хг = 2; 3) Х| = 1, хг=-|-?
27. Среди функций у=4~х2 + х, у=д/х+Т, у= —— выберите
ту, у которой в нуле самая большая производная.
Производная сложной функции
28. Вычислите производные:
1) у=(^+1)5; 2) у=л/^+Т; 3) y=Vl+^;
4) £/=((х-|-1)4—2)3; 5) у=М2х*-\-, 6) у = , 1 .
лА+т
Исследование функции с помощью производной
Монотонность
29. Исследуйте на монотонность и экстремум функции вида
у = хп, где п — натуральное число. Начните с конкрет-
ных значений п=1, 2, 3, 4. Сформулируйте общий резуль-
тат в зависимости от п.
30. Найдите промежутки монотонности для функций:
1) £/=-2х2 + Зх + 5; 2) £/==(х+1)2;
3) £/ = 2х2 —х; 4) // —6 —х —х2; 5) у = х3-^х;
6) г/ = х3—12х+ 1; 7) г/=-х3 + Зх + 2; 8) z/ = x3 + 3x+l;
9) z/ = x3 + 3x2-|-3x; 10) z/ = x3 —2х2 + 3х+1;
11) у = х4 — 4х3+Ю; 12) z/ = x4 —2х2 + 2;
13) у = х* — 2х3 + х2 — 2; 14) £/ = Зх5 —5х3 —ЗОх;
117
15) У=х+±-, 16) У= х——~\ X
1 Q\ X 191 X
io; У X2—1 ’ У х*+1 ’
91 \ 92^ 1 1
у х2 + х+1 ’ У (х-Н)2 X2
24) уХ
Экстремумы
17) У=х2+±-,
(ъг\\ х —2,5
2°) y=~V^~ '
23) у=х —-у/х-,
31. Исследуйте на экстремум следующие функции:
1) у = 3 —х2; 2) у=х2 + 4х;
3) у= 1 —х —х2; 4) у = 2х2—х+5;
5) у= 12х—х3; 6) у=х3 — 6х2;
7) У=^- + х2 —4х + 5; 8) у = 2х3 — 9х2 — 60х +1;
9) У=х4 —х2; Ю) у=х4 + 2х2 + 1;
Н) у = х4—х3; 12) у=(х+1)3-27 (х+1);
13) У=х+Т’ 14) X . У х2 + 5 *
15) У=х— 16) у = Х~^Х—~\/х.
32. Найдите точки остановки тела, двигающегося по следую-
щему закону:
I) * = <г~^+2 ; 2) 5 = 2/-!+^^-;
3) S=1=T’ , 4)
5) S== (f-2)2 F’ S= /2 —2/+1 ’
7) s = 2/3-6/-l; 8) s = 2/3—15/2 + 35/—13.
33. Сколько точек экстремума может иметь квадратичная функ-
ция? Тот же вопрос для кубической функции.
34*. Исследуйте вопрос о количестве точек экстремума куби-
ческой функции у=х3 + рх+^ в зависимости от р и q.
35. Найдите экстремумы следующих функций, разобрав отдельно
случаи а>0 и а<0:
1) £/ = а(х+1)2; 2) £/ = х4~;
3) £/ = х4 + ах2 + 6; 4) £/ = х3 + ах-|-L
36. Производная квадратного трехчлена у = ах2 + ftx + c в точках
3 и 8 равна соответственно 10 и 5. Найдите точку экстре-
мума функции и укажите, является ли она максимумом
или минимумом.
118
37. Функция £/ = (%—-а) (х2 — 1) имеет минимум в точке х = -^-.
В какой точке у нее максимум?
38. При каких а функции у=— х3 + Зах + 5 и у=х2 + (а+1)х
имеют минимум в одной и той же точке?
Построение графика
39. Проведите исследование функции и постройте ее график:
1) у—х*—х; 2) у=х2 + 2х; 3) у=1—х2;
4) у=2х2 + х+1; 5) у = 2 — х — х2; 6) у=—х2 + 2х —3;
7) у=х3 — Зх2+ 1; 8) у —Зх—х3; 9) у=х3 —12х;
Ю) £/ = х3 + Зх; 11) у = х3— Зх2; 12) у=х3- 12х2 + 27х;
13) £/ = 2х3 + Зх2 —2; 14) у = 2х3 — 9х2+ 12х — 3;
15) х3 । х2 У=Т+Т-Х’ 16) у=х4 —2х2 —3;
17) у = х4 + 2х3 —5х2; 18) у = (х—I)3 —3(х—1);
19) у = 3х4 —4х3—12х2+10; 20)
21) y=x+JL; 22) 1 у = х ; X 23) у-^;
24) у=т=р-; 25) X У-^-1 ; 26) y=J^rh
27) y=Vx2—х; 28) £/ = х — 2 д/х; 29) у=х-\/х —6х;
30) 31) = : 32) У=^~-
График функции и ее производной
40. По графикам функций (рис. 78) постройте графики их
производных.
119
41. Разбейте графики функций (рис. 79) на пары «функция и
ее производная».
42. Выберите из следующего списка формулу, задающую каждую
из функций, изображенных на рисунке 79:
1) у = х3+ 1; 2) у = 4х — х2; 3) У= I . 2 -у/х
4) */ = Зх2; 5) У=-у/х', 6) У = 1-4; X
7) у=х+-Ь 8) у = х + 5; 9) У = х2 । г .7 т+5х+т
Ю) У — —2х+4; Н) у= —2х —4; 12) У = — 2.
Нахождение числа корней уравнения
43. Найдите число корней уравнения:
1) х3 —Зх2 + 6х- 1 =0; 2) 5х3 —5х —3 = 0;
3) 12х4 — 12х3 — Зх2 — 5 = 0.
120
44. Сколько корней имеет уравнение х4-|-х3==10?
45. При каких а уравнение 4х3 — Зх = а имеет только один корень?
Доказательство неравенств
46*. Докажите неравенства:
1) 1+4—+*< 1если х>°;
Z О Z
2) 1— —5—С1— хД-х2.
1 4-х
Приложения производной
Механика
47. Высота камня, брошенного вертикально вверх со скоростью
и0 с начальной высоты от земли йо, меняется по закону
x = ho + vot— , где g=10 м/с2 — ускорение силы тяжести.
1) Найдите зависимость скорости камня от времени.
2) При йо = 20 м, и0 = 8 м/с найдите скорость камня
через 2 с. Зачем указано значение йо? Через какое время ка-
мень упадет на землю?
3) На какой высоте скорость обратится в 0?
4) Покажите, что энергия камня Е=^—\-mgh (где m —
масса камня) не зависит от времени.
48. Тело удаляется от Земли по закону $=Д (/Д-с)3.
1) Найдите закон, по которому меняется его скорость.
2) Вычислите ускорение тела.
3) Докажите, что сила, действующая на тело, меняется об-
ратно пропорционально квадрату расстояния $.
49. Докажите, что движение по кубическому закону s = a/3 +
+ bt2 -\-ct + d происходит с ускорением, меняющимся линейно.
50. Точка движется по закону s = 2 + 20/ —5/2. Найдите мгновен-
ную скорость в момент t = 0, t= 1, t = 2. Постройте график за-
висимости мгновенной скорости от времени.
51. Движение точки по оси х задано законом х (/)=-— Най-
дите мгновенную скорость в момент /=1, / = 2, / = 3. Обра-
тите внимание на знак скорости.
52. Точка движется прямолинейно по закону s = t3-}~3t2. Най-
дите скорость и ускорение в момент времени /=1.
53. Точка движется прямолинейно по закону Докажите,
что движение замедленное и что ускорение а пропорциональ-
но кубу скорости V.
54. Тело массой 5 кг движется прямолинейно по закону s = /2 —
— 3f + 2, где t измеряется в секундах, s — в метрах. Найдите
кинетическую энергию тела через 10 с после начала движения.
121
55. В какой момент времени будет иметь максимальную кинети-
ческую энергию тело, движущееся прямолинейно по закону
*-‘(м+)?
56. При равномерном движении тела по окружности угловой ско-
ростью тела называется угол поворота в единицу времени.
Дайте определение угловой скорости для неравномерного
движения.
57*. В следующих примерах дан закон движения в координатах:
1) r(3/; 4/-1); 2) r(2t;
з) тт?) ’ 4) F('2“1;'t'2-1»-
Найдите координаты скорости.
58*. Нарисуйте траектории, по которым движутся точки в пре-
дыдущей задаче.
59. Что можно сказать о скорости движения точки в задаче
57 (1)? Чему равна ее величина?
Электричество
60. При равномерном протекании заряда по проводнику силой
тока называется заряд, протекающий за единицу времени.
Дайте определение силы тока в общем случае.
61. Количество электричества, протекающее через проводник,
начиная с момента / = 0, задается формулой <? = 3/2-Н+2.
Найдите силу тока в момент времени /=3.
62. В какие моменты времени ток в цепи равен нулю, если ко-
личество электричества, протекающего через проводник,
задается формулой: a) q = б) q = t—V^+l?
63. Измерения величины заряда на* обкладках конденсатора по-
казали, что заряд q меняется со временем по закону
<7(0=3,05+6,11/—^
(/<10, время в секундах, заряд в микрокулонах). Найдите
закон изменения силы тока.
Другие приложения
64. Пусть Q (Т) — количество теплоты, которое необходимо для
нагревания 1 кг воды от 0° до Т° (по Цельсию). Известно,
что в диапазоне 0<Г<95 формула
Q (Г) = 0,3967 + 2,081 • 10-3 Г2-5,024-10“7 Т3
дает хорошее приближение к истинному значению Q (Т). Най-
дите, как зависит теплоемкость воды от температуры.
65. Если бы процесс радиоактивного распада протекал равно-
мерно, то под скоростью распада следовало бы понимать коли-
122
чество вещества, распавшегося в едини-
цу времени. На самом деле процесс не-
равномерен. Дайте определение скорос-
ти радиоактивного распада.
66. Длина стержня меняется в зависимос-
ти от температуры по закону
/=/0+0,001/+0,0001/2.
Найдите коэффициент линейного рас-
ширения при / = 5°С.
67. Что будет производной площади круга как функции от ра-
диуса и почему?
68. Обсуждая успехи своего ученика, учитель математики так
отозвался о нем: «Он очень мало знает, но у него положи-
тельная производная». Все поняли, что хотел сказать учитель:
скорость приращения знаний у ученика положительна, а это
есть залог того, что его знания возрастут. Подумайте, как вы
могли бы охарактеризовать три разные кривые роста знаний,
изображенного на рисунке 80.
Дифференциал и касательная
69°. Вычислите дифференциал функций:
1) у=х3; 2) t/ = x2 + 5x; 3) у=х4 —2-\/х;
4) s = 3/3+2/2-/+ 1; 5) S=nR2; 6) £(г) = /гг2--Ь
7) Ц7=3/3-^-; 8) F=±~, 9) u(t)=-±-.
I Г I —10
70°. Напишите уравнения касательных к графику функции
у = 2х2, проведенных в точках:
1) х=1; 2) х— — 1; 3) х=0; 4) х=—J-.
71. К гиперболе У—~ проведена произвольная касательная.
Докажите, что площадь треугольника, образованного этой
касательной и осями координат, равна 2.
Приближенные формулы
72. Вычислите приближенно с помощью дифференциала:
1) (1.002)6; 2) (0,997)3; 3) V1.0012;
4) д/0-984; 5) V1.015; 6) V6^6;
7) ——; 7 1,021 ’ Q\ 1 . 7 0,928 ’ 9) (2,003)5;
10) л/15,92; 11) Va.012; 12> 5,02 =
123
13) 2,012; 14) 5 043; 15 ) 9.9983;
16) Vh04; 17) л/0999; 18) Л/82;
19)doT; 20) оЖ; 2I)W; 22) 9Ж’
73. Даны функция y=f(x) и точка х0. Вычислите приближенно
значение у в точке Хо с помощью дифференциала:
1) у = 2х5, х0= 1,003; 2) у=х4+х2 +1, хо = 2,О4;
3) у = х2+-^-, х0=1,97; 4) у = 5л/х, хо = 4,О2.
74. Приближенное значение у/2 можно вычислить двумя спосо-
бами: а) представив 2 = 4 0—0) ; б) представив 2 = 1 + 1.
Какое из двух приближений будет более точным?
Наибольшее и наименьшее значения функции на отрезке
75. Найдите наибольшее и наименьшее значения функции на ука-
занном отрезке:
1) у = 2х3 + 3х2, [—1; 1]; 2) у = х3 — 6х2+1, [—1; 2];
3) у = 7 + 4х3-х4, [-1; 3]; 4) г/ = 5х—|-х3, [0; 2];
5) 6)
7) у=Л/х —х, [0; 4]; 8) у = х — 2 у/х, [0; 9];
9) 1/ = 7х3 + 9х2-Зх + 6, [-1; 1];
10) у = 2х3 — 15х2 + 36х- 13, [—у; 3 0
76. Найдите наименьший член последовательности ап:
1) ап==п2 — 7n + 1; 2) ап = п4 — 5п3 — Зп2.
77*. Докажите, что если |х|^2, то |х3 —Зх|^2.
Прикладные задачи на экстремум
78. Какую наименьшую площадь полной поверхности может
иметь цилиндр, если его объем равен V?
79*. Параболическим сегментом называется фигура, ограничен-
ная параболой и прямой, перпендикулярной к оси параболы.
Расстояние от вершины параболы до этой прямой называется
высотой сегмента, а длина отрезка прямой, высекаемого
параболой,— основанием сегмента. Какую наибольшую пло-
щадь может иметь прямоугольник, вписанный в параболи-
ческий сегмент с основанием а и высотой Я? (Одна из сто-
рон прямоугольника параллельна оси параболы, рис. 81.)
80*. Из пункта А, находящегося в лесу в 5 км от прямолинейной
дороги, пешеходу нужно попасть в пункт В, расположенный
124
на этой дороге в 13 км от пункта
Д. По дороге пешеход может дви-
гаться с максимальной скоростью
5 км/ч, а по лесу — с максимальной
скоростью 3 км/ч. За какое мини-
мальное время пешеход сможет
добраться из пункта А в пункт В
(рис. 82)?
81. Тело представляет собой прямой кру-
говой цилиндр, завершенный сверху
полушаром. Какую наименьшую пло-
щадь полной поверхности может
иметь это тело, если его объем ра-
вен V?
82. Объем правильной четырехугольной
призмы 8 см3. Какую длину должны
иметь сторона основания и высота
призмы, чтобы площадь ее поверх-
ности была наименьшей?
83. В основании пирамиды прямоугольный треугольник с гипоте-
нузой 2 см. Высота пирамиды 6 см. Найдите наибольший
объем пирамиды.
84. Найдите наибольший объем правильной треугольной пирами-
ды, у которой периметр боковой грани равен 6 см.
85. В прямоугольном параллелепипеде ABCDA'B'C'D' расстояние
АС равно 2^/2 см, ДД' = 1 см. Найдите площадь поверхности
параллелепипеда, имеющего наибольший объем.
86. Найдите число, которое, если сложить со своим квадратом,
даст наименьшую сумму.
87. Найдите положительное число, которое, если сложить с обрат-
ным ему числом, даст наименьшую сумму.
88. Найдите такое положительное число, чтобы разность между
ним и его кубом была наибольшей.
89. Требуется изготовить ящик (без крышки) с прямоугольным
основанием и заданным объемом V, отношение сторон основа-
ния которого равнялось бы k. Каковы должны быть размеры
ящика, чтобы его поверхность была наименьшей? Вычислите
размеры ящика при: 1) £=1, V = 32; 2) fe = 2, V = 36.
90. Бак цилиндрической формы должен вмещать V литров воды.
Каковы должны быть размеры бака, чтобы поверхность его
(без крышки) была наименьшей?
91. Периметр равнобедренного треугольника равен 2р. Какой
длины должны быть его стороны, чтобы объем тела, обра-
зованного вращением этого треугольника вокруг его основа-
ния, был наибольшим?
92. Через пункт О из пунктов А и В, находящихся от О на рас-
стоянии /1 и /2, едут два велосипедиста с постоянными ско-
ростями vi и V2 по прямолинейным дорогам, угол между
125
которыми 60°. В какой момент вре-
мени расстояние между велосипедис-
х тами наименьшее?
А 93. Стоимость эксплуатации катера, плы-
1 х вущего со скоростью у км/ч, состав-
’ х I ляет (90+0,4и2) рублей в час. С
какой скоростью должен плыть катер,
I чтобы стоимость 1 км пути была наи-
п г х меньшей?
<ои ио> х 94. Точка М — середина отрезка АВ.
Найдите точку X на этом отрезке,
Рис. 83 для которой произведение длин отрез-
ков АХ, MX и ХВ наибольшее.
95. В трапеции ABCD длины сторон АВ, ВС и CD равны 1,
AD>BC. Каким должен быть угол = Z-CDA, чтобы пло-
щадь трапеции была наибольшей?
96. На странице книги печатный текст должен занимать 150 см2.
Верхнее и нижнее поля страницы по 3 см, правое и левое —
по 2 см. Если принимать во внимание только экономию бу-
маги, то каковы должны быть наиболее выгодные размеры
страницы?
97. На двух стройплощадках возводятся два одноэтажных склада
общей площадью 600 м2. Стоимость постройки склада прямо
пропорциональна квадрату его площади. Кроме того, известно,
что строительство 1 м2 на второй площадке обходится на 40%
дороже, чем на первой. Какой должна быть площадь
каждого склада, чтобы стоимость строительства была наи-
меньшей?
98. Требуется выгородить прямоугольное пастбище площадью
1 км2 и разделить его на два прямоугольных участка. Какой
наименьшей длины забор при этом может получиться?
99. По одну сторону от стены высотой 30 м на расстоянии 10 м
от стены лежит груз, по другую сторону от стены по го-
ризонтальной площадке ездит кран. Башня крана имеет
высоту 20 м, а его стрела, прикрепленная к верхней точ-
ке башни, имеет длину I м и может быть расположена под
любым углом к горизонту. При какой наименьшей длине
/ стрелы кран может поднять груз через стену? (Трос крана
свисает вертикально с конца стрелы, его длина не ограничена;
рис. 83.)
КОНТРОЛЬНОЕ ЗАДАНИЕ К ГЛАВЕ II
Вариант 1
1. Вычислите производные и найдите их значения в точке х=\:
а) у = 2х2+-^-, б) у = (х2 — 1)(х24-2х — 3); в)
126
2. Исследуйте функцию у=х34-Зх2 и постройте ее график.
3. Дан закон движения материальной точки s = 2/2 —8/+11, где
$ — путь в метрах, t — время в секундах.
а) Вычислите скорость и ускорение движения.
б) В какой момент времени точка остановится?
4. Найдите наименьшее значение функции у=х+— на отрезке
[4; 5].
Вариант 2
1. Вычислите производные и найдите их значения при х = 4:
а) у=(3х—1)3+уг; б) ; в) у = -\/5 —х• (3 — х).
2. Дана функция y = f(x), где f(x) = 3x4—х2.
а) Исследуйте функцию и постройте ее график.
б) При каких значениях а уравнение f(x) = a имеет четыре
корня?
3. Закон движения тела имеет вид s=8 — 2/4-24Z2— 0,3/5. В ка-
кой момент времени тело имеет наибольшую скорость?
4. Вычислите приближенно 1,012.
Вариант 3
1. Вычислите производные и найдите их значения при х = 2:
a) t/=(2x2+1)4—-р; б) у=х^3~? ; в) у=^4х-Ух2-2х.
ух {Зх— 1)
2. Найдите наибольшее значение функции у=^х — х3 при поло-
жительных значениях х.
3. Приведенное уравнение газового состояния имеет вид:
(р+-^)(ЗУ-1) = 8Г,
где р, V и Т — приведенные значения давления, объема и тем-
пературы. Постройте изотерму (зависимость р от V) при крити-
ческом значении Т= 1.
4. а) Вычислите приближенно д/1»06.
б) Докажите неравенства
i+f-v<VT+^<i+f
при х>0и примените их для оценки погрешности вычисления
в пункте а).
А синуса график волна за волной
По оси абсцисс убегает.
Из студенческой песни.
Глава III
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
ВВОДНАЯ БЕСЕДА
1. Периодические процессы
В этой главе будет изучаться новый класс функций — триго-
нометрические функции. Они служат прежде всего для описания
разнообразных периодических процессов. С периодически повто-
ряющимися ситуациями человек сталкивается повсюду. Его жизнь
сопровождают различные астрономические явления — восход и
заход Солнца, изменение фаз Луны, чередование времен года,
положение звезд на небе, затмения и движения планет. Человек
давно заметил, что все эти явления возобновляются периоди-
чески. Жизнь на Земле тесно связана с ними, и поэтому неуди-
вительно, что астрономические наблюдения явились источником
многих математических открытий.
Биение сердца, цикл в жизнедеятельности организма, враще-
ние колеса, морские приливы и отливы, заполненность городско-
го транспорта, эпидемии гриппа — в этих многообразных при-
мерах можно найти общее: эти процессы периодичны.
Открывая утром газету, мы часто читаем сообщение об оче-
редном запуске искусственного спутника Земли. Обычно в сооб-
щении указываются наименьшее и наибольшее расстояния спут-
ника от поверхности Земли и период его обращения. Если сказа-
но, что период обращения спутника составляет 92 мин, то мы по-
нимаем, что его положение относительно Земли в какой-то момент
времени и через каждые 92 мин с этого момента будет оди-
наковым. Так мы приходим к понятию периодической функции как
функции, обладающей периодом, т. е. таким числом Г, что значе-
ния функции при значениях аргумента, отличающихся на Г, 2Т, ЗТ
и т. д., будут одинаковыми.
Астрономия, которая дает нам наиболее наглядное представ-
ление о периодических процессах, определяет положение объектов
в небесной сфере с помощью углов. Можно сказать так: в качестве
аргумента периодических функций очень часто выступает угол.
Поэтому в нашей беседе мы обсудим вопрос об измерении углов.
128
2. Углы и их измерение
Геометрический угол — это часть плоскости, ограниченная
двумя лучами, выходящими из одной точки, вершины угла. Чтобы
сравнивать углы, удобно закрепить их вершины в одной точке
и вращать стороны.
Как измеряют углы? В качестве единицы измерения геомет-
рических углов принят градус—часть развернутого угла.
Конкретные углы удобно измерять в градусах с помощью тран-
спортира. Многие оптические приборы также используют градус-
ную меру угла. Углы, получающиеся при непрерывном вращении,
удобно измерять не в градусах, а с помощью таких чисел, ко-
торые отражали бы сам процесс построения угла, т. е. вращение.
На практике углы поворота зависят от времени, и поэтому удобно
связать измерение углов со временем.
Представим себе, что зафиксирована не только вершина угла,
но и один из образующих его лучей. Заставим второй луч вращать-
ся вокруг вершины. Ясно, что получающиеся углы будут зависеть
от скорости вращения и времени. Можно считать, что вращение
происходит равномерно (с постоянной угловой скоростью). Тогда
поворот будет определяться путем, который пройдет какая-либо
фиксированная точка подвижного луча.
Если расстояние точки от вершины равно /?, то при вра-
щении точка движется по окружности радиуса R. Отношение
пройденного пути к радиусу R не зависит от радиуса и
может быть взято за меру угла. Численно она равна пути, прой-
денному точкой по окружности единичного радиуса.
Итак, пусть угол получен вращением подвижного луча от не-
которого начального положения. Его величина численно равна
пути, который пройдет точка этого луча, находящаяся на единич-
ном расстоянии от вершины.
Развернутый угол измеряется половиной длины единичной ок-
ружности. Это число обозначается буквой л. Число л было
известно людям с глубокой древности и с довольно большой
точностью. Первые десятичные знаки этого числа таковы:
л = 3,14159265358... .
Угол величиной л часто используется как самостоятельная
единица измерения углов — прямой угол равен -у-, угол в равно-
стороннем треугольнике равен Часто встречаются записи меры
о
5 2 л ж г *
углов в виде —л, —л, — и т. д. Угол, мера которого равна числу 1,
называют радианом. Он соответствует некоторому углу, чуть мень-
шему, чем -2-, ведь -^-«1,047.
О о
5 Заказ 836
129
Гаусс Карл Фридрих
(1777—1855) —
немецкий математик, астроном и физик.
Еще студентом написал «Арифметические ис-
следования», определившие развитие теории
чисел до нашего времени. В 19 лет определил,
какие правильные многоугольники можно по-
строить циркулем и линейкой. Занимался гео-
дезией и вычислительной астрономией. Соз-
дал теорию кривых поверхностей. Один из
создателей неевклидовой геометрии.
«Не считать ничего сделанным, если еще
кое-что осталось сделать».
К. Ф. Г а у с с
Так как на практике приходится иметь дело как с градусной,
так и с радианной мерой, то на микрокалькуляторе обычно
есть рычажок, регулирующий способ измерения используемого в
вычислениях угла. Фактически микрокалькулятор умеет перево-
дить градусы в радианы и обратно.
Выведем формулы для этого перевода. Достаточно сравнить
меры одного и того же угла, например прямого:
-^=90°,
откуда 1 ° =-^-«0,017.
Обратно можно выразить единицу (т. е. один радиан) в гра-
дусной мере: 1 =-^-90°=^-1°=(57,296)°.
В географии, астрономии и других прикладных науках исполь-
зуют доли градуса — минуту и секунду. Минута — это граду-
са, а секунда — минуты. Запишем соотношения между различ-
ными единицами измерения углов:
1 ° «0,017,
1
1« (57,296)° «57° 17'45".
Заметим еще, что обозначение градуса (минуты, секунды)
нельзя пропускать в записи, а обозначение радиана опускают.
С физической точки зрения угол — безразмерная величина, поэ-
130
тому имеют смысл записи: а = 0,23, а = 3,14, а = 0,01. Во всех
этих записях подразумевается, что угол а измерен в радианах.
Подведем некоторые итоги. Угол мы можем получить вращени-
ем подвижного луча. Радианная мера угла численно равна пути,
который проходит точка этого луча, отстоящая от вершины на
расстояние 1.
Движение точки по окружности во многом аналогично движе-
нию точки по прямой. Чтобы определить положение точки на пря-
мой, недостаточно знать путь, пройденный ею от начальной точки,
нужно указать еще направление движения. Обычно на прямой
фиксируют положительное направление, а положение точки опре-
деляют одним числом, которое может быть не только положитель-
ным (как путь), но и отрицательным.
Аналогично поступают и с вращательным движением. В ка-
честве положительного направления движения по окружности вы-
бирается движение против часовой стрелки. Угол задают числом
t (которое может принимать произвольное значение). Чтобы по-
строить угол f, на единичной окружности от неподвижной точки
откладывают путь, равный |/|, в направлении, определяемом
знаком числа t. Таким образом, для произвольного числа t мы пост-
роили угол /, определяемый двумя лучами — неподвижным и тем,
который проходит через построенную точку (рис. 84).
При таком обобщении понятия угла постепенно отходят от
его геометрического образа как части плоскости, лежащей между
двумя лучами. Фактически слово «угол» становится для нас си-
нонимом слова «число». Угол t (т. е. произвольное число t) может
выступать у нас в качестве аргумента тригонометрических функ-
ций. Изображать угол t нам будет удобно не в виде пары
лучей, а в виде точки единичной окружности. Для этого мы под-
робно рассмотрим вращательное движение.
3. Вращательное движение и его свойства
Представим себе маленький шарик, который равномерно вра-
щается по единичной окружности в положительном направлении
(т. е. против часовой стрелки). Будем считать, что в момент вре-
мени / = 0 шарик находился в положении А и что за время /=1
он проходит по окружности расстояние, равное 1. Половину
окружности шарик проходит за время, равное л, а всю окруж-
ность — за время 2л.
Обозначим через Pt точку на ок-
ружности, в которой шарик находится
в момент времени t. Для того чтобы
найти на окружности точку Pti надо от-
ложить от точки Pq=A по окружности
дугу длиной \t\ в положительном нап-
равлении, если />0, ив отрицательном
131
направлении (т. е. по часовой стрел-
ке), если /<0. Рассмотрим при-
меры.
1. Пусть /=-^-. Отложим по
окружности от точки Ро в положи-
тельном направлении путь длиной
Так как длина всей окружности
равна 2л, то точка Рп является се-
т
рединой дуги АВ (рис. 85).
2. Пусть -. Отложим от точ-
ки Ро путь длиной Заметим, что ^-=2л+-^-. Пройдя путь
длиной 2л, мы опять попадаем в точку А. Пройдя оставшийся
путь, мы попадаем в середину дуги АВ, Таким образом, точка Р9л
совпадает с точкой Рп. 4
4
3. Найдем теперь точку Р л. Для этого нам необходимо
и 3 и Л
проити в отрицательном направлении путь длиной —.
О
Таким образом, мы для каждого значения t можем построить
точку Pt. На языке механики аргумент t — это время, на языке
геометрии t — это угол.
Оси координат делят плоскость на четыре части. В зависи-
мости от того, в какую часть плоскости попадает точка Pti гово-
рят о том, в какую четверть попадает угол t. При этом полезно пом-
нить, что 1 радиан чуть меньше 60°, т. е. трети развернутого угла.
Перечислим некоторые свойства вращательного движения.
Свойство 1. Для всякого целого числа k точка Pt совпа-
дает с точкой Pt+2nk- Это свойство выражает периодичность враща-
тельного движения: если моменты времени отличаются на число,
кратное 2л, то шарик в эти моменты времени занимает одно
и то же положение.
Свойство 2. Если Pti = то найдется такое целое число k,
что t\ = /г + 2лй.
Свойство 3. Для всякого значения t точки Pt и Pt+n диа-
метрально противоположны.
Свойство 4. Для всякого значения t точки Pt и P-t сим-
метричны друг другу относительно оси абсцисс.
Свойство 5. Для всякого значения t точки Pt и P-t+n сим-
метричны относительно оси ординат.
Свойство 6. Для всякого значения t точки Pt и Рл сим-
метричны друг другу относительно биссектрисы первого и третьего
координатных углов.
132
г) д) е)
Рис. 86
Эти свойства легко объяснить с помощью рисунка 86.
Сделаем лишь пояснение к свойству 6. Возьмем две точки Ро
и Рп. Они симметричны друг другу относительно биссектрисы
~2
первого и третьего координатных углов. Чтобы построить точку Pti
надо от точки Pq двигаться в одном каком-то направлении на
расстояние |/|, а чтобы построить точку Рл , надо на такое же
расстояние двигаться от точки Рл, но в противоположном на-
т
правлении. Ясно, что при этом точки Pt и Рл при всяком t будут
оставаться симметричными друг другу относительно указанной
прямой.
Контрольные вопросы
1. Обратите внимание на следующие встретившиеся в тексте
ключевые слова и обозначения: угол, радиан, число л, точка
Pt. Приведите примеры их использования.
2. По каким формулам переводят градусную меру угла в ра-
дианную и наоборот?
133
3. Как построить произвольный угол /?
4. В чем состоит периодичность вращательного движения?
5. Каким углам соответствуют: а) диаметрально противопо-
ложные точки окружности; б) точки, симметричные друг другу
относительно оси абсцисс; в) точки, симметричные относительно
оси ординат; г) точки, симметричные друг другу относительно пря-
мой £/ = х?
6. Как связаны между собой углы t и если Pt — PtP
7. Приведите примеры периодических процессов.
§ 1. ОПРЕДЕЛЕНИЕ И ПРОСТЕЙШИЕ СВОЙСТВА
ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
1. Определение тригонометрических функций
Тригонометрические функции определяются с помощью коорди-
нат вращающейся точки. Рассмотрим на координатной плоскости
ху единичную окружность, т. е. окружность единичного радиуса с
центром в начале координат. Обозначим через Pq точку еди-
ничной окружности с координатами (1; 0) (рис. 87). Точку Ро бу-
дем называть начальной точкой. Возьмем произвольное число t.
Повернем начальную точку на угол /. Получим точку на единичной
окружности, которую обозначим через Pt.
Определение. Синусом числа t называется ордината точ-
ки Pt, косинусом числа t называется абсцисса точки Pt, где Pt
получается поворотом начальной точки единичной окружности на
угол t.
Если обозначить координаты точки Pt через х и у, то мы полу-
чим x = cos /, r/ = sin t или можно записать, что точка Pt имеет
координаты (cos /; sin t\
Так как координаты точки Pt (х; у), лежащей на единичной
окружности, связаны соотношением х2 + у2 = 1, то sin t и cos t свя-
заны соотношением
sin2 Z + cos21= 1 (или cos2 /sin2 / = 1),
которое называют основным тригоно-
метрическим тождеством.
Определение. Тангенсом числа t
называется отношение синуса числа t к
его косинусу, т. е. по определению
s cos t
Котангенсом числа t называется отно-
шение косинуса числа t к его синусу, т. е.
по определению
134
Тангенс числа t определен для тех значений /, для которых
cos/y=0. Котангенс числа t определен для тех значений t, для
которых sin /=/=0.
2. Периодичность
Тригонометрические функции являются периодическими функ-
циями.
Теорема. Число 2л является периодом синуса и косинуса.
Доказательство. Необходимо доказать тождества
sin (/ + 2n) = sin t, cos (/ + 2n) = cos t.
Значения тригонометрических функций определяются с по-
мощью координат вращающейся точки. Так как точки Pt и Р/+2л
совпадают, то совпадают и их координаты, т. е. cos Z = cos (/+ 2л)
и sin f = sin (/+ 2л), что и требовалось доказать.
Следствие. Верны тождества
tg(/ + 2n)=tgt ctg(< + 2n) = ctg t.
Действительно, tg (/-|-2л)= sl" = sm *. =tg t. Аналогии-
» । / cos(/ + 2n) cos/ &
но доказывается и второе тождество. Это означает, что
2л является одним из периодов тангенса и котангенса.
Равенство sin (/ + 2л) = 54п t верно при всех значениях t.
Подставляем в это равенство вместо t число / + 2л, получаем це-
почку равенств sin (/4-2л + 2л) = 51п (/-|-2n) = sin t, т. е. равенство
sin (7 + 4л) = sin t также верно при всех значениях t. Аналогично,
подставляя вместо t число / — 2л, получим тождество sin (/ —2л) =
= sin t. Можно сказать так, что раз 2л является периодом синуса,
то и 2-2л, —2л также являются его периодами. Получаем,
что всякое число вида 2лй (fe£Z) является периодом синуса.
Число 2л выделяется тем, что это наименьший положительный
период синуса. Аналогично 2л — наименьший положительный
период косинуса. У тангенса и котангенса наименьшим положи-
тельным периодом будет число л. Эти утверждения мы докажем
позже.
3. Знаки тригонометрических функций
Знаки тригонометрических функций определяются в зависи-
мости от того, в какой четверти лежит рассматриваемый угол.
Синус числа t есть ордината точки Pt. Поэтому синус положи-
телен в первой и второй четвертях и отрицателен в третьей и чет-
вертой.
Косинус числа t как абсцисса точки Pt положителен в первой и
четвертой четвертях и отрицателен во второй и третьей.
Тангенс и котангенс являются отношением координат. Поэтому
они положительны тогда, когда эти координаты имеют одинаковые
135
знаки (первая и третья четверти), и отрицательны, когда разные
(вторая и четвертая четверти). Знаки тригонометрических функ-
ций по четвертям приведены на рисунке 88.
4. Четность
Теорема. Синус — нечетная функция, т. е. при всех t вы-
полнено равенство sin (— t) = — sin t.
Косинус — четная функция, т. е. при всех t выполнено ра-
венство cos (— О =cos t.
Доказательство. Действительно, мы знаем, что для вся-
кого значения t точки Pt и P-t симметричны друг другу относитель-
но оси абсциссы (т. е. cos t = cos ( — /)), а ординаты противополож-
ны (т. е. sin t= — sin ( — /))> что и требовалось доказать.
Следствие. Тангенс и котангенс — нечетные функции.
Действительно, tg (— /)=— 2 = —sln;Z = — tg Л Аналогии-
но доказывается нечетность котангенса.
5. Формулы приведения
Значения тригонометрических функций острых углов можно
вычислить по таблицам или с помощью прямоугольного треуголь-
ника. Их вычисление для любого значения аргумента можно при-
вести к вычислению значений для аргумента у-]. Соот-
ветствующие формулы так и называются — формулы приведения.
Они основаны на симметрии вращательного движения.
Основные формулы:
sin (t4-л)= —sin t\
sin (л — /) = sin t\
sin —t — cos t\
cos (<4-n)= — cos t; (1)
cos (л —1)= —cos t; (2)
cos (-2—t ) = sin t. (3)
136
Формула (1) —это запись в координатной форме свойства 3
вращательного движения, формула (2) — это запись свойства 5,
а формула (3) — запись свойства 6.
С помощью периодичности и формул (1) — (3) можно привес-
ти вычисление синуса и косинуса любого числа t к их вычис-
лению для t, лежащего между 0 и -у-.
Из основных формул (1) — (3) можно вывести и другие фор-
мулы приведения:
sin ) = cos t\ cos )= — sin f. (4)
Доказательство.
sin (j-+0 = sin (-2—( — /)} = cos ( —/) = cos t,
cos (-£-+t) = cos (-2— (— t)) = sin (— t) = — sin t.
Аналогично выводятся формулы
sin )= — cos f; cos + t ) = sin t. (5)
Формулы приведения для тангенса и котангенса получаются
как следствие аналогичных формул для синуса и косинуса.
Например:
<+')
,inGr+')
— sin t
cos t
-tg/.
Мнемоническое правило для запоминания формул приведения
следующее:
1) Название функции не меняется, если к аргументу левой
части добавляется —л или +л, и меняется, если добавляется
число или zhy*.
2) Знак правой части определяется знаком левой, считая,
что /е(о; -=-) .
Примеры.
1. Вычислить sin-^-л. Представим ^-л так: ^-л = 6л+4-л.
о боб
Далее, sin sin (6n+-^-) = sin •^• = sin (я—2-) = sin -?-=4-.
о \ о/ 6 \ 6 / 62
137
2. cos——=cos f28л - •^ = cos(-^) = cos^=
= cos (л—2-)= — cos-j-= —i-.
А можно иначе:
cos ^—=cos (26n4~) = cos -y = COS (n+y-) = —cos y-= —
6. Значения тригонометрических функций
Вычисление значений тригонометрических функций имеет
длинную историю. Потребности точных астрономических наблю-
дений вызвали к жизни появление огромных таблиц, позволявших
производить вычисления с четырьмя, пятью и даже семью и более
знаками. На составление этих таблиц было затрачено много
усилий. Сейчас, нажав кнопку микрокалькулятора, мы можем мо-
ментально получить требуемое значение с очень высокой точ-
ностью. С помощью большой вычислительной машины нетрудно
найти, если нужно, значения тригонометрических функций с любой
степенью точности.
Некоторые соображения о значениях тригонометрических
функций надо помнить всегда, так как они облегчают вычисления.
1) С помощью формул приведения вычисление значения три-
гонометрической функции любого числа можно свести к вычисле-
нию функции угла, лежащего в первой четверти.
2) Достаточно знать значение лишь одной из тригономет-
рических функций. С помощью основных тождеств и зная чет-
верть, в которой лежит значение аргумента, легко найти зна-
чения остальных функций.
Примеры.
о
1. Пусть sin t=—— и t лежит в третьей четверти. Тогда
э
cos21= 1 — sin21 = —- и cos t ——так как косинус в третьей
четверти отрицателен. Получаем tg и ctg f =--•
2. cos/=-|-, 2л]. Получаем sin t =
= —tg t=-2д/2; ctg t=-------------
3 s v . s 2л/2 4
3. tg/= —10, и t лежит во второй четверти. Получаем
Ю5,= -^Г;
ct®'=-ik-
138
3) Полезно помнить значения тригонометрических функций
для углов двух «знаменитых» прямоугольных треугольников —
для равнобедренного и для треугольника с углами 30° 00 и
60° 00 . Эти значения обычно записывают с помощью радикалов
и при необходимости эти радикалы заменяют их приближенными
значениями (-\/2= 1,414..., -\/3= 1,732...). Сведем их в таблицу,
дополнив ее значениями 1=0 и /=-2-.
t sin t cos t tg t ctg/
0 0 1 0
л “6 1 2 уз 2 II Уз
я T ^1- II У2 2 1 i
Л T Уз 2 1 2 V3 л/З 3
Л ~2 1 0 — 0
7. Решение простейших тригонометрических уравнений
Для решения некоторых,особенно простых, но важных урав-
нений достаточно вспомнить определение тригонометрической
функции.
Примеры.
1. sin 1=0. Вращающаяся точка имеет нулевую ординату в
моменты времени t=0, л, 2л, .... а также /= — л, —2л, ... . В об-
щем виде множество этих значений можно записать в виде /=л/г,
k£Z. Таким образом, решением уравнения sin / = 0 будут числа
t = n,k, k£Z.
Запишем кратко решения еще нескольких уравнений, правиль-
ность которых предлагается проверить самостоятельно.
2. sin/=l, /=у-+2лй, k£Z.
3. sin /= — 1, /=у-+2л/г, k£Z.
4. cos t = 0, t=^-+nk, k£Z.
139
5. cos t — 1, / = 2nfe, k£Z.
6. cos t= — 1, f = n+2nfe, fegZ.
Все рассмотренные уравнения имеют бесчисленное множество
решений. Эти решения записываются в виде бесконечных серий
с помощью переменной (в наших примерах /г), которая может
принимать любые целые значения.
Теперь легко доказать, что 2л является наименьшим положи-
тельным периодом синуса и косинуса. Действительно, формула 3
показывает, что значение 1 синус принимает только в точках
f = y-+2nfe, fegZ. Расстояние между соседними точками этой по-
следовательности равно 2л, поэтому синус не может иметь поло-
жительный период, меньший 2л. Рассуждения для косинуса анало-
гичны.
Контрольные вопросы
1. Обратите внимание на следующие встретившиеся в тексте
ключевые слова: синус, косинус, тангенс, котангенс, периодич-
ность, формулы приведения. Приведите примеры их использова-
ния.
2. Дайте определения основных тригонометрических функций.
3. Какое число является наименьшим положительным перио-
дом синуса и косинуса?
4. Определите знаки тригонометрических функций в зависи-
мости от того, в какой четверти находится угол.
5. Что можно сказать о четности тригонометрических функций?
6. Какое вы знаете правило для запоминания формул приве-
дения?
7. Назовите значения тригонометрических функций углов
30°, 45°, 60°.
8. Какова область определения тангенса?
9. При каких углах котангенс угла не определен?
10. Значение sin t вам известно. Достаточно ли этого,
чтобы найти значения других тригонометрических функций угла /?
§ 2. ИССЛЕДОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ
ФУНКЦИЙ
1. Основные свойства синуса и косинуса
При введении тригонометрических функций мы обозначали
аргумент буквой /, так как буквы х и у были заняты —
они обозначали координаты вращающейся точки Pt. Сейчас при
исследовании мы вернемся к обычным обозначениям: х — ар-
гумент, у — функция.
140
Рассмотрим функции r/ = sinx и z/ —cosx.
1) Область определения. Синус и косинус числа х задаются
как координаты точки Рх, получающейся из точки Ро(1; 0)
поворотом на угол х. Так как поворот возможен на любой угол,
то областью определения синуса и косинуса является множество
R всех вещественных чисел.
2) Промежутки монотонности. Проследим за характером изме-
нения координат точки Рх, движущейся по окружности. При х = 0
точка занимает положение Ро (1; 0). Пока она движется по окруж-
ности, оставаясь в первой четверти, ее абсцисса уменьшается,
а ордината увеличивается. При х=—- точка займет положение
Рл (0; 1). Итак, в первой четверти синус (ордината) возрастает от
~2
0 до 1, а косинус (абсцисса) убывает от 1 до 0.
Когда точка переходит во вторую четверть, ордината начина-
ет убывать от 1 до 0. Абсцисса становится отрицательной и растет
по абсолютной величине, значит, косинус продолжает убывать от
0 до — 1.
В третьей четверти синус становится отрицательным и убывает
от 0 до — 1, а косинус начинает возрастать от — 1 до 0.
Наконец, в четвертой четверти синус возрастает от — 1 до 0 и
косинус возрастает от 0 до 1.
Монотонность синуса и косинуса по четвертям показана на
схеме VIII.
3) Точки экстремума. Координаты вращающейся точки меня-
ются между —1 и +1. Эти числа являются наименьшими и
наибольшими значениями синуса и косинуса. Если требуется ука-
зать абсциссы точек экстремума, то надо решить уравнения sin х =
= ±1 и cos х= ± 1, что мы проделали в предыдущем параграфе.
4) Промежутки постоянного знака и корни функции. Эти воп-
росы были нами также изучены в предыдущем параграфе. Мы
повторим их еще раз при построении графика.
5) Множество значений. Синус и косинус принимают любые
значения от —1 до +1, так как являются координатами точки,
движущейся по единичной окружности.
2. Графики синуса и косинуса
Для приближенного построения синусоиды можно поступить
так. Разделим первую четверть на 8 равных частей и на столько
же частей разделим отрезок р); y-J оси абсцисс. Удобно при
этом начертить окружность слева, как на рисунке 89. Пере-
несем значения синуса (проекции на ось у точек деления окруж-
ности) к соответствующим точкам оси х. Получим точки, лежа-
щие на синусоиде, которые нужно плавно соединить и продол-
жить кривую дальше, пользуясь симметрией.
141
Так мы получим график синуса на промежутке [б; . Так
как sin —х ) = sin , то график синуса должен быть
симметричен относительно прямой х=^-. Это позволяет построить
график синуса на отрезке [у-; л ] . Воспользовавшись нечетностью
синуса, получим график синуса на отрезке [—л; 0] симметричным
отражением построенной части синусоиды относительно начала
координат. Так как отрезок [—л; л] имеет длину, равную
периоду синуса, то график синуса на всей числовой оси можно
получить параллельными переносами построенной кривой.
График синуса мы построили, воспользовавшись его свойства-
ми. При этом к определению синуса мы обращались только при
построении графика на отрезке 0; -yj.
Построение графика на всей оси потребовало знания сим-
метрии вращательного движения (формулы приведения, нечет-
ность, периодичность). После того как график построен, полезно
вернуться к свойствам синуса и посмотреть, как они проявляются
на графике.
1. Функция r/ = sin х имеет период 2л. На графике это свойство
отражается следующим образом: если мы разобъем ось х на
отрезки длиной 2л, например, точками... —4л, —2л, 0, 2л, 4л, ...,
то весь график разобьется на «одинаковые» части, получающиеся
друг из друга параллельным переносом вдоль оси х. При этом вид-
но, что 2л — наименьший положительный период синуса.
2. Функция r/ = sinx нечетна. На графике это свойство
проявляется так: синусоида симметрична относительно начала ко-
ординат.
3. Функция r/ = sinx обращается в нуль при х = лй, fegZ.
На графике это точки пересечения синусоиды с осью абсцисс.
142
4. Функция r/ = sinx положительна при 2nfe<x<(2fe+1) л
и отрицательна при (2fe+1) л<х<(2/г-|-2) л, fe£Z. Указанные
промежутки соответствуют первой-второй (sinx>0) или третьей-
четвертой четвертям (sin х<0).
5. Функция у = sin х возрастает при —4-2лй^х^—-4-2л&
и убывает при -^-4-2лй^х^-у- + 2лй, k£Z. Указанные отрез-
ки соответствуют четвертой-первой и второй-третьей четвертям.
6. Множеством значений функции y = sinx является отрезок
[— 1; 1]. Действительно, проекции вращающейся точки на ось
заполняют отрезок [—1; 1]. На графике это свойство проявля-
ется так: синусоида расположена в полосе — и .при
этом проекции точек графика на ось у целиком заполняют отре-
зок [—1; 1].
График косинуса можно построить так же, как и график си-
нуса. Возможен и другой путь. Формулы приведения показывают,
что синус и косинус связаны между собой простыми соотношения-
ми. Воспользуемся, например, формулой cos x = sin (хД-—-) .
Эта формула показывает, что график косинуса получается сдвигов
синусоиды на у- влево по оси х (схема VIII).
Если изображать графики синуса и-косинуса в системе коор-
динат с одинаковым масштабом по осям, то синусоида получается
очень растянутой. Однако на практике величины х и у, связанные
с помощью тригонометрических функций, имеют различные едини-
цы измерения и необязательно изображать их в одном масштабе.
Если аргумент умножить на некоторое число, то синусоида
будет, как гармоника, сжиматься и растягиваться по оси х. При-
меры такого преобразования приведены на рисунке 90.
Если значение синуса умножить на число, то будет происхо-
дить растяжение (сжатие) по оси у.
Графики функций вида у —A sin (сохД-а) при различных Д, со, a
являются синусоидами. Эти функции описывают так называемые
Рис. 90
143
гармонические колебания — движение проекции вращающегося
шарика на ось или колебания конца упругой пружины.
Постоянные величины Д, со, а, задающие колебания, имеют
наглядный физический смысл: А — амплитуда колебания, со — его
частота, а — начальная фаза.
3. Исследование тангенса и котангенса
Если свойства синуса и косинуса мы получили, рассматривая
свойства движения точки по окружности, то для исследования
тангенса и котангенса нам нет необходимости возвращаться к
механической модели.
По определению тангенс числа х задается как отношение
sin х и cos х. Изучим свойства тангенса.
1. Областью определения функции r/==tgx=^-^ является
множество всех вещественных чисел, за исключением тех, в кото-
рых косинус обращается в нуль. Мы запишем это множество
следующим образом: л/г, kf^zj.
2. Тангенс — периодическая функция с периодом л:
tg (x + n)=sin(*+") =^^=tg X.
bX 7 cos(x+n) — COS X b
3. Тангенс — нечетная функция, т. е. tg( —х)=—tgx.
4. Функция r/ = tgx обращается в нуль одновременно с си-
нусом, т. е. при х = л/г, k£Z.
5. Функция £/ = tgx положительна в первой и третьей четвер-
тях и отрицательна во второй и четвертой.
Выберем для дальнейшего изучения тангенса какой-либо проме-
жуток числовой оси длиной, равной периоду, т. е. числу л.
Можно было бы выбрать отрезок от 0 до л, но это неудобно,
так как внутри этого отрезка есть точка х=-—•, в которой
тангенс не определен. Лучше выбрать промежуток ( —•
6. Тангенс возрастает в первой четверти. Действительно,
пусть 0<Х| <х2<у-. Тогда sin Xi <sin х2 (возрастание синуса) и
cosxi>cosx2 (убывание косинуса). Так как значения косинуса
положительны, то по свойству неравенств имеем —!—<——.
J Г COS Xi cos х2
Умножим это неравенство на неравенство с положительными
членами: sin Xi <sin х2. Получим tgxi<tgx2.
Тангенс возрастает также и в четвертой четверти. Действитель-
но, пусть ——<Х| <х20. Тогда имеем 0^ —х2< —Xi
144
Теперь числа ( — *2) и ( —Х|) лежат в первой четверти, и мы
можем воспользоваться тем, что в первой четверти тангенс воз-
растает: tg ( — x2)<tg ( — xi). Но так как тангенс — нечетная
функция, получим:
tg ( — х2) < tg ( — Х|) — tg Х2< — tg X, => tg Xi <tg Х2.
На промежутке (—о] тангенс отрицателен и возрастает.
На [О; -у) тангенс становится положительным и возрастает.
В итоге тангенс возрастает на промежутке ( —.
7. Какие же значения принимает тангенс? Когда х возрастает
от 0 до тангенс возрастает. При этом когда х приближается
к -2-, синус х близок к единице, а косинус близок к нулю. Поэтому
отношение sl”~~ становится сколь угодно большим. То, что любое
вещественное число может быть значением тангенса, видно из
рисунка 91. Построим ось, параллельную оси ординат с нача-
лом в точке Ро. Возьмем на этой оси точку, соответствующую
произвольно выбранному числу а. Соединим Оса. Получим точку
Р на окружности. Пусть х — число, принадлежащее (—
и такое, что (cos х; sin х) — координаты Р. Тогда tgx=^-^=
=-р=а. Мы показали, что областью значений тангенса является
вся числовая ось R.
Вообще на этой оси, которую часто называют осью танген-
сов, можно проследить все свойства тангенса.
145
8. Построим график тангенса. На промежутке |_0; график
тангенса можно построить по точкам, учтя, что тангенс строго
возрастает, в нуле обращаясь в нуль, а при приближении к -2-
становится сколь угодно большим (рис. 92).
Отразив построенную часть графика относительно начала
координат (тангенс — нечетная функция), получим график тан-
генса на промежутке( —2_; -2-) . Для построения полного графика
разобьем числовую ось на отрезки, перенося ( —2-; -2-) вправо
и влево на л, 2л, Зл и т. д.
График тангенса распадается на отдельные, не связанные
между собой части. Это вызвано тем, что в точках -2-4-л&, fe^Z,
тангенс не определен.
Замечание (о монотонности тангенса).
Мы доказали, что функция тангенс возрастает на ( —2-; -2-) .
Можно ли сказать, что тангенс возрастает на всей области опре-
деления? Нет. Достаточно посмотреть на график. Если взять
Х| а то Xi = 1, a tg х2 = — 1. Хотя %1 <х2, но tg Xi >
>tg х2. Нарушение монотонности связано с тем, что между точка-
ми %| и х2 лежала точка х = -2-, в которой тангенс не определен.
Однако можно сказать, что тангенс возрастает на каждом
промежутке, который целиком попадает в его область определения.
Свойства котангенса получаются так же, как и свойства
тангенса. Перечислим кратко эти свойства, оставляя их доказа-
тельство для самостоятельной работы.
1. Функция у = ctg х = определена при х=#лй, k£Z.
2. Функция y = ctgx периодична. Ее периодом является чис-
ло л:
ctg (х + л) = ctg X.
3. Функция y = ctgx нечетна: ctg ( — х) = — ctg х.
4. Функция y = ctgx обращается в нуль одновременно с коси-
нусом, т. е. при х = -2—|-л&, k£Z.
5. Функция y = clgx положительна в первой и третьей четвер-
тях и отрицательна во второй и четвертой.
6. Функция y = ctgx убывает на промежутке (0; л). Перенося
его на йл, получаем, что котангенс убывает на каждом про-
межутке (лй; л + лй).
146
7. Область значений котангенса — множество R всех вещест-
венных чисел.
8. График котангенса изображен на рисунке 93.
4. Производные тригонометрических функций
Пусть точка А движется с единичной скоростью . по
окружности радиуса 1 с центром в начале координат О в положи-
тельном направлении. Координаты точки А в момент времени t
равны cos t и sin t. Вектор мгновенной скорости точки А в мо-
мент времени t направлен по касательной к окружности в точке
А (рис. 94), и в силу теоремы о перпендикулярности касательной
к радиусу, проведенному в точку касания, вектор и перпендикуля-
рен вектору ОА.
Вычислим координаты вектора и. Отложив от точки О
вектор и, мы получим вектор ОВ, координаты которого равны
координатам вектора и. Далее, так как движение точки А по
окружности происходит с единичной скоростью, то длина век-
—
тора v равна 1, поэтому длина вектора ОВ также равна 1. Следова-
тельно, точка В лежит на окружности.
Вектор ОВ перпендикулярен вектору О А, поэтому если A = Pt,
то В = Р^Л. Таким образом, координаты вектора v = OB равны
cos^-y—= —sin t и sin Н ) =cos t.
С другой стороны, координаты скорости v являются производ-
ными от координат точки Д, следовательно,
(cos ty = — sin (sin /),==cos t.
Найдем производную функции у —A sin((of + a):
у' = Дсо cos ((о/ + а) = Д(о sin ((о/4-а + -£-) .
Рис. 94
147
Рассмотрим примеры.
1. r/ = sin х cos х,
у' = (sin х)' cos х + sin х (cos x)' = cos2 x — sin2 x.
2. r/ = sin 5x, £/' = 5 cos 5x.
3. y = cos^-, y' =—5-sin-^-.
4. y = 2 sin (3x—2-) , у' = 6 cos (3x—2-) .
5. y = 5 cos (-2—x) ,
f/'=4-(-!)•(— l)sin (-^-x)=-|-sin (-2— x) .
О \ О / О \ □ /
Вычислим теперь производную функции y = tgx. Так как
tg то по теореме о производной частного получаем:
(tg x)/==cos2x-(-sin2x) = ^
v ° 7 COS X COS X
Следовательно, (tg xY =—L— .
v 6 ' cos2 X
Аналогично
(ctg x)' =
— sin2 x —cos2 x
sin2 x
1
sin2 x ‘
Таким образом, (ctgx)'=—
У sin x cos X tgx Ctgx
У' cos X — sin x 1 cos2 X 1 sin2 x
Примеры.
1. z/ = tgx + ctgx,
/_____ 1_______1 _ sin2 x—cos2 x
& cos2 x sin2 x sin2x-cos2x
2. 9-2lg3x. у-=5^
3. 9 = 3cte(f-i),
148
5. Приближенные формулы
Главная приближенная формула: вблизи нуля sin t^t.
Доказательство. Дифференциал функции у = sin х ра-
вен dy = cosxdx. Найдем dy при х = 0. Так как cos 0=1, то при
х = 0 dy = dx. Найдем приращение функции:
Ay = sin Дх —sin 0 = sin Дх.
Так как kyxidy, то получим Ar/ = sin \x^dy = dx = Дх. Вместо
Дх можно написать t и получить sin t^t.
Эта формула дает тем точнее значение синуса, чем ближе t к
нулю. Возможность заменять sin t на t при маленьких зна-
чениях угла t широко употребляется в приближенных вычисле-
ниях. Можно дать различные интерпретации этой приближенной
формулы.
1. lirn-———== 1 — это запись того, что отношение приращения
функции к его главной части стремится к единице при стремлении
к нулю приращения аргумента.
2. Рассмотрим единичный круг. Пусть для простоты />0.
Тогда длина дуги АВ равна /, а длина отрезка ВС равна sin t.
Удвоим дугу АВ и отрезок ВС — дуга BD имеет длину 2/, а
хорда BD — длину 2 sin Л Соотношение sin/^/ означает, что
отношение длины хорды к длине стягиваемой ею дуги стремится
к единице, когда дуга стягивается в точку (рис. 95).
3. Рассмотрим касательную к синусоиде в начале координат.
Так как (sin x)' = cos х, a cos 0= 1, то уравнение этой касательной
у = х. Таким образом, заменяя вблизи начала координат график
синуса отрезком касательной, мы вычисляем приближенное значе-
ние синуса по формуле sin
Для получения других приближенных формул выпишем диффе-
ренциалы тангенса и косинуса:
zy —tgx, dy=-^-^dx\
y = cosx, dy=— sinxdx.
При х = 0 получим приближенное
значение тангенса:
tg Дх«Дх, tg t^t.
Применяя этот же прием к косину-
су, мы получим, что дифференциал ко-
синуса при х=0 равен —sin О-dx, т. е.
равен 0. Это означает, что главная часть
приращения косинуса равна нулю и в
первом приближении cos х « cos 0=1.
Можно получить более точную формулу
таким путем. Запишем cos х так:
149
cos x=^Jl —sin2 x. Заменим в этой формуле sin х на х и восполь-
зуемся приближенной формулой для квадратного корня:
Vl — sin2 х«-д/1 — х2« 1 -у-.
Полученная приближенная формула для косинуса вблизи точки
х = 0 весьма точна.
Более точные приближения можно получить с помощью формул
х$
sinx = x-T+—-..-
. х2 . х4
COS Х=\ - — .
Примеры.
1. Вычислить приближенно sin 0,03-tg 0,12.
sin 0,03«0,03, tg0,12«0,12, sin 0,03-tg 0,12«0,0036«0,004.
2. Вычислить приближенно sin 2°. Переводим 2° в радианную
меру: 2° «0,034. sin 2°«0,034.
Контрольные вопросы
1. Как определяются синус и косинус числа х?
2. Какова область определения синуса и косинуса?
3. В каких точках синус и косинус обращаются в нуль?
4. Как меняются знаки синуса и косинуса?
5. Каковы наименьшее и наибольшее значения синуса и коси-
нуса?
6. Являются ли точки, в которых синус (или косинус) при-
нимает наибольшее или наименьшее значение, точками экстре-
мума?
7. Сколько точек экстремума имеет синус (косинус)?
8. Сколько раз принимает свое наибольшее (наименьшее) зна-
чение синус (косинус)? Чему оно равно?
9. Какому неравенству удовлетворяют все значения синуса
(косинуса)?
10. Каково множество значений синуса (косинуса)?
11. Можно ли сказать, что синус (косинус) является монотон-
ной функцией?
12. На каких промежутках (в каких четвертях) синус (коси-
нус) возрастает (убывает)?
13. Какова область определения тангенса (котангенса)?
14. Каков период тангенса (котангенса)?
15. В каких точках тангенс (котангенс) обращается в нуль?
16. Как меняются знаки тангенса (котангенса)?
17. Что можно сказать о монотонности тангенса (котангенса) ?
18. Имеет ли тангенс (котангенс) точки экстремума?
150
19. Принимает ли тангенс (котангенс) наибольшее (наимень-
шее) значение?
20. Какова область значений тангенса (котангенса)?
21. Сколько раз принимает каждое свое значение тангенс
(котангенс)?
22. Чему равна производная синуса, косинуса, тангенса,
котангенса?
23. Каковы координаты вектора скорости вращательного дви-
жения?
24. По каким приближенным формулам можно вычислить си-
нус, косинус и тангенс угла, близкого к нулю?
§ 3. ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ
1. Формулы сложения
Тригонометрические функции связаны между собой многочис-
ленными соотношениями. Первая серия тождеств описывает связь
между координатами точки окружности — это так называемые ос-
новные соотношения. Эти соотношения позволяют выразить значе-
ния одних функций через другие (при одном и том же значе-
нии аргумента). Вторая серия тождеств происходит от симметрии и
периодичности в движении точки по окружности. Отсюда мы полу-
чаем формулы приведения. Третий источник тригонометрических
формул — это изучение поворотов. Поворот точки на угол а + 0
можно составить из композиции двух поворотов — на угол а и на
угол 0. Есть простые формулы, связывающие координаты то-
чек Ра, Рр и Ра+р. Эти формулы называются формулами сло-
жения.
Нашей целью является вывод формул, связывающих sin (а ±0),
cos (а ± 0), tg (а ± 0), ctg (а ± 0) с тригонометрическими функциями
углов а и 0. Достаточно вывести формулу косинуса разности, ос-
тальные формулы получатся как ее следствия.
Теорема. Косинус разности двух углов равен произведению
косинусов этих углов, сложенному с
произведением синусов:
cos (а — 0) = cos а cos 0 + sin а sin 0.
Доказательство. Построим
углы а и 0 с помощью единичной
окружности, т. е. точки Ра и Рр, такие,
что векторы ОРа и ОРр образуют уг-
лы а и 0 с положительным направле-
нием оси абсцисс. Угол между вектора-
ми ОРа и ОРр равен а — 0 (рис. 96).
151
Вычислим скалярное произведение этих векторов. По опреде-
лению скалярного произведения
ОРа • ОРр = | ОРа | • | ОРр | • cos (а - 0) = cos (а - 0)
(так как векторы ОРа и ОРр имеют длину, равную 1).
Теперь вычислим это же скалярное произведение с помощью
координат:
ОРа • ОРр = cos a cos 0 + sin а sin 0.
Сравнивая результаты вычислений, получаем требуемую формулу:
cos (а — 0) = cos а cos 0 + sin а sin 0.
Доказательство теоремы закончено. Выведем остальные формулы.
Косинус суммы. Сумму а + р представим как разность
а —( —Р) и подставим в формулу для косинуса разности:
cos (a + 0) = cos (a — (— 0)) = cos a cos ( — 0) + sin a sin ( — 0).
Воспользуемся тем, что cos( —0) = cos 0 (четность косинуса),
a sin( —Р)=—sin 0 (нечетность синуса). Получим:
cos (a + 0) =cos a cos 0 — sin a sin 0.
Синус суммы. Воспользуемся одной из формул приведения:
sin (a + 0)=cos (у— (a + 0)) = cos ((у-—a ) — 0 ) .
Теперь по формуле косинуса разности получим:
cos ((-£— a ) — 0 ) = cos (-2— a ) cos 0 + sin (-2— a ) sin 0.
Окончательно
sin (a + 0) = sin a cos 0 + cos a sin 0.
Синус разности sin (a —0) = sin (a + ( —0)) = sin a cos ( —0)+
-|-cos a sin ( —0)=sin a cos 0 —cos a sin 0.
sin (a —0) = sin a cos 0 —cos a sin 0.
В качестве примера вычислим sin 15°. Представим 15° как
разность 45° — 30°. Получим sin 15° = sin (45° — 30°) =
= sin 45° cos 30°-cos 45° sin 30° =^-^-^-±-=^/3- 1).
152
Тангенс суммы и разности. По определению tg(a + P) =
sin (a-1-6) гт 1
cos (ос + р) ' 1° Ф°РмУлам синуса и косинуса суммы имеем:
। / I q\___ sin a cos fl + cos a sin fl
°' cos a cos fl —sin a sin fl
Разделив числитель и знаменатель этой дроби на cos a cos 0,
получим:
Заменяя £
лучаем:
tg(a + (3)=tg«+tgP
g 1—tgatgfl ’
на ( —Р) и пользуясь нечетностью тангенса, по-
P' l+tgatgr
2. Формулы удвоения
Формулы сложения являются одними из основных формул, свя-
зывающих тригонометрические функции. Из них можно вывести
различные следствия. Полагая а = р, получим так называемые
формулы удвоения.
1. sin 2a = sin (a + a) = sin a cos a-f-cos a sin a = 2 sin a cos a;
sin 2a = 2 sin a cos a.
2. cos 2a = cos (a 4-a) = cos a cos a —sin a sin a =
= cos2 a —sin2 a;
cos 2a = cos2 a —sin2 a.
Заметим, что в формуле для cos 2a можно заменить cos2 a
на 1 — sin2 а или sin2 a на 1 — cos2 a. Получим две новые формулы:
cos 2a = 1 — 2 sin2 a, cos 2a = 2 cos2 a — 1.
3. tg2a = tg(a + a)=-lg“+tga =r^-;
1— tg a tg a 1— tg2 a
tg 2a =-2^“-.
S l-tg2a
3. Тригонометрические функции половинного угла
Из формул двойных углов cos 2а = 2 cos2 а — 1 = 1 —2 sin2 а
можно получить формулы для синуса и косинуса половинного угла.
Сначала запишем:
cos2 а=-£-(1 + cos 2а), sin2 а=-—(1 —cos 2а).
153
Затем в этих формулах подставив у вместо а, получим:
cos2 + cos а), sin2 — cos а).
Извлекая корень, получим:
I а I _/ 1— cos а I а I _/ 1+cosa
lsin~l = V—2—’ lC08ThV 2—•
^Для того чтобы раскрыть модули, надо знать, в какой четверти
лежит угол -у. )
Обилие тригонометрических формул связано с тем, что между
основными тригонометрическими функциями — синусом, косину-
сом, тангенсом и котангенсом — есть соотношения, которые позво-
ляют по-разному написать одно и то же выражение. Возникает
вопрос: нельзя ли выбрать одну какую-то функцию и через нее вы-
ражать все остальные? Если в качестве такой функции мы выбе-
рем синус, то во многих формулах появятся квадратные корни.
Так, например, выражая sin 2a через sin а, мы получим sin 2a =
= 2 sin a cos a = 2 sin a (±V* —sin2 a). Такие формулы неудобны.
Оказывается, что все тригонометрические функции от аргу-
мента х (и от пх при целом п) выражаются через тангенс
угла у- рационально, без квадратных корней. Выведем эти полез-
ные формулы.
Напишем формулы двойного угла для исходного угла у-:
sin х = 2 sin у cos у, cosx = cos2^—sin2 у.
Представим число 1 в виде 1 =sin2 у—(-cos2 у и поделим на
1 правые части последних формул:
2 Sin у COS у COS2 у — Sin2 у
sin х =------------, cos х —--------------.
Sin2 у 4- COS2 у Sin2 у + cos2 у
Поделим теперь числитель и знаменатель каждой дроби на
.9х • Х
sin Т х Sln ~2 х
cos2—- и заменим ------ на tg2-£- и -----на tg-£-:
cos2 у cos у
2 tg у l-tg2f
sin х =------, cos х=-------.
1 + tg2^ i+tg2f
154
Пользуясь этими формулами, можно функцию вида у —
= а sin %+&cos х + с представить в виде рациональной функции
от tg у.
Пример. Выразить у —2 sin х + 3 cos х— 1 в виде функции
от tg у.
о. X . , 2 Х
2tg-y l-tg-s-
2 sin х + 3 cos x — 1 = 2---1-3---------1 =
i+tg2f i+tg2f
4tgy + 3-3tg2y-l-tg2y -4tg2y + 4tg-i- + 2
•+tg2f l+tg2f
4. Преобразование суммы тригонометрических функций
в произведение и обратные преобразования
Пусть требуется преобразовать сумму sin a + sin р в произве-
дение. Используем следующий искусственный прием: напишем
тождества а=—уН—у1 и Р = “----------2 ’ заменим аиР вы-
ражениями, стоящими справа, в формулах для синуса суммы и раз-
ности:
sin a + sin 0 = sin (^y^+^^^ + sin -^£) =
=sin cos a~P + cos a + P sin g~^ +sin g + ^ cos g~^—
At At At At At At
- cos Sin ^-=2 sin COS .
sin a + sin 0=2 sin g^~P cos g~^ .
Аналогично выводятся еще три формулы:
sin a — sin 0 = 2 sin g~~cos
r 2 2 ’
cos a + cos 0 = 2 cos a + cos g~^ ,
cos a — cos 0 = 2 sin g+^ sin ^~g .
к 2 2
Выпишем подряд четыре формулы сложения:
1. sin (a + 0)=sin a cos 0 + cos a sin 0.
2. sin (a — 0) = sin a cos 0—cos a sin 0.
3. cos (a + 0) = cos a cos 0—sin a sin 0.
4. cos (a — 0)=cos a cos 0+ sin a sin 0.
155
Вычитая почленно из четвертого равенства третье, получим:
sin a sin 0 =-^-(cos (а — 0) — cos (а + Ра-
складывая третье и четвертое равенства, получим:
cos a cos р = --(cos (а — 0) + cos (а + 0)).
Складывая два первых равенства, получим:
sin a cos р = -^-(sin (a + 0) + sin (а —0)).
Мы рассмотрели различные тождества, связывающие тригоно-
метрические функции. Все их запомнить трудно, и приходится об-
ращаться к таблицам и справочникам. Важнее запомнить не сами
формулы, а то, какие функции между собой они связывают,
что с их помощью можно получить.
Контрольные вопросы
1. Чему равен косинус разности двух углов?
2. Как, зная формулу для косинуса разности, вывести другие
формулы сложения?
3. Приведите все известные вам формулы для косинуса двой-
ного угла.
4. Через какую функцию все тригонометрические функции вы-
ражаются с помощью рациональных формул?
5. Какой искусственный прием применяется для вывода фор-
мул для суммы и разности синусов и косинусов?
§ 4. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
1. Арксинус
Рассмотрим уравнение sinx = a. Так как областью значений
синуса является отрезок [— 1; 1], то это уравнение не имеет реше-
ний при |а\ >1. Пусть теперь |a| 1. Построим на одном чертеже
графики у = а и r/ = sinx (рис. 97).
156
По рисунку ясно, что прямая у = а пересечет синусоиду бес-
конечно много раз. Это означает, что при |а| ^1 уравнение
sinx = a имеет бесконечно много корней. Так как синус имеет
период 2л, то достаточно найти все решения в пределах одного
периода. По графику видно, что при |а| < 1 на отрезке [0; 2л] есть
два числа, или, можно сказать, два угла, синус которых равен а.
Если один из таких углов а, то другой л —а. Все другие
решения уравнения sin х = а, где |а| < 1, получаются из двух най-
денных с помощью свойства периодичности синуса.
Итак, пусть а — какое-либо решение уравнения sinx = a,
где |а| < 1. Тогда все решения этого уравнения получаются по
формулам
х = а + 2лй, х = л— а-р2лй, fe£Z.
Эти две серии решений иногда записываются одной формулой:
х = (—1)"а4-лп, n£Z.
Пример. Решить уравнение sin х = у.
Одно решение этого уравнения х=у-. Все остальные решения
получаются по формулам
x=4-+2nfe и х=л—£-+2л£=^-+2л&, k£Z.
О 0 0
Как мы уже выяснили, уравнение sinx=a при |а| 1 имеет
бесконечно много решений. Для одного из них имеется спе-
циальное название — арксинус.
Определение. Пусть число а по модулю не превосходит
единицы. Арксинусом числа а называется угол х, лежащий в пре-
делах от —тг Д° у» синус которого равен а.
Обозначение: х = arcsin а.
Итак, равенство х = arcsin а равносильно двум условиям:
sinx = a и —у^Сх^Су-. Обратим еще раз внимание на то, что
arcsin а существует лишь, если |а| 1.
Примеры.
1. arcsin 0 = 0.
2. arcsin у=у-.
з. arcsin (—L)=—2-.
Теперь решения уравнения sin х — а (при |а| 1) можно запи-
сать так: х = arcsin а + 2л/г, х = л — arcsin а + 2л/г, или в виде
одной формулы:
Jc=( — 1)* arcsin а + 2лЛ, k£Z.
157
Запишем некоторые тождества для арксинуса.
1. sin arcsin а = а.
Это тождество вытекает из определения арксинуса (arcsin а —
это такой угол х, что sin х = а).
2. arcsin (sin х) = х, если х£^—у; у].
Действительно, обозначим sin х через а. Тогда наше тождество
будет равносильно определению арксинуса: arcsin а = х, если
х£^—у-] и sinx = a. Заметим, что выражение arcsin (sin х)
имеет смысл при любом х, однако при х^—y-J оно не равно х.
3. arcsin ( — а) =—arcsin а.
Действительно, синусы от правой и левой частей равны:
sin (arcsin ( —а)) = — а и sin ( — arcsin а)= —sin (arcsin а) = —a.
В то же время правая часть доказываемого равенства — это угол,
принадлежащий отрезку у]. Поэтому левая и правая
части равны между собой.
2. Арккосинус
Так же как и в предыдущем пункте, при |а| > 1 уравнение
cosx = a решений не имеет; если |а| 1, то решений уравнения
бесконечно много.
Если а — какое-либо решение уравнения cos х = а, то — а так-
же есть решение этого уравнения, так как cos а = cos ( — а).
По графику или на единичном круге видно, что при |а|<1 в
пределах одного периода уравнение cos х=а имеет два решения.
Если а — одно из решений уравнения cos х = а, то все решения
исчерпываются двумя сериями:
x = a + 2jife, fe£Z; х=—а + 2лй, fe£Z.
Эти серии обычно записывают в виде одной формулы:
x=±a4-2nfe, fe£Z.
Пример. Решить уравнение cos х= —
Одно решение находится легко: х = ~. Запишем все решения
□
так: х= ±^+2л/г, k£Z.
□
Так же как и для синуса, выделяется одно определенное ре-
шение уравнения cos x = a и ему дается специальное название —
арккосинус.
158
Определение. Пусть а — число, по модулю не превосхо-
дящее единицы. Арккосинусом числа а называется угол х, лежа-
щий в пределах от 0 до л, косинус которого равен а.
Обозначение: х= arccos а.
Равенство x = arccosa равносильно двум условиям: cosx = a
и О^Сх^Сл. Арккосинус числа а существует лишь при |а| < 1.
Пример, arccos 0 —arccos arccos (—^-)=Д-л.
2 2 <5 \ 2 / 3
Решение уравнения cos х = а (при |а| 1) можно записать те-
перь в общем виде:
х = ± arccos а+2 лЛ, k 6 Z.
По каким причинам для значений арксинуса был выбран от-
резок £—, а для арккосинуса отрезок [0; л]?
Это объясняется тем, что на этих отрезках, во-первых, си-
нус и косинус принимают все возможные значения от — 1 до 1 и,
во-вторых, каждое значение принимается ровно один раз. Отрез-
ков с этими условиями бесконечно много, но при этом выбраны
отрезки «поближе к нулю».
Для арккосинуса можно вывести ряд тождеств.
1. cos (arccos а) = а.
Это тождество следует из определения арккосинуса.
2. arccos (cos х) = х, если xg[0; л].
Обозначим cosx = a. Получим определение арккосинуса:
arccos а=х, если х£[0; л] и cosx = a.
3. arccos ( — а) = л — arccos а.
Сначала вычислим косинус от левой и правой частей:
cos (arccos ( — а))= — a; cos (л —arccos а) = — cos (arccos а)= — а.
Если равны косинусы двух чисел, то это еще не означает, что
равны сами числа. Проверим, что правая часть принадлежит от-
резку [0; л]. (Так как левая часть тоже принадлежит этому
отрезку, то из равенства косинусов двух чисел теперь уже будет
следовать равенство самих чисел.) Итак, надо доказать, что
л —arccos а принадлежит [0; л]. Действительно, arccos а£[0; л],
— arccos а£[—л; 0], л—-arccos а£[0; л], что и требовалось до-
казать.
3. Арктангенс
Область значений тангенса (котангенса) — вся числовая ось.
Поэтому уравнения tg х = а, ctg х = а имеют решения при любом
а. В пределах одного периода л тангенс и котангенс принимают
каждое значение ровно один раз. Поэтому если известно од-
159
но решение уравнения tg х = а или ctg х = а, то все остальные полу-
чают прибавлением периода:
tgx = a, x = a-\-nk, k£Z,
ctgx = a, х = а4-л&,
где a — какое-либо решение соответствующего уравнения.
Примеры. Решить уравнения:
1. tg х= 1, x=^-+nk, k£Z.
2. ctgx=^, x=^-+nfc, k£Z.
Определения арктангенса и арккотангенса вводятся анало-
гично определениям арксинуса и арккосинуса, поэтому мы про-
ведем его короче.
Определение. Арктангенсом числа а называется угол
х^(—2-; , тангенс которого равен а.
Арккотангенсом числа а называется угол х(Ч0; л), котангенс
которого равен а.
Обозначения: х = arctg а и х = arcctg а.
Примеры.
1. arctg 0 = 0; arcctg 0=у-;
arctg (—1)=—arcctg ( — l)=-y.
2. Решить уравнения:
tg x = ao x = arcctg a-f-nfe, k£Z,
ctg x = a о x = arcctg a + nfe, k£Z.
Тождества:
1. tg arctg a=a; ctg arcctg a = a.
2. arctg (tgx)=x, если хб(—-у) ;
arcctg (ctg x) = x, если x£(0; л).
3. arctg (-—x) = —arctg x; arcctg ( —x) = n — arcctg x.
4. Решение тригонометрических уравнений
Тригонометрические уравнения встречаются в задачах, в кото-
рых из соотношений между тригонометрическими функциями тре-
буется найти неизвестные углы. Основными, чаще всего встречаю-
щимися тригонометрическими уравнениями являются уравнения
простейшего типа sin х = а, cos х = а, tg х — а и ctg х = а, которые
уже рассмотрены в предыдущих пунктах. Следует отметить, что
такие уравнения обычно имеют бесконечные серии решений, зада-
ваемые с помощью параметра, принимающего целые значения.
160
Более сложные тригонометрические уравнения обычно решают-
ся сведением их к простейшим с помощью различных алгебраи-
ческих и тригонометрических формул и преобразований. Рассмот-
рим некоторые приемы решения тригонометрических уравнений.
а) Уравнения, алгебраические относительно одной из тригоно-
метрических функций.
Примеры решения уравнений.
1. 2 sin2 *4-3 sin х — 2 = 0.
Это уравнение является квадратным относительно sin х. Кор-
ни этого квадратного уравнения sinx = y- и sinx=—2. Второе
из полученных простейших уравнений не имеет решений, так как
|sinx|^l, решение первого можно записать так:
х=-2—|-2л/г и х=я—2-+2яЛ=^Ч-2лЛ, k£Z.
О 0 0
Если в уравнении встречаются разные тригонометрические
функции, то надо пытаться заменить их все через какую-нибудь
одну, используя тригонометрические тождества.
2. 2 sin2 х —5 cos х —5 = 0.
Так как квадрат синуса легко выражается через косинус,
то, заменяя sin2 х на 1 — cos2 х и приводя уравнение к квадратному
относительно cos х, получим 2 (1—cos2 х) —5 cos х —5 = 0, т. е.
квадратное уравнение 2 cos2 х-|-5 cos х4-3 = 0, корни которого
3 3
cos х= — 1, cos х= ——. Уравнение cos х= —— решений не име-
ет. Решения уравнения cosx= —1 запишем в виде
x = n4"2nfe, k£Z.
3. tg х4-3 ctg х = 4.
Заменив ctg х на и приведя к общему знаменателю, полу-
чим квадратное уравнение tg2 х — 4 tg х4-3 = 0, корни которого
tg х= 1, tgx = 3, откуда
х = у—hnfe, x = arctg 34-лй, k£Z.
4. 2 sin x4-cos x = 2.
Если в этом уравнении заменим косинус на синус (по ана-
логии с предыдущими примерами) или наоборот, то получим урав-
нение с радикалами. Чтобы избежать этого, используют формулы,
выражающие синус и косинус через тангенс половинного угла, т. е.
2tgy l-tg2f
sin х=------- и cos х=-------.
l+tg2y l+tg2y
6 Заказ 836
161
Делая замену, получаем уравнение относительно tg у-:
4 tg f+l-tg2 f=2 (1 +tg2 f).
Квадратное уравнение 3tg2-|—4tg-£-+l=0 имеет корни
tgy-=L 0ТКУда
^-=-^+л/г, k£Z, х=у-+2лй, k^Z-,
-£-=arctg 4-+л;й, k^Z, x = 2arctg-|—|-2nfe, k£Z.
Л О о
б) Уравнения, решаемые понижением их порядка.
Формулы удвоения позволяют квадраты синуса, косинуса и
их произведения заменить линейными функциями от синуса и ко-
синуса двойного угла. Такие замены делать выгодно, так как они
понижают порядок уравнения.
Примеры решения уравнений.
1. Решить уравнение cos 2x + cos2 х=—.
Можно заменить cos 2х на 2 cos2 х— 1 и получить квадратное
уравнение относительно cos х, но проще заменить cos2 х
на -i-(l+cos2x) и получить линейное уравнение относительно
cos 2х:
cos 2x + 4-(1+cos 2х)=“2", cos 2х = -^-, x=±-^-+nfe, k£Z.
2. Решить уравнение sin4 x + cos4 х=|р
Подставляя вместо sin2 х, cos2 х их выражение через cos 2х,
получим:
-J-(l -cos 2х)2+у-(1 +COS 2х)2=|р
1 —2 cos 2x + cos2 2х+ 1 +2 cos 2x-|-cos2 2х=4-|т-;
ol
cos2 2х = 2-|т~ 1; cos22x=^-; cos 2x= ±-7-;
ol ol 9
2x= ±arccosk^Z\
x= ±-|-arccos-|-+-|-fc, k£Z.
162
в) Уравнения, решаемые после преобразований с помощью три-
гонометрических формул.
Иногда в уравнениях встречаются тригонометрические функ-
ции кратных углов. В таких случаях нужно использовать форму-
лы преобразования суммы в произведение.
Примеры решения уравнений.
1. sin x + sin 2% + sin 3x = 0,
(sin x + sin 3x) + sin 2x = 0,
откуда 2 sin 2x cos x + sin 2x = 0; sin 2x (2 cos x+ 1) = 0; sin 2x = 0;
2х = л£; x=^, k^Z,
или 2cosx =— 1; x— ±~-\-2nk, k£Z.
2. sin 3x sin 5x = sin x sin 7x.
Преобразуем произведение синусов в сумму:
X-(cos 2х —cos 8x)=-i-(cos 6х —cos 8х), cos 2x = cos 6х.
Полученное уравнение можно решить разными способами. Мож-
но воспользоваться формулами сложения и преобразовать в произ-
ведение. Удобнее воспользоваться условием равенства косинусов
двух углов 2х и 6х:
6х= ±2х4-2л/г, k£Z.
Получим два уравнения:
6x=2x4-2nfe, 4х = 2лЛ, х=^-, k£Z\
6х=—2х + 2лЛ, 8х = 2лЛ, k£Z.
Проверьте, что решения второй серии содержат в себе все
решения первой серии. Учитывая это, ответ можно записать
короче:
х=¥-, k£Z.
4
г) Однородные уравнения.
Решим уравнение sin2 х—5 sin х cos х + 6 cos2 х = 0.
Если считать, что sin х и cos х — члены первой степени,
то каждое слагаемое имеет вторую степень. Уравнение, в кото-
ром каждое слагаемое имеет одну и ту же степень, называется
однородным. Его можно решать делением на старшую степень
синуса (или косинуса). Делим наше уравнение на cos2 х. (При
этом мы не потеряем корней, так как если мы в данное уравне-
163
ние подставим cosx = 0, то получим, что и sinx = 0, что невоз-
можно.)
1Ш!^_5.2Ш_£+6 = 0; tg2 х-5 tg х 4-6 = 0;
tgx = 2, tgx = 3;
x = arctg 2 +nfe, x = arctg3 + nfe, fegZ.
Пример. 5 sin2 *4-3 sin x cos x — 4 = 0.
Заменяя 4 на 4 (sin2 x4- cos2 x), получим:
sin2 x-|-3 sin x cos x — 4 cos2 x = 0, tg2 x4~3 tg x —4 = 0;
tg x= 1, tg x = — 4,
x = -~4-nfe, x=—arctg 4 4-nfe, fegZ.
Контрольные вопросы
1. Обратите внимание на следующие встретившиеся в тексте
ключевые слова: арксинус, арккосинус, арктангенс, однородное
уравнение. Приведите примеры их использования.
2. Что такое arcsin а?
3. Какие тождества для арксинуса вы знаете?
4. При каких а определен arcsin а?
5. Какие значения принимает arcsin а?
6. Сформулируйте вопросы, аналогичные вопросам 2—5, для
arccos а и arctg а и дайте на них ответы.
7. Сколько решений имеют простейшие уравнения типа
sinx = a, cosx = a, tgx = a, ctgx = a?
8. Как, зная одно решение простейшего тригонометрического
уравнения, найти все его решения?
9. Какими формулами выгоднее пользоваться при решении три-
гонометрических уравнений и почему?
10. Придумайте несколько различных способов решения урав-
нения sin x-|-cos х = 1.
ЗАКЛЮЧИТЕЛЬНАЯ БЕСЕДА
Гармонические колебания
Гармонические колебания — это процесс, который может быть
описан функцией вида у — A sin (<ох4-а).
Примеры.
1) Колебания упругой пружины. Конец упругой пружины (точ-
ка Р) при ее сжатии или растяжении описывает колебатель-
ные движения. Если на прямой, по которой движется точка Р,
164
ввести координату х так, чтобы в положении равновесия хр = 0, от-
тянуть конец пружины в положительном направлении на расстоя-
ние Див момент времени / — О отпустить его, то зависи-
мость координаты точки Р от времени t (рис. 98) будет иметь сле-
дующий вид: х = Д cos (о/ = Д sin + » где — некоторый
коэффициент, характеризующий упругость пружины.
2) Электрический колебательный контур. Рассмотрим электри-
ческую цепь, состоящую из последовательно соединенных конден-
сатора С и катушки индуктивности L (рис. 99). Если эту цепь
замкнуть накоротко и считать, что в ней есть некоторый за-
пас энергии (например, ненулевой заряд в конденсаторе), то по
этой цепи пойдет ток, напряжение которого U будет меняться со
временем. При идеальном предположении отсутствия потерь в цепи
зависимость U от времени t будет иметь следующий вид:
(/= (/о sin ((о/ +а), где со — некоторая характеристика контура,
которая вычисляется через параметры конденсатора и катушки.
Константы Uq и а зависят от состояния цепи в начальный
момент времени.
Таким образом, гармоническое колебание у = А sin (со/Д-а)
определяется тремя параметрами: амплитудой Д>0, угловой ско-
ростью со>0 и так называемой начальной фазой а. Часто
вместо угловой скорости со говорят о частоте колебаний v, ко-
торая связана с угловой скоростью со (или иначе круговой
частотой) формулой co = 2nv. Функция у периодична. Ее основной
2л 1
период равен Г=—=—.
Колебания приходится складывать. В механике это связано
с тем, что на точку может действовать несколько сил, каж-
дая из которых вызывает гармонические колебания. В электро-
и радиотехнике сложение колебаний происходит как естественное
наложение токов. Оказывается, имеет место замечательный закон:
при сложении гармонических колебаний одной и той же частоты
получается снова гармоническое колебание той же частоты. На ма-
тематическом языке это означает, что сумма двух функций
у — А\ sin (со/Д-ai) и у=А2 sin (со/Д-аг) есть функция того же
вида: у —Аз sin (со/ Д-аз).
Достаточно научиться складывать функции вида у — А\ sin со/ и
Рис. 98 Рис. 99
165
y = A2 cos со/. Для их сложения применяется прием введения вспо-
могательного угла. Итак, рассмотрим выражение у = А\ sin <о/ +
+ Д2 cos со/. Оно похоже на формулу синуса суммы: sin ((о/ + а) =
= sin со/ cos а + cos со/ sin а. Числа А\ и А2 нельзя считать ко-
синусом и синусом, однако если их разделить на число
лМ?+^2, то тогда это будет возможно. Введем угол а с помощью
соотношений
cos а=—--1..- , sina = —.
а/лТ+л! л/лТ+л?
Сделаем преобразование:
Д| sin (0/4-Д2 cos со/ =
= -\/Д1+Д2 ( "dl -sin со/-|--COS О)/ ) =
V л/лТ+л? Vtf+Al '
=Дз sin (со/+ а), где Дз=лМ|+Д2.
Примеры.
1. £/ = sin % + cos х. Сделаем преобразование:
sin х + cos х = л/2 (—г sin *4—— cos х ) = л/2 sin (*4-—-^ .
М V2 / к 4 /
2. £/ = 3 sin 2*4-4 cos 2*. Введем вспомогательный угол а с по-
3.4^ *
мощью равенств cos а=—, sin а=—. Сделаем преобразование:
3 sin 2*4-4 cos 2* = 5(-|-sin 2*4--g-cos 2*^ = 5 sin (2*4-«).
2. Периодические функции
Тригонометрические функции являются периодическими. В об-
щем виде функция y = f(x) называется периодической, если су-
ществует такое число Г=#0, что равенство f (* + !) = /(*) выпол-
няется тождественно при всех значениях *.
Обычно среди периодов периодической функции можно выде-
лить наименьший положительный период, который часто называют
основным периодом. Все другие периоды функции являются це-
лыми кратными основного. График периодической функции состо-
ит из повторяющихся кусков, поэтому достаточно построить его
на отрезке изменения аргумента длиной, равной основному пери-
оду. На рисунке 100 изображены графики различных периоди-
ческих функций.
Приведем пример одной интересной периодической функ-
ции. Всякое число * можно представить в виде суммы его целой
и дробной частей. Целая часть числа * определяется как наиболь-
шее целое число, не превосходящее *, и обозначается [*]. Напри-
мер, [3]=3; [3,14]=3; [—3,14]=— 4. Дробная часть обозначается
166
{х} и равна по определению х — [х]. Функция у={х}=х — [х] являет-
ся периодической с основным периодом, равным единице. Ее
график изображен на рисунке 101.
Если функция y = f(x) периодична и ее периодом является
число Т, то и функция y=f (fex) будет периодической, причем ее пе-
т
риодом будет число Действительно, рассмотрим функцию
y=g(x), где g(x)=f(*x). Вычислим g(x+-
g (х+Х) =f (k (x+^)) (fex+ T)=f (kx).
Сдвиг аргумента не меняет период функции. Отсюда следует,
что функция у=А sin(<o/ + a), задающая гармоническое колеба-
Г 2л
= —.
Если Т является общим периодом двух функций f и gt то Т
остается периодом их суммы, произведения, частного. Правда,
как мы видим на примере тангенса, если Т является основным
периодом f и gt то это может быть не так для новых функций,
полученных из f и g арифметическими операциями.
Сумма двух функций с различными периодами необязательно
будет периодической. Интересен случай сложения двух функций
с различными, но очень близкими периодами. Рассмотрим, на-
167
пример, сумму функций у\ = sin o)it и r/2 = sin со2/, где а>| и со2 близки
друг к другу. Складывая синусы, получим
у. + у2 = 2 sin t. cos t.
Так как <0i«?(02, то <°1^— «<oi, а Поэтому
cos 1 при маленьких значениях t и yi-\-y2&2y.
Однако с ростом t множитель 2 cos tol у— t будет убывать.
«Ровное» гармоническое колебание типа у\ заменится «бие-
нием», график которого изображен на рисунке 102. Можно пред-
ставить себе, что «биение» — это колебание, амплитуда которого
медленно (и тоже периодически) меняется. Явление «биения»
можно наблюдать при наложении звуков близкой частоты, при
измерении величины океанских приливов, которые вызываются на-
ложением двух периодических процессов с близкими, но раз-
личными периодами — притяжением Солнца и притяжением
Луны.
3. Разложение на гармоники
Чистый звуковой тон представляет собой колебание с некото-
рой постоянной частотой. Музыка, которую мы слышим, представ-
ляет собой наложение различных чистых тонов, т. е. получается
сложением колебаний с различными частотами. Преобладание зву-
ка той или иной частоты (скажем, низких звуков или высо-
ких) связано с амплитудой соответствующих колебаний. Это
знакомое нам разложение звуков на чистые тона часто встречает-
ся при изучении различных колебательных процессов.
Можно сказать так: простейшие гармонические колебания яв-
ляются теми кирпичиками, из которых складывается любое коле-
бание. На языке математики это означает, что любую периоди-
ческую функцию можно представить с наперед заданной точностью
как сумму синусов.
168
Эйлер Леонард
(1707—1783) —
швейцарский математик и механик, акаде-
мик Петербургской Академии наук, автор ог-
ромного количества научных открытий во
всех областях математики. Эйлер первым
применил средства математического анализа
в теории чисел, положил начало топологии.
«Математика, вероятно, никогда не до-
стигла бы такой высокой степени совершенст-
ва, если бы древние не приложили столько
усилий для изучения вопросов, которыми се-
годня многие пренебрегают из-за их мнимой
бесплодности».
Л. Эйлер
Этот замечательный факт обнаружен еще в XVIII в. Д. Бернул-
ли при решении задачи о колебании струны. Это показалось
удивительным и невозможным по отношению к любой функции да-
же такому гениальному математику, как Л. Эйлер, который, кста-
ти, является автором всей современной символики тригонометрии.
Систематически разложения периодических функций в сумму си-
нусов (или, как говорят, на гармоники) изучал в начале XIX в.
французский математик Ж. Фурье, которые так теперь и назы-
ваются разложениями (или рядами) Фурье.
В качестве примера на рисунке 103 изображено приближение
к периодической функции у = {х} в виде суммы нескольких гар-
моник. Разложение произвольного периодического сигнала на гар-
моники является главным математическим аппаратом радиотех-
ники.
169
Контрольные вопросы
1. Какой формулой можно задать гармоническое колебание?
2. Чему равна амплитуда суммы двух гармонических колеба-
ний одной и той же частоты?
3. Какая функция называется периодической?
4. Приведите примеры периодических функций с периодом
Т=[.
5. Что можно сказать о периодичности суммы периодических
функций?
ЗАДАЧИ К ГЛАВЕ III
Измерение углов
Перевод из градусной меры в радианную
1. Выразите в радианах:
1) 1°; 2) 10°; 3) 15°; 4) 30°;
5) 45°; 6) 60°; 7) 70°; 8) 90°;
9) 120°; Ю) 135°; Н) 150°; 12) 210°
13) 225°; 14) 240°; 15) 320°; 16) 330°
Перевод из радианной меры в градусную
2. Выразите в градусах:
1) Л 75’ 2) —; 7 12 ’ 3) f; о 4) 7л. 9 ’
5) 2л . 3 ’ 6) 7) 1,5л; 8) Зя;
9) 0,25л; Ю) ^-л; 4 11\ 31 П) —g-л; 12) 101 12 Л'
Построение углов на единичной окружности
3. Постройте угол — а, если а имеет следующее значение:
1) Ю°; 2) 180°; 3) f; 4)
5> 6) 45°; 7) -30°; 8) -f
9) —л; 10) 270°; Н) -fn; 12) 1.
4. Постройте точки Ph соответствующие следующим значениям t:
1) 1; 2) 2; 3) 3; 4) 4; 5) 5; 6) —3;
7) 10; 8) 100л; 9) -^-л; 10) -4; 11) --Ut; 12) -У-л.
о их
170
5. Для каждого из приведенных значений t (t=-2-; 4-л;
\ О 2 о
5 7 3 \ 2,
—л; л; —л; —л 1 укажите такое значение t , что точки Pt
и Pt,:
1) диаметрально противоположны;
2) симметричны относительно оси абсцисс;
3) симметричны относительно оси ординат.
Движение по окружности
6. На единичной окружности разрешается делать два преобразо-
вания: поворот на 20° и симметрию относительно биссектрисы
угла хОу. Какие углы можно построить с помощью этих
преобразований?
7. На единичной окружности разрешается делать повороты на
углы и Можно ли с помощью этих поворотов построить
13
угол —л?
8. Две точки одновременно начали двигаться по единичной ок-
ружности из точки Pq в противоположных направлениях. Пер-
вая точка за 1 с проходит угол в положительном направле-
нии, а вторая за 1 с проходит угол в отрицательном
□
направлении. В какой точке окружности они встретятся в пер-
вый раз? Встретятся ли они когда-нибудь снова в точке Ро?
Найдите все точки встречи.
Прикладные задачи
9. Зубчатое колесо имеет 72 зубца. Выразите в градусах угол,
на который повернется колесо при повороте на 1 зубец, 30 зуб-
цов, 144 зубца, 300 зубцов.
10. Шкив скоростного электродвигателя делает 120 000 оборотов
в минуту. Определите угловую скорость вращения этого шки-
ва: 1) в градусах в секунду; 2) в радианах в секунду.
Исследование тригонометрических функций
Определение тригонометрических функций
11. Даны координаты точки Р, на единичной окружности. Вы-
числите sin t, cos t, tg t, ctg t:
° (“T; f); 2) Gl; —
3) (-f;
171
12. Найдите значения тригонометрических функций угла, образо-
—
ванного вектором ОР и осью х для следующих точек Р:
1) (-4; 3); 2) (1; -1); 3) (-5; -12); 4) (1; 3).
Периодичность
13. Докажите тождества:
1) sin (t — Ji) = sin (t + л);
3) tg (2/ —n) = tg (2/ + 5л);
14. Докажите равенства:
1) sin ---= sin ^-л;
6 о
3) tg(-^-) = tg^-«;
2) cos (t+f) = cos (t-^);
4) sin (7л —/) = sin (3л —/).
2) cos —= cos —-— ;
4) ctg‘15=ctg(-f«).
Знаки
15. Определите знаки следующих значений тригонометрических
функций:
1) sin 2) sin 2; 3) sin (-у-); 4) sin у-;
5) cos 6) cos 3; 7) cos (-у-); 8) cos у.;
9) tg(—2-л); 10) ctg-^; 11) tg 4; 12) ctg-£-«.
16. Определите знаки следующих чисел:
1) sin 280°; 2) cos 710°; 3) tg 100°;
4) ctg 910°; 5) sin-г-л; 6) cos-^л;
7) tg(-^-n); 8) ctg(iLn); 9) sin ( —) .
Четность
17. Выясните четность следующих функций:
1) у= —sin t\ 2) y — — cos t\
3) t/ = sin21\ 4) z/ = cos3 f;
5) t/ = sin t-cos t; 6) r/ = sin /4-cos t\
7) у = sin2/ — cos21; 8) r/ = sin 2x;
9) t/ = sin 5x; 10) r/ = sin 2%+ И
11) i/=sin (x+-J-) ; 12) z/ = cos (*+-J-)
13) y = tgx + ctgx; 14) £/ = tg 2x cos 4x;
15) z/ = tg 3x sin 2x; 16) COS X . У X ’
17) y=—.— ' V sin X 18) sin x + tgx У X
172
Значения тригонометрических функций
18. Вычислите:
1) sin 135°; 2) cos 135°: ; 3) cos 120°; 4) tg 150°;
5) ctg 225°; 6) sin 1110' 7) sin -^л; 8) 5 cos —л;
9) Ю) ctg ул; ii) sin n; 12) _ _ _ 3л . cos T'
13) tg 14) ctgfn; 15) sin -У-л; 0
16) sin2 402° +sin2 48° + tg2 225°;
17) sin2 99° + cos2 81° + ctg2 315°.
19. Существует ли число а, удовлетворяющее условию:
7 24
1) sina=—, cosa=—; 2) sin а=—0,7, cos а=—0,3;
25 25
3) sin а=-|-, cosa=—4) tg а=-|-, ctg а=—|-;
5) tga=-|-, ctga=-^-; 6) tga = 2+"\/3, ctga = 2—\/3?
20. Зная значение одной из функций и четверть, в которой лежит
угол, вычислите значения трех других тригонометрических
функций:
1) sin<=-J|, 2) cos л</<^;
3) tgt=-|-, л</<^-; 4) ctg t= -0,2, ^-</<2л.
Графики
21. Постройте графики функций:
Свойства тригонометрических функций
22. Найдите область определения функций:
1) t/ = sin2x; 2) t/= ‘ ; 3) t/=tgy;
4) i/ = ctg2x; 5^ У = -— 1 , ; 6) u=sin-\/x;
’ v Sinx+l ' у v
7) y = tgsinx; 8) t/ = sin tg x; 9) y = ^\ —sin x;
io) y=Vtg*; H) y= 2_ginx ; 12) y=tgx+ctgx.
23. Найдите промежутки монотонности функции:
1) t/ = sin (х—у) ; 2) i/=cos (х+у); 3) y = tg(x—у);
4) y=ctg (x+j-л ) ;5) t/=sin 2х; 6) t/=cosy-;
7) t/ = sin ( — х+у) ;8) t/ = cos( —2х).
24. Расположите числа в порядке возрастания:
1) sin 85°, sin 5°, sin 20°, sin 100°, sin 140°, sin 190°, sin 280°;
2) sin 1, sin 2, sin 3, sin 4, sin 5, sin 6;
o\ 5л •„ 13л 23л л 7л . 25л • 2л .
3) sin [2 , sin [2 , sin 12 , sm б , sin 6 , sin J2 , sin 3 ,
4) cos 95°, cos 15°, cos 30°, cos 110°, cos 150°, cos 200°,
cos 270°;
5) cos 1, cos 2, cos 3, cos 4, cos 5, cos 6;
6) cos -s-л, cos cos -У-л, cos -^-л, cos -7-л, cos cos
o Z о о 4 о о
_ 23л
COS — <
О
7) sin у, cos у л, sin-ул, совул, sin(—-у л
cos (—-УгЛ .
25. Найдите наибольшее и наименьшее значения функции:
1) j/ = 2sinx; 2) y = 3cos-5-; 3) t/ = 5sin(x—2-);
4) y = 2cos(y—2x) ; 5) t/ = sin2x; 6) t/=—‘ ;
7) y=2 coax ’’ -8) y=Vsin x; 9) t/=(l 4-sin x)2;
10) y=sin 4x4-5; 11) y=-—У—; 12) y=—!—
' 3 1—sinx 1 v cosx—1
26. Найдите область значений функции:
1) t/ = sin Зх; 2) у= — 3 cos2 х— 1;
3) t/ = 2cosx;
174
4) 7) • 2 £/ = sirr х; У= 1 —Ctg2 х; 5) 8) y = tg2 х; £/ = д/5 —sin х; 6) t/=(l Н-cos х)2;
9) у=~.—; sin X
10) t/= . 1 ,; 11) t/= . 1 • ' v sin x—1 ’ s sin x+2 Производные 27. Вычислите производную функции: 12) У — ^1~ cos X.
1) у —2 sin х; 2) 1 — 3 cos х . У 2 3) i/=3tgx-|-2ctgx;
4) 7) t/ = sin х cos х; У=—-. sin X 5) 8) 9 £/ = cos х; ^1ПХ_ X 6) 9) у=х2 sin х; у=^-^ ; sin X — COS X
Ю) t/ = sin 5х; Н) r/ = cosy-; 12) i/ = tg (2х+1);
13) t/=sin2 5х; 14) £/==cos (a — х); 15) t/=3tgf;
16) у=4- sin (2a- Зх); 17) у — sin 2х О-
28. Вычислите приближенно:
1) sin 5°; 2) cos 1,56-sin 3,18; 3) sin 181°;
4) sin2 0,09; 5) tg 179°; 6) tg3,l.
Тождественные преобразования
Основные тригонометрические тождества
29. Упростите:
1) sin4 а + 2 sin2 а cos2 а + cos4 а;
2) (sin а+cos а)2 + (sin а —cos а)2;
3) sin4 а — cos4 а + cos2 а;
4) cos2 а + sin4 а + sin2 а cos2 а;
5) cosa.tga,^ os
' sin2 а ®
6) sin а — cos a (tg а + ctg а);
7) (tga + ctga)2—(tga — ctg а)2;
8> (i+ctS“)Ghb-cl8“);
9* I + tg2« l+ctg*a ’ 1о» I +tg! a
1
l+ctg2a
30. Докажите тождества:
1) cos4 a — sin4 a = cos2 a — sin2 a;
9 \ 1_______ 1+tg2 a.
cos2 a—sin2 a 1 — tg2 a ’
175
3) ctg2 a —cos2 a = ctg2 a cos2 a;
sin2 a —tg2 «__tg4 a .
cos2 a —ctg2 a ctg2 a ’
4)
tga + ctgp_ tg a . l+ctg2a _
7 ctga + tgP tg p ’ 7 tga+ctga
7) (l-tga)2+(l+tga)2=^^-;
9) (sin a + tg a) (cos a + ctg a) = (l +sin a) (1 +cos a);
10) т——=sin2a; 11) *~ctg Y— — ctg y.
tga + ctga 7 1— tg 7 & '
31. Упростите:
cos2 ^2a —у ) + ctg2 (y+ 2a ) + l
sin2 (20с—у ) + tg2 (y+2a )+ 1
4) sin (180°-a) + cos (90° + a)-tg (360°-a) + ctg (270°-a);
ctg(|*-a) ctg2(2jt_a)_i
1—tg2(a —n) ctg(n + a)
6) sin (-2—a ) —cos (л — a)+tg (л —a) —ctg 0-л + а ) ;
7) tg2 (a-360°)-sin2 (a-270°) +cos2 (360° +a);
дч tg (270° —a) sin 130° cos 320° sin 270° .
ctg (180° —a) cos 50° sin 220° cos 360°
9) sin2 (26° + a) + sin2 (244°-a) + tg (113° +a) ctg (67°-a);
10) sin(y—a ) ctg (y-л + а ) cos (-|-л + а )+
4-ctg (л + р) ctg (у-л — p) .
Формулы сложения
32. С помощью формул сложения вычислите:
1) cos 15°, sin 75°, tg 105°, cos 165°;
/з _л/Гз
2) sin(a + P)» если sin а = cos 0=—j—
f<P<n;
2
176
4 5
3) tg(a — P), если sina=-r-, cos p=—, a, 0 — углы I чет-
верти.
33. Вычислите:
1) sin 13° cos 17° +sin 17° cos 13°;
2) sin 16° cos 29° -|- sin 29° cos 16°;
3) sin 78° cos 18° — sin 18° cos 78°;
4) sin 63° cos 33° — sin 33° cos 63°;
5) cos 66° cos 6° + sin 66° sin 6°;
6) cos 71° cos 26° + sin 71° sin 26°;
7) cos 20° cos 25° — sin 20° sin 25°;
8) cos 87° cos 33° — sin 87° sin 33°;
9) cos 8° cos 37° — cos 82° cos 53°;
10) sin 64° sin 34° — sin 56° cos 116°
34. Упростите:
2)
3)
4)
sin 3a cos 2a — cos 3a sin 2a;
cos 5a cos 3a + sin 5a sin 3a;
sin (a — P) cos p + cos (a — P) sin P;
sin (a + fl) + sin (a — fl) ,
sin (a + fl) — sin (a — fl) *
5)
sin (a -|- fl) — 2 cos fl sin a
cos (a-j-fl) — 2 cos a cos fl
35. Вычислите:
I)
3)
5)
tg 10° + tg 35°
1 — tg 10° tg 35° ’
l + tg67°tg7° .
tg67° —tg7° ’
tg 72°-ctg 48°
1 +tg 72° ctg 48°
2)
4)
tg73°- tg 13°
l+tg73° tg 13° ’
tg 20° + tg 25°
1 — ctg 65° ctg 70° ’
36. Найдите:
1) sin(v+a ) , если sin a=-|-, f);
2) sin(^— a ) , если О о О) P II 1 Сл|оо P а
3) / л cos (—— a \ о ) , если cos a=-^-, a 6 1 □ t)
4) , если tg a=2;
5) tg a, tg p, если tg ( x + tg p = 2; tg (a + P)=4.
Формулы удвоения
37. Вычислите:
1) cos2 15° —sin2 15°; 2) cos2-£—sin23) 2cos2-^-—1;
o 8 12
177
4) 1-2 sin2 О 5) sin 15° cos 15°; 6) sin 20° cos 20° cos 50°
7) sin 25° • sin 65° . 8) 9) tg 15° .
cos 40° i+tg2^’ о 1+tg2 15° ’
10) -tgy. , Q ft * И) 1+tg2 15° . 1 — tg2 15° ’
l+tg’T
12) sin 2a, cos 2a, tg 2a, если sin a=-^-, a — угол первой чет-
э
верти;
13) cos а, если cos -т-=-|-;
14) sin a, если sin -2-= —j-, ag(—2-; 0 ) ;
15) sin a, если sin -2-=—ag( —jv, 0).
Z □
38.
Упростите:
। ч (sin a 4-cos <*)2 .
' 14- sin 2a ’
Q4 cos 2a ,
’ sin a 4-cos a ’
2)
1 — sin 2a .
(cos a —sin a)2 ’
4) sin3 a cos a —sin a cos3 x.
39. Докажите тождество:
1) cos4 a — sin4 a = cos 2a;
2) cos4 a + sin4 a= 1—sin2 2a;
3) tg a + ctg a = . 2-- ; 4) tg y^+ctg ~-=4;
5) ctg a — tg a = 2 ctg 2a;
sin 2a 1 2 sin x — sin 2x .9 *
6) 1+соз“^а’ 7) 2 sin x+sin 2x~fg
Тригонометрические функции половинного угла
40. Найдите:
1) sin-i-; 2) cos ур 3) tg^;
4) sin-2-; 5) cos-2-; 6) tgf;
7) sin a, cos a, tg a, если tg -2-=3;
8) sin a, cos a, tg a, если ctg-2-=-|-.
41. Найдите sin-2-, cos-2-, если sin a=|^-, 0<a<-2-.
Z Z ZD £
178
42. Запишите следующие функции в виде функций от tg у:
1) j/ = sin х—2 cos х; 2) у = а sin x+b cos х;
оч 3 sin x+cos х— 1
' У sinx+cosx
Преобразование суммы тригонометрических функций
в произведение
43. Преобразуйте сумму тригонометрических функций в произве-
дение и упростите:
1) sin 75° +sin 15°;
3) cos 152° +cos 28°;
sin 25° +sin 15° .
sin 25° — sin 15° ’
7) cos 20° — sin 20°,
2) sin 78°-sin 42°;
4) cos 48° —cos 12°;
6) sin 20° +cos 40°;
8) sin2 a —sin2 0;
9) cos2 a — cos2 0;
1°) sin sin £;
11) cos у—COS73-; 12) sin
13) sin (40° + a) — sin (40° — a);
14) sin a + sin 2a + sin 3a 4- sin 4a;
15) cos a + cos 2a + cos 3a + cos 4a.
12) sin 4a-|-sin 2a;
44. Докажите тождество:
sin a + sin p__. a + p ,
cosa-|-cosp ® 2 ’
2)
cos----
sin a + sin p 2
sin a cos p +cos a sin p a + p’
3) sin a + cos a=-\/2 cos (a—yj ;
4) sin a —cos a=-\/2 sin (a—2-);
5) cos a-f-2 cos 2a + cos 3a = 4 cos2 уcos 2a;
6) cos a + cos 0 + cos y= 1 4-4 sin y-sinsin + если a, 0,
у — углы треугольника.
Преобразование произведения тригонометрических
функций в сумму
45. Преобразуйте в сумму:
1) cos 45° cos 15°; 2) sin^cos^-; 3) cos 20° cos 10°;
4) cos -—cos -2-; 5) sin y- sin y-; 6) sin -y-cos
1U D О о 1U О
179
7) sin 20° sin 10°; 8) sin 4a cos 2a; 9) sin 2a sin (a + 0);
10) cos a cos (a + 0); 11)2 sin a sin 2a sin 3a;
12) 8 cos (a —0) cos (a —y) cos (y —0).
Арксинус
46. Вычислите:
1) arcsin-^-; 2) arcsin (—1); 3) arcsin (—^
4) arcsin 1; 5) arcsin 2; 6) arcsin-y-;
7) arcsin 0; 8) arcsin-5-; 9) arcsin X \ z
47. Найдите значение выражения:
1) sin (arcsin-у-) ; 2) arcsin (sin -y-) ; 3) arcsin (sin -|-n
4) arcsin (sin x), если x£[-y-; «]•
48. Вычислите:
Арккосинус
1) arccos(—2) arccos(— 1); 3) arccos^-;
4) arccos 1; 5) arccos( —3); 6) arccos 0;
7) arccos (--у) ; 8) arccos (—^); 9) arccos-^-.
49. Найдите значение выражения:
1) cos arccos 2) arccos (cos у-) ;
3) arccos (cos (—£")) J 4) arccos (cos y-) .
50. Докажите тождество:
1) arcsin x +arccos x =-у-; 2) sin arccos x=-\/l —x2;
3) cos arcsin х = д/1 —x2.
Арктангенс и арккотангенс
51. Вычислите:
1) arctg д/3;
4) arctg (—1);
7) arcctg д/З;
10) arcctg д/З;
2) arctg 1;
5) arctg
8) arcctg 0;
11) arcctg (—Ц=) •
3) arctg 0;
6) arctg ( —д/З);
9) arcctg 1;
180
Обратные тригонометрические функции
52. Найдите значения выражения:
1)
4)
7)
9)
Н)
13)
sin (arcsin ; 2) cos (arccos ; 3) tg arctg 2;
ctg arcctg ( — 2); 5) tg (arctg (--1-)) ; 6) ctg (arctg ;
tg(arcctg(—|-)); 8) arcsin
arcsin (sin y-J ; 10) arccos (cos -2-) ;
arccos (cos 2); 12) arctg (tg -|-л ) ;
arctg (tg-J--) ; 14) arctg (tg 3); 15) arcctg (ctg 1).
53. Докажите тождества:
1) arctg x+arcctg x=-2-;
2) ctg (arctg x)=^; 3) sjn (arctg x)=~=^-.
Решение тригонометрических уравнений
Простейшие тригонометрические уравнения
54. Решите уравнения:
1) sin х = 0; 2) sin x= 1; 3) sin x = —
4) 1 sin Х = —: 5) sin x —2; 6) cos x = 1;
7) cos х = —- 1; 8) cos x = — 9) cos x=^-
Ю) cos x = — 3; 11) tgx = 0; 12) tgx = l;
13) 16) tgx=V3; ctgx= — 1. 14) tg*=-V; 15) ctg x = 0;
55. Найдите решения уравнений в указанных промежутках:
1) sin/= — 1, /£[0; 4л]; 2) cosx=l, /£[—л; Зя];
3) tg/ = l, /б[0; 4) cos/=—1~, /€[0; 2л];
5) sin/=—/€[—л; л]; 6) sin2/=-^-, /£[0; 2л];
7) cos2 /6[-л; л]; 8) sin2/=^-, /£[л; 5л];
181
9) tg2/=l; /£[—л; л];
11) sint-cost = 0, /£[0; 2л];
13) cos 2t = 0, /£[—л; л];
15) cos2t =— 1, /£[—л; л];
10) ctg2/ = 3, /6[0; 2л];
12) sin2/ = 0; ^[—у; у-
14) sin 27=1, /€[0; 2л];
16) tg 2t = 1, /6[0; л}
Уравнения алгебраические относительно одной
из тригонометрических функций
56. Решите уравнения:
1) sin 3x=0; 2) sin -y= 1 3) sin 2x = — 1;
4) cos-£-=0; 5) cos 2x = 1; 6) cos-*-=l;
7) tgy=0; 8) tg3x=l 9) tg2x= —1;
10) ctg 4x = 0; H) ctg-y=l 1; 12) ctg3x= —1;
13) sm (* + -g-)=— 14) sin2 2x = 1;
15) cos(f-f)=£; 16) COS2^1; 4 2 ’
17) tg(2x+f)=-V3; 18) tg2x=3;
19) n OQ oo| * + o>|jj V "|w 20) ctg2x=y-;
21) 2 sin2 x —3 sin x+ 1 =0; 22) 2 sin2 x—2 sin x = 1;
23) 2 cos2 x + cos x = 1; 24) 6 tg2 x + tg x— 1 =0;
25) 2 sin2 x + cos x—1=0; 26) 2 sin2 x + 5 cos x—4=0;
27) 4 cos2 x —3 sin x = 3; 28) 2 tg x—3 ctg x— 1 =0;
29) 3 tg2 x+ctg2 x=4; 30) sin x+-\/3 cos x= 1;
31) sin x —2 cos x=2; 32) sin (-2-+x ) + 3 cos x = 0.
Понижение порядка уравнения
57. Решите уравнения:
1) 4 cos2 x+cos 2х=5; 2) 4 sin2 х—cos 2х = 5;
3) sin 4% + cos2 2х = 2; 4) cos4-|-х —sin4-|-x=-i-;
5) cos2 x + cos2 2x+cos2 Зх=-|-;
6) sin2 Зх+sin2 4x + sin2 6x+sin2 7x = 2.
182
Использование различных тригонометрических формул
58. Решите уравнения:
1) sin 4х — sin 7х=0; 2) cos 3x4-cos 5х=0;
3) cos4x = cos5x; 4) sin 15x=sin 7х;
5) cos (Зх —-2-) = cos (*+-J-) ; 6) cos ^2x4—— cos
7) cos 3x = sin lOx; 8) sin 7x=cos 13x;
9) tg3x=tg5x; 10) ctg5x = ctgx;
11) sin x+sin Зх+sin 5x=0;
12) cos 2x+cos 4x — cos 3x=0;
13) cos 6x —cos 8x= 1 — cos 2x;
14) cos x 4-cos 2x4-cos 3x4-cos 4x=0;
15) 1 +cos Зх+cos 7x4-cos 10x = 0;
16) sin x4-sin 3x-)-sin 5x4-sin 7x=0;
17) cos 2x sin 4x=cos x sin 5x;
18) sin 2x cos 4x = sin lx cos 9x;
19) cos 7x cos 10x=cos 2x cos 15x;
20) sin 5x sin 3x +cos 7x cos x=0.
Однородные уравнения
59. Решите уравнения:
1) sin х=-£-cos х; 2) 3 sin2 x = cos2 х;
О
3) 3 sin2 х + 4 cos2 x= 13 sin x cos x;
4) sin2 x + 2 sin x cos x=3 cos2 x;
5) 7 sin2 x=8 sin x cos x — cos2 x;
6) 1 —3 cos2 x = 2 sin x cos x;
7) 6 sin2 x — 3 sin x cos x — cos2 x= 1;
8) 3 sin2 x + 2 sin x cos x = 2;
9) 6 sin2 x + 3 sin x cos x — 2 cos2 x = 3.
КОНТРОЛЬНОЕ ЗАДАНИЕ К ГЛАВЕ III
Вариант 1
1. Докажите тождество
cos2 a —sin2 а_1 — tg а
1 +sin 2а 1 +tg а *
2. Известно, что sin а=— и угол а лежит во II четверти.
Вычислите cos(f-а)-
183
3. Постройте график функции у = 2 sin (х—J .
4. Решите уравнение 7 sin х = 5 —cos2 х.
5. Найдите наименьшее значение функции
y = sin2 x+sin % +1.
Вариант 2
1. Докажите тождество
tg a sin а __tg a —sin а
tg а + sin a tg a sin а
2. Решите уравнение
cos2 % +cos2 2%4-cos2 Зх=-|-.
3. Дана функция £/ = sin х cos х.
а) Найдите ее наименьший положительный период.
б) Постройте ее график.
в) Найдите точки, в которых производная этой функции при-
нимает наименьшее значение.
г) Найдите приближенное значение функции при х = 0,012.
Вариант 3
1. В равнобедренном треугольнике угол при основании равен а.
а) Вычислите отношение k площади треугольника к сумме
квадратов его сторон.
б) Докажите тождество ----------Л-i—•
' 2 tga+3ctga
в) Найдите а так, чтобы fe=-~.
г) При каком а отношение k принимает наибольшее зна-
чение?
д) Найдите область значений отношения k.
2. Постройте график функции r/ = sin x-j-cos х.
О мир, пойми! Певцом — во сне —
открыты
Закон звезды и формула цветка.
М. Цветаева
Глава IV
ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ
ФУНКЦИИ
ВВОДНАЯ БЕСЕДА
1. Порядок роста и убывания функции
Функция — это основной математический инструмент для
изучения связей, зависимостей между различными величинами.
Чем большим запасом функций мы располагаем, тем шире и богаче
наши возможности математического описания окружающего мира.
Вслед за линейными мы подробно изучали квадратичные
зависимости. Так, путь при равноускоренном движении квадра-
тично зависит от времени; энергия падающего тела квадратично
зависит от его скорости; количество теплоты, выделяемой током,
текущим по проводнику, квадратично зависит от силы тока и т. п.
Степенные зависимости более высокого порядка также
встречаются на практике. Например, по закону Стефана — Больц-
мана излучательная способность абсолютно черного тела про-
порциональна четвертой степени его температуры. Масса шара
является кубической функцией его радиуса.
Если мы изобразим на одном чертеже (схема IX) графики
степенных функций вида y = xk (х>0) при положительных
значениях fe, то увидим, что, чем боль-
ше fe, тем быстрее при больших зна-
чениях х растут эти функции. Сте-
пенные функции образуют естест-
венную шкалу, позволяющую срав-
нивать рост различных функций со
стандартными, степенными функциями.
Аналогичная картина наблюдает-
ся и с убывающими функциями. Прос-
тейшая убывающая функция задает-
ся обратно пропорциональной зави-
симостью У=~~ (ОО, х>0). Изо-
бражая на одном чертеже (рис. 104)
185
Гильберт Давид
(1862—1943) —
немецкий математик, основатель Геттин-
генской математической школы. Гильберт
завершил начатое Евклидом. Ему принадле-
жит глубокое обобщение евклидовой геомет-
рии (гильбертовы пространства), он получил
важнейшие результаты в математической ло-
гике.
«Арифметические знаки — это записан-
ные геометрические фигуры, а геометри-
ческие фигуры — это нарисованные фор-
мулы».
Д. Гильберт
графики функций У=^г (х>0, k>0), видим, что, чем больше fe,
тем быстрее убывают эти функции при больших значениях х.
В естествознании и технике встречаются процессы, рост
или затухание которых происходит быстрее, чем у любой степен-
ной функции. С примерами быстро растущих функций человек
столкнулся очень давно. В древней легенде об изобретателе шах-
мат говорится, что он потребовал за первую клетку шахматной
доски одно пшеничное зерно, а за каждую следующую — вдвое
больше, чем за предыдущую. Человеку трудно представить себе
порядок величины 264— 1 (общее число зерен, плату за изобрете-
ние шахмат). Если грубо заменить 2|0= 1024 на 103, то 264 =
==24-260« 16-1018= 1,6-1019. Достаточно сказать, что расстояние
от Земли до Солнца в миллиметрах приблизительно равно
1,5-1014, так что, считая диаметр зерна за 1 мм, можно этим зер-
ном 100 тысяч раз уложить путь до Солнца.
Поразительное явление быстрого роста членов геометри-
ческой прогрессии, т. е. чисел вида cqn, отражено во многих
старинных задачах. Однако лишь с конца XVII в. стали система-
тически рассматриваться зависимости типа y = cqx, в которых
переменная х принимает не только целые значения. Такие функции
называются показательными.
Показательные функции, к изучению которых мы переходим
в этой главе, обладают замечательным свойством: скорость их
роста пропорциональна значению самой функции. Они как костер,
который, чем больше разгорается, тем больше в него надо
подкладывать дров.
Мы знаем, что скорость роста линейной функции постоянна,
квадратичной функции линейна и вообще производная степенной
функции, являясь меньшей степенью, растет медленнее, чем сама
функция. Необходимость изучения функций, у которых производ-
ив
ная пропорциональна самой функции, возникла с обнаруже-
нием различных законов естествознания, таких, как законы
размножения, законы радиоактивного излучения, законы движе-
ния в тормозящей среде и т. д. Как эти законы связаны с пока-
зательными функциями, мы обсудим в главе, посвященной интег-
ралу.
2. Определение степени с произвольным показателем
В основе определения показательной функции лежит понятие
степени. Как надо понимать выражение а'? Его определение
строится постепенно. Сначала надо вспомнить, что такое степень
с натуральным показателем, т. е. рассмотреть случай, когда t —
натуральное число. Запись 210 мы понимаем как произведе-
ние 10 одинаковых множителей, каждый из которых равен 2. В об-
щем виде если / = п — натуральное число, то запись ап означает
произведение п множителей, каждый из которых равен а.
Если t — отрицательное целое число, то его можно запи-
сать в виде / = — п, где п — натуральное число. Тогда d определя-
ется так: а' —Например, 2“10 по определению равно
Если / = 0, то d принимается равным единице, т. е. а°=1.
Заметим, что а1 при /^0 не определено при а=0.
Тем самым мы определили степень с произвольным целым
показателем. Дальнейшее обобщение понятия степени требует по-
ложительности основания а. Рассмотрим случай, когда t —
рациональное число. Его можно записать в виде дроби /=—, где
М m
m — целое число, п — натуральное число. По определению ап =
В частности,
Степень с произвольным вещественным показателем t опреде-
ляется следующим образом. Для числа t выбирается последова-
тельность рациональных чисел Л, /2,...»tn, ...9 задающая прибли-
жение числа t с любой степенью точности. Строится последо-
вательность степеней с рациональными показателями d'9 d\ ...,
dn,... . Оказывается, что эта последовательность задает прибли-
жение некоторого числа с с любой степенью точности. Это
число и называется степенью d.
Таким образом, мы определили степень d для положительного
основания а и любого показателя t.
Замечания.
1. Степень числа с натуральным показателем имеет смысл
не только для положительного, но и для любого основания, так
как эта степень определяется с помощью операции умножения, а
187
умножать можно любые числа. Поэтому имеют смысл равенства
( —З)3 4 = ( —3)-( —3)-( —3)= —27, (-1)100 = 1, (_Х)5 *=_±.,
09 = 0 и т. п. Степень с целым отрицательным показателем мо-
жет быть определена для любого числа, кроме нуля, так как ее
вычисление сводится к операциям умножения и деления. Опреде-
ление же степени с рациональным показателем требует операции
извлечения корня, которая выполнима, как правило, только для
положительных чисел. Поэтому мы с самого начала считаем осно-
вание степени положительным числом.
2. Степень с иррациональным показателем вычисляется
приближенно. Сначала мы задаем приближения к числу t с по-
мощью рациональных чисел, затем вычисляем степени с рацио-
нальным показателем. У нас остался невыясненным вопрос: как,
зная погрешность приближения числа t с помощью рациональ-
ного числа tni оценить погрешность приближения atn к числу а'?
3. Свойства степени
Операция возведения в натуральную степень имеет хорошо
известные свойства. Перечислим их.
1. аПх • ап2 = ап'+п\ т. е. при умножении степеней с одинаковыми
основаниями показатели складываются.
2. -—= аП1-П2, т. е. при делении степеней с одинаковыми осно-
а2
ваниями показатели вычитаются.
3. (аП1)П2==ап,П2, т. е. при возведении степени в степень показа-
тели перемножаются.
Для натуральных показателей эти свойства выводятся из
определения степени и свойств умножения. Аналогичные свойства
сохраняются для степеней с произвольными вещественными по-
казателями:
1) а',-а/2=а/,+'2;
3) (а')/2=а''2.
Доказательство свойств степени с произвольным вещественным
показателем проводится, начиная со случая натурального по-
казателя и переходя последовательно к целым, рациональным и
любым показателям.
В приведенных выше свойствах основание степени было одним
и тем же, а менялись показатели степени. Можно сформу-
лировать свойства степеней с одинаковыми показателями, но раз-
ными основаниями:
4) а\а2 = (а\а2У\
5)
аг \ а2 /
188
Контрольные вопросы
1. Что такое ап при натуральном и?
2. Как определяется степень с целым отрицательным показате-
лем?
3. Чему равна нулевая степень числа?
4. Как определить аг, где г — рациональное число?
5. Как вычислить степень ах при произвольном веществен-
ном х?
6. Какие свойства степеней вы знаете?
§ 1. ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ
1. Исследование показательной функции
Определение. Показательной функцией называется
функция вида у—а\ где а — фиксированное положительное
число.
При исследовании показательной функции будем считать, что
основание а=/= 1, так как при а = 1 функция получается постоянной.
Перечислим основные свойства показательной функции.
1. Область определения: множество всех вещественных чисел R.
2. Монотонность: при а>1 функция у = ах строго возрас-
тает, при 0<а<1 функция у = ах строго убывает (схема X).
3. Положительность: значения функции у = ах положительны
(при любом основании а>0).
4. Область значений: множество всех положительных чисел,
т. е. промежуток (0; +<»).
Свойство 1 подчеркивает, что степень ах определена при любом
вещественном показателе х. Доказательство свойств 2 и 3
показательной функции проводится так: эти свойства про-
веряются последовательно для натуральных, целых, рациональ-
ных показателей, а затем уже переносятся на произвольные ве-
щественные показатели.
Свойства показательной функции позволяют построить ее
график. Графики показательных функций при различных основа-
ниях показаны на рисунке 105.
Рассмотрим показательную функцию у = 2х. С ростом х зна-
чения этой функции возрастают очень быстро. Так, 210«Ю3,
2100«Ю30 и т. д. Если же брать отрицательные значения х,
то 2х будет быстро приближаться к нулю: 2~‘°«0,001; 2~100^
«10“3° и т. д. Это свойство показательной функции быстро уве-
личиваться, с одной стороны, и быстро приближаться к нулю,
с другой, хорошо видно на графике.
Вместе с функцией у = ах показательной функцией считают и
функцию вида у = са\ где с — постоянная. К такому виду мож-
но привести, например, функцию у = 2х+2, сделав преобразование:
2^+2 —2х.22 = 4*2х.
189
2. Производная показательной функции
Вычислим среднюю скорость роста показательной функции
у=ах на отрезке [х; х+Дх]:
\у = gx+Ax-g* g*(gAx—1) = . дАх-1
Дх Дх Дх Дх ’
Мы видим, что средняя скорость роста показательной
функции на отрезке [х; x-f-Ax] равна значению этой функции в точ-
ке х, умноженному на число . Исследуем, как ведет себя
это число при маленьких значениях Дх. Так как а°=1, то зна-
чение аДх при маленьких значениях Дх близко к 1. Если на графике
функции проведем секущую, проходящую через точки (0; 1) и
Дх_.
(Дх; аДх), то ее угловой коэффициент будет равен числу —==tg а
(рис. 106).
При Дх->0 секущая будет приближаться к касательной к
графику функции в точке (0; 1). Это означает, что будет
приближаться к произведению ах на значение производной при
х = 0. Итак, для нахождения производной функции у = ах надо
знать только значение этой производной в нуле. Если мы его
обозначим через fe, то получим формулу
(ax)'=ftax,
т. е. производная показательной функции пропорциональна самой
функции.
Как же найти коэффициент пропорциональности fe? Мы зна-
ем, что он равен угловому коэффициенту касательной, про-
веденной в точке (0; 1). Можно приближенно по графику вычислить
этот коэффициент. Так, известно, что для а=10 значение k«2,3,
поэтому (10х)'«2,3-10х.
С помощью знака предела коэффициент k можно записать так:
3. Число е
Посмотрим на графики показательных функций при различных
а (рис. 105). Все они проходят через точку М (0; 1). Про-
ведем в этой точке касательные к графикам. Мы видим, что, чем
больше основание а, тем «круче» касательная. Так, при а =
= 2 угловой коэффициент касательной равен 0,693, а при а =10
угловой коэффициент касательной равен 2,303. Ясно, что при
непрерывном изменении а от 2 до 10 угловой коэффициент каса-
тельной в точке М будет непрерывно меняться и найдется такое
190
Рис. 106 Рис. 107
Рис. 105
значение а, для которого этот коэффициент будет равен единице.
Такое основание а обозначается буквой е. Число е иррационально.
Его приближенное значение таково: е«2,718.
Итак, е — это такое число, что угловой коэффициент касатель-
ной к графику функции у = ех в точке х = 0 равен единице,
т. е. касательная в этой точке образует с осью абсцисс угол
45° (рис. 107).
Можно сказать иначе. Мы уже знаем, что производная
любой показательной функции пропорциональна самой этой функ-
ции. Число е — это основание, для которого коэффициент пропор-
циональности равен единице, т. е. е — это такое число, что произ-
водная функции у = ех равна самой этой функции:
(ех)'=е\
Функцию у = ех часто обозначают г/ = ехр х (читается: «Эксп от
х») и называют экспонентой. Экспонентами называют и функции
более общего вида: y — cekx. Подумайте, понятен ли вам смысл та-
ких распространенных выражений: «Численность бактерий растет
по экспоненте», «Сила тока затухает по экспоненте», «Его успе-
хи растут по экспоненте».
Контрольные вопросы
1. Обратите внимание на следующие встретившиеся в тексте
ключевые слова и обозначения: показательная функция, экспонен-
та, число е, ах, ехр х. Приведите примеры их употребления.
2. Перечислите свойства показательной функции.
3. Каково основное свойство производной показательной функ-
ции?
4. Известно, что производная показательной функции пропор-
циональна самой функции. Как найти коэффициент пропорцио-
нальности?
5. Как определяется число е?
6. Чему приближенно равно число е?
7. Чему равна производная функции у — ех?
8. Через какую точку проходят графики всех показатель-
ных функций вида у = ах?
191
§ 2. ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ
1. Логарифмы
Определение. Логарифмом числа а по основанию b на-
зывается показатель степени, в которую надо возвести а, чтобы
получить число Ь.
В качестве основания мы будем всегда брать положитель-
ное число а, отличное от 1.
В записи Ь = а1 число а является основанием степени,
t — показателем, b — степенью. Число t — это показатель степени,
в которую надо возвести основание а, чтобы получить число Ь,
Следовательно, t — это логарифм числа b по основанию а:
t = \oga b.
Можно сказать, что формулы а* = Ь и f = loga b равносильны, вы-
ражают одну и ту же связь между числами a, t и b (при
а>0, ау=1, &>0). Число t — произвольно, никаких ограничений
на показатель степени не накладывается.
Подставляя в равенство а* = Ь запись числа t в виде логариф-
ма, получаем равенство, называемое основным логарифмическим
тождеством:
al°Sab = b.
Представляя в равенстве t = loga b выражение b в виде степени,
получим еще одно тождество:
loga al = t.
Свойства логарифмов
Теорема. Верны следующие тождества, выражающие свой-
ства логарифмов:
1) loga 6|62 = loga b\-Н loga &2, т. е. логарифм произведения
равен сумме логарифмов множителей;
2) loga y-=loga&i — loga т. е. логарифм дроби равен раз-
ности логарифмов числителя и знаменателя;
3) \ogabk=k loga b, т. е. логарифм степени равен по-
казателю степени, умноженному на логарифм основания.
Доказательство.
Свойства логарифмов выводятся из свойств степеней с
помощью основного логарифмического тождества, выражающего
определение логарифма. Выведем для примера первое свойство.
Обозначим logafti=/i, \ogab2 = t2. По основному логарифми-
ческому тождеству имеем:
а*' =Ь\ и at2 = b2.
192
Перемножим эти равенства: at}-at2 = b\b2. По свойству степеней
а'|а'2 = а'|+'2> т. е. b\b2 = at} + t2. По определению логарифма t\ + /2 =
= loga b\b2, т. е. loga 6|62 = loga b\ + loga 62, что и требовалось до-
казать. Свойства 2 и 3 выведите самостоятельно.
Свойства степеней и логарифмов тесно связаны между собой.
Они фактически выражают одно и то же, только один раз
мы обращаем внимание на поведение самих степеней, а друге# —
на поведение показателей:
1) а''а/2 = а/| + '2,
2)
а2
3) =
10ga b[b2 = \0ga Ь\Ч- 10ga Ь2\
10ga-“=l°ga Ь\ — 10ga Ь2\
02
10ga bk = k 10ga Ь.
С помощью свойств логарифмов можно логарифмировать
выражения, составленные с помощью операций умножения, де-
ления и возведения в степень.
Примеры.
1. log* А =5 loga 2 4-4-loga 3-3 loga 5-4-|ogfl 1.
53 ^7 2 6
2. lOga 4 = 10ga3 + 3 + ^-l0gafe-2 loga (c + d).
3. A = 10xlogloX, logio A = 1 +(logio x)-logio x= 1 + (logic x)2.
Иногда приходится искать выражение по его логарифму.
Такую операцию называют потенцированием.
Примеры.
1. l0ga4=2l0ga3-^-l0ga2, Д = = = 2^.
22
2. loga Л = 1 +2 loga 6 — 3 loga с, А =^~ •
3. 10ga 4 = 10ga(x— l) + 10ga(x+l)-y-loga X, A = (£311Ж±11 .
2 V*
Замечание. Запись t = loga b имеет смысл лишь при b > 0.
Поэтому в тождествах, отражающих свойства логарифмов,
все выражения, стоящие под знаком логарифма, будем считать
положительными. При логарифмировании буквенных выражений
надо их раскладывать на множители так, чтобы все множители
были положительны. Например, пусть необходимо прологарифми-
ровать выражение А=х [х— 1). Сделать это можно лишь тогда,
когда Л>0, т. е. когда либо х<0, либо х> 1. Если х> 1, то оба
множителя х и х—1 положительны и мы можем записать:
loga A =loga х+ loga (X — 1) При Х>1.
7 Заказ 836 193
Если же х<0, то оба множителя отрицательны и А нужно раз-
ложить на множители так: А = ( — х) (1 — х), откуда
10ga = 10ga ( — x)+10ga (1 — х) При Х<0.
Аналогично loga х2 = 2 loga х при х>0 и loga х2 = 2 loga ( — х) при
х<0. С помощью модуля это можно записать короче:
logaX2 = 2 loga |х|.
Модуль перехода
В вычислениях в качестве основания а часто берется число
а =10. В то же время зачастую необходимы вычисления степе-
ней и логарифмов с разными основаниями. Возникает вопрос:
как связать между собой степени и логарифмы с разными осно-
ваниями?
Пусть дана степень Ь = а*. Мы хотим перейти к новому
основанию с, т. е. записать число а* в виде сх при некотором х. За-
писав равенство а‘ = сх и прологарифмировав его по основанию а,
получим f = xlogac, откуда х=^~-^. Так как а‘ = Ь, сх = Ь, то
можно с помощью логарифмов записать: / = loga ft, x=logc ft, от-
куда
logcft=-^-.
® 10ga C
Выведенную формулу называют формулой перехода от од-
ного основания логарифма к другому.
Таким образом, мы видим, что при изменении основания зна-
чения логарифмов изменяются пропорционально. Коэффициент
пропорциональности называют модулем перехода.
Отметим простые следствия выведенной формулы:
1)
2)
3)
logc a= с (положим в формуле перехода ft = a);
log^ft=-^A (положим в формуле перехода c — ak}\
log 1 ft=— loga ft (положим в предыдущей формуле
fe=-l).
С помощью логарифмов все степени можно привести к одному
основанию. Если в качестве основания берется число a = 10, то
соответствующие логарифмы обозначаются знаком 1g и называ-
ются десятичными. Можно записать:
a' = i(ylgfl)/= 10'lgfl.
Если в качестве основания берется число е, то соответствую-
щие логарифмы обозначаются знаком In и называются натураль-
ными:
^==e(lna)./ = e/ln^
194
Значения модулей перехода от десятичных логарифмов к на-
туральным и наоборот таковы:
In 10 = 2,303...,
'^-iTio-0'4343 -
2. Исследование логарифмической функции
Определение. Логарифмической функцией называется
функция вида y = loga х.
Напомним, что в качестве основания логарифмов выбирается
число а>0, отличное от 1.
Основные свойства логарифмической функции (схема X).
1) Область определения: множество всех положительных чи-
сел, т. е. промежуток (0; 4-оо).
2) Монотонность: если а>1, то логарифмическая функция
строго возрастает; если 0<а<1, то она строго убывает.
3) Область значений: множество всех вещественных чисел R.
Так как определение логарифмов основано на понятии степени,
то при доказательстве свойств логарифмической функции исполь-
зуют свойства показательной функции.
Свойство 1 в доказательстве не нуждается: оно опирается
на определение логарифма числа х, по которому необходимо, чтобы
число х было положительным.
Докажем свойство 2. Для этого сначала рассмотрим случай
а>1. Возьмем два положительных числа Х| и *2, такие, что
Xi <%2, и докажем, что loga х\ <loga х2. Обозначив первое из этих
чисел через второе — через /2, по определению логарифма
получим а*' = Х[, ah = x2. Если бы выполнялось неравенство /1^/2,
то по свойству монотонности показательной функции выполнялось
бы неравенство т. е. Х|^х2. Это противоречит условию.
Следовательно, t\<zt2i что и тре-
бовалось доказать. Случай 0<а<1
рассматривается аналогично.
Свойство 3 утверждает, что
всякое вещественное число t может
быть логарифмом некоторого числа
х. Так как степень а* определена
при любом /, то, взяв х = а\ полу-
чим loga что и требовалось до-
казать.
Графики логарифмических фун-
кций при различных основаниях по-
казаны на рисунке 108.
195
Графики функций у = ах и y = \ogax симметричны друг другу
относительно прямой у = х. Действительно, если точка Р(с; d) ле-
жит на графике функции у = а\ то d = ac. Но тогда c—\ogad
и точка Q(d\c) лежит на графике функции y = \ogax. Так как
точки Р (с; d) и Q (d\ с) симметричны относительно прямой у — х
(рис. 109), то симметричны и графики показательной и логариф-
мической функций.
Вместо логарифмических функций с произвольным основа-
нием удобно рассматривать функции вида r/ = clnx. Так как
loga x==i~* 'п то указанные функции исчерпывают все логариф-
мические функции.
Функция £/ = 1пх растет с ростом х, однако медленнее, чем
любая степенная функция вида y—xk (fe>0), в частности мед-
леннее, чем у = -у[х (схема IX).
3. Производная логарифмической функции
Рассмотрим две функции у = ех и £/ = 1пх. Мы знаем, что их
графики симметричны относительно прямой у — х. Это поможет
нам найти производную логарифмической функции, зная произ-
водную экспоненты. Возьмем точку Р (с; d) на графике экспо-
ненты (т. е. d = ec) и симметричную точку Q (d; с) на графике
логарифмической функции (т. е. c = lnd). Касательные к графи-
кам в этих точках тоже будут симметричны (рис. 109). Угловой
коэффициент k\ касательной к графику экспоненты равен значе-
нию производной функции у — ех при х = с, т. е. fei=ec, так как
(ех)' = ех. Пусть ои и аг — углы, образованные проведенными ка-
сательными с осью абсцисс. Из рисунка 109 ясно, что ai + a2=y-.
Так как k\ =tg ai =ес, то &2 = tg a2 = tg (-£—ai ) = ctg ai = -£-=
196
Таким образом, производная функции у = 1пх в точ-
ке x = d равна Можно написать:
(lnx)'=-U
Мы видим, что производная логарифмической функции t/==ln х
равна степенной функции у = х~'. Интересно заметить, что функ-
ция у = х~' не получается как производная какой-либо другой
степенной функции вида у = схк. Действительно, хотя (xk)r = kxk~x
при любом k, но получить значение k—1, равное —1, можно
лишь при /г = 0, а (х°)' = 0.
Так как logax = r—In х, то
(loga *)'=-!-—.
' ’ In О *
По формулам производной показательной функции (ех)' = ех
и (axY = kax, где k= lim ° - . Известно, что е1па—а и ах = екх,
где Л = 1п а. Поэтому (ах)' = kekx = kax, т. е.
(ах)' = (1п а) ах.
Примеры.
1. у = хех\ у'= ех ~t~xex = ех (1-j-x).
2. у=х\пх — х; у' = \п х+-^—1 = In х.
3. у = екх\ y' = kekx.
4. у = In kx\ у'=т~=—, или In kx = In fe + ln x; (In fex)'=—.
fix X x
Зная производные экспоненты и логарифма, можно получить
приближенные формулы для их вычисления.
Пусть у = е\ Хо = О, £/о = е°=1. Разность eh — e" = eh— 1 —это
приращение у на отрезке [0; h]. Вычислив dy при хо = О, получим
dy — y' (0) dx. Так как у' = е\ то г/'(0) = 1 • Заменив \у на dy и под-
ставив dx = h, получим приближенную формулу
etl — 1 « А, или eh« 1 + ft.
Более точная формула для вычисления экспоненты такова:
Пусть теперь z/ = lnx. Выберем х0=1, */о = 1п 1=0. Положим
dx = h и вычислим In (1 +ft). Найдем dy при хо=1. Так как
197
(In х)'=у-, то у' (хо)= 1 и dy = 1 -dx = h. Заменяя Ay = ln (1 + й) —
— In 1 = 1п(1+Л), получаем приближенную формулу
In (1
Более точная формула для вычисления логарифма такова:
2 /.4
1п(Ц-Л)=Л—f+... .
4. Вычисление логарифмов
Более 300 лет логарифмы использовались для облегчения
вычислений. Их основное достоинство — способность сводить
умножение к сложению по формуле logfl&1ft2 = loga b\-|-loga ft2.
Были составлены обширные таблицы логарифмов чисел, с по-
мощью которых можно легко переходить от чисел к их логариф-
мам и обратно.
Все таблицы логарифмов до 1950 г. являлись перепечаткой или
сокращением таблиц Бриггса. Генри Бриггс (1561 —1630) с очень
большой точностью (16 знаков после запятой) извлек подряд
57 квадратных корней из 10 и получил значения 10 2, 10 4 ,
2 1
10 8 , ..., IO2. Комбинируя эти значения, он получил ^густую сетку
чисел с известными десятичными логарифмами: 10 4 = 10 2 *10 4
и т. п. После этого десятичный логарифм любого числа х из про-
межутка [1; 10] с хорошей точностью находится округлением до
ближайшего известного.
Это огромная работа, и за 300 лет не нашлось никого, кто
повторил бы ее. Любопытно, что немного раньше Бриггса таблицу
натуральных логарифмов составил Джон Непер (1550—1617).
С появлением ЭВМ ситуация переменилась. Умножение по-
прежнему выполняется дольше, чем сложение, но логарифмиро-
вание требует еще больше времени. Поиск числа в таблице очень
дорогая операция для ЭВМ. Поэтому теперь значение логарифмов
как инструмента вычисления резко упало, а с распространением
калькуляторов оно сходит на нет. С другой стороны, сами по себе
логарифмические зависимости легко обрабатываются и использу-
ются при вычислениях на ЭВМ. Например, формула х* =
= ехр(£1пх) служит основным средством возведения в степень
(кроме Л= 1, 2, 3) на всех ЭВМ и на калькуляторах.
На современных ЭВМ (и на калькуляторах) значения In х и
ех вычисляют, пользуясь заранее найденными приближенными
формулами. По этим формулам вычисление логарифмов стано-
вится довольно простым. Пользователю ЭВМ никогда не прихо-
дится думать о вычислении логарифмов: на всех ЭВМ для этого
имеются стандартные программы.
198
5. Прикладные примеры
Во вводной беседе мы уже говорили о том, что многие процес-
сы описываются с помощью показательных функций. Почему так
происходит, это мы обсудим в следующей главе, а сейчас приведем
примеры зависимостей, в которых встречаются экспоненты и ло-
гарифмы.
1. Радиоактивный распад. Изменение массы радиоактивного
вещества происходит по формуле m —т02 г, где то— масса
вещества в начальный момент / = 0, m— масса вещества в мо-
мент времени /, Т — некоторая константа, смысл которой мы
сейчас выясним.
Вычислим значение m при t = T. Так, m (Г) = т0-2-1 . Это
означает, что через время Т после начального момента масса
радиоактивного вещества уменьшается вдвое. Поэтому число Т
называют периодом полураспада. Период полураспада радия
равен 1600 лет, урана-238 —4,5 млрд, лет, цезия-137 — 31 год,
иода-131 —8 суток.
Закон радиоактивного распада часто записывают в стандарт-
ном виде т = пгое т. Связь константы т с периодом полураспада
нетрудно найти:
= 2’' - -Т= -Г1'1 2‘45 Т
2. Рост народонаселения. Изменение количества людей в стра-
не на небольшом отрезке времени с хорошей точностью описыва-
ется формулой N — Noeat, где Уо — число людей при / = 0, У—
число людей в момент времени t, а — некоторая константа.
3. Барометрическая формула. Давление воздуха убывает с вы-
h
сотой (при постоянной температуре) по закону р = рое н, где
ро— давление на уровне моря (Л = 0), р — давление на высо-
те/!, Н — некоторая константа, зависящая от температуры. Для
температуры 20 °C величина Н^7,7 км.
4. Формула Циолковского. Эта формула, связывающая ско-
рость ракеты v с ее массой т, такова: и = иг1п^-, где иг —
скорость вылетающих газов, то — стартовая масса ракеты. Ско-
рость истечения газа при сгорании топлива vr невелика (в на-
стоящее время она меньше или равна 2 км/с). Логарифм растет
очень медленно, и, для того чтобы достичь космической скорости,
необходимо сделать большим отношение — , т. е. почти всю
т
стартовую массу отдать под топливо.
199
5. Коэффициент звукоизоляции стен измеряется по формуле
D = A 1g , где ро — давление звука до поглощения, р — давле-
ние звука, прошедшего через стену, А — некоторая константа, ко-
торая в расчетах принимается равной 20 дБ. Если коэффициент
звукоизоляции D равен, например, 20 дБ, то это означает, что
1g =1 и р()=10р, т. е. стена снижает давление звука в 10 раз
(такую звукоизоляцию имеет деревянная дверь).
Контрольные вопросы
1. Обратите внимание на следующие встретившиеся в тексте
ключевые слова и обозначения: логарифм, потенцирование, нату-
ральный логарифм, 1g х, In х, loga х. Приведите примеры их ис-
пользования.
2. Каковы основные свойства логарифмов?
3. В чем состоит основное логарифмическое тождество?
4. Какой формулой связаны между собой логарифмы по раз-
ным основаниям?
5. Какова область определения логарифмической функции?
6. Что можно сказать о монотонности логарифмической
функции?
7. Какова область значений логарифмической функции?
8. Как связаны между собой графики логарифмической и пока-
зательной функций?
9. Чему равна производная функции z/ = lnx?
10. По каким приближенным формулам можно вычислить
значения экспоненты и натурального логарифма?
§ 3. ПОКАЗАТЕЛЬНЫЕ И ЛОГАРИФМИЧЕСКИЕ
УРАВНЕНИЯ И НЕРАВЕНСТВА
1. Простейшие уравнения
Простейшее показательное уравнение — это уравнение вида
ах — Ь. Пусть основание а>0 и отлично от 1. Так как функция
у = ах строго монотонна, то каждое свое значение она принимает
ровно один раз. Это означает, что уравнение ах=Ь при /?>0
имеет одно решение, которое по определению логарифма равно
loga b. Если 6^0, то уравнение ах = Ь корней не имеет, так как ах
всегда больше нуля. Если число Ь записано в виде ас, т. е. если
уравнение представлено в виде ах — ас, то оно имеет один корень
х = с.
Сформулируем общий результат о решении простейшего
показательного уравнения (схема XI).
Теорема. Пусть а > 0 и а =# 1. Уравнение af (х) = а8 (х) равно-
сильно уравнению f (x) — g (х).
200
Доказательство. Докажем, что если af(х) = аё{х\ то
f(x) = £(x)- Действительно, так как показательная функция стро-
го монотонна, то из равенства ее значений ac = ad следует равенст-
во показателей c = d. Обратно: если f (x) = g (х), то а!{х) = аё{х).
Примеры.
1. 2Х=1 о2х = 2°ох = 0.
2. 9'=^-о32г=3*3о2х=-Зох=-
3. 3-4х = 2.32хо£=|-
4. 2-5x = 3x+l <s>lg 2 + х lg 5=(*+1) 1g 3 ox (1g 5 —lg 3) =
= |g 3 - lg 2 о .
5 6 Ig5 — lg 3
5. 2х2+х-3 = 8хо2х2+х-3 = 23х ox2 + x-3 = 3xo
-ох2 — 2х — 3 = 0ох1 = — 1, Х2 = 3.
Простейшее логарифмическое уравнение — это уравнение вида
logax = &. Оно имеет единственное решение x = tr при любом Ь.
Сформулируем общий результат о решении простейшего лога-
рифмического уравнения (схема XI).
Теорема. Уравнение logfl f (х) = loga g (х) равносильно
уравнению f (x)=g (х) при ограничениях f(x)>0, g(x)>0.
Доказательство. Пусть х — решение уравнения
loga f (x) = loga g (x). Тогда определены логарифмы чисел f (х) и
g (х), т. е. эти числа должны быть больше нуля. Потенцируя ра-
венство loga f (х) = loga g (х), получаем равенство f(x) = g(x). Об-
ратно, пусть х — решение уравнения f (x) = g(x), причем g(x)>0
и f(x)>0. Тогда равенство f(x) = g(x) можно прологарифми-
ровать, И МЫ получим loga f (х)= loga g (х).
Примеры.
1. Iog2 х = 0 о х = 2° = 1. 2. log3 х= 1 о х = 3.
3. log^ х= —1 ох = (-^-) =2.
2 Х 7
4. log2 (х—l) = log2 (5 —х)о х—1 =5 —х, х—1>0,
5—х>0 о х = 3.
Мы решили уравнение х—1=5 —х, а затем проверили, удов-
летворяет ли решение условиям х—1>*0 и 5 —х>>0. Заметим,
что если f (х) = g (х) и f (х) > 0, то тогда и g (х) > 0, т. е. из двух не-
равенств достаточно проверить только одно.
5. 1g (х2 — х — 3) = lg х о х2 — х — 3 = х, х>0^=>Х|=3,
х2= —1, х>0ох = 3.
201
2. Простейшие неравенства
Простейшее показательное неравенство — это неравенство ви-
да ах>Ь или ах<Ь (или ах^Ь, или ах^.Ь). Решение такого
неравенства нетрудно представить себе графически, построив
график показательной функции у = ах и проведя прямую у=Ь
(схема XI). Рассмотрим для примера два из 16 возможных
вариантов.
Пусть а>1 и Ь>0. Решением неравенства ах~^Ь является
промежуток [logo b; +<»), т. е. все числа x^logaft (схема XI).
Пусть а>1 и Ь^.0. Решением неравенства ах^Ь является
множество всех вещественных чисел R.
Примеры.
1. 2Х< 1. Ответ: х<0.
2- (т) ^(т) (т) • Ответ: х<~2-
3. 5х^—5. Ответ: решений нет.
4. (у-) >0- Ответ: х — любое число.
5. 5х<3-2хох lg 5<lg 34-х 1g 2ox(lg 5 — 1g 2)<lg 3.
Ответ: x
-lg2>0).
lg 3
Ig5-lg2
(в решении использовалось то, что lg 5 —
Можно сказать, что неравенство типа а!{х)>Ь мы решаем
логарифмированием. При логарифмировании неравенств надо
помнить два правила: 1) в обеих частях неравенства должны
стоять положительные числа; 2) при логарифмировании по осно-
ванию а>\ знак неравенства сохраняется, если же 0<а<1,
то знак неравенства меняется на противоположный.
Простейшее логарифмическое неравенство — это неравенство
вида loga х>ft (вместо знака > может стоять <, ^).
Аналогично показательному неравенству здесь также возможно
много вариантов (схема XI). Логарифмическое неравенство реша-
ют потенцированием. При этом надо помнить два правила: 1) при
переходе от выражения loga f (х) к выражению f (х) надо добавлять
условие f(x)>0; 2) если а>1, то при потенцировании знак не-
равенства сохраняется; если же 0<а<1, то знак неравенства
меняется на противоположный.
Примеры.
1. log2 х>0 ох> 1, х>0ох>1.
2. log2 х<1 ох<2, х>0 о 0<х<2, или х£(0; 2).
3. log2 , х-1>0оКх<3,
или х£(1; 3].
202
1
Рис. 110
X
4. Iog2 (x2—l)^log2 (x + 5). Сначала учтем условия x2—-l>0
и х+5>0. Решение этой системы неравенств изображено на
рисунке 110. Затем потенцируем: х2—1^х4-5^х2 — х--6<04>
о—2^х^3. Соединяя решения вместе, получим ответ:
— 2^х< —1 и 1<х^3, или [—2; — 1)0(1;3].
3. Введение новой неизвестной
Основной прием, с помощью которого решают показательные
и логарифмические уравнения и неравенства,— это введение новой
неизвестной. Поясним этот прием на ряде примеров.
1) Выражение показательных функций друг через друга.
X
рассмотрим выражения r/i=2x, г/2 = 22х, у3 = 2~\ у 4 = 2 2. Все
они могут быть алгебраически выражены друг через друга. На-
пример, у2 = у2, уз =—, У4=^[у\, У2 = -^т и т- Д- Алгебраическая
У\ Уз
связь между различными степенями может быть осложнена до-
бавлением в показателе степени постоянных слагаемых: г/5 = 2х+2,
£/б=22х-1, £/7 = 2|~х. Однако и сейчас несложно выразить эти
выражения, например, через у\. Получим £/5 = 22 - 2х = 4f/i,
£/б = 2-1 •22x=-^-£/i, £/7 = 2-2-х=—. К этому полезно напомнить
у
связь между различными основаниями. Например,-|-=2_|, 4 = 22,
2 , . v
у/2 = 22, 0,25 = 2 2 и т. п. Поэтому выражения ) >
«/9 = 4х+1, 4/ю = (л/2)-3х, у\\ =(0,25)~х также нетрудно выразить
через ус
_3х __3
Ув=^-, t/9 = 4-22x = 4z/f, 1/10 = 2 2 =у, 2,
У'
г/11=(2-2)-х = 22х = £/?.
Если в уравнении или неравенстве встречается несколько по-
казательных функций, то надо все их выразить через одну. Обычно
после этого показательное уравнение или неравенство превраща-
ется в алгебраическое.
Примеры.
1. 3-4Х-2х+3 + 8 = 22х+' - (у-)""' ~Х-
203
Пусть 2х=у. Тогда 4х = у2, 2х+3 = 8у, 22х+1 = 2у2, =2у.
Уравнение можно записать так: Зу2 — 8у + 8 = 2у2 — 2у о
ф>у2 — 6у + 8 = 0оу,=4, у2 = 2.
Возвращаясь к неизвестной х, получим 2' = 4ох=2;
2х = 2ох=1.
Ответ: Х| =2, х2 = I.
2. 2--(£Г’<1.
Делаем замену 2х =у. Неравенство перепишем таким образом:
«/ — “-< 1 о у2 — у — 2<0 (мы умножили неравенство на у, что
можно, так как = >0) о — 1 <z/<2. Так как 2Х> —1
верно при всех х, то остается решить неравенство 2х<2 о х<1.
Ответ: х<1. (Иначе ответ можно записать так: (— оо; 1).)
2) Выражение логарифмических функций друг через друга.
Рассмотрим выражения r/i = log2X, £/2 = log4X, £/3 = log2
~2
y4 = log^x. Используя модуль перехода, легко связать эти вы-
ражения между собой: y2=-^-yi, уз=—уь У4 = 2у^.
Свойства логарифмов позволяют по-разному записать связи
между выражениями. Например, £/5 = log2 х2 = 2f/i, £/6 = log2 л/* =
l/7 = log2 2х=1+yi, y8 = log2y-= — 1+Зу( и т. д.
Если в уравнении или неравенстве встречается несколько ло-
гарифмических функций, то надо (если не удается избавиться от
логарифмов потенцированием) выразить их через одну и свести
логарифмическое уравнение или неравенство к алгебраическому.
Примеры.
1. 1 + - 2- =1.
5-lgx т 14-lgx
Делаем замену lgx = r/. Получаем уравнение относительно у:
1 1 +у+2 (5-У)=(5~У) а +у)
оу2 — 5y + 6 = 0<^yi=2, У2 = 3.
Возвращаясь к неизвестной х, получим lgx = 2, х=100; lgx = 3,
х=1000.
Ответ. Х| = 100, х2 = 1000.
2. Iog3 X • log9 X • log27 X • log8| Х = .
□
Перейдем к основанию 3. Получим log9 x=-i-log3 х; log27X =
= -|-log3x; log8i x=-i-log3 х. Заменив log3 x на у, получим
204
y'Ty'Ty'Ty=i'^'kyi=T^y4 = iQ^>y===±2- ВозвРа-
щаясь к неизвестной х, получим log3x = 2, х = 9; log3x=—2,
Ответ: х,=9, Х2 = -^~.
3. x,gx-2<1000.
Логарифмируя, получим равносильное данному неравенство
(1g х — 2)lgx<3.
Положим lgx = y. Получим неравенство (у — 2)у<3о
оу2- 2у — ЗСОо — 1 <у<3.
Возвращаясь к неизвестной х, получим — l^lgxC3o
^<x<iooo.
Ответ: -^-^х^СЮОО, или в другой записи 1000 ].
4. Использование свойства монотонности функций
при решении показательных уравнений
Монотонность функций часто позволяет определить число кор-
ней уравнения, а иногда и найти их значения. Рассмотрим
примеры решения уравнений.
1. 22х = 5—-х.
В левой части уравнения имеем возрастающую функцию, а в
правой — убывающую. Следовательно, уравнение не может иметь
более одного корня (рис. 111). Один корень можно угадать:
х=1. Это число и является окончательным ответом.
2. 4х-3х = 1.
Рис. 1 1 1
205
Рис. 112
Одно решение х=1 легко найти подбором. Докажем, что
других корней нет. Перепишем уравнение так: 1 •
В правой части последнего уравнения сумма убывающих функций
т. е. значение £/=1 эта сумма может принять только один раз.
Ответ: х=1.
3. Сколько корней имеет уравнение ех = ах?
Изобразим схематически графики функций г/ = ех и у = ах
(рис. 112). При а<0 графики имеют одну точку пересечения.
При а>0 графики могут не пересекаться, касаться друг друга
или пересекаться в двух точках. Граничным значением парамет-
ра а, при котором происходит разделение основных случаев —
две точки пересечения или ни одной, является значение а, при
котором прямая у —ах является касательной к графику функции
у — ех в некоторой точке. Найдем это значение а. Пусть касание
произошло в точке х0, тогда производная функция у = ех в этой
точке равна а. Поэтому получаем уравнение ех = а, т. е. х0 = 1п а.
Точка с абсциссой х0 = 1па должна лежать как на графике
функции у = ех, так и на прямой у = ах. Получаем еХо = ах,
т. е. а = а In а, так как а=/=0, то In а= 1 и а = е.
Ответ: при а<0 один корень, при а>е два корня, при
а — е один корень, при Q^a<e корней нет.
Контрольные вопросы
1. При каких b показательное уравнение ах = Ь имеет корень?
2. Сколько корней имеет уравнение ах=Ь?
3. Как решать уравнение вида af(x) = ag(x)?
4. Сколько корней имеет уравнение logax=ft?
5. Как решать уравнение вида loga f (x) = log& g (х)?
6. Какие правила надо соблюдать при логарифмировании не-
равенств?
206
7. Какие правила надо соблюдать при потенцировании нера-
венств?
8. Какова алгебраическая связь между выражениями у\=ах
и у2 = акх7
9. Какова связь между выражениями: a) z/i = logax и у% =
= logftx; б) t/i = logax и z/2 = logo.x; в) j/! = logax и y2 = loga_. х?
10. Вы знаете одно решение уравнения. В каких случаях вы
можете доказать, что других решений нет?
ЗАКЛЮЧИТЕЛЬНАЯ БЕСЕДА
1. Взаимно обратные функции
Изученные в этой главе показательная и логарифмическая
функции являются взаимно обратными функциями. Подробное
ознакомление с этим понятием начнем с простых примеров.
Напишем формулу для вычисления площади круга по его ра-
диусу: S = n/c. Эта формула задает площадь круга S как функцию
его радиуса R, т. е. для каждого (положительного) числа R по
этой формуле вычисляется площадь круга S. Представим себе,
что надо решить обратную задачу: по данной площади круга S
/ с
вычислить его радиус. Для этого выразим R через S так: R=~\/— •
Новая формула задает радиус круга R как функцию его площа-
ди S. Полученные две функции S=S (R) и R = R(S) являются
примерами взаимно обратных функций.
Приведем еще примеры взаимно обратных функций:
1. у = 2х + 5 и х=-|—
2. г/ = х3, х^О, и x = V*A
3. у = 10х и x = lg у.
В каждом из указанных примеров соответствие между пере-
менными величинами, задаваемое взаимно обратными функциями,
одно и то же. В самом деле, зависимость между радиусом и пло-
щадью круга остается одной и той же: записывается ли она в
виде S = n/?2 или же в виде Точно так же функции
£/ = 2x4-5 и ----1- выражают одну и ту же зависимость между
переменными х и у.
Определение. Две функции fug называются взаимно
обратными, если формулы y=f (х) и x=g (у) выражают одну
и ту же зависимость между переменными х и у, т. е. если равенство
y—f (х) верно тогда и только тогда, когда верно равенство
*=g(y)--
207
y=f(x)ox=g(y).
Если две функции f и g взаимно обратны, то g называют
обратной функцией для f и, наоборот, f — обратной для g.
Как ответить на вопрос, что такое обратная функция для
функции f? Это можно сделать следующим образом: обратная
функция для функции f — это такая функция g, что f и g обра-
зуют пару взаимно обратных функций.
Как мы уже отметили, зависимость z/ = 2% + 5 и -----|-
между переменными х и у одна и та же. Эту же зависимость можно
записать и так: 2х —z/ + 5 = 0. Из последней формулы можно вы-
разить у как функцию от х, а можно и, наоборот, выразить х как
функцию от у. Эти две функции будут взаимно обратны.
Таким образом, исходным понятием является понятие зависи-
мости. Если есть некоторая зависимость между переменными х и у,
которая позволяет выразить у как функцию от х и х как функцию
от у, то эти две функции и являются взаимно обратными.
2. Графики взаимно обратных функций
При построении графиков взаимно обратных функций необхо-
димо внимательно следить за обозначениями переменных. Рас-
смотрим функцию f. Аргумент этой функции и ее значения можно
обозначить произвольными буквами. Так, в формулах у = ех, s =
= е\ N = e2 переменные обозначены различными буквами, однако
каждая из этих формул определяет одну и ту же показательную
функцию, экспоненту.
Определение взаимно обратных функций сформулировано на язы-
ке зависимостей. Чтобы определить, являются ли эти две функции
f и g (заметьте, здесь пока нет обозначений для переменных)
взаимно обратными, надо взять две переменные, например х и у,
составить две формулы y = f(x) и x = g(y) и затем определить,
задают эти две формулы одну и ту же зависимость между пере-
менными х и у или нет.
Различия в обозначениях переменных сказываются при
построении графиков функций. Пусть у нас есть две переменные
х и у, значения которых откладываются на выбранных координат-
ных осях, которые мы обозначаем этими же буквами х и у. Рас-
смотрим зависимости между х и у.
z/ = 2x-|-5;
У 5
г = —----•
2 2 ’
2х — z/4-5 = 0.
Ясно, что это разные записи одной и той же зависимости между
переменными х и у.
у = 2х+Ьох=^—|-^2х-// + 5 = 0.
208
Поэтому график каждой из этих зависимостей один и тот же —
он состоит из всех точек Р (х; у), координаты которых связаны
соотношением £/ = 2*4-5, справедливым тогда и только тогда,
когда х=-^----1“ или 2х —£/4-5 = 0 (рис. 113). Точно так же
график зависимостей £/ = ех и х = 1п£/ в системе координат (х; у)
один и тот же (и зависимость между х и у на самом деле одна
и та же; рис. 113).
Посмотрим на зависимость х=^------Она выражает х как
некоторую функцию от у. Аргумент этой функции обозначен бук-
вой £/, а значения — буквой х. Поменяем местами х и £/, т. е. рас-
х 5
смотрим зависимость У — ~^--ФунК1*ия осталась одной и той
же, но теперь ее аргумент обозначен, как обычно, буквой х, а зна-
чения — буквой £/. Построим график функции £/ = -^ 1- (напри-
мер, по двум точкам на рисунке ИЗ). Мы видим, что этот график
отличен от графика зависимости х=------
Как связаны между собой графики функций £/ = 2x4-5 и
х 5
У — ~2--Возьмем какую-либо точку на графике первой функ-
ции, например Р (0; 5). Поменяем местами координаты, т. е. рас-
смотрим точку Q (5; 0). Эта точка лежит на графике второй
функции 0 = -“ 1-. Точки Р (0; 5) и Q (5; 0) симметричны друг
другу относительно биссектрисы угла хОу, т. е. прямой £/ = х.
Из рисунка 114 видно, что при любых а и b точки Р (а; Ь) и Q (Ь-9 а)
симметричны друг другу относительно прямой £/ = х.
Теорема. Пусть fug — взаимно обратные функции.
Графики функций y = f(x) и y = g(x) симметричны друг другу
относительно биссектрисы угла хОу.
209
Доказательство. По определению взаимно обратных
функций формулы y=f(x) и x = g(y) выражают одну и ту же за-
висимость между переменными х и у, а значит, эта зависимость
изображается одним и тем же графиком — некоторой кривой С
(схема XII). Кривая С является графиком функции y = f(x).
Возьмем произвольную точку Р (а\ Ь)£С. Это означает, что
b = f(a) и одновременно a = g(b). Построим точку Q, симметрич-
ную точке Р относительно биссектрисы угла хОу. Как мы заметили
раньше, точка Q будет иметь координаты (ft; а). Так как a = g (ft), то
точка Q принадлежит графику функции y = g(x): действительно,
при x = ft значение у = а равно g(x). Таким образом, все точки,
симметричные точкам кривой С относительно указанной прямой,
лежат на графике функции y = g (х). Они исчерпывают этот график
целиком, так как аналогично показывается, что всякая точка
функции y = g(x) при указанной симметрии попадает на график
функции y=f(x). Теорема доказана.
На рисунке 115 изображены графики пар взаимно обратных
функций:
а) у = ех и у=1п х;
б) у = х2 (х^О) и у=^/х\
в) у = 2х — 4 и //=-*-+2.
3. Условие существования обратной функции
Дана функция y=f(x). Поставим следующий вопрос: при
каком условии существует функция, обратная к функции /? По оп-
ределению обратная функция к функции f строится так: из соот-
ношения y — f(x) надо х выразить как функцию от у.
Таким образом, самым простым ответом на поставленный воп-
рос будет такой: функция f имеет обратную, если из соотношения
210
y = f (x) переменную x можно однозначно выразить через у. Мы уже
знакомы с примерами функций, для которых это можно сделать.
Приведем примеры таких функций, для которых нельзя
однозначно выразить аргумент через заданное значение функции.
1. у= |х|. Для данного положительного числа у найдутся два
значения аргумента х, такие, что \х\=у. Например, если у = 2,
то х = 2 или х— —2. Значит, выразить однозначно х через у нельзя.
2. у = х2. Ситуация здесь такая же, как в предыдущем примере:
х = ^/у или х= —л/у.
3. r/ = sinx. При заданном значении у (где |у|<1) найдется
не по два, как в предыдущих примерах, а даже бесконечно много
таких значений х, что у = sin х. Здесь также х нельзя однозначно
выразить через у.
Сравним графически эти примеры с примерами, приведенными
ранее. Возьмем число yQ из области значений функции f и прове-
дем прямую у = уо, параллельную оси абсцисс. В ранее рассмот-
ренных случаях эта прямая пересекает график в одной точке,
т. е. можно по заданному значению у однозначно найти значе-
ние х. В последних трех примерах при некоторых у прямая пересе-
кает график более чем в одной точке: для этих значений у мы
не можем однозначно найти х, значит, эти функции не имеют
обратных.
Дадим геометрическую трактовку условия того, что функция
имеет обратную.
Функция y = f(x) имеет обратную, если всякая прямая у = уо
пересекает график функции y = f(x) не более чем в одной
точке (она может совсем не пересекать график, если у0 не
принадлежит области значений функции f).
Это же условие можно сформулировать иначе: уравнение
f(x)=yo при каждом у0 имеет не более одного решения.
Условие того, что функция имеет обратную, заведомо выполня-
ется, если функция строго возрастает или строго убывает. Дейст-
вительно, если f, например, строго возрастает, то при двух раз-
личных значениях аргумента она принимает различные значения,
так как большему значению аргумента соответствует большее зна-
чение функции. Следовательно, уравнение f(x)=y для строго мо-
нотонной функции имеет не более одного решения.
Показательная функция у = ах строго монотонна, поэтому
она имеет обратную — логарифмическую функцию y = logax.
Строго говоря, определение логарифма числа у требовало воз-
можности однозначно определить показатель х, такой, что ах — у,
т. е. чтобы из соотношения ах — у можно было однозначно выра-
зить х через у.
Мы знаем, что многие функции не имеют обратных. Если при
некотором b уравнение f(x) = b имеет более одного решения,
то функция y = f(x) обратной не имеет. На графике это означает,
что прямая у=Ь пересекает график функции более чем в одной
точке.
211
Многие изучавшиеся ранее функции не имеют обратных, на-
пример t/=x, y = sinx, y = tgx и т. п. С неоднозначностью
решения уравнения f(x) = b можно справиться следующим об-
разом: уменьшить область определения функции f так, чтобы ее
область значений не изменилась, но чтобы каждое свое значение
она принимала ровно один раз.
Примеры.
1. t/=x2, х^О.
2. у = х2, х^О.
3. y = sinx, xg[—у; у]
л . Зя ~|
2 ’ 2 J*
4» х* JT
. t/=sin X, хЯ —;
5. t/ = cos х, х£[0; л].
6. i/=tgx, хб(—у; у)
В каждом из приведенных примеров функция сохранила об-
ласть значений: для у = х2 это промежуток [0; +«>), для синуса
и косинуса это отрезок [— 1; 1], для тангенса это вся числовая ось.
В то же время, уменьшив область определения, мы добились
монотонности функции, а значит, и единственности решения
уравнения f(x)=b.
Каждая из выписанных выше функций имеет обратную. Для
обратных операций из примеров 1, 3, 5, 6 нами раньше введены
специальные обозначения:
1. у = х2, х^О о х — д/у.
3* s* Л Л I •
. y=sinx, х£ ——; — о x = arcsin у.
5. z/ = cosx, х£[0; л] о х=arccos у.
6. f/ = tg х, xg(— у-; y^ox=arctg у.
С помощью этих обозначений можно ввести функции, обратные
к тем, которые были перечислены выше:
1. £/ = V*-
3. у = arcsin х.
5. уarccos х.
6. у = arctg х.
Функции в пропущенных примерах 2 и 4 можно выразить через
уже введенные:
2. £/=— д/х является обратной функцией для функции у = х2,
х<0.
4. у = л — arcsin х является обратной функцией для функции
• г Г л Зл 1
y=sin X, хЕ[у; —J.
212
Проверим последнее утверждение:
а) Вычислим sin у:
sin (л — arcsin x) = sin arcsin х = х.
б) Проверим, что л—arcsin х имеет областью значений отре-
[-Ь ^]:
arcsin — arcsin х^ —л —arcsin х^ л—^-=у-;
л Зл
arcsin —— => л — arcsin х^. — .
4. Свойства взаимно обратных функций
1) Тождества. Пусть f и g— взаимно обратные функции.
Это означает, что равенства y = f(x) и x=g(y) равносильны.
Подставим одно из этих равенств в другое. Получим два тож-
дества:
Нё(уУ) = У и g(f (*))=*.
Примеры.
1. Пусть f — показательная, g— логарифмическая функция.
Получаем знакомые тождества:
— у и )Oga ах = х,
2. Функции у = х2, х^О и у = ^/х взаимно обратны. Имеем
два тождества:
(^/х)2==х и -\[х2 = х при х^О.
2) Область определения. Пусть f и g — взаимно обратные
функции. Область определения функции f совпадает с областью
значений функции g, и, наоборот, область значений функции f
совпадает с областью определения функции g.
Действительно, обратная функция к функции y = f(x) опре-
делена для всякого числа у, которое является значением функ-
ции f для некоторого числа х: мы берем равенство y=f(x)
и из него выражаем х как функцию от у. Это свойство наглядно
проявляется на графике: график функции y = f(x) совпадает
с графиком обратной функции x=g(y), только аргумент функ-
ции g откладывается по оси у. Ясно, что аргументы функции g —
это значения функции f и наоборот.
Пример. Область определения показательной функции —
вся числовая ось Я, а ее область значений — множество всех
положительных чисел. У логарифмической функции наоборот: об-
ласть определения — множество всех положительных чисел, а об-
ласть значений — все множество R.
213
3) Монотонность.
Теорема. Если одна из взаимно обратных функций строго
возрастает, то и другая строго возрастает.
Действительно, пусть f и g — взаимно обратные функции,
причем f строго возрастает. Докажем, что тогда и g строго воз-
растает. Пусть %| и х2 — два числа, лежащие в области опреде-
ления функции g, причем х\ <х2. Надо доказать, что g (%i)<g (х2).
Обозначим g(x\) = y\, g(x2)=y2. Числа у\ и у2 лежат в области
определения функции f, так как они являются значениями функ-
ции g. Предположим, что у\ ^у2. В силу монотонности функции f
имеем f (г/2). Но f {yi) = f {g (xi)) = X| и f (y2)=x2, т. е. Xi >х2,
что противоречит условию Х|<х2. Следовательно, у\<у?, что и
требовалось доказать.
5. Производная обратной функции
Выведем общую формулу производной обратной функции ана-
логично тому, как мы выводили формулу производной логарифми-
ческой функции. Пусть f и g — взаимно обратные функции.
Как найти производную функции g, зная производную функции f?
Графики функций y=f(x) и y=g(x) симметричны друг другу
относительно биссектрисы I угла хОу (рис. 116,а).
Возьмем какую-нибудь точку х = а и вычислим значение одной
из функций в этой точке: f (a) = b. Тогда по определению обратной
функции g(b) = a.
Точки (a; f (а)) = (а; ft) и (ft; g(ft)) = (ft; а) симметричны относи-
тельно указанной прямой /. Так как кривые симметричны, то
и касательные к ним симметричны относительно прямой /.
Из симметрии ясно, что угол одной из этих прямых с осью х
равен углу другой прямой с осью у. Если первая прямая образует
с осью х угол а, то ее угловой коэффициент равен k \ =tg а; тогда
214
вторая прямая имеет угловой коэффициент &2 = tg (-2—а) =
= ctg а = (рис. 116,6). Таким образом, угловые коэффициенты
прямых, симметричных относительно прямой /, взаимно обратны,
т. е. ^2=т“» или £|fe2=l.
Переходя к производным и учитывая, что угловой коэффициент
касательной является значением производной в точке касания,
делаем вывод:
Значения производных взаимно обратных функций в соответ-
ствующих точках взаимно обратны, т. е.
8' •
Напомним еще, что b = f(a) и a = g(b).
Замечание. В приведенных выше рассуждениях предпо-
лагалось, что k\ =/=0, т. е. касательные к кривым не параллельны
осям координат.
Приведем примеры нахождения производной обратной
функции.
1. y=f (х) = х3. Обратной функцией будет функция y = g(x) =
=\[х. Найдем производную функции g-.
а' ( 1 — 1 — 1
8 w 3(g(x))2 3 V?’
2. y=f(x) = sin x, хб[—у; у]-
Обратной функцией будет у = g (х) = arcsin х. Найдем про-
изводную арксинуса:
, / ч 1 1 1
0' (х) =----------=--------------= — .
ь v ' f' (g (х)) cos arcsin x
Итак, (arcsin xY = , 1 .
Аналогично вычисляется производная арктангенса:
(arctg х)' =------j-----=cos2 arctg x=
cos2 arctg x
__ 1____________1
14-tg2 arctg x 1 +x2
21&
6. Аксиоматическое определение показательной функции
Показательная функция y = f(x), где f(x) = ax, обладает за-
мечательным свойством:
0х' -аХ2 = ах'+х\ т. е. f (xi)-f (x2) = f (xi + х2).
Это свойство может быть положено в основу определения пока-
зательной функции.
Пусть функция f задана на всей числовой оси R и для любых
чисел Х|, х2 удовлетворяет соотношению
f(Xiyf(x2)=f(xt+X2).
Написанное соотношение называют функциональным уравнением.
Вопрос можно поставить так: каковы функции f с областью опре-
деления R, удовлетворяющие функциональному уравнению
f (Xi)-f (x2)=f(xi4-x2)?
Прежде всего функция f (х) = 0 удовлетворяет этому уравне-
нию. Будем считать, что f не является тождественным нулем. Из
функционального уравнения следует цепочка свойств функции [,
которые мы перечислим в виде серии нетрудных задач с указания-
ми на то, как их надо решать.
1) f(0)=l (рассмотреть f(x+0), где х — какое-либо число,
для которого f(x)=/=O).
2) f(x)^O для любого х (рассмотреть f(x+( — х))).
3) f (х)>0 для любых х (рассмотреть —Ну-))-
4) f ( — x) = f~' (х) (рассмотреть f(x+( — x))).
Обозначим f (1) через а.
5) f(n) = an, где n£N (рассмотреть f (1 +1 + -..+ 1)).
6) f( — п) — а~п, где n£N (воспользоваться 4) и 5)).
7) f где n^N (рассмотРеть f
8) f(r)==a\ где г — рациональное число.
Таким образом, мы видим, что значения всякой, не равной
тождественно нулю функции, определенной на всей числовой оси
и удовлетворяющей функциональному уравнению f (xi)-f (х2) =
= f (xi+x2), Для рациональных значений аргумента г совпадают
со значениями аг при некотором а. Для того чтобы сделать вывод
о том, что f (х) совпадает с ах при любом вещественном х, одного
функционального уравнения мало. Надо добавить еще какое-либо
свойство — монотонность или непрерывность. Вот почему, ста-
раясь избежать трудоемкого описания значений показательной
функции с помощью рациональных приближений, часто дают сле-
дующее определение показательной функции:
Показательная функция y=f (х) — это строго монотонная
функция, определенная на всей числовой оси и удовлетворяющая
функциональному уравнению f (xi)-f (x2)=f (х\+х2).
216
Контрольные вопросы
1. Какие две функции называются взаимно обратными?
2. Как расположены графики взаимно обратных функций?
3. Приведите примеры функций, имеющих обратную.
4. Сформулируйте различные условия обратимости функции.
5. Как связаны между собой области определения и области
значений взаимно обратных функций?
6. Как связаны между собой свойства взаимно обратных
функций?
7. Чему равна производная обратной функции?
8. Чему равны производные арксинуса, арктангенса?
9. Какими аксиоматическими свойствами можно задать пока-
зательную функцию?
10. Какому функциональному уравнению удовлетворяет ло-
гарифмическая функция?
ЗАДАЧИ К ГЛАВЕ IV
Степени
Порядок роста степенной функции
1. Какая функция растет быстрее (при больших х) :
у=\00х1 2 или £/ = 0,1х4?
2. Расположите в порядке скорости роста следующие функции:
1) у=2х; 2) У=^х', 3) у=х3;
4) у = х5; 5) у=^-< 6) у = х4.
3. Какая функция убывает быстрее:
*/ = -“— или =
57 10х 27 х2
4. Расположите в порядке скорости убывания следующие
функции:
1) у = 2) у = 3) у=±--, 4) У=-±; 5)
Х -yJX Х X ~\JX \Х2
Определение степени
5°. Запишите в виде степени двойки следующее число:
1) 8; 2) 1024; 3) -Ь; 4) -Ь; 5) 0,5; 6) 0,25;
7) д/2; 8) V*; 9) 10) 2 д/2^2; 11) 10; 12) е.
217
6°. Запишите в
виде степени с рациональным показателем:
5)
6) 3 4/9.
1) W;
1
7. Запишите с помощью радикалов:
_ в --
1) 3 5; 2) (т) 3; 3) 53,2;
4) 2-°’25; 5) (-1-) \ 6) 22-5т.
Свойства степени
8°. Упростите:
1) а5а7а12; 2) а"2Лг5; ( (
4) b^b^b3^ 5) 64-2^-2~3-г--®
9. Выполните действия:
1) 2-21 -27 •2'®; 2) ;
2 _2 \4^ '
, ч а 3 а 4 2 2
4) 4-4’ 5) ((а2)3)5;
а2 а 3
3) (b~lb3y~2b~3-,
61 (4+W)'
10*. Докажите тождество
ах + д-х^2 (дх-д~х^
11. Упростите:
2) -725^—2-5Л + (д/5)2х+4;
+ 49 2
4) 2Л-32~Х
(^2)2х+<
(л/3)2х~2
12*. Выясните, какое из чисел больше:
о
3) V3 или 4/6;
5) 1714 или 31";
4> (т) "л" (т)
г»3100 п9100
6) 23 или З2 .
218
Доказательство неравенств
13*. Докажите, что (1+x/^l+fex при xi>0.
14*. Докажите, что (1 + х)*1 + kx при 0k1, х^О.
15*. Докажите неравенства:
1) 2"<n! при п^4;
3) пп>(п+1)л_| при п>2;
2) 2п > п + 2 при п^5;
4) (1+—)"< (1+-ХТ
\ п / \ п + 1
п+1
Показательная функция
Монотонность
16°. Укажите, какие из следующих показательных функций воз-
растают, а какие убывают:
1) г/ = 5х; 2) у = Зх-1;
4)«=+П
5) t/ = 2-x; 6) у = Зх-4х;
График
17°. Постройте графики функций:
1)У=(-|-)Х; 2) у = 3) у = 2ех;
4) у— — 5ех; 5) у = 2>е~х\ 6) у = е3х.
18*. Постройте графики функций:
1) У = е х; 2) у = хе х; 3) у = ех sin х
4) у = е~х cos х; 5) у = е|х|; 6) y = eSinx.
19°. Докажите, что графики функций у = 2х и у= сим-
метричны относительно оси ординат.
20. Изобразите на одном чертеже графики функций y — ekx при
k = 0, ±1, ±2.
21. Изобразите на одном чертеже графики функций у—сех при
с=±1, ±2.
Производная
22. Вычислите производные:
1) у = 2ех-
4) у=х2е~х;
7) z/ = e~xcosx;
2) у = ех-\-е х;
5) y = e*sinx;
8) у==5л+1;
3) у=хех;
б)
9) у = ех + 2х.
219
Исследование функции
23°. Исследуйте функции и постройте их графики:
1) у=ех + е~х; 2) у=х2е~х', 3) у — ех—х.
24°. Найдите наибольшие и наименьшие значения функций:
1) у=2х, х£[—1; 1];
3) t/=x + e*, х£[— 1; 1];
5) у — ех — х, х£[ — 2; 2];
2) у=3~х, х€[0; 2];
4) у = ех sin х, х£[0; л];
6) у = 2х + 3\ х6[— 1; 0]
25*. Найдите области значений функций:
1) у = е^пх; 2) y=e~msx;
3) у=-\/1 —ех; 4) у = е~х sin х, х^О;
5) У=ТТ7г; 6) у = хе~х, х>0;
I “Г с
7) у=±-(ех + е~ху, 8) у = е~х\
Число е
26. Известно много формул для приближенного вычисления чис-
ла е. Самыми распространенными являются формулы
—-I—i—I--------------------!
1 ТЬ2Т 1-2-3 “ 1-2-...'П
которые при натуральных значениях п дают последователь-
ности приближенных значений е с любой степенью точности.
Выпишем первые члены этих последовательностей:
^(Ц-О^г, е2=(1+^-)2 = 2,25,
ё, = 1 +^=2, ё2=1+^+-г1?=ё1+|-=2,5, ... .
Организуйте с помощью микрокалькулятора вычисление е
по этим формулам с точностью до 10-4. Какая из двух формул
быстрее дает требуемое приближение?
Логарифмы
Определение логарифма
27°. Вычислите логарифмы:
1) loga a, loga 1, logo а5, loga-i-, loga-\/a, loga^o3;
2) log_i 4". log_i 2, log2 1, log2 8, log_i V2. log_i
2 2 2 2 2 2 2
220
28°. Вычислите:
1) logs 27; 2) !og+ 3) logs^-;
4) log2 д/2; 5) 6) logs 5 д/5;
7) log^ 2 д/2; 2 8) logys 4; 9) log^ V125-
29°. Вычислите:
1) 2iog2 3 . 2) 4log23; 3) 2los<3- 4) 27log3^
, Свойства логарифмов
30. Вычислите:
1) log62 + log63; 2) log6 2 — log6;
3) log^ 3 + log2 5; 4) logyj 12 —log^ 4.
5 5
31°. Прологарифмируйте данное выражение по основанию а:
1) Зд/Зй 2) 4 =x4;
3) л 6(a3-a2) . 2 1 1 » a3b4c 2 4) A=a3 (a-2) (a-5).
32. Прологарифмируйте:
1) А=^±_. 2) А= 5si7^ ;
’ Зйх-фс cos Зх tg 5х
3 / psinx
3) г
33°. Найдите А по его логарифму:
1) loga 4 = 3 + 2 logo loga X —4 loga у;
2) In 4 = In sin х —In cos х+-^-In х;
3) 1g 4 = — 1+-|-lg (x—l)+-|-lg (x+1) —3 1g x;
4) log2 A = log2 log2 5 —log2 log2 10;
5) log3 4 = log9 a —log27& + log2
Изменение основания логарифмов
34°. Замените все логарифмы логарифмами по основанию 2:
log2 a, log8a, log2 a, log^a, log3 a.
2 4
221
35. Вычислите:
1> log, 12 + Iog^ 3; 2)!^; 3) ;
8 Ю“9 ’ 10g2S y3
4) Iog4 5 • logs 6-log6 7-log7 8;
log3 5
5) log3 49-logyy 5-log25 27; 6) б™7; 7)
10g36 Z 10g72 Z
36*. Докажите тождество
lOgafc X =--j--!---j--.
10g0 x"*" 10g(, X
37. Найдите:
1) logs 9, если logi2 18 = a;
2) logo 15, если logV4s25 = a;
3) log25o 120, если log9 20 = a, lg 2 = 6.
Логарифмическая функция
Область определения
38. Укажите области определения следующих функций:
1) t/ = logax; 2) I/ = loga |x|j
3) f/ = loga(x+1); 4) t/=loga(—x);
5) t/ = loga(l— x); 6) t/ = log2(5 — 2x);
7) t/=log2(3 — x)4-log2(3+x);
8) t/ = log2 (9 —x2); 9) z/ = ln In x;
10) y = ln (ex— 1); 11) t/ = log2(x2 — x—6).
Монотонность
39°. Определите характер монотонности следующих функций:
1) f/=lgx; 2) z/ = lnx; 3) y = log2 х;
2
4) y = log2^-; 5) у= — Igx; 6) y=log2 |x|.
40. Что больше:
1) logs 2 или 0; 2) log^ 3 или 0;
5
3) logs 4“ или 0; 4) log । или 0;
d 3 2
5) logs 4 или 1; 6) log^ или 1;
222
7) log2 3 или log2 5; 8) log2 7 или Iog2 -y-;
9) log । 7 или log । 10; “з “3 10) log । 4- или log । 4 3 ° 3 '
И) log । 3 или — 1; 15 12) log । 3 или log । 5; 5 T
13) logs 2 или log5 2; 14) log । 3 или log । 3; ~7 "8
15) 2 logs 2 или —; □ 16) Iog2 7 или log3 8? График
41. Начертите графики следующих функций:
1) у = 1пх; 2) у = 1п-^-; 3) у = 1п( —х);4) у —In |х|;
5) у = 1пх2; 6) y = log2 4x; 7) y = log i 2х; 8) y=|lnx|.
~2
Исследование функции
42°. Вычислите производные:
1) у = 1п2х; 2) y=xlnx; 3)
4) у = е*1пх; 5) у = 1п(5х+1); 6) у = 1пд/х.
43°. Исследуйте функции и постройте их графики:
1) у=Зх-1^; 2) у = 1пх-^-;
□ □
3) y=xlnx; 4) У=~—Них.
44°. Найдите наибольшее и наименьшее значения функций:
1) у=1п х, х£ [у-; е j;
2) y = 31gx + 2, xg[l; 100];
3) у=х — In х, х£ е];
4) у=2х2 — In х, xg 1 j;
5) у=^-+1пх, хб е2].
45*. Найдите области значений функций:
1) y=21g3x; 2) y = lnsinx;
3) y = ln(ex+l); 4) y=log2-\/4 —*2;
5) y = lnx —ln(x+l); 6) y = log2 (x2 + x+1).
22.3
Приближенные вычисления
46. Вычислите с одним знаком после запятой:
1) е0,1; 2) е~0,2; 3) е1’2;
4) In 1,1; 5) In 0,8; 6) lg 10,1;
7) 20,2; 8) IO0,9; 9) lg 0,9.
Прикладные задачи
47. Вычислите период полураспада вещества, если за год его
масса уменьшилась в 10 раз.
48. Период полураспада вещества равен двум суткам. Через ка-
кое время его масса уменьшится в 1000 раз?
49. Выведите из барометрической формулы формулу для вычисле-
ния высоты подъема в зависимости от давления.
50. Коэффициент звукоизоляции кирпичной стены в один кирпич
равен 50 дБ. Каков коэффициент звукоизоляции стены в два
кирпича?
51. От т мг вещества через t мин радиоактивного распада оста-
лось п мг. Найдите его период полураспада.
52. К началу радиоактивного распада имели 1 г полония-218.
Через сколько минут останется 0,125 г полония, если его период
полураспада равен 3 мин?
53*. Период полураспада радиоактивного вещества равен 1 ч.
Через сколько часов его количество уменьшится в 10 раз?
Вычислите, какая доля радиоактивного вещества останется
через 1000 лет, если период его полураспада равен 1550 лет.
Уравнения и неравенства
Простейшие показательные уравнения
54. Решите уравнения: 2) Зх=9х+1; 3) 53х-' = 2;
1) 4х = 8;
4) 7'~4х=1; 5) 6) Зх2“4х = 9;
7) 4x = 26+*-A 8) 22'=2; 9) 2х+14-2х = 3;
Ю) 2Х=4; Н) 2х = 16; 12) 3х—— 1;
13) 2х = 3; 14) Зх=0; 15) 5Х = 1;
16) 3 х —3=0; 17) 32х=81; 18) 23х = 5;
Ю) дх2 —5x4-8 _д. 20) ух у2 —х. 21) 25х = 53-х;
22) 2х-Зх+1=81; 23) Зх.52х-з=45;
24) 2Х-3Х~1-52х = 3-104.
224
Простейшие логарифмические уравнения
55. Решите уравнения:
1) log4x = 2; 2) log5x=—2; 3) log^x = 4;
4) log2 (1 —3х)=3; 5) log2 (x2 —Зх+1) = 0;
6) log4 (2—x) = log2 3; 7) log2 (x —7) = log2 (11 — x);
8) log3 (x —5) = log3 (2 —x); 9) logs (x2 — 4x) = logs (3 — 2x);
10) log2x = 3; 11) log3x = 2; 12) lgx = 0;
13) log2 (2x-3)=-2; 14) log, 3 = 2;
2
15) logx5 = 0; 16) log6_xx = 2; 17) log? log3 log2 x = 0.
Показательные уравнения, приводящиеся к линейному
56. Решите уравнения:
1) зх+2-Зх+1+Зх = 21;
/ 1 \*~2
2) 4х-|~22х+' — (чУ =47;
3) 4х — 3^ = 3*+ 2 — 22х~';
4) 5-2Vx —3-2Vx“'==56;
5) 5'-х+(д-)Х-2 + 25~ =155;
6) 2х + 2х+'4-2х+2 + 2х+3 = ЗО;
7) 7-5х + 90 = 5х+2;
8) 4х+3 + 22х+2 = 51;
9) 4*+1_з* = з*+2_4*;
10) 2х + 2х+1 +2х+2 = 5х4-5х+1;
11) 18-4х + 2-9х = 36-4х+1-32х+3;
12) 4х-52х+1 =6- 10х.
Показательные уравнения, приводящиеся к квадратному
57. Решите уравнения: Зх+з' ~x=j-; 2Х + 2~Х _ 17 . 2'-2-' 15 ’ 32х-2-Зх = 3; 2-Зх+'—5*9х-2 = 81; 2-4х-5-6х + 3-9х = 0.
1) 3) 5) 7) 9) 2х+Ч-4х = 80; 72х-6-7х + 5 = 0; 101+х!-10'-х2 = 99; 3’4-3-' __о. з* з—х 4х + 6х = 2-9х; 2) 4) 6) 8) Ю)
8 Заказ 836 225
Логарифмические уравнения
58. Решите уравнения:
1) logi х —3 log, . + 2 = 0; 2) т=1_+_1_=1:
3) logi x + log3 х2 = 8; 4) lg3x2 = 8lgx;
5) log2x log4 x log8x logi6X=4-log i x;
d 2
6) log2x + logy2x+log2 X = 6;
7) log3x -£-+ logi X= 1; 8) logx (x—2)= — 1.
Показательные неравенства
59. Решите неравенства:
1) Зх+2 —Зх+'+Зх<21;
х-А х+1
3) 4х —3 2 <3 2 -22х“
5) 4х + 2х + 1 >0;
7) 2Х>1;
9) Зх>0;
11)
13) 32х~*-3х-1 >2;
15) 5х~'-5х + 5х+1>21;
17) 4х + 2х <20;
2) 2х+14-4х>80;
4) Зх + 3'~х>у-;
6) 4х + 2х+'<0;
8) 2Х>^-;
Ю) (2-)'<0;
12)
16)
Логарифмические неравенства
60. Решите неравенства:
1) lgx>l; 2) lgx<2; 3) log2x< — 1;
4) log05x>2; 5) lg (1
7) log2 (2x — 3)<3;
9) lg x + lg (x —3)<1;
11) lg(2x+3)<lg(x-l);
13) ____!____<<J_.
°’ log2(x-2) 2 ’
15) log^ x + iog3 x + log9 X
x)^2; 6) In x2< 1;
8) log2 (x+5)<-2;
10) (log2x)2<4;
12) 2 lg (x+2)> lg (x+4);
14) Iogx3<-1;
:-1;
226
16)
lg Юх
Igx
17) logs x2 + (logs x)2> 1 + logs 7;
18) x'og2X>4 log2 x;
19) log3 x —logx 3<-|-.
61*. Изобразите множество точек, координаты которых удовлет-
воряют неравенствам:
1) log2 (х + у)< 1; 2) log2(t/ —х2)<2.
62*. Докажите, что при всех х^2 выполняется неравенство
8х > 5х + 6х.
63*. Решите неравенство
3х+4х < 5х.
64*. Докажите неравенство
1п(1+х)<х при х>0.
Системы уравнений
65. Решите системы:
1) 13Х-5У = 75, 2) (3х —22!/ = 77, 3) (ху+2 = 10,
\3У-5Х = 45; 1 4 1х2у_, = 100;
132 —2^ = 7; 1
4) /2х + 2!/ = 6, 5) (ху=10, 6) (ху=\6,
lx + t/ = 3; [(lgx)(lgt/)=— 2; [ t/ + log2 х = 5.
Использование графика при решении уравнений
66. Решите уравнения:
1) 5Х = 7 —2х;
3) log2X = 3 —х;
5) 5Х = 27 —х;
7) х3 + 2х = 3;
2> (Я=£
4) X log2 (х+l) = log2 х + 7;
3
6) 2Х + 7Х = 32;
8) х logs х = 18.
67. При каких значениях а уравнение 1пх=х + а имеет хотя бы
один корень?
Обратная функция
Взаимно обратные функции
68°. Из соотношений между переменными х и у выразите каждую
из переменных как функцию от другой:
1) Зх + 5у=4; 2) (х-2)(у + 3)= 1;
3) x2 + t/2=l при х^О, 4) е* =—.
У
227
69. Из формул выразите t как функцию от s:
2
1) S = So + y (/ —/о);
3) s = soe ‘°;
2) s = a (/ —/о)3;
4) s = s0 In (1 +7-Y
\ to /
70. Найдите функции, обратные данным:
1) у = 5х — 1;
4) у = Л/1—х;
2) у = 2х+ |х| — 1;
5) у=ё'Гх-,
3) £/ = Vl —
6) у = In In x.
Графики взаимно обратных функций
71°. Для каждой из следующих функций найдите обратную и
постройте графики обеих функций, откладывая аргумент каж-
дой из них на оси абсцисс:
i)
3) у — х3, х^О;
5) z/ = ln(x—1);
2)
4) у = е х;
6) г/ = х2, х<0.
72. По графику функции (рис. 117) постройте график обратной
функции.
Условие существования обратной функции
73. На рисунке 118 изображены графики шести функций. Опреде-
лите по графику, какая из них имеет обратную, а какая нет.
74*. Разбейте область определения функции у = х2 — 2х на про-
межутки монотонности и для каждого из промежутков пост-
ройте обратную функцию.
75. Проверьте, что функция y = cosx, х£[л; 2л], имеет обратную,
и выразите ее через арккосинус.
Свойства взаимно обратных функций
76. Докажите, что если одна из взаимно обратных функций строго
убывает, то и другая строго убывает.
Рис. 117
228
Рис. 118
77. Докажите, что если одна из взаимно обратных функций не-
четна, то и другая тоже нечетна.
78. Может ли четная функция иметь обратную?
79. Какие из приведенных ниже равенств являются тождествами:
1) sin arcsin х = х;
3) cos arccos х = х;
2) arcsin (sin x) = x;
4) arccos (cos x) = x?
Какие условия надо добавить, чтобы все они стали тожде-
ствами?
80*. Проведите исследование функции у = arcsin (sin х) и построй-
те ее график.
Производная обратной функции
81*. Выведите формулу производной обратной функции, диффе-
ренцируя соотношение f (g(x))=x.
82*. Выведите формулу производной функции у = arccos х.
83. Вычислите производные:
1) £/ = arctgV*;
3) у = In In х;
2) £/ = arcsiny-;
4) у = arccos д/1 — *2-
Контрольное задание к главе IV
Вариант 1
1. Исследуйте функцию и постройте ее график:
у — ех — In х.
229
2. Решите уравнение
5~* — 5*+2 = 24.
3. Решите неравенство
log3 (х —3)+log3 (х-5)< 1.
4. Постройте график функции у = 2~х и по графику найдите
решение уравнения 2-х=-^-.
Вариант 2
1. Дана функция y = f(x'), где /(х) = 5х+тг-
э
а) Решите уравнение f (х) = 26.
б) Найдите наименьшее значение функции у.
в) При каком значении а функция y = f(x-\-a) является
четной?
2. Исследуйте функцию и постройте ее график: у = хех+1.
3. Решите неравенство
log3 X — log3 (x+2) + log3 (х2 — 4)< 1.
Вариант 3
1. Дана функция y=f(x), где f(x) = log2 (4х—12).
а) Найдите область определения функции у.
б) Решите уравнение f (х) = х.
в) Докажите неравенство f (х)<2х.
г) При каких значениях k уравнение f(x) = x + fe имеет
хотя бы один корень?
2. Решите неравенство
l0g, Д±1>-!.
3. Постройте график функции
f/=10g2 (х2 + х+1).
В одном мгновеньи видеть вечность,
Огромный мир — в зерне песка,
В единой горсти — бесконечность
И небо — в чашечке цветка.
У. Блейк, пер. С. Маршака
Глава V
ИНТЕГРАЛ И ЕГО ПРИМЕНЕНИЕ
ВВОДНАЯ БЕСЕДА
1. Задача интегрирования
Математика изучает различные связи между величинами. Важ-
нейшие примеры таких связей дает механическое движение. Мы
уже много раз обращались к примеру движения материальной точ-
ки по оси. Между положением (координатой) точки и ее скоростью
есть известная связь, лежащая в основе математического анализа:
скорость является производной от координаты по времени. Сама
операция нахождения производной называется дифференцирова-
нием. Обратная задача — нахождение положения точки по ее ско-
рости — решается с помощью другой математической операции,
называемой интегрированием.
Мы знаем много примеров пар величин, которые связаны между
собой так же, как положение точки и ее скорость. Нахождение
одной из этих величин, если известна другая, мы свели к операции
дифференцирования. Так, линейная плотность тонкого стержня
есть производная его массы по длине, мощность есть производная
работы по времени, сила тока есть производная заряда по времени
и т. д. С помощью обратной операции — интегрирования мы
научимся вычислять массу по заданной плотности, работу по из-
вестной мощности, заряд по заданной силе тока и т. д.
Прежде чем учиться вычислять интегралы, мы рассмотрим их
геометрический смысл. Начнем по-прежнему с задачи о механичес-
ком движении. Пусть точка движется с постоянной скоростью
v = vq. Графиком скорости в системе координат (/; v) будет прямая
v = и0, параллельная оси времени t. Если считать, что в начальный
момент времени' t = 0 точка находилась в начале координат,
то путь ее $, пройденный за время f, вычисляется по формуле
s = vot. Величина v^t представляет собой площадь прямоугольника,
ограниченного графиком скорости, осью абсцисс и двумя верти-
кальными прямыми, т. е. путь точки можно вычислить как площадь
под графиком скорости (рис. 119).
231
Обратимся к случаю неравномерного движения. Теперь ско-
рость можно считать постоянной только на маленьком отрезке
времени. Если скорость v меняется по закону v = v(t), то путь,
пройденный за отрезок времени [t; t + dt\, приближенно выразит-
ся произведением v а на графике — площадью прямо-
угольника со сторонами dt и v (t). Точное значение пути за отрезок
времени [/; t-\-dt] равно площади криволинейной трапеции,
заштрихованной на рисунке 120. Весь путь получится сложением
площадей таких криволинейных трапеций, т. е. выразится как
площадь под графиком скорости.
Аналогично если мы начертим график зависимости силы тока
от времени/ —/ (/) (рис. 121), то величина заряда q, перенесенного
током за отрезок времени [/; t + dt], приближенно вычислится
по формуле I {t)dt, т. е. представится площадью прямоугольника
со сторонами dt и / (/). Точную величину заряда можно вычислить
как площадь под графиком силы тока.
Таким образом задача интегрирования тесно связана с задачей
вычисления площади.
2. Геометрический смысл интеграла
Коротко об интеграле можно сказать так:
Интеграл — это площадь.
Способ вычисления площади, о котором пойдет речь в этой
главе, уходит корнями в глубокую древность. Еще в III в. до н. э.
великий Архимед вычислил площадь параболического сегмента с
помощью изобретенного им «метода исчерпывания», который через
две тысячи лет был преобразован в метод интегрирования. Прос-
тейшими фигурами, площади которых мы научимся вычислять,
являются криволинейные трапеции.
Определение. Пусть на координатной плоскости дан
график положительной функции f, заданной на отрезке [а; 6].
Подграфиком (или криволинейной трапецией) называется фигура,
ограниченная графиком функции f, прямыми х=ан х=Ь и осью
абсцисс.
Можно образовать криволинейные трапеции с помощью раз-
личных известных вам функций. Некоторые примеры их представ-
лены на рисунке 122.
232
Определение. Пусть дана положительная функция
определенная на конечном отрезке [а; 6]. Интегралом от функции
f на отрезке [а; Ь] называется площадь ее подграфика.
Итак, интеграл — это площадь. Если мы научимся вычислять
площади, то сумеем вычислить и интегралы, а тем самым многие
физические величины.
Прямое вычисление площадей некоторых фигур, а значит, и
интегралов от некоторых функций проделал еще Архимед. Однако
лишь в XVII в. Ньютону и Лейбницу удалось открыть общий
способ вычисления интегралов.
3. Интегральные суммы
«Метод исчерпывания» Архимеда хотя и не дал общего способа
вычисления площади, однако сыграл очень большую роль в мате-
матике, так как с его помощью удалось объединить самые разные
задачи — вычисление площади, объема, массы, работы, давления,
электрического заряда, светового потока и многие, многие другие.
Проиллюстрируем этот метод на простом примере. Предпо-
ложим, что нам надо вычислить объем лимона, имеющего непра-
вильную форму, и поэтому применить какую-либо известную фор-
мулу объема нельзя. С помощью взвешивания найти объем также
трудно, так как плотность лимона в разных частях его разная.
Поступим следующим образом. Разрежем лимон на тонкие дольки.
Каждую дольку приближенно можно считать цилиндриком,
радиус основания которого можно измерить. Объем такого ци-
линдра вычислить легко по готовой формуле. Сложив объемы
маленьких цилиндров, мы получим приближенное значение объема
всего лимона. Приближение будет тем точнее, чем на более тонкие
части мы сможем разрезать лимон.
Применим аналогичную процедуру для вычисления площади
подграфика. Рассмотрим подграфик функции f, заданной на от-
резке [а; Ь]. Разобьем этот отрезок на несколько частей. Площадь
233
Архимед
(ок. 287—212 до н. э.) —
греческий физик и математик. Ему при-
надлежит метод нахождения длин и площа-
дей, предвосхитивший интегральное исчисле-
ние. Закон Архимеда — один из фундамен-
тальных законов механики. «Внимательно чи-
тая сочинения Архимеда, перестаешь удив-
ляться всем новейшим открытиям геомет-
рии»,— сказал о нем Лейбниц.
«Легче найти доказательство, приобретя
сначала некоторое понятие о том, что мы
ищем, чем искать такое доказательство без
всякого предварительного знания».
Архимед
всего подграфика разобьется на сумму площадей более мелких
криволинейных трапеций. Каждую такую трапецию можно прибли-
женно считать прямоугольником. Сумма площадей этих прямо-
угольников дает приближенное представление о всей площади
подграфика. Чем мельче мы разобьем отрезок [а; ft], тем точнее
вычислим площадь.
Запишем проведенное рассуждение в виде формул.
Разделим отрезок [a; ft] на п частей точками х0 = а, хь ...» хп = Ь.
Длину fe-ro обозначим через \Xk=Xk — Xk-\- Составим сумму Sn =
= f (xi) Axi + ... + f (xrt) Дхп. Геометрически эта сумма представляет
собой площадь ступенчатой фигуры, заштрихованной на ри-
сунке 123.
Суммы вида Sn = f (xi) Дх|+ ...+ f (хп) Дхл называются интег-
ральными суммами для функции f.
Интегральные суммы дают приближенное значение площади.
Точное значение получается при помощи предельного перехода.
Представим себе, что мы измель-
чаем разбиение отрезка [a; ft] так,
что длины всех маленьких отрезков
стремятся к нулю (т. е. Дх* 0). Тог-
да площадь ступенчатой фигуры бу-
дет приближаться к площади подгра-
фика S. Можно сказать, что площадь
подграфика равна пределу инте-
гральных сумм, т. е.
S = lim Sn.
Тем самым и про интеграл можно
сказать так:
234
Интеграл равен пределу интегральных сумм.
С помощью интегральных сумм можно приближенно вычислять
самые различные величины. Приведем примеры.
1. Объем лимона. Обозначим толщину fe-й дольки через ДА*
(необязательно резать лимон на дольки одинаковой толщины),
а радиус ее через rk (k = 1, ..., п — это означает, что мы разрезали
лимон на п долек). Объем лимона приближенно представим
интегральной суммой
Sn = nr2\\h\ +... + лГпД/гл.
2. Работа. Предположим, что на точку, движущуюся по оси %,
действует некоторая сила F, направленная по той же оси. Мы
знаем, что если сила F постоянна, то работа равна Fs, где s —
путь, пройденный точкой. Предположим теперь, что F меняется
от точки к точке и нам известно ее значение F (х) в каждой точке х
некоторого промежутка [а; Ь]. Как найти работу А по перемеще-
нию точки из а в ft?
Разобьем отрезок [a; ft] на п отрезков. Будем приближенно
считать, что на каждом отрезке сила постоянна. В качестве посто-
янной силы на отрезке [х*_ i; xk] можно взять значение функции F
в одной из точек этого отрезка, например в точке х*. Работу
на fe-м отрезке пути приближенно можно представить как произ-
ведение F (x*)Ax*, а на всем отрезке — интегральной суммой:
А п = F (х ।)Дх 1 +... + F (хп)\хп.
Точное значение работы А получается предельным переходом:
A = lim Ап.
Способ вычисления пределов интегральных сумм оказался
очень трудным. Даже для простейших функций этот способ вы-
числения интегралов неприменим. Архимед сумел вычислить не-
которые площади, объемы, фактически находя пределы интеграль-
ных сумм для квадратичной функции. Однако этот результат
стоял особняком в математике до конца XVII в., когда было
выяснено, что задача нахождения площади обратна к задаче на-
хождения скорости.
4. Скорость роста площади
Рассмотрим положительную функцию f, заданную на отрез-
ке [a; ft]. Представим себе «переменную» криволинейную трапе-
цию, полученную следующим образом: закрепим левую стенку
х = а, а правую начнем двигать вдоль оси абсцисс. Такая
трапеция изображена заштрихованной фигурой на рисунке 124.
Ее можно считать подграфиком функции область определения
которой ограничена отрезком [а; х].
Обозначая площадь трапеции, т. е. площадь подграфика
функции f, заданной на отрезке [а; х], через S (х), получим новую
235
функцию S = S(x) (переменная площадь). Перечислим свойства
функции S. Она определена для всех х£[а; Ь], ее значение при х=а
равно нулю (трапеция вырождается в отрезок, и ее площадь равна
нулю), эта функция возрастает, и при х=Ь ее значение равно пло-
щади всего подграфика, т. е. интегралу от функции f.
Найдем скорость роста функции S и результат запишем в виде
теоремы.
Теорема (о скорости роста площади). Пусть f — положи-
тельная функция, S — переменная площадь ее подграфика. Тогда
производная функции S равна функции А т. е. S'(x)=f(x).
Итак, теорема утверждает, что производная переменной пло-
щади подграфика функции f равна самой функции f. Для дока-
зательства теоремы поступим так, как всегда поступают при вы-
числении производной.
Зафиксируем значение аргумента х и дадим аргументу при-
ращение Дх. Вычислим приращение функции: Д5 = 5 (х-|-Дх) —
— S (х). По рисунку 125 видно, что приращение площади есть пло-
щадь подграфика функции f, определенной на отрезке [х; х + Дх].
Если Дх достаточно мало, то площадь заштрихованной на ри-
сунке 125 криволинейной трапеции мало отличается от плошади
прямоугольника со сторонами f (х) и Дх, т. е. можно записать
приближенное равенство Д5«/(х)Дх. Отсюда мы делаем вывод,
что (х), т. е. производная функции S равна функции f, что
и утверждалось в теореме.
Замечание. В доказательстве
теоремы мы использовали такое сооб-
ражение: если отрезок [х; х + Дх] дос-
таточно мал, то площадь подграфика
функции f на этом отрезке мало отлича-
ется от произведения f (х)Дх. Но если в
точке х функция f имеет разрыв, то это
неверно, что хорошо видно на рисунке
126. Поэтому в формулировку теоре-
мы о скорости роста площади надо до-
бавить требование непрерывности фун-
кции f.
236
Подведем итог. Для функции f мы построили новую функ-
цию S — переменную площадь подграфика. Связь между функ-
циями f и S такова:
S — интеграл от функции f,
f — производная функции S.
Из этого видно, что нахождение интеграла (интегрирование)
и нахождение производной (дифференцирование) являются вза-
имно обратными операциями. Если мы знаем функцию f, то нахож-
дение функции S (площади подграфика функции f) есть задача
интегрирования функции f. Если же задана функция S, то на-
хождение функции f (скорости роста площади) есть задача
дифференцирования функции S.
5. Обозначение интеграла
Традиционно интеграл от функции y — f(x) на отрезке [а;/?]
обозначается так:
ь
5 f (x)dx.
а
Эта традиция имеет исторические корни. Интегральные суммы,
с помощью которых приближенно вычисляется интеграл, состав-
ляются из слагаемых вида f (х) Дх. Приближенное равенство
Д3«/(х) Дх может быть заменено точным равенством дифферен-
циалов dS = f (х) dx. Интеграл можно представить как сумму
«бесконечного числа дифференциалов». Знак интеграла J и есть
стилизованная запись буквы S — первой буквы слова «сумма»
на латинском языке:
ь
S = J f (х) dx.
а
Напоминаем, что площадь S можно получить суммированием
слагаемых вида f (х) dx. Около знака интеграла ставят пределы
интегрирования — концы отрезка [a; ft], на котором задана
функция f.
Переменная площадь S (х) запишется как площадь подграфика
функции f на отрезке [а; х], т. е. в виде интеграла с переменным
верхним пределом:
S (х) = $ f (х) dx.
а
Связь между функциями f и S, установленную в теореме о ско-
рости роста площади, можно записать так:
S' (x)=(Jf(x)dx)' = f(x).
237
6 . Выводы
1) Инте гр ад от положительной функции — это площадь ее
подграфика.
2) Интеграл можно приближенно вычислить с помощью ин-
тегральных сумм. Переходя к пределу, можно получить точное
значение интеграла.
3) Если рассмотреть переменную площадь подграфика функ-
ции f, т. е. интеграл от f с переменным верхним пределом, то
мы получим новую функцию S, производная которой равна функ-
ции f.
Определение интеграла нетрудно распространить на произволь-
ную функцию f, отказавшись от требования ее положительности.
Рассмотрим произвольную функцию, заданную на отрезке [а; Ь],
и ее подграфик, т. е. часть плоскости, ограниченную графиком f,
прямыми х = а, х = Ь и осью абсцисс. Этот подграфик состоит
из частей, лежащих выше оси абсцисс и ниже ее. Условимся
брать первые из них со знаком « + », а вторые — со знаком « —».
По определению интегралом от функции f называется сумма пло-
щадей частей ее подграфика, взятых с указанными знаками.
Контрольные вопросы
1. Обратите внимание на следующие встретившиеся в тексте
слова и обозначения: подграфик, интеграл, интегральная сумма,
интеграл с переменным верхним пределом. Приведите примеры их
использования.
2. Какие физические величины можно выразить как площади?
3. Что такое подграфик функции?
4. Что называется интегралом?
5. Как строится интегральная сумма?
6. Что такое интеграл с переменным верхним пределом?
7. В чем состоит связь между функцией и переменной пло-
щадью ее подграфика?
8. Как определить интеграл от функции, принимающей значе-
ния разных знаков?
9. Какое условие нужно наложить на функцию для справедли-
вости теоремы о скорости роста площади?
10. Чему равен дифференциал переменной площади подграфи-
ка функции f?
§ 1. ВЫЧИСЛЕНИЕ ИНТЕГРАЛА
1. Первообразная
Во вводной беседе мы установили, что интегрирование явля-
ется операцией, обратной дифференцированию. Вычисление ин-
теграла сводится к нахождению функции производная которой
равна заданной функции. Эту операцию мы рассмотрим отдельно.
238
Определение. Первообразной для функции f называется
такая функция Г, производная которой равна данной функции.
Иными словами, равенство
можно прочесть двумя способами: f — производная функции F
или F — первообразная для функции f. Для обозначения перво-
образной традиционно используют знак неопределенного интегра-
ла, т. е. интеграла без указания пределов интегрирования:
F (х) = $ f (х) dx.
Перечислим свойства первообразной.
1. Если F — первообразная для функции f, то F-+-C,
где С — константа, также является первообразной для той же
функции.
Действительно, (F + С)' = F' + С' = f + 0 = f.
2. Если F\ и F2 — две первообразные для одной и той же
функции f, то они отличаются на постоянное слагаемое.
Действительно, если F'x = f и F2 = f, то (Fi — F2)' = F\ — F2 =
— f — f = Функция, производная которой тождественно равна
нулю, является постоянной. Итак, F\ — F2^=C.
Таким образом, все первообразные для функции f получаются
из одной из них прибавлением к ней произвольной постоянной.
Надо помнить, что знак $ является «неопределенным» в том смыс-
ле, что он обозначает какую-нибудь первообразную.
3- (x) + g(x))dx = \f + J g (x) dx.
Действительно, пусть F и G — первообразные для функ-
ций f и g соответственно. Тогда F-\-G является первообразной
для функции f+g:
(F+G)' = F'+G' = f + g.
4. \cf (х) d = с J f (x) dx.
Доказывается аналогично.
Таблицу первообразных получают с помощью таблицы произ-
водных. Проверить таблицу можно, делая обратную операцию,
т. е. вычисляя производные.
f(x) 5 f (x)dx
1 X
X x2 У
xk, k=A — 1 x‘ + l *4-1
239
П родолжение
J f (x)dx
—, х>0 X In X
sin х — cos X
cos X sin x
ех ex
5. Линейная замена переменной.
Теорема. Пусть F — первообразная для функции f. Тогда
\f(kx + b) dx = ±-F (kx + b).
Действительно, вычислим производную от F(kx + b):
(F (fex + b))' = kF' (kx + b) = kf (kx + ft).
Отсюда yf(h + ft) является первообразной для функции
f (kx + b).
Отметим полезные следствия, которые можно внести в таб-
лицу первообразных.
fix) I f (x)dx
(kx + b)n, n=/= — 1 1 (kx-\-b')"+l k n-\-1
1 , x>a x — a In (x — a)
x x In a a =e -J—a' In a
sin (cox + ») I / . X cos (cox 4-a) co
cos (cox 4-a) — sin ((ox 4-a) (0
240
Заметим, что операция дифференцирования совершается фор-
мально — нужно запомнить несколько правил, и их будет доста-
точно для нахождения производных. Не так обстоит дело с ин-
тегрированием, например нет формулы для интегрирования
произведения и частного функций. Поэтому составлены обширные
таблицы интегралов (первообразных) и появляется новая зада-
ча — научиться преобразовывать вычисляемые интегралы, сводя
их к табличным.
Пример. Вычислить $ sin2 х dx.
В таблице интегралов нет интеграла от sin2 х. Однако можно
воспользоваться формулой sin2 х=-^-(1 — cos 2х). Для cos 2х
интеграл мы знаем, поэтому пишем так:
J sin2 х dx = \ -i-(l —cos 2х) dx = ±-( \dx — \ cos 2x dx) =
1 / 1 • \ x sin 2x
=-{x~Tsln 2x)=T—— •
2 . Теорема Ньютона — Лейбница
Знаменитая теорема, носящая имена основоположников мате-
матического анализа, гласит:
Интеграл равен приращению первообразной.
Запишем формулировку более подробно.
Теорема (Ньютона — Лейбница). Пусть f — данная функ-
ция, F — ее произвольная первообразная. Тогда
ь
\f(x)dx=F(b)-F(a).
а
Доказательство. Сначала проверим теорему, подста-
вив в правую часть известную нам первообразную для функции
f — переменную площадь S (х) подграфика функции f. По опреде-
ь
лению интеграла (х)dx = S (b) = S (b) — S (а), так как S(a) = 0.
a
Пусть F — произвольная первообразная для функции f. Тогда
она отличается от S на константу, но приращение функций
F и S будет одним и тем же: S (х) = F (х) + С.
ь
\f(x)dx=S(b)-S(a) = F(b)+C-F(a)-C = F (b) - F (а),
а
что и требовалось доказать.
Теорема Ньютона — Лейбница сводит вычисление интегралов
к вычислению первообразных (схема XIII).
241
Приведем примеры вычисления интегралов.
1. Вычислить Jx2dx. Решение оформляется так: выписывают
о
первообразную F для подынтегральной функции, ставят прямую
черту, около которой указывают пределы интегрирования, и
затем находят численное значение интеграла
л
“2
2. Вычислить $ sin 2х dx.
о
л
л
SI 1^1 1
sin2xdx=—— cos 2х I =——cos л+—cos 0= 1.
и । и 2 2
3. Свойства интеграла
Формула Ньютона — Лейбница сводит свойства интеграла
к свойствам первообразной, которые, в свою очередь, опираются
на свойства производной.
Теорема (линейность интеграла).
ь ь ь
S (f (х) 4-g (X)) dx = \f (х) dx+\g (х) dx; (1)
а а а
b b
\cf (х) dx=c\f (х) dx. (2)
а а
Доказательство. Пусть F и G — первообразные для
функций f и g соответственно. Тогда функция F-\-G является
одной из первообразных функции f + g. По теореме Ньютона —
Лейбница
ь ь
$(f W+Я W) dx=(F+ G) |0 = F (Ь)+ G (b)—F(a)—G (а)=
а
b b
= F(b)-F(d)+G(b)-G(d) = \f(x)dx + \g(x)dx.
а а
Вторая формула доказывается аналогично.
Отметим полезные следствия выведенных свойств:
ь ь ь
5 (f (x)—g W) dx = J f(x) dx— $ g (x) dx;
a a a
242
b
J(af (%) + ₽£ (x)) dx =
a
b b
=a$f (x)dx + p$g(x) dx.
a a
Ряд свойств интеграла является
следствием свойств площади, лежа-
щей в определении интеграла.
Теорема (аддитивность инте-
грала ).
Рис. 127
b с b
\f (х) dx = \f (х) dx+\f(x) dx.
а а с
Это свойство интеграла наглядно видно из свойств площади:
площадь всей криволинейной трапеции с основанием [а; Ь] есть
сумма площадей трапеций с основаниями [а; с] и [с; Ь] (рис. 127).
Это же свойство можно получить и вычислением. Пусть F —
первообразная для функции f. Тогда
с b
J f (х) dx= F(c)-F (a); J (х) dx = F(b)-F (с),
а с
Складывая почленно левые и правые части равенств, получаем:
с b
\f(x)dx+\f (х) dx = F (с) - F (a)+F(b)-F(c)=F (Ь) - F (a)=
a c
b
= \f(x)dx.
a
Доказанное свойство интеграла называют его аддитивностью
(от латинского слова addo — складываю).
а
Полезно отметить, что $f(x)dx = 0, так как F (a)—F (a) — Q.
а
Теорема (интегрирование неравенства). Если} (х) ^g (х),
то
b ь
\f(x) dx^\g(x) dx.
а а
Действительно, функция h(x)=f (x) — g (х) по условию неотри-
цательна. Следовательно, неотрицателен и интеграл от нее,
ь
являющийся по определению площадью подграфика: \h (х) dx^O.
а
243
Раскрывая левую часть по свойствам 1 и 2, получаем:
ь ъ ь
\h (х) dx = ^f (х) dx — \g (х) dx^O,
а а а
b b
т. е. f W dx > \g (х) dx, что и требовалось доказать.
а а
Примеры вычисления интегралов.
-2 л л
2 л л
•• $ (х —sinx)dx=j xdx—\ sinxdx = ^-|0 +cosx|0 =
° 0 0
=Z±—0+0 —1 «0,23.
8
2 2
2. i:-
=(2 —l)+(ln 2-In —l)=-y+ln2«2,19.
Контрольные вопросы
1. Что такое первообразная?
2. Перечислите свойства первообразной.
3. Как меняется первообразная при линейной замене аргумен-
та подынтегральной функции?
4. Сформулируйте теорему Ньютона — Лейбница.
5. Перечислите свойства интеграла.
6. В чем состоит аддитивность интеграла?
7. Как связаны между собой две первообразные для одной
и той же функции?
8. Как меняется при интегрировании амплитуда гармоническо-
го колебания?
9. Как меняется степень при интегрировании степенной функ-
ции?
10. Верно ли, что интеграл от любой степенной функции будет
снова степенной функцией?
§ 2. ПРИЛОЖЕНИЯ ИНТЕГРАЛА
1. Площадь
Пусть надо вычислить площадь какой-либо плоской фигуры Ф.
Введем на плоскости декартову систему координат. Тогда отдель-
ные куски границы фигуры Ф можно будет задать в виде графиков
244
некоторых функций. Сравнительно
простой случай изображен на рисун-
ке 128. Площадь фигуры Ф можно по-
лучить сложением и вычитанием
площадей подграфиков функций,
задающих границу. Так, в типичном
случае, изображенном на рисунке
128, площадь фигуры Ф получается
как разность подграфиков функций
f и g, т. е. выражается через интег-
ралы:
Рис. 128
ь ь
S=\f(x) dx — \g(x)dx.
а а
Примеры.
1. Найти площадь одной арки синусоиды (рис. 129,а),
л
S = $ sin xdx — — cos x |Q = 1 + 1=2.
0
2. Найти площадь фигуры, заключенной между дугами па-
рабол у = х2 и у = ^/х (рис. 129,6).
Данная фигура ограничена графиками двух функций:
f(x)=x2 и g(x) = x2. Искомая площадь вычисляется так:
til 1
С f -2 , ( 2. 2х2 I 1 X3 I* 2 1 1
S—dx \xdx- |0 |0—з 3 — 3-
О о
Вычисление площади с помощью интеграла изображено на
схеме XIV.
Вычисление площади — самое простое применение интеграла,
так как интеграл по определению у нас тесно связан с площадью.
Вычисление некоторых физических величин с помощью интеграла
потребует дополнительных рассуждений.
245
2. Схема применения интеграла
При знакомстве с понятием интеграла мы выделили три его
характеристики.
1) Интеграл от функции f есть площадь ее подграфика
(с учетом знака).
2) Интеграл есть предел интегральных сумм.
3) Интеграл от функции f есть приращение ее перво-
образной.
Любая из этих характеристик интеграла может служить осно-
вой для его приложений. Наиболее стандартным путем выражения
одной физической величины в виде интеграла от другой является
использование третьей характеристики интеграла как приращения
первообразной. Однако и две первые характеристики очень важны
в приложениях, так как позволяют получить геометрический
смысл связи между физическими величинами и простой способ
их приближенного вычисления.
Вернемся еще раз к величинам, которые вычисляются с по-
мощью интеграла. К таким величинам можно отнести перемеще-
ние, работу, массу, электрический заряд, давление, теплоту. К ним
можно присоединить геометрические величины — длину, площадь,
объем, свойства которых мы сейчас перечислим.
1. Величины можно рассматривать как функции отрезка. Пе-
ремещение вычисляется в зависимости от отрезка времени дви-
жения. Работа переменной силы при движении по прямой зависит
от пройденного отрезка пути. Массу тонкого неоднородного
стержня можно рассматривать как функцию от отрезков этого
стержня. Электрический заряд, протекающий через поперечное
сечение проводника, зависит от отрезка времени, за который мы
производим измерение.
2. Для вычисления этих величин с помощью интеграла нам
нужно знать скорость изменения этих величин. Изучая производ-
ную, мы привели примеры различных физических величин, явля-
ющихся скоростями изменения других величин. Так, скоростью
изменения перемещения (или расстояния) будет обычная ско-
рость. Скоростью изменения работы в зависимости от времени
является мощность, а скоростью изменения той же работы, но в
зависимости от перемещения является сила. Скорость изменения
массы — это ее плотность. Само слово «плотность» имеет такой же
универсальный характер, как слово «скорость», и им широко
пользуются: например, говорят, что сила — это плотность работы
по отношению к перемещению.
Если исходная величина нам задана в виде некоторой функ-
ции, то ее скорость (или плотность) мы найдем как производную
этой функции.
246
Примеры.
Скорость механического движения: v = ^- .
at
Линейная плотность стержня: р=^-.
dA
Мощность: N=——.
dt
Сила при перемещении по прямой: F==-^-.
Интеграл применяется тогда, когда известна скорость (плот-
ность) f искомой величины. Если искомую величину представить
в виде приращения некоторой функции F, то f является произ-
водной F, а тем самым F — первообразной для f. В итоге искомая
величина есть приращение первообразной для функции f, т. е.
интеграл от функции f.
Запишем то же самое с помощью формул. В качестве неза-
висимого аргумента выберем букву t. Пусть мы ищем величину F.
Рассмотрим ее значение на маленьком отрезке [/; t + dt]. Пусть
скорость изменения величины F обозначена через f. Эту связь
между величинами F и f можно записать в дифференциальной
форме:
dF = f (f) dt.
Тогда
ь
F — \f(t)dt.
a
Итак, схема применения интеграла сводится к следующему:
1) Записываем главную часть изменения искомой величины с
помощью дифференциалов:
dF = f(t) dt.
2) Переписываем значение F в виде интеграла:
ь
F=\f(t)dt.
а
3) Находим первообразную для функции f и вычисляем F
как разность значений первообразной на концах отрезка (схе-
ма XIII).
Замечания.
1. Отметим вольность в обозначениях, которая часто допус-
кается в приложениях. Мы ищем некоторую величину, например
массу стержня. Обозначаем ее какой-то буквой, скажем т. Мы
ищем массу данного конкретного стержня, и поэтому т будет
просто числом. Однако для нахождения т нам надо рассматри-
вать массу произвольного отрезка стержня. Ее мы снова обозна-
чаем т, хотя сейчас понимаем т как функцию. Для этого мы
вводим переменную массу — массу стержня от начальной точки до
247
точки х, и эту функцию от х тоже удобно обозначать той же
буквой т, чтобы записать соотношение для плотности: р =
= » или dm = pdx. Особой беды, что мы употребляем везде
одну и ту же букву, нет, зато это очень удобно.
2. Рассмотренные нами величины зависели от отрезка — отрез-
ка времени, отрезка прямой. Часто встречаются аналогичные ве-
личины, но зависящие от других областей. Так, масса произволь-
ного тела зависит не от отрезка, как это мы идеализировали для
тонкого стержня, а от области пространства. Работа при пере-
мещении по произвольной траектории зависит от частей этой
траектории. Давление на поверхность зависит от частей этой по-
верхности. Существуют более сложные интегралы, которые позво-
ляют вычислить величины, зависящие от частей кривой линии
(криволинейные интегралы), от частей поверхности (поверхност-
ные интегралы), от частей объема (объемные, или тройные, инте-
гралы). В некоторых простых случаях искомые величины удается
рассмотреть как функции отрезка и свести их нахождение к вы-
числению обычных интегралов. С примерами таких случаев мы
познакомимся при решении прикладных задач.
3. Работа
Пусть тело движется по оси х, в каждой точке которой при-
ложена некоторая сила F = F(x). Вычислим работу, которую надо
проделать при перемещении из точки а в точку Ь. На маленьком
отрезке пути от точки х до точки x-prfx можно считать силу
постоянной и равной F (х). Тогда дифференциал работы запишем
так: dA=F (х) dx. Отсюда получаем, что всю работу на отрез-
ке [а; Ь] можно записать в виде интеграла:
ь
A = \F(x) dx.
а
Эта формула позволяет вычислить работу при прямолинейном
движении.
Пример. Предположим, что в точку О помещен единичный
электрический заряд. Он создает электрическое поле. Мы знаем,
что на другой единичный заряд, помещенный в точку х, действует
сила, обратно пропорциональная квадрату расстояния, т. е.
f (х) = А-. Найти работу электрического поля по перемещению
единичного заряда из точки Х| в точку Х2.
Применяя формулу для работы, получим:
Х2 *2
A = \^-dx = k \
J х J х2
248
Для функции F (х) = -^- первообразную U (х) можно найти
по таблице: U (х) =——. Получим:
1 Х\ X । х । XI %2
Функция U (х)=называется потенциалом электрического
поля. Работа равна приращению функции U, т. е. разности по-
тенциалов на концах отрезка.
Используя геометрический смысл интеграла как площади, мы
можем представить работу как площадь подграфика для функции
U. Изобразим этот график для разобранного выше примера
(рис. 130).
4. Перемещение
Предположим, что точка движется по прямой (по оси х)
и нам известна скорость этой точки. Положение точки на оси бу-
дем считать функцией времени: % = %(/). Как найти перемещение
точки за промежуток времени [fi; /2] ?
Если скорость точки постоянна и равна и, то это перемещение,
которое мы обозначим через s, вычисляется так: s = v(tz — /1).
Пусть теперь эта скорость меняется и нам задан закон этого
изменения v = v(t). Рассмотрим отрезок времени [/; Глав-
ную часть перемещения As мы получим, если будем считать, что
на этом отрезке скорость постоянна и равна v (/). Получим
12
ds = v(t}dt, откуда s = \v(t)dt.
h
Если мы изобразим график скорости, то перемещение будет
задаваться площадью подграфика (рис. 131).
249
5. Масса
Масса произвольного тела является величиной, для вычисле-
ния которой нужен более сложный интеграл, чем тот, который
мы научились вычислять. Мы сможем написать формулу для вы-
числения массы тонкого стержня, т. е. такого тела, в котором
плотность меняется вдоль одного направления и которое можно
представить как отрезок тонкой проволоки с изменяющейся
плотностью.
Если стержень однороден, то его масса т пропорциональна
длине /, т. е. m = pdl, где р — коэффициент пропорциональности,
называемый линейной плотностью. Поставим задачу вычисления
массы неоднородного стержня, если нам известно, как меняется
плотность р. Представим себе, что стержень расположен вдоль
оси так, что он занял положение отрезка [0; /]. Тогда линейную
плотность р можно считать функцией от х, т. е. р = р(х),
заданной на этом отрезке. Возьмем отрезок [х; x + dx]. Считая на
нем плотность постоянной, получим dm = p (х) dx, откуда т —
= J р (х) dx.
о
Таким образом, масса стержня является интегралом от его
линейной плотности.
6. Электрический заряд
Представим себе переменный ток, текущий по проводнику.
Как вычислить заряд q, переносимый за интервал времени [а; Ь]
через сечение проводника? Если бы сила тока I не менялась со вре-
менем, то изменение заряда q равнялось бы произведению
I(b — d). Пусть задан закон изменения 1 = 1 (t) в зависимости от
времени. Тогда на малом интервале времени [/; t + dt] можно счи-
тать силу тока постоянной и равной 1 (/), a dq = l (/) dt, и, сле-
ь
довательно, q = \l (t) dt.
а
Мы представили такие величины как работа, масса, электри-
ческий заряд, перемещение, количество теплоты в виде функций
отрезка с заданной плотностью.
Можно сравнить приведенные сейчас примеры с физическими
примерами, обсуждавшимися при применении производной. Фак-
тически мы имеем дело с одними и теми же соотношениями вида
dF = f (х) dx, но смотрим на них по-разному. В первом случае нам
дана величина F, а мы ищем f. В этом случае f выступает как
производная F. Во втором случае нам дана величина f, а мы
ищем F. Тогда F является интегралом от f.
Составим из наших примеров таблицу.
250
Величины Соотношение в дифференциалах Вычисление производной Вычисление интеграла
А — работа F — сила W — мощность dA = F (x)dx dA = N(t)dt г / \ dA F(x)=—~ dx x2 A = j F (x) dx xi Z2 4 = \N(t) di <i
т — масса тонкого стержня р — линейная плот- ность dm = p (x)dx m= (x) dx xi
q — электрический заряд / — сила тока dq = l (/) dt '«-7, z2 4=\l(t}dt '1
s — перемещение v — скорость ds = v (/) dt Z2 s = \ v (t) dt h
Q — количество теп- лоты с — теплоемкость dQ = c (f)dt Z2 Q = C (t) dt '1
7. Решение прикладных задач
Задача 1. Пирамида Хеопса представляет собой правиль-
ную четырехугольную пирамиду высотой 147 м, в основании ко-
торой квадрат со стороной 232 м. Она построена из камня, плот-
ность которого 2,5 г/см3. Найти работу против силы тяжести,
затраченную при постройке.
Решение. Проведем вертикально вверх ось х с началом
у основания пирамиды. По этой оси будем измерять высоту подъе-
ма камней. Решим задачу в общем виде, а в ответ подставим
числовые значения. Пусть высота пирамиды равна Я, сторона
основания а, плотность камня р. Обозначим через А (х) работу,
которую надо совершить для постройки пирамиды от основания
до высоты х. Найдем сначала сторону у квадрата, получающегося
в горизонтальном сечении пирамиды на высоте х. Из подобия
треугольников получаем откуда у — — х). Рас-
смотрим тонкий слой пирамиды, расположенный на расстоянии х
от основания. Пусть толщина слоя равна dx. Слой можно при-
близительно считать параллелепипедом. Масса его dm равна
251
py2dx = p — x)2 dx. При подъеме этого слоя на высоту х была
проделана работа dA, равная (gdm)-x, где g— ускорение силы
тяжести, т. е.
dA =gp jpx (Я —х)2 dx.
Отсюда
A = A(H)=\dA = gp-£-\x(H — x)2dx =
о Н о
=-SJ<j(x//2-2//x2 + x3)dx=-^(//24—2//4-+т) 1о =
__ gpg2 ( Н4 2Н4 i Н4 \_ gpa2 „2
Я2 \ 2 3 “Г” 4 / 12 * *
Подставляя числовые данные а = 232 м, Я=147 м, р =
= 2,5 г/см3 = 2,5 т/м3, получаем А =2,37 • 1012 Дж = 2,4-105 тонно-
километров.
Задача 2. Квадратная пластина со стороной а погружена
в воду перпендикулярно ее поверхности, причем верхнее основа-
ние пластины находится на поверхности. Найти давление воды на
пластину.
Р е ш е н и е. На маленькую площадку площадью dS, располо-
женную на глубине х от поверхности, давит столб воды в виде ци-
линдра с основанием dS и высотой х. Давление dp будет при
этом равно pgxdS, где р — плотность воды, pxdS — масса цилинд-
ра. Возьмем полоску пластины шириной dx, находящуюся на глу-
бине х. Ее площадь dS равна adx. Отсюда dp = pgaxdx.
а 2 а з
Получаем р = \ pgaxdx — gpa~ | 0=^р-
Контрольные вопросы
1. Как вычислить площадь плоской фигуры с помощью интег-
рала?
2. Назовите примеры физических величин, которые можно
рассматривать как функции отрезка.
3. В чем состоит схема применения интеграла?
4. Что является плотностью работы как функции отрезка
пути?
5. Что является плотностью перемещения как функции отрезка
времени?
6. Что является плотностью массы тонкого стержня как функ-
ции отрезка этого стержня?
252
7. Что является плотностью электрического заряда как функ-
ции отрезка времени?
8. Что является плотностью количества теплоты как функции
отрезка времени?
9. Как в форме интеграла записать дифференциальную связь
dF — f (/) dt между величинами F, f и /?
10. Как вычислить некоторую величину, если задан график
ее плотности?
ЗАКЛЮЧИТЕЛЬНАЯ БЕСЕДА
1. Составление дифференциального уравнения
Вернемся к задаче про пирамиду Хеопса. Для вычисления
произведенной работы мы ввели две переменные величины: х —
высоту от земли, на которую подняты камни, и А — работу, ко-
торую надо проделать, чтобы построить пирамиду до высоты х.
Дальнейшие рассуждения дали нам соотношение между диф-
ференциалами этих величин: dA—F (х) dx, где F (x)—kx (Н — х)2 —
найденная нами функция. Полученное соотношение можно назвать
дифференциальным уравнением для нахождения А =А (х). Его
можно записать и с помощью производной: -=F(x), или
A' = F(x). Это уравнение очень простое: в нем производная
неизвестной функции выражена как функция от х. Отыскание са-
мой функции А сводится к операции интегрирования:
А (х) = $ F (х) dx.
о
Дифференциальные уравнения — это уравнения, связывающие
неизвестную функцию и ее производные.
Многие физические законы имеют вид дифференциальных
уравнений, т. е. соотношений между функциями и их производны-
ми. Задача интегрирования этих уравнений — важнейшая задача
математики. Некоторые дифференциальные уравнения удается
проинтегрировать в явном виде, т. е. записать искомую функцию
в виде формул. Для решения некоторых дифференциальных урав-
нений до сих пор не удается найти достаточно удобных формул.
В этих случаях применяются эффективные численные методы,
позволяющие с помощью вычислительных машин найти прибли-
женные решения. Мы не будем подробно изучать методы интег-
рирования дифференциальных уравнений, а рассмотрим только
примеры уравнений и их решений.
1) Уравнение механического движения.
Рассмотрим пример движения материальной точки массой т
по оси х под действием силы F. Обозначим через t время, v —
253
скорость, а — ускорение точки. Второй закон Ньютона ma = F
можно рассматривать как дифференциальное уравнение, если
записать ускорение а как вторую производную:
Уравнение mx" = F называют уравнением механического дви-
жения. В этом уравнении х = х (/) — неизвестная функция, mnF —
известные величины. В зависимости от физических условий сила F
будет задаваться по-разному и мы получим различные дифферен-
циальные уравнения. Рассмотрим несколько примеров.
1. Сила постоянна: F = const. Уравнение движения примет вид
г
х" =— = а (где а — постоянная).
т
2. Сила периодически меняется со временем, например, по
закону F = Fq sin (of. Уравнение движения имеет вид х" =
=—sin (of.
т
3. Сила пропорциональна смещению (движение идеально уп-
ругой пружины): F=— kx (fe>0), знак « —» указывает на то,
что направление силы противоположно направлению смещения.
Уравнение движения можно записать в виде х" = х.
4. Свободный радиальный космический полет — на точку
действует сила, обратно пропорциональная квадрату расстояния:
F= — . Уравнение движения: х"=—
5. Падение с трением — на точку действует постоянная сила
тяжести F\ = — mg и сила трения^Лг, пропорциональная скорости:
F2=—kx'. Уравнение движения имеет вид х" = — g--^~ х'.
Во всех приведенных уравнениях вторая производная неиз-
вестной функции х выразилась через время f, положение точки х
и ее скорость х'. Такое уравнение называют уравнением второго
порядка, так как в него входит вторая производная. Дифферен-
циальное уравнение для работы по постройке пирамиды Хеопса
является уравнением первого порядка, так как в него входит
только первая производная. Приведем еще примеры уравнений
первого порядка.
2) Радиоактивный распад.
Рассматривается радиоактивное вещество, масса которого т
меняется со временем: т = т (/). Экспериментальные данные дают
основание считать, что скорость изменения массы пропорциональ-
на массе вещества в данный момент, т. е. что ^-= — km, где
at
через k обозначен коэффициент пропорциональности (знак « —»
перед положительным коэффициентом k выписан для того,
чтобы подчеркнуть, что масса вещества убывает).
254
3) Народонаселение. ц С
Пусть население страны в момент време- - || + I
ни t выражается функцией L = L(t). Ес- I
тественным допущением будем считать, что \
за единицу времени народонаселение увели- р I
чивается на определенный процент. Если в ------1--1-----1
момент времени t число жителей равно L(/),
то за период времени [/; t^dt] появится при- ис' 32 .
мерно kL (/) dt новых жителей, т. е.
\L^kL(i) dt. Хотя величина L принимает целые значения, обыч-
но интересуются приближенными значениями L. Заменяя настоя-
щую функцию L функцией, принимающей значения непрерывно
и удовлетворяющей соотношению dL = kLdt, мы не сделаем боль-
шой ошибки. Таким образом, скорость роста функции L равна kL
и она удовлетворяет дифференциальному уравнению
—=kL.
dt
4) Электрическая цепь.
Рассмотрим электрическую цепь, состоящую из последователь-
но соединенных сопротивления и конденсатора (рис. 132). Будем
считать, что в цепи сделано короткое замыкание и конденсатор,
имевший начальный заряд, начинает разряжаться. Напряжение на
конденсаторе в момент времени t обозначим через U (/). Заряд
q (t) связан с напряжением U формулой q = CU, где С — емкость
конденсатора. Через сопротивление пойдет ток, который связан
с напряжением U формулой U——RI, где R — величина сопротив-
ления (закон Ома), а знак « —» связан с направлением тока.
Появление тока связано с изменением заряда q, и, значит, ве-
личина / является скоростью изменения заряда во времени:
/=^2- . Подставляя в эту формулу вместо / выражение —
а вместо q выражение CU, получим уравнение для напряжения:
rdU _ U „„„ dU _ I ,,
С ~~т~— Dr U.
dt я\ dt дС
Сделаем выводы. Многие явления природы и техники опи-
сываются дифференциальными уравнениями, т. е. уравнениями,
связывающими неизвестные величины и их производные. Вывод
дифференциальных уравнений основан на знании законов изу-
чаемых явлений.
2. Решение дифференциального уравнения
Дифференциальное и интегральное исчисление позволило за-
писать на математическом языке в виде дифференциальных урав-
нений различные законы и явления. За 300 лет существования это-
го раздела математики появились многие тысячи дифференциаль-
255
ных уравнений. Первое замечательное обстоятельство, которое
было замечено, состоит в том, что многие уравнения похожи друг
на друга. Сравним, например, три уравнения, полученные в при-
мерах 2, 3 и 4 предыдущего пункта:
din 1 d L 1 j d U Irr
—=—km\ ~—=kL', —=——U.
dt dt dt RC
Все они имеют один и тот же вид — скорость изменения иско-
мой функции пропорциональна значению этой функции. Решив
dx
уравнение — = fex, мы получим решения всех трех уравнений,
подставляя разные значения коэффициента пропорциональности k.
Здесь мы наблюдаем замечательное проявление силы матема-
тики — совершенно разные процессы привели к одной и той же
математической модели. Исследование этой модели дает нам
ответ как в разобранных задачах, так и во многих других, которые
приводят к аналогичному уравнению.
Аналогичное явление мы обнаружим позже и для уравнений
второго порядка.
Математики научились объединять вместе похожие уравнения,
классифицировать их. Так же как для простых алгебраических
уравнений были найдены в свое время формулы их корней, так и
для некоторых стандартных дифференциальных уравнений были
получены формулы их решений.
Решение дифференциального уравнения — это функция, при
подстановке которой уравнение превращается в тождество. Так
как операция дифференцирования выполняется просто, то всегда
нетрудно проверить, является данная функция решением диффе-
ренциального уравнения или нет.
Приведем примеры решений написанных ранее уравнений.
1) Функция х=^—Н wt + хо, где ио, хо — произвольные числа,
является решением уравнения х" — а. Действительно, вычисляя
производные, получаем x'=at + vQ, х" = а.
2) Функция х = ““гsin со/ является решением уравнения
Р
х" =—sin со/.
т
3) Функция х — A sin + где А и а — произвольные
числа, является решением уравнения х" ——— х.
4) Функция m = Ce~kt, где С — произвольная постоянная,
является решением уравнения т'= — km.
Проверьте самостоятельно, что функции, указанные в приме-
рах 2, 3 и 4, действительно являются решениями соответствую-
щих дифференциальных уравнений.
256
Чебышев Пафнутий Львович
(1821—1894) —
русский математик, основатель Петер-
бургской математической школы. Создал со-
временную теорию приближений, получил
глубокие результаты в теории чисел и теории
вероятностей. Чебышев придавал очень
большое значение прикладным задачам и за-
нимался теорией механизмов.
«Сближение теории с практикой дает са-
мые благотворные результаты, и не одна
только практика от этого выигрывает, сами
науки развиваются под влиянием ее.»
П. Л. Чебышев
Однако не для всех уравнений решения записываются так прос-
то. Так, для уравнения свободного космического полета написать
формулу решения довольно трудно. Часто удается исследовать ре-
шение дифференциального уравнения, не находя самого решения.
3. Уравнение показательного роста
Известно много процессов, в которых скорость изменения
какой-либо величины пропорциональна ее значению. К числу таких
процессов относятся радиоактивный распад, изменение народона-
селения и другие сходные процессы, связанные с размножением, а
также остывание тела, разряд емкости через сопротивление
и т. д.
Эти процессы описываются, как мы видели в начале параг-
рафа, дифференциальным уравнением первого порядка x'=kx
при различных значениях коэффициента k.
Как же решать уравнение x' = fex?
Мы знаем, что показательная функция обладает тем свойст-
вом, что ее производная пропорциональна ей самой. Таким об-
разом, функция x = ekt является одним из решений уравнения
х' = fex. Как найти все решения? Пусть z — произвольное решение,
т. е. пусть z' = kz. Запишем z в виде z = yekt, где у — новая
неизвестная функция. Подставив z в уравнение, получим:
(уек‘У = k (ye*1).
Вычислим производную слева:
(уе*')' = У'ек‘ + kyekt = е*'(t/' + ky).
Приравнивая полученный результат к правой части уравнения и
сокращая, получим £/' = 0, т. е. у = С. Таким образом, произврд-
9 Заказ 836 257
ная функции у равна нулю и у = С. Итак,
любое решение уравнения x'=dx имеет
вид x = Cekt, где С — константа.
Получаем решения рассмотренных вы-
ше уравнений.
Значение константы С определяют,
зная начальное значение искомой вели-
чины. Если в качестве начального момен-
та времени взято /=0, то значение С
как раз и равно значению искомой вели-
чины при / = 0. Так, если начальное напряжение на конден-
саторе равно 1/0, то конденсатор будет разряжаться по экспо-
ненциальному закону: U=UQe RC. При больших t значения U
будут приближаться к нулю. Графики показательных функций при
разных значениях k приведены на рисунке 133.
4. Уравнение гармонических колебаний
В п. 1 указано уравнение движения точки массой т, при-
крепленной к концу упругой пружины. Это уравнение имеет вид
тх"= — kx. Оказывается, что есть много задач, приводящих
к аналогичным уравнениям второго порядка.
Рассмотрим электрическую цепь, состоящую из последователь-
но соединенных конденсатора (с емкостью С) и катушки (с
индуктивностью L). Будем считать, что на конденсаторе есть
начальное напряжение, в цепи сделано короткое замыкание
и пошел ток через катушку. Обозначим через U — U (/) напряжение
на конденсаторе в момент времени t. Напряжение на катушке
(равное U (/) при выбранном направлении тока) пропорционально
скорости изменения тока /, проходящего через катушку, т. е.
Выражая обычным образом ток / через заряд /=^у-
и заменяя заряд q через CU, получим:
U = - L = - L = - L С .
Окончательно приходим к уравнению второго порядка отно-
сительно напряжения:
___х—и
dt2 LC
Итак, две разные на первый взгляд задачи физики — задача
колебания упругой пружины и задача разряда конденсатора
через катушку — привели к одному и тому же дифференциальному
уравнению второго порядка, только записанному в разных обозна-
чениях:
х"=-— х и
т LC
258
Разберем одно из них, обозначив константу, стоящую перед
искомой функцией, через — со2. Итак, рассмотрим уравнение х" =
= — (о2х. Это уравнение называется уравнением свободных
гармонических колебаний.
Проверим, что функция х = А cos ((о/4-а), где Лиа —
константы, является решением уравнения х"—— оз2х. Действи-
тельно,
х'= — о)Л sin ((д/ +а),
х" — — со2Л cos (со/ + а) = — со2х.
Оказывается, что, меняя Л и а, мы получим все решения
уравнения гармонических колебаний. Константы Лиа имеют
наглядный смысл: Л — это амплитуда колебаний, а — начальная
фаза. Значения Лиа находятся из начальных условий —
значений хих' в начальный момент времени. Графики гармони-
ческих колебаний при различных значениях Л, со и а приведены
на рисунке 134.
Уравнение гармонических колебаний получено нами при
идеальных предположениях, которые реально не выполняются.
Так, при колебаниях пружины часто приходится учитывать тре-
ние, а при изучении разряда конденсатора — внутреннее сопро-
тивление. Учет указанных условий вызывает добавление в урав-
нение члена, зависящего от первой производной (скорости). При-
ведем пример уравнения для тока I в цепи, изображенной на
рисунке 135:
Решения такого уравнения будут зависеть от соотношения
между параметрами L, /?, С.
Мы рассматривали так называемые свободные колебания. В
примере с электрической цепью это соответствует тому, что в ней
сделано короткое замыкание и ток идет только за счет началь-
ных условий (заряда, запасенного в конденсаторе). Если к этой
цепи подключить источник, задающий некоторое напряжение,
то мы получим новое уравнение, которое нетрудно вывести. Реше-
ния такого уравнения называются вынужденными колебаниями.
Они, конечно, зависят от подаваемого напряжения.
Рис. 134 Рис. 135
259
Мы рассмотрели некоторые примеры дифференциальных урав-
нений. При этом мы не ставили задачи научиться решать эти
уравнения: это предмет специального раздела математики, теории
дифференциальных уравнений, которая изучается в высшей
школе. Важно понять, что с помощью основных операций анализа
(дифференцирования и интегрирования) можно строить матема-
тические модели (дифференциальные уравнения) достаточно
сложных и важных процессов. Полезно иметь в виду и то, что
разные задачи могут приводить к одной и той же модели, что
делает наиболее часто встречающиеся уравнения особенно важ-
ными. К их числу относят уравнение показательного роста, урав-
нения свободных и вынужденных колебаний.
Контрольные вопросы
1. Что такое дифференциальное уравнение?
2. Как записать второй закон Ньютона в виде дифферен-
циального уравнения?
3. Приведите примеры дифференциальных уравнений механи-
ческого движения.
4. Каким дифференциальным уравнением описывается ра-
диоактивный распад?
5. Какому дифференциальному уравнению в первом приб-
лижении удовлетворяет функция, описывающая рост народона-
селения?
6. Напишите дифференциальное уравнение свободных гар-
монических колебаний.
7. Приведите примеры разных процессов, описываемых одним
и тем же дифференциальным уравнением.
8. Какой вид имеют решения уравнения показательного роста?
9. Чему равна частота колебания, описываемого уравнением
x" + fex = 0?
10. Как определяются значения констант, появляющихся при
решении дифференциальных уравнений?
ЗАДАЧИ К ГЛАВЕ V
Определение интеграла
Запись площади в виде интеграла
1°. а) Запишите с помощью интегралов площади фигур, изоб-
раженных на рисунке 136.
б) Нарисуйте фигуры, площади которых равны следующим
интегралам:
2 2 f f _____
1) \x2dx\ 2) \±rdx\ 3) sin xdx\ 4) \^-x2dx.
0 1 x 0 0
260
Рис. 137
Приближенное вычисление интеграла
2. Постройте на клетчатой бумаге систему координат с масшта-
бом «две клетки — единица длины». Найдите приближенные
значения следующих интегралов, построив графики подынтег-
ральных функций и вычисляя площади подграфиков «по клет-
кам»:
10
1) J 0,lx2dx;
о
10 10
2) ^dx; 3) ^5sin^-dx.
' J х 'J 10
Графическое вычисление интеграла
3. Для функций, графики которых изображены на рисунке 137,
постройте графики функций S = S(x), задающих переменную
площадь подграфика.
4. Какая фигура имеет большую площадь: полукруг радиуса 1
или фигура, заключенная между осью х и графиком функции
у=1—х4?
261
Рис. 138
5. Укажите на рисунке 138, какой функции соответствует график
какой первообразной.
6*. Табличное значение для \ex*dx равно 1,463 (е = 2,718).
о
е
Найдите J д/ln z dz.
7*. Найдите dx.
о
262
Составление интегральной суммы
8. Составьте интегральные суммы Sn для приближенного вычис-
ления следующих интегралов, разбивая отрезок интегрирова-
ния на п равных частей:
1
1) $x2dx;
о
2
1
3) \-yfxdx\
о
л/2
4) ) sin х dx.
о
Дайте геометрическую интерпретацию составленных интег-
ральных сумм.
9*. Докажите неравенства:
10 10
1) lgxdx<9; 2) lgxdx>4,5.
i i
Вычисление интеграла
Вычисление первообразной
10°. Найдите первообразные следующих функций:
1) у=1; 2) £/ = х; 3) У = 3х;
4) У=х9\ 5) у=Зх3 — 5х2 + х — 2; 6) Г3 y=f-l;
7) 1 . У=~ ’ 8) 9) у=л/*;
Ю) 1 у=—= ; Н) х3— 1 12)
2^/х X у/х
13) у = 3 sin х; 14) у=2 cos х; 15) y = sin 2х;
16) у=А cos <ох; 17) 1 у=—2—; и COS X
18) j/=cos2y-; 19) у=2^; 20) У = е~х\
21) 1+е2" . У- ? - 22) У = 2Х; 23) y = e3x+l-
24) У=Ю-Х; 25) II * |ю 26) У=7ТГ’
27) 1-1-Х2 . У=—— X 28) у=-—И—; у х 1 X—1’ 29) У=7ТТ;
30) х3 + х2 + х + 1 . У 3? 31) t/ = x3 + 2x2 — 5х+ 1; 32) z/ = (x — 2)3;
33) у=(1—2х)2; 34) У=±~т+* 35) х2— 1 У- х2 ;
36) 37) y = s'm x + cos х;
38) i/ = sin (Зх+у-
263
39) r/ = cos5x; 40) y = 2 sin x cos x;
41) r/ = sin x sin 3x; 42) r/ = sin 2x cos 4x;
43) = ; 44) y = ; 45) £/ = cos2x;
46) y = (ex + e~x)2; 47) £/ = ^1^7; 48) y= 10~\
Вычисление интеграла no формуле Ньютона — Лейбница
11. Вычислите интегралы:
1) 2 3 $ dx; 2) $5dx; 5 1 3) J xdx; 4) jjx2 dx;
- 1 0 -2 0
5) 4 1 J(3-2x)dx; 6) J 1 0 (x2+l)dx; 7) J (x2+2x)dx; -1
2 1 7
8) $(2x3 — x— 1) dx; 9) $ 0 - (2x2 —5x —7) dx; 10) № ; 1 2 x
2 4 1 8 13) \ ypdx; 14) 0 2 Vх
Н) 12) \^cdx;
15) 2 j 2*3+J*~2 dx; 8 16) j^' + Xx + l dx; 1 Vх
Л 7 л T
17) J sin 5x dx; 18) J cos x dx;
0 Л 5
л "4 7
19) f . X Xi \ sin—cos—dx; 0 2 2 20) cos2 -^-dx; Л
21) л 7 f ^x • J sin2 x л 4 22) { —; J COS X
23) J (sin x — 3 cos x — x) dx; 0 24) j tg2xdx;
264
2 I I
25) $ |х — 11 dx; 0 26) J х4 dx\ 0 27) ( •
28) Л 4 J sin 2х dx\ 29) 0 $ x3 dx\ 30) In 2 J e2x dx\
31) л ~ “4 л т J sin2 х dx\ 32) — i J x2dx; 33) 0 2л j I sin x| dx\
34) 0 4 J \[х dx\ 35) -1 1 д/l — x rfx; 0 36) 0 8 ( 3 V^+T ’
Приложения интеграла
Вычисление площади
12. Найдите площади фигур, ограниченных линиями:
1) х= — 1, х=2, у = 0 и у=х2-\-1;
2) у=0 и у= 1 —х2;
3) х=1, х=2, у = 0 и у=х2+1;
4) у—х2 —х — 5 и у=х — 2;
5) у=х2+х—4 и у=6—х2;
6) у—— х2+4 и у —2—х;
7) у=х2 + 2 и у=х+4;
8) y = sin х, х=-2~, х—л, у=0;
9) у—~~, х=1, х=3, у=0;
10) у= — х2 + 3х, у = 0;
П) у= — х2 — 2х, у=0;
12) у=2х, х= —1, х=1, у=0;
13) у=4-х2, х=0, у = 0;
14) у=9—х2, х=0, у=0, х—— 2;
15) у=х24-4, х=0, у = 0;
16) у=х2 и у=\[х\
17) у=х3 и y=Vx;
18) у=х—х2 и у—х2—х;
19) y=sinx и У=~^ х (xi>0);
20) у=2х—1 и у=д/х.
265
13*. а) Найдите площадь фигуры, заданной на координатной
плоскости условием у^х2, х>у2.
б) Найдите площадь фигуры, заданной на координатной плос-
кости условием 15 —7х^у<7 —Зх, у>0.
Работа
14. Из цистерны, имеющей форму прямого кругового конуса ра-
диусом основания R и высотой Я, выкачивают воду через вер-
шину конуса. Найдите совершаемую при этом работу. Найдите
численное значение работы при /? = 3 м, // = 5 м, считая
плотность воды р = 1 г/см3.
15. Найдите работу, совершенную при постройке великой еги-
петской пирамиды — пирамиды Хефрена, имеющей высоту
215 м и сторону основания 143,5 м. Ответ дайте в джоулях
и в тонно-километрах.
16. Два точечных электрических заряда +Ю“4 и —10-4 Кл на-
ходятся на расстоянии 10 см друг от друга. Найдите работу,
необходимую для того, чтобы развести их на расстояние 10 км.
Давление
17*. Вычислите давление воды на квадратную пластину со сторо-
ной а, погруженную в воду перпендикулярно ее поверхности,
считая, что верхнее основание пластины находится на рас-
стоянии h от поверхности воды.
Теплота
18*. Найдите количество теплоты, выделяемой переменным сину-
соидальным током I sin ((о/ +а) в течение одного перио-
да времени в проводнике сопротивления R.
Путь
19. Точка движется по оси абсцисс так, что скорость ее в про-
извольный момент времени t задается формулой v (t) =
= cos Найдите положение точки в момент времени
если в момент времени /=-~-она имела абсциссу, рав-
ную — 1.
Сила
20*. Найдите силу гравитационного взаимодействия между рас-
положенными на одной прямой материальной точкой массой m
и однородным стержнем длиной I и массой М. Расстояние от
точки до ближайшего конца стержня равно /.
266
Дифференциальные уравнения
Подстановка решения в уравнение
2
21. Найдите такое число а, что функция х = а/^ является реше-
нием уравнения х"=—
22. Проверьте, что функции у{=с\е\ у2 = с2в~2х являются реше-
ниями уравнения у" + у' — 2у = 0.
23. Пусть Х| и л2 — вещественные корни квадратного уравнения
t2 + pt + q = O. Докажите, что функции у\ = С\^'Х и у2 = С2^2Х —
решения дифференциального уравнения £/" + ру' + qy = O.
Интегрирование с учетом начального условия
24. Найдите функции f, удовлетворяющие условиям:
1) Г«=х2, Н2)= 1;
3) Г(х)=^(х>0), f(e)=l;
5) f'(x)=sinx, f (0) = 2;
2) f'(x) = e~x, f(0W-2;
4) Г(х)=^(х<0),Н-1)=1;
6) rW = 2cosxj(f)=3.
Линейное дифференциальное уравнение первого
порядка
25. Решите дифференциальные уравнения:
1) у' = 2у, 2) у'— — у, 3) 2у'=Ьу.
26. Период полураспада радиоактивного вещества равен 4,4 -109
лет. Через сколько лет останется 99,99% исходного количества
радиоактивного вещества?
27. Напишите закон радиоактивного распада, если известно, что
при / = /0 масса вещества /n(/o) = wo.
28. Скорость роста дрожжей пропорциональна их массе. Найдите
зависимость массы дрожжей от времени, если известно, что
при / —0 их масса была равна т0.
29*. Найдите коэффициент пропорциональности в предыдущей за-
даче, если известно, что прирост дрожжей через 2 ч больше,
чем прирост за первый час, на И кг, а начальное количество
дрожжей 100 кг.
30. Каким должен быть среднегодовой рост производства, чтобы
за 10 лет объем производства удвоился?
267
КОНТРОЛЬНОЕ ЗАДАНИЕ К ГЛАВЕ V
Вариант 1
л
т
1. Вычислите J cos 2х dx. Изобразите фигуру, площадь кото-
Л
Г2
рой представляет вычисленный интеграл.
2. Найдите площадь фигуры, ограниченной параболой у=х2 — 1
и прямой у=х + 1.
3. Точка движется по прямой. В начальный момент /=1 с ее
скорость равна 1 м/с, а затем уменьшается по закону о=-^-.
Найдите длину пути, пройденного точкой за 4 с от начального
момента времени.
4. Материальная точка движется по оси х. На нее действует
сила F, зависящая от положения точки: F=F{x). Как с по-
мощью интеграла выразить работу, совершаемую при пере-
мещении точки на отрезке [0; а] оси х?
Вариант 2
1. Вычислите интегралы:
л
4 I 4
a) ^л/xdx; б) J(x3 + 2x2 — 3)dx; в) Jsin3xdx.
1 0 л
д
2. Найдите площадь фигуры, ограниченной графиком функ-
ции y=cosx, осью х и прямой, проходящей
через начало координат и точку ) на графике ко-
синуса.
3. Задан закон изменения скорости движения материальной точ-
2
ки по прямой: о = 2 (<+1)^ (время t в секундах, скорость о
в метрах в секунду). Какой путь пройдет точка за 7 с от начала
движения (/ = 0)?
4. На рисунке 121 изображен график изменения силы тока /
в цепи в зависимости от времени t. Постройте график
зависимости от времени величины заряда q, переносимо-
го током.
268
Вариант 3
1. Вычислите интегралы:
л
I ____ I Т
a) J д/1 —х dx-, б) $ —; в) $ sin3xdx.
о ох+* о
2. Вычислите площадь петли, описываемой кривой, заданной
уравнением у2=х3+х2.
3. Тело массой 1 движется с ускорением, меняющимся линейно
по закону a (f) = 2t— 1. Какой путь пройдет тело за 4 единицы
времени от начала движения 1=0, если в начальный момент
его скорость равнялась 2?
4. Сила взаимодействия между двумя точечными массами пг и М
вычисляется по формуле F — k^-, где г — расстояние между
массами. Выведите интегральную формулу для вычисления
силы взаимодействия между точечной массой пг и однородным
стержнем массой М, длиной /, расположенным на одной пря-
мой с массой пг, причем расстояние от точечной массы до
ближнего конца стержня равно а.
Все животные равны. Но некоторые жи-
вотные более равны, чем другие.
Дж. Оруэлл
Глава VI
УРАВНЕНИЯ И НЕРАВЕНСТВА
ВВОДНАЯ БЕСЕДА
1. Выражение
Уравнение — это самая простая и самая распространенная
форма математической задачи. Заканчивая школьный курс, вы
накопили богатый опыт решения разнообразных уравнений.
Наступил момент, когда нужно привести свои знания в порядок,
разобраться в тех приемах и рассуждениях, которые вы обычно
проводили при решении уравнений, часто не обращая внимания
на их смысл.
Мы начнем повторение с понятия «выражение».
Выражение — это числа и буквы, соединенные знаками раз-
нообразных операций.
В начальной школе вы познакомились с простейшими арифме-
тическими операциями — сложением, вычитанием, умножением,
делением — и с их помощью составляли выражения такого, на-
пример, типа:
2а ~\~b
а — 2Ь
х2+ху+у2
х2-Ъху + у2
и др.
Появление новых операций — возведение в степень, логариф-
мирование, вычисление синуса, тангенса и т. д. — расширило
возможности в составлении выражений. Теперь можно составить
более сложные выражения, например такие:
log2 (а 2 — b 2)
sin%4-tg2w „
------ И др
arcsin ху
Числа и буквы, входящие в состав выражения, имеют разный
смысл. Число, как бы оно ни было записано, например
0,5; 0,4999... или как-то иначе, всегда конкретно, постоянно.
Буква же обозначает переменную, меняющуюся величину, ко-
торая может принимать разнообразные значения. Мы будем под-
ставлять в выражения вместо букв только числа. При подстанов-
270
ке в выражение вместо букв каких-то чисел мы будем получать
так называемые числовые выражения. Так, числовое выражение
получено из выражения подстановкой в
о — о • о • э э х — оху -г- у
него значений х = 3, // — 5.
Подставляя в выражение определенные значения букв, мы мо-
жем получить числовые выражения, не имеющие смысла. Бес-
смысленные числовые выражения получаются прежде всего тогда,
когда это выражение содержит невыполнимые операции над
числами, например деление на нуль, логарифмирование отри-
цательного числа, арксинус числа, большего единицы, тангенс
числа у и т. п. Другой причиной, приводящей к не имеющим
смысла числовым выражениям, является подстановка вместо букв
чисел, не входящих в область допустимых значений этих букв.
Например, если в выражении для производительности труда
участвует буква а, обозначающая число землекопов в бригаде,
9
то, подставляя значение а = 2— («два землекопа и две трети»),
I мы получим бессмысленное числовое выражение, хотя все опера-
ции над входящими в выражение числами формально осуществимы.
Областью допустимых значений (ОДЗ) выражения обычно на-
зывают множество всех значений букв, при подстановке кото-
рых выражение имеет смысл, т. е. превращается в осмысленное
числовое выражение.
Заметим, что если выражение содержит одну букву, то его
ОДЗ — это числовое множество, т. е. какое-то подмножество точек
числовой прямой. Если же букв, например, две, то ОДЗ выраже-
ния — это множество пар чисел и его можно изобразить в виде
области, расположенной на координатной плоскости.
Возьмем какое-либо осмысленное числовое выражение и про-
делаем все указанные в выражении операции над входящими в
него числами. Получим одно число — значение числового выраже-
ния. Возьмем буквенное выражение и подставим в него вместо
букв числа из ОДЗ (т. е. такие числа, чтобы выражение превра-
тилось в осмысленное числовое выражение). Вычислим значение
получившегося числового выражения. Это число называют значе-
нием выражения при выбранных значениях букв. Возможность од-
нозначно вычислить значение выражения при любых допустимых
значениях входящих в него букв позволяет определить функцию.
Вот почему говорят, что выражение можно рассматривать как
способ вычисления значений некоторой функции. Поэтому понятие
выражения и понятие функции близки между собой.
Два выражения считаются тождественно равными, если равны
их числовые значения при любых допустимых значениях букв,
входящих в это выражение. Тождество — это два тождествен-
но равных выражения, соединенные знаком равенства.
271
Примеры тождеств.
1. (a±b)2=a2 ±2ab-\-b2.
2. (а±&)3 = а3±3a2b + 3ab2±&3.
3. а2 — Ь2 = (а — Ь) (а + Ь).
4. a3±b3 = (a±b) (a2=Faft + &2).
Во всех приведенных тождествах ОДЗ выражений, стоящих
слева и справа, совпадают. Часто используют тождества, соеди-
няющие выражения, имеющие разные ОДЗ. В этом случае име-
ется в виду, что тождество выполняется на общей части ОДЗ
выражений, стоящих справа и слева. Поэтому без дополнительных
оговорок считаются тождествами следующие равенства вы-
ражений:
6. (7а)2 = а.
7. alogaX = x.
8. sin arcsin х — х.
9. tg x-ctg x = 1.
10. loga xy = loga X + loga y.
Иногда искусственно (какими-либо дополнительными условия-
ми) уменьшается ОДЗ выражений, составляющих некоторое
равенство. Тогда можно говорить о тождестве, выполняющемся
на некотором множестве. Так, если [х] обозначает целую часть
числа х, то равенство [х + -^-]=[х] является тождеством на
множестве целых чисел (но, разумеется, не является тождеством
в обычном смысле слова). Приведем более содержательные
примеры.
11. arcsin (sin х) = х — тождество на промежутке —£"»“£"]•
12. д/? = х— тождество на промежутке [0; +«>).
13. arcsin (sin х) = л— х — тождество на промежутке -у-].
Тождественное преобразование выражения — это переход от
одного выражения к тождественно равному выражению.
Самые «безобидные» тождественные преобразования — на-
пример, приведение подобных членов, сокращение дробей, исполь-
зование свойств степени и т. п.— могут привести к выражению,
у которого ОДЗ больше или меньше, чем у исходного выражения.
Это может оказаться существенным при решении уравнений, по-
этому информацию об изменении ОДЗ при тождественных пре-
образованиях полезно хранить в памяти (собственной, машинной
или просто в тетради).
272
2. Уравнение
Возьмем два числовых выражения и поставим между ними
знак равенства. Мы получим числовое равенство. Оно будет
верным или неверным в зависимости от того, равны или не равны
значения взятых числовых выражений. Классическими примерами
являются равенства 2-2 = 4 и «2-2 = 5».
Отметим еще раз, что, когда мы говорим «равенство двух
числовых выражений», мы вовсе не утверждаем, что эти два выра-
жения действительно равны. Соединить два числовых выраже-
ния А и В знаком « = » и говорить о получившемся равенстве
А =В можно независимо от того, верно или неверно сформу-
лированное нами утверждение А =В.
Возьмем два буквенных выражения и соединим их знаком ра-
венства. Получим уравнение. Таким образом, уравнение в первом
приближении можно понимать как равенство двух буквенных
выражений.
Равенство числовых выражений иногда называют «безуслов-
ным» равенством, т. е. равенством или безусловно верным, или
безусловно неверным. Уравнение с этой точки зрения можно счи-
тать «условным равенством» — при одних условиях ( т. е. при
одних значениях букв) оно может оказаться верным, при других —
неверным. Тождество — это равенство, верное при всех допусти-
мых значениях букв. Его тоже можно считать частным случаем
уравнения.
Уравнение — это не просто формальное равенство двух выра-
жений. Главное в понятии уравнения — это постановка вопроса о
его решении. Можно сказать, что уравнение — это равенство
двух выражений вместе с призывом найти его решения. Опишем
более точно, что же значит решить уравнение.
Буквы, входящие в состав уравнения (т. е. в состав выраже-
ний, образующих уравнение), называются неизвестными. Если та-
кая буква одна, то говорят, что мы имеем дело с уравнением с
одним неизвестным. Аналогично можно говорить об уравнении с
двумя, тремя и любым другим числом неизвестных.
Рассмотрим уравнение с одним неизвестным. Значение неиз-
вестного, при подстановке которого уравнение превращается
в верное числовое равенство, называется корнем уравнения.
Решить уравнение с одним неизвестным — значит найти все
его корни.
Возьмем уравнение с числом неизвестных, большим чем одно.
Например, рассмотрим уравнение с двумя неизвестными. Чтобы
получить из него числовое равенство, надо каждому неизвестному
придать определенное числовое значение, т. е. взять пару чисел.
Решить уравнение с двумя неизвестными — значит найти все
пары чисел, удовлетворяющих этому уравнению, т. е. такие, при
подстановке которых уравнение превращается в верное числовое
равенство. Одну такую пару тоже можно было бы назвать
273
Винер Норберт
(1894—1964) —
американский математик, создатель ки-
бернетики как «науки об управлении и свя-
зи в живом организме и машине». Работы
Винера являются основополагающими для
применения вычислительных машин в раз-
личных сферах человеческой деятельности.
Норберту Винеру принадлежит высказыва-
ние: «Вычислительная машина ценна ровно
настолько, насколько ценен использующий ее
человек».
корнем уравнения, но обычно так не говорят, а вводят понятие
«решение уравнения».
Решение уравнения с двумя неизвестными — это пара чисел,
удовлетворяющих этому уравнению.
Разумеется, и в случае уравнения с одним неизвестным можно
вместо слов «корень уравнения» говорить «решение уравнения».
Путаница может возникнуть из-за разного употребления слова
«решение». Можно сказать о решении уравнения как его корне.
При таком употреблении этого слова имеют смысл такие фразы,
как «уравнение имеет одно решение», «уравнение имеет три
решения», «уравнение не имеет решений». В речи часто исполь-
зуют словосочетание «решение уравнения» как процесс нахож-
дения его корней (решений). Можно сказать так: «Уравнение
имеет сложное решение», «Я не смог найти путь решения этого
уравнения». В процессе решения уравнения может обнаружиться,
что оно совсем не имеет корней (решений). В этом случае мы
скажем, что мы уравнение решили: доказали, что у него решений
нет.
Что означает найти корни уравнения? В школьной практике
при решении уравнений принято записывать ответ как результат
знакомых операций над числами, например:
х = Л/2,
v v V logs 5
x=sin-2-, х = 2^, x = arcsin4-.
5 о
В то же время при решении прикладных задач бывает необ-
ходимо представить ответ в десятичной записи с определенным
числом знаков после запятой. Такой ответ можно получить, ис-
пользуя калькулятор или другое вычислительное устройство.
Мы условились понимать под уравнением равенство, состав-
ленное из двух выражений. Мы уже говорили о том, что выра-
274
жение можно рассматривать как способ задания некоторой функ-
ции. Поэтому уравнение можно понимать как равенство, соеди-
няющее две функции. Пусть даны две функции от переменной х, на-
пример y=f(x) и y = g(x). Составим уравнение f(x) = g(x). Оно
получено приравниванием выражений f (х) и g(x). Пусть D\—D (f)
и D2 —D (g) — области определений функций f и g. Тогда D\ и О2
можно понимать как области допустимых значений выражений
f(x) и g(x). Общая часть областей D\ и О2, т. е. множество
D3==DiC|D2, является ОДЗ уравнения f (x) = g(x).
Полезно вспомнить, что подставлять в уравнение можно лю-
бое значение х. При каком-то значении х может получиться бес-
смысленное числовое выражение, а при х из ОДЗ получится
осмысленное числовое равенство. Если при этом оно окажется
еще и верным, то взятое число х является корнем уравнения.
Вернемся к вопросу о решении уравнения. Начнем с уравнения
с одним неизвестным х. В какой форме рекомендуется записы-
вать его ответ?
Уравнение может иметь один корень, например х=5. Тогда
ответ проще всего записать именно в этой форме: х = 5.
Уравнение может иметь несколько (конечное число) корней.
Ответ удобно записать в виде перечисления всех корней, давая
каждому значению х свой номер. Например, Xi —— 1, х2 = 0,
х3=1. Полезно корни располагать в порядке возрастания.
Уравнение может вовсе не иметь корней. В таком случае на-
гляднее всего это и указать в ответе словами: корней нет.
Тригонометрические уравнения (и вообще уравнения с перио-
дическими функциями) часто имеют бесконечно много корней,
которые можно записать в виде одной или нескольких последова-
тельностей. Скажем, возможна такая запись ответа:
х—-^-+л/г,
Встречаются уравнения, решения которых заполняют один или
несколько промежутков, которые и указываются в ответе, на-
пример: O^Cx^Cl или х — любое число.
Все корни (решения) уравнения образуют множество корней.
Слово «множество» не означает, что корней очень много («великое
множество»). Если множество корней обозначить одной буквой,
скажем X, то ответ может быть записан иначе. Примеры записи
ответов с употреблением теоретико-множественных обозначений:
X ={5}; Х = {— 1; 0; 1}; Х=0 (пустое множество, т. е. корней
нет; не надо путать знак пустого множества с обозначением нуля);
х=[0; 1]; х ={?-+nk/kez]; x=r.
Множество решений уравнения с двумя неизвестными состоит
из пар значений этих неизвестных. Важно помнить, что одна пара,
скажем х=1, г/ = 5,— это одно решение (а не два). К вопросу
о записи решения уравнений с несколькими неизвестными мы
вернемся в параграфе, посвященном системам уравнений.
275
3. Равносильность
Если идет дождь, то мы открываем зонт. Можно сказать, что
открывание зонта является следствием того, что идет дождь.
Если число делится на 6, то оно четно. Так же как и в первом
случае, можно сказать, что четность числа является следствием
его делимости на 6.
Пусть даны два уравнения А и В. Если каждый корень урав-
нения А является корнем уравнения В, то говорят, что урав-
нение В является следствием уравнения Д, и записывают
так: А => В (читается: «Из А следует В», или «В является
следствием Л», или «Если Д, то В»).
На языке теории множеств можно сказать короче: уравнение
В является следствием уравнения Д, если множество корней
уравнения А содержится в множестве корней уравнения В, т. е.
если Хлс=Хв, где ХА и Хв — упомянутые множества корней.
Переходя от одного уравнения к его следствию, мы не по-
теряем корней исходного уравнения, но возможно приобретем
лишние. Основой получения разнообразных следствий является
следующее простое соображение. Пусть а = Ь — числовое равенст-
во, a f — функция, определенная в точках а и Ь. Тогда равенство
f (a) = f (6) является следствием равенства а = Ь, т. е. если ра-
венство а = Ь верно, то верно и равенство f (a) = f(b) (если оно
имеет смысл).
Возьмем теперь уравнение, полученное приравниванием двух
выражений. Если функция f определена при всех значениях этих
выражений, то, вычислив значения функции f от обеих частей
уравнения, получим новое уравнение, являющееся следствием ис-
ходного. Это правило особенно удобно, если функция f определена
при любых числовых значениях переменных.
Приведем примеры. Возьмем уравнение д/х +1 = х2 + 1.
Следующие уравнения являются его следствиями (рядом за-
писана применяемая функция, а буквой г обозначен ее аргумент):
1. (V^+T)2 = (x2+1)2, f(z) = Z2.
2. д/Г+Т— 1 =-^2> f(z) = z-l. з. 2v7+r=2x’+l, f(z)=2*.
4. sin (-\/*+ 1)=sin (х2+ 1), f(z) = sinz.
Все функции f определены при любом z, поэтому получение
указанных следствий было формальной операцией.
5. Iog2 A/x+l=log2 (х2+1), f(z)=10g2Z.
6. V*+T=a/P+T, f{z)=^z.
7.
8.
7=7=-?ТГ- f (?)=+-
д x 4-1 x । 1 z
arcsin -уд/хД-1 = arcsin y(x2 + 1), f (z) = arcsin у.
276
В случаях 5—8 функции уже определены не при всех х.
Однако во всех случаях новые уравнения являются следствиями
исходного. Этот вывод уже не является формальным. Примеры
5—7 разберите самостоятельно. Пример 8 является существенно
более трудным и требует дополнительных сведений о корнях
исходного уравнения (докажите, что все его корни лежат на от-
резке [0; 1]).
Два уравнения называются равносильными, если каждое из
них является следствием другого, т. е. если каждый корень
одного из них является корнем другого.
Пусть уравнение А имеет множество корней ХА, а уравне-
ние В — множество Хв. Равносильность уравнений А и В обозна-
чается так: Л о В. По определению равносильность означает
выполнение двух условий: А => В (уравнение В является следстви-
ем уравнения А) иВ=>А (наоборот, уравнение А является след-
ствием уравнения В). На языке теории множеств равносильность
означает равенство ХА = ХВ.
Итак, у равносильных уравнений корни одни и те же. По-
этому основным способом решения уравнения является следую-
щий: с помощью перехода от одного уравнения к равносильному
стараются прийти к уравнению, решения которого находятся легко.
Основной способ получения следствия нам известен — вычис-
ление значений какой-либо функции от обеих частей уравнения.
Чтобы этот переход сохранял равносильность, надо, чтобы
возможен был обратный переход. Это всегда выполняется, если
новое уравнение получено с помощью функции, имеющей обрат-
ную. На этом соображении основаны теоремы о равносильности,
позволяющие утверждать равносильность пар уравнений, полу-
чающихся друг из друга с помощью взаимно обратных функций.
Сформулируем несколько таких теорем.
Запишем уравнение в символической форме:
□ = А,
где □ и А — два выражения, составляющие уравнение.
Теоремы помещены в левой колонке таблицы. В правой колон-
ке указаны взаимно обратные функции, с помощью которых эти
теоремы доказываются.
1. □ = А □ -|- а = A “h ci г=у—а 1 t z+a = y
2. □ = A $ а- □ =а- А 1 2=-y 1 t аг=</
277
3. ° II <=> II а > О а а * V — о Z= loga 4/ 1 t аг=у
4. <1 II <=>J □ □ г = Чу 1 t z3=y
Во всех этих случаях не было трудностей с областями оп-
ределения применяемых функций. Использование таких распрост-
раненных операций, как возведение в квадрат, умножение и деле-
ние на некоторую функцию, нахождение обратной величины и т. д.,
в общем виде не гарантирует равносильности. Например, возводя
в квадрат обе части уравнения, мы получаем следствие:
□ = Д => п2 = д2.
Вообще говоря, обратный переход неверен. Однако если из
последующего решения уравнения П2 = Д2 мы узнаем, что для его
корней выражения □ и Д имеют одинаковый знак, то можно
будет поставить стрелку в обратном направлении и найти корни
исходного уравнения:
□ 2=Д2=ф- □ = Д, если □ и Д одного знака.
Остановимся подробнее на некоторых полезных преобразова-
ниях уравнений.
1) Тождественное преобразование одной из частей уравнения
и перенос членов из одной части уравнения в другую с проти-
воположным знаком приводят к равносильному уравнению, если
при этом не происходит изменения ОДЗ. Например, уравнение
X ___ 1
х2 + 2 ~ 3
равносильно уравнению
х2 —Зх + 2 = 0.
В то же время уравнения
и lg(x_2)(x + 6)=l+lg2
lg(x-2) + lg(x + 6)=l+lg2
не являются равносильными (корни первого: х\ = — 8, *2 = 4;
корень второго: х = 4), так как логарифмирование произведения
уменьшило ОДЗ.
2) Переход к совокупности уравнений. Рассмотрим задачу,
в которой требуется решить несколько уравнений, а затем объе-
динить их корни. Можно сказать, что идет речь о решении со-
278
вокупности уравнений. Обычно совокупность обозначается с по-
мощью прямой скобки.
Пусть ОДЗ выражений □ и Д совпадают. Тогда уравнение
□ •Д=0 равносильно совокупности
Г п=о,
L Д=0.
Оговорка про совпадение ОДЗ не случайна. Так, уравнение
cosx-tgx = 0 не равносильно совокупности
cos х=0,
tgx = 0.
3) Переход к системе уравнений. Рассмотрим задачу, в которой
надо решить несколько уравнений и взять их общие корни (или
иначе найти числа, удовлетворяющие каждому из уравнений
системы). В систему можно объединять не только уравнения,
но и различные условия, ограничения, неравенства. Например,
решить систему
х2 + 2х — 3 = О,
х+1>0
означает, что надо решить первое уравнение и взять только те
его корни, для которых выполняется неравенство х+1>0.
Использование переходов от уравнения к совокупностям и
системам позволяет разнообразить схемы равносильных пере-
ходов. Покажем некоторые из них:
1)
° =0^1 П=0’
д Д =/=0;
J___1 „ ( □ = Д,
□ д I О =/=0;
3)
□2=д2,
- п>о,
кД >0,
□ = д
□2=д2,
□ <0,
Д <0;
4)
( 1g □ =lg Д,
"I D>0,
(lg(-D) = lg(-A),
I D<0,
L ( □ =0,
l Д =0.
Различные переходы от уравнения к совокупностям и систе-
мам изображены на схеме XV.
279
4. Неравенство
Почти все, что было выше сказано об уравнении, можно
дословно перенести и на неравенство. Прежде всего отметим, что
знаков неравенства четыре: > (больше), < (меньше),
(больше или равно), (меньше или равно). Мы будем
говорить о каком-либо одном из них.
Числовое неравенство получается соединением двух числовых
выражений знаком неравенства. Аналогично равенствам числовые
неравенства могут быть верными или неверными. В приведенных
ниже примерах все неравенства с нечетными номерами являются
верными, а с четными — неверными:
1) 3>2; 2) — 3> — 1; 3) 3>3; 4) 2>3;
5) -3<5; 6) 2<2; 7) 3<5; 8) -1<-2.
Приведем основные правила преобразования неравенств, ис-
пользуя знак следствия => и равносильности о.
1. а>Ь а — b >0 о b <а о b — а<0.
2. а>Ь о a + ob + с.
3.
4.
5.
{ => ас>Ьс.
{ с<0 ас<Ьс-
6. 0>a>b=^ — <-J-.
а о
Основой техники преобразования неравенств является следую-
щее общее соображение: пусть функция f монотонна на проме-
жутке, содержащем числа а и Ь. Тогда a<b f (a)<f (Ь), ес-
ли f строго возрастает; a<b => f (a)>f (6), если f строго
убывает.
Указанные выше свойства 3—6 получаются применением это-
го правила к функциям y = cz и У=~~- Аналогично для функ-
ций y — z2 и у = 2г можно записать:
7. a>b>Q=^a2>b2.
8. 0>a>b => а2<Ь2.
9. a>b^2a>2b.
Неравенство с одним неизвестным получается, когда соеди-
няют знаком неравенства два выражения, содержащие одну бук-
ву, или, что близко по смыслу, две функции от одной и той же пере-
менной. Аналогично можно рассматривать неравенства с двумя
и более неизвестными.
280
Ограничимся неравенствами с одним неизвестным. Область
допустимых значений (ОДЗ) неравенства—это множество
значений неизвестного, при подстановке которых получается
осмысленное числовое неравенство. Решение неравенства —
это такое значение неизвестного, при подстановке которого
получается верное числовое неравенство. Решить неравенст-
во — это значит найти, описать множество его решений.
Два неравенства называются равносильными, если множества
их решений совпадают. Одно неравенство является след-
ствием другого, если множество его решений содержит в себе
множество решений второго. Ясно, что каждое из равносиль-
ных неравенств является следствием другого.
Технику решения неравенств с помощью переходов, сохраня-
ющих равносильность, мы покажем на примерах в § 2.
5. Параметр
Посмотрим на знакомое уравнение ах2 4-ftx + c = 0. Выраже-
ние, стоящее в его левой части, содержит четыре буквы —
х, а, Ь, с. Хотя все эти четыре буквы равноправны, мы смотрим
на это уравнение как на квадратное уравнение относительно не-
известного х, считая а, Ь, с буквенными коэффициентами, па-
раметрами. Необходимость рассматривать уравнения с буквен-
ными коэффициентами возникает часто. Прежде всего это полезно
тогда, когда формулируются некоторые общие свойства, присущие
не одному конкретному уравнению, а целому классу уравнений.
Так, мы можем сформулировать свойства корней квадратного
уравнения, показательного уравнения ах = Ь, тригонометрического
уравнения sin (ох=а в зависимости от параметров а, Ь, со.
Разумеется, то, что в уравнении одни буквы мы считаем
неизвестными, а другие — параметрами, в значительной степени
условно. В реальной практике из одного и того же соотношения
между переменными приходится выражать одни переменные через
другие, т. е. решать уравнение относительно одной буквы, счи-
тая ее обозначением неизвестного, а другие буквы параметрами.
По традиции неизвестные обозначаются последними буквами
латинского алфавита — х, у, z, а параметры — первыми — а, Ь, с
или вообще буквами другого алфавита (например, греческими).
При решении уравнений и неравенств с параметрами чаще
всего встречаются две задачи:
1. Найти формулы для решений уравнения (неравенства),
выражающие эти решения как функции от параметров. Типичный
пример — формула корней квадратного уравнения.
2. Исследовать решения уравнения (неравенства) в зависи-
мости от изменения значений параметров. Скажем, встречается
такая задача: найти число корней уравнения в зависимости от
параметра или определить, при каких значениях параметра
уравнение не имеет корней. Очень часто исследование корней
281
в зависимости от параметра можно провести, не вычисляя самих
корней.
Пример. Дано уравнение х2 + 2х + а = 0 относительно неиз-
вестного х с параметром а.
1) При каких значениях а уравнение имеет два корня?
2) При каких значениях а уравнение имеет два корня, причем
один из них больше единицы, а другой меньше?
3) При каких значениях а сумма квадратов корней меньше
шести?
Решите этот пример самостоятельно.
Укажем ответы: 1) а<1; 2) а< — 3; 3) —1<а<1.
Контрольные вопросы
1. Обратите внимание на следующие встретившиеся в тексте
ключевые слова и обозначения: выражение, тождество, уравнение,
корень, решение уравнения, неравенство, решение неравенства,
=*>, о, ОДЗ. Приведите примеры их использования.
2. Что такое ОДЗ выражения?
3. Приведите примеры верных и неверных числовых равенств.
4. Что такое решение уравнения с тремя неизвестными?
5. Приведите пример уравнения, имеющего единственное ре-
шение.
6. Приведите пример уравнения, имеющего более одного, но
конечное множество решений.
7. Приведите пример уравнения, имеющего бесконечно много
решений.
8. Приведите пример уравнения, не имеющего решений.
9. Что означает, что одно уравнение является следствием
другого?
10. Одно уравнение имеет два корня: %i = 1, х2 = 3. Какие кор-
ни может иметь второе уравнение, чтобы первое уравнение было
его следствием?
11. Какие уравнения называются равносильными?
12. Первое уравнение является следствием второго, второе —
следствием третьего, а третье — следствием первого. Что можно
сказать о равносильности этих уравнений?
13. Что может произойти с уравнением, если мы обе его части
возведем в квадрат? Приведите примеры.
14. Что может произойти с уравнением, если мы прологариф-
мируем обе его части? Приведите примеры.
15. Чем отличается совокупность уравнений от системы урав-
нений?
16. Могут ли быть одновременно верными числовые неравен-
ства a<zb и а^Ь?
17. Какие неравенства называются равносильными?
18. Что может произойти при возведении обеих частей нера-
венства в квадрат?
282
19. Если некоторое неравенство вида А <В не имеет решения,
то что можно сказать о решении неравенства Д^В?
20. Решением какого уравнения можно заменить решение сис-
темы неравенств f Д^В,
В>Д?
§ 1. УРАВНЕНИЯ С ОДНИМ НЕИЗВЕСТНЫМ
1. Общие приемы
В простейших случаях решение уравнения с одним неизвест-
ным распадается на два шага — преобразование уравнения к стан-
дартному и решение стандартного уравнения. Второй шаг осу-
ществляется по известным формулам, которые всегда можно вос-
становить в памяти с помощью справочников. Есть они и в спра-
вочных материалах в нашем учебнике.
Перечислим стандартные уравнения, которые были нами
изучены.
1. Линейное уравнение ах-\-Ь — 0.
2. Квадратное уравнение ax2-\-bx-\-c — 0.
3. Простейшее степенное уравнение хп — а.
4. Показательное уравнение ах = Ь.
5. Логарифмическое уравнение \ogax = b.
6. Простейшие тригонометрические уравнения sinx = a,
cosx=a, tgx=a, ctgx = a.
Преобразование уравнения к одному из стандартных является
основным шагом в решении уравнения. Полностью алгоритмизиро-
вать процесс преобразования нельзя, однако полезно запомнить
некоторые наиболее употребительные приемы, общие для всех
типов уравнений.
1) Разложение на множители. Если уравнение равносильными
преобразованиями удается привести к виду □ • Л =0, то, как мы
уже отмечали, исходное уравнение равносильно совокупности двух
более простых уравнений Г П=0, при условии сохранения ОДЗ.
L А=0
Этот прием часто применяется при решении алгебраических
уравнений степени выше второй, при решении тригонометрических
уравнений. Соответствующие примеры будут приведены ниже.
2) Введение нового неизвестного. Посмотрите, не решая, на
следующий набор уравнений:
а) (х2 + 3х)2 + 2(х2 + 3х)- 120 = 0;
б) ^х2 + Зх+д/х2 + 3х+ 1 = 1;
В) 2х!+3х — 2*г+3х~'=-£-;
г) logi (х2 + 3х) — logz (х2 + 3х)=2.
283
В каждом из этих уравнений отме-
тим присутствие выражения х24-3х. Если
заменить его буквой у, т. е. положить у =
=х2 + 3х, то получим более простые урав-
нения относительно у.
а) у2 + 2у-120=0;
б) л/у+л/у+Т-1;
в) 2»-2?-'=у-;
г) logi у — log2z/ = 2.
Найдя из этих уравнений значения у, подставим их в соотно-
шение £/ = х24-Зх и вычислим корни исходного уравнения.
3) Графический метод. Рассмотрим уравнение с одним неизве-
стным f (х) = g (х).
Изобразим на одном рисунке графики функций y=f(x) и
y = g(x) (рис. 139). Точкам пересечения графиков этих функций
соответствуют те значения аргумента х, при которых совпадают
значения функций, т. е. корни данного уравнения.
Итак, абсциссы точек пересечения графиков функций y = f(x)
и y = g(x) являются корнями уравнения f(x) = g(x).
Например, для уравнения х2 = х-|-2 такими точками будут
Pi(-1; 1) и Р2 (2; 4), т. е. х> = — 1, х2 = 2.
Если уравнение имеет вид f (х) = 0, то в качестве функции, стоя-
щей в правой части, выступает функция £/ = 0. Графиком ее будет
ось х, поэтому корнями уравнения f (х) = 0 будут абсциссы точек
пересечения графика функции y = f(x) с осью х.
Графическая иллюстрация решения уравнения указывает на
первый взгляд и способ решения уравнения: строят в системе
координат две кривые и находят их точки пересечения. Действи-
тельно, если выбрать масштаб и построить графики достаточно
аккуратно, то можно приближенно найти точки пересечения и
их абсциссы — корни уравнения. Но для того чтобы найти коор-
динаты точек пересечения точно, как раз и нужно решить соот-
ветствующее уравнение! В то же время графическая иллюстрация
часто дает некоторые качественные отве-
ты, число корней, а также грубо указывает
отрезки на числовой оси, где эти корни
могут находиться. Рассмотрим в качестве
примера уравнение (х— 1)2=-у/х.
Построим графики функций, стоящих
в левой и правой частях.
Из рисунка 140 можно заключить,
что уравнение имеет два корня, один из
которых находится в интервале (0; 1), а
другой — в интервале (2; 3). Можно указы-
вать эти интервалы и более точно: (0; 0,5)
284
и (2; 2,5), еще более точно: (0,2; 0,3)
и (2,2; 2,3). (Действительно, нетрудно про-
верить, что при х = 0,2 имеем д/х<(х — I)2,
а при х = 0,3 уже д/х>(х—I)2; точно так
же при х = 2,2 левая часть уравнения
больше правой, а при х = 2,3 меньше.)
Вообще, вычисляя и сравнивая зна-
чения левой и правой частей уравнения,
можно найти корни с любой степенью точ-
ности.
Корни уравнения пятой степени х5 —Зх +
+ 1= 0 вообще нельзя записать с помощью
радикалов, но, построив достаточно точный график функции
£/ = х5 —Зх+1 (рис. 141), можно определить, что уравнение
имеет три корня в интервалах (—1,5; —1,3), (0; 0,5) и (1; 1,3).
2. Примеры решения уравнений
1) Алгебраическое уравнение х (х + 1) (х + 2) (х+3) = 120.
Если раскрыть скобки и привести подобные члены, то получится
уравнение четвертой степени. Общий прием решения уравнения
четвертой степени нам неизвестен, поэтому не будем торопиться
раскрывать скобки.
Первый способ. Воспользуемся симметрией левой части.
Перемножим первый и четвертый множители, а также второй
и третий. Получим (х2 + 3х) (х^ + Зх + 2)= 120. Теперь видно, что
после замены х2 + 3х = г/ уравнение сводится к квадратному
{/({/ + 2)=120.
Второй способ. Симметрией можно воспользоваться
иначе. Заметим, что числа х, x-f-l, xz+2, х + 3 расположены
з
на числовой оси симметрично относительно числа х + —. Сделаем
замену х+^-=у. Тогда х=у — -|-, х+ 1 =*/—у-, x + 2 = t/+^-,
з
x + 3 = i/ + —. Уравнение превращается в такое:
(«-!) ИВ
Теперь преобразования более очевидны: (у2 — -|-) (у2 — -^-) = 120-
Это так называемое биквадратное уравнение, приводящееся к
квадратному заменой y2 = z.
Третий способ. Перемножив все скобки, получим урав-
нение х4+6х3+11х2 + 6х—120 = 0. Попробуем подобрать корень.
285
Легко догадаться, что 2-3-4-5=120, поэтому х=2 является
корнем. Разделим левую часть уравнения на х — 2:
X4 + 6х3 4-11X2 + 6х - 120 = X4 - 2х3 + 8х3 - 16х2 +
+ 27х2 - 54х + 60х — 120 = (х — 2) (х3 + 8х2 + 27х + 60).
Теперь подбираем корень уравнения х3 4-8х2 4-27x4-60 = 0.
Можно угадать х=—5 (так как (~-5)*( —4)-( —3)-( —2)= 120).
Выделим множитель х4-5:
х34-5х24-Зх24-15х4-12х4-60=(х4-5) (х2 4-3x4-12).
У оставшегося квадратного трехчлена х2 4- 3x4- 12 вещественных
корней нет.
Четвертый способ. Он основан на тождестве
х (х4-1) (х4-2) (х4-3)4-1 =(x24-3x4- I)2 (см. задачу 3 в конце гла-
вы). Получаем:
(/+зх+1)>_121^[
Ответ: xt — —5, х2 = 2.
2) Уравнение с модулем | х2 + 2х | + х2 + х=5.
Уравнение равносильно совокупности двух систем:
( х2Н-2х+х2+х = 5, ( — х2 — 2х + х2+х = 5,
I х2 + 2х>0; |х2 + 2х<0.
Рекомендуем сначала решить квадратное неравенство
х2 + 2х>0.
Ответ: xi =—х2=1.
3) Иррациональное уравнение -^х-\-2=х.
Уравнение равносильно системе г х+2 = х2, Заметим, что
I х^0.
указывать ОДЗ (х+2^0) нет надобности, так как всякое решение
уравнения, полученного после возведения в квадрат, автомати-
чески попадет в ОДЗ: ведь если верно, что х+2 = х2, то x+2i>0,
так как х2^0. Наоборот, пропуск условия х^0 нарушает равно-
сильность.
Ответ: х=2.
4) Показательное уравнение 2х+1+22-х = 9.
Замена 2х=у немедленно приводит его к алгебраическому
2f/+y=9.
Ответ: х, = — 1, х2 = 2.
286
5) Логарифмическое уравнение log2 (Зх —х2)= 1 — log2 (х—1).
При потенцировании теряется информация об ОДЗ. Поэтому
выпишем ОДЗ в явном виде:
( Зх — х2>0,
|х—1>0.
Решением этой системы неравенств будет интервал (V; 3).
Теперь потенцируем, перенося логарифм в левую часть:
(Зх —х2) (х-1) = 2ох3-4х2 + Зх + 2 = 0.
Подобрав один корень х = 2, выделяем множитель (х —2):
х3 — 4х2 + Зх + 2 = х3 — 2х2 — 2х2 + 4х — х + 2 = (х — 2) (х2 — 2х — 1).
Корни квадратного множителя: х= 1 ±д/2. Сопоставляя с ОДЗ,
получаем ответ: Х| =2, х2= 1 + д/2.
24
6) Тригонометрическое уравнение 3 sin x-f-4 cos х = —.
Делаем замену sin х= ^2 , cos х= *^*2 , где / = tg-^-, и
получаем уравнение
3/ I 2 (1 —/2) _ 12
1+/2 “Г 1+/2 5 ’
откуда /1=-^-, ^2==ТГ’ т‘ е‘ х = 2 arctg-^-4-2лп, x=2arctg-^-+
+ 2лп. Так как уравнение несовместно с условием cos х = — 1, то
при переходе к тангенсу половинного угла потери корней не про-
изошло.
3. Приближенные методы вычисления корней
Во многих случаях при решении уравнений их корни находят
приближенно. Для этого в математике накоплены различные мето-
ды приближенных вычислений. Обычно они дают последователь-
ность приближений к искомому числу. Примером может служить
способ извлечения квадратного корня, знакомый из курса ал-
гебры.
Простейшим методом приближенного вычисления корней явля-
ется метод половинного деления. Допустим, что известен проме-
жуток [a; ft], на котором лежит искомый корень. Приближенно
строится график функции f на этом промежутке (например, так,
как это изображено на рисунке 142).
Вычисляя f (а) и f (ft), видим, что эти числа разных знаков:
f (а)<0, f (ft)>0. Вычисляем далее значение функции f в середине
отрезка [a; ft]. Из двух половин отрезка [a; ft] берем ту, на концах
которой знаки функции различны. Очевидно, корень х лежит
внутри нового отрезка. Совершаем с ним ту же процедуру: делим
287
его пополам, вычисляем значение функции f в точке деления и бе-
рем ту половину отрезка, на концах которой знаки функции f
различны. Так мы получим последовательность отрезков, длина
которых убывает и внутри которых лежит искомый корень. Это
и означает, что получена последовательность приближенных зна-
чений искомого корня.
И. Ньютону принадлежит так называемый метод касательных.
Об этом способе приближенного вычисления корней можно по-
лучить представление, рассматривая рисунок 143. Приближенные
значения корня получаются построением касательных к графику
функции. Уравнение касательной написать нетрудно, а затем нуж-
но найти точку ее пересечения с осью х, что и дает приближенное
значение корня функции.
Вместо касательных можно проводить хорды (рис. 144) и по-
ступать аналогично (метод хорд).
Контрольные вопросы
1. Сколько корней имеет линейное уравнение ах + Ь = 0?
2. Сколько корней имеет квадратное уравнение х2 + рх+^ = 0?
3. Сколько корней имеет уравнение хп = а при различных
п и а (п — натуральное число) ?
4. Сколько корней имеет простейшее показательное уравне-
ние ах = Ь при различных а и Ь?
5. При каких значениях а уравнение sinx = a не имеет ре-
шений?
6. В чем состоит графический метод решения уравнений?
7. Какие приближенные методы нахождения корней уравнения
вы знаете?
8. Почему при решении уравнения вида f (х) = 0 стараются
разложить на множители левую часть?
9. Придумайте тригонометрическое уравнение, которое с по-
мощью введения нового неизвестного сводилось бы к квадратному.
10. Придумайте показательное уравнение, которое с помощью
замены неизвестного сводилось бы к линейному.
288
§ 2. НЕРАВЕНСТВА
С ОДНИМ НЕИЗВЕСТНЫМ
1. Общие приемы
Решение неравенств (так же как и решение уравнений) обыч-
но распадается на два шага — преобразование неравенства к од-
ному из стандартных и решение стандартного неравенства. К
стандартным неравенствам мы отнесем следующие типы нера-
венств, изученные нами ранее (из возможных четырех знаков
неравенства мы выбираем один):
1. Линейное неравенство ах-±Ь>0.
2. Квадратное неравенство ах2 + Ьх + оО.
3. Степенное неравенство хп>а.
4. Показательное неравенство ах>Ь.
5. Логарифмическое неравенство logax>ft.
Решение стандартных неравенств было рассмотрено нами в
предыдущих главах.
Общие приемы решения уравнений и неравенств аналогичны.
Так же как и для уравнений, при решении неравенств помогает
разложение на множители. Как уже отмечалось, решение неравен-
ства вида □•Д>0 можно заменить решением двух систем
неравенств: /□>(), (□<(),
( Д >0 и ( Д <0.
В то же время если множители □ или л являются линейными
или произведениями линейных, то не стоит сводить решение
неравенства к системе: проще применить метод интервалов
(см. § 3 гл. I), который сильно сокращает количество вычислений.
Важнейшим методом решения неравенств является метод за-
мены неизвестного. Мы проиллюстрируем его примером ре-
шения неравенства
|22х + 3_2х + 5+19|
Прежде всего сделаем замену
2x+l=z, тогда 22x+2=z2 и неравен-
ство примет вид 12z2—16z + 19|<Z5.
Изобразим график квадратного трех-
члена y = 2zi— 16z (рис. 145). Реше-
нием неравенства |у + 19|^5, как
видно из графика, является объеди-
нение двух отрезков [zi; Z2] и [z3; z4],
где zi, z4 — решения уравнения у =
= — 14, a Z2, z3— решения уравне-
ния у= — 24. Решая эти уравнения,
находим zi = l, z2=2, z3=6, z4 = 7.
Учитывая, что функция z является
возрастающей, решаем стандартные
неравенства и записываем ответ:
[-1; 0]U[log2 6-1; log2 7- 1].
10 Заказ 836
2. Примеры решения неравенств
1) Алгебраическое неравенство
Перенесем правую часть влево, приведем к общему знаме-
нателю и разложим на множители числитель дроби:
— <0«ф>
х+1 ~х+3 х+2
x2 + 5x+6+2(x2 + 3x+2)-3(x2 + 4x + 3) п
(х+1)(х+2)(х + 3)
------—*+1 < 0 о -> 0
(х+1)(х+2)(х+3)-------------------------(х+ 1)(х+2) (х+3)
Применяя метод интервалов, с помощью числовой оси (рис. 146)
решаем неравенство и получаем ответ: х<—3, — 2<х< —1,
х> 1.
2) Иррациональное неравенство -\]х-\-2>х.
ОДЗ: х-|-2^0ох^—2.
Если иррациональное уравнение мы смело возводили в квад-
рат, так как всегда можно было проверить нарушение равносиль-
ности, подставляя корни полученного уравнения, то при решении
неравенства нужно поступать аккуратнее.
Заметим, что неравенство а>Ь, где а^О, &<0, является
всегда верным, какие бы значения указанных знаков ни под-
ставляли вместо а и Ь. Поэтому если х<0, то неравенство
-\/х4-2>х будет верным. Итак, все отрицательные числа, входя-
щие в ОДЗ, будут решениями неравенства. Нанесем их на число-
вую ось. Пусть х^О. Возведение в квадрат теперь не нарушает
равносильности:
х + 2>х2ох2 —х—2<0.
Корни квадратного трехчлена х, = — 1, хг = 2 наносим на чис-
ловую ось; решением неравенства будут числа 0^х<2.
Ответ: —2^х<2.
3) Логарифмическое неравенство log । —
Сначала преобразуем правую часть:
2.
[A_-2 = log2 10-2 =-log^ 10 —log—log,,
Рис. 146
290
Рис. 147
Стандартное логарифмическое неравенство log । D^log i -|-
{2
□ < —, Решаем каждое неравенство
э
□ >0.
системы методом интервалов, предварительно сделав преобразо-
вания:
х 2 — (2х2 —7х —4)
х2 —х —2 5 “ 5(х+1)(х-2) '
Корни числителя: х\ = ——, х2 = 4. Решение системы неравенств
изображено на рисунке 147.
Ответ: —^-^х<0, х^4.
Контрольные вопросы
1. Каким может быть множество решений линейного неравен-
ства?
2. Какие типы числовых множеств могут получиться в ответе
при решении квадратного неравенства ax^+ftx-f-c^O?
3. Какой вид может иметь множество решений неравенства
хп^а при различных п и а?
4. При всех ли а и b неравенство ах>Ь имеет хотя бы одно
решение?
5. Может ли логарифмическое неравенство logax<ft быть
верным при любом положительном значении х?
6. Можно ли при решении неравенства умножить обе его части
на х2 + 1?
7. Сформулируйте, что происходит с неравенством при умно-
жении обеих его частей на выражение f (х).
8. Приведите пример логарифмического неравенства, не имею-
щего решений.
9. Левая часть неравенства является произведением трех
линейных множителей (в правой части нуль). Подсчитайте, сколь-
ко случаев вам придется рассмотреть, перебирая все комбинации
знаков множителей, и сколько случаев, используя метод интер-
валов.
10. Приведите пример неравенства, множество решений кото-
рого состоит из двух чисел.
291
§ 3. СИСТЕМЫ УРАВНЕНИЙ
1. СпосоС подстановки
Системы уравнений появляются при решении задач, в которых
неизвестной является не одна величина, а несколько. Эти вели-
чины связаны определенными зависимостями, которые записы-
ваются в виде уравнений.
Если система имеет хотя бы одно решение, она называется
совместной. Если решений у системы нет, она называется несов-
местной. Слово «несовместность» наглядно показывает, что урав-
нения системы накладывают несовместимые друг с другом условия,
которым должны удовлетворять неизвестные. Например, система
I %4-£/ = 2 несовместна, потому что сумма чисел х и у не может
одновременно равняться единице и двум.
Одним из основных способов решения систем является способ
подстановки. Рассмотрим, например, систему двух уравнений с
двумя неизвестными х и у. Часто удается одно уравнение преоб-
разовать так, чтобы одно неизвестное явно выражалось как
функция другого. Тогда, подставляя его во второе уравнение, мы
получим уравнение с одним неизвестным. Приведем примеры.
1- ( х24-£/2 = 25, 2. f х24-£/2 = 5,
£/=1. = 3
3 __1_3_—2 4. ( 2х + Зг/= 4хг/,
\ху=Л. \*+У=Тху.
В каждой из четырех систем второе уравнение системы мож-
но решить относительно у, т. е. преобразовать к виду y = f(x):
1. х — у= 1 о у = х— 1.
2. х2 + у = 3о у = 3 —х2.
3. ху = 3оу = ^.
4. .
Тх-1
Подставляя y — f(x) в первое уравнение системы, получим
уравнение с одним неизвестным:
1. х2 + (х-1)2 = 25.
2. х2 + (3-х2)2 = 5.
3. —+х = 2.
X
4. 2х+—.
4х-1
292
Решая уравнение, находим его корни — значения неизвестно-
го х, а затем для каждого из них находим соответствующее зна-
чение у по формуле y = f(x):
1. х2 + (х—1)2 = 25 о 2х2 —2х —24 = 0.
2. х2 + (3 — х2)2 = 5 о х4 — 5х24-4 = 0 о х2 = 4, х2=1.
Уравнение имеет четыре корня, а система — четыре решения:
rxi = l, гх2= — 1, |х3 = 2, |х4—— 2,
(//1=2; (//2 = 2; (z/3= — 1; (r/4= — 1.
3. х-|-±-=2ох2-2х+1=0ох= 1.
Ответ: f х~ 1’
Ответ: rxi=0, г х2 = 1,
|//|=0; (//2 = 2.
Способ подстановки возможен не всегда, а кроме того, не
всегда выгоден и тогда, когда возможен. Часто из уравнений
системы удается получить новое уравнение — их следствие — бо-
лее простого вида. Так, в четвертом из рассматривавшихся выше
примеров можно, исключив произведение ху, стоящее справа,
получить:
2х4-Зг/ = 4х£/,
. 3 ’ =>4-(2x + 3u) = 4(x + u).
х + у = — Ху 2 v 1 v 1
Последнее соотношение является линейным, и из него соотно-
шение между х и у легче находится так: у = 2х.
Важным приемом, часто позволяющим упростить систему, яв-
ляется замена неизвестных. Так, во втором примере полезно за-
менить х2 на z и получить более простую систему:
( ? + у2=5,
[? + У = 3.
293
Системы двух уравнений с двумя неизвестными и их решения
можно изобразить графически на координатной плоскости. На ри-
сунке 148 изображены кривые уравнений написанных выше систем.
Точки пересечения кривых (а точнее, их координаты) — решения
систем.
Есть некоторые типы систем, для которых известны стандарт-
ные методы решения. Рассмотрим два из них: симметричные
системы и линейные системы.
2. Симметричные системы
Симметричными называются системы, составленные из выра-
жений, являющихся симметричными относительно всех неизвест-
ных. Приведем примеры различных симметричных выражений
для двух неизвестных: х и у.
1. U\=X-\-y. 2. U2 = xy. 3. U3 = X2 + */2.
4. щ = -—|—5-. 5. u5 = x3 + */3. 6. u6=——+ .
x У u у 1 X
294
Решение простейшей симметричной системы г х -\-у — а,
основано на теореме, обратной теореме Виета: х и у, удовлетво-
ряющие указанной системе, являются корнями квадратного урав-
нения /2 —а/ + р=0. Этот вывод можно получить, подставив из
первого уравнения во второе у — а — х.
Итак, для решения простейшей симметричной системы надо
составить квадратное уравнение с заданными суммой и произве-
дением корней и решить его. Найденные корни будут значения-
ми х и у.
Пример 1.|х-|-£/ = 3,
(ху = — 4.
Составляем квадратное уравнение t2 — 3t — 4 = 0, откуда
fi=4, /2== — 1. Ответ: jxi=4, г х2= — 1,
(//! = —1; (//2=4.
Решение других симметричных систем основано на том, что
всякое симметричное относительно х и у выражение можно выра-
зить через и = х + у и v = xy.
Приведем примеры таких выражений:
х2+у2 = (х + у)2 — 2ху = и2 —2v\
J__।_1 __ х+у _ и .
X ' у ху и ’
*3+у3=(*+г/) (х2 + г/2—ху) = и(и2 — 3v);
х — 1 । у— 1 х2-х-\-у2—у и2 — 2и—и
У ' х ху v
Делая в симметричной системе замену x4-r/ = u, xy = v, полу-
чаем более простую систему относительно и и и, а затем, найдя
численные значения и и и, приходим к решению простейших
симметричных систем: гх4-г/ = и,
(х£/=и.
Пример 2. ( х24-£/2 = 25,
( х + у = 7.
Далее решаем систему р + // = 7,
(ху=12.
Пример 3. ( х34-£/3 = 7,
[х2 + 3ху + у2= — 1.
Воспользуемся найденным выше выражением х3+у3 через
и И VI
295
( и (и2 — Зи) — 7,
( и2 + v = — 1.
Из второго уравнения v— — 1— и2 подставляем в первое:
и* + 3и (и2+1) = 7,
4u3 + 3u —7 = 0,
(и- 1) (4u2 + 4u + 7)=0,
и—1=0, а=1,
4u2 + 4u + 7 = 0 — корней нет.
Далее решаем систему (х-±у=\,
\ху = — 2.
3. Линейные системы
С системами линейных уравнений мы встречались ранее. В ос-
новном рассматривались системы двух линейных уравнений с дву-
мя неизвестными вида ( а\х-\-Ь\у — С\,
I а2х + Ь2у = с2.
Исследование этой системы можно повторить по информацион-
ной схеме XVI.
В практике встречаются системы линейных уравнений с боль-
шим количеством неизвестных. Так, в задачах математической
экономики можно найти системы, состоящие из нескольких сотен
уравнений с таким же примерно числом неизвестных. Для их ре-
шения разработаны мощные машинные методы. Эти методы
в основном имитируют знакомый вам метод подстановки, которым
в принципе можно решить любую такую систему. Основную
роль при этом играют компактные способы записи систем и их
преобразований. Представьте только себе: система из тысячи
уравнений с тысячью неизвестными содержит миллион коэффи-
циентов.
Рассмотрим более скромный пример — систему трех линейных
уравнений с тремя неизвестными:
p + 2y + 3z = 2,
J 2%4-Зг/ —4z= — 5,
(зх + */ + 2 = 3.
Будем решать систему методом исключения неизвестных. Что-
бы исключить х из второго и третьего уравнений, надо вычесть из
них первое, умноженное соответственно на 2 и на 3.
Получим систему
{x + 2r/ + 3z = 2,
_//-10z=-9,
— 5у — 8z= —3.
296
Удобно умножить второе и третье уравнения на ( — 1), а за-
тем из третьего уравнения вычесть второе, умноженное на 5. По-
лучим «треугольную» систему
{х -(- 2у Ч" == 2»
r/+10z = 9,
42z = 42.
Из последнего уравнения находим z=l. Подставляя в пре-
дыдущее уравнение, находим у=9 — 10= — 1.
Подставляя z=l, у= — 1 в первое уравнение, получим
*4-2 (— 1) + 3-1 =2, откуда х=1.
Ответ: х = 1, z/ = — 1, z = 1.
Показанный на этом примере способ решения линейной систе-
мы называется методом Гаусса по имени великого немецкого ма-
тематика, жившего в первой половине XIX в. Метод Гаусса с раз-
личными модификациями используется при решении линейных сис-
тем с помощью вычислительных машин.
Контрольные вопросы
1. Какая система уравнений называется совместной?
2. Приведите пример несовместной системы.
3. Что такое решение системы уравнений?
4. Как графически изобразить решение системы двух уравне-
ний с двумя неизвестными?
5. Каким методом решают линейные системы уравнений?
6. В чем состоит теорема, обратная теореме Виета?
7. Как выражается сумма квадратов чисел через их сумму
и произведение?
8. Приведите примеры симметричных относительно х и у выра-
жений.
9. Как симметричность выражения f (х; у) скажется на графи-
ке зависимости f (х\ у) = 0? Приведите примеры.
10. В чем состоит метод подстановки?
ЗАКЛЮЧИТЕЛЬНАЯ БЕСЕДА
1. Тождества
Мы определили тождество как равенство двух выражений,
справедливое при всех допустимых значениях букв, входящих в эти
выражения. Такая точка зрения свойственна теории функций —
мы рассматриваем две части равенства как функции и называем
эти части тождественно равными, если они совпадают как
функции, т. е. если они при одних и тех же значениях аргумента
принимают равные значения. Возможна другая точка зрения на
тождества, которая более тесно связана с алгеброй.
297
Колмогоров Андрей Николаевич
(1903—1987) —
советский математик, один из создателей
и автор общепринятой системы аксиом сов-
ременной теории вероятностей. Автор глубо-
ких идей и результатов в топологии, мате-
матической логике, гидродинамике и небес-
ной механике.
«Обобщение понятия часто бывает полез-
но для постижения его сущности».
А. Н. Колмогоров
В алгебре многочлен рассматривается не как функция, а
как некоторое формальное выражение, составленное из одночле-
нов. Мы умеем совершать различные операции над многочленами,
не задумываясь при этом над тем, какие значения можно подстав-
лять в многочлен вместо букв. В алгебре два многочлена равны,
если после приведения подобных членов окажется, что они сос-
тавлены из одинаковых одночленов, т. е. если выполняется фор-
мальное, почленное равенство. Так, проверяя тождество а3 — Ь3 =
= (а — b) (а2 + aft + £г), мы совсем не занимаемся подстановкой
в обе части значений аи b (тем более что неясно, сколько их надо
подставлять), а преобразуем правую часть и убеждаемся, что она
формально совпадает с левой.
Проверке формального совпадения многочленов может помочь
их запись, принятая в качестве стандартной. Например, если
многочлены от одной буквы х записывать по убывающим степеням
(как мы привыкли), то тождество многочленов будет означать ра-
венство их степеней и совпадение коэффициентов, стоящих на
одинаковых местах.
Возникает естественный вопрос: как связаны между собой
функциональное и алгебраическое определения тождества? Разу-
меется, если два многочлена равны формально, то они принимают
одинаковые значения при всех значениях букв. Обратное заклю-
чение составляет содержание трудной теоремы алгебры — теоремы
о тождестве. Поясним смысл этой теоремы для простейшего случая
многочленов от одной буквы х.
Прежде всего заметим, что от равенства f(x)=g(x) всегда
можно перейти к равенству f (x) — g (х) = 0, как бы мы ни определя-
ли понятие тождества. Это означает, что теорему о тождестве
можно доказывать в таком упрощенном варианте: если многочлен
F (х) при всяком значении х равен нулю, то этот многочлен нуле-
вой, т. е. не содержит ни одного ненулевого одночлена. Если
многочлен F (х) имеет степень п, то, оказывается, достаточно
298
подставлять лишь и 4-1 значение х. Иными словами, если мно-
гочлен F (х) степени п имеет п4-1 корень, то этот многочлен
нулевой. В такой формулировке теорема допускает уже не очень
сложное доказательство.
Итак, полезно запомнить, что ненулевой многочлен не может
иметь корней больше, чем его степень. Возможна другая формули-
ровка: если два многочлена степени п совпадают в п4-1 точке,
то эти многочлены формально равны. Последняя формулировка
очень полезна при доказательстве различных тождеств (см. за-
дачи) .
В применении к многочленам первой степени нам знакома
геометрическая формулировка этой теоремы: через две точки про-
ходит только одна прямая. Аналогично для совпадения двух
квадратных трехчленов достаточно равенства их значений в трех
точках.
Кроме равенства многочленов, можно определить равенство
дробей с алгебраической точки зрения: две дроби и
считаются равными, если формально равны многочлены f\ (x)g2 (х)
И g\ (x)f2 (х).
В более усложненном варианте алгебраический подход воз-
можен и к тригонометрическим тождествам. Так, тождествам,
содержащим степени sin х и cos х, можно придать условный
характер: доказать тождество, используя из тригонометрии лишь
соотношение sin2 x-j-cos2 х= 1. Такую задачу можно решить,
делая лишь алгебраические преобразования и не вспоминая о том,
что такое синус и косинус. Приведем пример условного тождества
в алгебре:
если а4-6 4-с = 0, то а3 4- b3 -}-с3 = 3abc.
Другие примеры условных тождеств приведены в задачах.
2. Доказательство неравенств
Наряду с тождествами — равенствами, выполняющимися тож-
дественно,— существуют тождественно выполняющиеся неравен-
ства, т. е. неравенства, верные при любых допустимых значениях
входящих в них букв. Приведем простейшие примеры таких тож-
дественно выполняющихся неравенств.
1) х2>0;
2) а2-\-Ь2-\-с2^0, причем равенство нулю возможно лишь
при а = Ь = с = 0;
3) х24-рх4"<7>0, если р2 — 4^<0.
Задачи на доказательство неравенств (т. е. на доказатель-
ство того, что неравенство выполняется при всех допустимых
значениях букв) решаются с помощью цепочки преобразований,
приводящей к равносильному известному неравенству.
299
Пример. Доказать неравенство где а^О, £>0.
Делаем цепочку преобразований:
а^-~оа4”^2 -у/ab о а —2 о (-\/а — V^)2^0-
Последнее неравенство всегда верно, следовательно, всегда верно
исходное.
Полученное неравенство (его называют неравенством о сред-
нем арифметическом и среднем геометрическом двух чисел) мож-
но применять к доказательству других неравенств. Убедитесь,
например, что следующие неравенства являются следствиями
доказанного:
1) при а>0;
2) если а& = 1, то а-\-Ь^2 (где а>0, 6>0);
3) если то (14-ai)(1+а2)>4 (где fli>0, а2>0);
4) a,+<’.3 4±£i±^>afecrf (где a>0, с>0, </>0).
Использование производной дает мощный способ доказатель-
ства неравенств с одной переменной. Этот способ основан на
следующем соображении: если в точке х0 выполняется условие
f(xo)>O и для всех х^х0 выполняется условие f' (х)>0, то для
всех х^хо верно неравенство f (х)>0 (разберитесь в справедли-
вости сформулированного правила).
Пример (неравенство Бернулли).
(1 + %)*> 1 + fex (где х^О, 1).
Для доказательства рассмотрим функцию y = f(x), где
f (x) = (14-x)*-l-fex. Имеем f (0) = 0, f' (x) = fe (1 +x/"‘-k =
= fe((l 4-x)/?~l — 1). Так как x^O, fe^l, to (l+x)*-1^! и
f' (x)>0. Значит, при xJ>0 функция f возрастает и при всяком
х^О имеем f(x)^f (0) = 0, что и требовалось доказать.
3. Алгебраические уравнения
Алгебраическое уравнение — это уравнение вида
xrt4“tin_ixrt 1 -р... -р а\х 4- ао = 0.
Число п называется степенью уравнения. Уравнение первой сте-
пени (или линейное уравнение) решается с помощью арифмети-
ческих операций. Формула для решения уравнения второй степени
(или квадратного уравнения) известна с глубокой древности. В нее
входит операция извлечения квадратного корня. Решение урав-
нения произвольной степени в течение многих веков считалось
основной задачей алгебры.
300
Постановка вопроса о решении алгебраического уравнения
может быть различной. Почему «не решается» данное нам уравне-
ние? Рассмотрим возможные ответы на этот вопрос.
1) Нам «не хватает» имеющихся чисел. Уравнение х2 + 2х +
-|-5 = 0 не имеет вещественных корней. Можно, конечно, на этом
утверждении остановиться. Однако полезно, как это было сделано
еще в XVI в., ввести комплексные числа, с которыми вы немного
знакомы. Комплексное число имеет вид a + ftz, где а и b — ве-
щественные числа, а символ i (мнимая единица) обозначает та-
кое число, для которого i2 = — 1. Комплексные числа х\ = — 1 — 2i
и х2 = — 1 + 2/ являются корнями написанного выше квадратного
уравнения.
Если мы разрешим числу х принимать не только вещественные,
но и комплексные значения, то отпадет вопрос существования кор-
ня алгебраического уравнения. В 1831 г. Гаусс доказал замеча-
тельную теорему, которую часто называют основной теоремой
алгебры: всякое алгебраическое уравнение имеет хотя бы один
комплексный корень.
2) Мы не можем разложить левую часть уравнения на мно-
жители. Возьмем, например, уравнение х5 + х+1=0. Не сразу
бросается в глаза, что левую часть можно разложить на множи-
тели:
х5+х+ 1 = х5 — х2 + х2 + х + 1 = х2 (х3 — 1)4-х2+х+1 =
= (х2+%+ 1) (х3 — Х2+ 1)-
После разложения на множители получим уравнения меньших
степеней: х2 + х+1=0 и х3 —х2+1=0. Однако этот прием про-
ходит далеко не всегда. Так, многочлен х5 —х+1 уже нельзя
разложить на множители с целыми коэффициентами. Известен
алгоритм, который позволяет разложить любой многочлен с целы-
ми коэффициентами на множители с целыми коэффициентами,
если это возможно. Частный случай применения этого алгоритма
мы неоднократно использовали: если многочлен xn + an_|Xn-l +
+ ... + ао с целыми коэффициентами имеет множитель вида х —с,
где с — целое число (являющееся, конечно, корнем многочлена),
то свободный член а0 делится на с. Эта теорема позволяет перебо-
ром делителей свободного члена и проверкой найти целые корни
многочлена с целыми коэффициентами.
3) Мы не знаем общей формулы для корней уравнения. Прос-
тая формула корней квадратного уравнения вызывала желание
математиков найти формулы корней уравнения более высокой
степени. В XVI в. эта задача была решена для уравнений 3-й
и 4-й степеней. Хотя эти формулы громоздки и не употребляются
для реального вычисления корней, принципиальное их значение
велико: они позволяют записать корни уравнений 3-й (и 4-й) сте-
пеней как некоторую функцию от коэффициентов этих уравнений.
Эта функция содержит операции извлечения корней 3-й (и 4-й)
степеней. Долго изучавшийся вопрос о том, существует ли
30!
формула, выражающая корни уравнения 5-й степени через его
коэффициенты с помощью радикалов, получил отрицательное
решение в работах Абеля (1802—1829) и Галуа
(1811 — 1832) в начале XIX в.
Итак, как правило, для алгебраического уравнения высокой
степени мы не можем указать общей формулы его корней. Для
приближенного вычисления корней используют методы анализа,
примеры которых мы рассматривали в § 1 этой главы.
Различные приближенные методы нахождения корней уравне-
ния часто используют следующее соображение, которое мы неод-
нократно отмечали раньше: если на концах промежутка функция
y = f(x) принимает значения разных знаков, то внутри этого про-
межутка уравнение f (х) = 0 имеет корень (рис. 142). Это утверж-
дение верно для всех непрерывных функций. С его помощью
нетрудно, например, доказать, что всякий многочлен нечетной
степени имеет вещественный корень. Например, кубическое урав-
нение x34-ax24-ftx + c = 0 всегда имеет хотя бы одно решение,
так как левая часть при больших по модулю и отрицательных х
меньше нуля (слагаемое х3 «перевесит» все остальные), а при
положительных больших х станет больше нуля.
Для разрывных функций сформулированное утверждение
может оказаться неверным, как показывает простой пример функ-
ции £/ = у-, не имеющей корней, но принимающей значения раз-
ных знаков.
Контрольные вопросы
1. Какие определения тождества многочленов вы знаете?
Чем они отличаются друг от друга?
2. Сколько корней может иметь многочлен степени п?
3. Каким количеством точек определяется многочлен п-й
степени?
4. В каком количестве точек достаточно проверить совпадение
значений двух многочленов четвертой степени, чтобы доказать
их тождественное равенство?
5. Приведите примеры тождественно выполняющихся нера-
венств.
6. В чем состоит неравенство для среднего арифметического
и среднего геометрического двух чисел? Предложите его обобще-
ние для п чисел.
7. Как с помощью признака монотонности функции можно
доказывать неравенства с одной переменной?
8. В чем состоит основная теорема алгебры?
9. Начиная с какого п не существует общей формулы реше-
ния уравнения n-й степени?
10. Может ли многочлен пятой степени не иметь веществен-
ных корней?
302
ЗАДАЧИ К ГЛАВЕ VI
Область допустимых значений выражения
1. Найдите ОДЗ выражений:
1)° X . x— 1 ’ 2) x+1 . x3 +1 *
3) x —2 . x2 + 4x—5 ’ 4) Vх 4-5;
5) -y/x — x2; 6) -\/x+2+-\/2 —x;
7) 1 . V*2—4 8) 1 . sin 2x *
9) tg 3x; 10) ctg(x+-J-);
H) tgx + ctgx; 12) 3^;
13) lg(l-2x); 14) 1 lg(x2—x)
2. Изобразите на плоскости xy ОДЗ выражений:
1)
X — У
5) Vх 4-у;
7) ^У — Х2-,
9) tg(x+y);
11) arcsin (х+у);
4) -\jl—x2—y2-,
6) Vx+Vy;
8) -----!-----;
COS X — cos у
10) log2xy;
12) arcsin x +arcsin y.
Тождества
3. Докажите тождества:
1) a6 — b6=(a — b) (a + b)(a2-\-ab-\-b2) (a2 —ab-\-b2\,
2) (a-\-b4-c)2=a2 -\-b2+c2-\-2ab-\-2bc + 2ac;
3) a3 + b3 + c3 — 3abc=(a + b + c) (a2-\-b2 + c2 — ab — be—ac);
4) (a+b)3 — a3 — b3 = 3ab (a + b)-,
5) a (a+1) (a+2) (a4-3)4- 1 = (a24-3a +1)2;
6) (л/?Нг14-а)(л/а?+’1-а)=1;
7) (a?4"^2) (O2 + &2) = (fl!|O2 4-^1^2)2 4"(a1^2— O2^l)2;
8) (o2 4" b2 4-c2) (oi 4" b2 4-ci)—(oiO2 4"^i^2 4"CiC2)2=
=(feic2 —b2Ci)2+(Cia2—c2ai)2+(aife2 —a2&i)2;
303
n\ (х-Ь)(х—с) , (х-с)(х—а) , (x-a)(x-b) ,.
' (a—b)(a—c) "Г (b — c)(b—a) “r (c-a)(c-b)
1 (П n2 (x~b)(x-c) । h2 । c2 (x—a)(x —<>) _ v2
' (a —Z>)(g —c) “T (b—c)(b—a) (c-a)(c-b) '
4*. Докажите условные тождества.
Если a+b + c = 0, то:
2) a5 6 + 65 + c5=-|-a&c(a2 + Z>2 + c2);
3) 5 (a3 + b3 + c3) (a2 + ft2 + c2) = 6 (a5 + b5 + c5);
лч /a — b । b — c । с — a \ / c . a . b \
4’ (.—+—+—) +r+—+7=7/
5. На каких множествах справедливы тождества:
1) 7(х—1)2=1—х; 2) lgx2 = 21g( —х);
3) |х2 — 2х| = 2х — х2; 4) logaax=x?
ОДЗ уравнения
6. Найдите ОДЗ уравнений:
1)° 77-7=7777; 2)° 7+=^=х;
3) 77^4 + 72^1=3; 4) ^CZZ=lg(4-x2);
5) log2(x2 —х—6)=—77; 6)* tg 79 —х2=1;
7)* arcsin 777=-2-; 8) lgx = arccosx;
9) 2 х =—\/х; 10)* 7sin х+7б—1.
Равносильность
7. Для каждой пары уравнений выясните, является ли одно из
них следствием другого. Предлагается форма ответа: (да,
да), (да, нет) и т. п. Например, ответ (нет, да) означает,
что второе уравнение не является следствием первого, а пер-
вое является следствием второго:
1) 2х—4=0 и х2 — х — 2 = 0;
2) х2 + 4х + 4 = 0 и х + 2 = 0;
3) х2+х-2=0 и х2 + 2х-3 = 0;
5) х3 = 27 и х3+7±_=27+гЬ_;
6) (х-3)(х + 2)=6 и (х-З)2 (х + 2)2 = 36;
304
7) х2 —х=1 и (x2 —x)2 = l;
8) x2—x+5=4 и (x2—x+5)2 = 16;
9) (x+1) (x-3)2=0 и (x+1)2 (x-3)=0;
10) ^/(x+l)2 = l и x=0;
12) (x+3)(x-2)=l и lg(x+3)(x-2)=0;
13) (x+3)(x-2)=l и lg (x + 3)+lg (x-2)=0;
14) (x—1)(4x5—l)=x—1 и 4x5 —1 = 1;
15) (x—2) (x3 —7)=x—2 и x3 —7=1;
16) x4=9 и x2=3;
17) ~\jx— 1 = 1 —x и x— 1 =(1 — x)2.
8. Добавьте дополнительные условия так, чтобы были равно-
сильны уравнения:
1) Н- = 1 и П = Д;
2) □ •Д = 0«ДиП = 0;
3) л/а = Д и П = Д2;
4) УЁГ=-/д и П = Д;
5) 21g □=! и □ 2 = 10;
6) □ = Д и sin D=sin Д;
7) Пд = 1 и Д =0;
8) ПД = П° и Д = 0;
9) I □ I = А и □ = Д.
9. Докажите следующие теоремы о равносильности неравенств:
1) гП>0, 2) га>о,
Г I Д>0, _ г1 Д>0,
□ •д>0о —>0о
□ <0,
Д<0;
3) 1 □ > log । □ <log । д;
305
5) f arcsin □> arcsin Д,
J |O|<1, oJ I □ I < 1,
[|Д|<1 (lAld;
6) l°l>A- [ □ < —A
7)
□ > A2,
A>0,
□ >0,
A <0.
Разложение на множители
10. С помощью разложения на множители приведите решение дан-
ных уравнений к решению более простых уравнений (не решая
сами уравнения):
1) х3 — Зх + 2 = 0;
2) 4х3 — 9х2 —х + 6 = 0;
3) 2 sin3 х — 5 sin2 х — 3sinx = 0;
4) 25х + 24х—5-23х + 3-22х-4-2х- 12=0.
11. Решите уравнения разложением левой части на множители:
1) х4 + 2х3-6х2 —7х+ 12 = 0;
2) х4 + 4х3 + 4х2+ 1 =0;
3) х5+х-2 = 0;
4) 1 + 2 sin х • cos х + sin х +cos х = 0.
Введение нового неизвестного
12. С помощью замены неизвестного приведите уравнения к более
простому виду (не решая получившихся уравнений):
1)° -\/х2 — Зх=х2 — Зх — 2;
2)* (Уб+у/35)х + (л/б -у/35)х=2;
3) 5 sin2 2х — 3sin2x = 2;
4) log2(x — 1) — logx—। 2= — 1.
Графическое решение
13*. Определите с помощью графика число корней уравнений:
1) 2Х = 3 —2х—х2; 2) log2 х=х2 + х —2;
3) sinx=-|-x—4) х5=10х—1.
306
Целые корни
14. Найдите целые корни уравнений:
1) х3 —6х2 +15х—14 = 0;
2) х3-6х2 +11х-6 = 0;
3) х5 — 2х4 — 4х3 + 4х2 — 5х + 6 = 0.
Алгебраические уравнения
15. Решите уравнения:
1) —г-----—=—!—•
’ 5x42 х—2 3-х ’
___6___I_3 _ 8______4___t
64-х — х2 х2 —4 х2—9 х2-|-х —6 ’
3) х4- 13х2 + 36 = 0;
4) Зх4—х2-2 = 0;
5) 2х6—Их3 —40 = 0;
6) 3(2х2 + Зх-2)2=8х2+4х-9;
7) (х2 + 3х — 4)2 + (х2 + Зх + 2)2 = 36;
8> (т+2)!+т='°;
9) (тт£-)2-тт£=20;
10) х4 + 2х3-6х2 + 2х+1 =0.
Уравнения с модулем
16. Решите уравнения:
1) |2х — 3|=5;
2) х2 + 2 |х2 —Зх|—5 = 0;
3) |2х+Н + |2-х|+х=11;
4) х |х|-3 |х2+х+1|+8 = 0;
5) ItttI ==2х + 6;
6)* 11 |х + 2| -5| -7| =5.
Иррациональные уравнения
17. Решите уравнения:
1) д/Зх2 —5х—12 = 10; 2) д/х2-5 = д/х+1;
3) 1 =х—\; 4) д/6 —х — х4 = х+ 1;
5) д/7+2-д/27^3=1; 6) д/С^+дДр^^-;
307
7) -\/5 + x2+75 — x2 = 4; 8) x/x—4 V* + 4 =3;
9) -\/x + 2 -\/x— 1 +"\/x —2 1—2;
10) V9Z^+V^=3-
Тригонометрические уравнения
18. Решите уравнения:
1) 2 cos (Зх- 1)=^-;
3) l_sin(2x—=-)=--J-;
□ \ □ / о
5) 2 + 2 tg х cos х=—!—+tg
7) cosxtgx = 0;
9) cos 2x = 2 sin2 x —3;
11) 4 — 3 cos2 x = 4 sin x cos x;
13) cos x—cos3 x=sin 2x;
15) 2 sin2 x + 5 cos x — 4 = 0;
17) 2 sin x + 5 cos x = 0;
18) cos2 x—3 sin x cos x + 2 si
19)* tg гт"т-"2 = л/3;
7 ь 1-I-х-Hr v
2) 3sin(f+f)=f;
4 л ftg (3x+l)=-7;
c; 6) tg3x=tgx;
8) sin x = sin x cos x;
10) tg(x+^-) + ctg x= -3;
12) 1+cos x=2 sin2 x;
14) sin6x=sin8x;
16) I+2 cos 2x = 8 cos x;
2 x=0;
20) sin x + cos x= — 1.
Показательные и логарифмические уравнения
19. Решите уравнения:
1)° 7Х = 343;
3) -Н=32;
(W
5) 2Х+3—2Х=112;
7) 2х+'+4х=8;
9) Зх+2=9х+1;
11) 4-Зх —9-2х = 5-6^;
13) 6х + 9х = 22х+1;
15> ^Нг=з';
17) е2х-'+ех=1+е-';
19) log8 (9х-3х-8) = 2;
2) 8Х=128;
4)° 11х-7=177-х;
6) 32х-2 + 32х = 30;
8) 5х=0,008;
/ л \ Зх— I Z е \ 2х — 9
"»+) =(f) ;
12) 2-25х — 5- 10х + 2-4х = 0;
14)* (д/7 + л/48)" + (V7-л/48)х= 14
16) |2Х- 11 + |2Х-2| = 1;
18) хх = 27;
20) х'« 1000х=тЬ-.
308
Алгебраические неравенства
20. Решите неравенства:
1) 2х2 + 5х-7<0;
3) х4-5х2 + 4>0;
5>
х2 4~ 2x4-3 _ о.
’ xs-4x+3'> d’
9) 5~7х <1;
’ х-Н ’
11) х (Х+ 1) (х+2) (х + 3)<
12)**г + ->>1.7 (x + -L);
2) Зх2-4х+1>0;
4) (х2 + х+1)2<5х2 + 5х-1;
gч хг-|~6х-|-15 q.
' х — 4 *
Q\ х— 10 1
») 7ЧТ<-Т’
ю) -LT-—+Чп->°;
' X— 1 X х-|-1
1 з \ 1 >
’ х24-2х-3 2x4-1 ’
Иррациональные неравенства
21. Решите неравенства:
1) л/2х + 7<х + 2;
3) -\/х + 9>х —3;
5) -\/8 —x+V* —3>3;
7)*
2) д/х + 4>х-2;
4) у'х2—х— 1 С1;
6) х-\/10 —х2>х2—6;
8) х + 8> 6 Vх—I-
Показательные и логарифмические неравенства
22. Решите неравенства:
1) l°g^ ( —х)>4;
3) 1g (х-5)-lg 2>-l-lg (Зх-20);
5) lg (x + 5)+lg (x-5)<2;
7) log3x + log3(x — 2)> 1;
9)° 2X>4;
11)° 2x+‘<-^-;
13)
15) |3x+2-11 <2;
2) log3(x-12)<2;
4) lg2 x + lg x3 + 2>0;
6) log^ (1 —2x)> — 1;
8) log, 2 <2;
10)° 9X>3;
12) 32x“'—3*-'>2;
14) 2X>5X;
16) log3_xx< —1.
309
Системы уравнений
23. Решите системы уравнений:
1) ( Зх + 5у=4,
I 7х—Зу = 24;
3) ( 2х2 — Зу2 = 24,
I 2х — Зу=О;
5) f x-j-xy=3,
t ху2 + ху3=12;
7) Г х~у + ху = 5,
I х — У—ху=— 7;
9) (2L+i.= 25
I ух 17 ’
(х2-|-у2 = 25;
11) f 2х — Зу — 6z= 10,
< x + y + 2z = 0,
^Зх + 2у —4z= —2;
2) г 2х—Зу=4,
| 4х — 6у = 5;
4) fx + 2y = 7,
J Зх—у—14,
1 2х+у=12;
6) ( х2 + у2 = 29,
1 ху=10;
8) ( х2-2ху+у2 = 25,
I 2х2 — 2ху—у2 — 11;
10) (x + 5y-2z = 5,
J 7х —Зу —4z = —9,
15х—y + 2z = 31;
191* ( ХУ — 1
’ 1 х+у 2 ’
XZ___ 1
2x—z ’
-J2—=1.
Зу -2z
Исследование систем с параметром
24. При каких значениях а прямые
(а+ 2) х + (а — 3) у + 2а — 1 =0
и
(а — 1) х + (2а — 6) у — (а — 1) = 0:
1) пересекаются; 2) параллельны; 3) сливаются?
25. При каких значениях т система
г (/п + 3) х + 2г/ = 2/?г,
I 2х-\-ту= 1
имеет единственное решение?
26. При каких значениях т системы уравнений имеют единствен-
ное решение, бесконечное множество решений, не имеют ре-
шений:
1) ( (т-рЗ) х — 2у = 5, 2) г (т — 5) х — 2у — т — 7,
|(т-Н)х + // = 7; [ (m+ 1) х + ту = 3т?
310
КОНТРОЛЬНОЕ ЗАДАНИЕ К ГЛАВЕ VI
Вариант 1
1. Решите системы уравнений:
а) (х+у — z=2, б) (х + у = 5,
J 2х — у — 2 = 0, |х2—у2 = 15.
1 Зх+2у—6z= — 2;
2. Решите графически:
а) 3х = 11 — х; б) г х2 -j-y2=4,
|х2 — у=2.
3. Выясните, какие из следующих неравенств имеют отрицатель-
ные решения:
а) х2 — 99х—100>0; б) -\/х —2>х;
в) 32х-х!>1; г) log2 x+log4 (х + 2)>2;
д) sin2x<4-.
4
Вариант 2
1. Решите системы уравнений:
a) (2x—y + z=4, б) (x(x+y + z) = 7,
J х+Зу —2z= —4, J у (x+f/+z)= 14,
1 3x4-i/ + 5z = 7; 1 2 (x4-z/-j-z) = 28.
2. Какие из следующих уравнений имеют ровно один корень:
а) 23х-5 = 3'-х; б) 9х2+12х+4 = 0;
в) х4 —х2—10=0; г) sin2 Зх+5 sin х= 11 tg2 5х;
Д) log3-^j-=l; е) е3х-' = 1— х?
3. Решите неравенства:
а) у/2*+3>х; б) logx(x+-£-)> — 1.
Вариант 3
1. Решите системы уравнений:
ху __ 1
Зх—2у
2xz___।
x-f-z ’
^3^2^___,
4y—z
6) rx2 + l/2=13,
I x3+y2 = 19.
311
2. Даны функции f(x)=x3 — х и g (х)=х3 -\-х.
а) Решите уравнение
2f(x)+g(x)=0.
б) Решите неравенство
в) При каких значениях а уравнение f (x) = ag (х) имеет ровно
три корня?
3. Решите неравенство
log, 2-log2x 2>log4x 2.
4. Сколько корней на отрезке [0; 1] имеет уравнение
8х (2х2 - 1) (8х4 - 8х2 +1) = 1 ?
ЗАДАЧИ НА ПОВТОРЕНИЕ
СВОЙСТВ ФУНКЦИЙ
Рациональные функции
1. Дано квадратное уравнение х2 —4x-f-a—1 =0.
а) При каких значениях а уравнение имеет два корня?
б) При каких значениях а уравнение имеет два положи-
тельных корня?
в) При каких значениях а уравнение имеет два корня, каж-
дый из которых больше единицы?
2. Дана функция z/ = f(x), где f (х)=х2+х+-т—.
X -f л -f* 1
а) Найдите область определения функции у.
б) Решите уравнение f (х) = 5.
в) Найдите наибольшее значение функции у на отрезке
[-5; 0].
г) При каких а уравнение f (х)=а имеет 4 корня?
3. Дана функция y = f(x), где f (х) = х2 (х— I)2.
а) Решите уравнение f (х)=4.
б) Найдите производную функции у.
в) Найдите промежутки возрастания функции у.
4. Дана функция y = f(x), где f (х) = 3х4 —х2.
а) Решите уравнение / (х)=.
б) Решите неравенство f (х)^2.
в) Постройте график функции у.
г) При каких значениях а уравнение f (х) = а имеет 4 корня?
5. Дана функция y = f(x), где f(x) = x4 —2х2.
а) Упростите выражение f (х+1) — f (х— 1).
б) В каких точках функция у принимает наименьшее значе-
ние?
в) Решите неравенство f(x)^—
г) Сколько корней имеет уравнение f (х) = 1пх?
6. Дана функция у=/(х), где f (х)=(х+3) (х+1) (х — 2).
а) Решите неравенство f (х)> 6 (х+ 1).
б) На каких промежутках функция у возрастает и прини-
мает только положительные значения?
313
в) Сколько корней имеет уравнение f (x) = Z? (х+1) в зависи-
мости от Л?
7. Дана функция y = f(x), где f (х) = 2х2 (х +1).
а) Найдите наибольшее значение у при х<0.
б) Решите неравенство f (х)>у-.
в) Сколько корней имеет уравнение y = kx в зависимости
от fe?
г) Есть ли на графике функции у пары точек, симметрич-
ные относительно начала координат?
8. Дана функция y = f (х), где
а) При каких значениях х функция у принимает положитель-
ные значения?
б) Найдите участки убывания функции у.
в) Решите уравнение f(x)=x2^1x_jr1 •
г) Сколько корней имеет уравнение f (х) = х2—1?
9. Дана функция y=f(x), где fU) = x2_gx+3
а) Решите неравенство / (x)=gC 1.
б) Найдите наибольшее значение функции у.
в) Решите уравнение f (х) = (2х)-1.
10. Дана функция y = f(x), где f (x)=log । .
а) Найдите область определения функции у.
б) Решите уравнение у= — 1.
в) Найдите область значений функции у.
11. Дана функция y = f(x), где f (х) = х3 — а2х+ 1, а>0.
а) Решите неравенство f(x)^l.
б) Найдите наименьшее значение функции у при х^О.
в) При каких а уравнение f (х) = 0 имеет три корня?
12. Дана функция у (х) = 3х (х— I)2.
а) Найдите экстремумы функции у (х) при х<1.
б) Решите неравенство t/(х)<6 (х—1).
в) Сколько различных корней имеет уравнение у (x) = kx в за-
висимости от fe?
г) Есть ли на графике функции у (х) пары различных точек,
симметричных относительно прямой Зх=1?
13. Дан многочлен Р(х) = х2 + (а-—3)х + а.
а) При каких а этот многочлен имеет хотя бы один корень?
б) Найдите сумму квадратов корней многочлена Р (х).
в) Найдите наименьшее значение суммы квадратов корней
многочлена Р (х).
г) При каких а многочлен Р (х) имеет два положительных
корня?
314
14. Дан многочлен Р (х)=х24-х —2.
а) При каких а число х=5 является корнем уравнения
РСх4-а) = 0?
б) При каких а все коэффициенты многочлена Р(х4-а) по-
ложительны?
в) Решите уравнение ~х-
г) Решите неравенство Р (х)«Р (х 4-а) >0.
15. Дана функция f (х)=х2 (х+ I)2 — 6х (х+1).
а) Решите уравнение f (х)4-8=0.
б) Решите неравенство f (х)>0.
в) Покажите, что f' (х)=2 (2x-j-1) (х24-х—3).
г) Найдите область значений функции f.
Иррациональные функции
16. Дана функция y=g(x), где g (х) = -\/х4-2.
а) Решите уравнение g (х)=х.
б) Решите неравенство g (х)>х.
в) При каких значениях а уравнение -д/*+а=х имеет два
корня?
17. Дана функция y = f(x), где f (х)=^+^ •
а) Найдите область определения функции у.
б) Решите уравнение f (х)= — 1.
в) Решите неравенство f (х)^-^_
18. Дана функция y = g(x), где g (х) = -73х4-44-л/х —4-
а) Найдите область определения функции у.
б) Решите уравнение g (х)=2 -\/х.
в) Сколько корней имеет уравнение g(x) = 2 тД4*а ПРИ поло-
жительных значениях а?
19. Дана функция t/ = f(x), где f (х) = д/6 —х4~л/х + 3-
а) Найдите область определения функции у.
б) Решите уравнение f (х)= 1 4-2 д/2.
в) Какие значения может принимать функция у?
20. Дана функция y = f(x), где f (х)=д/3— х4-д/х4-а.
а) Решите уравнение f (х) = 3 при а = 3.
б) Найдите область значений функции при а=3.
в) Найдите все значения а, при которых функция у имеет
максимум в точке х=1.
21. Стоимость контейнера, имеющего емкость V, находится по
формуле q (К)=-\/Д К34-Д, где А и В — постоянные величины,
V^l. Известно, что при V=1 и У=2 соответственно q = 3 и
<7 = 4.
315
а) Найдите А и В.
б) Величина f (V)=2-^ характеризует экономичность контей-
нера. При каком V значение f (V) минимально?
22. Дана функция f (х)=-\/2—хЦ-3.
а) Найдите область определения функции f (х).
б) Решите уравнение f (х) = 4х.
в) Решите неравенство f (х)>2х.
г) При каких значениях параметра а уравнение (f(x))2 —а2 =
=777— I имеет хотя бы одно решение?
23. Дана функция f (х) = д/2х —х2.
а) Найдите область определения функции f.
б) Решите уравнение f (х)=&.
в) Решите неравенство f (х)^х— 1.
г) Сколько корней имеет уравнение f (|х|) = а в зависимости
от величины параметра а?
24. Дана функция f (x) = xj(x — 1) (3—х).
а) Решите неравенство f(x)<^.
б) Решите уравнение f(x) = x —2.
в) При каких а неравенство f(x)<x+a справедливо для
всех х из области определения функции f?
25. Дана функция y=f(x), где f (х)=-\/х3 +1.
а) Найдите область определения функции f.
б) Решите уравнение f (х)=2х+1.
в) Решите неравенство f (х)<хЦ-1.
Показательные и логарифмические функции
26. Дана функция y=f(x), где f (х) = 4х — 2х+1.
Q
а) Решите уравнение f(x)=——.
б) Найдите наименьшее значение функции у.
в) При каких значениях а уравнение f (х) = а имеет два корня?
27. Дана функция y = f(x), где
f W = log^(3-x) + log2(3-x) + log , (3-x)+log4(3-x).
“2
а) Упростите выражение f (х).
б) Решите неравенство f (х)<3.
в) При каких значениях k все решения неравенства f(x)<fe
будут положительны?
316
28. Дана функция y = f(x), где f (x)=log2 (4х— 12).
а) Найдите область определения функции.
б) Решите уравнение f (х)=х.
в) Докажите неравенство f (х)<2х.
г) При каких значениях k разрешимо уравнение f (х) = /г+х?
29. Дана функция у=/(х), где f(x)=3-3
□ -р О
а) Решите уравнение f (х)=^-.
б) Найдите область значений функции.
30. Дано уравнение log3 (9х — 2-Зх + а)=0.
а) Решите уравнение при а= — 2.
б) При всех отрицательных значениях а найдите область
допустимых значений этого уравнения.
в) При каких значениях а уравнение имеет два корня?
31. Дана функция y = f(x), где f (х)= |о6^х+^+-1 .
а) Найдите область определения функции у.
б) Решите уравнение f (х)=-^-.
в) Решите неравенство f (х)^1.
32. Дана функция y = f(x), где f (х)=е~2х — 2е~х.
а) Решите неравенство f (х)^8.
б) Найдите область значений функции у.
в) При каких значениях а уравнение / (х) = а имеет два корня?
33. Дана функция у = /(х), где f (х) = у^г+^гр-•
а) Решите уравнение f (х)=-|-.
б) При каких значениях х функция у принимает отрицатель-
ные значения?
в) Найдите область значений функции у.
34. Дана функция y=f(x), где f (x) = log2 (х— 1) — log2 (х2+1).
а) Решите уравнение f(x)=log2 3 — 2 log2 5.
б) В какой точке функция у достигает наибольшего значения?
в) Решите неравенство f (х)> — 1 — log2 х.
35. Дана функция y = f(x), где f (x) = logg (1 — 4x) + log3 (х + 3).
а) Найдите область определения функции у.
б) Решите уравнение f (х)= 1.
в) Сколько решений имеет уравнение f (x) = log3 (х + 2 — а2)
в зависимости от а?
36. Дана функция y = f(x), где f (х)=1п (ех + 3е-х).
а) Решите уравнение f (х)=2 In 2.
б) Найдите область значений функции у.
в) При каких а уравнение f(x)=a имеет два положитель-
ных корня?
317
37. Дана функция у=/(х), где f (x) = log2 (4-х — 2'~х).
а) Найдите область определения функции у.
б) Решите неравенство f (х)>0.
в) Решите уравнение f (х)= — х.
38. Дана функция y = f(x), где f (x) = logx (6 — х).
а) Найдите область определения функции у.
б) Решите уравнение f (х) = 2.
в) Решите неравенство f (х)<0.
39. Дана функция y = f(x), где f(x) = log, log6 * +*
а) Вычислителе).
б) Найдите область определения функции у.
в) Решите неравенство f (х)>0.
40. Дана функция y = f(x), где f (x) = log2 (х+10) — log2(x+6).
а) Найдите область определения функции у.
б) Решите уравнение f (х)= 1.
в) Найдите наибольшее значение функции у на отрезке [2; 6].
г) При каких значениях k уравнение f (x)=log2 (k — х) имеет
два решения?
Тригонометрические функции
41. Дана функция y — f(x), где f (x)=log2 sin х.
а) Найдите область определения функции у.
б) Решите уравнение f (х)=—
в) С помощью графиков выясните, сколько корней имеет урав-
нение f (х)=х2 — 36.
42. Дана функция y = f (х), где f (x)=sin2 2х — cos 4х.
а) Решите уравнение f (х)=—
б) Найдите область значений функции у.
в) Найдите наименьший положительный период функции у.
43. Дана функция y = f(x), где f (х) = А sin 2х + В cos 2х.
а) Вычислите значение функции у при Л =5, В = 3, если
известно, что sin х = — и —л.
б) Найдите числа А и В так, чтобы выполнялись условия
f(f)-V2Kf'(^) = ^-
в) Какое наибольшее значение принимает функция у при
найденных значениях А и В?
318
44. Дана функция y = f(x), где f (x)=sin3xcosx—sin x cos3 x _
cos 4jc
а) Докажите тождество f (x) =—Цр.
б) Найдите наименьший период функции у.
в) Решите уравнение f (x) = tg 2х.
45. Дана функция y = f(x), где f (х)= j-lnx—|- ^°sx .
к ' l+cosx l+sinx
а) Докажите тождество f (х)=-------------г-.
1 + V2sin
б) Решите уравнение f (х) = 1.
в) Вычислите наименьшее значение функции у при 0^х<-^-.
г) При каких значениях а уравнение f (х) = а не имеет ре-
шений?
46. Дана функция y = f(x), где f (x) = sin4 x + sin4 (х+-^-).
К
а) Решите уравнение f (%)=—.
б) Обращается ли в нуль функция у?
в) При каких значениях х функция у принимает наименьшее
значение?
47. Дана функция z/ = f(x), где f (х) = 1 + sin 2х — sin х— cos х.
а) Докажите тождество f (x) = (sin x + cos х) (sin x+cos x— 1).
б) Решите уравнение f(x) = 2.
в) Найдите наименьшее значение функции у.
г) Найдите область значений функции у.
48. Дана функция y = f(x)y где f (x) = cos2 x + -^-cos2 2х.
а) Решите уравнение f (х)=1.
б) Найдите наименьшее значение функции у.
в) Сколько корней имеет уравнение f(x)=x^+l?
49. Дана функция t/ = f(x), где f (x)=tg (х—-^-) + tg (х+у-).
а) Докажите, что f(x)= ~
б) Решите уравнение f(x) = 3tgx.
в) Найдите наибольшее значение функции у на отрезке
[°;Я
50. На отрезке [0; л] задана функция y — f (х), где
f (x) = cos4 x + sin4 х.
а) Выразите у через cos 4х.
б) Найдите область значений функции у.
319
в) Решите уравнение f(x)=4~-
О
к
г) Решите неравенство f (х)< —.
51. В равнобедренном треугольнике угол при основании равен а.
а) Вычислите отношение k площади треугольника к сумме
квадратов всех его сторон.
б) Докажите тождество fe=~ ------Д—:.
’ 2 tga + 3ctga
в) Используя доказанное тождество, найдите а так, что-
бы
г) При каком а отношение k принимает наибольшее зна-
чение?
д) Найдите область значений отношения k.
52. В равнобедренном треугольнике угол при основании равен а,
длина боковой стороны равна а.
а) Докажите, что отношение k радиусов вписанного и опи-
санного кругов равно 2 cos a (1 — cos a).
з
б) Найдите а, такое, что k=—.
О
53. В треугольнике одна сторона равна а, противолежащий
угол равен один из оставшихся углов равен а.
а) Какие значения может принимать угол а?
б) Вычислить площадь S треугольника.
в) При каком значении а площадь S (а) принимает наиболь-
шее значение?
г) Постройте график функции S = S(a).
54. В равнобедренной трапеции основания равны а и 2а, острый
угол равен а.
а) Вычислите отношение k площади трапеции к сумме квад-
ратов всех ее сторон.
б) Докажите тождество k=~—,tg “,, .
2 tg a+ 11
в) Используя доказанное тождество, найдите угол а так,
чтобы Л=-|-.
г) При каком значении а отношение k принимает наибольшее
значение?
55. Один из углов треугольника равен отношение сторон,
заключающих этот угол, равно t.
а) Вычислите отношение k суммы квадратов всех сторон
треугольника к его площади.
б) Найдите наименьшее значение отношения k.
320
в) При каких значениях t выполняется неравенство
у 3
г) Постройте график функции y = k(f).
Системы уравнений
56. Дана система уравнений f x-j-y — a— 1,
( ху = 3а—8.
а) Пусть z — x2-j-y2. Выразите z через а.
б) При каких значениях параметра а система имеет единст-
венное решение?
в) Найдите наименьшее значение величины z, предполагая,
что система имеет решение.
57. Дана система уравнений ( х2 — ху-\-у2 = а,
I х + у=а.
а) Решите систему при а = 3.
б) Сколько решений имеет система в зависимости от а?
в) При каких а решения системы существуют и состоят
только из положительных чисел?
58. Дана система уравнений (2у — х2 — а,
| 2х=у2 —4.
а) Тождественными преобразованиями привести данную сис-
тему к виду ((х— 1)2 + (у— 1)2 = а + 6,
| (х+1)2 — (у+ 1)2 = а—4.
б) Решите систему при а = 4.
в) Докажите, что при а<—6 система не имеет решений.
59. Дана система уравнений с д[х —у —а,
| ^х-у= 1 —а.
а) Решите систему при а = 2.
б) При каких значениях параметра а система имеет единст-
венное решение?
в) При каких значениях параметра а система имеет реше-
ние (х; у), такое, что х^у2?
60. Дана система уравнений f tgx + tg у = а,
а) Решите систему при а=1.
б) При каких значениях параметра а система имеет решение?
в) При каких значениях параметра а система имеет такое
решение (х; у), что tg х^О, tg t/^0?
11 Заказ 836
ЛАБОРАТОРНЫЕ РАБОТЫ
Лабораторная работа № 1
Цель работы: исследование экспериментально заданной
функции по ее графику.
1. Составьте таблицу долготы дня в вашей местности, отме-
тив ее в 24 точках — по две точки на каждый месяц. (Если вы
будете определять долготу дня по печатному календарю, то учтите,
что он дает данные для широты Москвы.)
2. Вычислите в каждой точке отклонение h долготы дня от 12 ч.
(Вычисления ведите в часах с точностью до 0,1 ч, для нахождения
h вычтите из долготы дня число 12.)
3. Постройте график функции h по точкам.
4. Проведите исследование функции h по графику. По-
старайтесь объяснить смысл каждого пункта исследования.
5. Ответьте дополнительно на следующий вопрос: когда дол-
гота дня возрастает быстрее всего?
Лабораторная работа № 2
Цель работы: изучение углового коэффициента прямой.
Точка движется по координатной плоскости (/; у) в течение
отрезка времени 0^/^7. При t — О точка находится в начале
координат. Траектория точки — ломаная с вершинами Ро, Pi,
Pi, Рз, Pi, Ръ, Ръ, Pi- В точку плоскости Pt (где /=0,1, .... 7) дви-
жущаяся точка приходит в момент времени t. От точки Pt до точ-
ки Pt+i она движется по прямой, угловой коэффициент которой
kt вычисляется по формуле kt — t2 — yt, где (/; yt) — координаты
точки Pt-
1. Вычислите последовательно координаты точек Pt.
2. Постройте траекторию точки.
3. Вычислите угловые коэффициенты ко, ki, .... ко звеньев
ломаной.
4. Напишите уравнения прямых PqPi, Р1Р2, Р2Р3, РзР^, Р*Ръ,
РзРб-
322
Лабораторная работа № 3
(два варианта)
Цель работы: изучение механического и геометрического
смысла производной.
Вариант 1
На рисунке 149 изображен график зависимости пути некото-
рого движения от времени.
а) Вычислите среднюю скорость движения на отрезках време-
ни [0; 1], [-2; 1J [—3;3], [-1; 3].
б) В каких точках скорость движения равна нулю?
в) Вычислите приблизительно скорость движения в начальный
момент времени (/=—3) и в конечный (< = 3).
г) Найдите точки, в которых скорость равна 1.
д) В какой момент времени скорость движения наибольшая?
е) Начертите примерный график скорости.
Вариант 2
Перечертите (лучше всего на миллиметровку) график функции,
изображенный на рисунке 150.
а) Выберите 3—4 точки графика, проведите в них касательные
и вычислите приближенно их угловые коэффициенты.
б) В какой точке касательная параллельна оси х? Что можно
сказать о скорости изменения функции в этой точке?
в) В какой точке касательная расположена круче всего? Что
можно сказать о скорости изменения функции в этой точке?
г) Найдите точки, в которых касательная наклонена к оси под
углом 45°.
д) В каких точках угловой коэффициент касательной отрица-
телен?
е) Нарисуйте примерный график изменения углового коэффи-
циента касательной.
323
Лабораторная работа № 4
Цель работы: пример построения математической модели
механического движения.
Теннисный мячик сброшен с высоты Но = 1,6 м. При каждом
отскоке мяч теряет половину кинетической энергии.
1. Найдите скорость и0 первого падения мяча на землю, исполь-
зуя равенство кинетической и потенциальной энергии в этот мо-
мент: mgHo=^-, где £ = 9,8 м/с2.
2. а) Докажите, что скорость и\ первого отскока связана со
скоростью ио падения мяча соотношением ui=^=- и0.
б) Выразите скорости второго, третьего и т. д. отскоков иг, ^з,...
через скорость у0. Верно ли, что иг вдвое меньше Vo?
в) Используя формулу связи между кинетической и потенци-
альной энергией, покажите, что при каждом отскоке высота подъе-
ма уменьшается вдвое.
3. а) Покажите, что между вторым и третьим отскоками за-
висимость Н от t такова: // = 2,8/— 4,9/2.
б) Определите время между первым и вторым отскоками,
вторым и третьим.
в) Найдите уравнение движения между третьим и четвертым
отскоками.
г) Проверьте, что время между третьим и четвертым отскоками
вдвое меньше времени между первым и третьим.
д) Обозначьте время между fe-м и (fe+ 1)-м отскоками через Tk\
докажите, что Tk=^Tk-\\ Tk=±-Tk-2-
-у/2
4. Используя результаты проведенного исследования, построй-
те график зависимости H —
5. а) Постройте последовательность моментов падения мяча
на землю: /|, /2 = /i + Ti, /3=/24-Т2, ... .
б) Найдите предел последовательности /*, который покажет
время движения мяча до полной остановки.
в) Каким точкам на графике соответствуют моменты отскоков?
Можно ли провести в этих точках касательные?
Лабораторная работа № 5
Цель работы: использование тригонометрических функ-
ций для параметрического задания кривой.
Точка Р движется в координатной плоскости. Ее координаты
в момент времени t задаются формулами rx = 5cos/,
। у = 4 sin /.
1) Составьте таблицу значений х и у в зависимости от t на
отрезке 0^/^СЗ, взяв значения t через 0,2 (т. е. / = 0; 0,2; 0,4; ...;
2,6; 2,8; 3,0). Вычисление значений х и у ведите с точностью до 0,1.
324
2) Постройте точки с найденными координатами, выбрав под-
ходящий масштаб по осям х и у. Соедините построенные точки
плавной кривой.
3) Найдите координаты точек Pt при/=—0,4; —1; —2; —2,6.
Постройте эти точки. Соедините все построенные точки плавной
замкнутой кривой. Эта кривая называется эллипсом.
4) Найдите точки, в которых х принимает наибольшее или
наименьшее значение. Найдите точки, в которых у принимает
наименьшее значение. При каких значениях t обе координаты
точки Pt возрастают?
5) Нанесите точки с координатами Fi ( — 3;0) и F2 (3; 0).
Измерьте с помощью линейки расстояния от некоторых из по-
строенных точек до точек Fi и F2. Убедитесь в том, что сумма
расстояний IPF1I + IPF2I постоянна. Точки F\ и F2 называются
фокусами эллипса.
6) Докажите тождества:
(5 cos /+ 3)2 + (4 sin /)2 = (54-3 cos /)2,
(5 cos t — 3)2 + (4 sin f)2=(5 — 3 cos /)2.
7) Докажите, что PFj =5 + 3 cos/, PF2 = 5 — 3 cos /, и полу-
чите равенство PFi+PF2=10.
Лабораторная работа № 6
Цель работы: приближенное вычисление корня уравнения
с помощью микрокалькулятора (МК).
1. Постройте в крупном масштабе график функции r/ = cosx
на отрезке [О; yj и график функции у = х. Найдите графически
приближенное решение уравнения cos х = х. Сколько корней имеет
уравнение cosx = x?
х2
2. Воспользуйтесь приближенной формулой cos х« 1 — — для
приближенного нахождения корня уравнения cosx = x. Сравните
найденное значение с полученным графически.
3. Итерационный метод (от слова «итерация» — последова-
тельное приближение) решения уравнения cosx = x основан на
следующей процедуре. В качестве начального приближения х0 бе-
рется произвольное число на отрезке [О; -у-]. Затем вычисляется
xi =cos хо, затем x2 = cos xi (т. е. cos cos хо) и т. д. В общем виде
хп+| =cos хп. Введите в МК найденное ранее приближенное зна-
чение корня. Многократно нажимая кнопку «cos», убедитесь в том,
что с некоторого момента высвечиваемое на МК число не меняется,
т. е. для него cosx=x. Выпишите найденное значение корня.
4. Повторите процедуру, начиная с различных значений х0.
Что можно сказать о монотонности последовательности прибли-
жений Хо, Х|, х2, х3, ...?
325
5. Изобразите в крупном масштабе часть графика на отрезке
[х—0,1; где х — найденный корень. Возьмите хо=х—0,1
и изобразите на графике последовательные приближения к корню.
6. Добавьте на предыдущем чертеже кривую, симметричную
графику функции y=cos х относительно прямой у=х. Используй-
те эту кривую для геометрического изображения последова-
тельности приближений.
Лабораторная работа № 7
Цель работы: изучение влияния погрешности вычисления
t на погрешность вычисления а1.
1. Составьте таблицу значений 10' при / = 0,01; 1,01; 2,01; 3,01;
4,01; 5,01; 6,01, записывая результат с двумя знаками после
запятой.
2. Заметьте, что каждое заданное значение t имеет вид / = /о +
+ 0,01, где to — целое число от 0 до 6. Составьте таблицу значений
10'—10'° (с точностью до 0,01).
3. Сформулируйте, чему равна погрешность вычисления 10', ес-
ли погрешность вычисления t равна 0,01.
4. Вычислите 103+л—103 при Л=0,1; 0,01; 0,001; 0,0001.
5. Сформулируйте, чему равна погрешность вычислений 103+Л
в зависимости от h.
6. С какой погрешностью нужно вычислить h, чтобы погреш-
ность вычисления 103+Л была не больше 0,1, т. е. чтобы
|103+A-103|<0,l?
Лабораторная работа № 8
Цель работы: приближенное вычисление натурального
логарифма числа а с помощью формулы (а*)'=(1п а) ах.
1. Постройте график функции у— 10ft на отрезке [—0,5; 0,5],
выбирая значения h с шагом 0,1 (т. е. взяв й=—0,5; —0,4; ...;
0,4; 0,5). Масштаб по оси у выберите так, чтобы можно было откла-
дывать значения у с точностью до 0,1.
2. Проведите касательные к построенному графику в точках
й= —0,5, Л=0 и й=0,5. Вычислите доступными вам средствами
угловые коэффициенты этих касательных (с точностью до 0,1).
3. Составьте таблицу значений выражения —— при Л =
= ±0,3; ±0,2; ±0,1. Каково (с точностью до 0,1) значение пре-
дела этого выражения при h -► 0?
4. Вычислите отношения где /(Л)=10Л,
И —0,5) )(0) / (0,5)
взяв значения производной из п. 2. Убедитесь в близости этих
отношений к найденному в п. 3 числу In 10.
5. Вычислите значения Ina при а = 0,5; 2; 2,7; 3 по прибли-
женной формуле In ал—— (с точностью до 0,1).
326
Лабораторная работа № 9
Цель работы: приближенное вычисление интеграла с по-
мощью интегральных сумм.
1. Выберите одну из трех функций, указанных в задаче 2 (гл. V).
2. Составьте таблицу значений функции, разбив область опре-
деления на равные части длиной Ах=1.
3. Вычислите две интегральные суммы, выбирая значения
функции для первой суммы на левых концах промежутков
[х,-; Xi-f-Ax], а для второй суммы на правых.
4. Приведите геометрическую иллюстрацию вычисляемой
площади и интегральных сумм.
5. Сопоставьте ответ с полученным в задаче 2 результатом
и со следующими значениями площадей, найденными с точностью
до 0,01:
io IP IP
\ 0,1 x2dx« 33,33; \— dx ж 23,02; \ 5 sin ^dx«31,83.
J J x J 10
о 1 о
Лабораторная работа № 10
Цель работы: приближенное решение дифференциально-
го уравнения методом Эйлера.
Задача. Найти решение дифференциального уравнения
у' = у — х2, удовлетворяющее начальному условию уо = 2 при Хо = 0.
1. Проверьте, что функция у = х2 + 2x4-2 является точным ре-
шением поставленной задачи.
2. Ломаная строится, начиная с точки Pq (0; 2). Значения
х=х* берутся на отрезке [0; 1], начиная с х0 = 0, с шагом h так:
хл+1 =Xn + /i. Значение у — уп вычисляется по формуле уравнения
прямой i/n+i =Уп+Уп*Л, начиная с уо = 2. Угловой коэффициент у'п
находится из дифференциального уравнения у'п=уп-{-х1. Составь-
те таблицу значений хл, ул, у'п для отрезка [0; 1] при шаге й = 0,2.
3. Постройте ломаную РцР\...Ръ из найденных точек Pk (х*; у*).
Постройте график точного решения на отрезке [0; 1]. Найдите наи-
большее отклонение Д1 точного решения от приближенного.
4. Повторите вычисления п. 2 с шагом h = 0,1. Постройте
новую ломаную. Вычислите новое отклонение Д2. Во сколько раз
точнее (т. е. каково отношение получилось приближение
при уменьшении шага вдвое?
Лабораторная работа № 11
Цель работы: графическое решение кубического уравне-
ния.
1. На листе миллиметровой бумаги начертите график кривой
у=х3 при —2<х<2.
327
2. Постройте точки Ро (0; — 1) и Pt 0) при / = 0,2; 3,5; 4,5.
3. Докажите, что абсциссы точек пересечения кривой у=х3 *
и прямой P0Pt являются корнями уравнения х3 —/х4-1=0.
4. Найдите корни уравнения х3 — tx+ 1 =0 при t=0,2; 3,5;,4,5.
5*. Проверьте, что подстановка z=\[qx—где q = c—v- +
, приводит уравнение z3 4-az2 + bz + c=0 к уравнению
х3 — /х+ 1 =0 при /=(^— b ) q~\
6. Решите уравнение х3 4-Зх2 4-0,75x4-2 = 0.
Лабораторная работа № 12
Цель работы: приближенное вычисление корней уравне-
ния.
1. Постройте по 3—4 точкам график функции у = х5-\-х— 1 на
интервале [0; 1].
Вариант 1 (метод половинного деления)
2. Составьте программу вычисления значений функции у =
= Х54“Х— 1.
3. Вычислите значения у в точках х = 0,5; 0,75; 0,875; 0,8125;
0,78125.
4. Постройте последовательность для нахождения корня:
[0; 1]; [0,5; 1]; [0,75; 1]; [0,750; 0,875].
Продолжите вычисления до тех пор, пока не получится интер-
вал длины, меньшей чем 2-10~5, на концах которого у принимает
значения разных знаков.
2.
3.
4.
Вариант 2 (метод касательных)
Составьте программу для построения последовательности
г —г У" — 4х"+1
"+l Хп 5xi+l 5xi+l •
Выберите х( = 1 и вычислите хг, Хз, ..., х7.
Вычислите Х7-4-Х7—1.
Вариант 3 (метод хорд)
2. Составьте программу для построения последовательности
(х„;у„) по формулам | хп+, = х„ — ,
3. Выберите (xi; f/i)=(0; — 1) и (хг; z/2)=(l; 1) и вычислите
(х3; уз), ..., (х)5; уц>).
СПРАВОЧНЫЙ МАТЕРИАЛ
Основные обозначения
R — множество всех вещественных (действительных) чисел
Z — множество всех целых чисел
АГ — множество всех натуральных чисел
— возрастает, убывает, стремится к преде-
лу (о функции)
£—принадлежит, не принадлежит (лежит, не лежит —
о числах, точках)
U —объединение (множеств корней, решений и других мно-
жеств)
=>, о — следовательно, равносильно (если... то, тогда и только
тогда в формулировках теорем, свойств, при решении уравнений
и неравенств)
D (f) — область определения функции f
&f — приращение функции f
df — дифференциал функции f
f' — производная функции f
ь
j f (х) dx — интеграл от функции f на отрезке [а; Ь].
Функции и графики
1) Линейная функция y=kx-\-b. График — прямая.
2) Квадратичная функция у = ах2-\-Ьх + с. График — парабо-
ла с вершиной в точке ).
329
1 1 X
5) Рациональная функция у = х+—, у=— — , y=-^Y и т.п.
6) Показательная функция у = ах.
7) Логарифмическая функция y = logax.
8) Тригонометрические функции y = sin шх, y=coscox, у =
= tg сох, y = ctg сох.
9) Обратные тригонометрические функции у— arcsin х, у =
= arccos х, у = arctg х, у — arcctg х.
Преобразование выражений
1) Алгебраические выражения
а2 — Ь2=(а + &) (а — Ь\
a3 — b3—(a — b)(a2+ab + b2),
a3-\-b3=(aA-b)(a2—ab + b2),
(а ± b)2 = а2 ± 2аЬ -|- Ь2,
(а ± Ь)3=а3 ± За2 6 + ЗаЬ2 ± Ь3,
(а ± Ь)4 = а4 ± 4а3Ь + Qa2b2 ± 4аЬ3 4- Ь\
1 —х"=(1 —х)(1 4-х+х2 +... + хл-'),
^ + »х + с-0((х + А.)г-^),
ad — b(\
ax-\-b _1 ас \
cx+d с ( , d Г
\ ’+~)
2) Экспоненты и логарифмы
a'°s‘x=x, logaxy = logax4-logay,
ах = ех'па, loga “-= loga х—logo у,
У
logf, Х = £|2-£ , \ogaXk = k loga X,
lOga a
10gaV^=— , 10gaZ> = —!— .
& v n & log* a
3) Тригонометрические функции
sin2 x+cos2 x= 1, cos—x) =sin x,
330
sin(f-x)=cosx.
ct8x~Я7-. te(f-x)-ctgx,
1+le’'=+; c,s(f-
sin (a±P) = sin a cos p±cos a sin p,
cos (a±p)=cos a cos pepsin a sin p,
sin 2a=2 sin a cos a,
cos 2a=cos2 a — sin2 a = 2 cos2 a— 1 = 1 —2 sin2 a,
1 +cos a=2 cos2 1 —cos a=2 sin2 -y,
sin 3a = 3 sin a cos2 a — sin3 a, cos 3a=cos3 a—3 sin2 a cos a,
sin a + sin p=2 sin ^y£ cos ^y£,
cos a + cos p = 2 cos cos a^- ,
sin a — sin p = 2 sin cos ,
cos a — cos p = — 2 sin a sin g~P ,
sin a cos p=-^-(sin (a + P) + sin (a —P)),
sin a sin p = -y(cos (a —P) —cos (a + P)),
cos a cos p=-y (cos (a + P) + cos (a — p)),
2 tg у l-tg2y 2 tg y
sin a=------- , cosa=-------- , tga =----— .
l+tg2y l+tg2y 1- tg2y
Z z
4) Обратные тригонометрические функции
arcsin (—x)= — arcsin x,
arccos (—x)=n— arccos x,
arctg (—x) = —arctg x,
7
sin (arcsin x)=x,
cos (arccos x)=x,
tg (arctg x)=x,
cos (arcsin х)=д/1 —x2, arcctg (—x)= —arcctg x,
331
sin (arccos х)=д/1 —x2, arcsin x+arccos x=-^-,
sin (arctg x) = , tg (arcsin x)= ,
arcsin 0=0, arctg 0 = 0, arccos 0=-^-, arcctg 0=y-,
arcsin4"=4-, arctgT=T' arccos 4-=^, arcctg^ =-^-,
arcsin=-£-, arctg l=-£-, arccos=-2-, arcctg 1=-£-,
2 4 ® 4 2 4 b 4
arcsin^- =-7-, arctg д/3=^-, arccos^ =-£-, arcctg д/3=-£~,
Z о о Z о о
arcsin 1 =-j-, arccos 1 =0.
Производные и интегралы
(и + v)' = и' + v', (u (ax))' = au' (ax),
(!«)' = lu', (un)' =nun~'u',
(ии)' = и'и + ии', (u (y))'= u'(y) v',
/ u\'u'v — uv'
Функция у Производная у' Первообразная \ydx
xn —, x>0 X sin x cos X sin cox COS (OX tgx e ax arcsin x nxn~1 1_ x2 COS X — sin x (or COS (OX — (o sin (ox 1 cos2 X ex ax In a 1 Vl-xJ «4-1 In X — cos X sin x 1 COS (OX (0 1 . Sin (OX (O 6х r~a‘ In a
332
Формулы для приближенных вычислений
VT+^i+f-Т'гЬ
Z О 1 “ГЛ
1 +—х-^- х2,
(1 1 + kx-{-k х2, sinx«x—у-,
cosx«l—tgx«x+^-,
^»1+х+^-, 1п(1+х)«х-^-.
Решение уравнений
ах 4-6 = 0 (а^О), х=—
ах24-Ьх+с = 0 (а#=0), х i ,2 = ~ - —~ , (если Ь2 — 4ас<0,
то корней нет);
ax=b, x = logo b-, logax = ft х=аь;
sinx=a, х = arcsin а+ 2л£, х=л — arcsin a-\-2nk;
cos х = а, х= ± arccos а + 2лЛ;
tgx = a, х = arctg а + nk;
ctgx=a, x=arcctg а+лЛ;
sin x=0, x = kn; cos x=0, x=-~|- nk\
tgx=0, x=kn; ctg x=0, х=-£-+л/г.
Некоторые известные соотношения
ai+^+-+a">^fl,a2.„ani ^.^о,
(fl2 -|-G2 Ч" ••• 4*On) (^1 4" ^2 4“ ••• “Ь ^n)^(Ol^l 4-02^2 4“ ••• 4"Onbn) »
(14-a)h> 14-Ла, а> —1, Л>1.
ззз
l+2+3 + ... + n=^±l),
1 +3+54-..-+(2n-l)=n2,
1-2~2-3~ " ' n(n + l) n + I ’
Бином Ньютона
(a + b)n=an+nan ~1 b + л(л~^ • an ~ 2b2 +...+• a2b n~2
+ nabn~l +bn.
Треугольник Паскаля (биномиальные коэффициенты)
1
1 1
1 2 1
13 3 1
1 4 6 4 1
15 10 10 5 1
1 6 15 20 15 6 1
1 7 21 . 35 35 217 1
ЗАВИСИМОСТИ
Прямая Гипербола
У; 1 У=ХХ ПЕРЕМЕННЫЕ t- бремя 5 - расстояние V - скорость У) f 1 11 1 . Х1ч
0 X т- масса s/7 X
Е - энергия р - давление
Парак X 1ола у=ах2 V - объём U - напряжение I - сила тока Т - температура х - абсцисса Окружи У часть хг+у2=/?г
у - ордината Р - точка \ 0 у х
0 X ©
335
ЛИНЕЙНАЯ ФУНКЦИЯ
у=кх+Ь
Модуль - это расстояние
М(х) _
X О X
х
МОДУЛЬ
M(xt) М(хг)
о
Расстояние - это модуль
М<*-0 м+м‘
Х} О X Х~Х,
|^'| = |^|=|х-х,|
\х\=2<=>х=±2
-2 О 2
|х|<2 <=>-2<Х<2
zlx|>2^
----1--ъ
-2 0 2
|х|>2 <=>х<-2
или х>2
336
КВАДРАТИЧНАЯ ФУНКЦИЯ
ПРОИЗВОДНАЯ
Аргумент х
Функция y=f(x)
Приращение
аргумента Дх
срункции. Ду=f (х+Дх) - f(x)
Средняя скорость
ПроизВодная y'=Jim^
У
с
кх+Ь
хп
1
X
Vx
sinx
COSX
еХ
Lnx
у'
О
к
ПХпЧ
1
р
1
2\Гх
COSX
-sinx
ех
X
337
ИССЛЕДОВАНИЕ ФУНКЦИИ
Функция у Производная у'
Монотонность
EZD <=> у'^
У Гч~~1 <=> у'^0
\ const I <=> у/= О
Экстремумы
Перегиб
sin и cos
• корни ПК
max $+2як
min -£ + 2як
338
исследование exp и Log
339
340
ИНТЕГРАЛ
Теорема Ньютона-Лейбница
ь
Jf(x)dx= F(b)-F(a)
а
ВЫЧИСЛЕНИЕ ПЛОЩАДИ
С ПОМОЩЬЮ ИНТЕГРАЛА
341
РАВНОСИЛЬНОСТЬ
Помни про ОДЗ
Помни про ОДЗ
СИСТЕМА ДВУХ ЛИНЕЙНЫХ УРАВНЕНИЙ
OjX + b^^q - прямая If
а2х + Ь2у = с2- прямая 12
Исключение:
а2 в2 с2
(Ш)
Решений
бесконечно много:
X-любое число
у-С/~М
1 у ь,
Главный случай:
#2 ^2
Решение единственно:
х __С1^2~С2^1
о а^Ь2 — а2Ь1
y. = afC2~a2<=1
afb2-a2bf
ОТВЕТЫ
ГЛАВА I
4. 1) 0,432 > 0,429; 3) л>3,14; 5) -А>—1. 7. 1) з) .
8. 1) 0,28; 3) 0,2855714...; 5) 0,533... . 10. 1) 0,99...9; 3) .... 99...9. 16. а=2, Ь=3.
17. а, = 1, b, = 1; а2=2, *2=у • 18. . 20. =3^/3г‘. 21. S^x^fi^x1.
23. 1) {/=л/4/?2-х2, х£[0; 2/?]; 3) S = x-j4R'2-x2. 24. t=Z^. 26. а =
kVQ
= уг(^Ь-р\ 28- S=sh 38-а=2- 40- ’) х=А±1; 3) R; 5) [0; 1)U(1; + со);
7) х=#=0; 9) х<1, или ( — оо; 1]. 46. а)
У=*
1 при х<-1, 47. 1) f(g(x)) =
— х при х£[— 1; 0],
х при х£[0; 1],
1 при х> 1.
-jrfT-uWS-^ + i; з> Н«М)-ь’. s(/w>-sx>; S) №(»))-,.
( 1 при х<0, 2 —Зх
S (f W)=| 2 при х>0. * 5
з
; 9) и =-----у и, и=£0', и=——V, и=#=0.
□ Z
у= —|х|; 5) o=V?;
69. 1) -5; 3) -4;
□
5) 4; 7) -4; 9) -100. 70. 1) х=4; з) х=-4 ; 5) х=з; 7) х=4 •
<J Z О / 1Z
7 3 3
72. 1) х>——; 3) х<-; 5) х>3; 7) *>2; 9) х>-. 73. 1) -1; 3; 3) {/наим =
= —4, наибольшего значения нет. 76. 1) у=2х—3; 3) {/=4x4-1-
77. 1) —1; 3) 0. 78. 1) {/=4x4-4 (прямая АВ); {/=—Зх—1
<5 <5
1 3
(прямая ДС); у = 2х— 1 (прямая ВС); 3) у=—— х-|-— (пРямая ЛА11);
#=х-|-1 (прямая ВМ2); у = 7х— 1 (прямая СМз). 82. |х— 5|=2; Х|=3, Хг = 7.
5 3
84. 1) — 1; 3; 3) —; -у ; 5) корней нет; 7) — 1; 4; 9) — 2^х^ — 1; 11) х>2;
13) 2; 15) ±3; ±5. 85. 1) (-оо; - 1](J[1; + оо); 3) (-оо; -4]|J[0; + оо);
5) (_оо; -1)и(5; 4-оо); 7) (-1;4); 9) [0;1]; И) (—оо; 1); 13) (4;4);
15) [—7; —3]U[3; 7]. 86. 1) 3,1; 3) 10-л2; 5) ->/5 — 2; 7) х-3 при х>3, 3-х при
343
рз
св
Р9
i
__2_
28. 1) 5(д/х+1)4—3) ---- 1 —; 5) 2х2(2х3-1) 3. 30. 1) —:
2 v* 4 д/1 + ^/х• -\Jx
+ оо J ; 5) (— оо; -|- оо); 9) : (— оо; + оо),
+ оо);"-^ : (-«; 0]; [-1; 1 ]; 17) : [1; + оо),
: (— оо; 0); (0; 1]; 21)^*" : (—оо; —1], [1; --- [—1; 1]. 31. 1) max:
(0; 3); 5) min: (—2; —16), max:
n (1 n
4 / \д/2 4 /
max: (0; 0); 13) min: (1; 2); max:(—1; —2). 32. 1) у; 5) нет. 34. При p>0
и любом q экстремумов нет; при р<0и любом q один минимум и один максимум.
36. max: ^13; -у-“Н ) •
38. а=1. 43. 1) 1; 2) 1; 3) 2.
44.
70.
21)
k
2. 45. |а|>1. 69. 1) dy = 3x2dx\ 5) dS = 2nRdR\ 9) du=-т.—-r^dt.
1) i/ = 4x-2; 3) y=0. 72. 1) 1,012; 5) 1,005; 9) 32,24; 13) 4,04; 17) 0,999;
1,9954. 73. 1) 2,03; 3) 4,39. 75. 1) Наим.: 0, наиб.: 5; 5) найм.: —у, наиб.: 1;
283
9) найм.: уу, наиб.: 19. 76. 1) аз = сц= — 11.
Глава III
*• *> 15); 3> П ; 5> Т= 7) Й ; 9) Н) 4я; 13> 4 я* 15) V "• 2- *> ,2°:
3) 22°30'; 5) 120°; 7) 270°; 9) 45°; 11) —930°. 9. 5°; 150°; 720°; 1500°. 10. 720 000
град/с; 12566 рад/с. 11. 1) sin/ = y, cos t=—, tg t =—у , ctg/=—у;
3) sin/=-^ , costg^=-V3, ctg/=А .15.1) —; 3) + ;5) -; 7) -;
9) +; 11) +. 16. 1) —; 3) —; 5) +; 7) —; 9) —. 17. 1) Нечетная; 3) четная;
5) нечетная; 7) четная; 9) нечетная; 11) ни четная, ни нечетная; 13) нечетная;
15) четная; 17) четная. 18. 1) ; 3) —у 5) 1; 7) ; 9) —1; 11) 0; 13) 1;
z z Z
15) —у; 17) 2. 19. 1) Существует; 3) существует; 5) существует. 20. 1) cos/ =
5 . . 12 5 . 5 2
= -13 tg ‘-У ’ Ctg <= "12 ; 3) Sin t= ’ C0S ‘-’ Ctg t =
=^-. 22. 1) (—оо; +оо); 3) х#=лЛ, k£Z-, 5) хф —£- + 2лЛ, k$Z. 24. 1) sin 280°,
5 2
sin 190°, sin 5°, sin 20°, sin 140°, sin 100°, sin 85°; 3) sin n, sin ,
O 12
345
sin — л, sin— л, sin — , sin —л, sin — л; 5) cos 3, cos 4, cos 5, cos 2, cos 1,
lx lx О о 1^
COS 6. 25. 1) //иаим = 2, !/наиб = ^» 3) !/наим= 5, //наиб”^; 5) !/Наим = 0’ //наиб=
7) //наим^-^” ’ ^наиб”!» 9) //наим = ®» //наиб=^- 26. 1) [ 1; 1]; 2) [ 2; 2];
5) [0; Ч-оо); 7) (-оо; 1} 27. 1) у' = 2 cos х; 3) / = 1+3 tg2 х-2 ctg2 х; 5) i/' =
= — 2 sin х cos х;
, —2ctgx 2cosx
7) и' =---: — =----:—я— ;
sin X Sin X
ЛЧ , cosx-hsinx
9) l/' =------H----
* cos2 X
(cos x-|-sin x) tg x __ sin3 x+cos3 x—2 cos x t _____1_ . x
(sin x—cos X)2 cos2 x (sin x—cos x)2 ’ f У — 2 Sln 2 ’
,ov 1Л . R к-x / 1 , 2 cos 2x cos 3x+3 sin 2x sin 3x
13) 10 sin 5xcos5x; 15) i/'=---- ; 17) y' --------------.
n X COS OX
cos T
29. 1) 1; 3) sin2 a; 5) sin a; 7) 4; 9) 0. 31. 1) tg2 2a; 3) 1; 5) 1; 7) 1; 9) 2.
33. 1) y; 3) у ;5)y;7)^;9)^.34.1)sina;3)sina;5) -tg(a-p). 35.1) 1;
31 3 ; 51 i ” " T: 3> 5+jfe— " T 3> T S) T;
7) 4-; 9) -f ; H) —r- ; l3> —1 > 15> 38- >) *; 2) 3> cosa-sina;
" л/3 ** «о
4( --L sin 4a. 40. I> V2~VS . 3, 2-Д 5) o/gJ-V2 ; 7) q.S; 0,8; 0,75
d, . a 3 4 „ „
41. sin—=—; cosa=—. 42. 1) y=----------- ; 3) //=1 +
2 5 5 l+tg2f
4 4 X 1 4 2 X
4tgy - 1- tg2y /g
H-----------43. 1) ; 3) 0; 5) ctg 5° tg 20°; 7) sin 25°;
2tgy+l—tg2y
13 5
9) — sin (a + p) sin (a — 0); 11) —2 sinл sin — л; 13) 2 sin a cos 40°;
15) 4 cos у cos a cos у a. 45. IJ-L^.V3 ; 3) У3 _|__L cos ю°; 5)
4(cosl£-cos lir) ; 7) +4C0S I0°; 9) +cos(a —₽)—C0S(3a + P)):
11) (sin 4a —sin 6a + sin 2a). 46. 1) 45°; 3) —60°; 5) не существует; 7) 0;
9) —45°. 47. 1) -j-; 3) 48- 0 ; 3) -g-; 5) не существует; 7) ;
9) 49. 1) 3) —51. 1) 3) 0; 5) 7) 9) 11) |л.
3 oo 3 oo43
52. 1) 4; 3) 2; 5) ~ J 7) —; 9) ; 11) 2; 13) ; 15) 1. 54. 1) nk,
□ Ox4! 1U
3 7
k^Z\ 5) нет решения; 9) ±-^-+2л/г, k£Z\ 13) -^- + л/г, k£Z. 55. 1) -у л, ^-л;
О О XX
346
5> -у; 9) -% , % ; И) 0, у, «. у , 2л; 13) -% , --J,
у, у ; 15) -у, 56. 1) ±k, kEZ; 5) ±^+лЛ, *6Z; 9) -у+у*.
kez-, 13) (-1)*£—£+лл, kEZ-, 17) -±л+4л, kez-, 21) (-1)‘-£+л*,
4+лй, fegZ; 25) ±4-л+2лй, 2лА, kEZ; 29) ±-?-+л/г, +л/г, kEZ.
2 о 4 о
57. 1) л*, kEZ; 5) ±4+-т*. ±4+"*, ktz- 58- >) -4-л*. ±4 +
О 4 3 Oil
+у, feez; 5) -Д+у. §4-лЛ, kEZ; 9) yft, fegZ; 13) у+уЛ;
^k, nk, kEZ. 59. 1) arctg 4+лЛ, kEZ; 5) arctg 4+лЛ, x=-^-+nk, kEZ;
о о 7 4
9) arctg ( — 2) +л/г, k£Z.
ГЛАВА IV
2 _2
1. 0,lx4. 2. x5; x4; у ; 2x; x 3 ; -Jx.
_i_i j
5. 1) 23; 5) 2"'; 9) 2 20; 10) 2 4 . 6.
1_5 2
8. 1) a24: 5) 27. 9. В 28: 5) a5.
з 10 4 ±. 1 . _L 1 . ±
x* ' x^[x ' x ' 3-x/x5" ’ -yfx
1)3^; 5) (4)"^ ’• О 7t4 J 5) V37-
, 5 /V 5 /7Г
11. 13.3- 12. 1) Vi9<V23;
Г I 1 13
5) 17’“ >31". 25. 1) I —; el; 5) (0; 1). 27. 1) 1; 0; 5; - 1; у; у; 2) 2; — 1; 0; —3;
-у ; у. 28. 1) 3; 5) -±-. 29. 1) 3; 2) 9; 3) л/З; 4) 4. 30. 1) 1; 2) 1; 3) -2; 4) 2.
a3h2 -\lac~' --
33. 1) A =---— ; 5) 4=^—=—. 34. log2a~'; log2 \[a; log2 a 2 ; log2 a2;
yA -y/x yb
35.1)6; 5) 6)5. 37. 1) 2(2a~1} ; 2) ;
log2 3 3 3 (z — a) 2 (b — a)
3> 2?42^(9M+1~- 38’ *> <0; +TO); 5> %<I; 9) Hi +~). 40. 1) log32>0;
5) log34>l; 9) logj 7>logj 10; 13) log52>log62. 42. 1) / = —; 5) / =
3 3 x
=57УТ • 44- ° г/(4’) = _|’ yW=1' 2) ^(0=2. У (100)=8; 3) у (1)= 1, i/(e)=
= e-l; 4) j/(y)=y + ln2, </(l) = 2. 45. 1) (-oo; + oo); 2)(-«;0];
3) (0; 4-co); 4) (-co; 1]; 5) (-oo;0); 6) [log2 у; + oo ) . 47. 7 = ^ (лет).
347
48. t = § (суток). 49. /i(p)=//-ln — . 51. Т = --Ц---. 52. / = 9 мин.
In 2 р log2m — log2 и
3 1
54. 1) х= —; 5) х= —; 13) x=log23; 17) х=2; 21) х=1. 55. 1) х=16; 5) х = 0,
х=3; 9) х=-1. 56. 1) х=1; 5) х=-1; 9) x=2-log23. 57. 1) х = 3;
5) х=±1; 9) х=0. 58. 1) х = 9, х = 3; 5) х=1, х = -^-. 59. 1) х^1;
5) (—оо;+оо); 9) (-оо;+оо); 13) (1;+оо); 17) (-оо;2). 60. 1) х> 10;
5) х< -99; 9) 3<х<5; 13) х>6. 65. 1) х=1, у=2;
5) ( х= 100, Г х=-, 66. 1) х=1; 2) х= 1; 3) х = 2; 4) х = 3; 5) х=2;
\у=То : Ъ=100-
6) х=1; 7) х=1; 8) х=9. 68. 1) , у=^^-- 3) x = VTZ77, У =
о Э
=7П7?; 4) x=-lnj/, у = ±. 69. 1) /=£^+/0; 2) /=-^+/0;
3) / = /01п —; 4) / = /0(е^-1). 70. 1) ; 3) = 4) j/=l-x2;
s 5
5) #=ln2 х; 6) у = ее*. 71. 1) # = 2х-|-2; 3) у=^/х, х>0; 4) у = — In х; 5) у = е*-\- 1;
6) у=^. 83. 1) / = -—L—2) </'=—4=; 4)
2 Vх (1 + х ) х -у/х2 — 1 1 х
ГЛАВА V
3 5 г2 9 -
10. 1) х; 5) -^-х4-4х3+---2х; 9) -=-х2 ; 13) -3cosx; 17) tg х; 21) -е~х +
4 □ 2 3
+ е*; 25) 2 In |х|; 29) x-ln |х+ 11; 33) -4-(1-2х)3 = 4-(2х-I)3; 37) -cosx +
О о
+ sin х; 41) —z-sin 4x-|--^-sin 2х; 45) 4“ sin 2x4--^-. 11. 1) 3; 5) —6; 9) —;
о 4 4 2 3
13) 17) 4-; 21) 1; 25) 1; 29) —J-; 33) 4. 12. 1) 6; 3) ; 9) In 3;
13) ; 17) 11 . 19. _2. 24. 1) 1; 5) -cosx + 3. 25. 1) у=Се2\
О ZU Z □ □
2) у = Се~’-, 3) у=Се~2
ГЛАВА VI
1. 1) х=/=1; 5) 0<х<1; 9) х^= ±4- + 4-яп; 13) х<4>. 5. 1) х<1; 3) [0; 2}
о 3 2
6. 1) х#=±1; 3) 0; 5) (-оо; -2)U(3; 5)U(5; + оо). 8. 1) Д #=0; 5) □ >0;
348
9) Д >0. 14. 3) x=l; -2; 3. 15. 3) x = ±2, ±3; 5) x=2,
Q
1. 16. 1) x= —1; 4; 5) x=-2; -y. 17. 1) x = 7;
—LT; 5) x=10; 9) x<2.
О
18. 5) x= ±-^- + 2л/г; 9) x = -^- +л/г; 13) x = ^ ; 18) x=-^- +л/г, x = arctg +л/г.
О Z Z 4 Z
19. 1) x=3; 5) x=4; 9) x=0; 13) x=0; 16) [0; I]; 19) x=2. 20. 1) (-y; *):
5) (3; + oo)U(—°°; -2); 9) (-oo; -l)u(y’. + «>)• 2l- l) [—3.5; —3]U[1;
+ oo); 5) (4; 7); 7) [1; 5] 22. 2) (12; 21]; 5) (5; 5^5); 8) (0; 1) (J (л/2; +«>); 14) x<0.
23. 1) (3; -1); 7) (2; 3), (-3; -2); 10) (4; 3; 7).
ОГЛАВЛЕНИЕ
Предисловие.......................................................... 3
Глава I. Функции и графики........................................... 5
Вводная беседа................................................. —
§ 1. Понятие функции.......................................... 11
§ 2. Чтение графика........................................... 15
§ 3. Линейная функция......................................... 21
§ 4. Преобразование графиков...................................28
Заключительная беседа......................................... 35
Задачи к главе I...............................................45
Глава II. Производная и ее применение................................65
Вводная беседа................................................. —
§ 1. Вычисление производной....................................73
§ 2. Исследование функции с помощью производной .... 80
§ 3. Приложения производной....................................92
Заключительная беседа.........................................104
Задачи к главе II..............................................ПО
Глава III. Тригонометрические функции...............................128
Вводная беседа................................................. —
§ 1. Определение и простейшие свойства тригонометрических
функций.......................................................134
§ 2. Исследование тригонометрических функций..................140
§ 3. Тождественные преобразования.............................151
§ 4. Тригонометрические уравнения.............................156
Заключительная беседа.........................................164
Задачи к главе III............................................170
Глава IV. Показательная и логарифмическая функции-..................185
Вводная беседа................................................. —
§ 1. Показательная функция....................................189
§ 2. Логарифмическая функция..................................192
§ 3. Показательные и логарифмические уравнения и неравенства 200
Заключительная беседа.........................................207
Задачи к главе IV.............................................217
350'
Глава V. Интеграл и его применение...................................231
Вводная беседа................................................. —
§ 1. Вычисление интеграла......................................238
§ 2. Приложения интеграла......................................244
Заключительная беседа..........................................253
Задачи к главе V...............................................260
Глава VI. Уравнения и неравенства....................................270
Вводная беседа................................................. —
§ 1. Уравнения с одним неизвестным.............................283
§ 2. Неравенства с одним неизвестным...........................289
§ 3. Системы уравнений........................................292
Заключительная беседа..........................................297
Задачи к главе VI.............................................303
Задачи на повторение свойств функций ................................ 313
Лабораторные работы..................................................322
Справочный материал..................................................329
Ответы ..............................................................343
Сведения о пользовании учебником
№ Фамилия и имя ученика Учебный год Состояние учебника
В начале года В конце года
1
2
3
4
5
Учебное издание
Башмаков Марк Иванович
АЛГЕБРА И НАЧАЛА АНАЛИЗА
Учебник для 10—11 классов
средней школы
Зав. редакцией Т. А. Бурмистрова
Редактор Л. Н. Белоиовская
Младшие редакторы М. В. Зарвирова, Е. В. Казакова
Художники В. В. Костин, Б. Л. Николаев
Художественный редактор Ю. В. Пахомов
Технический редактор Н. А. Киселева
Корректор М. Ю. Сергеева
ИБ № 13909
Подписано к печати с диапозитивов 08.05.91 Формат 60x90/16. Бум. офсетная. Гарнит. Литературная. Печать
офсетная. Усл. печ. л 22,0+0,25 форз. Усл. кр.-отт. 22,75. Уч.-изд. л. 18,61+0,42 форз. Цена 2р. 50 коп.
Ордена Трудового Красного Знамени издательство «Просвещение» Министерства печати и массовой информа-
ции РСФСР 129846, Москва, 3-й проезд Марьиной рощи, 41.
Отпечатано при посредстве В/О «Внешторгиздат»
Отпечатано Графишер Гросбетриб Пёснек ГмбХ - Эйн Мондрук-Бетриб
Gedruckt bei Graphischer GroBbetrieb PoBneck GmbH • Em Mohndruck-Betrieb
и?