Математический анализ. Функции одного переменного Ч.1 и 2 - Шилов Г.Е.

Автор: Шилов Г.Е.
Теги: математика математический анализ теория множеств учебное пособие теория вещественных чисел теория пределов теория рядов
Год: 1969
Похожие
Математический анализ. Функции нескольких переменных Ч.1 и 2
Математический анализ (функции одного переменного). Части 1 и 2
Математический анализ (функции одного переменного). Часть 3
Сборник задач по математическому анализу. Топ 3. Функции нескольких переменных
Текст
                    Г.Е.Шилов
МАТЕМАТИЧЕСКИЙ АНАЛИЗ (ФУНКЦИИ ОДНОГО ПЕРЕМЕННОГО)
части1 и 2
Книга представляет собой учебное пособие по курсу математического анализа.
Она не является учебником и не следует официальным программам курса
математического анализа, хотя формально знаний основ анализа не
предполагается. Книга рассчитана в первую очередь на студентов, знакомых уже с
элементами дифференциального и интегрального исчисления и желающих
углубить свои знания. В гл. 1 дается аксиоматическое построение теории
вещественных чисел. В гл. 2 излагаются элементы теории множеств и теории
математических структур. Гл. 3 посвящена метрическим пространствам. В гл. 4
строится общая теория пределов, использующая упрощенную схему фильтров
Картана. В гл. 5 рассматривается понятие непрерывности и изучаются
элементарные трансцендентные функции. В гл. 6 излагается теория рядов—
числовых и функциональных. Гл. 7—8 посвящены собственно
дифференциальному исчислению, а гл. 9—интегральному исчислению. Гл. 10
вводят читателя в теорию аналитических функций; ее методы используются, в
частности, в гл. 11 о несобственных интегралах.
ОГЛАВЛЕНИЕ
Предисловие	6
ЧАСТЬ ПЕРВАЯ
ВВЕДЕНИЕ В АНАЛИЗ
Глава 1. Вещественные числа	13
§ 1.1.	Первоначальные сведения о	13
множествах
§ 1.2.	Аксиомы вещественных	16
чисел
§ 1.3.	Следствияиз аксиом	18
сложения
§ 1.4.	Следствияиз аксиом	19
умножения
§ 1.5.	Следствияиз аксиом	22
порядка
§ 1.6.	Следствияиз аксиомы о	25
верхней грани
§ 1.7.	Принцип Архимеда и его 29
следствия
§ 1.8.	Принцип вложенных	35
отрезков Кантора
§ 1.9.	Расширенная область	36
вещественных чисел
Дополнение к главе 1. Логическая 38
символика
Задачи	39
Историческая справка	40
Глава 2. Элементы теории	41
множеств
§ 2.1.	Операции над множествами	41
§ 2.2.	Эквивалентность множеств	43
§ 2.3.	Счетные множества	46
§ 2.4.	Множества мощности	49
континуума
§ 2.5.	Понятие о математической 50
структуре. Изоморфизм структур
§ 2.6.	Пространство п измерений	55
§ 2.7.	Комплексные числа	60
§ 2.8.	Общее понятие функции.	65
График
Задачи	67
Историческая справка	68
Глава 3. Метрические	70
пространства
§ 3.1.	Определения и примеры	70
§ 3.2.	Открытые множества	78
§ 3.3.	Сходящиеся	81
последовательности и
гомеоморфизм
§ 3.4.	Предельные точки
§ 3.5.	Замкнутые множества
§ 3.6.	Всюду плотные множества и
замыкания
§ 3.7.	Полные пространства
§ 3.8.	Пополнение
§ 3.9.	Компактность
Задачи
Историческая справка
Глава 4. Общая теория пределов
§ 4,1. Определение предела
§ 4.2.	Общие теоремы о пределах
§ 4.3.	Пределы числовых функций
§ 4.4. Предельные точки функции
§ 4.5.	Функции, неубывающие по
направлению
§ 4.6.	Основные теоремы о
числовых последовательностях
§ 4.7.	Пределы векторных
функций
Задачи
Историческая справка
Глава 5. Непрерывные функции
§ 5.1. Непрерывные функции на
метрическом пространстве
§ 5.2. Непрерывные числовые
функции на числовой оси
§ 5.3. Монотонные функции
§ 5.4. Логарифм
§ 5.5. Экспонента
§ 5.6.	Тригонометрические
функции
§ 5.7.	Приложения
тригонометрических функций
§ 5.8. Векторные непрерывные
функции векторного переменного
§ 5.9. Последовательности
функций
Задачи
Историческая справка
Глава 6. Ряды
§ 6.1.	Числовые ряды.
Знакоположительные ряды
91
95
97
100
107
111
119
121
122
122
131
132
139
141
144
148
151
153
154
154
162
165
169
172
181
188
195
203
208
210
211
211
§ 6.2.	Ряды с любыми	219
вещественными членами
§ 6.3.	Действия с рядами	221
§ 6.4.	Ряды векторов	227
§ 6.5.	Ряды функций	236
§ 6.6.	Степенные ряды	238
Задачи	242
Историческая справка	246
ЧАСТЬ ВТОРАЯ
ДИФФЕРЕНЦИАЛЬНОЕ И
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
Глава 7. Производная	249
§ 7.1.	Определение производной 249
§ 7.2. Второе определение	258
производной
§ 7.3.	Дифференциал	260
§ 7.4.	Теоремы о конечных	262
приращениях
§ 7.5.	Расположение кривой	264
относительно своей касательной
§ 7.6.	Правила Лопиталя	268
Задачи	270
Историческая справка	273
Глава 8. Высшие производные	274
§ 8.1.	Определения и примеры	274
§ 8.2.	ФормулаТейлора	277
§ 8.3.	Анализ поведения функции	280
в окрестности данной точки
§ 8.4.	Высшие дифференциалы	285
§ 8.5.	Ряд Тейлора	286
§ 8.6.	Экспонента и	289
тригонометрические функция в
комплексной области
§ 8.7.	Гиперболические функции 294
Задачи	297
Историческая справка	299
Глава 9. Интеграл Римана	300
§9.1.	Определение интеграла и	300
теоремы существования
§ 9.2.	Зачем нужен интеграл?	314
§ 9.3.	Интеграл как функция	321
верхнего предела
§ 9.4.	Техника неопределенного 327
интегрирования
§ 9.5.	Вычисление определенных 338
интегралов
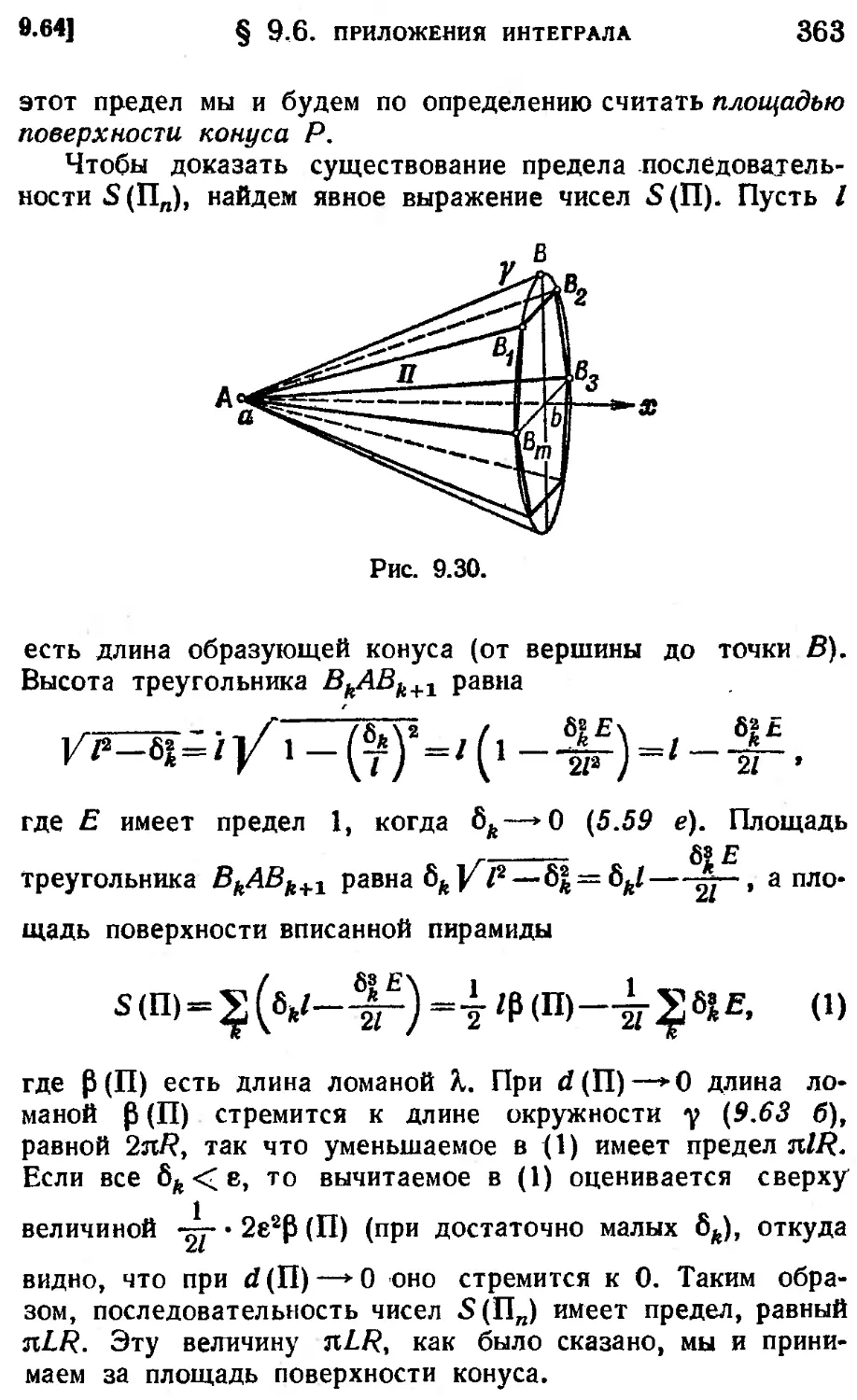
§ 9.6.	Приложения интеграла	348
§ 9.7.	Интегрирование и	373
дифференцирование
последовательности функций
§ 9.8.	Интегрирование и	379
дифференцирование по параметру
§ 9.9.	Криволинейные интегралы 385
Задачи	393
Историческая справка	396
Глава 10. Аналитические функции 397
§ 10.1.	Определения и примеры	397
§ 10.2.	Криволинейные интегралы	406
от комплексных функций
§ 10.3.	Теорема Коши и ее	414
следствия
§ 10.4.	Вычеты и изолированные	428
особые точки
АЛФАВИТНЫЙ
Абель 122,210
Абсолютная величина вещественного
числа 23
Автоморфизм п-мерного
пространства 58
-------тождественный 59
—	структуры 51
Адамар 70, 451
Аналитическая функция 398
---вещественная 427
---целая 424
Аналитическое продолжение 288, 426
Арган 69
Аргумент комплексного числа 189
—	функции 65
Ариабхата 210
Арифметико-геометрическое среднее
152
Арифметическая степень
множества 40
—	сумма множества 39
§ 10.5.	Отображения и	440
элементарные функции
Задачи	450
Историческая справка	453
Глава 11. Несобственные	455
интегралы
§ 11.1.	Несобственные интегралы 455
первого рода
§ 11.2.	Несобственные интегралы 468
второго и третьего рода
§ 11.3.	Вычисление несобственных 473
интегралов с помощью вычетов
§ 11.4.	Несобственные интегралы, 483
содержащие параметр
§ 11.5.	Гамма-функция и бета-	495
функция Эйлера
Задачи	508
Историческая справка	509
Указания и ответы к задачам	510
Алфавитный указатель	523
УКАЗАТЕЛЬ
Арифметическое произведение
множеств 39
Архимед 13, 29, 246, 349, 350, 395
Архимеда принцип 29
Асимптотическая единица 138
— принадлежность 131
Базис 57
Барроу 273
Бернулли И. 273, 453
Бернулли Я. 273
Бесконечно удаленная точка 436
Бесконечность 36
Бета-функция 497
Больцано 40, 121, 209, 210, 246, 273
Больцано - Вейерштрасса принцип 94
Бомбелли 69
Борель 121
Брус замкнутый 157
— открытый 157
Бурбаки50, 68, 121,273
Бюрги 210
Валле-Пуссен 509
Вейерштрасс 40, 209, 210, 273, 454
Вектор 55
— единичный 73
— нормированный 73
Верхний предел 139, 147
Верхняя грань 17
----точная 18
Вессель 69
Вещественная часть 62
Взаимно однозначное соответствие
44
Включение 14
Вложенных промежутков система 35
Внутренняя точка 72
Высшие дифференциалы 285
Вычет 429
— логарифмический 431
Гамма-функция 495
—, асимптотическое выражение 503
— в комплексной области 506
—, формула дополнения 500
Гармоническая функция 405
Гаусс 40, 69,210, 246, 453
Гёдель 40 Гейне 209
Гентцен 40
Гильберт 11, 40
Гиперболические функции 294
----обратные 333
Гипергеометрический ряд 243
Гомеоморфизм 85
Гомеоморфные метрики 86
Гранди 211, 246
Граница множества 318
Грассман 69
График функции 66
Грегори 299
Группировка членов ряда 223
Грушни В. В. 67
Даламбер 211, 453
Дарбу 396
Двоичная система 34
Дедекинд 40, 210
Десятичные знаки 32
Диаметр 72
Дирихле 69, 509
Дифференциал сложной функции 262
— функции 261, 401
----высшего порядка 285
Дифференцирование интеграла по
параметру 381
— несобственного интеграла по
параметру 486
— последовательности функций 377
Длина вектора 73
— дуги 320, 356
----как функция параметра 361
----эллипса 359
— окружности 359
Дополнение множества 42
Дробная часть 30
Дю-Буа-Раймон 396
Евдокс 40
Евклид 40
Единица 17
— асимптотическая 138
Единичный вектор 73
Зависимое переменное 65
Замкнутый контур 388
Замыкание 98
Зендель 210
Знаки включения 14
Значение функции 65
Изолированная точка 106
Изоморфизм структур 51
Индукции математической метод 20
Интеграл криволинейный 385
— Лапласа 480
— неопределенный 323
— несобственный абсолютно
сходящийся 462
----второго рода 468
----первого рода 455
----расходящийся 456
----сходящийся 456
----третьего рода 470
----условно сходящийся 462
----определенный 323
— по замкнутому контуру 388
— Римана 301
----, его пределы 302
----на брусе 318
----на компакте 316
— Стилтьеса 346
----криволинейный 385
— типа Коши 414
— Френеля 508
— Фурье 476
----особый 481
Интегральная сумма 301
Интегрирование по параметру 379.
485
— по частям 326, 338, 467
----многократное 394
— последовательности функций 373
— через подстановку 326, 343, 467
Интегрируемая мажоранта 489
—	функция 302
Интервал 28
—	смежный 96
—	составляющий 80
Интрезок 29
Иррациональные числа 20
Казорати 454
Кантор 40, 41, 49, 68, 121, 210
Кантора принцип вложенных
отрезков 35, 37
КартанА. 153
Касательная 249
Катеноид 366
Кеплер 349
Клеро 396
Колебание функции 160
----в точке 394
Компакт 111
—	нагруженный 317
Компактное метрическое
пространство 111
Комплексно сопряженные числа 62
Комплексные числа 60
Конечные точки 436
—	числа 37
Континуум 49
Конфниальные последовательности
Координаты вектора 55, 57
Корень аналитической функции 423
-------кратности к 423
—	n-й степени 26
Коши 40, 121 122,153,154,209,210,
246, 273, 299. 396, 453, 455, 509
Коэн И. 68
Коэффициенты Лорана 434
—	Тейлора 421
Кратность корня 201
Кривая кусочио-гладкая 356
Криволинейный интеграл 385
Критерий Дю-Буа-Раймона 394
—	Лебега 394
— Коши для векторного ряда 229
---для предела векторной
функции 151
---для предела по направлению
130
---для равномерной сходимости
206,488
-------сходимости несобственного
интеграла 457
----------числового ряда 212
----------числовой
последовательности 101, 145
— Римана 394
— Хаусдорфа 114
Круговые функции 297
Крылов А. Н. 292
Кэлн 69
Лагранж 453
Лебег 121, 396
Лейбниц 273, 298, 299, 302, 343, 396,
453,455
Лемма Жордана 479
— о замкнутых шарах 105
— о конечном покрытии 118
Линейная зависимость 56
Линейно упорядоченное множество
51
Лобачевский 16, 69
Логарифм 169
— натуральный 179
Логарифмирование 174
Лопиталь 273
Лузин Н. Н. 455
Люилье 273
Люстерник Л. А. 115
Максимальное из двух чисел 23
Максимум локальный 260
Меиголн 246
Мера Жордана 318
Метод математической индукции 20
Метрика 70
Метрическое пространство 70
---компактное 111
---локально компактное 111
---полное 101
---предкомпактное 113
Минимальное из двух чисел 23
Минимум локальный 260
Мнимая часть 62
Многочлен Тейлора 277
Множества геометрически равные 78
Множество 13
—	бесконечное 13
—	вещественных чисел 16
—	всюду плотное 97
—	жорданово 318
—	замкнутое 95
—	конечное 13
—	линейно упорядоченное 61
—	мощности континуума 50
—	несчетное 49
— ограниченное 28
---в метрическом пространстве 71
---сверху 17
---снизу 25
—	открытое 78
—	пустое 13
—	счетное 46
Модуль вещественного числа 23
—	комплексного числа 189
Мощность множества 45
Мур 153
Направление 122
Натуральные числа 19
Невозрастающая последовательность
145
Независимое переменное 65
Немировский А. С. 243
Неограниченное множество 72
Неопределенный интеграл 323
Неотрицательное число 23
Непер 210
Неположительное число 23
Непрерывность односторонняя 164
—	равномерная 159
Неравенство Коши 75
—	Коши - Буняковского 75
—	треугольника 70
—	четырехугольника 71
— Юнга 354
Несобственный интеграл второго
рода 468
---первого рода 455
---третьего рода 470
Несчетное множество 49
Неубывающая
последовательность 145
Нижний предел 139, 147
Нижняя грань 25
---точная 25
Новиков П. С. 40
Норма вектора 73
Нормированный вектор 73
Нуль 16
— аналитической функции 423
Нуль аналитической функции
кратности к 423
Ньютон 246, 273, 298, 299, 300, 396,
455
Область 78
— односвязная 414
— связная 398
Обратная функция 167
Обратное вещественное число 17
Обратные гиперболические функции
333
— тригонометрические функции 186
Объединение множеств 14, 41
Объем множества 318
— шара 372
Ограниченная последовательность
145
— сверху последовательность 145
— снизу последовательность 145
Односторонняя непрерывность 164
Окрестность точки 72
Определенный интеграл 323
Ортогональные векторы 192
Особая точка изолированная 435
------устранимая 435
Особые точки кривой 361
Остаточный член формулы Тейлора в
интегральной форме 339
----------в форме Лагранжа 279
Отображение 195
— конформное 440
— непрерывное 195
Отражение 78
Отрезок 28
Отрицательное число 23
Оттервал 29
Паламодов В. П. 67
Пеано 40
Первообразная 322
Пересечение множеств 15, 41
Перестановка членов ряда 224
Периодическая функция 185, 292
Период функции 185, 292
Пикар 439
Площадь криволинейной трапеции
314,348
— круга 350
— плоской фигуры 315, 389
------в полярных координатах 355
—	поверхности вращения 365
—	эллипса 352
Поверхность сферы 366
Поворот 192
Подмножество 14
—	истинное 14
Позиционная запись вещественных
чисел 32
Показатель степени 21
Поле комплексных чисел 61
—	числовое 17
Полна 397, 451
Полнота системы аксиом 51
Положительное число 23
Полукасательная левая 267
Полукасательная правая 257
Полюс п-го порядка 435
Полярные координаты 188
---в пространстве 194
Полярный радиус 189
—	угол 189
Пополнение 107
Последовательности конфниальные
107
Последовательность 65
—	невозрастающая 145
—	неубывающая 145
—	ограниченная 145
---сверху 145
---снизу 145
—	расходящаяся 81
—	сходящаяся 81, 123
—	фундаментальная 100
— функций 203
Постоянная Эйлера 462
Потенцирование 174
Правила Лопиталя 268
Предел по направлению 122
-------на подмножестве 125
Предельная точка подмножества 93
---последовательности точек 91
-------чисел 147
---функции 140
--------верхняя 139
--------нижняя 139
Предкомпактное метрическое
пространство 113
Преобразование Абеля 230
—	подобия 60
Признак Абеля—Дирихле для рядов
230
--------для несобственных
интегралов 465
--------равномерной сходимости
интегралов 494
—	Вейерштрасса 239
—	Даламбера 214
—	Коши 214
— Лейбница 220
---для интегралов 462
— Раабе 218
— сравнения 213, 458
—	сходимости интегральный 459
Пример Ван-дер-Вардена 271
Принцип аргумента 451
—	максимума 450
Произведение бесконечное 244
—	вещественных чисел 17
—	множеств 41
---прямое 65
—	ряда на число 221
—	рядов 222
Производная 249
—	вторая 274
—	левая 257
—	логарифма 254
—	обратной функции 253
—	односторонняя 257
—	по множеству 397
—	порядка п 274
—	правая 257
—	сложной функции 252
—	степеннйй функции 255
Производная тригонометрических
функций 255
—	частная 402
Промежуток 29
Пространство вещественное п-мерное
55,73
—	евклидово п-мерное 74
Противоположное число 17
Птолемей 210 Путь 385
Равномерная непрерывность 159
—	сходимость 204
Равномощность множеств 45
Радиус сходимости 211
Разбиение 300
—	, его параметр 300
—	последующее 302
—	с отмеченными точками 300
Разложение рациональной функции
на простейшие дроби 202
—	целой функции на простейшие
дроби 452
Расстояние 70
—	между подмножествами 120
—	от точки до множества 120
Расходящаяся последовательность 81
Рациональные числа 20
Региомонтан 210
Рефлексивность 45
Риман 396
Риманова поверхность 447
Ролль 273
Ряд абсолютно сходящийся 220
-------векторный 229
—	векторов 227
—	гармонический 217
—	гипергеометрический 243
—	двусторонний 233
---, симметричное суммирование
235
—	знаконеотрицательный 211
—	знаконеположительный 211
—	знакоотрицательный 211
—	знакоположительный 211
— Лорана 434
---, главная часть 434
---, правильная часть 434
— сгруппированный 223
— степенной 240
---, радиус сходимости 241
— Тейлора 287, 421
—	условно сходящийся 220
—	функций 236
---, равномерная сходимость 239
---, сумма 237
—	числовой 211
---, отрезок 211
---, расходимость 211
---, сходимость 211
---, частные суммы 211
Свертка 491
Свертывание 493
Сдвиг 78
Сеге 397
Симметричность 45
Система двоичная 34
—	троичная 34
Скалярное произведение 73
Сложная функция 157
Слой 66
Смежный интервал 96
Соприкасающаяся парабола 281
Составляющий интервал 80
Сохоцкий Ю. В. 454
Среднее интегральное 307
Средняя ордината 307
Стевни 13
Степенная функция 174
Степень арифметическая множества
40
—	вещественного числа 20
Стилтьес 396
Стокс 210
Структура математическая 50
Сумма арифметическая множеств 39
—	вещественных чисел 16
—	множеств 4 1
—	рядов 221
Сфера 72
Сходимость равномерная 204
---внутри области 421
Сходящаяся последовательность 81,
123
---, предел 81
Счетное множество 46
Тейлор 299 Теорема Абеля 241
—	Абеля — Лиувилля 335
—	Больцано 163
—	Бэра 105
—	Вейерштрасса 158
—	Гейне 159
—	Дирихле 225
—	единственности аналитической
функции 425
— Коши 262,414
—	Коши — Адамара 237
—	Лагранжа 263
—	Лиувилля 427
—	о вычетах 431
—	о среднем 307, 409
—	Римана 226
—	Ролля 262
—	существования корня многочлена
197,452
—	Фрагмена - Линделёфа 453
—	Хаусдорфа 107
—	Штейница 245
—	Эрмита 146
Тождество Эйлера 245
Торричелли 273
Точка выпуклости вверх 265
---вниз 265
—	изолированная 106
—	конденсации 119
—	непрерывности 154
—	перегиба 265
—	разрыва 154
— существенно особая 436
Транзитивность 45
Трансцендентные числа 50
Тригонометрические функции 181
---в комплексной области 290
---обратные 186
Троичная система 34
Угол между векторами 191
Уравнение Лапласа 405
Условия Коши—Римана 403
Успенский В. А. 16
Фермн 249, 272
Флюента 396
Флюксия 300, 396
Формула Валлиса 394
— Дирихле 508
— Коши 417
— Лейбница 274
— Ньютона -Лейбница 323, 342, 409
— Тейлора 277
----, остаточный член 279, 339
— Фруллани 508
Формулы Эйлера 291
Фреше 121
Фробениус 64, 69
Фундаментальная
последовательность 100
Функций, эквивалентные по
направлению 137
Функция 65
— аналитическая 398
----вещественная 427
----в точке 398
----целая 424
— бесконечно большая 133
----по сравнению 137
----дифференцируемая 286
----малая 133
----по сравнению 137
—	векторная 65
—	вещественного переменного 65
—	возрастающая 165
— выпуклая вверх 265, 271
----вниз 265, 271
—	гармоническая 405
—	гладкая 274
----п-го порядка 274
—	Дирихле 312
—	дифференцируемая в точке 249
---по множеству 398
—	дробно-линейная 442
—	кусочно-гладкая 326
—	кусочно-непрерывная 310
—	кусочно-постоянная 311
—	многозначная 66
—	монотонная 165
— невозрастающая 165
---по направлению 143
— неотрицательная по направлению
133
— непрерывная в точке 154
---на множестве 155
---слева 165
---справа 165
— неубывающая 165
---по направлению 141
— п-кратно-дифференцируемая 274
-------по множеству 400
—, область значений 65
—, — определения 65
— обратная 167
— ограниченная 132, 133, 149
---по модулю 132
---сверху 132
Функция ограниченная снизу 132
—	однозначная 66
—	однолистная 442
—	отрицательная бесконечно
большая 133
—	положительная бесконечно
большая 133
—	положительная по направлению
133
—	равномерно непрерывная 159
—	Римана 208
—	сложная 157
— степенная 174, 443, 445
—	убывающая 165
—	характеристическая 318
Харди 337
Хаусдорф 41, 121
Целая аналитическая функция 424
—	часть 30
Целое кратное 29
Целые числа 20
Частная производная 402
Частное вещественных чисел 19
Чеботарев Н. Г. 335
Числа иррациональные 20
—	комплексные 60
—	конечные 37
—	натуральные 19
—	рациональные 20
Числа трансцендентные 50
—	целые 20
Число е 146
—	неотрицательное 23
—	неположительное 23
—	отрицательное 23
—	тс 184
—	положительное 23
Числовая ось 25
Числовое поле 17
Числовой ряд 211
---, отрезок 211
---, расходимость 211
---, сумма 211
---, сходимость 211
---, частные суммы 211
Шар 72
—	замкнутый 72
—	открытый 72
Шварц Г. 450
Штифель 209
Эйлер 69, 210, 299, 453, 609
Эквивалентные множества 44
Экспонента 172, 444
—	в комплексной области 289
Экстремум локальный 260
Эллиптические интегралы 335
Энгельс 247
Ячейка 316
—	, ее мера 317
ПРЕДИСЛОВИЕ
Математический анализ есть большая область математики,
связанная с понятиями функции, производной и интеграла.
К настоящему времени эта область обнимает большое ко-
личество меньших областей—дифференциальные уравнения
(обыкновенные и в частных производных), интегральные
уравнения, функции комплексного переменного, дифферен-
циальную геометрию, вариационное исчисление и другие.
Но если содержание математического анализа можно считать
установившимся, то во взглядах на его структуру происхо-
дят значительные перемены. В классическом курсе 20-х годов
Э. Гурса весь анализ представлен как бы на огромной рав-
нине— на едином уровне абстракции; в книгах нашего вре-
мени большое внимание уделяется выявлению в анализе
различных «этажей» абстракции, т. е. различных «структур»
(Бурбаки), характеризующих математико-логические основы
исходных построений. Обращение к основам приводит к яс-
ности существа дела, освобождая математика от учета кон-
кретной индивидуальности объекта, а понимание существа
дела позволяет немедленно включить в рассмотрение новые
объекты с иной индивидуальностью, но с тем же глубинным
устройством.
Так, было известно доказательство Пикара существования
и единственности решения дифференциального уравнения,
основанное на методе последовательных приближений искомой
функции на отрезке другими функциями, получающимися по
определенным правилам. А затем был сформулирован (Бана-
хом и другими) «метод неподвижной точки», которым была
доказана та же теорема. Он обнаружил существенную часть
в доказательстве Пикара: наличие сжимающего оператора
в некотором метрическом пространстве. Вся же обстановка —
числовые функции на отрезке, дифференциальное уравнение —
ПРЕДИСЛОВИЕ
7
оказалась несущественной. В результате «метод неподвижной
точки» не только сделал более прозрачным, «геометрическим»
доказательство теоремы Пнкара, но и дал возможность, раз-
вивая заложенную в нем идею, доказывать множество теорем
существования, где речь шла даже не о функциях на от-
резке и не о дифференциальных уравнениях. То же отно-
сится к геометрии гильбертова пространства, к исчислению
дифференцируемых функционалов и многому другому.
В этой книге мы излагаем основные концепции матема-
тического анализа применительно к функциям одного пере-
менного. Однако «одно переменное» мы понимаем в несколько
расширенном смысле. Дело в том, что для таких основных
понятий анализа, как предел и непрерывность, разница между
классическими случаями одного и нескольких переменных
не столь существенна; в этих главах мы предпочитаем вести
изложение в оптимальной общности, понимая под «одним
переменным», например, точку метрического пространства.
Но когда дело доходит до дифференцирования и интегри-
рования, разница между указанными классическими случаями
становится уже весьма ощутимой, и мы ограничиваемся там
функциями «на Самом деле» от одного переменного—вначале
вещественного, а затем комплексного. Однако значения этих
функций лишь вначале числовые; далее они векторные, даже
принадлежащие к нормированному пространству, что откры-
вает широкий круг приложений. Аналитические функции
составляют в нашем построении неотъемлемую часть анализа.
Мы не касаемся в этой книге всей обширной области диф-
ференциального и интегрального исчисления функций не-
скольких переменных, изложение которой требует по крайней
мере еще целого тома.
Мы не ввели в книгу интеграл Лебега, поскольку в рас-
сматриваемых здесь задачах анализа встречаются лишь
непрерывные функции (или функции, обладающие конечным
числом точек разрыва), для интегрирования которых доста-
точно интеграла Римана. В более высоких задачах анализа,
например в теории интегральных уравнений, решающая роль
интеграла Лебега неоспорима. Но изложение теории интеграла
Лебега в данной книге могло бы переакцентировать внимание
читателя в специфические тонкости теории функций действи-
тельного переменного и теории меры. Поэтому мы оставили
за рамками книги интеграл Лебега и его приложения.
8
ПРЕДИСЛОВИЕ
Хотя формально у читателя не предполагается знаний
сверх школьного курса, но все же было бы весьма полезным,
если бы он, читатель, был знаком с построением графиков,
с дифференцированием и интегрированием и их простейшими
геометрическими применениями*). Данная книга не пред-
назначена служить элементарным учебником по курсу мате-
матического анализа; скорее ее нужно рассматривать как
пособие, предназначенное для самостоятельного чтения, про-
думывания, сопоставления друг с другом различных аспек-
тов теории. Отдельные места лектор может использовать
в лекционном курсе и в семинаре повышенного типа. Этой же
цели служат - приведенные в книге задачи; среди них нет
задач, преследующих выработку технических навыков (таких
задач достаточно в распространенных задачниках), и приво-
димые задачи иллюстрируют и развивают излагаемую общую
теорию.
Книга состоит из трех частей. Первая часть «Введение
в анализ» и вторая часть «Дифференциальное и интеграль-
ное исчисление» лежат перед читателем; третья часть
«Избранные главы современного анализа» выйдет в свет не-
сколько позднее отдельно.
Систематическое изложение предмета начинается в первой
части с теории вещественных чисел (гл. 1). Под вещест-
венными числами мы понимаем набор объектов, удовлетво-
ряющих некоторым определенным аксиомам. Существуют
и иные построения теории вещественных чисел, где то, что
мы принимаем за аксиомы, доказывают, исходя (в строгом
изложении — например в известном курсе Ландау) из аксиом
натуральных чисел и теории множеств. В обоих типах по-
*) Для начинающих я позволю себе рекомендовать свою брошюру
«Математический анализ в области рациональных функций» (готовится
к выпуску). В ней предмет анализа—функции, производные,
интегралы—описывается в применении к рациональным функциям
(частным двух многочленов). Работая над ней, я надеялся, что начи-
нающий читатель будет заинтересован перспективой, открывающейся
при овладении методами дифференциального н интегрального исчис-
ления; с другой стороны, он убедится, что одних рациональных функ-
ций недостаточно, что в полную силу методы авализа будут действо-
вать именно за пределами области рациональных функций; он будет
предупрежден об опасности формального, некритического использова-
ния этих методов и будет подготовлен к необходимости глубокого
изучения основ, предваряющих изучение дифференциального и инте-
грального исчисления в достаточно полной общности.
ПРЕДИСЛОВИЕ
9
строений отсутствует весьма существенный элемент—дока-
зательство непротиворечивости аксиом. По-видимому, в со-
временной математике не существует построения теории
вещественных чисел, свободного от этого недостатка. Вопрос
здесь далеко ие технический, а упирающийся в самые основы
математического мышления. Во всяком случае, раз это так,
расположение начального пункта в общей схеме анализа
становится, в общем, не очень существенным, и мы выбираем
его по соображениям наибольшей возможной близости к соб-
ственно аналитическим построениям. В гл. 2 после небольшого
экскурса в теорию множеств вводятся понятия математи-
ческой структуры и изоморфизма. В качестве иллюстрации
устанавливается единственность (с точностью до изомор-
физма) структуры вещественных чисел. Вводятся структуры
n-мерного пространства и поля комплексных чисел.
Гл. 3 посвящена теории метрических пространств.
В гл. 4 развивается общая теория предела. Основой теории
являются, с одной стороны, множество Е с выделенным в нем
направлением (упорядоченной системой подмножеств с пустым
пересечением—образованием, несколько более ограничитель-
ным, чем фильтр А. Картана, но для анализа вполне доста-
точным), с другой,— функция, определенная на множестве Е
со значениями в метрическом пространстве. В такую схему
укладываются все пределы, рассматриваемые в анализе, от
предела числовой последовательности до производной и ин-
теграла. В следующей гл. 5 после первоначальных теорем
о непрерывных числовых функциях на числовой оси вводятся,
с помощью функциональных уравнений, логарифм (из кото-
рого обращением получается экспонента) и тригонометри-
ческие функции. Среди приложений рассматриваются алгебра
и топология комплексных чисел н теорема о существовании
корпя у многочлена с комплексными коэффициентами.
В гл. 6 мы рассматриваем теорию рядов (числовых, сте-
пенных, функциональных).
Вторая часть книги открывается седьмой главой о произ-
водной. Главы 7 и 8 содержат собственно дифференциальное
исчисление. Формула и ряд Тейлора приводят к естественному
распространению вещественного анализа в комплексную об-
ласть. В гл. 9 содержатся наряду с общей теорией интеграла
Римана также и некоторые ее приложения. Для дальнейшего
развития анализа становится настоятельно необходимой
10
ПРЕДИСЛОВИЕ
техника аналитических функций, которая излагается
в гл. 10. Теория аналитических функций оказывается,
в частности, весьма полезной при вычислении несобствен-
ных интегралов, которым посвящена следующая гл. 11.
Система нумерации ясна из примера: символ 10.37 б озна-
чает «глава 10, параграф 3, пункт 7, подпункт б». Номера пунк-
тов, указанные на колонтитулах, позволяют быстро найти не-
обходимое место. Аналогично формула 10.37 (4) есть чет-
вертая формула пункта 10.37. В пределах одного пункта
формулы обозначаются просто порядковыми номерами. Рисунки
и задачи нумеруются в пределах главы.
Пользуюсь случаем выразить благодарность коллегам,
с которыми я обсуждал различные вопросы, затронутые
в книге; в особенности это относится к Н. В. Ефимову,
М. А. Крейнесу, Е. В. Майкову, А. Д. Соловьеву, Л. А. Ту-
маркину, 3. Я. Шапиро (Москва), В. М. Борок, Я. И. Жи-
томирскому, Б. Я. Левину (Харьков). Неоценимую идейную
поддержку мне оказывал ныне покойный Б. Л. Гуревич.
Рядом весьма ценных улучшений я обязан М. С. Аграновичу
и Н. И. Плужниковой.
Автор
Математика есть единая симфония бескоиечиого.
Д. Гильберт
ЧАСТЬ ПЕРВАЯ
ВВЕДЕНИЕ В АНАЛИЗ

ГЛАВА 1
ВЕЩЕСТВЕННЫЕ ЧИСЛА
Мы приходим к выводу, что не существует никаких аб-
сурдных, непостижимых, неправильных, необъяснимых
илн глухих чисел, ио что среди чисел существует такое
совершенство и согласие, что нам надо размышлять дин
и ночи иад их удивительной законченностью.
Симон Стевин (1634)
§ 1.1. Первоначальные сведения о множествах
1.11. Когда рассматривают несколько каких-нибудь объ-
ектов («элементов»), употребляют такие слова, как «сово-
купность», «собрание», «множество». Например, можно го-
ворить о множестве студентов в аудитории, о множестве
песчинок на пляже, о множестве вершин многоугольника или
о множестве его сторон. Указанные примеры обладают тем
свойством, что fe каждом из них соответствующее множество
состоит из определенного.числа элементов (которое можно
оценить, ограничить, хотя, может быть, практически и не-
легко установить точно*)). Такие множества мы будем на-
зывать конечными.
В математике часто приходится иметь дело с совокуп-
ностями, состоящими не из конечного числа объектов; про-
стейшими примерами служат множество всех натуральных
чисел 1, 2, 3, ... и множество всех точек отрезка**). Та-
кие множества мы будем называть бесконечными.
К числу множеств мы относим и пустое множество —
множество, не содержащее ни одного элемента.
Как правило, мы будем обозначать множества большими
буквами А, В, С, ____, а нх элементы—:малыми буквами.
*) «Некоторые люди, о, царь Гелон, воображают, что число пес-
чинок всей суши бесконечно велико.. . Я, однако, приведу доказа-
тельства, с которыми н ты согласишься, что я в состоянии назвать
некоторые числа, .. . превосходящие число песчинок в куче, равной
земному шару» (Архимед, Псаммит илн Исчисление песчинок).
**) Точные определения объектов, которые- рассматриваются в
§ 1.1 в качестве примеров, будут приведены ниже. Здесь они имеют
лишь иллюстративное значение.
14	ГЛ. 1. ВЕЩЕСТВЕННЫЕ ЧИСЛА	(1-12
Запись а£А (или ЛЭ а) означает, что а есть элемент мно-
жества А; запись а^А, или а£А, или А$а, означает, что а
не есть элемент множества А. Запись АсВ (или ВгзЛ) озна-
чает, что каждый элемент множества А является элемен-
том множества В; в этом случае множество А называют
подмножеством множества В. Наиболее широким из подмно-
жеств множества В является, очевидно, само множество В,
наиболее узким — пустое множество. Любое из остальных
подмножеств множества В непременно содержит элементы
из В, причем заведомо не все его элементы. Каждое из
таких подмножеств называется истинным подмножеством.
Знаки С, 9 > cz, 23 называются знаками включения. Если
имеют место включения АсВ, ВсА, то это означает, что
каждый элемент множества А является элементом множе-
ства В и, обратно, каждый элемент множества В является
элементом множества А; таким образом, множества А и В
состоят в данном случае из одних и тех же элементов и,
значит, совпадают друг с другом. Этот факт записывается
равенством Л = В. Аналогичная запись для элементов а = Ь
означает просто, что а и b есть один и тот же элемент.
Существуют различные формы задания множеств. Наибо-
лее простая состоит в указании всех элементов множества,
например: Л = (1, 2, ..., п, ...). Иная часто употребляе-
мая форма состоит в указании свойств элементов множества,
например: А = {х:х2— 1 <0} есть множество всех х, для
которых выполняется указанное после двоеточия неравенство.
1.12. Рассмотрим две простые операции, которые можно
производить над множествами: объединение н пересечение.
Опишем сначала операцию объединения множеств. Пусть
даны множества А, В, С, ... Рассмотрим совокупность всех
элементов, каждый из которых принадлежит хотя бы к од-
ному из множеств А, В, С, ... Эта совокупность есть
новое множество, которое и называют объединением мно-
жеств А, В, С, ...
Так, объединение множества Л= (6, 7, 8, ...} (всех нату-
ральных чисел, больших чем 5) и множества В — (3, 6, 9, ...}
(всех натуральных чисел, делящихся на 3) есть множество
5={3, 6, 7, 8, 9, 10, ...}
(всех натуральных чисел, за исключением 1, 2, 4 и 5).
1-12J	§ 1.1. ПЕРВОНАЧАЛЬНЫЕ СВЕДЕНИЯ О МНОЖЕСТВАХ 15
Введем теперь операцию пересечения множеств. Пересе-
чением множеств А, В, С, ... называется совокупность
элементов, входящих в каждое из указанных множеств.
Так, в предыдущем примере пересечением множеств
А = {6, 7, 8, 9, 10,
В = {3, 6, 9, 12, ...}
является множество
Z?={6, 9, 12,
Может оказаться, что множества А, В, С, ... не имеют
ни одного общего элемента. Тогда их пересечение есть пустое
множество; в этом случае говорят, что множества А, В, С, ...
не пересекаются. Например, три числовых множества
А = {1, 2},	В={2, 3},	С={1, 3}
не пересекаются (хотя каждые два из них имеют общие
элементы).
Можно рассматривать объединение и пересечение как
конечной, так и бесконечной совокупности множеств. На-
пример, можно построить объединение множеств точек всех
прямых на плоскости, проходящих через заданную точку О.
Этим объединением будет, очевидно, множество всех точек
плоскости. Пересечением указанных множеств будет мно-
жество, состоящее из единственной точки О.
Для объединения множеств употребляются знаки S и и,
так что, например, запись
5=2-^» или S = U А
V=1	V=1
обозначает объединение множеств Alr Аа, ...,	...
Для пересечения множеств употребляются знаки JJ и f|,
так что, например, запись
D = ТТ А. или D= П А,
V=1	V=1
обозначает пересечение множеств Av Aa, ..., Av, ...
16	ГЛ. 1. ВЕЩЕСТВЕННЫЕ ЧИСЛА	П-21
§ 1.2.	Аксиомы вещественных чисел
Приводимое ниже определение исходит из простейших
свойств чисел, известных частично из повседневного опыта,
частично из школьного курса*). Мы не определяем отдель-
ное вещественное число—мы определяем сразу всю сово-
купность вещественных чисел как множество элементов
с некоторыми отношениями и действиями.
Свойства отношений и действий задаются системой
аксиом.
Аксиомы разбиты на четыре группы; в первую группу
входят аксиомы сложения, во вторую — аксиомы умножения,
в третью — аксиомы порйдка, четвертая группа состоит из
одной-единственной аксиомы — аксиомы о верхней грани.
Определение. Множество элементов х, у, z, ...
называется совокупностью R вещественных (или действитель-
ных) чисел, если для этих объектов установлены следующие
операции и отношения;
1.21.	Операция сложения: каждой паре объектов
х, у поставлен в соответствие объект г, называемый суммой
х и у и обозначаемый х-)-у, так, что при этом выполняются
условия:
а.	х-)-у=у-)-х для любых х и у из R.
б.	(х+у) + ^ = х-|-(у + г:) для любых х, у, z из R\
поэтому выражение х +у + z имеет однозначный смысл.
в.	Существует такой элемент в R, обозначаемый 0 (нуль),
что х-| О = х для любого x£R.
*) Про аксиому о верхней грани (1.24) лишь с большой натяж-
кой можно сказать, что она известна «из повседневного опыта». Но и
аксиома Евклида о существовании единственной параллели, лежащая
в основе геометрии, находится в таком же положении. Опыт не дик-
тует иам с полной однозначностью математические аксиомы; между
опытом и системой иауки лежит еще этап формирования аксиом, ко-
торые—в рамках одного и того же опыта—могут быть одними или
совсем другими. И как наряду с евклидовой геометрией существует
и неевклидова (геометрия Лобачевского) с аксиомой о существовании
многих прямых, параллельных данной, проходящих через заданную
точку,—так и наряду с приводимой теорией вещественных чисел
существуют иные, в которых не всякое ограниченное множество имеет
точную верхнюю грань (см., например, В. А. Успенский, Лек-
ции о вычислимых функциях, М„ 1960, § 12).
1.24]
§ 1.2. АКСИОМЫ ВЕЩЕСТВЕННЫХ ЧИСЕЛ
17
г.	Для любого х £ R существует элемент у, называемый
противоположным к х, такой, что х-(-у — 0.
1.22.	Операция умножения: каждой паре объек-
тов х, у поставлен в соответствие объект u£R, называемый
произведением х и у и обозначаемый х-у (или ху), так, что
при этом выполняются условия:
а.	ху—ух для каждых х и у из R.
б.	(ху) z = x (yz) для каждых х, у, z из /?; поэтому
выражение хуг имеет однозначный смысл.
в.	Существует такой элемент в /?, отличный от 0 и
обозначаемый 1 (единица), что х  1 = х для каждого х € R-
г.	Для каждого х Ф 0 в R существует элемент и, назы-
ваемый обратным к х, такой, что их—1.
д.	Для каждых х, у, z из R справедливо равенство
x(y + z) = xy + xz.
Последняя аксиома связывает операцию умножения с вве-
денной выше операцией сложения (1.21).
Совокупность объектов х, у, ..., удовлетворяющих ак-
сиомам 1.21—1.22, называется числовым полем, или просто
полем.
1.23.	Отношение порядка: для каждых двух эле-
ментов х, у из R справедливо одно (или оба) из отношений
х^.у (х меньше или равно у) или у^х со следующими
свойствами:
а.	х х для каждого х; из х ^.у, у х следует х —у.
б.	Из х =Су, у z следует х z.
в.	Из х^у для любого z из R следует х -)-z ^y-j-z.
г.	Из 0 х, 0 <у следует 0 ху.
Отношение х <Jy записывается также в виде у х
(у больше или равно х). Отношение х^у при х#=у записы-
вается в виде х < у (х меньше у) или у > х (у больше х).
1.24.	Множество AaR называется ограниченным сверху,
если существует такой элемент z£R, что х z для каж-
дого х£А-, это отношение записывается в форме Л^г.
Всякое число z, обладающее по отношению к множеству А
указанным свойством, называется верхней гранью множест-
ва А. Верхняя грань Zq множества А называется точной
18
ГЛ. 1. ВЕЩЕСТВЕННЫЕ ЧИСЛА
[1.31
верхней гранью множества А, если любая другая верхняя
грань z множества А больше или равна z0. Точная верхняя
грань множества А обозначается sup Л*). Теперь мы сфор-
мулируем последнюю аксиому:
Аксиома о верхней грани. Всякое ограниченное
сверху множество Ac.R обладает точной верхней гранью.
Далее мы будем выводить логические следствия из при-
веденных выше аксиом; совокупность этих следствий даст
полный набор тех свойств системы вещественных чисел,
которые используются при построении математического ана-
лиза.
§ 1.3.	Следствия из аксиом сложения
1.31.	В множестве R существует лишь единственный нуль.
Действительно, допустим, что в R имеются два нуля:
0х и 02. Тогда, используя аксиомы 1.21а и в, мы получаем
О, = 0, 4" 0о 0« 4“ 0. —' 0о-
1.32.	В множестве R для каждого элемента X сущест~
вует лишь единственный противоположный элемент.
Допустим, что для элемента х нашлось два противопо-
ложных элемента уг и у2, так что х-4-У1 = л:-4-у2 = О. Тогда
по аксиомам 1.21а—в мы имеем
Уч = 0 +у2 = (* +ji) + У2 = х + (Ji+у2) = х + (Уа +У1) =
= (х + Уа) +У1 = 0 +У1 =У1-
Элемент, противоположный элементу х, обозначается
через —х. Сумма * + (—у) записывается также в виде х—у
и называется разностью х и у. Элемент, противоположный
сумме, есть сумма элементов, противоположных каждому
слагаемому: действительно, —х—уЦ-(х-4-у) =—х—У +
+ х+у— —х + х—у+у = 04-0 = 0.
1.33.	Уравнение
a-]-x = b	(1)
имеет в R единственное решение, равное Ь—а.
!) Supremum—высшее (лат.).
1ЛЗ] § 1.4. СЛЕДСТВИЯ ИЗ АКСИОМ УМНОЖЕНИЯ	19
Действительно, прибавляя к обеим частям равенства (1)
число —а, находим, используя аксиомы 1.21а — в,
а-\- х— а~ а— а-\- х = х — х = Ь — а,
так что если решение существует, то оно равно b—а. Но
b — а есть решение, так как
аЦ-(&—а) = а-)-Ь-\-{ — а)-= « + (— a)-]-b = O-\-b = b.
§ 1.4.	Следствия из аксиом умножения
1.41.	а. В множестве R существует лишь единственная
единица.
Допустим, что в R имеются две единицы 1Х и 12. Тогда,
используя аксиому 1.22а, мы получаем
11= 1х-12 = 12.
б. В множестве R для каждого элемента х=/=0 сущест-.
вует лишь единственный обратный элемент.
Допустим, что для элемента х имеются два обратных
элемента и z2, так что xz1=l, xz2=l. Тогда по аксио-
мам 1.22а — в мы имеем
z2 = 1 • Z2 = (Х£1) z2 = X (£х£2) = X (z2£x) = (*Z2) Z1=l-Z1 = Zv
1.42. Элемент, обратный к элементу х, обозначается
1	„ 1
через —. Элемент —, обратный к произведению ху, равен
х	ху
произведению элементов, обратных к х и у: действительно,
Произведение х — записывается также в виде — и на-
зывается отношением {частным) х и z.
1.43. Определение. Числа 1, 2=14-1, 3 = 24-1, ...
..., л = (л—1)4-1,	называются натуральными. Таким
образом, множество натуральных чисел может быть опреде-
лено как наименьшее числовое множество, содержащее число
1 и вместе с каждым числом л содержащее число л4-1-
Во многих задачах требуется установить, что некоторое чис-
ловое множество А (например, множество тех натуральных
20	ГЛ. 1. ВЕЩЕСТВЕННЫЕ ЧИСЛА	[1.44
чисел л, для которых верно предложение Тп, зависящее
от п) содержит все натуральные числа. Метод математиче-
ской индукции по натуральным числам, применяемый в таких
задачах, состоит в том, что проверяются условия:
1) А содержит число 1;
2) если А содержит некоторое натуральное п, то оно
содержит и п-\-1.
Из сказанного выше ясно, что в этом случае А содер-
жит все натуральные числа, что и требуется.
Мы видим, что обоснованность метода индукции выте-
кает из самого определения натуральных чисел.
1.44. а. Натуральные числа, им противоположные и нуль
называются целыми числами.
б. Частные — , где т, п — целые и п 0, называются
п ’
рациональными числами.
в. Все остальные вещественные числа называются ирра-
циональными.
1.45. Уравнение
ax = b (а=£0)	(1)
имеет в R единственное решение, равное
Действительно, умножая обе части равенства (1) на -i-,
находим
1 .	.	/ 1	\	.	Ь
— (ах) = — a]x=i-x = x= —,
а '	'	\ а )	а ’
Ь „ b
так что если решение существует, оно равно —. Но —
есть решение, так как
Ь /	1 \ ,	. .	,
а- — = а-— о = 1 -Ь=Ь.
а \ а /
1.46.	По определению при п — 1, 2, ...
Хп = X ... X.
п раз
Очевидно, xn-xm = xn+m и (xn)M = xn"! при любых нату-
ральных п и ш. Число п в выражении хп называется пока-
1-47]	§ 1.4. СЛЕДСТВИЯ ИЗ АКСИОМ умножения	21
зателем степени. Распространим понятие показателя степени
на все целые числа. Положим для любого х О
х°= 1,
Проверим, что формулы
771	- д* 71 "Ь Т71
(xn)m = хпт
(1)
остаются справедливыми для любых целых п и т. Пусть
п > 0, т= —р < 0, причем р п; тогда
^^-.хп-р.хр
хР
J_ —, хп~Р — хп + т
Если р > п, то по 1.42
п vtn__хп , _L_ v-n .	_хп • — .	1 — I — хп+т
хР хпхР-п хп хР~п хР-п
Если же т =—р < О, л=—q < 0, то также по 1.42
vtn. vn___L_ _2_ ____— хт + п
ХР хЧ хР+4
Аналогично проверяется справедливость второй формулы (1).
1.47,	а, Для любого x^R имеет место равенство
0-х = 0.
Действительно,
О - а: + 1 • а; — (0 + 1) х = 1 • х — X,
0-х+1-х = 0-х-[-х,
откуда
х — 0-х-[-х;
в силу 1.33, 0-х = х— х = 0.
Отсюда следует, что 0 не имеет обратного, поскольку
равенство 0-х =1 невозможно. Таким образом получается
оправдание школьного правила: «на нуль делить нельзя».
б. С другой стороны, из ху = 0 и х=£0 следует, что
у = (— • х )у — — (ху) = — • 0 = 0.' Таким образом, если про-
\ X i X	X
извещение равно нулю, то (по меньшей мере) один из мно-
жителей равен нулю.
22
ГЛ. 1. ВЕЩЕСТВЕННЫЕ ЧИСЛА
[1.48
1.48. Всегда при и=#0, ®=^=0
и ‘ v uv '
Действительно,
ХУ-\-уи
UV
1 .	.	1	.1 X . у
— (хг/4-vw) = — -xv-\---уи —-----к—.
UV '	1 ' ’ uv uv' и V
1.49. Для любого x£R
— X = (--1) X.
Заметим, что обе части равенства определяются незави-
симо, так что равенство требует доказательства. Мы имеем
по 1.47 а
(—1)х + * = [(—1)+ 1]-х = 0-х=0,
откуда и следует требуемое.
Следствия §§ 1.3 —1.4 обеспечивают для вещественных
чисел выполнение всех тождеств элементарной алгебры (би-
ном Ньютона, формулы суммирования прогрессий, свойства
детерминантов и т. п.).
§ 1.5.	Следствия из аксиом порядка
1.51.	Связи порядка с операцией сложения,
а. Если х^.у, y^z и x = z, то x=y = z.
Действительно, у^.г=х, так что у^.х, откуда по
аксиоме 1.23а у~х, что нам и требуется.
Из а непосредственно вытекает
б.	Из х <у, y^z следует х < z. Аналогично из х^.у,
у <Zz следует х <Zz.
в.	Отношения x?gZy, О^у— х,	yt^~—х, х—у^О
эквивалентны.
Действительно, прибавляя к обеим частям первого не-
равенства —х и применяя 1.23 в, получаем второе; прибавляя
к обеим частям второго —у, получаем третье; прибавляя
к обеим частям третьего х, получаем четвертое и, прибавляя
к обеим частям четвертого у, возвращаемся к первому.
г.	Из х<у следует x-\~z <.y-\-z для любого z£R.
Действительно, из х<_у заведомо следует, что x^Zy и
Но если бы имело место равенство x-\-z-
=y-\-z, то, прибавляя к обеим его частям —z, мы получили
1.53]	§ 1.5. СЛЕДСТВИЯ ИЗ АКСИОМ ПОРЯДКА	23
бы х—у, что по условию не имеет места. Поэтому x-\-z<Z
< y + z.
д.	Если XjSgj^, ..., хп^уп, то хх4-. . . +хп<ау1+  • • -\-уа;
при этом если хотя бы для одной пары Xj, yj имеет место
неравенство Xj<iyj, то и Xj + ... + xn <J1 + ... +jn-
Действительно, по аксиоме 1.23 в
причем если хотя бы для одной пары ху-, у}- имеет место
неравенство х,- < у}-, то в силу г в соответствующем месте
преобразования появитсй знак <, который сохранится и в
дальнейших местах в силу г. Таким образом, одноименные
неравенства можно складывать. В частности, из хг 0, ...
..., х„ 0 следует $ = хг +    + хп 0, причем если хотя
бы для одного j мы имеем Xj <0, то и s < 0. Аналогичный
факт справедлив при замене всех знаков на и < на >.
е.	Отношения х<у, 0<у— х, —у <—х, х—_у < 0
эквивалентны.
Это выводится из д так же, как в выводилось из аксиомы
1.23 в.
1.52.	Определение. Если xZ>0 (х > 0), число х
называется неотрицательным (положительным)-, если х^О
(х < 0), число х называется неположительным (отрицатель-
ным). Число 0 одновременно неположительно и неотрица-
тельно.
1.53.	Определение. Пусть даны два вещественных
числа х и у и, например, х у. Тогда х называется мини-
мальным из чисел х и у, что обозначается x = min{x, j},
а у называется максимальным из чисел х и у, что обозна-
чается у —max (х, у}. По индукции можно определить
min {х1э . .., х„} и max {хт, .. ., х„} для любого (конечного)
набора чисел xlf ..., хп (например, max {х1У ..., хл} =
= max {max (хь ..., х,,^), хД).
Число | х | = max {х, —х} называется модулем, или абсо-
лютной величиной, числа х. Таким образом, |х| = х, если
xZ>0, и | х|=—х, если xs^O; для любого х число |х|
неотрицательно и |—х| = |х|.
24
ГЛ. 1. ВЕЩЕСТВЕННЫЕ ЧИСЛА
[1.54
1.54.	а. При а>0 неравенство | х | а равносильно
двум неравенствам х^а, —х^а или же —а^х^а.
б. Для любых двух вещественных чисел х, у
I х +у | < | х | +|у|.
(1)
Действительно, если х, у оба неотрицательны или оба
неположительны, то неравенство выполняется по определе-
нию модуля. Если же, например, х^>0, ау^О, то
X +у < X < X + |у | = | X [ + |у |,
—х—у<— j' = b’KI*l + b’l.
так что | х +у | = max {х +у, —х—у}	| х | + |у |, а это и
требуется.
в. Из (1) по индукции следует, что
| Х! + . . . + Хп I | Xj | + . . . + I Хп |.
1.55.	Связи порядка с операцией умножения,
а. Если х > 0, у > О, то ху > 0.
б.	Если х^.у, то для любого z > О
xz^.yz.
Утверждение а вытекает из аксиомы 1.23 г с учетом 1.47 б.
Утверждение б следует из неравенства
yz —xz = (у—х) z	0
в силу 1.23 г.
в.	Используя 1.47 б, в б можно заменить всюду на <.
г.	В частности, при х > 1 мы имеем х2 > х, а при
0 < х < 1 мы имеем х2 < х.
д.	Если х^.у, 0<z^.u, то xz^Lyz^Zyu, так что при
указанных условиях неравенства можно перемножать.
е.	В частности, при 0<х <у всегда х2<_у2, .. .,хп<_уп.
ж.	Если х^О, yZ>0, то ху^.0; если х^О, у^О,
то ху 0.
Действительно, в первом предположении —х^О и по
аксиоме 1.23 г и свойству 1.49 имеем (—х)у =—1-х-у =
= —(ху)^0, откуда ху^О. Во втором предположении
—у^О и, используя первый результат, получаем —xys^O,
ху^О. Во всех случаях знаки можно заменять на <.
34 В частности, при любом х=#0 имеем х2 = х- х> 0.
Отсюда 1 — 1 • 1 > 0; далее, по 1.51 г 2 = 1-(-1 > 1 -(-0=1,
3 = 2+ 1 > 2 и т. д.
l.ei] § 1.6. СЛЕДСТВИЯ ИЗ АКСИОМЫ О ВЕРХНЕЙ ГРАНИ 25
И. Для всех х, у справедливо равенство | х -у | =
1.56. Если х > 0, то -—>0; из 0<х<у следует
Первое утверждение следует из х- — =1 >0 и 1.55 ж.
Умножая неравенство 0 < х < у на —
г	J	VII
получаем второе.
р
частности, все рациональные числа —, где р и у—на«
туральные числа, положительны.
1.57. Следующий принцип часто используется в доказа-
тельствах:
Если число z неотрицательно и меньше любого положи-
тельного числа, то z — 0.
Действительно, если z > 0, то по условию мы должны
иметь z < z, что невозможно (см. 1.23).
§ 1.6. Следствия из аксиомы о верхней грани
Совокупность R всех вещественных чисел будем называть
также числовой осью, асами вещественные числа—ее точками.
1.61. В 1.24 дано определение множества, ограниченного
сверху. Рассмотрим теперь множество, ограниченное снизу.
Множество EczR называется ограниченным снизу, если су-
ществует такой элемент z^R, что для всякого х£Е;
это соотношение записывается в форме z Е. Всякое число z,
обладающее по отношению к множеству Е указанным свой-
ством, называется нижней гранью множества Е. Если Е
ограничено сверху, т. е. если существует такое у, что
Е^.у, то множество —Е (множество всех чисел — х для
х£Е) ограничено снизу, поскольку из х^у следует
—х^—у, при этом —у есть нижняя грань множества —Е.
Обратно, если Е ограничено снизу, то по тем же сообра-
жениям —Е ограничено сверху, и если к] есть нижняя
грань множества Е, то —т] есть верхняя грань множест-
ва —Е.
26
ГЛ. 1. ВЕЩЕСТВЕННЫЕ ЧИСЛА
[1.62
Нижняя грань у0 множества Е, ограниченного снизу, на-
зывается точной нижней гранью множества Е, если любая
другая нижняя грань множества Е меньше или равна у0. Точ-
ная нижняя грань множества Е обозначается infF*).
Теорема. Всякое множество Е, ограниченное снизу,
имеет точную нижнюю грань, и она равна —sup (—Е).
Действительно, множество —Е ограничено сверху, и по
аксиоме 1.24 существует число £ = sup(—Е). Покажем, что
—g = infF. Мы имеем для х£Е всегда —х<^£, откуда
—£ х; таким образом, —£ есть нижняя грань множества Е.
Пусть т] есть любая другая нижняя грань множества Е.
Тогда —т] есть верхняя грань множества —Е м согласно
определению, —i]^sup(—F) = |; отсюда —£, что и
требуется.
1.62. а. Если Е и F ограничены сверху и EczF, то
supF sup F; если Е и F ограничены снизу и EczF, то
infF^= inf F.
Действительно, в первом случае sup F является верхней
гранью для F и тем более для EczF\ поэтому supF^supF.
Таким же образом во втором случае infF является нижней
гранью для F и тем более для Ec.F, поэтому inf F^ inf Е.
б. Если для любых х£Е и у £F выполнено неравенство
то Е ограничено сверху, F—снизу и sup F^ infF.
Действительно, множество Е ограничено сверху любым
y£F, поэтому supF существует и supF^j для любого
у g F. Отсюда следует, что F ограничено снизу числом sup F;
значит, sup F inf F.
1.63. Здесь будут доказаны существование и единствен-
ность корня л-й степени из любого положительного числа.
Теорема. Для всякого вещественного х>0и целого
л > 0 существует и притом единственное вещественное у > О,
такое, что уп = х.
Это число обозначается у/х (корень п-й степени из х).
Доказательство**). Рассмотрим множество А всех
положительных z таких, что zn^x. Это множество огра-
*) Infimum—низшее (лат).
**) По книге У. Рудин, Основы математического анализа,
«Мир», 1966, гл. 1.
1-63]	§ 1.6. СЛЕДСТВИЯ ИЗ АКСИОМЫ О ВЕРХНЕЙ ГРАНИ
27
ничено сверху (числом 1, если х^1, и числом х, если
х^1). Положим
у = sup А.	(1)
Покажем, что уп~х. Пусть у"<х, х—уп — Е. Для любого
положительного h 1 мы имеем по формуле бинома Ньютона
(у + h)n =уп + пуп 1h+n2 йгуп~г +  • • =
=yn-\-h пуп~г -|- —/гу"~а + .  . J sgZ
^Уп + h [лу”’1	+ ...] =
=уи+Ч(1+у)"-у"]-
Можно взять
, ' е
(!+{/)"-Уп '
тогда мы получим (у + /г)" ^у" + е = х, что противоречит
определению (1). Таким образом, уп~^х. Пусть у" > х,
уп—х = е. Для любого положительного /к; 1 мы имеем
(у—h)n—yn—nyn~1h + n^y^h2— ... =
=ук —h ^лу'г-1 —~^yn~2h+ ..
^y"—h пуп~г-\-’~-~-yn~ih-\-..
^yn—h nyn-l-i-^^yn-2+ •  •] =
=y"—A[(l+y)n—y"].
Можно снова взять
h < e
^<J+y)n-yn’
тогда мы получим
(у—h)n ~^уп—е = х,
что опять противоречит определению (1). Таким образом,
уп — х, что и требовалось.
Единственность корня следует из неравенства yi!<y"
при у!<у2 (1.55 е).
28
ГЛ. 1. ВЕЩЕСТВЕННЫЕ ЧИСЛА
(1.64
1.64. Для любых двух положительных х и у
П/-------------------	п/~ п/---
(1)
Пусть £ = у/х, 1]= y/у, т= у/ху. Мы имеем £" = х,
т)п =у; тогда (£т])п =	= ху = т". В силу доказанной
единственности корня
т= {/ху = ^.
что и требуется.
Аналогично доказывается, что для положительного х и
любых целых m, п > 1
V V х.	(2)
1.65. Поскольку (—х)"=(—1)"хп, при п четном урав-
нение уп — х > 0 имеет, кроме положительного решения
У1= \/х, отрицательное решение у2 =— {/х; уравнение
же у" =- х < 0 не имеет вещественных решений. При нечет-
ном п уравнение у" = х>0 имеет в области вещественных
чисел единственное решение у — у/х. В этом случае и урав-
нение уп = х < 0 также имеет (единственное) решение
У= — V И-
Формулы 1.64 (1), (2) позволяют построить обычным
образом всю элементарную алгебру выражений, содержащих
корни из вещественных чисел, в частности, формулы для
решения квадратных и более сложных алгебраических урав-
нений, которые рассматриваются в элементарной алгебре.
1.66. Множество Е, ограниченное сверху н снизу, назы-
вается ограниченным с обеих сторон, или просто ограниченным.
Всякое ограниченное множество имеет точную верхнюю
грань sup£ и точную нижнюю грань inff.
Примерами ограниченных множеств служат отрезки и ин-
тервалы.
При а < b совокупность всех вещественных чисел х,
удовлетворяющих неравенству	называется отрез-
ком с левым концом а и правым концом b и обозначается
через [а, Ь]. Совокупность всех вещественных чисел х,
удовлетворяющих неравенству а < х < Ь, называется интер-
валом с левым концом а и правым концом b и обозначается
(а, Ь). Концы отрезка принадлежат отрезку, концы интервала
1.71]
§ 1.7. ПРИНЦИП АРХИМЕДА И ЕГО СЛЕДСТВИЯ
29
не принадлежат интервалу. Тем не менее
sup [о, b] = sup (a, b) = b, inf [о, £] = inf (а, Ь) — а.
Впрочем, терминологию нельзя считать установившейся.
Иногда отрезок называют замкнутым интервалом, а интер-
вал—открытым отрезком. Встречаются также и «полузамк-
нутые» или «полуоткрытые» отрезки и интервалы; так,
множество {х:а < x^b} = (a, /?] называют полуинтерва-
лом, открытым слева и замкнутым справа, а множество
{х: а х < Ь} = [о, Ь)—полуинтервалом, открытым справа
и замкнутым слева*). Отрезки, интервалы и полуинтервалы
мы будем называть промежутками.
Для единства терминологии иногда точку а также назы-
вают отрезком и пишут а = [а, а] = {х:а^х
§ 1.7.	Принцип Архимеда и его следствия
1.71.	Если х—вещественное число, а п—целое число,
то числа пх называются целыми кратными х.
Принцип Архимеда**). Если х > 0, а у—произ-
вольное вещественное число, то существует такое целое крат-
ное пх числа х, для которого (п— 1)х^_у, пх >у.
Доказательство. Предположим, что для всех целых
р выполняется неравенство рх^.у. Это значит, что множе-
ство А всех чисел {рх} ограничено и имеет число у своей
верхней гранью. По аксиоме 1.24 существует точная верхняя
грань множества {рх}, | = supA. Число £—х < £ уже не яв-
ляется верхней гранью множества А; поэтому существует та-
кое/?, что рх > |—х. Отсюда (р-[- 1) х > В и £ не может быть
верхней гранью множества А. Полученное противоречие
доказывает существование целого числа р, для которого
рх ~>у. Аналогично существует целое число q, для которого
qx<Zy, очевидно, q^p. Перебирая все пары (q, #4-1),
(#+1, #Ч~2), ..., (р — 1, р), найдем среди них такую,
например (л—1, л), для которой (л—1)х^.у, а пх >у.
*) Для таких множеств предлагались в свое время названия
«интрезок» и «оттервал», однако при всей их целесообразности в оби-
ход они ие вошли.
**) В других современных аксиоматических теориях веществен-
ных чисел принцип Архимеда, наряду с принципом Кантора (§ 1.8),
входит в состав аксиом; при таком построении аксиома о верхней
грани (1.24) становится теоремой.
30
ГЛ. 1. ВЕЩЕСТВЕННЫЕ ЧИСЛА
[1.72
В частности, если х = 1, мы получаем, что для любого
у существует такое целое л, что п — \^.у<п. Число
п—1 называется целой частью числа у и обозначается [у].
Число у—[у] называется дробной частью числа у и обозна-
чается (у). Таким образом, всякое число у есть сумма своей
целой части и своей дробной части: у=[у] + (у)-
1.72.	Заменяя всюду в 1.71 сложение умножением, полу-
чаем следующий мультипликативный*) вариант принципа
Архимеда:
Если х > 1, у > 0, то существует такой целый показа-
тель п, что
хп~г^у, хп>у.
1.73.	Если в условии принципа Архимеда число у также
положительно, то положительно и число п > — . Умножая
X
X
последнее неравенство на —, приходим к следующему за-
ключению:
Для любых х > 0 и у > 0 существует такое натуральное
У
число п, что — <~х.
’ п
Как следствие получаем: при любом у > 0
inf М, п= 1, 2, ... 1 =0.	(1)
Действительно, множество в скобках состоит из положи-
тельных чисел, поэтому его нижняя грань неотрицательна.
Но по * доказанному она не может быть положительной;
отсюда вытекает (1).
1.74.	Следствие. Каждая из систем полуоткрытых
промежутков
(0, у]=> (о, f]z> ... 2Э (о,	... (у > 0),	(1)
(а, а -|-у]	(а, й + у] Z3 ... О ^а, й +	(2)
[а—у, a) Z) [а—о ...	(3)
имеет пустое пересечение.
*) От слова multiplicator—умножающий (лат.).
1.76]
§ 1.7. ПРИНЦИП АРХИМЕДА И ЕГО СЛЕДСТВИЯ
31
Действительно, если бы промежутки системы (2) имели
общую точку Jj, то |—а была бы общей точкой системы (1);
и если бы промежутки системы (3) имели общую точку щ,
то а—т] была бы общей точкой системы (1). Но промежутки
системы (1) не могут иметь ни одной общей точки в силу
1.73, что и доказывает утверждение.
1.75.	Теорема. Каждый интервал (а, Ь) содержит
рациональную точку.
Доказательство. Пусть h = b—а>0 и п—‘целое,
большее, чем ± (существующее по принципу Архимеда)', так
что -i- < h. По принципу Архимеда найдется такое т, что
т - т+1 „	m+1	. 1 , ,
— £-'« <—— . При этом----------— <о— а, так что
п	п	п	п
и4-1 . . т	s	г .	..
  п' < Ь. Таким образом, а < —< Ь, ~— g (а, Ь), что
и требовалось.
На самом деле между а и b существует даже бесконеч-
ное множество рациональных чисел, поскольку, применяя
/т-М .\
приведенное рассуждение к интервалу ( —, b 1, мы полу-
чим новое рациональное число у, —у < Ь, и про-
цесс можно продолжать неограниченно.
1.76.	Для заданного вещественного числа £ обозначим
через совокупность всех рациональных чисел
и через 'Р, совокупность всех рациональных чисел г £.
Множество N, ограничено сверху (числом £), множество
ограничено снизу (числом £).	1
Теорема, supNr_ = £ = infР^.
Доказательство. Пусть supN. = а. Так как
для каждого s g N„, то по определению точной верхней грани
имеем	Предположим, что а<£. По 1.75 имеется
рациональная точка pg (а, £). Так как р < то p£N^,
откуда вытекает p^sup^=a, что противоречит включе-
нию pg (а, £). Следовательно, неравенство а<£ невоз-
можно, откуда a = supM = £. Аналогично доказывается, что
£ = infPr
32
ГЛ. 1. ВЕЩЕСТВЕННЫЕ ЧИСЛА
[1.77
1.77.	Позиционная десятичная запись веще-
ственных чисел. Мы проверим здесь, что с помощью
последовательности из знаков 0, 1, 2, ..., 9 можно запи-
сать любое вещественное число.
Положим 9+ 1 = 10.
Пусть > 0. В силу 1.72 существует (и однозначно
определен) такой показатель р, что
Ю*+1.
Имея р, найдем число 0О (из набора 1, 2, ..,, 9) такое,
что
6о-Ю/’<|<(0о+1).1О₽.
Число 0О также определено однозначно, так как промежутки
0-1О*<х< (04-1)-1О/?
при различных 0 = 0, 1, ..., 9 не пересекаются. Далее,
имея 0О, найдем число 0Х (из набора О, 1, 2, ...,9) такое,
что
0О- Ю^ + 0Г 10r-i<^£ < 00.10f + (0Х+ П-1ОР"1.
Продолжая этот процесс неограниченно, мы получим после-
довательность символов (цифр от 0 до 9)
6О0Д... (0О=# 0).	(1)
Для указания числа р поступаем так: если р 0, ставим
запятую между символами Qp и 0j,+1; если р < 0, т. е.
р =—q, q > 0, перед последовательностью (1) пишем до-
полнительно q нулей и после первого из них ставим запя-
тую. С учетом этого условия в записи отражено и число р.
Итак, каждому вещественному числу £, мы поставили
в соответствие по указанному правилу символ вида (1), воз-
можно, с несколькими нулями впереди и с запятой на неко-
тором месте. Этот символ называется десятичной позицион-
ной записью числа цифры 0О, 0Ъ ... в их взаимных
положениях (позициях) в последовательности (1) называются
десятичными знаками числа Для числа 1 десятичная
запись имеет вид 1,000...; аналогичный вид имеет десятич-
ная запись для чисел 2, 3, ..., 9. Для числа 10 десятич-
ная запись имеет вид 10,000 ... Для чисел вида с не-
10*
1.77]
§ 1.7. ПРИНЦИП АРХИМЕДА И ЕГО СЛЕДСТВИЯ
33
отрицательными целыми s и t («десятично рациональных»)
и только для них в символе (1) не более чем t цифр после
запятой отлично от 0.
Мы утверждаем, что в символе (1) не может быть так,
что, начиная с некоторого места, все цифры являются
девятками. Действительно, наличие всех девяток, начиная
с номера п после запятой, означало бы, что число £ лежит
в промежутках
, 9	,10	,	1
л + Ю» S < л + 10» r‘ 10"-1 ’
.99	। 9 । 10 — ।	1
Г +	ю»+1^= + г + ю»+ юп+1 Л+ 10"-1 ’
.9.9	.	9 g .	1
Г + Тб”+ 10"+1+ ' ’ ' + 10»+*^=^ + Г + 10"-1 ’
но все вместе эти промежутки не имеют ни одной общей
точки {1.74).
Обратно, пусть дана произвольная последовательность
цифр от 0 до 9
TiT2...
(2)
с запятой на некотором месте, причем не все т,- суть нули
и как угодно далеко имеются цифры, отличные от 9. Пока-
жем,- что существует число £>0, для которого (2) совпадает
с представляющим его символом (1).
Пусть тт—первая отличная от 0 цифра в (2). Запятая
находится или правее хт на <7^5 0 цифр (не считая хт), или
левее хт на t 1 цифр (считая хт); во втором случае по-
ложим q = —t.
Теперь положим
| = sup {10*-Tm + Ю9-1-тт+1-|- 10*-2-тт+2+ ... 4-
k
и покажем, что десятичное разложение этого числа £ сов-
падает с (2). Пусть фиксировано натуральное число s, затем
34
ГЛ. 1. ВЕЩЕСТВЕННЫЕ ЧИСЛА
(1.78
выбрано г > s так, чтобы т„/+г^8, и пусть k > г произ-
вольно. Тогда, суммируя геометрическую прогрессию,
найдем
10?~‘s+1’.rra+i+1+ ... + 10*-'.ти+г+ ... + 10*-*.ти+л <
<9-10’"и+1,4- ... 4-9- 109-г4- ... 4-9- Ю9-*—10«-r =
„ Ю^-^+п—109~(ft+u
= 9 . Ar--___AA±--------109-r < 109-s — IO9-'.
1 —10-1
Поэтому
£ = sup {109-Tra + • • • + 109-s.Tm+5+ ... 4- 109-*.Tffi+J<
< 109-Tm-|~ • • • 4- 109-^ти+.,4- 109-s- IO9-' <
<109.Tm+...4-109-i(Tra+,+ l).
Итак, при любом s = 0, 1, 2, ...
109.T„,4-...+109-s.Tra+,<|<
< 109-Tm4- • • • + 109-i (Tffl+i4-1).
Полагая здесь s = 0, 1,2, ... и вспоминая определение
числа р и знаков 0о, 0Ь ... числа £, мы находим p~q,
®о —6i = 'tm+i> , откуда н следует совпадение Деся-
тичного разложения числа £ с символом (2).
Если £ < 0, то —| > 0, и поэтому
В —	. . .,
как было показано выше; мы полагаем по определению
В=~ Tfr2...
Наконец, для £ = 0 мы полагаем
£ = 0,0000 ...
Этим завершается построение позиционной десятичной
системы.
1.78.	Вместо числа 10 можно взять какое-либо другое
целое число Р > 1. Соответствующая позиционная система
обозначений вещественных чисел называется Р-ичной пози-
ционной системой. Наиболее часто, кроме десятичной, ветре-
1.81]	§ 1.8. ПРИНЦИП ВЛОЖЕННЫХ ОТРЕЗКОВ КАНТОРА 35
чаются двоичная и троичная системы, где Р есть соответ-
ственно 2 илн 3. В двоичной системе для записи любого
вещественного числа используются лишь цифры 0 н 1,
а в троичной — цифры 0, 1 и 2.
§ 1.8.	Принцип вложенных отрезков Кантора
1.81.	Пусть на вещественной оси R указана некоторая
совокупность промежутков, обладающих тем свойством, что
из каждых двух промежутков этой совокупности один со-
держится в другом. Такую совокупность будем называть
системой вложенных промежутков.
В 1.74 мы видели, что система вложенных промежутков
может не иметь в пересечении ни одной точки. Промежутки,
которые рассматривались в 1.74, были полуоткрытыми. Тем
более система вложенных открытых промежутков (интерва-
лов) может не иметь ни одной общей точки. Однако если
рассматриваемые промежутки содержат оба своих конца, т. е.
являются отрезками, общая точка всегда имеется; этот факт
составляет содержание следующего важного предложения:
Принцип вложенных отрезков Кантора. Для
всякой системы Q вложенных отрезков [а, ft] существует
точка, принадлежащая ко всем отрезкам этой системы. Точнее
говоря, существуют
|=sup {a:[a,ft]£Q};
г)= inf {ft: [a, ft] €Q}.
Тогда Е Т) и отрезок [£, ц] есть пересечение всех отрез-
ков системы Q.
Доказательство. Пусть Е = {а : [a, ft] £Q} есть
множество левых и F— {ft: [а, ft] £ Q} множество правых концов
отрезков системы Q. Для любых двух отрезков [а1, ft1]c:[a2, ft2]
системы Q мы имеем а2^С	так что любое а £ Е не
превосходит любого b£F. Из 1.626 следует, что числа | и т],
указанные в формулировке теоремы, существуют и удовлетво-
ряют неравенству £ Для любого [a, ft]€Q мы имеем
a<EE<Z»]^Cft, так что [a, ft] о [|, г]], откуда и JJ[a, ft] э [|, т]].
Нетрудно убедиться, что JJ [a, ft] состоит только из точек
отрезка [£, т]]: для любой точки х, не входящей в отрезок
36
ГЛ. 1. ВЕЩЕСТВЕННЫЕ ЧИСЛА
[1.82
[I, л1» например, по той причине, что х < найдется
левый конец а, для которого х < а < | = sup {«}, и, сле-
довательно, х не принадлежит соответствующему отрезку
[а, £>]. Если | = т], то, говоря об отрезке [|, т]], мы подра-
зумеваем эту точку | = Т].
1.82.	В каком случае пересечение системы вложенных
отрезков состоит из одной единственной точки? Ответ дается
следующей теоремой:
Теорема. Пересечение системы Q вложенных отрезков
состоит из одной единственной точки тогда и только тогда,
когда для любого е > 0 е системе Q имеется отрезок [a,
длины b — а<Е.
Доказательство. По принципу Кантора пересечением
отрезков системы Q является отрезок [|, т)], который сво-
дится к одной точке, если т] = |. Если т]#=|, то длина
каждого отрезка [а, А] о [|, т]] системы Q не меньше, чем
т] — поэтому если в системе Q имеются отрезки произвольно
малой длины, то их пересечением является одна точка. Об-
ратно, поскольку т] = inf {b: [а, £>] €Q}> | = sup{a:[a, £>] g Q},
в системе Q для заданного 8>0 есть отрезок	для
которого —е/2, и отрезок [а2, д2], для которого
fc2<T]-}-8/2. Если, например, [ах, гэ [«2> д2], то мы имеем
а2'^а1 > | — е/2, Ь2 < »] + е/2. Если | = т], то Ь2 — а2 < 8,
так что в системе Q имеется отрезок длины < 8, н теорема
доказана.
§ 1.9.	Расширенная область вещественных чисел
1.91.	Определение. Расширенная область /? веще-
ственных чисел состоит из совокупности R всех веществен-
ных чисел и двух символов, или точек, —оо и оо (точ-
нее, -|- оо) (минус бесконечность и плюс бесконечность).
На эти символы распространяются отношения порядка
по следующему правилу:
для каждого х g /?;
для каждого x£R;
1.94] § 1.9. РАСШИРЕННАЯ ОБЛАСТЬ ВЕЩЕСТВЕННЫХ ЧИСЕЛ 37
В расширенной области сохраняются аксиомы порядка
1.23 а — г. Обычные вещественные числа в отличие от симво-
лов — оо и оо называют конечными.
1.92.	Для каждого непустого множества EcR опреде-
ляются величины supf и inff по следующему правилу.
Если Е не содержит точки оо и ограничено сверху (см. 1.24),
то supf сохраняет смысл, указанный в 1,24\ в остальных
случаях (т. е. если Е содержит оо или, хотя и не содер-
жит оо, но не является ограниченным сверху) полагаем
sup£'=oo. Аналогично, если Е не содержит точки —оо
и ограничено снизу, число inff сохраняет смысл, указанный
в 1.61’, в остальных случаях полагаем inf£=—оо. Таким
образом, в системе R всякое непустое множество имеет
точную верхнюю и точную нижнюю грани.
1.93.	Если а^21>—две точки из R, то множество
[а, />] = {х R' а х Ь}
называется отрезком с концами а и Ь, а множество
{a, b) = {х £R: а < х < Ь)
называется интервалом с концами а и Ь.
1.94.	Сформулируем обобщение принципа вложенных
отрезков на область R. Пусть на расширенной прямой R
указана некоторая совокупность Q вложенных (в том же
смысле, что и в 1.81) отрезков [а, Ь\. Утверждается, что
все они содержат некоторую точку x£R. Действительно,
пусть Л есть множество всех левых концов отрезков си-
стемы Q и В—множество всех правых концов отрезков этой
системы. Положим
£ = sup Л, i] = inf В.
Так же как и в 1.81, доказывается, что и что пе-
ресечение всех отрезков [a, СQ совпадает с отрезком
[£, т)] и, следовательно, не пусто.
38
ГЛ. 1. ВЕЩЕСТВЕННЫЕ ЧИСЛА
Дополнение к главе 1
Логическая символика
При записи математических рассуждений целесообразно
использовать экономную символику, уже давно применяемую
логиками. Мы укажем здесь лишь несколько самых простых
и употребительных логических символов*).
Если нас интересует не сущность некоторого предложе-
ния, а взаимосвязь его с другими предложениями, мы можем
обозначить это предложение одной буквой. Тогда символ
а=>Р означает: «из предложения а следует предложение р».
Знак а<==>р означает «предложения аир эквивалентны»,
т. е. из а следует р и из р следует а.
Запись ух£Е:а означает: «для каждого х£Е выпол-
няется предложение а». Запись gjg^P означает: «суще-
ствует элемент у £F, для которого имеет место предло-
жение Р».
Например, предложение «число | есть точная верхняя
грань множества Л» (/.24) можно записать следующим
образом:
(а)	(т. е. для каждого х£А имеет место
неравенство х |) и,
(б)	(т. е. для каждого Ь, не меньшего,
чем любой элемент множества А, выполняется неравенство
Запись а означает «не а», т. е. отрицание предложения а.
Например,
а<==фР<==ф(а<==фР), а=фР<==ф(Р=фа), а<==>а.
Построим отрицание утверждения ух££:а (для каждого х £ Е
имеет место свойство а). Если высказанное утверждение не имеет
места, то, следовательно, свойство а имеет место не для каждого
х £ Е и, значит, существует элемент х £ Е, для которого свойство а
не имеет места: Vх € £:аф==ФЭХ € Е'.а.
Построим отрицание утверждения g у £ Е: Р (существует у £ Е,
обладающий свойством Р). Если это утверждение неверно, то указан-
ного у £ Е не существует, т. е. для каждого у £ Е свойство Р
*) Подробнее см., например, в книге: В. А. Успенский,
Лекции о вычислимых функциях, гл. 2, Физматгиз, 1960.
ЗАДАЧИ
39
не выполнено:
i7e^₽<==^>v У € Е-.$.
Таким образом, черта над знаком у или g превращает его, соответ-
ственно, в знак а или у и переносится на свойство, стоящее после
двоеточия.
Например, отрицание приведенного выше утверждения (б) имеет
вид _ _____________ _______________
(б)	yb А: b Эг £ <==^> gb Si А: b :& £ <£==£> g Ь S: А: b < J
(существует Ь, не меньшее любого х £ А, не превосходящее £).
Подробнее, с расшифровкой знака bS=A:
(б)	эЬ < I, ух g A:x<b.
Рассмотрим еще следующее предложение:
(в)	уе>О:дх£А, х>|—е (для каждого е>0 существует
х £ А, превосходящее £—е).
Построим отрицание этого предложения:
(в)	ge > 0:yx g А, х > g—е<==^>де > 0:yx g А,	х<|—е.
Заменяя здесь |—е иа Ь, можно записать этот результат так:
(в)	Э.Ь < |:ух £ А, х^Ь.
Мы замечаем, что (в) совпадает с (б). Отсюда следует, что (в)
совпадает с (б), т. е. в определении точной верхней грани утвержде-
ние (б) можно заменить утверждением (в).
Мы видим, что, оперируя логическими символами, можно прихо-
дить к содержательным теоремам. Разумеется, в данном случае цепь
рассуждений можно было бы провести и без употребления логических
символов. Но в дальнейшем во многих случаях указанная «логиче-
ская алгебра» будет полезна. Мы не будем ее применять в самом
тексте книги, поскольку не стремимся к максимальной экономии места,
но рекомендуем читателю использовать ее в самостоятельной работе.
ЗАДАЧИ
1.	Показать, что для любых вещественных чисел х и у выпол-
няется неравенство
|х—{/|->||х|—|у||,
а для любых х, уА, ..., уп—неравенство
I A—J/i— • •  — уп | Ss || х | — | {/! I—... —| уп ||.
2.	Арифметической суммой А + В числовых множеств А и В
называется совокупность всех сумм х-]-у, где х £ А, у £ В. Дока-
зать, что если А и В ограничены сверху, то и A-f-B ограничено
сверху н
sup (А + В) = sup A-|-sup В.
3.	Арифметическим произведением АВ числовых множеств А и В
называется совокупность всех произведений х-у, где х £ А, у £ В.
40
ГЛ. 1. ВЕЩЕСТВЕННЫЕ ЧИСЛА
Доказать, что если А и В ограничены сверху и состоят из положи-
тельных чисел, то и АВ ограничено сверху и
sup (AB) = sup Л-sup В.
4.	Арифметической п-й степенью множества А называется сово-
купность всех чисел х", где х £ А. (Заметим, что, вообще говоря,
А2 А-А.) Доказать, что если А состоит из положительных чисел н
ограничено сверху, то и Ап ограничено сверху и
sup (A") = (sup А)п.
5.	Если вся совокупность вещественных чисел разбита на два
непустых и непересекающихся подмножества А и В, таких, что а < Ь
для всех а £ А, b £ В, то существует одно и только одно число у,
такое, что а < у < b для всех а £ А и b £ В («дедекиндово сечение»).
Историческая справка
По-видимому, первая теория, эквивалентная современной теории
вещественных чисел, была построена древнегреческим математиком
Евдоксом; она изложена в «Началах» Евклида (русское издание:
Гостехиздат, 1948, т. 1, кн. V). Преследуя в основном чисто логи-
ческие цели, эта теория была мало приспособлена для вычислений и
алгебраических построений. Современные теории ведут начало скорее
от работ Гаусса (1812), Больцано (1817), в особенности от знаменитого
«Курса алгебраического анализа» Коши (1821), где в качестве основа-
ния, считающегося очевидным, был принят принцип вложенных
отрезков. Следующий шаг был сделан Дедекиндом, Вейерштрассом н
Кантором (к 1872 г.), которые—разными путями—определили веще-
ственные числа с их свойствами, исходя из рациональных чисел *).
Таким образом, определение системы вещественных чисел было при-
ведено к определению системы рациональных чисел и тем самым
к определению системы натуральных чисел. В связи с этим впервые
были сформулированы и аксиомы натуральных чисел, именно, Дедекин-
дом в 1888 г. и Пеано в 1891 г. Разумеется, сразу же возник вопрос
о непротиворечивости арифметики натуральных чисел с ее аксиомами;
Д. Гильбертом (1900) он был включен в число основных проблем
математики XX века. Гильберт указал и допустимые («финитные»)
средства' для такого доказательства; однако Гёдель (1931) показал,
что этими средствами проблема в принципе не может быть решена.
«Трансфинитными» средствами непротиворечивость арифметики была
доказана Гентценом (1936) и П. С. Новиковым (1943). С законностью
применения таких средств далеко не все математики согласны. См.
П. С. Новиков, Элементы математической логики, Физматгиз, 1959.
*) С изложением теории Дедекинда («дедекиндовы сечения»)
можно познакомиться по книге П. С. Александров и А. Н.
Колмогоров, Введение в теорию функций действительного пере-
менного, ГТТИ, 1938; с изложением теории Кантора («фундаменталь-
ные последовательности») по книге В. В. Н е м ы ц к и й, М. И.
Слудская, А. И. Черкасов, Курс математического анализа,
т. 1, Гостехиздат, 1944.
ГЛАВА 2
ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
Бессмертная заслуга Георга Кантора в том, что он
отважился вступить в область бесконечного, не побояв-
шись нн внутренней, ни внешней борьбы не только
с мнимыми парадоксами, широко распространенными
предрассудками, приговорами философов, но и с преду-
беждением, высказанным многими великими математи-
ками. Этим самым он стал создателем новой науки —
теории множеств.
Ф. Хаусдорф, Теория множеств (1927)
Математика (греч. mathema — знание) — наука о ма-
тематических структурах (множествах, между элементами
которых определены некоторые отношения).
Философский словарь (ИПЛ, 1968)
§ 2.1. Операции над множествами
2.11. Мы рассмотрим здесь несколько подробнее операции
над множествами, введенные в 1.12. Напомним определения
этих операций. Если имеются множества А, В, С, ..., то
совокупность всех тех элементов, которые принадлежат
хотя бы одному из этих множеств, называется объединением
множеств А, В, С, ... Совокупность всех тех элементов,
которые входят в каждое из множеств А, В, С, ..., назы-
вается пересечением множеств А, В, С, ...
Объединение 5 множеств А, В, С, ... называют иногда
суммой и записывают в форме 5 = Л4-В + С-}-...; пересе-
чение D называют произведением и обозначают D = АВС...*).
Некоторые основания для таких «арифметических» наимено-
ваний имеются. Например, для любых трех множеств А, В,
С справедливо равенство
(Л + В)С = ЛС + ВС.
Напомним, что два множества считаются равными, если
каждый элемент одного из них есть в то же время элемент
другого. Приведем доказательство написанного равенства
как простой, но типичный образец рассуждений о равенствах
множеств.
Мы должны показать, что каждый элемент х, входящий
в (Д-(-В)С (левая часть), входит в АС-j-ВС (правая часть)
и, обратно, каждый элементу, входяГций в ЛСЦ-БС, входит
*) Не путать с «арифметической суммой» и «арифметическим про-
изведением», введенными в задачах к гл. 1.
42
ГЛ. 2. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
[2.12
и в (Л2?) С. Пусть сначала х принадлежит (А-(-В)С.
Будучи элементом пересечения множеств А 4- В и С, элемент х
должен входить в каждое из них; таким образом, мы имеем
х ^АА-В и х £ С.
Так как х входит в объединение А и В, то х входит хотя
бы в одно из слагаемых, например в А. Но включения х£А,
х С влекут за собой х £ АС, откуда х £ АС+ВС. Если же
х входит не в А, а в В, то таким же образом получаем
х£ВС, х £АС + ВС, что и требовалось. Обратно, если у
принадлежит сумме АС-\ВС, то у принадлежит одному из
слагаемых, например у£ВС. Но тогда у£В ну£С; далее,
из у^В следует у£А-}-В и окончательно j £ (Л-j-2?) С.
Случай у £ АС разбирается аналогично, чем доказательство
и завершается.
Следует, однако, заметить, что далеко не все арифме-
тические правила переносятся на операции с множествами.
Например, для множеств А, В, С имеют место формулы
А + А = А,
А-А — А,
А + ВС = (А + В) (Л + С),
уже непохожие па обычные арифметические равенства. Мы
предлагаем читателю самостоятельно убедиться в справед-
ливости этих формул.
2.12. Введем теперь новую операцию — операцию допол-
нения.
Если множество В является подмножеством множества А,
то совокупность всех элементов множества А, не принадле-
жащих В, называется дополнением множества В до множе-
ства А и обозначается СВ или А—В*).
Отметим очевидные формулы
С (СВ) = А—(А—В) = В,
(А—В) + В = А.
Заметим, что для двух произвольных множеств А и В фор-
мула
(А + В)—В = А,
) С—начальная буква слова «complement»—дополнение (франц.)
2.12]
§ 2.2. ЭКВИВАЛЕНТНОСТЬ МНОЖЕСТВ
43
вообще говоря, неверна; она верна только в случае, когда
А и В не имеют общих элементов.
Из более сложных формул отметим следующую, которая
часто будет далее встречаться:
С2В»=ПСВ-	О)
v	V
прочитать ее можно так: дополнение к объединению неко-
торых тожеств есть пересечение их дополнений.
Докажем справедливость этой формулы. Пусть х£ С 2 Bv‘,
тогда	это означает> чт0 ПРИ любом v мы имеем
x£Bv, т. е. x£CBv; но тогда	Обратно, если
__	V
то x£CBv при любом V, т. е. x£Bv при любом
V
у; но тогда x£^Bv, т. е. x^.C^Bv, что и требовалось,
v	v
Применяя к обеим частям равенства (1) еще раз операцию
С и полагая Av — CBV, мы получим формулу
2сд-сТИ	(2)
V	V
т. е. дополнение к пересечению некоторых множеств есть
объединение их дополнений.
Приведенные результаты можно соединить в форме
общего правила: переставляя символ дополнения С со знаком
2 (или П), нужно заменить V на ТТ (соответственно Ц
на 2)-
§ 2.2.	Эквивалентность множеств
Мы хотим теперь установить правила, по которым можно
было бы сравнивать различные множества по запасу эле-
ментов в них.
Для конечных множеств здесь никакой проблемы нет:
пересчитывая элементы каждого из двух конечных множеств
А и В, мы можем непосредственно выяснить, какое из этих
множеств более богато элементами по сравнению с другим.
Естественно называть конечные множества А и В экви-
валентными, если число элементов в них одинаково. Это
44
ГЛ. 2. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
[2.21
определение эквивалентности, однако, непосредственно не.
переносится на случай бесконечных множеств. Мы сейчас
придадим ему другую форму, в которой перенесение на беско-
нечные множества уже станет возможным. Для этого заметим,
что при установлении эквивалентности или неэквивалентно-
сти конечных множеств А и В на самом деле нет необхо-
димости в пересчете элементов того и другого множества.
Например, если множество А есть множество слушателей в
аудитории, а В есть множество стульев в этой же аудито-
рии, то, вместо того чтобы пересчитывать отдельно слуша-
телей и отдельно стулья, можно предложить каждому слу-
шателю занять один из свободных стульев, и тогда станет
сразу ясно, без всяких подсчетов, эквивалентны указанные
множества или нет.
Процедура, которая производится в указанном примере,
описываемая абстрактным образом, есть установление вза-
имно однозначного соответствия между множествами А и В.
2.21.	Определение. Если каждому элементу множе-
ства А каким-либо образом сопоставлен единственный элемент
множества В и при этом всякий элемент множества В ока-
зывается сопоставленным одному и только одному элементу
множества А, то говорят, что между множествами А и В
установлено взаимно однозначное соответствие. Множества
А и В в этом случае и называются эквивалентными.
Это новое определение эквивалентности годится для
любых множеств, не обязательно конечных; так, например,
бесконечное множество А натуральных чисел 1, 2, ... экви-
валентно множеству В целых отрицательных чисел —1;
— 2, ..., причем взаимно однозначное соответствие между
множествами А и В устанавливается посредством правила:
каждому числу п£А сопоставляется число —п£В.
Точно так же множество натуральных чисел 1, 2, ...
эквивалентно множеству всех четных положительных чисел
2, 4, ...: соответствие между ними осуществляется по
правилу п-^-Чп.
На этом примере мы видим, что множество может быть
эквивалентно своему истинному подмножеству; ситуация
такого рода, разумеется, может иметь место лишь для бес-
конечных множеств. Соответствие между элементами х£А
и у £В обозначается х++у.
2.22]
§ 2.2. ЭКВИВАЛЕНТНОСТЬ МНОЖЕСТВ
45
Отношение эквивалентности обозначается знаком
Легко видеть, что это отношение симметрично (т. е. А~А),
рефлексивно (если А~В, то В~А) и транзитивно (если А~В,
а В ~ С, то А~ С). Если два множества эквивалентны, то
говорят также, что они равномощны, имеют одну и ту же
мощность.
2.22.	Примеры. Отрезок [0, а], а > О, эквивалентен
отрезку ГО, 1]: соответствие осуществляется по формуле
х е [о,	= ах£[О, а]. Любые два отрезка [а, А] и
[a-J-Л, равной длины Ь—а эквивалентны: соответст-
вие осуществляется по формуле х£[а,	*-»у = х-[-Л
£[а + Л, & + Л]. Поэтому вообще любые два отрезка число-
вой оси эквивалентны. Точно так же эквивалентны любые
два интервала числовой оси. Соответствие х+->у = — уста-
навливает эквивалентность интервала 0 < х < 1 и полуоси
у > 1, соответствие х*-*у
всей
= -г-:—— эквивалентность
1
числовой оси и интервала (— 1, 1).
Докажем теперь, что отрезок [а, 6] эквивалентен интер-
валу (а, Ь). Рассмотрим произвольную последовательность
А точек отрезка [a, Z>], включающую два его конца:
х1=а, х2=Ь, х3, ..., хп, ... Тогда х3, xt, ... ле-
жат в интервале {а, Ь), так же как и остальные точки
отрезка [a, ft], не попавшие в выбранную последователь-
ность. Установим соответствие между точками отрезка и
интервала по следующему правилу:
хг «-► х3,
х2 «->
Хп -*-«+2»
у£А+*у.
Это соответствие, очевидно, взаимно однозначно. Таким
образом, отрезок [а, д] и интервал (а, Ь) эквивалентны.
Используя полученные ранее соответствия, заключаем, что
любой интервал эквивалентен любому отрежу, полуоси и
всей числовой оси.
46	ГЛ. 2. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ	[2.31
§ 2.3.	Счетные множества
2.31.	Определение. Множество, эквивалентное мно-
жеству всех натуральных чисел 1,2, ..., называют счетным
множеством.
Можно сказать иначе: множество счетно, если все его
элементы можно занумеровать всеми натуральными числами.
Приведем несколько простых теорем о счетных множествах.
2.32.	Всякое бесконечное подмножество В счетного мно-
жества А также счетно. Действительно, элементы множества В
можно заново перенумеровать по порядку их следования
в А (причем, поскольку В бесконечно, придется для нуме-
рации использовать все натуральные числа).
2.33.	Объединение конечной или счетной совокупности
счетных множеств есть счетное множество.
Доказательство. Рассмотрим сначала случай двух
множеств. Пусть имеются счетные множества A = (ax, а2, ...)
и В=(61, Ь2, ...). Выпишем в одну строку все элементы
обоих этих множеств по следующему правилу:
а1< ^1! й2> ^2’ й3, *3> • • •
Теперь все эти элементы можно заново перенумеровать по
порядку следования в строке. Элемент, встречающийся два
раза (т. е. такой, который входит и в А, и в В), естест-
венно, приобретает номер в первый раз, а во второй раз
пропускается. В результате каждый элемент объединения
множеств А и В получит свой номер, что и требуется.
Так, множество всех целых чисел 0, ±1, ±2, ...
счетно, как объединение двух счетных множеств 1, 2, 3, ...
и 0, —1, —2, . . .
Совершенно аналогичным образом теорема доказывается
в случае трех, четырех или вообще любого конечного числа
счетных множеств. В случае счетной совокупности счетных
множеств
-^1={й11> й12>  • а1п> • • •},
^2= {й211 й22> • • •» й2п> • • •}»
Л = {ЙЛ1> ЙЛ2> akm •••}»
изменение будет только в том, что правиле? для записыва-
2-35]	§ 2.3. СЧЕТНЫЕ МНОЖЕСТВА	47
иия всех элементов всех этих множеств в одну строку при-
дется применить несколько иное, например по группам эле-
ментов с равной суммой индексов:
а11> а21» й12> а31> й22> а13> а41> а32> й23> й14> • • • >
в остальном же доказательство не изменяется.
2.34.	Множество всех рациональных чисел (т. е. чисел
р	.
вида , где р и q—целые числа) счетно.
Действительно, множество всех рациональных чисел есть
объединение следующих счетных множеств:
1)	множества Аг всех целых чисел п = 0, ±1, ±2, ...;
2)	множества А2 всех дробей вида -у, п = 0, ± 1, ± 2,... ;
3)	множества А3 всех дробей вида у, п = 0, ±1, ±2, ...;
k) множества Ак всех дробей вида у , п = 0, ±1, ±2, ...;
Множества А1г А2, ..., Ак, ... составляют счетную сово-
купность множеств; так как каждое из них счетно, то в силу
2.33 и их объединение счетно, что и утверждалось.
2.35.	Если
Л = («1, а2, ..., ак, ...) и B = (blt b2, ..., Ьп, ...)
— счетные множества, то множество всех пар (ак, Ь„)
(k, п= 1, 2, ...) также является счетным.
Действительно, множество всех этих пар можно пред-
ставить в виде объединения счетной совокупности счетных
множеств
А ={(«!> *1)- («г. *г)> •••,(«!, Ьп), ...},
Л2 = {(«2, *i)> («2- *2),	bn), ...},
= {(ak, bj, (ak, b2), ..., (ak, bn), ...},
и в силу 2.33 оно является счетным множеством.
48
ГЛ. 2. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
[2.36
Этому примеру можно придать геометрический смысл:
паре (ak, bn) отвечает точка на плоскости с координата-
ми ak, bn‘, мы видим, в частности, что множество всех
точек плоскости, обе координаты которых рациональны,
счетно.
2.36.	Множество всех многочленов Р (х) = а0 + с^х
... + апхп (любых степеней) с рациональными коэффициен-
тами а0, alt ..., ап счетно.
Множество всех многочленов указанного вида есть объеди-
нение счетной совокупности множеств Ап(п — О, 1, 2, ...),
где Ап означает множество многочленов степени ^л. По-
этому, имея в виду теорему 2.33, достаточно показать, что
каждое из множеств Ап счетно. При л = 0 речь идет о счет-
ности множества самих рациональных чисел, которая уста-
новлена в 2.34. Далее будем действовать по индукции:
предположим, что доказана счетность множества Ап, и до-
кажем счетность множества Лп+1.
Каждый элемент множества Ап+1 можно записать
в виде
Q(*) + cn+i*"+1.
где Q(x)—многочлен степени ^Сл с рациональными коэф-
фициентами, т. е. элемент множества Ап, и лп+1 — рацио-
нальное число.
Множество многочленов Q(x) по предположению счетно,
и множество чисел ап+1 также счетно. Таким образом, каж-
дому элементу множества Лп+1 можно сопоставить пару
(Q(x), ап+1), каждая из составляющих которой пробегает
счетное множество значений. В силу 2.35 множество Лп+1
также счетно, что и требовалось.
2.37.	Множество всех алгебраических чисел (т. е. корней
многочленов с рациональными коэффициентами) счетно.
Согласно 2.36 все многочлены с рациональными коэффи-
циентами мы можем занумеровать натуральными числами,
так что эти многочлены будут образовывать последователь-
ность
PjW, Pz(x)......Р„(х), ...
Но каждый из указанных многочленов имеет некоторое ко-
2.42]
§ 2.4. МНОЖЕСТВА МОЩНОСТИ КОНТИНУУМА
49
нечное число корней (см. 5.87). Выписывая в одну строку
сначала все корни многочлена (х), затем все корни много-
члена Р2(х) и т. д., мы получаем возможность занумеровать
и все алгебраические числа, что и требовалось.
§ 2.4.	Множества мощности континуума
Существуют бесконечные множества, элементы которых
нельзя перенумеровать натуральными числами. Такие множе-
ства называются несчетными. Типичным примером несчетного
множества является континуум—множество всех точек ка-
кого-либо отрезка.
2.41.	Теорема (Г. Кантор, 1874). Множество всех то-,
чек отрезка 0 х 1 несчетно.
Доказательство. Допустим, что, напротив, множе-
ство всех точек отрезка [0, 1] счетно и все их можно рас-
положить в последовательность хх, х2, . ..,хп, ... Имея
эту последовательность, построим следующим образом по-
следовательность вложенных друг в друга отрезков.
Разделим отрезок [0, 1] на три равные части. Где бы ни
находилась точка хх, она не
менно всем трем отрезкам
может принадлежать одновре-
среди них можно указать такой, который не содержит точки хг
(ни внутри, ни на границе); этот отрезок мы обозначим через
Дх. Далее, обозначим через Д2 ту из трех равных частей
отрезка Дх, на которой не лежит точка х2. Когда таким
образом будут построены отрезки ДхзэД2зэ ... зД„, мы обо-
значим через Д„+1 ту из трех равных третей отрезка Дп,
на которой не лежит точка хп+1; и т. д. Бесконечная после-
довательность отрезков Д1гэД2гэ... в силу теоремы 1.81
имеет общую точку £. Эта точка £ принадлежит каждому
из отрезков Д„ и, следовательно, не может совпадать ни
с одной из точек хп. Но это показывает, что последова-
тельность хх, х2, ...,хп, ... не может исчерпывать всех
точек отрезка [0, 1], вопреки первоначальному предположе-
нию. Теорема доказана.
2.42.	Мы видели, что все рациональные числа отрезка
[О, 1] составляют счетное множество. Остальные числа от-
резка называются иррациональными. Мы видим теперь, что
50
ГЛ. 2. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
[2.43
иррациональных чисел «значительно больше», чем рацио-
нальных: точнее говоря, иррациональные числа образуют
заведомо несчетное множество (иначе, если бы множество
иррациональных чисел было счетным, то было бы счетным
и множество всех чисел отрезка 0 <1 х 1, как объедине-
ние двух счетных множеств). Более того, так как алгебраи-
ческие иррациональные числа (корни многочленов с рацио-
нальными коэффициентами) образуют также счетное множе-
ство (2.37), то несчетное множество составляют числа, не
являющиеся корнями многочленов с рациональными коэффи-
циентами, — трансцендентные чисЛЗ".
Между прочим, приведенное рассуждение доказывает и
само существование трансцендентных чисел, нисколько не
очевидное заранее.
2.43.	Определение. Всякое множество, эквивалентное
множеству всех точек отрезка [0, 1], называется множест-
вом мощности континуума.
Мы видели, что множества точек любого отрезка [a, ft],
любого интервала (а, 0) и, наконец, всей прямой —оо < х < оо
эквивалентны множеству точек отрезка [0, 1]; следова-
тельно, все они имеют мощность континуума.
§ 2.5.	Понятие о математической структуре.
Изоморфизм структур
2.51.	С некоторой общей точки зрения математика имеет
дело только с множествами. Но богатство той или иной
математической теории зависит от дальнейших связей между
элементами (и подмножествами) множеств, изучаемых в дан-
ной теории. Эти связи формулируются абстрактным образом
с помощью аксиом. Примером' служит система вещественных
чисел, рассмотренная в гл. 1: она представляет собой мно-
жество, элементы которого удовлетворяют некоторой опре-
деленной, достаточно сложной системе аксиом. Множество
с дальнейшими условиями (на элементы и подмножества) на-
зывают математической, структурой. Точное определение мате-
матической структуры должно было бы содержать общее оп-
ределение таких «условий», и мы предпочитаем его не приво-
дить *), ограничиваясь словесным описанием и рядом примеров.
*) См. Н. Б у р б а к и, Теория множеств, гл. IV, «Мир», 1965.
2.53]	§ 2.5. ПОНЯТИЕ О МАТЕМАТИЧЕСКОЙ СТРУКТУРЕ 51
2.52.	Две структуры с одинаковыми типами условий на-
зываются изоморфными, если между их элементами можно
установить взаимно однозначное соответствие так, что при
этом соответствии сохраняется выполнение или невыполне-
ние условий, определяющих структуру. Всякая структура
изоморфна самой себе: тождественное отображение, очевидно,
взаимно однозначно, и при нем сохраняются все условия,
которым подчинены элементы и подмножества структуры.
Но возможны и нетождественные отображения структуры на
себя, сохраняющие описывающие структуру условия; такие
отображения называются автоморфизмами структуры.
Рассмотрим для примера структуру линейно упорядочен-
ного множества. Так называется множество Е элементов
х, у, ... с тем дополнительным условием, что для каждых
двух различных элементов х, у установлено одно из отно-
шений («меньше») или у < х, причем если х<у и
у < г, то х < z. Примером может служить (расширенная)
числовая ось или любое подмножество числовой оси с обыч-
ным отношением порядка. Два упорядоченных множества Ех,
Е2 называются изоморфными, если между ними установлено
взаимно однозначное соответствие так, что из хг ^Е1,у1 £Elt
х1<Су1 Для соответствующих элементов х2 gЕ2 и у2 £ £2
следует х2<у2. В этом смысле вся числовая ось изоморфна
любому интервалу; но она не изоморфна отрезку (у отрезка
есть наименьший элемент, у оси—нет). Автоморфизмом ли-
нейно упорядоченного множества является любое его взаимно
однозначное отображение на себя, сохраняющее порядок:
если	хг соответствует х2, yt соответствует у2, то
х2 <.у2. Для интервала (0, 1) как линейно упорядоченного
множества формула у — хп при любом фиксированном п за-
дает автоморфизм.
Возможны структуры, система аксиом которых определяет
структуру с точностью до изоморфизма; иначе говоря, воз-
можно, что всякие две структуры с данной системой аксиом
изоморфны. Говорят в таком случае, что система аксиом дан-
ной структуры полна и что сама данная структура единственна.
2.53.	В качестве примера рассмотрим вопрос о единст-
венности системы вещественных чисел. Мы назвали в гл. 1
системой вещественных чисел совокупность объектов, удов-
летворяющих определенным аксиомам (1.21 —1.24).
52
ГЛ. 2. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
[2.54
Поставим вопрос: единственна ли система объектов, удов-
летворяющих всем этим аксиомам? Изоморфны ли две струк-
туры вещественных чисел? Более точно: если имеется два
экземпляра системы вещественных чисел, можно ли устано-
вить между их элементами такое взаимно однозначное соот-
ветствие, при котором результатам сложения и умножения
чисел первой системы соответствуют результаты одноимен-
ных операций во второй системе, при котором сохраняется от-
ношение порядка между соответствующими элементами и
при котором точные границы соответствующих множеств
соответствуют друг другу? Ответ на этот вопрос положи-
тельный и дается следующей теоремой, доказательство ко-
торой проводится в 2.54—2.58.
Теорема. Пусть имеется два экземпляра Rv и R2 си-
стемы вещественных чисел; числа первой системы будем снаб-
жать индексом 1, числа второй системы — индексом 2.
Утверждается, что между числами х± £ и х2£ R2 можно
установить взаимно однозначное соответствие, обозначаемое
знаком так, что при этом будут выполняться следующие
свойства:
1)	из х1~х2, у1~у2 следует х1+у1^ х2+у2>
2)	из х1~х2, >1~Уг следует хгу2~ х^;
3)	из хг^х2, у!.~у2, х1<у1 следует х2 <у2;
4)	если множество A1cRl ограничено сверху, то множе-
ство А2 соответствующих элементов из R2 также ограничено
сверху и
sup Д ~ sup А2.
2.54.	Приступая к доказательству теоремы 2.53, мы мо-
жем отметить, что теоретико-множественная эквивалентность
систем Rv и R2 следует уже из возможности представления
чисел каждой системы бесконечными десятичными дробями
(1.77). Мы используем здесь иной подход, более приспособ-
ленный для проверки свойств 1)—4). Обозначим через Q±
и Q2 множества рациональных чисел из систем R± и R2.
Между и Q2 устанавливается естественное взаимно одно-
значное соответствие по самой записи рациональных чисел
,	m гт	ч.
в форме —. При этом, очевидно, выполняются свойства
1) — 3), так как указанные операции выражаются непосред-
ственно через символы m и п. Если теперь g Rt —любое
2.56]	§ 2.5. ПОНЯТИЕ О МАТЕМАТИЧЕСКОЙ СТРУКТУРЕ
53
число, то по 1.76 мы имеем
Bi = sup (Вх) = inf Pt (gj,
где (|j) означает множество рациональных чисел 1\
а Рг (£i) — множество рациональных чи<;ел	при этом
всегда r1^sl. Обозначим через N2 множество рациональ-
ных чисел системы /?2, соответствующих рациональным чис-
лам из множества Л/^^) ^т. е. имеющих туже запись ,
и через Р2—множество рациональных чисел системы Р2,
соответствующих числам из множества	Мы имеем
r2 <1 s2 для всяких r2 £ N2 и у2 £ Р2 и по 1.62 б sup N2 <1 inf Р2.
Так как все рациональные числа в системе Р2 попадают либо
в N2, либо в Р2, то между числами a2 = supAr2 и 02 = inf Р2
нет рациональных чисел. А это значит, что а2 = (32, иначе
по 1.75 между а2 и (32 нашлась бы рациональная точка.
Теперь поставим в соответствие числу	число £2 =
=а2 = Р2£А’2. Указанное соответствие, по симметрии, вза-
имно однозначно.
2.55.	Проверим теперь выполнение свойств 3) и 4). Если
х1<у1, мы найдем, пользуясь 1.75, рациональное число fj,
хг < t\ < у^, для соответствующих чисел х2, г2, у2 по са-
мому определению соответствия будем иметь х2 < г2 < у2,
так что 3) выполнено. Пусть Аг ограничено сверху и =
= supA1, и пусть А2—множество, соответствующее и
g2—число, соответствующее Мы имеем ^^л^для лю-
бого	откуда х2 Для любого х2£А2 и, следо-
вательно, ^2^supA2. Если supA2<£2, то имеется число
(даже рациональное) у2 такое, что л:2<у2<^2 для любого
х2£А2, откуда x1<y1<Bi для любого и для у1У
соответствующего у2. Но тогда sup Аг ^.уг < в противо-
речии с предположением. Таким образом, supA2 = £2, чем
доказано 4).
2.56.	Для доказательства свойств 1) и 2) установим
две леммы.
а.	Лемма. Пусть даны вещественные числа у и г и ра-
циональное число r>y-]-z; существуют рациональные числа
и>у, v>z такие, что и-^т> = г.
54
ГЛ. 2. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
[2.57
Доказательство. Пусть г—(y-\-z) — h. В качестве и
возьмем любое рациональное число в интервале (у, у-)-Л)и
положим v = r—и; очевидно, v > г—(y~\-h) = z, что и тре-
буется.
б.	Лемма. Пусть даны положительные числа у и z и
рациональное число г > yz; существуют рациональные числа
и>у, такие, что uv=r.
Доказательство. Пусть h. В качестве и возь-
мем любое рациональное число в интервале (у, уй) и поло-
г	г
жим 17= — ; очевидно, ‘P>-^ = z, что и требуется.
2.57.	Теперь проверим выполнение свойства 1). Пусть
~ х2, ух ~у2,	+У1 ~ =И= х2 4-у2 и пусть, например,
2'2>х2+у2. Выберем рациональное число /2 € (х2 + у2, z2).
По лемме 2.56а существуют рациональные числа и2 > х2,
>у2, «2 + ‘п2 = /2. Для соответствующих чисел zlt tlt ult
мы имеем хг < и1г у1 < vlf Xi+yx < + = Но так как
/2 < z2 ~	то 4 < х1Ту1 в противоречии с предыду-
щим. Предположение z2 < х2 Ц-у2 исключается аналогично.
2.58.	Переходя к свойству 2), рассмотрим его вначале
для положительных хг и ylt которым по 3) соответствуют
положительные же х2 и у2. Пусть хгуг ~ z2 =0= х2у2 и пусть,
например, z2 > х2у2. Выберем рациональное число /2 £ (х2у2,
z2). По лемме 2.566 существуют рациональные числа п2 > х2,
®2>J2, u2v2 = t2. Для соответствующих чисел zlt flt иъ vr
мы имеем х± < ult уг < vlt х1у1 < u1z>1 — tx. Но так как
t2 < z2 ~ Xjylt то < хгуг в противоречии с предыдущим.
Предположение z2 < х2у2 исключается аналогично. Случай,
когда один из множителей равен 0, очевиден.
Переходя к общему случаю и имея в виду правило знаков,
достаточно проверить, что —1-х1~— 1-х2. Пусть —bjq
соответствует элементу z2. По 1) равенство —1 • Xj-|-jq = О
влечет z2~i-x2 = 0, откуда z2 =—Пх2, что и требовалось.
Тем самым наша теорема полностью доказана.
2.59.	Мы показали, что существует единственная с точ-
ностью до изоморфизма система вещественных чисел. Оста-
новимся еще на вопросе о том, каковы автоморфизмы этой
2.62]
§ 2.6. ПРОСТРАНСТВО п ИЗМЕРЕНИЙ
55
системы. В соответствии с 2.52 автоморфизмом системы /?
мы называем взаимно однозначное отображение /?—>/?, со-
храняющее результаты сложения и умножения, отношение
порядка и точную верхнюю грань. Покажем, что такое ото-
бражение R—может быть только тождественным. Будем
обозначать через х' тот элемент из R, в который при рас-
сматриваемом автоморфизме переходит элемент х. Элемент Г
есть единица в поле /?, поскольку для любого х мы имеем
Г-х' = х'\ в силу единственности единицы (1.41а) мы имеем
Г = 1. Отсюда 2'= 1'4-Г = 2, ..., п'= (п— 1)'-|-Г = л;
( т V т' т ,,
( —1 == — = —. В силу единственности противоположного
элемента (1.32) мы имеем	. Таким образом,
наш автоморфизм оставляет на месте систему рациональных
чисел. Но тогда он оставляет на месте и каждое веществен-
ное число, поскольку в силу 1.76 для каждого
| = sup N.,
где Л/.— класс рациональных чисел, не превосходящих £, а
наш автоморфизм сохраняет отношение порядка и верхнюю
грань. Итак, рассматриваемый автоморфизм есть тождествен-
ное отображение | —> £.
§ 2.6.	Пространство п измерений
2.61.	Определение. Пусть дано натуральное число л;
обозначим через Rn совокупность всех комплексов («векто-
ров») из л вещественных чисел
х = (хъ ..., хп).
Числа хх, ...,хп называются координатами вектора х.
Будем считать, что вектор x = (xt, ..., хп) равен вектору
у = (ух,	в том и только в том случае, когда выпол-
няются равенства х1=у1, ..., хп—уп.
Совокупность Rn называется п-мерным вещественным,
пространством.
2.62.	Введем в пространстве Rn операцию сложения по
формуле
(хх, ...,хп) + (у1, ...,уп)=-(х1+у1, ...,Хп+уп). (1)
56	ГЛ. 2. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ	[2.63
Покажем, что для операции сложения в Rn выполнены
аксиомы сложения 1.21, в которых под символами х, у, ...
понимаются уже элементы пространства Rn. Пусть х =
= (*ь	х„), у = (уь ..., уп), z = (zY, ..., zn). Мы имеем:
a.	=	..., хп+уп)=у + х.
б.	(x+j)-]-2=(X1-j-J1-]-2’1, • • • ,	+	= Х +
+ (j + 2’)-
в.	Для вектора 0 = (0, 0, .. ., 0) («нуль-вектор») выпол-
няется равенство х + 0 = (хх + 0, ..., х„ + 0) = х.
г.	Для каждого х £ Rn существует противоположный эле-
мент у такой, что х+у = 0; а именно, можно положить
У = (—х1г ..., —х„).
Вместе с аксиомами а) — г) выполняются все следствия
из них, выраженные в предложениях § 1.3.
2.63.	Введем в пространстве Rn операцию умножения на
любое число a£R по формуле
а(хь ..., х„) = (ах1, ...,ах„).	(1)
Очевидно, что справедливы формулы:
а(х+^) = ах + ау;	(2)
(а-|-Р) х = ах + Рх;	(3)
1-х = х;	(4)
а(Рх) = (аР)х.	(5)
2.64.	Векторы
х<1> = (х<п, ..., х“>), ..., х<т = (х<т>, .... х<пт>)
пространства Rn называются линейно зависимыми, если
существуют такие постоянные Clt ..., Ст, среди которых
есть отличные от нуля, что
С1х«>+...+Стх‘и> = 0.	(1)
Если же равенство (1) возможно только при Сх= .. . =Ст~ 0,
то векторы х11’, ..., х(т> называются линейно независимыми.
Векторное равенство (1) в силу 2.62 (1) и 2,63 (1) эквива-
2.66]
§ 2.6. ПРОСТРАНСТВО п ИЗМЕРЕНИЙ
57
лентно п числовым равенствам
С^’+...+Qxr^O,
С1Х^+.'.. +СтхГ = 0.‘
Поэтому в силу известных теорем теории систем линейных
уравнений *) линейная зависимость векторов х(1), ..., xw>
эквивалентна тому, что ранг матрицы || х}*’ || меньше т.
В частности, в Rn систему п линейно независимых векторов
можно задать с помощью любой квадратной матрицы || x|-ft> ||
из п строк и столбцов с отличным от 0 определителем.
Всякие же л + 1 векторов пространства Rn линейно зависимы.
2.65.	Пусть Д, ..., fn — какая-либо система п линейно
независимых векторов пространства Rn. Тогда для любого
вектора g£Rn в силу линейной зависимости векторов Д, ...
..., Д, g существует линейная зависимость
СО^+СЛ+=0,	(1)
причем заведомо Со=^(), иначе оказались бы линейно зави-
симыми векторы Д, ..., Д. Поэтому равенство (1) можно
разрешить относительно g; мы получим равенство вида
^=«1/1+• • •+aj„.	(2)
Числа аь ..., а„ называются координатами вектора g отно-
сительно базиса j\, ..., Д.
Так, выбирая в качестве векторов Д, ..., fn векторы
е1 = (1,0, ...,0), ..., е„ = (0, 0, ..., 1),	(3)
получаем для любого вектора х = (х1; ..., х„) С Rn
х =	+ ... + хпе„,
так что числа хь ..., хп являются координатами вектора х
относительно специального базиса еь ..., е„(3).
2.66.	Пусть Д, .. ., Д — фиксированный базис в простран-
стве Rn. Если g= + ... + а„Д И й = рхд + ... + р„Д,
то по свойствам 2.63 (2) — (3)
h .=	Д + -.. + (а„ + ₽„) Д,
Cg~ CajД + ... -j- Ca.nfn при любом числе С,
*) См., например, Г. Е. Шилов, Математический анализ, Ко-
нечномерные линейные пространства, «Наука», 1969, ЗЛ2. В даль-
нейшем обозначаем эту книгу КЛП.
58
ГЛ. 2. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
[2.67
так что сложению векторов и умножению вектора на число С
отвечают, при любом базисе, сложение соответствующих
координат и умножение их на это число С. Можно сказать,
что отображение, ставящее в соответствие любому вектору
х = (хг, ...,хп) вектор «=(«!, ..., а„), где ...,а„ —
координаты вектора х относительно фиксированного базиса
/i,	есть автоморфизм (2.52) л-мерного простран-
ства /?„.
2.67.	Вообще, в соответствии с определением автомор-
физма математической структуры (2.52) автоморфизмом
п-мерного пространства Rn мы назовем такое взаимно одно-
значное отображение х' = Л(х) пространства Rn на себя,
что выполняются условия:
а.	А(ах) = аА(х) для любого x£Rn и любого a£R.
б.	Л(х+у) = Л (х) + Л (у) для любых х и у из Rn.
Из свойств а и б легко получить более общую формулу:
( р	\	р
в.	АI 2 akxk ) — 2 (хл) Для любых векторов xlt ...
\Л= 1	/	k=l
..., хр и любых вещественных аь ..., ар.
Найдем общее выражение автоморфизма А через коор-
динаты вектора х. -Пусть х = (хг, ..., хп) и х'=А(х) —
= (Xi, ..., х’п). Пусть, далее, еу-=(0, ..., 1, ..., 0) и e'j =
— А (еу) = (ау1, ...,ajn). Мы имеем
и	/ п \ п
х' = 2 xkek = А (х) = А ( 2 *jej) = 2 xjA (*/) =
\/=1	/	/=1
п	/ п	\ п	/ п	\
== 2 Xj	( 2	ajkek ) ~ 2	( 2	ajkxj ) ek >
;=1	\ft=l	/ k=l	\i=l	J
откуда
n
4=2 ajkXj.	(1)
/= i
Таким образом, автоморфизм А задается в координатах
системой линейных соотношений (1). Так как эти формулы
должны давать взаимно однозначное отображение простран-
ства Rn на себя, то по основным теоремам линейной алгебры
(см. КЛП, 4.76) матрица ||а/лН невырождена:
det||O7ft||=#0.
2.67]
§ 2.6. ПРОСТРАНСТВО П ИЗМЕРЕНИЙ
59
Обратно, всякая невырожденная матрица || ау7е || по фор-
мулам (1) задает отображение пространства Rn в себя, удов-
летворяющее условиям а, б и взаимно однозначное, т. е.
определяет автоморфизм пространства /?„. Итак, автомор-
физмы пространства Rn описываются посредством невырож-
денных матриц по формулам (1).
Рассмотрим несколько примеров. Автоморфизм I, опреде-
ляемый матрицей
1 0 ... О
О 1 ... О
О 0 ... 1
переводит каждый вектор в себя самого; это—тождественный
автоморфизм. Автоморфизм Лу-, определяемый матрицей
f-я строка
О
(не выписанные элементы — нули) увеличивает в Zy- раз /-ю
координату каждого вектора; он называется растяжением
в Ху- раз по /-й оси. Автоморфизм, определяемый матрицей
К
О
(V2..-W0),
по каждой оси производит растяжение: по первой—в	раз,
по второй — в Z2 раз и т. д. Если все числа
совпадают, то соответствующий автоморфизм, определяемый
60
ГЛ. 2. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
[2.71
матрицей
X	0
X
О	X
(^=#0),
каждый вектор х переводит в вектор Хх. Такой автоморфизм
называют преобразованием подобия с коэффициентом подо-
бия X.
§ 2.7.	Комплексные числа
2.71.	Естественно возникает вопрос, можно ли в /^мер-
ном пространстве Rn ввести операцию умножения векторов
друг на друга так, чтобы в результате получался снова
вектор из /?„и были выполнены аксиомы умножения 1.22 а—д.
Оказывается, это можно сделать при л = 2, например,, по
следующему правилу. Пусть е1 = (1, 0), е2 = (0, 1); каждый
вектор z£R2 можно записать в виде z = (x, у) = хе1 + уе2,
где х к у—координаты вектора z относительно базиса elt е2.
Положим
Cj	^1^2	^2^1 — ^2» @2 —	^1*
Распространим это умножение на все векторы z = xe1-\-
-\-уе2^-^2 nQ линейному закону: если w = ue1-{-ve2, то
zw = (хег +уе2) (иех -пе2) = хие{ + xw1e2 -(-уие2е1 +yve% =
= (хи—yv) ех + (xt'-f-ya) е2.
Короче, определение умножения в R2 таково:
zw = (x, у)(и, v) = (xu—yv, xv-[-yu).	(1)
При этом, очевидно,
a.	wz = (их—vy, vx + иу) = zw.
б.	Если ,у = (а, Р), то
(zw) у= (хиа—yva—хтф—пуР, х«р—у©р Н-хто+уиа) =
= (х (иа—•пР)—у (т'а+«Р), х (wx + zzp)+y (иа—•£$)) =
= z(wy).
2.72]	§ 2.7. КОМПЛЕКСНЫЕ ЧИСЛА	61
в.	Для точки е = (1, 0) и любого z—(u, v) мы имеем
(1, 0)(и, v) = (u, v).
г.	Для любой точки (х, у) =# (0, 0) имеется обратный
элемент, именно
(и, v) = ^2+г/2, —	•
Действительно,
(х,у)(и, г») = (х2+г/2 + Х2^_г/2> х2+у2~x2+i/2) = (1’ °)'
д.	Для любых трех точек z = (x,y), w = (u, v), у = (а, P)
(z + w) у — zy + wy.
Действительно,
(2 + w)-y = (x + «, y + ®)(a, ₽) =
= ((x + «)a —(y + v) P, (x + a)P + (y+®)a) =
= ((xa—yP) + («a—®P), (*P +ya) + («Р + i»a)) =
= (xa—yP, xP~|-ya) + (Ka—®P> «P + ^a) =
= {x, y) (a, P) + («, Ш Р) = гу+и»у.
Таким образом, для введенного нами умножения в /?а выпол-
няются все аксиомы 1.22а — д. Вместе с ними выполняются
и все следствия из них, указанные в предложениях § 1.4.
2.72.	Определение. Пространство /?2 с операциями
сложения 2.62 (1) и умножения 2.71 (1) называется полем
комплексных чисел и обозначается через С. Совокупность
вещественных чисел R вкладывается взаимно однозначно в С
по правилу
х«-»(х, 0),
причем сохраняются операции сложения и умножения, по-
скольку
(х, 0) + (у, 0) = (х +у, 0), (х, 0) (у, 0) = (ху, 0).
Поэтому комплексные числа (х, 0) мы будем называть ве-
щественными числами и писать (х, 0) = х.
Таким образом, базисный вектор е1 = (1, 0) получает
обозначение 1. Второй базисный вектор еа = (0, 1) обозначим
через г. Каждое комплексное число (х, у) можно теперь
62
ГЛ. 2. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
[2.73
записать в форме x-r-iy. По определению мы имеем г2 = е2=
——е1 = (—1,0) = —1, так что в области комплексных
чисел из числа —1 можно извлечь квадратный корень. Вто-
рым квадратным корнем из —1 является число —i, поскольку
(—/)2=(—l)2i2 = —1. Других квадратных корней из -—1
(кроме i и —г) среди комплексных чисел нет: действительно,
если для некоторого z£C мы имеем г2 =—1, то z2-)-! =
=	— Z) = 0, откуда в силу 1.47 б (с учетом сказан-
ного в 2.71) z+t = 0 или z— i = 0, т. е. z = i или z =— i.
Правило умножения 2.71 (1) можно записать в форме
(х + iy) (и iv) = (хи —yv) -{- i (xv + уи),
что соответствует обычному правилу перемножения двучле-
нов с учетом равенства /2=—1.
Для данного z = х 4- iy число х называется вещественной
частью z, а число у называется мнимой частью z; мы пишем
x = Rez, _у = Im г.
2.73.	Комплексные числа z = x-r-iy и z — x—iy назы-
ваются комплексно сопряженными.
Справедливы следующие утверждения:
а.	Соотношение л = г равнозначно тому, что z вещест-
венно.
_12Г 2---1 1 2 J для любых комплексных и z2.
в. z1z2 = z1-z2 J
Доказательство, (а) Соотношение x-]-iy = x — iy
равносильно у = 0, т. е. z = x-\-iy в этом и только в этом
случае вещественно.
(б	) Пусть = хх + tji, z2 = х2 + iy2; тогда
^1 + ^2 = (X1 + X2) — 1’(л+^а) = (Х1—4У1)-т-	_ _
+ (хг—(Уг)= zi + zv
(в) Аналогично
*1* *2 = (*1х2	~ * (*1 У 2 + X2J1) =
= (Xi — iyx) (х2 — iy2) = zt • z2.
В частности, из в следует, что справедливо соотношение
г. az=az для любого вещественного а.
2.75]
§ 2.7. КОМПЛЕКСНЫЕ ЧИСЛА
63
2.74.	Единственность системы комплексных
чисел.
Теорема. Если в двумерном пространстве R2 введено
умножение элементов друг на друга, удовлетворяющее акси-
омам 1.22, то в R2 можно найти линейно независимые век-
торы gt и g.2 такие, что gl^g^ gl = — gi, gig2 = g-2gi = g2-
Доказательство. В силу аксиомы 1.22 в в /?2 сущест-
вует элемент 1, отличный от 0; положим gi=l. Пусть,
далее, А—любой вектор, линейно независимый с gx. Мы имеем
/1 = «51-г РА с некоторыми вещественными а и р. Для
вектора А = fY Ц- ygx =?= 0 (у вещественно) мы имеем
(А + У51)а =/? + 2уА + y25i = «51 + РА + 2уА + у25ь и если
взять у =— Р/2, мы получим /| = (а + у2)51. Вещественное
число а-ф-у2 не может быть равным 0 по 1.47 а. Оно не
может быть также положительным, так как тогда мы полу-
чили бы
(А — Ка + У2 51) (А Н- /«ту2 5i) = О
в противоречии с 1.47 б. Итак, a-j-y2 = — б, 6 >
,	1 г	« (а+?'3)£1
А на 52 = р^А. находим g* == — 51-
0. Заменяя
Равенства
5i52 = 525i = 52 вытекают из того, что gr есть единица.
Теорема доказана.
Из этой теоремы следует, что между любыми двумя дву-
мерными пространствами с умножением, удовлетворяющим
аксиомам 1.22, можно установить взаимно однозначное соот-
ветствие с сохранением операции умножения, т. е. соответ-
ствующие структуры (двумерные пространства с умножением)
изоморфны.
2.75.	Автоморфизмы системы комплексных
чисел. Мы видели в 2.59, что единственным автоморфизмом
системы вещественных чисел является тождественный авто-
морфизм | Определение автоморфизма области комплек-
сных чисел таково: взаимно однозначное отображение z —+z’
плоскости С на себя называется автоморфизмом, если для
любых zY и z2 из С и любого вещественного а выполнены
следующие условия:
1)	^1 + z2Y = z'l + z'2;
2)	(ztz2)’ = z[z'2,
3)	(az) — az[.
64
ГЛ. 2. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
[2.76
Свойства 1) и 3) показывают, что рассматриваемый авто-
морфизм является автоморфизмом системы С как двумерного
пространства (2.67). Свойство 2) говорит, что этот авто-
морфизм должен сохранять операцию .умножения.
Нетождественный автоморфизм системы С можно задать
правилом
x-j-iy —-> х—iy.	(1)
Покажем, что система С не имеет других нетождественных
автоморфизмов. Пусть (х + iy)' есть элемент, в который
переходит элемент х + iy при некотором автоморфизме.
Из 3) следует, что
Vz' = (l-z)' = z',
так что 1' есть единица системы С; в силу единственности
единицы имеем Г=1. Для любого вещественного х по 2)
х' = (х •1)' = х-1' = х-1 = х, так что автоморфизм оставляет
на месте всю совокупность вещественных чисел. Далее, по 2)
(i')2 = t2 = —1,
откуда i' есть либо i, либо —i (2.72). В первом случае
находим
(х + iy)' = х' i'y' = x~\~iy,
а во втором
(х + iyY = х' + i’y' = х— iy,
что и доказывает наше утверждение.
Изучение комплексных чисел будет продолжено в гл. 5
(5.72 и далее).
2.76.	Возможно ли при л >2 для векторов пространства Rn
ввести операцию умножения с выполнением аксиом 1.22 а—д?
Оказывается, нет: существует теорема Фробениуса, согласно
которой- -при п > 2 это сделать невозможно. Мы не будем
останавливаться на доказательстве этой интересной теоремы *).
*) См., например, А. Г. Курош, Лекции по общей алгебре,
гл. 5, § 8, стр. 277 и далее, «Наука», 1962.
2.82]	§ 2.8. ОБЩЕЕ ПОНЯТИЕ ФУНКЦИИ. ГРАФИК	65
§ 2.8.	Общее понятие функции. График
2.81.	Пусть имеются множество X, состоящее из эле-
ментов х, и множество Y, состоящее из элементов у. Пусть
каким-то способом/каждому элементу х £ X поставлен в соот-
ветствие элемент y£Y; тогда соответствие х—>у (или
у=/(х)) называется функцией с областью определения X
и областью значений Y.
При этом х называется независимым переменным (или
аргументом) функции /(х); у называется зависимым пере-
менным (или значением) функции.
Подчеркнем, что в определении функции нет надобности,
чтобы каждый y£Y был значением f(x) при некотором
х£Х, и не требуется, чтобы разным значениям х соответ-
ствовали разные значения у. (Если оба эти условия выпол-
нены, то мы имеем дело с взаимно однозначным соответст-
вием (2.21), которое есть частный случай функции.) Если
область значений Y функции /(х) есть числовая ось /?,
функция /(х) называется числовой функцией. Если Y есть
векторное пространство /?„ (§ 2.6), функция /(х) называется
векторной функцией.
Если область определения X функции /(х) есть число-
вая ось R, или расширенная числовая ось R (1-91), или
множество Е с R, то / (х) называется функцией веществен-
ного переменного.
Если область определения функции /(х) есть множество
натуральных чисел 1, 2, 3, ..., то функция /(х)—иначе
обозначаемая через /(л) или /„—называется последова-
тельностью точек множества Y. Заметим, что понятие после-
довательности точек множества не сводится к понятию
подмножества (не более чем счетного): в последователь-
ности точки могут повторяться, а в подмножестве—нет.
Так, последовательность Д = a, f% — a, = а, ... (а—фик-
сированный элемент множества У) вовсе не есть то же
самое, что один элемент а; последовательность j\ = a,
fz — bn fs=a> /ъ=а, fa=bs, ... вовсе не есть счетное
подмножество {а, Ьъ b2, bs, ...} множества Y.
2.82.	Введем понятие прямого произведения двух произ-
вольных множеств. Прямым произведением множеств X и Y
мы назовем множество Р(Х, У) всех пар (х, у), где
к
ГЛ. 2. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ

первый элемент взят из множества X, а второй — из множе-
ства Y. Равенство двух пар (х, j) и (х', у') определяется
условиями х' = х, у’=у. Так, вещественная плоскость (/?2)
есть прямое произведение двух вещественных прямых.
Фиксируем в множестве Y элемент _у0 и рассмотрим под-
множество из всех точек (х,у0)£Р(Х, Y). Это подмножество,
очевидно, эквивалентное подмножеству X, называется слоем
в Р(Х, IQ, отвечающим элементу х. Все прямое произведение
Р(Х, У) является объединением различных слоев, эквивалент-
ных множеству X (и друг другу).
2.83.	Если имеется функция y=f(x) с областью опре-
деления X и областью значений Y, мы назовем ее графиком
подмножество прямого произведения Р(Х, У), состоящее из
тех пар (х, j), для которых y=f(x). Это определение
в случае А' = /?1 и Y=R± совпадает с обычным определе-
нием графика вещественной функции числового аргумента.
В практически важных случаях график числовой функции
вещественного переменного представляет собой некоторую
линию на плоскости (х, _у). Если область определения X
функции /(х) есть плоскость х = (х1, х2), а область зна-
чений есть числовая ось, то график есть некоторое мно-
жество в Rs, которое часто можно представить себе в форме
некоторой поверхности. Если область определения X функ-
ции /(х) есть вещественная ось, а область значений Y есть
плоскость j =	j'), то график функции /(х) также есть
множество в Rs; но на этот раз его удобнее представлять
себе как линию (с каждой плоскостью х = const она пересе-
кается лишь в одной точке). Все рассмотренные примеры пред-
ставляют собой важнейшие объекты математического анализа,
и в дальнейшем они будут систематически рассмотрены.
2.84.	Замечание об «однозначных» и «много-
значных» функциях. В силу самого определения 2.81
каждая функция сопоставляет каждому элементу х£Х один
элемент y£Y и в этом смысле «однозначна». Иногда встре-
чается выражение «многозначная функция» в том смысле,
что каждому элементу х£Х поставлен в соответствие не
один элемент множества Y, а несколько элементов. Можно
было бы расширить определение функции в этом направле-
нии; однако это привело бы к затруднениям при определе-
ЗАДАЧИ
67
нии действий с такими «функциями», и мы не будем произво-
дить такое расширение. Но кое-где термин «многозначная
функция» будет удобен. А именно, иногда в единой фор-
муле (например, с целью сокращения записи) объединяют
несколько однозначных функций; такое объединение назы-
вают «многозначной» функцией. Например, «двузначная
функция»
j =	ха (—Is^xs^l)
есть просто объединение двух однозначных функций
=	— х2, у2 = х — (1— х2	(—l^x^l).
ЗАДАЧИ
1.	Доказать, что указанные ниже множества являются счетными:
а) Множество всех интервалов а < х < b с рациональными кон-
цами.
б)	Множество всех коиечно-звенных ломаных на плоскости
с вершинами в рациональных точках.
2.	Доказать, что следующие множества или конечны, или счетны:
а) Множество попарно не пересекающихся интервалов, заданных
на оси.
б)	Множество замкнутых самопересекающихся линий в форме
восьмерки (заданных на плоскости), не имеющих попарно общих
точек.
в)	Множество М вещественных положительных чисел при усло-
вии, что все конечные суммы 2 */> х/ € AI, ограничены фиксиро-
ванным числом А.
Замечание. В. В. Грушнн и В. П. Паламодов доказали
аналогичные утверждения для множества непересекающихся фигур
на плоскости, имеющих тройные точки (как у буквы Т), а также
для множества непересекающихся фигур в пространстве, содержащих
особые точки типа «кнопки» или участки типа «листа Мёбиуса» *).
3.	Разложить множество натуральных чисел 1, 2, ... в счетную
совокупность попарно не пересекающихся счетных множеств.
4.	(Задача-шутка.) I. Как рассказывал математик X, к нему
как-то в гости пришли его друзья братья N. В передней они сняли
шляпы и повесили их на вешалку. Когда они собрались уходить и
стали надевать шляпы, оказалось, к величайшему конфузу хозяина,
что одной шляпы не хватает. В переднюю за это время никто не
заходил.
II.	Когда братья N снова пришли в гости к X (в шляпах), они
опять повесили шляпы на вешалку в передней. Когда они стали,
*) См. Успехи математических наук 17, вып. 3 (105) (1962),
стр. 163—168.
68
ГЛ. 2. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
уходя, надевать шляпы, одна шляпа оказалась лишней. Хозяин и
гости твердо помнили, что до их прихода иа вешалке не было ни
одной шляпы.
III.	В следующий раз гости надели шляпы н ушли, а хозяин,
проводив гостей иа улицу и вернувшись, обнаружил, что шляп на
вешалке оказалось столько же, сколько было до ухода гостей.
IV.	Наконец, в четвертый раз гости пришли без шляп, а уходя,
воспользовались шляпами, оставшимися от прошлого посещения.
Проводив гостей, хозяин опять увидел шляпы на вешалке,— столько
же, сколько было до прихода гостей.
Как объяснить все эти парадоксальные события?
5.	Если к бесконечному множеству А добавить конечное или
счетное множество В, то в сумме получится множество, эквивалент-
ное исходному множеству А.
6.	Доказать, что множество I иррациональных чисел и мно-
жество Т трансцендентных чисел имеют мощность континуума.
7.	Множество всех последовательностей, состоящих из нулей и
единиц, имеет мощность континуума.
8.	Множество всех возрастающих последовательностей . натураль-
ных чисел
(О <)fej < k2 < ... < kn < ...	(1)
имеет мощность континуума.
9.	Множество всех последовательностей натуральных чисел
mlt m2, .... mn, ...	(2)
(не обязательно возрастающих) имеет мощность континуума.
10.	Множество всех последовательностей вещественных чисел
................................... Еп. •••)
имеет мощность континуума.
11.	Множество всех точек «-мерного пространства при любом
л=1, 2, ... имеет мощность континуума.
12.	Множество Е всех функций y=f(x) на отрезке [0, 1] с об-
ластью значений из двух различных точек имеет мощность, не рав-
ную мощности континуума.
13.	Множество всех подмножеств множества А не эквивалентно
самому А.
Историческая справка
Основные идеи теории множеств были сформулированы впервые
в конце XIX века в работах Г. Кантора и с тех пор проникли
в самые разные области математики, в значительной мере завершив
формирование ее языка. См. Ф. Хаусдорф, Теория множеств,
ОНТИ, 1937. На рубеже XIX и XX веков обнаружилось, что тради-
ционная логика в теории множеств приводит к противоречиям. Воз-
никшая драматическая ситуация, поставившая под сомнение все
достижения математики, получила разрешение в создании аксиома-
тических систем теории множеств, где фиксировались не только свой-
историческая СПРАВКА
69
ства объектов, но и допустимые логические средства. См. П. Коэн,
Теория множеств и континуум-гипотеза, «Мир», 1969.
Роль структур в математике подчеркнута Н. Бурбаки в статье
«Архитектура математики» (1948)*). Многотомное сочинение Бур-
баки «Элементы математики» (начало выходить с 1939 г.) посвящено
представлению всей математики как системы структур. Но к на-
стоящему времени (1969) издание еще далеко не закончено; а так
как, по-видимому, математика неисчерпаема, то оно вряд ли когда-
нибудь и будет закончено на сколько-нибудь естественном месте.
 Многомерные координатные пространства были введены Кэли и
Грассманом (1846). Комплексные числа появились значительно раньше,
еще в XVI веке, у итальянских алгебраистов при решении алгебраи-
ческих уравнений; в «Алгебре» Бомбелли (1579) уже описаны пра-
вила действий с выражениями вида a -f- bf/'—i. Поскольку в то вре-
мя комплексным числам не могли приписать никакого реального
смысла, их называли «мнимыми», «абсурдными» и т. д. до тех пор, пока
Гаусс (1797; независимо Бессель 1798, Аргаи 1806) не интерпрети-
ровал их как точки плоскости с соответствующими координатами.
В 1903 г. Фробениус установил несуществование л-мерных прост-
ранств со сложением и умножением, удовлетворяющим всем аксио-
мам 1.21—1.22 при л > 2.
В конце XIX века, с развитием теории множеств, стало ясно,
что и представление комплексного числа a-f-ЬУ —1 в виде фор-
мальной пары (а, Ь) ничем не хуже геометрического представления.
Общее определение функции (2.81) было сформулировано (для
числовых функций) Н. Й. Лобачевским (1834) и Дирихле (1837), а
еще ранее, но в менее определенной форме, Эйлером (1751) и яви-
лось итогом длительной работы математиков XVIII века; это опре-
деление отделило общее понятие функции от (все расширяющегося
с ходом развития математики) понятия аналитического представле-
ния. См. Н. Н. Лузин, Функция (Собрание сочинений, т. 3, изд.
АН СССР, М„ 1959, стр. 319—344).
*) См. Н. Б у р б а к й, Очерки по истории математики, ИЛ, М.«
1963, стр. 245—259.
ГЛАВА 3
МЕТРИЧЕСКИЕ ПРОСТРАНСТВА
Единственное, чего в настоящее время не хватает
теории множеств, чтобы занять должное место в ана-
лизе, это общей концепции предельного перехода
Ж. Адамар (1900)
Метрические пространства представляют собой одну из
важнейших математических структур. В частности, она
лежит в основе общей теории пределов, излагаемой в гл. 4.
§3.1. Определения и примеры
§3.11	. Определение. Произвольное множество А1 не-
которых элементов («точек») х, у, ... называется метриче-
ским пространством, если: имеется правило, которое позво-
ляет для любых двух точек х, у указать число р (х, у)
(«расстояние от х-,,до у»), причем это правило удовлетво-
ряет следующим требованиям (аксиомам):
а.	р (х, у) > 0 при х =^у\ р (х, х) = 0 для любого х.
б.	р(у, х) = р(х, у) для любых х и у (симметрия рас-
стояния).
в.	р(х, г)^р(х, у) + р(у, х) для любых х, у, z («не-
равенство треугольника»).
Неравенство треугольника имеет следующее геометри-
ческое происхождение: в элементарной геометрии сторона
xz треугольника xyz имеет длину, не превосходящую суммы
длин двух других сторон ху и yz.
Правило, которое позволяет по паре точек х, у про-
странства М находить число р (х, у), называют метрикой
пространства М.
Заметим, что любое подмножество М' с М метрического
пространства М само является метрическим пространством
с той метрикой, которая была задана во всем простран-
стве М.
Укажем сразу же некоторые простейшие следствия из
аксиом а—в:
3.12]
§ 3.1. ОПРЕДЕЛЕНИЯ И ПРИМЕРЫ
71
г.	Для любых элементов хъ ..хп метрического про-
странства М имеет место неравенство
р(*1,	*2) + р(х2> *з)+---+р(*п-1» х„)
(обобщение известной теоремы элементарной геометрии:
замыкающая ломаной имеет длину, не большую, чем сумма
длин звеньев ломаной). Для доказательства последовательно
применяется аксиома в-:
Р(*р *«)<Р(-Ч, х2) + р(х2, х„)<
<P(*i, х2) + р(*2, *з) + р(*з> *»)<
<p(Xi, x2)-f-p(x2,	х„).
д.	Для каждых четырех точек х, у, z, v метрического
пространства М имеет место «неравенство четырехугольника»
|р(*, У)~p(z, ®)|<р(х, z) + p(y, v) (1)
Действительно, по г мы имеем
Р^, J)<P(«, z) + p(z, ®) + р(г>, у),
р (z, р (z, х) + р (х, у) + р (у, V),
или
Р (*. у) —Р (Z, т)< р (х, Z)4-р(г», у),
P(z, V) — р(х, у)<р(2, х) + р(Ь ®).
Правые части этих неравенств совпадают по аксиоме б.
Левые части отличаются знаком; отсюда следует (1).
е.	Полагая в неравенстве (1) v=y, получаем
|Р(*. У}~P(z, _у)|<р(х, г)	(2)
(в элементарной геометрии: разность двух сторон треуголь-
ника не больше третьей стороны).
3.12.	а. Множество В в метрическом пространстве М
называется ограниченным, если расстояния от какой-либо
точки а£М до всех точек Ь£В ограничены фиксированной
постоянной. В этом случае ограничены фиксированной
постоянной и расстояния между любой другой фиксирован-
ной точкой с и всеми точками множества В, а также рас-
стояния между любыми двумя точками множества В. Все
это следует из неравенства треугольника
Р(Ь, с)^р(Ь, а)+р(а, с).
72
ГЛ. 3. МЕТРИЧЕСКИЕ ПРОСТРАНСТВА
[ЗЛ2
Величина
diamB = sup р (х, у)
хев, уев
называется диаметром (ограниченного) множества В.
б.	Для M = (вещественная ось) ограниченность мно-
жества В в смысле а равносильна его ограниченности
в обычном смысле (1.66), поскольку в данном случае и
одна и другая означают, что множество В помещается на
некотором (конечном) отрезке.
в.	Множество В в метрическом пространстве Ж назы-
вается неограниченным, если для любого вещественного С
в множестве В существует пара точек х, у с р (х, у) > С.
В этом случае и для любой фиксированной точки a £ М
при любом С можно найти точку х£В, для которой
р (а, х) > С; в противном случае множество В было бы
ограниченным и по доказанному (а) были бы ограничены
расстояния между любой парой его точек.
г.	Определения ограниченного и неограниченного метри-
ческого пространства получаются соответственно из а и в
при В = М.
д.	Совокупность всех точек х метрического простран-
ства М, расстояния до которых от данной точки х0 меньше
заданной величины г > 0, так что
Р (х, х0) < г,
называется шаром (точнее, открытым шаром) радиуса г;
точка х0 есть центр этого шара. Совокупность всех точек х,
удовлетворяющих неравенству
Р(*, xQ)^r,
называется замкнутым шаром радиуса г с центром в х0.
Наконец, точки, находящиеся точно на расстоянии г от точки
х0, так что
р(х, х0) = г,
образуют сферу радиуса г с центром в х0.
е.	Любой шар с центром в точке х0 называется окрест-
ностью этой точки. Точка х0 называется внутренней точкой
множества Е с М, если она входит в Е вместе с некото-
рой своей окрестностью.
3.14]
§3.1. ОПРЕДЕЛЕНИЯ И ПРИМЕРЫ
73
3.13.	Примеры.
а.	Любое множество М на вещественной прямой
является метрическим пространством с расстоянием р (х, _у)=
=| х—у |.
Выполнение условий 3.11 а—в следует из обычных
свойств модуля (1.54 6). Если М—вся прямая, то откры-
тый шар радиуса г с центром в точке х0 есть интервал
|х0—х | < г;
замкнутый шар радиуса г с центром в точке х0 есть отрезок
I*—*o]<G
сфера радиуса г с центром в х0 есть пара точек
х — х0 + г.
б.	Точно так же множество М в плоскости /?2 или
в трехмерном пространстве Rs является метрическим про-
странством, если считать расстоянием между точками (для
определенности —в Я3) x=(gr, g2, g3) и у = (ifc, т]а, т]3)
обычное геометрическое расстояние:
Р (X, у) = V& - П1)а + (£а - Т]а)а + (£3 - V-
Неравенство треугольника (аксиома в) превращается здесь
в обычное геометрическое неравенство: третья сторона
треугольника не больше суммы двух других сторон. Более
общий пример рассматривается в следующем пункте.
3.14.	а. Рассмотрим л-мерное вещественное простран-
ство Rn (2.61). Пусть х и у—два любых вектора из Rn,
x = (h, ..., U. J = nJ- Число
п
(х,	(1)
называется скалярным произведением векторов х и у. Число
1х1 = ’|/Л^^=К(х, х)>0
называется длиной, или нормой, вектора х. Вектор х, для
которого |х|= 1, называется единичным, или нормирован-
ным.. Наличие скалярного произведения, как мы увидим
74
ГЛ. 3. МЕТРИЧЕСКИЕ ПРОСТРАНСТВА
[3.14
далее, позволяет построить в пространстве Rn геометрию
с использованием длин и углов. Пространство Rn со ска-
лярным произведением (1) называют евклидовым, п-мерным
пространством.
Определим расстояние между векторами х — (£ъ ...,£„)
и у= (т]А, ..., т]„) как длину вектора х—у, т. е. по формуле
р(х, j)= + ]/ 2
k=i
(2)
Покажем, что выполнены аксиомы 3.11 а—в. Выполнение
первых двух очевидно; несколько более сложной является
проверка выполнения аксиомы в. Она эквивалентна проверке
неравенства
|х+у|<|х| + |у|.	(3)
Действительно, (3) получается из искомого неравенства
Р (х, у) С Р (х, z) + р {у, z)	(4)
заменой у на —у и г на 0; в свою очередь неравенство (4)
получается из неравенства (3) заменой х на х—z и у на
—y + z.
Чтобы доказать -(3), несколько более подробно рассмот-
рим скалярное произведение (1). Очевидно, оно обладает
следующими свойствами:
1)	(х, у) —(у, х);
2)	(ах, у) = а(х, у) для любого вещественного а и лю-
бых х, у из Rn;
3)	(X -f-y, z) = (х, z) -f- (у, z) для любых х, у, z из Rn;
4)	(х, х)^0 для каждого x£Rn.
Мы докажем неравенство (3), исходя только из свойств
скалярного произведения 1) — 4). Для этого рассмотрим
выражение
<р(X) = (х—Ку, х—Ку) — (х, х) — 2%(х, j) + X2(y, у) =
= Л—2ХВ + СХ2,
где А = (х, х), В — (х, у), С = (у, у). По 4) <р (%)	0 при
всех % £ R. Таким образом, трехчлен <р (%) не может иметь
двух различных вещественных корней, поскольку при нали-
чии таковых он принимал бы значения разных знаков. От-
сюда следует, что величина Ва—ДС=(х, у)а—(х, x)(j,j)
3.14]
§3.1. ОПРЕДЕЛЕНИЯ И ПРИМЕРЫ
75
(находящаяся под радикалом в формуле решения квадрат-
ного уравнения) не может быть положительной. Следова-
тельно,
(х, у)2^(х, х)(у, у) = |Х|2.|у|2)
откуда
|(х, у)К|х|-|у|.	(5)
Это неравенство называется неравенством Коши — Буняков-
ского. Далее,
Iх ОI2 = Iх +Л х+у) = (х, х) + 2(х, _у) + (У, J’X
^|х|2 + 2|х|.|уЦ-|у|2 = (|х| + Ь|)2,
откуда следует (3).
Таким образом, пространство Rn с введенным в нем
расстоянием (1), а также и любое подмножество EczRn с тем
же расстоянием являются метрическими пространствами. Нера-
венство (5) в координатах (х = (|х, . .., £„), у = (т)!, ..., т]„))
принимает 'следующий вид (неравенство Коши):
(6)
Аналогично неравенство (3) в координатах принимает вид
Неравенство 3.11 (2) при у = 0, £ = (&х, ..., £„) принимает
вид	___________
(в)
Все неравенства (6) — (8), справедливые при любых вещест-
венных |х, ..., т)х, ..., т]„, Ci, • L, весьма часто
применяются в анализе в разного рода оценках, даже без
всякой связи с геометрическим источником этих неравенств —
теорией метрических пространств.
Отметим еще полезную цепь неравенств:
шах ||л—т]л1^р(х,^) = 1/ У(^ —T]ft)2<
1<fe<n	Г_ 1
max |£ft—nft|. (9)
1 < k < n
176
ГЛ. 3. МЕТРИЧЕСКИЕ ПРОСТРАНСТВА
[3.14
Для доказательства перейдем от очевидного неравенства
(£л~ Пл)2^^(£л~ Пл)2
к его следствию (1.55 е)
Ил ~ Пл К']/'£ (£л~Пл)2-
Переходя здесь в левой части к максимуму по k, получаем
первое из неравенств (9). С другой стороны, мы имеем
5 (£л—Пл)2 < £ max (£А—т]л)2 = л • max	—Пл)2 =
= n [max|^ —T)J]2,
откуда следует и второе из неравенств (9).
б. Как описать в л-мерном пространстве /?„ ограничен-
ные множества? Если множество Лс/?я ограничено, то
ограничены фиксированной постоянной расстояния всех то-
чек х = (£ь ..., |п) £ А от какой-либо точки пространства
/?„, например от нуля. Иными словами, существует такая
постоянная Ь, что для всех х£А
Ь1 = |/
Но тогда при каждом А=1, 2,
|£лК*П
..., п для х С А также
(Ю)
т. е. каждая из координат точек х £ А ограничена на ве-
щественной оси. Обратно, если множество AczRn таково,
что каждая из координат его точек ограничена на вещест-
венной оси, так что существует постоянная Ь, удовлетво-
ряющая неравенству (10) при всех k=l, ..., ли всех
х £ А, то и
так что множество А ограничено в пространстве /?п. Итак,
множество AcRn ограничено тогда и только тогда, когда
множество значений всех координат точек х£А ограничено
на числовой оси.
3-16)	§ 3.1. ОПРЕДЕЛЕНИЯ И ПРИМЕРЫ	77
3.15. Для метрических пространств как математических
структур можно в соответствии с 2.52 ввести определение
изоморфизма, которое в данном случае называется изомет-
рией. Два метрических пространства называются изометрич-
ными, если между элементами этих пространств можно
установить взаимно однозначное соответствие, сохраняющее
величину расстояния между соответствующими парами эле-
ментов.
Например, два отрезка равной длины на числовой оси
с ее естественной метрикой изометричны, два отрезка раз-
ной длины — не изометричны. Всякая фигура на плоскости
изометрична своему зеркальному отражению относительно
какой-нибудь прямой. Заметим, что в л-мерном пространстве
изометрия, переводящая сумму любых двух векторов х и у
в сумму их образов (линейная изометрия), сохраняет и ска-
лярное произведение, что следует из равенства
x+^) = (x, х) + 2(х, _у) + (У. У)-
Вот два простых примера изометрических отображений
в себя л-мерного евклидова пространства /?„:
а.	Зеркальное отражение относительно плоскости х„ = 0:
каждый вектор х = (£ь ..., £„) переводится в вектор
^' = (11, •••, Ui. -и-
б.	Сдвиг на вектор Р = (Pi, • • •, Рп): каждый вектор
х = (£х, ..., £„) переводится в вектор
* + ₽ = (£i+₽i, .... £П + Р„)-
Заметим, что при р 0 это отображение не является
автоморфизмом пространства Rn (2.67): оно не оставляет
на месте начало координат.
в. Вообще, если существует изометрическое преобразо-
вание л-мерного пространства /?п в себя, при котором мно-
жество Gcz/?„ переходит в множество FczRn, эти множе-
ства Ои F называются геометрически равными, в соответствии
с терминологией элементарной геометрии (хотя и не в со-
ответствии с самим определением равенства, которое
в элементарной геометрии дается только для фигур специ-
ального вида).
3.16. Метризация прямого произведения
метрических пространств. Пусть и ТИ2—два
метрических пространства; индексами 1 и 2 будем снабжать
78	ГЛ. 3. МЕТРИЧЕСКИЕ ПРОСТРАНСТВА	[3.21
соответственно обозначения метрики и точек этих про-
странств. Пусть 7И = 7И1х^/И2 — прямое произведение мно-
жеств и-Д (2.82), т. е. совокупность всех пар х = (хъ х2),
xi €	х2 £ М2. Введем в множестве М метрику по сле-
дующему правилу: если х — (хг, х2), у = (У1, у2), то
Р (х,у) = р [(хх, х2), (у15 у2)] = max {рх (хьyj, р2 (х2, у2)}. (1)
Проверим выполнение аксиом 3.11 а — в. Если х=/=у, то
Х1¥=У1 или х2#=у2, т. е. PxfXb уг) > 0 или р2(х2, у2) > 0;
в обоих случаях в силу определения (1) и р(х, у) > 0.
Если же х=у, то х1=у1, х2=у2, откуда р1(х1, уг) = 0,
р2 (х2, у2) = 0 и, следовательно, р (х, у) = 0. Таким обра-
зом, выполнена аксиома а. Далее, р(у, х) = max {рг (у1; Xj),
Р2(Л- x2)} = max{p1(x1, ух), р2(х2, у2)} = р(х, у), так что
выполнена аксиома б. Наконец, пусть z = (zr, z2); оценим
р(х, z) = max{pj(хь zt), р2(х2, z2)}. Пусть для опреде-
ленности р (х, z) = рх (хХ) гг); тогда мы имеем
р(х,г) = р1(х1, ^XpifXi.yJ + Pifyi, z1)^p(x,y)+p(y,z),
чем доказано выполнение аксиомы в.
Заметим, что метрика (1) на каждом слое (х, z) с фикси-
рованными 6 7Иа (2.82) совпадает с метрикой пространства Mlt
так что каждый слой (х, z) не только эквивалентен, но и
изометричен пространству При этом формула (1)—не
единственный способ введения метрики в прямом произведе-
нии пространств Afj и ЛГ2. Могли бы быть использованы
и другие формулы, например
р (х, у) = Pi (хь ух) + р2 (х2, у2)	(2)
или
р(х, у) = Ур!(хъ У1) + р1(х2, у2).	(3)
Мы предоставляем читателю проверку аксиом метрики
в случаях (2) и (3).
§ 3.2.	Открытые множества
3.21.	Множество U в метрическом пространстве М на-
зывается открытым множеством или областью, если каждая
точка х0 множества U является внутренней точкой этого
множества, т. е. входит в это множество вместе с неко-
3.23]
§ 3.2. ОТКРЫТЫЕ МНОЖЕСТВА
79
торым открытым шаром (радиус которого может зависеть
от точки х0) с центром в точке х0.
Так, открытый шар с центром в точке хх
U= {х: р(х, хх) < г}
есть открытое множество. Действительно, пусть х0 С U,
так что р(х0, хх) = 0 < г. Рассмотрим шар Uo с центром
в точке х0 радиуса г0 < г—0; мы утверждаем, что шар Uo
целиком входит в шар U. В самом деле, для любого х G Uo
по неравенству треугольника
р(х, хг)СР(х, х0) + р(х0, хх) < г0 + 0 <г,
что и требуется.
3.22.	Теорема. Объединение любой совокупности откры-
тых множеств и пересечение любой конечной совокупности
открытых множеств снова являются открытыми множествами.
Доказательство. То, что объединение открытых
множеств является открытым, ясно из самого определения
3.21. Остановимся на вопросе о пересечении конечного чи-
сла открытых множеств. Пусть точка х0 принадлежит
открытым множествам £7Х, U2, ..., Um и входит в первое
из них вместе с шаром радиуса гх (с центром в х0), во
второе — с шаром радиуса г2 и т. д.; тогда шар с центром
в х0 радиуса min(rx, г2, ..., rm) содержится в каждом из
множеств Z7X, U2, ..., Um и, следовательно, содержится и
в их пересечении.
Для бесконечной совокупности открытых множеств при-
веденное рассуждение не пройдет, так как минимум (вернее,
точная нижняя грань) бесконечного множества положитель-
ных чисел может быть равным нулю. И действительно,
пересечение бесконечного числа открытых множеств
Un = (x‘- Р(*> хо)<^-}	(л=1, 2, ...)
содержит только те точки х, для которых р(х, хо) = О,
т. е., согласно аксиоме 3.11 а, только точку х0; это пе-
ресечение не является, вообще говоря, открытым множеством.
3.23.	На оси —оо < х < оо всякий интервал (а, р)
(ограниченный или неограниченный) есть, очевидно, откры-
тое множество. Открытым множеством является также
80	ГЛ. 3. МЕТРИЧЕСКИЕ ПРОСТРАНСТВА	[3.23
конечное или счетное объединение интервалов (av, £v)
(v= 1, 2, ...). Покажем, что каждое открытое множество U
на оси есть конечное или счетное объединение интервалов
без общих точек.
Рассмотрим произвольную точку х € U. Согласно опре-
делению точка х входит в множество U вместе с некото-
рым шаром, т.е. вместе с некоторым интервалом оси, содержа-
щим точку х. Мы построим сейчас наибольший интервал, со-
держащий точку х и содержащийся целиком в множестве U.
Обозначим через 5 множество точек, лежащих правее х
и не принадлежащих U. Если 5 пусто, то вся полупрямая
(х, ос) входит в U. Если множество S’ не пусто, то оно
обладает точной нижней гранью Эта точка £ заведомо
не входит в U, так как у любой точки множества U есть
окрестность, целиком входящая в U и не содержащая тем
самым ни одной точки множества S, а точка как точная
нижняя грань множества S, в любой своей окрестности
содержит точки из S. В частности, Очевидно также,
что весь интервал (х, £) входит в U.
Аналогичное построение произведем слева от точки х;
мы получим там содержащийся в U интервал (т)< х), левый
конец которого не входит в U (или этот интервал есть вся
полупрямая (—оо, х)).
Итак, по заданной точке х £ U мы построили интервал
(т], ^), принадлежащий множеству U и такой, что каждый
его конец, если он не лежит в бесконечности, уже не
входит в множество U. Такого рода интервалы называются
составляющими интервалами открытого множества U.
Если два составляющих интервала (т^, и (г]2, |2)
имеют общую точку х0, то они целиком совпадают; дей-
ствительно, неравенство, например, < |2 невозможно,
так как точка с одной стороны, как внутренняя точка
интервала (х0, £2) должна принадлежать множеству U,
а с другой стороны, как концевая точка интервала (х0, ^х)
она не может входить в U. Поэтому все множество U есть
объединение составляющих интервалов, не имеющих попарно
общих точек. Такое объединение не может быть более чем
счетным, поскольку в каждом из составляющих интервалов
множества U можно выбрать по рациональной точке (/.75),
а множество всех рациональных точек —счетное множество
(2.34). Тем самым наше утверждение полностью доказано.
3.32]
§ 3.3. СХОДЯЩИЕСЯ ПОСЛЕДОВАТЕЛЬНОСТИ
81
§ 3.3.	Сходящиеся последовательности
и гомеоморфизм
3.31.	Сходящиеся последовательности. Рас-
смотрим последовательность {х„} = {х1, ..., хп, ...} то-
чек метрического пространства М. Будем говорить, что
эта последовательность сходится к точке х (ЕМ (и обозна-
чать этот факт символом хп —+ х), если для любого е > О
можно указать такое натуральное N, что при каждом л N
выполняется неравенство
р(х, х„)<б.
Иначе говоря, последовательность хп сходится к х,
если в любой шар с центром в точке х попадают все точ-
ки этой последовательности, начиная с некоторой (и тем
самым вне этого шара остается лишь конечное число ее
точек).
При этом точка х называется пределом последователь-
ности хп, что обозначается символом *)
х — lim х„.
П СО
Символ хп —-» х читается «х„ сходится к х» или, под-
робнее, «при п—+<х> последовательность хп сходится к х
по метрике р». Если для данной последовательности хп не
существует точки х, для которой было бы справедливо
соотношение хп —+ х, последовательность хп называется
расходящейся.
3.32.	Примеры.
а.	Если М есть числовая ось, M=R, с метрикой 3.13 а,
р(х, _у) = |х— _у|,
то определение 3.31 приобретает следующий вид: последо-
вательность вещественных чисел хх, х2, ... сходится к
числу х, если для любого б > 0 можно указать такое N,
что при каждом п^> N выполняется неравенство
Б.
) limes—предел (лат.)
82
ГЛ. 3. МЕТРИЧЕСКИЕ ПРОСТРАНСТВА
(3.32
Так, последовательность точек хп = — (л = 1, 2, ...)
на числовой оси (с ее метрикой 3.13 а) сходится к точке
х = 0: действительно, для заданного е>0 возьмем нату-
ральное ; для каждого nZ^ N имеем 0<хп = —
< е, так что соответствующие точки хп попадают в
шар радиуса е с центром в точке х = 0.
б.	Покажем, что из соотношений x = limxn, у —limyn
П -> сс	П -> сс
в метрическом пространстве М следует соотношение р (х, у) =
— lim р (хп, уп) на числовой оси. (Это свойство называют
СО
иногда «леммой о непрерывности расстояния».)
Для заданного е > 0 найдем номер М так, чтобы при
л > W выполнялись неравенства
Р (х, хп) < у, р (у, у„) < у;
тогда по неравенству четырехугольника 3.11 (1) при этих
же л>Л'
|р(х, у) — р(х„, у„)|<р(х, хп) + р (у, у„) < е,
что и требуется.
в.	Хотя общая теория пределов рассматривается в гл. 4,
нам уже здесь понадобятся некоторые простые свойства
сходящихся числовых последовательностей. Прежде всего
покажем, что для числовых последовательностей хп, уп из
соотношений
х = limхп, у = limy„, х„<у„ (л=1, 2, ...)
следует неравенство
х^у.
Действительно, допустим, что х >у, ипустье = х—у >0.
Найдем такой номер 7V, что при л > 7V выполняются нера-
венства
1х„—х !<-%, |у„— у\<-^-
Тогда
хп>х — У = (у + е)—У >^у„—yj + e—У=у„
в противоречии с предположением, и утверждение доказано.
3.32]
§ 3.3. СХОДЯЩИЕСЯ ПОСЛЕДОВАТЕЛЬНОСТИ
83
г.	Проверим, что для числовых последовательностей хп, уп
из соотношений
х — lim хп, у — limy„
следует, что
x+_y = lim(x„ +_у„).
Найдем для заданного е > 0 номер N так, чтобы при
nZ^N выполнялись неравенства
I*—*п|<у.	Ь|<| •
Тогда при этих же л >АГ выполняется и неравенство
I (х +.У) — (хп +у„) | = | (х—хп) + (у—уп) | <
<|х — х„| + |у— уп\<е,
что и требуется.
д.	Для трех числовых последовательностей х„, уп, zn из
соотношений
x = limx„, _y = lim уп,
П -> со	п -* оо
z = hmzn, xn+yn<zn (л=1,2, ...)
следует неравенство
x+y<z\
этот факт непосредственно вытекает из в и а.
е.	Пусть М есть /я-мерное вещественное пространство
с метрикой 3.14 (2): если x = (gb ... , gj, J = (Пь • • •> ДД
то
Р (X, у) = |/"— Г]*)2.
Утверждается, что сходимость последовательности век-
торов хп = (1п1, .... lnm) к вектору х = (£х, ... , %т) рав-
носильна сходимости m числовых последовательностей
* ^11 • • • > *
(1)
Действительно, пусть выполнены предельные соотноше-
ния (1). Для заданного е > 0 мы можем найти такой номер N,
что при каждом л > М выполняются все неравенства
84
ГЛ. 3. МЕТРИЧЕСКИЕ ПРОСТРАНСТВА
(3.33
так что и
max
k
^>nk —'^k
В
V"m
Для этих же п > М в силу второго из неравенств
3.14 (9) имеем
/ tn	__
Р (х„,_ х)=1/ 5 (lnk —	/т max | lnk — Ъ* | < е,
у	k — 1	k
так что хп —> х по метрике пространства Rm.
Обратно, пусть хп—>х по метрике пространства Rm.
Для заданного е > 0 найдем такой номер N, что при каж-
дом tt> N выполняется неравенство
/ т
р(хп,х)=1/ S(U—U2<e-
f k — 1
Но тогда в силу первого из неравенств 3.14 (9)
max | lnh—lk | < р (х„, х) < е,
k
так что каждая последовательность £nfc сходится к числу
(k = 1, ... , т), что и требовалось.
3.33 а. Проверим, что если последовательность хп схо-
дится, то только к одному единственному элементу простран-
ства М. Пусть хп—> х и вместе с тем хп—»-у. Тогда для
заданного е >0 мы найдем номер N, начиная с которого
выполняются оба неравенства
Р (х, хп) < е,
Р (Л хп)<е,
откуда по неравенству треугольника
Р (х, у)< р (х, х„) + Р (хп, у) < 2е.
Так как е>0 произвольно мало, то по 1.57 р (х, у) = 0,
откуда в силу аксиомы 3.116 х—у, что и требуется.
б. Покажем, что если последовательность х1( х2, ...
сходится, то она ограничена в пространстве М; иначе гово-
ря, числа р (хп, Ь), где Ь — какой-нибудь элемент простран-
ства М, образуют на числовой оси ограниченное множество
(ср. 3.12 а).
3.34)
§ 3.3. СХОДЯЩИЕСЯ ПОСЛЕДОВАТЕЛЬНОСТИ
85
Действительно, пусть p = limjcn; найдем для какого-ни-
П -> оо
будь е > 0, например для е = 1, такое число N, что при
n^>N выполняется неравенство р (хп, р)<е=1. Пусть,
далее, Z) = max {р (хг, р), .... p(x^, р)}. Тогда при лю-
бом п— 1, 2, ... мы имеем р (х„, тах{1, £)}, что и до-
казывает ограниченность последовательности х1г х2,   
3.34.	Гомеоморфизм метрических прост-
ранств. Во многих вопросах анализа играет роль не явное
выражение метрики пространства, а только то, какие после-
довательности точек при данной метрике являются сходя-
щимися и какие—расходящимися. В связи с этим введем
следующее определение:
а.	Два метрических пространства М' и М" называются
гомеоморфными, если между их точками можно так устано-
вить взаимно однозначное соответствие, что из сходимости
Хп —> х’ в М' следует сходимость соответствующих точек
х'п —>• х" в М" и, обратно, из сходимости х'п —> х" в М"
следует сходимость соответствующих точек х^ —► х' в М.'.
Указанное взаимно однозначное соответствие называется
гомеоморфизмом.
б.	Следующая теорема дает критерий того, что неко-
торое взаимно однозначное соответствие между точками
метрических пространств является гомеоморфизмом.
Теорема. Пусть ~ есть взаимно однозначное отображе-
ние метрического пространства М' с метрикой р' (х', у') на
метрическое пространство М" с метрикой р"(х", у"). Отобра-
жение ~ тогда и только тогда есть гомеоморфизм, когда
для любого х' £М' и любого е' > 0 существует такое > О,
что отображение ~ переводит шар {у" £ М":р" (х”, у") < е"}
в шар {у' £М':р' (х', у’) < е'}, и, наоборот, для любого
г" > 0 существует такое е' > 0, что отображение ~ пере-
водит шар {j'	:р' (х', у’) < ев шар
{у"еМ":р"(х", у") < е"}.
Доказательство. Пусть отображение ~ есть гомео-
морфизм, так что для любой последовательности Хп—+х'
мы имеем х'п —* х" и обратно. Фиксируем точку х' € М'
и число е' > 0. Если не существует числа ё", о котором
говорится в формулировке теоремы, то для любого л= 1,2, ...
шар {у" €7И":р" (х",у")< 1/л} при отображении ~ переходит в
86
ГЛ. 3. МЕТРИЧЕСКИЕ ПРОСТРАНСТВА
[3.34
множество, имеющее точки вне шара {у' £ М’ :р' (х', у') < е'}.
В частности, для любого л=1, 2, ... мы можем указать
точку у'п £ М", для которой р" (х", Уп) < -i-, р' (х', Уп)
Таким образом, у'п-~^х", но у'п не сходится к х', что про-
тиворечит предположению о гомеоморфности отображения
Следовательно, по данному е' > 0 можно найти е", о
котором говорится в формулировке, если отображение ~
есть гомеоморфизм. Меняя местами в этом „ рассуждении
М' и М', по данному е" > 0 мы сможем найти требуемое е'.
Обратно, пусть для любого х' £ М' и любого' е' > О
можно найти нужное е". Покажем, что из х" х" сле-
дует х'п-+ х'. Возьмем произвольно е' >0, найдем соответ-
ствующее е" и затем номер 7V такой, что при n"^N выпол-
няется неравенство р" (х", х") < е". Применяя отображение ~
и пользуясь предположением, получаем р' (х'п, х') < е'. Таким
образом, х'п -* х'. Проводя то же рассуждение от М" к М',
получим, что из х'п-^х' следует х^-*х". Теорема доказана.
в.	Можно устанавливать различные метрики на одном и том
же множестве Е, превращая его тем самым в различные
метрические пространства. Будем называть две метрики р' (х, у)
и р" (х, у) на одном и том же множестве Е гомеоморфными,
если тождественное отображение х~х является гомеомор-
физмом получающихся метрических пространств М' и М".
г.	Применяя для ситуации, описанной в в, критерий б,
получаем следующую теорему:
Теорема. Две метрики р' и р", заданные на одном и
том же множестве Е, гомеоморфны тогда и только тогда,
когда для любого х£Е и любого е' > 0 существует такое е!‘,
что шар {у: р" (х, у) < е"} содержится в шаре {у: р' (х, у) < е,’},
и наоборот, для любого е," > 0 существует такое е', что шар
{у:р'(х, у) < е'} содержится в шаре {у:р"(х, у) < e'J.
д.	В качестве примера рассмотрим три метрики на пря-
мом произведении М метрических пространств Мг и М2 (3.16):
ра}(х, t/) = max {Pifxj, уг), р2(х2, у2)};
р{2Цх, У)=р1(х1,	+	У2)>
р(3> (х, у) = Vpl (хг, уг) 4- р| (х2, у2).
Все они гомеоморфны на М. Это вытекает из справедли-
вости неравенств
шах {а, Ь} [Лг2 + & a -f- b 2 max {a, b) (1)
3.35)	§ 3.3. СХОДЯЩИЕСЯ ПОСЛЕДОВАТЕЛЬНОСТИ	87
для любых неотрицательных чисел а и Ь. Более подробно:
пусть, например,	тогда
max {a, b} = b = У Ь2 У а2 + b2 а2 + 2аЬ + Ь2 =
= а-|-6^26 = 2тах {а, Ь},
откуда и вытекает (1).
3.35.	Мы введем, далее, метрику на расширенной число-
вой оси R (1.91), гомеоморфную на множестве — оо <х <оо
обычной метрике 3.13а. Для этого вначале рассмотрим одну
специальную функцию.
а.	Рассмотрим функцию переменного х,— оо < х < оо:
/(х)=тги-	(1)
Дополним ее определение условиями
/( —оо)=—1, /( + оо)=+1,
так что функция f(x) определена на расширенной вещест-
венной оси R. График функции/(х) представлен на рис. 3.1.
В б, в и г мы выведем некоторые нужные нам неравенства,
связанные с этой функцией.
б.	Очевидно, что f(x) > 0 при х > 0 и f(x) < 0 при х<0,
а /(0) = 0. Далее, при любом конечном х мы имеем
f( — х)= — f(x) и
I ftд-и_ I*!__ < .М+.1. = 1	(2)
I/WI —1_|_|Х|	1 + |х|	W
в.	Покажем, что для любых х и у из R
l/w-	х-у|.	(3)
При х > О, у О мы имеем
I/(х) —f (у) I = |	~~Т+у |= (1 +х) (1 +у) ।х ~У I-
88	ГЛ. 3. МЕТРИЧЕСКИЕ ПРОСТРАНСТВА	[3-35
При х^О, у О таким же образом
№)- /Ы1=|т^— г=?Н (Г=даЬ)^к- у\-
При х^О, t/^О мы имеем
!/(*)-/(</) 1^ I/O) |+/(<0=
= .	[ х [ + у = —x-j-y=lx — yl;
1 + | х [ 1 1+у	1 1 1 а	। » I
наконец, при х!>0, у^ХО по предыдущему
I/(х)— f(y) |= I/O»)— f (х) | < 1.У—х |= | х—у |,
что и требуется.
г.	Пусть для некоторых хиуи0<6<1 мы имеем
|/(х)|<1—6, |/(у) |< 1-6.
Тогда
к—у| ^-^-1/(•*)—/(У) I-	(4)
Для доказательства сначала разрешим (1) относительно х.
При х > О, когда | х | = х, мы имеем
при х^О, когда |х|=—х, мы имеем
Таким образом, при х 0, у О
I — I 0х)	| —
—|_£W~Afo) I—+J_ \f zx)_/ (v) I
Если x^O, y^O, to —x^O, —y^ 0 и по преды-
дущему
k— y|=l— y—(—*)K^I/(— y)— f(—x) 1 =
=-^|/k)-/(y)|-
3.35]	§ 3.3. СХОДЯЩИЕСЯ ПОСЛЕДОВАТЕЛЬНОСТИ	89
Если х^О, у^О, то
|Х у|_|х|+>(-пта- + -т--ж^
с-i-ll/wi +ГСм)1 =
если х^О, у^О, то по предыдущему
I х— у | = ]у—х | <	1/(у) —/(х) [ =	|/(х) —/(у) |,
что и требуется.
д.	Теперь рассмотрим на расширенной числовой оси R
(1.91) следующую числовую функцию г(х, у) от пары точек
х, у:
г(х, у) = |/(х) — /(у)|.	(5)
Здесь /(х)—функция, введенная в а.
Теорема. Функция г(х, у) (5) есть метрика на R; на
множестве R конечных точек — оо < х < оо она гомеоморфна
обычной метрике
Р(Х, У) = |х—у|.	(6)
Геометрический смысл метрики г(х, у) легко усмотреть
из,рис. 3.1. Именно, в качестве нового расстояния г(х, у)
между точками х и у горизонтальной оси принята длина
соответствующего отрезка вертикальной оси [/(х), /(у)].
Доказательство теоремы. Проверим выполнение
аксиом 3.11 а — в. Выполнение аксиомы б (аксиомы симмет-
рии) следует непосредственно из определения (5). Выполне-
ние аксиомы а (г(х, у) равно 0 при х=у и положительно
при х#=у) следует также из определения и из неравен-
ства (3). Выполнение аксиомы в (аксиомы треугольника) сле-
дует из неравенства
Г (x,z) = \f(x)— /(z)|<|/(x) — /(у)| + |/(у)— /(г)| =
= r(x, y)+r(y, Z).
Проверим, что на множестве R конечных точек метрики
г (х, у) и р(х, у) гомеоморфны.
Пусть хп х по метрике (6). Для заданного е > 0 най-
дем такой номер N, что при п выполняется неравенство
90
ГЛ. 3. МЕТРИЧЕСКИЕ ПРОСТРАНСТВА
[3.35
|х„—х|<е. Тогда по неравенству (3) для тех же n~^N
Г (х„, X) = | / (х„) — f (X) | < | хп — X | < Е,
так что хп -> х и по метрике (5).
Пусть теперь хп -* х по метрике (5). Мы имеем |/(х) | < 1;
положим |/(х)|=1—26, 0<6<-^-. Для заданного е>0
найдем номер N так, чтобы иметь при n~^N
r(xn, x) = \f(xn)— /(х)| < min (е, 6)-62.
Тогда при этих же n~^N
|/(*„) IС |/(*) | + min (е, 6) 62 С |/(х) 14-6=1—6,
и так как также |/(х)|=1—26<1—6, можно применить
неравенство (4):
Р(*„> лг)=|х„—х|^-^-|/(х„)—/(x)|^min(E, 6)^е.
Следовательно, х„ -> х и по метрике (6). Теорема доказана.
е.	Что представляет собой в метрическом пространст-
ве R с метрикой (5) шар радиуса с > 0 с центром в точке оо?
По определению это есть совокупность тех х € R, для ко-
торых выполнено неравенство
(7)
Ограничимся наиболее важным случаем, когда с мало, с^1.
Тогда, поскольку для х < 0 значения /(х) отрицательны и
/(оо)—/(х) > 1, неравенству (7) могут удовлетворять лишь
значения х 0. Неравенство (7) теперь принимает вид
1 х _____ 1	,,
1-|-х 14-*^С’
или, что то же,
Итак, искомый шар {х:г(х, оо)с) есть промежуток
—— l^x^oo. Аналогично шар радиуса с^1 с центром
в точке —оо есть промежуток —оо^х^--------~+1-
3.41)	§ 3.4. ПРЕДЕЛЬНЫЕ точки	91
В частности, последовательность точек 1, 2, 3, ... в про-
странстве /? попадает, начиная с некоторого номера, в любой
шар с центром в точке оо, так что в пространстве /? мы
имеем
lim л = оо;
п-*оо
в то же время указанная последовательность в пространстве
R, очевидно, никакого предела не имеет.
ж. Следует отметить, что пространство R с метрикой
(5) изометрично отрезку [-1, 1] с его обычной метрикой.
Соответствие R ~ [—1,1 ] осуществляется по правилу
оно по нашему построению взаимно однозначно, и расстояние
между точками х, y£R по метрике (5) равно обычно-
му расстоянию между соответствующими точками f(x)
и Ду)-
Отбрасывая здесь крайние точки (—оо и оо простран-
ства R и —1, 4-1 отрезка [—1, 1]), получаем изометрич-
ность вещественной оси R с метрикой (5) и интервала
(—1, 1) с его обычной метрикой. Используя д, получаем,
что метрическое пространство R с его обычной метрикой
гомеоморфно интервалу (—1, 1), — факт, который, впрочем,
легко проверить и непосредственно.
§ 3.4.	Предельные точки
3.41.	Пусть снова {х„} есть последовательность точек
метрического пространства М. Будем говорить, что точка
у£М есть предельная точка последовательности {х„}, если
для любого е > 0 и любого натурального N можно найти
такой номер n~^N, для которого
р(_У, хп)<е.
Иначе говоря, точка у является предельной точкой по-
следовательности хп, если в любой шар с центром в у
попадают точки последовательности с произвольно большими
номерами, хотя, быть может, и не все точки с номерами
как у сходящейся последовательности. Сходящаяся
последовательность хп—» х имеет, очевидно, точку х своей
предельной точкой, а других предельных точек уже не имеет
92
ГЛ. 3. МЕТРИЧЕСКИЕ ПРОСТРАНСТВА
[3.42
(доказательство аналогично приведенному в 3.33 а). Несхо-
дящаяся последовательность может не иметь предельных
точек, а может их иметь в любом количестве. Так, после-
довательность точек х„ = (—на числовой оси
(с ее обычной метрикой) имеет две предельные точки —1
и 4- 1 (и не сходится ни к одной из них); последователь-
ность хп = л(-1)” имеет одну предельную точку у = 0, но не
сходится к ней; а если записать в единую последователь-
ность все рациональные точки оси (2.34), то любая точка
оси будет предельной для этой последовательности.
3.42.	При наличии у последовательности х1г ..., хп, ...
предельной точки у из последовательности хп всегда можно
выбрать подпоследовательность, сходящуюся к у. Именно,
если у есть предельная точка последовательности хп, то для
каждого т в последовательности хп существует точка
хъп(пт >яи-1)> для которой р (у, хПт) <	\ подпоследова-
тельность, составленная из точек хп„ хПг, ..., очевидно,
сходится к точке у. Обратно, если у некоторой последова-
тельностих„имеетсяподпоследовательность	2,..,),
сходящаяся к какой-до точке у £ 7И, то эта точка у, оче-
видно, есть предельная точка для всей последовательности хп.
Таким образом, мы получаем второе определение предельной
точки: точка у есть предельная точка последовательности хп,
если у последовательности хп имеется подпоследователь-
ность, сходящаяся к точке у.
3.43.	Второе из приведенных определений предельной
точки опирается только на понятие сходящейся последова-
тельности. Так как гомеоморфизм метрического простран-
ства М в метрическое пространство М' сохраняет сходя-
щиеся последовательности, мы приходим к выводу: если
точка у£М является предельной для последовательности
хп£М, а пространство М' гомеоморфно пространству М, то
точка у'£М', соответствующая точке у при рассматри-
ваемом гомеоморфизме, является предельной для последова-
тельности соответствующих точек х'п£М'.
В частности, если на одном и том же множестве М
введены две различные, но гомеоморфные метрики р и р'
3.44]
§ 3.4 ПРЕДЕЛЬНЫЕ ТОЧКИ
93
и точка у£М является предельной точкой последователь-
ности хп по метрике р, то она является предельной точ-
кой последовательности хп и по метрике р'.
3.44.	а. Пусть А есть подмножество метрического про-
странства М. Будем говорить, что точка у £М есть пре-
дельная точка подмножества А, если в любой окрестности
Vr(y) = {х-.р(х, у) < г} точки у можно указать точку х£А,
отличную от самой точки у.
Приведенное определение предельной точки подмножества
по форме несколько отличается от определения предельной
точки последовательности; это объясняется тем, что по-
следовательность точек множества есть иное понятие, чем
подмножество, поскольку в последовательности точки могут
повторяться, а в подмножестве—иет (ср. 2.81). Так, точки
О и 1 являются предельными точками последовательности
О, 1,0, 1, ..., но не являются предельными точками мно-
жества из двух точек 0 и 1.
Однако выводы 3.42 и 3.43, относившиеся к предельным
точкам последовательностей, справедливы и для предельных
точек подмножеств. Если у есть предельная точка множе-
ства АсМ, то из множества А можно выбрать последова-
тельность различных точек, сходящуюся к у (тем же приемом,
что и в 3.42); и обратно, если из множества А можно
выбрать последовательность различных точек, сходящуюся
к некоторой точке у £ М, то эта точка у является предель-
ной для множества А. Отсюда следует сохранение предель-
ных точек множества А при гомеоморфизме метрического
пространства М (в силу 3.43).
б.	Пример. Пусть множество А на вещественной оси
ограничено сверху (снизу), и пусть ^ = зирЛ (г] = inf У1) не
входит в множество А; покажем, что £ (г]) есть предельная
точка для множества А.
Проведем доказательство для точки £ = sup.4. В силу
самого определения точной верхней грани для любого п =
= 1, 2, ... существует точка хп£А такая, что £—<
Поскольку, по условию мы имеем хп^^.
Число £, таким образом, оказывается предельной точкой
множества А, что и требовалось.
94
ГЛ. 3. МЕТРИЧЕСКИЕ ПРОСТРАНСТВА
[3.45
3.45.	Желательно иметь общие предложения, позволяющие
судить о существовании предельных точек у достаточно
широкого класса множеств или последовательностей. Полез-
ным предложением такого рода является следующая теорема:
Теорема («принцип Больцано—Вейерштрасса»), Каж-
дое бесконечное множество точек на отрезке [g, b]czR имеет
хотя бы одну предельную точку.
Доказательство. Если на некотором отрезке [с, d]
имеется бесконечное множество Е, то хотя бы на одной из
с, —I и —, al отрезка [с, d] имеется
бесконечное подмножество множества Е. Пользуясь этим
очевидным соображением, мы, отправляясь от отрезка
[а, й] = Дг с заданным на нем бесконечным множеством то-
чек А, построим последовательность вложенных отрезков
Д1оД2о ..., где каждый последующий составляет половину
предыдущего и несет на себе бесконечное подмножество
множества А. По принципу Кантора 7.87 у этих отрезков
имеется общая точка х0; покажем, что она является пре-
дельной для множества А. Возьмем любой интервал V с
центром в точке х0, скажем, длины 6 > 0. Пусть п таково,
*	6
что длина отрезка Д„ меньше -%', включая в себя точку х0,
он целиком содержится в интервале V. Вместе с отрезком Д„
в интервал V попадает бесконечное число точек множества А;
следовательно, х0 есть предельная точка множества А, что
и требовалось.
3.46.	Аналогичное предложение справедливо для после-
довательностей:
Теорема (принцип Больцано—Вейерштрасса для после-
довательностей). Каждая последовательность точек на от-
резке [с, Ь\ имеет хотя бы одну предельную точку.
Доказательство повторяет приведенное в 3.45 с учетом
того факта, что в последовательности точки могут повто-
ряться.
3.47.	На всей вещественной оси R имеются бесконечные
множества без предельных точек (например, 1, 2, 3, ...).
Но на расширенной вещественной оси R, метризованной по
правилу 3.35 д, снова каждое бесконечное множество обла-
3.51]
§ 3.5. ЗАМКНУТЫЕ МНОЖЕСТВА
95
дает предельной точкой; это следует из того, что R изо-
метрично отрезку [-1. 1] с его обычной метрикой (3.35 ж),
а свойство точки быть предельной сохраняется при изоме-
трическом отображении (и даже при гомеоморфизме, как мы
видели в 3.43).
3.48.	Следующее утверждение дает достаточное условие
отсутствия предельных точек:
Последовательность хг, х2, . .., у которой все расстояния
р (хт, хп) ограничены снизу положительной постоянной С,
так что р (хт, хп) С, не имеет ни одной предельной точки.
Действительно, пусть у есть предельная точка последо-
вательности хп; в этой последовательности заведомо имеются
С	С
такие точки хт и хп, т^=п, что р (у, хт) <	, р (у, хп) < у ,
а тогда
Р (*и. *п) < Р (хт, У) + Р (Л х„) < С
в противоречии с предположением.
§ 3.5.	Замкнутые множества
3.51.	Определение. Множество ПсМ называется
замкнутым, если оно содержит все свои предельные точки.
Примеры, а. Отрезок	замкнут на вещест-
венной прямой, а полуинтервал а х < b не замкнут, так
как его предельная точка b не принадлежит ему.
б.	В любом метрическом пространстве шар
U = {х:р(х, х0)^г}
есть замкнутое множество (поэтому он и называется замкну-
тым шаром).
Действительно, возьмем любую точку хг, не принадле-
жащую шару U, так что р (х0, хх) = гх > г. Мы утверждаем,
1 ,
что в шаре с центром в точке х. и радиусом -к-(г,—г) нет
точек шара U: если бы такая точка нашлась, то, обозна-
чив ее через z, мы имели бы
р (х0,	Р (х0, г) + р (хг, г)С^ + 4 (Г1—И = i (ri + r) < г!
96
ГЛ. 3. МЕТРИЧЕСКИЕ ПРОСТРАНСТВА
[3,52
в противоречии с равенством р (х0, хх) = гг. Поэтому точка
ие может быть предельной точкой для множества U.
3.52.	Замкнутые множества в метрическом пространстве
М тесно связаны с открытыми множествами этого простран-
ства. Именно, имеет место следующая теорема:
Теорема. Множество U, дополнительное в метрическом
пространстве М к замкнутому множеству F, всегда открыто.
Множество F, дополнительное к открытому множеству U,
всегда замкнуто.
Доказательство. Пусть F—замкнутое множество
и U—его дополнение; покажем, что U открыто. Рассмотрим
произвольную точку х0 £ U; мы должны показать, что имеет-
ся шар, определяемый неравенством вида
Р (х, х0) < г,
целиком входящий в множество U.
Допуская противное, мы должны предположить, что в
любом шаре с центром в точке х0 имеются точки множе-
ства F. Но тогда, согласно второму определению предель-
ной точки, точка х0 является предельной для множества F.
Так как F замкнуто, то мы должны были бы иметь x0£F,
что противоречит предположению x0£U. Итак, U открыто.
Переходим ко второй половине теоремы. Пусть множество U
открыто и F—его дополнение; покажем, что F замкнуто.
Любая точка х0, принадлежащая U, входит в U вместе с
некоторым шаром и поэтому не может быть предельной
точкой множества F. Таким образом, предельные точки
множества F могут быть только в самом F, и следовательно,
F замкнуто. Теорема доказана.
3.53.	а. Вспоминая 3.23, мы получаем общее описание
всех замкнутых множеств на прямой —оо < х < оо: каждое
замкнутое множество на прямой получается удалением ко-
нечной или счетной совокупности интервалов без общих точек.
Выбрасываемые интервалы, которые служат составляющими
интервалами дополнительного открытого множества, назы-
ваются смежными интервалами данного замкнутого множества.
б. Ограниченное сверху (снизу) замкнутое множество А
всегда содержит свою верхнюю (нижнюю) точную границу:
в предположении противного эта точная граница была бы
3.61J	§ 3.6. ВСЮДУ ПЛОТНЫЕ МНОЖЕСТВА И ЗАМЫКАНИЯ
97
предельной точкой для А (3.446) и множество оказалось бы
незамкнутым.
3.54.	Используя известные нам свойства открытых мно-
жеств в метрическом пространстве (3.22) и указанную только
что связь между открытыми и замкнутыми множествами, мы
можем утверждать, что объединение конечного числа замк-
нутых множеств и пересечение любой совокупности замкну-
тых множеств суть снова замкнутые множества.
Действительно, пусть даны замкнутые множества Fy
(v пробегает некоторую совокупность индексов) и пусть
Uy—дополнительные открытые множества. По формуле 2.22(1)
мы имеем
сП^=2 CFy=^uy.
V	V	V
Множество открыто, поэтому дополнительное к нему
V
множество П Л замкнуто.
v
Если v пробегает конечную совокупность индексов, то
П Ц>, согласно 3.22, есть открытое множество; по фор-
муле 2.12 (2)
с!Х=Псе;=Пс;;
V	V	V
поэтому 2г, замкнуто, что и требовалось.
§ 3.6.	Всюду плотные множества и замыкания
3.61.	Всюду плотные множества. Множество А
в метрическом пространстве М, по определению, распола-
гается всюду плотно по отношению к множеству ВсМ,
если всякая точка х£В или сама входит в А, или является
предельной точкой для А. Иными словами, А располагается
всюду плотно относительно В, если в любом шаре с цент-
ром в точке х В имеется точка у £ А.
Если при этом АсВ, то говорят, что А всюду плотно
в В. Так, множество рациональных точек всюду плотно на
числовой оси —оо < х < оо, множество точек (тг, ..., гп)
с рациональными координатами всюду плотно в «-мерном
евклидовом пространстве.
98
ГЛ. 3. МЕТРИЧЕСКИЕ ПРОСТРАНСТВА
[3.62
3.62.	Свойство «всюду плотности» обладает транзитив-
ностью в следующем смысле: если множество А расположено
всюду плотно относительно множества В, а множество В,
в свою очередь, расположено всюду плотно относительно
множества С, то А расположено всюду плотно и относи-
тельно С. Действительно, для заданного е > 0 и заданной
точки z£C мы можем найти точку у£В такую, что
р(_у, ^)< у; затем мы можем найти точку х£А такую, что
р (х, .у) <	; в итоге при любом е > 0 мы можем найти по
заданной точке г £ С такую точку х £ А, что р (х, г)
р (х, .у) + р(.у, г) < е. Это и означает, что А всюду плотно
относительно В.
3.63.	Замыкания. Пусть А — множество в метриче-
ском пространстве М; обозначим через А множество, состоя-
щее из всех точек множества А и всех предельных точек
множества А. Множество А называется замыканием множе-
ства А. Если А — замкнутое множество, т. е. А содержит
все свои предельные точки, то А = А. В общем случае Az>A.
Если А —А, то это означает, что все предельные точки
множества А вхоДят в Л и, следовательно, А замкнуто.
Таким образом, высказывания «А замкнуто» и «А = А» рав-
носильны. Если известно, что АсА, то, учитывая, что всегда
ДзэД, мы имеем Д = Д, так что А замкнуто.
3.64.	Покажем, что замыкание любого множества А всегда
есть замкнутое множество. Заметим вначале, что в силу
самих определений всякое множество всюду плотно в своем
замыкании. В частности, А всюду плотно в Д, Д всюду
плотно в своем замыкании Д. Но тогда, в силу транзитив-
ности свойства всюду плотности, А всюду плотно в Д, т. е.
каждая точка множества А есть или точка множества Д,
или предельная точка множества Д. Отсюда АсА, и, сле-
довательно, А замкнуто.
Так, замыкание множества рациональных точек на оси
— оо < х < оо совпадает со всей осью.
3.66J	§ 3.6. ВСЮДУ ПЛОТНЫЕ МНОЖЕСТВА И ЗАМЫКАНИЯ 99
3.65.	Покажем, что замыкание А ограниченного множе-
ства А есть ограниченное множество и diam Л = diam/1.
Так как Ас А, то diam Л diam Л. Далее возьмем в мно-
жестве А произвольно точки х и у и для заданного е > О
найдем такие точки х£А, у^А, что р(х, х)<-|-)
Р О', < у - Тогда
Р {х, У)^Р (*> *) + Р (*. У) + Р (У, >) < у + diam А +	,
откуда
diam А = sup р (х, у) е + diam А,
и, поскольку в > 0 произвольно,
diam А diam А.
В соединении со сказанным выше получаем, diam А = diam А,
что и утверждалось.
3.66.	Пусть F—замкнутое множество и GcF—область
в метрическом пространстве М. Покажем, что существует
такая область Н с F, содержащаяся в области G вместе со
своим замыканием, что
FcHcHcG.
Для доказательства обозначим через d (х) расстояние от
точки х £ G до внешности области О, т. е. величину
d (х) = inf р (х, у).
у g М - О
Для каждого x£G величина d (х) положительна, поскольку
точка х входит в область G вместе со своей окрестностью.
Положим множество И равным объединению всех открытых
шаров с центрами в точках х £ F и радиусами, равными
-g-d(x). Очевидно, что FcH\ по 3.22Н—область. Покажем,
что замыкание Н множества Н содержится в области G.
Предположим противное: существует точка у £ НП (М—О),
100
ГЛ. 3. МЕТРИЧЕСКИЕ ПРОСТРАНСТВА
(3.67
Найдем последовательность zn£H, zn-^>-y и последователь-
ность	р(хп, z„)^yd(x„). Мы имеем
d(xn)^p(x„, у)^р(х„, zn) + p(zn, y)^±-d(xn)+p(zn,y).
Отсюда
d (х„) < 2р (z„, у), р (х„, у) < 2р (z„, у),
так что у — lim хп £ Fc G. Мы получаем противоречие с пред-
положением у £ М— G. Итак, Нс G, что и требовалось.
3.67.	В частности, если F ограничено (3.12а), то функ-
ция d(x) допускает оценку (х0—фиксированная точка F)
d(x) = inf р(х, у)^
у€ М — G
< inf [р(х, х0) + р(х0, y)]^diamF+d(x0). (1)
M-G
Поэтому множество Н, построенное в 3.66, ограничено вместе
с множеством F, так как из определения Н и из (1) сле-
дует, что
diam diam Z7-! - 2 sup d (х)	3 diam F+ 2d (х0).
xeF
§ 3.7.	Полные пространства
3.71.	а. Последовательность точек хь х2, ... метриче-
ского пространства М называется фундаментальной, если
для любого е существует номер N такой, что для v~^N и.
p^N выполняется неравенство р (х„, хи)^е.
б.	Любая сходящаяся последовательность xlt х2, х
является фундаментальной: действительно, по неравенству
треугольника
P(*v,	(х„ Х) + р(х, хД
н если х„ —> х, то правая часть для достаточно больших
v и р становится меньше любого заданного е > 0.
в.	Любая фундаментальная последовательность xlt х2, ...
ограничена. Для доказательства найдем номер N так, что
при	p^N выполняется неравенство р (х„, хр)^ 1.
Тогда для любого v=l, 2, ... мы имеем
р(х„, х^С
тах{р(хх, xN),
1
. .. , pfXjy.x, Хд,)} (vCM,

3.72]
§ 3.7. ПОЛНЫЕ ПРОСТРАНСТВА
101
так что расстояния от точек xlt х2, ... до точки xN ограни-
чены фиксированной постоянной.
г.	Определение. Метрическое пространство М назы-
вается полным, если в нем всякая фундаментальная после-
довательность сходится к некоторому элементу этого
пространства.
3.72.	Примеры.
а.	Покажем, что вещественная числовая ось R с метрикой
Р(х, у) = |х—у|
является полным метрическим пространством.
Иначе говоря, числовая последовательность хг, х2, ...
является сходящейся тогда и только тогда, когда для любого
е > 0 существует такой номер N, что при любых п> N,
m>N выполняется неравенство | хп— хт | < е.
В этой форме теорема а имеет название «критерий
Коши». Для доказательства будем рассуждать так:
Пусть хъ х2, ... —фундаментальная последовательность
вещественных чисел. В силу 3.71b она ограничена; для каж-
дого т=\, 2, ... положим
««= inf хп, bm = sup хп.
п^т	п^т
Очевидно, что при любом т выполняются неравенства
Ьт^-Ьт+Ъ откуда [ат, Ьт]=>[ат+1, Ьт+1].
По принципу Кантора 1.81 имеется точка p£R, принад-
лежащая всем отрезкам [ат, Ьт], т—1, 2, ... Покажем,
что р = iim х„. Для заданного е>0 найдем номер N так,
П-*- 00
чтобы при n^N, m^N иметь
рК> =
Фиксируем здесь m — N и будем полагать л = ДГ4-1,
N + 2, ... Поскольку все значения хп при n>N отстоят
от xN не далее чем на е, то и числа aN и bN отстоят от
xN не далее чем на в. Число р лежит на отрезке [ад, bN],
поэтому для всех п > N мы имеем
IР—х„ | С bN—aN = (bN—х„) 4- (хл— aN) С 2е.
Таким образом, хп—*р, что и требовалось.
102
ГЛ. 3. МЕТРИЧЕСКИЕ ПРОСТРАНСТВА
[3.72
б.	Интервал (0, 1) представляет собой метрическое про-
странство с обычной метрикой числовой оси. Последователь-
ность у, -у, •	••• является фундаментальной в
этом метрическом пространстве, но не имеет в нем предела;
поэтому интервал (0, 1) не есть полное пространство.
Этот пример, в частности, показывает, что свойство
полноты пространства существенно зависит от выбора мет-
рики и может не сохраниться при переходе к гомеоморфной
метрике; действительно, метрические пространства в примерах
а и б гомеоморфны (3.35ж), но одно из них полно, а вто-
рое—неполно.
в.	Покажем, что т-мерное вещественное пространство Rm
с метрикой 3.14 (2) полно. Пусть х„ = (Вв1, ...,
(п=1, 2, ...) — фундаментальная последовательность век-
торов пространства Rm. Для заданного е > 0 найдем номер N
так, чтобы при р > N, q~> N иметь
По неравенству 3.J4 (9) для любого k и р, q > N имеем
Мы видим, что каждая числовая последовательность
£ k(k = 1, . . ., m) фундаментальна на числовой оси. Применяя
а, получаем существование пределов
£* = lim lpk (k= 1, ..., m).
p CD
Образуем вектор x = (g1, ..., Н,и). Снова no 3.14 (9)
|*~{^k — ^/г)2<К/итах|^ — gpfc|. (1)
Теперь для заданного e > 0 найдем номер N так, чтобы
при р > N выполнялись все неравенства
1^-Ер«1<р=	<‘='...”»
3.74]
§ 3.7. ПОЛНЫЕ ПРОСТРАНСТВА
103
Тогда для этих же значений р, как видно из (1), и
|х — XF| < 8,
откуда следует, что последовательность векторов хп схо-
дится к вектору х. Итак, пространство Rm полно, что и
утверждалось.
3.73.	а. Пусть полное метрическое пространство М
является частью (с той же метрикой) метрического про-
странства Р. Покажем, что М замкнуто в Р. Пусть у£Р —
предельная точка множества М и последовательность хп
точек 7И сходится к точке у. Так как последовательность
х„ фундаментальна (3.71 б) и пространство М полно, то
в М имеется предел z — lim хп. В силу единственности
со
предела (3.33а) у = z € 7W, что и требуется.
б.	Обратно, замкнутое подмножество А полного метри-
ческого пространства М, рассматриваемое как самостоятель-
ное метрическое пространство (с метрикой, заимствованной
из 7И), является полным пространством. Действительно,
всякая фундаментальная последовательность yv£ А сходится
в 7И (поскольку М полно), и ее предел принадлежит мно-
жеству А в силу предположенной замкнутости этого мно-
жества.
в.	В частности, любой отрезок [a, ft] на числовой оси
как замкнутое подмножество (3.51 а) полного метрического
пространства (3.72 а) является полным пространством.
3.74.	Для числовой прямой имеет место принцип вложен-
ных отрезков Кантора (1.81): всякая система вложенных друг
в друга отрезков имеет общую точку. Для полного метриче-
ского пространства можно указать различные аналоги этого
предложения.
а.	Пусть в множестве М выделена некоторая совокуп-
ность Q непустых подмножеств А, В, ..., обладающих тем
свойством, что из каждых двух подмножеств этой совокуп-
ности одно содержится в .другом. Такую совокупность Q
будем называть системой вложенных подмножеств.
Лемма. Пусть в полном метрическом пространстве М
выделена система Q вложенных подмножеств А, В, ... Если
среди них имеются подмножества как угодно малого
104
ГЛ. 3. МЕТРИЧЕСКИЕ ПРОСТРАНСТВА
(3.74
диаметра (3.12 а}, то существует такая точка р£М, что
для любой ее окрестности Vr (р) = {х:р (х, р) < г} можно ука-
зать множество A£Q, целиком содержащееся в Vr(p).
Доказательство. По условию, для любого пг — 1,
2, 3, ... имеется множество A = A„,€Q с diam А. —.
Пусть хт— любая точка из Ат. Так как при п>ти или
АпсАт, или Атс.Ао, то заведомо р(хв, хга) Л, так что
последовательность xlt хг, ... фундаментальна. Пусть
р= lim хт; покажем, что эта точка р удовлетворяет тре-
т-^оо
бованиям леммы. Пусть е>0 произвольно; найдем такое п,
что р(р,	и diam . Тогда для любого х£Ап
имеем
Р(Р, Х)^р(р, Ха} + р(Хп, х)^^ + ^- = Е,
так что AncVe(p), что и утверждалось.
б.	Замечание. В условиях леммы а может существо-
вать лишь единственная точка р, удовлетворяющая требова-
ниям леммы. Действительно, если q—другая точка, также
удовлетворяющая требованиям леммы, так что р(р, ?) =
= 2е>0, то шары Vs(p) и Ve(q) не пересекаются; вместе
с тем, по лемме а, существуют множества А и В в системе
Q такие, что AcVJp), Bc.V^(q)- но это противоречит
тому, что одно из множеств А, В должно быть вложено
в другое.
в.	Лемма. Пусть в дополнение к условиям леммы а все
множества системы Q замкнуты. Тогда точка р, удовлетво-
ряющая требованиям леммы, входит в каждое из множеств
системы Q.
Доказательство. Пусть точка р не входит в неко-
торое множество В. Поскольку В замкнуто, существует
такое е > 0, что шар Ve (р) не пересекается с множеством В.
По лемме а, существует множество целиком содержа-
щееся в шаре Пе(р). Очевидно, это множество А не пере-
секается с множеством В, и мы снова получаем противоречие.
Лемма доказана.
г.	Следующий частный случай леммы в часто употреб-
ляется.
3.75J
§ 3.7. ПОЛНЫЕ ПРОСТРАНСТВА
105
Лемма о замкнутых шарах. В полном метриче-
ском пространстве последовательность вложенных друг
в друга замкнутых шаров
v=l,2, ...,
радиусы которых rv монотонно стремятся к нулю при v —> оо,
имеет общую точку.
д.	Замечание. Если на числовой оси имеется после-
довательность вложенных друг в друга отрезков, то общая
точка у них существует всегда, независимо от того, стре-
мятся их длины к нулю или нет. В метрическом простран-
стве, даже полном, может существовать последовательность
вложенных друг в друга шаров без общей точки. В качестве
примера рассмотрим пространство, образованное из счетной
последовательности точек х1, х2, ... с расстоянием, опре-
деленным по формуле р(х„, хп+р) = 1 4--^-(л= 1,2, ...).
Это пространство удовлетворяет всем аксиомам метрического
пространства. Оно полно, так как в ием нет несходящнхся
фундаментальных последовательностей (вообще нет фунда-
ментальных последовательностей из различных точек). Шар
Vn радиуса 1 + -^ с центром в хп содержит точки хп,
х„+1, ... и не содержит никаких других точек. Очевидно,
00
... и П V„ пусто.
1
3.75.	а. Теорема (Бэр). Если полное метрическое про-
странство М представлено в виде счетной суммы своих зам-
кнутых подмножеств Аъ А2, ..., то по меньшей мере одно
из этих подмножеств содержит целиком некоторый шар
пространства М.
Доказательство. Допустим противное: ни одно из
множеств Л1Э А2, ... не содержит целиком никакого шара.
Пусть хх— точка, не входящая в множество Аг; так как А±
замкнуто, то существует шар 1/г (х1) = {х:р(х, х1)^г1},
свободный от точек множества Аг. Внутри шара К1/2 (хх) есть
точка х2, не лежащая в множестве А2; вместе с ней в мно-
жество А2 не входит некоторый шар Vrj (хг). Можно считать,
что l/z (x1)oVZa(x2) и г2< ~. Продолжая таким же об-
106
ГЛ. 3. МЕТРИЧЕСКИЕ ПРОСТРАНСТВА
[3.75
разом далее, мы построим последовательность шаров
УГ1 (Xjjz) Vr2 (x2)r>... так, что весь шар УГп(хп) не пере-
секается с множеством Ап (л=1,2, ...). Общая точка х0
всех этих шаров, существующая по лемме 3.74 а, не при-
надлежит ни к какому из множеств А2, ..., что проти-
СО
воречит условию	U Ап. Теорема доказана.
И=1
б.	Пример. Покажем, что множество Z всех иррацио-
нальных точек отрезка М=[а,Ь] не может быть представ-
лено в виде счетной суммы замкнутых подмножеств отрезка 7И.
со
Действительно, если бы мы имели Z= U Ап, где Дпо:7И —
п — 1
замкнутые множества, то и весь отрезок М был бы пред-
ставлен в виде счетной суммы замкнутых подмножеств (счет-
ной совокупности множеств Ап и счетной совокупности
одноточечных множеств, содержащих по одной рациональной
точке). Так как отрезок М=[а, £] есть полное пространство
(3.73 в), мы получили бы противоречие с теоремой
Бэра.
в.	В 2.41, используя теорему о вложенных отрезках, мы
доказали, что множество точек отрезка [0, 1] несчетно.
Мы можем установить теперь справедливость аналогичного
утверждения и для широкого класса полных метрических
пространств.
Предварительно введем следующее определение: точка
х0 метрического пространства М называется изолированной,
если некоторый шар р (х, х0) < 6 не содержит ни одной
точки пространства 7И, кроме самой точки х0. Например,
пусть 7И есть некоторое множество точек оси —оо< х <оо
с обычной метрикой; тогда есть изолированная точка,
если имеется интервал, содержащий точку х0 и не содер-
жащий более ни одной точки множества /И.
Лемм а. Полное метрическое пространство Л'Т, если оно
состоит лишь из счетного множества точек, содержит изоли-
рованную точку.
Доказательство. Каждая точка есть замкнутое
подмножество метрического пространства. Применяя теорему
Бэра, получаем, что в данном случае некоторая точка х0
пространства М содержит некоторый шар Vz(x0); это воз-
можно, лишь если точка х0 изолирована.
3.82J
§ 3.8. ПОПОЛНЕНИЕ
107
Отсюда получаем:
г.	Всякое полное метрическое пространство М без изоли-
рованных точек несчетно.
Замечание. Это утверждение перестанет быть спра-
ведливым, если отказаться от предположения, что в прост-
ранстве М нет изолированных точек. Соответствующим при-
мером может служить любое счетное замкнутое множество
(например, последовательность, сходящаяся к пределу, и ее
предел) на прямой, рассматриваемое как самостоятельное
метрическое пространство.
§ 3.8.	Пополнение
3.81.	Теоремы, доказанные в 3.73—3.75, используют
существенно'полноту метрического пространства 7И. И в даль-
нейшем полнота метрических пространств будет играть
важную роль. Что касается неполных пространств, то,
оказывается, каждое такое пространство можно включить
в некоторое полное пространство.
Теорема (Ф. Хаусдорф). Пусть М—метрическое
пространство (вообще говоря, неполное). Существует пол-
ное метрическое пространство М (называемое пополне-
нием пространства М), которое обладает следующими
свойствами'.
1)	М изометрично некоторой части Л'^аМ;
2)	плотно в 7И.
Всякие два пространства М, М, удовлетворяющие усло-
виям 1) и 2), изометричны между собой.
Доказательство дается в 3.82—3.87.
3.82.	Назовем две фундаментальные последовательности
{yv} и {s'v} пространства М конфинальными, если lim p(_yv,zf) = 0.
V—> сс
Например, всякие две последовательности пространства 7И,
сходящиеся к одному и тому же пределу, являются конфи-
нальными, а сходящиеся к разным пределам не являются
конфинальными. Две фундаментальные последовательности,
конфинальные с третьей, конфинальны и между собой.
Поэтому все фундаментальные последовательности, которые
можно построить из элементов пространства 7И, можно раз-
бить на классы так, что все последовательности, входящие
108
ГЛ. 3. МЕТРИЧЕСКИЕ ПРОСТРАНСТВА
[3.83
в один класс, конфинальны между собой и любая последо-
вательность, не входящая в этот класс, не конфинальна ни
с одной последовательностью класса. Из таких классов — мы
будем обозначать их Y, Z, ... — мы и будем строить новое
пространство М. Подлежит определению лишь величина рас-
стояния между классами Y и Z. Мы определяем ее по формуле
р(У, Z) = Iimp(yv, zv),	(1)
V-> co
где {у J—любая фундаментальная последовательность из
класса Y, a {zv} —любая фундаментальная последовательность
из класса Z. Нужно, конечно, прежде всего проверить, что
указанный предел существует и не зависит от выбора после-
довательностей {у,} и {zj в классах Y и Z. По неравенству
четырехугольника (<?.//(!))
I Р ^v) Р(.У11 + р.> ^v + p.) I Р (,У»> J'v + p.) Р (^1>1 ^» + р)>
откуда следует, что числа р (у„ z„) образуют последова-
тельность, удовлетворяющую критерию Коши. Таким обра-
зом, limp(yv, zv) существует. Если {у'} и {z'}—другие
фундаментальные последовательности в классах Y и Z, то,
снова применяя неравенство четырехугольника, находим, что
IР (Уч, zv)—р (уч,, 4) I < Р (jv, Уч) + Р (zv, zv) -> 0,
поэтому последовательность р (у^, z'v) имеет тот же предел,
что и последовательность р(у„, zv). Таким образом, опре-
деление расстояния между классами не зависит от выбора
фундаментальных последовательностей в этих классах.
3.83.	Теперь мы должны проверить, что величина
Р(^> ^) = Hmp(yv, zv)
*V-> со
удовлетворяет аксиомамметрического пространства^.// а—в).
Аксиома 3.11а.'. p(F, Z) > О при Y^Z, р(У, У) = 0
проверяется следующим образом. Прежде всего по построе-
нию функции р мы имеем p(F, У) = 0, ибо в формуле 3.82 (1)
можно положитьyy — zv. Далее, предположим, чтор(У, Z)=0.
Это означает, что для любой фундаментальной последова-
тельности {у,} из класса Y и любой фундаментальной после-
довательности {zv} из класса Z имеет место равенство
3.85]	§ 3.8. пополнение	109
lim р(у„ г„) — 0. Но тогда {у,} и {zv}—конфинальные по-
V“> СО
следовательности и класс Y должен совпадать с классом Z.
Таким образом, если р(У, Z) = 0, то Y—Z\ отсюда следует,
что при Y=f=Z имеем р(У, Z) > 0, что и требуется.
Аксиома 3.116'. р(У, Z) = p(Z, У) выполнена по построе-
нию.
Проверим аксиому 3.11 в: р(У, U) р (У, Z) -|-р (Z, U).
Пусть {yj, {zj, {uj—фиксированные фундаментальные
последовательности из классов У, Z, U соответственно.
Искомое неравенство получается в результате перехода
к пределу (3.32 в—г) в неравенстве
P (Л> uv) Р (У». zj + р (^, и,).
Проверим теперь для пространства М все утверждения,
сформулированные выше в теореме о пополнении.
3.84.	Покажем, что М содержит подмножество Л4Х, изо-
метричное пространству М. Каждому элементу у £ М поста-
вим в соответствие класс УсЛ1, содержащий последователь-
ность у, у, у, ... (т. е. класс всех последовательностей,
сходящихся к у). Если по этому правилу точка у соответ-
ствует классу У и точка z—классу Z, то
р(У, Z) = limp(y, z) = p(y, z).
Отсюда следует, что совокупность /Их соответствующих
классов У есть часть пространства М, изометричная 'прост-
ранству М.
3.85.	Проверим, что Afx плотно в М: Пусть У—произ-
вольный класс нз /И и {yj—фундаментальная последова-
тельность из класса У. Рассмотрим последовательность
классов У,, У2, ..., У„, ..., где Уи определяется последо-
вательностью уи, ур, ..., т. е. отвечает элементу уи в соот-
ветствии А1 —► /Их. Для заданного е > 0 найдем номер р0 так,
чтобы при р > р0 иметь р (уи+/,, уи) е. Тогда
р(Т, F ) = Um(yv,y)<e.
V-+ со
Но это означает, что класс У есть предел классов У^. Так
как класс Уи принадлежит по построению множеству /Их, то
тем самым доказано, что плотно в М.
110
ГЛ. 3. МЕТРИЧЕСКИЕ ПРОСТРАНСТВА
[3.86
3.86.	Покажем, что М—полное пространство. Пусть
У,, У2, ... —фундаментальная последовательность элементов
из М. Для каждого класса Yv найдем класс Z^c/Hj так,
чтобы иметь р (У„, Z„) <, и пусть zv£M есть элемент,
соответствующий классу Zv. Мы утверждаем, что последо-
вательность {zv} фундаментальна в пространстве 7И. Дейст-
вительно,
Р(^>	= ZF)<p(Zv, У,)+р(У„ Уи) + Р(^,
<Р(^>	+ при	И-^оо-
Фундаментальная последовательность {zv} определяет неко-
торый класс ZcTW; покажем, что класс Z является пределом
в М последовательности У„. Для заданного е > 0 при доста-
точно большом v^v0 имеем
p(Z, yv)<p(Z, ZJ+p(Z„ У„) = 1ипр(гц, ^) + 1<е.
сю	v
Таким образом, всякая фундаментальная последовательность
У,о:7И имеет в М предел, что и требовалось.
3.87.	Наконец, покажем, что любое метрическое прост-
ранство 7И, обладающее свойствами 1) и 2), изометрично
пространству 7И.
Действительно, пусть и ТИ2— подмножества прост-
ранств М и 7И, изометричные пространству /И и, следова-
тельно, изометричные друг другу. Мы должны продолжить
эту изометрию с множеств Мг и ТИ2 на пространства М и М.
Возьмем любой элемент УсТИ и рассмотрим последователь-
ность элементов УгсЛ11, сходящуюся к У. Соответствующая
последовательность Zvc:M2 во всяком случае фундамен-
тальна, так как в силу изометрии между и ТИ2 взаимные
расстояния между элементами последовательности Zv такие
же, как между элементами последовательности У,. Так как
М полно, то в М имеется элемент Z = lim Zv. Этот элемент
_	V-* со
ZaM поставим в соответствие взятому элементу УсТИ.
Он определен однозначно, поскольку конфинальные после-
довательности в М соответствуют конфинальным последо-
3.91]
§ 3.9. КОМПАКТНОСТЬ
111
вательностям в М и замена последовательности Yv на конфи-
нальную приводит к замене последовательности Zv также на
конфинальную. Указанное сопоставление взаимно однозначно
и исчерпывает все элементы М и 7И. Нам остается показать,
что оно является изометрическим. Пусть элементы У и У'
пространства 7И соответствуют элементам Z и Z' простран-
ства М и при этом
У = lira Ут,
y' = lirnyv (Ут, Yv из Al!).
Если, далее, Zv и Zv — элементы из ТИ2, отвечающие эле-
ментам Yv и yv, то p(Zv, Zv) = p(yv, Yv) и в силу леммы
о непрерывности расстояния 3.326
p(Z, Z') = limp(zv, Zv)=limp(yv, У^) = р(У, У'),
V-> 00	V~+ cd
что и требуется. Тем самым теорема 3.81 доказана пол-
ностью.
3.88.	Предположим, что данное метрическое простран-
ство М есть часть другого полного метрического простран-
ства М*. Тогда в качестве пополнения М можно взять за-
мыкание М множества М в пространстве /И*. Действительно,
Л4 как замкнутое подмножество полного пространства М*
есть полное пространство (3.73 б); затем оно содержит
внутри себя 7И в качестве плотного подмножества. Оно удов-
летворяет, таким образом, условиям доказанной теоремы и
в силу этой теоремы может служить пополнением простран-
ства М.
§ 3.9.	Компактность
3.91.	а. Определение. Метрическое пространство М,
в котором каждая (бесконечная) последовательность точек
имеет предельную точку, называется компактным простран-
ством, или компактом. Метрическое пространство М, в кото-
ром для каждой точки а £ М имеется компактный шар
{х £7И:р (а, х) с}, называется локально компактным про-
странством.
112
ГЛ. 3. МЕТРИЧЕСКИЕ ПРОСТРАНСТВА

Если метрическое пространство М компактно, то каждое
бесконечное подмножество ЕсМ имеет предельную точку.
Действительно, бесконечное подмножество в Е содержит бес-
конечную последовательность хх, х2, ... различных точек,
и ее предельная точка будет и предельной точкой множе-
ства Е. Обратно, пусть каждое бесконечное подмножество
метрического пространства М имеет предельную точку;
покажем, что М компактно. Пусть хг, х2, ... —любая после-
довательность точек из М (не обязательно различных).
Если в этой последовательности фактически участвует лишь
конечное число различных точек пространства М, то заве-
домо хотя бы одна из них повторяется бесконечное число
раз, п тогда она и будет предельной точкой последователь-
ности хъ х2, ... Если же в этой последовательности уча-
ствует бесконечное множество различных точек М, то пре-
дельная точка этого бесконечного множества будет и пре-
дельной точкой всей последовательности. Таким образом,
данное выше определение компактного пространства экви-
валентно следующему: метрическое пространство компактно,
если каждое его бесконечное подмножество содержит пре-
дельную точку.
б.	Примеры. Отрезок «^х^£ на числовой оси яв-
ляется компактом {3.45). Вся числовая ось R не является
компактным пространством, так как, например, последова-
тельность 1, 2, ..., п, ... не имеет в R не одной пре-
дельной точки. Но пространство R является локально ком-
пактным пространством. Расширенная числовая ось R с мет-
рикой г (х, у) {3.35 д) компактна. Множество рациональных
точек отрезка [a, f>] с метрикой числовой оси не является
ий компактным, ни локально компактным.
в.	В 3.43 мы отметили, что свойство данной точки быть
предельной для последовательности х„ не нарушается при
переходе к новой метрике, гомеоморфной исходной. Так
как определения компактного и локально компактного про-
странства опираются лишь на понятие предельной точки,
то мы делаем вывод, что свойство пространства быть ком-
пактным или локально компактным не нарушается при пере-
ходе к новой метрике, гомеоморфной исходной.
Так, вещественная ось R является локально компактным
пространством и в обычной метрике р (х, у) — | х —у |, и
₽ метрике г (х, у) {3.35 д).
3.93]
§ 3.9. КОМПАКТНОСТЬ
113
3.92.	а. Теорема. Каждое компактное пространство
полно.
Доказательство. Пусть хг, х2, ... — фундамен-
тальная последовательность точек компактного простран-
ства М, и пусть х0—предельная точка этой последователь-
ности. Покажем, что x0 = litnxn. Для заданного 8>0 иай-
дем сначала номер N так, чтобы при от > Л/, п> N иметь
Р (xn, xm) < е/2 , и затем номер р > N так, чтобы было
р (хр, х0) < е/2. Тогда для всех л > /V
Р (*„, *о) < Р (*». хр) + р (хр, х0) < в,
откуда и вытекает утверждение.
б.	Теорема. Компактное подмножество М метриче-
ского пространства Р замкнуто в Р.
Это следует из а и 3.73а.
в.	Пусть М—компактное подмножество метрического
пространства Р, и GczP—открытое множество, содержащее
М. Образуем открытое множество Л4В, являющееся объеди-
нением всех открытых шаров радиуса б с центрами в точ-
ках множества М. Утверждается, что существует такое
б > О, при котором MBczG.
Для доказательства, допуская противное, для каждого
п = 1, 2, ... найдем две точки х„£Л1, уп£Р—G, для кото-
рых р (х„, у„) <	. Последовательность х„ лежит в ком-
пакте М, и из нее можно выбрать сходящуюся подпоследо-
вательность; вводя новую нумерацию и отбрасывая ненуж-
ные точки, можно считать, что х„-»х g М Так как
Р(УП. *Хр(К> хп) + р(хп, х)^ — + р(хп, х), то и уп-»-х.
Но множество Р— G замкнуто, поэтому х £ Р— G в про-
тиворечии с предыдущим. Тем самым утверждение доказано.
3.93.	а. Некоторым расширением класса компактных про-
странств является класс предкомпактных пространств*).
Метрическое пространство М называется предкомпактным,
если в нем каждая последовательность точек содержит фун-
даментальную подпоследовательность. Если при этом М
*) В литературе нет единой терминологии. Иногда называют
предкомпактные пространства компактными, а компактные в нашем
смысле—компактами.
114
ГЛ. 3. МЕТРИЧЕСКИЕ ПРОСТРАНСТВА
[3.93
полно, то эта фундаментальная последовательность будет
и сходящейся, и пространство /И оказывается компактным.
Таким образом, полное пр ед компакт ное пространство явля-
ется компактным. Обратно, компактное пространство явля-
ется полным (3.92 а) и, очевидно, пр ед компактным. Интер-
вал (а, Ь) числовой оси дает простой пример предкомпакт-
ного, но не компактного пространства.
б.	Теорема. Каждое пред компакт ное пространство
ограничено.
Доказательство. Мы будем доказывать, что неог-
раниченное пространство непредкомпактно. В неограничен-
ном пространстве М расстояния от любой точки а до осталь-
ных точек	в совокупности не ограничены (3.12 в).
Пользуясь этим, фиксируем произвольно точку х±£ М и
затем индуктивно построим последовательность точек
х2, х3, ... так, чтобы выполнялись неравенства
И-1
Р (*„+!> хп)> 2p(xft+1, хй)+1	(Л= 1, 2, ...).
k=l
Тогда по 3.11 г при п > m
Р (хп, >
Р (Хп’ Хп-1) — [р (Хп-11 Xn-2) + •  • “Гр (XZB + 1> х/я)]
>р(х„, x„_x) — 2p(xft+1, хк) > 1,
k=l
так что из последовательности хп нельзя выбрать фунда-
ментальной подпоследовательности. Тем самым пространство М
не предкомпактно, что и утверждалось.
в.	Критерий Хаусдорфа. Для проверки предком-
пактности метрическое пространство М иногда целесооб-
разно включить изометрически в более широкое метрическое
пространство Р. В предположении изометричности включе-
ния MczP назовем множество BczP Е-сетью множества
МсР, если каждая точка х множества М отстоит не далее
чем на е от некоторой точки у£В. Таким образом, объеди-
нение всех шаров радиуса е с центрами в точках множест-
ва В содержит все множество М.
Вообще, если объединение некоторых множеств Ua содер-
жит множество /И, говорят, что множества Ua в совокуп-
3.93]	§ 3.9. компактность	115
ности покрывают множество М, или же что они образуют
покрытие множества 714. Таким образом, можно сказать, что
множество В есть е-сеть для множества 714, если совокуп-
ность всех шаров радиуса е с центрами в точках множе-
ства В покрывает множество /И*).
Теорема (Ф. Хаусдорф). Множество 714, расположен-
ное в метрическом пространстве Р, предкомпактно (в мет-
рике Р) тогда и только тогда, когда для любого е > О
в Р имеется конечная Е-сеть для 714.
Доказательство. Пусть 714 предкомпактно, и пусть
задано е > 0. Покажем, что существует конечная е-сеть для
множества 714. Возьмем произвольную точку хг £ 714. Если
все остальные точки множества 714 находятся от точки
на расстоянии ^е, то сама точка х1 представляет е-сеть
для 714 и построение закончено. Если же среди точек мно-
жества 714 имеются такие, которые отстоят от хг дальше
чем на е, то мы выберем среди них произвольную точку х2.
Если теперь каждая точка множества 714 отстоит не далее
чем на е или от точки xlt или от точки х2, то х1 и х2
образуют конечную е-сеть для 714 и построение закончено;
в противном случае построение можно продолжить.
По построению каждая новая точка хп отстоит от каж-
дой из предшествующих х1г х2, ..., х„_г дальше чем на
е. Поэтому, если бы процесс можно было продолжать не-
ограниченно, мы получили бы бесконечное подмножество
xlt х2, ..., хп, ... множества 714, заведомо не содержащее
ни одной фундаментальной последовательности, что проти-
воречило бы предкомпактности 714. Так как 714 предком-
пактно, то процесс закончится после конечного числа шагов;
в результате мы получим конечную е-сеть для множества 714.
Обратно, пусть в пространстве Р имеется при каждом
е > 0 конечная е-сеть для множества 714; покажем, что 714
предкомпактно. Рассмотрим произвольное бесконечное под-
множество Лс714; мы должны выбрать в А фундаменталь-
ную последовательность. В качестве первой точки этой по-
следовательности возьмем любую точку х0 £ А. Применяя
условие теоремы прие=1, мы можем покрыть множество Л
*) «Если в каждой точке множества В, являющегося е-сетью для
множества 714, зажечь фонарь, освещающий шар радиуса е, то будет
освещено все множество 714». (Из лекций Л. А. Люстерника.)
116
ГЛ. 3. МЕТРИЧЕСКИЕ ПРОСТРАНСТВА
[3.94
конечным числом шаров радиуса 1; среди них имеется
такой—обозначим его через Ult—который содержит беско-
нечное подмножество A±czA. Выберем в А± любую точку
хху=х0. Применяя условие теоремы при e = -g-, мы можем
покрыть множество Лх конечным числом шаров радиуса
у; среди них есть шар U2, который содержит бесконечное
подмножество Л2сЛх. Выберем любую точку х^А^, не
совпадающую ни с х0, ни с хх. Продолжая таким же обра-
зом далее, мы построим цепочку бесконечных подмножеств
ЛэЛхэA^zd ... ззЛ,зз... (причем каждое из множеств Л,
rr 1 \
содержится в шаре Uv радиуса — 1 и, кроме того, после-
довательность различных точек х0, хх, х2, ..., xv, ...,
где xv £ Av. Мы утверждаем, что последовательность
х0, xii хг> _фундаментальна. Действительно, при р < v мы
2
имеем С^гзЛцГзЛ,,, поэтому р (хр х,)< —. Эта величина
стремится к нулю при р —>оо; значит, последовательность
х0, х1г ... фундаментальна, что и требовалось.
3.94.	В качестве применения этого признака покажем,
что любое ограниченное множество М в п-мерном евклидо-
вом пространстве P = Rh предкомпактно. Действительно,
для любого m в том шаре пространства Р, который содер-
жит ограниченное множество М (3.14 б), существует лишь
конечное число точек, все координаты которых имеют вид
k ,
—, к—целое, а множество всех таких точек, очевидно,
при достаточно большом m образует е-сеть для М.
3.95.	Отметим еще следующий простой признак пред-
компактности: множество М в метрическом пространстве Р
предкомпактно, если для любого е > 0 можно указать в Р
предкомпактное множество Ве (может быть, и бесконечное),
являющееся ъ-сетью для М.
Доказательство этого признака весьма просто.Мы утвер-
е _
ждаем, что при заданном е конечная -^--сеть Z для множе-
ства Ве/2, существующая в силу предкомпактиости Де/2,
3.96J
§ 3.9. КОМПАКТНОСТЬ
117
есть конечная е-сеть для множества Л4. Действительно, для
произвольной точки х£7И по условию найдутся такая точка
У € Ве/ъ, что р (х, у) , и такая точка z £ Z, что р (у, z)
< ; но тогДа Р (х, z) р (х, у) + р (у, z) е, что и утвер-
ждалось. Таким образом, при любом е > О множество Л1
обладает конечной 8-сетью и, следовательно, предком-
пактно.
3.96.	а. Пополнение М любого предкомпактного мно-
жества М есть компакт. В самом деле, множество Л4, по-
скольку оно плотно в /И, является е-сетыо для множества
М при любом е > 0. По условию М предкомпактно; отсюда
по 3.95 и М предкомпактно; а так как М полно, то оно есть
компакт, что и требовалось.
б.	Замыкание М любого предкомпактного подмножества
М полного метрического пространства Р компактно. Это
следует из а и из замечания 3.88, в силу которого в каче-
стве пополнения множества М можно взять его замыкание
в Р.
в.	Предкомпактное подмножество М полного метриче-
ского пространства Р является компактом тогда и только
тогда, когда оно замкнуто в Р.
Действительно, если подмножество М замкнуто в пол-
ном метрическом пространстве Р, то оно само является
полным метрическим пространством (3.73 б). Если при этом
М предкомпактно, то, согласно 3.93 а, М есть компакт.
Обратное утверждение следует из 3.92 б.
г.	Соединяя 3.93 в и 3.96 в, получаем:
Теорема. Множество М в полном метрическом про-
странстве Р является компактом тогда и только тогда,
когда оно замкнуто в Р и для каждого е > 0 в Р имеется
конечная s-сеть для М.
д.	Множество М в пространстве Rn является компактом
тогда и только тогда, когда М замкнуто и ограничено в Rn.
Действительно, если М—компакт, то множество М замк-
нуто (3.92 б) и ограничено (3.93 б); если множество М огра-
ничено в Rn, то оно предкомпактно (3.94), а в силу пол-
ноты/?,, (3.72 в) из замкнутости предкомпактного множества М
118	ГЛ. 3. МЕТРИЧЕСКИЕ ПРОСТРАНСТВА	[3.97
следует его компактность (3.96 в). В частности, замкну-
тый шар {лт:| л: — х0|^г) есть замкнутое (3.516) и огра-
ниченное множество; поэтому в пространстве Rn всякий зам-
кнутый шар компактен.
е.	Каждое компактное множество М на числовой оси
ограничено и содержит свои точные границы.
Действительно, множество М ограничено и замкнуто (д);
остается применить 3.53 б, и утверждение доказано.
3.97.	Часто используется следующее предложение отно-
сительно компактов:
Лемма о конечном покрытии. Если компактное
подмножество К метрического пространства Р покрыто семей-
ством В={Ва\ открытых подмножеств пространства Р, то
существует конечное подсемейство Blt ..., Вт семейства В,
также покрывающее компакт К.
Доказательство. Допустим противное: никакое ко-
нечное подсемейство семейства В не образует покрытия
компакта К.
Поскольку К—компакт, согласно 3.93 в для каждого
е> О имеется конечное число шаров (замкнутых) ..., Llmi
радиуса е, покрывающих компакт К. Если бы для каж-
дого из шаров U.(j=\, ..., тг) существовало конечное
подсемейство Bj семейства В, покрывающее шар Uj, то,
объединяя эти подсемейства, мы смогли бы выделить из
семейства В конечное подсемейство, покрывающее весь ком-
пакт К. Поэтому хотя бы один из шаров Uj, например Ult
не может быть покрыт никаким конечным подсемейством
семейства В.
Придадим числу е последовательность значений 1, у ,
-i-, ...; для каждого п у нас имеется шар t7i/n (хп) радиуса
О
— с центром в точке хп, который не может быть покрыт
никаким конечным подсемейством семейства В. Пусть х —
предельная точка последовательности хп. Точка х входит
в некоторое множество Ва вместе с некоторым шаром U (х)
радиуса р. Начиная с некоторого номера, в шар U?(x) попа-
дают шары U1/n (х„) с как угодно большими номерами. По-
этому указанные шары покрываются даже только одним
множеством Ва в противоречии с построением. Лемма доказана.
ЗАДАЧИ
119
3.98.	Принцип вложенных отрезков (1.81) с числовой
оси мы перенесли (3.74) на полное метрическое пространство,
заменив в формулировке отрезки на замкнутые подмноже-
ства с произвольно малыми диаметрами. Если эти подмно-
жества компактны, никаких других предположений уже не
нужно:
Теорема. Всякая система Q вложенных непустых ком-
пактных подмножеств метрического пространства имеет об-
щую точку.
Доказательство. Фиксируем в системе Q один из
компактов Ко. Если теорема неверна, то для каждой точки
х£К0 найдется компакт Кх (tQ, не содержащий точки х.
Так как Кх есть замкнутое множество (3.92 б), то сущест-
вует окрестность точки х, не пересекающаяся с Кх. Ука-
занные окрестности, построенные для каждой точки х £ Ко,
образуют покрытие компакта Ко; по 3.97 из этого покры-
тия можно выделить конечное покрытие. Обозначим окре-
стности, составляющие конечное покрытие, через V1, , .., Vn.
Пусть Klt ..., Кп — компакты из системы Q, не пересекаю-
щиеся соответственно с Vlt ..., Vn. Пересечение ... Кп не
имеет общих точек ни с одной из окрестностей ..., V„
и не пересекается поэтому с компактом Ко. Таким обра-
зом, пересечение КаКг...Кп пусто. С другой стороны,
поскольку Q—система вложенных множеств, всякое конеч-
ное пересечение множеств этой системы есть снова множе-
ство этой системы и, в частности, не может быть пустым.
Полученное противоречие доказывает справедливость тео-
ремы.
ЗАДАЧИ
1.	Множество предельных точек любого подмножества А метри-
ческого пространства /И обозначим через А'. Далее, по индукции
определяется множество А(п> = (А(п-п)'. Для заданного п построить
на прямой множество А так, чтобы А(п> было непустым, а А*"*1’
пустым.
2.	Доказать, что множество А' замкнуто, каково бы ни было
АсМ.
3.	Дано множество	для которого при некотором п мно-
жество А(п) счетно. Доказать, что А счетно.
4.	Точка х на прямой называется точкой конденсации несчетного
множества А, если в любой окрестности точки х имеется несчетное
множество точек множества А. Доказать, что у всякого несчетного
120
ГЛ. 3. МЕТРИЧЕСКИЕ ПРОСТРАНСТВА
множества А имеются точки конденсации; более точно, почти все его
точки, кроме, может быть, счетного множества, являются точками
конденсации.
5.	Если множество Е на прямой покрыто произвольной системой
интервалов, то из этой системы можно выделить не более чем счет-
ную подсистему, также покрывающую Е.
6.	Величина
р(х, Л) = 1п1р(х, у)
уеА
называется расстоянием от точки х до множества А. Доказать, что
для замкнутого множества А соотношения
р(х, Л)=0, х£А
эквивалентны; если же А не замкнуто, то они не эквивалентны.
7.	Доказать, что для любого множества А в метрическом про-
странстве М совокупность точек х, для которых р (х, Л) < в, открыта,
а совокупность точек у, для которых р (у, Л) < в, замкнута.
8.	Даны два непересекающихся замкнутых множества Fj и Г2
в метрическом пространстве М. Построить непересекающнеся откры-
тые множества U1 и Uz так, чтобы U^F^ U^F^ я иг я U2 не
пересекались.
9.	Пусть М —ограниченное метрическое пространство. Определим
для любых двух подмножеств АсМ и ВсМ величину
р(Л, B) = sup{p(x, В), р(у, Л)}.
хе А
уев
Показать, что всевозможные замкнутые подмножества Л, В, ... в М
образуют метрическое пространство, если определить расстояние
между двумя замкнутыми подмножествами по этой формуле. Пока-
зать, что это пространство полно, если М полно, н компактно, если
М компактно.
10.	Если метрическое пространство М состоит из п < 4 точек,
то существует метрическое пространство М', изометричное М и
расположенное в евклидовом пространстве	Для пЭ=4 такое
утверждение уже, вообще говоря, неверно.
И. Пусть Rn означает евклидово пространство Rn с присоеди-
ненной точкой оо. Ввести на Rn метрику г так, чтобы на Rn она
была гомеоморфной обычной метрике р (3.14) и чтобы всякая по-
следовательность xCT£/?n, неограниченная в обычной метрике, имела
бы оо предельной точкой.
12.	Решить задачу 11, заменив пространство Rn произвольным
неограниченным метрическим пространством М.
13.	В задаче 11 вместо рассмотренных прямых (см. указание
к задаче 11) использовать прямые, проходящие через центр сферы Sn.
Какой набор «бесконечно удаленных» элементов обеспечит существо-
вание предельной точки (в новой метрике) для всякой последователь-
ности точек xm£.Rti-
ИСТОРИЧЕСКАЯ СПРАВКА	121
Историческая справка
Первое корректное определение предела числовой последователь-
ности было дано Больцано (1817), а затем Коши (1821) в его курсе
по алгебраическому анализу. В частности, Больцано впервые ясно
сформулировал «критерий Коши» и даже попытался его обосновать;
но его рассуждение «за полным отсутствием какого бы то ни было
определения действительных чисел, не было и не могло быть ничем
иным, кроме порочного круга» (Бурбаки). Сам Коши получил свой
критерий из принципа вложенных отрезков, который считал очевидным.
Понятие предельной точки открытого и замкнутого множества
(сначала на оси, затем в евклидовом n-мерном пространстве) и тео-
ремы о структуре этих множеств на оси были даны Кантором в 70-х
годах XIX века. Теорема о выделении конечного покрытия была
впервые доказана (для отрезка) Борелем (1895, для случая, когда
исходное покрытие счетно) и Лебегом (1902, для любого исходного
покрытия). В 1906 г. Фреше ввел понятие метрического простран-
ства, в рамках которого получили естественное обобщение понятия
предыдущего периода; кроме того, Фреше ввел понятия полноты и
компактности метрического пространства.
Еще более широкие возможности открыло понятие топологичес-
кого пространства (Хаусдорф, 1914), о котором мы здесь только упо-
мянем. См. Ф. Хаусдорф, Теория множеств, ОНТИ, 1937.
ГЛАВА 4
ОБЩАЯ ТЕОРИЯ ПРЕДЕЛОВ
Превосходное сочинение г. Коши «Курс анализа По-
литехнической школы», которое должен прочесть всякий
аналист, любящий строгость в математических изыска-
ниях, служило мне проводником.
Нильс Абель (1826)
§4.1. Определение предела
4.11.	Определение. Пусть дано произвольное мно-
жество Е; система S непустых подмножеств А, В, ... мно-
жества Е называется направлением, если для каждых двух
подмножеств A£S, B£S выполняется одно из включений
Аа.В или Во: А и пересечение всех А £6’ пусто.
4.12.	Опр еделение. Пусть на множестве Е задана
функция у=/(х), значения которой принадлежат к метри-
ческому пространству 7И с расстоянием р (3.11). Будем го-
ворить, что функция-у = f(x) имеет предел по направлению S,
если существует такая точка р £ 7И, что при любом е > О
можно найти множество А£.$, во всех точках которого
выполняется неравенство
Р [Г. /(*)] < е.
В этом случае точка р называется пределом функции
f(x) по направлению S. Вся описанная ситуация обознача-
ется символом
p = lim/(x).	(2)
S
Пишут также f(x)—+p или просто f(x)—+p.
S
В 4.13—4.16 рассматриваются примеры.
4.13.	Пусть Е—множество всех натуральных чисел
1, 2, ... Направление В определим как систему всех под-
множеств АпаЕ вида
А„ = {л, л-J-l, «4-2, ...}	(л=1, 2, ...).
4.14]
§ 4.1. ОПРЕДЕЛЕНИЕ ПРЕДЕЛА
123
Очевидно, из всяких двух множеств Ап, Ат одно содер-
жит другое; далее, пересечение всех множеств Ап (п = 1,2, ...)
пусто. Таким образом, система S действительно есть направ-
ление. Это направление обозначается п—«-оо. Функция
y—f(x) в данном случае есть последовательность точек
Уг, у2, • • • 1 Ут    метрического пространства М. Согласно
нашему определению, последовательность уп имеет предел
по направлению 5, т. е. при л—* оо, если существует такая
точка рСАТ, что для любого е>0 можно найти такой
номер N, что для всех п~^ N выполняется неравенство
P(j„, Р)<е.
Последовательность точек имеющая предел р, называ-
ется сходящейся к р. Очевидно, это определение совпадает
с тем, которое было дано в 3.31. Обозначение 4.12 (2) приоб-
ретает видр= limy,,.
п -> оо
4.14.	а. Пусть Е = есть вещественная полуось {х:а^ х}.
Направление S определим как систему всех подмножеств
A.cRa вида
А={х£/?+:х>£}.
Очевидно, что 3' есть направление в смысле 4.11. Это на-
правление обозначается х—«-ф-оо. Согласно нашему опре-
делению, функция f(x), определенная при х^а (со значе-
ниями в метрическом пространстве М), имеет предел по
направлению «5, т. е. при х—«--(-оо, если существует такая
точка р£М, что для любого е>0 можно найти такое
число £, что для всех х^| выполняется неравенство
Р(Р, /(*))<е.
Точка р называется пределом функции f(x) при х—«-оо;
соответствующая запись имеет вид
р = lim/(x).
X -> со
б.	Если M—R есть числовая прямая, мы получаем оп-
ределение числовой функции, имеющей предел при х—>-оо,
именно: числовая функция /(х), определенная при х^а,
имеет пределом число р при х—«-оо, если для любого е > О
существует такая точка что для всех х £ выполняется
неравенство
Гр—/(*)] < е.
124
ГЛ. 4. ОБЩАЯ ТЕОРИЯ ПРЕДЕЛОВ
[4.15
в.	На вещественной полуоси R~а = {х: х а} вводится
направление х—> — оо. Оно определяется как система всех
подмножеств B^czR^ вида
B^{x£R-a-.x^l}Ri.
Согласно нашему определению, функция f(x), определенная
при х^я, имеет предел р при х—+— оо, если для любого
е > О можно найти такое число что для всех х £ вы-
полняется неравенство
Р(Р,
или, для числовой функции f(x),
|р— /Wl<6-
г.	Аналогично на числовой оси вводится направление
х —> ± °0, или, что то же, | х | —> оо. Направление | х | —> оо
образовано всеми множествами {х:|х|^С}. Таким образом,
приобретает определенный смысл выражение
lim /(х).
1*1-* «>
4.15.	а. Пусть Е есть метрическое пространство. Пред-
положим, что точка' а£Е не есть изолированная точка в Е,
иными словами, что любой шар UT{a) = {х £Е\р(х, а) <г}
содержит, кроме точки а, еще некоторые точки из Е. Тогда
направление х —>- а определим как совокупность всех шаров
UT{a) = {x^,E\p(a, х)<г}, из которых выброшена цент-
ральная точка а. Предположение о том, что а не есть изо-
лированная точка, означает, что каждое из множеств U (а) не
пусто; выполнение остальных свойств направления очевидно.
Согласно нашему определению, функция /(х), определенная
на Е (со значениями в метрическом пространстве М), имеет
предел при х—+ а, если существует точка рgМ, для кото-
рой при любом е > 0 можно найти число 6 > 0 так, что
для всех х€Ц(я) (т. е. для всех х=£а, удовлетворяющих
неравенству р (х, а) < 6) выполняется неравенство
Р (/(*)>
Обозначение 4.12 (2) принимает вид
Р = lim /(х).	(1)
х -> а
4.16]
§ 4.1. ОПРЕДЕЛЕНИЕ ПРЕДЕЛА
125
Точка р, как и в других случаях, называется пределом
функции f(x) при х —► а*).
б. В частности, если /?=/?, M=R, мы приходим к сле-
дующему определению:
Направление х —> а есть совокупность всех интервалов
{а—б, а 4-6), из которых выброшена центральная точка а.
Числовая функция f(x), определенная на числовой оси /?,
имеет в точке a£R предел р, если для любого е > 0 най-
дется такое б > 0, что из соотношений |х—а| < б, x£R,
х=£а вытекает неравенство
!/(*)—
Обозначение (1) сохраняется без изменения:
p = lim /(х).
х-> а
в. Примеры 4.13 и 4.14 а—в в действительности явля-
ются частными случаями определения 4.15 а. Проверим это
для примеров 4.14 а—в. На вещественной оси R можно
ввести метрику пространства R (3.35 5); тогда направления
х —*— оо и х—>--|-оо, описанные в 4.14 а, совпадут с на-
правлениями х—> — оо и х—»--]-оо (4.15 а), где —оо и оо
рассматриваются как точки метрического пространства R
(если учесть 3.35 е).
4.16.	Предел по направлению на подмноже-
стве.
а. Пусть имеется множество Е с выделенным в нем на-
правлением 5. Фиксируем множество GaE и рассмотрим
семейство множеств GA, где А—любое множество из на-
правления 5. Предположим, что все множества GA не пусты.
Тогда, поскольку пересечение этих множеств пусто (вместе
с пересечением всех Л^5), система их снова образует на-
правление, которое мы обозначим через GS. Пусть на мно-
жестве Е задана функция f(x) со значениями в метрическом
пространстве М. Если существует lim/(х), равный р, то,
s
очевидно, существует и lim/(x), также равный р. Но если
GS
*) В этом определении значение функции f(x) при х—а не иг-
рает роли. Функция f (х) может даже и не быть определенной в точке
х=а.
126
ГЛ. 4. ОБЩАЯ ТЕОРИЯ ПРЕДЕЛОВ
[4.16
известно, что существует lim/(x), то lim/(x) может и
os	s
не существовать. Установим следующее предложение,
дающее условие эквивалентности двух рассмотренных пре-
делов:
Лемма. Если множество G содержит некоторое множе-
ство В из направления S, то из существования lim / (х) сле-
OS
дует существование lim f (х) ( = lim	Если же множество G
S	GS
не содержит целиком никакого B^S, а метрическое простран-
ство М содержит хотябы две различные точки, положимр и q^=p,
то существует функция f(x) со значениями в М, для которой
iimf (х)—р, a lim/(x) не существует,
os	s
Доказательство. Пусть GzoB, B£S и lim/(x)=p.
os
Для задавного е > 0 найдем в направлении GS множество GA,
но всех точках которого выполняется неравенство
р(/(х), р)<е. Множество GA содержит множество ВА,
которое само есть или В, или А и потому входит в направ-
ление 5. На множестве ВА также выполняется неравенство
р(/(х), р)<е. Отсюда следует, что lim/(x) существует
s
(и равен р).
Пусть множество G не содержит целиком никакого B£S
и Н есть дополнение к G (до всего Е). Положим /(х)
равной р при х £ G и равной q при х£Н. Возьмем
е < -i- р (р, q). Если бы существовал lim/(x) = Z, то для
2	s
некоторого A £S мы имели бы р (/(х), t) < е при нсех х g А
Но оба множества GA и НА по условию не пусты; беря по
очереди х £ GA и х € НА, получаем, что должны быть вы-
полнены оба неравенства р (р, t) < е, р (q, t) < е, откуда
р (р, q)^p(p, 0 + p(?i 0 < 2е в противоречии с опреде-
лением е. Тем самым лемма полностью доказана.
б. Если функция /(х) определена только на множестве
G, то запись lim/(x) не имеет прямого смысла. В случае,
s
когда G содержит какое-либо из множеств направления 5,
мы полагаем по определению lim/(x) = lim/„(x), где
S	S
lim/£(x) — произвольное продолжение функции /(х) с G
4.16]	§ 4.1. ОПРЕДЕЛЕНИЕ ПРЕДЕЛА	127
на нее Е. По доказанному, результат имеет смысл и не
зависит от способа продолжения f(x) с G на Е.
В частности, предел последовательности ylt у%, ... ,уп, ...
(4.13) естественно определен не только тогда, когда по-
следовательность jj, у2, ... задана для всех индексов
1,2, ..., но и тогда, когда она задана лишь для всех ин-
дексов п, больших некоторого п0; при этом limj/„ не зави-
П -> 00
сит от значений ух, ..., уп<1, которые нам почему-либо за-
хотелось бы ввести в рассмотрение. Аналогично определение
lim f(x) (4.14) требует лишь знания значений функции f(x)
Х~> <ю
при х, больших какого-либо х0, и не зависит от значений
f(x) при х^х0. Таким же образом определение lim f(x)
х-+ а
(4.15) требует лишь знания значений функции f(x), как
говорят, только «вблизи точки х — а», т. е. в некотором
шаре р (х, а) < г, х^= а.
в. Вернемся к случаю, когда множество G, пересекаясь
с каждым из множеств A g 5, не содержит целиком ни од-
ного Как и выше, обозначим через /7дополнение к G
до всего Е. Рассмотрим семейство HS множеств НА, где А
пробегает S. Так как в рассматриваемом случае никакое НА
не пусто, система HS также образует направление и мы
можем говорить о существовании или несуществовании
lim/(x). Если существует lim/(x)=p, то существуют
HS	s
lim/(x) и lim/(x), также равные р. Однако пример, приве-
os	HS
денный во второй части доказательства леммы а, показы-
вает, что из существования lim f(x) и lim f(x) не следует
GS	HS
существование lim/(x).
s
Теорема. Если существуют lim/(x) и lim/(x) и эти
GS	HS
пределы совпадают, то существует и lim/(x).
s
Доказательство. Пусть p = lim/(x) = lim/(x). Для
GS	HS
заданного е > 0 найдем А и В в 5 так, чтобы в точках
множеств GA и НВ выполнялось неравенство
Р(/(х),р)<£.	(1)
128
ГЛ. 4. ОБЩАЯ ТЕОРИЯ ПРЕДЕЛОВ	[4.17
Из двух множеств А, В одно вложено в другое, напри-
мер, АсВ. Тогда неравенство (1) заведомо выполняется в
точках множества GA и в точках множества НА, следова-
тельно, и в точках множества А= GA-\- НА. Так как е>0
произвольно, то lim/(x)=p, что и утверждалось.
4.17.	Взаимно однозначные отображения
множества Е и соответствующие преобразо-
вания пределов.
а.	Пусть множество Е отображено взаимно однозначно
на множество F, так что каждому х£Е соответствует не-
которое у = со (х) € F. Пусть на множестве Е задано на-
правление 5 из множеств АсЕ. Пусть BcF есть образ
множества А при отображении со. Совокупность Т всех мно-
жеств В образует направление на F, поскольку из свойств
взаимно однозначного отображения со следует, что множе-
ства В, так же как и множества А, вложены друг в друга
и пересечение их пусто. Пусть, далее, на множестве Е
задана функция f(x) с значениями в метрическом простран-
стве Определим на множестве F функцию g(y) формулой
g(y)=g(®(x))=f(x).	(1)
Теорема. Функция g(y) имеет предел по направлению Т
тогда и только тогда, когда функция /(х) имеет предел по
направлению S, и при этом
liin/(x) =
S	т
Доказательство. Пусть существует	=р.
т
Для заданного е > 0 найдется множество В £Т, для кото-
рого р(^(у), р) < е при у£В. На соответствующем мно-
жестве мы имеем
Р p)=Q (*)), р) < е,
так что jD = lim/(x). В силу симметрии построения верно
s
и обратное, что и завершает доказательство.
б.	Из соображений 4.16 б вытекает, что предыдущий
результат сохраняется, если взаимно однозначное отобра-
жение ю определено не на всем Е, а только на каком-либо
подмножестве
4.18]
§4.1. ОПРЕДЕЛЕНИЕ ПРЕДЕЛА
129
Рассмотрим два примера.
в.	Пусть Е есть полуось	и _у =—х есть
отображение полуоси Е на полуось F= < — а}. На Е
выберем направление х —► оо. Соответствующее направление
на F, очевидно, есть направление у —>—оо. В силу а пре-
делы liraf(x) и Ига/(—у) существуют или не существуют
X -> оо	У-+— СО
одновременно, и если они существуют, то равны:
lira /(х)= lira /(—у).
г.	Пусть Е есть отрезок |х—х0]^1 с выброшенной
точкой х0 и F есть множество 1. Формула _у =—5—-
X Xq
определяет взаимно однозначное отображение Е на F. На-
правлению х —»х0 на отрезке Е отвечает направление
|_у | —»- оо на множестве F. В силу а пределы lira f(y) и
I у I -»“
ига/(----) существуют или не существуют одновременно
х-+хл V* хо/
и, если существуют, равны:
lira /(j) = lim /f-L-Y
| у I -> OS	X-+ x„	*0 /
4.18.	Определение предела, данное в 4.12, зависит, есте-
ственно, от метрики, заданной на пространстве М. Однако
при замене метрики р (х, у) гомеоморфной метрикой г (х, у)
(3.34 в) соотношение
lim/(x)=p	(1)
s
сохраняется для метрики г (х, у), если оно было выполнено
для метрики р (х, у). Для доказательства мы используем
критерий гомеоморфности, указанный в 3.34 г. Пусть соот-
ношение (1) выполнено в метрике р и метрика г гомеоморфна
метрике р. Пусть задано е > 0; мы должны найти такое
во всех точках которого выполняется неравенство
r(f(x), р) < е.
(2)
В силу критерия 3.34 г по заданному е>0 мы можем
найти такое 6 > 0, что из р(р, у) < 6 следует г(р,у)< е.
По найденному 6 возьмем А £ S так, чтобы при х £ А иметь
Р (Дх), Р) < б-
130
ГЛ. 4. ОБЩАЯ ТЕОРИЯ ПРЕДЕЛОВ
[4.19
Но тогда при х £ А выполняется и (2), что нам и нужно.
Очевидно, что верно и обратное: если соотношение (2)
выполнено в метрике г, а метрика р гомеоморфна метрике г,
то соотношение (1) выполнено и в метрике р.
4.19.	Критерий Коши. Критерий Коши существова-
ния предела числовой последовательности, приведенный
в 3.72 а, может быть перенесен на общий случай в пред-
положении, что функция f(x) принимает свои значения
в полном пространстве.
Теорема. Функция f(x), определенная на множестве Е
с выделенным направлением S, принимающая свои значения
в полном метрическом пространстве Л1, имеет предел по
направлению S тогда и только тогда, когда выполняется
критерий Коши-, для любого е > 0 существует такое множе-
ство В gS, что
P[/U'). /(^")]<е	(1)
для всех х'£В, х"£В.
Доказательство. Пусть выполнено условие крите-
рия Коши. Рассмотрим в пространстве Л4 совокупность всех
множеств /(Д), где Д^^. (Множество/(Д) есть множество
всех значений функции f(x), принимаемых ею на множе-
стве Д.) Так как’множества Д£б’ образуют вложенную
систему, то и множества /(Д) образуют вложенную систему
(на М). Как видно из неравенства (1), среди множеств /(Д)
имеются множества как угодно малого диаметра. Поэтому,
в силу полноты пространства М и леммы 3.74 а, в М имеется
такая точка р, что в любом шаре V, (р) = {у £ М: р (у,р) < е}
содержится целиком одно из множеств f(B), B£S, так что
для всех х € В мы имеем
Р (/(*), р)<е.
Но это в означает, что функция /(х) имеет по направ-
лению 5 предел, равный р.
Обратное утверждение не требует предположения о пол-
ноте пространства М. Пусть f(x) имеет по направлению 6’
предел, равный р. Найдем для заданного е > 0 множество
В «S’, для всех точек которого выполнено неравенство
р[а/(х)] c-J;
4.23]
§ 4.2. ОБЩИЕ ТЕОРЕМЫ О ПРЕДЕЛАХ
131
тогда для любых х' и х" из В имеем
Р [/(-*'), /(И] СР [Р, /(*')] + Р [₽,/(*")] Се,
что нам и требуется.
§ 4.2.	Общие теоремы о пределах
Пусть Е— снова произвольное множество с выделенным
в нем направлением 5, и пусть f(x) — функция, заданная
на Е, со -значениями в метрическом пространстве М.
4.21.	Если функция f(x) постоянна на Е, т. е. во всех
точках множества Е принимает одно и то же значение
р£М, то ее предел по направлению S существует и равен р.
Очевидно, требуемое неравенство 4.12 (1) выполняется
в данном случае при любом е > 0 на каждом A g S.
4.22.	Функция f(x) может иметь по направлению S лишь
единственный предел.
Действительно, пусть
р = lim/(x) ft М и q = gAl.
s	s
Для заданного e > 0 найдем множество 4cS, во всех точ-
ках которого выполняется неравенство
Р (/(*), Р) С г,	(1)
и множество BczS, во всех точках которого выполняется
неравенство
P(/W, ?)С8.	(2)
Пусть, например, АсВ. Тогда во всех точках множества А
выполняются оба неравенства (1)и(2). Пусть х£А — любая
точка, тогда из (1) и (2) следует, что
Р(Р, ?)^Р(/(-«),р) + р(/(х), ?)^2е.
Поскольку е > 0 произвольно мало, мы имеем р (р, q) = О,
т. е. p = q, что и утверждалось.
4.23.	Функция f(x) называется асимптотически принад-
лежащей множеству Gc М, если существует множество
во всех точках которого f(x) принадлежит 6.
132	ГЛ. 4. ОБЩАЯ ТЕОРИЯ ПРЕДЕЛОВ	(4.31
Теорема. Если lim/(х)=р и множество GcM содер-
s
жит некоторый открытый шар с центром в точке р, то функ-
ция f(x) асимптотически принадлежит G.
Доказательство. Пусть G содержит шар V =
—	Р) < еЬ Найдем множество во всех точках
которого выполняется неравенство р (/(х), р) < е. Это озна-
чает, что во всех точках множества А выполнено и включе-
ние f(x)^VcG, что и требуется.
§ 4.3.	Пределы числовых функций
4.31.	а. В §§ 4.3—4.6 мы будем строить теорию пре-
делов для числовых функций, т. е. функций f(x), принима-
ющих свои значения на числовой оси (расширенной или нет).
Специфика таких функций определяется наличием на число-
вой оси метрики, порядка и арифметических операций. Соб-
ственно, мы знаем там даже две разные метрики: обычную
метрику р (х, у) = |х—у |, действующую в области R конеч-
ных чисел, и метрику г(х,у) (3.35 д), действующую в рас-
ширенной области R. Но в области R эти метрики гомео-
. морфны (3.35 д); отсюда следует (4.18), что существование
или несуществование конечного предела
p = lim/(x)
s
не зависит от того, какая из метрик, р или г, использована
в определении этого предела.
б.	Пусть на множестве Е заданы две функции: /(х) и
g(x) со значениями в R. Мы пишем f (x)^g(x), если для
любого х0£Е выполняется неравенство/(х0) ^^(х0). Функ-
ция /(х) называется ограниченной сверху на множестве Е,
если существует такое конечное число С, что для всех х£Е
выполняется неравенство /(х)^С. Функция /(х) называется
ограниченной снизу на Е, если существует такое конечное
число С, что для всех х С Е выполняется неравенство / (х) С.
Функция /(х) называется ограниченной с обеих сторон (или
ограниченной по модулю, или просто ограниченной), если су-
ществует такое конечное число С, что для всех х g Е выпол-
няется неравенство |/(х) | С.
В каждой точке х0£Е, где обе функции /(х) и g(x)
конечны, мы определяем сумму /(х)+^(х) как результат
4.34]
§ 4.3. ПРЕДЕЛЫ ЧИСЛОВЫХ ФУНКЦИЙ
133
сложения соответствующих значений f(x0) и g(x0). Анало-
гично определяются вычитание, умножение и деление; по-
следнее (для данной точки х0) возможно, лишь если знаме-
натель в этой точке отличен от нуля.
4.32.	В развитие определения 4.23 будем называть чис-
ловую функцию /(х)
(а) неотрицательной (положительной) по направлению S,
(б) ограниченной (сверху, снизу) по направлению S,
(в) бесконечно малой по направлению S,
(г) положительной бесконечно большой по направлению S,
(д) отрицательной бесконечно большой по направлению S,
если, соответственно,
(а)	существует множество A g 5, на котором функция
f(x) неотрицательна (положительна);
(б)	существует множество В £ 5, на котором функция
f(x) ограничена (сверху, снизу); пишут /(х) = О(1);
(в)	lim/(x) = 0 (т. е. для любого е>0 существует мно-
s
жество B£S, на котором |/(х) | < е); пишут /(х) = о(1);
(г)	для любого C£R существует множество B£S, на
котором" f(x) > С; в этом случае будем писать lim f(x) = оо;
s
(д)	для любого С £R существует множество В£S, на
котором f (х) < С; в этом случае будем писать lim f(x) = —оо.
s
4.33.	Соотношение lim/(x)=p равносильно соотношению
s
lim[/(x)—р] = 0.
Это следует из определений предела и расстояния на чис-
ловой оси R:
р(а, Ь) = \а—&|.
4.34.	а. Лемма. Пусть lim f(x)—p; для любого е>0
s
существует такое A£S, во всех точках которого выполня-
ются неравенства
|/(х)—Р|< 8, если р конечно,
/(х) > если р— -(-оо,
/(х) <--------—, если р — — оо.
134
ГЛ. 4. ОБЩАЯ ТЕОРИЯ ПРЕДЕЛОВ
[4.34
Утверждение леммы есть непосредственное следствие
теоремй 4.33 с учетом рассматриваемой метрики (на R и
на R).
б.	Пусть р у=0 и конечно; тогда можно найти такое
в > О, что интервал (р—е, р~Ье) не содержит точки 0 и
состоит тем самым из чисел того же знака, что и само р.
Отсюда:
Если функция f(x) имеет по направлению S предел р > О,
то f(x) положительна по направлению 5; если f(x) имеет
по направлению S предел < 0, то f (х) отрицательна по
направлению S.
Результат верен также для р — оо и р = —оо, что не-
посредственно видно из а.
в.	Следующее предложение представляет собой своего
рода обращение предложения б:
Если f(x) неотрицательна по направлению S и имеет
предел р, то р^О.
Действительно, если бы было р < 0, то по свойству а
существовало бы множество	на котором f(x) < 0.
С другой стороны, так как f(x) неотрицательна по направ-
лению У, существует множество B£S, на котором f(x) 0.
Поскольку АВ не пусто, получаем противоречие.
г.	Подчеркнем, что при заключении «от предела» (б)
сохраняется знак > 0 (или < 0, но без равенства), а при
заключении «к пределу» (в) сохраняется знак 0 (или 0,
с равенством). Если известно только, что р 0, то о знаке
функции /(х) на множествах нельзя делать никаких
заключений, она может принимать как положительные, так
и отрицательные значения. Если известно, что /(х) >0 на
некоторых А £ У, то предел р может быть положительным,
а может быть и нулем.
д.	Будем говорить, что/(x)^Cg(x) (/(х) < g(x)) по на-
правлению S, если разность £г(х)—f (х) неотрицательна
(положительна) по направлению 5.
е.	Если f(x) и g(x) имеют по направлению S соответ-
ственно пределы р и q и f(x)^.g(x) по направлению S, то
p^q. (Следует из определения и из в.)
ж.	Если f(x) и g(x) имеют пределы р и q и р <q, то
f(x)<g(x) по направлению S. (Следует из б.)
4.36]
§ 4.3. ПРЕДЕЛЫ ЧИСЛОВЫХ ФУНКЦИЙ
135
з.	Если f (х)	g(х)	h (х) по направлению S и f(x) и
h (х) имеют одинаковый предел р = lim f(x) — lim h (x), то g(x)
s s
также имеет предел no направлению S, равный p.
Достаточно рассмотреть случай р — 0, заменив в против-
ном случае /(х) и g(x) на /(х)—р и g(x)—p (4.33). Для
заданного е > 0 найдем множество А £ 5, на котором
/(х)1<е и |Л(х)|<е; очевидно, на множестве А также
^(х)|<е, что и требуется.
4.35.	а. Если f(x) и g(x) ограничены по направлению S,
то f (х) + g(x) и f(x)-g(x) также ограничены по направле-
нию S.
Действительно, пусть на множестве Л £5 выполняется
неравенство |/(x)|<ZC1 и на множестве BgS выполняется
неравенство |^(х)|<СС2. Если, например, Лез В, то для всех
х£А выполняются неравенства
|/(х) + 5'(х)|^С14-С2 и |/(x)g-(x)KC1Ca,
что нам и требуется.
б.	Если f(x) и g(x)— бесконечно малые по направлению S,
то f(x) + g(x)— также бесконечно малая по направлению S.
Пусть для заданного е > 0 мы нашли множества Л £ S
и B£S, на которых соответственно |/(х)|<-|-, |g-(x)| <
<	! если, например, АсВ, то для всех х£Л
|/(х) + ^(х)|<е,
что и требуется.
в.	Если f(x) ограничена по направлению S, a g(x)—
бесконечно малая по направлению S, то f(x)g(x) — беско-
нечно малая по направлению S.
Действительно, пусть на множестве Л^5 выполняется
неравенство |/(х)|^С и для заданного е > 0 мы нашли
множество В £ 5, на котором выполняется неравенство
| g(x) |	. На АВ выполняется неравенство |/(х)^(х) | е,
что нам и требуется.
4.36.	а. Если \imf(x)—p, Umg(x) — q, то функция
S	S
f(x) ~[£(х) имеет на S предел, равный p-\-q.
136
ГЛ. 4. ОБЩАЯ ТЕОРИЯ ПРЕДЕЛОВ
[4.37
Действительно,	f(x) + g(x)—(p + q) = (f(x) — />) +
+(^(х)—q), как сумма бесконечно малых, есть бесконечно
малая (4.35 б).
б.	Если lmf(x)=p, \img(x) = q, то функция f(x)g(x)
s	s
имеет на S предел, равный pq.
Действительно,	f(x)g(x) —pq=fg—fq+fq—pq~
—f(g—q)-\~q(f—P)’, каждое из слагаемых есть бесконечно
малая по 4.35в.
в.	Если lim/(x)=p^0, то тг-с ограничена по направ-
s	I 'х>
лению S.
Действительно, найдем множество А £ S, на котором
|/(х)	(4.34 а); для мы имеем	что и
требуется.
1
г.	Если lim/(x) — р^О, то -z-т—имеет предел по направ-
s	IW
лению S, равный —.
Действительно, ~—Р) есть бесконеч-
но малая по в, 4.33 и 4.35 в.
д.	Если lim^(x) — q, Yimf(x)—p^0, то —~ имеет пре-
s.	s	I \х)
дел по направлению S, равный .
Это следствие биг.
4.37.	а- Если lim/(x) = 0, то limr-i—=оо, и обратно',
s	s I / WI
если lim|g-(x)] = оо, то lim-i- =O.
s	s SW
Заключение вытекает из равносильности неравенств
1/(х)|<еи ^>1.
б.	Если lim/(x) = oo, то lim [—/(х)]=—оо. Если
S	S
lim/(x) = oo и lim^(x)=p >0, то \mf(x)g(x) = ca\ если
s	s	s
же lim g(х) — р < О, то lim/(х) g(х) = — оо. Это—непосред-
s	s
ственные следствия определений 4.32 (г), (д).
4.38]
§ 4.3. ПРЕДЕЛЫ ЧИСЛОВЫХ ФУНКЦИЙ
137
4.38.	Определение. Пусть f(x) и g(x)—две функции
на множестве Е с направлением S. Функция f(x) называется
бесконечно малой по сравнению с g(x) (или, если g'(x) сама
есть бесконечно малая, бесконечно малой высшего порядка
по сравнению с g(x)), если
lim^==0.
s S(x)
В этом случае пишут
/(*) = о (g(x)).
Функция f(x) называется бесконечно большой по сравнению
с g(x) (или, если g(x) сама есть бесконечно большая, бес-
конечно большой высшего порядка по сравнению с g(x)),
если
f(x)
g(x)
= оо.
lim
s
Функции f(x) и g(x) называются эквивалентными (по на-
правлению 5), если
s SH
а.	Из 4.37 а следует: если f(x)—бесконечно малая
по сравнению с g(x), то g(x)— бесконечно большая по
сравнению с f(x).
б.	Если f(x) и g(x) эквивалентны и существует предел
s h (*)
где h(x)—некоторая функция на Е, то существует и предел
s М*)
который также равен L. Действительно,
f(x) = g(x) f (х)__,
й(х) h(x)g(x)
по 4.36 б. Таким образом, при вычислении предела отношений
числитель {а также, конечно, и знаменатель) можно заменять
эквивалентной функцией,
138
ГЛ. 4. ОБЩАЯ ТЕОРИЯ ПРЕДЕЛОВ
(4.39
4.39.	Символ Е.
а.	Символ Е обозначает функцию, имеющую (по данному
направлению) предел 1. (Более правильным было бы обозна-
чение Е (х), но для сокращения аргумент к не пишут.)
Функцию Е, в соответствии с 4.23, будем называть асимп-
тотической единицей. Очевидно, произведение и частное двух
асимптотических единиц есть снова асимптотическая единица.
б.	Лемма. Если lim«(x) = 0, то при любом натураль-
s
ном р
(1 +«(х)И= 1 +рЕи (х).	(1)
Доказательство. По формуле Ньютона
(1 + «(х))Р = 1 +ри (х) +	«2 (х) + ... + up (х) =
= 1 +ри(х) [1 +^и(х) + ... +-1 и?-1 (х)] =
= 1 -\-ри(х)-Е,
поскольку предел выражения в скобке равен 1 (4.36 а, б).
в.	Асимптотические единицы часто приносят пользу при
вычислении пределов. Пусть, например, надо найти
Iim (1+х)Р-(1+х+х2)?
х-> 0 (1 +2хУ-(1-2х+х»Г
(р, q, г, s — натуральные числа).
По определению и лемме б мы имеем
(1 4-хУ’= 1 -(-рхЕг; хх2= х х) = хЕ2;
(1 + х + х2)? = (1 + xErf = 1 + qxE2E3 = 1 + qxEit
(1 + 2x)r= 1 + 2xr£s, 2x—x3 = 2x ^1—у x2^ = 2xEe,
(1 — 2x + x3)s = (l — 2xfe)s = 1 — 2xsEeE4 = 1 —2xsEe;
(l + x)F-(l+x+x2)? _ (1+рх£г)-(1+9х£4) _
(1 +2x)r—(1— 2x4-x3)-'	(1 +2xr£5)—(1—2xs£8)
t pE-L—gEj	p—q
2r£6 + 2s£8	2(r+s)’
и вычисление закончено.
г.	Предел рациональной функции R(x) при
х —> + оо. Рассмотрим рациональную функцию
п / а<>х,п+а1хгп-1 + ...+аг„
W Ьох" + М"-1+---+^
ао=АО, Ьо^О.
4-41)	§ 4.4. ПРЕДЕЛЬНЫЕ ТОЧКИ ФУНКЦИИ
139
При | х | —> оо мы имеем
„ ут ( 1 । °1 1 ,	, Д/л 1
I “Г	“Г •  • Г т I vtnp п
\ Др х a,Q х j аох Oq т—пр
+ b°X'‘E2 ~b°
\ UQ л	"о X, /
Отсюда, в силу правил 4.36—4.37, если т^п,
| 0 при т<.п,
lim /? (х) = { Qo
|xl -> а>	| у- при т~п.
При от > п функция R (х) имеет бесконечный предел того
или иного знака, в зависимости от выбранного направления
(х —+ + оо или —оо), от знака ~ и от четности или нечет-
ко
ности величины от—л. Мы предоставляем читателю разоб-
раться в возникающих здесь возможностях.
§ 4.4.	Предельные точки функции
4.41.	Рассмотрим предельное поведение числовой функ-
ции f (х) со значениями в расширенной области вещественных
чисел R (§ 1.9). Для каждого множества положим
az = inf {/(х):х£ Д}, bA = sup {f(x):x € А}-,
в области R обе указанные величины существуют и аА ЬА.
Так как всякие два множества А и В системы S вложены
друг в друга, то и всякие два отрезка [ал, Л>л], [ов, ftB]
вложены один в другой. Положим
£ = 5ирал, 1]=1п!£л;	(1)
Ле5	Ле$
в силу обобщенного принципа Кантора (1.94) и
[L т)]= П [«л. ^1-	(2)
лез
Число S g R называется нижней предельной точкой (или ниж-
ним пределом) функции f(x) по направлению S, число т] С /?
называется верхней предельной точкой (или верхним пределом)
функции f(x) по направлению S; это записывается так:
g=lim/(x), T]=lim/(x).
140
ГЛ. 4. ОБЩАЯ ТЕОРИЙ ПРЕДЕЛОВ
(4.42
4.42.	Из равенства (2) (4.41) можно вывести следующий
результат: при любом е > 0 существует такое множество
A£S, что
аА = inf {f(x):x £А} > В—е,
fez = sup{/(x):xCX}<r] + e.
(Если £ принадлежит/?—R, то полагаем £ — е = £; анало-
гично т)-|-е = 'П, если rjg/?— /?.)
4.43.	Как следствие получаем: если | — т], то функция f(x)
имеет предел по направлению S, равный = т); если % и т]
конечны и £ = T], то £ = 7] есть конечный предел функции f(x)
по направлению S.
4.44.	Обратно, если функция f(x) имеет предел по на-
правлению S, равный р, то отрезок [£, ?)] = JJ [ал, при-
AtS
водится к единственной точке р, так что Е, = т]=р.
4.45.	Для выяснения смысла введенных понятий дадим
еще следующее определение (ср. определение 3.41):
Число y£R называется предельной точкой функции f(x)
по направлению S', если для любого е > 0 и для любого
А £ S’ существует такая точка х £ А, что
|/(х)—у|< е, если у конечно;
f(x) >	, если у = оо,
f(x) < ——, если- у = — оо.
Если функция f(x) имеет по управлению 5 предел р,
то р есть предельная точка функции f(x) по направлению S’,
однако обратное, вообще говоря, не имеет места.
4.46.	Покажем, что для любой предельной точки y£R
функции f(x) выполняются неравенства £ ^у ^т], где £ и
определены в 4.41.
Действительно, если у есть предельная точка функции
f(x) по направлению S, то для любого А С S’
аА = inf {/(х):х G 4} sgTy < sup {f(x): x £ A} = bA
и, следовательно, J€П [“л,	=	*1]-
4.51]	§ 4.5. ФУНКЦИИ, НЕУБЫВАЮЩИЕ ПО НАПРАВЛЕНИЮ 141
С другой стороны, сами точки £ и т) всегда суть предель-
ные точки функции f(x) по направлению S, так что опре-
деление 4.41 согласуется с 4.45. Проверим это утверждение
для точки g. Если | есть конечное число, то для заданного
е>0 существует такое Ло£5, что — ад0 < у , и,
следовательно, для каждого Дс:Л0 мы имеем
откуда также — аА < —. Таккак аА = inf {/(х):х £ Л},
то существует точка х£А, для которой 0^/(х)— аА < ~
и, следовательно,
|/(х)-£|<е.
Для каждого ВоЛ0 также имеется такая точка х, которую
можно взять из множества Ао. Таким образом, Е есть пре-
дельная точка функции /(х) по направлению S. Доказатель-
ство для случая, когда	— /?, а также доказательство
аналогичного утверждения для точки т] проводятся по той
же схеме.
4.47.	Следствие. Множество всех предельных точек
функции fix) на расширенной прямой не пусто, и его точными
[границами являются точки £ = lim/(x) и T] = lim/(x).
—	s
4.48.	Если функция /(х) имеет предел по направлению S,
равный р, то, как мы видели, | = т]=р; в этом и только
в этом случае число р есть единственная предельная точка
функции /(х) по направлению 5.
§ 4.5.	Функции, неубывающие по направлению
Числовая последовательность ylt у2, ..., у,„ ... назы-
вается неубывающей, если ут ...	• • •
Сформулируем аналогичное определение для числовой
функции у=/(х), заданной на произвольном множестве Е
с выделенным направлением 5.
4.51.	Определение. Числовая функция /(х) назы-
вается неубывающей по направлению S, если для любых
множеств А С 5, В £ S из того, что В Z)A, следует неравенство
sup {f(x):x£B — A} ^inf {/(х):х £ Л}.	(1)
142
ГЛ. 4. ОБЩАЯ ТЕОРИЯ ПРЕДЕЛОВ
[4.52
4.52.	Примеры.
а.	Если f={l, 2, ...}, то функция y=f(x) есть чис-
ловая последовательность уг, _у2, ... Пусть, как обычно,
направление 5 на Е задано множествами Л„ = {п, п-\-1, .. .},
л=1, 2, .. . Покажем, что в этом случае определение 4.51
совпадает с нашим исходным определением неубывающей
последовательности.
Пусть последовательность /„—неубывающая в смысле
определения 4.51. Для множеств Ап = {п-ф 1, ...} и Вп —
= {/z, zz-J- 1, ...} мы имеем Вп — /!„={«}, так что условие
4.51 (1) влечет
/„<inf {fp-.P > п} </„+1.
Обратно, из выполнения неравенств/х^/2^    ^/„^- • •
следует для любого А = {/,„ fn+l, . ..}££ и АсВ =
= К, Л+1, -	что sup{/(x):xGB — А} =
= sup{/ft, ...,/, ,_х} =/„_!</„ = inf {/(х):х£ А}, так что
последовательность /(х)— неубывающая в смысле опреде-
ления 4.51.
б.	Если E = R* есть вещественная полуось а^.х с на-
правлением S, определенным подмножествами Ar= {х £R„:х~^
то функция /(х) является неубывающей при х—>оо
тогда и только тогда, когда из а ^.у < z следует f(y)
Действительно, пусть функция /(х) является неубываю-
щей в смысле определения 4.51. Тогда для множеств Ау и
Az, Ayzz>Az, т. е. при у < z, мы имеем
/(j)<sup {/(x):j<x <4<inf {/(х):х> 2} </(£)•
Обратно, если для любых у < z из R% мы имеем f(y)
то функция/(х) — неубывающая в смысле определения 4.51,
так как если х' £ А—Az (т. е. j^x' <z) и х" £AZ (т. е.
х"^г), то /(x')<f/(x") и по 1.626
sup {/ (х'): х' £ {Ау — 4г)} < inf {/ (х"): х" б Az}.
4.53.	Теорема. Если функция f (х) не убывает и огра-
ничена сверху по направлению S, то она обладает пределом
по направлению S:lim/(x) = sup {/(х):х б А\, где XgS—
s
любое множество, на котором /(х) ограничена сверху.
4.54]	§ 4.5. ФУНКЦИИ, НЕУБЫВАЮЩИЕ ПО НАПРАВЛЕНИЮ 143
Доказательство. Пусть fix) ограничена сверху на
множестве Д£5. Положим р = sup {fix)'.x£A}. Для задан-
ного е > 0 найдем точку х0 £ А, для которой
Р — £<f(x0)^p.
Так как пересечение всех множеств системы 5 пусто, то
существует множество В £ $, не содержащее точки ха. Оче-
видно, из двух возможных включений А^В, В^>А в данном
случае реализуется первое, А^В. Так как fix) не убывает
по направлению S, то
inf {/(х):х£В}> sup {f(x):x^A — B}^f(x0) >р — е.
С другой стороны, из BczA следует
sup {f (х): х £ В} sup {f (х): х £ Д} =р
(см. 1.62 а). Таким образом, всюду на В
p — e.<f(x)^p,
что и завершает доказательство.
Для неубывающей функции fix), имеющей предел р по
направлению S, используется запись fix)/ р или просто
f(x)Sp.	s
4.54.	Числовая функция fix) называется невоэрастающей
по направлению S, если для любых множеств А £ 5, B£S
из того, что B:dA, следует неравенство
inf {f(x):x£B—Д}	sup {f(x):x € А}.
Для невозрастающих функций справедлива теорема, анало-
гичная 4.53'.
Теорема. Если функция fix) не возрастает и ограни-
чена снизу по направлению S, то она обладает пределом,
по направлению S:
р = lim fix) = inf {f(x):x £ A},
s
где A£S — любое множество, на котором функция fix)
ограничена снизу.
Эта теорема немедленно получается из теоремы 4.53,
если заметить, что в условиях нашей теоремы функция
—fix) не убывает и ограничена сверху на направлении $
и что если p = inf {/(х):х£ Д}, то по 1.61
sup {— fix): х б Д} = — р.
144
ГЛ. 4. ОБЩАЯ ТЕОРИЯ ПРЕДЕЛОВ
[4.55
Для невозрастающей функции f(x), имеющей предел р,
используется запись f(x)\p или просто f(x)\p.
s
4.55.	Теорема. Если функция f(x) на направлении S
не убывает и не ограничена сверху, то
lim f(x) — оо
s
(см. 4.32 (г)).
Действительно, пусть задано число С; так как функция
f(x) по направлению S не ограничена сверху, то в любом
множестве В£ S найдется точка х0 £ В, в которой f (х) > С.
Фиксируя В, найдем на направлении <9 множество А с: В, не'
содержащее точки х0. По условию
C^sup {f(x):x£B—{/(х):х£/1};
следовательно, во всех точках множества А выполняется
неравенство
и наша теорема доказана.
4.56.	Аналогичный факт имеет место для функции f(x),
невозрастающей по направлению «S’:
Теорема. Если числовая функция f(x) на направле-
нии S не возрастает и не ограничена снизу, то lira f(x) = — со.
s
Доказательство сводится к применению 4.55 к функции
-/(*)•
§ 4.6.	Основные теоремы о числовых последовательностях
4.61.	Мы применим здесь общую теорию §§ 4.3—4.5
к случаю числовых последовательностей. Определение пре-
дела числовой последовательности мы дали еще в 3.32 (а).
Напомним его здесь. Числовая последовательность {y,J =
— {ji>  • , Уп<   •} (Уп 6 R) называется сходящейся к числу
р /?, если для каждого е > 0 существует такое натураль-
ное N, что при всех n~^N выполняется неравенство
|Р—К1<е-
4.63]	§ 4.6. ТЕОРЕМЫ О ПОСЛЕДОВАТЕЛЬНОСТЯХ	145
Число р в этом случае называется пределом последова-
тельности уп, что записывается в форме
Р =
Если числа уп рассматривать как точки расширенного
пространства R, то определение конечного предела остается
таким же, но становятся возможными и бесконечные пре-
делы. Последовательность	уп, ..., сходящаяся
в пространстве R к +оо, является в пространстве R рас-
ходящейся; в отличие от других расходящихся последова-
тельностей мы будем такую последовательность называть
расходящейся к 4-°°- Аналогично определяется последова-
тельность, расходящаяся к —оо.
4.62.	Критерий Коши 4.19 для числовых последо-
вательностей совпадает с приведенным в 3.72:
Последовательность чисел хх, .. ., хп, .. . имеет (конечный)
предел тогда и только тогда, когда для любого е > О суще-
ствует такое число N, что при всех mZ^N, n^N
\xm~xn\<E.
4.63.	а. В соответствии с определением 4.32 (б) после-
довательность хъ ..., хп, ... называется ограниченной
сверху при п—>оо (снизу, просто ограниченной), если суще-
ствуют число С и такое число N, что для всех n^N вы-
полняется неравенство хп-^С(хп~^С, |х„|^С). Впрочем,
условию	не удовлетворяет только конечное число
натуральных чисел от 1 до N; поскольку множество чисел
хь . .., Хдг ограничено, в условии ограниченности последо-
вательности величину N можно не упоминать; можно опу-
скать также слова «при п—>-оо».
б.	Далее, в соответствии с определениями 4.51 и 4.54
последовательность хъ х2, ... называется неубывающей
(невозрастающей) при п—>-оо, если существует такое N,
что при выполняется неравенство х„+1^х„ (х„+1^х„).
в.	В силу теоремы 4.53 всякая ограниченная сверху
и неубывающая последовательность хг, х2, ... имеет при
п—->-оо предел. Аналогично (4.54) имеет предел последова-
тельность Хр х2, ..., ограниченная снизу и невозрастающая.
146
ГЛ. 4. ОБЩАЯ ТЕОРИЯ ПРЕДЕЛОВ
[4.63
Если же неубывающая (невозрастающая) последова-
тельность не является ограниченной сверху (снизу), то она
стремится к оо (—оо) (4.55, 4.56).
г.	Пример. Рассмотрим последовательность чисел
«.-(1+4)" (”=1.2....);
покажем, что эта последовательность имеет при п —* оо
конечный предел. Действительно, по формуле бинома Ньютона
«.-(l+D’-l + l+s-^TT^+ff-" Г -+ =
=i+i+4('-4)+i(i-4)(i-4)+- •
'с возрастанием п в этой сумме увеличиваются й число сла-
гаемых, и каждое слагаемое, так что числа ип возрастают.
k
Далее, заменяя 1—— на 1, получаем
ип< 1 + 1+й' + ^+-- •+i<
1 —!_
II	1	2п+1
<1+1+- + -+.. .+- = 1+-^<1+2=3,
т
так что последовательность ип ограничена сверху. Приме-
няя в, убеждаемся в существовании предела последователь-
ности и„. Этот предел обозначают буквой е:
е = lim
Из сказанного ясно, что 2<е<(3. Более точное вычис-
ление показывает, что е = 2,71828... Можно доказать, что
число е иррационально (см. задачу 14 к гл. 8), и даже что
оно трансцендентно (теорема Эрмита *)).
*) См., например, Г. М. Фихтенгольц, Курс дифференциаль-
ного и интегрального исчисления, т. 2, п. 319, стр. 146, Гостехиз-
дат, 1966.
4.65]	§ 4.6. ТЕОРЕМЫ О ПОСЛЕДОВАТЕЛЬНОСТЯХ	147
4.64.	Приведем еще определения и факты, относящиеся
к предельным точкам числовых последовательностей. В соот-
ветствии с определением 4.45 точка называется пре-
дельной точкой последовательности хп, если для любого
е>0 и любого N найдется номер n~^N такой, что
| хп—11 < е, если g конечно,
х„>1/е, если £ = оо,
хп < — 1/е, если | = —оо.
Для каждого п положим
=	х„+1, . ..}ея,
Z>„ = sup{x„, х„+1,
Согласно 4.41 отрезки [п„, />„] расширенной числовой оси
образуют вложенную последовательность с пересечением
т)], где | = sup ап, T] = inf Ьп. Все предельные точки по-
следовательности хп содержатся в отрезке [|, т)], причем
сами точки | и т] всегда являются предельными и назы-
ваются нижним и верхним пределом последовательности;
это обозначают так:
| = lim хп, т) = lim хп.
Если В = Л> последовательность хп имеет предел
Если |=т] и конечно, то последовательность хп имеет ко-
нечный предел £ = т]. Обратно, если последовательность хп
имеет предел р, то £ = q = р и последовательность хп
имеет число р своей единственной предельной точкой.
4.65.	Предел последовательности и предел
функции. Если функция f{t), определенная при
имеет при t —> оо предел, скажем lim/(/)=/?, то последо-
со
вательность чисел
К=/(«) (П — целые, большие Zo)
имеет тот же предел р {4.16 а).
Обратное заключение о существовании предела функции
f(x), определенной при х^ х0, при наличии предела после-
довательности f{n) уже несправедливо. Так, функция
148
ГЛ. 4. ОБЩАЯ ТЕОРИЯ ПРЕДЕЛОВ
(4.66
— (дробная часть х, 1.71) не имеет предела при
X —*оо, хотя /(л) = (л) = 0 имеет пределом 0.
4.66.	Однако имеет место следующая теорема.
Теорема. Функция f(x), определенная при х^х0,
имеет предел при х —* оо тогда и только тогда, когда каж-
дая последовательность f(xn) (где хп~^х0—любая после-
довательность, расходящаяся к оо) имеет предел.
Доказательство. 1) Если f(x) имеет при х —>• оо
предел р, то этот же предел р имеет и любая последова-
тельность f(xn), гдех„—>-оо.
Это снова вытекает из 4.16 а.
2)	Если f(x) не имеет предела при х—>-оо, то не вы-
полняется критерий Коши 4.19. Поэтому при некотором
h > 0 для любого п можно найти такие точки х'п > п,
х'п > п, что
!/«)-/«) \>h.
Рассмотрим последовательность
Хг, Х2, • • •> Хп, Хп, •
(1)
Очевидно, она стремится к оо, и последовательность
соответствующих значений функции f(x)
f(x'i), f(x'i), f(x’J, /«), .
не имеет предела, так как (1) показывает, что для этой
последовательности не выполняется критерий Коши.
Изложенные факты не исключают, однако, того что в спе-
циальных случаях, используя дополнительные свойства функ-
ции f(x), можно делать выводы о существовании ее предела
при х—>оо на основании существования lim/(л).
СО
§ 4.7. Пределы векторных функций
4.71.	Рассмотрим здесь функции f(x) со значениями
в л-мерном пространстве Rn (2.61). Поскольку л-мерное
пространство является метрическим, определение предела
по направлению 5 применимо, и для такого предела спра-
ведливы свойства, указанные в § 4'.2. Но и некоторые
свойства пределов для функций с числовыми значениями,
4-73}
§ 4.7. пределы Векторных функций
149
перечисленные в §§ 4.3—4.5, сохраняются для функций со
значениями в Rn, именно те, которые связаны со свойствами
линейных операций и не связаны с использованием порядка.
Перечислим их вкратце.
4.72.	Для функций со значениями в л-мерном простран-
стве Rn определены следующие операции:
а.	Сложение: если функции f(x) и g{x) принимают
свои значения в пространстве Rn, то их сумма, т. е. функ-
ция, равная при каждом хп£Е сумме /(хо) + ^(хо)? также
есть функция со значениями в Rn.
б.	Умножение на вещественную функцию:
если функция f(x) принимает значения в пространстве Rn,
а функция <х(х) имеет вещественные значения, то их про-
изведение, т. е. функция, равная при каждом хп£Е произ-
ведению а(х0)/(х0), также есть функция со значениями
в пространстве /?„.
в.	Для случая п — 2, когда векторные функции /(х),
g(x) можно истолковать как комплекснозначные, по прави-
лам действий с комплексными числами определены произ-
ведение /(х) • g(x)
частное
fW
g(x)
(последнее — при
и
Е(х)^О).
4.73.	а. Соотношение lim/ (х) =р g Rn равносильно соот-
s
ношению lim[/(x)—р] = 0 и соотношению lim|/(x)—р| = 0.
s	s
б.	Функция /(х) со значениями в Rn называется огра-
ниченной по направлению S, если существует конечное
число с и множество	во всех точках которого вы-
полняется неравенство |/(х)|^с.
Если f(x) и g(x) ограничены по направлению S, то
функция f(x)-\-g{x) также ограничена по направлению S.
в.	Если limf(x)=p£Rn, lim g (х) = q С Rn, то функция
s	s
f(x)-\-g(x) имеет по направлению S предел, равный p-\-q'.
Ит [/ (х) + g (х)] = lim f (x) + lim g (x).
150
ГЛ. 4. ОБЩАЯ ТЕОРИЯ ПРЕДЕЛОВ
[4.74
г.	Если lim/(x) —р £ Rn, lim а (х) = I £ R, то функция
s	s
a(x)-f(x) имеет по направлению S предел, равный 1р:
lima(x)/(x) = lima(x)-lim f(x).
s	s s
д.	Для случая л = 2, когда векторные функции f(x),
g(x) можно истолковать как комплекснозначные, так что
имеет смысл операция умножения, имеем: если lim f (х) =р £ С,
s
limg(x)=v€C, то Vmf(x)-g(x)=pq и lim^--=2- (послед-
S	5	S 6W <7
нее при 95^0).
е.	Пример. Определим в плоскости С комплексных
чисел z=x-\-iy направление z —>оо как совокупность всех
множеств Аг вида
4={д€С-.|г|>г}.
Очевидно, свойства направления (4.11) здесь выполнены, и
мы можем для функций f(z), определенных при | г |	г0,
говорить о существовании или несуществовании предела
lim/(z). В частности, для функции f(z)~ — , определенной
г-> со	2
при д=/=0, мы имеем
lim — - О,
г-», 2
поскольку при любом е > 0 на множестве
A1/E = ^zeC:\z] >у|
мы имеем |/(z) | = Д- < е. Далее, для любого многочлена от
I2 1
1
переменного —, т. е. многочлена вида
а0+^+---+^
с комплексными коэффициентами а0, а1г . . ., ап, в силу в и д
4.74.	Функцию f(x) со значениями в n-мерном простран-
стве Rn можно записать в форме
/(х) = (Л(х), ...,/„(X)),
ЗАДАЧИ
151
где fk(x)— координаты вектора f(x), представляющие собой
числовые функции. При этом имеет место неравенство
(3.14 (9))	______________
max |Д (х) —fk (у)	/2 V/(х) — fjСУ)]2<
6=1, ...» п	j = l
п
< 2 1Л(*)-Ж (1)
/=1
Отсюда мы делаем следующий важный вывод:
Теорема. Функция f(x)£Rn тогда и только тогда
имеет предел по направлению S, когда каждая из числовых
функций (х), ..., fn (х) имеет предел по направлению S.
4.75.	Сформулируем для пространства Rn критерий Коши
(4.19), справедливый в силу полноты Rn (3.72 в).
Теорема (критерий Коши в Rn). Функция f(x)
со значениями в Rn имеет предел по направлению S тогда
и только тогда, когда для любого г > 0 существует такое
множество A £ S, что для любых двух точек х и у из А
\f(x)-f(y)\^e.	(1)
ЗАДАЧИ
1.	Доказать, что если сходится последовательность xn£R, то
сходится и последовательность | хп |. Верно ли обратное?
2.	Для любых двух вещественных последовательностей ап и Ьп
lim ап + lim bn < lim (ап + Ьп)	lim ап+lira bn,
lim ап + lim br Ss lim (ап + bn) lim ап + lim bn.
3.	Если последовательность ап сходится, то и любая ее переста-
новка ап,, апз, ..., аПк, ... сходится к тому же пределу. Следует
ли сходимость последовательности из сходимости некоторой ее пере-
становки?
4.	Если последовательность ап сходится, то для любой последо-
вательности Ьп имеем
fim (ап+b„) = lim ап + lim b„.
5.	Если для некоторой последовательности ап и любой последо-
вательности Ьп
lim (ап+bn) — lim ап + lim b„,
то последовательность ап сходится.
152
ГЛ. 4. ОБЩАЯ ТЕОРИЯ ПРЕДЕЛОВ
6.	Пустьx1==a,x2 = b,x3=-^-(a^b), .... х„=-^(х„_1+хп_2), ...
Найти limx„.
7. Пусть а > 0, х0 > 0 и
(«-0- ’ 2- •••)•
хп /
Доказать, что lim хп = У а.
8.	(Арифметико-геометрическое среднее Гаусса). Пусть а > О,
b >0; положим хг=а, У1—Ь, ..., х„+1=Ух^, Уп+1 —...;
доказать, что числа хп и уп имеют общий предел.
9.	Если max {plt .... pm\ = pY (pi >0, рт> 0), то и
lim У ^pnk=P1.
k=i
10.	Прямая y=kx-]-b называется асимптотой кривой y=f(x) при
х —* + со, если
lim ff (х)—(kx-|- /?)]=0.
Х->+«0
Доказать, что кривая y=f(x) в том и только в том случае обла-
дает при х—>- + оо. асимптотой, если одновременно существуют пре-
делы
lim
lim Г/(х)—х lim
+ со L	v->+co х J
11.	Пусть f (х)—функция, определенная на метрическом простран-
стве М, со значениями в метрическом пространстве Р. Будем говорить,
что точка р£Р есть «усиленный» предел функции f (х) при х-+а£М,
если для любого е > 0 найдется такое б > 0, что для всех х£М
таких, что р(х, а) < б (не исключая и точки х=а), выпол-
няется неравенство р (f (х), р) < е. «Усиленный» предел не входит
прямо в схему 4.12 предела по направлению. Показать, что точка
pgP тогда и только тогда является «усиленным» пределом функции
f (X) при х а, когда р есть предел функции f (х) по направлению х-»-а
и при этом f (a)=p.
12.	Пусть у(х)—функция, определенная на множестве X с выде-
ленным в нем направлением S = {Aa}, со значениями в метрическом
пространстве У; пусть г (у)—функция, определенная на Y, со значе-
ниями в метрическом пространстве Z. Сложная функция г (х) = г [у (х)]
определена на множестве X и принимает свои значения в простран-
стве Z. Пусть существуют пределы
р=1йпр(х)£У, q — lim z(i/)^Z.
5
ИСТОРИЧЕСКАЯ СПРАВКА
153
Справедливо ли утверждение, что существует lim г (х)? Если он
s
существует, совпадает ли с qt
13.	В условиях задачи 12 доказать следующие предложения:
а)	Если существует множество A£S, на котором р(х) не при-
нимает значения р, то г(х) имеет предел, равный р.
б)	Если существует множество A£S, на котором р(х) тождест-
венно равна р, то г(х) имеет предел г (р).
в)	Если на каждом множестве A£S функция р(х) принимает
и значение р, и значения, отличные от р, то функция г(х) имеет
предел тогда и только тогда, когда д = г(р) (т. е. q есть «усиленный»
предел функции г (р) при р —> р), и в этом случае
lira z (х) = q.
S
Историческая справка
Первое корректное определение предела числовой функции было
дано Коши в 1821 г. в его «Курсе алгебраического анализа». Коши
установил основные теоремы о существовании разного рода пределов,
в частности пределов монотонных функций и последовательностей.
Он же ввел понятия верхнего и нижнего пределов. Более общие
понятия предела были предложены Шатуновским (1923), Муром и Сми-
том (1923). Сходимость «по направлению» есть частный случай схо-
димости «по фильтру» А. Картаиа (1937). См. Н. Бурбакй, Общая
топология, Физматгйз, 1958.
ГЛАВА 5
НЕПРЕРЫВНЫЕ ФУНКЦИИ
Моей главной целью было согласовать строгость,
которую я вменял себе в обязанность в изложения моего
курса анализа, с простотой, вытекающей из непосред-
ственного рассмотрения бесконечно малых количеств.
О. Коши (1823)
§5.1	. Непрерывные функции на метрическом
пространстве
5.11.	Пусть задана функция f(x) на метрическом про-
странстве М со значениями в метрическом пространстве Р.
Пусть а^М—фиксированная не изолированная точка (4.15 а).
Рассмотрим направление ха (4.15 а), образованное ша-
рами Ur(a)= {х:р(х, а)^.г} с выброшенной точкой а.
а.	Определение. Функция f(x) называется непре-
рывной при х = а (а точка а при этом называется точкой
непрерывности функции f(x)), если
lim f(x)=f(a).
х->а
Иначе говоря, функция f(x) непрерывна при х — а, если
для любого е > 0 существует такое б > 0, что из р (х, а) < б
следует
P(f(x), f(a)) < 8.
(1)
Для числовой функции f(x) неравенство (1), естественно,
записывается в виде
|/(X)— /(«)| < 8.
б.	Из 4.66 следует второе определение непрерывности:
функция f(x) непрерывна при х=а, если для любой после-
довательности хп -»- а (в М) непременно f(xn) —*f(a) (в Р).
в.	Каждая изолированная точка а£М, по определению,
считается точкой непрерывности функции f(x).
5.13]	§ 5.1. НЕПРЕРЫВНЫЕ ЧИСЛОВЫЕ ФУНКЦИИ	155
г.	Определение. Точка х0, не являющаяся точкой
непрерывности функции f(x), называется ее точкой разрыва.
д.	Определение. Функция, непрерывная в каждой
точке пространства Л1, называется непрерывной на М.
е.	Определение непрерывности функции /(х) в точке а
зависит, естественно, от метрики, заданной на пространст-
вах М и Р. Но гак как это определение может быть сфор-
мулировано в терминах сходящихся последовательностей (б),
то свойство функции быть непрерывной в точке а, а также
и на всем множестве М, не нарушается при замене мет-
рики в пространствах М и Р на гомеоморфные (3.34).
5.12.	а. Очевидным примером непрерывной функции с об-
ластью определения М и областью значений Р является
постоянная:
f(x) = у0,
где у0 — фиксированная точка пространства Р (4.21).
б.	В качестве второго примера рассмотрим расстояние
р (х, а) от фиксированной точки а. Это есть некоторая
числовая функция в метрическом пространстве М. Ее непре-
рывность в каждой точке х = х0 пространства М следует
из 3.32 б.
5.13.	Дальнейшие предложения, относящиеся к случаю
числовых функций, дают возможность строить широкие
классы непрерывных функций.
а.	Если числовые функции f(x) и g(x) непрерывны при
х = х0, то h (х) =/(х)+£(х) также непрерывна при х = х0.
Это—следствие из 4.36 а.
б.	Если f(x) и g(x) непрерывны при х — х0, то р(х) =
=/(х)-^(х) также непрерывна при х = х0.
Это—следствие из 4.36 б.
в.	Если f(x) и g(x) непрерывны при х = х0 и g(xo)#=O,
. . f (х)
то q (х) = также непрерывна при х — х0.
Это — следствие из 4.36 д.
г.	Числовая функция у = х, определенная на числовой
оси R, очевидно, непрерывна на R. Из предложений а, б к
в следует, что любой многочлен а0 + агх	апхп не-
прерывен на R всюду и что любая рациональная функция
156
ГЛ. 5. НЕПРЕРЫВНЫЕ ФУНКЦИИ
[5.14
, . ao+aix+...+°т№	г> т
г (х) = ,	,-------т- непрерывна на R всюду, кроме
тх
точек, где ее знаменатель обращается в 0.
д.	Числовая функция у — (k-я координата вектора
х — (^, ..., £„)), очевидно, есть непрерывная функция
в л-мерном пространстве /?„. Из предложений а — в следует,
что любой многочлен от координат вектора х непрерывен
всюду на Rn и любая рациональная функция от координат
вектора х непрерывна, на Rn всюду, кроме точек, где ее
знаменатель обращается в 0.
5.14.	Пусть /(х) —непрерывная функция, определенная
на метрическом пространстве М, со значениями в метриче-
ском пространстве Р. Пусть, далее, G с. Р — некоторое мно-
жество и Н= {х ?Af:/(x) С G}.
а.	Если G открыто, то и Н открыто.
Действительно, пусть х0^Н,	f(x0)£G и V=
= {у€Р:р(у, f (Хо)) < е} есть шаР с центром в точке/(х0),
лежащий в области G. Пусть найдено 6 > 0 так, что из
р(х, х0) < 6 следует р(/(х), /(х0)) < е. Тогда шар U=
= {х:р(х, х0) < 6} лежит в Н.
б.	Если G замкнуто, то и Н замкнуто.
Действительно, дополнением в М множества {х:/(х)£С}
является множество {х:/(х)^Р—G}, которое в данном
случае открыто в силу а.
в.	Следствие. Если f(x) — числовая непрерывная
функция, то при любом вещественном c£R множества
{x£M-.f(x)<c},
{xg2W:/(x) > с}
открыты, а множества
{х:/(х)С4>
{х:/(х)>с},
{х:/(х) = с}
замкнуты.
г.	Если /j(x), ..., fm(x) — непрерывные числовые функ-
ции, то при любых вещественных аг, ..., ап, Ьг, ..., bm
5.15]
§ 5.1. НЕПРЕРЫВНЫЕ ЧИСЛОВЫЕ ФУНКЦИИ
157
{из R) множество
{x:a1<f1(x)<b1, ..., am<fm{x) <bm} (1)
открыто, а множество
{x’.a1^f1{x)^b1, ...,	(2)
замкнуто.
Это получается из в на основании теоремы о пересече-
нии открытых {3.22) и замкнутых {3.54) множеств.
д.	В силу предложения г многие фигуры элементарной
геометрии, описываемые системами неравенств (1) или (2),
оказываются соответственно открытыми или замкнутыми.
Так, в л-мерном пространстве множество вида
{х:а1<х1<Ь1, ..., а„<х„<У
открыто, а множество вида
{х-.а^х^Ьь ..., ап^хп^Ьп}
замкнуто; первое называется, открытым брусом, а второе —
замкнутым брусом.
На плоскости х1г х2 /и-угольник, описываемый m нера-
венствами вида ajX^-YbjX^ <С с}- {j=~ \, .. ., m), есть откры-
тое множество — открытый /и-угольник; если же в этих
неравенствах заменить знаки < на знаки , то получится
замкнутый m-угольник. Аналогично в л-мерном пространстве
выделяются открытые и замкнутые многогранники с по-
мощью неравенств, связывающих линейные функции от
координат.
Те из перечисленных фигур, которые замкнуты и при
Этом ограничены, являются компактами в силу 3.96 д.
5.15.	Непрерывность сложной функции
а.	Пусть М, N, Р—метрические пространства с рас-
стояниями p^, рр. Пусть y=f{x)—функция с областью
определения Al и с областью значений/V, а г = ф(у)—функ-
ция с областью определения N и с областью значений Р.
Сложная функция z — <р [/(*)] == h (х) определена в М и
принимает свои значения в Р.
Теорема. Если y=f{x) непрерывна при х = х0, а
z~-<p{y) непрерывна при у=уй—/{х$), то функция z — h{x)
непрерывна при x — xQ.
158
ГЛ. 5. НЕПРЕРЫВНЫЕ ФУНКЦИИ
[5.16
Доказательство. Пусть задано е > 0. Из условия
lim ф(у) = ф(_Уо) найдем число т>0 так, чтобы из
рЛ,(у, у0) < т вытекало рр (ф (у), ф (у0)) < е. Далее, из усло-
вия lim f(x)=f(x0) по имеющемуся т найдем такое 6 > О,
чтобы из рЛ1(х, х0) < б следовало рЛ,(у, Уо) = Pyv(/(*)>
/(х0)) < т- Тогда прирЛ1(х, х0) <бмы имеемpP(h(x), h(x0))=
= рр(ф(/(х)), ф(/(х0))) = рр(ф(у), ф(у0))<е, что и тре-
буется.
б.	Если f(x)—непрерывная функция, определенная на
метрическом пространстве М, со значениями в метрическом
пространстве N и b£N—фиксированная точка, то числовая
функция
Л(х) = р(/(лг), Ь),
есть непрерывная функция от х£М.
Это — следствие из а и 5.12 б.
В частности, если на метрическом пространстве М не-
прерывна числовая функция f(x) (со значениями в R), то
непрерывна и функция |/(х) | = р(f(x), 0).
5.16.	Непрерывные функции на компакте.
На метрическом компакте М (3.91 а) непрерывные функции
обладают некоторыми специальными свойствами, которые
мы рассмотрим здесь и в 5.17.
а.	Теорема. Множество всех значений непрерывной
функции f(x), определенной на компакте М, само компактно.
Доказательство. Пусть f(xk), ..., /(х„), ...—
произвольная последовательность значений непрерывной
функции f(x), определенной на компакте М. Выберем из
последовательности точек хк, ..., хп, .. . сходящуюся
последовательность xnk(k=\, 2, ...); пусть, например,
хПк —> а. Так как функция f(x) непрерывна при х=а, то
f(Xnk) —*/(«). Таким образом, из последовательности f(xn)
выделена сходящаяся подпоследовательность, что и нужно.
б.	Следствие (теорема В е й е р ш т р а с с а). Не-
прерывная числовая функция (со значениями в R), опреде-
ленная на компакте М, ограничена и достигает на М своих
точных границ, т. е. если cc=inf/(x), P = sup/(x), то
существуют такие точки q £ М, р£М, что a = f(q), $—f(p).
5.17]	§5.1. НЕПРЕРЫВНЫЕ ЧИСЛОВЫЕ ФУНКЦИИ	159
Доказательство немедленно получается из а и свойств
компактного множества на числовой оси (3.96 е).
в.	Пусть в условиях б компакт М есть отрезок а х b
числовой оси, и пусть f(a)=f(b). Тогда можно утверждать,
что хотя бы одна из точек р, q, удовлетворяющая усло-
виям теоремы Вейерштрасса, имеется в интервале (а, Ь).
Действительно, если функция f(x) постоянна и равна f(a),
то в качестве точки q—p можно взять любую точку интер-
вала (а, Ь). Пусть f(x) непостоянна и, например, среди
ее значений имеются ббльшие, чем f(a). Тогда 0=
=sup/(x) >/(а). По теореме Вейерштрасса существует
точка рё[а> #], в которой /(р)=0. Но /(а) =/(£)< 0,
поэтому р£(а, Ь), что и требуется. Если f(x) принимает
значения меньшие, чем f(a), то аналогичное рассуждение
проводится для точки q, где достигается inf/(x).
5.17.	Равномерная непрерывность.
а.	Определение. Функция у = /(х), определенная на
метрическом пространстве 7И, со значениями в метрическом
пространстве Р, называется равномерно непрерывной на М,
если для любого е > О существует такое 6 > 0, что из
р]*!, х2) < б следует р [/(*!), /(х2)]<в, каковы бы ни
были точки хъ и х2 из /И.
Очевидно, что всякая равномерно непрерывная функция
является непрерывной в каждой точке пространства М.
Однако в общем случае из непрерывности функции f(x)
на пространстве /И не вытекает ее равномерная непрерыв-
ность. Например, функция у= х2 непрерывна на полуоси
0^х<оо (5.13 г), но не равномерно непрерывна на ней,
поскольку
— *2 = (*i — *2) (*i + -Ч)
и из условия |хх— х2|<б заведомо не следует, что
| х[— х|| ограничено какой-либо постоянной,
б.	Для случая, когда М есть метрический компакт, спра-
ведлива следующая теорема.
Теорема (Гейне). Непрерывная функция y=f(x),
определенная на метрическом компакте К, со значениями
в метрическом пространстве Р равномерно непрерывна
на К.
160
ГЛ. 5. НЕПРЕРЫВНЫЕ ФУНКЦИИ
(5.17
Доказательство. Допустим, что функция f(x) не
является равномерно непрерывной на К. Тогда для некото-
рого е > 0 и любого 6 > 0 существует пара точек х', х"
в К, для которой р(х', х") < 6, но р(/(х'), /(х"))^е.
Придадим числу б последовательно значения 6=1,
-i-, ..., — , ... Для каждого &==—• найдем соответству-
ющую пару точек х„ и х"п так, что р(х„, x'„)<6 = -i-, но
p[/U«)> /Un)] >8.	(1)
Поскольку К—компакт, из последовательности х’п можно
извлечь сходящуюся подпоследовательность хП1, х„2, ...
.... х'„к, х0 € /С Так как p(x'„fc, х„к) < -Ь, то
nk
Р *о)*СР (хпк, хПк)+р(х"м Хо) * 0>
так что также и х^, х^, ..., х"Пк ...	Xq. в точке
х = х0 функция у = /(х) определена и непрерывна; для
имеющегося е найдем 60 > 0 так, чтобы
Р [/U)> /Uo)] < у
при р(х, х0) < б0. Так как хПк —> х0, хПк —>• х0, то послед-
нему неравенству удовлетворяют все точки хП([, хПк, начи-
ная с некоторого номера. Поэтому для этих точек
Р [/U«J. f Uo)] < у > Р [UnJ, f Uo)] < у
и, следовательно,
р[/ийк), /U„k)] <8,
что противоречит (1). Теорема доказана.
в.	Колебание функции. Пусть снова /(х) есть
функция, определенная на метрическом пространстве М, со
значениями в метрическом пространстве Р. Образуем число-
вую функцию
0/(6)= sup p(/Ui), /U2))-
Р Ut. xj < б
Ее аргументом является положительное число 6. Если
функция f (х) равномерно непрерывна на М, то со/(6) ко-
нечна для всех достаточно малых б и, согласно определе-
5.18J
§ 5.1. НЕПРЕРЫВНЫЕ ЧИСЛОВЫЕ ФУНКЦИИ
161
нию равномерной непрерывности,
lim ю.(б) = 0.	(2)
6->0
В частности, если Месть компакт, этот факт всегда имеет
место в силу теоремы Гейне.
Обратно, если toy (б) конечна при достаточно малых
б > 0 и выполняется равенство (2), то функция f(x) равно-
мерно непрерывна на пространстве М.
Функция со»(б) называется колебанием функции f(x) на
пространстве М.
г.	Для числовых функций f(x) (т. е. принимающих зна-
чения на числовой оси Рг с обычным определением расстоя-
ния р(/, ^) = |/—^|) функция (Оу(б) обладает следующими
свойствами:
1)	<o/+g (6X^(6) +(0^(6);
2)	(ол/ (б) = Л(0у (б) (Л > О—постоянная);
3)	(б) < sup |/(х) | - (о* (б) ©у (б) sup k(x) |.
Выполнение первых двух свойств следует непосредст-
венно из определения. Для доказательства третьего свойства
нужно воспользоваться неравенством
|/(-Ч) £(*1)g(xz) | =
= |Л*1И(*1)~/(*iH(X2) +/(*1) g(Xz) -f(x2) g(Xz) | <
< 1/(^1) I k(*i)—g(xz) I + |/(X1) -f(xz) 11 g(xz) I <
C sup 1/ (X) I  I g (Xj)—g (x2) I +|/ (xj -f (x2) I • sup j g (x) |.
5.18.	Непрерывные функции двух перемен-
ных. В анализе часто приходится иметь дело с непрерыв-
ными функциями от двух (и более) переменных. Пусть
Afj и УЙ2—метрические пространства с метриками рх и р2.
Функцию /(хп х2), аргументы которой суть точки х1£М1,
х2 €Af2, а значения—точки метрического пространства Р,
называют непрерывной по совокупности аргументов xlt х2
при хг = х[, х2 = х®, если для любого е>0 можно найти
такое б > 0, что из рх (х2, х?) < б, р2 (х2, х°) < 6 следует
p[/(Xi, х2), /(х$, х°)]<в. Нетрудно убедиться, что это
определение, по сути дела, не является новым и совпадает
162
ГЛ. 5. НЕПРЕРЫВНЫЕ ФУНКЦИИ
(5.21
с определением непрерывности функции f{xlf х2) как функ-
ции одного аргумента х = (х1( х2)—точки произведения
М = М1хЛ4г метрических пространств и. М2. Напом-
ним (3.16), что в прямом произведении М метрика вводится
по правилу: если х = (хх, х2), у — (уг, у2), то полагают
Р(*. У) = тах [pi (*!> У1)> Р2(*2. Ь)]- Функцию двух аргу-
ментов f(xx, х2) можно считать функцией f(x) от точки
* =	ее непрерывность в точке x° = (xj, х®) озна-
чает, что для любого е > 0 существует такое 6 > 0, что
из р (х, х°) = max [pj (х1( х®),	р2(х2, х®)] < 6 следует
|/(х)—/(х°)|<е. Так как неравенство р(х, х°) < б рав-
носильно двум неравенствам р1(х1, х?) < 6 и р2(х2, х®)<б,
то два приведенных определения непрерывности равносильны.
На произведении Л4 = /И1х7И2 мы указали еще две мет-
рики (3.16). Поскольку в 3.34 д мы убедились, что они
гомеоморфны метрике, использованной выше, нам нет нужды
их выписывать; из 5.11 е следует, что запас непрерывных
функций (со значениями в фиксированном пространстве Р)
будет одним и тем же для любой из этих трех метрик.
§	5.2. Непрерывные Числовые функции
на числовой оси
5.21.	а. В §§’5.2—5.7 мы рассматриваем функции f(x)
переменного х, изменяющегося по множеству Ё, лежащему
на расширенной числовой оси R, с метрикой г (х, у) про-
странства R (3.35 д). Значения функции f(x) предполагаются
лежащими также в пространстве R с той же метрикой.
Впрочем, если х0 конечно или /(х0) конечно, то, поскольку
в конечной области метрика г(х, у) гомеоморфна обычной
метрике р(х, j) = |x—у|, в вопросах, связанных с непре-
рывностью функции /(х) при х = х0, можно (соответственно
для значений х или /(х)) использовать и обычную метрику
(3.13 а).
б. Рассмотрим с этой точки зрения рациональную функцию
f(r\= ^n + e‘ixn-1+---+an
60х“+М'в~1+ --.+bm ’
определенную при x£R, за исключением тех точек, где
знаменатель обращается в нуль. Если ее доопределить и в
5.22]	§ 5.2. НЕПРЕРЫВНЫЕ ФУНКЦИИ на числовой оси 163
точках + оо дополнительными условиями
/(— oo) = lim f(x), /(oo) = lim f(x)
X->—OO	оо
(существование этих пределов в R было доказано в 4.39 г),
то полученная функция, со значениями в R, будет сохранять
непрерывность и в точках ±
в. Лемма. Если, числовая функция f (х) £R непрерывна
при x = a£R, то для любого е > 0 существует такой шар
Vt с центром, в точке а, т. е. множество вида
| х — а | < б, если а конечно,
1
X > -т-, если а = 4- оо,
о
1
х < —г-, если а= — оо,
о
во всех точках которого выполняется неравенство
|/(х)—/(а)|<е, если f(a) конечно,
f(x)>±, если f(a)= ф-оо,
/(х)<—г, если/(а)= —оо.
В частности, шар Vt можно выбрать так, что во всех
его точках значения функции f(x) будут иметь тот же знак,
что и число f(a), если f(a)=£0.
Это утверждение следует из 4.34 а, б, определения мет-
рики в R (в частности, 3.35 е) и определения непрерывности.
5.22.	Теорема (Больцано). Если числовая функция
f(x)£R непрерывна на отрезке [а, и на концах
отрезка принимает разные по знаку значения, то внутри
отрезка существует точка с, в которой /(с) = 0.
Доказательство. Пусть для определенности
/(а) < 0, f(b) > 0. По 5.21 в неравенство f(x) < 0 сохра-
няется при всех х, достаточно близких к а, неравенство
f(x) >0 сохраняется при всех х, достаточно близких к Ь.
Положим
с — sup {х ё [а, &]:/ (х) < 0}.
164
ГЛ. 5. НЕПРЕРЫВНЫЕ ФУНКЦИИ
[5.23
В силу сказанного точка с не может совпадать ни с точ-
кой а, ни с точкой Ь. Согласно определению точной верхней
грани, при х' > с мы имеем /(х')^0, и для любого б > О
существует х" > с—б, для которого f(x") < 0. Таким обра-
зом, в любой окрестности точки с существуют такие точки х'
и х", что /(х')^0, /(х")<0. Но по 5.21 в это невоз-
можно, если /(с) =^0. Поэтому /(с) = 0, что и требуется.
5.23.	Следствие. Если функция f(x) непрерывна на
отрезке [a, b], A=f(a)^f(b) = B и число С заключено
между числами А и В, то существует такая точка с £ [а, 5],
что f(c) = C.
Действительно, /(х)—С непрерывна вместе с функцией
f(x) и удовлетворяет условиям теоремы Больцано. Применяя
теорему, получаем требуемое.
5.24.	Односторонняя и двусторонняя непре-
рывность. Для дальнейшего рассмотрим некоторые типы
направлений в области R конечных вещественных чисел.
В соответствии с определением 4.15 б направление х—* а
(=^= ±оо) определяется как совокупность всех интервалов
(а —Л, а + Л), 0< Л < Ло, с исключенной точкой а. Направ-
ление х / а мы рпределим как совокупность всех интервалов
(а — h, а), направление х\а—как совокупность всех
интервалов (a, a-j- h) (0 < h < Ло).
Если функция f(x) определена в интервале (а—Ло, а),
можно ставить вопрос о существовании или несуществовании
предела lim/(x), который обозначается (если существует)
х/а
через f(a — 0). Если функция /(х) определена в интервале
(а, а-\-Нй), можно ставить вопрос о существовании предела
Пт/(х), который обозначается через /(a-f-O). Если функция
/(х) определена в интервалах (а —Ло, а -|- h0) (за исключе-
нием, быть может, самой точки а), можно ставить вопрос о
существовании предела lim/(x). Поскольку при любом h,
Х-+а
O<.h<.ho,
(а—h, а) с (а — h, a-\-h) — {а},
(а, a-\-h)cz(a — h, a~j-h) — [a},
(а — h, a-\-h) — {а} = (а—h, a) U (a, a-f-й),
Б.31]
§ 5.3. МОНОТОННЫЕ ФУНКЦИИ
165
можно применить результаты 4.16, полагая
Е = {х R:x=^=a}, G={x£R:x <а}, Н— {х £R:x > а}.
В применении к рассматриваемому случаю эти результаты
приводят к следующему заключению: из существования
lim/(x)=p следует существование пределов lim/(x) =
x-t-a	х/а
= lim/(x)=p, и обратно, из существования и равенства
х\а
пределов lim/(x) = lim f(x) —р следует существование пре-
х/'а
дела lim/(x)==p.
х~+а
Предположим, что функция /(х) определена и при
х = а. Равенство lim/(x) —f(a), как мы знаем, определяет
х-*а
класс функций, непрерывных при х — а. Равенство f(a) —
= lim f(x) определяет класс функций, непрерывных слева
х/ а
при х — а. Равенство f(a) — lim/(x) определяет класс
х\о
функций, непрерывных справа при х—а. Функция f(x),
которая непрерывна в точке а и справа, и слева, непре-
рывна при х = а.
§ 5.3.	Монотонные функции
5.31.	Пусть числовая функция /(х) со значениями в R
определена на множестве EczR. Если из х^Е, у£Е, х<у
всегда следует какое-нибудь (фиксированное) иа четырех
неравенств
(a)	f{x)<f(y),
(б)	/(х)</(у),
(в) f{x)>f(y),
(г) /(х)>/(у),
функция /(х) соответственно называется: (а) возрастающей
на Е\ (б) неубывающей на Е-, (в) убывающей на Е; (г) не-
возрастающей на Е. Во всех четырех случаях функция /(х)
называется монотонной на Е.
166
ГЛ. 5. НЕПРЕРЫВНЫЕ ФУНКЦИИ
[5.32
5.32.	Если возрастающая {или убывающая) функция при-
нимает некоторое значение С, то только при одном значении
х. Невозрастающая {или неубывающая) функция может при-
нимать одно и то же значение во многих точках.
Результаты 5.33—5.36 формулируются и доказываются
для неубывающих функций; аналогичные формулировки для
невозрастающих функций мы предоставляем привести чита-
телю.
5.33.	Пусть х0£Е не есть левый конец отрезка Е =
= [a, ft], на котором определена неубывающая функция f{x).
Функция f{x) является неубывающей по направлению
Е {х / х0) в смысле 4.51\ так как при этом она ограничена
сверху на этом направлении (например, значением /(х0)),
по теореме 4.53 существует
f(x0—0) = lim / (х) = sup (х): х < х0, х£Е}.
Е(х/ х„)
Аналогично, рассматривая направление Е(х \ х0) и приме-
няя теорему 4.54, мы приходим к существованию предела
/(хо4-О)= lim /(х) = inf {/(х):х > х0, х^Е}
Е(х\х„)
для любой точки х0, отличной от правого конца отрезка
[a, ft]. Для точек а и ft мы положим, по определению,
f(a-O)=f(a), f(b + Q)=f{b).
5.34.	Так как для любых х"^Сх0 и х'^х0 мы имеем
Дх")^/(х0)^/(х'), то по 1.62 /(хо-О)^/(хо)<
^/(хо4-О). Если /(х0—О)=/(хо), функция f{x), согласно
сказанному выше, непрерывна слева при х = х0. Если
f (хо)=/(хо4-О), функция f{x) непрерывна справа при
х = х0. Равенство /(х0—О)=/(хо4-О) и вытекающее из
него равенство /(х0—О)=/(хо)—/(х04 0) являются необ-
ходимыми и достаточными условиями непрерывности неубы-
вающей функции f (х) при х = х0.
5.35.	Рассмотрим случай f(x0 — О)</(хо4-О). Такая
точка х0 есть заведомо точка разрыва функции f (х). Слева
от точки х0 значения функции /(х) не превосходят f(x0—0),
5.38]
§ 5.3. МОНОТОННЫЕ ФУНКЦИИ
167
справа от точки х0 значения функции f(x) не менее, чем
/(хо-|-О); значение f (х0) лежит в промежутке
М/(*о-О), /(хо + О)].
Но это значит, что все числа в промежутке I, кроме,
быть может, одного, вообще не являются значениями
функции f(х). Отсюда следует часто используемое доста-
точное условие непрерывности неубывающей функции:
5.36.	Если функция f(x), неубывающая на отрезке
[а, 6], принимает при х£[а, Ь] каждое значение из отрезка
f(a), /(£)], то f(x) непрерывна на [а, й].
Действительно, в этом случае исключается неравенство
f(x0 — 0) < f (х0 -Д 0) в какой-либо точке х0 £ [а, Ь\. По-
этому в силу 5.34 функция f(x) непрерывна в каждой точке
х0€[а, />].
Указанное условие и необходимо {5.23).
5.37.	Обратная функция.
Определение. Пусть функция y = f{x) определена
на некотором множестве Е и принимает на Е значения у
из множества F; пусть функция ф(у) определена на мно-
жестве F и принимает значения на множестве Е. Функция
ф (у) называется обратной к функции /(х), если ф[/(х)] = х
всюду на Е и /[ф(у)]=у всюду на F.
5.38.	а. Теорема. Пусть числовая функция y=f(x)£R
определена, непрерывна и возрастает на отрезке [a, b\ с R.
Тогда на отрезке [/(а), /(£>)] существует функция ф(у), °б~
ратная к функции f(x); эта функция ф(у) также непрерыв-
ная и возрастающая.
Доказательство. Для	у=/(а) = Л	положим
ф(Л)=«; для у = f {Ь) = В положим ф(В) = й, для любого
f{b)) положим ф(у) равной тому (единствен-
ному) значению с, для которого
f(c) = C.
Таким образом, функция ф (у) определена на [Д, В], причем
Для любых х С [а, Ь], у g [Д, В]
Ф [/(*)] — х, /[ф(у)]=у.
168
ГЛ. 5. НЕПРЕРЫВНЫЕ ФУНКЦИИ
[6.39
Очевидно, что из уг<у2 следует х1<х2, т. е. ф(уг)<
< ф (у2), так что функция ф (у) возрастает. Ее непрерыв-
ность следует из того, что она принимает все значения
в промежутке а^х^5 (5.36). Теорема доказана.
б. Рассмотрим теперь случай, когда функция/(х) задана
не на отрезке, а на интервале, н покажем, что он приво-
дится к предыдущему. Пусть функция y—f(x) определена,
непрерывна и возрастает на интервале (а, Ь) £ /?. Положим
Д=/(а) = 11т/(х), В —f (b) — limf (х) (5.33); теперь функ-
х/Ь
ция /(х) определена уже на отрезке [а, 5], причем и на
этом отрезке непрерывна и возрастает. Применяя доказанную
теорему, получаем: существует функция ф (у), определенная,
непрерывная и возрастающая на отрезке [Л, В] с/?, обратная
к функции f(x). Рассматривая /(х) только на интервале
(а, Ь), приходим к следующему результату:
Теорема. Для функции у—f(x), определенной, непре-
рывной и возрастающей на интервале (a, b)cR, существует
обратная функция ф (у), определенная, непрерывная и воз-
растающая на интервале
(A, B)£~R, где
А=lim f (х),В = lim f (х).
х/'Ь
5.39. График обрат-
ной функции. Если имеет-
ся график возрастающей чи-
словой функции у—f (х) на
отрезке [а, 5], то график обрат-
ной функции, естественно,дол-
жен быть построен на отрезке
® [Д,В], где A=f(a), B=f(b).
Если эти отрезки отложить
на одной и той же оси, то
график обратной функции х = ф(у) получается из графика
функции у=/(х) отражением относительно биссектрисы
координатного угла: действительно, точка (х, у=/(х))
после отражения относительно биссектрисы переходит в
точку (у, х = ф(у)) (рис. 5.1)
Б.41]
§ 5.4. логарифм
169
§ 5.4. Логарифм
5.41. Теорема. При х > 0 существует и единственна
функция y=f{x), удовлетворяющая следующим условиям:
1) /(Ху)=/(х)+/(у) для любых положительных х, у;
2) /(а) = 1 для заданного а > 1;
3) f(x)—возрастающая функция: если x<Zy, то f(x) <
Доказательство*). Сначала, предполагая сущест-
вующей функцию f(x), найдем ее выражение. Из 1) следует
/(1)=2/(1), откуда /(1) = 0. Далее, из 1) и 2) следует,
что f(an) — nf(a) = n при любом натуральном п. Согласно
1.72, для любого л>1 можно найти такое т, что
^x"<am+1. Поскольку f(x) возрастает, из неравенства
am^x"<am+1 следует f(am) = m^.f(xn) = nf(x) <
</(am+1) — /»+ 1; таким образом, для любого л^1 можно
найти такое т, что

Тем самым число f(x) определено однозначно как общая
[т /п+П	„
— , —— произвольно малой длины.
Теперь мы определим функцию f(x), используя приве-
денные соображения. Положим «j=l, л2= 2, ..., nk = 2k
и для данного k найдем тк так, чтобы иметь
ami< хПк	ать+1.
Этим определяется отрезок	. Покажем, что
[ГПь+л /Пь+1+П
 	— лежит в предыдущем.
пй+1 nk+l J
Действительно, из неравенства
атк хПк <
следует, что
a2mk х2пк — xnk+1 < а2 (mk+Dt
откуда mk+1^2mk, mk+1 + 1 ^2(тк+ 1),
nk ~ 2nfe nk+i nk+i "" 2nft	nk
*) По книге Ж. Дьедонне, Основы современного анализа,
«Мир», 1964, гл, 4,
170
ГЛ. 5. НЕПРЕРЫВНЫЕ ФУНКЦИИ
[5.42
Таким образом, отрезки	*j образуют вложенную
последовательность и по принципу Кантора 1.81 имеют
общую точку; по 1.82 она единственна, так как длины
отрезков при Л—-> оо стремятся к 0. Возьмем в качестве
значения f(x) число, отвечающее общей точке всех этих
отрезков.
Покажем теперь, что построенная функция /(х) удовлет-
воряет условиям 1)—3). Пусть заданы х и у; найдем для
заданного k такие mk и что
хПк <С 1,
@Рк ^^упк	,
так что
/'(х)	-1-	—	.
nk	nk	nk
Отсюда
amk+pk (xy)nk amk4-Pk+2,
(1)
так что
С другой
™k + Pk < f ,x х < mk+pk + 2
nk y'"" nk
стороны, из (1) следует, что
</(х) +/CV) <^+РЛ±2 .
rLk	nk
Таким образом,
9
поскольку nk произвольно, мы применяем 1.57 и приходим
к выполнению равенства 1).
Для х = а получаем очевидное равенство /(а) = 1. Для
любого х > 1 существует такое п, что а хп, и, следова-
тельно, согласно определению функции f(x) мы имеем
/(х)^—. В частности, для любого х>1 мы имеем
/(х)>0. Поэтому f(xy) =/(х)+/(у) >f(x) при любом
у > 1 и функция f(x) возрастающая; теорема доказана.
5.42.	Функция f(x), удовлетворяющая условиям 1) — 3)
5.41, существование и единственность которой мы доказали,
называется логарифмом от х при основании а и обозначается
5.43]
§ 5.4. логарифм
171
через logcx. Формулы 1) — 3 )5.41 теперь можно записать так:
logfl(xj) = logcx + logcj;	(1)
logfla = l;	(2)
если x<j, то logc х < logB<y.	(3)
Далее, из (1) вытекают следующие формулы:
logaxn = п logax при любом натуральном п; (4)
logo 1 = loga 1г = 2 loga 1, откуда
logo 1=0;	(5)
loga (х • у) = logo 1 = logo х + logo у = °»
откуда
log(I j =—logox;
следовательно,
logo = logo X — logo У-	(6)
Поэтому формула (4) справедлива для любого целого п.
5.43.	Покажем, что логарифм есть непрерывная функция
от х. Для заданного е>0 найдем и> — и положим h —
е
— {/а. Так как hn = a, то п loga h — loga hn = loga a = 1,
так что logaft = -^-, logfly=——. Таким образом, в про-
1 ,
межутке -^-^х^Л выполняется неравенство
— е <----log_ х sSC — < е,
п °й п ’
что доказывает непрерывность функции logax при х=1.
При любом у0 и у = ху0, <Z х <Z h, мы имеем logoj =
= logo X + logo-Уо» так что
I loga^—logo.ro I = I logo х I < е.
Так как интервал	hyo'j включает в себя некоторый
интервал (у0—6, _у0 + б), то отсюда следует непрерывность
функции logax при х=у0.
172
ГЛ. 5. НЕПРЕРЫВНЫЕ ФУНКЦИИ
[5.44
5.44.	Установим связь между логарифмами при разных
основаниях а и Ь. Рассмотрим функцию
Очевидно, она удовлетворяет условиям 5.41 1) и 3) опре-
деления логарифма и, кроме того, равенству
Л^) = гН = 1-
' ' logo Ь
В силу установленной единственности логарифма мы имеем
f(x) = logbx. Таким образом, прн любых а>1, £>1,
х > 0 справедлива формула
iogax = logab-logbx.	(1)
5.45.	Отметим предельные соотношения
lim logax= оо, lnnlogox=;—оо.
х -> оо	х\0
Первое, в силу теоремы 4.55, следует из того, что при
х —* оо функция logc х возрастает и не ограничена (поскольку,
например, logc(a") = « для любого п). Второе приводится
к первому в силу равенства
loga (х ~) = Iog“ х + ,og« log« 1 = °*
Указанные соотношения позволяют дополнить определение ло-
гарифма условиями logo0= —оо, logGoo = oo, причем logox
оказывается функцией со значениями в R, непрерывной при
О^Сх^С оо.
§ 5.5.	Экспонента
5.51.	Непрерывная возрастающая функция у == loga х по
теореме об обратной функции 5.38 допускает обратную
функцию, которая называется экспоненциальной функцией,
или экспонентой, и обозначается у = а*. Экспонента опреде-
лена при всех вещественных х, а значения ее—положитель-
ные числа. Таким образом,
aiogax— Х) loga (ах) = х.
(1)
5.53]
§ 5.5. ЭКСПОНЕНТА
173
С другой стороны, мы имеем при любом натуральном п
loga(а.. .а) = logaа + ... + logaа = п.
(п раз)
Последнее равенство показывает, что обозначение ах согла-
суется с прежним обозначением ап = а...а для натураль-
ного п.
Если х—1/n, мы получаем loga«'/n = l/n, откуда
пlogfla1/n = logo(a*/n)n—	(а'/п)п = с,
т. е. а'/п есть корень л-й степени из а (1.63).
5.52.	Как и функция у = logo х, обратная функция у = а*
также возрастает и непрерывна при всех х. Имеют место
следующие равенства:
(ах)г = ахг	(2)
для любых вещественных х, у, г. Действительно, пусть
х = loga В, у = loga т), тогда
ах+У = а,о8о 6+ >°Sa П — aIogB = ах. ау;
аналогично доказывается (2).
Заменяя в 5.44 (1) х на Ьх, получаем
loge (bx) = loga Ъ  logb Ьх = х loga b.	(3)
5.53.	Определения логарифма и экспоненты можно рас-
пространить на случай основания ftg(0, 1). А именно, по-
лагая о = —, a >1, мы имеем по определению (и учитывая
формулу 5.44 (1))
logb х =	=-k>gax=- logI/4x.
Таким образом, функция logbx убывает при увеличении х;
свойства же, аналогичные свойствам 5.41 1) и 2), сохраняют-
ся. Далее,
таким образом, t>loei>x = а~ loet>x — а1оеах = х и
log6 (bx) = — logfl (а~х) = х,
174
ГЛ. 5. НЕПРЕРЫВНЫЕ ФУНКЦИИ
[5.54
так что сохраняются формулы 5.51 (1), а также и следую-
щие из них формулы 5.52 (1) и (2).
Переход от х к ах называется потенцированием, переход
от х к logax—логарифмированием.
5.54.	С экспонентой тесно связана степенная функция с
произвольным вещественным показателем, определенная при
х > 0 согласно 5.51 с заменой а на х и х на а:
у=ха.
Эта функция выражается через экспоненциальную и логариф-
мическую по формуле
у = (fclOEft xja _ fra logj x	( ] )
при любом b > 1, откуда следует ее непрерывность по тео-
реме 5.15. Из этой же формулы после замены хна pq(p, q > 0)
и использования 5.42 (1) и 5.52 (1) следует равенство
(pq)a=pa-qa.	(2)
5.55.	Предельные соотношения для лога-
рифма и экспоненты. Имеют место следующие
предельные соотношения:
lim bx — s	[	оо, если b [	0, если b <	> 1, : 1;	(1)
	[	0, если а '	> 1,	
lim ах = \			(2)
х->-00	1	к оо, если а <	С 1;	
	[ оо, если а '	> 1.	
lim loga х = >			(3)
	[ —оо, если а <	4 1;	
1	( —оо, если а '	> 1,	
lim logo х = х\0	।	[ ф- оо, если а <	С 1;	(4)
	[ оо, если b	>о,	
lim хь = s *->CO	'	[	0, если b <	СО;	(5)
	[	0, если b	>0,	
lim хь= s			(6)
х\0	1	[ оо, если b <	с о.	
5.55]
§ 5.5. ЭКСПОНЕНТА
175
Доказательство. Первое из соотношений (1) сле-
дует из того, что ft* при ft > 1 и х —> оо возрастает и не
ограничена (ее значения заполняют область определения
функции y = log0x, т. е. всю числовую ось); второе вы-
водится из первого заменой ft на . Соотношения (2) полу-
чаются из (1) заменой х на —х. Первое из соотношений
(3)	установлено в 5.45\ второе получается из первого в силу
определения log0 х при а < 1. Из (3) заменой х на по-
лучается (4). Соотношения (5) и (6) получаются логариф-
мированием с использованием (1) —(4).
Полученные соотношения позволяют нам представить
себе графики экспоненты, логарифма и общей степенной
функции (рис. 5.2—5.4).
176
ГЛ. 5. НЕПРЕРЫВНЫЕ ФУНКЦИИ
[6.56
Функция ах при а > 1, определенная при х € R, допу-
скает доопределение в точках ±оо:
a~№ = Q, о+е0 = оо,
и после этого оказывается непрерывной на R (со значени-
ями в R). Если о< 1, последнее утверждение будет спра-
ведливым, если мы положим
= оо, а+“=0.
5.56.	Прежде чем переходить к дальнейшим предельным
соотношениям, докажем лемму.
ап
Лемма, lim — = оо при любом а > 1 и любом вещест-
венном г.
Действительно, возьмем число Ь в промежутке (1, а).
В силу свойства 5.54 (2) имеет место равенство
an+i ап а	,,,
\ ' п)
Правая часть равенства (1) в силу непрерывности функции
хг в точке х = 1 стремится при п —»- оо к а и поэтому,
начиная с некоторого номера n — N, становится больше,
чем Ь. Тогда
Л+» aN .
(N+iy^ Nr ’°’
aN+* аН+1	N
(N+2Y^(N + l)r’	Nr '° ’
(N+ k)r Nr ’ ° ’
и равенство
lim bk = oo
fe->€0
(вытекающее из 5,55 (1)) убеждает нас в справедливости
леммы.
5.58]	§ 5.5. экспонента	177
5.57.	Укажем дальнейшие предельные соотношения для
логарифма и экспоненты, связанные с леммой 5.56.
Теорема. Справедливы предельные соотношения:
.. я*
11Л1-г = оо;	(1)
ljm!°^ = 0;	(2)
lim хр log0 х = 0;	(3)
lim х(*П = 1;	(4)
limx1/xP=l.	(5)
х->со
Здесь а > 1, г—любое вещественное число, р—любое поло-
жительное число.
Доказательство. Если для данного х > 0 мы най-
дем п такое, что л^х < л-|-1, то
ах ап 1 ап+1
откуда, используя лемму 5.56, получаем (1). Соотношение
(2) получается из (1) заменой х на log0x и возведением
в степень Р — у- Заменяя в (2) х на у, получаем (3). На-
конец, (4) получается из (3) с помощью потенцирования,
а (5) из (4)—заменой * на у. Таким образом, экспонента
у = ах, а > 1, при х —► оо возрастает быстрее, чем любая
степенная функция хг. Логарифмическая функция
у = log6 х (b > 1),
наоборот, при х —► оо возрастает медленнее, чем любая
степенная функция х₽(0>О).
5.58.	Учитывая связь между пределом функции /(х)
при х-юор пределом последовательности f(n) при п—>оо
178
ГЛ. 5. НЕПРЕРЫВНЫЕ ФУНКЦИИ
[6.59
(4.65), мы можем написать следующие пределы последова-
тельностей:
	lim bn = J Л->СО	|	[оо, если b > (0, если b <	1, 1	(1)
(следует	из 5.55 (1)); limlog„« = J П-*СС	1	[оо, если а [—оо, если а	> 1, < 1	(2)
(следует (следует	из 5.55 (3)); lim nb = J П->00	J из 5.55 (5));	[оо, если b > [0, если b <	о, 0	(3)
	lim = оо (а п-мг> П	> 1, —ОО <	г < оо)	(4)	
(следует	из 5.57 (1));			
	lim!« = П->ОО п	0 (а > 1, р '	>0)	(5)
(следует	из 5.57 (2)); lim f/л = 1 п-ж>			(6)
(следует	из 5.57 (5) при р=1).			
5.59. Согласно	Экспоненциальная функция 4.63 г,			н число е.
	lim (1 +1?	f = e = 2,71828...		(1)
а. Рассмотрим функцию f(x) = -ф при х 0. Оказывается, что также			1)'	определенную
	lim ( Х~>СС k	>+!)'=«•		(2)
Подчеркнем, что непосредственно из соотношения (1) это
еще не вытекает (4.65), нужно использовать специфику
функции f(x). Для заданного х > 1 найдем натуральное
п = п(х) так, чтобы иметь л^х<л-|-1; тогда прн х—*оо
5.59]
§ 5.5 ЭКСПОНЕНТА
179
также и п—>оо. Мы имеем
Правые части в этих двух неравенствах имеют один и тот
же предел е, когда п—>оо. Для заданного 8>0 найдем
такое N, что при каждом л > N обе правые части отли-
чаются от е меньше чем на в. Тогда при х > N-f-1 про-
межуточная величина	также будет отличаться от
е менее чем на в. А это и означает справедливость (2).
б. Покажем, что также
Действительно, при у —> оо мы имеем
1 V-’' _ (У~х\~у _	1	_ ( У V
у) \ У )	/'«/—IV kJ/—1/
откуда, заменяя у на —х и используя а и 4.17 в, полу-
чаем требуемое.
в. Из б, в частности, вытекает, что
— результат, который нетрудно было бы получить и прямо из
определения е (1).
г. Теорема.
lim loga(1+z)=logae.
z-> о z
(4)
Доказательство. Имеем log<?.P^z^ — loga(l -f-z)z ;
полагая =	, приходим на основании а, б и непрерывности
логарифма к нужному результату.
180
ГЛ. 5. НЕПРЕРЫВНЫЕ ФУНКЦИИ
[5.59
Формула (4) выглядит особенно просто, если за основа-
ние а взять число е. Логарифмы с основанием е называются
натуральными логарифмами и обозначаются так:
loge х = log nat х = In х.
Для натуральных логарифмов формула (4) записывается
в виде
ЦтН1±£) = 1.	(5)
z->o 2
Используя асимптотическую единицу Е (4.39), можно
записать результат еще следующим образом:
In(1 + z) = zE (Е —j-1 при г—> 0).	(6)
д. Теорема.
ft->o h loe«e
(7)
Доказательство. Положим ah—1 — у; тогда ah—
= l+y. *==logfl(l+-^) и
1
0й — 1	X 1
М1Ч4) М1+4)л’
откуда в силу а и б, непрерывности логарифма и соответ-
ствия направлений h —>-0 и х—► ± оо и следует требуемое
(4.17 а). Используя натуральные логарифмы, можно написать
проще;
.. ей—1
llmSr-=k	(8)
й->о "
Та же формула с асимптотической единицей Е:
eh— \-\-Eh, £->-1 при Л—>0.	(9)
е. Следующая теорема интересна тем, что хотя в ее фор-
мулировке число е отсутствует, однако ее было бы трудно
доказать без привлечения числа е и связанных с ним пределов.
Теорема. При любом вещественном р
limQ+y-.1 =р.	(Ю)
я—ъ-п	*
5.61]	§ 5.6. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ	181
Доказательство. Используя (6) и (9), находим
In (1 +«)==z£'1, 1+а = егЕч
(1 +г.)л==ерг£1 = 1 +^^£2= 1 -j-pzE, (11)
что и требуется.
Между прочим, из соотношения (11) видно, что резуль-
тат 4.39 б, доказанный там для натуральных р, справедлив
для всех вещественных р.
ж. Отметим специально соотношение (11) для р——1:
1^=1-*Е.	(12)
Более общее и часто применяющееся соотношение: при
«¥=Р
l±5gl=i+(a_p)z£ (Ei, Es, Е-+ 1 при г->0). (13)
Оно получается из (12) простыми преобразованиями:
|±g=(1+azEj (1 - р^ед=
— 1 -J- azE±—$zE2E3—a^>z2E1E2E3 =
= 1 + z (aEy— $Е2Е3~ uf>zEAEJ:3);
поскольку последняя скобка, очевидно, имеет пределом
а — Р, получаем окончательно (13).
§ 5.6.	Тригонометрические функции
5.61.	Определения тригонометрических функций, приня-
тые в геометрии, опираются не на аксиомы вещественных
чисел, и мы эти определения не будем рассматривать. В
тригонометрии выводятся соотношения
sinajc-|-cosax= 1;	(1)
sin (х +у) — sin x cosy 4- sin у cos х;	(2)
cos (х4-у) = cos х cosy—sin	x sin y;	(3)
. sinx	,..
0 < sin x < x <----- (4)
COS X	' ’
при достаточно малом x>0, например при 0 < х < е0.
Мы определим sin х и cos х как функции, заданные при
всех вещественных х и удовлетворяющие соотношениям
182
ГЛ. 5. НЕПРЕРЫВНЫЕ ФУНКЦИИ
[5.62
(1)	— (4). Позднее, в гл. 8, мы дадим доказательство суще-
ствования и единственности таких функций; ближайшие рас-
смотрения, строго говоря, являются условными (если суще-
ствуют функции sin х и cosx, удовлетворяющие (1)—(4),
то ..хотя мы не будем этого специально оговаривать.
5.62.	Полагая в 5.61 (1)—(3) х=у = 0, получаем сле-
дующие равенства:
sin2 0 + cos2 0=1;	(1)
sin 0= 2 sin 0-cos 0;	(2)
cos 0 = cos2 0 — sin20.	(3)
Из (2) следует: или sin 0 = 0, или cosO = -i. Но из (1)
и (3) мы получаем
1 4- cos 0 = 2 cos2 0,	(4)
откуда видно, что равенство cos 0 = у невозможно. Поэтому
sin0 = 0, и из (1) следует, что cosO = +l. Равенство (4)
позволяет выбрать из этих двух значений cos 0 единственно
возможное cos 0=1. Итак,
sin 0 = 0, cos0=1.	(5)
5.63.	Заменяя в 5.61 (2), (3) у на —х и используя 5.62 (5),
имеем
О = sin х cos (— х) + sin (— х) cos х,
1 = cosx cos (— х)— sin х sin (—x).
Разрешая эту линейную систему относительно sin (—х)
и cos (—х), получаем
sin (—х) = — sin х, cos (—х) = cos х. (1)
Вычитая из равенства 5.61 (2) то же равенство, в котором
у заменено на —у, и используя (1), находим
sin (х 4-у) — sin (х —у) = 2 sin у cos х.
Совершая аналогичную процедуру с равенством 5.61 (3),
получаем
cos (х 4~.у)—cos(x—_у) = —2 sin х sin_y.
5.64]	§ 5.6. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ	183
Заменяя в полученных формулах х-]-у на а, а х—у
на р, так что х = 2  , у =	, записываем эти фор-
мулы в виде
sin а— sin р = 2 sin —cos ;	(2)
„	„ . а+р . а—р	п
cos а—cos р = —2 sin —g-1- sin •	(3)
5.64.	а. Из 5.61 (1) следует, что при всех х
| sin х |	1, | cos х |	1.
б. Пользуясь а и 5.63 (2), (3), мы докажем непрерыв-
ность функций sin х и cos х. Пусть х>у и разность
х—у достаточно мала. Тогда
1 •	-in- х—у\	x-j-yl -
I sin х — sin у I = 2 sin —g-2 cos —~
__________________ . (x—y) , _ x—у
<2 2 sin  2 < 2 —-x—y,
откуда следует непрерывность функции sin х. Аналогично
1	I с 1 . х-4-у
I cos х — cosy I = 2 sin —
• x—у . x—y~
Sin 5^2 Sin ~~	X —y,
откуда следует непрерывность функции cosx.
в. Из соотношения 5.61 (4) с учетом теоремы 4.34 з
следует, что
.. sinx .	...
hm-—=1,	(1)
х\о Л
поскольку 5.61 (4) дает для 0 < х < в0
1	sin х	।
cos х х
а крайние члены этого неравенства при х\0 имеют пре-
дел 1. Учитывая 5.63 (1), мы имеем также
.• sinx	sin(—х) .	,о.
lim----= lim ——-=1.	(2)
х7о х (-х)\о х
Объединяя формулы (1) и (2), получаем
lim
sin х
(3)
о
X
184
ГЛ. 5. НЕПРЕРЫВНЫЕ ФУНКЦИИ
[5.65
5.65.	а. Покажем теперь, что функция у = cos х при
х > 0 обращается (в некоторых точках) в нуль. Положим
0 = inf {cosx}. Если 0 > О, то из 5.63 (2) следует, что
Х>0
при достаточно малом х и любом т=1, 2, ...
sin (m+l)x— sin /»х^20 sin у >0;
поэтому величины sin тх неограниченно возрастают вместе
с т, что противоречит 5.64 а. Таким образом, 0 = 0. По-
кажем, что существует точка х0, в которой cosx0 = 0.
Если при х > 0 всюду cos х > 0, то из 5.63 (2) следует,
что функция sin х возрастает и соответственно (в силу
5.61 (1)) cosx убывает. Поскольку inf {cosx} = 0, най-
Х>0
5
дется такая точка z0, что cos х < при х > г0 и, сле-
довательно, sinx = prl—cos2x > у- . При y = x>z0
формула 5.61 (2) дает
•^ < sin 2х = 2 sin х cosx < 2• 1
А —12
13 — 13 ’
что невозможно. Итак, имеются точки, где cosx обращается
в нуль.
б.	Положим
-2- = inf {x>0:cosx = 0}.	(1)
Число л/180 называется градусом-, таким образом, л/2 = 90
градусов (90°). Так как функция cosx непрерывна, то
cos-y=0, sin -у = 1. На отрезке £о, функция sin х воз-
растает, a cosx убывает. Далее, формулы 5.61 (2), (3)
дают
. / л . А .л . л.
sin I ~2 ”1“ х / = sin у cos х + cos -у sin х = cos х,	(2)
(Л  \	Л	 Л 		/п.
-у-|-Х 1 =COS -у COSX— Sin-g-SinX =—sin X, (3)
откуда
sin (х-|-л) = cos (х-|--у) =—sin х,	(4)
cos(x-|-n) = —sin(x-|--yj= — cosx. (5)
5.66]
§5.6. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
185
в.	Далее,
sin (х + 2л) = — sin (х 4- л) = sin х,	(6)
cos (х 4-2 л) = — cos (х 4-л) = cos х.	(7)
Функция	удовлетворяющая при некотором Т
и всех х уравнению /(х4- Т) =/(х), называется периоди-
ческой, число Т называется ее периодом. Мы видим, что
функции sinx и cosx—периодические функции с перио-
дом 2л. На протяжении одного периода 2л знаки этих
функций, определенные по формулам (2)—(5), чередуются
следующим образом:
Мы видим, что если при данном х sinx=£O и cosx^O,
то по знакам sinx и cosx можно однозиачио указать ту
четверть промежутка 0 < х < 2л, где находится х.
На рис. 5.5 показаны графики функций sin х и cosx.
(На данном этапе мы еще не можем обосновать указанную
на графиках выпуклость кривых; это будет сделано в даль-
нейшем, в 7.55.) Число л равно 3,14159... (задача 15 к
гл. 9).
5.66. Лемма. Если для некоторых х и и выполнены
равенства
sin (х 4- и) = sin и,
cos(x4-«) = cosu,
0)
то x = 2lm, где k есть целое число.
186
ГЛ. 5. НЕПРЕРЫВНЫЕ ФУНКЦИИ
[5.67
Доказательство. Решая систему уравнений
sin (х + w) = sin х cos и + cos х sin и = sin и,
cos (х -р и) — cos х cos и — sin х sin и = cos и
относительно cos х н sin х, находим
cosx=l, sinx = 0.	(2)
В промежутке 0^х<2л эти уравнения, как следует
из 5.65, удовлетворяются лишь при х = 0. Вследствие су-
ществования у функций cos хи sin х периода 2л уравнения
(2) удовлетворяются при х = 2/гл (А = 0, ±1, ±2, ...)
и не удовлетворяются ни при каких других значениях х.
Лемма доказана.
5.67. Мы видели, что функция sinx возрастает на от-
резке [0, л/2]; в силу равенства sin (— х) = — sin х она
возрастает даже на отрезке [—л/2, л/2], изменяясь от —1
до +1. По теореме об обратной функции 5.38 на отрезке
[—1, 1] определена обратная функция, которую обозначают
arcsinx; эта функция возрастает, непрерывна и принимает
свои значения в промежутке [—л/2, л/2]. Функция
cosx=sin + возрастает на отрезке [—л, 0], изме-
няясь от —1 до ф-1; поэтому на отрезке [—1, 1] опреде-
лена обратная к ней функция, которую обозначают arccosx.
Эта функция возрастает, непрерывна и принимает свои зна-
чения в промежутке [—л, 0].
Так как по 5.65 (2)
• ( , я \
sin ( х + I = cos х,
то, обозначая общее значение этих величин через «, находим
, л
х = arccos и,	х 4- -g- — arc sin и
и, следовательно, при любом ug [—1, 1]
Л
arccos и -|- у — arc sin и.	(1)
Можно определить и другую функцию arccos и, используя
убывающую ветвь функции cosx на отрезке [0, л]. Здесь
5.68]
§ 5.6. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
187
Вместо формулы
обратная функция будет также убывающей на отрезке
[—1, 1] и изменяющейся от л до 0.
sin I х -]- -у 1 = cos х, связывающей
функции sinx и cosх на тех участках,
где мы строили обратную функцию,
на этот раз нужно использовать фор-
мулу sin l-g—x)=cosx, откуда вместо
формулы (1) получается
arccos и = —arcsin и.	(2)
Для предупреждения возможной пута-
ницы можно обозначать первую из введен-
ных нами обратных функций к cosx —
возрастающую — через arccosB и, а вто-
рую— убывающую — через	arccosy и.
Графики функций arcsin х, arccosBx, arccosyx показаны на
рис. 5.6.
Имеются и другие функции на [—1, 1], которые с тем
же правом можно считать обратными к sin х и cos х, но
мы ограничимся приведенными.
5.68. Положим, далее,
,	sinx
tg х =---.
°	cosx
Эта функция определена всюду, кроме точек, где cos х = О,
т. е. кроме точек х = у4-Ал, А = 0, + 1, + 2, ... При этом
lim tgx= + oo,
lim tgx = — оо.
Из равенств 5.65 (4), (5) следует, что функция tgx имеет
период л. Из поведения функций sin х и cos х на интер-
вале	следует, что tgx в этом интервале воз-
растает, заполняя своими значениями всю числовую ось.
По теореме об обратной функции существует обратная
функция arctgx, определенная на всей числовой оси,
188	ГЛ. 5. НЕПРЕРЫВНЫЕ ФУНКЦИИ	[5.71
возрастающая, непрерывная и изменяющаяся в интервале
Рассмотрение остальных тригонометрических функций
. 1 1 1 л
ctax = T—, secx =-------, cosec х — -.— и им обратных мы
° tg х ’	cos х	sin х	r
предоставляем читателю.
§ 5.7.	Приложения тригонометрических функций
5.71.	Полярные координаты на плоскости.
Для каждой точки (х, у) в вещественной плоскости /?2 при
х2 -|-у2 =#0 выполняется равенство
х2 I У2 _,
X2 + j/2 X2 + у2
Определим число 0 в промежутке 0^0 < 2л из условий
cos 0 =--.х , sin 0
+ /х2+у2
(1)
5.72] § 5.7. ПРИЛОЖЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ 189
Искомое 0 существует и единственно: при х > 0, у > 0 это
следует из формулы 5.61 (1), непрерывности и монотон-
ности cos 0 и sin 0 при 0 < 0 < -у и следствия из теоремы
Больцано 5.23; в остальных случаях—из формул 5.65 (2)—(5)
и правила знаков 5.65 (8). Число© называется полярным углом
точки (х, у). Для точек с х > 0, у = 0 полярный угол
равен 0, для точек с х — 0,у > 0 он равен -у = 90°, для точек
су = О, х < 0 он равен л = 180° и для точек с х = 0, у < 0 он
равен -у л = 270°. Впрочем, иногда удобнее, воспользовавшись
периодичностью функций sin 0 и cos 0, под 0 понимать не
только решение системы (1) в [0, 2л), но и любое веще-
ственное число, отличающееся от этого решения на число,
кратное 2л. Число
г = У х2+у2	(2)
называется полярным радиусом точки (х, у). Формулы (1)
можно записать в форме
х = г cos 0, у = г sin 0.	(3)
Числа г и 0 называются полярными координатами точки
(х, у); они определены всюду, кроме точки х = 0, у = 0,
где г=0, а величина 0 не имеет смысла. Координатная линия
г = const есть окружность
x2+y2 = r2;
координатная линия 0 = const есть луч
^ = tg0.
5.72.	Тригонометрическое представление
комплексных чисел. Пусть г = х-\-1у^д—комплекс-
ное число (§ 2.7). Используя равенства 5.71 (3), можно
это число представить в форме
z — г (cos 0 4* i sin 0),	(1)
где 0 и г определены по формулам 5.71 (1), (2). В этой
записи г называется модулем комплексного числа z, а 0 —
аргументом г*). Пишут г — | z |, 0 = argz.
*) Не надо путать с понятием аргумента функции (2.81).
190	ГЛ. 5. НЕПРЕРЫВНЫЕ ФУНКЦИИ	[5.73
Если
г1 — rl (cos +1 sin 61),
z2 = ra (cos 03 + i sin 02),
то, перемножая эти равенства и используя 5.61 (2), (3),
получаем
гхг2 = гхг2 [(cos 0j cos 62 — sin 0t sin 02) +
+ i (cos 0г sin 02 + sin 0X cos 02)] =
= rj2 [cos (0X + 02) + I sin (0X + 02)].	(2)
Таким образом, при умножении комплексных чисел их
модули перемножаются, а аргументы складываются.
5.73.	В частности, для любого z=^0 из 5.72 (2) сле-
дует, что при любом натуральном т=1, 2, ...
2J"=r'n(COSff!0 + / sin w0).	(1)
Используя формулу (1), мы решим уравнение
zm = w,	(2)
где w—заданное комплексное число. При w = 0 имеется
очевидное (единственное) решение z — Q. Поэтому будем
считать w=#0,
tv~ R (cos co -f- i sin to).
Будем искать z в форме 5.72 (1), где г и 0 подлежат
определению. Равенство (1) приводит к уравнению
rm (cos + i sin m0) = R (cos to + i sin co),
откуда
rm cos mQ = R cos co, rm sin mQ = R sin co. (3)
Возводя эти равенства в квадрат и складывая, находим
г2/я = Rp"
это уравнение в области положительных чисел имеет един-
ственное решение
r = '^R.
Сокращая теперь равенства (3) на rm = R, получаем
cos WZ0 = cos со, sin /Й0 = sin со.
5.74]	§ 5.7. ПРИЛОЖЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ функций 191
В силу 5.66, где положено и = со, х и = тв, так что
х = т6—со, мы имеем тв—со = 2Ал, т. е.
0=<o+2fax (ft = 0, ч-1, ±2, ...).
При k = 0, 1, ... , т—1 получается т различных ре-
шений уравнения (2)
zk—y/R [cos
2kn
m
---) 4-1 Sin
m J 1
Остальные значения k дают для 0 значения, отличаю-
щиеся на какое-либо кратное 2л от уже найденных, и
поэтому не дают новых корней
уравнения (2).
Найденные корни (4) распола-
гаются в вершинах некоторого пра-
вильного m-угольника с центром в
начале координат (рис. 5.8).
5.74.	Угол между век-
торами в /г-м ерном про-
странстве. Имея векторы
* = (*1..хп) £Rn,
У—(Уъ ••,Уп)^^
R=\, <0 = 192°.
мы составляем их скалярное произведение (3.14 (1))
(х, у)= % хкуь.
k= 1
Учитывая неравенство Коши—Буняковского 3.14 (5)
мы можем при х О, у =£ 0 найти число со,
из условия
л,
(х, У)
cos со = -г--,--.--, .
\*1-Ы
Число со называется углом между векторами х и у и обо-
значается (А.у)- Если со = О, т. е.
(х, ^) = |х|- [>],
192
ГЛ. 5. НЕПРЕРЫВНЫЕ ФУНКЦИИ
[5.75
то векторы х и у линейно зависимы. Действительно,
в этом случае уравнение
0 = (х—"Ку, х—'Ху) = (х, х)—2А(х, у) + ^а(у, у) =
= |х1а-2Л|х|.|у| + Ла|у|а=(|х|-Л|у|)а
I I
имеет решение А, = -|^-; следовательно, при этом А
х = Ау.
Аналогично, если со = тт, т. е. (х, у) =— |х|«|у|, векторы
х и у линейно зависимы; на этот раз связывающий их
множитель отрицателен.
Если to = л/2, т. е. (х, у) = 0, векторы х и у назы-
ваются ортогональными. Это последнее определение есте-
ственно распространяется и на случай, когда один из век-
торов х, у (или оба) есть 0:- нуль-вектор оказывается
ортогональным к любому вектору х.
Применим полученное определение к двум векторам на
плоскости. Пусть вектор xg/?2 имеет полярные координаты
{р, ф}, а вектору—полярные координаты {г, г|з}. Соот-
ветственно прямоугольные координаты векторов х = (хх, х2)
и у — (уь у2) имеют вид
Xj — р cos <р,	х2 = р sin <р, У1 — г cos ф, у2 = г sin ф.
Поэтому, согласно общему определению,
,	(х, у) pr(coscocosф-4-sin<рsinф) .	„.
cos (>у)=тМи=—рг~ —	= cos (•₽ -
Отсюда угол (х, у) между векторами х и у есть то из вы-
ражений ф—тр2/гл или гр—ф-|-2Ал, которое заключено
между Ойл.
5.75.	П о в о р о т ы. а. В плоскости /?2 поворотом на угол 0
называется преобразование, оставляющее на месте начало
координат н переводящее каждый вектор х 0 с поляр-
ными координатами {р, ф} в вектор х' с полярными коор-
динатами {р, ф-|-0}.
Запишем преобразование поворота в прямоугольных
координатах. Пусть в прямоугольных координатах х = (хх, х2),
5.75]	§ 5.7. ПРИЛОЖЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ 193
х'— (xj, xj). Мы имеем
xj = р cos (<р + 0) = р (cos <р cos 0— sin ф sin 0) ==
= хх cos 0—х2 sin0,
xj — р sin (ф 4- 0) — р (sin ф cos 0 + cos ф sin 0) =
= x1sin0 + x8cos0;
это и есть искомые формулы поворота в прямоугольных
координатах. По самому определению поворот не меняет
длины любого вектора. Покажем, что поворот не меняет
и угла между двумя векторами. Если ф и ф—полярные
углы двух векторов х и у, то полярные углы векторов
х' и у', получающихся после поворота, равны ф -|-0 и ф-|-0.
Угол го между векторами х и у определяется из уравне-
ния cos го = cos (ф — ф), угол со' между векторами х' w у" —
из уравнения cos со' = cos [(ф + 0) — (ф + 0)]; так как и го
и со' заключены в пределах от 0 до л, то со = го', что и
требуется. Определитель из коэффициентов построенного
линейного преобразования, очевидно, равен 1.
б.	Обобщим определение преобразования поворота на
n-мерное евклидово пространство. Поворотом, или ортого-
нальным преобразованием, называется такое линейное пре-
образование х' = и (х), или в координатах
xj=K11x1+...+K1„x„, ’I
......................} (1)
х'п = ^щХ1 + ...+иппХп, I
при котором не меняются длины векторов и углы между ними,
и det||uyft|| = l.
Найдем условия на коэффициенты иуА, обеспечивающие
выполнение поставленного требования. Пусть ej —
= (0........ 1.......0) (/=1, ..., л) и ej=u(ey). Век-
, i
торы е1г ... , еп должны быть ортогональными и нормиро-
ванными (3.14 а) вместе с векторами ..., еп. Из (1)
следует, что ej = (uly., ... , лпу), поэтому"мы должны иметь
, . ..	( 1 при «==/,
(eii ej) —	Ut<illkj — I 0 При t^=j.	(2)
Мы утверждаем, что условия (2) и достаточны для того,
чтобы преобразование (1) было преобразованием поворота.
194
ГЛ. 5 НЕПРЕРЫВНЫЕ ФУНКЦИИ
[5.76
Действительно, пусть х' = и(х), у' = и(у) определены по
формулам (1); тогда
(*'. y') = ^xky’k= ukiX^^ukjy^ =
Д (Jj	“*/) Х‘У' = J Х‘У‘= (Х’ У)’
откуда следует сохранение и длин векторов,и углов между
ними. Можно показать, что при л=2 приведенное опреде-
ление совпадает с определением а (задача 19).
5.76.	Полярные координаты в пространстве.
Вычислим угол ау- между вектором х = (х1, ..., хп) и ба-
зисным вектором Су=(О, ..., 1, ..., 0) в л-мерном евкли-
довом пространстве Rn. По общей формуле 5.74
/ч (х, еу) ху
cos а,- = COS (X, е,.) = ;—п—; =:—г •
I v ’ J’ |х|-|ву|	]х|
Отсюда прямоугольные координаты вектора х можно запи-
сать в форме
Ху= | X | COS (X, Су), х= |x|(cos(x, ..., cos(x, еп)). (1)
Углы Оу=(х,ву) и |х | называются полярными коорди-
натами вектора х. Между величинами аь ..., а„ имеется
связь
gcos2ay=£ =
Угол между векторами х и у по их полярным углам
аь ..., a„ и fj, ..., р„ можно записать формулой
cos (х?у) = |	= cos ax • cosPi + ... + cos a„ • cos p„.
Если co = (<o1, ..., <o„) есть единичный вектор, |<o|=l,
то числа <0у, как видно из (1), суть косинусы углов между <о
и соответствующими базисными векторами: <Oy=cos(co, еу).
В частности, коэффициенты ujk преобразования поворота
5.75 (1) как координаты единичных векторов ej имеют
прямой геометрический смысл: коэффициент и,у есть коси-
нус угла между вектором е'- и базисным вектором е{.
5.82]
§ 5.8. ВЕКТОРНЫЕ НЕПРЕРЫВНЫЕ ФУНКЦИИ
195
§ 5.8. Векторные непрерывные функции векторного
переменного
5.81.	Рассмотрим функцию у=/(х), областью опреде-
ления которой является множество G в л-мерном евклидо-
вом пространстве а областью значений /я-мерное евкли-
дово пространство Ет. Такая функция называется отобра-
жением множества GcEn в Ет. Поскольку Еп и Ет — ме-
трические пространства (3.14), результаты § 5.1 применимы
к отображениям. В соответствии с общим определением
5.11 отображение y = f(x) называется непрерывным при
x — a^G, если lim f(x) = f(a), или, иначе говоря, если для
х~> а
любого е>0 существует такое 6 > 0, что из |х— а|<6
следует
\f(x)—f(a)\<e.
Через | | в данном случае обозначаются, естественно, рас-
стояния в пространствах Еп и Ет.
5.82.	Если записать функцию y=f(x) в координатах,
мы получим систему равенств вида
•••> xj^f^x),
ym=fm(X1, . . ., Х„) =/и (X),
в которых участвуют т числовых функций переменного
х = (хъ ..., хп). Из 4.74 следует, что соотношение
lim f(x)=f(a)
х-+а
равносильно т соотношениям для числовых функций
lim /1(х)=/1(а),
а
I»™ fm(x) =fm(a).
х-+ а
Поэтому отображение y=f(x) непрерывно при х = а тогда
и только тогда, когда при х = а непрерывны все т число-
вых функций /х(х), ..., /т(х).
196
ГЛ. 5. НЕПРЕРЫВНЫЕ ФУНКЦИИ
[5.83
5.83.	На непрерывные отображения переносятся некото-
рые из доказанных нами в § 5.1 теорем о числовых непре-
рывных функциях. А именно:
а.	Если./(х) и g(x) —векторные функции (отображения),
непрерывные при x = x0£G, то функция f (х)-(- g(x) также
непрерывна при х = х0.
б.	Если а (х)— числовая функция, определенная в О и
непрерывная при х — Х0, a g(x)—отображение G в Rm,
непрерывное при х — х0, то а(х)^(х) есть отображение G
в Rm, также непрерывное при х = х0.
в.	Если y—f(x)—отображение, непрерывное в точке
х — х0, то |/(х)| есть числовая функция, непрерывная при
х = х0.
5.84.	Рассмотрим функцию w=/(z), определенную на
множестве G в евклидовой плоскости £2, с областью зна-
чений также в плоскости Е2. При этом z = (x, у), w=(u, v)
можно считать комплексными числами. Функция w=f(z)
называется комплексной функцией комплексного аргумента.
В соответствии с 5.81 функция w=/(z) непрерывна в (не-
изолированной) точке z = a£G, если lim /(z)=/(a), или,
z -> а
иначе говоря,если для любого е > 0 существует 6 > 0 такое,
что из | г — а | < 6 следует
|/(z)— /(a)|<e.
Согласно 5.82 функция w =f (z) = и (z) -J- iv (z) непрерывна
при z — a тогда и только тогда, когда обе вещественно-
значные функции u(z) и v(z) непрерывны при z = a.
Согласно 5.83а,б вместе с комплексными непрерывными
функциями f(z) и g(z) непрерывны при z—a их сумма
/(z)-j-g(z) и произведение функции f(z) на любую вещест-
венную функцию а (г), непрерывную при z — a. Используя
известные действия с комплексными числами, мы можем до-
бавить к этим свойствам следующие:
а.	Если f (z)u g(z)—две комплексные функции, непрерыв-
ные при z — a, то произведение f(z)g(z) также непрерывно
при z—a.
б.	Если f(z)— комплексная функция, непрерывная при
I
Ц4
Z= а, причем f (а)	0, то
непрерывна при z—a,
5.86]	§ 5.8. ВЕКТОРНЫЕ НЕПРЕРЫВНЫЕ ФУНКЦИИ	197
в.	Если f(z) и g(z)—две комплексные функции, непре-
рывные при z~a, причем g(a)=£0, то также непре-
рывна при z=a.
Эти утверждения вытекают из соответствующих свойств
пределов (4.73 д).
5.85.	Функция w = z, очевидно, непрерывна при каждом
z — х + iy. В силу 5.84 каждый многочлен w — Р (в) — aQzn +
. 4-ап с комплексными коэффициентами а0,..., ап
есть непрерывная функция от г и каждая рациональная
функция
да. = р (г). = аог"+---+<г»
™ Q (г)	60г,л
непрерывна всюду, кроме тех значений z, для которых
Q (z) = 0.
5.86.	Теорема о существовании корня. Чис-
ло z0, удовлетворяющее уравнению P(zo) = 0, называется
корнем многочлена P(z). В вещественной области имеются
многочлены, не имеющие корней (пример: Р(х) = ха-]-1).
«Основная теорема алгебры» состоит в том, что в комплексной
области каждый многочлен, отличный от постоянной, имеет по
крайней мере один корень. Здесь мы докажем эту теорему.
а.	Лемма. Пусть P(z)—некоторый многочлен. Для лю-
бого положительного А существует такое R, что при | z | R
выполняется неравенство |Р(г)|^Л.
Доказательство. Мы имеем при а0 0 и z 0
/5(z) = a0zn + a1zn“1 + ... Ч-ап =
= «ozn Г1 +-^-+____•
Так как предел скобки при z —>- оо равен 1 (4.73 е), то
существует число такое, что при | z |	/?г
и, следовательно,
198
ГЛ. 5. НЕПРЕРЫВНЫЕ ФУНКЦИИ
[5.86
Если взять теперь |г|^/?>/?1, то неравенство
р(г)]>1|со!1^1"^4|со1/?П>Л
п /’
выполняется при R > 1/ 2 :—т, что и доказывает лемму.
' I °о1
б.	Лемма. Пусть P(z)— некоторый многочлен степени
п~^\. Если P(zo)=/=O и задано число 60 > О, то сущест-
вует точка zly | zr —z0 |	60, для которой | P(zT) | < | P (z0) |.
Доказательство. Вначале рассмотрим случай z0 = О,
Р(0)= 1. Пусть ak—первый из коэффициентов an_lt ...,
а0, отличный от 0. Тогда
P(z) = 1 +akzk+    +aozn= 1	[1 +//(z)],
где
Я(г) = ^1г+..,
' о*	“k
Так как, очевидно, Н(0) = 0, то в силу непрерывности мно-
гочлена Н (z) существует круг |г|^6^б0, в котором
выполняются условия
\Щг) | ^4’б'г । ak I < Е	(О
Определим zt из уравнения
4 = _,
1	fife
которое разрешимо (5.73), причем, очевидно, | zx | = 6. Тогда
IР (*i) I = 11 + akzi + akziH (zi) I =
что и требуется.
В общем случае, пользуясь соотношением
Р (*) =	аЪгП~к = ак Kz — zo)
мы можем расположить многочлен P(z) по степеням z—z0:
P(z)^ 2 bk (z ~z0)n~k, P (*o) = ^0^0.
k = 0
5.86]
§ 5.8. ВЕКТОРНЫЕ НЕПРЕРЫВНЫЕ ФУНКЦИИ
199
Если мы заменим здесь z—z0 на £, то получим
P(*) = M>0(£),
где
^(□=1+£ч+.--+гЧп.
°0
Так как | P(z) | = |ft0 |>|P0 (£) |, то задача сведена к преды-
дущей.
в.	Мы можем теперь доказать основную теорему.
Теорема. Каждый многочлен Р(z) = а^п +... + ап
(п 1, а0 =# 0) в комплексной плоскости имеет по край-
ней мере один корень.
Доказательство. Функция | Р (z) | неотрицательна;
положим
а = inf {| P(z) |}.
Z(=C
Далее, используя лемму а, можно найти такое R, что при
| z |	R выполняется неравенство
\P(z) |>а + 1.
Поэтому при вычислении а значения Р (z) вне круга | z | R
уже не играют роли. Мы можем написать
а= inf {|P(z)|}.
I z 1
Но круг V = {| z | R} в отличие от всей плоскости С есть
уже компактное множество (3.96 д). В силу теоремы 5.16 б
непрерывная функция |P(z)| достигает в некоторой точке
z0 £ V своей нижней грани:
|P(z0)| = a.
Если а = 0, то P(z0) = Q. Покажем, что предположение
P(Zq)=£0 ведет к противоречию.
Точка z0 лежит внутри круга V, так как на его грани-
це, т. е. при | z | = R, уже выполняется неравенство
1. Таким образом, некоторый малый круг
\z—z0|^60 лежит целиком в круге V. По лемме б в этом
круге можно найти такую точку что |P(zx) | < |P(z0) |.
Но это означает, что a=|/’(z0)| не является точной ниж-
ней гранью функции |P(z0)| в круге V. Полученное проти-
воречие показывает, что P(zo) = O, и теорема доказана.
200	ГЛ. 5. НЕПРЕРЫВНЫЕ ФУНКЦИИ	{6.87
Б.87. Из алгебры известно*), что для любых двух мно-
гочленов P(z) и Q (z)=^0 можно найти путем деления и
выделения остатка два других многочлена S(z) и R (z) та-
ких, что
P(z) = Q(z)S(z) + R(z),	(1)
где или R(z) = 0, или степень R (z) (остатка) ниже степени
многочлена Q(z); многочлен P(z) при этом называется де-
лимым, Q(z)—делителем, а 5 (z)—частным. Сумма степеней
делителя и частного равна степени делимого. Здесь z есть
просто символ, не обязанный быть каким-либо числом, и
многочлен P(z) есть некоторое формальное выражение,
определяемое совокупностью коэффициентов а0, ..., ап,
с естественными правилами сложения и умножения. При
подстановке в равенство (1) вместо z произвольного ком-
плексного числа это равенство перейдет в равенство между
получающимися числами.
Пусть, в частности, Q(z) = z—zr. Тогда R(z) имеет
нулевую степень, т. е. является постоянной. Если при этом zx
есть корень многочлена P(z), то постоянная R(z) равна
нулю; действительно,
R (z)^R (zj = Р (zt)-S (zj (zr -zj = 0.
Разложение (1) принимает вид
P(z) = S(z) (z—zr),
где многочлен S (z) имеет степень n—1.
Повторяя этот процесс в применении к многочлену
S (z) = S1(z), мы получаем
5 (z) == (z) = S2 (z) (z — Zg),
где za есть корень многочлена (z) и тем самым и много-
члена P(z); степень многочлена S2(z) равная—2. Продол-
жая таким образом далее, мы можем снизить степени
последовательных частных до нулевой, в результате чего
получится разложение
P(z) = S0(z—Zj).. .(z—zn),
*) См. например, А. Г. К у р о ш, Курс высшей алгебры, М.,
1968, гд. 5.
5.88]	§ 5.8. ВЕКТОРНЫЕ непрерывные функции 201
где 50—постоянная, a zt, ...,z„—корни многочлена Р(г).
Они могут быть не все различными? объединяя скобки с оди-
наковыми корнями, мы получим Окончательную форму разло-
жения многочлена на множители
P(z) = S0(z-z^...(z-zh)%	(2)
где числа гъ ..., гк уже все различны. Показатели гх,..., гк
называются кратностями соответствующих корней. Раскры-
вая скобки, мы можем убедиться, что число So совпадает
со старшим коэффициентом многочлена P(z).
5.88.	а. Разложение рациональных функций
на простейшие дроби. Для данных двух многочленов
Рг(г) и P2(z) (например, с комплексными коэффициентами)
можно построить их общий наибольший делитель D(z) —
многочлен наибольшей степени, на который делятся без
остатка Ру (z) и Р2 (z) *). Доказывается, что существует
представление
D (г) = Pi (z) Sj. (z) + Р2 (z) S2 (z),
где 5x(z) и S2(z) — новые многочлены от z.
Очевидно, всякий корень многочлена D(z) ёсть корень
обоих многочленов Px(z) и P2(z). Поэтому, если Px(z) и
P2(z) не имеют общих корней, их общий наибольший де-
литель есть постоянная, которую можно считать равной 1.
б.	Рассмотрим рациональную функцию
Q(z)
Px(z) Pa(z) ’
где Px(z) и P2(z) не имеют общих корней. Согласно ска-
занному, существуют такие многочлены (z) и <Sa (z), что
Px(z)Sx(z)-|-P2(z)Sa(z)==l
и, следовательно,
Q{z) = Q (г) Ру (z) Sx (z) + Q (z) Р2 (z) S\ (z).
Разделив обе части этого равенства на Px(z)P2(z), получим
Q(z)	Q&Sy(z) , Q(z)Sg(z)
Pi(z)P2(Z) Pt(z) Py(z) 
) См. А. Г. К у p о ш, там же.
202
ГЛ. 5. НЕПРЕРЫВНЫЕ ФУНКЦИИ
[5.89
Можно продолжить эту операцию, разлагая Pr(z) и P2(z)
далее на множители без общих корней. Используя для мно-
гочлена P(z) представление 5.87 (2), мы таким путем мо-
жем построить разложение рациональной функции в сумму
<?(2) =	<?(2)	= у
р(г) So (г-zj' ... (z-z^ 2- (г-г/р '
Располагая каждый из числителей Qj(z) по степеням соот-
ветствующей разности z—Zj, мы можем, далее, от разло-
жения (1) перейти к разложению
<2)
/= 1 ' m= 1	J
где T(z)—многочлен, а А/т—числа. Формула (2) называется
L .	Q (г)
разложением рациональной функции на многочлен и про-
* И/
стейшие дроби *).
5.89.	Многочлены с вещественными коэф-
фициентами.
а.	Если Р (z) = a„zn -f- an_lzn~1 + ... + a0 есть многочлен
с вещественными коэффициентами и z0 есть число, ком-
плексно сопряженное с числом z0, то, согласно 2.73,
Р(г0) = апг"+ ... +a0 = anzS+ ... ±a0 = P(z0). (1)
В частности, если г0—корень многочлена P(z), т. е. P(z0) = 0,
то равенство (1) показывает, что и P(zo)~O, т. е. что z0
также есть корень многочлена P(z).
б.	Пусть z0 = x0 + iy0, z0 = x0—iy0; тогда (z—z0) х
X (z — z0) = (z~x0—iy0) (z —x0+iy0)=(z—x0)2+yl Раз-
делив многочлен P(z) на трехчлен с вещественными
*) В алгебре доказывается и единственность такого разложения;
см. А. Г. К у р о ш, там же, гл. 5. На теореме единственности
основан «метод неопределенных коэффициентов» для фактического
построения разложения (2), с которым можно познакомиться по книге
Г. М. Фихтенгольц, Курс дифференцильного и интегрального
исчисления, т. 2, гл. VIII, и. 262, Гостехиздат, 1948.
5,91]
§ 5.9. ПОСЛЕДОВАТЕЛЬНОСТИ ФУНКЦИЙ
203
коэффициентами (z—xt)2-\-yl, получим
Р (z) = [(Z — х0)2 +у?] Л (z),
где Pi(z)—снова многочлен с вещественными коэффициен-
тами. Это позволяет преобразовать разложение 5.87 (2)
к вещественной форме, объединив множители с комплексно
сопряженными корнями; при этом вместо 5.87 (2) получается
разложение на множители с вещественными коэффициентами
Р(г) = М(г—*1)2+Я]г* • • • [(*—X
X(z—xfc+1)'*+. • • • (z — xp)rp, (2)
где xx ± iyi, • • •, xk ± % — невещественные корни много-
члена P(z), a xk+l, ..., xp—вещественные его корни с
соответствующими кратностями г1э ..., гр. В частности,
невещественные корни Xj-yiyp- и —iyj имеют одну и ту
же кратность.
в.	Аналогично разложение на простейшие дроби 5.88 (2)
для многочленов Q(z) и P(z) с вещественными коэффициен-
тами может быть преобразовано к виду
— Ttz\ 4. V J V Л/«»+гД/«» I 
Р ( ri А- \
+ L {L(r4r :
/=Н-1 Vm=l J I
соответствующая выкладка предоставляется читателю.
§ 5.9.	Последовательности функций
5.91.	Рассмотрим сначала последовательность функций
/г(х), /2(Х), ..., /п(х), ...,	(1)
заданных на произвольном множестве Е, со значениями
в метрическом пространстве М. Будем говорить, что после-
довательность (1) сходится на множестве Е, если каждая
последовательность вида
/1 (Хо)> /г (Хр), ..., fn (х0), ... (х0£Е)
имеет в М предел. Этот предел, зависящий, естественно,
от точки х0, мы обозначим через /(х0); тем самым мы
204
ГЛ. 5. НЕПРЕРЫВНЫЕ ФУНКЦИИ
[5.92
А (*) ='
получаем функцию f(x), которая, по определению, является
пределом последовательности функций f„(x):
/(х)= lim/„(x).	(2)
п-+к
Таким образом, равенство (2) означает, что для каждого
е > 0 и каждой точки х0(ЦЕ найдется номер N (зависящий
от в и от точки х0) такой, что для всех « > N
Р[/(*о).	(3)
5.92.	Примеры.
а.	Последовательность числовых функций
fn{x)=-^-f(x)
сходится к нулю в области определения числовой функции
/(X).
б.	Последовательность числовых функций fn (х) = х"
сходится в промежутке —1<х^1. Ее предел/(х) есть
функция, равная 0 при х < 1 и 1 при х = 1.
в.	Последовательность функций
п sin пх при О X ,
О	при х л
сходится в каждой точке х £ [0, л] к 0. Заметим, что мак-
симальное отклонение функции fn (х) от предельной функции
/(х), равное п, в этом примере не только не стремится
к 0, но даже неограниченно возрастает.
5.98.	Вообще говоря, предельная функция последователь-
ности /п(х) может не обладать свойствами, которыми обла-
дают сами функции fn(x). Так, в примере 5.92 б функции
/„(х) непрерывны на [0, 1], а предельная функция разрывна.
Чтобы иметь возможность сказать что-то определенное от-
носительно предельной функции, обычно приходится налагать
условия на характер сходимости.
В следующем определении сформулировано одно из важ-
нейших условий такого рода.
Определение. Последовательность функций 5.91 (1)
называется равномерно сходящейся к предельной функ-
5.95]
§ 5.9. ПОСЛЕДОВАТЕЛЬНОСТИ ФУНКЦИЙ
205
ции f(x) на £, если для любого е > 0 можно найти номер N
так, что для любой точки х0 £ Е при л > N выполняется
неравенство
P[/W> fn (*о)]<8-
(1)
Отличие от предыдущего определения 5.91 состоит в том,
что здесь одни и тот же номер N годится сразу для всех
точек х0£Е, в то время как в определении 5-91 номер А/
зависел еще от выбора точки х0. Поэтому неравенство (1)
следует заменить неравенством
supp[/(x), /„(х)]^е
хеЕ
(2)
для всех	N=N(г).
В примере 5.92 а сходимость последовательности fn(x)
к своему пределу была равномерной, а в примерах 5.92 б, в —
неравномерной.
Целесообразность введенного определения подтвержда-
ется следующими теоремами.
5.94.	Теорема. Если каждая из функций fn(x) огра-
ничена, т. е. для фиксированной точки р£М выполняются
неравенства
Р [fn (X),	(л=1, 2, ...),
и последовательность fn(x) сходится на Е равномерно, то
предельная функция f (х) также ограничена.
Доказательство. Найдем для заданного е > 0, на-
пример е=1, номер N так, чтобы иметь при n^N и каж-
дом х£Е
Р [/„(*). /(х)]Се=1.
Отсюда при каждом х£Е
Р [/(*), .Р]<Р [/(*), /jv(*)]+p[/a(*),
и мы видим, что функция f (х) ограничена.
5.95.	Теорема. Если Е есть метрическое пространство
и каждая из функций последовательности fn(x) непрерывна
в точке х0£Е, то в случае равномерной сходимости после-
довательности fn(x) предельная функция f(x) также непре-
рывна в точке х0.
206	гл. 5. непрерывные функции	[5.96
Доказательство. Для данного е > 0 найдем номер N
так, чтобы при всех п~^ N и всех х£Е иметь
р[Л(х),/(х)]<|.	(1)
Так как функция fN(x) непрерывна при х = х0, существует
такое 6 > 0, что при всех х в шаре V= {р (х, х0) < 6}
выполняется неравенство
p[/jv(*)> Zjv(^o)] *	е 3" ‘	(2)
Запишем неравенства (1) для точек	х V и	х0 и n = N:
P[Zyv(^o)> /(*<>)] =	е -У ’	(3)
P[/jv(*), /(*)]<	е ^У’	(4)
Из (2)—(4) следует, что при х € V
Р [/(*), /(*о)] < 8,
что и означает непрерывность функции /(х) при х = х0.
5.96.	Как следствие получаем:
Теорема. Предел равномерно сходящейся последова-
тельности непрерывных функций f„(x) на метрическом про-
странстве Е есть непрерывная функция на Е.
5.97.	Если метрическое пространство М есть лч-мерное
вещественное пространство Rm, так что функции /„(х) Суть
функции с векторными значениями, неравенства 5.93 (1) и
5.93 (2) принимают соответственно вид:
]7(Хо)-А(ХО)]<8	(1)
при каждом х0^Д и	х0);
sup |/(х0)—/„ (х0) [ < е	(2)
хеЕ
при каждом n~^N(e,).
5.98.	В этом же случае (M=Rm) для равномерной сходи-
мости имеет место критерий, похожий на критерий Коши 4.75.
Критерий Коши для равномерной сходимо-
сти. Последовательность функций fn(x), определенных на
5.98]	§ 5.9. ПОСЛЕДОВАТЕЛЬНОСТИ ФУНКЦИЙ
207
множестве Е и принимающих значения в пространстве Rm,
сходится на множестве Е равномерно тогда и только тогда,
когда для любого е > 0 существует номер N такой, что для
всех n^N, p~^N
sup |/„(х)—/г(х)|<е.
х£Е
Доказательство. Пусть функции /„(х) сходятся
равномерно на £ к функции /(х). Тогда для заданного в > 0
мы возьмем номер N так, чтобы при любом и любом
х£Е иметь
|/„(х)-/(х)|^|.
В частности, и для номера р~^ N при любом х £Е
|/г(х)-/(х)|^|.
Отсюда при любом х£Е и указанных лир
\fn (*)— /г(х)1=^е-
Следовательно, и
sup |/„(х)— / (х)|<е.
хеЕ	г
Обратно, пусть выполнено условие теоремы. В частности,
прн фиксированном х0££ для последовательности векторов
/г(х0), .. .,/„(х0), ... выполнен критерий Коши в Rm (4.75).
Поэтому в силу теоремы 4.75 последовательность /„(х0)
сходится в Rm к некоторому вектору, который мы обозначим
через /(х0). При всевозможных х = х0£Е получаем функцию
/(х) со значениями в Rm. Покажем, что f„(x) сходится к
/(х) равномерно.
В неравенстве
IAU)—
перейдем к пределу при р—>-оо. В силу непрерывности
расстояния (5.12 б) мы имеем при всех х£Е и n~^N
|/»W-/(х)|<е,
что и означает равномерную сходимость fn(x) к /(х).
Теорема доказана.
208
ГЛ. 5. НЕПРЕРЫВНЫЕ ФУНКЦИИ
Примечание. В условии и утверждении этой теоремы
можно заменить пространство Rm на любое полное метри-
ческое пространство. Мы вернемся к этим вопросам в даль-
нейшем, в гл. 12.
ЗАДАЧИ
1.	Дана числовая функция y=f(x), определенная в окрестности
точки хв. Известно, что для каждого о > 0 существует такое е > 0,
что из | х—х01 < 6 следует | f (х)—-f (хв) | < е. Непрерывна ли функция
f(x) при Х=Хд?
2.	Пусть для каждого е > 0 существует такое 6 > 0, что из
[f (x) — f (хв)[ < е следует |х—хй| < 6. Непрерывна ли функция
t(x) при х=х0?
3.	Доказать непрерывность функции у=[х |.
4.	Исследовать на непрерывность функции у = (х) (дробная часть х)
и У = [х] (целая часть х) (1.71).
5.	Доказать, что функция Римана
[ 1	т	„
. I —, если х=— есть несократимая дробь,
/(*)=< п	п
' 0, если х иррационально,
непрерывна в иррациональных и разрывна в рациональных точках оси.
6.	Если числовые функции f (х) и g (х) непрерывны, то и функции
max {f (х), g(x)}, min {f (x), g(x)}
также непрерывны.
7.	Если числовая функция f (х) непрерывна при х£[а, Ь] и х(, ...
..., х„—любые точки этого отрезка, то существует точка х0£[а, Ь],
в которой
= (*«)]•
8.	Если ограниченная монотонная функция f (х) непрерывна на
интервале (а, Ь), конечном или бесконечном, то она равномерно не-
прерывна на (а, Ь).
9.	Монотонная функция f(x), определенная на (—оо, оо), удо-
влетворяющая функциональному уравнению f (x-f-y) = f (x) + f (у),
имеет вид
f (х) = ах.
10.	Указать на (—оо, <») участки равномерной сходимости по-
следовательности функций

ЗАДАЧА
209
11.	Доказать, что соотношение 5.61 (4) не есть следствие соотно-
шений 5.61 (1)—(3), а соотношение 5.61 (1) не есть следствие соотно-
шений 5.61 (2)—(4).
12.	Функция j (х) определена при — об < х < об, и для любых
двух точек Xi < х2 и любого с£([ (хг), f (х2)) имеется точка хс£(хъ х2),
в которой f(xc)=c. Непрерывна ли функция f(x)?
13.	Проверить таблицу значений:
X	SlHX	СО$ X	tgx
л	1	/3	/3
6	2	2	3
л	V2	/2	1
4	2	2	
Л т	Гз 2	1 2	/3
14.	-Пусть f (х)—вещественная функция, определенная на отрезке
[а, Ь]. Доказать, что множество тех точек с£[а, Ь], для которых
lim f (х) существует и отличен от f (с), не более чем счетно.
х~>с
15.	Пусть 7 = 0, 7Х 12 ... 1„ ...—десятичная запись (7.77) Веще-
ственного числа t, < 1. Пусть, далее, п, < л2 < ... <	<...—
некоторая подпоследовательность последовательности натуральных
чисел. Исследовать на непрерывность функцию
ЦО=о, tnjtn2...tn/i...
16.	Доказать, что множество М точек в плоскости, расположен-
ных на единичной окружности Г с центром в начале координат и
имеющих полярные углы 1, 2, .... п........всюду плотно на Г.
17.	Функция f (х), определенная и непрерывная на множестве Р,
всюду плотном на некотором компакте М, обладает непрерывным
продолжением на все М (т. е. существует функция F (х), определенная
и непрерывная на М и совпадающая на Р с f (х)) Тогда и только
тогда, когда f (х) равномерно непрерывна на Р.
18.	Доказать, что вещественная функция f (х), определенная и
неубывающая в промежутке (а, Ь), может иметь не более счетного
множества точек разрыва.
19.	Показать, что поворот в «-мерном пространстве (5.766) при
п=2 есть поворот в плоскости на некоторый угол (5.76 а).
20.	Если в определении поворота в n-мерном пространстве
(5.766) отбросить требование det|| U/k [|=1, то получающееся линей-
ное преобразование, если оно не есть поворот, есть «поворот с от-
ражением», т. е. результат последовательно произведенных отраже-
ния	.... £л-1=£л-1, ёл = —U и поворота.
210	ГЛ. 5. НЕПРЕРЫВНЫЕ ФУНКЦИИ
Историческая справка
Первое корректное определение непрерывности для функции ве-
щественного переменного было дано Больцано (1817), а затем Коши
(1821). Оба они, используя «критерий Коши», получили теорему о про-
межуточном значении (5.22). Теорема 5.16 б об ограниченности не-
прерывной функции и о достижении ею точных границ была (для
отрезка) найдена Вейерштрассом (около 1860). Определение равномер-
ной непрерывности и соответствующая теорема о непрерывных функ-
циях (5.17 б) (для отрезка) были получены Гейне (1870).
Показательная функция с дробным показателем была известна
давно (Штифель, 1544); уже на этом раннем этапе было замечено,
что произведению степеней отвечает сумма показателей и что такое
свойство может быть использовано для вычислений. Первые таблицы
логарифмов были составлены Непером (1617) и Бюрги (1620). Полное
определение показательной функции и логарифма и доказательство
непрерывности этих функций были даны в середине XIX века, как
только появились достаточно разработанные теории вещественных
чисел
Тригонометрические функции (как отрезки в круге) были известны
в древности (первая таблица синусов составлена Птолемеем во II ве-
ке н. э.). Индийские математики знали формулу 5.61 (1) (Ариабхата,
V век). Формулы 5.61 (2) и (3) получены немецким математиком
Региомонтаном (XV век). Современные обозначения тригонометриче-
ских функций были введены Эйлером (XVIII век).
Существует иное аксиоматическое построение теории тригономе-
трических функций, не требующее предположения о существовании
решений некоторых функциональных уравнений и основывающееся
на соображениях теории непрерывных групп (Н. Б у р б а к и, Общая
топология. Числа и связанные с ними группы и пространства, гл. VIII,
Физматгиз, 1959.)
Проблема существования комплексного корня у всякого много-
члена с комплексными коэффициентами была поставлена еще
в XVII веке; в XVIII веке было дано несколько ее решений, но все
они не были и не могли быть строгими до построения развитой теории
вещественных чисел и непрерывности. Первое строгое доказательство
с явным указанием роли непрерывности было дано Гауссом (1799);
недостающие места здесь заполнились в результате работ Больцано
(1817), Коши (1821) и в конечном счете Дедекинда—Кантора—Вей-
ерштрасса (1874).
Понятие равномерной сходимости последовательности функций
и роль этого понятия в сохранении непрерывности были указаны
Стоксом и Зейделем (1847—1848) н затем Коши (1853); впрочем, ранее
для частного случая аналогичная теорема была уже у Абеля (1826).
РЯДЫ
ГЛАВА 6
По-разному расставляя скобки в выражении 1 — 1 +
+ 1 — 1+...,я могу по желанию получить 0 или 1.
Но тогда нет ничего невозможного в предположении о со-
творении мира нз ничего.
Гвидо Гранди (1703)
Что касается меня, то признаюсь, что все рассуж-
дения и вычисления, основанные на ие сходящихся ря-
дах... всегда кажутся мие крайне подозрительными.
Жан Даламбер (1748)
§6.1. Числовые ряды. Знакоположительные ряды
6.11. а. Пусть Gj, яа, .. ,,а„, ... — последовательность
вещественных чисел. Образуем частные суммы
si — aii
«.= ^ + «2,
s„ — «1 + «г + • •  +
Определение. Если последовательность чисел
sb sa, . . ., sn, . . . сходится к конечному пределу а, то мы
будем говорить, что числовой ряд
а1 + а2 +    + ап +
(1)
сходится и его сумма равна числу а = lim sn. Если же после-
ZZ->00
довательность чисел а2, ..., sn, ... расходится, будем
говорить, что ряд (1) расходится, и не будем приписывать
ему никакой суммы.
Числа аг, а2, ... называются членами ряда (1). Всякая
конечная сумма am+1-j-  • • +«„ называется отрезком ряда (1).
Если все числа аг, ..., ап, ... положительны (неположи-
тельны, неотрицательны, отрицательны), ряд (1) называется
знакоположительным (знаконеположительным, знаконеотри-
цательным, знакоотрицательным).
212
ГЛ. 6. РЯДЫ
[6.11
б.	Пример. Рассмотрим числовой ряд
1 4-x-f-x2+хи-1+...,
(2)
где х — некоторое фиксированное число. Частные суммы
этого ряда вычисляются по формуле суммы геометрической
прогрессии
Если | х | < 1, то при п —> оо мы имеем хп —> 0, откуда
следует, что величины sn имеют предел
(3)
Таким образом, при | х | < 1 ряд (2) сходится и его сумма
имеет значение (3).
Если х=1, то, очевидно,
s„= 1 + ... + 1 = л
и, следовательно, ряд (2) расходится. При х = —1 имеем
аг=1, а2 = 0, а3=1, а4 = 0, ...
так что последовательность sn, оставаясь ограниченной, не
имеет предела, и ряд (2) также расходится. Наконец, при
| х|> 1 величина | sn | с ростом п неограниченно возрастает,
так что ряд (2) опять-таки расходится.
В итоге мы получаем: ряд (2) сходится при | х | < 1
и имеет сумму (3), а при | х |	I расходится.
в.	Критерий Коши для ряда. Применяя к после-
довательности частных сумм а2,... , sn,... критерий Коши
(3.72) и учитывая, что при т<п мы имеем sn—sm =
= cm+1+ • • • + а„, получаем критерий Коши для ряда:
Ряд (1) сходится тогда и только тогда, когда для любого
е > 0 существует такое число N, что при всех m~^N, п^> m
1йт+1+ •••+««!<»•
г.	В частности, если ряд (1) сходится, то для любого
е>0 существует такое N, что при n^N
т. е. lim о„ = 0.
со
6.13J § 6.1. ЧИСЛОВЫЕ РЯДЫ. ЗНАКОПОЛОЖИТЕЛЬНЫЕ РЯДЫ 213
Таким образом, у сходящегося ряда ^4- ... 4-а„ + .. •
последовательность его членов аг, ..., а... стремится
к нулю. Соотношение ап —> 0 является, следовательно, не-
обходимым условием сходимости ряда аг + • • • + ап + -  •
Но имеются и расходящиеся ряды аг 4- ... -}-ап 4- ..., у кото-
рых также ап —* 0 (пример в 6.15 6), так что условие ап —> О
не является достаточным условием сходимости ряда.
д. Другое необходимое условие сходимости ряда выте-
кает из 3.33 б: всякая сходящаяся последовательность ограни-
чена. Поэтому у всякого сходящегося ряда ах + ... + ап 4- ...
последовательность его частных сумм ..., sn, ... ограни-
чена. Это условие, являясь необходимым условием сходи-
мости, также не является достаточным. Так, частные суммы
ряда 1 —14-1 — 1 4- • • • ограничены, однако он не является
сходящимся.
6.12. В дальнейших пунктах 6.13 — 6.17 мы рассмотрим
знаконеотрицательные ряды. У знаконеотрицательного ряда
суммы $!, $2, ... образуют неубывающую последователь-
ность. Поэтому если частные суммы а2, ... знаконеотри-
цательного ряда ограничены (при п —> оо), то этот ряд яв-
ляется сходящимся. Мы видим, что для знаконеотрицатель-
ного ряда необходимое условие 6.11 д является и доста-
точным.
6.13. а. На этом свойстве основан признак сравнения-.
Если знаконеотрицательный ряд at 4~ ае + ' '' + ап 4~ • • •
сходится, то сходится и всякий знаконеотрицательный ряд
4* ^2 + • • • 4* Ь„-}-...,
для которого существуют постоянная с и номер N такие,
что для всех n~^N выполняются неравенства Ь„^.са„.
Действительно, пусть s = 4- <?2 + • • • и °и=А4- • • • 4~^п;
мы имеем при п> N
— bi 4- • • • + Ьп гС Ьг 4-... 4- fyv4- с (aN+i 4-F ап) С
<^14~ • • • +^v+cs-
б. Пример. Если члены знаконеотрицательного ряда
4- &2 4~ • •  удовлетворяют неравенствам
bns^c8n (n = N, AZ4-1, •••),
где с > О и 0 sC 6 < 1, то ряд Ьг 4- Ла 4" • • • сходится.
214
ГЛ. 6. РЯДЫ
[6.14
Действительно, можно применить признак сравнения, по-
лагая в нем ап = 8" и используя 6.11 б.
6.14.	Следующие два признака основаны на рассмотре-
ниях 6.13.
а.	Признак Даламбера. Если для знакоположи-
тельного ряда
«1 + ^2+ • • • +аи + аи+1+ • • •	(О
выполняется неравенство
л->оо an
(2)
то ряд (1) сходится. Если
(3)
оо
то ряд (1) расходится.
Доказательство. Если выполнено (2), то для не-
которого 6 < 1, начиная с некоторого номера N, выпол-
няется неравенство
Отсюда
C7V+1	СЛ'+2	®C7V+1	• • • > aN+k	• • •»
и сходимость ряда (1) следует из 6.13. Если же выполнено
(3), то, начиная с некоторого номера N, выполняется не-
равенство
2^±1> 1	(л = Л/, 7V+ 1, ...);
отсюда aN+! > aN, aN+2 > aN+1, ..., так что члены ряда
не стремятся к 0; следовательно, в силу 6.11г ряд (1)
расходится.
Пример. Ряд
, 1-2	1-2.3	1-2-3-4
1 + 1-3+ Ь3.'5+ 1-3-5-7+ * ‘ •
сходится, поскольку
Оп + 1 __	1	1
ап 2п -J-1 *" 2
6.15] § 6.1. ЧИСЛОВЫЕ РЯДЫ. ЗНАКОПОЛОЖИТЕЛЬНЫЕ РЯДЫ 215
б.	Признак Коши. Если для знакоположительного
ряда
Й1 + й2 + • • • + ап + • • •	(4)
выполняется неравенство
lim < 1,	(5)
оо
то ряд (4) сходится. Если же
lim у/ ап > 1,	(6)
то ряд (4) расходится.
Доказательство. Если выполнено (5), то для не-
которого 0 < 1, начиная с некоторого номера N, выпол-
няется неравенство
< е>
откуда при
ап < О",
и ряд (4) сходится по 6.13. Если выполнено (6), то для
любого номера N найдется число л > N, для которого вы-
полняется неравенство
V ап> 1»
откуда
й«> 1;
таким образом, члены ряда (4) не стремятся к 0 и в силу
6.11 г ряд расходится.
Пример. Ряд
4+(1У+(Я+(Я+...
сходится, так как
я/ТГ” _ n-f-l	1
V п ~ in—1	"2 •
6.15.	Укажем еще один полезный признак сходимости,
найденный Коши,
216
ГЛ. 6. РЯДЫ
[6.15
Если	ап~^ ... ^0, то ряд^ап схо-
дится или расходится вместе с рядом
S2fta2fc.	(1)
m
Действительно, рассмотрим сумму и возьмем число
k так, чтобы иметь 2k > т. Тогда
О1+ — 4~С/Л^а1+  • • +a2k-i =	4~ (й2 + °з)4~ •  • +
+ (с2*-» + • • • + а2*->)	Й1 + 2а2 + . • • + 2ft-1 o2ft_,.,
00
Если ряд ^2Aa2fc сходится, то правая часть ие превосходит
суммы этого ряда. Следовательно, частные суммы аг+... -}-ат
00
ограничены и У ап сходится. С другой стороны, если k та-
ково, что 2й < т, мы имеем
а1 + • • • + ат а1 4" • • • 4~ ®2* = Й1 + й2 + (Й3 4~ й«) + • • • +
+ («afc-i+1+ • • • + c2fc) °i + °г + 2а4 + • • • 4-2й 1o2/t =
— ~2 (а1 4" 2°2 4" ^а4 4~ • •  4~ 2fto2s)
СО
и из расходимости ряда ^2йа2& следует расходимость
ряда
СО
Примеры, а. Ряд У и — сходится при р > 1 и расхо-
дится при 0^р ^1.
В самом деле, при р 0 члены ряда не возрастают
и можно применить признак Коши. Соответствующий ряд (1)
имеет вид
СО	05	ОО
Е^ = Х2"(1_/?) = ХаП> где « = 21~л
1	1	I
и результат следует из примера 6.136 с учетом того, что
при р > 1 мы имеем 21-^ < 1, а при 1 имеем 21-^^ 1.
6.16J § 6.1. ЧИСЛОВЫЕ РЙДЫ. ЗНАКОПОЛОЖИТЕЛЬНЫЕ РЯДЫ 217
Отметим, что
1 . 1 _ 1 1
(п+1И ' пР ~ /п+1 л 1 у
\ П /	\ ' п )
так что признак Даламбера в данном случае неприложим.
00
б.	В частности, ряд . — расходится. Каждый член этого
ряда, начиная со второго, есть среднее гармоническое двух
ОО
соседних членов *), поэтому ряд , — называется гармони-
ческим..
СО
в.	Ряд 7.------— сходится при р > 1 и расходится при
п loggn
O^p^l (если основание а > 1). Здесь в силу неубывания
логарифма (5.42) также можно применить признак Коши.
Соответствующий ряд (1) имеет вид
2”	___ж	1	__ 1 х 1
Zu 2" (logc2")P ~ Zu (п \o&fi)P ~ (logc2)P Zu пР ’
и вопрос о сходимости приводится к примеру а.
6.16.	Используя для сравнения ряды 6.15 а тл в, можно
устанавливать сходимость или расходимость многих типов
рядов, для которых признаки Даламбера 6.14 а или Коши
6.14 б не действуют.
Заметим вначале, что сравнивать можно не только члены
рядов, но и отношения соседних членов.
00	00
Лемма. Если для знакоположительных рядов ип u^vn
при всех достаточно больших п выполняется неравенство
un vn
аз	оо
и ряд сходится, то сходится и ряд
(1)
*) Число а называется средним гармоническим чисел b и с, если
1=1(1+1)
а	с )'
218
ГЛ. 6. РЯДЫ
[6.17
Доказательство. Пусть неравенство (1) выполняется
при n = N, /V1, N + 2, ... Перемножая левые и правые
части неравенств (1), написанные для n = N,
.. ., N-\-p, находим
uN + p ^VN + p
un "" vn
или
UN+p'^^'VN+p’	(2)
поскольку неравенство (2) справедливо при всех р — 1, 2, ...,
СО
сходимость ряда следует из 6.13.
6.17.	а. Теорема (признак Раабе). Если для зна*
СО
неположительного ряда ^ип отношение соседних, членов
можно записать в виде
(£-> 1 при л —оо, ср. 4.39),
ОО
то ряд сходится при а > 1 и расходится при а < 1.
Доказательство. Положим	v„ = -4 ; тогда по
” пР
5.59 е, ж
Vn+i	\	1	_ . рЕ
vn («+))/> /	_1_у рЕ п ’
\ "Г п )	' п
Если а>1, возьмем	а); тогда при достаточно
больших п
ип+1  t / 1 рЕ Уп+1'
ип	п	п vn
00
Поскольку в данном случае ряд сходится (6.15 а), из
00
6.16 вытекает сходимость ряда Ус„. Если а< 1, возьмем
6.21]	§ 6.2. РЯДЫ С ЛЮБЫМИ ВЕЩЕСТВЕННЫМИ ЧЛЕНАМИ 219
р£(а, 1); тогда при достаточно больших п
уп+1 _	__ un+i
vn	п	п ип ’
СО
и если бы ряд £И„ сходился, то по 6.16 сходился бы и ряд
со
Но последний в данном случае (р < 1) расходится,
00
следовательно, расходится и ряд
б. Пример. Рассмотрим ряд (у и б не есть числа
О, —1, —2, .... —п, ...)
у у(У+1)---(т+п—1)	,. v
Z-fi(6+l)...(6+n_ ij-	U)
_	un + 1 v + n	n ,	0 — у o „
В данном случае	— =------т- = 1----—- E. По а ряд
J un o+n 1-lA
n
(1) сходится, если б—у > 1, и расходится, если б—у < 1.
§ 6.2. Ряды с любыми вещественными членами
6.21. Для ряда
а1 + аг+• • •• • •	U)
с любыми вещественными членами рассмотрим знаконеотри-
цательный ряд
|а1| + |й2|+...+|«„1+• •.	(2)
Теорема. Если ряд (2) сходится, то и ряд (1) сходится.
Доказательство. Для заданного е > 0 найдем номер
N так, чтобы при л > N выполнялось неравенство
1 am+l I + • • • +l°nl < е-
Для указанных тип также
I ат + 1 +  • • + ап I СI arn + l 1 + • • • + | ап I < е,
так что для ряда (1) выполнен критерий Коши, и теорема
доказана.
220
ГЛ. 6. РЯДЫ
[6.22
6.22.	Ряд (1), для которого сходится ряд (2), называется
абсолотно сходящимся.
Может оказаться, что ряд (1) сходится, а ряд (2) рас-
ходится (пример будет указан ниже); в этом случае ряд (1)
называется условно сходящимся.
6.23.	Признак Лейбница. Если а2^ а3 .
и ап —>- 0, то знакочередующийся ряд
°1—йг + аз—««+ •••
сходится.
Доказательство. Мы имеем
^2n + l~ S2n-1 а2п^~ °2n+l ^S2n-lt
S2n + 2 = S2n 4" а2п+1	а2п+2 S2n<
так что последовательность s2, st, ... не убывает, а после-
довательность s3, ... не возрастает. При любом k и п k
S2 ^4 ^4 ^4 • • • ^4 S2n ^4 S2n 4" а2п+1 = S2n + 1	• • • ^4 ^2й+1>
так что последовательность s2, s4, ... ограничена сверху
любым числом s2ft+1; таким образом, £= lim s2n^s2k+1 при
П-> со
любом k. Но в таком случае lim s2n служит нижней грани-
п -> 00
цей всех s2ft+1; поэтому существует lim s2n+1 и
п -> ос
В = lim s2n	lim s2n+1 = т].
П“> ОО	00
Далее, имеем О^т]— B^s2n+i—szn — asn+i> так как по
условию а2п+1 —> 0, то £ = т] = lim sn (4.64), что и требуется.
«-►СО
6.24.	Примеры.
а. Ряд
1—2“4“35—4«+-”	(а > 0)>
согласно признаку Лейбница, сходится. При а > 1 он схо-
дится абсолютно (6.15 а). При 0 <	1 он сходится лишь
условно, так как соответствующий ряд из абсолютных величин
1 j—।
1 । За ' 4а ' ” • ’
расходится (6.15 а).
6.31]
§ 6.3. ДЕЙСТВИЯ С РЯДАМИ
221
б.	В частности, сходится знакопеременный ряд
1“4 + Т'“т+-'-
В дальнейшем (9.74) мы укажем величину его суммы,
в. Рассмотрим ряд
СО
_ у (у+1). •(?+«—О
" 6(6 + 1)...(6+п— 1)’
—1, —2, ...
П=1
у, бу=0,
Этот ряд
Покажем, что
абсолютно сходится при 6>у+1 (6.17 6).
он сходится (условно) и при 6 > у. Так как
«л+1 !	6—у Е
ип	п
(6.17 б), то, если 6 > у, мы имеем ип+1 < ип, во всяком
случае при достаточно больших п. Для применения признака
Лейбница остается установить, что lim «„=0. По 5.59 г и
ж имеем
lnii£±l= In Г1 —$	е \ =— -—- Е' (Е’ —> 1 при п—+ оо);
\	**	/	Л
jnto:=1n^+...+1nte. = _(6_T)£^-,
11	"	fe=l
откуда вследствие расходимости гармонического ряда (6.15 б)
In ип+1 —> — оо и, следовательно, и„+1 —> 0, что и требуется.
§ 6.3.	Действия с рядами
6.31.	Определения. Пусть имеются два числовых ряда
а1 + а2+...+а„+...,	(1)
+ ^2 + • • • +	+ • • •	(2)
а.	Ряд
(O14-&1) + (а2 + &2) + • • • + (ап + ^п)+ • • •	(3)
называется суммой рядов (1) и (2).
б.	Если а—число, то ряд
аа1 + аа2+...+аа„+...	(4)
называется произведением ряда (1) на число <Х,
222
ГЛ. 6. РЯДЫ
(6.32
в.	Ряд
«1^1 + (а1^2 + ^1сг) + (°1^3 + °2^2 + °з^1) + • • •	(5)
называется произведением рядов (I) и (2).
Все эти определения, без каких-либо предположений
о сходимости рядов, носят формальный характер. Содержа-
тельный смысл они приобретают в следующей теореме.
6.32.	Теорема.
00	00
а. Если ряды (1) и (2) сходятся и ^ак—А, ^Ьк — В,
1	I
СО
то ряд (3) также сходится и 2(ал
00
б. Если ряд (1) сходится и = Л, то ряд (4) также
I
00
сходится и
I
00	00
в.	Если ряды (1) и (2) сходятся, ^ак = А, "£bk = В
1	1
и хотя бы один из. этих рядов сходится абсолютно, то ряд (5)
сходится и его сумма равна А-В.
п	п
Доказательство, (а) Если Л„=2ал,
I	I
п
т0 2 (°*+ £*)== Л„ + В„ имеет пределом Л-]-В.
1
п	п
(б) Если Ап = ^ак, то 2 ctGft == имеет пределом «А
1	I
п	п	п
(в) Положим An = ^ak, Bn^^bk, cn=^akbn_k,
Cn~^ck. Пусть сходится абсолютно ряд так что
1	I
со
О = 2Н*1<°°- Числа Ап ограничены, поскольку последо-
I
вательность Alt А2, . .. сходится; пусть 7W=sup|H„|. Числа
|ЛИ — Ат | Ап | -(- \Ат | ограничены числом 2М. Для задан-
6.34]
§ 6.3. ДЕЙСТВИЯ С РЯДАМИ
223
ного 8 > 0 найдем номер N так, чтобы при п'_> иметь
п	«о
Y.ak и X 1М^4^- Тогда прп n^N
k—m	k—N
AfPn— | = I («2 + • • • + °n) + (°з +  • • +fin) ^n-l +
+  • • 4- anb21 I aa + ...+a„|-|ft„| +
+ |аз+ • • • +Gn|-|^n-i|+ ... +
так что lim C„= lim AnBn = А- В, и теорема доказана.
«~>О0	И->00
Если оба ряда (1), (2) сходятся неабсолютно, теорема в
перестает быть справедливой (см. задачу 5).
6.33.	Группировка членов ряда. Пусть дан ряд
ai + аъ + • •  + ап + • • •	(1)
Пусть, далее, т1 < /и2< •   —возрастающая последователь-
ность натуральных чисел. Положим
ах = Oi + ... + ат„
С62 = l +  •  + ат,,
О-п —	”Ь • • • ^mni
Определение. Ряд
«1 + «а+••+«„+•••	(2)
называется сгруппированным рядом (1).
Теорема. Если ряд (1) сходится, то и ряд (2) сходится
к той же сумме.
Действительно, при любом п
«1 + аг+ ...+а„ = Я1+ ...+«Ип,
и при п —> оо правая часть имеет пределом сумму ряда (1).
6.34.	Более интересен вопрос, при каких условиях из
сходимости ряда (2) следует сходимость ряда (1). В общем
224
ГЛ. 6. РЯДЫ
[6.35
случае это не имеет места; так, ряд 1 —1 + 1 — 1 + • • • не
сходится, в то время как сгруппированный ряд (1 — 1) +
+ (1 — !)+••• сходится (к сумме 0). Сходимость ряда (1)
есть следствие сходимости ряда (2) при некоторых допол-
нительных условиях, формулируемых в теоремах а и б.
а.	Теорема. Если ряд (1) знакоположителен и ряд (2)
сходится, то и ряд (1) сходится.
Действительно, при любом п
а1 + • • • + ап а1 + • • • + ап + • • • + атп =
— О1 + • • • + гС S ak>
так что частные суммы ряда (1) ограничены; далее остается
применить 6.12.
б.	Теорема. Если ап—+0 и число элементов каждой
группы ограничено постоянной (т. е. тп—тп_1^.М при
всех п), то из сходимости ряда (2) следует сходимость
ряда (1).
Действительно, для заданного п найдем mk и тк+1 так,
чтобы иметь
mk^n^mk+1.
Тогда, если sn = аг + ... + ап, oft = 04 + ... + мы имеем
°>l=l amk+i Н----------1-aJsCM- max |ау| -> о>.
I > тк
при А-»оо, откуда следует, что числа sn имеют тот же пре-
дел, что и числа ок.
6.35.	Перестановки членов ряда. Пусть
ai + °2 + • •  + ап + • • •
(1)
— некоторый ряд.
Определение. Если т^, т2, ... есть некоторая пе-
рестановка множества натуральных чисел, то ряд
+ ^2 + • •  + Ьп + ...,
(2)
где Ьп = аПп(п=1, 2, ...), называется перестановкой
ряда (1).
Теорема. Если ряд (1) сходится иап 0 (n= 1, 2, ...),
то ряд (2) сходится и имеет ту же сумму.
6.36]
§ 6.3. ДЕЙСТВИЯ С РЯДАМИ
225
Доказательство. Для каждой частной суммы ряда(2)
ап — + • • • + Ьп	(3)
найдется частная сумма ряда (1)
sm(n} — Й1 + й2 + • • • + йи(л»	(4)
которая включает в себя все члены суммы (3). В свою оче-
редь, мы можем найти частную сумму ряда (2), которая
включает в себя все члены частной суммы (4):
ОЛЧп) = ^1+ • • • +^»+ • • • + ^V(n>-
Поскольку й„^0 при любом п, мы имеем
ап sm (л)	(5)
Первое из найденных неравенств дает
°n s«a(n) SI
так что ряд (2) сходится; пусть о—его сумма. Очевидно,
т (л) и N (л) не менее, чем л, и поэтому вместе с л неогра-
ниченно возрастают. Переходя к пределу в (5) при п —► оо,
получаем
о
откуда o = s, и теорема доказана.
6.36.	Теорема (Дирихле). Если ряд 6.35 (1) сходится
абсолютно, то ряд 6.35 (2) также сходится абсолютно и
имеет ту же сумму.
Доказательство. Абсолютная сходимость ряда (2)
следует из 6.35. Для заданного е > 0 найдем номер N та-
кой, что	—x|<y и при m~^N выполняется неравен-
п
ство У. | у. Пусть р0—такое число, что всякая
m
частная сумма ор ряда (2) при р~^р0 содержит первые N
членов' ряда (1). Тогда при любом р^р0 разность ор—sN
содержит лишь члены ряда (1) с номерами, большими N;
поэтому рд,—откуда и
к—swl + lsw—ор|<е.
Тем самым ор —► s, что и требуется.
226
ГЛ. 6. РЯДЫ
(6.37
6.37.	Совершенно иная картина имеет место для условно
сходящегося ряда.
Теорема (Риман). Если ряд 6.35 (1) сходится условно
и заданы произвольно числа	{на расширенной веще-
ственной оси), то существует такая перестановка 6.35 (2)
ряда 6.35 (1), что
limo„ = a, lirno„=p.
Доказательство. Поскольку ряд 6.35 (1) сходится, его члены
стремятся к 0. Поэтому существует лишь конечное число номеров п,
для которых | ап | превосходит данное положительное число в. Это
позволяет выбирать из любой совокупности членов ряда 6.35 (1)
наибольший (или наибольший по модулю). Отделяя в этом ряде по-
ложительные и отрицательные слагаемые и выбирая последовательно
наибольшие (наибольшие по модулю) члены, мы можем составить два
ряда: ряд
Р1+Р2+• • •+₽п+• • •>	(1)
образованный из всех положительных слагаемых ряда 6.35 (1), рас-
положенных в порядке убывания, так что Pi^р2^..и ряд
9i + 9а + - • • + Яп + • • •.	(2)
образованный из абсолютных величин всех отрицательных слагаемых
ряда 6.35 (1) также в порядке убывания, так что qi^q2^. • 
Мы утверждаем, что оба эти ряда расходятся.
В самом деле, еслй бы оба ряда (1) и (2) сходились, имея суммы
s и о, то ряд 6.35 (1) сходился бы абсолютно, поскольку любая ко-
нечная сумма | щ |+ ... +|а„ | не прееосходила бы суммы s-j-C-
Рассмотрим случай, когда один из рядов (1), (2) сходится, а другой
расходится. Предположим, например, что сходится ряд (2), а расхо-
дится ряд (1). Частные суммы s„ ряда 6.35 (1) с возрастанием п
вбирают в себя все большее количество членов из ряда (1) и ряда (2);
члены из ряда (1) дают как угодно большую сумму, в то время как
члены из ряда (2) могут дать лишь ограниченную компенсацию.
Таким образом, s„—> оо и ряд 6.35 (1) не может быть сходящимся.
Аналогичная картина, с изменением знака, будет иметь место в случае
сходимости ряда (1) и расходимости ряда (2). Итак, оба ряда (1) и
(2) расходятся.
Теперь мы строим из членов рядов (1) и (2) новый ряд по сле-
дующему правилу (для случая, когда а и f конечны). Частные
суммы Sn ряда (1) неограниченно возрастают; найдем номер щ так,
чтобы иметь
Р1+ • • • +рщ-1 < Р < Р1 + • • • + Pnt
(если уже pt > 0, считаем л1 = 1). Далее, найдем иомер mj так, что-
бы иметь
Р1+ • • • +Рщ—91— •   —Qm, < a «S Pi + ... +₽щ—91— • • • —9лц-1-
6.41]	§ 6.4. ряды векторов	227
Затем—номер п2 так, чтобы иметь
Р1 + • • • +₽«!—41— • • • —9zHi+P«1+l+ • • • +Р«а-1 < ₽ <
<	Р1+ • • • +Рп,—41— • • • —4mi+Pm+i+ • • • +pnj*
Затем—номер т^ так, чтобы иметь
Р1+ • • • +Рт — 41— • • • — 4mi + Pni + l+ • - • +Ро3 — 4mi + l—• • •—4я>а<
<	«<Р1+ •.. +Рщ—41— • • • —4и1 +
+ Рщ+1+ • • - +р«а — 4mi+l—• • • —4и2-1*
Продолжим это построение иеограииченио. Мы получим ряд
^1 + ^2 +— +6п+—»	(3)
представляющий собой некоторую перестановку ряда 6.35 (1). Пока-
жем, что ряд (3) удовлетворяет требуемому условию.
а.	Точки а и р являются предельными точками последовательно-
сти частных сумм ряда (3).
Действительно, частные суммы ряда (3) с номерами п1г ni+ffli+
+ п2, .... n1-j-m1-f-n2-j- ... -j-wife-i+nfe, ... отличаются от числа р
соответственно не более чем на р„г, рП2, ..., рП), ..., и эти вели-
чины стремятся к 0; аналогично частные суммы ряда (3) с номерами
zij-f-Wn пj-f-т 1 + п2+т2, ..., п1-}-т1-}-п2-}-т2-}- • - • -Ьп^-рт^, ...
отличаются от числа а соответственно не более чем на qmt, qmv ...
... > qm , и эти величины также стремятся к 0.
6.	Вне отрезка [a, f] нет предельных точек последовательности
частных сумм ряда (3).
Действительно, если, например, у > Р и у — р = й > 0, мы найдем
,	h
номер nk так, чтобы иметь рЛ( <	; тогда все частные суммы ряда
(3) с номерами, большими, чем П1 + /П1+ ... -[~mk^l-4-nk, не превос-
ходят Р + рП/1 < ₽+-^- и не подходят к точке у ближе чем иа ~.
Очевидно, предложения а н б доказывают теорему в случае ко-
нечных аир. Если одно, или оба, из чисел аир бесконечны,
построение должно быть несколько видоизменено; мы можем предо-
ставить читателю его выполнение.
В частности, мы можем положить а = р = р, и тогда ряд (3) будет
сходиться к числу р. Мы видим, что, переставляя должным образом
члены условно сходящегося ряда, можно добиться его сходимости к
наперед заданному значению суммы.
§ 6.4.	Ряды векторов
6.41.	Определение сходимости можно сформулировать
для ряда векторов из пространства Rn в полной аналогии
с определением 6,11 сходимости числового ряда, именно:
228
ГЛ. 6. РЯДЫ
[6.42
Пусть а1г ..., ат, ...—последовательность векторов
пространства Rn. Образуем частные суммы
s^a&R,»
sa=Gi + Ga€^B,
—cl + as+ • • •
Если последовательность частных сумм , sm, ... схо-
дится в пространстве Rn, то мы будем говорить, что век-
торный ряд
й1 + йаН----~Ьея>Н-----	(1)
сходится и его сумма равна вектору s — lim sn. Если же
п-^со
последовательность векторов slf ..., sm, — расходится,
будем говорить, что ряд (1) расходится.
6.42.	Поскольку сходимость в пространстве Rn приводится
к сходимости по каждой координате (3.32 е), мы можем
сказать, что ряд из векторов
•••» Gln)> G2=(G21» •••> G2n)> •••
..., am=(aml, ..., amn), ...
сходится тогда и только тогда, когда сходятся все числовые
ряды
аи + G21 + • • • + апл + • • •»
G12 + G22 + • • • + атй + • - • »
+ G2n + • • • +	+ •••;
при этом сумма ряда 2Gm есть вект°Р Р — (Ръ •••, Рп)>
каждая составляющая pk которого есть сумма соответствую-
оо
щего числового ряда 2 amk-
m= 1
6.43.	Поскольку критерий Коши выполняется в примене-
нии к векторным функциям, в частности к векторным после-
довательностям (4.75), он справедлив и для векторных рядов:
6.46]
§ 6.4. РЯДЫ ВЕКТОРОВ
229
Критерий Коши для векторного ряда.
Векторный ряд at 4- с2 4- • • • + ат + • • • («га € сходится
тогда и только тогда, когда для любого е > 0 существует
такое число N, что при всех п~> m~^N
lG«+l + • • • + Gn| < е-
6.44.	В частности, для всякого сходящегося векторного
ряда всегда limc„ = 0.
6.45.	Применяя критерий Коши, так же как и в 6.21,
получаем следующее достаточное условие сходимости:
Если сходится числовой ряд
|с1| + |а2|+• • •+lGml+• • •> (U
го сходится и векторный ряд
<h + °2 + • • • + am + • • •	(2)
Ряд (2), для которого сходится числовой ряд (1), назы-
вается абсолютно сходящимся. Если ряд (1) расходится,
а ряд (2) сходится, последний называется условно сходя-
щимся.
6.46.	Для векторных рядов остаются в силе результаты
6.32 а и 6.32 б о почленном сложении рядов и умножении
на числа. Результат 6.32 в об умножении рядов, вообще
говоря, уже не имеет смысла, поскольку не определено
умножение векторов. Остаются в силе результаты 6.33 и
6.34 б, касающиеся группировки членов ряда, и 6.36 о пе-
рестановках членов ряда. Обратные теоремы, включая тео-
рему Римана, получают своеобразные формулировки; они
указаны в задачах 17—22.
Ряды с комплексными слагаемыми, как векторные ряды
в /?2, укладываются в приведенную схему. Кроме приведен-
ных выше общих результатов, здесь сохраняется и теорема
об умножении рядов 6.32 в:
Если ряды из комплексных чисел
g1 + g2 + - • • +Gra+ • • • >	(1)
+ ^а + • • • + + • • •	(2)
230
ГЛ. 6. РЯДЫ
[6.47
сходятся и хотя бы один из этих рядов сходится абсолют-
но, то сходится и ряд
а1Р1 4" (й1^2 + й2^1) + (й1^3 + й2^2 + й3^1) 4~ - • •	(3)
и его сумма равна произведению сумм рядов (1) и (2).
Доказательство полностью повторяет доказательство
теоремы 6.32 в.
6.47.	Для неабсолютно сходящихся векторных рядов мо-
жет принести пользу признак Абеля — Дирихле. Он осно-
ван на одном специальном преобразовании конечных вектор-
ных сумм, которое называется преобразованием Абеля.
а.	Пусть даны числа аг, ..., ат и векторы Ьх, ..., Ьт.
Положим
a'i = a2—«1, а'2=а3—а2, ... , ат^ = ат—ат_и
= В2 = Ь1-\-Ь2, ... , Вт —bt-[-...-\-Ьт.
Теорем а (преобразование Абеля). Для любых чи-
сел cq, ..., ат и векторов blt ..., Ьт имеет место равенство
tn	tn—l
%akbk = amBm--'£akBk (m=2, 3,...).	(1)
k=i	k-\
Доказательство будем вести по индукции. Для m = 2
равенство (1), очевидно, выполняется:
а1Ь1 + а262 = а2 (bt + #2) — (а2—aj Ьг.
Допустим, что равенство (1) выполнено для некоторого но-
мера т; покажем, что оно выполняется и для следующего
номера т-^-1. По предположению индукции, мы имеем
т+1	т
ь=1
nt— 1
=	2«^fe + am+1&ra+1.
1
Мы хотим доказать, что справедливо равенство
т— 1
«л — 2 a'kBk+«ra+i^+i=
/?=1
т—1
= ат+1Вп.+1— 2 a'kBk~а'твт.	(2)
I
6.47]
§ 6.4. РЯДЫ ВЕКТОРОВ
231
т—1
Сокращая в (2) на 2 a'kBk, получаем
fe=l
Н ат+1Рт+1 ат+1^т+1 ат^гл
= «т + 15Я + 1 —(««, + ! —«И)£И-
Отбрасывая сначала атВт и сокращая затем на ат+1, при-
ходим к равенству Ьт + 1 = Вт+1— Вт, очевидно, верному. Воз-
вращаясь по цепочке произведенных преобразований, получаем
(2), что и требуется.
б.	Отметим неравенство, вытекающее из (1): если
ал>а2> ...	и	(А=1, ... , п), то
т
fe=l
2Са1е
(3)
Действительно, в данном случае ] атВт | атС агС,
a'k^.O и
т— 1
2 «А
1
= с
т—1	т—1
<c2(-aft) =
1 1
(«i—«2) + - • •	aj] = C (ax —am)	Cc^\
поэтому (3) вытекает из (1).
в.	Признак Абеля—Дирихле для векторных
рядов. Ряд
1&тЬт	(4)
1
сходится, если числа ат\0 и векторы Bm = b!-\~.. .-\-Ьт
ограничены, | Вт | С.
Доказательство. Применим оценку (3) к отрезку
ряда (4). Мы получим
2 «Л
k—p
2Схар,
где
Сх= sup |f> 4-.-- + М= sup |(^ + ...+^) —
_(й1+...+^_1)|= sup	Х|С2С.
р<г<<7
232
ГЛ. 6. РЯДЫ
(6.47
Полученная величина стремится к нулю при р оо и
любом q~>P- Таким образом, для ряда (4) выполнен крите-
рий Коши 6.43, так что ряд сходится.
г.	Признак Лейбница 6.23 является частным случаем
признака Абеля—Дирихле. Этот частный случай получается,
если считать п=\ и положить В1=1, Ве = —1, В3=1,
В4 = —1,... Но и при л=1 признак Абеля—Дирихле имеет
более широкое поле применения, чем признак Лейбница.
Рассмотрим вещественные ряды (л=1)
СЮ
У а,„ sin тВ,	(5)
о
2 cos тВ	(6)
о
и ряд из комплексных чисел
00
2 (cos тВ Д- i sin тВ).	(7)
тс=0
Выясним, при каких значениях 0 указанные ряды сходят-
ся. Положим z ~ cos 0 4- i sin 0; при этом (5.72) |z|= 1 и
zm = cos тВ 4- i sin тВ.
Далее,
2 (cos kB 4- I sin A0) — 2 z* — ~ i ~ 7—
fc = O	fe=O 1 i
m
2(cos£04-T sin kB)
k = 0
______2_______
1—cosO—isinO)
________2________
V(1 —COS 6)2 4- sin2 6
(8)
Мы видим, что величина
т
2 (cos Л0-Н’ sin £0)
k=0
остается ограниченной при т оо, если 0=^0, ±2л, ±4л,...
Предположим теперь, что числа ат, убывая, стремятся к нулю.
Тогда к ряду (7) применим признак Абеля — Дирихле; в силу
этого признака ряд (7) сходится, если ат\В и 0=4=0, ±2л,...
6.48]
§ 6.4. РЯДЫ ВЕКТОРОВ
233
При этих же условиях сходятся и ряды (5) и (6), посколь-
ку они представляют собой вещественную и мнимую части
ряда (7). Ряд (5) сходится и при 0 = 0, ±2л,..., так как
все его члены при этих значениях 0 обращаются в 0.
д.	Из оценки (8) следуют аналогичные оценки в вещест-
венной области
m
У COS&0
k=0
m
У sin/г0
fe=o
(9)
Эти оценки часто используются в работе с признаком
Абеля — Дирихле.
е.	Для частного случая ат = гт(г<1) легко написать
явное выражение для суммы рядов (5)—(7). Именно, сумми-
руя геометрическую прогрессию, находим
СП
о
1
1— ге№
Отделяя здесь вещественную и мнимую части, получаем
1	___ 1—re~ll>________1—г cos 6-|-tr sin 6
1—re'6 — (1—re'0)(l—re~'6) — 1—2rcos6+r2 ’
откуда
У, rm cos mQ = Re У rmeimi — -. 1~f c0^y—. ,
1—2rcos64-ra
о	о
У rm sin /И0 = Im V. rmeimi = sin ,
1—2rcos64-r2
о	о
6.48.	Двусторонние ряды.
а.	Пусть имеется «двусторонне бесконечная» последова-
тельность векторов ..., а_п, ..., a_t, а0, alt ..., ап, ...
Мы определяем сумму «двустороннего ряда»
2 ak	(О
— 00
234
ГЛ. 6. РЯДЫ
[6.48
как предел частной суммы — выражения
2 ak
—т
при т, п, независимо стремящихся к бесконечности, при
условии, что этот предел существует. Иначе говоря, ряд (1)
сходится и имеет сумму s, если для каждого е > 0 суще-
ствует номер М такой, что при любых т, п> N выпол-
няется неравенство
п
«— s ak
-т
е.
(2)
б.	Следующая теорема приводит вопрос о сходимости
двустороннего ряда к вопросу о сходимости односторонних
рядов.
Теорема. Ряд (1) сходится тогда и только тогда,
когда сходятся оба «односторонних» ряда
со	оо
2Х « 2 й-*;
О	1
(3)
если они сходятся и
О	1
то сумма s ряда (1) равна А-\-В.
Доказательство. Пусть ряды (3) сходятся. Для
любого е > О можно найти номер 7V такой, что при п > N,
m>N
п
A-l£ak
о
m
B~lLa-k
1
Отсюда
п
— m
это означает, что ряд (1) сходится и имеет суммой число
А + В.
6.49]
§ 6.4. РЯДЫ ВЕКТОРОВ
235
Обратно, если сходится ряд (1), то из неравенства (2)
следует, что при любых р > N, q > О
откуда вытекает по критерию Коши 6.43, что сходится
“	00
ряд ак. Аналогично доказывается сходимость ряда У a к,
»	1
и теорема доказана.
в.	Пример. Двусторонний ряд
—
со
сходится всюду при t^Rr, если 21 с»|<°°; он сходится
— со
всюду, за возможным исключением точек t — 0, ± 2л,
± 4л, ..., если с„\ 0, с_„\0 (л—>-(-оо) (ср. 6.47 г).
6.49.	а. Симметричное суммирование двусто-
ронних рядов. Двусторонний векторный ряд
(1)
— со
называется симметрично суммируёмым, если существует пре-
дел при п —> оо его симметричных частных сумм
п
= п = 0, 1, 2, ...;	(2)
— п
в этом случае предел s сумм (2) называется симметричной
суммой ряда (1).
Если ряд (1) сходится в смысле 6.48, то, очевид-
но, он симметрично суммируем и его симметричная сумма
совпадает с обычной суммой. Но не всякий симметрично
суммируемый ряд является сходящимся в смысле 6.48. На-
пример, двусторонний ряд из чисел ак, равных 1 при k > О,
О при k= Q и —1 при /г < О, является симметрично сумми-
руемым (и его симметричная сумма равна 0), но не является
сходящимся в смысле 6.48.
б. Симметричная суммируемость двусторонних рядов так-
же приводится к обычной сходимости:
236
ГЛ. 6. РЯДЫ
[в.51
Теорема. Двусторонний ряд (1) симметрично суммируем
тогда и только тогда, когда сходится односторонний ряд
а0 + ^(ак + а_к),	(3)
fe=i
и в случае сходимости ряда (3) его сумма совпадает с сим-
метричной суммой ряда (1).
Доказательство. Теорема вытекает из очевид-
ного совпадения л-й частной суммы ряда (3) и л-й симмет-
ричной частной суммы (2) ряда (1).
Симметричное суммирование используется, например,
в теории тригонометрических рядов вида
— Л
(часть III, гл. 14).
в. Пример. Двусторонний ряд
e~lnt	e-2lt e-it git e2lt	enlt
• •• n •• •	2	г + т+т + ‘- •+'7г + ,,‘
сходится при всех t #= 0, ± 2л, ± 4л, ... (6.48 в), но при
1 — 0, ± 2л, ± 4л, -... не сходится, поскольку при этих t
не выполнены условия теоремы 6.48 б. Однако при всех
значениях он является симметрично суммируемым, так
как всюду сходится ряд
“ etkt__e—tkt _	“	sin	kt
2-i k	2-i k
k=i	i
(6.47 г).
§ 6.5. Ряды функций
6.51. Ряды функций уже встречались в нашем изложе-
нии (§ 6.4 и др.). Приведем здесь общие определения и
т-еоремы, относящиеся к сходимости таких рядов. Рассмот-
рим ряд
л1(х) + са(х)+...+л„(х) + ...	(1)
из функций со значениями в Rm, определенных на произ-
вольном множестве Е. В соответствии с 5.91 и 5.93 сфор-
6.54]
§ 6.5. ряды функций
237
мулируем определения сходимости и равномерной сходимости
ряда (1).
а.	Определение. Если последовательность частных
сумм ряда (1)
S1(x) = C1(x),
s2(x) = fli(x)4-a2(x),

сходится на множестве Е, мы говорим, что ряд (1) схо-
дится на множестве Е, и предел функций sn(x) называем
суммой ряда (1).
б.	Определение. Если последовательность sn (х)
сходится на множестве Е равномерно, мы говорим, что
ряд (1) сходится на множестве Е равномерно.
6.52.	Критерий Коши 5.98 для ряда из векторных функ-
ций формулируется следующим образом:
Ряд 6.51 (1) является равномерно сходящимся на мно-
жестве Е тогда и только тогда, когда для любого в > 0 су-
ществует такой номер N, что при всех N, р > п, х£Е
I ап+1 (х)4-...+ар(х)|<е.
6.53.	Для ряда 6.51 (1) можно сформулировать и простое
достаточное условие равномерной сходимости;
Признак Вейерштрасса. Если
sup |ап(х)| = а„
хсе
со
и ряд сходится, то ряд (1) сходится равномерно.
1
Это предложение вытекает из 6.52, оценки
I &п+1 (х)+ ... +ар(х) 1^а„+1+ ... -\-ар
и критерия Коши для сходимости числового ряда (6.11 в).
6.54.	Следующие теоремы являются непосредственными
следствиями теорем 5.94—5.95.
238
ГЛ, 6. РЯДЫ
(6.62
а.	Теорема. Если ряд 6.51 (1) состоит из ограниченных
функций со значениями в Rm и сходится равномерно на Е,
то и его сумма s (х) ограничена на Е.
б.	Теорема. Если ряд 6.51 (1) состоит из непрерывных
функций на метрическом пространстве Е со значениями в Rm
и равномерно сходится на Е, то сумма ряда (1) является
также непрерывной функцией на пространстве Е со значе-
ниями в Rm.
§ 6.6.	Степенные ряды
6.61.	В комплексной области особый интерес представ-
ляют степенные ряды.
Определение. Ряд вида
а0 + аг (z—z0) + а2 (z—z0)2 + ... + ап (z—za)n + ..., (1)
где z — x-[-iy, zQ — xQ-\-iyQ, а коэффициенты a0, alt ...—
комплексные числа, называется степенным рядом.
6.62.	Представляет интерес выяснение области сходимо-
сти этого ряда—совокупности тех значений z, для которых
ряд 6.61 (1) сходится. В этом направлении имеется следующая
Теорема (Коши — Адамар). Положим
-^- = Йт /Ы,
где верхний предел рассматривается в расширенной числовой
области. Ряд 6.61 (1) сходится, притом абсолютно, во всякой
точке z с \z—z01 < R и расходится во всякой точке z
С |г—z0| >/?.	________
Примечание. Если Ит \ ап | = оо, считают R = 0.
Если lim 1 ап | = 0, считают 7?=оо, и в этом случае
в теореме утверждается, что ряд 6.61 (1) сходится при каж-
дом г£С.
Доказательство. Рассмотрим случай конечного
R=/=0. Пусть
I z—z01 <----.
lim 1 «„ |
Это неравенство можно записать в форме
| z—z01 lim У | ап | = lim ^1а„Цг—г0|" < 1,
6.63]
§ 6.6. СТЕПЕИНЫе РЯДЫ
239
откуда на основании признака Коши 6.14 б и 6.45 следует
сходимость ряда 6.61 (1).
Если же
lz~zo\ > — у;—:»
lim |/ | о„ |
то таким же образом
\г—z0|lim =	!/\ап(г—z0)n| > 1,
и в силу того же признака 6.14 б и 6.44 ряд 6.61 (1) рас-
ходится.
Доказательства для случаев R = 0 и /?=оо мы предо-
ставляем читателю.
6.63.	Теорема 6.62 показывает, что область O£R2 схо-
димости степенного ряда 6.61 (1) есть круг радиуса R, поэтому
число R называется радиусом сходимости ряда 6.61 (1). То-
чнее, область G содержит все внутренние, точки этого круга
(те z, для которых |z—z0|<7?) и не содержит ни одной
внешней точки (где [z—z0|>R). Что же касается точек
на самой окружности \z—z01 — R, то здесь могут предста-
виться различные возможности.
СС п
Примеры, а. Ряд — сходится при всех г, так как
= lim	Нт 1 =
П->со ty Пп n-+ u> п
оо
б.	Ряд	сходится только при z — Qt так как
1
= lim %/ пп — lim п — оо.
в.	Ряд ^n*zn при любом фиксированном а имеет радиус
1
сходимости 1, поскольку по 5.58 (6)
lim —= lim f= 1.
П-» 05 1/ Па n 05 (	- I
Ml” /
Однако при a^ssO ряд не сходится ни в одной точке окруж-
ности | z | = 1, так как его члены не стремятся к 0. При
а< — 1 ряд сходится в каждой точке окружности | z | = 1,
и притом абсолютно, в силу 6.15а. Если —1^а<0, то
ряд расходится при z=l, но сходится при всех zy=l,
\z | = 1 (ср. 6,47 г).
240
ГЛ. 6. РЯДЫ
[6.65
6.64.	Пусть степенной ряд 6.61 (1) имеет радиус схо-
димости R. Поставим вопрос: является ли этот ряд равно-
мерно сходящимся в круге \z— z0|<7?? Ответ, вообще
говоря, отрицателен; так, если бы ряд
\+z+z*+...
равномерно сходился в своем круге сходимости |z|< 1, то
его сумма была бы ограниченной {6.54 а); но его сумма рав-
на (6.11 б) и не является ограниченной в круге |г| < 1.
Тем не менее справедлива теорема:
а.	Ряд 6.61 (1) сходится равномерно в любом, круге
|г—г0 К/?!</?.
Действительно, при \z — z01 Rx справедлива оценка
\an{z— z0)n|<|a„ |/?5,
а ряд из чисел [ ап | R" сходится, как мы видели в доказа-
тельстве теоремы Коши—Адамара 6.62. Тем самым в круге
| z |	/?! можно применить признак Вейерштрасса 6.53, ко-
торый и приводит к нужному результату.
б.	Как следствие из а и 6.54 а, б получаем:
Сумма s(z) ряда 6.61 (1) есть ограниченная и Непре-
рывная функция в любом круге | z—z01	Rr.
Тем самым функция s(z) непрерывна во всем круге
\z—z0\ < R, так как каждая точка этого круга лежит и в не-
котором меньшем круге \z—Но ограниченной во
всем круге | z—z01 < R она может и не . быть, как мы
только что видели.
6.65.	Как мы знаем, на границе круга сходимости сте-
пенной ряд может сходиться, может и расходиться. Но если
ои сходится в граничной точке zlt то оказывается, что
в область его равномерной сходимости можно включить весь
отрезок, идущий из центра круга в точку zr. Для доказа-
тельства достаточно рассмотреть случай го=О, z1=f1>0.
СО
Теорема Абеля. Если степенной ряд Уantn сходится
о
в точке > 0, то он сходится равномерно на отрезке
Доказательство. Для заданного е > 0 мы должны
найти такое N, что при p^N, q~^N будет иметь место
6.вв]
§ 6.6. СТЕПЕННЫЕ РЯДЫ
241
неравенство I У} anin
I р+х
образование Абеля 6.47 (1), полагая ak — (
..., q; р <_q пока произвольны):
< е при всех 111	/1. Применим пре-
t \к . ,k
Т) ’ Ьк = аА
я
р+1
я
Я-1
п
Выбираем
У. ak^i
р+1	р+1
N так, чтобы из p^N,
k=p+i
следовало
е
•g-; тогда мы получим оценку
q
я-i
maxV
е . . е
1+_тах
Е , Е
что и требовалось.
6.66.	Примеры.
а.	Ряд
7	с»2	у??
1+р+^ + -.(0<а<1)
сходится при всех |z|== 1, z=£ 1 (6.47 г). По теореме Абеля
6.65 он сходится равномерно иа каждом радиусе круга
| z |	1, ведущем в любую точку z0, где | z01 = 1, z0 =# 1
(не следует думать, что он сходится равномерно на сово-
купности точек всех этих радиусов!).
б.	Ряд
у, «(«+!)• • .(<x-pn—1) „-1
2- р(р+1)...ф+п-1)г
я= I
(а, Р отличны от 0, —1, —2, ...),
если р>а-|-1, сходится при z— 1 (6.17 б), следовательно,
сходится при |z |< 1 и равномерно сходится на отрезке
242
ГЛ. 6. РЯДЫ
[6.67
О х 1. Этот же ряд, если Р > а, сходится при z = — 1
(6.24 в), следовательно, равномерно сходится на отрезке
— 1 si №С0.
6.67.	Оказывается полезным следующий вывод из тео-
ремы Абеля:
Теорема. Пусть функция f(x) непрерывна при
а при 0^х<хх справедливо равенство
f(x)= ^а„хп.
я=0
Тогда если сходится ряд
2 апх">	U)
л=0
ТО
f(xl)~ ^апх1-
п=0
Доказательство. Положим для всех х g [0, xj
j^a„xn = s(x).	(2)
Так как ряд (1) сходится, то по теореме Абеля ряд (2)
сходится равномерно на [0, xj. Поэтому в силу 6.65 б
функция s(x) непрерывна на [0, xj. Так как по условию
f(x) также непрерывна на [0, хх] и f(x) = s(x) для
Оз^х < хь то
f(Xj)= litn/(x) = lim s (x) = s (xj = 2a„x?,
X-+X1	n = 0
что и требуется.
ЗАДАЧИ
1.	Пусть ап > 0 (n= 1, 2, ...) и ?2±1= 1 ——+	, где числа
0^2	Zi Z2-
СО
| р„ | ограничены, | 0„ | < С. Доказать, что ряд ап расходится
1
(Гаусс).
ЗАДАЧИ
243
2.	Гипергеометрический ряд Гаусса (а, р, у отличны от чисел
Г (а, р, у, х)=1+£
Л=1
а(а+1)...(а+п-1)р(Р+1)...(Р+п-1)
п! у(у+1)...(у+п—1)
при |х| < 1 абсолютно сходится, при |х| > 1 расходится; еслих=1,
то он сходится (абсолютно) при у > а+р, расходится при yca-j-P;
если х= — 1, то он абсолютно сходится при у > а-|-Р, условно схо-
дится при —1<у—(а+Р)<0, расходится при у—(а-|-Р)«£—1.
СО
3.	Если ап^ап+1 > 0 (п=1, 2, ...) и ряд сходится, то
1
, 1
ап есть бесконечно малая величина сравнительно с —.
Примечание. Не существует функции <р(п), стремящейся к О
быстрее, чем — , которую можно было бы поставить в формулировке
вместо -i- (А. С. Немировский).
СО
4.	Пусть ряд 2 ап сходится (оп > 0); доказать, что существует
1
последовательность t>i<62 с... <6„<..., lim t>„= оо, такая, что ряд
сс
2 апЬ„ также сходится.
1
5.	Показать, что при умножении на себя сходящийся ряд
переходит в расходящийся.
6.	Доказать, что для ряда Лейбница 6.23 разность между полной
суммой ряда и суммой п первых членов по модулю не превосходит
модуля (п-|-1)-го члена.
со
7.	Доказать, что радиус сходимости степенного ряда ап (г—гД",
о
V °п+1	1
для которого существует Inn	равен —.
«-►со С1п	Г
со
8.	Если о„^0 для всех п=1, 2, ... и f (f) = ^'Jantn
о
при 0 < t < 1, то у функции f (t) существует при t —>• 1 предел,
СО
равный
о
244
ГЛ. 6. РЯДЫ
9.	Пусть числа ал*^0 (п=1, 2, 3, ...( Л=1, 2, ...) и Ьп
(п=1, 2, ...) удовлетворяют условиям:
1)	°пА<^п При любых Л=1, 2, ... ц_п=1, 2, ...,
2)	2 Ь„ < «,
п= 1
3)	limo„k=o„(n = l,2,...).
А-»«>
со	со
Положим V anA=sfc(^=*« 2, ...) и 2 ak=s- Доказать, что
n=i	k=i
s= lim Sb.
k~+ CD
10.	Бесконечные произведения. Пусть zlt z2, ...
..., z„, ...—последовательность комплексных чисел. Говорят, что
бесконечное произведение
СО
П z* = z1z2...zfc...
А=1
п
сходится, если последовательность чисел Рп = JJ z* (n=l, 2, ...)
А=1
сходится к конечному пределу Р 0; число Р называют величиной
се
произведения JJ г*.
1
Доказать, что из сходимости бесконечного произведения следует
соотношение lim z„ = l.
СЮ
11.	(Продолжение.) Пусть хг > 0, х2 > 0, ..., хп > 0, ...; про-
СО
взведение JJ xh сходится тогда и только тогда, когда сходится ряд
£=1
се
2 logfcXfe (при произвольном основании b > 1).
А=1
12.	(Продолжение.) Положим xs = l-|-a>s. Если все «вводного
СЮ
знака, то произведение JJ (1 -|- со*) сходится тогда и только тогда,
k=\
аз
когда сходится ряд 2 cos. (Если сод. изменяют знаки, результат не
fe=i
будет иметь места; см. задачу 15 к гл. 8.)
ЗАДАЧИ
245
13.	Доказать, что при | х | < 1 справедливо равенство
(1 +х) (1 + х2) (1 4-х*) (1 4-х8).. .(1 +х2"-1)...
14.	Доказать тождество Эйлера
(х > 1, ръ р2....рп, ... —последовательность всех простых чисел).
С» 1
15.	Доказать, что ряд / t — (pk—простые числа) расходится.
Л= 1Pk
16.	Пусть [qk]—последовательность воех натуральных чисел,
десятичное представление которых (/.77) не содержит ни одной де-
03
вятки. Сходится или расходится ряд / —?
17.	Рассматривается ряд
ui+ua+ • - • +“m+ • ••	(1)
векторов евклидова пространства Д„. Вектор p£Rn называется век-
СО
тором абсолютной сходимости ряда (1), если ряд У;(р, ит) сходится
1
абсолютно. Доказать, что ряд (1) сходится абсолютно тогда и только
тогда, когда каждый вектор p^Rn есть вектор абсолютной сходимости
этого ряда.
18.	(Продолжение.) Вектор q£Rn называется вектором абсолют-
ной расходимости ряда (1), если векторы ряда (1), попадающие в лю-
бой телесный угол, содержащий вектор q, образуют абсолютно
расходящийся ряд. Доказать, что ряд (1) абсолютно расходится тогда
и только тогда, когда у него есть хотя бы один вектор абсолютной
расходимости.
19.	(Продолжение.) Пусть fej < fe2 < • • • —некоторая последова-
тельность, состоящая из натуральных чисел, и /1 </г < • • •—после-
довательность остальных натуральных чисел. Ряды	• и
t(/i+u/a+ • -  называются дополнительными частями ряда (1). Дока-
зать, что если одна из дополнительных частей сходящегося ряда
сходится, то сходится и другая, и всякая перестановка членов ряда (1),
не меняющая порядка следования членов в каждой из частей, не
меняет суммы ряда.
20.	(Продолжение.) Если ряд (1) сходится условно и q есть
вектор абсолютной расходимости ряда (1), то существует такая часть
«ft,-}- ... ряда (1), для которой составляющие слагаемых по вектору q
образуют абсолютно расходящийся ряд, а ортогональные составляю-
щие—абсолютно сходящийся ряд.
246
ГЛ. 6. РЯДЫ
21.	(Продолжение.) Если каждый вектор е 0 есть вектор абсо-
лютной расходимости ряда (1), то любой вектор f£Rn является
суммой ряда, получающегося некоторой перестановкой ряда (1).
22.	(Продолжение—теорема Штейница.) Для всякого условно
сходящегося ряда (1) область сумм при всевозможных перестановках
членов есть линейное многообразие в Rn, ортогональное подпрост-
ранству А всех векторов абсолютной сходимости и проходящее через
сумму проекций членов ряда (1) на А (определенную однозначно)!
Историческая справка
Суммирование бесконечных геометрических прогрессий со знаме-
нателем, меньшим 1, производилось уже в древности (Архимед).
Расходимость гармонического ряда была установлена итальянским
ученым Менголи в 1650 г. Степенные ряды появились у Ньютона
(1665), который полагал, что степенным рядом можно представить
любую функцию. У ученых XVIII века ряды постоянно встречались
в вычислениях, но далеко не всегда уделялось внимание вопросу
о сходимости*). Точная теория рядов начинается с работ Гаусса
(1812), Больцано (1817) и, наконец, Коши (1821), где впервые дано
современное определение суммы сходящегося ряда и установлены
основные теоремы.
*) Что не раз использовалось и для антинаучных спекуляций.
Так, в 1703 г. бенедиктинский монах и теолог Г. Гранди, манипули-
руя с рядом 1 — 1 +1 — .... «доказывал» существование бога.
Из всех теоретических успехов знания вряд ли ка-
кой-нибудь считается столь высоким триумфом человече-
ского духа, как изобретение исчисления бесконечно
малых.
Ф. Энгельс
ЧАСТЬ ВТОРАЯ
ДИФФЕРЕНЦИАЛЬНОЕ
И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ

ГЛАВА 7
ПРОИЗВОДНАЯ
Чтобы отыскать максимум или минимум количества
f (х), надо составить выражение f (x±h)- f (х), где h есть
неопределенное число. Затем, освободив это выражение
от дробей и радикалов и сделав приведение подобных
членов, нужно разделить полученное выражение на это
неопределенное h. Полагая затем в оставшихся членах
Л=0,_ мы имеем некоторое уравнение, содержащее бук-
ву х, корни которого и есть максимумы и минимумы.
П. Ферма (1629)
Мы можем теперь перейти к определению одного из
основных понятий математического анализа—к определению
производной.
§ 7.1. Определение производной
7.11. Пусть имеется вещественная (конечная) функция
y=f(x), определенная в интервале (а, Ь). Пусть х0£(а, Ь);
составим отношение
(xo + M(a>	(1)
Если это отношение имеет (конечный) предел при h—>0, мы
говорим,.что функция /(х) дифференци-
руема при х — х0, и полагаем
Ит f(xo+6)—f (*<>) =
ь->о h
=г(*о) ==[/(*)];=*.•	(2)
Число f (х0) называется производной
функции f(x) при х = х0.
Геометрически отношение (1) есть угловой коэффициент
хорды, пересекающей график функции y=f(x) в точках с
абсциссами х0 и х04-Л(рис. 7.1). Выражение (2) есть угло-
вой коэффициент некоторой прямой, проходящей через
точку (х0, у0); мы назовем ее касательной к графику функ-
ции f(x) в точке с абсциссой х0.
250
ГЛ. 7. ПРОИЗВОДНАЯ
[7.12
7.12.	Если функция у— f(x) имеет производную при
х = х0, то отношение (1) ограничено при h—>0, например,
постоянной с; отсюда при всех достаточно малых | h |
|/(х0 + h)— f(x0) К с | h |,
и, следовательно, функция f(x) непрерывна при х = х0.
произ-
водной. Пусть функции f(x) и g(x) определены в интер-
вале (а, Ь) и дифференцируемы при х = х0. Тогда функции
число),
7.13.	Основные правила вычисления
/(*) + £(*),	а/(х)	(а—любое вещественное
f(x)-g(x), дифференцируемы при х = х0 (последняя —
в случае	и имеют место следующие равенства:
(1)
(2)
(f(x) + g(x))x=XB=f (x0) + g' (х0);
(а/(х))х=Хо = а/'(х0);
(f(x)-g(x))x=Xa-=f'(x0)g(x0)+f(x0)g’(x0);	(3)
f (л) Y SM f' (*<>)—g' fa) f M
,g(x) J x=x0	g2 fa)
(4)
Доказательство. (1) Имеем
(f fa+h)+g fa 4- h))—(f fa)+g fa))
h
. ffa+A)—ffa) , gfa + A)—gfa)
~ h + h
и результат следует из 4.36 а.
(2)	Имеем
а/ fa+А)—а/ fa) „ f fa+h) — f fa)
h	“ h
и результат следует из 4.36 б.
(3)	Имеем
f fa+h)g(x0+h)—f fa)gfa) =
h
__ ffa+/z)gfa+/i)—f fa)gfa+/z)	Hx^gfa+A)—ffa)gfa) _
“	h	+	h
и результат следует из 4.36 б и 4.36 а с учетом 7.12.
7.14]
§ 7.1. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ
251
Имея в виду (3), для доказательства (4) достаточно рас-
смотреть случай /(х) = 1. Тогда
g(xo+/0 g(Xn)
gix^+hy—gixo)
g(*o)g(*o+/0 ’
и результат следует из 4.36 д с учетом 7.12.
7.14.	Примеры.
а.	Постоянная f(x) = c имеет, очевидно, производную,
равную 0.
б.	Функция f(x)^=x имеет производную, равную 1.
в.	Учитывая 7.13, находим, что каждый многочлен
Р (х) = «охп + СрХ”-1 Н--ь ап
и каждая рациональная функция
Р(Х)_ C(lX” + c1Xn t-H.-.+On
Q(x)
имеет производную, во всяком случае в точках хп, где
Q(xo)=^O.
Производные рациональных функций можно вычислять,
используя формулы 7.13 (1) — (4) и формулу
(хп)' = пхп~\
(1)
получающуюся по индукции из 7.13 (3).
г.	Производная от произведения п множителей вычисля-
ется по формуле
+Л (х) Л (X) ... /„ (X) +... +А (х)/2 (х).. .fn (ху,
это доказывается по индукции на основании формулы 7.13 (3).
д.	Найдем производную от детерминанта, составленного
из дифференцируемых функций:
№(х) =
«и (х) «12 (X) ... и1п (х)
«21 (х) п22 (х) ... о2„ (х)
«„1 (X) «я2 (х) ... «„„ (X)
Согласно определению, детерминант Я7(х) есть алгебра-
ическая сумма п\ слагаемых с определенными знаками, каждое
252
ГЛ. 7. ПРОИЗВОДНАЯ
[7.15
из которых есть произведение л множителей, взятых по
одному из каждого столбца и каждой строки детерминанта.
Дифференцируя каждое слагаемое по правилу г и собирая
сначала члены, в которых продифференцирован множитель
из первого столбца; затем члены, в которых продифферен-
цирован множитель из второго столбца, и т. д., получаем
формулу
«'11W «12 (*)
«21 (х) и22(х)
Г(х)==
uln (X)
Ч2п (X)
«Л1 (X) ип2 (X) ... ипп (X)
«11 (х) и12(х)
«21 (*) «22 (X)
«1„ (х)
U2n (X)
ип1(х) ип2(х) ... ипп(х)
«11 (X) и12(х) ... и1п(х)
«21 (*") «22 (*") • • • и2П (х)
Unl (X)
Un2 (х)
• • •	(х)
7.15.	а. Производная сложной функции. Если
y~f(x) дифференцируема при х = х0, a z = g(y) определена
в интервале, заключающем точку y0=f(x0), и дифференци-
руема при у=у0, то сложная функция 2 = ^[/(х)] диф-
ференцируема при х~х0, причем
x'(x0) = g'(y0)f'(x0).	(1)
Доказательство. Согласно определению произ-
водной,
У —Уо=f(x)—f (х0) = (х—х0) [/' (х0) + е (х)],
е(х)—>-0 при х—*"Х0,
g(y)—g(y0) = (у— Уо) [£' (Уо) +6 (_У)]>
6(у)—0 при y-fy0.
Поэтому
z(x)— z(x0) = g[f(x)] —g[f (х0)] —g(y) —^(у0) =
= (у—Уо) [£' (Уо) 4- 6 Су)] =
= (X — Хо) [/' (Хо) + 8 (X)] [g, (у0) + б (у)].
7-1в1	§ 7.1. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ	253
Когда х—*хОк как мы видели, е(х)—>-0. Далее, в силу
непрерывности функции /(х) в точке х0 мы имеем также
у—>Уо и, следовательно, 6 (у)—>0. Переходя к пределу в
равенстве
~^Хо) = [/' (хо) + е (*)] UHjo) + 6 (у)],
A AQ
получаем требуемый результат из 4.36 б.
б. Пример. Производную от функции
(1+х2)88
можно было бы найти по правилам 7.14, развернув вначале
бином по формуле Ньютона. Однако в данном случае проще
представить функцию как сложную:
у = а88, и=1-^х2.
При этом
у' (и) — 99а88, а' (х) = 2х
и по (Г)
у' (х) = 99а88-2х = 99 (1 -J-x2)88 -2х.
7.16.	Производная от обратной функции.
Пусть дана функция, у =/(х), непрерывная.и возрастающая
в интервале (а, Ь}, и пусть х = ф(у)—обратная функция,
определенная, во всяком случае, в окрестности точки
у=у0=/(х0), х0^(а, Ь). Тогда если функция y=f(x)
дифференцируема при х = х0 a f (х0)	0, то функция
х=ф(у) дифференцируема при у—у0 и
Доказательство. Рассмотрим отношение
<Р(У)—<Р(Уо)	(1ч
У—Уо ’	' '
Согласно определению обратной функции,
<р(у) = х, ф(у0) = х0, у=/(х), у0=/(х0),
так что соотношение (1) можно записать в виде
X —Хд________1
f(x)—f(x0)	Г(х)—/(х0) 
254
ГЛ. 7. ПРОИЗВОДНАЯ
[7.17
Так как взаимно обратные функции одновременно непрерывны
(5.38), то из у—*уп следует х—>х0, и так как /(х) по
условию дифференцируема при х —> х0, то
Ф (У)—Ф (У<>)	1
У—Уо Г (*о) ’
что и требуется.
7.17.	Производная логарифма и связанных
с ним функций.
а.	Пусть y=logox. При х0 > 0 имеем
1
logc (Хо + ^) —logaXp _ ]no. ( x„+h\ Л _
h	ёа { х„ J
“М1+£Г’тМ1+4)”
в силу 5.59 г. Итак,
(logaX)'x=^ = -^|^.
Ло
Особенно простой -вид эта формула имеет при а = е, когда
речь идет о натуральном логарифме (5.59 г):
(1п*)'=4-	(П
б.	Найдем производную от функции у = 1п( — х), опре-
деленной при х < 0. По правилу 7.15 а дифференцирования
сложной функции мы получаем
[1П(-Х)]' = —(-x)'=~4-(-l)=i.	(2)
' Дг	Л/	Л/
Формулы (1) и (2) можно объединить в одну формулу,
справедливую при всех х^=0:
(1п|х|)' = 1.	(3)
в.	Экспонента х — аУ есть обратная функция к функции
j»=lognx; поэтому, согласно 7.16, мы имеем
(ау)и-и« = —;— =	= т~— = аУ° 1°&> а =	1п а.
\	log^ logee logae
7-18]	§ 7.1. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ	255
Заменяя у0 на х, —оо < х < со, получаем формулу
(ах)' = ах In а.	(4)
Особенно просто эта формула выглядит при а — е:
(ех)' = ех.	(5)
г.	Производная степенной функции с про-
извольным показателем. Функция
у=ха,
определенная при х > 0 (5.54), может быть записана в форме
у = еа I” х.
Отсюда следует, что у нее имеется производная, которую
мы можем выписать по правилу 7.15, используя результа-
ты а—в. Мы получаем
У (х) = е“|п*-—=осх“-1.	(6)
В частности, при а натуральном, как и следовало ожидать,
получается формула 7.14 (1).
д.	По образцу этого примера может быть найдена про-
изводная более сложной функции
y=f (х)« (*> = eS М,n f W;
вычисление мы предоставляем читателю.
7.18.	Производные тригонометрических
функций и обратных к ним.
а.	Для функции у — sin х мы имеем, согласно 5.63,
sin (x-f-Л)— sin х = 2 sin у cos (x-f-y) >
откуда
. h
sin (x-|-/i)—sinx sln 2 I h \
-  h---------= —•C0S^+2-)-
2
Используя 5.64 в и непрерывность функции cosx, находим
. .	,, sin (х+Л)—sin х
(sin х) = lim-*—---------= cos x.	(1)
256
ГЛ. 7. ПРОИЗВОДНАЯ
[7.18
б.	Далее, используя формулы 5.65 (2), (3), получаем
(cosx)'= pin	4-х)j = cos(4р4-*) = —sinx. (2)
2k л-1
в.	Наконец, по правилу 7.13 (4) при х#=——л, k — Q,
±1, ±2, ...
sinx V _ cos2x-|-sin2x _	1	_.
v s \ cosx J	cos2x COS2X * w
г.	Если x = arc sin u,u = sin x, то, согласно правилу 7.16,
л . .л ,	,
при —-2-<x<-g-H —1 <«< 1
(arc sin «)' =	= —-— =---r ......—-----. 1	. (4)
(sinx)' cosx	4-/i—sin2 x	+K1—«a
д.	Аналогично при —л < x < 0 и — 1 < и < 1
,4/1	1
(arc cos «) — -г.-ту- =---.— =
К	' (cos %) sin X
=--------z---...  = 4— J,., . (5)
— р 1 — cos2x	у 1.—ы2
Выражение (5) можно было бы получить из (4), используя
равенство 5.67 (1)
arc cos « 4“ -тг = arc sin и.
Точнее говоря, равенство (5) относится к возрастающей
функций arc cos и, которую мы в 5.67 обозначили через
arccosB«. Для убывающей функции arccosy« равенство (5)
должно быть заменено на равенство
(arc cosv и)' =---г 1
у	V1—и2
е.	Наконец, при —< х < у, — оо < и < оо
(аГС tg «)' = .. 1	= COS2 X =	|	5 „.	(6)
'	° 1 (tgx)	l-j-tg^x	1 +u2	' '
Производные остальных тригонометрических функций и
обратных к ним мы предоставляем найти читателю.
7.19]
§7.1. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ
257
7.19.	О д н о с т о р о н и и е производные.
а.	Пусть функция /(х) определена в промежутке
х0^х< Ь. По определению она обладает правой производ-
ной при х = х0, если существует
f (х0) = lim f.fa+/1)~fa)
пр ° ft\o h
Величина /рр (x0) иначе обозначается через /'(Xo + O).
б.	Аналогично, в том случае, когда функция /(х) опре-
делена в промежутке а<х^х0, она обладает левой про-
изводной при х = х0, если существует
f {Хо) =Um ffa+^)-ffa)
левУ 01 h/T)	h
31g
Рис. 7.2.
Величина /^ев (х0) иначе обозначается через /' (х0 — 0).
в.	Если функция /(х) определена в интервале (а, Ь),
содержащем точку х0, можно говорить о левой и правой
производных в точке х0. При этом если существует про-
изводная f (х0), то, разумеется, существуют и производные
/пр (Хо) И /лев (*<>)’ причем /пр (Хо) = Лев (*о) = /' (*<))• Но
может быть и так, что Лр(х0) и/^ев(х0) существуют, а
/' (х0) не существует (рис. 7.2).
Если существуют /^р (х0) и f'nm (х0)
и имеет место равенство /' (х0) =
=/'ев (х0), то, как легко проверить,
существует и f (х0) (ср. 4.16 в).
г.Луч, определяемый уравнением
y=f(x0) +Лр (х0) (х—х0)
называется правой полукасательной к кривой у=/(х) при
х = х0. Аналогично луч, определяемый уравнением
.У=/(*о)+Лев (*о) (х—х0)	(х<х0),
называется левой полукасательной к кривой у = /(х) при х=х0.
д. Следующее предложение обобщает на односторонние
производные теорему 7.16-.
Пусть функция у =/(х) непрерывна и возрастает в интер-
вале (а, Ь) и х = <р(_у) — обратная функция. Если функция
258
ГЛ. 7. ПРОИЗВОДНАЯ
[7.21
y=f(x) имеет при х = х0 правую производную f (х0 + 0)
то функция <р (_у) имеет при y0=f (х0) правую производную
<р' (_у0 + 0) и при этом
’,'<>"+<”=7гтат-
Доказательство проходит по тому же пути, что и в 7.16,
с использованием только значений х х0 и у у0.
§ 7.2. Второе определение производной
7.21. Мы обратимся теперь к анализу общих свойств
дифференцируемых функций. Прежде всего рассмотрим еще
один подход к определению производной, важный для даль-
нейшего. Будем строить линейные функции	которые
при х — х0 имеют то же значение, что и данная функция
y=f(x)', их можно описать уравнением
уА = А(х—х0)+/(х0) = Л-й+/(х0)	(Л = х—х0). (1)
Две такие функции, скажем уА = А(х— х0) +/(*о) и ув —
= В (х—х0) +/(х0), отклоняются друг от друга на вели-
чину, пропорциональную х—х0:
Уа ~Ув=(а —в) (х—х0) = (А—В) h.
Попробуем иайти среди функций (1) такую, которая имеет
отклонение от функции y=f(x), бесконечно малое выс-
шего порядка (4.38) сравнительно с h — x—х0, т. е. та-
кую, что
у—Ул = е(Л)-/г,	(2)
где е (Л) стремится к 0, когда h -> 0.
Допустим, что искомое А найдено. Тогда из (2) следует,
что
f (х)—Л/i—f(x0) = f(xB+h)—f(x0) _А = е 0,
так что отношение
/(хр+й)—f (х0)
h
имеет при h -► 0 предел, равный А. Таким образом, если
искомая линейная функция существует, то функция f(x)
дифференцируема при х — х0 и f (х0) есть искомый коэффи-
циент А.
7.23J	§ 7.2. ВТОРОЕ ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ 259
7.22. Обратно, если функция f(x) дифференцируема при
х = х0, мы имеем
_/' (Хо) = 8 (А) _ 0,
откуда
/ (х0 + А) — [/' (Хо) А +/ (ХО)] = е (й) • й,	(1)
так что линейная функция от h — x—х0
К=/'(Хо)А+/(хо)
удовлетворяет нашему условию: ее отклонение от функции
f(x) есть бесконечно малая величина высшего порядка
сравнительно с h—x—х0.
Прямая на плоскости (х, у), определенная уравнением
У—f' (х0)(х—х0)+/(х0),
согласно определению 7.11, является касательной к кривой
у=/ (х) при х = х0. При любом е > 0 найдется 6 > 0, для
которого |е(й)| < е при | h | < 6;
поэтому при указанных h
— Eh^f(x)—f'(x0)h—f(x0)^
<ей,
пли
/(х0) + [/' (х0) — е]К/(х)<	Рис. 7.3.
</(х0) + [Г(х0) + е]А. (2)
Неравенство (2) имеет следующий геометрический смысл:
график функции, дифференцируемой в точке х = х0, в доста-
точной близости к точке х0 проходит между двумя прямыми,
составляющими с касательной произвольно малый угол
(рис. 7.3).
7.23.	Как следствие получаем:
а.	Если /' (х0) > 0, то существует такое б > 0, что при
0<й<6
/(х0-Л)</(х0)</(х0 + й).	(1)
б.	Если же f (х0) < 0, то соответственно при 0 < Л < 6
/(х0-й)>/(х0)>/(х0 + й).	(2)
260
ГЛ. 7. ПРОИЗВОДНАЯ
[7.24
7.24.	На этом свойстве основано правило для вычисле-
ния точек локального экстремума.
Определение. Будем говорить, что в точке с £ (а, Ь)
функция f(x) имеет локальный максимум, если существует
такое h > 0, что при всех xg (с—h, c-^h)
/(х)С/(с)
(рис. 7.4). Аналогично будем говорить, что в точке eg (а, Ь)
функция f(x) имеет локаль-
ный минимум, если существует
такое h > 0, что при всех
xg (с—h, c-^-h)
/W>/(c)
(рис. 7.5). Точки локального
минимума или локального мак-
симума называются точками
Рис. 7.5.
локального экстремума. Если
функция f(x) дифференцируема при х = с и/'(с)=#0, то
неравенства 7.23 (1) и (2) показывают, что точка с не мо-
жет быть точкой локального экстремума. Отсюда следует,
что во всякой точке локально-
го экстремума дифференцируемой
функции f(x) выполняется ра-
венство
/'(с) = 0-	(1)
Поэтому, чтобы найти точки
локального экстремума (всюду)
дифференцируемой функции, следует проанализировать урав-
нение (1). Искомые точки заключены среди его решений.
Однако возможны и случаи, когда /'(с) = 0, но локального
экстремума нет; например, это имеет место для функции
f (х) — Xs при с = 0. Подробнее анализ эстремумов прово-
дится дальше, в § 7.5 и § 8.4.
§ 7.3.	Дифференциал
7.31.	Из равенства 7.22 (1) видно, что приращение
функции f(x) при переходе независимого переменного х от
значения х = х0 к значению х = х0 + Л складывается из
7.33]
§ 7.3. ДИФФЕРЕНЦИАЛ
261
двух частей: первая, /' (х0)й, линейна относительно смеще-
ния h переменного х, а вторая, е(й)й, бесконечно мала
сравнительно с h. Геометрически первая часть учитывает
приращение, измеряемое до касательной, а вторая часть —
приращение от касательной
до самого значения /(х0-)-й)
(рис. 7.6). Слагаемое /' (х0) h
называется главной линейной
частью приращения функции.
Таким образом, из сущест-
вования производной вытека-
ет возможность выделения в
приращении функции главной
линейной части. Обратно, как
показывают приведенные рас-
суждения, возможность
Рис. 7.6.
выделения
главной линейной
части
из приращения функции обеспечивает существование про-
изводной.
7.32.	Дифференциал. Пусть f(x) дифференцируема
при x — xQ. Величина й = х—х0 обозначается иначе через
dx, величина /' (x0)h = /' (x0)dx обозначается через dy (х0)
или просто dy. Число dy называется дифференциалом функ-
ции f(x) в точке х — х0 при дифференциале независимого пе-
ременного dx. Таким образом, dy есть линейная функция от dx.
Имея dx и dy, мы можем записать f (х0) в форме от-
ношения дифференциалов
7.33.	Правила вычисления производных, описанные в § 7.1,
приводят к соответствующим правилам вычисления диффе-
ренциалов. А именно, умножая на dx левые и правые части
формул 7.13 (1)—(4), находим
d (а/) = ad/;
d[f-g\=fdg+dfg‘,
l_g J g2(*o)
(1)
(2)
(3)
(4)
последнее равенство имеет место, как и 7.13 (4), при ус-
ловии, что =/=0.
262	гл. 7. производная	Р-34
7.34.	Дифференциал сложной функции. Фор-
мула 7.15 (1) после умножения на dx дает
dz—g' (у0)у' (x0)dx = g' (y0)dy.
Но если бы у было независимым переменным, а не функцией
от х, то дифференциал функции z мы написали бы, согласно
определению, точно так же:
dz=g'(y0)dy.
Таким образом, дифференциал функции не зависит от того,
является ее аргумент независимым переменным или функцией
от нового переменного.
Этот факт можно использовать при практическом диф-
ференцировании сложных функций. Например, производную
от (х2+1)8в (7.15 б) можно вычислить через дифференциал
d (х2 + 1 )88 = 99 (х2 + 1 )B8d (х2 + 1) = 99 • (х2 + 1)«®  2xdx,
откуда
((х2 + 1 )в9)' =	= 99 (х2 + 1 )88 • 2х.
§ 7.4.	Теоремы о конечных приращениях
7.41.	Теорема Ролля. Если (конечная) функция f(x)
непрерывна на отрезке [а, (может быть, бесконечном),
причем f(a)=f(b), и дифференцируема во всех точках ин-
тервала (а, Ь), то существует точка с£(а, Ь), для которой
f'(c) = 0.
Доказательство. В силу 5.16 в существует точка
с£(а, Ь), в которой выполняется равенство f(c) — sup{/(х)}
(или /(c) = inf {/(х)}). Таким образом, с есть точка локаль-
ного экстремума функции /(х). По 7.24 имеем /'(c) —О,
что и требуется.
7.42.	Следствие. Если функция /(х) непрерывна на
отрезке [а, &] и дифференцируема на интервале (а,Ь)и если всю-
ду на (а, Ь) имеет место неравенство f (х) =/= 0, то f (b)^=f(a).
Доказывается от противного с применением 7.41.
1АЪ. Теорема Коши. Если (конечные) функции f(x) и
g(x) непрерывны на отрезке а х b (может быть, бесконеч-
7.44]	§ 7.4. ТЕОРЕМЫ О КОНЕЧНЫХ ПРИРАЩЕНИЯХ 263
ном) и дифференцируемы во всех внутренних точках отрезка,
причем g' (х) не обращается в нуль, то существует точка
с С (а, Ь), для которой
f(b)—f(a) _ Г (с)	,,
g(b)—g(a) g'(c)'	v 1
Доказательство. Заметим, что g(b) ^g(a) в силу
7.42. Функция ф(х)=/(х)—Ag-(x) с любой постоянной А
вместе с функциями f(x) и g(x) непрерывна на отрезке
[а, Ь] и дифференцируема во всех его внутренних точках.
Подберем А так, чтобы для функции ф(х) выполнялось ус-
ловие теоремы Ролля ф(&) = ф(а). Для А мы получим урав-
нение
f(a) — Ag(a)=f{b)—Ag(b),
откуда
f(ft)-f(g)
g(b)—g(a) •
Применим теорему Ролля: существует точка с £ (а, Ь), в
которой
#'(4=о.
Отсюда и следует (1).
7.44.	Следствие (теорема Лагранжа). Если
функция f(x) непрерывна на конечном отрезке [а, ft] и диф-
ференцируема в его внутренних точках, то существует такая
точка с С (а, Ь), что
Для доказательства нужно в
положить g{x) = x. Формулу (1)
но записать в виде
f(b)=f{a)+f' (с) (Ь-—а);
в этом виде она называется формулой
конечного приращения. Геометрически с — такая точка на от-
резке [a, ft], что касательная к кривой y—f(x) в соответ-
ствующей точке (с, /(c)) параллельна хорде, соединяющей
точки (a, f(a)) и (ft, /(ft)) (рис. 7.7).
264
ГЛ. 7. ПРОИЗВОДНАЯ
[7.45
7.45.	Следствия.
а.	Если f (х) > 0 всюду в (а, Ь), то функция /(х) воз-
растает на [а, &].
б.	Если /'(х)<0 всюду в (а, Ь), то функция f(x) убы-
вает на [а, 6].
в.	Если /'(х) = 0, то f(x) постоянна.
Для доказательства заменим в 7.44(1) а на х', b на х",
где [х', х"] с [а, &].
Далее,
(а)	если /' (х) > 0, мы получим
/(х") =/(х') + (х’-х')/' (с) >/(*');
(б)	если f (х) < 0, то
/(х") =/(х') + (х"-х')Г (с) </(X');
(в)	если же /' (х) = 0, то
/(х") =/(х') + (х"—х')/' (с) ^У(х'),
что и доказывает утверждение.
г.	Пример. Пусть /(x) = sinx, /'(x) = cosx. В про-
межутках —~4-2йл<х<-^- + 2£л функция cosх положи-
тельна (5.65), и мы делаем вывод, что в этих промежутках
функция sinx возрастает; в промежутках -2-2kn < х <
Зя
< — +2Лл функция cosx отрицательна, и, следовательно,
функция sinx убывает. Аналогично, если положить /(х) =
— cosx, f'(x) =—sinx, мы получим, что в промежутках
(2k—1)л<х<2£л функция cosx возрастает, а в проме-
жутках 2kn < х < (2^+ 1)л — убывает. (Собственно говоря,
такого рода выводы мы делали и в 5.65, ио рассуждения
здесь более короткие.)
§ 7.5.	Расположение кривой относительно
своей касательной
7.Б1	. Пусть функция у = f (х) непрерывна на интервале
(а, Ь), содержащем точку х0, и обладает в sjom интервале
производной /'(х). Мы рассмотрим здесь взаимное распо-
ложение графика функции у =*f(x) и ее касательной,
7.52]
§ 7.5. РАСПОЛОЖЕНИЕ КРИВОЙ
265
проведенной в точке с х = х0:
Y(x)=f(x0)+f (х0)-(х—х0).
Введем следующие определения. Точка х0 называется
точкой выпуклости вверх функции /(х), если в окрестности
точки х0 (кроме самой этой точки) выполняется неравенство
/(х)< Y(х), или, иначе говоря, если график функции /(х)
в окрестности точки х0 располагается ниже касательной,
проведенной в точке х0. Аналогично точка х0 называется
а хд b
Рис. 7.8.
точкой выпуклости вниз функции /(х), если в окрестности
точки х0 выполняется неравенство
то же, если график функции распо-
лагается выше касательной. Если
каждая точка х £ (а, Ь) есть точка
выпуклости вверх(вниз)для функции
у = /(х), то функция/(х) называет-
ся выпуклой вверх (вниз) на интервале
(а, Ь). Точка х0 называется точкой
перегиба функции /(х), если при
х< х0 кривая/(х) располагается по
одну сторону, а при х > х0—по
/(x)>F(x), или, что
другую сторону от касательной, проведенной в точке х0.
Рис. 7.8—7.10 иллюстрируют указанные случаи.
Ниже даются достаточные (аналитические) условия осу-
ществления того или иного из рассматриваемых случаев.
7.52.	а. Если при всех т]ё(х0, Ь) выполняется неравен-
ство f (т]) < f (х0), то кривая f(x) располагается при х^> Хц
ниже касательной, проведенной в точке Хд.
266
ГЛ. 7. ПРОИЗВОДНАЯ
[7.53
б.	Если при всех г] € (х0, выполняется неравенство
f fa) > f (хо)> то кривая f(x) располагается при х > х0
выше этой касательной.
Действительно, в первом предположении для х > х0 по
формуле Лагранжа имеем
/(х)=/(х0) +/' (TJ) (х—х0) < /(х0) +/'(*0) (X—Хо) = Y(х),
что и требуется; при втором предположении рассуждение
аналогичное.
7.53.	Аналогично если при всех £ £ (а, х0) выполняется
неравенство f (£) > f (х0), то кривая f (х) располагается
при х < х0 ниже касательной, проведенной в точке х0; если
при всех х0) выполняется неравенство f (£) </' (х0),
то кривая f (х) располагается при х <_х^ выше этой каса-
тельной.
Доказательство получается, так же, как и в 7.52, при-
менением формулы Лагранжа к отрезку [х, х0].
7.54.	Комбинируя возможности, описанные в 7.52 и 7.53,
приходим к следующим результатам:
Если при всех £ g {а, х0) и т| £ (х0, Ь) выполняется нера-
венство
ГЮ>Г(х0)>/'(п),
то х0 есть точка выпуклости вверх для функции /(х); если
при всех £ g (а, х0) и г] £ (х0, Ь) выполняется неравенство
h),
то х0 есть точка выпуклости вниз для функции /(х). Нако-
нец, если для всех £ £ (а, х0) и г] G (х0, Ь) выполняются не-
равенства
или неравенства
то х0 есть точка перегиба функции f(x).
7.55.	Далее, непосредственно получается вывод:
Если функция f (х) возрастает при а <_х <.Ь, то функ-
ция f(x) выпукла вниз в интервале (а, Ь); если f (х) убы-
7.57]
§ 7.5. РАСПОЛОЖЕНИЕ КРИВОЙ
267
вает при а < х < /\ то /(х) выпукла вверх в интервале
(а, Ь).
При мер.'Положим f(x)=sinx, f (x) = cosx. Так как в про-
межутках (2k—1) л < х < 2/гл функция cosx возрастает (7Л5), то в
этих промежутках функция sinx выпукла вниз; так как в проме-
жутках 2йл < х< (2fe-j- 1) л функция cosx убывает, то в этих про-
межутках функция sin х выпукла вверх. Аналогично в промежутках
(1 х	г з х
2k-]- — J я < х < 2fe + -g-1 л функция cos х выпукла вниз, а в про-
межутках ^2k—^л<х<	л—выпукла вверх. (Этим
обоснован вид графиков функций sinx и cosx, приведенных в 5.65.)
В 8.32—8.33 будут даны аналитические условия для выде-
ления точек выпуклости и точек перегиба, Основанные на
свойствах высших производных функции /(х).
7.56.	Если f (хо) = О, то Y(х)=/(х0) и касательная,
проведенная при х = х0, горизонтальна. Если при этом х0
есть точка выпуклости вниз, т. е. кривая /(х) располага-
ется над касательной, то в окрестности точки х0 мы имеем
/(х)>/(х0) и, Следовательно, х0 есть точка локального
минимума функции /(х). Аналогично если при /' (х0) = О
точка х0 есть точка выпуклости вверх, то она является
точкой локального максимума. Мы получаем теперь из 7.54
следующие достаточные условия для минимума или макси-,
мума:
Теорема. Пусть f'(xo) = O. Если при этом для всех
£ (Е (а, х0) и т| (Е (х0, Ь) выполняются неравенства
/'(IX о, /'(т|) > О,
то х0 есть точка локального минимума функции /(х). Если,
наоборот, для всех £ £ («, х0) и т] (Е (х0, Ь) выполняются
неравенства
/'(!)> о, /'(ч)<о,
то х0 есть точка локального максимума функции /(х).
7.57.	Пусть, как и в 7.56, /'(хо) = О и при всех
I ё («, х0), ’l ё (х0, выполняются неравенства
/' (I) < 0, /' (т|) < 0.
268
ГЛ. t. ПРОИЗВОДНАЯ
[7.61
Тогда, согласно 7.53, точка х0 есть точка перегиба для
функции /(х): кривая у = f(x) переходит в точке х0 с одной
стороны касательной на другую сторону, так что в этом
случае точка х0 заведомо не является ни точкой минимума,
ни точкой максимума. Аналогичное положение имеет место
в случае, когда при всех £ £ (а, х0), т] £ (х0, Ь) выполняются
неравенства
Z'(В)>0, Г(п)>0.
§ 7.6.	Правила Лопиталя
Теоремы, приведенные в этом параграфе, часто бывают
полезны при вычислении пределов.
7.61.	Первое правило Лопиталя. Пусть (конеч-
ные) функции f(x) и g(x) непрерывны на отрезке [а, /?]
(может быть, бесконечном) и дифференцируемы в интервале
(а, Ь), и пусть g' (х) 5^ 0 всюду в (а, Ь). Пусть, далее,
известно, что
£(«)=/(«) = 0.
Тогда говорят, что отношение
ляет собой неопределенность вида -д-
при х \ а представ-
Теорема. Если при указанных условиях
lim
хХх а
f (X)
g'W
= А
(на расширенной числовой оси), то и
lim
/(х)
g(x)
А.
Доказательство. Сначала предположим, что
—оо < А < оо. Для заданного е > 0 выберем х0 так, чтобы
в интервале (а, х0) выполнялось неравенство
Применим теорему Коши 7.43 к отрезку [а, х0],
где а < х < х0; в силу этой теоремы существует такая
7.62)
§ 7.6. ПРАВИЛА ЛОПИТАЛЯ
269
точка с £ (а, х0), что
f(x) (x0)—f (а) _ f (с)
g(x) g(x0)—g(a)	g'(c)
и, следовательно, для всех х, a <Zx х0,
f (x)		<	\ 8.
g(x)	1 1 g (c)		
Это и означает, что Д = Ит ~	.
x^aS(x)
В случае, когда А бесконечно, неравенство (1) заме-
f'(x)	f’{x) .	1
нится неравенством ~> — или	< —— в зависи-
мости от знака А, в остальном доказательство не меняется.
7.62.	Второе правило Лопиталя. Пусть функции
/(х) и g(x) непрерывны и дифференцируемы в интервале
(а, Ь) (может быть, бесконечном) и g’ (х) не обращается
в нуль в (а, Ь). Пусть известно, что g(a) =f(a) — оо; тогда
говорят, что отношение при х \ а представляет собой
неопределенность вида —.
Теорема. Если при указанных условиях
lim
х \ а
f{x)
g'(x)
= А
(на расширенной числовой оси), то и
lim
х \ а
f(x)
g(x)
= А.
Доказательство. Пусть сначала А конечно. Для
заданного е >> О выберем х0 так, чтобы в интервале (а, х0)
выполнялось неравенство
| Г (х)
I g' (х)
—А
8.
(1)
Определим функцию D(x, х0) из условия
f(x)
g(x)
f(x)—f (х0)
g(x)—g(XQ)
D (x, x0).
270
ГЛ. 7. ПРОИЗВОДНАЯ
(7.62
Мы имеем
g(x)—g(x0) t g(X„)
D<x’ = {2)
f(x)	g(x)
при x —► а. Применяя к отрезку [х, х0] теорему Коши,
получаем, что для некоторой точки с £ [х, х0]
f (*) _ f (с) . Г) (х х \ — ? Ю I F (с) гп (х х \_11
g(x) 8'(с)	’ 0	8' (с) g' (с) I ’ 0
Отсюда для тех х, для которых |£)(х, х0) — 11 < е, на-
ходим
л| + |-4^||£)(х, х0)—1|<
lg(*)	1^4 8 (с) I Ч 8 (с) I v ’ °
Се+(Н| + е)е.	(3)
Так как 8 произвольно мало, то lim	= А, что и тре-
х -> а & \х'
бовалось.
В случае, когда А—оа, неравенство (1) заменяется не-
равенством	а неРавенство (3)—неравенством
f(x)	Г (с)	1
g(x)	g'(c) ’ 2 ’
имеющим место при х, достаточно близких к Л, в силу (2).
В случае А=—оо проводится аналогичное рассуждение.
ЗАДАЧИ
1.	Пусть f (х) определена при а^х<Ь и при любых и х2 из
[a. bj удовлетворяет неравенству
lf(x^—f(x2)\<Clxl—xi]1+a, а>0.
Доказать, что /(х) постоянна.
2.	Пусть f (х) определена и дифференцируема при х > с. Пусть,
далее, limf'(x)=0. Тогда при любом h > 0
lim [f(x+ft)-f(x)]=O.
Х-* оо
3.	Функция f(x), имеющая на отрезке [а, Ь] непрерывную про-
изводную, равномерно дифференцируема на [а, Ь]; иными словами,
для любого е > 0 существует такое б > 0, что из | Xt—х21 < 6,
ЗАДАЧИ
271
Г (*1)
xi. Хъ£[а. 6] следует неравенство
f (x2)—f (*i) I . „
1 < e-
4.	Показать, что функция «/=x2sin-^- всюду дифференцируема
на [0, 1], но ее производная не является непрерывной.
5.	У функции f(x), всюду дифференцируемой на [а, Ь], произ-
водная принимает любое значение между f' (а) и f (Ь) (теорема Дарбу).
6.	Если функция f (х) выпукла вниз на (а, Ь) (7.51), то для
любого х£ (а, Ь) имеет место неравенство
f (х) < ¥ (х)	,
т. е. график функции f(x) лежит не выше хорды, соединяющей
точки с абсциссами а и Ь.
7.	Результат задачи 6 приводит к более общему (чем в 7.51)
определению выпуклости функции 7, ие опирающемуся на ее диф-
ференцируемость: функция y=f(x) называется выпуклой (вниз) на
[о, Ь], если иа любом интервале (а, 0) с [а, Ь] ее график прохо-
дит ие выше хорды, соединяющей точки с абсциссами а и 0, т. е.
при любом х£(а, 0)
f м /(₽)(*—<*)+/(«)(₽—*)
‘И)	•
Доказать, что для любых точек xlt . . ., хр отрезка [о, Ь] и любых
р
чисел . ., Хр, таких, что 0<Ху<1 (/== 1........р) и У 1,
/ р \ р
л 2 V/) < 2 М (*/)•
\/= 1 / 1-1
8.	(Продолжение. В задачах 8—13 используется определение
выпуклости, введенное в задаче 7.) Показать, что функция / (х) вы-
пукла на отрезке [а, Ь] тогда и только тогда, когда при х > а > а
наклон хорды
р(а,х)=^х)-^и).
есть неубывающая функция от х при каждом фиксированном а.
9.	(Продолжение.) Функция f(x), выпуклая на отрезке [а, Ь],
непрерывна в каждой точке х£(а, Ь) н имеет конечную левую и пра-
вую производные, причем
/лев^Х/прОО-
10.	(Продолжение.) Если f(x) выпукла на [а, Ь], то функции
/лев (х) и f (х) ие убывают и для любых а и 0, а < а < 0 < Ь,
f  {гЛ^. Н0)—Л«) _ f 
I пр	Р а	/лев (г)"
272
ГЛ. 7. ПРОИЗВОДНАЯ
11.	(Продолжение.) Всякая выпуклая на [a, Ь] функция f (х)
имеет производную всюду на [«, Ь], кроме, возможно, счетного мно-
жества точек.
12.	Пусть f (х) дифференцируема на fa, b] и для любой пары
точек а, р, где a<a<f^b, существует единственная точка у
такая, что
Показать, что или f (х), или —f (х) выпукла на [а, Ь].
13.	Если функция у — f (х) выпукла вниз в окрестности точки
х0£(а, Ь), то ее график лежит не ниже правой и левой полу каса-
тельных в точке х0, т. е.
f (*) Ss (х—х„) f „р (х0) + f (х0)	(х > х0),
f (х) Sa (х—Х0) £,ев (хп) + f (х0)	(х < х0).
14.	Дифференцируемая кривая y=f(x), определенная при
asjxsgjoo, тогда и только тогда обладает асимптотой y=kx-[-b
(гл. 4, задача 10), когда существуют пределы
k= lim f (х), b= lim [f (x)—xf (x)J.
a>	oc
15.	Если функция f (x) определена в отрезке [a, b] и в интервале
(a, b) существует производная f (х), имеющая при х \ а предел р,
то это число р есть правая производная функции / (х) прн х=а.
16.	Если функция f(t) возрастает при 0«£/<Ь, а при 0 < <s£b
обладает убывающей производной f (f) (при t ~>0 производная
может неограниченно возрастать), то
17.	(Пример Ван-дер-Вардена.) Положим
(х при 0<х=С-^-,
j
1—X При -g-<X< 1
и продолжим эту функцию затем на всю ось с периодом 1. Положим,
далее,
Фп(*)=^<Ро (4"х).
Функция qn(x) имеет период 4-п и производную всюду, кроме уг-
ловых точек с абсциссами равную -f-1 или—1. Пусть, наконец,
ОО
п= I
Показать, что f (х) непрерывна, но ни в одной точке не имеет про-
изводной.
ИСТОРИЧЕСКАЯ СПРАВКА
273
Историческая справка
Дифференциальное исчисление (вместе с интегральным) появи-
лось в XVII веке; рассмотренное вначале в частных случаях многими
учеными в геометрическом и кинематическом аспекте (Ферма, Тори-
челли, Ролль, Барроу), оно было сформулировано общим образом
в конце века И. Ньютоном и Г. Лейбницем*). Лейбниц ввел символ
, .	-	du	„ ,,
дифференциала и обозначение для производной. Ньютон, затем
Лейбниц и его ученики, в первую очередь братья Якоб и Иоганн
Бернулли, применили методы дифференциального исчисления к мно-
гочисленным проблемам геометрии, механики и физики. Для физиче-
ских применений центральную роль сыграло истолкование скорости
движения как производной от пройденного пути по времени.
Первый трактат по дифференциальному исчислению «был напи-
сан в 1691—1692 г. Иоганном Бернулли в качестве пособия для одного
маркиза, который показал себя хорошим учеником» (Бурбаки). Этот
маркиз, Гийом Франсуа де Лопиталь, опубликовал в 1696 г. упомя-
нутый трактат, чем и составил себе имя в истории науки. По-види-
мому, исторически более правильно было бы называть «правила До-
пита ля» правилами Бернулли. Точное определение производной, осно-
ванное на определении предела, дано лишь у Коши **); со времени
Коши «существование производной, в которое до тех пор можно
было только верить, становится вопросом, изучаемым обычными сред-
ствами анализа» (Бурбаки). Примеры непрерывных функций без про-
изводных были указаны Больцано (1830, опубликовано в 1930) и
Вейерштрассом (1860, опубликовано в 1872). В обосновании анализа
лекции Вейерштрасса в Берлинском университете явились следующим
этапом после Коши.
*) По этим вопросам первая публикация Лейбница относится
к 1684 г., первая публикация Ньютона — к 1687 г.; но оба они,
как видно из переписки, владели методами нового исчисления и ра-
нее этих лет.
**) Еще раньше Люилье (1786); но работа последнего не приш-
лась ко времени н не имела продолжения, хотя и была увенчана
премией Берлинской Академии наук.
ГЛАВА 8
ВЫСШИЕ ПРОИЗВОДНЫЕ
Если первая производная позволяет нам для данного
момента времени описать характер какого-либо движе-
ния, то вторая — помогает проникнуть в его скрытые
причины.
В. Томсон и В. Тэт. Введение в натуральную фи-
лософию (1867).
§8.1	. Определения и примеры
8.11.	Если числовая функция y—f(x) имеет производную
у' — f (х) в интервале (с, й) и если функция f (х), в свою
очередь, дифференцируема на (а, Ь), то производную функ-
ции f (х) мы будем обозначать через у" = f (х) и называть
второй производной от функции /(х). Продолжая таким об-
разом, мы получим на интервале (а, Ь) функции
/(х), f(x), f(x), ...,/м(х).....
причем /*п)(х) при любом л>1 есть производная от
Функция /<л>(х) называется л-й производной, или
производной порядка п от f(x); если существует функция
/<л> (х), то1 функция /(х) называется п-кратно дифференци-
руемой на (а, Ь). Если функция f (х) существует и непре-
рывна, функция /(х) называется гладкой-, если функция
/<л) (х) существует и непрерывна, говорят, что функция /(х)
имеет гладкость п-го порядка. Сама функция /(х) считается
своей производной нулевого порядка:
/(х)=/«”(х).
8.12.	Действия с производными высших по-
рядков. В предположении л-кратной дифференцируемости
функций /(х) и g(x) в интервале (а, Ь) имеют место сле-
дующие формулы:
(/(х) + ^(х))‘л> =/<"> (х) + g™ (х);	(1)
(а/ (х))(л) = а/(л) (х) (а—любое вещественное число); (2)
п
(/(х)-^(х))</г)= 2 Ckf{k\x) g{n~k} (х) (формула Лейбница), (3)
*=о
где С„—	—биномиальные коэффициенты.
к!
8.14]
§ 8.1. ОПРЕДЕЛЕНИЯ И ПРИМЕРЫ
275
Доказательства равенств (1) и (2) получаются последо-
вательным дифференцированием равенств 7.13 (1), (2). До-
казательство (3) проведем по индукции. Если (3) верно для
некоторого п, то, дифференцируя еще раз, находим
п
2 С* [/<*>gtn-k+ri£.(«-*)] =
п	п+1
п
=A-(n+1,+ 2
k=i
п+1
k=0
на основании формулы С£+1 = С^Ц-С*-1. Мы видим, что из
справедливости формулы (3) для показателя п вытекает ее
справедливость для показателя л + 1; так как она справед-
лива для л=1, то отсюда следует ее справедливость для
любого л.
8.13. Следующая таблица высших производных для часто
встречающихся функций будет полезна в дальнейшем:
f м	Г W	f" (x)	f" U)		f<"' (x)
ха	axa-J	a(a—l)x“~2	a (a— l)x X(a—2)x“-3		a (a—1)... X X(a—n-|-1) x“~n
еах	ае°х	a2e°*	ase“x		ane°x
1п X	1 X	1 X2	2 X3		> *"з 1 s X 1 3 1
sin bx	b cos bx	—b2 sin bx	—b3 cos bx		bn sin I bx-\-n -g- ]
cos bx	—bsin bx	—b2 cos bx	-|-b3 sin bx		bn cos ^bx-|-n
8.14.	Производные многочлена и его разло-
жение по степеням х—а. При дифференцировании
многочлена каждый раз его степень снижается на единицу.
Если многочлен имеет степень л, то после л-кратного диф-
ференцирования мы получим постоянную; производные же
порядка л -|-1 и выше обращаются в 0.
276	гл. 8. высшие производные	18.14
Всякий многочлен Р(х) степени п можно расположить
по возрастающим степеням х—а, где а—любое число,
с помощью замены х = (х — а)-{-а; именно, если
Р (х) = 2 akxk>
А=0
то мы имеем
Р(х) = Р[(х~а)+ а]= а^Цх а]к,
k=0
что можно записать в форме
P(x) = b0 + b1(x—a) + b2(x—a)2-j- .. .+b„(x—a)n. (1)
Коэффициенты b0, Ьг, ..., Ьп можно выразить через произ-
водные многочлена Р(х) в точке а. Полагая в (1) х — а,
находим
Р(«)=Л-
Дифференцируя (1) по х, находим
Р’ (х) = ^+2й2 (x-a)+3ft3 (х-п)2+... +nb„ (х—а)п~\ (2)
Подставляя сюда х=а, получаем
Р'(*) = *!•
Дифференцируя (2), получаем
P"(x) = 2&2 + 2-3ft3(x-a)+ ... + ф-1)Мх-аГ2.(3)
Полагая здесь х = а, находим
P"(a) = 2ft2.
Продолжая таким же образом далее, получаем при любом
Л = 0, 1, ..., п
F^(a)=1-2.. ,k-bk.	(4)
Таким образом, при k — 0, 1, .... я мы имеем
(считая 0!= 1), и разложение (1) можно записать в форме
п
Р (х) = ^^^(х — а)к.	(5)
л=о
8.21]
§ 8.2. ФОРМУЛА ТЕЙЛОРА
277
§	8.2. Формула Тейлора
8.21.	Если функция f(x) непрерывна на конечном отрезке
[a, ft], а в интервале {а, Ь) обладает производными до
(л-(-1)-го порядка включительно и ее производные до п-го
порядка включительно имеют предельные значения fM(a)*)
(Лг = О, 1, ..., л), то существует точка с£(а, Ь) такая, что
п
/(ft) = S	+	(1)
Л=0	Р
Формула (1) называется формулой Тейлора.
Для п = 0 эта формула превращается в формулу Лагранжа
7.44 (2). Для многочлена л-й степени /<п+1) (х) = 0, и мы
получаем формулу 8.14 (5).
Лемма. Если функции F(x) и О(х) непрерывны на
отрезке [a, ft] и (п-[-))-крат но дифференцируемы в интер-
вале (а, Ь), причем G(fc) (х) не обращается в нуль в (а, Ь) и
(х) и GM(x) имеют пределы при х—+а, равные О
(А=0, 1, ..., л), то существует точка с£(а, Ь), в которой
F (Ь) _ Яп+1’(с)
G(b) — G(n+1) (с) •
Действительно, по теореме Коши 7.43 имеется точка
сг £ (а, Ь), в которой
F(b)—F(a) _ F{b)	F'(cd
G(b)—G(a) G(b)	G'(Cl)‘
Применяя теорему Коши еще раз к промежутку (а, сх),
получаем существование точки с2£(а, сх), для которой
F(fe) F'(C1)	F’icd-F'ja)	F" (c2)
G (b) G‘ (C1) O' (ci) - O' (a)	G" (c,) '
Продолжая таким образом дальше, найдем после л шагов
точку с £ (а, сп), для которой
F (b) F™ (сп) _ F(n> (с„)—F‘«> (а) _ F‘« + »(с)
G (Ь) — G‘"> (с„)— О‘«> (с„)—G‘"> (а)	G‘«+ «(с) ’
что нам и требуется.
*) Введенные здесь предельные значения f (а) в действительности
являются соответствующими правыми производными (задача 15 к гл. 7),
но это обстоятельство для нас не играет роли.
278
ГЛ. 8. ВЫСШИЕ ПРОИЗВОДНЫЕ
[8.22
Доказательство формулы Тейлора. Положим
в лемме
F(x)=/(x)-£/‘«(a)^-
*=о
О(х) — (х—а) "+1.
Функция Г(х) имеет производные до порядка п + 1 вместе
с функцией /(х). Функция О(х) имеет производные всех
порядков, причем ее производные до порядка п положи-
тельны при х > а. При этом, согласно 8.14 (4),
n	~1(т>
так что Flm} (а}~	(а)—/<т,(а) = 0 при т = 0, 1, ...,л.
По той же формуле G(m> (<z) = 0 при т=0, 1, ..., п. Таким
образом, выполнены все условия леммы, и можно ее при-
менить. При этом, очевидно,
+<«+» (х)=/‘«+1‘ (х),
О*«+п (х) = (Л4-1)|.
Применяя лемму, получаем: существует точка с £ (а, Ь)
такая, что
F(b)
G(b)
(6—a)K+i	(n-f-l)l
что и дает искомую формулу (1).
8.22.	Замечание. Мы рассмотрели случай а < Ь. Но
доказательство формулы Тейлора можно провести точно
таким же образом и для случая b < а, так что положение
точки Ь=£=а в действительности безразлично; в обоих слу-
чаях точка с лежит между а и Ь.
8.23.	Формулу 8.21 (1) часто пишут в форме

8.24]
§ 8.2. ФОРМУЛА ТЕЙЛОРА
279
Многочлен степени п, стоящий в начале правой части,
называется многочленом Тейлора. Величина
f(n + l) м
R„(x,	=	&
называется остаточным членом формулы Тейлора (в форме
Лагранжа). Если/<п+1,(х) при х —» а ограничена, то остаточ-
ный член Rn при х—> а есть бесконечно малая высшего
порядка по сравнению с (х — а)" (4.38)\ в соответствии
с принятым в 4.38 обозначением мы можем написать
Я„ = о((х —а)”).
В частности, для х < О нли х > 0, как нетрудно про-
верить, имеют место следующие разложения:
е*=1+х + -|г+...+^- + о(хп);	(3)
у2	у4	у 2 П
cosx=l —ir + f--••+(-! )"(Jijr + o(x2n+1); (4)
у-2	1*2 R +1
Sin x - x--... + (-1)”	+0 (x2"«); (5)
y2 y3	ytl
In(1 +X)= x-^+^— ... +	+ o (X«); (6)
(1 +x)“= 1 +ax + ^-y=^x2+ • • •
* * • +	x” + о (x«). (7)
8.24.	Роль формулы Тейлора состоит в том, что она
позволяет функцию f(x)— возможно, сложной природы —
заменить сравнительно простой функцией—многочленом —
с ошибкой 8.23(2), которая в ряде случаев допускает
простую оценку н может быть сделана достаточно малой.
Если известно, что
sup |/(и> (х) | = М„ (h)	(л=0, 1, 2, ...),
c<x<c+h
то для остаточного члена 8.23(2) мы получаем оценку
1Ш
Mn+i (К) , п+1
(«4-1)1	'
(1)
280	гл. 8. высшие производные	[8.31
Величину справа мы обозначим со = со (л, h). Можно поста-
вить три естественные задачи, связанные с определением
одной из величин со, л, h через две остальные:
(а)	Даны лий, найти со (л, й); иными словами, найти
оценку сверху для ошибки, получающейся при замене функ-
ции f(x) на интервале (a, a-]-h) ее многочленом Тейлора
л-й степени.
(б)	Даны л и со, найти й; иными словами, найти тот
интервал (а, а + й), на котором гарантируется, что ошибка
от замены функции f(x) ее многочленом Тейлора л-й сте-
пени не превзойдет дайной величины со.
(в)	Даны й и со, найти л; иными словами, найти степень
многочлена Тейлора, для которого ошибка от замены им
функции f(x) в данном интервале (а, а 4-й) не превзойдет
данной величины со.
В конкретных случаях все эти задачи решаются более
или менее элементарным счетом (см. задачу 10).
Те же задачи можно поставить и для интервала (а — й, а)
и решать их таким же путем.
§ 8.3. Анализ поведения функции в окрестности
данной точки
8.3Г	. В § 7.5 мы изучали расположение кривой y=f(x)
относительно ее касательной, проведенной при х = х0.
Аналитическим аппаратом служили значения /'(^при х^=х0.
Мы вернемся здесь к этому же вопросу, но вместо исполь-
зования множества значений f'(x) используем лишь одно
значение f"(x) при х = х0.
Теорема. Пусть функция y=f(x) имеет в интервале
(а, Ь), содержащем точку х0, первую производную f (х),
а в самой точке х0 и вторую производную f" (х0). Если
Г (*о) > 0, 70 хо ес7Ь точка выпуклости вниз для функции
f(x); если f ” (х0) < 0, 70 хо есть точка выпуклости вверх
для этой функции.
Доказательство. Пусть /" (х0) > 0; применяя
к функции /' (х) результат 7.23 а, получаем, что существует
б > 0 такое, что при 0 < й < ё
/' (*q—й) < /' (х0) < /' (х0 4- й),
8.34]
§ 8.3. АНАЛИЗ ПОВЕДЕНИЯ ФУНКЦИИ
281
Это позволяет для интервала (х0—6, х0 + б) применить
результат 7.54, который и завершает доказательство. Слу-
чай /" (х0) < 0 анализируется аналогично.
8.32.	Полученный результат позволяет дать новые доста-
точные условия минимума и максимума:
а.	Если в условиях 8.31 мы имеем f (хо)=О и f" (х0) > О,
то точка х0 есть точка локального минимума функции f(x).
б.	Если в условиях 8.31 мы имеем f (хо)=О и f" (х0) < О,
то точка хй есть точка локального максимума функции f(x).
Оба результата следуют из 8.31 и 7.56.
8.33.	Какую дополнительную информацию о свойствах
функции f (х) может дать знание значений f"(x) не только
в точке х0, но и в окрестности этой точки? Оказывается,
зная/"(х), мы можем описать расположение кривой у =/(х)
в окрестности точки х0 по отношению к «соприкасающейся
параболе»
F (х) ==/ (х0) +/ '(х0) • (х—х0) 4-" (х0) • (х—х0)2. (1)
а.	Теорема. Если при всех Т]€(хо, Ь) выполняется
неравенство	то кривая y~f(x) при х > х0
располагается выше соприкасающейся параболы (1). Если при
всех т]€(Хо, Ь) выполняется неравенство f" (rj) </" (х0), то
при х > х0 кривая у = /(х) располагается ниже параболы (1).
Доказательство. В первом предположении при
х > х0 по формуле Тейлора с л = 2 имеем
/(X) =/(х0) +/' (х0)-(х-х0) -Ц/" (с) (х—х0)2 >
> f (*о) +/'(хо) (X - Х0) + ~f” (х0) (х — х0)2 = Г (х),
что и утверждается. Для второго предположения рассужде-
ние аналогично.
б.	Аналогично если при всех £ £ {а, х0) выполняется
неравенство /" (В) >/" (-^о)» т0 кривая y=f(x) при х < х0
располагается выше параболы (1); если при всех х0)
выполняется неравенство /"(£)</" (х0), то кривая у —f (х)
при х < х0 располагается ниже параболы (1).
8.34.	Рассмотрим, в условиях 8.33, случай, когда
f"(xo) — O. В этом случае соприкасающаяся парабола 8.33 (1)
282
ГЛ. 8. ВЫСШИЕ ПРОИЗВОДНЫЕ
(8.35
вырождается в прямую, касательную к кривой y—f(x)
в точке х0:
У (x)=f(x0) +/'(х0) • (х—х0).
Комбинируя результаты 8.33, мы приходим к следующим
выводам:
Теорема. Если в условиях 8.33 мы имеем f"(xo) = O
и при всех х^хй выполняется неравенство f"(x) > f"(x0),
то для функции f(x) точка х0 есть точка выпуклости вниз.
Если привсех х=^ х0 выполняется неравенство f" (х) < /" (х0),
то для функции f(x) точка х0 есть точка выпуклости вверх.
Если при всех Z; g (а, х0), т] Е(х0, Ь) выполняются неравенства
/"(&)< о </"(ц)
или неравенства
то точка х0 есть точка перегиба функции f(x).
Подчеркнем, что последние два предположения оказы-
ваются достаточными условиями для того, чтобы точка х0
была точкой перегиба.
8.35.	Как и выше по отношению к f (х), вместо исполь-
зования множества значений /"(х) мы можем использовать
одно значение (х) в самой точке х0. Пусть функция /(х)
на интервале (а, Ь) Э х0 обладает производными f (х) и
/" (х), а в самой точке х0—производной f" (х0).
Теорема. Если f'"(x0)^>0, то кривая y=f(x) при
х > х0 располагается выше параболы 8.33 (1), а при
х < х0—ниже этой параболы. Если же /"'(хо)<0, то
картина противоположная: при х < х0 кривая располагается
выше параболы 8.33 (1), а при х > х0 — ниже этой параболы.
Доказательство. Пусть (х0) > 0. Применяя
к функции /"(х) результат 7.23 а, получаем, что сущест-
вует такое 6 > 0, что при 0 < h < б выполняется неравен-
ство
/"(х0—Л)</"(х0) </"(х04-Л).
К интервалу (х0—б, х04-б) теперь можно применить
теоремы 8.33 а, б, которые и приводят к нужным резульг
тэтам.
8.37]
§ 8.3. АНАЛИЗ ПОВЕДЕНИЯ ФУНКЦИИ
283
8.36.	Для случая /"(хо) = 0 получаем: если /"(хо) = 0,
f'" (хо)=£0, то х0 есть точка перегиба функции f(x).
В случае /"• (хо) = О вопрос остается открытым (если
мы желаем использовать только значения функции и ее
производных в самрй точке х0). Можно привлечь значения
последующих производных (см. задачу 11).
8.37.	В разного рода вопросах, связанных с изучением
поведения функции в окрестности данной точки, полезной
бывает еще одна форма записи формулы Тейлора, исполь-
зующая символ Е (4.39). Пусть в окрестности точки а
функция /(х) обладает производными до порядка
причем fw(о)у=0, а (х) ограничена. Тогда формулу
Тейлора 8.23 (1) можно записать в следующей форме:
f(a+h) = f(a)+hf («)+...
kn-l	fjn
+ + (<Z)£’ П)
где E, как и раньше, означает величину, стремящуюся к 1
(при h—>0). В данном случае, очевидно,
F_. , h f‘”+»(c)
1 п +1	(а) •
В частности, отметим формулы, вытекающие из (1) (при
указанных ниже значениях п) и	8.13 (или 8.23 (3)—(7)):	
ех = 1 + хЕ	(л=1);	(2)
cos х = 1 — — Е	(л = 2);	(3)
sin х = хЕ	(л=1);	(4)
In (1 4-х) = хЕ	(л=1);	(5)
(14-х)’=1+ахД	(л=1);	(6)
последняя формула была получена нами еще в 5.59 е. Более точные формулы, вытекающие снова из		(1) и
8.23 (3)—(7), таковы: у2 е*=1+х+^-Д	<«=2);	(2')
у2	у4 cosx= 1	2’ + -^-е	(л = 4);	(3')
X3 „ sin х = х —Е О	(л=3);	(4')
284	гл. 8. высшие производные	[8.38
1п(1 + х) = х + ^-£-	(л==2);	(5')
(д=2).	(6')
8.38.	Примеры,
а. Найти
lim e*~c2sx.
х о sin х
Решение. Используя формулы 8.37 (2)—(4), находим
(у2 \	х
	2	/	2	, j
sin х ~~	хЕ_Е
(Можно было бы воспользоваться н правилом Лопнталя 7.61.)
б. Найти
lim	.
х -» о In (14-х2)
Решение. Используя формулы 8.37 (2), (5), (6), находим
(у 2 Х& \
 1——Е)
1п(1+х2)	х2£
3 р % F
-2Е-ТЕ 3
Е “* 2 ’
Здесь применение правила Лопиталя потребовало бы сложных вычис-
лений.
в. Каково расположение кривой
в окрестности точки х = 0?
Решение. По формуле 8.37 (4')
так что lim {/==—. Более точный ответ требует привлечения и более
х-»0	6
точной формулы для sin х, именно
sinx=x__+—£
8.42]
§ 8.4. ВЫСШИЕ ДИФФЕРЕНЦИАЛЫ
285
(вытекающей из 8.23 (5)). Мы получаем здесь
у 6 120С’
так что в точке х=0 функция y=f(x) имеет локальный максимум.
§ 8.4.	Высшие дифференциалы
8.41.	Предположим, что функция y=f(x) определена
в интервале (а, Ь) и имеет в нем производные до л-го по-
рядка включительно. Дифференциалом, п-го порядка функ-
ции f(x) называется функция от двух независимых пере-
менных х и dx, определяемая равенством
dny =s dnf(x)=^fM (х) (dx)n.
Если dx считать постоянным, то, очевидно, dny= d(dn~1y).
При наличии dny можно записать л-ю производную в форме
отношения
В частности, для y~f(x) = x мы имеем
dy — dx, d2y = d3y ... = 0.
8.42.	Вычислим второй дифференциал от сложной функ-
ции j=/[<p (х)]. Согласно определению 8.41
д2у = {/[<Р (•*)]}" (dx)2 = [/' [<Р] -<Р' (*)]' (йх)2=
=/" [ф (х)] • [ф' (X) dx]2 +f' (ф) • ф" (х) (dx)a=
=f"l4> (x)]-(dtp)2+f' (ф)ф"(х) (dx)2.	(1)
Если бы ф была независимой переменной, то мы имели бы
^=Г[ф](^Ф)2.
Мы видим, что в отличие от первого дифференциала вто-
рой (и высшие) меняются, если независимое переменное
становится зависимым, т. е. функцией от нового незави-
симого переменного. Впрочем, для случая, когда независи-
мое переменное подвергается лишь линейной замене, второй
и последующие дифференциалы сохраняют свое выражение.
В этом случае ф(х) = Ах-|-Д (А и В—постоянные), поэтому
ф"(х) = 0 и второе слагаемое в (1) исчезает. Дифференцируя
286
ГЛ. 8. ВЫСШИЕ ПРОИЗВОДНЫЕ
[8.43
далее, последовательно получаем
d3j=/'" [<р (х)] [<р' (х) dx]3=/"' [q> (х)] (dtp)3.
dny = f{n) [<p (x)] [q/ (x) dx]"=/(”> [<p (x)] (d<p)",
поскольку члены, содержащие высшие производные от <р,
обращаются в нуль.
8.43.	Формула Тейлора 8.21 (1) в дифференциалах (а = х,
Ъ—a = dx) приобретает следующий вид:
п
f(x + dx) = X^dkf(a) + ^^dn+1f(c).
k=. о
§ 8.5.	Ряд Тейлора
8.51.	Рассмотрим функцию _у=/(х), имеющую в интервале
(а, Ь) производные всех порядков n = 0, 1, 2, ... Такие
функции будем называть в дальнейшем бесконечно диффе-
ренцируемыми. Выберем точку х0€(а, и напишем формулу
Тейлора:
/(х)=/(х0)+/(х0)(х—х0) + . . .
• • • + f—^ “ *о)П + R"(х’ Х«К
Предположим, что для данного х с возрастанием п вели-
чина остаточного члена стремится к 0. Это означает, что
бесконечный ряд
7(Хо)+/' (-«о) (х—х0) + ...	(х—х0)« 4-.. .=
(1)
п = 0
сходится и имеет своей суммой число /(х). Таким образом,
значение функции /(х) при данном х является суммой ряда
по степеням х — х0:
/(х) =/(х0) +/' (х0) (х—х0) + . . . + --	х0)п-|- ...
8.53]
§ 8.5. РЯД ТЕЙЛОРА
287
Ряд (1) для бесконечно дифференцируемой функции f(x)—
вне зависимости от его сходимости и суммы—называется
рядом Тейлора функции f(x). Нам следует выяснить, для
каких функций /(х) н в каких областях ряд Тейлора схо-
дится и имеет суммой значение самой функции f(x); иными
словами, для каких функций и в каких областях остаточный
член формулы Тейлора стремится к 0.
8.62. Лемма. Если в интервале (а, Ь) при некоторых
В > 0 и С > 0 выполняется неравенство
sup |/<«>(х)|<С (л = 0,1,2, ...)	(1)
а П1 хЦа.Ь)
(т. е. последовательность чисел, стоящих слева, ограничена),
то остаточный член формулы Тейлора стремится к 0 во всех
точках х£(а, Ь), для которых |х— xftl<-g-.
1	и 1 D
Доказательство. Запишем формулу для остаточного
члена
(у_г„У> + 1
Rn(x, ло) = 4мЛ)Г"^<"+1,(с) (с между х и Хо)-
Мы имеем в силу (1)
I Rn х0) I <	CBn+1 (п + 1)! = С (В I х - х01)«+‘,
что при [х—х0 [ <	стремится к 0, когда п—> оо.
8.53.	Рассмотрим несколько примеров.
а.	Для многочлена у — f(x) степени m неравенство S.52 (1)
выполняется тривиальным образом, поскольку /<т+1) (х) и все
последующие производные равны 0. Таким образом, всякий
многочлен разлагается в ряд Тейлора; впрочем, этот ряд
сводится к конечной сумме, которую мы уже рассматривали
в 8.14.
б.	Пусть f(x) = ex. Мы имеем /(п)(х) = е* и в,проме-
жутке [—Ь,
sup ех = еь.
Поэтому выражение
sup | f(n) (х) | еь
п\Вп п! В"
288
ГЛ. 8. ВЫСШИЕ ПРОИЗВОДНЫЕ
(8.54
с возрастанием п стремится к 0 и, следовательно, при любом
фиксированном b является ограниченным при п—>оо. Таким
образом, ряд Тейлора для функции ех сходится к ех на
отрезке [—Ь, й] любой длины; иначе говоря, он сходится
к ех при всех вещественных х. Итак, для всех х
у2 уЗ	vtt
^=1+х+^ + ^+...+^+...	(1)
в.	Пусть f[x) = sin х. Мы имеем |/(n) (х) |	1 ив любом
промежутке [—b, ft]
sup | fM (x) |	1
B"-n!	'
Эта последовательность ограничена независимо от Ь. Таким
образом, функция sin х также разлагается в ряд Тейлора,
сходящийся на всей вещественной оси:
уЗ у5 у?
sinx = x—а+тт-7г+-..	(2)
г.	Точно таким же образом и функция cosx разлагается
в ряд Тейлора, сходящийся на всей вещественной оси:
у2	уб
cosx=l--J-+^—(3)
8.64. Отметим, что наличие разложений 8.53 (2) и (3)
доказывает единственность функций sin х и cos х, которые
мы определили в 5.61 как решения некоторых функциональ-
ных уравнений. Для завершения их теории нам нужно, от-
правляясь от разложений 8.53 (2), (3), показать, что вы-
полняются указанные в 5.61 функциональные уравнения
и неравенства; это будет проведено в 8.68.
8.55. Аналитическое продолжение. Пусть
известно, что функция /(х), бесконечно дифференцируемая
в интервале (а, Ь), разлагается в нем в ряд Тейлора
сю
f(x) = ^ck(x—x0)k, ck^.	(1)
k=0	к'
Рассмотрим этот ряд в комплексной области, заменив вещест-
8.62]	§ 8.6. ЭКСПОНЕНТА В КОМПЛЕКСНОЙ ОБЛАСТИ
289
венный аргумент х на комплексный z = x-\-iy:
СО
2 ck(z — x0)k.
k=0
(2)
Область сходимости этого ряда есть круг некоторого ра-
диуса R с центром в точке х0 (6.52). Число R во всяком
случае таково, что весь интервал (а, Ь), где сходится ряд (1),
содержится в круге \z—х0|</?, поскольку нам известно,
что во всех точках вне круга сходимости степенной ряд
расходится. В точках z£(a, b) сумма ряда (2) по условию
равна f(x). Сумма ряда (2) в остальных точках круга схо-
димости есть некоторая функция от г; мы назовем ее ана-
литическим продолжением функции f(x) в комплексную
область и обозначим через f(z). В частности, если ряд (1)
сходится для всех вещественных х, то ряд (2) сходится для
всех комплексных z и аналитическое продолжение функции
f(x) оказывается определенным во всей комплексной пло-
скости.
§	8.6. Экспонента и тригонометрические функции
в комплексной области
Применим общие результаты 8.55 к экспоненте и триго-
нометрическим функциям.
8.61.	Ряд Тейлора для функции ех
у2	уП
e*==l + x + f+...+^+...
сходится при всех вещественных х; следовательно, ряд
ex=l+z+^+...+^+...	(1)
сходится при всех комплексных г, определяя экспоненту ег
во всей плоскости переменного г.
8.62.	Аналогично ряд Тейлора для функции sin х
уЗ у5 у7
8шх=х-зГЧ-5Г-7Г +
290
ГЛ. 8. ВЫСШИЕ ПРОИЗВОДНЫЕ
[8.63
и ряд Тейлора для функции cosx
Х^1 Х^ Xе
cosx~ 1 2Г + 4[ ёг+ • • •
сходятся при всех вещественных х; следовательно, для всех
комплексных г определены функции
sinz = s—3Г+5Г— • ••,	(1)
z3 z4
+	(2)
которые являются аналитическими продолжениями тригоно-
метрических функций sinx и cosx.
Как видно из формул (1) и (2), в комплексной плоскости
(как и на вещественной оси) справедливы равенства
sin (—z) = — sin z,	(3)
cos(—s) = cosz,	(4)
выражающие нечетность функции sin z и четность функции
cos г в комплексной плоскости.
8.63.	Из разложений 8.61 (1) и 8.62 (1), (2) вытекает
замечательная связь между экспонентой и тригонометри-
ческими функциями, существующая в комплексной области.
А именно, заменяя в разложении 8.61 (1) z на iz, мы нахо-
дим, что при любом z
tz 11-	• г® 1 г4 1
е — 1-^iz -gj i зг + -4г+ • • • —
f i гг г4 \ . . [ г3 г5 \
V1 2!	4!	•••J+Z(k2	3| + 5Г
= cos z + i sin z.	(1)
Таким образом, экспонента линейно выражается через sin z
и cos г. Заменяя в (1) z на —г, получаем также (с учетом
8.62 (3) и (4))
е~'г = со5г—/sins’.	(2)
Из (1) н (2) следуют формулы
g*z—
sinz==__;	(4)
8.64J	§ 8.6. ЭКСПОНЕНТА В КОМПЛЕКСНОЙ ОБЛАСТИ
291
впрочем, их можно было получить и непосредственно из
формул 8.61 (1) и 8.62 (1), (2). Формулы (1)—(4) называ-
ются формулами Эйлера.
Для вещественного г, равного 6, мы получаем из (1)
еп = cos 6 -f- i sin 0.	(5)
Мы видим, что комплексное число е'6 при вещественном 0
имеет модуль, равный 1.
Для любого комплексного числа 2^0 в 5.72 мы имели
тригонометрическое представление
х = г (cos 0 + i sin 0),
где г есть аргумент числа z, а 0—его модуль. Равенст-
во (5) позволяет этому же комплексному числу z дать «экс-
поненциальное представление»
z = n?'e.	(6)
8.64.	Дальнейшие свойства экспоненты основаны на сле-
дующем факте:
Л е м м а. Для любых комплексных гг и zz имеет место
равенство
ez>+z> _ gzt. gz,^
Действительно, мы имеем
ez* = 1 +гг +£+ ...,
_2
e*>=l+z2 + ^+...
Так как эти ряды сходятся абсолютно, то применима теорема
об умножении (6.46), которая дает
e^.e^=l+(z1 + zz) + ^+z1zi + ^ +
* \3! * 2! • 1 ‘ 1  2! * 3! / ‘ *
= l+(z1+za) +(£1^ + (Л1±^+...=ег1+г11
что и требуется.
292
ГЛ. 8. ВЫСШИЕ ПРОИЗВОДНЫЕ
[8.65
8.65.	В частности, для вещественных х и у и z — x-j-iy
е2 = ех+‘У = ех • е'У = ех (cosj-f-Z sinj) =
= е* cosyiex siny;	(1)
эта формула явно выделяет у функции ег вещественную
и мнимую части.
Равенство (1) обнаруживает одну интересную особенность
функции ег в комплексной плоскости, а именно, ее перио-
дичность; Вообще, функция /(z) называется периодической
функцией с (комплексным) периодом Т, если для всех z из
области определения функции f(z) выполнено соотношение
f^+T)=f(z).
В частности, для f(z) = ez и Т =2ni имеем по (1)
gZ+глг = gx+iy+snl = gx+i <у+ал) —
= ех [cos (у -Ь 2л) -р i sin (у -|=- 2л)] = ех [cosy i sin у] = ег, (2)
так что функция f (z) = ez оказывается периодической функ-
цией с чисто мнимым периодом Т = 2л/. Поэтому и для лю-
бого k = 0, ±1, ±2, ...
ez+2nki-- ez.
Напротив, функции eiz и e~iz имеют в комплексной пло-
скости вещественный период Т =2л. Например, для f(z) — eiz
мы получаем из (2), заменяя там г на iz,
f(Z-(- 2Л) = el <г+2Я) = giz+zni = eiz =
Функции sinz и cosz, рассматриваемые во всей комп-
лексной .плоскости, в силу формул 8.63 (3), (4) вместе с eiz
и e~iz также оказываются периодическими с вещественным
периодом 2л.
Полагая в (1)z = /л, получаем весьма интересную
формулу *):
ezn = _L
*) «Эта замечательная формула Эйлера как бы символизирует
единство всей математики: в ней —1 представляет арифметику, i —
алгебру, л—геометрию и а—анализ» (Д. Н. Крылов).
8.68J	§ 8.6. ЭКСПОНЕНТА В КОМПЛЕКСНОЙ ОБЛАСТИ 293
8.66.	С другой стороны, перемножая равенства 8.63 (1)
и (2) и используя лемму 8.64, мы находим, что
е'г.е_,'г = е° = 1 = (cosz4- i sin z) (oosz—i sin z) =
= cos2 z 4- sin2 z.	(1)
Таким образом, функции cosz и sin z н в комплексной
области удовлетворяют первому из функциональных уравне-
ний, которыми мы в свое время определили эти функции
(5.61 (1)). Из уравнения (1), однако, уже нельзя делать
вывода, который мы сделали в свое время в вещественной
области,—что функции sin z и cosz ограничены по модулю
числом 1,—поскольку их значения сами суть комплексные
числа. Более того, равенства 8.63 (3), (4), в которых z за-
менено на iy, показывают, что функции cos (iy) и i sin (zy) (их
аргумент чисто мнимый, если у—вещественное число) нео-
граниченно возрастают при у -► ±оо.
8.67.	Пусть zx и z2—произвольные комплексные числа.
Заменяя в разложениях 8.63 (1) и (2) z на zx и на z2 и
перемножая, находим
е' tel+г’> = cos (Zj 4- z2) -f- i sin (zx + z2) = eiz' • е'г> =
= (cos zx + i sin zx) (cos z2 + i sin z2) =
= (cos zx cos z2— sin zt sin z2) + I (cos zx sin z2 4- sin zx cos z2)
и аналогично
e_'(z‘+z>’ = cos(z14-2'2)— i sin (Zj-f-Zg) = e~iZl-e~iz* =
— (coszx—i sin zx) (cosz2—i sin z2) =
= (cos zx cos z2 — sin zx sin z2)—i (cos zx sin z2 -f- sin zx cos z2).
Складывая и вычитая полученные разложения, находим
cos (zx + z2) = cos zx cos z2—sin zx sin z2,	(1)
sin (zx -f-^г) = sin zx cos z2 4> cos zx sin z2,	(2)
что дает нам распространение на комплексную область функ-
циональных уравнений 5.61 (2) и (3).
8.68.	В частности, если мы принимаем за определения
функций sinx и cosx ряды 8i62 (1) и (2), мы видим, что
294
ГЛ. 8. ВЫСШИЕ ПРОИЗВОДНЫЕ
[8.71
при этом удовлетворяются функциональные уравнения 5.61
(2) и (3). Покажем, что при достаточно малых положительных х
выполняется и неравенство 5.61 (4)
sin х <
sinx
cosx ‘
(В
х
Из разложения 8.62 (1) можно заключить, что
sinx = x—— "§•£)>	(2)
где Е стремится к 1 при х —* 0. Поэтому при достаточно
малых х мы имеем Д > и скобка в (2) меньше 1, откуда
н следует первое из неравенств (1).
Далее, из разложения 8.62 (2) следует представление
**2
cos х — 1 —g Е,	(3)
где Е —> 1 при х —>- 0. Отсюда (с учетом 8.37 (6))
=х(1-?£)(,+тЕ)=1(,+т£);	<4>
„ 1 ,
здесь при достаточно малых х мы имеем к. > у и скобка
становится больше 1, что и доказывает наше утверждение.
Таким образом, функции, удовлетворяющие соотношениям
5.61 (1)—(4), могут быть определены рядами 8.62 (1) и (2).
Единственность решений этих уравнений была уже доказа-
на (8.54).
§	8.7. Гиперболические функции
8.71.	Определим функции комплексного переменного
^2	9>6
chz=14--2i-4--jj--{--gi-4-...,	(1)
sh* = * + i + i+---	(2)
Указанные ряды сходятся при всех комплексных z. Первая
функция называется гиперболическим косинусом г, вторая —
8.73]	§ 8.7. ГИПЕРБОЛИЧЕСКИЕ ФУНКЦИИ	295
гиперболическим синусом z. Они обозначаются cos hyp z и
sin hyp г или, короче, shz и ch г.
8.72.	Учитывая разложение 8.61 (1)
Z2 Z3
e* = i+*+-|r+£r+...
и его же с заменой z на —z
с-г=1_г+__|г+..„
экспоненты ez и е~г мы можем выразить через полученные
функции ch z и shz:
ez — ch z -ф sh г,
e-z = chz—shz.
Разрешая полученные уравнения
находим:
char=y (ez4-e-2),
shz — у (ez—e~z).
В частности, для действительных
chx = у(с* + «“*),
shx = y (ех— е~х).
относительно shz и chz,
Рис. 8.1.
Графики этих функций даны на рис. 8.1.
8.73. В комплексной области гиперболические функции
тесно связаны с тригонометрическими. Именно, заменяя
в 8.72 (1) и (2) z на iz, находим
cos z = -^(e'z-)-e~/z) = ch iz,	(1)
I sin z =	(eiz—e~iz) = shiz.	(2)
Снова заменяя iz на z, получаем
ch z = cos (— iz) = cos iz,	(3)
sh z — i sin (—iz) — —i sin iz.	(4)
296	гл. 8. высшие производные	18.74
Таким образом, тригонометрические функции получаются из
гиперболических функций заменой аргумента z на iz (с точ-
ностью до множителя i у синуса). Геометрически умножение
аргумента на I означает поворот в плоскости на прямой
угол (5.72).
Специально отметим формулы (х и у вещественны)
sin (х + iy) = sinx- cos iy 4- cos x • sin iy =
= sin x-chy + i cos x-shy,	(5)
cos (x + iy) = cos x • cos iy— sin x • sin iy =
= cos x-chy— i sinx-shy.	(6)
Эти формулы получаются из (1) и (2) и 8.67 (1) и (2).
8.74	. Мы имеем, далее,
ch2 г—sh2z = cos2(i£)4-sin2(i£) = 1;	(1)
ch (гг 4- г2) = cos i (гг -)~z2) = cos izL cos iz2 — sin izt sin iz2 —
= ch z± ch z2 4- sh zt sh z2;	(2)
sh (zr 4- z2) = — i sin i (zt 4- г2) =
= —i [sin izt cos iz2 4~ cos izt sin iz2] =
= sh zt ch z2 4- ch sh z2.	(3)
В частности,
ch 2г = ch2 z 4- sh2 z,	(4)
sh 2г = 2 sh z ch z.	(5)
Далее, для вещественных x и у
sh (х 4- iy) — sh x ch iy 4- ch x sh iy =
= sh x cosy 4-1 ch x sin у,	(6)
ch (x 4- iy) — ch x ch iy 4- sh x sh iy —
= ch x cosy 4- i sh x sin у.	(7)
8.75	. Наконец, отметим формулы дифференцирования для
вещественных х:
(ch х)' = у (ех -\-е~х)' =~(ех—e_*) = shx,
(sh х)' = -±-(ех—е~х)' = у (ех 4- е~*) = ch х.
ЗАДАЧИ
297
Мы видим, что в некоторых отношениях гиперболические
функции устроены проще, чем тригонометрические. Название
«гиперболические функции» объясняется тем, что кривая на
плоскости (х, у) с параметрическим представлением
х = ch t, y = sht
представляет собой гиперболу х2—_у2=1. Для тригономе-
трических функций соответствующая кривая
х = cos t, у sin t
есть окружность х2Д.у2=1, поэтому тригонометрические
функции иногда называют круговыми функциями.
ЗАДАЧИ
1.	Показать, что функция e~1,x‘ имеет на отрезке [—о, а] произ-
водные всех порядков, но не представляется в форме ряда Тейлора
по степеням х.
2.	Показать, что функция {/=x3"sin — имеет при х—0 произ-
водные до n-го порядка включительно, a i/”+1)(0) не существует.
3.	Доказать, что если все корни многочлена Р (х) вещественны,
то и все корни многочленов Р' (х), Р" (х), ..., Р’"-1’(х) также веще-
ственны.
4.	Пусть f (х) ограничена и имеет непрерывные ограниченные
производные f (х) и f (х) на (— оо, оо). Пусть (/ = 0, 1, 2)
Mj= sup | f{P (x)l- Доказать, что
“<*<"	M3<2M0MP
5.	Показать, что вторую производную f (х) (если она существует)
можно получить предельным переходом из значений функции f (х)
в трех соседних точках, именно
f” (х) = lim —2/ (Х~Ь^)~Ь/ (x4~2fe) ф
д-*о	Л®
Написать аналогичную формулу для Д”’(х).
6.	Если выпуклая вниз функция f (х) (гл. 7, задача 7) имеет при
х = х0 вторую производную, то /"(хо)^О.
7.	Если всюду на [а, 6] выполняется неравенство f (х) > 0, то
кривая y=f(x) выпукла вниз на [а, Ь].
8.	Доказать, что функция to = sin г не имеет иных нулей в ком-
плексной плоскости, кроме вещественных нулей 0. ± л, ± 2л, ...
9.	Доказать, что функция ra=sinz по модулю ограничена снизу
положительной постоянной на множестве точек всех окружностей
|г| =	п' п = 0, 1,2, ...
298
ГЛ. 8. ВЫСШИЕ ПРОИЗВОДНЫЕ
10.	(а) Оценить ошибку от замены функции ех в отрезке [0, 1]
ее многочленом Тейлора 10-й степени, (б) В каком отрезке [0, й]
многочлен Тейлора 10-й степени для функции ех отклоняется от нее
не больше чем на 10-’? (в) Какой степени многочлен Тейлора для
функции ех отклоняется от нее в отрезке [0, 1] не больше чем на
10-’?
11.	В промежутке (а, Ь), содержащем точку хв, функция f (х)
обладает производными до порядка п, а в самой точке хв—производной
порядка л-f-l. Известно, что f' (х0) = ... =fin> (хв) — 0, /|п+1) (хо)?=0.
Описать расположение кривой y—f(x) относительно ее касательной
в точке х0 в следующих предположениях:
(а) /<'!+«(^о)>0.
(б) /!"+1’(*о) > о,
(в)	< 0,
(г)	+	< 0,
п четно;
п нечетно;
п четно;
п нечетно.
12.	Если функция f (х) в окрестности точки а допускает пред-
ставление
/(а+й)=/(а)+Лй+о(й),
то /' (а) существует и равна А (7.21). Предположим, что функция f (х)
в окрестности точки а допускает представление
f (a+h)=f(a)+f' (a)h+ j-Bh*+o(h>).
Верно ли, что существует /" (а)?
13.	Доказать неравенство
п	1
е k! < п-п! *
k=o
п
14.	Используя тот факт, что nt есть целое число, дока-
k=o
зать, что е иррационально.
15.	Результат задачи 12 гл. 6 становится неверным без
предположения о том, что все одного знака. Показать, что
СО
при и* — (—l^-y— произведение ТТ (1 +сод,) расходится, хотя
Vk	Л=1
® (—1)* —
ряд 2 сходится. При ^k—e	—1 обратная картина.
/?=1
ИСТОРИЧЕСКАЯ СПРАВКА
299
16.	Показать, что при —2л < х < 2я, п = 1,2,х^О вы-
полняются неравенства
У2 у4	2
2Г+-4Г-“-(4Й=2)!<СО8*<
ха х4	xin
< 1	2! +1Г "’+ (4п)! ’
17.	Пользуясь неравенствами задачи 16 при п=1, получить для
числа л оценки
3,11 < л < 3,18.
Историческая справка
Высшие производные появились вместе со всем аппаратом диф-
ференциального исчисления и систематически применялись Ньютоном
и Лейбницем в конце XVII века к задачам геометрии, механики
и физики. В приложениях к задачам механики существенное зна-
чение имело истолкование ускорения при движении как второй про-
изводной от пути по времени; основной закон механики (второй за-
, кон Ньютона) связывает силу, действующую на какое-либо тело, с
ускорением, вызванным ею, и массой этого тела.
Ряды для элементарных функций были еще раньше исследованы
Ньютоном и Дж. Грегори (1660-е годы). На комплексную область эти
ряды были в следующем столетии распространены Эйлером. Работа
Тейлора, в которой появился «ряд Тейлора»,' относится к 1715 г.;
впрочем, эквивалентные построения ранее встречались и у Ньютона,
и у Лейбница. В течение всего XVIII века математики—явно или
неявно—считали, что «всякая функция» представляется своим рядом
Тейлора; лишь Коши впервые (1823) устанавливает точные условия
сходимости ряда Тейлора к данной функции и проводит отчетливое
различие между сходимостью этого ряда вообще и сходимостью к
данной функции.
ГЛАВА $
ИНТЕГРАЛ РИМАНА
Площадь кривой есть непрестанно рождающееся ко-
личество, увеличивающееся непрерывной флюксией, про-
порциональной ординате кривой.
Исаак Ньютон, Математические начала
натуральной философии (1687)
§9.1. Определение интеграла и теоремы
существования
Интеграл—наряду с производной—важнейшее понятие
классического математического анализа.
9.11.	Разбиение с отмеченными точками.
Если на отрезке а х b указана система точек
х0, xi> • • •> хп такая, что
а =~х0 Хг хп = Ь,
то мы говорим, что нам задано разбиение отрезка [а, Ь] на
промежутки [xft, xfc+1]; сами точки х0, хг, ..., х„ называются
точками деления отрезка [а, £]. Если, кроме того, в каждом
промежутке [xft, xfc+1] выбрана точка
xk ^== xk+i
(* = О, 1,
л-1),
то мы говорим, что нам задано разбиение с отмеченными
точками £0,	..., £„_!• Разбиение обозначается буквой П,
или, подробнее,
П — [с — хо 5^	-*-1	51 Х2 • • •

Разность xk+1 — xk обозначим через А.хк. Число й(П) =
= max Axk называется параметром разбиения П.
9.12.	Ин тегральная сумма. Рассмотрим на от-
резке [а, (конечную) функцию у=f(x). По данному
9-13]	§ 9.1. ОПРЕДЕЛЕНИЕ ИНТЕГРАЛА	301
разбиению (1) можно построить «интегральную сумму»—число
п-1
5п(/)=2/(идхА.
k—o
9.13.	Интеграл. Число / называется интегралом
(Римана) от функции f(x) по отрезку [a, ft], если для любого
е > 0 найдется такое 6 > 0, что при любом разбиении П
с </(П)<6 имеет место неравенство
|/-5п(/)|<е.	(1)
Это определение можно рассматривать в свете общего
определения предела, данного в 4.12. А именно, мы рас-
сматриваем множество Е, элементами которого являются раз-
биения П с отмеченными точками. Для заданного р > 0
обозначим через Ef подмножество в Е, состоящее из всех
разбиений П, для которых d (П) < р. Очевидно, любые два
множества ЕР1 и ЕРг вложены одно в другое, и пересечение
всех Ер пусто. Поэтому множества Ef определяют направле-
ние S' на множестве Е, которое можно использовать для
построения предела функций, заданных на Е. Именно, опре-
деление 4.12 в применении к данному случаю формули-
руется так:
Число I есть предел функции S (П), заданной на множе-
стве разбиений П с отмеченными точками, по направлению S,
если для любого е > 0 существует такое б > 0, что из
d (П) < б следует неравенство
|/-S(II)|<e.	(2)
Предел по указанному направлению S на множестве всех
разбиений с отмеченными точками мы будем также называть
пределом при неограниченном измельчении разбиения.
Мы видим теперь, что если функция S (П) построена по
функции f(x), как указано в 9.12, то существование пре-
дела S (П) по направлению S, т. е. при неограниченном
измельчении разбиения П, равносильно существованию инте-
грала от функции f (х). Интеграл обозначается также сим-
волом
ь
5 /(*) dx,	(3)
°
302
ГЛ. 9. ИНТЕГРАЛ РИМАНА
[9.14
напоминающим исходную интегральную сумму. Однако в то
время как символ интегральной суммы содержит указание
на действия, приводящие к ее вычислению, символ интеграла
пока что «неразъемен», так что в нем не имеется в виду
умножать f(x) на dx и затем «интегрировать». Целесооб-
разность принятого обозначения интеграла (а, например,
ь
не §/(*)) будет ясна из дальнейшего*). С другой стороны,
а
ясно, что для величины интеграла не играет роли обозначе-
ние независимого переменного, так что, например,
ь	ь	ь
\f(x)dx=\f(l)dl = \f(t)dt=...
а	а	а
Числа а и b называются границами, или предалами инте-
грала (3); а есть его нижний, Ъ есть его верхний предел.
Для данной функции f(x) ее интеграл вовсе не обязан
всегда существовать. Далее мы докажем (9.14 и 9.16), что
всякая непрерывная функция и некоторые простые разрывные
функции обладают интегралом; напротив, сильно разрывные
функции (как, например, функция Дирихле (9.17)) не имеют
интеграла. Функция f(x), определенная на [а, £] и обладаю-
щая интегралом, называется интегрируемой на (а, ft].
9.14.	Здесь мы докажем существование интеграла для
непрерывной функции y—f(x) на отрезке [а, ft].
а.	Обозначим через соДб) колебание функции f(x) на
отрезке [а, ft]: <oz(6) = sup	|/(х')—/(х")|- Напомним
1лг'-лг" | <б
(5.17 в), что для непрерывной функции f(x) на отрезке [а, ft]
всегда lim ю. (6) = 0.
л-»о '
б.	Разбиение П' = [с =	х^. .^Хр = ft]
мы назовем последующим по отношению к разбиению П =
=[а = х0^ |0хп = ft], если каждая из точек
х0, ..., хп входит в число точек х'о, ..., х’р (так что набор
*) «Предупреждаю, чтобы остерегались отбрасывать dx—это
ошибка, которую часто допускают и которая препятствует продвиже-
нию вперед, так как тем самым лишают неделимые, как здесь dx, их
общности, ... из которой проистекают бесчисленные трансфигурации
и эквипотентаости фигур» (Лейбниц, 1686).
9.14]
§9.1. ОПРЕДЕЛЕНИЕ ИНТЕГРАЛА
303
х'в, ..х’р получается добавлением к набору х0, ..., хп
некоторых новых точек деления); при этом на отмеченные
точки не налагается никаких новых условий. Теперь
установим две простые леммы.
в.	Лемма. Если разбиение П удовлетворяет условию
d (П)	6, то для всякого последующего разбиения П'
|5п'(/)—Sn(/)|<ioz(6)(fe-a).	(1)
Доказательство. При переходе от разбиения П
к разбиению П' каждый отрезок [xft, xft+1] заполняется но-
выми точками деления и новыми отмеченными точками; не-
сколько изменяя обозначения, их можно записать так:
xk~xM^	mk-i^xkmk~ Xk+1.
Часть интегральной суммы 5П', приходящаяся на отрезок
mfc-l
[*ft. Xfe+J, ™еет ВИД 2 №*№ХЫ №xkj = xk,j+i—xiJ-
Слагаемое /(£fc) Axft интегральной суммы 5П мы можем
т*-1
также записать в виде суммы У /(Б*)Ах>у.
7=о
Мы имеем
Шк-1	тк-1	«к-1
2 Жу)Ахй/- 2 №)Axft/= 2
/=о	/=о	7=0
и поскольку d (П) < б,
тк-1	Шк-Х
2 /(^.)Axfc/- 2 /(U Axfc/
7=о	/=о
mk-i
< 2 1/(^у)-/(и1А^7<Ю/(6)Ахл.
/=о
Суммируя по индексу k, получаем
12 2 f	^Xki~^ f	Axft | < и, (6) (ft—с),
и лемма доказана.
г.	Лем м а. Для двух (произвольных) разбиений Пг и П2
с «/(ЩХб, d (П2) < 6
|5n,(/)-SnI(/)|<2a>/(6)(ft-a).	(2)
304	ГЛ. 9. ИНТЕГРАЛ РИМАНА	(9-15
Для доказательства построим новое разбиение П3, исполь-
зуя все точки деления разбиений Пх и П3 в качестве точек
деления, а отмеченные точки взяв произвольно. Разбие-
ние П3 является последующим по отношению и к разбие-
нию Пх, и к разбиению П2. По лемме в
] $п, (/) - 5П, (/) К «>, (б) (f> - а),
|5П1(/)-^п.(6) (Ь—а),
откуда и вытекает (2).
д.	Теперь мы можем доказать основную теорему.
Теорема. Всякая непрерывная функция f(x), опреде-
ленная на отрезке [с, Ь], интегрируема на [а, Ь].
Доказательство. Имея в виду критерий Коши суще-
ствования предела по направлению (4.19), достаточно пока-
зать, что для любого е > 0 существует такое б > 0, что
из d (Hi) б, d (П2) б следует

Так как. функция f(x) непрерывна на [а, б], то для задан-
такое б > 0, что а, (6)	;
> ' '^2(6—а)
ного е > 0 можно найти
Но тогда по лемме г для любых двух разбиений Пг и П2
с d (П) б выполняется неравенство
Ип, </)-5п. (/) К 2 2^) (Ь-а) = е.
Таким образом, критерий Коши удовлетворен, и теорема о
существовании интеграла для непрерывной функции доказана.
9.15.	Мы будем иметь дело и с интегралами от более
широкого класса функций. Здесь мы приведем некоторые
общие свойства интеграла в предположении только его суще-
ствования, не опираясь на какие-либо специальные свойства
функций, к которым он применен.
а.	Если функция f(x) интегрируема на отрезке [а, Ь] и
k — постоянная, то функция kf(x) также интегрируема на
Га, й] и
ь	ь
kf(x)dx —f(x) dx,	(1)
a	a
т. e. постоянную можно выносить за знак интеграла.
9.15]
§ 9.1. ОПРЕДЕЛЕНИЕ ИНТЕГРАЛА
305
В самом деле, для любого разбиения П
л-1	л-1
Sn (kf) = 2 kf (У \Xj = k 2 f (M Axy = kSn (f);
1 = 0	j=0
правая часть имеет предел при неограниченном измельчении
ь
разбиения П, равный k^ f(x) dx; отсюда следует, что и
а
левая часть имеет этот же предел, что и дает равенство (1).
б.	Если функции f(x) и g(x) интегрируемы на отрезке
[a, ft], то и функция f(x)-[-g(x) интегрируема на [а, ft] и
ъ	ь	ъ
J [/(x) + g(x)]dx= J/(x)dx + J^(x)dx,	(2)
а	а	а
т. е. интеграл от суммы равен сумме интегралов.
Действительно, для любого разбиения П
л-1
sn(/+^) = 2 [№)+№)] Аха=
о
л-1	л-1
= 2 f (U Axfc + 2 №) Axfc = Sn (/) + Sn (£);
k=o	fc=o
переходя к пределу при неограниченном измельчении раз-
биения П, получаем существование интеграла от функции
f (х) + g(х) и равенство (2).
в.	Всякая интегрируемая функция f(x) ограничена.
Пусть функция /(х) не ограничена на [a, ft]. Рассмот-
рим произвольное разбиение П= {а = х0 хг^  •.
хп_1 <1 хп = ft}. Хотя бы в одном из промежутков [ху, Ху+1]
функция /(х) также не является ограниченной. Тогда, фик-
сируя отмеченные точки в остальных промежутках и меняя
в том промежутке, где /(х) не ограничена, мы можем по-
лучать сколь угодно большие (по модулю) значения инте-
гральной суммы. Поэтому суммы 9.12 не могут иметь предела.
г.	Интегрирование неравенств. Если интегри-
руемые на [a, ft] функции f(x) и g(x) удовлетворяют
неравенству
fM^g(x).
306
ГЛ. 9. ИНТЕГРАЛ РИМАНА
[9.15
то и
ь
$/(х) йхС
а
Ъ
J glx) dx.
а
(3)
Действительно, интегральные суммы Зп (/) и Зп 1g} для
одного и того же разбиения П с одними и теми же отмечен-
ными точками gy- удовлетворяют неравенству
п	п
Sn (/)= 2 /(g7) Аху< 2 gfy) Аху= Зп lg),
/=i	/=i
откуда (3) получается переходом к пределу при d(П) —> 0.
Д. В частности, если интегрируемая функция f(x} на от-
резке [а, /’] ограничена сверху, скажем, числом М, то
ь	ь
<\)f(x)dx^SlMdx = M(b — а}.	(4)
а	а
е. Аналогично если интегрируемая функция fix) на от-
резке [a, ft] ограничена снизу числом т, то
ь
m(b—a}^f{x}dx.	(5)
а
ж. В частности, если функция fix} неотрицательна,
можно взять /я = 0, и, следовательно, ее интеграл также
неотрицателен. Если функция /(х) неположительна, то
в (4) можно положить 2И=0, и мы получаем, что и ее
интеграл неположителен.
з.	Для функции f[x}, ограниченной с обеих сторон,

получается двусторонняя оценка интеграла
ь
mlb—а}^. J/(x)dx^A^lb—а),
а
(6)
Величина
b
^ra^flx}dx
а
9.15]
§9.1. ОПРЕДЕЛЕНИЕ ИНТЕГРАЛА
307
называется (интегральным) средним, функции f(x). Из (6)
вытекает следующее неравенство для среднего («теорема о
среднем»):
ь
m^-^^f(x)dx^M.	(7)
а
Если функция f(x) непрерывна на [a, ft], то, взяв в ка-
честве чисел m и М ее нижнюю и верхнюю точные грани
и воспользовавшись теоремой Больцано 5.22, мы заключаем,
что имеется точка £ € [а, ft] такая, что
ь
b±^f(x)dx=f£).
а
Число /(В) называется средней ординатой функции f(x) на
отрезке [a, ft],
и.	Если интегрируемы функции f(x) и |/(х)|*), то,
интегрируя неравенство
- |/(х)|С/(х)С|/(х)|,
находим
ь	ь	ь
— $|/(x)|dx< J f(x) dx < $ l/W | dx,
a	a	a
откуда
b	b
\f(x)dx C J |/,(x)|dx.
a	a
к.	Если функция f(x) интегрируема на отрезке [а, с] и
на отрезке [с, ft], то она интегрируема и на отрезке [а, ft] и
Ь	с	b
J f(x)dx=^f(x)dx+	^f(x)dx.	(8).
а	а	с
Возьмем для доказательства	любое разбиение П отрезка
[a, ft]:
П = [а = х0 хг	хт с хт+1	хп~ ft].
*) Из интегрируемости функции f (х) на самом деле следует ин-
тегрируемость функции | f (х) | (см. задачу 7).
308
ГЛ. 9. ИНТЕГРАЛ РИМАНА
[9.15
Соответствующая интегральная сумма с отмеченными точка-
ми (А =0,1, ..., л—1) преобразуется следующим образом:
п—1	т—1
5п (/) = 2 f = 2 f (U A xk+
ft=0	а?=о
л- 1
+/(^)Дхи+ 2 №)Дх*=
k=m+ 1
т-1
= 2 /(^)ДхА+/(с)(с—хт)+/(с)(хст+1—с) +
k=0
л-1
+ 2 /(UA^ + [/(U)~/(c)]Axm =
= Sn. (/) + Sn, (/) + [/(£.)-/(«)] Дхи,	(9)
где Щ и П2— некоторые разбиения отрезков [а, с] и [с, д].
При неограниченном измельчении разбиения П разбиения
П± и П2 также неограниченно измельчаются, а последнее
слагаемое в (9) стремится к нулю (так как интегрируемая
функция f(x) по в ограничена, а длина промежутка Дхт
стремится к нулю). Поэтому правая часть в (9) имеет пре-
дел, равный
с	b
$7(х) dx+ $/(*) dx.
а	с
Левая часть в (9), со своей стороны, имеет предел
ъ
J/(x)dx, откуда и следует (8).
а
л.	Обратно, если функция f (х) интегрируема на отрезке
[a, t], то она интегрируема на отрезках [а, с] и [с, &],
где а < с <_Ь. Мы ограничимся доказательством для отрезка
[а, с]; доказательство для отрезка [с, 6] проводится ана-
логично. Любое разбиение отрезка [а, с]
П= [a = x0^g0^x1<g1< ... <xffl = c]
можно дополнить до разбиения П отрезка [a, /?]:
II [п = X|)S^t'-^Х,.; | |. ,^^Xn
Для второго разбиения
П' = [a = x;<g^x'1^gK ... СХр=с]
9.16)
§9.1. ОПРЕДЕЛЕНИЕ ИНТЕГРАЛА
309
возьмем то же самое дополнение:
II = [а = Х0^^0 Хх	5и1	^~т+1	‘ %п ^]-
Так как /(х) интегрируема на [а, &], то для заданного
е > 0 существует 6 > 0 такое, что из d (П) < 6, d (IT) < 6
следует неравенство
РпОЭ—%•(/>! <е.
Но в данном случае, очевидно,
5п (/) -5П' (/) = 5п (/)-Sn- (/),
поэтому для всех разбиений П и П' с d (П) < 6, d (IT) < 6
|Sll(/)-Sn- (Z)| < 8.
Таким образом, для интегральных сумм функции /(х) на
отрезке [а, с] выполнен критерий Коши для направления
d (П) —» 0. Отсюда следует интегрируемость функции f (х)
на отрезке [а, с].
м. Несколько раз применяя предложение л и используя к,
приходим к следующему результату:
Если функция /(х) интегрируема на отрезке [а, Ь] и
а — с0<с1 < ... < с„ = £>, то /(х) интегрируема на каждом
из отрезков [ck_1, cft] и
&	Ct	сп
J/(x)dx = $/(х) dx-\- ... -J- У /(x)dx.
а	СО	сп—	1
н. Наконец, отметим одну полезную оценку отклонения
интеграла от интегральной суммы.
Если функция f(x) интегрируема на [а, и d (П)	6,
то
ь
^f(x)dx-Sn(f)
а
—а).
Это неравенство получается из неравенства 9.14 (1) пре-
дельным переходом при d (П')—*-0.
9.16. Теперь мы покажем, что интеграл существует и
для некоторых разрывных функций. Правда, класс разрывных
функций, которые мы здесь рассмотрим, еще невелик, но он
уже вполне достаточен для всех ближайших приложений.
310
ГЛ. 9. ИНТЕГРАЛ РИМАНА
[9.16
а.	Пусть функция h (х) равна 0 при а < х < Ь и имеет
произвольные значения h (а) и h(b). Покажем, что h(x) ин-
тегрируема иа [a, ft] и
ь
^h(x)dx = 0.	(1)
а
Действительно, интегральная сумма для функции h(x)
по любому разбиению П приводится к виду
*(Bo)Ax0 + *(B„_i) Дх„_1,
где Л (|0) есть 0 или h(a) и ft(B„_i) есть 0 или ft(ft).
Когда d (П) —► 0, это выражение, очевидно, стремится к 0,
что и требуется.
б.	Пусть функция /(х) непрерывна при a^x^ft. Пусть
(х) совпадает с /(х) при а < х < ft и имеет произвольные
значения («) и j\ (ft). Тогда функция (х) интегрируема
на [a, ft] и
ь	ь
\fl(x)dx=^f(x)dx.	(2)
а	а
Действительно, функция Л(х)=/Х(х)—/(х) удовлетво-
ряет условиям а; поэтому она интегрируема и выполняется
равенство (1). Тогда в силу 9.15 6 интегрируема и функция
/1 (х) =/(х)-|-/г (х), причем в силу 9.15 6 и (1) имеет место
(2), что и требуется.
в.	Функция /(х) называется кусочно-непрерывной на
отрезке [a, ft], если существует такое разбиение
а = Xf> < *1 <
< x„ = ft,
что /(х) непрерывна в каждом интервале xk < х < xk+1 и
имеет конечные пределы /(хо + О), /(хх—0), /(хх-|-0),
/(х2—0), ... , f{xn—0) (значения же в самих точках xk
может иметь какие угодно). Покажем, что каждая кусочно-
непрерывная функция f(x) на отрезке [с, ft] интегрируема на
этом отрезке.
Обозначим через Д(х) функцию, определенную на от-
резке xk х ^xfc+1, совпадающую внутри этого отрезка
с функцией /(х) и принимающую на концах отрезка соот-
ветствующие предельные значения /(xft4~0) и /(xft+1—0).
9.16]
§9.1. ОПРЕДЕЛЕНИЕ ИНТЕГРАЛА
311
Функция fk(x) непрерывна на [xft, xfe+1]; в силу б функция
f (х) интегрируема на [xft, xft+1] и
*ir+i
J f(x)dx = fk (*) dx.
Xk	xh
Применяя 9.15 к, получаем, что функция f(x) интегрируема
на всем отрезке [с, б], что и требовалось.
По 9.15 м мы имеем также
Ь	п-1 xk+t	п_, хк+,
^f{x)dx = 2 J f(x)dx— 2 $ fk(x)dx,
a	k=0 хк	k=0 хк
так что вычисление интеграла от кусочно-непрерывной
функции приводится к вычислению интегралов от непрерыв-
ных функций.
г. В частности, интегрируема
функция
всякая ку сочно-постоянная
Ло = const при
11г — const при
А(х) = {
а = х0 < х < х1(
*1 < X < х2,
Й„_1= const При Х„_х < X < хп=Ь,
и ее интеграл равен
Ь	Я-1 xk + t
\ Л (х) dx = 2 h (*) dx =
a	£ — О хк
П - 1	xk+1	П — I
= 2 Afe J dx = 2 fik(xk+l-xk).
k-o	~.	k-o
Между прочим, отсюда следует, что интегральная сумма
•^п(/) (^-^2) для всякой функции /(х) есть интеграл от
некоторой кусочно-постоянной функции йц (х) — именно, при-
нимающей в промежутке хк < х < хк+1 постоянное значе-
ние hk=f(lk).
д. Теорема. Пусть g(x)^O — кусочно-непрерывная
функция и
ь
$^(x)dx = 0.	(3)
а
312
ГЛ. 9. ИНТЕГРАЛ РИМАНА
[9.17
Тогда g(x) может быть отличной от нуля лишь в конечном
множестве точек.
Доказательство. Пусть сначала g(x) непрерывна;
покажем, что в этом случае из (3) следует g(x) = 0. Дей-
ствительно, если g(x) ф. 0, то существует точка с, а ^.с^.Ь,
где g(x) > 0, и в силу непрерывности функции g(x) имеется
целый промежуток ос^хй^Р, где g(x)^g0> 0. Мы имеем
ь
а
fl
g(x)dx=§ g(x)dx + J g(x)dx^
a	x((a, (3)
₽
> У g(x) dx >(₽ — a) g0> 0,
a
что противоречит (3). Таким образом, (3) влечет g(x) = 0.
Пусть теперь g(x)—кусочно-непрерывная функция и
с0 = а < сх < ... < ср = Ь — ее точки разрыва. Тогда по в
Ь	р_1ск + ,
\g(x)dx = 2 J g(x)dx — 0,
а	*=° ск
и так как каждое слагаемое неотрицательно, то
e/c+i
Ос
g(x) dx — 0
(/г = 0, ..., р— 1).
Функция g(x) непрерывна внутри промежутка (cft, cft+1),
поэтому во всех внутренних точках этого промежутка
g-(x) = 0. Возможными точками, где g(x) > 0, могут быть
только точки с0, ..., ср, которых конечное число. Теорема
доказана.
9.17. Мы установили интегрируемость кусочно-непрерыв-
ных функций; такие функции имеют лишь конечное число
точек разрыва*). Как обстоит дело с интегрируемостью
функций, имеющих бесконечное число точек разрыва? Рас-
смотрим функцию Дирихле % (х), равную 0 в каждой ирра-
циональной и 1 в каждой рациональной точке отрезка
*) Можно доказать, что всякая ограниченная функция с конеч-
ным числом точек разрыва интегрируема. См. задачу 9,
9-18]	§ 9.1. ОПРЕДЕЛЕНИЕ ИНТЕГРАЛА	313
[О, 1]. Для любого разбиения П, если точки взять
рациональными, мы получим интегральную сумму
равную 1; если же точки (для того же разбиения П)
взять иррациональными, интегральная сумма	^xk
будет равна 0. Значит, для функции Дирихле не существует
предела интегральных сумм при неограниченном измельчении
промежутка [0, 1], и, следовательно, она неинтегрируема.
Таким образом, граница между интегрируемыми и неин-
тегрируемыми функциями проходит где-то в области функ-
ций с бесконечным множеством точек разрыва. Существует
теорема, согласно которой функция f(x) интегрируема по
Риману тогда и только тогда, когда множество всех ее
точек разрыва при любом е > 0 может быть покрыто конеч-
ной или счетной совокупностью промежутков с суммой длин
< е (задача 9). Но при необходимости интегрировать раз-
рывные функции более целесообразно применять другую,
более общую, чем римановская, схему интеграла — интеграл
Лебега *).
9.18. Определенный интеграл в пределах
от b до а, где	Пусть /(х) интегрируема на
а х Ь. По определению полагаем
а	Ъ
\f(x)dx= _\f(x)dx.	(1)
Ь	а
Теперь уже для любых а, р, т€[а, fr] оказывается спра-
ведливой формула
v	₽	v
J/(x) dx = J/(x) dx + J/(x) dx	(2)
a	a.	₽
при любом взаимном расположении точек а, р, у на отрез-
ке [а, Ь\. Действительно, для а < р < у эта формула была
доказана в 9.15 к. Возьмем какое-либо иное расположение
точек а, р, у, например у < р < а. Тогда по доказанному
J f(x) dx = J f (x) dx + J f (X) dx.
V	V	₽
*) См., например, Г. E. Шилов и Б. Л. Гуревич, Ин-
теграл, мера и производная. Общая часть, М., 1967, гл. II.
314
ГЛ. 9. ИНТЕГРАЛ РИМАНА
[9.21
Теперь, используя (1), получаем
V	а	₽	а
J /(х) dx — — J/(х) dx — — J/(x) dx — J/(x) dx==
а	V	V	₽
₽	V
= J/(x)rfx + ^f(x)dx,
a	₽
что и требуется; при любом другом расположении а, Р, у
рассуждение аналогичное.
Отметим, далее, равенство,	немедленно	следующее	из	(1):
a	b	b
-±F^(x)dx=--^~^f(x)dx = T^^f(x)dx. (3)
b	а	а
Используя	для	правой части (3) оценку	9.15 (7), получаем
inf f (х) = от <	J/(x) dx < М = sup/ (х),
ь
так что в оценке среднего безразлично, имеет ли место
неравенство а < b или противоположное неравенство b < а.
§ 9.2.	Зачем нужен интеграл?
Мы продемонстрируем здесь применение понятия интег-
рала в математическом анализе на двух геометрических
примерах (9.21 и 9.28), откладывая подробное изложение до
§9.6.
9.21.	Площадь криволинейной трапеции.
Из элементарной геометрии известно понятие площади для
простых геометрических фигур, например, ограниченных от-
резками прямых. А что такое «площадь» фигуры, ограни-
ченной какими-нибудь иными линиями? Элементарная геометрия
не дает определения площади такой фигуры*).
*) Площадь круга в элементарной геометрии вычисляется на
самом деле не элементарными средствами (с привлечением пределов)
и поэтому не идет в счет.
9.21]
§ 9.2. ЗАЧЕМ НУЖЕН ИНТЕГРАЛ?
315
Естественно исходить нз следующей аксиоматической пред-
посылки: площадь фигуры Ф есть число, которое не больше,
чем площадь S любой объемлющей элементарной фигуры
(например, составленной из многоугольников), и не меньше,
чем площадь s любой объемлемой
элементарной фигуры (рис. 9.1).
Поскольку (согласно теоремам
элементарной геометрии) всегда
мы имеем (1.62 6)
su р s inf 5,
где верхняя грань в левой части бе-
рется по всем элементарным фигурам,
объемлемым фигурой Ф, а нижняя
грань в правой части — повеем элементарным фигурам, объем-
лющим фигуру Ф. Если sup s = inf 5, то для площади фигуры Ф
единственно возможным значением становится общая вели-
чина sup s и inf 5. Применим это общее соображение к слу-
чаю криволинейной трапеции — фигуры Ф, ограниченной
снизу отрезком [а, Ь\ оси х, сверху — графиком непрерывной
функции y=f(x)^O, с боков — ординатами этого графика
при х = а и х = Ь. Рассмотрим разбиение n=[a = xosg
^хп = Ь], причем точку [xk, xfc+1]
выберем так, чтобы функция f(x) в этой точке достигала
максимального (на [xk, xft+1]) значения, которое мы обо-
Рис. 9.2.
значим через Mk. Соответствую-
щую интегральную сумму
Sn(f) = ^M^xk
k-0
можно истолковать как площадь
элементарной фигуры, образован-
ной «выступающими прямоуголь-
никами» и содержащей фигуру Ф
(рис. 9.2). Если же выбрать точку
Bfc € [хл, **+1] так, чтобы функция f(x) в этой точке достигала
минимального (на [xft, xfc+1]) значения, которое мы обозна-
чим через mh, то соответствующую интегральную сумму
316
ГЛ. 9. ИНТЕГРАЛ РИМАНА
[9.22
можно истолковать как площадь элементарной фигуры, об-
разованной «вложенными прямоугольниками» и содержащейся
в фигуре Ф (рис. 9.3). Поэтому всякое число S, которое могло
бы претендовать на звание «площади фигуры Ф», в соот-
ветствии с нашей посылкой долж-
но удовлетворять неравенству
Sn(/)^S^Sn(/).
Но, с другой стороны, если у
функции f(x) есть интеграл (а
для непрерывной функции мы это
доказали в 9.14), то при неогра-
ниченном измельчении разбиения
П суммы (/) и Sn (/) имеют
общий предел /; таким образом, мы приходим к единствен-
но возможному определению площади фигуры Ф:
ь
$=1=^/(х)(1х.
а
9.22.	Для завершения построения следовало бы убедиться в том,
что приведенное определение площади криволинейной трапеции удов-
летворяет выдвинутой выше аксиоматической предпосылке в приме-
нении ко всем элементарным фигурам, а не только к тем специальным,
которые участвовали в определении. Этот факт действительно верен,
но доказательство его кропотливо, и к тому же все рассуждение
является лишь частным случаем общих построений теории измерения
площадей и объемов. Поскольку указанный факт нам в этой книге
не понадобится, мы предпочитаем дать читателю общий очерк теории
измерения, отсылая за деталями к литературе *).
9.23.	Мы начнем с описания определения интеграла Римана на
метрическом компакте. Пусть К—компакт (3.91). Некоторые подмно-
жества компакта К будем называть ячейками.-, при этом предполага-
ется выполнение следующих свойств:
1)	сам компакт К и пустое множество суть ячейки;
2)	пересечение двух ячеек есть ячейка;
3)	для любого б > 0 существует разбиение компакта К на ко-
нечное число взаимно не пересекающихся ячеек, диаметры которых
(3.12а) не превосходят 6. *•)
*•) См., например, А. Я. X и н ч и н, Краткий курс математи-
ческого анализа, М., 1953, гл. 27; Г. Е. Шилов, Математический
анализ, III.17—III.24, изд. МГУ, 1967, стр. 5 и далее.
9-24]	§ 9.2. зачем нужен интеграл?	317
Предположим, далее, что каждой ячейке Q поставлено в соответ-
ствие неотрицательное число mQ, называемое мерой ячейки Q, и при
этом всякий раз, когда ячейка Q есть объединение непересекающих-
ся ячеек Q1( ... , Q„, выполнено условие аддитивности
mQ=mQ1 + ...+mQn.	(1)
В дальнейшем компакт с системой ячеек и мерой будем называть
нагруженным, компактом. На нагруженном компакте можно устано-
вить схему интегрирования по аналогии со схемой интеграла Римана
на отрезке, описанной в § 9.1.
Пусть дана функция f (х), определенная на нагруженном ком-
пакте К. Рассмотрим разбиение П компакта К на конечное число
непересекающихся ячеек Qj....Qp. Обозначим через d (П) макси-
мальный из диаметров ячеек Qlt ... , Qp. Выберем в каждой ячей-
ке Qj произвольную точку и составим интегральную сумму
р
sn(D = 2^/>mQ/-	<2>
7=1
Число /f) называется интегралом Римана от функции f (х) по
нагруженному компакту К, если для любого е > 0 найдется такое
б > О, что при любом разбиении П с d (П) < б имеет место нера-
венство
|Zf-Sn(f)|<e.
Иными словами, интеграл Римана от функции fj (х) есть предел
интегральных сумм (2) при неограниченном измельчении разбиения П.
Это определение укладывается в общую схему предела по направле-
нию, как и в случае отрезка (9.13). Можно доказать—так же, как
в 9.14 для отрезка,—что всякая непрерывная функция ft (х) интегри-
руема на нагруженном компакте К.
9.24.	Примеры.
а.	Пусть К—отрезок [а, Ь] с его обычной метрикой. Ячейками
будем называть всевозможные промежутки а<х<Р, а<х<Р,
а«£х<р, а<х<Р, где а < Р; длину соответствующего промежутка
будем считать мерой ячейки. В этом случае мы приходим к обычному
интегралу Римана на отрезке (9.13).
б.	Пусть К есть брус в «-мерном пространстве, выделяемый
неравенствами
«1 Xi Ь\, .   , ап хп Ьп,
с обычной метрикой евклидова пространства (3.14). Ячейками будем
называть подбрусы Q бруса К, выделяемые неравенствами ос1<х1<
«sPt, ..., а„«£х„<р„, а также неравенствами, получающимися
из написанных здесь заменой некоторых знаков < на <. Мерой
п
бруса Q будем называть его объем, т. е. число JJ (Р*—«*)• Легко
ft=o
318	ГЛ. 9. ИНТЕГРАЛ РИМАНА	[9.25
проверить, что все требования, наложенные на систему ичеек и их
меру, здесь выполнены. Получающийся интеграл называется в данном
случае интегралом Римана по п-мерному брусу К.
9.25.	Будем говорить, что множество Z в нагруженном компакте К
имеет (жорданову) меру 0, если при любом е > 0 оно может быть
S
покрыто конечным числом ячеек , Qs с 2 mQj < е, причем каж-
i=i
S
дая точка x£Z есть внутренняя точка (3.21) множества U Qj- Имеет
I	i=i
место теорема (обобщающая теорему об интегрируемости кусочно-
непрерывной функции 9.16): каждая ограниченная функция f. (х) на
нагруженном компакте К, непрерывная вне некоторого множества
меры 0, интегрируема.
9.26.	Каждому множеству Е С К сопоставим характеристическую
функцию У,е1х)' равную 1 на Е и 0 вие Е. Будем говорить, что
множество Е имеет объем (меру), если функция f.(x) интегрируема,
и в этом случае число тЕ = 1ур назовем объемом (мерой Жордана)
множества Е. Для каждого множества меры 0 его объем равен 0.
Из основных свойств интеграла вытекает, что из Et с Ег следует
mE1<m£’2 (если эти объемы существуют), и если имеется разло-
жение множества Е, имеющего объем, в конечное объединение мно-
жеств Elt ... , Es, также имеющих объемы и не пересекающихся,
то тЕ = тЕ1-(- • •  JrmEs (аддитивность объема).
Какие же множества ЕаК имеют объем? Можно судить о на-
личии объема у множества Е по свойствам его границы. Границей
множества Е называется множество точек х£К, предельных одно-
временно для Е и для его дополнения (т. е. точек, в любую окрест-
ность которых входят как точки Е, так и точки К—Е). Имеет место
следующая теорема: множество Е С. К имеет объем тогда и только
тогда, когда мера его границы равна 0. Такие множества в даль-
нейшем будем называть жордановыми множествами. В частности,
для каждой жордановой ячейки ее объем есть ее исходная мера.
Для жордановых множеств свойство аддитивности объема можно
усилить следующим образом: если жорданово множество Е есть ко-
нечное объединение жордановых множеств Ег, ... , Es, не имеющих
попарно общих внутренних точек, то mE — mEl-\-...-\-mEs.
9.27.	В n-мерном брусе (9.246) можно указать простой и вместе
с тем достаточно богатый класс жордановых множеств. А именно,
жордановым является всякое ограниченное множество, граница ко-
торого есть объединение конечного числа поверхностей с уравнения-
ми вида
Ху — фу (Хц ... , Ху—1, Ху^-1, ... I Хп),
9.27]
§ 9.2. ЗАЧЕМ НУЖЕН ИНТЕГРАЛ?
319
где фу—непрерывная функция (от точки (jq....X/-i, Х/+ь • • • > хп),
пробегающей некоторую область в (и—1)-мерном пространстве).
В частности, всякий многогранник (множество, ограниченное конечным
числом плоскостей) является жордановым множеством.
Как мы говорили в 3.16 в, множества G и F в л-мерном евкли-
довом пространстве Rn называются геометрически равными, если су-
ществует изометрическое преобразование пространства Rn в себя, при
котором множество F переходит в множество G. Доказывается,. что
геометрически равные жордановы множества имеют и равные объемы.
Это имеет место, в частности, если G получается из F сдвигом (3.16 6),
отражением относительно какой-либо плоскости (3.16 а), поворотом
(5.75). Далее, если жорданово множество G получается из жорданова
множества F растяжением вдоль некоторого направления в Я раз (2.67),
то mGr=-l.mF. Если жорданово множество G получается из жорда-
нова множества F растяжением в раз по оси xlt в Я2 раз по оси
х.2,	, в раз по оси хп, то mG = X1 ... Kn-mf. Наконец, если G
получается из F растяжением по всем направлениям в одно и то же
число раз, положим в X раз, т. е. G подобно F с коэффициентом
подобия Я, то mG = knmF.
На плоскости (п — 2) фигура, описанная в 9:21,—криволинейная
трапеция, ограниченная линиями х = а, х=Ь, y = f(x)^O,—является
жордановым множеством, если функция f (х) непрерывна, и по общей
теореме 9.26 имеет объем (который при и = 2 следует, конечно, на-
зывать площадью). В силу указанных в 9.26 свойств объема он за-
ключен между объемами элемен-
тарных фигур, описанных в 9.21,
и, следовательно, равен приведен-
ному там выражению—интегралу
Римана от функции f (х) по отрез-
ку [о, Ь].
В соответствии со сказанным
выше площадь фигуры, составлен-
ной из конечного числа криволиней-
ных трапеций (или геометрически
равных таким трапециям) (рис. 9.4),
также можно записать через рима-
новские интегралы.
Таким образом, теория измере-
ния площадей на плоскости в зна-
чительной мере приводится к вычис-
лению интегралов Римаиа. Следует
Сложная фигура, рассеченная на 4
криволинейные зрапецш.
Рис. 9.4.
все же заметить, что эта теория не
на все естественные вопросы спо-
собна дать ответы; в частности, в ней только для конечного объеди-
нения множеств, имеющих объемы, гарантируется существование объ-
ема. Более общая теория—лебеговская, допускающая и счетные
объединения,—более сложна*).
*) См., например, Г. Е. Шилов и Б. Л. Гуревич, Интеграл,
мера и производная, 2-е изд., «Наука», М., 1967.
320
ГЛ. 9. ИНТЕГРАЛ РИМАНА
[9.28
9.28.	Длина дуги кривой. В элементарной геометрии
известно понятие длины отрезка и длины ломаной, состав-
ленной из отрезков. Длина дуги окружности определяется
как предел длин вписанных и описанных ломаных. Не оста-
навливаясь на уточнении этого
определения (необходимом по
причине недостаточной четко-
сти школьного определения
предела), мы попробуем сразу
сформулировать аналогичное
определение для дуги произ-
вольной кривой L, заданной на
y=f(x)
Рис. 9.5.	отрезке [а, й] с помощью
функции у = f(x). Рассмотрим
разбиение П= [а = х0 х± <1 <2 х2 ...
= с не фиксированными пока точками |0, .. .
... , и построим ломаную Ln с вершинами в точках
(х0, Jo)> • • • 1 (хп> Уп), где Ук=/(хк)- Эта ломаная вписана
в кривую L (рис. 9.5). Длина s (Ln) ломаной £п может быть
найдена по формуле (Ахк = хк+1 — хк, Ьук=ук+1—Ук)
п— 1	_______
s(Ln)= 2/М+М.
k=0
Предположим, что функция /(х)имеет производную f'(x).
Тогда, используя теорему Лагранжа 7.44, можно выбрать
точку gft£(xft, хл+1) так, чтобы иметь
Выражение длины ломаной £п теперь приводится к виду
п—1	__________
S (£п) = 2/1 +[Г(^)]2Д^.	(1)
*=0
Это выражение есть интегральная сумма для функции
g(x) = /1 + [/'W]2, составленная по разбиению П с ука-
занными отмеченными точками Во, В. £„_v Если функ-
ция g(x) интегрируема, то при неограниченном измельчении
разбиения П суммы (1) имеют пределом величину
ь
S Ki+[/W<**;
9-31]	§ 9.3. ИНТЕГРАЛ КАК ФУНКЦИЯ ВЕРХНЕГО ПРЕДЕЛА 321
таким образом, мы приходим к определению длины s (L)
дуги L в форме
ь
= \ /1 + [/'(x)]2dx.
а
9.29.	В вычислительном плане сказанное здесь имело бы
малую цену, не слишком отличаясь от тавтологии, если бы
для вычисления интегралов не было никакого иного пути,
кроме прямого определения, данного в 9.13. В действитель-
ности имеются эффективные средства вычисления интегралов,
они излагаются в §§ 9.4 и 9.5.
В § 9.3 производится некоторая предварительная под-
готовка; при этом получаются результаты, важные сами по
себе.
§ 9.3.	Интеграл как функция верхнего предела
9.31.	Пусть f(x) — интегрируемая функция на отрезке
[а, й]. Интеграл
X
F(x)=$f(t)dt,
а
(мы обозначили здесь переменное под знаком интеграла че-
рез t, чтобы не путать его с х, стоящим в верхнем пределе)
является функцией от числа х, которое может принимать
все значения от а до Ь. В силу оценки
|F(x')-F(x")| = J < sup |/(х)|-(х"—х')
х'	xc[a,b]
функция F(х) непрерывна.
Попробуем найти производную от этой функции в ка-
кой-либо точке х —с. В силу свойства 9.18 (2) мы имеем
(C+h	с
£ (c+.^-F (£)=!) J
v а	а
c+h
= И ЛО dt.
С
(1)
322	гл. 9. интеграл римана	[9.32
Полученная величина есть среднее от функции f(x) по от-
резку [с,с + ti\ *).Положим mh= inf f(x),Mh = sup /(x);
xe[c,c+h]	xe[c, c+h]
тогда по неравенству 9.15(7) (см. также 9.18(3)) мы имеем
c+h
с
Если функция f(x) непрерывна справа при х = с, то
при k\0 имеют место соотношения mh-+f(c) и zWA->/(c).
Таким образом, предел выражения (1) существует и равен f(c).
Это означает, что у функции F (х) в точке х — с имеется
правая производная, равная f(c). Аналогично, если f(x)
непрерывна слева при х — с, по тем же причинам при h^Q
выражение (1) имеет предел f(c). В частности, у функции
F (х) в каждой точке х = с (двусторонней) непрерывности
функции f(x) имеется двусторонняя производная, или про-
стопроизводная, равная f (с). При х = а и х = Ь функция F(x),
опять-таки в предположении соответствующей односторон-
ней непрерывности f(x) в этих точках, обладает в них одно-
сторонней производной, левой при х = Ьи правой при х—а,
соответственно равной f(b) и f(a).
9.32.	Вычисление интегралов с помощью
первообразных функций. Пустьу=/(х)— кусочно-
непрерывная функция на отрезке [а,£]. Всякая непрерывная
функция G(x), определенная на отрезке [а, />] и в каждой
точке непрерывности х функции f(x) обладающая произ-
водной, равной f(x), называется первообразной по отношению
к f(x) на [а, £]. Так, например, функция хп есть первооб-
разная по отношению к функции пхп~1. Для любой ку-
сочно-непрерывной функции f(x) мы построили первообраз-
ную в 9.3F.
X
F(x)=\f(t)dt.
а
Вместе с какой-либо первообразной G(x) и всякая функция
G1(x) = G(х) + С также есть первообразная по отношению
к f(x); таким образом, у функции f(x) оказывается беско-
нечное множество первообразных, отличающихся друг от
*) Если/1 <0,полагаем по определению [с, c-|-/i] = {x:c-|-teSx<:c}.
9.32}	§ 9.3. ИНТЕГРАЛ КАК ФУНКЦИЯ ВЕРХНЕГО ПРЕДЕЛА 323
друга на постоянную. И обратно, всякая первообразная
Н(х) от функции f(x) имеет вид G(x)-(-C, где G(x)— какая-
то фиксированная первообразная. Действительно, в каждой
точке непрерывности функции f(x) мы имеем (Н (х)— G(x))' =
= f(x)—f(x) = 0. Поэтому Н(х) — G(x) постоянна на каж-
дом интервале непрерывности f (х) (7.45 в); а так как
Н(х)— G(x) непрерывна на всем [а, ft] вместе с Н(х) и
G(x), то Н(х)— G(x) постоянна на [а, Ь].
Этот факт открывает следующую возможность вычис-
ления интегралов с помощью первообразных функций. До-
пустим, что мы знаем какую-то первообразную О(х) от функ-
ции f(x); тогда любая другая первообразная, и в частности
функция F(x), отличается от G(x) на постоянную, так что
X
F(x)=^f(t)dt=G(x) + C.	(2)
а
Чтобы найти постоянную С, положим х= а; тогда, очевид-
но, F(a)=0, и, следовательно, С——G(a). Полагая в (2)
х=Ьу находим
ь
^f(f)dt—G(b) — G(a).	(3)
а
Таким образом, для вычисления интеграла от (кусочно-
непрерывной) функции f(x) по отрезку [a, ft] следует найти
какую-либо из первообразных G(x) функции f(x) и составить
разность G(b) — G(a).
Формула (3), полученная, по существу, Ньютоном и Лейб-
ницем, является важнейшей формулой анализа, связывающей
дифференциальное исчисление с интегральным.
Совокупность всех первообразных функций называется
та^же неопределенным интегралом от функции f(x) и обо-
значается через
$/(*) dx
(без указания пределов); в противоположность этому интег-
рал 9.13 называется определенным интегралом.
Равенство (3) записывают также в форме
Ь	х=Ь
^f(x)dx = G(x) s
а	х-а
b
G(x) ;
а
324
ГЛ. 9. ИНТЕГРАЛ РИМАНА
[9.33
запись справа указывает, что нужно в функцию G(x) под-
ставить значение х = Ь, затем в эту же функцию подставить
х — а и второе число вычесть из первого.
Рис. 9.6.
Так, например, согласно сказанному,
ь	ь
пхп-1dx — хп — Ьп.
о	о
Этот результат имеет следующий гео-
метрический смысл: площадь, ограничен-
ная дугой АС параболы {п—1)-й степени
= участком АВ оси абсцисс 0^
х Ь и ординатой ВС в точке х — Ь,
равна — -й части площади прямоугольни-
ка ABCD (рис. 9.6).
9.33.	d и J как взаимно обратные операции.
Пусть /(х)— непрерывная функция, определенная на от-
резке [a, ft], и F (х)— ее неопределенный интеграл, так что
F' (х) =/(х). Рассмотрим выражения d^f(x) и ^dF(x).
По определению неопределенного интеграла
d ^f(x)dx = d[F(x) + С] = F' (х) dx —f(x) dx.
Таким образом, в комбинации d знак d сокращается со
знаком J. С другой стороны, по определению дифференци-
ала и неопределенного интеграла
J dF(x) = J F’ (x)dx = F(x) + C.
Таким образом, в комбинации d знак J сокращается
со знаком d, но при этом следует в правую часть добавить
постоянную.
9.34.	Общие правила неопределенного ин-
тегрирования. Применяя знак \ к известным правилам
9.37]	§ 9.3. ИНТЕГРАЛ КАК ФУНКЦИЯ ВЕРХНЕГО ПРЕДЕЛА 325
дифференцирования 7.33—7.34 и используя результат 9.33,
мы можем получить, соответствующие правила неопределен-
ного интегрирования. Имеются в виду следующие правила
дифференцирования:
d(ku) = kdu	(k— постоянная);	(1)
d (и + -и) — du -j- dv;	(2)
d(uv) ~udv-\-v du.	(3)
Если u — u(t), то
dF(и) = F' (и) du = F' (и) и' (t) dt	(4)
(дифференцирование сложной, функции).
9.35.	Применяя знак J к равенству 9.34 (1) и переписы-
вая результат справа налево, находим при k0:
kdu = J d (ku) — kuС = k (иCt) = du (1)
(«постоянный множитель можно выносить за знак неопреде-
ленного интеграла»).
9.36.	Применяя знак J к равенству 9.34 (2), получаем
^(du-\-dv) = J d (в+ !>) = «	J + J (1)
(«неопределенный интеграл суммы равен сумме неопределен-
ных интегралов»).
9.37.	Применяя знак J к 9.34(3) и используя 9.36(1),
получаем
J (и dv + v du) = udv-\- J vdu= d (uv) = и • v -|- C.
Записанное в форме (С включена во второй интеграл).
\iudv=uv—yvdu,	(1)
это равенство называется формулой интегрирования по час-
тям. Оно позволяет найти \ и dv, если известен \ v du.
326
ГЛ. 9. ИНТЕГРАЛ РИМАНА
[9.38
9.38.	Формулу 9.34 (4) мы используем следующим обра-
зом. Пусть и = и (t) — функция с непрерывной производной,
определенная на отрезке	и принимающая значения
в отрезке А и В', пусть, далее /(и) — непрерывная функ-
ция, определенная при Л^и^В. Рассмотрим два неопре-
деленных интеграла
F(e)= J/(e)de и G(t) = §f(u (t)) и' (t) dt.
Первый есть функция от и, определенная на отрезке [Л, В],
второй—функция от t, определенная на отрезке [а, 0]. По-
кажем, что приа^/^p справедливо равенство
Г [и (t)]~G(t) + C.
(1)
Для этого достаточно показать, что совпадают дифферен-
циалы правой и левой частей. По формуле 9.34 (4) мы имеем
dF [и (/)] = F' (и) и' (/) dt=f(u (/)) и' (t) dt,
а по определению неопределенного интеграла
dG(t)=f(u (/)) и' (/) dt.
Отсюда вытекает равенство (1). Оно позволяет сформу-
лировать правило интегрирования через подстановку: в не-
определенном интеграле / (и) du можно заменить и на функ-
цию от t, причем du заменяется на и' (/) dt, согласно пра-
вилу преобразования дифференциалов. Иными словами, свой-
ство инвариантности дифференциала распространяется и на
дифференциалы, стоящие под знаком неопределенного интег-
рала.
В дальнейшем мы увидим, как работают все эти правила,
на многочисленных примерах.
9.39.	В заключение этого параграфа мы докажем одно
простое, но важное предложение, обратное по отношению
к теореме 9.31.
Функция F(x) называется кусочно-гладкой на отрезке
[п, &], если она непрерывна на [а, и всюду, кроме конеч-
ного числа точек, имеет производную, которая является ку-
сочно-непрерывной функцией на отрезке [а, &].
9.41J § 9.4. ТЕХНИКА НЕОПРЕДЕЛЕННОГО ИНТЕГРИРОВАНИЯ 327
В 9.31 мы фактически установили, чго для кусочно-непре-
рывной функции f(x) ее интеграл
F(x) = \f(t)dt
а
является кусочно-гладкой функцией. Обратно, пусть имеется
кусочно-гладкая функция G (х) и f(x)— ее кусочно-непрерыв-
ная производная. Так как G(x) есть первообразная для f(x)
(9.32), то справедливо равенство 9.32 (2)
G(x)= J/(Z) d/ + O(O).
а
Таким образом, всякая кусочно-гладкая функция G(x) с
точностью до постоянного слагаемого есть интеграл от неко-
торой кусочно-непрерывной функции с верхним пределом х.
§ 9.4.	Техника неопределенного интегрирования
9.41.	Интегрирование многочленов.
а.	Применяя знак J к формуле
d (хп) = nxn~ldx (л=1, 2, ...),
получаем после замены п—1 на m и деления на п = т-}-\
1
xmdx = --—rТ + С	(т=0, 1, 2, ...),
m_|_l	।	\	>	>	1	'>
где С—произвольная постоянная.
Отсюда по правилам 9.35—9.36 для любого многочлена
Р (х) = а0 4- агх 4- ... 4- апхп мы находим, что
Sy-2	Y^ 1
P(x)dx = aox4-fl1-§-4- ... 4-си_^4-с.	(1)
б.	В некоторых случаях экономнее пользоваться другими
правилами. Например, для вычисления интеграла
J х (х24- 1)500 dx
нецелесообразно развертывать бином (,х24- 1)500 по формуле
Ньютона и применять затем общую формулу (1); лучше
328
ГЛ. 9. ИНТЕГРАЛ РИМАНА
[9.42
ввести подстановку и = х24-1 и воспользоваться правилом
9.38, которое приводит к немедленному вычислению:
f х (х2 + 1 )Б0° dx = f и 500 ±du = • -Ст + с =
J	Z	Z О v 1
~nw(*4-')-+c.
В случае интеграла
Jx3 (х2+ 1)600 dx
уместно применить правило интегрирования по частям 9.37,
полагая «=х2, dv = х (ха + 1)Б0°dx; тогда, согласно преды-
дущему примеру, "1(^2’(х2+1)501> du= 2х dx и, следова-
тельно,
У Xs (х2+ 1)Б0° dx = uv — §vdu=
__ х* / „г I i \бо1____f (xa~bl)501-2xdx______
1002 ' i" б. 7 J 1002	~
_ x2 (X2 + 1 )s°i	(x2 +1 )Б02 . r
~	1002	1002-502
9.42.	Интегрирование рациональных функ-
П /дЛ
ций. Требуется проинтегрировать функцию ~	>
где 7?(х) и Q(x) — многочлены с вещественными коэффи-
циентами.
а. Если степень числителя больше или равна степени
знаменателя, то, произведя деление, можно преобразовать
/(х) к виду
/(х) = Р(х)+^,
где степень S (х) уже меньше степени Q(x). Как интегри-
ровать многочлен Р(х), мы уже знаем {9.41), поэтому огра-
„ X 8 (х)
ничимся правильной дробью .
б. Пусть х15 х2, ..., xk — вещественные корни много-
члена <2(х), zv zlt ..., zm, zm—комплексные невеществен-
ные корни (вместе с каждым корнем z — а-|-/р по 5.89 а
9.42] § 9.4. техника неопределенного интегрирования 329
комплексно сопряженная величина z = a—/0
ется корнем той же кратности).
S (х)
В силу 5.89 в рациональная функция
также
может
явля-
быть
разложена на простейшие рациональные функции (простей-
шие дроби):
S (х) _ Ац .	Л12			 A2i .
Q (х) ~ х—хх (х—хх)2 '	(х—Xi)r* х—Хг '
Дц+СцХ .	, _£1£1+_£1у/_ ]
*	(х-а^ + Р?	’ ‘ ‘	[(X-«1)2 + Р?]’*
I	I । Bmqm тдт %
(х-аи)2 + ₽т	’ ’ ’	((х-ага)2 + Р^1’“ ’
и вопрос сводится к интегрированию простейших дробей.
в.	Интеграл
f dx
J (х-х^Р
при р =# 1 можно найти из равенства
d (х—Xjp-P — (1 — р) (x — Xj}~p dx:
интегрируя обе его части, мы получаем
+С = (.-,)(L^- + С- <”
г.	При/9=1 следует воспользоваться равенством 7./7 (5),
которое после умножения на dx д.ае.ч
d (In I х — х,|) = —х- ;
отсюда
f 7—=ln I	(2)
Заметим, что формулы (1), (2) имеют место в проме-
жутке [а, &], не содержащем точки (иначе подынтеграль-
ная функция не будет кусочно-непрерывной и нельзя дей-
ствовать по 9.32).
д. Интеграл
С Ах+В______dx
J [(х-а)2 + р2]“аХ
330
ГЛ. 9. ИНТЕГРАЛ РИМАНА
[9.42
подстановкой х — a=fiu приводится к более простому виду:
Cu4-D
(u2+ 1)“
du.
Если здесь D — 0, то подстановкой и2 + 1=Ф интеграл
вычисляется до конца:
Р Cw du __С Р dv___
J (u2 + l)m — Т J Vй "
С 1 С _______	С	I С wz *"> 1 •
_ 2(l-m)»“-1T 1“2(l-m)(u2-H)l'-1 + 4, т
^-ln|i/; + C1 = yln(M24-l) + C1,	т=\.
е. Остается рассмотреть интеграл
~ J (иа + 1)“ 
Если т = 1, то
С du
\ arc tg и,
J и2+1	& ’
как вытекает из формулы дифференцирования 7.18 е. Пусть
/и > 1. Применим к (3) формулу интегрирования по частям,
1	.	,	2ти du ..
полагая	== "У, так чт0 = ~~ (u2+i)«+i- Мы получим
. С du _______ и , „ С и-и du
!т — j („2 _[_])« — (и2_[_ 1)»> +J («a + l^+i -
_ и	, 9 I С (и2+1) du Р du 1 _
— (i/2+l)“ 1	(J(u2+l)«+l J(«2+l),/! + 1J
(U2| 1)*» +	^rn + T^i
откуда
.	_ 1 и	.2m—1 .
•m+1 -	(Ц2_|_ 1)« H 2m ‘m'
Эта формула выражает /m+1 через Im и рациональную функ-
цию. Используя ее для т=\, находим значение /2 =
= J(i?W=TG^w+^arctg" + c- Полагая w=2, на‘
ходим значение /3, и т. д.
В итоге каждая рациональная функция обладает неопре-
деленным. интегралом, выражающимся через рациональные
функции, логарифмы и арктангенсы..
9.43]	§ 9.4. ТЕХНИКА НЕОПРЕДЕЛЕННОГО ИНТЕГРИРОВАНИЯ 331
На практике для определенного интегрирования рацио-
нальных функций имеется много вспомогательных приемов,
которые мы не излагаем*).
9.43. Интегралы, приводящиеся к интегра-
лам от рациональных функций. Интегралы некото-
рых типов приводятся к интегралам от рациональных функций
(или, как говорят, рационализируются) с помощью некото-
рых стандартных подстановок. В дальнейшем /? означает
рациональную функцию от одного или двух аргументов.
а.	Интеграл
У R (ех) dx
рационализируется подстановкой ех — и, х = 1пи, dx =	.
б.	Интеграл
J R (tg х) dx
рационализируется подстановкой tgx = «, х —arctgn, dx —
=	• Рациональными от tgx, в частности, являются
функции
cos2х = , , ! „ ; sin2x=l—cos2x; cos2x = cos2x—sin2x;
1 + tg2 X
sin 2x = 2 sin x cos x = 2 tg x cos2 x.
Поэтому интеграл
f R (sin 2x, cos 2x) dx
также рационализируется подстановкой tgx = K.
Заметим, что функции sin х, cos х уже не являются
рациональными функциями от tgx (например, потому, что
tg х имеет период л, a sin х и cos х имеют период 2л).
Но они являются рациональными функциями от «=tg-^- :
2tg|	l-tg2y
sin х=--------; cos х =-------
i+tg2<	i+tg^
*) См., например, Г. М. Фихтенгольц, Курс дифференциального
и интегрального исчисления, т. 2, «Наука», 1967.
332
ГЛ. 9. ИНТЕГРАЛ РИМАНА
(9.44
а так как при этом dx
2 du
j-q~2 , то интеграл
j 7?(sin х, cosx)dx
X
рационализируется подстановкой tg-g- = «.
9.44. Интегралы от иррациональных выраже-
ний. Рассмотрим интеграл
У/?(х, j)dx,	(1)
где у есть некоторая функция от х. Если х и у можно
одновременно представить рациональными функциями от
нового переменного t, так что х = х(7)> J=J(O» т0 инте-
грал (1) очевидным образом рационализируется:
j 7? (х, у) dx — j R {х (Г), у (/)) х' (/) dt.
а. Пусть, например, у = У ах -f- b; тогда рационализирую-
щую подстановку можно взять в форме ах -|- b = /2, х =
= |('2-*), y=t-
Jt?(x, Vах + b)dx = ^R (72 — b),
t: г>	t/ox-l-b
б. В случае _у=
действует тот же прием:
ах 4-6
сх 4~ d
= t2, y=t,
t2d—b
a—ct2 ’
х
в.	Но квадратичная иррациональность y = l' ax2 4- bx 4- c
уже не рационализируется подстановкой ах2 4- bx 4- с = 7s,
так как при этом х не является рациональной функцией от
t. Здесь будем поступать иначе. Выделяя под корнем пол-
ный квадрат (х—а)2 и заменяя (х —а) на при надле-
жаще подобранном Р, приводим квадратный корень к одному
из трех видов:
У1 = У1 —и2-, у2 = И + и2; _уа = j/и2 — 1.
г.	В первом случае подстановка и = sin ф (или cos ф = и)
приводит интеграл (1) к уже рассмотренному виду (9.43)
R(u, ]/1 — u2)du= I 7? (sin ф, cosф) cosф dtp.
9.44] § 9.4. ТЕХНИКА НЕОПРЕДЕЛЁННОГО интегрирования 333
Примеры:
С du С cos <в dtp Р ,	.	, у-,	,п.
I   — = \ ——- = \ da> — <р — arc sin и 4- С	(2)
J cos<p J т т
(подстановка и = sin ср);
P_d»---= PsinOde fde = e = arccosa + C*)	(3)
J i<l—u2 J — sine J
(подстановка a = cosip).
Различие результатов, полученных разными подстанов-
ками, не должно нас смущать: согласно общей теории, ре-
зультаты могут отличаться на постоянную, и, действительно,
имеется формула 5.67 (1)
arc cos и у = arc sin и.
д.	В случае у2 = V1 + и'
перболическая подстановка
a = sh6,1 +«2= 1 4-sh2,6=
— ch2 6, так что
$7? (а, ]/1+«2) du =
= J R (sh 6, ch 6) ch 6 d&.
Пример:
P du _____Pch0d0___
J 1^1 +a2 J ch 6 ~
— J dG = 6 = ar sh и -f- C (4)
аналогичную роль играет ги-
Рис. 9.7.
(подстановка a = sh8).
Функция arsha (рис. 9.7) есть обратная функция по
отношению к sh0. (В 9.61 ж мы увидим, каков ее геомет-
*) Область определения функции cos 0 в данном случае—отрезок
[—л, 0]. Мы имеем +V1—и2 =—sinO и используем обратную воз-
растающую функцию arc cosB и (5.67). С обратной убывающей функ-
цией arc coSy и была бы получена формула
Р du	, „
I ------= —arc cosv а 4-С.
J^l—ua	y
334
ГЛ. 9. ИНТЕГРАЛ РИМАНА
[9.44
рический смысл, в частности, почему принято обозначение
ar; area означает по-латыни «площадь».) Эту функцию можно
записать и через известные нам функции, разрешив относи-
тельно 0 уравнение
е6—е-6	1
и = sh 0 = —2— = —
ев —-
е'
Мы имеем при этом е9=	-\-и2 (так как е6 > 0, то
знак минус нужно отбросить), откуда
0 = ar sh и = In (и 4- ]/1 + и2)-
е. Наконец, в случае у3 = )/и2—1 пригодна гиперболи-
ческая подстановка и = ch 0, и2 — 1 = ch2 0—1 = sh 2 0, так что
7? («, J/и2 — 1) du = J 7? (ch 0, sh 0) sh 0 dO.
Пример:
du Р sh 0 d0 p	. r~,
-t== \ —7-5-= \ d0 = 0 = archtz + C (5)
J she J	v '
(подстановка u = ch0).
Функция ar ch и (рис. 9.8) есть обратная функция по
отношению к ch0. Аналогично предыдущему, ее можно
получить, разрешив относитель-
но 0 уравнение
« = ch6 = ^ =
При этом е® = и	и2 — 1 (г0"
дятся оба знака), откуда
0=ar ch «=1п(и±)Ли2— 1).
Г рафики функций и= ar sh 0,
zz = arch0 получаются обычным путем, т. е. отражением гра-
фиков функций « = sh 0 и и = ch 0 относительно биссектрисы
координатного угла (5.39). Они подтверждают однозначность
функции ar sh 0 и двузначность функции ar ch 0.
9-45] § 9.4. техника неопределенного интегрирования 335
9.45.	Эллиптические интегралы. В том случае,
когда многочлен Р(х) имеет степень п > 2, интеграл
J R(x, УР(х))ах,	(1)
вообще говоря, не выражается через элементарные функ-
ции*) (теорема Абеля — Лиувилля; доказательство можно
найти в статье Н. Г. Чеботарева, УМН 2, № 2 (1947),
или в т. 1 Собрания сочинений Н. Г. Чеботарева,
изд-во АН СССР, 1950). При л = 3 и л = 4 интеграл (1)
называется эллиптическим, при п > 4 — гиперэллиптическим.
Имеются два важнейших эллиптических интеграла (1-я и
2-я нормальные формы Лежандра):
sin ф	ф	'
F (k, <р)^ f dt — = f  dQ ,
о /(1-Р)(1-^)(<=«1пе>^ 1-fe2sin2e
sin ф_______ ф
E(k, Ф) = J у dt = JKl- A2sin2ede,
0	(Z = sin6) 0	}
1.
При A=0 оба интеграла дают одну и ту же функцию:
<р	<р
F(0, ф) = d6 = (p,	Е(0, ф) = d6 = cp.
о	о
При А=1 оба интеграла выражаются через элементарные
функции
sin <р
Г(1,ф)= С "	1„>+<1*’=1 1„1+$И;
J l—t2 2	1—и о 2	1— sinф’
о
9Шф
u.	Р	] sin®
£(1, Ф)= \ dt—ti = sinф.
о
Функции F(k, ф) и E(k, ф) табулированы; таблицы этих
функций имеют два входа (для значения переменного ф и
*) То есть те, которые получаются из аргумента х и веществен-
ных параметров применением конечного числа алгебраических опера-
ций (сложение, вычитание, умножение, деление), логарифмирования,
потенцирования, взятия тригонометрических и им обратных функций.
336
ГЛ. 9. ИНТЕГРАЛ РИМАНА
[9.45
параметра k = sin а). Краткая таблица значений этих функ-
ций приводится ниже:
\ a Ф \	E(k, ф)					F(ft, <p>			
	90°	60°	45°	30°	0°	30°	45°	60°	90°
0°	0	0	0	0	0	0	0	0	0
30°	0,50	0,51	0,51	0,52	0,52=4 О	0,53	0,54	0,54	0,55
45°	0,71	0,73	0,75	0,77	0,78 = 4 4	0,80	0,82	0,85	0,88
60°	0,87	0,92	0,96	1,01	1,05 = 4 О	1,09	1,14	1,21	1,32
90°	1	1.21	1,35	1,48	l.S7=|	1,69	1,85	2,16	
График на рис. 9.9 дает представление о ходе измене-
ния функций F(k, <р) и E(k, <р) при разных значениях k.
Эллиптические функции появляются при вычислении дли-
ны дуги эллипса (9.63 в) откуда и возникло их название. Они
Рис. 9.9.
применяются во многих задачах анализа и изучены в настоящее
время не менее, чем круговые (тригонометрические) функции.
Можно показать, что общий эллиптический интеграл
f R(x, Уaxi-\-bx3 + cx2-\-ex+f)dx
9.46]	§ 9.4. ТЕХНИКА НЕОПРЕДЕЛЕННОГО ИНТЕГРИРОВАНИЯ 337
приводится элементарными преобразованиями к 1-й и 2-й
нормальным формам Лежандра, к элементарным функциям
и, возможно, к «нормальной форме 3-го рода» с двумя пара-
метрами h и k:
С___________________________
J (1 -|-/i sin2 <р) V1 —fe2 sin2 ip
(см. цитированный выше курс Г. М. Фихтенгольца,
т. 2, гл. I).
9.46.	Другие типы часто встречающихся ин-
тегралов.
а.	Пусть Р(х)— многочлен. Интеграл
J /э(х) ех dx
равен линейной комбинации интегралов вида
Im= хтех dx.
Интеграл 1т путем интегрирования по частям (и—хт,
exdx = dv; du = mxm~l dx, v=ex) приводится к виду
Im = еххт — т J xm~lex dx = exxm—rnlm_1
и, так как /0= ^exdx = e*-]-C, допускает полное вычисление
в элементарных функциях.
б.	Аналогично допускают полное вычисление интегралы
J Р (х) In х dx, J Р (х) cos х dx, Р(х) sin xdx.
в.	Напротив, не могут быть выражены через элементар-
ные функции интегралы
С вх	Р du
\—dx = I,— (интегральный логарифм);
J х (ех=и) J ш и
С sin х ,	.	„	,
\ —— dx	(интегральный синус);
J -°s х dx	(интегральный косинус).
Доказательства последних утверждений имеются в книге:
Г. Харди, Интегрирование элементарных функций, М., 1935,
338
ГЛ. 9. ИНТЕГРАЛ РИМАНА
[9.51
§ 9.5.	Вычисление определенных интегралов
9.51.	Интегрирование по частям для опреде-
ленных интегралов.
а.	Пусть и и v—кусочно-гладкие функции. Так как
uv есть первообразная для своей производной uv'-\-vu',
то по формуле Ньютона — Лейбница 9.32 (2)
ь	ь
J {uv'+vu')dxs^ J (и di)v du) — uv
а	а
Иначе можно написать
Эта формула дает правило интегрирования по частям для
определенного интеграла.
Л,2
б.	Пример. Вычислим интеграл Im= sin'® х dx. Интегрируя
о
по частям, находим
И/2
J sin"1-1
о
xd(— cos х) =
= — sin'"-1 cosx
Я/2	п/2
+ («— О j
О	О
sin7”-2 x-cos2 xdx.
Внеиитегральный член в результате двойной подстановки обращается
в нуль; поэтому мы получаем
л/2
7т = (т —1) sinw~2 х(1 — sin2х)dx = (m — 1) /лл_2—(т—1)/т,
о
откуда
л/2
С Л
Так как /0 = 1 dx^-y, то при четном т = 2п
о
Л/2
, С - j — 1 2п—3	3	1 л	(2п—1)1! я
/2„=Jsin xdx = 2п  2п_2---4 • у • -J--	2. (1)
о
9-52]	§ 9.5. ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ 339
П/2
Так как /j= finxdx=l, то при нечетном т = 2п+1
о
Л/2
, С • » . .	2«	2/1—2	4 2 ,	(2«)П
1гч+1- J sin »+ xdx-2n+1 • 2п_f'' 3 " j '	(2n-f-l)!!' W
о
9.52.	а. Формула Тейлора с остаточным чле-
ном в интегральной форме. Рассмотрим вначале
интеграл
ь
^/(х) (Ь — х)п dx.
а
Считая функцию f{x) кусочно-гладкой, применим интегри-
рование по частям:
ь	ь	ь
р(х) (ь-x)» dx=-f(X)
a	a a
b
Используя равенство (1) для функции /(х), имеющей на
отрезке [а, Л] непрерывные производные до порядка п и
кусочно-непрерывную производную /1п+1) (х), последователь-
по получаем
ъ
f(b)-f(a) = $ f (х) dx = /' (a) (b-a) +
a
b
+ J/"(X) (fe-x) dx=/' (a) (b—a) + y/"(a) (b —a)2 +
a
b
+ 4 J f" M (b-x^dx = ... =/' (a) (&-a) +
a
+ 4/" {a)(b-a)2 + ... + ±/<«>(a)(fc_a)n +
b
+ -^-^r'!+1>(x)(b-x)'!dx.
a
340	ГЛ. 9. ИНТЕГРАЛ РИМАНА	(9-52
Отсюда получается формула Тейлора
f(b)=f(a) +f (a) (b—a) +	(Ь-а? + ...
где
Rn = -^fin+1>(x)(b-x)"dx	(3)
а
есть остаточный член в интегральной форме Коши.
б.	Из неравенств
ь
max/<п+ п (х)• J (Ь — х)п dx —
^(-^ТпГтах/<п+^>(х)’
7?„^-^-min /<п+1>(х)- J (Ь—х)п dx=>
можно получить и лагранжеву форму остаточного члена
(8.23 (2))
^ = ^RF/<n+1>(c)
в предположении, что функция /<п+1>(х) непрерывна и, сле-
довательно (5.23), любое промежуточное значение между
минимальным и максимальным принимается ею в некоторой
промежуточной точке с.
в.	В качестве приложения рассмотрим для функции
/(х) = (1+х)“	(4)
вопрос об области сходимости к ней ее ряда Тейлора (8.51).
В этом случае формула Тейлора (2) имеет вид (при а = 0,
Ь = х)
(1 +*)“= 1 +«х + ^=^х2+ ... +	-(«-»++
+ {Х'{Х~1«1 (0С~П) S+0а_"-1 (х—f)" di.
9-52]	§ 9.5. ВЫЧИСЛЕНИЕ ОПРЕДЕЛЁННЫХ ИНТЕГРАЛОВ 341
При | х | < 1 и t между 0 и х
2
X ’
1
t
X
— < 1—л
X
Поскольку х и х—t одного знака,
<1— t
X
и, следовательно,
Поэтому
f(x-Q"
J (1 + 0"
о
(1 +t)a-1dt
О
где С=С(х,а). Отсюда
Обозначим величину справа через а>п. Мы имеем
поэтому, если | х | < 1, величины (оп стремятся к 0. Таким
образом, остаточный член (3) стремится к 0 при | х | < 1.
Следовательно, для — 1 < х < 1 имеет место разложение
(1 +х)‘= 1 + ах +с^-^>х*+  • •
g(g— I) ... g(a—п + 1) х„
(5)
Если а отлично от натурального числа (когда справа—много-
член), то ряд справа расходится при |х | > 1 и достаточно
больших п (отношение последующего члена к предыдущему
больше 1), поэтому радиус сходимости ряда (5) равен 1.
Заменяя в (5) вещественное переменное х на комплекс-
ное z = x-^iy, получаем аналитическое продолжение функ-
ции (4) в круг |z| < 1:
(I +z)-= 1 +»Z	.
-+--~+г+7'‘Ч:1> г"+-- <6>
342
ГЛ. 9. ИНТЕГРАЛ РИМАНА
19.53
Например, для а — — 1 получается известная уже фор-
мула суммирования убывающей геометрической прогрессии
(6.11 б):
1 “Г 4
г.	Ряд (6) можно записать в форме
(1 +z)“= 1 +(-а) (-z) + (~ ^(*~a)(-z)2+ ... +
(—<х) (1 —а) ... (n-1—a)
"+	1-2 ... n ' Z'
Применяя результаты 6.66 б, получаем: если 1>—a4-1,
т. е. a> 0, ряд (6) сходится при —z = 1, т. е. при д = — 1.
В силу 6.67 мы получаем интересное равенство
1 „ a(a~!)2)
1-2	1-2-3
= 0;
(7)
по доказанному, оно справедливо при всех a > 0.
Если 1>—а, т. е. а>—1, ряд (6) сходится при
— z =— 1, т. е. при z=\\ в этом случае 6.67 приводит
к равенству
11	।	।a<a-(«-ад.
при a > — 1.
справедливому
Равенства (7) и (8) обобщают на нецелые показатели
известные свойства чисел	ПРИ натуральных
Аил:
С* 4-С1п4-С£+---4-С£
= 2"
с°-СА4-0>----+(-1)«с« = о.
9.53.	Для а > b остается справедливой формула Нью-
тона— Лейбница 9.32 (2):
а
f (х) dx = F(a)—F(b)	(F'(x)=f(x)).
ь
9.54]	§ 9.5. вычисление определенных интегралов 343
Действительно, по 9.18 мы имеем
а	b
J/(x) dx = — J /(х) dx = — [В (b)—В (в)] = F(a) —F(b).
b	a
9.54.	Интегрирование при помощи подста-
новки в определенных интегралах. Предположим,
ь
что нам задан интеграл ^f(u)du, где /(в)—функция, не-
а
прерывная в отрезке [а, &]. Пусть u(t)—функция, опре-
деленная в некотором отрезке [а, Р], обладающая на нем
непрерывной производной, причем и (а) —а, и($) = Ь. Фор-
мальная замена переменной и = и (t) приводит к равенству *)
ь	6
$ f(u)du = $ f[u(t)]u'(t)dt.	(1)
и—a	t—a
Спрашивается, при каких условиях это равенство действи-
тельно имеет место. Естественной предпосылкой является
возрастание функции u(t) на отрезке [а, Р]. Но, оказы-
вается, формула (1) справедлива и в более общем случае,
когда функция u(t) не является монотонной и даже когда
значения функции и (t) выходят за пределы отрезка [а, &],
в котором определена функция /(в), лишь бы только функ-
ция /(в) допускала непрерывное продолжение на тот более
широкий отрезок [Д, В] о [а, &], в котором принимает свои
значения функция в(/) при [а, Р]. Именно, имеет место
следующая теорема:
Теорема. Если функция u(t) на отрезке [а, Р] при-
нимает значения в отрезке [Д, В] ZD [а, Л] и имеет на [а, Р]
непрерывную производную, а функция f(u) непрерывна на
[Д, В], то формула (1) справедлива.
Доказательство. Пусть В (в) есть первообразная
для функции / (в) на отрезке [Д, В] и функция G(t) — перво-
образная для функции f(u(t))u' (/) на отрезке [а, Р]. По
9.38 имеет место равенство
 F(a(0)=G(0+C.
*) Поэтому-то Лейбниц и предостерегал от отбрасывания dx в обо-
значении интеграла (см. сноску на стр. 302). Вероятно, «трансфигу-
рация» по Лейбницу н означает переход от f(u) к f (и (t)).
344
ГЛ. 9. ИНТЕГРАЛ РИМАНА
[9.55
Поэтому
h
J/(a)d« = F(&)-F(a) = F(B(P))-F(B(a)) = G(P)-G(a)=
а
₽
=!/(«(/))«' (t) dt,
a
и теорема доказана. Равенство (1) выражает правило при-
менения подстановки в определенном интеграле; подчеркнем,
что вместе с заменой функции под знаком интеграла изме-
няются соответственно и пределы интеграла. Так как фор-
мула Ньютона — Лейбница справедлива и при а (9.53),
то случай а>р не исключен, и, применяя правило подста-
новки, мы можем не интересоваться, в естественном ли
порядке стоят пределы интеграла до и после подстановки.
9.55.	Простейшие следствия и примеры.
а.	Интеграл от «сдвинутой» функции. Пусть
f(x) определена на отрезке [а, &]; тогда «сдвинутая» функ-
ция f(x—h) определена на отрезке b-\-h\ и имеет
место равенство
64-л	ь
j f(x—h)dx = f(x) dx.
aj-h	a
Для доказательства достаточно применить подстановку
х — h= и.
б.	Покажем, что интеграл от периодической *) функции
f (и) имеет одно и то же значение на любом промежутке
длины Т периода функции f(u). Действительно, найдем
число шТ (т—целое) между а и а 4- Т; запишем
а+Т	тТ	а+Т
§ f(u)du = J f(u)du+ f(u) du;
a	a	mT
в первом из интегралов произведем подстановку и —
— (ш—\)T=t, а во втором — подстановку и — mT—t; так
*) То есть удовлетворяющей соотношению f (х-\-Т) = f (х)
(ср. 5.65).
9.55]	§ 9.5. вычисление определенных интегралов 345
как в силу периодичности f(u) мы имеем
+	то
а+Т	Т	a-(m-l)T	Т
J /(K)d«= J /(0^ + J f(t)dt=\f(i)dt;
a	a-(m-1) Т	О	О
что и требуется.
в.	Пример. Покажем, что при любом у>0 и любом
натуральном k имеет место равенство
я	л
sin2TAxdx = J cosPkxdx.	(1)
-л	-л
Для доказательства, используя равенство sina = cos^— aj
и затем подстановку —kx = ku, находим, что
л ,
Л	Л
f sin2rkxdx= cos2T —kx] dx — f cos^udu;
J	J	\ z	J	J
-л	-л	л _
~2k~n
применяя предложение б, получаем (1), что и тре-
буется.
Для 2у, равного целому числу т, значение интеграла (1)
было найдено в 9.51 б. Для -у= 1 сразу получаем из
равенства
л	л
J (sin2 kx 4- cos2 kx) dx = J l-dx = 2n
-Л	- Л
значение интегралов
Л	л
У sin2kxdx= J cos2fexdx = n.
-л	-л
г. Интеграл от «отраженной» функции. Имеет
место равенство
ь	ь
f (х) dx — \f(b—x)dx.
о	о
346
ГЛ. 9. ИНТЕГРАЛ РИМАНА
[9.56
Действительно, подстановка и = Ь—х дает
ь	о	ь	ь
J f(b—x)dx =— ^f(u)du = ^f(u)du — ^f(x)dx.
0	6	0	0
9.56.	Мы закончим наши общие рассмотрения одним
важным общим понятием.
Интеграл Стилтьеса. Пусть в промежутке [а, &]
заданы две функции: f(x) и g'(x). Рассмотрим разбиение
П = {а= х0 < ... < х„ = промежутка [a, Z?] с отмеченными
точками	Лу+J; далее, как обычно, положим
d (П) = так (ху+1—ху). Интегральной суммой Стилтьеса на-
зывается число
$п (/, g) = i ftej) [g(XJ+1)—g(Xj)].	(1)
Число I называется интегралом Стилтьеса от функции
f(x) по функции g(x) на отрезке [a-, ft], если для любого
е > 0 найдется такое 6 > 0, что при любом разбиении
П с d (П) < 6 имеет место неравенство | /—5п(/, g) | < е.
Иначе говоря, интеграл Стилтьеса есть предел интег-
ральных сумм (1) при неограниченном измельчении раз-
биения П. Интеграл Стилтьеса обозначается символом
ь
^f(x)dg(x).	(2)
а
Например, всегда справедливо равенство
ь
J dg(x)=g(b)-^g (а),
а
Мы не будем в этой книге заниматься интегралом
Стилтьеса с общих позиций*) и докажем только теорему
существования его в самом простом случае, когда f(x) не-
прерывна на [a, ft], a g(x) обладает на [а, Ь\ непрерывной
производной. В этом случае интеграл Стилтьеса, как мы
увидим, приводится к обычному интегралу.
Если функция g(x) дифференцируема, то ее приращение
на промежутке [ху-, ху+1] можно записать с помощью
*) См. Г. Е. Шилов и Б. Л. Гуревич, Интеграл, мера
и производная, Общая часть, гл. 2, «Наука», М., 1967.
9.56]	§ 9.5. ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ 347
теоремы Лагранжа 7.44:
=	g(Xj} = g'	Cj^(Xj, х/+1).
Поэтому
/2—1	/2—1
2 /(В/ Ag' (х/ = 2 /(£,) g' (9)
i=o	/=о
= 2 f (с/ g' (с/ Ах- + 5 [/(^)—/(с •)] g' (с •) Ах •=
/=0	/=0	7
п—1	/2—1
= 2 f (с7) g' (Cj) \x •+ 2 Ejg' (Cj) &Xj,	(3)
/=0	/=0
где все числа |ey| при достаточно мелком разбиении П не
превосходят заданного е > 0. При этом
п- 1
2 E g’ (с) Ах • < Е  max I g’ (х) | (Ь — а),
j=0	а<х<Ь
так что второе слагаемое справа в (3) стремится к нулю
при неограниченном измельчении разбиения П. Первое сла-
гаемое в(3) есть интегральная сумма для функции f(x)g'(x)
и с измельчением разбиения П стремится к пределу, равному
ь
^f(x)g’(x)dx.	(4)
а
Мы видим, что при указанных предположениях (/(х) непре-
рывна, g(x) имеет непрерывную производную) интеграл
Стилтьеса существует и равен обычному интегралу (4).
Можно получить формулу, аналогичную (4), в предполо-
жении, что /(х) только кусочно-непрерывна (при непрерыв-
ности g’ (х)) или что g' (х) только кусочно-непрерывна (при
непрерывности /(х)). Если функции /(х) и g' (х) одновре-
менно кусочно-непрерывны, то при совпадении точек их раз-
рыва интеграл Стилтьеса перестает существовать.
В общем случае легко получаются следующие свойства
интеграла Стилтьеса, аналогично соответствующим свойст-
348
ГЛ. 9. ИНТЕГРАЛ РИМАНА
[9.61
вам интеграла Римана (а, р— числа):
ь
J [«V1W +«2/2 (*)]<*£(*) =
а
b	ь
= «1$ /1 (*) dg(x) + «2 $ A (*) dg(x);	(5)
а	а
Ь
$ Дх) d [р^ (х) + p2g2 (х)] =
а
b	b
= Pl $ / W dgl (X) + Р2 $ f(x) dg2 (х);	(6)
а	а
Ь	с	Ь
\f(x)dg(x)=\f(x)dg(x)+\f(x)dg(x);	(7)
а	а	с
b	Ь
\f(x) dg(x)=f(x)g(x) I* — ^g(x)df(x),	(8)
о	a
если существуют интегралы в правых частях.
§ 9.6. Приложения интеграла
9.61. Вычисление площадей. Как мы видели
в 9.21, вычисление площадей достаточно простых фигур
на плоскости приводится к вычислению определенных инте-
гралов. Если речь идет о вычислении площади криволинейной
трапеции, ограниченной снизу
отрезком [а, Ь] оси х, свер-
ху— непрерывной кривой у =
= /(х)^>0, с боков — орди-
натами х = а, х = Ь, то эта
площадь выражается интегра-
лом (рис. 9.10)
О»	о	ь
Рис. 9.10.	I=^f(x)dx. (1)
а
Если фигура Ф не является криволинейной трапецией,
но может быть представлена как объединение криволинейных
трапеций без общих внутренних точек, то площадь фигуры
Ф есть сумма площадей этих трапеций. Более общим обра-
зом, площадь любой фигуры, представляющей собой объеди-
9.61]
§ 9.6. ПРИЛОЖЕНИЯ ИНТЕГРАЛА
349
нение простых (жордановых) фигур без общих внутренних
точек, равна сумме площадей этих простых фигур.
Вернемся к определению площади в форме интеграла (1).
Оно действует, если /(х)^0. Если/(х)^С0 (рис. 9.11),
то /^СО и величина / дает площадь, ограниченную участком
Рис. 9.12.
оси, двумя ординатами и кривой, со знаком минус. Если же
f(x) меняет знак в промежутке [а, &], то интеграл / дает
алгебраическую сумму площадей: со знаком плюс—отвечаю-
щих тем участкам оси, где /(х)^0, и со знаком минус:—
отвечающих тем участкам, где /(х)^СО (рис. 9.12).
Примеры.
а. Как следует из 9.32, площадь, ограниченная кривой у=х2
над участком оси 0 < х < Ь, равна -g- от площади соответствующего
прямоугольника (правило Архимеда). Выведем сейчас более общую
формулу Кеплера (из «Стереометрии винных бочек», 1615):
ь
Г*	Г	(а ~b \	"1 Ь~—а
J f (х) dx= р (a)+4f	(b)J —;	(2)
a
эта формула справедлива, если f (х) есть многочлен не выше 3-й сте-
пени (рис. 9.13). Перенося начало координат в среднюю точку отрезка
[а, Ь], можно переписать ее в
форме
с
§ f(x)dx~
— с
=[f(-c)+4f(0) + f(c)]y.
(3)
Заметим теперь, что если формула (3) верна для некоторой функции
f(x), то она верна и для kf(x) при любом k, и если она верна для
некоторых функций f(x)ng (х), то она верна и для функции /' (х)	(х).
350
ГЛ. 9. ИНТЕГРАЛ РИМАНА
(9.61
Это позволяет нам, если мы желаем установить ее справедливость
для функции вида f (х) = A -\-Вх-'гСх2-\-Dx\ проверить ее только
для функций ?л(х)=1, fi(x)=x, /2(х)=х2, f3(x)=xs. Для функции
f0(x)=l она, очевидно, справедлива. Для функций Д(х) и /3(х)
(нечетных) обе части равенства (3) обращаются в 0, так что формула
также справедлива. Наконец, для функции f2(x) формула (3) при-
водится к правилу Архимеда; таким образом, она верна для всех
многочленов степени не выше 3.
б.	Площадь круга х2+_у2^г2. По соображениям
симметрии можно написать (рис. 9.14)
S=4^_ydx = 4^ ]г!— x2dx.
о	о
Полагая х — г cos 0, dx =— г sin 0 dG, находим:
0	п/2	п/2
5- = —4r2 J sin20d0 = 4r2 J sin2© d0 = 4r2 f -~c°s2erf0 =
л/2	0	0
л/2	л/2
= 2ra ( c?0 — 2r2 ? cos 20 dG = nr2—r2 sin 201 "/Z = nr2.
X	X	'o
Таким образом, число л/2, введенное нами ранее как
первый положительный корень функции у — cosx (5.65), по-
лучает интерпретацию как половина площади круга радиуса 1.
в.	Для площади сектора круга х2+_у2^г2, или, в пара-
метрической форме, х = г cos 0, _y = rsin0, ограниченного
лучами 0 = 0О, 0 = 0!, 0 0О < 0Х < у (рис. 9.15), имеет
место представление
S(0o,01) = ^(O, Oj-StO.Oo),
9.61]
§ 9.6. ПРИЛОЖЕНИЯ ИНТЕГРАЛА
351
так что достаточно сосчитать лишь S’ (0, 60) при любом
0О € [о, у! (рис. 9.16). Мы имеем
rcose0	г
S’(О, 0о) = J xtg60dx+ У У г*—x2dx —
О	г cos е0
oCOS °-^ео+гЧ Sin26d6 =
" I и	v)
о
л	00
г2 cos2 0О а д । 9 С 1 —cos 20 ,п
=------2---' ^ео + г J -------2-----rf6==
О
г2 sin 26
4~~~
г2	г2
= у COSa0otg0o + T0o
Таким образом, получаем
5(0О. е1)=у(е1-0о).
(4)
Эта же формула, как нетрудно проверить, справедлива для
любого сектора с раствором О^0Х—0О < 2л.
г.	При растяжении вдоль оси у в k раз площадь 5 криво-
линейной трапеции (рис. 9.17) увеличивается в k раз. Это
вытекает из равенства
ь	ь
Sk= kf(x) dx = k^f(x) dx
а	а
(если не вспоминать общих сообра-
жений 9.27).
Рис. 9.17.
д. При растяжении вдоль оси х в k раз площадь S’ криво-
линейной трапеции (рис. 9.18) увеличивается в k раз. Для
352
ГЛ. 9. ИНТЕГРАЛ РИМАНА
[9.61
__	Х^ tfi
е. П л ощ а д ь э л л и п с а. Эллипс= 1 получается
из круга х2ф-у2 = 1 растяжением в а раз по оси х и в b раз
по оси у (рис. 9.19). Так как площадь круга радиуса 1
равна it, то, применяя результаты примеров г и д, находим
•^эллипса = ЛаЬ.
Рис. 9.20.
ж. Геометрический смысл обратных гипер-
болических функций. Рассмотрим гиперболу х2 —у2— 1
и найдем площадь сектора АВС (рис. 9.20). Эта площадь
задается интегралом
X
Г-= J у— 1 du,
1
8.61]
§ 9.6. ПРИЛОЖЕНИЯ ИНТЕГРАЛА
353
который мы вычислим подстановкой и = с11/:
х	arch*
§ У и2 — 1 du = J sh21 di.
1	о
Так как ch 2/=cli2/—[ sh2/ и l=ch2/—sh2/,тоsh2)/ =
отсюда
ar ch*
J C ch 2/— 1
7= J 2
0
Заметим, что sh 2/=2 sh / ch /; поэтому sh 2/=2 Vch2/ — 1 ch /
и, следовательно,
[xVx2 — 1 — ar ch x] =X Vx2 — 1 —У ar chx.
£
2
ar chx
r=o
Первое слагаемое есть площадь треугольника ОВС; таким
образом, у ar chx есть площадь сектора ОАС и, следова-
тельно, 5 = ar ch х есть площадь
сектора ОС'АС (рис. 9.21). Обра-
щая эту формулу, получаем пара-
метрическое представление гипер-
болы
х = ch S’, у = х2 — 1 = sh S.
Собственно, мы уже и раньше от-
мечали, что кривая с параметриче-
ским представлением х = ch /, у = sh /
есть гипербола; но только теперь
мы обнаружили геометрический
смысл параметра /, который оказал-
ся площадью сектора, определен-	рис 921.
ного данной точкой гиперболы.
Это представление полезно сопоставить с параметри-
ческим представлением окружности
х = cos 6, у — sin 0.
Здесь 0 есть полярный угол АОС; но эта же величина
есть и площадь сектора ОС'АС (рис. 9.22). Таким
354
ГЛ. 9. ИНТЕГРАЛ РИМАНА
[9.Щ
образом, и для окружности, и для гиперболы площадь сектора
может быть взята в качестве основного параметра.
3. Неравенство Юнга. Пусть_у=/(х) (0 х < оо) —
возрастающая непрерывная функция, причем /(0) = 0,
f (оо)= оо. Пусть x~g(y) — обратная функция (5.38), которая
в данном случае также непрерывна и возрастает от х = 0
до х = оо. Положим для х > О, у О
F(x)=\f(№,
О
У
о
Утверждается, что для любых х > 0, у > 0 имеет место
неравенство
xy^.F(x) + G(y),	(5)
которое называется неравенством Юнга. Оно очевидно из
геометрических .соображений (рис. 9.23); мы не сомневаемся,
что читатель сможет построить и аналитическое доказа-
тельство. Заметим еще, что неравенство (5) обращается
в равенство лишь при_у=/(х).
Неравенство Юнга служит основой для многих других
неравенств, важных в анализе. Отметим здесь частные случаи:
1
прлагая f (х) = хр~\ g(y) =ур~1, получаем неравенство
ху^-+—	(— + — = 1Y	(6)
z р q	\р q /’	' ‘
9.62]
§ 9.6. ПРИЛОЖЕНИЯ ИНТЕГРАЛА
355
а полагая j = ln(x+l), х — еУ— 1, получаем неравенство
хуг^(х + 1) In (* + 1)~ х-±еУ — у—1.	(7)
Оба неравенства (6) и (7) справедливы для любых х^О,
9.62. Площадь в полярных координатах. Рассмотрим
уравнение кривой в полярных координатах (рис. 9.24) г — г (<р) и вы-
числим площадь сектора ОАВ, ограниченного двумя лучами
Ф = а и ф = Р и дугой линии г = г(ф), заключенной между ними.
Сектор ОАВ есть жорданово множество и в
силу общей теории (9.27) имеет площадь,
которая заключена между площадью любого
жорданова множества, содержащего сектор
ОАВ, и площадью любого жорданова мно-
жества, содержащегося в секторе ОАВ. Пусть
П = {а=<р0«£ф1< ... <<р„ = р}
есть разбиение участка (а, Р] изменения ко-
ординаты ф и, как обычно,
Afe<P = <Pfe+i—<Pfe. mk= min г (ф),
q>fc < ф< фь+1
Мк = max г(ф).
Фк<Ф<Фк+1
Обозначим через Рк точку (<рк, г(<рк)) иа кривой г = г(ф). Нам из-
вестно выражение 9.61 (4) для площадей секторов, ограниченных
лучами 0 = Фтг н 0 = ф6+1 и дугами окружностей радиуса тк и Мк
(рис. 9.25). Используя эти выражения, мы замечаем, что величина S,
которую мы желаем определить, должна удовлетворять неравенствам
п-1	п—1
1	У т1Дфл<5<± У М|ДфЛ.
2	fe=0	*=0
356
ГЛ. 9. ИНТЕГРАЛ РИМАНА
[9.63
Но если функция г —г (ср) непрерывна, то при неограниченном из-
мельчении разбиения П обе суммы справа и слева стремятся
к одному и тому же пределу
у jr2(<p)dq>;
а
таким образом, эта величина и есть площадь фигуры ОАВ.
Пример. Кривая r = asinm<p (при т нечетном) называется
«-лепестковой розой (рис. 9.26). Соотношение
л/т	л
-х- \ a2 sin2 тер dtp = 9— \a2sin2^<ftp
показывает, что площадь одного лепестка «-лепестковой розы равна
(1/«)-й части от площади лепестка «однолепестковой розы» r=a sin <р
(которая, между прочим, есть обычная окружность).
9.63. Длина дуги. Еще в 9.28, определяя длину
дуги как предел длин вписанных ломаных, мы получили для
длины дуги кривой j=/(x) между точками х = а и х = Ь
выражение (в предположении существования интеграла)
ь
£-= $	+ [/' (х)]2 dx.	(1)
а
В общем случае кривую у можно описывать параметри-
ческими уравнениями, задавая текущие координаты точки
кривой как функции от некоторого параметра t. Таким об-
разом, на плоскости мы будем иметь два уравнения: х = х (/),
у=у (0:в трехмерном пространстве—три уравнения: х = х (/),
y=y(t), z = z(t); в л-мерном пространстве будем иметь
л уравнений:
х1 = х1(0, х2 = x2(f),..., х„ = х„(0.	(2)
Будем предполагать, что функции Xj(t) определены на
отрезке а t b и имеют кусочно-непрерывные производные.
В этом случае кривую у будем называть кусочно-гладкой.
Пусть П — {а — i0 < i\ < ... < tp = b} — разбиение от-
резка [«, &]. Каждой точке tt соответствует точка АГ, на
кривой у, имеющая координаты хх (<,-), . ..,x„(<f). Соединяя
точки М( отрезками, получим ломаную AfgAfj ... Мр, длина
9.63]
§ 9.6. ПРИЛОЖЕНИЯ ИНТЕГРАЛА
357
которой может быть найдена по формуле
р-1 Г п
sP= 2 1/ 2 [*/ (^i+i) xj (h)]2-
r i=o г i=i
Здесь мы имеем в силу кусочной гладкости функций Ху(/)
fy+i
Xj (^i+l) XJ (ty = J xl (^)
ti
Запишем этот интеграл в виде х} (f() Д/; + 8,уД/г., где в слу-
чае, когда if есть точка разрыва функции x'f(i), под Ху(/;)
мы понимаем xJ^+O). Отсюда
II xj (^+1) — xj (t.) I — \x'i (ii) I MiI < I e<7I Mt.
В силу неравенства 3.14 (8)
и, далее,
I xj (^i+l) — Xj 12	2 1/ 2 I Xf (tj) I 2 Д/(-
i=0 ' j=l
p — 1 f n
<21/ 2|ef/|«A^. (3)
/=o r /=1
Величина eiy- допускает оценку
I i tlcl	I
le./l= дГ | x'j(ti)]dt C max |x;(/)—xXM-<4)
Сумму справа в (3) разобьем на две части: в первую отне-
сем слагаемые, соответствующие промежуткам непрерывности
всех во вторую—промежуткам, содержащим точки
разрыва хотя бы одной из х,- (/). Так как в промежутках
непрерывности функции x'j(t) равномерно непрерывны, то,
если	есть промежуток непрерывности х}(/), мы
имеем max | X/ (/)—х) (t-) | г^со (d (П)), где © (и)—бесконечно
малая величина вместе с и, a d (П), как обычно, есть max Д/(..
358
ГЛ. 9. ИНТЕГРАЛ РИМАИА
[9.63
Если в промежутке Д/,- функция х/(/) терпит разрыв, то
правая часть в (4) допускает оценку
шах | x'j (/)—x'j (tj) | • Д/(-	M-
где M—некоторая постоянная. В итоге величина справа
в (3) получит оценку
ш(й(П))(&-а)+ЛГ£'Д/,.,
где 2' относится к промежуткам, содержащим точки раз-
рыва хотя бы одной из x'j(t). Так как этих точек фикси-
рованное число, то с измельчением разбиения П сумма 2'
стремится к 0; одновременно стремится к 0 и величина
to (d (П)). С другой стороны, функция
/21У-ю|l 2 * * S
/=1
также кусочно-непрерывна и выражение
l-и / = 1
есть ее интегральная сумма, которая при d (П) —► 0 имеет
предел
\Xj(V>\*dt.
(5)
Теперь из неравенства (3) мы усматриваем, что при d (П) —* О
и величина Lp имеет предел, равный интегралу (5).
Итак, длина дуги кривой (2) между значениями t = a и
t — b, определенная как предел вписанных ломаных, в пред-
положении кусочной гладкости функций Xj(t) существует
и выражается интегралом (5).
При п=2 получается формула (хг = х, х2=у)
ь
S = $ V[*' (0]2 + [У (О]2dt.	(6)
а
Если здесь в качестве параметра t взята координата х, то
мы возвращаемся к формуле (1).
9.63]
§ 9.6. ПРИЛОЖЕНИЯ ИНТЕГРАЛА
359
Примеры.
а.	Длина дуги цепной линии у = ch х между точками
с абсциссами х = 0 и х = Ь (рис. 9.27) равна
ь	ь
s = J /1 —sh2x dx = J chx dx = sh£.
о	о
б.	Длина дуги окружности x — r cos 6, y — r sin 0, огра-
ниченной лучами 0=©! и0=02,	<
<02^2л, согласно (6), равна
es ________________
а = J ]/r2 sin2 0 +r2 cos20 d0 =
= H02-01).
В частности, при 0X = 0, 02 = 2л, получа-
ем, что длина полной окружности радиу-
са г равна 2лг. Таким образом, Число л по-
лучает новую интерпретацию как отно-
шение длины окружности к ее диаметру.
в.	Длина дуги эллипса
х = a cos t, у = b sin t, b~y> а
с	b2 ~~~а2
с эксцентриситетом е = у —-—--------- на участке
т	т
s= J ]/а2 sin2/ + fe2c'os2/d/= Jp^a2 sin2/-|-№(l — sin2/)df=
о	о
т	т
= J У Ь2—(Ь1—a2)sin2/ dt = b^ У1—s2 sin2 / dt—b-E(e, T),
о	о
где Е(е, Т)— эллиптическая функция Лежандра (9.45).
г.	Длина одного витка у — sin х синусоиды также вы-
ражается эллиптическим интегралом
Я/2	П/2
s—	J	+ cos2 х dx = J У 2— sin2xdx =
о	о
Л/2_______________
^У2 у 1—sin2 x-dx = /2‘ffy, -70.
О
360
ГЛ. 9. ИНТЕГРАЛ РИМАНА
[9.63
Впрочем, здесь нет ничего удивительного, так как эллипс,
получаемый косым сечением прямого кругового цилиндра,
становится синусоидой при разворачивании этого цилиндра
на плоскость.
д.	В отличие от площади, при растяжении какой-либо
из осей длина дуги кривой не преобразуется, вообще говоря,
сколько-нибудь простым образом; даже для ломаной линии
при указанном растяжении длина каждого звена умножается
на свой коэффициент, зависящий от угла этого звена с на-
правлением растягиваемой осн.
Однако если растяжение в k раз производится сразу
по всем осям (т. е. мы имеем дело с преобразованием по-
добия), то, очевидно, в k раз увеличивается длина каждого
отрезка, каждой ломаной и, как следствие, длина каждой
кусочно-гладкой дуги.
е.	Пусть s0 обозначает длину хорды у0, соединяющей
точки Л=7И0 и В=Мр кусочно-гладкой кривой у. Так как
в силу неравенства треугольника каждая ломаная М0Мг ... Мр
имеет длину sp^ s0, то и длина s самой кривой у удовлетворя-
ет тому же неравенству
So-
Таким образом,
С другой стороны, если хорду у0 стягивать в точку Мо
так, что точка В стремится к точке А, то отношение
п
имеет пределом 1, если V [х] (а) ]®	0.
9.63]
§ 9.6. ПРИЛОЖЕНИЯ ИНТЕГРАЛА	361
Мы приходим к следующему важному результату:
Длина дуги кусочно-гладкой кривой у есть бесконечно
малая, эквивалентная длине стягивающей ее хорды, когда
соответствующее приращение параметра стремится к 0.
ж.	Дуга как функция параметра и как пара-
метр. Пусть кривая L задана параметрическими уравнениями
=	хп = хп(т:),
где Xj (т) —кусочно-гладкие функции. Длина кривой L от
значения т=адо значения x — t
есть кусочно-гладкая функция от I. Ее производная по t
вие точек разрыва x'j(t)
^'(0=]/2,W(0]2	(п
непрерывна и неотрицательна, так что a (t) не убывает.
Если х'1 (/), ..., х'п (/) нигде вместе не обращаются в нуль
(а в точке разрыва одновременно не обращаются в нуль ве-
личины	и величины xj (f—0)), то на каждом про-
межутке одновременной непрерывности функций (t) можно
применить теорему об обратной функции: в этом случае
существует обратная функция t — t (s), также непрерывная,
возрастающая и обладающая производной, которая, как видно
из формулы 7.16 (2), кусочно-непрерывна вместе с А
тогда и все функции Xj(t) можно представить в виде функ-
ций от а, причем также непрерывных и с кусочно-непрерыв-
ными производными. В частности, если t означает длину дуги,
то из (7) следует, что
(8)
Точки, в которых все функции xj (t) обращаются в нуль,
называются особыми точками-, параметрическое представление
с параметром—дугой, как мы видим, возможно на участках
кривой, не содержащих особых точек.
362
ГЛ. 9. ИНТЕГРАЛ РИМАНА
[9.64
9-64. Площадь поверхности вращения. Дана
кривая /. = {у =/(х) ^>0, х g [a, ft]}. При ее вращении
вокруг оси х образуется поверхность Р, площадь которой мы
желаем определить (рис. 9.28).
Пусть сначала функция
f(x) линейна, /(х)== kx +
тогда поверхность Р называет-
ся конусом, (рис. 9.29); линия
у = kx + bi называется обра-
зующей конуса, точка А пересе-
чения образующей с осью —
вершиной конуса, окружность
у, полученная вращением точки
В,—направляющей окружно-
стью. Площадь поверхности конуса определяется следующим
образом. Выберем иа окружности у точки В1, ..., Вт и
соединим их последовательно отрезками друг с другом и
с вершиной А; получится, во-первых, замкнутая ломаная
Рис. 9.29.
{В1..	= во-вторых,—система равнобедренных тре-
угольников BjAB2, ..., BmABlt образующих в совокупности
вписанную пирамиду П (рис. 9.30). Площадь поверхности
пирамиды П мы определим как сумму S (П) площадей со-
ставляющих ее треугольников. Положим BkBk+1 = 2bk
(А=1, ..., т) и d(П) = maxРассмотрим произвольную
k
последовательность вписанных пирамид Пх,..., Пв,...
с d(H„)—*0; оказывается, что числа 5(П„) имеют предел,
который не зависит от специального выбора этих пирамид;
9.64]
§ 9.6. ПРИЛОЖЕНИЯ ИНТЕГРАЛА
363
этот предел мы и будем по определению считать площадью
поверхности конуса Р.
Чтобы доказать существование предела последователь-
ности S (П„), найдем явное выражение чисел S (П). Пусть I
Рис. 9.30.
есть длина образующей конуса (от вершины до точки В).
Высота треугольника BkABk+1 равна
где Е имеет предел 1, когда	—>0 (5.59 е). Площадь
,----- 6*£
треугольника BkABk+1 равна 8ky Р—8% = 8к1-, а пло-
щадь поверхности вписанной пирамиды
/ 6s Е\ 	1
s (П) = £ (8к1—±~) = 1 /₽ (П)—±	(1)
где Р(П) есть длина ломаной X. При d (П)—*0 длина ло-
маной р (П) стремится к длине окружности у (9.63 б),
равной 2л/?, так что уменьшаемое в (1) имеет предел nlR.
Если все < 8, то вычитаемое в (1) оценивается сверху
величиной • 2е®Р (П) (при достаточно малых 6ft), откуда
видно, что при d (П) —»0 оно стремится к 0. Таким обра-
зом, последовательность чисел 5(П„) имеет предел, равный
iiLR. Эту величину nLR, как было сказано, мы и прини-
маем за площадь поверхности конуса.
364
ГЛ. 9. ИНТЕГРАЛ РИМАНА
[9.64
Площадь поверхности «усеченного конуса» (рис. 9.31),
получающегося при вращении вокруг оси х отрезка прямой
y = kx~\-b, мы определим как разность площадей поверх-
ностей двух конусов с образующими Lt и £2 и радиусами
оснований соответствен-
но и Т?2. Мы получим
величину
л Т2/?2)=
=л (Z.J £2) (/?j +
поскольку £^2 = £27?i,
£1 Ri
или, что то же, =
А2
как легко получить из
соображений подобия.
Величина £т—£2 есть
очевидно, длина отрезка образующей конуса.
Переходим теперь к общему случаю, причем вместо кривой
>=у(х) будем рассматривать кривую в параметрической
форме
L = {x — x(t), y=y{t)^O,	х (а) = а, х (Р) = Ь).
Площадь поверхности вращения этой кривой вокруг оси х
определим, как предел площадей поверхностей,. полученных
вращением вокруг оси х ломаных, вписанных в кривую £.
Пусть П = {а = t0 tr	tn — Р} — разбиение проме-
жутка [а, Р] и £„—ломаная с вершинами в точках
(х(70), У(^о))»	y(in))t k-e звено этой ломаной
имеет длину Д/А = |/Дл’* + Aj|, где &xk = x(fk+1)—x(tk),
При вращении А-го звена этой ломаной
вокруг оси х получается усеченный конус, поверхность ко-
торого равна л (Уй+Уй+1) A/fc; суммируя по всем звеньям,
получаем выражение площади поверхности вращения ломаной
=	(л+Л+1)А/б-
Предположим теперь, что функции х (t) и у (/) обладают
непрерывными производными х' (/) и у' (/). Тогда выражения
Ах| и Ду£ можно преобразовать по формуле Лагранжа 7.44,
9.64]
§ 9.6. ПРИЛОЖЕНИЯ ИНТЕГРАЛА
365
и мы получим
рп=(**) +у (**+i)] у Iх' (UP+iy (пл)]2
где точки ^к и т]л находятся в промежутке (tk, tk+1). На-
ряду с выражением Рп рассмотрим величину
п— 1	_________________
рп = 2л£у (tk) v[х' (ik)]* + [у' (/*)? Ык.
Величина есть интегральная сумма для непрерывной
функции 2лу (/) ]/[х'(/)]2-]-[у'(/))2 и при неограниченном
измельчении разбиения П имеет пределом число
₽
5 = 2л $ y(i) V[х' (О]2 + [у' (/)] * dt. (2)
а
Покажем, что и величина Рп при неограниченном измельче-
нии разбиения П имеет этот же предел. Достаточно про-
верить, что
lim [Р£-Р„]=0.
d (П) -> О
Действительно, для заданного е > 0 можно найти 6 > 0 такое,
что из | /'-— /1 < 6 следуют неравенства | х' (/') — х' (/) | < е,
1У (О—У (01 < е, |у (/')— у (/) | < е. Если d (П) < 6, то,
в частности,
У (^+i) =У + eie. I ei I < 1.
У(1и)=У(и+ез8. РзК1.
так что
[> (60 +у (^+1)1 VIх' О2+[У (nft)]2=
= (2у (tk)+е18) V (х' (tk)+е28)2+(у' (tk)+е3е)2=
= (2у (^) + е18) V[X' (/fe)]2 + [y (^)]2 + ее4,
где 1641	2 шах [ | х' (t) Ц- \у' (/) | + е]. Для любых а, Ь > О
имеют место неравенства*)
♦) Первое из них очевидно; второе_есть неравенство треуголь-
ника в R2 для векторов (У а, 0) н (0, Vb).
366
ГЛ. 9. ИНТЕГРАЛ РИМАНА
[9.64
поэтому
=	+	|06| <1.
В нашем случае можно написать
К[х' (и]2+[У(^)12+ее4=
= /[*' (6J12+[У (U12+е6
где 1651	1. Отсюда
Рп-Рп— 2 л Jjу (tk) V[х' (/fc)]2 + [у' (^)j2 +
+ л j (2у (U + 0ie) [^[*' (**)]а+[У (*й)]2+06Ke6J =
k- о
=	[х' (Q]2+ [У О2 + 2лу (tk) 66 /ёЩ +
-J- л6166е|/< 80J;
очевидно, эта величина стремится к нулю вместе с е, что
нам и требуется.
Итак, формула (2) дает выражение для искомой площади
поверхности вращения в предположении существования и
Рис. 9.32.

непрерывности у’ (/) и х'(/). При t^x она приводится
к виду
ь
5 = 2л $у(х)К 1 + [У (x)]zdx.
а
9.65]
§ 9.6. ПРИЛОЖЕНИЯ ИНТЕГРАЛА
367
Примеры.
а.	Поверхность сферы радиуса R. Сфера есть поверх-
ность вращения полуокружности x—R cos 0, у— R sin 0, 0 л
(рис. 9.32). Поэтому, согласно формуле (2),
л
S = 2n J R sin 0 У R2 sin® 0-f-R2 cos® 0d0=
о
n
= 2nR2 J sin 0d0 = 4«/?®.
о
б.	Катеноид—поверхность вращения цепной линии относительно
оси х (рис. 9.33). Мы имеем здесь у=ch х, у' =&hx, У 1-|-</'2=chx,
ch®xdx=2n

[ sh 2x , | |+a	, , „ , „ ,
= л—к----h* =n(sh2fi-l-2a).
L 2 J|-o
9.	65. Общая схема использования инте-
грала. Пусть нам нужно вычислить некоторую величину v.
Предположим, что эта величина есть одно из значений
функции v(x) переменного х, меняющегося в промежутке
[a, ft], например ® = ®(ft). Если мы сможем для каждого
х е[а. указать главную линейную часть dv приращения
Д® функции 'о(х) при переходе от х к x-|-dx в форме
dv—f(x)dx
(В
и если мы знаем ®(а), то задача в принципе сводится к вы-
числению интеграла
ь
v(b) = v(a) + \f(x)dx.	(2)
а
Действительно, коэффициент /(х) в главной линейной
части приращения функции есть производная от функции
®(х), поэтому наша задача сводится к проблеме восстанов-
ления первообразной, которая и решается с помощью ин-
теграла (2).
В некоторых случаях, когда составление равенства (1)
встречает затруднения, но можно получить неравенство вида
dv^.f(x) dx,
368
ГЛ. 9. ИНТЕГРАЛ РИМАНА
[9.65
мы, интегрируя его, получаем оценку величины v(b):
ь
v(b)^.v (а) + J f(x) dx.
а
Следует иметь в виду, что при составлении выражения dv
(в отличие от А©) можно пренебрегать малыми высшего по-
рядка по сравнению с dx. Это соображение часто упрощает
задачу.
Рассмотрим несколько простых примеров.
а.	Какую работу нужно произвести, чтобы 1 кг массы поднять
с поверхности Земли за пределы земного тяготения?
Пусть W (Л) означает работу, необходимую для поднятия 1 кг
на высоту h. Сила F = F (h), с которой Земля притягивает массу 1 кг,
находящуюся на высоте h м над уровнем моря, по закону Ньютона
равна С•	, где R—радиус Земли. Постоянную С.можно найти
из условия, что эта масса на уровне моря притягивается Землей
с силой в 1 кг веса (= 9,8 кг • м/сек2). Отсюда С — R2, F (К) = кг'
Переместим нашу массу с высоты ft на высоту ft 4- Aft м. Считая на
этом участке силу F (п) постоянной, получаем работу
R2
dW = F dh=,  n„ dh кг-м.
(h-\-R)2
В действительности сила F не постоянна на промежутке [ft, ft+Aft],
но учет ее изменения на этом промежутке привел бы к появлению
в выражении dW малых высшего порядка (~ AF-Aft), в то время
как нам нужны только малые первого
порядка по сравнению с dh.
Теперь по формуле (1) получаем ве-
личину работы, необходимой для под-
нятия 1 кг на высоту И:
н
С R2
W = J (h+R)2d,t
h=0
= п_____W_
R H + R
При весьма большом
становится пренебрежимо малой (в этом
случае и говорят «за пределами земного тяготения», так как для
дальнейшего удаления практически уже не приходится расходовать
работу против силы притяжения Земли). Поэтому истинный ответ
есть W =6,4-10е кг-м.
б.	Воронка с верхним сечением S, нижним s и высотой Н на-
полнена водой (рнс. 9.34). Известно, что скорость истечения из ниж-
Я2 io _
< /? = 6,4-10® кг-м.
Н величина тт-.—л
п
9.65]	§ 9.6. ПРИЛОЖЕНИЯ ИНТЕГРАЛА
369
него отверстия в тот момент, когда высота столба воды над ннм есть Л,
равна
v(h)~y2gh (g=9,81 м/сек3).
За сколько времени вся вода выльется из нижнего отверстия?
Обозначим через S (Л) сечение воронки на уровне h=h(t) над
нижним отверстием и через v=v(t) объем воды в воронке в мо-
мент времени t. За промежуток времени (f, <+Д/] через нижнее
отверстие воронки вытечет v-s-dt = y 2gh-s.-dt см3 воды (мы считаем,
что за это время скорость истечения остается постоянной, так как
учет ее нзменеиия привел бы к появлению малых высшего порядка,
а нам нужны только малые первого порядка по сравнению с dt).
Эту же величину dv мы получим, считая, что вытекающий объем
равен объему цилиндра с высотой dh и сечением S(h) (в действи-
тельности вытекающий объем есть объем усеченного конуса, но
разница составляет малую высшего порядка по сравнению с dft).
Получаем равенство
S (h)dh= У 2gh-s-dt,
откуда
dh -S
У 2gh	H2 У Н2
Интегрируя по t от 0 до Т и учитывая 9.54, получаем
7	Н
БуЛ=БГ=——
о	о
откуда
2 S И
5 s V 2g'
в. Оценка площади p-о крести ости плоской
кривой. Геометрическое место V?(L) точек всех кругов
радиуса р, центры которых лежат на заданной кривой L,
называется р-окрестностью кривой L (рис. 9.35). Кривую L
будем считать кусочно-гладкой; можно доказать, что при
этом множество Vp (Z) имеет площадь. Мы покажем здесь,
что площадь Sf(L) множества Vf(L) допускает оценку
5р(£Х2лр«(£)4-лрг,	(2)
где s (L) есть длина кривой L.
Для доказательства введем на кривой L в качестве па-
раметра длину дуги s, отсчитываемую от начальной точки
Л($ = 0) до конечной точкиВ(« = «0) (9.63 ж). Пусть Sf(Le)
есть площадь р-окрестности дуги кривой L, определяемой
370
ГЛ. 9. ИНТЕГРАЛ РИМАНА
[9.65
промежутком	изменения параметра s. Пусть Qp
есть круг радиуса р с центром в точке С (s — о). Возможные
положения точек С' £ L, отвечающих значениям параметра s
в промежутке о s о + d.s, заключены в круге радиуса ds
с центром в точке С (рис. 9.36). Возможные положения точек
Рис. 9.36.
кругов радиуса р с центрами в точках С' заключены в круге
Qp+di радиуса p-f-ds с центром в точке С. Поэтому полное
приращение величины 5р (Ls) при переходе параметра $ от
значения а к значению о 4- ds не превосходит разности пло-
щадей кругов Qp+ds и Qp, т. е. величины
л (р + ds)s—лра — 2лр ds + л (ds)a.
Для главной линейной части этого приращения получаем
оценку
dSp (Ls) 2лр ds.
Интегрируя по s в пределах от 0 до $0, находим
Sf(L)~Sf(L0)^2nps{L).	(3)
Так как 5р (£0) == лра, из (3) следует (2).
г.	Объем тела с известными горизонталь-
ными сечениями. Из общей теории измерения объемов
следует, что объем прямого цилиндра с жордановым основа-
нием 5 и высотой Н равен SH (рис. 9.37). Пусть имеется
произвольное тело, у которого сечение Vh, проведенное
на высоте h, жорданово и имеет площадь 5 (й) (рис. 9.38).
Предположим, что контур сечения Vh меняется непрерывно
9.65]
§ 9.6. ПРИЛОЖЕНИЯ ИНТЕГРАЛА
371
с изменением высоты й; это означает, что для любого е > О
найдется 6>0 такое, что при \h—h' | < б проекция на
плоскость основания границы сечения Vh- проходит в 8-окре-
стности проекции на ту же плоскость границы сечения Vh
(в). Тем самым разница площадей сечений Vh и Vh- не пре-
восходит площади этой окрестности и, согласно в, оцени-
вается сверху числом C&L, где L—число, ограничивающее
сверху длины контуров всех горизонтальных сечений.
Рис. 9.38.
Обозначим через v (h) объем тела, ограниченного сверху
сечением Vh, При переходе от йкй + йй главная линейная
часть приращения -о (й) может быть записана в форме 5 (й) dh,
как если бы в промежутке [й, h-\-dti\ тело представляло
собой цилиндр; действительное приращение объема от-
личается от приведенной величины на малую высшего по-
рядка по отношению к dh. Итак,
dv = S(h) dh-,
интегрируя, получаем
н
v=\S(h)dh. (4)
о
д.	Объем конуса А" вы-
соты Н с площадью S верхнего
сечения (рис. 9.39). Сечение на высоте й, по соображениям
/ ь \2
подобия, имеет площадь 5 (й) = 5 • I -д- j . Отсюда
н
о
372
ГЛ. 9. ИНТЕГРАЛ РИМАНА
[9.65
е.	Объем шара радиуса /?. Площадь сечения на вы-
соте h (над центром) равна л (Я2—й2) (рис. 9.40). Отсюда
R
2 J л (7?2—й2) dh = 2л
о
= 2л^-5)=4я/?3-
\	0/0
ж.	Для тела вращения формулу (4) можно переписать
в виде
н
» = л^ r2(h)dh,	(5)
о
где г(й) есть радиус сечения на высоте й.
Рис. 9.40.
з.	Объем тела, вырезанного из шара радиуса R парабо-
лоидом вращения с вершиной в центре шара (рис. 9.41).
Уравнение параболоида 2az = x2+j2; отсюда площадь се-
чения параболоида плоскостью на высоте й (над центром
шара) равна л-2ай. Площадь сечения шара на высоте й равна
л(/?2—й2). Пересечение поверхности шара и поверхности
параболоида происходит на высоте z0, определяемой из
уравнения 2az0 = /?2—z2; таким образом, z0=—aа2 + R2
и
z0	R
v= J л-2ай</й-|- J л (7?2-г-й2) dh.
О	г0
Полученные интегралы легко вычисляются; выкладку пре-
доставляем читателю.
9.71]	§ 9.7. ИНТЕГРИРОВАНИЕ ПОСЛЕДОВАТЕЛЬНОСТИ
373
и.	При растяжении тела в k раз вдоль какой-либо оси
его объем возрастает в k раз (доказательство такое же, как
в 9.61 г-д для плоского случая). Отсюда, например, долу-
,	.	4	.
чается, что объем эллипсоида с полуосями а, о, с равен -и- паре,
О
4
поскольку шар радиуса 1 имеет объем -^-л, а наш эллип-
О
соид получается из шщра растяжением в а раз по оси х,
в b раз по оси у и в с раз по оси z.
§ 9.7. Интегрирование и дифференцирование
последовательности функций
9.71.	Рассмотрим последовательность интегрируемых
функций /х (х), /2 (х), ...,/„ (х), ... на отрезке а х Ь,
сходящуюся всюду на [a, ft] к некоторой функции /(х).
Поставим следующие вопросы:
(а)	Будет ли функция /(х) также интегрируемой!
(б)	Если ответ на (а) положительный, справедливо ли
равенство
ь	ь
lim \fn(x)dx—\f(x)dx'i	(1)
л-* «о	а
Оказывается, что в общем случае ответ на оба поставлен-
ных вопроса отрицательный.
(а)	Пусть /„(х) равна 1, если х£[0, 1] имеет вид у ,
где q^.n, н равна 0 в противном случае. Таким образом,
функция /„ (х) отлична от 0 лишь в конечном числе точек,
и потому (9.16 в) интегрируема (с Интегралом, равным 0).
Последовательность /„(х) имеет в каждой точке отрезка
[0, 1] при л—>оо предел /(х), равный 1 в рациональных
точках и 0 в иррациональных точках. Функция /(х) не ин-
тегрируема (9.17).
(б)	Пусть /„ (х) равна л sin лх при 0 х и равна 0
при х л. Эта последовательность /„ (х) имеет предел
в каждой точке х£[0, л], равный 0. Предельная функция,
очевидно, интегрируема, и ее интеграл по отрезку [0, л]
374
ГЛ. 9. ИНТЕГРАЛ РИМАНА
[9.72
равен 0. Однако
л	л/п
J/n(x)rfx = J nsin/zxdx = 2,
о	о
и равенство (1) заведомо не выполняется.
9.72.	Положительного ответа на вопросы 9.71 (а), (б)
можно ожидать, если на сходимость последовательности fn (х)
будут наложены дополнительные условия. Таким дополнитель-
ным достаточным условием является равномерная сходимость
функций /п(х) к своему пределу /(х), определенная нами
в 5.93. Напомним определение в применении к нашему слу-
чаю: последовательность Д (х), /2 (х), ... сходится к функ-
ции /(х) равномерно на [а, ft], если для любого е > 0 най-
дется такое N, что при всех х£ [a, ft] и п N выполняется
неравенство |/(х)—/„(х)|<е.
Теорема. Если последовательность интегрируемых
функций fx(x), /2(х), ... сходится к функции /(х) равно-
мерно на [a, ft], то /(х) также интегрируема и имеет место
предельное соотношение
X	X
lim $/„(£)<*£ = $/<£><*£
а	а
равномерно на [а, ft]. В частности,
ь	ь
lim	=
а	а
Доказательство. Для любых разбиений П и П'
отрезка [a, ft] и любого л=1,2, ... мы имеем
5п(/) = 5п(/„) + 5п(/-/п),	(1)
Sir (/) = Sn- (fn) + Sn(/—/„).	(2)
Для заданного е > 0 найдем номер п так, чтобы всюду на
[a, ft] выполнялось неравенство
тогда, очевидно,

|Sir (/-/„)
9.73]	§ 9.7. ИНТЕГРИРОВАНИЕ ПОСЛЕДОВАТЕЛЬНОСТИ
375
Так как функция /„(х) интегрируема на fa, ft], а следова-
тельно, и на [а, х] (9.15 л), то существует 6 > 0 такое, что
для любых разбиений П и П' с d (П) < 6, d (ГТ) < б
Ип(Д)-5П'(/„)|<|.
Но тогда для этих же разбиений из (1) и (2) следует
|$n(/)-Sn'(/)|<|Sn(/J-Sn'(A)| +
+ 15П (/-/„) | + |Sn-(/-/„) |<
=С 4 +	—а) +	i (ft—а)» в.
2 1 4(6—а)'	' 1 4(6—а)'	'
Это означает, что для интегральных сумм функции /(х) вы-
полнен критерий Коши, откуда по теореме 4.19, применен-
ной к рассматриваемому направлению й(П)—>-0, и следует
существование интеграла.
Для доказательства второй части теоремы заметим, что
XX	X
J/(g)^-J/„(g)^ - $[/(£)-/„(E)NI <
С $ !/(!)-/„ (I) | dg < е (Х-Й) <в(ft-c) (3)
для всех номеров п, для которых при всех х выполняется
неравенство
|/(х)—/„(х)|<8.
(4)
Так как последовательность fn (х) равномерно сходится к/(х),
то неравенство (4) выполняется при заданном в для всех
номеров п, начиная с некоторого N; отсюда и следует тре-
буемое.
9.73.	Теорема 9.72, доказанная для последовательности
функций, немедленно переносится на функциональный ряд:
Теорема. Если ряд интегрируемых функций
<Р1 (х) + <Р2(х)+ ...+ф„(х)+ ...
(1)
376
ГЛ. 9. ИНТЕГРАЛ РИМАНА
[9.74
сходится к сумме S (х) равномерно на [а, 6], то S (х) также
интегрируема и имеет место предельное соотношение

равномерно на [а, 6]. В частности,
а Ь	6
1 о	а
(2)
(3)
Доказательство получается немедленно из равно-
мерной сходимости к S(x) частных сумм ряда (1) и из тео-
ремы 9.72.
9.74.	Примеры. Ряды
j-L- = 1 —х 4- Xs—ж8 + . .
bfTa =1 — *2 + **—хв + ..
(D
(2)
сходятся равномерно на любом промежутке [—Ь, й],0<#< 1.
Интегрируя их почленно от 0 до t, получаем новые ряды
.	t2 t3
1п(1+0 = /—г + т-"-’	(3)
/3 /о
arctg/ = /—(4)
также сходящиеся равномерно на [—Ь, д], 0 < b < 1. Так как
ряды справа в (3) и (4) сходятся и при, f = 1, а функции слева
в этих равенствах непрерывны при 0 t 1, то, используя
6.67 и 5.68, получаем
1п2=1-14-4-...,	(5)
т=1-1+4-”-	<6)
9.75.	С помощью теоремы 9.73 можно разлагать в сте-
пенные ряды многие неэлементарные функции. Например, ин-
тегрируя разложение
sin f .___Z1_______t9 ,
t ~ 1	3! +5!~71 +•••>
8.77]	§ 9.7. ИНТЕГРИРОВАНИЕ ПОСЛЕДОВАТЕЛЬНОСТИ 377
сходящееся равномерно на любом отрезке [-*-7', 7], получаем
разложение в степенной ряд интегрального синуса
также сходящееся равномерно на любом отрезке 7, 7].
9.76.	Поставим вопросы, аналогичные вопросам 9.71 (а),
(б), для операции дифференцирования. Пусть имеется по-
следовательность дифференцируемых функций на отрезке
ZiU). /2(*). •••>	...»
сходящаяся всюду на [а, Ь] к функции f(x). Спрашивается:
(а) Будет ли функция f(x) дифференцируемой?
(б) Если ответ на (а) положительный, справедливо ли
равенство
f'(x) — limf,n(x)f	(1)
Снова ответ на оба поставленных вопроса отрицатель-
ный—даже при равномерной сходимости последовательности
А(х):
(а)	Последовательность дифференцируемых функций на
[-1.4-1]
fn (*) = |* |1 + “
равномерно на [— 1, 4-1] сходится к функции f (х) = | х |,
уже не имеющей производной при х = 0.
(б)	Последовательность функций на [0, л]
= пх
равномерно сходится к 0. Предельная функция, очевидно,
дифференцируема. Но равенство (1) не выполняется: после-
довательность (х) = cos пх не сходится ни в одной точке,
кроме х = 0.
9.77.	Положение изменится, если мы предположим равно-
мерную сходимость производных. При этом оказывается, что
378
ГЛ. 9. ИНТЕГРАЛ РИМАНА
(9.78
относительно последовательности самих функций хп (f) можно
предположить уже много меньше:
Теорема. Если последовательность кусочно-гладких
(9.39) функций xn(t) сходится хотя бы в одной точке t0
отрезка [а, &], а последовательность их производных x’n(t)
сходится равномерно на [а, к кусочно-непрерывной функ-
ции g(t), то последовательность функций хп (t) сходится
равномерно на [а, Ь] к некоторой кусочно-гладкой функции
х (I) с производной x'(t)= lim x'n(t) = g(t) в точках непре-
п~* сс
рывности функции g(t).
Доказательство. Для функции хп (t) мы имеем, со-
гласно 9.32,
t
xn(t)-xn(Q=-\xn(l)dl,	(1)
^0
и по теореме 9.72 функции xn(t)—х„(10) равномерно схо-
дятся на отрезке [а, &]; а так как числа хп(10) имеют предел,
то равномерно сходится сама последовательность xn(t).
Обозначим ее предел через х (I). Переходя к пределу в ра-
венстве (1) и снова используя теорему 9.72, получаем
t
х (t)—x(t0)=\g(l)dl.
*0
Так как функция g(i) по предположению кусочно-непрерыв-
на, то согласно 9.31, функция x(t) дифференцируема всюду,
кроме точек разрыва функции g(t), и при этом в точках
непрерывности g(t) имеем х' (t) = g(f) — lim *„(/), что и тре-
бовалось.
9.78., Сформулируем аналогичную теорему для ряда.
Теорема. Если ряд из кусочно-гладких функций
ui (х) + и2 (*) + • • • сходится хотя бы в одной точке отрезка
[а, &], а ряд из производных и\ (х) + ... сходится равно-
мерно на [а, Ь] к кусочно-непрерывной сумме s(x), то ряд
из функций ип (х) сходится равномерно на [а, Ь] к некоторой
кусочно-гладкой функции g(x) с производной g' (х), равной
s(x) в точках непрерывности функции s(x).
Для доказательства к последовательности частных сумм
рассматриваемого ряда нужно применить теорему 9.77.
9.82]
§ 9.8. ИНТЕГРИРОВАНИЕ ПО ПАРАМЕТРУ
379
§ 9.8. Интегрирование и дифференцирование
по параметру
9.81. Пусть дана числовая функция /(х, t) от аргумента х,
пробегающего отрезок Д = {а^х^&}, и аргумента t, про-
бегающего метрическое пространство М. Пусть эта функция
f(x, t) равномерно непрерывна по совокупности аргументов
х, t или, что то же, равномерно непрерывна на метрическом
пространстве Q=AxAf (5.18 и 5.17 а).
Теорема. При указанных условиях функция
ь
Ф(О= $/(х, f)bx (t£M)
а
равномерно непрерывна на пространстве М.
Доказательство. Обозначим через
COZ(6)= sup |/(х', t')— f(x", Г)|
| X' — X” I < б
P (/'. /") < С
колебание функции f(x, t) на пространстве Q (5.17 в). Для
заданного е > 0 существует такое 60 > 0, что при 6<60
имеем со/(6)<е. Пусть p(f, f)^6<S0; тогда
ь
|Ф(Г)-Ф(Г)| = J [/(х, t')—f(x, t")\dx <
а
b
<$!/(*>	t")\dx^<i>f(i>)(b—а).
откуда
(0ф(6)= sup |Ф(/')—Ф(Г)| ^.&t(8)(b—a)<&(b—а),
р (/', п < б	'
что доказывает равномерную непрерывность функции Ф(0
на М.
9.82. Пусть
и непрерывна в
Тогда
вещественная функция f(x, f) определена
прямоугольнике Q= {а х b, c^.t^.d}.
b ( d	d ( Ь
$ |$/(х, f)dtldx = $ {$/(х, t)dxldf. (1)
а (.с	/ с 1а	/
380
ГЛ. 9. ИНТЕГРАЛ РИМАНА
[9.82
Доказательство. Положим
ь
ф(/)= J/(x, f)dx
а
d
F(x) =$/(*, t)dt (a^x^b).
В силу 9.81 функции Ф(/) и F(x)—непрерывные функции
своих аргументов. Далее, напомним, что разность между
интегралом от непрерывной функции G(t) по отрезку [с, d]
и ее интегральной суммой, построенной по разбиению П
с <*(П)<д, имеет оценку (9.15 н)
т—1
d
? G(t)dt— 2 G(UM, ^aG(6)(d—c).
C	i=°
В частности, для разбиения П отрезка [с, d] с </(П)<6
имеем
d
I
c
“	т — 1
J/(x, t}dt- 2 f{x,tj)Mj ^f(6)(d-c).
С	i=°
Интегрируя это неравенство по х, получаем (9.15з)
f(x, t)dt
f(x, ij) Д/J dx
^©z(6) (d—c)(b—a).
(3)
С другой стороны, в силу той же оценки (2), примененной
к функции Ф(/), мы имеем
“	т — 1
\ Ф (t)dt— 2 ф(6) Д^7 ==
с	1=0
с (г	1	т-1 (с	1
=	t)dx\dt— 2
с 1а	/	1=0 (0	J
^(£>ф (6) (d—с)	(t)f (6) (b — a) (d—с).
Так как, очевидно,
* (т -1	"I	т-1
П S	6)Дб} dx =	2	I \/(х,
a I i=0	J)	1=0	U
д^,
9.84]
§ 9.8. ИНТЕГРИРОВАНИЕ ПО ПАРАМЕТРУ
381
то из (3) и (4) следует, что
ь
d ( ь
а
d
\f(x, f)dt dx —
dt
с
2coz (6) (b—a) (d—c),
и так как правая часть может быть сделана произвольно
малой, то справедливо равенство (1), что и требуется.
9.83.	Пример. Положим в теореме 9.82 f(x, 1) = хг.
х£ [0, 1], Р] (а^О, Р>0); мы получим
1 (₽ \ ₽ (1
dt.
О \а /	а \ 0	)
Вычисляя внутренние интегралы, находим значение опре-
деленного интеграла
г -4=£. dx=.
J 1пх	1+а
о
Это значение было бы затруднительно вычислить обыч-
ными приемами, описанными в §§ 9.4—9.5, поскольку неопре-
„	х®—х®
деленный интеграл от j не выражается в элементарных
функциях.
9.84.	Теорема. Если функция f(x, t) определена при
a^.x^.b, c^.t^.d и в окрестности точки tog(c, d)
обладает непрерывной производной по аргументу t:
ft(Xt 0= hm /ои+до-г(х. о ,
At -» О	Л‘
р—м<fi.
то справедливо равенство
ь	ь
а	а
при любом ^оё[с, d].
Доказательство. Поскольку функция f't(х, f) непре-
рывна в прямоугольнике ах ^.b, t0—б/	+ б, к ней
382
ГЛ. 9. ИНТЕГРАЛ РИМАИА
[9.86
можно применить теорему 9.82; используя формулу Ньюто-
на—Лейбница (9.32), мы получаем, далее, при любом
*ё[*о—^о+ fi]> чт0
« /6
$ 1 $ (х, t) dx
to la
b / t	\
dt = J j J ft (x, f) dtl dx =*
ь J°	ъ
= $/(*» t)dx—\f(x, t0)dx.
a	a
Левая часть равенства имеет производную по t, равную
подынтегральной функции (9.31). Следовательно, и правая
часть равенства имеет эту же производную. Но второе сла-
гаемое в правой части не зависит от t, и его производная
по t равна 0. Приравнивая производные от правой и левой
части и полагая t = t0, приходим к равенству (1). Теорема
доказана.
9.85.	Пример. Интеграл
Л/2
/(/)== J 1п(<2—sin2x)dx (t > 1)
о
не вычисляется приемами § 9.4. Однако в силу теоремы
9.84 (ее условие здесь, очевидно, выполнено) имеем
л/2
р _ С 2< dx___________я
1 ~ J <2—sin2
о
(здесь первообразная уже вычисляется—с помощью 9.436).
Отсюда, интегрируя по t, можно восстановить значение
интеграла I(t):
/(П = fyfe' dt=«Н* +V?-i)+c.
Чтобы найти значение С, в равенстве
Л/2
С= § 1п(£2—sin2x)dx—л1п(<4-]/<2—1) =
о
Л/2	____
f . (, sinaxA , .	*+K*2-i
— 1 In ( 1----dx —л In —,
J \ t2 )	t
о
9.86]
§ 9.8. ИНТЕГРИРОВАНИЕ fto ПАРАМЕТРУ
383
справедливом при всех t > 1, будем переходить к пределу
при t —»- оо, или при т = у—>0. Заметим, что функция
In (1 —t2 sin2 х)
определена и непрерывна в прямоугольнике 0^х^-у,
О^т^то<1, поэтому, в силу 9.81, функция
п/2
Ф (т)= J In (1 —т2 sin2 х) dx
о
непрерывна при О^т^то. Следовательно,
Л/2
0 = Ф(0)= ПтФ(т)= Пгй 1п(1—T2sin2x)dx.
t-f 0	Т->- 0 о
С другой стороны,
lim л In	—1 — я lim In (1 -р ]Л1 —т2) — п 2«
t-r 00	'	Т-» о
Окончательно получаем С ——л1п2и
,,,,	1
/(О = л 1п -^2-----.
9.86.	Рассмотрим несколько более сложный случай, когда
не только подынтегральная функция, но и пределы интеграла
зависят от параметра t.
а.	Теорема. Пусть функция f(x, t) непрерывна при
а ^.х^.Ь, c^.t^.d, а производная f't (х, t) существует
и непрерывна при а^.х^Ь, |/—101	6. Пусть, далее,
функция ср(/) определена, непрерывна и дифференцируема
при 11 —10 I < б и принимает свои значения в отрезке а^х^Ь.
Тогда функция
ч>(0
Ф(0= $ f(x, t)dx
а
дифференцируема при t = t0 и
ч>(Л>)
Ф' (U = J ft (X, t0) dx +/(ф (tg), tg)^' (tg).	(1)
384
ГЛ. 9. ИНТЕГРАЛ РИМАНА
[9.87
Доказательство. Положим Ф (t) = Ф1 (/) 4- Фа (/),
где
4>W
= J f(x,t)dx, Ф2(/) = $ f(x,t)dx.
о	4>W
Функция Фг (t) по теореме 9.84 имеет при t — t0 производную
<Р (Q
ф;^о)= $ Л(*. t0)dx.	(2)
а
Производную от Ф2 (i) найдем непосредственно. Мы имеем
Ч> (М-АГ)
= 1 J f(x, t0 + M)dx~
Ч> (/о)
=Ф«о+Д0-<р«о)^(е> /о+до
в силу теоремы о среднем 9.15 з; число 0 заключено между
<P(U и <р (/0—|-А/). В силу сделанных предположений отно-
сительно функций f(x, t) и <р (/) полученное выражение при
0 имеет предел
Фии=<₽'(и-/(ф(и, Q.	(3)
Из (2) и (3) следует (1), и теорема доказана.
б.	Пусть, в частности, с = а, d = b, <f(f) = t Мы полу-
чаем формулу
/	tr
t)dx	*о)<*х+/(*о, t0),	(4)
о	t=t0 a
справедливую в предположении, что f(x, t) непрерывна при
а 5^ х ^.b, а t b и что f't (х, t) существует и непрерывна
в окрестности точки t = t0.
9.87.	Пример. Найдем производную по х от функции
4W = (7ZTijij(^-«)n"1/(«)^ (л=1, 2, ...), (1)
а
где f (x)—функция, непрерывная при
9.91]
§ 9.9. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
385
По формуле 9.86 (4) (где t заменено на х, а х—на в)
4 М = (ТТЛ)! J («-1) (^-«)""7 (и) du +	f (х) =
= 4-iW-
При этом, очевидно, /в(а) = 0, так что
X	X
= $4-!
а	а
х
Заметим, кроме того, что I1(x) = J/(iz) du.
а
Отсюда следует, что 1„(х) есть результат п последо-
вательных интегрирований функции f(x) в пределах от а
до х,— иначе говоря, результат операции, обратной к
л-кратному дифференцированию. Формула (1) представляет
результат этой операции в виде однократного интеграла
с параметром.
§ 9.9.	Криволинейные интегралы
9.91.	Криволинейный интеграл Стилтьеса.
Рассмотрим кривую L в л-мерном пространстве Rn с урав-
нениями Xj=Xj(t) (/=1, 2, ..., л), где функции Xj(t)
определены на отрезке [а, 6], непрерывны и обладают не-
прерывными (или кусочно-непрерывными) производными. Кри-
вую с выбранным направлением на ней (определяемым по
направлению роста t от а к Ь) будем называть путем.
Согласно 9.63 ж, если 2 [х/ (t + О)]2 и 2 [*/ (*—О)]2 не об-
ращаются в нуль, на пути L можно ввести в качестве пара-
метра длину дуги s, отсчитываемую от некоторой фиксиро-
ванной точки А.
Рассмотрим участок пути L от точки A (s = 0) до точки
B($=S). Обозначим через П разбиение дуги АВ последо-
вательными точками А = Л10,	..., Мр = В. Соответст-
вующие значения параметра s, именно
s (А) = 0 s (Afj) —	s (В) = sp — S,
386
ГЛ. 9. ИНТЕГРАЛ РИМАНА
[9.91
образуют разбиение отрезка [0, <$] вещественной оси.
Как обычно, полагаем
d(П) = max(sy+1—sy) = maxAsy. (/=1, ..., р—1).
Пусть на пути АВ заданы вещественные функции /(Af)
и g(M). Составим сумму
р-1
2 f(M]) к(Жу.+1)-^(ЖУ.)],	(1)
/=о
где точка M'j лежит на дуге Afy-Afy+1, так что s (Af') =
= $/€[$/, $/+1]. Предел при й(П)—>0 суммы (1), если он
существует, называется криволинейным интегралом Стилтьеса
по дуге АВ от функции f(M) по функции £r(Af) и обозна-
чается через
J f(M)dg(M).	(2)
АВ
Например, всегда имеет место равенство
£d^(Af) = g(B) — g(A).
АВ
Если функция g(Af) на дуге АВ постоянна, то, очевидно,
j /(Af)dg-(Af) = O.
АВ
Если существует один из написанных ниже интегралов,
то существует и второй и имеет место равенство
$ f(M) dg{M) = — \ dg(M).
AB	BA
Когда путь AB задан параметрическими уравнениями
xfc=xft(/) (А=1, ...,л), a ^t^b, функции /(А!) и g-(Af)
можно считать функциями от параметра t:	g=g(t)'<
тогда интегральная сумма (1) может быть записана в форме
р-1
2 /М	<z/+r <3>
/=0
При неограниченном измельчении разбиения пути АВ раз-
биение отрезка [а, />] изменения t также неограниченно
9.91]
§ 9.9. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
387
измельчается, поскольку в силу наших условий t есть диф-
ференцируемая функция длины дуги s и по формуле Лагранжа
Д/у=Г (Ву) Asy,
Обратно, по тем же причинам неограниченному измель-
чению разбиения отрезка [a, fc] отвечает неограниченное
измельчение разбиения пути АВ. Поэтому суммы (1) и (3)
имеют предел одновременно, и вопрос о существовании кри-
волинейного интеграла Стилтьеса (2) приводится к вопросу
о существовании обычного интеграла Стилтьеса (9.56):
ь
\f(t)dg(t),	(4)
а
который для гладкой g(t) есть интеграл Римана 9.56(A).
Поэтому справедливы формулы, аналогичные 9.56 (5)—(8):
$ [«Vi (Af) + “2/2 (АО] dg(M) =
АВ
= «!$/! (М) dg (М) + а2 $ /2 (Ж) dg(M)-,	(5)
АВ	АВ
$ /(^)d[Pi^i(^) + ₽2^(^)l =
Ав
= ₽1 $ /(Ж)^(^) + р2 $ f(M)dg2(M);	(6)
Ав	АВ
$ f(M)dg(M) =
Ав
= $ f(M)dg(M)+ $ f(M)dg(M) (АВЭС)-, (7)
АС	СВ
J /(A4)^(A4)=/(A4)^(A4)|J-£g(A4)d/(Al),	(8)
Ав	Ав
если существуют интегралы в правых частях.
Часто встречается комбинация криволинейных интегралов
по одному и тому же пути
$ /1 (М) dgl(M) +...+ $ fp(M) dgp (М)-
АВ	Ав
388
ГЛ. 9. ИНТЕГРАЛ РИМАНА
[9.92
она записывается короче так:
J А И*) dgl (Ж) + ... +fp (Ж) dgp (Ж) =
Кв
= J fidgl+...+fpdgp
Кв
(без скобок). В предположении непрерывности функций f}(t)
и кусочной гладкости функций gj (t) она вычисляется по пра-
вилу 9.56(4)
ь
J [А (0^(0 + • • • +4>(0^(0]<».	(9)
/=а
9.92.	Примеры. Найдем криволинейные интегралы
4= $ (х2— y2)dx, /2= $ (х2 — y2)dy,
Кв	Ав
где АВ—дуга параболы у = х* между точками Д = (—1, 1)
и В = (1, 1) (рис. 9.42). В первом случае можно взять за
Рис. 9.42.
параметр х, и мы получаем
Во втором случае нельзя
брать за параметр у, так
как одному значению у отве-
чают две точки на дуге.
Поэтому снова возьмем за параметр х; по 9.56 (4) на-
ходим
1
/8 = J (х2— x4)2xdx =
-1
2х4	2х6~1 I1
.4	6 J 1-х
9.93.	Интеграл по замкнутому контуру. Если
конечная точка В пути АВ совпадает с начальной точкой А,
©.94]
§ 9.9. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
389
путь АВ называется замкнутым контуром. Интеграл по замк-
нутому контуру L часто обозначается через
L
Величина интеграла (1) не зависит от выбора начальной
точки А, так как по 9.91(7) для любой другой точки А'
J fdg = J fdg+ J fdg =
AA'A	AA'	A7/
= J fdg+ J fdg — J fdg.
/Fa ~aa' /Faa-
Но интеграл (1) зависит от выбора направления обхода
контура, так как при перемене направления обхода на про-
тивоположное все разности g(Mj+1)—g(Mj) меняют знак,
то при такой перемене направления обхода меняет знак и
интеграл (1). При желании указывают направление обхода
стрелкой
Ь	L
Впрочем, такое указание может принести пользу лишь на
плоскости (л = 2).
9.94.	Вычисление площади плоской фигу-
ры с помощью криволинейного интеграла.
Пусть имеется плоская фигура
(рис. 9.43), ограниченная кривыми
,у = ф1(х) (сверху) и _y=q>2(*)
(снизу). Ее площадь равна
ь	ь
S=J<Pi(x)dx— $<p2(x)dx. О)
а	а
Заметим теперь, что по само-
му определению оба написанных
интеграла можно считать криволинейными интегралами, так
что
L,	L,
390
ГЛ. 9. ИНТЕГРАЛ РИМАНА
[9.94
Далее, можно написать
S=^ydjc-\- J у dx (—L2
Lt -l2
затем добавить (равные 0)
Рис. 9.44.
есть £2, проходимая от В к Л),
интегралы по боковым верти-
кальным отрезкам (если тако-
вые имеются); объединение
всех этих интегралов даст
интеграл по замкнутому кон-
туру
S = ^ydx =—^ydx. (2)
Таким образом, площадь фи-
гуры можно записать через
криволинейный интеграл по ее контуру L.
Можно установить и более симметричную формулу. Имен-
но, меняя ролями координаты х и у, находим аналогично
(рис. 9.44)
d	d
c	c
= х dy — J х dy = J x dy + J x dy = ф x dy.	(3)
7-g	7-4	7-3	— 7-4	L
Складывая (3) и (2) и умножая на 1/2, получаем
5 =	jdx.	(4)
Формула (4) может оказаться предпочтительнее фор-
мулы (1) при удачном выборе параметра. Например, для
эллипса x=acos/, _y=bsin/ мы непосредственно получаем
2л
S = у ф х dy — у dx = у У ab [cos21 + sin2 /] = л ab.
L	t=0
Формулу (4) полезно сопоставить с формулой
в	в
$ xdy+y dx = ^d(xy) = xy 1^ = х (В)у (В) — х (А)у (Д);
А	А
9.95]
§ 9.9. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
391
для замкнутого контура Г мы получаем всегда
$ xdy dx = 0.
г
Аналогично для любого замкнутого контура Г и непрерыв-
ных /(х), ф(.у)
<fif(x)dx~0; <fiq(y)dy=0.
9.95.	Аппроксимация интеграла по кривой
интегралами по ломаным. В этом пункте мы ограни-
чимся криволинейными интегралами вида
$-/1(Af)dx1+...+/„(M)dx„.
(П
Здесь предполагается, что L есть путь в л-мерном
пространстве, определяемый параметрическими уравнениями
Xy=Xy(f).	/=1, п, где функции х'/(1) не-
прерывны и У [х;- (/)]2 > 0. (Впрочем, можно считать их
и кусочно-непрерывными; тогда мы разобьем путь L на ко-
нечное число дуг, где функции xj (t) будут непрерывными.)
Интегралы вида (1) допускают следующую оценку через
длину s(L) пути L:
|$/1(жмх1+...+/„(/иихп|
max
Met
(2)
Действительно, если рассмотреть интегральную сумму,
составленную для некоторого разбиения П, мы получим,
применяя неравенство Коши (3.14 (6)),
р-1 п	р-\ Г п	Г п
С2 1/ 2 HW 1/ 2
j=0 ft=l	/ —0 F к=1	Г к=1
max
м
п	р— 1
ал7,
392
ГЛ. 9. ИНТЕГРАЛ РИМАНА
[9.96
где ДЛу. есть длина хорды	Поскольку сумма длин
этих хорд как длина ломаной МдЛ41 ... Мр не превосходит
длины s(L) самой дуги L, переходя к пределу, получаем
неравенство (2).
Далее, мы будем предполагать функции A (Af), .. .,fn (Af)
определенными и непрерывными не только на самой кривой L,
но и в некоторой ее окрестности, в которую попадают все
ломаные с достаточно мелкими звеньями, вписанные в L.
Пусть П={й = ^0^/1^ ^.tp = b}— разбиение отрезка
[а, #], на котором меняется параметр t, и пусть £п есть
ломаная с последовательными вершинами в точках А=А10,
Afj, ..., Мр = В кривой L, отвечающих значениям tQ, tlt ..tp
параметра t. Утверждается, что
lim J A (Af) dX1 + ... +/„ (Al) dxn =
«ЦП)->0
= J A (Al) dX1 + .. . +/„ (A4) dxn. (3)
L
Отсюда следует, что, зная интегралы по всем ломаным
в некоторой области пространства Цп, мы сможем найти
и интегралы по всем кривым, проходящим в этой области.
Соотношение (3) достаточно доказать для одного сла-
гаемого:
lim J fk(M}dXk=^fk(M)dXk.
(4)
В доказательстве индекс k будем подразумевать, не вы-
писывая его явно. Пусть задано 8 > 0; найдем 6 > 0 так,
чтобы при d (П) < 6
| J / (Al) dx -f (Mj) AxyI <8
(5)
и чтобы из p(Af, Al') < 6 следовало |/(Af)—/(Af')|<s.
Рассмотрим сначала одно звено ломаной £п, например
А1уА1у+1. Здесь мы можем написать, используя оценку (2),
J /(Al7)dx=/(A17) J dx =/(Al,) Дх7
AfjAfj+i	Af jM j+i
9.95]
ЗАДАЧИ
393
и
| $ /(M)dx-/(M7)AxJ =
= |	J	f(M)dx- J /(Afy)dx| =
= |	S	If (M) - f (M7)] dx | < 8 s (Mj
Суммируя по всем звеньям, получаем
Ир-i	I p-i
f(M) dx — 2 f(Mj) bxj < 8 2 s (ALAL+1) = 8 s (£n).
ьп	/=o	/=o
(6)
Так как числа s(£n)— длины ломаных £п— ограничены (их
предел есть длина дуги £), то неравенства (5) и (6) имеют
своим следствием соотношение (4). Поэтому верно и (3).
ЗАДАЧИ
1.	Если /(х)—периодическая функция на (— оо, оо), то функция
X
F(*) = p(&)dg
а
может быть представлена как сумма периодической и линейной
функций.
2.	Если f (х) и <р (х) Ss 0 ограничены и интегрируемы на [а, ft],
причем <р(х) не убывает, то существует точка ££(а, ft] такая, что
ь	ь
J f(x)<p(x)dx=<p(b—0) J f(x)dx.
а	Е
Если <р(х)^0 не возрастает, то существует точка i)€[a> Ч
такая, что
6	П
f (х) <р (х) йх=ф (a+0) f (х) dx.
а	О
3.	Если f (х) и ф (х) ограничены и интегрируемы иа [a, ft], причем
Ф (х) монотонна, то существует точка Jjgfa, ft] такая, что
ь	Е	ь
р (*) ф (*) dx=<p (a+ 0) р (х) dx+ф (Ь—0) J f (х) dx
а	о	J
(«вторая теорема о среднем»).
394	ГЛ. 9. ИНТЕГРАЛ РИМАНА
4.	Доказать формулу многократного интегрирования по частям
ь
У uu(n+1) (х) dx=
а
ь
= [uvM—. ~|~(—1)" u(n)o] |* + (— 1)”+1 J ы(п+1> vdx
а
при соответствующих предположениях о гладкости функций и и о.
5.	Для данной (ограниченной) функции / (х) и отрезка [а, f>]
полагаем
w If; а, ₽] = sup |f (х')—f(x")|.
х', к" € [а, ₽]
Доказать, что функция f (х) интегрируема на [а, Ь] тогда и только
тогда, когда
п-1
lim У to ff; х/+1] (х/+1—ху) = О,
<!(П)->0 у-=0
где ri={a = x0<X!< ... <х„ = й}, d(H) = max (х/+1 — ху) (критерий
i
Римана).
6.	Доказать, что монотонная ограниченная функция интегрируема.
7.	Если функция f (х) интегрируема, то н функция | f (х) | инте-
грируема.
8.	Колебанием функции f (х) в точке с называется выражение
to[f; с]= inf toff; а, ₽], а < с < (J.
а, р
Доказать, что ограниченная функция f (х) интегрируема на [a, 5]
тогда и только тогда, когда для любых е > 0 и 6 > 0 множество то-
чек с£[а, Ь], в которых toff; cj^e, можно заключить в конечное
число интервалов с суммой длин <6 (критерий Дю-Буа-Раймона).
9.	Доказать, что ограниченная функция f (х) интегрируема на
[а, Ь] тогда и только тогда, когда для любого 6 > 0 множество всех
точек разрыва функции f (х) можно заключить в конечное или счет-
ное множество интервалов с суммой длин (критерий Лебега).
10.	Пусть функция f (х) интегрируема. Доказать, что функция
1
-- — также интегрируема, если она ограничена.
/
11.	Интегрируя неравенство sin2"+lx< sin2”x< sin2B-1x по
промежутку 0<х<-^ н используя формулы 9.51 (1), (2), получить
формулу Валлиса (1656)
я	2-2-4-4 ... 2и-2п	_ ТТ *
"2 ~ „X ЬЗ-3-5 ... (2п-1)(2п + 1) - 11 “Т 
4ц2
ЗАДАЧИ
395
12.	Пусть функция f(x) непрерывна на отрезке [Д, В], содержа-
щем точки а н b (расположенные как угодно). Пусть, далее,
П = {с=х0, хг, .... x„ = b}—любой набор точек отрезка [Д, В]
(расположенных любым образом). Составим «обобщенную интеграль-
ную сумму»
л—1
sn(/)=	о
/=о
где точка расположена произвольно между точками х,- и x,+i.
п- 1
Доказать, что при	|х<+1—ху| <С и <1(П) = тах | ху-+1—ху|—>0
/=о
величина (1) имеет предел и
Ь
lim sn (Л = О (х) dx.	(2)
й(П)-0	j
п- 1
13.	Если в задаче 12 снять условие	| х,-+1—ху-|<С или
i=o
допустить кусочную непрерывность функции f (х), величина (1) уже
не будет иметь предела.
14.	(А кси ом этическое определение интеграла.)
Допустим, что каждой кусочно-непрерывной функции f (х) на отрезке
[а, Ь] и каждому промежутку [а, р| <z [с, Ь] поставлено в соответ-
ствие число (/), удовлетворяющее следующим условиям:
1) /₽ (kf) = fe/P (/) при любой постоянной k;
V (Л+'£(£)=/£(/+£) для любых кусочно-непрерывных
f(x) и g(x);
3)	/₽(1) = р-а;
4)	/а(0 = /а(/) + 4(Л при любых а < у < Р;
5)	| /₽ (Л | < С sup | f (х) | с фиксированной постоянной С.
Тогда для любой кусочно-непрерывной функции f (х)
₽
fy=\f(x)dx.	(3)
сс
15. Для точного вычисления числа л можно было бы использо-
вать ряд 9.74(6), но он сходится медленно. Показать, что справед-
ливо разложение
6 = ру + 3^5 ~ 3^7 “1	) =0,523599 ....
уже вполне пригодное для практического вычисления л.
396
ГЛ. 9. ИНТЕГРАЛ РИМАНА
Историческая справка
Геометрические задачи, которые в современных обозначениях
ь ь
записываются через J х dx или х2 dx, рассматривал еще в древно-
а	а
сти Архимед. Создание интегрального исчисления в нашем смысле
слова с его выходами в геометрию, механику и физику—дело XVII
века, и в основном Ньютона и Лейбница. Производную Ньютон
называл флюксией, первообразную—флюентой. Лейбницу принадле-
жат обозначения d и и свод правил неопределенного интегриро-
вания. Криволинейные интегралы появились впервые у Клеро (1743).
Точное определение интеграла как предела интегральных сумм
дано впервые Коши (1821). С этим определением, наконец, можно
было ставить вопрос о существовании интеграла для функций того
или иного класса. Коши предложил доказательство существования
интеграла для непрерывной функции; однако, за отсутствием поня-
тия равномерной непрерывности, доказательство Коши не было
корректным. Первое корректное доказательство существования инте-
грала от непрерывной функции было дано Дарбу (1875). Необходимые
и достаточные условия интегрируемости (разрывной) функции были
указаны в разных формах последовательно Риманом, Дю-Буа-Рай-
моном, Лебегом на протяжении второй половины XIX века. Стилтьес
цвел свое новое понятие интеграла в 1894 г. в связи с некоторыми
специальными задачами; в XX веке это понятие стало широко при-
меняться и в общих вопросах. В 1902 г. новое более широкое
понятие интеграла ввел Лебег; в современной математике оно играет
решающую роль, во-первых, потому, что совокупность интегрируемых
по Лебегу функций может быть оформлена в полное нормированное
пространство (см. часть третья, гл. 12), во-вторых, потому что это
понятие сделало возможным описание класса всех первообразных
функций по их внутренним свойствам. См. Б. Г. Гуревич и
Г. Е. Шилов, Интеграл, мера и производная, 2-е изд., «Наука»,
М., 1967, гл. 4.
ГЛАВА 10
АНАЛИТИЧЕСКИЕ ФУНКЦИИ
Мы можем, таким образом, сравнить аналитическую
функцию с организмом, отличительной особенностью
которого является как раз то, что воздействие на любую
его часть вызывает солидарную реакцию всего целого.
Г. Полиа и Г. Сеге
Задачи и теоремы из анализа (1924)
§ 10.1.	Определения и примеры
10.11.	В этой главе мы будем рассматривать функции
f(z), определенные на множестве Е в плоскости Сг комплекс-
ного переменного z и принимающие значения на плоскости
Cw комплексного переменного w.
Определим сейчас производную по множеству Ec.Cz от
функции f(x) в неизолированной точке z0£E.
а.	Определение. Число А называется производной
по множеству Ес.Сг от функции -w—f{z) в неизолирован-
ной точке z0 £ Е, если для любого 8 > 0 существует такое
6 > 0, что из | z — z01 < 6, z g Е, z^z0 следует неравенство
|д—Нг)—f (?о)1 < е число д обозначается при этом также
через f'E (z0). Число А, очевидно, есть предел отношения
f (г)—f (г0)	ц)
Z Zq
Е
по направлению z z0, которое определяется совокупно-
стью пересечений с множеством Е всех кругов \z—z01 р
с выброшенной центральной точкой z0. Это определение по
форме напоминает определение производной от вещественной
функции в вещественной области (7.11). Определение про-
изводной от функции вещественного переменного (7.11)
является частным случаем приведенного: чтобы получить 7.11,
в качестве Е нужно взять интервал вещественной оси, со-
держащий точку Ztf= х0. Однако при внешнем сходстве между
производной в вещественной и в комплексной областях име-
ется ряд существенных различий, которые будут ясны из
дальнейшего.
398
ГЛ. 10. АНАЛИТИЧЕСКИЕ ФУНКЦИИ
[10.11
б.	Если F есть часть множества Е и z0— неизолирован-
ная точка множества F (тем самым и неизолированная точка
множества Е}, то из существования производной /е (z) сле-
дует существование f'F(z) и равенство
fF(z)=f'E(z\
Таким образом, из дифференцируемости по большему мно-
жеству следует дифференцируемость по меньшему. Обратное,
конечно, несправедливо, что будет видно на простых примерах.
в.	Если функция w=/(z) дифференцируема в точке
z£E по множеству Е, то отношение (1) ограничено прн
z —> z0, например, постоянной С; тогда при z g Е и доста-
точно малых |z— z0|
|/(2)-/(zo)I < C\z — z0|,
и, следовательно, функция/(z) непрерывна на Е при z=z0.
г.	Определение. Функция -w=f (z), обладающая про-
изводной по множеству Е в каждой точке множества Е,
называется дифференцируемой в Е.
д.	Определение. В соответствии с определением 3.21
множество G в плоскости Сг, которое вместе с каждой точ-
кой z0 содержит некоторый круг |z—z0|<r (г может
зависеть от z0), называется открытым множеством, или
областью.
Область G называется связной, если любые две ее точ-
ки z0 и zx можно соединить друг с другом кусочно-глад-
кой линией, лежащей целиком в G.
е.	Определение. Если G есть открытое множество
в Сг, то функция /(z), дифференцируемая в О, называется
аналитической в G*}. Производная аналитической функции
по открытому множеству G обозначается через /' (z) (без
указания области О). Аналитическая функция в каждой
точке z0 g G дифференцируема по любому множеству Е, со-
держащему z0 в качестве неизолированной точки, и при этом
/е<2о) = /' <2о)-
ж.	Определение. Функция f(z) называется анали-
тической в точке z0, если существует область G^z0, в ко-
торой функция /(z) определена и аналитична.
) Синонимы: голоморфная функция, регулярная функция.
10.13]
§ 10.1. ОПРЕДЕЛЕНИЯ И ПРИМЕРЫ
399
1,
10.12.	Примеры.
а.	Функция f{z\ = z является аналитической всюду на
плоскости Сг, поскольку в этом случае
f (z) —/(z0) _z—z0
Z Zq z z0
и f (z) при каждом z0 равна 1.
б.	Функция f(z)=z = x— iy в любой точке z0 является
дифференцируемой по любому лучу Е, исходящему из точки z0,
так как
f(z)—f (zn)	z—z„ _	.	.
=-----2-= — 2 arg (z — zA,
z—z0 z—z0	°'’
и, следовательно,
7e(z0) = —2arg(z —z0).
Но это же равенство показывает, что f(z)—z не может
быть дифференцируемой по множеству Е, содержащему два
разных луча, выходящих из точки г0. Тем более z не явля-
ется аналитической функцией от z ни в какой точке z0 С Cz.
10.13.	Общие свойства производной. Формаль-
но теми же рассуждениями, что в 7.13 и 7.15, получаются
следующие правила действий с функциями, дифференцируе-
мыми по множеству Е в точке z0.
а.	Если функции f(z) и g(z) дифференцируемы при z = z0
по множеству Е, то функции af{z) (а — любое комплексное
число), f(z) + g(z), f(z)g(z), также дифференцируе-
ё
мы по множеству Е при z = z0 (в последнем случае предпо-
лагается, что g(zo)^0). При этом имеют место формулы
(для z = z0):
(af(z))’E = af'E(z);	(1)
(f(z) + g(z))'E=fE{z}+gE(z};	(2)
(f(z) gWE =fE (z}g(z) + f(z) gE (z);	(3)
(	= 4/z)g(z)—/(z)gE (z)
U(z)/£	g2(z)	‘	'
б.	Если функция w =/ (z) дифференцируема по мно-
жеству E при z=z0, а функция p = <p(w) определена
400
ГЛ. 10. АНАЛИТИЧЕСКИЕ ФУНКЦИИ
[10.14
в множестве F, содержащем все точки w—f(z) для z£E,
достаточно близких к z0, и дифференцируема по F при
iD = ii)0=f(zb), то сложная функция p(z) = <p (/(.?)) диффе-
ренцируема по Е при z=z0 и
Ре(*о)=Ф>(^о)-/е (*<>)-
в.	Из правил (1), (3) и 10.12 а следует, что всякий мно-
гочлен Р (z)—aozn + " х+... ап является аналитической
функцией с производной
Р' (z)=(aozn + a1zn~1+ ... 4-а„)' =
= naoz"-1 + (n—l)a1zn-z+ ... 4-fln_v
г.	Далее, из правила (4) следует, что и всякая рацио-
,	Р(г)
нальная функция, т. е. отношение двух многочленов
P(z) и Q(z), является аналитической всюду, кроме корней
знаменателя Q(z).
10.14.	Высшие производные. Высшие производные
функции f(z) по множеству Е определяются, как и в случае
вещественного переменного, индуктивно:
Л"+" = [Лп) (2)]е (Л = 1, 2, . . . )
в предположении, что эти производные существуют. Функ-
ция /(г), имеющая по множеству Е производные до порядка п,
называется п-кратно дифференцируемой по множеству Е.
Для л-кратно дифференцируемых по множеству Е функ-
ций f(z) и g(z) справедливы формулы:
[а/(£)]£* = ctf(E (z) (а — любое комплексное число); (1)
[/(г) + g (*)]£ ’ = Лп) (г) + d?’ (г);	(2)
[/(г)-^(г)]’Еп) =	(г) g{E~k} (z).	(3)
Эти формулы доказываются так же, как доказывались соот-
ветствующие формулы для функций вещественного перемен-
ного в 8.12.
10.15.	Дифференциал.
а.	Как и в случае вещественного переменного (7.31),
10.16]
§ 10.1. ОПРЕДЕЛЕНИЯ И ПРИМЕРЫ
401
приращение функции w=f(z), дифференцируемой по мно-
жеству Е в точке гй, можно представить в форме
f(z} — f(z0)=f'E (z0) (z —z0) + e (z, z0) (z—z0),
где e(z, z0) — величина, стремящаяся к нулю при z—>z0.
Первое слагаемое есть главная линейная часть приращения
функции. Величина z—z0 обозначается через dEz или, ко-
роче, dz, величина /e(z0)-(z—z0) — через dw или dw(zb).
Таким образом, производную fE (z0) мы можем написать
в форме
dw___dw
dEz dz
/е (z0)
б.	Так же как и в 7.33—7.34, устанавливается справед-
ливость следующих формул:
Для любой дифференцируемой по множеству Е функции
w=/(z) и любой комплексной постоянной а
d (aw) = adw;	(1)
для любых двух дифференцируемых по множеству Е
функций и w2
d (wt + w2) = dwx + dw2,	(2)
d (w1w2) = wxdw2 + d-Wi • w2;	(3)
. fwA w,dw-l—w1dw2 .	. . ,
d U/=—(при (Zo) 0)- (4)
в.	Если w=f(z) дифференцируема по множеству E при
z — z0, a функция p=<p(w) определена на множестве F,
содержащем все точки w=f(z), и дифференцируема по F
при w=w0=/(z0), то dp = <p' (w) dw=q>' (w) w' (z) dz, так
что дифференциал функции не зависит от того, является ее
аргумент независимым переменным или функцией другого
независимого переменного.
10.16*. Условия Коши—Римана. Вначале введем
определение частной производной.
Для функции F(x, у), определенной в области G плоско-
сти вещественных переменных х, у, выражение
Iim F(x0+h, y0)—F(x0, у0)
402	ГЛ. 10. АНАЛИТИЧЕСКИЕ ФУНКЦИИ	[10.16
если оно существует, называется частной производной от
функции F(x, у) по переменному х в точке (х0, y0)<z.G.
Аналогично выражение
lim F(x0, yB+h)—F(xB, у„)
ft-^o	h
называется частной производной от функции F(x, у) по
переменному у в точке (х0, у0) £ G. Первое из указанных
„	*	dF (хв, ув)
выражений обозначается через —, второе — через
'X У0) ИЛИ’ короче’ через Fx=F* (хо, Jo) и Fy=Fy (хо, Jo)-
Пусть w=/(z)=«(z) + /w(z)=o(x, y)-]-iv(x, у) диф-
ференцируема при z= z0 = х0 + «у0 по множеству Е, содер-
жащему точку z0 и некоторые отрезки, включающие эту
точку и параллельные вещественной и мнимой оси.
Положим z= z0-{-h£E, где h вещественно. Тогда z =
= z0-|-A = (x0 + A, у0) и
f (z)—/(г») __n(zB+fe)—“(z0) , .t>(z„+ft)—t>(zn)
z—z0	h '	h 	\ >
Существование предела отношения (1) приводит к сущест-
вованию пределов
u(xB-\-h, у„)—и(х6,у0) _ди(хв, ув)
h “о	h	дх ’
Iim	Уо)—У(хв, ув)  dv(x„, у0)
h дх
и равенству
(2)
Положим z = z0-\- ih£E, где h вещественно. Тогда
z = z0+ ih = (x0, у0 + h) и
/(z)—Hz0) = M(z0 + ife)—и(г0)	. v(zB+ih)—v (z„) =
z—z0	ih ’’	th
___u(xB, y0-\-h)—и (xB, t/0) . t> (x0, yB-\-h)—v (xB, yn)
~	ih	'	h
10.17J	§ 10.1. ОПРЕДЕЛЕНИЯ И ПРИМЕРЫ	403
Существование производной fE (z0) приводит к существованию
пределов
Ит «(-Ч). yo+h}—u(xQ, у0) ди(х0, уп)
h-+o	h	дУ
ffa. Уо+ft)—t>(xn, у0) _ dv (x0, yn)
h™	h	dy
и равенству
f \— idU <X0' У") I dV (*0. Уп)	/OS
/e(Z0)_ —4—-----------------•	(3)
Сравнивая (2) и (3), находим, что в каждой точке z0, где
существует f'E(z0), выполняются равенства
ди (хо, Уп) _ dv (х0, у„)
дх	ду	’	(4)
dv (хв, у„)   ди (х0, уд)	'
дх	ду ’
называемые условиями Коши — Римана.
10.17*. В частности, если функция f(z) аналитична
в окрестности точки z0, то условия Коши — Римана выпол-
няются в каждой точке этой окрестности. Оказывается, что
и обратно, выполнение условий Коши — Римана в окрестности
точки z0 при дополнительном условии непрерывности функ-
ди ди dv dv ,	.	.
ций дх ’ ду ’ дх ’ ду обеспечивает аналитичность функции f(z)
в этой окрестности. В самом деле, пусть h=p-{-iq настолько
мало, что z0-|-/z лежит в пределах указанной окрестности.
Составим разность
/(Z0 + ft)-/(Z0) =
= [и (*4^Ж+«,(*+м+?)]~[«(-«, j) + Zv(x,y)] =
= [и(х+р, y + q) — и(х, j)]+i [«’(*+/’, y + q)—v(x,j)].
(1)
Преобразуем выражения в квадратных скобках следующим
образом. Мы имеем
\и(*+Р, y + q) — u(x,y) =
= [«(*+/>,	u(x,j + 9)] + [u(x,^ + ^)—W(X,Jf)].
Применим к первой из разностей как функции от х формулу
Лагранжа 7.44-, получим
y-\-q)—u(x,y^q) = ux(xA-^iP, y + q)P,
404
ГЛ. 10. АНАЛИТИЧЕСКИЕ ФУНКЦИИ
(10.17
где их означает производную по х, а 0!—число между 0 и 1.
Аналогично, применяя формулу Лагранжа по переменной у,
находим
u(x,y-\-q) — и(х, у) — иу(х, y-\-62q)q.
Аналогичные преобразования произведем со второй квадрат-
ной скобкой в (1). В результате получим
f (z + h) — f (z) = [ux (x + 0XP, у + q) P + uy (x, у + 02?) q] +
+ 1 [vx (х + взР, y + 4)P + vy(x,y + Qtq) ?].
Используя условия Коши—Римана, можно эту же разность
записать так:
f(z + h)—f{z) = [ux(x + eip, y + q)p + uy(x,y + e2q)q] +
+ К (* У + 04?) q—иу (х + 03р, у + ?)/>].
В силу предположенной непрерывности функций их и иу мы
имеем, далее,
/ (z + Л) — f (z) = их(х, у) (р + iq)—iuy (х,у)(р + iq) +
+ 81(Р, ?)/’ + ег(Р.?)?.
где е,г(р, q) и е2(р, q} стремятся к 0 вместе с р и q. По-
этому
f(z-f-ft)—f(z)	.	,	. .	, , ej (р, о) р + е» (р, q) а
= их (х, у)—iuy (х, у} +
Оценим последнее слагаемое. Мы имеем	—-т- <11,
ImTjI*1’ “’“У"
I	1 < I е. (₽, 9) I +1 в,(Л ,) I.
Так как последняя величина стремится к 0 вместе с р и q,
то при h —> 0 величина (2) имеет предел, равный их—iuy.
Это и означает существование производной у функции f(z)
при z = z0, равной ux(z0) — iuy(z0). Теорема доказана.
Можно сформулировать вариант условий Коши — Римана
в виде критерия, необходимого и достаточного для анали-
тичности, введя понятие дифференцируемой функции двух
переменных. (См. задачу 6).
10.18]	§ Ю.1. ОПРЕДЕЛЕНИЯ И ПРИМЕРЫ	405
10.18*. В дальнейшем (10.34) мы увидим, что всякая
аналитическая функция f(z) имеет и производные второго
(и любого высшего) порядка. Посмотрим здесь же, какие
вытекают отсюда следствия для вещественной и мнимой
части функции f(z). Мы обозначим через —вторую
частную производную функции и(х,у) по переменному х
(т. е. вторую производную от функции и(х,у) по перемен-
ному х в предположении, что второе переменное у не меняет-
ся и поэтому функция и(х,у) есть функция только от х).
Аналогичный смысл имеет вторая частная производная
дги(х, у)
ду* 
Рассуждая так же, как в 10.16, мы получаем равенства
f"i\	if / w	д (ди	.dv\	дги . d2v
f(z)=(f (z)) =ч- д—H	=
J ' '	v ' "	dx \dx	dx j	dx*	1 dx2
_ 1 d / 1 du .______ дги	. d2v
i dy \ i dy'dy)	dy"1	1 dy*
Сравнивая вещественные и мнимые части, находим
д2ы . й2и_» d2t> d2t>______
+	— dx2 ' dy2-
Вообще, уравнение
д2Ф(х. у) , д2ф(х, у)
дх* ду2
называют уравнением Лапласа-, непрерывные вещественные
функции, удовлетворяющие ему в данной области G, называ-
ются гармоническими функциями в области G. Мы видим, что
мнимая и вещественная части аналитической функции в обла-
сти G суть функции, гармонические в этой области.
Обратно, каждая гармоническая функция и(х, у) в об-
ласти G является вещественной частью некоторой аналити-
ческой функции f(z) (и, разумеется, мнимой частью анали-
тической функции if(z)). Мы убедимся в этом в 14.49 в
(часть третья).
Две гармонические функции и(х, у) и v(x,y), являю-
щиеся вещественной и мнимой частью одной аналитической
функции f(z), т. е. связанные условиями Коши—Римана
10.16, называются сопряженными гармоническими функциями.
406	ГЛ. 10. АНАЛИТИЧЕСКИЕ ФУНКЦИИ	[10.21
§ 10.2. Криволинейные интегралы
от комплексных функций
10.21. Мы будем рассматривать криволинейные интегралы
по кусочно-гладким путям (9.91) в комплексной области.
В 9.91 были определены криволинейные интегралы
Стилтьеса вида
\f(M)dg(M),
L
где /[Ж(01—кусочно-непрерывная функция, а ^[Ж(0]—
функция с непрерывной производной, обе вещественные. Этот
интеграл приводится к обычному определенному интегралу
ь	ь
[Ж(0] dg [Ж(/)] = р [Ж(/)] -в[~^dt,
а	а
где [а, 6] — отрезок изменения параметра t, которому отве-
чает путь L. Сейчас мы обобщим это определение на слу-
чай, когда функции /(Ж) и g(M) принимают комплексные
значения.
Если функция /(Ж) принимает комплексные значения
/(Ж)=/1(Ж) + //2(Ж), где j\(M) и f2(M) вещественны, то
криволинейный инте'грал Стилтьеса определяется по фор-
муле
$/(Ж) dg(M) = $ Д (Ж)dg(M) + i\f*(Ж)dg(M)
L	L	L
(функция g(M) вещественна). Аналогично, если /(Ж) веще-
ственна, a g(M) комплексна, так что ^(Ж) = §-1(Ж)4-/§-2(Ж),
то полагаем
$ f (Ж) dg(M) = \f(M) dgl (М)+i\f (М) dg2 (Ж).
L	L	L
Когда обе функции /(Ж)=/1(Ж) + //а(Ж) и §-(Ж) =
= gt (Ж) -]-igz (Ж) принимают комплексные значения, естест-
венно получается определение
$ /(Ж) dg(M) = $ а (Ж) dgl (Ж) -а (Ж) dg2 (Ж) +
L	L
+ / { A (Ж) dg2 (М) 4-А (Л1) dgr (Ж).
L
10.21]
§ 10.2. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
407
На плоскости (л = 2) для g(x, y) = z = х-\-iy v.f(x,y) =
= и. (х, у)iv (х> у) получаем формулу
^f(x,y)dz = udx—vdy-\-i udy-\-vdx. (1)
L	L	L
В этом случае возможно дать и прямое определение ком-
плексного интеграла (1), именно
$/(x,_y)dz = Игл £/(>: , .у) Аг-,	(2)
L	4(П)-»о
где П—некоторое разбиение пути L, Zj—(Xj,yj) есть
j-я точка деления и &Zj=Zj+1—Zj. Действительно,
5 f(xj, У]} &/= 2 и (Xj, jy) Ах,— 2 v (х, у Л Ду +
/ = 0	/ = 0	7 = 0
+ / 2 «(Xj; у/> Ьу}- 4- i 2 v (Xj., yj) ЛХ/,
1=0	j=0
что при d (П) —* 0 имеет пределом как раз величину (1). Из
представления (2) легко получаются основные свойства инте-
грала: равенство
$ [«х/i (* J) 4- «2/2 (*, J)] dz =
L
=“1 $ /1 (*> j) dz 4~ «2 $ Мх, У) dz (3)
L	L
для любых интегрируемых функций j\(x,y) и f2{x,y) и лю-
бых комплексных постоянных ах и аа; равенство
$ f{x,y)dz = J f(x,y) dz+\jf(x,y)dz, (4)
Е	L,	L2
где L — кусочно-гладкий путь, состоящий из двух примыкаю-
щих друг к другу частей Lr и £а с тем же направлением
интегрирования; оценка
^$|/(x,jO|ds^sup !•«(£)» (5)
L	L	Z^L
где s(L) — длина пути L.
Иногда для уточнения какого-либо свойства пути интегри-
рования или просто для большей наглядности используются
408
ГЛ. 10. АНАЛИТИЧЕСКИЕ ФУНКЦИИ
[10.22
специализированные знаки интегралов, например
L L L L L L
И Т. П.
Здесь первое из обозначений указывает, что интеграл
вычисляется по замкнутому контуру L; второе и третье
уточняют направление интегрирования; четвертое и пятое
показывают, что интегралы берутся по некоторым прямым
в указанных направлениях; шестое—что интеграл берется
по замкнутому пути, представляющему собой полуокружность
с ее диаметром, в указанном направлении. Вообще смысл
того или иного специализированного обозначения становится
ясным из контекста или чертежа.
10.22. Рассмотрим последовательность функций fn(z),
определенных на множестве, представляющем собой кусочно-
гладкий путь Lc:Cz. Пусть функЦии /п(г) равномерно на
этом пути сходятся к функции f(z). Если функции fn(z)
непрерывны на L, то и предельная функция f(z) непрерывна
на L (5.96).
а.	При сформулированных условиях имеет место равен-
ство
$/(2)dz = lim \fn(z)dz.
L	L
Действительно, из 10.21 (5) получается оценка
5 [f(z)—fn(z)]dz S^max|/(z)—fn(z)\-s(L),
I	A
которая и приводит к нужному результату.
б.	Если при этом функции fn(z) и f(z) зависят от неко-
торого параметра А, пробегающего множество Л., так что
в более точной записи fn(z)=fn(z,k), f(z)=f(z,"k), и
сходимость fn (z, К) к f (z, А) равномерна относительно А,
так что
sup |/„(z, A)— f(z, А) | —> 0,
г, К
то и функции
F„(K) = \f„(z, ?.)dz
L
10.23]
§ 10.2. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
409
сходятся к функции
— $/(*> tydz
L
равномерно по Х£Л.
Это следствие той же оценки 10.21 (5):
$ [f<z,	k)] dz I < sup (z, h)—/(z, A) | .$ (L).
L	| z.X
10.23.	Теорема о ср ед нем. Если f(z) кусочно-не-
прерывна на гладком пути L = {z:z — z(f),	и
если z'(fo)=£O, a f(z) непрерывна при z — z0 = z (t0), то
lim
г->-г0
J
L (z,z0)
где L(z,z0)— участок пути L между точками z и zQ.
Доказательство. Для случая /(<г)=/(г0) = const
утверждение теоремы вытекает непосредственно из опреде-
ления интеграла. Поэтому в общем случае можно считать,
что f (z0) = 0, вычитая в противном случае постоянную вели-
чину f(z0) из функции f(z). Для заданного 8>0 найдем
б > 0 так, чтобы из z£ L, [z—z0[ < б следовало |/(z)| < 8.
Тогда по 10.21 (5)
f(z)dz <
8-S(£ (z, z0)).
L (Z,ZO)
Поэтому
I 5 f^dz
I t(Z, z„)
S(L(Z,Z0))
|2—Z0|	| 2 — 20| *
(1)
Но по предположению о гладкости пути L отношение длин
участка пути и стягивающей этот участок хорды стремится к 1
при z —> z0 (9.63 е). Поэтому при достаточно малых \z—z0\
оценку (1) можно заменить оценкой
1
2—20
J f(z)dz
L (z,z„)
<28,
откуда и следует утверждение теоремы.
410
ГЛ. 10. АНАЛИТИЧЕСКИЕ ФУНКЦИИ
[10.24
10.24.	Рассмотрим функцию /(z, £) двух комплексных
переменных; переменная z = x-\-iy пробегает в z-плоскости
кусочно-гладкий путь L, а переменная £ = g it) пробегает
в ^-плоскости кусочно-гладкий путь А. Предполагается, что
функция f(z, £) непрерывна по совокупности аргументов,
т. е. для любого е > 0 можно указать 6 > 0 так, что
из \z—z'[^6,	z,z'£L, £, следует
|/(г\ С )—f(z, £)|<e. Тогда каждый из интегралов
/(S)=J/(Z,?)dZ, J(z) = $/(z, t,)d£	(1)
L	Л
представляет собой непрерывную функцию от соответствую-
щего переменного и
J H/(z, £)d£ldz=$ H/(z,t>)dz\dt>. (2)
Аналогичная теорема для функций вещественных пере-
менных у нас была доказана в 9.82. Поскольку, как мы
видели выше, интеграл по комплексному пути линейно выра-
жается через интегралы по вещественному переменному,
наше утверждение немедленно следует из теоремы 9.82.
10.25.	а. Пусть w=f(z)—функция, дифференцируемая
по множеству Е, содержащему кусочно-гладкий путь L с нача-
лом в точке z0 и с концом в точке zr. Тогда справедлива
формула Ньютона — Лейбница
^fL(z)dz = f(z1)—f(z0).
L
В самом деле, пусть z = z{t), t0^t— параметри-
ческое представление пути L с кусочно-гладкой функцией z(t},
и пусть F(t) = f(z (/)). Тогда, по теореме о производной
сложной функции 10.13 б,
fi(z)dz(t) = dF(t),
откуда
t,
J4 (z) dz = J dF(t) = F(fl)-F(io)=f(zl)~f{z0)t
I-	ц
что и требуется.
10.26]
§ 10.2. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
411
б.	В частности, если w=/(.?)—аналитическая функция
в области О, то мы имеем
$ /' (z)dz=f(Z1)— f(z0)
L
для любого кусочно-гладкого пути L, соединяющего точки
z± и z0 (и проходящего целиком в области G). Отсюда сле-
дует, что интеграл от f (z) по всякому замкнутому кусочно-
гладкому пути Lc.G равен 0.
в.	Так, интеграл по замкнутому пути L от всякого мно-
гочлена
P{z) = a0 + a1z+ ... +a„zn
равен 0, поскольку многочлен P(z) есть производная от
многочлена
г2
Pi(z)=aoz + «Х-2--4-
zn + t
• • • +ап «+т•
10.26.	Свойство 10.25 6 можно обратить. Пусть в связной
(10.11 д) области G задана функция <p(z), относительно
которой известно, что ее интеграл по всякому кусочно-глад-
кому замкнутому пути L в области G
равен 0:
ф ср (z) dz = 0.
L
Утверждается, что существует функ-
ция f(z), определенная и аналитиче-
ская в области G, такая, что /' (z) =
Рис. 10.1.
Для доказательства фиксируем в
области G произвольно точку z0 и рассмотрим любую дру-
гую точку z и кусочно-гладкий путь £г £ G, соединяющий
z0 с z. Положим
7(г)=$ф(М.
Значение f(z) не зависит от выбора пути, ведущего из г0
в z. Действительно, из двух таких путей zopz и zQqz можно
образовать замкнутый путь гдгйрг (рис. 10.1), интеграл по
412
ГЛ. 10. АНАЛИТИЧЕСКИЕ ФУНКЦИИ
[10.27
которому, по условию, равен 0; следовательно,
Jq>M= J J ч>ю^= $<р(М-
z„pz	z„qz	zqz^pz	z„pz
Докажем, что f(z)— аналитическая функция.
Возьмем для данного z число р > 0 так, что круг ра-
диуса р с центром в точке z лежит еще в области G.
Пусть, далее, h—комплексное число, [й|< р. Поскольку
путь из z0 в z~'rh можно выбирать в области G произвольно,
мы построим его присоединением к уже имеющемуся пути
из z0 в z отрезка, соединяющего z и z-\-h. Тогда
f(z+h)-f(z)= J ф(М-$ф(М= J ч>(М
ZO	20	2
И
z+ft
S f(cm.
Z
Эта величина при Л -> 0 имеет предел, равный ср (z) в
силу 10.23, откуда и следует аналитичность f(z).
10.27.	Рассмотрим функцию двух комплексных переменных
f(z, £): переменная z = x-\-iy пробегает в z-плоскости об-
ласть G, переменная £ пробегает кусочно-гладкий путь Л.
Предполагается, что функция f(z, £) при каждом ££ Л ана-
литична в G и что ее производная f'z(z, £), как и сама
функция f(z, £), непрерывна по совокупности аргументов z g G,
£ёЛ. Образуем функцию
Ф (*)=$/(*,
л
Теорема. При указанных условиях функция Ф(г) ана-
литична в области G.
Доказательство. Рассмотрим функцию
Ф(*)=
л
10.28]
§ 10.2. КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ
413
Мы утверждаем, что для любого замкнутого пути LtzG
имеет место равенство
J ф (z) dz = 0.
L
Действительно, по 10.24 и 10.25 б
= 0.
L
Л
В силу 10.26 существует функция Фо (z), аналитическая
в области G, для которой функция ф(г) есть производная,
причем снова по 10.24
z	г
фо U) = ( ф (a) da == (
г.	I
Л
р/г(а, QWjda^
dald£=J/(z, g)dg-J/(z0,g)dg.
‘ Л	Л
Поскольку Ф0(г) отличается от Ф(г) на постоянную, мы
видим, что Ф(г) вместе с Ф0(г) есть аналитическая функ-
ция в области G.
10.28.	Рассмотрим функцию, определенную выражением
F^=^dl,	(1)
где /(g) непрерывна на кусочно-гладком пути Л, а точка z
лежит вне этого пути. Функция F(z), таким образом, опре-
делена в области О, дополняющей контур Л до всей пло-
скости Cz. Через Gp обозначим совокупность тех точек
области G, для которых sup|z— g| > р. Любую наперед
заданную точку z£G область Gp включает в себя при до-
статочно малом р. Заметим теперь, что функция
/С,
аналитична по z в области G и, более того, обладает в G
производной любого порядка:
f <П) /«	__	f (С)
/г Vе > W (g____г)п + 1 "
414	ГЛ. 10. АНАЛИТИЧЕСКИЕ ФУНКЦИИ	(10.31
Эти производные, очевидно, непрерывны по совокупности
аргументов z£Gf при любом р и аналитичны по z
в области G. Применив теорему 10.27, получаем:
Теорема. Функция F(z), определяемая выражением (1),
аналитична в области G и, более того, обладав! производ-
ными всех порядков, которые также являются аналитичес-
кими функциями. При этом
FM(z) = n\
' ' J (С—z)ra+l
A
Интеграл (1) называют обычно интегралом типа Коши.
§ 10.3.	Теорема Коши и ее следствия
В этом параграфе собраны центральные результаты те-
ории аналитических функций (открытые в основном Коши.)
10.31. Связная область G (10.11 д) называется односвяз-
Рис. 10.2.
ной, если любой многоуголь-
ник, контур которого лежит
в области G, можно предста-
вить в виде конечного объе-
динения треугольников, принад-
лежащих данной области вместе
со своей внутренностью. Так, от-
крытый круг и любая выпуклая
область (т. е. вместе с любыми
двумя точками содержащая сое-
диняющий их отрезок) односвяз-
ны, а, например, круговая по-
лоса rt < | z | < г2 неодносвязна
(рис. 10.2).
10.32.	Теор емаКоши. Для аналитической функ-
ции/(г) в односвязной области V
$ f(z)dz=0
L
по любому замкнутому пути L, целиком расположенному
в области V.
Доказательство. В 9.95 мы доказали, что интеграл
по кривой линии есть предел интегралов по ломаным; поэтому
10.32]	§ 10.3. ТЕОРЕМА КОШИ И ЕЕ СЛЕДСТВИЯ	415
нам достаточно доказать теорему Коши для многоугольника.
Так как область V односвязна, то в пределах этой области
можно разбить многоугольник L на треугольники Т1г .Тт;
при этом (рис. 10.3)
(fif(z)dz=(J) f(z)dz+ ... +(fif(z)dz
L	Tt	Tm
(интегралы по внутренним сторонам взаимно сокращаются,
так как эти стороны проходятся дважды и в противоположных
направлениях); поэтому достаточно доказать теорему Коши
для треугольника.
Рассмотрим произвольный треугольник Т в области V и
обозначим его периметр через р, а абсолютную величину
интеграла
$ f(z) dz
г
через с. Разобьем треугольник 7 на четыре равных тре-
угольника 7j, Т2, Т3, 74, соединяя отрезками середины его
сторон (рис. 10.4). Тогда
и, следовательно, хотя бы для одного из них, например для
Т(, выполняется неравенство
$f(z)dz
Ti
416
ГЛ. 10. АНАЛИТИЧЕСКИЕ ФУНКЦИИ
[10.32
Треугольник Tt мы также разобьем на четыре равных
треугольника 7П, ..., T{i и найдем среди них такой, поло-
жим Тц, для которого
/ f{z)dz	ff{z)dz
Гц	Tt
Этот процесс будем продолжать неограниченно; мы полу-
чим последовательность вложенных друг в друга треуголь-
ников, положим ТХ=Т{, 72=7',у, ..., для которых
M/{z)dzl>-£.
(1)
Каждый треугольник Тп (взятый с внутренностью) есть
компактное множество в плоскости Сг = /?2 {5.14 д), и в силу
3.98 на плоскости имеется точка г0, лежащая во всех этих
треугольниках.
В этой точке, как и во всех точках области V, функция
f{z) дифференцируема, и из определения производной мы
можем получить, что для любого е > 0 существует S > 0
такое, что при |г—z0|<6
Л*) =/(*o)4V4*o) (*“*<>)+Я1(*> *о),	(2)
где ]/?i (z, z0) | < е|z—z0| {10.15}. Остаток —во всяком
случае непрерывная (по z) функция вместе с другими частями
равенства (2). Оценим теперь интеграл от f {z) по треуголь-
нику Тп, содержащемуся в круге радиуса 6 с центром в z0,
используя соотношение (2). Мы имеем
^f(z)dz = ^f{z0)dz+f'(z0)^{z—z0)dz+^R1{z, z0) dz.
Тп	ТЛ	Тп
Первые два слагаемых в силу 10.25 в равны 0. Так как
периметр треугольника Тп равен то в силу оценки (2)
для Rx
§ f{z}dz =	.
Т»	Тп	I
Сравнивая это неравенство с неравенством (1), получаем
с
4"
Ра
4" ’
С Ер2.
10.33]
§ 10.3. ТЕОРЕМА КОШИ И ЕЕ СЛЕДСТВИЯ
417
Так как е можно взять произвольно малым, то с = 0, и те-
орема Коши доказана.
10.33.	Формула Коши.
а.	Круг |z— а|<7? с исключенной точкой z = a являет-
ся одним из примеров неодносвязной области. Функция
-—аналитична в этой области (и неаналитична
(г—а)т '	'
во всем круге ]z—а [</?). Вычислим интеграл
dz
(г—а)т ’
где L есть окружность радиуса г < R с центром в точке а.
В качестве параметра возьмем полярный угол <р; тогда
z—а = ге1^, (z—a)m = rmeim<fl, dz = trendy, и мы получаем
2л
т——=	С	dtp	—
у (z—a)m	J	Y
l	<p=o
( , „ pi 12л
-------------J =0	(m#=l),	(1)
i(l —m)|o	'	'	'
= < 2л
I i ^d<p = 2ra	(m=l).	(2)
\ о
При m = 1 наш интеграл равен 2га #=.0, что, между
прочим, показывает существенность условия односвязности
в теореме Коши.
б.	Отметим, далее, следующее	т J
важное общее свойство интегралов ..........."	\
по замкнутым путям в неодносвяз- /7,	—\
ных областях. Если в области V (	Г[_
(вообще говоря, неодносвязной) оп- \.	S J
ределена аналитическая функция	S
f{z) и заданы два замкнутых ку-
сочно-гладких пути Lr и L2, как	Рис. 10.5.
показано на рис. 10.5, которые
вместе с некоторой соединяющей их кусочно-гладкой ли-
нией Т ограничивают односвязную область, то
ф f(z) dz = faf(z)dz.
(3)
418
ГЛ. 10. АНАЛИТИЧЕСКИЕ ФУНКЦИИ
[10.33
Действительно, имея указанную односвязную область,
установим на ограничивающем ее сложном замкнутом кон-
туре L следующее направление обхода: контур будем
проходить в положительном направлении (против часовой
стрелки), контур А2—в отрицательном направлении (по ча-
совой стрелке), а соединяющую их линию Т—дважды в
противоположных направлениях (рис. 10.5). По теореме
Коши 10.32
0 = £f(z) dz = ф f(z) dz-}- $ f(z) dz + f (г)dz f(z)dz,
L	Lt	т	т	l2
откуда и следует (3), если учесть изменение знака криво-
линейного интеграла при перемене направления обхода
(9.91).
На рис. 10.5 дан не самый общий случай взаимного рас-
положения контуров Z.J и L2, но нам и этого случая будет
достаточно.
в.	Этим соображением мы воспользуемся для вычисления
интеграла
L г~а
по пути L, обходящему вокруг точки а в положительном
направлении. Функция /(?) предполагается аналитической
в односвязной области V, содержащей точку а и контур L.
.	f(z) ,	,
Функция г -, вообще говоря, имеет особенность при z = а
(т. е. может в этой точке не быть дифференцируемой),
поэтому интеграл / может быть не равным нулю. Но так как
f (<г)
г__а аналитична вне а вместе с функцией /(z), то по ска-
занному. выше интеграл I не изменится, если мы сожмем
контур L в окружность малого радиуса е с центром в точке а.
Положим
/(г)=/(ц) + /?(д).
Функция непрерывна вместе с функцией f(z) при z^= а,
а при z—>а имеет предел f (а), поэтому она ограничена в
10.34]
§ 10.3. ТЕОРЕМА КОШИ И ЕЕ СЛЕДСТВИЯ
419
I R (г) I____	~
окрестности точки а; пусть, например, ^/И. 1огда
f (z)rfz
z—а
Ф
[z-a|=e
f (z) dz __
z — a
= /(») Ф Ф	(4)
|z-a|=e	|z-a|=e
Первое слагаемое, с учетом 10.33(2), равно 2ш'-/(п). Со-
гласно оценке 10.21 (5) для второго слагаемого мы получаем
ф

г—а
М • 2ле;
таким образом, второе слагаемое стремится к нулю вместе
с Е. Но так как остальные два члена в равенстве (4) посто-
янны, то второе слагаемое справа также постоянно; следо-
вательно, оно равно нулю, и мы получаем ответ
f (z) dz 
г—а
2nif(a),
или
/<“)=ЙФ
f(z)dz
z—а
(5)
Формула Коши (5) является одной из важнейших формул
теории аналитических функций: она выражает значение ана-
литической функции внутри контура L в форме интеграла
по контуру L от ее граничных значений.
10.34.	Теорема. Функция w=f (z), аналитическая в
области G, обладает в этой области производными любого
порядка, которые также являются аналитическими функциями.
При этом
где интеграл берется по любому пути L, обходящему в об-
ласти G вокруг точки z в положительном направлении.
Действительно, формула Коши 10.33(5) показывает,
что f(z) представима в области G интегралом типа Коши,
и остается применить теорему 10.28.
420	ГЛ. 10. АНАЛИТИЧЕСКИЕ ФУНКЦИИ	[10.35
10.35.	а. Теорема. Всякая функция w = f(z), анали-
тическая внутри круга У = {г:|г—г'о|^г}> разлагается
в степенной ряд
/(*) = |Х (*-*<>)".	(1)
сходящийся внутри круга V.
Доказательство. Мы исходим из формулы Коши
J ' 2niu £—z ’
справедливой для контура Л = {£:|£—z0| = r—6} и любой
внутренней по отношению к Л точки z. При этом
1   1_________1_____ 1	( г—z0 \л
£—z	z0	z—z0 — £—z0 2- V Zo J ’
1 Г	п = 0
Полученный ряд сходится равномерно по £ на Л в силу
оценки
и признака Вейерштрасса 6.53. В силу теоремы 10.22 б
Л п=0
-VU-Z 1" 1 Ах
Z0) 2nj<y(^-z0)«+i’
/1=0	Л
что и дает искомое разложение. При этом мы получаем и
формулу для коэффициента ап:
п - 1 Ах Ж	/91
" 2ntY^-z0)«+i-	<2)
Л
б. В силу 10.34 мы имеем
Это позволяет усилить формулировку теоремы а:
Теорема. Всякая функция <w—f(z}, аналитическая
внутри круга	—z0| < г}, разлагается в этом круге
10.36]
§ 10.3. ТЕОРЕМА КОШИ И ЕЕ СЛЕДСТВИЯ
421
е степенной ряд
об
= X ^fM^o)(z-zor.
«=0
(4)
Ряд (4) называется рядом Тейлора для аналитической
функции f(z) в круге V.
в. Следствие. Если функция f(z) аналитична в круге
V={z:[z—z0| < г} и fw(zo) = O (л = 0, 1, 2, ...), то
f(z) = 0 в круге V.
10.36. а. Будем говорить, что последовательность (ряд)
функций fn(z), определенных в области О, сходится равно-
мерно внутри G, если сходимость этой последовательности
(этого ряда) равномерна на любом компакте Q, целиком
лежащем в области G.
Для дальнейшего заметим, что вокруг компакта Q, ле-
жащего в области G, всегда можно обвести замкнутый
кусочно-гладкий контур, проходящий в области G. Действи-
тельно, каждую точку z0£Q можно покрыть открытым
кругом V={z:]z—z01 < р}, лежащим вместе с границей
в области G. Из полученного покрытия компакта Q в силу
3.97 можно выделить конечное покрытие Vlt ..., Vm. Гра-
ница области V= Vj_ U - •. U Vra представляет собой замкну-
тый кусочно-гладкий контур, состоящий из конечного числа
дуг окружностей; по построению он проходит в области
G—Q и обходит вокруг Q, что и требуется.
б. Теорема. Если последовательность аналитических
функций fi (z), f2 (z), ... в области G сходится равномерно
внутри G к некоторой функции f(z), то f(z)—также ана-
литическая функция в G. Последовательность производных
любого порядка f[m (z),	(z), ... сходится равномерно
внутри G к соответствующей производной flm(z) функции
f(z).
Доказательство. Мы имеем по формуле Коши 10.33
для любого замкнутого пути Ac G, обходящего вокруг
данной точки z £ G. Переходя к пределу при п —* оо и
422
ГЛ. 10. АНАЛИТИЧЕСКИЕ ФУНКЦИИ
[10.37
пользуясь теоремой 10.22 а, находим
Л в
т. е. f(z) также представима интегралом типа Коши и потому
аналитична в G.
Для доказательства второй части теоремы напишем пред-
ставление 10.34 для функций /<”” (z) и
^(z\ - wl & f(S)dg f(jn>	A fn(t)<K
7 (Z’~ 2iti a (£—z)CT+1 ’	7/1 2ni 7 (g—z)m+1 ’
где интегралы берутся по замкнутому кусочно-гладкому пути
LczG, обходящему в положительном направлении вокруг
заданного компакта QcG. Так как функция	при
£g L, z£Q ограничена по модулю величиной , где
d — inf I £—z I, и последовательность /_(£) на контуре L
f (Г\
равномерно сходится к /(£), то последовательность _ *я, —
f (О
на контуре L сходится к	равномерно относительно
параметра z£Q и можно применить 10.22 6. Теорема дока-
зана.
10.37.	а. Здесь мы установим теорему, обратную к тео-
реме 10.35'.
Теорема. Сумма степенного ряда
f(z} = ^an{z—z0)n	(1)
аналитическая функция внутри круга G—{z:[z—г0|<г}
сходимости этого ряда, и всюду внутри G справедлива
формула
f'(z) = a1 + 2a2(z—z0) + 3a3(z—z0}2+...
Доказательство. По теореме 6.64 а степенной ряд
сходится равномерно в любом круге G', лежащем внутри
круга сходимости G и имеющем тот же центр.
Но любой компакт QaGлежит в таком круге G'. Действи-
тельно, предполагая противное, мы смогли бы указать в
10.37]	§ 10.3. ТЕОРЕМА КОШИ И ЕЕ СЛЕДСТВИЯ	423
компакте Q последовательность точек zlt z2, zs, ... с
\zn—z0 | —> г, и в компакте Q содержалась бы любая предель-
ная точка этой последовательности. Но для мы имели
бы \zm—что противоречило бы условию QdG.
Поэтому можно применить теорему 10.36 б. Так как функ-
ции (z—z0)n аналитические, то по 10.36 6 ряд (1) представ-
ляет аналитическую функцию внутри G, что и утверждается.
Вторая часть теоремы следует из второй части 10.36 б.
6.	В частности, мы имеем
(e*)' = (l + z + -^+...y = l+z+-J+...=e*,	(2)
(sinzr^^-gr+gj—.. J =1—2i- + 1T-...=coSz, (3)
/ z^ z4 \f	z3 z^
(“SZ)'^1—2Г+41---J =-г+зГ—5T+-” = “sinZ’ (4)
( Z3 Z6	\ r	2%	2^
(sh*)' = (z+3! +5T+-J =l+2f+4r+--=chz,	(5)
(ch z)' = ^1+ —+ ^j-+. • • j =z+^j-+-gp + ... =sh z. (6)
Впрочем, формулы (3)—(6) можно было бы получить и из формулы
(2), используя известные нам выражения тригонометрических и гипер-
болических функций через экспоненту (8.63 и 8.72).
в.	Радиус сходимости ряда (L) естественно связывается
со свойствами аналитичности функции f(z). Именно, круг
сходимости ряда (1) есть наибольший круг с центром в z0,
в котором функция f(z) является аналитической, посколь-
ку во всяком круге аналитичности функции f(z) она пред-
ставляется, по 10.35, своим рядом Тейлора.
Так, радиус сходимости ряда
^z) = TFF = 1-z2+24-ze + ---	(7)
равен 1, и ближайшие к точке zo = 0 особенности функции f (z) нахо-
дятся в точках г= ± i, на расстоянии 1 от точки г0. Оставаясь в
вещественной области, нам было бы трудно объяснить по поведению
функции f (х) причины расходимости ряда (7) при z=± 1.
г.	Точка z = a называется нулем., или корнем, аналити-
ческой функции w=f(z), определенной в области G$a,
если /(а) = 0. Эта точка точнее называется нулем (корнем)
кратности k, если /(о)=/' (о) = ...	(<z) = 0, fiky(a) #=0.
424
ГЛ. 10. АНАЛИТИЧЕСКИЕ ФУНКЦИИ
[10.38
Таким образом, в окрестности нуля кратности k для
аналитической функции f(z) справедливо разложение в ряд
Тейлора, начинающийся с (z—а)к:
fW=т - °)*+{z ~c)fc+1 + • •'
Можно написать также
f(z) = (z—a)kg{z),
где
g(z)
1<кЦа)
kl
(ft+1)1
[z— a)+ ...
аналитична в окрестности точки а (как сумма сходящегося
степенного ряда), а следовательно, и во всей области G
(как частное аналитических функций f(z) и (z—а)к), и при
этом g(a) = Д-/(«(а)у=0.
10.38.	Функция, аналитическая во всей плоскости С,
называется целой аналитической функцией. По 10.35 целая
функция f(z) разлагается в ряд Тейлора
7(z) = |x*"	(^о=0),	(1)
сходящийся во всей плоскости.
Теорема (Лиувилль). Целая аналитическая функция
f(z), ограниченная по модулю во всей плоскости С, есть
постоянная.
Доказательство. Пусть при всех z С С выполнено
неравенство
Напишем выражение 10.35 (2) коэффициентов ряда, рассмат-
ривая в качестве контура А окружность радиуса R с центром
в начале координат:
а — — (Ъ f	(2)
л
В силу неравенства 10.21 (5) мы имеем
.	1^1 А _ „ А
1°”!^ 2л	•
10.39]
§ 10.3. ТЕОРЕМА КОШИ И ЕЕ СЛЕДСТВИЯ
425
Поскольку в этом неравенстве величину /? можно взять
произвольно большой, мы получаем
а„ = 0 при п= 1, 2, ...
и, следовательно,
f (z) — а0 = const,
что и требовалось.
10.39.	а. Теорема (теорема единственности
аналитической функции). Если аналитическая функ-
ция <р (z) в связной области G равна 0 на последователь-
ности точек zlt z2, ... , сходящейся к точке z0 £ О, то
<р (z) == 0 в области G.
Доказательство. В силу теоремы 10.35 функция
<р (z) в любом круге	— z0|<r}cG есть сумма
степенного ряда:
(p(z) = c0 + c1(z — z0) + c2(z — z0)2+...	(1)
Сначала мы покажем, что <p(z) = 0 в круге V. Для этого
достаточно показать, что все числа с0, сх, с2, ... равны 0.
Вместе с рядом (1) рассмотрим степенные ряды
<Р1 (z) = ci + c2 (z— z0) + c3(z — z0)2+ ... ,
<р2(z) = c2 + c3(z — z0) + ci(z—z0)2+	,
Каждый последующий ряд получается из предыдущего вы-
читанием свободного члена и делением на z — z0. Поэтому
все эти ряды сходятся в том же круге, что и исходный
ряд (Г), и функции <pm (z), согласно 6.64 б, непрерывны при
z = z0. Мы имеем, далее, по индукции
<р (zn) = 0,	с0 = <p(z0) = lim <р (zn) = 0;
Л -> CD
<Р1 (-gB) = <P(Z")Zz (г°~ = 0> С1 = <Р1(*о) = Ига <Р1(^«) = 0;
*0	п СС
%, (zn) =	1(Zn)	— = о, cm = <pffl (z0) = lim <pm (zn)=0;
40	л-*-co
...............................................................
В итоге все c,= 0, что и утверждалось.
426	ГЛ. 10. АНАЛИТИЧЕСКИЕ ФУНКЦИИ	[10.39
Мы доказали, что ф (z) = 0 в некотором круге V
с центром в z0. Пусть теперь — любая точка области G.
Так как G — связная область, то существует кусочно-глад-
кий путь L cz G, соединяющий точки z0 и zr.
Положим d = inf р (z), где р (z) — радиус наибольшего
круга с центром в точке z С L, лежащего внутри G; вели-
чина d положительна в силу компактности L. По доказан-
ному ф (z) == 0 в круге Vo с центром в z0 и радиуса d.
Двигая центр круга радиуса d вдоль линии L, мы видим,
что ф (г) = 0 внутри этого круга при любом положении
центра на линии L. Завершив путь в точке z1( мы получаем
равенство ф (дД = 0. Теорема доказана.
б.	Теорема. Если две аналитические функции f(z) и
g(z) в связной области G совпадают на последовательности
точек zlt ..., z„, ... , сходящейся к точке z0 С G, то
f(z)^=g(z) в области G.
Доказательство. Положим f(z)—	= ф (г);
функция ф (z) аналитична в G вместе с f(z) л g(z) л удов-
летворяет условиям теоремы а. Применяя а, получаем, что
ф(,г) = 0 в области G, и, следовательно, f(z)=g(z) всюду
в области G. Теорема доказана.
в. На свойстве б основана идея аналитического продол-
жения функций. Пусть функция /1 (г) аналитична в области
Gt и функция Д (z) аналитична в области G2, имеющей
с Gr непустое связное пересечение Go. Пусть известно,
что в области Go имеется последовательность точек
zlt z2, ... , zn, .. . , сходящаяся к точке z0£ Go, такая, что
Д (?„) = Д (?„) (л=1, 2, ....). Тогда, по доказанному,
функции Д (г) и Д (z) совпадают во всей области Go;
функция f(z), равная Д (z) в Gt и f2(z) в G2, определена
однозначно в области G=G1(jG2 и является аналитической
в области G. Говорят в таком случае, что функция f(z)
есть аналитическое продолжение функции j\(z} из Gx в G.
Из сказанного следует, что аналитическое продолжение
(z) из области Gr в область G может быть лишь единст-
венным.
СО
г.	Пример. Функция Д (г) -= гпв круге | z | < 1 опре-
о
делена (как сумма ряда) и аналитична. Функция f(z)
1—z ’
10.39]
§ 10.3. ТЕОРЕМА КОШИ И ЕЕ СЛЕДСТВИЯ
427
определенная всюду, кроме z=\, дает аналитическое про-
должение функции Д (z) на всю плоскость С с выброшен-
ной точкой z=\.
д.	Теорема. Если в точке а все производные (а)
функции f(z), аналитической в связной области G^a,
обращаются в нуль (k = 0, 1, 2, ...), то f(z) = 0 в G.
Доказательство. Рассмотрим круг V =
— {z:fz — с|<г}, лежащий целиком в области G. В силу
теоремы 10.35 в функция f(z) в этом круге тождественно
равна нулю, и нам остается применить теорему 10.39 а.
е.	Пример: вещественные аналитические
функции. Функция f(z), аналитическая в связной обла-
сти G, содержащей точки вещественной оси, называется
вещественной аналитической функцией, если все ее значения
на вещественной оси сами вещественны.
Поскольку значения производной у аналитической функ-
ции f (z) на вещественной осн можно вычислить по значе-
ниям самой функции f(z) только на вещественной оси, мы
видим, что у вещественной аналитической функции ее
производная /' (z) — также вещественная аналитическая
функция. Таким же образом и все остальные ее производ-
ные f(z), f" (z), ...—также вещественные аналитические
функции. Разложение функции f(z) в ряд Тейлора с центром
разложения в точке z0 на вещественной оси
/(*) = 2сп(г—z0)n
о
имеет вещественные коэффициенты ап —	/<п) (z0). Поэтому
в пределах круга	сходимости	этого	ряда	мы	имеем
___ со	со
/(*)= 2	an(z—zo)n= 5	an(z~ zo)n=f(z)-
о	о
Теорема. Вещественная аналитическая функция f(z)
удовлетворяет условию
f(z)=f(z)
для любой точки z £ G, для которой также z £ G.
Доказательство. Оставляя в области G только
те точки, которые входят в G вместе с комплексно со-
пряженными, можно считать, что область G симметрична
428
ГЛ. 10. АНАЛИТИЧЕСКИЕ ФУНКЦИИ
(10.41
относительно вещественной оси. Обозначим через О+ ту
часть области G, которая находится в верхней полупло-
скости, и через О~—ту, которая находится в нижней
полуплоскости. Определим в области G+ новую функцию
Л (*)=/(*),
используя значения f(z) для z£G~. Для любой точки
z0£G+ из разложения в ряд Тейлора
ОО
/(г)= S an(z—z0)n
о
получается разложение функции Д (z) в степенной ряд
Л(г) =/(*) = 2 an{z— z0)" = S«R(* — *о)">
о	о
откуда следует, что функция Д (г) — аналитическая в G+.
Но вблизи вещественной оси функция /, (z), как мы видели
выше, совпадает с функцией /(z). Применяя б, получаем,
что fv(z)=f(z) всюду в G+. Меняя ролями G+ и G~,
получаем, что f(z)s^f(z) и всюду в G~. На веществен-
ной оси, очевидно, f(z)=f(z). Таким образом, f{z)s=f(z)
всюду в G, что и требовалось.
§ 10.4. Вычеты и изолированные особые точки
10Л1. Вычеты. Если функция f(z) аналитична в области
G и в этой области взят замкнутый кусочно-гладкий путь L,
то по теореме Коши 10.32
L
Часто приходится иметь дело с интегралом
И)
L
взятым по замкнутому пути, внутри которого *) имеются
*) Более точно: внутри ограниченной области, границей кото-
рой является путь L.
10.42] § 10.4. ВЫЧЕТЫ И ИЗОЛИРОВАННЫЕ ОСОБЫЕ ТОЧКИ 429
особые точки функции f(z). Такой интеграл, вообще говоря,
отличен от нуля. Примером служит интеграл Коши 10.33 (5):
1 £ <р(£И£
2ni'j С-г
L
ф И,
(2)
где <р (z) аналитична в односвязной области G, содержащей
путь L. Рассмотрим случай, когда функция f(z) в (1)
имеет в области О, содержащей контур L, единственную
особую точку z=^a (особую в том смысле, что в этой
точке f(z) или не определена вовсе, или хотя и опре-
делена, но не является дифференцируемой по области G).
Значение интеграла (1) в этом случае не зависит от выбора
пути L (при условии, что он обходит один раз вокруг
точки а в положительном направлении). Оно называется
вычетом, функции f(z) в точке z=a и обозначается так:
Выч [f(z)]2=a.
10.42. Рассмотрим некоторые примеры,
а. Интеграл
2ni (у Р (£)
где P(z)— многочлен, имеющий при z = a простой корень
(так что /э(а)=0, Р' (а) =0=0) и не имеющий других корней
в области G, a g(z)— функция, аналитическая в области G.
Можно написать
Р(г) = Ьг (z — a)+b2 (z — a)2+... = (z — a) Рг(г),
где Pi (z) = bi + b2(z — a) + • • • — многочлен, равный при
z = a величине Ьг = Р' (а) =0= 0 и не имеющий корней при
z£G. По формуле Коши 10.41 (2)
] __ 1 t. g(£)	1 £.	_ g(a) g(a)
йк-^РК)^ 2шФа-а)Рх(?) Pi(a) Р' (а) ’
L	L
и вычет функции /Сг)=|г^' ПРН г = а найден:
Выч[/(г)]г=й=/=|^.	(1)
б. Интеграл
/ = — dt
2m<$ Р&)а1”
430
ГЛ. 10. АНАЛИТИЧЕСКИЕ ФУНКЦИИ
[10.43
где многочлен P(z), в отличие от только что рассмотрен-
ного случая, имеет при z = a /n-кратный корень, так что
^»=И=0-
Можно написать
P(z) = (Z-«)“P„(z),
где
Рт(г)^Ьт-\-Ьт^(г— а) + ... , Рт(а) = Ьт
Разложим
Тогда
т\
1	£ (z)	~
функцию ъ 7 \ в Рнд Тейлора по степеням z— а:
#^) = с0 + с1 (z — a) + c2 (z—a)2+...
г т \с)
g(z)_ g(z)
P(z) (z—a)mPm(z)
___ C0 I______C1
(z —a)m' (z—a)m~l
C^ + cm + cm+1(z~a)+...
При интегрировании no L сохранится лишь член, содержа-
щий коэффициент ст_1 (10.33 а). По 10.35 б он имеет
значение
1	r _	1	(	\(m-D
2ш^ Р&)	(m-\)\\Pm(z))z=a
1	/g(z)(z—a)mym-1)
= (т —1)1	Р17) Jz=a •
Итак, в рассматриваемом случае, когда P(z) имеет лг-кратный
корень при z = а,
g(z)~l _	1	Г g(z) (г—а)'д~| (m -1)
Е(г)]г=а (m—1)! L р(г) J z=
10.43. Если нам нужно вычислить интеграл 10.41 (1) по
замкнутому пути, внутри которого находится не одна,
а несколько (конечное число, например т) особых точек
аг, ... , ат функции f(z), то можно воспользоваться ра-
венством
Z,
т
= 2 Выч[/(2)]г=ор	(1)
10.44] § 10.4. ВЫЧЕТЫ И ИЗОЛИРОВАННЫЕ ОСОБЫЕ точки 431
где Llt ... , Lm — замкнутые кусочно-гладкие пути, каждый
из которых обходит лишь одну особую точку. Доказатель-
ство этого равенства (называемого основной теоремой о
вычетах) очевидно из теоремы Коши и из рис. 10.6, где
показан исходный путь L, пути Llt ... , Lm и соединяющие их
пути, проходимые дважды в противоположных направлениях.
Пример. Найдем
ф г2—2рг-(-1 ’ Р>Х-
|г|=1
Из двух корней знаменателя, произведение которых равно 1,
один, z-i, находится внутри, а другой, z2,— вне единичного
круга (рис. 10.7). Именно, в формуле для корня квадратного
трехчлена
Zi'2=p±Vp*— 1
при р > 1 знак минус отвечает корню zr, а знак плюс —
корню z2. В точке zr знаменатель имеет простой корень,
и по формуле 10.42 (1)
ф г2—2pz-|-l	2TO2(z—р)
|г| = 1
10.44. Логарифмический
__
вычет. Рассмотрим
интеграл вида
7V— — f dz
Л 2тф f(z) ’
L
(1)
где функция f(z) аналитична в области G, содержащей
432
ГЛ. 10. АНАЛИТИЧЕСКИЕ ФУНКЦИИ
[10.45
замкнутый контур L, а на самом контуре не обращается
в 0. Если она и внутри контура L не обращается в нуль,
то по теореме Коши 10.32 интеграл (1) равен нулю. Если
функция f(z) имеет нули внут{5и контура L, то по теореме
единственности 10.39 а этих нулей конечное множество;
обозначим их через ..., zm, а их кратности — через
klt .  , km. В соответствии с 10.43 интеграл N можно
представить в виде суммы аналогичных интегралов
/ =1	ч
где внутри контура £у- имеется уже только один нуль Zj
кратности kj. Для сокращения записи положим гу=а, kj—k.
В окрестности точки а мы имеем
/(?) =ck(z~a)k + ck+Az—a)ft+1+ ... , cfe¥=0,
f'(z} = kck(z—a)ft-1 + (A+ l)cft+1(2—a)k+ ....
f (Z) = 1 . feCfe+(fe+D Cfe + l(Z —c)+... = <p (z)
/(г)	г—a'	ck+ck+1(z—a)+... z—a’
где <p (z)— аналитическая функция в окрестности точки a,
принимающая в самой точке а значение <р(а)=6. Поэтому
^-dz = ~.fc\ dz = q> {a) — k.
г) 2т^г-а	'
Li
tn	tn
n= 2	2
j=i	f=i
есть целое положительное число, равное
сумме кратностей всех нулей функ-
ции f(z), находящихся внутри конту-
ра L.
Интеграл N называется логариф-
мическим вычетом функции f(z) от-
носительно контура L. Смысл этого
названия будет ясен из дальнейшего
(10.57).
10.45. Ближайшие пункты посвяща-
ются «качественному анализу» поведе-
ния функции в окрестности изолиро-
ванной особой точки. Средством для этого анализа являет-
ся разложение рассматриваемой функции в ряд по положи-
2ni ф1 f
Ч
В итоге
10.45) § 10.4. ВЫЧЕТЫ И ИЗОЛИРОВАННЫЕ ОСОБЫЕ точки 433
тельным и отрицательным степеням z— а, называемый рядом
Лорана.
Рассмотрим функцию тю=/(г), аналитическую в круго-
вой полосе С={/'0<|г — а|</?0}> где </?0^°°
(рис. 10.8). Выберем числа г и /? так, чтобы иметь
r0 < г < R < /?0. Тогда по теореме Коши, примененной
к односвязной области, полученной разрезанием круговой
полосы Q вдоль радиуса, не проходящего через z, при
г<|г — а|</? имеем
'W 2ni	£-z ЪИ £-г •
|z-a|=R	|z-a|=r
В первом интеграле используем разложение
Во втором интеграле используем разложение
1_________1	____1 _	1	___ у (£—а)п
t,— г~ (?—а)—(г—а)~~	г—a' t g—а	^(г— а)п+1 '
г—а
По признаку Вейерштрасса (ср. 10.35 а) оба разложения
равномерно сходятся на соответствующих контурах инте-
грирования. Поэтому, применяя 10.22 а, можно написать
f(z) = ^cn(z—a)n+^cn(z—a)n,	(1)
где
1 &
2ni	ЧГ (?—а)«+*
|z-a|=«'b	'
J f(№
2ni j (£—a)n+1
k |z-a|=r
при л>0,
при п
<0.
Впрочем, поскольку подынтегральная функция ^__^п+Г
аналитична в круговой полосе Q, интегралы можно брать
по любой окружности \z— а[= р, p£(rQ, /?р), и даже по
434	ГЛ. 10. АНАЛИТИЧЕСКИЕ ФУНКЦИИ	[10.45
любому замкнутому кусочно-гладкому пути, обходящему в
пределах полосы Q один раз вокруг ее внутренней части
в положительном направлении.
В частности, если го=0, коэффициент с_х есть как раз
вычет функции f(z) в точке z-=a (10.41).
Сумма (1) короче записывается в форме
f(z) = ^cn(z — а)п.	(2)
Полученное выражение можно рассматривать и как предел
суммы %cn(z— а)п, когда р —»- — оо, q—> оо независимо
п=р
друг от друга, т. е. как сумму двустороннего ряда (6.48 а);
это следует из сходимости обоих рядов-слагаемых в пра-
вой части (1) и теоремы 6.486.
Ряд (1), или (2), называется рядом Лорана для функции
•w=f(z) в полосе Q. Согласно теореме 10.22 6 он сходит-
ся равномерно при	По функции f(z) он
определяется единственным образом, поскольку для любого
т=0, +1, +2, ... при г0 < р < /?0 из (1) следует
J f(z) (z—a) mdz = ^cn J	(z—a)~m+ndz =
|z—o|=P	— cd |z—a|=p
Слагаемое f + (z) = ^cn(z—a)n называется правильной
— co
частью ряда Лорана, слагаемое f~(z)—^cn(z — а)п—
главной частью ряда Лорана. Числа сп называются коэффи-
циентами Лорана.
Правильная часть ряда Лорана есть ряд по положитель-
ным степеням z — а, сходящийся при \z — а | = /? и, следо-
вательно, сходящийся во всем круге \z — a\^.R0 (6.62),
включая и всю внутреннюю часть ]z — а | г0, не входя-
щую в круговую полосу Q.
Главная часть ряда Лорана есть ряд по отрицательным
степеням z — а, сходящийся при \z — al = r. Если положить
1
z — а = -^, мы получим ряд по положительным степеням
10.46] § 10.4. ВЫЧЕТЫ И ИЗОЛИРОВАННЫЕ ОСОБЫЕ точки 435
сходящийся при |£| = у и, следовательно (6.62), сходящий-
ся при всех — ; поэтому главная часть ряда Лорана
сходится при всех \z — а | > г0, включая и всю внешнюю
часть \z— а ] 7?0, не входящую в круговую полосу Q.
10.46. Изолирован ные особые точки. Рассмот-
рим случай функции w=f(z), аналитической в круге
]z — а | < 7?0 всюду, за исключением центральной точки а.
В области 0 < \z — а) < функцию f(z) можно разложить
в ряд Лорана
/(*) = (1)
— 00
В зависимости от структуры этого ряда изолированная
особая точка а получает одно из следующих наименований:
а.	Если все коэффициенты Лорана сп с п < 0 равны О,
точка а называется устранимой особой точкой функции f(z).
В этом случае в области 0 < \z — <z[ < 7?0 функция f(z)
представима рядом
f(z)-Ycn(z~a)n,
сумма которого есть аналитическая функция во всем круге
\z — а | < /?0, включая точку z = a, равная с0 при z = a.
Поэтому, если дополнительно положить /(«)=с0, мы полу-
чим аналитическую функцию в круге \z — и |</?0 без осо-
бенности в точке z = c. Этим объясняется название «устра-
нимая особая точка».
б.	Если все коэффициенты Лорана сп с п <—tn, где
m > 0, равны 0 и с_т^0, точка а называется полюсом.
m-го порядка функции f(z).
в.	Если имеются отличные от нуля коэффициенты Ло-
рана с„ с отрицательными номерами п, как угодно больши-
ми по модулю, точка а называется существенно особой
точкой функции f(z).
г.	Для общности результатов мы дополним здесь комп-
лексные плоскости переменных z и w символическими точ-
ками z—oo, w=oo (^бесконечно удаленными точками»).
Символом z—» оо будем обозначать направление на плос-
кости z, образованное из множеств Аг= {г:| z | > г}, где
436
ГЛ. 10. АНАЛИТИЧЕСКИЕ ФУНКЦИИ
(10.46
г пробегает все положительные числа (или хотя бы все
числа, большие некоторого г0); аналогичный смысл будет
иметь символ w —* оо (4.73 е). Прежние точки z и w (отличные
от введенных z = oo и те»=оо) будем называть конечными
точками. Пусть S есть какое-нибудь направление на плос-
кости z; будем говорить, что для данной функции w=/(z)
имеет место предельное соотношение lim/(z)=oo; если для
s
любого г можно найти такое множество Ar£S, во всех
точках которого выполняется неравенство

Таким образом, приобретают точный смысл выражения
lim /(г)=оо, lim/(z) = £, lim f(z) = oo
z-+ a	z	z -> со
(где а и b — конечные точки). Например, имеют место ра-
венства
lim
z—a
1
(z—a)m —
оо;
lim<p(z)/(z) — оо, если lim q> (?) = &=# 0, Iim/(z) = oo;
z~*a
lim <p (z) = оо тогда и только тогда, когда lim — 0.
z-»a	z—a
Далее, аналогично 4.45, будем говорить, что точка w= оо
есть предельная точка для функции f(z) по направлению S,
если для любого г можно в каждом множестве Аг £ 5 указать
точку zr, в которой выполняется неравенство

Функция /(z), не являющаяся ограниченной по направ-
лению <5>, необходимо имеет предельную точку w=co.
д.	Рассмотрим случай, когда функция/(z) определена
и аналитична в области G={z:|z|>/?}. В силу общей
теоремы 10.45 она разлагается в области G в ряд Лорана
/(z) = 2c„z\
— Q0
(2)
10.48] § 10.4. ВЫЧЕТЫ И ИЗОЛИРОВАННЫЕ ОСОБЫЕ точки 437
Преобразование z~~^ переводит область С? в область
Н— < £:0 < | £| <	> и функцию f(z) в функцию
<рЮ = 2ЧГп.	(3)
— со
Будем говорить, что функция f(z) имеет в точке оо
соответственно устранимую особую точку, полюс или су-
щественно особую точку, если одноименную особую точку
имеет функция <р (£) при £ = 0. Иначе говоря, точка z=oo
является для функции f(z) устранимой особой точкой, если
в разложении (2) отсутствуют члены с положительными
показателями; полюсом порядка т, если в разложении (2)
коэффициенты ат+1,	ат+2, ... равны 0, а коэффициент
ат =/= 0; существенно особой точкой, если в разложении (2)
имеются члены с произвольно большими показателями.
Далее мы изучим поведение функции f(z) вблизи изоли-
рованной особой точки во всех указанных случаях.
10.47.	Если в разложении 10.46 (1) с„= 0 при п <—т,
т> 0, так что
f(z)= 2 с» (* — <*)">
п—-т
то мы можем положить
ф (z) = (z — a)mf(z) = с_т + с_т+1 (z — а) + ...
Функция ф(г) имеет при z=a устранимую особую точку
и при дополнительном условии ф(а)=с_т становится ана-
литической в круге [z — а | < /?0, отличной от 0 при£ = а.
Отсюда
f(z) =
<p(z)
(z—а)т
Так как ф(а)=^0, при z —> а функция f(z) стремится
к бесконечности (10.46 г).
К этому типу относятся подынтегральные функции в при-
мерах 10.42 а, б, где мы вычисляли вычеты.
10.48.	Пусть теперь а есть существенно особая точка
функции f(z).
438
ГЛ. 10. АНАЛИТИЧЕСКИЕ ФУНКЦИИ
[10.48
Прежде всего покажем, что функция f(z) не может быть
ограниченной в окрестности существенно особой точки z — a.
Так как правильная часть /+ (z) заведомо ограничена вблизи
точки z — а, то из ограниченности /(г) следовала бы огра-
ниченность главной части f~ (z). Ряд
со
f~	— а)п
сходится при всех z^=a (10.45). Поэтому, заменяя z — а
1
на , мы получим ряд
ф(0= 2U“-
п=1
сходящийся во всей плоскости Если функция f~ (z) ог-
раничена при 0<|г — а|^е, то функция <р(£) ограничена
при | | > y • Н° при | С | < ~- функция <р (^) также огра-
ничена (вследствие Своей непрерывности), поэтому <р (£)
ограничена во всей плоскости С- По теореме Лиувилля
(10.38) <р(£) есть постоянная, и так как <р (0) = 0, мы по-
лучаем <р (£) == 0,_ откуда и с„ = 0 при всех п < 0 в проти-
воречии с предположением.’ Итак, f(z) не является ограни-
ченной при Z—+ а, т. е. точка оо есть предельная
точка функции f(z) при z —. Пусть теперь А — любое
конечное комплексное число. Если значение А принимается
функцией f(z) в каждой окрестности точки а, то тем самым
А есть и предельное значение f(z) при z—>а. Если же
в некоторой окрестности точки а функция f (z) не принимает
значения А, то функция <р (г) =	не имеет иных
особых точек в указанной окрестности, кроме самой точки а.
Если точка а есть полюс или существенно особая точка
функции <р (z), то по доказанному существует последователь-
ность zn —► а, для которой <р (zn) —► оо, и, следовательно,
f(zn)->-A, так что А есть предельное значение функции
f(z) при z—* а. Наконец, рассмотрим случай, когда точка
z—a есть устранимая особая точка функции <р(.г). В этом
случае по доказанному существует конечный предел
b— lim <р (z).
z -+а
10.49J § 10.4. ВЫЧЕТЫ И ИЗОЛИРОВАННЫЕ ОСОБЫЕ точки 439
Так как существует последовательность zn —> а, для кото-
рой	то
Ь =	= f (*п)~А = °-
Можно положить
<p(z) = (z — a)mty(z),
где ф(а)=^0, т~^\. Функция —аналитична в окрест-
V и)
ности точки а и допускает разложение в ряд Тейлора
_LJ = feo + fe1^-«)+...,	™e*0=~.
Таким образом,
f (z) = А 4-	= А 4- —а)И (г) =
= A + (z~a)~m[b0 + b1(z — a)+...],
и мы видим, что ряд Лорана для функции f(z) имеет лишь
конечное число слагаемых в главной части в противоречии
с предположением.
Итак, в существенно особой точке любое значение А
в расширенной плоскости z является предельным значением
функции f(z) при z —а*).
10.49.	С другой стороны, поведение функции f(z)
в окрестности изолированной особой точки можно описывать
независимо от предыдущего в следующей системе взаимно
исключающих характеристик:
(1)	функция f(z) ограничена в некоторой окрестности
точки а;
(2)	функция f(z) имеет при z —> а предел оо;
(3)	функция f(z) имеет при z~> а по крайней мере два
предельных значения, одно из которых есть оо.
*) Имеется более точная теорема Пикара, в силу которой в лю-
бой окрестности существенно особой точки функции f (z) каждое
значение А (кроме, возможно, одного) фактически принимается
функцией f (г), притом бесчисленное множество раз. См. И. И. П р и-
валов, Теория функций комплексного переменного, М., 1966.
440
ГЛ. 10. АНАЛИТИЧЕСКИЕ ФУНКЦИИ
[10.51
Результаты 10.46—10.48 таковы:
устранимая особая точка есть точка типа (1);
полюс есть точка типа (2);
существенно особая точка есть точка типа (3).
Но так как и классификация 10.46, и классификация по
типам (1)—(3), каждая в своих терминах, описывает взаимно
исключающим образом все возможные типы поведения функ-
ции f(z) в окрестности изолированной особой точки, то
справедливы и обратные заключения:
точка типа (1) есть устранимая особая точка;
точка типа (2) есть полюс;	*
точка типа (3) есть существенно особая точка.
Подчеркнем, что эти высказывания нетривиальны. Так, на-
пример, первое из них утверждает, что функция, аналити-
ческая и ограниченная в окрестности точки а, на самом
деле имеет при z—> а конечный предел; оно получает обо-
снование лишь в результате анализа поведения функции
в окрестности полюса и в окрестности существенно особой
точки, проведенного нами в 10.47—10.48.
С учетом 10.46 д все эти выводы полностью переносятся
на случай изолированной особой точки в бесконечности.
В частности, если функция /(z) является аналитической
при всех z, | z | > л, мы приходим к следующим предло-
жениям: если при этом функция w=f (z) имеет на беско-
нечности единственную предельную точку w=oo, то /(z)
есть многочлен; всякая целая функция f(z), не являю-
щаяся многочленом, любое число да £ G имеет своим пре-
дельным значением при z—* оо.
§ 10.5.	Отображения и элементарные функции
10.51.	Конформное отображение. Рассмотрим
линейную функцию
w=b(z — z0)+®0=s/(z),	(1)
где z0, да0, b=£0 — некоторые комплексные числа. Очевидно,
/(z0)=®0. Далее, w — w0= b(z — z0), откуда
Iw — w0|=|&|.|z- *o|>	(2)
arg (да — w0)=argb + arg(z—z0)	(3)
(с точностью до слагаемого, кратного 2т$). Равенства
10.52)	§ 10.5. ОТОБРАЖЕНИЯ И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ 441
(2), (3) показывают, что отображение -w=f(z) имеет сле-
дующую геометрическую природу: каждый круг \z— z0|^p
растягивается в | b | раз по всем направлениям, поворачивает-
ся вокруг центра z0 на угол aTgb и затем накладывается
центром на точку w0.
Пусть теперь w=f(z) — произвольная аналитическая
функция, определенная в окрестности | г—z0|^p точки z0,
причем/' (г0) =	f(z0} — w0. Мы имеем в этом случае
в силу определения производной
w=w0 + b(z—z0) + E(z, z0)(z — z0),	(4)
где 8 (z, z0) —► 0 при z —z0.
Равенство (4) показывает, что отображение w=f(z)
с точностью до малых второго порядка описывается фор-
мулой (1), так что с указанной точностью оно представляет
собой результат последовательного поворота вокруг центра z0
на угол argb, растяжения в |Ь| раз и наложения центром
на точку w0. Отображение такого рода называется кон-
формным в точке z0 с характеристиками k= | b | n0=argM
Таким образом, аналитическая функция w = /(z) осущест-
вляет конформное отображение во всякой точке z0, в кото-
рой f (z0) Ф 0. В частности, при конформном отображении
линии, образующие в точке г0 угол а, переходят в линии,
образующие в точке tv0 тот же угол а.
10.52.	Теорема. При f (z0) =/= 0 некоторая окрестность
точки z0 переходит в окрестность точки w0 взаимно одно-
значно.
Это утверждение, разумеется, очевидно в случае функции
10.51 (1), когда можно прямо разрешить уравнение отно-
сительно z, но в общем случае требует доказательства.
Рассмотрим окрестность G точки z0, в которой функция
f(z) — w0 обращается в нуль лишь единственный раз, при
z = z0; поскольку нули аналитической функции f(z) —
изолированы (10.39 а), такая окрестность всегда существует.
Пусть L — контур, ограничивающий область G. Тогда в силу
10.44
так как единственный нуль функции /(z) —w0 имеет крат-
ность 1.
442
ГЛ. 10. АНАЛИТИЧЕСКИЕ ФУНКЦИИ
[10.53
Функция ОТ W
2ni 2 f ($)—«’
определена при ч/и—ч/и0 (где она равна 1) и для близких
значений w, например при |w — w0|<e, поскольку знаме-
натель не обращается в нуль на контуре L не только при
w = w0, но и для всех достаточно близких значений w.
Она непрерывно зависит от w по теореме 10.24. Но так
как эта функция принимает лишь целые значения (10.44),
она равна 1 и для всех близких значений w. А это озна-
чает, в силу 10.44, что внутри контура L функция f(z)— и>
обращается в нуль один раз, т. е. для любого w1, |wx — w0 |<е,
имеется в окрестности О одна и только одна точка где
f(zt) — wr. Теорема доказана.
10.53.	Обратная функция. В условиях 10.52,
в силу взаимной однозначности отображения f(z),
имеется обратная функция z=q>(w), осуществляющая обрат-
ное отображение окрестности точки w0 в окрестность точ-
ки z0. Покажем, что г=(р(да) — также аналитическая функ-
ция. Для этого рассмотрим отношение
ФИ~Ф (te0)^Az
W—WB	&W ‘	' J
При w —> w0 мы имеем z —-> z0: если бы у функции <р (w)
при w —> w0 нашлась вторая предельная точка zlt то мы
бы имели f (z0) = w0= что по доказанному невозможно.
Поэтому существует предел отношения (1), равный
Az 1	1	._.
lim ~ ---------— — г—— ,	(2)
lim— Г(го)
г ->• z„ A Z
что доказывает дифференцируемость функции <р(и>) при
W — w0.
10.54.	Однолистные функции. Функция <w = f (z),
определенная и аналитическая в области G на плоскости z
и отображающая ее взаимно однозначно в область Н на
плоскости w, называется однолистной в G. Мы увидим
(10.596), что у однолистной функции всюду f'(z)=^=0.
10.56]	§ 10.5. ОТОБРАЖЕНИЯ И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ 443
По 10.52 однолистной является любая аналитическая функ-
ция да=/(г) в окрестности точки z0, где /'(го)=^О.
10.55.	Дробно-линейная функция. Линейная
функция, рассмотренная в 10.51,
w=b{z — z0)-Yw0,	(1)
очевидно, однолистна во всей плоскости z.
Функция w=-|- осуществляет взаимно однозначное и
конформное в конечных точках отображение расширенной
плоскости z на расширенную плоскость w„ причем
точка г=0 переходит в точку те»=со и точка z~ оо
переходит в точку w=0. Можно считать, что линейная
функция (1) также отображает расширенную плоскость z
в расширенную плоскость w, переводя точку z— оо в w= оо.
Общую дробно-линейную функцию
az-f-b	,	,	, гл
w — —г-т , где Ъс^аа, с^=0.
сг-j-a
можно рассматривать как результат последовательного при-
менения линейной функции, функции вида и еще одной
линейной функции: это следует из представления
а , Ьс—ad
W с +с (cz-f-d) '
Поэтому дробно-линейная функция также осуществляет
взаимно однозначное отображение расширенной плоскости z
„	d
на расширенную плоскость w. При этом точка z ——— пе-
реходит в точку w— оо, а точка z—оо переходит в точку
10.56.	Степенная функция w— zn, п> 1, и ей об-
ратная. Здесь мы имеем, во всяком случае при | arg г | <	,
|«>| = |z|n, arg w =/г arg z.	(1)
Из формул (1) видно, что функция <w=zn отображает вза-
имно однозначно внутренность угла —сс < argz <	— на
444
ГЛ. 10. АНАЛИТИЧЕСКИЕ ФУНКЦИИ
(10.57
угол в плоскости w, выделяемый неравенствами
— ла < arg w < ла.
Наибольший угол — а < arg z < а, в котором функция w=zn
остается еще однолистной, имеет раствор ; он ото-
бражается этой функцией на всю плоскость w, из которой
удалена вещественная отоицательная полуось.
Обратная функция, обозначаемая, естественно, г =
отображает взаимно однозначно указанную область в плоско-
л	. л
сти w на внутренность угла----— < arg г < — в плоскости z.
В точке z=0 функция w = zn определена и сохраняет
аналитичность, однако конформность отображения в этой
точке отсутствует; это связано с тем, что в точке 0 про-
изводная функции zn равна 0, если л> 1.
10.57.	Экспоненциальная функция ®=ег и ей
обратная. Здесь мы имеем
е2 = ех+,У — ех (cosу + г sin j).
В частности, |ег] = е*, arg j + 2£л (k= 0, ±1, ±2, ...).
Каждая горизонтальная прямая у=у0 в плоскости z пере-
ходит в плоскости-w в линию u=e*cos_y0, v= ех sin_y0; это
есть луч, выходящий из начала координат в плоскости w
под углом у0 к положительному направлению оси и. Полоса
в плоскости z, выделяемая неравенствами —а<_у<а<л,
отображается функцией w = e* взаимно однозначно в угол
в плоскости w, выделяемый неравенствами
—а < argw < а.
Наибольшая полоса —а <_у < а, в которой функция w=<?z
остается еще однолистной, имеет ширину 2а = 2л (так что
а—л); она отображается функцией w=ez взаимно одно-
значно на область W в плоскости w, получаемую удале-
нием из этой плоскости вещественной отрицательной полу-
оси. В этой области W определена и аналитична обратная
функция, которая, естественно, обозначается ^=lnw. Для
действительных положительных w эта функция совпадает
с известной функцией Inw, определенной в 5.41. Далее,
из равенства |ег|=е* следует, что x = ln|ez|; учитывая,
10.58]	§ 10.5. ОТОБРАЖЕНИЯ И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ 445
что одновременно у= arg е2, мы имеем
In to = z = х + iy = In [ e2 | + I arg e2 — In | w [ 4- i arg 10,
что позволяет отделить в функции In 10 вещественную и
мнимую части. Из равенства е21+г’ = ег* ега обращением полу-
чается соответствующее свойство логарифма
In • w2) = In w1 -j- In io2.
Найдем производную от логарифма. Поскольку (е2)' = е2
(10.37), мы имеем по формуле 10.53 (2)
(In -ze/)' =	—-4=—.
'	' (ег) е2 ш
Отсюда следует, на основании теоремы о первообразной
(10.25), что функция z= In ю в области W может быть пред-
ставлена в форме интеграла
In w = In w0 -j- у	,
где путь интегрирования есть любая кусочно-гладкая линия,
соединяющая в области W точку io0 с io. Проще всего взять
w0= 1; тогда 1п«/о=О, и мы получаем
W
w' (г)
---7~Г > ЧТО
оу(г)
в 10.44.
Производная от сложной функции In w (z) равна
поясняет термин «логарифмический вычет»
Функция In w определена теперь для всех io, кроме веще-
ственных отрицательных; отрицательные числа пока еще
не имеют логарифмов. Немного погодя мы укажем полную
область определения логарифма, включающую и отрица-
тельные числа.
10.58.	Общая степенная функция io = z\ где
Л—положительное число. Эта функция определяется по фор-
муле
ю= е11п2
при условии, что z не есть вещественное отрицательное
число. Угол —а < arg г < а < min (л, •?•) функцией In г
446	ГЛ. 10. АНАЛИТИЧЕСКИЕ ФУНКЦИИ	[10.59
переводится в полосу —а < Im In z < а; умножение на Л
эту полосу переводит в полосу —аХ < ImXlnz < аХ, и по-
следующее потенцирование переводит полученную полосу
в угол в та-плоскости, выделяемый неравенствами
—аХ < argw < аХ.
Наибольший угол —а < argz < а, в котором функция w—
— zy остается еще однолистной, имеет (при Х^1) раствор
2 а —	( а = 4г”5) и отображается этой функцией во всю
плоскость w, из которой выброшена вещественная отрица-
тельная полуось.
Производная функции w—zx по общим правилам равна
(ех1пг)' = ezln2-(X 1пд)Л — — е^,пг = Xz>-1.
10.59.	Неоднолистность и римановы поверх-
ности.
а.	Рассмотрим функцию
w=(z—z0)n,	л>1,
в окрестности \z—z0|<p точки z0. Будучи однолистной
в пределах угла —arg(z—zo)	эта функция, хотя
и аналитическая, не,является однолистной во всей окрест-
ности точки z0. Окружность L — {(z—z0| = p} отображается
в плоскости w на окружность Л = ни | = рп}, но когда пе-
ременное z один раз пробегает окружность L, функция w—zn
пробегает соответствующую окружность Л уже п раз.
б.	Аналогичная картина имеет место для окрестности
л-кратного нуля z0 любой аналитической функции
w=f{z)=cn(z—z0)"-|-cn+J(z—z0)"+1+- • • , с„#=0, л>1.
Действительно, если G есть окрестность точки z0, в преде-
лах которой нет других нулей функций f(z) и /' (z), и
LcG—замкнутый контур, обходящий вокруг точки z0, то
согласно 10.44 логарифмический вычет функции f(z) отно-
сительно контура L равен п:
_±_с на.
L
По соображениям непрерывности, как и в 10.52, для
10.59]	§ 10.5. ОТОБРАЖЕНИЯ И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ 447
любого ни, достаточно малого по модулю, имеем также
2ш J f(£)-W а1= П'
Отсюда следует, по 10.44, что значение <w принимается функ-
цией f(z) в окрестности О, с учетом кратностей, п раз.
Но так как по условию /' (z) не имеет других нулей в об-
ласти G, кроме точки z0, мы видим, что любое значение
w=^0 принимается фактически функцией f(z) в п различ-
ных точках. В указанных случаях для восстановления вза-
имной однозначности отображения вводят понятие римановой
поверхности. Мы не будем здесь формулировать общее опре-
деление рнмановой поверхности, а ограничимся лишь двумя
характерными примерами.
в.	Для случая функции w=(z— z0)n риманова поверх-
ность строится следующим образом. Берутся п экземпляров
обычной плоскости w с отож-
дествленной—для всех экземпля-	г и
ров—точкой w=0, разрезанных	_________/
вдоль вещественной отрицатель-	/	/у
ной полуоси. Далее листы склей- /	f/j
ваются (т. е. производится coot- / д е/Ь
ветствующее отождествление) /
следующим образом: верхний край /	‘
разреза на первом листе склей-	** &
вается с нижним краем разреза /
на втором листе, верхний край /
разреза на втором листе—с ниж-	/
ним краем разреза на третьем г-и
листе, и т. д. , верхний край	рис g
разреза на л-м листе — с ниж-
ним краем разреза на первом листе (рис. 10.9). (Фактически
в трехмерном пространстве произвести такое склеивание, без
дальнейших самопересечений, невозможно, но это несущест-
венно.) При этом на каждом листе сохраняется первоначаль-
ная комплексная координатная система. Теперь отображение
<w~zn можно рассматривать как взаимно однозначное ото-
бражение полной плоскости z на построенную риманову по-
верхность. А именно, поставим в соответствие точке г= р > 0
точку tw=p" на первом листе. При движении z по окруж-
ности [z [= р в положительном направлении w==zn будет
448	ГЛ. 10. АНАЛИТИЧЕСКИЕ ФУНКЦИИ	(10.59
двигаться в положительном направлении по первому листу
римановой поверхности и, когда точка z дойдет до границы
области однолистности, указанной в 10.56, т. е. до значения
zc arg z = -^-, точка ч» будет иметь аргумент argw=n,
т. е. будет находиться на луче, по которому первый лист
склеен со вторым. При дальнейшем движении точки z в том
же направлении точка ни перейдет на второй лист, затем
на третий и т. д. и после полного оборота точки z вокруг
Z—0 вернется к исходному положению иа первом листе. Мы
получили искомое взаимно однозначное отображение плоско-
сти z на построенную (вместо плоскости «/) риманову по-
верхность. На этой римановой поверхности определена об-
ратная функция, которую мы по-прежнему обозначаем z —
—	; она отображает взаимно однозначно построенную
риманову поверхность на плоскость г.
Всем п различным точкам на построенной римановой по-
верхности с одной и той же комплексной координатой
отвечают л различных точек гй, ... , гп_1 на плоскости z;
их модули равны | ни | , а аргументы определяются равен-
ством
1
argzA = — (argw-J-2/гл), Л = 0, 1,..., л—1.
В частности, при л=2 и w= —1 получаем
г/—Г	• • (2Л-|-1)л	, .
—1 = « sm - y = ±Ч
в полном соответствии с основным правилом алгебры комп-
лексных чисел.
г.	Чтобы построить риманову поверхность, восстанавли-
вающую взаимную однозначность для функции w = ez, сле-
дует взять бесконечное (счетное) количество экземпляров
w-плоскости, занумерованных всеми целыми числами от — оо
до 4-оо, и склеить их в точке z = 0 и вдоль разреза по
вещественной отрицательной полуоси, приклеивая верхний
край разреза на Л-м листе к нижнему краю на (й4~1)-м листе
(рис. 10.10). Указанная в 10.57 область однолистности функ-
ции «/ = ег, т. е. полоса —отобразится взаимно
однозначно на нулевой лист (без разреза). Если точка z
будет двигаться по вертикали х=х0 от точки _у = 0 до
10.59J § 10 5. ОТОБРАЖЕНИЯ И ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ 449
точки у —л, точка w будет на нулевом листе описывать
полуокружность радиуса до верхнего берега разреза.
Если точка z будет двигаться вверх дальше, через значение
_у = л, то точка w перейдет через разрез, окажется на вто-
ром листе и будет описывать на
нем окружность того же радиу-
са; когда точка z перейдет через
значение j = 3n, точка w еще
раз перейдет через разрез и ока-
жется на третьем листе и т. д.
Обратная функция z = lnw
дает взаимно однозначное отоб-
ражение построенной римановой
поверхности на полную плоскость
z. При этом значениям w на л-м
листе отвечают значения z в по-
лосе (2л—1) л < у < (2л-}- 1) л.
Таким образом, функция, обрат-
ная к функции w = е2, есть функ-
ция бесконечнозначная, она обозначается через Ln и»; все
ее значения заключены в формуле
Ln w = In [ w | -}- i arg w,
где учитываются все возможные значения argw.
В частности, если w есть вещественное отрицательное
число w — —р, р>0, мы получаем
Ln(—р) = 1п|р| + (2Л+1)лх (Л = 0, ±L ±2, ...),
причем нет никаких сколько-нибудь естественных соображе-
ний, которые могли бы выделить из всех выписанных значе-
ний какое-либо одно.
д.	Аналогично можно строить римановы поверхности для
других аналитических функций. При этом в общем случае
в отображении w—f(z) участвуют римановы поверхности
как для переменного z, так и для функции w.
Для построения римановой поверхности функции f(z)
следует заготовить достаточное число идентичных между
собой листов, соответствующих области определения функ-
ции /(z), и провести на них разрезы, разделяющие эту
область на части, в которых функция f(z) однолистна; да-
лее следует склеить края разрезов на различных листах
450
ГЛ. 10. АНАЛИТИЧЕСКИЕ ФУНКЦИИ
(подобно тому как это делалось в примерах в и г) с целью
обеспечить взаимную однозначность получающегося отобра-
жения всей римановой поверхности для переменного z на
всю риманову поверхность для переменного и».
Точки, при обходе вокруг которых по окружности про-
извольно малого радиуса значения функции f(z) переходят
на новый лист, играют особую роль в структуре римановой
поверхности; они называются точками разветвления функ-
ции f(z). Для любой точки г0, не являющейся точкой
разветвления функции f(z), существует окрестность, в ко-
торой функция f(z) приводится к набору однозначных
аналитических функций; у точки разветвления не существует
окрестности с таким свойством.
В примерах виг точками разветвления были точки 0 и оо.
Более подробно строение римановых поверхностей для
различных функций рассмотрено в книге А. И. Маркуше-
вича «Краткий курс теории аналитических функций», Гос-
техиздат, 1957. Современное состояние общей теории рн-
мановых поверхностей описано в книге Дж. Спрингера
«Введение в теорию римановых поверхностей», ИЛ, 1960.
ЗАДАЧИ
СО
1.	Если радиус сходимости ряда f (г) = ^апгп равен 1 и все ап
о
положительны, то z=l есть особая точка.
СЮ
2.	Если ряд 2 апгп имеет радиус сходимости 1 и на окруж-
о
ности | г | = 1 единственной особой точкой является полюс порядка т,
то | ап\^Апт~1, где А — постоянная.
3.	(Принцип максимума.) Пусть /(г)—аналитическая функция
в области G, ограниченной контуром Г, и пусть
sup |f(z)|.
гег
Тогда | f (г) | М в области G. Если | f (z0) | — М в некоторой внут-
ренней точке z0£G, то f (z) постоянна в области G.
4.	Если функция f (г), аналитическая внутри круга | г | < R,
удовлетворяет в нем неравенству (z)| М и если f(Q) = Q, то
М . ,
И (г) I < -R-1 г |
(Г. Шварц).
ЗАДАЧИ
451
5.	Если функция f (г) аналитична в круге | z | < /?, то функция
In М (р), где М (р) = max | f (г) |, есть выпуклая функция от 1п р
|z |=р
(Ж; Адамар).
6.	Вещественная функция и (х, у) называется дифференцируемой
в точке (х0, у0), если существуют числа Аи и Вп такие, что в неко-
торой окрестности точки х0, у0 справедливо представление
и (х0+h, yB+k)=u (х0, ув) + Auh+Bak+e, (h, k),
g
где I /, ij’ i ь i—* О ПРИ —* 0’	0- Доказать> что комплексная
I Л I -f- | К I
функция w=u(x, y)-f-iv(x, у) тогда и только тогда имеет производ-
ную w' (z0), когда функции и (х, у) и v (х, у) дифференцируемы в
точке z0=*xe-j-iye и АЙ = ВО, Ао=— Ва.
_ _	,	az-j-b
7.	Доказать, что дробно-линеиная функция w= сг_|_^ перево-
дит в себя семейство всех окружностей (включая и прямые, которые
можно считать окружностями с бесконечно удаленным центром).
СЮ
8.	Рост функции f (г) = 2 anzn можно оценивать с помощью
о
функций
Ж(р)= max |f (г) |,
I z |=p
^(р^екпи"-
о
Очевидно, М (р) <	(р). Но Mt (р) не слишком быстро возрастает
сравнительно с М (р): при любом о > 0 имеет место неравенство
М (г+6).
9.	Пусть в области G, ограниченной контуром L, функция f (г)
аналитична, за исключением, возможно, конечного числа полюсов, и
на контуре L отлична от нуля. Когда г обходит L в положительном
направлении, точка w—f (z) описывает некоторую замкнутую кривую.
Ее число оборотов (вокруг точки ш=0) равно числу нулей функции
И*) н области G за вычетом числа полюсов (принцип аргумента).
10.	Известно, что последовательность аналитических функций
f„(z) (л = 1, 2, ...) сходится к функции f(z)+O равномерно внутри
области G (10.36 а). Пусть Z—множество всех нулей всех функций
fn (г) н области G. Тогда множество нулей функции f (z) (считая
m-кратный нуль за т нулей) в области G совпадает с совокупностью
всех предельных точек множества Z внутри области G.
СО
11.	Если ряд У g(n)(z) сходится хотя бы в одной точке г, где
о
функция g(z) аналитична, то g(z)—целая функция и указанный ряд
сходится при всех г равномерно в каждом круге (Г. Полна).
452
ГЛ. 10. АНАЛИТИЧЕСКИЕ ФУНКЦИИ
12.	Указать области однолистности, построить римановы поверх-
1 ( , 1 \
иости и наити точки разветвления у функции w==~2' 1г~Ь~ 1 •
tt)=cosz и им обратных z — w ± У щ2—1, z=Arccost0.
13.	Доказать равенство
i Arc cos w= Ln (w ± Уз2 — 1).
14.	Если функции f± (г), ..., fn (г) аналитичны в области G, то
функция | fi (г) | + ... +1 fn (г) | не может достигать максимума
внутри G.
15.	Аналитическая функция f(z), определенная во всей плос-
кости г, отображает всю плоскость в верхнюю полуплоскость. Дока-
зать, что f(z) есть постоянная.
16.	Вывести теорему о существовании корня у алгебраического
многочлена Р (z) (5.Е6) из теоремы Лиувилля 10.38.
17.	Вывести теорему о существовании корня многочлена Р (г)
(5.86) из теоремы о логарифмическом вычете (10.44).
18.	Вывести теорему о существовании корня многочлена Р (г)
(5.86) из принципа максимума (задача 3).
19.	Аналитическая функция f (г) определена во всей плоскости,
•за исключением точек гь г2, ... , z„, ... , в которых эта функция
имеет простые полюсы с вычетами Ьх, Ьп, ... Допустим, что
множество {z: | f (z) | < С} при некотором С содержит семейство ок-
ружностей Гп с центром z=0 радиусов Рп—> оо. Доказать, что
СЮ
Z(2) = f(0)+X ьп
1 z-z„ гп)
(разложение f (г) иа простейшие дроби).
20.	Пусть g(z) аналитична во всей плоскости и имеет простые
pr (z)
нули в точках гь z2, ... Допустим, что для функции f(z) =
выполнены условия задачи 19. Показать, что
g'(Q> г 03 1	г
^(г)=^(0)ее(О) П у 1—— W"
»=1 Ц
21.	Доказать, что справедливы разложения
ИСТОРИЧЕСКАЯ СПРАВКА
453
22-	Пусть функция f (г) аналитична в области G =
г: —а «С arg z < а < -g- > и удовлетворяет условиям
|/ (г)| < Аев 1 2 1 в области G;
И (?) I < 1 на лучах arg г = ± а.
Тогда | f (г) | < 1 но всей области G (Фрагмен—Линделёф).
23.	Пусть функция f (z) аналитична в верхней полуплоскости G
и удовлетворяет условиям
|Z(x)l<c	(—оо < х < оо)
и при любом е > О
|/(z)|< Леее|г| для всех z£G.
Тогда | f (z) | < с при всех z£G.
24.	Пусть f (z)—целая аналитическая функция, удовлетворяющая
условиям
IZ (•*)!< с, inf Р(х)|=0 (—оо < х < оо)
и при любом е>0
P(z) |<Леее,г| для всех z£G.
Тогда f(z) = O.
Историческая справка
В конце XVII и в начале XVIII века накопилось уже много
фактов относительно свойств элементарных функций, в которых
вместо вещественного аргумента подставлен мнимый (комплексный).
Не имея геометрического представления комплексного чирла (которое
было указано лишь Гауссом в 1799 г.) и рассуждая по аналогии,
математики той эпохи часто приходили к парадоксальным результа-
там. Так, Лейбниц и И. Бернулли спорили о том, каковы логарифмы
отрицательных чисел—мнимые или действительные, причем ни тот, ни
другой не имел какого бы то ни было определения логарифма в
комплексной области; такое определение, учитывающее многознач-
ность логарифма, было дано Эйлером в 1749 г. «Условия Коши —
Римана» для функций, заданных степенными рядами, были впервые
указаны Даламбером (1752) и Эйлером (1777). Термин «аналитическая
функция» идет от книги Лагранжа «Теория аналитических функций,
содержащая принципы дифференциального исчисления, освобожден-
ные от всякого рассмотрения бесконечно малых или умаляющихся,
пределов или флюксий и сведенные к алгебраическому анализу
конечных количеств» (1797), где под аналитической функцией пони-
мается сумма степенного ряда. Впрочем, Лагранж даже не ставил
вопроса о сходимости своих рядов (иначе он неминуемо принужден
был бы апеллировать к изгнанному им понятию предела). Работы
454	ГЛ. 10. АНАЛИТИЧЕСКИЕ ФУНКЦИИ
Коши (начавшиеся с 1814 г.), в которых содержится ряд центральных
теорем теории аналитических функций, основаны на том же опреде-
лении, но с четким выявлением смысла сходимости рядов и с ясной
геометрической картиной комплексного переменного; также у Коши
впервые рассматривается криволинейный интеграл по комплексному
аргументу, определение которого он сводит к определению обычного
интеграла по вещественному переменному отделением вещественной
и мнимой части. Он указал способ вычисления интегралов аналити-
ческих функций по замкнутому контуру с помощью вычетов. С другой
стороны, Коши связал аналитичность функции с ее дифференцируе-
мостью по комплексному переменному; это последнее свойство он
называл моногенностью. Анализ особых точек однозначной функции,
связанный с использованием ее ряда Лорана (1843), был одновременно
произведен русским математиком Ю. В. Сохоцким и итальянцем
Казорати (1868) и несколько позднее Вейерштрассом (1876).
ГЛАВА 11
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
Интегральное исчисление немного бы стоило, если
бы первообразная не разыскивалась в конечном виде, но
всегда требовала бы тоже перехода к пределу; в этом
случае ие было бы никакого прогресса . . . Вся огромная
заслуга Ньютона н Лейбница состояла именно в конеч-
ной выразимости результата фактически невыполнимой
операции ... С тех пор минуло более 250 лет и по пути
Ньютона и Лейбница прошло немало сильных людей.
Никто нз них не смог продолжить дела основоположни-
ков анализа бесконечно малых и ие мог указать другого
метода выражать в конечном виде результат суммирова-
ния бесконечно малых... Лишь на долю Коши, сильней-
шего аналитика XIX века, выпала честь дать особый
прием, названный им исчислением вычетов, с помощью
которого во многих случаях, там, где нам изменяет ис-
пытанный метод первообразных Ньютона и Лейбница,
можно выражать в конечном виде результат суммировав
иия бесконечно большого числа бесконечно малых сла-
гаемых.
И. Н. Лузин,
Исаак Ньютон, как математик н натуралист (1943)
§ 11.1. Несобственные интегралы первого рода
11.11. Пусть функция у = f (х) определена при а^х=С
оо и принимает комплексные значения. Определение ин-
теграла от комплекснозначной функции можно считать из-
вестным из 10.2Г, именно, если /(x) = ii(x)-|-i'u(x), где
и(х) и v(x) вещественны, мы полагаем по определению
ь	ь	ь
J f (x)dx = J и (x)dx i J v (x)dx.
a	a	a
Таким образом, интегрируемость функции f(x) по отрезку
[а, равносильна одновременной интегрируемости по этому
отрезку функций и(х) и v(x).
Пусть функция f(x) интегрируема (например, кусочно-
непрерывна) на каждом конечном промежутке а х b < оо,
где а фиксировано, а b произвольно. Мы желаем придать
смысл «несобственному интегралу 1-го рода»
\f(x)dx.	(1)
а
Рассмотрим комплексную функцию от аргумента Х^а
х
ЦХ)= [f(x)dx.	(2)
456
ГЛ. 11. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
(11.11
Определение. Если при X —> сю функция 1(Х} имеет
конечный предел то мы называем несобственный инте-
грал (1) сходящимся и полагаем по определению
Пт
Х'-> со
X
^f(x)dx =1.
и
(3)
Если при X —> оо функция I(X) не имеет конечного предела,
мы называем интеграл (1) расходящимся и не приписываем
ему никакого значения.
х
xadx =
СО
Примеры, а. Несобственный интеграл x“dx.
1
Так как
уа+1______________________1
-МЛ- п₽и
1пХ при а = — 1,
то интеграл сходится при а < — 1 и расходится при
—1.
СО
б. Несобственный интеграл ^созхб/х.
о
Так как
х
cos х dx = sin X
о
не имеет предела при X оо, то интеграл расходится.
СО
в. Несобственный интеграл elx dx.
о
Так как
о
не имеет предела при X —> оо,то интеграл расходится.
11.12]
§ 11.1. ИНТЕГРАЛЫ ПЕРВОГО РОДА
457
11.12.	К рите рий Коши и эквивалентные ус-
ловия сходимости. Утверждается, что следующие че-
тыре предложения эквивалентны'.
а.	Существует такое I, что для любого е > 0 найдется
Хо > а такое, что для каждого Х~^Х0
х
|/—/(Х)| = |/—J/(x)dx|<e.
а
б.	Для любой последовательности Хп—+<х> числа 1(Хп)
имеют (конечный) предел.
в.	Для любой последовательности Хп —> оо ряд
Xn+i
2№+1н№2 $ мах
И	X
сходится.
г.	Для любого е > 0 существует такое X а, что при
Х’^Х, Х"^Х
|/(Х')-/(Х")|=| J/(x)dx|<8
X’
(критерий Коши).
Предложение а есть просто определение предела функции
/ (X) на бесконечности. Предложение г есть критерий Коши
для существования этого предела. Предложение б представ-
ляет собой эквивалентное условие на языке последователь-
ностей (4.66). Наконец, предложение в выражает обычную
связь между сходимостью ряда и сходимостью последова-
тельности его частных сумм. Итак, предложения а—г эк-
вивалентны.
В предложении б существенно, что речь идет о любой
последовательности Хп—>оо. Если известно, что для неко-
торой последовательности Хп —> сю числа 1(Хп) имеют пре-
дел, то это еще не означает, что интеграл (1) сходится.
Например,
2НЛ
cosx dx-- О,
о
но интеграл 11.11 б расходится,
458
ГЛ. 11. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[11.13
11.13.	Случай неотрицательной подынтег-
ральной функции.
а.	Рассмотрим несобственный интеграл
СО
J f(x)dx
а
(1)
с неотрицательной функцией f(x). Тогда первообразная
х
I(X) — J f(x)dx не убывает; если I (X) не ограничена на (а, оо),
а
то при X -+ оо она стремится к + оо и мы говорим, что
интеграл (1) расходится к +оо; если / (X) ограничена на
(а, оо), то sup/(Х) = lim /(X) (4.53) и интеграл (1)
X -> оо
СХОДИТСЯ.
б.	Признак сравнения формулируется следующим
образом: если на (а, оо) заданы две неотрицательные инте-
грируемые на каждом конечном промежутке функции J\(х)
и fz(x) и j\(x)^.cf2(x) при х~^Х0, то из сходимости ин-
теграла от f2 (х) следует сходимость интеграла от (х),
из расходимости интеграла от (х) следует расходимость
интеграла от f2 (х).
Все эти выводы следуют из неравенства
х	х
4 (Х)-/х (Хо) = J Л (x)dx < с J /2 (x)dx= с (/2 (Х)—12 (Хо)),
х0	Х„
имеющего место для любого X > Хо, и из сходимости ин-
теграла с ограниченной первообразной /(X) (а).
в.	Пример. Интеграл от рациональной функции
^-dx
<2 (х) ах
(а > 0),
(2)
где Р(х) и Q(x)^=0— многочлены (с комплексными коэф-
фициентами) степеней соответственно р и q, сходится,
если + и расходится, если ^<1р-|-1.
I р (х) I
Действительно, если q^p-i-2, то -щ-у s
с
—, и
X2 ’
грал (2) сходится, поскольку для сравнения можно
функцию(11.11а). Пусть теперь q^.p~\-\. Тогда
инте-
взять
У Ра-
11.14]
§ 11.1. ИНТЕГРАЛЫ ПЕРВОГО РОДА
459
я .	Р (х)
циональной функции х имеется ненулевая целая часть;
можно положить
xwT а°хт++ • • • +	+«»+
где т^О, аоу=О, степень Р1(х) ниже степени Qi(x). Отсюда
Р (*) — а хт~г I 4-а
Q(x) — °х	• +ат-1
1 PiW
х Qilx)’
J Q (*)
a
X
.. +V1 {X-a)+amln^+ Clglg dx .
flI	L* t/ * WI JA}
a
Последнее слагаемое, по только что доказанному, имеет
конечный предел (степень знаменателя по крайней мере на
2 выше степени числителя), сумма же остальных слагаемых
заведомо не имеет предела, так как по модулю стремится
к оо . Поэтому в данном случае интеграл (2) расходится.
г.	Пример. Для многочлена Р (х) = а0 хт + ... ~\-ат
с вещественными коэффициентами и а0>0 при больших х
справедлива двусторонняя оценка
поэтому
III	<	111	<
сходится, если — > 1, и расходится, если —	1 .
11.14.	Интегральный признак сходимости
числового ряда. Пусть аг +«2+ ... есть ряд с поло-
жительными невозрастающими членами, так что an+i^an
(л=1,2, ...), и пусть, далее, у=а(х) — положительная
невозрастающая функция, такая, что а(п) = ап. Из рис. 11.1
4€0
ГЛ. 11. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
{11.14
видно, что
п
а2-\-	a (x}dx^a1-\-ai+ ... +a«_v	(1)
i
Из неравенства (1) вытекает: если сходится интеграл
\ а (х) dx, то сходится ряд 2 ап> и если расходится интег-
1 1
03	со
рал \ a(x)dx, то расходится и ряд У, ап. Это — интеграль-
1	1
ный признак Коши сходимости числового ряда.
и расходится при 1 (11.11 а). Отсюда заново получается
со
результат о сходимости ряда 2}-jnpn а>1 и его расхо-
I
димости при а^1 (6.15 а).
б. Равенство
00	со
С dx С du ,	.	. ,.
1 -1 • „ = \ —(п= 1п х, а>1)
J xln“x J иа '	’	'
a	In а
со
показывает, что несобственный интеграл J - сходится
а
при а > 1 и расходится при а^1. Соответственно ряд
СО
У, - j^a— сходится при а > 1 и расходится при
2
а<1 (6.15 в).
11.14]
§ 11.1. ИНТЕГРАЛЫ ПЕРВОГО РОДА
461
в. Используя геометрические соображения такого типа,
как в начале пункта, можно получать различные оценки для
остатков сходящихся рядов и для частных сумм как сходя-
щихся, так и расходящихся рядов. Например, из рис. 11.2
мы непосредственно получаем:
ОО	05
у 1	Р dx ___ 1 р 1___________
J 7	L(«-i)A~1
Л—П	п-1
Из рис. 11.1 при а (х) = у имеем
(Х>1).
Таким же образом из рис. 11.3 вытекает неравенство
п (	k + ,1	\
У, |aft— \ a
л=1 i. k *
причем величина слева возрастает при увеличении п.
Обозначая ее предел через С и производя суммирование,
462	ГЛ. 11. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	[11.15
получаем, что
п	п+1
У. ak = С a(x)dx + c—уп, уп \ 0.	(2)
k=i i
Для случая ряда ak— постоянная С была вычислена впер-
вые Эйлером (1734): С— 0,5772... Постоянная Эйлера часто
встречается в анализе. Равенство (2) в этом случае прини-
мает вид
1+т+4+---+^=1п(л+1)+°’5772---~^’ ^\°-
11.15.	Абсолютная и неабсолютная сходи-
мость несобственных интегралов. Рассмотрим
несобственный интеграл
со
$/(x)dx,	(1)
а
где /(х)—кусочно-непрерывная комплексная функция. Если
сходится интеграл
СО
Sl/(x)|dx,	(2)
а
то сходится и интеграл (1), поскольку при любых X' и X”
по 10.21 (5)
X"	X"
J f(x)dx < 5 |/(х) I dx
X'	X'
и можно применить критерий Коши. В этом случае интеграл
(1) называется абсолютно сходящимся, а функция f(x) —
абсолютно интегрируемой на (а, оо). Но интеграл (1) мо-
жет сходиться и при расходимости интеграла (2); в этом
случае интеграл (1) называется условно или неабсолютно
сходящимся. Существуют признаки сходимости, применимые
к неабсолютно сходящимся интегралам.
11.16.	Признак Л е йб н и ц а. Рассмотрим несобствен-
ный интеграл
со
J/(x) dx,
а
H’leJ	§11.1. ИНТЕГРАЛЫ ПЕРВОГО РОДА	463
где функция /(х) вещественна. Пусть < а2 < . . . <
< ап < ... есть последовательность всех корней функции
f(x) на (а, оо), причем ап—->-оо, f(x)>0 при a2n— i < х<
<а2пи/(х)<0 при а2п < х < а2п+1 (рис. 11.4). Числа
ап + 1
bn= $ f(x)dx	(1)
On
образуют знакочередующуюся последовательность. Если для
них выполняются условия признака Лейбница для числового
Рис. 11.4.
ряда (6.23), т. е. если для всех n — N, Д;+1, N +2, ...
выполняется неравенство | Ьп |	| btl+11 и |tn| \ 0, то интег-
рал (1) сходится.
Для доказательства найдем при заданном X такое п,
что а„^Х^ап+1. Тогда
х	at	х
J/(x) dx = ^f(x) dx + [fex + ... +&„_!] + $/(x)dx.
d	Cl	an
Первое слагаемое справа постоянно. Сумма в квадратных
скобках при п —> оо имеет предел в силу признака Лейб-
ница для ряда. Последнее слагаемое по модулю не превосходит
“n+i
S |/(х) |dx=|M
С»
и в силу условия стремится к нулю при п-—>-оо. Отсюда
следует существование предела у левой части, что нам
и нужно.
Примеры, а. Рассмотрим интеграл
СО
g(x) sinxdx,	(2)
а
464
ГЛ. 11. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
(11.16
где g(x)>0 и g(x) \ 0 при х —> оо. Последовательные
корни функции £-(x)sinx при х>а суть x=kn, (k 4-1) л, —
Поскольку, очевидно,
g (х) | sin х |	g (х 4* л) | sin (х 4- я) |,
мы имеем
(m + I) п
|&J = $ £(х) | sin x | dx >
mn
(m+1) л
$ ё(х 4-я) | sin (x 4-я) |dx="
mil
(m+2) л
= $ g(x] | sin x I dx = I bm+11;
(m+1) n
далее,
(m+1) n
\bm |= g(x) | sin x | dx ng(mn)—>0 при m—>oo.
тл
Таким образом, условия признака Лейбница выполнены,
и интеграл (2) сходится.
ОС
Если J g(x)dx < оо, то интеграл (2) сходится абсолют-
а
а:
но. Покажем, что при g(x) dx = оо интеграл
а
сп
^g-(x)|sinx[dx	(3)
а
расходится. В промежутке (т—1) л 4~ <Сх	тл — ~ дли-
2	1
ны у л имеют место неравенства | sin х | у , g (х) g (тл);
поэтому
Л
_	тл--^-
тл	6
J g(x) | sinx\dx J	g(x)| sin x\dx^
(т-1)л	л
'	(m- I) Л+ —
О
_	,	.	1	2
^ё(тл) - у у л.
11.17]
§ 11.1. ИНТЕГРАЛЫ ПЕРВОГО РОДА
465
Но ряд из чисел g(mn) расходится, так как расходится
соответствующий интеграл
со	со
§ g (хп) dx = — § g(u) du	(и=пх).
а	ал
Поэтому расходится и интеграл (3) согласно 11.12 в.
б. Интеграл
СО
sin (x'i) dx, у > 0,	(4)
а
сводится подстановкой хт = и к интегралу
— С
V J
ь
sin и  и v du.
который по предыдущему сходится при
— 1 < О, т. е.
V
при у > 1 (можно применить признак Лейбница и непосредст-
венно к интегралу (4)).
Заметим, что в сходящемся интеграле (4) подынтеграль-
ная функция sin (хт) не стремится к нулю при х—>оо, как
можно было бы ожидать на основании формальной аналогии
с рядами. На самом деле аналогом теоремы «.общий член
сходящегося числового ряда стремится к нулю» является не
предложение «подынтегральная функция сходящегося несоб-
ственного интеграла стремится к нулю при х —► оо»,—как
мы видим, неверное,— а другое предложение: «интеграл от
подынтегральной функции сходящегося несобственного ин-
теграла, взятый по интервалу фиксированной длины, уда-
ляющемуся в бесконечность, стремится к нулю». Иными
словами, при любом h > О
х+Л
lim f f(u)du — Q-,
X -> 00	„
это вытекает немедленно из критерия Коши 11.12 г.
11.17.	а. Признак Абеля—Дирихле. Рассмотрим
несобственный интеграл
оо
^g (x)s(x)dx.	(1)
а
466
ГЛ. 11. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[11.17
Если (комплексная) функция g(x) обладает кусочно-не-
прерывной абсолютно интегрируемой на (а, оо) производной и
стремится к 0 при х—>-оо, a s(x) имеет ограниченную
первообразную G(x), |G(x)|^C, то интеграл (1) сходится.
Для доказательства воспользуемся интегрированием по
частям:
<7	4
^g(x) s (х) dx—g(x) G(x) I’ — J G(x)g' (x)dx (p<q).
p	‘ p
Здесь внеинтегральный член допускает оценку
I g(q) G(q) — g(p) G(p) | sC 2C max {| g(p) |, | g(q) |}
и, следовательно, стремится к нулю при р, q оо. Инте-
гральное слагаемое допускает следующую оценку:
ч
G(x)g' (x)dx
р
ч
| g' (х) ]dx,
р
откуда следует, что оно также стремится к нулю при р —>- оо,
^->оо. Таким образом, для интеграла (1) выполняется кри-
терий Коши 11.12 г, и, следовательно, интеграл сходится.
б. Пример. Рассмотрим интеграл
J Q(x)
eiax dx
(a£R, a=^0),
(2)
где P(x) и Q(x)— многочлены от x (с комплексными коэф-
фициентами), причем степень многочлена Q(x) на единицу
выше степени многочлена Р(х) и Q(x) не имеет корней
р М
в промежутке (а, оо). Положим g(x) =	. , s(x) = eiax.
W (Л)
P'Q__PQ'
Тогда g'(x) =— 2	 есть рациональная функция, у кото-
рой числитель имеет степень по крайней мере на 2 ниже,
чем знаменатель. Поэтому g' (х) обладает абсолютно схо-
дящимся интегралом (11.13 в). Функция s(x) = eia-x имеет
е‘ах
ограниченную первообразную . Таким образом, условия
для применения признака а выполнены, и интеграл (2) схо-
дится.
11.18]
§ 11.1. ИНТЕГРАЛЫ ПЕРВОГО РОДА
467
в. Для вещественной функции g(x) условие признака а
можно несколько видоизменить; именно, в этом случае до-
статочно предположить, что g(x) стремится к нулю моно-
тонно, обладая кусочно-непрерывной производной. Действи-
тельно, в указанном предположении функция g' (х) не меняет
знака и
^|^(х)|йх = ^g'(x)dx =|^(Х)— ^(а)|
имеет конечный предел при X-> оо, так что | g' (х) | интег-
рируема.
Условия на функцию s (х) остаются прежними.
11.18. Интегрирование по частям и через
подстановку в несобственном интеграле. Фак-
тически мы уже не раз пользовались этими приемами в кон-
кретных случаях; выскажем теперь некоторые общие сооб-
ражения. Достаточно проверить, что возможно произвести
указанные действия на конечном промежутке (а, X), и затем
перейти к пределу при X -> оо. Так, если интегрирование
по частям на промежутке («, X) дает
J /(х) g(x) dx =/(х) G(x) £ — $ f(x) G(x) dx,
то можно написать и равенство
\f(x)g(x)dx=f(x)G(x)\“ — $/'(х) G(x)dx
в предположении, что по крайней мере два из написанных
трех предельных выражений существуют (тогда, очевидно,
будет существовать и третье). Здесь внеинтегральный член,
в частности, определен так:
/(*)G(x)|“= lim/(x)G(x)
<а Х-*а>
= lim [/(X)G(X)-/(a)G(a)].

468
ГЛ. 11. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
(11.21
Аналогично, если в результате подстановки х = х (и) мы
пришли к равенству
х	и
dx — ^f(x(u))u' (x)dx
a	b
и при этом из X -> оо следует U В ( оо ) и обратно, то
справедливо равенство
f (х) dx = J f(x (и)) и' (х) dx,
а	b
если существует хотя бы один из написанных интегралов
(тогда существует и второй).
§ 11.2.	Несобственные интегралы второго
и третьего рода
11.21.	Н е с об с т в е н н ы е интегралы второго
рода.
а.	Рассмотрим комплексную функцию f(x), заданную
в конечном промежутке [а, 6], интегрируемую в каждом
промежутке [я-]-в, £], но', возможно, не интегрируемую (на-
пример, не ограниченную) на всем отрезке [а, #]. Мы желаем
придать смысл «несобственному интегралу 2-го рода»
а
(1)
Для этого рассмотрим функцию от в
ь
/(в)= $ f(x)dx.
а+в
Если при в —> О это выражение имеет конечный предел,
положим I, то мы говорим, что несобственный интеграл 2-го
рода (1) сходится, и приписываем ему значение
ъ
I— lim/(e) = lim [ f(x)dx.
е -> 0	е -> Ос+е
11-21]	§ 11.2. ИНТЕГРАЛЫ ВТОРОГО И ТРЕТЬЕГО РОДА 469
Если при в -> 0 функция /(е) не имеет предела, мы говорим,
что несобственный интеграл (1) расходится, и не приписы-
ваем ему никакого значения.
б.	Если интеграл
ь
I=\f(x)dx	(2)
а
существует как обычный определенный интеграл, то он
существует и в нашем новом определении и имеет то же
значение I. Действительно, если интеграл (2) существует
в обычном смысле, то функция f(x) ограничена вместе с ее
вещественной и мнимой частью (9.15 в); пусть, например,
1/(х)| < С. При любом е > 0 имеем
Ь	а+в	b
^f\x)dx =	^f(x)dx,
а	а	а+е
(3)
причем
с+е
J f(x)dx
а
Отсюда следует, что при е —► 0 предел второго интеграла
в правой части (3) существует и равен интегралу в левой
части, что и требуется.
в.	Приведенное определение а очень похоже на опре-
деление несобственного интеграла 1-го рода (т. е. с беско-
нечным верхним пределом). И действительно, интеграл 2-го
рода прямо приводится к интегралу 1-го рода с помощью
1 п	-
подстановки х—а — — . Поэтому можно всю теорию несоб-
ственных интегралов 2-го рода вывести из теории интегра-
лов 1-го рода. Можно теорию строить и параллельно, фор-
мулируя заново соответствующие теоремы. Мы предоставляем
читателю сформулировать для интеграла 2-го рода критерий
Коши, признаки сравнения, определение и теорему об абсо-
лютной сходимости, признак Лейбница и признак Абеля—
Дирихле. Отметим только некоторые специфические для
интегралов 2-го рода конкретные факты, существенные в
приложениях.
470
ГЛ. И. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[11.22
11.22. а. Для применения признака сравнения, как всегда,
важно иметь широкий набор «эталонных» интегралов. Тако-
выми для интегралов 2-го рода служат чаще всего интегралы
вида
ь
ЬДг-	<4
а
Мы имеем
dx
(х—а)х
!— Ь L(fc—“)К-1
е
(А=/=1),
(k=l);
поэтому интеграл вида (1) сходится при А. < 1 и расходится
при А 1.
б. Применяя признак сравнения, получаем: если при х € (а,Ь)
выполняется неравенство
(х—а)
С2
(х—а)* ’
то интеграл 11.21 (1) сходится при А<1 и расходится
при А 1.
в. Рассмотрим, в частности, интеграл
ь
| In х |т dx.
о
(2)
При малых х мы имеем |Inх |с |х |при любом а>0
(5.57 (3)). Можно взять а = -у ; сравнивая теперь интеграл
(2) с интегралом
х 2dx,
о
сходящимся в силу а, получаем, что и интеграл (2) схо-
дится при любом у.
11.23.	Несобственные интегралы третьего
рода. Пусть комплексная функция f (х) задана в проме-
11.23]	§ 11.2. ИНТЕГРАЛЫ ВТОРОГО И ТРЕТЬЕГО РОДА 471
жутке (а, Ь), концы которого могут быть и в бесконечности
(т. е. значения а=—оо, Ь= Ц-оо допускаются). По отно-
шению к функции f(x) будем называть точку с особой
в следующих случаях:
а)	точки с = — оо, -|-оо, если они являются концевыми
точками промежутка (а, Ь), всегда считаются особыми;
б)	точка с, лежащая внутри (а, Ь), называется особой,
если функция f(x) не является интегрируемой в обычном
смысле ни в какой окрестности этой точки; концевая точка
с считается особой, если f(х) не интегрируема ни в какой
односторонней (со стороны промежутка (а, Ь)) окрестности
этой точки.
Будем предполагать, что функция f(x) обладает не бо-
лее чем конечным числом особых точек и что вне этих
точек она непрерывна или кусочно-непрерывна. Мы хотим при-
дать смысл «несобственному интегралу 3-го рода»
ь
\f(x)dx.	(1)
а
Выбирая между каждыми двумя соседними особыми точ-
ками с(-, с1+1 неособую точку ру, мы получим совокупность
промежутков вида (с,-, р,) и (р;, с;+1), имеющих только по
одной особой точке на границе. Определим сначала интег-
ралы от функции f(x) по таким промежуткам, как несобст-
венные интегралы 1-го и 2-го рода:
pi	Pi
^f(x)dx = lim ^f(x)dx,
a	x-ci x
O + t	x
^f(x)dx= lim ^f(x)dx.
pt	x-»c;+lpi
Только если все получающиеся несобственные интегралы
сходятся, мы будем приписывать смысл интегралу (1); имен-
но, положим
Ь	Z P i	0'4-1
J/(x)dx=2] \f(x)dx + 5 f{x)dx
О	10	Pi
(2)
Нужно проверить, что результат не зависит от выбора
точек Pi. Проверим это для одного из промежутков [с;, с;+1].
472
ГЛ. И. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
(11.24
Пусть ct < Pi < < cz+1. Тогда
«t	QI
что и требуется. (В промежуточной выкладке мы не выпи-
сывали подынтегральных выражений, поскольку они не ме-
нялись.)
11.24.	Пример. Рассмотрим интеграл
dx_________
... \х—сп[ап’
— оо < ех
с„<оо. (1)
Особые точки: — оо, сх, .
pi
оо.
Ci
J сходятся тогда и только тогда, когда
Pi-i
множители ограничены в окрестности точ-
Ро “
ки cz). Интегралы J и j
Cl
az < 1 (остальные
сходятся тогда и только тогда,
—®	Рп
когда ссх ... +ап > 1. Итак, интеграл (1) существует тогда
и только тогда, когда выполнены условия
ах< 1, ... , а„< 1, ах +
Заметим, что интеграл
'л
dx
11.31)	§ 11.3. ВЫЧИСЛЕНИЕ С ПОМОЩЬЮ ВЫЧЕТОВ 473
получающийся из (1) при л=1, не сходится ни при
каком значении а. При всяком а расходятся и оба интег-
рала
с
Р dx
J (с-х)“ ’
dx
§ 11.3. Вычисление несобственных интегралов
с помощью вычетов
11.31. Интеграл от рациональной функции.
Рассмотрим несобственный интеграл от рациональной функ-
ции— отношения двух многочленов Р(х) и Q(x) (с комп-
лексными коэффициентами):
dx.
(1)
Он сходится, если знаменатель не имеет вещественных
корней и степень числителя по крайней мере на две едини-
цы меньше, чем степень знаменателя (11.13 в).
Как вычислить значение этого интеграла?
Можно, разумеется, взять неопределенный интеграл от
Р(х)
рациональной функции по правилам 9.42 и подставить
пределы —оо и оо. Но, оказывается, иногда быстрее при-
менить методы, связанные с аналитической природой функ-
Р(х)
ЦИИО>-
Функция комплексного переменного
P(z)
равная
аналитична всюду в плоскости переменного г, за исключени-
ем конечного числа точек—корней знаменателя. Рассмот-
рим в верхней полуплоскости замкнутый кусочно-гладкий
контур L, образованный отрезком [—R, Z?] вещественной
оси и полуокружностью
Cr= {z=Re‘4,
где R настолько велико, что вне полученного полукруга
уже нет в верхней полуплоскости ни одного корня знаменателя.
474
ГЛ. 11. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[11.31
Внутри этого полукруга имеется, вообще говоря, некоторое
число корней знаменателя, например alt ... , ад (рис. 11.5).
В силу формулы 10.43 (1) мы
получаем выражение
Устремим теперь R в оо.
,,	+	I P(z) I А
На полуокружности Сд мы имеем ~Q(z) =5= в СИЛУ
условия на степени многочленов Р (z) и Q(z), где А — некото-
рая постоянная; поэтому
|ШЛ|<ЛЯК_.М.
CR
Отсюда следует, что интеграл
R
С л
J <2(Х) dx
-R
имеет пределом при R —» оо
теграл (1) сходится, то он
интеграла (3). Итак,
(3)
величину (2). Но так как ин-
должен совпадать с пределом
<z
.• dx = 2ni V Выч
QW	Хм
Р(х)
Р(г)
(4)

а.	Если корни а,, ... , aq простые, то по формуле 10.42 (1)
Р(а7)
Выч
z=aj
и, следовательно,

(5)
11.31]
§ 11.3. ВЫЧИСЛЕНИЕ С ПОМОЩЬЮ ВЫЧЕТОВ
475
„	(* dx _ . 1 [
Пример:	\	2ш -уг—	= л.
н J *2+1	22 |2=г-
— со
б.	Если корни йъ .. . , ад кратные, так что корень
имеет кратность kj, то вместо формулы 10.42 (1) мы должны
использовать более общую формулу 10.42 (2)
Выч [4Я-1	= -1 Г(г-а,
I Q(z) jz=aj	(kj—1)! ['	7 Q(z) Jz=aj
так что
*	о
f Нттг dx = 2га’ У (b 1 пГ [“ а№ -77гг1 {kj~1 ’ • (6)
J QW	Zj (kj— 1)! L >' Q(z) Jz=aj ' '
— 05	z= 1
Пример:
CO
S (a:2+1)2 =2ra [(2—02 (22+1Ji]z=i =
— co
= 2л/
1 T _.	4ш I	л«• 1 л
(2+»)2jz=i- (z + i)3 |z=f~— 4m8p-—•
О	1Л	Г P (*) J
в.	Замечание. Интеграл \ dx мы привели к сум-
J Ч (Л)
Р (z)
ме вычетов (умноженной на 2л/) функции в верхней
полуплоскости, рассматривая контур L, составленный из отрез-
ка [—/?, /?] и полуокружности Сд= [z = Reirf, 0^<р^л}.
Но таким же образом можно рассуждать и с контуром L~,
составленным из отрезка [/?, —/?] (проходимого справа налево)
и полуокружности C^—{z—Re‘^, л^<р^2л} в нижней
полуплоскости; мы получим
= i-^dz=
z=bk Q (2)
= С
J Q (*)
R
2л/ Выч
k=i
«h
CR
где Ьг, ... , br—корни многочлена Q(z), лежащие в нижней
полуплоскости.
476
ГЛ. И. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[11.32
Переходя к пределу при /? —»-оо, найдем
сс	R	г
Г Р(х) .	1- С Л О - Vo Г Р(г)1
\ - и У4- dx = lim \ - ; ; dx ----- —2ш / , Выч -^гН-
J <2W	ew	LQ(z)Jz=bk
-«	-R	1
(7)
Полученный результат по форме отличается от резуль-
тата (4). В действительности они, конечно, совпадают, тйк
что разность этих результатов, т. е. умноженная на 2га'
Р (г)
сумма вычетов функции-^-— во всех корнях Q(z), как в
верхней, так и в нижней полуплоскости, равна 0.
Это можно показать и непосредственно. Как мы знаем,
эта сумма вычетов совпадает с интегралом
2п‘Я^	(8)
по полной окружности радиуса /?, достаточно большого,
чтобы она содержала внутри все корни Q(z). Этот интеграл
не зависит от R и в то же время допускает оценку
I fo^dzlc max I £Ж2л/?^ ~2л7?0.
l|Zi^«Q(z) I iz 1=7?Кит Я2
Таким образом, интеграл (8) равен 0. Отсюда
Г Р (z)l	.	Г Р (z)l
ЕВыч |да.|г=^+ЕВь14 [та] z=bk =°-
/=i	*=i
11.32. а. тегралы вида	Инте гр алы Фурье. Часто встречаются СО	ИН-
	f(x)eiaxdx, — сс	(1)
	со J /(х) cosoxdx, — со	(2)
	со J /(х) sin ox dx, — сс	(3)
содержащие	вещественный параметр о; они называются	
интегралами Фурье,
11.32]	§ 11.3. ВЫЧИСЛЕНИЕ С ПОМОЩЬЮ ВЫЧЕТОВ
477
Если выполнено условие
|/(х) | dx < оо,
— со
то все три интеграла Фурье абсолютно сходятся. Если при
| х | -> оо функция /(х) вещественна и монотонно стремится
к нулю, интегралы (2) и (3) сходятся при о#=0 (ср. 11.16 а),
но, вообще говоря, неабсолютно. Если при этом /(— х) =/(х)
(т. е. функция /(х) четна), то интеграл (3) равен нулю,
если же /(—х)=—f(x) (функция /(х) нечетна), то интег-
рал (2) равен нулю. Кроме того, имеется очевидная связь
со	со	со
f (х) eicx dx = f (х) cos ox dx + i J f (x) sin ox dx,
— CO	— co	— co
так что в случае вещественной /(х) интегралы (2) и (3)
представляют вещественную и мнимую части интегра-
ла (1).
б. Общая теория ' интегралов Фурье будет рассмотрена
в гл. 15 (часть третья). Здесь мы ограничимся вычислением
интегралов Фурье для некоторых классов функций. Часто
бывают полезны методы контурного интегрирования.
Пусть /(х)=-75у-( есть рациональная функция и поли-
Ч (Л)
ном Q (х) имеет степень по крайней мере на единицу выше
степени полинома Р(х) и не обращается в 0 при вещест-
венных х. В этом случае интегралы (1) — (3) сходятся (11.17 б);
мы сейчас их вычислим.
Пусть аг, ... , ат — корни многочлена Q (х), лежащие
в верхней полуплоскости. Образуем замкнутый контур Z,+,
состоящий из отрезка [ — /?, /?] вещественной оси и полу-
окружности С#— {г=Ре'ч,	Тогда согласно
10.43 (1)
л	сл
• -v Г р (z) • 1
= 2ш2^выч e‘ozJ .	(4)
/=1 1
478
ГЛ. И. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
(11.32
Покажем, что при о > О
Нт А'222- eiazdz=0.
R-+и 3. Q (z)
с«
(5)
Если у О, о^О, то | efoz |= | е‘°*-°£|== g-w 1. Поэтому
если степень многочлена Q{z) по крайней мере на две еди-
ницы выше степени многочлена P(z), доказательство соот-
ношения (5) можно провести точно так же, как в 11.81.
в.	Если степень многочлена Q(z) лишь на единицу выше
степени многочлена P(z), то рассуждение 11.81 не прохо-
дит. Для. этого случая мы установим следующую лемму.
Лемма. При о>0 справедливо неравенство
(с — постоянная).
Доказательство. Так как sin (л—ф) = sin ф, то до-
статочно рассмотреть интеграл
Л/2
о
составляющий
при R 1
ровно
половину предыдущего. Мы имеем
Л/2	Л/в
g-Rc sin
о	о
Л/2
'Мф = g-Яс sin _|_ (J g-Rc sin ф^ф
л/в
Л/в	Л/2
е-давшф^ф
О о	л/6
g- Rc Sin Ф
_ л
Ro cos
О
-С*?5#. е-Яаяпф^ф^.
cos—тг-
1 / 1
Ro ( л.
\COS -7-
' n
поскольку функция ие~и при и > 0 ограничена. Лемма доказана.
11.32]	§ 11.3. ВЫЧИСЛЕНИЕ С ПОМОЩЬЮ ВЫЧЕТОВ 479
г.	Следствие (лемма Жордана). Если функция
f(z) определена и аналитична в полуплоскости Imz^O при
| z | р и при этом
lim sup |/(z)|=0,
|2 |=Я
то для о > О
lim & f (z)eiaz dz = 0.
R № J
CR
Доказательство. Применяя лемму в, находим
f(z)ei0Zdz = f(z)eiox е~°и Rei(f dtp
О
л
<lsup	J e~Rasin,‘d(p^~ sup |/(г)|->0при/?->-оо,
о	z£Cr
что и требуется.
д.	Теперь завершим вычисление интеграла (1) для
Р (г)
^(z)~ Q (г)' Так как эта функция прн достаточно больших
[z\ удовлетворяет неравенству
|q((z) |> |Z| ’
то из леммы Жордана следует выполнение равенства (5).
Интеграл Фурье от функции f(z) получается теперь при
о > 0 из (4) предельным переходом при R—> оо:
5	вмч
-00	1— 1
iaz
Jz=aj'
е.	Если о < 0, то проведенное рассуждение теряет силу,
так как на дуге Сд функция е‘ох неограниченно возрастает.
В этом случае аналогичное построение мы проведем не в верх-
ней, а в нижней полуплоскости. Обозначим через СЦ полу-
окружность [z = Re‘^,	настолько большого ра-
диуса, что все корни blt ..., br многочлена Q(z) в нижней
480
ГЛ. 11. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[11.33
полуплоскости оказываются внутри нее; тогда
, fit
L	+«	са
= 2га У Выч Г е '“1
“i LQ(z) Jz=6k
Интеграл по полуокружности CR допускает оценку
CR
2л
С L^Lei«xe-<,y
J <2 (z)	Y
Л
Л
max I I • R • J eRosin<j> ^<p
гбСд	о
и в силу леммы стремится к нулю при R —юо. Отсюда
сс	R
С ^~-eiaxdx~ lim С ~~elexdx =
J <2(х)	fi_00 J Q(x)
— oo	— 7?
= — 2га У Выч Гe ,02l
L<2(z) Jz=bfc’
.	,	P(x)
значение интеграла Фурье от функции при
что дает
о < 0.
ж.	При о=0 интеграл Фурье (1) становится интегралом
Р (х)
от рациональной функции и при разнице степени числи-
теля и знаменателя на единицу не существует.
з.	Пример (интеграл Лапласа)-.
f xel°x dx		2га Выч —2гаВыч J	Г zefff2 1
		|_z2 +1 zeiaz - _z2 + lj
J _ со		
= 1ле~"	(о>0),
2=1
= —тев (о<0).
2= — I
х^^х
Заметим, что неопределенный интеграл от функции । не
выражается в элементарных функциях.
11.33. Особые интегралы Фурье. Интегралы
Фурье 11.32 (2) и (3) иногда могут существовать и для
11.33]	§ 11,3. ВЫЧИСЛЕНИЕ С ПОМОЩЬЮ ВЫЧЕТОВ 481
функций f(x), имеющих особенности на самой оси х, если
эти особенности компенсируются соответствующими нулями
функций sin ах или cos ах. Для примера рассмотрим важный
в математической физике интеграл
СО
sin ох ,
-------dx
X
— со
(сходимость которого получается по признаку Лейбница
со
Р etax
11.16). Интеграл Фурье i ~^~^х в Данном случае не су-
— со
шествует.
Рассмотрим контур L, образованный последовательно
отрезком [—/?, —е] вещественной оси, малой полуокруж-
ностью
СЕ — {z = ее''?, О^ф^л},
отрезком [е, /?] вещественной оси и большой полуокружностью
ГR = {z= Re‘4, О^ф^л}
(рис. 11.6). Ввиду отсутствия особенностей функции elez!z
внутри контура L
— Е
Г	р „tex
и на самом этом контуре мы имеем
A pttiX	п plCZ
— dz+ I +A1 ^-dz = Q.
Применяя лемму Жордана, получаем при о>0
г«
482
ГЛ. И. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[11.33
Далее,
.	cos ох
поскольку в силу нечетности функции —-— ее интегралы
по отрезкам [—R, —е] и [е, /?] взаимно уничтожаются.
Наконец,
где
\eiaz— 11
<С max ------- ел Me,
ZSC, I 2 I
eiaz— 1
так как функция —-— непрерывна и тем самым ограничена
вблизи z=0. Устремляя е к 0 и R к оо, получаем
00
С sin ах .	...
\ —— dx — л.	(1)
— 00
Если о < 0, то sin ох= — sin (—о) х, где —о > 0, поэтому
СО	со
Г sin ох ,	г sin (—о)х ,
\ -----ах — — \ -------1--— dx = — П.
J X	J X
— GO	— СО
Как следствие получаем (Эйлер, 1781)
*	.	—	при	а	> О,
С	sin ах ,	2	1	'	...
= '	л	(2)
о	—у	при	а< 0.
•1.41]	§ 11.4. ИНТЕГРАЛЫ, СОДЕРЖАЩИЕ ПАРАМЕТР 483
Аналогичный метод позволяет вычислять более сложные
интегралы
С
J QW *
— ее
где Q(x)=£0 (см. задачу 5).
§ 11.4.	Несобственные интегралы,
содержащие параметр
11.41.	Интеграл Фурье является примером несобственного
интеграла' с параметром. Рассмотрим любой несобственный
интеграл, для простоты 1-го рода, содержащий вещественный
параметр о:
со
/(о) = ^y(t,o)dt.	(1)
а
Мы предполагаем, что он сходится при каждом значении о
из некоторого промежутка а^о^Р; нас интересуют
свойства результата интегрирования /(о) как функции от а.
А именно, мы желаем выяснить:
(а)	Если функция y(t, о) непрерывна по о, будет ли I(о)
непрерывной функцией от о?
(б)	Справедлива ли формула интегрирования по параметру

y(t, o)dt
do
dt?
(в)	Если функция у (/, о) дифференцируема по о, спра-
ведлива ли формула дифференцирования
°)d/=
а	а
Рассмотрим в качестве примера интеграл
С sin to .,
J—
о
484	ГЛ. 11. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	[11.42
сходящийся при всех о и вычисленный в 11.33', мы име-
ли там
/(0) =
л
2
л
~2
при О
при о
0.
0.
Кроме того, очевидно, /(0) = 0.
Таким образом, несмотря на непрерывность подынтег-
„ .	sin ta
ральной функции —— по параметру о, результат интегри-
рования /(о) в данном случае терпит разрыв при о=0.
Следовательно, ответ на вопрос (а) в общем случае отри-
„ тт	d sin to
нательный. Далее, в данном случае мы имеем	—• —
= cos ta и формула дифференцирования (в) не имеет места
уже по той причине, что интеграл в правой части равенства
оказывается расходящимся. И хотя в данном примере фор-
мула интегрирования (б) оказывается справедливой, мы уже
понимаем, что это происходит из-за специальных свойств
.	sin tor,	„
функции ——>. В задаче 6 указан пример, где ответ на
вопрос (б) также отрицателен. Общий положительный ответ
на вопросы (а)—(в) требует дальнейших условий на харак-
тер сходимости несобственного интеграла (1).
Хотя мы проведем здесь необходимые построения для ин-
тегралов 1-го рода, соответствующие определения и теоре-
мы могут быть непосредственно перенесены и на интегралы
2-го и 3-го рода; проверку этого мы предоставляем чита-
телю.
11.42.	Определение. Несобственный интеграл с па-
раметром
Ца)= ^у (t, a)dt,	(1)
а
сходящийся при каждом значении а из некоторого мно-
жества S, называется равномерно сходящимся на S (или по
а •$), если для любого е > 0 существует такое N, что при
11.44]	§ 11.4. ИНТЕГРАЛЫ, СОДЕРЖАЩИЕ ПАРАМЕТР
485
любом p~^N и любом agS
c)dt
Возьмем произвольно числа hn/оо и составим последова-
тельность функций
а+Л„
/„(а)= J а)Л (л=1, 2, ...).
(2)
Если интеграл (1) сходится равномерно на множестве S, то
последовательность (2) в том же промежутке равномерно
сходится к своему пределу, которым служит интеграл (1).
11.43.	Теорема. Если S есть метрическое пространство,
функция у (1, о) равномерно непрерывна на каждом произведе-
нии SX [а, аЦ-Л], 0 < h < оо, и интеграл 11.42 (1) сходится
равномерно на S, то /(о)— непрерывная функция от а на
множестве S.
Доказательство. По теореме 9.81 функция 1п(а)
непрерывна при o^S. По теореме 5.96 функция /(о), как
предел равномерно сходящейся последовательности непрерыв-
ных функций, также непрерывна при о £5. Теорема доказана.
11.44.	Теорема. Если функция у (t, о) непрерывна по
совокупности (I, с) на каждом прямоугольнике
S = {(/, о): а t	а + h, 0 < h < оо; а а р}
и интеграл 11.42 (1) сходится при а 0^(3 равномерно по
а, то функция
У(0= a)da
обладает сходящимся несобственным интегралом по про-
y(t, o)dt>do
Доказательство. По теореме 9.72 из равномер-
ной сходимости непрерывных (11.43) функций 1п (о) к I (а)
486
ГЛ. IT. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[11.45
следует, что
₽	Р
V I(o) do — lim {ln(p)do.	(2)
П—кев "
С другой стороны, по теореме 9.82
₽	Р ( a+fln	ч	a + hn ( Р	х
J/„(a)do=^< J y(t,o)dt\do= J <
a	a ' a	'	a V a	>
Поэтому равенство (2) можно переписать в форме
р	°+лп
(/(о) do= lim f
*	п—Ь- Oft "
y(t, о) do
di.
(3)
Но существование предела
означает существование
y(t,	(11.126).
Теорема доказана.
справа для любых hn / оо
несобственного интеграла
Поэтому из (3) получаем (1).
11.45.	а. Теорема. Если частная производная
y'o(t, о) непрерывна по совокупности (I, о) в любом пря-
моугольнике а^о^р,	0 < h < оо , ин-
CD
теграл §уа (t, о) dt сходится при а о Р равномерно по о
а
оо
и сходится интеграл у (t, a) dt, то функция
а
со
/(о)= Jy (t, о) dt
а
существует при а о р, дифференцируема по о и
<Х>	00
o)dt = ^ya(t, o)dt.	(1)
а	а
11.45]	§ 11.4. ИНТЕГРАЛЫ, СОДЕРЖАЩИЕ ПАРАМЕТР
487
Доказательство. В силу теоремы 9.84
a+hn	a+hn,
= J У(*> G)dt= jj yo(t, c)dt.
а	а
По условию последовательность функций /„(а) сходится
равномерно на отрезке а^о^р, а последовательность
функций /„(о) сходится в точке а=а. В силу теоремы 9.77
последовательность 1п (о) сходится равномерно на отрезке
а^Со^Ср, ее предел /(а) есть дифференцируемая функция
от а(Е[а, р] и
Г (с) = lim/' (а).
п~>ос
Тем самым доказаны существование и дифференцируемость
по а интеграла
СО
/(о) — Vу (t, о) da— lim/„ (а)
и равенство (1).
б. Для аналитических функций теорема а приобретает
несколько измененную формулировку.
Предположим, что функция у (t, s) определена при t € (а, оо)
hs£G, где G—некоторая область в плоскости « = а~4-гт;
пусть, далее, у (t,s) аналитична по sgG при каждом t и
непрерывна по совокупности (/, $) в каждом «цилиндре»
вида	{$: |s — s0| ^p}cG(O < h < оо). Будем
говорить, что интеграл
00
s}dt, s^G,	(2)
а
сходится равномерно внутри G, если он сходится при каж-
дом s£Gn если для любого компакта QczG и любого 8 > О
существует такое M=/V(e, Q), что
00
J y(t,s)dt
N
< 6
при любом S € Q-
488
ГЛ. 11. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[11.46
Теорема. Если интеграл (2) сходится равномерно внут-
ри G, то функция
I(s)=^y (t,s) dt
а
аналитична внутри G и
00
Г ($) = (t,s)dt.
а
Доказательство. В силу теоремы 10.27 функция
4(«)= $y(*,s)df
а
*п
аналитична по s, и при этом Гп (s) = j Х (Л$) dt- Далее,
а
функция In (s) при п -* оо равномерно внутри G сходится
к функции I (s); поэтому в силу теоремы 10.36 функция l(s)
аналитична в G. Вейлу той же теоремы 10.36 функции I'n{s)
сходятся в области G к функции Г ($); отсюда
Ьп
/'($)= lim {y's(t,s)dt
«-*“ а
сю
= J y’s (М dt,
а
что и требуется.
11.46. Критерий Коши для равномерной схо-
димости интегралов. Несобственный интеграл
^y(t, o)dt
а
(1)
с параметром о, пробегающим некоторое множество S, схо-
дится равномерно на S тогда и только тогда, когда для
любого е > 0 найдется такое число N, что при любых p^sN,
q^N, c^S
у (t, о) dt 8.
(2)
11-47]	§ 11.4. ИНТЕГРАЛЫ, СОДЕРЖАЩИЕ ПАРАМЕТР
489
Доказательство. Пусть интеграл (1) сходится рав-
номерно на 5. Для заданного е > 0 найдем число Аг так,
чтобы иметь
СО
y(t, c)dt
р
(3)
при любом p^N и любом ngS. Пусть, далее, q^N, так
что и
СО
y{t, o)df
я
в
2
(4)
Из неравенств (3) и (4) следует (2), чем доказана не-
обходимость критерия Коши. Обратно, если выполнено не-
равенство (2), то интеграл (1) при каждом сходится
в силу 11.12 г. В неравенстве (2) перейдем к пределу при
<7—>-оо; мы получим
ОО
у (/, о) dt
Е
для всех p^N и всех a g S, что и означает равномерную
сходимость интеграла (1) на множестве 5. Теорема доказана.
11.47. а. Критерий Коши в свою очередь служит основой
для получения частных признаков равномерной сходимости.
Одним из простейших является «мажорантный признак».
Пусть имеется неотрицательная функция /(/) со схо-
дящимся интегралом
00
\f(t)dt.	(1)
а
Мы будем называть ее интегрируемой мажорантой для всякой
функции J (/), такой, что |_у (/) | =5^/(0-
Теорема. Если функция у (t, о) при всех о£3 обла-
дает одной и той же интегрируемой мажорантой f (t), то
интеграл
У у (t, a) dt
а
сходится равномерно на 3-
490
ГЛ. 11. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[11.47
Это утверждение выводится из неравенства
Ч	q	q
^y(t, o)dt С $ |j(*,O)|J f(t)dt
ppp
путем применения критерия Коши 11.46.
б. Пример. Покажем, что несобственный интеграл
СО
cosol—COS Pt ,.
-------I2-----dt
О
1)	(2)
сходится равномерно по параметру о в промежутке 0	1. Для
этого установим справедливость неравенств
( 2
COS Gt—COS pf I |
12 M 2
при
при
l=a= 1,
KI
при всех о и p в промежутке [0, 1].
Первое из приведенных неравенств очевидно. Для доказатель-
ства' второго применим формулу, вытекающую из формулы Тейлора
8.23 (4):
а2!2
cos at = 1---g- + 1*G (a, 1),
где при | a |< 1, 111< 1
ю<«.	<4-
Отсюда при 0<o<l, 0<р<1, 0<1<1
I cos of—cos Pf | |E^+,.(0(O| 0_0(р. щЬ । + 1 +  <2,
что и требуется.
Функция
/(1)=J i2 при * — 11
1 2 при (К К 1
определяет, таким образом, интегрируемую мажоранту для всех
.	„ cosot—cos pi „	,, _
функции ------------—, о, р g[0. И- Поэтому интеграл (2) сходится
равномерно по о при og[0, 1] и, следовательно, представляет собой
непрерывную функцию от о в этом промежутке. Мы найдем ее
явное выражение в 11.49 б.
11.48J	§ 11.4. ИНТЕГРАЛЫ, СОДЕРЖАЩИЕ ПАРАМЕТР 491
11.48.	Свертка двух функций. Сверткой двух
комплексных функций g(i) и /(/), определенных при
— оо < t < оо, называется интеграл 3-го рода
ОС
h(t)= \f(o)g(t —с) da.	(1)
— 00
Эта функция определена не всегда. Далее указываются
условия ее существования и ее свойства.
Теорема. Если f(t) и g(t) непрерывны, ограничены
и абсолютно интегрируемы на оси —оо < / < оо, то h(t)
существует при каждом t, непрерывна, ограничена и абсо-
лютно интегрируема на оси —оо < / < оо, причем
СО	СО	00
h(t}dt = J f (t) dt J g(t)dt.
— co	— oc	— ос
Доказательство. Если | g(t) | < С, подынтегральная
функция допускает оценку |/(о) g(t—о)	1, откуда
следует, что интеграл (1) сходится и притом равномерно по
параметру а£( — оо, оо). Далее, функция h(t) (1) ограничена,
поскольку
ОС	ОС
)А(0|< J |/(o)||^U-o)|da^C J |/(o)|do.
— со	— со
Покажем, что подынтегральная функция непрерывна по
совокупности аргументов в каждом конечном прямоугольнике
а^а^р. Пусть	и |/(/)|^С. Для
заданного е > 0 найдем 6 > О так, чтобы из о' —о" | < 6,
о', о"С [а, Р] следовало |/(о')—/(о")|<е и из —	<26,
t', t"£[a — р, b — al следовало |g-(Z')— g(t") | < 8; тогда
при |о'—о"|<6, \t’—/"|<6 мы имеем
| (/' —о') —(/"—о") | <26
и при o', o"€[a, Р], t', t"g[a, b]
I f (o') g (f—o') — f (a") g (f—о") К
<|/(o')-/(o")||^(f-o')| +
+ l/(o") 11 g(t'-a')-g(f-c") | < Ce + Ce - 2Ce,
что и означает непрерывность функции f(o)g(t—a) по
совокупности аргументов в указанном прямоугольнике. В силу
теоремы 11.43 функция h(t) непрерывна по t.
492	ГЛ. 11. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	[11.48
Теперь проверим абсолютную интегрируемость h (t). Для
этого заметим сначала, что функции |/(о) | и |^(/)| удов-
летворяют тем же условиям, что и /(о) и £(/); следова-
тельно, интеграл
00
$ |/(о) ||£•(*—о)|Жт
— со
также сходится равномерно по t, причем подынтегральная
функция непрерывна по совокупности I и о в любом прямо-
угольнике	Применяя к этому интегралу
теорему 11.44, находим
*Г	1 г со	\
J	Ш |/(o)|k(/-a)|do>^ =
— Т	-т '-ос	'
cd	( Ъ	А
= У |/(а)п J k(*—o)|dQda=
— ос	' — X	'
ос	г T-U	X
= У1/(°)Н $
-ос	'-Т-О	*
СО	г СО	х	СО	00
< У |/(а)К У	|/(o)|do,
— 00	' — 00	*	— 00	— 00
00
откуда следует существование интеграла У |й(/)|«Я. На-
конец, снова по теореме 11.44
У h(t)dt= ( / ( f(v)g(t — o)dol dt=
—X	— X	'-ос CO	г X	x = $ /(°) т $ g(t —	do = -oc	V-T	' CD	r- CD = $/(o) —co	1 00	] t- 00	00 = $ g(t}dt J f{o)do~ — OC	— oc	CO	, x-O	\ У /(<*){ У — ОС	V—T~O	' g{t)dt do= о l> T 00	г	4 У/(о)< У -ao	l]/-a|>x	'
11.48]	§ 11.4. ИНТЕГРАЛЫ, СОДЕРЖАЩИЕ ПАРАМЕТР 493
Мы докажем, что последний интеграл стремится к 0 при
т—>-оо, чем и будет доказано последнее утверждение тео-
ремы. Для заданного е > 0 найдем р так, чтобы
J |/(o)|do<e,
l<j| >о
и затем т так, чтобы
$	1^(0 \dt< е.
Тогда мы будем иметь


С 5 1/(о)Н $ к(0|^ра+
|О|>С	1~<»	'
+ S S
юко	чл>т-е	J
/ас	С»	\
|	|^(0|^+ J |/(0)|d0>,
V — оо	— иэ	*
откуда и следует утверждение. Теорема доказана.
Операция свертки, или свертывание, функций/(/) и g(t)
обозначается знаком *. Мы доказали, что
СО	оо	оо
J [/(0* g(t)]dt= $	$ g(t)dt.
— оо	— 00	— оо
Замечание. Если в собственном интеграле
с
М0 = \f(o)g(i — G)do
-т
494
ГЛ. И. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[11.49
сделать подстановку t—a=t], c — t—т], мы получим
t+z
hz(t) = J fit —
t-x
Переходя к пределу при т —оо, находим
ОС
/(0*5г(0=Л(0= $	— o)do =
— CD
СО
= $ Л* ~ П)=£(*) */(0,
— оо
так что свертка симметрична относительно функций /(?) и g(t).
11.49.	Признак Абеля — Дирихле равномер-
ной сходимости интегралов.
а.	Этот признак может быть использован в некоторых
случаях, когда мажорантный признак 11.47 а непригоден.
Рассмотрим интеграл
ОО
^u(t)v(t, c)dt, a£S.	(1)
а
Если (комплексная) функция u(t) обладает кусочно-непре-
рывной абсолютно интегрируемой производной и стремится
т
J v(t, о) dt
а
к нулю при t—>оо, а
С, где С не зависит ни
от Т, ни от о £S, то интеграл (1) сходится равномерно на S.
т
Для доказательства положим
V (Z, о)= ^(6, o)d6
а
и воспользуемся интегрированием по частям:
т,	т,	Т'
^u(t)v(t, c)dt = u(t)V(t, о)| — Ju'(/)V(/, o)dt.
т	т	т
Здесь мы имеем, как и в 11.17 а,
\u(T)V(T, a) — u(T)V(T, о) |< 2Сmax {u(Т), и (Т')}-,
Т’	Т'
$«(/)©(/, o)dt ^Ч.Си(Т)-\-С^ и' (t)dt = SCи (Т).
т	т
11.51]	§ 11.5. ГАММА-ФУНКЦИЯ И БЕТА-ФУНКЦИЯ ЭЙЛЕРА 495
В силу наших предположений полученные величины стре-
мятся к 0 при Т—>оо, что и требуется.
СО
_ ,,	..	siii to ,, зт .	.
б.	Пример. Интеграл \—=	был вычислен
о
нами в 11.33. Покажем, что ои сходится равномерно в любом
отрезке 0 < а<о <р. Действительно, при t -> оо функция — стре-
мится к 0 и имеет непрерывную и интегрируемую производную
— 1 /I2, а
Т
cos То—cos ао
о
а
так что признак Абеля—Дирихле можно применить. Интегрируя
по параметру og[a, Р) и используя 11.44, получим значение рас-
смотренного в 11.47 интеграла
dt =
cos at—cos р/ dt —
о
₽
C sin to .
) —i— dc
a	,

C sin to ..
]~rdt
о
a
<fo=y(P—а)-	(2)
Поскольку, как было там доказано, он сходится равномерно при
agio. 1], мы можем перейти к пределу при а-^0 в равенстве (2).
Мы получим значение нового несобственного интеграла
fl — cos р/	Р1П 2 ,, пр
J-----= 2 I —~ dt = -~.	(3)
о	о
§ 11.5.	Гамма-функция и бета-функция Эйлера
11.51.	Гамма-функция Эйлера Г (т) определяется фор-
мулой
Г(т)=	(1)
о
Этот несобственный интеграл 3-го рода представляется
в виде суммы интеграла 1-го рода
СС
$ F-ie^dt
1
496
ГЛ. И. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[11.52
и интеграла 2-го рода
1
J t^e^dt;
о
первый сходится при любом вещественном т, второй сходится
при любом т > 0.
Поэтому Г (t) определена равенством (1) для всех т > 0.
Если т^а>0, то подынтегральная функция 1х~1е~г обла-
дает интегрируемой мажорантой	поэтому на любом
отрезке [а, Р] интеграл (1) сходится равномерно и по
теореме 11.43 представляет собой непрерывную функцию
от т. Таким образом, Г (т)—непрерывная функция от т на
(О, оо). Производная по т подынтегральной функции имеет
вид Л-11п/-е~* и обладает интегрируемой мажорантой
1а~Чп1-е~* на любом отрезке 0<а^т:^р, а так как
функция Л-1 In t- непрерывна по t £ [О, оо) при каждом
т > 0 и непрерывна по t и т в любом прямоугольнике
а^т^р, то согласно теореме 11.45а функция
Г (т) имеет производную
00
Г' (т) = ^tz-1\nt-e-idi
о
(Т > 0),
которая непрерывна по тем же причинам, что и сама функ-
ция Г (т). Можно продолжать дифференцирование, каждый
раз применяя теорему 11.45 а; таким образом, Г(т) имеет
производные всех порядков.
11.52.	Из определения 11.51 (1) интегрированием по
частям получаем
со	оо	со
Г (т) = J	J
о	<=о	о
или
Г(т + 1) = тГ(т).	(1)
Равенство (1) называется основным функциональным урав-
нением для гамма-функции. Применяя его несколько раз,
получаем
Г(т+п)=(т + /г-1)(т-Ьл-2)...(т + 1)тГ(т);	(2)
11,53]	§ 11.5. ГАММА-ФУНКЦИЯ И БЕТА-ФУНКЦИЯ ЭЙЛЕРА 497
таким образом, если мы знаем значения гамма-функции в ка-
ком-либо промежутке длины 1, мы сможем найти ее значения
в остальных точках полуоси т > 0. Поскольку
Г(1)= Je-<d/=l,
о
мы получаем, что
Г(« + 1) = п(п— 1). . . 1 —п\.
Отсюда видно, что гамма-функция является распростране-
нием на все положительные числа функции л!, определенной
лишь для натуральных значений п. Далее, из непрерывно-
сти Г (т) при т= 1 и из (1) следует, что при т—>-0
Г(т) = ^=_У-^оо.
11.53.	Бета-функция и ее связь с гамма-
функцией. Интеграл
1
В(Р, 0=$x/’-1(l-x)‘?-1dx,	(1)
о
являющийся функцией двух параметров р и q, называется
бета-функцией Эйлера. Он существует для всех положитель-
ных значений р и q-. при р, q~^ 1 как собственный, при
остальных значениях р и q как несобственный интеграл,
g
Подстановка х = -j-q-g преобразует интеграл (1) к виду
П/	\ С б*’-1*®
В J (1-1-0)/’+“7 ’	№
О
Покажем, что бета-функцию можно выразить через гамма-
функцию.
Сделав в выражении для гамма-функции
Г (т) = J dt
о
498
ГЛ. 11. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[11.53
подстановку /=0_у, мы получим
о
е~9У dy.
Заменим здесь т на p-\-q и 0 на 1 -|- 0:
<ю
Г + — С vP+9-l е~У е-^У dv.
о
Умножим обе части этого равенства на 0Г 1 и проинтегри-
руем от 0 до п:
п	п ,00
г (Р+Q} J Ш 0/” 1Ур+9~1 е'у е'*у dy I de- (3)
о	о ' о	'
При п —► оо левая часть стремится к Г(р + ^)В(р, q).
Подынтегральная функция в правой части имеет инте-
грируемую мажоранту пР-1yP+q~x е~У, поэтому согласно тео-
реме 11.44 интегралы можно переставить:
где функция
ny
Fn{y) = $ 1Р~1е-' dt
О
при п —* оо стремится к функции Fly), равной 0 при j=0
и равной постоянной Г (р) при у > 0. На отрезке 0 у ^.Ь
эта сходимость неравномерна (что видно хотя бы из разрыв-
ности предельной функции). Но на любом отрезке h ^.у
11.53]	§ 11.5. ГАММА-ФУНКЦИЯ И БЕТА-ФУНКЦИЯ ЭЙЛЕРА 499
где й>0, сходимость F„ (у) —> F(y) уже равномерна, поскольку
пу	nh
О < Г (р)—^ tP-1 е-1 dt (р) — ^ tP~le~tdi.
о	о
Кроме того, поскольку Fn(y) стремится к F(y) возрастая,
у совокупности функций у4-1 е~У Fn (у) имеется интегрируе-
мая мажоранта уч~г е~У Г (р); поэтому в силу теоремы 11.43
ОС	<ю
lim ( у®-1 е~У Fn( у) dy—Г (р) \уЧ~ге~У dy.
h
С другой стороны, при любом h > О
h	h
\у9^ е~У F„(y)dy^r(p) ^yg~1dy = r(p)^-. (4)
v	J	Ч
О	О
Для заданного 8 > 0 выберем h > 0 так, чтобы иметь
Г(Р)7<-3-	(5)
Далее, при выбранном h найдем N такое, чтобы при л>М
иметь
СЮ
0< Г(р) ^уЧ~1е~У
h
00
dy—^уЧ-'е-У Fn(y)dy<.^. (6)
h
Наконец, заметим, что при выбранном h
0< Г(р)Г(9)—Г(р) ^уч-^е-У dy =
h
h
= Г (р) У у4’1 е~У dy < Г (Р) у < у •
О
(7)
Из неравенств (4), (5), (6), (7) следует, что
00
о< Г(р)Г(?) — \)у9~1е~У Fn(y)dy < е,
О
500
ГЛ. 11. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
(11.54
откуда следует, что
lim \уч~1е~У Fn(y)dy = T (р)Г(д).
о
Теперь, переходя к пределу в (3), получаем
<8)
Это и есть искомое выражение бета-функции через гам-
ма-функцию.
11.54.	Многие тригонометрические интегралы в свою
очередь выражаются через бета-функцию. Так, произведя
в интеграле
Я/2
| sin*’-16 cos’-10 d0
О
подстановку sin20=x, получим
1 = J X(P-l)/2 (!—*)(?-l)/2
0
-H
0
dx
J7__j
x) 2	dx = ±B
11.55.	Формула дополнения для гамма-функ-
ции. Полагая q = \—р, из формулы 11.53 (8) получим
СО
Г(р)Г(1-р)=В(р,
о
(1)
Этот интеграл можно вычислить до конца. Рассмотрим вна-
чале аналитическую функцию
в плоскости комплексного переменного z, разрезанной по
вещественной положительной полуоси. Эта функция опре-
11.55]	§ 11.5. ГАММА-ФУНКЦИЯ И БЕТА-ФУНКЦИЯ ЭЙЛЕРА 501
делена однозначно, если на верхнем крае разреза положить
w (•*: + «)) = гт-
I -р Л
(2)
где хР~г берется в смысле 5.54. На нижнем крае разреза,
совершив обход в положительном направлении вокруг на-
чала координат, мы получаем
z = х — 10 = хе2л1,
w(x— г'О) = ~^еИя(Р_1)	(3)
Рассмотрим замкнутый кон-
тур L (рис. 11.7), состоящий
из отрезка [0, /?] (/?>1) оси
х на верхнем крае разреза, ок-
ружности радиуса R с цент-
ром в начале координат и отрез-
ка [/?, 0] на нижнем крае разреза.
Внутри контура L имеется одна
особая точка функции rw(z~)—
полюс первого порядка при z=—1. В силу 10.42 а
J (z) dz — 2ni  Выч w (z)	= 2nze'JIt/’_1).
L	z=- 1
С другой стороны,
R	e
J -w (д) dz = § w (x 4- z’0) dx + 5	C2) dz + $ w(x—z‘0)dx. (5)
L	0	CR	R
Dp—i
При | z | — R мы имеем | <w (г) |	cR?~\ откуда при
Р<1
2ncRP-1 —<-0.
(6)
R
Переходя в равенстве (5) к пределу при R —> оо и исполь-
зуя (2)—(5), находим
2л1е1мР~» = С dx-(\— е2л«Р-х>)
J 14-х	4	'
о
502
ГЛ. 11. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[11.56
И, следовательно,
CxP~1dx „ . efn(p-i)	2л/
I -----=2ш------------= ----------------=
J 14-Х	]_е2го<р-1>
О
л	л
sinir(p— 1) sin пр’
Таким образом, мы получаем
Г(р)Г(1-р) = В(р, 1-р)=^-.	(7)
Эта формула называется формулой дополнения для гамма-
функции. В частности, полагая в ней р-Х]?,, находим
г(|)=/л.	(8)
Используя основное функциональное уравнение, получаем
г(|)=|41/л,...,г(2-фи^гл.
На рис. 11.8 дан график гамма-функции при 0<р^5.
11.56.	С помощью гамма-функции можно вычислить важ-
ные интегралы, встречающиеся в теории вероятностей:
00
/т= J xme~axtdx (а>0,/я> —1).	(1)
О
Именно, подстановка ax2 = t, х = 1/ — , dx = ~~ -^L.-
r а ’	2 уЛ at
11.57]	§ 11.5. ГАММА-ФУНКЦИЯ И БЕТА-ФУНКЦИЯ ЭЙЛЕРА 503
приводит интеграл 1т к виду
/ = 1.	2 Г Ат-D/2 -f _	1	г (m-HA
«	2 a(m+l)/2 J 1 e ul~ 2a(m+l)/2 1	2 J’
0
В частности,
/0=	=	(2)
о
11.57.	Асимптотическое выражение для гам-
ма-функции. При больших значениях т величина гамма-
функции
ОО
Г(т)= J iz~1e~tdf
О
допускает простое асимптотическое представление.
а. Лемма. Пусть функция f(x)^0 определена при
х > 0, равна 0 при х= 1, монотонно убывает при 0 < х < 1
и монотонно возрастает при х > 1, в окрестности точки х = 1
допускает представление
f(x) = a (х— 1)2+ (х— 1 )2+2г ф (х),
б > 0, | ф (х) | М, о > 0,
и при х с > 1 удовлетворяет неравенству
|/(х)|>бх, t> > 0.	(1)
Тогда
СО
7(s) = <\je~'-fwdx	(2)
О
при s —► оо есть бесконечно малая, эквивалентная j/"~ .
Доказат ельство. Сходимость интеграла (2) при s>0
следует из оценки (1). Мы имеем при 0<е< 1
/ 1 —е	1 +е	с	оо у
Z(s) = < S + S + $
' 0	l-g 1+е с I
504	ГЛ. 11. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ	[11.57
Далее, при достаточно малом е по условию
I-e	-S — е*
J	< е-^О-е) <е 2 з	(3)
О
С	S в *
J e~siM dx<(c — 1)е“^(1+е><(с — l)e“S 2‘е , (4)
1+е
С е-«/(х) dx	{ e~six dx	= e	S^C	.	(5)
J	J	®
c	c
Переходя к вычислению	интеграла	от	1—е до 1+е, заме-
чаем, что в этом промежутке
| e-s(x- 1)2+2Чи _ 1 | =
= | S (X — 1 )2+ 2в4 (X) + у S2 (X — 1 )2<2+2в> 42 (х) + . . . | <
<Afse2+2e+y Af2s2e2l2+2e> +... <2Afse2+2e,
если только
Afce2+2e<y.	(6)
Число е у иас пока произвольно; положим для s —оо
1
B=S 2 + 6»
Тогда
2 + 26	6
se2+2®=s 2+6 =$ 2+6—(s—>оо)
и условие (6) заведомо выполняется. С другой стороны, при
указанном выборе е
_А_
se2 —s 2+®==s2 + 6—»-оо	(s—+оо).
Теперь при s—»-оо и любом х£(1—е, 1+е) по построению
| e-s(x-i)2+2<4>u) — 1 |	2Afce2+26 —р 0,
11.57]	§ 11.5. ГАММА-ФУНКЦИЯ И БЕТА-ФУНКЦИЯ ЭЙЛЕРА 505
так что
гЧ»-1)’+м1И=1 +о(1),
где о(1) —»-0 при у—> оо. Поэтому
14-е	1+е
J e~sf^dx = j e"Sfl(*-1)1(l+o(l))dx =
1-е	1-е
= [l+o(l)] f e-s***-1’1 dx= [1 + o(l)]f e-^du.
J	V sa J
l-8	—elzsa
Так как e ]/ у —* оо, то последний интеграл при у —оо имеет
предел (11.56)
e~u*du=}f п,
— GO
так что
eV sa
J	e~’a*du = pT(l +o(l)),
— e Vsa
где o(l)—>0 при s—> оо. Итак,
e-^«dx=(l+o(l))
Что касается остальных слагаемых (3), (4), (5), то в силу
равенства ye3 = yfi/(2+e^ все они при у—> оо стремятся к О
по экспоненциальному закону. Следовательно,
со
7(y) = Je-^>dx=(l+o(l))
О
“/si'+’O’i-
что и требуется.
б. Теперь преобразуем выражение гамма-функции к та-
кому виду, чтобы можно было использовать лемму. Мы имеем
506
ГЛ. 11. НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
[11.58
при подстановке t=sx
со	со
Г ($+ 1)	dt= s5+1 xse~sx dx =
о	о
со	со
= ss+1 J e-s-f+sln-fdx = ss+1e“sJ e-s(x-inx-ij	=
о	о
со
= ss+1e~s e~sf<х) dx,
о
где
f(x)=x — Inx — 1.
Функция f(x), как нетрудно проверить, удовлетворяет усло-
виям леммы. При этом /(1)=/' (1)= 0, /"(1)= 1, /"'(1) =
= —2; в окрестности точки х=1
lim Е==1«
2	15	л--» I
так что постоянная а равна 1/2. Применяя лемму, находим
11	X
[ 1+ о (1)] « № + 2 e~s )/<2л,
что и дает искомое асимптотическое выражение.
В частности, если s=n — натуральное	число, то
Г(л-|-1) = л!, и мы получаем
п\ тип 2 е~п У 2л
(формула Стирлинга, 1730).
11.58. Гамма-функция в комплексной обла-
сти. Формула, определяющая гамма-функцию,
СО	со
Г (z)= J tz~1e~t dt = J e(z-i)inf e-t fit	(1)
о	0
пригодна не только для вещественных значений z > 0, но
и для некоторых комплексных z. А именно, если z — x-^iy,
х > 0, то интеграл (1) также сходится, поскольку подын-
11.58]	§ 11.5. ГАММА-ФУНКЦИЯ И БЕТА-ФУНКЦИЯ ЭЙЛЕРА 507
тегральная функция
e(x+iy- 1) In t e-t — e(x- 1) In t e-teiy In t __ fx-\e-t eiy In t
лишь множителем e‘vint, по модулю равным 1, отличается
от функции fx~1e~t. Таким образом, формула (1) непосред-
ственно позволяет определить Г (z) для всех z=x-]-iy
с х > 0, т. е. во всей (открытой) правой полуплоскости G
плоскости z. Интеграл (1) сходится равномерно внутри G,
поскольку для любого компакта Qc:G величина d=infx
zeG
положительна и имеется интегрируемая мажоранта
По 11.45 6 функция Г (z) аналитична в области G.
Исследуем возможность аналитического продолжения
функции Г (z)в левую полуплоскость. Для этого используем
уравнение 11.52 (2)
Г(г + л) = г(г + 1)...(г + л-1)Г(Д	(2)
Оно было доказано для вещественных значений z. Но так
как обе части равенства представляют собой, очевидно,
аналитические функции от z в области G, то из совпадения
их на вещественной оси следует в силу теоремы единствен-
ности 10.39 б их совпадение во всей полуплоскости G.
Переписывая равенство (2) в виде
Г	= 2(z+l).(..tz + n—1) ’
обратим внимание на то, что правая часть определена и ана-
литична при всех z с Rez >—п, за исключением значений
z = 0, —1, ..., —«4-1. Используя теперь формулу (3)
для определения гамма-функции, мы получаем аналитическое
продолжение ее -в область G„= {z:Rez > —п}. При разных п
получаются формально различные определения, но в силу
единственности аналитического продолжения (10.39 в) раз-
личные определения дают для любого z одно и то же зна-
чение функции Г (z). Так как п можно взять произвольно
большим/ функция Г (z) оказывается определенной во всей
плоскости z, за исключением изолированных особенностей
в точках z = 0, 1, ..., —
Из формулы (3) видно, что все эти особенности являются
полюсами первого порядка. Можно вычислить и вычет функ-
ции Г (г) в полюсе z= —«4-1, используя формулу 10.42 (1);
508
ЗАДАЧИ
именно
Выч Г (z)
I ______________Г (zj-n)___I __
|z=-n + l	z(z-j-l) (Z-f-n— 2)|z=-n + l
_ Г (1)	-(-I)"-1
(—•!)(—2)..n-|-l)	(n—1)1
ЗАДАЧИ
1.	Доказать формулу Дирихле
f ! f хх-у-1(1 — x—уУ~1Цх, y)dy\dx —
о 1y=o	I
1 fl-У	Л
= H $ хх-^-1(\-х-уУ~Ч(х, y)dx\dy,
0 x=0	J
где 0<Х<1, 0<p<l, 0<v<l, f(x,y) непрерывна при
o<x<i, i.
2.	Доказать формулу Фруллани
P(ax)-f(fcx)rfx^,40)inA,
J х	' а
о
где а > О, b > 0, если f (х) непрерывна при 0<х < оо и интеграл
со
f f (х) .
I i-l-c dx сходится.
J х
I
3.	Используя интегрирование в комплексной плоскости, найти
CD
Z(p) = ^e-.P*!dx,
о
где Rep^O.
4.	Найти интегралы Френеля
СО	со
Fi = J sin (х2) dx, F2 = cos (х2) dx.
о	о
5.	Найти особый интеграл Фурье
Р (х) sin х
Q(x) —х
/ =
dx,
где Р(х) и Q (х)—многочлены, причем степень Р (х) не превышает
степени Q (х) и Q (х) не обращается в 0 при вещественных х.
ИСТОРИЧЕСКАЯ СПРАВКА
509
6.	Показать, что
S {I dy== ~ 2” S {j (М7^} dx^ “L
Нет ли противоречия с теоремой 11.44?
7.	Обозначим через L путь в плоскости комплексного перемен-
ного s, состоящий из участка [е, + оо) вещественной оси, проходи-
мого справа налево, окружности | s | = е, проходимой в положительном
направлении, и участка [е, +оо) вещественной оси, проходимого
слева направо. Показать, что справедлива формула
Г (z) =--!— ( e~ssx~1ds,
e2niz—1 J
L
дающая представление гамма-функции при любом комплексном z,
кроме ее полюсов.
Историческая справка
Многие конкретные несобственные интегралы были вычислены
в XVII и XVIII веках, еще до точного определения сходимости
несобственного интеграла, данного Коши лишь в 1821 г. Коши ука-
зал также снособ вычисления несобственных интегралов с помощью
аналитического продолжения и теории вычетов. Абсолютно сходя-
щиеся интегралы были выделены Дирихле (1854), равномерно сходя-
щиеся—Валле-Пуссеиом (1892). Гамма-функция и бета-функция были
введены и изучены Эйлером (1730-е годы).
УКАЗАНИЯ И ОТВЕТЫ К ЗАДАЧАМ
К главе 1
1.	Указание. Имеем
откуда
I х | = | х—у-Уу | < | х—у 14-1 у I,
1*1—у[-
Заменить здесь х на у и у на х.
2.	Указание. Проверить для числа sup А + sup В выполнение
всех свойств точной верхней грани множества А-\-В.
3.	Указание. Проверить для числа sup A-sup В выполнение всех
свойств точной верхней грани множества АВ.
4.	Указание. Действовать аналогично тому, как в задачах 2 и 3.
5.	Указание. Множество А ограничено сверху; у = sup А.
К главе 2
1.	Указание. Использовать 2.35—2.36.
2.	Указания, а) В каждом из имеющихся интервалов можно
выбрать по рациональной точке, б) Внутри каждой из двух половин
восьмерки выбрать по точке с рациональными координатами, в) Вне
любого отрезка [0, е] может лежать лишь конечное число точек М.
3.	Указание. Обратить построение 2.33.
4.	Указание. Братьев N было счетное множество.
5.	Указание. Пусть С—счетное подмножество в А и D = A—С.
При этом A = D-j-C, A-f-B=D-}-C-]-B; использовать эквивалент-
ность множеств С и СВ.
6.	Указание. Пусть В есть множество рациональных чисел; ис-
пользовать задачу 5, полагая А = /. Аналогично в случае множе-
ства Т.
7.	Указание. Рассматриваемое множество А есть объединение
двух множеств: множества последовательностей, содержащих лишь
конечное число нулей, и множества последовательностей, содержащих
бесконечное число нулей. Первое счетно, второе имеет мощность
континуума, поскольку находится во взаимно однозначном соответ-
ствии с множеством точек отрезка, взятых в двоичной записи (см.
1.78, р = 2). Использовать задачу 5.
УКАЗАНИЯ И ОТВЕТЫ К ЗАДАЧАМ
511
8.	Указание. Каждой последовательности (1) поставить в соот-
ветствие последовательность нз нулей и единиц, с единицами на
местах с номерами k2, ... Использовать задачу 7.
9.	Указание. Каждой последовательности (2) поставить в соот-
ветствие возрастающую последовательность
ky=mY, кг=тг + т2..... *л = т1+-.- + ^„,
10.	Указание. Используя задачу 9,
поставить в соответствие таблицу
каждому символу £ можно
5~
/Пц т12 ... т1п ..
т21 т22    m2n ..
aipi тр2   . трп ..
элементы которой—натуральные числа. Эту таблицу можно записать
единой последовательностью, как в 2.33, после чего снова применить
задачу 9.
11.	Указание. Соответственно упростить решение задачи 10.
12.	Указание. Пусть каждому t£[0, 1] поставлена в соответствие
функция ft(x)£E. Набор Wc:E функций ft (х) не исчерпывает
всего £, поскольку функция <f (х), значение которой в каждой точке
х отлично от значения функции fx (х), не входит в W.
13.	Указание. Обобщить идею решения задачи 12, заменив [0, 1]
иа Л и задав каждое подмножество ВсЛ с помощью функции,
равной 1 на В и 0 вне В.
К главе 3
1.	Указание. Если Л = {1,	, ...} , то Л' = {0}, А" пусто.
Построить итерацию.
2.	Указание. Любая предельная точка множества Л' является
предельной точкой множества Л.
3.	Указание. Достаточно рассмотреть п=1. Точка множества Л,
не являющаяся предельной для Л, может быть покрыта интервалом
с рациональными концами, не содержащим других точек множества Л.
Использовать задачу 1 (а) к гл. 2.
4.	Указание. Точку, не являющуюся точкой конденсации мно-
жества Л, можно покрыть интервалом с рациональными концами,
содержащим самое большее счетное множество точек множества Л.
5.	Указание. Отметить те интервалы с рациональными концами,
которые входят в интервалы покрытия, и оставить по одному из
интервалов покрытия, содержащих лк
8.	Указание. Положить t/i= U
хег,
логично определить U2.
10.	Указание. Для п=3 построение производится с помощью
пары окружностей. Пространство М из четырех точек х1( х2, х3, х4
ой отмеченный интервал.
у:р(х, у) <-1р(х,В2)каиа-
512
УКАЗАНИЯ И ОТВЕТЫ К ЗАДАЧАМ
с расстояниями
р(Х1, Х2) = р(х2, х3) = р(*з. яЛ^рСЧ, *1)=Ь
р(*1> *з) = Р(*2> ~«) = 2
уже не изометрично никакому подмножеству евклидова простран-
ства Rs.
11.	Указание. Рассмотреть сферу S„c7?n+i радиуса 2 с центром
в точке (0, 0, О, 1). Отобразить в S„ пространство RncRM,
состоящее из точек (£ь ...,	0), используя прямые, проходящие
через точку (0, 0, ..., 0, 2). Поставить саму эту точку в соответ-
ствие точке оо £ Rn. В качестве метрики г взять обычную метрику
пространства для точек Sn («стереографическая проекция»).
12.	Указание. Фиксируя точку а£М, для каждой пары точек
х, у найти в евклидовой плоскости R2 тройку точек А, X, У с теми
же взаимными расстояниями (задача 10). Новое расстояние г (х, {/)
определить путем стереографической проекции на сферу S2, касаю-
щуюся в точке А.
13.	Ответ. Два элемента на каждую прямую, проходящую
через начало координат.
К г ла в е 4
1.	Указание. См. задачу 1 к гл. 1. Рассмотреть последователь-
ность х„ = (—1)" (п=1, 2, ...).
2.	Указание. Пределы lim и lim являются пределами некоторых
последовательностей.
3.	Ответ. Следует.
5.	Указание. Если ап^ -> lim ап < lim ап, положить, например,
О	при п = п^, k= 1, 2...
lima„—lima„ при n ?= nk.
6.	Ответ, lim x„ = — a+b.
О «5
7.	Указание. Для последовательности е„=——1 получить
У а
уравнение и оценку
_	_вп . еп
е”+1-2(1+е„)< 2 •
8.	Указание. уп < уп+1 < хп+1 < хп.
9.	Указание. Пусть рг= ... =pr > Pr+i^ • • • Рт* тогда
(Рь\п
~ = 0 при k > г.
PiJ
11.	Указание. Использовать определение предела по направле-
нию х а.
УКАЗАНИЯ И ОТВЕТЫ К ЗАДАЧАМ
513
12.	Ответы на оба вопроса в общем случае отрицательны. При-
меры: пусть Х = {1,2, ..., п,...}, S = {n -> со}, Y = {0, 1, Ч2, */3, . .},
Z = {0, 1}; пусть, далее, й(2л)=1/2п,	(2« +1) = 0, р2(п) = 0
(п=1, 2, ...), z(0) = 1, z(i/)=0 при у # 0. Тогда z(y,(n)) не имеет
предела при п-> оо, а г(у2(п)) имеет предел, равный 1 # limz(i/).
13.	Указание, а) и б) устанавливаются непосредственно, в) сле-
дует из 4.16 в
К г лав е 5
1.	Ответ. Нет.
2.	Ответ. Нет.
3.	Указание. Использовать задачу 1 к гл. 1.
4.	Ответ. Обе функции разрывны при целых х и непрерывны
при всех остальных х.
7.	Указание,
п
.....£„}=С-4	••>£"}•
।
8.	Указание. Использовать существование /(а-|-0) и f (Ь—0).
9.	Указание. Положить х = 1ор(/ и применить 5.41.
10.	Ответ: [ — оо, —1—6]; [ — 1 + 6, 1—6]; [1 -|-6, оо); 6>0 —
любое.
11.	Указание. Рассмотреть пары функций sin ах, cosox; a* sinx,
ах cos х.
12.	Указание. Рассмотреть для примера функцию
(sin — при х / 0,
х
0 при х=0.
13.	Указание. Использовать формулы 5.61 (1)—(3).
14.	Указание. У всякой точки с, обладающей свойством
|limx(0—х (с) | 3s <? > 0, существует окрестность, в которой ни одна
t - > с
другая точка не обладает этим же свойством.
15.	Ответ. Функция х(0 непрерывна всюду, кроме тех точек,
для которых все знаки 1п2, .... начиная с некоторого,—де-
вятки.
16.	Указание. Если дуга АосГ не содержит точек множества
М, то дуги Aj = A — 1, А2 = А—2 и т. д. также не содержат его
точек. Дуги Ао, An Д2, ... равной длины, находясь на окруж-
ности Г, не могут не пересекаться. Если, например, дуга Aft пере-
секается с дугой Aft+ m, то объединение дуг Aft, Aft+m, &fe+2m.
покрывает всю окружность Г
17.	Указание. Пусть q—любая точка множества М — Р и
Pi, рг, ...—последовательность точек Р, сходящаяся к q. Показать,
исходя из равномерной непрерывности функции f (х) на Р, что
последовательность значений / (ра) имеет предел, который не зависит
514
УКАЗАНИЯ И ОТВЕТЫ К ЗАДАЧАМ
от выбора последовательности pt, р3, сходящейся к точке q.
Положив f(q)= lim f(pn), проверить непрерывность этой функции
Л-» 00
иа всем М.
18.	Указание. Интервалы (/(а—0), /(а 4-0)) не пересекаются
при разных а.
К главе 6
1.	Указание. Применить 6.16, положив v„
вать 5.59 (6), (11) и (13).
2.	Указание. Использовать признаки § 6.1
3.	Указание. Для любых п и т < п
(л—т)а„^ат+1+...+а„^гт = 2 ап>
m-j-l
1
—:---. ИСПОЛЬЗО-
П 1g Л
и задачу 1.
П
откуда пап^^—^гт.
4.	Одно из решений. Пусть для каждого л=1, 2, ... найден
“	1
номер N = N(ri), для которого V	при N(n)^m<
m—N	П
< IV (л 4-1) положить Ьт = п.
5.	Указание. Использовать неравенство k (л—Л)<;л2 (k= 1, 2,...
..., л—1).
6» УкОЗйНИё, ^2n ®	&2п +1 — ®2/1
7.	Указание, Применить признак Даламбера 6.14 а.
8.	Указание, Существование предела следует из неубывания f (t)
CD
и ее ограниченности; при этом L s lim f (f) У] an. С другой сто-
<-♦1	о
N	со
роиы, для любого е > 0 можно подобрать N так, что 2an>Sa« е’
о	О
N	сю
и затем выбрать t так, что ^1antn > 2a«—е-
о	о
9.	Указание. Та же идея, что в задаче 8.
10.	Указание. zn = P„+1/P„.
п
11.	Указание. logtp„ = 2 lo8bxk-
k=i
12.	Указание. Использовать 5.59е.
13.	Указание. Вычислить (1 —х) рп.
14.	Указание. Разложить-----j— в геометрическую прогрессию.
1____
Рх
15.	Указание. Тождество Эйлера справедливо и при х— 1; в этом
случае обе части равенства бесконечны.
УКАЗАНИЯ И ОТВЕТЫ К ЗАДАЧАМ
515
16.	Указание. Количество чисел, заключенных между 10т 1—1
и 10м—1 и записываемых без цифры 9, равно 9я1—9™-1. Поэтому
9___J 92___9	93_92
искомая сумма меньше, чем —j---1 —|——|- ... = 80.
17.	Указание. Длина вектора не меньше, чем длина любой его
проекции, и не превосходит суммы длин всех проекций на оси.
18.	Указание. Использовать компактность сферы в Еп.
19.	Указание. Использовать теорему 6.32 а (6.46).
20.	Указание. Пусть ZJ V2 • - • —последовательность телесных
углов, содержащих вектор q, таких, что sup sin (х, e)=<Jm\0,
xevm, |х|=1
СО
причем	Последовательно выбирать в ряде (I) члены, содер-
1
жащиеся в V2, V2, ..., сумма длин которых заключена между 1 и 2.
21.	Указание. Для п—1 утверждение совпадает с утверждением
теоремы Римана 6.37. Пусть f£En—любой вектор и £„-i—его
ортогональное дополнение. По индукции существует перестановка
ряда (1), у которой сумма проекций на £„-1 равна заданному век-
тору в Далее, выбрать часть ряда, для которой составляющие
по f образуют ряд, сходящийся к 4-00, а ортогональные составля-
ющие сходятся абсолютно (задача 20). Дополнительная часть ряда
имеет составляющие по вектору f с суммой —оо. Переставляя их,
получить заданную проекцию на вектор f. На величину суммы орто-
гональных проекций эта перестановка не повлияет (задача 19).
22.	Указание. Применить к ортогональному дополнению под-
пространства А результат задачи 21.
К главе 7
1.	Указание, f (x)s0.
2.	Указание. Использовать теорему Лагранжа 7.44.
3.	Указание. Использовать теорему Лагранжа 7.44.
4.	Указание. Мы имеем у'(0)=0, но у'(х) не стремится к 0 при
х —*• 0.
5.	Указание. Достаточно рассмотреть случай f (а) < 0 < f (b)
и доказать существование точки с£(а, b) с f (с)=0. Точка, где f (х)
достигает наименьшего значения, является искомой.
6.	Указание. От противного, с использованием теоремы Лаг-
ранжа 7.44.
7.	Указание. Если искомое неравенство верно для точки
Х={ЛЬ ....	и Для точки	....	то оно
верно для всего отрезка в Rp, соединяющего эти две точки. Для
точек вида А/={0, ..., 1, ..., 0} оно очевидно; отсюда перейти
к любому набору Х=|Л1, .... ХД.
8.	Указание. Неравенство
f (х)—f (w)^f (Р)—f (я)
х—а	~ р—а
(а < х < Р)
эквивалентно определению выпуклой функции в задаче 7.
516
УКАЗАНИЯ И ОТВЕТЫ К ЗАДАЧАМ
9.	Указание. В неравенстве
f(x)—/(а) /(Р)—/(«) f (Р)—/(х)
х—а р—а
₽—х
при р \ х получается существование fnp (х) и равенство f (х 4- 0) =
= f (х), а при а У х—существование /лев (х) и равенство f (х—0) = f (х).
10.	Указание. Следствие неравенства задачи 9.
11.	Указание. Интервалы (^лев(х), fnp (х)), построенные для
каждой пары точек, в которых не существует f (х), не пересекаются.
12.	Указание. Из условия задачи следует, что кривая y=f(x)
имеет с каждой своей хордой общими точками лишь концы хорды и,
следовательно, располагается либо выше, либо ниже хорды. Перейти
по непрерывности от хорды с концами, имеющими абсциссы а, Ь,
к любой хорде.
13.	Указание. Если на кривой y=f(x) при х > х0 есть точка
(хх, f (xj)), лежащая ниже полукасательной, то кривая должна про-
ходить ниже хорды, соединяющей точки с абсциссами х0 ихь Исполь-
зовать 7.22 (2).
14.	Указание. К пределам, указанным в задаче 10 к гл. 4, при-
менить правило Лопиталя.
,,	т.	f(a-\-h)—f (а)	.
15.	Указание. К отношению ——1—!-2-£- применить формулу
Лагранжа
16.	Указание. Угловой коэффициент касательной в точке х„=—
нр превосходит углового коэффициента хорды, проведенной через
точки х„+1 и хп.
17.	Указание. Фиксируя т для данного х0, возьмем приращение
Тогда приращения всех од, (х), начиная с т-й, будут
равны нулю. Функция ОД,-1(х) имеет интервалы без угловых точек
2
длины —; тот из них, который содержит точку х0, содержит вместе
с ней и один из интервалов ^х0, х0 + —j или ^х0, х0——J . На
этом интервале и все предшествующие функции од (X), k < т—1,
не имеют угловых точек; приращения их будут по модулю равны
приращению аргумента. В итоге мы получим
т- I
Д/(х) у &<Pfe (х)
Дх	&х
fe=0
_ Д/ (х)	. п
Поэтому дх не имеет предела при Дх —► 0.
четному числу при т четном,
нечетному числу при т нечетном.
УКАЗАНИЯ И ОТВЕТЫ К ЗАДАЧАМ
517
К главе 8
1.	Указание. Все производные функции e~i/x2 при х=0 равны 0;
для доказательства использовать задачу 15 к гл. 7.
2.	Указание. Найти и оценить главный член в формуле Лейбница.
3.	Указание. Использовать должное число раз теорему Ролля.
4.	Указание. Рассмотреть точку хв, в которой | f (х0) | > Мг—е,
и учесть, что f (x)—f (х„) S== f (хв) (х—хв) — М2	.
5.	Ответ.
f (x)—nf (x+h) + —" g-- f (x+2h) — ... + (— 1)« f (x+nh)
f<"»(x)=Um--------------------------------------------------------
h-+0	n
6.	Указание. Если f" (x0) < 0, то кривая y=f(x) в окрестности
точки х=хв лежит под своей касательной (8.32). Учесть задачу 13
к гл. 7.
7.	Указание. Наличие хорды, лежащей хотя бы частично под
кривой, приводит к существованию точки (х0, f (хв)), в окрестности
которой кривая лежит под касательной; неравенство f" (х) > 0 это
исключает.
8.	Указание. Использовать формулы 8.73 (5); оценить снизу
sin г по модулю, учитывая, что ch у > sh у.
9.	Указание. Для | у | > в использовать оценку, вытекающую из
задачи 8. Для |{/| < в учесть, что |cosxj> 1—6.
10.	Ответ, (а) <о < 10”’; (б) /К 1,03; (в) п5а10. В частности,
ошибка от замены числа е суммой 1+не превосхо-
дит 10-7.
11.	Ответ на рисунке:
		f(n+1)(xo)*0
п четно		
п нечетно		
		
12.	Ответ. Нет. Можно построить пример, используя задачу 2.
518
УКАЗАНИЯ И ОТВЕТЫ К ЗАДАЧАМ
18.	Указание. Использовать неравенство

14.	Указание. Если е рационально, то nle при некотором л есть
целое число.
15.	Указание. Использовать формулы 8.37 (2') и (5').
16.	Указание. В некоторой окрестности 0 искомое неравенство
заведомо выполняется. Если во всем промежутке [—2л, 2л] оно на-
рушается, то имеется точка х0 Ф 0, в которой неравенство обра-
щается в равенство. К промежутку [0, х0] применить теорему
Лагранжа 7.44.
17.	Указание. Положить х=л/2.
К главе 9
1.	Указание. Угловой коэффициент линейной составляющей
равен
о
где Т—период функции f(x).
2.	Указание. Рассмотреть правую часть как (непрерывную)
функцию от £, вначале считая f(x) сохраняющей знак.
3.	Указание. Если <р(х), например, убывает, то <р(х)—<р(а+0),
также убывает и неотрицательна.
4.	Указание. Применить индукцию по п. Другой способ: заменить
Ь на х, продифференцировать по х и убедиться в совпадении резуль-
татов. К исходной формуле вернуться интегрированием, убедившись,
что при х—а обе части равенства совпадают.
5.	Указание. Соответственно обобщить доказательство теоремы
9.14 д.
6.	Указание. Применить критерий Римана (задача 5).
7.	Указание. Учитывая неравенство
применить критерий Римана.
8.	Указание. Использовать критерий Римана.
9.	Указание. В критерии Дю-Буа-Раймона (задача 8) положить
,11	х	б в б
е= 1, тг ,	и вместо б писать соответственно -я- , т , -я- , . •.
2 о	2	4 о
10.	Указание. Использовать критерий Лебега.
11.	Указание. В неравенстве
Г (2л)1!	1	л	Г (2л)1! 1* 1
|_(2л—1)!1] 2л4-1-	2 ** [(2л— 1)11J 2л
отношение крайних членов стремится к 1.
УКАЗАНИЯ И ОТВЕТЫ К ЗАДАЧАМ
519
12.	Указание. По данному е > 0 найдем 6 (е) из условия равно-
мерной непрерывности функции / (х) на отрезке [А, В]. При d (П)<6
имеем
f (£/) (*>+!—*/) = J f(x) dx+ez | x/+1—xj I,
XJ
где | в,-1 < e.
n-1
13.	Указание. Если 2 I x/+i—x/l не ограничивается, ошибки
7=o
от замены f(£/)(xy+1—xj) на соответствующий интеграл (2) могут
нарастать неограниченно при суммировании по Если f (х) имеет
хотя бы одну точку разрыва, ошибка от указанной замены не будет
малой.
14.	Указание. Пользуясь 1)—4), проверить (3) для любой кусоч-
но-постоянной функции f (х). Пользуясь 5) и аппроксимируя данную
кусочно-непрерывную функцию кусочно-постоянной, получить (3).
15.	Указание. Подставить в 9.74 (4) /=1/Уз.
К главе 10
1.	Указание. Пусть z — 1 есть точка аналитичности функции f (z).
 , ftfe) (11
Имеем f (г) = у t ' (г—1)®(| г—1 | < р), где на основании зада-
о
чи 8 к гл. 6
f(l) = lim / (z)=2afe> •••• /°”(1) = 2*(й— 0 •• (Л—я + 1)а*»
0	0
а на основании следствия из теоремы Абеля (6.67) и задачи 15 к гл. 7
f(e«) = 2a*e'*9, .... fw (e«)=2akk(k—!).. .(k—n + l)e‘M,
о	о
ип) (eZ6\
откуда видно, что ряд \	—- (г—е1Г1)п сходится при | г—е;б1 < р.
OS	<30
2.	Указание. Исходить из равенства	М“.
__	___ о
где lim b„ | < 1.
3.	Указание. Рассмотреть отображение ц|=/(г) в окрестности
точки z0.
о
520
УКАЗАНИЯ И ОТВЕТЫ К ЗАДАЧАМ
4.	Указание. Применить принцип максимума к функции .
5. Указание. Требуется доказать соотношение (rt < г2 < г3)
In М (г2) <
1п г2— In гг
1п г3 — In г,
In М (г3)	In М (гг).
' 1п г3—In t\ '
Рассмотреть функцию zaf (z), где а—такое число, что r“Af(r!) =
=	(r3)-
6.	Указание. Использовать метод 10.16.
7.	Указание. Проверить отдельно для функций az, z-}-b, —, ис-
пользовать 10.55.
8.	Указание. Оценить выражения ап в 10.38 (2).
9.	Указание. Подсчитать приращение аргумента при обходе
вокруг каждого нуля и полюса по малой окружности.
10.	Указание. Использовать 10.44.
X ₽(И1,(а) .
11.	Указание. Пусть g (z) = / ,	 (г—а)т; тогда
о
”	k
|g<“4z)+...+gon+n’(z)l= У te'm’(a)+...+g(ra+n+fc,(a))(-£=^
ft=o
Л!
12.	Ответы, а) Каждый лист римановой поверхности функции
ts>(z)—вся плоскость с разрезом по линии, соединяющей точки +1
и —1 (например, по отрезку вещественной оси [ — 1, 1] или по до-
полнительной части вещественной оси); риманова поверхность дву-
листна, листы склеиваются по краям разреза: нижний край первого
листа с верхним краем второго; точки разветвления — 1 и +1 на
плоскости w. На плоскости z области однолистности: внутренность
единичного круга и внешность его. б) На плоскости г области одно-
листности—полосы kst < х < (fe-f-1) л (й = 0, ±1, ±2, ...); обрат-
ная функция z = Arc costs) бесконечнозначна; для построения рима-
иовой поверхности следует на каждом листе плоскости w провести
разрез по вещественной оси от —оо до —1 и от +1 до 4-оо.
Верхний край левой половины разреза на Л-м листе склеивается
с нижним краем левой половины разреза на (Л+ 1)-м листе, верхний
край правой половины разреза на /г-м листе—с нижним краем пра-
вой половины разреза на (Л—1)-м листе.
13.	Указание. Использовать представление cos г через экспо-
ненту.
14.	Указание. Рассмотреть функцию c1f1 (г) + ... -f-cnfn (г), где
числа c/i выбраны так, что | ck | — 1 и в точке г0 максимума
I fi (г) |+ • • • +1 fn (z) I имеет место равенство
clfl (го)+ • • • +сп/п (zo) = l fl (го) 1 + • ••+!/« (го) I'
УКАЗАНИЯ И ОТВЕТЫ К ЗАДАЧАМ
621
15.	Указание, Использовать 10.49.
16 Указание. Рассмотреть .
Р (г)
17. Указание.
Проинтегрировать
шого радиуса.
18. Указание.
гает максимума в
19. Указание.
Р' (z) п , g(z)
р	. где g(z) ограничена при z—► оо.
это соотношение по окружности достаточно боль-
Если Р (г) не обращается в нуль, то
конечной точке.
дости-
» С f(№_
2sti J g—z
ftzft-z
где суммирование распространяется на все полюсы f (г) внутри кон-
тура Гп. С другой стороны,
1	1 Cffodt, z Р f(&d£,=
2ni j £—z	2ni J g	—z)
Г n	Г»	r„
~Zk	z)
*	Гп
последний интеграл стремится к 0 при п —» оо.
20.	Указание. О бесконечных произведениях см. задачу 10 к
гл. 6. Разложение на простейшие дроби, данное в задаче 19, проин-
тегрировать и пропотенцировать.
21.	Указание. Использовать задачу 9 к гл. 8. Для первого раз-
пг,	, , sin z
ложения в задаче 20 положить g (г) =---.
22.	Указание. Рассмотреть функцию
/(г)е-вЛ
в секторе | arg z | < а, | z | < г и применить принцип максимума.
23.	Указание. Применить задачу 22 к функции f (z) е,Тг (-у > 0)
в каждой из четвертей, составляющих верхнюю полуплоскость, и
получить оценку
| f (г) е'",г | < max |с, mJ,	— шах а£е(8_1>г.
Если > с, то функция | f (г) | достигает максимума в некоторой
точке мнимой оси, что при f(z)^ const невозможно (задача 3).
Поэтому т7<с, | f (г) | <с | е_'Тг|; устремить здесь у к нулю.
24.	Указание. Применить задачу 23 и теорему Лиувилля.
522
УКАЗАНИЯ И ОТВЕТЫ К ЗАДАЧАМ
К главе 11
1. Указание. Доказать формулу для внутреннего треугольника,
где подынтегральная функция непрерывна, и перейти к пределу.
2. Указание.
Р	Р	Р	ар	ftp
fСf f^dx=
J х	J X J X J X J x
a	a	a	aa	ba
ba	ftp
(* f(x) , f f(x) ,	£	, b .. ., b
= \ '-^dx—\ '-^dx = f ft) In----------/(tl)ln—,
J x	j	x	' a " a
aa	ap
aa. < g < ba, a₽ < T) < ftp.
1 /~7c	__
8.	Ответ. I (p) = — у — с подходящим значением у p. Ис-
пользовать в качестве контура сектор, образованный отрезком оси х,
отрезком луча ф=ф0 и дугой окружности с центром в начале
координат.
4.	Указание. Использовать задачу 3.
Ответ. Ft=Fs=± |/ у.
5.	Ответ.
I=2л< Выч
Р(х) sin х-]
.QW х J ’
где сумма распространяется на все корни многочлена Q(x) в верхней
полуплоскости.
6.	Ответ. Интеграл с бесконечным пределом не является равно-
мерно сходящимся по параметру у.
7.	Указание. Сраввить значения s2-1 на участке [в, +оо], про-
ходимом в одном и в другом направлениях.
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Абель 122, 210
Абсолютная величина вещественного
числа 23
Автоморфизм л-мерного пространства
58
------тождественный 59
—	структуры 51
Адамар 70, 451
Аналитическая функция 398
---вещественная 427
---целая 424
Аналитическое продолжение 288, 426
Аргаи 69
Аргумент комплексного числа 189
—	функции 65
Ариабхата 210
Арифмети ко-геометр ичес кое с р едиее
152
Арифметическая степень множе-
ства 40
—	сумма множества 39
Арифметическое произведение мно-
жеств 39
Архймед 13, 29, 246, 349, 350, 395
Архимеда принцип 29
Асимптотическая единица 138
—	принадлежность 131
Базис 57
Барроу 273
Бернулли И. 273, 453
Бернулли Я- 273
Бесконечно удаленная точка 436
Бесконечность 36
Бета-фуикция 497
Больцано 40, 121, 209, 210, 246, 273
Больцано -е Вейерштрасса принцип 94
Бомбелли 69
Борель 121
Брус замкнутый 157
—	открытый 157
Бурбаки 50, 68, 121, 273
Бюрги 210
Валле-Пуссеи 509
Вейерштрасс 40, 209, 210, 273, 454
Вектор 55
—	единичный 73
—	нормированный 73
Верхний предел 139, 147
Верхняя грань 17
--- точная 18
Вессель 69
Вещественная часть 62
Взаимно однозначное соответствие 44
Включение 14
Вложенных промежутков система 35
Внутренняя точка 72
Высшие дифференциалы 285
Вычет 429
—	логарифмический 431
Гамма-функция 495
—	, асимптотическое выражение 503
—	в комплексной области 506
—, формула дополнения 500
Гармоническая функция 405
Гаусс 40, 69, 210, 246, 453
Гёдель 40
Гейне 20.9
Геитцеи 40
Гильберт И, 40
Гиперболические функции 294
---обратные 333
Гипергеометрический ряд 243
Гомеоморфизм 85
Гомеоморфные метрики 86
Гранди 211, 246
Граница множества 318
Грассман 69
График функции 66
Грегори 299
Группировка. членов ряда 223
Грушин В. В. 67
Даламбер 211, 453
Дарбу 396
Двоичная система 34
Дедекинд 40, 210
Десятичные знаки 32
Диаметр 72
Дирихле .69, 509
Дифференциал сложной функции 262
— функции 261, 401
---высшего порядка 285
Дифференцирование интеграла по
параметру 381
— несобствениого интеграла по пара-
метру 486
— последовательности функций 377
Длина вектора 73
— дуги 320, 356
---как функция параметра 361
---эллипса 359
— окружности 359
Дополнение множества 42
Дробная часть 30
Дю-Буа-РайМои 396
524
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Евдокс 40
Евклид 40
Единица 17
— асимптотическая 138
Единичный вектор 73
Зависимое переменное 65
Замкнутый контур 388
Замыкание 98
Зейдель 210
Знаки включения 14
Значение функции 65
Изолированная точка 106
Изоморфизм структур 51
Индукции математической метод 20
Интеграл криволинейный 385
— Лапласа 480
— неопределенный 323
— несобственный абсолютно сходя-
щийся 462
--- второго рода 468
--- первого рода 455
---расходящийся 4 56
---сходящийся 456
--- третьего рода 470
---условно сходящийся 462
---определенный 323
— по замкнутому контуру 388
—	Римана 301
---, его пределы 302
---иа брусе 318
---на компакте 316
—	Стилтьеса 346
—	— криволинейный 385
—	типа Коши 414
—	Френеля 508
— Фурье 476
---особый 481
Интегральная сумма 301
Интегрирование по параметру 379,
485
— по частям 326, 338, 467
------ многократное 394
— последовательности функций 373
— через подстановку 326, 343, 467
Интегрируемая мажоранта 489
—	функция 302
Интервал 28
—	смежный 96
—	составляющий 80
Иитреаок 29
Иррациональные числа 20
Казорати 454
Каитор 40, 41, 49, 68, 121, 210
Кантора принцип вложенных отрез-
ков 35, 37
Картан А. 153
Касательная 249
Катеноид 366
Кеплер 349
Клеро 396
Колебание функции 160
— — в точке 394
Компакт 111
— нагруженный 317
Компактное метрическое простран-
ство 11 1
Комплексно сопряженные числа 62
Комплексные числа 60
Конечные точки 436
—	числа 37
Континуум 49
Конфинальные последовательности
107
Координаты вектора 55, 57
Корень аналитической функции 423
—--	--кратности k 423
—	п-й степени 26
Коши 40, 121. 122, 153, 154, 209,
210, 246, 273, 299. 396, 453, 455
509
Коэн П. 68
Коэффициенты Лорана 434
—	Тейлора 421
Кратность корня 201
Кривая кусочн^хладкая 356
КрнволинейныЙинтеграл 385
Критерий Дю-Буа-Раймона 394
—	Лебега 394
—	Кошн для векторного ряда 229
---для предела векторной функции
151
-— —для предела по направлению
130
--- для равномерной сходимости
206. 488
---— сходимости несобственного
интеграла 457
--------- числового ряда 212
--- — — числовой последователь-
ности 101, 145
— Римана 394
— Хаусдорфа 114
Круговые функции 297
Крылов А. Н. 292
Кэли 69
Лагранж 453
Лебег 121, 396
Лейбниц 273, 298, 299, 302, 343,
396, 453, 455
Лемма Жордана 479
—	о замкнутых шарах 105
—	о конечном покрытии 118
Линейная зависимость 56
Линейно упорядоченное множество 51
Лобачевский 16, 69
Логарифм 169
—	натуральный 179
Логарифмирование 174
Лопиталь 273
Лузин Н. Н. 455
Люилье 273
Люстериик Л. А. 115
Максимальное из двух чисел 23
Максимум локальный 260
Менголн 246
Мера Жордана 318
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
525
Метод математической индукции 20
Метрика 70
Метрическое пространство 70
---компактное 111
---локально компактное 111
--- полное 101
--- предкомпактное 113
Минимальное нз двух чисел 23
Минимум локальный 260
Мнимая часть 62
Многочлен Тейлора 277
Множества геометрически равные 78
Множество 13
—	бесконечное 13
—	вещественных чисел 16
—	всюду плотное 97
—	жорданово 318
—	замкнутое 95
—	конечное 13
—	лннейио упорядоченное 51
—	мощности континуума 50
—	несчетное 49
—	ограниченное 28
---в метрическом пространстве 71
—	— сверху 17
		- снизу 25
—	открытое 78
—	пустое 13
—	счетное 46
Модуль вещественного числа 23
— комплексного числа 189
Мощность множества 45
Мур 1 53
Направление 122
Натуральные числа 19
Невозрастающая последовательность
145
Независимое переменное 65
Немировский А. С. 243
Неограниченное множество 72
Неопределенный интеграл 323
Неотрицательное число 23
Непер 210
Неположительное число 23
Непрерывность односторонняя 164
—	равномерная 159
Неравенство Кошн 75
—	Кошн - Буияковского 75
—	треугольника 70
—	четырехугольника 71
— Юнга 354
Несобственный интеграл второго
рода 468
---первого рода 455
---третьего рода 470
Несчетное множество 49
Неубывающая последовательность
145
Нижний предел 139, 147
Нижияя грань 25
—	— точная 25
Новиков П. С. 40
Норма вектора 73
Нормированный вектор 73
Нуль 16
—	аналитической функции 423
Нуль аналитической функции крат-
ности k 423
Ньютон 246, 273, 298, 299, 300,
396, 455
Область 78
—	одиосвязная 414
—	связная 398
Обратная функция 167
Обратное вещественное число 17
Обратные гиперболические функции
333
—	тригонометрические функции 186
Объединение множеств 14, 41
Объем множества 318
—	шара 372
Ограниченная последовательность 145
— сверху последовательность 145
— снизу последовательность 145
Односторонняя се прерывность 164
Окрестность точки 72
Определенный интеграл 323
Ортогональные векторы 192
Особая точка изолированная 435
--- устранимая 435
Особые точки кривой 361
Остаточный член формулы Тейлора
в интегральной форме 339
—	—----в форме Лагранжа 279
Отображение 195
—	конформное 440
— непрерывное 195
Отражение 78
Отрезок 28
Отрицательное число 23
Оттервал 29
Паламодов В. П. 67
Пеано 40
Первообразная 322
Пересечение множеств 15, 41
Перестановка членов ряда 224
Периодическая функция 185, 292
Период функции 185. 292
Пикар 439
Площадь криволинейной трапеции
314, 348
— круга 350
— плоской фигуры 315, 389
------в полярных координатах 355
—	поверхности вращения 365
—	эллипса 352
Поверхность сферы 366
Поворот 192
Подмножество 14
—	истинное 14
Позиционная запись вещественных
чисел 32
Показатель степени 21
Поле комплексных чисел 61
— числовое 17
Полна 397, 451
Полнота системы аксиом 51
Положительное число 23
Полукасательиая левая 257
526
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Полукасательиая правая 257
Полюс п-го порядка 435
Полярные координаты 188
---в пространстве 194
Полярный радиус 189
— угол 189
Пополнение 107
Последовательности конфииальные
107
Последовательность 65
— невозрастающая 145
—	неубывающая 145
—	ограниченная 145
---сверху 145
--- снизу 145
—	расходящаяся 81
—	сходящаяся 81, 123
—	фундаментальная 100
—	функций 203
Постоянная Эйлсрз 462
Потенцирование 174
Правила Лопиталя 268
Предел по направлению 122
-------на подмножестве 125
Предельная точка подмножества 93
---последовательности точек 91
------- чисел 147
---функции 140
------- верхняя 139
—------иижняя 139
Предкомпактное метрическое прост-
ранство 113
Преобразование Абеля 230
—	подобия 60
Признак Абеля — Дирихле для рядов
230
-------для несобственных интегра-
лов 465
—	— — — равномерной сходимости
интегралов 494
—	Вейерштрасса 239
—	Даламбера 214
—	Коши 214
—	Лейбница 220
—	— для интегралов 462
—	Раабе 218
—	сравнения 213, 458
—	сходимости интегральный 459
Пример Ван-дер-Вардена 271
Принцип аргумента 451
—	максимума 450
Произведение бесконечное 244
—	вещественных чисел 17
—	множеств 41
		прямое 65
—	ряда на число 221
—	рядов 222
Производная 249
—	вторая 274
—	левая 257
—	логарифма 254
—	обратной функции 253
—	односторонняя 257
—	по множеству 397
—	порядка п 274
—	правая 257
—	сложной функции 252
—	степейнбй функции 255
Производная тригонометрических
функций 255
—	частная 402
Промежуток 29
Пространство вещественное п-мериое
55, 73
—	евклидово п-мерное 74
Противоположное число 17
Птолемей -210
Путь 385
Равномерная непрерывность 159
—	сходимость 204
Равномощиость множеств 45
Радиус сходимости 211
Разбиение 300
—	, его параметр 300
—	последующее 302
—	с отмеченными точками 300
Разложение рациональной функции
на простейшие дроби 202
—	целой функции иа простейшие дро-
би 452
Расстояние 70
—	между подмножествами 120
—	от точки до множества 120
Расходящаяся последовательность 81
Рациональные числа 20
Региомонтан 210
Рефлексивность 45
Риман 396
Рима нова поверхность 447
Ролль 273
Ряд абсолютно сходящийся 220
-------векторный 229
—	векторов 227
—	гармонический 217
—	гипергеометрический 243
—	двусторонний 233
---, симметричное суммирование 235
—	знаконеотрнцательный 211
—	зиаконеположительный 211
—	знакоотрицательный 211
— знакоположительный 211
—	Лорана 434
---, главная часть 434
---, правильная часть 434
—	сгруппированный 223
—	степенной 240
---, радиус сходимости 241
—	Тейлора 287, 421
—	условно сходящийся 220
— функций 236
---равномерная сходимость 239
---, сумма 237
— числовой 211
---, отрезок 211
— —, расходимость 211
---, сходимость 211
---. частные суммы 211
Свертка 491
Свертывание 493
Сдвиг 78
Сеге 397
Симметричность 45
Система двоичная 34
— троичная 34
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Скалярное произведение 73
Сложная функция 157
Слой 66
Смежный интервал 96
Соприкасающаяся парабола 281
Составляющий интервал 80
Сохоцюйй Ю. В. 454
Среднее интегральное 307
Средняя ордината 307
Стевин 13
Степенная функция 174
Степень арифметическая множества 40
—	вещественного числа 20
Стилтьес 396
Стокс 210
Структура математическая 50
Сумма арифметическая множеств 39
—	вещественных чисел 16
—	множеств 41
— рядов 221
Сфера 72
Сходимость равномерная 204
---внутри области 421
Сходящаяся последовательность 81,
---, предел 81
Счетное множество 46
Тейлор 299
Теорема Абеля 241
—	Абеля — Лиувилля 335
—	Больцано 163
—	Бэра 105
—	Вейерштрасса 158
—	Гейне 159
— Дирихле 225
— единственности аналитической
функции 425
— Коши 262, 414
—	Коши — Адамара 237
—	Лагранжа 263
—	Лиувилля 427
—	о вычетах 431
—	о среднем 307, 409
—	Римана 226
—	Ролля 262
—	существования корня многочлена
197, 452
—	Фрагмеиа — Линделёфа 453
—	Хаусдорфа 107
—	Штейн ица 245
—	Эрмита 146
Тождество Эйлера 245
Торричелли 273
Точка выпуклости вверх 265
---вниз 265
—	изолированная 106
—	конденсации 119
—	непрерывности 154
—	перегиба 265
—	разрыва 154
— существенно особая 436
Транзитивность 45
Трансцендентные числа 50
Тригонометрические функции 181
---в комплексной области 290
---обратные 186
Троичн'ая система 34
Угол между векторами 191
Уравнение Лапласа 405
Условия Коши — Римана 403
Успенский В. А* 16
Ферм£ 249, 272
Флюента 396
Флюксия 300, 396
Формула Валлиса 394
—	Дирихле 508
—	Коши 417
—	Лейбница 274
— Ньютона—Лейбница 323, 342, 409
—	Тейлора 277
---, остаточный член 279, 339
—	Фруллани 508
Формулы Эйлера 291
Фреше 121
Фробениус 64, 69
Фундаментальная последовательность
100
Функции, эквивалентные по направ-
лению 137
Функция 65
— аналитическая 398
---вещественная 427
---в точке 398
---целая 424
— бесконечно большая 133
------— по сравнению 137
---дифференцируемая 286
--- малая 133
------по сравнению 137
—	векторная 65
—	вещественного переменного 65
— возрастающая 165
— выпуклая вверх 265, 271
---вниз 265, 271
—	гармоническая 405
—	гладкая 274
---n-го порядка 274
—	Дирихле 312
—	дифференцируемая в точке 249
---по множеству 398
—	дробио-лииейная 442
—	кусочно-гладкая 326
—	кусочио-непрерывиая 310
—	кусочно-постоянная 311
—	многозначная 66
—	монотонная 165
— и е во эра стающая 165
---по направлению 143
— неотрицательная по направлению
133
— непрерывная в точке 154
---иа множестве 155
--- слева 165
--- справа 165
—	неубывающая 165
—	— по направлению 141
—	п-кратно-диффереицируемая 274
------по множеству 400
—	, область значений 65
—	, — определения 65
—	обратная 167
— ограниченная 132, 133, 149
---по модулю 132
—	— сверху 132
528
АЛФАВИТНЫЙ
УКАЗАТЕЛЬ
Функция ограниченная снизу 132
—	однозначная 66
—	однолистная 442
—	отрицательная бесконечно большая
133
—	положительная бесконечно боль-
шая 133
—	положительная по направлению
133
—	равномерно непрерывная 159
—	Римана 208
—	сложная 157
—	степенная 174, 443, 445
—	убывающая 165
—	характеристическая 318
Числа трансцендентные 50
— целые 20
Число е 146
— неотрицательное 23
— неположительное 23
— отрицательное 23
— л 184
— положительное 23
Числовая ось 25
Числовое поле 17
Числовой ряд 211
----, отрезок 211
— —, расходимость 211
----, сумма 211
----, сходимость 211
----, частные суммы 211
Харди 337
Хаусдорф 41, 121
Целая аналитическая функция
424
— часть 30
Целое кратное 29
Целые числа 20
Частная производная 402
Частное вещественных чисел 19
Чеботарев Н. Г. 335
Числа иррациональные 20
—	комплексные 60
—	конечные 37
—	натуральные 19
—	рациональные 20
Шар 72
—	замкнутый 72
—	открытый 72
Шварц Г. 450
Штифель 209
Эйлер 69, 210, 299, 453, 509
Эквивалентные множества 44
Экспонента 172, 444
— в комплексной области 289
Экстремум локальный 260
Эллиптические интегралы 335
Энгельс 247
Ячейка 316
—, ее мера 317
Ниже приводится содержание третьей части, которая выйдет
отдельным изданием в 1970 году.
ЧАСТЬ ТРЕТЬЯ
ИЗБРАННЫЕ ГЛАВЫ СОВРЕМЕН ИОГО АНАЛИЗА
Глава 12. Основные структуры современного анализа.
Глава 13. Дифференциальные уравнения.
Глава 14. Ортогональные разложения.
Глава 15. Преобразование Фурье.
Глава 16. Пространственные кривые