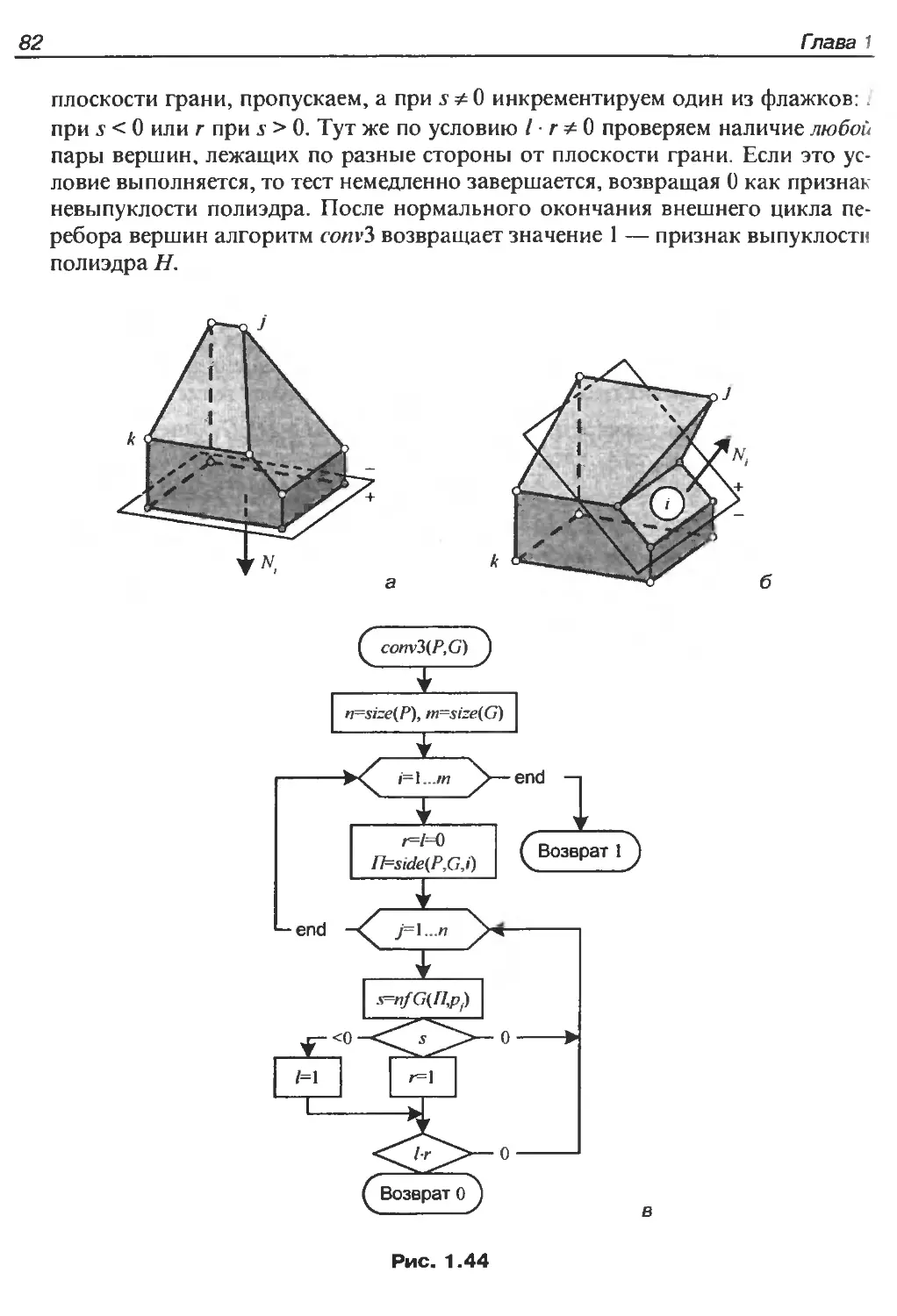
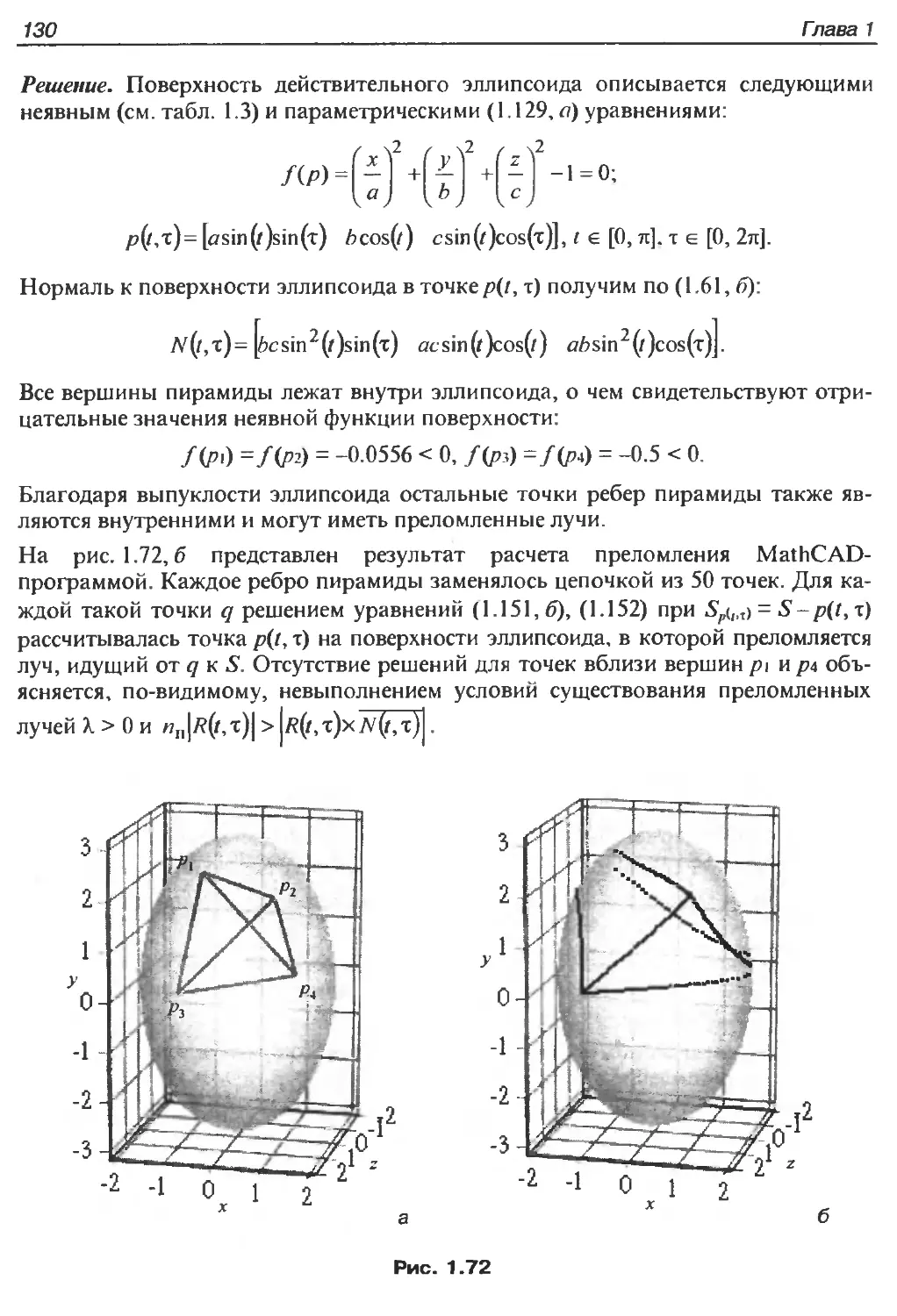
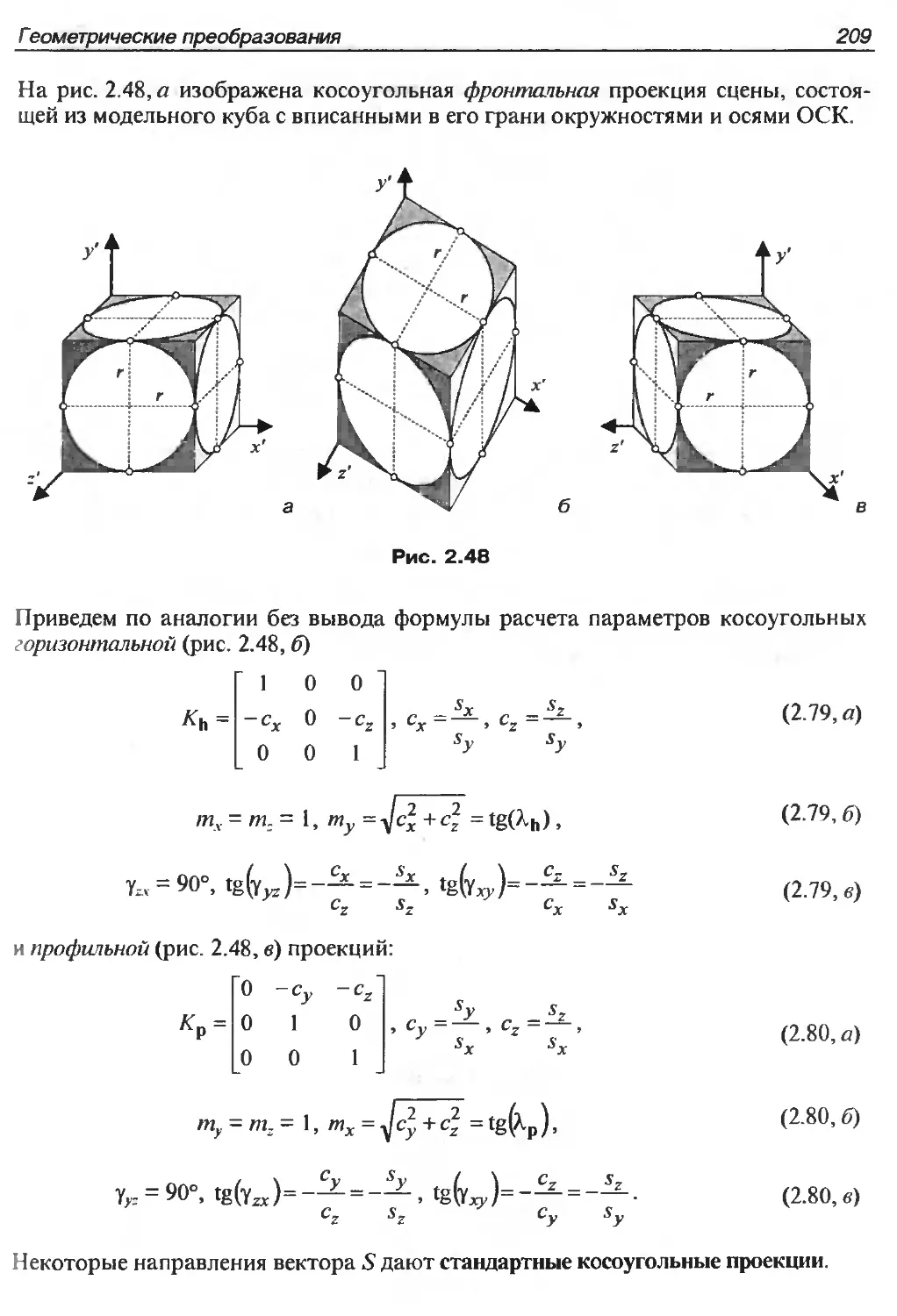
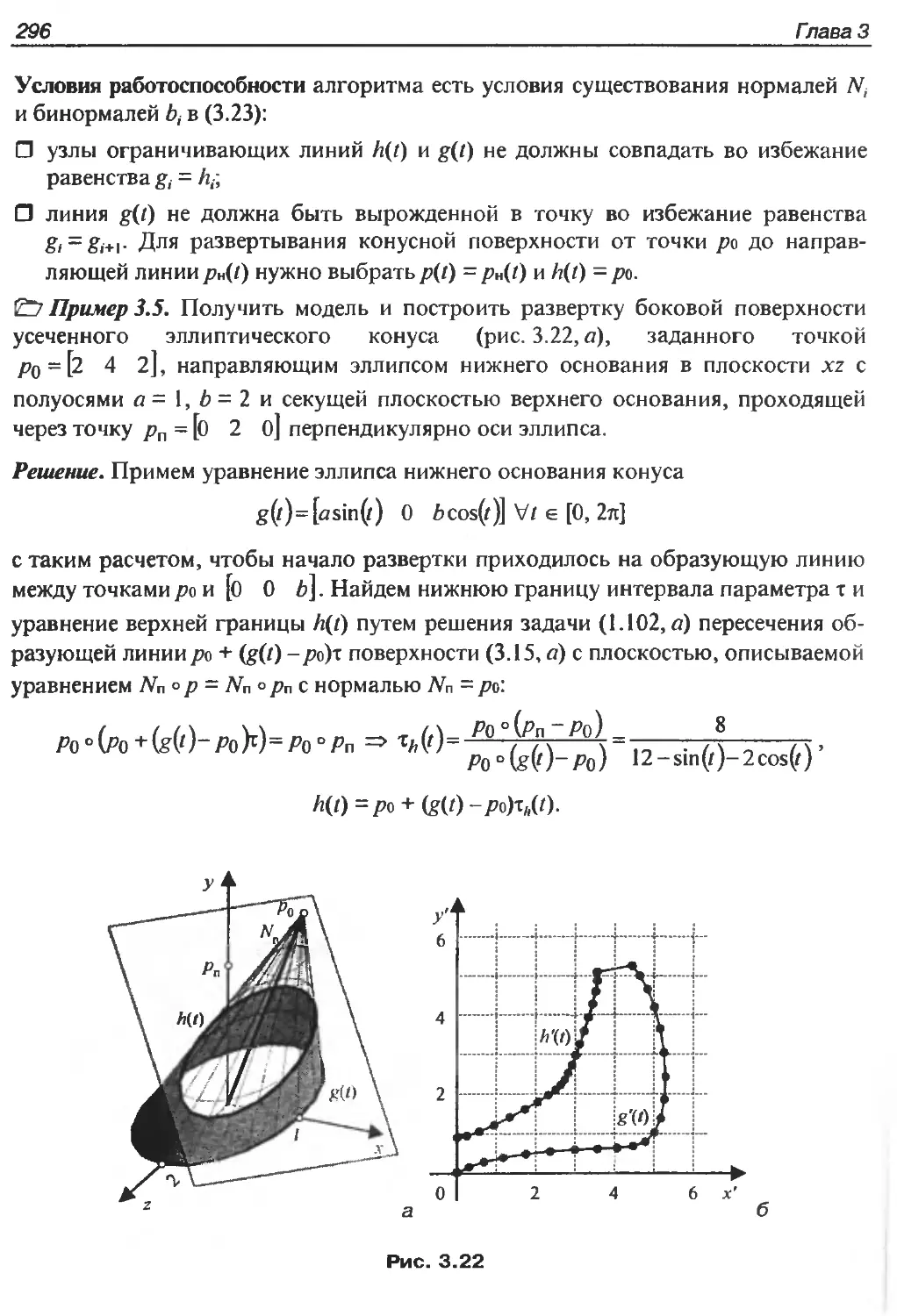
Автор: Никулин Е.А.
Теги: математика информатика компьютерные науки высшая математика компьютерная графика издательство бхв-петербург
ISBN: 5-94157-264-6
Год: 2003
Текст
Е. А. Никулин
КОМПЬЮТЕРНАЯ ГЕОМЕТРИЯ
И АЛГОРИТМЫ
МАШИННОЙ ГРАФИКИ
Геометрические основы компьютерной графики
Аффинные и проективные преобразования
Математические модели поверхностей и объектов
Геометрические задачи визуализации
УЧЕБНОЕ ПОСОБИЕ
Е. А. Никулин
КОМПЬЮТЕРНАЯ ГЕОМЕТРИЯ
И АЛГОРИТМЫ
МАШИННОЙ ГРАФИКИ
Санкт-Петербург
«БХВ-Петербург»
2003
Никулин Е. А.
Компьютерная геометрия и алгоритмы машинной графики. —
СПб.: БХВ-Петербург, 2003. — 560 с.: ил.
В книге приведено максимально полное изложение геометрических и
алгоритмических основ современной компьютерной графики: математи-
ческие модели графических элементов на плоскости и в пространстве, фун-
даментальные законы геометрической оптики и основанные на них алго-
ритмы построения оптических эффектов, методы геометрических преобра-
зований, анализа и синтеза моделей линий, поверхностей и объектов,
геометрические задачи визуализации — комплекс алгоритмов 2d- и 3d-
отсечения и удаления. Материал сопровождается большим числом иллюст-
раций, блок-схем алгоритмов и примеров их реализации.
Для студентов вузов и специалистов, изучающих компьютерную графику
и занимающихся разработкой новых алгоритмов
и прикладных графических программ
Группа подготовки издания:
Главный редактор
Зав. редакцией
Редактор
Компьютерная верстка
Корректор
Дизайн обложки
Зав. производством
Екатерина Кондукова
Григорий Добин
Нина Седых
Натальи Смирновой
Наталия Першакова
Игоря Цырульникова
Николай Тверских
Рецензент:
кафедра вычислительной техники Нижегородского государственного техни-
ческого университета (зав. кафедрой член-корреспондент РАН, профессор
В. В. Кондратьев)
Содержание
Введение................................................................1
Основные обозначения и соотношения......................................5
Глава 1. Геометрические основы компьютерной графики.....................9
1.1. Графические элементы на плоскости................................12
1.1.1. Модели прямой линии на плоскости............................13
1.1.1.1. Неявное уравнение прямой................................13
1.1.1.2. Нормальное уравнение прямой..............................15
1.1.1.3. Параметрическая функция прямой..........................16
1.1.1.4. Уравнения прямой, проходящей через две точки............17
1.1.1.5. Уравнения прямой в отрезках.............................18
1.1.2. Взаимное положение графических элементов на плоскости.......18
1.1.2.1. Коллинеарность точек.....................................18
1.1.2.2. Взаимное расположение прямых............................19
1.1.2.3. Взаимное расположение точки и прямой.....................19
1.1.2.4. Построение прямой, наименее удаленной
от совокупности точек.............................................21
1.1.2.5. Пересечение двух прямых..................................24
1.1.2.6. Уравнения пучка прямых и биссектриса угла...............25
1.1.2.7. Тесты свойств графических элементов на плоскости........27
1.1.2.8. Тесты ориентации точки относительно полигона............32
1.1.2.9. Алгоритмы пересечения на плоскости......................42
1.1.2.10. Площадь и геометрический центр полигона................48
1.1.2.11. Алгоритмы генерирования случайных полигонов............51
1.1.3. Квадратичные и параметрические кривые.......................54
1.2. Графические элементы в пространстве.............................60
1.2.1. Модели плоскости в пространстве.............................62
1.2.1.1. Неявное уравнение плоскости.............................62
1.2.1.2. Нормальное уравнение плоскости..........................63
1.2.1.3. Параметрическая функция плоскости.......................64
1.2.1.4. Уравнения плоскости, проходящей через три точки.........66
1.2.1.5. Уравнения плоскости в отрезках..........................66
1.2.1.6. Модели линии в пространстве.............................67
1.2.2. Взаимное положение графических элементов в пространстве.....69
1.2.2.1. Коллинеарность точек....................................69
1.2.2.2. Компланарность точек....................................69
IV
Содержание
1.2.2.3. Точка и прямая............................................70
1.2.2.4. Точка и плоскость.........................................70
1.2.2.5. Построение плоскости, наименее удаленной
от совокупности точек..............................................71
1.2.2.6. Взаимное расположение двух прямых.........................73
1.2.2.7. Взаимное расположение прямой и плоскости..................74
1.2.2.8. Две плоскости.............................................75
1.2.2.9. Пучок плоскостей и биссекторная плоскость.................76
1.2.2.10. Пересечение плоскостей...................................77
1.2.2.11. Модель полиэдра..........................................77
1.2.2.12. Тесты свойств графических элементов в пространстве.......80
1.2.2.13. Тесты ориентации точки относительно полиэдра.............83
1.2.2.14. Алгоритмы пересечения в пространстве.....................85
1.2.3. Квадратичные и параметрические поверхности....................89
1.3. Основные задачи геометрической оптики.............................99
1.3.1. Пересечение луча с поверхностью..............................100
1.3.2. Отражение луча от поверхности................................106
1.3.3. Преломление луча на поверхности..............................107
1.3.4. Прямая и обратная трассировка лучей...........................110
1.3.5. Лучевые методы построения оптических эффектов.................112
1.3.5.1. Тень.....................................................116
1.3.5.2. Отражение................................................121
1.3.5.3. Преломление..............................................128
Глава 2. Геометрические преобразования..................................139
2.1. Аффинные преобразования..........................................140
2.1.1. Основные понятия и соотношения...............................140
2.1.2. Элементарные аффинные преобразования.........................144
2.1.2.1. Перенос..................................................144
2.1.2.2. Масштабирование..........................................144
2.1.2.3. Сдвиг....................................................145
2.1.2.4. Вращение.................................................148
2.1.2.5. Табличный расчет тригонометрических функций..............149
2.1.3. Сложные аффинные преобразования..............................154
2.1.3.1. Методы расчета матрицы сложного преобразования...........155
2.1.3.2. Кинематический метод построения объектов.................170
2.1.3.3. Кинематическая задача перемещения в пространстве.........182
2.2. Проективные преобразования.......................................194
2.2.1. Ортографические проекции.....................................196
2.2.2. Аксонометрические проекции...................................197
2.2.3. Косоугольные проекции........................................207
2.2.4. Центральные (перспективные) проекции.........................211
2.2.5. Проективные алгоритмы сложных преобразований.................221
2.2.5.1. Проецирование пространственных линий на плоскость........223
2.2.5.2. Стереографические проекции...............................228
Содержание
V
2.2.5.3. Картографические проекции..............................231
2.2.5.4. Построение сцены с подвижным наблюдателем.............242
2.2.5.5. Проективные алгоритмы построения оптических эффектов...247
Глава 3. Математические модели поверхностей и объектов...............261
3.1. Методы моделирования поверхностей.............................261
3.1.1. Методы изображения поверхностей...........................262
3.1.1.1. Выбор проекции изображения............................263
3.1.1.2. Каркасные поверхности.................................264
3.1.1.3. Точечные поверхности..................................268
3.1.1.4. Модели освещенности и закрашивание поверхностей.......271
3.1.2. Кинематические поверхности................................278
3.1.2.1. Поверхности вращения, переноса и комбинированные......282
3.1.2.2. Линейчатые поверхности и их развертки..................289
3.1.2.3. Нелинейчатые поверхности..............................307
3.1.3. Кусочно-определенные поверхности..........................324
3.1.4. Сплайны...................................................329
3.1.4.1. Сплайновые кривые.....................................330
3.1.4.2. Сплайновые поверхности................................339
3.1.5. Фрактальные множества.....................................347
3.1.5.1. Фрактал Мандельброта и алгоритмические фракталы.......348
3.1.5.2. Геометрические фракталы...............................353
3.1.5.3. Свойства фракталов....................................370
3.1.6. Графические поверхности...................................376
3.2. Модели объектов в пространстве................................379
3.2.1. Каркасные модели. Платоновы тела..........................381
3.2.2. Граничные модели..........................................393
3.2.3. Сплошные модели...........................................395
Глава 4. Геометрические задачи визуализации..........................405
4.1. Логические операции со списками...............................405
4.1.1. Объединение списков отрезков............................408
4.1.2. Пересечение списков отрезков............................411
4.1.3. Исключение списков отрезков.............................413
4.2. Методы отсечения..............................................416
4.2.1. Регулярное плоское отсечение отрезка......................420
4.2.2. Произвольное плоское отсечение отрезка....................423
4.2.3. Произвольное плоское отсечение полигона...................429
4.2.4. Объемное отсечение отрезка................................432
4.2.5. Объемное отсечение полигона и полиэдра....................434
4.2.6. Логическое конструирование ЗФобъектов.....................442
4.2.7. Дополнительные задачи отсечения на плоскости..............448
4.2.7.1. Отсечение выпуклого полигона полуплоскостью...........448
4.2.7.2. Расчет ядра произвольного полигона....................452
4.2.7.3. Пересечение выпуклых полигонов........................453
VI
Содержание
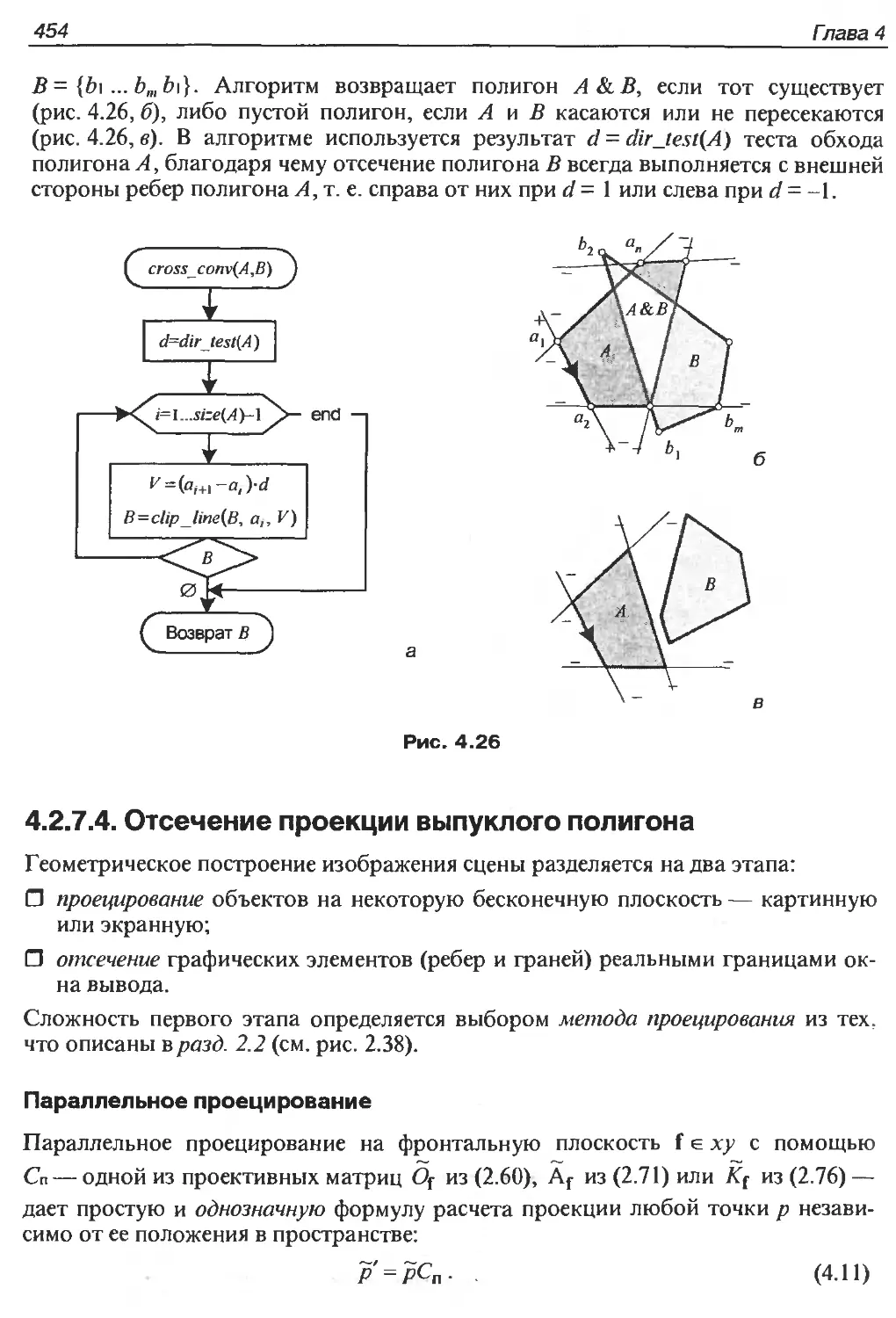
4.2.1.4. Отсечение проекции выпуклого полигона..................454
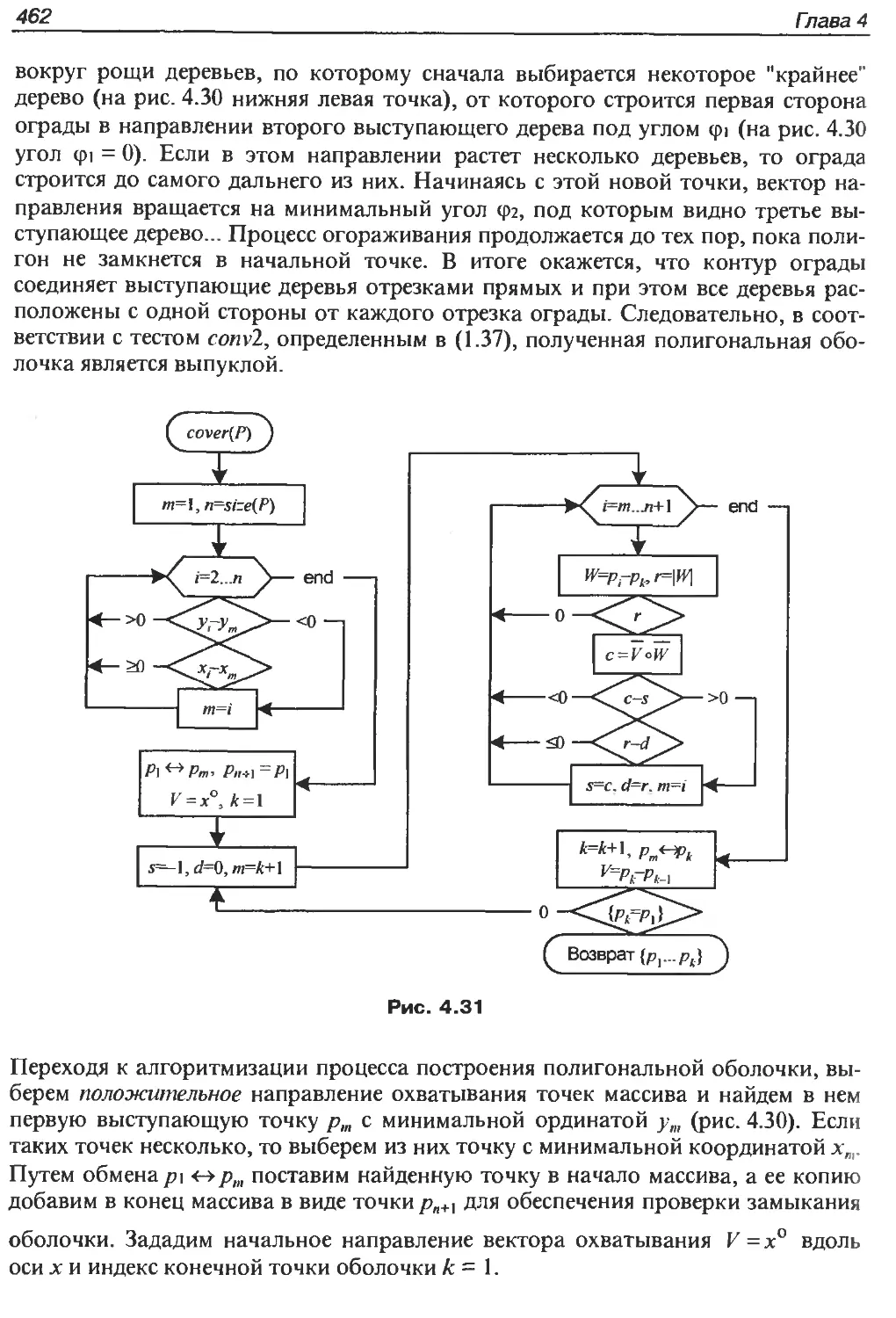
4.2.7.5. Выпуклая полигональная оболочка массива точек..........461
4.2.7.6. Полигонализация массива точек..........................464
4.2.7.7. Разрезание невыпуклого полигона........................468
4.2.7.8. Триангуляция полигона..................................472
4.2.8. Дополнительные задачи отсечения в пространстве.............484
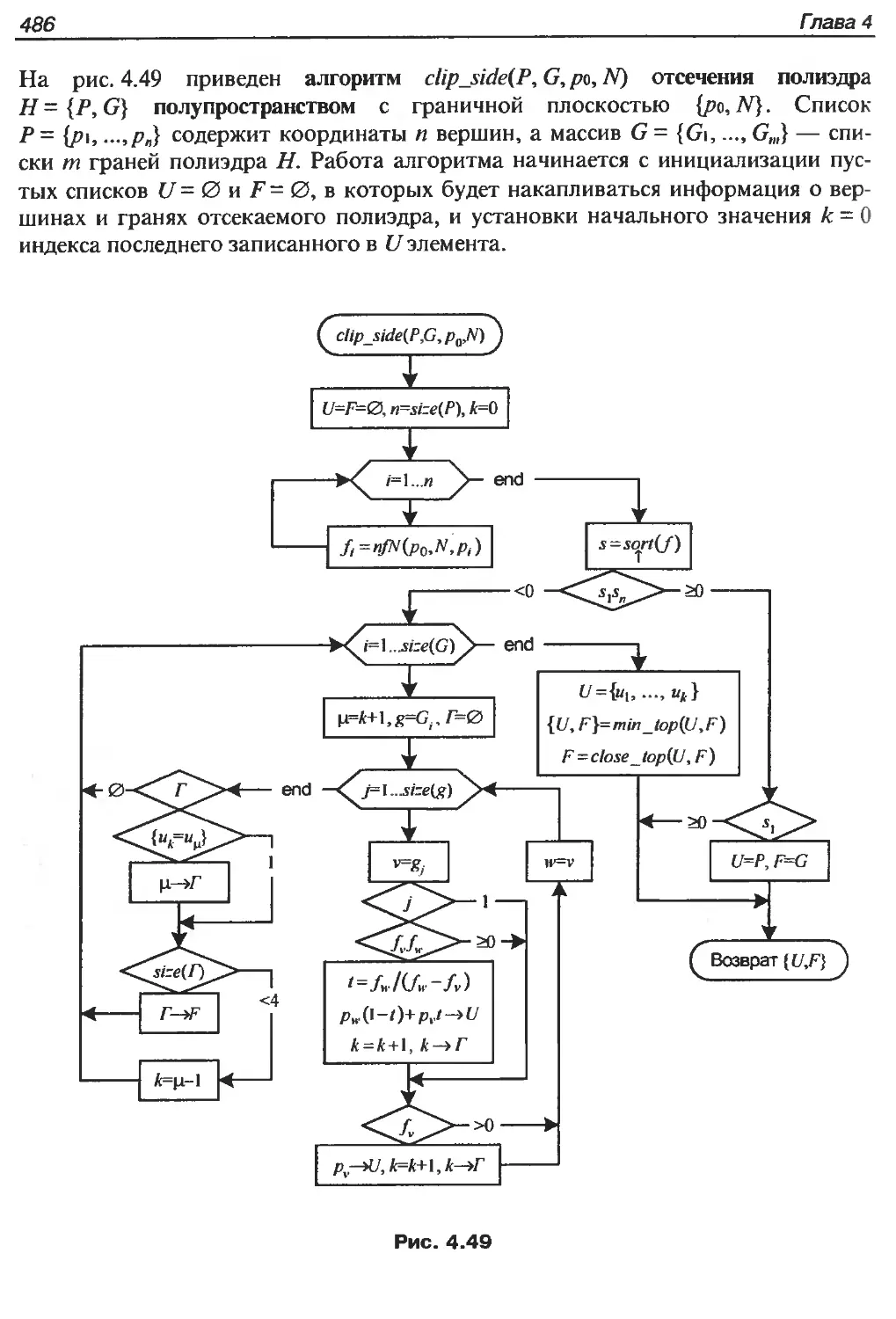
4.2.8.1. Отсечение выпуклого полиэдра полупространством.........484
4.2.8.2. Сечение выпуклого полиэдра плоскостью..................493
4.2.8.3. Расчет ядра полиэдра...................................495
4.2.8.4. Пересечение выпуклых полиэдров.........................496
4.2.8.5. Выпуклая полиэдральная оболочка массива точек..........498
4.3. Методы удаления................................................504
4.3.1. Предварительная обработка моделей объектов.................509
4.3.1.1. Выбор мировой системы координат........................509
4.3.1.2. Построение охватывающих оболочек.......................513
4.3.1.3. Разбиение граней.......................................523
4.3.1.4. Отбраковка нелицевых граней и нормировка векторов......530
4.3.2. Удаление невидимых линий...................................533
4.3.3. Удаление невидимых граней..................................539
Заключение............................................................545
Список литературы ....................................................549
Введение
В основании бесконечно развивающегося здания компьютерной графики крае-
угольными камнями лежат фундаментальные дисциплины — аналитическая гео-
метрия и оптика, скрепленные раствором — искусством программирования.
Возникнув из потребностей рынка, развития информатики и вычислительной
техники, компьютерная графика изучает методы построения изображений раз-
личных геометрических объектов и сцен.
Главными этапами построения изображения являются:
23 моделирование как искусство применения методов математического описания
объектов и сцен, природа которых может быть самой различной: обычные
геометрические фигуры и тела в двух- и трехмерном пространстве; естествен-
ные явления природы — горы, деревья, облака и другие объекты; огромные
массивы чисел, полученных в различных экспериментах, и многое другое;
71 визуализация (отображение) как искусство построения реалистичных изобра-
жений объемного мира на плоском экране дисплея ЭВМ, заключается в пре-
образовании моделей объектов и сцен в статическое изображение или
фильм — последовательность статических кадров.
В отличие от плоских изображений реальных трехмерных объектов, которые на
фотографиях автоматически выглядят натурально благодаря действию в приро-
де оптических законов, синтезированное компьютерное изображение будет по-
хоже на реальное лишь при мастерском владении как методами моделирования
геометрических форм, так и средствами их достоверной визуализации. Таким
образом, компьютерную графику можно рассматривать как искусство создания
реалистичной иллюзии действительного мира. Эта сторона ее применения нашла
наиболее яркое воплощение в системах виртуальной реальности — комплексах
аппаратных и программных средств имитации окружающей среды с помощью
визуальных, акустических, тактильных и других эффектов.
С другой стороны, методами компьютерного синтеза стало возможным создание
и нереальных, фантастических изображений и эффектов, без чего не обходится
ни одна популярная компьютерная игра или кассовая голливудская кинолента.
Подлинное второе дыхание компьютерная графика придала рекламному бизнесу
благодаря умению создавать анимированные, т. е. оживленные, персонажи рек-
ламируемых товаров.
Из более серьезных областей применения компьютерной графики можно назвать:
□ системы автоматизированного проектирования (САПР), в которых осущест-
вляется интерактивное взаимодействие конструктора и синтезированного с
помощью компьютера изображения создаваемого изделия или сооружения;
2
Введение
□ автоматизированные системы научных исследований (АСНИ), в которых
осуществляется визуализация результатов экспериментов в виде трехмерных
статических или динамических изображений, интерпретирующих огромные
массивы первичных данных;
□ распознавание и обработка изображений в системах искусственного зрения,
авиационной и космической картографии, медицинской томографии и т. д.
В качестве исходного материала могут быть отсканированные изображения,
космические снимки, данные локации и т. п. Компьютерное преобразование
этих данных в зримые геометрические образы помогает достаточно просто
понимать суть происходящих процессов людям, далеким от вычислительной
техники.
Таким образом, интерес к машинной графике проявляют представители самых
различных специальностей: программисты компьютерных игр, конструкторы,
технологи, физики, биологи, медики, дизайнеры, кинорежиссеры, художники-
мультипликаторы, клипмейкеры и др. Неудивительно поэтому, что постоянно
ощущается острый дефицит литературы, раскрывающей возможности примене-
ния научных методов в современной компьютерной графике. К такого рода из-
даниям и относится настоящая книга. Наиболее близким к ней по духу является
фундаментальный тандем книг [25, 26] по основам машинной графики. К удач-
ным изданиям последнего времени хотелось бы отнести также [5, 18. 23] и осо-
бенно [36].
Глубоко уважаемый автор последней книги, как и большинство других авторов,
отстаивает "подход программиста" при овладении знаниями в области компью-
терной графики. Цель его книги — научить приемам решения простейших задач
трехмерной графики, не останавливаясь на детальном исследовании излагаемых
алгоритмов и оптимальных методов их реализации.
Конечно, можно успешно водить автомобиль, не зная в деталях, что происходит
под капотом. Но компьютерная графика— не массовое увлечение, а удел спе-
циалистов своего дела, знающих предмет изнутри. Основное содержание на-
стоящей книги составляет детальное изложение методов и алгоритмов реали-
стичного изображения как статических, так и динамических объектов и сцен.
Автор глубоко убежден в том, что гораздо интереснее и важнее понимать и
уметь самому реализовать скрытые закономерности изображения сложных объ-
ектов, чем с восхищением наблюдать, как эти изображения создаются чужими,
пусть и более совершенными графическими программами.
Автор сознательно не приводит текстов программ на каком-либо алгоритмиче-
ском языке, т. к. мода на языки программирования преходяща (сохранившиеся
кое-где книги с программами на раритетных ныне языках Basic, Fortran и Algol
[20,24,31] не вызывают ничего, кроме умиления), стиль работы каждого про-
граммиста уникален, а алгоритмы, изложенные на понятном для всех языке
формул и блок-схем, универсальны и существенно более долговечны. Книга при-
звана вооружить читателя удочкой— методами, алгоритмами и особенностями
их реализации, а не готовой рыбкой — текстами программ; побудить его рабо-
тать своей головой, а не использовать чужие решения.
Введение
3
По аналогичной причине книга не является инструкцией пользователя какого-
нибудь популярного графического пакета. Более того, она не содержит ни одно-
го названия подобных программ, простое упоминание которых лет через пять
вызовет лишь снисходительную улыбку читателя по причине их безнадежной
древности. Единственное исключение сделано уникальной программе MathCAD
[22], которую автор использовал для создания геометрически достоверных ри-
сунков и решения многочисленных примеров, иллюстрирующих работу алго-
ритмов. И снова читатель будет лишен удовольствия сравнить свое искусство
программирования в среде MathCAD с авторским, поскольку в книге сознатель-
но не приведено ни одного листинга конкретной программы.
Этому есть еще одно объяснение. Курс "Компьютерная графика", читаемый ав-
тором на протяжении ряда лет в Нижегородском государственном техническом
университете, предполагает выполнение лабораторных работ, где излагаемые в
книге алгоритмы программируются в среде MathCAD. Для того чтобы доста-
вить студентам удовольствие от самого процесса получения самостоятельного
решения, тексты программ не включены в содержание книги.
Автор выражает благодарность студентам факультета информационных систем
и технологий Нижегородского государственного технического университета за
роль подопытных кроликов, которую они доверчиво играли в процессе изучения
курса, являясь одновременно экспертами методов и алгоритмов, излагаемых в
книге. Нет границ признательности автора к членам своей семьи, в течение ряда
лет терпеливо наблюдавших спину своего мужа и отца, работающего за компь-
ютером над созданием и бесчисленными исправлениями этой книги. Спасибо
всем неравнодушным за моральную поддержку!
Основные обозначения
и соотношения
S — символ, обозначающий начало алгоритма или примера.
S — символ, обозначающий конец алгоритма или примера
R" — евклидово пространство размерности п
х°, у° и z° — ортогональные векторы единичной длины (орты), направлен-
ные по осям декартовой системы координат xyz.
f, h и р — фронтальная (ху), горизонтальная (xz) и профильная (yz) координат-
ные плоскости декартовой системы координат.
К = [их Уу]- Vxx° + УуУ° G R2 — вектор в плоскости ху с координатами Vy
и модулем (длиной) |и| = ^Vx + Vy .
V = \Кх Vy Vz ]= Vxx° + Vyy° + V:z° G R3 — вектор в пространстве xyz с коор-
динатами Vx, Vy, И. и модулем | V |= -Jk2 + Vy + Vz .
О„ e R" — нулевой вектор или блок вектора размерности п.
О„х„, g R"x"' — нулевая матрица или блок матрицы размерности п х т.
V = [v 1] G R”+l — расширенный вектор V, дополненный координатой, равной
единице.
V = [V О] G R”+l — расширенный вектор V, дополненный координатой, равной
нулю.
- V
—нормированный вектор Иединичной длины.
И|| И7 и V# W— соответственно, параллельные и непараллельные векторы V
и W.
VlWii V JJV — ортогональные и неортогональные векторы Vи W.
Z.VWили Z(V,IV) — угол между векторами Vи W.
6
Основные обозначения и соотношения
V о W = Kv • JVX + Vy • Wy + V. • W. — скалярное произведение векторов V и W.
Другое выражение для скалярного произведения V ° W = |И] • | - cos(ZVW) по-
зволяет найти косинус угла между векторами Vv,W:
cos(z VW) = И т
ИИ
Vo W- 0 — шест ортогональности векторов Vи XV.
V°W = ±1 — тесты параллельности (при +1) и антипараллелыюсти (при -1)
векторов V и W.
। । / ч— V°W ( —\—
рги^И =|И| cos(ZVW)W =-— W = [V ° W)W — проекция вектора V на вектор W.
И
рг/уИ =К-ргд,К = K-(k<>7v)/V — проекция вектора Vе R3 на плоскость П,
имеющую вектор нормали N.
N = f^xw= Vx
= Nxx° + Nyy° + Nzz° — векторное произведение векто-
И7,
ров V е R3 и W е R3, имеющее координаты
и модуль |Л'| = |IZ] jW] sin(ZVJV). Отсюда получаем значение синуса угла между
векторами в пространстве:
sin(zrfr)=iL-r-!r.
и-и
|ИхИ/| = 0— тест параллельности (антипараллельности) векторов I'eR3 и
W е R3.
{/л pi —Рп} — ломаная линия (полилиния), заданная списком точек в порядке их
соединения pi -> pi^> ... -> рп.
{pi pi...Р„Р>}— многоугольник (полигон), заданный списком точек-вершин в
порядке их обхода по замкнутому контуру pi —>pi -> ... -+р„^> pi.
V/(r)= —-----вектор градиента скалярной функции/векторного аргумента V.
dV
Нпе(а, Ь) — функция рисования отрезка прямой линии ab на плоскости ху.
diagfTV/, । ... М„п \ — квадратная матрица М е R"*" с диагональными элемента-
ми Ми и недиагональными элементами = j.
Основные обозначения и соотношения
7
£„=diag[l ... 1] — единичная их/1-матрица.
G R(«+1H"+1)
М =
О|Х„ ! 1
— расширенная матрица М, дополненная нижней
диагональной единицей.
и
tr(A/)= ^Мц — стед квадратной матрицы М е R"x".
/=1
rang(A/) — ранг матрицы М, равный числу ее линейно независимых строк или
столбцов.
г , [1, если выполняется условие cond-,
{cond j= {
[О, если не выполняется условие cond.
if (cond : a, b) =
а при cond ФО
b при cond = О
— условный оператор.
sgn(x) = if(x >0:1, if(х<0: -1,0))=
1 при х > 0
0 при х = 0 — знак действительного числа х.
-1 при х < 0
mod(«, b) — остаток от деления действительного числа а на действительное чис-
ло Ь * 0. Знак остатка равен знаку числа а. Дробная часть числа х равна
mod(x, 1).
[хJ — округление числа х до ближайшего целого числа m < х.
fx"| — округление числа х до ближайшего целого числа М > х.
[_x + 0.5j или [х-0.5"| — округление числах до ближайшего целого числа.
md(x) — случайное число, равномерно распределенное в интервале (0, х). Слу-
чайное число в интервале (а, Ь) равно а + tnd(b - а). Случайное целое число в ин-
тервале [/', /л] генерируется как |_« + rnd(m +1 - z?)J.
L = {/1,..., /„} — список п скалярных переменных.
Lp - {pi, ...,р„} — список п точек, элемент которого есть вектор координат точки.
Ls - {«1 bi,..., а„ Ь„} — список п отрезков, элемент которого есть пара векторов
концевых точек отрезка.
Lm = {Li,.... L,„} — группа m списков, элемент которого есть список типа L или Lp.
Гт = {Ci,..., Г„,} — массив m групп списков, элемент которого есть массив спи-
сков типа Lm.
size(S) — функция расчета числа элементов структурированного объекта 5.
sort(L) — функция сортировки элементов списка (вектора) L по критерию с.
С
Глава 1
Г еометрические основы
компьютерной графики
Реалистичность восприятия человеком сложного компьютерного изображения
определяется умением разработчика математической модели изображаемого
объекта или процесса достоверно повторить на экране его развитие в простран-
стве и во времени. Модель включает в себя систему уравнений и алгоритмов их
реализации. Математической основой построения модели являются уравнения,
описывающие форму и движение объектов. Все многообразие геометрических
объектов является комбинацией различных примитивов— простейших фигур,
которые в свою очередь состоят из графических элементов — точек, линий и по-
верхностей.
Положение точки в R” задается радиус-вектором p = [pj р% ... р„], имеющим
п координат/>i и разложение
Р = [р\ Р2 ••• Pn\=T,Piei (11)
1=1
по п линейно-независимым базисным векторам е\ -е- еп. Совокупность базисных
векторов и единиц измерения расстояний вдоль этих векторов составляет систе-
му координат (СК). В пространствах размерностей п < 3 вместо цифр использу-
ются синонимы в виде буквенных обозначений координат. Например, первой
координате можно сопоставить букву х, второй — букву у, а третьей — букву z.
Если при этом векторы е{ = х°, е2 = у° и = z° нормированы и взаимно орто-
гональны, то xyz является декартовой СК — наиболее распространенной систе-
мой координат.
Для описания формы графических объектов, задания расположения объектов в
пространстве и их проекций на экране дисплея используются различные СК,
наиболее удобные в каждом конкретном случае. Перечислим системы, приме-
няемые в настоящей книге, и кратко охарактеризуем их назначение:
3 неподвижная мировая система координат (MCK) xyz содержит точку отсчета
(начало координат) и линейно независимый базис, благодаря которым стано-
вится возможным цифровое описание геометрических свойств любого графи-
ческого объекта в абсолютных единицах;
10
Глава 1
П экранная система координат (ЭСК) x>y,Z:, в которой задается положение
проекций геометрических объектов на экране дисплея. Проекция точки в ЭСК
имеет координату z3 = 0. Тем не менее, не следует отбрасывать эту координа-
ту, поскольку МСК и ЭСК часто выбираются совпадающими, а, кроме того,
вектор проекции [хэ у-} о] может участвовать в преобразованиях, где нуж-
ны не две, а три координаты;
а система координат сцены (СКС) хс ус Zc. в которой описывается положение
всех объектов сцены — некоторой части мирового пространства с собствен-
ными началом отсчета и базисом, которые используются для описания поло-
жения объектов независимо от МСК;
□ объектная система координат (ОСК) хо уо zo, связанная с конкретным объек-
том и совершающая с ним все движения в СКС или МСК.
По умолчанию будем полагать, что все координаты задаются в МСК.
В R2 наиболее распространены ортогональная декартова (х,у) и полярная (г, <р)
системы (рис. 1.1, а), связанные друг с другом следующими соотношениями:
Рис. 1.1
В R3 наиболее распространены ортогональная декартова (х, у, z), цилиндрическая
(р, у, <р) и сферическая (г, <р, \р) системы (рис. 1.1,6), связанные друг с другом сле-
дующими соотношениями координат:
□ декартова СК с цилиндрической СК:
x = psin(<p), z=rcos(<p),
I----- v (1.3, а)
p = Vx2+z2, tg(<p)=-;
П декартова СК со сферической СК:
x = rsin(<p)sin(v), y' = rcos(v), - =rcos(<p)sin(ip),
/~2 2 2 ( \ x ( \ Vx2 +z2 (1-3,6)
r=Vx +/+* , tg(<p)=-, tg(v) =--------------;
z У
Геометрические основы компьютерной графики 11
23 цилиндрическая СК со сферической СК:
p = rsin(v) _y = rcos(y),
Г2 2 / \ Р (1-3, в)
/• = Vp +у ’ tg(v)=--
У
Для единообразия терминов и алгоритмов мы будем работать в правой декарто-
вой СК, оси которой ориентированы в пространстве так, что вращения ортов
х°—>у°, у° —> z° и z° —>х° происходят в положительном направлении, т. е.
против часовой стрелки с точки зрения наблюдателя, находящегося на конце
третьего свободного орта.
Взаимосвязь координат графического элемента может быть описана неявным
.равнением f(p) - 0 и параметрической функцией p(t). Частным случаем неявного
описания является явная форма, в которой одна из координат выражена через
другие. Это возможно лишь для некоторых простейших линий и поверхностей.
Не все графические элементы могут быть описаны неявными функциями. Наи-
более универсальным является параметрическое описание каждой из п коорди-
нат графического элемента соответствующей функцией времени, угла поворота
или других параметров.
Целью настоящего краткого экскурса в вычислительную геометрию, не претен-
дующего на исчерпывающую полноту и строгость, является систематизация
формул, необходимых для работы с графическими объектами, приведение их к
алгоритмическому виду. Это отличает компьютерную графику от обычной, в
которой свойства и взаимосвязь графических объектов визуально воспринима-
ются глазами человека и интеллектуально интерпретируются его мозгом. С ме-
тодами решения задач классической геометрии можно познакомиться, например,
в [6,7].
Компьютерная или вычислительная геометрия оперирует не с рисунками, а с
числами (координатами точек, векторов, матрицами преобразований, списками
данных) и отношениями между ними, выраженными также в цифровой форме.
Исходная информация, обработанная специальными алгоритмами, преобразу-
ется в другие цифровые данные, интерпретируемые как искомый результат —
модель объекта, его экранное изображение, отношения между объектами сцены
и т. п. Подробное изложение основ вычислительной геометрии приведено в
[24, 29].
Рассмотрим основные соотношения между графическими элементами на плоско-
сти R2 и в пространстве RA Все основные формулы будут записаны в координат-
ной и векторной формах. Векторная форма компактнее координатной и пред-
почтительнее для понимания и программирования алгоритмов, хотя и требует
несколько больших машинных ресурсов— объема памяти и времени счета. Уве-
личение ресурсов объясняется наличием в векторах и матрицах фиксированных
элементов (единиц и нулей), с которыми иногда выполняются бесполезные
арифметические операции.
Выше приведены основные обозначения и соотношения векторной алгебры. Са-
мые трудоемкие матричные операции — обращение квадратной п х «-матрицы
12
Глава 1
М и расчет ее определителя — рекомендуется выполнять с максимально возмож-
ной точностью простым в программировании рекуррентным алгоритмом Левер-
рье—Фаддеева [10]:
а, = Li+l = ML, - a,E„ V/ = 1, п,
, ' (1-4)
=—, |л/| = (-1)"_1осп.
аи
1.1. Графические элементы на плоскости
Точка на плоскости имеет две степени свободы. Расстояние между двумя пючка-
мир]=[х] <Р|]и р2 = [х2 У21=Ь Отравно:
|Р| _ Рг|= -х2 У + (У1 _ У2 Y — в декартовой СК,
Vr<2 +г2 ~ 2г]Г2 cos(<P] - ф2 ) — в полярной СК.
(1.5)
Линия на плоскости имеет одну степень свободы. Уравнения линии в неявной
(НФ) и параметрической (ПФ) формах имеют следующий вид:
НФ: f (х, у) = 0 или f(p) = 0; (1.6, а)
ПФ: р(0 = [4) Я')]- С1-6’6)
В любой регулярной (гладкой и некратной) точке на линии р0 = [х0 ^0]= p(t0)
возможна линеаризация кривой (рис. 1.2), т. е. проведение к ней касательной пря-
мой, уравнения которо! Nx(x-x0) + i НФ’ ' N - #(*,>') 1 имеют вид: VyG’->’o) = 0 N _#(Х’У [«"(р-р»)=о; (|.7>я) Wo p(‘)=po +^; или _ dp(t) (1-7,6) co.Xo d* Po ен к линии и по свойству градиента на-
х dx х(/)=х0 ПФ: х dt Вектор нормали N = [/V ’ у ’ dv Хо,Уо у _v(z)= -ИО + ) у _ <Й) х ' у d' хо>Хо х TVj,] ортогонал
правлен в ту сторону, где f(p) > 0. При замене уравнения линии на -f(p) = 0 на-
правление нормали меняется на противоположное.
Направляющий вектор линии V ~[кх Гу] начинается в точке ро и направлен по
касательной к р(1) в сторону увеличения I. Для перехода от одной формы (1.7) к
геометрические основы компьютерной графики
13
другой необходимо выбрать одно из двух ортогональных направлений нормали
относительно направляющего вектора. Из условия ортогональности
N о V= 0 => Nx Vx + Ny Vy = О
получаем способ быстрого преобразования V N или N -> Г:
□ координаты исходного вектора переставляются местами;
J у одной из координат полученного вектора меняется знак.
Рис. 1.2
Например, если дан вектор К = [1 2], то после перестановки координат он ста-
новится равным [2 1], а после изменения знака, например, у первой координаты
получим вектор W = [-2 1], направленный влево от V. Проверка показывает,
что векторы V и N ортогональны:
No V=(-2)- 1 + 1 -2 = 0.
Для единообразия изложения материала примем правую ориентацию нормали,
означающую, что при движении точки по линии вектор N направлен перпенди-
кулярно вправо от вектора V. Таким образом, связь векторов нормали и направ-
ения прямой будет следующей:
**]• <18)
1.1.1. Модели прямой линии на плоскости
Рассмотрим способы задания прямой на плоскости в различных формах.
1.1.1.1. Неявное уравнение прямой
Неявное уранение прямой задается тремя коэффициентами А, В и D, составляю-
щими вектор F = [а В о]:
НФ: Ах + By + D = 0 или [р 1]° Т = р ° F = 0 . (1-9)
14
Глава 1
Хотя бы одно из чисел А или В должно быть ненулевым. Если оба коэффициента
А * 0 и В * о, то прямая проходит наклонно к осям координат и пересекается с
ними в следующих точках (рис. 1.3. я):
— D
А
— D
В
О
При А = 0 и В * 0 уравнение By + D = 0 описывает горизонтальную прямую, а
уравнению Ах + D = 0 при А * 0 и В = 0 соответствует вертикальная прямая. От-
метим ограниченность "школьного" способа приведения неявного координатно-
го уравнения к явному виду
у(х)=-—х- —
В В
и построения линии по точкам в желаемом интервале л g [xmm, Хтах]. Этот способ
неприменим для вертикальных прямых с коэффициентом В = 0 и единственной
координатой л = -D / А всех точек таких прямых.
Прямая f{p)=p°F = Q проходит через начало координат при /(О?) = £) = ().
Благодаря ее свойству разделять пространство плоскости на два подпространст-
ва с противоположными знаками f(p), неявное уравнение позволяет с минималь-
ными вычислительными затратами (за два умножения и два сложения) опреде-
лить по условию f(q) — 0 принадлежность произвольной точки q прямой линии,
а также ориентацию двух точек а и b относительно прямой (рис. 1.3, а).
П при (Z>) > 0 точки лежат по одну сторону от прямой;
П при f(a) -f(b) < 0 — по разные стороны от прямой.
Для построения прямой по уравнению Ах + By + D = 0 необходимо и достаточно
иметь либо две несовпадающие точки ро и р\, через которые она проходит, либо
точку ро и направляющий вектор V, с помощью которого вторая точка вычисляется
как р\-ро+ V. Сравнивая формулы (1.9) и (1.7, я), заключаем, что координатами
вектора нормали можно принять коэффициенты неявного уравнения А и В:
# = [л в].
Тогда по (1.8) получаем направляющий вектор неявной прямой
У = [-В А].
Рассмотрим два способа выбора точки = [х0 jq].
1. Первое, что приходит на ум — выбрать ее в том месте, где прямая пересекается
с осью х при А * 0 или с осью у при А - 0 (только для горизонтальной прямой):
p0=if А:
О
А
О
В
(1.10, а)
Несмотря на легкость понимания, этот способ не самый лучший для про-
граммирования из-за наличия альтернативы выбора точки в зависимости от
коэффициента А.
Геометрические основы компьютерной графики
15
2. Вычислим ближайшую к началу координат точку ро (рис. 1.3, а) методом наи-
меньших квадратов (МНК) путем решения экстремальной задачи
|/?|2 - р ° р -» min
с ограничением р о N + D = 0. Для этого составим функцию Лагранжа
Щр, X) = 0.5(р ° р) + к(р ° N + £>).
Из условий ее экстремума
ЭЗ(р,Л) ЭЗ(М) .. n п
—- = л + XN = От , — = p°N + D = 0
др Р 2 ЭЛ
получим
и оптимальное решение
Ро =77^7^ = 2 D (1.10,6)
NoN а1+ Вл '
Данное решение безальтернативно по сравнению с (1.10, а), более удобно в
программировании и эффективнее в вычислении. Поэтому далее будет ис-
пользоваться преимущественно оно.
Таким образом, координатная и векторная параметрические формы прямой,
заданной вектором С = [л В £>], принимают вид
х{() = --AD--- Bt
А +В или p(t)= - - [И в]+[-£ A]t. (Ill)
А2 + В2
1.1.1.2. Нормальное уравнение прямой
Нормапьное уравнение прямой {/?о, N}, заданной точкой ро и вектором нормали N,
выводится из условия ортогональности векторов N и р-ро для всех точек р,
принадлежащих прямой (рис. 1.3, б):
НФ: Nx(x-xo) + ^(y-j'o) = 0 или (p-po)°N = O; (1.12,а)
ПФ: х(/) = хо - Ny t, y(t) - j'o + Nx t или p(t) - po + Vt, (1.12,6)
r = [-^. aJ.
Сравнивая (1.12, a) c (1.9), получим зависимость вектора неявного уравнения от
параметров нормального уравнения:
F = [w -р0о^. (1.13)
16
Глава 1
Неявная функция
f(p) = (Р-ро) 0 N
позволяет оценить положение точки р относительно прямой не только по знаку
возвращаемого ей значения, но также и относительно направления нормали:
П при f(a) > 0 точка а лежит в том полупространстве, куда направлена нор-
маль, а угол Z(« - ро, N) острый;
П при f(b) < 0 угол Z(b -ро, N) тупой, а точка b и нормаль находятся по разные
стороны от прямой (рис. 1.3, б).
1.1.1.3. Параметрическая функция прямой
Параметрическая функция прямой {ро, V), проходящей через точку ро в направле-
нии вектора V(см. рис. 1.3, б), и эквивалентное ей уравнение в НФ будут иметь вид:
ПФ: x(l) - хо + Vj, y(t) = уо+ Vyt или p(t) = ро+ Vf, (1.14, а)
НФ: VyX- + D = О, D =-fyo + f = ^-p0‘>4 (1.14,6)
где N = [ку -Кх]. Параметрическая форма удобна для задания и построения час-
тей прямой — отрезков и лучей. Для этого в (1.14, д) необходимо указать преде-
лы изменения параметра I. Например:
П бесконечный интервал -оо < t < оо не ограничивает протяженность бесконеч-
ной прямой',
Рис. 1.3
'еометрические основы компьютерной графики
17
□ задание / > 0 дает луч, выходящий из точки ро в бесконечность в направлении
вектора К;
□ конечный интервал to < t < h определяет отрезок прямой между точками
ро + Vto иро + Vt\.
Благодаря левой ориентации направляющего вектора V относительно вектора
нормали N, эквивалентная нормальной форме функция
f(p)={р - Ро)° Н “ vx]= Р ,/°
позволяет определить положение точки относительно направления движения по
прямой:
□ при f(a) > 0 точка а лежит справа, так что угол Z(<7 -ро, V) положительный;
□ при f(b) < 0 угол Z(Z> -ро, Г) отрицательный, а точка b лежит слева от прямой.
1.1.1.4. Уравнения прямой, проходящей через две точки
Неявная форма уравнения прямой, проходящей через две точки Д = [«д ау] и
Ь = [лх /Гу] (рис. 1.3, в), выводится из условия принадлежности прямой этих то-
чек и точки р = [х >]:
НФ:
= 0.
(1.15, а)
Выбрав направление движения по прямой от точки а к точке Ь, получим направ-
ляющий вектор V - b - а и параметрическую модель линии:
ПФ: х(/) = д, + (bx - ax)t, y(t) = а} + (by - ay)t или p(t) = а + (b- a)t. (1.15,5)
Условие существования прямой очевидное: 1Р]# 0, т. е. а * Ь.
При изменении параметра от t = 0 до t - 1 движение точки происходит внутри
отрезка ab от точки а до точки Ь. Ниже рассматриваются свойства плоских мно-
гоугольников (полигонов), определяемые ориентацией векторов нормалей к их
сторонам. С учетом принятого соглашения (1.8) внешняя ориентация нормалей к
сторонам полигона обеспечивается при его обходе против часовой стрелки.
Соответствующая данному способу задания прямой функция
/(р) =
позволяет определить нахождение точки р относительно движения по прямой от
л до Ь. При f(p)> 0 точка р лежит справа от прямой, а при f(q) < 0 точка q нахо-
дится от нее слева.
р-а
Ь-а
18
Глава 1
1.1.1.5. Уравнения прямой в отрезках
Неявное уравнение прямой в отрезках и hy, одновременно не равных нулю и
отсекаемых прямой на осях х и у (рис. 1.3, г), получим из уравнения (1.9) при
D - -1 с учетом соотношений Л, = -D /А v\hf = -DIB:
T~ + T~~i=0 =>М + Л^’-Л.Д = 0=>F = [ft>, hx -hx/iy]. (1.16,д)
r/r П,,
Выбрав на прямой две точки а = о], 6 = [о hyJ, получим ее направляющий
вектор
V = b-a = [-hx Лу]
и координатные параметрические функции прямой в отрезках:
ПФ:
x(t) = Av(l - /), y(t) = hyt.
(1.16,5)
1.1.2. Взаимное положение
графических элементов на плоскости
Рассмотрим некоторые полезные формулы, тесты и алгоритмы, описывающие
свойства и взаимное расположение точек, прямых и полигонов на плоскости.
Для получения необходимых результатов активно используются тесты ортого-
нальности и параллельности векторов, приведенные в перечне основных обозна-
чений и соотношений.
1.1.2.1. Коллинеарность точек
Три точкир,, р-. ир, коллинеарны, т. е. лежат на одной прямой (рис. 1.4, а), если
X!
х2
х3
J1
У2
Уз
1 =0 или
Pl~Pl
P3~Pl
(1-17, д)
Обобщение (1.17, а) на произвольное число точек р\ 4- рп:
Pi Р1~Р\
rang Р2 = 2 или rang РЗ~Р\
-Рп. _Рп ~ Р\ _
(1.17,6)
геометрические основы компьютерной графики
19
Точка р лежит на отрезке ab при нулевом угле между векторами р - а и b-р\
(р-а) о (b-р) = |/з-о| • |6-р\. (118)
Значение параметра I, соответствующее положению точки p-a + (b- a)t на
трямой относительно ее отрезка ab, вычисляется с помощью скалярного произ-
ведения:
(р-а) ° (b - а) - (b-a)l о (Ь-а) - \Ь- д|2 • I,
откуда
(р-а)о(й-а)
‘-(Ь-аУ(Ь-аУ <119)
1.1.2.2. Взаимное расположение прямых
Лее прямые совпадают (рис. 1.4,6), если
V,
НФ: Fi x Fi = О з ; ПФ: I 1Z2 = 0 n- P2O~PlO = 0
Лее прямые параллельны (рис. 1.4, в), если
НФ: = 0; ПФ: ?1 = 0
w2 V2
Расстояние между параллельными прямыми равно:
^ = |ргм(р20 -Pio)| = |(P2O -pio)o?/i|;
ПФ:
Р20~ РЮ
И
|Р20 - Р10 “ РГГ (Р20 “ Р10
= |Р2О “/’IO -((Р20 -Р1О)°П) Pi|.
Лее прямые ортогональны (рис. 1.4, г), если
НФ: м о № = 0; ПФ:
Ki о V2 = 0.
(1.20)
(1.21)
(1-22, а)
(1.22,6)
(1.23)
1.1.2.3. Взаимное расположение точки и прямой
Уравнения перпендикуляра, опущенного из точки q = \gx qy \ на прямую, заданную
э НФ или ПФ (рис. 1.4, д), выглядят следующим образом:
НФ: Ny(x-q,)-Nx(y-qy) = 0^>Nj_=[Ny -aJ, Fj_ = (1-24,0)
ПФ: px(t) = q + N t илиp±(f) = q + Vj, где = [ly ~TXJ. (1-24,6)
20
Глава 1
Расстояние от точки q до прямой равно:
НФ:
(125,«)
ПФ:
q-_Po
v
= \я - Ро - РГг (<7 - Ро )| = \я - Ро - ((? ~ Ро)°
(1-25,6)
d =
Зеркальное отражение точки q от прямой лежит на перпендикуляре к прямой на
расстоянии 2d от q в сторону, противоположную проекции вектора q-po на
нормаль N (рис. 1.4,6):
Нф: ‘7, = <7-2ргЛг(9-ро)=<7-2((д-ро)°^)л?; (1.26,д)
ПФ: / = ?-2(9-р0-рги(9-р0)) = 2р0-9-2((<7-р0)ои)г. (1.26,6)
& Пример 1.1. Отразить треугольник pi р-> рз с вершинами р\ = [о о], р2 = IP 11
и р3 = [2 О] от прямой линии, проходящей через точки а = [3 0] и b = [2 2]
(рис. 1.5).
Решение. Находим направляющий вектор прямой И = 6-о = [-1 2], по формуле
(1.8) нормаль N = [2 1] и квадрат ее длины 2УоУ=5. Пусть ро = а, тогда по
(1.26, а) последовательно для точек р\,р-з ирз вычисляем отраженные точки
Pi = Pi ~
2(p,-a)oN
NoN
N:
p{ = [0 0]-0.4([-3 0]° [2 1] )[2 1]=[4.8 2.4],
еометрические основы компьютерной графики 21
Р2=[0 1]-0.4([-3 1]о[2 1])[2 1]=[4 з],
Рз = [2 0]-0.4([-1 0]о[2 1] )[2 1]=[з.6 0.8]. □
1.1.2.4. Построение прямой, наименее удаленной
от совокупности точек
Рассмотрим интересную задачу, связанную с понятием расстояния от точки до
-рямой линии. Допустим, в R" (здесь при решении задачи на плоскости ху будем
зюлагать п = 2) задано m > 2 произвольных точек pi ч-рш. Сформируем из них
матрицу
(1.27)
Lp™
Так как в общем случае точки не коллинеарны, то не существует ни одной прямой
^(р) = 0, для которой все числа с/, = f (рд обращаются в ноль. Другими словами,
асстояния |с/,| / |Л] от точек р, до прямой с нормалью N, вычисленные по (1.25, а) и
пропорциональные с/„ не могут быть одновременно все нулевыми (рис. 1.6).
Рис. 1.6
22
Глава 1
Построим аппроксимирующую прямую {ро, N}, наименее удаленную от совокупно-
сти точек ph путем решения экстремальной задачи
т
^d, —> min .
i=l
С целью уменьшения неопределенности зададим ограничение |7V| = 1, поскольку
ориентация прямой линии зависит лишь от направления, а не от длины вектора
нормали. При выполнении данного ограничения числа г/, являются алгебраиче-
скими, т. е. со знаками, расстояниями от точек до прямой. Из пяти рассмотрен-
ных выше способов описания прямой линии выберем неявную форму (1.9) с век-
тором F = pV £>], имеющим минимальное число скалярных параметров, равное
трем при п = 2. При таком выборе вектор d е R"' расстояний от точек до прямой
принимает вид
d = FPr = h'Pv + D [1 ... 1],
m
а квадрат его длины равен
|j|2 = dd'{ = [nP{ + D |1
= NP^PN^+ID ^p, N1+mD2 = NPTPNT+2mD(NoC)+mD2,
где точка
с =
1
-Yp.
m ,=1
(1.28)
есть геометрический центр массива точек /?,. Задача аппроксимации решается
методом наименьших квадратов путем минимизации функции Лагранжа
s(/v,DA)=|d|2+^|2-iJ= (]29
= NPrPNT + 2mD{N ° с)+ mD2 + 2.(/\WT -1).
Из условий ее экстремума
1 — = NpTp + mDc + XN =
2 dN
- — = m(NoC)+mD = 0, — = MVT-1=O
.2 dD V 7 dA
(1.29,6)
"еометрические основы компьютерной графики 23
* свойства произведения скалярного произведения двух векторов на третий вектор
(а о b) • с = a (bTc)
следует, что
D = -N°c, N(pTP-mcIc + XEn)=On. (1.29, в)
Сравнение выражений для коэффициента D в (1.29, в) и (1.13) убеждает, что все
~рямые, доставляющие экстремум S(N, D, X), проходят через точку ро - с.
Второе соотношение в (1.29, в) представляет собой однородную систему линей-
ных алгебраических уравнений относительно координат вектора N. Она имеет
нетривиальное решение 7V> О„ при нулевом определителе матрицы ХЕ„ - М, где
Л/=/псгс-РтРе R"x". (1-29, г)
Следовательно, множитель Лагранжа X есть одно из п собственных чисел
• значений), a N— соответствующий ему нормированный собственный вектор
матрицы М. Количество собственных значений квадратной матрицы равно ее
размерности. В случае п = 2 симметричная матрица М имеет две действительные
.ебственные пары {Xi, 2V1} и {Хг, N?}, причем при Xi * Хг [см. 9, 13, 32].
Это означает, что прямые, доставляющие экстремум функции 3(Л\ D, X), орто-
гональны. Вычисление собственных чисел и векторов матрицы — хорошо отра-
ботанная процедура вычислительной математики, например, в [10,27,32]. Сле-
дует обратить внимание на нормирование собственных векторов в том случае,
ясли алгоритм их вычисления не делает эту операцию сам.
Возникает закономерный вопрос: какой из полученных векторов N\ или Nz сле-
дует выбрать в качестве нормали искомой прямой? Ответ очевиден: тот, чья
_рямая доставляет минимум функции Лагранжа (1.29, а). Ведь условия (1.29,6)
_ают лишь экстремальные значения, которые при D = -N о с и [IV] = 1 равны
S = NprpNr о с)2 = -NMN'V = -l.NN1' = -X > 0.
Этсюда следует, во-первых, что все собственные числа матрицы М не положи-
-ельны, во-вторых, что минимум функции Лагранжа доставляет собственная
_ара {X, N} с максимальным значением X = max{Xi, Хг) и соответствующим ему
з ектором N— нормалью искомой прямой {с, N}.
Для удобства построения найденной прямой линии можно перейти от ее нор-
мальной формы (1.12, а) к параметрической форме (1.14, а) с вектором
1 =["А\ Ли-
ставшаяся собственная пара матрицы М с минимальным собственным числом
лает максимум функции Лагранжа и ортогональную (при Xi * Хг) прямую (на
тис. 1.6 она изображена пунктиром), пересекающуюся с оптимальной прямой в
точке с.
& Пример 1.2. Построить прямую линию, наименее отклоненную от точек
₽-. = [1 2], р2=[2 1], Рз = [з l],P4 = h 1]ир5=[2 2] (см. рис. 1.6).
24
Глава
Решение. Из заданных точек составим матрицу (1.27) и найдем их центр (1.28):
1 2
2 1
Р = 3
с_ Pl+P2 + ft + P4+P5._[Lg 14]
1 1
2 2
Вычислим по (1.29, г) матрицу М и ее собственные параметры:
М =5
1-4]
1 2 3 I 2~[ Г1 2 3 1 2
2 1112 2 1112
-2.8 0.6
0.6 -1.2
2.1 =-3,2.2 = -1, Nj =[-0.949 0.316], = [0.316 0.949].
Отделив максимальное значение К = 2.2, получим параметры неявной формы ис-
комой прямой:
W = [0.316 0.949], D = -N-> с = -1.897.
Таким образом, аппроксимирующая прямая описывается неявным уравнением
0.316л+ 0.949^- 1.897 = 0
или параметрическими функциями
л(/) = 1.8 - 0.949/, у(/) = 1.4 + 0.316/.
Алгебраические расстояния от точек до этой прямой равны dt =0.316.
di = -0.316, di = Q,d^- -0.632 и ds = 0.632, а минимум функции Лагранжа состав-
ляет -Omin — I.
Для сравнения на рис. 1.6 построена пунктирная прямая, соответствующая соб-
ственной паре {2.1, М}. Расстояния от нее до заданных точек равны dt =0.949,
di = -0.316, //з = —1.265, //4 = 0.632 и ds = 0, а значение функции Лагранжа
Зшах = 3 > 3min, что подтверждает правильность решения задачи. □
1.1.2.5. Пересечение двух прямых
Важнейшей задачей геометрии на плоскости является расчет точки д пересечения
двух прямых (рис. 1.7, а), который в зависимости от формы их задания выполня-
ется следующим образом:
TVj]= ho0М Р20о^2]=>
НФ: (1.30, а)
=> q = hо ° Pio ojV2l гГ wJ] ;
Геометрические основы компьютерной графики
25
ПФ:
рю+ Vltl =Р2О+ V2t2=> [1, t2 ] = (р20 ” Р\ О)
'Г| Г'
.-У1.
(1.30,6)
=> q= рю + Viti.
Условия существования решений в (1.30)
I ^7 М2 | * 0 или
У\
-V2
*0
равносильны непараллельности прямых.
Введем функцию вычисления угла между векторами V и W
ang(y,iv) = if d =
И
IV
*0: sgn(</), 1 -arccos
И<>1Г
(131)
как угла кратчайшего вращения от V к W. По свойству скалярного произведения
векторов модуль угла равен arccos^о (v)e [о, л], а правильный знак определяет-
ся по ненулевому знаку определителя d матрицы, построенной на этих векторах.
При <7=0 векторы Vи Wлинейно зависимы, а знак sgn(<7) = 0 в (1.31) игнориру-
ется. Это может быть в двух случаях:
Л при параллельности векторов угол между ними нулевой, a arccos(l) = 0;
□ при антипараллельности векторов угол между ними развернутый, а по (1.31)
получим arccos(-l) = л.
Таким образом, угол пересечения двух прямых находится с помощью функции
(1.31) как
у = ang(Ni,Nl) или у = ang(Vt, Иг). (1-32)
1.1.2.6. Уравнения пучка прямых и биссектриса угла
Уравнения пучка прямых, заключенных между двумя прямыми (рис. 1.7, б), выво-
дятся следующим образом:
НФ:
^А„Ы=(1-Х)л0>)+Л/20,);
/2V’)=Po^2
(1.33,0)
ПФ:
Pt(f)= Рю (|-30’б)
< \ я
Р2\Ч~ Р20 + ^21
РА+10=Я+Ул+1^
(1.33, б)
Изменение параметра пучка в интервале 0 < X < 1 дает такие промежуточные
прямые, что вращение векторов N^+t и f\+i происходит по кратчайшим углам от
начальных положений Nt и Vi до конечных положений ТУг и Иг. Уравнение
(1 33, б) можно также рассматривать как параметрическую (с параметром X) мо-
26
Глава 1
дель прямой линии, соединяющей точки исходных
рг = q + 12/ при фиксированном значении параметра I.
прямых р\ = q + Г1/ и
Рис. 1.7
На основе этой трактовки несложно и без вычисления углов решается задача
построения дуги окружности радиуса г. заключенной в створе между векторами
Ki и Иг, выходящими из точки q (рис. 1.7,в). Точки дуги Jx+i, соответствующие
параметру X е [0, 1], вычисляются по формуле
= q + Vw,
в которой нормируемый вектор lx+i находится по (1.33,6). Для изображения
дуги в виде ломаной линии, состоящей из N отрезков между точками di и di,
можно разбить диапазон изменения параметра К на У равных интервалов
(рис. 1.7, в построен при N - 5), сформировать набор значений X = i / N Vi = 0, N,
рассчитать векторы Kx+i и точки дуги Jx+t, после чего соединить эти точки от-
резками прямых.
Уравнения биссектрисы угла между двумя прямыми получим по уравнениям
(1.33) с параметром X = 0.5 только при |7Vi| = |Уз| или |Г1| = |Кг|, т. е. когда тре-
угольник с вершиной в точке q и сторонами Г, и Гг является равнобедренным,
у которого биссектриса совпадает с медианой. В противном случае можно ис-
кусственно создать равнобедренный треугольник со сторонами |Гг|Г1 и |Г||р2
равной длины |К|| • |К2|. В результате параметры биссектрисы можно найти по
формулам
Гб«с = |7V2|Fi + IM|Г2, Рбис(/) = q + Гб.,с/, Гбис = ] г2| И1 + IF1|И2. (1.34)
Геометрические основы компьютерной графики
27
Расчет биссектрис бывает необходим, например, при построении окружности,
вписанной в треугольник (рис. 1.7, г). Как известно, ее центр лежит в точке пере-
сечения любых двух биссектрис внутренних углов этого треугольника. При по-
строении биссектрисы внутреннего угла следует учитывать направления под-
ставляемых в (1.34) векторов сторон треугольника: они должны либо оба
выходить из вершины, либо оба в нее входить. При несоблюдении этого правила
по (1.34) будет построена биссектриса дополнительного угла треугольника, а
окружность окажется вневписанной.
Итак, допустим, что вершины треугольника находятся в точках a, b и с. Вычис-
лив векторы сторон
Ki = b - a, Иг = c-b, Из = а-с,
найдем по (1.34) направляющие векторы биссектрис двух внутренних углов
Ва = | Из| И -1И||Из, В„ = |И1|Иг -1Иг|Иь
Тогда центр вписанной окружности о лежит на пересечении параметрически за-
данных прямых {а,В„} и {Ь,В,,} и может быть вычислен методом (1.30,6), а ее
радиус г есть расстояние от точки о до прямой {а, И|}, вычисляемое по (1.25, 6).
1.1.2.7. Тесты свойств графических
элементов на плоскости
Рассмотрим вначале тесты, основанные на свойстве сепарабельности прямой
f(p)-0 разделять плоскость на два подпространства с противоположными зна-
ками функции f(p).
□ Тест ориентации точки р = [х у] относительно прямой заключается в про-
верке знака числа ftp), для вычисления которого в зависимости от способа
задания прямой в разд. 1.1.1 используется соответствующая функция nf ♦, где
означает варьируемый третий символ "F", "TV", "V" или "2" в имени функ-
ции:
nfF(f,p)=poF ;
nf Ntpo, N,p) = tp -po) ° M
(1.35, a)
(1.35,6)
nfV(p0,V,p) =
P-PV
V
(1.35, в)
nf2(a,b,p) =
p-a
b-a
(1.35, г)
Все точки q справа от прямой, т. е. со стороны ее нормали, дают значения ка-
ждой из этих функций nf * > 0, а слева — nf * < 0. Для доказательства данного
факта подставим, например, в функцию (1.35,6) точку q = ро + Vt + XN, пра-
вую при X > 0 и векторе V ± N (рис. 1.8):
nfNtpo, W, 9) = (И/ + ХЛЭ о W = (Ио Д')/ + Л) = 0 • / + Л|ЛП2 > 0.
28
Глава 1
Рис. 1.8
Так как значение f (q) не зависит от коэффициента t, отсчитываемого вдоль
направляющего вектора V, то линии постоянных уровней f (р) проходят па-
раллельно прямой и также являются прямыми. Как следствие, получим рас-
стояние от точки q до прямой, равное
и совпадающее с (1.25, а)
Ввиду простоты вычисления функция f (р), реализуемая на практике одной из
функций nf * в (1.35), идеально подходит для сортировки точек относительно
прямой линии на правые, левые и лежащие на ней. Тест ориентации точки от-
носительно прямой применяется в алгоритмах, связанных с обработкой то-
чек, вершин полигонов, а также во многих других задачах вычислительной
геометрии.
□ Тест пересечения прямой линии f(p) = 0 с полигоном Р = {ptp2 — рпР\}, имею-
щим произвольное направление обхода вершин, выполняется с помощью сле-
дующей функции:
crossl(f, Р) = {3 1 <J <i<n -.ftp,) f(pj) < 0}. (1.36)
Прямая пересекает полигон, если существует хотя бы одна пара вершин, ле-
жащих от нее по разные стороны (рис. 1.9, а).
Обсудим некоторые подходы к реализации теста в виде конкретного алго-
ритма, стремясь получить его наиболее эффективным в смысле минимальной
трудоемкости.
Следует ясно понимать, что нужно сравнивать положение относительно пря-
мой линии не только смежных вершин полигона р, и р,+), а всех различных
пар вершин {р„р7}, т. к. прямая может, пересекая полигон только в вершинах,
не пересечь ни одного ребра внутри (рис. 1.9, б). Свойство сепарабельности
позволяет по разным знакам чисел /(р,) и f(p) обнаружить вершины р, и р7,
лежащие по разные стороны от пересекающей полигон прямой. Если же не
еометрические основы компьютерной графики
29
найдется ни одной пары разносторонних вершин, то прямая и полигон не пе-
ресекаются.
Число всех пар из и вершин полигона равно n (и + 1) / 2. Если решать задачу
алгоритмизации теста (1.36) "в лоб" (с двумя вычислениями f(p) для каждой
пары вершин), то при больших значениях и (например, когда некоторая
замкнутая кривая аппроксимируется полигоном с числом сторон порядка не-
скольких тысяч) трудоемкость теста будет пропорциональной п2, т. е. недо-
пустимо большой. Уменьшения этой зависимости до линейной можно дос-
тичь с помощью специальных приемов. Рассмотрим некоторые из них:
• во внешнем цикле i = \,n вычисляем значения Si=f(p}. Во внутреннем
цикле j = l, i-l V/ > 1 анализируем знак произведения 5,^ (заметим, что
число Sj = f(p]) уже вычислено). При SjSj < 0 тест немедленно завершается,
возвращая 1 — признак пересечения прямой с полигоном. После нормаль-
ного окончания внешнего цикла алгоритм возвращает 0 — признак отсут-
ствия пересечения либо касания прямой с полигоном;
Рис. 1.9
30
Глава 1
• в цикле z = l, п вычислим значения s,=f(p,), а затем сделаем сортировку
вектора л. Результат тестирования возвращается числом res = sgn($i s„).
При res = -1 крайние элементы si и s„ имеют разные знаки, что означает
пересечение прямой с полигоном. По сравнению с предыдущим алгорит-
мом данный вариант теста способен различить касание (res — 0) и отсутст-
вие пересечения прямой с полигоном (res = 1). В качестве недостатка отме-
тим наличие операции сортировки, трудоемкость лучших методов
которой оценивается зависимостью п log(zz) < п2 [13, 24];
• наилучший, по мнению автора, алгоритм теста пересечения представлен
блок-схемой на рис. 1.9, в и использует три флажка, сигнализирующих о
наличии вершин полигона слева (флажок /), справа (флажок г) и точно на
прямой (флажок е). Вначале все флажки сбрасываем в ноль. В цикле i = 1, п
вычисляем значение 5 = f(pd и устанавливаем в единицу один из флажков: I
при 5 < 0, е при 5 = 0 или г при 5 > 0. Тут же по условию / • г 0 проверяем
наличие любой пары вершин полигона по разные стороны от прямой. Если
это условие выполняется, то тест немедленно завершается, возвращая 1 —
признак пересечения прямой с полигоном. После нормального окончания
цикла обхода вершин алгоритм возвращает значение е- 1, равное 0 при
касании или -1 при отсутствии пересечения прямой с полигоном.
□ Тест выпуклости полигона Р = {pt ...рпр}}'.
conv2(P) = {sgn(«/2(p,_|,p„^,+l)) = const] Vz =1, и, гдеро =р„,p„+i =pt. (1-37)
У выпуклого (convex) полигона все углы Ар^р^-ц одного знака. Другими
словами, при обходе выпуклого полигона по замкнутому контуру в произ-
вольном направлении каждая вершина р,+, расположена относительно ребра
p,_i р, одинаково для всех значений г. слева при положительном направлении
обхода и справа при отрицательном (рис. 1.10, а). Благодаря свойству сепа-
рабельности в процессе обхода невыпуклого полигона рано или поздно обяза-
тельно произойдет инверсия знака числа 5 = nf2(pi_f,pi,pn.l) по сравнению со
знаком числа c = nf2(p„,px,pi) в начальной вершине pf, как показано на
рис. 1.10, б.
Блок-схема теста выпуклости приведена на рис. 1.10, в. По сравнению с (1.37)
алгоритм conv2 стал способен определять наличие у полигона развернутого
угла при вершинер, по нулевому значению nf2(pi_t,pl,pM) = 0.
Определенная блок-схемой функция conv2 возвращает 1 для выпуклого поли-
гона, 0 для невыпуклого и -1 для полигона, имеющего хотя бы одну вершину
с развернутым углом.
□ Тест самопересечения полигона Р = {р, ...р„р^\
self test(р) =
В i?е [1, п - 2], j е [z + 2, п -1 + {z > 1}]:
{fijftjvx < о}П {/>/,,/+1 <0}
где п > 3, afj = zz/2(p„pf+l,py) — значение НФ (1.35, г) прямой отрезка PiP,+i в
точке р}. Полигон является самопересекающейся замкнутой ломаной линией,
метрические основы компьютерной графики 31
если у него существует хотя бы одна пара пересекающихся отрезков. Два от-
резка PiPi+l и PjPj+\ пересекаются друг с другом, если концы одного находятся
по разные стороны от прямой другого и наоборот. Интервалы изменения ин-
дексов i и j выбраны так, чтобы были протестированы все пары не смежных
ребер полигона:
• индекс i перебирается в интервале от 1 до и - 2;
• при / = 1 индекс j перебирается в интервале от 3 до п — 1;
• при i > 1 индекс j перебирается в интервале от i + 2 до и.
Рис. 1.10
Функция self_test возвращает I при наличии самопересечения полигона и О
при его отсутствии. Для того чтобы тест был способен обнаруживать не
только "чистые" пересечения несмежных ребер, но и их касания, используемое
в нем логическое условие должно быть записано немного сложнее:
<о}п{б, Дж < о}и{4 АЛ1 < о}п <о}.
32
Глава 1
1.1.2.8. Тесты ориентации точки относительно полигона
Рассмотрим тесты ориентации точки q = [x у] относительно полигона
Р= {pt ...p„pt}.
О Выпуклый тест
conv! _ test{f], Р) =
-1, если sgn(/}) = const Vz = 1, л;
1, если 31 < j < i < п: fifj< 0;
(1.38)
0, если не ±1
определяет внутреннее положение точки дВНу относительно выпуклого полиго-
на при одинаковых знаках чисел f = ч/Цр^р^Цыц}, вычисленных по (1.35, г)
для всех ребер p,pt+\ (рис. 1.11,а). Любую внешнюю точку q»m тест обнаружи-
вает по разным знакам чисел / и у", соответствующих ребрам р,р^+1 и PjPj+i
(рис. 1.11,6). Как и в тесте cross!, здесь также нужно сравнивать положение
точки q не только относительно соседних ребер полигона p,p,+i и р/+|А+2> а
всех различных пар ребер р,р,+| и PjPj+i Наконец, все точки, не идентифици-
рованные как внутренние или внешние, считаются граничными точками qrp.
Тесты cross! и conv!_test имеют много общего и фактически являются двойст-
венными формами общего метода обработки точек и прямых на основе свой-
ства сепарабельности прямой. Схожесть тестов наглядно иллюстрируется
блок-схемой алгоритма conv!_test, изображенной на рис. 1.11, в.
В соответствии со знаком числа 1, возвращаемым тестом для внешних точек,
назовем внешнее подпространство полигона положительным. Внутреннее
пространство полигона будем считать отрицательным согласно знаку воз-
вращаемого значения -1. Все точки <уГр на границе полигона (в вершинах или
на ребрах) дают значение conv!_test(qrf>, Р) = 0.
Если тест (1.38) проводится в экранной системе координат, то все расчеты яв-
ляются целочисленными и максимально быстрыми.
Рис. 1.11, а, б
еометрические основы компьютерной графики
33
Рис. 1.11, в
□ Габаритный тест
gab2_test(q, Р)={х< pxmin }U {х > pxmax } U
г . г г (1-39,0)
U V < Pjmin J U V7 > Pjmax J
определяет по возвращаемому значению gabl_test - 1 гарантированную не-
принадлежность точки q произвольному полигону Р путем сравнения ее коор-
динат с габаритами полигона— минимальными и максимальными коорди-
натами его вершин р, V/ = 1, п:
/\rnin = min {р,Л.} , /\rnax = ГПаХ {р,Л} , p,,min = ГШП , р;тах = ГПаХ {р0,} . (1.39, б)
Полностью габаритный тест задачу ориентации не решает, возвращая значе-
ние 1 только для тех внешних точек qme, которые расположены вне габарит-
ного прямоугольника (рис. 1.12, а). Результат gabl_test = 0 означает, что точ-
ка находится внутри габаритного прямоугольника, но не может быть
однозначно идентифицирована как внешняя, внутренняя либо граничная.
Тем не менее, благодаря своей простоте габаритный тест применяется во мно-
гих алгоритмах для быстрого обнаружения заведомо непересекающихся гео-
метрических объектов, что освобождает от необходимости решения трудоем-
ких задач внешнего и внутреннего отсечения.
34
Глава 1
Точечный тест (1.39) легко обобщается, как показано на рис. 1.12, б, на слу-
чай полигона Q - ... q,„ q{\ с габаритными координатами
(7Л-тт — Hiin{^,4}, qxmm = max{r/,A}, qymin — , ^max = max {<5^}:
gab! _ poly(Q,P} = {<7xmax < Pxmin }U {<7xmin > Рутах }U
U {?ymax < Pymin }U {vyrnin > Рутах }•
(1.40)
□ Угловой тест основан на вычислении и анализе алгебраической суммы углов
б, = £(Vh Г/+1) между смежными векторами = p.-q, соединяющими точку q
с вершинами р„ при обходе произвольного полигона Р по замкнутому контуру
в произвольном направлении. Тест основан на следующем опыте: наблюда-
тель, просматривающий вершины полигона из внутренней точки qBKy, совер-
шает вокруг себя полный оборот (рис. 1.13, а), а из любой внешней точки
^вне — ни одного оборота (рис. 1.13, б).
Воспользуемся для вычисления угла между двумя векторами функцией ang,
определенной в (1.31) и возвращающей радианную меру угла. Тогда при всех
ненулевых векторах Г, радианный вариант углового теста примет вид
п
^ang(yhyi+x)
i=l
О < Я => Чине ®
2л > л => <7ВНу е Р.
(1.41)
В связи с неизбежными погрешностями, возникающими при суммировании
углов, вычисляемых с помощью приближенной функции ang, в (1.41) нельзя
сравнивать результат ни с нулем, ни с 2л: он всегда будет хоть на немного, но
отличаться от этих чисел. Предлагается взять пороговое значение, равное л:
оно ни при каких погрешностях не даст неверного результата тестирования.
Граничная точка qvp обнаруживается по следующим признакам:
• если при расчете векторов будет получен нулевой вектор длиной
|Г,] = 0, то тестируемая точка совпадает с вершиной д;
геометрические основы компьютерной графики
35
• если при расчете углов 8, будет получен развернутый угол с модулем
|8j = л, то тестируемая точка лежит на ребре р, (рис. 1.13, б).
Резюмируя сказанное, получим алгоритм rad_test(q, Р) радианного углового
теста ориентации точки q относительно произвольного полигона Р
(рис. 1.13, в). Поскольку для вычисления угла б, нужна лишь пара смежных
векторов Vj и К;+1, то при обходе вершин полигона можно вычислять текущий
вектор Г, а в конце цикла запоминать его в векторе W для использования в
следующей итерации, экономя тем самым память компьютера. Алгоритм воз-
вращает 1 для внешних точек, -1 для внутренних и 0 для граничных.
Рис. 1.13
Ввиду важности места, занимаемого угловым тестом в задачах компьютерной
графики, обсудим как явные, так и скрытые недостатки алгоритма rad_test:
• необходимо нормировать все ненулевые векторы Vh что связано с опера-
циями вычисления квадратного корня и деления, которые относятся к не-
36
Глава 1
целочисленным операциям с плавающей точкой, выполняющимся гораздо
медленнее операций с целыми числами;
• вычисление угла в (1.31) тригонометрической функцией arccos произво-
дится путем суммирования бесконечного степенного ряда до сходимости
по точности, предусмотренной компилятором используемого языка про-
граммирования. Этот итерационный процесс с плавающей точкой также
не отличается высоким быстродействием;
• вычисления с плавающей точкой приводят к накоплению погрешностей
при суммировании степенных рядов и углов в (1.41). В связи с этим обна-
ружение граничной точки q е р^р,+\ с помощью сравнения |8,| = л на прак-
тике должно быть заменено условием
||8,|-л|<е,
где е — экспериментально подобранная минимальная константа, надежно
поглощающая ошибки округления;
• при малом € необходимо иметь число л с максимально возможной точно-
стью, а не как обычно задают Р1= 3.1415926. Фактически это означает,
что если константа л отсутствует в используемом языке программирова-
ния, то она должна вычисляться с машинной точностью. Для этого можно
воспользоваться абсолютно, но медленно сходящимся степенным рядом
к=0
(-1)*
2k +1
Модифицируем радианный угловой тест так, чтобы расчет углов 8, с высокой
точностью стал не обязателен. Будем считать углы в целочисленных октан-
тах. Руководствуясь неравенствами на рис. 1.14, сопоставим вектору
Г = [х у] октантный угол 1 < v < 8 и функцию вычисления октантного угла
oct(V), возвращающую 0 при х = у - 0 и целое число ve {1, 2,..., 8} при |Р] * 0.
Как и в радианном тесте, получение нулевого значения v, = oct(pt-q) означает
принадлежность точки q границе полигона в его вершине р, и немедленное за-
вершение теста с возвращением нуля.
5
хсу<0
о
8 J
у -х<у<0
0<х<-у
у<х<0
Рис. 1.14
Геометрические основы компьютерной графики
37
При q *р, Vz = 1, п вычислим приращения октантных углов Д, = v,+1 - Vj на пе-
реходах р,-»р,+|. Для получения кратчайших угловых приращений необхо-
дима коррекция величин и знаков октантных углов с |Д,| > 4:
• если Д, > 4, то Д, = Д, -8; (1.42, а)
• если Д, < -4, то Д, = Д,- + 8; (1-42, б)
• если Д,,= ±4 и/= nf2(Pi,pi+l, q) * 0, то Д,, = -4sgn(/). (1.42, в)
Поясним коррекцию в (1.42, в). Значение |Д,| = 4 возможно в трех случаях рас-
положения точки q в окрестности ребра PiPi+\, при которых угол Ap,qpi+[
близок к развернутому или равен ему:
• точка находится точно на ребрер,р,+| (на границе полигона Р, рис. 1.15, а).
Этот факт устанавливается проверкой f— 0 и завершает тест, возвращая 0;
• при/> 0 точка лежит справа от отрезкаpjpi+l, а Д; = -4 (рис. 1.15, б);
• при f < 0 точка лежит слева от отрезка р, р,+1, а Д, = 4 (рис. 1.15, в).
Обозначим за oct_cor(q, а, Ь) функцию вычисления октантной меры угла Z.aqb
и его коррекции по (1.42). Тогда целочисленный октантный тест, аналогичный
радианному тесту (1.41), принимает вид
" / \ (0=>q£P;
|±8s(p (1.43)
Точка q является внешней относительно полигона Р, если суммарный октант-
ный угол поворота вектора Vt при обходе вершин р, по замкнутому контуру ра-
вен нулю. Точка лежит внутри полигона, если этот угол ненулевой. Наконец,
точка находится на границе полигона, если либо при oct(pi -q) = 0 она совпада-
ет с вершинойр„ либо при |Д,| = 4 и и/2(р„р,+1, q) = 0 она лежит на ребрер,р,+1.
Обозначим за oct_test(q, Р) функцию октантного углового теста ориентации
точки q относительно плоского полигона Р = {р, ...p^}, возвращающую -1
для точки внутри полигона, 1 — вне полигона и 0 — на его границе. Блок-
схема октантного теста построена на рис. 1.15, в. Пунктиром выделена часть
алгоритма, в которой происходит вычисление и коррекция приращения ок-
тантного угла по (1.42).
Рис. 1.15, а, б, в
38
Глава 1
Рис. 1.15, г
& Пример 1.3. Определить ориентацию точек эд =[4.5 з], q2=[2.5 Л и
<?3 =[1.5 1.5] относительно невыпуклого полигона Р = {ptpz.-.pi} с верши-
нами эд = [1 2], р2 = [2.5 0.5], рз = [2 2.5], р4 = [4 0.5], р5 = [5 4],
Рб = [3 3] и р7 = [1.5 4.5] (рис. 1.16).
Решение. Для первой тестируемой точки эд = [х] ] вычислим октантные
углы векторов Vt = р,- qx и их приращения:
Vi -5, V2 = 6, vs = 5, 1’4 = 6, vs = 2, V6 = 5, г? = 4, V8 = 1’| = 5;
А, = 1, Дг - -1, Дз = 1, Д4 = -4, Дз = 3, Дб = -1, Д7 = 1.
Без коррекции приращения угла на ребре pups сумма октантных приращений
равна нулю, что не соответствует внутреннему положению точки. Подставив
координаты точки в функцию прямой (1.35, г) ребра p4ps
n/2(p4,ps, эд) - 3.5Х| - j, - 13.5 = -0.75 < 0,
получим по (1.42, в) скорректированное значение Д» = 4 и скорректированную
сумму 5 = 8. Согласно (1.43) точка q{ лежит внутри полигона.
еометрические основы компьютерной графики
39
Для второй точки qi октантные углы и их приращения равны:
i’i = 4, V2 = 7, и = 3, V4 = 8, vs = 2, V6 - 2, v? = 3, vg = v, = 4;
Ai = 3, Д2 = -4, Аз = 5 = -3, Ад - -6 = 2, As = 0, Аб = 1, A? = 1.
Значение функции прямой для ребрар2рз в точке q2
nfl(p2,pi, qi) - 2x2 + 0.5^2 - 5.25 = 7.75 > 0
положительно, поэтому Аг = -4, а сумма приращений октантных углов s = 0.
Из (1.43) следует, что точка q2 является внешней.
Наконец, для точки qi на первом же ребре pt р2 получим приращение октант-
ного угла Д( = 8 - 4 = 4. Подставив координаты этой точки в функцию ребра
Р\Рг
nf2(px,pi, qi) = 1.5хз + 1.5>'з- 4.5 = 0,
заключаем, что точка qi принадлежит границе полигона. □
С помощью суммирования углов можно алгоритмически определить направ-
ление обхода вершин полигона. Установим граничную точку
в середине последнего ребра p„pt и вычислим алгебраическую сумму углов
вращения векторов Е, = Pj-qr? при обходе вершин отр, дор„ (см. рис. 1.13, б).
Если общее направление обхода вершин полигона против часовой стрелки,
то этот суммарный угол равен л [рад] или +4 октанта. При обходе вершин по
часовой стрелке, т. е. в отрицательном направлении, знак суммарного угла
отрицателен.
Глава ’
40
Отсюда получаем два варианта теста dir_test(P) направления обхода веришь
полигона Р ~ {pt Р„Р{}, возвращающего знак направления обхода (1—
против часовой стрелки, либо -1 — по часовой стрелке):
• радианный тест направления обхода
cftr_tetf(p)=sgn -<7гр,Р,+1 “«ftp) ;
(1.44, а>
• актантный тест направления обхода
( н~\
dir _ test (р) = sgn oct _ cor
(1.44.6)
гораздо более эффективный, чем радианный тест, благодаря целочис-
ленным и не итерационным вычислениям.
□ Лучевой тест ориентации точки q относительно произвольного полигона Р
заключается в выпускании из этой точки в произвольном направлении V луча
p(t) -q + И \/l> О и подсчете числа его пересечений с ребрами полигона. Па-
раметры пересечения луча с отрезками р, + (д,+,- д,)т V0 < т < 1, непараллель-
ными вектору V, находятся по следуемой из (1.30, б) формуле
к
' v г' —
V/ = \,п.
_Р/-Р1+Г
(1.45)
Анализ параметрических пар {г„ xj дает следующие критерии ориентации
точки относительно полигона:
• точка является внутренней, если число пар {/, > 0,0 < т, < 1} нечетно
(рис. 1.17, а);
• точка является внешней, если число таких пар четно, в том числе и равно
нулю (рис 1.17,6);
• точка лежит на границе полигона, если найдется хотя бы одна пара
{/, = 0,0<т,< 1} (рис. 1.17,в).
Особенности лучевого теста:
• неопределенность числа пересечений при прохождении луча точно через
вершину р, при х, = 1 или вершину /?,+| при х, = 0 (рис. 1.17, а, б). Необходи-
мо повторить тест заново с другим направлением луча К;
• требуется расчет по (1.45) (с плавающей точкой и вычислением обратной
матрицы) параметров пересечений луча со всеми ребрами полигона.
Обозначим за ray2_lesl(q, Р) функцию лучевого теста ориентации точки q от-
носительно плоского полигона Р, возвращающую результат:
• -1, если точка находится внутри полигона;
• 0, если точка на границе полигона;
• 1, если точка вне полигона.
еометрические основы компьютерной графики
41
Блок-схема алгоритма лучевого теста приведена на рис. 1.17, г. Направление
луча задается вектором V = [cos(<p) sin(<p)] единичной длины со случайным
углом <р - rnd(2n), равномерно распределенным в интервале (0, 2л). Парал-
лельность луча и /-го ребра PiPi+l устанавливается тестом (1.21) по нулевому
значению определителя обращаемой в (1.45) матрицы.
Расчет четности числа пересечений луча с ребрами полигона ведется с помо-
щью флажка f, устанавливаемого сначала как для внешней точки в 1 и инвер-
тируемого при каждом пересечении ребра лучом. В результате после завер-
шения обхода полигона возвращаемое значение f автоматически будет равно
1 для внешней или -1 для внутренней точки.
Рис. 1.17
42
Глава '
1.1.2.9. Алгоритмы пересечения на плоскости
П Перенесение отрезка прямой линии ab с отрезком cd.
Когда в (1.30, б) ищется пересечение не бесконечных прямых, а их отрезков
то кроме проверки непараллельности прямых необходимы дополнительные
проверки 0 < г < I и 0 < т < 1 принадлежности точки их пересечения одновре-
менно обоим отрезкам. Составим алгоритм расчета точки q и параметров t и *
пересечения отрезков ab и ed, возвращающий признак пересечения:
• -1, если прямые отрезков параллельны (не пересекаются) или совпадают
(точка пересечения не определена);
• 0, если непараллельные отрезки не пересекаются;
• 1, если отрезки касаются или пересекаются.
При непараллельности отрезков возвращаются значения параметров и точке
пересечения прямых, на которых лежат эти отрезки. При возвращении значе-
ния cross_segm = 1 эта точка одновременно является точкой пересечения от-
резков.
& cross_segm(ab, cd, t, т, q)
V
с — d
{ V=b-a, M =
И матрица направляющих векторов
если |М| = 0, то возврат -1;
[г т]=(с-а)л/ 1;
q = а + Г[;
возврат {О < t < 1}П{О < т < 1};
ю
И тест параллельности прямых
// параметры пересечения прямых
И точка пересечения прямых
И тест пересечения отрезков
Максимальная трудоемкость алгоритма составляет 11 операций сложе-
ния/вычитания и 10 операций умножения/деления. Сравним эти затраты со
вторым вариантом того же алгоритма, основанным на использовании неяв-
ных функций (1.35, г).
& cross_segm(ab, cd, t, т, q)
{fa~nf 2(C d, a), f, = nf 2(c, d, b)', // НФ точек а и b относительно cd
fc = nf 2(a, b, c), fd = nf 2(a, b, d)\ И НФ точек с и d относительно ab
если f. = fd, то возврат -1; // тест параллельности прямых
f f
t = ———, т = ———; // параметры пересечения прямых
fa-fb fc-fd
q - a + (b- a)t; // точка пересечения прямых
возврат {faft, < 0}П {fefd - тест пересечения отрезков
}О
геометрические основы компьютерной графики
43
Несмотря на кажущуюся простоту второго варианта, его трудоемкость вдвое
выше— 41 арифметическая операция, в числе которых 27 сложений/вы-
читаний и 14 умножений/делений. Далее с именем cross_segm будем свя-
зывать более эффективный первый вариант функции расчета пересечения от-
резков.
□ Пересечение отрезка ab с полигоном Р = {рх ... рпр\}.
Требуется отсечь от отрезка те его части, которые находятся вне полигона
(рис. 1.18, а). Здесь мы рассматриваем задачу внешнего отсечения отрезка вы-
пуклым полигоном. Другие варианты отсечения обсуждаются в конце этой
главы и в гл. 4.
Рис. 1.18
На рис. 1.18,6 построена блок-схема алгоритма clip2_cross(ab, Р) отсечения
отрезка ab выпуклым полигоном Р, основанного на расчете пересечений пря-
мой {а, Ь}, несущей отрезок, с отрезками PiPj+x — сторонами полигона. Алго-
ритм возвращает через аргумент ab неотсеченный фрагмент отрезка внутри
полигона, а сама функция clip2_cross возвращает признак видимости отрезка
ab в "окне" полигона Р:
• 0, если отрезок находится вне полигона и целиком им отсекается;
• 1, если отрезок весь или частично расположен внутри полигона.
44
Глава 1
Работа алгоритма начинается с инициализации счетчика пересечений к = 0 и
вычисления направляющего вектора отрезка V=b-a. Далее выполняется
обход ребер полигона PtPt+i Vi = 1, п и расчет пересечений с ними не самого
отрезка ab, а несущей его прямой a + (b - a)l с помощью функции cross_segm.
Если возвращаемое ею значение не отрицательно и прямая пересекает ребро
(это обнаруживается по условию 0 < т < 1), то счетчик пересечений к инкре-
ментируется, а параметр I сохраняется в переменной оА.. По достижении двух
пересечений (к = 2) дальнейший обход выпуклого полигона прекращается.
Концевые точки неотсеченного отрезка [«, Л] рассчитываются с помощью
табл. 1.1 в зависимости от значений = Z, и а2 = tj параметра /, при которых
прямая пересекла ребра PtPi+\ и р}р1+\. Две ячейки {о|<0,о2>1} и
{о, > 1, о2 < 0} соответствуют внутреннему положению отрезка, при котором
он не отсекается. В ячейках {о, < 0, о2 < 0} и {о, > 1, о2 > 1} формируются от-
резки [а, а] и [Ь, Ь} нулевой длины, которые обрабатываются алгоритмом как
полностью отсеченные с возвращением нуля. Остальные ячейки таблицы со-
ответствуют частичному отсечению отрезка ab и стягиванию его внешних
концевых точек на границу полигона — в точки а + Ео( и а + Ро2.
Таблица 1.1
о2 < 0 0 < о2 < 1 а2 > 1
о( < 0 [а, а] [а, а + Ра2] М
0 <о( < 1 [а, а + PcJ [а + Vcst,a + ЕО|] [а + Го,, Л]
о( > 1 [«,*] [а + Го,, Л] [М]
Естественное завершение цикла обхода вершин полигона означает, что пря-
мая отрезка ab либо касается полигона, либо не пересекает его вовсе
(рис. 1.18, а). В обоих случаях алгоритм завершается возвращением нуля.
Возможно и второе решение задачи отсечения отрезка полигоном на основе
выпуклого теста ориентации точки (1.38). Оно представлено на рис. 1.19
блок-схемой алгоритма clip2_test(ab, Р) отсечения отрезка ab выпуклым поли-
гоном Р = {р{ ...p„pt}, работающего следующим образом.
& Шаг 1. Инициализируем список L= {0, 1}, в который будем записывать
значения параметра t е [0, 1] положения точек на прямой p(t) - а + (b - a)t.
Начальный состав списка соответствует концевым точкам отрезка а = р(0) и
Ь=р(1).
Шаг 2. Рассчитываем не более двух пересечений отрезка ab с отрезкамиPiPi+\,
i= 1,2,... Значения параметра пересечения t добавляем в список L.
Шаг 3. Сортируем список L по возрастанию, после чего точки qk = p(Lk) раз-
бивают отрезок ab на непересекающиеся фрагменты общим числом не более
трех.
''еометрические основы компьютерной графики
45
Рис. 1.19
Шаг 4. С помощью выпуклого теста ориентации conv2_test определяем внеш-
нее либо внутреннее положение каждого фрагмента [%, %+|]са/> относи-
тельно полигона по его средней точке (рис. 1.18, а)
=a+Lk+Lk+ly
к 2 2
Внутренний фрагмент, удовлетворяющий условию corv2_test{mk, Р) = -1, воз-
вращается через аргумент ab наряду с признаком отсечения clip2_test = 1. При
отсутствии внутреннего фрагмента отрезок отсечен полигоном целиком, а
возвращаемый признак отсечения равен нулю. □
Из-за наличия теста ориентации conv2_test алгоритм clip2_test имеет ббльшую
трудоемкость по сравнению с алгоритмом clip2_cross, но его идейная основа
лучше приспособлена для решения других задач отсечения:
• при внутреннем отсечении отрезка выпуклым полигоном (рис. 1.20, а) от-
бор неотсеченных фрагментов выполняется по условию их внешней ори-
ентации conv2_lest(mlc, Р) = 1. Число таких фрагментов может быть от нуля
(весь отрезок лежит внутри полигона) до двух (средняя часть отрезка эк-
ранируется полигоном);
• при отсечении отрезка невыпуклым полигоном необходимо вместо вы-
пуклого теста conv2_test использовать угловые rad_test, oct_lest или луче-
вой ray2_test тесты для определения ориентации средних точек фрагмен-
тов относительно произвольного полигона. При внешнем отсечении
(рис. 1.20, б) отбираются фрагменты, средние точки которых лежат внутри
полигона, а при внутреннем (рис. 1.20, в)— фрагменты со средними точ-
ками вне полигона.
46
Глава 1
Рис. 1.20
□ Пересечение полигона А = {а, ... anat] с полигоном В = {Л| ... Ь„, Л,}.
Требуется найти общую часть полигонов, принадлежащую как А, так и В.
т. е. их логическое произведение А &.В. Здесь мы рассматриваем пересечение
только выпуклых полигонов. Логические операции с произвольными полиго-
нами детально изучаются в гл. 4.
Общие принципы расчета пересечения поясним на примере выпуклых поли-
гонов А = {«! а2 аз 04 at} и В = {/>, Ь2 Ьз b4 bsbt}, изображенных на рис. 1.21, а.
• Сначала функцией clip2_test(aiOn.l, В) X/i = l,n выполняем внешнее отсече-
ние ребер полигона А полигоном В, который в этой операции играет роль
отсекателя. В результате получаем список отрезков Ls = {qx а2, а2 q2,
q3q4}.
• Далее функцией clip2_test(bjbj+l, A) = выполняем внешнее отсечение
ребер полигона В отсекателем А и добавляем в список Ls новые отрезки
6| ?2,<7l ^4И93&,.
• Из элементов полученного списка
Ls = {q, а2, а2 q2, q3 q4, q2, q} q4, q3 *,}
собираем замкнутый контур соединением отрезков друг с другом совпа-
дающими концами. Берем первый отрезок q, а2, а среди оставшихся элемен-
тов списка Ls ищем отрезок, любой из концов которого совпадает с точкой
а2. Этот отрезок а2 q2 образует с qt а2 цепочку С = {qt а2 q2}. Среди оставших-
ся элементов Ls находим продолжение цепочки — отрезок b} q2. После его
присоединения к концу С точкой q2 цепочка принимает вид С = {q} а2 q2bt}.
Продолжая процесс поиска и присоединения отрезков до полного исчерпа-
ния списка Ls, получим окончательный вид замкнутого контура
С= {?! a2q2b} q3q4qx}.
Если полигоны А и В не пересекаются, то после обоюдного внешнего отсече-
ния их ребер список Ls остается пустым, вследствие чего и результат опера-
ции А & В пуст.
еометрические основы компьютерной графики
Рис. 1.21
Аналогичным образом формируется объединение полигонов А + В (рис. 1.21, б).
• Выполнив внутреннее отсечение ребер полигона А отсекателем В, получим
список отрезков Ls = , q2 аз, аз ш, ш q3, qtat}.
• В результате внутреннего отсечения ребер полигона В отсекателем А до-
полняем список Ls отрезками q2 b2, Ь2 Ьз, Ьз qt, qt bt, bt bs и bs qs.
• Из одиннадцати отрезков полученного списка Ls формируем замкнутый
контур
С = {«1 qt Ьз b2 q2 аз at q3 bs bt qtat}.
Если полигоны А и В не пересекаются, то их объединение состоит из двух
фрагментов, при сборке которых нужно после присоединения очередного от-
резка к имеющейся цепочке сравнить ее новый конец с началом. При совпа-
дении этих точек первый фрагмент собран. Из оставшихся в списке Ls отрез-
ков собираем второй замкнутый контур.
Описанный метод сборки нескольких фрагментов из общего списка их ребер
применяется при вычислении исключения A -i В полигона В из полигона А
(рис. 1.21, в).
• Выполнив внутреннее отсечение ребер полигона А отсекателем В, получим
список отрезков Ls = {a, q}, q2 аз, аз at, at цз, qt а,}.
• Внешнее отсечение ребер полигона В отсекателем А дополняет список Ls
отрезками b} q2, ср qt nq3bx.
• Из восьми отрезков полученного списка
Ls - {а, <?|, q2 аз, аз at, at q3, qta},bx q2, qx qt, q3 b\}
собираем первый замкнутый контур
С\ = {«1 qx qtaj.
Из пяти отрезков, оставшихся в списке Ls= {q2a3, аз at, atq3, btq2, q3bt},
формируем второй фрагмент
С2= {q2 аз at q3 b} q2}.
48
Глава 1
Если весь полигон А лежит внутри полигона В, то первые два этапа отсече-
ний дают пустой список Ls, вследствие чего и результат операции A -i В пуст.
1.1.2.10. Площадь и геометрический центр полигона
Рассмотрим методы вычисления площади S и геометрического центра g полигона
Р = {р, ...р„Р\}.
О Простейшим полигоном является треугольник {abca} (рис. 1.22). Его площадь
может быть найдена несколькими способами [13]:
• расчет по формуле Герона
5Д =7л(А-| a-fe|)(A-|fe-c|)(A-|c-a|),
требует вычисления длин его сторон |я - Ь\, - с|, |г - а| и полупериметра
^_|а-Л| + |Л-с|+|с-а|
2
ценой четырех итерационных приближенных вычислений квадратного
корня. Все эти затраты делают формулу Герона наименее эффективным
инструментом расчета площади треугольника;
• известная из тригонометрии формула
S& = 0.5|Л - а| • |с - а| • sin(Zbac),
равносильная половине произведения длины стороны ab на длину высо-
ты, опущенной на нее из вершины с, также включает приближенные вы-
числения длин векторов У= Ь-а, №=с-аи синуса угла между ними;
• сравнение последнего выражения с нормой векторного произведения векторов
Г = \Кх ^у о]е ХУ и ~ К Wy о]е ху позволяет записать его в виде
Рис. 1.22
Геометрические основы компьютерной графики
49
Введем функцию алгебраической площади треугольника {abca}
o(a,b,c)=0.5
b-a
с-a
= 0.5«f2(a,c,fc),
(1.46)
сводящуюся к неитерационному вычислению с помощью функции nf2, опре-
деленной в (1.35, г), половины значения НФ вершины Ъ относительно сторо-
ны ас. Знак алгебраической площади о(«, Ь, с) совпадает как с ориентацией
точки b относительно прямой {а, с}, так и с направлением обхода вершин
треугольника {abca}.
Окончательное выражение площади треугольника принимает следующий вид:
S& = |а(а, Ь, с)|. (1-47, а)
Геометрический центр треугольника расположен в точке пересечения его ме-
диан и делит каждую из них в отношении 2:1. Отсюда получаем
2( Ь + с А а + Ь + с
—°J=—5—• (!-47,<Э
□ Выпуклый полигон {/?, ...p„pt} после разрезания диагоналями, проведенными
из вершины pt (рис. 1.23), представляет собой объединение (п-2) непересе-
кающихся треугольников {р\Р2р^Р\} -5- {Р\Рп-\РпР\}, площади которых S, и
геометрические центры gi вычисляются по (1.47):
Представляя совокупность треугольников системой точечных масс S,, закреп-
ленных в точках g, [15], получим площадь и геометрический центр выпуклого
полигона:
(1.48, б)
я-1
л-1 ^SiSi
S=2Si,g = ^—
1=2 d
Рис.1.23
50
Глава 7
□ Площадь невыпуклого полигона можно вычислить по (1.48,6), выполнив его
триангуляцию — разрезание на непересекающиеся треугольники (рис. 1.24, а).
Задача триангуляции произвольного полигона достаточно сложна. Некото-
рые алгоритмы триангуляции рассматриваются в гл. 4. Между тем, после не-
большой модификации метод (1.48) может работать и с невыпуклыми поли-
гонами (рис. 1.24, б):
Рис. 1.24
Знаки площадей о, треугольников {р, р,р,¥} р,} совпадают с направлениями
их обхода. Фрагменты треугольников, лежащие вне полигона, суммируются в
(1.49) с противоположными знаками четное число раз, в результате чего их
площади взаимно сокращаются. Фрагменты треугольников внутри полигона
суммируются с противоположными знаками нечетное число раз. Таким обра-
зом, алгебраическая площадь полигона включает площади только внутрен-
них фрагментов и только однократно. Геометрический центр полигона также
является взвешенной алгебраической суммой центров треугольников с учетом
знаков их площадей.
Знак алгебраической площади полигона совпадает с общим направлением
обхода его вершин. Вот мы и получили самый быстрый тест направления об-
хода полигона
dir to/(/J)= sgn
л-l '
> А'+1’А') I
(1.50)
имеющий трудоемкость 8л - 15 арифметических операций. По эффективности
тест (1.50) даст сто очков вперед полученным в (1.44) радианному и октант-
ному тестам направления обхода полигона.
гнеметрические основы компьютерной графики 51
1.1.2.11. Алгоритмы генерирования случайных полигонов
3 процессе создания и отладки алгоритмов компьютерной графики необходимы
образцы различных графических объектов, служащие исходными данными для
моделирования. Принципиально различаются два типа данных:
П задаваемые вручную и позволяющие добиться верного решения задачи при
заранее известном ответе. Сложность ручного задания заключается в искус-
стве заранее предвидеть все нюансы задачи, поставить нужные цифры в нуж-
ное место так, чтобы за минимальное число испытаний пройти по всем вет-
вям алгоритма и добиться его правильной работы;
□ задаваемые случайно и позволяющие увеличить объем и статистическую дос-
товерность работы алгоритма. При большом числе испытаний со случайны-
ми исходными данными и хорошо продуманной системой диагностики рано
или поздно должны быть обнаружены все имеющиеся в алгоритме ошибки
вычислительного характера.
Имея в распоряжении функцию rnd(x)— генератор равномерно распределенных
случайных чисел (РРСЧ) в интервале (0, х), можно построить генераторы других
—ипов случайных равномерно распределенных данных:
□ а + rnd(b -а) — генератор РРСЧ в интервале (a, by,
□ [п + md(m +1 - w)J — генератор целых РРСЧ в интервале [л, т];
□ Г; = а + rnd(b - a) Xfi = 1, и — генератор случайного вектора V е R”, элементы
которого есть РРСЧ в интервале (a, by
□ К = [cos(<p) sin(<p)] — генератор единичного вектора на плоскости со случай-
ным углом направления <р = глб/(2л);
□ V = [sin(<p)sin(v) cos(v) cos(<p)sin(y)] — генератор единичного вектора в трех-
мерном пространстве со случайными углами места <р = rnd{2n) и азимута
V - rnd{n) (см. рис. 1.1,6).
Разработаем два алгоритма генерирования случайных полигонов — системы слу-
женного количества (не менее трех) случайных точек на плоскости, последова-
~ельно соединенных друг с другом не пересекающейся замкнутой ломаной лини-
ей со случайным направлением обхода вершин.
Т Случайный произвольный полигон строится следующим методом (рис. 1.25, а).
2D Шаг 1. Из заданной точки Т как из центра проводим лучи под углами
0° < ср < 360° к оси х. Начальное значение угла ф( = 0°, а последующие углы
рассчитываем путем приращения
фл+1 = Фл + Дфл
на случайные значения Дф„ = rnd(&). Максимальное приращение углов
120° < © < 180° выбираем с таким расчетом, чтобы минимальное число лучей
было равно трем.
52
Глава 1
Шаг 2. Вдоль лучей откладываем расстояния
r„ = a + rnd(b - a),
генерируемые как РРСЧ в интервале (а, Ь). Таким образом, получаем верши-
ны полигона
Рп=Т+^kos(<p„) sin(<p„)],п = 1,2,...
ШагЗ. Генерируем РРСЧ d = rnd(2), равновероятно принадлежащее как ин-
тервалу (0, 1), так и интервалу [1, 2). При d> 1 нумеруем вершины полигона Р
в обратном порядке.
Шаг 4. Возврат Р. □
Воплощая описанный метод в алгоритм, получаем функцию rpoly(T,a,b,®)
генерирования случайного произвольного полигона (рис. 1.25, б).
и=0, <р=0
>360
n=n+\,r=a+rnd(b-a)
— p„=7’+/-[cos(q>) sin(<₽)]
<p=<p+rnt/(0)
md(2)
б
Рис. 1.25
Автором проведен статистический анализ числа сторон генерируемых поли-
гонов в зависимости от параметра © е {90°, 120°, 150°, 180°} на выборке в
10 000 испытаний. Процентное соотношение n-угольников приведено на
рис. 1.26. Соотношение положительного и отрицательного направлений об-
хода оказалось очень близким к 1 : 1.
П Случайный выпуклый полигон строится следующим методом (рис. 1.27, а).
& Шаг 1. Размещаем первую вершину полигона р} в исходной точке Т и за-
даем начальный угол ср, = 0°. Очередную вершину рл+|, п - 1,2,... получаем
путем проведения из предыдущей вершины ря луча под углом
фл+| = фл + Аф,
^метрические основы компьютерной графики
53
со случайным приращением Д<р„ = rnd(&) и откладывания вдоль этого луча
расстояния
rn = a + rnd(b - a),
генерируемого как РРСЧ в интервале (а, Ь). Максимальное приращение углов
90° < © < 180° выбираем с таким расчетом, чтобы минимальное число лучей
было равно трем.
Рис. 1.26
□ 90
120
□ 150
180
Шаг 2. Полученную точку
<1 = Рп + гп 1СО8(фл ) sin (фи Я
тестируем, начиная со значения п = 2, на пригодность быть вершиной выпук-
лого полигона, т. е. на попадание в заштрихованную область. Точка q долж-
на, во-первых, лежать левее прямой {Т,рг}, во-вторых,— правее прямой
{рп, Г}. Только при одновременном выполнении этих условий сохраняем точ-
ку q как очередную вершину полигона рл+|.
Шаг 3. По окончании цикла генерируем РРСЧ d = rn</(2), равновероятно при-
надлежащее как интервалу (О, I), так и интервалу [I, 2). При d> I переставля-
ем вершины полигона Рв обратном порядке.
Шаг 4. Возврат Р. О
Воплощая описанный метод в алгоритм, получаем функцию rcpoly(T,a,b,@)
генерирования случайного выпуклого полигона (рис. 1.27, б).
Гистограммы числа сторон генерируемых полигонов в зависимости от пара-
метра © е {90°, 120°, 150°, 180°} на выборке в 10 000 испытаний приведены на
рис. 1.28. Соотношение положительных и отрицательных направлений обхо-
да оказалось практически равным.
54
Глава 1
Рис. 1.27
Рис.1.28
□ 90
120
□ 150
180
1.1.3. Квадратичные и параметрические кривые
Кривые второго порядка (квадратичные кривые) на плоскости описываются ко-
ординатным уравнением в НФ
f (х, у) — Ах2 + By2 + 2Еху + 2Gx + 2Jy + D = 0 (1.51, а)
Геометрические основы компьютерной графики
55
или в векторном виде
/(р)= PFpT = °, где F =
A E\G
Е__В_ | J
G j]D
^1
Al
Ai
D
A=^11-
(1.51,6)
Вектор нормали к кривой в точке ро е f(p) вычисляется по (1.7, а) путем диффе-
ренцирования (1.51):
Для любой квадратичной кривой три величины
1}=А+В,12 = |Fn| = АВ-Е2, h = И
(1.53, а)
называются инвариантами, не изменяющими значения относительно невырож-
денных преобразований переноса и вращения, изучаемых в гл. 2. Число
A G В J
G D +J D
/2 -
= I}D-G2-J2
(1.53,6)
есть полуинвариант относительно преобразования вращения. Знание легко вы-
числяемых инвариантов и полуинварианта позволяет быстро определить тип и
каноническое уравнение кривой по уравнениям (1.51) и табл. 1.2.
Таблица 1.2
11 /3 Невырожденные кривые с 1з * 0 Вырожденные кривые с/з = 0
-^-<0 /1 Действительный эллипс Точка вырожденного эллипса
12 *0 N -с + сч К 1 <3 2 -1 = 0 о II ГЧ N -0 + сч К 1 Q
Центральные кривые с Z2*0 -^->0 /1 Мнимый S W W шлипс 2 + 1 = 0
/2 *0 К | Q Г ипербола 2 / \2 -И -1 [b J = 0 Две асимптоты вырожденной гиперболы Z \2 Z ч2 (*] _fz] =0
56
Глава 1
Таблица 1.2 (окончание)
Л — Невырожденные кривые с h * 0 Вырожденные кривые с/., = ()
Нецентральные кривые с 11 = о Парабола , \2 М -z=o 1J /2<0 Две параллельные прямые / \2 (-1 -1=0 1° J
Г2 =0 Мнимая прямая / л2 [-) +1=0 1 a J
Г2 >0 Одна двойная прямая (-1 +1=0 \а J
Неявная форма непригодна для построения кривых и используется для анализа их
свойств по инвариантам и расчета пересечений. Исключением являются редкие
случаи функций, явно выраженных через одну из координат.
Рассмотрим взаимное расположение квадратичной кривой и прямой линии. Под-
ставим параметрическое уравнение прямой p(t) -q + Vt в неявное векторное
уравнение (1.51,6):
f21
^2Т1
D
[q + Vt
1]т= 0 =>
=> (<у + Vt)Fx t(q + Vt)T + 2(g + +0=0.
Раскрыв скобки, получим квадратное уравнение
at1 + 2bt + с = О
с коэффициентами
a = VFxxVT, b — (qFxx+F2X)FT, c = qFxlqT + 2qF2X+D.
В зависимости от их значений и дискриминанта
d = Ьг-ас
(1.54)
(1.55, а)
(1.55,6)
(1.55, в)
Геометрические основы компьютерной графики 57
возможны следующие решения задачи пересечения прямой с квадратичной кри-
вой (рис. 1.29):
□ при {а >0} прямая (1) пересекает кривую в двух различных точках
Pi = q + Vtt и р2 = q + Vt2 с параметрами
-b-Jd -b+Jd
h =-------<ti =-----; (1.56, a)
a a
П при {а*0}П{</ = 0} прямая (2) касается кривой в единственной точке
р, = q + Vtt с параметром
-6
г1- —; (1.56,6)
□ при {а = 0 }П {б *0} прямая (3) пересекает кривую в единственной точке
Р\= q+ Vtt с параметром
'|=^Ь (1.56,6)
□ при {а = о}Г) {б = 0}П {с = О} прямая касается вырожденной нецентральной кри-
вой (прямой линии) в бесконечном множестве точек;
□ в остальных случаях прямая (4) не имеет с кривой ни одной общей точки.
Рис. 1.29
Параметрическая (Ъорма как самая гибкая и универсальная наиболее распро-
странена для описания и построения геометрических объектов благодаря разно-
образию выбора функций, задающих движение точки по направлениям ее степе-
ней свободы. Параметрическая функция p(t) квадратичной кривой может быть
получена следующими способами.
58
Глава 1
□ Заменой аргументов хну канонического уравнения из табл. 1.2 функциями
одного параметра (например, t) на основе известных тождеств
cos2(/) + sin2(z) = 1, ch2(/) - sh2(/) = 1.
Простейший пример— окружность единичного радиуса. Ее каноническое
уравнение х2 + у2 - 1 = 0 допускает подстановку
x(t) = sin(0, y(t) = cos(Z).
□ Суперпозицией одновременных движений точки вдоль координатных осей из
заданного начального положения. Например, сложение гармонических коле-
баний по осям координат л(0 = cos(/), y(j) - sin(z), записываемое в векторной
форме как
с(/)= cos(r)x° +sin(t)y° =[cos(/)
sin(t)] VO < t < 2л ,
(1.57)
дает вращение точки по окружности единичного радиуса из начального по-
ложения л(0) - 1, у(0) = 0 (рис. 1.30, а). Направление вычисленного по (1.7, б)
вектора скорости и(г)= [~sin(t) cos(ОН 4) ортогонально влево от вектора
с{1) соответствует вращению точки против часовой стрелки.
Вращательное движение является основой для построения более сложных транс-
цендентных кривых: фигур Лиссажу, спиральных, циклических и полярных.
П Фигуры Лиссажу образуются суперпозицией разночастотных колебаний
вдоль ортов СК:
x(t) - cos(co47), y(l) = sin(co,z) или p(t)= [cos(coJt.r)sin(coJ,/)j.
На рис. 1.30, б изображена такая фигура, построенная при соЛ = 4, со, = 7 в ин-
тервале изменения параметра t е [0, 2л].
Рис.1.30
Геометрические основы компьютерной графики
59
□ Спиральные кривые описываются моделью p(t) = r(t)c(t) и образуются враще-
нием точки по дуге монотонно изменяющегося радиуса г(/). Примеры:
• спираль Архимеда (рис. 1.31, а) имеет равномерно увеличивающийся радиус
r(t) = го + Г]/;
• спираль Бернулли (рис. 1.31,6) образуется при экспоненциально изменяю-
щемся радиусе r(t) = roer,t;
• радиус параболической спирали, изображенной на рис. 1.31, в, описывается
зависимостью r(t) = r0 +rt-Jt .
Параметры го — г(0) и rt задают начальный радиус и характеристику его из-
менения за один оборот спирали, т. е. за приращение t на 2л.
Рис. 1.31
□ Простейшие циклические кривые описываются векторной параметрической
функцией
/’(О - Ри(0 + rc(tol), (1.58)
где pu(t) — траектория переносного движения центра окружности радиуса г,
по которой одновременно вращается точка с угловой скоростью со. На
рис. 1.32, а изображена циклическая кривая при pa(t) = 3c(t), г = 2, со = 3.5 и
t е [0, 4л].
П Многие известные трансцендентные кривые [8, 13] задаются полярной функци-
ей г(ср). После подстановки
t = (р, х(Г) = r(/)cos(/), y(i) = r(/)si n(/)
получим параметрическую функцию кривой p(t) - r(t)c(t). Например:
• улитка Паскаля (рис. 1.32,6) описывается следующими соотношениями в
неявной, полярной и параметрической формах:
(х2 + у2 - ах)2 - Ь2(х2 + у2) = О,
г(ф) = а cos(cp) + Ь, p(t) = (а cos(cp) + £)<?(/);
60
Глава 1
• трисектриса (рис. 1.32, в) описывается соотношениями
л'2(х - а + b) + j2(.v + Ь) - О,
г(<р)= acos(<p)~
Ь
cos(<p)
, р(/)= acos(r)-
Ь
cos(/)
Рис. 1.32
1.2. Графические элементы
в пространстве
Точка в пространстве имеет три степени свободы. Расстояние |/л-р2| между
двумя точками р\ и ргв разных системах координат вычисляется следующим об-
разом:
П в декартовой СК
</ = V(xi + (У1 -Л'г)2 +(Z1-Z2)2
□ в цилиндрической СК
= ^Р? +Р2 _2p|P2cos((P] -фг)+ G1 ~У1У ’>
□ в сферической СК
d = -J/F+,F~2,l,2(sin(Wl)s'n(W2)+Cos(W|)cos(V2)cos((P| -Фг))4"^! ~У2?
Поверхность имеет две степени свободы. Уравнения поверхности в неявной и па-
раметрической формах имеют следующий вид:
НФ: f(x, у, z) = 0 или f(p) = 0; (1.59, о)
ПФ: р(/,т)= [х(/,т) y(t,t) z(/,t)]. (1.59,6)
геометрические основы компьютерной графики
Любая реальная поверхность ограничена в пространстве либо в силу своей
замкнутости (например, сфера, эллипсоид или тор), либо благодаря системе не-
равенств, наложенных на ее координаты или параметры:
НФ: z) > 0 или у(р) > 0; (1.60, а)
ПФ: т) > 0. (1.60, б)
Особенность ограниченной поверхности в том, что при расчете ее пересечения с
другим графическим объектом могут быть получены точки или линии, лежащие
на поверхности (1.59), но не удовлетворяющие условиям (1.60). Следовательно,
результат пересечения должен всегда тестироваться по всем необходимым услови-
ям существования.
В регулярной точке поверхности р0=[х0 -о]= p(fo,^o) функция p(t, т) не-
прерывно дифференцируема по своим аргументам и обладает свойством [13]
, ,2 ,, 2
xt yt + zt
хт Ут Ут -т
d(x,j)/d(/,T) Э(>’,с)/3(/.т)
3(z,x)/3(/,T)
*0.
Точки поверхности, в которых частные производные
д(х,у) d(y,z) d(z,x)
d(t,T) ’ д(1,т) ’
равны нулю или не существуют, называются особыми. Эти точки образуют ребра
(линии самопересечения поверхности или пересечения двух поверхностей) и вер-
:иины (точки пересечения трех поверхностей), где производные не определены.
В регулярной точке поверхности ро существует единственная касательная плос-
кость (рис. 1.33), описываемая координатными и векторными уравнениями в
неявной и параметрической формах:
Рис.1.33
62
Глава 1
ЛГх(^-^о)+Л'^6/->’о)+ЛГг(г-го)=О fw°(p-po)=o
*х=Л|х у , , Ky=fy\ , ^=/;ix v / PV=V/G’)L
'ХО’ГО’*О Л zlx0,y0,Z0 '*0>Л0’гС ^0
ПФ:
(1.61, я)
x(t,т)= х0 + Fxt + ИСт,Vx = x.'l , Wx = xJ
\ / U X X X tlpo’ X T|po
yfa)=y0 +Vyt+WyT,Vy =y't\Po,Hx =^|po.
z(z,t)=z0 +rzt + Wzr,Vz =z't\po,^z =z;|po
p(z,r)= p0 +rt + WT;
= p'A , w = P'x\ ; O-61-6)
'W 'Po
VxW *O3.
Вектор нормали N = N
TV,] направлен в ту сторону поверхности, где
f(p) > 0. Направляющие векторы И± N и W± N должны быть непараллельны. Они
составляют с нормалью
уу = КХ1Е =
уг
W, wz
vx
wx
vx
wx
vy
Wy
(1.62)
правую тройку векторов. Это означает, что вращения И—> W, fV-yNnN-yV
происходят в положительном направлении, т. е. против часовой стретки с точки
зрения наблюдателя, находящегося на конце третьего свободного вектора.
1.2.1. Модели плоскости в пространстве
Рассмотрим способы задания плоскости в различных формах.
1.2.1.1. Неявное уравнение плоскости
Неявное уравнение плоскости задается четырьмя коэффициентами А, В, С и D,
составляющими вектор F = [а ВС !>]:
НФ: Ах + By + Cz + D = 0 или [р l]oF = poF = 0. (1.63)
Хотя бы одно из чисел А, В или С должно быть ненулевым. Если все коэффици-
енты А * 0, В 0 и С 0, то плоскость проходит наклонно ко всем осям коорди-
нат, пересекаясь с ними в точках (рис. 1.34, а)
, D , D , D
пх =---, п.=---, А_ =---.
х А у В ‘ С
Но, например, при >4=0, и CV 0 уравнение By + Cz + D - 0 описывает
плоскость, параллельную оси х и ортогональную координатной плоскости yz-
при А *0, В = 0 и С = 0 уравнению Ах + D = 0 соответствует плоскость, ортого-
нальная оси х и параллельная плоскости yz.
Плоскость /(/>)= Р ° У - 0 проходит через начало координат при f (Оз) = D = 0.
Благодаря ее свойству разделять пространство на два подпространства с проти-
~еометрические основы компьютерной графики
63
воположными знаками f (р), неявное уравнение позволяет с минимальными вы-
числительными затратами — за три умножения и три сложения — определить по
Условию f(q) = 0 принадлежность плоскости произвольной точки q, а также ори-
ентацию двух точек а и Ь относительно плоскости:
□ при f(a)f (Ь) > 0 эти точки лежат по одну сторону от плоскости;
□ при f(a) f(b) < 0 — по разные стороны от плоскости.
Для перехода от неявного описания плоскости к следующему нормальному опи-
санию необходимо найти любую ее точку ро и вектор нормали N. Сравнивая
(1.63) с (1.61, а), заключаем, что координатами вектора нормали можно принять
коэффициенты неявного уравнения А, В и С:
# = В с].
Приведем два способа получения точки р0 = [х0 у0 z0].
1. Выберем ее в месте пересечения плоскости с осью координат, соответствую-
щей ненулевому коэффициенту в (1.63):
0 — 0 , 0 0—1. п .
В J [ С JJI (1.64,67)
Несмотря на легкость понимания, этот способ не самый лучший для про-
граммирования из-за наличия альтернативы выбора точки в зависимости от
коэффициентов А и В.
2. Вычислим ближайшую к началу координат точку ро путем решения МНК-
задачи |р|2-р °р -> min с ограничением р ° N + D = 0. Аналогично (1.10,6)
решение имеет вид
в с]- <‘М0
1.2.1.2. Нормальное уравнение плоскости
Нормальное уравнение плоскости {ро, А}, заданной точкой ро и вектором нормали
.V, совпадает с (1.12, а) и выводится из условия ортогональности векторов N и
”-ро для всех точекр, принадлежащих плоскости (рис. 1.34,6):
НФ: Nx(x - хо) + Ny(y - >о) + Nz(z - zo) = 0 или (p- ро) ° N =0. (1 -65)
Зависимость вектора неявного уравнения от параметров нормального уравнения
совпадает с (1.13):
F = [7V-P00./V]. (1.66)
С помощью функции
f(p)-(p-po)°N (1.67)
64
Глава 1
можно определить ориентацию точки р относительно плоскости:
□ при f(a)>0 точка а лежит в том полупространстве, куда направлена нор-
маль, а угол Z(o -ро, N) острый;
□ при f(b) < 0 угол Z.(b-ро, N) тупой, а точка b и нормаль находятся по разные
стороны от плоскости.
Рис. 1.34
Таким образом, плоскость является двусторонней границей, разделяющей про-
странство R3 на положительное и отрицательное полупространства в соответст-
вии со знаком функции ftp). Назовем сторону плоскости, обращенную в поло-
жительное полупространство, лицевой, а обратную сторону — нелицевой.
1.2.1.3. Параметрическая функция плоскости
Параметрическая функция плоскости {ро, V, И7}, заданной точкой ро и направле-
ниями линейно независимых векторов К и W (рис. 1.35, а), имеет следующий вид:
ПФ:
х(/,т) = х0 + Vxt + Wxi;
y(t,T) = yG+Vyt+ WyT или p(t,i) = po + Vi + tVi;
z(t,T) = z0 + Vzt + W,t.
(1.68)
Условие линейной независимости направляющих векторов эквивалентно усло-
вию их непараллельности V х W* Оз.
Параметрическая форма удобна для задания как всей бесконечной плоскости,
так и ее полубесконечных и конечных частей. Для этого в (1.68) задаются соот-
ветствующие интервалы изменения параметров t и т. Например:
□ бесконечные интервалы -оо</<оои-а><т<ооне ограничивают протяжен-
ность бесконечной во всех направлениях плоскости',
П задание бесконечного -оо < t < х и полубесконечного т > 0 интервалов опре-
деляет полуплоскость, находящуюся от прямой ро + Vt по одну сторону с век-
тором W\
Геометрические основы компьютерной графики 65
□ бесконечный -оо < t < х и конечный 0 < т < 1 интервалы задают полосу шири-
ной \W\, протяженную вдоль вектора К;
□ конечные интервалы 0 < f < 1 и 0 <т< 1 определяют параллелограмм между
четырьмя точками ро,ро + V,po + IV и ро + V+ IV;
□ конечные интервалы 0 < г < 1 и 0<т<| дают треугольник с вершинами в точ-
ках ро, ро + V и ро + V + W.
Переход от параметрического описания плоскости {ро, Г, И7} к нормальному
no, N} и неявному {У7} описаниям заключается в вычислении по (1.62) вектора
нормали N, а по (1.66) — вектора F:
N=VxW,F = [N (1-69)
Ортогональность векторного произведения V х W к векторам-сомножителям
озволяет использовать его в качестве нормали. Эквивалентная (1.67) функция
ZGO = (Z7 — Ро) ° (И х ИО (1.70)
определяет ориентацию точкир относительно плоскости {ро, V, И7}:
□ при /(<?)> 0 точка а лежит в положительном полупространстве, откуда вра-
щение от вектора V др вектора W выглядит положительным (против часовой
стрелки). При этом угол /.(а -ро, N) острый;
Э при f(b) < 0 угол Z.(b -ро, N) тупой, а точка b находится в отрицательном по-
лупространстве (с нелицевой стороны плоскости).
Более сложной является неоднозначная обратная задача выбора подходящих
направляющих векторов на основе единственного вектора нормали (рис. 1.35,6).
Выберем произвольный вектор Н, не параллельный N, например, любой из коор-
динатных ортов co°#2V, где со е J7}, и по свойству ортогональности векторов
в векторном произведении получим желаемое решение:
Н = if ()V || х° : у°, х°), V=HxN*Oi, W=Nx Г* Оз. (1-71)
Рис. 1.35
66
Глава 1
1.2.1.4. Уравнения плоскости,
проходящей через три точки
Неявная форма уравнения плоскости, проходящей через три точки а, b и с
(рис. 1.36,«), выводится из условия принадлежности плоскости этих точек и точ-
ки р = [х >>]:
Выбрав направляющие векторы плоскости V-b-aw W = с- b, получим пара-
метрическую модель плоскости, проходящей через три точки:
ПФ: p(t) = а + (b - a)l + (c-b)t. (1.72,6)
Условие существования плоскости следующее: |7V] * 0 или (Ь - а) х (с - Ь) * Оз. Это
означает, что три точки не должны лежать на одной прямой.
Эквивалентная (1.70) функция
f(p) = (p-a)°((b-a)x(c-b)) (1 73)
позволяет вычислить ориентацию точки р относительно плоскости {«, Ь, с} При
ftp) > 0 точка р лежит в положительном полупространстве, откуда обход тре-
угольника {abca} выполняется против часовой стрелки.
Ниже рассматриваются свойства многогранников (полиэдров), обусловленные
ориентацией векторов нормалей к их граням. С учетом принятого соглашения
(1.8), внешняя ориентация нормалей к граням полиэдра обеспечивается при обходе
его граней против часовой стрелки, если смотреть на каждую грань из внешнего
полупространства.
1.2.1.5. Уравнения плоскости в отрезках
Неявное уравнение плоскости в отрезках hx, hy и h., одновременно не равных ну-
лю и отсекаемых плоскостью на осях л, у и z (рис 1.36, б), получим аналогично
(1.16):
нф: 'Г+й“ + 'Г_1 =° F = hxhy -hxhyhz\. (1.74,а)
Пу
Выбрав на плоскости точки
a=[hx 0 0], 6 = [о hy б], с = [0 0 hz],
получим ее направляющие векторы
r=b-a = [-hx hy б], W =c-b = [о -hy Лг],
'еометрические основы компьютерной графики
67
я по (1.72, б) — координатные и векторную функции:
ПФ:
х(/.т) = Лх(1-/);
= или p(t)=[hx(\-t) hy(t -i) h,x]
(1.74,6)
z(t,i) = hzx.
1.2.1.6. Модели линии в пространстве
Линия в пространстве имеет одну степень свободы и является либо пересечением
^вух поверхностей, либо кинематическим следом движения некоторой точки в
-ространстве. Соответственно, имеем две формы модели пространственных линий'.
НФ: {/iG0= 0}n{/2G,)= °); ПФ: /?(/)= [x(z) 4) 4)1
Неявная форма требует решения системы нелинейных уравнений относительно
координат х, у, z точки р и для практического применения неудобна. Парамет-
рические функции прямой линии в пространстве в векторном виде полностью
совпадают с (1.14,«) и (1.15, б):
p(l) = ро+ Vt и р{1) = ро + (b- а)1.
В координатном виде они дополняются аппликатами
z(t) - zo + V.t и z(l) = zo + (b, - a.)l.
Получим уравнения прямой как линии пересечения двух плоскостей (рис. 1.37).
Рис. 1.37
68
Глава 1
(1 75)
П В неявной форме плоскости заданы векторами F(=[^ О]] и F2=\n2 D2],
Прямая их пересечения p(t) =ро + Vt имеет неизвестные элементы ро и V. Для
их нахождения запишем систему двух уравнений плоскостей (1.63):
[р 1]Н
_°1 D2.
Полученное векторное уравнение эквивалентно недоопределенной системе двух
скалярных уравнений с тремя неизвестными, не имеющей единственного реше-
ния. Прямоугольная матрица |tV|T N2 ]е R3x2 не обращаема. Получим бли-
жайшее к началу координат МНК-решение, минимизируя функцию Лагранжа
3(р, Л) = 0.5(р о р) + Л о <р(р>),
в которой X е R2 — вектор множителей Лагранжа, а
<р(р)=рк ]+[Р) D2]
есть соответствующая (1.75) векторная функция связи координат точки р. Диф-
ференцируя 5(р, Л) по векторным аргументам, получим систему уравнений
^1'
Л2.
^2
Подставляя решение первого уравнения
д%(р,Л)/др = p + Л
dQ{p,X)/dX = p[V|T
= o3;
]+[d, d2]=o2.
(1.76)
p = -A
во второе, получим вектор множителей Лагранжа
А = Ь1 *2]] •
Подстановка его в первое уравнение (1.76) дает МНК-решение уравнения (1.75):
К
Ро =
-[d, Я,]! hT №>r]
N2.
(1.77)
= -[/?! Г>2]
Щ o/V,
о TV2
N\°N2
n2 ° n2 n2
Если обе плоскости заданы в НФ элементами {рю, N\} и {рж,№}, то в (1.77)
следует подставить D\ ~ -рю ° Ni и D2- -ртя ° №.
Направляющий вектор прямой ортогонален обеим плоскостям:
К = № х №.
'еометрические основы компьютерной графики
69
Условие существования решения V* Оз есть также и условие невырожденно-
сти обращаемой в (1.77) матрицы:
MW -(^1 °Af2)2 = H2N2(’ -cos2(zy^2))=
= |7V| |21#212 sin 2 (ХУ] W2) * 0 •
Это означает, что плоскости не должны быть параллельными.
П В параметрической форме плоскости заданы точками рю, рго и направляю-
щими векторами V\, JVi, V2 и W2 (рис. 1.37). Параметры рю и V искомой пря-
мой определяются путем перехода (1.66) к неявным формам плоскостей и ре-
шения задачи (1.77).
1.2.2. Взаимное положение графических
элементов в пространстве
Рассмотрим некоторые полезные формулы, тесты и алгоритмы, описывающие
гвойства и взаимное расположение точек, прямых, плоскостей и многогранников
полиэдров) в пространстве.
1.2.2.1. Коллинеарность точек
Три точки pi, р2 и рз коллинеарны, если
(рг-рО X (p.3-pi) = Оз или I(p2-pi) о (p.3-pi)| = |p2-pi| • |рз-р1|. (1-79,«)
Обобщение на произвольное число точек pi -г рп:
rang Pl Pl = 2 или rang Р1~Р\ РЗ~Р\ = 1
_Рп_ Рп~ Р\.
(1.79,6)
Проверка принадлежности точки р отрезку ab выполняется по тесту (1.18), а зна-
-ение параметра t, соответствующее положению точки р = а + (b - a)t на прямой
относительно отрезка ей, вычисляется по (1.19).
1.2.2.2. Компланарность точек
Четыре точки р\,рг,рз и рь компланарны, т. е. лежат в одной плоскости, если
Р\
Р2
Рз
Р4
= 0 ИЛИ ((рг-pi) х (рз-pi)) о (P4-P1) = 0.
(1.80)
70
Глава 1
Размерность пространства R'", натянутого на п точек pt р„, вычисляется на ос-
нове определения ранга матрицы как числа ее линейно-независимых строк или
столбцов:
т — rang Р\ Р1 -1 = rang Р1~Р\ Рз~Р\ <т!п{з, п-1}. (1.81)
РП. Рп~ Р\_
1.2.2.3. Точка и прямая
Рассмотрим расположение лючки q и прямойp(t) = ро + Vt (рис. 1.38, а).
Точка принадлежит прямой, если
Н - Оз, где Н = (q-ро) х V.
Уравнение перпендикуляра, опущенного из точки q на прямую, имеет вид:
p_i.(Z) = Q + ^±1, где = Н х V.
Расстояние от точки q до прямой выражается следующей формулой:
d
= |<7-po|sin(a)=|(9-po)xp|
(1.82)
(1.83)
(1.84)
IM
КГ
Уравнения плоскости, проходящей через точку q ортогонально прямой, имеют вид:
НФ: ^of±=0,F±=[k -q°r]; ПФ: pv(t, т) = q + Vj + Ят. (1.85)
1.2.2.4. Точка и плоскость
Рассмотрим расположение точки q и плоскости (рис. 1.38, б).
Точка принадлежит плоскости, если
НФ: q°F = 0; ПФ: (q-po) о (V х IV) = 0. (1-86)
Параметрические уравнения перпендикуляра, опущенного из точки q на плоскость.
имеют вид:
НФ: Pi.(l) = q + Nl; ПФ: pjj) = q + Nt, N = V * W. (1.87)
Расстояние от точки до плоскости находится так:
d = |prw (<? - ро )| =|(? - Ро )° W|= |(<7 - Ро )° Р х И''] • 88)
Зеркальное отражение точки q от плоскости расположено на перпендикуляре к
плоскости на расстоянии 2d от q в сторону, противоположную проекции вектора
q-ро на нормаль N, и вычисляется по формуле (1.26, а).
Геометрические основы компьютерной графики
71
Уравнения плоскости, проходящей через точку q параллельно заданной плоскости,
следующие:
НФ: =0, Л[| =[# ПФ:
/?ц(/,т)=9 + К/ + И/т. (1.89)
Рис. 1.38
1.2.2.5. Построение плоскости,
наименее удаленной от совокупности точек
Рассмотрим задачу, связанную с понятием расстояния от точки до плоскости.
Допустим, в R3 задано т > 3 произвольных точек р\ + рт. Так как в общем случае
точки не компланарны, то не существует ни одной плоскости f(p) = 0, для кото-
рой все числа J, = f (рд обращаются в ноль. Другими словами, расстояния |J,| / |7V]
отточекр, до этой плоскости, вычисленные по (1.88) и пропорциональные dh не
могут быть одновременно все нулевыми (рис. 1.39).
Рис. 1.39
72
Глава 1
Алгоритм построения аппроксимирующей плоскости {ро, N}, наименее удаленной
от совокупности точек р„ аналогичен двумерному алгоритму, полученному в
(1.29). Применительно к размерности пространства п - 3 он имеет следующий вид.
& Шаг 1. Сформируем из точек р, т х 3-матрицу Р и найдем их геометрический
центр с:
Р\
1 т
L^pi-
mi=\
Р =
(1.90, а)
\_Pm_
Шаг 2. Вычислим собственные значения Xi, Хг, Хз и соответствующие им норми-
рованные собственные векторы Nt, N2, № симметричной 3 х 3-матрицы
М = тсТс-Р7Р. (1-90,6)
ШагЗ. Определив собственную пару {ХА, Nk} с максимальным значением
ХА = тах{Х,}, получим элементы вектора F = pV Z?] неявного уравнения иско-
мой плоскости (1.63):
N=Nk,D = -N°c.
(1.90, в)
□
Вместо неявной формы плоскости можно использовать ее нормальное уравнение
(р - с) о W = 0. Для построения более удобна параметрическая форма
p(t, т) = с + Vt + Wt,
направляющие векторы которой Си Wнаходятся по (1.70).
Оставшиеся две собственные пары матрицы М дают плоскости, ортогональные
оптимальной (при различных собственных числах) и пересекающиеся с ней в
геометрическом центре точек с.
& Пример 1.4. Построить плоскость, наименее отклоненную от точек (см. рис. 1.39)
Р1=[1 0 2], р2 = [4 3 4], р3 = [б 3 1], р4 = [5 5 0], р5 = [4 1 1].
Решение. Следуем шагам алгоритма (1.90).
Шаг 1. Р =
1
4
6
5
4
0
3
3
5
1
2
4
1
0
1
2.4 1.6].
Шаг2. М = 5с1с-РхР =
-14
-И
4
-11
-15.2
3.2
4
3.2
-9.2
1 5
t еометрические основы компьютерной графики 73
Xi = -3.475, 7V, = [- 0.74 0.65 -0.15];
Хг ——4.865, TV2 = [0-073 0.304 0.95];
Хз = -27.06, N3 =[-0.67 -0.69 0.27].
Шаг3.&= 1, W = [-0.74 0.65 -0.15], D = 1.64.
Таким образом, аппроксимирующая плоскость описывается неявным уравнением
-0.74* + 0.65у - 0.15z + 1.64 = 0.
_1тя получения направляющих векторов выберем вектор Н = [1 0 о], не парал-
лельный вектору N. Тогда по (1.70) получим направляющие векторы
К = [0 0.15 0.65], И7 = [0.45 0.49 -0.11]
и параметрические функции плоскости
x(t, т) = 4 + 0.45т, X - 2.4 + 0.15г + 0.49т, z(t, т) = 1.6 + 0.65Z - 0.11т.
Алгебраические расстояния от заданных точек до этой плоскости равны
J =0.594, <72 = 0.026 (точка рг почти лежит в плоскости), г/з = -1, Л = -0.632 и
лз = -0.82, а минимум функции Лагранжа составляет 3min = 3.475. О
1.2.2.6. Взаимное расположение двух прямых
Исследуем расположение в пространстве двух прямых pi(h) = рю + Viti и
л(гз) = р2о + Vi ti (рис. 1.40).
Прямые совпадают, если
К =03}n{V|| = О3},где Гх= Ki х V2, 7V|| =(р20~Р\0)хК1 • (1.91)
Прямые параллельны, если Кх - Оз. Расстояние между параллельными прямыми
равно
^ = j(/?2O_/’lo)x^j О-92)
Уравнения плоскости, проходящей через две параллельные прямые, имеют вид:
НФ: poFj|=0, F|। = [1V11 _Pio°^||]> (1-93,fl)
ЛФ: p(t,x)= рю + (р2о-рю)1 + V]t. (1-93,6)
Прямые лежат в одной плоскости при (р2о-рю) ° = 0. Угол их пересечения равен
у = arccos (и 1 ° И 2) (1 -94)
и представляет собой неотрицательный угол кратчайшего вращения от вектора
1 к вектору Vi, видимого со стороны ортогонального им вектора V± = V\ х Vi.
Уравнения плоскости, проходящей через две пересекающиеся прямые, имеют вид:
НФ: p°Fx=0, Fx = [k± P1O°K1J; (1.95,с)
74
Глава 1
ПФ: p(t, т) = р\о + V\t + Уп.
Точка пересечения прямых находится аналогично формуле (1.30, б):
q — рю + KiZi =/>2о + Viti,
г 1 / л т т1 Г -и о^Т1
где Н1 г2]-(р2О_Р1о)г1 _f/2j ., ., ., .,
(1.95, б)
(1.96)
Прямые ортогональны, если У\ ° Иг = 0.
Прямая, соединяющая скрещивающиеся прямые по кратчайшему пути, имеет на-
правляющий вектор И± = И1 х Иг и проходит ортогонально им обеим через точки
qi = рю + Till, qi =/>го + Viti.
Параметры ti и ti находятся по формуле (1.96). Уравнение кратчайшей прямой
есть />j_(Z) = q\ + У±1. Кратчайшее расстояние между скрещивающимися прямыми
равно
Рис.1.40
(1.97)
1.2.2.7. Взаимное расположение прямой и плоскости
Рассмотрим расположение прямойpi(t) - рю + V\t и плоскости (рис. 1.41).
Прямая принадлежит плоскости, если
НФ: =0}П{р10оИ = 0}; (1.98, а)
ПФ: {у} о(ихИ/)=0}П{(р|о-/’о)0(^х^) = 0}. (1.98,6)
Прямая параллельна плоскости, если
НФ: И1оДг=0; ПФ: И|О(ИхИЭ = 0. 0")
Расстояние от прямой до параллельной ей плоскости равно
d = |(ао ~ Ро)° = |(Р1 о - Ро)° r xWZ| • (1.100)
еометрические основы компьютерной графики
75
Прямая ортогональна плоскости, если
НФ: И1х/У = Оз; ПФ: И х (Их И7) = Оз. (1.101)
Одной из основных задач компьютерной графики является расчет точки пересе-
ления произвольной прямой с плоскостью, аналогичный расчету (1.30) пересечения
двух прямых на плоскости:
НФ:
(9-ро)°Лг = О (р0-pi0)°N (po~Pio)°n iz .
=> t —-----------=> q — рю "I----------И ,
9 = Рю + 1/1/ р1оДГ
(1.102, а)
ПФ:
q =рю + Ии =ро + Ит + WQ, где [/
т б]=(ро-Рю)
(1.102,6)
-W
Условие существования решения: У\ ° N*0 — прямая не параллельна плоскости.
Угол между прямой и нормалью к плоскости находится аналогично (1.94):
Л = arccos ° arccos^o ИхМ7). (1.103)
Уравнения плоскости, проходящей через прямую ортогонально заданной плоско-
~ти, имеют вид:
НФ: роЕ±=0,где Fx = ^x-p1o<’Ar±L^±= И х^ (1.104,а)
ПФ: р(г,т)=рю+ Иц/ + (Их №)т. (1.104 6)
У -ловие единственности решения: Hi х W * Оз — прямая не ортогональна плоскости.
Р«
Рис. 1.41
1.2.2.8. Две плоскости
Исследуем расположение в пространстве двух плоскостей (см. рис. 1.37).
Плоскости совпадают, если
НФ: {л,1Х^2=ОзЮ{(Р20-Ло)°л;2=0}; (1.105, а)
ПФ: {(И|хИ'1)х(И2хИ'2) = 03}П{(р20-/’1о)°(^х»2) = 0}. (1.105,6)
76
Глава 1
Плоскости параллельны, если
НФ: Мх№ = Оз; ПФ: (Hi х Ил) х (И2 х IV2) = Оз. (1.106)
Расстояние между параллельными плоскостями равно
^ = |(Р20-/’1о)оЛГ1| = |(Р20 -Рю)°И х*н|- (1.107)
Плоскости ортогональны, если
НФ: МоДГ2 = 0; ПФ: (Ki х WY) ° (И2 х 1И2) = 0. (1.108)
Одной из основных задач компьютерной графики является расчет прямой пересе-
чения двух плоскостей, выполненный в (1.75)-(1.78). Здесь дополнительно при-
ведем формулу для вычисления угла пересечения плоскостей, аналогичную (1.94):
у = arccos^[ ° N2)= arccos^ хИ) ° И2 х РИ2 ) • (1.109)
Уравнения плоскости, проходящей через точку ро ортогонально двум плоскостям.
имеют следующий вид:
НФ: р о = 0, где F± = [Wx_Po °^±]> = Ni х N2", (1.110, а)
ПФ: p(t, т)-ро + (И| х Wi)t + (И2 х ГИ2)т. (1.110,6)
1.2.2.9. Пучок плоскостей и биссекторная плоскость
Уравнения пучка плоскостей, заключенных между двумя плоскостями (рис. 1.42, а).
имеют вид:
НФ: роГЛ+1 =0, гдеЛ+i =(1-X)Fi+ XF2; (1.1 И,я)
ПФ: a+i(z,t) = (1 -М(Рю+ H.Z+ И'1т) + Х(р20+ У21+ ^2t). (1.111,6)
Изменение параметра пучка в интервале 0 < Л < 1 дает такие промежуточные по-
ложения плоскостей, что вращение нормалей происходит по кратчайшему
углу от начального положения N\ до конечного положения N2. Модели (1.111)
представляют собой линейные комбинации точек исходных плоскостей, соответ-
ствующих равным значениям параметров t и т.
Параметры диссекторной плоскости получаются из (1.111) при Л = 0.5 и уравни-
вании длин векторов, определяющих исходные плоскости:
Ибис = |№|Fi + |М |И2, Ибис = I и2| И| + I Vi IИ2, 1Ибис = IW\ + | Wi | W2. (1.112)
Расчет биссекторных плоскостей бывает необходим, например, при построении
сферы, вписанной в четырехгранник. Ее центр о лежит в точке пересечения трех
биссекторных плоскостей внутренних телесных углов, примыкающих к одной из
треугольных граней, а радиус г есть расстояние от точки о до плоскости любой
грани, вычисляемое по (1.88).
>: метрические основы компьютерной графики
1.2.2.10. Пересечение плоскостей
' чка пересечения трех плоскостей (рис. 1.42, б) определяется из условия ее при-
надлежности этим плоскостям:
4Ф к Пк ?2 ^3Т]=Оз^ Рх=-к D2 D3][^t Nj /Vj]-';(l.ll3,a)
1Ф: Ру=[р|0°^1 Р20 ° ^2 РЗО ° ^з! 1мТ ^2 ^3 ] , М = х И7/- (1.113,6)
сювие существования единственного решения |^т N2 Nj| * 0 — линейная
независимость нормалей плоскостей, что равносильно существованию и попар-
~?й непараллельности линий пересечения плоскостей.
Рис. 1.42
71? формулам (1.113) рассчитываются вершины полиэдра как точки пересечения
эскостей трех смежных граней.
~ ?е сечение п плоскостей в одной точке рх, вычисляемой по (1.113) на основе па-
раметров первых трех плоскостей, возможно при условии
rang[^ F2 ... F„T]=3,
аккумулирующем требования совместности системы линейных уравнений в
13. о), предъявляемое теоремой Кронекера—Капелли [8—10] о равенстве ран-
матриц [с/ F2 ... F„t]h [v]T N2 ... ], и единственности ее решения,
•’ределяемой полнотой ранга матрицы [л^ N2 ... Л^], который должен
•ль равен трем.
1 2.2.11. Модель полиэдра
“ереходим к изучению полиэдров — замкнутых пространственных объектов, ог-
раниченных плоскостями. Среди объемных тел полиэдры занимают такое же
. лое место, как и полигоны среди плоских фигур. Благодаря планарности всех
78
Глава '
граничных поверхностей полиэдра существенно упрощается расчет его пересече-
ний с различными геометрическими примитивами и другими полиэдрами. По-
мимо того, что в природе существует множество собственно полиэдральных
объектов (пять правильных многогранников, призмы, пирамиды и т. п.), чаете
криволинейные граничные поверхности аппроксимируют системой полигональ-
ных граней, что превращает гладкие объекты в полиэдры.
Подробное изучение свойств полиэдров отложим до гл. 3, а здесь приведем наи-
более оптимальную модель полиэдра Н - {Р, G}, состоящую из двух массивов:
П координатного списка пв вершин Р = {/?], ... ,р„в}, пронумерованных в произ-
вольном порядке. Благодаря однородности элементов списка может быть
удобнее организовать и использовать вершины полиэдра в виде матрице,
вершин в нормальной или расширенной формах (применяется в преобразова-
ниях, изучаемых в гл. 2):
□ топологического массива списков пГ граней G = ]Gi,..., Gn? j. Элемент массива
G, ={?,], ..., gin , g/i} представляет собой список номеров (целочисленных ин-
дексов) tij вершин полигона /'-ой грани, перечисленных в порядке их обхода по
замкнутому контуру.
В рамках такого метода организации структуры данных полиэдра доступ к ег<
конкретной вершине с номером gy осуществляется в два этапа.
1. Из списка G, считывается j-ый элемент v = gy.
2. Из списка Р считывается элемент pv.
Массив G содержит сведения о порядке соединения ребрами вершин полиэдра,
описанных в списке (матрице) Р. При этом описание каждого ребра, соединяю-
щего вершины р, и pj, дважды встречается в списках граней либо в виде последо-
вательности {..., i, j,...}, либо как {...,у, i,...}.
Для примера построим модель полиэдра, состоящего из пв = 11 вершин и пг = 7 гра-
ней (рис. 1.43):
0 0 3 3
5 2 2 2
4 0 4 4
5 0 0 0
0 6 6 0
4 4 0
1 1 0
0 6 0
,G = {G1,G2,...,G7},
(1-115)
где
0 6 6 0
G, = {1, 2, 3, 5,1}, G2 = {2, 3.10, 7, 6, 2}, G3 = {З, 4, 5, з},
G4 = {3, 4, 9.10,3}, G5 = {7,8,9,10, 7}, G6 = {5, 4,9, 8,11,1,5},
G7 = {1, 2, 6,11,1}
еометрические основы компьютерной графики
79
Рис. 1.43
Зля работы с полиэдрами нам будут необходимы две функции, возвращающие:
□ полигон вершин i-ой грани полиэдра {Р, G}:
side(P,G,i)=\pgii... PgjnjPgi}}', (l.l 16)
Т. вектор нормали к плоскости полигона Р - {pi ...р„р\} е R3:
norm(P) - (pz - pi) х (рз - pi). (1. 117)
Пространственная ориентация плоскости полигона задается направляющими
векторами V = pi-p\, W - рз-рзи нормалью N- V х W по первым трем некол-
-меарным вершинам р\,р2 ирз. Со стороны внешнего полупространства, в кото-
рое направлена нормаль, обход вершин полигона выглядит положительным,
роисходящим против часовой стрелки (см. рис. 1.36, а).
Зля обеспечения внешней ориентации нормали i-ой грани полиэдра
Nj = Vt х Wj = norm(side(P, G, i)) (1. 118)
аужно руководствоваться следующими правилами:
Т вершины в списке G, должны перечисляться в положительном направлении с
точки зрения внешнего наблюдателя;
□ если полигон грани не выпуклый, то первые три вершины должны составлять
выпуклый угол;
□ если направление нумерации вершин в списке G, оказалось отрицательным,
то следует перенумеровать их в обратном порядке:
С/—{g/b Sin,Si2’ &il}’
ГТ если нормаль к какой-либо грани не вычисляется по (l.l 18), а задается внешне
ориентированной вручную, то направление обхода вершин в списке этой
грани безразлично.
80
Глава ‘
С учетом сказанного скорректируем некоторые списки в (1.115) так, чтобы вы-
числяемые по (1.118) нормали ко всем граням полиэдра стали внешними:
G2 = {2,6,7, 10, 3, 2},G4 = {3, 10, 9,4,3},
G6= {1,5,4,9, 8, 11, 1},G? = {1, 11,6,2, 1}.
1.2.2.12. Тесты свойств графических элементов
в пространстве
Рассмотрим тесты, основанные на свойстве сепарабельности плоскости f(p) = (.
разделять пространство на два подпространства с противоположными знакам.
/(Р).
П Тест ориентации точки р относительно плоскости заключается в проверке зна-
ка числа f(p), для вычисления которого в зависимости от способа задания
плоскости в разд. 1.2.1 используется соответствующая неявная функция nf ♦:
ttfF{F,p)= p°F\
(1.119, а,
nfN(po, N,p) = (р-ро) ° N\
Р-Ро
п/пфо>^г,р)=(р-Ро)°(1/><яг)= V
W
р-а
nfl(a, b, с, р)=(р-а)° ((б -а)х(с-7>)) = b-а
(1.119, б)
(1.119, в)
(1.119,г)
с-Ь
Дополнительно определим еще одну функцию ориентации точки р относи-
тельно плоскости полигона Р-{р\рзрз ...p„pi} е R3:
P-Pt
nfG(P,p)=(p-pi)onorrnfaр2р3}) = р2 -р,
РЗ~Р2
(1.119, d)
Внешнее полупространство, в которое направлена нормаль плоскости, назы-
вают положительным согласно знаку всех определенных выше функций
nf ♦ > 0. Для доказательства построим к плоскости {ро, V, нормаль
N = V х W, выберем точку q - ро + Vt + Wi + KN, которая при X > 0 лежит во
внешнем полупространстве, и вычислим, например, значение (1.119, б):
nfN(po, N,q) = (Ft + Wx + KN) ° N = (У o N)t + (И7° N)x + K(N°N) = > 0.
To, что величина f(q) не зависит от координат t и т, отсчитываемых вдоль
направляющих векторов V и W, означает, что поверхности постоянных уров-
'-.'метрические основы компьютерной графики 81
ней f (р) проходят параллельно плоскости f(p) = 0 и также являются плоско-
стями. Как следствие, получим расстояние от точки q до плоскости, равное
и обобщающее (1.88).
Ввиду простоты вычисления функция f(p), реализуемая на практике одной из
функций nf* в (1.119), идеально подходит для сортировки точек относительно
плоскости на внешние, внутренние и лежащие на ней. Тест ориентации приме-
няется в алгоритмах, связанных с обработкой точек, вершин полигонов, а так-
же во многих других трехмерных задачах вычислительной геометрии.
□ leer пересечения плоскости f(p) = 0 с полиэдром Н — [Р, G}, имеющим список
вершин Р= {/?],...,/>„}, идентичен двумерному аналогу (1.36) с блок-схемой,
изображенной на рис. 1.9, в и применимой с точностью до имени функции:
cross3(f, Р) - {3 1 <j <i<n :f(p,) f(p)<0}. (1.120)
Плоскость пересекает полиэдр, если существует хотя бы одна пара вершин
‘PnPj}, лежащих от нее по разные стороны.
Свойство сепарабельности плоскости позволяет по разным знакам значений
НФ /(р,) и f(p^ обнаружить вершины полиэдра р, и рр лежащие по разные
стороны от пересекающей его плоскости. Если же не найдется ни одной па-
ры разносторонних вершин, то пересечение отсутствует. Функция (1.120)
возвращает 1 как признак пересечения. В отсутствие оного тест возвращает -1,
а при касании полиэдра с плоскостью вершиной, ребром или гранью — зна-
чение 0.
□ Тест выпуклости полиэдра Н - {Р, G}, заданного списками вершин
Р = {pi, ...,р„} и граней G = {G....G,,,}:
conv3(P, G) = {sgn(n/G(side(P, G, i),ру)) = const} V/ = 1, m, j = 1, n: jiGr G 121)
У выпуклого полиэдра нет нн одной пары вершин, лежащих по разные сторо-
ны от любой грани (рис. 1.44, а). Напротив, в невыпуклом полигоне всегда
найдутся грань G, и пара вершин {р,,рА}, находящиеся по разные стороны от
плоскости этой грани (рис. 1.44, б). Свойство сепарабельности плоскости по-
зволяет обнаружить у полиэдра невыпуклую грань 77, = side(P, G, I) по проти-
воположным знакам чисел nfG(JIi,p^ и п/СЩ^р,} в вершинах р^П, и
рк ё IJh не входящих в состав грани 77,.
Наилучший, по мнению автора, алгоритм тестирования выпуклости полиэдра
представлен блок-схемой на рис. 1.44, в и в цикле i = \,m использует два
флажка, сигнализирующих о наличии вершин слева (флажок Г) и справа
(флажок г) от плоскости i-й грани 77 = side(P, G, z). В начале внешнего цикла
обхода граней оба флажка сбрасываем в ноль. Во внутреннем цикле обхода
вершин р} вычисляем значение s - nf G(TI,p^. Вершину сг = 0, лежащую в
82
Глава 1
плоскости грани, пропускаем, а при 5^0 инкрементируем один из флажков:.
при 5 < 0 или г при j > 0. Тут же по условию I • г 0 проверяем наличие любой
пары вершин, лежащих по разные стороны от плоскости грани. Если это ус-
ловие выполняется, то тест немедленно завершается, возвращая 0 как признак
невыпуклости полиэдра. После нормального окончания внешнего цикла пе-
ребора вершин алгоритм convi возвращает значение 1 — признак выпуклости
полиэдра Н.
Рис.1.44
еометрические основы компьютерной графики
83
1.2.2.13. Тесты ориентации точки
относительно полиэдра
Рассмотрим тесты ориентации точки q относительно полиэдра Н = {Р, G}, задан-
-ого списками вершин Р - {pi, и граней G = {Gi,G,,,}.
□ Выпуклый тест
сотЗ _ test (у, P,G) =
-1, если fi < О V/ = 1, т\
1, если 3/ 6 [1, т]: fi > 0;
(1.122)
0, если не ±1
аналогичен плоскому тесту (1.38) и определяет положение точки относитель-
но выпуклого полиэдра с одинаково ориентированными нормалями (например,
всеми внешними) по знакам неявной функции (1.119, <Э)
f=nf G(nh q), где 77, = side(P, G. i).
Все внутренние точки <?Вну лежат с одинаковых сторон от всех граней ГЦ. Для
юбой внешней точки qKHe всегда найдется пара граней 77, и Пр относительно
которых она расположена с разных сторон. Наконец, все точки, не идентифи-
цированные как внутренние или внешние, считаются граничными точками qr?,
расположенными на гранях, ребрах или вершинах выпуклого полиэдра.
Алгоритм выпуклого теста conv3_test функционирует согласно блок-схеме,
показана на рис. 1.45.
Рис. 1.45
84
Глава 1
В соответствии со знаком числа 1, возвращаемого тестом для внешних точек,
назовем внешнее пространство полиэдра положительным. Внутреннее про-
странство будем считать отрицательным по знаку числа -1, возвращаемого ал-
горитмом для всех точек из этого пространства. Все точки на границе полиэдра
(в вершинах, на ребрах или гранях) дают нулевой результат тестирования.
П Габаритный тест
gab3 _ test(q, Р) = {х g [xnlin, xmax ]}U{y Й [vmin, >’nlax ]}U{z g [zmin, zmax ]} (1.123, a)
определяет по возвращаемому значению gab3__test = 1 гарантированную не-
принадлежность точки q произвольному полиэдру Н = {Р, G} путем сравнения
ее координат с габаритными параметрами полиэдра. Тест (1.123, а) легко
обобщается на случай полиэдра со списком вершин Q — {</1,..., q,„\. имеющего
габаритные параметры
= min{</„}, ^.min - min{gf>.}, = min{<7,.},
qxnm - max{qix}, qymax = max{^0.}, = max {<?,.}: (1.123,6)
gab3 _ poly(Q,P) = IJ (k1JIllax < ^min Ю {<7(i)min > ^max })
ШЕ{х,Х,2}
П Лучевой Зй-тест аналогичен плоскому варианту (см. рис. 1.17, г) со следую-
щими изменениями:
• генерируется вектор V е R3 со случайными углами места <р = rnd(2n) и ази-
мута \|/ = rnd(n) (см. рис. 1.1,6);
• по (1.102, б) рассчитываются параметры [г, т, oj и точка с, = ^ + Кг, пе-
ресечения лучаp(t) = q + Vt X/t > 0 с плоскостью z-ой грани П, - side(P, G, i):
• блок проверки условий 0 < т, < 1 заменяется тестом ориентации точки с,
относительно полигона z-й грани. Для /7, в виде параллелограмма это
{О < т, < 1}П{О < Oj < 1}, для треугольника — {0 < 0, < т, < 1}.
В результате получается алгоритм ray3_test(q, Р, G) лучевого теста ориентации
точки q относительно полиэдра Н - {Р, G}, блок-схема которого приведена на
рис. 1.46. В общем случае для проверки принадлежности точки произвольно-
му плоскому полигону применяются 26-тесты ориентации (1.38)—(1.45).
Предварительно выполняется преобразование системы координат так, чтобы
фронтальная плоскость ху совпала с плоскостью полигона. В гл. 2 рассматри-
вается алгоритм MAPI расчета матрицы такого преобразования Ск. В изме-
ненной системе координат x'y'z' становится возможным применять плоские
тесты ориентации. Обозначим результат такого теста ле {-1,0, 1}. Решение
о принадлежности точки полиэдру выносится на основе следующих правил.
Точка не принадлежит полиэдру, если число пар {/, > 0, г, = -1} равно нулю
или четно. Точка лежит внутри полиэдра, если число этих пар нечетно. Точка
принадлежит границе полиэдра, если имеется хотя бы одна пара {/, = 0, л, < 0}.
^метрические основы компьютерной графики
85
хлгоритм ray3_test, использующий 2с1-тест rayl_test, так же возвращает числа
-1,0 или 1 в соответствии с принятым решением о расположении точки. Все не-
достатки плоского лучевого теста присущи и его пространственному аналогу.
Особенно это касается случаев пересечения лучом ребра или вершины полиэд-
ра, когда требуется повторить тест с новым случайным направлением луча V.
Пространственный вариант углового теста отсутствует из-за неопределенно-
;ти геометрического понятия знака телесного угла.
2.2.14. Алгоритмы пересечения в пространстве
“ Пересечение отрезка ab с плоским Зй-полигоном Р.
Когда ищется пересечение не просто прямой с плоскостью, а их частей — от-
резка с полигоном, то параметрическая форма решения (1.102,6) предпочти-
тельнее неявной (1.102, я) благодаря возможности проверки принадлежности
точки q отрезку ab по условию 0 < / < 1, а полигону Р по плоскому тесту ори-
ентации. Последнее тестирование выполняется в измененной системе коорди-
нат. в которой плоскость полигона Р является фронтальной.
Составим алгоритм расчета точки q и параметра t пересечения отрезка ab с
плоским полигоном Р - {р\ ...p„pi}. Алгоритм возвращает через свое имя
iross_side признак пересечения:
• -1 — отрезок и полигон параллельны (не пересекаются) или их плоскости
совпадают (точка пересечения не определена);
86
Глава 1
• 0 — непараллельный отрезок не пересекается с полигоном;
• 1 — непараллельные отрезок и полигон касаются или пересекаются.
В двух последних случаях через аргументы функции возвращаются параметр t
и точка пересечения q.
& cross_side(ab, Р, t, q)
{Н - b-a, V = p2-pi, W = рз-рг,
N=VxW;
если N ° H = 0, то возврат -1;
И направляющие векторы
// нормаль к плоскости полигона
// тест параллельности (1.99)
-а
// расчет параметров пересечения
-W
q = а + Hr,
возврат {О < t < 1 }П{qe Р};
И точка пересечения прямой с плоскостью
И тест пересечения отрезка с полигоном
} О
□ Пересечение отрезка ab с полиэдром Н = {Р, G}, заданным списками вершин
Р = {^i, ...,р„} и граней G = {Gi,..., G„,}.
Требуется отсечь от отрезка те его части, которые находятся вне полиэдра
Здесь мы рассматриваем задачу внешнего отсечения отрезка выпуклым поли-
эдром. Другие виды отсечения обсуждаются в гл. 4.
На рнс. 1.47 приведен алгоритм clip3_cross(ab, Р, G) внешнего отсечения отрез-
ка ab выпуклым полиэдром {Р, G}, основанный на расчете пересечений пря-
мой {а, Ь}, несущей отрезок, с плоскостями граней полиэдра. Он возвращает
через имя сИрЗ_сгол$ признак ориентации отрезка относительно полиэдра:
• 0 — отрезок целиком отсечен полиэдром и находится вне его;
• 1 — отрезок весь или частично расположен внутри полиэдра. Через аргу-
мент ab возвращаются концевые точки не отсеченного полиэдром фраг-
мента отрезка [a, Z?].
Эти точки рассчитываются с помощью табл. 1.1 в зависимости от значений
= tj и С2= tj параметра t, при которых прямая пересекла грани G, и Gj. Две
ячейки {о < 0, 02 > 1} и {о > 1,02 < 0} соответствуют внутреннему положе-
нию отрезка, при котором он не отсекается. В ячейках {oi < 0,02 < 0} в
{oi > 1,02 > 1} формируются отрезки [а, а] и [b,b] нулевой длины, которые
интерпретируются алгоритмом как полностью отсеченные с возвращением
нуля. Остальные ячейки таблицы соответствуют частичному отсечению от-
резка ab и стягиванию его внешних концевых точек на границу полиэдра.
Естественное завершение цикла обхода граней означает, что прямая отрезка
ab либо касается полиэдра, либо не пересекает его вовсе. В обоих случаях ал-
горитм завершается возвращением нуля.
fметрические основы компьютерной графики
87
Рис. 1.47
Возможно и второе решение задачи отсечения отрезка полиэдром с использо-
ванием выпуклого Зб-теста ориентации (1.122). Оно представлено на рис. 1.48
блок-схемой алгоритма clip3_test(ab, Р, G) отсечения отрезка ab выпуклым по-
лиэдром Н = {P,G}. Алгоритм возвращает такие же результаты, что и рас-
смотренный выше алгоритм clip3_cross. Его идейная основа и словесное опи-
сание аналогичны 2<1-варианту clipl_test отсечения отрезка полигоном
•см. рис. 1.19), в связи с чем они здесь подробно не излагаются. Отметим лишь
.'гтичия Зб-алгоритма:
• в цикле с переменной i перебираются грани полиэдра, а не ребра полигона;
• пересечение отрезка ab с i-ой гранью П = side(P, G, i) рассчитывается
функцией cross_side(ab, П, t, q), возвращающей в случае пересечения при-
знак cross_side = 1 и соответствующий параметр t е [0, 1];
• используется определенный в (1.122) Зб-тест conv3_test ориентации точки
относительно выпуклого отсекателя.
Несмотря на то, что алгоритм clip3_test имеет большую трудоемкость в срав-
нении с алгоритмом clip3_cross (дополнительно выполняется от одного до
88
Глава i
трех тестов conv3_test), его идейная основа лучше подходит для решения дру
гих задач отсечения:
• при внутреннем отсечении отрезка выпуклым полиэдром (рис. 1.49, а) от-
бор неотсеченных фрагментов выполняется по условию их внешней ориен-
тации conv3_test(nik, P,G)= 1. Число таких фрагментов может быть от н\
ля (весь отрезок лежит внутри полиэдра) до двух (средняя часть отрезка
экранируется полиэдром);
• при отсечении отрезка невыпуклым полиэдром нужно вместо выпуклого
теста conv3_test использовать лучевой тест ray3_test для определения ори-
ентации средних точек фрагментов относительно произвольного полиэдра
При внешнем отсечении отбираются фрагменты, средние точки которых
лежат внутри полиэдра, а при внутреннем — фрагменты со средними точ-
ками вне полиэдра (рис. 1.49, б).
clipi_test(ab,P,G)
________2L_________ ________1
k=0. l=b-a.L=‘.()li L=sqrt(L) -----------►<*=!...jiz
• ’ * ’ ’ т i=l...size(G) ^-end ► c=cross_side(ab,side(P, G,i),t,q) I- 4 <1 — k=k+l, t —> L <2 —2 Рис.1.48 °4-4Л<\ c —-n a a i /и=а+0.5(Л* + Lk+I)V c = conv3_tesi(m, P,G) — >0 — ab={a+LkV,a+Lk+y } Возврат {c=-l} 1 ft 6
Рис.1.49
~еометрические основы компьютерной графики
89
1.2.3. Квадратичные и параметрические
поверхности
Поверхности второго порядка (квадратичные поверхности) описываются урав-
- ением в неявной форме с векторным аргументом:
Лр)=р Г р7 =0,
де
А Е Q\H
Е В G \ J
Q G С | К
(1-124)
F2, D
ЛТ1 = ^11 . ^12 =/=21-
юрмаль и матрица касательной плоскости в точке ро g f(p) в соответствии с
61, а) и (1.66) равны
- 2(P0Fl 1 + ^21 )>
'?кас = к-А)°'Ч-
(1.125)
Для любой квадратичной поверхности четыре величины
/ = А + В,
/2 =
Е В G A Q
В G С+ Q С
(1.126, а)
h = |Fn|, h = |f]
«ваяются инвариантами относительно преобразований переноса и вращения, а
«ела '2 = И В G J н + D А В J J D Q + н с к К D ’ А Е Н (1.126,6)
О II + Q н с к к D + Е В J Н J D
уть полуинварианты относительно преобразования вращения. Они позволяют
эютро определить тип и каноническое уравнение поверхности по уравнению
124) с помощью табл. 1.3, 1.4.
Таблица 1.3
Л Невырожденные поверхности, Л + 0 Вырожденные поверхности, /4=0
/4 > 0 /4 < 0
/i/з > 0 Мнимый эллипсоид Действительный эллипсоид Точка вырожденного эллипсоида
Центральные поверхности, И /2 > 0 (х/а^+О/й)2 + (с/с)2+ 1=0 (х/а)2 + (у/й)2 + (с/с)2-1=0 (х/д)2 + (у/й)2 + (с/с)2 = 0
/з*0 /i/з < 0 или /2<0 Однополостный гиперболоид Двуполостный гиперболоид (х/а)2-(у/й)2+(с/с)2+1=0 Конус вырожденного гиперболоида (х/а)2 - 0/й)2 +(=1с? =0
Нецентральные Гиперболический параболоид Эллиптический параболоид Цилиндры и пары плоскостей
поверхности, /з = 0 (х/аУ -(y/b)-(z/cf =0 (х/а)2-(у/й)+(с/с)2 =0 (табл. 1.4)
Таблица 1.4
/з' h h > 0 /2<0 /2 = 0
Цилиндры, Д * 0 и rang(F) = 3 Эллиптический (x/a)2 + (с/с)2 -1=0 Г иперболический (х/ст)2 - (с/с)2 -1 = 0 Параболический (х/а)2 + (c/cf =0
Пары плос* костей, rang(F) = 2 Прямая пересечения плоскостей (х/а)2 + (с/с)2 = 0 Пересекающихся (х/а)2-(с/с)2 =0 Параллельных (х/аУ -1=0
/з=0 rang(F) = 1 Совпадающих (х/а)2 = 0
Глава
Геометрические основы компьютерной графики
91
Неявная форма неудобна для построения поверхностей и используется при анали-
зе их свойств по инвариантам и решении задач пересечения методом трассиров-
ки лучей.
Исследуем взаимное расположение квадратичной поверхности {F} с прямой линией
q. И] и с плоскостью {q, V, IV}.
□ Первая задача фактически решена в (1.54)—(1.56). Анализируя варианты ре-
шения квадратного уравнения at2 + 2bt + с - 0 из (1.55) с коэффициентами
а ~ ^11^Т> = 1 + ^21 ХТ> с = ЧГ\ 1(?т + ^-Ч^п + D
и дискриминантом d — Ь2- ас, заключаем:
• при {а*0}А{б/>0} прямая пересекает поверхность в двух различных точ-
ках р\ - q + Vt\ и pi - q + Vti с параметрами
• при {а*0}П{б/ = 0} прямая касается поверхности в единственной точке
р\= q + Vt\ с параметром
-Ь
zi —;
а
• при {а = 0}П{б^0} прямая пересекает поверхность в единственной точке
р\ - q + Vt\ с параметром
-с
Л-----;
1 2b
• при {а = 0}П{/> = 0}П{с = 0} прямая касается нецентральной поверхности в
бесконечном множестве точек;
• в остальных случаях прямая не имеет с поверхностью ни одной общей
точки.
□ Подставим параметрическое уравнение плоскости p(t, т) = q + Vt + Wt в не-
явное векторное уравнение квадратичной поверхности с матрицей F из
(1.124):
(д + Vt + lVr)Ft i(q + Vt + (Vt)T + 2{q + Vt + FTt)^ +0 = 0. (1.127)
После упрощения получим квадратичное уравнение связи параметров / и т в
скалярном или матричном видах
t
at2 + Ьт2 + 2еП + 2gt + 2jx + d=0 и б(/,т)= [г
т]©
(1.128, a)
т
= 0
92
Глава
со следующей симметричной матрицей 0 и коэффициентами a, b, d,e,gu j:
а
0= е
е g
b j
j d.
a = EF1IET, b^WF^W1, d = qFllqr +2qF2}+D,
e = FFuJVT, g=(qFli+F2i)F\ J =(qFll+F2i)WT
(1.128,6)
S
Налицо полная аналогия (1.128) с уравнениями (1.51) квадратичных кривых
на плоскости. Вычислив по (1.126) инварианты h+h и полуинвариант Г-
матрицы О, по табл. 1.2 определим тип кривой пересечения квадратичной по-
верхности с плоскостью:
• действительный эллипс, гипербола и парабола образуются в большинстве
случаев сечения плоскостью криволинейной квадратичной поверхности
(эллипсоида, параболоидов, гиперболоидов, цилиндров и конуса);
• мнимый эллипс и мнимая прямая означают отсутствие пересечений и каса-
ний поверхности и плоскости;
• точка вырожденного эллипса означает касание поверхности плоскостью е
точке;
• две асимптоты вырожденной гиперболы образуются при сечении конуса
плоскостью, проходящей через его вершину;
• две параллельные прямые образуются при сечении цилиндра плоскостью
параллельной его оси;
• одна двойная прямая образуется при касании плоскостью нецентрально?
поверхности.
В тех случаях, когда неявное уравнение в (1.128, а) может быть приведено к
явному виду t = <р(т) или т = \|/(z), возможно получение явных ПФ
/>(т) - ро + Еф(т) + Wz или p(l) = ро + Vt + HAp(z)
пространственных кривых пересечения плоскости с квадратичной поверхно-
стью. Иначе необходимо найти параметрические зависимости t = ф(о) и
т = у(о). Тогда кривая сечения будет описываться ПФ
р(т) = ро + Тф(о) + Bty(o).
Параметрическая форма p(t, z) поверхности второго порядка может быть поле-
чена следующими способами.
□ Заменой аргументов х, у, z канонического уравнения функциями двух пара-
метров (допустим, t и т) на основе известных тригонометрических тождеств
cos2(z) + sin2(z) = 1, ch2(z) - sh2(/) = 1.
Простейший пример — сфера единичного радиуса. Ее каноническое уравне-
ние х2 + у2 + z2 - 1 = 0 допускает, например, подстановки
x(t, т) = sin(z),p(G т) - cos(z)sin(T), z(t, т) - cos(z)cos(t).
еометрические основы компьютерной графики
93
Гораздо более сложен поиск подстановок для произвольного уравнения вто-
рого порядка. Данная задача решается методом геометрических преобразова-
ний канонической поверхности в заданную, с которым можно ознакомиться,
например, в [10, 26, 32].
Л Суперпозицией одновременных движений точки вдоль координатных осей из
определенного начального положения. Например, сложение гармонических
колебаний x(t, т) = sin(z) и z(t, т) = cos(z) вдоль осей х и z с независимым от них
равномерным движением y(t, т) = т вдоль оси у дают боковую поверхность
кругового цилиндра. Если движение вдоль оси у сделать зависимым, например,
y(l, т) = йт, то получим цилиндрическую винтовую линию с шагом 2л й. Деталь-
ное изучение кинематического метода построения параметрических кривых и
поверхностей продолжим в следующих главах.
Эбязательными элементами параметрической формы являются интервалы изме-
-ения параметров гит, необходимые и достаточные для описания точек всей по-
?ерхности или любого ее желаемого фрагмента.
:еалистичное изображение гладкой поверхности на экране дисплея — сложная
ждача, состоящая в передаче ее формы за счет правильного расчета освещенно-
~и видимых точек. Упрощенное построение поверхности заключается в изо-
бражении ее каркаса— совокупности линий, передающих форму поверхности.
Для этого выполняется дискретизация непрерывных параметров
t — to, h, ..., t„, Т = То, Т|,..., т,„,
* организуются вложенные циклы вывода на экран каркасных линий p(t„ т) и
Л г, т7). Пересечение линий дает ячейки треугольной или четырехугольной формы.
Наиболее простое изображение непрозрачной поверхности заключается в за-
крашивании всех точек видимой ячейки постоянным цветом, соответствующим
освещенности усредненной точки ячейки, например, ее центра. Существуют и
более сложные методы закраски поверхностей, некоторые из которых будут рас-
смотрены в гл. 3.
Основные трудности некинематического подхода к составлению уравнений квад-
ратичных поверхностей:
Д невозможность описания единственным векторным уравнением гиперболиче-
ских и двуполостных поверхностей из-за постоянства знака функций ch(z) > О
и р > 0;
□ назначение интервалов изменения параметров, обеспечивающих существова-
ние и единственность поверхности в желаемой области пространства;
Д выбор из множества вариантов функций подстановки, обеспечивающих
вычисление нормали = p't х р'Т к поверхности во всех ее регулярных
точках;
□ неизвестный заранее вид каркасной сетки {p(th T),p(t, Ту)}, выясняемый только
после практического построения поверхности.
94
Глава '
На рис. 1.50 с помощью программы MathCAD построены некоторые квадратич-
ные поверхности из табл. 1.3, 1.4 по их каноническим уравнениям с численным^
значениями масштабных коэффициентов a - \,Ь — 2ис = 3:
Рис. 1.50
П действительный эллипсоид (рис. 1.50, а):
p(z,x)= [asin(Z)sin(x) 6cos(Z) csin(Z)cos(x)]
ze[o, л], те [о, 2л].
(1.129, с.
еометрические основы компьютерной графики
95
Как пример неудачной подстановки приведем другую модель эллипсоида
cos(t) bt с
sin(x)
(1.129,6)
ze [-1,1, те [о, 2л],
у которой частная производная
-aZ cos(t) -ct sin(x)
----z— ----1
не вычислима в точках [о +Ь о] при t = ±1, хотя нормаль
2V(z,t) =
- bc^l-t2 cos(t) act at
sin(x)
существует во всех точках поверхности эллипсоида, а при t = ±1 вычисляется
вручную разрешением неопределенности типа 0/0;
□ однополостный гиперболоид (рис. 1.50,6):
/>(z,t)= [ach(/)sin(r) 6sh(z) cch(z)cos(x)]
ze (—°o,°o), те [о, 2л]; (1.130)
71 двуполостный гиперболоид (рис. 1.50, в) с матрицей
F = diag
1_
2
-1
Ь2
описывается двумя параметрическими функциями верхней (+) и нижней (-)
полостей:
р(г,т)= [ash(Z)sin(T) ±Ach(z) csh(Z)cos(T)]
ze [0,oo), те [0,2л];
□ эллиптический конус (рис. 1.50, г):
p(z,t)= [az sin(T) bt cZcos(t)]
ze (—°0,00), те [о, 2 л];
(1.131)
(1.132)
□ седловая поверхность гиперболического параболоида (рис. 1.50,6) наиболее
удачно описывается в параметрической форме как
р(/, т) = [az sin(T) - bt2 cos(2t)
ze [0,°o), те [0,2л].
(1.133, a)
96
Глава
В учебниках и справочниках [13,26] ошибочно приводятся параметрически
модели гиперболического параболоида типа
p(z, т) = [az сЬ(т) bt2 cZsh(x)]
/ е (-оо, °°), те (-«>, °°),
описывающие его поверхность только в половине пространства. Правильна
было бы составить отдельные выражения для верхних и нижних полосте
(рис. 1.50, е):
azch(x) bt2 cZsh(T)j — верхние правая илевая,
] (1.133, с
aZsh(x) -bt cZch(T)] — нижние передняя изадняя.
Эти полости соединяются друг с другом на вычислительно недоступных (Z —> ±=с
асимптотических прямых |х/«| = |z/c|, что не позволяет изобразить всю повер'
ность как единое целое. Следовательно, модель гиперболического параболоид.
(1.133, б) во всем проигрывает модели (1.133, я) и является неверной;
П эллиптический параболоид (рис. 1.50, ж):
p(z,x)= [aZsin(T) bt2
/е[0,°°), те [0,2 л];
ct cos(t
(1.13-
П эллиптический цилиндр (рис. 1.50, з):
р(/,т)= [asin(T) bt ccos(t)]
ze (-moo), те [о, 2л];
П параболический цилиндр (рис. 1.50, и)\
p(z,T)=[aT bt ст2]
z е (—о°, оо), т е (—°°, оо).
& Пример 1.5. Классифицировать поверхность, описываемую неявным урав
нением
f (х, у, z) = 2х2 + у2 - 3z2 + xz - 2у + z - 1 = О,
и линию пересечения этой поверхности с плоскостью, заданной отрезками /гч = 3
hy.= 2 и h. — 1, отсекаемыми ею на осях координат.
Решение. Составим по (1.124) матрицу поверхности и вычислим ее инварианты:
F = ’4010 0 2 0 -2 10-61 0 -2 1 -2
h = 0, Z2 = 4 0 0 2 + 2 0 0 -6 + 4 1 1 -6 = -29,
4 1 /3=2 5 1 -б 50, Z4 = И = 192.
По классификации, приведенной в табл. 1.3, это соответствует поверхности о<-
нополостного гиперболоида, плоскими сечениями которого могут быть эллипс
парабола или гипербола.
еометрические основы компьютерной графики
97
Сформируем по (1.74, б) параметры описания плоскости
Ро = [3 0 о], К = [-3 2 0], JK = [-3 0 1]
и вычислим коэффициенты квадратного уравнения (1.128):
a = 44, b = 24, е = 33, g = 40, j = 32, d = 34.
По его инвариантам
Л = 68 > 0, h = -33 < 0, h = -98 < О
: помощью табл. 1.2 определяем, что линия пересечения является гиперболой,
описываемой неявным уравнением
22/2 + 12т2 + 33/т - 40Z - 32т +17 = 0.
Задав величину ЛЛ = 4, мы получим в сечении гиперболоида плоскостью параболу
; уравнением
36г2 + 25т2 + 60zt - 68г - 59т + 31 = 0
и инвариантами
1\ = 122 > 0, h = 0, h = -392 < 0.
При hx = 5 сечение дает эллипс
54г2 + 42т2 + 95zt -104г- 94т + 49 = 0
с инвариантами
Л = 192 > 0, h = 47 > 0, h = -768 < 0. □
27 Пример 1.6. Построить тень каркаса пирамиды с вершинами
Р1=[з 4 -1], р2=[1 4 2], р3=[5 3 2], р4 = [2 2 о]
ча поверхности эллипсоида с полуосями г, = 2, ry = 1, г. = 3 и центром в точке
-=[-2 1 -2]. Источник света удален в бесконечность в направлении
1=[4 2 1] (рис. 1.51).
ешение. По каноническому уравнению эллипсоида из табл. 1.3 и заданным па-
раметрам получим неявное уравнение
А2
У-су
2
-1 = 0 => 9х2 + 36у2 + 4z2 + 9х - 18j + 4z + 52 =0,
> по (1.124) следующую матрицу Fи ее блоки:
9 0 0 18 '
0 36 0 -36
0 0 4 8
18 -36 8 52
0 36 0
0 0 4
18
, F2)=[18 -36 8],Z) = 52.
9 0 0
98
Глава 1
Рис. 1.51
Так как в квадратном уравнении (1.55) коэффициент
a(p) = LFnLT = 292*0
не зависит от расположения точки р, то пересечение луча р- Lt с квадратичной
поверхностью определяется знаком дискриминанта d(p) = ЬЦр) - а(р) с(р) с ко-
эффициентами
Ь(р) = -(рЛ 1 + ^21Х-Т = -8 - 34х - 72j> - 4z,
с(р) = pF\iPJ +2pFi\ +D=9x2 +36y2 + 4z2 + 36*-Uy + 16z +52 .
Вычислим дискриминанты и действительные точки тени для четырех вершин
пирамиды
, . 6(A)+ , w. —Л.
P,=Pi+------—------6 V/ = l,4:
«(А>
b(pi) = -400, c(pi) = 517, d(pi) = 9036 > 0 => р{ =[-1.177 1.911 -2.044];
b(pi) - -376, c(pi) = 496, t/(p2) = -3456 < 0;
6(рз) = -412, с(рз) = 613, d(pi) = -9256 < 0;
Ь(рГ) = -224, f(p4) = 160, = 3456 > 0 => p\ = [-0.263 0.868 -0.566].
Отрицательные значения d(pi) и d(pi) означают, что лучи, проходящие через
вершины pi и рз, не пересекаются с поверхностью эллипсоида. Следовательно,
ребра пирамиды pi pi, р\ рз, pipy Pi pt и рз pt, инцидентные этим вершинам, не
могут полностью проецироваться на поверхность. □
В общем случае тень прямолинейного отрезка р,р} на криволинейной поверхно-
сти может быть одной линией, разрываться на несколько линий или вообще от-
сутствовать. Концы отрезка могут не иметь тени, а внутренние его точки могут,
“"еометрические основы компьютерной графики
99
например, ребро pi рз. Предлагается следующий численный метод расчета криво-
тнейной тени каркасного объекта, ребра которого в общем случае — криволи-
нейные отрезки. Метод гарантирует достоверное построение тени каркасного
объекта на произвольной квадратичной поверхности, а при достаточно частой
дискретизации ребер — гладкость изображений криволинейных теней.
Шаг 1. Ребра каркаса разбиваются на достаточно малые прямые отрезки.
Шаг 2. Для каждого отрезка вычисляются дискриминанты его концов и dj.
Шаг 3. Если {dj > 0}Г| {dj> О}, то по (1.56, а) рассчитываются ближайшие к источ-
нику света точки
, bj+y[dj , bj+-Jdj
Pi = Pi +---Pj=Pj+------------L
at aj
пресечения лучей pt-Lt и Pj-Lt с квадратичной поверхностью. В противном
.лучае тень отрезка отсутствует.
Шаг 4. Рассчитывается изображение отрезка прямой p'jp'j на экране дисплея. О
1.3. Основные задачи
геометрической оптики
Построение компьютерного изображение трехмерных объектов и сцен основано
-л методе трассировки лучей, моделирующем процесс распространения световых
лучей от момента их испускания источниками до взаимодействия с объектами
сцены и попадания в приемник. Основная идея метода сводится к повторению на
ЭВМ всех геометрических преобразований, которые бы совершил световой луч
.ч а пути источник — объект — приемник (глаз наблюдателя). Хотя действитель-
-ых лучей бесконечно много, обычно ограничиваются трассировкой выбороч-
-ых лучей, достаточных для достижения желаемой реалистичности изображения
-лены— совокупности объектов и окружающего их интерьера. Например, для
•'зображения полностью видимого отрезка прямой линии достаточно проведе-
-ия всего двух лучей через его концевые точки. Расчет тени отрезка на криволи-
-ейной поверхности требует проведения большого числа лучей через внутренние
очки отрезка. Эти точки должны быть выбраны с такой дискретностью, чтобы
оманая линия (изображение тени отрезка) выглядела гладкой дугой.
Ключевая задача метода трассировки лучей — определение освещенности произ-
=ольной точки поверхности и части световой энергии, содержащейся в отражен-
-ом и преломленном лучах. Освещенность создается первичной энергией источ-
-иков света и вторичной энергией лучей, отраженных от других объектов сцены.
Отсутствие освещенности означает затененность точки. Существование и интен-
сивность вторичной энергии определяются оптико-механическими свойствами
материалов— прозрачностью, цветом, шероховатостью и отражательной спо-
собностью поверхности.
100
Глава 1
Для каждого луча решается задача пересечения с объектами сцены. Распростра-
няясь прямолинейно, луч либо проходит мимо всех объектов и покидает про-
странство сцены, либо пересекает первый встретившийся на его пути объект.
В точке пересечения часть световой энергии поглощается материалом поверхно-
сти, а оставшаяся часть энергии первичного падающего луча претерпевает рас-
щепление на вторичные лучи — отраженный и преломленный. Соотношение по-
глощенной, отраженной и преломленной энергий луча определяется большим
числом факторов. Это и физико-механические, и оптические свойства материала
поверхности, и ее ориентация в пространстве, и спектральный состав луча, и
т. д., и т. п.
Каждый из вторичных лучей распространяется до пересечения со следующей по-
верхностью, порождая третичные лучи, и т. д. Любое взаимодействие с поверх-
ностью уменьшает суммарную энергию отраженных и преломленных лучей. По-
глощение энергии происходит также при распространении луча в не абсолютно
прозрачной среде. Таким образом, через определенное число столкновений с по-
верхностями объектов интенсивность луча становится меньшей некоторого по-
рогового значения и отслеживание процесса его распространения прекращается.
Абстрагируясь от волновой природы оптического излучения, будем руково-
дствоваться законами геометрической оптики [16]: прямолинейности распростра-
нения луча в однородной среде (принцип Ферма), отражения, преломления и об-
ратимости хода светового луча. Наибольшую сложность расчета взаимного
положения луча с произвольной поверхностью имеют задачи пересечения, отра-
жения и преломления. Рассмотрим в общих чертах содержание и алгоритмы ре-
шения задач геометрической оптики.
1.3.1. Пересечение луча с поверхностью
Принцип прямолинейности распространения света в однородной среде позволя-
ет построить алгоритм расчета пересечения луча с ограниченной поверхностью,
изображенной на рис. 1.52.
Рис. 1.52
еометрические основы компьютерной графики
101
& Шаг 1. Рассчитываются все точки q'j пересечения луча
p(t) = q + Vt, t > О
: неограниченной поверхностью. Для этого решается скалярное уравнение
f(q + Vt) = О
относительно параметра t, если поверхность задана в НФ уравнением f(p) = 0.
Если она определена параметрической функцией р(т, 6), то решается векторное
•равнение
q + Vt = р(т, 6)
относительно трех параметров t, т и 6. Отсутствие действительных решений t
означает, что несущая луч (/) прямая не пересекает поверхность.
Шаг 2. Список полученных точек <?' сортируется по возрастанию значений th и
«з него исключаются элементы с Z, < 0, не принадлежащие лучу. Если оставшийся
писок пуст, то луч (2) не пересекает поверхность.
Шаг 3. Ищется ближайший к началу списка элемент, для которого выполняются
оловия у(<?')>0 или у{т„ 6,} > 0 принадлежности точки <?' ограниченной по-
зерхности. Невыполнение любого из этих условий означает, что луч (3) не пере-
текает поверхность внутри ее границ. Найденный элемент является искомой точ-
«ой q' на луче (4). □
Рассмотрим вычислительные аспекты расчета пересечения прямой с поверхно-
стью. Точное аналитическое решение уравнений f (q + Vt) = 0 или q + Vt = р(т, 6)
зчззможно лишь для некоторых простейших поверхностей первого (плоскость в
НФ или ПФ) и второго (в НФ) порядков. Эти решения получены в (1.102) и 3d-
зарианте (1.54)—(1.56). Пересечение луча q + Vt с более сложными поверхностя-
ми находится численными методами. Рассмотрим некоторые из них.
Корни скалярного уравнения f(q+ Vt) - 0 можно найти любым известным чис-
*енным методом решения нелинейных уравнений [13, 19]: проб, касательных,
:екущих, итераций и т. п. Простейший для программирования и не требующий
зачисления производной d f I At метод проб заключается в трассировке луча от
течки q в направлении вектора Vс шагом Az. В точках траектории
Pi = q + Vt, = q + iVM, i = 0, 1, 2,...
-еявная функция поверхности имеет значения f=f(pd Первый же найденный
нтервал [l„ z,+,], на котором выполняется условие ff-ц < 0, пропорционально
дробится точкой
(0) = lz+ik +lzk/+i
1ФЫ
са два интервала [t„ т(0)] и [т(0>, /,+,]. Из них выбирается интервал [z',z-+]] с разно-
дачными концевыми значениями НФ, для которых /(z,')/(z'+1) < 0. Дихотомиче-
102
Глава
ский процесс дает последовательность значений {т<Л>} и заканчивается при дос
тижении желаемой точности е по аргументу |т,Л+|> - т<*>| < е или (и) функци,
|/(т<Л+|>)-/(т<*))| < е.
Основные проблемы метода:
П компромиссный выбор шага Аг: достаточно малого, на котором не будет че^
ного числа пересечений лучом поверхности, ограничивающей малый объем,
в то же время достаточно большого для получения приемлемого машинног
времени расчета;
П необходимость ограничения пространства распространения луча габарит
сцены на случай, если пересечения не существует.
Параметрическая форма поверхности р(т, 6) не имеет такого индикатора пересе-
чения ее лучом, каким в НФ является инверсия знака функции f(p). Будем искап
в пространстве параметров 1, т и 6 корни уравнения q + Vt = р(т, 0), доставляю-
щие нулевое значение целевой функции
J(t, т, 6) = \q + Vt -р(т, 6)|2 > О,
т. е. квадрату расстояния между лежащими на одной вертикали точками луча »
поверхности.
Алгоритм МНК-решения задачи минимизации J(t, т, 6), стартуя с начальны-
приближений to = 0, то и 6о, обновляет параметры по итерационной формуле
k+i L+1 е/+1]=к Ь 6,] + [Л/, Лт, Л6,], г = 0, 1,2,... (Ы37)
Различные методы оптимизации отличаются способами расчета вектора обнов
лений [Л/, Лт, Л6, ]. Метод градиентного спуска полагает
[Л/, Лт, Ле,]=-у,ГД/„т„е,) (1.138, л
и имеет скорость сходимости, зависящую от выбора шага настройки у„ что само п
себе представляет нетривиальную задачу. Квадратичной скоростью сходи мост
обладает метод линеаризации, заключающийся в замене по (1.61,6) поверхности t
текущей точке р(т„ 0,) касательной плоскостью р(т„ 6,) + 1^Лт, + И<Л6„ расчете пс
(1.102, б) вектора обновлений и нового приближения точки пересечения
V
[Л/, Лт, Ле/]=(р(т,,е,)-<7-Иг,) -К,-
-Wi
=> р,+| = р, + VM, (1-138, б
до сходимости по аргументу ||А/, Лт, Л0, ]| < е или (и) функции J(/„ т„ 0,) < е
Большое число поверхностей являются периодическими по одному или обою-
параметрам т и 6. Например, если период т функции р(т, 0) по параметру т раве-
2л, то
р(т, 6) = р(у + тк, 0) VA- = 1,2,...
' еометрические основы компьютерной графики
103
Формула обновления (1.137) может вывести параметр за допустимый интервал
О < Tmin < т < Ттах < т. Во избежание потери решения на третьем этапе алгоритма
пересечения, где проверяются условия допустимости параметров ш(тп„ 6п,) > О,
необходимо после каждого обновления сдвигать значение т,+! на целое число
периодов по формуле
т,+1 = mod(mod(T,+1, ш) + т, т) е [0, т). (1139)
Итерационные методы оптимизации являются локальными (сходятся к локаль-
ному минимуму J(t, т, 6), причем необязательно нулевому), в связи с чем требует-
ся выполнить несколько расчетов с различных начальных значений то и 6о, на-
пример, равномерно распределенных в областях их допустимых значений.
Полученные решения группируются на прямой q + Vt в окрестностях точек ее
пересечения с поверхностью. Далее выполняется сортировка, описанная во вто-
ром и третьем шагах алгоритма пересечения.
Пример 1.7. Из точки q = [10 1 о] выпущен луч p(t) = q- Vt в направлении,
задаваемом вектором V = [-2 -0.1 -0.2]. Рассчитать пересечение луча с по-
верхностью, описываемой явным уравнением
у = f(x,z)=e~a^x +z ^cos(coxx)cos(cozz)
с параметрами а = 0.02, а. = 1 ио. = 0.5 (рис. 1.53, а).
Решение. Так как уравнение поверхности задано в явной форме, будем решать
задачу пересечения как задачу поиска корней функции
h(t) = y(t)-f(x(t),z(t)) = 1 -0.1z-/(10-2z,-0.2z)
зависимости вертикального расстояния от точки p(z) = [x(z) y(t) z(z)] до по-
верхности. Из ее графика, приведенного на рис. 1.53, б, видно, что луч пересекает
поверхность в пяти точках. Ввиду некоторой сложности расчета производной
d/i / dz зададим шаг трассировки луча AZ = 0.1, допустимую погрешность е = 10”
и выполним поиск первой точки пересечения методом проб.
Реализация метода в среде MathCAD показала, что необходимо выполнить 45 ша-
гов трассировки для достижения интервала Z е [4.5,4.6] с разнозначными значе-
ниями Л(4.5) = 0.0808 и /?(4.6) = -0.066. Пропорциональное дробление этого ин-
тервала еще за 4 итерации дало параметр пересечения Zi = 4.553155 с абсолютной
погрешностью |/?(Zi)| = 5.208 • 10” < 10” и точку
</= [0.8936 0.5447 -0.91 Об].
Заметим, что половинное дробление интервала [4.5, 4.6] с той же погрешностью
потребовало бы 14 итераций. Задание слишком большого шага трассировки
Az> 1.1 приводит к пропуску первых двух ближайших точек пересечения луча с
поверхностью и получению сразу третьей точки <73 = [-0.9861 0.4507 -1.098б]
с параметром Z3 = 7.678274. □
104
Глава '
& Пример 1.8. Рассчитать пересечение луча, выпущенного из точю
q = [-8 0 8] в направлении V = [4 0.5 -4], с параметрической поверхностьк
(рис. 1.54, а)
р(т,0)= [(1 + т-sin(x))cos(6) 1 -cos(x) -(т -sin(x))sin(0)]
V0.1л<т< 1.4л. 0<0<1.5л.
Решение. Луч р(/) = [-8 + 4/ 0.5/ 8-4/], />0, пересекает поверхность р(т, 0) в
трех точках. Найдем их методом линеаризации (1.137) и (1.138,6), минимизируя
целевую функцию
J(t, T,Q) = \p{t)-p(T,Q)Y
с начального приближения /о = 0 и девяти сочетаний начальных приближений
то е {0.1л, 0.75л, 1.4л}, Оо е {0,0.75л, 1.5л}.
На рис. 1.54,6 изображены пространство параметров т и 0, допустимая область
их изменения, начальные приближения {то, Оо} и результаты сходимости алго-
ритма линеаризации с погрешностью е = 106:
□ приближения {0.1л, 0} и {1.4л, 0} дают сходимость к точке qx с параметрам
/1 = 3.061, ti = 1.322л, 01 = 0.25л;
□ приближение {0.75л, 0} дает сходимость к точке qi с параметрами ti = 2.307.
Т2 = 0.549л, 02 = 0.25л;
□ приближение {0.1л, 0.75л} дает лишь относительную сходимость к парамет-
рам / = 5.911, т = 7.128л, 0 = 0.25л и ненулевому установившемуся значению
J — 3.827 * 0, в связи с чем этот вариант в список анализа не включается;
Геометрические основы компьютерной графики 105
□ приближения {0.75л, 0.75л} и {0.75л, 1.5л} дают сходимость к точке q\ с па-
раметрами Гз = 1.744, тз - 0.459л, Оз = 1.25л;
□ приближение {1.4л, 0.75л} дает сходимость к точке q4 с параметрами
Га = 2.07, Т4 = -0.511л, 64 = 0.25л;
□ приближение {0.1л, 1.5л} дает сходимость к точке q'5 с параметрами
is = 1.917, is = -0.487л, 0s = 1.25л;
□ приближение {1.5л, 1.5л} дает сходимость к точке q'f, с параметрами
Ге = 0.732, те = 1.719л, бе = 1.25л.
Рис. 1.54
Таким образом, сортируя точки q' по возрастанию параметра /, > 0, получим
упорядоченный список точек L = {q'^, q'^, q$, q4, q'z, q{}, расположенных на луче
q + Vt в порядке удаления от начала луча — точки q.
106
Глава 1
На третьем этапе исключим из списка L точки, параметры которых не удовле-
творяют условиям 0.1л <т< 1.4л и 0<0< 1.5л. Это, во-первых, точка % пере-
сечения луча с продолжением поверхности при те > 1.4л, изображенной
на рис. 1.55,а для интервалов параметров 0<т<3.4л и 0<0<2л. Во-вторых,
это точки и с отрицательными значениями т. Первая в оставшемся спи-
ке точка
<73 = <7 + 1.744И = [-1.026 0.872 1.02б|
и является точкой q' пересечения луча с заданной поверхностью. На рис. 1.55, б
изображены графики итерационных процессов поиска параметров г„ и 0,. □
Рис. 1.55
1.3.2. Отражение луча от поверхности
Зеркальное отражение луча от поверхности (рис. 1.56) строится по следующим
законам отражения.
□ Отраженный луч q' + Mt находится с той же стороны поверхности, что и па-
дающий луч q + Vt,a эти два луча лежат в одной плоскости с вектором норма-
ли N, построенным в точке пересечения прямого луча с поверхностью q’.
□ Равенство скоростей падающего и отраженного лучей: |Р] = |М|.
□ Равенство углов падения а и отражения р.
Найдем нормальную и тангенциальную составляющие падающего луча:
Кк = РГА' V = |K|cos(ZPW)/V = |К|(Ё о N)N = (И о N)N,
Иц =Г-ГХ = K-(KoAf)Af.
Геометрические основы компьютерной графики
107
Рис. 1.56
На основе законов отражения вычислим составляющие и сам вектор отраженно-
го луча:
ml = -r± = -(r<>jv)/v, л/ц = r-(r<>jv)/v,
. (1.140)
М = М± +Л/|| =Г-2(Го NJN.
Таким образом, алгоритм расчета отражения луча от зеркальной ограниченной
поверхности имеет следующий вид.
Шаг 1. Решается задача пересечения луча q + Vt с ограниченной поверхно-
стью. Если точка q' отсутствует, то луч проходит мимо поверхности.
Шаг 2. По (1.61), (1.62) вычисляется нормаль N к поверхности в точке q'.
Шаг 3. По (1.140) находится направляющий вектор М отраженного луча q' + Mt. □
1.3.3. Преломление луча на поверхности
Идеальное преломление луча на поверхности раздела двух сред с показателями
преломления ш и ш (рис. 1.57) строится по следующим законам преломления.
□ Преломленный луч q’ + Rt находится с другой стороны поверхности, чем па-
дающий луч q + Vt, а эти два луча лежат в одной плоскости с вектором норма-
ли N, построенным в точке пересечения прямого луча с поверхностью q'.
Рис. 1.57
108
Гпава 1
□ Скорость распространения луча в каждой среде обратно пропорциональна ее
показателю преломления. Отсюда следует соотношение длин векторе.
|Л| = Лп| V], где пП = nt / т — относительный коэффициент преломления.
□ Углы падения а и преломления у удовлетворяют закону Снеллиуса—Декарта
msin(a) = n2sin(y). (1.141
Вычислим нормальную и тангенциальную составляющие вектора преломленног:
луча:
I = |/?|sin(y>f| = ^|r|sin(a)lf | = (ko7v)v),
откуда следует вектор
у
R = Rl +/?||=ипИ +лп sgn
|2 —
- nnV <>N N ,
(1.142
Существование преломленного луча в среде с меньшим показателем преломле-
ния П2 < т (например, при переходе из воды в воздух) возможно при положи-
тельности подкоренного выражения в (1.142), что совпадает с известным в опти-
ке неравенством [16]:
|И|2-«п|их//|2 > 0 => |К| > лп|гxn| => 1 > лп sin(a).
(1-143)
При падении луча на оптически менее плотную среду под углом a>arcsin(l I пп)
наблюдается оптический эффект полного внутреннего отражения, при котором
преломленный луч отсутствует.
Таким образом, алгоритм преломления луча на ограниченной поверхности разде-
ла сред имеет следующий вид.
£7 Шаг 1. Решается задача пересечения луча q + Vt с ограниченной поверхно-
стью. Если точка q' отсутствует, то луч проходит мимо поверхности.
Шаг 2. По (1.61), (162) вычисляется нормаль Nk поверхности в точке q'.
Шаг 3. Если не выполняется условие (1.143), то преломленный луч отсутствует.
Шаг 4. По (1.142) находится направляющий вектор R отраженного луча q' + Rt. CZ
I& Пример 1.9. Из точки q = [б 0 0] воздушной среды (m » 1) выпущен луч в на-
правлении V = [-4 О 1J. Найти точку его пересечения со стеклянным (пг » 1.52)
эллипсоидом, имеющим полуоси гд-— 1, гу = 2, г. = 3 и центр в точке с = [о -1 -1].
а также направления отраженного и преломленного лучей (рис. 1.58).
геометрические основы компьютерной графики
109
Решение. Составим неявное уравнение f{x,y,z) = 0 и матрицу F эллипсоида по
его каноническому уравнению из табл. 1.3:
+ -1 = 0 => 36х2 + 9^2 +4z2 + 18_р + 8z - 23 = О,
I rz J
F = 36 0 0 0 9 0 0 0 4 0 ' 9 4
0 9 4 Г-23_
36
9 0 , F21=[0 9 4], D = 23.
0 0
0 4
Вычислим коэффициенты и дискриминант квадратного уравнения (1.55):
a = 580, b = -860, с = 1273, <7 = 1260.
Так как {а * 0}П {d > О}, то прямая p(t) = q+ Vt пересекается с поверхностью эл-
липсоида в двух различных точках с параметрами
-b-qd , -b + yjd ,
/, =---— = 1.422, t2 =-------= 1.544 .
a a
Ближайшая к источнику точка пересечения имеет координаты
q = [0-314 0 1.422].
Для расчета отраженного и преломленного лучей вычислим по (1.61, а) вектор
нормали в точке падения:
N = [72x' 18/+ 18 8z'+8]= [22.59 18 19.37].
На рис. 1.58 этот вектор, имеющий длину |7V] = 34.78, изображен для удобства в
четыре раза короче.
Рис. 1.58
110
Глава 1
По (1.140) и (1.142) определяем векторы направлений отраженного и преломлен-
ного лучей, предварительно вычислив значения
пп =1/1.52=0.658, 77=[0.65 0.518 0.557], Г <>77 = -2.041 <0,
VxN =[-0.518 2.878 -2.07], |их77| =3.582 , |г|2-^|их77|2 = 11.445 >0:
A/ = r-2(r°7v)v = [-l-348 2.113 3.274],
R = n^y-n„
\2 +ппУ ° N N = [-2.603
-0.695 -0.315]. □
1.3.4. Прямая и обратная трассировка лучей
На основе закона обратимости можно построить путь светового луча как в пря-
мом направлении от источника L к объекту и от него в приемник S, так и в об-
ратном — от приемника к объекту и источнику. Каждый из методов трассиров-
ки лучей моделирует соответствующий процесс распространения света и имеет
свои отличительные черты.
В методе прямой трассировки генерируется пучок лучей L + V\t, выходящих из
источника во всевозможных направлениях У\, Уг,... На рис. 1.59 показаны вари-
анты распространения лучей в сцене, включающей отражающие, преломляющие
и поглощающие свет объекты.
Рис. 1.59
Большинство лучей, испущенных источником, не попадает в приемник, а значит,
и не влияет на формируемое в нем изображение. Лишь очень малая часть лучей
Геометрические основы компьютерной графики
111
после всех отражений и преломлений в конце концов попадет в приемник, созда-
вая изображение сцены в его рецепторах. На шероховатых поверхностях возни-
кает множество диффузно отраженных лучей. Все их нужно программно генери-
ровать и отслеживать, что лавинообразно увеличивает сложность задачи
трассировки.
Прохождение луча в неидеальной среде сопровождается рассеянием и поглоще-
нием световой энергии на ее микрочастицах. Эти физические процессы чрезвы-
чайно сложно адекватно моделировать на ЭВМ с ее конечными вычислитель-
ными ресурсами. Практически ограничиваются применением коэффициента за-
тухания энергии луча на единицу пройденного им расстояния. Аналогично вво-
дятся коэффициенты уменьшения энергии луча при его отражении и преломле-
нии на поверхности раздела сред. С учетом этих коэффициентов отслеживается
уменьшение энергии всех первичных и вторичных лучей в процессе их блужда-
ния в пространстве сцены. Как только энергия некоторого луча становится
меньше заданного абсолютного уровня или уменьшается в заданное число раз,
трассировка данного луча прекращается.
Таким образом, главным недостатком метода прямой трассировки является его
большая трудоемкость и малая эффективность. При реализации данного метода
большая часть работы по расчету пересечений лучей с объектами оказывается
проделанной впустую. В следующем разделе предпринимаются некоторые по-
пытки сокращения числа рассматриваемых прямых лучей путем решения урав-
нений, полученных на основе законов оптики и моделей поверхностей.
После недолгих размышлений становится ясно, что для отсекания лучей, не по-
павших в приемник, достаточно рассматривать наблюдателя .S’ в качестве источ-
ника обратных лучей В соответствии с методом обратной трассировки проложим
трассу луча S + Vt в направлении V от точки .S’ к какой-нибудь точке на поверх-
ности некоторого объекта (рис. 1.60, а). По вышерассмотренным методикам рас-
считываются вторичные, третичные и т. д. лучи.
Рис. 1.60
112
Глава 1
В результате для каждого первичного луча строится дерево трассировки
(рис. 1.60, б), ветви которого составляют вторичные лучи. Ветвление трассы за-
канчивается, когда луч (7) выходит за пределы сцены или (2) встречается с не-
прозрачным телом, поглощающим свет, или (5) попадает в источник света, или
(4) когда его интенсивность падает ниже порога чувствительности, или, наконец.
(5) когда число расщеплений первичного луча становится слишком большим для
имеющихся машинных ресурсов. В результате прямая световая энергия (цвет и
интенсивность), попавшая в приемник из направления V, слагается из энергий
терминальных вершин дерева с учетом их потерь при распространении в оптиче-
ских средах.
Метод обратной трассировки фактически аккумулирует все лучи, в действитель-
ности приходящие в приемник из определенного направления независимо от и.\
начала. Это позволяет видеть и изображать на экране:
□ непрозрачные объекты, поглощающие обратные лучи;
□ прозрачные объекты, через которые благодаря преломлению наблюдателю
видны другие объекты;
□ отражения объектов на зеркальных поверхностях, в том числе и блики, соот-
ветствующие попаданию обратных лучей в источник света;
□ тени, образующиеся в точках поверхности, заслоненных от источника други-
ми объектами;
□ другие разнообразные оптические эффекты.
Количество "зондирующих" обратных лучей, подвергаемых трассировке, огра-
ничено числом точек на поверхностях объектов сцены, видимых из точки .S’ и
перебираемых с конечным шагом пространственного квантования, обусловлен-
ным разрешением экрана. Благодаря этому объем вычислительных затрат в ме-
тоде обратной трассировки существенно уменьшается по сравнению с методом
прямой трассировки. Возможно разумное комбинирование двух методов трасси-
ровки для оптимизации алгоритмов и снижения их трудоемкости.
Очевидно, что трассировка лучей носит характер рекурсивной процедуры, кото-
рая будет сама себя вызывать, как только выяснит, что анализируемый луч от-
ражается или преломляется. Ббльшая часть вычислений при реализации методов
трассировки приходится на расчет пересечений лучей с поверхностями, в связи с
чем они применяются для изображения оптических эффектов в сценах с неболь-
шим числом объектов.
1.3.5. Лучевые методы построения
оптических эффектов
Применим методы прямой и обратной трассировки лучей для решения задач по-
строения оптических эффектов: тени, отражения и преломления. Сразу отметим
Геометрические основы компьютерной графики
113
некоторые геометрические и вычислительные особенности, порождаемые нели-
нейностью поверхности, на которой строится оптический эффект:
□ эффект может быть фрагментарным, т. е. созданным не всеми точками объек-
та, а лишь теми, в которых выполнены все условия существования эффекта на
некотором участке поверхности;
□ эффект непрерывного объекта может быть разрывным, когда тень от двух
близких точек объекта падает на разные участки поверхности, удаленные
друг от друга в силу ее криволинейности и самоэкранирования;
□ эффект одной точки может быть множественным, когда его видно не в одной,
а в нескольких точках поверхности, где одновременно выполнены все условия
существования эффекта;
□ большинство численных методов решения нелинейных уравнений имеют ло-
кальный характер сходимости, а результат их работы зависит от выбора на-
чальных приближений неизвестных. Следовательно, для получения достовер-
ного результата— всех и именно тех точек поверхности, в которых
наблюдается эффект, — необходимо выбирать начальные приближения в ок-
рестности сходимости к глобальному (нулевому) минимуму целевой функции.
С учетом первых трех геометрических особенностей становится ясно, что
глобальных минимумов целевой функции может быть несколько.
Таким образом, качественный алгоритм построения оптического эффекта на
нелинейной поверхности должен быть способен:
□ выполнять декомпозицию объекта на множество не связанных между собой
точек, каждая из которых обрабатывается независимо от других;
□ генерировать вычислительный процесс с множества различных начальных
приближений неизвестных параметров. Период пространственной дискрети-
зации (расстояние между элементами этого множества) выбирается на основе
Зб-аналога теоремы Шеннона—Котельникова, т. е. так, чтобы узлы дискре-
тизации оказались во всех возможных областях притяжения минимумов целе-
вой функции;
□ накапливать достоверные решения и отбрасывать недостоверные, достав-
ляющие целевой функции локальный, а не глобальный минимум;
□ фильтровать накопленный массив решений, т. е. удалять из него либо сразу
туда не записывать решения, совпадающие с уже существующими или близ-
кие к ним;
□ фрагментировать отфильтрованные решения в компактные группы;
□ максимально использовать возможности параллельных вычислений, зало-
женные в операционной системе и выбранном языке программирования. Во-
обще говоря, методы трассировки лучей по самой своей природе идеально
подходят для организации параллельной обработки данных.
В целом следует признать, что лучевые алгоритмы в совокупности с другими
алгоритмами Зб-графики требуют для своей работы значительных машинных
ресурсов и на современных персональных компьютерах работают пока еще мед-
114
Глава 1
ленно, особенно при моделировании динамических сцен. Собственно говоря,
основной прогресс в развитии компьютерной техники есть постоянное совер-
шенствование аппаратных и программных Зб-ускорителей. Нет сомнений, что в
ближайшее время задачи построения самых сложных оптических эффектов будут
быстро решаться в реальном времени.
Множество сложных геометрических объектов может быть представлено сово-
купностью простейших графических элементов — точек и отрезков, а поверхно-
сти, на которых строятся оптические эффекты, аппроксимированы системой
плоских граней. Отсюда ясна актуальность решения задач построения оптиче-
ских эффектов точек и отрезков на плоскости. В связи с этим подробнее рас-
смотрим построение оптических эффектов на плоскости для точки и отрезка,
заданного двумя концевыми точками.
Желательно иметь описание плоскости элементами нормальной формы {po,N}.
Если плоскость задана элементами параметрической формы {ро, V,W}, то по
(1.69) ее нормаль равна N - V х W. Возможно, на плоскости задан полигон
Р = {pi ...рпр\} с числом сторон п > 3, по которому должно выполняться отсече-
ние оптического эффекта. Тогда принимаем точку ро = pi, а по (1.117) вычисляем
нормаль N - погт(Р). Непосредственное использование тестов ориентации и ал-
горитмов отсечения, описанных в разд. 1.1.2, возможно при совмещении плоско-
сти эффекта с координатной плоскостью ху методом аффинного преобразования
системы координат с помощью функций MAPI, MAPI или МАР4, определенных
в гл. 2.
При построении тени должно быть задано положение источника света. В зави-
симости от его удаленности от объекта возможны два случая, отличающиеся
свойством параллельности лучей (рис. 1.61):
П источник, например, светильник, расположен в конечно удаленной точке L.
Различные точки пространства q связаны с ней непараллельными расходящи-
мися из L прямыми лучами q + V41 либо сходящимися в L обратными лучами
q - V41 с векторами направления
Непараллельность лучей приводит к искажению формы тени объекта (У), что
делает ее перспективное изображение более естественным;
Рис. 1.61
Геометрические основы компьютерной графики
115
71 источник, например, Солнце, бесконечно удален от объекта в направлении
вектора L. Источник можно считать бесконечно удаленным, если минималь-
ное расстояние между ним и объектом хотя бы на порядок, т. е. в 10 раз, пре-
вышает максимальный габарит объекта. При этом условии максимальный
угол расхождения лучей не превышает значения arctg(O.l) = 5.7°, что доста-
точно близко к 0°. Такая идеализация позволяет считать прямые q + V41 и об-
ратные q - V41 лучи параллечьными с векторами направления
V4^-L
для всех точек q, упрощает построение тени (2), делает возможным примене-
ние групповых матричных методов обработки точек, описанных в гл. 2, но не
дает перспективного изображения.
При построении оптических эффектов необходимо знать положение их наблю-
дателя. В зависимости от его удаленности от объекта также возможны два слу-
чая, отличающиеся свойством параллельности лучей (рис. 1.62):
□ наблюдатель расположен в конечно удаленной точке 5. Различные точки про-
странства q соединены с ней непараллельными сходящимися в 5 прямыми лу-
чами q + S4t либо расходящимися из 5 обратными лучами q- S4t с векторами
направления
Sg = S-q.
Непараллельность лучей делает перспективное изображение оптического эф-
фекта (5) реалистичным, но усложняет его расчет;
21 наблюдатель бесконечно удален от объекта в направлении вектора 5. Конечно
удаленного наблюдателя можно считать бесконечно удаленным, если мини-
мальное расстояние между ним и объектом хотя бы на порядок больше мак-
симального габарита объекта. Такая идеализация позволяет считать прямые
q + S41 и обратные q-S4t лучи параллельными с равными векторами направ-
ления
S4 = S
для всех точек q, упрощает построение оптических эффектов, делает возмож-
ным применение групповых матричных методов обработки точек, но не дает
перспективного изображения (4).
Рис.1.62
116
Глава 1
Используя устоявшуюся терминологию [36], будем впредь называть конечно
удаленного наблюдателя и источники света "ближними", а их же, удаленных в
бесконечность,— "дальними". Каждый из этих режимов, как отмечалось чуть
выше, имеет свои преимущества и недостатки, но применять их следует, руково-
дствуясь конкретными геометрическими условиями.
Переходим к изучению лучевых методов построения оптических эффектов точек
и отрезков на произвольной поверхности и более детально — на плоскости.
1.3.5.1. Тень
Тень точки q на произвольной поверхности образуется в точке q' пересечения с
ней прямого луча q + V4t. При дальнем источнике света рекомендуется задавать
вектор его направления в виде V4 = -yL с коэффициентом удаленности у, во мно-
го раз большим отношения максимального габарита сцены к длине вектора L.
Задача построения тени точки на произвольной поверхности решена в
разд. 1.3.1. Более сложный, чем точка, графический объект представляется сис-
темой точек, для которых тени строятся однотипно.
Возможность пересечения прямого луча q + V4t с плоскостью {/>о, N] в точке q'
(рис. 1.63) определяется числом
= v4 о N.
При v4 = 0 луч (?) проходит параллельно плоскости, нигде ее не пересекая. Если
то по (1.102,6) находим параметр и точку пересечения прямой {q, с
плоскостью {ро, N}:
Ср0~<7)°/У
9
(1.144)
Рис.1.63
Геометрические основы компьютерной графики
117
При 1Ч = 0 точка q лежит в плоскости {ро, N} и согласно (1.144) совпадает со сво-
ей тенью: д' = q. При t4 > 0 луч (2) пересекает плоскость впереди точки q и дает
действительную тень д'. Условие существования тени 1Ч > 0 геометрически озна-
чает, что векторы ро - q и V4 одинаково ориентированы относительно плоскости,
т. е. образуют с нормалью N однотипные углы: либо оба острые, либо оба ту-
пые. При условии -1 < t4 < 0 луч (5) пересекает плоскость в точке q' раньше, чем
доходит до точки q, а при t4 < -1 луч (4) вообще удаляется от плоскости. Таким
образом, при t4 < 0 тень является мнимой.
Важным аспектом построения тени является ее видимость наблюдателем. Даже
если тень точки существует, она будет невидима, когда наблюдатель и падающий
зуч находятся по разные стороны от плоскости. Тогда отпадает необходимость
самого расчета тени. Таким образом, условия видимости и существования тени
точки имеют следующий вид:
{vpoo<0}n{^>0}, где vpo =Vpo o/V, o = Spo °N. (1145)
Первое в (1.145) условие видимости тени геометрически означает, что векторы
Гро и Sp(j противоположно ориентированы относительно плоскости, т. е. из
двух углов и ^SpoN один острый, а другой — тупой.
Построение тени отрезка ab на плоскости {ро, N} (рис. 1.64) требует анализа
взаимного расположения концевых точек отрезка а и b относительно плоскости
и источника. Каждая концевая точка q- а либо q - Ь может располагаться в од-
ном из четырех положений:
□ при v4 - 0 на равном с источником удалении и по одну сторону от плоскости;
□ при {v? * О}П {(. < -1} дальше от плоскости, чем источник;
118
Глава 1
П при Ivg * 0]Я f-1 < tq < 0j по разные с источником стороны от плоскости;
П при \Vg * О/Cl\tq > Oj между источником и плоскостью.
В табл. 1.5 приведено 16 возможных вариантов образования тени отрезка ab:
Таблица 1.5
b а v^O
G.<-l гй> I
v„ = 0 — — d -> 2d- b' b' —> c'
— — d->2d-b' b'->2b'-a'
-I < t„ < o <•/ —> 2d -a' d -> 2d - a' — [d,b'}
tB> I a' -> c' a' —> 2a' - b' [a',d] {a',b'\
П в пяти вариантах тень отсутствует (прочерки в таблице): если оба конца ab
расположены не ближе к плоскости, чем источник (/), либо оба они лежат по
другую сторону от плоскости, чем источник (2);
П в трех случаях тень имеет вид отрезка qi qr. когда один из концов ab находится
между источником и плоскостью, а другой там же (3) либо ниже плоскости (4).
Точка пересечения отрезка с плоскостью вычисляется как
d = а +
(ро -а)°7У
(b-a)° N
(b-a)-,
□ в восьми вариантах тенью отрезка является полубесконечная прямая — луч
ср —> qi, начинающийся в точке ср и уходящий через точку qi в бесконечность
в направлении qi-q\. Например, при {vfl -0}П{^ - 0} луч L —> а параллелен
плоскости, и только один конец отрезка b имеет действительную тень
qx=b’ = q +
(ро ~q)°N
Vb'
В качестве второй точки луча тени (5) можно принять вычисляемую по (1.144)
проекцию qi — с' средней точки отрезка с = 0.5(п + Ь). При
{ta <-1}П{-1 — tb <0} концы отрезка (6) имеют мнимые тени а' и Ь', но, тем
не менее, отрезок отбрасывает тень в виде луча, выходящего из точки d в на-
правлении точки d + (d-b') = 2d- b'.
Геометрические основы компьютерной графики
119
В связи с возможностью существования тени отрезка в виде луча необходимо
модифицировать описанные в разд. 1.1.2 алгоритмы отсечения clip2_cross и
.iip2_iest так, чтобы они могли работать не только с отрезком ab, но и с лучом
.7 -> Ь. Рассмотрим два варианта модификации.
1. Луч а-^Ь заменяется отрезком [а, а + (Ь - а)у] с коэффициентом у -> оо.
2. В модифицированный вариант функции clip2_cross(ab, Р, mod) введем допол-
нительный аргумент mod, задаваемый равным 0, если ab — отрезок [а, А], и 1,
если ab — луч я —> Ь. При mod = 1 изменения алгоритма на рис. 1.18, б мини-
мальны и заключаются в том, что расчет концов неотсеченной части луча
а-+Ь вместо табл. 1.1 выполняется по более простой в программировании
табл. 1.6.
Таблица 1.6
Ci 02 < 0 0 < 02 < 1 02 > 1
oi < 0 [п,п] [а. а + Рог] [я, а + Гог]
0 < 01 < 1 [а, а + loi] [я + F01, а + Гог] [я + Fbi, а + Гог]
О| > 1 [я, а + Fbi] [я + Fbi, а + Гог] [я + Fbi, а + Гог]
& Пример 1.10. Построить тень пирамиды с вершинами
А=[3 4 -1],Р2 =12 4 2], р3=[5 3 2], р4 = [2 2 О]
(а плоскость, заданную отрезками A, = 1, Ал. = 2, А. = 3, от источника света, рас-
положенного в точке L = [4 2 1] . Направление на дальнего наблюдателя зада-
ется вектором 5 = [1 1 /7]. Проанализировать изменение тени при удалении
источника в бесконечность вдоль вектора L (рис. 1.65).
Решение. Плоскость тени описывается уравнением в отрезках (1.74, а)
х у z ,
—+—+-=1
1 2 3
или неявным уравнением 6х + Зр + 2z - 6 =0 и имеет вектор нормали
\ = [б 3 2]. Выбрав на плоскости точку р0 = h.z° = [О 0 з], оценим по (1.145)
зидимость точек тени:
Vpo=Po-L = [-4 -2 2], vPo=-26, 5ро =5, а = 14.29 => vpoo< 0.
120
Глава 1
Рис.1.65
Условие видимости выполнено. Приступаем к расчету тени точек по формулам
Vt - pj - L, vt - Vj° N, tj = ———° N , p' = Pj +Vjtj:
V;
r(=[-l 2 -2], VI = -4*0, Л = 5.5>0,|p[=[-2.5 15 -12]|;
F2=[-2 2 1], V2 =-4 *0,12 = 5.5 >0,|p'2 = [-9 15 7.5]|;
И3=[1 1 l],v3= 11 *0,1з = -3.364 <0, p3 =[1.636 -0.364 -1.364];
И4 = [-2 0 -1], V4 = -14*0,/4 = 0.857>0,|p4 = [0.286 2 -0.857].
Удовлетворяющие условию существования тени 1,->0 значения h, 1г и 14 означа-
ют, что ребра пирамиды р\рг, ргрь и р\ р* имеют на плоскости действительные
тени. Отрицательное значение 1з сигнализирует, что точка рз отстоит от плоско-
сти дальше источника и у нее есть только мнимая тень р3. Следовательно, тени
ребер pi рз, р2рз и р4рз представляют собой расходящиеся на плоскости лучи
р' + ИуТ (z е {1, 2, 4}, т > 0) с направляющими векторами И7, = р'-р3 и общей
задней точкой схода р3.
На рис. 1.66, я изображена рассчитанная MathCAD-программой сцена, вклю-
чающая оси координат, объект, источник света, теневую плоскость и тени ребер
объекта на ней. Ракурс, соответствующий направлению на дальнего наблюдате-
ля S = [1 1 V7] в системе координат сцены, является диметрической проекцией
Геометрические основы компьютерной графики
121
на ортогональную к наблюдателю плоскость и очень наглядно отображает
трехмерный мир на плоскости.
Рис.1.66
Заменив в исходных данных положение источника света L на yL, рассчитаем
тень объекта при у > I — удалении источника в бесконечность вдоль вектора L.
На рис. 1.66, б приведены положения тени пирамиды при у = I, у = 1.5 и у = 100.
Последнее значение у соответствует практически дальнему источнику света.
Анализ изображений тени показывает, что с удалением источника она уменьша-
ется в размерах, достигая в пределе у -> оо размеров объекта. При этом умень-
шаются и ее перспективные искажения. □
1.3.5.2. Отражение
Отражение точки q от произвольной поверхности p(t, т) наблюдается в такой
точке q’ е р(1,т) (см. рис. 1.56), где выполняются все перечисленные в разд. 1.3.2
законы отражения. Векторы падающего
этраженного M(t, т) лучей и нормали, вычисляемой по достаточно сложной
формуле (1.61,6) как
Э/ Эх
гвязаны уравнением отражения прямого луча (1.140):
= p(t,i)-q-2^p(t,i)-q)° a(z,t))v(/,t).
(1.146, a)
122 Глава '
Из принципа обратимости лучей следует соотношение
= -М-2(-М °n]n,
откуда получаем более простое по сравнению с (1.146, я) уравнение отражена-
обратного луча
p(t, t)-q = M(l ,т)-2(м(г, т)° 7V(t, t))w(z, т). (1.146, f
Отраженный луч начинается в точке р(1, т) и с точностью до скалярного множи-
теля X имеет вектор направления на наблюдателя
Л/(/,т) = Х5;,(„т), (1.147
где
Spti.-o = S
при дальнем и
= S-p(t, т)
при ближнем наблюдателе. Знак числа X служит индикатором направления от-
раженного луча относительно наблюдателя. При X > 0 отражение действитель-
ное, а при X < 0 — мнимое, т. к. отраженный луч удаляется от наблюдателя в пре
тивоположном направлении.
Решение уравнений (1.146, я) либо (1.146, б) совместно с (1.147) относительнс
всех допустимых переменных {г, т, Х>0} имеет перечисленные в начале
разд. 1.3.5 свойства, изучаемые здесь более подробно, и следствия из них:
П отражение может быть множественным-, решение представляет собой набор
разных точек q'k = р(1к,Тк)’ £> 1, в которых наблюдатель видит отражени»
одной и той же точки q на произвольной нелинейной поверхности p(t, т);
П отражение может быть разрывным- нельзя соединять точки отражения друг с
другом, даже если соответствующие точки объекта были соединены, напри-
мер, ребром;
П отражение может быть фрагментарным: возможно, что решение {г,т,Х>0
пусто, а отражение отсутствует.
& Пример 1.11. Построить отражение пирамиды из примера 1.10 (см. рис. 1.65
от криволинейной поверхности из примера 1.7 (см. рис. 1.53, я), описываемой
явным уравнением
у = f(x,z) = е~°^ +г ^cos(roA..Y)cos(a)-z), я = 0.02, (од = 1, ш. = 0.5.
Направление на дальнего наблюдателя задается вектором 5 = [1 1 1], соответ-
ствующим изометрической проекции.
Геометрические основы компьютерной графики
123
Решение. Составим неявное уравнение поверхности y-f{x, z) = О и по (1.61,а)
вычислим нормаль к ней в точке p(x,z)= [х f(x,z) z]:
Эх OZ
e-o(r +z Jcos^T^^OXCOS^xJ + CO^Sin^x))
е +г )cos(a\x)(2nzcos((i)-z)+coz sin(cozz))
Нелинейное векторное уравнение (1.146,6) с вектором М(х, z) = ).S принимает
следующий вид:
p(x,z)-q = >S S—^(x,z)l.
v 2V(x,z)o2V(x,z) j
Его численное решение относительно х, z и X > 0 дает точки тени q' = р(х, z). При
X < 0 отражение отсутствует и не изображается.
На рис. 1.67 изображена рассчитанная MathCAD-программой изометрическая
проекция сцены, включающая объект, зеркальную криволинейную поверхность
и отражение в ней объекта. Каждое ребро пирамиды заменялось цепочкой из
21 точки. Начальные приближения {х, z} выбирались из всевозможных сочета-
ний (всего их 24) элементов списков хе {1, 3,4, 5, 7, 10} иге {1, 3, 5, 7}. Анализ
отражения убеждает, что оно, действительно, имеет множественные и фрагмен-
тарные свойства. □
Рис.1.67
124 Глава 1
В частном случае плоской параметрической поверхности {ро, V, W} с нормалью
N = V х W = const и ближнего наблюдателя подстановка в (1.146, а) выражения
M(t, т) = Х(5 - p(t, т))
и свойство ортогональности (И/ + ИЛт)° N — 0 дают нелинейное уравнение
- р0 - Vt - Wx) = Ро + Vt + Wx - q - 2((p0 - q)° N )?7.
Его точное решение
[а Р Л]=(<7-р0
-2((g-po)o7v)y)
Po-S
а Р
t --, х — ——
Л +1 Л +1
(1.148, а)
определено при вектореро - 5, не лежащем в отражающей плоскости.
При дальнем наблюдателе подстановка
M(t, т) = XS
в (1.146, б) дает следующее линейное уравнение и его точное решение при SLN:
Po + Vt + Wx-q = AS-2A.(Son)n => [/
* = (<7 - Ро)
W
2($о N )у-S
(1.148,6)
В обоих случаях отражение точки q действительно при X > 0 и наблюдается на
поверхности неограниченной плоскости в точке q' = ро + Vt + Wx.
Задача построения отражения точки на плоскости имеет простое геометрическое
решение (рис. 1.68). Вычислим по (1.26, а) симметричную к плоскости точку
q°-q + 2^j)Q-q)o N^l (1.149)
Рис. 1.68
Геометрические основы компьютерной графики
125
и выпустим из нее луч q° +S^ot. Наблюдатель видит отражение точки q в точке
q=q°+^0~q°^NSo (1.150)
пересечения луча с плоскостью. Тип отражения определяется соотношением зна-
ков чисел v4 - (q-ро) ° N и о = Spo ° Л' . При vvo > 0 точка q и наблюдатель рас-
положены по одну сторону от плоскости, а вычисленное по (1.150) отражение (Г)
действительно. При vvo < 0 по одну сторону от плоскости находятся наблюда-
тель и точка q° (2), а отражение является мнимым.
Точки q° и q' лежат на одном прямом луче q° —> S' и визуально сливаются в од-
ну точку. Зрительная система человека размещает отражение объекта за зерка-
лом, а не на его поверхности. Контур зеркала является как бы окном, через кото-
рое наблюдатель рассматривает виртуальный (кажущийся) объект. Таким
образом, для расчета отражения точки q от зеркальной плоскости достаточно
найти по (1.149) симметричную точку q° и при выполнении условия vvo > 0 счи-
тать ее действительным отражением.
Построение отражения отрезка ab на плоскости {ро, N} (рис. 1.69) начинается с ана-
лиза взаимного расположения концевых точек отрезка а и b относительно плоскости
п наблюдателя. Четыре варианта этого расположения приведены в табл. 1.7:
Таблица 1.7
а v,,a < 0 i’Ao > 0
v„o<0 k И
v„o > 0 k, *°]
□ наблюдатель видит полное отражение а°Ь°, если оба конца отрезка (7) рас-
положены с ним по одну сторону от плоскости;
□ отражение отсутствует (прочерк в таблице), если оба конца отрезка (2) рас-
положены по другую сторону от плоскости, чем наблюдатель;
2) в двух случаях наблюдается неполное отражение q°d при пересечении отрез-
ком (3) плоскости в точке
. (ро -о)° TV I, \ ,
d = а+ —л.----(b-а) е ab.
(b-a)°N
126
Глава 1
& Пример 1.12. Построить отражение пирамиды с вершинами
Pl=[2 2 -2], р2 = [1 3 1], р3 = [4 2 -1],р4=[1 0 -1]
от плоского зеркала в форме параллелограмма, три вершины которого отсекают
на осях координат отрезки hx = 1, hy - 3 и h. = 2. Наблюдатель находится в точке
S' = [1 1 л/я]. Сравнить отражения при удалении наблюдателя в бесконечность
вдоль вектора yS' при у > 1 (рис. 1.70).
Рис. 1.70
Решение. Плоскость зеркала описывается неявным уравнением 6л + 2^ + 3z -
- 6 - 0 и имеет нормаль У = [б 2 3]. Выбрав на ней точку ро=й-з°=[О 0 2],
Геометрические основы компьютерной графики
127
вычислим индикаторы у, = (д-ро) ° N ориентации вершин /?, относительно плос-
кости, а по (1.149) — вершины симметричной пирамиды
„о _ „ . 2С’о-Р|)°Л'
Pt ~Р‘+-----------
Л» Л
А:
Vl = 4 > 0, = [1 02 1.673 -2.49];
V2 = 9>0, Р2 =[-1-204 2.265 -0.102];
v3= 19 > 0, р$ =[-0.653 0.449 -3.327];
V4 = -3 < 0, р4 = [1.735 0.245 - 0.63з].
Поскольку о = (S -ро) ° N = 10.485 > 0, то из всех вершин пирамиды лишь р$ на-
ходится с наблюдателем по разные стороны от плоскости зеркала и не имеет
действительного отражения. Вычислим точки
. (ро _ PiN \
<4 = Pi + 7-----ГД7^4 ~ Pi pip4
\Р4 ~Pi)°N
пересечения бесконечной плоскости {ро, N} с ребрами пирамиды, смежными с
вершиной/м (рис. 1.71, а):
</14= [1.429 0.857 -1.429], d24 = [1 0.75 -0.5], d34 = [1.409 0.273 -1].
Таким образом, отражение пирамиды от бесконечной плоскости зеркала состав-
ляют отрезки р°р2, /2]°р£, р2р3, p?dl4, p2d24 и p3d34.
Второй этап расчета отражения состоит в проецировании всех объектов сцены
ча некоторую картинную плоскость, допустим, координатную плоскость ху.
Проецирование является центральным, т. к. как наблюдатель как бы испуска-
ет проецирующие лучи из центра— конечно удаленной от сцены точки
5 = [vx sy s,J. Не вдаваясь пока (до подробного изучения в гл. 2) в методику
центрального проецирования, отметим ее сходство с алгоритмом построения
тени, в котором глаз наблюдателя является источником обратных лучей.
Заключительный этап состоит в отсечении проекций отрезков отражения поли-
гоном проекции зеркала. На рис. 1.71, а изображена рассчитанная MathCAD-
программой центральная проекция сцены. Пунктиром обозначены отсеченные
фрагменты отрезков отражения.
Заменив в исходных данных положение наблюдателя 5 на yS, рассчитаем отра-
жения пирамиды при удалении наблюдателя в бесконечность вдоль вектора 5.
Для ряда значений у = 1, у = 2 (рис. 1.71, б) и у = 5 (рис. 1.71, в) углы горизон-
тального обзора сцены составляют соответственно 106°, 56° и 23°. Последний
случай практически эквивалентен дальнему наблюдателю с коэффициентом
128
Глава 1
у -> оо. Соответствующий ракурс с вектором направления 5 = [1 1 V8] является
кабинетной косоугольной проекцией на плоскость ху и широко применяется для
отображения трехмерного мира на плоскости. Анализ изменения отражения по-
казывает, что с удалением наблюдателя уменьшаются как его размеры, так и
перспективные искажения. О
Рис. 1.71
1.3.5.3. Преломление
Преломление точки q на произвольной поверхности p(t,x) раздела двух сред с
показателями преломления т и пг наблюдается в такой точке q'ep(t,t)
(см. рис. 1.57), где выполняются все перечисленные в разд. 1.3.3 законы прелом-
ления. Векторы падающего
Vv(i, т) = p(t, т) - q,
преломленного R(t, т) лучей и нормали
Э/ Эт
связаны уравнением преломления прямого луча (1.142):
я=Яп2
sgn((p-9)oA)j|(p-9)|2
(1.151,«)
(р-?)+«п
~nn(p-q)°N
Геометрические основы компьютерной графики
129
Из принципа обратимости лучей следует уравнение преломления обратного луча'.
Преломленный луч начинается в точке p(t, т) и с точностью до скалярного мно-
жителя X имеет вектор направления на наблюдателя
Л(Г,т) = ^,т), (I-152)
где
= S—p(t, т)
при ближнем и
Sp(iO = S
при дальнем наблюдателе. Знак числа X служит индикатором направления пре-
ломленного луча относительно наблюдателя. При X > 0 преломление действи-
тельное, а при X < 0 — мнимое, т. к. преломленный луч удаляется от наблюдателя
в противоположном направлении.
Дополнительные условия существования действительного преломления, озна-
чающие отсутствие эффекта полного внутреннего отражения, имеют вид, анало-
гичный (1.143):
|р-?| >«n|G’-?)x/v| (1.153)
Решение уравнений (1.151, я) либо (1.151,6) совместно с (1.34, в) и (1.34, г) отно-
сительно всех допустимых переменных {t, т, Л > 0} имеет перечисленные в начале
разд. 1.3.5 свойства, изучаемые здесь более подробно, и следствия из них:
□ преломление может быть .множественным— решение представляет собой
набор разных точек q'k = А > 1, в которых наблюдатель видит пре-
ломления одной и той же точки q на произвольной нелинейной поверхности
P(t, т);
23 преломление может быть разрывным — нельзя соединять точки преломления
друг с другом, даже если соответствующие точки объекта были соединены,
например, ребром;
“1 преломление может быть фрагментарным — возможно, что решение {/, т, X > 0}
пусто, а преломление отсутствует.
±7Пример 1.13. Внутри янтарного эллипсоида с полуосями а = 2, b-З, с =2,
центром в начале координат и коэффициентом преломления т = 1.6 находится
пирамида (рис. 1.72, а) с вершинами
Р\ =1-1 2 -1], р2 = [1 2 1], р3 = [-1 0 1J. Р4=[1 0 -О-
Построить преломленное изображение пирамиды, видимое наблюдателем из
точки 5 = [4 4 1б] воздушной среды с коэффициентом преломления пг - 1.
130
Глава 1
Решение. Поверхность действительного эллипсоида описывается следующими
неявным (см. табл. 1.3) и параметрическими (1.129, г?) уравнениями:
- A2
- -1=0;
c J
.2
ч2
£ |
ь
Лр)= -
И
р(/,т)= [asin(/)sin(T) 6cos(/) csin(r)cos(r)], t e [0, л], т g [0, 2л].
Нормаль к поверхности эллипсоида в точке p(t, т) получим по (1.61,6):
7V(/,t)= [6csin2(/)sin(r) acsin(f)cos(z) fl6sin2(/)cos(T)].
Все вершины пирамиды лежат внутри эллипсоида, о чем свидетельствуют отри-
цательные значения неявной функции поверхности:
/(Р-) =/(р) = -0.0556 < 0, f(p.) =f(p<) = -0.5 < 0.
Благодаря выпуклости эллипсоида остальные точки ребер пирамиды также яв-
ляются внутренними и могут иметь преломленные лучи.
На рис. 1.72, б представлен результат расчета преломления MathCAD-
программой. Каждое ребро пирамиды заменялось цепочкой из 50 точек. Для ка-
ждой такой точки q решением уравнений (1.151,6), (1.152) при Spi„T) = S-p(t, т)
рассчитывалась точка p(t, т) на поверхности эллипсоида, в которой преломляется
луч, идущий от q к 5. Отсутствие решений для точек вблизи вершин p^ и рь объ-
ясняется, по-видимому, невыполнением условий существования преломленных
лучей X > 0 и пп |т?(/, т)| > |/?(г, т)х а(/, т)|.
Рис.1.72
Геометрические основы компьютерной графики
131
Благодаря выпуклости поверхности эллипсоида (сравните ее с поверхностью в
примере 1.1J) практически при любых начальных приближениях параметров t(0\
т<°) и Х<°> алгоритм построения преломления приводит к одинаковому результату.
Это относится даже к тем случаям, когда начальная точка p(t(0>, т(0)) находится на
противоположной к наблюдателю стороне поверхности эллипсоида. Кажущийся
на первый взгляд логичным выбор начального приближения p(tm, т(0>) в точке
пересечения отрезка qS с поверхностью эллипсоида приводит к решению допол-
нительной нелинейной задачи поиска этой точки, которая также требует задания
начальных условий. В итоге трудоемкость задачи возрастает вдвое.
Из двух вариантов оптического алгоритма, решающих нелинейные векторные
уравнения преломления прямого (1.151, а) и обратного (1.151,6) лучей, второй
вариант проявил себя лучше как по скорости сходимости (машинному времени
расчета), так и по более широкой области сходимости, что отразилось в боль-
шем числе полученных точек изображения пирамиды внутри эллипсоида. □
Получим геометрические решения задачи преломления точки на плоскости для
разных вариантов удаленности наблюдателя.
□ При дачьнем набтюоателе требуется найти на плоскости с нормалью N такую
точку q’, чтобы преломленный в ней луч имел направление 5 (рис. 1.73).
В первую очередь с помощью векторного или скалярного произведений нор-
мированных векторов S и N вычислим значение
g = sin(y)=|SxA'| = ^l-(soJvy <1, (1154)
откуда получим
/22
tg(y) = -j g-, sin(a)=—, cos(a)=^—tg(a)=-y=J=.
Рис. 1.73
132
Глава 1
Проведем из точки q ортогональную плоскости прямую q + Nt и луч q + St.
параллельный преломленному лучу, до их пересечения с плоскостью в точках
o' = q+ ((/?о ~q)°N)N, р =q + S- (1.155)
5 о /V
Выбор точки q' на луче о' —>р' обеспечивает компланарность падающего,
преломленного лучей и нормали. Рассматривая прямоугольные треугольники
q o'р' и q o' q' с общим катетом q o', вычислим искомую точку преломления на
плоскости раздела сред:
g' = o'+^)(Jj'-o’')=o'+ I 1-g {р-o'). (1.156)
w) Ьп-g2
Зрительная система человека размещает преломленное изображение точки q в
точке qn с той же стороны от плоскости, что и точка-образ, на равном рас-
стоянии от точки cf '.
qn = q'-\q'-q\s
(1.157)
Отношение расстояний от точек qn и q до плоскости составляет число
_ cos(y) j 1-g2
cos(a) yn2-g2
I 1-g2
^-(g/Wn)2
При наблюдении объекта, находящегося в более плотной оптической среде,
из менее плотной среды (пп > 1) он кажется приподнятым, как бы находящимся
'еометрические основы компьютерной графики 133
ближе к плоскости преломления, чем в действительности (г) > 1). Наоборот,
при наблюдении из более плотной среды (лп < 1) объекты кажутся отстоящи-
ми от плоскости дальше (q < 1). На рис. 1.74 построены графики зависимости
q(y, лп) кажущейся глубины преломленной точки при взгляде на нее под углом
у из воздуха в воду (лп = 1.33), в стекло (лп = 1.52), в алмаз (лп = 2.42) и из во-
ды в воздух (лп = 0.75).
Рассмотрим условия существования преломленного луча.
• Во-первых, это соотношение знаков чисел
у = (q - ро) ° N, и = S о N,
характеризующих взаимное расположение точки и наблюдателя. При
vvo > 0 луч q + St удаляется от плоскости. При vvo < 0 точка q и наблюда-
тель расположены по разные стороны от плоскости раздела сред, что яв-
ляется необходимым условием видимости эффекта преломления.
• Во-вторых, это условие существования решения в (1.156). При лп > 1 всегда
будет sin(a) < sin(y), точка q' располагается между точками о' и р', а пре-
ломленный луч всегда существует. При лп < 1 точка q' лежит на продолже-
нии луча о' -> р' лишь в отсутствие эффекта полного внутреннего отраже-
ния, т. е. при sin(a) = g / лп < 1— условии определенности подкоренного
выражения в (1.156). Например, при переходе луча из воздуха в воду
(лп = 0.75) предельное значение угла преломления ynp = arcsin(nn) = 48.8°
достигается при угле падения а—>90°. Пунктирный график на рис. 1.74
стремится в бесконечность при у —> упр и объясняет, почему из-под воды
весь воздушный мир виден, во-первых, лишь в конусе с углом раствора
2упр = 97.5°, а во-вторых, — приподнятым.
При лп <g < 1 получим значение sin(a) > 1: не найдется ни одного падаю-
щего луча, который преломится в более плотную среду в направлении век-
тора 5. Например, при взгляде из-под воды под углом у > упр видна лишь
отражающая поверхность.
Таким образом, решение задачи преломления действительно при
{v^o < о}п {о < g < лП}. (1.158)
& Пример 1.14. Пирамида с вершинами
Р1=[1 3 1], P2 = [i 3 3], Рз = [3 1 1], р4 = [о О 1]
погружена в стеклянный аквариум, доверху наполненный водой (лв = 1.33), так
что вершины pi и рг находятся в воздухе, а вершины рз и рь — в воде. Размеры
аквариума dx = 3, df = 2 и d.= 3. Построить изображение каркаса пирамиды без
• чета преломления лучей в тонких стенках аквариума. Вектор направления на
дальнего наблюдателя равен S = [2 1 з]. На рис. 1.75, а приведен эскиз сцены с
аквариумом без воды.
134
Глава ‘
Решение. Изображения погруженных частей ребер пирамиды искажаются из-за
преломления лучей на поверхностях раздела воды и воздуха. По положительные
знакам координат вектора 5 заключаем, что плоскостями преломления являютс:
передняя (фронтальная), верхняя (горизонтальная) и правая (профильная) стены
аквариума. Зададим их общую точку Po=[dx dy Jz]=[3 2 з] и нормали
единичной длины Nf = z°, Nh =у°, Np =х°. Вычислим точки
пересечения ребер пирамиды р,р} с поверхностью верхней грани {ро, Nh}:
J]3 = [2 2 0.5], dl4 = [0.667 2 О.ЗЗЗ],
d23 = [2 2 2], J24 = [0.667 2 2.333].
Отрезки пирамиды pt pi, pt dti, pt du, pi du, pi du находятся в воздухе и виднь
наблюдателю без искажений. Отрезки du pi, du pi, du pi, du pi и pi pi, находящиеся
в воде, имеют преломления на бесконечных плоскостях {ро, Nt}, {ро, А'ь} и {ро, NP}.
т. к. для всех их точек q выполнены все условия в (1.158):
v4 < 0, or = 3 > 0, Oh = 1 > 0, оР = 2 > 0 => or < 0, v? оь < 0, v4 оР < 0;
пп = л» = 1.33 gf - 0.598 < лп, gh = 0.964 < пп, gP - 0.845 < пп.
После вычисления по (1.155) и (1.156) преломлений подводных отрезков они от-
секаются полигонами ближних к наблюдателю граней аквариума. Проиллюст-
рируем это на примере ребра pi pi. Точки pi и pi имеют следующие преломления
на плоскостях фронтальной, горизонтальной и профильной граней аквариума:
РЗГ=[3.9 1.45 3], рзь = [3.583 2 1.875], ^р=[з 1 1],
/4г=[0.9 0.45 З], рдц =[1.166 2 2.749], Р4Р=[3 0.781 3.342].
Рис.1.75
Геометрические основы компьютерной графики
135
После отсечения отрезков P3fP4f, РзьАю РзрР4р полигонами соответствующих
граней получим отрезки, изображенные пунктиром на рис. 1.75, а.
Конечный результат расчетов, выполненных с помощью программы MathCAD,
показан на рис. 1.75,6. Там же изображены преломления задних ребер аквариу-
ма в трех его ближних гранях, вычисленные аналогично преломлениям ребер
пирамиды.О
□ При ближнем наблюдателе найдем на плоскости {ро, N} такую точку q', что-
бы преломленный в ней луч прошел точно через точку 5 (рис. 1.76). В отличие
от случая с дальним наблюдателем здесь нельзя сразу найти значение
g = sin(y).
Опустим из точек q и 5 перпендикуляры на плоскость {ро, N} до пересечения с
ней в точках
o' = q+((p0-q)oN^, P' = S + ((pq-S)oN^. (1.159)
Вычислив расстояния
</ = |р' - о'|, - \о' - ql, hs - |р' - 5|,
составим уравнение с одним неизвестным g для суммы d = d4 + ds длин отрез-
ков d4 = h4 tg(a) и ds = hs tg(y):
g |o-_g| + _g |p'_5|=|p'_o-|. (1.160)
V«n-g2 Vi-g2
Ввиду отсутствия аналитического решения оно должно искаться каким-либо
численным методом. В качестве начального приближения можно использо-
вать значение
(о> _ |р'-°1
8 М’
136
Глава ’
соответствующее а = у и прохождению луча от q до S через точку с'. Поел,
решения нелинейного уравнения (1.160) найдем соотношение длин отрезков
8 = d4! ds, наблюдаемое на плоскости преломление
q' = о'+
a
и аналогичную (1.157) виртуальную точку </п:
6 =
пт
V«n-g2
S-<7
(1.161
Рассмотрим условия существования преломленного луча:
• при /л = т луч от точки q до точки S’ идет без преломления (а = у) по крат-
чайшей прямой {q, S}, пересекающей плоскость в точке с';
• при «1 > П2 точка q' смещается в сторону точки о' в такое положение, где
sin(y) / sin(a) = пп > 1;
• при т < П2 всегда найдется положение точки между точками с' и р' с со-
отношением углов sin(y) / sin(a) - пп < 1. Отличие от варианта преломле-
ния с дальним наблюдателем заключается в том, что угол преломления у
для различных точек q не фиксирован, а образуется согласно закону Снел-
лиуса—Декарта (1.141) таким образом, что все виртуальные точки qn вид-
ны наблюдателю в конусе с углом раствора 2arcsin(«n). Вне этого конуса
наблюдается эффект полного внутреннего отражения.
Таким образом, решение задачи преломления на плоскости действительно при
т?о < О, где vq ={q~po)°N, о = (S-р0)°М (1.162)
Построение преломления отрезка ab на плоскости {/>о, N} требует анализа че-
тырех вариантов взаимного расположения концевых точек отрезка а и b от-
носительно плоскости и наблюдателя, отраженных в табл. 1.8:
Таблица 1.8
а ~~~ _ V;,O < 0 > 0
уао < 0 [o', b'] [o', J]
тао > 0 ]d,b’} —
• наблюдатель видит полное преломление a'b', если оба конца отрезка распо-
ложены с ним по разные стороны от плоскости;
• преломление отсутствует, если оба конца отрезка и наблюдатель распо-
ложены по одну сторону от плоскости;
Геометрические основы компьютерной графики
137
• в двух случаях наблюдается неполное преломление q'd при пересечении от-
резком ab плоскости (ро, 7V} в точке
<,=й+КцМ(6_й)бо6.
Пример 1.15. Фотокамера лежит в воде на дне круглого бассейна радиусом
R = 5 м на глубине Л = 2 м и смещена от центра на расстояние г = 3 м. Над бас-
сейном построен купол в виде каркасной полусферы радиусом R с угловым ша-
гом параллелей и меридианов, равным 30° (рис. 1.77). Рассчитать изображение
купола в камере.
Рис.1.77
Решение. Зададим систему координат с началом в центре поверхности воды и
юзицией камеры 5 = [г -Л о]. Плоскость преломления имеет нормальное
описание {ро, N} с элементами р$ = [О 0 0]h7V=[0 1 о].
Параметрическая модель гладкой поверхности полусферы приведена в (1.129, я):
р(/,т)= /?[sin(z)sin(x) cos(z) sin(z)cos(x)] V/ e [0, л / 2], т e [0, 2л].
Для получения узлов каркаса — точек пересечения п = 3 параллелей и m = 12 ме-
: идианов — выполним дискретизацию параметров:
--- ---- 2 л
I, = i л, = j Дт V/ = 0, п, j = 0, т, , Дт = —.
1п т
Тогда узлы будут размещены в точках qhj = p(ih т,), z-я параллель образована со-
единением отрезками узлов qp q„„, а j-ый меридиан — узлов qo, -г- qnj.
Решая уравнения (1.159)—(1.162) при пП = 1 / 1.33 = 0.75 для каждой точки qih по-
лучим точки q'tj и узлы виртуального каркаса q^. Соединяя их в порядке, анало-
138
Глава 1
гимном соединению узлов в меридианы и параллели, получим изображения
преломления каркаса на поверхности воды и виртуального каркаса (рис. 1.78,«).
Рис.1.78
На рис. 1.78, б преломление изображено так, как его видит подводный наблюда-
тель. Радиус окружности, заключающей в себе все преломленное изображение,
равен 2.28 м, а угол раствора конуса видимости с учетом глубины залегания на-
блюдателя h = 2 м составляет
2arctg [ | ~ 2arcsin(«n) = 97.5°. □
I h J
Глава 2
Г еометрические
преобразования
В этой главе мы рассмотрим законы движения геометрических объектов на
плоскости и в пространстве, а также методы изображения объектов и сцен на
экране дисплея в различных ракурсах и проекциях. Цель изучения данных вопро-
сов— овладение математическим языком описания динамики и визуализации.
Профессиональный художник интуитивно чувствует, как нужно изображать
объемный мир на плоском холсте. Реалистичностью экранного изображения
компьютерная программа обязана математически строгому расчету фаз движе-
ния объектов на основе закономерностей геометрических преобразований.
Геометрическое преобразование — это отображение р' = f(p) точки р е R" п-
мерного пространства образа в точку р'е R” «'-мерного пространства прообра-
за. Геометрические преобразования делятся на нелинейные (например, отражение
в кривом зеркале) и линейные. Линейное преобразование точки описывается век-
торным уравнением
р' = рА + В
(2-1)
с матрицами преобразования Ае R"x” и Be Rlx" , не зависящими от векторар.
В зависимости от размерности пространств п, п' и свойств матрицы А линейные
преобразования делятся (рис. 2.1) на невырожденные (аффинные) и вырожденные
(проективные). Свойства аффинного преобразования (АП):
п = п', rang(J) = п,
что означает квадратность и невырожденность матрицы А. Существование
обратной матрицы А~} позволяет по точке прообраза р' восстановить точку об-
раза р:
р-(р'-В)А~1. (2.2)
При проективном преобразовании т < п и не существует обратной матрицы А~1,
поэтому однозначное восстановление образа по прообразу невозможно из-за поте-
ри информации об одной или нескольких координатах образа.
140
Глава 2
Рис. 2.1
2.1. Аффинные преобразования
2.1.1. Основные понятия и соотношения
Аффинное преобразование (от англ, affinity — родство) имеет следующие свойства:
□ отображает «-мерный объект в «-мерный — точку в точку, линию в линию,
поверхность в поверхность;
□ сохраняет параллельность линий и плоскостей;
□ сохраняет пропорции параллельных объектов— длин отрезков на парал-
лельных прямых и площадей на параллельных плоскостях.
Эти свойства позволяют строить прообразы полигонов на плоскости и полиэд-
ров в пространстве по конечному набору т точек их вершин:
Далее вершины р- соединяются прямыми линиями (ребрами) в нужном порядке.
Система вершин и ребер составляет каркасную (проволочную) модель полиэдра.
Для получения объемной модели определяются и закрашиваются видимые грани.
Преобразование вектора V - pi-p\, соединяющего точки р\ и pi,
V' = Р2~р'\ - р^А + В-Р\А-В = (Р2 ~Р})А = УА (2.4)
показывает, что преобразование В, воздействуя на оба конца V, не влияет на Р.
Геометрические преобразования
141
Любая комбинация N последовательных АП
At,В, А2,В2 4n,bn
Ро Pl P/v>
где/л =ро At + В,pi - pi А2 + Bi = ро Ai Ai + B\ Ai + В2И по индукции
N N N
P?v =РоПА + ЦА П4/~PoA + B> (2.5,a)
,=1 ,=i j=j+i
j<N
A,В
эквивалентна одному АП р0 —» pN с матрицами преобразования
А = Ai А2... An,
В = (... (BiA2 + Bi) Аз + ... + B^i) An + BN. (2’5’
Этот алгоритм использует операции сложения и умножения матриц. Он доста-
точно трудоемок в расчете матрицы В.
Комбинация N преобразований вектора V согласно (2.4) и (2.5) также не зависит
от наличия в этих преобразованиях переносных составляющих:
(2.6)
i=i
С целью упрощения и унификации записи геометрических преобразований вво-
дится понятие расширенного пространства (РП) R"+l, в котором (п + 1)-я коор-
дината равна фиксированному числу — единице или нулю. Координаты точки
р = [р 1] или вектора V = [р о] в РП часто называют однородными. Наиболее
гачное. по мнению автора, объяснение этому спорному термину приведено в [35].
Преобразование (2.1) точки в РП принимает вид
А О„х1
В 1
или р
р С, где С =
A О„х1
В 1
е ^(п+1)х(и+1)
(2.7)
есть матрица преобразования в РП с обратной матрицей
А~1
— ВА~1
Оих1
1
уписывающей обратное преобразование в РП р = р' С 1, равносильное (2.2).
Цепочка из N преобразований в РП
_ С, ~ с2 cN ~
Ро Pl Pn
142
Гпава 2
эквивалентна одному преобразованию с матрицей
c=f[Q.
i=i
(2.8»
По сравнению с алгоритмом (2.5) матрица преобразования в расширенном про-
странстве рассчитывается единообразно— с помощью только перемножения
матриц. Унификация — основное преимущество выполнения АП в однородных
координатах, позволяющее без лишних раздумий правильно записать и быстрс
вычислить матрицу сложного преобразования С как произведение матриц эле-
ментарных преобразований С,. Несмотря на то, что для этого требуется выход е
пространство R"+l, количество арифметических операций в общем итоге даже
снижается, да и программирование (2.8) гораздо проще, чем (2.5, б).
К недостаткам преобразований в расширенном пространстве можно отнести:
□ избыточную размерность расширенных матриц и векторов:
□ фиксированные элементы последнего столбца [о ... О if, потребляющие
машинные ресурсы;
□ необходимость контроля и коррекции фиксированных элементов после мат-
ричных операций в связи с возможным накоплением погрешностей машинно-
го округления.
В отличие от (2.3), одновременное групповое преобразование точек может быть
выполнено по более простой матричной формуле
Р\
Рт
(2.9)
Преобразование вектора V = pi-pi согласно (2.4) и (2.7) выполняется в РП сле-
дующим образом:
А О«х1
В 1
[Г о]=[г 0]
или V' = V С.
(2-10)
Смещение произвольной точки р при ее преобразовании по (2.1) равно
d{p)-p'-р-р(А -Е„) + В.
Точку рИ, остающуюся в процессе АП неподвижной, можно найти, решая уравне-
ния рн =рИА + В или d(pH) - О„:
рн = В(Е„-А)'. (2.11)
Условие существования точки р»— невырожденность матрицы Е„-А. Точка,
неподвижная при всех допустимых значениях матриц А и В, называется центром
преобразования.
Геометрические преобразования
143
Невырожденное преобразование прямой и плоскости, описываемых в неявной форме
векторным уравнением pF1 =0 , изменяет их матрицу F следующим образом:
p'F'1 = pCF'T = pFT =0 F = F'CT,
(2-12)
Читателю предлагается самостоятельно убедиться, что перенос плоскости из при-
мера 1.10, имеющей вектор коэффициентов неявной формы С = [б 3 2 -б], в
начало координат с помощью любой из матриц
II ст 1 000' 0 10 0 0 0 10 -1 0 0 1 ,С2 = ’1 0 0 О' 0 10 0 0 0 10 0-201 >Сз = '1 0 0 0' 0 10 0 0 0 10 .° 0 ~3 L
дает вектор F' = [б 3 2 о].
Важным свойством линейных преобразований является равенство модулей опре-
делителей ||Л|| = ||С]| матриц АП изменению площади (в R2) и объема (в R3) преоб-
разуемого объекта, что позволяет быстро вычислять эти важнейшие параметры
геометрических фигур по известным их исходным значениям и матрицам преоб-
разований.
Знание координат (п + 1)-ой пары точек образа и прообраза, не лежащих в про-
.транстве R"-1, позволяет вычислить матрицы С и С-1 методом парных точек:
(2.13)
Здесь обязательно нужно контролировать последние столбцы полученных матриц.
Часто бывает удобнее оставить объект неподвижным, а преобразованиям под-
вергать систему координат. Это пассивное АП описывается матрицей Ск = С1,
обратной к матрице С такого же активного преобразования объекта. Дополним
метод парных точек (2.13) формулами расчета матриц прямого и обратного пре-
образований СК
Ск
(2.14)
в которых Pi+Pn+i и Pi+p'n+i — расширенные формы одноименных точек в
исходном и конечном положениях СК. После вычисления матрицы Ск любая
точка р, имеет в новой СК координаты р' = /5,СК, а любой вектор V - pi-р\ пре-
образуется в вектор
Й' = ЙСК.
(2.15)
144
Глава 2
2.1.2. Элементарные аффинные преобразования
Все множество аффинных преобразований может быть сведено к следующим
элементарным преобразованиям (ЭП).
2.1.2.1. Перенос
Перенос (transfer) всех точек объекта на вектор tsp в неподвижной СК
(преобразования / на рис. 2.2, а и б) описывается уравнением
р'=р + tsp
и матрицами переноса
A=En,B~tsp, T(tsp) =
Еп
Еп Олх1
-tSp 1
= 7’Ч(Д^).
(2.16)
0/7X1
I
Переносное смещение d - tsp не зависит от положения точки. Неподвижная точ-
ка согласно (2.11) удовлетворяет уравнению
рн О„хл = tsp.
При ненулевом переносе tsp О„ она отсутствует, а при tsp = 0„ все точки про-
странства неподвижны. Определитель матрицы переноса |7'| = 1.
2.1.2.2. Масштабирование
Масштабирование (растяжение, сжатие, отражение) вдоль осей координат опи-
сывается координатными уравнениями
х' = тхх, у' - т}.у, z' - m.z
с коэффициентами тх, ту и т. — диагональными элементами матриц масштаби-
рования'.
Рис. 2.2
геометрические преобразования
145
При = -1 точка отражается вдоль оси со е {х, у, z] от координатной плоско-
сти со = 0. Если все коэффициенты и» = my = tn. = -1, то точка кососимметрично
отражается относительно начала СК. На рис. 2.2 изображены операции:
□ масштабирования 2 в R2 матрицей Л/(2, -1);
□ отражения 3 в R2 вдоль оси х матрицей М(-\, 1);
□ отражения 4 в R3 вдоль оси у (от плоскости xz) матрицей Л/(1, -1, 1);
□ отражения 5 в R3 от оси z матрицей М(-\, -1, 1);
□ отражения 6 в R3 от начала координат матрицей
Неподвижная точка, подвергаемая масштабированию, удовлетворяет уравнению
рн diag[l-w?x 1-ту j 1-/иг]=О„ .
При тш = 1 неподвижны все точки на оси со. Центр масштабирования находится
з начале координат, т. к. только точка рн = О„ остается неподвижной при произ-
вольных масштабных коэффициентах тш.
Масштабирование с нечетным числом отрицательных коэффициентов изменяет
"опологические свойства преобразуемых объектов. В частности, направление об-
хода вершин полигона при таком масштабировании меняется на противополож-
ное. Возможность подобных эффектов необходимо предусматривать в алгоритмах,
равильность работы которых зависит от направления обхода. Примером может
.лужить задача определения видимости плоской грани полиэдра по направлению
ее рассчитываемой нормали, зависящему от направления обхода вершин полигона
грани. Если оно положительно и нормаль внешняя, то грань видима. Зеркальное
тражение полигона этой грани имеет отрицательное направление обхода и внут-
реннюю нормаль, рассчитываемую по тем же формулам, что и нормаль самой гра-
-•и. Таким образом, отраженная грань, реально видимая в зеркале, будет иденти-
фицирована программой как невидимая и не отобразится на экране.
Определитель матрицы масштабирования равен |Л/| = ту т.. У матрицы от-
ражения с коэффициентами тш = ±1 он равен |Л/| = (-1)*, где к— число инверти-
руемых координат преобразуемой точки. Например, при отражении вдоль одной
хн получим |Л/| = -1. В результате инвертируются направления обхода всех от-
ражаемых полигонов без изменения их площадей, а также объемов полиэдров.
При неравных масштабных коэффициентах преобразование масштабирования
изменяет углы между векторами, площади, объемы и форму геометрических фи-
;>р. Неравномерное растяжение или сжатие вдоль осей координат— простей-
ший способ получения эллипса из окружности и эллипсоида из сферы.
2.1.2.3. Сдвиг
Гдвиг (shift) вдоль направлений осей СК или их комбинации описывается сле-
гающими координатными уравнениями и матрицами сдвига в R2 и R3:
x' = x+sy Г 1 $ ’
* 7 => S2 = (2.18, а)
У =y + syxx 1/ху 1 .
146
Гпава 2
x' = x + Sxyy + SxzZ Г 1 Sy* Szx
y' = SyxX + y + SyzZ => S3= 1 szy
z = szxx+szyy+z |_5xz syz 1
(2.18,6)
Параметры сдвига задаются недиагоналъными элементами матриц Si и &. Коэф-
фициент матрицы сдвига Sg есть единица смещения вдоль оси I, пропорциональ-
ного j-ой координате.
Сдвиговое смещение
d = p(S„-E„) (2.19)
зависит от положения точки р, что и отличает его от переноса. Неподвижная
точка удовлетворяет уравнению
рн(5„ - Е„) = О„.
Если в матрице S„ все недиагональные элементы со-ой строки — нулевые, то пр.
сдвиге неподвижны все точки, лежащие на оси со. Две нулевые строки матриць
S„ - Е„ дают множество неподвижных точек на координатной плоскости. Центр
сдвига при произвольных параметрах матрицы S„ находится в начале координат.
Важно отметить, что если в матрице сдвигового преобразования элемент Sg * (
не единственен, то векторы смещения (2.19) не параллельны, а сдвиг осуществля-
ется одновременно вдоль нескольких осей СК, и его нельзя заменить последова-
тельностью одноосевых сдвигов:
1 0 1 syx
sxy I]|о 1
I
sxy
syx 1 syx
1 + 1ЛУ 1
Преобразование сдвига может иметь вырожденную матрицу с нулевым опреде-
лителем, например,
1 О
1
О
1
Размерность пространства, натянутого на точки сдвинутого в Rn объекта, равна
рангу матрицы 5„. Следовательно, при rang(S„) < п преобразование сдвига не
является аффинным.
На рис. 2.3, а приведены примеры преобразований сдвига на плоскости с матри-
цами (2.18, а) и сдвиговыми смещениями (2.19):
П отрезка (У) матрицей
52 =
1
-2
О
I
с параллельными векторами смещений d = [-2y о] || х° и множеством не-
подвижных точек, лежащих на оси х;
Геометрические преобразования
147
□ квадрата (2) и круга (3) матрицей
с непараллельными векторами смещений d = [-2y х].
Рис. 2.3
На рис. 2.3, б выполнены преобразования объемной фигуры в пространстве:
J сдвиг (/) вдоль оси у матрицей
1 -2 О
$з=0 1
0
I
0 0
с параллельными векторами смещений d = [о -2х 0] 11 у° и множеством
неподвижных точек, лежащих в плоскости yz;
□ сдвиг(2) матрицей
1
0 0
1 0
-1 1
с векторами d = [- у -z -z о];
сдвиг (5) вырожденной матрицей
^3 =
о
1
о
о
1
о
ранга 2, в результате чего все точки прообраза лежат в плоскости x-z = 0.
148
Гпава 2
2.1.2.4. Вращение
Вращение (rotation) точки на плоскости ху вокруг начала координат (рис. 2.4, а)
описывается следующими координатными уравнениями:
х' = rcos(a + <p)= х cos(<p)~ ysin(<p}
у' = г sin (а + <р) = х sin (<р)+ у cos(<p),
откуда следуют матрицы вращения в положительном (против часовой стрелки) и
отрицательном (по часовой стрелке) направлениях:
««.МЛ
sin(cp) cos((p)
> Л("ф)=
cos(<p)
sin(<p)
-sin(<p)
cos(<p)
(2.20)
= /?T(<p)= 7?-'(<p).
Рис. 2.4
При вращении точки в пространстве вокруг осей правой системы координат
(положительные направления вращений удовлетворяют правилу буравчика и
показаны на рис. 2.4, б) матрицы вращений получим из соответствующих урав-
нений:
□ х" - х, у' - y’cos(<pv) - zsin(<pv), z' - ysin(<pv) + zcos(<pv),
1
О
Лг(<Рх) =
О
cos(<pj
-sin(<pj
sin(<pJ > ^(-<px)=/?x’(<px);
(2.21, a)
cos(<pj
О
0
□ x' - xcos(tpy) + zsin((p;,), y' = y, z’ - -xsin((p>) + zcos(<p>),
-sin^J
0
cos(<pj
«Ру) ('Ч’у)’
(2.21,6)
О x' - xcos((pz) - J’sin(<p_), y' = xsin(<p,) + j cos((p.), z' = z,
Геометрические преобразования
149
cos(<pz) stn(<p_) О
-sin(<pz) cos(<pz) О
(2.21, в)
О О 1
Преобразование вращения не изменяет углы между синхронно вращающимися
векторами, площади, объемы и форму геометрических фигур, а также топологи-
ческие свойства полигонов. Определители всех матриц вращения равны единице.
Благодаря свойству ортогональности
R1 R = RR1 = Е„
при изменении знака угла вращения на противоположный обращение матриц
вращения заменяется их транспонированием:
/?-'(<р)=/?т(<р).
Векторы смещения вращательного движения
d = P(R^) - Е„)
(2.22)
образуют цилиндрическое векторное поле, ось симметрии которого <о содержит
множество неподвижных точек. Центр всех вращений на произвольные углы во-
круг любых осей координат располагается в начале СК.
Строго говоря, вращение не является элементарной операцией, т. к. его можно
представить последовательностью масштабирования и сдвига:
cos(<p) sin(<p) cos(ф) О I Г 1 tg(<p)-l
— sin(cp) cos(<p) 0 cos(<p) — tg(<p) 1
Тем не менее ввиду простоты понимания, распространенности и важности места
вращательного движения в системе геометрических преобразований целесооб-
разно считать вращение элементарным, а не сложным преобразованием.
2.1.2.5. Табличный расчет
тригонометрических функций
Весьма важным в практике применения матриц вращения является быстрый рас-
.ет тригонометрических функций угла и наоборот — угла по значениям его три-
гонометрических функций. Актуальность этой проблемы объясняется присутст-
вием преобразования вращения практически в каждом сложном преобразовании
и высокой частотой выполнения этой операции, в том числе и во вложенных
циклах. Использование встроенных в языки программирования функций cos и
sin, вычисляемых суммированием рядов Тейлора, конечно, заманчиво, но не-
практично из-за их невысокого быстродействия.
Еще меньшая скорость сходимости у обратных тригонометрических функций, из
которых во встроенной библиотеке обычно имеется только функция arctg. От-
150
Гпава 2
сутствующие функции arcsin и arccos можно вычислить либо создав собственные
варианты этих функций
asin(x) = if | x |< 1: arctg
acos(x) = if x: arctg
(2.23, a)
(2.23, 6)
либо суммируя до сходимости по заданной погрешности е соответствующие ря-
ды Тейлора:
( \ 1 3 3 5
arcsin(x)= хч---х ч-------х
2-3 2-4-5
~ 2А+1
3-5 7
ч---------X
2-4-6-7
2* ,
^->2Л + 1
А=1
i=2
2 ’
2 ’
arccos(x) = y - arcsin(x).
Оба ряда у границ области |х| < 1 сходятся очень медленно (более 4000 итераций)
и с недопустимо большой ошибкой (до 0.0086 рад, т. е. 0.5°) при абсолютной по-
грешности е = 10“6.
В настоящее время наиболее быстрым и популярным считается табличный метоо
вычисления тригонометрических функций с кусочно-линейной интерполяцией
между узлами сетки. Суть его в том, что при запуске прикладной программы
один раз с высокой точностью вычисляется N + 1 узловое значение наиболее вос-
требованной в машинной графике монотонно убывающей функции с(х) = cos(x)
в интервале х е [0, л / 2] с шагом Ах = л / 2N. Таким образом, в оперативной па-
мяти компьютера создается 2 х (Л7 + 1)-матрица (таблица) узлов сетки
х,- = (Ах, с, = cos(x,) V/ = О, N.
При вычислении тригонометрических функций cos(x) и sin(x) произвольный ар-
гумент х циклическим смещением
х = х - 2sgn(x)n
приводится в интервал [-л, л]. Далее используются известные тождества, сужаю-
щие интервал до [0, л / 2]:
cos(x) = c(x),
cos(x) = -с(л - x),
cos(x) = c(-x),
cos(x) = -c(n + x),
sin(x) = с(л / 2 - x);
sin(x) = c(x - л / 2);
sin(x) = -с(л /2 + x);
sin(x) = -с(-л / 2 - x).
(2.24, a)
(2.24, 6)
(2.24, e)
(2.24, г)
Геометрические преобразования 151
Вычисляя значение с(^) по аргументу 0<£<л/2, определим индекс i = [^/AcJ,
при котором х, < < х1+, (рис. 2.5). Тогда приближенное линейно интерполиро-
ванное значение функции равно
с(£)=с< +(g+i ~ci) г-' •
Рис. 2.5
Допустим, составлена таблица {х„с,} с крупным шагом Дх = 0.01745 рад = 1° и
задан аргумент х = -14.2 рад. Сместив его на два периода, получим
х = -14.2 + 4л = -1.6336 рад = -93.6°.
Вычислим по (2.24, г) функции cos(x) и sin(x):
Д £ = л + х - 1.508 рад => i = 86, «6 = 0.06976, m = 0.05234, откуда
-<"(0^-0.062789,
в то время как cos(x) = -0.069792. Абсолютная и относительная погрешности
интерполяции составили 2.25 • Ю-6 и 3.59 • 10~5;
“1 £, = -л/2-х = 0.06283 рад => z = 3, сз = 0.99863, С4 = 0.99756, откуда
-с(О» -0.99799,
тогда как sin(x) = -0.998027. Абсолютная и относительная погрешности ин-
терполяции составили 3.648 • 10~5 и 3.655 - 10-5.
Расчет обратных тригонометрических функций 0 < arccos(«) < л (рис. 2.6, а) и
-- / 2 < arcsin(«) < л / 2 (рис. 2.6, б) аргумента -I < а < 1 начинается с поиска ин-
декса z, для которого с,.ц < |«| < с,. С помощью линейно-интерполяционной функции
L(a,i) = xl +——— Дх
Q+l -Q
152
Гпава 2
получим приближенные значения
, ч f при «>0;
arccos(a) = ( ( .
[ 7Г-£(-я,/) при а<0;
. z ч [ тг/2 - L(a,i) при п>0;
arcsm(a)=( , . ,
[ L(~ a,i)-n/2 при a<0.
(2.25, a)
(2.25, б)
Рис. 2.6
Вычислим по таблице {л„ с,}, i = 0,90, функции arccos(«) и arcsin(n) для a = -0.98.
Так как ci i = 0.982 и сп = 0.978, то i = 11. Тогда по (2.25) находим
arccos(n) «л - L(-a, i) = 2.941445 рад;
arcsin(n)~ L(-a, i)-n!2--\.370648 рад.
Точные значения углов равны, соответственно, 2.941258 рад и -1.370461 рад
Даже при такой крупной сетке, построенной с шагом 1°, максимальная абсолют-
ная погрешность вычисления обратных тригонометрических функций на грани-
цах интервала -1 < a < 1 составила 4.767 10 4 рад или 0.03°.
В заключение приведем примеры нелинейных элементарных преобразований.
Геометрические преобразования
153
Пример 2.1. Получить матрицы кручения и изгиба вокруг координатных осей.
Решение. Деформация кручения характеризуется линейно возрастающим углом
вращения слоев материала, ортогональных оси кручения, при удалении от не-
подвижного основания. Кручение так же соотносится с вращением, как сдвиг с
переносом.
Вывод матрицы кручения вокруг оси х аналогичен выводу матрицы (2.21, а).
Пусть а— погонный угол кручения, т. е. дополнительное вращение, приходя-
щееся на единицу длины (на рис. 2.7, а изображено кручение параллелепипеда
при а = 9°). Тогда координатные уравнения и матрица кручения имеют вид
х' = х Г1
у' = ycos(ax)-zsin(ax) => B^.(a)= О
z/ = ysin(ax)+zcos(ax) О
О
cos(ax)
-sin(ax)
О
sin(ax)
cos(ax)
/?x(ar).
Аналогично получаются матрицы кручения вокруг осей у и z:
и$(Р) = я,(РЯ
FK(y) = Rfyz).
Рис. 2.7
Кручение превращает прямую ро + Vt, не ортогональную оси кручения, в винтовую
•ривую. Следовательно, это нелинейное преобразование не является аффинным.
В отличие от кручения при деформации изгиба угол поворота точки вокруг оси
изгиба пропорционален ее удалению. Матрицы преобразования изгиба вокруг
- оординатных осей, зависящие от погонных углов a, р и у (на рис. 2.7, б изобра-
жен изгиб параллелепипеда вокруг оси z с коэффициентом у = 4.5°), равны
Dx(a)=/?/a7/ + z2l Dy(p)=/?Jp7x2+z2l Dz(y)=Rz(yJx2+y2
154
Гпава 2
Изгиб превращает прямую линию ро + И/, не параллельную оси изгиба, в спи-
ральную кривую (см. рис. 1.31, а). Следовательно, и это нелинейное преобразова-
ние не является аффинным. □
2.1.3. Сложные аффинные преобразования
Сложным (комбинированным) называется преобразование, реализующее цепоч-
ку не менее, чем из двух элементарных преобразований. Отметим, что почти все
аффинные преобразования не коммутативны, т. е результат цепочки преобразова-
ний зависит от порядка их выполнения. Для цепочки из двух ЛП с матрицами Ci и
Сг некоммутативность означает C1C2# С2С1. Например, комбинации вращения
объекта вокруг оси со е {х, у, z} на угол ср и переноса на вектор Д/> имеют разные
матрицы сложного АП:
Лш(ср)г(Дд) =
Яш(ф) О„х1 Е,
_°1х„ 1 JL^
* 7'(Др)я(и(ср) =
О«х1 _ Лш(ф) О„х|
1
^со(ф) О«х1
ДрЛш(ср) 1
Др
п
Как исключение, попарно коммутативны лишь преобразования перенос - перенос и
масштабирование — масштабирование-.
Т(\р^Т(\Р2) =
\тх, Шу, т2
Еп
Др1
При выполнении преобразований не теряйте из виду систему координат! Напри-
мер, вращения куба вокруг оси \, а затем вокруг оси у, оставшейся неподвиж-
ной, дают матрицу R, R, и конечное положение куба, показанное в конце цепоч-
ки 1 - 2 на рис. 2.8. Если забыть направление оси у и второе вращение куба сде-
лать вокруг отклоненного ребра, которое вначале было вертикальным ((цепочка
1 - 5)), то матрица полного АП с учетом вращения системы координат вокруг
оси х, поворота куба и возврата в исходное состояние будет равна
RX\R~XRVRX)= R,.RX # RXR.,.
л \ л у х / ух х у
Разные конечные положения кубов наглядно доказывают, что преобразования
вращения не коммутативны.
Геометрические преобразования
155
Рис. 2.8
2.1.3.1. Методы расчета матрицы
сложного преобразования
Рассмотрим два метода расчета матрицы сложного преобразования С в задачах с
произвольным расположением осей вращения, прямых и плоскостей отражения.
□ Метод разложения (декомпозиции) сложного движения объекта на N элемен-
тарных движений, описываемых матрицами С, относительно координатных
осей и плоскостей неподвижной СК. Тогда по (2.8) получим
.V
с = ПС
1=1
Разложение процесса на составные части — отличительная черта "методов
серого ящика", в которых форма (начальное и конечное состояние объекта)
наполняется содержанием (промежуточными состояниями и способами их
достижения) не единственно возможным образом. Задача и искусство про-
граммиста состоит в оптимизации состава ЭП.
Полезным приемом, часто облегчающим выбор ЭП, является временный пере-
вод системы координат матрицей Ск в такое положение, где оси вращения,
прямые и плоскости отражения становятся координатными. В измененной СК
выполняются необходимые элементарные АП с общей матрицей Q. Восста-
новление системы координат в исходное положение описывается матрицей
1 Таким образом, сложное АП имеет матрицу
с=скеск-‘.
156
Гпава 2
При расчете матрицы Ск необходимо помнить об инвертировании знаков па-
раметров элементарных преобразований — вектора переноса начала коорди-
нат и углов вращений СК вокруг ее осей.
□ Метод парных точек, определяющий матрицу АП по трем (на плоскости) или
четырем (в пространстве) парам линейно независимых точек образа и прооб-
раза. Это принципиальное безразличие к способам перехода от начального к
конечному состоянию объекта — явный признак "метода черного ящика".
Обращаемые в (2.13) и (2.14) матрицы всегда будут невырождены при усло-
вии, что тройки точек не коллинеарны, а четверки — не компланарны. Наи-
лучшая обусловленность матриц достигается при ортогональности систем
векторов, построенных на выбранных точках образа и прообраза.
Читателю предлагается оценить эффективность метода парных точек на сле-
дующих примерах.
& Пример 2.2. Рассчитать матрицу преобразования треугольника р\pi pi в тре-
угольник /?4psрь (рис. 2.9).
Решение. Подставив вершины треугольников в (2.13), сразу получаем необходи-
мую матрицу АП:
-4 2 ’Г 2 з Г -1.375 1.25 О'
с= -3 -1 1 4 -1 1 = -1.125 1.75 0
-1 1 1 -1 5 1 -1.25 4.5 1
Вот и все. А теперь попытайтесь угадать последовательность и параметры эле-
ментарных преобразований, переводящих треугольник pt pi pi в треугольник
рьрьрь, вычислить матрицы этих преобразований, сравнить их произведение с
вышенайденным результатом — и вы почувствуете разницу методов! □
Геометрические преобразования
157
& Пример 2.3. Рассчитать масштабный коэффициент цэ и матрицу Сэ пропор-
ционального отображения прямоугольного окна {Xmin 4- Лщах, Jniin 4- J'rnax} В ПЛОС-
КОСТИ ху МСК в центр окна ЭСК {left 4- right, up 4- down] (рис. 2.10).
Рис. 2.10
Решение. Обозначим коэффициенты прямоугольности окон в МСК и ЭСК:
Tmax ~Tmin _ down-up
*max-*min ’ ’ right-left'
\ пропорциональных окон коэффициенты прямоугольности р и рэ равны, а окно
МСК отображается во все окно ЭСК. В этом случае матрица Сэ наиболее просто
находится методом парных точек (2.13) при п — 2. Хотя задача решается на
плоскости, но с целью использования ее результата для преобразований в про-
странстве выберем четыре пары некомпланарных точек в МСК и ЭСК:
Р1 = Ь-min >’min О] Лэ = № down °L
Р2 = [*min Утах б] -4 р2э = [/e/Z up О],
P3=knax Утах о] -> р3э = [ngA/ up О],
7° 7°
“ z3 •
Тогда
*min Tmin ® 1 -1 left down 0 1
С, = xmin Утах ® I left up 0 1
Xmax Утах ® 1 right up 0 1 (2.26)
0 011 .° 0 1 1.
1 _ right-left _ down-up
*max — *min Tmax-Train
В случае непропорциональных окон получим матрицу Сэ методом разложения,
выполнив цепочку элементарных преобразований исходного окна в МСК.
158
Гпава 2
Шаг 1. Перенос центра окна в начало МСК матрицей
т — т([ г v о!) гпр г _ xmin +-vmax _ J’min +J’max (2.27, л)
Л-Ml xu о];,гдехц-- , >’ц--------
Шаг 2. Пропорциональное масштабирование окна по осям координат и измене-
ние направления оси у матрицей
A/=diag[p3 -цэ 1], где рэ
right - left
------------ при рэ > р;
Xmax xmin
down - up
------------ при рэ < р.
-Утах .Уmi и
Шаг 3. Перенос центра окна в точку р31( в ЭСК матрицей
гг о left + right _up + dow
^2 — \ Iх цэ Л’цэ OJA r^e хиэ > 7’цэ —
Матрица полного преобразования равна
(2.27, б)
(2.27. в)
Мэ 0 0 О'
Сэ =7jA/72 = 0 "Рэ 0 0
0 0 1 0
хцэ — М-ЭХЦ З’цэ *‘М-э7?ц 0 1
(2.27, г)
Коэффициенты этой матрицы дают прямые уравнения пересчета координат точ-
ки из МСК в ЭСК (координата z3 вектора /?э = рСэ при этом не используется):
Хэ — Хцэ + Цэ(Л" “ Хи), Уз — J'in — Цэ(у У и). (2.28)
Описанный алгоритм гарантирует, что любое изображение в прямоугольном
окне без искажений отобразится в любом желаемом окне дисплея, заполнив его
максимально полностью и симметрично относительно центра.
Если при расчете масштабного коэффициента рэ по (2.27, б) заранее неизвестны
границы окна МС К, целиком вмещающего сцену, можно задать значение jx> = 40
из тех соображений, что один сантиметр экрана (40 пикселов) соответствует од-
ной единице длины в пространстве МСК. Наконец, можно выбрать единицу
длины в МСК равной размеру пиксела экрана 0.25 мм. Тогда рэ = 1, что сильно
упрощает матрицу (2.27, г) и координатные уравнения (2.28):
1
О
О
О 0 0
о
I
о
о
ХЦЭ Х11
-1
о
Уцз+Уц 0 1
, Хз = Хиэ - Хи + X, Уз = >'иэ + >‘и - у.
(2.29)
'еометрические преобразования
159
Сравним методы вычисления матрицы сложного АП на примере весьма распро-
гграненной операции изменения пространственной ориентации системы коорди-
iam, заключающейся в совмещении начала СК с точкой о, а какой-либо коорди-
натной оси, допустим, z— с направлением заданного вектора И* Оз (рис. 2.11).
Положение других осей в измененной СК не регламентируется. Данное преобразо-
вание применяется, например, в алгоритмах вращения (/) вокруг заданной прямой
о, И} или отражения (2) от произвольной плоскости вдоль ее нормали И.
Рис. 2.11
Решение задачи достигается за два преобразования.
Перенос начала координат в точку о, описывается матрицей 7(-о).
2. Поворот оси z в направлении вектора V, выходящего из начала новой СК.
Обозначим нерасширенную матрицу этого преобразования Л(К).
Расширенная матрица полного преобразования СК равна
С(о,Р)=7’(-о)л(г).
Рассмотрим различные методы вычисления матрицы поворота Л(К).
Метод разложения
Алгоритм, основанный на методе разложения, рассматривается во многих учеб-
никах по машинной графике [5, 26, 33, 34] и состоит в нахождении проекции
V = [l’v К_] вектора Vна координатную плоскость л/ (у разных авторов вариан-
ты алгоритма отличаются выбором плоскости проецирования) и выполнении
звух вращений СК xyz (рис. 2.12):
□ первое вращение вокруг оси у на угол а, у которого
cos(a)= -р-, sin(a) = -j^-, где |v| = + И,2 .
Система координат после этого занимает положение x'y'z', в котором ось z'
совпадает с направлением вектора v;
160
Глава 2
□ второе вращение вокруг новой оси х' на угол -Р, у которого
v К
cos(p)=j—, sin(p) = -p7
Система координат после этого занимает требуемое положение x"y"z", в ко-
тором ось z" совпадает с направлением вектора V.
Рис. 2.12
Таким образом, матрица поворота СК по методу разложения равна
ЯР(Ю = кЛ(Р). (23°)
Всегда ли верно это решение? Очевидно, что оно не является таковым при |v| = О,
когда К || _у°. В этом случае угол а не определен, а совмещение орта z° с векто-
ром V достигается не за два, а за одно вращение СК матрицей
ЯР(Ю = ^v(sgn(K,)90°).
Однако, и при V#y° у метода (2.30) имеются скрытый недостаток и особенно-
сти программной реализации, которые даже не обозначены и не обсуждаются в
перечисленных выше учебниках:
□ при расчете матриц вращения по (2.21) возможно использование неверных
аргументов, вычисленных с помощью функции arccos в интервале [0°, 180°], в
то время как углы изменяются в интервалах
-180° < а < 180°, -90°<Р<90°.
Так же некорректно определение угла а (но не р!) функцией arcsin в интервале
[-90°, 90°]. Следовательно, угол а должен вычисляться с учетом знака его си-
нуса, т. е. функцией (1.31) с векторными аргументами [гх Vz\ и [о 1]. Итак,
в (2.30) углы вращений находятся следующим образом:
(2.31)
геометрические преобразования
161
□ поскольку матрицам вращения требуются, собственно, не сами углы, а их коси-
нусы и синусы, которые в рассматриваемой задаче явно выражены через эле-
менты вектора V, то практичнее создать модификации матриц вращения (2.20) и
(2.21) с двумя аргументами с и 5— косинусом и синусом угла вращения:
(2.32)
Эти матрицы рекомендуется использовать даже в тех случаях, когда исход-
ным является угол вращения <р: вычислив один раз с = cos(<p) и a - sin(cp), под-
ставить их в (2.32) вместо двукратного вычисления в (2.20) и (2.21);
□ прямая подстановка
и
Id
cos(a)=-pj-, sin(a) = -J^, cos(p)=£L sin(₽) =
M P'l И
в матрицы вращений (2.30) и их ручное перемножение приводит к весьма гро-
моздкой записи матрицы АР(1/), которую автор здесь сознательно не приво-
дит, дабы не искушать читателя этим порочным методом разработки алго-
ритмов компьютерной графики. Во-первых, в процессе ручных выводов
очень легко наделать ошибок. Во-вторых, вместо элегантного перемножения
матриц в одной строке программы поэлементное описание матрицы АР(Г~)
требует много строк — это путь к разбуханию программного кода, источник
дополнительных ошибок и затрат времени на отладку программы.
Матрицы некоторых сложных преобразований на плоскости, вычисленные ме-
тодом разложения, приведены в табл. 2.1.
Таблица 2.1
Преобразование Матрица преобразования
I , Масштабирование I от точки о Т(-о}м(р1х,ту}т(р) = тх 0 0 ту (\-тх)ох ^-ту 0 0 )°у
Отражение от точки о Т(-о)м(-\,-\)т(о) = -1 о о’ 0-10 2ох 2о.. 1
162
Гпава 2
Таблица 2.1 (продолжение)
Преобразование Матрица преобразования
Отражение от прямой {о, И} cos(a)=r4, sin(a)=-r^f- И И г(- о)«(- а)М (-1,1 )« (а ) т(р) =
= 2sin2(a)-1 -2cos(a)sin(a X - 2 cosl a)sin(a) C
) l-2sinz(a) С Y 1
X ~ 2cos(a)(oAcos(a) + o(,sin(a)) Y = 2sin(a)(ovcos(a) + o;.sin(a))
Отражение от прямой у = ax + b о = Ьу°, а = arctg(rt), |л| < оо T (1-Г72И1 + О2 2оД1 + о2) -2ab/^ + a2} 7(1-1)л(с ) WG 2Z>/(1 с)т(^°)= + «2) o’ W) ° +«2) 1
Отражение от прямой х - а T -ах°)л/(-1, 1 )7’(ax°)= -1 0 o' 0 1 0 2a 0 1
Отражение от прямой у = b T (-Ьу°)м(\,-\} '1 0 O' 0-10 0 2b 1
Отражение от прямой у = х Л(45°)Л/(-1, l)«(-45°) = 0 1 o' 1 0 0 0 0 1
Отражение от прямой у — -х Л(-45°)Л/(-1, 1) Я (45°) = 0-10 -10 0 0 0 1
Вращение вокруг точки о на угол <р г(-о)л(ф)г(о)= X = ov(l - сг Y= о,(1 — с< cos(<p) sin(<p) 0 -sin(<p) cos(<p) 0 X Y 1 )s(<p)) + o,,sin(<p) >s(<p)) - ovsin(<p)
Геометрические преобразования
163
Таблица 2.1 (окончание)
Преобразование Матрица преобразования
Сдвиг вдоль прямой {о, V} cos(a)=7^-, sin(c/.)=— и и Г(-о)/?(-а) ' 1 0 О' sxy 1 0 0 0 1 Л(а)г(о)
Матрицы сложных преобразований в пространстве приведены в табл. 2.2.
Таблица 2.2
Преобразование Матрица преобразования
Масштабирование от точки о = Т(^- о')м{р1х,ту, тх 0 0 ту 0 0 (l-wjox (l-wy)< mz )г(о) = 0 o' 0 0 mz 0 ^~mz)°z 1
Отражение от точки о Г(- о) м(-1,-1 -1)7(0) = -1 0 0 O' 0-100 0 0-10 2or 2ov 2oz 1 _ X у Z J
Отражение от прямой {о. V] cos(a)=—, sin(cc)= —, V V cos(₽)=i^, sin(P) = -^, V = ^x2+^ №у°: Т(- o)Ry (- a)Rx (₽)Л1(-1,-1, 1К (- р)Лу (а) т(р )
VII/ Г(-о)л/(-1, 1,-1)г(о) = -1 0 0 o' 0 10 0 0 0-10 1ox 0 2o_. 1
164
Гпава 2
Таблица 2.2 (продолжение)
Преобразование Матрица преобразования
7’(-о)Л/(1,-1,-1)Т’(о) = 10 0 0 0-100 0 0-10 0 2оу 2о, 1
r||z° т(-о)м(-1,-1, 1)Т’(о) = '-1 0 0 ( 0 -1 0 С 0 0 1 С 2ог 2о., 0 )'
Отражение от плоскости {о.М cos(a) = -^-> sin(a)=-^-, V V eos(₽).^. sin(P)-^. V = Jn* + N* Т(- o)Ry (- а)/?х(₽)Л/(1, 1,-1)7Ц- р)ял, (a)T(o)
*117° Г(-о)Л/(1,-1, 1)Т’(о) = '1 0 0 О' 0-100 0 0 10 0 2оу 0 1
7V || л°: 7’(-о)Л/(-1, 1, 1)Т’(о) = '-1 0 0 О' 0 10 0 0 0 10 2ох 0 0 1
Геометрические преобразования
165
Таблица 2.2 (продолжение)
Преобразование Матрица преобразования
^|z°: 7’(-о)Л/(1, 1,-1)г(о) = ’1 0 0 O’ 0 10 0 0 0-10 0 0 2o_ 1
Вращение вокруг прямой {о, V} на угол <р cos(a)= —, sin(a)= —, V V ,, V cos(₽)=i^.sin(₽)=^, v = + V2 • s“ ~ sgnfVJ V#y°: Г(- o)Ry (- a)Rx (₽Я (<p)/?x (- ₽)/?, (а) т(о)
= Г К/: г(-0)^^<р)г(0)= cos(<p) 0 -.s^sir^q)) 0 0 10 0 sin(<p) 0 cos(<p) 0 ox(l-cos(<p))- o o2(l-cos(<p))+ j ~syoz sin(ф) + syox sin(<p)
= Г||х°: T(-o)Rx(sx(p)-T(o) = rl 0 0 O' 0 cos(<p) 5xsin(<p) 0 0 -5xsin((p) cos(<p) 0 o>,(l-cos((p))+ oz (1 - cos(<p))- ! + sxo2sin(<p) -5^о>з1п(ф)
166
Гпава 2
Таблица 2.2 (окончание)
Преобразование Матрица преобразования
= П^°: г(-о)Йг(уг<р)г(о) = cos((p) .s , sin (ср) 0 0 - j_sin((p) cos(<p) 0 0 0 0 10 ox(l - cos((p))+ Oy(l — cos(<p))— j + .v_o>, sin(cp) -j.oxsin((p)
Экономичный метод разложения
Экономичный вариант метода разложения заключается в вычислении вектора
нормали =z°xrе ху и двух вращений системы координат (рис. 2.13):
П на угол а вокруг оси z;
П кратчайшего вращения на угол р вокруг новой оси у'.
Рис. 2.13
Судя по интервалам изменения углов -180° < а < 180° и 0° < р < 180°, формулы их
расчета и матрицы поворота следующие:
а = if (|/V|:ang(y°, /v), о), p = arccos(z° о r), Jjp(Ю = A-(-a) Л,(-р). (2.33)
Метод парных точек
Для получения 3 х 3-матрицы Л(Р) методом парных точек найдем в пространстве
три неколлинеарные точки, в которые перейдут концы ортов х°, у° и z° после
Геометрические преобразования
167
поворота системы координат (рис. 2.14). Одна из этих точек на конце вектора
V— прообраз z°. В общем случае при K#z° выберем прообразы векторов у0 и
х° на концах векторов нормали = z° х V е ху и бинормали И7 = Лгх И. Длины
векторов N и W равны — это необходимо для неискаженного преобразования
углов из СК x'y'z' в СК xyz. Подставляя точки образа {х°, у°, z0} и прообраза
{И7, N, К} в нерасширенный вариант (2.14), получим
4(П=
Особый случай — параллельность векторов К11 z°, при которой z° х К = О3.
Специальный выбор векторов
N = Ky°, И7=#хЙ=|К,|л0
обеспечивает ортогональность, равномасштабность и правую ориентацию трой-
ки {IV, N,V} базисных векторов системы x'y'z' как при V ТТ z°, так и при
Г TJ- z°. Эти три свойства необходимы для правильного отображения в СК xyz
как величины, так и знака угла вращения, выполняемого в СК x'y'z'.
Обобщая сказанное, запишем алгоритм расчета матрицы поворота системы коор-
динат методом парных точек в следующем виде:
WxK
W = if( |z°or|<l: z°xr, ЛП(И)=
(2.34, a)
168
Гпава 2
Метод парных точек позволяет сразу найти матрицу полного преобразования
системы координат, равную Т(-о) Ап(У), без разложения на промежуточные пре-
образования:
Сравнение методов (2.30), (2.33) и (2.34) по критериям понятности, простоты вы-
вода, краткости записи, вычислительной эффективности ставит впереди всех, по
мнению автора, метод парных точек. К сожалению, все рассмотренные методы
страдают условностью, т. е. зависимостью алгоритмов от особых случаев ориен-
тации вектора V. Видимо, единый алгоритм для произвольных положений этого
вектора отсутствует, а те методы, что предлагаются в учебной литературе —
лишь частные случаи, не учитывающие особых ситуаций. Опыт курсового про-
ектирования студентов под руководством автора показывает, что эти ситуации
встречаются не так уж и редко. Внешне они проявляются во внезапном заверше-
нии программы из-за попытки деления на ноль при обращении вырожденной
матрицы.
Гораздо проще, чем в Зб-варианте, вычисляется матрица преобразования систе-
мы координат на плоскости. Допустим, требуется совместить начало координат с
точкой о, а оси у придать направление вектора V (рис. 2.15). Такое преобразова-
ние полезно делать при расчете отражения и масштабирования относительно
произвольной прямой {о, И}.
Рис. 2.15
Приведем без лишних рассуждений очевидные формулы расчета матрицы пре-
образования системы координат Ск:
П по методу разложения
a = ang(y°,r), Ср(о,К)=7’(-о)л(-а); (2.35)
Геометрические преобразования
169
□ по методу парных точек
N = га(-90°)= [vy
(2.36)
Пример 2.4. Построить отражение треугольника на плоскости с вершинами
Р]=[о О], Р2=[0 1] и Рз=[2 О] от прямой линии, проходящей через точки
Р4 = [з О] и р5 = [2 2] (рис. 2.16).
Рис. 2.16
Решение. Вычислим направляющий вектор и нормаль заданной прямой линии:
Г = р5-р4=[-1 2], W = r/?(-90°)=[2 1].
Последовательность действий для построения отражений р' исходных точек р,
(i - 1,2, 3) может быть, например, следующей.
Шаг 1. Получим по (2.35) матрицу преобразования системы координат
методом разложения на два элементарных преобразования: перенос начала ко-
ординат на вектор рь и вращение на угол а, у которого
170
Гпава 2
Второй вариант матрицы преобразования системы координат получим методом
парных точек (2.35) по двум тройкам точек {л°,> °, О2} и {^б.р5,/м}:
-0.2
0.4
0.6
О
О
I
Читателя не должно смущать несовпадение полученных матриц: видимо, матри-
ца СкР эквивалентна иной, чем в матрице Скп, последовательности элементарных
преобразований, которые, по сути дела, нас не интересуют. Главная цель— по-
лучение матрицы преобразования системы координат— достигнута с помощью
метода парных точек быстрее и проще.
Шаг 2. Отражение вдоль оси х' описывается матрицей М = diag[— I 1].
ШагЗ. Восстановление исходной системы координат описывается матрицами
1 0
2 О
О 1
Шаг 4. Матрица сложного АП
'-0.6
С = СкрМ С~р = СКНМ Cjt =
-0.8
4.8
-0.8 0
0.6 0
2.4 1
одинакова для обоих методов расчета матрицы изменения СК, что подтверждает
вывод о неединственности способа выполнения сложного преобразования.
Шаг 5. Координаты отраженных точек рассчитаем групповым методом (2.8):
Р\ Г Р\ Г '0 0 Г -0.6 -0.8 О' 4.8 2.4 Г
Р1 1 = Р2 1 с = 0 1 । -0.8 0.6 0 - 4 3 1 .С
РЗ 1 Рз 1 2 0 I 4.8 2.4 1 3.6 0.8 1
2.1.3.2. Кинематический метод построения объектов
Аффинные преобразования — основа кинематического метода построения пара-
метрических объектов (кривых и поверхностей), генерирующего состояния объ-
екта из заданных начальных состояний точки, отрезка, окружности как функции
некоторого параметра, имеющего физический смысл времени движения. Конеч-
ным результатом преобразований являются не уравнения объекта, а его изобра-
жение на экране. Построение изображения эффективнее выполнять не по слож-
ным аналитическим уравнениям, а непосредственно по обобщенной векторной
Геометрические преобразования
171
модели, задав желаемое начальное состояние объекта, необходимые матрицы
преобразований и интервалы изменения параметров. Простейший пример: для
построения окружности кинематическим методом достаточно задать:
□ начальное состояние точки, например, р(о)= [1 О];
□ возрастающие значения параметра в интервале t е [0, 2л];
□ векторное уравнение p(t) = р(0)7?(/), моделирующее вращение точки на еди-
ничном расстоянии от начала координат. Параметр t имеет физический
смысл угла между векторами р(0) и pit).
Для повышения эффективности своей работы программистом должна быть соз-
дана библиотека матричных и графических функций, процедур и алгоритмов.
Такой стиль разработки программ делает их модульными и компактными, луч-
ше читаемыми, удобными в отладке и внесении корректив в структуру и пара-
метры модели.
При решении же задач анализа необходимы координатные уравнения состояний
объекта, получаемые обычно кропотливыми ручными выкладками либо с по-
мощью возможностей символического процессора MathCAD, либо какой-
нибудь другой "умной" математической программы.
Рассмотрим основы кинематического принципа конструирования линий. Кривая
изображается на экране последовательностью точек p(t,), соединенных отрезка-
ми прямых. Визуальная близость полученной ломаной линии к гладкой кривой
определяется плотностью размещения узловых точек по периметру кривой. Оп-
тимальная плотность пропорциональна кривизне кривой, при этом минималь-
ное расстояние между соседними точками должно быть порядка одного пиксела.
Для получения такого распределения необходим анализ скорости V(l) - dp(t)l dr
движения точки по кривой. Например, вектор скорости движения по окружности
получается как
at
так и ручным выводом, и покоординатным дифференцированием уравнения
(1.57):
4)=[1
0]
cos(r)
-sin(r)
sin (l)
cos (t)
= [cos (t)
sin (r)] => Г (r)= [-sin (t)
cos (r)|.
(2.37)
Анализ модуля векторной функции |И(/)| = 1 показывает, что точка движется по
окружности с постоянной скоростью, поэтому оптимальным является равномер-
ное распределение значений параметра /, = г'Д/ VZ = 0, п по интервалу [0, 2л] с по-
стоянным шагом дискретности Дг = 2л In. При таком выборе параметрической
модели окружности соседние точки с, и с,+1 = с,Я(Дг) равноотстоят друг от друга
как по углу Дг = const, так и по периметру:
Ig+i - Gl = 2sin(Ar / 2) = const.
172
Глава 2
Соединение точек отрезками прямых аппроксимирует окружность правильным
«-угольником (рис. 2.17, а). С учетом масштабного множителя из (2.27, б) зна-
чения
П = 2тЩэ, Д/ = 1 / Цз
достаточны для того, чтобы расстояние между узловыми точками было равно од-
ному пикселу, а многоугольник точно совпал с окружностью. В действительности
уже при Д/ = 10 / рэ многоугольник визуально не отличается от окружности.
Возможны и некинематические параметрические модели окружности, напри-
мер, удовлетворяющие каноническому уравнению х2 + у2- 1 =0 функции коор-
динат x(t), y(t) и вычисленный их дифференцированием вектор направления
движения V(t)\
*(')=
I-/2
1 +t2
2t
1 + Z2
=> г(/)=2
(2.38)
Зависимость модуля вектора скорости движения от параметра t означает, что
при постоянном шаге Д/ точки (х(/,) _>’(/,)] распределены по окружности (кривой
постоянной кривизны) неравномерно (рис. 2.17, б). Кроме того, точка [-1 0],
соответствующая значениям параметра t = ±оо, вычислительно недоступна. Сле-
довательно, дробно-рациональная модель (2.38) неудачна, хотя по ней точки ок-
ружности рассчитываются быстрее, чем по тригонометрической модели (2.37).
Еще менее удачна некинематическая модель
x(t) = t, >’(/)=71^Z2 V/е [-1, 1].
Во-первых, по ней строится не вся окружность, а лишь ее верхняя половина.
Нижняя половина имеет ординату y(f)= -71-Z2. Во-вторых, вектор скорости
Е(/)= 1
в крайних точках [±1 о] при t -+ ±1 невычислим. В-третьих, нелинейная зави-
симость модуля скорости |к(/)| = 1/71 ~/2 от параметра t также дает неравно-
мерное распределение точек по периметру (рис. 2.17, в).
Проведенный сравнительный анализ трех моделей одного и того же графическо-
го объекта показывает, насколько компетентно нужно подходить к выбору как
уравнений модели, так и ее параметров для получения достоверного и качест-
венного изображения объекта на экране дисплея.
Геометрические преобразования
173
Рис. 2.17
Параметрические уравнения произвольного эллипса на плоскости с центром в точ-
ке Рц ~ 1хц >’н]> полуосями а, b и углом наклона большой полуоси а получим за
три преобразования (масштабирования, вращения и переноса) окружности c(t)
(рис. 2.18):
р(/)=4)
cos(a)
-sin (а)
sin (а)
cos(a)
+ Рц,
а О
О b
х(/)= acos(a)cos(r)- fesin(a)sin(r)+ хц,
y(t)= asin(a)cos(t)+Z>cos(a)sin(t)+_>’u.
(2.39)
Рис. 2.18
Модуль
v(/) = |к(г)| = sin2 (/)+ Л2 cos2 (f)
вектора скорости
г(/)= с'(г)л/(а,*)/?(а)=
= [-<7cos(a)sin(r)-fesin(a)cos(/)-asin(a)sin(r)+fecos(a)cos(/)J
174
Гпава 2
движения точки по эллипсу зависит от параметра 1 (рис. 2.19, а): в точках апогея
с максимальной кривизной скорость минимальна (v = min{a,/>}), в точках пери-
гея с минимальной кривизной — максимальна (v = шах{а, />}). Следовательно,
при аппроксимации эллипса полигоном плотность распределения его вершин р, по
периметру должна быть переменна: максимальна на участках апогея и минималь-
на на участках перигея.
Точное решение задачи распределения связано с исчислением эллиптических ин-
тегралов. Простейшее же решение — равномерное распределение t, = iAi с шагом
Л/ = 2л / п — благодаря непропорциональному масштабированию окружности в
(2.39) при а * b фактически приводит к нужному результату (рис. 2.19, б): график
8(z) плотности распределения точек p(z,) по периметру эллипса, приведенный на
рис. 2.19, а, обратно коррелирует с графиком скорости v(z). Оптимальные значе-
ния числа сторон полигона и шага дискретности
2тт
иэ = [~2лцэтт{а,б}~|, Дгэ = —
иэ
дают минимальные расстояния между точками эллипса в один пиксел на участ-
ках с максимальной кривизной.
В частном случае при а - Ь = г и а = 0 эллипс превращается в окружность ра-
диуса г с центром в точке рц = [хц уц]:
р(г) = гс(г)+рц = [rcos(f)+xu rsin(f)+yu]. (2.40)
Наилучшее качество аппроксимации окружности правильным /г-угольником
достигается при выборе параметров моделирования
— |~2лу.эг"], Az0 — .
«о
Геометрические преобразования
175
Произвольную окружность в пространстве радиуса г с центром в точке pu е R3,
лежащую в плоскости {pu, N}, получим несколькими способами.
□ По методу разложения подвергнем окружность единичного радиуса <"(/) е ху
с нормалью z° трем активным преобразованиям:
• масштабированию до радиуса г;
• совмещению нормали с вектором N;
• переносу центра в точку рц.
Векторное уравнение окружности
p(r) = r[c(z) О] А~‘(/V)+ рц
(2.41)
использует обратную матрицу преобразования системы координат AP(J7) с
аргументом V= N, вычисляемую в разд. 2./.J./ двумя способами:
• по варианту (2.30), (2.31) поворот z° —> W выполняется вращениями, изо-
браженными на рис. 2.20, а. Обозначив вектор проекции нормали
v = [/Vv 0 /Vz]gxz,
получим алгоритм
arcsin
Ny
(2.42, а)
Рис. 2.20
а
• по экономичному варианту (2.33) два вращения обеспечивают кратчайший
поворот z° —> (рис. 2.20, б). Вычислив вектор
W = z°xNe ху,
176
Гпава 2
получим алгоритм
a = if (|РК|: angle(y°, IV), б), Р = arccos(z° °n],
л1(н)=пУШ«)- <2'42,6)
Для иллюстрации сказанного составим по (2.42, б) аналитические уравнения
произвольной окружности в зависимости от ориентации нормированной
нормали W = [л^. Ny 7VZ]:
• при N#z° для вектора W = z° Nx о] длиной w = ^Nx + Ny *0
и параметров углов
cos(a)= —, sin(a)= Nv/w, cos(p) = N., sin(P) = w
w z/
получим координатные функции
x(t) = r(cos(a)cos(p)cos(r)-sin(a)sin(())+xu =
= хц + — (nxNz cos(/)- Nv sin (f)),
w Л
j(r) = r(sin(a)cos(p)cos(r)+cos(a)sin(r))+ Ju = (2-43)
= Ju + — (NyNz cos(/)+ Nx sin(r)),
w
z(()= -rsin(jp)cos(/)+zu = zu -nvcos(/)5
• в особом случае при N || z° в (2.43) имеет место вычислительная неопреде-
ленность типа 0/0 из-за того, что Nx = Ny = w = 0. Поэтому, полагая
IV = у0, a = 0 и cos(p) =/V, = ±1, получим уравнения окружности, не яв-
ляющиеся следствием уравнений (2.43) и потому не имеющие права на заб-
вение при программировании и анализе:
х(/) - г N. cos(z) + %ц, j(f) - г sin(r) + z(r) = zu. (2.44)
Применение метода разложения в задачах со сложными преобразованиями
требует развитого пространственного воображения и учета особых случаев,
что часто игнорируется и рано или поздно приводит к сбою программы.
Кроме того, преобразование по варианту (2.42, а) не дает поворота векторов
z° —> N по кратчайшему углу.
П Получим уравнение окружности суперпозицией колебаний точки вдоль двух
ортогональных векторов V и W, лежащих в плоскости {рц, N} (рис. 2.21).
В соответствии с (1.71) выберем произвольный вектор H#N, вычислим орто-
гональные нормали векторы
V = HxN, 1V = NxV
Геометрические преобразования
177
и составим комбинацию взаимно ортогональных гармонических колебаний
вокруг центра ри:
p(t) = pu + rcos(t)v + rsin(z)H/.
(2.45)
Рис. 2.21
При W#z° примем H = z°, тогда
K = [-Wy Nx о], fF = [-/VxW, -NyNz ^2],где w^N^ + Ny *0.
Подставив эти выражения в (2.45), получим аналогичные (2.43) выражения
x(z) = хц ~—(nv cos(z)+ NXNZ sin (/)),
w
y(t) = yu+ — (Nxcos(t)-NyNzsin(t)], (2.46, a)
w
z(l) = zu + rwcos(z).
При W || z° примем H = x°, тогда, подставив в (2.45) векторы
К = [0 -Nz 0],fF = [~l О О],
получим аналогичные (2.44) функции
x(z) = хц - rsin(z), j’(z) - J u - rN. cos(z), z(Z) = zu. (2.46, 6)
Таким образом, метод суперпозиции в конечном итоге эквивалентен методу
разложения, но существенно проще его как для анализа, так и для практиче-
ского построения окружности в пространстве.
178
Гпава 2
П По методу парных точек, основанному на расширенном варианте (2.34, б).
вычислим ортогональный нормали N = [д\. Ny Wz] вектор
W = if z°x7/L z°*N, Nzy°
с помощью которого получим уравнение окружности
?(')=М) о 1]с-’(рц, /7)=
= [rcos(t) rsin(t) 0 1 -rcos(z)-rsin(t)]
Pu+WxN
Pu + W_
Pu + N
Pix
1
1
1
1
(2.47)
Применение метода парных точек, в котором задаются лишь начальное и ко-
нечное состояния объекта, позволяет исключить из процесса разработки ал-
горитмов сложных преобразований выбор промежуточных ЭП, расчет их
матриц, учет особых условий ориентации объекта относительно системы ко-
ординат и другие тонкие моменты, непонимание которых может привести к
нежелательным визуальным эффектам.
Циклические кривые
Циклические кривые образуются сложением относительного движения точки по
окружности с переносным движением центра окружности по кривой рц(/)
(рис. 2.22, а):
p(t) = r(t)c(mt)Q + pu(t). (2.48)
В этом уравнении:
□ r(t) — закон изменения радиуса окружности;
’еометрические преобразования
179
<о — частота относительного вращения, согласованная с переносным движени-
ем и равная числу оборотов точки c(&t) при изменении t на 2л;
"о Q— матрица управления начальным состоянием и направлением вращения
точки по окружности. На рис. 2.22, б приведены значения матриц Q, дающих
начальные условия на осях координат и оба направления.
В ^елом закон движения (2.48) расширяет возможности формулы (1.58).
Получим уравнения некоторых циклических кривых.
1 Циклоида — это траектория движения точки окружности радиуса г при ее ка-
чении без скольжения по прямой у - 0 (рис. 2.23). Пусть в (2.48) со = 1, тогда
отсутствие скольжения означает переносное движение
Рц(/)='-[' 1J-
При изменении параметра t на 2л центр окружности смещается по оси х на
расстояние 2лг — длину ее периметра. Выберем матрицу
/ \ / х Го -Г
0 = Л/(1,-1)/?(-9О°)= о
такую, что вращение точки c(t)Q = [—sin(/) -cos(/)] происходит из начально-
го положения [б -1] по часовой стрелке. Объединяя найденные элементы
движения, получим векторную и координатные уравнения циклоиды
р(г)=г[г l]-r[sin(r) cos(z)],
| x(r)=r(r-sin(r)),
lj(O=r(1-cos0)-
Трехмерный аналог этой кривой — циклоидная поверхность, по которой дви-
жется точка сферы, катящейся по плоскости. Подобная поверхность изобра-
жена на рис. 1.55, а. Ее параметрическую модель можно получить, вращая
циклоиду вокруг оси j:
р(г,т)=r]f-sin(/) l-cos(r) 0]/?>,(т)=
= r[(/-sin(/))cos(r) l-cos(z) (sin(r)-/)sin(T)].
180
Гпава 2
Кинематическому методу формирования разнообразных параметрических
поверхностей посвящен основной материал, изложенный в гл. 3.
□ Эпициклоида представляет собой траекторию движения точки окружности
радиуса г при ее качении без скольжения снаружи окружности радиуса
(рис. 2.24). Переносное движение описывается формулой
Pu(')=('-o + '-)[sin(r) cos(z)].
Рис. 2.24
При изменении параметра t на 2л центр внешней окружности совершает
со = Го / г + 1 оборотов вокруг внутренней. Матрица Q такая же, как у циклои-
ды. Подставляя найденные элементы движения в (2.48), получим параметри-
ческие уравнения эпициклоиды
p(z) = (r0+r)[sin(z) cos(z)]-r [sin(coz) cos(coz)],
x(z)=(r0 + r)sin(z)-rsin
y(t) = (ro + r)cos(z)-
П Гипоциклоида— траектория движения точки окружности радиуса г при ее
качении без скольжения внутри окружности радиуса го (рис. 2.25). Перенос-
ное движение описывается формулой
Pu(') = ('-o-'-)[sin(z) cos(z)|.
При изменении параметра z на 2л центр внутренней окружности совершает
со = го / г - 1 оборотов по периметру внешней. Матрица
О Г
-1 О
2 = я(90°)=
"еометрические преобразования
181
дает вращение точки c(t)Q = [-sin(r) cos(/)] против часовой стрелки из на-
чального положения [о 1]. Подставляя найденные элементы движения в
(2.48), получим уравнения гипоциклоиды
р(0== (го-г)[5*п^) cos(f)]+r[-sin(ftw) cos(d>/)],
Рис. 2.25
□ Коническая винтовая линия с углом раствора 2а и шагом й (рис. 2.26) образу-
ется сложением равномерного переносного движения по оси у и спирального
относительного движения в плоскости xz, подобного движению, изображен-
ному на рис. 1.31, а:
Д,)=^[0 , 0|+“^[4) 0fc(-90") =
271 271
= — [sin(a)cos(r) cos(a) -sin(a)sin(r)].
2л
□ Замкнутая спиральная линия, N витков которой равномерно навиты на по-
верхность тора с осевым радиусом го и радиусом витков г (рис. 2.27), образу-
ется сложением вращения точки по окружности
Ро(О = 4с0 0]+[го 0 о]
182
Гпава 2
и вращения этой окружности с W раз меньшей частотой вокруг оси у:
р(')= =
rsin(z) -(r0 + rcos(z)sinj
Vz = 0, 2tlV.
2.1.3.3. Кинематическая задача
перемещения в пространстве
Продолжая изучение методов сложных преобразований, рассмотрим кинемати-
ческую задачу перемещения в пространстве. В компьютерной графике непрерыв-
ное движение объекта изображается последовательностью состояний (фаз.
кадров) — элементов дискретного множества его положений во времени и про-
Геометрические преобразования
183
странстве. Цель кинематического анализа и синтеза — изучение и имитация реа-
листичного движения графических объектов, выявление в алгоритмах движения
методических ошибок и непредвиденных эффектов.
Движущийся в R" объект как система связанных точек имеет 2л степеней свобо-
ды: п координат центра масс и п параметров угловой ориентации. Естественно,
что наличие формул движения всех основных точек объекта (например, вершин
полиэдра) полностью решает задачу кинематики, т. е. позволяет построить изо-
бражение объекта в любой момент времени. Однако такая полная информация
)б объекте, во-первых, не всегда имеется в наличии, а во-вторых, она избыточна.
Согласно методу парных точек для идентификации состояния объекта достаточ-
но знания координат его (н + 1)-ой точки, чтобы рассчитать матрицу преобразо-
вания из предыдущего состояния и групповым методом получить координаты
летальных точек. Этот метод основан на принципе пространственно-временной
огерентности — сохранении взаимной ориентации точек объекта при его дви-
жении в пространстве и во времени.
При неполной информации об объекте логично полагать, что согласно принципу
минимального действия он движется по экономичной траектории — кратчайшим
направлениям переноса центра масс и поворота собственной оси. Без учета вра-
щения объекта вокруг своей оси и его состояние Р - {о, V} задается центром
базовой точкой) о и вектором V направления оси и. Возможно, что объект так-
же подвергается преобразованию подобия — равномерному масштабированию во
зсех направлениях относительно своего центра. Изменение размеров объекта
можно моделировать изменением длины вектора V.
3 машинной графике применяются два метода кинематического расчета перехо-
да Р( —> Рм объекта из предыдущего состояния в последующее.
□ Рекуррентное вычисление состояний
Рм =pici \/i= 1,2,...,
начиная с состояния Pi (рис. 2.28, а). Начальное состояние либо исходно зада-
ется элементами {oi, Pi}, либо рассчитывается по формуле
Л=?оСо
из состояния Ро подобного объекту примитива— объекта единичных разме-
ров, центр которого о0 расположен в начале СК, а вектор Vo ориентирован
вдоль некоторой координатной оси. Ниже будет показано, что матрица
сложного преобразования С, может описывать как прямой переход Р,-> Р,+),
так и переходы Р, -> О„ -> Р,+) через начало координат.
Достоинство рекуррентного метода в возможности реализации экономично-
го движения при специальном выборе матриц С,. Недостатком метода явля-
ется относительная сложность расчета таких матриц. Метод рекомендуется
использовать в экономичном варианте при неполной информации о движе-
нии объекта.
184
Гпава 2
□ Итеративное вычисление состояний объекта
Vz= 1,2,...
из состояния примитива Ро (рис. 2.28, б). В рамках данного подхода все гео-
метрические объекты сцены исходно задаются примитивами, которые часто
являются виртуальными, т. е. реально не существующими в сцене объектами.
Примитивы удобны для выполнения преобразований относительно осей ко-
ординат — масштабирования и вращений, после чего следует перенос центра
объекта в нужную точку пространства о,- В следующее состояние Р,+] объект
опять переносится из начала координат, будучи предварительно подготовлен
для этого необходимыми преобразованиями масштабирования и вращения.
Положительными аспектами итеративного метода являются:
• экономия на переносах Р, —> О„ объекта в начало координат, которые тре-
буются в одном из вариантов рекуррентного метода;
• возможность использовать меньшее число примитивов, чем объектов сцены.
Недостаток метода заключается в том, что два перехода Ро —> Pt и Ро —> Р,+
могут быть не эквивалентны одному экономичному переходу Р, —> Pi+l. Визу-
ально это проявляется в виде эффекта нежелательного вращения движущегося
объекта вокруг своей оси. Метод рекомендуется использовать при полностью
определенных законах движения объекта.
Рис. 2.28
Переходим к разработке кинематических алгоритмов— методов вычисления
матриц преобразования состояний объекта с не полностью определенными эле-
ментами движения. Итак, пусть даны два состояния объекта {oi, И1} и {02, Vi} с
центрами в точках oi, 02 и векторами направления осей V\, V2. Относительное
изменение размеров объекта охарактеризуем коэффициентом подобия
Геометрические преобразования
185
Попытаемся получить матрицу экономичного преобразования {oi, Vi} —» {02, Кг}
по кратчайшим направлениям переноса 01 —> 02 и вращения V\ —> Кг. Кратчайшее
изменение направления от V\ до V2 означает одновременный поворот всех точек
объекта, перенесенного из oi в 02, на один и тот же минимальный угол у до со-
вмещения V\ с V2 (рис. 2.29).
Рис. 2.29
□ По методу разложения, основанному на преобразовании (2.30), выполним
переход из {01, Ki} в {02, Кг} за пять фаз с соответствующими матрицами:
• Ф1: {01, Ki} —> {Оз, Ki} — перенос из 01 в начало координат матрицей K(-oi);
• Ф2: {О3, К}—> {о3, |К||г° }— совмещение вектора Ki с осью z матрицей
Л(К.);
• ФЗ: {о3, |K||z° }-» {03, |К2|г°} — масштабирование матрицей М(р, ц, ц);
• Ф4: {о3, |K2|z° }—» {О3 , К2}— совмещение вектора |K2|z° с Кг матрицей
• Ф5: {Оз, Кг} -> {ог, Кг} — перенос из начала координат в ог матрицей Цог).
С учетом того, что фазы Ф2 и Ф4 включают до двух ЭП, суммарное число ЭП
достигает семи. Матрица полного АП вычисляется по достаточно длинной
формуле
С = Г(-оД(к1)Л/(щ и, (2.49)
На рис. 2.30 изображены выполняемые по описанному алгоритму фазы пре-
образования несимметричного объекта — двухцветного флажка, древко ко-
торого задает вектор направления К. Оказывается, что конечное состояние
{ог, Кг} не полностью совпадает с результатом экономичного движения, изо-
браженным на рис. 2.29. Совпали лишь концы вектора Кг. Остальные точки
186
Гпава 2
объекта дополнительно поворачиваются вокруг оси на угол вплоть до значе-
ния 180° при |са - аз| = 180°.
Рис. 2.30
В чем причина такого нежелательного эффекта? Очевидно в том, что сложное
АП (2.49) не является экономичным: четыре элементарных вращения объекта
на углы -со, Pi, az и -Рз, не лежащие в одной плоскости, не дают в совокупно-
сти кратчайшего угла. Таким образом, метод разложения с промежуточной
ориентацией объекта вдоль координатной оси не может дать экономичного ал-
горитма решения кинематической задачи.
□ В экономичней варианте алгоритма по методу разложения явно присутствует
кратчайшее вращение объекта на угол у > 0. заключенный между векторами
Vi и I'z (см. рис. 2.29). Значение этого угла у = arccos(p) определяется скаляр-
ным произведением р = Ио^2. Ось кратчайшего вращения ортогональна
плоскости {оз, Vi, Vz} и имеет направление нормали N= Vi х Из. В случае
И1 || К2, когда |р| = 1, можно выбрать вектор N = хоз0, ортогональный к V\ и
орту со0 # V\, где со 6 {х, у, z}.
Фазы преобразования объекта (рис. 2.31) и их матрицы следующие:
• Ф1: {oi, Vi} -> {Оз, Vi} —перенос из точки oi в начало СК матрицей Т(-о\).
• Ф2: {х,у, z} -> {д', у', z'}— совмещение оси z с нормалью N матрицей
Лэр(А);
• ФЗ: {o3,pKf}—>{О3, 1'1} — вращение вокруг оси z матрицей 7?.(arccos(p)).
которую экономичнее вычислять по варианту (2.32) как
Я2,| р, 71-р2
ь метрические преобразования
187
без использования тригонометрических и обратных тригонометрических
функций;
• Ф4: {%', у', z'} —> {х, у, z} — восстановление СК матрицей /^(Л7);
• Ф5: {О3, И^}—> {О3, рИ^} —масштабирование матрицей Л/(р, р, р,);
• Ф6: {Оз, Кг} —> { 02, Иг} — перенос из начала координат в точку ог матрицей
ЦО1).
Рис. 2.31
р = И[оИ2, Ц = т—т
В итоге матрица сложного АП, включающего до восьми ЭП, вычисляется по
следующему алгоритму:
, N = И] xif(|p| < 1: И2, if(|K|z|<|И||: z°, у0
(2.50)
С = г(- О| Яр (А)Л2^р, Vl-P2^-* (р, р, р)т(о2 )-
71 По методу парных точек построим две ортогональные системы векторов,
связанные с исходным и конечным состояниями объекта (рис. 2.32):
• вычислив нормаль N- Vi х Иг (если И| || Иг, то при И(#г° полагаем
N = И| хг°, а при И[ || z° — N = И| ху°) и бинормаль Wi = Hi х N, получим
исходную систему векторов на четырех точках:
{01, oi + Ki, oi + N, oi + (Hi};
• вычислив коэффициент подобия р = |Иг|/|И1| и бинормаль (Иг - Иг х N,
получим конечную систему векторов на четырех точках:
{ог, ог + Иг, ог + рА, 02 + (Иг}.
188
Гпава 2
Рис. 2.32
В связи с простотой, экономичностью и дальнейшим широким использовани-
ем оформим алгоритм решения кинематической задачи методом парных то-
чек в виде функции расчета матрицы аффинного преобразования по двум па-
рам точек, возвращающей матрицу АП объекта из состояния {/л, И} в
состояние {pi, Из}.
£7 МАР2(о\, Hi, oi, Vi)
{ N = t\ xif(|n oF2|<1: И2, if(|r1;|<|И]|: z°, /)), M =
возврат матрицы
°1 11 1 °2 1'
о,+И] 1 о2+И2 1
o\+N 1 о2 1
oi+^xW 1 + ^2 * N 1
(2.51)
}О
Ортогональность векторов обращаемой в (2.51) матрицы обеспечивает ее
наилучшую обусловленность. Единственное условие существования реше-
ния — ненулевые векторы V\ и Иг. Численные значения матриц, вычисленных
по алгоритмам (2.50) и (2.51), совпадают, т. к. кинематическая задача имеет
единственное экономичное решение. Трудоемкость же метода парных точек
существенно меньше.
Расчет матрицы преобразования системы координат из состояния {oi, И|} в
состояние {oi, Иг} выполняется функцией
MAP2(oi, Из, oi, И) = МАР2(о\, И|, 02, Иг)'.
В качестве параметров начального состояния можно выбрать начало координат
oi = Оз и один из ортов, например, И] = z°. Тогда преобразование с матрицей
Ск(о,и) = MAP2(o,P,O3,z°)
'еометрические преобразования
189
переводит начало СК в точку о, а ось z' ориентирует по направлению вектора
V. Положение осей х' и у' не регламентируется. Такая неопределенность ори-
ентации системы координат вполне допустима в задачах на преобразования
относительно только одной оси. Например, это вращение вокруг оси {о, И
на угол выполняемое матрицей
или отражение от плоскости {о, N} с помощью матрицы
Ск (o,n)m(\, 1, -1 )С“* (о, /V).
Сравним три алгоритма (два по методу разложения и один по методу парных
точек) и два подхода (рекуррентный и итеративный) решения кинематической
задачи на примере движения плоского полигона Р через последовательность со-
стояний Р\ -> Pi Pm -> Pi, равномерно распределенных по окружности
радиуса г в плоскости ху (рис. 2.33). Состояние Р, задается точкой центра поли-
гона и вектором нормали к его плоскости:
о, = z-x°Pz((z-1)Av), /V, = _у°Рг((/-1)Ду), где Avy = 2л / m.
Соединение соседних состояний каждой из вершин полигона отрезками прямых
з совокупности с изображением самих полигонов дает поверхность, классифи-
цируемую в гл. 3 как трубчатая. Скручивание продольных каркасных линий на-
глядно свидетельствует о вращении полигона вокруг своей оси (нормали) на пе-
реходах между состояниями. На рис. 2.34, а изображена полностью определенная
^талонная поверхность без осевого вращения, поперечные сечения которой
состояния полигона) рассчитаны по формуле
Pi = Р0Лл.(-л/2)Лг(/Д^)г(о,) Vz = 1, m (2.52)
гри in - 36, где Ро 6 ху — состояние полигона с центром в начале координат и
чормалью z°.
190
Гпава 2
Наилучшие результаты — полное совпадение с эталоном — дали экономичные
алгоритмы на основе рекуррентного подхода со следующими матрицами преоб-
разований на переходе Р,^> Рм\
□ по рекуррентному методу разложения (2.50)
=^xif(|p,|<l: Ni+l, if(pvj<pv,|: z°, >° )),
/ /---rx (2.53)
C, = т(-о, )Лэр(^ )R2 J p„ 71 -p2 pip1 (w, )t(om );
П по рекуррентному методу парных точек (2.51)
С/ = MAP2(oh Nh oM, Ni+l).
(2.54)
Остальные алгоритмы проносят полигон через состояния Р, неэкономично, с до-
полнительным вращением вокруг нормали, что визуально наблюдается как
скручивание продольных каркасных линий. Алгоритмы различаются степенью
неравномерности угла скручивания по траектории движения полигона:
□ по методу разложения (2.49) как в рекуррентной, так и итеративной формах
неравномерная скрутка поверхности (рис. 2.34, б) наблюдается на тех участ-
ках, где вектор А, меняет знак абсциссы 7V,v, из-за чего происходит вращение
полигона на некоторый угол, вплоть до 180° (см. рис. 2.30);
Рис. 2.34
Геометрические преобразования
191
□ итеративные методы экономичного разложения (2.50) и парных точек (2.51)
дают равномерное скручивание (рис. 2.34, в), объясняемое тем, что экономич-
ные переходы полигона Ро —» Р, и Ро —> Р,+) не эквивалентны экономичному
рекуррентному переходу Р, —> Р,+|.
На рис. 2.34, г, д, е показаны результаты моделирования переходов полигона по
траектории произвольно расположенной в пространстве окружности. Рекур-
рентные алгоритмы экономичного метода разложения (2.53) и парных точек
(2.54) еще раз подтвердили свою работоспособность (см. рис. 2.34. г) в отличие
от других изученных алгоритмов моделирования (см. рис. 2.34, д, е).
Может возникнуть естественный вопрос: если есть точный метод кинематиче-
ского расчета (2.52), то зачем нужны другие алгоритмы, некоторые из которых
дают нежелательные визуальные эффекты движения? Ответ прост: в общем слу-
чае движение может быть не полностью определенным. Например, трубчатая
поверхность формируется протягиванием контура ее поперечного сечения по
траектории осевой линии, но как ориентирован контур в каждом сечении — этот
момент не оговаривается. Изображение такой поверхности выглядит неестест-
венно, если ее продольные каркасные линии проходят не параллельно осевой
линии, а закручиваются вокруг нее. Желаемый вид поверхности достигается с
помощью экономичных рекуррентных алгоритмов движения, которые дают ми-
нимальное или вообще нулевое кручение продольных линий.
Общий неоостаток рассмотренных методов кинематических преобразований
состоит в их нечувствительности (разной степени) к вращению объекта вокруг
собственной оси из-за недостаточности задания только двух пар точек
.01,01 + И1} и {ог, 02 + Иг} на оси движения. Если известна третья пара точек
oi + W\ и ог + W-l вне оси, то матрица преобразования {oi, Hi, IVi} —> {02, Иг, №2}
находится по (2.13) после расчета нормалей
м - И1 X * Оз, N1 = Иг X W2 * Оз
и четвертой пары точек 01 + Ni и 02 + N2.
Оформим данный метод в виде функции расчета матрицы аффинного преобразо-
вания по трем парам точек, возвращающей матрицу преобразования объекта из
.остояния {01, И|, 1И|} в состояние {02, Иг, W2}.
МАРЗ>(о\, Hi, Wi,02, Иг, ГИг)
возврат матрицы
°1
°1 + ,i
°1 + ИхИ/1
11 'Г О2 1
1 о2 + И2 1
1 о2 + w2 1
1J [о2+И2ХИ/2 1
(2-55)
192
Гпава 2
Для преобразования СК из исходного положения [О3, х°, y°,z° j необходимо
знать ее новое начало о и неколлинеарные векторы Ии W, задающие новые на-
правления осей х' и у'. Матрица такого преобразования СК равна
Ск=Л/Л/’з(о, V, W,O3,x°,y°\
Наконец, если известны четыре пары некомпланарных точек объекта в началь-
ном и конечном состояниях, то для расчета матриц преобразования объекта С и
системы координат Ск используются формулы (2.13) и (2.14) при и = 3. Состоя-
ния объекта могут быть также полностью определены точками oi, 02 и тройками
некомпланарных векторов {Ki, tZi} и {V2, Wz, U2}. Для этого случая введем
функцию расчета матрицы аффинного преобразования по четырем парам точек.
£7 MAP4(oi, Vi,Wi, Ui,O2, V2, Wz, U2)
{возврат матрицы
01
Oi+Kj
Ol+W7!
,°i +Ц
1 1 б>2 1
1 O2 + V2 1
1 o2+W2 \
1 С>2 + ^2 1
(2.56)
Эту функцию можно использовать для преобразования координат точки р из
исходной СК {о3, х°, y°,z0} в другую декартову (не обязательно правую и ор-
тонормированную) систему координат с началом в точке о и осями х', у', z', на-
правления и масштабы которых заданы базисными векторами V, Wn U:
р' = рСк, где Ск = MAP4^o, V, W, U, О3, х°, у°, z°). (2.57, a)
Аналогично решается задача преобразования точкир е R2 из СК {о2, х°, j0} в
другую декартову СК, имеющую начало в точке о и базисные векторы V и W:
о 1 -1 ’0 0 1
Р = рСк, где Ск = о + И 1 1 0 1
о + И' 1 0 1 1
(2-57, б)
Преобразование координат— полезный инструмент определения принадлежно-
сти точки q некоторым специальным геометрическим объектам при выполнении
совокупности условий-неравенств для координат прообразов q', вычислен-
ных по (2.57):
□ плоским параллелограмму П и треугольнику Т с одной из вершин в точке о и
выходящими из нее векторами сторон V и W (рис. 2.35):
П: 9? = {0<х'<1}П{0<У<1}; (2.58,а)
Т: = {?>0}п{у'>0}П{х+/< 1}. (2.58,6)
Геометрические преобразования
193
Рис. 2.35
Например, для параллелограмма П с элементами о = [б -1], Г = [2 з] и
И7 = [-2 1] получим матрицу преобразования
91= [7 2], 92= [-4 2], 93=[-3 1]
имеют в СК {о, V, И7} координаты
9j= [0.875 0.375], 92 = [-0.5 4.5], д'ъ = [-0.625 3.875].
По (2.58, а) определяем, что точка 91 лежит внутри параллелограмма, а точки
92 и 93 — вне его. Эти же точки в системе координат треугольника Т с элемен-
тами о =[-6 4], Г = [4 -2], ^ = [1 -5] и матрицей преобразования
0.278 -0.111 1
Ск = 0.056 -0.222 1
1.444 -0.222 1
имеют координаты
q{ = [3.5 -1], 92 = [0.444 0.222], 93 = [0.667 О.ЗЗЗ].
По (2.58, б) определяем, что 91 е Т, 92 е Т, а точка 93 принадлежит границе Т;
□ объемным параллелепипеду П и треугольной пирамиде Т с одной из вершин в
точке о и выходящими из нее векторами ребер V,WnU(рис. 2.36):
П: = {О<х'< 1}П{О<у< 1}П{0< z< 1}; (2. 59,а)
Т: 9? = {/>0}n{y'>0}n{z,>0}n{x' + y + z,<l}.
(2. 59, б)
194
Гпава 2
Рис. 2.36
2.2. Проективные преобразования
Проецирование (от лат. projectio — выбрасывать вперед) — это отображение
трехмерного объекта на двухмерную картинную плоскость (КП). Получение
проекции базируется на методе трассировки лучей: из центра проецирования S
(проектора) проводятся лучи через каждую точку объекта до пересечения с КП
(рис. 2.37). След, образуемый точками пересечения лучей с КП, составляет проек-
цию объекта. Если фокусное расстояние F во много раз больше габаритов объек-
та и расстояния d от источника лучей до объекта, то пучок проецирующих лучей
можно считать параллельным, а источник — дальним. Такая идеализация ото-
бражения объемного мира на плоский экран облегчает построение проекций, за
что приходится платить ухудшением реалистичности изображений.
Рис. 2.37
Геометрические преобразования
195
За длительное время развития цивилизации придумано множество способов изо-
бражения объемных объектов на плоскости, более или менее точно передающих
их геометрическую форму. Поскольку проецирование— не аффинное преобра-
зование и в принципе необратимо, то любая проекция всегда содержит в себе
ошибку (лучше сказать — неопределенность) восстановления координат объек-
та-образа. Назначение того или иного метода проецирования состоит в умень-
шении неопределенности восприятия наиболее значимых свойств объекта за счет
менее значимых. Например, архитектурный чертеж фасада здания абсолютно
точно передает геометрическую ширину и высоту как всего фасада, так и его
деталей, за счет полной неопределенности их глубины.
К числу важнейших свойств метода проецирования относится достоверность
восприятия объекта наблюдателем по его проекции, т. е. узнаваемость объекта
по его плоскому изображению. Если свойство достоверности восприятия объяв-
ляется доминирующим, то наилучшей может стать "живая" проекция с далеко не
минимальной геометрической неопределенностью. Например, изометрическая
проекция несет искаженную информацию о размерах объекта во всех трех изме-
рениях, но лучше передает форму объекта в целом по сравнению с изображением
объекта в "фас".
ПРОЕКЦИИ к ( Параллельные ( Центральные Косоугольные ) Ортогональные ) Аксонометрические Виды ) К \ 1 Гриметрические Главные Диметре*. -е <ие ^Вспомогательные) V у Изометрические Левый Нижний Рис. 2.38 — С одной точкой схода . С двумя точками I схода ± С тремя точками ' схода Фронтальный ►^Горизонталоный ) Поофильный Задний
На рис. 2.38 приведена общепринятая классификация проекций, используемых для
изображения трехмерных объектов или сцен на картинной плоскости. С учетом
вышесказанного следует признать, что наилучшей проекции не существует. Во-
196
Гпава 2
первых, критерий выбора проекции определяется ее назначением — достижение
геометрической точности или получение эстетического удовлетворения. Во-
вторых, "на вкус и цвет товарищей нет": автор данной книги, например, предпо-
читает диметрическую аксонометрическую проекцию (это видно по большинст-
ву рисунков), тогда как некоторые эстеты без ума от изометрии с ее чересчур
правильной и скучной симметрией.
Для лучшего восприятия ориентации объектов в пространстве мы иногда будем
рисовать вместе с проекциями объектов еще и проекции осей МСК x'y’z', СКС
хсУсгс или ОСК xoyozo. Эти проекции создаются по тем же алгоритмам, кото-
рые используются для изображения объектов.
2.2.1. Ортографические проекции
Для получения ортографических проекций (видов) оси ОСК ориентируются па-
раллельно осям МСК, вдоль которых направляются пучки проецирующих лучей.
Так как последние оказываются перпендикулярными координатным плоскостям,
то в виде теряется информация о координате вдоль оси координат, параллель-
ной пучку (рис. 2.39, о). Отдельные виды необратимы. Восстановление 3d-
объекта возможно не менее чем по двум его видам, содержащим совместно все
три координаты.
Рис. 2.39
С целью точной передачи размеров деталей в инженерной практике применяются
чертежи в составе трех главных видов (рис. 2.39, б):
□ спереди или фронтальный (front) на КП f (ФКП), совпадающую с координат-
ной плоскостью МСК ху. У проекции р' точки р координаты равны
х' = х, у' = у, z' = 0;
Геометрические преобразования 197
□ сверху или горизонтальный (horizon) на КП h — плоскость MCK xz. Коорди-
наты проекции точки р равны
х' — х,у' — 0, z' = z;
□ справа или профильный (profile) на КП р— плоскость MCK yz. Координаты
проекции точки р равны
х' = 0, у' = у, z' = z.
Если сплошной (не каркасный) объект имеет сложную форму, которую нельзя
передать с помощью главных видов, то как исключение в чертежах приводятся
вспомогательные виды: левый, нижний и задний.
Матрицы видового проецирования
Of=diag[l 1 0], Oh=diag[l 0 1], Ор =diag[o 1 1] (2.60)
вырождены, что подтверждает невозможность восстановления по формуле (2.2)
всех трех координат точки только по одному ее виду.
Область применения видов — машиностроительное черчение, архитектура и дру-
гие приложения, требующие точных измерений по чертежу линейных и угловых
размеров объектов благодаря параллельности измеряемых элементов плоскостям
проецирования. Особое значение имеет фронтальное ортогональное проецирова-
ние с матрицей Of как последняя фаза аксонометрического проецирования.
Создание на плоскости иллюзии объемности с помощью только одного изобра-
жения объекта возможно двумя способами.
□ Во-первых, объект вместе с его ОСК подвергается преобразованиям враще-
ния вокруг двух или трех неколлинеарных осей, в то время как проецирую-
щие лучи остаются перпендикулярными к проективной плоскости. Так полу-
чаются ортогональные аксонометрические проекции.
□ Во-вторых, можно направить проецирующий пучок под углом к КП, осветив
тем самым объект сбоку. Так образуются косоугольные проекции и их оптиче-
ский аналог — тени объектов на плоскости.
2.2.2. Аксонометрические проекции
Выберем для определенности фронтальную КП проецирования и последователь-
ность вращений объекта и его ОСК х0 уо zo:
<Р, -> <р ч -> <рг.
Такая очередность поворотов дает привычную вертикальную ориентацию про-
екции у' оси у0 при произвольных углах первых двух вращений (рЛ. и <рА. Лишь
третье вращение ОСК на угол <р. поворачивает проекцию этой оси на такой же
угол. В результате получим ориентацию ОСК относительно ФКП, изображен-
ную на рис. 2.40.
198
Гпава 2
Рис. 2.40
Задача аксонометрии (от греч. axon — ось, metreo — измерять) состоит в опреде-
лении координат проекций точек, осевых масштабов тх, тг пи и ориентации
проекций осей ОСК х', у' и z' на ФКП. Рассчитаем матрицу сложного преобра-
зования (трех вращений) объекта в неподвижной СК xyz:
ff'xr mxy mxz
myx myy myz
mzx '»zy
(2.61)
Ее (/,у)-ые элементы
тхх = cos(<py)cos((p,)- sin (<рЛ. )sin (<рЛ. )sin (<р,),
тху = cos(<Py)sin(<рг)+ sin(<px)sin(<pj;)cos(<p,), mxz =-cos^^sinjcp^.
тух = - cos(<px )sin (<рг ), myy = cos(<px )cos(<p.), myz = sin (<px ),
/wzx = sin ((p^, )cos((p_)+ sin(<px )cos(<pj; )sin(<p,),
mzy =sin(<p>,)sin((p-)-sin(<px)cos(<p},)cos((p_), = cos((px)cos(<p>1)
(2-62)
есть j-ые координаты z-ых ортов ОСК. Получим соотношения для расчета углов
уЛ, хрЛ. и vp. наклона осей ОСК к ФКП:
sin(vx)=wxz
sin^^/w^,
sin(yz )= mzz
= -cosfajjsin^,
= sin(q>J,
= cos(<pA.)cos((p>,),
(2.63)
Геометрические преобразования
199
из которых следуют независимость углов фти от угла <р. последнего в (2.61)
вращения и условие связи углов
sin2(xpv) + sin2)^) + sin2(\p_) = 1. (2.64)
Оно означает, что свободно могут быть выбраны только один или два угла на-
клона осей ОСК к ФКП. Примеры:
□ фд. = 45°, фЛ = 30° => sin2(v;) = 0.25 => фг = 30°;
□ vpv = 45°, = 45° => sin2(vp>.) = 0 => ф(. = 0°;
□ = 90° => - ip = 0°.
Из (2.63) следует решение обратной задачи: для получения желаемых углов vj/v,
и углы вращения ОСК следует выбирать из условий
<рд. = ф,„ = -arcsin
sin(yJ
cos(w,.)
= arccos
sin(y..)
(2-65)
Масштабные коэффициенты осевых искажений
тх = +п1^у = ф -cos2(<px )sin2 (<pj;) = cos(vx) ^ 1,
my = ijmjx + m}y = |cos((pv )| = cos(vj; )< 1,
m. = + m^y = ^1 - cos2 (<pY )cos2 (<p v) = cos(y _) < 1
(2.66)
есть длины отрезков — проекций ортов ОСК на КП. Из (2.64) и (2.66) следует
условие взаимосвязи масштабов:
7 7 7
mi + mi + mi =2.
Л z *-
(2.67)
Как и в (2.64), свободно могут быть выбраны только один или два масштаба.
Иногда нужно обеспечить желаемые соотношения масштабов
тх : ту : т: = А\.: ку : к..
Тогда, приняв ж, = г/<„ из условия (2.67) получим
А2+А2+А2 ' 'ykx+ky+kz
(2.68)
Ориентация проекций осей ОСК на ФКП может быть определена, например,
углами у,„ уду, у,.. и у., (рис. 2.41). причем у + уу: + у.д. = 360°:
cos(yj; )= = cos(<pr ) => Yr = Ф- ; (2.69, а)
200
Гпава 2
тххтух + тху+туу _ siп (<ру )sin (фу )
>Пх>ПУ ^l-cos2fax)sin2^)
myxmzx +туу+ mzy _ - sin (фх )соз(фу)
mymz ^1-СО52(фх)сО82(ф5,)
(2.69, 6)
cos(y.J
mzxmxx + mzy + тху
mztnx
__________cos2(<Px)sin((p>,)cos((p>,)__________
'1 - cos2 (фх )sin 2 (фу )^1 - cos2 (фх )cos2 (фу )
-90°«ру<0° -90°«ру<0°
-90°«рх<0°
0°«р>.<90°
0°«рх<90°
0°«р>,<90°
Рис. 2.42
Геометрические преобразования
201
Изобразим на рис. 2.42 ориентации осей х'. у', z' и моделей кубов в зависимости
от знаков углов <рЛ и <рг Из анализа (2 69) следуют выводы:
□ только углы <рд и <рЛ. определяют коэффициенты осевых искажений и углы ме-
жду проекциями осей ОСК;
□ только угол ф. последнего поворота ОСК определяет угол уу вертикальной ори-
ентации проекции ОСК на ФКП. Именно поэтому вращение ОСК вокруг оси z
выбрано последним, чтобы без него можно было получать разнообразные ра-
курсы изображения объекта с привычным вертикальным расположением оси у'.
Часто при построении аксонометрической проекции задаются масштабами т„
ту. и т., соответствующими единичным отрезкам на осях х',у' и z'. Тогда осталь-
ные параметры ортогональной аксонометрической проекции можно рассчитать
по вытекающим из (2.66) формулам:
. , j 2
cos2 (фх) = т2 , cos2 (ф^, )= —
ту
cos(vx)=wx, cos(vr)=/wJ„ cos(vz)=/w2, (2.70)
2 2 2
cos2(Yxy)= cos2(yyz)= —cos2(yZx)= —
1 - my 1 - mz 1 - mx
Полная матрица ортогонального аксонометрического преобразования на ФКП
с учетом последней операции проецирования равна
Af - Ryxz°t ~
тух
та
тху 0
Шуу 0
mzy 0
(2.71, о)
Для того чтобы проекция имела вертикальную ориентацию оси у' (уу = 0), пово-
рот объекта вокруг оси z не нужен, что следует из (2.69, а). При ф. = 0 матрица
фронтального аксонометрического проецирования вычисляется как матрица
сложного преобразования
Af = Ryx Ot
и с учетом (2.71, я) и (2.62) принимает вид
sinfajJsin^tp.J
cosfaj
-sinfojcos^
-cosVPxJsin^J
sin(<Px)
cos(cpA. )cos (ф^,)
cos (ф^ ) sin (фх )sin (ф^) 0
0 cos (фх) 0
sin^,) - sinfax )cos (ф^ ) 0
(2.71,6)
202
Гпава 2
Во многих задачах (построение теней и зеркальных отражений, расчет освещен-
ности поверхностей и т. д.) требуется знать вектор направления на источник про-
ецирующих лучей, выраженный в объектных координатах. В МСК это вектор S.
Например, при фронтальном ортогональном проецировании S = [o 0 1], при
горизонтальном— S = [o 1 О], профильном— S' = [1 0 б]. Преобразование
сцены матрицей С изменяет и координаты вектора S в ОСК. Их легко получить с
помощью обратного преобразования, описываемого матрицей С-1. Координаты
вектора наблюдателя в ОСК вычисляются по формуле (2.15):
So = S С’1.
Обратная к (2.61) матрица равна
yxz К: Кх Ку KyXZ,
откуда получаем вектор источника в ОСК:
(2-72, а)
В частном случае фронтальной аксонометрии с вектором S = [о 0 1] и матри-
цей Ryx с учетом (2.62) получим
S0=['Wjc myz [“cos(<Px)s'n(4)>) ^(фх) cos(tPx)cos(<P>)]- (2.72,6)
Рассмотрим построение аксонометрической проекции окружности p(t) радиуса г.
лежащей в плоскости П под углом к КП, равным 90° — хр < 90°. Ее проекцией яв-
ляется эллипс p'(t) с полуосями а - г и b - г sin(xp) < г, ориентированными относи-
тельно проекции нормали к П как b || N' и а ± N' (рис. 2.43, а).
Рис. 2.43
Геометрические преобразования
203
Так как координатные плоскости ОСК образуют с ФКП углы 90° - то длины
н ориентации полуосей эллипсов как проекций окружностей на гранях модель-
ного куба (рис. 2.43, б) равны
«f = г ± z, ah = г ± у, Ор = г ± х,
bt = || z', = гф-Шу || у, bp = || x.
CD Пример 2.5. Построить аксонометрическую проекцию куба со вписанными в
его грани окружностями при соотношении масштабов mx : my: т. = 6:5:4.
Решение. Вычислив по (2.68)
= 0.1612, тх
6с ® 0.967, mf = 5с ® 0.806, т: = 4с ® 0.645,
определим по (2.69, б) углы ориентации проекций осей ОСК
уд>. = 101.2°, уу: = 150.6°, у., = 108.2°,
а по (2.73) длины полуосей эллипсов
af = «ь = af = г, bt - 6.164r, bh - 0.592г, bf — 0.255г,
являющихся фронтальными проекциями окружностей радиуса г на передней,
верхней и правой гранях куба. Изображение объекта приведено на рис. 2.43, б.
Для его построения по (2.69, а), (2.70) и (2.71,6) рассчитаны следующие углы
вращения объекта и матрица проецирования:
0
<Р,
0.949
-18.4°, <рЛ = 36.3°, <р_. = 0°, Аг = 0
-0.316
-0.187
0.806
-0.562
0 .□
о
Таким образом, мы рассмотрели основы аксонометрии— методики построения
иамой общей триметрической ортогональной проекции, у которой все осевые
масштабы попарно не равны друг другу. Количество триметрических проекций
бесконечно, стандартная триметрия отсутствует.
В диметрических проекциях два из трех масштабов равны друг другу, что дает
три варианта выбора углов вращения ОСК.
23 Если тх - ту * т., то из (2.66) получим sin2(cpr) = tg2(q> J, откуда
|<Рх| = |агс1Й'п(<Рт))|
тх =ту =М<Рх)|.
ту =V2|sin(<px)|,
со52(у>2)=сов2(у,х) =
tg(<Px)
^(2<Рх)’
6f = r>/|cos(2<px)|, 6h =bp =r|sin(<px)|.
204
Гпава 2
Например, выбрав фл = -60°, получим tg2(ipv) = 0.75. Из четырех возможных
углов выберем
Фх = arctg
и определим параметры диметрической проекции куба на рис. 2.44, а:
тх = ту = 0.756, т. = 0.926, уЛ, = у,Л. = 110.7°, уху - 138.6°.
□ Если ту = т. тх, то из (2.66) получим соя2(фЛ) = tg2^v), откуда
^x| = |arctg(cos^_J)|,
тх = V2|sin(фх)| ’ ту = mz ~ |cos(<Px)|’
cos2(vJ=cos2(,J = |^il,
bf =bh = r|sin(vJC)|, bp =r^\cos(2(px)\.
Например, выбрав фЛ = -30°, получим tg^J = 0.75. Из четырех возможных
углов выберем
V3
<рх = arctg — ~ 40.9°
и определим параметры диметрической проекции куба на рис. 2.44, б:
тх = 0.926, ту = mz = 0.756, уху = у.Л. = 110.7°, yyz = 138.6°.
□ Если тх = т,* ту, то из (2.66) получим sin2^,) = со52(ф>), т. е. выбор углов
вращения ОСК должен быть таков: фЛ е {+45°, ±135°), фЛ. — любой. Тогда па-
раметры диметрической проекции имеют вид
73-со8(2фх)
тх = mz =------------, ту = |cos(Vx )|,
2, 2, 1-соб(2ф )
cos (^)-cos <^>°3_cos(2/i).
bf = bp = lCOSJl*)lr, bh = /jsinfa, )|.
Например, выбрав фЛ = -45° и фЛ.= 15°, получим параметры диметрической
проекции куба на рис. 2.44, в:
тх = тг = 0.73, ту = 0.966, уху = yyz = 104.5°, yxz = 151 °.
В стандартной диметрической проекции соотношение масштабов составляет
тх : my:mz = 2 : 2 : 1.
Геометрические преобразования
205
Фл=45°,
Ф, =35.26°,
<рг=30°
Рис. 2.44
Тогда по (2.34) определяем
9%/9 -v9
mx = mv =--------= 0.943 , m =-------~ QA11,
x y 3 3
а остальные параметры этой проекции (рис. 2.45) равны
v7 г
Yr = Yxv = 131.4°, y,.v = 97.2°, b{ = -yr = 0.882г, = Ар =- = 0.333г.
Рис. 2.45
206
Глава 2
Для получения стандартной диметрии углы вращения ОСК должны быть заданы
в соответствии с (2.70) равными
<P_V
-20.7°, <рх =arccos
= 19.47° ,ф.
0°,
тогда матрица проецирования и вектор источника по (2.71,6) и (2.72,6) будут
равны
л /?2 о 0 ' 0.935 -0.118 О'
А = ^*дим 0 8 V9 0 0 0.943 0
ГТ -0.354 -0.312 0
1 7
-, - 0
V8 V 72
Ядам 4 1 V7]=[l 1 2.646].
(2-74)
При построении ортогональной изометрической проекции выбор углов
ния ОСК фг и <рЛ. связан условием тх = ту = т.. Тогда из (2.68) получаем
враще-
т, = J— =0.816,
а из (2.70) и (2.73) следуют соотношения
cos2 (ф,) = р cos2(v>,)=|,
cos2 cos2(y^)= cos2(yzx)=-^-,
6f = 6ь = bp = -4=r = 0.577r.
v3
Из этого можно сделать следующие выводы:
□ изометрическая проекция объекта может быть получена вращением его на
углы ф> е (±45°, ±135°} и фЛ. е {±35.26°, ±144.74°};
□ проекции осей ОСК ориентированы под углами, кратными 60°;
□ проекции всех окружностей на координатных плоскостях ОСК подобны, от-
личаясь лишь ориентацией осей.
На рис. 2.44, г построена изометрическая проекция куба при углах вращения
ФЛ - 45°, фу - 35.26° и ф. - 30°.
Стандартная изометрическая проекция (рис. 2.46) получается при углах враще-
ния объекта
<Р, = -45°,
= arccos
= 35.26°,
Фг
0°,
еометрические преобразования
207
mx .niy.m, = 1:1:1
Рис. 2.46
имеет симметрично ориентированные под углами ух> = уу: = yv. = 120° проекции
осей ОСК, а матрица проецирования и вектор источника согласно (2.71, б) и
(2.72, б) равны
Sroo=[l 1 О-
(2.75)
2.2.3. Косоугольные проекции
Косоугольное проецирование отличается от ортогонального тем, что в нем для
объемного видения объекта пучок параллельных проецирующих лучей не орто-
гонален КП. При этом сам объект и его ОСК остаются неподвижными. Соответ-
ственно, 5кос - S. Косоугольное проецирование — основной инструмент для по-
строения тени объекта на плоскости и отражения объекта в плоском зеркале.
Как показано на рис. 2.47, вектор направления на проецирующий пучок
5 = |лЛ. sy sz ] составляет с нормалью к ФКП угол проецирования Хг такой, что
a +sy
tg уч )- •
sz
Параметрическая функция луча, проходящего через точку р = [х у z] в на-
правлении .8, есть р- St. Этот луч пересекает ФКП в точке р' = [х' у z']. Из
\ словия
z' -- z - s. tf = 0
208
Глава 2
получим параметр пересечения Ии остальные координаты точкир' е f:
Z , Sx , Sy
If = —, X =x——z, у = y——z.
sz sz sz
В векторной форме
P' = pKt
косоугольное проецирование на ФКП описывается матрицей
Kf - 1 0 o’ 0 1 0 ~ сх ~су 0 Sx Sy > сх=—. СУ= — sz sz
(2-76)
Получим коэффициенты осевых искажений, проецируя косоугольно орты ОСК
на ФКП:
П 0 01 1 0 о’
0 1 0 - 0 1 0 z=>mx = my = 1, mz=y/cx+Cy = tg(Zf)
0 0 1 ~СХ ~Су 0
(2.77)
Углы ориентации проекций осей ОСК на ФКП определяются условиями
улу = 90°, tg(y>2)=-^ = -^, tg(yzJ=-^ = -^.
с_у Sy сх sx
(2.78)
Окружности в плоскостях, параллельных КП, проецируются в окружности, т. е.
без искажений (рис. 2.48). Это главное отличие и основное преимущество косо-
угольного проецирования перед аксонометрическим, позволяющее избежать по-
строения эллипсов с произвольной ориентацией полуосей.
еометрические преобразования
209
На рис. 2.48. а изображена косоугольная фронтальная проекция сцены, состоя-
щей из модельного куба с вписанными в его грани окружностями и осями ОСК.
Рис. 2.48
Приведем по аналогии без вывода формулы расчета параметров косоугольных
горизонтальной (рис. 2.48, б)
1
О
о о
О — cz
О 1
сх= —> cz
Sy
*z
Sy ’
(2.79, a)
mx = m.= 1, my=-Jcx+cz = tg(Zh),
/ \ CY SY { \ C- s,
Yza = 90°, tg(y )= —, tg(y^)= —- = —*-
c7 s. CY SY
(2.79,6)
(2.79, e)
и профильной (рис. 2.48, в) проекций:
s= 0 -Су — cz 0 1 0 0 0 1 sy sz , Cy=—, cz=-^-, sx sx (2.80, a)
ту = т. - 1, тх = jCy + cz = tg(zp ), (2.80,6)
90°, tg(Yzx)=-^ = - cz —, tg(y^)= sz J Cy Sy (2.80, e)
Некоторые направления вектора 5 дают стандартные косоугольные проекции.
210
Гпава 2
□ Кабинетная проекция (косоугольная фронтальная диметрия), изображенная
на рис. 2.48, а. образуется при S= [l I 2V2]. Тогда по (2.76)—(2.78) опреде-
ляем ее параметры:
т, = ту - 1, т. = 0.5, уд> = 90°, = у.Л. = 135°,
= 0.354, SKa6=[l 1 2V2],
"kt - arctg(0.5) ~ 26.6°, сх =с,
1 0 0 1 0 0
^каб 0 1 0 0 1 0 (2.81)
1 1 0 -0.354 -0.354 0
2V2 2V2 -
Данная проекция наиболее наглядна и проста в построении. Часто кабинет-
ной проекцией ошибочно называют построенную на бумаге в клетку косо-
угольную проекцию с соотношением масштабов тх :ту :т2 =2:2:близ-
ким к соотношению 2:2:1 кабинетной проекции.
□ Каеальерная или военная проекция (косоугольная фронтальная изометрия)
изображенная на рис. 2.49, образуется при выборе S = [1 1 ^]. Тогда по
(2.76)—(2.78) определяем параметры проекции:
тх = ту = т. = 1, уДД1 = 90°, у>5 = у.Л. = 135°,
Хг = arctg(l) = 45°, cx=cv = -J= = 0.707, 5кав=[1 1 Ji],
V2
^кав
1
о
1
о
-0.707
0 0
1 0
-0.707 0
(2.82)
Рис. 2.49
Геометрические преобразования 211
По сравнению с кабинетной проекцией лучи при кавальерном проецировании
проходят более полого, под большим углом к КП. Из-за этого проекции объек-
тов выглядят вытянутыми и несколько неестественными. В то же время каваль-
ерная проекция удобна для измерения длин отрезков, параллельных осям коор-
динат. Геометрическая точность и способность отображать объем объясняют
использование в старину кавальерных проекций в фортификационном деле.
□ Зенитная проекция (косоугольная горизонтальная изометрия) образуется при
выборе направления проецирования S = [1 2 у!з]. Тогда по (2.74) находим
ее параметры:
тх = ту - т. = 1, у.А. - 90°, yV), = 120°, уу. - 150°,
Xh = 45°, cx = 0.5, cy = 2il = 0.866, 5зеи = 1 2 7з],
1 0 0 10 0
^•зсн -- 0 2 2 -0.5 0 -0.866 (2.83)
0 0 1 0 0 1
Данная проекция представляет наклонный вид на объект сверху. В аэрофото-
съемке используется зенитная диметрия — вид с высоты птичьего полета — с
углом наблюдения Хм ~0° и соотношениями осевых масштабов и координат
точки наблюдения
2 2 2 2
тх: ту :т:= 1 : ky : 1, sx+sy = kysy.
Выбор коэффициента сжатия высоты
ку = ctg(Xh) « 1
позволяет изображать на чертеже вытянутые вверх объекты — горы, небо-
скребы, башни и т. д.
Если перед косоугольным проецированием выполнить вращения объекта, то по-
ручим косоугольную триметрию — наиболее общий вид параллельного проеци-
рования, в котором осевые масштабы связаны условием, обобщающим (2.67):
тх +ту +т% = 2 + tg2(X). (2.84)
2.2.4. Центральные (перспективные) проекции
При построении центральной проекции (ЦП) используются однородные коорди-
аты и эквивалентные векторы. Декартовы [х у z 1] и однородные
j Ь с h\ координаты расширенного вектора связаны соотношениями
а Ь с
Т’ У = ~Г’
h n n
(2.85)
212
Гпава 2
Назовем операцию (2.85) приведением однородного вектора к декартовой форме, в
которой h = 1. Эквивалентность векторов
\hx hy hz h]~ [х у z 1]
означает, что они имеют равные соответствующие декартовы координаты. За-
дание масштаба h * 0 позволяет без арифметических операций изменить сразу
все координаты в 1 / h раз.
Возможны два способа работы с однородными векторами:
□ все операции проводятся с векторами в декартовой форме, а полученные од-
нородные векторы сразу переводятся по (2.85) в декартову форму;
П операции проводятся с однородными векторами по специальным формулам,
а перевод в декартову форму выполняется только на последнем этапе вывода
изображения на экран дисплея.
Основные операции с однородными векторами:
Г) сложение и вычитание
Ь fy]+[p2 h2]~ y-
P2
_h2
1 ~\p\h{+P2h2 МгЬ
1
□ умножение вектора на скаляр
£
h
а[р /г]~а
ар
h
1
1 ~ р
h
а
П скалярное произведение векторов
[р] Л]]°[р2 Л2]~ -^- ° -p-V-'0/2 ~Ь°Р2
И ДМ hh2
М2];
□ векторное произведение векторов
[pi М1а> = M2L
(М IM М2
Рассмотрим методику получения центральной проекции точки р = [х у г] на
фронтальную КП от точечного проектора с координатами 5' = [vx sy дг]
(рис. 2.50). Через точку р проходит прямой луч, описываемый параметрической
функцией
5 + (р - S)t X/t > 0.
В отличие от параллельного проецирования, не все точки пространства имеют
центральные проекции, а лишь те, которые вместе с КП лежат по одну сторону
от проектора, т. е. удовлетворяют условиям z < s. при s. > 0 или z > s. при s. < 0.
Геометрические преобразования
213
Рис. 2.50
Координаты р' = [/ у о] проекции точки р на ФКП находим из условия z' = О
пересечения луча с плоскостью ху:
z' = s. + (z- s.)tt — 0 => If = — = £ h ’ (2.86, a)
, 7 \ x - cxz
Пол И ЭК1 учаем yp швалент [/ у Ди iS y • X f ’ h у = sy + (y sy)tf - hy , sx Sy 1 . cx =—Cy=^~, Cf =—, n = sz л sz sz авнения в однородных координатах hx' = х-cxz, hy' - у- cyz, hz' — 0,h — ное декартово решение в координатнс z' 1]~ [hx' hy hz' й]=[х у z 1] 1 - Cf z. 1 - CfZ й и векторной форм 1 0 0 0 ' 0 10 0 ~cx ~cy 0 ~cf 0 0 0 1 (2.86, 6) (2.87) ax: , (2.88)
р'~рЦ{. 4
Это и есть решение задачи центрального проецирования точки на фронтальную
плоскость, получаемое за два этапа:
□ расширенный вектор координат точки умножается на матрицу Цг,
□ полученный однородный вектор преобразуется в декартову форму.
214
Гпава 2
Между этапами следует выполнить проверку значения h. Условие существования
центральной проекции tr > 0 согласно (2.86, а) равносильно условию h > 0. Ем\
удовлетворяют точкир\,рг ирз на рис. 2.50. При h < 0 центральной проекции точки
на ФКП не существует. В частности, если луч .S' —параллелен ФКП, то z = v.
Л = 0, а проекция р'д является вырожденной, т. е. удаленной в бесконечность:
Тем не менее конечная величина отношения
У _y~sy
X X-Sx
задает на ФКП направление на точку р'4. Наконец, если луч S -урз сразу после
испускания удаляется от КП, то на первом этапе расчета центральной проекции
получим h < 0 и —мнимую проекцию точки рз.
Не трудно заметить сходство механизмов центрального проецирования и обра-
зования тени точки q на плоскости по формуле (1.144) (см. рис. 1.63): в обоих
процессах прообраз q’ может быть действительным (при h > 0 и 1Ч > 0), мнимым
(при h < 0 и t4 < 0) или вырожденным (при Л = 0 и 1’, = 0). Есть и отличие: точка,
расположенная относительно проектора за плоскостью проецирования, имеет
действительную центральную проекцию, но не имеет действительной тени. Дру-
гими словами, плоскость проецирования является прозрачной (часто она вообще
виртуальная, т. е. мысленно подразумевается, но в действительности не сущест-
вует), а плоскость тени реальная и непрозрачная, иначе, выходящие из источника
лучи, обтекая объект, не создавали бы на ней освещенность вокруг тени.
При удалении проектора от ФКП в бесконечность центральная проекция объек-
та вырождается в параллельную. При этом, если:
П проектор удаляется в ортогональном к картинной плоскости направлении, то
kJ < со, к,1 < со, KI сх ~ су = ct=0,
а в (2.88) получим Цг = Of— матрицу ортогонального фронтального проеци-
рования из (2.60);
П проектор удаляется в неортогоналъном к КП направлении, то
|.v.| -> оо, 0 * |сЛ.| <оо, 0 * |су| < <ю, а = О,
a Iff = Kt— матрица косоугольного фронтального проецирования из (2.76).
Важнейшее свойство центрального проецирования, давшее ему второе назва-
ние, — перспективное (от лат. perspicio — ясно вижу) схождение проекций парал-
лельных линий. Изучим это интересное явление, благодаря которому плоские
изображения выглядят объемно и реалистично.
Геометрические преобразования
215
Центральной проекцией отрезка прямой линии, например, р\рз на рис. 2.50,
также является отрезок р[р^ на прямой пересечения ФКП с плоскостью, про-
ходящей через три точки: S,pt и рз. Подставим уравнение прямой p(t) = ро + Vt
в (2.88)
МО y(t) z(t) 1]Z4 =
= [x0 + Ext-cx(z0+E,t) y0 + Vyt-cy(z0+V.t) 0 l-cf(z0+K/)]~
*0 ~ cx-0 + (^x ~cx^z)? - CyZ0 + (*У ~ )f 0 J Г //Л '(Л
l-c{z0-CfVzt \-CfZ0-cfVzt
В том, что полученные координаты проекции x'(t) и y'(t) описывают прямую ли-
нию, нетрудно убедиться, вычислив наклон этой линии:
dy' _ dy'/dt _ (1 ~ cf zo У у ~ ~ cf zo Уz _
dx' dx'/dt (1 - cf z0 )VX - (cx - cf z0 )VZ
Gz ~z0)vz
Gz -z0)Vx-(sx-z0)f/z
= const Vt.
Таким образом, прямая линия проецируется также в прямую линию, но с нерав-
номерной шкалой: движение точки по прямой p(t) с постоянной скоростью V дает
неравномерное движение ее проекции p'(t).
Убедимся также, что предельное положение (точка схода) проекции прямой ли-
нии ро + Vt
Pcf = lim p'(t)= sx —+sz
Vz
(2.89)
не зависит от расположения точки ро, а определяется только координатами ис-
точника 5 и направляющего вектора V. Все параллельные прямые, не парал-
лельные плоскости проецирования, имеют на перспективной проекции одну и ту
же точку схода. Ее можно просто получить, проведя из точки 5 прямую 5 + Vt до
'’ересечения с ФКП. Если эта прямая параллельна проективной плоскости, то
точка схода отсутствует.
Из сказанного следуют выводы:
□ центральные проекции пучка параллельных прямых сходятся в одну общую
точку (2.89);
□ условие существования точки схода: V, 0 — пучок параллельных прямых не
должен быть параллелен плоскости проецирования:
□ если V. - 0, то точка схода вырождена, т. е. удалена в бесконечность, а проек-
ции параллельных прямых, параллельных картинной плоскости, параллельны.
216
Гпава 2
Аналогично (2.86)—(2.89) выводятся формулы для центрального проецирования
на горизонтальную
1 0 0 0
Uh = ~сх 0 ~сг -А» Л„ S7 1 > сх=—, cz=~, ch= —
0 0 1 0 Sy Sy
0 0 0 1
(2.90)
К. Sv
Pch sx ~SV x tz •> У A 0 sz ——sv 17 У у = S—
и профильную КП:
^P = 6 Cy Cz Cp 0 10 0 0 0 10 0 0 0 1
(2.91)
Можно обойтись и одним фронтальным проецированием, поворачивая объект к
проектору нужными гранями. Но если картинная поверхность состоит более чем
из одной плоскости, то лучше использовать совместно разные виды перспектив-
ных проекций для уменьшения числа геометрических преобразований и времени
расчета.
Центральные проекции условно классифицируются (см. рис. 2.38) по числу точек
схода изображения куба или параллелепипеда. Например, проекции каркасных
кубов на рис. 2.51 имеют одну (а), две (б) и три (в) точки схода по числу пучков
параллельных ребер, не параллельных плоскости ху. Второй объект получен
вращением первого вокруг вертикальной оси. Третий объект — вращением вто-
рого вокруг оси, параллельной оси х. Условность классификации ЦП означает,
что изображения других объектов могут вообще не иметь ни одной точки схода
(например, тетраэдр) или более трех таких точек (октаэдр).
Построение центральной проекции отрезка ab требует анализа четырех вариан-
тов расположения его концевых точек а и Ь относительно плоскости проециро-
вания и проектора в зависимости от значений параметров hu и
П при {йа > 0}П {hb > б} отрезок а'Ь' есть действительная проекция отрезка ой;
П при {ha <0}П{й6 <0} проекция отрезка отсутствует в силу мнимости
(вырожденности) ЦП обоих его концов;
□ в оставшихся двух вариантах проекцией является луч, начинающийся в точке
действительной проекции и уходящий в бесконечность в направлении, проти-
Геометрические преобразования
217
воположном точке схода отрезка. Например, при {Ла > 0}П {hb <о} и направ-
ляющем векторе V = b - а по (2.88) и (2.89) вычисляем точки
а' ~ аЩ, Ьс =
Sy vz Sz
О
по которым строим проекцию отрезка в виде луча а' —> 2а' - Ьс.
При {Ло < 0}П {hb > О} получим проекцию-луч b' -> 2Ь' - ас, где
Ь'~ЬЦ{, ас =
VH
Sy Vz Sz
О
«РсЗ
Рис. 2.51
& Пример 2.6. Построить проекцию отрезка прямой ab на угол первого октан-
та, образованный пересечением координатных плоскостей ху и zy. Координаты
проектора .S' = [2 I 4], концов отрезка а = [О 1 б] е zy и 6 = [3 2 О] е ху
(рис. 2.52).
218
Гпава 2
Решение. Рассчитаем по (2.88) и (2.91) матрицы центрального проецирования на
фронтальную и профильную плоскости:
1 0 0 0 '0 -0.5 -2 -0.5
Uf = 0 -0.5 1 -0.25 0 0 0 -0.25 > Up 0 0 1 0 0 1 0 0
0 0 0 1 0 0 0 I
Найдем однородные и декартовы координаты проекций концов отрезка на эти
плоскости:
Рис. 2.52
Из четырех проекций только две ap=a и b'{ =b являются действительными
Проекции a'f и Ь'р — мнимые, лежащие на отрицательных продолжениях лучей
5 —> а и 5 —> Ь, что подтверждается значениями hj - -0.5 < 0 и /гЛР = -0.5 < 0.
Геометрические преобразования
219
Таким образом, мы имеем по одной точке проекции a'pezy и bf еху на гори-
зонтальной и фронтальной картинных плоскостях. Полная проекция отрезка ab
состоит из двух отрезков, для построения которых нужны еще две точки — по
одной на каждой плоскости проецирования. Например, вычислив направляю-
щий вектор К = b-a = [-3 -1 б] и по (2.89) и (2.91) точки схода
Pcf = 4
3 0 , Рср - о
8
3
(их можно построить графически, проведя через точку 5 прямую, параллельную
ab, до пересечения с плоскостями f и р), получим параметрические уравнения лучей
p{(f)=b'+(b'(-pcf}tf =[з 2 о]+[-1 1/3 0]rf V/f>0,
Рр(') = «р + U - Pep )tp = [О 1 б]+ [0 2/3 - 2]rp V/p > 0.
При it = tf - 3 лучи пересекаются в точке с = [б 3 б] на оси у, обеспечивая пе-
реход проекции отрезка с одной проективной плоскости на другую.
Используя мнимые проекции b'pGzy и а'{еху, получим альтернативные (2.92)
параметрические уравнения лучей
Pf (t) — bf + (bf ~ af = [з 2 o]+[—3 1 oj/g*
Рр(‘)=ар + ("p _/>p)fp =[° 1 6l+[° 2 -6]fpVrp>0,
пересекающиеся при tr-tp- 1 в точке с = [б 3 б].
В итоге центральной проекцией отрезка ab является ломаная линия acb. Однако,
если не проверять все точки проекций на мнимость, будет получена неверная
ЦП, состоящая из двух отрезков abp и ba'f. □
Одним из видов центрального проецирования является так называемая
"обратная перспектива". Построение изображений объемных тел в этом ракурсе
широко применялось в византийской и унаследовавшей ее традиции древнерус-
ской живописи. Ее яркими представителями являются знаменитая икона Андрея
Рублева "Троица" XV в. (рис. 2.53, а) и миниатюра из Евангелия XVI в.
(рис. 2.53, б). Визуально обратная перспектива отличается от прямой тем, что в
ней из двух одинаковых фигур крупнее выглядит та, которая расположена от
наблюдателя дальше, что придает изображению некоторую ирреальность, неес-
тественную потусторонность.
Рассмотрим геометрическую модель метода обратной перспективы и построение
с помощью этой модели изображения объекта. Желаемый эффект достигается
отделением активного процесса формирования проекции от пассивного процес-
са ее созерцания. В соответствии с названием метода разместим наблюдателя и
проектор 5 по противоположные стороны от ФКП (рис. 2.54), а именно:
□ направление на дальнего наблюдателя зададим ортом z°;
220
Гпава 2
П положение проектора S = [о О -У7] на фокусном расстоянии F от ФКП за-
дадим так, что минимальная аппликата объекта znnn > -F, а объект целиком
располагался бы между наблюдателем и проектором.
Рис. 2.53
Рис. 2.54
Таким образом, расчет обратной перспективы точки р = [х у z] выполняете»
по формуле (2.88) с матрицей и координатами проекции
'1 0 0 0 '
0 1 0 0 , Fx , Fy
Ц[ ~ , х - , у -
0 0 0 F 1 F + z F + z
0 0 0 1
(2.93)
Геометрические преобразования
221
На рис. 2.55 приведена рассчитанная по (2.93) обратная перспективная проекция
сцены, состоящей из квадратного подиума и стола с квадратной крышкой, на
которой лежит, немного свесившись вперед, книга в форме параллелепипеда.
Рис. 2.55
2.2.5. Проективные алгоритмы
сложных преобразований
Проективные преобразования кроме своего непосредственного назначения —
(зображения сцены в желаемом ракурсе— могут применяться для быстрого по-
строения:
□ различных фигур и изображений на плоских и криволинейных поверхностях;
□ сцен от первого лица, изображаемых с позиции подвижного наблюдателя;
□ простейших оптических эффектов — теней, отражений, преломлений.
Основное преимущество проективных алгоритмов — возможность группового
преобразования точек по (2.9), т. е. параллельных вычислений по одним и тем же
формулам для всего множества точек. Такой подход к организации вычисли-
тельного процесса составляет серьезную конкуренцию алгоритмам трассировки
см. разд. 1.3), в которых проводятся индивидуальные лучи через каждую точку
аждого объекта. Процесс трассировки более трудоемок по сравнению с группо-
вым преобразованием и имеет преимущество лишь при малом числе точек и вы-
сокой сложности их преобразования.
Для расчета групповых преобразований по (2.8) и (2.9) необходимо сформиро-
вать матрицу координат Q. Ее строками являются расширенные формы:
□ точек р, =[р, 11 — центров объектов, концов отрезков прямых, вершин по-
лигонов;
□ векторов Ё; = б] — скоростей движений и направлений осей вращений;
□ нормалей N, = [Д', б] к плоскостям граней полиэдров, теней и отражений.
222
Глава 2
При групповой организации координат всех объектов сцены в одной матрице
общее преобразование сцены матрицей С выполняется за одно умножение:
Q' = QC.
Если требуется выполнить индивидуальное преобразование т-го объекта сцены
матрицей С<я,>, то можно объединить строки координат этого объекта в блок
Q<m>, тогда
Q /<т> __ Q<’"> Q<ni>
Построение изображения Зб-объектов на плоском экране дисплея может быть
выполнено двумя способами (рис. 2.56).
П Двухэтапное преобразование координат точек
• из МСК в СК ФКП с помощью Сп — одной из проективных матриц Of
Af, К{ или Це.
Qr~QCn. (2.94.«)
• из СК КП в ЭСК с помощью матрицы С, из (2.26) или (2.27):
C, = CfC,. (2.94,6)
Двухэтапный метод применяется при посзроении изображения сложной сце-
ны, состоящей из множества объектов. Между первым и вторым этапами ре-
шаются задачи визуализации изображения:
• отсечения графических элементов, нс попавших на КП;
• удаления невидимых элементов, заслоненных другими элементами;
• освещенности видимых поверхностей;
• расчета различных оптических эффектов — отражений, преломлений, теней
При использовании центрального проецирования после первого этапа вы-
полняется приведение координат к декартовой форме.
Рис. 2.56
П Преобразование координат точек из МСК сразу в ЭСК:
— Qf Сп,, где Си, — Сп С,.
(2.95»
''еометрические преобразования
223
Одноэтапный метод удобен для параллельного проецирования одиночных
выпуклых объектов прямо на экран дисплея. Решение задачи отсечения вы-
полняется быстрыми целочисленными алгоритмами в ЭСК.
Совмещение ЭСК с МСК превращает двухэтапное преобразование (2.94) в одно-
этапное (2.95). Если при этом ось z, направлена к наблюдателю, то в левой ЭСК
направления всех вращений будут обратными по сравнению с правой СК, что
нужно учитывать при выборе параметров матриц вращений (2.21).
При выводе элементов изображения на экран дисплея сразу после их расчета и
при низком быстродействии ЭВМ наблюдается неприятный эффект "мерцания",
при котором последовательность вывода замедлена и видна в реальном времени.
У странение мерцания и "дергания" изображения достигается методом двойной
буферизации [36], т. е. разделения массивов памяти, используемых для формиро-
вания изображения и вывода его на экран. Если используемый программой гра-
фический режим имеет хотя бы две страницы видеопамяти (буфера кадра), то
одна из них выбирается пассивной видимой страницей, а другая — активной
и невидимой. После построения всего изображения на активной странице по
командам прикладной программы выполняется переключение страниц.
В отсутствие второй видеостраницы в качестве буфера используется массив
>перативной памяти размером с окно вывода, откуда данные блочно, т. е. быст-
ро, копируются в видеопамять. Этот способ предпочтительнее, т. к. запись в ОЗУ
выполняется быстрее, чем в видеопамять, но он требует от программиста созда-
ния собственной библиотеки растровых функций построения прямых, окружно-
стей, полигонов и решения задач заливки, отсечения, вывода текста, решаемых
встроенными библиотечными функциями любого развитого языка программи-
рования.
2.2.5.1. Проецирование пространственных линий
на плоскость
Применим проекционный подход к построению изображений графических объ-
ектов на различных поверхностях. Вначале рассмотрим некоторые методы про-
ецирования пространственных линий на плоскость, в том числе и на плоскость
•крана. Они могут быть полезны программисту, создающему библиотеку функ-
дий построения различных геометрических фигур.
Общий подход к проецированию полностью детерминированной линии p(t) е R3
из МСК на плоскость экрана заключается в расчете по (2.95) матрицы проециро-
вания Ст, выборе значений параметра t„ вычислении узловых точек р, = />(/,), их
экранных проекций рЭ1 = рц, )СПЭ и соединении каждой пары соседних точек
стрезком прямой линии функцией Ипе(рь, p>.,t \)-
Проецирование обладает полезным свойством: локальные участки кривой p(f),
ча которых вектор К(/) = dp(t) / dr составляет с нормалью к проективной плоско-
сти малые углы, имеют на проекции p,(t) большую кривизну и сгущение узлов.
Оптимальным является распределение узлов на кривой линии по следующему
принципу: плотность точек р, пропорциональна кривизне самой кривой, а не ее
224
Гпава 2
проекции. Для изображения отрезка прямой достаточно проекций всего двух его
концевых точек.
Проецирование пространственной окружности на плоскость эквивалентно аф-
финному сжатию плоской окружности в эллипс. Как показано на рис. 2.19, это
преобразование автоматически сгущает удаленные от центра эллипса точки рЭ;, в
то время как узлы р, распределены по окружности равномерно.
Рассмотрим методы проецирования некоторых не полностью определенных ли-
ний. Начнем с построения правильной n-сегментной ломаной линии
Р = {р< ...р„ри+|}, вписанной в дугу окружности, с параметрами:
□ f = {ро, N} — плоскость окружности;
□ ро — центр окружности;
□ N — нормаль к плоскости окружности;
□ pi — первая вершина ломаной линии;
□ 5 рад — угол раствора дуги окружности.
Наиболее рациональный путь решения задачи состоит в построении образа ло-
маной линии Ро е хр путем л-кратного вращения орта х° вокруг оси z на уго~
у = а/п, преобразовании образа в заданное положение Р на плоскости f и, на-
конец, проецировании на картинную плоскость или экран (рис. 2.57).
Рис. 2.57
Наличие трех элементов ро, pi и N, связанных с плоскостью f, позволяет постро-
ить матрицу Со преобразования из СК xyz в СК x'y'z' с помощью функции
МАРУ, определенной в (2.55). Зададим ее аргументы
oi = Оз, = z°, И7! = х°, 02 = ро, И2 = N, Wi= р\ -ро
Геометрические преобразования
225
так, чтобы образ точки р\ был в х°, а коэффициент масштабирования по осям х
и у был одинаковым и равным г = |/л -ро|. Отметим, что если задать Vi - N, то
коэффициент масштабирования в направлении оси у будет равен r|7V], а ломаная
линия Р е f будет вписана в дугу эллипса, а не окружности.
На основе сказанного составим функцию проецирования дуги правильной лома-
ной линии с матрицей проецирования Сп.
S'pro_arc(p$, N,pi,a, п, Сп)
R = R(a I ny, // матрица вращения на угол ц/
С = МАРз(рз,г°,х°, Po,N,pi - Ро)сп i И матрица проецирования
р = х° , рэ = рС ; И образ первого узла и его проекция
Vi = l, п И цикл построения сегментов ломаной линии
{Я=Рй // запоминание проекции /-го узла
р = pR\ И расчет образа (/ + 1)-го узла
Рз = рС; // проекция (i + 1 )-го узла
line(q, рз); И проекция отрезка ломаной линии
Задание специальных значений аргументов функции pro_arc позволяет проеци-
ровать различные пространственные линии.
□ при a - 2л получим проекцию правильного п-угольникст,
□ при достаточно большом значении п ломаная линия практически совпадает с
дугой окружности. Например, выбор л = р80а/л^ располагает узлы ломаной
линии на дуге описанной окружности через один градус. Следуя рекомендаци-
ям, изложенным в комментариях к рис. 2.14, получим оптимальное значение
ap.trN,
"=ПМ~’
где г = \р\ -/?о|, а цэ — вычисляемый по (2.27, б) масштабный коэффициент пе-
рехода из ОСК в ЭСК. Если все координаты и размеры элементов в МСК за-
даны в пикселах, то ц, = 1;
□ для проецирования окружности задаются а = 2л и большое число сторон ап-
проксимирующего окружность правильного полигона, например, п - 360 или
его оптимальное значение
Иэ'-
|«|
226
Гпава 2
Проекция представляет собой вписанный в эллипс н-угольник, плотносте
расположения вершин которого пропорциональна кривизне эллипса, а ми-
нимальное расстояние между вершинами составляет один пиксел.
В описанном методе положение окружности в пространстве задается центром р
и точкой pi, лежащей в плоскости {ро, N} и определяющей радиус окружное™
г = |pi -ро|. Часто исходными параметрами окружности могут быть ро, N и г, чтс
делает ее построение неоднозначным, т. к. при этом остается неизвестной началь-
ная точка pi. В условиях неполной определенности можно вычислить матрицу С
преобразования из СК xyz в СК x'y'z' с помощью функции MAPI из (2.51) с ар-
гументами
OI = Оз, И] =2°, 02 = ро, V2=rN.
Взяв теперь начало окружности образа в х°, получим точку р| = х°С0, лежашук
в плоскости {ро, N} на расстоянии г от точки ро.
Реализуем все сказанное в виде функции проецирования окружности радиуса г
лежащей в плоскости {ро, N}.
& pro_circle(r,po, N, Сп)
Н И число вершин аппроксимирующего полигона
R = Rz(2n/ л); // матрица вращения на угол между вершинами
С = MAP2\pj,z°, р^, rN ; И матрица проецирования
р = х° , рэ= рС ; V/ = 1, п И образ первой вершины и ее проекция И цикл построения сторон полигона
p=pR\ Рэ=РС', // запоминание проекции i -ой вершины // расчет образа (/ + 1)-ой вершины И проекция (/ + 1)-ой вершины
line(q,pi)-, } } О И проекция ребра полигона
С помощью функции pro_circle были построены изображения окружностей, впи-
санных в грани кубов, на рисунках данного раздела.
& Пример 2.7. Построить в диметрической проекции изображение глобуса, со-
стоящее из параллелей с шагом 30°, меридианов с шагом 45° и контура. Ради} с
глобуса г, угол склонения вправо в плоскости хр равен фск = 23.5°.
Геометрические преобразования
227
Рис. 2.58
Решение. Желаемое склонение глобуса достигается вращением матрицей
0.917 -0.4 O'
RCK =^Z(-<PCK) = VK Z \ < Vlx / 0.4 0.917 0
0 0 1
Диметрические проекции пяти параллелей, имеющих общие векторы нормалей
Vn = >'°/?ск, различные радиусы и центры
г(ап) = rcos(a„), рц (ап) = г sin (ап )у° RCK
.гроятся функцией
pro_circle(r(aB),pll(ci.B),Nn, АДИМСЭ) Van е {0°, ±30°, ±60°}.
Диметрические проекции четырех меридианов, имеющих отличающиеся друг от
друга векторы нормалей
A(aM)=[cos(aM) 0 sin(aM)]/?CK,
'бщие нулевые центры и радиусы г, строятся функцией
pro_circle(r,Oj,N(aM), АДИМСЭ) VaM е {0°, 45°, 90°, 135°}.
Эртогональная фронтальная проекция контура глобуса создается большой ок-
эужностью в его сечении, перпендикулярном вектору S' = [1 1 л/У] из (2.74), и
: гроится функцией
pro circle^",Oj,S,OfC3). □
228
Гпава 2
2.2.5.2. Стереографические проекции
Во многих приложениях (компьютерные игры, тренажеры, авто- и авиасимуля-
торы, управление манипуляторами и т. п.) важно создать восприятие глубины
сцены, максимально близкое к реальной действительности. Проецирование на
плоскость из единственного центра равносильно монокулярному зрению, кото-
рое дает неполное ощущение трехмерности окружающего мира. Оно, конечно,
лучше параллельного проецирования, которое вообще не способно к передаче
глубины из-за бесконечной удаленности наблюдателя. Система монокулярного
зрения человека преобразует двухмерную картинку на близкой к сферической
поверхности сетчатке глаза в объемную, используя следующие "подсказки" на
подсознательном уровне [26]:
□ геометрическая перспектива — схождение в одну точку параллельных прямых;
□ воздушная перспектива— ослабление толщей атмосферы цветового контра-
ста и разрешающей способности глаза;
□ параллакс движения— ближние к глазу объекты смещаются на плоскости
проекции больше, чем дальние;
□ относительный размер знакомых наблюдателю объектов;
□ экранирование (перекрытие) дальних объектов ближними;
□ фокусирующая аккомодация — зависимость напряжения фокусирующих мус-
кулов глаза от расстояния до объекта.
Система бинокулярного зрения обрабатывает дополнительную информацию:
□ угол сведения оптических осей глаз;
□ несогласованность местоположения проекций объекта на двух сетчатках, ис-
пользуемая мозгом для оценивания расстояния до объекта.
Программная имитация бинокулярного зрения состоит в разработке алгоритма
построения стереографической проекции— двух центральных проекций на об-
щую КП от двух разнесенных в пространстве проекторов (рис. 2.59). Пусть рас-
стояние между глазами (оптическая база) равно 2D. Зрительная система фоку-
сирует взгляд в некоторой точке — центре визуальной массы объекта или группы
объектов, находящемся от наблюдателя на фокусном расстоянии F.
Проведем через центр визуальной массы фронтальную плоскость проецирования
ортогонально направлению взгляда. Глаза наблюдателя (проекторы) находятся
в точках
5лев=[-П 0 F],Snp=lD О Г]
и фокусируются под углом сведения
( DA
y = arctg^— .
Если D « F, то у« 0° и оба глаза видят объект практически одинаково. При
сравнимых расстояниях D и F изображения, формируемые в сетчатке каждого
глаза, отличаются друг от друга, чем и достигается эффект объемности при со-
Геометрические преобразования
229
единении мозгом двух картинок в одну. Наиболее комфортные для зрения усло-
вия и наилучший стереоэффект достигаются при tg(y)®0.1, откуда у® 6°
и Fa Ю£>. Например, при среднестатистической базе 2D = 70 мм получим
F= 35 см — оптимальное гигиеническое расстояние для чтения, письма и точной
ручной работы.
Рис. 2.59
Стереоизображение состоит из двух центральных проекций объекта, рассчитан-
ных отдельно для каждого глаза. Рассматривание стереопары производится с
нулевым углом сведения глаз. Преобразования произвольной точки р в проек-
ции левого и правого глаз состоят из операций вращения вокруг соответствую-
щего глаза на углы
флев = Y, фпр “ —у
и центрального проецирования на ФКП, описываемого по (2.88) матрицами
' 1 0 0 0 ' 1 0 0 0
0 1 0 0 0 1 0 0
^лев D 0 0 ’ Цпр - 0 0
F F F F
0 0 0 1 0 0 0 1
Таким образом, построение стереопары {рЛев,рпр} точки р выполняется по сле-
дующим формулам:
Рлев ~ рТ(—£лев)Ку(О)Т(8лев)Цлев ,
(2.96)
Рпр ~ <7)^('^пр)^пр •
На рис. 2.60 построено стереоизображение трех четвертей глобуса радиуса
R - 20 мм при фокусном расстоянии F= 300 мм и оптической базе 2D = 70 мм.
Рассматривать стереопару рекомендуется с расстояния 30 см с непрозрачной пе-
регородкой между глазами на линии, разделяющей пространства левого и пра-
вого изображений.
230
Глава 2
Рис. 2.60
Кроме пространственного существуют и другие методы разделения стереопар [5]
□ цветовое: изображение левого глаза строится, например, красным цветом.
правого — зеленым, а для просмотра используются цветные очки. Вместе
цветовых фильтров можно использовать поляризованные. Недостаток спосо-
ба в том, что по сути дела можно формировать только простые каркасные
изображения, но зато реализация метода проста и полностью использует про-
странственное разрешение дисплея;
□ пространственно-временное: изображение для левого глаза строится в четных
строках экрана, для правого — в нечетных, а для просмотра используются
электронные или электромеханические очки, перекрывающие соответствую-
щий глаз на время прорисовки четных или нечетных строк. Этот подход мо-
жет быть реализован на дисплеях с чересстрочной разверткой, позволяв
выводить быстро меняющиеся динамические цветные полутоновые изобра-
жения, но с уменьшением вдвое разрешения по вертикали;
□ временные: для левого глаза используется одна страница видеопамяти, для
правого — другая, а их переключение происходит с достаточно большой час-
тотой кадровой развертки. Для перекрытия глаз также должны использо-
ваться электронные или электромеханические очки. Пространственное раз-
решение по строкам здесь не теряется;
□ наилучшие условия для восприятия стереоизображений созданы в системах
виртуальной реальности, где в специальные очки или шлем вмонтирован би-
нокулярный монитор из двух мини-дисплеев. На них подаются картинки
рассчитанные отдельно для каждого глаза. Программа с помощью механиче-
ских, инфракрасных или электромагнитных датчиков отслеживает повороть
головы и, возможно, глаз, что создает удивительный эффект "погружения в
действительность" со стереоскопическим изображением и изменением сцены в
реальном времени в зависимости от движений головы или глаз наблюдателя
В перспективе создание систем с лазерной прорисовкой изображений непо-
средственно на сетчатке каждого глаза.
Геометрические преобразования
231
Карты вовсе не безгрешны
И в пределах разных норм
Нарушают верность линий,
Площадей, углов и форм.
2.2.5.3. Картографические проекции
К типичным, широко распространенным и общеизвестным представителям
сложных проективных преобразований относятся картографические проекции,
применяемые для составления плоских географических карт поверхности Земли.
Последняя, являясь приближенно эллипсоидом вращения с соотношением эква-
ториального радиуса к полярному 1.00336 : 1 [28], не может быть развернута на
плоскость без складок и разрывов. В связи с этим фактом здесь уместно привести
стихотворение известного картографа А. В. Гедымина:
Изучая суть проекций,
Надо помнить положение:
С переходом сферы в плоскость
Неизбежны искажения.
Искажения, возникающие на карте, являются расплатой за удобство, которое мы
получаем при пользовании плоским изображением вместо глобуса. Характер
искажений зависит от способа проецирования и от вида картографической сет-
ки — системы меридианов и параллелей на карте, т. к. в нее, как в "прокрустово
ложе", приходится вгонять изображения материков. В зависимости от неиска-
жаемого параметра принято следующее деление карт [3]:
□ равноугольные — проекции Меркатора, сохраняющие угловые соотношения и
конфигурацию фигур за счет искажения их площадей. В таких проекциях
строятся навигационные карты, используемые в судовождении;
□ равновеликие— проекции Ламберта, сохраняющие соотношения площадей
фигур в разных частях карты за счет искажений их конфигураций, особенно
сильных на краях карты. Такие проекции применяются для создания полити-
ческих карт, где важно показать правильное соотношение размеров различ-
ных стран;
□ равнопромежуточные — эквидистантные проекции с равными расстояниями
между определенными линиями (параллелями или меридианами) картогра-
фической сетки во всех частях карты;
□ произвольные — проекции, которым свойственны в разной степени как угло-
вые, так и площадные, и дистантные искажения.
Типовыми операциями картографической съемки являются преобразования ко-
ординат образа из системы координат земной поверхности в другую систему,
описывающую прообраз на поверхности проецирования, и развертывание по-
следней на плоскость. Считая Землю сферой радиуса г = 1, зададим сферические
координаты точки на ее поверхности вектором р = [1 ф у], в котором
□ ф° е [- 180°, 180°] — долгота, отсчитываемая от Гринвичского меридиана;
□ у° е [-90°, 90°] — широта, отсчитываемая от параллели экватора.
Радианное а и градусное а° измерения угла связаны соотношением
о 180
а =----а.
л
232
Гпава 2
Системами координат проективной поверхности могут быть полярная, цилиндри-
ческая или коническая.
Механизм построения любой картографической проекции таков, что проектор и
наблюдатель находятся по разные стороны от проективной поверхности. Такая
проекция фактически является обратной перспективой (см. рис. 2.54), что хорошо
заметно на некоторых видах карт. Важно отметить, что создание картографиче-
ских проекций при неподвижном проекторе не всегда возможно. В этих случаях
используются формулы прямого преобразования координат, которые аналити-
чески выводятся в рамках проективного метода с подвижным проектором.
Искажение какого-либо геометрического параметра образа характеризуется от-
ношением к нему того же параметра прообраза на плоской карте. Примем в ка-
честве образа прямоугольник на экваторе сферы с длинами сторон а по долготе
и b по широте. Обозначим длины сторон фигуры прообраза а' и Ь'. Эта фигура
будет близка к прямоугольнику лишь при достаточной малости значений а « 1
и b « 1. Определим коэффициенты долготного т^, широтного тч„ углового mz и
площадного ти искажений'.
Му
lim —
а
lim
тЛ=—^~ ,тЛ = mvmv.
(2.97)
На равноугольных и равновеликих картах будет, соответственно, тг - I
и тя = 1.
Для визуального оценивания искажений построенные ниже карты содержат про-
екции черных квадратов, размещенных в разных местах поверхности сферы. При
аналитическом выводе коэффициентов искажений в различных картографиче-
ских проекциях (для этого автор использовал возможности символического про-
цессора MathCAD) благодаря малости длин отрезков а и b можно считать, что
на широте у они имеют измерения a sec(vp) по долготе и b по широте.
В зависимости от формы и положения проективной поверхности наиболее рас-
пространены следующие виды картографических проекций.
Азимутальные проекции
При построении азимутальной проекции проецирование точки сфер!
р = [1 <р у] выполняется на плоскость, касающуюся сферы в некоторой точке
р0=[1 Фо Фо] (рис. 2.61). Для превращения этой плоскости во фронтальную
расположим начало системы координат х'у'г' в ро, а ее ось у' направим по каса-
тельной к меридиану фо, который на карте будет расположен вертикально. Такое
сложное преобразование системы координат описывается матрицей
Са = Яу(-фоЖфоН-г°)-
'еометрические преобразования
233
Рис. 2.61
Расположив проектор в точке [о О -F] на оси z', проходящей через центр сфе-
эы — точку [О О -1], получим матрицу проецирования (2.93)
1 О О
ООО
О
О
F-1
1
-огда с учетом взаимосвязи (1.3, б) сферических и декартовых координат полу-
чим азимутальную проекцию точки:
у 0 1]~ [sin(ip)cos(v) sin(v) cos(ip)cos(v) l]ca2/f. (2.98)
?адавая различные фокусные расстояния, получают следующие разновидности
'зимутальной проекции'.
□ при F=1 (проектор в центре сферы) строится гномоническая проекция,
для которой характерно разрежение линий сетки при удалении от центра
карты. При выборе F> 1 становится возможным построение карты целого
полушария;
□ проекция, соответствующая F=2, называется стереографической. Проектор
располагается в диаметрально противоположной точке -ро;
□ проекция, построенная при фокусном расстоянии F>2, называется внешней,
т. к. проектор находится вне сферы;
□ при F—> оо азимутальная проекция вырождается в орпгографическую, при этом
проецирующие лучи параллельны, а линии сетки сгущаются от центра карты
к ее периферии.
При всех значениях фокусного расстояния искажения отсутствуют в точке каса-
-ия плоскости со сферой.
234
Гпава 2
Варьируя расположение плоскости проецирования, получают следующие азиму-
тальные картографические проекции:
П полярную-, плоскость касается сферы в полюсах при кро = ±90°. Сетка полярной
карты состоит из концентрических окружностей параллелей и радиальных
прямых меридианов. Коэффициенты долготных и широтных искажений, вы-
численные по (2.97) при \ро = 90°, равны
F _ (F-l)sin(y)+l „
W<₽ F-l+sin(y)’ (f-l+sin(y))2 (299)
Полярную проекцию точки р = [1 <р у] удобнее описывать не декартовым
(2.98), а полярным вектором [р ср —ср01 с модулем р и коэффициентом ши-
ротного искажения mv:
p(v. F)- Vmma = /7^...
F-l+sin(y) Эу
Например, при F= 1 получим параметры гномонической проекции
р = ctg(y), mw - sin-'(y), = sin 2(y),
/nz = sin '(y), - sin 4(y),
искажающей как углы, так и площади. Аналогичны свойства и ортографиче-
ской проекции с параметрами
р = cos(y), m,f = 1, mv = тг = = sin (у).
На рис. 2.62, а в этой проекции построена карта северного полушария. Таким
образом, с точки зрения искажений гномоническая и ортографическая проек-
ции являются произвольными.
Уравнивая в (2.99) коэффициенты и /hv, получим способ построения ази-
мутальной равноугольной карты Меркатора как стереографической (при
F= 2) проекции с параметрами
2cos(y) 2 , 4
Р = ;—г-7-^ > "'<р = '«v = 7—“ГТ ’ = 1 ’ = 7-----ГАТТ
l + sin(y) ф l + sin(y) (l + sin(y))2
На этой карте, как видно из рис. 2.62, б, сохраняются пропорции фигур в раз-
ных ее частях при увеличении площади в четыре раза на краю по сравнению с
центром.
Равнопромежуточная полярная проекция с линейным модулем р = л / 2 - с
имеет постоянный шаг параллелей и коэффициенты искажений
= 1, /«ф = тя
л/2-у cos(y)
----> т2--------------•
cos(y) л/2 - у
Геометрические преобразования
235
Она реализуется при переменном фокусном расстоянии
F(е [_!!_, з] Vlp6[o.„/21.
v ' n/2-v-cos(v) [л-2 J
Оптимальное по среднеквадратичному критерию
л/2
( (p(v,^)-("/2-v))2dV -э min
J F
О Г
постоянное расстояние проектора от плоскости, дающее наиболее равномер-
ную сетку параллелей, составляет 2.8.
Практичный метод построения равнопромежуточных карт заключается в
распрямлении каждого меридиана на плоскость проецирования, что как раз и
описывается формулой
p(V)=y-V.
Равномерный масштаб позволяет изобразить всю поверхность земного шара
внутри одной окружности, что и реализовано (без Антарктиды) в эмблеме
Организации Объединенных Наций (рис. 2.62, в). На внешних краях такая
карта имеет максимальные искажения;
Рис. 2.62
П экваториальную', плоскость параллельна оси вращения сферы и касается па-
раллели vpo = 0° в точке с долготой <ро. Соответствующий меридиан <ро распо-
ложен на карте вертикально в центре. Дуги остальных меридианов сходятся
на полюсах. Линия экватора на карте горизонтальна; параллели изображены
236
Гпава 2
дугами, кривизна которых уменьшается при удалении центра проецирования.
В экваториальной стереографической (она является равноугольной) или внеш-
ней проекциях обычно строятся карты полушарий Земли, например, восточ-
ного при сро = 90°, фо = 0° и F= 2 (рис. 2.62, г). В этом ракурсе хорошо прояв-
ляются свойства обратной перспективы;
□ косую-, плоскость занимает произвольное касательное к сфере положение, а
алгоритм проецирования дан в (2.98). Применяется, во-первых, для изобра-
жения земного шара в наклонном положении, в котором кривые линии па-
раллелей и меридианов наглядно подчеркивают его объемность (рис. 2.62, д).
Во-вторых, косая азимутальная проекция дает малые искажения карты ло-
кальной области земной поверхности, для чего параметрам фо и фо задаются
значения координат географического центра этой области. Например, на
рис. 2.62, е построена гномоническая карта Гренландии и ее окрестностей с
центральной точкой фо = -40° и фо = 70°. Для изображения диагонально про-
тяженной области можно изменить в (2.98) матрицу преобразования на
Са = Ry (- ФО )RX (vo }RZ (y)H- z° )
с углом у между диагональю области и параллелью.
Цилиндрическая проекция
При построении цилиндрической или панорамной проекции точка сферы проеци-
руется на боковую поверхность охватывающего сферу цилиндра, после чего тот
развертывается на плоскость. В зависимости от положения оси цилиндра отно-
сительно оси вращения сферы цилиндрические проекции делятся на продольные
(все параллели горизонтальны, а меридианы вертикальны и равно отстоят друг
от друга), поперечные и косые. На линии касания цилиндра со сферой искажения
отсутствуют, а при удалении от нее увеличиваются. Горизонтальные искажения
присущи всем цилиндрическим проекциям, а вертикальные зависят от способа
образования проекции.
Получим алгоритм проецирования точки р = [1 Ф ф] на поверхность продоль-
ного цилиндра, касающегося сферы по экватору. Без внесения дополнительных
широтных искажений эту криволинейную поверхность можно заменить верти-
кальной плоскостью х’у', касающейся цилиндра по меридиану ф (рис. 2.63). Та-
кое преобразование системы координат описывается матрицей
Сц(фМД-<р)т(-7°).
Разместив проектор в точке [о 0 - г] на оси z', рассчитаем по (2.93) матрицу
Ц(. Развертывание боковой поверхности цилиндра эквивалентно переносу про-
екции на расстояние ф вдоль оси х'. Таким образом, проекция точки
р = [1 ф ф] на развертке цилиндра вычисляется следующим образом:
q’ ~ [8т(ф)соя(ф) sin(v) cos^)cos(v) l]Cu(<p)//f,
п Г 3 <2100)
р =q + фх =|ф h 0j.
Геометрические преобразования
237
Рис. 2.63
Аналитическое выражение для ординаты проекции
F-l+cos(y)
позволяет исследовать влияние фокусного расстояния /'на искажения цилиндри-
ческих карт. Коэффициенты долготных и широтных искажений, вычисленные по
(2.97), равны
1 (F-l)cos(v)+l г dh(w, F)
При F = 1 (проектор в центре сферы) получим зависимость
Л(у/) = tg(y)
с коэффициентами искажений
m4, = cos-2(y), тл = cos_|(v)> /,;в = со5~3(ц/).
Эта проекция, сильно искажающая на высоких широтах как углы, так и площа-
ди, является произвольной.
Уравнивая в (2.101) коэффициенты и тц„ получим дифференциальное уравнение
дл(у/, е)________________________________1
Этр cos(v)
Его решение
h(\y) = Injsec(vp) + tg(vp)| = X(v)
238
Гпава 2
есть лямбда-функция [13] широты 1|/. Равноугольная цилиндрическая проекция
Меркатора (рис. 2.64, а) с коэффициентами искажений
= 1, тя = cos“2(\|>)
проективно строится при переменном фокусе
FW=W^^e0.u]vVe[O.,/2).
Оптимальное по среднеквадратичному критерию
л/2
j (A(v,F)-A(v))2dv —> min
о F
постоянное значение фокусного расстояния, дающее наименьшие угловые иска-
жения, равно Fх 1.275. Изображение полюсов в проекции Меркатора невозмож-
но, а приполярные области имеют большие искажения площадей.
При F-> оо все проецирующие лучи горизонтальны,
h(\y) = sin(vp),
а коэффициенты искажений равны
mv = cos(vp), mz = cos2(y), /»и = 1.
Таким образом, это равноплощадная цилиндрическая проекция Ламберта
(рис. 2.64, б). На ней параллели сгущаются от экватора к полюсам.
Наконец, равнопромежуточная цилиндрическая проекция (рис. 2.64, в) получается
при использовании линейной формулы
А(у) = v
с коэффициентами искажений
mv. = 1, /«z = cos(vp), т,? = тя = cos '(у).
Реализующий эти свойства проектор имеет переменное фокусное расстояние
F(. vQ-eosW) Е Г^_ Л Vv е [0_ , 2|
y-sin(y) L71-2 J
Оптимальное по среднеквадратичному критерию
п/2
/ (л(у,т)-у)2<1у —> min
о f
постоянное значение фокуса, дающее наиболее равномерную сетку параллелей,
равно Т» 2.8.
Геометрические преобразования
239
Рис. 2.64
Коническая проекция
При построении конической проекции точка сферы р = [1 <р у] проецируется
на боковую поверхность надетого на сферу конуса, после чего тот развертывается
на плоскость. Сетку конической карты составляют концентрические дуги парал-
лелей и радиальные прямые меридианов.
Для уменьшения радиальных (широтных) искажений проективный конус должен
касаться сферы по средней параллели картографируемой области уо * О (при
уо = 0 конус становится цилиндром, и для построения карты должен использо-
ваться алгоритм (2.100)). На этой параллели карты искажения отсутствуют, а
при удалении от нее увеличиваются. Угол между меридианами <pi и <рэ на кониче-
ской развертке равен |<pi - <рг| sin(yo). Измерив его, можно определить параллель
уо, на которой объекты изображены без искажений.
Для удобства пользования картой задается средний меридиан <ро, который на
развертке должен быть вертикальным. Коническая проекция применяется для
изображения протяженных по долготе областей средних широт 20° < |у°| < 70°
(Россия, США, Канада), хотя и способна отобразить на одной карте объекты в
разных полушариях.
Получим алгоритм проецирования точки р = [1 <р у | на поверхность конуса,
касающегося сферы по параллели уо. Без внесения дополнительных широтных
искажений эту криволинейную поверхность можно заменить вертикальной
плоскостью х'у', касающейся конуса по меридиану ср (рис. 2.65). Матрица такого
преобразования системы координат равна
CK(y)-^,(-<pK(y0)r(-z°).
240
Гпава 2
Рис. 2.65
Разместив проектор в точке [о 0 - F] на оси z', рассчитаем по (2.93) матрицу
Цг. Развертывание поверхности конуса эквивалентно переносу системы коорди-
нат в его вершину на вектор
v = ctg(v0)Z
(2.102)
и вращению проекции вокруг оси z' на угол
у = (ф- сро) sin(vpo).
Таким образом, проекция точки сферы р = [1 ф у] на развертке конуса вычис-
ляется по следующим формулам:
q' ~ [sin^)cos(y) sin (у) cos^)cos(y) 1]ск(ф)//г,
р/ = ?'т(-г)Л2(у).
Ее положение можно описать также полярным вектором [р у] с модулем
р(ф, V0,F) = ctg(V0) - Fsin(v Vo)
F-l + cos(ig-v0)
и используемым в (2.102) углом
у = (ф-фо) sin(yo),
отсчитываемым от вертикальной проекции меридиана фо. Исследуем влияние
фокусного расстояния F на искажения углов и площадей. Коэффициенты дол-
готных и широтных искажений, вычисленные по (2.97), равны
_p(v,V0,F)sin(v0) _ (F-l)cos(v-v0)+l _ -Эр(у,у0, f)
W(₽ cos(v) ’ (F_] + cos(v_Vo))2 Эф (2.103)
Геометрические преобразования 241
При F= 1 (проектор в центре сферы) получим зависимость
p(w) = ctg(vpo) - tg(y - уо)
и коэффициенты искажений и m , сильно отличающиеся от единицы на ши-
ротах, далеких от уо. Следовательно, эта проекция является произвольной.
Уравнивая в (2.103) коэффициенты mv и получим дифференциальное уравнение
Эр(у,у0, С)_ -p(w,Wp, /7)sin(y0)
Эу cos(y)
с начальным условием р(уо, уо, F) - ctg(yo), решение которого есть
р = ctg(y0 )esi"^X^o НМ) = ctg(Vo / sec(y0)+tg(yo)Yin(Vo) = )
sec(y)+tg(y) J
Равноугольная коническая проекция Меркатора (рис. 2.66, а) с коэффициентами
искажений
= 1, тя = r2(y, уо) sin2(yo) cos~2(y)
проективно строится при переменном фокусном расстоянии
) __ (ctg(Vo )~ r(w, Wo)) (1 - cos(y - Wo))
0 ctg(yo)-r(w,Wo)-sin(w-Wo)
Приравнивая в (2.103) произведение коэффициентов /иф и mv к единице, получим
дифференциальное уравнение
Эу sin(w0)
с начальным условием р(уо, уо, F) = ctg(yo), решение которого есть
Р = 72 + ctg2(Wo)-2sin~l(Wo)sin(‘P) = z(w, Wo)
Равноплощадная коническая проекция Ламберта (рис. 2.66, 6) проективно стро-
ится при переменном фокусном расстоянии
\ (ctg(Wo)~/(w,Wo)) (l-cos(w~Wo))
0 ctg(wo)-/(w,Wo)~sin(w-Wo)
Наконец, равнопромежупючная коническая проекция с постоянным шагом па-
раллелей (рис. 2.66, в) имеет коэффициенты искажений
cos(w) -1
тш = 1, wz =-—7—г—--------х—7—v, w<p = = '«z
cos(y0)-(w-Wo)sin(Wo)
и строится либо по формуле
р(у) = ctg(yo) - (у - уо),
242
Гпава 2
либо проективным методом при переменном фокусном расстоянии
= (ctg(Wo)-(v-Wo))(l-cos(w))
ctg(vo)"(v-Vo)-sin(v)
Рис. 2.66
2.2.5.4. Построение сцены
с подвижным наблюдателем
Далее рассмотрим методы построения сцены с подвижным наблюдателем, пере-
мещающимся в трехмерном пространстве по некоторой траектории. Это типовая
задача, решаемая при разработке компьютерных игр, в которых объекты сцены
изображаются в перспективной проекции так, как их видит перемещающийся в
пространстве наблюдатель. Положение объектов в MCK xyz описывается мно-
жеством точек р,; векторов Г, и Nh расширенные формы которых р,, Й, и N,
составляют строки матрицы координат Q. Объекты могут быть как неподвиж-
ными относительно МСК (здания, рельеф местности, интерьер комнаты и др.),
так и подвижными (герои игры, средства их передвижения, деревья, окна, двери,
лифты зданий и др.).
Для того чтобы составить модель сцены, представим, что перед глазами наблю-
дателя на фокусном расстоянии F находится прямоугольная рамка, через кото-
рую он рассматривает окружающий мир (рис. 2.67). Соотношения длин горизон-
тальной, вертикальной сторон рамки и фокусного расстояния g-.v.F
определяют горизонтальный а и вертикальный Р углы обзора:
a = 2tg( —|, P = 2tg| —|.
^2F J (.2F J
Геометрические преобразования
243
Рис. 2.67
Среднестатистический глаз человека имеет углы обзора a » 150° и [3 — 110° [17].
Отсюда следует оптимальная пропорция параметров рамки
g: v:F«7.5: 3: 1,
при которой видимая область сцены заполняет всю рамку.
Зададим положение рамки траекторией движения ее центра s(t), вектором нор-
мали к плоскости Z(t), направленным к наблюдателю, и вектором Y(t) ± Z(/)
ориентации вертикальной (относительно наблюдателя) стороны. В центре рамки
разместим начало подвижной системы координат наблюдателя (СКН) хи Гн z» с
ортами
Л)=Г(<). ^(0=Z(r). (2.104)
С помощью матрицы (2.55) преобразования из МСК в СКН
//(/)= MAP3^(t), О3, у°, z° ) (2.105)
вычисляются координаты элементов сцены в СКН:
Q„(t) = Q(t) H(t). (2.Ю6)
При выбранном расположении СКН наблюдатель находится на оси zH в точке
S(l)=s(t)+FZ(t),
244
Гпава 2
имеющей в СКН постоянные координаты SH =[о О F], что упрощает уравне-
ния (2.86) центрального проецирования точки [xH(z) _ун (')
4(z)=
(2.107)
Проекция точки действительна при zH < F, в противном случае точка находится
сзади наблюдателя и через рамку не видна. Кроме того, невидимыми для наблю-
дателя являются точки с zH < F. Их действительные проекции отсечены прямо-
угольником рамки, т. е. не удовлетворяют условиям видимости
(2.108)
Рассмотрим подробнее особенности формирования в реальном времени парамет-
ров положения рамки в пространстве. При разработке программы, отображаю-
щей сцену глазами подвижного наблюдателя, определенным командам, пода-
ваемым с клавиатуры или мышью, назначаются соответствующие движения
наблюдателя и связанной с ним рамки. Возможна, например, следующая система
клавишных команд управления'.
П <Т> или <>L> — смещение вдоль оси zH на расстояние -d. (вперед) или гЛ
(назад);
□ <Shift>+<T> или <Shift>+<!>— смещение вдоль оси на расстояние dy
(вверх) или -dy (вниз);
□ <Shift>+«-> или <Shift>+<-» — смешение вдоль оси хн на расстояние -dx
(влево) или dx (вправо);
□ <<—> или <—» — поворот вокруг оси j’n на угол ф,. (влево) или -фЛ (вправо);
□ <Ctrl>+<T> или <Ctrl>+<4>— поворот вокруг оси х„ на угол -cpv (наклон
вперед) или <рЛ (наклон назад);
П <Ctrl>+<<-> или <Ctrl>+<—>> — поворот вокруг оси zH на угол <р. (наклон
влево) или -ф. (наклон вправо);
□ отсутствие команды означает остановку в текущем положении.
Для большего правдоподобия оси вращений виртуальной рамки должны прохо-
дить не через ее центр, а через точку S(t) расположения действительных глаз на-
блюдателя. Оси вращений при этом параллельны осям Хн, у» и zH. В самом общем
виде движение рамки описывается в СКН матрицей преобразования
Сн=7'(-5н)ЛЛ(±фх)^(±ф^К(±фг№)Н[±^ ±dy ±JZ]) (2.109)
с соответствующими каждой команде значениями и знаками углов вращений и
координатных смещений. Во избежание бесполезных умножений на единичные
матрицы можно каждой конкретной команде сопоставить более простую, чем
(2.109), матрицу АП. Например, в приведенной выше системе команд клавише
Геометрические преобразования
245
<Т> соответствует матрица Сн = r[-dzzo), а поворот влево по команде <<->
отрабатывается с помощью матрицы Сн = T(-SH )Ry (<Р3, .
Важная проблема при разработке программ с подвижными элементами — обна-
ружение и отработка столкновений наблюдателя с объектами сцены и объектов
друг с другом. Столкновение наблюдателя с каким-либо объектом можно обна-
ружить, например, тестами ориентации (1.122) и (1.123) точки S(t) внутри этого
объекта. Столкновение объектов обнаруживается по расположению любой вер-
шины одного объекта внутри другого (рис. 2.68, а) либо по пересечению любого
ребра одного объекта с любой гранью другого (рис. 2.68, б).
Рис. 2.68
Поведение наблюдателя и объектов при столкновении определяется их подвиж-
ностью и упругими свойствами. Например, при столкновении с неподвижной
стеной наблюдатель должен остановиться либо упруго от нее отскочить. Оста-
новка означает отмену команды управления, приведшей к столкновению. Упру-
гий отскок, удовлетворяющий законам отражения (см. рис. 1.56), требует расчета
соответствующей команды. Аналогично отрабатываются столкновения объек-
тов друг с другом. Ниже приводятся алгоритмы с остановкой при столкновении
наблюдателя с объектами сцены.
Пусть
□ tk, к = 0, 1, 2,... — вырабатываемые по сигналам таймера ЭВМ моменты оп-
роса устройств — источников команд управления;
□ 5о, Zo и Уо— параметры начального положения рамки и вычисляемая по
(2.105) матрица пересчета начальных координат из МСК в СКН;
□ H0=MAP3^0,Yo,Zo,03,y0,z°)-
TJ Qo — матрица начальных координат элементов сцены.
Циклический алгоритм расчета перспективного изображения динамической сце-
ны в зависимости от команд управления можно реализовать объективным и
субъективным методами, отличающимися тем, какая система координат при-
нимается неподвижной (см. рис. 2.67). В обоих методах на k-ом шаге движения
вычисляются матрицы Снк и С^т> \/т = \,М собственных движений рамки в
СКН и М объектов в МСК (у неподвижных элементов сцены матрицы движе-
246
Глава 2
ний единичные). Матрицы Нк и Нк+\ на соседних шагах моделирования связа-
ны соотношением
Нк+1 = ЯкСнк
В объективно неподвижной МСК xyz движения наблюдателя и объектов рассчи-
тываются независимо друг от друга. Проецирование выполняется на подвижную
картинную плоскость, поэтому для визуализации сцены (отсечения проекций объ-
ектов контуром рамки, удаления невидимых элементов, закрашивания видимых
поверхностей) требуется преобразование координат всех объектов из МСК в
СКН. На к-ом шаге алгоритма моделирования вычисляются:
□ по (2.106) матрица координат объектов в СКН
QHk = Qk Як,
центральные проекции объектов и визуализация сцены на экране дисплея;
□ по (2.109) матрица СнЛ и матрица движения наблюдателя в МСК
Ск=ЯкС11кЯк1-, (2.110)
П прогноз параметров рамки и наблюдателя на (к + 1 )-ом шаге:
?А+1 = ^кск> zk+i = zkck>
(2.1П)
Sji+i =fy+i +FZk+\, Hk+l = HkCHk ;
П прогноз координат объектов сцены на (к + 1)-ом шаге:
Qk'”> = Qkn,>Ckm> (2.112)
□ если точка Sjt+i принадлежит хотя бы одному из in е [1, М\ объектов, то вы-
полняется остановка:
«+i = sk, Zk+\ = Zk, Qffi = Qkm>, = Hk (2-113)
Субъективно (с точки зрения наблюдателя) полагая неподвижной СКН уК zH.
мы должны перед циклом моделирования пересчитать начальные координаты
всех объектов сцены из МСК в СКН по формуле группового преобразования
Сно= Qo я0.
Движение объекта в СКН есть суперпозиция двух движений: собственного и от-
носительного, обратного движению рамки. Проецирование сцены выполняется
на неподвижную фронтальную плоскость рамки. На Л-ом шаге алгоритма моде-
лирования вычисляются:
□ центральные проекции объектов и визуализация сцены на экране дисплея;
□ по (2.109) матрица Снл и матрицы собственных движений объектов в СКН:
с"^ = ЯкХСкт>Нк Ут = Гм- (2.114)
'еометрические преобразования
247
21 прогноз координат объектов сцены на (к + 1)-ом шаге:
йХ1 = Сн2 V/» = ЦИ , Hk+l = HkC~l; (2.115)
□ если точка SN = [о 0 с] принадлежит хотя бы одному из m е [1, М\ объек-
тов с координатами Q^+i, то выполняется остановка:
= (2.116)
равнительный анализ двух методов построения сцены с подвижным наблюда-
телем свидетельствует о несколько меньшей трудоемкости субъективного подхо-
да, в котором все расчеты ведутся в системе координат, жестко связанной с на-
блюдателем. С учетом направленности ее оси zH навстречу наблюдателю и
зыраженности всех координат сцены относительно картинной плоскости субъ-
ективный метод идеален для реализации алгоритмов визуализации как на про-
ламином, так и на аппаратном уровнях.
2.2.5.5. Проективные алгоритмы
построения оптических эффектов
Переходим, наконец, к изучению проективных алгоритмов построения оптиче-
:ких эффектов— тени объекта на плоскости, отражения от зеркальной плоско-
сти и преломления на плоской границе раздела двух сред. В разд. 1 3.5 эти задачи
решались методом трассировки путем поиска точек пересечения множества све-
*овых лучей с поверхностью проецирования. Это универсальный способ по-
:гроения эффектов на произвольной криволинейной поверхности. Для каждого
л> ча задача пересечения решается индивидуально, что требует больших машин-
ных ресурсов и не позволяет применять групповые методы преобразований, т. к.
при неплоской поверхности отсутствует единая для всех точек объекта матрица
проецирования.
Роль проекторов в моделировании оптических эффектов играют две точки:
Э L — источник прямых лучей, создающих тень;
2J S— позиция наблюдателя, выступающего в роли приемника прямых и ис-
точника обратных лучей.
Особенности дальнего и ближнего расположения этих элементов сцены относи-
тельно объекта и плоскости проецирования эффекта обсуждаются в коммента-
риях к рис. 1.61, 1.62.
На рис. 2.69 построена схема вычисления оптических эффектов на плоскости
f = {ро, N} от исходной точки q в МСК до экранного изображения ее оптическо-
го эффекта 9, в ЭСК. Данная схема является развитием двухэтапного процесса,
изображенного на рис. 2.56, и использует три самостоятельные СК со своими
матрицами преобразований.
248
Гпава 2
Рис. 2.69
□ Система координат плоскости f— в ней формируется оптический эффект.
Для перехода из МСК в СК f требуется вычислить матрицу
Ск =MAP2(p0,N,O3,z°\
делающую плоскость построения эффекта фронтальной. В базисе СК f рас-
ширенные формы точки qt, вектора Кг, источника Lt и наблюдателя St нахо-
дятся следующим образом:
• qf = qCK, ближние Lf = LCK и S{ = SCK ;
• = ЙСК, дальние Lf = LCK и Sf = SCK.
Координаты векторов Lt (при построении тени) или St (при построении от-
ражения или преломления) определяют параметры матриц Kt косоугольного
(2.76) или Цг центрального (2.88) проецирования на фронтальную плоскость f.
что дает проекцию эффекта
Qt = Qf^f или Qf ~ QfHf
Дополнительным шагом вычисления эффекта отражения является ортого-
нальное отражение
Qf =QfM{
с матрицей Л/f =diag[l 1 -1], после чего находится проекция
Qf = Qf ^f или Qf ~ Qf 4f
Вычисление проекций эффектов всех точек объекта позволяет определить не-
обходимые габариты плоскости f или, при заданных габаритах f, отсечь не
попавшие на нее элементы алгоритмами clipl_cross (см. рис. 1.18) или
clipljtest (см. рис. 1.19).
"еометрические преобразования
249
После каждой операции центрального проецирования точки qf ~ qfL[f или ее
отражения q'( ~qt(MfLff) проверяется условие Лг> 0 существования действи-
тельной проекции q'{. При выполнении этого условия она приводится по
(2.85) в декартову форму. Индикатор правильности вычисления проекции в
базисе СК f — значение z\ = 0.
Проекцию эффекта в СК f можно получить сразу из образа в МСК как
q’f ~ qCf с помощью матрицы Cf, вычисляемой в зависимости от вида эффек-
та и типа проецирования как
Ср = СкК{ либо Ct — СкЦг
для нахождения тени и преломления или
Cf = CK(A/fAf) либо Cf =CK^A/fZ/f j
при расчете отражения.
□ Мировая СК, переход в которую из СК f осуществляется с помощью матрицы
С”1. Возможно получение эффекта в МСК сразу из образа в МСК как
q'~qCM с помощью матрицы
cw=cfc-'.
□ Экранная СК, переход в которую из МСК дает окончательное изображение
оптического эффекта q'3 ~ q'Cm и выполняется с помощью матрицы Спз из
(2.95). Без учета преобразования из СК картинной плоскости в ЭСК можно
считать, что Спз — одна из проективных матриц О{, Af, Kf или Ц(, завися-
щих от положения наблюдателя 5. Эффект объекта должен выводиться на эк-
ран раньше самого объекта q3 ~ qCm для недопущения экранирования объек-
та его эффектом.
Если требуется изобразить на плоскости f какую-либо текстуру, сетку или просто
гладкую окраску, то ее точки pt легко проецируются на экран преобразованием
Рз ~ Pf (‘ к ^пэ)-
Поверхность построения эффекта должна выводиться на экран раньше самого
эффекта для недопущения экранирования эффекта и объекта поверхностью.
Теоретически возможно построение эффекта на экране сразу из образа в МСК
по формуле
Чэ ~ Я ^Рм^т) >
т. е. за одно матричное умножение. В этом простом и чрезвычайно эффективном
методе таится возможность расчетной ошибки в том случае, когда обе матрицы См
и Спз содержат центральное проецирование, а нелинейная операция приведения
250
Глава 2
расширенного вектора к декартовой форме выполняется только один раз. Напри-
мер, в задаче построения тени при ближних источнике и наблюдателе имеем
СМ = СКЦ(СК 1 , Ст = z/кп f-
Аналогичный случай имеет место и при расчете отражения с ближним наблюда-
телем, где
См =СКМ(Ц(СК 1 , Ст = 1/кги.
Для получения на экране достоверного изображения можно идти двумя путями:
П разделить одношаговый процесс на два преобразования, каждое из которых
имеет по одному декартову приведению, например,
<7f ~ <7(CK/Zf ), q'3 ~ qf (cK*/ZKnf )
В промежутке между этими действиями может решаться задача отсечения
проекции эффекта ограниченной плоскостью f в ее системе координат;
□ использовать альтернативный путь от точки q до изображения ее эффекта q"
на рис. 2.69 с одним центральным преобразованием, например,
Теперь задача отсечения решается в ЭСК. Отсекателем является проекция огра-
ниченной плоскостью f, а объектом отсечения — экранная проекция эффекта.
Преимущества проективных методов проявляются только при групповой обработ-
ке данных, когда за одно матричное умножение вычисляются проекции сразу всех
точек объекта. Как только возникает необходимость поточечных операций, ско-
рость работы проективных алгоритмов резко снижается из-за замены параллель-
ных вычислений последовательными. Такое бывает, когда разные точки одно к
объекта отличаются свойствами существования эффекта. Например, тень объекта
пересекающегося с плоскостью проецирования, создается лишь теми его точками,
которые находятся относительно плоскости со стороны расположения источника
света (см. рис. 1.64) Если в процессе движения объекта такая ситуация возможна,
то придется искать пересечение с плоскостью отрезков его ребер и полигонов гра-
ней. При этом возникают новые точки, отрезки и полигоны. Все это выбивает про-
ективный алгоритм построения тени из русла группового метода.
Аналогичная картина наблюдается при расчетах преломления, отражения, цен-
трального проецирования, отсечения проекции контуром ограниченной плоскости
проецирования. Следовательно, групповой подход имеет ограниченное применение.
Рассмотрим подробнее проективные алгоритмы построения оптических эффек-
тов с учетом проблем их существования и видимости.
Тень
Тень точки q на плоскости f является косоугольной (при дальнем источнике L
либо центральной (при ближнем источнике) проекцией q' е f (см. рис. 1.63). Про-
геометрические преобразования
251
ективный алгоритм построения тени точки q на ограниченную плоскость f имеет
следующий вид.
t? Шаг 1. Вычисляются qf = qCK и Lt— векторы точки и источника в СК f. При
Lt. qt. < 0 источник и точка не лежат по одну сторону от плоскости, тень не су-
ществует, и алгоритм завершен.
Шаг 2. Координаты вектора Lf дают матрицу Лт либо Ц{.
Шаг 3. Вычисляется действительная проекция
Й~?сг=Ь Уг zf Лг1
точки <7 на f. При ht < 0 она не существует и алгоритм завершен. На этом шаге
используются матрицы Cf =CKKt либо Ct- СкЦг.
Шаг 4. Если точка q'{ 6 f , т. е. лежит внутри границ плоскости f, то тень видима
и на КП или экран выводится ее проекция
<7э ~‘Уг (--к СПЭ).О
& Пример 2.8. Решить проективным методом задачу построения тени каркасной
лирамиды на плоскость f (см. пример 1.10) при расположении источника света в
точке А = [б 3 1.5], т. е. при у= 1.5 (см. рис. 1.65). Изобразить на плоскости
прямоугольную сетку с единичным шагом, целиком вмещающую тень объекта.
Решение. Плоскость тени описывается в неявной форме вектором нормали
\=[б 3 2] и точкой p^ = hzz° = [о 0 3], которую примем за начало СК
гг rr zt. Пустим из нее оси лт, zf || N и yr е f в направлении точек
р5=Лхл°=[1 0 б], р6 = р0 + N = [б 3 5],
Py=Po+N*(p5-po)=[-9 20 °J-
1 аким образом, в СК лтyr zt плоскость f является фронтальной.
Получим по (2.14) матрицы прямого и обратного перехода от МСК к СК f:
Ро 1 -1 О3 г 0 0 3 1’ -1 0 0 0 Г
Ск Р5 1 Рб 1 Р5 ~ Рб~ Ро Ро х° 1 2° 1 = 1 6 0 3 0 1 5 1 Vio” 0 0 0 0 7 1 1
J>1 Р1~ Ро У° 1 -9 20 0 1 0 7л/Т0 0 1
’ 0.316 -0.407 0.857 О’ ‘ 0.316 0 -0.949 О’
= — 0 0.949 0.904 -0.136 0.429 0.286 0 0 К и = -0.407 0.857 0.904 0.429 -0.136 0.286 0 0
2.846 0.407 — 0.857 1 0 0 3 1
252
Гпава 2
Вычислим положение источника в СК f и необходимые матрицы проецирования:
Af=[6 3 1.5 1]СК = [3.32 0.474 6 1],
1 0 0 0
0 10 0
Щ = -0 .553 -0.079 0 -0.167 •>
0 0 0 1
-0.158 -0.474 0 -0.143
-0.237 0.87 0 -0.071
Сг = C.J7r =
-1.107 -0.158 0 -0.048
3.32 0.474 0 1.143
Определяем координаты точек р\ + рь и их проекций в СК f:
Plf Г Pl Г ’4.743 2.936 3.143 f
P2f 1 — P2 1 cK = 1.581 2.936 3.143 1
P3f 1 P3 1 2.53 0.813 5.286 1
P4f I Pi 1 3.476 1.4 1.714 1
Pl Г ’ 3.004 2.688 0 0.476 6.309 5.645 0 Г Pit f
P2 1 Cr - -0.158 2.688 0 0.476 -0.332 5.645 0 1 P2i 1
P3 I ^1 -0.395 0.395 0 0.119 -3.32 3.32 0 1 P3i 1
Pi 1 2.53 1.265 0 0.714 3.432 1.771 0 1 .Pit 1
Все аппликаты точек Lt и р,годного знака и, кроме того, все значения Л,г > 0, сле-
довательно, вся пирамида имеет действительную тень на плоскости f. Абсциссы
и ординаты проекций p'f дают целочисленные границы
-4 <лг < 7,0 <yt < 6
прямоугольника на плоскости f, целиком вмещающего тень объекта.
На рис. 2.70 построена диметрическая проекция сцены с вектором направления
на дальнего наблюдателя S = [l 1 VT], заданным в примере 1.10. Матрица
Спз = Аднм приведена в (2.74). Расчет сцены выполняется в следующей последова-
тельности:
П с помощью функций
/гне([о 0 0]Адим, [б 0 о]адим),
/ще([о 0 о]Адим, [о 7 0]Адим),
0 о]Адим, [о О 7]Адим)
Геометрические преобразования
253
рисуем оси координат: ось х длиной 6, ось у длиной 7 и ось z длиной 7.
Длины осей определены по максимумам соответствующих координат всех
точек сцены;
Рис. 2.70
□ строим прямоугольную сетку с единичным шагом на плоскости тени:
//ие([л| О О 1]СК Адим, Ьт 6 О 1]СК Адим)\/х|- ——4,7,
/Ц["4 Л О 1]С-’АДИМ, [7 уг 0 1]Ск-‘Адим)ууг =06;
□ рассчитываем диметрические проекции точек тени р^Ск Адим V/ = 1,4 и со-
единяем их шестью прямыми согласно топологии объекта;
□ рассчитываем диметрические проекции точек объекта р, АДИм Vz = l, 4 и со-
единяем их шестью прямыми согласно топологии объекта;
□ рассчитываем диметрическую проекцию источника £АДим.
2]
Отражение
Отражение точки q от плоскости f является косоугольной (при дальнем наблю-
дателе S) либо центральной (при ближнем наблюдателе) проекцией q' е f отра-
женной точки q° (см. рис. 1.68). Проективный алгоритм построения отражения
точки q от ограниченной плоскости f имеет следующий вид.
Шаг 1. Вычисляются qt =qCK и St— векторы точки и наблюдателя в СК f.
При St, qt, < 0 наблюдатель и точка не лежат по одну сторону от плоскости, от-
ражение не существует, и алгоритм завершен.
Шаг 2. Координаты вектора St дают матрицу Kt или Це
254
Гпава 2
Шаг 3. Вычисляется проекция q' точки q° иа f:
Qi -qCf=[x( у{ z{ /?f].
Здесь используется матрица Cf = CKMfKf либо Q =CKMiUl.
Шаг 4. Если точка q'f е f , т. е. лежит внутри границ плоскости f, то отражение
видимо и на КП или экран выводится проекция
9э ~ (*“К ^пэ)-
& Пример 2.9. Решить проективным методом задачу построения отражения
каркасной пирамиды от плоского зеркала из примера 1.12 (рис. 1.70). Наблюда-
тель находится в точке S =2[1 1 л/sj-
Решение. В указанном примере установлено, что вершина пирамиды ри не может
иметь отражения в зеркале, т. к. она с наблюдателем расположены по разные
стороны от его плоскости. Там же найдены точки
т/14= [1.429 0.857 -1.429], d24 = [1 0.75 -0.5], d34 = [1.409 0.273 -1]
пересечения ребер /л р4, pipu и pi pt с бесконечной плоскостью зеркала. Таким
образом, отражение пирамиды создается отрезками pi pi,p\ ръ.ргpi.pi du,pi du и
Pi du.
Вычислим необходимые векторы и матрицы проецирования с учетом, что плос-
кость зеркала описывается в неявной форме нормалью N = [б 2 3] и точкой
Ро = [о 0 2], а вершины полигона зеркала находятся в точках
w,=/7zz°=[0 0 2]=р0, т2 =hxx° = [1 0 б],
т3 = hyy° = [О 3 б], т4 = гщ +т3 -т2 = [“1 3 2]:
/«1 Г -1 о3 г ‘ 0.447 -0.256 0.857 О'
/и2 1 |/и2 -«1|х° 1 0 0.958 0.286 0
/И] + N 1 1 -0.894 -0.128 0.429 0
т\ + N х (т2 - /П]) 1 |?/||от2-лф0 1 1.789 0.256 -0.857 1
[Sf 1]=[2 2 2^8 1]ск= [-2.376 0.938 3.853 1],
1 0 0 0
0 10 0
0.617 0.617 0 -0.26
0 0 0 1
Геометрические преобразования
255
1 0 0 0
S = [2 2 5.657] ^спэ = 0 1 0 0
-0.354 -0354 0 -0.177
0 0 0 1
' -0.21 -0.23 0 0.13
1 -0.403 0.923 0 0.043
С(угп ~ Ск^гСк Cjyj ~
отр К I к ПЭ -0.958 0.469 0 -0.112
1.21 0.23 0 0.87
Учитывая предупреждение о возможных ошибках декартова приведения, нахо-
дим групповым методом экранные проекции точек полигона зеркала, пирамиды
н ее отражения:
w3 Г 1 1 1_ С = ^пэ '-0.707 1 0 -1.707 -0.707 0 3 2.293 0 0 0 0 0.646 1 1 0.646 - '-1.094 1 0 -2.641 -1.094 0 3 3.547 0 0 0 0 1 1 1 1 = /«1э ™2э «Зэ ™4э 1 1 1 1
Pl 1 '2.707 2.707 0 1.354' 2 2 0 Г Р э 1'
Р2 1 0.646 2.646 0 0.823 0.785 3.215 0 1 Р2э 1
РЗ ^14 1 1 с ^пэ = 4.354 1.934 2.354 1.362 0 0 1.177 1.253 3.7 2 0 1.544 1.088 0 1 1 G »3э 1 ^14э 1 >
^24 1 1.177 0.927 0 1.088 1.081 0.852 0 1 6 24э ।
Уз4 1 - 1.763 0.626 0 1.177 1.498 0 532 0 1 0 Г34э к -
- Pl - ' 1.901 2.554 0 1.44 1.32 1.773 0 г - Р1э 1
Р2 -1.168 2.301 0 1.018 -1.147 2.261 0 1 Р2э 1
РЗ ^14 1 1 О>тр = 0.523 1.934 1.625 1.362 0 0 1.588 1.253 0.329 1.544 1.023 1.088 0 0 1 1 РЗз 7]4э 1 1
^24 1 1.177 0.927 0 1.088 1.081 0.852 0 1 ^24э 1
^34 1 1.763 0.626 0 1.177 1.498 0.532 0 1 ^34э 1
По этим данным на рис. 2.71 построено изображение сцены, полностью совпа-
дающее с картинкой на рис. 1.71, б. Отсеченные фрагменты проекций ребер пи-
рамиды изображены пунктиром. Из всех ребер лишь проекция pi, рз, не подвер-
глась отсечению экранной проекцией полигона зеркала {ть /м?, лйэ пи? шь}, т. е.
ребро рз рз целиком видно в зеркале. Ребра pi рз, р\ рз и отрезки ребер pi du, рз
видны в зеркале частично, а отрезок pj3d'l4j полностью отсечен проекцией зер-
кала. □
256
Гпава 2
Рис. 2.71
Преломление
Разработка проективного алгоритма преломления осложняется изломом лучей,
проходящих от точек объекта к наблюдателю, на границе раздела сред с показа-
телями преломления Аналогично лучевому алгоритму преломления
(см разд. 1.3.5.3) рассмотрим два случая удаленности наблюдателя от плоскости
преломления f и соответственно два варианта расчета в базисе f значения
g = sin(y) для угла преломления у.
1. Наблюдатель бесконечно удален от плоскости f в направлении S, составляю-
щем с нормалью к f угол преломления с синусом (1.154)
(2.117)
не зависящим от положения точки q. Следовательно, угол падения а и вектор
падающего луча V также не зависят от q, а точка преломления q' g f является
косоугольной проекцией q на плоскость f (см. рис. 1.73).
Получим направление проецирования Vt масштабированием вектора наблю-
дателя Sr в ортогональном к f направлении:
Vt = Sr М( 1, 1, X), где Л =
tg(?) »n~g2
tg(«) V 1-g2 ’
"1
= —
«2
(2.118)
Теперь становится возможным сформировать по (2.76) матрицу косоугольно-
го проецирования Kt. необходимую для расчета точки преломления q\.
Решение (2.118) определено при 0 < g < пп, что является условием отсутствия
полного внутреннего отражения и совпадает с (1.158). Так как направление
проецирования не зависит от положения точки q в среде с показателем пре-
ломления т, то возможно групповое преобразование всех точек объекта, нахо-
дящихся в этой среде.
257
Геометрические преобразования
2. Наблюдатель находится в конечной точке St (см. рис. 1.76). В отличие от парал-
лельного проецирования здесь проявляется эффект аберрации', продолжения
падающих лучей q —э q' для разных точек среды с показателем преломления т
не пересекаются в единственной точке, которую иначе можно было бы считать
центром проецирования. Действительно, т. к. теперь g * const, то высота
. ds . %tg(v)
Г tg(«) tg(«)
Мп-g2
v i-g2
на которой продолжение падающего луча пересекает вертикаль p'S, зависит
от расположения точки q. Это причина отсутствия единой матрицы централь-
ного проецирования и невозможности группового преобразования всех точек
объекта.
Решая задачу индивидуально для каждой его точки, вычислим такое значение
g = sin(y), при котором луч q —> q' после преломления попадет точно в наблю-
дателя 5. Составим аналогичное (1.160) нелинейное уравнение:
' / 2g 2 lgfcl+ / g 2 lSfcl= -4k)2 + -Qfy)2 (2.119)
v^n-g V,_g
Оно всегда имеет численное решение g, удовлетворяющее условию 0 < g < пп.
Далее по (2.118) находим вектор Vt, а по (2.76)— матрицу косоугольного
проецирования Kt.
Оформим проективный алгоритм построения преломления точки q на ограничен-
ной плоскости f раздела двух сред в следующем виде.
&Шаг1. Вычисляются qf = qCK и St— векторы точки и наблюдателя в СК f.
При St-qt. >0 наблюдатель и точка не лежат по разные стороны от плоскости,
преломление не существует, и алгоритм завершен.
Шаг 2. По (2.117) либо (2.119) находится значение g. Если g g (0, Пп), то прелом-
ление не существует, и алгоритм завершен.
Шаг 3. Координаты вычисленного по (2.118) вектора Eir дают матрицу Kt.
Шаг 4. Вычисляется проекция q' точки q на плоскость f:
<7f ~ <?Cf = [л-f yf z{ /if].
Здесь используется матрица C{ = CKKf.
Шаг 5. Если точка q'{ е f , т. е. лежит внутри границ плоскости f, то преломление
существует и на КП или экран выводится ее проекция
<7Э ~'<?(CfCK Спэ).
□
258
Глава 2
I& Пример 2.10. Решить проективным методом задачу построения преломления
каркасной пирамиды на гранях стеклянного аквариума из примера 1.14
(см. рис. 1.75, а). Вершины пирамиды равны
^=[1 3 1],р2 = [1 3 з], Л = [з 1 1],р4 = [0 0 11-
Пересечение ребер пирамиды с поверхностью воды (верхней гранью аквариума)
происходит в точках
</13 = [2 2 0.5], J14 = [0.667 2 0.333], б/2з = I2 2 2], б/24 = [0.667 2 2.333].
Размеры аквариума d, = 3, dr = 2 и d: - 3. Вектор направления на дальнего на-
блюдателя равен S = [2 1 з].
Решение. Построение сцены включает:
□ изображение верхней, передней и правой граней аквариума;
□ изображение не погруженных в воду отрезков р\ pi,p\ d\3,p\ dw,pi da и pi da’,
□ расчет преломления и отсечения погруженных отрезков du рз, duр4, daрз и
da рь в трех гранях аквариума.
Прежде всего определим аксонометрическую проекцию, в которой должна изо-
бражаться сцена. Найдем по (2.72. б) минимальные углы вращения сцены, даю-
щие желаемый вектор S':
sin(<Px)=^- => <px=arcsin
= 15.5°;
tg(<Py)=^ => <Py =-arctg(2/3)= -33.69°.
Тогда по (2.71, б) получим матрицу трнметрнческого проецирования
А = 79/13 -д/2/91 0 0 д/13/14 0 -74/13 -79/182 0 0.832 -0.148 О' 0 0.964 0 -0.555 -0.222 0
Экранные проекции вершин каркаса аквариума и концов отрезков надводной
части пирамиды вычисляются как
'0 0 0 ' 0 0 0‘
dx 0 0 2.496 -0.445 0 Pl 0.832 2.743 0’ Ply
0 dy 0 0 1.927 0 P2 -0.832 2.075 0 Р2э
0 0 ct A = -1.664 -0.667 0 dl3 A = 1.387 1.52 0 = d\33
dx dy 0 2.496 1.482 0 dl4 0.37 1.754 0 dl4j
dx 0 dz 0.832 -1.112 0 d23 0.555 1.186 0 d23s
0 dy dz -1.664 1.26 0 d24. -0.74 1.31 0 _d243 _
dx dy <4 0.832 0.815 0
Геометрические преобразования
259
и на изображении (рис. 2.72) соединены друг с другом в соответствии с тополо-
гией обоих каркасов. Для ориентирования приведена сетка экранной системы
координат.
Рис. 2.72
Построение преломления рассмотрим на примере ограниченной плоскости верх-
ней грани аквариума. Найдем
□ матрицу преобразования системы координат, совмещающую эту грань с
фронтальной плоскостью f:
’10 0 О'
~СпУ о 0010
Ск = RX - \T(-d..z°) = ;
к \2j J 0-100
0 0-21
□ вектор наблюдателя в новой СК f:
Sf=SCK=[2 -3 1 О];
□ вектор направления падающих лучей (2.118):
g = -^13/14 = 0.964 <лп = 1.33 => Л. = 3.43 => =[2 -3 3.43];
□ матрицу косоугольного проец фования: 1 0 О' 0 10; -0.583 0.875 0
□ матрицу преобразования исходных точек из МСК в экранные проекции их преломлений: ' 0.832 -0.148 0 О' ~ 0 0.281 0 0
СПр _CK^fC к А = к -0.555 -0.222 0 0 1.365 0 0 ’ 1
260
Глава 2
□ групповым методом находим точки в ЭСК, необходимые для расчета пре-
ломления пирамиды и задних ребер аквариума в его верхней грани:
РЗ Г 1.941 0.979 0 Г РЗэ 1“
Р4 1 -0.555 1.143 0 1 Р4э 1
^13 1 1.387 1 52 0 1 ^13э 1
J14 1 0.37 1.754 0 1 4/|4э 1
^23 1 0.555 1.186 0 1 ^23э 1
^24 1 — Hip -0.74 1.31 0 1 = ^24э 1
О 1 0 1.365 0 1 оэ 1
dxX° 1 0.832 1.217 0 1 1
dyy° 1 0 1.646 0 1 dyy° 1
dzz° 1 -0.555 1.143 0 1 О N ^3 i 1
По этим данным на рис. 2.73, а построены преломления погруженных в воду от-
резков пирамиды и результат отсечения их проекцией верхней грани аквариума с
помощью функции clipl_cross (отсеченные фрагменты показаны пунктиром).
Решая аналогичные задачи для передней и правой граней аквариума, получим
изображения преломлений пирамиды на рис. 2.73.6 и 2.73, в. Объединяя все по-
строенное на рис. 2.72 и 2.73 в одно целое, получим изображение сцены на
рис. 1.75, б. □
Глава 3
Математические модели
поверхностей и объектов
В процессе построения сцены решаются геометрические и оптические задачи.
К первоочередным относятся геометрические задачи формирования поверхно-
стей, составления моделей объектов сцены, композиции объектов в пространстве
сцены, отсечения элементов сцены, не попавших в отображаемую область, уда-
ления невидимых элементов отображаемой области. В результате получается
эскиз сцены.
Далее решаются оптические задачи реалистичного изображения объектов: за-
крашивание поверхностей с учетом их цвета, освещенности и ориентации в про-
странстве, расчет теней, отражений и более сложных оптических эффектов —
полутеней, переотраженнй, бликов, полупрозрачности и т. п. При этом могут
появиться новые виртуальные, т. е. кажущиеся, объекты, которые усложняют
эскиз сцены. Таким образом, построение сцены — процесс многошаговый. По
окончании формирования изображения в буферной памяти ЭВМ оно выводится
на экран дисплея.
3.1. Методы моделирования
поверхностей
Поверхность — это граница, отделяющая пространство, принадлежащее объек-
ту, от внешнего мира. Модели поверхностей играют важную роль в конструиро-
вании, производстве и изображении объемных объектов. Очевидными примера-
ми областей их применения являются:
ZJ проектирование корпусов и оболочек в машиностроении — автомобилей,
кораблей, самолетов и их отдельных деталей;
ZJ разработка программ обработки поверхностей для автоматических станков;
ZJ дизайн изделий легкой промышленности — мебели, посуды, обуви и одежды;
ZJ визуализация экспериментальных данных о границах раздела сред в естествен-
ных науках— медицине (компьютерная томография), геологии и локации
(построение рельефа поверхности Земли, морского дна, космических объектов).
262
Гпава 3
Из всех аспектов изучения поверхностей наибольший интерес, на наш взгляд,
представляют методы конструирования математических моделей поверхностей и
их реалистичного изображения на плоскости. В соответствии с этими двумя ка-
тегориями на рис. 3.1 представлена схема классификации поверхностей, раскры-
тие которой составляет содержание данной главы. Логично начать углубленное
изучение поверхностей со способов их изображения, чтобы потом можно было
иллюстрировать методы построения моделей в наглядной графической форме.
Рис. 3.1
3.1.1. Методы изображения поверхностей
Изображение является мощным графическим средством зрительного восприятия
геометрической информации. Далеко не каждый человек может построить в сво-
ем воображении объемную фигуру по ее словесному описанию или уравнениям
математической модели. Основная задача компьютерной графики, собственно, и
Математические модели поверхностей и объектов 263
состоит в преобразовании геометрических моделей в наглядные визуальные
формы, реалистично отображающие на плоскости строение и ориентацию объ-
ектов, расположенных в пространстве.
Как только появляется необходимость изобразить на экране дисплея какую-либо
поверхность, тут же возникает множество вопросов.
□ Какими изобразительными средствами можно достоверно передать форму
поверхности?
□ Как выбрать удачный ракурс изображения, раскрывающий на плоском экра-
не особенности строения объекта?
□ Как закрасить изображение поверхности, наиболее точно подражая игре све-
та и тени на поверхности реального объекта?
Начнем рассмотрение этих проблем в логически обоснованном порядке.
3.1.1.1. Выбор проекции изображения
Выбор проекции изображения осуществляется из арсенала методов параллельно-
го или центрального проецирования, подробно рассмотренных в гл. 2. Как пра-
вило, конструируемая поверхность ориентирована своими осями симметрии па-
раллельно координатным осям, поэтому ее орнюграфическая проекция на
координатную плоскость выглядит невыразительно (рис. 3.2, а). Для большей
наглядности поверхность рекомендуется повернуть в пространстве так, чтобы
были видны характерные детали ее рельефа, а выпуклости как можно меньше
заслоняли впадины. Такой ракурс характеризуется углами разворота <рт и накло-
на <pv, модули которых рекомендуется выбирать в интервале 20° -г 60°
(тримешрическая проекция). Большинство иллюстраций в книге выполнено в
стандартных проекциях, хорошо передающих глубину объекта в пространстве:
диметрической с углами <рЛ « -20°, <рЛ » 20° (рис. 3.2, б) и изометрической с углами
® -45°, <рх« 35° (рис. 3.2, в). Углы наклона <рх, близкие к 0° и 90°, делают изо-
бражение плоским, со скрытыми важными деталями рельефа (рис. 3.2, г).
Наиболее правдоподобно выглядит центральная проекция объекта, предвари-
тельно развернутого в пространстве на диметрические или изометрические углы.
Это более сложное, чем параллельное проецирование, преобразование содержит
дополнительную операцию (2.85) приведения расширенных векторов к декарто-
вой форме. Близость наблюдателя, собственно, и создает эффект перспективы.
Он заметен при фокусном расстоянии, сравнимом с размерами объекта. Удален-
ный от сцены наблюдатель видит все ее объекты в параллельных лучах. Из-за
этого размеры проекций не зависят от приближения или удаления объектов, а
смысл и эффект центрального проецирования здесь теряется.
Таким образом, перспективная проекция рекомендуется для изображения про-
тяженных в глубину сцены статических объектов, а также динамичных сцен, в
которых наблюдатель и объекты перемещаются по глубине пространства.
Переходим к выбору метода отображения рельефа поверхности. Не принимая
всерьез совершенно не информативное решение выводить поверхность моно-
264
Гпава 3
хромно закрашенным внешним контуром (рис. 3.2, д) (это годится лишь для пло-
ских полигонов и построения теней), выделим два наиболее распространенных в
компьютерной графике способа изображения неплоских поверхностей: каркас-
ный (рис. 3.2, е, ж) и точечный (рис. 3.2, а—г). Возможна также комбинация этих
методов (рис. 3.2, з).
Рис. 3.2
3.1.1.2. Каркасные поверхности
Многие прикладные программы Зб-графики для быстрого эскизного изображе-
ния поверхности выводят на экран дисплея не все ее точки, а лишь то их неболь-
шое количество, которое достаточно реалистично передает характер искривле-
ния поверхности в пространстве. Совокупность таких точек образует каркас —
систему линий на поверхности. Эти условные линии разбивают ее на ячейки, гра-
ничащие друг с другом по ребрам, которые соединяются в вершинах (узлах).
В зависимости от способа описания поверхности строятся соответствующие кар-
касные линии.
□ Параметрическая поверхность p(t, т) изображается параметрическими линиями
p{th т) и p(t, ту) (см. рис. 3.2, е), которые рассчитываются следующим образом:
• задаются целые числа п и пг, определяющие индексную сетку {i,j}, в кото-
рой i = 0, п, j =
• выполняется дискретизация параметров
t - to, t\,..., t„, т = TO, Tl, ..., т,„
Математические модели поверхностей и объектов
265
и создается параметрическая сетка {z„ ту}. В простейшем случае она может
быть равномерной с интервалами дискретности:
Az, = z, - z,~1 = const Vz, Ат,- = т= - т, -1 = const V/;
• вычисляются узлы p(th Ту) и циклически строится каркасная сетка из про-
екций отрезков между узлами
=0,/и) V/= 0, и, р^Х/г =0, п, T^X/j =0,т.
□ Неявная поверхность f(x,y,z) = 0 изображается семействами линий уровня
или изолиний (рис. 3.2, ж)
х ~ ХУЬ У ~ УУр z ~ ZW-’
расчет которых на примере изолиний х = ху„ параллельных координатной
плоскости yz, следующий:
• задается п значений уровней xyi X/i = 1, п;
• рассчитываются сечения поверхности плоскостями, параллельными плос-
кости yz, путем «-кратного решения нелинейного уравнения
f(xy„y,z)-() X/i = \,n.
Если поверхность допускает явное описание, например, у(х, z), то изоли-
ния ху, превращается в аналитическую однопараметрическую функцию
p(z)=[*yi >(*y<’Z) ZL
При существовании явного описания z(x,y) для построения используется
однопараметрическая функция
р(у)= fcyz У zfryz»y)]-
В [36] описан эффективный численный "метод маркированных квадратов",
-троящий линии уровня поверхности, описываемой явной функцией z(x, j). Ме-
тод основан на пространственной интерполяции функции двух переменных меж-
ду узловыми значениями z(J на прямоугольной сетке (л„
Важный момент при построении каркасных моделей — разумный выбор числа
лнтервалов дискретизации, определяющего размер ячеек и расстояние между
аркасными линиями. Малое число крупных ячеек делает изображение криволи-
нейной поверхности грубым и угловатым (рис. 3.2, з). Наоборот, при большой
плотности каркасных линий они сливаются друг с другом и скрывают под собой
рорму и цвет поверхности. Некоторым компромиссом может быть построение
гамих кусочно-линейных линий с малым шагом дискретизации одного парамет-
ра, а выбор расстояния между ними — с А-кратным шагом дискретизации друго-
го параметра:
p^i^jX/j = 0, km) Vz = 0, к,..., кп, p(z, VZ = 0, кп, ту ) V/ = 0, к,..., кт .
266
Гпава 3
При этом ячейки выглядят крупными и объемными, а ребра — криволинейными.
Реальные же ячейки, построенные на всех узлах ру, в к раз мельче и лучше ап-
проксимируют криволинейную поверхность.
Ячейки каркасных поверхностей могут быть:
□ прозрачными и непрозрачными;
□ объемными и плоскими, которые называются гранями-,
□ полигональными и криволинейными.
Для изображения прозрачной каркасной поверхности (см. рис. 2.58) достаточно
вывести на экран все ее ребра в произвольном порядке. Такая картинка часто
выглядит как набор линий, неоднозначно передающих глубину поверхности,
воспринимаемую каждым человеком по-своему.
Изображение непрозрачного каркаса (см. рис. 2.60) включает только ячейки, ви-
димые наблюдателем. Для их определения необходимо выполнить процедуру
удаления невидимых ячеек или их фрагментов, заслоненных другими ячейками.
Рассмотрим два простейших алгоритма, решающих эту задачу визуализации пу-
тем упорядочения вывода экранных проекций ячеек.
□ Алгоритм Робертса, предназначенный для построения выпуклых замкнуты
поверхностей с плоскими гранями, выводит на экран только лицевые грани,
обращенные внешней стороной к наблюдателю. Идентификация z-ой грани
заключается в оценке угла видимости у, = ZN, S, между векторами наблюда-
теля S, и внешней нормали N, (рис. 3.3, а). Ячейка является лицевой при ост-
ром угле видимости, и это быстро определяется из условия
А,- о S, > 0
без вычисления самого угла. Порядок вывода лицевых граней произволен.
Рис. 3.3
Математические модели поверхностей и объектов
267
Модификация алгоритма Робертса для невыпуклых поверхностей заключается
в присвоении каждой грани определенного приоритета вывода по правилу:
чем внутреннее находится грань, тем выше у нее приоритет (рис. 3.3, б). По-
прежнему, выводятся только лицевые грани, но теперь в порядке уменьшения
приоритетов. Порядок вывода граней с равными приоритетами произволен.
Данный метод обеспечивает корректное экранирование внутренних ячеек
внешними при наложении их экранных проекций.
Незамкнутая выпуклая каркасная поверхность (см. рис. 2.60) также может
быть изображена модифицированным методом Робертса, если внутренним
сторонам ячеек присвоить высший приоритет и определять их видимость по
правилу N, о S, < 0, где N, — внешняя нормаль к плоскости /-ой ячейки.
□ Алгоритм художника предназначен для изображения произвольных поверхно-
стей и выводит на экран все ячейки целиком по мере их приближения к на-
блюдателю. Проекции ближних граней могут частично или полностью нало-
житься на ранее построенные проекции дальних граней подобно тому, как
художник наносит на холст один мазок поверх ранее нанесенного мазка, тем
самым скрывая последний от зрителя.
Метод основан на вычислении удаленности (глубины) d, центров ячеек с,
(в разных вариантах алгоритма используются и другие опорные точки ячеек)
от наблюдателя, сортировке и выводе ячеек в порядке уменьшения элементов
вектора d. При наблюдателе, находящемся в конечной точке Л1, глубина точки
с, равна расстоянию
dt = |с,-Я (3-1, а)
а в вычислительном аспекте более эффективно использовать квадрат рас-
стояния (3.1, а) как скалярное произведение
//2=(c,-S)o(C/-S). (3.1,6)
В случае наблюдателя, бесконечно удаленного в направлении вектора S, рас-
стояния от него до всех точек также бесконечны. Впрочем, для сортировки
можно использовать и относительные глубины, отсчитываемые вдоль любой
оси d, противоположной направлению вектора А (рис. 3.4). Запишем проек-
цию точки с, на вектор А:
Cl Cj°S
prSCi=tiS, где /,=-г.
|5|2
Рис. 3.4
268
Гпава 3
Увеличение значения I, означает приближение точки с, к наблюдателю. Сле-
довательно, в качестве эквивалента глубины, который должен уменьшаться с
ростом можно принять легко вычислимое скалярное произведение
di--c,oS. (3.1, в)
Алгоритм художника отличается высоким быстродействием, но, к сожале-
нию, имеет серьезный недостаток-, ячейки каркаса должны быть примерно
одинакового и достаточно малого размера по сравнению с габаритами поверх-
ности. При определенном ракурсе разновеликие ячейки могут вывестись на
экран в неверном порядке, что иллюстрируется на рис. 3.5 изображениями
боковой поверхности цилиндрической призмы с прямоугольными гранями.
Ориентация поверхности на рис. 3.5, а выбрана так, что центр первой грани
ci расположен к наблюдателю чуть-чуть ближе, чем центр второй грани с:.
Вращение объекта всего лишь на угол <рЛ, - 2° из-за большой протяженности
первой грани расположило точку п немного дальше точки сг, из-за чего вто-
рая грань была выведена на экран позже первой и неестественно перекрыла ее
(рис. 3.5, б).
Общим недостатком рассмотренных алгоритмов, выводящих грани целиком,
является невозможность правильного изображения двух пересекающихся ячеек
каждая из которых видна лишь частично (см. рис. 2.68). Более совершенные ме-
тоды удаления невидимых элементов рассматриваются в гл. 4.
3.1.1.3. Точечные поверхности
Каркасные линии как средство передачи рельефа поверхности в действительно-
сти не существуют. К тому же, будучи искусственно нанесенными на поверх-
ность, они занимают часть ее площади, иногда значительную. Наиболее реали-
стичным является точечное изображение криволинейной поверхности с
индивидуальной закраской каждой ее видимой точки. Эффект объемности дос-
тигается благодаря игре цвета, света и тени в исполнении искусного программи-
ста-художника.
Некоторые методы реалистичного закрашивания поверхностей рассматриваются е
следующем разделе. А здесь сосредоточимся на конструктивной задаче опреде-
ления порядка вывода точек криволинейной поверхности на экран.
‘Математические модели поверхностей и объектов
269
. амым распространенным алгоритмом визуализации произвольных поверхно-
.тей является простой и достаточно эффективный метод z-буфера, аппаратно
теализованный во всех современных графических ускорителях. Сущность метода
включается в переборе точек поверхности и записи в видеопамять цветовых ко-
з?в ближайших к наблюдателю точек. Для реализации процесса сортировки то-
-ек по глубине сцены в памяти ЭВМ создаются две матрицы:
Д буфер глубины Z, хранящий параметры удаления точек сцены, ближайших к
наблюдателю и видимых им. Объем z-буфера равен width х height слов, где
width - right - left + 1, height - down -up+ 1
есть размеры прямоугольного окна вывода на экране дисплея (см. рис. 2.10), а
разрядность слова Nz определяется числом уровней 2Л’7 квантования уда-
ленности точек от наблюдателя;
И буфер кобра F, хранящий цвета точек окна вывода Объем буфера кадра равен
width х height слов, разрядность которых Nr определяется числом уровней
2 ' квантования цветовых оттенков.
Алгоритм работы метода z-буфера поясняется блок-схемой, приведенной на
Рис. 3.6. Перед началом обработки поверхностей объектов сцены выполняется
щиализация буферов глубины и кадра фоновыми значениями дальности и цве-
"3. Фон — это любая картинка, заполняющая окно вывода в отсутствие объек-
тов. Дальность фона задается числом, большим удаленности самой дальней точ-
• и сцены от наблюдателя. Например, это может быть максимальное число
Тлзрядной сетки процессора ЭВМ, условно говоря, оо.
Поверхности или их отдельные ячейки проецируются на экран, отсекаются
"эаницей окна вывода, после чего начинается сканирование точек каждой про-
;<цпи, которые можно перебирать в произвольном порядке. Эта процедура назы-
вается разложением проекции в растр — двумерную матрицу пикселов, закра-
_-.1ваемых независимо друг от друга. Для каждой точки растра рэ = [лэ уэ о]
-еобходимо найти образ р = [х у z] на соответствующей поверхности, ис-
-о.тьзуя ее уравнение. Физически это означает, что из точек растра проводятся
.санирующие лучи в направлении наблюдателя и производится расчет точек пе-
тесечения этих лучей с поверхностями. Понятно, что из нескольких точек, нани-
анных на (цД-ый луч, наблюдатель увидит лишь самую ближайшую. Именно
ту точку и следует изобразить на экране путем записи ее цвета су в </,Д-ый пиксел
'?фера кадра. Если на луче нет ни одной точки, то цвет пиксела остается фоновым.
Метод вычисления глубины d точки р к наблюдателю S’ зависит от используемой
проекции изображения поверхности:
3 при ортографическом фронтальном проецировании система координат сцены
остается неподвижной, вектор наблюдателя, ортогональный картинной плос-
кости, равен S = z°, а в качестве эквивалента глубины точки можно с помо-
щью (3.1, в) принять число d = -z;
270
Гпава3
□ при аксонометрическом проецировании на фронтальную плоскость МСК все
объекты описываются в СК сцены, развернутой в пространстве матрицей R}
из (2.61) на углы <pr <pv и ср.. Нормированный вектор наблюдателя в системе
координат сцены находится по (2.72, а) и одинаков при любых углах враще-
ния <р.:
5 = [0 0 1]/?^ =[-cos(9x)sin(9>,) sinfaj cosfajcos^)].
В стандартных аксонометрических проекциях удобнее использовать ненор-
мированные формы этого вектора, приведенные в (2.74) и (2.75):
£дим = [1 1 М^изо = [1 1 11-
Преобразование pf = pRyxz = [*f yf Zf ] дает аппликату точки в МСК, рав-
ную zt. Тогда вычисленная по формуле
d = -zt
Математические модели поверхностей и объектов
271
глубина точкир будет уменьшаться по мере ее приближения к наблюдателю.
Другой более быстрый способ заключается в вычислении по (3.1,в) эквива-
лента глубины точки
d--р ° S
относительно бесконечно удаленного наблюдателя, связанного с координатой
zr соотношением d = -zr |5"|;
“1 при центральном проецировании на фронтальную плоскость МСК расчет глу-
бины по формуле (3.1, а) как d = \р - Л'| (расстояние от точки р до наблюдателя
5) требует вычисления квадратного корня. В вычислительном аспекте выгод-
нее ассоциировать глубину с квадратом расстояния (3.1, б)
d=(p-S)°(p-S),
вычисляемым всего за восемь арифметических операций.
После нахождения величины d проверяется состояние (/,у)-го элемента z-буфера
Ztj. При d < Zu точка р находится к наблюдателю ближе, чем другие точки по-
верхности (или фон), имеющие такие же экранные координаты [/ у]. В z-буфер
записывается новое состояние Z,; - d. а в элемент буфера кадра Ftj — код цвета
точки с, вычисленный с помощью излагаемых чуть ниже моделей освещенности
и формул закрашивания.
По окончании перебора точек поверхностей всех объектов содержимое буфера
кадра копируется в окно вывода на экране дисплея, начиная со строки up и
столбца left.
3.1.1.4. Модели освещенности
и закрашивание поверхностей
При решении задачи закрашивания сконструированной поверхности програм-
мист оказывается один на один со сложной дилеммой-
□ с одной стороны, ему нужна модель взаимодействия света и материала, кото-
рая бы максимально соответствовала реальным физическим процессам;
□ с другой стороны, реализация этой модели в графической системе не должна
сильно перегружать компьютер.
Понятно, что никакая программа на самом мощном компьютере не в состоянии
проследить пути всех лучей, пронизывающих пространство сцены (см. рис. 1.61),
чтобы рассчитать энергетические и спектральные характеристики света, прихо-
дящего к наблюдателю из всех видимых им точек. Следовательно, нужна такая
модель расчета освещенности, которая была бы достаточно простой, не отсле-
живала путь каждого луча, но создавала на экране распределение цветового по-
ля, визуально близкое к реальной действительности.
Цвет закраски непрозрачной поверхности определяется множеством факторов,
важнейшими из которых являются
□ физико-механические и оптические свойства поверхности, определяющие ее
собственный цвет;
272
Гпава 3
□ освещение поверхности внешними источниками света;
□ ориентация поверхности относительно источников и наблюдателя;
□ цветовая палитра используемого графического режима.
Цвет и свет неразрывно связаны. Нельзя говорить о цвете того или иного пред-
мета, не указав, каким светом его освещают. В повседневной жизни мы рассмат-
риваем цвет как свойство материалов. Спелый помидор— красный, весенняя
трава— зеленая, небо — голубое, сера— желтая, снег— белый, а сажа— чер-
ная. Естественно, мы оцениваем цвет предметов и материалов при дневном свете.
Более того, привычные цвета знакомых вещей кажутся нам таковыми и при
иных условиях освещения: ночью снег и при освещении красной лампой про-
должает казаться нам белым. Мы также говорим о цвете световых потоков и
считаем цвет свойством света, как, например, цвет лучей светофора, прошедших
через красный, желтый или зеленый светофильтр.
Являются ли эти бытовые определения цвета правильными? Очевидно, нет. Ведь
окраска незнакомого предмета в сумерках и при люминесцентном освещении
различна, а световой луч в темноте вообще невидим (не проявляет своего цвета),
если он не попадает непосредственно в глаз, ни с чем не пересекается и в воздухе
нет пыли. Цветовые свойства света и объектов проявляются лишь тогда, когда
прямые или косвенные лучи попадают в глаз наблюдателя. Объективные наблю-
дения показывают, что материалы и свет не являются цветными.
Великий Исаак Ньютон, изучая свет в своей книге "Оптика" (1704), четко уста-
новил: "В действительности явно выраженные лучи ... не являются цветными
В них нет ничего, кроме определенной способности и предрасположения вызывать
у нас ощущение того или иного цвета" [1]. Таким образом, вместо того, чтобы
говорить: "Этот свет красный", более правильно было бы сказать: "Цвет, вызы-
ваемый этим светом, красный". В психофизическом аспекте цвет есть характери-
стика светового стимула или просто цветовой стимул, который вызывает опреде-
ленное ощущение у стандартного наблюдателя, имеющего нормальное цветовое
зрение.
Построение реалистических изображений включает как физические, так и пси-
хологические аспекты. Свет после взаимодействия с окружающей средой попада-
ет в глаз, где в результате физических и химических процессов вырабатываются
электромагнитные импульсы, которые далее идут по нервным волокнам в мозг
Восприятие света мозгом в виде цвета — приобретаемое свойство, и во всем ви-
димом диапазоне оно доступно лишь человеку и высшим животным —приматам.
Зрительная система воспринимает электромагнитную энергию в диапазоне волн
Л = [380 нм, 780 нм] как видимый свет. Он попадает в приемник (глаз) двумя пу-
тями (см. рис. 1.59). Во-первых, непосредственно от излучателя— тогда свет
имеет цвет излучателя. Во-вторых, косвенно в результате отражения или пре-
ломления на поверхности раздела оптических сред. При распространении он ис-
пытывает поглощение, рассеяние на частицах среды и поляризацию составляю-
щих электромагнитной волны. Эти факторы изменяют исходные параметры
излученного света — его спектральный состав и интенсивность.
Математические модели поверхностей и объектов 273
Таким образом, цвет отраженного света определяется как цветом излученного
света, так и поглощающими, отражательными и преломляющими свойствами
оптической среды, выступающей в роли косвенного источника вторичных лучей.
Например, желтая поверхность желта только при освещении белым светом, т. к.
она отражает красную и зеленую компоненты, которые, смешиваясь в глазу,
воспринимаются как желтый цвет. При освещении красным светом поверхность
будет красной, а синим — черной.
В зависимости от состава спектра и распределенной по нему энергии свет бывает:
□ белым, содержащим все цвета спектра от фиолетового до красного, имеющие
равную и максимальную энергию;
□ ахроматическим, содержащим все цвета примерно равной, но не максималь-
ной энергии. Уровень средней энергии определяет степень серости цвета. Чем
меньше энергия, тем он выглядит чернее. Ахроматический источник кажется
белым, а отраженный или преломленный ахроматический свет— белым, се-
рым или черным. Белыми выглядят объекты, отражающие более 80% белого
света, черными — менее 3%. Промежуточные значения коэффициента отра-
жения дают оттенки серого цвета;
□ хроматическим или окрашенным, содержащим комбинацию различных цве-
тов неравной энергии. Доминирующий энергетический всплеск определяет
преобладающую окраску цвета;
□ монохроматическим, содержащим узкополосную спектральную составляющую
света, воспринимаемую как цветовой тон. Установлено [I], что нормальный че-
ловеческий глаз может различить около 200 цветовых тонов, из которых толь-
ко четыре унитарных цвета (красный, желтый, зеленый и синий) не восприни-
маются как смеси. Все другие цветовые тона рассматриваются как смеси
унитарных тонов, например, оранжевый как смесь красного и желтого.
Из существующих теорий цветного зрения лучше других объясняет его свойства
трехцветная теория Ломоносова—Юнга—Гельмгольца [I, 14, 16, 17]. Согласно
ей — и зто подтверждено экспериментально — сетчатка глаза содержит свето-
чувствительные рецепторы трех типов с областями чувствительности в коротко-
волновой (фиолетово-синей), средневолновой (зеленой) и длинноволновой
(желто-красной) областях спектра. Наличие трех независимых каналов воспри-
ятия человеком всего цветового богатства окружающего мира позволяет любой
цветовой оттенок представить трехмерным вектором
с = [с,. cg cj (3.2)
интенсивностей красной (red), зеленой (green) и синей (blue) составляющих. Це-
тесообразно каждую из компонент выражать в независимой от цветовой палит-
ры относительной форме— числами в интервале от 0 до 1. Белый, черный, крас-
ный, зеленый и синий цвета описываются соответственно векторами [1 1 1],
[0 0 О], [1 0 О], [б 1 О] и [о 0 1]. Все градации серого имеют равные цве-
товые компоненты cr = cg = сь.
274
Гпава 3
Разнообразие оттенков определяется числами битов n„ ng и nh кодирования цве-
товых компонент. Например, в палитре "High color" 16-битовый код цвета слага-
ется из пг = 5, = 6 и пь = 5 разрядов. Три байта цветового кода палитры "True
color" поровну разделены между компонентами: nr = нк - nb ~ 8.
Вектору относительного цвета в nK, п,,} -разрядной палитре соответствуют
округленные до ближайших целых чисел абсолютные цветовые коды
r = [l?"r -l)cr +0-5J, g =
-lk+0.5
, б=У?"‘-’к+0-51
(3.3)
Например, вектор с = [0.6 1 0.8] бледно-зеленого цвета кодируется по форме -
лам (3.3) в палитре "True color" числами г = 153, g = 255 и b = 204.
Наблюдатель видит тот или иной неизлучающий объект лишь благодаря отра-
жению его поверхностью падающих на нее лучей. Отражательные свойства по-
верхности не одинаковы для различных участков спектра. Это объясняет нали-
чие у нее собственного цвета
c0 = [c0r c0g cofe] (3.4, «I
определяемого спектральным составом отраженного света при освещении это
поверхности белым рассеянным светом. Можно считать, что цветовые компоненть
0 < сою < 1 Vco 6 {г, g, b} (3.4, б)
равны коэффициентам диффузного отражения красной, зеленой и синей состав-
ляющих фонового светового потока, имеющего спектр белого цвета.
Падающий на поверхность луч имеет некоторый спектральный состав, которьи
мы также будем описывать вектором относительных интенсивностей
J = [jr Jg Эй],где0< J,a< 1 Vco е {r,g,6}.
Допустим, сцена содержит т точечных источников света Lh i е [1, т]. Для вычис-
ления видимого цвета произвольной точки р на поверхности объекта строите*
следующая система векторов (рис. 3.7):
Рис. 3.7
Математические модели поверхностей и объектов
275
внешняя нормаль N, направление которой в любой точке плоской полиго-
нальной грани Р = {/?1 pi ...р„р\} постоянно и равно
N - norm(P) = (pi-pi) х (рз-pi), (3.5, a)
а у криволинейной поверхности вычисляется в каждой ее точке как
w-idd
dp
при неявном описании f(p) =0 или
Эр(<,т)хЭр(/,т)
Э/ Эт
(3.5,0
(3.5,0
при параметрическом описании p(t, т);
□ вектор 5 направления наблюдателя, составляющий с нормалью угол видимо-
сти точки
\р - Z.(N, S), cos(v)= N°S ; (3.6, a)
□ векторы Vt: = p - L, падающих от источников £, лучей, составляющих с внеш-
ней нормалью углы падения
ai = Z(N,-Vi), cos(a,)=-7Voi<; (3.6,0
□ векторы М, отраженных лучей источников L,, вычисляемые по (1.140) как
и составляющие с нормалью углы а„ а с вектором наблюдателя S углы боково-
го отражения
р, = Z(S, Мд, cos(P,) = S о Л/7. (3.6, в)
Основной вклад в интенсивность отраженного поверхностью света вносят сле-
дующие факторы.
□ Отражение фонового освещения, падающего на поверхность равномерно со
всех направлений. Оно аккумулирует излучение большого числа мелких и
распределенных источников, окружающих объект со всех сторон, включая
небо, облака, многократные отражения от соседних объектов, рассеяние в
мутной среде и т. д. Замена всего этого множества излучателей одним услов-
ным источником фонового света позволяет избежать вычислений бесчислен-
ного количества трасс третьестепенных лучей, которые не позволяют графи-
ческой системе формировать изображение в реальном масштабе времени.
Теперь при моделировании можно просто считать, что каждая точка поверх-
ности объектов сцены освещена одинаково с интенсивностью
J<1> = 1/фг J$b 1 гДе 0 < /фю < 1 Vco е {г, g, b}.
276
Гпава
Энергия этого света частично поглощается материалом поверхности, а час-
тично отражается в виде вторичного излучения. Коэффициент диффузно! .
отражения зависит от длины волны падающего света. Как указывалось выше
совокупность трех таких коэффициентов составляет вектор со собственног.
цвета с элементами (3.4, б).
Поскольку фоновое освещение не является направленным, то его отражение
имеет диффузный характер, а интенсивность отражения одинакова во все
направлениях. У реальных поверхностей диффузное отражение не идеаль-
ное — диаграмма направленности вторичного излучения поверхности (7 н^
рис. 3.7) зависит от угла видимости у в (3.6, а). При у -> 90° наблюдатель ви-
дит некоторое потемнение поверхности из-за уменьшения охватывающего ее
телесного угла и заключенной в этом угле световой энергии. Смоделировать
эту закономерность можно с помощью коэффициента, равного cosv(\p), где
v < 1 — показатель равномерности диффузного рассеяния. Задание v — 0 мо-
делирует идеальное диффузное отражение, одинаковое во всех направлениях
и отсутствие потемнения поверхности при скользящем взгляде.
Таким образом, интенсивность отражения фонового освещения равна
<"Ф<, = coo, cosv(v) /фю V(o е {г, g, b}. (3.7. a
□ Отражение направленных лучей, приходящих в точку р от источников L,. Ос-
вещенность, создаваемая идеальным точечным источником L, ослабляется п.
мере его удаления от анализируемой точки р по закону обратных квадратов
т. е. пропорционально числу
у = (Г2, где d = \L -р\.
Применение этого теоретически правильного закона дает слишком резкое bi
зуальное почернение изображения поверхности при ее удалении от источник
в отсутствие других источников света, в том числе и фонового. В задаче пс-
строения тени объекта от точечного источника света она имеет очень резки
контраст с освещенной зоной. Большая маневренность в регулировании ос-
вещенности и смягчении светотеневого контраста в компьютерной графи» ?
достигается с помощью обратно-квадратичного множителя [36]
Aq + k\d +
с экспериментально подбираемыми коэффициентами Ао, к\ и кг.
Достигнув поверхности, направленный луч претерпевает поглощение, отра-
жение и, возможно, преломление. Нас интересует отраженный свет. Он состс-
ит из двух составляющих, отличающихся по механизму возникновения.
• Диффузное отражение направленного луча обусловлено шероховатость*
поверхности, т. е. наличием на ней микрограней, отражающих луч пр>**—
мерно одинаково во все стороны. Поверхность с идеальным диффузные
отражением называется ламбертовой, а характер отражения описываете»
законом Ламберта — пропорциональностью интенсивности отражен г
энергии косинусу угла падения (3.6, б). Физически этот закон объясняет?»
уменьшением световой энергии, попадающей на единицу площади п -
Математические модели поверхностей и объектов
277
верхности, при увеличении угла падения от 0° до 90°. Диффузное же рас-
сеяние этой энергии как и фоновой происходит равномерно во все сторо-
ны поверхности, а ее видимый цвет определяется избирательным отраже-
нием (коэффициенты отражения есть компоненты собственного цвета сог,
cog и соД направленных лучей с интенсивностями
m
с№> = Cow cosv (v)X vk )cos(a, )j/co Vco g {r, g, b}. (3.7, 6)
i=i
• Зеркальное отражение направленного луча возникает на достаточно глад-
кой поверхности и обусловлено концентрацией отраженных лучей пре-
имущественно вдоль вектора идеального отражения М. Чем зеркальнее
поверхность, тем более острой является диаграмма направленности отра-
женного излучения (2 на рис. 3.7). Эта диаграмма хорошо моделируется
зависимостью cosM(P,) интенсивности зеркальных лучей от угла бокового
отражения (3.6, в). Ее действие проявляется в появлении на поверхности
ярких бликов в тех точках, где углы Р, = 0.
0 Коэффициент резкости бликов ц » 1 регулирует ширину диаграммы
направленности. Идеальному зеркалу соответствует значение р = оо.
При построении отражения от металлов рекомендуется выбирать
100 < р < 500. Малые значения р < 100 соответствуют наиболее распро-
страненным материалам с обычными оптическими свойствами — неме-
таллам и окрашенным поверхностям. Идеальная ламбертова поверх-
ность характеризуется коэффициентом р = 0.
0 Важное свойство зеркального отражения— слабая зависимость его
спектра от собственного цвета поверхности. Будем считать, что блики
имеют цвет падающих лучей, а доля зеркально отраженной энергии ре-
гулируется коэффициентом 0 < кз < 1.
Таким образом, интенсивность зеркального отражения по каждой цве-
товой компоненте рассчитывается следующим образом:
т
сзю = кз X y(< )cosH (₽< )Лю v“ G {т к, Ь}. (3.7, в)
i=i
Закон вычисления компонент вектора интенсивности отраженного от поверхно-
с ги света называется функцией закраски. В [5, 11, 23, 25, 33 - 36] рассматривается
множество функций закраски. В (3.7) мы получили основные факторы, влияю-
щие на формирование цвета поверхности согласно модели отражения Фонга
'25, 36]. По принципу суперпозиции результирующая функция закраски точки р,
имеющей вектор собственного цвета со и освещенной фоновым светом интенсив-
ности /ф и т источниками с интенсивностями Jh расположенными в точках £,,
принимает следующий вид:
„ , V4 c0c0cosv(v)cos(a,)+^3cos^(p/) ,
са> с0юcos (ЖУфю + / < 2
i=l k0 +k\\p-Li\ + k2\P-Li\
(3.8, я)
VtOG {/-, g, б}.
278
Гпава 3
Подставив в (3.8, а) выражения (3.7) косинусов углов гр, а, и р, через их скаляр-
ные произведения, получим расчетный вариант функции закраски Фонга
(у о о s)v (у о и),
✓ 9 **
м ко+к{\р-фк2\р-ЬХ
(3.8, б)
Vco G {г, g, b}.
У криволинейной поверхности нет постоянного направления нормали, из-за чег>.
каждая ее точка имеет на экране индивидуальную закраску. Кроме того, эта по-
верхность может сама себя экранировать. Большую сложность представляет от-
бор таких точек, которые в совокупности образуют экранное изображение без
проколов и наложений пикселов друг на друга. Перечисленные факторы пре-
вращают вывод криволинейных поверхностей в наиболее сложную задачу ви-
зуализации, решаемую, как правило, на последнем этапе.
Наиболее просто выполняется закрашивание параллельной проекции плоско;
грани, которая не может самоэкранироваться (см. рис. 3.3). Благодаря неизмен-
ности угла между векторами нормали N и бесконечно удаленного наблюдателя S
цвет закраски плоской грани постоянен во всех ее точках. Верх примитивизма —
заливка экранной проекции грани цветом со. Более реалистично выглядит грань
цвет закраски которой вычислен по упрощенному по сравнению с (3.8, б) законг
VlOG {г, g, fe},
(3.8, в.
учитывающему только диффузные составляющие отражения и ориентацию по-
верхности относительно источников света и наблюдателя.
Разбиение поверхности на плоские полигональные ячейки, вершины которьп
удовлетворяют условиям планарности (1.81), выполняется несколькими спосо-
бами. Один из них состоит в разрезании объемных ячеек на треугольники — все-
гда плоские полигоны. Второй метод заключается в выборе узлов дискретизации
поверхности (сферы, цилиндра, конуса, тора и т. п.) с учетом ее симметрии так
чтобы все ячейки стали плоскими (см. рис. 1.50).
3.1.2. Кинематические поверхности
Кинематические поверхности формируются непрерывным движением в про-
странстве некоторой линии по определенной траектории. Параметрически!
уравнения кинематической поверхности имеют вид
p(i, с) = ро(т) А(1, т) + рн(0
(3.9, а-
или в расширенном пространстве
р(б Т) = Ро (т)с(о т), где С(г, т)=
Л(г,т)
Рн(')
Озх1
1
(3.9,с
Математические модели поверхностей и объектов
279
Математическая модель (3.9) включает следующие кинематические элементы
(рис. 3.8):
□ ро(г) — исходное состояние образующей линии с центром (базовой точкой) в
начале координат;
□ рн(0 — направляющую линию, вдоль которой переносится центр образующей
линии;
□ A(t, т) — матрицу преобразования линии />о(т), согласованного с траекторией
МО;
□ интервалы изменения параметров 1 е [/о, /„] и т е [то, т,„].
Рис. 3.8
Фиксация центра образующей линии в точках рн(Ц) дает поперечные каркасные
тинии р(ц, т). Фиксированные точки ро(ту) в процессе движения образуют про-
дольные каркасные линии p(t, т;).
Правильный выбор кинематических элементов имеет важнейшее значение при
юнструировании поверхностей. Для любой пары значений параметров {/, т}
функция p(t, т) должна быть:
21 вычислимой. Примером поверхности, не вычислимой в некоторых точках,
служит модель (1.133, б) гиперболического параболоида (см. рис. 1.50, ё). Вы-
числимая модель той же поверхности на рис. 1.50, д задается параметриче-
ской функцией (1.133, а);
□ однозначной— это важно при расчете пересечений поверхности с другими
геометрическими объектами (отрезками, лучами, плоскостями и т. д.) для ис-
ключения нескольких решений этой задачи. Уж на что проста кинематическая
модель сферы
/>(/,т)=[sin(r) cos(т) о]лДг) = [sin(x)cos(t) cos(t) -sin(x)sin(/)j (3.10)
280
Гпава 5
как поверхности вращения окружности sin(x)№ + cos(t)p° G ху вокруг оси 1
так и для нее часто задают интервалы параметров t е [0, 2л] иге [0, 2л], исхо-
дя только из свойств периодичности тригонометрических функций sin и cos
Тем самым каждая точка такой поверхности имеет минимум двойное пара-
метрическое описание. Например, точке [1 0 о] соответствуют две napi
параметрических координат [t = 0, т = л / 2} и {I = л, т = Зл / 2}.
Гарантией правильного выбора интервалов изменения параметров функци.
p(t, т) является учет кинематики формирования поверхности, а именно, пре -
хождение образующей линии не более одного раза по одному и тому же уча-
стку пространства. Например, сферу (3.10) с однозначным описанием точе-
можно получить либо вращением полной окружности (т е [0, 2л]) на угол 180:
(t е [0, л]), либо вращением полуокружности (т е [0, л]) на угол 36(,:
(t е [0,2л]). Второй вариант предпочтительнее, т. к. он дает на поверхности
одну линию склейки вместо двух;
□ дифференцируемой— это необходимо в алгоритмах визуализации, исполь-
зующих нормаль для расчета видимости и освещенности точек поверхност:
В каждой точке p(t, т) должны существовать направляющие векторы каса-
тельной плоскости
г(,л)=^=рдт)^)+*нЦ
dt dt dz _ I
от ат от
и образующий с ними правую тройку вектор нормали
N(t, т) = K(Z, т) х W(t, т). (3.12. a
Для того чтобы нормаль была ненулевой и вычислимой во всех точках по-
верхности, векторы K(z, т) и W(t, т) не должны быть нулевыми или параллель-
ными. Это принципиальное условие работоспособности многих алгоритм 1
удаления, например, Робертса, и моделей закрашивания, например, (3.8).
Неудачная модель эллипсоида с невычислимыми по (3.11) на полюсах (Z = -
векторами V(l, т) приведена в (1.129, б). В то же время не следует идеализирова-ъ
модель (1.129, о), поскольку ее векторы
и(/,т)= [ncos(/)sin(T) -fesin(z) ccos(z)cos(t)],
^(дт) = |«sin(/)cos(t) 0 -csin(/)sin(T)]
дают по (3.12, о) нормаль
7V(z,t) = |cZ>sin2(r)sin(r) acsin(z)cos(z) a/>sin2(/)cos(T)]
нулевой длины на полюсах эллипсоида при t = 0 и t = л. В остальных точках
верхности нормали имеют переменную длину (рис. 3.9, о). В алгоритмах виз ь-
лизации важно направление вектора нормали, а не его длина. Например »
Математические модели поверхностей и объектов
281
(3.8, б, в) используется вектор /V единичной длины. Поэтому вместо (3.12, а)
лучше сразу вычислять нормированную нормаль
N(t, т)=г(/, т), (3.12,6)
а при получении N(t, т) = Оз в особых точках, например, в полюсах эллипсоида,
следует отдельно задавать нужное направление единичного вектора нормали
(рис. 3.9. б):
N(tfi)=y°, N(t,n)=-y°.
Рис. 3.9
На любом локальном участке поверхность является двухсторонней, причем сто-
роны могут различаться собственным цветом и освещенностью. В случае непро-
зрачной замкнутой поверхности нет смысла тратить машинные ресурсы на изо-
бражение ее заведомо невидимой внутренней стороны. У незамкнутых или
полупрозрачных поверхностей деление сторон на внешнюю и внутреннюю по
принципу видимости наблюдателем условно Назовем внешней ту сторону по-
зерхности, которая обращена к вектору нормали (3.12). Алгоритмы визуализа-
ции, использующие нормаль, отображают именно внешнюю сторону. Противо-
положная сторона поверхности является внутренней и для ее визуализации
используется вектор антинормали, равный -N(t, т).
Неудачный выбор кинематических элементов модели (3.9) может привести к не-
ожиданному эффекту инверсии внешней стороны. Например, в модели сферы
(3.10) с интервалами изменения параметров t е [0, л] и те [0, 2л] половина по-
верхности при 0 < т < л обращена нормалями внутрь, а другая половина — на-
чужу сферы (рис. 3.9, в). Причина этого явления — инверсия направления векто-
ра F(r, т) вдоль оси у при переходе параметра т через значение л, в результате
чего изменилось на противоположное и направление вектора N(t, т).
Итак, синтез кинематической модели поверхности заключается в корректном
зыборе всех ее элементов Расчет точек p(t, т) производится непосредственно в
векторной форме (3.9). Тем не менее, иногда мы будем приводить и координат-
ные выражения x(t, т), у(1, т) и z(t, т) для тех читателей, которые, мягко говоря, не
любят векторы, матрицы и операции с ними.
282
Гпава 3
3.1.2.1. Поверхности вращения,
переноса и комбинированные
В зависимости от характера движения образующей линии ро(т) поверхность мож-
но получить ее вращением, переносом вдоль направляющей линии рн(0 или ком-
бинированием различных аффинных преобразований. Простейшая кинематиче-
ская поверхность вращения вокруг координатной оси о е {л, у, z} описывается
функциями
p(t,x) =po(T) A(t), p(z,t)=p0(t)c(z)
с матрицами АП
A(t) = RM, C(f)=R^t).
Плоскости, проходящие через ось вращения, пересекают поверхность по мери-
дианам. Главный меридиан лежит в плоскости, параллельной картинной плоско-
сти, и проецируется на нее без искажений (см. пример 2.9). Плоскости, ортого-
нальные оси вращения, пересекают поверхность по параллелям. Параллель с
наибольшим диаметром называется экватором, с наименьшим — горлом, с нуле-
вым — полюсом (рис. 3.10, а).
У поверхности переноса
p(t,T)-pAs)+pH(t)
образующая движется без вращения и масштабирования (А = Ез) вдоль направ-
ляющей линии (рис. 3.10, б). Во избежание получения вырожденных в линию
участков поверхности кинематические элементы модели (3.9) нигде не должны
быть параллельны:
dPo(TL А.О)
di dz
Рис. 3.10
Математические модели поверхностей и объектов 283
В вырожденных точках поверхность имеет параллельные векторы lz(z, т) || W(t, т)
и по (3.12, а) нулевую нормаль, что неприемлемо для работы алгоритмов визуа-
лизации.
Многие поверхности могут быть получены как вращением, так и переносом. На-
пример, круговой цилиндр формируется вращением прямой линии вокруг па-
раллельной ей оси либо переносом окружности вдоль прямой, ортогональной
плоскости окружности.
Наибольшее разнообразие поверхностей достигается комбинированием преобра-
зований образующей линии при ее движении вдоль направляющей. Так, мас-
штабированием ро(т), зависящим от угла вращения т, на поверхности можно соз-
дать различные волны (рис. 3.10, в), лепестки (см. рис. 3.2) и другие
формообразования. Перенос масштабируемой образующей ортогонально на-
правляющему вектору dpH(Z) / dz формирует разнообразные каналы и трубопро-
воды переменного сечения. Последовательность преобразований отражена в
структуре матрицы C(t, т). Например, масштабирование образующей линии ро(т)
матрицей M(t), вращение вокруг оси ш и движение по направляющей траектории
рн(0 дает комбинированную поверхность, изображенную на рис. 3.10, в, с матри-
цей сложного преобразования
С(/)=М0Асо(/Ж0).
Рассмотрим задачу восстановления кинематических элементов модели (3.9) по
координатным функциям x(t, г), y(t, т) и z(i, т) поверхности вращения образую-
щей линии Po(T)=lxo(T) >'о(т) z0(t)] вокруг какой-нибудь одной координатной
оси co е {x,y,z}. Ее решение необходимо, например, для правильного задания
интервалов изменения параметров гит. Выполнив преобразование вращения
1х(/,т) j(z,t) 4,т)]=А>(т)М0,
сведем его результаты в табл. 3.1.
Таблица 3.1
Ось х(1, Т) j(', t) Z(t, t)
(0 = X Хо(т) _Fo(t)cOS(Z) - Zo(T)sin(/) J’o(T)sin(Z) + Zo(t)cOS(Z)
W = у Ao(t)COS(0 + Zo(r)sin(/) -Ao(T)sin(Z) + Zo(r)cos(z)
СО = Z Ao(t)COS(Z) - J’o(r)sin(Z) Ao(r)sin(Z) + y0(r)cos(z) Zo(t)
Анализ координатных функций параметрической поверхности начинается с по-
иска в них выражения, не содержащего функций cos(z) и sin(z). Это дает имя оси
д. вокруг которой вращается образующая, и первую координатную функцию
(т). Сравнивая оставшиеся координатные функции в (о-ой строке табл. 3.1, оп-
ределяем вторую и третью координаты в ^о(т). Если образующую линию задать в
какой-либо координатной плоскости, то вторая координата будет содержать
284
Гпава 3
cos(/), а третья — sin(z). После восстановления вида образующей задаем интерва-
лы изменения параметров / и т с учетом соображений об однозначности поверх-
ности и направлении ее нормали, высказанных выше.
Возможно, что согласование исходной функции p(t, т) с табл. 3.1 потребует об-
мена в ней параметров t <-> т так, что образующая станет po(t) — функцией пара-
метра t, а матрица вращения Rw(t) — параметра т. В этом случае формула расче-
та нормали (3.12, а) принимает вид
Id/ J ( dr J
& Пример 3.1. Построить кинематическую модель верхней полости кругового
конуса (см. рис. 1.50, г), заданной функцией (1.132) с параметрами а - с = 1, как
поверхности вращения.
Решение. Сопоставив координаты
x(t, т) = zsi п(т), y(t, т) = bt, z(t, т) = /cos(t)
с табл. 3.1, заключаем, что вращение образующей ро(!) с элементами
Jo(Z) = bl, Xo(Z) = 0, Zo(Z) = i
выполняется вокруг оси у с помощью матрицы
А(т) = Rv(t).
В итоге поверхность конуса формируется следующим образом (рис. 3.11): пряма»
линия
/2о(/)=[0 bt tjeyz
Рис. 3.11
Математические модели поверхностей и объектов 285
вращается вокруг оси у в положительном направлении. Для получения верхней
полости конуса высотой h следует задать интервалы изменения параметров
t е [0, h/Ь\ и т е [0, 2л].
Построив в любой точке поверхности векторы
dr cos(t) 0 -sin(i)
b 1] 0 sin(r) 1 0 0 cos(t) = [sin(x)
dx d -sin(x) 0 cos(t) 0 - cos(t) 0 0 0 -sin(x) = [/cos(t)
b cos(t)],
касательные к поперечной и продольной каркасным линиям,
нормали
JV(f,T)=[-fosin(x) t -Ztfcos(x)]
0 -/sin(r)|,
получим вектор
переменной длины, направленный во внутреннее полупространство конуса. В вер-
шине конуса при t = 0 получим нулевой вектор 7V(0, т). Нормировка нормали при-
водит к существующему во всех точках внутренней поверхности конуса вектору
^вну(/,'г)= —[- frsinfr) 1 -6cos(x)].
Vfc2+1
Нормаль внешней поверхности конуса имеет вид
A^BHe(^'t)=^BHy(t,'r)=-y=L=[fesin(x) -1 £>cos(t)]. О
лМ2+1
EZ? Пример 3.2. Построить внешнюю половину трех четвертей эллиптического
тора с полуосями образующего эллипса а, b и радиусом направляющей окруж-
ности г.
Решение. Выберем образующую и направляющую окружности
PoW=JO^(-T)=[sin(T) cos(t) ojexy,
/7н(/)=гх°^у(/)=г[СО5(/) 0 -sin(t)]exz,
а также интервалы изменения параметров t е [0, Зл / 2] и т е [0, л], обеспечиваю-
щие формирование нужной части тора (рис. 3.12). Масштабируя линию ро(т) по
осям х и у матрицей М =diag[a b 0] и вращая ее вокруг оси у, получим матрицу
преобразования
A(t)=MRy(t)=
acos(/) 0
0 b
0 0
-asin(/)
0
0
286
Глава 3
Рис. 3.12
Подставив найденные кинематические элементы в (3.9), получим модель поверх-
ности эллиптического тора
J р(/,т)= [(asin(t)+r)cos(/) 6cos(t) -(asin(x)+r)sin(z)]
| Vze [о, Зл/2] те [о, л]. (3.13)
Возможна и другая последовательность преобразований образующей />о(т): сна-
чала она масштабируется матрицей М, затем переносится вдоль оси х на рас-
стояние г, наконец, вращается вокруг оси у. Матрица сложного преобразования
дает модель р(/,т)= p0(x)c(z), в точности совпадающую с (3.13). С
Ё7 Пример 3.3. Полоска бумаги длиной / = 2лг и шириной 2h сворачивается в
кольцо и перед склеиванием один из ее концов перекручивается п раз. Получить
математическое описание образованной при этом ленты Мебиуса.
Решение. Зададим образующий отрезок прямой
р0(т) = Лхг°е х Vt е [-1, I]
и последовательность таких преобразований, чтобы за один оборот по направ-
ляющей траектории
Рн(') = r[cos(z) 0 -sin(z)o]e xz Vi e [0, 2л]
он повернулся вокруг своего центра на угол тс.
П первое преобразование — вращение вокруг оси z на угол nt / 2;
П второе преобразование — вращение вокруг оси у на угол t;
П третье преобразование — перенос в точку pH(t).
Математические модели поверхностей и объектов
287
Подставив в (3.9) матрицу
получим модель поверхности ленты Мебиуса
nt 1
Т J
V/g[o. 2л} те[-1, 1].
р(/,т)= Г + АТСО!
/х , • I nt
cos(z) Ат sin —
, nl \ , .
г-Ат cos — I sm(/)
На рис. 3.13 построена лента Мебиуса (о) при и = 1 и (б) при « = 6.
Рис. 3.13
Другая последовательность преобразований образующего отрезка ро(т): сначала
он вращается матрицей R:(nt / 2), затем переносится вдоль оси х на расстояние г,
наконец, вращается матрицей Ry(t). Матрица полного преобразования
дает модель р(/,т)= р0(т)с(г), совпадающую с приведенной выше. □
& Пример 3.4. Построить модель объекта "шапочка с помпоном" (рис. 3.14).
Решение. Сформируем направляющую линию, по которой будет двигаться центр
образующей фигуры. Ее первый участок (ось шапочки) есть четверть окружно-
сти радиуса п; второй участок (ось помпона)— прямая линия длиной 2гз
(рис. 3.15,«):
q[cos(f) sin(z) о] при 0<Z<Tt/2,
Н [_/i0 + cos(2/)) Г] О] при л/2 < t < л.
Сконструируем образующую линию из окружности
р0(т)= [cos(x) 0 sin(x)]exz,
288
Глава 3
изменяя ее форму и размер следующими параметрическими коэффициентами:
□ функцией масштабирования
ш(т) = 1 + 0.25|sin(4T)|,
создающей на поверхности продольные выпуклости;
□ функцией радиуса
при О <г <тс/2,
4)=
гз
I 71)
-r2sin(2z) прил/2<7<л,
создающей на первом участке коническое от гз до 0, а на втором — сфериче-
ское от 0 до п и опять до 0 изменения радиуса поперечного сечения поверхно-
сти (рис. 3.15, б).
Рис. 3.15
Далее кривая ш(т) г(/) /><>(?) вращается вокруг оси z на угол
ф(')=
t при 0 < / < л/2,
л/2 при тг/2<1<п
Математические модели поверхностей и объектов
289
(рис. 3.15, б), а затем ее центр переносится в точку рЦ). Совокупность окружно-
сти /?о(т), матрицы полного преобразования
C(t, т) = /и(т) r(/) 7t(<P(O)
и интервалов изменения параметров t е [0, л] и т е [0, 2л] составляет модель ис-
комой поверхности, которая благодаря своему рельефу выглядит вполне реали-
стично и без каркасных линий (см. рис. 3.14). □
3.1.2.2. Линейчатые поверхности и их развертки
По типу образующей линии поверхности делятся на линейчатые и нелинейчатые
(см. классификацию на рис. 3.1). Линейчатые поверхности формируются движе-
нием прямой образующей линии. Развертываемые линейчатые поверхности мо-
гут быть разложены на плоскость без разрывов, складок и искажений длин ли-
ний и площадей фигур.
П Цилиндрическая поверхность образуется движением прямой по направляющей
линии pH(t) параллельно заданному вектору W(рис. 3.16):
p(t, т) - рЦ) + И7т. (3.14)
Рис. 3.16
Условие невырожденности цилиндрической поверхности в линию (оно же есть
условие существования нормали) — непараллельность вектора W вектору
v' At
касательному к направляющей линии.
□ Коническая поверхность образуется движением прямой, проходящей через
неподвижную точку ро и направляющую линию pH(t) (рис. 3.17). Составим два
варианта моделей конической поверхности, отличающихся направлением из-
менения параметра т:
p(t, т) = ро + (pH(t)-ро)т,р(1,0) = ро, p(t, 1) = p»(fy, (3.15, а)
p(t, т) = p„(t) + (ро-pH(t))T,p(l, 0) =pH(t),p(t, 1) =ро. (3.15, б)
290
Гпава 3
Рис. 3.17
Условие невырожденности конической поверхности — непараллельность векторов
и(дт) = dAtfr) W(t) = p„(i) - ро.
dt
П Торсовая поверхность образуется движением прямой по касательной к на-
правляющей линии p»(i) (рис. 3.18):
/>(<•’)= <3|6>
СИ
Рис. 3.18
Условие невырожденности торсовой поверхности — непараллельность векторов
и(г,т) = ^нЮ + ^0 W^=AP^
d/ d/2 dr
На направляющей линии (при т = 0) эти векторы равны, следовательно, нор-
маль к поверхности вырождается в нулевой вектор. Если pH(t) — плоская кри-
вая, то векторы V и W ей компланарны, нормаль имеет постоянное направле-
ние, а поверхность торса является плоскостью, хотя и не с самой простой
кинематической моделью. ЕслиpH(t) — прямая с нулевой кривизной
д2Рн(0_о
dr2 3’
то V(t) — W(t), а торсовая поверхность вырождается в прямую линию.
Математические модели поверхностей и объектов
291
Указание в моделях (3 14)—(3.16) интервалов изменения параметров делает ли-
нейчатую поверхность ограниченной линиями g(l) и A(z). Например, при т е [то, т,„]
получим
g(t) = p(t, то), h(i) = p(t, т,„).
Границы могут быть также результатом пересечения образующих прямых с дру-
гими поверхностями (точка пересечения прямой с плоскостью находится по
(1.102)). В этом случае границы интервала параметра т становятся зависимыми
от параметра г.
т е [to(Z), t„,(z)] => g(t) = p(t, to(Z)), h(t) = p(i, т,„(/)).
Рассмотрим задачу построения развертки линейчатой поверхности— плоской
замкнутой фигуры, вырезав которую из листа упругого материала (бумаги, цел-
лулоида, жести и т. п.) и свернув, можно получить исходную поверхность без
складок, разрывов и искажений длин линий. В рсзд. 2.2.5 мы уже строили раз-
вертки простейших линейчатых поверхностей — круглых прямых цилиндра и
конуса— вместе со спроецированными на них изображениями контуров мате-
риков. Аналитические методы развертывания таких поверхностей основаны на
преобразовании декартовых координат точки р = [х у z] в криволинейные
координаты, соответствующие типу поверхности.
П Положение точки на поверхности круглого прямого цилиндра радиуса р опи-
сывается в цилиндрической СК ординатой по оси у и углом азимута <р е [0, 2л],
отсчитываемым, например, от оси z декартовой СК (см. рис. 1.1,6). Не аф-
финное преобразование (1.3, а) декартовых координат точки р = [х у z] в
цилиндрические координаты ри = [р у <р] устанавливается нелинейными
функциями
p(p)=Vx2+z2 , <р(р) =
при х > 0,
(3.17)
Заметим, что декартовы координаты точки
х = psin(<p), z - pcos(<p)
получаются из цилиндрических за одно аффинное преобразование вращения:
[х у z]=[0 у р]Яу(<р). (3.18)
Допустим, поверхность круглого прямого цилиндра (3.14) с кинематическими
элементами
pH(/)=a[sin(z) 0 cos(/)] Vz е [/о, z„], IV =у°
ограничена линиями g(z) и h(t), а отрезки go ho и g„ hn лежат на меридианах. На ос-
нове точки ho вычислим по (3.17) радиус цилиндра р и начальный меридиан (ро.
292
Гпава 3
Расположим плоскость развертывания х'у' касательно к цилиндру по отрезку
go ho с у' (рис. 3.19, а). Так как длина дуги параллели между меридианами сро и
<р равна р- (<р — <ро), то развертка точки р = [х у z] с найденным по (3.17)
меридианом <р имеет координаты
Х' = Р . (ф _ <р0), у' = у.
Для того чтобы развертка была непрерывной вдоль оси х'. перед ее вычисле-
нием повернем цилиндр вокруг оси у на угол —сро, после чего отрезок go ho бу-
дет иметь угол <р = 0, а остальные точки поверхности — углы азимута в ин-
тервале (0,2л]. В итоге мы получили следующий алгоритм развертывания
точки р круглого прямого цилиндра на плоскость x'j':
а = р(Ло), сро = <р (ho), р = [аф(рЛ^(-ср0)) у]- (3.19)
Вычислим по этому алгоритму развертки точек граничных линий g\ и /г'.
Фигура, заключенная между ними и отрезками g^ и g'ntfn, является раз-
верткой ограниченной цилиндрической поверхности (рис. 3.19, 6).
Рис. 3.19
□ Положение точки на поверхности круглого прямого конуса с углом раствора
Ф е [0, л] описывается в сферической СК расстоянием г до вершины конуса и
углом азимута <р е [0, 2л] (см. рис. 1.1,6). Преобразование (1.3, б) декартовых
координат точки р = [х у z] в сферические координаты рк = [г <р \у] ус-
танавливается нелинейными функциями (3.17) и
r(p) = LpI, v(p) =
(3 20)
Декартовы координаты точки
х = rsin(<p)sin(\p), у = rcos(y), z = rcos(cp)sin(vp)
Математические модели поверхностей и объектов 293
можно получить из сферических за два преобразования вращения:
[х у z]=[0 г 0К(ф)/?,,(ф). (3.21)
Допустим, поверхность круглого прямого конуса (3.15, о) с кинематическими
элементами
ро - Оз, pH(z)= [arsin(f) b tzcos(z)] Vz е [Zo, z„]
ограничена линиями g(t) и A(z), а отрезки go ho и g„ h„ лежат на меридианах. На
основе точки ho (или go при ho - Оз) вычислим по (3.20) угол раствора конуса
Ф и начальный меридиан фо.
Расположим плоскость развертывания х'у' касательно к конусу по отрезку
go ho с у' (рис. 3.20, а). Дуга параллели между меридианами <ро и <р имеет длину
rsin(v)(<p-<p0)
и развертывается на плоскость х'у' в виде дуги с радиусом г и углом
у = _(ф _ (p0)sin(4/),
отсчитываемым от оси у'. Для того чтобы развертка была непрерывной в на-
правлении вращения у, перед ее вычислением повернем конус вокруг оси у на
угол —<ро, после чего отрезок go ho будет иметь угол ф - 0, а остальные точки
поверхности — углы азимута в интервале (0, 2л]. В результате мы получили
следующий алгоритм развертывания точки р круглого прямого конуса на
плоскость х'у':
<ро = <p(go), 8 - v(go), у = -sin(8) ф(рД/-фо)), р = [о |/т|]/?(у). (3.22)
Рис. 3.20
294
Гпава 3
По этому алгоритму вычислим развертки точек граничных линий g- и h'.
Фигура, заключенная между ними и отрезками g'oh'o и g'„h'„, является раз-
верткой ограниченной конической поверхности (рис. 3.20, б).
Точное построение развертки произвольной линейчатой поверхности — не круг-
лых или не прямых цилиндров и конусов, а также торсов, — сопряжено с трудо-
емким исчислением длин дуг кривых линий в криволинейных системах коорди-
нат. Рассмотрим приближенный и понятный даже ребенку метод развертывания
путем отрезания от поверхности узких полосок и укладывания их на плоскости
плотно друг к другу.
Выполним дискретизацию параметра направляющей линии: t = th i = \,n. В ре-
зультате гладкие граничные линии заменяются кусочно-линейными аппрокси-
мациями с узлами g, = g(/,) и h.~ а поверхность— последовательностью п
соединенных друг с другом четырехугольных полосок g,g/+l hi+i h, (рис. 3.21,17).
При вырождении какой-либо ограничивающей линии в точку (например, вер-
шины конуса) полоски будут треугольными. Увеличение числа п приближает
полигональную аппроксимацию развертки к истинной криволинейной.
Сформируем (2/1 + 3) х 3-матрицу S, в строках которой будем сохранять векторы
sk е R3 \fk = 0, 2/1 + 2 разверток узлов в следующем порядке:
go -> gi -> ... -> g„ -> -> ... ho -> go.
Начнем строить развертку на плоскости х’у' с фиксации точек
50 = 52в+2 = Оз, S2„+1 = К - go|Z е У
Рис. 3.21
Последовательно при каждом i = 0, п -1 отрезая от поверхности и укладывая на
плоскость развертки очередной полигон {g,g,+l Л,+| ^g,}, совмещаем пары точек
{g„ и {/?,, 52„+| J, а точку g,+l — с плоскостью х'у' (рис. 3.21, б). Расчет матрицы
такого преобразования методом парных точек (2.13) требует две четверки не-
Математические модели поверхностей и объектов
295
компланарных точек образа и прообраза. Две пары точек {g„ h,} и J2„+l-,} уже
известны. Построим векторы нормалей и бинормалей, на концах которых полу-
чим еще по две пары точек:
Ni = (gi+i - gi) x (Л, - g, 6, = (hj -g^x Ni,
H, = К|z° 1 x'y, P, = ta/z+i-z -S, )xHj e x'y'.
Вычислим матрицу присоединения z-ой полоски поверхности к ребру 5, S2„+l-,- по-
строенной части развертки:
Это позволяет дополнить строки матрицы .S' двумя точками j,+l и s2n~, — разверт-
ками точек g,+l и Л,+|:
$+1 = Sz+lQ. ?2zz-Z = hi+\CiO{ <325)
По окончании отрезания и укладывания полосок первые два столбца матрицы S
содержат абсциссы х' и ординаты у' вершин полигона развертки, третий же
столбец аппликат z' остается нулевым.
Источниками погрешностей изложенного алгоритма развертывания являются:
П конечное число полосок п, на которые разрезается линейчатая поверхность;
П проективный метод получения точки с координатой Z2„+]_,- = 0. Если
z-ой полигон поверхности {g,g,+l hi+l hjgi} не планарный, то после фиксации
трех точек g„ h, и g,+l четвертая точка Лж останется вне плоскости х’у’. Орто-
гональное проецирование в (3.25) искажает размеры и форму z-ro полигона
развертки. Последовательное накопление искажений приводит к тому, что
построенная развертка является не точной, а приближенной.
Таким образом, алгоритм приближенного построения развертки линейчатой огра-
ниченной поверхности на плоскости имеет следующий вид.
& Шаг 1. Вычисляются концы go и ho начального положения образующего от-
резка и соответствующие им точки развертки $о = sin+2 = Оз и .s^n+i = |^о _£о|т°-
Шаг 2. В цикле z = 0, и-1 вычисляются:
О концы образующего отрезкаgi+l и й/+|;
□ по (3.23) нормали Nh Н, и бинормали р,;
О по (3.24) матрица преобразования С,;
□ по (3.25) точки развертки \+, и
Шаг 3. Вывод ребер развертки функцией lineis^, s^+|) X/k = 0,2n +1. □
296
Гпава 3
Условия работоспособности алгоритма есть условия существования нормалей /V,
и бинормалей Ь, в (3.23):
П узлы ограничивающих линий h(t) и g(t) не должны совпадать во избежание
равенства g, = Л,;
□ линия g(i) не должна быть вырожденной в точку во избежание равенства
Si~St+i- Для развертывания конусной поверхности от точки ро до направ-
ляющей линии pH(t) нужно выбрать p(t) = pH(t) и h(t) - ро.
& Пример 3.5. Получить модель и построить развертку боковой поверхности
усеченного эллиптического конуса (рис. 3.22, а), заданного точкой
р0 = [2 4 2], направляющим эллипсом нижнего основания в плоскости xz с
полуосями а= 1, Ь= 2 и секущей плоскостью верхнего основания, проходящей
через точку рп = [о 2 о] перпендикулярно оси эллипса.
Решение. Примем уравнение эллипса нижнего основания конуса
g(t)=[asin(t) 0 Z>cos(t)] Vz е [0, 2л]
с таким расчетом, чтобы начало развертки приходилось на образующую линию
между точками ро и [о 0 й]. Найдем нижнюю границу интервала параметра т и
уравнение верхней границы h(t) путем решения задачи (1.102, о) пересечения об-
разующей линии ро + (g(z) -ро)т поверхности (3.15, о) с плоскостью, описываемой
уравнением Nn°p = Nn°pnc нормалью 2Vn = ро:
Po°(/’o+(g(')-A))c)=A)°A1 => ч(')= Р0°^П.\ Р0\ = й—ПЛП-----------(Л’
Po°(g(')-Po) 12-sin(z)-2cos(z)
fi(l)=po + (g(t)~po)xll(t)-
Рис. 3.22
Математические модели поверхностей и объектов
297
Таким образом, боковая поверхность усеченного конуса описывается векторной
функцией с зависимыми интервалами параметров:
p(t,t) = [l + (O.5sin(f)-l)r 2(1-т) l + (cos(t)-l)r]
V/e[o, 2л], те -------1 .
12 -sin(f)-2cos(z)
На рис. 3.22. б по алгоритму (3.23) - (3.25) построена развертка усеченного ко-
нуса. □
& Пример 3.6. Получить уравнения и построить развертку торсовой поверхности,
образованной движением отрезка длиной I = 3 по касательной к первому витку
цилиндрической винтовой линии с радиусом г = 1 и шагом d - 1.5 (рис. 3.23, а).
Решение. Направляющая винтовая линия описывается параметрической функцией
рн(/)= rsin(r) — rcos(t) Vz е [0, 2л].
2л
Необходимый в уравнении (3.16) вектор производной
^h(z)_ rcos0 -rsin(f)
dt 2л V
имеет независимую от параметра t длину
dt 2л
Это дает постоянные границы интервала изменения параметра т в модели торсо-
вой поверхности:
р([,т)= [r(sin(f)+Tcos(t)) 5(г + т) r(cos(z)-Tsin(/))]
V/ е [о, 2л], те [0,тЛ ], X/, = —L----= 2.92 .
Vr2 +б2
Рис. 3.23
298
Гпава 3
Данная поверхность имеет постоянный угол X наклона нормали к горизонталь-
ной плоскости во всех точках:
N(<, т) = хТ) = /-т[8cos(r) -г —5sin(r)],
z \ /Vv г
sin (Л)=-г-4 = —, = -0.97 => X = -76.6°.
И V7777
Свойство равнонаклонности торсовой поверхности используется при сооруже-
нии поворотов на скоростных автодорогах, велотреках, водостоках и т. п.
Приняв g(Z)=pH(/) и /?(/)= р(7, тЛ), строим развертку торсовой поверхности
(рис. 3.23, б). Вырезав ее по всему контуру и подняв за левый верхний угол на
высоту d= 1.5, получим исходную торсовую поверхность. □
Косые (неразвертываемые) линейчатые поверхности согласно классификации,
приведенной на рис. 3.1, образуются при движении прямой по двум или трем
направляющим линиям. В случае двух направляющих образующие прямые долж-
ны удовлетворять одному дополнительному условию. Например, они должны
быть ориентированы под определенным углом к некоторой плоскости 77. В зави-
симости от вида направляющих косые поверхности делятся на:
П цилиндроиды, у которых обе направляющие кривые;
П коноиды с кривой и прямой направляющими;
П косые плоскости с двумя прямыми направляющими.
Методика получения модели косой поверхности с двумя направляющими g(t), h(t)
и образующими, параллельными плоскости П(У, W) (рис. 3.24), следующая.
1. Фиксируем параметр t и точку на линии g(t).
2. Через точку g(l) проводим плоскость g{l) + Vtn + Wxn параллельно плоскости 77.
3. Находим параметр th и точку Л(/й) пересечения этой плоскости со второй на-
правляющей:
g(l) + Vln + Wxn = /т(7й) => => h(th(j)). (3.26)
4. Составляем модель косой поверхности:
P<J, т) = g(f) + (Л(/„(0) - g(0K (3.27)
Рис. 3.24
Математические модели поверхностей и объектов 299
Требования к направляющим линиям g(z) и h(t):
□ плоские направляющие не должны быть компланарны или параллельны
плоскости П, иначе уравнение (3.26) либо не имеет решений, либо имеет их
бесконечное множество;
□ направляющие не должны пересекаться, иначе в (3.27) при = g(t) функ-
ция p(t, т) не будет иметь две степени свободы.
& Пример 3.7. Получить модель цилиндроида. образованного движением концов
отрезка с постоянным фазовым сдвигом <р по двум направляющим окружностям
радиусами г\ и тг, расположенным соосно в горизонтальных параллельных плос-
костях на расстоянии d (рис. 3.25, а).
Решение. Запишем уравнения направляющих окружностей с учетом фазового
сдвига вращения концов образующего отрезка:
g(z) = / Jcos(/) 0 sin(z)], /?(z)=r2|cos(/ + <p) d sin(z + <p)].
Модель искомой поверхности между направляющими линиями имеет вид
p(z,x)= g(z)+ (/?(z)- g(z))x =
= [r2 cos(z + фХ + ri cos(/)(l - т) di r2 sin (z + <p)r + q sin(z)(l - t)]
Vze[0, 2л], tg [o, 1].
Условие постоянного фазового сдвига равносильно условию постоянного угла "К
между образующими прямыми и плоскостью xz:
W
sin (/) = r-q- = .
KI -^d2 + r2 + r2 ~ 2r1r2 cos(tp)
= const Vz, где W = = h(t)-g(t).
Эт
d
Рис. 3.25
Например, при ip^0 и <р*л изучаемая линейчатая поверхность одновременно яв-
ляется квадратичной поверхностью однополостного гиперболоида (см. рис. 1.50, в).
300
Гпава 3
При <р * 0 получим боковую поверхность усеченного конуса (рис. 3.25, б) с углом
наклона образующих прямых
кт(Л)= , .
При л = Г2 это поверхность цилиндра. Наконец, при <р = л все образующие пря-
мые имеют общую точку
о о'
fl +Г2
и образуют поверхность двуполостного конуса (см. рис. 1.50, г).
Рис. 3.26
Метод формирования криволинейной поверхности из отрезков прямых имеет
практическое применение при разработке очень прочных, но легких, ажурных и
красивых конструкций башен, телевышек, опор и т. п. На рис. 3.26 построена
четырехступенчатая модель известной "башни Шухова". Каждая следующая сту-
пень строится преобразованиями масштабирования и переноса предыдущей сту-
пени. О
& Пример 3.8. Получить модель поверхности винтового коноида, образованной
при горизонтальном движении отрезка прямой по оси у и N виткам цилиндриче-
ской винтовой линии с радиусом г и шагом d (рис. 3.27).
Решение. Зададим уравнения направляющих линий
g(/) = [rsin(r) & rcos(r)], = [0 t О],
Математические модели поверхностей и объектов
301
где 5 = dl 2л, а также направляющие векторы горизонтальной плоскости V =х°
и W =z°. Подставив эти исходные данные в (3.26), получим векторное уравнение
[/•sin(r) + tn 8/ rcos(r) + T/y]= [о l). О],
из которого следует lh(l) = 5/ и модель поверхности винтового коноида (3.27):
р(/,т)=[г(1 -r)sin(z) & r(l -t)cos(z)] V/ е [0, 2лЛ^, т е [0, 1].
Рис. 3.27
Практическое применение данная поверхность находит в конструкциях различ-
ных винтовых движителей, перемещающих материалы (снег, песок, вязкие жид-
кости, воду, мясо) и несущие их транспортные средства (снегоходы) вдоль оси
винта. □
S Пример 3.9. Получить модель поверхности косой плоскости, образованной
скольжением прямой образующей по скрещивающимся прямым направляющим
линиям: первая линия проходит через точки А = [б 0 1] и В = [-1 1 б], вто-
рая— через точки С = [о 0 -1] и D = [1 1 о]. Во время движения образую-
щая должна быть параллельна плоскости с направляющими векторами
И = [о 1 о]иИ/ = [-1 0 1] (рис. 3.28).
Решение. Подставив в (3.26) уравнения направляющих прямых
g(z)=z4 + (B-z4> = [-Z t 1-/],
X г , (3.28)
Л0=с + (о-с)/ = [г t Z-1J,
получим векторное уравнение
[-z-T/? t + tn 1-г + т^]=[г/( th //,-1], (3.29)
302
Гпава 3
из которого следуют зависимость
hM = 1 -1
и модель косой плоскости (3.27):
р(г,т)=[т-г г + т-2/т 1-г-т].
(3.30)
Рис. 3.28
Уточним характер движения образующей прямой по направляющим отрезкам
АВ и CD. Подставив в (3.30) т - 0 и т - 1, получим с учетом (3.28)
p{t, O) = g(t), р(м)=[1-' 1-f -d=A(!-O-
Это означает, что образующая движется по направлению g(r) и против направ-
ления h(l). В частности, при I - 0 она проходит через точки А и D, а при t = 1 —
через В и С, оставаясь все время параллельной плоскости { V, И7}.
Выразив из координатных функций
х(1, т) = т - г, y(t, т) = t + т - 2/т, z(l, т) = 1 -1 - т
параметры t = 0.5(1 -x-z) и т = 0.5(1 + x-z), получим неявное уравнение косой
плоскости х1 - z1 - ly + 1 = 0 — поверхности второго порядка со следующе>-
матрицей (1.124) и инвариантами 7i + Л:
10 0 0
0 0 0 -1
0 0-10
0-101
Л = 0, /2 =
0 0 0 -1
+ +
0 0-1 о
1,
1
о
о
1
о о
/3 = 0
0 0 = 0, h = 1 > 0.
о
0 -1
Математические модели поверхностей и объектов
303
По классификации табл. 1.3 это гиперболический параболоид. Его сечения коор-
динатными плоскостями следующие (рис. 3.29, а):
□ X = 0 => у = 0.5(1 - z2) — парабола (7) в плоскости yz\
□ = 0 => х2 = z2 - 1 — гипербола (2) в плоскости xz\
□ z = 0 => у = 0.5(1 + х2) — парабола (3) в плоскости ху.
Что касается названия поверхности, то оно объясняется просто. Возьмем плоский
квадратный лист бумаги ABCD за противоположные края и повернем их в раз-
ные стороны, воспроизводя преобразование кручения (см. рис. 2.7, а). Скручен-
ная из плоскости фигура получила название "косая плоскость".
Поверхность (3.30) получена по (3.27) как линейная интерполяция между направ-
ляющими g(t) и й(1 - I). Однако, если строить ее без учета условия параллельно-
сти образующей линии плоскости {К, И7}, то при образующих прямых (3.28) по-
лучим косую плоскость
p(6t)=g(z)(l-T)+/?(/)r = t(2T-l) t (z-1)(2t-1)J. (3.31)
Рис. 3.29
Это тоже гиперболический параболоид, имеющий в отличие от (3.30) иную ори-
ентацию в пространстве. Как видно из рис. 3.29, б, при построении поверхности
(3.31) образующая линия все равно остается всегда параллельной, но теперь уже
к плоскости xz. О
В зависимости от вида трех направляющих, которые не должны друг с другом
попарно пересекаться, среди косых поверхностей выделяются:
□ однополостные гиперболоиды, у которых все направляющие — прямые;
О косые цилиндры с двумя прямыми и третьей кривой направляющими;
□ конусоиды, имеющие две кривые направляющие и одну прямую.
304
Гпава 3
Методика получения уравнения p(t, т) косой поверхности с тремя направляющими
g(t), h(t) и u(t) (рис. 3.30) имеет следующий вид.
1. Фиксируем параметр t и точку на линии g(z).
Рис. 3.30
2. По (3.15, а) строим конусы на направляющих Л(0 и u(t) с общей вершиной g(z):
h^h > И,) = g{t) + {h(th )-g(t))Th,
. ) = g(/)+ (w(r„ )- g(/)K.
3. Находим прямую пересечения этих конусов, которая является образующей
косой поверхности:
(Л(0,) -g(0)T/, = -g(r))T„ => kh(t,) - u(t„) = (k-\)g(t), (3.32)
где k-xhlт„. Решая векторное уравнение (3.32) относительно переменных
k(t), th(t) и z„(z), получим модель искомой поверхности в любой из двух форм:
P(t, т) = g(t) + (A(z;,(O) - g(0K
P(t, т) = g(z) + (w(z„(z)) - g(z))t. (333)
С7 Пример 3.10. Классифицировать и построить модель поверхности, образо-
ванной движением прямой линии по трем скрещивающимся прямым направ-
ляющим g(t) = [1 Z 0], A(z)=[0 1 /], w(f)=[z 0 1] (рис. 3.31).
Решение. Уравнение (3.32) имеет вид
[- tu к kth — l]=[fc—1 (£-l)z о],
откуда находим
и параметрические функции поверхности:
х(/,т)=! + ~,y{t, т) = z( 1 - т), z(z, т) = т. (3.34)
Математические модели поверхностей и объектов
305
Рис. 3.31
Исключив параметры
получим неявное координатное уравнение
ху + xz + yz - х - у - z + I = 0.
Эта поверхность второго порядка имеет следующие матрицу (I. I24) и инварианты:
0 1 I -1
10 1-1
110-1
-1 -1 -1 2
/| = 0, /2 = -3, /з = 2 * 0, /д = 1 > 0.
(3.35)
По классификации табл. 1.3 получили однополостный гиперболоид.
Анализируя координатную функцию x(t, т) в (3.34), приходим к выводу, что она
имеет разрыв при t = 1 Следовательно, построение непрерывной поверхности по
модели (3.34) возможно в два приема. На рис. 3.31 приведена лишь часть по-
верхности в интервале изменения параметра t е [-10, 0.99]. Другая часть при
е [1.01, 12] построена на рис. 3.32, г?. В обоих случаях интервал изменения вто-
рого параметра т е [-5, 5]. Каждое из этих двух изображений в диметрической
проекции мало похоже на однополостный гиперболоид из-за неудачного сочета-
ния его ориентации в пространстве и выбранного ракурса. Совместное изобра-
жение двух поверхностей в произвольной триметрической проекции (рис. 3.32, б)
убеждает в том, что это именно однополостный гиперболоид, аналогичный изо-
браженному на рис. 1.50, б. На его поверхности есть две линии разрыва, неза-
метные благодаря специально подобранному ракурсу. Одна из них соответству-
ет неопределенности поверхности при t = 1, другая получается из-за конечных
пределов интервала параметра t вместо теоретически бесконечных пределов. □
306
Гпава 3
Рис. 3.32
& Пример 3.11. Получить модель поверхности усеченного конусоида, основа-
ниями которого являются окружность радиуса г и квадрат а х а, а высота равна
d (рис. 3.33).
Рис. 3.33
Решение. В силу симметрии объекта построим модель p°(t, т) поверхности его пе-
редней грани, образованной движением прямой по следующим направляющим:
П четверти дуги окружности
g(r) = r[cos(/) 0 sin(/)| Vz g [0, 2л];
Математические модели поверхностей и объектов
307
□ отрезку прямой линии между точками [g d о] и [о d q\ при q =
Л(/)= [</(1-/) d qt\ X/t g [0, 1];
□ прямой w(/)=[o t 0] || J’°.
Составив уравнение (3.32)
kd-tu &??/,]= [(A-l)rcos(/) 0 (k-l)rsin(r)],
эпределим
>t0- sin(,)
sin(/) + cos(/)
и первую в (3.33) модель передней грани:
0/ \ л \ i х aTcosfr) , л \ . / \ arsing)
р°(/,т)= r(l-T)cos(0+—-7-----77ч dx r(l-?)sin(f)+ . / "7Л •
2sin(/ + n/4) 2sin(/ + n/4)
Поверхности остальных трех граней конусоида получаются с помощью враще-
ния поверхности p°(t, т) вокруг оси j:
p‘(t,x) = p°(t,T)Ry(-m/2) V/ = 1?3 , t g [0, л/2],т g [0, 1]. □
3.1.2.3. Нелинейчатые поверхности
Нелинейчатые поверхности формируются по формуле (3.9) только кривыми об-
разующими /?о(т), которые в процессе движения вдоль направляющей pK(t) могут
"рансформироваться матрицей A(t, т), что дает большое разнообразие поверхно-
стей. В частности, циклическая поверхность создается движением окружности или
ее дуги (см. рис. 3.8). Если плоскость образующей окружности постоянно под-
держивается ортогональной направляющей кривой, т. е. нормаль к плоскости
тараллельна направляющему вектору г(/) = p„(f), то такая циклическая поверх-
чость называется каналовой. Толщина канала определяется функцией изменения
садиуса образующей окружности г(0, входящей сомножителем в состав матрицы
4 ([, т). Поверхность канала постоянного радиуса г называется трубчатой.
Рассмотрим вычислительные аспекты построения каналовой поверхности. Преж-
де всего необходимо задать кинематические элементы модели (3.9). В целях уни-
фикации в большинстве задач будем использовать образующую окружность
единичного радиуса с нормалью z° и центром в начале координат:
PoW=cos(t)x0+ып(т)>’° = [cos(t) sin(x) о]ел-у. (3.36)
Эднако для исключения дополнительных вращений на углы ±90° иногда более
делесообразным может оказаться выбор окружности
р0(т)=cos(t)j° +sin(r)z° е yz
308
Гпава 3
с нормалью х° или
А>(т)= cos(T)-° + 81п(т)г0 е xz
с нормалью j°. Задание интервала изменения параметра т, имеющего геометри-
ческий смысл угла дуги окружности, определяет степень замкнутости каналовой
поверхности. При т е [0, 2л] получим замкнутый канал. Выбор меньшего интер-
вала позволяет построить разрез поверхности вдоль меридианов и увидеть ее
изнутри (см. рис. 3.8).
Важным элементом модели каналовой поверхности является скалярная функция
r(t) изменения радиуса окружности поперечного сечения канала вдоль направ-
ляющей траектории. Аналитическое представление этой зависимости конкрет-
ной формулой во многих отношениях предпочтительнее. Его преимущества —
это точность, компактность записи, простота вычисления при любых допусти-
мых значениях параметра, возможность аналитического, т. е. точного, диффе-
ренцирования. К сожалению, это представление возможно лишь в самых про-
стых случаях (рис. 3.34). Например, у трубчатой поверхности (2) r(t) - го, канал
конусного типа (2) получим при r(t) = ro+ r\t, а чуть более сложный гофриро-
ванный канал может быть сформирован равномерным переносом окружности
переменного радиуса r(t) - го + nsin(coz) (3) или r(t) - ro + n|sin(oM)| (4).
Рис. 3.34
Аналитическая форма функции часто бывает чрезмерно сложной в записи, вы-
числении и дифференцировании. Выгоднее становится задание n + 1 узловых
точек {th г,} W = 0, п и восстановление аналитической зависимости r(t) в классе
функций, сочетающем хорошее приближение к узлам и малые межузловые укло-
нения с небольшим числом варьируемых параметров и простотой вычислений
К таким функциям относятся степенные, полиномиальные и кусочно-полино-
миальные (сплайновые), экспоненциальные и гармонические.
В вычислительной математике разработано много интерполяционных и при-
ближающих формул [13]. Наиболее востребованы методы полиномиальной ин-
терполяции и приближения Лагранжа и наименьших квадратов. Напомним крат-
ко их суть.
П Интерполяционный полином Лагранжа и его производная
” ” 1
,=0 >=°z' Z/
i=o 7=0Z'
7*'
fl ГТ
£=0 Z' Z*
k*i, k*j
(3.37)
Математические модели поверхностей и объектов 309
не нуждаются в каких-либо дополнительных, кроме узлов и параметра /, дан-
ных, т. е. являются формулами прямого действия. Недостаток метода —
сложность программирования и малое быстродействие интерполирования в
реальном времени.
□ Интерполяционный МНК-полином и его производная
'•(0= Xе/ > (3.38)
1=0 (=1
требуют предварительного расчета вектора коэффициентов полинома
с ~ fco С1 cn 1 с помощью матрицы Вандермонда W - [и,7] и вектора узлов
С/ = [г0 п ... г„]:
Wy=tj V i = 0,n, j-0,n => с - U W~l. (3.39)
Необходимость обращения (n + I) х (и + 1)-матрицы W компенсируется ма-
лой трудоемкостью интерполирования по формулам (3.38).
□ Аппроксимационный МНК-полином и его производная
ш т
Г(‘)='ЁСА ''(f)=^icit,~ (3.40)
1=0 i=l
отличаются от интерполяционных полиномов (3.37) и (3.38) способностью
сглаживать погрешности узловых данных за счет степени т < п. Вектор
с = [с0 ci — ст] находится с помощью матрицы Грама G- [#,,] и вектора
узлов U = [z7q W| ... ит]:
п . . ___ _______ п ___
v i = 0.m, j=0,m, щ=i = 0.m ^>c-UG~'. (3.41)
k=0 k=0
При m - n векторы с в (3.39) и (3.41) совпадают. Аппроксимация полиномами
степени т, меньшей числа интервалов л, используется для устранения межуз-
ловых осцилляций, которыми грешат интерполяционные полиномы высоких
степеней при большом числе узлов.
Следующий важный элемент кинематической модели в целом и каналовой по-
верхности в частности— направляющая линия pH(t) движения центра образую-
щей. Она должна быть гладкой, т. е. непрерывно дифференцируемой по t, иначе
з точках излома или разрыва вектор направления - dpH(t) I dt будет не опре-
делен. Второе интуитивно понятное требование к направляющей состоит в том,
чтобы при каждом значении г радиус ее кривизны [13, 29]
310
Гпава 3
был не меньше радиуса образующей окружности r(z). В противном случае обра-
зующие точки с вогнутой стороны направляющей линии будут совершать по-
пятное движение, а поверхность p(t, т) окажется не гладкой, а смятой.
Как и в случае скалярной функции радиуса, применяется аналитическое и узло-
вое задание векторной функции Преимущества первого метода описань
выше. Однако очень часто выражения координатных функций линии pH(t), даю-
щих ей желаемое расположение в пространстве, либо слишком громоздки, либс
их получение превращается в непосильную задачу. Тогда становится целесооб-
разным применение численных методов восстановления направляющей линии пс
конечному числу узлов рн, V/ = 0, л.
Полиномиальное приближение векторной функции рн(0 е R3 выполняется пс
алгоритмам (3.37)—(3.41) индивидуально для каждой координаты лн(0, )’н(/) и
2н(0- Интерполяционные методы обеспечивают точное прохождение направ-
ляющей кривой через заданные в пространстве узлы, но при большом числе уз-
лов возможны большие межузловые осцилляции решения. Аппроксимация пс
МНК целесообразна для понижения степени векторного полинома и уменьшен,!»
осцилляций за счет появления ошибок сглаживания.
Направляющая траектория может быть неплоской и неаналитической, может не
иметь ни одного прямолинейного или постоянной кривизны участка, т. е. може*
представлять собой произвольную кривую. Для отслеживания ее направлена»
необходим вектор производной Г(/)= p'H(t\ Его можно получить дифференци-
рованием координатных функций лн(0, У«(1) и z„(l) либо аналитически, в tow
числе по (3.37), (3.38) и (3.40), либо численно, например, по трехточечным фор-
мулам [13] для схем с равноотстоящими узлами при ti+l - Z, - At:
у _ ~3pHQ +4рн| — Рц2 у _ Phi + \ ~ Рш-1 у _ ^Рнп ~4Рни-1 Рнп-2 (3 4"1
0 2Д/ ’ ' 2Д/ ’ " 2Д/
Наибольшую сложность при синтезе каналовой поверхности представляет расче-
матриц преобразований A(t) или C(t), обеспечивающих ортогональность плоское
образующей окружности /?0(т) r(t) A(t) вектору V(j), касательному к кривой р„{
движения центра окружности. Конечно, если эта кривая полностью аналитическ>
определена и состоит из простейших участков (отрезков прямых или дуг окружно-
стей с известными радиусами и координатами центров), то можно и без знанк*
касательного вектора нужным образом сориентировать образующую окружность
в начале координат, изменить ее радиус согласно зависимости r(f) и перенести
центр в точку p,<(t) Именно такой подход к формированию кинематических по-
верхностей был применен при решении примеров 3.2—3.4.
Здесь читателю рекомендуется освежить в памяти подходы (рекуррентный и ите-
ративный на рис. 2.28) и методы (два варианта разложения на рис. 2.30, 2.31 •
парных точек на рис. 2.32) решения кинематической задачи, подробнейшим об-
разом рассмотренные в разд. 2.1.3.3. Анализируя представленные алгоритмы и
результаты их моделирования (см. рис. 2.34), заключаем, что расчет матриц аф-
финных преобразований следует выполнять по экономичным рекуррентным алг -
Математические модели поверхностей и объектов
311
ритмам (2.53) и (2.54), из которых предпочтительнее второй вариант, основан-
ный на методе парных точек.
Обобщая изложенное, сформулируем рекуррентный алгоритм построения сечений
каналовой поверхности p(tjy т) V/ = 0, п при заданной в (3.16) образующей окруж-
ности ро{х) е ху, функции изменения радиуса r(t) и произвольной направляющей
кривой pH(t) с касательным вектором C(t):
C0=MAP2^)3,z°, рМ r(z0H0)) => P<to^ = P0№0,
Ci = MAPZ^pJtj), pH(ti+i), r(/,+i)и(/,+1)) => р^+1,т)=р(1,,т)С/.
Работоспособность алгоритма иллюстрируется на рис. 3.35, а, где построен каркас
трубчатой поверхности с радиусом трубки г = 0.3 и направляющей траекторией
[-1 sin(z) cos(f)]v 0<t<n,
,[cos(z) sin(z) -l]V n<t<2it,
[1 sin(z) -cos(f)]V 2л</<3л,
[-cos(z) sin(z) l]V3n<z<4n
; производной — вектором направления
[o cos(z) -sin(f)] V 0<Z<n,
[—sin(f) cos(f) o]v 7i<Z<27t,
[o cos(z) sin(z)] V2n<t <3n,
[sin(z) cos(z) o] V3n<z<4n.
Осевая линияpH(t) интересна тем, что на ней есть восемь точек, где вектор K(z) ста-
новится параллельным одной из координатных осей, и в их окрестностях возмож-
но скручивание поверхности, построенной по неэкономичному алгоритму. Не
трудно убедиться, что алгоритм (3.43) строит каналовую поверхность верно.
Итеративный алгоритм, основанный на методе парных точек
C(z) = WlP2(o3, z°, рн (l) => p(t, t) = p0 , (3.44)
позволяет получить сечение каналовой поверхности при любом значении пара-
метра Z экономичным преобразованием примитива ро(т) из начала координат в
~очку pn(t). Однако переходы между соседними сечениями не являются эконо-
мичными, что подтверждается скручиванием продольных линий поверхности на
рис. 3.35, б и делает алгоритм (3.44) не самым лучшим для построения каналовых
поверхностей.
Наконец, худший алгоритм построения каналовой поверхности — итеративный
зариант неэкономичного метода разложения (2.49) с матрицей сложного АП
-1(0, вычисляемой по (2.30), (2.31):
Я(Г) = 1 (r(z)) =>p(Z, т) = r(z) /?о(т) A(t) + pH(t). (3.45)
312
Гпава 3
Рис. 3.35
Методические ошибки алгоритма очевидны (рис. 3.35, в). Перекручивание сосед-
них сечений на угол вплоть до 180° происходит на тех участках, где К(0 »0, г
функция Кх(г) меняет знак. При этом вычисляемый по (2.31) угол а скачком изме-
няется с ±90° на +90° при почти неизменном угле р « ±90°. Матрица сложного АП
4'(П=^(-₽ХМ
обратная к матрице (2.30), выполняет вращение почти горизонтальной окружно-
сти ро(т) ЛЛ(-Р) вокруг оси у на угол а последним — отсюда понятна причина
перекручивания поверхности на вертикальных участках. Тем не менее, мы будеч
использовать алгоритм (3.45) для получения аналитических моделей каналовых
поверхностей.
& Пример 3.12. Из проволоки длиной / = 100 и радиусом г = 1 изготовлена прх-
жина путем навивки с шагом Л = 6 на боковую поверхность цилиндра радиусо«
гц = 3 (рис. 3.36, а). Затем пружина была поставлена вертикально на плоскость и
под действием собственного веса и упругости сжалась так, что два нижних витка
соприкоснулись (рис. 3.36, б). Построить модели и изображения поверхностен
свободной и сжатой пружин.
Решение. Выберем образующую окружность (3.36), а направляющую кривую
свободной пружины в виде цилиндрической винтовой линии с равномерным ша-
гом h и числом витков
пв = - , = 3.87:
у14712(гц+гУ+й2
/’св(/)=[(гц+г)81п(г) kCB1 (ru+r)cos(z)] Vze[o, 2лив]. (3.46,
Благодаря постоянному коэффициенту наклона
ксв = h / 2л = 0.955
ординаты направляющей Jcb(0 = kCBt (график 1 на рис. 3.37) касательный вектор
*/cB(')=[('i1+'-)cos(r) ксв -(гц +r)sin(/)] (3.47)
Математические модели поверхностей и объектов
313
всюду составляет с плоскостью xz равный угол
₽св = arctg
^св
'11+''
= 13.43°.
Рис. 3.37
Построение изображения трубчатой поверхности свободной пружины на
рис. 3.36, а выполнено по алгоритму (3.43).
Так как направление винтовой линии (3.46) нигде не приближается к верти-
кальному, то получение аналитической модели поверхности свободной пру-
314
Гпава 2
жины возможно по формуле (3.45). Подставив в нее кинематические элементь
/2о(т),/?св(0,
/^cn(z) — 7?v(—Рсв) R.(J + л / 2)
и выполнив необходимые преобразования, получим координатные функции по-
верхности:
х(г,т)= (ru + г -rcos(t))sin(z)- (/i«B/7/)cos(r)sin(c),
у{(,т)= (2лив(гц +r)z-//)sin(T)+A//2n,
z(/, т) = (гц + г - г cos(?))cos(/)+ (hnBr//)sin(/)sin (т),
V/g [б, 2n«B], tg [б, 2л]
У сжатой пружины (рис. 3.36, б) каждый виток нагружен весом лежащих выше
него витков. Не углубляясь в дебри теоретической механики, будем считать, чтс
направляющая кривая p^(t) имеет ординату )'сж(1) с линейно возрастающим наклоном
- at + b
(график 2 на рис. 3.37):
Рсж(0=[(гц+г)5'п(/)
О Sat2 +ht + c
(3.49)
Касательный вектор Кж(/) также увеличивает угол своего наклона Рсж(/) с рос-
том t:
^c>K(/)=[('ix+'')C0S(/) al + b
- (гц + r)sin(f)], Рсж (/) = arctg
at+b
(3.51»
Подставив в алгоритм (3.45) кинематические элементы р0(т),рсж(1) и
Лсж(/) = Rx{—Рсж) Ry(t + л / 2),
получим координатные функции поверхности сжатой пружины:
*сж(/’т)= ('ц + ''-rcos(r))sin(/)—, - . =^cos(r)sin(T}
, \ + r) I \ 7
З’сжу‘,т)= । ——— -sin(T)+0.5gr +bt + c,
+(at+b^
гсж(бт)= (ru+r-rcos(x))cos(r)+-, Г^Г+Ь^ sin(r)sin(c),
Vzg [о, 2лисж], tg [о, 2л]
(3.511
Для практического построения этой поверхности необходимо определить неиз-
вестные величины а, Ь, с и Лсж. Не учитывая достаточно сложной зависимость
числа витков пружины от степени ее сжатия (в действительности оно немногс
Математические модели поверхностей и объектов
315
увеличивается при сжатии) и полагая лСж = Пв, запишем исходные требования к
сжатой пружине в виде трех соотношений относительно неизвестных a, Ь и с:
Э верхний конец сжатой пружины ненагружен, следовательно, он имеет значе-
ние наклона Аък(2ллв) как у свободной пружины ксв'.
2ппЛа +Ь = —
в 2л
(3.52)
□ начальная ордината направляющей уо = _уСж(0) с учетом упора сжатой пружи-
ны о плоскость xz и наклона ее нижнего торца на угол Ро равна rcos(Po)
(рис. 3.38):
(3.53)
Рис. 3.38
□ ордината направляющей _yi - уСж(2л) в конце первого витка, касающегося сво-
его начала с углом наклона Pi > Ро, равна
y° + cos(p0) cos(P|)
4л2<7 + 2nb = —-—I + г)2 + b2 + л/(гц + r)2+ (2ла + b)2
(3.54)
Численное решение системы уравнений (3.52)—(3.54) при I- 100, r = 1, ru = 3 и
h = 6 дало значения коэффициентов а = 0.03, b = 0.224, с - 0.998 и изображение
сжатой пружины на рис. 3.36, б. □
& Пример 3.13. Построить поверхность топологического объекта, называемого
"бутылка Клейна" (рис. 3.39, а). Эта объемная фигура интересна тем, что ее кор-
пус плавно переходит в ручку, которая, входя в корпус у горлышка, внутри со-
единяется с ним, образуя замкнутую одностороннюю поверхность (рис. 3.39, б).
316
Гпава 3
Удалив фрагмент корпуса в месте входа в него ручки, можно показывать фокус:
налитая вода при наклоне бутылки не выливается, а скапливается внутри у гор-
лышка.
Рис. 3.39
Решение. Построение весьма замысловатой поверхности бутылки Клейна — хоро-
шая иллюстрация богатых возможностей, гибкости, но и капризной непредсказуе-
мости метода параметрической интерполяции (3.38), (3.39). Именно отсутствие
простых аналитических выражений координат направляющей линии pH(t) и функ-
ции изменения радиуса r(t) вынуждает строить их как интерполяционные кривые.
Расположим на плоскости ху десять узловых точек рн, = [хн, Ун, О] V/= 0,9
направляющей рн{1) в наиболее характерных местах изменения направления и
толщины канала (рис. 3.40, а). В каждом узле pHj зададим радиус г, образующей
окружности, переносимой ортогонально направляющей линии. Для изображе-
ния поверхности каркасом с равномерной плотностью поперечных сечений зада-
дим приращения параметра А/, пропорционально округленным до целых чисел
расстояниям между узловыми точками |/?„ /+1 -рн,|- Все необходимые для интер-
поляции данные сведены в табл. 3.2.
Таблица 3.2
i 0 1 2 3 4 5 6 7 8 9
tj 0 2 20 35 53 63 88 109 119 124
Хн/ 0 0 0 0 10 20 20 1 0 0
Уч 50 48 30 15 0 0 25 35 45 50
Г/ 2 4 6 13 8 5 3 2 2 2
Математические модели поверхностей и объектов
317
Ручное вычисление по (3.39) векторов коэффициентов интерполяционных поли-
номов девятой степени сх, су, сг является непреодолимо сложным, в чем убеждает
значение определителя матрицы Вандермонда 1^ = 2- 1073. Полученные с помо-
щью MathCAD методом (3.38) интерполянты хн(/), .МО и r(t) (рис. 3.40, б) ис-
пользовались для построения каналовой поверхности бутылки Клейна по алго-
ритму (3.43).
Рис. 3.40
Решение задачи интерполяции крайне чувствительно к выбору числа и располо-
жения узловых точек, причем рост числа узлов увеличивает степень полинома и
межузловые осцилляции. Похожий эффект наблюдается и при недостаточном
числе узлов. Например, исключив как будто бы лишний узел рИ2, лежащий на
прямой /?н1 рнз, получим направляющую линию с сильной осцилляцией, изобра-
женную пунктиром на рис. 3.40, а. СЗ
Квадратичные поверхности описываются алгебраическими неявными уравнения-
ми/(р) = 0 типа (1.124). Параметрические формы поверхностей второго порядка
уже изучались нами в разд. 1.2.3, однако там шла речь об их получении не дви-
жением линий в пространстве, а подбором подходящих функций подстановки
x(t, т) z(t, т), удовлетворяющих уравнению f(x, у, z) = 0. Но именно кинемати-
ческий метод с целенаправленным выбором элементов движения позволяет по-
лучить поверхность с желаемым расположением каркасных линий, внешней
(если она необходима) ориентацией нормалей и корректными интервалами из-
менений параметров. При наличии кинематических элементов pH(l) и р0(л) по-
строение векторов V(t, т), W(t, т) и N(t, т) выполняется буквально "на пальцах", а
не путем трудоемких вычислений по (1.61, б) и (1.62).
Изучая линейчатые поверхности, мы убедились, что некоторые квадратичные
объекты — цилиндры, конусы, однополостные гиперболоиды и гиперболические
318
Гпава 3
параболоиды — могут быть сформированы движением прямой линии. Поверх-
ности с осевой симметрией можно строить либо вращением специально выбран-
ной образующей линии вокруг этой оси, либо переносом вдоль нее окружности
переменного радиуса. Составим, например, модель кругового эллипсоида
+/+z2-l=0
двумя способами:
□ вращением половины эллипса
/?0(т)= [tzcos(t) sin(x) 0]е ху Vt е [0, л]
вокруг оси х матрицей A(t) = R^J) Vt g [0, 2л] при pH(t) - Оз (рис. 3.41, а). То-
гда по табл. 3.1 получим модель
/?(/,т)= [czcos(t) cos(z)sin(r) sin(r)sin(r)]. (3.55)
Проведя в любой точке поверхности касательные векторы V и W в направле-
нии увеличения параметров t и т, построим нормаль N = V х IV, которая для
модели (3.55) является внутренней;
Рис. 3.41
□ переносом образующей окружности
р0(т) = С® cos(t) sin(x)]G yz Mr e [0, 2л]
вдоль направляющей прямой
Рн (')=[« cos (/) 0 о] II х° \/1 е [0, л]
с одновременным ее масштабированием матрицей A(t) = sin(/)£3 (рис. 3.41, б).
Подставляя эти кинематические элементы в (3.9), получим параметрическую
модель эллипсоида
p(t,t)= [acos(z) sin(z)cos(r) sin(z)sin(r)|, (3.56)
Математические модели поверхностей и объектов 319
формально совпадающую с (3.55) с точностью до имен параметров. Модель
(3.56) имеет внешнюю ориентацию нормалей, что видно по расположению
векторов V и W.
Второй способ ближе к универсальному кинематическому методу формирования
произвольной квадратичной поверхности сложным АП образующей окружно-
сти единичного радиуса. Процесс синтеза целесообразно разделить на два этапа.
□ Строится модель нормированной канонической поверхности с масштабными
коэффициентами а = b - с = 1 в координатных функциях (1.129)—(1.136):
р«(1, т) - r(t) ро(г) + рн(0- (3 57)
Ниже приведены возможные варианты кинематических элементов для построе-
ния нормированных поверхностей, изображенных на рис. 1.50: r(t)— функции
изменения радиуса окружности /?0(т) в процессе ее переноса вдоль направляю-
щей прямой pn(t). По умолчанию выбрана образующая окружность
/?0(т)= |sin(r) 0 cos(t)]g xz Vt е [0, 2л]
(лишь при построении параболического цилиндра используется другая кривая):
• для действительной сферы (1.129, а)
r(t) - sin(r), /’„(/')= [О cos(/) О] Vr е [0, л]; (3.58, а)
• для однополостного гиперболоида (1.130)
r(t) = ch(r), Рн(/)= [° sh(z) е (~°°> (3.58, б)
• для двуполостного гиперболоида (1.131) с верхней (+) и нижней (-) полостями
r(t) = sh(r), рн(/)=[° ±ch(f) о] VZ е (-оо, со); (3.58, в)
• для круглого конуса (1.132)
r(t) = t, pH(t)= [О bt о] Х/l е (-оо, со); (3.58, г)
• для построения гиперболического параболоида (1.133, а) переносное движе-
ние точек образующей окружности должно зависеть от параметра т:
r(t) - t, рн([,х)= |о t2 cos(2t) o] \/t e [0, оо), т e [0, 2л]; (3.58, d)
• для круглого параболоида (1.134)
r(t) = t, pH(t)= [o t2 o] Vr e [0,co); (3.58,e)
• для круглого цилиндра (1.135)
r(t) = 1, AiO)= [0 1 0] Vr e (-oo, co); (3.58, ж)
• для построения параболического цилиндра (1.136) используется отличная от
предыдущих вариантов образующая кривая в виде параболы:
р0(т)=[т 0 т2], r(t)= 1, (3.58,з)
pH(t)= [О t О] Vr е (-оо, со), т е (-оо, со).
320
Глава 3
□ Построение произвольной квадратичной поверхности выполняется последова-
тельностью аффинных преобразований канонической модели (3.57) с кинема-
тическими элементами (3.58), соответствующими типу поверхности. В общей
сложности достаточно четырех аффинных преобразований — масштабирова-
ния, двух вращений и переноса:
p(t, т) = pK(t, т) М(а, b, с) 7?Л(\|/) Я/<р) + Ри, (3.59)
где а, b и с — желаемые коэффициенты масштабирования по осям х, у и z; хр и
<р — углы ориентации (см. рис. 1.1,6) той оси симметрии квадратичного объ-
екта, которая в канонической форме является вертикальной; рк— центр
квадратичного объекта.
Сложное преобразование р(г,т)= рк(г,т)С с матрицей
С = М(а, b, c)Rx MRylfpyrtpu)
устанавливает между матрицами FK и F неявной формы (1.124) соотношения,
аналогичные (2.12):
р Fр1 =ркСFC1 р^ =рк FK р^ =0 => FK=CFСТ, F = C~lFK^. 0-60)
Нас интересует обратная задача нахождения параметров а, Ь, с, хр, <р и ри пре-
образования (3.59) по известным матрицам Fh Fk. Так как все матрицы к F
при любом к * 0 описывают одну и ту же поверхность, то матрицы НФ FK и F
являются конгруэнтными с точностью до еще одного неизвестного скалярного
множителя к\
FK=kCFCT. (3.61)
& Пример 3.14. Построить нелинейчатую кинематическую модель однополост-
ного гиперболоида (см. рис. 3.32, б), заданного матрицей неявной формы (3.35).
Решение. Анализируя линейчатый метод получения гиперболоидной поверхно-
сти, заключаем, что ее центр расположен в точке
ри = [0.5 0.5 0.5],
а ось симметрии имеет направление Г = [1 1 1] и углы ориентации
у = arctg(V2 )= 54.7е, <р = 45°.
В модели (3.59) осталось определить коэффициенты масштабирования а, b и с
Вычислим по (3.60) матрицу FKi канонической поверхности при а = Ь = с = 1:
’ 0 1 1-1' ’1/^ 0 -1/V2 0
F = 10 1-1 110-1 , Cl =Лх(у>>,(ф)7'(рц)= 1М i/V£ 1М -2/^ 1/>/з 0 i/Тб о
-1 -1 -1 2 °-5 0.5 0.5 1
Математические модели поверхностей и объектов
321
откуда
-1 0 0 0
0 2 0 0
^К1 = 0 0 -1 0
0 0 0 0.5
Построенная по каноническому уравнению однополостного гиперболоида
(табл. 1.3) матрица
FK=diag[l -1 1 -1]
связана с матрицей Fu и масштабными коэффициентами соотношением
FK =A diag[a2 b2 с2 l]fKl.
Отсюда получаем
k--2, a = с = \/у[2 =0.707 ,b - 0.5.
В результате матрица сложного преобразования принимает вид
1/2 О
э/з/б х/з/б
л/з/б -д/з/з
0.5 0.5
-1/2 0
х/з/б 0
л/з/б 0
0.5 1
а координатные функции искомой поверхности однополостного гиперболоида
(рис. 3.42) получаются на основе канонических элементов (3.58, б) модели (3.57)
следующим образом:
[*(',?) У'('л) z(r,r) 1]= (т(/)р0(т)+ рн(г))С =
= [ch(f)sin(r) sh(r) ch(r)cos(r) 1JC,
322
Гпава 3
x(t, т) = 0.5(1 + ch (f)sin (с)) + (л/з /б )(sh (/) + ch (/)cos(t)) ,
y(t. т) = 0.5 + (л/з/б)^)-2ch(f)cos(t)) .
z(t,x) = 0.5(1 - ch (z)sin(c)) + (>/з/б)(5Ь(г)+ ch(z)cos(r)).
Весьма трудоемкая проверка убеждает, что полученные параметрические функ-
ции координат удовлетворяют неявному уравнению ху + xz +yz-x-y-
z + 1 = 0, соответствующему матрице неявной формы (3.35). □
Поверхности высших порядков описываются алгебраическими неявными уравне-
ниями f(p) — 0 или параметрическими функциями p(t, т) со степенями координат
или параметров выше второй. Высокие степени полиномов координатных функ-
ций могут быть лишь формальным признаком высокого порядка поверхности.
Например, поверхность
/?(г,т)= [л/^2 +т3) z4+t- 1 z4+t + 1]
четвертого порядка относительно параметра t и третьего порядка относитель-
но т описывает плоскость — поверхность первого порядка. Действительно, вы-
числив по (1.62) направляющие векторы и нормаль
r = ^V2z 4/3 4/3], И7 = |зл/2т2 1 1], М=2л/2(бА2-1) [О 1 -1],
обнаруживаем постоянное направление последней для всех значений 1 и т, что
является доказательством того, что поверхность с такой нормалью является
плоскостью.
Трансцендентные поверхности имеют трансцендентные координатные функции в
неявных уравнениях f(p) = 0 или описаниях кинематических элементов— обра-
зующих и направляющих кривых. Наибольшую трудность представляет изобра-
жение неявных поверхностей f(x,y, z) = 0, не допускающих параметризацию,
либо с взаимно не выражаемыми координатами. В разд. 3.1.1.2 в общих черта?
описан метод построения линий уровня — сечений поверхности плоскостями, па-
раллельными координатным плоскостям.
Изображение сложной неявной поверхности облегчается, если:
□ уравнение f (х, у, z) = 0 разрешимо относительно некоторой координаты, на-
пример, у = <р(х, z). Параметризация
p(x,z) = [x (p(x,z) z]
позволяет построить каркас из линий уровня р(х„ z) и р(х, zjy,
□ сложная функция f (х, у, z) факторизуема, т. е. представляется произведением
более простых функций / (х, у, z). Тогда поверхность/(х, у, z) = 0 объединяет
все поверхности /(х,р, z) = 0, которые могут строиться независимо друг от
друга.
£? Пример 3.15. Построим следующие поверхности.
1. Аналог гауссовской функции плотности вероятности двух переменных
<p(x,z)=e-(* +z )
Математические модели поверхностей и объектов
323
как параметрическую поверхность p(x,z) = [x <p(x,z) z] колоколообразного
вида (рис. 3.43, а) и на ее основе "холмистый рельеф" как сумму масштаби-
руемых по осям координат гауссовских поверхностей
z)= X Л,ф(Ух, (х -сх, \ yzi (z -czi)). (3.62)
i=\
Параметры /-го холма (впадины) задаются следующими числами:
• Л, — высотой (глубиной при А, < 0);
• с„- и с., — координатами вершины;
• Уxi и У:, — коэффициентами крутизны склонов в направлении осей х и z.
Рис. 3.43
Рельеф на рис. 3.43, б построен суммированием четырех холмов и одной впа-
дины с векторами параметров v, = [й, cxi czi yxi yZ(],/ = 1,5:
vj=[1.5 -1 -1.5 2 2],v2=[1 0 0 1.4 2],v3=[1.2 1.5 -0.5 2 0.7],
v4 = [1 -1.5 I 2 1.2], v5 =|-0.8 0.5 1 0.5 1.2].
2. Поверхность четвертого порядка, описываемая неявным уравнением
f (х, у, z) = 36х4 - 1 бу4 + 36z4 - 140х2у2 + 153x2z2 - 20y2z2 - 216x3 + 864xj’2 -
-864xz2 + 144x2 - 1168j2 + 1116z2 + 864x- 1152 = 0.
С помощью символической функции Factor программы MathCAD разложим
функцию f (х, у, z) на два множителя:
/i (х, у, z) = х2 - 4у2 + 4z2 - 4, fz (x, у, z) = 36x2 + 4y2 + 9z2 - 216x + 288.
Следовательно, искомая поверхность является объединением двух квадра-
тичных поверхностей (рис. 3.44):
= 0 — однополостного гиперболоида с по-
луосями а = 2, Ь = с = 1;
324
Гпава 3
О
г ( V
/2(х,у,г) = 36 (х-3)2+ |
2
I -1
z
2
a - 1, b = 3, с = 2 и центром в точке [з 0
эллипсоида с полуосями
0].
Рис. 3.44
= 0 —
3.1.3. Кусочно-определенные поверхности
В предыдущих разделах обсуждались вопросы создания и свойства поверхно-
стей, для которых известны глобальные неявные или параметрические описания
Однако на практике сложная поверхность часто формируется как совокупность
сегментов с индивидуальными геометрическими моделями. Типичными приме-
рами являются автомобильные кузова, фюзеляжи и крылья самолетов, корпуса
кораблей, лопасти турбин и вентиляторов, скульптуры, фигуры людей и живот-
ных, оболочки с отверстиями и другие поверхности, отдельные части которых
представляются в кусочном виде, подобно лоскутному одеялу. Кусочное пред-
ставление бывает также необходимо для описания нерегулярных поверхностей с
нарушениями непрерывности (разрывами) или гладкости (изломами).
Часто исходная информация о поверхности является неполной, т. е. отсутствует
аналитическое выражение, позволяющее вычислить координаты любой точки
внутри любого имеющегося сегмента. Кусочная модель сегмента поверхности
восстанавливает это описание по ограниченному набору данных. В зависимости
от объема этих данных рассмотрим три кусочно-интерполяционные модели. По-
лагаем, что сегмент имеет форму объемного четырехугольника. Треугольный
сегмент является частным случаем четырехугольного при вырождении одной из
его граничных линий в точку, что никак не ограничивает работоспособность
алгоритмов интерполяции.
П Одной из самых простых является билинейная кусочная поверхность, заданная
четырьмя узловыми точками woo, woi, wto и wii (рис. 3.45). Такой минимальный
объем исходных данных встречается, например, в машиностроительных
САПР, в которых специальными щупами измеряются координаты отдельных
Математические модели поверхностей и объектов
325
точек поверхности сложной детали и по ним строятся кусочные модели всех
сегментов.
Рис. 3.45
Если к поверхности сегмента не предъявляется никаких других требований,
кроме прохождения через заданные узлы, то наиболее оптимальным является
вычисление ее произвольной точки как линейной интерполяции между
противоположными границами mooz/io и moi мн. Зададим в параметрической
плоскости квадрат {zg{0, 1},tg{0, 1}}, четыре вершины которого [г т] со-
ответствуют узловым точкам объектного пространства м,т. Линейно интерпо-
лированные граничные линии
м,о(О = моо + (мю — uoo)t = моо( 1 — Z) + uiot,
m,i(Z) — Moi + (мп — Moi)Z = Moi (1 — Z) + wnZ
являются отрезками прямых. Зафиксируем значение первого параметра в ин-
тервале z g [0, 1] и построим линейную интерполяцию граничных точек сег-
мента m,o(z) и m,i(z) по второму непрерывному параметру 0 < т < 1:
т) = w,o (0(1 - 0+ «zi (')г = «00 0 - ОС - 0+ Що'(1 - 0+ «010 - 0т + «11«, (3.63)
что также является отрезком прямой. Идентичный результат получим при
интерполяции граничных точек
мот(т) = моо(1 - т) + MoiT, мц(т) = мю( 1 - т) + мпт
при фиксированном значении т g [0, 1] по непрерывному параметру 0 < z < 1:
p(z, 0 = «от (ОО - 0+ «к (О' = «00 (1 - Об “ 0+ «01С - 0т + «ю'(1 - 0+ «11п-
В соответствии с классификацией на рис. 3.1 билинейная поверхность является
косой плоскостью, а согласно примеру 3.9, где рассматривалось движение пря-
мой образующей по двум скрещивающимся прямым направляющим, она же
представляет собой квадратичную поверхность — гиперболический параболоид.
Таким образом, при узловом задании кусочной поверхности она представля-
ется набором независимых четырехугольных'сегментов косых плоскостей с
326
Глава 3
прямолинейными каркасными линиями. Если четверка узлов сегмента ком-
планарна. то интерполяционная поверхность между ними — обычная плос-
кость.
Также плоскую форму принимает билинейная поверхность, заданная тремя
узлами. Например, подставив в (3.63) точки woi = wn, получим билинейную
поверхность
p(t, т) = woo( 1 - 0(1 ~ т) + wioZ(l - т) + woit
с направляющими векторами
V(t, т) = (wio - woo)(l - т), W(t, т) - (woo - wio)Z + woi - woo
и нормалью
N(t, т) = (1 - t)(wio - woo) x (woi - woo)
постоянного направления, что доказывает планарность поверхности трехуз-
ловой линейной интерполяции.
П Далее рассмотрим построение гранично-линейной кусочной поверхности, за-
данной двумя граничными линиями g(t) и h(t) (рис. 3.46), причем их параметр в
границах сегмента изменяется в интервале t е [0, 1]. Здесь требуется больший
объем исходных данных: аналитические описания указанных граничных ли-
ний или возможность их получения методами полиномиальной (3.37)—(3.41)
или иной интерполяции.
Рис. 3.46
Поскольку поведение сегмента между граничными линиями не регламентиро-
вано, то для вычисления его произвольной точки выбираем линейную интер-
поляцию по параметру 0 < т < 1 между граничными точками g(t) и h(t) с рав-
ными значениями параметра Г.
p(l, "0 = g(0(l - т) + Л(0т- (3.64
Согласно классификации, приведенной на рис. 3.1, это линейчатая поверхность
с двумя направляющими, причем в качестве дополнительного условия ее по-
строения выступает общий параметр t согласованного движения прямой обра-
Математические модели поверхностей и объектов 327
зующей по граничным линиям. Каркасные линии р(/„т) являются отрезками
прямых, а линии p(t, т7) образуют систему полиморфных кривых, переходящих от
одной формы к другой, а именно — от линии p(t, 0) = g(Z) к линии p(t, 1) = h(f).
Небольшую сложность при подготовке исходных данных для интерполиро-
вания кусочной поверхности представляет нормализация отрезков граничных
линий— приведение параметра t в интервал [0, 1]. Допустим, граничный уча-
сток сегмента находится на линии l(t) в интервале изменения ее параметра
t е [r„, rj с любым соотношением между числами г„ и th. Тогда нормализован-
ная граничная линия сегмента имеет параметрическое описание
g(0 = /О» + (О ~ Qt) Vr e [0, 1]. (3.65)
□ Наиболее сложным в построении линейно интерполяционным объектом явля-
ется граничная кусочная поверхность, называемая в [26, 29] линейной поверхно-
стью Кунса. Она задается четырьмя граничными линиями g(l), h(f), /(т) и г(т), об-
разующими объемный четырехугольник с угловыми точками (рис. 3.47)
woo = g(0) - 1(0), wio = g( 1) = ДО), woi - h(O) = /(1), wn = h( 1) - r(l).
Рис. 3.47
Как и в предыдущем случае, все граничные линии сегмента должны иметь па-
раметрическое описание в интервалах t е [0, 1] и т е [0, 1], иначе к ним необ-
ходимо применить операцию нормализации (3.65).
Выберем следующие краевые условия фиксации параметров гит:
• t = 0 на линии /(т);
• t - 1 на линии г(т);
• т = 0 на линии g(t);
• т = 1 на линии h(t).
Первоначально кажется, что для вычисления произвольной точки гранично
определенного сегмента можно использовать двухпараметрическую линей-
ную интерполяцию по методу (3.64):
P(t, т) = g(r)(l - т) + Л(г)т + /(т)( 1 - г) + Дт)г.
328
Гпава 3
Однако эта формула дает несовпадение с исходными данными во всех угло-
вых и граничных точках. Например, вместо угловой точки woo получим
р(0,0) = g(0) + /(0) = 2woo * woo,
а граничная линия g(t) интерполируется искаженной кривой
p(t, 0) - g(t) + woo( 1 - Z) + mot^g(t).
Причина ошибок — двойное вхождение угловых точек в формулу интерполя-
ции. Скорректируем ее вычитанием лишних слагаемых:
p(t, т) = g(t)(1 - т)+ й(/)т + /(т)(1 - z)+r(r)t -
-«00 О _,)С “т)-иО10 -z)t-wi,zt
(3.66)
Теперь не трудно убедиться, что правильность интерполяции восстановлена:
р(0, 0) = g(0) + /(0) - woo = woo
p(t, 0) = g(t) + Z(0)( 1 - z) + r(0)t - woo(l - Z) - wioZ = g(z).
В кинематическом аспекте поверхность (3.66) формируется движением поли-
морфной образующей по двум направляющим. Ее каркасные линии состав-
ляют две системы полиморфных кривых:
• P(t„ т) — от р(0, т) = /(т) кр(1, т) = г(т);
• p(t, г,) — от p(t, 0) = g(t) к p(t, 1) = h(t).
Сложная поверхность, состоящая из множества сегментов, конструируется
как система кусочных поверхностей, соединенных друг с другом по гранич-
ным линиям. Общий недостаток рассмотренных методов кусочной интерпо-
ляции — негладкость поверхности в точках и на линиях стыковки сегментов,
поскольку модели поверхностей сегментов строятся индивидуально без учета
взаимного влияния.
Испытаем алгоритмы (3.63), (3.64) и (3.66) на примере построения кусочной
поверхности зуба. Зададим в пространстве 17 узловых точек, образующих
каркас полигональных сегментов, организованных по схеме 2x8 (рис. 3.48):
Рис. 3.48
Математические модели поверхностей и объектов
329
• билинейная кусочная поверхность, изображенная на рис. 3.49, а, состоит из
восьми плоских треугольников и восьми косых четырехугольников;
• продольные граничные линии сегментов гранично-линейной поверхности,
построенной на рис. 3.49, б, получены полиномиальной трехточечной ин-
терполяцией по (3.38) и (3.39), при этом линейчатые поверхности всех сег-
ментов неплоские;
• наиболее эстетично в сравнении с предыдущими моделями выглядит по-
верхность зуба с гранично-кусочными сегментами, все граничные линии ко-
торых являются интерполяционными полиномами (рис. 3.49, в).
Рис. 3.49
3.1.4. Сплайны
Кусочно-линейная интерполяция кривых линий отрезками прямых и поверхно-
стей плоскими сегментами дает нулевой порядок непрерывности. Негладкость
полученного решения выражается в изломах, т. е. разрывах производных в узло-
вых точках. Для повышения порядка непрерывности используются более глад^
кие функции интерполяции, чем линейные. Широко распространенные в прак-
тике интерполирования полиномы Лагранжа (3.37) или Ньютона имеют степени,
зависящие от числа узлов. Их главный недостаток— большие межузловые ос-
цилляции, появляющиеся уже при степенях полиномов, равных 6 -? 8. При числе
узловых точек кривой, большем десяти, интерполяция глобальным полиномом
становится непрактичной.
Более предпочтителен другой подход— использование кусочной интерполяции
гюдкими полиномами невысоких степеней (сплайнами). Подробное изложение
теории и практики сплайн-интерполяции приведено в [20, 26, 29]. Из богатого
многообразия сплайновых методов приближений кривых и поверхностей мы
рассмотрим построение интерполяционных сплайн-функций по оригинальному
330
Глава 3
алгоритму, вычисляющему сразу все параметры кусочных полиномов решением
системы линейных алгебраических уравнений (СЛАУ) высокого порядка, и его
рекуррентной модификации, требующей обращения матриц только четвертого
порядка независимо от числа узлов.
Для обеспечения непрерывности сопряжения кусочных полиномов в узловых
точках линии или поверхности по нулевой, первой и второй производным дос-
таточно использовать кубические сплайны, дающие минимум интегральной кри-
визны сплайнового объекта. Интерполяционным кубическим сплайном называется
кусочно-определенная функция, обладающая следующими свойствами:
П она проходит через все узлы интерполяции;
□ на каждом интервале интерполяции описывается кубическим (линия р,(0) или
бикубическим (поверхность рДг, т)) полиномом;
□ кусочные полиномы гладко, т. е. с непрерывными первой и второй производ-
ными, сопрягаются друг с другом в узлах интерполяции.
Механический аналог кубического сплайна— гибкий упругий стержень, прохо-
дящий в пространстве через заданные узловые точки при определенных краевых
условиях. Повинуясь физическим законам, стержень занимает положение с мини-
мумом потенциальной энергии изгиба, пропорциональной интегральной кривизне
л ,
XJo'ftVd'-
/=1
Аналитическое решение этой экстремальной задачи имеет вид кусочно-
кубической параметрической функции.
Рассмотрим методы получения кубических сплайнов и их использование.
3.1.4.1. Сплайновые кривые
Даны узловые точки
У, z,]V/=0, п,
пронумерованные в порядке их соединения в конструируемой сплайновой кривой
(рис. 3.50).
Рис. 3.50
Математические модели поверхностей и объектов
331
Число интервалов интерполяции равно п. Координатные
xi (0— s0xi +slxit + s2x^ + s3xi* ’
У^)- s0yi + slyit + s2yd + s3yi^ >
+i 0)~ s0zi "* slzi^ "* s2zi^ "* s3zit
и векторная
s0xi s0yi s0zi
/?,(,)= [1 / t2 f3]s, ^I>7 Sjz/
____ 9где oy —
V/e [o, </,], z = l, и s2xi s2yi s2zi
s3xi s3yi s3zi
(3.67)
функции сплайна содержат 12л неизвестных коэффициентов— элементов мат-
риц Sj. Их однозначное определение требует составления и решения совместной
системы 12л скалярных или 4л векторных уравнений, исходя из перечисленных
свойств сплайна.
□ Условия фиксации сплайна в узловых точках р,(0) = и p,(d,) — и дают 2л век-
торных уравнений
[10 0 O|Sj =«,_!,[) di d2 </?]$, =и,-Vz = l^. <3-68>
□ Условия двойной гладкости сплайна во внутренних узлах
Pi (di) = Pi+l (°) > A'U ) = A+l (°)’
т. e. непрерывности двух производных
p;(r)=[o 1 2t 3r2]s,, /<(/)= [o 0 2 6/].S„
дают 2(л - 1) уравнений
[о 1 2d. 3^2k=[0 1 О 0]s,+I, (369)
[о 0 1 Зб7,Х =[О 0 1 o]si+1 V/ = l, и-1.
□ Оставшиеся 4л-2л-2(л-1) = 2 векторные уравнения составляют краевые
условия, налагаемые на параметры сплайна в крайних узлах w и ин. Они могут
варьироваться в зависимости от специфики строящейся кривой:
• свободные концы с нулевой кривизной
Х(°)= P'Adn)=°3
дают уравнения
[0 0 1 O]Sj = О3, [0 0 1 Зб/„К=О3; (3.70,а)
332
Глава 3
замкнутый сплайн должен кроме совпадения узлов ио - и„ удовлетворять
условиям гладкого сопряжения концов
Р$)=РгМ, Р1'(0)= Pn(dn):
[О 1 О 0]S,=[0 1 2dn 3d* К,
, [о 0 1 o]S] = [о О 1 3<js„;
• закрепленные концы с направлениями
а(о)=Го, p'M = Vn
дают уравнения
[О 1 0 o]s, = Ио, [о 1 2d„ 3d^]S„=P„. (3'70>в)
Могут быть и смешанные краевые условия с соответствующими уравнениями
(3.70). Например, для сплайна со свободным концом в узле ио и заданным на-
правлением Vn в узле и„ уравнения краевых условий примут вид
[о 0 1 0]$!=03,[0 1 2dn 3dl\Sn=Vn.
Совокупность уравнений (3.68) - (3.70) дает СЛАУ
QS= U => S = Q~>U (3.71)
с матрицами (верхние буквенные индексы в блоках 0 и Qi соответствуют вари-
антам краевых условий в (3.70))
Й1 Qi ОдХ4 О 4x4 А'
Q= О 4x4 . а О 4x4 О 4x4 С1.Л-1 • С>4х4 Qi 64 . е R4"x4", S = А. 6 r4"x3, и = е R4nx3
0 0 ' 'о 0 0 0
d] 0 0 0 0
2dt 3dj > Qi - 0 -i 0 0
1 3di_ 0 0 -1 0
0 0 0 0' '0 0 0 o'
eja) = 0 0 0 0 0 0 10 , ej6)=e2> eiB) = 0 0 0 0 0 10 0
0 0 0 0 0 0 0 0
'10 0 o' '10 0 o'
e?) = 1 dn d„ d3n 0 0 0 0 , o^=oln, eiB) = 1 dn d2n d3n 0 0 0 0 >
0 0 1 3dn 0 1 2dn 3d„
Математические модели поверхностей и объектов
333
Поясним принцип формирования матричных блоков Qiit Q2, Q3, Q4 и U,. Выпол-
нив блочное умножение в (3.71), получим развернутую запись СЛАУ в виде
Й1^1 + б2$2 -Ц>
й,л-1^л-1 +£?2‘<’л =^и-1»
£?3^1 + £?4*$л = ^п
(3.72)
Отсюда видно, что уравнениям (3.68) соответствуют первые две строки всех бло-
ков, уравнениям (3.69)— третья и четвертая строки всех блоков, кроме 0, (h и
Uj. Оставшиеся две строки заполняются согласно краевым условиям (3.70).
Особенности обращаемой в (3.71) матрицы Q.
□ высокая размерность 4п х 4л, что все-таки меньше размерности 12л х 12л, ко-
торая бы получилась при группировке неизвестных в виде вектора, а не блоч-
ной матрицы 5;
□ сильная разреженность, т. е. большое относительное содержание нулей, из-за
чего при решении СЛАУ выполняется много бесполезных арифметических
операций с нулем;
□ блочно-ленточная структура. Это свойство вкупе с невырожденностью бло-
ков Qti позволяет свести задачу одновременного нахождения всех матриц
Sj к- S„ к их последовательному вычислению при меньшей размерности обра-
щаемых матриц. Подставляя цепочкой матрицы
в последнее уравнение (3.72), получим рекуррентный алгоритм расчета пара-
метров кубического сплайна:
v/=«-i, 1.
334
Гпава 2
Знание параметров сплайна позволяет провести гладкую кривую через узловые
точки, используя координатные или векторное уравнения (3.67). Для получени»
промежуточных точек между узлами z'-ый интервал «,] дробится на N/ рав
ных частей А/, = df 1 N,. Вычисленные точки
Pi (k^ti) = [1 АА/,- (кЫ; У (k&i f ]s, Vk = 0, Nt
соединяются отрезками прямых. Отрезки на разных интервалах будут примерь
равной длины Л, если принять значения
пропорциональными длинам хорд, соединяющих узлы. При h = 1 и задании ко-
ординат узлов в пикселах сплайновая кривая будет выглядеть на экране дисплее
почти предельно гладкой.
До сих пор предполагалось, что известны интервалы [0, <7J изменения параметре
t на каждом из / = 1, п интервалов интерполяции. Поскольку узловые точки
могут располагаться в пространстве неравномерно, то значения d, должны быт«=
пропорциональны длинам дуг p,{t). Пока сплайн не построен, эти длины неиз-
вестны. Учитывая, что сплайновая кривая является наиболее гладкой, можно п
методу хордовой аппроксимации [26] принять значения
di= |«, — w,-i|
равными расстояниям между соседними узлами.
Можно, конечно, задать равные параметрические длины всех интервалов d, - 1 и
строить так называемый нормализованный сплайн, параметры которого рассчи-
таны по алгоритму (3.73) с постоянными числовыми матрицами (Д и Qu. Поле-
ченное решение отличается от сплайна с хордовой аппроксимацией чисел dt ка*
формой, так и меньшей гладкостью, а при равномерной дискретизации парамет-
ра t еще и разной плотностью промежуточных точек pKtk) на коротких и длин-
ных интервалах.
& Пример 3.16. Построить параметрическое семейство нормализованных куби-
ческих сплайнов в плоскости ху по трем узлам
w0 = [2 б], W| = [б 1], w2 — [б б]
с направлениями концов
г0=х[1 1], к2 = [-1 1]
для различных значений параметра X.
Математические модели поверхностей и объектов
335
$2(*)=U -mW'U (М-аег'ц),
51(л)=й-'(с/1 -Q2sM,
откуда
s,(x)=
X
-4.75-1.75Х
2.75 + 0.75Х
О
X
3.25-1.75Х
-2.25 + 0.75Х
> s2(x)=
О
-1.25-0.25Х
3.5 + 0.5Х
-2.25-0.25Х
1
-0.25-0.25Х
-3.5 + 0.5Х
2.75-0.25Х
2
Уравнения семейства сплайновых кривых на каждом из двух интервалов интер-
поляции и общее уравнение сплайна со сквозным параметром t имеют следую-
щий вид:
Pl(t,Х)=[2 + Хг-0.25(19+ 7Х>2 + 0.25(11 + ЗХ>3 Хг + 0.25(13-7Х>2 +0.75(Х-3>3 |,
Р2М =
= [-0.25(5 + Х> + 0.5(Х - 7>2 + 0.25(11 - X)/3 1 - 0.25(1 + X)/ + 0.5(Х - 7>2 + 0.25(11 - X)/3 ],
р(/,х)=
/?|(г,Х) при0</<1,
/?2(^_1Л) при1</<2.
На рис. 3.51, а построены сплайновые кривые для значений параметра
X е {-1, 1,3}, изменяющего вектор Vo направления сплайна в узле но. Отличие
графиков друг от друга свидетельствует о зависимости параметров и формы
сплайна как от направлений, так и от модулей концевых векторов Vo и V„. Дру-
гими словами, эти векторы характеризуют скорости изменения точек сплайно-
вой кривой в концевых узлах. Для сравнения пунктиром построен нормализо-
ванный сплайн со свободными концами.
336
Глава 3
На рис. 3.51, б приведены графики координат x(l. 1) и y(l, 1), состоящие из отрез-
ков кубических парабол, гладко сопрягающихся на границах интервалов интер-
поляции. О
& Пример 3.17. Построить трубчатую поверхность топологического объекта
известного как "узел Эшера" (рис. 3.52).
Рис. 3.52
Решение. Согласно (3.9) для построения каналовой, в том числе и трубчатой по-
верхности, необходимо иметь уравнение ее направляющей кривой рн(1). Ввид.
отсутствия аналитических выражений для координат xH(t) 4- zH(t) построим эта
замкнутую линию методом сплайн-интерполяции. Выберем семь узлов интерпо-
ляции в наиболее характерных точках пространства (рис. 3.53, а) при а= 14
Ь = 10, с = 4:
мо=мб = 1а с ui=la ~с м2= [-а cL
«3 = [/> а -с], = [с —b a],W5=[-c b а].
Математические модели поверхностей и объектов
337
Длины интервалов изменения параметра зададим по методу хордовой аппрок-
симации:
d\ =d^=d5 = 2^b2 + с2 =21.54, <72 =d$ =d(, = -J (я + б)2 + (a + c)2 -^(Zj-c)2 =33.35.
Рассчитав no (3.73) при условиях (3.70, 6) матрицы параметров сплайна
16 4 -10 16 -4 10
0.54 -0.627 0.284 -0.679 0.1 0.777
51 = , s2 = -0.044
-0.019 0.0019 0.067 -0.038 0.032
-0.0003 0.0005 -0.002 _ 0.001 -0.0005 0.0005
-10 16 4 10 16 -4
0.284 0.54 -0.627 0.777 -0.679 0.1
53 = , 54 =
0.067 -0.019 0.0019 -0.044 -0.038 0.032
-0.002 - -0.0003 0.0005 0.0005 0.001 -0.0005
4 -10 16 -4 10 16
-0.627 0.284 0.54 0.1 0.777 -0.68
s5 = 0.0019 0.067 -0.019 ,s6 = 0.032 -0.044 -0.038
0.0005 -0.002 -0.0003 -0.0005 0.0005 0.0011
получим направляющую кривую
Phi 0=[1 Z t2 t3 J5, tfZ e [0, d], i = Гб,
Рис. 3.53
координаты которой ,xH(z) 4-zH(z) в сквозном времени z е [0,164.7] изображены на
рис. 3.53, б. Каркас трубчатой поверхности узла Эшера на рис. 3.52 построен по
алгоритму (3.43) при r(z) = 3 и направляющих векторах И,(г) = [о 1 It 3z2pz. □
338
Глава .
Пример 3.18. Построить каналовую поверхность бутылки Клейна (приме:
3.13), используя узловые данные табл. 3.2 для сплайн-интерполяции направляю-
щей линии и радиуса образующей окружности.
Решение. Число интервалов интерполяции, судя по табл. 3.2, равно девяти, а и
параметрические длины <7, = г, - варьируются от d\ = 2 до dt, - 25. С учете*
различия в длинах более чем на порядок будем строить ненормализованнь
сплайновые функции.
Выберем краевые условия сплайнов:
П для линии p»(t) е R3 — закрепленные концы с направлениями
К0=[0 -1 о], К9=[о 1 О];
□ для функции радиуса r(t) е R1 — свободно закрепленные концы.
Результаты расчетов представлены на рис. 3.54 параметрическим p»(t), декарто-
выми Xh(z), J'h(z) и r(t) графиками, а на рис. 3.55, а— изображением каналово»
поверхности p(t, т). В сравнении с глобальной полиномиальной интерполяции
(см. рис. 3.39, 3.40) сплайн-интерполяция дает более гладкие решения на тех •
узловых точках (эстетические свойства объектов здесь не обсуждаются).
Рис. 3.54
На рис. 3.54, а пунктиром изображена нормализованная сплайновая кривая /м
а соответствующая каналовая поверхность построена на рис. 3.55, б. Нал>
ухудшение гладкости решений из-за неравномерного расположения узлов инт-" г-
поляции. □
Математические модели поверхностей и объектов
339
Рис. 3.55
3.1.4.2. Сплайновые поверхности
Дано (л + 1)(/н + 1) точек — узлов интерполяции
uij = U Уу zij ] V/ = 0, и, j = 0, те
з порядке их соединения в каркасе конструируемой сплайновой поверхности.
Индексы узлов i и j составляют сетку из пт прямоугольных ячеек (рис. 3.56). Каж-
дая (г',у)-ая четырехугольная (при совпадении соседних узлов некоторые ячейки
могут оказаться и треугольными) криволинейная ячейка поверхности описывается
бикубическим полиномом
лЛт)=[1
V/ е [о, </, ],
(3.74)
: трехслойными (по одному слою на каждую координату х,у и z) матрицами ко-
ффициентов Sy е R4X4X3, содержащими в сумме 48л/;г неизвестных параметров.
Их однозначное определение требует составления и решения системы из 16ллг
зекторных уравнений, исходя из условий, которым должен удовлетворять бику-
бический сплайн.
Д Условия фиксации поверхности в узлах:
А(0, 0) = л,_|.Л|,р,у(0, 8;) = u^.^Pi/di, 0) = и^,ру(ф, 8;) = Uy. (3.75)
Гпава 3
340
Рис. 3.56
О Условия двойной гладкости сплайна во внутренних узлах
Р^'}(д,,г)= рЙДо.т) Vtg f),67}
РуТТН'’б/)=Рич1(^0) V/e{o,J,}.
4n)U’6/)=H"iUi(o-o). P^(0,6y)=P^y+1(rf,4>0)
с производными
i it зг2Х
и частными производными
4П)('>*)=[о 1 2г 3r2Jsv
2т
Зт2
□ Краевые условия, налагаемые на производные сплайна в граничных узлах и,о, и^.
и(>] и u„j. Они могут варьироваться в зависимости от специфики решаемой задачи
• свободные границы дают условия нулевой кривизны поверхности на краях
4'’(4л)= р,Н,о)= .
r!fVo)=p£>(<.5j=P,W(<>,t)=^>fc.^=03 <3'77-‘
V/g{0, d,} ie{)>6J}>
Математические модели поверхностей и объектов
341
• замкнутый сплайн должен кроме условий совпадения узлов Wj - unj и
и/> - uim удовлетворять условиям гладкого сопряжения границ:
Р|;\о,г)= Р|у\о,г)= VTGk^,},
Рл\'-°)= Л’Л'ЛЛ V/e{o,dJ,
^’(0.0)’ Г&Ч U. 67-.). )= p£k»).
Могут быть и другие комбинации краевых условий. Например, возможен
сплайн цилиндрического типа с замкнутыми границами в узлах щ = uim и
свободными границами в utj и и„г Здесь не рассматриваются закрепленные
границы с заданными направлениями касательных векторов V\j, VaJ, C,i и Vitll,
т. к. эти краевые условия требуют задания большого объема неочевидных ис-
ходных данных.
Совокупность уравнений (3.75) - (3.77) составляет линейную систему
(3.78)
с матрицами
QS&= U^S= QlU&l
’01 02 • • О4Х4 ©4x4 Г-Su • *^1/77
0= С*4х4 . 0з ®4х4 ©4x4 • 0\,п-1 .. О4Х4 eR4"*4", s = $nl • С °/1/77 _ £ r4hx4«ix3
©11 02 • O4X4 04x4 T Ц1 . •• uim
e = 04x4 . 03 ©4x4 ©4x4 • ©l,wi-1 O4X4 02 ©4 . G R4"7*4™ у _ Pnl ^nm _ G R4nx4z”x3
блоки которых представляют собой матрицы
’10 0 0 ’ ’10 0 0 ’ 00 0 o’
1 di d? d? 1 5i 5? 0 0 0 0
01,= 0 1 2</, Ml , 6 1, = 0 1 25, 35? > 02 = 0-100
0 0 1 3dt 0 0 1 35; 0 0-10
’0 0 0 O' 1 00 o’ 1 00 o’
0ia) = 0 0 0 0 0 0 10 > Q(A a) = 1 0 dn dn dK 0 0 0 , ®4a) = 1 0 ° f” 0 0 S°!L
0 0 0 0 0 0 1 3>d„ 0 0 1 35m
342
Гпава 5
e3(6)=e2,^6M«>^6)=®i^
О3 О3'
Uti = Uy О3 О3 е R4x4x3
У Оз О3 О3 03
°з О3 О3 О3
Блоки Qi и Qu матрицы Q реализуют краевые условия в узлах гц; и unj, а блок
Ql и ©4 матрицы © — в узлах н,| и и,т.
Вычисление по (3.78) выполняется отдельно для каждого координатного ело»
трехмерных матриц U и 5. Из-за непреодоленной автором сложности матричнь
преобразований не удалось вывести рекуррентный алгоритм расчета параметре
бикубического сплайна, аналогичный алгоритму (3.73).
Каркасное изображение сплайновой поверхности благодаря криволинейны»
каркасным линиям является гладким в отличие от полигонального каркаса, по-
строенного на тех же узловых точках. Возможность расчета по (3.74) любы
промежуточных точек позволяет строить сплайновую поверхность с более ме.~
кими ячейками без нового расчета параметров сплайна. Для этого межузловыс
интервалы
k-l,y-b
дробятся соответственно на N; и Л/, равных частей Д/, = </, / N, и Дт, = 8;- / Л/;. Вс;
ячейки будут примерно равновеликими h х q-параллелограммами, если принять
max -------------1 *
й,„] n
При неравномерном распределении узловых точек в пространстве рекомендуете»
задавать параметрические длины интервалов d, и т, на основе метода хордов.
аппроксимации, усредняя расстояния между противоположными парами узле-
вых точек:
1 wi-l,/-l|+|wy м'-1,/| s-
л. = I—1--------- 1 1 у, 5 .
' 2 1
2
Задавая все значения dt8, - 1, получим нормализованную сплайновую повер i-
ность, параметры которой рассчитаны по алгоритму (3.74)—(3.78) с постоя—
ными числовыми матрицами Qi, ©i, Qi и ©4. Полученное решение отличаете»
от сплайна с хордовой аппроксимацией чисел </, и 8, как формой, так и хул-
шей гладкостью, а при равномерной дискретизации параметров гит еще »
разной плотностью промежуточных каркасных линий на коротких и длинн»
интервалах.
Математические модели поверхностей и объектов 343
Сплайновое описание поверхностей, приходя на смену полигональному, начина-
ет широко применяться в промышленных САПР для изображения корпусов ав-
томобилей, судов, самолетов, в медицине (компьютерная томография), карто-
графии (отображение рельефа местности), компьютерных играх (изображение
трехмерных объектов, в том числе и людей) благодаря возможности получения
зналитической формулы p(t, т) гладкой оболочки по ее экспериментальным уз-
ловым точкам utj. Имея уравнение поверхности, мы получаем возможность дос-
тупа к любой ее точке, преобразования, изображения в желаемой проекции, рас-
юта пересечений с другими поверхностями, изготовления натурной модели,
лрограммирования станка с числовым управлением и т. д.
2^ Пример 3.19. Построить нормализованную сплайновую поверхность со сво-
бодными границами по девяти точкам
^оо = [-1 о -1], «01 = [о -I -1], «02 = [1 о -1];
«Ю = [-1 1 о], «и=[о О о],«12=[1 1 0];
«20 ~ [“ I 0 1], «21 ~ [б ~' I 11 ’ w22 ~ t б 1],
принадлежащим гиперболическому параболоиду х2 - у - z2 = 0.
344
Гпава 3
Sx = -1 1 0 0 | 0 1 о o' 0 00010000 0 000'0000 0 0 0 0 > 0 0 0 0 0 -1.5 0 0.5 1 -1 0 1.5 -0.5' 1.5 0 0 0 I 1.5 0 0 0 0 000'000 0 -0.5 0 0 0 < -0.5 0 0 0
-i i о о! о 1 оо о oooloooo о oooloooo 0 000'0000 , Sy 1 -1.5 0 0.5 ! 0 0 1.5 -0.5 о ooolooo 0 -1.5 0 0 0 1-1.5 0 0 0 0.5 0 0 0 | 0.5 0 0 0
S2
-10 0 0
10 0 0
0 0 0 0
0 0 0 0
0 0 0 0
10 0 0
0 0 0 0
0 0 0 0
-10 0 0
10 0 0
0 0 0 0
_о_ о_о__о
0 0 0 0
10 0 0
0 0 0 0
0 0 0 0
Рис. 3.57
Подставив матрицы параметров в модель бикубического сплайна (3.74), пс г
чим координатные функции поверхностей четырех ячеек
Рц(?,т)=[т-1 1.5(г — t)+O.s(t3 -г3) г-1],
Р12^,т)=[т — 1 + l.s(r+ т2)—O.s(r3 +т3) г-1],
Математические модели поверхностей и объектов
345
Р21(^т)= [т“1 1 ~ 1-5+ т)+0.5(^3 + т3) г],
P22(f’T)=[c 1.5(т2 — Г2)+0.5^3 -т3) г],
каждая из которых локально определена в интервалах изменения параметров
/ е [0, 1] и те [0, 1]. Полное изображение сплайновой поверхности с узлами ин-
терполяции приведено на рис. 3.57. Каркасные линии построены через интерва-
лы дискретности А/ - Ат = 0.2. О
& Пример 3.20. Допустим, необходимо построить достоверное изображение
некоторого рельефа по измерениям высоту множества точек его плана {х;, z7}.
В качестве источника координат используем модель поверхности (3.62). Нало-
жим на план местности (карту линий равных высот) регулярную сетку с размера-
ми ячеек Ах = Az = 0.5 и координатами узлов
х,- = -2 + 0.5/ V/ = Ojj, Zj = -2 + 0.5j V/ = 0Л
после чего построим на этой 81-узловой сетке нормализованную сплайновую
поверхность со свободными границами (рис. 3.58). Налицо практически полная
идентичность этого изображения с образцом (см. рис. 3.43, б) благодаря выбору
частой сетки и совпадению ее узлов с вершинами и впадиной рельефа.
Рис. 3.58
Однако вдвое более редкое размещение 25 узловых точек с координатами
х,. = -2 + i V/ = 0~4, z; = -2 + j V/ = 0~4
дает сплайновую поверхность (рис. 3.59), существенно отличающуюся от образ-
да. Это объясняется выбором слишком редкой пространственной дискретизации
Лх = 1 и Az = 1, при которой почти все пиковые точки поверхности (кроме обо-
значенной цифрой 2) не совпали с узлами интерполяции и оказались "не заме-
зенными" алгоритмом построения сплайна.
346
Гпава 5
Рис. 3.59
Целенаправленным смещением всего лишь четырех узлов удалось на нерегуляр-
ной 25-узловой сетке получить сплайновую поверхность (рис. 3.60), весьма близ
кую к регулярной 81-узловой поверхности. Однако данный искусственный спо-
соб минимизации числа узлов интерполяции не отменяет изложенного ни,;
правила. О
Рис. 3.60
Вывод (пространственный аналог теоремы Шеннона—Котельникова)', при
строении сплайновой поверхности выбор интервалов дискретизации ограничен <
ху минимальными размерами элементов интерполируемого объекта. Для получ
достоверного изображения значение интервала дискретности по некоторой кос
нате должно быть хотя бы вдвое меньше длины минимального элемента.
В разд. 3.1.3 рассматривались три метода построения кусочно-определенных г-:~
верхностей. Сплайн-интерполяция — это еще один метод, дающий, возмож-
Математические модели поверхностей и объектов
347
наиболее гладкие решения. Для иллюстрации сказанного построим сплайновую
поверхность зуба по семнадцати узлам u9 V i = 0,2, 7 =0,8, изображенным на
рис. 3.48. Наиболее подходящими краевыми условиями сплайна являются замк-
нутость по границам и,о = up и свободные границы ио} и uij.
Поверхность зуба, построенная по алгоритму (3.74)—(3.78) и изображенная на
рис. 3.61, является, несомненно, более гладкой и эстетически привлекательной по
сравнению с результатами работы других методов интерполяции (см. рис. 3.49).
Рис. 3.61
3.1.5. Фрактальные множества
Многие объекты окружающего мира обладают свойством "самоподобия" или
геометрической инвариантности к пространственному масштабу. Если рассмат-
ривать эти объекты в разном масштабе, то постоянно обнаруживаются подоб-
ные фундаментальные элементы. Так, строение Вселенной от Метагалактики до
атома описывается сходными моделями типа "ядро—спутники"; строение гори-
стой поверхности или изрезанность морского берега выглядят примерно одина-
ково и с космической высоты, и с высоты птичьего полета, и с уровня человече-
ского роста. Все отличие лишь в разрешающей способности восприятия
изображения. Вообразим съемку береговой линии кинокамерой с трансфокато-
ром, имеющим регулируемое, но конечное угловое разрешение. При "наезде"
камеры на объект взору открываются неразличимые ранее фрагменты, сходные
по структуре с фрагментами предыдущего уровня разрешения. Такой процесс
укрупнения масштаба изображения принципиально отличается от увеличения
фотографии по ее негативу или от растяжения выделенного фрагмента растро-
вой картинки, при которых усиливается зернистость без появления новых более
мелких фрагментов.
Математическое описание бесконечно дробимых объектов уравнениями линий
или поверхностей чрезвычайно громоздко из-за необъятного количества мель-
348
Гпава 3
чайших фрагментов. Для преодоления этой трудности математиком Исследо-
вательского центра корпорации IBM Бенуа Мандельбротом в 1975 г. был вве-
ден термин "фрактал" (от лат. fractus — раздробленный, разбитый), а в 1982 г
опубликована основополагающая книга "Фрактальная геометрия природы"
где описаны фрактальные множества, их свойства, методы получения и изо-
бражения.
3.1.5.1. Фрактал Мандельброта
и алгоритмические фракталы
Мандельброт исследовал предельное (при к -» со) поведение последовательности
комплексных чисел
-i+i =zk +с. к = 0, \,2,... ,zo = с (3.79, а)
при различных значениях комплексных чисел с. Вместо арифметических опера-
ций с комплексными числами можно моделировать на плоскости ху движение
точек Zfr = [х£ у//], задаваемое двумя рекуррентными уравнениями координат:
**+1 = хк -Ук + Л+1 = 2а*Л + Су, £ = 0,1,2,..., Ло = cY, ^0 = су. (3.79, б)
Последовательность zk с ростом числа итераций демонстрирует поведение двух
типов (рис. 3.62) в зависимости от выбора начальной точки с = [сх с^]. Ее эле-
менты, эволюционируя по плоскости, либо постепенно уходят в бесконечность
(7), либо всегда остаются в определенной замкнутой области, совершая цикличе-
ское движение (2) или сходясь в точку (3). Математиками строго доказано, что
если при некотором к модуль |zA.| > г.шп, где гшт =2 — минимальный радиус рас-
ходимости множества Мандельброта, то далее последовательность расходится и
lim |^|=о°.
Л—
Множество точек с, для которых последовательность (3.79) не расходится, назы-
вается множеством Мандельброта. Весьма сложно доказывается [21], что это
множество связно.
Графическая интерпретация множества Мандельброта удивительно красива и
бесконечно разнообразна (рис. 3.63, 3.64). Для ее получения зададим исходные
данные итерационного процесса (3.79):
□ прямоугольное окно С с разрешением п х т точек;
□ значение гшш = 2;
□ максимальное число итерации ктах.
Условимся, что если точка zk вышла за пределы круга радиуса rmin, то расходи-
мость достигнута за к < ктЛх итераций и процесс (3.79) останавливается. При
|zA.| < rmin ВПЛОТЬ ДО к — А^тах расходимость отсутствует.
Математические модели поверхностей и объектов
349
2
I
О
-1
-2
-3
Рис. 3.62
Для каждой точки с,у 6 С, i = \,n, j = \,m запустим итерационный процесс и
сформируем матрицу М, элемент которой mtj е [1, Лтах] равен номеру итерации к,
на которой процесс был остановлен. Далее возможны варианты изображения
фрактального множества на плоскости или в пространстве.
□ В плоском варианте визуализации выведем матрицу М на экран как растр,
сопоставив элементам некоторую палитру из А'тах цветов. Например, мож-
но выбрать радужную палитру, у которой цвета и оттенки от фиолетового до
красного (или градации серого цвета) распределены по диапазону чисел мат-
рицы либо линейно (чем быстрее расходится последовательность в некоторой
точке с,7, тем темнее ее цвет), либо по другому закону. Яркие изображения
дают палитры с чередующимися контрастными цветами.
На рис. 3.63 приведены примеры использования различных палитр. В центре
черным цветом изображена область комплексной плоскости, содержащая все
множество Мандельброта. Окружающие центральный рисунок изображения
представляют масштабированные области в соответствующих квадратах. Все
фрактальные множества рассчитаны с разрешением 600 х 600 точек при
&гоах = 50-5- 200 (чем сильнее увеличение, тем больше максимальное число ите-
раций). Картинки верхнего ряда окрашены с помощью радужной палитры со
случайным порядком цветов.
□ Полагая числа т1} высотами некоторой поверхности в точках с,7, можно по-
строить объемное изображение множества Мандельброта или его части
(рис. 3.64), которое при специально подобранном освещении может выглядеть
и как скала с плоской вершиной (рис. 3.64, а), и как водопад (рис. 3.64, б}, и как
горная пещера (рис. 3.64, в).
350
Гпава 3
Рис. 3.63
Рис. 3.64
Математические модели поверхностей и объектов
351
Типичный фрактал, каким является множество Мандельброта, представляет со-
бой иерархический объект, состоящий из родительского тела в форме кардиоиды
и многочисленных потомков, повторяющих форму предков, от которых они от-
ветвляются. Самоподобие элементов фрактала хорошо прослеживается на
рис. 3.63. Связность множества означает, что его элементы, даже самого малого
размера, которые Мандельброт назвал "фрактальной пылью", не обособлены, а
соединены тончайшими нитями в одно целое. Продолжая процесс увеличения
пограничных областей, мы всюду видим бесконечное разнообразие форм, пора-
жающих гармонией, великолепием и поразительным сходством с изображениями
регулярно-хаотических явлений природы — молний, снежинок, ледяного узора,
инея на ветвях деревьев, кораллов, паутины, солнечных протуберанцев, звездных
скоплений, космических снимков поверхности Земли, колючей проволоки и т. п.
И все это неожиданное разнообразие порождено казалось бы несложным детер-
минированным алгоритмом (3.79) и небольшим объемом исходных данных для
его моделирования — границ области С, ее размеров лит, параметров останов-
КИ Anin и &тах. Поневоле хочется считать, что фрактальная геометрия описывает
природные формы, по-видимому, изящнее и точнее, чем евклидова.
"Почему геометрию часто называют холодной и сухой? Одна из причин заклю-
чается в ее неспособности описать форму облака, горы, дерева или берега моря.
Облака— это не сферы, горы— не конусы, линии берега— не окружности, и
кора не является гладкой, и молния не распространяется по прямой <...> Приро-
да демонстрирует нам не просто более высокую степень, а совсем другой уровень
сложности. Математики <...> предпочли все больше и больше отдаляться от
природы, изобретая теории, которые не соответствуют ничему из того, что мож-
но увидеть или почувствовать ..." (Б. Мандельброт, [21]).
Фрактальное множество Мандельброта принадлежит к классу алгоритмических
фракталов. При наличии достаточно развитой фантазии можно придумать мно-
жество других итерационных процедур общего вида
zk+l = F(zk, с), k = G,\,2, (3.80)
порождающих различные изображения. Например, если в (3.80) подставить
функцию
F(?k,c)=z£+c
с целым числом и > 2, то получим симметричное фрактальное множество, объе-
диняющее n - I множество Мандельброта. На рис. 3.65, а построена почти ре-
альная шестилучевая фрактальная снежинка, соответствующая значению п - 7.
Еще один алгоритмический фрактал получается на основе знаменитой формулы
(3.79). Ее модификация заключается в том, что комплексное число с фиксируется,
а элемент mtj матрицы М задает начальное значение zo, перебираемое дискретно
в области С. Результат моделирования этого алгоритма в области Се [-1, 1] +
+[-1, 1] i при с - 0.36 + 0.36 I, называется фракталом Жюлиа (рис. 3.65, б). Естест-
венно, возможны теоретически бесконечно глубокие погружения внутрь этого
фрактального множества, изображение которого напоминает фотографии спи-
352
Глава 3
ральных галактик, и всегда будут проявляться важнейшие свойства фракталов —
симметрия и самоподобие. Практическая глубина погружения ограничена раз-
личимостью точек Су, т. е. разрядностью процессора.
Рис. 3.65
Реализация третьего фрактального алгоритма
, -3~*+1
“Zr+l 3 ’
названного в [23] "Ньютон", показана на рис. 3.65, в. Итерационный процесс
(3.80) останавливается при
|“Zr+l — 1| — rmin >
где rmin « 1 — радиус кругов сходимости с центрами в точках (1,0), (0, i), (-1,0)
И (0, -i), Либо При ДОСТИЖеНИИ к = ктах.
Фрактальные свойства можно обнаружить в самых, казалось бы, обычных алго-
ритмах. Например, при расчете корней функции f (z) в комплексном пространст-
ве итерационным методом zt.+l = k(zt) обычно полагают, что области сходимости
начальных приближений zo к корням z<°> *- z^ имеют фиксированные и гладкие
границы. Моделирование, однако, показало, что они, в действительности, фрак-
тальны. Для доказательства этого факта на рис. 3.66 построены области сходи-
мости к восьми корням полинома
/(z)=n(-2«),
1=1
четыре из которых z<’> - -2, z<2> = 0, z<3> = 1 и z<4> = 3 — действительные числа, а
четыре образуют две комплексно-сопряженные пары z<5 6> - -3 ± i и z<7 8> = 1 ± 3 i.
Для вычисления корней, обозначенных на плоскости ху белыми точками, ис-
пользовался итерационный метод Ньютона
Математические модели поверхностей и объектов
353
с условием остановки |/(zi+| )| < 0.01. Принадлежность начальной точки zo к об-
ласти сходимости корня z<’> определялась по минимальному расстоянию
\zk -z^| —> min VZ = 1,8.
Рис. 3.66
При внимательном рассмотрении изображения на рис. 3.66, с можно увидеть
восемь главных областей и множество маленьких "островков" вблизи их границ.
Масштабные увеличения приграничных областей выявляют новые элементы
фрактального множества, неразличимые при меньших разрешениях
(рис. 3.66, б, в). Таким образом, моделирование работы итерационных алгорит-
мов вычислительной математики практически доказало фрактальность областей
сходимости корней нелинейных уравнений.
3.1.5.2. Геометрические фракталы
В отличие от алгоритмических фракталов представители другого класса — гео-
метрических фракталов — реально осязаемы и могут быть до некоторого раз-
решения, позволяемого остротой зрения мастера, умением и твердостью его рук,
изготовлены из проволоки (линейные объекты), тонкого листа фольги (пло-
щадные объекты) или в объеме. Геометрические фракталы строятся на основе
исходной фигуры — линии, полигона, полиэдра — путем ее дробления и выпол-
нения аффинных и логических преобразований (объединения или исключения)
полученных фрагментов. Метод построения фрактального объекта может быть
как итерационный, так и рекурсивный, причем последний чаще бывает богаче
возможностями и проще в программировании.
Рассмотрим, например, процесс формирования плоской линии Коха — линейного
фрактального объекта, строящегося на отрезке прямой ab путем разбиения его
на три равные части ас, cd и db, построения на средней части равностороннего
треугольника с вершиной е и удаления отрезка cd. В результате отрезок ab пре-
вращается в ломаную линию acedb (рис. 3.67, а). Эта простая процедура повторя-
354
Гпава 3
ется многократно для каждого отрезка полученной линии (рис. 3.67, б, в) до тех
пор, пока длины разбиваемых отрезков не станут меньше заданного значения 5.
Так как после первого же разбиения отрезок становится полилинией, то способ
построения фрактала Коха на отрезке естественно обобщается на ломаную ли-
нию, заданную списком вершин Р = {pt pi...р„} (рис. 3.67, г), в том числе и
линию, замкнутую в полигон (рис. 3.67, д). В частном случае полигона в виде
правильного треугольника получим фрактал, называемый "снежинкой Коха"
(рис. 3.67, е).
Для того чтобы линия Коха, построенная на выпуклом полигоне, не имела само-
пересечений, она должна находиться с его внешней стороны. Это легко обеспе-
чить, определив по (1.50) направление обхода полигона D = dir_test(P). Тогда
при D - 1 точки е строятся справа, а при D = -1 — слева от отрезков.
Составим итерационный алгоритм построения линии Коха KOCHit(P, D, 5, т) на
ломаной линии Р- {pt pi ...р„} с ориентацией, заданной числом D е {-1, 1}, ми-
нимальной длиной разбиваемого отрезка 5 и максимальным числом итераций т
(рис. 3.68).
Работа алгоритма начинается с формирования матрицы вращения
Rot = R(-Dn 13)
на угол 60° в направлении -D. Далее в цикле итераций к = 1, т определяется чис-
ло звеньев ломаной линии n-size(P), формируется список L= {pi} из первой
вершины полигона Р и начинается цикл обработки отрезковPiP,+{ Xfi = 1, д-1:
П находится третья часть вектора направления г-го отрезка
к= А+1~А
3
Математические модели поверхностей и объектов
355
Если 3| F] < 5, что означает достижение предела разбиения отрезка, то в спи-
сок L добавляется очередная вершина p,+t и цикл выполняется для следующе-
го значения i = i+ 1;
Рис. 3.68
□ в противном случае в список L добавляются новые точки
с = pt + V, е - с + V • Rot, d - р,-н - V
и вершина pt. Точку е можно найти и без использования матрицы вращения
Rot. Достаточно с помощью (1.8) построить £>-стороннюю нормаль
N - D^y - ЕЛ ] и получить точку
е = с + 0.5(и +
как вершину правильного треугольника {cdec} (см. рис. 3.67, а).
По завершении обхода всех отрезков ломаной Р = {pip2...pn} линия Коха на
А'-ой итерации разбиения сформирована. Список L переименовывается в Р и
цикл итераций выполняется для следующего значения к = к + 1 и нового списка Р.
По достижении значения к = т алгоритм завершает работу возвращением спи-
ска Р вершин ломаной Коха в порядке их следования. В случае необходимости
готовый фрактал рисуется на экране как последовательность отрезков между
вершинами списка Р.
356
Глава 3
Гибкие правила прекращения разбиения отрезка позволяют управлять видом
линии Коха. Например, если задать значение б - 0, то на всех отрезках ломаной
независимо от их длины будет выполняться ровно т итераций разбиения. При
задании достаточно большого числа итераций т отрезки будут дробиться до тех
пор, пока все их длины не станут меньше значения 5.
Для исключения "холостой" работы, когда все отрезки стали короче 5, а до зна-
чения к = т еще далеко, в алгоритме KOCHit используется флажок /, обнуляе-
мый в начале итерации и устанавливаемый в единицу после первого разбиения
отрезка. Если же на некоторой итерации не было ни одного разбиения, то по
признаку/= О алгоритм прекращает работу и возвращает список Р.
Рекурсивная функция построения линии Коха KOCHrec(L, b, D, 5, гес) настолько
проста, что нет необходимости оформлять ее в виде блок-схемы. Получив
на входе список L вершин построенной части линии Коха (последняя из них яв-
ляется началом следующего отрезка ab), точку Ь, параметры D, 5 и число гес раз-
биений отрезка ab (по одному за каждую рекурсию), функция работает следую-
щим образом.
& KOCHrec(L,b,D,b,rec)
{<•/ = Ц,-м, V=(b-a)/3',
если {гес = 0}U{3r|<5}, то
// начало отрезка и треть его вектора
// условия остановки разбиения отрезка
Нпе(а, Ь)',
возврат L};
с - а + V, d = с + У,е = с + V R(-Dk I 3);
L = KOCHrec(L, c, D, 5, rec -
L - KOCHrec(L, e, D, 5, rec -
L - KOCHrec(L, d, D, 5, rec -
возврат KOCHrec(L, b, D, 5, rec - 1);
1);
1);
1);
// добавление в список новой точки
// рисование отрезка
// выход из рекурсии
// точки разбиения отрезка
// разбиение отрезка ас
И разбиение отрезка се
// разбиение отрезка ed
И разбиение отрезка db
Перед первым обращением к функции нужно в список L занести начальную точ-
ку отрезка или ломаной, на которой строится фрактал Коха. Например, одно-
кратное вычисление
L = KOCHrec(a, b, D, 5, гес)
строит /^-ориентированную линию Коха на отрезке ab и формирует в L список ее
вершин. Для построения фрактала на ломаной {/л pi ...рп} создается начальный
список L = {pt}, а затем в цикле
L = KOCHrec(L,ph D, 5, rec) Vz = 2, п
рисуются линии Коха на отрезках р,.
Математические модели поверхностей и объектов
357
Минимальные изменения функций KOCHit и КОСНгес позволяют итерационно
либо рекурсивно строить на средней части каждого отрезка не равносторонний
треугольник, а квадрат, как показано на рис. 3.69, а. В результате получаются
интересные фрактальные узоры в виде непрерывных непересекающихся ломаных
линий. На рис. 3.69, б, в эти линии построены на сторонах квадрата
Р— {р\ргрзрлр 1} по рекурсивному алгоритму с параметрами 5 = 0, тес = 2,
тес — 3 и с чередованием ориентации точек е и f на смежных уровнях рекурсии.
А если в цикле перечисления сторон квадрата обращаться к рекурсивной функ-
ции с параметром (-!)'£>, то получится не менее красивый фрактальный узор,
изображенный на рис. 3.69, г.
Рис. 3.69
Обладая симметрией и завораживающей гармонией, геометрические фракталы
Коха и подобные им линии имеют несомненное эстетическое значение и практи-
ческое применение как выразительные элементы оформления различных узоров
и орнаментов.
Пожалуй, наиболее популярным линейным геометрическим фракталом, служа-
щим такой же визитной карточкой фрактальной темы, как и множество Ман-
дельброта, является ветвь папоротника (рис. 3.70). Разработаем рекурсивный
алгоритм построения изображения этого фрактального объекта. Целесообраз-
ность использования рекурсии основана на подобии всей ветви любому ее листу.
Ключ к успешному решению задачи имитации объектов природы — точное со-
блюдение пропорций их элементов. Заключим оригинальное изображение ветви
в прямоугольное окно и проведем необходимые линейные и угловые измерения
между опорными точками pt> 4-рз, лежащими на концах ветви и двух нижних ли-
358
Глава 3
стьев. Вычислим длину листа d = [оо -рз|, высоту окна Ло - r/cos(<po) и коэффици-
енты пропорций
. _ h) ~л| , _ ко -^1
Ч-------'1---’ *2 - ,
(3.81)
m, , I" ~ ^1 h. - gj, . I'v ^1.
1 d 2 d d
Составим следующую рекурсивную функцию построения ветви папоротника.
Ро
Рис. 3.70
& fern(pv, h, ц/, side, 8, rec)
{если {rec = 0}lJ < б}, то выход; // выход из рекурсии
Р1 = Ро + [о *1#) , Pi = Ро + fa ; Н точки ветвления
line(po, pi)', И рисование линии в окне О
fern(pi, mih, у - side(ipi + сро), -side, 8, rec - 1); // построение листа в окне 1
fern{pi, mih, у + side(tyi + сро), side, 8, rec - 1); // построение листа в окне 2
fern(pi, mih, у - side(^s - <po), side, 8, rec - 1); // построение листа в окне 3
При обращении к функции ей передаются данные, определяющие расположение
ветви в окне:
□ РО = tx0 Уо] — координаты начальной точки на осевой линии окна;
□ h — высота ветви;
□ Ф — угол отклонения ветви от вертикали;
Математические модели поверхностей и объектов
359
□ side = ±1 — направление изгиба ветви вправо (+1) или влево (-1) от оси окна;
□ 5 — минимальная длина ветвящегося отрезка;
□ тес — максимальное число рекурсий ветвления.
На каждом уровне рекурсии в текущем окне 0 высотой h алгоритм вычисляет
точки pi и pi, лежащие на осевой линии окна на расстояниях \popt\ = kth и
[ро- kih от точки ръ, затем рисует отрезок ръpi и трижды рекурсивно вызывает
себя с параметрами подобных окон 1,2 и 3:
□ точками ветвления pt,pi и рг,
□ высотами пп h, mi h и ms h\
□ углами отворота от осевой линии -(<р। + <ро), (рз + (ро и —((рз - (ро);
□ направлениями изгиба листьев относительно изгиба ветви согласно схеме на
рис. 3.71, а;
□ параметром 5;
□ декрементированным значением rec - 1.
Предусмотрено два альтернативных условия прекращения ветвления:
□ по исчерпанию заданного числа рекурсий гее,
□ по достижению длины отрезка ki h, меньшей пороговой длины 8.
Задание 8 = 0 позволяет построить ветвь точно за тес рекурсий. При этом общее
число отрезков, составляющих изображение ветви, равно
Nrec = 1 + 3(1 + 3(1 + ... + (1 +3)))=УЗ'-' =О.5(ГС-1). (3.82)
<=1
Ветвь на рис. 3.71, б построена при тес = 5 и состоит согласно (3.82) из 121 отрез-
ка, причем многие из них имеют размеры меньше пиксела и просто не видны.
Задание параметра 8 > 0 при достаточно большом значении тес вынуждает алго-
ритм строить ветвь до тех пор, пока длина всех ее отрезков не станет меньше 8.
Такой прием позволяет регулировать густоту ветви, глубину вложения рекурсий
и сильно от нее зависящие необходимые машинные ресурсы. Оценка максималь-
ной глубины рекурсии, необходимой для достижения разрешения 8, следует из
соотношения
^2м3^0 < 5 >
откуда получаем
(3.83)
360
Глава 3
Рис. 3.71
Ветвь папоротника на рис. 3.71, в построена по угловым измерениям оригинала
ветви на рис. 3.70 и коэффициентам (3.81):
(ро» 14.9°, ср। » 37.7°, <р2« 36.8°, срз« 17.6°; (3.84)
кл = 0.0483, к2 = 0.162, пи = 0371,тг = 0.336, тз = 0.849. (3.85)
Высота экранного окна задана равной h = 200, минимальная длина рисуемого
отрезка 5 = 0.5. Фактическая глубина рекурсии и количество цветовых оттенков
изображения составили г = 30, что точно удовлетворяет оценке (3.83):
гео
1п(0,0077)
1п(0.849)
Для повышения реалистичности изображения ветви можно с переходом на сле-
дующий уровень рекурсии уменьшать толщину рисуемой линии, а также изме-
нять ее цвет. Наиболее реалистичные фрактальные изображения, лишенные
строгой гармонии, так не свойственной объектам природы, строятся методом
управляемой случайности.
Суть метода в том, что в детерминированный процесс сознательно вносятся помехи
с желаемыми стохастическими параметрами. В алгоритме построения ветви папо-
ротника можно, например, случайно смещать точки ветвления р\ и рг вдоль осевой
линии или вносить небольшие изменения в углы ветвления epi (рз. На рис. 3.71, г
показана реализация алгоритма со случайными воздействиями на углы ср> (р?
из (3.84) аддитивных помех т?и/(20°) - 10°, равномерно распределенных в интервале
(-10°, 10°). Где-то в лесу я видел именно такую ветку папоротника!
По алгоритмам, устроенным подобно рассмотренному, можно получать изо-
бражения фрактальной травы, кустарников и деревьев. Вся изюминка заключа-
ется в выборе небольшого числа параметров, определяющих форму растения.
Например, функция fern использует девять глобальных параметров к\, кг, пи пг
и (ро 4- (рз. В совокупности с аргументами общее число скалярных данных, необ-
ходимых для построения фрактального изображения ветви папоротника, равно 16
Математические модели поверхностей и объектов
361
Вместе с текстом программы это не сравнимо с объемом массива, необходимого
для хранения изображения ветви в любом из графических форматов, даже наи-
более плотно упакованном.
Вот парадокс! Такие сложные изображения создаются с помощью чрезвычайно
малого числа исходных данных. Здесь кроются богатые практические возможно-
сти фрактальной геометрии: описывая объекты на фрактальном языке, мы мо-
жем значительно уменьшить объем информации, необходимой для построения
изображения, хранения его в памяти компьютера или передачи по сети. А внося
в алгоритм элементы управляемой случайности, можно получать такие разнооб-
разные, неожиданные и изумительно красивые изображения, что никакой самый
изощренный фантазер не сможет придумать всего того, на что способна одна
простая фрактальная программа.
Строительными элементами площадных (именно площадных, а не двухмерных)
геометрических фракталов служат плоские полигоны, чаще всего трех- и четы-
рехугольники. Самым знаменитым фракталом этого класса является треугольник
Серпинского, строящийся путем разбиения треугольника — не обязательно рав-
ностороннего — средними линиями на четыре подобных треугольника, исклю-
чения центрального и рекурсивного разбиения угловых треугольников до полу-
чения площадных элементов желаемого или минимально видимого разрешения
(рис. 3.72). Существует простой стохастический алгоритм поточечного построе-
ния треугольника Серпинского [36], работа которого иллюстрируется на
рис. 3.73, а.
Рис. 3.72
& Шаг 1. Внутри исходного треугольника pi рг рз генерируется случайная точка:
t - rnd{\), т = rnd(l - t),qo = pi + (pi-pi)t + (рз-/л)т.
В более детерминированном варианте алгоритма точка
_Р1+р2+Рз
<70 -----~----
выбирается в центре треугольника.
Шаг 2. Задается число т итераций генерирования случайных точек.
362
Гпава 3
Шаг 3. В цикле k = 1, т генерируется случайное целое число — номер
и = [гл7б/(з)~|е {1, 2, з}
одной из вершин треугольника р„, с помощью которой вычисляется и рисуется
точка
®——
в середине отрезка рг. СЗ
Благодаря выбору точки qo внутри треугольника р\ piрз центр отрезка qo р„
(точка q\) никогда не окажется внутри центрального треугольника, отмеченного
на рис. 3.73, а пунктиром. При достаточно большом числе итераций т генери-
руемые точки qk образуют случайный узор, предельная форма которого стремится
к треугольнику Серпинского. Результат работы алгоритма при т = 20 000 пока-
зан на рис. 3.73, б. Следует отметить, что небольшое число начальных точек </,
все-таки может попасть в запретные области. В частности, это случится при вы-
боре точки qo в центре треугольника pi pi рз. Тогда точка q\ всегда окажется в
центре любого из угловых треугольников, т. е. в запретной области.
Рис. 3.73
Внеся в алгоритм три изменения, а именно
П задание четырех точек в пространстве р\ pi,
П выбор начальной точки по формуле
qo = pi + (pi pi)t + (рз-р\)т + (pi - pi)0 e R’,
где l = rnd(\), т = rnd(\ - t) и 0 = rnd(l - t - t),
□ интервал генерирования случайного номера вершины
и = [гиг/(4)"|е {1, 2,3, 4},
получим стохастический алгоритм построения треугольной пирамиды Серпинско-
го— объемного фрактального объекта, аналога одноименного треугольника
Результат работы этого алгоритма за т = 5 000 итераций показан на рис. 3.73, в
Математические модели поверхностей и объектов 363
В задачах компьютерной графики фрактальная технология получила наиболь-
шее распространение при формировании объектов природного ландшафта —
линии горизонта, неровных поверхностей, холмов, гор, каньонов и прочих нере-
гулярных образований. Построение основано на рекурсивном разбиении исход-
ного объекта средними точками и смещении этих точек по методу управляемой
случайности. Начальные объекты выбираются из простых геометрических фи-
гур — отрезков, треугольников, прямоугольников, тетраэдров. Управление слу-
чайными параметрами алгоритма заключается в уменьшении смещения средних
точек элементов по мере уменьшения их средних размеров.
Изучение методов формирования объектов фрактального ландшафта начнем с
построения фрактальной ломаной линии (ФЛЛ) на некотором базовом отрезке ab.
В практических применениях она может изображать след молнии, траекторию
случайного блуждания некоторой частицы (броуновское движение) или линию
горизонта неровной местности. Эта хорошо заметная линия разделяет светлую
область неба, где рисуются фрактальные облака, и темную область земли с
фрактальными деревьями и травой.
Построение ФЛЛ еще проще, чем линии Коха, особенно в рекурсивном исполне-
нии. Обозначим за rf (о) функцию генератора центрированных (с нулевым сред-
ним) случайных чисел (ГСЧ), распределенных по некоторому закону с параметром
разброса о. Например, это может быть равномерное распределение в интервале
(-о,о) или нормальное распределение со среднеквадратичным отклонением
(СКО), равным о. Нецентрированные случайные числа со средним значением р
генерируются по формуле р + rf (о). При необходимости можно использовать и
другие менее распространенные законы распределения случайных чисел.
На рис. 3.74 показаны первые три шага разбиения отрезка ab с управляемо-
случайными ортогональными смещениями средних точек разбиваемых отрезков.
Величина \cd\ конкретного смещения средней точки отрезка с есть реализация
ГСЧ rf (Х|яй|). где X — коэффициент пропорциональности параметра разброса о
к длине отрезка \ab\. Например, при использовании равномерного ГСЧ
rf (а) = rnd(2c) - ст е (—ст, ст)
смещение средней точки будет равновероятно в интервале (-Х, X) единиц длины
отрезка.
Рис. 3.74
Рекурсивная функция FLLrec(L, b, "К, 5, гес) построения фрактальной ломаной с
аргументами L (список вершин построенной части линии, последняя точка кото-
рого а является началом следующего отрезка ab), точку Ь, параметры X, 5
364
Гпава 3
(минимальная длина разбиваемого отрезка) и гес (глубина рекурсии) работает
следующим образом.
£7 FLLrec(L, b, А, 5, гес) {a-LsiM, V=b-a; если {rec = 0}U {| К| < б}, то И начало отрезка и его вектор И условия остановки разбиения отрезка
{b->L; line(a,b)', возврат L}; И добавление в список новой точки И рисование отрезка // выход из рекурсии
с = a + 0.5 V, d = с + V • 7?(-л / 2) • rf (А| И]); И средняя точка и ее смещение
L = FLLrec(L, d, А, 5, rec - 1); И разбиение отрезка ad
возврат FLLrec(L, b, А, 5, rec - 1); И разбиение отрезка db
} □
Построение ФЛЛ на отрезке ab осуществляется однократным вычислением спи-
ска ее вершин L = FLLrec(a, b, К, 5, гес). Для генерирования фрактала на базово
ломаной линии {pipi...p„} инициализируется начальный список L = {pi}, после
чего в цикле
L - FLLrec(L,pj, А, 5, rec) \/i = 2, и
строятся ФЛЛ на базовых отрезках рг1 р,.
На рис. 3.75 показаны три реализации алгоритма FLLrec на базовом отрезк.
единичной длины с применением равномерного ГСЧ, параметров
А е {0.1,0.2, 0.3}, 5 = 0 и гес - 8. При моделировании с разными значениями г
установлены следующие закономерности, проявившиеся в некоторых реализаци-
ях ансамбля:
П при 0.2 < А < 0.3 линия имеет участки с попятным движением, т. е. перестае-
быть однозначной в ортогональном направлении к базовому отрезку;
П при А > 0.3 на ломаной линии появляются петли, что затрудняет ее использо-
вание, например, как линии горизонта.
Таким образом, алгоритм рекомендуется использовать при значениях параметра раз-
броса ГСЧ А < 0.2, нежелательно — при 0.2 < А < 0.3 и противопоказано при А > 0.3.
Для выработки дальнейших практических рекомендаций по использованию ал
горитма FLLrec с равномерным ГСЧ предпримем небольшое статистическое ис-
следование. Каждая ФЛЛ, построенная за гес рекурсий разбиения отрезков сре_
ними точками, состоит из n = + 1 вершин _у,],/е[1,л] и имее~
индивидуальные максимальное и среднеквадратичное отклонения от базовогс
горизонтального отрезка:
(3.86
Математические модели поверхностей и объектов
365
Важной статистической характеристикой ломаной линии {pi pi ...р„], отражаю-
щей ее непрямолинейность, является коэффициент удлинения — отношение сум-
мы длин отрезков ломаной к расстоянию между ее концами:
Х|р, - А+1|
у = 1=1_______
|Р1-Рл|
(3.87)
Зададим число М = 30 и набор значений X, = 0.01/ V/ =0, М . Для каждого X, рас-
считаем ансамбль из N = 1000 ФЛЛ с вычисленными по (3.86) отклонениями Т]А. и
<зк, а по (3.87) — коэффициентами уА.. Рассчитаем средние параметры ансамбля
। N 1 TV j 7V
Вер 77 °ср 7ср 77 (3.88)
” А=1 ” k=l /v А=1
Соответствующие графики приведены на рис. 3.76. Первые две зависимости хо-
рошо аппроксимируются линейными функциями, а третья — параболой:
Цср(А) « ТК / 3, Оср(Х)» 0.2Х, уср(А) « 1 + 6АА (3.89)
Рис. 3.76
366
Гпава 3
Итак, в (3.89) нами получены усредненные зависимости максимального и сред-
неквадратичного отклонений и коэффициента удлинения фрактальной ломаной
линии от параметра разброса X генератора равномерно распределенных случай-
ных чисел. Теперь стало возможным как оценить полосу нахождения линии го-
ризонта вокруг базового отрезка при заданном значении X, так и задать X сооб-
разно желаемому поведению ФЛЛ.
Для формирования ФЛЛ на Зб-отрезке ab с помощью функции FLLrec, рабо-
тающей в плоскости ху, перейдем в промежуточную систему координат, у кото-
рой ось абсцисс направлена вдоль ab. При любом положении отрезка матрица
преобразования СК легко вычисляется с помощью функции МАР2 из (2.51). За-
пишем функцию построения пространственной ломаной фрактальной линии на
отрезке ab е R3 в следующем виде.
& FLL3(a, b, X, 5, гес)
{Ск = МАР2^,Ь~а,О3,х°)-, // матрица преобразования СК
L = FLLrec{aCK,bСк,Х,5,гес)-1; // список вершин ломаной линии в R4
возврат L;
Как и с функцией FLLrec, построение ФЛЛ на отрезке ab е R3 осуществляется
однократным вычислением списка ее вершин
L = FLL3(a, b, X, 5. гес).
Для генерирования фрактала на базовой ломаной линии /л рг ...р„ инициализи-
руется начальный список L = {/л}, после чего в цикле
L = FLL3(L, ph X, 5, rec) Vi = 2^n
строятся ФЛЛ на базовых отрезках рН1 р,.
В последующих задачах мы будем использовать функцию FLL3 с параметром
5 = 0. Таким образом, форму ФЛЛ между точками а и b будут регулировать все-
го два параметра:
О X определяет относительное отклонение ФЛЛ от базового отрезка и согласи
рекомендациям, разработанным выше, должен задаваться из условия X < 0.3;
□ гес устанавливает фиксированное число отрезков ФЛЛ, равное
N(rec) = 2rfC
и возрастающее вдвое при увеличении числа разбиений на единицу.
Следующий объект фрактального ландшафта— фрактальная кусочная поверх-
ность (ФКП), гладкий аналог которой — кусочная поверхность Кунса, постро-
енная на рис. 3.47, — описывается моделью (3.66). Практическое применение
ФКП — изображение небольшого участка рельефа, водной поверхности, разве-
вающегося на ветру флага, смятого листа бумаги...
Математические модели поверхностей и объектов
367
Зададим в пространстве четыре узла uoo, woi, wio, wh и построим на базовых отрез-
ках woo wio, woi wn, woo woi и wio wh соответствующие граничные линии горизонта g,
А, 1и г (рис. 3.77). С помощью функции FLL3 рассчитаем граничные ФЛЛ:
g = 7?b£3(woo, W| о, А, 0, rect), h = ।, W] ।, А, 0, rect),
/ = FA£3(wqq,Wo],A, 0, гесх\ г - FLL3(u^,Un, А, 0, гест).
(3.90)
Рис. 3.77
Очень важный момент в этой задаче — равенство числа вершин в парах линий
{g, h} и {/,/}, потому что дальше мы сопоставим (л, + 1)-ой паре точек {g„A,}
значения параметра
=^-,где =2^',
h
а (лт + 1)-ой паре точек {/,, /)} — значения параметра
т.=^-,гдепг=2гесС
ит
Числа гес, и гест можно задавать равными, исключая случаи сильной вытянуто-
сти ячейки вдоль одного из направлений t или т.
Теперь по уравнению непрерывной модели (3 66) вычислим узлы ФКП:
Pij = 8,(' -ъ)+^j+ G(1 -4)+ ^4 “"00(1 -4)(1 -ъ)-«ю4(1 -ъ)-
-«01(1-4)т~м114ту V/ = 0, nt,j = G, nx , nt=2rec', nx=2rec\
В целях иллюстрации работы алгоритма (3.90), (3.91) на рис. 3.78 построены
фрактальные поверхности на одном и том же наборе некомпланарных узлов woo,
woi, wio, wn, но с разными значениями параметра разброса А равномерного ГСЧ.
Налицо влияние этого коэффициента на характер рельефа: от чуть холмистой
равнины при А»0.1 (рис. 3.78,6) до сильно пересеченной горной местности при
А « 0.3 (рис. 3.78, в). Кстати, если задать А = 0, то алгоритм создаст прямолиней-
368
Гпава 3
ные граничные линии g, h, I, г и детерминированную поверхность типа косой
плоскости, изображенной на рис. 3.45.
Рис. 3.78
Логическое завершение темы фрактального рельефа — построение фрактальной
полигональной сети (ФПС) как объединения фрактальных кусочных поверхно-
стей в единое целое. Практическое применение фрактальных сетей — изображе-
ние протяженных рельефных ландшафтов с разнообразными топографическими
свойствами участков.
Допустим, в пространстве задано (п + !)(/«+ 1) узлов иу X/i = 0,n, j=0,m, про-
нумерованных в порядке их соединения в крупноячеистую базовую сеть
(рис. 3.79). Для удобства организуем объемную матрицу
м00 и0т
^пХтхЗ
ип0 • ипт
Рис. 3.79
с элементами векторного типа. Простое wn-кратное выполнение алгоритма
(3.90), (3.91) с индивидуальными граничными ФЛЛ каждой ячейки не дает не-
прерывного сопряжения кусочных поверхностей смежных ячеек (рис. 3.80, а)
Для обеспечения непрерывности ФПС необходимо, чтобы ее ячейки имели общие
Математические модели поверхностей и объектов
369
граничные линии, рассчитанные функцией FLL3. Лишь после этого наступает
черед расчета внутренних узлов кусочных поверхностей по формуле (3.91).
В результате получаем следующий алгоритм FPS(U, X, 5, гес,, гест) построения
фрактальной полигональной сети на базовой сети с матрицей узлов U е R"x",x\
& Шаг 1. Рассчитываем m + 1 граничную ФЛЛ базовых ячеек вдоль направле-
ния t:
{v^=wOj, = FLL3^\uj j,X, 0, rectj Vz = l, zz}v/ = O, zn. (3.92)
Шаг 2. Рассчитываем и + 1 граничную ФЛЛ базовых ячеек вдоль направления т:
{ =uoj, = FL12^'\uij,X,0,recxj V/ = l,/n} Vz = O,n. (3.93)
Шаг 3. Во вложенном цикле i: = 0, n -1, j = 0, m -1:
П из списков уСТ и v(/+l\ каждый из которых содержит по п • n, + 1 точек, где
nt = 2гес‘ , формируем массивы n, + 1 вершин граничных линий (z, у)-ой ФКП:
р = I г(7) AJ) ) д _ ( VO+D v(7+|) vO+>) И 94)
* I in, ’ 1П/+1-’ (/+1)«, J’ n I % > %+1-’ r(z+l)nzh
П из списков и и’('+|), каждый из которых содержит по т- п,+ 1 точек, где
z^ = 2геСт , формируем массивы nx + 1 вершин граничных линий (z, у)-ой ФКП:
/ = {wW w(0 w(0 | r = { WG+D wG+l) w*'.4;1) }; (3.95)
1 j"t+i (y+iKJ 1 jnx O+0«tj ’
П во вложенном цикле v = 0, nt , p = 0, nx рассчитываем узловые точки ФКП
(z, у)-ой ячейки как подмножество узлов общей ФПС:
Pin,+v. уят+р = Sv О — т)++ — 0+— Mi у(1—ОО-т)—
V ц (3.96)
- "Z+I, - т}~Щ, J+1 (1 -')*- «1+1,у+1^ где t = —, т = —.
J ’J J nt nx
Шаг 4. Выводим ФПС как параметрическую поверхность, заданную узловыми
вершинами р^ Vz = 0,2rec‘ n +1, j = 0,2ГССт т +1 . □
На рис. 3.80, в приведено изображение горного ландшафта, построенного по ал-
горитму FPS на основе базовой сети с организацией 7x7 узлов. Центральное
ядро базовой 5 х 5-сети позаимствовано из примера 3.20 (см. рис. 3.60), а по кра-
ям к нему добавлено предгорье. Для оживления пейзажа в ландшафт вставлено
горное озеро с волнистой поверхностью, моделируемой функцией типа
у(х, z) — y4sin(cn)cos(ox).
Для создания ФПС были выбраны следующие формообразующие параметры:
гес, - гес, = 5, X = 0.4. Кстати, благодаря тому, что специально выбрано значение
X > 0.3, горы и получились такими складчатыми.
370
Гпава 3
Рис. 3.80
3.1.5.3. Свойства фракталов
После беглого знакомства с отдельными представителями бесконечно разнооб-
разного фрактального мира можно поговорить об основных свойствах и законо-
мерностях строения фрактальных объектов. Прежде всего отметим, что фрак-
тал— это не линия или поверхность в виде привычных уравнений. Фракталы
выражаются не в первичных геометрических формах, а в алгоритмах, которые
трансформируются в геометрические формы с помощью компьютерной про-
граммы.
Отличительной особенностью большинства фрактальных алгоритмов является
их преимущественно рекурсивный характер, хотя некоторые фракталы можно
строить и итерационным методом, наглядное подтверждение чему — линия Коха
и алгоритм ее построения KOCHit (см. рис. 3.67, 3.68). Теоретически глубина ре-
курсии фрактала бесконечна. Окончательным результатом бесконечно повто-
ряющегося цикла рекурсии является предельное изображение. Его можно опреде-
лить вычислением суммы бесконечной геометрической прогрессии, но
невозможно достичь в рамках самого процесса. Глубина рекурсии ограничена
размерами изображения и разрешающей способностью дисплея отображать са-
мые мелкие его детали. Примером вычисления глубины рекурсии фрактального
алгоритма при заданном разрешении служит формула (3.83). При растяжении
выделенной области с одновременным пропорциональным уменьшением разме-
ра минимального элемента алгоритм продолжает рекурсию до нового предела
разрешения с появлением новых, невидимых ранее, элементов.
Математические модели поверхностей и объектов 371
Нами рассмотрены два типа фрактальных алгоритмов: детерминированные и
стохастические. Алгоритмы первого типа абсолютно воспроизводимы: они да-
ют идентичные изображения независимо от числа повторений. Стохастические
алгоритмы дают большее разнообразие форм благодаря элементам управляемой
случайности. Это же делает случайное фрактальное изображение неповторимым,
что иногда является недостатком из-за невозможности заранее предвидеть ре-
зультаты длительного расчета.
По принципу преобразования элементов между итерациями или уровнями рекур-
сии фрактальные алгоритмы делятся на линейные и нелинейные. Нелинейный фрак-
тал представлен множеством Мандельброта и другими алгоритмическими фракта-
лами, рассмотренными выше. Линейное фрактальное множество образуется
рекурсией аффинных преобразований определенного геометрического объекта.
Преобразуемый элемент может перемещаться, вращаться, сжиматься, отражаться
произвольным образом при условии, что прямые линии остаются прямыми. При-
мерами линейных фрактальных алгоритмов служат функции построения всех объ-
ектов, изображенных на рис. 3.67—3.80. К ним же относятся алгоритмы построе-
ния объемных фрактальных объектов, показанных на рис. 3.81.
Рис. 3.81
По характеру изменения объема пространства, занимаемого фрактальными объ-
ектами, между соседними уровнями рекурсии алгоритмы и производимые ими
объекты делятся на аддитивные и q бтративные. Большинство известных фрак-
талов относятся к аддитивным, т. к. в процессе дробления появляются новые
элементы, увеличивающие объем занимаемого фракталом пространства. К суб-
тративным можно причислить треугольник и пирамиду Серпинского, а также
показанный на рис. 3.81, б куб со стремящимся к нулю предельным объемом.
Почему мы так уверенно говорим, что обычная линия одномерна, полигон
двухмерен, а полиэдр трехмерен? Ведь ясно, что показателем размерности объек-
та служит не размерность пространства, в котором он существует, а что-то дру-
гое. Линия может проходить и в трехмерном пространстве, тем не менее она од-
372
Гпава 3
номерна. То же касается и поверхности — двухмерного объекта, который может
существовать и на плоскости, и располагаться в пространстве RA
Независимо от природы или метода построения у всех фракталов есть одно важ-
ное общее свойство, характеризующее степень их раздробленности и предельные
свойства. Это некоторое характеристическое число D, называемое фрактальной
размерностью. Следуя идее Мандельброта, ее можно определить подсчетом чис-
ла элементов N, принадлежащих фрактальному множеству, при различных раз-
решениях 5 — минимальных линейных размерах элементов. При достаточно ма-
лом 5 выполняется условие
N • <5D « const.
Задав малые значения 5i, бг и подсчитав соответствующие числа Nt и №, из ус-
ловия
= ^282
получим оценку размерности фрактала:
iog(/v2/M)
Это соотношение приблизительное потому, что при определении принадлежно-
сти элементов объекту по принципу "да / нет" число N округляется до целого.
Иначе пришлось бы учитывать дробные части элементов, что требует разреше-
ния, меньшего 5. Поэтому правильнее будет определить предельную форму раз-
мерности:
D = lim при 5/+| < 8'- (3.98)
iog(5i78i+i) J
При выборе разрешений 5, совсем не принципиально условие их кратности. Од-
нако, если при уменьшении разрешения в целое число раз
постоянен предельный коэффициент увеличения числа элементов
kN = lim
Ч ", J
то получим более простую, чем (3.98), формулу расчета размерности фракталь-
ного объекта:
°=1^=1о8‘«‘Л" <3”
Например, если при каждом уменьшении линейного разрешения в два раза числе
элементов увеличивается втрое, то размерность фрактального объекта оценива-
ется числом D = log23 ® 1.585.
Математические модели поверхностей и объектов
373
Вычислим по (3.98) размерность плоской замкнутой фигуры с постоянной гра-
ницей. Зададим разрешение пространства плоскости Si = 1, построим растр с
шагом 5i и подсчитаем число "пикселов" растра, центры которых закрываются
фигурой. Оно равно М = 9 (рис. 3.82, а). Уменьшив разрешение до & = 0.5, полу-
чим число новых "пикселов" № = 43 (рис. 3.82, б) и размерность
Di = log2(43 / 9)» 2.2563.
Рис. 3.82
Продолжая двойное уменьшение 5, получаем последовательность
Z>2 = log2(167/43)» 1.9574,
Лз = log2(683 / 167) » 2.032,
Z>4 = log2(2 7331683)» 1.9962,
Ds = log2(l 0 90312 733) » 1.9999,
достаточно быстро сходящуюся к размерности плоского нефрактального объек-
та, равной D = 2.
В отличие от привычных геометрических объектов, фрактальное множество не имеет
постоянной границы. Она дробится с каждым уменьшением разрешения. У аддитив-
ных фракталов происходит приращение "вещества", у субтративных — его сокраще-
ние. В результате размерность фрактала может быть дробной! Это свойство фрак-
тальных множеств является их очередной удивительной особенностью.
Использование формул (3.97)—(3.99) предполагает, что фрактал состоит из од-
нородных элементов, как, например, линия Коха или треугольник Серпинского.
Однако не все фрактальные множества таковы. Ветвь папоротника или фрак-
тальная ломаная линия и построенные на ее основе поверхности (ФКП и ФПС)
сложены из элементов разной длины или площади. Для вычисления размерно-
стей таких объектов введем понятие среднего фрактального элемента длиной 5,
площадью б2 или объемом б3. Количество фрактального "вещества" (назовем это
массой фрактала М) в зависимости от числа степеней свободы фрактала п связа-
но с числом средних элементов У длины б соотношением
М = N-8”.
374
Гпава 3
У линейного фрактала масса равна суммарной длине всех его отрезков, у пло-
щадного — сумме площадей, а у объемного — сумме объемов элементов.
Прежнее определение размерности можно сформулировать в обобщенной форме:
_ п
“ [ l-log(4+IM)/log(y/+1/y,)J ’ (3-100)
где под массой Л/>0 подразумевается длина линейного фрактала с n = 1, пло-
щадь площадного фрактала с п = 2 или объем объемного фрактала с п - 3. Из
(3.100) следует:
□ при ненулевой предельной массе фигуры ее размерность совпадает с числом
степеней свободы и. Следовательно, не все фрактальные множества имеют
дробные или отличные от числа степеней свободы размерности,
П если предельная масса аддитивного фрактала с Л/,+| > М, неограниченно воз-
растает, то его размерность D > п и может быть дробной;
П если предельная масса стремится к нулю, то такой субтративный фрактал с
Л/,+| < Л/, имеет размерность D < п и также может быть дробной.
Рассчитаем размерности рассмотренных нами выше фрактальных объектов.
□ У линии Коха (см. рис. 3.67, а, б, в) на каждой итерации (или уровне рекурсии)
один отрезок заменяется четырьмя отрезками втрое меньшей длины. Следо-
вательно, б,, = З1 ', Nt-4‘ и по (3.99) этот линейный фрактал имеет размер-
ность D = log.,4 ~ 1.262. Аналогично получаем, что прямоугольные линии Ко-
ха, изображенные на рис. 3.69, имеют размерность D = logj5 ® 1.465. То, что
обе размерности больше единицы, говорит о бесконечной предельной длине
этих аддитивных фракталов.
□ У "снежинки" Коха (см. рис. 3.67, е) как площадного фрактала с уменьшением
линейного разрешения б, = 3* ' число треугольных элементов растет следую-
щим образом:
7V1 = 1,№ = 9М + 3,Уз = 9№+ 12,..., NI+l =9У, + 3-4/-1 = 0.2(8-9М -3 -4'-1).
По определению (3.98) при lim (У/-ц/У|)=9 получим D = logj9 = 2. Таким
/—>«5
образом, несмотря на аддитивность фрактала, его размерность п не дробная, а
равна двум — размерности геометрической фигуры с постоянной границей
Этот результат объясняется конечнои предельной площадью фрактала
ч/З э '’А
Л/„ = -у УмбВ, = =^~ = 0.693 .
□ Каждый элемент треугольника Серпинского (см. рис. 3.72) при разбиении
заменяется тремя подобными треугольниками с вдвое меньшими линейны-
ми размерами. Поэтому по (3.99) размерность этого площадного фрактала
D = log?3 « 1.585 То, что она меньше двух, есть признак субтративного
Математические модели поверхностей и объектов 375
фрактала со стремящейся к нулю площадью. Действительно, т. к. б, — 2|J и
Nj = З'1, то
□ Аналогично получим размерность объемного тетраэдра Серпинского
(см рис. 3.73, в), равную D - log24 = 2 < 3— признак стремящегося к нулю
объема фрактала. Интересно, что предельная площадь боковой поверхности
его элементов бесконечна:
б, = 2'"', N, = 16’1 => Л/м = — = — 4“ = оо.
4 4
□ Ветвь папоротника (см. рис. 3.71) относится к линейным фракталам с неодно-
родными элементами: один отрезок длиной / за рекурсию обрастает тремя от-
резками длиной mi I, m21 и >m I. С учетом коэффициентов (3.85) относитель-
ная прирастаемая масса за одну рекурсию составляет
т = /Mi + m2 + тз = 1.556.
Подставив в (3.100) вычисленное в (3.82) число отрезков А, = 0.5(3'- 1) и мас-
су линейного фрактала
. . , , (. 2 /-11 , т' ~ 1
Л7, =A2^0V + ,m+w + — + т 1=^2^0------’
т-1
получим размерность ветви папоротника
D =----?---= 1.674 >1.
1 - log3 т
□ Фрактальная ломаная линия также является стохастическим линейным фрак-
талом с неоднородными элементами. Оценим размерность фракталов на
рис. 3.75, генерируемых функцией FLLrec(a, b, X, 5, гес) при б = 0 за гес = 8 ре-
курсий, с учетом зависимости (3.89) коэффициента удлинения уср(Х) от пара-
метра X равномерного ГСЧ. Так как из Nt = 1 отрезка длиной М\ - 1 получа-
ется Nt - 2ГК - 256 отрезков общей длиной Мг = Уср(Л) ® 1 + 6Х2, то
О(Х) =-------U-----л > n = 1.
1^°ё256 V + 6^- J
Например, 0(0.1) * 1.011, 0(0.2) ® 1 04, 0(0.3) ® 1.084. За неимением результа-
тов статистических исследований фрактальных кусочных поверхностей и по-
лигональных сетей автор не может доложить читателю об их размерностях,
но, очевидно, что они немного больше двух.
□ Аналогичный изображенному на рис 3.82 эксперимент по расчету размерно-
сти множества Мандельброта (см. рис. 3.63) при разрешениях б, = 0.1 • 2*“' дал
значения D, = log2(A/+l / А,), совершающие затухающие колебания в интервале
[1.995, 2.005] вокруг предельной размерности D - 2 (рис. 3.83). Это означает,
376
Гпава 3
что данный фрактал нельзя уверенно отнести ни к аддитивным, ни к субтра-
тивным фрактальным множествам, и он имеет конечную и ненулевую пло-
щадь предельного изображения.
Рис. 3.83
В заключение темы перед последним цитированием "отца фракталов" хотелось
бы вновь повторить, что репертуар фрактальных объектов неисчерпаем. Каж-
дый объект является завершенным и единственным в своем роде алгоритмом —
единицей смыслового значения фрактального языка. Овладев языком фракта-
лов, можно изобразить дерево или гору так же просто, как архитектор описыва-
ет здание с помощью чертежей на языке традиционной геометрии. Благодаря
эстетической привлекательности и бесконечной глубине содержания фракталь
привлекают внимание исследователей, дизайнеров и программистов к освоении
этого класса математических объектов.
"Красота многих фракталов тем более поразительна, что открылась совершение
неожиданно: мы хотели построить— с чисто учебной целью— всего лишь ма-
тематические диаграммы, и можно было ожидать, что они окажутся сухими и
скучными <...> Трудно найти человека, равнодушного к фракталам. Многн.
считают, что знакомство с фрактальной геометрией подарило им совершение
неповторимые эстетические впечатления и обогатило новым научным опытом
В этом смысле фракталы безусловно оригинальны настолько, насколько это во-
обще возможно" (Б. Мандельброт, [21]).
3.1.6. Графические поверхности
Графическая поверхность описывается множеством отдельных точек, принадле-
жащих этой поверхности. Поточечное описание применяется в тех случаях, когд.
поверхность очень сложная, негладкая ни в одном своем фрагменте, имеет pa i-
рывы, отверстия и другие нарушения непрерывности. Это могут быть грунтовь :
поверхности, рентгеновские снимки, компьютерные томограммы, данные лока-
ции и т. п. Практическая цель изучения графических поверхностей заключается i
приобретении умения строить разноракурсные изображения и анимацию объек-
тов, ограниченных графическими поверхностями.
Математические модели поверхностей и объектов
377
Согласно современной терминологии дискретные элементы пространства назы-
ваются вокселами (VOlume piXEL), т. е. объемными пикселами. Вексельная тех-
нология подразумевает разбиение пространства на отдельные элементы и рас-
сматривает их как неделимые. В отличие от математических точек, вокселы
имеют ненулевой объем. Исходная информация о графической поверхности, со-
стоящей из «в вокселов, задается массивом координат, организованным как ли-
нейный список Р = |/7|,...,р„в} без учета или с частичным учетом взаимной бли-
зости точек, либо как л х т х 3-матрица (при нт = ив), соседние элементы
которой соответствуют физически близким вокселам.
Для создания впечатления о целостности графической поверхности ее элементы
юлжны отстоять друг от друга на некотором оптимальном расстоянии. Опти-
мальная частота пространственной дискретизации вокселов должна быть та-
кой, чтобы их изображения заполняли все пикселы экранного окна вывода без
проколов и наложений (рис. 3.84). Например, если размер пиксела равен 0.25 мм,
а масштаб изображения 1 / 1000, то оптимальный интервал съема точек состав-
ляет 25 см.
Рис. 3.84
Редкое расположение вокселов характерно скорее для независимых точек, чем
для структурно упорядоченной поверхности (рис. 3.85, а). Не самым худшим
способом заполнения пустых промежутков между редкими вокселами является
увеличение их диаметра с небольшим перекрытием друг друга (рис. 3.85, б). При
большой частоте съема резко возрастают машинные ресурсы, необходимые для
хранения и обработки всех точек. Однако это не улучшает степени детализации
изображения, т. к. его дополнительные точки не могут быть помещены между
пикселами экрана. Избыточность дискретизации может быть полезна в том слу-
чае, если в дальнейшем потребуется увеличить графическое разрешение экрана
или масштаб изображения (рис. 3.85, в).
Рассмотрим особенности визуализации вексельных поверхностей. В начальном
приближении воксел можно считать кубиком, а еще удобнее— шариком, равно-
мерно окрашенным в некоторый цвет со. Также могут использоваться прозрач-
ные вокселы. Введение атрибута прозрачности позволяет быстро изменять ви-
димость отдельного воксела или группы вокселов без их физического удаления
из массива данных.
378
Гпава 3
Рис. 3.85
Равномерная окраска изображения воксела на экране естественна, когда егс
диаметр составляет примерно один пиксел. Для более крупного изображения
вокселов можно использовать круги с равномерной (рис. 3.86, а) или градиент-
ной заливкой. Последняя может быть как центральной (рис. 3.86, б), так и сме-
щенной в направлении источника света (рис. 3.86, в). Эффект бархатистой по-
верхности создается путем изображения вокселов в виде аэрозольных пятен с
радиально уменьшающейся плотностью точек (рис. 3.86, г).
Рис. 3.86
Простейшие способы изменения цвета или оттенка цвета равномерного окраши-
вания вокселов используют следующие направления сортировки:
□ вдоль некоторой оси координат МСК, например, по высоте (см. рис. 3.85);
О вдоль направления на наблюдателя S, используя для сортировки точек р, чис-
ла dj = |р; - при ближнем или d, - -р, ° 5 при дальнем наблюдателе;
П комбинирование этих двух способов: например, выбор цвета воксела по неко-
торой координате, а оттенка цвета — по удаленности воксела от наблюдателя.
Максимально реалистичное окрашивание воксела по методу Ламберта (3.8)
требует знания направления нормали к поверхности в месте его расположения.
Ввиду неаналитичности и недифференцируемости вексельной поверхности ап-
проксимируем ее полиэдром, для чего каждую точку соединим ребрами с не-
сколькими (минимум с тремя) ближайшими с ней точками. Пусть ближе всех к
точкер, расположены точки рррк и р,. Вектор нормали Nt вычислим усреднением,
а еще проще — суммированием
N^N^ + N^ + N.j
трех нормалей к треугольным граням p,PjPk,PiPkPi иPiP/Pj (рис. 3.87):
Nijk = пот({р,рурк}), Nikl = погт({р,ркр,}), NHJ = ло/ти({р,р,р,}).
Математические модели поверхностей и объектов
379
Наиболее сложен поиск ближайших к р, точек поверхности путем сортировки
скалярных произведений
(Pj-Pi) ° (Pj ~Pi) = \Pj-Pi\2 V/ = 1, nB ,j * i.
Полный перебор требует очень больших вычислительных затрат. Рациональнее
изображать графическую поверхность методом, подобным алгоритму z-буфера
(см. рис. 3.6):
3 определяются экранные координаты всех вокселов
[х,э у1э 0 1|=[х, у, z, 1]сэ,
где Сэ — матрица преобразования пространственных координат точки в эк-
ранные;
О из каждой группы точек с равными координатами {хъ, отбирается одна
видимая точка /?,, ближайшая к наблюдателю S, т. е. с минимальным значени-
ем dj = fa - 51 при ближнем или dt - ~р, ° 5 при дальнем наблюдателе;
□ вычисляется нормаль Nf и по (3.8) цвет окраски этой точки, который для про-
стоты можно принять равным
сю = pV ° s|c0co Vco е {г, g, b}.
Подводя итог сказанному, заключаем, что сложная и ресурсоемкая задача изо-
бражения графической поверхности затруднена отсутствием аналитического
описания поверхности. Для ускорения перебора сначала находятся видимые во-
кселы, которые затем изображаются шариками, окрашенными соответственно
направлению нормалей.
3.2. Модели объектов в пространстве
Объект есть часть пространства, заключенная между некоторыми границами.
Границы играют важную роль в моделировании объектов компьютерной графи-
ки. Именно благодаря их непрозрачности объекты становятся видимыми, а от-
380
Гпава 3
ражательные свойства ограничивающих поверхностей определяют их цветовое
восприятие. Взаимная ориентация графических объектов также выполняется от-
носительно их границ. В алгоритмах трассировки рассчитываются пересечения
лучей с объектами в их граничных точках. Для ускорения расчетов в задачах
ориентации и пересечения сложные объекты часто окружаются виртуальными
габаритными оболочками простой формы в виде сферы или параллелепипеда.
На рис. 3.88 приведена классификация моделей пространственных объектов. Наи-
большее распространение получили три основных типа моделей [11]: каркасные,
граничные и сплошные. Каркасная конструкция в виде проволочной сетки, охва-
тывающей объект по линиям пересечения ограничивающих его поверхностей, яв-
ляется простейшим и самым примитивным способом передачи формы объемного
тела. Проволочные модели применяются для быстрого, не требующего детальной
визуализации, эскизного изображения объектов и их габаритных оболочек.
Рис. 3.88
Граничное описание включает перечень всех элементов, создающих границы объ-
екта— тонкие оболочки, под которыми находится пустое пространство. К гра-
ничным элементам объекта относятся:
□ грани— ограниченные поверхности, отделяющие внутреннее пространство
объекта от внешнего;
П ребра — линии пересечения граней;
П вершины — точки пересечения ребер.
Вершины, инцидентные (принадлежащие) одному и тому же ребру, как и грани,
имеющие общее ребро, являются смежными.
Количественное соотношение между числами вершин »в, граней лг и ребер иР замк-
нутого объекта устанавливается удивительно простой формулой Эйлера [7, 13]:
лв+лг=лр+2. (3.101)
Граничное моделирование информативнее каркасного и позволяет выполнять
более реалистичную визуализацию объектов. Каркасное изображение гранично
определенной модели строится достаточно легко, т. к. задание ребер присутству-
ет в структуре данных явным образом. Определенную трудность представляет
Математические модели поверхностей и объектов
381
выполнение над объектами булевых операций, при которых появляются новые
граничные элементы, требующие расчета пересечений линий и поверхностей.
Сплошная, объемная или твердотельная модель охватывает все точки внутри и
на поверхности объекта. Описание сплошными телами подразумевает перечис-
ление вокселов— мельчайших Зб-ячеек, заполняющих объект, либо конструиро-
вание сложной формы как композиции небольшого числа простых объемных
примитивов (куб, сфера, конус, цилиндр), с которыми выполняются необходи-
мые аффинные преобразования. Последовательность конструирования описыва-
ется древовидной структурой, терминальными вершинами которой являются
примитивы, нетерминальными — операторы над ними, а ветвями — матрицы
преобразований промежуточных форм.
Сплошные модели органично приспособлены к работе в системах логического
конструирования сложных форм. Алгоритмы выполнения булевых операций
(объединения, пересечения и дополнения) с Зб-объектами являются составной
частью данного способа моделирования, область применения которого — раз-
личные САПР твердотельных конструкций, системы архитектурного проектиро-
вания и им подобные.
3.2.1. Каркасные модели.
Платоновы тела
Назначение каркасной модели Зб-объекта— отражать форму его граней. В за-
висимости от их свойств выбираются методы построения каркасного изображе-
ния. В случае плоской грани вполне достаточно вывода ее ребер (рис. 3.89, а). За-
метим, что условие планарности вершин грани (1.81)— только необходимое
условие планарности всей грани. Следовательно, информация о свойствах гра-
ничных поверхностей объекта должна быть априорно известной.
Адекватное восприятие объемной грани невозможно без вспомогательных кар-
касных линий, проведенных в междуреберном пространстве. Особенно это важ-
но в случае планарности вершин грани, когда информация о дополнительных
точках поверхности в принципе необходима. В подтверждение сказанного на
рис. 3.89, б изображен объект, имеющий неплоскую грань с теми же планарными
вершинами, что и на рис. 3.89, а. Очевидно, что без промежуточных каркасных
линий реальная форма объемной грани не воспринимается. Для построения карка-
са криволинейной поверхности грани с известными граничными элементами мож-
но использовать алгоритмы кусочно-линейной интерполяции (см. разд. 3.1.3), а
при задании дополнительных узловых точек внутри грани и на ее ребрах могут
быть полезны методы сплайн-интерполяции (см. разд. 3.1 4.2).
Каркасное изображение объекта с прозрачными гранями, построенное без учета
удаленности ребер от наблюдателя, выглядит двусмысленным: восприятие фор-
мы и ориентации тела в пространстве у разных наблюдателей индивидуально.
Один из них видит параллелепипед на рис. 3.89, а как бы сверху, для другого на-
блюдателя ближними и видимыми являются передняя, левая и нижняя грани.
Большей реалистичности и однозначности восприятия можно достичь несколь-
382
Гпава 3
кими способами: утолщением ребер видимых граней (рис. 3.90, а), пунктирным
изображением (рис. 3.90, б) или вообще удалением невидимых ребер (рис. 3.90, в).
В любом из этих случаев необходимо выполнять упорядочивание граней объекта
по удаленности от наблюдателя и определять их видимость. Некоторые алго-
ритмы решения задач данного типа в общих чертах рассмотрены в разд. 3.1.1.
Рис. 3.90
Описание каркаса Зб-объекта включает следующие действия.
П Нумерация элементов каркаса — вершин, ребер и граней. Для этого чаще ис-
пользуются сквозные (одноиндексные) номера, хотя иногда могут быть удобнее
двухиндексные номера. Например, при сквозной нумерации вершин р, Vz = 1, zzB
двухиндексное обозначение гу несет информацию о том, что объект имеет реб-
ро, соединяющее вершины р, и р}. На рис. 3.91 построен и пронумерован сквоз-
ным образом объект, состоящий из /г» - 9 вершин, пг = 7 граней и пР — 14 ребер.
Не трудно убедиться в справедливости формулы Эйлера (3.101).
П Задание или расчет координат вершин относительно начала координат
(абсолютный метод) или некоторой базовой точки (относительный метод)
и сохранение их в пв х 3-матрице координат Q. В качестве базовой точки
можно выбрать центр симметрии объекта или любую вершину каркаса. От-
носительные координаты вершин предпочтительнее абсолютных, т. к. при
геометрических преобразованиях объекта достаточно выполнить одну груп-
повую операцию
£' = £С
(3.102)
Математические модели поверхностей и объектов
383
вместо вычисления координат каждой вершины по сложным формулам аф-
финных преобразований.
Рис. 3.91
□ Задание топологии каркаса, т. е. указание порядка соединения вершин ребра-
ми. Это можно осуществить следующими способами:
• в каждом из /?р списков-столбцов матрицы ребер R = [/?( ... ] записы-
ваются два номера вершин, соединенных ребром. Например, топология
объекта, изображенного на рис. 3.91, описывается матрицей ребер
12344567168798
23415673581929
Список R, может дополнительно содержать атрибуты /-го ребра: цвет,
толщину, стиль линии (сплошная, пунктирная и т. п.) и другие характери-
стики. Матрица ребер не содержит явной информации о составе граней
каркаса, поэтому ее используют для изображения каркасной поверхности
с прозрачными ячейками, не требующими расчета их видимости и окраски
в зависимости от направления нормали;
• в каждом из лг списков массива граней G = {G|,..., Gn } записываются но-
мера вершин грани в порядке их обхода по замкнутому контуру в выбран-
ном направлении. Крайние элементы списка G, = (g/i, ..., g/„ > gzl J совпа-
дают: они соответствуют одной и той же вершине QgСписок Gj может
дополнительно содержать атрибуты /-ой грани: прозрачность, цвет, види-
мость, координаты вектора нормали и т. п. Если грани имеют разное чис-
ло ребер, то списки в G будут неравной длины. Например, топологию гра-
ней, изображенных на рис. 3.92, можно описать списками
G, = {1,2, 3, 4, 1},G2= {3, 4, 5,6,7,3},Сз= {1,5, 6, 8, 1}, G4 = {1,4, 5, 1},
G5= {2,3,7, 9, 2},G6= {6,7, 9, 8, 6}, Gi = {1,8,9, 2, 1}.
384
Гпава 3
Рис. 3.92
Если для объектов с числом граней лг < 10 перечисленные действия можно вы-
полнить вручную, то более многогранные каркасные модели должны строиться
исключительно алгоритмически. Серьезному программисту рекомендуется соз-
дать библиотеку моделей разных тел и алгоритмов их формирования.
Построение каркаса с помощью введенных массивов выполняется путем пооче-
редного сканирования списков используемого топологического массива:
О по списку Rj на экране рисуется ребро между вершинами Q и Qr При этом
каждое ребро каркаса выводится только один раз. Недостаток кодирования
топологии матрицей R заключается в сложности определения всех ребер, вхо-
дящих в состав конкретной грани;
П по списку G, на экране рисуется замкнутый контур /-ой грани. Недостаток
метода в том, что большинство ребер каркаса (а в замкнутых объектах — все
ребра) выводится дважды. Применение кодирования топологии матрицей G
оправдывается при построении непрозрачного каркаса, когда требуется вы-
являть лицевые грани и вычислять их окраску по направлению вектора нор-
мали. Плоскость /-ой грани определяется точкой Qg и нормалью
Nj - norm(side(Q, G, i)). (3.103)
Для ускорения вычисления нормали можно включить ее координаты в струк-
туру списка грани, а при геометрическом преобразовании поверхности мат-
рицей С пересчитывать по формуле (2.10):
/V' = /V,C. (3.104)
Второй вариант — включить векторы Nj в массив координат Q и выполнять
совместное преобразование вершин и нормалей по (3.102).
Математические модели поверхностей и объектов
385
Перед тем, как перейти к изучению алгоритмов построения правильных много-
гранников и производных от них тел, сделаем некоторые важные дополнения.
П Для правильной визуализации непрозрачных граней все нормали к ним
должны иметь одинаковую ориентацию — либо внешнюю, либо внутреннюю.
Если /-ая грань является плоским и выпуклым полигоном, то вычисленная по
(3.103) нормаль будет иметь внешнюю ориентацию при направлении ее обхода
против часовой стрелки с точки зрения внешнего наблюдателя. Таким обра-
зом, два списка граней объекта на рис. 3.91 следует формировать в виде
G2 = {3, 6, 7, 5, 4, 3}, Gs = {2, 9, 7, 3, 2}.
Обход невыпуклой плоской грани против часовой стрелки должен начинаться
с такой вершины, чтобы угол между первыми тремя вершинами полигона
был выпуклым. Например, топологию грани, заштрихованной на рис. 3.93,
можно описать списком {1,2, 10,9,6,5, 1}, но не {10,9,6,5, 1,2, 10}.
Рис. 3.93
Все сказанное здесь о необходимости правильного выбора направления об-
хода граней следует учитывать, если нормаль к грани рассчитывается по трем
ее первым точкам. Если же вектор Nt получается способом, независимым от
порядка перечисления вершин в списке грани G,, то этот порядок может быть
произвольным.
О Для описания полигона с отверстием введем фиктивное ребро ij, связываю-
щее внешний и внутренний контуры полигона между /-ой и /'-ой вершинами
(рис. 3.94, а). Отразим это добавлением в список грани индексов
Второй отрицательный индекс пары {... i, -j,...} означает, что при сканирова-
нии списка ребро /J не должно изображаться. Направление обхода полигона
должно быть таким, чтобы он оставался все время слева. Например, тополо-
гию передней грани объекта на рис. 3.94, б можно определить списком
{1,2,3,4,-12, 11,-19, 18, 17, 19,-11, 10,9, 12,-4, 1}.
386
Гпава 3
Рис. 3.95
Каркасные модели могут быть естественными или аппроксимирующими объек-
ты с гладкими криволинейными граничными поверхностями. К естественным
относятся модели полиэдров, из которых выделяются пять платоновых тел
(рис. 3.95). Число этих фигур определяется числом способов соединения однород-
ных правильных полигонов в вершине полиэдра. Допустим, к вершине примыка-
ют т > 3 правильных п > 3-угольников. Сумма их внутренних углов, каждый из
которых равен = 180° - 360° In, должна быть меньше 360°, т. к. телесный угол
при вершине не должен быть плоским Из условия т < 360° и естественных
геометрических соображений получаем систему неравенств
т(п — 2)<2и,
п>3,
т>3,
имеющую всего пять целочисленных решений {п, т}, изображенных на рис. 3.96:
П {3,3}—тетраэдр («);
□ {4, 3} — гексаэдр (б);
П {3, 4} — октаэдр (в);
□ {3, 5} — икосаэдр (г);
П {5, 3} — додекаэдр (д).
Математические модели поверхностей и объектов
387
Рис. 3.96
Приставка перед греческим корнем "эдр” означает число граней полиэдра пг. Для
любого «г-эдра число ребер равно пР - nrnm / 2, а число вершин определяется по
формуле Эйлера (3.43):
«в - 2 - Пг - nrnm / 2.
Рассмотрим экономичные, т. е. с минимумом ручных расчетов, методы построения
платоновых тел, координаты ив вершин которых отсчитываются относительно
начала координат— центра симметрии. Массив G, содержащий списки равной
длины и + 1, будем задавать пг х (и + 1)-матрицей. Добавим к параметрам тела
П длину ребра d\
П радиус описанной сферы Re,
П длину ребра описанного куба dK.
Зная эти величины, можно управлять относительными размерами тел:
П деление матрицы Q на дает тела, вписанные в сферу радиуса Rc - 1;
□ деление матрицы Q на d дает тела с ребрами единичной длины d - 1.
Переходим к детальному изучению моделей платоновых тел.
П Тетраэдр (и - 1, пг = 4, иР = 6, пв - 4)— простейший правильный полиэдр,
построение которого в привычном виде (см. рис. 3.95, а) — вовсе не триви-
альная задача из-за необходимости ручного расчета координат вершин. Вра-
щая тетраэдр, вписанный в куб (рис. 3.97), на углы
<ру = -45°, <рЛ = arctg(V2 )= 54.7°,
получим желаемое положение тетраэдра с параметрами
-1 1 -1' 1 3 2 Г
04- 1 1 1 -1 -1 1 Пу^уК^х)’ G4 = 1 2 1 4 4 1 3 1 , d = 2^2 , Rc = Л, А = 2.
1 -1 -1 2 3 4 2
388
Гпава 3
Рис. 3.97
П Гексаэдр (и = 4, пг = 6, пР = 12, п» = 8) или в просторечии куб прост в построе-
нии и расчете параметров (рис. 3.97):
1 5 2 6 1
1 -1
-1 1
-1 1
1 -1
1 -1
-1 -1
7
6
8
5
3 5 1
4 7 1
4 6 2
3 8 2
3 7 4 8 3
d=2, Rc=Ji,dK = 2.
П Октаэдр (и = 3, иТ = 8, иР - 12, пЕ - 6) также просто строится
(рис. 3.98) и имеет параметры
на основе куба
^8= 1
-1 о
о о
О -1
°т
-1 , 68 =
о
1
2
5
1
1112 2
3 4 5 3 6
2 3 4 6 5
1112 2
3 4Т
d — V2 , Ас — I, б/к — 2.
Рис. 3.98
О
О
1 О
О О
О 1
4 5
6 6
3 4
Математические модели поверхностей и объектов
389
□ Икосаэдр (и = 3, «г = 20, иР = 30, пЕ = 12) конструируется по следующему алго-
ритму (рис. 3.99).
Рис. 3.99
& Шаг 1. В окружностях сечений у = ±Л цилиндра единичного радиуса
х2 + z2 - 1 строятся правильные пятиугольники 1-3-5-7-9-1 и 2-4-6-8-10-2
(рис. 3.99, а) с координатами вершин
х, = cos(36°z), z, - sin(36°z), у, = (-1)'~'h V/ = 1,10 .
Шаг 2. Соединяя вершины 1-2-3-4-5-6-7-8-9-10-1, получим десять средних тре-
угольных граней икосаэдра с длиной горизонтальных ребер
Из условия получения равносторонних треугольников
h - ао|=V^+^+O-^i)2 = fa2 =d
получим значение h = 0.5.
Шаг 3. Вычислив радиус описанной сферы
7?с = |л| = Vх!2 +^2 +z\ = ’
построим две вершины р\ । = [0 Rc 0] и Р]2 =[0 ~RC О]. Соединяя их с
вершинами pi -5-рю, как показано на рис. 3.99, б. получим пять верхних и пять
нижних граней икосаэдра. □
В результате получаем следующие параметры модели икосаэдра:
0
020= h
Lzi
Х2 *3 х4 х5 х6 х7 *8 *9 *10 0
— h h — h h - h h —h h — h Rc
z2 Z3 z4 z5 z6 z7 Zg z9 zl0 0
-Rc
0
*1
390
Гпава 3
13 57912345678 9 10 2 4 6 810
11 11 11 11 11 3 3 5 5 7 7 9 9 1 1 12 12 12 12 12
3 5 7 9 12446688 10 10 2 10 2 4 6 8
13579123456789 10 2468 10
П Додекаэдр (и = 5, th = 12, иР = 30, гъ = 20) — наиболее сложное платоново тело.
Оптимальный метод его построения заключается в предварительном созда-
нии икосаэдра и соединении центров его смежных граней ребрами
(рис. 3.100). Отсюда получаем формулу расчета строк 02^ матрицы коор-
динат вершин додекаэдра на основе матриц икосаэдра £720 и G20:
0 2 £ Q20^G20,i) V/ = h20 .
3*=1
Рис. 3.100
Матрица граней додекаэдра и остальные его параметры равны
1 1 2 3 4 5 7 9 11 13 15 16
5 2 3 4 5 1 8 10 12 14 6 17
G12 = 4 8 10 12 14 6 9 11 13 15 7 18
3 7 9 11 13 15 18 19 20 16 17 19
2 6 8 10 12 14 17 18 19 20 16 20
1 1 2 3 4 5 7 9 11 13 15 16
„ / 2-^5+5 , /5 + V5 125+ 11^5
Rr — л-------, d = J------, cL .
с V 12 V 18 V 18
Математические модели поверхностей и объектов
391
Путем построения дополнительных надстроек на гранях правильных полиэдров
создаются различные объекты сфероидной и звездчатой форм. В первой группе
объектов все вершины полигонов надстроек находятся на описанной вокруг по-
лиэдра сфере; во второй группе надстройки над гранями полиэдра имеют форму
лучей.
□ Для создания сфероидного объекта с параметрами {п, пв, nr, Q, G, d, Rc} каж-
дая из и? граней полиэдра (например, грань {/л pi ...p„pt} на рис. 3.101) заме-
няется надстройкой из (и + 1)-ой грани. Центральная грань подобна исход-
ной, ее вершины р,„ -^рт+п-\ лежат на прямых, соединяющих центр полиэдра с
серединами ребер грани {pi pi ...p„pt}, на расстоянии Rc от центра:
Pm = (pi +Рг)' Rc ’ Рт+1 = (?2 + Рз)’ Rc , - > Рт+„-\ = (рЯ +Р1)' Rc
Рис. 3.101
Боковые грани pt р,„}, {p„,pipm+l},... ,(p„on-iP„Pm-^} (равнобедренные,
но не правильные треугольники) соединяются с соседними надстройками. За-
мена одной старой грани на (п + 1)-у новую грань алгоритмически означает
выполнение следующих действий:
• «в = ив + п, а в матрицу Q добавляется и новых строк;
• Иг - пг + и, а в массив G вместо списка, описывающего заменяемую грань,
вставляется и новых списков.
Выполнив аналогичные замены всех граней исходного полиэдра, получим
модель сфероидного объекта, вершины которого лежат на поверхности опи-
санной сферы. На рис. 3.102 изображены объекты этого класса, построенные
на гексаэдре (а), октаэдре (б) и икосаэдре (в). Возможно итеративное над-
страивание граней сфероидного объекта. После нескольких итераций объек-
ты становятся близкими к правильным полиэдрам, но ими не являются: не все
их грани — правильные полигоны, что отчетливо видно по несимметрично-
сти каркасной сетки. На рис. 3.102 показан результат двукратного надстраи-
вания граней на гексаэдре (г), октаэдре (б) и икосаэдре (е).
392
Гпава 3
Рис. 3.102
П Звездный объект на правильном полиэдре конструируется путем надстройки
над каждой его гранью прямой пирамиды. Например, для грани {pi рз ...p„pi}
на рис. 3.103 вершина пирамиды находится в точке
Рис. 3.103
Коэффициент а задает длину луча в единицах расстояния от центра объекта
до грани полиэдра. При a < 1 лучи направлены внутрь объекта. Замена одной
старой грани на п новых треугольных граней {p„,pi рг}, {ртргрз},..., {p„,p„pi}
алгоритмически означает выполнение следующих действий:
• Ив = ив + п, а в матрицу Q добавляется новая строка координат точки р,„;
• Дг = Дг + п-1, а в массив G вместо списка, описывающего заменяемую
грань, вставляются п новых списков.
Математические модели поверхностей и объектов
393
Выполнив аналогичйые замены всех граней полиэдра, получим модель звезд
ного объекта. На рис. 3.104 изображены объекты данного класса, один из ко-
торых построен на додекаэдре с коэффициентом a - 0.75, а два других — на
сфероидных объектах с а - 2.
Рис. 3.104
3.2.2. Граничные модели
Граничная модель представляет объект системой элементов, создающих его гра-
ницы (поверхности, края поверхностей и указатели пересечения поверхностей), и
топологической информации о соединении элементов друг с другом. Структура
данных модели включает:
П матрицы неявного описания плоскостей Ft и квадратичных поверхностей Fi.
Аффинное преобразование с матрицей С дает следующие преобразованные
матрицы плоскостей и квадратичных поверхностей:
F{ = C~tFl,
□ элементы неявного или параметрического описаний поверхностей высших
порядков и трансцендентных поверхностей;
□ коэффициенты параметрических функций и интервалы изменения парамет-
ров, задающие края граничных поверхностей — линии их пересечения;
П топологические матрицы граничных поверхностей.
При моделировании объекта границами структура данных строится одновре-
менно с процессом создания модели. Благодаря явному присутствию в этой
структуре уравнений поверхностей и линий их пересечения легко решается зада-
ча каркасного изображения объекта. В отличие от каркасной модели с плоскими
гранями граничное описание позволяет изображать нелинейную поверхность
каркасом с криволинейными ячейками.
Основной проблемой граничного описания является выбор возможных форм
задания поверхностей. Так как поверхности в большинстве случаев непрозрач-
ны, то для их правильной визуализации требуется, как уже неоднократно отме-
394
Гпава 3
чалось, внешняя ориентация нормалей ко всем точкам поверхностей. Для обеспе-
чения этого требования применяется метод заведомо внутренней точки рт\
□ в неявной форме описания поверхности ±f(p) = 0 одна из возможных функций
+f(p) или -f(p) выбирается по правилу размещения точки рт в области, где
значение f (р) < 0:
/+(p) = -sgn{/(pBH)}/(p). (3.105)
В частности, матрицы поверхностей первого и второго порядков корректи-
руются так:
F/ = -sgn{ рвн ° Fi }Fi, F2+ = -sgn{pBHf2 pBHT }f2. (3.106)
Это означает изменение знаков всех элементов матрицы F на противополож-
ные, если для заведомо внутренней точки выполняется условие f (рвн) > 0;
□ в параметрической форме p(t, т) ориентация нормали N = Fx W определяется
направляющими векторами V = p't и W = р'х. При обмене параметров t <-> г в
функции p(t, т) нормаль меняет направление на противоположное. Это же
происходит при расчете нормали по формуле N = W х И. Из двух возможных
параметрических форм выбирается та, в которой угол между нормалью в
точкеро и вектором рт-ро, направленным в заведомо внутреннюю точку /?вн.
тупой'.
рвн. (рви ~ро) ° N <0, где N = V х W, V =
at
„ ’ дг
Ро
Ро
(3.107)
Это условие выполняется для любой внутренней точки выпуклого объекта и
близкой к ро внутренней точки невыпуклого объекта. Если для исходного урав-
нения p(t, т) условие (3.107) не выполняется, то его нужно либо заменить на
р(х, t), либо вычислять нормаль как N = Wх V.
Условие близости двух точек ро и рвн-ро весьма важно. Построим, например,
нормаль к замкнутой поверхности эллиптического тора с моделью (3.13)
р(г,т)= [(asin(T)+r)cos(r) 6cos(t) -(asin(x)+r)sin(/)]
Уг,те [О, 2л], г > а, г>Ь (3.108)
в точке р0 = [О 0 - (г - а)], соответствующей параметрам to - л / 2 и то = Зл / 2:
И = [-(r + asin(T))sin(r) 0 -(г + asin(r))cos(/)] |f =[-(г-а) 0 0],
W - [acos(r)cos(x) -6sin(T) — czsin(f)cos(r)J | =[0 b о],
‘0>Т0
N = -(г - а) 0
о =[о о
-б(г-а)].
X
0 b
о
Математические модели поверхностей и объектов 395
Она направлена внутрь тора. Выбор близкой к ро внутренней точки
Рвн = С® 0 _ г] подтверждает эту направленность:
(рвн-ро) ° N = ab(r -a)> 0.
Корректируем (3.108) путем обмена параметров t <-> т:
р(г,т)= [(nsin(r)+r)cos(c) 6cos(t) -(asin(/)+r)sin(x)] Vr, т g [0, 2л]. (3.109)
Теперь нормаль N = [О 0 7>(г-а)] является внешней к поверхности тора
(рис. 3.105):
(рвн — ро) ° N — -ab(r - a) < 0.
Рис. 3.105
Однако, если выбрать не близкую к ро, но тоже внутреннюю точку
Рвн = [О 0 И, то тест (3.107) дает ложный ответ:
(Рвн -p0)°N = (2r + a)(r-a)b>0.
Многие объекты не являются замкнутыми, и часть их внутренней поверхности
может быть видна одновременно с внешней (см. рис. 3.2, 3.8, 3.10, 3.12, 3.25 и
др.). Для визуализации внутренних поверхностей они должны быть описаны как
внешние. Другими словами, каждая тонкая оболочка, претендующая на двухсто-
роннюю видимость, рассматривается как две граничные поверхности p(t, т) и
р(т, t) с противоположно ориентированными внешними нормалями. Если какая-
либо внутренняя поверхность не видна ни при каких ракурсах, то включать ее
описание в граничную модель нет необходимости.
3.2.3. Сплошные модели
Сплошная модель включает в объект как граничные, так и внутренние точки.
Это позволяет, во-первых, производить декомпозицию сложного объекта на про-
стые составляющие— примитивы (кубы, сферы, конусы, пирамиды, призмы
и т. д.); во-вторых, строить разнообразные композиции из простых примитивов.
Процесс композиции заключается в выполнении аффинных преобразований
396
Гпава 3
примитивов для создания нужных форм в нужном месте пространства и булевых
операций с формами для создания единого объекта. Это очень напоминает
строительный конструктор, позволяющий создавать разнообразные по архитек-
туре сооружения из типовых блоков. За счет небольшого числа примитивов и
всего четырех булевых операций конструктивный подход к описанию сложных
объектов и сцен позволяет уменьшить объем памяти и трудоемкость процесса
построения сцены.
Простейшая декомпозиция заключается в разбиении пространства сцены на ку-
бические или сферические ячейки, называемые вокселами (рис. 3.106, а), и уста-
новлении состояния каждой ячейки — свободна она или занята объемом тела.
Структура данных вексельного объекта представляется трехмерной n х т х I-
матрицей битов состояний ячеек пространства сцены.
Рис. 3.106
При построении разрезов или сечений сплошных тел требуется временно уда-
лить группу вокселов. Эту операцию удобно выполнять, управляя атрибутом
прозрачности: выводу на экран подлежат только непрозрачные вокселы, а про-
зрачные можно даже не исключать из описания объекта для быстроты восста-
новления его неразрезанной модели.
Вексельный метод моделирования прост, но требует большого объема памяти
для описания крупных Зб-объектов с хорошим разрешением. Если у вексельных
поверхностей лишь один тонкий слой "вещества", то в объемном варианте этого
метода объект состоит из множества слоев вокселов, и, что досадно, большинст-
во внутренних ячеек, находящихся в глубине тела, практически никогда не будут
видны, занимая, тем не менее, уйму машинной памяти.
Уменьшение требуемых ресурсов достигается применением:
□ различных методов сжатия данных, аналогичных методам архивации фай-
лов. Например, по методу группового кодирования можно хранить в памяти
карту горизонтального плана некоторого вексельного пейзажа размером
п х т. Каждая ячейка этой матрицы плана хранит всего два числа — мини-
мальную и максимальную ординаты столбика вокселов, расположенного над
данной клеткой (рис. 3.106, б). Это равносильно затратам памяти на хранение
Математические модели поверхностей и объектов 397
всего двух слоев и дает выигрыш в скорости вывода вокселов на экран, со-
кращая число обращений к массиву данных;
□ пирамидально-ячеечной структуры объекта, начинающей его описание с
крупных кубических ячеек и рекурсивно разбивающей частично заполненные
ячейки на подъячейки меньшего размера, пока не будет достигнуто желаемое
пространственное разрешение. При этом наиболее мелкие ячейки группиру-
ются на границе объекта, а его внутренность охвачена небольшим числом
крупных ячеек. У каждой ячейки-кубика изображается не более трех лицевых
граней. Применение сферических вокселов более просто в визуализации, но
сложнее в заполнении ими пространства объекта, т. к. приходится решать за-
дачу вписывания сферы в область с криволинейными границами.
Конструктивное моделирование представляет объекты комбинацией простых пло-
ских и объемных примитивов. Простота примитивов означает относительную ма-
тематическую простоту и удобство конструирования из них произвольных тел.
Плоский примитив есть часть плоскости, ограниченная криволинейной замкнутой
линией или полигоном. Объемный примитив есть часть пространства, ограничен-
ная функционально описанными поверхностями первого и второго порядка. Вы-
бор минимальных порядков граничных поверхностей обусловлен необходимостью
аналитического решения задачи пересечения с ними светового луча.
Каждый примитив имеет граничное описание. Исходное положение примитивов
"ожно выбрать в начале координат, т. е. описывать их геометрию в собственных
объектных координатах. Многообразие конструкций достигается аффинными
преобразованиями примитивов. Например, граничное описание цилиндрического
примитива состоит из:
□ матрицы F6oK=diag[l 0 1 -1] боковой поверхности цилиндра единичного
радиуса;
□ матриц FlllI>K = [О -1 0 б] и FBep = [б 1 0 -1] торцевых плоскостей, ор-
тогональных оси цилиндра;
Г) уравнений линий пересечения боковой поверхности с торцами:
Рниж(')=[со5(г) о sin(r)], pBep(/)=[cos(r) 1 -Sin(r)].
Рассмотрим правила построения комбинаций примитивов. Множество примити-
вов П1, Пз, ... , все пространство I и пустое пространство 0 образуют булеву ал-
гебру со следующими логическими операциями (символ означает точку).
1 Отрицание (дополнение до I) примитива П:
•е (-1П), если »g П. (3.1Ю)
Выполнение этой операции означает:
• изменение направлений нормалей ко всем граничным поверхностям на
противоположные;
• матрицы F, плоскостей и квадратичных поверхностей заменяются на мат-
рицы -f);
398
Гпава 3
• направления обхода полигональных граней заменяются на противопо-
ложные;
• параметрические функции p(t, т) заменяются на функции р(т, t).
П Объединение (сложение) примитивов Пу и П/
•е (П, + Пу), если («е n;)U(«e Пу). (3.111)
Выполнение этой операции заключается в расчете пересечения всех поверхно-
стей примитивов П, и Пу. Поверхность объекта П, + Пу формируется из внеш-
них частей поверхности П, относительно Пу и из внешних частей Пу относи-
тельно П,-.
П Пересечение (произведение) примитивов П, и Пу:
•е (П, & Пу), если («е Пу)П(«е Пу). (3.112)
Поверхность объекта П, & Пу формируется из внутренних частей поверхности
П, относительно Пу и из внутренних частей П, относительно П,.
□ Исключение (вычитание) примитива Пу из примитива П<
•е (П,--1 Пу), если (•еПу)П(»йПу). (3.113)
Поверхность объекта П, -i П, формируется из внешних частей поверхности П,
относительно Пу и из внутренних частей П, относительно П,.
Логические операции подчинены следующим основным законам булевой алгебры:
П законам отрицания
-Л = 0, -п0 = I, Ч-П) = П; (3.114)
П коммутативным законам
П,. + П, = Пу + П„
Пу & Пу = Пу & П,-; (3115)
□ ассоциативным законам
(Пу + Пу) + П, = Пу + (П7 + П,),
(Пу & Пу) & пд = Пу & (Пу & ПО; (3-116)
□ дистрибутивным законам
(П, + Пу) & Пд. = П, & Пд. + Пу & Пд,
П, & Пу + Пд - (П, + Пд) & (Пу + Пд); (3-117)
□ законам двойственности де Моргана
-.(Пу+Пу) = (-Пу)&( Ч)
—’(Пу & Пу )=ЬПу)+
□ законам идемпотентности
П, + П, = Пу,
Пу & Пу = Пу; (3119)
Математические модели поверхностей и объектов
399
□ законам поглощения
(П, + П,) & П, = П„
П,. & П,- + П, = П,.
(3.120)
Последовательность логических операций над примитивами при конструирова-
нии объекта называется его булевым описанием. Любое булево выражение, опи-
сывающее объект О, можно представить в виде объединения 2Л пересечений N
объектов о,— примитивов и их отрицаний:
2n ( N
Л=1
(3.121)
где о,С, означает воздействие на объект о, аффинного преобразования с матрицей
С,. Данная каноническая форма булева описания может быть минимизирована
широко известными в булевой алгебре методами карт Карно, диаграмм Эйлера
(Венна) и т. д. [13].
Полная сплошная модель объекта включает его минимальное булево описание
совместно с данными о типе каждого примитива, его граничной моделью, опти-
ческими свойствами каждой поверхности и матрицами аффинных преобразова-
ний на каждом шаге конструирования сложного объекта или сцены.
Процесс композиции можно изобразить в виде бинарного дерева с правилом об-
хода "от листьев к корню". Терминальные вершины (листья) означают исходные
примитивы; узлы — логические операции; ветви — аффинные преобразования;
корень— объект или сцена. Не лишне будет еще раз напомнить формулы аф-
финных преобразований матриц плоскостей и квадратичных поверхностей:
f'=c~'f , т/=с_|т(с“1)г.
Правила логического конструирования позволяют формальными методами рас-
считать положение точки относительно замкнутого объекта. Оно определяется
трехзначной функцией принадлежности <р(р, П) точки р примитиву П:
-1, если р внутри П;
0, если р на поверхности П;
1, если р внеП.
(3.122)
Пусть выпуклый примитив П ограничен N поверхностями/(р) - 0 V/ = 1, /V, нор-
мали которых внешне ориентированы по правилам (3.105)—(3.107). Функция
принадлежности точки р примитиву П вычисляется аналогично тесту (1 122):
-1, если //(/>)< О V/ = 1,JV;
<р(а п)=1 1> если З/е [1Л1: Л(р)>0;
0, если не ±1.
(3.123)
400 Гпава 3
Точка лежит внутри выпуклого примитива, если в ней все значения f(p) < 0. Точ-
ка лежит вне примитива, если хотя бы одна из функций / (/?) > 0. Точка принад-
лежит поверхности выпуклого примитива, если хотя бы одна из функций поверх-
ностей в этой точке обращается в ноль, а остальные функции неположительные.
Требование выпуклости примитива принципиально. Для убедительности доста-
точно вычислить по (3.123) функцию принадлежности точки, находящейся под
гранью {5, 6, 7, 8, 5} объекта на рис. 3.93:
Ф(р, П) = 1,
т. к. существует грань {9,10,11,12,9}, относительно которой эта внутренняя
точка расположена снаружи.
Правило (3.123) совместно с логической формулой (3.121) позволяет формально
вычислить ориентацию точки относительно сложного объекта, полученного
композицией выпуклых примитивов. Решение этой задачи актуально для его
визуализации. В методе трассировки световой луч пересекает множество поверх-
ностей различных примитивов (расчеты пересечений луча с плоскостью и квад-
ратичной поверхностью даны в гл. 1). Из всех точек пересечения отбираются
точки, принадлежащие границам объекта, а из них— ближайшая к источнику
света или наблюдателю. Таким образом, нужно уметь вычислять ориентацию
точки относительно комбинированного объекта. В табл. 3.3 приведены функции
принадлежности точки объектам А,Ви их логическим комбинациям. Объекты
не обязательно должны быть выпуклыми. Главное, чтобы расчет по (3.123) вы-
полнялся для выпуклых примитивов.
Таблица 3.3
А в ->А А&В А +В А -> В
-1 -1 1 -1 -1 1
-1 0 1 0 -1 0
-1 1 1 1 -1 -1
0 -1 0 0 -1 1
0 0 0 0 0 0
0 1 0 1 0 0
1 -1 -1 1 -1 1
1 0 -1 1 0 1
1 1 -1 1 1 1
Особенность трехзначной логики, заключающаяся в том, что -10 = 0, накладыва-
ет ограничение на расположение примитивов с совпадающими границами. Во
Математические модели поверхностей и объектов
401
избежание ошибки расчета положения точки на общей границе двух объектов,
когда ф(р, А) = ф(р, В), должны быть запрещены совпадения границ в двух опера-
циях (рис. 3.107), отмеченных в табл. 3.3:
□ внутреннее касание границ при объединении объектов. По табл. 3.3 определя-
ем ф(рц А + В) — 0, хотя в действительности точка pt лежит внутри объекта
А+В-,
□ внешнее касание границ при операции исключения объектов. Согласно
табл. 3.3 имеем ф(рг, А - В) = 0, хотя в действительности точка pi лежит вне
объекта A -п В.
Рис. 3.107
Для исключения запрещенных совпадений границ между объектами А и В можно
изменить один из примитивов, например, В, так, чтобы было ф(р„ В) = -!. Те-
перь по табл. 3.3 функции принадлежности определяются верно:
ф(р|, А + В) = -I, ф(р2, А ->В)= I.
22J Пример 3.21. Составить описание объекта, изображенного на рис. 3.108, а, и
вычислить принадлежность объекту точек
<7,=[1 3 3], 92=[2 3 3],93=[3 3 3].
Решение. Выбрав примитивы П| (куб на рис. 3.108, б) и Пз (призму на
рис. 3.108, в), составим бинарное дерево композиции объекта (рис. 3.108, г). Бу-
лево описание объекта имеет следующий вид:
О = (П1С1) & (П2С2) -1 (П1С3).
Сформируем массивы неявного описания плоскостей объектов П1, Пг и матрицы
аффинных преобразований Ci 4- Сз:
1 0 0 -1 0 О’ 0 1 -1 0 О’
0 0 1 0 0 1 0 0 -1 0 0 -1 , П2 = 1 1 0 0 0 0 -I 0 0 -1 (3.124)
-1 -1 -1 0 0 0 -1 -1 0 0 0
402
Гпава 3
Рис. 3.108
Матрица Сз выбрана так, чтобы внешние грани объектов IIiCi и ГПСз не совпа-
дали. Обходя дерево от листьев к корню, формируем массив матриц плоскостей
объекта:
~0 1-10 О'
1 00-10
1 0 0 0 -1’
-8-80 0 0
I 0'
1 о
I -1 ’
-4 -7 -7 2 2 0
Математические модели поверхностей и объектов
403
1 0 0 -10 0 О'
(П,С,)&(П2С2)= 0 1 0 0-10 1 0 0 1 0 0 -1 1 >
-6 -6-60 0 0-8
1 0 0-1 0 0 0 0 -1 1 0 0
0 10 0 -101 100 1 0
о =
0 0 10 0-11 1000 1
-6 -6 -6 0 0 0-8-84-2 -2 -2
По формуле (3.123) вычислим функции принадлежности точек q\ + qj примити-
вам П1С1, П2С2 и П1С3, а по табл. 3.3 — всему объекту О:
□ фп = <p(<7i, П1С1) = -1, ф12 - ф(<?|, П2С2) = -1, фи = ф(<?1, П1С3) - 1:
фП & ф!2 -1 ф13 — (—1) -1 1 = -1,
из чего следует, что точка qi находится внутри объекта О;
□ ф21 = ф(<?2, П1С1) = -1, ф22 = ф(<?2, П2С2) = -1, ф23 = ф(<?2, П|Сз) = 0:
ф21 & ф22 —1 ф23 - (—1) -10 = 0,
откуда следует, что точка qi лежит на поверхности объекта О;
□ Ф31 - ф(#з, П1С1) = -1, фзг = ф(<?з, П2С2) = -1, фзз = ф(^з, П1С3) -- -1:
ф31 & ф32 -1 фзз = (-1) -1 (-1) = 1,
откуда следует, что точка <?з лежит вне объекта О. □
Глава 4
Геометрические задачи
визуализации
В этой главе рассматриваются методы решения главных геометрических задач
визуализации — отсечения элементов, не попавших в область отображения сце-
ны, и удаления элементов, заслоненных (экранированных) другими элементами
от наблюдателя. В результате на экране дисплея формируется изображение, не-
сущее наблюдателю важнейшую информацию о пространственном строении
объектов сцены и их взаимном положении. Последующие более тонкие и трудо-
емкие оптические алгоритмы делают изображение реалистичнее и красивее.
Сложность геометрических задач визуализации привела к появлению большого
числа различных способов их решения. Некоторые из них разработаны в расчете
на специализированные приложения и учитывают их нюансы, другие более уни-
версальны, имеют широкий круг применения, но менее проработаны в частно-
стях. Не следует считать, что разработка алгоритмов визуализации в настоящее
время завершена. Усвоив основные идеи методов отсечения и удаления, описы-
ваемых в этой и других книгах, читатель сможет самостоятельно разобраться в
новых появляющихся алгоритмах или разработать свои алгоритмы примени-
тельно к конкретному приложению.
4.1. Логические операции со списками
Для работы с данными, объем которых заранее неизвестен, используются дина-
мические массивы— списки различных типов данных. Поскольку настоящая
книга не является учебником по программированию, то в планы автора не вхо-
дит рассмотрение разнообразных типов списков, методов их структурной орга-
низации и программной реализации. Квалифицированным программистам все
это хорошо известно, а просто любопытным читателям можно войти в курс де-
та, например, по книгам [5, 30] и не стареющей во все времена "библии програм-
миста" [12].
Перечислим операции со списками:
□ вычисление размера списка size(L) — числа содержащихся в списке L элементов;
□ инициализация пустого списка L = 0. Размер пустого списка 5/ze(0) = 0;
406
Гпава 4
П добавление е—> L нового элемента е в конец списка L с увеличением размера L
на единицу;
□ исключение L-,em списка L элемента, значение которого равно е. Если такой
элемент в списке найден, то после его исключения размер списка
size(L) = size(L) - 1,
в противном случае список L не изменяется. Возможен вариант операции ис-
ключения из списка всех элементов, равных е. Тогда значение size(L) умень-
шается на число исключенных элементов;
П слияние (конкатенация [4]) двух списков L\ и Lt в список L - L\ v Lt, вклю-
чающий все элементы каждого списка независимо от их суммарной кратности
в списке L. Размер конкатенации
size(L) = size(Li) + size(LiY,
П объединение (дизъюнкция) двух списков L\ и Lt в список L = L\ U L2 мини-
мальной длины путем записи в него объединений элементов L\ и Lt. Размер
объединенного списка
size(L) < size(Li) + sizefLT);
П пересечение (конъюнкция) двух списков Li и Lt в список А = А|Г)А2 мини-
мальной длины путем записи в него пересечений элементов L\ и Lr,
П исключение L\ Lt из списка L\ пересечений с элементами списка Lx,
П сортировка sort(b) элементов списка L по критерию с. Чаще всего критерием
С
сортировки является возрастание или убывание элементов либо самого спи-
ска L, либо какого-нибудь другого списка.
Логические операции со списками скалярных (L) и векторных (£/?) переменных
имеют переборный характер. Рассмотрим их выполнение на примере списков
скалярных данных L\ - {а\, ...,а„} и Lt = {Z>i, Ввиду простоты действий с
множествами точек ограничимся словесным описанием алгоритмов.
П Алгоритм слияния L- Lw Lt заключается в создании списка L = L\ и пооче-
редном добавлении b}^> Lb него всех j = 1, т элементов списка Lt.
П Алгоритм объединения L = A] U L2 можно реализовать двумя методами—ао-
дитивнъш (с добавлением элементов) и субтративным (с удалением элементов):
• после инициализации пустого списка L = 0 в него последовательно добав-
ляются элементы a, VZ = 1, п и b, X/j = 1,т, не содержащиеся в текущем спи-
ске L;
• из конкатенации L = L\ v Lt исключаются все кратные элементы путем их
попарного сравнения.
Удаление из произвольного списка L всех кратных элементов выполняется с
помощью операции A = A(J0. По аддитивному методу из списка L как ис-
407
еометрические задачи визуализации
точника данных в список L (приемник данных) будут скопированы (через
вспомогательный буферный список) только некратные элементы. По субтра-
тивному методу элементы конкатенации Lv(Z> = L попарно сравниваются друг
с другом и в приемник L копируются только непересекающиеся элементы.
□ Алгоритм пересечения L = Ц П £2 также может быть выполнен аддитивным и
субтративным методами:
• после инициализации пустого списка L - 0 в него добавляются элементы
О; = bj, общие для обоих списков-сомножителей;
• из списка Z. = A]U0 исключаются элементы, не совпадающие ни с одним
из элементом Ьг
□ Алгоритм исключения L = Li -л Li также реализуется двойственным образом:
• после инициализации списка £ = 0в него добавляются элементы a^fy
первого списка, отсутствующие во втором списке;
• из списка Л = £( U0 исключаются элементы, совпадающие хотя бы с од-
ним из элементов bj.
Не трудно видеть, что аддитивные варианты всех алгоритмов предпочтительнее
еубтративных как по трудоемкости, так и по автономности, т. е. независимости
от алгоритмов выполнения других логических операций.
Теперь рассмотрим логические операции со списками отрезков
Lsi = {<?i ... = {ci di,..., c„,d„,},
размещенных на плоскости или в пространстве. В отличие от списков типа L и
Lp, элементы которых являются объектами нулевой длины, в списках типа Ls
зозможно частичное совмещение отрезков «,/>, и c}dj, лежащих на одной прямой.
Эти отрезки необходимо выявить либо отличающимися друг от друга тестами
коллинеарности (1.20) на плоскости или (1.91) в пространстве, либо едиными,
работающими в пространстве любой размерности, тестами:
□ параллельности пар векторов {/?, - я„ dj - с;} и {bt - ah Cj - о,}:
bi-ajodj-cj\ = ] :~а, °Cj,-a,,| = 1 }; (4.1, a)
□ (1.17, б) в R2 — он же (1.79, 6) в R3 — расположения четырех точек а„ bit Cj и <7;
на одной прямой:
rang
(4.1,6)
В алгоритмах, изложенных ниже, будет использован тест (4.1, я), позволяющий
этсеять неколлинеарные отрезки уже после первой проверки на параллельность.
В то же время вариант теста (4.1, б) также вполне эффективен. Он срабатывает,
если тестируемая 3 х //-матрица (// — размерность пространства R", содержащего
408
Гпава 4
отрезки) не имеет ни одного ненулевого 2 х 2-минора, общее число которых рав-
но трем при и = 2 или девяти при п = 3. Достоинство этого теста — отсутствие
вычислений длин векторов и их нормировки. Эти две операции выполняются
приближенно и служат источниками вычислительных погрешностей, тогда как
расчет определителей в (4.1,6) является целочисленным и может производиться
непосредственно с экранными координатами точек.
После нахождения пары коллинеарных отрезков с множеством их точек совер-
шается необходимая операция. Наиболее эффективный алгоритм обработки
списков отрезков основывается на комбинированном аддитивно-субтративно.м
методе.
4.1.1. Объединение списков отрезков
Изображенный на рис. 4.1, а алгоритм объединения Z.S|UAa2 списков отрезков
Ls\ и Ls2 начинает работу со слияния исходных списков в конкатенацию
Ls = Ls\ v Ls2 = {wi h’i, ..., U/W,}
cl = n + m элементами
w, и; = Ojbj Vi = l,n, u„+, и’„+, = c,d, Vi = l.m.
Определим направляющий вектор z-го отрезка
Vi = Wj-u, Vi = 1,1.
До тех пор, пока / > 2, т. е. список Ls содержит более одного элемента, итератив-
но выполняются следующие действия.
& Шаг 1. Перебираем пары отрезков цЛ V i = 2,1 и zz;w; V j = \, z-1, пока не
будет обнаружена коллинеарная пара. Два отрезка с номерами i и j коллинеар-
ны, если (рис. 4.1,6):
П параллельны векторы И, и Vj, т. е.
ро^ = 1;
П параллельны векторы F, и и} - и„ т. е.
|г, °(м7 -м,)| = 1.
Если ни одна пара элементов Ls не удовлетворяет этим условиям, то алгоритм
возвращает текущий список Ls и заканчивает свою работу.
Шаг 2. Для найденной пары отрезков {м, ,и'„ zz, и1,} по (1.19) вычисляем координа-
ты t и т точек Uj и и’; в одномерном пространстве их общей прямой, при этом на-
чало координат лежит в точке и„ а единица— в точке и-, (рис. 4.1, в). Если ока-
жется, что I > т, то путем обмена параметров t <-> т обеспечиваем
сонаправленность объединяемых отрезков (рис. 4.1, г).
Геометрические задачи визуализации
409
Шаг 3. Тестируем перекрытие отрезков u, w, и u,Wj по логическому пересечению
числовых интервалов [0, 1] и [г, т]. При t > 1 или т < 0 отрезки не имеют ни одной
общей точки и остаются в списке без изменения (рис. 4.1, г). В противном случае
при z<l (рис. 4.1, д) и т>0 (рис. 4.1,е) вычисляем дизъюнкцию
pq=UjWj \JujWj — новый отрезок, концевые точки которого р и q имеют в мас-
штабе отрезка upWj координаты min{0, t} и max{ 1, т} соответственно.
Шаг 4. Элементы ци; и и;и’; исключаем из списка Ls, а отрезок pq в него добавля-
ем. Декрементируем размер списка / = / - 1 и переходим на проверку условия /> 2
перед шагом 1. □
а
Рис. 4.1, а
410
Глава 4
Рис. 4.1, б, в, г, д, е
Внешний цикл алгоритма заканчивается, когда в Ls не останется ни одной парь
перекрывающихся коллинеарных отрезков, либо размер списка / станет равным I
Возвращаемый алгоритмом список содержит все попарно непараллельные от-
резки списков Lsi и Ls2, а также все дизъюнкции коллинеарных отрезков.
Особенностью изложенного алгоритма является первоначальное формирование
конкатенации Ls-Lsis/Lsi, в которой все отрезки являются равноправными
независимо от их принадлежности исходным спискам. Следовательно, алгоритм
объединения списков отрезков можно применять для дизъюнкции отрезков одного
списка Ls с помощью операции Ls = Ls U 0.
& Пример 4.1. Рассчитать объединение двух списков отрезков
Ls\ = {oi bt, (i2 b2, as bi} и Ls2 = {c\d\,C2d2,csds}. Взаимное расположение отрезков
показано на рис. 4.2, а. Для наглядности отрезки немного смещены от несущит
их прямых.
Решение. Формируем конкатенацию из / = 6 отрезков (рис. 4.2, б), которые гра-
фически будем обозначать направлениями и номерами в списке Ls. В поиске
коллинеарных перекрывающихся отрезков перебираем пары {2, 1} (не коллине-
арны), {3, 1} (коллинеарны, но не перекрываются), {3, 2}, {4, 1}, пока не находим
нужную пару отрезков {4, 2}, для которых значения параметров 0 < t < 1 и т > 1
Следовательно, концы объединенного отрезка равны
р - Ci + (dt - ci) • min{0,1} - о,
q = ci + (dt - ci) • max{ 1, t} = bi.
После удаления из списка Ls второго, четвертого отрезков и добавления нового
отрезкаpq нумерация элементов становится такой, как изображена на рис. 4.2. 6
Геометрические задачи визуализации
411
Повторяя поиск из I = 5 элементов списка, находим пару перекрывающихся от-
резков {3, 2}, для которых t > 1 и т < 0. Так как t > т, то после обмена получим
t < 0, т > 1 и концевые точки р = di и q - ci. Удалив второй, третий и добавив но-
вый отрезок pq, получим размер списка / = 4 и новую нумерацию его элементов,
показанную на рис. 4.2, г.
Аналогично, при объединении в этом списке третьего и второго перекрываю-
щихся отрезков получим t > 1 и 0 < т < I. После обмена параметров будет нуж-
ное соотношение 0 < i < 1 < т и концевые точки объединенного отрезка р = сз и
q = a. Удаление двух отрезков и добавление отрезка pq дает список из / = 3 эле-
ментов (рис. 4.2, д).
Анализ расположения этих отрезков показывает, что среди них нет ни одной
перекрывающейся пары. Таким образом, мы получили окончательный состав и
расположение отрезков объединения списков Ls\ и Lsi, изображенные на
рис. 4.2, е. □
4.1.2. Пересечение списков отрезков
Алгоритм пересечения Lsl ГШ2 списков отрезков Lsi и Lsi (рис. 4.3, а) построен
по аддитивному методу. Сначала инициализируется пустой список Ls = 0, в ко-
торый будут добавляться конъюнкции pq = albjr\cJdj каждого отрезка списка
Lsi с каждым отрезком списка Lsi. В том случае, когда любой из исходных спи-
сков пустой, т. е. имеет нулевой размер, алгоритм возвращает пустой результат и
заканчивает работу.
412
Гпава 4
Пересечение отрезков аД и с7Д не пусто, если они:
□ коллинеарны, т. е.
{|Й о (dj - Cj )| = 1 }П {|Й ° (с, - а,) | = 1},
где Г =Л, -о,;
□ перекрывают друг друга при
{г <1}П{т > 0},
где t и т > t — вычисляемые по (1.19) координаты точек с7 и d, в масштабе от-
резка аД. Если окажется, что t > т, то путем обмена г т делаем отрезки со-
направленными.
Концевые точки конъюнкции р и q имеют в масштабе отрезка аД координаты
тах{0, /} (рис. 4.3, б) и min{ 1, т} (рис. 4.3, в) соответственно.
Рис. 4.3, а
Геометрические задачи визуализации
413
Рис. 4.3, б—е
I& Пример 4.2. Рассчитать пересечение двух списков отрезков
Lsi = (ai bi, azbi, asbs} и Lsi = (ci dt, скЬ, csds}. Взаимное расположение отрезков
показано на рис. 4.3, г.
Решение. Инициализируем список Ls = 0. В поиске коллинеарных перекрываю-
щихся отрезков {etibj, Cjdj} первой находим пару {aibi, ск/i}, для которой значе-
ния параметров t < 0 и 0 < т < 1. Следовательно, первый отрезок, помещенный в
список Ls, имеет концевые точки, изображенные на рис. 4.3, д:
pi = as + (bi-ai) max {0, /} = as,
qt - яг + (bs - ог) • min{ 1, т} = dt.
Вторая пара отрезков {asbs, csds} характеризуется параметрами 0 < т < 1 < I. По-
сле обмена 0 < t < 1 < т получим второй отрезок списка Ls с концевыми точками
ps - ds и qs = bs. Наконец, третья пара {asbs, csds} с переставленными параметра-
ми t < 0 и т > 1 добавляет в Ls отрезок ps qs = as bs.
Окончательный состав списка Ls изображен на рис. 4.3, е. □
4.1.3. Исключение списков отрезков
Алгоритм исключения Lsi Lss отрезков списка Lss = {ci dt,..., c„,d„,} из отрезков
списка Lsi - {atbt,... ,a„b„} изображен на рис. 4.4, а. Принципиальное отличие
операции исключения отрезков от других логических операций с отрезками и от
исключения списков скаляров и точек заключается в возможности получения
более одного результирующего отрезка при полном перекрытии отрезка Cjdj от-
резком л, 6,.
414
Гпава 4
Рис. 4.4, а
Геометрические задачи визуализации
415
Рис. 4.4, б—к
Вначале формируется список Ls = Lsi = {hi ..c l = n элементами
w, и’, = a, b,. Если список Lsi пуст, т. e. m = 0, то алгоритм возвращает Ls и закан-
чивает работу. Иначе, пока размер исключаемого списка I = size(Ls) > 0, произ-
водится аналогичный предыдущим алгоритмам поиск пары перекрывающихся
отрезков {и,и’(, Cjdj} Vz = l,/, j = 1, m . В зависимости от их ориентации, опреде-
ляемой значениями координат I и т > I концевых точек с, и в масштабе отрезка
iijWi (при т < t выполняются обмены параметров (нти точек с} <-> т/,), возможны
следующие варианты действий:
□ при I < 0 и т > 1 отрезок и, и1, целиком перекрывается отрезком Cjdj (рис. 4.4, 6);
□ при 0 < t < 1 неперекрытая часть U/Cj отрезка zz,w, добавляется в Ls (рис. 4.4, в);
□ при 0<т< 1 неперекрытая часть djW, отрезка и,и’/ добавляется в Ls
(рис. 4.4, г).
416
Глава 4
После этого отрезок ii/W,- удаляется из списка Ls. В связи с изменениями разме-
ра списка Ls и нумерации его элементов алгоритм повторяет анализ отрезков с
начала.
Завершение работы алгоритма, не считая упомянутого случая т = 0, происходит
либо при получении пустого списка Ls = 0, когда все отрезки а,7>, перекрыты
отрезками Cjdj, либо при исчерпании пар перекрывающихся отрезков {и,и’„ Cjdj}.
I& Пример 4.3. Рассчитать исключение отрезков списка Lsi = {ci dt, cidi, csds} из
отрезков списка Lst - {a\b\,aib2,asbs}. Взаимное расположение отрезков пока-
зано на рис. 4.4, д.
Решение. Создаем список Ls с тремя элементами иги’, = а,6, и ищем пары пере-
крывающихся отрезков {UjWj.Cjdj}. Первой находим пару {ii2W2,c\d\}, для кото-
рой 0 < t < т < 1 (рис. 4.4, е). Исключив из Ls отрезок иг W2 и добавив два отрезка
аг а и dt Ьг, получим конфигурацию, изображенную на рис. 4.4, ж.
В следующей паре отрезок иг W2 (под ним теперь скрывается аз Ьз) полностью пе-
рекрыт отрезком С2 d2 и поэтому удаляется из Ls (рис. 4.4, з).
Анализируя третью пару отрезков {пзи’з, сзЛ} с параметрами (после обмена)
О < t < 1 < т, удаляем из Ls отрезок из из и добавляем туда dt d3. В получившейся
конфигурации отрезков (рис. 4.4, и) нет ни одной перекрывающейся пары.
Окончательный состав списка Ls показан на рис. 4.4, к. Q
4.2. Методы отсечения
Отсечение (clipping) есть процедура обнаружения и исключения из дальнейшего
анализа элементов сцены (линий, поверхностей, объектов), которые не попадают
в видимую область, отображаемую на экране. Эта операция выполняется одной
из первых в процессе визуализации. Она позволяет существенно снизить трудо-
емкость расчета сложной пространственно протяженной сцены за счет раннего
исключения из дальнейшей обработки многих объектов в условиях ограничен-
ной видимости. Помимо задачи визуализации алгоритмы отсечения могут ис-
пользоваться в системах конструктивного моделирования для выполнения логи-
ческих операций с плоскими и пространственными объектами и построения
сечений, в различных тестах ориентации, при построении оптических эффек-
тов — теней, отражений и преломлений — на ограниченных поверхностях, для
создания многооконного интерфейса прикладных программ со сложной, т. е. не
прямоугольной, формой окон и т. д., и т. п.
Объект, устанавливающий границы области отсечения, называется отсекателем.
В зависимости от размерности, области действия, сложности формы и средств
реализации отсекатели бывают:
□ плоскими (2d), например, окно на экране дисплея, в котором строится изо-
бражение сцены. Такое не слишком трудоемкое отсечение производится на
конечной стадии отображения объемной сцены, многие элементы которой,
возможно, не попадут в окно;
Геометрические задачи визуализации
417
□ объемными (3d), например, призма (при параллельном проецировании) или
пирамида (при центральном проецировании) видимости — это полиэдры, в
основаниях которых лежит картинная плоскость, а боковые грани ориенти-
рованы параллельно лучу зрения наблюдателя. Более трудоемкое в сравнении
с плоским, отсечение по объему исключает заведомо невидимые элементы
сцены из дальнейшего анализа, т. е. до расчета их взаимного положения с
другими элементами. Это дает значительную экономию машинных ресурсов;
□ внешними, отбрасывающими элементы сцены, находящиеся вне отсекателя.
Последний играет роль ограниченного окна, через которое объекты сцены
видны наблюдателю;
□ внутренними, отбрасывающими элементы сцены внутри отсекателя. Послед-
ний играет роль ограниченной ширмы, которая загораживает объекты сцены
от наблюдателя;
□ регулярными, имеющими форму плоской (прямоугольник) и объемной
(параллелепипед) фигур, ориентированных по координатным осям. Для этих
простейших форм отсекателей разработаны специальные упрощенные, но за-
то и более быстрые алгоритмы отсечения;
□ нерегулярными, имеющими произвольную форму. Алгоритмы, работающие с
такими отсекателями, более сложные и ресурсоемкие;
□ аппаратными, реализованными микропроцессорными средствами СБИС цен-
трального процессора, контроллеров, графических ускорителей и т. д. Обыч-
но аппаратные отсекатели ограничиваются простейшими — регулярными
или выпуклыми — 2d- и Зб-формами;
□ программными, создаваемыми в отсутствие аппаратного отсекателя или не-
стандартных ситуаций отсечения. Программные алгоритмы часто имеют не-
достаточное быстродействие в приложениях, ориентированных на процессы,
протекающие в реальном времени.
В гл. 1 нами уже рассматривались некоторые методы внешнего выпуклого отсече-
ния отрезка на плоскости и в пространстве. Эту операцию выполняют функции
clip2_cross (см. рис. 1.18), clip2_test (см. рис. 1.19), clip3_cross (см. рис. 1.47) и
clip3_test (см. рис. 1.48). В разд. 1.3.5.1 было рассмотрено два варианта модифи-
кации этих алгоритмов для выполнения внешнего выпуклого отсечения луча. В
рамках тех знаний было затруднительно построить систематическую методоло-
гию различных видов отсечения, перечисленных выше. Теперь это стало воз-
можным, в связи с чем далее разрабатывается пакет алгоритмов отсечения, рас-
сматриваемых в порядке возрастания их сложности.
Структурная схема пакета приведена на рис. 4.5. Форма модулей алгорит-
мов отсечения условно отражает форму отсекателя: регулярный, выпуклый, не-
выпуклый, плоский или объемный. Отсекаемые этими модулями фигуры
(отрезки, полигоны или полиэдры) показывают решаемые алгоритмами задачи
внешнего или внутреннего отсечения. Округлые модули выполняют вспомога-
тельные функции, необходимые для работы основных алгоритмов. Стрелки,
соединяющие модули, обозначают использование модуля-источника модулем-
приемником.
418
Гпава 4
Рис. 4.5
Сравним две тактические схемы выполнения отсечения на примере построения
проекции Зб-сцены, включающей объект— плоский полигон Р- {р\ргртр\},
отсекатель — полигон О - {oi от оз 04 oi} в плоскости f, источник света 5 и тень
Геометрические задачи визуализации
419
объекта Р на окно О. Схемы отличаются местом, занимаемым в них операцией
отсечения.
□ Схема отсечения в пространстве сцены целесообразна, если отсекатель пред-
ставляет собой прямоугольник (рис. 4.6, а). Здесь полностью применим про-
ективный алгоритм построения тени, описанный в разд. 2.2.5.4. Согласно ему
сначала вычисляются проекции
Pit = PiCf
точек объекта на f, затем по простому алгоритму выполняется отсечение по-
лигона Pf окном
о{=оск
в такой системе координат, где отсекатель является регулярным. Матрицу Си
преобразования системы координат можно вычислить по формуле (2.14), вы-
брав четыре пары точек:
{Оз, oi}, {|о2 -О||х°, 02}, {|о4 -ojj0, о4}, {|Af|z°, Oi +Wf},
где Nt - (ог - oi) х (04 - oi) — нормаль к плоскости f. Наконец, координаты
видимого в О полигона тени преобразуются в экранные с помощью мат-
рицы Ск'спэ.
Рис. 4.6
□ Схема отсечения в плоскости экрана целесообразна в том случае, когда отсе-
катель является произвольным полигоном (рис. 4.6, б). Сначала рассчитыва-
ются экранные проекции полигонов окна
д„=бсп
и полной тени объекта
Л1 = >
а отсечение выполняется в экранной системе координат Хэуэ перед отображе-
нием сцены.
420
Гпава 4
Таким образом, практически всегда отсечение тени произвольным полигоном
выполняется быстрее по второй схеме. Аналогична картина и при построении
отражения объекта в полигональном зеркале. Выигрыш достигается за счет ис-
ключения расчета промежуточных точек на плоскости тени или зеркала, преоб-
разования СК и получения результата отсечения сразу в виде экранной формы.
4.2.1. Регулярное плоское отсечение отрезка
Простейшим внешним 2б-отсекателем является прямоугольное окно О на кар-
тинной плоскости или на экране дисплея, заданное координатами сторон хп, лъ.
ун, ув или вершин
°ЛН — Ун]» °лв — (*л Ув ] > °ПВ — 1ХП Ув1> ®ПН — ["'П Ун]
(рис. 4.7). К такой форме отсекателя сводится множество типовых задач селек-
тивного изображения элементов сцены. Например, составной частью алгорит-
мов построения оптических эффектов является проверка принадлежности точк!1
ограниченной поверхности. Если эта поверхность— плоский прямоугольник,
то, преобразуя его во фронтальное и ориентированное вдоль осей окно, прихо-
дим к регулярному виду отсекателя.
Внешнее отсечение точки р = [х у] регулярным прямоугольным окном О вы-
полняется элементарным габаритным тестом (1.39, а):
[хл, хп]}П{уб [у„, Ув1}=^Р6 О,
[{х£ [хл, xnJ}U{уй [ун, Ув]}=>^£ О.
Более сложна задача внешнего отсечения отрезка p\pi (рис. 4.7, а). Возможны
следующие варианты ориентации отрезка и регулярного окна-отсекателя:
□ отрезок целиком расположен в окне, если для обоих концов отрезка тест (4.2)
дает результат
{/?! g о}П{/?2 6 О}= I;
□ отрезок целиком лежит вне окна, достаточным условием чего является распо-
ложение обеих точек р\ и pi снаружи любой из сторон окна (тест (1.40)):
р\pi g О: gab2_poly(p\pi, О) = 1. (4.3)
Внешнее положение отрезка возможно и при невыполнении условия (4.3), что
подтверждает верхний правый отрезок на рис. 4.7, а;
□ отрезок расположен в окне частично, пересекая его стороны один или два раза.
Основным в процедуре плоского отсечения является расчет точек пересечен^
заданного отрезка с отрезками — сторонами окна. Для этого можно использо-
вать функцию cross_segm, разработанную в гл. 1. Там же представлены алгорит-
мы внешнего отсечения отрезка clip2_cross и clip2_test, использующие функцию
cross_segm для получения нужного числа точек пересечения отрезка со сторона-
ми отсекателя.
Геометрические задачи визуализации
421
Рис. 4.7
Произвольно ориентированный на плоскости отрезок пересекается с регуляр-
ным окном не более двух раз и не более одного раза с каждой его стороной.
С целью уменьшения расчетов пересечений, требующих обращения матрицы,
желательно как можно раньше отделить заведомо внутренние и внешние отрез-
ки, а для остальных полностью или частично внешних отрезков запомнить ин-
формацию о сторонах окна, с которыми потенциально возможно их пересечение.
Для этого каждой концевой точке отрезка = [хд у^ ] поставим в соответствие
трехзначный логический код
Ek = ek\ ek2 екз ek4, (4.4, a )
четыре разряда которого однозначно описывают ориентацию точки относи-
тельно каждой из четырех сторон регулярного окна по порядку его обхода:
ekt - sgn(xn - хА), ek2 - sgn(yk - jB), ед.з = sgn(xA. - хп), e*4 = sgn(yH - yk). (4.4,6)
Определим отношения E * а, означающие, что все разряды логического кода Е
удовлетворяют условиям е, с символом отношения * е {=, А <, <, >, >}. Тогда
точка рк, находящаяся внутри регулярного окна, имеет код £( = -1, а в коде гра-
ничной точки Ек < 0 нулевые разряды (один или два) означают расположение
точки на соответствующих сторонах окна.
Поразрядные логические операции с кодами Ei и Ег выполняются согласно
табл. 3.3. Из нее следует:
□ признак расположения всего отрезка pi рг внутри окна есть Е\ & Ег < 0;
□ признак заведомого расположения отрезка вне окна— невыполнение условия
Е\ + Ei < 0.
Оставшиеся после этих двух проверок отрезки содержат по одному или два
внешних концов. Со стороны внутреннего конца, если он есть, частично види-
мый отрезок обязательно пересекает какую-нибудь сторону окна. Со стороны
422
Гпава 4
внешнего конца отрезок может пересечь не более одной из двух сторон окна,
для которых eki = 1.
На рис. 4.8, а представлен разработанный на основе метода логических кодов
алгоритм reg_outclip2(p\pi, О, Ls) внешнего отсечения отрезка р\рг регулярным
окном, векторы вершин которого составляют массив
О = {Рлн Олв Опв Опн Олн} = {О| 02 03 04 05}
в порядке, соответствующем очередности формирования разрядов в логическом
коде (4.4). Алгоритм возвращает признак видимости отрезка в окне:
□ О — весь отрезок расположен вне окна и невидим;
□ 1 — отрезок видим в окне целиком или частично.
На рис. 4.8, б приведен алгоритм reg_inclipl(p\рг, О, Ls) внутреннего отсечения
отрезка р\рг регулярным окном О, возвращающий признак видимости отрезка
вне окна:
□ О — отрезок целиком невидим, т. е. расположен весь внутри окна;
□ 1 — отрезок видим вне окна целиком или частично одной частью;
□ 2— отрезок видим частично двумя частями. Внутреннее отсечение в отличие
от внешнего может расщепить отрезок на два фрагмента (см. рис. 4.7, б).
Рис. 4.8, а
Геометрические задачи визуализации
423
б
Оба алгоритма регулярного отсечения отрезка сохраняют его видимые фрагмен-
ты в списке Ls, заранее созданном для запоминания неотсеченных элементов
сцены. Это может быть обычный массив отрезков или более сложно организо-
ванная структура, дополнительно содержащая параметры tn и тп, вычисленные
функцией cross_segm. После отсечения всех объектов сцены накопленное содер-
жимое списка используется последующими алгоритмами визуализации.
4.2.2. Произвольное плоское отсечение отрезка
Усложним отсекатель— пусть он будет произвольным выпуклым «-угольником,
заданным массивом векторов вершин О = {oi ... о„ oi}. Подобные отсекатели
возникают, например, при построении тени или отражения отрезка на полиго-
нальном участке плоскости. Приняв за основу алгоритмы отсечения на рис. 4.8,
внесем в них следующие минимальные изменения:
□ цикл i = 1 ... 4 заменим циклом i — 1 ... и;
□ изменим правила расчета «-разрядного логического кода £* ориентации точки
рк относительно сторон выпуклого окна. Построим по (1.8) внешние нормали
Nj = (о/+1 —о,)т?(—90 )— ~°i,y °i,x ~°i+l,x]
424
Гпава 4
к сторонам окна, обходя его вершины против часовой стрелки. Тогда значе-
ние разряда ekj определяется знаком угла между вектором рк - о, и нормалью
N, (рис. 4.9):
eki = sgn((p*. - о,) ° N,) V/ = 1,л.
(4.5)
Рис. 4.9
Обозначим модифицированные таким образом алгоритмы произвольного вы-
пуклого внешнего и внутреннего отсечения как
outclip2(p\pi, О, Ls), inclip2(p\pi, О, Ls).
Они возвращают число неотсеченных фрагментов отрезка.
Сравнительный анализ трудоемкости (числа расчетов пересечений прямых) род-
ственных алгоритмов outclip2, clip2_cross и clip2_test показывает эффективность
метода логических кодов, ускоряющего решение самой массовой задачи геомет-
рической визуализации: благодаря анализу этих кодов алгоритм outclip2 обра-
щается к функции cross_segm лишь тогда, когда потенциально возможно пересе-
чение отрезка с окном. Алгоритм clip2_cross поочередно рассчитывает все
пересечения до тех пор, пока их число не станет равным двум. Конкуренцию ме-
тоду пересечений составляет алгоритм clip2_test, способный благодаря тес-
ту ориентации отделять внешние фрагменты отрезка от внутренних. В связи с
этим он весьма перспективен, но имеет большую трудоемкость, чем алгоритм
clip2_cross.
Дальнейшее усложнение отсекателя', пусть он будет произвольным невыпуклым
полигоном, возможно, с отверстиями и несвязными фрагментами. Рассмотрим
три способа описания произвольных отсекателей и соответствующие алгоритмы
отсечения ими отрезка ab.
1. Полигон отсекателя задается списком вершин О — {си ... o„oi} в порядке об-
хода его по замкнутому контуру в произвольном направлении. Описываемый
ниже метод пересечений не нуждается в логических кодах (4.5). Он рассчиты-
вает пересечения отрезка со всеми сторонами окна, т. к. в отличие от выпук-
лого алгоритма clip2_cross заранее неизвестно максимальное число пересече-
Геометрические задачи визуализации
425
ний. Алгоритм, конечно, работоспособен и с регулярными, и с выпуклыми
отсекателями, но менее эффективен в этих случаях из-за бесполезных расчетов
в среднем около половины пересечений.
Отсечение отрезка ab окном О основано на идее, заложенной в алгоритм
clip2_iesi (см. рис. 1.19), и выполняется следующим образом.
&Шаг1. Инициализируем список чисел L = {0, 1}, определяем возвращае-
мые значения
5, = cross_segm(ab, о^,+\, th т„ q,) Vi = l,n
функции расчета пересечений отрезка со сторонами полигона и формируем
логическую сумму
Z, = £U|J,fU >0:0>°)
/=1
в виде неупорядоченного списка параметров точек пересечения на отрезке
/(О = a + (b - a)t,
включая параметры его концевых точек t = 0 и t = 1.
Шаг 2. Сортируем список по возрастанию элементов
L = sort(L),
после чего точки rk = /(ЛА) разбивают отрезок на непересекающиеся фрагмен-
ты [/*., лА.+|] с постоянной ориентацией относительно полигона.
Шаг 3. С помощью тестов ориентации (см. рис. 1.15, 1.17) средних точек
т _ rk + rk+l _ „ . Lk + Lk+\ (h
-------------a+----------(0 - a)
определяем расположение каждого фрагмента относительно полигона Р. Ви-
димые фрагменты изображаются на экране или добавляются в список Ls не-
отсеченных элементов.
Шаг 4. Ls = Ls U 0 и возврат size(Ls). □
& Пример 4.4. Выполнить внешнее и внутреннее отсечение отрезка ab невы-
пуклым окном О - {oi ... on oi} (рис. 4.10, а).
Решение. Инициализируем список L = {0,1} и рассчитаем параметры пересече-
ния отрезка со сторонами окна, дополняя L параметрами Z, граничных точек:
• cross_segm(ab, 0102, lt,Ti,qt) = 1, /1 = 0, п = 0 => L = L\Jtl= {0,1};
• cross_segm(qb, 02 оз, /2, тг, qi) = 0, ti — 1.12, тг = 1.98;
• cross_segm(ab, 03 04, /з, тз, qi) = 0,Гз = 0.57, гз = 2.98;
• cross_segm(ab, 04 05, /4, т 4, qi) = 0, /4 = 0.94, Т4 = 1.31;
426
Гпава 4
• cross_segm(ab, 05 os, ts, ts, qs) - 1, ts = 0.85, ts = 0.47 => А = Z, U/5 = {0,1, /5 };
• cross_segm(ab, оьот, 1ь, ть,дь)~ \,tb = 0.7, Тб = 0.53 => L = LUtb = {о, 1, z5, /6};
• cross_segm(ab,OTO%,tT,Ti,qT) - 1, ti = 0.57, т? = 0.48 => L = L U/7 = {0,1, /5, tf,,ty};
• cross_segm(ab, os 09, ts, ts, qs) = 0, ts = 0.49, те = -0.26;
• cross_segm(ab, 09 010, /9, T9, <79) = 0, /9 = 0.85,19 = -2.53;
• cross_segm(ab, оюon, /ю, тю, <710) = 0. /10 = 0.19, тю = 2.34;
• cross_segm(ab, on 012, /11, th, 911) = 0, /11 = 0.57, th = -2.02;
• cross_segm(ab, 01201, /12, T12, <712) =1, tn = О, тп = 1 =>
=> L = L{jt\2 = {0,1,/5,^, Z7}.
Далее сортируем элементы списка по возрастанию 0 < 1т < ts < ts < 1 и отби-
раем точки л = а, гг = qi, гз = qs, rn- qs и rs- b (рис. 4.10, б). Наконец, угло-
вым тестом, примененным к средним точкам пп пи, определяем, что внутри
окна находятся непересекающиеся фрагменты пп и пп, а вне окна— фраг-
менты Г2 ГЗ И Г 4 Г5.
Трудоемкость алгоритма составляет двенадцать расчетов пересечений пря-
мых и четыре теста ориентации точки относительно полигона. □
2. Желание сократить число расчетов пересечений с помощью логических ко-
дов, формируемых корректно только для выпуклых отсекателей, приводит к
конструктивному методу — описанию произвольного окна булевой комбина-
цией выпуклых полигонов, индивидуальному отсечению отрезка каждым
примитивом и логическим операциям с полученными списками неотсеченных
фрагментов отрезков.
Внешнее и внутреннее отсечения отрезка ab невыпуклым полигоном
О = 0(01,..., Оа) конструктивным методом выполняются следующим образом.
& Шаг 1. Инициализируем пустые списки Lsi=0Xfi = \, со и функцией
внешнего отсечения outclipl(ab, О,, Ls,) добавляем в них внутренние относи-
тельно О, фрагменты отрезка ab.
Геометрические задачи визуализации
427
Шаг 2. Формируем список не отсеченных отсекателем О фрагментов отрезка ab:
• при внешнем отсечении Ls = £l(Lst,... , Lsl;1):
• при внутреннем отсечении Ls = {ab} -i Q(Lst,..., Lsa).
Шаг 3. Возврат size(Ls). □
Результат внутреннего отсечения отрезка ab можно получить и иначе. Вы-
полнив внутреннее отсечение функцией incliplipb.O^Ls1"^ V/ = l,со, получим
списки Ls}", дополняющие соответствующие списки внешнего отсечения
Ls°ut до целого отрезка ab. Из законов двойственности де Моргана (3.118)
следует двойственная логическая формула:
Lsin=^№(Ls^,...,Ls^}.
Двойственность означает формальный обмен логических операций "+" и
Например, двойственны формулы
А В + С и (А + (I В)) & С.
Практически всегда предложенная в алгоритме формула расчета списка
Ls'" ={^}^Q(£5r",...,Z.4u')
менее трудоемка, чем двойственная ей формула
& Пример 4.5. Решить пример 4.4 конструктивным методом.
Решение. Представим отсекатель комбинацией
О — Ot Oi + Оз
выпуклых примитивов Ol = {он 0120130140ц}, 01 = {02| 022023021} И
Оз — {оз, 032 оззоз4 оз1} (рис. 4.11, а). Внешние отсечения отрезка ab сторонами
примитивов формируют списки отрезков
Ls\ = {<714<71з}, Lsi = {</21 qn}, Lsi - {адзз}.
Первая операция Lsi Lsi дает список Lsti = {quqmqnqti}. Вторая операция
£.V|2 и£.?з дает результат внешнего отсечения
Ls'“" = {aq33,qnq\3}.
Список видимых отрезков внутреннего отсечения отрезка ab отсекателем О
имеет вид
Ls"1 = {ab} -i {адзз, qnqti} - {q33qn,q\3b}.
Трудоемкость алгоритма составляет шесть расчетов пересечений прямых и
две (три — для задачи внутреннего отсечения) логические операции со спи-
сками отрезков. □
428
Гпава 4
3. Разновидностью конструктивного метода является представление невыпукло-
го отсекателя объединением непересекающихся выпуклых примитивов:
O = (JO, , OjHOj=0 Vi* j.
i=i
(4.6)
Это эквивалентно разрезанию (ручному или алгоритмическому [25]) полигона
на простейшие выпуклые фигуры (трех- и четырехугольники), для которых
задача отсечения решается индивидуально с помощью функций
*сИр2{рЬ,С>1,Ьз*}, где символ означает "out" или "in". В результате созда-
ются непересекающиеся списки отрезков Ls*,Ls*^. Состав результирующе-
го списка Ls* зависит от вида отсечения:
• для внешнего отсечения
Lsou' =ijLsfu>-,
/=1
• для внутреннего отсечения работает двойственная формула
Lsin=f\Lsf.
z=l
Рис. 4.11
& Пример 4.6. Внутреннее отсечение в примере 4.4 методом разрезания.
Решение. Разрежем отсекатель на выпуклые примитивы О\ = {он 0120130140ц}.
Ог - {ог, 022023024021} и Ог = {оз| оз2озз034оз)} (рис. 4.11,6). Сначала формиру-
ем списки внешних отрезков
Ls\ - {bq\i},Lsi ~ {ab},Lsi = {0934, bqn}.
Пересечение этих списков есть
Ls = Ls\ A LS2 A Ls^ = {734 <71з, 6<7зз}.
Трудоемкость метода составляет семь расчетов пересечений прямых и две ло-
гические операции со списками отрезков. □
Геометрические задачи визуализации
429
Анализ трудоемкости методов отсечения, основанных на представлении отсека-
теля комбинацией выпуклых примитивов, показывает, что они заметно сокра-
щают число расчетов пересечений прямых. К недостатку конструктивных мето-
дов, затрудняющему их применение, отнесем сложность алгоритмизации выбора
выпуклых примитивов и синтеза булевой формулы описания невыпуклого окна.
Из всего вышесказанного следует вывод: конструктивный метод имеет высокую
эффективность в задачах невыпуклого отсечения.
Обозначим алгоритмы невыпуклого внешнего и внутреннего отсечения отрезка ab
отсекателем О как
outdip2_segm(ab, О, Ls) и indip2_segm(ab, О, Ls).
4.2.3. Произвольное плоское отсечение полигона
На основе разработанных методов отсечения отрезка перейдем к решению глав-
ной задачи плоского отсечения произвольного полигона Р произвольным полиго-
нальным отсекателем О. Если полигон каркасный, то эта задача сводится к по-
следовательному отсечению ребер. Непустым результатом отсечения сплошного
полигона является полигон. При этом возможна фрагментация видимых элемен-
тов полигона, т. е. расчленение его на несвязные фрагменты. Алгоритм отсече-
ния должен сформировать все эти фрагменты и описать каждый из них анало-
гично описанию исходного полигона Пусть, например, даны полигон
Р- {pipzpspapi} и окно Oi = {oi 02 оз од 05 Об О7О|} (рис. 4.12). Внешнее отсечение
(а) дает два полигона
Pi = {pi q\ ОбЦьр\}, Pi = {qiqsquqsqi},
а внутреннее (б) — два полигона
Рз = {piqiqspnqbObqipi}, Pt = {рз^дф^з}.
Рис. 4.12
Основная идея поиска внешне (внутренне) не отсеченных фрагментов полигона
воплощается в двухэтапном процессе:
П внешнее (внутреннее) отсечение сторон полигона окном;
П внешнее (внешнее) отсечение сторон окна полигоном.
430
Гпава 4
На каждом этапе неотсеченные отрезки накапливаются в неупорядоченном спи-
ске Ls. Затем эти отрезки сцепляются в замкнутые контуры концами с совпа-
дающими координатами. Результат сцепления сохраним в массиве списков
Аш = {/.|, ...,Ln] замкнутых контуров— видимых фрагментов исходного поли-
гона. Число ик элементов массива равно числу полученных контуров. Каждый
элемент Lm есть список Lk = {lk , ... lk,mkh,\\ вершин k-го замкнутого контура —
/иА-угольника. Перед сцеплением из Ls нужно удалить кратные отрезки, которые
появляются при внешнем отсечении полигонов с совпадающими границами
(например, отрезок см/м на рис. 4.12, в).
Возможен случай, когда при отсечении должен получиться полигон с одним или
несколькими отверстиями (см. рис. 3.94,6). При этом в массиве списков Lm будут
присутствовать непересекающиеся контуры: охватывающий и соответствующее
число вложенных в него. Критерий охватывания контура L, контуром £, имеет вид
Lj с L, : {/у ц е £j }П {li v g Z.y} Vv = 1, , р = 1, , (4.6)
т. е. все вершины £, лежат внутри £й а все вершины £, лежат вне £,, что определяется
тестами ориентации — габаритным и угловым. Условия (4.6) проверяются для ка-
ждой пары списков £, и Lj. В случае их выполнения формируется новый список
Л = {4,1 ••• Ф ^/,1 ••• Ф 4,1} (4.7)
со специальными элементами Ф, вставляемыми между концами фиктивного реб-
ра полигона. Список Lj исключается из Lm.
Функция cont(Ls) формирования замкнутых контуров из отрезков списка Ls, воз-
вращающая список типа Lm. имеет следующий вид.
& Шаг 1. Инициализация пустого списка Lm = 0 и номера списка k = 1. Если
Ls = 0, то видимые фрагменты полигона отсутствуют и перейти на шаг 6.
Шаг 2. Начало первого отрезка в Ls принимается за начало к-го контура Lk, а
конец — за конец контура. Сам отрезок удаляется из Ls.
Шаг 3. В списке Ls ищется отрезок, любой из концов которого совпадает с кон-
цом контура. Отрезок присоединяется к контуру этим концом, второй его конец
становится концом контура Lk, а сам отрезок удаляется из списка Ls. Формиро-
вание контура в Lk заканчивается при совпадении его конца с началом.
Шаг 4. Если Ls * 0, то к = к + 1 и перейти на шаг 2.
Шаг 5. Контуры в Lm проверяются по (4.6) на охватывание, и при необходимо-
сти по (4.7) формируются списки контуров с отверстиями.
Шаг 6. Возврат Lm. □
Если видимые фрагменты имеют общую точку на границе окна (рис. 4.12, в), то в
ней возможно неоднозначное продолжение контура. В этом случае следует про-
считать все возможные варианты замыкания контура от точки разветвления и
выбрать из них кратчайший вариант. Отрезки, удаленные в не выбранных вари-
антах, должны быть восстановлены в списке, а в выбранном варианте—- удале-
ны из списка.
Геометрические задачи визуализации
431
Алгоритмы внешнего
outclipl_poly(P, О, Lm)
либо внутреннего
inclipl_poly(P, О, Lm)
отсечений полигона Р- {р\ ...pnpi} полигональным окном О - {oi ... o,„oi}, воз-
вращающие число неотсеченных фрагментов, имеют следующий вид.
& Шаг 1. Инициализация пустого списка Ls = 0 и расчет числа вершин поли-
гонов
п = size(P) - 1, m = size(O) - 1.
Шаг 2. Внешнее либо внутреннее отсечение п ребер полигона Р отсекателем О с
помощью функции
outclip2_segm(pjpi+\, О, Ls) либо inclip2_segm(pipi+\, О, Ls) Vi = 1, п.
Видимые внутренние либо внешние фрагменты сторон Р добавляются в Ls.
Шаг 3. Внешнее отсечение m ребер полигона О отсекателем Р с помощью функции
outclip2_segm(pioi+\, Р, Ls) Vi = 1, m .
Видимые внутренние фрагменты сторон О добавляются в Ls.
Шаг 4. Формирование замкнутых контуров в массиве списков Lm = cont(Ls U 0).
Шаг 5. Возврат size(Lm). □
Пример 4.7. Внутреннее отсечение полигона Р = {p\pipipip\} невыпуклым
окном О = {oi oi оз 04 os Об 07 oi} (рис. 4 12, б).
Решение. Последовательно отсекая части сторон Р, лежащие внутри О, получим
первый список отрезков
£ji - {q\pi,piqi,qipi,psqt,qspi,p^q6}.
Аналогично отсечение частей сторон полигона О вне отсекателя Р дает второй
список
Lsi - {qi qi, qs qi, q\ Об, 06 qe}.
Просматривая объединенный список видимых отрезков Ls = Ls} U Ls2. формиру-
ем первый замкнутый контур
Рз = {(71 pi qi qs р* qt оь q\}.
Из оставшихся в Ls - {qip3,psqi, qzqt} трех отрезков составляем второй замкну-
тый контур
Pi = {qipsq^qs},
после чего список Ls = 0. Таким образом, после отсечения число видимых фраг-
ментов равно двум, они не удовлетворяют условиям охватывания (4.6), а массив
списков фрагментов имеет описание Lm = {Рз, Pi}. □
432
Гпава 4
I& Пример 4.8. Внешнее и внутреннее отсечения невыпуклого полигона
Р- {/’1/22/23/24/25/2)} невыпуклым ОКНОМ 0= {oi О2ОЗО4О)} (рис. 4.12, в).
Решение. Внешнее и внутреннее отсечения сторон Р окном О дают списки отрезков
Ls\ = {<71 <72, оьрь,p*ps,psqi}, Lsi - {p\q\,q2pi,p2p3,p30n,q3p\}.
Внешнее отсечение сторон О отсекателем Р дает список отрезков
Lsi = {q^qi, qion, otp^}.
Получаем списки сторон полигонов отсечений Lsout = Ls{ U Ls^ и Ls,n = Ls2 U Ls3 c
одним отрезком 04/24 в каждом списке (второй такой же отрезок удален при объ-
единении списков).
Начиная фрагментацию списка Ls"‘" с отрезка q\ qi, формируем замкнутый контур
Ps = {q\q2O^pnpsq3q\},
после чего ЛУ"" = 0. В результате массив Lm"'" - {Ps} содержит один замкнутый
контур.
Фрагментация списка внутреннего отсечения Ls'" дает два замкнутых контура:
Рь = {p\q\qip\}, Рз = {qipipiOnqi}.
В результате получаем массив из двух замкнутых контуров Lm'" = {Рь, Рз}. □
4.2.4. Объемное отсечение отрезка
Обобщим методику плоского отсечения на трехмерное пространство. Наиболее
распространенные формы ЗФотсекателей — призма и пирамида видимости —
возникают, например, при параллельном и центральном проецировании
(рис. 4.13). Сечение этих полиэдров картинной плоскостью дает окно с изобра-
жением части сцены, находящейся внутри отсекателя, боковые грани отсекателя
направлены к наблюдателю, а передняя и задняя грани могут не участвовать в
отсечении, т. е. быть пассивными.
Рис. 4.13
Геометрические задачи визуализации 433
Цель объемного отсечения— выявление активных объектов на ранней стадии
расчета сцены — до ее проецирования на картинную плоскость. Это существен-
но экономит машинные ресурсы и, главное, не загружает компьютер бесполез-
ной работой с заведомо невидимыми объектами.
Второй пример Зб-отсечения — логические операции со сплошными телами:
□ объект А + В образуется объединением внутренних отсечений тела А телом В,
тела В телом А и пересечения тел А и В\
□ объект А & В есть объединение внешних отсечений тела А телом В и тела В
телом А;
□ объект А -1 В формируется объединением внутреннего отсечения тела А телом
В и внешнего отсечения тела В телом А.
Методика отсечения обогащает формальные правила конструирования сложных
объектов из примитивов, описанные в комментариях к определениям (3.110)—
(3.113).
Рассмотрим последовательно задачи Зб-отсечения точки, отрезка прямой линии,
плоского полигона и полиэдра. Взяв за основу алгоритмы плоского отсечения,
внесем в них необходимые изменения. Для работы с полиэдрами нам потребуются
определенные в (1.116) и (1.117) функции side(P,G,i) и попп(Р), позволяющие
вычислить нормаль к /-ой грани полиэдра Н = {Р, G} как
N = norm(side(P, G, /)).
Простейший регулярный Sd-отсекатель — параллелепипед с шестью гранями,
параллельными координатным плоскостям (рис. 4.13, а). Положение точки рк
относительно граней отсекателя описывается логическим кодом Ek = e*i ... ek5ekt>,
четыре разряда которого определены в (4.4), а два последних разряда
ек5 = sgn(z*. - ze), екь = sgn(z« - z*.) (4.9)
ориентируют точку по глубине сцены относительно ближней и дальней граней
отсекателя с аппликатами ze и гд.
Аналогично (4.5) вычисляется лг-разрядный логический код точкирк
ekj=sgn^pk -og.yN/)\/i = ],nr (4.10)
относительно лг граней произвольного выпуклого отсекателя. Также аналогично
плоскому варианту признаки полной видимости и заведомой невидимости отрезка
р\pi во внешнем отсекателе есть, соответственно, выполнение условия
Ei & Ei < 0
и невыполнение условия
E\+Ei< 0.
Основой Зб-отсечения является расчет точек пересечения отрезка p\pi с гранями
отсекателя с помощью функции cross_side (см. разд. 1.2.2). Если отрезок совпа-
дает с плоскостью какой-либо грани (при этом возвращается значение
434
Гпава 4
cross_side = -1), то нет нужды решать задачу плоского отсечения отрезка поли-
гоном этой грани в ее СК, т. к. прямая отрезка в этом случае пересекает и другие,
не параллельные ей грани.
Выполнив все необходимые изменения функций reg_oulclip2, reg_inclip2, outclipl.
inclip2, outclip2_segm и inclip2_segm, получим Зд-алгоритмы регулярного, выпук-
лого и произвольного отсечений отрезка
reg_outdip2>(p\pi, О, G, Ls), reg_inclipi(pt pi, О, G, Ls),
outclip?>(p\pi, 0, G, Ls), inclip2>(p\pi, O, G, Ls),
outclip?>_segm(p\pi, 0, G, Ls), inclip2>__segm(p\pi, 0, G, Ls),
возвращающие в списке Ls неотсеченные окном О фрагменты отрезка p\pi
На рис. 4.14 показано, как выглядит алгоритм внешнего выпуклого отсечения
oulclip2>.
Рис. 4.14
4.2.5. Объемное отсечение
полигона и полиэдра
Следующая задача рассматривает пересечение в пространстве двух произволь-
ных плоских полигонов Р= {р} ...рпр\} и О = {oi ...о,„о|} (рис. 4.15). Требуете»
найти все отрезки, по которым полигоны взаимно пересекают друг друга.
Геометрические задачи визуализации
435
Рис. 4.15
Составим алгоритм cross_poly(P, О, dim, Ls) расчета пересечения произвольных
плоских полигонов Р и О, возвращающий признак пересечения:
П -1 — плоскости полигонов параллельны и не совпадают;
ПО — полигоны не пересекаются;
П 1 — полигоны пересекаются по отрезкам, добавляемым в список Ls\
П 2— плоскости полигонов совпадают, а в списке Ls возвращаются отрезки
сторон полигона Р, находящиеся внутри отсекателя О.
Параметр dim е {2, 3} определяет размерность пространства, в котором заданы
полигоны.
& Шаг 1. Вычислив нормали к полигонам
NP = norm(P), No - norm(O)
и матрицы преобразования системы координат
СР = MAP2(pi,T^,O3,z°); Со = MAP2^,No,O3,z°),
проверяем ориентацию плоскостей Р и О'.
П если {ЛГрХДГо=О3}А{ЛГр°(л - о,) Ф О}, то возврат -1;
П если {ЛГрХДГо=О3}А{ЛГр«>(л -oj) = 0}, то выполняется внешнее отсечение
полигона Р отсекателем О в системе координат, где их общая плоскость
фронтальная
{ЛО} —С>’ >{Р ,О'}, Ls' — 0, outclipl_poly(P’, О', Ls’), Ls'———>Ls ,
и возврат 2;
П если dim - 2, то возврат 0.
Шаг 2. Для каждого ребра Р и О вычисляем булевы переменные
Sj - cross_side(PiPi+\,O,t,q,) \/i = \,n ,n = size(P) - 1,
q, = cross_side(OjOp\, P, x, rj \/j = \,m , m — size(O) - 1.
436
Глава 4
Если число пересечений ребер с полигонами
” т г 1
>0}+£{оу >о}<2 ,
i=l /=]
то возврат 0.
Шаг 3. Формируем неупорядоченный список точек пересечения ребер с полигонами:
Lp = 0~
q, -* Lp Vi: л, > 0;
5 -> Lp Vj: > 0;
Lp = Lp U 0 , M = size(Lp).
Сортируем неповторяющиеся точки в Lp вдоль прямой, на которой они распо-
ложены:
|Zp2 “iPlI
5ort(z,p)-> {Lpx,..., LpM }.
~tk
Шаг 4. Преобразовав точки списка Lp в системы координат полигонов Р и О по
формулам
Lp Ср > Lp , {Lp, б?} —С-“ ->{Lp', О"},
с помощью подходящего 2d-niecma ориентации из коллекции тестов, приведен-
ных в гл. I, определяем принадлежность центра каждого фрагмента LpkLp>.
обоим полигонам:
{0.5(Л/4 + Lp'k+i )е Р'}П {0.5(Lp£ + Lp^+i )е О'}.
Фрагменты, удовлетворяющие этому условию, добавляются в список Ls неотсе-
ченных элементов.
Шаг 5. Возврат 1. СИ
На основе функций cross_poly, outclip?>_segm и inclip?>_segm составим алгоритмы
внешнего
ouldip?>_poly(P, О, G, U, F)
либо внутреннего
inclip?>_poly(P, О, G, U, F)
отсечений плоского полигона Р= {pt ...рпр\} произвольным полиэдром, заданным
массивами координат вершин О и топологии граней G ={0] ... Gn ).
& Шаг 1. Инициализация пустого списка Ls = 0 и расчет размера списков:
п = size(P) - 1, «г = size(G).
Геометрические задачи визуализации
437
Шаг 2. Расчет пересечения полигона Р с каждой гранью полиэдра отсекателя:
cross_poly(P, side(O, G,j), 3, Ls) = 1, пг.
Шаг 3. Расчет отсечения каждого ребра Р полиэдром G соответствующей
функцией
outclip‘i_segm(pipM, О, G, Ls) либо inchp3_segm(plpi+x, О, G, Ls) Vz = 1, п.
Шаг 4. Формирование видимых контуров в массиве списков
Lm = cont^Ls U 0) •
Шаг 5. Сохранение списков массива Lm в массивах U и F.
Шаг 6. Возврат Lm. □
Результат отсечения — видимые фрагменты полигона, возвращенные списком
через имя функции и сохраненные в массивах координат вершин U, топологии
граней F = {5, •••, Рп^ }• Число элементов массива Нравно числу хранящихся в
нем фрагментов. Каждый элемент Fk содержит список номеров вершин замкнуто-
го контура k-то фрагмента. Номера fkt есть номера вершин фрагмента в U. На
пятом шаге алгоритма выполняется копирование координат точек из Lm в мас-
сив U и формирование списков Fk в соответствии со списками Lmk. Фиктивное
ребро, признаком которого является элемент Ф между двумя точками списка
Lmk, оформляется в списке Fk парой номеров вершин с отрицательным вторым
номером, как это описано в разд. 3.2.1.
Для экономии памяти и однозначности нумерации вершин рекомендуется сохра-
нять в массиве U только отсутствующие в нем точки. Если отсечение полигона
полиэдром — самостоятельная задача, то перед вызовом функций outclip3_poly
или inclip3_poly нужно инициализировать пустые массивы U= 0 и F= 0.
& Пример 4.9. Рассчитать внешнее и внутреннее отсечения треугольника ptpipi
с вершинами
Л=[0 5 0], р2=[1 1 5], Рз=[8 0 1]
невыпуклым полиэдром с вершинами
О] = [о 0 о], о2=[4 О о], о3=[4 О 2],о4=[2 0 2],
о5 = [2 0 б],о6=[0 0 6], 07= [0 2 0], о8=[0 2 б],
о9=[2 2 6], о10=[2 2 2],оп=[4 2 2],О]2=[4 2 б]
и массивом топологии G - {Gt,..., Gs} со списками граней (рис. 4.16)
Gi = {1,2, 3,4, 5,6, 1},G2= {7,8,9, 10, 11, 12, 7}, G3 = {6, 5, 9, 8, 6},
Gt = {5,4, 10, 9, 5}, Gs= {4,3, 11, 10, 4},G6= {3, 2, 12, 11,3},
Gi = {2, 1,7, 12, 2},Gs = {1,6, 8, 7, 1}.
438
Гпава 4
Рис. 4.16
Решение. Инициализируем массивы U = {pi, р2, рз} и F= 0.
На первом шаге получаем список
Lst - {hl2,hU,lsk,lih,l9lw}
отрезков пересечения полигона Р со второй по шестую гранями отсекателя О
С остальными гранями полигон не пересекается. Координаты точек 1\ /ю сле-
дующие:
/, = [0.75 2 3.75], /2= [2 2 2.78],/З=[3 2 2], /4=[Д 2 1.22],
/5=[2 0.86 4.43],/6 = [2 2 2.78],/7= [4 1.46 2], /8 = [з 2 2],
/9 = [4 2 1.22],/10= [4 1.46 2].
На втором шаге рассчитываем точки
^=[0.75 2 3.75], <72= [2 0.86 4.43]
пересечения ребер полигона Р с гранями отсекателя О, после чего формируем дв
списка отрезков:
П Lsi = {<71 pi,piq2} — внутри отсекателя;
П Lsy - {pi q\, дгрз,рзр\} — вне отсекателя.
Геометрические задачи визуализации 439
В результате получаем неупорядоченные списки отрезков внешнего и внутренне-
го отсечений полигона полиэдром
Lsout = Lsi U Ls2 , Lsin = Ls\ U Ls3.
На третьем шаге, учитывая совпадение точек
/1 = q\,h = U, h = Is, /4 = /9, /5 = qi, /7 = ho,
формируем замкнутые контуры в двух массивах
Lm'““ — {/1 /2 /5pi h, h /4 /7 /3}, Lm'" = {h h Isрзp\ h, b /4 /7 /3}.
Проверяя угловым тестом (в системе координат, в которой полигон Р является
фронтальной плоскостью) полученные контуры на охватывание, обнаруживаем,
что контуры в списке LnP удовлетворяют критерию (4.7): второй контур охва-
тывается первым. После коррекции по (4.8) массив контуров внутреннего отсе-
чения принимает вид
£ш'" = {/i 11Ьрзр\ /1Ф /з/4/7/з Ф /1}.
Он содержит внешний контур h 111зрзр\ h с отверстием bhhb.
На четвертом шаге формируем массивы вершин и списков фрагментов:
(/ = {p\,pi,p3, 1\, 11, Is, Ь, /4, 11},
7^"'= {{4,5,6, 2, 4}, {7, 8, 9, 7}}, F" = {{4, 5,6,3, 1, 4,-7, 8, 9, 7,-4}}. Q
Переходим к последней и главной задаче Зб-отсечения произвольного полиэдра
Н\ = {Pi, Gi} произвольным полиэдром Hi - {Pi, G2}. Исходные объекты заданы
массивами координат вершин Р\, Pi и топологии граней Gi, Gi.
Основная идея объемного внешнего (внутреннего) отсечения аналогична плос-
кому варианту: накопление неотсеченных элементов в процессе внешнего
(внутреннего) отсечения Н\ отсекателем Hi и внешнего отсечения Hi отсекателем
Н\. В результате формируются массив координат вершин U и неупорядоченный
список Fнеотсеченных фрагментов граней.
При Зб-отсечении также возможно расчленение Н\ на несвязные объемные
фрагменты. Алгоритм отсечения должен сформировать все эти фрагменты, т. е.
описать каждый из них аналогично описанию исходного полиэдра. Это означает
упорядочение массива F и разделение его на группы списков граней замкнутых
полиэдров. Принцип фрагментации — сцепление граней друг с другом ио общим
ребрам до получения замкнутого объекта. Результат фрагментации представляет
собой массив групп списков Гт = {//«],..., Гтп^ ] замкнутых полиэдров— неот-
сеченных фрагментов исходного полиэдра. Число п$ элементов массива равно
числу полученных фрагментов. Каждый элемент Гт есть группа
Гтк - {г*],..., Г^, } списков граней £-го замкнутого полиэдра — шА.-гранника).
440
Гпава 4
Функция frag(U, F) формирования замкнутых фрагментов из граней массива спи-
сков F, возвращающая массив групп списков типа Гт, имеет следующий вид.
& Шаг 1. Инициализация пустого массива Гт - 0 и номера фрагмента к = 1
Если F- 0, то видимые фрагменты отсутствуют, и следует возврат Гт.
Шаг 2. Первый список массива F принимается за начало /с-ой группы и перено-
сится из F в массив Гтк.
Шаг 3. Для каждого нефиктивного ребра из Гтк ищется совпадающее с ним не-
фиктивное ребро в массиве Fc концами и UF_ . В случае удачи весь спи-
сок F, переносится в массив Гтк. Формирование фрагмента в Гтк заканчиваете?
при просмотре всех содержащихся в нем ребер.
Шаг 4. Если F* 0, ток-к + 1 и перейти на шаг 2.
Шаг 5. Возврат Гт. □
Внешнее
outclip3_hedr(P\, Gi, Pi, Gi, U, Гт)
либо внутреннее
inclip3_hedr(P\, Gi, Pi, Gi, U, Гт)
отсечение полиэдра Hi = {Pi,Gi} полиэдром Hi = {Pi, Gi} выполняется следую-
щим алгоритмом, формирующим в массивах U и Гт координаты вершин в
группы списков фрагментов, а также возвращающим число фрагментов.
& Шаг 1. Инициализация пустых массивов списков U- 0 и F= 0.
Шаг 2. Внешнее
оШсИрЪ_ро1у{П„ Pi, Gi, U, F)
либо внутреннее
inclipl_poly(Hh Pi, Gi, U, F)
отсечение т = size(Gt) граней
П; = side(Pt, Gi, i) Vz = 1,
полиэдра H\ отсекателем Hi. Вершины и списки неотсеченных фрагментов гра-
ней Hi добавляются в U и F.
Шаг 3. Внешнее
outclip‘i_poly{side{Pi, Gi,j), Pi,Gi, U,F) V/ =1, n2
отсечение ni = size(Gi) граней полиэдра Hi отсекателем Н\. Координаты вершн-
и списки неотсеченных фрагментов граней Р2 добавляются в массивы UuF.
Шаг 4. Формирование неотсеченных фрагментов в массиве
Гт =frag(U, F).
Шаг 5. Возврат size(Tm). Q
'еометрические задачи визуализации
441
Пример 4.10. Рассчитать внешнее и внутреннее отсечения треугольной пира-
миды Н - {Р, Г}, заданной списками вершин и граней
Р = {Р1,Р2>РЗ,Р4}={11 5 3], [1 1 4], [5 1 о], [5 0 б]},
Г= {Гц Г2, Гз, Гл} = {{1,3,2, 1}, {1,2,4, 1}, {1,4, 3, 1}, {2,3,4, 2}},
невыпуклым отсекателем, заданным в примере 4.9 списками вершин
О - {oi,..., 012} и граней G = {Gi,..., Gs}.
Решение. На рис. 4.17 приведен эскиз сцены с выделенными отрезками, по кото-
рым грани полиэдров пересекаются друг с другом:
Рис. 4.17
П {/1/2, 1з1л}, {Ы2}, {1б1з} и {/7/4} — отрезки пересечения грани Л с гранями G2,
G4, Gs и Сь;
□ {k /1} и {/9 /в} — отрезки пересечения Л с G2 и G4;
П {/5/9}, {/е/ю} и {/7/10}—отрезки пересечения Л с Сл, Gs и Gt>.
Координаты точек 1\ 4- /ы следующие:
/|=[1.5 2 3.75],/2= [2 2 3.25],/3= [3.25 2 2], /4=[4 2 1.25],
Z5=[2 1 З],/6=[3 1 2],/7=[4 1 1],/8=[2 2 3.94],/9= [2 0.75 4.5],
/10=[4 0.83 2].
Перед вычислением отсечения {Р,Г} отсекателем {О, G} инициализируются пус-
тые массивы списков U = 0, F”" - 0 и F" = 0.
442
Глава г
Внешнее отсечение граней /7, = side(P, Г, i) Vz = 1,4 функцией
oulclipl_poly(nh О. G. U, F""‘)
добавляет в массив F°‘“ фрагменты
F\ ~ {/i hlspilx}, Fi = {/3/4/7hh}, F3 — {Ishpihh},
Fs — {Is hpi /5}, Fs — {/б/юЛ/б}-
Внутреннее отсечение
indipi_ро1у(П„ О, G, U, F'”)
добавляет в Fm фрагменты
Ft = {pipilildifolshl\pi}, Fi = {pi /1 khp^pi},
Ft, - {pip4p3pi}, F9 = {Isltfoohpspsbls}.
Внешнее отсечение
ouidip3_poly(Qj, P, Г, U, F'"") либо ouldipi_poly(Qp P, Г, U, Fm)
граней Qj = side(Q, G,j) \/j = 1,8 полиэдром {P, Г} добавляет в массивы F“" либо
F" неотсеченные фрагменты
Fio = {/2/1 kb], Pi 1 - {Uhon /4}, Fn — {foblshfo},
F13 = {/з/б/юоп /3}, Fh = {/10/7/4on /10}.
В процессе последовательного формирования неотсеченных фрагментов созда-
массив из 15 вершин:
U— {/i, /2, Is,pi, /з, /4, /7, /б, fo, b,p\,ps,ps, 011}.
Фрагментация списков Fm" и Fm функциями frag(U, F""') и frag(U, F'n) дает мас-
сивы групп списков
Гт"'11 = {{Fi, Fio, F12, Fi, Fs}, {Fi, Fn,Fu, Fs, F13}},
Гт= {{Ft, Ft, F9, Fu, Fi 1, F13, Fn, F10, Fi}}. Q
4.2.6. Логическое конструирование Sd-объектов
В завершение разработки комплекса методов отсечения получим на их основе
алгоритмы выполнения бинарных логических операций с объектами А и В:
П объединения А + £;
П пересечения А & В,
П исключения А -> В.
Эти алгоритмы воплощают в реальность описанный в разд. 3.2.3 метод конст-
руктивного моделирования сложных объектов на плоскости и в пространстве. Н.
рис. 4.18 показаны результаты логических операций А + В, А & В, А -> В и В - а
с двумя Зб-объектами: пирамидой А и сферой В.
Геометрические задачи визуализации
443
В разд. 4.2.3 и 4.2.5 были фактически разработаны плоские и объемные варианты
алгоритмов выполнения двух логических операций:
П операция пересечения А & В - В & А эквивалентна внешнему отсечению поли-
гона на плоскости (см. рис. 4.11, а) или полиэдра в пространстве
(см. рис. 4.17) с помощью функций
outclipl_poly(A, В, Lm), outdip3_hedr(A, GA, В, GB, U,Гт);
П операция исключения А В эквивалентна внутреннему отсечению полигона
на плоскости (см. рис. 4.11,б) или полиэдра в пространстве (см. рис. 4.17) с
помощью функций:
inclipl_poly(A, В, Lm), inclip3_hedr(A, GA, В, GB, U, Гт).
Рассмотрим порядок выполнения третьей логической операции — объединения.
В плоском варианте граница объекта
а + в = (я-.я)и (я-л)и (А & В)
формируется из отрезков трех непересекающихся групп (рис. 4.19):
П фрагментов сторон полигона А вне полигона В;
П фрагментов сторон полигона В вне полигона Л;
П пересекающихся фрагментов сторон А и В.
Рис. 4.19
444
Гпава 4
Получаем следующий алгоритм addl(A,B,Lm) объединения полигонов
А = {oi ... <7n«i} и В - {Ь\ ... ЬтЬ\}, формирующий массив списков фрагментов
объекта А + В и возвращающий через имя функции add! число его сторон.
& Шаг 1. Инициализация пустого списка Ls = 0.
Шаг 2. Внутреннее отсечение n = size(A) - 1 сторон полигона А отсекателем В
функцией
inclip2_jegm(fi,ai+i, В, Ls) X/i = I,и.
Внешние фрагменты сторон А добавляются в Ls.
Шаг 3. Внутреннее отсечение т = size(B) - 1 сторон полигона В отсекателем А
функцией
inclip2_segm(bj bj+], А, Ls) = .
Внешние фрагменты сторон В добавляются в Ls.
Шаг 4. Формирование списков отрезков
jLs> = {б?1 аг, О2Оз,..., a„a\},LsB = {61 bz, bibz,... , b„,bi}
и добавление их пересечения в список Ls'.
LsA (~}Lsb —> Ls .
Шаг 5. Формирование замкнутых контуров в массиве списков Lin = cont(Ls).
Шаг 6. Возврат size(Lm). □
Аналогично строится алгоритм add3(A, GA,B, GB, и,Гт) объединения полиэдров
НА = (A, GA) и Нв- (В, GB), формирующий в массивах U и Гт координаты вер-
шин и группы списков фрагментов объекта А + В, а также возвращающий через
имя функции addS число его фрагментов.
& Шаг 1. Инициализация пустых массивов списков U- 0 и F- 0.
Шаг 2. Внутреннее
inclipS__poly(side(A, GA, i), В, GB, U, F) \/i = i,n
отсечение n — size(GA) граней полиэдра HA отсекателем Нв. Координаты вершин
и списки неотсеченных фрагментов граней НА добавляются в массивы U и F.
Шаг 3. Внутреннее
inclipS_poly(side(B, GB,j), A, GA, U,F) X/j = I, m
отсечение m = size(GB) граней полиэдра Нв отсекателем НА. Координаты вершин
и списки неотсеченных фрагментов граней Нв добавляются в массивы U и F.
Шаг 4. В циклах i = l,n , j = 1, т функцией
cross_poly(side(A, GA, i), side(B, GB,j), 2, Lm)
Геометрические задачи визуализации 445
вычисляем пересечения пар граней GAi и GBj, лежащих в одной плоскости. Если
возвращенное значение cross_poly = 2, то добавляем списки массива Lm в масси-
вы U и F.
Шаг 5. Формирование массива
Гт = frag(C. F)
и возврат size(Tiri). О
I& Пример 4.11. Сконструировать объект из примера 3.21 (см. рис. 3.77, а).
Решение. Опишем примитивы П| = {Р, Gi} (см. рис. 3.77, б) и Пг = {Р, Gz}
(см. рис. 3.77, в) массивами координат вершин
Р = {[0 0 оЦ1 О ol [0 1 0|[0 О 1J [1 1 Oj fl О 1J [0 1 1J [1 1 1]}
и топологии граней
Gi = {{1,3,5,2,1}, {1,4,7,3,1}, {1,2,6,4,1}, {8,7,4,6,8}, {8,6,2,5,8}, {8,5,3,7,8}},
G2 = {{1, 3, 5, 2, 1}, {1,2,6, 4, 1}, {1,4, 3, 1}, {2, 5, 6, 2}, {3, 4,6, 5,3}}.
Объект конструируется по формуле
О = (LIiCi) & (П2С2) -л (П1С3) s Gi & О2 -1 Оз
с матрицами преобразований Ci, С2 и Сз из (3.51). Выполнив необходимые пре-
образования вершин примитивов, получим три выпуклых объекта Oi = {Pi, Gi},
Oz= {Pz, G2} и Оз - {Рз, G3}— операнды логических операций (рис. 4.20, а) с
новыми матрицами вершин
Pl - 6Р = {ОН, ... , 018},
Р2 = 8Р= {021, ... , 028},
Р3={|2 2 2Ц4 2 2][2 7 21(2 2 7}[7 7 2j[4 2 7][2 7 7][4 7 7]}.
°31 °32 °33 °34 °35 °36 °37 °38
Инициализируем пустые массивы U - 0 и Гт = 0. Первая логическая операция
конъюнкции Од - Oi & О2 выполняется функцией
outclip3_hedr(P\, Gi, Р2, G2, U, Гт).
Рис. 4.20
446
Глава 4
В табл. 4.1 показана последовательность внешних отсечений граней Oi отсекате-
лем Ог, граней Ог отсекателем О\ и накопления данных в массивах U и Гт = {F}.
В результате получаем описание объекта <?4 = {U, F} (рис. 4.20, б) с десятью вер-
шинами Oi -е- Uio и десятью гранями Ft + Fio. Объединение F = F\J0 исключает
из массива Играни Fi, Fs и Fi, совпадающие, соответственно, с гранями Ft, F3 и
Fi. Фрагментация frcig(U, F) сцепляет оставшиеся грани в один фрагмент
F= {Ft, Fi, Ft, Fs, Fs, Fa, Fio}.
Таблица 4.1
Грани Oi и Ог Отсечение Массив U Фрагменты Fi
{oil O|3O|5OI2O||} {on 013015012011} O11>O13>O15>°12 Ц u2 Щ U4 Ft = {1,2, 3,4, 1}
{oil 014017 013OI 1} {0110149192013011} °14,<7b92 u5 u6u2 Fi= {1,5, 6,7,2, 1}
{oil 0120160140ц} {Oil O12OI6O14OI1} 016 = Us Fs = {1,4, 8, 5, 1}
{O|8 017 OI4OI6 018} {qt oiAOttqsqt} qs = U9 Fa= {6, 5, 8,9, 6}
{018016012015018} {^3 016 012 015^4^3} qA = Uio Fs = {9, 8, 4,3, 10,9}
{018015013017018} {<74 015 013 <72 <74} Ft— {10,3,2,7, 10}
{O2I 023 025 022 021} {on 013015012011} F7= {1,2, 3,4, 1}
{02l 022 026 024 02l} {oil O12OI6O14OI1} Fs= {1,4, 8. 5, 1}
{O2I 024023 021} {011014471 92013011} F = {1,5, 6,7,2, 1}
{O22 025 026 O22} {0}
{O23 024 026 025 023} {929193(74(72} Fio= {7,6,9, 10,7}
Вторую операцию О = Оа -п Оз выполним функцией
iiidip?>_hedr{U, F, Рз, Оз, U, Гт)
без инициализации массивов U и Гт. В результате в U добавятся вершины
qs = Un, qt = Un, qi = Uis, qs = Uia, 031 = Uts, 032 = Utt,
а в массиве Гт будет сформирован один фрагмент
{Fi, F2, Ft, Fs, Fs, Fa, Fit, F12, F13, Fia, Fts, Fib}
Геометрические задачи визуализации
447
из двенадцати граней объекта О, изображенного на рис. 4.20, в. В дополнение к
табл. 4.1 обозначено
Fw = {6, 11, 12, 7, 6}, Fn= {13,9, 10, 14, 13},Fu= {15, 16, 14, 12, 15},
Fm= {15, 11, 13, 16, 15},Fi5= {15, 12, 11, 15} и/V {16, 13, 14, 16}. □
В заключение хотелось бы на рис. 4.21 проиллюстрировать возможности конст-
руктивного метода моделирования примерами конструирования из выпуклых
примитивов сложных объектов— фонаря, лавочки, шахматного коня и макета
Нижегородского кремля. Изображения построены с помощью программы
3dLoCon (трехмерный логический конструктор), разработанной магистром Ни-
жегородского государственного технического университета Дмитрием Васиным
под руководством автора книги.
Рис. 4.21
448
Гпава 4
4.2.7. Дополнительные задачи отсечения
на плоскости
В каждом сложном алгоритме существуют определенные секреты и приемы, по-
могающие выполнять его более эффективно, с меньшими затратами машинных
ресурсов. Иногда это достигается предварительным решением некоторых не-
сложных задач, облегчающих решение основной задачи. Именно такие вспомо-
гательные задачи, имеющие отношение к трудоемкой процедуре отсечения, рас-
сматриваются в данном и следующем разделах. Предлагаемая ниже коллекция
алгоритмов несколько выбивается из идейного русла пакета алгоритмов отсече-
ния, изображенного на рис. 4.5. Каждый описываемый здесь алгоритм имеет са-
мостоятельное значение, а некоторые из них могут использоваться как альтерна-
тивные методы решения задач отсечения.
4.2.7.1. Отсечение выпуклого полигона полуплоскостью
Как известно, прямая линия разделяет плоскость на две области, в которых не-
явная функция линии f(p) имеет противоположные знаки. Каждая область явля-
ется неограниченной выпуклой полуплоскостью. Далее полуплоскостью будем
называть отрицательно определенную часть плоскости, во всех точках которой
/(р)<0.
Рассмотрим задачу нахождения области пересечения нескольких полуплоско-
стей. Если эта область не пуста, то она безусловно выпукла как пересечение вы-
пуклых областей. Способ решения задачи заключается в последовательном рас-
чете пересечения текущей выпуклой области с очередной полуплоскостью
(рис. 4.22). В результате после каждого шага область пересечения либо не изме-
няется (если она целиком лежит в отсекающей полуплоскости), либо сужается,
либо становится пустой (если пересечение с полуплоскостью отсутствует). В по-
следнем случае обработка оставшихся полуплоскостей прекращается.
Рис. 4.22
Геометрические задачи визуализации 449
Выберем наилучший способ задания границы полуплоскости. Сравнивая методы
описания прямой линии, рассмотренные в гл. 1, и варианты (1.35) вычисления
неявной функции f(p), заключаем, что наиболее практичны параметрическая
форма {ро, К} с функцией nfV(po, V,p). Для описания прямой им достаточно че-
тырех чисел, а для вычисления f(p)— пяти арифметических операций. Такие же
затраты ресурсов имеют нормальная форма прямой {ро, N} и функция
nf N(po,N,p), но мы остановимся на параметрической форме, т. к. направление
прямой удобнее задавать направляющим вектором И, чем нормалью N.
Наибольшая трудоемкость вычисления f(p)— семь арифметических операций в
(1.35, г) — у способа задания прямой двумя точками, т. е. четырьмя числами. Ка-
залось бы, что наиболее предпочтительна неявная форма (1.9), в которой прямая
описывается всего тремя числами— элементами вектора /7 = [и В Т>],— а
функция nfF(F,p) вычисляется за четыре операции. Однако расчет F по (1.13)
требует еще трех арифметических операций, что в итоге делает неявную форму
не только неудобной, но и невыгодной.
Если отсекаемая область не является замкнутым полигоном, возникает естест-
венный вопрос о способе описания такой неограниченной области. Для преодоле-
ния неопределенности зададим начальный полигон
big_box - {pipipsp^pi}
в виде выпуклой ограниченной квадратной области с координатами
|л| < BIG, И < BIG,
где BIG— максимально возможное конечное число, надежно обеспечивающее
пересечение с big_box любой возможной прямой (см. рис. 4.22). Таким образом,
задача пересечения неограниченных полуплоскостей сводится к поочередному
отсечению ими большого, но ограниченного выпуклого полигона справа от век-
торов направлений граничных прямых.
Алгоритм clip_line(P,po, F) отсечения выпуклого полигона Р= {pi ...p„_ipi =р„}
полуплоскостью с граничной прямой {ро, И} приведен на рис. 4.23. Работа алго-
ритма начинается с инициализации пустого списка U = 0 и расчета пересечения
прямой с ребрами полигона. Для этого вычисляются значения НФ
f=nfV(p0, V,p)
во всех вершинах полигона, после чего производится сортировка вектора f
s = sort
?
по возрастанию его элементов и сравнение значений крайних элементов полу-
ченного вектора j:
□ при 51 s„ > 0 полигон с прямой не пересекается, но может касаться ее одной
вершиной либо одним ребром. В случае 5i < О весь полигон Р находится в от-
секающей полуплоскости и возвращается алгоритмом без изменения. Иначе
при 51 > 0 полигон целиком отсекается полуплоскостью, а алгоритм возвра-
щает пустой результат U = 0;
450
Глава 4
□ при 5u„ < 0 существует хотя бы одна пара вершин {р,,р}}, лежащих по разные
стороны от прямой {ро, V}. Так как полигон выпуклый, то прямая пересекает
его ровно в двух точках. Отрезок секущей линии между этими точками совме-
стно с частью полигона, лежащей в полуплоскости, составляет искомый по-
лигон U.
clip_Une(P, p^V)
Возврат U
Рис. 4.23
Для расчета области пересечения прямой с полигоном Р организуем новый цикл
i = 1, п обхода вершин /?, с добавлением в список U:
П точек /?,, находящихся в полуплоскости или на ее границе. Эти точки обнару-
живаются по ранее вычисленным отрицательным значениям/ < 0;
П точек
Qi= Р, + (Рм -Pfri
пересечения ребер полигона PiPM с отсекающей прямой {ро, V} при условии
Л/ж<о,
Геометрические задачи визуализации
451
означающем, что вершины />, и pi+l находятся по разные стороны от прямой.
Значение параметра
в точке пересечения z-го ребра с прямой при разностороннем расположении
вершин Pj и pi+i всегда удовлетворяет условию 0 < /, < 1.
По окончании цикла проверяется замкнутость полученной в списке U ломаной
линии путем сравнения ее крайних вершин L/i и Uk, где k - size(U). При совпаде-
нии этих точек алгоритм возвращает полигон U = {U\,..., СА.-|, Uk = СД}. Однако,
если первая вершина отсекаемого полигона р\ лежит вне полуплоскости, то
крайними вершинами ломаной U - {СЛ,..., Uk} являются две точки пересечения.
Замыкание ломаной линии до полигона выполняется добавлением точки U\ в
конец возвращаемого списка U.
На основе описанного метода отсечения работает алгоритм построения выпукло-
го полигона сот_poly (рис. 4.24), полезный в различных задачах компьютерной
графики. Алгоритм выполняет поочередное отсечение выпуклого полигона
Р - big_box случайно сгенерированными полуплоскостями. Секрет получения
всегда непустого решения — в способе выбора отсекающих линий, у которых на-
чало координат всегда лежит слева от векторов направлений, т. е. в отрицатель-
ных полупространствах.
Рис. 4.24
На плоскости задается или случайно генерируется точка q = [x у]*О2, через
которую проводится отсекающая прямая {q, N] с вектором нормали N = q и на-
правляющим вектором
F=A-7?(90°)=[-y х].
452
Гпава 4
Отрицательное значение неявной функции (1.35, в) в точке с координатами [о 0]
nf V(q, V, Ог) = nf N(q, q, O2) = -q ° q < 0
доказывает, что начало системы координат находится слева от любой построен-
ной таким способом прямой. Генерирование полуплоскостей и отсечение ими
полигона Р продолжается до тех пор, пока в координатах его вершин имеются
габариты исходного полигона — числа BIG или -BIG. При полном отсечении от
Р всех границ объекта big_box алгоритм возвращает полученный выпуклый по-
лигон как решение задачи построения случайного выпуклого полигона.
Область применения метода отсечения выпуклого полигона полуплоскостью
обширна: это целый круг задач, связанных с изображением сцен, отдельных объ-
ектов и оптических эффектов внутри ограниченных выпуклых окон, граней, зер-
кал... Задачи отсечения с невыпуклым полигоном и/или невыпуклым отсекателем
могут быть сведены к объединению выпуклых решений после разрезания невы-
пуклых фигур на выпуклые фрагменты, в частности, на треугольники. Алгорит-
мы разрезания произвольных полигонов изучаются в конце разд. 4.2.7.
4.2.7.2. Расчет ядра произвольного полигона
Ядро полигона — это множество точек, из которых напрямую видны все его вер-
шины [18, 24]. Две точки полигона р, и р, взаимно видны друг другу, если весь
отрезок p^j принадлежит полигону. Любой выпуклый полигон совпадает со
своим ядром (рис. 4.25, а), но не каждый невыпуклый полигон имеет ядро, что
видно из сравнения рис. 4.25, б с рис. 4.25, в.
В обиходном смысле ядро К полигона Р— это то, что останется от исходной
неограниченной плоскости после отрезания от нее ножницами всего, что находится
по одну сторону от линий разреза — сторон полигона Р — по завершении обхо-
да его ребер. Выбор положительного направления обхода приводит к отсечению
Р отрицательными полуплоскостями его ребер, что позволяет использовать для
этой операции алгоритм clipjine.
Заметим, что описанная процедура вовсе не равносильна разрезанию полиго-
нальной фигуры в процессе обхода ее сторон. При наличии у полигона невыпук-
лых вершин последовательное отсечение удаляет некоторые ребра, формирую-
щие ядро, в результате чего от полигона остается нечто большее, чем его ядро
(рис. 4.25, г).
Алгоритм kern_poly(P) расчета ядра полигона Р = {р\ ...рпр\] работает в соответ-
ствии с блок-схемой, приведенной на рис. 4.25, д. Вначале с помощью функции
dir_tesi(P), наиболее удачный вариант которой приведен в (1.50), находится на-
правление обхода d е {+1, -1} исходного полигона Р, а начальное значение от-
секаемого полигона К устанавливается равным big_box. Затем для каждого реб-
ра PiPi+i вычисляется вектор направления Vi = Pi+i-Pi и выполняется отсечение
полигона К прямой этого ребра: справа при d = 1 либо слева при d = -\. Если
после очередного отсечения полигон К окажется пустым, то ядра полигона Р не
существует, а алгоритм возвращает пустой результат К - 0.
Геометрические задачи визуализации
453
Рис. 4.25
4.2.7.3. Пересечение выпуклых полигонов
Близкой к задаче нахождения ядра полигона является реализация булевой функ-
ции А & Б пересечения выпуклых полигонов А и В. Если в алгоритме kern_poly
заменить Р на А, К на В и отсекать от полигона В фрагменты, не принадлежащие
полуплоскостям сторон полигона А, то получим полигон, принадлежащий как
А, так и В, т. е. их пересечение А & В, если оно, конечно, существует. Оно же яв-
ляется ядром объединения выпуклых полигонов А + В.
Из этих соображений на рис. 4.26, а построена блок-схема алгоритма
cross_coiiv(A,B) расчета пересечения выпуклых полигонов А = {oi ... a„at} и
454
Гпава 4
В = {b\ ... b,„bt}. Алгоритм возвращает полигон А&В, если тот существует
(рис. 4.26, б), либо пустой полигон, если А и В касаются или не пересекаются
(рис. 4.26, в). В алгоритме используется результат d — dir_test(A) теста обхода
полигона А, благодаря чему отсечение полигона В всегда выполняется с внешней
стороны ребер полигона А, т. е. справа от них при d - 1 или слева при d = -1.
Рис. 4.26
4.2.7.4. Отсечение проекции выпуклого полигона
Геометрическое построение изображения сцены разделяется на два этапа:
П проецирование объектов на некоторую бесконечную плоскость — картинную
или экранную;
П отсечение графических элементов (ребер и граней) реальными границами ок-
на вывода.
Сложность первого этапа определяется выбором метода проецирования из тех,
что описаны в разд. 2.2 (см. рис. 2.38).
Параллельное проецирование
Параллельное проецирование на фронтальную плоскость f е ху с помощью
Сп — одной из проективных матриц Of из (2.60), Af из (2.71) или К{ из (2.76) —
дает простую и однозначную формулу расчета проекции любой точки р незави-
симо от ее положения в пространстве:
Р=рСП- . (4.11)
Геометрические задачи визуализации 455
Физически безусловное существование проекции объясняется удалением проек-
тора в бесконечность, откуда проецирующие лучи доходят параллельным пуч-
ком до каждой точки сцены и всегда пересекаются с неограниченной плоскостью
проецирования.
Проецирование более сложных, чем точка, графических объектов (отрезков, ло-
маных линий, полигонов) выполняется путем расчета по (4.11) проекций р' всех
формообразующих точек р, 3<1-объекта Р. В результате получаем плоскую про-
екцию объекта Р'.
На втором этапе производится внешнее отсечение отсекателем О:
П отрезка а'Ь' с помощью функций clip2_cross(a'b',O) (см. рис. 1.18),
clip2_test(a'b', О) (см. рис. 1.19), reg_outclip2(a'b', О, Ls) (см. рис. 4.8, а) или out-
clip2(a'b', О, Ls)',
П полигона Р'— функциями outclip2_poly(P',O,Ls) или cross_conv(P', О)
(см. рис. 4.24, а).
Центральная проекция
Центральная проекция р' = [х' у о] точки р = [х у z] на фронтальную
плоскость f от ближнего проектора 5 = [sx sy sz] вычисляется по (2.86):
Л = 1-— => p=S+£^-. (4.12)
sz h
Существование проекции точки условно и зависит от знака числа h. При h > О
луч пересекает плоскость f, а проекция (4.12) действительна. При Л < 0 с проек-
тивной плоскостью пересекается лишь обратное продолжение луча, создавая
мнимую проекцию. Наконец, при h — 0 луч параллелен f, а проекции точки с ко-
ординатой z = s, не существует.
Все формы центральной проекции отрезка ab в зависимости от значений h„ и hh
приведены в табл. 4.2. Действительная проекция может быть отрезком а'Ь' при
{Ла > 0}П {hb >0} или лучом (два варианта), для расчета направления которого
используется невырожденная точка схода (2.89)
Таблица 4.2
а Л„<0 А„> 0
Л„<0 — b' —> 2Ь' -рс
йй>0 а' —> 2а' - рс [а', 6']
456
Гпава 4
s,
(4.13)
проекций прямых с направлением V = b - а.
Функции внешнего отсечения отрезка а'Ь' выпуклым отсекателем О те же, что и в
задаче параллельного проецирования. Отсечение луча а' -> Ь' может быть выпол-
нено функцией clip2_cross(a'b', О) совместно с табл. 1.5 либо любой другой функци-
ей отсечения отрезка [а’, а' + (а' - 6')у] при задании достаточно большого числа у.
Принципиальное отличие центрального проецирования полигона Р = {р\ ...р„р\}
от параллельного заключается в том, что когда не все точки р, имеют действи-
тельные проекции с параметром /г, > 0, то на плоскости f образуется незамкнутая
и неограниченная проекция Р' (рис. 4.27), не пригодная для использования в
функциях outclip2_poly(PО, Ls) и cross_conv(PО). Применим для решения за-
дачи отсечения полигона Р' выпуклым полигональным окном О функцию
clip_line. Поскольку она работает с неограниченным отсекателем — полуплоско-
стью, то по свойству коммутативности внешнего отсечения назначим отсекае-
мым объектом полигон О, а граничными линиями полуплоскостей — прямые, на
которых лежат действительные проекции ребер полигона Р.
В табл. 4.3 приведены все варианты выбора параметров отсекающей прямой
{ро, У} е f в зависимости от значений hu и hh, вычисленных по (4.12) для концов
проецируемого отрезка а и Ь. По этой таблице выбираются аргументы {ро, 11
функции clip_line(0,po, V) при отсечении полигона О действительной проекцией
Геометрические задачи визуализации
457
ребра Pipi+] полигона Р. Если ни одна из вершин р, не имеет действительной про-
екции, то отсутствует вся проекция полигона Р.
Таблица 4.3
а Л„<0 ЛЛ>0
Лй<0 — {b',pc-b'}
йо>0 {а', а'-рс] {o', b' -а'}
Как определить направление обхода фигуры Ропределяющее ориентацию от-
секающих полуплоскостей относительно их граничных прямых? Ввиду возмож-
ной незамкнутоспш линии Р' применение теста dir_test(P') в общем случае не-
возможно. Тем не менее, задача легко разрешима с точки зрения дальнего
проектора S ". Достаточно вычислить ортогональную замкнутую проекцию по-
лигона Р " = POt е f, найти направление ее обхода dir_test(P "), инвертировать
его при расположении проекторов S и S " по разные стороны от плоскости по-
лигона Р и использовать полученное значение d в аргументе d- V функции
clip_line. Кстати, если проектор лежит в плоскости полигона Р, то проекция Р'
вырождается в неполигональную фигуру нулевой площади (отрезок, луч или
бесконечную прямую), что равносильно отсутствию проекции.
Итак, выкристаллизовывается следующий алгоритм clip_pro(P, О, S) отсечения
центральной проекции полигона Р = {pi ...р„р\} е R3 выпуклым окном О е f,
возвращающий часть проекции Р' <^О внутри окна О либо пустое решение 0
(рис. 4.28).
& Шаг 1. По (1.119, г) находим значение неявной функции
f = nf3(pi,p2,p3, S).
Если f = 0, то проектор лежит в плоскости полигона Р, а алгоритм возвращает
пустое решение 0 = 0.
Шаг 2. Определяем направление обхода
d = dir_test(P Ot)
ортогональной проекции Р на плоскость проецирования f и корректируем его
умножением на sgn(/). Признаку существования действительной проекции при-
своим значение 5 = 0.
Следующие шаги 3 -ь 6 выполняются в цикле i = 1, size(p}-\ для каждого отрезка,
направленного от точки р, = ак точке pi+\ = b.
Шаг 3. По (4.12) вычисляем значения
ha =1-—, /%=1-—.
s„ s,
458
Гпава 4
Рис. 4.28
Проекции концов отрезка
a — S +
a — S
ha
b' = S +
b-S
hb
Геометрические задачи визуализации 459
действительны, соответственно, при h„ > 0 и hh > 0. В любом из этих случаев ус-
танавливаем признак 5=1.
Шаг 4. При выполнении условия
К > o}n{hb < o}U{ha < 0}n{hb > о}
один из концов отрезка ab имеет действительную, а другой — мнимую проек-
цию. Для расчета направления линии отсечения вычисляем по (4.13) точку схода
Pc=s~ , Sz- -(b-a).
bz -az
Шаг 5. Выбираем по табл. 4.3 параметры прямой отсечения — точку ро и на-
правление V.
Шаг 6. При {/га > О} U {fy, > о} выполняем отсечение полигона О полуплоскостью
с граничной прямой {ро, V}. Если в результате получим О = 0, то алгоритм воз-
вращает пустое решение.
Шаг 7. При 5 = 1 возвращается полигон О, иначе — пустое решение О = 0. □
& Пример 4.12. Наблюдатель находится в точке S = [о 0 F] на фокусном рас-
стоянии F - 30 от фронтальной плоскости проецирования. Построить перспек-
тивное изображение плоского пятиугольника Р с вершинами
Pl = [4 -4 14], /?2=[4 4 2б], р3=[0 8 34], р4=[~4 4 30],
Р5=[-4 -4 18]
внутри прямоугольного фронтального окна О с габаритами -15<х<15 и -
10 <у < 10 (см. рис. 4.27).
Решение. Вычислив по (4.12) числа Л, = 1 - z, / F, равные
/и = 0.533 > 0, !п = 0.133 > 0, Из = -0.133 < 0, Л4 = 0, hs = 0.4 > 0,
и анализируя их знаки, заключаем, что вершины полигона р\, pi и рз имеют по
(4.12) действительные проекции
= [7.5 -7.5 О], рз = [30 30 0], Р5=[-10 -10 о],
тогда как вершины рз и р4 таких проекций не имеют. Следовательно, лишь ребра
p\pi и рзр\ образуют на плоскости ху действительные проекции в виде отрезков
р[р2 и Р5Р1 Проекции ребер ргрз и рьрз, для которых hi Из < 0 и Л4Л5 < 0, пред-
ставляют собой лучи, векторы направлений которых Vi и Ct вычислим по
табл. 4.3 с помощью точек схода (4.13):
Рс2=5----— (рз-Р2)=&5 -15 0]=> К2=^-рс2=[15 45 о];
z3“ z2
Pc4 = s——(р5-а)=[о -20 0]=> И4 = Рс4-р5 =[10 -10 0].
z5“z4
460
Глава 4
Оставшееся ребро рзр4 не проецируется на фронтальную плоскость ни в каком
виде (рис. 4.29), т. к. целиком находится сзади проектора.
Рис. 4.29
Таким образом, центральной проекцией замкнутого полигона {р\ргрзр4р5р\} на
плоскость ху является фигура
Р1Р2 ->°°...°°-> p'sP\
с незамкнутой границей в виде двух отрезков р'\Р2, PsP\ и двух лучей {р2, И2}
{ps,r4}. Удаленность части границы в бесконечность не позволяет считать эту
фигуру полигоном и определить направление ее обхода. Для выполнения данной
операции построим ортографическую проекцию Р"^ху путем обнулен»»
z-координат вершин р, (см. рис. 4.27). Направление обхода Р" положительно и
п/3(р\,рг,рз, S) = 256 > О,
поэтому d = 1 и отсечение полигона О полуплоскостями будем выполнять справе
от их граничных линий {ро,-, И,}.
Начинаем обход ребер полигона Р и отсечение окна О линиями их проекций
Первая же прямая {р{, р2 -р[} отрезает от О правый нижний угол. Вторая пря-
Геометрические задачи визуализации
461
мая {р2, И2} не изменяет окна, полностью лежащего слева от нее. Третье ребро
рзр4 не создает отсекающей полуплоскости. Прямая {p's,^} отсекает от окна
левый нижний угол. Наконец, последняя прямая {/25, р\ -/4} отсекает от остат-
ка окна нижний треугольник. В итоге центральная проекция полигона Р на ог-
раниченное плоское окно О представляет собой шестиугольный полигон, зани-
мающий большую часть окна. □
4.2.7.5. Выпуклая полигональная оболочка массива точек
Допустим, на плоскости задан массив Р — {р\,рг, ...,р„} из п >2 точек
Pi =[*i Л']- Выпуклая полигональная оболочка массива точек есть объединение
всех полигонов, построенных на точках этого массива как на вершинах. Ее мож-
но также представить как выпуклый полигон минимальной площади, накры-
вающий все точки массива (рис. 4.30).
Рис. 4.30
По отношению к оболочке точки массива делятся на внутренние и граничные,
принадлежащие сторонам полигона оболочки. Граничные точки, образующие
вершины этого полигона, назовем выступающими. На отрезки между высту-
пающими вершинами могут попасть другие граничные точки. Задача построе-
ния выпуклой оболочки заключается в поиске выступающих точек и формиро-
вании из них замкнутого контура.
Алгоритм cover(P), решающий задачу построения выпуклой оболочки, представ-
лен блок-схемой на рис. 4.31. Он воплощает простой метод построения ограды
462
Гпава 4
вокруг рощи деревьев, по которому сначала выбирается некоторое "крайнее"
дерево (на рис. 4.30 нижняя левая точка), от которого строится первая сторона
ограды в направлении второго выступающего дерева под углом <pi (на рис. 4.30
угол (pi = 0). Если в этом направлении растет несколько деревьев, то ограда
строится до самого дальнего из них. Начинаясь с этой новой точки, вектор на-
правления вращается на минимальный угол фг, под которым видно третье вы-
ступающее дерево... Процесс огораживания продолжается до тех пор, пока поли-
гон не замкнется в начальной точке. В итоге окажется, что контур ограды
соединяет выступающие деревья отрезками прямых и при этом все деревья рас-
положены с одной стороны от каждого отрезка ограды. Следовательно, в соот-
ветствии с тестом convl, определенным в (1.37), полученная полигональная обо-
лочка является выпуклой.
*=*+|. Р„^Рк
V~Pt~Pk-\
о
( Возврат {p,...pt}
Рис. 4.31
Переходя к алгоритмизации процесса построения полигональной оболочки, вы-
берем положительное направление охватывания точек массива и найдем в нем
первую выступающую точку рт с минимальной ординатой у,„ (рис. 4.30). Если
таких точек несколько, то выберем из них точку с минимальной координатой х„,.
Путем обмена pi <->р,„ поставим найденную точку в начало массива, а ее копию
добавим в конец массива в виде точки рл+1 для обеспечения проверки замыкания
оболочки. Зададим начальное направление вектора охватывания V =х° вдоль
оси х и индекс конечной точки оболочки к - 1.
Геометрические задачи визуализации
463
Далее организуем внешний цикл поиска выступающих точек р„, и накопление их
в начале массива путем обмена p„,<r+pk. Во внутреннем цикле / = Л + 1, и + 1 для
каждой точки р, вычисляется вектор пробного направления W = р,рк. При нену-
левой длине этого вектора г = \W] 0 (данная проверка позволяет отсечь кратные
точки, которые не должны входить в оболочку) находим скалярное произведение
c = cos((p)=f/oW'e [-1, 1].
Перебрав точки р, Xfi > к, находим точку р„„ видимую из точки рк под минималь-
ным углом <р = Z(E, И7), т. е. при максимальном значении с. Если таких точек не-
сколько, то выбираем из них самую дальнюю от рк. Инкрементировав индекс
к — к + 1, сделаем ее путем обмена р,„ <-> рк новой выступающей точкой оболоч-
ки. Новый вектор направления положим равным V~ рк. -pk-t.
Внешний цикл и построение оболочки заканчиваются при совпадении точки рк с
начальной точкой р\. Алгоритм возвращает субмассив вершин оболочки
{pt - А }
Статистическое моделирование алгоритма cover(P) со случайными выборками
случайного числа точек показало его высокую надежность и быстроту работы.
По сравнению с описанным в [18] алгоритмом giftwrapHull, основанным на мето-
де "заворачивания подарка" [24], наш алгоритм правильно строит оболочку и в
том случае, когда в массиве есть кратные и коллинеарные точки.
Применительно к задаче отсечения расчет выпуклой оболочки может быть поле-
зен, например, при построении тени выпуклого полиэдра Р на ограниченной
плоскости f. Можно, конечно, решать задачу внешнего отсечения проекции каж-
дой грани полиэдра контуром плоскости f. Тогда после закрашивания одинако-
вым темным цветом все теневые полигоны сольются в один общий выпуклый
полигон тени.
Для достижения той же цели более эффективно будет вычислить точки — проек-
ции вершин полиэдра на бесконечную плоскость, совпадающую с f, построить
выпуклую оболочку этих точек, а затем только один раз выполнить внешнее от-
сечение оболочки замкнутым контуром f и закрашивание полученного полигона
цветом тени.
Функция cover может быть также полезна как генератор выпуклых полигонов.
& Пример 4.13. Построить выпуклую оболочку массива точек pi три с тремя
кратными точками pi =рц,рз =pi upt = р% (см. рис. 4.30).
Решение. Анализируя координаты точек, находим самую нижнюю левую на-
чальную вершину оболочки рз. Переставив ее с точкой р\ и добавив копию в ко-
нец массива, получим (нумерация точек сохранена в исходном виде, хотя в дей-
ствительности она меняется согласно месту точек в массиве)
Р= {рз | ргр\ pips ...рирз}.
Вертикальная черта отделяет вершины построенной части оболочки от осталь-
ных точек массива.
464
Гпава 4
Вторую выступающую точку ищем по принципу уменьшения положительного
угла cpi между векторами Г = [1 о]и = /2, -рз. Просматривая точкиp3,pi,pt,pb.
находим, наконец, точку рч с углом <р< = 0. После перестановки рч с рз массив
принимает вид
Р = {рзрч I/?! Pt ...pt /22/210 .../2|5/2з}.
Следующий угол срг между векторами V -рч-рз и W, = р, -/29 будет минималь-
ным для выступающей точки pis, обменяв которую с pi, получим следующий со-
став массива и в его начале — построенную часть оболочки:
Р = {рз /29/215 |/24 .../28 /22 Р10 ... pit pi рз} .
После нахождения четвертой выступающей точки рз и обмена ее с точкой pt мас-
сив принимает вид
Р - {РЗР’>Р15Р2\РЗР6РТ psptpiopu pnpispitpi рз}.
Обнаружение выступающей точки /27, совпадающей с первой вершиной оболочки
рз, завершает работу алгоритма. Окончательный состав полигона оболочки сле-
дующий:
Р= {/23/29/215/22/27}.
Полигон является замкнутым из-за совпадения точек рз и рз. Как видно, благо-
даря этому совпадению точка рз, специально помещенная в конец массива, не
пригодилась. Но если бы точка рз находилась в другом месте, то алгоритм за-
кончил бы свою работу при обнаружении совпадения начальной точки рз с ее
копией в конце массива. □
4.2.7.6. Полигонализация массива точек
Свойство видимости всех вершин полигона из любой точки его ядра наводит на
мысль о возможности такой сортировки массива точек Р - {pi,рз,... ,р„}, что все
они могут быть соединены замкнутым полигональным непересекающимся конту-
ром и будут видны из некоторой, например, первой точки массива (рис. 4.32).
Описываемый алгоритм полигонализации массива точек poly_point(P), блок-
схема которого приведена на рис. 4.33, основан на выполнении сортировки то-
чек по возрастанию угла вращения луча pt /2,- V/ = 2, и ,/2, * pi, не допуская пересе-
чения ребер строящегося полигона друг с другом и исключая из списка вершш-
кратные и содержащие развернутый угол точки.
Сначала формируется массив Q = {<71,..., q„,} из т < п точек/2, *р\ и по (1.31) вы-
числяются углы
(р, =«27g(x°,^)e (-л, л]
между векторами [1 О] и F} = g,-/2i. Затем точки q, сортируются по возрастании
углов ф„ и к полученной ломаной линии {71 <72... q„} по краям добавляется точка pi.
Геометрические задачи визуализации
465
Рис. 4.32
Рис. 4.33
Будет ли замкнутый полигон Р = {p\q\ ... решением задачи полигонализа-
ции массива точек, как это утверждается в [18]? Ответ утвердительный почти
всегда для произвольного набора точек. Однако возможны случаи, нарушающие
данный порядок формирования полигона. Соответственно, дальнейшие дейст-
вия следующие:
□ если существуют соседние лучи р\ —> q, ир\ -ь qi+l с углом вращения
<Р,-1 - <Р, >
466
Гпава 4
т. е. больше развернутого, то полигон Р = {piqi ... q„,pi} является самопересе-
кающимся (рис. 4.34, а). В таком случае можно выбрать другой замкнутый
полигон Р - {г?! ... q,pi qr4 ... q,„ <71} с ядром в точке qr,
Рис. 4.34
□ если полученный массив Р имеет на одном отрезке прямой группу соседних
точек, то вершинами полигона могут быть только концевые точки этого от-
резка. Удаление лишних вершин выполняется алгоритмом формирования ми-
нимального полигона mm_poly{P) (рис. 4.35) в процессе обхода вершин поли-
гона Р по замкнутому контуру.
Работа алгоритма начинается с инициализации начального значения индекса
т = 1 и выполнения цикла i = 2, size(P) тестирования точек р, на способность
быть вершинами минимального полигона. Совпадающие с р,„ точки р, про-
пускаются, а остальные проверяются функцией (1.35, г) на принадлежности
прямой ребра p„,-t р,„. Если
nf1<p„,-i,p„„pd * О,
то после инкрементирования индекса т = т+ 1 не коллинеарная с прямо*
{p,„-i,p,„} точка Pi сохраняется как вершина полигона рт.
Коллинеарная с отрезком рт-\Р,„ точка р, может располагаться относительна
него в одном из следующих положений:
• спереди (рис. 4.34, б) при условии
тогда она заменяет точку р,„;
• сзади (рис. 4.34, в) при условии
(Pi0 (Pm-Pm-i) < О,
тогда делаются замены р,„ -> р„г1 и р, -> р,„;
• внутри, тогда она пропускается.
Геометрические задачи визуализации
467
Рис. 4.35
По завершении обхода в начале массива Р оказываются накопленными m
вершин минимального полигона {pi ...р,„}. Перед его возвращением выпол-
няется последняя проверка условия
nfl(p\,p2,p„r{) = О,
выявляющая возможную коллинеарность точек р„,-\,р\,р2. При обнаружении
данного факта возвращаемый полигон заменяется на {pi ...рпГ\ рг}.
Функция poly_poinl может быть полезна как генератор произвольных полигонов
для различных тестов и задач.
Самостоятельное значение имеет и функция min_poly, которую рекомендуется
использовать для удаления из полигона избыточных элементов, затрудняющих,
например, расчет нормали к его плоскости. Это кратные вершины (между ними
ребра нулевой длины) и вершины, имеющие развернутый угол 180° между при-
мыкающими к ним коллинеарными ребрами.
& Пример 4.14. Построить полигон на точках pi -г pis из примера 4.13.
Решение. Вычислим углы (в градусах) ориентации каждой, кроме рп, точки мас-
сива относительно pi:
Pi Р2 РЗ Р4 PS Pf> Pl P8 P9 P10 P12 Pl3 P14 P15
ф, I 149° -108° 26° 108° -56° -108° 26° -37° 90° -90° 180° 180° 90°
468
Гпава 4
Угловая сортировка, выполненная MathCAD-программой, расположила точки
массива Q в следующем порядке:
<li Рз Р7 Р12 Рб Р9 Р4 Ръ Р\5 Pw Р5 Р1 Р\3 Р\4
ф, -108° -108° -90° -56° -37° 26° 26° 90° 90° 108° 149° 180° 180=
Так как приращения углов между каждой парой соседних точек меньше л, то
замкнутый контур обхода точек массива имеет вид
Р = {p^pipnphpvptpspispwpspipispwpi}.
Приступая к минимизации этого массива, отбираем точки pi, рз, пропускаем
кратную точку pi = рз, добавляем ри. Следующая точка рь коллинеарна отрезкч
рзрп и лежит впереди него, поэтому точку ри заменяем точкой ре. Она, в свои
очередь, заменяется коллинеарной точкой рч, лежащей впереди отрезка рзрь. Да-
лее к списку добавляется вершина рз, а кратная точка рг = /м пропускается. Вер-
шина pis, лежащая впереди отрезкарчрз, заменяет точку рз.
Следующими вершинами минимального полигона становятся точки рю, pi (она
заменила точку ps, т. к. лежит впереди отрезка piops),pi3 и ри. Последняя точка р
лежит сзади коллинеарного отрезка р\зри, поэтому в соответствии с рис. 4.34. в
последние звенья минимального полигона {... pipispupi} заменяем на
{...pipupi}.
В результате получаем полигон
Р- {pipypspispiopipupi}. □
4.2.7.7. Разрезание невыпуклого полигона
Для успешной работы некоторых алгоритмов невыпуклого отсечения необходи-
мо уметь выполнять разрезание невыпуклого объекта на выпуклые составляю-
щие. Эта операция представляет и самостоятельный интерес. Она заключается в
построении границ, по которым исходный объект распадается на выпуклые не-
пересекающиеся фрагменты. Желательно, чтобы число фрагментов было мини-
мальным.
Разрезание может быть ручным и алгоритмическим. Ручное разрезание заведомо
известного невыпуклого объекта, естественно, может свести число фрагментов к
минимуму за счет интеллектуальных способностей человека. Если же объект вы-
числяется в процессе работы программы и заранее неизвестны его конфигурация
и даже сам факт выпуклости, то необходимы алгоритмы проверки выпуклости и
разрезания невыпуклого объекта на выпуклые фрагменты.
Разработаем метод разрезания полигона Р= {pi ...pnpi} хордами— продолже-
ниями его ребер (рис. 4.36). Ясно, что будучи выпуклым, в частности, треуголь-
ным, полигон не нуждается в разрезании, т. к. продолжения ребер проходят сна-
ружи него. Невыпуклый же полигон можно начинать резать с любогс
невыпуклого угла. Поэтому исходный полигон Р необходимо проверить тестоо
выпуклости conv2(P), приведенным в (1.37). Идейная основа этого теста — одно-
сторонняя ориентация вершин у выпуклого полигона— пригодна для обнарч-
Геометрические задачи визуализации
469
жения невыпуклого угла Z.pipiJi.lpl.>2 при вершине по совпадению знака числа
nf Up,,pi+l,рм) с направлением обхода полигона d = dir_test(P).
Рис. 4.36
Далее нужно рассчитать все пересечения луча р,~уркц за точкой с ребрами
Pi+iPi+i’ — >PnPt, — , Pi-zPi-i и найти минимальный параметр пересечения 0 > 1, но-
мер к ближайшего пересеченного ребра, ближайшую точку пересечения
9=А + (Р.+|-А)6
и линию разреза рм q, по которой полигон Р разделяется на два фрагмента Pi и Рг.
Для простоты формирования списков вершин фрагментов будем после каждого
обнаружения выпуклого угла делать левый циклический сдвиг списка вершин по-
лигона Р~ {pipi ...pnPi} (рис. 4.37) функцией
LCShift(P) - {р2рз...p„pip2}. (4.14)
Pl Pl p„ Pl
Рис. 4.37
Теперь, благодаря сдвигам, тестируемая на выпуклость вершина имеет постоян-
ный номер р2, луч р\рг проверяется на пересечение с ребрами рзр*,... ,рп-\Рп, а
полигон разрезается на два фрагмента
Pt = {/?! 9A+I -P„Pi}, Pi = {p2P3...pkqp2}.
470
Гпава 4
При совпадении найденной точки q с вершиной полигона Р у одного из фраг-
ментов появятся кратные вершины, которые должны быть удалены. Возможно
также совпадение луча с какой-либо стороной разрезаемого полигона
(см. рис. 4.36), в результате чего один из фрагментов будет иметь вершину с раз-
вернутым углом. Поэтому фрагменты перед дальнейшим разрезанием необходи-
мо минимизировать алгоритмом min_poly (см. рис. 4.35).
Описанная процедура разрезания невыпуклого полигона на два фрагмента ре-
курсивно применяется для полигонов Pi и Рг. Примерное дерево рекурсии, тер-
минальные вершины которого есть искомые выпуклые полигоны, изображено на
рис. 4.38. Выход из рекурсии с записью Р в массив списков Lm осуществляется
при условии, что тест выпуклости полигона дал результат conv2(P) = 1.
Рис. 4.38
Реализация всего сказанного в виде рекурсивной функции cut_poly(P, Lm) разре-
зания полигона Р изображена на рис. 4.39. Функция формирует массив Lm вы-
пуклых фрагментов и возвращает их количество. Перед внешним обращением к
функции необходимо инициализировать пустой массив Lm = 0, в который внут-
ри функции будут добавляться выпуклые фрагменты, отрезанные от исходного
полигона.
Необходимость расчета множества пересечений прямых полностью уничтожает
все преимущества алгоритмического метода разрезания при построении функций
отсечения outclip2_segm и inclip2_segm. Ручной метод разрезания невыпуклого
полигона имеет меньшую трудоемкость, чем алгоритмический. Тем не менее
алгоритм cut_j)oly незаменим в задачах разрезания полигонов заранее неизвест-
ной конфигурации, которая может быть решена только алгоритмически, а не
вручную.
& Пример 4.15. Проиллюстрируем работу алгоритма cut_poly на примере разре-
зания невыпуклого полигона Р- {р\ ...рцр\}, изображенного на рис. 4.36. Тест
(1.50) дает положительное направление обхода </ = clir_jest(P) - 1. Дерево рекур-
сивного разрезания полигона показано на рис. 4.38.
Решение. Начинаем первый уровень рекурсии с проверки выпуклости угла
Z/л ргрз. Так как п/2(р\,рг,рз) - -6 < 0, то с учетом знака числа с!> 0 заключаем
Геометрические задачи визуализации
471
что этот угол выпуклый. После левого циклического сдвига вершин исходный
полигон принимает вид
Р - {ргрз ...рир\рг}.
Вот теперь из равенства знаков чисел d и п/2{рг,рз,р^) = 8 > 0 следует, что вер-
шина рз является невыпуклой. Для удобства анализа работы алгоритма номера
вершин оставлены без изменения.
Лучpi-^рз пересекается с ребрамирюри, рчртз, ртзрн ирир\. Из всех точек пе-
ресечения ближайшей к рз является точка qi, совершенно случайно совпавшая с
вершиной рн. Таким образом, первоначальный полигон разрезался по отрезку
psqi на два полигона:
Pi - {p2qipiipi2pi3pupipi}, Pi - {рзрьрзръртрърчркщхрз}.
472
Гпава 4
На втором уровне рекурсии полигон Pt, имеющий кратные вершины qi = рц и
лежащие на одной прямой линии соседние вершины рг, q\ и р\г, минимизируется
алгоритмом min_poly до вида Pi - {ргр1гр1зрир1рг}. Далее этот полигон разре-
зается на фрагменты
/’ll-\р2Я2Р\4Р\Р2}={р?Я2Р\Р2} , ^12 -{р\2Р\ЗЯ2Рп} ,
а другой полигон Рг — на фрагменты
Рг\ = {рзq3p9pioqip3p4ps}, ^22 ={РбРуР8ЧзРб} •
На третьем уровне рекурсии с помощью теста convl обнаруживается, что поли-
гоны Рп, Р\г и Рз2— выпуклые и в дальнейшем разрезании не нуждаются. Ос-
тавшийся полигон Рг\ на четвертом уровне разрезается на составляющие части
^211 -{р994Р4Р5<73Р9} > ^212 ~ {р\0<71 Рз<74Р\0} ,
которые на последнем пятом уровне тестируются как выпуклые.
Таким образом, исходный полигон Р оказался разрезан на пять выпуклых фраг-
ментов, которые записались в массив списков в следующей последовательности:
Lm = {Pn,Pi2, Р211, Р212, Ргг}.
□
4.2.7.8. Триангуляция полигона
Триангуляцией называется операция разрезания полигона на треугольники. Она
часто используется для сведения решения типовых задач (пересечения, отсечения,
удаления и т. п.) в области, имеющей сложную конфигурацию, к совокупности
задач, решаемых в области треугольника— простейшей геометрической фигу
ры. Что дает замена многоугольника набором треугольников?
□ Значительно упрощается тест ориентации точки q относительно треугольни-
ка piргрз. Достаточно записать разложение вектора
q -pi - Vt + Wt
по векторам сторон треугольника V = рг-pi и W = рз- pi, затем по методу
Грама [9, 10] составить систему двух линейных уравнений из скалярных про-
изведений
(q-P\)°V = V °Vt + V °Wx
(q-P\)°W = V °Wt + W °Wt.
и найти ее решение — коэффициенты разложения по базису {V, И7}:
(p~Pi)°^l
уоу yoW
V о W W°W
з-1
(4-15)
Геометрические задачи визуализации 473
Тогда из (2.58, б) следует, что при
{/>0}П{т>0}П{/ + т<1} (4.16, п)
точка лежит внутри треугольника, при
{/ < o}U {t < 0}U {/+ т > 1} (4.16, б)
она расположена вне треугольника, а в остальных случаях — на его границе.
Обращаемая в (4.15) матрица с определителем
|F]21 W\2 - (Vо W)2 = |F]21 И2]2 sin2(ZVW) = |p2 -pi|2 |/>з -pi|2 sin2(Zp3p\pi) > 0
невырождена при угле Zp3pipi, не нулевом и не развернутом, т. е. при некол-
линеарности вершин треугольника р\ргрз.
□ Благодаря минимальному числу сторон треугольного полигона быстро вы-
полняются операции переборного типа, к которым относятся отсечение и
удаление. Априорная выпуклость треугольника позволяет существенно упро-
стить все алгоритмы обработки полигонов путем использования только их
выпуклых вариантов.
□ Структура данных для хранения m треугольников может иметь вид обычной
матрицы размерности 3 х 4 х т, а не более сложно организованных массивов,
структур и списков.
□ Обобщение алгоритма триангуляции плоского полигона на криволинейную
поверхность позволяет заменить последнюю сеткой треугольников, для кото-
рых значительно проще решаются все задачи визуализации, в том числе за-
крашивания всех точек треугольной грани в однородный цвет благодаря ее
планарности.
В принципе триангуляция произвольного полигона может быть выполнена мо-
дифицированным алгоритмом cut_poly(P), завершающая часть которого приведе-
на на рис. 4.40, а. Суть модификации состоит в том, что в массив Lm вместо вы-
пуклого л-угольника Р= {pi ...p„pi} добавляется п - 2 треугольников
{рхргрзрх}, {ptpsptpi},..., {pip„-tp„pi},
полученных разрезанием полигона диагоналями р\рз,... ,р\р„-\ (рис. 4.40, б).
Можно разрезать выпуклый полигон и другим способом (рис. 4.40, в) — на л
треугольников
{ср\р2С}, {cpipic}, ..., {cp„pic}
с дополнительно вычисленной вершиной — точкой геометрического центра по-
лигона
Хотя при этом получается большее число треугольных фрагментов, но зато они
имеют менее вытянутую форму, чем при разрезании диагоналями.
474
Глава 4
Недостаток применения алгоритма cut_poly(P) для триангуляции состоит в том.
что полигон разрезается хордами, пересечение которых с ребрами создает новые
точки. Да и число полученных треугольников далеко от минимального.
Рассмотрим более быстрый и экономичный метод триангуляции, в котором по-
лигон рекурсивно разрезается на части диагоналями (рис. 4.41). Задача заключа-
ется в поиске диагонали удовлетворяющей следующим условиям:
□ она является внутренней диагональю полигона;
□ она не пересекает и не касается не смежных с ней сторон полигона.
Рис. 4.41
Геометрические задачи визуализации
475
Рекурсивный алгоритм триангуляции полигона Р= {pt ...p„pt}, реализующий эти
условия, приведен на рис. 4.42. Работа функции tri_poly(P, Lm) начинается с ми-
нимизации исходного полигона, необходимой для исключения из него кратных и
коллинеарных вершин. Если полученный полигон оказался треугольником
(л = 3), то он добавляется в возвращаемый список Lm.
Рис. 4.42
Дальнейшие действия выполняются с нетреугольным полигоном. В случае его
выпуклости, что быстро проверяется тестом conv2{P) - 1, полигон можно сразу
разрезать диагональю pt рз.
У невыпуклого полигона сначала ищется вершина, из которой можно провести
разрезающую диагональ. Для этого годится не каждая выпуклая вершина, чему
пример — точка ри на рис. 4.41. В то же время из любой невыпуклой вершины р,
напрямую видна хотя бы одна несмежная вершина рг Поиск невыпуклой верши-
ны выполняется путем циклического сдвига вершин полигона функцией LCShift,
476
Гпава 4
определенной в (4.14), до тех пор, пока значение nf2{p„,pi,pi) не станет того же
знака, что и направление обхода d = dir_test(P). Благодаря сдвигам невыпуклая
вершина и начало разрезающей диагонали всегда будут находиться в точке pi, а
доступ к остальным вершинам полигона становится более простым.
Второй конец диагонали рк, к е [3, л - 1], должен, во-первых, лежать относитель-
но ребра р\рг с внутренней стороны полигона, где значения d и n/2(pi,p2,p*)
имеют разные знаки. Во-вторых, отрезок pi рк не должен пересекаться или ка-
саться ни с одной из следующих сторон полигона PiPi+\, несмежных с вершинами
pi и рк, откуда следует, что к + 1 < i < и - 1. Благодаря выбору начальной точки pi
в невыпуклом угле такая точка рк и разрезающая диагональ pi рк существуют все-
гда. Для ускорения процесса поиска после обнаружения пересечения диагональю
стороны PiPt+i значение к приравнивается к I.
Разрезание полигона диагональю pi рк реализуется рекурсивным обращением к
функции tri_poly со следующими аргументами-полигонами:
Pi = {pipk ...p„pi},P2= {pi ...pkpi}.
Примерное бинарное дерево рекурсии, терминальные вершины которого пред-
ставляют собой искомые треугольники, показано на рис. 4.43. Функция форми-
рует массив Lin, содержащий выпуклые фрагменты разрезанного полигона, и
возвращает их число. Перед внешним обращением к функции необходимо ини-
циализировать пустой массив Lm = 0, в который внутри функции tri_poly будут
добавляться треугольники, отрезанные от исходного полигона.
& Пример 4.16. Проследим работу алгоритма на примере триангуляции невы-
пуклого полигона Р~ {pi ...pupi} (см. рис. 4.41). Тест (1.50) направления обхода
полигона дает значение d = dir_test(P) = 1. Дерево рекурсивного разрезания по-
лигона изображено на рис. 4.43.
Рис. 4.43
Геометрические задачи визуализации
477
На первом уровне рекурсии после двух циклических сдвигов по условиям d> 0 и
л/2(д2,рз,Д4) = 8 > О
находим невыпуклую вершину рз, которая становится началом полигона:
Р = {рзрл ...рырхргрз}.
Для удобства анализа работы алгоритма номера вершин оставлены без изменения.
Последовательная проверка точек рк на левое (при d = 1) расположение относи-
тельно ребра рзрл и диагоналей рзрк на непересечение с остальными ребрами,
начиная с ребра pk^pk+i, дает значение к= 10. Таким образом, исходный поли-
гон разрезался диагональю рзрю на два фрагмента:
Pi = {рзрю ...pupiргрз}, Рг = {рз ...рюрз}.
На втором уровне рекурсии у полигона Pi сразу находим невыпуклую вершину
рз и диагональ разрезаниярзри, которой он разрезается на фрагменты
Ри = {рзри ... рюр1 ргрз}, Р\2 = {рзР10Р11Рз}
У полигона Рг находим ближайшую невыпуклую вершину рь и диагональ рьръ,
которой он разрезается на фрагменты
Ри = {рьрьрчрюрзр*рзрь},\Р22={Р(,РтРъР(,}
На третьем уровне обнаруживаем, что полигоны Рп и Ргг являются треугольни-
ками и дальнейшему разрезанию не подлежат. Сохраняем их в предварительно
инициализированном списке Lm. Полигон Ри, имеющий четыре вершины рг,рз,
ри и pi2 на одной прямой, минимизируем до Ри — {pi2pi3pupi ргри} и разрезаем
диагональю рпри на фрагменты
Pin = {pnpupipipii}, Л12 ~ {Р12Р13Р14Р12?
Полигон Рг1 разрезаем диагональю рьрч на фрагменты
Рги = {рьрчрюрзр^рзрь}, Р2\2 ={РбРзР9Рб}-
На четвертом уровне рекурсии полигон Pin, имеющий три вершины рг,рп,рю на
одной прямой, минимизируем до треугольника
Ли ={Р14Р1Р2Р14)
и сохраняем в списке Lm. Полигоны Риг и Р212 также являются треугольниками
и добавляются в Lm. Оставшийся полигон Рги разрезаем диагональю рю/м на
фрагменты
Р2111 = {рюрьрзрьрърю}, Р2112 ~{Р|ОРзР4Р|о}-
На пятом уровне обнаруживаем, что полигон Ргиг является треугольником, и
записываем его в Lm. Полигон Р2111 разрезаем диагональю рюрз на фрагменты
Р21111 = {рюрзрьрчрю}, Р21112 = {P10P4P5P10} •
478
Гпава 4
На шестом уровне рекурсии треугольник Ри 112 добавляем в Lm, а Риш разрезаем
диагональю рюрь на фрагменты
^11111 -{/’ю/’бРоРю}, ^11112 -{£1О/’5/’бР1о}>
которые на последнем седьмом уровне добавляем в Lm как треугольники.
В результате работы алгоритма полигон Р оказался разрезан на девять тре-
угольников, которые записались в список Lm в следующей последовательности:
Lm = {Pin, Р112, Р12, Р211111, Р211112, Р21112, Р2112, Р212, Р22}. □
После небольшой модификации алгоритм tri_poly можно использовать для раз-
резания произвольного полигона диагоналями на выпуклые, но не обязательно
треугольные фрагменты. Суть модификации в том, что проверка треугольности
полигона {л = 3} заменяется на проверку его выпуклости {сош'2(Р) = 1}, а сле-
дующее после вычисления dir_test(P) тестирование conv2(P) исключается
(рис. 4.44, а). При разрезании полигона диагоналями не возникает новых точек,
как это происходит при работе алгоритма cut_poly (см. рис. 4.36).
Моделирование показывает, что невыпуклый полигон обычно разрезается диа-
гоналями на несколько треугольников и один выпуклый не треугольный фраг-
мент. Например, полигон Р на рис. 4.44, б разрезался на шесть треугольников
{рир\ргры}, {рпркрирп}, {рзрюрирз},
{рюрзр^рю}, {рьрърчрь}, {рбртркрь}
и один пятиугольник {рюр^рзрьрчрю}.
Рассмотренные нами алгоритмы разрезания cut_poly, tri_poly и все их модифика-
ции имеют общий недостаток: получаемые фрагменты имеют заранее непредска-
зуемые размеры и форму. Большое различие в габаритах и сильная вытянутость
отдельных фрагментов затрудняют решение некоторых задач визуализации, на-
пример, сортировки граней по удаленности от наблюдателя (см. рис. 3.5), ис-
пользуемой в алгоритмах удаления невидимых элементов.
Разработаем метод триангуляции с контролируемыми размерами получаемых
треугольников, длины сторон которых не должны превышать значения h. Идея
метода, эскизно намеченная в [19], заключается в поиске у полигона
Р = {pi ...p„pi} выпуклой вершины р,„ с минимальным внутренним углом
у = min {|<р,|}, где (р, = Z(p/-i -phpt+[ -р,)
(рис. 4.45, а), и отрезании от этого угла в зависимости от его величины одного
(рис. 4.45, б), двух (рис. 4.45, е) или трех (рис. 4.45, г) треугольников с длинами
сторон, не превышающими h. В двух последних случаях нужно так расположить
вершины треугольников с, d и е между векторами г и и’, чтобы длины всех отрез-
ков не превышали значения h.
Предлагается следующая методика вычисления этих точек, основанная на поня-
тии пучка прямых линий (1.33, б). Сформируем параметрический вектор
w(X)=r(X)Vfl(- W), гдег(Х) = (1 -Х)М + Х|и|, X е [0,1], (4.17)
Геометрические задачи визуализации
479
длина которого г(Х) и угол отклонения у = от вектора г являются линейны-
ми функциями X. При изменении параметра в интервале X е [0, 1] этот вектор
переходит из положения ы(0) = v в положение и(1) = w, равномерно увеличивая
свою длину от |у| до |wj и угол вращения от 0 до у.
Теперь становится возможным расположить вершины отрезаемых треугольни-
ков в точках, вычисляемых с помощью вектора (4.17):
a=pm + v,b = p,„ + и»;
с = p,„ + w(0.5);
d = р,„ + w(l / 3), е = р„, + и(2 / 3).
(4.18, а)
(4.18, б)
(4.18,в)
Рис. 4.44
480
Гпава 4
Для уменьшения общего числа треугольников предлагается при расстоянии ме-
жду точками а и Ь, меньшем значения h, отрезать всегда один треугольник
{pmabp„,} независимо от величины угла у. Так как |v| < h и |wj < А, то этот тре-
угольник удовлетворяет габаритному ограничению.
Моделирование описанного метода триангуляции показало, что когда длины
сторон полигона, примыкающие к вершине р,„, становятся меньше габаритного
параметра А, часто возникает коллизия с отрезанием треугольников. Отрезок ab
может пересечь некоторые стороны полигона либо вычисленные по (4.18) точки
с, d или е могут оказаться за его пределами (рис. 4.45, д). После отрезания тре-
угольников новый полигон перестает быть частью старого. Он становится само-
пересекающимся либо изменяет направление обхода на противоположное. По-
нятно, что дальнейшая триангуляция такого полигона недопустима.
Предлагается следующее решение этой проблемы. Перед отрезанием треуголь-
ников сохраним копии полигона Р' и списка отрезанных треугольников Lm'. а
после отрезания проверим обновленный полигон Р на самопересечение тестом
selfjtest, рассмотренным в гл. 1. При положительном результате этого теста либо
при изменении направления обхода полигона, проверяемого тестом (1.50), вос-
становим сохраненные в Р' и Lm' данные и будем уменьшать в (4.17) длины век-
торов г, и’ и отрезать треугольники с новыми вершинами (4.18) до тех пор, пока
полигон Р не перестанет самопересекаться или изменять направление обхода.
На рис. 4.46 построен алгоритм contri_poly(P, А) контролируемой триангуляции
полигона Р с габаритным параметром А, который реализует описанные выше
идеи. Работа алгоритма начинается с инициализации пустого массива Lm = 0, в
Геометрические задачи визуализации
481
который будут добавляться списки вершин отрезанных треугольников, и вычис-
ления направления обхода полигона
D = dir_test(P),
необходимого в функции (4.17) и для исключения анализа невыпуклых углов
<р, > 180°. Дальнейший процесс выполняется циклически до отрезания последнего
треугольника. После каждого отрезания полигон изменяет свою конфигурацию,
число п и список вершин Р= {pi ...р„р\}. Рассмотрим вычисления, выполняемые
в одном цикле алгоритма.
conlri poly(P,h)j
Lm=0, D=dir_test(P)
У — Pm-l Pm’W — Pm+l Pm
> p2 —> P,n=size(P)-t,V=n
k,
/=2 ... n >— end -►
l={m=n}
P'=P. Lm'=Lm
<p=ang(pi-i-phpM-Pt)
D-ai
fl<P <V}
V=|<p|,m=i
kv=kv + \
kw=kw+\
P=P\ Lm=Lm'
{pmbap„}-^Lm
P = Lp} vLp2
V t W
a = Pn,+T’ b=Pm+—
kv kw
LPi={Pm>—.Pm-iBJa
Lp2 =iU{pro+..,P„+/}
3
c = Pm+u(i/2)
{pmcapm}-+Lm
{pmbcpm}->Lrn
P = Lpt vcvLp2
si:e(P)
Q Возврат Lm
D
dir tesnP)
0
self testtP)
d = pm+u№)
e = Pm+u(2/3)
{pmdap„,}^Lrn
{pmedp„}^>Lm
{pmbepm}^>Lm
P = Lptv{d,e}vLp2
k
Рис. 4.46
&Шаг1. Для унификации вычисления внутренних углов /-Pt-iPiPt+i, включая
угол /-PnPi рг при вершине pi, добавляем в список Р вершину pi и вычисляем чис-
ло и = size(P) - 1, при котором р„ =pi и p„+l = pi.
482
Гпава 4
Шаг 2. Вычисляем с помощью функции (1.31) внутренние углы полигона
(р, = ang(p,_,-рь рм -р) V/ = 2, и.
Пропуская вогнутые вершины, знаки углов которых совпадают со знаком числа
D, находим вершину р,„ с минимальным выпуклым углом у = |ср„,| < 180°. При
этом индекс т заключен в интервале [2, и].
Шаг 3. На сторонах угла у разместим точки а и Ь, отстоящие от вершины р,„ не
дальше, чем на величину h. Проще всего было бы отложить от точки рт отрезки
длиной h, но при этом в конце отрезания некоторого ребра может получиться
очень короткий остаток длиной, много меньшей Л, что в свою очередь даст очень
маленький треугольник. Процедура равномерного разбиения ребер полигона со-
стоит из начальных установок некоторых величин и их циклических настроек.
Установочная фаза включает:
□ вычисление векторов сторон полигона при вершинерт:
V = Pm-i -Рт, W = pm^ -р„;,
□ расчет целых кратностей длин сторон к числу Л:
к -М к _|И.
n h
□ расчет целой кратности угла к углу 60° = л / 3:
л
□ формирование корректировочного индекса /, равного 1 при т = л и 0 в про-
тивном случае;
□ сохранение копий полигона и списка треугольников:
Р' = Р, Lm' - Lm.
Циклическая фаза разбиения ребер, примыкающих к вершинер„„ включает:
□ вычисление векторов сторон треугольников, длины которых не превышают
значения Л:
V V
v =—, w = —;
□ вычисление по (4.18, а) вершин треугольников, лежащих на ребрах р„,_\рт и
РтРт+\-
a=Pm + V,b=Pm + w;
□ формирование двух списков вершин нового полигона, расположенных до и
после точки р,„:
( LP\ = {pi+b Pm—l }u a,
,..r 1 (4.19, a)
[ LP1 =^Uipm+i,
Геометрические задачи визуализации 483
Вместо операций объединения формирование списков точек Lp\ и Lpi можно
выполнить и другим способом — с помощью условной функции if, прове-
ряющей совпадение точки a с p„ri и точки b с р„,+й
LP\ = if(pra-l = a {?!+/, - > Pm—I }> {pi+/, > Pm-l > «})> 19
Lp2 = if (Аи+1 = b {pm+l» ••• > Pn+l}. Pm+\. Pn+l })
Шаг 4. В зависимости от длины отрезка ab и значения к, вычисленного на шаге
3, возможны три варианта отрезания треугольников и формирования списка
вершин нового полигона Р (рис. 4.45, б, в, г):
□ если \a - Z>| < h или к = 1, т. е. у < 60°, то добавляем в массив Lm один тре-
угольник {р,„Ьар„}, а список Р формируем конкатенацией списков Lp\ и Lpi.
полученных в (4.19). После добавления в Lm последнего отрезанного тре-
угольника полигон вырождается в отрезок Р- {pipipi}. Поэтому при выпол-
нении условия size(P) < 4 алгоритм заканчивает работу и возвращает список
Lm со всеми содержащимися в нем треугольниками;
□ при к = 2, т. е. при 60° < у < 120°, вычисляем по (4.18, б) точку с, добавляем в
массив Lm два треугольника {р,„сарт} и {р,„Ьср„}, а список Р формируем кон-
катенацией списка Lp\, точки с и списка Lpr,
□ при к - 3, т. е. при 120° < у < 180°, вычисляем по (4.18, в) точки d и е, в массив
Lm добавляем три треугольника {p„,dap„,}, {p,„edp,„} и {p,„bep„}, а список Р
формируем конкатенацией списков Lp\, {d, е} и Lpz.
Шаг 5. Проверяем самопересечение нового полигона Р:
s = selfjest(P).
При $ = 0 и dir_test(P) = D переходим на шаг 1. В противном случае:
□ инкрементируем коэффициенты разбиения ребер:
кх. = кх. + 1, кК = к№ + 1;
□ восстанавливаем копии полигона и списка треугольников:
Р-Р', Lm - Lm';
□ переходим на шаг 3.
□
По окончании работы алгоритма contri_poly все возвращенные им в массиве Lm
треугольники имеют такие же направления обхода, как и у исходного полигона Р.
В заключение покажем результаты работы алгоритма контролируемой триангу-
ляции полигона, взятого из примеров 4.15 и 4.16, с разными значениями h
(рис. 4.47). Следует отметить, что при задании числа h большим максимальной
длины ребра полигона размеры получаемых треугольников ограничиваются
лишь расстояниями между соседними вершинами. Таким образом, функцию
contri_poly можно использовать также и для разрезания полигона на максималь-
но крупные треугольники, что проиллюстрировано на рис. 4.47, г решением при
h = 6. Эта способность изложенного алгоритма решать обычные задачи триан-
гуляции, несомненно, повышает его универсальность и полезность.
484
Гпава 4
Рис. 4.47
4.2.8. Дополнительные задачи отсечения
в пространстве
Представленные в предыдущем разделе алгоритмы имеют интуитивно понятные
трехмерные обобщения. Рассмотрим некоторые из Зб-алгоритмов отсечения,
которые могут оказаться полезными при решении различных задач компьютер-
ной графики.
4.2.8.1. Отсечение выпуклого полиэдра
полупространством
Аналогично определению полуплоскости, данному в разд. 4.2.7.1, назовем полупро-
странством ту часть пространства, во всех точках которой неявная функция плос-
кости отрицательна, т. 0. Эту сторону плоскости назовем внутренней.
Рассмотрим задачу нахождения области пересечения полупространств. Если эта
область не пуста, то она безусловно выпукла как пересечение выпуклых 3d-
областей. Решение задачи заключается в поочередном отсечении текущей вы-
пуклой области очередным полупространством (рис. 4.48). В итоге после каждо-
го отсечения область либо не изменяется — когда она целиком лежит в полупро-
странстве, либо сужается, либо становится пустой — если пересечение с
полупространством пусто, после чего обработка оставшихся полупространств
прекращается.
Выберем метод задания границы полупространства. Сравнивая методы описа-
ния плоскости, рассмотренные в гл. 1, и варианты вычисления неявной функции
f(p) в (1.119), заключаем, что наиболее практичны нормальная форма {до, А}
(шесть чисел) и функция nfN(po, N,p) (семь арифметических операций). Казалось
бы, что неявная форма (1.119, а), в которой прямая описывается всего четырьмя
элементами вектора F = [A В С £>], а функция nfF(F,p) вычисляется за
шесть операций, более предпочтительна. Однако расчет F по (1.66) требует еще
пяти операций, что в итоге делает неявную форму невыгодной. Еще большую
Геометрические задачи визуализации
485
ресурсоемкость имеют параметрическая (1.68) и трехточечная (1.72) формы
плоскости и соответствующие им функции (1.119, в) и (1.119, г).
Рис. 4.48
Когда отсекаемая область не является замкнутым полиэдром, возникает естест-
венный вопрос о способе описания такой неограниченной области. Для преодоле-
ния неопределенности зададим начальный полиэдр
BIG_BOX = {Ра BIG, Ga}
в виде выпуклой ограниченной области гексаэдра, изображенной на рис. 4.48
пунктиром, с интервалами изменения координат
|x|<B/G, h|<Z?ZC7, |z|<5/G,
где BIG— достаточно большое конечное число, надежно обеспечивающее пере-
сечение с BIG_BOX любой возможной плоскости. Матрица координат вершин
гексаэдра Ра и массив списков его граней
1 -1-1 1 1 -1 -1 1 т
Ро = 1 1-1-1 1 1-1-1 5
1 1 1 1 -1 -1 -1 -1
Pl Р2 РЗ Р4 РЗ Рб Pl Р&
za следующие:
Ga = {Gi, Gi, Gi, G4, Gs, Ge},
Gi = {1,2, 3, 4, 1},
Gi= {1,4,8,5, 1},
Gs = {1,5, 6, 2, 1}, (4.20)
G4 — {2,6, 7, 3, 2},
Gs= {3, 7, 8,4,3},
G6= {5, 8,7,6,5}.
Таким образом, задача пересечения неограниченных полупространств сводится
к поочередному отсечению ими от ограниченного выпуклого полиэдра частей,
лежащих с внешних сторон граничных плоскостей.
486
Гпава 4
На рис. 4.49 приведен алгоритм clip_side(P, G, ро, N) отсечения полиэдра
H={P,G} полупространством с граничной плоскостью {po,N}. Список
Р = {/ц, ...,р„} содержит координаты п вершин, а массив G = {Gi,..., G„,} — спи-
ски т граней полиэдра Н. Работа алгоритма начинается с инициализации пус-
тых списков U=0n F=0, в которых будет накапливаться информация о вер-
шинах и гранях отсекаемого полиэдра, и установки начального значения к = О
индекса последнего записанного в Uэлемента.
__________*___________
U=F=0, n=si:e(P), А=0
/=1 ...и
end
f,=nfN(p(J,N,p,)
<0
s=sqrt(J)
аз
1=1...я:
M?=*+l,g=Gf, Г=0
U={ut, ..., u*}
{U, F}=min _top{U,F)
F = close top(Jj,F}
v^r
Q Возврат {t/,F}
sice(F)
U=P, F=G
Рис. 4.49
Геометрические задачи визуализации
487
В связи с повышенной сложностью пространственных построений целесообраз-
но как можно быстрее установить факт пересечения плоскости с полиэдром ана-
логично тому, как это делает тест cross!, определенный в (1.120). Для этого вы-
числяются значения неявной функции во всех вершинах полиэдра
f = nf N(po, N, pft 1, n,
после чего элементы вектора/сортируются по возрастанию:
5=5ОГ/(/).
При 5i5„>0 полиэдр расположен относительно плоскости односторонне, воз-
можно, касаясь ее вершиной, ребром или гранью. Если к тому же si < 0, то весь
полиэдр Н находится внутри отсекающего полупространства и возвращается
алгоритмом без изменения как {/*, G}. Иначе при 5i > 0 полиэдр целиком отсека-
ется полупространством, а алгоритм возвращает {0, 0}.
В случае si s„ < 0 существует хотя бы одна пара вершин {phpj} по разные стороны
от плоскости {ро, N}, пересекающей полиэдр минимум по трем граням. Не отсе-
ченные полупространством грани должны входить в искомый полиэдр {U, F}.
Для его расчета организуем цикл i = 1, m обхода граней G,, в котором будем до-
бавлять в список U координаты, а в массив F— списки вершин, оставшихся по-
сле отсечения. Перед началом обработки /-ой грани установим в переменной
ц = k + 1 индекс начальной вершины этой грани и инициализируем список Г - 0
индексов неотсеченных вершин.
Центральная часть алгоритма, выполняющая отсечение грани полупространст-
вом, заключается в обходе вершин ее полигона согласно списку g = G,h форми-
ровании неотсеченного контура, лежащего с внутренней стороны секущей плос-
кости [ро, N}. В этот контур включаем вершины pg,j^ [1, s/ze(g)], лежащие в
полупространстве, а также точки пересечения ребер с плоскостью. Найденные
точки добавляем в список U, а индекс к инкрементируем и добавляем в Г.
По завершении обхода грани Gh убедившись в непустоте списка Г (при Г = 0 вся
грань отсечена плоскостью), проверяем замкнутость полученного контура. При
Щ * добавляем индекс ц в Г. Далее проверяем число неотсеченных вершин
грани. Для того чтобы грань была как минимум треугольной, число элементов
ее списка должно быть не менее четырех. В этом случае список Г добавляем в
массив F. Число новых точек в списке U, меньшее четырех, бывает при отсечении
грани, которая касается плоскости с внешней стороны одной вершиной или од-
ним ребром. Для аннулирования этих вершин устанавливаем индекс к в исход-
ное значение р - 1, которое он имел перед началом отсечения грани.
По окончании обхода всех граней исходного полиэдра из списка U берутся пер-
вые к элементов — вершины искомого полиэдра. Массив F содержит списки его
граней, но не всех\ На завершающем этапе алгоритма clip_side с массивами U и F
выполняются две важные операции.
1. Минимизация топологического описания полиэдра. После отсечения граней по-
лиэдра координатный список U всегда имеет кратные точки, т. к. каждая
488
Гпава 4
вершина входит в состав не менее трех смежных граней, получаемых незави-
симо друг от друга. Устранение кратности вершин выполняет приведенный
на рис. 4.50 алгоритм min_lop(P, G) минимизации топологии полиэдра, задан-
ного списком вершин Р = {pi, ...,р„} и массивом списков граней
Работа алгоритма начинается с копирования первой точки списка Р в список
U и установки к - 1 размера списка простых вершин U. Последующие верши-
ны Pt \/i = 2,п поочередно проверяются на совпадение с простыми вершинами
Wy \/j = 1 ,к . Если совпадение найдено, то во всех списках g = Vp = 1, т эле-
менты gY,у е [l,s/ze(g)], равные /, заменяются на j. В противном случае вер-
шина Pi является простой, что влечет за собой следующие действия:
• инкрементирование индекса к = к + 1;
• запоминание простой вершины ик = р,;
• поиск в списках граней элементов, равных i, и замену их на к.
Геометрические задачи визуализации
489
По окончании отбора простых вершин алгоритм возвращает список вершин
U = и обновленный массив списков граней G минимизированного
полиэдра.
2. Замыкание топологии полиэдра. Дело в том, что при отсечении полигонально-
го объекта по алгоритму clip_side не может появиться новой грани — сечения
полиэдра плоскостью. Вершины этой грани рассчитываются алгоритмом не-
зависимо друг от друга и в отдельный список не собираются В результате ис-
комый полиэдр оказывается незамкнутым, т. е. без одной грани в массиве G.
Идея нахождения единственной отсутствующей грани основана на следующей
закономерности. Если в замкнутом полиэдре некоторое ребро ркр,„ соединяет
две грани с номерами i и j, то индексы его концов дважды входят в состав
списков Gj и Gj как {..., к, т,...} либо {..., т, к,...}. В незамкнутом полиэдре
ребро сечения входит лишь в один список грани, что позволяет обнаружить
все такие ребра и сформировать из них замкнутый контур.
На рис. 4.51 приведен алгоритм close _top(P, G) топологического замыкания
полиэдра с формальными параметрами— списком вершин Р = {р\,...,р„} и
массивом списков граней G = {Gi,..., G,„}. Работа алгоритма начинается с
инициализации симметричной квадратной матрицы инцидентности вершин
полиэдра 1 е R"*". Поочередно сканируя содержимое списков g = Gi =
инкрементируем (g7, #,+1)-ые элементы матрицы I, ведя таким образом подсчет
кратностей ребер, соединяющих вершины полиэдра. По окончании сканиро-
вания сумма симметричных элементов матрицы инцидентности 7Л/ + 1,к равна
кратности ребра ркр,.
Для иллюстрации сказанного допустим, что при отсечении шестигранника,
изображенного на рис. 4.52, получены следующие списки вершин и граней:
Р ~ {/’1,7’2,рз,/?4}, G = {Gi, Gi, Gs},
Gi = {1,2, 3, 1},G2= {1,2,4, 1},G3 = {1,3, 4, 1}.
Тогда матрица инцидентности принимает следующий вид:
О 2 1 О’
0 0 11
1 0 0 1 (421)
2 0 0 0
Второй этап алгоритма close jop — формирование двухстрочной матрицы R,
столбцами которой являются индексы вершин ребер единичной кратности.
Сканируя наддиагональные элементы V/= 1, л-1, j = 1 + 1,п, добавляем в
матрицу R столбец [/ /Jr при выполнении условия
490
Глава 4
Рис. 4.51
Рис. 4.52
Геометрические задачи визуализации
491
Одновременно заполняем единицами вектор z, анализируемый на следующем
этапе. Просматривая наддиагональный треугольник матрицы (4.21), получим
матрицу ребер
2
2 3
4 4
и вектор z = [l I ]]. Следовательно, грань сечения полиэдра составляют
ребра единичной кратности ргрз,ргрь и рзрь.
На третьем и последнем этапе неупорядоченные ребра сечения соединяются
совпадающими вершинами в полигон (подобная задача на плоскости решается
функцией cont, описанной в разд. 4.2.3). Сначала в список g заносятся индек-
сы Rn и Rn. Тот факт, что первый столбец матрицы R использован, фиксиру-
ется установкой значения zi = 0. Далее и до тех пор, пока вектор z не станет
нулевым, т. е. в матрице R не будут использованы все столбцы, выполняется
поиск такогоу-го столбца R, для которого 0 и один из двух элементов Ry
или Ry равен последнему индексу в списке g. Оставшийся элемент добавляет-
ся к g, а устанавливаемое значение z; = 0 блокирует использованиеу-го столб-
ца в дальнейшем поиске. При блокировке в матрице R всех столбцов список g
готов: он содержит индексы вершин недостающей грани полиэдра.
Возвращаясь к задаче отсечения на рис. 4.52, получаем g - {2,3} и
z = [o 1 1], затем g - {2,3,4} и z = [o I б], наконец, g={2,3,4,2} и
z = [б 0 б]. Последний состав списка g описывает полигон {ргрзр^рг} сече-
ния полиэдра плоскостью.
Сформированный список индексов вершин новой грани добавляется в массив
G, и алгоритм close_top заканчивает свою работу, возвращая обновленный
массив G. Завершая решение задачи на рис. 4.52, добавим к массиву граней
полиэдра новую грань в виде списка Gi = {2, 3, 4, 2}.
На основе метода отсечения полиэдра полупространствами разработан алгоритм
conv_hedr построения выпуклого полиэдра (рис. 4.53), полезный в различных за-
дачах компьютерной графики, например, для отладки ЗсЬтестов и алгоритмов на
случайных выпуклых полиэдрах. Алгоритм заключается в поочередном отсече-
нии от исходного выпуклого гексаэдра
BIG_BOX = {Ра • BIG, Gn}
внешних частей относительно случайных плоскостей. Для получения всегда не-
пустого решения выберем способ генерирования отсекающих плоскостей, у кото-
рых начало координат всегда находится в отрицательных полупространствах.
Пусть в пространстве задана или случайно сгенерирована точка q, через кото-
рую должна проходить отсекающая плоскость {q, N}. Выбрав вектор нормали
N = q, получим отрицательное значение неявной функции плоскости в начале
координат:
f (Оз) = -q ° q < 0 \/q * Оз.
492
Гпавг
Рис. 4.53
Поэтому отсечение полиэдра Н полупространством с граничной плоскостьк
{q, q} сохраняет начало системы координат внутри Н. Процесс генерирована
плоскостей и отсечения ими полиэдра продолжается до тех пор, пока координа-
ты вершин получающегося полиэдра имеют числа BIG или -BIG. При полно*
отсечении от объекта BIG_BOX его исходных границ функция conv_hedr возвра-
щает искомый выпуклый полиэдр. На рис. 4.54 показано несколько случайны
полиэдров, сгенерированных описанным алгоритмом.
Рис. 4.54
Область применения метода отсечения выпуклого полиэдра полупространс--
вом обширна: это задачи отсечения объектов границами ограниченных облас-
тей видимости (призмы или конуса на рис. 4.13), построения сечений выпуклы
объектов плоскостями, расчета ядра полиэдра, пересечения выпуклых полиэ_
ров и т. п.
Геометрические задачи визуализации 493
4.2.8.2. Сечение выпуклого полиэдра плоскостью
Задача расчета сечения выпуклого полиэдра плоскостью фактически решается на
последнем этапе алгоритма clip_side (см. рис. 4.49), где функция close_top(U, F)
формирует полигон сечения, замыкающий топологию неотсеченного полиэдра.
Возвращаемый алгоритмом clip_side результат в виде двух массивов {U, F} мож-
но использовать для выделения из него полигона сечения С. Если плоскость и
полиэдр пересекаются, то координаты вершин полигона С возвращаются в мат-
рице U*P среди других вершин неотсеченного полиэдра, а список вершин сече-
ния находится в конце массива списков F^G. Если сечение отсутствует, то алго-
ритм возвращает либо {0,0}, либо {Р, G}. Так или иначе, для получения
полигона С нужна дополнительная обработка возвращаемых массивов U nF.
На рис. 4.55 показано, как нужно модифицировать заключительную часть алго-
ритма clip_side (правую часть блок-схемы, приведенной на рис. 4.49) для того,
чтобы он возвращал полигон сечения С. В отсутствие пересечения плоскости с
полиэдром, т. е. при sis„>0, возвращается пустой полигон. В противном случае
выполняется отсечение полиэдра полупространством плоскости {ро, N}, после
чего список g = F^.^ записанный в массив F последним, используется для фор-
мирования полигона С из точек ug. Xfi = 1, size(g).
{U, F}= mintoplJU ,F)
F = close _top(U, F)
Рис. 4.55
Задача, казалось бы, решена. Однако то обстоятельство, что модифицированный
алгоритм clip_side выполняет избыточные вычисления вершин и граней, не при-
надлежащих сечению, побуждает к разработке самостоятельного алгоритма, на-
494
Глава 4
ходящего только точки пересечения полиэдра с плоскостью, составляющие вер-
шины полигона С.
Такой алгоритм cutJiedr(P,G,po,N) построения сечения полиэдра H={P,G\
плоскостью {ро, N} приведен на рис. 4.56. Его работа начинается с инициализа-
ции полигона С - 0 и тестирования пересечения полиэдра с плоскостью. Отсор-
тировав по возрастанию значения неявной функции во всех вершинах полиэдра
f- nf N(po, N,p?) X/i= 1, fi,
принимаем решение о необходимости расчета сечения. При si s„ > 0 сечение от-
сутствует, а алгоритм возвращает С - 0. Если числа si и sn имеют разные знаки,
то вершины полиэдра находятся по разные стороны секущей его плоскости.
cut_hedr(P,G, pa,N)
____________I___________
n=si:e(P), C=R=0, k=0
pw(\~t)+pvt^>U
Рис. 4.56
Геометрические задачи визуализации
495
Полигон сечения С формируется из отрезков по которым плоскость пересе-
кает полигональные грани выпуклого полиэдра. По мере нахождения этих от-
резков будем записывать их концевые точки в столбцы матрицы R следующего
формата:
Л = ГЯ! а2 - ak
_b\ ^2 -
Перед началом цикла расчета отрезков пересечения плоскости с гранями ини-
циализируем пустую матрицу R - 0, а перед началом обработки грани G, —
пустой список точек U— 0. В процессе обхода ребер грани добавляем в U вер-
шины, лежащие в плоскости сечения, и точки пересечения ребер с этой плоско-
стью. После обхода грани при условиях, что в списке U ровно две точки и они в
любом сочетании [г/, г/2 Г или [м2 Щ не встречаются ни в одном из столбцов
R<J> , формируем из точек U новый столбец матрицы R.
Кратный отрезок в сечении полиэдра появляется при касании двух смежных гра-
ней с плоскостью по их общему ребру. А если какая-нибудь грань касается плоско-
сти единственной вершиной, то ее список U будет иметь всего одну точку. Для ис-
ключения ошибок обработка данной грани завершается без изменения матрицы R.
На завершающем этапе из отрезков-столбцов непустой матрицы R (их в ней не
менее трех) формируется полигон сечения С. Метод соединения отрезков совпа-
дающими концами до получения замкнутого контура использован нами в функ-
ции close_top. Теперь отличие в том, что матрица R состоит не из индексов, а из
векторов.
Для иллюстрации работы алгоритма на рис. 4.54 построены сечения случайных
полиэдров случайными плоскостями.
4.2.8.3. Расчет ядра полиэдра
Ядро полиэдра Н— это множество точек К, из которых видны все вершины по-
лиэдра (рис. 4.57, а). Любой выпуклый полиэдр совпадает со своим ядром
(рис. 4.57, б), но не каждый невыпуклый полиэдр имеет ядро (рис. 4.57, в). В оби-
ходном смысле ядро— это то, что остается от неограниченного пространства
после отсечения его полупространствами плоскостей граней полиэдра.
По этому способу на рис. 4.57, г построен алгоритм kernJiedrtP, G) расчета ядра
полиэдра Н- {Р, G} с матрицей вершин Р и массивом списков граней G. Вначале
устанавливаются исходные параметры отсекаемого полиэдра К= BIG_BOX. За-
тем в цикле i = 1, size(<G) выполняется внешнее отсечение К плоскостями всех гра-
ней полиэдра Н:
П формируется полигон z-ой грани полиэдра П = side(P, G, z) и вычисляется век-
тор ее нормали N - погт{П)\
П выполняется отсечение полиэдра К = {U, G} полупространством этой грани с
помощью функции clip_side(U, F, П\, N)\
496
Глава 4
П проверяется размер матрицы U. Если на каком-то шаге результат отсечения
окажется пустым, то ядро полиэдра отсутствует, а алгоритм возвращает пус-
той массив {7=0.
Для того чтобы отсечение плоскостью грани выполнялось с внешней стороны,
нормаль к грани всегда должна быть внешней. Это достигается выбором поло-
жительного направления нумерации вершин грани, если смотреть на нее снару-
жи полиэдра. Дополнительное условие предъявляется к описанию грани, имею-
щей форму невыпуклого полигона (например, задней шестиугольной грани
полиэдра Н на рис. 4.57, а). В ее списке G, первые три вершины должны состав-
лять выпуклый угол. Только тогда определенная по трем точкам нормаль (1.118>
будет внешней.
4.2.8.4. Пересечение выпуклых полиэдров
Аналогично плоской задаче пересечения полигонов реализация булевой функ-
ции А & В пересечения выпуклых полиэдров А и В основана на отсечении объек-
Геометрические задачи визуализации 497
та В полупространствами граней объекта Л. В результате получим объект А & В,
принадлежащий как Л, так и В, т. е. являющийся пересечением этих объектов.
Из этих соображений на рис. 4.58, а построена блок-схема алгоритма
kem_hedr(A, GA, В, GB) расчета пересечения выпуклых полиэдров {Л, GA} и {В, GB}.
Алгоритм возвращает пересечение объектов Л & В, если оно существует
(рис. 4.58, б), либо пустой массив координат, если Л и В лишь касаются друг дру-
га или вообще не пересекаются. Принципиальное требование к объекту Л, плос-
костями граней которого выполняется отсечение объекта В, является внешняя
ориентация нормалей ко всем граням GAi. Внешняя ориентация нормалей к гра-
ням объекта В не обязательна.
Рис. 4.58
Идентификация направления нормалей выполняется методом внутренней точки,
описанным в разд. 3.2.2. У выпуклого полиэдра со списком вершин А = {oi,
легко вычислимой внутренней точкой является геометрический центр
Сформировав по (1.116) полигон Z-ой грани П = side(A, GA, i) и вычислив по
(1.117) нормаль N - попп{ГТ), определим знак j- числа nfN(Jh,N,c), где П> —
первая вершина полигона П. При j = -1 точка с находится в отрицательном по-
498
Гпава 4
лупространстве грани, ее нормаль — внешняя, а отсечение объекта В плоскостью
{/7|, N} будет выполняться с внешней стороны. В противном случае 5 = 1, а для
отсечения должна быть использована антинормаль, равная -N.
Если окажется, что после очередного отсечения матрица вершин полиэдра В ста-
ла пустой, то дальнейший перебор граней объекта А теряет смысл, и алгоритм
заканчивает работу, возвращая пустой результат.
Для иллюстрации работоспособности алгоритма на рис. 4.58, в построен каркас-
ный полиэдр А & В— пересечение двух случайных выпуклых полиэдров А и В.
сгенерированных алгоритмом conv_hedr.
4.2.8.5. Выпуклая полиэдральная
оболочка массива точек
Допустим, в пространстве задано произвольное число п точек р, V/ = 1, п. Выпук-
лая полиэдральная оболочка массива точек Р = {pi, ...,р„} представляет собой вы-
пуклый полиэдр минимального объема, охватывающий все точки массива напо-
добие покрова из эластичной ткани. По отношению к оболочке точки массива
делятся на внутренние и граничные, принадлежащие вершинам, ребрам или гра-
ням оболочки. Граничные точки, образующие вершины, назовем выступающи-
ми. Задача построения полиэдральной оболочки заключается в отборе из всех
точекр, некоторых выступающих точек и построении на них полигонов граней с
одновременным формированием матрицы вершин оболочки U и массива спи-
сков граней G.
Алгоритм coverl(P), решающий задачу построения выпуклой Зё-оболочки, пред-
ставлен на рис. 4.59. Прежде всего он проверяет возможность существования
оболочки с помощью теста (1.81). Если размерность пространства, натянутого
на точки массива Р, меньше трех, то расширенная п х 4-матрица вершин
Pl
1Рп.
имеет неполный ранг, меньший четырех. При этом оболочка, обтягивающая
точки, не имеет объема, поэтому алгоритм возвращает пустой результат {0, 0}.
При наличии принципиальной возможности построения оболочки ее формиро-
вание выполняется в три этапа.
1. На первом этапе ищутся три неколлинеарные точки {р^РрР^}, плоскость ко-
торых не пересекает оболочку и потому способна быть плоскостью ее первой
грани. Условие неколлинеарности точек по тесту (1.79, а)— существование
вектора нормали
W = <Pj - А) х (л - А) * °з-
Геометрические задачи визуализации
499
Рис. 4.59
Для исключения повторных сочетаний индексы точек перебираются в интер-
валах i = 1, и - 2, j = i +1, п -1 и k = j +1, п. Искомая плоскость будет найдена
тогда, когда из всех точек массива не будет найдено ни одной пары точек,
лежащих от плоскости по разные стороны. Это легко проверяется тестом
cross3, определенным в (1.120). В качестве параметра/— имени функции рас-
чета ориентации точки относительно плоскости — наиболее экономично ис-
пользовать функцию/(р) = nfNipt, N,p), определенную в (1.119, б).
2. На втором этапе формируется полигон первой грани полиэдральной обо-
лочки как выпуклой полигональной оболочки точек, лежащих в плоскости
{ph N}. Вычислив матрицу преобразования
C = MAP2{phN,O3,z°),
рассчитаем координаты
Q = PC
всех точек массива Р в новой системе координат, в которой плоскость {/>,, N}
является фронтальной. Затем отберем в массив О точки q, = [х, у, zj,
имеющие координаты z, = 0. Из этих точек с помощью алгоритма cover
(см. рис. 4.31) сформируем выпуклую оболочку Н. Обратным преобразованием
и=нс~х
500
Гпава 4
получим полигон U = {ш,w„,} вершин первой грани оболочки в исходной
системе координат. Список вершин первой грани устанавливаем в первом
элементе списка G, равном Gi = {1,т}.
Для корректного обращения с функцией cover, работающей с точками на
плоскости ху, в алгоритме cover! используются матрицы
1 О О
О 1 о
1 о
Л/2з ~
л/32 ~ о 1
-Л/23
.° 0
преобразующие точки из R2b R3 и обратно с сохранением координат хи у:
[х У’]л/2з=[х У О], [х у z]M32=[x у].
3. На третьем этапе запускается поиск второй грани оболочки, примыкающей
к первому ребру первой грани нош. Затем к ней нужно будет присоединить
новые примыкающие грани, и так до тех пор, пока оболочка не станет замк-
нутой. По окончании формирования полиэдра оболочки алгоритм миними-
зирует ее топологию функцией min_top (см. рис. 4.50) и возвращает парамет-
ры полиэдральной оболочки {U, G}.
Процесс присоединения новых граней оболочки к уже существующим имеет ре-
курсивный характер и реализует простой способ включения света во всех комна-
тах здания, соединенных друг с другом коридорами. По этому способу при входе
в темную комнату нужно включить в ней свет и начать обход по периметру, от-
мечая двери, открываемые для входа в комнаты следующего уровня. Войдя в
освещенную комнату, следует вернуться назад и перейти к следующей неотме-
ченной двери. В конце обхода всех дверей текущей комнаты нужно вернуться
через ее первую дверь в комнату предыдущего уровня и продолжить обход ее
неотмеченных дверей. Процесс автоматически завершится, когда будут отмече-
ны все двери первой комнаты.
На рис. 4.60 представлен рекурсивный алгоритм gran(P, U, G, ab) формирования из
точек списка Р грани, примыкающей к отрезку ab. Алгоритм получает на входе
список Р, отрезок ab, массивы вершин U — {ш,..., ит} и списков граней
G= {Gi,..., Gy} текущей оболочки, а возвращает ее обновленную модель {U, G}
Методика нахождения примыкающей грани следующая.
4. На первом этапе в списке Р ищется такая точка что плоскость {a, N} с
нормалью
N = (Ь - а) х (ptа) Оз
удовлетворяет двум условиям:
• во-первых, она не совпадает ни с одной из уже имеющихся граней G
Х//=1,у. Проверка совпадения плоскости {a,N} с плоскостью j-ой грани
П = side(U,G,j), имеющей нормаль Н — погт(П), выполняется с помощью
теста (1.105, а). При |7V х = 0 и N ° (П\ - а) = 0 плоскость {я, N}, совпа-
дающая с плоскостью П, не может нести новую грань;
Геометрические задачи визуализации
501
granfP ,U,G ,ab}
______________X______________
n = size(P\ m = size(U\ 4=size(G)
N = (b~a)x(pi -b)
П =side(U,G,j\ H =norm(H)
C = MAPi(a,N,O3,z°)
Q = PC, k=0
{U,G}=gran(P,U,G,n,nM )
Рис. 4.60
• во-вторых, она не пересекается с оболочкой, т. е. среди элементов списка Р
нет ни одной пары разносторонних точек. Это легко проверяется тестом
cross! с аргументом f(p) = nf N(a, N,p). При cross! = 1 плоскость {a, N} пере-
секает оболочку и не может быть плоскостью грани выпуклого полиэдра.
Если после перебора всех значений i = 1, п не будет найдено ни одной плоско-
сти {a,b,p}, удовлетворяющей перечисленным условиям, то функция gran
возвращает параметры полиэдра без изменения. Это первое условие выхода из
рекурсии по отсутствию новой грани, примыкающей к отрезку ab.
2. На втором этапе формируем полигон (у+ 1)-ой грани полиэдральной обо-
лочки как выпуклую полигональную оболочку точек, лежащих в плоскости
{a, N}. Вычислив матрицу преобразования
С = Л7Л/>2(«,Л',О3,г0),
найдем координаты
<2 = РС
502
Гпава 4
всех точек массива Р в новой системе координат, в которой плоскость {я, N}
является фронтальной. Затем отберем в массив О точки =[х, у, z,] с ко-
ординатами z, = 0. Из этих точек с помощью алгоритма cover сформируем вы-
пуклую оболочку Н. Обратным преобразованием
П = НС]
получим полигон П = {П\,Пк} вершин новой грани в исходной системе
координат. Точки /7, добавляем в массив U, а индексы их расположения в
этом массиве устанавливаем в элементе <7у+| = {ш + 1,..., т + к}.
3. На третьем этапе организуем циклическое обращение функции gran самой к
себе в форме
{U, G} = gran(P, U, G, ГЦ, Пм) V/ = 1Д-1.
Это означает разветвление дерева рекурсии на к - 1 направление по числу
сторон полигона П. Некоторые из этих ветвей окажутся тупиковыми по пер-
вому условию выхода из рекурсии. Другие ветви, возможно, сами будут вет-
виться. Для исключения захода в грань предыдущего уровня рекурсии вы-
полняем проверку на несовпадение отрезка ПкПм с входным отрезком либо в
прямом ab, либо в обратном Ьа порядке следования концевых точек. По вто-
рому условию выхода из рекурсии — завершению цикла перебора ребер гра-
ни — функция gran возвращает обновленную модель оболочки {U,G}.
I& Пример 4.17. Проследим работу алгоритма cover! на примере построения по-
лиэдральной оболочки массива семи точек pi ч- р?, из которых рг и рд pi являются
выступающими, точка рз — внутренней, точки pi и ри+ pi — компланарными, а
pi -е- рз — коллинеарными (рис. 4.61, о).
Рис. 4.61
Геометрические задачи визуализации
503
Перебирая индексы / = 1,5, j = / + 1,6 и k = j +1,7, тестируем тройки
на способность нести плоскость грани выпуклого полиэдра:
□ тройка точек {р\,рг,рз} коллинеарна;
□ плоскости всех троек {/л, рърь} + {рцрърт} и {/л, рз,ри} + {рцрз.р?} пересе-
кают множество Р\
□ наконец, находим подходящую тройку точек {pi,/M,ps}. В ее плоскости лежат
еще две точки pt и рт, так что полигональная оболочка пяти точек, форми-
руемая алгоритмом cover во вспомогательной системе координат, имеет вид
17 - {ргрьрьрзрт} = {щ W2W3W4Ws},
а список первой четырехугольной грани равен G\ = {1, 2, 3, 4, 5}.
Начиная поиск грани, примыкающей к первому ребру pipe, функция gran нахо-
дит точку рц а алгоритм cover формирует полигон
{рьргртрь} = {utuiusw)}
второй треугольной грани Gi = {6, 7, 8, 9}. На втором переходе ищется третья
грань, примыкающая к первому ребру второй грани рьрг. Результат поиска —
точка /м и плоская оболочка трех точек
{p^pipip^} = {uioWll W12UI3}
треугольной грани G3 - {10, 11, 12, 13}. Третий переход на уже существующую
грань Gi, примыкающую к первому ребру третьей грани рьръ, является тупико-
вым, а следующий переход дает примыкающую к ребру ргрь четвертую грань
{ptpspipi} = {пи ms Щб ип}
со списком вершин G4 = {14, 15, 16, 17}. Аналогично, пятый переход через ребро
pips на грань Gi является тупиковым, а шестой переход через ребро pspi откры-
вает пятую треугольную грань
{pspipips} = {И|8Ш9М20П2|}
со списком вершин Gs - {18, 19, 20, 21}. Оба перехода с этой треугольной грани
на Gi и Gi являются тупиковыми. Они завершают обход Gs и возвращают алго-
ритм через четвертую и третью грани (их обход также оказался завершенным) на
грань G2.
Оставшийся тупиковый переход через ребро ргрз на грань Gs возвращает поиск
на первую грань Gi, а алгоритм — в функцию covert со списком вершин
U = {piptpupspi\p6p2pip6\pip6p2pi\p^psp2pi\psp2pips} = {wi ... W21}
и списками граней Gi + Gs. После минимизации топологии этого полиэдра полу-
чим следующую модель выпуклой полиэдральной оболочки (рис. 4.61, б):
U- {piptptpspi} = {u\ uiiowus}, G - {Gi, G2, G3, G4, Gs},
Gi = {1,4, 3, 2, 1}, G2 = {2, 5, 1,2}, G3 = {3, 5, 2, 3},
G4= {3,4, 5, 3},Gs= {4, 1,5,4}.
□
504
Гпава 4
4.3. Методы удаления
Удаление невидимых линий и поверхностей является, пожалуй, наиболее сложной
задачей визуализации. Она заключается в построении на экране дисплея проек-
ций лишь тех графических объектов— линий, поверхностей, тел,— которые
видны наблюдателю с его точки зрения (см. рис. 2.56, 2.67) Невидимость объек-
тов обусловлена двумя причинами. Во-первых, некоторые из них находятся вне
поля зрения наблюдателя — сбоку или сзади от него. Исключением этих объек-
тов из списка визуализации занимается задача отсечения. Объекты второй груп-
пы могут быть полностью или частично заслонены (экранированы) другими
непрозрачными объектами, расположенными ближе к наблюдателю. Идентифи-
кация таких объектов и реалистичное изображение их на экране дисплея состав-
ляют задачу удаления невидимых элементов
Необходимость решения этой задачи неизбежно возникает при переходе от кар-
касной модели объекта с прозрачными ячейками к модели с непрозрачными
гранями. Это существенно повышает реалистичность и информативность вос-
приятия объекта. Например, типичное изображение куба каркасом из двенадца-
ти ребер со всеми прозрачными гранями (рис. 4.62, а) не позволяет однозначно
судить о его действительной ориентации относительно наблюдателя. Удаление
невидимых ребер помогает избавиться от неоднозначности восприятия объекта
(рис. 4.62, б. в), даже если ячейки каркаса не закрашены, т. е. бесцветны или мо-
нохромны.
Рис. 4.62
Эффект экранирования дальних объектов ближними легко объясним с позиций
обоих методов трассировки лучей, рассмотренных в разд. 1.3.4. Пусть вдоль не-
которой определенной прямой в глаз наблюдателя направлены прямые лучи, из-
лученные источниками или отраженные поверхностями, которые можно рас-
сматривать как источники вторичных прямых лучей. Лишь луч от самого
ближнего к наблюдателю источника не встретит на своем пути преград и благо-
получно достигнет своей цели, а глаз увидит в данном направлении точку,
имеющую цвет источника луча. Остальные прямые лучи того же направления
поглотятся или рассеются на встреченных объектах (рис. 4.63).
Полагая, что из глаза наблюдателя вдоль той же прямой испущен обратный луч
проследим его путь до первого пересечения с ближайшей непрозрачной поверх-
ностью. Точки пересечения с остальными объектами, "нанизанные" на продол-
Геометрические задачи визуализации
505
жение обратного луча, оказываются экранированными, поэтому глаз их не ви-
дит (рис 4.64).
Рис. 4.63
Несмотря на кажущуюся очевидность и простоту, удаление невидимых линий и
поверхностей является достаточно сложной задачей визуализации, требующей
расчета пересечений множества графических объектов друг с другом с привлече-
нием больших машинных ресурсов. Поэтому существует целый ряд разнообраз-
ных алгоритмов ее решения, включая и методы, опирающиеся на аппаратные
средства.
Алгоритмы удаления классифицируются по следующим признакам (рис. 4.65).
□ Во-первых, по типу объектов. Здесь водораздел проходит между объектами с
разным числом степеней свободы, т. е. между линиями и поверхностями. Не-
обходимость в удалении невидимых линий возникает при работе как с сугубо
двухмерными Зб-объектами, например, тонкими нитями или осями коорди-
нат— равноправными элементами сцены,— так и каркасными поверхнос-
тями с непрозрачными ячейками, пересекающимися по ребрам-отрезкам,
некоторые из которых могут быть невидимы (см. рис. 4.47). Конечно, подав-
ляющее число объектов машинной графики обладает некоторой поверхно-
стью, отчего и методы, ориентированные только на удаления линий, пред-
ставляют меньшинство в общей массе алгоритмов данного назначения.
506
Глава 4
Рис. 4.65
□ Второе, чем различаются алгоритмы удаления — это используемые модели
объектов, из которых основными являются аналитические (явные и неявные).
параметрические и полигональные. Применение аналитического описания по-
верхностей иногда бывает предпочтительнее для быстрого решения
задач ориентации и пересечения как этапов общей задачи удаления. Боль-
шинство алгоритмов удаления работает с поверхностями, представленными
системой полигональных плоских граней, в основном, треугольников. Пара-
метрическую поверхность, описываемую векторной функцией p(th т/ можно
рассматривать как частный случай полигональной сети, состоящей из четы-
рехугольных ячеек — полигонов {/?,; A+bjA+ij+i Рьj+\ P,ji
□ Третий признак классификации — по способу выбора рабочего пространства.
• объектные алгоритмы работают в физической системе координат сцены.
Элементы объектов — вершины, ребра, грани, объемы — расчленяются на
фрагменты, позволяющие упорядочить их по удалению от наблюдателя.
Результат представляет собой список видимых элементов, вычисленных с
машинной точностью, никак не связанной с растровыми свойствами кар-
тинной плоскости. В связи с этим объектные алгоритмы иногда называют
непрерывными. Изображение видимых объектов, полученное в объектном
окне, переносится на экран дисплея (см. рис. 2.56) простым пересчетом по
(2.28) объектных координат в экранные пикселы.
Трудоемкость простейших объектных алгоритмов, сравнивающих поло-
жение каждого из No объектов с оставшимися объектами, оценивается
квадратичной зависимостью No . Недостаток непрерывных методов — их
достаточно высокая сложность;
• экранные алгоритмы выполняют удаление проекций невидимых элементов
объектов в системе координат экрана. Путем перебора по строкам, столб-
цам или в ином порядке конечного числа пикселов экрана находят точки
Геометрические задачи визуализации
507
пересечения сканирующего луча со всеми объектами сцены. В результате
на луче, соединяющем наблюдателя с (/,/)-ым пикселом (/ е [0, п - 1],
j е [0, m - 1]), формируется набор конкурирующих точек. Пиксел закра-
шивается цветом точки, ближайшей к наблюдателю (см. рис. 4.64). Сте-
пень детализации генерируемого изображения ограничена разрешающей
способностью экрана (п пикселов по горизонтали и m по вертикали), из-за
чего экранные алгоритмы называют дискретными. Всем им свойственны
ошибки дискретизации, особенно явно проявляющиеся при масштабном
увеличении изображения.
Ресурсоемкость простейшего дискретного алгоритма, сравнивающего
проекцию каждой из No граней с каждым из пт пикселов, пропорциональ-
на произведению Notim и, например, при п = /и®512 намного превышает
трудоемкость объектного алгоритма с числом объектов No ~ 1000. В связи
с бурным развитием технологии СБИС и резким удешевлением электрон-
ной памяти вопрос ресурсов практически снят с повестки дня. Это позво-
лило относительно простым дискретным алгоритмам визуализации (не
только удаления, но также закрашивания пикселов, геометрического и
цветового сглаживания) внедриться в программное обеспечение видео-
адаптера каждого современного персонального компьютера (об этом под-
робнее чуть ниже);
• гибридные алгоритмы работают как с самими объектами в пространстве,
так и с их экранными проекциями, объединяя преимущества и отстраняясь
от недостатков простейших алгоритмов, неся в себе целый ряд разного ро-
да оптимизаций.
Большинство алгоритмов удаления включает в себя сортировку. Главная сорти-
ровка ведется по геометрическому расстоянию от поверхности, ребра или точки
объекта до точки наблюдения. Смысл сортировки по глубине в том, что чем даль-
ше расположен объект от наблюдателя, тем больше вероятность, что он будет пол-
ностью или частично заслонен другим объектом, более близким к наблюдателю.
Дополнительная сортировка объектов по горизонтали и/или вертикали позволяет
оценить действительную возможность перекрытия проекций объектов на экране
дисплея. Весьма эффективно в этом смысле применение габаритных тестов и охва-
тывающих оболочек различной степени иерархии: от оболочек отдельных объек-
тов до оболочек кластеров — групп пространственно связанных объектов.
Для повышения эффективности визуализации путем учета предыстории состояния
сцены часто используется свойство ее когерентности, т. е. тенденции неизменяемо-
сти параметров в малой области. Выделяют несколько видов когерентности:
□ когерентность в картинной плоскости: если данный пиксел соответствует
проекции некоторой грани, то, скорее всего, соседние пикселы также соответ-
ствуют точкам этой же грани;
П когерентность в объектном пространстве', если данная грань видима, то со-
седняя грань также видима;
□ временная когерентность при создании анимации: свойства видимости объек-
тов в соседних кадрах, вероятнее всего, сохраняются.
508
Гпава 4
Громадный объем вычислений предъявляет жесткие требования к аппаратному
обеспечению компьютера — процессору, оперативной памяти и системной шине,
по которой данные передаются в видеоадаптер, а также к самому видеоадаптеру.
В последнее время появились специализированные устройства обработки изо-
бражений — графические ускорители, решающие задачи визуализации на аппа-
ратном уровне и делающие экранные алгоритмы предпочтительнее объектных.
Поскольку центральный процессор не всегда способен достаточно быстро обра-
ботать громадный поток данных, эта задача перекладывается непосредственно
на специализированную плату-акселератор, имеющую "на борту" собственный
графический процессор и дополнительную память для буферизации данных.
Применение графических ускорителей позволяет распараллелить и тем самым
ускорить процесс обработки информации.
Взаимодействие "ускоряемой" программы с тем или иным набором микросхем
осуществляется с помощью драйверов, а на программном уровне — графических
библиотек. Из наиболее популярных библиотек можно назвать Direct3D в сос-
таве пакета DirectX, OpenGL и QuickTime3D. Графические Зб-библиотеки, или
так называемые интерфейсы программных приложений (API — Application
Programming Interface), предназначены для того, чтобы с помощью некоторых
общих методов обработки графических данных облегчить и ускорить процесс
создания приложений, использующих трехмерную графику— объемные объек-
ты, свет, оптические эффекты, перспективу, деформации и т. д. При работе над
тем или иным графическим эффектом программисту необходимо обратиться к
библиотечной функции, передать ей требуемые параметры и получить готовый
результат. Многие графические библиотеки, например, Direct3D, рассчитаны на
комбинированную работу как с акселераторами, так и с центральным процессо-
ром. Если акселератор в системе не найден или не поддерживает данную функ-
цию, то библиотека "переложит" всю работу на центральный процессор и эф-
фект все равно будет достигнут, правда, за счет несколько большего времени.
В зависимости от сложности сцены (числа ее элементов), типа объектов
(выпуклые или невыпуклые), наличия пересечения объектов друг с другом, сте-
пени компромисса между желаемой скоростью и реалистичностью визуализации
существующие алгоритмы удаления более или менее учитывают эти и другие
особенности. Следует ясно понимать, что не придумано еще универсального ме-
тода решения задачи удаления.
Разработка нового алгоритма, аккумулирующего достижения отдельных мето-
дов, нередко выливается в чрезвычайно громоздкую процедуру, медленно рабо-
тающую даже с простыми сценами. Понятно, что для обработки информации в
реальном времени с частотой более 30 кадров в секунду, например, в програм-
мах авиатренажеров или "крутых" компьютерных игр (между прочим, двигате-
лей компьютерного прогресса), такие алгоритмы не годятся. С другой стороны,
в компьютерном кинематографе временной фактор отходит на второй план:
здесь более важна глубокая проработка оптических эффектов, позволяющая
достичь небывалой реалистичности или, наоборот, фантастичности изображе-
ния. По мере создания более быстрых алгоритмов и способных их реализовать
видеокарт всегда будут возникать новые потребности в скорости, детальности и
минимальной стоимости обработки данных.
Геометрические задачи визуализации
509
4.3.1. Предварительная обработка
моделей объектов
Есть два принципиальных подхода к уменьшению времени, затрачиваемого на
визуализацию сцены в целом и решение задачи удаления в частности как наибо-
лее сложной задачи визуализации. Во-первых, это максимально возможное со-
кращение вычислений; во-вторых, распараллеливание вычислительного процесса.
Не вдаваясь в детали реализации второго метода с помощью многопроцессор-
ных и транспьютерных систем [II], а также конвейерной организации вычисле-
ний [36], рассмотрим некоторые тактические приемы, позволяющие ускорить
процесс вывода изображений за счет сокращения вычислений.
4.3.1.1. Выбор мировой системы координат
Весьма эффективным средством упрощения векторных и матричных вычислений
является удачный выбор МСК xyz, с которой связываются положения наблюдате-
ля и проективной плоскости. Как показано в разд. 2.2.5.3, такой системой является
СК наблюдателя xHyHzH. В СКН, играющей роль МСК, основные геометрические
элементы и соотношения приобретают следующие наиболее простые формы.
□ Плоскость проецирования совпадает с фронтальной плоскостью ху. На ней
организуется регулярное симметричное окно-отсекатель с координатами цен-
тра и габаритными размерами
Хи = j-'u = о, -g < X < g, —V < у < V.
Через это окно наблюдатель как бы смотрит на окружающий его мир
(см. рис. 2.67). Габариты окна g и v либо задаются априорно, либо определя-
ются габаритами
left < Хэ < right, up <уэ< down
экранного окна вывода (см. рис. 2.10) и масштабным множителем цэ:
(4.22)
right — left _ down — up
2цэ 2цэ
Соотношения (2.28) между проекцией р = [х' у о] некоторой точки на
картинную плоскость и ее экранной проекцией р3 = [хэ у3 о] принимают
следующий вид:
left + right , up + down ,
хэ = — - + V , Уэ =-----~ - ВэУ ;
, _ хэ - V.Slfft + right) , _ 0.5(ир + down)-уэ
Мэ Мэ
(4-23)
(4-24)
510
Глава 4
□ В случае дальнего наблюдателя вектор его направления S = [о 0 1] ориенти-
рован вдоль оси z, матрица проецирования равна матрице Ot из (2.60), орто-
графическая проекция точки р = [х у z] есть
р' = [х' у z']=[x у 0],
а экранные координаты проекции рассчитываются по (4.23) при х' = х и
У' = У-
Во многих алгоритмах удаления требуется восстановить положение точки р
по ее экранной проекции />э (рис. 4.66). Благодаря простоте ортографического
проецирования координаты точки равны координатам проекции (4.24):
х-х’,у=у'. (4.25)
Рис. 4.66
Для восстановления z-координаты нужна некоторая дополнительная инфор-
мация о поверхности, которой принадлежит точкар.
В случае неявного описания поверхности неявным уравнением f(x, y,z) = 0
находится его аналитическое или численное решение
Z = <р(х,у).
При параметрическом описании поверхности векторной функцией
р(цт)=[х(/,т) z(/,t)]
составляется система двух нелинейных уравнений
(х(/,т)=х',
I <4-26)
аналитическое или численное решение которой относительно параметров t и
т определяет недостающую координату z(t, т).
Геометрические задачи визуализации
511
В частном случае плоскости, не параллельной оси z, получим несколько вари-
антов расчета z-координаты в зависимости от способа описания плоскости в
разд. 1.2. Г.
• при неявном описании матрицей |/1 В С £>] с коэффициентом С * О
(плоскость не параллельна оси z) из уравнения
Ах + By + Cz + D = О
получим
Ax + By + D
z=------Q-----; (4.27, п)
• при нормальном описании плоскости ТОЧКОЙ р0 = [х0 Zq | и вектором
нормали N = [/Vx Ny 7V_], не ортогональным оси z, из (4.27,п) и соот-
ношений
А = N„ В = Ny, С = N:*0, D = -Nxxo - Nyyo - N. zo
получим
(x-x0)/Vx+(y-y0Xv
z = z°--------nI--------; (427’
• при параметрическом описании плоскости точкой р0=[х0 уц z0] и не-
параллельными векторами V = [гх Vy Г_] и W = [fTx Wy ITZ], плос-
кость которых не параллельна оси z, путем подстановки координат векто-
ра нормали
Кх =
уг
иг
Ny
Уг
Wz
Уу Ух
х , N,=
Wx’ г Wx
Vy
Wy
*0
в (4.27, б) получим
Z - ZQ + [х - хо
У~Уо1
Ух
*х
иг wz
/ J L. —1
(4.27, в)
В СКН с вектором S = z° сортировка глубины точек р, по убыванию скаляр-
ных произведений J, = -pt ° S превращается в сортировку аппликат z,
(см. рис. 3.4). Аналогичное упрощение происходит при нахождении лицевых
граней полиэдра с помощью теста Nt° S > 0, который в СКН становится про-
стым анализом знаков аппликат внешних нормалей N:i. Грань является лице-
вой при выполнении условия Nd > 0.
□ Ближний наблюдатель находится в точке S’ = [б 0 г] оси z на фокусном
расстоянии 0 < F< оо от картинной плоскости (рис. 4.67).
512
Глава 4
Рис. 4.67
Центральное проецирование выполняется по (2.88) с помощью матрицы
10 0 0
0 10 0
ООО -1/F
ООО 1
либо по аналогичным (2.107) координатным формулам
, Fx
х =----
F-z
(4-28)
Экранные координаты проекции точки находятся по (4.25).
Восстановление координат {x,y,z} точки р по ее экранным координатам
начинается с вычисления по (4.24) значений х' и у'. При неявном опи-
сании f(x,y, z) = 0 поверхности, пересекающейся с лучом зрения в точке р,
координаты последней находятся решением системы двух линейных уравне-
ний, полученных из (4.28), и нелинейного уравнения поверхности:
Fx + x'z = x'F,
Fy + у 'z - yF,
/(x,y,z) = 0.
(4.29)
При параметрическом описании поверхности функциями x(t, т), y(t, т) и z(t, т)
координаты лежащей на ней точки находятся решением системы двух в об-
щем случае нелинейных уравнений
Fx(/, т)+ х 'z(l, т)= x'F,
Fy(/,T)+y'z(t,z)=y'F
(430)
относительно параметров {г, т) и подстановкой их в функцию z(r, т).
Геометрические задачи визуализации
513
В частном случае плоской поверхности получим несколько вариантов расчета
координат точки р в зависимости от способа описания плоскости:
• при неявном описании плоскости матрицей [а ВС £>]:
Fx + x'z = x'F, F О A
Fy + y'z = yF, => [x у z]=[x/F yF -£>] 0 F В
Ax + By + Cz + D = 0 x’ у C
(4.31, fl)
Без применения матричных операций после ручных преобразований вы-
ражение (4.31, о) принимает вид
CF + D , CF + D , Ax'+By+D
х = - — ---—— х, у =----------у , z = — -----F; /л з । к\
Ax+By'-CF Ax+By'-CF Ax+By'-CF
• при нормальном описании плоскости {/?о, N} применяем формулы (4.31) с
коэффициентами
А = Nx, В = Ny, C = NZ,D = -ро о М (4.32)
• при параметрическом описании плоскости {ро, V, Ж} вычисляем нормаль
N - Vx И'и применяем формулы (4.31) с коэффициентами (4.32).
Также представляет интерес решение (1.102, а) задачи пересечения луча
р' + Vt, проведенного из точки р' = [х' у' о] в направлении наблюдателя
Г=5-д' = [-х -у Г],
с плоскостью {ро, N}:
„ = ' . _ (S-p0)°N , (др - д> W
Р Р VoN (S-p')oNP (S-p)oN
(4.33)
В СКН с ближним наблюдателем S сортировка точек д, по уменьшению их
дальностей <7, превращается в сортировку по уменьшению длин векторов
S- р/ = —Ро,) (S- р'). м 34)
" (5-д,М^ '
Основной недостаток выбора СКН в качестве рабочей системы — необхо-
димость пересчета в нее координат всех объектов и матриц преобразований,
задаваемых обычно в СК сцены. Подробное обсуждение особенностей рабо-
ты в этой субъективно неподвижной системе координат приведено в
разд. 2.2.5.3.
4.3.1.2. Построение охватывающих оболочек
Метод оболочек получил широкое распространение в системах машинной гра-
фики благодаря резкому сокращению трудоемкости решения задач трассировки
лучей и визуализации. Суть метода в том, что сложный 3<!-объект с большим
числом разнообразных (полигональных или криволинейных, плоских или объ-
514
Гпава 4
емных, выпуклых или невыпуклых) ячеек окружается (вручную или автоматиче-
ски) виртуальной выпуклой оболочкой существенно более простой формы, чем
объект. Назначение оболочки:
П локализовать часть пространства, содержащего объект;
П заменить выполнение вычислительных операций со сложной поверхностью
объекта операциями с его простой оболочкой.
Модели оболочек добавляются к списку моделей объектов сцены либо состав-
ляют отдельный список оболочек. Оболочки обновляются после каждого гео-
метрического преобразования, приводящего к изменению их моделей.
Трудоемкость метода оболочек пропорциональна суммарному числу граней
оболочек всех объектов сцены
Аг — АоЛго,
где /ко— среднее число граней оболочки одного объекта. Уменьшение трудоем-
кости оценивается коэффициентом простоты оболочек
где пг — среднее число граней объекта.
Вот лишь некоторые задачи компьютерной графики, в которых применение ох-
ватывающих оболочек наиболее эффективно в смысле экономии машинных ре-
сурсов:
П практически все алгоритмы, использующие трассировку лучей. Метод трасси-
ровки лежит в основе некоторых алгоритмов удаления. Расчет пересечения
лучей с объектами сцены занимает от 75% до 95% всех вычислений [33], при-
чем большая часть расчетов при малой степени заполнения сцены объектами
выполняется бесполезно по причине прохождения большинства лучей мимо
всех объектов. Поэтому при обработке сцены желательно как можно раньше
исключить такие лучи из рассмотрения путем быстрой оценки их непересече-
ния с простыми оболочками;
П обработка столкновений движущихся объектов. При этом проверяется взаим-
ное проникновение элементов одного объекта внутрь другого (см. рис. 2.68).
что связано с расчетом попарных пересечений ребер с гранями и выполнения
тестов ориентации точек относительно полигонов и полиэдров. С помощью
оболочек можно быстро обнаружить заведомо непересекающиеся объекты;
П в системах анимации, моделирования и автоматизированного проектирова-
ния сложных многозвенных конструкций практикуется эскизное изображение
звеньев сложной формы в виде охватывающих их оболочек-параллеле-
пипедов (рис. 4.68, а). Это повышает эффективность проектирования и уско-
ряет вывод по сравнению с каркасной моделью (рис. 4.68, 6), не говоря уж о
сплошной (рис. 4.68, в), за счет исключения трудоемкой визуализации слож-
ных поверхностей и оптических эффектов. Аналогичный прием используется
в программах архитектурного и ландшафтного дизайна, заменяющих на ста-
дии эскизного проекта сложные архитектурные сооружения условными
Геометрические задачи визуализации
515
"коробками" для ускорения композиционных, транспортных, акустических,
инсоляционных (солнечное освещение), аэродинамических и других инженер-
ных расчетов.
Рис. 4.68
Наиболее распространены три типа оболочек'.
П сферические;
П габаритные;
П полигональные.
Кроме геометрической формы оболочки характеризуются:
П способом построения — ручным, полуавтоматическим или автоматическим;
П плотностью облегания объекта;
П сложностью модели — числом ее параметров и трудоемкостью применения;
П зависимостью параметров оболочки от геометрических преобразований ох-
ватываемого объекта.
Сферические оболочки
Сферическая оболочка (рис. 4.69, а) строится автоматически и отличается от дру-
гих оболочек минимумом параметров, простотой построения и использования,
но, с другой стороны, невысокой плотностью облегания. Положение сферы в
пространстве однозначно задается точкой центра с и радиусом г. В первом при-
ближении, достойном его простоте, центр сферической оболочки объекта с вер-
шинами р( можно принять в его центре тяжести
с=-Ха>
п i
516
Гпава 4
а радиус оболочки равным
г =тах|/>, -с|.
Аффинные преобразования вращения и переноса, не изменяющие форму объек-
та, не влияют на значение г, тогда как масштабирование объекта приводит к из-
менению радиуса оболочки. Таким образом, у сферической оболочки любого
движущегося жесткого объекта изменяются только координаты центра с.
Расчет пересечения прямой линии p(t) = ро + Vt с квадратичной поверхностью
(см. разд. 1.2.3) сводится к решению квадратного уравнения (1.55), для составле-
ния которого нужно иметь матрицу F квадратичной формы поверхности из
(1.124). Однако тест пересечения луча со сферой интересуют не сами точки пере-
сечения и даже не значения параметра t в этих точках, а лишь факт наличия или
отсутствия пересечения. Достаточно вычислить расстояние от точки с до прямой
{ро, V}, равное по (1.84)
^ = |(с-Ро)хП >
и сравнить его с радиусом г. При d > г луч и сфера гарантированно не пересекаются.
Рис. 4.69
Так же просто с помощью двух сферических оболочек с параметрами {ci,n} и
{с2, гг} оценивается взаимная ориентация объектов 1 и 2 (рис. 4.69, б). Тестом
заведомого непересечения этих объектов является выполнение условия
d = |ci - сг| > ri + Г2.
Некоторые авторы [11] предлагают вместо сферической использовать эллипсоио-
ную оболочку, оси которой ориентированы вдоль осей координат. Конечно та-
Геометрические задачи визуализации 517
кая оболочка может дать чуть более плотное облегание объекта, но при этом
теряются все преимущества сферической оболочки. Выполнение операций с не
самым простым квадратичным объектом, каким является эллипсоид, — слишком
дорогая цена такой замены.
Габаритные оболочки
Габаритная оболочка объекта с вершинами р,=[х, у, z, ] строится автомати-
чески как описанный шестигранник, форма которого зависит от положения на-
блюдателя. В сцене с дальним наблюдателем, имеющим вектор направления
S = z°, оболочка принимает форму регулярного параллелепипеда, грани которого
параллельны координатным плоскостям СКН (рис. 4.70). Габаритные координа-
ты объекта
Xmin = min{x,},^min = min{>',}, zmin = min{z,},
Лжах = max{A,},j'niax = max{>,}, Zmax = max{z,}
определяют принадлежащее его оболочке замкнутое пространство
{г 6 [xmjn , Xmax {у € [}’rnin ’ Jtnax ]}n{z
tmin» гтах ]}•
При диагональном расположении сильно вытянутого объекта его габаритная
оболочка имеет очень малую плотность облегания.
Для получения полиэдральной модели параллелепипеда {О, G} из модели куба
(4.20) вычислим его центр
с = 0-5 [*min + *тах -Уггпп + -Утах zmin + zmax 1
518
Глава 4
и полудлины сторон
— 0.5(Xmax — Xmin). dy — 0.5(j;max —J’rnm). d- — 0.5(Zmax — Zram).
Тогда матрица вершин оболочки и массив списков граней равны
O = PaM(dx,dy, dz)T(c\G = Ga.
В алгоритмах удаления, использующих трассировку лучей для сортировки точек
по глубине сцены, габаритные оболочки-параллелепипеды применяются для бы-
строго обнаружения объектов, не пересекаемых лучами. Габаритный тест пере-
сечения объекта с прямой p3+z°t, проходящей через экранную точку р3 парал-
лельно боковым граням оболочки, состоит в вычислении по (4.24) координат
точки р' в системе координат наблюдателя и проверке условия
{xmin < х < хтах }Г1 {Угтп < У < Утах } (4-35)
их принадлежности прямоугоэьной проекции оболочки. Расположение начала
луча вне габаритного прямоугольника означает гарантированное непересечение
объекта лучом.
Оболочки-параллелепипеды широко применяются в габаритных тестах взаим-
ной ориентации графических объектов, сводящихся к простой проверке пересе-
чения интервалов их координат. Примерами использования габаритных оболо-
чек для быстрого обнаружения заведомо непересекающихся объектов служат
функции gab?>_tesi и gab3_poly, определенные в (1.123).
В сцене с ближним наблюдателем, находящимся в точке S = Fz°, габаритные
оболочки объектов имеют форму усеченных пирамид с вершинами 5 (рис. 4.71).
Задняя и передняя прямоугольные грани оболочки параллельны плоскости про-
ецирования и лежат, соответственно, в плоскостях
Zmm = min{z,}, Стах = max{z,}.
Плоскости боковых трапециевидных граней образуют (левая с правой, а нижняя
с верхней) минимальные углы раствора по горизонтали и вертикали. В результа-
те все точки объекта заключены между этими плоскостями. Тангенсы углов на-
клона плоскостей gmin, graax, I’min, Vmax к оси z и габаритные координаты прямо-
угольной проекции оболочки на плоскость *)’ находятся следующим образом:
( X ( &min m*n „ > £max max ', lj vmin = m'n —— , Vmax = ГПаХ - пип 1 * шал 1AF~z‘) 1 xmin — ^£>min ’ xmax — Л&тах > J’min = X x> yt "I (4.36, a) '--v у Утах — ^vmax •
Геометрические задачи визуализации
519
Полиэдральная модель усеченной пирамиды {О, G} включает массив списков
граней куба G = Gn из (4.20) и матрицу вершин
&min^
v max Н
zmin
&min^
vmax^
zmax
Smax^
vmax^
zmax
gmaxH grnin^
vmax^ vmin^
zmin zmin
&min^
vmin^
zmax
gmax/i
vm'm^
zmax
gma*H
vm'm^
zmin
где
H — F — Zmin, h — F — Zmax.
Рис. 4.71
Эти данные можно использовать для визуализации оболочки как любого друго-
го полиэдра, а также в иных целях, например, при решении различных задач пе-
ресечения.
В алгоритмах, использующих трассировку лучей для сортировки точек по рас-
стоянию до ближнего наблюдателя, габаритные оболочки-пирамиды применя-
ются для быстрого обнаружения объектов, не пересекаемых сканирующими лу-
чами, сходящимися в цензре проецирования. Габаритный тест пересечения
объекта с прямой р' + (S -р')1, соединяющей точку р' е ху с наблюдателем S, за-
ключается в проверке условий
{•’min < х < •’max }l"l {Vmin < У <Утах} (4.36,6)
ее принадлежности прямоугольной центральной проекции оболочки. Расположе-
ние начала луча вне габаритного прямоугольника означает гарантированное
непересечение объекта с этим лучом.
Оболочки-пирамиды применяются в габаритных тестах взаимной ориентации
графических объектов, сводящихся к проверке пересечения их угловых интерва-
лов [gmin, gmax], [Vmin, Vmax] И КООрдИНаТНЫХ интервалов [Zmin, Zmax]. НаПрИМер, ана-
520
Глава 4
логично тесту (1.123, а), использующему оболочку-параллелепипед, строится
перспективный вариант габаритного теста ориентации точки q = [х у z] с уг-
ловыми координатами
относительно объекта Р, имеющего пирамидальную оболочку с параметрами
(4.36, а):
gM_ {g & min ’&max ]}U {г£ [vmin ’vmax ]}U {- £ l?min >zmax ]}•
Недостатки габаритной оболочки заключаются, во-первых, в зависимости ее
параметров от преобразований объекта; во-вторых, как уже говорилось, в малой
плотности облегания объекта при вытянутости его формы и диагональном рас-
положении относительно координатных плоскостей.
Полиэдральные оболочки
Полиэдральная оболочка строится как выпуклый полиэдр {О, G} несложной фор-
мы, плотно облегающий объект. Как правило, такая оболочка строится один раз
и претерпевает синхронно с объектом все геометрические преобразования. Спо-
соб построения оболочки, в основном, ручной— путем интерактивного выстав-
ления вокруг объекта точек о, (вершин оболочки) и формирования на них граней
GjC непрерывным тестированием:
П выпуклости получаемого полиэдра {О, G} функцией conv3(O, G) из (1.121);
П нахождения всех вершин объекта р, в пределах границ выпуклого полиэдра
{О, G} с помощью функции conv3_test(ph О, G) из (1.122).
Автоматизация построения плотной полиэдральной оболочки возможна при
наличии у объекта симметрии или если имеется алгоритм синтеза выпуклых по-
лиэдральных оболочек массива точек. Для поверхности, полученной вращением
некоторой образующей линии р0(т) = [х0(т) >'0(т) о] вокруг оси/’, можно инте-
рактивно задать на плоскости ху минимальное число точек о, так, чтобы лома-
ная линия {oi ог... о„} огибала образующую, нигде с ней не пересекаясь
(рис. 4.72). Непрерывное вращение этой ломаной вокруг оси / дает криволиней-
ную поликоническую боковую поверхность (рис. 4.73, о).
Для получения полиэдральной оболочки впишем каждый усеченный конус в
правильную усеченную пирамиду с по > 3 боковыми гранями. Поскольку у пра-
вильного л0-угольника соотношение радиусов описанной и вписанной окружно-
стей равно [13] sec(\|/o), где = л / по, то вершины оболочки лежат на меридианах
поверхности вращения ломаной линии {ojo^... о'„}, полученной растяжением по-
лилинии {oi ог... о„} вдоль оси х в sec(\)/o) раз. Угол между образующими мери-
дианами равен 2хр0, следовательно, вращение каждой точки о', не являющейся
полюсом, дает по вершин оболочки, рассчитываемых по формуле
Ру = (2Vo7'И V/ = 1, «о •
Геометрические задачи визуализации
521
Рис. 4.72
Благодаря осевой симметрии расположения этих точек четырехугольные грани
оболочки являются планарными.
Рис. 4.73
Таким образом, с учетом верхней и нижней По-угольных граней топологические
параметры полиэдральной оболочки в полном соответствии с формулой Эйлера
(3.101) равны
//в - И По, пг = (л - 1 )по + 2, пР - (2л - 1 )По.
Если одна из крайних точек сч либо о„ является полюсом, то
//в = (л - 1)Ло + 1, Лг = (л - 1)Ло + 1, Лр = 2(л - 1)Ло.
Наконец, если обе эти точки выбраны на оси вращения, то
Лв = (Л - 2)Ло + 2, Лг = (л - 1 )llo, пР - (2п - 3)ло.
Для иллюстрации изложенного метода на рис. 4.72 построены две полиэдраль-
ные оболочки одного и того же объекта вращения при ло = 4 (6) и ло = 6 (в).
522
Гпава 4
Полностью автоматический синтез полиэдральной оболочки может быть вы-
полнен с помощью алгоритма cover3, описанного в разд. 4.2.8.5 (см. рис. 4.59).
Достаточно сформировать массив Р вершин объекта, перечисленных в произ-
вольном порядке, и алгоритм возвратит модель выпуклого полиэдра
{О, G} = cover3(P),
плотно обтягивающего объект по выступающим вершинам.
Недостатки автоматического метода'.
П задание большого числа точек криволинейной поверхности для увеличения
плотности ее облегания дает слишком много граней оболочки, что нарушает
принцип ее простоты по сравнению с объектом;
П задание слишком малого числа точек криволинейного объекта приводит к
выпячиванию его отдельных частей из построенной "оболочки", которая в
этом случае таковой не является. Выходом из этой ситуации является добав-
ление выступающих точек к списку вершин построенного полиэдра и по-
вторный расчет оболочки.
Кластерные оболочки
Дальнейшее развитие метода оболочек, повышающее эффективность визуализа-
ции, основывается на понятии кластерных групп пространственно связанных
объектов и приводит к построению иерархического дерева оболочек. Начальный
уровень иерархии состоит из одного кластера сцены, чья оболочка охватывает
все ее содержимое. Например, сцена компьютерной игры в футбол состоит из
объектов второго уровня иерархии — поля, двух ворот, игроков наподобие фи-
гуры, изображенной на рис. 4.68, и мяча. Тело человека не является единым объ-
ектом и состоит из соединенных между собой относительно подвижных частей
(головы, шеи, туловища, рук и ног) — объектов третьего уровня иерархии. Кла-
стер группы конструктивно связанных объектов имеет собственную оболочку.
Процедура кластеризации выполняется до получения терминальных вершин ие-
рархического дерева — неделимых объектов со своими оболочками.
Построенные кластерные оболочки обрабатываются в иерархическом порядке,
начиная с кластера сцены. Если луч не пересекает его оболочку, то он не может
пересечь и ни одного из входящих в него объектов, что позволяет сразу исклю-
чить их из списка обработки. В противном случае на пересечение с лучом прове-
ряются оболочки кластеров следующего уровня иерархии. Если луч не пересека-
ет некоторую оболочку, то ее кластер и все содержащиеся в нем объекты и
кластеры исключаются из дальнейшего анализа.
В случае пересечения кластера лучом описанная процедура обхода кластерного
дерева рекурсивно повторяется до тех пор, пока не будут рассмотрены все объ-
екты. Когда луч пересекает оболочку некоего объекта, тот заносится в список
активных объектов. По завершении обхода дерева число элементов в списке ак-
тивных объектов, как правило, намного меньше общего числа объектов сцены,
подвергаемых обработке.
Геометрические задачи визуализации
523
Кластеризация значительно сокращает расчет пересечений лучей с оболочками и
в целом повышает эффективность алгоритма визуализации сцены. Трудоемкость
метода кластерных оболочек пропорциональна log(№) « Nr при Nr» 1.
4.3.1.3. Разбиение граней
В предыдущих разделах мы изучили алгоритмы разбиения (разрезания) плоского
полигона на выпуклые фрагменты и треугольники (cut_j>oly, tri_j>oly, contri_j>oly).
Там же было кратко сказано о месте операции разбиения в арсенале инструмен-
тов компьютерной графики. Приведем еще некоторые аргументы в пользу выпол-
нения разбиения на предварительной стадии визуализации объектов:
□ насколько это возможно, рекомендуется избегать операций с невыпуклыми
объектами, существенно более сложных в сравнении с алгоритмами обработ-
ки выпуклых фигур. Однократные затраты на выпуклое разбиение, например,
алгоритмом cut_j>oly, невыпуклых взаимно перекрывающихся или пересе-
кающихся полигонов (см. рис. 4.15) несравнимы с многократным решением
задачи визуализации этой конструкции в различных ракурсах;
П определенные трудности обычно вызывает визуализация неплоской грани.
Во-первых, нормаль к ее поверхности не имеет постоянного направления, из-
за чего цвет закраски этой грани индивидуален в каждой ее точке
(см. рис. 3.45—3.47). Во-вторых, неплоская грань типа косой плоскости при
определенном ракурсе наблюдения может экранировать саму себя и проеци-
роваться на картинную плоскость невыпуклым и, возможно, самопересекаю-
щимся полигоном (см. рис. 3.29, б). Аппроксимация такой грани системой
треугольников — всегда плоских полигонов — избавляет от перечисленных
проблем. Для этого можно использовать, например, алгоритм tri_poly\
П некоторые алгоритмы удаления правильно работают с равновеликими гра-
нями, близкими по форме к правильным полигонам (равносторонним тре-
угольникам и квадратам), но не всегда верно отображают грани вытянутой
формы, намного отличающиеся друг от друга габаритными размерами
(см. рис. 3.5). Решение становится возможным после разбиения таких граней
на примерно равновеликие фрагменты желаемой формы. Для этого можно
использовать, например, алгоритм contri_poly\
П в зависимости от удаленности наблюдателя один и тот же объект под разны-
ми углами зрения может выглядеть как мелко, так и крупно. Если в исполь-
зуемом алгоритме визуализации не применяется никаких методов сглажива-
ния, то приближение наблюдателя к криволинейной поверхности делает ее
изображение крупноячеечным, как бы сотканным из лоскутков с четко раз-
личимыми границами. В этом случае целесообразно разбивать поверхность
на фрагменты с постоянными угловыми размерами. При этом линейные раз-
меры фрагментов изменяются пропорционально расстоянию от наблюдателя
до поверхности;
□ одной из основ САПР объектов с распределенными параметрами является
метод конечных элементов [19,20], основанный на разбиении объекта на
большое число мелких частей. В области конечного элемента определенные
524
Глава 4
свойства объекта считаются постоянными, а их изменение происходит на
границах элементов. Таким образом, разбиение играет в системах проектиро-
вания сложных распределенных объектов основополагающую роль.
В сценах с подвижным наблюдателем весьма эффективно адаптивное разбиение,
смысл которого заключается в следующем. С дальней дистанции мелкие детали
объекта не различимы (сливаются) из-за конечного углового разрешения здоро-
вого глаза человека 8Р « Г = 0.00028 рад, обусловленного ненулевым расстояни-
ем между светочувствительными рецепторами. Для осмысления этой малой ве-
личины достаточно сказать, что круглый диск диаметром d. = 0.25 мм виден под
углом 8р с расстояния d. /8Р®1 м. Значит, поверхности удаленных объектов
можно разбивать на малое число крупных граней. При "наезде" наблюдателя на
объект предельное линейное разрешение ЛР = г8Р — промежуток между различи-
мыми точками — уменьшается пропорционально расстоянию г от наблюдателя
до объекта (рис. 4.74).
Рис. 4.74
Вторым фактором, ограничивающим линейное разрешение изображения на эк-
ране дисплея, является конечный размер пиксела графического режима, в кото-
ром работает прикладная программа. В режиме с максимальным разрешением
видеоадаптера можно принять диаметр пиксела равным d. = 0.25 мм. Тогда с
учетом масштабного коэффициента цэ, вычисленного по (2.26) или (2.27,6), по-
лучим предельное линейное разрешение ЛР = цх/..
Объединяя обе оценки и принимая во внимание, что самый малый различимый
элемент имеет размер ЛР, а минимальный просвет между элементами также равен
ЛР, получим следующую оценку минимального габаритного параметра разбиения'.
Amin = 2max{r8P, цэ</.}. (4.37)
Таким образом, выбор размера ячеек разбиваемой поверхности должен осущест-
вляться из условия h > hmm, не забывая при этом, что значение hmtn дает предельно
малые размеры различимых элементов изображения и делает визуализацию
чрезвычайно трудоемкой. На практике, конечно, можно задавать параметр h в
несколько раз большим.
Геометрические задачи визуализации
525
Алгоритм адаптивного разбиения имеет явно выраженные фрактальные свойст-
ва в смысле бесконечности процесса приближения модели, составленной из пло-
ских граней, к реальной гладкой поверхности.
Выделим основные типы поверхностей разбиения'.
□ параметрические р(1, т), определенные в узловых точках p:j = p(th т;) сетки
t е {Го,..., t„}, т е {то, ...,т,„} (рис. 4.75, а), и полигональные, заданные списком
точек-вершин Р — {р\ ...ркр\} в порядке обхода границы поверхности по
замкнутому контуру (рис. 4.75, б).
Рис. 4.75
Переход от параметрического описания к полигональному заключается в
формировании замкнутого контура из к - 2(п + т) граничных точек:
Р - {роор\о ...p,fiP,.\ -р„трп^т .ротро.т_1 ...роо}. (4.38)
При этом возможно слияние нескольких вершин в общем полюсе, порож-
дающее кратность этих точек и необходимость ее устранения перед началом
разбиения.
Обратное преобразование полигональной поверхности в параметрическую, в
общем случае, невозможно из-за ее произвольной формы и нерегулярного
распределения вершин по контуру полигона;
□ плоские и объемные в зависимости от определяемой по (1.81) размерности
пространства, натянутого на точки поверхности. Разбиение плоских граней
на более мелкие плоские же грани имеет целью приведение их размеров к од-
ному порядку для облегчения решения задачи удаления, а также разрезание
невыпуклых граней на совокупность выпуклых фрагментов.
Еще одна и, пожалуй, главная причина, по которой объемные поверхности
подвергаются разбиению по алгоритму триангуляции, — это получение мо-
делей с плоскими гранями. Параметрические поверхности симметричных объ-
ектов — в основном, тел вращения — могут быть разбиты на плоские грани и
более чем треугольной формы. Благодаря симметрии все вершины такой гра-
ни удовлетворяют в (1.81) условию т = 2.
526
Глава 4
Дробление параметрической поверхности целесообразнее всего выполнять в про-
странстве параметров {t, т} с последующим прямым расчетом точек поверхно-
сти p(t, т). Следует помнить, что нелинейности в координатных функциях
x(t, т) -е- z(t, т)— источник искажений формы ячеек, построенных в пространстве
{t, т}, при их отображении на криволинейную поверхность.
Рассмотрим некоторые способы разбиения параметрической сетки.
П Уменьшение (не обязательно кратное) интервалов дискретизации
Az, = r,+i - Z,, Ат, = ту+| - ij.
Фактически на прежнюю поверхность натягивается новая, более густая сетка,
что увеличивает число ячеек и уменьшает их размер. Например, при кратном
уменьшении AZ, в N, а Ат, в М раз каждая ячейка дробится на N М прямо-
угольных ячеек (рис. 4.76, а)
П Разбиение каждой прямоугольной ячейки диагоналями на два или четыре
треугольника, причем во втором случае центр параметрической ячейки нахо-
дится в точке бу = 0.5^ + Г,-+1 т, + т,+1 ] (рис. 4.76, б).
П Переход от параметрической сетки к граничному прямоугольнику с четырьмя
вершинами и его триангуляция по алгоритму contri.jtoly с желаемым значени-
ем А, выбираемым с учетом (4.37) (рис. 4.76, в).
Рис. 4.76
Геометрические задачи визуализации
527
Эффективность описанных методов разбиения объемной параметрической по-
верхности обусловлена решением задачи фактически в двумерном пространстве
ее параметров и простотой прямого расчета положения фрагментов в простран-
стве по известной зависимости p(t, т). К недостаткам метода можно отнести ис-
кажения формы фрагментов при переходе из плоского параметрического про-
странства на криволинейную поверхность. Особую осторожность нужно
соблюдать при разбиении параметрических прямоугольных ячеек, примыкаю-
щих к полюсам поверхности, на которой они имеют форму треугольников
(см. рис. 1.50, а, в—ж). При разбиении такой ячейки на два треугольника один
из них вырождается в отрезок со всеми вытекающими отсюда сложностями его
визуализации как грани.
Сложность разбиения полигональной поверхности, заданной граничным конту-
ром Р - {р\ ... pkpk+x= р\}, зависит от ее планарных свойств, т. е. близости к
плоскости. Ориентация плоской грани характеризуется единым для всех ее точек
вектором нормали N, заданным в нормальном описании {ро, N}, либо вычислен-
ным по параметрическому описанию {ро, V, W} как N- Vx W, либо построен-
ным по любым трем неколлинеарным точкам php и р, как N = погт({р„Ррр}).
Точки объемной поверхности некомпланарны, но если она не очень выпуклая,
то по методу Ньюэла [25] строится аппроксимирующая плоскость {pi,7Vcp} с
нормалью
к к
Ncp = YNi =(А -PJX(P21 ~Л)+£(а -Рм)х(л+1 -Pz)>
z=l z=2
полученной усреднением нормалей
Ni = погт({рк,,рьр!+1})
к плоскостям треугольников при вершинах полигона (рис. 4.77). Оптимальная
аппроксимирующая плоскость {ро, N}, наименее удаленная от совокупности то-
чек {/л, ...,рк}, строится по алгоритму (1.90).
Рис. 4.77
528
Глава 4
Промелькнувшее выше определение поверхности "не очень выпуклая" означает,
что локальные нормали 7V, к вершинным треугольникам составляют с прямым и
обратным направлениями усредненной нормали Nep не слишком большие углы,
скажем, не более 30°. Наличие нормалей, почти ортогональных к направлению
Nep, означает, что полигональная поверхность может иметь складку, т. е. описы-
ваться неоднозначной функцией z' - <р(х', у') в системе координат x'y'z', в которой
аппроксимирующая плоскость является фронтальной. Однозначное описание
поверхности объемной грани гарантирует, что любые ортогональные к плоско-
сти {/?|, Лер} (или {ро, 7V}) прямые пересекают поверхность один, а грань— не
более одного раза.
Рассмотрим два метода, благодаря которым становится возможным применение
алгоритмов двухмерного разбиения объемных граней, как параметрических, так и
полигональных.
1. С помощью матриц (2.60) или простым обнулением одной из координат мас-
сив точек поверхности S проецируется на некоторую координатную плос-
кость МСК. Для минимизации проективных искажений выбирается такая
плоскость, нормаль которой со0 — один из ортов х°, у° или z° — составля-
ет с нормалью плоскости (аппроксимирующей плоскости) грани наименьший
угол, а со-ая координата нормали имеет наибольший модуль |7VM|. Второй при-
чиной выбора плоскости, например, ху, может служить наличие явного опи-
сания поверхности, например, z = <р(х, у).
Далее выполняется разбиение орто графи ческой проекции 51', результатом чего
является массив проекций точек разбиения QПоследнее, что нужно сде-
лать, — это получить точки массива Q на исходной поверхности путем расчета
пересечения с ней проецирующих прямых q' + uPt (рис. 4.78, а). При выборе
проективной плоскости ху с нормалью ю° = z° это делается по (4.25)—(4.27).
Недостатки ортографического проецирования объемной грани заключаются,
во-первых, в возможности получения на проекции самопересекаюшегося по-
лигона, недопустимого для работы алгоритмов разбиения. Как иллюстрация
сказанного на рис. 4.78, а построены три ортографические проекции кусоч-
ной полигональной поверхности, из которых одна— профильная проекция
Sp — является самопересекающейся. Отсутствие самопересечений — третье
ограничение в выборе проективной плоскости. Тест self_test{P) проверки
плоского полигона Р на самопересечение приведен в гл. 1.
Во-вторых, восстановление точек разбиения грани по их ортографическим
проекциям вносит масштабные искажения тем большие, чем больше угол на-
клона нормали плоскости грани N к проективной плоскости.
2. Разбиение выполняется в плоскости (аппроксимирующей плоскости) самой
грани {ро, N} (рис. 4.78, б). Преобразование поверхности S в систему коорди-
Геометрические задачи визуализации
529
нат x'y'z', в которой плоскость разбиения является фронтальной, выполняется
с помощью матрицы
Ск = MAPl{p0,N, O3,z°).
Рис. 4.78
Вычислив проекцию S' -SCKOt, делаем ее разбиение, а полученный массив
точек Q ' на плоскости х'у' преобразуем на плоскость {ро, N} по формуле
Q"=&c?.
Если исходная поверхность 5 плоская, т. е. совпадает с {po,N}, то ее разбие-
ние фактически готово:
Q = Q".
В случае объемной поверхности восстановление точек «у, массива Q на исход-
ной поверхности производится путем расчета пересечения с ней проецирую-
щих прямых q" + Nt. При неявном описании поверхности грани выражением
/(р) - 0 решается скалярное уравнение
Ж+м)=о
относительно параметра t. При параметрическом описании p(t, 6) решается
система трех скалярных уравнений
q*+Nt= /?(т, б)
относительно параметров t, т и 0. Так или иначе, после нахождения числа t
получим точку пересечения qt =q"+Nt.
С сожалением приходится констатировать, что применение алгоритмов разреза-
ния плоских фигур для разбиения объемной поверхности связано с численным
решением нелинейных уравнений пересечения, что вкупе с проективными иска-
жениями делает данный метод весьма трудоемким.
530
Глава 4
4.3.1.4. Отбраковка нелицевых граней
и нормировка векторов
Процесс создания реалистичного изображения сцены можно представить как
графический конвейер, на который различные объекты ставят свои элементы —
точки, отрезки, полигоны — для последующей обработки. Пройдя через участки
геометрических преобразований в пространстве, проецирования на картинную
плоскость, отсечения окном вывода, элементы поступают на этап удаления, где
определяется их взаимное экранирование и степень видимости наблюдателем.
В результате из видимых фрагментов формируется растр изображения в желае-
мой цветовой палитре— цветной, черно-белой, в градациях серого и т. п. Одно-
временно с расчетом растра выполняется цветовой расчет (тонирование по [36]),
после чего готовая картинка из буфера кадра выводится на экран.
Сразу после размещения объектов сцены в пространстве становится возможным
определить, какие графические элементы не будут видны наблюдателю целиком
по причине их полного экранирования другими элементами. Эти элементы целе-
сообразно немедленно отбраковать (снять с конвейера), чтобы не тратить ма-
шинные ресурсы на их дальнейшую бесполезную обработку. Когда отбраковка
касается граней, то эти грани называются нелицевыми, т. е. не обращенными
"лицом" к наблюдателю.
Задача идентификации и отбраковки нелицевых граней имеет два аспекта: алго-
ритмический и геометрический. Алгоритмический аспект имеет следующий
смысл: если используемый алгоритм удаления не основан на изображении толь-
ко лицевых граней, примером чего является описанный в разд. 3.1.1.2 алгоритм
художника, то отпадает сама необходимость их обнаружения, не говоря уж об
удалении из конвейерного списка. Таким образом, не для всех алгоритмов уда-
ления отбраковка лицевых граней может быть одинаково полезна, хотя, несо-
мненно, вреда она не принесет, сократив размер списка обрабатываемых граней.
Геометрический аспект основан на том соображении, что у любой поверхности
как границы раздела пространства есть две стороны. Мы сейчас не будем вни-
кать в строгое топологическое определение стороны поверхности, а используем
обиходное понятие сторон листа как двумерных сущностей, кратчайший переход
между которыми выполняется путем прокола листа. Какую из двух сторон на-
звать внешней (наружной), а какую внутренней? Может ли быть лицевой внут-
ренняя сторона?
Ответы на эти вопросы зависят от вида модели объекта, его замкнутости и по-
зиции наблюдателя. Внешней условно назовем сторону поверхности замкнуто-
го объекта, видимую наблюдателем из неограниченного подпространства
(рис. 4.79, а). У объекта, описываемого сплошной 3<1-моделью, внутренняя сто-
рона поверхности вообще отсутствует в том смысле, что ее нельзя увидеть из-
нутри по причине отсутствия внутренней полости. При разрезании сплошного
тела с помощью булевой операции исключения, которую можно выполнить
функцией inclip3_hedr, его поверхность изменяется, но всегда остается внешней
(рис. 4.79, б). Таким образом, лицевые (в смысле— потенциально видимые)
участки поверхности сплошного тела могут располагаться только на ее внеш-
Геометрические задачи визуализации
531
ней стороне, а описания внутренних поверхностей в моделях данного класса
отсутствуют.
Рис. 4.79
Внутренняя сторона поверхности замкнутого граничного объекта существует,
может иметь цвет, отличающийся от цвета наружной стороны, но остается неви-
димой, пока поверхность непрозрачна. Установление ненулевого процента про-
зрачности какой-либо ее части делает обе ее стороны доступными для наблюде-
ния (см. рис. 1.75, 4.73). При разрезании граничного объекта он становится
незамкнутым, что эквивалентно замкнутому граничному объекту с полностью
прозрачными гранями разреза (рис. 4.79, в). Так или иначе, лицевые участки
замкнутой граничной поверхности могут располагаться на обеих ее сторонах, а
модель объекта данного класса должна содержать двустороннее описание гра-
ничной поверхности.
Определения внешней и внутренней сторон поверхности незамкнутого объекта
бессмысленны, т. к. обе стороны могут быть видны одновременно и никакой из
них нельзя отдать предпочтение (см. рис. I.50, 2.60, 3.10, 4.79, б). Модель незамк-
нутой криволинейной поверхности всегда должна быть двусторонней, и на каж-
дой стороне могут быть одновременно как лицевые, так и нелицевые участки.
Признаком лицевой ориентации j-ой грани или касательной плоскости к выпук-
лой поверхности является острый угол ц/, между векторами внешней нормали Nt и
направления на наблюдателя 5, (см. рис. 3.3, а), а самым простым ее тестом —
положительный знак скалярного произведения 7V, ° S, > 0. Более того, как гово-
рилось в разд. 4.3.1.1, при выборе системы координат, в которой вектор дальне-
го наблюдателя равен S = z°, отбраковка превращается в простой анализ знаков
аппликат внешних нормалей У.у.
Что означает термин "двустороннее описание" поверхности или грани? Для про-
стоты обычно пренебрегают толщиной листа, разделяющего пространство. Та-
ким образом, определяющие бесконечно тонкую поверхность точки на противо-
положных ее сторонах совпадают. Лишь нормали N к внешней и -N к
внутренней сторонам имеют противоположные направления (рис. 4.80). Следо-
вательно, модели противоположных сторон поверхности могут использовать
общее параметрическое p(t,i) или полигональное Р - (р> ...р„р\} описание, но
разные нормали, либо общий вектор нормали и два знака 1 и -1, с которыми он
должен применяться каждой из сторон.
532
Гпава 4
Рис. 4.80
В заключение необходимо отметить, что небольшое ускорение визуализации
может быть достигнуто с помощью предварительной нормировки
всех векторов V (имя V— обобщающее, вместо него может быть любое другое
обозначение вектора), модули которых |F| используются более одного раза. Со-
кращение времени достигается за счет:
□ исключения многократных вычислений квадратного корня |и| = —
достаточно медленной операции, выполняемой с помощью разложения в сте-
пенной ряд;
□ отсутствия необходимости в не самой быстрой арифметической операции
деления, т. к. длина нормированного вектора |и| равна единице.
Укажем несколько типовых случаев использования нормированных векторов:
□ расчет расстояний между различными графическими элементами;
□ трассировка лучей и расчет по (1.146)—(1.162) оптических эффектов
(отражений и преломлений) на произвольных поверхностях и, в частности, на
плоскостях;
П вычисление угла между векторами по (1.31) либо косинуса угла
cos(ZW)=ro^.
Этот расчет необходим, например, для нахождения лицевых граней и закрас-
ки поверхности по (3.8) на основе закона диффузного отражения Ламберта.
В связи с этим рекомендуется сразу после вычисления нормировать вектор
направления S дальнего наблюдателя и векторы нормалей N, ко всем граням
полиэдров и во всех необходимых точках криволинейных поверхностей.
Переходим к изучению методов удаления невидимых элементов. Разработано ве-
ликое множество алгоритмов удаления. Часть их описана в книгах [2, 5, 11, 18,
19, 20, 23, 25, 31,33—36], другая часть — в библиографии к ним, остальные менее
популярные методы оказались вне пределов упоминания, что, однако, не лишает
Геометрические задачи визуализации
533
их права на существование. Одни алгоритмы просты, но применимы только в
частных случаях; другие— более универсальны, но и трудны для понимания,
сложны в программировании и требуют больших машинных ресурсов.
Многообразие методов удаления, их названий (функциональных и именных) и
продолжающаяся разработка новых методов свидетельствует об активности и
перспективности исследований в этом направлении. Наиболее обстоятельное,
полное, детальное (объем списка эпитетов стремится в бесконечность) изложение
различных методов удаления приведено в книге Д. Роджерса [25]. Здесь же автор
не претендует на открытие новых алгоритмов, а всего лишь предпринимает по-
пытки оригинального решения задач этого класса в надежде, что его решения
будут востребованы.
Будем полагать, что все отрезки о,й, и лицевые грани Lpt, подвергаемые анализу
на видимость, собраны в двух общих списках
Ls = {oi b\ ... anb„}, Lm = {Lp\ ... Lpm}
независимо от их принадлежности отдельным объектам. Использование иной
организации данных будет оговорено в каждом конкретном случае.
4.3.2. Удаление невидимых линий
Элементарный способ (называть его алгоритмом слишком амбициозно) изобра-
жения выпуклого каркасного тела с непрозрачными плоскими гранями, полно-
стью экранирующими собственные невидимые ребра (см. рис. 4.62, б, в), заклю-
чается в выводе экранных проекций контуров всех лицевых граней на том
основании, что каждое ребро, принадлежащее видимой грани, также является
видимым. При этом ребра между двумя лицевыми гранями рисуются дважды.
Вовсе не факт, что дополнительные вычисления, необходимые для исключения
кратного вывода ребер, будут выгоднее, чем их отсутствие.
Если видимые ребра некоторого k-го выпуклого полиэдра необходимы для
дальнейшей работы, то из них нужно сформировать список Lsk, в котором крат-
ные элементы, естественно, недопустимы. Для этого просматриваются списки
вершин граней
где ХА. — список индексов граней к-го объекта в массиве списков Lm, и по алго-
ритму, приведенному на рис. 4.1, я, вычисляется объединение ребер лицевых гра-
ней выпуклого полиэдра
Lsk = U jkjA,7+i}> (4.39)
у=1
в котором по сравнению с простой конкатенацией кратные отрезки отсутствуют.
Рассмотрим общую задачу определения видимости отрезков, произвольно распо-
ложенных относительно плоских полигональных граней. Отличие этой задачи от
534
Гпава 4
предыдущей состоит в допущении пересечения отрезков с гранями и их частичной
видимости вследствие частичного экранирования (см. рис. 2.68).
Вначале разработаем алгоритм экранирования (shielding) отдельно взятого отрез-
ка ab отдельно взятой полигональной выпуклой гранью Р= {pt ...рпр\} в зависимо-
сти от их ориентации относительно друг друга и наблюдателя. Обозначим вектор
направления отрезка V = b - а. Будем рассматривать два типа наблюдателя:
П бесконечно удаленного в постоянном направлении Н - S от всех точек отрез-
ка (рис. 4.81, я);
П ближнего, расположенного в точке 5 в направлении H=S-a от точки а
(рис. 4.81, б).
Рис. 4.81
Первое, что делает отрезок невидимым,— это его совпадение с лучом зрения,
что быстро проверяется тестом
|ГхЯ] = 0.
Такой отрезок имеет вырожденную в точку экранную проекцию и должен быть
исключен из анализа экранирования всеми гранями.
Второй особый случай касается совпадения луча зрения с плоскостью грани. Это
вырождает ее проекцию в отрезок нулевой площади, который не в состоянии
экранировать никакой другой объект. К тому же, если все грани сцены прошли
предварительную обработку, то совпадающая с лучом грань не является лицевой
и будет отбракована.
Обратные лучи, проведенные из глаза наблюдателя до точек не параллельного
им отрезка ab, лежат в плоскости зрения П = {a, N} с нормалью N = V х Н. Экра-
нирование отрезка гранью Р возникает при одновременном выполнении двух
условий:
П грань пересекается с плоскостью зрения. Отрезок их пересечения cd можно най-
ти по алгоритму сечения полиэдра бесконечной плоскостью cut_hedr(P. G, a, N)
535
Геометрические задачи визуализации
(см. рис. 4.56), использующему список G={Gi}, состоящий из одной грани
Gi = {1,..., п, 1}. Достоинство этого алгоритма— предварительное тестиро-
вание пересечения по (1.120) и возвращение пустого списка при отсутствии
пересечения. Это означает, что отрезок ab не экранируется полигоном Р, или,
другими словами, экранируется пустым отрезком;
П обратные лучи, проведенные от наблюдателя до точек отрезка ab (но не
дальше!), по пути пересекают хотя бы часть или весь отрезок cd.
Расчет отрезков, экранирующих ab, проведем в следующем порядке.
Е7 Шаг 1. Аналогично (4.15) найдем параметры разложения векторов
с - a = Vt, + Нт,, d-a = Vt,, + Нт,,
в базисе {V, Н}.
/с тс (с-й)«И (с-а)оН И ° И V°H
td (d ~ a}° H (d ~ °)° H V ° H H ° H
(4.40)
Шаг 2. Выполним внешнее параметрическое отсечение отрезка cd областью ви-
димости т > 0, при необходимости смещая параметры задних точек с или d на
границу т = 0:
□ при {тс > 0}Г) {tj > о} весь отрезок cd расположен от наблюдателя не дальше,
чем отрезок ab, поэтому значения параметров, вычисленные в (4.40), не изме-
няются;
□ при {тс > 0}Г) {tj <0} (этот случай изображен на рис. 4.81) ближняя часть cd
расположена со стороны точки с, поэтому смещению подвергаются парамет-
ры точки d.
tc +{td~ ‘с
Tc~Td
(4.41, а)
П при {тс < 0}Г){т</ > о} смещаются параметры точки с:
к
0
(4.41,6)
□ при {тс < 0}П {т^ < о}и {тс < о}П {cd < О} весь отрезок cd отстоит от наблюда-
теля дальше, чем ab, т. е. экранирование отсутствует.
Шаг 3. При наличии эффекта экранирования спроецируем ближнюю к наблюда-
телю часть сечения грани плоскостью
{а + Vt, + Нт,, а + Vt,, + Нт,,}
на прямую отрезка ab:
П при дальнем наблюдателе параллельное проецирование дает точки
а = а + Vtc, Р = а + Vtd, (4.42, а)
536
Гпава 4
П при ближнем наблюдателе по правилам центрального проецирования получим
(442 б)
о
На рис. 4.82 приведен алгоритм shield_segni_conv(ab, Р, S, mod) экранирования
отрезка ab плоской полигональной выпуклой гранью Р= {/ц ...p„pi}. Наблюда-
тель задается вектором 5 и типом удаленности mod е {0, 1}. равным нулю при
бесконечном и единице при конечном удалении. Алгоритм возвращает экрани-
рующий отрезок на прямой, проходящей через точки а и Ь, либо пустой отрезок
при отсутствии экранирования.
Рис. 4.82
Вспоминая, что в нашей коллекции есть алгоритм cross_poly расчета пересечения
двух плоских полигонов (см. рис. 4.15), используем его для решении задачи экра-
нирования отрезка ab произвольным, в том числе и невыпуклым полигоном
Р= {pt —PnPt} (рис. 4.83). Смысл идеи в том, что все отрезки, по которым Р пе-
ресекается с полигоном (не плоскостью!) видимости П, экранируют отрезок ab и
Геометрические задачи визуализации
537
не нуждаются в параметрическом отсечении по формулам (4.41). Достаточно для
каждого отрезка с,Д, из списка Ls', возвращенного функцией
cross j>oly(P, П, 3, Ls') = 1,
найти по (4.40) параметры концевых точек {td, т„-} и {/</,, спроецировать эти
точки по (4.42) на прямую отрезка ab и сформировать конкатенацию получен-
ных отрезков а, р,.
Что касается способа задания полигона видимости, то для ближнего наблюдате-
ля это треугольник П = {abSa}, а для дальнего — полубесконечная полоса. Ана-
логично способу представления полуплоскости (см. разд. 4.2.7.1) зададим доста-
точно большое число BIG, заведомо превышающее максимальную глубину
сцены. Тогда полосу видимости можно заменить конечным полигоном
П = {a, b, b + BIG -S,a + BIG S,a}.
Описанный метод реализован в виде алгоритма shield_segm(ab, Р, S, mod) экрани-
рования отрезка ab плоской полигональной гранью Р- {pt ...рпр\} с наблюдате-
лем, задаваемым параметрами 5 и mod е {0, 1} (рис. 4.84). Алгоритм возвращает
список экранирующих ab отрезков, лежащих на прямой, проходящей через точки
а и Ь, либо пустой список при отсутствии экранирования.
538
Гпава 4
Рис. 4.84
Несмотря на простую блок-схему, алгоритм достаточно трудоемок, т. к. основан
на сложном алгоритме cross_ро1у. Поэтому в задачах визуализации объектов, все
грани которых являются выпуклыми полигонами, рекомендуется использовать
более простой и быстрый алгоритм shield_segm_conv.
Завершим раздел разработкой алгоритма удаления отрезков списка
Ls = {a,bh..., a„bn}, экранированных плоскими полигональными гранями, со-
ставляющими массив списков Lm= {Lpt,Lp„,}. Если грани этого массива не
проходят отбраковку, то читатель должен самостоятельно дополнить алгоритм
расчетом их нормалей 7V, = norm(Lpt), скалярных произведений о,f = N, ° S и рабо-
тать только с лицевыми гранями, для которых ст, > 0.
Каркасное изображение сцены создается как самостоятельными отрезками, так и
ребрами лицевых граней. Есть еще отрезки взаимного пересечения граней, от-
сутствующие в исходных данных. Они рассчитываются по алгоритму crossjwly.
Все эти отрезки объединяются в общий список Lso. Для каждого отрезка LsOj, не
совпадающего с лучом зрения, формируется список экранирующих отрезков Lsb,
после чего исключение LsOi -i Lsj, добавляется в список видимых отрезков Lsb.
На основе сказанного разработан и представлен на рис. 4.85 алгоритм
hide_segm(Ls, Lm, S, mod) удаления отрезков списка Ls, экранируемых полиго-
нальными гранями списка Lm с наблюдателем, задаваемым параметрами S и
Геометрические задачи визуализации
539
mod е {О, 1}. Алгоритм возвращает список отрезков в границах их видимости
наблюдателем в объектном пространстве.
Рис. 4.85
4.3.3. Удаление невидимых граней
Простейший способ изображения выпуклого сплошного полиэдра заключается в
произвольном порядке вывода экранных проекций всех его лицевых граней и
представляет собой один из вариантов метода Робертса (см. разд. 3.1.1). Благо-
даря выпуклости объекта его грани видимы либо невидимы целиком. Все неви-
димые грани являются нелицевыми, и на этом основан принцип их отбраковки,
рассмотренный в разд. 4.3.1.4. Смежные грани пересекаются друг с другом толь-
ко по общим ребрам, а несмежные грани не пересекаются. Таким образом, у вы-
пуклых полиэдров исключена частичная видимость граней.
Рассмотрим общую задачу определения видимости плоских полигональных гра-
ней, произвольно расположенных относительно друг друга. Она решается при
изображении как отдельных невыпуклых тел, возможно, имеющих отверстия и
540
Гпава 4
самопересечения, так и совокупности пересекающихся тел. В отличие от выпук-
лой задачи здесь возможна частичная видимость граней вследствие их взаимного
экранирования, в том числе и за счет пересечения друг с другом (см. рис. 2.68).
Сначала изучим эффект экранирования отдельно взятой плоской грани Q другой
плоской гранью Р в зависимости от их ориентации относительно друг друга и
наблюдателя. Экранирование поверхности подобно оптическому эффекту обра-
зования тени и заключается в попадании части или всей поверхности Q в тене-
вую зону И, находящуюся за гранью Р. В итоге наблюдатель видит лишь часть
грани Q, находящуюся вне теневой зоны.
В случае дальнего наблюдателя область Н представляет собой незамкнутую
призму с основанием Р (рис. 4.86, а), а при ближнем наблюдателе это будет не-
замкнутая усеченная пирамида с передней гранью Р и без задней грани
(рис. 4.86, б). Задача экранирования эквивалентна внутреннему отсечению поли-
гона Р областью Н.
Рис. 4.86
Геометрические задачи визуализации 541
Единственное, что мешает использовать для такого отсечения алгоритм
mclip?>_j)oly, разработанный в разд. 4.2.5,— это бесконечная протяженность те-
невой зоны в глубину сцены. Аналогично ранее примененному методу представ-
ления неограниченных полупространств зададим достаточно большое число
BIG, заведомо превышающее максимальную глубину сцены. Тогда бесконечная
теневая зона полигона Р = {р\ ...р„р\} заменяется конечным полиэдром
Н- {O,G} с параллельными передней и задней гранями. Координаты его 2п
вершин, составляющих массив О = {oi,..., О2Л}, в зависимости от типа наблюда-
теля, задаваемого параметром mod е {О, I}, вычисляются следующим образом:
Pt при i < п;
Oj = . , (4 43)
Pi-n-BIG \S~mod - Pi-n)npHi>n.
Грани полиэдра Н опишем массивом G = {Gi, Gi, Gi,..., Gn+i} co списками
G] ={1, ..., n, 1} G? = {2/7, 2/7-1, ...,w + l, 2//}
___ (4.44)
Gj+j = {/, n + i, mod(/7 + z +1, n\ mod(z +1, n\ /} Vz = 1, n.
Введем вспомогательную функцию shadow(P, S, mod) формирования параметров
полиэдра теневой зоны грани Р - {р\ ... р„р\) с наблюдателем, задаваемым пара-
метрами 5 и mod е {0, 1}. Функция возвращает рассчитанные по (4.43) матрицу
координат полиэдра G и по (4 44) массив списков граней G.
Вот теперь, при наличии конечного полиэдра Н, можно использовать его в каче-
стве внутреннего отсекателя грани Q, экранированной гранью Р. После вычис-
ления параметров теневого полиэдра
{О, G} - shadow(P, S, mod)
и отсечения им полигона Q по алгоритму
inclip?>_poly(Q, О, G, U, F)
получим список полигонов — видимых фрагментов Q.
На рис. 4.87 приведен алгоритм hide_poly(Lm, S, mod) удаления полигональных
граней списка Lm, невидимых наблюдателем, задаваемым параметрами S и
mod е {0, 1}. Алгоритм возвращает список полигонов— видимых фрагментов
исходных граней.
Алгоритм рассчитывает попарное экранирование m граней массива списков
Lm= {Lpi,..., Lp„,} путем внутреннего отсечения граней Q = Lp, Vi = \,m тене-
выми полиэдрами граней Р = Lp, Mj =1,/и, j * i. В зависимости от размера и
содержимого вспомогательного списка Lm', возвращенного алгоритмом
inclip?>_poly, возможны следующие варианты действий:
□ если список Lm' пустой, то грань Q полностью экранирована гранью Р
(рис. 4.88, а) и удаляется из списка Lm\
□ если Lm' содержит один элемент, то это может быть либо полигон исходной
полностью видимой грани Q (рис. 4.88, б), либо один видимый фрагмент час-
542
Гпава 4
тично экранированной грани Q (рис. 4.88, в). В первом случае, т. е. при
Lm' = Q, алгоритм переходит к проверке экранирования полигона Q следую-
щей гранью Р, а во втором элементы списка Lm' добавляются в список Lm, а
Q из него исключается;
□ если в списке Lm' более одного элемента (рис. 4.88, г), то все видимые фраг-
менты частично экранированной грани Q добавляются в список Lm, a Q из
него исключается.
При любом изменении размера или содержимого списка граней Lm, выполнен-
ном в результате отсечения, алгоритм переходит на начало обработки обнов-
ленного списка. Если перед очередным циклом обработки список Lm содержит
единственную грань, то алгоритм заканчивает работу с возвратом этой грани.
Геометрические задачи визуализации
543
По окончании обработки список Lm содержит не экранирующие друг друга по-
лигональные фрагменты видимых наблюдателем граней, которые алгоритм воз-
вращает как результат своей работы. Далее эти полигоны можно проецировать
на экран или использовать в последующих расчетах.
Рассмотренный алгоритм hidej)oly содержит важный элемент оптимизации, по-
зволяющий сократить число переборов пар {Q, Р} с помощью флажков полной
видимости граней. Флажок z-ой грани f является ее неотделимым атрибутом, та-
ким же, как число и координаты вершин, цвет, нормаль и другие параметры. Он
участвует во всех списковых операциях вместе со своей гранью. Перед началом
обработки граней все т флажков сбрасываются в ноль.
Грань Q = Lpt, не экранированная ни одной гранью Р = Lpj,j ф i, является полно-
стью видимой наблюдателем, поэтому после перебора всех граней Р флажок /
устанавливается в единицу. Больше эта грань не будет участвовать в проверках
экранирования и в отсечении ни как объект Q, ни как экран Р. Новые полигоны,
добавляемые в Lm, снабжаются своими флажками полной видимости, устанав-
ливаемыми в ноль. В конце обработки списка Lm флажки всех его полигонов
становятся равны единице.
В заключение хочется еще раз подчеркнуть, что автор не ставил своей целью эн-
циклопедический охват всех существующих алгоритмов удаления, которые мож-
но найти во многих книгах по компьютерной графике, а попытался проторить
свою, пусть и неширокую, тропинку в безбрежном пространстве решений про-
блем визуализации сложных геометрических объектов.
544
Гпава 4
На сегодняшний день наиболее эффективное решение графических задач обес-
печивает конвейерная архитектура, реализованная как программными, так и
аппаратными средствами [36]. В будущем, совершенно очевидно, графические
СБИС станут работать быстрее, степень их интеграции многократно возрас-
тет, а стоимость уменьшится. Это является предпосылкой тотального наступ-
ления методов распараллеливания графических вычислений, обеспечивающих
более высокое качество изображения, учет большего числа источников света и
глубину проработки разнообразных световых эффектов. Следовательно, поль-
зователь такой графической системы получит возможность включать в ото-
бражаемую сцену больше объектов с самыми разнообразными оптическими
свойствами, которые будут моделироваться так же, как они происходят в при-
роде — быстро и параллельно.
Заключение
Поздравляю тебя, вдумчивый читатель, с тем, что ты успешно дочитал до конца
мою книгу! Надеюсь, что она не показалась тебе слишком заумной, непонятной
и скучной. Ведь первоначально она задумывалась как небольшое внутривузов-
ское методическое пособие по основным геометрическим понятиям и взаимоот-
ношениям объектов на плоскости и пространстве, адаптированным к использо-
ванию в компьютерной графике. Но лишь выйдя из-под клавиш и начав
самостоятельное существование, рукопись, как и полагается своенравному чаду,
перестала слушаться своего создателя и начала диктовать свои требования по
дальнейшему развитию. В результате она разрасталась, захватывала все новые и
новые темы, пока не стала такой, какой ты, читатель, ее видишь перед собой.
И ведь неймется, негодной, так и заставляет автора дополнять, исправлять, при-
думывать новые примеры...
Пришла, в конце концов, пора остановить этот бесконечный процесс и предста-
вить на суд общественности сей скромный труд, весьма далекий от совершенст-
ва. Я надеюсь, что книга будет полезна как для первоначального знакомства с
основами компьютерной геометрии и графики, так и для кропотливого изучения
ее материала студентами, преподавателями, программистами и научными ра-
ботниками — теми, для кого она создавалась.
Главным посылом, который подвигнул меня заняться сочинительством, была
неудовлетворенность уровнем и содержанием книг по компьютерной графике,
изданных как десять лет назад, так и продаваемых в настоящее время. Вся лите-
ратура по вычислительной геометрии и компьютерной графике отчетливо де-
лится на три группы:
1. Книги теоретического плана [24], посвященные глубокому анализу свойств
геометрических объектов и алгоритмов. К сожалению, материал подобных
научных трудов, при всем огромном уважении к их авторам, не усваивается
средним студентом технического вуза, и большой труд оказывается затрачен
впустую.
2. Книги, рассчитанные на неподготовленного читателя, в которых рассматрива-
ются простейшие геометрические соотношения и алгоритмы, а решение более-
менее сложных задач дается на уровне добрых пожеланий [2, 5, 23, 31,33, 34, 35].
Даже в таких основательных изданиях, как [25], и то можно встретить "советы"
такого типа: "... разрезать невыпуклое тело плоскостью, несущей выбранную
грань" (с. 204). Как это сделать не на словах, а с помощью конкретного алго-
ритма — ни слова, ни намека. Приведенная выдержка взята из предлагаемого
Д. Роджерсом алгоритма разрезания невыпуклого полиэдра, по которому не-
возможно написать программу без какого-либо домысливания.
3. Книги, посвященные описанию общеизвестных графических программ,
большую часть которых занимает обучение пользованию кнопками меню и
546
Заключение
изображение различных окон и экранных форм. Конечно, это очень интерес-
но, но хотелось бы не только видеть результат нажатия какой-нибудь кнопки,
но и знать, как он получился, т. е. по какому алгоритму рассчитан. Надеюсь,
читатель понимает, что овладение компьютерной графикой на уровне внеш-
них визуальных эффектов есть не истинное знание этой науки, а лишь навык
работы с конкретной прикладной программой. Суть происходящих в ней ин-
формационных процессов глубоко скрыта за видимой легкостью получения
результата одним щелчком мыши.
В своей книге я попытался нащупать "золотую середину" между излишней ака-
демичностью и дилетантством, сделав ее доступной и полезной широким слоям
студентов, программистов и научных работников.
В Заключении хотелось бы заострить внимание читателя на тех моментах новиз-
ны, которыми данная книга отличается от других изданий. Что касается содер-
жания книги в целом, то это иллюстрация практически всех изучаемых алгорит-
мов блок-схемами, по которым можно поводить пальцем, проследить порядок
выполнения операций в зависимости от различных условий, другими словами,
заставить работать несколько механизмов усвоения читателем материала книги.
В главе Г.
□ приведен полный систематизированный свод основных геометрических соот-
ношений между графическими элементами на плоскости и в пространстве;
□ разработано множество различных тестов, позволяющих максимально быст-
ро установить необходимые свойства графических объектов и взаимоотно-
шения между ними;
□ рассмотрен комплекс основных задач геометрической оптики и лучевых ме-
тодов построения оптических эффектов как на плоской, так и на криволиней-
ной поверхности.
В главе 2:
□ обоснован метод парных точек, позволяющий вычислять матрицы сложных
преобразований объектов и системы координат по их начальным и конечным
состояниям без разложения на элементарные преобразования;
□ в зависимости от количества известных точек в начальном и конечном по-
ложениях объекта предложено три алгоритма расчета матрицы преобразо-
вания;
□ разработаны экономичные итеративные и рекуррентные кинематические ал-
горитмы перемещения объектов с не полностью определенными элементами
движения;
□ подробно излагаются теория и методы построения параллельных и централь-
ных проекций;
□ разработаны проективные алгоритмы сложных преобразований, в том числе,
построения проекций пространственных линий на плоскость, стереографиче-
ских проекций, свойства и методы построения различных картографических
проекций, алгоритмы изображения динамичных сцен от первого лица и. на-
конец, проективные методы построения оптических эффектов на плоскости.
Заключение
547
В главе 3:
□ приведена полная схема классификации поверхностей, представляющая мето-
ды конструирования их математических моделей и реалистичного изображе-
ния на плоскости;
□ предложены алгоритмы построения разверток линейчатых поверхностей;
□ разработан экономичный рекуррентный алгоритм построения каналовых
поверхностей на основе метода парных точек;
□ рассмотрены методы построения кубических сплайновых кривых и поверхно-
стей, в том числе и в рекуррентной форме, позволяющей снизить порядок об-
ращаемых матриц до четвертого;
□ изучаются свойства, методы получения и изображения фрактальных мно-
жеств, включая фрактальные ломаные линии и полигональные сети.
В главе 4'.
□ разработаны алгоритмы выполнения логических операций со списками от-
резков;
□ разработан пакет алгоритмов отсечения различных графических элементов
на плоскости и в пространстве и на этой основе метод логического конструи-
рования трехмерных объектов;
□ предложена коллекция алгоритмов решения классических задач вычисли-
тельной геометрии, связанных с отсечением на плоскости и в пространстве,
включая отсечение полигона полуплоскостью, а полиэдра— полупростран-
ством, а также построение выпуклых оболочек и разрезание полигонов;
□ предложены оригинальные алгоритмы удаления невидимых линий и граней,
основанные на алгоритмах пакета отсечения.
С окончанием работы над книгой у меня осталось чувство ее незавершенности,
недосказанности всего, что задумывалось и просилось быть раскрытым. К мо-
менту выхода книги в свет накопилось несколько тем, которые мне хотелось бы
увидеть во втором издании, если оно когда-нибудь состоится. Вот что планиру-
ется добавить:
□ в раздел 2.1— задачу построения квадратичной поверхности, описываемой
произвольным неявным уравнением второго порядка, сводящуюся к вычис-
лению матрицы сложного аффинного преобразования канонической поверх-
ности, тип которой идентифицирован по инвариантам заданной поверхности;
□ в раздел 2.2— задачу преобразования Зс1-объектов, позволяющую свести ко-
соугольное и центральное проецирование к параллельному с помощью пред-
проективных искажений;
□ в раздел 2.2.5— задачу проецирования на криволинейные поверхности, ре-
шаемую методом преобразования системы координат, включая наложение
текстур;
□ раздел 2.3— восстановление состояния трехмерного объекта по его парал-
лельным и перспективным, включая стереографические, проекциям;
548
Заключение
□ в раздел 3.1.3 — развитие теории кусочно-определенных поверхностей;
□ в раздел 3.1.4 — развитие теории сплайновых поверхностей;
□ в раздел 3.1.5 — алгоритмы фрактального сжатия данных;
□ в разделы 4.2.7 и 4.2.8— алгоритмы решения новых задач отсечения на плос-
кости и в пространстве;
□ главу 5 "Оптические задачи визуализации", посвященную детальному изуче-
нию основных физических и психофизических понятий света, цвета и их
свойств в объеме, необходимом для обоснования цветовых систем и решения
оптических задач визуализации — построения различных моделей освещен-
ности, алгоритмов закрашивания поверхностей, расчета сложных оптических
эффектов;
□ главу 6 "Анимация", посвященную разработке алгоритмов построения дина-
мических полиморфных объектов и сцен в реальном времени;
□ другие темы и задачи, которые созреют к моменту подготовки второго изда-
ния книги.
Я не могу не поблагодарить главного редактора издательства "БХВ-Петербург"
Кондукову Екатерину Владимировну и заведующую редакцией Кузьмину Анну
Сергеевну за принятие ответственного решения об издании моей книги, за тер-
пение, благожелательность и требовательность, проявленные ими при подготов-
ке книги.
Буду рад получить от читателей критические замечания по материалу книги,
сообщения об ошибках или опечатках, любые пожелания об улучшении содер-
жания и оформления ее будущих изданий. Мой адрес e-mail: nea@mail.nnov.ru.
почтовый адрес: 603600, Нижний Новгород, ул. Минина, 24, Нижегородский
государственный технический университет, кафедра "Вычислительная техника",
Никулину Евгению Александровичу.
Всегда готов к взаимовыгодному сотрудничеству.
С уважением ко всем читателям
Евгений Никулин
Список литературы
1. Агостон Ж. Теория цвета и ее применение в искусстве и дизайне. — М.: Мир,
1982, — 184 с.
2. Амерал Л. Машинная графика на языке С. В 4-х кн. Пер. с англ. — М.: Сол
Систем, 1992.
3. БерлянтА. М. Картография: Учебник для вузов.— М.: Аспект Пресс,
2001, —336 с.
4. Борковский А. Б. Англо-русский словарь по программированию и информа-
тике (с толкованиями). — М.: Рус. яз., 1989. — 335 с.
5. Вельтмандер П. В. Машинная графика: Учеб, пособие в 3-х кн.— Новоси-
бирск: Новосибирский гос. ун-т, 1997.
6. Вернер А. В., Кантор Б. Е., Франгулов С. А. Геометрия. Ч. I. Учебное посо-
бие. — СПб.: Специальная литература, 1997. — 352 с.
7. Вернер А. В., Кантор Б. Е., Франгулов С. А. Геометрия. Ч. II. Учебное посо-
бие. — СПб.: Специальная литература, 1997. — 320 с.
8. Воеводин В. В. Линейная алгебра. — М.: Наука, 1980 — 400 с.
9. Воеводин В. В., Кузнецов Ю. А. Матрицы и вычисления. — М.: Наука,
1984. —318 с.
10. Гантмахер Ф. Р. Теория матриц. — М.: Наука, 1988. — 548 с.
И. Иванов А. П., Батраков А. С. Трехмерная компьютерная графика. — М.:
Радио и связь, 1995. — 224 с.
12. КнутД. Искусство программирования. В 3-х томах.— М.: Издательский
дом "Вильямс", 2001.
13. Корн Г., Корн Т. Справочник по математике (для научных работников и
инженеров). — М.: Наука, 1978. — 832 с.
14. Кривошеев М. И., Кустарев А. К. Цветовые измерения. — М.: Энергоатом-
издат, 1990. — 240 с.
15. КухлингХ. Справочник по физике. — М.: Мир, 1983. — 520 с.
16. Ландсберг Г. С. Оптика. — М.: Наука, 1976. — 928 с.
17. Луизов А. В. Цвет и свет. — Л.: Энергоатомиздат, 1989. — 256 с.
18. Майкл Ласло. Вычислительная геометрия и компьютерная графика на C++:
Пер. с англ. — М.: Бином, 1997. — 304 с.
19. Математика и САПР. В 2-х кн. Кн. 1. Пер. с франц. / Шенен П., Коснар М.,
Гардан И. и др. — М.: Мир, 1988. — 204 с.
550 Список литературы
20. Математика и САПР. В 2-х кн. Кн. 2. Пер. с франц. / Жермен-Лакур П.,
Жорж П. Л., Пистр Ф., Безье П. — М.: Мир, 1989. — 264 с.
21. Пайтген Х.-О., Рихтер П. X. Красота фракталов. Образы комплексных ди-
намических систем. — М.: Мир, 1993. — 176 с.
22. Плис А. И., Сливина Н. A. MathCAD 2000. Математический практикум для
экономистов и инженеров: Учеб, пособие.— М.: Финансы и статистика,
2000. — 656 с.
23. Порев В. Н. Компьютерная графика. — СПб.: БХВ-Петербург, 2002. — 432 с.
24. Препарата Ф., Шеймос М. Вычислительная геометрия: Введение. — М.:
Мир, 1989. —478 с.
25. Роджерс Д. Алгоритмические основы машинной графики. — М.: Мир,
1989, —512 с.
26. Роджерс Д., Адамс Дж. Математические основы машинной графики. — М.:
Мир, 2001. — 604 с.
27. Уилкинсон Дж. X. Алгебраическая проблема собственных значений. — М.:
Наука, 1970. — 564 с.
28. Физические величины: Справочник//Составители: А. П. Бабичев, Н. А. Бабуш-
кина, А. М. Братковский и др. / Под ред. И. С. Григорьева, Е. 3. Мейли-
хова. — М.: Энергоатомиздат, 1991. — 1232 с.
29. ФоксА., Пратт М. Вычислительная геометрия. Применение в проектирова-
нии и на производстве. — М.: Мир, 1982. — 304 с.
30. Фостер Дж. Обработка списков: Пер. с англ. — М.: Мир, 1974. — 71с.
31. ХирнД., Бейкер М. Микрокомпьютерная графика.— М.: Мир, 1987.—
352 с.
32. Хорн Р., Джонсон Ч. Матричный анализ. — М.: Мир, 1989.—655 с.
33. Шикин Е. В., Боресков А. В. Компьютерная графика. Динамика, реалисти-
ческие изображения. — М.: ДИАЛОГ-МИФИ, 1995. — 288 с.
34. Шикин Е. В., Боресков А. В. Компьютерная графика. Полигональные моде-
ли. — М.: ДИАЛОГ-МИФИ, 2000. — 464 с.
35. Эйнджел Й. Практическое введение в машинную графику.— М.: Радио и
связь, 1984. — 136 с.
36. Эйнджел Э. Интерактивная компьютерная графика. Вводный курс на базе
OpenGL, 2-е изд. — М.: Издательский дом "Вильямс", 2001. — 592 с.
Е. А. Никулин
. КОМПЬЮТЕРНАЯ ГЕОМЕТРИЯ
И АЛГОРИТМЫ
МАШИННОЙ ГРАФИКИ
Рассматриваются геометрические и алгоритмические основы
компьютерной графики, математические модели объектов на
плоскости и в пространстве, законы геометрической оптики и
алгоритмы построения оптических эффектов, методы геометри-
ческих преобразований, анализ и синтез моделей, алгоритмы
отсечения и удаления на плоскости и в пространстве. Пособие
предназначено для студентов вузов и специалистов, интересу-
ющихся компьютерной графикой и занимающихся разработкой
графических программ.
Графические элементы на плоскости и в пространстве
Лучевые и проективные методы построения оптических эс
Методы построения и изображения поверхностей
Логическое конструирование трехмерных объектов
Комплекс алгоритмов отсечения и удаления на плоскости
и в пространстве
ИНТЕРНЕТ-МАГАЗИН
www-romputerppo^_
БХВ-Петербург
198005, Са»т-П(Г“рбург,
Измайговскач пр.. 29
E-rpait: FiaiKSbhv.ru
Interact www.bhv.ru
тал (812) 251-42-44
ISBN 5-94157-264-6