Теория железобетона с трещинами - Карпенко Н.И.

Автор: Карпенко Н.И.

Теги: железобетонные конструкции

Год: 1976

Похожие

Общие модели механики железобетона

Железобетонные конструкции. Том I. Сопротивление железобетона

Железобетонные конструкции. Часть 1. Сопротивление железобетона

Железобетонные конструкции. Том II. Строительная механика железобетона

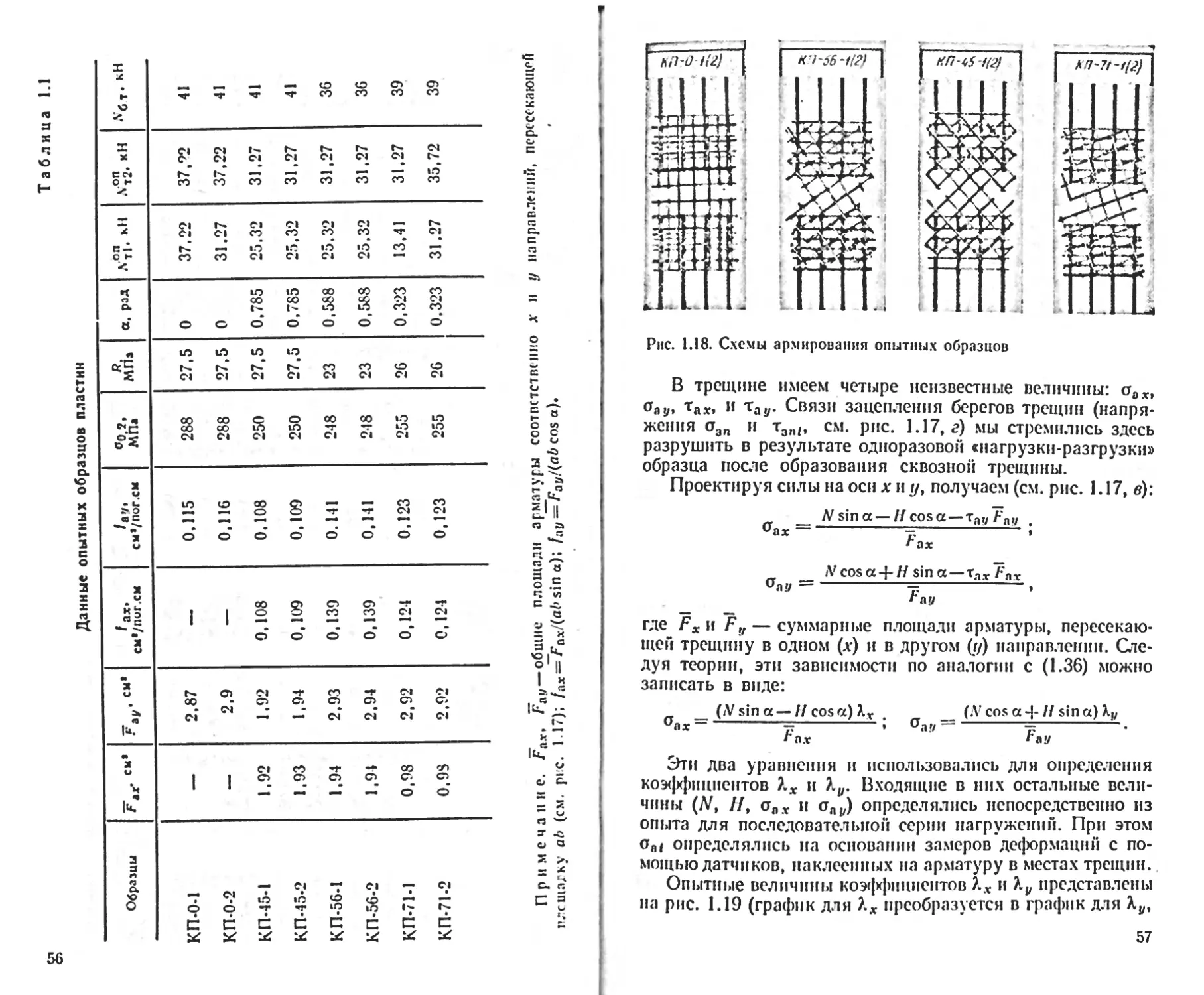
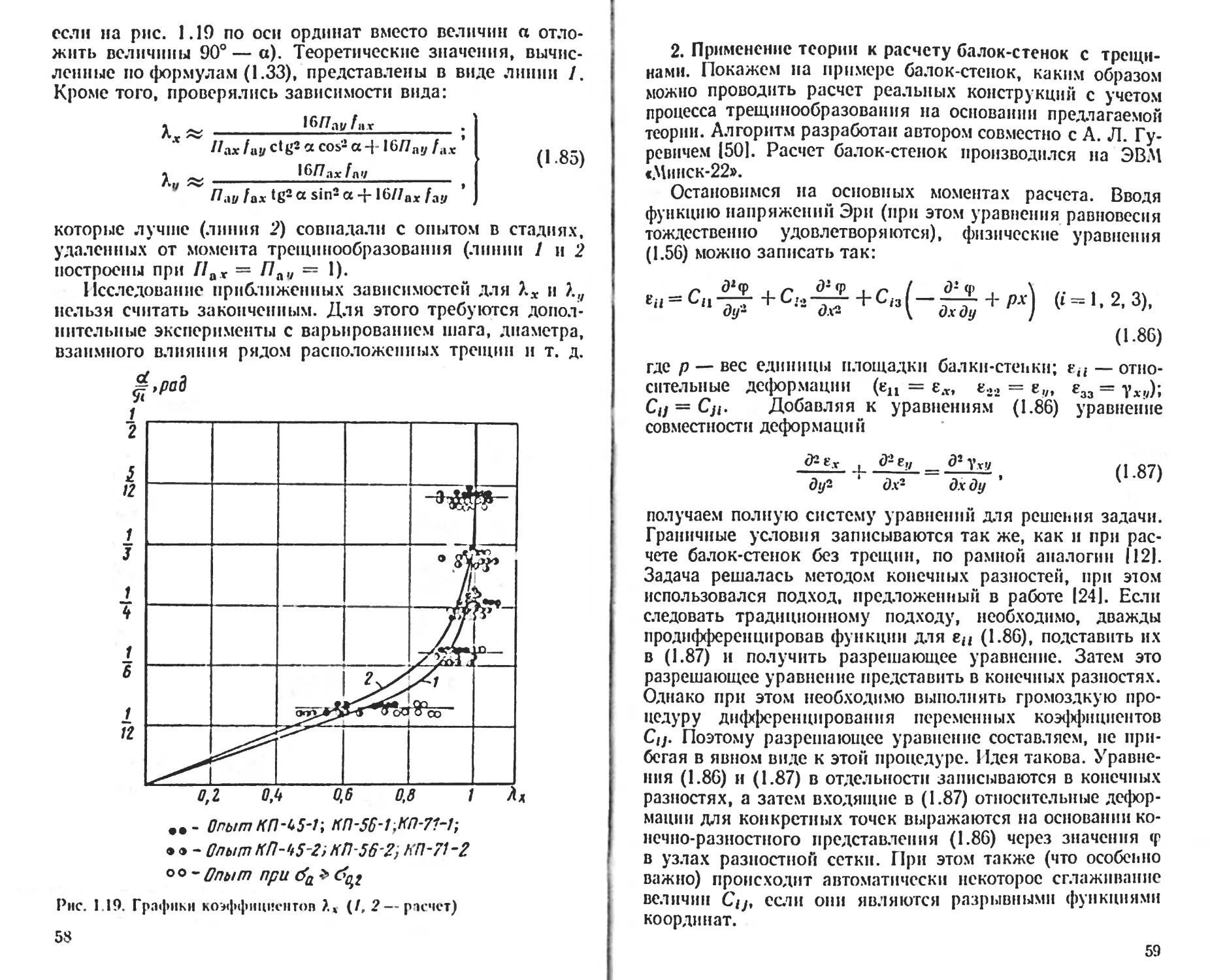
Текст

И. И. К а р п е н к о,
д-р техн, наук
ТЕОРИЯ
ДЕФОРМИРОВАНИЯ
ЖЕЛЕЗОБЕТОНА
С ТРЕЩИНАМИ
л
МОСКВА
СТРОП ИЗДДТ
1976
УДК «24.012.45.044
Печатается по решению секции литературы по
строительной физике и конструкциям редакционного
совета Строй издата.
Карпенко Н. И. Теория деформирования железо-
бетона с трещинами. М.» Стройиздат, 1976.
Изложена теория деформирования железобе-
тона с трещинами при сложном напряженном состоя-
нии применительно к расчету плосконапряженных
пластин типа балок-стенок, плит, элементов обо-
лочек (в условиях моментного напряженного состоя-
ния) и стержней (в условиях кручения и изгиба с кру-
чением). Рассмотрен расчет конструкций на трещнно-
стойкость, жесткость (с учетом различных схем тре-
щин) и прочность (с описанием критериев, характе-
ризующих разрушение). Приведены эксперименталь-
ные исследования и даны примеры расчета.
Книга предназначена для научных и инженерно-
технических работников научно-исследовательских и
проектных организаций.
Табл. 2, ил. 67, список лит.: 98 назв.
30205 — 230
О47(О1)-7ь ~ 10576
ф Стройиздат, 1976.
ПРЕДИСЛОВИЕ
Железобетон — основной конструкционный материал
в строительстве наших дней — отличается рядом особен-
ностей, которые необходимо учитывать для надежного про-
ектирования разнообразных конструкций и сооружений,
возводимых из этого материала. Одна из таких особенно-
стей — работа конструкций при наличии трещин в бетоне,
которая либо отвечает их состоянию в условиях нормаль-
ной эксплуатации, либо требует исследования при рассмот-
рении возможных неблагоприятных воздействий.
Хотя наличие трещин так или иначе учитывалось из-
давна в теории железобетона ври расчетах прочности, се-
годня надо с достаточным приближением оценить и влия-
ние трещин на деформации конструкций и ширину раскры-
тия этих трещин для обеспечения сохранности арматуры.
Эти задачи до сих пор удовлетворительно решены только
для стержневых элементов, подвергающихся действию из-
гиба и осевых сил. Для плит, стенок, оболочек, а также
для балок при воздействии крутящих моментов и попереч-
ных сил задача не имела достаточно общего решения, не-
смотря на- некоторые имеющиеся предложения частного
характера.
Предлагаемая работа Н. И. Карпенко в основном за-
полняет этот пробел, открывая возможность проследить
работу конструкций от упругой стадии вплоть до ста-
дии, близкой к исчерпанию их несущей способности. Она
позволяет перекинуть мост и к предельному состоянию
по прочности, если оно может быть оценено методом пре-
дельного равновесия.
В книге не исчерпываются все вопросы, относящиеся
к рассматриваемой проблеме. В частности, в ней не осве-
щается- влияние ползучести бетона, изучаются не обо-
лочки в целом, а их элементы. Опа, однако, представ-
ляет собой крупный вклад в теорию железобетона, имею-
щий большое и непосредственное практическое значение.
Можно быть уверенным, что публикация книги
Н. И. Карпенко не только поможет практическому ис-
пользованию предложенной нм теории, но побудит также
других исследователей к разработке не исчерпанных в
ней вопросов.
Д-р техн, паук, проф. А. А. Гвоздев
3
ВВЕДЕНИЕ
Большинство железобетонных конструкций работает
с трещинами, которые зачастую качественно изменяют ха-
рактер их напряженно-деформированного состояния. Тео-
рия расчета стержневых элементов с учетом трещин была
предложена В. II. Мурашовым и значительно развита
А. А. Гвоздевым, С. А. Дмитриевым, Я. М. Немировским
и др. Роль этой теории в развитии отечественной науки
о железобетоне велика. Однако такие конструкции, как
балки-стенки, плиты перекрытий, оболочки, стержни,
испытывающие кручение в сочетании с изгибом, и элемен-
ты конструкций, работающие в условиях сложного напря-
женного состояния, не могут быть рассчитаны по указан-
ной теории. Впервые это было показано на примере опер-
тых по контуру плит еще в ранних исследованиях
А. А. Гвоздева. С. М. Крылова и А. Н. Королева, которые,
собственно, и послужили толчком к поискам более общих по-
строений в этой области. Однако многие из перечисленных
выше конструкций до сих пор рассчитываются методами
теории упругости без учета особенностей железобетона,
хотя в настоящее время созданы достаточные предпосылки
для перехода на новые методы их расчета, учитывающие
как трещины, так и другие виды неупругих деформаций
железобетона. В данной книге в систематизированном ви-
де изложены результаты исследований автора по разра-
ботке теории деформирования железобетона с трещинами
при сложном напряженном состоянии и построению мето-
дов расчета указанных конструкций.
В первой главе рассматриваются основы теории дефор-
мирования железобетона с трещинами при плоском напря-
женном состоянии, включающей расчет конструкции на
трещиностойкость (образование трещин и их раскрытие),
жесткость (расчет деформаций с учетом трещин) и проч-
ность (расчет до разрушения отдельных элементов конст-
рукции с указанием критериев, характеризующих разру-
шение). Приводятся методики экспериментальных исследо-
4
ваннн, и на примере расчета балок-стенок указываются
способы, применения теории к расчетам плоских конст-
рукций с учетом трсщпнообразования.
Вторая глава посвящена теории деформаций пластин
и элементов оболочек с учетом совместного действия
изгибающих и крутящих моментов и нормальных и каса-
тельных сил. Вследствие действия моментов картина воз-
никающих здесь трещин значительно усложняется, поэто-
му все указанные в первой главе виды расчетов конкрети-
зируются применительно к этой более сложной картине.
Представлены экспериментальные исследования, и на при-
мере изгибаемых в двух направлениях плит приведены
практические способы применения теории к расчету кон-
струкций с трещинами, работающих в условиях момент-
ного напряженного состояния.
В третьей главе дано приложение теории к решению
задач но расчету деформаций при кручении и изгибе с
кручением железобетонных стержней после появления в
них трещин.
Необходимо отметить, что ряд важных вопросов, отно-
сящихся к рассматриваемой проблеме, предстоит решить
в дальнейшем. К ним относятся вопросы учета ползуче-
сти бетона, остаточных деформаций при повторных
нагружениях, особенностей поведения конструкций при
динамических воздействиях и др. Еще многое предстоит
сделать по применению теории к практическим расче-
там (включая разработку способов интегрирования систем
нелинейных дифференциальных уравнений) и оптималь-
ному проектированию различных конструкций. Тем не
менее представленные исследования уже доведены до оп-
ределенного логического завершения, и их внедрение
в практику проектирования железобетонных конструкций
позволит с большей точностью подойти к их расчету и
конструированию.
Автор выражает благодарность д-ру техн, наук, проф.
А. А. Гвоздеву и д-ру техн, наук, проф. С. М. Крылову
за ценные советы при проведении исследований.
ГЛАВА I
ТЕОРИЯ ДЕФОРМИРОВАНИЯ ЖЕЛЕЗОБЕТОНА
С ТРЕЩИНАМИ ПРИ ПЛОСКОМ
НАПРЯЖЕННОМ СОСТОЯНИИ
Теория предназначена для расчета плоских железобе-
тонных конструкций, работающих в своей плоскости, после
появления в них трещин. К таким конструкциям могут
быть отнесены балки-стенки, перемычки, стеновые панели
и другие пластины, которые до появления в них трещин
могут рассчитываться на основании уравнений плоской
задачи теории упругости. Чтобы сохранить преемствен-
ность, напряженное состояние железобетона в таких конст-
рукциях и после трещинообразования будем называть ус-
ловно плоским, хотя здесь и возникают новые особенности.
Теория, изложенная в данной главе, построена на основа-
нии обобщения последних исследований автора 135, 44),
выполненных в развитие более ранних его исследований
1191 (соавтор А. А. Гвоздев) (30, 31).
§ 1. Характерный элемент
и компоненты его напряженного состояния.
Схемы непересекающихся и пересекающихся трещин
1. К постановке исследований. Разработка теории де-
формирования железобетонных элементов с трещинами при
плоском напряженном состоянии включает решение следу-
ющих задач: вывод физических уравнений, связывающих
деформации с усилиями, вывод зависимостей для определе-
ния напряжении в арматуре и бетоне, ширины раскрытия
трещин и других, характеризующих поведение конструк-
ций с трещинами в малой пластине у точки Л1 (рис. 1.1, о),
а затем применение указанных зависимостей для расчета
напряженно-деформированного состоянии конструкции
6
в целом. Физические зависимости устанавливаются на ос-
новании теоретического анализа и моделирования харак-
тера деформирования с трещинами указанных малых в пла-
не пластинок (характерных элементов типа АОВС на
рис. 1.1, б), мысленно выделяемых из конструкций, рабо-
тающих в условиях плоского напряженного состояния.
Ввиду того, что длины граней пластинок предполагаются
хотя и малыми, но конечными, усилия вдоль них могут
несколько изменяться. При выводе физических зависи-
мостей этим в основном пренебрегаем.
Рис. 1.1. Характерная пластина и компоненты сс напряженного со-
стояния
7
Роль характерных элементов подобна в какой-то сте-
пени роли призм, использующихся для определен ня
свойств бетонов. Однако в данном случае используется
не экспериментальный, а теоретический путь исследова-
ния свойств материала с определением на основании
экспериментов лишь некоторых параметров теории.
С усложнением напряженных состояний характерные
элементы и их напряженные состояния будут также услож-
няться (главы 2 и 3). Использование характерных элемен-
тов дает возможность проводить анализ в общем виде (для
комплекса конструкций), нс привязываясь к конкретному
объекту.
Смоделировав свойства элементов с трещинами в малом,
переходим к расчету реальных конструкций (к решениям
в большом).
2. Обобщенное плоское напряженное состояние эле-
мента без трещин. Касательные и нормальные напряжения,
действующие по граням характерной пластинки (см.
рис. 1.1, б), будем приводить к касательным (AZXI/, Afwv) и
нормальным (А’х, Л'\) погонным силам, приложенным на
уровне ее серединной поверхности. В общем виде для же-
лезобетона усилия Л'х. А',р Л’х,, — составные величины
(см. §3гл. 1), однако при рассмотрении работы элементов
до появления трещин влиянием армирования во многих
случаях можно пренебречь (вопросы учета армирования
указаны в работах 123, 37)1, рассматривая конструкции
как чисто бетонные. При этом
^Х A If N хц & ух 0*0
где ах. тту— соответственно нормальные и касатель-
ные напряжения в бетоне.
В элементах реальной толщины может возникать не-
который эффект объемного напряженного состояния и,
вследствие этого, напряжения могут несколько изменять-
ся по толщине (пунктирная линия / на рис. 1.1, «). В же-
лезобетоне этот э<|х}х?кт может усиливаться из-за наличия
арматуры. Однако этим пренебрегаем, принимая средние
напряжения в бетоне по толщине элемента. Такое плоское
напряженное состояние, как известно, называется обобщен-
ным. Напряжения и усилия растяжения здесь и далее при-
няты за положительные. Эти же усилия нанесены на схе-
мах. Сжимающие напряжения необходимо вводить во все
формулы со знаком минус. Для рассматриваемых плоских
элементов соблюдается закон парности касательных сил
8
(Л'Х!/ = Л'9Х). Обозначим через Л',,, Nt, Nllt и Nln погонные
усилия на наклонных площадках пластины (см. рис. 1,1, б).
Выделяя из пласт пики треугольные элементы (рис. 1.1, д, е)
и проектируя приложенные к их граням усилия на оси
х и у, получаем:
Nx — Az„ sin2 а -1- Nt cos2 а—(Nnl 4- Af/n) sin a cos a;
/V,; — Az„ cos2 a + A\ sin2 a 4 (.V,d 4- Л^„) sin a cos a;
NxU — (A'n — Azr) s*n a cos a + A,K sin2 a—A\„ cos2 a;
N,JX = (.V„—Nt) sin a cos a— Nnt cos2 a 4- Ntn sin2 a.
При NXIJ = N,IX (A'nl = Ntn) последние два уравнения
становятся одинаковыми. Заменяя в (1.2) индексы «х» и «у»
соответственно на «и» и «/» (и наоборот), а также угол а на
— а получаем уже значения Л',,, Nt, Nnt в функции от Nx,
Л\„ Nxy. Приравнивая при этом производные dNn!da и
dNt/da нулю, получаем следующие уравнения для опре-
деления главных направлений, по которым Nn и Л\ до-
стигают экстремальных значений (эти главные усилия ни-
же обозначаются как AfMartC и AfMm„ а углы их наклона a
как ar):
tg2a = lg2ar = (Л\„ + Л^/^-Л',). (1.3)
Направления эти взаимноортогональны и для них каса-
тельные силы Nnl + A'm = 0 или (при Nnl = Nln) Nnt =
= Ntn = 0. Формулу (1.3) можно записать (при Nxy =
= NIIX) и по-иному:
etga = ctg«r=(AzMai:c—Nx)/Nyxium tg«r = (AzMfll.c—Ny)/Nxv.
(1-4)
Эти выражения легко получить па основании рис. 1.1, г,
проектируя силы на осн х и у. Главные силы или напряже-
ния (Л\,а,.с = оМ!11!сЛ, = ом„„й) определяются в функ-
ции от сил Nx, Ny, NXy но известным формулам из сопро-
тивления материалов.
Величины Nx, Nv, Nvx, NXI, образуют тензор второго
ранга. В данном случае, ввиду того что Nyx = NX!„ тензор
будет симметричным. Как известно, тензорами называют
объекты, нс зависящие от преобразования координат (ин-
вариантные объекты). Тензоры могут быть различного ран-
га (первого и выше, вектор есть тензор первого ранга).
Составляющие тензора называются компонентами (тензоры
конкретизируются через компоненты). Векторы имеют
9
одну компоненту, тензоры второго ранга четыре
компоненты, которые записываются в виде Ntj9 где i, /
индексы (индексами могут быть различные буквы, например
сг>и«//», рангтензора равен количеству индексов его компо-
нент). Ниже мы используем иетензорные обозначения, заме-
няя двойные индексы типа хх на х, у/у/ на // (например, вмес-
то Nxx записываем Л\). При преобразовании координат
компоненты тензора изменяются. Однако, что удобно, эти
изменения происходят по общим для каждого ранга зако-
нам и таким, что в целом сам объект, который компоненты
характеризуют, остается неизменным (например, напряжен-
ное состояние пластинки не изменится от того, что его за-
ладим компонентами Nnt Nnt или Л\, Л\;, Nxy). Мы
неоднократно будем иметь дело с объектами второго ранга,
например относительными деформациями, моментами,
погонными площадями арматуры. Все они будут преобра-
зовываться при повороте осей координат согласно урав-
нениям (1.2), и для них будут также справедливы зави-
симости (1.3) и (1.4).
3. Схемы трещин н условия их образования. Изучают*
ся сквозные трещины, которые образуются при двух
видах напряженных состояний: «растяжение-растяжение»
(оба главных напряжения являются растягивающими)
и «растяжение-сжатие» (<тмпкс > 0, оМ111, < 0). В первом
случае возможно образование двух схем трещин: непере-
секающихся (рис. 1.2, а) и пересекающихся (рис. 1.2, б).
Во втором случае образуются только непересекающиеся
Рис. !.2. Схемы трещин
/ — иепсресскающихся; б — пересекающихся
10
трещины. Пересекающиеся трещины встречаются редко.
Будем полагать, что трещины образуются по главным
площадкам, когда главные усилия превысят некоторую
предельную величину Л;б.т» названную усилием трещи-
нообразования 137]. При этом, если
^макс ^б.т » Мри б.т»
образуются непересекающиеся трещины. Если
^макс ^б.т И Л м ин > Кб.т.
(1.6)
образуются пересекающиеся трещины.
Угол наклона трещин а к осн х можно определить из
уравнения (1.3) или (1.4) по усилиям в момент трещнно-
образования.
Необходимо отметить, что важен лишь сам факт существо-
вания двух схем трещин—пересекающихся и непересекаю-
щихся, а условия их образования могут быть приняты лю-
быми, однако представленные условия лучше всего со-
гласуются с экспериментами. Полагаем также, что в
процессе деформирования главная площадка может откло-
няться от площадки трещины (т. е. от своего положения
в момент трещинообразования). Вопрос о возможных из-
менениях ориентации трещин рассматривается в § 7.
Известно, что линия трещины представляет собой неко-
торую зигзагообразную кривую, а не является прямой
даже на небольшой длине. Угол а, вводимый в расчет, —
это усредненный угол наклона трещин в пределах харак-
терного элемента (так называемый угол спрямленной в ма-
лом трещины, показанной пунктирной линией ав на
рис. 1.2, а)
Положительные значения углов наклона трещин а от-
считываем от оси х против часовой стрелки, а отрицатель-
ные— наоборот (см. рис. 1.2, а), обычно ограничивая их
значения интервалами 0 ...90° и 0...—90°.
Усилие образования трещин равно:
/Vf, т —- A’p/?p/i,
(1-7)
гдсА'р — коэффициент, учитывающий влияние оМ|||| на
уменьшение /?,, — прочности бетона при одно-
осном растяжении (сокращенно коэ<|х|)ициент вли-
яния плоского напряженного состояния).
В некоторых случаях 1501 учитывалось допол-
нительно влияние усадки на Rp путем умножения правой
II
части зависимости (1.7) на коэффициент *у (согласно
СНиП П-В. 1-62*, А’„= 1-0.8).
Для определения коэффициента А’р данные
советских и зарубежных исследователей 16, -31 по изуче-
нию прочности бетонов при плоских напряженных состо-
яниях, полагая, что при <тмакс > 0 условия разрушения
бетонов могут характеризовать образование трещин в же-
лезобетоне. Попытки учета этого явления при расчете тре-
щиностойкостн даны в 17, 28, 37 и др. ]. Обобщая данные
этих исследовании, принимаем:
А’р=1
’(I — 2с)
I—2стр
/Ир-|^мин1Ж1р). (18)
где /?||Р — призменная прочность бетона1; с — коэффици-
ент, зависящий от марки бетона (для марок бетона 600 и
выше с = —0,3, для марки 500 с = —0,25; для марки 400
с == —0.05, для марки 300 с = 0,15; для марки 200 и ниже
с = 0,35), влияние марки бетона учитывается на основа-
нии работы (281.
При напряженных состояниях «растяжение-растяже-
ние» можно принимать kv 1 или для унификации, на-
пример расчетов на ЭВМ, определять также по формуле
1.8).
§ 2. Общая характеристика деформирования элементов
с трещинами и начальные зависимости
Остановимся в основном на наиболее часто встречаю-
щейся схеме непересекающихся трещин, а на некоторые
принципиальные отличия, возникающие при пересекаю-
щихся трещинах, укажем по ходу этого изложения.
1. Сцепление арматуры с полосами бетона. С образо-
ванием непересекающихся трещин бетон разделяется по
одному из направлений трещинами на отдельные блоки
(полосы бетона между трещинами), пронизанные арматур-
ными стержнями. Арматурные стержни после трещинооб-
разования не терпят разрыва и таким образом соединяют
отдельные полосы бетона в единой системе. Совместное де-
формирование такой системы обеспечивается за счет сцеп-
1 В расчетах трещи постой костя и жесткости элементен при-
нимаются нормативные значения /?пр и /?р (или /?||р1| и /?Р11),
а в расчетах прочности — расчетные величины.
12
Рис. 1.3. К анализу сцепления арматурных стержней с полосами
бетона между трещинами (/т—расстояние между трещинами)
/ — арматурный стержень: 2 — полоса бетона; Л. 4 — рядом расположенные
трещины; 5 — биссектриса угла между трещинами: ат — ширина раскрытия
трещины; ТпН — контактные касательные напряжения; ш — взаимные смеще-
ния арматуры и бетона у контакта (ugi — величина смещения арматуры отно-
э
снтслыю берега трещины); са/ —нормальные (осевые) напряжения армату-
с
ры (0*4 — максимальные напряжения арматуры в трещинах; <Ja<* — средние
напряжения арматуры на участках между трещинами)
лени я (связи по контакту) арматуры с бетоном между тре-
щинами (рис. 1.3). В качестве примера рассмотрим схему
сцепления одного из арматурных стержней, расположен-
ных вдоль некоторого произвольного направления i. Здесь
и далее индекс i обозначает, что рассматриваемые явления
относятся к стержням любых направлений (i = .г, //, ...).
Касательные напряжения тсц1 приводят к изменению
нормальных (осевых) напряжений арматуры элемента
13
на участках между трещинами (рис. 1.3, б). За счет сил
сцепления происходит постепенная передача усилии с ар-
матуры на бетон и вовлечение полос бетона в работу кон-
струкции.
В модели фигурируют два вида напряжении в арма-
туре — в трещине (о8<) и средние на участках между
трещинами (о8ь см. рис. 1.3, б). Как известно [69, 70J,
в теории балок с трещинами связь между этими величина-
ми осуществляется с помощью коэффициента фа В. И. Му-
рашова (о' = фа<т8). В нашем случае
<& = <г<нФаь (1-9)
т. е. каждое направление стержней вводится со своим па-
раметром усреднения фа<. Средние относительные дефор-
мации арматуры
где Еа — модуль упругости арматуры; £а< — средние
модули деформации арматуры.
Формула (1.10) требует уточнения для упругопластн-
ческой стадии деформирования арматуры. В железобетон-
ных элементах с трещинами пластические деформации
арматуры на участках между трещинами распределяются
неравномерно — в трещине они достигают максимума,
а с удалением от трещины затухают или вообще равняются
нулю (арматура продолжает деформироваться в упру-
гой стадии). В связи с этим простая замена модуля упруго-
стн арматуры Еа на секущий модуль деформации Еа (обыч-
но [67J записывают Enl — Eai vn/, где va< — коэффициент, оце-
нивающий пластические деформации арматуры) в формуле
(1.10) приводит к завышению расчетных деформаций над
опытными. Для определения средних деформаций арматуры
в этой стадии можно использовать предложение Н. М. Му-
лине и Ю. П. Гущи, разработанное применительно к расче-
там балочных элементов [671. Саеду я этим исследованиям,
eai можно определять и для этой стадии по формуле (1.10),
где под E'ti понимаем величину
= ^а/(Фа1 ^а/)> (1-11)
где Па1 = ( I 4-----------
\ Vai Фа/ фа/ /
Здесь i|'i« — коэффициент оценки средних пластических
деформаций арматуры на участках между трещинами
(он определяется согласно работе I67J); Па1 — обобщенный
коэффициент влияния пластических деформаций в арматуре
на ее средние деформации еа/. В упругой стадии деформиро-
вания арматуры Пя1 = 1, так как voj = 1.
Важной особенностью связей бетона и арматуры у кон-
такта является то, что при этом происходят взаимные
смещения gt одного материала относительно другого и на-
рушается условие совместности относительных деформа-
ций арматуры и бетона. Это приводит к тому, что арматура
может получать большие удлинения, чем удлинения бето-
на, в результате чего и раскрываются трещины. Пример-
ная эпюра смещений на участках между трещинами пред-
ставлена на рис. 1.3,6. Она носит кососимметричный ха-
рактер. Максимальных значений, равных ugl, смещения
gi достигают в трещине. По мере удаления от трещины
к середине полосы бетона они затухают до нуля. Точки
Ot нулевых смещений (при некоторой идеализации) можно
принять расположенными посередине полосы бетона (на
линии ед, рис. 1.3, о). В этих точках перемещения арматуры
будут равны перемещениям бетона. Линии типа ед названы
линиями совместных перемещений арматуры и бетона. Ко-
сосимметричный характер эпюр gt и наличие таких ли-
ний позволяют принимать в модели перемещения стержней
вдоль трещин в среднем равными перемещениям точек полос
бетона у контакта в этом же направлении. Кроме того, если
некоторые арматурные стержни расположены в полосах
бетона и направлены вдоль трещин (вдоль ед), то лишь
для них можно считать приемлемым условие совместности
осевых относительных деформаций арматуры и бетона.
Величину ugl можно определить в функции от сред-
них деформаций арматуры еа| и бетона еб{ на участках
между трещинами:
“gi = (eal —ec,)/i = (eal —e6l) 0,5ZT/sin(a + 00, (1.12)
где длина отрезка стержня Ц определяется согласно
рис. 1.3, в (Ц ^0,0,').
У границы конструкции, а также у единичной трещи-
ны (последний вопрос рассмотрен ниже при определении
/т в § 4) будут однозначные эпюры сцепления. Необходимо
еще отметить, что в чистоте взаимные смещения gt возмож-
ны лишь при арматуре весьма гладкого профиля.
15
При других профилях в величину добычно 1791 вклю-
чают собственные смещения арматуры относительно бето-
на н часть особо повышенных перемещений слоя бетона
у контакта с арматурой по сравнению с перемещениями
бетона, окружающими этот слой. Эти повышенные пере-
мощения связаны с раздроблением контакта вокруг стерж*
ня некоторой сетью мелких трещин 149] и с другими явле-
ниями (72, 791. Однако изучение самой природы сцепления
арматуры с бетоном выходит за рамки данной работы. Здесь
и ниже мы пренебрегаем в пределах малых элементов вза-
имными углами наклона рядом расположенных трещин,
изображая их параллельными (считаем, что изменение
углов достаточно учитывать лишь при переходе от одного
элемента к другому). Однако этой предпосылки можно и не
вводить. При учете взаимного наклона соседних трещин
изменится в основном лишь способ определения расстоя-
ния между трещинами /т (его следует определять согласно
рис. 1.3, г в виде суммы длин отрезков О{ b и Ot а или при-
нимать /т = 2(0/ Ь) — 2(01 а), а основные формулы остают-
ся практически без изменения.
2. Тангенциальные перемещения стержней в бетоне и
связанные с ними явления (учет нагельного эффекта). Кро-
ме осевых gt арматурные стержни в бетоне испытывают
тангенциальные (направленные нормально к оси t) пере-
мещения (на рис. 1.3 они не показаны). Тангенциальные
перемещения (смещения) точки О/ стержня относительно
берега трещины обозначены в виде vgl. Таким образом,
в общем виде смещения арматуры в трещине характеризу-
ются двумя величинами: ugi и vgt (рис. 1.4, а) Если с ве-
личинами ugl связаны нормальные aal напряжения арма-
туры в трещинах, то с величинами vgl — касательные та/
напряжения (рис. 1.4, б). Связи между vgl и та/ можно
установить теоретически, как для некоторых микробалок,
заделанных в бетонное основание, или на основании экс-
периментов записать в виде
i Qi — Kxi Та/
| sin (а 4-р<) |
sin (« + Р»)
(113)
где Ku(Kxi = Ku'Fnl)—функции податливости стерж-
неи сдвигу (Fa/ — площадь стержня). Функции | sin (а+
+ P/)|/sin (а-г р/) искусственно введены в (1.13), чтобы
согласовать принимаемые ниже правила знаков для та/
Рис. 1.4. К анализу танген-
циальных перемещений ар-
матуры в бетоне и связан-
ных с ними явлений
/ — реальные: 2 — абсолютно
гибкие и 3 — абсолютно жесткие
на изгиб арматурные стержни
и Vgi (касательные напряжения, вращающие элемент па
рис. 1.4, а по часовой стрелке вокруг точки б( независимо от
знаков а, приняты за положительные).
Для упрощения некоторых промежуточных выкладок
зависимости (1.13) будем использовать в виде:
. б,5/т тп/
х> sin (а 4- Р/) Ей ’
(1.13а)
гп„ „ _ | sin(a4-p,)| Ей
где tlxi —----——---------1\хь
U । Di «р
выражая податливость сгержней перемещениям vgi через
податливость смещениям ugl при рг>1 = 0 и коэффициенты «т/.
Указанные явления в свою очередь зависят от раскрытия ат
трещины и взаимного сдвига А ее берегов.
Поясним физическую сущность новых явлений на при-
мере рис. 1.4, в. Проследим, как перемещается в полосе бето-
на между двумя трещинами абсолютно гибкий (пунктир-
ная линия 2) и абсолютно жесткий на изгиб стержень
(сплошная линия 3) при раскрытии трещин. Абсолютно
17
ибкий стержень у берегов трещины испытывает загиб
к берегу трещины (располагается вдоль главной линии
ракрытия трещины СС|), а в толщине бетона его перемещения
совпадают с перемещениями бетона у контакта. Абсолютно
жесткий стержень испытывает (кроме осевых) вынужден-
ные тангенциальные (направленные нормально к i) пере-
мещения в полосах бетона (на рис. 1.4, в— область этих
перемещений заштрихована). Тангенциальные перемещения
приведут к возникновению напряжений смятия бетона асМ/
под арматурой. В результате отпора бетонного основания
в стержне возникают изгибающие моменты и поперечные
силы. Причем в точках изменения кривизны стержня О/ и
Of, лежащих на осях трещин, изгибающие моменты равны
нулю (некоторые моменты возникают лишь вследствие
взаимного перекоса берегов трещины, но ими пренебрега-
ем), а поперечные силы достигают максимума. Эти попереч-
ные силы мы и учитываем, вводя в расчет средние (по тол-
щине стержня) касательные напряжения в арматуре
в трещинах та1 (та| = Qi/Fai)» где (?/ — поперечная сила
в точке Of; Га/ — площадь стержня. Реальная арматура 1
(см. рис. 1.4, а), обладая конечной жесткостью на изгиб,
занимает промежуточное положение между стержнями 2 и
3- Однако и ее осевая линия проходит через точки О/,О/ и
Of, и все указанные явления для жесткого стержня 3 со-
храняют силу.
3. Условия совместности перемещений стержней в
трещине. Перемещения ugl и vgl стержней различных
направлений, пересекающих трещину на некотором малом
отрезке, не могут быть произвольными, а будут связаны
друг с ^другом и с величинами ат и Д; это показано на
рис. 1.5, а9б9 из которого следует, что главные векторы
перемещений стержней разных направлений будут равны
вектору и (модуль этого вектора и = сб\ рис. 1.5, а). Не-
трудно видеть, что ugi и vgl или 0,5 аг и 0,5 Д—это состав-
ляющие главного вектора по некоторым ортогональным
направлениям (ниже мы оперируем лишь с модулями век-
торов, а их положительные направления показываем на
схемах) и таким образом они взаимно связаны между собой.
Например, проектируя 0,5 Д и 0,5 ат на направление i и на
нормаль к i (рис. 1.5, в), получим соответственно ugi и vgc.
^/ = 0,5aTsin(a + p/)^0,5Acos(a-|-p/);
vgl = 0,5ят cos (а + ₽,) + 0,5Д sin (а + р,). ' '
18
Рис. 1.5. Связь перемещений стержней в трещине и с рас-
крытием ат и сдвигом берегов трещин А
/ — положения стержня после раскрытия трещин; 2 — начальное положение
стержня в бетоне
Условия (1.14) можно записывать по-разному. Для
дальнейших исследований удобно выразить все перемеще-
ния через две величины: иех и ивч — осевые смещения
стержней, расположенных вдоль осей х и у. Проектируя
ийХ и ивУ на направления, представленные на рис. 1.5, в,
ПОЛУЧЯРМ /ппн п -t- Л •• ~ ' cuv>\.
11 gi = ugx cos Р, 4- ugV sin pz; vgt = ugu cos pz —
ugx s*n Pz, ugx = vgy‘, ug,j = vgx,
0,54 = ugu sin a- ugx cos a; 0,5nT = uglJ cos a4
+ Wina OV-v.//)•
(115)
Зависимость (1.14) или (1.15) представляет собой усло-
вия совместности перемещений стержней в трещине.
Выражая на основании первого уравнения (1.15) ugx и
ucV через остальные перемещения и подставляя (поочеред-
но) полученные выражения во второе уравнение (1.15),
можно записать последнее в виде:
^ugicmfit—un
81
пли п р,
8 cos р.
Указанное ограничение на применимость формул (1.15)
н (1.16) следует из того, что при a = 0 или a = ±90°
одна из величин (ugx или ugy) обращается в нуль (так как
19
сдвиг стержней, расположенных вдоль трещин, равен нулю)
н формулы в общем виде не могут приниматься для выра-
жения главного вектора и при этих углах.
4. Зацепление берегов трещин через бетонные связи. В
моменты, близкие к началу образования трещин, могут еще
сохраняться некоторые бетонные связи между краями тре-
щин (в виде бетонных мостиков, рис. 1.6, а). При определен-
ном направлении сдвига берегов трещин, показанном на
рис. 1.6, а сплошными стрелками, бетонные мостики будут
работать на внецеитренное сжатие и воспринимать неко-
торые усилия в трещине. Представим связи зацепления
равномерно распределенными по длине участков трещин и
обозначим возникающие в них погонные силы зацепления
через Л/Эп и ,V3n< (рис. 1.6, б). Обозначая удлинение элемен-
та на отрезке расстояния между трещинами /т через а°, а
относительные сдвиги двух соседних линий типа ед на
рис. 1.3, а— через Д°, можно записать.:
зп ж hEma^lit\ Nsnt »
(1-17)
где Езп и E3nt— секущие модули деформаций связей за-
цепления.
Рис. 1.6. К анализу зацепления берегов трещин при сдвиге (САГ — бе
тонные мостики)
20
С некоторым приближением можно предположить, что
функции £Эп будут подобны функциям изменения модуля
деформации бетона в конце ниспадающей ветви диафрагмы
е—а растяжения бетонных образцов (рис. 1.6, в) при е=д?//т
и о = Лишь в первом приближении можно
принимать E3nt « Езп. Явление зацепления остается
практически неизученным, поэтому в расчетах силами за-
цепления пока пренебрегаем. Однако при выводе теоре-
тических зависимостей силы зацепления учитываем, ис-
пользуя формулы (1.17). Могут быть и другие виды зацепле-
ния (рис. 1.6, г), но учет их наиболее существен при раз-
грузке.
5. Деформации и напряжения в полосах бетона между
трещинами. Полосы бетона между трещинами выполняют
две важные функции. С одной стороны, из-за сцепления
бетона с арматурой они приводят к уменьшению средних
напряжений и деформаций арматуры на участках между
трещинами; с другой, воспринимают усилия, действующие
на площадках, нормальных к трещинам, и определяют
при непересекающихся трещинах деформации элемента
вдоль трещины; при пересекающихся трещинах последние
функции теряются и остается лишь первая. Характер на-
пряженного состояния бетона между трещинами можно
проследить на основании рис. 1.7. (abed—прямоуголь-
ный элемент полосы бетона между трещинами.) Рассмот-
рим сначала изменение напряжений в бетоне по сечениям
типа ink, параллельным трещине. Бетон выключается
из работы только в трещинах (но линиям cd и ab), где все
усилия (если не считать некоторых связей зацепления)
передаются на арматуру. По мере продвижения в глубь
полосы бетона часть усилий с арматуры (из-за сцепления)
постепенно передается на бетон. Поэтому в бетоне по ли-
ниям типа ink возникают нормальные и касательные на-
пряжения, средние величины которых обозначены как
об„ и Тг, nt- 11з-за дискретного влияния стержней арматуры
действительные эпюры напряжений в бетоне могут носить
некоторый криволинейный характер, но теория учитывает
средние величины.
11а площадках типа 1>с и ad природа касательных и нор-
мальных напряжений в бетоне является более сложной,
где Ос/ и тг>(„ — средние величины этих напряжений. Одна
часть из них связана с действием внешней нагрузки на
полосы бетона вдоль трещин, а вторая часть — с влиянием
растянутой арматуры, пересекающей не только трещины,
21
но и одновременно площадки типа Ьс и ad. Способы учета
этих факторов указаны в § 3 и 4. Средние относительные
де<|>ормац||и полос бетона между трещинами можно принять
равными:
1 / Ч 1 / ч
*Ъп .. (®0n Pii^Ol)» ^Ot(®Gt Pii ®6>i)’
». || Си
То nt .. . _ (^0nt 4‘^б tn)»
(I +|'||) СП
(1.18)
где Е„, р„ — соответственно секущий модуль и коэффициент
поперечной деформации бетона в полосах между трещина-
ми.
Ввиду действия напряжений сцепления бетон вокруг
арматуры работает в условиях объемного напряженного
состояния и лишь на некотором удалении от контакта этот
э<рфект исчезает. Некоторые локальные напряжения смя-
тия возникают под арматурой вследствие тангенциальных
се перемещений в бетоне (см. рис. 1.4, о). Влияние всех
этих локальных эффектов на повышение деформативности
бетона можно учесть косвенным образом (при определении
модуля деформаций полос бетона Ёп).
6. Дополнительное влияние деформаций полос бетона
на деформации арматуры. Как указывалось выше, в тре-
щине все усилия передаются на арматуру, вызывая в ней
определенные напряжения и дс<|юрмации. Природа допол-
ни гельных деформаций арматуры иная. Она связана с на-
Рис. 1.7. К анализу напряжен-
ной» состояния полос бетона
между трещинами (/ — арма-
турные стержни)
Рис. 1.8. к пояснению физия-
сьон сущности дополнител1.н1.
напряжений Оа( и дсформащ-
гц арматуры
пряжениями бетона на площадках, нормальных к трещи-
нам. Чтобы пояснить происходящие при этом явления, нач-
нем с примера. Выделим элемент полосы бетона между дву-
мя трещинами в виде некоторой призмы (рис. 1.8, где
двумя боковыми гранями призмы служат берега трещин)
и рассмотрим поведение забетонированного в нее стержня
сс при ее сжатии (oCf — напряжения сжатия бетона; пунк-
тиром показана призма после деформаций). Точку Ot стерж-
ня поместим в центре призмы и примем ее за начало отсчета
перемещений призмы при указанном сжатии. Рассмотрим
два граничных случая — в первом случае (см. рис. 1.8, а)
сцепление бетона с арматурой такое, что соблюдается усло-
вие совместности перемещений арматуры и бетона, во вто-
ром (см. рис. 1.8,6) — сцепление полностью нарушено
и стержень лишь закреплен в одной точке О/.
В первом случае при деформировании призмы стержень
переместится в положение с'с' и укоротится на величину,
равную:
(с' е')—(сс) = 2е0/ /, = 2еа/
где ббь еа< — относительные деформации арматуры и бето-
на; 2 li — длина отрезка сс. Этот пример показывает, что
в арматурных стержнях возможны деформации и напряже-
ния, несвязанные с указанными в п. 1 напряжениями арма-
туры в трещинах. Они названы дополнительными.
Во втором случае (при полностью нарушенном сцеплении)
стержень повернется вместе с каналом бетона и займет по-
ложение e'c*. При этом длина его не изменится (сс = с"с") и
он будет выдвигаться с обеих сторон призмы. В этом случае
при любых деформациях бетона eaJ = 0.
Выше рассмотрены два граничных случая. Поведению
реального стержня частично будут присущи элементы как
первого (они будут преобладать в момент трещинообра-
зовання, когда сцепление еще слабо нарушено), так и вто-
рого случаев (элементы второго случая начинают преобла-
дать с раскрытием трещин и нарушением сцепления). Все
эти явления будут учтены, если принять:
еп<«еб<фиь (119)
£ДС (1— — коээ(1х|)иц,иенты влияния на
при частично разрушенном сцеплении арматуры
с бетоном. Выражение для является приближен-
23
tim.M, no в принципе удовлетворительно моделирующим
изменение этого коэффициента. Действительно, в момент
трещинообразования (при фат х 0»2) ф,н 8, а к мо-
менту разрушения (при фа( — 1) ф„| -> О.~
Остановимся на определении величин воь с которыми
в общем виде связаны дополнительные деформации и на-
пряжения арматуры. Полагаем, что величины е,-,( зависят
лишь от напряжении ойг и tj,,, на площадках, нормальных
к трещинам, и связанных с ними деформаций г о/ 11 Tg/>..
Пренебрегая коэ<]и]>ициснтом поперечной деформации, мож-
но записать (выделяя их из общих деформаций (1.18)]:
e6i Л
Тй/И—Tfl(„ ^11* *\>П 0, £"|| Eq vu, (1.20)
где Ес,— модуль упругости бетона; vu—коэффициент
неупруги.х де<|юрмаций полос бетона вдоль трещин.
Считаем, что природа остальных напряжений (о^,, и
TCnt) связана с тсц/ и изменением oai и их влияние уже
учтено выше при определении средних деформаций арма-
туры по формуле (1.10).
В принципе представленное разделение деформаций
бетона не лишено некоторых условностей, однако они не
сказываются заметно на точности модели. Формула (1.19)
для гл/ записана в предположении нс стесненных сдвигов
арматуры относительно краев трещин. Возможное уточне-
ние fui в связи с этим указано в § 4.
§ 3. Способ учета армирования.
Понятия усилий и относительных деформаций
для железобетонных элементов с трещинами
I. Армирование. Рассматриваемые схемы армирования
плоской конструкции или ее отдельных областей (элемен-
тов и Эг) показаны на рис. 1.9. (схемы /—5). Начнем изу-
чение с наиболее общей схемы / — схемы трехслойного
армирования, выделив се отдельно (рис. 1. 10, «) Стой арма-
туры i (i = 1,2, 3 или .г, у, 3) представляет собой часто рас-
положенные стержни одного /-го направления и характе-
ризуется в своей плоскости (рассматриваются лишь слои,
параллельные срединной поверхности пластинки) углом
Pi наклона стержней к осн х и параметром армирования
fai — Е al/S„ (1.21)
21
Рис. 1.9. Изучаемые схемы ар-
мирования (Л — арматурные
стержни; Лу — арматура, заме-
няющая стержень Л; Г — грани-
ца конструкции)
Рис. 1.10. К определению коэффициентов армирования
а — общая схема армирования: б, <j, г —к определению коэф-
фициентов армирования для одною слоя арматуры на наклон-
ных площадках ab
25
где Fai и S| — соответственно площади стержней и расстоя-
ния между ними.
Например, прямоугольная арматурная сетка представ-
ляет два плотно прилегающих слоя армирования. Если
однотипных (с одинаковым р() слоев несколько, то fai пред-
ставляется как сумма аналогичных коэффициентов всех
этих слоев. Армирование предполагается симметричным
относительно срединной поверхности (случаи несимметрич-
ного армирования рассмотрены в главе 2), поэтому все слои
условно переносим на эту поверхность. Для рассматрива-
емых схем Р, = 0; р, = 90°. Важно отмстить, что в даль-
нейшем задание площадей арматуры в виде fai сочетается
с учетом рассмотренных в § 2 свойств поведения отдельных
стержней в бетоне.
Поясним определение коэффициентов армирования
fai на наклонных площадках ab длиной, равной единице
(рис. 1.10, б) на примере одного /-го слоя арматуры. Ве-
личина' fai характеризует площадь арматуры, пересекаю-
щей единичную площадку, расположенную перпендикуляр-
но к направлению стержней (т. е. площадку а' Ь). Вращая
а' b вокруг точки Ь, видим, что поток стержней, пересекаю-
щих площадку, будет уменьшаться. Пусть, например, от-
резок а' b в результате поворота занял положение а Ь, где
а— угол наклона а b к оси х. Тогда площадь арматуры
fab пересекающей alt, будет равна:
fai = /а<(«' W (а' Ь) = fat (а" Ь),
так как длина отрезка а' b — 1. Согласно рис. 1.10, б дли-
на отрезка
(a b) — (ab) cos (90°—а— Р,) = sin (Р, -|- а),
в результате
fai = fai sin (Р, + а).
Для стержней, параллельных соответственно осям х и
{/(рис. 1.10,в,г), получим (учитывая, что Р, = 0, рз — 90"):
fax = fa х(«<>) = fax sin fay = fay H) « fay COS a. (1.22)
Площадь арматуры, пересекающей единичную площад-
ку, нормальную к аЬ, обозначим в виде /в«|. По аналогии
с формулой (1. 21):
fa'i = fai COS (Pi + a)
(1-23)
26
Обозначая проекции площадей армирования на нормаль
^касательную к площадке ab и к площадке, нормальной
к ab, в виде Fn, Ft, Ftn и Fnt, получаем:
Fn = 2 fai sin2 (a + ₽,); Ft = v fa( cos2 (a + p
i i
Fnt~Ftn “ fat sin (a -{- P/) cos(a -j- p().
(1.2-1)
Полагая в уравнениях (1.24) a = 90°, получаем вели-
чины Fx, Fy, Fxy, характеризующие проекции площадей
арматуры на единичных площадках, параллельных осям
х и у. Однако Fx, Fu и FxU можно получить и по формулам
тина (1.2), заменяя в них N на F. Таким образом, они
образуют симметричный тензор. На тензорный характер
параметров армирования впервые обратил внимание
А. А. Гвоздев 115], анализируя условия текучести армату-
ры в железобетонных плитах.
Как и тензор напряжений, симметричный тензор арми-
рования имеет главные осн, в которых касательные ком-
поненты (типа Fnl) обращаются в нуль. Их направления
определяются по формуле (1.3).
В реальных конструкциях, кроме сеточного армирова-
ния, могут устанавливаться отдельные стержни арматуры
(схема 5 на рис. 1.9, в). Такую схему армирования заменя-
ем схемой 5а (подобной схеме 3), распределяя арматуру
в пределах некоторого малого шага 6. Если дискретная арма-
тура расположена у границы конструкции, схему 5 мож-
но заменить схемой 56 так, чтобы учесть возможную кон-
центрацию касательных усилий на уровне дискретной арма-
туры и увязать это с условиями на границе. При этом ар-
матура распределяется на два малых элемента — Э2 и Э3,
где к граничному элементу Э3 относится небольшое коли-
чество арматуры (лишь такое, чтобы можно было рассмат-
ривать ее работу с учетом трещин).
Однако в ряде случаев, когда стержни будут располо-
жены на значительном расстоянии один от другого, от прин-
ципа задания арматуры в виде fat будем отказываться,
учитывая дискретное расположение арматуры. Такие за-
дачи рассматриваются в главе 3.
2. Усилия. Погонные силы i\’x, N,/t Nxl/ представляются
как составные величины, состоящие из усредненных уси-
27
лнй, воспринимаемых арматурой (Мах, ...) и бетоном
(Л'б*. ...) (рис. 1.11, а, б, в), т. е.
Nx “ А/вж 4- А/ бх; Nу = A/av т* А^бу, №ху ^&хи “Ь (>хт
(1-25)
Лишь по линиям трещин составляющие усилий бетона
равны нулю.
А'Пл. А'а,;, A’nvv—это проекции нормальных и касатель-
ных усилий в арматуре, пересекающей грани элемента,
на нормаль и касательную к граням (/Va,z, A'axI/, Nc,x и A'r,xV
показаны на рис. 1.11, б, в, г), отнесенные к единицам их
длины.
В связи с нарушением совместности деформаций арма-
туры и бетона одноименные усилия арматуры и бетона могут
быть как одного, так и разных знаков. Например, при чис-
том сдвиге А/ах «« —/Vбх н Nuu ——N6!) (рис. 1. 11, О). 11нте-

Рис. 1.11. К пояснению понятия усилий Nx, Ny и Nly Для элементов
с трещинами
/ — арматурные стержни: 2 — трещины*. 3 — эпюры осевых напряжспиЛ в ар-
матуре между трещинами: 4 и 5 — действительные и усредненные эпюры и<>р
мальиых и касательных сил в бетоне
Рис. 1.12. К пояснению понятия относительных деформаций
для элементов с трещинами
ресно отметить, что до появления трещин при чистом сдви-
ге Ntx = Nex = 0; Nay = N= 0- Особенно существен-
ными могут быть касательные силы в бетоне Naxy'.
Все теоретические исследования, как правило, будем
вести, используя суммарные величины Nx, Nu и Nxy. Для
них будут справедливы зависимости (1.1)— (1.4).
3. Относительные деформации элемента с трещинами
(рис. 1.12, а, г) складываются из двух частей: средних от-
носительных деформаций от раскрытия трещин и сдвига
их берегов (рис. 1.12, б) и средних относительных дефор-
маций полос бетона между трещинами (рис. 1.12, е):
г" 4*сбп» 8«“сб<’ Vni—j F To nt — т/п Уп(»
^tn Т^Том. Тл/ "i ~ To/ir
(1.26)
29
Остановимся на свойствах величин уравнений (1.26).
Составляющие углов сдвига =#= Ул» у Ynt. поэтому
величины еп, е<, у{л и уя/ преобразовываются при поворо-
те осей координат, как компоненты несимметричного тен-
зора согласно (1.2), при этом Nnt н Ntn заменяются на у},/ и
у{„. В осях, совпадающих с направлениями арматурных
стержней, преобразованные таким образом компоненты
совпадают с относительными удлинениями и углами пово-
рота арматурных стержней (если пренебречь некоторым
перегибом стержней в трещине). Величины en, e.t и 4-у„(
преобразовываются как компоненты симметричного тен-
зора, при этом Nnt н Ntn заменяются на Получаемые
при этом относительные углы сдвига в осях хну равны
среднему углу поворота стержней двух ортогональных на-
правлений ~ | (у!у + у[л). Указанные зависимости
и преобразования легко вывести по аналогии с выводом
условий совместимости (1.15), выражая дополнительно
перемещения арматуры через относительные деформации.
Выражения (1.26) удобны для пояснения физической
сущности относительных деформаций железобетонных
элементов с трещинами. Однако непосредственно их при-
менять из-за неизвестных аг и Д весьма затруднительно.
Используем более простой подход. Выше указывалось,
что, преобразовывая компоненты тензора относительных
деформаций (1.26) к осям, совпадающим с направлениями
арматуры, получим средние относительные удлинения ар-
матуры на участках между трещинами. Вдоль трещин де-
формации элемента совпадают с деформациями бетона. Все
это позволяет подойти к определению относительных де-
формаций элемента с трещинами через определение
осевых относительных деформаций арматуры и полос бето-
на вдоль трещин и в итоге получить простым путем компо-
ненты деформаций, эквивалентные компонентам (1.26).
При схеме пересекающихся трещин относительные де-
формации определяются (это показано ниже) только через
деформации арматуры. Некоторые особенности возникают
также при одноосном армировании (см. § 5).
Различаем два вида углов поворота граней элемента.
Один вид—углы у„/ и у’„ (рис. 1.12, г), связанные с напря-
женным состоянием элемента. Другой вид—это возмож-
30
ный поворот всего элемента как жесткого тела. Исключая
жесткий поворот по такой схеме, как и в теории упругости
(например, [51), получаем:
ди
♦
Г дх *
(1.27)
где и, v— перемещения элемента вдоль осей х и у.
Таким образом, несмотря на то, что ух!/ Ф у’х ф
приходим к тем же уравнениям, что и в классической тео-
рии упругости. Исключить жесткий поворот из уравнений,
отдельно связывающих у’^ и у'х с перемещениями, невоз-
можно. Ниже используем только величины ех, н ух,,.
§4. Анализ напряженно-деформированного
состояния элементов с непересекающнмися трещинами
при основных схемах армирования
Для упрощения теоретических выкладок сначала
определяем деформации элемента от действия усилий Nn
и Nnt> приложенных по сечению, совпадающему с трещи-
ной, а затем учитываем влияние усилий и Ntn, прило-
женных по сечению, нормальному ж трещинам.
Рассматриваем в общем виде трехслойное армирование
(схема / на рис. 1.9, б) и его частный случай — двухслой-
ное армирование (в виде прямоугольной сетки, схема 2).
1. Общая постановка задачи по определению напряже-
ний в арматуре в трещинах и средних деформаций элемен-
та, связанных с действием сил N,, и N„t. Установим за-
висимости между напряжениями в арматуре в трещинах и
силами Nx, N„, Nx,t и Л^. Для этого выделим из харак-
терного элемента треугольную призму oab (рис. 1.13) так,
чтобы ее’наклонная грань ab прошла по трещине, а две ос-
тальные— вдоль осей х и у. Как ив § 2, ста( и Tai (i =х,
у, 3)—нормальные и касательные напряжения в арматуре
в трещинах. Размер грани ab в дальнейшем исключается,
поэтому его сразу принимаем равным единице. При этом
площади арматуры разных направлений, пересекающих
ab, определяются по формулам (1.21), а общие усилия ар-
матуры в трещинах равны величинам тпJef и oaJcu (см*
рис. 1.13). Кроме усилий в арматуре при небольшом раск-
рытии трещин в ней могут оставаться связи по бетону (си-
лы зацепления берегов’трещин N3n и Nant на рис. 1.13 вы-
31
несены отдельно). Длины граней аО и ОЬ соответственно
равны 1 sin а и 1 cos а, поэтому приложенные к ним общие
усилия будут равны Nx. sina, ...» Nyx cos а. Проектируя все
силы, приложенные к граням призмы аОЬ, на оси х и у, по*
лучаем:
Nx sin a + Nux cos a = aax fax sin a 4- aa3 fa3 sin (a 4-
4-₽3) cos ₽3—та!, fau cos a—та3 fa3 sin (a 4- ₽3) sin ₽3 4-
4- N3n sin a—Nanl cos a;
Nu cos a 4- Nxy sin a = <таУ fay cos a 4- <та3 fa3 sin (a 4-
+₽з) sin p3 4- тазе)ах sin a 4- та3 fa3 sin (a 4- 03) cos 034*
4-jV3n cos a 4-^3 nt sin a.
(1.28)
В эти уравнения входят семь неизвестных величин: шесть
напряжений в арматуре (<таЬ xaJ ) и величины ^nf и Nan.
Для их определения кроме условий (1.28) необходимы до*
полнительные уравнения, которые устанавливаем, исполь-
зуя все условия совместности деформаций арматуры (1.15),
кроме второго уравнения, которое записывается в виде
выражения (1.16). В эти уравнения вместо их1 и ие1
подставляем их значения из (1.12) и (1.13 а). При этом в за-
висимостях (1.12) предварительно принимаем e6J л; О и
Рис. 1.13. К опре-
делению напряже-
ний в арматуре
в трещинах
32
выражаем eai через oai по формулам (1.10); в результате
получаем:
(Сяз~ебзНт ~ еа»1т _____________ gn*2l------- ;
Ugi ~ 2 sin (а 4- Р,) ~ 2 sin (а + ps) 2£а'з sin (а 4- р3)
„ °ax G . .. — pal> It
g 2£axsma 2£ai,cosa
Кроме уравнений (1.15) и (1.16) используем зависи-
мости (1.17), подставляя в лих вместо Д° и а? соответствен-
но величины Д и ст, найденные из пятого и шестого урав-
нений (1.15). В результате уравнения (1.15), (1.16) и (1.17)
при i = 3 запишутся в виде:
раз рах CQS Рз .
£аЗ sin (а+Рз) £ах SintZ
оау sin Ра
Еаи cos а
(1.29)
_ Одх Еар COS Ct e
Ъ» Т/ • •
пгп sm а
I у ОА
г —hp ( аах 1 \.
ЭП — '‘^зп I • I "Т7 |»
\ Сах /
(тау Eax sin а #
£,'₽ cos а
d \ т + М
£lt 6 У »’ лх3
COS Рд ^ах \
\ Еаз sin (а + Рз) sin а Eax sin а sin р3 /
— £а3 $*п (а 4- Рз) / _ Пар__________On> sin рз
лтЗ \ Еа|/ cos а cos Рз sin (а + р3) cos р3
(1.30)
Подставляя значения (1.30) в (1.28) (при этом первое
выражение для та9 подставляется в первое уравнение (1.27),
а второе выражение во второе уравнение), получаем:
ЛГХsin а + Nуxcos а = <j f sin а 4-
лх
+ааз/аз sin (а 4- рз) cos рз + Х4 oaj/ [Лу sin а;
Ny cos а 4- jVx„ sin а = -!-orav f cos а 4-
+ Ъ ga3 /аз sin (a 4- Рз) Sin p3 4- X4 <jax fax cos a>
2 3«. 63|
(1.31)
33
I . hw /, w cos2 а . g»3 /яа sin2 (a + p3) ।
X, Г«лС(,/Их*|"2а "* £««tl/axsin2a
+ (£jn+ ctg1 a); ± ==!-}-
/;« /at Atf
b*. /„r sitHa
Елц nxf /ay cos2 a
/;»з sin2 (a + P.i) /а»
'»fl/»« cos2 a
(1.32)
(£.„ 4~ ^3>i, lg"a)«
h
E»v lav
^4 ~ i (^.m
Etulay
X4--^-(EJ(1-Ein/).
cat /аг
При записи (1.28) в виде уравнения (1.31) такие второсте-
пенные факторы. как нагельный э<|х|>ект и зацепление
берегов трещин, влияющие на напряжения в арматуре
в трещинах, учитываются с помощью коэффициентов Л(
(/ « .г, у, 3, 4, 5). Уже качественный анализ зависимостей
(1.32) показывает, что на Лх и основное влияние оказы-
вают углы наклона трещин а и соотношения коэффициен-
тов армирования. Учитывая это и данные экспериментов
(III, удалось упростить выражения (1.32), приняв:
I _ t l W.iv/;«vCos2a , //л.г/лэ sin2 (а-|-р3) .
*х //а?//ах"о sin-’а //аз/ах «о s«n*a
I | , Яду/аг sin2 a //av/a3 Sin2(a-I-Pt) .
я ах Iлу”оСО52а Паз/ау «0 cos2 a
(1.33)
"о
где п0 л: 13—17 (в расчетах мы принимали п„ т 16).
31
Решая совместно уравнения (1.31) и (1.29), получаем
(при ^4 = ^ = °):
(<Vx-r Nyx dfi а) ^х с1а . (Д !/+ Хху tg а) с2а )
а*3 [лхЕахФ 1ауЕауФ
(Л\ + Хух ctg а) \х (Хх + Л\7Х ctg а) X" с*ft Х3
°аХ= /ах ЦхЕа<Ф
(Ху 4- ХхУ tg а) Ху Х3 - .
/ f <Ь С1аС2а'пЗлх»
lay lax Lay ч>
(Ху + Л ху tg <х) Ху (Ху -|- Хху tg а) ХуСоаХ3
fay 1ауЕауФ
(УгЧ* А ху ct g а) Хх Х7 с । ас2а fa3X3
1ах1ау^ахФ
где
. / I . /a3flaKv^3 . /аз^ц^у хз \
\£аЗ /а-v^ax fay^ay /
с. = cos2 ₽3 ctg а sin рз cos рз= -S?s Рз5|П <а+Рд) .
,u sin а
с, = sin2 рз 4- tg а sin рз cos рз = sin Рз5ш(«+р3) .
cos а
(1.34)
(1.35)
Принята следующая последовательность вывода (1.34).
Напряжения оПх и оау на основании (1.31) выражались
в функции от сил и напряжений оп3 и подставлялись
в уравнение (1.29). Определив таким образом о,3, из
предыдущих выражений можно определить оПх и onjz.
При /аз = 0 формулы (1.34) значительно упрощаются:
^ах (^х "1" ^'ух ^'хИпх' | zj
°ау = (Ny -|- Nxy tg a) ku/faiJ. J
Напряжения в арматуре оах, оа7 и оаз не изменятся,
если напряженное состояние, направление трещин и схема
армирования изменяются зеркально-отображенным спо-
собом (схема рис. 1.14, а перейдет в схему рис. 1.14, б).
Здесь и ниже правило отсчета углов а принято обратным
правилу отсчета углов Р/ (см. рис. 1.2, «).
Средние деформации арматуры еа< (/ = л‘, у, 3) опреде-
ляются по формулам (1.10). Из предыдущего анализа сле-
дует, что величины rnJ непосредственно связаны с раскры-
тием трещин, поэтому вдоль трещин (вдоль оси /) еп» = 0.
2’
35
Учитывая это, на основании второго уравнения (1.2)
можно записать:
еа| = 0 = рах cos’а + еау sin2 а — уахУ sin а cos а,
откуда
Уаху = faxctga -I- faj, tg се.
(1.37)
Нетрудно заметить, что использование формулы (1.37)
для определения величины уахУ связано с некоторыми осо-
бенностями. Формула будет справедлива при всех углах,
кроме а = 0° и а = 90°, когда она переходит соответст-
венно в зависимости еах = eat = 0 и еау = еа| = 0. Одна-
ко, чтобы не выделять отдельно случая а = 0° и а = 90°,
можно поступать так. Предполагая, что величина уаху при
малых (а -*• 0) и больших (а -► 90°) углах изменяется нез-
начительно. принимать:
при 0 а 5°
при 90° а 85°
а ~
(1.38)
Отклонения ± 5° соответствуют реальному разбросу
углов наклона трещин. Кроме того, при а = 0“ и а = 90°
величины Ух7 будут во многих случаях равны нулю, поэто-
му возможная неточность в определении жесткости на сдвиг
при этих углах практически не скажется на точности рас-
чета. Более точно случаи, когда а = 0° и а = 90°, рассмот-
рены в § 5. Величины еах, еау и уахУ представляют части
общих деформаций элемента, вызванные действием сил Nn
и Nnt. Подставляя значения напряжений оах и oa(Z из (1.34)
Рис. 1.14. Случаи на-
пряженного состоя-
ния и трстинообразо-
вания
а — прямой; б —зеркаль-
но отраженный
36
вуравнения (1.Ю) >• (1-37), получаем:
е = ^- = Сац Nx 4- Cai2 Nu 4- Cal3 Nyx',
Eax
eay ~ ~ ^al2 ^x + O>22 M, + Ca23 NXy,
Eay
Tax!/ = £ai3 Nx + Qn23 ^y + ^аЗЗ Л\у»
где
_?.x XxZ3 cig/а» .
fax Eax (fax Qu:)2 Ф
p_________?.i;___/•* ?-3 C?g fa3 .
322 “ fay^y (fayt'ay)-* '
r r ?.х^!Лз<Час2а/а» .
LaJI —ca21— . f P, F, ... ’
fax I ay ^ax Lay®
Qj13 = Сац ctg Ct -f- Cai2 tg Ct,
Qi^3 = 0i22 CC 4’ 0112 C tg Ct,
Qi33 — 0122 tg" а 4* 2Cal2 4* Qin ctg2 Ct.
(1.39)
(1.40)
Величины Ф, cw и cw определяются по формулам
(1.35). Полагая в формулах (1.40) /пз = 0, придем к коэф-
фициентам жесткости Cai] для армирования (схема 2 на
рис. 1.9.) в виде прямоугольной сетки.
2. Деформации полос бетона между трещинами и их
влияние на общие деформации элемента. Выше (п.1) рас-
смотрены лишь деформации, связанные с действием уси-
лий Nn и Nnt, приложенных по линиям трещин. Общие де-
формации элемента также зависят от усилий Nt и Л’|п и свя-
занных с ними деформаций бетона, определяемых из урав-
нении (1.20). Деформации бетона в осях х и у равны’(прн
этом^юполнительно присоединим к ним еще и выражения
ДЛЯ ₽G.f)’
fcx= ₽6tcos2a— T6fnsinacosa = (o6rcos2a —
-тС(п sin a cos a)/£n = (a6x cos2 a —
~T6wx sin a cos a)/£„;
ебу — (Обу sin2 ct—t6vV sin a cos ct)/£n;
37
Гб, И I—(п<-.х ; п6и) sill a cos а | тОл., cos2 а -|-
-г tepxsiira|/£u:
*’б< = 1°бх«*2а I-а6чsiira — (тбхУ
I T^Jsinacosal/E,,;
(I -41)
компоненты fc,x, еОи и находим, преобразовывая сна-
чала Ffif II 2 «Уб/п ' ^'аУбп!» 3 3<1ТеМ Обо *^ба/ И ^б/п по
формулам (1.2); при этом еЛ„ = 0; об„ = 0.
Выразим на основании (1.25) напряжения в бетоне через
общие усилия:
Обх = Л^бх/Л “ ('VA — Л'ах)/Л;
tyjW : " С'^» ^пч) h’
^бл» ~ ^б»х “ ОУх» ^ахч)
(1 -42)
При определения средних усилий арматуры пренебре-
гаем касательными напряжениями в стержнях, считая,
что они существенны лишь в малой области у трещин, и
учитываем только средние нормальные напряжения арма-
туры, равные оа1фп/. Заменяя в (1.24) /а, на /п|фа| оа1 и
полагая а =* 90 , получаем:
^пя“ 2L ^а/Фи//а/COS Р,-,
I
N ay e °а/ Фа/ fai Р/•
i
(1 43)
ЛатР » ^aux i ®а/ Фа/ fai Pi COS Р/.
i
В дальнейшем выражения (1.43) подставляются в (1.42),
а последние в (1.41). В результате, например,
е» =» е61 [Nx cos2 a }• /Vy si n2 a — 2NxV si n a cos a —
— aaxfaxtax «»’ «~а«У Фа» fav SIH2 a — <Ta3 фа3 fn3 COS2 X
X (а + р3)|/(ЛЕ„). (1.44)
Подставляя в формулы (1.41) преобразованные по ана-
логия с зависимостями (1.44) значения ая1 из (1.34) или
(1.39), получаем окончательные выражения для ect, eCv и
rot. С этими величинами связаны дополнительные относи-
тельные деформации арматуры eav, eav и raf. Они и харак-
теризуют то дополнительное влияние, которое оказывают
38
деформации полос бетона на общие деформации элемента
с трещинами. Согласно (1.19):
• ®пх ®бх Фих’ ®ау ®бу ФпУ •
(1.45)
Используя первое уравнение (1.45) и преобразования
типа (1.2), можно определить дополнительные углы пово-
рота арматуры в бетоне:
Таху “ ®ах ct6 а -I- Cay tg a—e6</(sin а cos а). (1.46)
В итоге величины еПх, еп,, и уПх7 выражаются функциями
от общих сил Nx, Ny и Nxu. Указанный точный путь вывода
дополнительных деформаций ведет к весьма громоздким
выражениям и не дает возможности выявить и отбросить
сразу некоторые второстепенные члены. Чтобы этого из-
бежать, используем приближенный вывод окончательных
зависимостей (1.45), рассмотрев два граничных случая.
Первый случай соответствует началу образования тре-
щин и еще практически ненарушенному сцеплению арма-
туры с бетоном. Полагая для этого случая
Фп< 1» М бх ~ ^Х» ^7 Му, N Сху М ху,
из уравнений (1.41)—(1.46) получаем:
., sin 2а
— Д' их------
ух 2ЕпЛ
sin 2а
— Д'vM - — —
~ кг cos- а
еах = Мх-- -
еау ~ Му
sin2 а
2Е„ А
А, sin 2а sin 2а
cos* а
Xll г • '
2EU А
sin2 а
ух ‘ 7" V
(1.47)
Второй случай соответствует практически полностью
нарушенному сцеплению арматуры с бетоном. При этом
Фп< « 0, а фП| яг 1 и зависимости (1.45) и (1.46) запишут-
ся так:
епх яг 0; еа„ яг 0; ynxf яг — ec,/(sin a cos а). (1.48)
Пусть fn3 = 0, при этом напряжения в арматуре будут
определяться из (1.36). Подставляя о„Л. и ап„ из (1.36) в вы-
ражение (1.41), а последнее в (1.48) и учитывая, что для
39
roft стадии без особой погрешности можно принять
\1—~ (I—М « к получаем:
О
0:
Yax»« (2 + ctg2а4-
+ Ли1й2а)/(Е„Л).
(1.49)

« 0;
При [пз Ф 0 можно использовать зависимости:
0;
₽аУ ~ 0;
ТахУ хУ (2 ”1" fах Eax С113 etg 6С 4"
(1.49а)
4” /а У ^ау Сг23 iga) Ci А»
где Сщз и Сиз определяются согласно (1.40).
Значения 7ат, г„„ и уЯх„ между граничными случаями,
описываемыми (1.47) н (1.49а), определяем по интерполя-
ции, используя в качестве интерполяционных множите-
лей коэффициенты ф||х и фп7. В результате:
₽ах Citi А\ 4" Сиз ^ух- еаУ ^622 Му 4*
+С»33 ”хУ’
ТахУ ~ С13 Мх + Cj23 Ny -г Срзз Л ху,
(1.50)
где, учитывая зависимости (1.20) для Е„, имеем:
tn г с<><2 а .
6.1 = г~77 ’
£б Л\п
1Г„7 sin 2а
623 ----------.
2/:с Av„
_ «Г,,» sin 2а .
613---------Т7Г~.----»
2£6*vI(
г tfnySinSa .
'-'б'4’ — _ •
£бйу„
Сбзз —Try I Ф„х si »2 « 4- ф11Ч cos2 а + (1 4-
Тп^оЛ
+ fax Еах С„з ctg а) (1 — ф„х) -I- (1 +
4- fay ^ау Ca23 ig 6t) (1 Фп'/)1*
(1.51)
Ниже для ортогонального армирования (при /л3 = 0)
нашли применение и более простые зависимости (1.51),
в которых полагали

1.
И
(1.52)

в результате:
СбП « cos2а/(£б Л): Cci3 » Сб23 л; — sin 2а/(Еб Л);
Сс„ « sin2 а/(Еб Л); Сбзз Ц- [ 1 4- (1 4-
Lq/i
-Hxctg2a) фах/vn4-(1 4- К tg2a) ^a!,/vn] =
= -L (Л-1
£'o h \ Vn
Смысл обозначения группы величин, входящих в Cq33
в виде 2/vn— 1, будет ясен из дальнейшего [с.м. (1.54)].
Сравнивая уравнения (1.50) с (1.47), видим, что вели-
чины Сац отличаются лишь коэффициентами фпх, фп!/
и (2/vn—1). Это дает возможность в дальнейшем (при
исследовании более сложных задач) не повторять громозд-
кого вывода окончательных зависимостей (1.50), а сразу
записывать их на основании простых зависимостей (1.47),
умножая их величины Сац на указанные коэффициенты.
Для дальнейших исследований могут еще понадобиться
величины еа< = е(, соответствующие уравнениям (1.50).
Подставляя (1.50) в (1.4G), получаем
ifnx cos2 а
а. /V
I у
sin2 а
sin а cos а
ху
X 1Фпх 4" Фиу 4~ 0 4" fax Eax £al3 а) 'fax 4* (1 4“
4-tga) ~ [при предпосылках (1.52) и
/аз — 0]
Nx cos2 а
Л\/ sin2 а 2.Vxy sin а cos а
£б Л Ес hvn
(1.54)
Таким образом, коэффициент vn характеризует влия-
ние разрыхления полос бетона трещинами и влияние напря-
женного состояния арматуры при частично нарушенном
сцеплении на деформативность полос бетона между трещи-
нами.
Остановимся на возможном уточнении представленных
зависимостей. Указанные на рис. 1.8, б сдвиги арматуры
относительно бетона (обозначим их как uKi и v^i) могут
в стесненных условиях приводить к возникновению в ар-
матурных стержнях в трещине дополнительных напряже-
нии (аа| и тп<), образующих самоуравиовешенную систему
41
сил. Этот случай можно описать так. Два уравнения (для
определения оа1 и та<) получаем, приравнивая пулю проек-
ции этих сил в трещине на оси х и у. Остальные уравнения
составляем на основании уточненных выражений (1.20) и
(1.12):
'Гц/ ^g/ (^а/ ^б/) I
и использования условий совместимости (1.15), в которых
и . и заменяются на ugl и vk</. Фактические напряже-.
ния в арматуре в трещине равны сумме оа1 и oai. Однако
вопрос о необходимости учета величин ол1 еще требует ис-
следования.
3. Физические уравнения для элементов с трещинами
них связь с обобщенным законом Гука для анизотропных
материалов. Общие деформации элемента с трещинами со-
гласно уравнениям (1.26) равны сумме величин (1.39)
и (1.50):
^х " ^ах "1* еах’ ^У ^ау “1" ^ау*
ТхУ ~ ТахУ "1" VахУ
(1.55)
или
(1.56»
₽х = ^х *1” ^42 ” У *1* ^43 ух'
еу = С12 ^х + ^22 Nv -J- Саз Nxy\
ТхУ ~ ^43 *Vx *1“ ^23 ^У ‘1* ^33 ХУ'
где, если принять приближенные значения (1.53) дляСсо,
42
_ (J _ tgg Cog /аз tg a
32“ fayE^
^x ^з ^j/x c2a faa ctg a sin 2a
fax Iay t ay “^6
__ Kyctg2 a \v^3g|a/fl3ctg2a
’ /ax Eax Улх Е'ахГ- Ф
l,z tg2 a \z c2a faз tg2 «
/ау E^y (/ay Ф
2XxX(/X3C|a c2a/n3 ( j /2 \
fax fay Eax E а{/Ф EqIi Vjj j
Коэффициент C33 при a = 0° и a = 90° необходимо
определять с учетом рекомендации (1.38). Уравнения (1.55)
по форме совпадают с обобщенным законом Гука для ани-
зотропных материалов 18]. При этом матрица коэффициен-
тов жесткости является симметричной относительно глав-
ной диагонали, проходящей через коэффициенты Сц, хотя
из-за нарушения сцепления арматуры с бетоном симметрия
коэффициентов может несколько нарушаться, но это нару-
шение оказывается пренебрежимо малым. Главные коэф-
фициенты Сц являются положительными величинами, а
побочные Сц (i #= /) имеют любые знаки. Эти свойства
присущи.н обобщенному закону Гука. Различие состоит
в способах получения Сц,, в их выражениях, кроме того,
коэффициенты Сц, в данном случае являются не констан-
тами, а некоторыми функциями, зависящими в свою очередь
от усилий. Таким образом, железобетон с трещинами де-
формируется подобно физически нелинейным анизотроп-
ным материалам.
Если при изменении знака касательных усилий зеркаль-
но-отображенно (см. рис. 1.11) изменяются угол наклона
трещин н схема армирования (что в железобетонных кон-
струкциях при симметричной нагрузке, как правило, вы-
полняется), то знаки С13 и Со3 будут так же изменяться.
Обычно:
при yVx,z>0 С|3>0 и С23>0; |
при Nx,j<Z0 С13<0 и С.,3<0. I
(1.58)
•S3
Эго приводит к тому, что оси симметрии паи ряжен но-де-
формированного состояния конструкции, существующие
до трещишюбразования (когда модель деформирования
материала принимается изотропной), продолжают сохра-
няться и после трещинообразования (когда имеем общий
случай анизотропии). Такие свойства в теории анизотроп-
ных материалов при общем случае анизотропии не прояв-
ляются. В нашем случае они приводят к значительному
упрощению при решениях задач и качественно иным реше-
ниям.
Выше рассматривалась серия трещин с расстояниями
/т. Вели трещина одна, свойствами (1.56) будет обладать
прилегающая к трещине полоса шириной 2ГТ, где Тг — рас-
стояние от трещины до области, где контактные сдвиги
весьма малы. Зависимости (1.56) носят масштабный харак-
тер, т. е. действуют в пределах элементов, размеры граней ко-
торых соизмеримы с /г или /т. Поэтому к значительному
дроблению элементов при решении задач стремиться не
следует (за исключением случаев, когда необходимо учиты-
вать быстрое изменение углов наклона трещин в пределах
какой-либо области).
Несмотря на некоторые формальные и не формальные
отличия, сложная задача расчета железобетонных пластин
с учетом трещинообразования в принципе сводится к рас-
чету пластин из некоторого эквивалентного анизотропного
материала, свойства анизотропии которого приобрета-
ются и изменяются в соответствующих областях конструк-
ции в процессе трещинообразования.
Присоединяя к физическим уравнениям (1.5G) извест-
ные из теории упругости геометрические и статические урав-
нения, а также соответствующие граничные условия, кото-
рые записываются так же, как для анизотропных пластин
1621, получим замкнутую систему уравнений для расчета
железобетонных пластин с трещинами.
4. Ширина раскрытия трещин. Де<|х)рмацию еп элемента
перпендикулярно к липни трещин (вдоль оси л) можно вы-
разить, используя значение первого инварианта тензора
де<|х’рмаций:
Fn =••» pt -г ew—et или гя„ — гх Ь г,,—гг—ебл.
(1.59)
где ton — деформации бетона; га„ — деформации, связан,
ные с раскрытием трещин (гп = ебп -}- ?а„).
41
Ширина раскрытия трещин
flr = 8ап^т “ (®х "Ь ®v““’®r) ^т» (1.60)
гдеех, еи, е, определяются согласно формулам (1.55) и (1.54)
В*практических расчетах нашел пока применение приб-
лиженный вариант формулы (1.60):
Дт (^ах “Г ®ар)‘т»
(1.61)
не учитывающей влияние полос бетона на дополнительные
сдвиги арматуры и ширину раскрытия трещин (см. п. 7,
§ 2), однако это упрощение еще требует исследования и,
очевидно, будет не всегда приемлемым. Формула (1.61)
получается из (1.60) при условиях (1.47).
Рассмотрим поведение арматурных стержней произ-
вольного /-го направления в момент трещинообразования
(рис. 1.15, о). Напряжения у первой трещины ab в момент
образования смежной трещины cd обозначим через Gat,
а напряжения в арматуре в момент, предшествующий трещи-
нообразованию, —через о®/. По аналогии с теорией
В. И. Мурашева [691 для одноосного напряженного состоя-
ния примем, чго смежная трещина возникает на таком рас-
стоянии /т, при котором напряжения в арматуре, ввиду
действия сил сцепления между арматурой и бетоном, умень-
т О
шатся с величин оа/соответственно до величин оа/, а усн-
Рнс. 1.15. К определению расстоянии между трещинами (Ф — фраг-
менты поверхности пластины с трещинами)
/ — арматурный стержень; 2 — эпюра изменения растягивающих напряженнЛ
арчзпрноч стержне; ab — первая трещина; cd — линия образования смеж-
ной трещины
45
лня в бетоне соответственно возрастут от нуля у трещины
до значений, вызывающих образование новой трещины.
Исходя нз указанных предпосылок можно записать:
fai Vaifnl — Тсц/(l—= А, I/, 3, ....), (1.62)
где о>/ — коэффициенты полноты эпюр касательных на-
пряжений; т,.ц/ — максимальные касательные напряже-
ния сцепления стержней i с бетоном; S/ — периметры пло-
щадей [я1, причем fni/Si^ (Ц/4 (dt— диаметры стержней).
I !з рис. 1.15, а следует, что
/т- = 2/т1 sin (а + р,).
При учете изменения угла наклона трещины cd по
сравнению с углом ab (согласно рис. 1.3, г) следует прини-
мать
2i / (___________!______।______* ~ I*
1 2 т \ sin (a-f-p,) sin («х + р,) / sin(ac + p,)'
При этом в окончательных формулах вместо а будет фигу-
рировать ас.
В момент после трещннообразования оя1 можно пред-
ставить в виде
o-Vsin(a + p,)
М1 тсц/ $1
(1.62а)
где о^| — дополнительные напряжения в арматуре, вы-
званные перераспределением усилий с бетона на арматуру
по линии трещины. В момент перед трещинообразованием
(рис. 1.15, б)
Л’х 4- Nx4 etga - Nv + /VI7tga « Лгг,.т.
(1.63)
Подставляя в формулы (1.34) вместо усилий величину
<Vo.t, согласно (1.63), и заменяя оа1 на о^ь получаем значе-
ния Ojj. Подставляя в(1.62 а) поочередно вместо оя1 найден-
ные их значения о?,, о'\ и оа3, получаем три значения /т, из
которых в качестве расчетного выбирается максимальное
значение (47]. При {я3 = 0;
/т — Р /|ХГ_ цх sin а; /т — цу ip, cos а, (1.61)
lax lay
где
Mi = </i/4; t]i /?р/(т^цо>,).
16
Здесь действительное расстояние /т будет равно максималь-
ному расстоянию из найденных двух величин. Коэффици-
енты Л/ можно принимать равными коэффициенту н из
СНиП П-В. 1-62*. 1
Наряду с теоретическими зависимостями для /т может
использоваться и полуэмпирическая зависимость, которая
оказывается в ряде задач более удобной. В ней сделана по-
пытка учесть как выявленное выше влияние углов накло-
на трещин а и значений kp, так и влияние некоторых вели-
чин (диаметра и процента армирования), входящих в эмпи-
рическую формулу новых норм для ог, предложенную
Ю. П. Гущей 126].
Определяем промежуточные величины:
П = fax sin® а + /ajCOS2 CL\
fl
-r/a3siif(a + p3);
14 fnx sin2 a + du fay cos2 a +
4-d3fa3sin2(a4-p3)]/F„.
(1.65)
По аналогии c dc определяется и величина i]c, где вместо
dx, dy и d3 подстанавливаются величины %, и ц3, оце-
нивающие профиль арматуры (они принимаются равными
коэффициентам ц из работы [261).
Зависимость для определения расстояний между трещи-
нами имеет вид
1т=kDе0 ilc (3,5 -100 Fn/h) Vd-dc (1 - (0,15 F°/F n) x
X | sin 2a 11,
(1.66)
где следует принимать (3,5—100Fn/A) 1,5; d0 = 3,2 cm —
размерная константа (эталонный диаметр); kD определя-
ется согласно формуле (1.8) и принимается 0,3; е0 —
эмпирический коэффициент, зависящий от вида напряжен-
ного состояния (моментное или безмоментное).
Результаты статистической обработки чисел е0 показали,
что формулы (1.61) и (1.66) при е0 ~ 2,3 приводят к сред-
ним значениям для ат, при е0 та 3,5 получаются средние
значения максимальных ат, а при е0 = 3 — значения сред-
них ат с обеспеченностью 4-2 о (о — среднеквадратич-
ное отклонение). Исходя из рекомендаций новых норм
расчет необходимо вести при с0 та 3, а согласно
СНиП П-В. 1-62* — при с’о та 2,6.
§ 5. Анализ напряженно-деформированного
состояния элементов с непересекающимися трещинами
при частных схемах армирования.
Элементы с пересекающимися трещинами
1. Элементы с одноосными схемами армирования (схемы
.? и 4 на рис. 1.9.) Рассмотрим сначала элементы со схемой 3.
Полагая в уравнениях (1.28) fau = /а3 = 0, получаем:
Nx sin а + Nux cos а = oax [ах sin а -Ь Л',,п sin а — cos а:
Ny cos а -|- NxV sin а = тах f„x sin а А’.,„ cos а 4- .VaH( sin а.
(1.67)
Принимая в (1.12) гсх яг 0 и учитывая связи (1.15)
между uKi и vKi, окончательные уравнения (1.15) для схе-
мы 3 можно переписать так:
А = 2vgx sin а — еах /т ctg а; ат = 2vgx cos а 4- eaх
ea!Z - 2^gx cos а//т- (1.68)
Выражая vgx через тах по формуле (1.13) и подставляя
ат и Д вместо о? и Д° в (1.17), получаем зависимости для N3n
и Л^эпь которые вводим в (1.67). В результате:
Мх sin а 4- NVx cos а = —— oax fax sin а 4-
+ 2Лтах(£ЗП E3nt)K-.x cos а | sin a |//T;
Ny cos а + Nxy sin а = тах fax sin а 4-
Лтх
(1.69)
I r 2E3nthK ..I sin а I , 2EanhK „cos2 а
где ----= 1 4------------—------L -|-------—------
G fax l-r fax I si n Ot |
I
«X
Elnh Fa nt h COS3 Ct
1 ax fax ‘ Eax fax sini Ct
(1.70)
Пренебрегая в уравнениях (1.69) членами, содержащи-
ми (Е3 п — Езп(), можно записать:
Л х 4-Л ctg g 3 Л у ctg а + Л х(/ у
ах^ f Лих» ^ях {
/ах /ах
(1.69а)
48
Определив oav по формуле (1.10), находим е, Величи
ну еау получаем из (1.68) и (1.13), а г, „ — пз л ™ и .
;:х“хол"л'к >|,а“"м",я>' "эд. I™™;
Спц = КхЩях Е'м)\ Са13 = Хох Сtg а/(£а'х/ );.
ca22 = 2ZTX /\ Tl I sin a l,'(fax /Т tg2 aj.
Са>з = Са22 tgcc; г О-Н)
Сазз= Са(| ctg*a-f-Са22 tg2a. ]
Зависимости (1.71) теряют силу лишь при « = 0 Выше
указывалось, что формула (1.40) для Са33 требует уточне-
ния при а = 0 и a = 90°. Формула (1.71) представляет собой
уточненное выражение Са33 для ортотропного армирования
(когда /а3 = 0) при а = 0. Случаи a = 90° получается из
рассмотрения схемы 4 (см. рис. 1.9, б). Формально зависи-
мости для элементов с 4-й схемой армирования можно полу-
чить, если заменить в формулах (1.69)—(1.71) индекс х
на у, и, наоборот, в полученных выражениях изменить знаки
при тау и вместо а подставить (90° — а). Кроме того, в за-
висимостях (1.71) индекс «1» заменяется на <2», и наоборот.
Дополнительные деформации еах, еач и уа опреде-
ляются по формулам (1.50) и (1.51), где следует принять-
для схемы 3:
fny — /аз — 0; фау — 0; — 7.0х, фпУ — 1, (1.72)
для схемы 4:
fax = /оз = 0; фах — О'» — ’lux ‘ 1-
(1.73)
Суммируя одноименные величины (еах с еах, ,..), при-
ходим к общим физическим зависимостям типа (1.56).
2. Неполная система физических уравнений для элемен-
тов со схемами армирования 3 и 4. Рассмотрение неармнро-
ванных областей с трещинами. Рассмотрим случай, когда
не только силы зацепления (Лгзп и Л'апГ), но и касательные
напряжения в арматуре та< можно принять равными нулю,
т. е. когда арматура не может сопротивляться сдвигу. 1 Нач-
нем со схемы 3. Из формулы (1.67) получим:
— (Л^хЧ- Nyx ctg «) /лх»
NF cos a -J- Л’,,, sin a = 0.
(1-74)
49
Зная оах, можно определить епх. Величина деформации
элемента от раскрытия трещин вдоль оси у (сохраним для
нее условно обозначение еа9)при известных значениях сил
/Vx, 'Ny и Nxu не может быть определена. Для определения
еа„ уже дополнительно необходимо знать деформации кон-
тура, окружающего рассматриваемый элемент, вдоль
оси у.
Систему физических уравнений, нз которой, зная силы
малого элемента, можно определить лишь часть его относи-
тельных деформаций, назовем неполной, в отличие от си-
стемы (1.55). Последняя система названа полной.
Если в конструкции встречаются элементы с неполной
системой физических уравнений, можно при расчетах посту-
пать так. Вводить величину еа„ как неизвестную и допол-
нять систему физических уравнений вторым уравнением
(1.74). Величина еах определяется по формуле (1.10), а
Тпх» — по (1.37). Суммируя еах, еа„ и yaxj,c еах, eajz и уах(/,
которые определяются согласно (1.50) при условиях (1.72),
получаем следующую неполную систему физических урав-
нений:
ех — Nx Сп 4- N,JX С13‘,
~ Рау Ф NУ ^623 Ф ^хУ ^613'
Уху — у ‘ ь ® Т Лгх С и -р Ny C(j23 -р
Ф Nxy (Са11 ctg2 а -Р Ссзз),
(1.75)
где Сл/у определяются по (1.51) с учетом (1.72), а Calj~
по (1.71) при ZOx = 1. Система (1.75) дополняется вторым
уравнением (1.74).
Заменяя в зависимостях (1.74) и (1.75) индекс «х» на
индекс «//» и наоборот и а на (90° — а), получаем формулы
для элементов, армированных по схеме 4.
Для неармнрованного элемента с трещинами, зная силы,
можно определить лишь его деформации вдоль трещин
1г( по (1.41)1. Их можно представить формулами (1.47),
оставив условно обозначения еах, еа„ и уаху.Эти величины
можно также определить согласно (1.50) и (1.51) при выпол-
нении условий (1.72) и (1.73). Деформации, связанные с рас-
крытием трещин, задаем двумя неизвестными величинами:
еах и Fay Величина уахи определяется по (1.37). Суммируя
50
величины eaj[c₽ax» ....получаем:
= £*611 4" N ху ^613>
еу — еяу 4" Nu С022 -J- Nxy C^i3,
Уху = еах с tg2a-f-ea!/ tg2 а+М,Сб13+
4* Ny Со «з 4* Nxy С Сзз.
Неполная система (1.76) дополняется двумя статически-
ми уравнениями:
Nx sin а 4- Nvx cos а = 0; Nu cos а 4- A\(/sin а~0, (1.77)
которые следуют для данного случая из уравнений (1.67).
3. Схема пересекающихся трещин. Рассмотрим два слу-
чая.
1. Случай, когда силы зацепления и касательные напря-
жения в арматуре (та<) можно принять равными нулю.
Как указывалось выше, при схеме пересекающихся трещин
бетон разрывается трещинами по двум и более направле-
ниям и в результате полностью теряет способность самосто-
ятельно воспринимать усилия и характеризовать деформа-
ции элемента по какому-либо направлению. Он играет лишь
вспомогательную роль, оказывая влияние на средние де-
формации арматуры через коэффициенты фа/.
На основании рис. 1.16, а получим (по аналогии с (1.24)1
fai COS (fij -{- а),
I
^n = ^oaJajsin2(p, + a);
Ntn = ®ai fat $'П (Pi т
i
-I-a) cos (pH-a)-
(1 -78)
В данном случае по двум ортогональным площадкам ком-
поненты тензора сил совпадают с компонентами тензора
усилий арматуры в трещинах (правые части зависимости
(1.78)1. Если трещины не ортогональны, такое совпадение
будет по двум (и более при большем числе пересекающихся
трещин) наклонным площадкам. Однако можно показать, что
если компоненты тензора сил совпадают минимум по двум
непараллельным площадкам, то тензоры равны. Из этого
следует, что уравнения типа (1.78) в принципе необяза-
тельно составлять для осей трещин. Правые части уравне-
ний (1.78) можно записать в осях х и у и приравнять к уси-
51
лиям Л'х, Nv и Nxv (при этом индексы «л» и «/» заменяются
на «х» и «у» и а — 90°). Таким образом, напряжения в ар-
матуре в пересекающихся трещинах не зависят от направ-
лений трещин. Для трехосного армирования напряжения
в арматуре в трещинах о0Х, оа1/ и ап3 можно непосредственно
определить из формул (1.78). Деформации арматуры опре-
деляются согласно (1.10). Средние деформации арматуры
совпадают с общими деформациями элемента с трещинами
(т. е. еа1 = е<). Зная деформации элемента по трем направ-
лениям, легко определить углы сдвига ух„, используя пре-
образования типа (1.2), и получить полную систему физи-
ческих уравнений.
Для двухосного армирования (при /а3 = 0):
«х = ^Vx/(fax £L); е7=ад/а7^); =/Vwx = 0. (1.79)
Однако ух„ #= 0, т. е. в данном случае приходим к непол-
ной системе физических уравнений.

Рис. 1.16. К анализу схемы пересекающихся трещин
52
Рассмотрены случаи, когда число направлений арматуры
не превышает трех. При большем числе направлений задача
определения напряжений anJ и деформаций становится внут-
ренне статически неопределимой. Путь ее решения таков.
Составляем три уравнения типа (1.78) и к этим уравнениям
добавляем уравнения типа (1.2), связывающие относитель-
ные деформации элемента по направлениям i > 3 с дефор-
мациями по трем выделенным (базисным) направлениям.
Из многоосного армирования для пересекающихся трещин
практически интерес еще может представить схема с че-
тырьмя направлениями стержней.
2. Случай, когда касательные силы зацепления N3Xy
и ух и касательные напряжения в арматуре тах и тзу не
равны нулю (рис. 1.16, б, в). В этом случае напряжения в ар-
матуре в пересекающихся трещинах могут несколько зави-
сеть от их ориентации. Рассмотрим при армировании в виде
прямоугольной сетки трещины, проходящие нормально
к стержням арматуры. Пусть прямоугольные блоки бетона
между трещинами еще способны сопротивляться танген-
циальным перемещениям стержней. Нормальные напря-
жения Стах и сау будут определяться по формулам (1.79),
а деформации е{ = 8П{ — по (1.10). Новый элемент в этом
случае — появление жесткости на сдвиг.
Касательные силы (см. рис. 1.16):
Nyx = Nayx + ^ayfayi Nxy = У3ху + Taxfax- (1.80
Согласно (1.13) и (1.17) можно записать (рис. 1.16, г):
^зУх ^^ЛУХ^ТУ9 ^ЗХУ Xax = ~ &xlKxxi та7 ~ &yi Подставляя (1.81) в (1.80), получаем: л'.,-»—-; Л'-"=с-'/ С33 «ту с33 1 1 Л Г 1 . 1 АР - нЬдух I * pw JXJ С33 ь33 Окончательно можно записать: Yx!/ - -г- + сзз + Л\у СЬ = Чу Чх -зхУ^хх' 1 К.,. 1 (181) • 1 тх - + Л^- 0 82) Уху (Сзз -!- Сзз)- (1.83)
53
При выводе формул (1.82) и (1.83) мы считали, что де-
формации таковы, что можно еще пренебречь в уравнениях
(1.80) возможным искривлением стержней у трещин и изме-
нением их ориентации.
Ширина раскрытия трещин вдоль оси х (ахх) и вдоль
осн // (аг9) равна:
**х Gx Gx (/пх^лл)» (1.8-1)
§ 6. Экспериментальные исследования
и применение теории к расчету плоских конструкций
I. Опыты на железобетонных пластинах с фиксиро-
ванной трещиной (исследование параметров }.х и /.„). Схе-
мы проведения экспериментов представлены на рис. 1.17.
Опыты проводились на прямоугольных железобетонных
пластинах, имевших в среднем сечении (по /—/) клино-
видные вырезы. При центральном растяжении пластин
силой N по линии аЬ возникла трещина. В этой трещине
и изучались напряжения в арматуре. Ввиду того что пло-
щадь сечения образцов в местах вырезов была примерно
в 2 раза меньше площади сечений остальных областей пли-
ты, трещина aft оставалась фактически единственной вплоть
до разрушения образца. Таким образом, место прохождения
трещины было известно. Пластинки в местах предполагае-
мых трещин армировались таким образом (рис. 1.18), чтобы
арматурные стержни пересекали линию aft под разными уг-
лами; это давало возможность изучать поведение арматуры
при разном ее наклоне к линиям трещин,.
Для испытания пластин была законструирована спе-
циальная установка, позволявшая вести испытания образ-
цов по двум схемам. При первой схеме (см. рис. 1.17, а)
пластина подвергалась центральному растяжению силами
/V, которые равномерно передавались на четыре точки с
обеих сторон образца. При второй схеме дополнительно
устанавливалась система боковых динамометров. В процес-
се растяжения образца в динамометрах возникали горизон-
тальные силы 7\ и Ts вследствие того, что они препятство-
вали сдвигу берегов трещин. Последние приводил и к воз-
никновению на площадке трещины касательной силы Н
(см. рис. 1.17, б, в). Силу Н легко можно определить из
уравнения моментов сил, приложенных к половине образна,
относительно верхней линии динамометров (Д-1. Д-4 —
динамометры).
54
Рис. 1.17. Схема опытов на пла-
стинах с одной фиксированной
трещиной
а — первая схема испытания пластинок:
б — вторая схема испытания пластинок
(Д-1...Д 4 — кольцевые динамометры):
«—•статическая схема: г—к учету спя-
зсП по бетону в трещинах: / — направ-
ление сдвига предполагаемой трещи
ны 2, 3 — неподвижные (при испытани-
ях) опоры динамометров: 4 — подвиж-
ные опоры; 5 — жесткие диафрагмы;
6 — приспособления для замера сдвига
берегов трещин; 7 — уровни располо-
жения двух арматурных сеток; 8 — точ-
ки приложения силы .V по толщине
пластины: Я — металлические прокладки
Было испытано восемь образцов железобетонных плас-
тин. Каждые два образца имели одинаковые характеристи-
ки (табл. 1.1). Величина N°i характеризует опытную на-
грузку появления первой трещины. Первые трещины появ-
лялись у вырезов и имели, как правило, небольшую длину
(порядка 2—3 см). N™ — нагрузка образования сквозной
трещины по сечению /—/.
Образцы КП-45-1, КП-56-1 и КП-71-1 испытыва-
лись по схеме/, а образцы КП-45-2, КП-56-2 н КП-71-2—
по схеме 2.
55
Данные опытных образцов пластин
56
Рис. 1.18. Схемы армирования опытных образцов
В трещине имеем четыре неизвестные величины: оах,
Оау. Ъх. и тау. Связи зацепления берегов трещин (напря-
жения аэп и тзп/, см. рис. 1.17, г) мы стремились здесь
разрушить в результате одноразовой снагрузки-разгрузки»
образца после образования сквозной трещины.
Проектируя силы на осн х н у, получаем (см. рис. 1.17, в):
______ N sin a — // cosa—та>,
стах__------------ >
• ах
, Л7 cos а + Н sin а—тлх 7'лг
ал?/ — = »
* ау
где Fx и Fy — суммарные площади арматуры, пересекаю-
щей трещину в одном (л) и в другом (//) направлении. Сле-
дуя теории, эти зависимости по аналогии с (1.36) можно
записать в виде:
__ (/V sin а — /7 cosa) t __ (Д’cos а Ч-77 sin а)
<пх “ т? » ^а?/ 75
гпх Гау
Эти два уравнения и использовались для определения
коэффициентов и Х/7. Входящие в них остальные вели-
чины (7V, //, олх и олр) определялись непосредственно из
опыта для последовательной серии нагружений. При этом
an< определялись на основании замеров деформаций с по-
мощью датчиков, наклеенных на арматуру в местах трещин.
Опытные величины коэффициентов лх и представлены
на рис. 1.19 (график для 1Х преобразуется в график для
57
если на рис. 1.19 по осн ординат вместо величин а отло-
жить величины 90° — а). Теоретические значения, вычис-
ленные но формулам (1.33), представлены в виде линии /.
Кроме того, проверялись зависимости вида:
16/7ау fИ,г .
Hax fay « cos2 а 16/7пу fax ’
f ay
Паи fax tg2 a sin2 а + 16//ax fay ’ .
(1.85)
которые лучше (линия 2) совпадали с опытом в стадиях,
удаленных от момента трещинообразования (линии / и 2
построены при ПаХ = ПаУ — 1).
Исследование приближенных зависимостей для и ).;1
нельзя считать законченным. Для этого требуются допол-
нительные эксперименты с варьированием шага, диаметра,
взаимного влияния рядом расположенных трещин и т. д.
... Опыт КП45-1; КП-56-1,КП-714;
• ® - Опыт КП-Ч5-2; КП-56'Zj КП-71 -2
° ° ~ Опыт при См;
Рис. 1.19. Графики коэффициентов ?.»• (/, 2— расчет)
2. Применение теории к расчету балок-стенок с трещи-
нами. Покажем на примере балок-стенок, каким образом
можно проводить расчет реальных конструкций с учетом
процесса трещинообразования на основании предлагаемой
теории. Алгоритм разработан автором совместно с А. Л. Гу-
ревичем 150). Расчет балок-стенок производился на ЭВМ
«Минск-22».
Остановимся на основных моментах расчета. Вводя
функцию напряжений Эри (при этом уравнения равновесия
тождественно удовлетворяются), физические уравнения
(1.56) можно записать так:
(1 = 1. 2, 3),
(1.86)
где р — вес единицы площадки балки-стенки; — отно-
сительные деформации (ен = ел, е.,., = е,;, е33 = ух„);
Сц = Сц. Добавляя к уравнениям (1.86) уравнение
совместности деформаций
tee* , д- ец _ д'-
ду- * дх2 дх ду ’
(1.87)
получаем полную систему уравнений для решения задачи.
Граничные условия записываются так же, как и при рас-
чете балок-стенок без трещин, по рамной аналогии |12|.
Задача решалась методом конечных разностей, при этом
использовался подход, предложенный в работе 124]. Если
следовать традиционному подходу, необходимо, дважды
продифференцировав функции для ец (1.86), подставить их
в (1.87) и получить разрешающее уравнение. Затем это
разрешающее уравнение представить в конечных разностях.
Однако при этом необходимо выполнять громоздкую про-
цедуру дифференцирования переменных коэффициентов
Сц. Поэтому разрешающее уравнение составляем, не при-
бегая в явном виде к этой процедуре. Идея такова. Уравне-
ния (1.86) и (1.87) в отдельности записываются в конечных
разностях, а затем входящие в (1.87) относительные дефор-
мации для конкретных точек выражаются на основании ко-
нечно-разностного представления (1.86) через значения <р
в узлах разностной сетки. При этом также (что особенно
важно) происходит автоматически некоторое сглаживание
величин Сц, если они являются разрывными функциями
координат.
59
Решением системы уравнении будут значения <р в узлах
сетки. Определив «р, ио ([юрмулам (1.80) находили ех, г,, н
з затем из уравнений (1.27) определяли перемещения
и и v, при этом применялись центральные и односторонние
разности и учитывалась симметрия по осп х. Разностная
сетка была 6x9. Система уравнений решалась шагово-ите-
рационным методом последовательных приближений с не-
которыми особенностями. Эти особенности подробно рас-
смотрены в главе 2 при описании алгоритма расчета изги-
баемых плит, на примере которых впервые проверялась при-
нятая организация расчета. Если поля усилий отличались
в точках на очередных итерациях не более чем на 5%, то
считалось, что достигнута сходимость процесса, и перехо-
дили к следующему шагу нагружения, расчет начинали
с нагрузки, при которой трещин еще нет. Давая нагрузке
определенные приращения, постепенно прослеживали пе-
реход балки-стенки в отдельных точках из одной стадии
в другую, фиксируя процесс образования и развития тре-
щин.
Остановимся на стадиях работы конструкции в отдель-
ных точках, их определении и моделировании, полагая,
что в процессе нагружения элементы балки-стенки у точек
разностной сетки проходят следующие стадии деформиро-
вания: упругую и упругопластическую без трещин и упру-
гую и упругопластическую с трещинами. В последнем слу-
чае учитывалось развитие пластических деформаций в ар-
матуре в трещинах. В зависимости от стадии деформирова-
ния изменялись лишь коэффициенты С lh системы (1.86).
Стадию без трещин считали справедливой при
Л\,акс < Л'0.т. (1-88)
Величина Л’б.т определяется по формуле (1.7).
В стадии без трещин в общем виде модель бетона прини-
малась в виде модели нелинейного ортотропного материала,
осн ортотропии которого проходят вдоль осей п и /, сов-
падающих с направлениями площадок главных усилий
^макс ”
В осях ортотропии /1 и I физические уравнения имеют
вид (они уточнены но сравнению с (50|):
Л'п A’d'cfl+ffl) .
А'бл Л (Л'бП"Н-£б/)Л ’
^пРб(1 + »0 , .\'t .
(Есп т + i:bl)h ‘ £б/л’
Тп/ -- ^nt ,
h
I , 2)i6(I+m)
“r----------- I
i'ot Ь’бп»» + ^б< )
(1.89)
I
i<5n
60
Где III — | Л\макс^^мп111'
модули деформаций. При
< 0; Л^ыин < 0)
Рб 0,2; ЕОп и £С( — секущие
двухстороннем сжатии (Л\1а1*с <
(« = «,/);
1 мин I
Л/?пр кс
1;
(1.90)
с0 = 0,85 + 0,25
Зт
1 + 2}/т3
где kc определяется ниже по формуле (1.104); R — марка
бетона.
При напряженном состоянии «растяжение-сжатие» E6t
вычисляется по формуле (1.90), где kc = 1, ас0 заменяется
на (1 4- 0,5Лр), находится по формуле (1.8);
При А/Макс 0,5/Vq, т Eq, п Eq,
При Ломакс 0,5т ^б. п 0,5 Eq Nq, т/Л\|а|;с
(1.91)
При напряженном состоянии «растяжение-растяжение»
ЕбП и Eq{ определяются по формулам (1.91), где лишь при
определении Eq( Л\,а1!С заменяется на ЛГММн.
Для удобства при расчетах уравнения (1.89) необходимо
преобразовать к осям х и у. Эти преобразования легко вы-
полнить, используя (1.2). В результате для уравнений (1.86)
получаются следующие коэффициенты:
В (37, формулы (7G), (77)] указано, как учесть армату-
ру в матрице
Появление трещин определялось на основании (1.5).
Угол а вычислялся по формулам (1.4) для момента трещино-
образования и в дальнейшем считался известным.
61
Образование трещины приводит к изменению выраже-
ний для коэффициентов Сц в уравнениях (1.86). Коэффи-
циенты Сц определялись по формулам (1.57).
Входящие в Ctj величины vu находились по приближен-
ной формуле (3.16) из главы 3. Модули арматуры Е'ах
и E'ail до появления пластических деформаций вычислялись
по формуле (1.10), где:
Фа/ = 1 — 0,7.V0T '<таЛк 0,15 < фа/ < 1. (1.92)
В упругонластической стадии работы арматуры для оп-
ределения Е’„х и Ej у использовались формулы (1.11) и (2.77).
Коэ<|м|)ициенты пластичности vaZ, входящие в эти зависи-
мости, определялись по формуле (6) из работы (671.
Проанализируем данные расчета балок-стенок № 101 и
ЮЗ из опытов II. М. Нильсона (971. Эти данные частично
представлены на рис. 1.20.
Балка-стенка № 103: L — Н — 200 см; й = 8 см. Ци-
линдрическая прочность бетона Rn = 37 МПа (R = 7?ц/0,83).
Балка-стенка армировалась по всей высоте сеткой из про-
волоки диаметром 6 мм и тагом стержней 10х 10 см (/ах —
~ — 3.14 • 0.6М • 10 — 0,0282). Полные данные пред-
ставлены в работе (50|.
Балка-стенка № 101: L — Н — 100 см; й = 8 см; 7?ц =
— 41 МПа. Армирование было аналогично армированию
балки-стенки № 103. Пз рис. 1.20, а можно заметить, что
появление первых трещин (как в опыте, так и при расчете)
не приводило к резкому (скачкообразному) увеличению
прогибов.
Для всех рассчитанных конструкций наблюдалось значи-
тельное перераспределение усилий с развитием трещин.
Так, растянутая зона поднималась вверх, растягивающие
усилия Л'х по нижней грани уменьшались, а сжимающие по
верхней грани значительно (в 2—3 раза) увеличивались
(по модулю). На характер перераспределения растягиваю-
щих усилий в нижней зоне балок-стенок (кроме
трещин) оказало влияние также сравнительно раннее на-
чало развития неупругих деформаций в нижней арма-
туре.
Касательные усилия Nxv увеличивались в верхних и
уменьшались в нижних сечениях (до 30%), где была разви-
тая схема трещин, при этом в процессе растрескивания ор-
динаты максимальных касательных усилий несколько сме-
62
Рнс. 1.20. Графики проги-
бов и схем развития трещин
в балкс-стенке № 103 из
опытов П. М. Нильсона (Pl
d° т
и гт —соответственно тео-
ретическая и опытная на-
грузка трещинообразования;
Л — армирование)
а — прогибы (/ — опыт; 2 — рас-
чет); б —расчетные трещины
при нагрузках Р - 75—222 кН;
в — опытные трещины при на-
грузке Р-225 кН
щались: наверху — к точке приложения нагрузки Р, а
внизу — к опорам.
Отношение высоты балок-стенок к пролету заметно ска-
залось на характере перераспределения усилий N,r В
квадратной балке-стеике в зонах с трещинами, особенно
вблизи середины, наблюдалось существенное (до двух раз
и более) уменьшение сжимающих усилий Nyt а в сечениях,
лежащих над опорами, сжимающие усилия увеличивались
(в 2 раза и более). В прямоугольной балке-стенке Ле 103
этот эффект был выражен уже заметно слабее.
Характер развития теоретических трещин подобен опыт-
ному (рис. 1.20, б, в),
63
Рис. 1.21. К иллюстра-
ции процесса раз-
грузки
/ — разгрузка нслинсЛно*
упругого тела; 2 — рас-
четная линия разгрузки
и попторноЛ нагружи:
J — действительная ли-
ния разтрузкн. 4 — линия
иоптеркой нагрузки
Таким образом, анализ показывает, что расчет балок-
стенок необходимо производить с учетом трещин. Пред-
ставленная теория и разработанный на ее базе метод рас-
чета удовлетворительно описывают напряженно-деформи-
рованное состояние таких конструкций с учетом развития
трещин и нсупругих деформаций в арматуре и бетоне.
3. Учет локальных разгрузок при расчете балок-стенок.
В зависимостях (1.55), а следовательно и в (1.86), не учи-
тываются эффекты, связанные с разгрузкой. В то же время
расчет пластин на ЭВМ показал, что даже при увеличении
нагрузки пропорционально одному параметру (пропор-
циональном нагружении) после образования трещин про-
исходит перераспределение усилий и в отдельных точках
возможна локальная разгрузка. Это явление учитываем
так. Пусть в момент, предшествующий разгрузке, в некото-
рой точке О жесткостныс коэффициенты равны Clk. Если
в точке О происходила разгрузка, величины Cih не умень-
шались, а принимались равными Clh. Таким образом, раз-
грузка происходила по формулам (1.55) при Clh « C(k.
Процесс, который при этом происходит, легко представить
на примере деформаций центрально-растянутой железо-
бетонной призмы с трещинами, где
N — сила растяжения, а е — соот-
ветствующие ей относительные удли-
нения призмы. Примем, что призма
нагружается до некоторого уровня N
(точка О на рис. 1.21), а затем на-
чинается разгрузка. Жесткость приз-
мы, соответствующую силе Л', обо-
значим в виде C,v. Действительная
разгрузка произойдет по линии 3.
При закреплении жесткости Cn рас-
четная разгрузка произойдет по ли-
нии 2, а при использовании нелиней-
ного упругого тела — по линии /.
Очевидно, что разгрузка по линии 2
гораздо ближе соответствует действи-
тельности, чем по модели нелиней-
ного упругого тела, и при малых ло-
кальных разгрузках отклонения ли-
нии 2 от 3 мало скажутся на точности
расчета. При более точном подходе
деформации в уравнениях (1.55) не-
61
обходимо подразделять на обратимые и необратимые, при
нагрузке оперировать с их суммой, а прн разгрузке —
с обратимой частью.
§7. Условия прочности для элементов
плоских конструкций и их связь
с деформационной теорией
Начнем с элементов, уже имеющих трещины. Прочность
железобетонных элементов с трещинами будет зависеть от
двух факторов — прочности по арматуре и прочности по
бетону1. Составить единые’условия прочности, которые бы
учитывали эти два фактора, не удается, так как физическая
природа их различна. Поэтому факторы рассматриваем
в отдельности, устанавливая два вида условий.
1. Условия прочности элементов по арматуре притя,»0.
Пусть для начала конструкция армирована стерж-
нями, имеющими идеальные площадки текучести (от1 —
пределы текучести стержней). Будем полагать, что в момент
исчерпания прочности стержни всех направлений по неко-
торым линиям (трещинам разрушения) достигают теку-
чести. Кроме того, пренебрегаем касательными напряже-
ниями та/ в стержнях. Обозначим угол наклона линий теку-
чести к оси х через ат. Принимая в уравнениях (1.28) вместо
Ou величины от/, а вместо а -* ат и полагая та{ = 0, N3n =
= Nanl = 0, получаем:
+ (2. от1 fat cos pf sin Р/ — Nxy jeos aT = 0;
oT/ fa< sin2 3 Р/ — ) cos ar 4-
4- (S oTl fai sin Р/ cos pf — Лгж!/) sin aT = 0.
(1.93)
В этой системе однородных линейных уравнении sin aT и
cos aT одновременно не могут быть' нулями, значит опреде-
литель системы должен обращаться в нуль. Раскрывая
1 Для приопорных участков важной является также прочность
сцепления арматуры с бетоном, однако этот вопрос в книге не рас-
сматривается.
3 Зак. C3I
Ь5
определитель, получаем
— <\i fbi cos’ Р/ — Nx } Q <Тт| fnt Sin2 р.
(1.94)

Это и есть условие прочности элементов по арматуре, ко-
торое выведено в работах (33, 351; оно представляет, как
будет показано ниже, развитие известного условия
Л. Л. Гвоздева для изгибаемых плит на случай плоского на-
пряженного состояния. Если арматура не достигла теку-
чести, условие (1.94) будет выполняться в виде указанного
неравенства.
Величины, заключенные в скобках условия (1.94), со-
стоят из разности компонентов тензора предельных усилий
арматуры и компонентов тензора действующих усилий. Их,
следуя терминологии проф. А. А. Гвоздева [20]. называем
компонентами тензора запаса прочности по арматуре. Ис-
черпание прочности наступает в момент, когда на какой-то
площадке компоненты тензора предельных усилий в арма-
туре и компоненты тензора действующих усилий совпадают.
Естественно, на этой площадке компоненты тензора запаса
обращаются в нуль, т. е. для тензора запаса это будет глав-
ная площадка. Из этих соображений следует, что нормаль-
ные компоненты тензора запаса не могут быть отрицатель-
ными величинами (т. е. не может быть площадки, на которой
действующие усилия превышают те, которые способна вос-
принять арматура), отсюда:
(SoTJaicos2 Pi — Nx) 0; (SoT1/afsin2p, - ЛГу) > 0, (1.95)
i i
т. e. наряду с (1.94) должны всегда выполняться условия
(1.95).
Решая совместно уравнения (1.93), получаем также
lgar= ±] (^arJa/sin2p| — Nu]l(loTJa|Cos2p|—Ах).
(1.9G)
где знак < ±» будет обратен знаку величины
(EoT|/a<sin Picos pi — А'ш). Таким образом, линии теку-
чести могут не совпадать с первоначальным (в упругой ста-
дии) наклоном трещин а.
Представленная выше деформационная теория будет
состыкована с условиями прочности, если учесть в ней изме-
66
пение наклона трещин от а в упругой стадии работы армату-
ры до ат в предельной стадии и пренебречь в этой стадии ка-
сательными напряжениями тар Однако последняя предпо-
сылка является приближенной и при деформационном рас-
чете ее можно не вводить.
Предполагаем, что углы наклона трещин начинают изме-
няться в момент начала текучести (обычно принимали при
0,9<гт«) стержней одного из направлений (это можно опреде-
лить в процессе деформационного расчета). Обозначим ком-
поненты тензора усилий, соответствующие этому моменту,
через Л*, Ng и Nxy. Пусть ц0 — коэффициент, на который
необходимо умножить усилия N1, №у и N?y, чтобы условие
(1.94) выполнялось в виде равенства. Значение его можно
определить, подставляя в (1.94) для указанного момента
вместо Ny и Nxy соответственно i]0Ax, и
Аналогично определяются и промежуточные значения этого
коэффициента, которые обозначим в виде ц. В предельной
стадии 1] = 1. В упругопластической стадии углы наклона
трещин а можно определять по линейной интерполяции
между а упругой стадии (обозначим этот угол в виде ау) и
углом ат в функции от коэффициентов ц (при их изменении
от i]o Д° ’1 = 1)-
Если применяется арматура с упрочнением, то вместо
Oji можно подставлять о£ 2< (условные пределы текучести
стержней, соответствующие остаточным деформациям 0,2%)
и определять изменение угла наклона трещин от ау до ат
так же, как это указано выше. Однако, в отличие от идеаль-
но пластической арматуры, посте достижения а — ат рас-
чет можно не прекращать, а производить до тех пор, пока
стержни хотя бы одного из направлений не достигнут проч-
ности на разрыв. При этом может изменяться также вели-
чина ат, однако в первом приближении этим можно пре-
небречь.
Степень внутреннего перераспределения усилий, кото-
рая необходима для реализации указанного выше пласти-
ческого состояния, может оцениваться по разности |ат—о|.
Судя по данным некоторых экспериментов, армирование
(при тяжелых бетонах) должно подбираться так, чтобы
|ат — а| < 15 — 20° (хотя это ограничение еще требует
уточнения). При подборе ортогональной арматуры необ-
ходимо иметь в виду указанное ограничение на ат — а1
и учитывать тот факт, что расход арматуры на элемент
уменьшается по мере приближения ат к 45° (это легко дока-
зывается ИЗ условия <JT (fax fay) = ПИП ).
3‘
67
2. Условия прочности элементов по арматуре с учетом
та| и других факторов. Будем рассматривать эти вопросы
на примере ортогонального армирования при В. «= О
₽з = 90°. /аз = 0.
Условие прочности (1.94) для этого случая примет вид
(сттх/ах Nх) (<Уту [йу Nу)— Nxy— 0. (1.97)
Рассмотрим, как изменится условие (1.97), если теку-
честь в арматуре будет достигаться при совместном дейст-
вии нормальных <та( (их в пластической стадии обозначаем
в виде o*J и касательных та< напряжений. Согласно усло-
вию пластичности Мизеса
- Уаг<—ЗтЬ (I = х, у).
Заменяя для этой стадии в (1.28) аа/ на o*t, полагая jV3n=
= Want =0 (хотя в принципе ввести их в условие проч-
пости не трудно) и исключая угол а, получаем [по аналогии
с выводом (1.94) из (1.93)1:
(Nх~otK fax) (Nу~оfя,,) (Nx,J—xuvfa,/) (.Vx7—тах/ах) О
(1.98)
или, если использовать при этом вместо (1.28) уравнение
(1.31):
(Т- o*tifax- Nx\(4-otyfay-Ny}-Nly^O. (1.98а)
Сравнивая (1.98а) с (1.97), можно установить, что каса-
тельные напряжения, с одной стороны, влияя па о*х, умень-
шают прочность элемента с трещинами, а с другой стороны,
за счет Хх и (?.х, 1) увеличивают ее. При величинах
та< < 0,2оТ| можно принять « ат| н прийти к выводу,
что касательные напряжения в арматуре несколько увели-
чивают прочность.
Заменяя в (1.94)
агх ,,а о'х;).х\ ат;/ на о'и/).и и of3 На Z3oJ3, (1.986)
получаем условие типа (1.98а) для трехслойного армиро-
вания.
Условия прочности, установленные с учетом та<, более
точно описывают состояние элемента в предельной стадии,
однако требуют доработки по более точному определению
величин тЯ| или Zf.
68
Рассмотрим явление, которое может приводить к пони-
жению прочности. Можно представить себе случай, особен-
но при однородном напряженном состоянии элемента с раз-
витой системой трещин, когда из-за разброса углов наклона
трещин полное перераспределение усилий произойти не смо-
жет и арматура л-направления достигнет текучести по од-
ним трещинам, а арматура //-направления — по другим.
Такое явление будем называть явлением раздвоения линий
текучести. Пусть в результате такого раздвоения отклонения
углов наклона трещин неполной текучести от теоретической
липни полной текучести составят ± р. Тогда, заменяя ат
на (ат+₽) в первом уравнении (1.93) и на (ат —0) — во вто-
ром и исключая из полученной системы ат, вместо условия
(1.97) получим следующее:
1(^тх fax Nх) COS Р Nxy S1П 0] [(<Ттр fay - jVy) COS 0 —
—NxV sin 0] — [Nxy cos р + (oTxf0x—Nx) sin0~] [Nxy cos 0 +
+ (orJav —M(/)sinp] = 0. (1.99)
Непосредственное сравнение этого условия с (1.97) по-
казывает, что оно будет приводить к понижению прочности.
Реальный разброс трещин может составить 5° (т. е. 0 =
= 5е). Очевидно, в большинстве случаев указанные поло-
жительные и отрицательные явления будут компенсиро-
вать друг друга и их можно будет не учитывать.
3. Условия прочности элементов с трещинами по бе-
тону. Прочность элементов с трещинами при напряженных
состояниях «растяжение-сжатие» не может беспредельно
увеличиваться за счет увеличения армирования, воспри-
нимающего в трещинах растягивающие усилия, так как от
сжатия может произойти разрушение полос бетона между
трещинами. Чтобы этого избежать, необходимы ограниче-
ния по прочности бетона. Однако поведение бетона между
трещинами будет уже иным, чем в сплошном теле. Полагаем,
что разрушение полос бетона между трещинами происходит
в момент, когда максимальные по модулю главные сжимаю-
щие напряжения в бетоне ог>. мин превысят величину /?„,
где Rn — характеристика прочности полос бетона между
трещинами на сжатие (устанавливается на основании
экспериментов P18J). В среде между трещинами, кроме уси-
лий вбетоне, будуттакже усилия в арматуре, пронизываю-
щей полоски бетона. Па участках между трещинами будем
G9
учитывать средние напряжения в арматуре, обозначая н.к
как Одр Величины оа/ из-за сцепления арматуры с бетоном
даже в стадии ее текучести могут быть меньше аналогичных
напряжений в трещинах, т. е. oaJ от1. Пусть наклонная
грань призмы проходит не но трещине, а по площадке раз-
рушения бетона (см. рис. 1.13). Заменяя ав1 на о',, N3n на
Rtlh и полагая та/ » 0, N3nt «О, уравнения (1.28) можно
преобразовать к виду (1.93). Решая их, по аналогии с (1.94),
получаем
RH Л + °ai /al COs2 Pi ) h Г Nу —
(1.100)
Напряжения oaJ определяются из деформационного рас-
чета.
Величина
Ra « 2,51/Я0Япр.
(1.101)
где /?0 = 1 МПа (размерная константа).
Значение /?„ было установлено на образцах, подверг-
нутых кручению, где могут влиять факторы, не встречаю-
щиеся при деформировании пластин. Возможно также (по
мнению А. А. Гвоздева), что прочность Ra будет зависеть
от отношения ^МаКСЛУМ1|||. Поэтому величина Rn еще
требует исследования. Однако факт понижения прочности
бетона между трещинами на сжатие по сравнению с приз-
менной прочностью /?пр не вызывает сомнения.
Рассмотрим еще один вопрос. Пусть имеется ортотроп-
ное армирование и значительно нарушенное сцепление ар-
матуры с бетоном, так что фа< -> 1 и (1 — ?.<) -*• 0. Тогда,
подставляя значение (1.36) для аа4 вместо oaJ в формулу
(1.100), получаем
(Я..Л - Nxy ).х etg «)(/?,/! - Nxu ly tg a) - N'Xy > 0,
(1.102)
т. e. приходим к выводу, что на прочность бетона между тре-
щинами основное влияние в осях, совпадающих с направ-
лениями арматуры, оказывают касательные силы, а роль
нормальных сил мала. Хотя в общем случае такой вывод
сделать нельзя.
70
4. Прочность элементов без трещин при двухстороннем
сжатии (Аммане <0; А\,11Н < 0). Вопросам прочности бетон-
ных элементов при объемном и плоском напряженном состоя-
нии посвящены многие работы отечественных и зарубеж-
ных исследователей. Они подробно представлены в моно-
графиях 16 и 23], авторы которых также внесли большой
вклад в решение рассматриваемой проблемы, хотя здесь
и остается много нерешенных вопросов.
Ниже мы рассматриваем лишь один частный случай двух-
стороннего сжатия, но делаем попытку описать его более
тщательно и в виде, удобном для увязки с деформацион-
ными зависимостями (1.89). Экспериментальные исследо-
вания различных авторов убедительно показывают, что
при двухстороннем сжатии происходит увеличение проч-
ности бетонов. Учитывая это условие прочности бетона при
двухстороннем сжатии, можно записать:
| | (1.103)
где Ас — коэффициент, учитывающий, влияние двухосного
сжатия на увеличение прочности элементов,
k ~ । । 3Rp Г ।_____/ (1 с) (>и — 0.65) \- .
С У?пр L \0,65-рс(/л—0,65)/
/П = -'-чакс
А мин
(1.104)
(величина 3RP принята с некоторой осторожностью). Не-
обходимо иметь в виду, что сжимающие напряжения везде
приняты за отрицательные, поэтому |A\,„,| >|Л'М.1КС|.
Коэффициенты с зависят от марки бетона, и их значения
можно принимать такими же, как и в выражении (1.8) для
«р.
При расчете железобетонных элементов в ряде случаев
необходимо учитывать армирование. Компоненты тензора
усилий в этом случае будут составными величинами. По-
этому в зависимостях (1.103) и (1.104) вместо общих главных
усилий N„WI и А/Макс должны фигурировать главные уси-
лия бетона (А^-мик » А^г, Ма.<с). Эти условия также можно
представить в виде (1.100), где вместо /?„ следует подста-
вить RBPkc. Напряжения в арматуре о°( могут быть опре-
делены из условий совместности относительных деформаций
бетона н арматуры 137] (епх=ех == оах/Епх; г?лу1Еау = и
т. д.), которые для элементов без трещин могут считаться
справедливыми (за исключением приопорных участков).
71
«опорных участков eat — С; = dgtldxt. Кроме того,
к ^.нм уравнениям, чтобы получить замкнутую систему
уравнений, необходимо добавить функции сцепления
т = f(gt) и известные статические уравнения для стержня
_ <0 <)<тм
ГЛАВА 2
.МОМЕНТНАЯ ТЕОРИЯ ГЛАДКИХ ПЛИТ
И ЭЛЕМЕНТОВ ОБОЛОЧЕК С ТРЕЩИНАМИ
§ 1. К изложению теории. Краткий обзор
Основная цель исследований заключается в выводе
физических уравнений для железобетонных плит и оболо-
чек при разнообразных схемах трещин. Исследования про-
водим на примере изучения работы с трещинами некоторых
малых в плане характерных элементов, выделяемых нз кон-
струкции. Ввиду того, что прн этом принципиальных раз-
личий между характером работы малого элемента плиты
и оболочки не будет, мы придерживаемся следующей схемы
изложения теории. Рассматриваем в основном пластины,
для оболочек лишь указываем особенности применения
установленных зависимостей к их расчету.
Изложение теории начинаем с рассмотрения самого
общего случая, касающегося совместного действия на
элементы всех трех моментов (изгибающих и крутящих)
и трех сил (нормальных и касательных).
Рассматриваемые элементы считаем такими, что можно
пренебречь влиянием поперечных сил на их деформатив-
пость и прочность как до, так и после появления трещин.
В силу принятых ниже гипотез (п. 4, § 1) рассматривае-
мые плиты относятся к категории тонких плит. Если
возможно пренебречь действием поперечных сил, то полу-
ченные выводы можно распространять и на пластины сред-
ней толщины. К тонким плитам в теории упругих изотроп-
ных плит относят такие, у которых (Л//)$^0,1; для оболочек,
кроме того, (It IRt) 0,05, где Л—толщина, Rt—мини-
мальный радиус кривизны, I — меньший размер в плане.
Для пластин средней толщины Л.7 0,2. С появлением
72
тпещин эти характеристики гибкости плит нуждаются
руточнении и могут приниматься лишь как весьма при-
ближенные, однако очевидно, что более жесткими они не
становятся.
Идея построения данной модели плит с трещинами пред-
ложена автором в работах [30,31]. Дальнейшее развитие эта
идея нашла в работах [21, 32, 37, 47 и др.1.
Экспериментальные исследования проводились автором
совместно с С. М. Крыловым и А. В. Бильчеико [9, 21], а
описанные способы расчета плит на ЭВМ с учетом процесса
трещннообразования разработаны совместно с Л. II. Яри-
ным и А. Л. Гуревичем [24, 38].
Используя установленные нами физические зависимости,
Л. И. Ярнн построил способ расчета на ЭВМ цилиндриче-
ских оболочек с трещинами [83], а В. I I. Соломин и И. II. Ши-
шов-способ расчета круглых фундаментных плит [76].
И. Е. Прокопович и А. Ф. Яременко [74, 84] дополнительно
учли деформации ползучести при расчете плит с трещинами
по теории автора. Однако объем книги не позволяет под-
робнее остановиться на всех этих исследованиях, как и на
исследованиях других авторов. Укажем только, что попыт-
ки иных подходов к расчетам отдельных конструкций с тре-
щинами сделаны: для пластин—в работах А. А. Гвоздева,
С. М. Крылова и А. Н. Королева [55,57]; Е. А. Палатни-
кова(73];Я-Д. Лифшица иМ. М. Онищенко [63]; Л. Н. Зай-
цева [29]; Ф. Леви [94]; В. Н. Байкова и В. Ф. Владимиро-
ва [3]; Г. А. Гениева и Г. А. Тюлина [22]; В. М. Бондарен-
ко, И. Т. Тнмко и А. Л. Шагина [10]; В. В. Чижевского
[82] и др.; для оболочек—в работах X. X. Лауля [59];
И. Е. Милейковского [641; 10. В. Чнненкова [80] и др.
Частичный обзор исследований дан в работе [75].
Особенности применения теории к расчету предвари-
тельно-напряженных конструкций изложены в рабо-
92. Схемы трещин и схемы армирования.
Предпосылки и гипотезы предлагаемой теории
I. Классификация трещин и условия, описывающие их
образование. Характер деформирования железобетонных
пространственных конструкций в областях с трещинами
зависит от схемы трещин, т. е. ориентации трещин относи-
тельно направлений армирования, взаимного пересечения
73
^/иш, возникновения трещин на одной или обеих по-
верхностях элемента, характера прохождения трещин по
толщине элемента (сквозные или несквозные трещины).
Сквозные трещины встречаются при безмоментном напря-
женном состоянии или при дополнительном действии не-
больших моментов. Предполагается, что трещины нормальны
к срединной поверхности элементов.
Разнообразие трещин в элементах можно свести к шести
схемам.
I -я схема — пепересекающиеся трещины проходят на
одной из поверхностей: нижней (схема /«) или верхней
(схема 16); при этом в элементах имеется растянутая зона
с трещинами и сжатая зона без трещин (рис. 2.1, а, б; эле-
менты 9t, и Э.,).
2-я схема — элемент пронизан непересекающимися
сквозными трещинами (рис. 2.1, в; элемент Э3).
3-я схема — трещины разных направлений имеются одно-
временно на нижней и верхней поверхностях элемента
(рис. 2.1, г; элемент 5t). Они часто встречаются в угловых
зонах плит, где действуют большие крутящие моменты.
В верхней и нижней зонах имеются полосы бетона между
трещинами, воспринимающие силы сжатия (они представ-
ляют своеобразный тип «сжатых зон», пронизанных трещи-
нами).
4-я схема — на одной из поверхностей элемента — ниж-
ней (схема 4а, рис. 2.2, а, а, а, элемент Э5) или верхней
(схема 46) проходят пересекающиеся трещины двух и более
направлений.
5-я схема — элемент пронизан пересекающимися сквоз-
ными трещинами (рис. 2.2, б; элемент Эв).
6-я схема — на одной из поверхностей имеются непере-
секающиеся, а на другой пересекающиеся трещины (рис.
2.2, в; элемент Э-).
Все схемы могут быть разделены па две крупные группы:
группа Н—непересекающпхся трещин (см. рис. 2.1), к ко-
торой относятся схемы 1, 2,3, и группа П— пересекаю-
щихся трещин (см. рис. 2.2), к которой относятся схемы
4, 5 и 6.
Срормулнрусм условия, при которых возникает та или
иная схема трещин. Этот вопрос сводится к рассмотрению
условий трещинообразования.
Условие отсутствия трещин в железобетонных плитах
при равенстве нулю нормальных енл предложено в работе
74

г.<оролева и С. М. Крылова 155] и записывается в виде
ЛI мак с С AU.t = Л’ЯР/ЗД (2.1)
где А10>т — упругопластический момент трсщинообразова-
ния, отнесённый к полоске плиты шириной
6=1.
Формула для Л10.т предложена Б. Г. Скраматаевым.
В условии (2.1) учитывается развитие неупругих деформа-
ций в бетоне растянутой зоны, но не учитывается армиро-
вание, которым можно пренебречь 1551.
Рассмотрим более общие условия трещипообразования
для элементов, подверженных совместному действию момен-
тов и нормальных сил. Предложение сводится к распростра-
нению теории ядровых моментов трещипообразования стерж-
невых систем, предложенной Л. А. Гвоздевым и С. М. Дмит-
риевым 117], на более сложные железобетонные конструк-
ции плит и оболочек. Этот вопрос с учетом произвольного
армирования подробно рассматривался в работе автора
137]. Здесь же остановимся лишь на идее этих условий и
приведем их выражения без учета арматуры.
4 •/ схема трещин
jа схема трещин 6-х схема трещин
Рис. 2.2. Схемы пересекающихся трещин
а, с7. а — фрагменты попсрхностсА плиты с 4 А схсмоЛ трещин; б —то же.
с Б А схемой; а — то же. сИ схсмоА трещин (остальные обозначения см. на
рис. 2.1)
76
Две поверхности в элементе, отстоящие от соенпв.п-
верхности на расстоянии гле г __ », У сРединнои по-
ветственно верхней и нижней поверхностями’оназовсм Соот'
Величина г„ определяется как даяполоски птеты поЛ^'’^’
ле сопротивления материалов. плиты по форму-
Введем два новых тензора ядровых мми»».
пойнтам,. Ж„х. Л|„„ „ Л-1,,,,, где МОМС"ТОВ: с ком-
= Л(> + Л1„ = м„ + .V,r„; = Л(^ +
т NХуГп, о)
а другой с компонентами ' '
М” " -ЛМ-+ У” = ~Л,‘ + N> г„;
Л/,„----Л/„ + Л'„гп. (23)
иоет?пХо™хХ«Гво™Х-™
поверхности. Определяем экстремалы,ыеховдн^та?
зоров ядровых моментов ЛЕ, Af '1';;,поненты тен-
н величины нормальных сил''сД' ямм" Л/,ял”?'!С’л^я-
аналогичных площадках ядровых моментов я” ”а
При совместном действии сил и момм.™» ™
Л/с.т следует уточнить и кроме нее ввести ionn™u™4“Hy
величину Мб.г. На основании работ (37, 511 можно^апи-
Л4б.т = kNkvRtJi 3,5. (2.4)
Здесь kN—коэффициент, учитывающий влияние нормаль-
ных сил на изменения момента трещииообра-
зования (2.1), где:
при Л/?р > JVnl > 0 /г.у» 1—0,4Arnl/(/?p/0; 1 -2 5«
приЛГя1<0 kN 1 -0,4 [Л\11/(/»/?п1,)г]. )
При N„t < 0 коэффициент k,N принят с некоторым прибли-
жением и требует уточнения. Последние исследования, вы-
полненные в НИИЖБ, указывают также на необходимость
снижения в этом случае и величины г„; с некоторым при-
ближением при Nnl < 0 можно принять
В формуле (2.4) коэ<|х(>нциснт /гп учитывает влияние двух-
осного напряженного состояния на момент трещинообразо-
вання (при NM > 0 kp = 1, при N„2 < 0 kp определяется
177
по'формулс fT.9), где вместо AZMII11 вводится величина
С некоторым приближением можно также принимать
*Р « 1 - (^15//?,.рЛ)2.
Аналогично определяется величина Л1б.т- В этом случае
в формулах для A’.v и А’р вместо Л7,,, и -V„, подставляются
величины Л’я! и Л',,». Условие отсутствия трещин форму-
лируется так:
для нижней зоны элемента:
м
А1„. макс
А^б.т»
я. мин
< Afe.t;
(2-7)
для верхней зоны элемента:
А1я. макс Мб.т« А1я. мин Afg,T.
(2.8)
Если нарушается первое условие (2.7), то образуется
трещина по схеме 1а (см. рис. 2.1, а), которая проходит по
площадке действия главного ядрового момента Л1я.макс*
Угол наклона этой площадки (трещины) к оси х в момент
нарушения первого неравенства (2.7) можно определить из
известного выражения
1g СС = (А1я. макс—А/ду)/Л1я xj. (2-9)
При нарушении первого неравенства (2.8) образуются
трещины по схеме 16 (см. рис. 2.1, б). Угол наклона верх-
ней трещины к оси х определяется по аналогии с формулой
(2.9):
tg а' = (ЛЦ. макс-(2.9а)
Одновременное нарушение первого условия (2.7) или
первого условия (2.8) и дополнительного неравенства N„x
0,75^p/i указывает на образование трещин по схеме 2
(см. рис. 2.1, в). Дополнительное неравенство устанавли-
вается на основании предположения, что сквозные трещины
образуются в момент, когда по сечению имеет место одно-
значная трапецеидальная эпюра растягивающих нормаль-
ных напряжений, равных на одной из крайних и срединной
поверхности а на другой крайней поверхности — нулю.
Одновременное нарушение первого неравенства (2.7)
и первого неравенства (2.8) указывает на образование тре-
щин по схеме 3 (см. рис. 2.1, г).
Нарушение двух неравенств (2.7) указывает на образо-
вание трещин по схеме 4а (см. рис. 2.2, о), а нарушение двух
неравенств (2.8) — по схеме 46.
78
Предполагаем, что одновременное нарушение условий
(2.7) и неравенств /V(ll < 0,75/?.,Л и Л',р < 0,75/?.,А или
(2.8) н неравенств < 0,750 и N'„2 < 0,75/?Ji ведет
к образованию трещин по схеме 5 (см. рис. 2.2, б).
Одновременное нарушение условия (2.7) и лишь одного
из неравенств Nnl 0,75/?рА или <: 0,75/?рА или
условий (2.8) и лишь одного из неравенств N’nl 0,75/?рЛ и
дг'з < 0,75/?гЛ указывает на образование трещин (см.
рис. 2.2, в). Необходимо отметить, что дополнительные огра-
ничения по величине 0,757? Ji справедливы лишь для момента
перехода элемента из стадии без трещин в стадию с соот-
ветствующей схемой трещин. Если трещины уже есть, пе-
реход трещины из несквозной в сквозную может быть опре-
делен по напряжениям в бетоне над трещиной или под
ней.
2. Общая схема армирования. Рассматриваем в общем
виде элементы, армированные шестью слоями, три из кото-
рых (/ = 1. 2, 3) расположены у их нижней поверхности
и три (i=l', 2', 3') —у верхней (рис. 2.3, а). На рис. 2.3, б,
в нижние слои армирования выделены отдельно. В плоско-
сти хОу нижний слой i характеризуется 1см. (1.21)] углом
р, наклона стержней i к осн х и коэффициентом армирова-
ния /ai (fa! и ₽/ — характеристики верхних слоев). Расстоя-
ние от середины нижнего слоя i до верхней поверхности
пластины обозначим через hit а расстояние от середины слоя
i до нижней поверхности — через Л,'. Обычно два слоя в
верхней зоне (например, i — 1, 2) и два слоя в нижней зоне
(< = 1, 2) представляют собой ортогональные сетки, на-
правление стержней которых совмещаем с направлением
осей координат хну (т. е. 0t = 0[ =0; 02 = 02 = 90е).
Третьи слон характеризуются рядом стержней, установ-
ленных под некоторыми произвольными углами 0- и 0з
к плоскости хОг.
Полагая коэффициенты армирования отдельных слоев
равными нулю, можно получить практически почти все
встречающиеся частные схемы армирования. Для схем
с пересекающимися трещинами трехслойное армирование
не применяется, поэтому учитываем лишь двухслойное ар-
мирование в виде прямоугольной сетки.
В дальнейших расчетах еще каждую тройку слоев будем
совмещать в один обобщенный слой (т. е. переносить на один
уровень). Срединная поверхность нижнего (верхнего) обоб-
щенного стоя отстоит от верхней (нижней) поверхности
79
>ны на расстоянии h0 (Ло), где
Л| fal + 7л! + Лэ f.)3 .
’ »
/а1 + /а2 +/аЗ
hi-
л;/згьл^:.2+^/'5
f:t+/;2+/a'3
(2.Ю)
где fni определяются по формуле (1.21).
Чтобы компенсировать неточность, связанную с совме-
щением слоев армирования на один уровень, необходимо
величины, вычисленные по формулам (1.21), умножить на
корректирующие множители, а именно:
/»1—0,5.гт
/(□ ~~О.5хт
л;-о.5х;
л;-о.5х; *
(211)
где xt iixj — соответственно высота сжатой зоны бетона над
трещинами нижней зоны и под трещинами верх-
ней зоны элемента. В практических расчетах
выражения (2.11) можно заменить более про-
стыми:
fal ~ ^а/ (^о ^i)>
fa'i « F'al h'i/(lli S').
(2.11a)
Смысл выражений (2.11) и (2.11a) будет ясен из способа
определения напряжений в арматуре, указанного ниже.
В дальнейшем в обозначениях fai, fai индекс «1» будем
заменять на х, индекс «2» — на у (т. е. /а1 = [лх, —
~fav)-
3. Некоторые общие особенности деформирования эле-
ментов с трещинами, принципы их моделирования. Для
элементов с первой схемой трещин (для примера предполо-
жим, что трещины имеются на нижней поверхности Эх на
рис. 2.1) укажем на следующие характеристики, положен-
ные в основу расчетной модели. Трещины делят элемент по
толщине на две зоны: верхнюю над трещинами и нижнюю
с трещинами. Понятие о нсдеформированной срединной по-
верхности, даже при чисто моментном напряженном состоя-
нии, теряет свой смысл. Усилия передаются через свобод-
ные от трещин слои бетона и обобщенный слой армирова-
ния. Для удобства решения задачи действие напряжений по
вертикальным сечениям системы заменяется действием обоб-
щенных величин: моментов и.нормальных сил, приложен-
ных на уровне срединной поверхности. Выражения для
80
ян
Условные обозначения
б слоя армирования
1,2,3)
арматурный стер'
жень, Far площади
стерженей
Рис. 2.3. Схема армиро-
вания элемента пластины
а —элемент; б —слои арми-
рования; в — расчетная схе-
ма армирования (НС А и
ВС А — обобщенные слон ар-
мирования: нижний и верх-
ний)
моментов и нормальных сил в функции от напряжений
в арматуре и бетоне находятся иными путями (§ 3), чем в тео-
рии упругих пластин. Закон парности крутящих момен-
тов может быть принят лишь с некоторым приближением.
В верхней зоне над трещинами работает слой бетона.
В нижней зоне с трещинами бетон выключается нз работы
только в местах трещин, где все усилия передаются через
арматуру.
Ранее уже подчеркивалось, что железобетон представ-
ляет собой двух компонентную систему и появление трещин
приводит к нарушению сплошности одного компонента (бе-
тона), и то, в данном случае, лишь в одном направлении —
перпендикулярно к трещинам. Вдоль трещин полосы бето-
81
(например, заштрихованная полоса на рнс. 2.1, а) будут
самостоятельно воспринимать усилия и определять дефор-
мативность элементов в этом направлении. Наличие сил
сцепления между арматурой и полосами бетона обеспечи-
вает их совместную работу. Напряжения и деформации в рас-
тянутой арматуре и верхнем сжатом бетоне на участках
между трещинами распределяются неравномерно. Вблизи
трещин они увеличиваются, с удалением от трещин — зату-
хают. Однако расстояние между трещинами обычно мало
по сравнению с размерами плит в плане, что позволяет
усреднить деформации арматуры и бетона на участках между
трещинами по аналогии с тем, как это сделано в теории
В. И. Мурашова [18, 691. Коэффициенты усреднения не
содержат определенных размеров элемента, что особенно
важно, а выражаются соответственно в функции от макси-
мальных напряжений в арматуре в трещинах и бетоне над
трещинами, а последние связываются с компонентами тен-
зора моментов и нормальных сил.
Элементы со 2-й и 3-й схемами трещин отличаются от
элементов с 1-й схемой тем, что у них нет сплошной сжатой
зоны бетона. При 2-й и 3-й схемах трещин характерно
активное участие арматуры и полосок бетона между тре-
щинами в работе элемента как в верхней, так и в нижней
его зонах. Элементы с трещинами группы П отличаются от
элементов с трещинами группы Н принципиально тем, что
бетон в зонах с трещинами ввиду нарушения сплошности по
двум и более направлениям уже не может самостоятельно
воспринимать усилия и определять деформации элемента
в каком-либо направлении (бетон в зоне с трещинами играет
второстепенную роль, оказывая лишь влияние на деформа-
ции арматуры).
4. Основные гипотезы.
а. Гипотеза прямых нормалей применительно к плитам
с трещинами. Рассмотрим этот вопрос на примере элементов
с 1-й схемой трещин (когда трещины в нижней зоне). Пусть
1234— прямоугольное сечение элемента по высоте некото-
рой плоскостью nOz (рис. 2.4, о; 1—2 — линия на сжатой
поверхности; 4—3—линия па уровне обобщенного слоя
армирования). В процессе изгиба плиты прямоугольник
123 4 искривляется (рнс. 2.4, в). При этом после появления
трещин боковые стороны 1—4 и 2—3 также искривляются
(пунктирные линии L на рис. 2.4, в) и арматура несколько
смещается относительно бетона в зависимости от удаления
от линии трещины. Однако полагаем, что если провести
82
6)
Рис. 2.4. К определению кривизн дли элементов с трещинами
касательные к линиям 1—2 и 4—3 в точках / и 4 (или 2 и 3)
и восстановить к ним нормали, то нормали точек 1 и 4 (или
2 и 3) совпадают (пройдут по прямым 1—4 и 2—3). В этом
суть модификации гипотезы прямых нормалей применитель-
но к элементам с трещинами. Совпадение нормалей легко
позволяет определять среднюю кривизну линий 1—2 и 4—3.
Известно, что средняя кривизна плоской линии Л = а/МЛГ
(рис. 2.4,6; Л1ЛГ — длина дуги; а—угол между каса-
тельными в точках М и ЛГ, рад). По аналогии с этим кри-
визна линии 1—2: kn = а/(1 + е„), а линии 4—3: k„ =
= а/(1 4- е„), где е„ и еп — средние относительные удли-
нения отрезков 1—2 и 4—3 (здесь и ниже мы оперируем с де-
формациями как с положительными, знак выявляется на ста-
дии выражения их через усилия). Используя гипотезу сов-
падения нормалей, можно получить:
а « tg а « AL//j0 = (еп — е^)/Л0
Учитывая это, окончательно получаем

ъ*
кп
Ло(1+е')
Ло О + ел)
/S' Ь ---
кп —
(2-12)
где принято (1 + г,,) (1 + е„) » 1.
83
•величину gn' Рудем~вазывать кривизной элемента по на-
правлению п и относить к его срединной поверхности.
Таким образом, кривизна элемента с трещинами по лю-
бому направлению может быть выражена через относитель-
ные деформации на двух поверхностях (эти поверхности
в дальнейшем называются расчетными) по этому направле-
нию и расстояние между расчетными поверхностями. По
предложению А. А. Гвоздева формула (2.12) впервые начала
широко использоваться для расчета балок с трещинами.
Искривление слабо изогнутой поверхности, согласно
работе (771, будет характеризоваться, например в осях х и у,
тремя величинами: изгибными кривизнами kx и ku (по на-
правлению х и у) и кривизной кручения kxy. По аналогии
с (2.12) их можно выразить через средние деформации на
верхней (ех, е'и, ,yY^)i< нижней (ех, е„,5-уХ!/) поверхностях
Л* м
так:
2ЛхУ = ^-^.. (2.13)
Поясним дополнительно вывод зависимости для kxy.
Согласно [771 кривизны являются тензорными величинами,
в результате
kn = kx sin’ а + k„ cos ’а + 2kxg sin a cos а,
a с другой стороны,
(ex — e*) sin* а 4- (fy—e*) cos» а+(Уху—Уху) sin a cos a
Ло
Сравнивая два последних выражения, приходим к зави-
симости (2.13) для kxy.
Формуле (2.12) можно дать еще одну трактовку, если
усреднение деформаций производить на базе расстояния
между трещинами. Дспланация линий 1—4 и 2—3 будет
увеличиваться по мере приближения к трещинам и умень-
шаться где-то посередине между трещинами. В. И. Мурашев
(691 и некоторые другие авторы при исследовании балок
с трещинами полагали, что посередине между трещинами
линии типа 1—4 и 2—3 можно принять прямыми. Тогда
средние (на базе расстояния между трещинами) кривизны
М
любой поверхности внутри Ло, параллельные линиям 1—9
и 4-3, могут быть определены по формулам (2 12) а спел
нне деформации элемента по толщине бу!ут распределять™
по линейному закону (рис. 2.4, г; линйя 7 или S) Нами
мер, на уровне срединной линии 5—6 h р
еоп = ел + (еп tn)-~-h/h0. (2.14)
Таким образом, применительно к указанным средним
деформациям элемента с трещинами можно считать споа-
ведливои гипотезу прямых нормалей для всей толщины
элемента. Очевидно, с большей точностью эта гипотеза 6v
дет выполняться для сечений элемента вдоль третий
Кроме трех кривизн, деформации элемента с трещинами
будем характеризовать тремя средними деформациями
и’ох» и Тоху) на уровне срединной поверхности опоеле-
ляя их по формулам (2.14). Для элементов со сквозными
трещинами кривизны могут выражаться через деформации
элемента на уровне нижнего и верхнего обобщенного слоя
армирования.
В отличие от пластин в оболочках, величины k k
kxy будут представлять собой приращения кривизн
б. Как и в теории упругих плит и оболочек, принимаем
статическую гипотезу, согласно которой влияние напряже-
нии на площадках, параллельных срединной поверхности
при расчете деформаций можно не учитывать. ’
§3. Анализ напряженного
и деформированного состояния элементов
при различных схемах трещин
1. Элементы плит с первой схемой трещин. Схематиза-
ция работы бетона над трещинами. Определим отдельно
деформации элемента от действия усилий в трещинах и на
площадках, нормальных к трещинам.
Напряжения и деформации элемента от действия уси-
лии9 приложенных по сечению 3 совпадающему с трещиной.
Рассмотрим первоначально элементы с нижними трещина-
ми (рис. 2.1, а и 2.5, п). Выделим из элемента треуголь-
ную призму, отсеченную по нижней трещине (рис. 2.5, б).
В трещинах усилия передаются через арматуру, которая
воспринимает продольные и касательные к направлениям
стержней усилия. Эти усилия прилагаются непосредствен-
но в местах трещин, на чертежах они схематически выне-
85
сены за пределы трещины. Усилиями зацепления берегов
трещин тина ^Vail и Л\п# пренебрегаем. Обозначим высоту
бетона над трещинами через .гг. Эпюры напряжений в бето-
не над трещинами являются криволинейными, кроме того,
в бетоне над трещиной возможны еще некоторые растяги-
вающие напряжения. Однако влиянием растянутого бетона
над трещинами пренебрегаем и в расчет вводим прямоуголь-
ные эпюры сжимающих напряжений бетона над трещинами.
Принятие указанной выше схематизации работы бетона
над трещинами обладает тем преимуществом, что позволяет
установить аналогию между средними модулями деформа-
ций бетона и арматуры в пластинах и балках и использо-
вать* выражения последних (с некоторой модификацией)
также и для расчета пластин и оболочек и, таким образом,
сделать модель доступной для расчетов.
При анализе деформаций бетона пренебрегаем влиянием
арматуры, расположенной в сжатой зоне, и поперечными
деформациями бетона.
Расчетная схема представлена на рис. 2.G (abc— средин-
ная поверхность). Составляем два уравнения равновесия
моментов относительно осей / и // (оси проходят через центр
тяжести сжатой зоны параллельно осям х и у}:
(Мх + Nx z6) sin а + (AfUx + NUxz6) cos a =
= KL si» “ + a.3 /азsin (a + P3) cosp3—
— Ta-/ fav cos a—таЭ fa3 sin (a + p3) sin p3] r,
(Afu + ?c) cos a + (Af,y + NxV zG) sin a =
= l°av /a v cos a + aa3/a3 sin (a + p3) sin p3 4-
+ Tax fax sin a 4- Ta3 fa3 sin (a + p3) cos p3] z.
(2.15)
Можно установить аналогию между уравнениями (2.15)
и (1.28), записанными для трехслойного армирования.
В результате решения уравнения (2.15) придем к форму-
лам (1.34) для напряжений в арматуре стах, аау и оаз, где
необходимо заменить:
Л’х на (Mx + Nxzc)/z; Nv на (Л1,, Ny zc)/z\
Nyx на (МУх+ Nyxz0)/z', NxV на (MxV + Nxvz6)z.
(2.16)
Деформации арматуры ея< определяются по формулам
(1.10).
Составляя два уравнения равновесия моментов относи-
тельно нижнего обобщенного слоя армирования, получаем
86
Рис. 2.5. К анализу первой схемы трещин
а- элемент с нижней трещиной; б-схема напряжений в бетоне и апмлтгпл
по сечению, совпадающему с трещиной; / — края тпешнны- 7—ЛЛ?МаТ>ре
бетона над трещиной; 3 — растянутая зона бетона над трещиной я Зона
Рис. 2.6. Рас-
четная схема
усилии и напря-
жении в арма-
туре и бетоне
на площадке
нижней тре-
щины
87
значения проекций напряжений в бетоне над трещинами на
ОСН X И у (оСх II Обу)-
о6х = — [(Л/я—za) sin а + (МУх—NVx ?а) cos а]/(глт);
а0. у = — 1(Л1„—t\'y za) cos а+(AfхУ—Nxy za) sin a]/(zxT).
(2-17)
Нормальные Gon и касательные тСп| напряжения в бето-
не над трещиной раины:
об п ~ обх sin а + сс,у cos а;
тбп| = —• <Vx cos а + °СУ sin а.
Предполагаем, что бетон над трещинами деформируется,
как некоторый ортотропный материал. Сначала определяем
составляющие общих деформаций отдельно от усилий иа
площадках, проходящих по трещинам, и площадках, нор-
мальных к трещинам, а затем их суммируем.
Средние деформации элемента на верхней поверхности
от действия Обп н тСп| равны:
Рбп = ос„/£б: Тбп« = тСл</£б; «6/ = 0, (2.19)
где Ес — модуль деформации бетона на верхней сжатой по-
верхности перпендикулярно к трещинам.
Используя преобразования компонентов тензора при
повороте осей координат и выражения (2.19), получаем
средние деформации бетона вдоль осей х и у:
е<5* = обх sin а/Еб', ебу = сгбу cos а/£б- (2.20)
Кривизны (kx, k'y, k't) и относительные деформации эле-
мента на уровне срединной поверхности (с-ох. «о» и е^) от
действия напряжений, прилохсеииых по сечению трещины,
определяются по формулам (2.13) и (2.14):
~ (?ах~~ ^бх)/Ла, ^р = (®пУ Сб^)/Ло1 kt = О, )
f tix = 0,5(еахЛ/Ло4- с0е'6х)-, (2.21)
0,5 (?ау/|//|а-f-еа ₽бр), Cof== 0, J
где е0 = 2 — /ь'Л0.
Кривизну кручения элемента — величину k'xv и вели-
чину сдвига на уровне срединной поверхности уо*р можно
88
определить из условия k't = 0 и = 0, используя пре-
образования (1.2): 7 н
2k ху = кхсtgа + ку tgа = (еах—е'бх) с 1 gа/Л0 +
+ (eav—e6V)tga/ft0:
Чоху = еох с tg a + tg a = 0,5 (еах 4-
+ е0 e&r) ctg a 4- 0,5 (еаа й/Л0 + сэ е^) tg a.
(2.22)
При выводе общих жесткостиых коэффициентов для их
упрощения будем принимать е0 « 1, что равносильно пере-
несению срединной поверхности на середину h0.
Используя зависимости (1.10), (2.15), (2.16) и (2.17),
легко выразить значения относительных деформаций и зна-
чения кривизн в функции от Мх, Ми, Мхи, Мих и
Ny, Nxu, Nyx. ’
Рассмотрим некоторые особенности расчетных формул
для случая, когда непересекающиеся трещины проходят в
верхней зоне элемента (см. рнс. 2.1, 6; схема 16). Эта схема
аналогична предыдущей, поэтому остановимся на ней крат-
ко. Чтобы отличить параметры схемы 16 от аналогичных
параметров схемы 1а (см. рис. 2.1, а), запишем их с верх-
ними штрихами. Например, угол наклона трещин а обо-
значается как а' и т. д.
Рассматривая равновесие треугольной призмы, отсечен-
ной верхней трещиной (рис. 2.7), находим напряжения в
Рис. 2.7. Расчетная схема усилий и напряжений на площадке верх-
ней трещины
верхней арматуре ол'х, а.’,7 и о.'3 11 проекции напряжений
в бетоне над трещинами Об* и аву-
Сбх = |(Л 1Х 4- Лх г') sin а' 4- (Л/ух + Ь'их 2->) cos а' ]/(х' г');
оСи = ((Л1, 4- Ь'и cos а' 4- (Л1х9 + Л\у sin а' )/(*; г').
(2.23)
Напряжение в арматуре о'3, оах и ®аУ определяются по
формулам (1.34) и (1.36), где необходимо заменить:
Nx на (—Л1Я+ Л’хгб)/г'; Хи на (—Afv 4- NyZ'^lz'-, |
NUx на (—MUx+NVxzc)z,\ Nxy на (—МхУ+N хУ z^/z’, J
(2-24)
а всем остальным величинам присвоить верхние штрихи.
Средние относительные деформации еа/ верхней арма-
туры и бетона на нижней поверхности и е<зУ вдоль осей
х и у от действия усилий, приложенных по сечению верх-
ней трещины, равны:
£ai = GailE»l у, 3), 1
«• в г*» I
Pct — oCxsin а'/сб; e6y = O6yCOsa’/E6, J
где Е2 — то чт0 Еб, но для нижней поверхности бетона,
а Еа|— тоже, что E'al, но для верхней поверхности арма-
туры.
Кривизны и относительные деформации элемента на
уровне срединной поверхности при схеме трещин 16 опре-
деляются из выражений (2.21) и (2.22), где необходимо за-
менить:
на еах, ?ау'.
е'бк, zt,y на Гбх, ГбУ; Ло на ho-
(2.26)
О возможном уточнении представленных выше формул.
Рассмотрим, как изменятся представленные выше фор-
мулы, если учесть криволинейность эпюр напряжений в сжа-
той зоне бетона и влияние напряжений в бетоне растянутой
зоны под трещинами. Моделированием этих явлений в бал-
ках детально занимался 51. М. Немировский 1711.
Предположим, что эпюры <тбх и геометрически по-
добны, тогда они будут иметь один коэффициент полноты
эпюры напряжений w„(0,5 юп 1) и центры тяжести
90
SHiiop совпадут. Проекции погонных ven лий п ~
будут равны: o6xw„xT; oCtzWnxT. Обозначим беТ°Не
тонных усилий растянутого бетон л ™м проекции по-
Npx и #Р1/, а их расстояния от арматувы и п^ещ"по» через
сжатой зоны—через 2р.б „ г„ "т''™’Рз тяжес™
жим, что моменты сил растяжения N * » v ’ ° ' Предпо-’,°-
сжатого бетона можно выразить в Фпш ,„„₽!L0T!!0SHTe-lbH0
моментов всех сил, вычисленных пти^ ” 0Т оСобц*енных
и //-// (см. рис. 2.6), т. е относительно осей /-/
А/рх^р.б = IM* 4" 4" (Мух 4* ctg air
NnuZn б — 4* yZa ~}“ (Мхр т tg ®1^6ii
Г J • •
Г< п1 ФУнкЧия влияния растянутого бетона (О
Обозначим:
Гб2 — 1 4“ I’GlZp.a'Zp. б» ГбЗ 1 ^х^б1^б^р.а/2’а^р.б-
Повторив вывод представленных выше формул с учетом
дополнительных предпосылок, придем к следующим уточ-
нениям: в формулах (2.16) вместо величины г следует под-
ставить величину z/(r6l 4- 1); в формулах (2.17) величину
гхт следует заменить на zxTwn/r62, а величину га на
zar^lr^ Таким образом, учет растянутого бетона приводит
к уменьшению напряжений в растянутой арматуре и уве-
личивает значения напряжений в бетоне сжатой зоны.
В представленной теории плит, как и в теории балок
с трещинами, указанные факторы учитываются за счет не-
которого изменения значений хт, Е^, Е'а по сравнению с их
действительными значениями так, чтобы в итоге получались
правильные значения средних деформаций арматуры и бето-
на, а отсюда и величины жесткости. По не всегда в эквива-
лентных величинах хт, Еб и Е<ч удастся полностью учесть
все указанные выше факторы, поэтому вопрос еще требует
исследования.
Определение напряжений и деформаций плиты от дей-
ствия усилий, приложенных по сечению, нормальному к на-
правлению трещины. Для этого выделим из характерного
элемента (см. рис. 2.5, о) треугольную призму (рис. 2.8),
наклонная грань которой пройдет перпендикулярно к ли-
ниям трещин. Па основании этого рисунка определим сум-
марные нормальные и касательные напряжения в верхнем
91
(п/ и т,'и) и нижнем (<т, н т,п) волокнах бетона. Чтобы не
усложнять расчета, влияние пластических деформаций на
изменение формы эпюр напряжений учитываем приближен-
но, в результате:
По мере удаления от трещины в глубь полосы бетона
величины этих напряжений несколько изменяются. Однако
это не учитывается при вводе их средних значений на участ-
ках между трещинами. В св
ных напряжений т/п итС/п в 5
веденных по трещине и норм
Рис. 2 8. К определению напряже-
ни А на площадке, нормальной
к площадке трещины
а —эпюры напряжения в сечениях бе-
Гона, нормальных к направлениям трс*
тип от моментов; б — то же. от дейст-
вия нормальных сил; в— общая схема
моментов и нормальных сил. приложен-
ных к граням прямоугольной приемы
/МО/.'.М'О'
Изи с этим парность касатель-
1есте пересечения сечений, про-
алыю к ней, может не соблю-
даться (см. формулы (2.18)
и (2.27)].
Значения <о1 и ю2 опре-
деляются в зависимости от
формы эпюр напряжений
т(л, т?п, °t и о/. Эпюры ка-
сательных и нормальных
напряжений принимаются
геометрически подобными.
Исследования коэффициен-
тов <•>! и о)2 для плит пред-
ставлены в работе 121].
Приведем данные из этой
работы. Когда в верхней
и нижней зонах эпюры
напряжений прямоуголь-
ные, а в верхней тре-
угольные, о>1 = 0,875;
о)2 == 1,74. Когда в верх-
пей и нижней зонах эпю-
ры прямоугольные, (Oj =*
= о>2 ~ 1,5; для треуголь-
ных эпюр <02 = <|)2 = 1.
Примем, в общем виде,
что полоски бетона на верх-
ней поверхности деформн-
92
руются при некотором секущем модуле бетона Ес , а в
нижней —при Ес.н-Части средних деформаций элемента
на верхней поверхности от действия о'( и т/_ опреде-
ляются по аналогии с (2.19): г
еб< = ог//Еб.в; Тбм = Т/'„/Ес.в; 8бП = 0. (2.28)
Используя преобразования (1.2) компонент тензора от-
носительных деформаций при повороте осей координат,
получим величины относительных деформаций е, и е
вдоль осей х и у: ** вя
eex = (ot cos2a—T('„sina cosa)/Ee.B;
«.» = («« sin2 a-hT^sin acosa),'E6.B.
(2.29)
Выражая величины a't и т/п по формулам (2.27) в функ-
ции от Мп и Л4П», а последние [на основании (1.2)1 — через
Мх, Му, МХу и Nx, Nu, Nxy, получаем:
6(Af xcos2 a—Myx sin a cos a)
/<2Ы1£б.в
Afxcos2 a — Nyx sin a cos a
Еб.ъЬ ’
6(.ИЦ sin2 a—Л1ху sin a cos a)
ft2 Wj Ес.»
Ny sin2 a—#xl< sin a cos a
Еб.вЛ
(2.29а)
Аналогично определяются деформации полосок бетона
на нижней поверхности элемента. Формулы для определе-
ния этих деформаций (е„х и еп„) вдоль осей хн у можно по-
лучить из выражений (2.29а), заменив перед первыми слагае-
мыми знак минус на плюс, <ож на <о, и Ебв на Еоп. При тре-
щинах, проходящих в верхней зоне элемента, в получен-
ных выражениях необходимо заменить а на а'.
Кривизны элементов (k’x, k’v и k"n) и деформации на уров-
не срединной поверхности (еох. foy и еоп), вызванные уси-
лиями, приложенными к полосам бетона между трещинами,
равны:
А’х— \^||Х ^Вх)/Й, Ку— V1IJZ ®ву)/Й, Ад V,
Сох — 0,5 (е„х -j- евх), &оу = 0,5 (г-цу Ф* ®ву)* 0.
(2.30)
93
Кривизну кручения — величину k*„ и величину сдвига
Тохр — определяем по аналогии с (2.22), используя =
= 0 и eSn = 0;
= (с«х ~®вх) ‘б ct/h (ец>/ вва) etg cc//i, | (2 31)
= 0,5 (Сцх + eDX) tg ос 0,5 (ену -f- eny) etg ос. J
Выражения (2.30) и (2.31) выведены в предположении,
что при учете вклада полос бетона между трещинами в об-
щие деформации элемента можно не учитывать частичное
нарушение сцепления арматуры с бетоном и влияние усилий
в арматурных стержнях, пересекающих площадки, нор-
мальные к трещинам. Подробно эти два фактора проанали-
зированы в § 4 главы 1. Следуя результатам этого анализа,
можно приближенно учесть указанные факторы так. В вы-
ражениях (2.30) величины е||Х и ell!Z записываются в функции
от сил и моментов и в этой записи для енХ и ену производится
замена:
Л1Х, Мух, Nx, Nyx умножаются на фпХ; )
Л(у, МХу, Ny, NXy умножаются на фиУ. /
В выражениях (2.31) величины е„х и е„у также записы-
ваются в функции от сил и моментов и в этой записи для
с1|Х н ен» производится замена:
только Мх и Nx умножаются на ф11Х; )
только Му и Nu умножаются на фиУ. j (2.33)
Указанные выше замены производятся, если трещины
распсложсны в нижней зоне. Если трещины расположены
в верхней зоне, в выражениях (2.30) замены производятся
в членах еиХ и еву, а именно:
Мх, Мих, Nx, Nux умножаются на ф„х;
Му, Мхи, Ny, Nxy умножаются на фпУ, .
а в выражениях (2.31):
Мх и Nx умножаются на ф™;
Му и Nu умножаются на ф,'|у.
(2.31)
(2.35)
Общие кривизны элемента пластины равны сумме вели*
чин (2.21), (2.22) и (2.30), (2.31) или (2.26) и (2.30), (2.31):
kx = kx + k’x-, ky = ky-]-k’y; kxy = kXy + k'Xy, (2.3G)
91
По аналогии с кривиз-
нами полные относитель-
ные деформации на уров-
не срединной поверхности:
Рнс. 2.9. Расчетная схема усилий и
напряжений в сквозной трещине
Yoxi,= Y<w “г Toxir (2.37)
Выражая в (2.36) и
(2.37) составляющие кри-
визн и относительных де-
формаций в функции мо-
ментов и сил на основа-
нии представленных выше зависимостей, придем к оконча-
тельным выражениям для полных кривизн и относительных
деформаций срединной поверхности. Они приведены в § 4
данной главы.
2. Элементы со 2-й схемой трещин. Пусть элемент про-
низывает сквозная трещина (см. рис. 2.1, в). Выделим из
этого элемента треугольную призму (рис. 2.9), наклонная
грань которой пройдет по сквозной трещине. Составляя по
два уравнения равновесия моментов относительно нижнего
и верхнего обобщенного слоев армирования и решая эти
уравнения так же, как (2.15), придем к выражениям для
и Оаь «а! и еа\, которые будут аналогичны (1.34) и (2.25)
с видоизменениями (2.16) и (2.24). В указанных выражениях
применительно к элементам со сквозной трещиной необхо-
димо внести лишь следующие изменения: при определении
оях, ” ааз принимать zo = га; при определении
о'ж, И принимать Z'6 = Zn, z' = Z. Величины Za, z’t и Z
определяются на основании рис. 2.9.
Кривизны и деформации срединной поверхности от дей-
ствия усилий, приложенных по сечению сквозной трещины,
определяются из выражений (2.21) и (2.22), где необходимо
заменить ег,г и на гат и е»,/, Ло на z; 0,5 h.'li0 на z'a'z,
е0 на za/z. При выводе обобщенных жесткостных коэффи-
циентов (для их упрощения) будем принимать:
Za/z X za/z Tti 0,5 Z.
Суммарные кривизны и относительные деформации оп-
ределяются как сумма их составляющих (2.21), (2.22), (2.30)
и (2.31). При этом, так как трещина сквозная, в выражения
(2.30) вносятся коррективы (2.32) и (2.34), а в (2.31) — кор-
95
рективы (2.33) и (2.35) одновременно для е„х, еи1/ и евХ,
ев„. 2-я схема трещин является переходной от моментного
к безмомснтному напряженному состоянию, формулы для
которого могут быть получены при Л1Х = Му = Л1ху = 0.
3. Элементы с 3-й схемой трещин (см. рис. 2.1, г; Э4) —
характерный элемент пересекают две несквозные трещины,
из которых одна расположена в нижней зоне, вторая —
в верхней (случай двух трещин разных зон). Можно пред-
ставить себе случай, когда трещины в обеих зонах располо-
жены под произвольными не зависящими друг от друга уг-
лами. Будем рассматривать лишь наиболее распространен-
ную схему, когда плоскости, проведенные через нижнюю и
верхнюю трещины, взаимно ортогональны (а' = 90° 4- а).
Анализ работы элемента с ортогональными трещинами
разных зон сводится к рассмотрению двух призм, одна из
которых отсечена сечением, совладающнм с нижней трещи-
ной (см. рис. 2.6), а вторая — с верхней (см. рнс. 2.7).
Для определения напряжений арматуры и бетона спра-
ведливы формулы (2.15) — (2.26). Суммируя приращения
кривизн и деформаций срединной поверхности, полученные
из рассмотрения указанных призм (т. е. величины (2.21),
(2.22) с аналогичными величинами (2.26)), получаем выраже-
ния для общих кривизн и относительных деформаций сре-
динной поверхности. При этом в величины (2.21) вносятся
коррективы (2.32), в величины (2.22) — коррективы (2.33),
в величины (2.21), вычисленные с учетом (2.26),— корректи-
вы (2.34) и в величины (2.22), вычисленные с учетом (2.26), —
коррективы (2.35).
4. Элементы с 4-й схемой трещин (см. рнс. 2.2, а; Эь).
Они будут нами рассмотрены при ортогональном армиро-
вании, которое является для элементов с указанными схе-
мами трещин наиболее распространенным.
На рис. 2.10 отдельно выделен рассматриваемый элемент
с двумя трещинами в нижней зоне (схема 4а), проходящими
по граням элемента. Нормальные напряжения в арматуре
в трещинах и бетоне над трещинами можно получить, изу-
чая отдельно работу элемента в сечении, проходящем по
трещине, нормальной к оси х, и в сечении, проходящем по
трещине, нормальной к оси у. Формулы для определения
нормальных напряжений и деформаций в арматуре и бетоне
для элементов со схемой 4 можно получить из формул
(2.15) — (2.26) для элементов со схемами трещин 1 (при
этом формулы для схемы 4а получаются из формул для схе-
мы 1а, а формулы для схемы 46 при трещинах в верхней
Уб
Рис. 2.10. К анализу работы
элемента с ортогональными пе-
ресекающимися трещинами на
растяжение н изгиб
Рнс. 2.11. К анализу ра-
боты элемента с ортого-
нальными пересекающи-
мися трещинами на сдвиг
и кручение
зоне — из формул для схемы 16, см. рис. 2.1, а, б и 2.2, а),
если в них при вычислении аах (о’ах), абх (осх) и t'6x (ejj
положить (данные в скобках относятся к схеме 46):
а = 90° (а* = 90°); хт = х7Х (х[ = л^Д
z6 = zCx & = - £бх (Е< = £2Д 1 J
а при вычислении аау, (оаД аб1/, (а^) НЕб^бу)
принять:
сс = 0 (сс =0), Ат = %ту (^т = ятД (2 38а)
Zq = z^y (zc = Zcy)\ Ес = E^y (Еб = Есу)-
Общие кривизны и деформации срединной поверхности
определяются по формулам (2.21) при вычислении входя-
щих в них величии с учетом правила (2.38).
Формулы (2.22) становятся непригодными. В связи
с этим остановимся на более точном определении кривизны
кручения kxy и относительного сдвига т0Х1/ для элементов
с пересекающимися трещинами 151» 581. Нормальные напря-
жения в бетоне сжатой зоны определяются с учетом
двух высот сжатой зоны xTX и (cwM- Рис-
При определении касательных напряжений (рис. 2.11)
вводим среднюю высоту сжатой зоны хт.с l.vT.c = (л\х +
+ л'т!/)1 н определяем некоторые усредненные значения ка-
*1 Зак. 631
97
сатсльных напряжений в бетоне (тсХ!/) и арматуре (тах
и тпв).
Уравнения моментов касательных сил относительно цент-
ра тяжести эпюр тОх1/. тах и тпи запишутся так:
т.с Л, — О
xV ^б.С
VX 4* ^vx ^6-с
лх/ах^с ®
(2.39)
откуда и определяются величины тсХ!,, та7 и тах. Углы
сдвига на верхней сжатой поверхности и на уровне растя-
нутой арматуры по аналогии с (1.83) можно определить по
формулам:
(2.40)
где б'б — модуль деформаций бетона на сдвиг (определяет-
ся как для ортотропного материала),
(2-41)
Здесь Дх и — сдвиг берегов трещин, расположенных
соответственно вдоль осей х и у; Кхх и КХу— функции по-
датливости стержней сдвигу (их можно принять, например,
на основании исследований [11]).
Кривизна кручения определяется по формуле (2.13),
а Тоху « 0,5 (ус'у + уХ7). Более подробно эта методика рас-
смотрена в работе [58].
Если считать, что арматура не работает на сдвиг и
тах == тП1/ » 0, то величина уху не может быть выражена
через усилия Л1Х7 и Nxy. При этом можно определить лишь
величину
Уху —ху!б<> ~ (—^хУ Nху 2а)/^с^т.С^б* (2.42)
Окончательная система уравнений для решения такой
задачи имеет вид:
= (ух7 Уху)/(2Л0)=Уху/(2А0) (NxyZa—МхУ)/(2йо?схт.сОб)»
Yoxi, ~ 0,5ул7 + 0.5 (—Л1ху + za)/(zcхт,с Об)» (2.43)
Мух 4* МУх гб-г = 0,
98
т. е. мы приходим к неполной (см. § 5 главы 1) системе физи-
ческих уравнений, в которой величина ух„ фигурирует как
неизвестная наряду с Л1Ху и NXy и находится в процессе
решения задачи, хотя в общем число уравнений (вместо пер-
вых двух) увеличивается на единицу и будет достаточным
для решения задачи. При равенстве нормальных сил нулю
вместо физических уравнений имеем:
= 0; NХу — 0, <2.44)
при этом элемент не обладает жесткостью на сдвиг и круче-
ние, и величины kXIJ и уОху могут быть любыми.
Выше мы рассмотрели схему 4а, аналогично рассматри-
вается и схема 46, когда пересекающиеся трещины располо-
жены в верхней зоне элемента.
Использование более точных зависимостей (2.40) пока
встречает затруднения в связи с малой исследованностью
и громоздкостью функций Кхх и Кху. Поэтому в практичес-
ких расчетах нашли применение либо зависимости (2.43) и
(2.44), либо приближенные зависимости для ух„ и kxy, кото-
рые указаны выше.
Выше был рассмотрен случай, когда пересекающиеся
трещины нормальны к стержням прямоугольной арматур-
ной сетки. Исходя из исследований (п. 3, § 5 главы 1) можно
предположить, что если касательными напряжениями
та( можно пренебречь, то полученные выше при та< = 0 за-
висимости применимы к элементам с другими схемами
(см. рис. 2.2, а, а ) пересекающихся трещин.
5. Элементы с 5-й схемой трещин (плиту пронизывают
две пересекающиеся сквозные трещины (см. рис. 2.2, б).
Все формулы, характеризующие напряжения и деформации
элемента с этой схемой, можно получить из формул для эле-
мента со 2-й схемой трещин, если в них принять:
при вычислении оах и вах а = 90°;
при вычислении <та1/ и с’ау а = 0°.
При определении сдвигов можно использовать зависимо-
сти типов (2.40) или (2.43), определяя их отдельно для ниж-
него и верхнего обобщенных слоев армирования. Могут
быть справедливы и зависимости (2.44).
6. Элементы с 6-й схемой трещин (см. рис. 2.2, в). Их
можно изучать, выделив у верхней и нижней арматуры два
слоя и рассмотрев деформации одного слоя, как при непе-
4» 99
(2.45)
ресекающихся трещинах, а второго — как при пересекаю-
щихся.
В заключение отметим следующее. Если в зоне с пере-
секающимися трещинами к ортогональным стержням доба-
вить еще стержни одного или двух других направлений, не
совпадающие с осями х и у, то такая система может в осях
хи у весьма значительно повысить жесткость на сдвиг. Этот
вопрос можно рассмотреть, используя теорию главы 1.
7. Некоторые особенности определения ширины раскры-
тия трещин. Этот вопрос подробно рассмотрен в § 4 главы 1
и в работах 117, 37J. Укажем лишь на те изменения, которые
необходимо внести в расчетные формулы главы 1 в связи
с действием моментов. Ширина раскрытия трещин определя-
ется по формуле (1.61), а расстояние между трещина-
ми — но формулам (1.64), в которых необходимо заменить
Л на kpkfjW6r/z, (2.46)
где U”6.T — упругопластический момент сопротивления се-
чения полоски плиты шириной b = 1 (1Гб т =
= Л2/3,5).
В приближенной формуле (1.66) для определения 1Ч сле-
дует е0 уменьшать в 1,2 раза, хотя это еще требует
исследования. Эта формула применима при faxlh, fay!h
> 0,003.
8. Особенности рассмотрения элементов круглых плит
с трещинами. Рассмотрим две схемы армирования круглых
плит; радиально-кольцевую (рнс. 2.12, а) и в виде прямо-
угольной сетки (рнс. 2.12, б).
Расчет плит с трещинами при 2-й схеме трещин удобнее
выполнять в декартовой системе координат, при этом все
указанные выше зависимости для прямоугольных плит мо-
гут непосредственно использоваться и для решения пред-
ставленной задачи. При решении задачи в полярной системе
координат необходимо выразить моменты и силы Мх, Му,...,
Nxy в функции от моментов и сил в полярной системе,
т. е. через Мг, Л4П,..., Л1гл,'где г — радиальная координата;
1] = гО (0 — угловая координата, рад). Переход от Afx,
ЛТ,,, k Мг, Л1л... производится по формулам (1.2), где
а следует заменить на 90° — 0.
Расчет круглых плит при радиально-кольцевой схеме
армирования удобно выполнять в полярной системе. В этом
случае во всех зависимостях индекс «х» следует заменить
индексом «г», а <//» — индексом «р. Так, параметры армиро-
100
вания при этом в радиальном/аг и кольцевом /ап иаппавте-
ниях равны: /ап "“"Р^в-те
• «г FaJSn /ап = Рап^п*
где Sr и Sn— шагн стержней (см. рнс. 2.12, а);
Par и ^ап площади кольцевых и радиальных стержней
Более точные величины /аг и /а„ определяются по фор-
мулам (2.11), где индексы «л» и «у» заменяются индексами
«г» и «п». Аналогичные замены производятся также при опре-
делении напряжений в арматуре, бетоне и при опредетении
деформаций и кривизн. Формулы для них получаются при
следующих предпосылках. Пусть в общем случае напри-
мер при некоторой несимметричной нагрузке, трещины на-
клонены под произвольными углами g к оси г. . Л л я опреде-
ления напряжении в арматуре в трещине и бетоне над тре-
щинами выделим у точки П треугольную призму abc (abc—
одновременно срединная поверхность призмы, рис. 2.12, в).
Известно, что для малого элемента abc кривая ab может быть
заменена на прямую, а криволинейный треугольник abc
Рнс. 2.12. К анализу физических зависимостей
а —при ря лиа л ыю-кольцевой схеме армнровдзависимостей дли плит
схеме армирования; и. г - к рассмотрению фи тичсх mix завит
при радиально кольцевой схеме армирования
101
можно рассматривать как прямоугольный треугольник.
Коэффициенты армирования /аг и /пп определяются у сере-
дины элемента (у точки II) и принимаются но плану рас-
сматриваемого малого элемента постоянными. Анализируя
напряженное состояние призмы abc, по аналогии, с тем,
как это выполнено в и. 1 §3, можно установить зависимости
для напряжений в арматуре в трещинах и бетоне над трещи-
нами, а затем перейти к определению деформаций. Схема
вывода этих и других зависимостей в осях г и ц при радиаль-
но-кольцевой схеме армирования полностью подобна схеме
их вывода, представленной в пп. I—7 в декартовых осях
х и y.QiMit зависимости также подобны. Это правило перехо-
да сохраняется и для схем пересекающихся трещин
(рис. 2.12, г).
9. Особенности рассмотрения элементов оболочек с тре-
щинами. Выше уже указывалось, что для оболочек величи-
ны kx, kv и kxy представляют собой приращения кривизн.
Рассмотрим некоторые другие особенности.
Пологие оболочки. Установленные выше зависимости бу-
дут полностью применимы к пологим оболочкам. Вывод
физических зависимостей для оболочек, прямоугольных
в плане (рис. 2.13, а), будет таким же, как и для прямоуголь-
ных плит; для оболочек, круглых в плане, необходимо учи-
тывать особенности, указанные выше в п. 8. Все это вы-
текает из того, что геометрия пологих оболочек отождеств-
ляется с геометрией их проекций на плоский план и не
требует особых пояснений.
Непологие оболочки. Сформулируем сначала правила
перехода к физическим зависимостям для оболочек, а затем
укажем на их обоснование. Для непологих оболочек (чтобы
сохранить представленные выше физические зависимости
без изменений) мы должны принять, что оси х и у являются
не декартовыми осями координат на плане оболочки, а пред-
ставляют собой ортогональную криволинейную систему
координатных линий на ее срединной поверхности (будем
ниже совмещать линии х и у с главными линиями кривизны
оболочки). В общем случае криволинейными являются также
арматурные стержни. При этом арматурные стержни двух
направлений предполагаются расположенными вдоль осей
х и у, а арматура третьего направления (если она имеет-
ся) считается наклонной к координатным линиям х под не-
которыми углами Рз (рис. 2.13, б). Расстояния (i ~ х,
у, S) между стержнями i-ro направления измеряются по ли-
ниям на поверхности, нормальным к i (рис. 2.13, б, в). Что-
102
Трещина,
д)
'Л
Трещина.
анализу физических
НСЬ
Рис. 2.13.
зависимостей для оболочек
/ — арматура х-направлення: 2 —арма-
тура {/-направления; 3 —арматура /-на-
правления; 4 — касательная плоскость
Ry
НСА
бы компенсировать некоторую неточность предпосылок,
указанных ниже, можно вместо S/ принять приведенные
к срединной поверхности величины S/ (см. рнс. 2.13, в).
Определение параметров ft и приведение трехслоиного арми-
рования к некоторому обобщенному слою с параметрами
/а» производятся по формулам (2.10) — (2.11, а). Все выра-
жения пп. 1—7 при такой трактовке величин, входящих
в эти выражения, сохраняют силу и для непологих оболочек.
Теперь рассмотрим некоторое обоснование этих положе-
нии. Выделим характерный элемент ekmn у некоторой точ-
ки П так, как показано на рис. 2.13, г, д (ekmn — одновре-
менно срединная поверхность выделяемого элемента). Нач-
нем анализ с известных положений. Пусть элемент ekmn
мал (стянут к точке /7) и работает в упругой стадии без тре-
щин. Поступая известным образом (см., например, с. 17 и
18 книги 1541), получаем значения моментов в функции от
103
напряжений (ох, ау,...) на гранях элемента:
0.5Л
0.5/1
где г—расстояния рассматриваемых слоев от срединной
поверхности.
Аналогично записываются и другие обобщенны» усилия.
В технической теории оболочек при определении Мх, Л1
как правило, принимают (например (1, 13, 54) и др.)
(1 + ~ (1 + —— ~ 1
\ Ry / \ Rx )
и приходят к тем же выражениям для погонных изгибающих
моментов и сил, что и в теории пластин; при этом окончатель-
ные соотношения упругости для оболочек такие же, как и
для пластин, с той лишь разницей, что вместо кривизн фи-
гурируют нх приращения. Формулы для моментов при усло-
вии (1 4- zIRi) At 0 можно получить и более наглядным об-
разом, заменив при рассмотрении трапецеидальный элемент
с криволинейными поверхностями (см. рис. 2.13, г) на неко-
торый параллелепипед (рис. 2.13, е). При этом нижняя и
верхняя поверхности элемента принимаются равными сре-
динной поверхности, а геометрия срединной поверхности
в свою очередь отождествляется с геометрией ее проекции
на касательную плоскость в точке П (см. рис. 2.13, д). Ана-
логично при нашем выводе физических зависимостей для
оболочек с трещинами характерный трапецеидальный эле-
мент заменяется на параллелепипед.
Отметим одну особенность. В нашем случае элемент с тре-
щинами не может быть принят сколь угодно малым, а будет
иметь конечные размеры. Какие ограничения в связи с этим
должны быть поставлены? Пусть наибольшее расстояние
точек элементаekmn от касательной плоскости равно/, а наи-
меньший размер его в плане равен а. Тогда, воспользовав-
шись гипотезой пологих оболочек можно указать, что отож-
дествлять геометрию поверхностей характерного элемента
с их проекциями на касательную плоскость в точке П можно,
ec.3n/.'a<g- (назовем это условием пологости характерного
элемента в малом). Здесь условие ортогональности двух
линий армирования требуется для плит и оболочек, так как
оно принято при выводе всех зависимостей пп. 1—7. Для
оболочек, работающих при безмоментиом напряженном со-
lul
Рис. 2.14. к определению знаков усилий и приращений кривизн
и — положительные направления усилий, принятые н данной работе; и — встре-
чающиеся положительные направления усилии в теории оболочек
стоянии, можно использовать результаты главы 1, а также
исследования статьи 144]. Последние позволяют учесть
любое косоугольное армирование.
Обратим внимание еще на правило знаков. На рис. 2.14
показаны принимаемые в книге положительные значения
моментов нормальных, касательных и перерезывающих
(Qx, Qy) сил. Перерезывающие силы находятся как произ-
водные от моментов. Приращения кривизн (i = х, у)
считаются положительными, если они увеличивают вогну-
тость элемента книзу (уменьшая указанный на рис. 2.14, а
радиус кривизны /?/). Такое же правило можно встретить
в книге 177]. В теории оболочек получило распространение
правило знаков, представленное на рис. 2.14, б. Оба правила
оказываются идентичными, если определить понятие верх-
ней и нижней поверхности (верхнего и нижнего армирова-
ния) исходя из направления оси z. Нижнее армирование
располагается у поверхности г = + 0,5 h, а верхнее —
у z — — 0,5 h. Например, если исходить из рис. 2.14, б,
то на рис. 2.13, г (при условии, что ось z направлена вверх)
будет представлен элемент с трещинами в верхней зоне.
§ 4. Окончательный вид физических уравнений.
Общая постановка задачи расчета плит
и оболочек при различных схемах трещин
I. Физические уравнения и обобщенные выражения же-
сткостей для элементов со схемами непересекающихся тре-
щин. Подставляя в выражения (2.36) и (2.37) для прнраще-
105
ний кривизн (kx, k,„ kxy) и относительных деформаций сре-
динной поверхности (гох. е0». Тох») значения составляю-
щих, выраженных в функции от моментов (Л1Х, Л1„, Л1Х!/)
и нормальных сил (А'х, Ny, Nxy) на основании установлен-
ных в § 3 зависимостей, получаем (при Мху = Мух, AXJZ =
« Nyx) следующую систему шести уравнений:
kx = Вц Л1Х 4 В I-, ЛГ„ -}• В Л1УХ 4- Bj । Ах 4*
4- В*_> Nу -{- В*з А’9х;
ky == В|2 Л fx Ь В22 ЛI у 4- В 23 Л f хУ "4*
В|2 Ах + В*2 А7 4- B-*j Аха;
2А>*ху “ В13 A/jf "Г Влд М„ -р В 13 Л/Ху -р
•г В|з Ах 4* В*з А’у 4* В*з AxV;
*ох — 1 А/х 4- С?2 Л1У *Р CJз Л1хУ 4-
р С, । Nx -р С|2 А„ -р С|з Аух;
р(>у = С*2 ЛГХ 4- С?2 Л1У + С*з Л1ху -р-
4- Cl2 Ах -р С 22 N и -р С«з AXJZ;
То ХУ = С13 Л/х т Cj3 Л1у т С33 Afxy -р
*р С)3 Ах г С;з ;Yy -р Сзз lVху.
(2.47)
где Вц, В*/, Ct), Сц (i, j — 1, 2, 3) — жесткостные коэффи-
циенты матрицы жесткости.
Такое разделение жесткостных коэффициентов связано
с их определенным физическим смыслом. Жесткости В1} ха-
рактеризуют влияние моментов на изгиб и кручение элемен-
та, а Сц — влияние нормальных сил на относительные де-
формации срединной поверхности. Своеобразную роль иг-
рают жесткости В*/ и С*,. Жесткости Вц характеризуют
влияние на изгиб и кручение элемента нормальных сил,
а С*/, наоборот, влияние моментов на относительные дефор-
мации срединной поверхности. Как видно из (2.47), указан-
ные группы жесткостных коэффициентов обладают опреде-
ленной симметрией, так при i j:
Вц — Вц', B*,j = B*i\ Сц — Cjf. C*i = C*fi.
Кроме того, исследования показывают, что коэффициенты
B*i и C*i оказываются весьма близкими по своим значениям,
и можно Припять
в:,« с;,.
(2.48)
106
При условии (2.48) матрица жесткости оказывается сим-
метричной относительно главной диагонали, проходящей
через Вц и Сц, что значительно упрощает решение задач.
Коэффициенты матрицы жесткости зависят от схем тре-
щин. Однако при анализе жесткостных коэффициентов,
выведенных для элементов при различных схемах трещино-
образовання, было установлено, что, несмотря на различие,
все они имеют много общих, но повторяющихся в различных
комбинациях параметров. Это дало возможность формально,
в целях более компактной записи и удобства в использова-
нии при расчете элементов на ЭВМ, составить на основании
конкретных значений жесткостных коэффициентов их обоб-
щенные выражения так, чтобы из последних можно было’
получить жесткости для элементов с любой схемой трещин.
Обобщенные значения жесткостей можно записать в виде:
B1i=ol4-ai'4-o3-|-O3 4-614-6i'4-(634-6i)cos2a;
В„, = о2 4" 02 4* о4 4* Од 4- (’г 4* ^2 т (63 Ч" 6®) sin2 а;
В33 = («1Ч- Ч- о3 4- аз) ctg2 а 4- («2 Ч- 62) tg2 а' 4-
4- (а. 4- Ь, Ч- ЯдЧ- Од) tg2 а 4- (of 4 bi) ctg2 а' 4-
4-63Ч-64—2(ав4-ОбЧ-я74- oi);
Bin = — (oe 4- Об 4 Q-г 4* 07);
В 1з = (Oi + о34- оз 4- 61) ctgа4-(of 4*bi)ctgа' —
—(63 4- 64) sin а cos а—(ав 4 а74 07) tg а—Об tg а';
В.23 = (о2 4 о® 4- од 4- 6«) tg а 4- (oi 4- Ь'з) tg о.' —
—(Ь3+Ь4) sin acosa—(ae+a.+ai) ctgа—о® ctga';
Bii=nti—tni+m3;
B22 = nin—mj4-»V
B33 = (»«i 4- Юз) ctg2 а 4- (nin 4- m 1) tg2 а—
—mi clg2a' —/nitg2a' —
— 2 (?g Oe -|- ?a tlj—Zб Об ?a 0?)i
В12 ~ — (Zg О® ‘I’ О- Об Zn O7),
Bi3~('»i4 m3)ctg a—onctga'-I-ZcOetga' —
— G’o oe 4- 2'3 (t-. — 07 ?n) tg a:
(2.49)
(2.50)
B*2s — (tn, 4- Щд) tg a—mi tg a' 4 «6 ctg a' —
— (^o,-| o7?a — «7 ^n) ctg a;
107
Cn 0 5 (Ло n, -I- Ло nJ+г«з)+ O.O8 (Лз ц,2 + Л4 u'i) Л2 cos2«;
C22 — 0,5 (Ло nt 4- ho «2 + *n4) 4- 0,08 (b3 w2 4- bt wt) Л2 sin2 a;
C33 = 0,5 (Ло n, + гп3) ctg2 a + 0,5 (Ло n2 4- гп4) tg2 a 4-
4- О.бЛо ПI Ctg2 a' + 0,5/10 nJ tg2 a' + 0.08Л2 (b3 w2+b, »,) -
—Ло 4 at—го «в Ло—г (z'a а7 4- za al);
Ct2 = — °.5 (Лэгс ав + Ло *б Об) — 0,5г (г'л а- 4- га al);
С,3 = 0.5 (Ло n, -|- гп3) ctg a + 0,5 Ло п! ctg a' —
—0.5 (г0 Ло ав 4- гга' а7 + гга о?) tg a—0,5го Л о «о tg а' —
— 0,08/i2 (/>з U’., + />4 u'j) sin a cos a:
C23 0.5 (Ло n2 + ?n4) tg a -b 0,5/ii /i’> tg a' —
— 0.5 (гв hv я, -г o7 + гга a 9 ctg a—0,5/ii z'6 a’6 ctg a' —
—0,08h2 (b3 w3 + Л4 ui4) sin a cos a;
(2.51)
Cu == 0,5/iv(a4—6J —0,5/iS (al —bl) + rn3;
C22 = 0,5/io (a4—b2) — 0,5/io (aJ—bi) 4- zn4;
C’j — (0,5/io (n,—bt) + tn3 ] ctg2 a —
—0,5/iJ(fl; — /)|')ctg2 a' +10,5Ло (a2—b.,) + ni4]tg2 a —
— O,5/io («2 — bi) tg2 a'—h0 a„ 4- /10 ai — z (a7—a7);
<42= —O,5(/ioa3—/ijao)—0,5г (o7—«/);
Cm = 10,5/io («,—Л,) + /«3I ctg a —
—0.5/ii(«,' — bl)ctga'—0,5(/i„oe+га7—za'7) tga +
4-0.5/1^а^ tga';
C23 = |0,5Ло(а,—A.,) rni4]tga—
- 0,5/1 i(o'. - bi) tga'—0,5(/iofle + г«7—za}) ctga 4-
4- O.5/io Об ctg a',
(2.52)
где
fl — (j _
Еаг/аг?Л0 у Е'х/агФ j
a’ - 11 - Л•
ел'г/;.ф' л
108
Оъ =

Е* Е' Р Р Ф'
^ах * ах lay
(2.53)
a6=a6l(zh0Y, аб=аз/(г'1^); а-=а3/гг; ai=a'5/z”;
b,=
sin2 а
bi =
sin2 а
блт
Ь3 —
Л.» =
cos-а
cos* а
и
и
б ЛТ 4“0
6
Eo.ii ^’1 h3
«! = Яд z6 + Л| z„; П|' = flj zc, -|- г'л‘,
пй = a., zc b., za;
11г2 = (1'2 2q 4* Ь'2 2д\ “ G3 Za 4~ Оз Za»
//д = Яд za 4- Яд za,
/п1 = я1г0—/>!Zn; mJ = fljz6—/>{ z'a\
til A Я A Zq bg Za f
П12 = d‘2 ^0“*^2 ^.1» Я1з = Я3 Za Я3 Za»
/Ид — O|Za— Яд' Z,.
109
Полагая в обобщенных выражениях жесткостей опреде-
ленные коэффициенты (a,, bt, a'i и bi) равными нулю и произ-
водя некоторые замены, чтобы учесть факторы (2.32) —
(2.35), можно получить жесткости для элементов при всех
схемах трещин. Так, при получении жесткостей для эле-
ментов со схемой трещин 1а (трещины в нижней зоне элемен-
та, см. рис. 2.1, а) следует принять
а! = а3 — оз = b{ = at=aj = b2 = а2 = Яб == °? = а? = 0 (2.54)
и заменить в жесткостях с индексами «11» и «В»(в Ви, В13,
Сц, ^13< Сп. £13' ^11» ^1з) ^3 ИЯ &зФи х-
При получении жесткостей для элемента со схемой тре-
щин 16 (см. рис. 2.1, б) следует принять
ai — аз = = а1 = 6., = а, = ов — о- = а? = 0 (2.55)
и заменить в жесткостях с индексами «22» и «23» Ь4 на 64фп у.
Кроме того, в тригонометрических функциях, стоящих прн
Ь3 и Ь4, следует заменить а на а'.
При получении жесткостей для элемента со 2-й схемой
трещин (сквозных, см. рис. 2.1, в) следует принять
ai = — a3 = b3 = а{ = Ь\ = а2 — Ь2 — ав — Об=0 (2.56)
н заменить: в жесткостях с индексами «11» и «13» Ь3— на
Мпх и Ь4 на б4фпХ; в жесткостях с индексами «22» и «23»—
Ь, на б3фп у и Ь4 на Ь4 ф„р.
Прн получении жесткостей для элемента с 3-й схемой тре-
щин (трещины в нижней и верхней зонах, см. рис. 2.1, г)
следует принять
о3 = о} =-- о4 — а\ — Ьл = b4 = a7 = ai = О (2.57)
и заменить: в жесткостях с индексами «11» и «13» bt на
M'lix* и Ь{ на Ьл|пх, а в жесткостях с индексами «22» и «23»—
bt на б|ф||7 и bt на Прн a = 0 и a = 90° выражения
(2.49) — (2.52) для В33, С33, С33 и В33 будут неточными.
Для получения более точных значений можно применять
зависимости (1.38).
Прн выводе жесткостных коэффициентов (2.49) — (2.53)
для их большей унификации и упрощения некоторые вто-
ростепенные члены были отброшены. Более точные значения
жесткостных коэффициентов представлены в работах 137,47|.
Выражения для физических (£»*» B3V,...) и геометрических
(*т» •••) величин, входящих в жесткостные коэффициен-
ты, приведены в § 5.
но
2. Физические уравнения для элементов со схемами пере-
секающихся трещин. Исследования §3 приводят (при /а3 =
= /аз = 0) к следующим физическим зависимостям для
элементов с пересекающимися трещинами, проходящими
нормально к стержням прямоугольных арматурных сеток:
Zrx = BllAlx-|-B;1/Vx;
Ку *“ В22 ^у Т ^22 У*
^^ХУ ^33 МХУ *•* ^33 ХУ>
®ОХ ^”11 ^Х >' ^-11
ТохЧ ^33 МХУ Т
С33 N ХУ
(2 58)
Нашли применение также измененные выражения (2.58),
где вместо последних зависимостей для /гху и уоху использо-
вались зависимости (2.44).
Жесткости элемента с 4-й схемой трещин (см.
рис. 2.2, а). Выражения для жесткостей Вн, В’,, Сп и
CJt формально следуют при учете преобразований (2.38)
из соответствующих выражений (2.49) — (2.54) для жест-
костей элемента с 1-й схемой трещин; аналогично, используя
преобразования (2.38а), получаем жесткости В22, Взг, С22
и С^2. При этом здесь и ниже жесткости элемента со схемой
Затрещин (см. рис. 22, а) получаются из аналогичных жест-
костей элемента со схемой трещин 1а (см. рис. 2.1, о), а же-
сткости для схемы 46 слехукя из жесткостей для схемы 16.
Жесткости с индексами <33» устанавливаются на основании
формул п. 4 § 3 данной главы или приближенно вычис-
ляются так. Определяются по два (при а as 5° и а х 85е)
значения жесткостей В33, В33, С33 и CJ, для элемента
с 1-й схемой трещин (в данном случае схема 1а) и в полу-
ченных выражениях хт заменяется на хТХ, z — на гг, z^ —
на ?б.с (^б.с — см. рнс. 2.10, 2.11) и Ес— на 0,5 Go, где
Go определяется согласно (2.41). Суммируя по два значения
В33, ..., CJa, получаем значения соответствующих жестко-
стей для элементов со схемой трещин 4а.
б). Выражения для жесткостей элемента с 5-й схемой
трещин. Жесткостные коэф шцненты элемента с этой схе-
мой будут определяться по формулам для аналогичных же-
сткостей элемента со 2-й схемой, где лишь следует принять:
при определении Вп, В*п, Си и С‘, а = 90°;|/959)
прн определении В22, Взг, С23 и CJ, а = 0° J •
и, кроме того, учесть, что /п3= f'a3 = 0.
Приближенные выражения для жесткостей с индексами
<33» определяются по аналогии с тем, как это указано прн
111
рассмотрении элементов с 4-й схемой трещин. Находятся но
два (при а « 5° и а » значения жесткостей Взэ, В33,
С33 и Сзз для элемента со 2-й схемой. Жесткости элемента
с 5-й схемой трещин определяются в виде суммы этих двух
значений (В33 в виде суммы двух значений В33 и т. д.). Же-
сткости с индексами «33» определяются приближенно. Спо-
собы определения более точных жесткостей указаны в п. 4
§ 3 главы 2.
При выводе уравнений (2.58) предполагалось, что пере-
секающиеся трещины нормальны к стержням прямоуголь-
ной арматурной сетки. С некоторым приближением (2.58)
можно использовать и для элементов со схемами пересе-
кающихся трещин, проходящих под углами к стержням ар-
матуры (см. рис. 2.2, а, а). Но этот вопрос еще требует ис-
следования.
Жесткости элементов с 6-й схемой трещин устанавлива-
ются на основании указаний п. 4 § 3, а физические уравне-
ния записываются в виде (2.47).
3. Физические уравнения для элементов без трещин.
Кроме областей с трещинами в пластинах и оболочках
будут области, свободные от трещин. Можно выделить две
стадии работы элементов без трещин: упругую и упруго-
пластическую (связанную с развитием неупругих деформа-
ций в бетоне). В упругой стадии справедливы известные фи-
зические уравнения изотропных пластин и оболочек 113,
541, которые можно записать в виде (при рс ~ 0):
Мх ~ D (кх 4- Рб к у), Nх = Е<5 Л (Eqx 4* Рб ®оу)» 1
MxV = D(l — РоНх/, Л^(, = £сЛ(рбе0х-1,-е07); I (2.60)
Л/„ = D (рб kx 4- ки); Nxy = G6 hyQxy, J
где D — цилиндрическая жесткость (D = E<,li4 (1 — р?));
G6 — модуль сдвига бетона (6б = Еъ12 (1 + р0))-
Неупругие деформации в бетоне могут развиваться как
в зонах с большими растягивающими напряжениями, так и
в зонах с большими (по модулю) сжимающими напряжения-
ми. Если учитывать лишь влияние неупругих деформаций
при растяжении, то упругую стадию можно считать справед-
ливой при выполнении двух неравенств:
^^<1. макс 0,5 Л/б. т> Мя. макс 0,5 Л4б. т- (2.61)
При нарушении одного или обоих неравенств (2.61) мож-
но приближенно считать, что сами зависимости (2.60) не из-
менятся, но модуль деформации бетона Ец и цилиндр и чес-
112
кая жесткость D уменьшатся. Более точные физические
зависимости для плит в упругопластической стадии можно
установить, используя ортотропную модель деформирова-
ния бетона, представленную в п. 2 § 6 главы 1.
4. Общая постановка задачи расчета плит и оболочек
с трещинами. Нетрудно видеть, что и общие физические
уравнения (2.47) по форме совпадают с общими физическими
уравнениями для анизотропных пластин и оболочек в общем
виде анизотропии. Ортотропная схема (2.58) получается при
ортотропном армировании лишь для случаев, когда трещины
проходят нормально к стержням арматурной сетки. Таким
образом, и в данной, более общей теории, наличие и ха-
рактер трещин отражаются только на свойствах анизотро-
пии и влияют на физическую сторону задачи, т. е. на зави-
симости между напряжениями и деформациями, моментами
и кривизнами, а также между напряжениями и обобщенными
величинами: моментами и нормальными силами. Геометри-
ческие уравнения, уравнения равновесия и граничные усло-
вия можно записывать так же, как и в теории сплошных
пластин и оболочек.
Так, полная система уравнений для расчета пологих
оболочек имеет вид (при правиле знаков, представленном
на рис. 2.14, а):
а) физические уравнения (2.47) или (2.58);
б) геометрические уравнения 1131;
, d*u> , . _______ а2» . , ____ .
дх2 ду2 дх ду
ди dif ди д2 f
Env=---------“ =-----------— u»
0 дх дх2 ду dy2
ди 2 d*f
дх дх ду
du
VoxV" dy
где и и v — перемещения точек срединной поверхности вдоль
осей х и у, w — прогибы (перемещения вдоль оси z); f —
уравнение срединной поверхности оболочки;
в) статические уравнения 113, 54):
дЛМ
a2 Afy|>
дхду
дН,
дх
*Ln
ду*
dN
dy
дх ду
Рх=°>
а2 , <
ду*
и "Ь Pi= о*
(2-63)
d\fx\
дх
— Nx -1-
113
где рх, ра, р, — проекции вектора нагрузки р па оси коор-
динат х, у, г.
Уравнения для пологих оболочек предложены В. 3. Вла-
совым (131. Обычно представленные системы сводят к двум
(если использовать функцию напряжений) или трем (в пере-
мещениях) разрешающим уравнениям. Однако ввиду того
что жесткости Ви, B*Jt Си и Сц уравнений (2.47) и (2.58)
являются функциями координат (они зависят от напряжен-
ного состояния), при составлении разрешающих уравнений
необходимо учитывать ряд важных особенностей. Частично
они указаны в работе (24] и приведены в § 6.
§ 5. Переменные физические
и геометрические параметры
жесткостных коэффициентов
1. Параметры жесткостных коэффициентов для элемен-
тов со схемами непересекающихся трещин. Важным элемен-
том расчета являются формулы для определения различных
переменных величин, входящих в выражения (2 53) для
жесткостей Blh, B*k, Cik и С**. Параметры зависят от схемы
трещин и армирования, ориентации трещин относительно
направлений арматуры, а также напряженного состояния
элемента у рассматриваемой точки. Способ определения не-
которых величин уже указывался выше. Так, угол наклона
трещин а и а' к осям хну можно определять по формулам
(2.9) и (2.9а), а коэффициенты и — по формулам
(1.85). Из оставшихся неопределенными основную роль иг-
рают четыре вида параметров: средние модули деформаций
арматуры Е»х и Е'аи, средний модуль деформаций бетона над
трещинами и высота сжатой зоны бетона над трещиной
хт (для зон с верхними трещинами это будут соответственно
величины ЕаХ, EaV, Ес и xj), а также средние модули деформа-
ций полосок бетона между трещинами. Три первых вида па-
раметров имеют свои прототипы в теории расчета балок
с трещинами, поэтому встал вопрос, нельзя ли найти анало-
гию в способах определения параметров для более простого
и более сложного случаев. Специальные экспериментальные
исследования показали, что такая аналогия имеется. В ре-
зультате для определения части параметров теории уда-
лось в основном использовать модифицированные формулы
норм, а также выполненные в последнее время в лаборато-
рии теории железобетона НИИЖБ исследования О. А. Ко-
ковина (561, Н. М. Мулина и Ю. П. Гущи (25,67] по уточне-
на
нию этих параметров для стадии работы элементов, близкой
к разрушению (как известно, формулы норм по определению
деформаций на эту стадию не распространяются). Выраже-
ния для параметров теории рассматривались в работах
19, 38, 52, 53].
Элемент со схемой трещин 1а (см. рнс. 2.1, о). Вычистим
некоторые предварительные величины. Изгибающий момент
Мп, нормальная Nn и касательная Nnt силы на наклонной
площадке, проходящей по трещине, равны:
Afn = Мх sin2 а 4- Л/v cos2 а 4- 2Мх!/ sin а cos а;
Л^п = Wx sin2 а 4- Nv cos2 а 4- 2Л xj, sin а cos а;
Nnt — (Ми --Nx) sin a cosa—Nxy (cos2 a—sin2 a).
Для того чтобы иметь возможность рассчитывать эле-
менты вплоть до стадии, близкой к разрушению, необходимо
определить ряд величин, характеризующих эту стадию.
Представим их пока с некоторым приближением, достаточ-
ным для расчета деформаций, а при окончательной оценке
прочности предельные величины уточним. Проекции усилий
текучести в арматурных стержнях на нормаль и касатель-
ную к площадке трещины (на оси п и /) равны:
= отх fax sin2 a 4- ату fay cos2 a 4-
4-а1Я/аз»1п2(а4-р;,);
Nant = (CTT.V L»— °тх /ах) Sin Ct COS Ct —
— °тз /аз sin (a 4- P3) COS (a 4- P3),
(2.64)
гдс<тТ|—пределы текучести арматуры или условные пре-
делы текучести оп>2/ (если арматура не имеет пло-
щадки текучести).
Высота сжатой зоны над трещинами текучести равна:
= V, Л» = Л?» +1 II Rw, (2.65)
где — относительная высота сжатой зоны для момента
текучести арматуры; см. сноску на стр. 12
(при использовании СНиП П-В. 1-62* в (2.65) и
последующих формулах § 5 и § 7 главы 2 сле-
дует /?„,» заменять на /?;; или /?„).
Обычно различают 137, 681 два случая разрушения эле-
ментов:
1) вследствие текучести арматуры или достижения ар-
матурой величин о02( (i = х, у, 3), если явно выраженной
площадки текучести нет;
2) в результате разрушения бетона сжатой зоны до до-
стижения арматурой предела текучести (величин с0 2< и
Or,)-
Первый случай можно считать реальным прн
5г» (2.66)
где 5,- — граничная высота сжатой зоны (может быть опре-
делена по формулам работы 1681). Прн использо-
вании СНиП П-В. 1-62* и марках бетона 400 и
ниже можно полагать 5Г « 0,55.
Переходим к определению относительной высоты ^сжа-
той зоны элемента при его разрушении. Если выполняет-
ся условие (2.66), можно поступать так: для идеально пла-
стической арматуры принимать 5р = 5т. а для арматуры
с упрочнением придерживаться следующего алгоритма опре-
деления 5р- Вычисляем промежуточную величину:
= 11 -г — 1) (1 — cos2(a -г ₽i)J, (2.67)
где т.,«, /п,» — коэффициенты, учитывающие возможность
возникновения в арматуре в момент разрушения элемента
напряжений, превышающих величины о0 г1 соответственно
в трещинах, нормальных к арматуре, и трещинах, располо-
женных под углами к направлениям арматурных стержней.
Величина /на« вычисляется по формулам работы 1681. Вели-
чина для наклонных трещин здесь принята осторожно
и требует еще специальных исследований.
Подставляя в формулы (2.64) вместо величин а0<!/ вели-
чину /н^Оо.л, получаем средине усилия арматуры Л'?п
и Л’ап/, соответствующие разрушению элемента. Подставляя
в формулу (2.65) вместо Nan и Nant величины и Л'Г„/,
получаем значение 5р.
Как поступать, если условие (2.66) нарушается, остается
не совсем ясным. Можно рекомендовать пока лишь следую-
щий приближенный прием. Для момента разрушения вво-
дятся одинаковые (средние) напряжения ал в стержнях
разных направлений, которые выражаются по формулам
новых норм в функции от Ер. При этом в (2.65) индексы <т»
заменяются на <р», и в выражения для величин Nan и Л’алг
вместо от( подставляются значения <та. Решается получен-
ие
ное квадратное уравнение и находится неизвестное значе-
ние Ер.
Переходим к последующим вычислениям. Определяем
моменты (текущие— Л1бП » моменты Men, соответствующие
Е = Ер) всех усилии, приложенных к сечению трещин, от-
носительно уровня нижнего армирования, а также величину
эксцентрицитета еп:
Afgn — Мп Nnza,
Л12п = /?прЛбЕР(1-О,5е₽);
&П ~ ^6п1 Мп
(2.68)
(момент Мбп аналогичен заменяющему моменту М3, а еп —
эксцентрицитету <?, которые фигурируют в формулах норм
по определению жесткости балочных элементов).
Находим условные коэффициенты нижнего армирования
рп = FJh\ Ра — Fnlh, где Fn и F„ определяются по форму-
лам (1.65).
Зная указанные выше величины, можно вычислить вы-
соту сжатой зоны лт для любого уровня нагрузки. Для оп-
ределения хт (или Е) можно использовать формулу СНиП
Н-В.1-62* с дополнением О. А. Коковина 1561, заменив
в ней величины моментов, значения Ер и другие вычисляе-
мые для балок, на аналогичные обобщенные величины,
представленные выше; в результате получим:
•^т — £ — I ?н “I" (?т
(2.69)
где
/I — А — Л^бп/^о^ир*
Ли
(2.70)
С = 3 при с = 5 'р<^-
117
Средний модуль деформации.сжатого бетона в направле-
нии, перпендикулярном к трещинам, можно принять рав-
ным [38]:
^б = ^в'’бХ/фб. (2.71)
где —начальный модуль деформации бетона;
vc, Фб — коэффициенты, аналогичные коэффициентам
v и ф из норм (фб « 0.9);
X—коэффициент, учитывающий увеличение деформа-
тивностн сжатого бетона над наклонными к арматуре тре-
щинами (введен на основании исследований 191),
X = 1 — 0,2 _sin2 2а,
|*П (а-ъ2)
(2.72)
где Ебт—относительная высота сжатой зоны в момент тре-
щинообразования.
Можно также использовать формулы [9]:
при 5 > х = 1 -0,5 $ Г1 Ра рп~' sin2 2а;
при g<5p X=l-0.5|(^)->paft„-,sin22a.
Коэффициент ve в общем виде можно вычислить по моди-
фицированной формуле О. А. Коковина:
vc=(0,5-ASn)/(l —0.88 S„), (2.73)
где А = 0.5—S„ =-^-;
£б ^пр
Выражения для величин, характеризующих дефор.матнв-
ность полос бетона вдоль, трещин, можно принять равным
(при Л/Я.М1Ш > 0):
« w, « 1; £б в « £б. н » £б f 1 — 0,25 ( —Г .
L \ Мб. т I .
(2.71)
Более точные выражения этих величин для плит приведены
в работе 138].
Средние модули деформаций арматуры £н определяются
по формуле (1.11). Следует указать лишь способы опредс-
118
ления величин фп/, vnJ и фу, входящих в эти формулы. На-
ходим предварительные величины:
Afax = ]МХ 4" (Mxv + ^xv ctg ®] \х»
Мпу = [Afy 4* Nv Zq 4* (Afxv “Ь ^xu ^б) tg ct] . (2.75)
Ma3 = Max cos2 ₽3 4- Ma!z sin2 p3; mt = Ma</Af6. T
(j = x,t/,3).
Для определения фа< можно использовать модифициро-
ванную формулу Ю. П. Гущи (251:
0,15 <фа/ = 1,25 — stiu — /i0(l — т,).'(3,5—2//1,)сп. (2.76)
Из (2.76) следует, что для плит, рассчитываемых без
учета нормальных сил (при /аз = 0):
0,15<ф9х= 1,25—s
0,15 ^фау= 1.25—s
_______Мб. т_________.
(Л1х4"М|/х с^б а) ^х
Мб. т________________
(5fv + M
ху tg а) ку
(2.76а)
Эти формулы проверены на основании представленных
ниже экспериментов. Более общая формула (2.76) записана
по аналогии. Также (при некоторой модификации), следуя
работе 1671, можно принять:
di cos 6/
100 oaf
аО, 2 I

(2.77)
где 6/ — угол между направлением арматуры i н нормалью
к трещине (при i = xcos б{ = cos а; при i — y cos б/ — sin а;
при I = 3 cos б/ = sin (а -Ь 03); d( — диаметры стерж-
ней; кроме того, cos б( 0,4.
В расчетах плит (см. § 6) принималась диаграмма растя-
жения арматурных сталей в виде ломаной линии, состоящей
из трех прямых отрезков. Согласно этой диаграмме
Vaj =---------------
(<т.Н — °1)
(о3—О/) аЯ1
—щ ] 4-01 (о3—о>)
(2.78)
119
где прн оа। 0,9 <т0.« (1-й участок диаграммы) а, = 0
(v«i = О*, при 0,9 ст0.г < °ai < а0.а (2-й участок) о, « 0,9
аол» °л = °о.ъ -va = vo,si ПРН аол<'°а1^ав (3-й участок)
— Оо,1> = ^а» '*1 = 'в-
Для определения величин v0 3 и vB можно использовать
формулы работы 167).
Плечо внутренних пар усилий в трещине, а также их
расстояния от срединной поверхности (согласно рис. 2.6)
равны:
^ = Л0(1 O.oj), Zg Ло(1 £), za 0,5Ло. (2./9)
Элемент со схемой трещин 16. Для элемента с этой
схемой в формулы (2.65) — (2.79) необходимо внести сле-
дующие коррективы:
1) формальные, заменив: а на а'; на /а»; 2Л на г';
Л« на Л'; хт на xj; £б на гб на z'e, обп на а'(,п, на 0/;
Е'Л1 на ЕаГ, оа1 на о,/ и т. д. (структура формул прн этом не
изменяется);
2) специальные, заменив знаки перед моментами Мх,
Mv, Л1 Яу н Л1„ на обратные.
Элемент со 2-й схемой трещин. Величины E'ai и Eat
определяются с использованием формул (2.75) — (2.78) так
же, как аналогичные величины для схем 1а и 16. В отличие
от формул (2.74), можно принять (при Л1Я.МШ1 >0 и
Л (я.мин > 0):
Прн переходе к полностью безмоментному напряженному
состоянию формулы (2.80) можно уточнить на основании ис-
следований, представленных в главе 3.
Элемент с 3-й схемой трещин. Параметры жесткостей
элемента с 3-й схемой можно определить по тем формулам,
по которым определяются одноименные с ними параметры
жесткости элемента с 1-й схемой трещин.
Элементы со схемами пересекающихся трещин. Для
элемента с двумя пересекающимися трещинами характерис-
тики его жесткостей вдоль первой и второй трещин будут
различными. В связи с этим для 4-й схемы трещин вводятся
два значения модулей деформации бетона: Е'бх и Е'(,и (или
120
Е’вх.Еби Для схемы *9 вместо Еб (или Еб) и две высоты
сжатой зоны бс«она над трещинами: хтх и хти (или xl* и
х', ) вм*~’и хт (*т)- Однако между элементами с I-й и 4-й
семами трещин имеются связи перехода, описываемые пра-
вилами (2.38) и (2.38а). Используя эти правила, формулы
для параметров жесткостей элемента с 4-й схемой трещин
можно получить из формул для параметров жесткостей эле-
мента с 1-й схемой. Более подробно коэффициенты представ-
лены в работе 138]. Выражения для параметров жесткостей
элемента с 5-й схемой трещин можно получить из аналогич-
ных выражений для параметров жесткостей элемента со 2-й
схемой по правилам перехода (2.59).
2. Экспериментальные исследования. Исследования про-
водились на плитах, шарнирно-опертых по контуру, и на
специальных образцах плит. Здесь имеется возможность
остановиться кратко лишь на исследованиях образцов,
представляющих наибольший интерес (особенно в методи-
ческом плане — методику можно использовать для проведе-
ния дальнейших исследований). Подробно эксперименталь-
ные исследования описаны в работах ПО и 27].
Эксперименты проводились А. В. Бильченко под руко-
водством автора в Харьковском Промстройниипроекте. Они
использовались для проверки формул теории, описывающих
поведение плит в областях с трещинами, расположенными
под углами к стержням арматурной сетки (т. е. в областях
с 1-й схемой трещин, изучение которых представляло осо-
бый интерес). Такие области характерны для плит, где дей-
ствуют изгибающие и крутящие моменты. Однако на натур-
ных конструкциях, например плитах, опертых по контуру,
количественная оценка результатов эксперимента оказы-
вается затруднительной, поскольку сама конструкция яв-
ляется статически неопределимой. Методика эксперимен-
тов позволяет, с одной стороны, изучать поведение плит
с наклонными трещинами, а с другой, — непосредственно
из опыта определять величины изгибающих и крутящих
моментов.
Образцы плит были двух типов: прямоугольные
(рис. 2.15, а) и круглые (рис. 2.15, в). Размеры прямоуголь-
ных плит в плане в среднем составляли 140 X 82 см прн
толщине h = 6 и 8 см. Диаметр круглых плнт был равен
120 см. Кубиковая прочность бетона к моменту испытания
составляла 20—35 МПа. Плиты армировались прямоуголь-
ными сетками (ортотропное армирование), расположенными
близ растягиваемой прн изгибе поверхности образцов. Дна-
121
-
..лй был 6 и 8 ММ, шаг стержней в сетках составлял
метр стерж» еи выхода стержней и» боковые поверх-
около Ю см. в пеЛ.сматривались отгибы стержней или
„ости $ для их надежной анкеровки. ^кн
приварка ортогональные стержни сеток) по-разному
(вернее, взаимно орт t пряМоугольных пластин
ориентировались к н стержней одного из направ-
им. рис. 2.U а)- * г обознач,1М черсз а (ввнду того, что
пХ, У к-рых « О „ №
‘)
<
Рис. 2.16. Схема установ-
ки для испытаний косо-
армированных плит
/ — плита; 2 — блок с шарни-
рами; 3 — поперечные опор-
ные балки; 4 — тяжи; 5 —
цельная металлическая пла-
стина; 6 — гилродомкрат;
7 — цилиндрические шарни-
ры под плитой; 8 — фраг-
мент нсподнижной опорной
рамы
будем называть косоармированными. Испытания проводи-
лись так, что трещины проходили параллельно короткой
стороне пластины (параллельно линии kd на рнс. 2.15, а),
поэтому а являлся еще и углом наклона трещин к направле-
ниям стержней арматурной сетки. Зга же идея лежит в ос-
нове испытания круглых плит. Оси хну будем совмещать
с направлениями стержней так, как показано на рис. 2.15, а.
Ось п направляется перпендикулярно, а ось /— параллель-
но к линиям трещин. Было учтено некоторое влияние нерав-
номерного выхода стержней на боковые края плиты, в ре-
зультате:
fax~ ^'ax^ch ~ Sill ®)’
fay ~ f ayl^cd ~ I'ny/(^ COS «)•
где /’nr, Fnv — площади всех стержней соответственно х и
у направлений, пересекающих в исследуемой зоне Со линии,
параллельные линии kd (т. е. линии будущих трещин);
/Г(|, — длины отрезков типа cd и ck (см. рнс. 2.15, б).
Величины уточнялись согласно (2.11а).
Установка для испытаний плит приведена на рис. 2.16, а.
Нагрузка Р от гидродомкрата 6 прикладывалась к центру
прямоугольника fken жесткой металлической пластины 5,
а затем с помощью тяжей и жестких подвесных
123
поперечин 3 передавалась непосредственно через длинные
(пунктирные линии на рис. 2.16) цилиндрические шарни-
ры 7 на плиту. Тяжи 4 имели шарнирное соединение
с поперечинами 3 и пластиной 5. Усилия в тяжах 4 за-
мерялись с помощью динамометров Д—/, Д — 2, Д — 3
и Д — 4 (эти усилия обозначим соответственно через Pt,
Р2, Р3, Р4). Рассматривая равновесие опорной пластины 5,
можно установить (рис. 2.16, б), что Р2 = Pt = Р3;
Л + Рз = Рз -г Р4 = 0.5Р.
Из рис. 2.16 и этих уравнений следует, что в зоне Со
плит могла возникнуть лишь комбинация чистого изгиба
с чистым кручением или в частном случае (при Р2 — Р2 =
= Р3 = PJ мог проявиться чистый изгиб. Пусть Л1„ —
нормальный, а Мп1 — крутящие моменты на площадках,
параллельных kd в зоне Со (см. рис. 2.15, в), тогда Мп1 =
= 0,5 b (Р3—PJ.tr, Мп = Q,5PA.b.
Нагрузка прикладывалась небольшими ступенями. В на-
чале испытания установка центрировалась так, что Pt —
— Р2 — Р3 = Р4 и это состояние автоматически сохраня-
лось вплоть до образования трещин (т. е. до образования
трещин плиты работали как балочные). Трещины появля-
лись в зоне Со и проходили параллельно линии kd. С по-
явлением трещин (как это следует из теории) плита прев-
ращалась в зонах с трещинами в анизотропную систему,
в результате в осях п и t могли появиться углы закручива-
ния, являющиеся функцией Л1п. Представленная на
рис. 2.16 схема препятствовала закручиванию (последнее
могло несколько проявиться лишь из-за податливости тя-
жей), в результате в зоне Со кроме моментов Мп могли воз-
никать моменты Мп1. Таким образом, опыты дали возмож-
ность проверить формулы теории для областей плит, где
площадки трещин могут не совпадать с площадками главных
моментов, а также выявить случаи, когда это может быть.
Аналогичные результаты можно также получить на осно-
вании испытания круглых плит по методике А. А. Гвоздева
и П. Ленкеи (611.
При передаче нагрузки на тяжи по схеме рис. 2.16, в
крутящие моменты Alnf будут равны нулю (Pt = Р2 —
= Ра = Р4 — 0,25Р). Такая схема также может использо-
ваться для испытания косоармированиых плит.
Представленные схемы необходимо рассматривать как
задачи плит с задаваемыми граничными условиями и напря-
женным состоянием, на основании которых можно проверить
124
основные положения теории расчета плит с трещинами и
определить коэффициенты (параметры), входящие в общие
выражения для жесткостей.
В процессе испытаний (в наших опытах) в исследуемой
зоне Со фиксировались: относительные деформации растяну-
той арматуры, деформации сжатого бетона на верхней по-
верхности плиты, прогибы в середине плиты по отношению
к краям зоны Со (пунктирные линии на рис. 2.16, а), а так-
же ширина раскрытия трещин. Деформации арматуры и
бетона замерялись тензорами на базе около 10 см, прогибы
фиксировались прогибомерамн, а ширина раскрытия тре-
щин — микроскопами с ценой деления 0,05 мм. Таким об-
разом, анализ теоретических зависимостей можно было
проводить по четырем величинам, непосредственно опреде-
ляемым из опыта.
По величинам Л1П и Л1п( (Л1( = 0) определяли моменты
Мх, Му и Л1 Ху. Величины хт вычисляли по формуле (2.69),
а затем находили г. Величины Ло. fax и fay определяли сог-
ласно (2.10) и (2.11а).
Средние деформации арматуры находили по формулам
(1.11) с учетом (1.36), (2.16) и (2.76а), а величину ах — с уче-
том (2.46).
Напряжения обп и средние деформации fon — Обп Ев
сжатого бетона на верхней поверхности пластины в направ-
лении, перпендикулярном к трещинам (вдоль осн л), опре-
деляли по формулам (2.71) — (2.73а).
Остановимся на коэффициенте %. Еще в опытах 1211
было отмечено, что угол наклона трещин а к арматурным
стержням влияет на деформации бетона Сел. т. е. при а 0
и а Ф 90° деформации увеличиваются при одинаковых вы-
численных значениях о<Л. Этот фактор и учитывается с по-
мощью X- Рассматриваемые опыты показали, что кроме
а на величины коэффициента X влияет также степень нагру-
жения, и он может определяться но формуле (2.72) или
(2.72а). Коэффициент X определялся как отношение дефор-
маций бетона Ебп в сопоставимых плитах при а #= 0 н
а = 0.
Исследуемые косоармированные пластины имеют еще и
то преимущество, что позволяют сравнительно просто вы-
числять прогибы, которые вдоль линии п (см. рис. 2.15, а)
будут определяться как для обычных балочных плит с той
лишь разницей, что кривизна А’п должна вычисляться по
иным зависимостям. Согласно § 3 (более подробно этот
125
вопрос рассмотрен в работе 133]), можно записать (с не-
которым пр ибл ижснием):
где величина епп характеризует относительные деформации
элемента на уровне арматуры в направлении оси п. Для
элементов, армированных при а — 90°, еа7 = 0, эта форму-
ла переходит в известную формулу норм. Опыты подтверди-
ли, чго в косоармпрованпых плитах прогибы увеличиваются.
Получено удовлетворительное (рис. 2.17) соответствие
теоретических и опытных значений средних деформаций
арматуры ев и бетона кЛ„, прогибов с и ширины раскрытия
трещин ат. Полные данные сопоставления приведены в ра-
боте |9|, где также представлены результаты обработки опы-
тов зарубежных исследователей 192, 951 (проанализирова-
ны данные около 35 плит).
На рнс. 2.17 представлены графики для прямоугольных
плит со следующими характеристиками: /( — 2: Л = 5,4 см;
/|ж =» 4,08 см; hy = 3,45 см; fax = faM = 0,0274 см; а =
= 45°; Л' — 4: Л = 5,8 см; hx — 4,4 см; hv = 3,69 см;
/ах = 0,0432 см; [а1/ = 0,0274 см; а = 45°; К — 6: Л =
= • 5,8 см; hx = 4,32 см; Л„ = 3,6 см; fax = 0,0635 см;
/., - 0,0153 см; а = 45°. *
Рнс. 2.17. Графики опытных и теоретических значении относитель-
ных деформаций бетона ?лп> арматуры и прогибов к*
126
§ 6. Расчеты железобетонных плит на ЭВМ
с учетом процесса трещннообразования
1. Описание алгоритмов. Рассмотрим практические спо-
собы расчета плит с использованием изложенной выше
теории. Решения осуществлялись на ЭВМ «Минск-22». Пли-
ты подвергались нагружению силами, нормальными к сре-
динной поверхности, а силы Nx, Ny и Nxu были равны ну-
лю. Нагрузка увеличивалась пропорционально одному пара-
метру (т. е. принималось пропорциональное нагружение).
Плиты армировались прямоугольными сетками, распола-
гаемыми близ поверхностен с трещинами, и стержни сеток
ориентировались вдоль осей х и у (при [а3 = 0). Было раз-
работано два алгоритма [24, 38J.
. •_ Первый алгоритм. Система (2.47) при учете (2.62) для
плит имеет вид:
= Вп Мх + В12 Ми 4- В13 Мих,
дх*
—= в1п Мх + В2. Mv + В,3 Л4«;
- 2-?Т- = Мх+Воз Л1у + Вяз Мхи;
дхду
dWy 2 а» ли
дх» дхду ду- И'
(2.81)
(2.82)
где р — функция вертикальной нагрузки.
Жесткостные коэффициенты В, 3 и В23 являются знакопе-
ременными:
В|3 > 0, Во, > 0 при Л!х|/ > 0;
В13<0, Во3<0 при Л1У„ < 0.
(2.83)
Как уже указывалось, уравнения (2.81) совпадают по
форме с аналогичными выражениями для анизотропных пла-
стинок 1621. В связи с (2.83) в железобетонной плите с тре-
щинами будут сохраняться те же оси симметрии напряжен-
но-деформированного состояния, что и в изотропной пласти-
не. Это свойство в теории анизотропных пластин не встре-
чается, а здесь оно приводит к упрощениям и качественно
иным результатам при решении задач. Чтобы исключить
дифференцирование переменных жесткостей Ви в стадии
127
работы плиты с трещинами, уравнения (2.81) и (2.82) не
смолились к одному разрешающему уравнению (относитель-
но и*), а использовались в представленном виде. Прием этот
известен в строительной механике. Например, в работе
1611 исходные уравнения (только первого порядка) исполь-
зовались для расчета изотропных оболочек.
Плита разбивалась разностной сеткой, и уравнения
(2.81) и (2.82) представлялись в конечных разностях. Ис-
пользовались вторые центральные разности [36]. Уравнение
равновесия (2.82) считалось пригодным для любой стадии
работы плиты, уравнения (2.81) изменялись в зависимости
от того, в какой стадии работы находилась та или иная точ-
ка плиты. Полагали, что в процессе нагружения элементы
плиты, выделяемые у рассматриваемых точек сетки, прохо-
дят следующие стадии деформирования: упругую и упруго-
пластическую стадии без трещин, упругую и упругоплас-
тическую с трещинами (последняя связана с развитием
пластических деформаций в арматуре в трещинах). Блок-
схема программы приведена на рис. 2.18.
Для рассматриваемых плит Л1я.макс = Мялке ЛДмакс =
= — ...а Л1б.т определяется согласно (2.1), в резуль-
тате условия трещинообразования (2.7) и (2.8) значительно
упрощаются. Упругая стадия работы плиты без трещин
считалась справедливой при 0,5 А1б.т < А1макс < Мъ.т
Для этой стадии справедливы формулы (2.60) теории упру-
гих плит, согласно которым
= ^23 “ 0j Вц = &22 ~~ 1/D} В12 = Рб Д» 1?33 =
= 2[(l-p0)DJ. (2.84)
Упругопластическая стадия ограничивалась неравенст-
вом 0,о А/б.т А/с.т-
Для этой стадии характерно постепенное падение же-
сткостей за счет развития неупругих деформаций в растяну-
той зоне бетона. В расчетах использовались скорректиро-
ванные выражения (2.81), где цилиндрическая жесткость
D заменялась значениями жесткости
£),=£)[ 1-0,4 (А1 макс — 0,5 МО.т)/Л1б.т]. (2.85)
В плитах встречаются 1, 3 и 4-я схемы трещин
(см. рис. 2.1, а, в и 2.2, а). Уравнения (2.83) зависят от схем
трещин. Так, для схем 1 и 3 лишь В12 = О, остальные же-
сткости имеют один и тот же порядок. Для 4-й схемы трещин
128
Рис. 2.18. Блок-схема расчета плит
5 з.ж. 631
129
принимали [приближенно, более точными будут выражения
(2.58)1:
Bis = Вг9 = Blt = 0; = 0. (2.86)
Для выявления точек плиты, вблизи которых образуют*
ся трещины, проверялись условия трещипообразования
(2.7) и (2.8) (при решении задач методом конечных разностей
условия трещипообразования и возникновение определен-
ных схем трещин можно рассматривать лишь для элементов,
мысленно выделяемых у отдельных точек поля плиты).
Согласно условиям трещипообразования элемент плиты у за-
данной точки работает без трещин до тех пор, пока главные
моменты Л/Ма11<. и Л[мии не превысят по абсолютной величине
значения момента трещипообразования Л1с.т- При этом,
если Л/Макс > Afc.T; |Л/мИ11|<Л/б.т. на нижней поверх-
ности элемента плиты у рассматриваемой точки образуется
одна трещина (по схеме 1а), которая пройдет по площадке
А^мтсс* при Af,laBc > Л[б.т, б.т н элементе обра-
зуется схема <3; при AfMnBC>Afc.T; >Me.t возникают
две пересекающиеся трещины (схема 4)\ при | Л[МПкС | <
< Л[с.т: — Л/мин > Л/б.т на верхней поверхности возни-
кает схема /б; при—/Имакс > Л1С.Т; — Л1МШ, > Л16.т на
верхней поверхности возникает схема 46.
Выявленные у точек схемы трещин запоминались и
в дальнейшем фигурировали как известные. Учитывался
лишь возможный вариант их изменения (в процессе нагруже-
ния в точках плиты с одной трещиной могли образоваться
две трещины).
Гипотеза трещипообразования по главным площадкам
использовалась только для выявления схем трещин. В про-
цессе нагружения (вследствие перераспределения усилий)
площадки трещин могли отклоняться от главных площадок.
В качестве метода решения задач был принят шагово-
итерационный метод последовательных приближений, поз-
воливший моделировать нелинейный процесс деформирова-
ния плиты. В качестве начальной (первого шага) принима-
лась нагрузка, соответствующая упругой работе плиты без
трещин. Для первой итерации следующего шага нагрузки по
упругому полю жесткостей вычислялось поле моментов (на-
зовем его обобщенно Мп) и поле прогибов. По этому решению
анализировались условия трещннообразовання у точек,
выявлялись элементы с трещинами и без трещин и в зависи-
мости от установленной стадии работы элементов плиты
у точек вычислялось новое поле жесткостей (обобщенно Вп).
130
По полученному полю жесткостей Вп снова определялось по-
ле моментов и прогибов на следующей итерации Мп+1.Если
решение Л1п+1 отличалось от решения Мп на величину,
большую заранее заданной точности, переходили к следую-
щей итерации. При этом матрицу жесткостей Вп+1 считали
не по решению Afn+It а по полусумме решений Л/п и
Л4п+1, сглаживая, таким образом, процесс возмущения
поля моментов, возникающий вследствие того, что непрерыв-
ный физический процесс образования трещин в плите моде-
лируется итеративным методом. Процесс считался сошед-
шимся, если моменты и прогибы на очередных итерациях от-
личались во всех точках не более чем на 3%.
Пусть Mn+J и Bn+J— соответственно окончательное
поле моментов и жесткостей для данного шага по нагрузке.
Было опробовано несколько вариантов перехода к первой
итерации следующего k-vo шага по нагрузке. Исследования
эти имели лишь одну цель — сократить число итераций
на очередном шаге. Наиболее рациональным оказался такой
переход, когда жесткости (для первой итерации А-го
шага) определялись так. В точках, где арматура в трещинах
работала в упругой стадии, значения Вк находились по зна-
чениям моментов, умноженным на коэффициент нагрузки с:
с = + 0,5 (ph — pn)]fpn,
где рк — нагрузка данного шага;
рп — нагрузка предыдущего шага.
В точках, где арматура работала в упругопластической
стадии с трещинами, полагали Bh = Bn+J.
Если для всех точек принимали Вк = Bn+J, число ите-
раций возрастало, однако результаты окончательного реше-
ния практически совпадали.
Укажем еще на ряд обстоятельств. На каждом шаге ве-
личины коэффициентов Bth сравнивались с величинами, по-
лученными по предыдущему решению и запоминались боль-
шие (чем больше В/к, тем меньше жесткость плиты в точках).
В результате при локальных разгрузках жесткостиые коэф-
фициенты не восстанавливались (в ряде точек в процессе
трещипообразования могли возникать малые разгрузки).
При возникновении в элементах поля плиты пересекаю,
щихся трещин матрица линейных конечно-разностных урав.
нений модифицировалась таким образом, что крутящие мо.
менты для них принимались согласно (2.44) равными нулю.
5*
131
Принятые положения приводили к быстрой стабилиза-
ции поля жесткостей на каждом шаге и сходимости итера-
тивного решения.
В описанном алгоритме как бы моделировался процесс
поведения конструкции под нагрузкой от начала ее загруже-
ння и до появления больших пластических деформаций.
Прежде чем перейти к новой ступени нагружения исследо-
валась предыстория работы конструкции с трещинами. Бы-
ли сделаны попытки пренебречь предысторией и сразу опре-
делить поле моментов и прогибов для заданной ступени
(шага), приняв в качестве первой итерации упругое решение,
соответствующее данной нагрузке. Одиако не для всех за-
дач таким образом полученное решение и указанное выше ре-
шение с учетом предыстории полностью совпадали. Из рас-
смотренных нами двух примеров хорошее совпадение было
для опертых по контуру квадратных плит при равномерной
нагрузке, при сосредоточенной нагрузке решения могли от-
личаться. Расхождение увеличивалось по мере удаления от
начала трещинообразования. Очевидно, хорошего совпаде-
ния обоих решений можно ожидать лишь для конструкций,
где перераспределение усилий, вследствие трещинообра-
зования, будет небольшим.
Второй алгоритм. При решении задач в конечных раз-
ностях с использованием уравнений (2.81) и (2.82) прихо-
дится сталкиваться с большой системой линейных алгебраи-
ческих уравнений. В связи с шагово-итерационным методом
ее решение требует больших затрат машинного времени.
Был разработан второй алгоритм, лишенный этого недостат-
ка. Уравнения системы (2.81) разрешались относительно
моментов [241:
A/a=-(Dai-^-+DA3-^- + 2D,(3^-) (Л=1,2,3),
\ их2 оу2 охру J
(2.87)
где' Л/i = Л/х; Л(2 = Му; Л43 = Мху. Жесткости Dh) =
“ / при этом Dh) — DJh (при k У= /).
Используя известные выражения для вторых централь-
ных разностей [361, уравнения (2.87) для точки i (рнс. 2.19, а)
можно записать так:
«1=nl о;, + ч Ц, + о>-Л1'„=41 о;, +
+ ч1Ц1 + ч1.^,; (2.88)
—»;=п1»(2+чо;2-ьп1,о;з.
132
Н* ^'а т «•’{>)/(/»*); — (и1,.—2u’j 4-u’jJ/A*;
Пху = (“'«{ &g ^’гп Дрн)> п — Ax/AyJ
wa, к’/—прогибы в точках a,i... разностной сетки:
М‘, М‘,М‘ —моменты в точке i.
*4
Записываем также уравнение равновесия (2.82) в конеч-
ных разностях, например для некоторой точки 33. Это урав-
нение имеет вид (см. рис. 2.19, б):
(МГ + M3i -2 МГ)/п- + (/И;’ + -Л1”)/2 п +
+ (М33 4- М*3 ~ 2Л133) --=-р Д®. (2.89)
Верхние индексы указывают на точки, к которым отно-
сятся моменты Мх, М„ и Л1Х(/.
Подставляя в (2.89) значения моментов, выраженных
через прогибы по формулам (2.88), придем к разрешающему
(относительно прогибов) уравнению для точки 33. В это
уравнение будут входить прогибы 25 точек // прн /, / = 1,
2, 3, 4, 5 и, кроме того, жесткости девяти точек krn Ik, т =
= 2, 3, 4).
Можно заметить, что при таком подходе получаем систе-
му разрешающих уравнений, совершенно эквивалентную
тон, которая получается прн использовании четырех урав-
нений (2.82) и (2.83). Однако число уравнений сокращает-
ся в 4 раза. Это приводит к значительной экономии машин-
ного времени (на ЭВМ «Минск-22» в 15—20 раз). Решением
системы уравнений на каждой итерации являются прогибы
в узлах разностной сетки. Зная прогибы, по формулам (2.88)
можно определить моменты. Итерационный процесс быстро
сходится. Время решения представленных ниже задач
Рис. 2.)9. К составлению уравнений в конечных разностях
133
(с учетом всей цепочки шагов) составляет около 15—25 мин.
В остальном второй алгоритм не отличается от первого.
Составление разрешающих уравнений было автоматизиро-
вано.
При указанном способе составления разрешающих урав-
нений необходимость в явном дифференцировании жест-
костей отпадает и производится их автоматическое сглажи-
вание в случае, если жесткости являются не гладкими функ-
циями координат. При традиционном способе вывода разре-
шающих уравнений необходимо накладывать условие диф-
ференцируемости жесткостей. Попытки применить конеч-
но-разностную аппроксимацию таким образом составленных
уравнений приводили к расходящемуся процессу счета на
ЭВМ.
Укажем на некоторые особенности учета граничных ус-
ловий при использовании разрешающих уравнений. Пусть
на кромках ab и cb (см. рнс. 2.19, б) имеется шарнирное опи-
рание 1771, тогда на ab: ьу = О, Мх = 0; на cb: w = 0,
Mv = 0.
Было опробовано два варианта учета этих граничных
условий. В первом варианте условия Л1х = 0 или Му = 0
на границе учитывались непосредственно на первом этапе
в уравнениях типа (2.89) при составлении их применитель-
но к разрешающим уравнениям для точек, лежащих на
линиях ed и ef (линиях, ближайших к границам ab и cb).
Выражения (2.87) для моментов Л1хи на границах ab и cb
представлялись в односторонних конечных разностях (в ка-
честве последних использовались известные выражения
в виде двух членов нтерополяционной формулы Ньютона
(361), а остальные моменты выражались через прогибы с по-
мощью уравнений (2.88). В составленные таким образом
уравнения законтурные точки выходить не будут. Этот спо-
соб позволяет сократить число уравнений.
Второй вариант учета граничных условий был таким.
Разрешающие уравнения (за исключением уравнения для
точки е) и граничные условия Мх — 0 или Му = 0,
представленные в виде (2.87), записывались в цент-
ральных конечных разностях. Лишь для выражения мо-
мента МХу в угловой точке с (этот момент входит в урав-
нение типа (2.89) для точки е) использовались односторон-
ние разности, чтобы исключить из рассмотрения законтур-
ную точку i (см. рис. 2.19, б). В составленные таким образом
уравнения входят некоторые прогибы одного ряда закон-
турных точек и, естественно, число уравнений увеличнвает-
134
ся. Однако при обоих вариантах записи граничных условий
некоторые различия были лишь для точек, прилегающих
к контуру.
Укажем еще на особенность составления граничных ус-
ловий для свободного края. Пусть, например, край cb сво-
боден, тогда на этой границе 177]
ЛГ-О;-^-+2-^2. =о.
ду дх
Чтобы выразить второе уравнение для границы в функции
от прогибов, поступали так: представляли это уравнение
в центральных (или односторонних) разностях, а затем уже
входящие в это уравнение моменты различных точек заменя*
ли их значениями, выраженными в функции от прогибов
на основании уравнений (2.88) или аналогичных уравнений,
записанных в односторонних разностях. В этом случае,
чтобы избежать дифференцирования жесткостей, применяет-
ся тот же прием, что и при составлении разрешающих урав-
нений. Укажем еще на одну особенность, которая встречает-
ся при записи граничных условий для опертых по контуру
плит. Как известно (8GI, углы таких плит при нагружении
могут приподниматься (если их не закрепить от подъема).
Чтобы это учесть, вертикальные перемещения угловых точек
выражались (на основании экспериментов) в виделинейной
функции от прогибов центра плиты. Эти зависимости и учи-
тывались непосредственно при записи граничных условий.
Подробно этот вопрос рассмотрен в работе (36].
Для решения системы уравнений использовались стан-
дартные программы.
2. Сравнение результатов расчета и опыта. По описан-
ной выше программе было просчитано большое число плит
из опытов Г. Баха и О. Графа 185, 861; В. Гелера и X. Амоса
[881; А. А. Гвоздева, С. М. Крылова н автора 121]. Исследо-
вания выполнялись автором совместно с Л. И. Яриным и
А. Л. Гуревичем [21, 381.
Данные некоторых просчитанных опытов представлены
в табл. 2.1. Плиты различались граничными условиями, раз-
мерами в плане, маркой бетона, толщиной, коэффициентами
армирования (некоторые плиты имели переменное по полю
армирование), а также видом загруженпя (равномерная и
сосредоточенная нагрузка). Плиты 924, 946 и 951 были пере-
армированы (разрушение их происходило от раздробления
бетона сжатой зоны до достижения арматурой текучести).
135
№ п/п Образцы пл нт axb, м На- груз- ка Схема опи- рания Л. см лх, см Л1/’ см S^. см Sy, см
Опыты Г. Баха и
1 825. 826. 827 2X2 Р-16 у 12,2 10.8 10.1 10 10
2 846, 847 Р-16 j 12.1 10,7 10 10-14,3 9,3—14
3 8-15 2X2 Р-1 j 12.1 10,7 10 10—14,3 9,3—14
4 842. 843 2X2 Р-16 8.1 6.7 6 ГО—14,3 8,8—14,5
5 844 2X2 1 л 8.1 6.7 6 10-14,3 8,8—14,5
6 828, 830. 811 2x2 р-16 / 8.1 6.7 6 10 8.8
7 831. 837. 840 2X2 р-16 у 12,1 10.7 10 10 9,3
8 921. 916, 951 2X2 р-16 у 8.1 6,6 5,6 6 5
9 863, 866. 868 3x2 Р-2! / 12.1 10,8 10,1 10 10
10 860. 861. 862 4 Х2 Р-32 у 12.1 10.8 10,1 10 10
11 1062 3x2 Р-1 2 14 12,5|11,4 10 10
Опыты В. Гелера
12 709, 710 3X3 Р-64 3 15 13 12 13-7 13—7
13 711, 712 3XL5 Р-64 3 14.9 12,9 12,1 12—12,5 17-18
14 713, 714 1.5X3 Р-64 2 15,1 13,1 12,3 12—12,5 16,7
Примечание. Р-16, Р-24, Р-32 и Р-64 — модели рапномерной
ных по полю плиты; Р-1—сосредоточенная нагрузка в центре плиты
136
мм F . ах см 1 =>£»» 'av s • . см °т* МПа %• МПа Ку Си- новия проч- ность, МПа Схемы опирания
О. Графа [85, 8G]
7,2 0,0407 0,0107 408 592,9 26,5 CiPMJI 1
/ 0.0385 0,0275 0.0414 0,0265 108 592,9 26,5
cri । 1 ; 1 1 1 ' |.
7 0,0385 0,0275 0,04 И 0,0265 408 592,9 26.5
1 д "t зс* t —
7,1 0,0395 0,0276 0,045 0,0273 408 592,9 26,5 и “ ч
7,1 0,0395 0,0276 0,045 0,0273 408 592,9 26,5
7,2 0,0407 0,0463 108 592,2 26,5 , 5 Слепа 2 £
7,2 0,0-107 0,0437 408 592,9 26,5 *сь —' г
10,1 0,133 0,16 529,2 782,9 14,6 _а
1 г 1
7 0,0385 0,0385 427,9 597.9 26,5
7 0,0386 0,0385 427,9 597,9 26,5
11 0,096 0,096 |348 447,3 24.7 СлемаЗ
и X. Амоса [88] Р £ ь го —— <
10,2 0,063 0.117 0,063 0,117 320 455 28 L «
т
10,2 0,0655 0.068 0,048 0,0455 320 455 27,3 . — Cfc‘cinvu край о Тс черные оперы
10,2 0,0655 0,068 0,0492 320 455 27
нагрузки в виде 16, 24, 32 и 64-х грузов, равномерно распределен
(на площадке 12,5x12,5 см).
137
Таким образом, можно было всесторонне оценить при-
емлемость теоретических решении. Рассмотрим сначала
квадратные опертые по контуру плиты прн равномерной
нагрузке. Теоретические и опытные прогибы сравнены на
рис. 2.20 и 2.21. На рис. 2.20 отдельно показано, как изме-
няется график,«нагрузка — прогибов центре плиты в зави-
симости от стадии ее работы (без трещин, с трещинами, с тре-
щинами после начала текучести арматуры). 1крсход из одной
стадии в другую характеризуется переломами на указанных
графиках. Однако эти переломы зависят от вида нагрузки
н граничных условий и не всегда носят ярко выраженный
Рис. 2.20. Графики прогибов плит № 825, 826 и 827 из опытов Г. Баха
а О. Графа
а — в центре плит; б, в —по линиям it—21 и ?5—X при Р-81 кПв
138
Рис. 2.21. Графики прогибов в центре квадратных плит
139
характер. Теоретические прогибы удовлетворительно со-
гласовывались с опытом не только в центре, но и по всему
полю плиты (рис. 2.20, б, в). Кроме прогибов исследова-
лись н другие вопросы. На рис. 2.21 представлены опытные
р? и теоретические р? значения нагрузок, соответствующих
началу трещннообразования в плитах. Имеется хорошая
сходимость опыта и теории. Анализ решении, полученных
по теории упругих пластинок, и решений с учетом трещин
показал, что моменты в обоих случаях представляют собой
величины одного порядка (расхождение 5—30% с увели-
чением к углам), в то время как прогибы отличаются на по-
рядок (расхождение в 3—12 раз).
Рнс. 2.22. Графики прогибов плит, нагруженных в центре
сосредоточенной нагрузкой
д —прогибы в пентре плит SH н 815; б, в—прогибы плиты 845 при Р«»70 кН
по линиям 2/—27 к
1 !0
Рнс. 2.23. Схемы развития трещин на нижней поверхности плиты
844 в процессе нагружения сосредоточенной в центре нагрузкой
(Р= 17—50 кН)
а —опыт; б —расчет
На рис. 2.22 приведены данные сравнения опытных и те-
оретических значении прогибов в квадратных опертых по
контуру плитах, нагруженных сосредоточенной в центре
плиты нагрузкой. В этих плитах армирование было пере-
менным (уменьшалось от центра к контуру). Сходимость
теории и опыта хотя и была удовлетворительной, однако
имели место особенности, очевидно, связанные с тем, что
141
в расчетах не учитывались мембранные и поперечные силы.
Так, на отдельных графах прогибов можно отметить неко-
торые резкие переломы, кроме того, после начала текучести
в арматуре теория в ряде случаев опережала (на 20—30%)
опыт. В плитах, нагруженных сосредоточенной нагрузкой,
после появления трещин наблюдалось явно выраженное пе-
рераспределение усилий (моменты в центре плиты умень-
шались по сравнению с данными упругого расчета на 20—
35%). Интерес представляет сравнение опытного и теорети-
ческого процессов развития трещин под нагрузкой. Эти
данные для плиты 844 представлены на рис. 2.23, где верх-
Рис. 2.24. Прогибы
fl-в центре прямоугольных плит 863, н 868; б —то же. 860, 861 и 862
142
Ч)
6)
Р-29 кПа

Р ^38 кПа
Рк53 кПа
Р* 70 кПа
Рис. 2.25. Схемы развития трещин на нижней поверхности плиты 8G6
в процессе нагружения равномерной нагрузкой (р « 29—70 кПа)
а — опыт; б — расчет
143
Рис. 2 26. Графики прогибов в центре опытных плит В. Гелера и
X. /\моса
ний ряд схем относится к данным опытов Г. Баха и О. Гра-
фа, а нижний представляет собой их теоретическое описа-
ние. Схемы трещин размещены в последовательности возра-
стания нагрузки. Эти схемы показывают, что теория удов-
летворительно описывает процесс трещинообразования-
Представлеиные выше детальные сравнения данных опыта
и теории были выполнены на только для квадратных опер;
тых по контуру плит. Сравнены также результаты расчета
и опыта для прямоугольных шарнирно-опертых по четырем
сторонам плит (рис. 2.24 и 2.25), прямоугольных и квадрат-
Пли^а 7*з
Р*П*Па
Р*26*Па
Плита 712
Р-12*Па
Р-32*Па
() Р*Н*Па
Р*20*Па
f)
Р’ПкЛа
р* 30 к Па.
Рис. 2.27. Схемы развития трещин на ннжнен поверхности плит
710 и 712
а — опытные; б — теоретические
141

них плит, опертых в четырех угловых точках (рис. 2.26
и 2.27) прн равномерной нагрузке.
Анализ этих результатов показывает, что предложенная
теория деформирования плит с трещинами и изложенный
способ расчета хорошо описывают напряженно-деформиро-
ванное состояние железобетонных плит, начиная с упругой
стадии работы и кончая состоянием, близким к разрушению.
Алгоритмы расчета, разработанные на основе этой теории,
позволили получить теоретически весьма детальную и близ-
кую к действительной картину процесса образования и раз-
вития трещин и прогибов по полю различных плит в процес-
се нагружения. Расчеты позволяют также определять ши-
рину раскрытия трещин и анализировать напряженное со-
стояние в любой области конструкции.
§ 7. Условия прочности для плит
и оболочек с трещинами
1. Условия пластичности К. Йогансена и А. А. Гвоз-
дева для изгибаемых плит. Развитие условий пластичности
для железобетонных элементов с трещинами берет свое на-
чало от работ К. Йогансена 190] и А. А. Гвоздева (15] по из-
гибаемым плитам. Ими рассматривалась идеально пласти-
ческая арматура с диаграммой в виде диаграммы Прандтля,
при которой понятия условий прочности и условий теку-
чести или пластичности элемента по арматуре можно ото-
ждествлять. Условие К. Йогансена было сформулировано
применительно к выдвинутой им теории прочности железо-
бетонных плит, армированных прямоугольной сеткой
(рис. 2.28, а), по линиям излома и имело вид (для линий из-
лома, расположенных в нижней зоне плиты, рис. 2.28, а, б):
Мп = Д1ТХ sin 3 ат 4- AfT!Z cos2 <хт, (2.90)
где Мп — изгибающий момент на линии излома; А1тх
и А1Т1/—предельные моменты усилий текучести в арматуре
(Mtx = <y„Jnxr, Мхи = ат.Л^. где z - п.течо внутренней
пары усилий); ат — угол между арматурой х-направления
и площадкой текучести, проходящей по линии излома.
Теория линий излома К. йогансена представляет собой
не что иное, как определение несущей способности плит
кинематическим способом теории предельного равновесия,
который дает оценку несущей способности сверху. Кроме то-
го, имеется статический способ теории предельного равно-
весия, дающий оценку несущей способности снизу. Теоре-
145
тическое обоснование метода предельного равновесия в его
современном виде и доказательство теорем о нижней и верх-
ней границах несущей способности даны А. А. Гвоздевым
114, 161. Однако на самом методе предельного равновесия
и работах, использующих или развивающих этот метод, мы
не останавливаемся и рассматриваем лишь условия пластич-
ности железобетона, нашедшие применение в этом расчет-
ном аппарате.
Неизвестной величиной в условии (2.90) является угол
«т, который К. Иогансен предлагал определять из экспе-
риментов. В этом отношении более общими оказались ус-
ловия текучести арматуры А. А. Гвоздева, предложенные
в работе 115). Условия были рассмотрены применительно
к сложному косоугольному армированию, однако, чтобы
иметь возможность сравнить их с условиями (2.90), рассмот-
рим вывод условий для нижнего ортотропного армиро-
вания. А. А. Гвоздевым было установлено, что предельные
моменты усилий текучести в арматуре образуют симметрич-
ный плоский тензор, который был назван тензором сопро-
тивления. Разность тензора сопротивления и тензора дей-
ствующих моментов была названа тензором запаса проч-
ности. Эта терминология А. А. Гвоздева оказалась весьма
удачной. Она неоднократно использовалась при анализе
более общих условий. Для рассматриваемого армирования
компонентами тензора сопротивления будут: Мтх, Мти
Рис. 2.28. К анализу условий пластичности
для плит (Ф —фрагмент поверхности пли-
ты с линией текучести арматуры)
/ _ арматура; 3 — линия текучести арматуры; 3 —
сжатая зона; 1 — линия на срединной поверхности
плиты
146
и Mtхи = 0, а компоненты тензора запаса прочности со-
ставят:
Л* — (Л1тх MJ), Ау = (Try MJ)', Axy = {Mtxy —
Мху) ~ Мху*
Зная величины Лх, Л,, и АХ:„ легко определить главные
компоненты тензора запаса прочности: ЛМ1Ш и Лмакс.
Площадка, на которой компоненты тензора запаса обра-
щались в нуль, и являлась площадкой текучести, а условие
текучести арматуры, предложенное А. А. Гвоздевым, имело
вид
Л„И11 = 0. (2.91)
Используя известные выражения для главных компо-
нентов плоского тензора, можно легко преобразовать усло-
вие (2.91) к виду
(Mtx — MJ) (М1и — MJ) — М'Ху = 0. (2.91а)
Однако А. А. Гвоздев записал свои условия в более простой
форме позже, в работе 120], а раньше (иным способом) это
сделали Ш. Массоне и М. Сав I95J. Условие (2.91) является
более надежным, чем (2.90), так как оно автоматически учи-
тывает наиболее опасные (при данном армировании и напря-
женном состоянии) площадки текучести. Формула для оп-
ределения ориентации площадок текучести арматуры дана
в работе 120]:
tg ат = ± V (Мгу-Му)1(МГх-Мх). (2.92)
Условие (2.90) преобразуется к виду (2.91) или (2.91а)
лишь при значениях ат, найденных по формуле (2.92).
Остальные предпосылки, принятые при выводе формул
(2.90) и (2.91), являются общими. Предполагается, что:
1) все стержни достигают текучести по некоторым площад-
кам; 2) в стержнях возникают лишь нормальные (направ-
ленные вдоль оси стержня) напряжения; 3) в процессе де-
формирования стержни не изменяют своей первоначальной
ориентации. Эти предпосылки стали классическими при
оценке работы арматуры в пластической стадии.
С момента своего появления условие К. Погансена (за-
рубежным исследователям условия А. А. Гвоздева долгое
время оставались неизвестными) неоднократно подвергалось
критике. Для нас в первую очередь представляет интерес
критика предпосылок, принятых при выводе этого условия.
147
Наибольшим нападкам подвергалась указанная выше тре-
тья предпосылка и делались попытки изменить ее. Так,
в работе Р. Вуда 1981 была выдвинута идея «полного
перегиба», согласно которой арматура при текучести в тре-
щинах перегибается так, что становится нормальной к тре-
щине (рис. 2.28, в). В этом случае в условии (2.90) величины
sin’a и cos’a заменяются на sina и cosa, что, естественно,
приводит к значительному увеличению расчетной несущей
способности. Позже М. Квицинский выдвинул идею «непол-
ного перегиба» [91), которая приводила к меньшему, чем у
Р. Вуда, увеличению несущей способности. Однако еще рань-
ше вопрос о перегибе арматуры затрагивался в работе
Н. В. Ахвледиани и В. Н. Шашимелашвилн 12]. Они и мно-
гие зарубежные исследователи пришли к выводу, что для
арматуры реальных диаметров явление перегиба можно не
учитывать. Видимо, это явление может, несколько ска-
зываться при исследованиях на моделях, где применяет-
ся мягкая арматура диаметром, соизмеримым с шириной
трещин.
Экспериментальная проверка условий (2.90) и (2.91)
проводилась многими исследователями (обзор их дан в ра-
боте 1751). Б. Баус и С. Толачча 1871 пришли к выводу, что
эти условия при определенных соотношениях главных мо-
ментов приводят к занижению прочности. Подобные данные
можно встретить также в работе Ш. Массона 1951. Согласно
1871, предельный момент в плите увеличивался на 30%,
если в перпендикулярном направлении прилагался равный
ему момент. Эти данные вызвали постановку более деталь-
ных экспериментов (эксперименты Ш. Массоне критику-
ются в работе ПОИ), которые показали хорошее согласова-
ние условия (2.90) с экспериментами. Среди этих экспери-
ментов необходимо отметить опыты Р. Леншоу и М. Созена
192,93J. Условия типа (2.91а) с учетом совместного действия
моментов и сил были рассмотрены в работах автора 1331
и С. Морли [961. Согласно (331 условия (2.91а) приняли
вил:
(М„ - - Af,)(AfT1, - Nyza - М„)~
-(Мху + МХ1/0)« = 0 (2.93)
(гб показано на рнс. 2.28, а).
Запись условий типа (2.93) для сложного армирования
дана в работе [391, а в [37! они дополнены условиями проч-
на
пости по бетону сжатой зоны, рассмотрен важный вопрос
определения г и zc и др. Способы применения условий (2.92)
и (2.93) для определения несущей способности плит и обо-
лочек по методу предельного равновесия разработаны в ра-
ботах М. И. Рейтмана, Б. 10. Мирзабекяна и других иссле-
дователей 134, 66, 751.
2. Вывод общих условий прочности по арматуре н бе-
тону для элементов с различными схемами трещин. Проч-
ность элементов зависит от характера развития в них трещин
и других факторов. Классификация схем трещин, по кото-
рым происходит разрушение, подобна той, которая дана
в § 2 для упругой стадии работы арматуры, однако величи-
ны а и ат могут быть в общем виде различными.
Ниже рассматриваем случай разрушения (см. п. 1 § 5)
по арматуре и бетону.
Элементы с 1-й схемой трещин. Прочность по арма-
туре. Рассматриваем элементы, армированные в общем виде
шестью слоями арматуры. Характеристики армирования,
способы приведения слоев армирования в один обобщенный
слой и другие параметры принимаются такими же, как в § 2.
Однако все слои приняты (в отличие от § 2) косоугольными.
Различаем арматуру: 1) имеющую значительную гори-
зонтальную площадку текучести (арматуру с диаграммой,
близкой к диаграмме Прандтля) и 2) не имеющую такой пло-
щадки. В первом случае прочность арматуры характери-
зуется одной величиной—пределом текучести от<, а во вто-
ром— двумя величинами: условным пределом текучести
o0t2i и условным пределом прочности ор/. Для элементов
с несквозными трещинами ор< ~ m(i o0.2i, где я» ц опре-
деляется по формуле (2.67) при замене а на ат.
Рассмотрим сначала вывод условий прочности (или пла-
стичности) элементов при арматуре с площадкой текучести.
Пусть трещины расположены в нижней зоне элемента и
верхняя арматура отсутствует. Пренебрегаем для пласти-
ческой стадии касательными напряжениями в арматуре,
полагая та1 = 0 (учесть их можно, заменяя в окончательных
зависимостях от/ согласно (1.986)1. Выделим из конструкции
малую в плане треугольную призму толщиной h так, чтобы
наклонная грань ее прошла по площадке текучести (тре-
щине, где течет арматура), и две боковые грани — вдоль
плоскостей хОг и yOz (рис. 2.29, а). Составляя два урав-
нения моментов всех сил, приложенных к граням призмы,
относительно осей, проходящих параллельно осям х и у
149
Рис. 2.29. К выводу условий текучести арматуры для элементов с 1-й
схемой трещин
через центр тяжести бетона сжатой зоны (точку е), полу-
чаем:
Ахх sin ат + Лх7 cos ат = 0;
АуУ cos ат + Hx!zsinaT = 0, (2.94)
где
Лх= 2 «Wai (Ло—0,5xpCOS®pi —Л4Я —
—0.5 (Л—хр;
Л99 = 2 стт/ Au (Ло—0.5 хр sin® pi—M,J—
-0,5Ny(h-x;)-,
AXV= 2XJaiC»o—0,5 Xp sin Pi cos Pi —
Mxy 0,5 NxU (Л —xp.
(2.95)
Исключая из (2.94) угол ат, придем к условию пластич-
ности:
Ахх АУУ~'Аху 0,
(2.96)
150
где Ахх^-О, Avv^0, а исключая величину Аху,—
к условию
tg «т = ±УАуи/Ахх. (2.97)
Здесь знак «±» обратен знаку величины Аху. Неизвестной
величиной в (2.95) является высота сжатой зоны х? над
рассматриваемой трещиной, где течет арматура. Точное
определение х? в общем виде представляет собой весьма тру-
доемкую задачу, поэтому остановимся на приближенных
способах. Обозначим усилия, приложенные к бетону сжатой
зоны над указанной трещиной, через Лгбп и Л'бп/. Проек-
тируя все силы в трещине на плоскость, нормальную к тре-
щине, и на плоскость трещины, получаем:
Л^бп (®т •'Pi)’
I
Мот = Nnt + X сгт1 fai sin (а + ₽(),cos (а + р4).
(2.98)
Ha площадке, нормальной к трещине, будем учитывать
влияние коэффициентов сцепления бетона с арматурой
(фа<) на уменьшение напряжений в арматуре, принимая
средние напряжения, равными оа4фа{. В результате
Л'б/ = — - °т( Фа! /а* COS2 (ССТ + ₽4),
i
(2.99)
кроме того, примем Notn = Л'Сп4. В общем виде в элементе
могут быть две высоты сжатой зоны: одна (хт = х?я) над
трещиной и вторая (xj4) в сечениях, нормальных к тре-
щинам (рис. 2.29, б). Величины их легко поддаются опре-
делению лишь для частного случая, когда площадки nut
будут главными площадками (при N6nl = 0) и напряжения
в бетоне достигнут величин /?„р. В этом случае приняв
хг1П = х?ь a xL = хЬ (рнс. 2.29, в), получим (при Л'вп <
< 0; Nct < 0):
== ^бп/^пр' *^т2 ~~~ 6t ^пр-
Если величин /?цр достигнут лишь напряжения над пер-
вой трещиной, то верным будет только первое условие, а ве-
личина х?2 может быть любой. При всех этих случаях xji
не зависит от х[2- Теперь подвергнем этот элемент допол-
нительному воздействию усилий При этом, чтобы на-
пряжения сжатой зоны нс превысили /?|1Р, высота сжатой
151
зоны должна
(рис. 2.25, г)
Полагаем,
Н6п < 0)
быть максимум увеличена на величину
A.V* — | У бп< | Rw.
что в общем случае можно принять (при
Ат ~ Ат1 4” —( ^бп 4" I | )/^ир—I ЛГп4"
+ °г/ fbi sin2 (аг ч- Pl) + | A’,lt + v qt/ fa( sin (<xT +
+ Р/Ros (aT -I- pj |]//?„p,
(2.100)
причем значение xTtt может быть любым или равным:
А'я (— ^6< + l^otn l)/^un— (—+
+ 2 СТт1 Фа* fai COS2 (at + pj) + |Л/П< + 2 °т< /а * sin (а -|-
+ Pi) cos (а + Pi) 11/ЯвР. (2.101)
В выражение для xj входит значение ат, поэтому окон-
чательные значения для xj можно установить, решая урав-
нения (2.1(H)) и (2.97) методом последовательных прибли-
жений. Для первого приближения можно принимать ат =
= «. Определив х[, находим окончательные значения (2.95)
для а затем проверяем выполнимость условия (2.96).
Но корректным совместное решение уравнений (2.97)
и (2.100) будет лишь при условиях, соответствующих вы-
полнению условия (2.96) в виде равенства. Чтобы это учесть,
можно предложить следующий приближенный алгоритм,
вводя экстраполяционный множитель т^0, для определения
напряженного состояния предельной стадии. Принимаем
«т = « и определяем xj. Находим ЛАу по формулам (2.95),
предварительно умножив все моменты и силы на i]0. Под-
ставляя значения Ak) в равенство (2.96), находим коэффи-
циент 1)0. Умножаем моменты и силы, входящие в урав-
нения (2.97), и для ат (2.100), на rf0 и в таком виде решаем
их для определения xj н «т. Затем находим окончательные
значения /1А; и проверяем выполнимость условия (2.96).
Остановимся еще на одном приближенном приеме. Если
оси х и у совпадают с главными осями армирования (см. п. 1
§ 3 главы 1), то при определении Ah) по формулам (2.95)
можно поступать так. Определять, используя уравнение
(2.100), два значения xj: xj = xL прн ат = 90° и х? = х^
152
при ат = 0°. В первом случае Nn = Л\, а во втором Nn =
» Nu. В дальнейшем в выражении для Ахх х? заменяется
на Хм, а в выражении для Ауи xj заменяется на х^. При
определении ЛХ!/ принимается xj = 0,5 (xj, + х^). При
этом необходимость знания углов аг при определении AhJ
отпадает. Найденные таким образом значения Ah) пригод-
ны также и для условий прочности элементов с 4-й схемой
трещин.
Подставив в формулы (2.94) — (2.100) вместо от( вели-
чину Оо.з//П^> придем к условиям прочности элемента.
Анализируя формулу (2.97) для ат, нетрудно заметить,
что углы наклона площадок текучести и разрушения могут
не совпадать с углами наклона трещин упругой стадии.
Поэтому, чтобы продолжать расчет деформаций вплоть до
разрушения элементов, необходимо вводить функции изме-
нения угла наклона трещин от а до ат. Один из таких прие-
мов указан в § 7 главы 1.
Условия прочности элементов по бетону. Пусть пре-
дельная высота сжатой зоны, соответствующая разрушению
этой зоны, равна Хр, а площадка, на которой напряжения
в бетоне достигают предельной величины /?пр, проходит под
некоторым углом ад к оси х (рис. 2.30). Усилия к граням
призмы прикладываются так, как показано на рис. 2.29, а.
Составляя два уравнения моментов всех сил, приложенных
к призме относительно осей, проведенных через точку а
на уровне обобщенного слоя армирования параллельно осям
х и у, получаем:
Бхх sin аБ 4- Бху cos аг, = 0; Буу cos аБ + Бху sin аБ -
= 0, (2.102)
где
S„=Mo-Afx-HVx(/io-0,5/i); Буу~ '
= —Му + У у (Ло 0,5/i); юз
БхУ=— Mxy + NxV(ltt-0,5hy, Мб=
= Лр 0,5 хр.
4
Решая уравнения (2.102), получаем
РххБуу-Б'Ху>0. (2.104)
153
Методика определения х₽ = £р частично уже указы-
валась в п. 1, §5. Остановимся на алгоритме ее уточнения.
По формулам (2.100) и (2.101) определяются величины х?
и Хи при ат = а. Эти величины сравниваются с гранич-
ным значением высоты сжатой зоны хг = 5^0, определяе-
мой согласно п. 1 § 5. Если нарушается одно из условий
х? хг и Хи хг, значит имеется случай разрушения по
бетону. В дальнейшем определяются средние напряжения
в арматуре, соответствующие этому случаю, и по формулам
(2.100) и (2.101), с учетом найденных напряжений в арма-
туре и ат = а, уточняются окончательные величины xj
и Хн. Максимальная из них и принимается как х£. Для
арматур классов А-I и А-П и бетонов марки не выше 400
Мс ~ 0,4 Л;/?„ (/?„ — см. СНиП П-В. 1-62*).
Остановимся еще на влиянии двухосного сжатия на уве-
личение прочности бетона сжатой зоны. Чтобы учесть этот
фактор, после определения х£ можно поступать так. Опре-
делять действия моментов и сил на верхний слой бетона
(если сжатая зона находится в верхней зоне) в виде приве-
денных сил:
Л/; = (—Мх + za)/z; м; = (—Му + za)/z;
Nxy = (—MX,J + NxyZa)lz\ z — h0—0,5xp,
находить Ммакс Н_ Nu„n И, если Л^ксСО II Л’хин<0,
определять т = N мт! Ынам и по формуле (1.104) находить
коэффициент увеличения
прочности бетона kc. Уточненное
Рис. 2.30. К анализу схемы
пересекающихся трещин
Рис. 2.31. К анализу прочности
бетона сжатой зоны
154
значение предельного момента ЛГб определяется по формуте
(2.103), где /?„р заменяется на Ruvkc. ''
Элементы с 4-й схемой трещин. Текучесть в арматуре
достигается по двум и более пересекающимся трещинам
Рассмотрим наиболее опасный случай, когда эти пересе-
кающиеся трещины проходят вдоль главных осей армиро-
вания, совмещая направление осей х и у с направлениями
главных осей (рис. 2.31), где площадки текучести совме-
щены с гранями прямоугольного элемента). В элементе
имеются две высоты сжатой зоны xjx и xj„. Для касатель-
ных сил вводим среднюю высоту х,с = 0,5 (xjx 4- xj.).
Предельные усилия в арматуре дают на каждой грани эле-
мента нормальные моменты относительно середины х,х и
x,v и касательные моменты относительно середины х. .
Вычитая из этих величин приведенные к тем же уровням
одноименные обобщенные моменты (величины Л1 ’, ц
Мxv плюс моменты от действия сил Л’х, Л’„ и Л’х„), получаем
функции запаса прочности элемента по арматуре ’ Л хх,
А у у, АХу. Как они получаются из (2.95) при двух значениях
высот сжатой зоны, указано при анализе первой схемы тре-
щин (см. приближенный прием). В момент наступления теку-
чести по двум линиям будут соблюдаться равенства:
Ахх = 0; Ауу = 0; Яху = 0. (2.105)
Таким образом, равенство (2.9G) для схем пересекаю-
щихся трещин распадается на три равенства (2.105). Проч-
ность элемента по бетону сжатой зоны оценивается так же,
как и при первой схеме трещин.
Выше рассматривались случаи, когда площадки текуче-
сти пронизывают нижнюю зону. Если имеются аналогич-
ные схемы трещин, но расположенных в верхней зоне, то
в представленные зависимости необходимо внести следую-
щие изменения: вместо характеристик нижнего армирования
(°ti. fob hf, рь Ло) подставить характеристики верхнего ар-
мирования (о,/, /а,-, hi, Р/, Л’), а также изменить знаки
перед изгибающими и крутящими моментами (Л1х, ЛТ„, ....
Л1П, ... Мп1, •••) на обратные. Компоненты тензора запаса
прочности для верхнего армирования будут определяться
по формулам (2.96) с учетом этих замечаний и, естествен-
но, схем трещин.
Элементы с 3-й схемой трещин. Обозначим через а
расстояние от нижнего обобщенного слоя армирования до
нижней поверхности, а через а' — аналогичное расстоя.
155
ние or верхнего обобщенного слоя армирования до верхней
поверхности. Для элементов с третьей схемой трещин не-
обходимо записывать два условия типа (2.94): отдельно для
нижнего и отдельно для верхнего армирования. Компонен-
ты тензора запаса прочности Ahj можно определять по фор-
мулам (2.97), приняв лишь при оценке нижнего армиро-
вания х? = 2 а ~ 2 (Л — Л'), а верхнего (кроме учета
указанных выше замечений) xj — 2 а = 2 (Л — Ло).
Таким образом, для элементов с 3-й схемой трещин нет
проблемы определения высоты сжатой зоны, и проверка
прочности по арматуре значительно упрощается.
3-я схема характерна для зон, где действуют большие
крутящие моменты, которые наряду с растяжением арма-
туры приводят к сжатию верхних и нижних полосок бетона
между трещинами. В результате возможно разрушение этих
полос бетона от сжимающих сил. Проверку прочности полос
бетона на сжатие следует производить для двух слоев бе-
тона: верхнего (толщиной х₽ = 2 а') и нижнего (толщиной
Хр = 2 а). Идею проверки рассмотрим на примере нижнего
слоя. Действие моментов и нормальных сил на нижний слой
можно свести к силам Nx, Ny и N ху, где
;VX = (.Wx + Nx ?а)/г;
= Ofy 4- Ny za)fz", Nxy = (Afxy -Ь iVXp za)/z\
z — h— a—a' = h0 + h't—h;
Zt = 0,5h—a’ = hg — 0,5h.
В дальнейшем расчет сводится к проверке условия (1.100)
для пластины толщиной Л = 2 а, где вместо сил Nx, Nv
и NX4 следует принять соответственно Nx, Nu и Nxu, однако
вопрос о величине /?„ остается здесь неисследованным.
Схемы сквозных трещин. Проверка прочности верхней
и нижней арматуры выполняется так же, как и для 3-й
схемы. В случае сквозных трещин одного направления при
оценке прочности полос бетона на сжатие изгибающими мо-
ментами можно пренебречь и расчет свести к проверке ус-
ловия (1.100), как при безмоментном напряженном состоя-
нии. Естественно, средние усилия в арматуре в этом случае
следует определять с учетом всего (нижнего и верхнего)
армирования и полной толщиной It.
3. Условия текучести для объемного напряженного со-
стояния железобетона с трещинами. Выше рассматрива-
ло
пись плиты и оболочки, которые по терминологии упругих
плит и оболочек можно отнести к тонким. В случае толсто-
стенных плит и оболочек (например, массивных фундамен-
тов, стенок реакторов и т. д.). расчет необходимо произ-
водить с учетом объемного напряженного состояния. Здесь
укажем лишь на идею и окончательные выражения, не
приводя подробностей вывода. Вывод условий для различ-
ного армирования дан в работах (35, 39,40|.
Пусть арматура расположена вдоль трех декартовых
осей х, У и г. При этом вводятся три коэффициента армиро-
вания: Нах» Hau ” Маг. каждый из которых равен площади
арматуры соответствующего направления, отнесенной к
единице площади площадки, проведенной нормально к это-
му направлению стержней. Обозначим компоненты тензора
напряжений у рассматриваемой точки через ож, оу, о.,
т т и трг. Считаем, что исчерпание прочности наступает
тогда?"когда по некоторой, в общем виде наклонной к трем
декартовым осям, площадке стержни всех направлений до-
стигают величины oTt. Выделяя в осях х, у и г малый тет-
раэдер так, чтобы наклонная его грань прошла по площадке
текучести,’и проектируя все приложенные к его граням
силы на оси х, у и z, получаем систему трех однородных
уравнений относительно направляющих косинусов площад-
ки. Решением такой системы является равенство нулю ее
определителя, что и приводит к следующему условию
(в осях х, у и z, совмещенных с направлениями арматуры):
(®тхМах Ox)(oTIZ[la!Z ОиХОтгМаг- °;) 4* Хху ХхгХуг —
Т2г(°тхМах ®х) — Т*г(<Тт рЩ у —
~ ау)~ т5и(оТ.-Маг — ОК) = 0, (2.106)
при этом величины (<хТЛрпх — ох), (<rTJ/pa„ — oj
И (СГтгМаг — °г) не МОГуТ бЫТЬ отрицательными.
При Щх = Маи = Маг = Ма; Отх = Оти = °тг = От УСЛО-
вие (2.105) преобразуется к виду.
(ОтМа)3 — (ОтМа)2 Л + (<4‘aKs ~ G = 0. (2.107)
где /ц /2 и /3 — инварианты тензора напряжений.
ГЛАВА 3
ДЕФОРМАЦИИ ЭЛЕМЕНТОВ ЖЕЛЕЗОБЕТОННЫХ СТЕРЖНЕЙ
С ТРЕЩИНАМИ ПРИ КРУЧЕНИИ И ИЗГИБЕ С КРУЧЕНИЕМ
В основу теоретических разработок положены: 1) новый
расчетный элемент с винтообразной поверхностью трещины
(позволяет правильно учесть дискретное расположение про-
дольной арматуры и другие факторы); 2) изложенная в гла-
ве 1 теория определения углов сдвига в железобетонных
элементах с трещинами и 3) некоторые геометрические и
статические зависимости, заимствованные (с рядом особен-
ностей) из теории кручения замкнутых тонкостенных про-
филей Л. А. Уманского 178]. Изучены случаи, касающиеся
чистого кручения или комбинации кручения с чистым из-
гибом и действием продольной силы. При этом сначала рас-
смотрены пустотелые элементы с замкнутым контуром, а
затем указаны особенности расчета элементов сплошного
сечения. Расчет элементов при совместном действии изги-
бающих, крутящих моментов и поперечной силы еще нахо-
дится в стадии разработки и в книгу не включен.
Основы рассматриваемого теоретического подхода к рас-
чету деформаций железобетонных стержней с трещинами
при кручении и изгибе с кручением сформулированы авто-
ром в работах 141, 461. Особенности применения его к эле-
ментам различного сечения, экспериментельная проверка
теории и исследование параметров жесткости элементов даны
в работах автора, Э. Г. Елагина и Т. П. Чистовой {43, 45,
811. Обобщение этих исследований (с попыткой упрощения
теории) дано в настоящей книге. Здесь автор не касается
вопросов прочности. Прочность может оцениваться по ме-
тодике Н. Н. Лессиг [60 и др.), хотя при доработке пред-
ставленная методика может быть распространена и на оцен-
ку несущей способности. Частичные исследования этого
вопроса представлены в работе 148).
§ 1. Силовые поверхности. Поток касательных сил.
Геометрические выражения для углов закручивания
1. Определение потока касательных сил от кручения
в элементе с трещинами. Расположим осн Ох и Ог в плоскости
поперечного сечения стержня, а ось Оу будем совмещать с
осью стержня, т. е. с линией центров тяжести площадей
его поперечных сечений (рис. 3.1). Рассматриваемые эле-
менты армируются отдельными продольными стержнями
158
Рис. 3.1. К определению потока касатель-
ных сил в железобетонном элементе с тре-
щинами
/ — хомуты; 2 — продольная арматура
арматуры, направленными вдоль осн О//, и замкнутыми по-
перечными стержнями—хомутами. Через центры тяжести
продольной и поперечной арматуры проводим две поверх-
ности, пересечение которых с поперечными сечениями стер-
жня происходит по линиям хомутов Лх.н линиям продоль-
ной арматуры Лп так, как показано на рис. 3.1, а. Эти по-
верхности будем называть силовыми или расчетными по-
верхностями продольной и поперечной арматуры. Действие
крутящего момента Мк на основании работы 178] можно
представить в виде потока касательных сил N„t. В эле-
менте с трещинами силы N)Jt располагаются на линиях хо-
мутов Лх, а обратные им силы Ntl/ (рис. 3.1,6) — на поверх-
ности продольной арматуры, т. е. на тех поверхностях, на
уровне которых происходит передача касательных сил че-
рез трещины. Прн этом Nyt ф NtV. Некоторое смещение
силовых поверхностей может произойти лишь вследствие
возможной работы отдельных стержней арматуры на соб-
ственный изгиб, а также из-за зацепления берегов трещин.
В теоретических построениях перемещаем поток касатель-
ных сил Nyt на силовую поверхность с линией Ло, распо-
ложенной по середине между Лх и Лп. При этом Nv, — Ntv
(рис. 3.1, в) (s — текущая координата, отсчитываемая по
ливни Ло от некоторой точки). На основании рис. 3.1, г
можно записать:
<ШК = N„tdsr0 = Nu^!w0,
где dii>0 = dsr0 — дифференциал удвоенной секториаль-
ной площади (на рис. 3.1, г величина
0,5 du>0 заштрихована).
Интегрируя по замкнутому контуру, получаем
АГц — J Л^, d (Oq — (3.1)
где <oo — удвоенная площадь, ограниченная замкнутой
линией Ло.
2. Выражения для углов закручивания. Установим вы-
ражения для углов закручивания, исключая нз данной ста-
дии, в отличие от 178], лишь использование физических за-
висимостей типа закона Гука.
Пусть на контуре Ло известны углы сдвига уау. Полные
перемещения точек контура в его плоскости обозначим че-
рез w, проекцию щ на касательную к контуру—через и,
а перемещения, перпендикулярные к плоскости контура
направленные вдоль осн у),—через v (и характеризуют деп-
ланацию сечения). Угол закручивания (поворота) сечения
обозначим через О, тогда
где <р — относительный угол закручивания.
Пусть известно, что сечение поворачивается вокруг
полюса А (рнс. 3.2, а). При этом некоторая точка а на кон-
туре переместится в положение а' (аа' — wj. Из рнс. 3.2, а
имеем:
и = w cos ф; w = r0 tg О « ro0; r0 = r0/cos ф,
откуда
и = Ого-
Дифференцируя и по у:
ди/ду = г0 дЬ/ду = г0 <р
и подставляя это выражение в известное уравнение
duldy 4- dvlds = yyt,
получаем
dv = (y,v—qrjds.
(3.2)
160
Рис. 3.2. К определению углов закручивания
Здесь принято, что v не зависит от у, поэтому dv заменяется
на dv, однако окончательная формула для <р нс изменится,
если v будет зависеть от s и у.
Из (3.2) следует:
» = $(?«—4>го) ds + v0,
л
где v0 — значение функции v в начале отсчета координаты s
(в точке а0).
При полном обходе контура ввиду его замкнутости по-
лучим v = о0, тогда

0.
Учитывая, что rods = d<i)0, получаем общую формулу
ф = — yvs ds. (3.3)
<оо J
Если некоторый криволинейный контур разбит на п
отрезков длиной sn и в пределах каждого отрезка кривой
углы сдвига равны y"v (рнс. 3.2, б), то
(3.3а)
6 Зак, 631
161
Эта формула и будет применяться нами для практических
расчетов. Как видно, окончательное выражение для <р не
зависит от места выбора полюса А (см. рнс. 3.2, а).
Рассмотрим выражения для ф, касающиеся некоторых
распространенных железобетонных профилей.
Прямоугольный профиль (см. рис. 3.2, в)
где у" . у"„. Ти»—углы сдвига указанных на рис. 3.2,в
Л ЯР ** У ~
стенок.
Кольцевой профиль при чистом кручении (рис. 3.2, г):
= YpO/Го.
(3-5)
где г0 — средний радиус трубы.
Кольцевое сечение при изгибе с кручением (рис. 3.2, д).
При рассмотрении изгиба с кручением кольцевых сечений
расчетная линия сечения разбивается на четыре отрезка
(1—3, 3—4, 4—2, 2—1) и для каждого отрезка в расчет
вводится свой усредненный угол сдвига. Согласно этой схе-
ме (обозначая Ф 360э = 0), получаем
ф=lift,+v;0 (। - 2р)+2₽Y;0]/(2ro).
(3.6)
Узкий прямоугольник. Пусть имеется сечение в виде уз-
кого прямоугольника ( рис. 3.2, е). Полагая для такого се-
чения = 0, получаем
Ф==(Тх»4 Т^)/2Л0-
Сравнивая эту формулу для <р с формулой (2.13) для
кривизны кручения kxu в тонкостенных элементах, видим,
что они совпадают.
§ 2. Расчет деформаций трубчатых элементов
при чистом кручении
и совместном действии кручения и продольной силы
1. Теория расчета. Геометрические характеристики коль-
цевого сечения рассматриваемых труб представлены на
рис. 3.3, а. Сечение армировано однорядной кольцевой
и продольной арматурой, где Fa,t — площадь всех стержней
продольной арматуры, равномерно распределенной по коль-
162
Рис. 3.3. К определению напряжении в арматуре в трещинах труб-
чатого образца (4 — хомуты; 5 — продольная арматура)
цу радиусом гп; Fao — площадь одного витка кольцевой
арматуры; ик — шаг кольцевой арматуры; гк — радиус
оси кольцевой арматуры; — наружный радиус трубы;
г — внутренний радиус трубы. Средний радиус г0 =
= 0,5 (гк + гп).
Коэффициенты армирования:
/я у — ^""ауД^ЛГо), /*0 ^"аО^к/Оо ®н)*
Чтобы компенсировать неточность, связанную с совме-
щением потока касательных сил на уровень продольной
арматуры, действительный коэффициент До умножен на
гк/г0,а при определении вместо га вводится г0.
6* 163
Пусть по толщине трубы действуют касательные силы
Nyo и погонные нормальные Ny. Учитывая (3.1), получаем:
« Л'о, = Л1к/(2лг;); Ny = Л7(2лг0), (3.7)
где N — продольная сила.
При выводе расчетных формул примем усилия Ny по-
ложительными (растягивающими). Если силы Ny являются
силами от предварительного обжатия, то в расчетные фор-
мулы их необходимо вводить со знаком минус. Принимаем
в момент, близкий к моменту трещипообразования, нормаль-
ные и касательные напряжения постоянными по толщине
элемента:
ау - Л'/|л(/?2 - г2)); т = 3 Л1 Л2л(Я3 - г»)]. (3.8)
где т определяется по формуле пластического кручения.
Пусть величина ау в момент трещипообразования из-
вестна, тогда, используя гипотезу образования трещин по
главным площадкам, можно получить 1431:
Л1К.Т = С/з)л (R3—Г3) Rp(Rp-ou);
(3-9)
tga = /(ftp—<jvj//?p.
где 4fK.T — крутящий момент трещипообразования (фор-
мулы можно уточнить, согласно (1.9), приняв
вместо /?р величину Rpkp).
Особенностью элементов при кручении является то,
что трещины в них развиваются по винтообразным поверх-
ностям и в связи с этим углы наклона трещин по толщине
будут несколько изменяться. Учтем это при определении
напряжений. Для вычисления нормальных (<тао» °а>/) и ка-
сательных (та0, та!/) напряжений в арматуре в трещинах
выделим из трубы (см. рис. 3.3, о) призму abca'b'c' так
(рнс. 3.3, б), чтобы ее грань ebe'b' прошла по трещине, а
две остальные грани были параллельны координатным ли-
ниям. В расчетах продольную и кольцевую арматуру со-
вмещаем на один средний уровень — поверхность 12 3
(рнс. 3.3, в).
Из рис. 3.3, б следует, что если на внешней поверхности
трубы угол наклона трещин к поперечному сечению равен
а, то угол наклона трещин а0 к поверхности 12 3 можно
определить из выражения
R tga = r9 tg a0.
(3.10)
164
Проектируя все силы, приложенные к силовой поверх-
ности 12 3, на оси s и у, придем к уравнениям (1.28), исклю-
чая из которых та0 и тОр, получаем по аналогии с (1.36):
аа0 = (NуО Ctg сс0—Тар fap ctg ао)//аО =
(^уО ctg Яо) Ао/До!
&аУ = №у "•* tg^o ТаоДо tga0)//ap =
(^У 4" l^Oy tg Ctg) Xp//ay,
где Ao и Ар определяются no (1.85).
В дальнейшем (на схемах) будут встречаться обозначения:
NaO <Га0 /а0 'Т Тар fayCtg СС0;
~ &ау fay 4" ТаО faO tg <Х0.
(3-12)
В итоге вывода (3.11) приходим к формулам главы 1,
в которых следует заменить: индекс <х» на индекс «О»; <а>
на «а0»; h на (/? — г). Учитывая это, средние деформации
арматуры еао, еаи и сдвиги уаор можно определять по фор-
мулам (1.10) и (1.37),-Дополнительные деформации арма-
туры еао и еа„ и сдвиги уаор по формулам (1.50).
Общие удлинения и сдвиги элемента со. и уоу опре-
деляются из выражений (1.56) при /аз = 0. Так,
УОу — C23Nу 4* C33Nyo, (3.13)
где С23 и С33 определяются в виде суммы (1.40) и (1.51)
или (1.40) и (1.53), т. е. принимаются равными (1.57).
Углы закручивания, учитывая (3.5), (3.7), (3.13), равны:
<Р = NyCi3fr0 + Л1кС33/(2лг’). (3.14)
Напряжения в бетоне, вызванные действием предвари-
тельного напряжения в моменттрещипообразования, равны:
<Т„=- -[o’1, (315)
где Fay, .Fay — соответственно суммарные площади про-
дольной напрягаемой и ненапрягаемой арматуры; о"у —
предварительные напряжения за вычетом потерь от усадки
и ползучести; о”у — напряжения в ненапрягаемой ар-
матуре от ползучести и усадки; п — Елу(Еъ.
Учитывая (3.15), по формулам (3.7) и (3.8) определяются
величш/ы У,;. Формулы (3.11) дают для прсдварительно-
напряженных образцов лишь приращения напряжений в тре-
щинах. Так, полные напряжения в напрягаемой арматуре
165
будут суммироваться из величин оау, определяемых по
(3.11), и величин (а"у — I па у |). При кручении потерн
от упругого обжатия не восстанавливаются, так как бетон
вдоль осей s и у не удлиняется, поэтому и вычитается
величина пви. Ширина трещин может определяться по фор-
мулам (1.61), (1.64) и (1.66).
2. Выражения для физических величин—параметров,
входящих в Ci3 и С33. Некоторые упрощения. Коэффициен-
ты фло и фа» определялись по формулам (L92), а входящие
в эти формулы величины УПт — по (1.7). При этом величины
NCrt дополнительно умножались на коэффициент k,lt учи-
тывающий влияние усадки 1см. пояснение к (1.9)1; А,, =
= 0,9 для ненапрягаемых образцов и ky = 1 — для образ-
цов с напрягаемой арматурой. Согласно работе 1431:
v„ « 0,15 + (.Ик.т/?к/Л4к/?кв)г.
(3.16)
где /?к — кольцевая прочность бетона [271; R° — кольцевая
прочность, соответствующая величине 58 МПа.
Методически коэффициент vn определялся по опытным
значениям деформаций бетона вдоль трещин eot путем срав-
нения их с расчетными [см. формулу (1.54)1. При этом опыт-
ные значения еб(, определяемые по показаниям датчиков,
приводились к уровню продольной арматуры уменьшением
на коэффициент rJR.
Исследования на трубах [431 показали, что упрощения
(1.52) вполне допустимы. Кроме того, оказалось, что вели-
чины еа,, и еао в трубах не превосходят 7% величин еп„
и еао. поэтому в формулах (1.53), (1,55) и (1.57) их можно
не учитывать, полагая:
е.о « 0; еау « 0 (однако уаху Ф 0), (3. 17)
т. е. принимать:
Сои ~
Сб! 3 ~
(3.18)
3. Обсуждение результатов эксперимента и теории.
Были отобраны эксперименты, выполненные в НИИ/КБ
Э. Г. Елагиным.
Эксперименты производили, на образцах кольцевого
сечения наружным диаметром 30 см, внутренним—около
20 см, длиной 3-3-1 см. Арматура для продольных стержней —
класса А-1П, из стали марки 35ГС, диаметром 10 и 14 мм
(12 стержней в сечении), поперечная—класса Л-I, диамет-
J66
Рис. 3.4. Схемы трещин в трубчатых образцах при кручении
я — теоретическая; 6 — опытная
ром 6,5 мм, шагом 4 и 8 см (г к = 13,2 и 13,4 см; ги = 12,3 см).
Опытная кольцевая прочность составляла 27—44 МПа.
Переменным» были следующие факторы: сечение про-
дольной и поперечной арматуры, марка бетона, предвари-
тельное напряжение арматуры.
Было испытано десять образцов: шесть из них с пена-
прягаемой арматурой (образцы ОК-7, ОК-2, ОК-4, ОК-14
нОК-15) и четыре—с напрягаемой (образцы ОНК-7, ОНК-8,
ОНК-14, ОН К-15), в которых предварительному напря-
жению подвергались 50?о продольных стержней. Испытание
на кручение производили па специальной установке
НИИЖБ. Подробные данные опытных образцов, а также
методика их испытания приведены в работе 127].
Для испытанных образцов были установлены опытные и
теоретические величины момента трещинообразовання ЛГК.Т»
значения углов наклона трещин к кольцевой арматуре «,
величины средних деформаций арматуры го и н бетона
вдоль трещин в,, углов закручивания <р, ширины раскры-
тия трещин пт. Таким образом, проверка теории осуществ-
лялась по шести непосредственно определенным из опыта
основным величинам. г
В среднем отношение опытных моментов трещинооора-
зовапия к расчетным составило 0,9. В вычисленных зна-
чениях влияние начальных напряжении от усадки нс \чи-
167
Мй.кНм 0НК-1Ь ОНК-15
168
Рис. 3.6. Графи-
ки углов закру-
чивания трубча-
тых образцов
тывалось, что, очевидно, и привело к завышению данных
теории.
Для образцов с ненапрягаемой арматурой опытные уг-
лы наклона трещин а были равны 43—5Г, а теоретические —
45°, соответственно для образцов с напрягаемой арматурой
они составили 47—53° и 53—60°. Схемы трещин приведены
на рис. 3.4.
Опытные и теоретические значения относительных де-
формаций кольцевой го и продольной еу арматуры пред-
ставлены на рис. 3.5, причем по опытным величинам пост-
роены три кривые (сплошные линии), соответствующие ми-
нимальным, средним и максимальным значениям деформации
арматуры. Теория (пунктирные линии) дает средние вели-
чины деформаций арматуры, которые хорошо согласукься
со средними опытными величинами. Максимальные и мини-
мальные значения го и гр показывают, что в данном случае
возможно существенное затухание напряжении в арматуре
от трещины в глубь полос бетона. Представленные на рис. 3.
:б9»
графики убедительно показывают, что деформации арма-
туры после образования трещин в значительной степени
зависят от величины касательных сил Л\о и Nov.
Правильность модели в общем виде могут характери-
зовать углы закручивания. Результаты расчета и опыта
приведены на рис. 3.6. От момента появления трещин и до
• 0,1 0,2 0,3 0,1 0,2 0} 0.1 0.2-0,3 0,1 0,2 0,3
—средний ------максимальный}
минимальный J
------расист
Рнс. 3.7. Графики ширины раскрытия трещин трубчатых обратной
.170
начала появления неупругих деформаций арматуры опытные
н теоретические величины углов закручивания отличаются
не более, чем на 10?6. Некоторое отклонение теоретических
углов закручивания от опытных в начале работы труб с тре-
щинами н при нагрузках, близких к текучести арматуры,
может объясняться неточностью определения коэффициен-
тов фаг п0 формулам, заимствованным из расчета централь-
но-растянутых элементов.
Опытные и теоретические значения ширины раскрытия
трешнн, которые определялись по формулам (1.61), (1.64), —
линия 1 и по формулам (1.61), (1.66) — линия 2, приведены
на рис. 3.7. На этих графиках нанесены три вида опытных
значений ат (минимальные, средние и максимальные). Как
видно, теоретические значения располагаются близко
к средним опытным величинам.
Таким образом, рассматриваемая теория деформирова-
ния железобетона с трещинами при плоском напряженном
состоянии удовлетворительно согласуется с результатами
испытания труб на кручение.
§3. Расчет деформации трубчатых элементов
при совместном действии изгибающих
и крутящих моментов и продольной силы
1. Теория расчета. Для этого случая остаются справед-
ливыми формулы (3.7), (3.8), (3.10) и (3.15), полученные для
чистого кручения. Перенесем кольцевую и продольную ар-
матуру на уровень г0. Выделим из трубы элемент, ограни-
ченный с левой стороны витком некоторой винтообразной
поверхности (с осью 0у), с правой — кольцевым сечением
н вдоль оси Оу — некоторым радиальным сечением 12 4 3
(рнс. 3.8, а). В нижней растянутой зоне винтовая поверх-
ность предполагается проходящей по поверхности трещины.
В сжатой зоне она пронизывает сплошное сечение. Элемент
ддя удобства показа сил развернут на 180° по сравнению
с рнс. 3.3. С правой стороны к кольцевому сечению прило-
жены: Л1к— крутящий момент; Л1„ — изгибающим мо-
мент; N — продольная сила, которая принята растягиваю-
щей. При наличии сжимающей силы, например силы от
предварительного обжатия, знаки перед Лг в расчетных
формулах следует изменить на обратные. С левой поромы
(по винтовой поверхности) указанные выше усилия уравно-
вешиваются усилиями в продольной и кольцевой арматуре
и бетоне сжатой зоны. Все погонные силы прикладываем на
17!
уровне силовой поверхности с радиусом г„. Зга поверхность
с силами выделена отдельно (рис. 3.8, б). Угол наклона тре-
щины и0 на уровне силовой поверхности при чистом кру-
чении не изменяется. 11ри изгибе с кручением углы наклона
трещин «, а следовательно и а0, изменяются по высоте об-
разца. В расчетной модели это учитываем приближенно,
принимая два значения а: а" и а“ (см. рис. 3.8, б) (индекс
«н» относится к углу наклона трещин на части наружной
поверхности трубы, лежащей ниже плоскости хОу). На си-
Рнс. 3.8. К анализу напряженного состояния железобетонной трубы
при совместном действии изгибающего и крутящего .моментов н нор-
мальной силы *
С сжатая зона; Р — растянутая зона с трещинами; Т — трещины
172
1Овой поверхности углы трещин равны а« и а;. По аналогии
'с (З.Ю):
7?tga" = rotga«; Я tgaB = rotgaj (3.19)
Поясним другие обозначения: Ф — угол между двумя ра-
диальными сечениями, ограничивающими сжатую зону,
Ф = 2лр (3.20)
(В — относительная величина сжатой зоны); Na0, Nay —
см. формулы (3.12); Nav и Nao — проекции на оси у и s по-
гонных (отнесенных к единице длины винтообразной линии)
нормальных и касательных сил в бетоне сжатой зоны. По-
гонные силы Nv для сжатой зоны обозначены в виде N'v.
Напряжения в арматуре в трещинах нижней зоны (о"у и
о;0) и напряжения (оа(/ и оа0) в арматуре в трещинах верх-
ней зоны, расположенной выше плоскости хОу, определя-
ются по формулам (3.11), где в первом случае а0 заменяется
на а!, а во втором—на aj. Это легко установить, рассмат-
ривая равновесие треугольного элемента Э, (на рис. 3.8. б, в)
по аналогии с рассматриванием элемента 123 (на рис. 3.3, в).
Однако изменение пока неизвестно, поэтому можно оп-
В в
рсделнть лишь оао и оао-
Найдем некоторые промежуточные величины. Действие
усилий Nao, Naa, приложенных к винтовым линиям, и уси-
лий Noy, приложенных по линии 5—6 (см. рнс. 3.8, б) в пло-
скости уОг, эквивалентно действию изгибающего момента
Л1Я К и осевой силы N„. Согласно рис. 3.8, б:
^ = nr0^(tga« + tgag). (3.21)
Момент Мя.к вычисляем по частям. Обозначая часть
момента А1„.к, которую дают силы Nov относительно оси
Ох, через А11,к. получаем:
Ali.K = Л'к го = лго Noy Об «о + tgao)-
Соответственно часть момента Ми.к, которую дают силы
X,е и Агао относительно оси Ох, обозначим в виде А1и.к •
Для нижней зоны:
сШ"к = ydy sin 0 = Nvo r0 у sin OdO.
Для верхней зоны элемента (рис. 3.7, б, г):
dM”K = jVa0 у sin Ods/cos a; = Го У s*n
173
Так как функции //для нижней и верхней зон различны:
при —0,5л00,5л у — r0Otget";
при 0,5л1,5л // = -1‘Лго1ба'(;4-го(0—0,5n)tgaj,
то оба выражения для d.U„.K интегрируем раздельно и ре-
зультат суммируем. Вычисляя таким образом Л!"ж. на-
ходим общий момент:
А».|.к = Л11.К + Л1"к *= 2;V₽0 г0* (tg a; -tg аов). (3.22)
Будем полагать при выводе расчетных формул, что усилия
Nay и Л'ао не зависят от 0, а зависят лишь от уровня на-
грузки. Это предпосылка равносильна предпосылке о пря-
моугольных эпюрах напряжений, принимаемой в расчете
деформаций элементов кольцевого сечения при изгибе, пред-
ложенном В. М. Баташевым и С. А. Дмитриевым 141. В этом
случае центры тяжести эпюр Nay и Noy (см. / — /и
// — //, на рнс. 3.8, б) отстоят от осн Ох соответственно на
расстоянии:
_ га sin лр . _ rasin лр
” Л(|-Р)’-С лр •
Обозначая z = хр -J- хс, получаем:
z==zosin лр/[лр(1 — р>|; xc = z(l—₽);
Xp = zp. (3.23)
Составляя сумму моментов всех правых и левых сил от-
носительно осн // — //, получаем значения средних напря-
жений в продольной арматуре в трещинах (при этом пола-
гаем « 1):
и __ + к । Л-|-Л|5
Составляя сумму
/ — /, получаем
____________________
cos а"
Рау (1 — Р) г Рау
моментов всех сил относительно осн
А1и+Л1ц.к—(‘V-J-Л'к) хр
2лг0 Р*
(3.25)
На основании рис. 3.8, г можно записать:
Aa<,/cos a" = N’Ov tg aj 4- N'u-
(3.25а)
По аналогии с формулой (15) работы (41 запишем:
Л р 2лг0 0 = /7₽<тр (1 + рр n«>a.c/v0), (3.256)
171
гдс a’ _ средние нормальные напряжения в бетоне сжатой
зоны; F — площадь кольцевого сечения; = 7ag/F;
п = 'Ели1Е9(Еаи, £б —модули упругости соответственно
продольной арматуры и бетона); toa.c — коэффициент
полноты эпюры напряжений в арматуре сжатой зоны, равный
0,55; Vo « 0.5 — произведение двух коэффициентов: vc, учи-
тывающего развитие неупругих деформаций в бетоне сжатой
зоны, и w6t,, учитывающего полноту эпюры о’и.
Подставляя значение N'u из (3.25 б) в (3.25 а), а послед-
нюю зависимость в (3.15), получаем
Ми +А1ц.к—((У-f- Л’|;)—Af0v 2л tg cc" r0] Xp
fM+MM
(3.26)
В начале § 3 мы указывали, как использовать формулы
(3.11) для определения средних напряжении о"^. Прирав-
нивая выражение (3.11) для о",, и выражение (3.24), полу-
чаем значение силы NtJ ниже плоскости хОу:
МиЧ-АГи.к
9 Хр [70!;(1-р)г
fav ho# Igo".
Перейдем к определению деформаций сдвига и углов
закручивания.
Углы сдвига yotf (с.и. рис. 3.2, д) определяются по тем же
формулам, что и углы уо„ в § 2, в которых лишь аа следует
заменить на aj и погонные силы Ny вычислить по формулам
(3.26). При этом можно вводить упрощения (3.18).
Углы сдвига убр сжатой зоны. Как и в главе 2, будем при-
нимать, что бетон сжатой зоны деформируется как неко-
торый ортотропный материал, оси ортотропии которого
пройдут вдоль и перпендикулярно к винтообразной линии.
Обозначая модуль деформации бетона перпендикулярно
к винтовой линии через Е^п. а вдоль линии—через £с/.
по аналогии с (1.89) получаем при рб ~ 0);
Top = V sin 2aS
‘ Еб/
(3 27)
где т находится по формуле (3.8).
Углы сдвига Vo*, можно принять равными 0,5 (ущ. 4*
4- yov). Определив уЗр, y"w и уб_». по формуле (3.6) вычис-
лим относительный угол закручивания ф.
17-
Найдем напряжения в крайнем фибровом волокне бетона
{вдоль линии ab, см. рнс. 3.8, а) и в нижнем стержне ар-
матуры:
о; л; о;/юбу; о'^ « о* /шлу,
(3.28)
где ыау — коэффициент полноты эпюры напряжений в ар-
матурных стержнях по высоте элемента (в эк-
сплуатационной стадии <да„ « 0,75; <об!/ ж
ж 0,66).
Средние деформации в крайних волокнах равны:
Кривизны элемента в плоскости уОг, а также удлинения
на уровне осн Оу определяются традиционным способом:
А’у — (вау — ®р)/(^? 4* Го)>
—%) R/(R+r0).
(3.30)
Окончательно зависимости для ky, еои и <р можно запи-
сать в виде:
ky — Ba Л1„ 4- Вп Мк 4- В,v N;
ф = Ми 4- DK Л1К 4- D,v 2V;
eov = Мк 4-С,у /V,
(3.31)
где Bj, Dj и С, (J = и, к, N) — жесткостные коэффициенты
матрицы жесткости.
Ширину раскрытия трещин можно вычислять подфор-
муле
— (еао 4~ еа^) /т,
(3.32)
где /т вычисляется по (1.66) при е0 = 2,9.
2. Параметры теории и сопоставление теории с экспе-
риментом. Модули деформации бетона сжатой зоны:
Еы Rq Ебп Rqi
где v6 « 0,75; фб » 0,9.
<76
(3.33)
Относительная высота сжатой зоны:
Р=Рс.тП -ь о»1 А* Д 0 >1 Ркр Рб.тЖ 3.П
Д = (Af„-Mn.T)/(Mn.p-AfD.T),
це д/ —изгибающий момент в момент образования
трацщЦопределяется по формулам работы [27]); ЛГ„.Р —
такой же момент в стадии разрушения элемента (опреде-
ляется по формулам работы [60]); 05,т — значение 0 в мо-
мент посте образования трещины; 0кр — значение 0 в ста-
дии разрушения (определяется согласно [45]).
м Величина 0б.т определяется из выражения (8) работы
I-I), где следует принять (в [4] 0С.Т обозначается как аб.т):
o6.v = (N0-N-NK.T)/Fa
(7П — приведенная площадь кольцевого сечения).
Углы наклона трещин определяются так:
а" «
0,5 (а + а'); а®
где а — угол наклона трещин у точки 9 (см. рис. 3.8, а);
а' — угол наклона трещин в нижней точке 1.
Исследования [45] показали, что значения углов а и а'
можно определить, используя следующие эмпирические
зависимости (при х > 0,2):
ctg 2а'« 4-------;
4хТГ. 4T₽p/i-ov/Rp
Мк .
Ми ’
х =
ctg 2а « cy/(4Rp у I — O„//?P),
(3.35)
где ^7т.к~ пластический момент сопротивления при кру-
чении; U'o — момент сопротивления приведенного сечения;
У — коэффициент, учитывающий неупругие свойства бе-
тона (принимается по табл. 34 СНиП П-В.1-62*); <т„—пред-
варительное напряжение бетона [см. формулу (3.15)1.
Формулы для а" и а" еще требуют уточнения.
Значения коэффициента фП1/ можно вычислять по эм-
пирическим формулам (27) — (31) работы [4]. При этом вхо-
дящее в формулу (27) работы [4] значение AL _ принима-
лось равным 0,8 Л1П.Т.
В соответствии с проведенными исследованиями вели-
чину коэффициента фво можно определять по формуле
фа0 = 1 _ о,4 (1 + Л1п.т/Л1и)Л1п.,ЛИи. (3.36)
7 Зак. 631 177
Для проверки теории и определения ее параметров были
обработаны результаты обширных экспериментов, ранее
проведенных в НИИЖБ Э. Г. Елагиным на обычных и пред-
варительно-напряженных трубчатых образцах (их харак-
теристики аналогичны характеристикам образцов, приве-
денных в § 2). Получено удовлетворительное согласование
теории с опытом. На рис. 3.9, а, б дано сравнение опытных
и теоретических значений прогибов и углов закручивания.
Полные результаты экспериментальной проверки пред-
ставлены в работе (45).
Рнс. 3.9. Графики для трубчатых образное при изгибе с кручением (из
опытов Э. Г. Елагина)
а — прогибов; р — углов закручивания
178
5Ч. Расчет деформаций прямоугольных стержней
ври совместном действии изгибающих
крутящих моментов и продольной .силы
1. Теория расчета элементов коробчатого сечения со
сиознычи трещинами. При этом трещины имеются по всему
периметру стержня. Элемент армирован четырьмя продоль-
ным стержнями (где 2 Fay — площадь двух продольных
стержней, установленных в нижней зоне элемента, а
2 fj,—площадь двух верхних продольных стержней),
и поперечными стержнями (в виде хомутов), установлен-
ным с одинаковым шагом их. Коэффициент поперечного
армирования fa = Fax/ux, где Fax — площадь одного по-
перечного стержня (хомута). Схема коробчатого сечения
и линии расположения арматуры в сечении показаны на
рис. 3.10, а, б. Согласно принципам расчета, совмещаем
расположение хомутов и продольной арматуры на одну си-
ловую поверхность, располагая ее линии а0 и Ьо посередине
между линиями ац, ах и Ьи, Ьх (см. рис. 3.10, б), и находим
приведенные значения площадей арматуры:
Fay=Fay (ап -I- а)/(а0 фа);
F'y « F*u (ап + а)/(а0 + а);
fa fa (Рх. 4" ®х)/(«о 4" Fq) •
(3.37)
Поток касательных сил представлен на рис. 3.11. При
расположении касательных сил на уровне одной расчетной
поверхности
Nyx Nyi — Л1 к 2 йубу.
(3.38)
Выделим из конструкции элемент, ограниченный с пра-
вой стороны коробчатым сечением, с левой — одним витком
поверхности трещины и снизу — некоторым продольным
сечением / 5 15 16 (рис. 3.12, а). На основании этого эле-
мента будем определять напряжения в арматуре в трещинах.
Предполагаем, что поверхность трещины проходит по не-
которым винтообразным сечениям 1 5 9 10; 9 10 11 12; 11 12
13 14 и 13 14 15 16 так, что соблюдается равенство длин
отрезков:
^1-» = 4-10» 4-11 ~ 4—12’ 4—13 == 4—14’ 4-13 = 4-1в* (3.39)
7’
179
Рис. ЗЛО. К расчету коробчатых элементов с трещинами на кручение
а — коробчатый элемент; б — схема армирования сечения; / — иижние про-
дольные стержни; 2 — верхние продольные стержни; 3 — поперечные стержни
(хомуты)
В этом случае ось винтовой поверхности 1 5 9 10 про-
ходит параллельно оси // через eit аналогично осн осталь-
ных винтовых поверхностей проходят через точки е», е3,
Для круглых и квадратных сечений точки е2, е3 и et
совпадают с центром тяжести сечения (точкой О).
Крутящие и изгибающие моменты, приложенные с пра-
вой стороны элемента (здесь элемент для удобства показа
сил повернут на 180°), вызывают усилия в продольной и
поперечной арматуре, пересекающей винтообразную тре-
щину (еще некоторые касательные силы действуют вдоль
сечения 1 5 15 16). Все силы приложены на уровне силовой
поверхности, которая выделена отдельно (рис. 3.12, б).
Если углы наклона трещин на наружной поверхности вер-
тикальных стенок, нижней и верхней горизонтальных сте-
нок обозначить соответственно через а, ан и а", тогда,
учитывая (3.39), аналогичные углы наклона трещин
Рис. 3.11. К определению потока касательных сил
а — коробчатый элемент; б — нижняя стенка коробчатого элемента
180
Рис. 3.12. К определению напряжений в арматуре в трещинах
а — схема расчетного элемента; б —схема усилий на силовой поверхности эле-
мента; в — схема касательных усилий в продольной арматуре в трещинах
(а0, aj и aj) на уровне стенок силовой поверхности получим
из выражений:
otga = aotgao; Mga" = ^Sa“ = ^otg«5- (3.39а)
Обозначим: a02 — нормальные напряжения в хомутах
вертикальных стенок у линий трещины; оаг.— нормаль-
ные напряжения в хомутах нижней (i-«n>) и верхней (»-«в>)
горизонтальных стенок у линий трещин; са(, — нормаль-
ные напряжения в нижних («-«н») и верхних (i-«B») стерж-
нях продольной арматуры. Кроме нормальных напря-
181
женин в стержнях продольной арматуры будем учитывать
возникновение касательных напряжений и сил. Схема этих
касательных сил (Р/, 7’!,', Т\ и Тх) вынесена отдельно и по-
казана на рис. 3.12, в. Силы TJ и уменьшают величины
напряжений оаг, силы Т” — величины напряжений о"х,
а Г; — величины напряжений о"х. На основной схеме
(см. рис. 3.12, в) этот факт учитывается косвенно в силах
Nai, A'u.r и которые представляются так:
ЛГаг = /а + (П + ЛМ* -Ю = °*:
№ = OU!Z -I- 2Т«/121 _26 = О?х/аЛ":
= (Та9 fa 2Т2/123- 25 = Oar fa/l”,
(3.40)
где X, X" и Х“— коэффициенты, которые, как и в главе 1,
учитывают влияние касательных сил в арматуре. Естест-
венно, некоторые касательные силы и напряжения могут
возникать и в хомутах. Учитывая все это, выражения для
X, Хн и X® по аналогии с (1.112) можно записать так:
*'= 1 б/а/[ (/1 + /а М tg «о I /«о) ctg2 а' + 16Д]; |
ь =16/a/[/i + 0.5/а а01 tg а£+tg а; | /Ьо] ctg2 а0+16/n]t j (3 41)
где Л = 2/-а>0; F'ty)!a0.
Усилия в нижней (»-«н») и верхней (»-<в») продольной
арматуре обозначим в виде Nlail. И ниже индекс «<» будет
принимать лишь эти значения («и», «в»).
Проектируя силы, приложенные к граням треугольных
элементов 3,, Э., и Э3 соответственно на оси z и х, полу-
чаем:
Ло dy—Nyx dy ctg «о = 0; Nai dy—MVi dy ctg a0 = 0,
откуда, учитывая (3.40), находим:
aL = ArpxX'ctgao//a: ^az = ^|(IXctga0//a. (3.42)
Определим некоторые промежуточные величины
(см. рис. 3.12, б). Силы Nat, Nax и N”x, приложенные к
винтовой линии трещины, и усилия Nxu, действующие по
182
линии 17—21, дают относительно осн х момент М„ , рав-
ный:
Vt Vt
Мы. к = J Wai ydy - J Наг ydy + 0,5 Nxy аа [2o0 tg а04-
0 yt
4-M<g а? 4-tg a»)J, (3.43)
где yt — aotgao; y3 = aotgao 4- 60tga;;
y3 - 2aotgao 4- &otgaJ.
Произведя интегрирование, получим:
М„.к = 0,5 A^X!/a060(tga« — tgaj). (3.44)
Кроме момента Л1„.к, указанные выше силы будут да-
вать проекцию на ось Оу, равную ЛГ„, где согласно
рнс. 3.12, б:
Wk = Wx„[2aotgao 4- Mg«! + tga;)). (3.45)
При чистом кручении, когда a0 = а" = а;, Л1и.к = 0.
Составляя уравнения моментов относительно граней 17—
18 и 19—20 элемента (см. рис. 3.12, б), получаем:
Afn + Afir. к ,
Н 1»КТ'
** ay
____ Afk+jV Ми+Мц.к
Vay_-------------•
2^o
(3.46)
В случае сжимающей силы N (например, силы от пред-
варительного обжатия) знаки перед N следует изменить
на обратные.
Средние относительные деформации поперечной арма-
туры вертикальных (еП1) и горизонтальных (е.ах, ₽“*) стенок
и верхней и‘нижней продольной арматуры (e"w,
логин с (1.10) равны:
Оаг 'Га I _ °.'х 'In . I _ o‘au t' ч
еа» = —г----• -----7 • SaD-----р •
£а ьа ьа
по ана-
(3-47)
По аналогии с (1.37) определим средние углы сдвига
вертикальных (уауг), нижней (т"₽х) и верхней (уЗрх)
горизонтальных стенок элемента:
4x=eixctgao + ei/gao:
Таих = еах с{б «О + °-5 + е»!/) {g ao-
183
При выводе формулы для величины уаиг учитываем до-
полнительно то обстоятельство, что верхняя и нижняя гра-
ни элемента деформируются неодинаково (е"х ¥= е”ч)-
Для таких элементов, следуя работе 1411, вводим в (3.48)
средние величины относительных продольных деформаций
указанных граней. Кривизны элемента ku в плоскости уОг
и относительные удлинения на уровне осн Оу (е0„) равны:
II I
а у ।
e'v). (3.49)
Определим деформации элемента, связанные с напря-
жениями и деформациями полосок бетона между трещинами,
исходя из приближенных предпосылок. На общие деформа-
ции элемента возможная при этом погрешность не окажет
заметногр влияния.
Пренебрегая некоторым неравномерным распределением
касательных напряжений т в стенках элемента, вводим в
расчет усредненные значения т, определив их из формул
пластического кручения (см., например, [5]);
т « Af К/1ГПК; IV'n.K = 2h(ab - bh - ah + 4йг/3). (3.50)
Усредненные нормальные напряжения по середине бо-
ковых стенок (<Тр), в верхней и нижней горизонтальных стен-
ках (о* и (ty вычислим по формулам:
Здесь F — площадь коробчатого сечения; И7п и — упру-
гопластический момент сопротивления сечения при из-
гибе:
1,751ГО, где — момент сопротивления при-
веденного сечения при упругом изгибе.
Зная величины т, о^, о” и о", по формулам главы 1
можно определить относительные деформации и сдвиги эле-
мента от деформаций полосок бетона между трещинами.
Так, согласно (1.50), (1.53) и (3.18), сдвиги вертикальных
стенокнижней (у"^) и верхней (yS ^) горизонталь-
181
пых стопок равны:
ТаУг :— т (2 V,,)/ (Eg V||) —
-°у sin 2ct0/(2Ec) « т(2-v„)/(E6v„);
Та их = т (2 — Vn)/ (Еб Vq) —
— °‘и sin 2а'0/(2Еб) « т (2 - v')/(Ec ?').
(3.52)
Величинами епж и еа!/ согласно (3.17) пренебрегаем.
Следовательно, можно пренебречь также некоторыми при-
ращениями кривизн, связанных указанными деформациями
полосок бетона.
Определим суммарные углы закручивания. Полные уг-
лы сдвига стенок (yyz, у"х и т”Л) равны:
У Ух •= Ya ух + Та у/.
I I ,
Ту* ~ Та их + Та их-
(3.53)
Углы закручивания определяются по формулам (3.4).
В итоге всех вычислений придем к физическим зависимо-
стям (3.31), где жесткостные коэффициенты матрицы жест-
кости Bj, Djn Сj (J = и, к, N) имеют вид:
185
Полагая в представленных выше зависимостях нормаль-
ные силы и моменты равными нулю, получим формулы для
чистого кручения.
2. Параметры теории. Пусть известны осевая сила N
и отношение х = Al^Afn. Значения крутящего момента
ЛЦ.т, соответствующие образованию трещин на нижней
(/-<»<») и верхней (/-«в») поверхностях и посередине боковых
поверхностей (/-«б»), определяются из уравнений:
Лу/?р (Лу/?р—о^)—”*/» Мк.»— Tylt^n. к* (3.54)
Здесь о/ вычисляется по формуле (3.51), где F заменяется
на yJinF, а 1ГП.„ — на lV’rin kn !A.\v — см. по формуле
(2.5)1; ku » 0,8 прн /?р = я; — согласно СНиП П-В. 1-62*
и kp = 1 прн определении Rp по новым нормам. При боль*
186
ших напряжениях сжатия вместо Яр в (3.52) необходимо
вводить ApflplcM. (1.7)]. Углы наклона трещин равны:
tg2a' = 2т/о[. (/-«и», «в», «б»).
Коэффициенты, входящие в (3.47), равны:
ф' = 1 - [0,4 + 0,3 (м'к. т/Л41()2] Ml. ,/ Мк
(у=.«н», «в», «б»)
^=1,05—0,85Л4к.т/А1к (i = «n>, «в»),
где ф®=Фа.
(3.55)
(3.56)
Коэффициенты v„ для полос бетона между трещинами:
Vn = сРау + 0,45 (Ml. tlM^‘;
Hay ~ (^ау Т Fау)/
где V„ = Vn,
(3.57)
с = 10 для элементов коробчатого сечения (этот коэффи-
циент исследовался при толщине стенок Л « 0,1 b, b —
больший размер сечения) и с = 3 для элементов сплош-
ного сечения. О применимости теории к расчету элементов
сплошного сечения указано в п. 4. Выражения (3.56) и (3.57)
получены Т. П. Чистовой [81] на основании эксперимен-
тов.
3. Дополнительные особенности расчета элементов
сплошного сечения. Выше формулы построены так, что тол-
щина стенок элемента Л не ограничивается и дает переход
к сплошному сечению. Но имеются дополнительные особен-
ности, которые остались пока не учтенными.
В элементах коробчатого сечения прн кручении тре-
щины сразу же после их появления проникают на всю тол-
щину стенок. В элементах сплошного сечения трещины в мо-
мент их образования проникают лишь на некоторую часть
сечения. В результате в центре сечения некоторое время
остается ядро бетона, свободное от трещин, которое влияет
на напряжения в арматуре. Прн этом часть крутящего мо-
мента (Л1К1) воспринимается сеченном с трещиной, а другая
часть (/ИК2) — нетреснувшим бетонным ядром (рис. 3.13).
187
(3.58)

KI-
С ростом крутящего момента величина Л11(1 приближается
к Мк. Согласно исследованиям Т. П. Чистовой:
.. *. Л _ ( Л1"
л
Напряжения в арматуре элементов сплошного сечения
определяются по формулам п. 1, где Л1К заменяется на Л1
При изгибе с кручением влияние бетонного ядра сечения
следует учитывать для случая спиральных трещин, разви-
вающихся по всему контуру сечения. При наличии сжатой
зоны бетона без трещин влиянием бетонного ядра можно
пренебречь, приняв ~ Мк.
5. Деформации элементов с несквознымн трещинами.
Можно принять, что формулы (3.37) — (3.42) остаются без
изменения. Другие величины определяем на основании
расчетного элемента, представленного на рис. 3.14, а. В от-
личие от расчетного элемента, для конструкции с несквоз-
ными трещинами рассматриваемый элемент с левой стороны
ограничивается винтообразной поверхностью, проходящей
по трещинам лишь в растянутой зоне. В сжатой зоне эта
поверхность проходит по сечению сплошного тела (площад-
ке главных сжимающих напряжений, установленной для
момента трещинообразования), где ав — угол наклона
верхней винтовой линии этого сечения к оси х (в отличие от
угла наклона а“ — верхней
трещины на рис. 3.12). Эти
различия носят формальный ха-
рактер, так как зависимости
(3.39а) остаются в силе. Сило-
вая поверхность показана на
рис. 3.14,6, где введены следую-
щие обозначения новых величин:
Nax, Na«, Naz ~ Проекции
касательных и нормальных сил,
приложенных к винтообразной
линии, проходящей посередине
сечения сжатой зоны, на оси х,
у и z; хг — высота сжатой зоны
элемента; х'т — высота сжатой
зоны на силовой поверхности;
О с — точка приложения равно-
действующей СИЛ /VUr, Nay И
Naz‘, 0,5 ас — расстояние от
Рис. 3.13. К анализу алия-
ния бетонного ядра сечения
при кручении стержней
сплошного сечения
/ — сечение с трещиной: 2 — нс
треснувшее бетонное ядро: 3—
внутренняя поверхность услов-
ного коробчатого элемента, за-
меняющего сплошной элемент

188
Рис. 3.14. К определению напряжений в арматуре и бетоне в элементе
с несквознымн трещинами
о — расчетный элемент; б — схема усилий на силовой поверхности
срединной поверхности сжатого слоя верхней стенки до
центра тяжести сечения (точки О). Для упрощения расчет-
ных формул (без существенной погрешности) на рнс. 3.14, б
допущена одна неточность: линия ab несколько отклоняет-
ся от винтообразной поверхности верхнего сечения. Однако
этим пренебрегаем, приняв а" ~ а;. При хт > h (h —
толщина стенки) х'7 = хх — 0,5ft. В других случаях и
для прямоугольных сплошных сечений х^ = 0,5хт. Напря-
жения в продольной арматуре и бетоне сжатой зоны опре-
делим, приняв, что величины N„u имеют одинаковое зна-
чение по всему периметру срединной линии сжатой зоны
(рис. 3.14, б). Положение равнодействующей величин Nay
(координату е0 точки Ос) можно определить из уравнения
v Л ( 2л-; . \
---------------------г — ^aiAo I । 11 »
cosa0 2 cos a" \cosa0 cos a J/
189
откуда, полагая cos а0 ~ cos а; (предварительные расчеты
показали, что это не должно приводить к заметной погреш-
ности), получаем
с0 «[Лт'(ис—л\) 4 0,5 b0 ac]l(2xi 4 b0).
Составим уравнение моментов всех сил, приложенных к
расчетному элементу относительно оси I—1 (см. рис. 3.14, б):
At,, 4- Л'<’0 4 А1„.к 4- — 2^Уа1/(О,5по 4- е0) = 0,
откуда получим:
о", - [Л1„ + ЛГ„. „ 4- е0 (/V 4 iVK)l/(2/Г, (0,5по 4 e0)L (3.59)
Уравнение моментов всех сил, приложенных к расчет-
ному элементу относительно линии 17—18, имеет вид:
;Valz/cos a* ~ - pt„ 4 At„. к- (N 4- :
: 1(2л-г' 4-Ьо) (О,5ло 4- U1. (3.60)
При эгом по аналогии с выводом зависимости для е0 при-
нимаем cos «о « cos«J. Нормальные силы A/v в сжатой зоне
определим из уравнения проекции сил, приложенных к
треугольному элементу на ось у:
— Naylcos a J—jV^j, tg a;.
(3.61)
Средине напряжения в бетоне сжатой зоны равны:
a; = iV;/7r, (3.62)
где нрн хт Л хт = Л; при хт < h хг = хг.
Подставляя в это . выражение значение Nv из (3.61)
и учитывая (3.60), а также то, что хт(2хт 4- М « ^б с» где
FO c — площадь бетона сжатой зоны, получаем
о; - -pflt 4 Af„. к—у (Лг 4- NK) ]/[F0.с х
X (0,5«о 4 с0)J —Nxu tg a’/xf. (3.63)
Касательные напряжения т в сжатой зоне можно опре-
делить но формулам (3.50).
Средние деформации в нижней зоне и углы сдвига y”t
определяются по формулам (3.47), (3.48) и (3.53) при Л«н».
Принимая ортотропную модель деформирования бетона
190
сжатой зоны, по аналогии с (3.27) и (3.29) на силовой по
верхности сжатой зоны получаем:
Ср (cos2 a'lEto 4. sjn2 j
+ 0,5т (llEb, — ]/£',) sjn
Тг|/ = т(1/£бп4-1/£^)4_0 5а'л/£' ..p, .
и\4L-6n—l/E6l) sin 2c^. (3.64)
Для упрощения расчета n (3.6-1) а» МПЖ11Л
на а". ' ' ао можно заменять
Средние углы сдвига боковых стенок v Л„
„о ^рмудам (3.48) „ (3.53), гда ,|в)бход;».
(3.4), где о, заменяется на о’з (о °+"» )'а1'™ ф 110 *0Р,'УДе
i ,ЛЛрРа”Окы""Я " №|X>|,Mll!"' сжатой „озера-
(ros««)£(„+ sin,a./£.i) +
+ 0,5т (I /£Сп — I/£б() S|-n 2а„ р
Кривизны элемента kt. и относитрлг <п,л «лл
ределяются по формулам (З'.ЗО) и (3 49? д^’?рма,и'» оп-
. я ё;, где а, заменяется „а I, 1 ^5^ I «
В окончательном виде физическпо
I ваются как уравнения (3 31) гле жрст!.-г?раВИС,,11я записы*
ты Вт, D, „Ст 0 = «,»! ХХ™с «оэфф-ншен-
j следующий вид: * 1ы жесткости имеют
I
I
191
(0,5 л0 4*^o) / cos2 an
<°б. у
si»a <x" \ (tgctp —tg«o)
Ect / 2f0. c(O,5<?o+<?o)
tg qg 2a0 tg ce04-6q (tg q” + tg <xg)
a0 b0 xt -Eq, c (O.5ao-j-fo) b0
Qq
*2h^ (О,5яо -f“ ^o)
cos2 a®
Ебл
^'y J 1
2F" Еа Еб.с<об.у
«Jr
sins an \ 1
~T' J ’
Ect /.
Dlt =
I >4 rip
fro sin 2ag
fc.c(°.5oo+fo)
tgao
—[*u tg «2 + (0»5«o + <u) tg «ol —
£a
t f
Ебп Еы *
cos2a5 । sin2 a°
Ecn Ea /1
и in
“ 2&0(0,5а0+?о)
t"s,(a<>tgao+Mgao)
(0,5ap -|- fp) '{•д X,
. 2/а Ea a0 tg2 q“ ' /a£aaoMg2ao
^a^e° tg a0 )
^0 }
n2ag + (O,5q°+fo) X
(tgqj — tgq")
o --------------------
J 2Eo. c (O.S^o + ^o)
4 \ Ебл E
XO | sin2q%
t Еб/
tgao j 2flotgao-p^o (tgeo4~t|
) bt^Xr 2Гб.c (0,5oo4“^o) bQ
sin 2a°
21Гп.к
Ебл
“4 (O,5o0 + «у) -г
Ебг/
4-2*0
Ect / _ 1^пк Ect
2(0,5до+ро) (2—vn)
vH
л
192
Du = '
2&0 (0,5oq €q)
л"
тар
4F"y Ea
Qq bt sin 2g?
4/^6. c (0i5ao4~eo)
at tg «о
Ein
COS2 ftp
Ебп
Ect
sin2 a?
h"
Lip
cos2a" . Sin2 a"
2 (O,5go+ ^o) *
l'vEa Ъ.с<»(>у
Еб.п
Ect
1 (°o tg °o+*>o tg ao) 4“y
4(O.5«o+eo)| 2F"Eab0
^*9
Величины ЮСм « 0,66, Ебл и Е'ы можно вычислить по
формулам (3.33), заменяя в них Е'6п на Е« и на-
оборот; а? « — а?. Здесь, чтобы получить переход к
случаю чистого изгиба, необходимо величины Мкл и Мк
в формулах (3.54) и (3.55) заменить соответственно на
mLt и Ми, где Alf,.T — изгибающие моменты, соответ-
ствующие образованию трещин в разных зонах. Это лег-
ко выполнить для моментов трещинообразования, зная х.
При х =/= 0 и х = const можно использовать формулы (3.54)
и (3.55) без изменения. Высота сжатой зоны вычисляется
как для изгибаемого элемента по формулам норм прн мо-
193
/7
Рис. 3.15. О длине характерного элемента. Дополнительные напряжс
ния сжатия полос бетона при кручении элемента с трещинами
менте, равном Ма + Л1И.К, и осевой силе, равной N 4- NK,
где Л4Я.К и NK определяются по (3.44) и (3.45).
В своих исследованиях Т. П. Чистова, обработав около
200 балок, сравнила результаты теоретических расчетов
с данными опытов советских и зарубежных исследований
и получила удовлетворительное их совпадение 181 и др.].
В заключение остановимся на двух факторах, важных
для понимания предлагаемой теории.
1. Рассматривая характерные элементы, представлен-
ные на рис. 3.7, 3.12 и 3.14, можно придти к неверному
выводу, что длина элемента, к которой следует относить уста-
новленные зависимости, равна проекции винтообразной
трещины на плоскость хОу (например, отрезку 15—1 на
рис. 3.12, а). В действительности полная развертка тре-
щины представляет собой лишь удобную условность, а все
полученные выражения относятся к малой зоне, прилега-
ющей к вертикальным сечениям и равной по длине пример-
но расстоянию между трещинами. В этом легко убедиться
на основании рис. 3.15, а, б, где за счет горизонтальных сече-
ний, расположенных равномерно по периметру элемента
и характеризующих переход из одной спирали трещины на
другую, элемент может быть стянут до небольшой зоны у вер-
194
текального сечения, но при этом выражения для напряже-
нии будут такими же, как и полученные согласно рис. 3.12.
2. Выделяя треугольные элементы типа на рис. 3.15, б
и проектируя силы на ось можно заметить, что для равно-
весия сил к бетону должны быть приложены сжимающие
силы NCy даже в случае чистого кручения (рис. 3.15, в,
для простоты рассмотрим случай чистого кручения). Общий
вектор этих сил для всего сечения уравновешивается силами
растяжения в арматуре (рнс. 3.15, г), в результате по
сечению в сумме горизонтальные силы в арматуре и бетоне
равны нулю, хотя в отдельности в арматуре и бетоне между
трещинами неизбежно возникают нормальные напряжения.
В этом заключается условность понятия чистого кручения
для железобетона с трещинами. При изгибе с кручением на
это поле усилий, естественно, будет накладываться поле
нормальных усилий от изгиба.
СПИСОК ЛИТЕРАТУРЫ
1. Амбарцумян С. А. Теория анизотропных оболочек М., Физ-
матгиз. 1961.
2. Ахвледиани Н. В., Шаишмелашвили В. Н. К вопросу несу-
щей способности оболочек. Сообщения АН ГрузССР, т. 18, № 2.
1957.
3. Банков В. Н., Владимиров В. Ф. Исследование железобе-
тонных плит на ЭВМ «Урал -2» с учетом действительной жесткости
на кручение. Труды VI Всесоюзной конференции по бетону и же-
лезобетону, 1-я секция НТО. М., Строниздат, 1966.
4. Баташев В. М.. Дмитриев С. А. Расчет прогибов и ширины
раскрытия трещин железобетонных элементов кольцевого сечения.
«Бетон и железобетон», 1965, № 2.
5. Безухов Н. И. Основы теории упругости пластичности и
ползучести. М., «Высшая школа», 1961.
6. Берг О. Я. Физические основы теории прочности бетона
и железобетона. М., Госстрой издат, 1961.
7. Берг О. Я., Смирнов Н. В. Об оценке прочности элементов
конструкций при плоском напряженном состоянии. — В сб.: «Тран-
спортное строительство», 1965, № 9.
8. Бехтерев П. /Аналитические исследования обобщенного за-
кона Гука. Издание автора, ч. I и II. 1925.
9. Бнльченко А. В., Карпенко Н. И. Экспериментальная про-
верка и исследование параметров теории деформирования железо-
бетонных плит с трещинами, работающих в двух направлениях.—
В сб. ИИИЖБ: Прочность и жесткость железобетонных конструк-
ций, под ред. С. А. Дмитриева и С. М. Крылова. М.» Строниздат,
1971.
10. Бондаренко В. М., Тнмко И. Т., Шагин А. Л. Расчет желе-
зобетонных плит и оболочек метолом интегрального модуля де-
формаций. Изд-во Харьковского Университета. Харьков, 1967.
11. Васильев А. И., Катин И. И., Шитиков Б. А. Работа заклад-
ных деталей при совместном воздействии сдвигающих и нормаль-
ных сил. «Промышленное строительство», 1971, Л*2 7.
12. Варвак П. М. Развитие и приложение метода сеток к расче-
ту пластинок, т. I и II. Изд-во АН УССР, Киев, 1949 и 1952 гг.
13. Власов В. 3. Общая теория оболочек. М., Гостехиздат, 1949.
14. Гвоздев А. А. Определение величины разрушающей на-
грузки для статически неопределимых систем, претерпевающих
пластические деформации. Труды конференции по пластическим
деформациям. At., 1936. М.—-Л., Изд-во АН СССР, 1938.
15. Гвоздев А. А. Метод предельного равновесия в применении
к расчету железобетонных конструкций. Инж. сб., 1949, т. 5, вып. 2.
16. Гвоздев А. А. Расчет несущей способности конструкций
по методу предельного равновесия. М.» Стройиздат, 1949.
196
17. Гвоздев А. А., Дмитриев С. А. К расчету предварительно-
напряженных, обычных железобетонных и бетонных сечений по
образованию трещин. «Бетон и железобетон», 1957, № 5.
18. Гвоздев А. А., Дмитриев С. А., Немировский Я. М. О рас-
чете перемещений (прогибов) железобетонных конструкций по про-
екту новых норм (СНиП 11-В. 1-62) «Бетон и железобетон», 1962,
№ 2.
19. Гвоздев А. А., Карпенко Н. И., Работа железобетона с тре-
щинами при плоском напряженном состоянии. «Строительная ме-
ханика и расчет сооружений», 1965, № 2.
20. Гвоздев А. А. К вопросу о предельных условиях (услови-
ях текучести) для ортотропных сред и для изгибаемых железобе-
тонных плит. — В сб.: Строительная механика. М., Строниздат,
1966.
21. Гвоздев Л. А., Карпенко И. И., Крылов С. М. Теоретическое
и экспериментальное исследование работы железобетона с трещи-
нами при плоском однородном и неоднородном напряженном состо-
яниях. — В сб. ИИИЖБ: Совершенствование расчета статически
неопределимых железобетонных конструкций, под ред. Л. А. Гвоз-
дева и С. М. Крылова. М., Стройиздат, 1968.
22. Гениев Г. А., Тюпии Г. А. Некоторые вопросы теории упру-
гости и пластичности железобетона при наличии трещин. — В сб.
ЦНИИСК им. Кучеренко: Новые методы расчета строительных
конструкций», под ред. А. Р. Ржаннцына. М., Стройиздат, 1968.
23. Гениев Г. А., Кисюк В. Н., Тюлин Г. А. Теория пластич-
ности бетона и железобетона. М., Стройиздат, 1974.
24. Гуревич A. JI., Карпенко Н. И., Ярин Л. И. О способах
расчета железобетонных плит на ЭВМ с учетом процесса трещи но-
образования. «Строительная механика и расчет сооружений»,
1972, № 1.
25. Гуща Ю. П. Исследование изгибаемых железобетонных
элементов при работе стержневой арматуры в упругопластической
стадии. Автореферат кандидатской диссертации, НИИЖБ, 1968.
26. Гуща Ю. П. Исследование ширины раскрытия нормальных
трещин. — В сб. ИИИЖБ: Прочность и жесткость железобетонных
конструкций, под ред. С. А. Дмитриева и С. М. Крылова. М., Строй-
издат, 1971.
27. Елагин Э. Г. Исследование работы железобетонных эле-
ментов кольцевого сечения с напрягаемой и ненапрягаемой армату-
ры при совместном действии изгибающего и крутящего моментов.—
В сб. НИИЖБ: Влияние скорости нагружения, гибкости и крутя-
щих моментов на прочность железобетонных конструкций. М.,
Стройиздат, 1970.
28. Залесов А. С., Ильин О. Ф. Несущая способность железо-
бетонных элементов при действии поперечных сил. «Бетон и желе-
зобетон». 1973, № 6.
29. Зайцев Л. И. Расчет прогибов железобетонных квадрат-
ных плит, заделанных по двум смежным сторонам и свободно
опертым по двум сторонам. «Бетон и железобетон», 1964, № 7.
30. Карпенко И. И. Теоретический анализ работы железобе-
тона с трещинами при плоском напряженном состоянии. Теорети-
ческое н экспериментальное исследование способов расчета желе-
зобетонных плит с трещинами. Тезисы докладов lull научно-техни-
ческой конференции молодых научных сотрудников ИИИЖБ, ПЭМ
Ц11ИИС Госстроя СССР. М., 1963, 1964.
197
31. Карпенко Н. И. Особенности работы железобетона с тре-
щинами при плоском напряженном состоянии и расчет железобетон-
ных плит. Автореферат кандидатской диссертации. М.» НЦИЖБ,
1964.
32. Карпенко Н. И. К расчету прогибов железобетонных плит
с трещинами, работающих в двух направлениях. — В сб:. Железо-
бетонные конструкции. Тула, Изд-во Политехнического ин-та, 1965.
33. Карпенко Н. И. О работе железобетонных плит с трещинами.
Труды VI Всесоюзной конференции по бетону и железобетону,
V-секция НТО Стройиндустрии. М., Стройиздат, 1966.
34. Карпенко Н. И., Рсйтман М. И. Нижняя граница несущей
способности и оптимальное проектирование железобетонных плит.—
В сб.: Труды VI Всесоюзной конференции по теории оболочек и
пластинок. М., «Мир», 1967.
35. Карпенко Н. И. О работе железобетона при сложном на-
пряженном состоянии в упругой и упругопластической стадиях.
— В сб. института Московского отделения Гипроннсельхоза «Иссле-
дование конструкций здания и сооружений для сельского строи-
тельства». М., Стройиздат, 1967.
36. Карпенко Н. И., Крылов С. М., Рейтмаи М. И., Скрыпнико-
ва Р. А., Ярин Л. И. Расчет железобетонных плит с трещинами
с помощью ЭЦВМ. «Вычислительная и организационная техника
в строительстве и проектировании», вып. 11-2. М., Гипротис, 1967.
37. Карпенко Н. И. Теоретическое исследование перемещений,
условий трещннообразования, ширины раскрытия трещин и усло-
вий прочности элементов с трещинами железобетонных плит и обо-
лочек. — В сб. ЦНИИЭПсельстроя: Исследования конструкций
зданий и сооружений для сельского строительства, вып. 2-1. М.,
Стройиздат, 1968.
38. Карпенко Н. И., Ярин Л. II. Исследование работы железо-
бетонных плит на ЭЦВМ с учетом образования трещин. — В сб.
ЦНИИЭПсельстроя: Исследования конструкций зданий и сооруже-
ний для сельского строительства, вып. 2-1. М., Стройиздат, 1968.
39. Карпенко Н. И. Условия текучести арматуры железобетон-
ных сред с трещинами. «Строительная механика и расчет сооруже-
ний», 1968, № 2.
40. Карпенко Н. И., Рсйтман М. И. Деформирование железо-
бетона при течении арматуры. «Прикладная механика», т. IV, вып.
10. Киев, 1968.
41. Карпенко И. И. О некоторых уточнениях расчета
деформаций железобетонных плит и оболочек с трещинами. — В сб.
ЦНИИЭПсельстроя: Исследования конструкций зданий и сооруже-
ний для сельского строительства, вып. 2-2. М., Стройиздат, 1969.
42. Карпенко Н. И. К определению деформаций стержневых
железобетонных коробчатых элементов с трещинами прн кручении.
Реферативный сб. ЦИНИСа: Межотраслевые вопросы строительства.
«Отечественный опыт», 1970, А? 10.
43. Карпенко Н. И., Елагин Э. Г. Деформации железобетонных
трубчатых элементов, подвергнутых кручению после образования
трещин. «Бетон и железобетон», 1970, А? 3.
44 . Карпенко Н. И. К расчету железобетонных пластин и
оболочек с учетом трещин. «Строительная механика и расчет соору-
жен и й», 1971, А? 1.
45. Карпенко И. И., Елагин Э. Г. Деформации железобетонных
тр убчазых элсмснтсв с трещинами при изгибе с кручением — В сб.
198
Прочность и жесткость железобетонных конструкций, под ред.
С. А. Дмитриева и С. М. Крылова. М., Стройиздат, 1971.
46. Карпенко Н. 11. К расчету деформации железобетонных
стержней с трещинами при изгибе с кручением. — В сб. НИИЖБ:
Теория железобетона, посвященном 75-летию со дня рождения
Л. А. Гвоздева. М.. Стройиздат, 1972.
47. Карпенко Н. И. Теоретическое исследование деформаций
железобетонных пластин и оболочек с трещинами при сложном
армировании. — В сб. НИИЖБ: Воздействие статических, дина-
мических и многократно повторяющихся нагрузок на бетон и эле-
менты железобетонных конструкций, под ред. А. А. Гвоздева, М.,
Стройиздат, 1972.
48. Карпенко Н. И. О двух общих условиях прочности для же-
лезобетонных элементов с трещинами. Доклады НИИЖБ на VII Все-
союзной конференции по бетону и железобетону. М.» Стройиздат,
1972.
49. Карпенко Н. И. К построению модели сцепления арматуры
с бетоном, учитывающей контактные трещины. «Бетон и железо-
бетон», 1973, № 1.
50. Карпенко Н. И., Гуревич A. J1. О расчете железобетонных
балок-стенок с учетом трещин. «Строительная механика и расчет
сооружений», 1974, № 1.
51. Карпенко Н. И. Теория деформирования железобетона
с трещинами при сложном напряженном состоянии и ее приложе-
ния к расчету балок-стенок, плит, элементов оболочек и стержней,
подвергнутых кручению и изгибу с кручением. Автореферат дис-
сертации на соискание ученой степени д-ра техн. наук. М., Изд-во
ВНИИМЕТМЛШ, 1973.
52. Карпенко Н. И., Кукуиасв В. С. Трещиностойкость и жест-
кость железобетонных плит с трещинами при совместном действии
моментов и мембранных сил. В монографии НИИЖБ: Предельные
состояния железобетонных конструкций, под ред. С. А. Дмитрие-
ва. М.. Стройиздат, 1976.
53. Карпенко Н. И., Ярин Л. И., Селиванова Ю. Н. Вычисле-
ние коэффициентов физических уравнений при расчете стен желе-
зобетонных цилиндрических силосов. — В сб. ЦНИИЭПсельстроя:
Строительные конструкции, здания и сооружения, № 9, М.» 1974.
54. Колкунов Н. В. Основы расчета упругих оболочек, М.,
«Высшая школа», 1963.
55. Королев А. Н., Крылов С. М. Способ расчета прогибов
железобетонных плит, опертых по контуру, и безбалочных пере-
крытий при действии кратковременной нагрузки. Труды НИИЖБ,
вып. 26, 1962.
56. Коковин О. А. Деформации изгибаемых и внецентренно
сжатых элементов при кратковременно действующей нагрузке
в стадиях, близких к разрушению. — В сб. НИИЖБ: Прочность
и жесткость железобетонных конструкций», под род. А.А. Гвоздева.
М., Стройиздат, 1963.
57. Крылов С. М. Перераспределение усилий в статически
неопределимых железобетонных конструкциях. М.» Стройиздат,
1964.
58. Кукунаев В. С. Линеаризация физических уравнений для
схем пересекающихся трещин при расчете железобетонных плит
с трещинами с учетом совместного действия моментов и мембран-
ных сил. В сб. НИИЖБ: Влияние неупругнх свойств железобетона
199
на работу и распределение усилий в статически неопределимых кон-
струкциях» под род. С. М. Крылова М., 1975.
59. Лауль X. X. Цилиндрические железобетонные оболочки
с трещинами в растянутой зоне. Труды Таллинского политехни-
ческого нн-та, серия А, № 45, 1953.
60. Лесснг Н. Н. Определение теоретической несущей способ-
ности железобетонных элементов кольцевого сечения, работающих
на изгиб с кручением. — В сб. НИИЖБ: Влияние скорости нагру-
жения, гибкости и крутящих моментов на прочность железобетон-
ных конструкций. М., Стройиздат, 1970.
61. Ленке и П. Некоторые вопросы расчета железобетонных
плит по методу предельного равновесия. — В сб. НИИЖБ: Совер-
шенствование расчета статически неопределимых железобетон-
ных конструкций, под ред. А. А. Гвоздева и С. М. Крылова. М.,
Строй нздат, 1966.
62. Лехницкий С. Г. Анизотропные пластинки. М., Гостехиз-
дат, 1963.
63. Лифшиц Я. Д., Онищенко М. М. Расчет железобетонных
плит с учетом трещи необразован и я и ползучести. «Строительная
механика и расчет сооружений», 1962, № 6.
64. Милейковскин И.* Е. Приближенный расчет цилиндри-
ческих оболочек открытого сечения с учетом трещин. Сб. ЦНИИСК
«Экспериментальные и теоретические исследования по железобе-
тонным оболочкам». М., Госстройиздат» 1959.
65. Милейковскин И. Е. К расчету пологих оболочек на ЭЦВМ
«Строительная механика и расчет сооружений», 1965, К® 4.
66. Мнрзабекян Б. Ю., Ройтман М. И. Определение несущей
способности и оптимальное проектирование железобетонных оболо-
чек с помощью линейного программирования. — В сб. ЦНИИЭП-
сельстрой: Исследование конструкций зданий и сооружений для
сельского строительства, вып. 2.1. М., Стройиздат, 1968.
67. Мул ин Н. М., Гуща Ю. П. Деформации железобетонных эле-
ментов при работе стержневой арматуры в упругопластнчсской
стадии. «Бетон и железобетон», 1970, № 3.
68. Мулин Н. М., Гуща Ю. П. Арматура и условия ее работы
в конструкциях. «Бетон и железобетон», 1971, К® 5.
69. Мурашов В. И. Трещиноустойчнвость, жесткость и проч-
ность железобетона. М., Машстройнздат, 1950.
70. Немировский Я. М., Никитин Н. В. О коэффициенте ф для
расчета жесткости железобетонных элементов «Бетон и железобе-
тон», 1958, № 2.
71. Немировский Я. М. Исследование напряженно-деформи-
рованного состояния железобетонных элементов с учетом работы
растянутого бетона над трещинами и пересмотр на этой основе тео-
рии расчета деформаций и раскрытия трещин. — В сб. НИИЖБ:
Прочность и жесткость железобетонных конструкций, под ред.
А. А. Гвоздева. М., Стройиздат, 1968.
72. Оатул А. А. Основы теории сцепления арматуры с бетоном.
Сб. трудов ЧПИ, № 46. Челябинск, 1967.
73. Палатников Е. А. Расчет железобетонных плит покрытий
аэропортов. М., Оборонгиз, 1961.
74. Прокопович И. Е.. Яременко А. Ф. Исследование работы
железобетонных плит с учетом трещинообразования и ползучес-
ти.—В сб.: Проблемы ползучести и усадки бетона (по материалам
200
^бГ°№С77°Ю1974° CoDeu*a,l,,fl)* М-» Изд-во ЦНИИС Минтранстроя,
75. Реитман М. И. Новые методы расчета пространственных
железобетонных конструкций. — В сб. ЦНИИЭПсел встрой:
Исследования конструкций зданий и сооружений для сельского
строительства, вып. 2—1. М., Стройиздат, 1968.
76. Соломин В. И., Шишов И. И. О расчете круглых фундамент-
ных плит с учетом особенностей деформирования железобетона.
«Строительная механика и расчет сооружений», 1972, № 1.
77. Тимошенко С. П., Войновский-Крнгер С. Пластинки и
оболочки. М., Госбизматгнз, 1963.
78. Уманский А. А. Кручение и изгиб тонкостенных авнаконст-
рукцнй. М., Оборонгиз, 1939.
79. Холмянскнй М. М. Закладные детали сборных железобе-
тонных элементов. М., Стройиздат, 1968.
80. Чннепков Ю. В. Расчет железобетонных цилиндрических
оболочек по трещи постой кости, жесткости и прочности. «Строитель-
ная механика и расчет сооружений», 1969, № 4.
81. Чистова Т. П. Экспериментальное исследование деформа-
тнвности обычных железобетонных элементов коробчатого и сплош-
ного прямоугольного сечения при чистом кручении. — В сб.:
Прочность и жесткость железобетонных конструкций, под ред.
С. Л. Дмитриева и С. М. Крылова. М., Стройиздат, 1971.
82. Чижевский В. В. Построение расчетной схемы изгибаемой
железобетонной плиты с трещинами. — В сб.: Совершенствование
железобетонных конструкций для промышленного строительства.
Сб.- трудов Уральского Промстройниипроекта, № 27. Свердловск,
1970.
83. Ярин Л. И. О расчете железобетонных оболочек-силосов в
стадии эксплуатации с учетом развития трещин. «Строительная
механика и расчет сооружений», 1974, Кз 3.
84. Яременко А. Ф. К расчету железобетонных плит с трещи-
нами при длительном действии нагрузки. Сб.: Строительные кон-
струкции, вып. XVIII. Киев, «Вудивельник», 1971.
85. Bach G. Versuche mit zweiseitig auflicgcnden Eiscnbcton-
platten bei konzentrierter Belastung. Helt 52. Berlin, 1923.
86. Bach G. und Graf O. Versuche mit allseitig auflicgcnden,
quadratischen und rechteckigcn Eiscnbctonplattcn. Berlin, 1915.
87. Bans B.,Tolaccia S. Calculc a la rupture des dalles on beton
arme et etude experimentale du criterc de rupture en flexion pure.
Annales, Tlnstitut Technique du Batiment et des Travaux Publics,
Paris, v. 17, N 1, 1963.
88. Gehler W., Amos H. Versuche mit kreuzwcisc bewehrten
Platten Heft 70. Berlin, 1932.
89. Huber M. G. Die Grundlagcn einer rationalien Bercchnung
dor kreizweise dcwchrten Eisen bctonplatten, z. ust. Ing-v, 11—30,
1914.
90. Johansen K. W. Bruchmomente der Kremzwcise bewehrte
Platten Abhandhingcn I. V. В. H., 1932.
91. Kwiecinski M. \V. Some on the Yield Criterion for a Reinfor-
ced Concrete Slab. «Magazine of Concrete Research», vol. 17, No 52,
Sept. 1965.
92. Lenschow R. J., Sozen M. A. Yield criterion for reinforced
concrete under biaxial moments and forces. 'The national Science
Foundation University of Illinois Urbana, 1966.
201
No 56, Paris, 1966
94
matlon des dalles diniensionnees _ Paris, I960,
ropcen du biton, Bulletin d In . no 'p|astiguc des Constructions.
Mnccnnot Ch., have г»- ___ioeq
л и * i Mnfe on Yield Criterion for
93. Lenschow R. J., s°zen.,^p'' du Biton, Bulletin d'Inf.
Reinforced Concrete Slabs. Counts Europ
, Paris, 1966. „лиinns de fissuration et de defor-
L Levi F. Controle des сот Hmite ultime. Comite Eu-
•------- ёП .1 м Calcul Plastiguc des Constructions.
95. Massonet Ch., Save M. CHcui rB *lles> l963.
VoLJ1* .?rVctTST POnathe viel I criterion of an orthogonally reinfo.
96. Morley С. T. On the yieiu « lg6(_
reed concrete slad .{na|vsis of Reinforced Concrete Slabs.
97. Nilsen M.P. L'''v^aalyGi 26. Copenhagen, 1964.
Ada9P°WoodnRaH.Cap|das‘ic and elastic design of slabs and plates.
London, Thames, 1961..
ОГЛАВЛЕНИЕ
Стр.
Предисловие............................................ 3
Введение............................................... 4
Глава /. Теория деформирования железобетона с трещинами
при плоском напряженном состоянии...................... 6
§ 1. Характерный элемент и компоненты его напряженно-
го состояния. Схемы непересекающихся и пересекающихся
трещин................................................. 6
§ 2. Общая характеристика деформирования элементов с
трещинами и начальные зависимости.....................12
§ 3. Способ учета армирования. Понятия усилий и относи-
тельных деформаций для железобетонных элементов с тре-
щинами.................................................24
§ 4. Анализ напряженно-деформированного состояния эле-
ментов с непсресекающнмнся трещинами при основных схе-
мах армирования........................................31
§ 5. Анализ напряженно-деформированного состояния эле-
ментов с иепересекающимнся трещинами при частных схе-
мах армирования. Элементы с пересекающимися трещинами . 48
§ 6. Экспериментальные исследования и применение тео-
рии к расчету плоских конструкций......................54
§ 7. Условия прочности для элементов плоских конструк-
ций и их связь с деформационной теорией................65
Глава 2. Моментная теория гладких плит н элементов обо-
лочек с трещинами.................................... 72
§ 1. К изложению теории. Краткий обзор.................72
§ 2. Схемы трещин и схемы армирования. Предпосылки и
гипотезы предлагаемой теории...........................73
§ 3. Анализ напряженного и деформированного состояния
элементов при различных схемах трещин..................85
§ 4. Окончательный вид физических уравнении. Общая
постановка задачи расчета плит и оболочек при различ-
ных схемах трещин.....................................Ito
203
Стр.
§ 5. Переменные физические и геометрические параметры
жесткостных коэффициентов..............................114
§ 6. Расчеты железобетонных плит на ЭВМ с учетом про-
цесса трещи необразованна..............................127
§ 7. Условии прочности для плит и оболочек с трещинами . 145
Глава 3. Деформации элементов железобетонных стержней
с трещинами при кручении и изгибе с кручением .........158
§ 1. Силовые поверхности. Поток касательных сил. Геомет-
рические выражения для углов закручивания..............158
§ 2. Расчет деформаций трубчатых элементов при чистом
кручении и совместном действии кручения и продольной
силы...................................................162
§ 3. Расчет деформаций трубчатых элементов при совмест-
ном действии изгибающих н крутящих моментов и продоль-
ной силы...............................................171
§ 4. Расчет деформаций прямоугольных стержней прн сов-
местном действии изгибающих и крутящих моментов и про-
дольной силы...........................................179
Список литературы......................................196
НИКОЛАИ ИВАНОВИЧ КАРПЕНКО
ТЕОРИЯ ДЕФОРМИРОВАНИЯ ЖЕЛЕЗОБЕТОНА
С ТРЕЩИНАМИ
Научный редактор — Л. Ф. Милованов
Редакция литературы по строительным материалам
и конструкциям
Зап. редакЦисЛ И. А. Рабинович
Редактор С. Б. Обухова
Мл. редактор Э. И. Федотова
Внешнее оформление художника М. Ибрагимова
Технические редакторы И. Г. Бочкова.
Т. В. Кузнецова
Корректор II. И. Чугунопа
Слано в набор 5 1 1976 г. Подписано в печать I.VI 1976 г.
Формат 81Х!(«’/„ д. л. Бумага типографская № 2.
10.92 уел. печ. л. (уч.нзд. л. 10.68). Тираж 4<ию нт
Над. № AVI—44tX>. Заказ № 631. Цена 73 кон.
Стройилдаг
103006, Москва, Каляевская ул. д. 23а
Московская типография № 4 Союзполиграфпрома
при Государственном комитете Совета Министров СССР
по делам и<дательств. полиграфии и книжной торговли.
Москва, И-41, Б. Переяславская ул.» д. 40