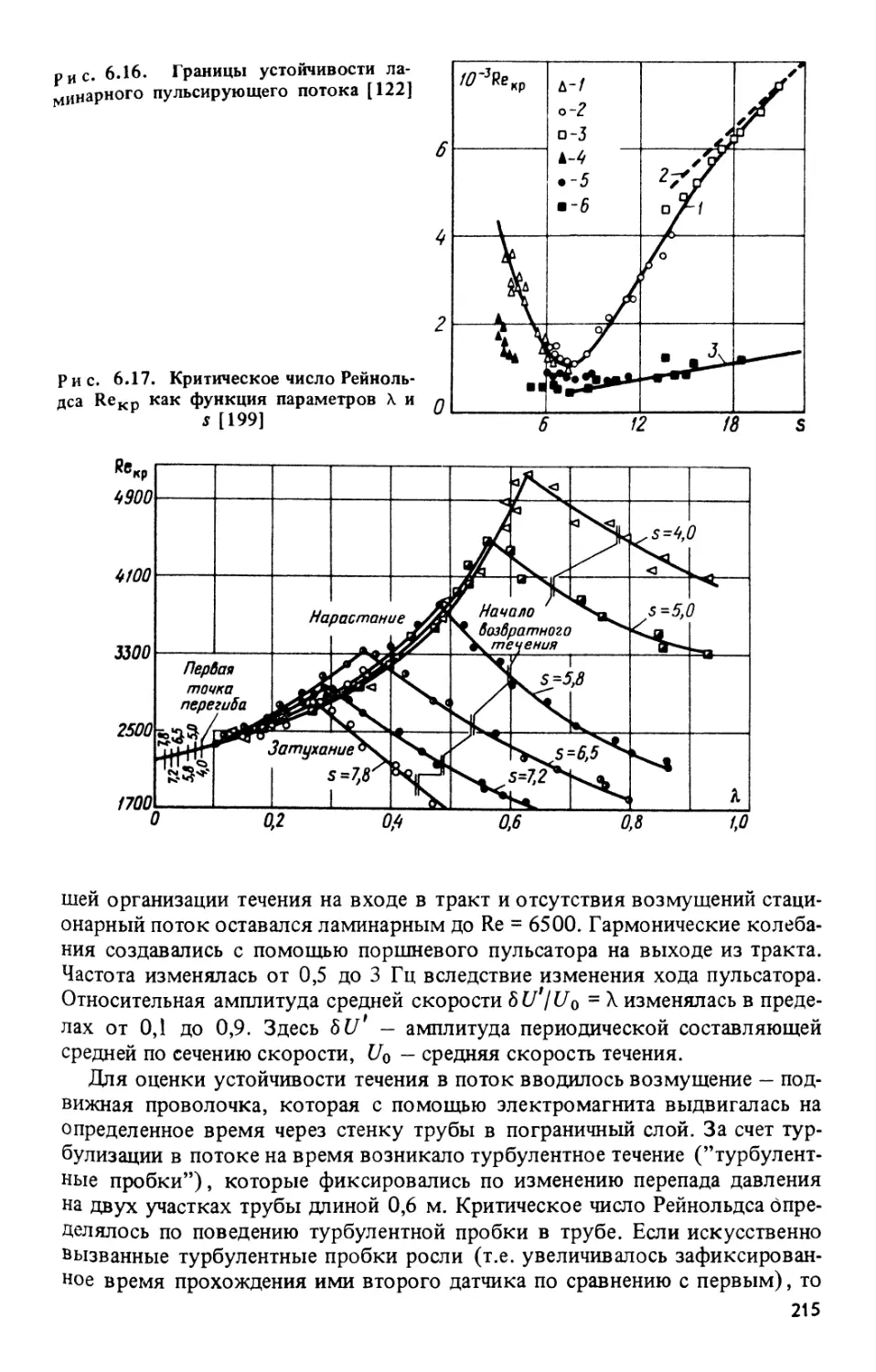
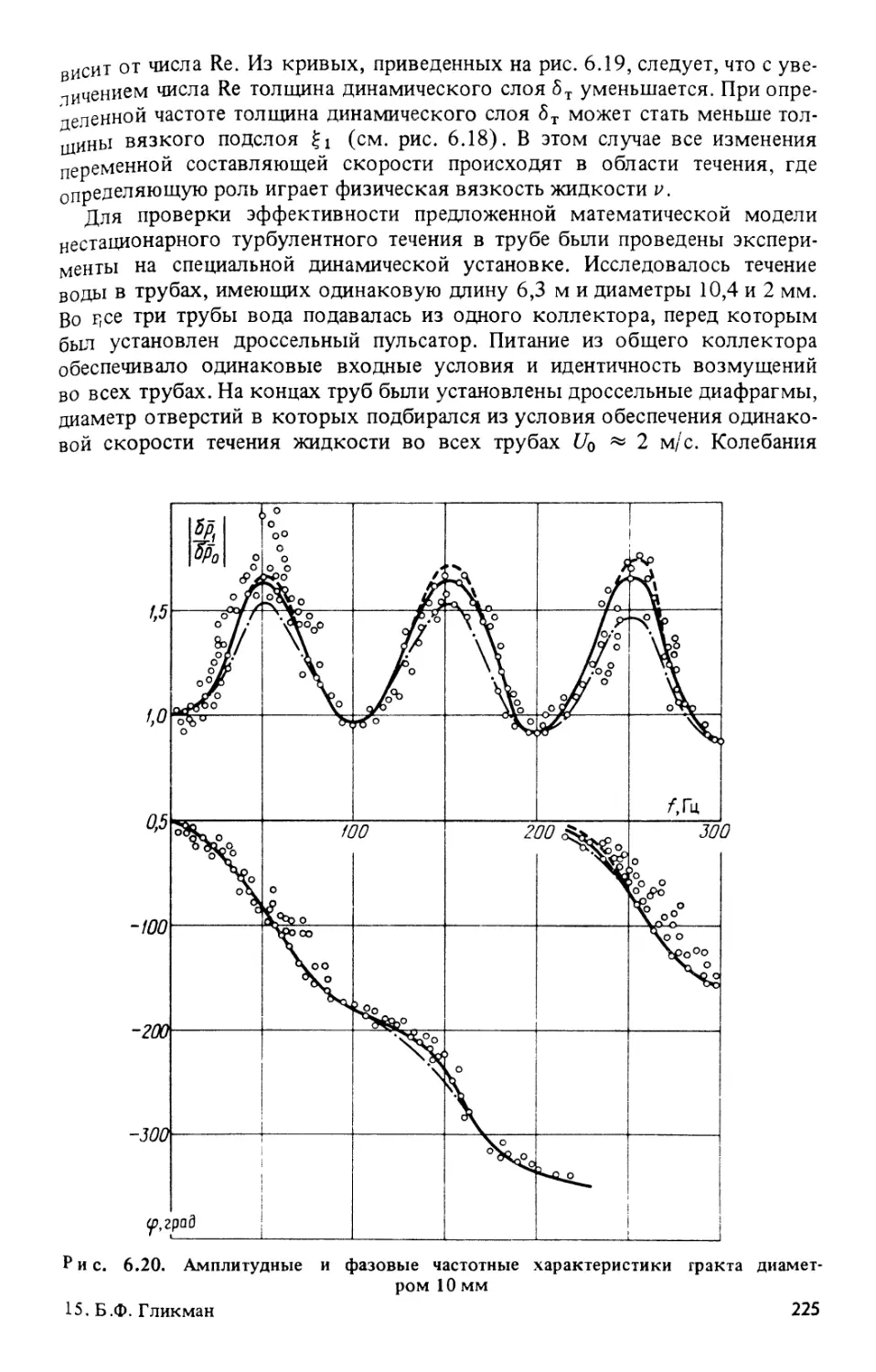
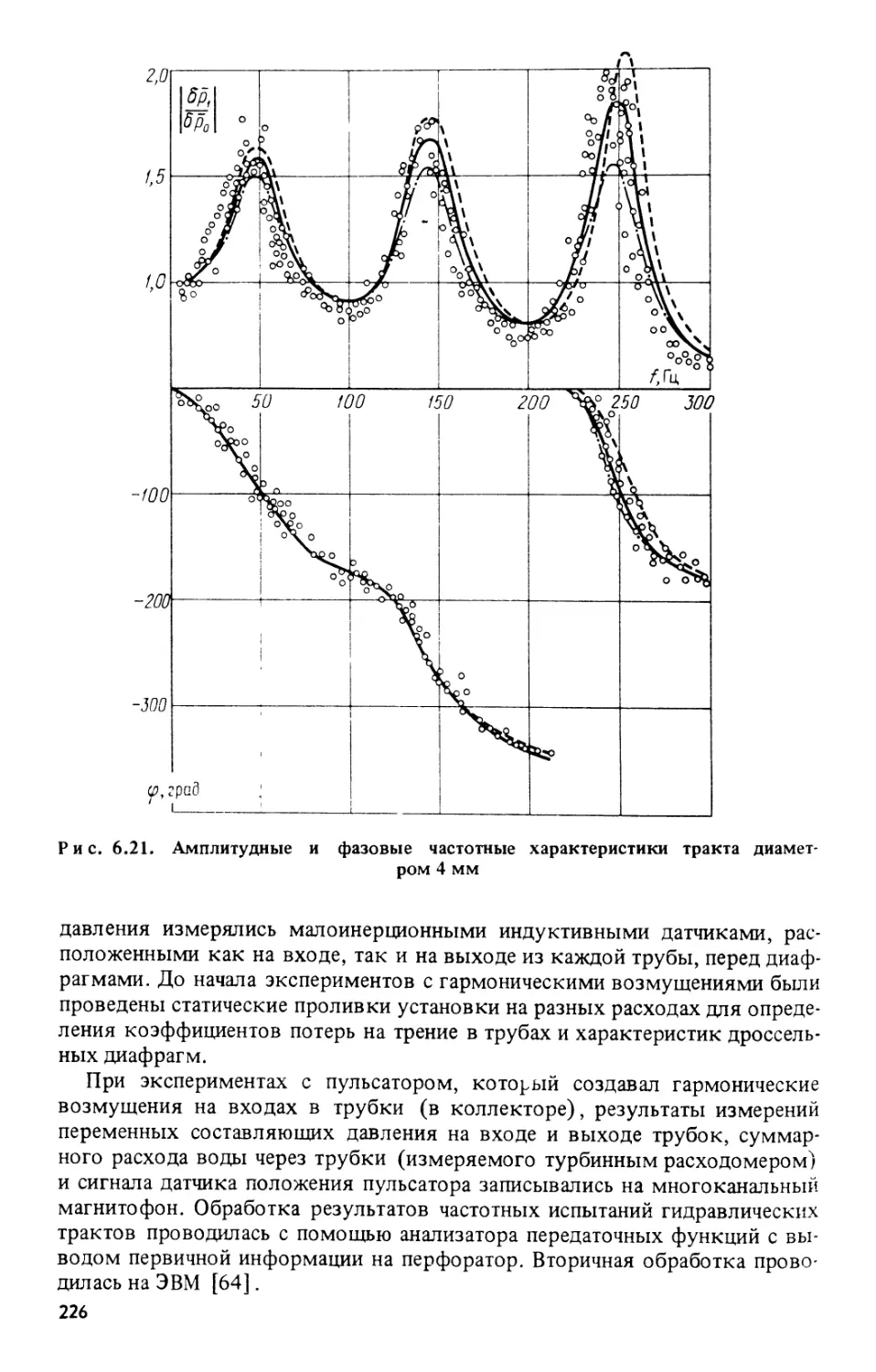
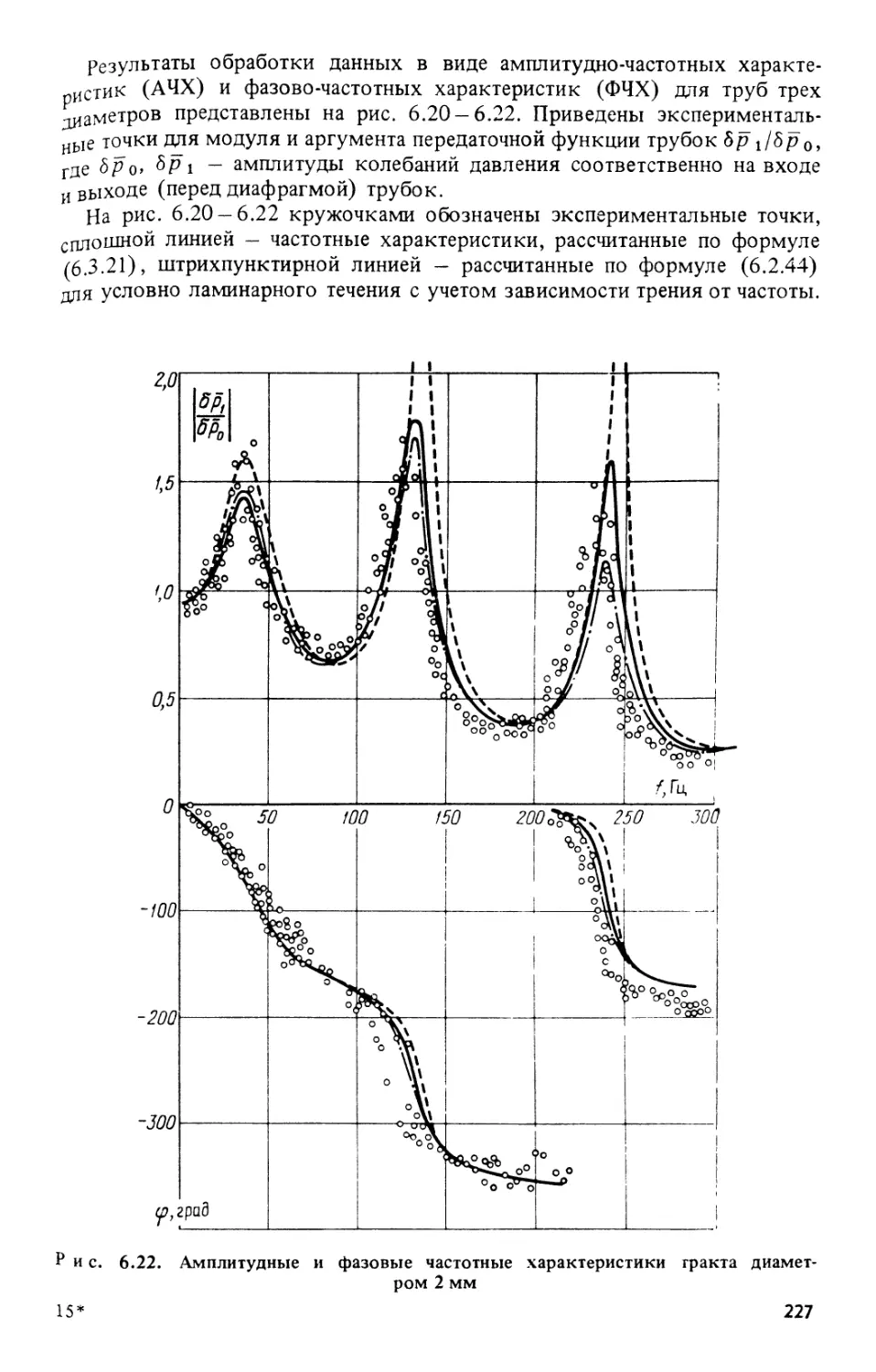
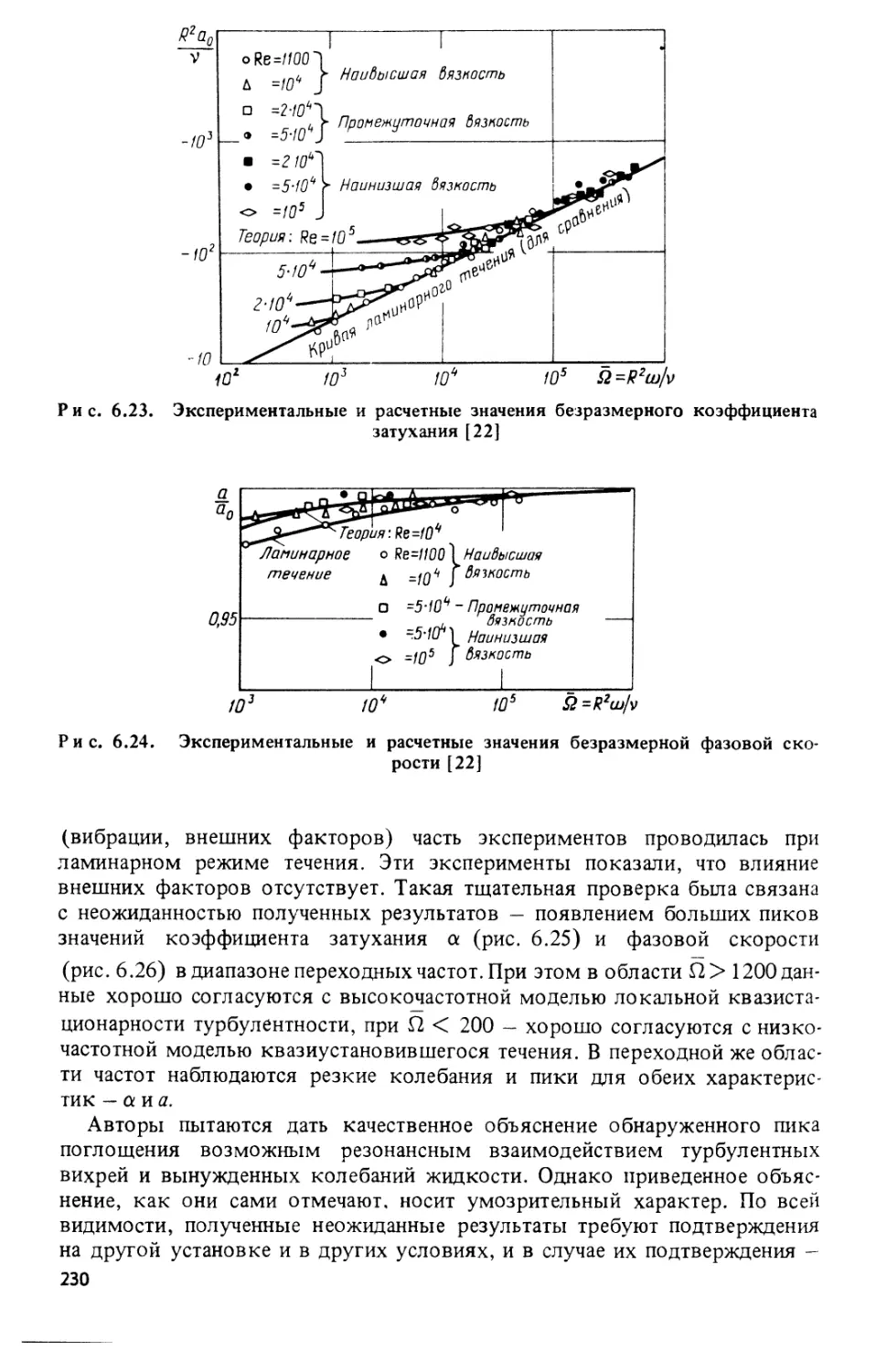
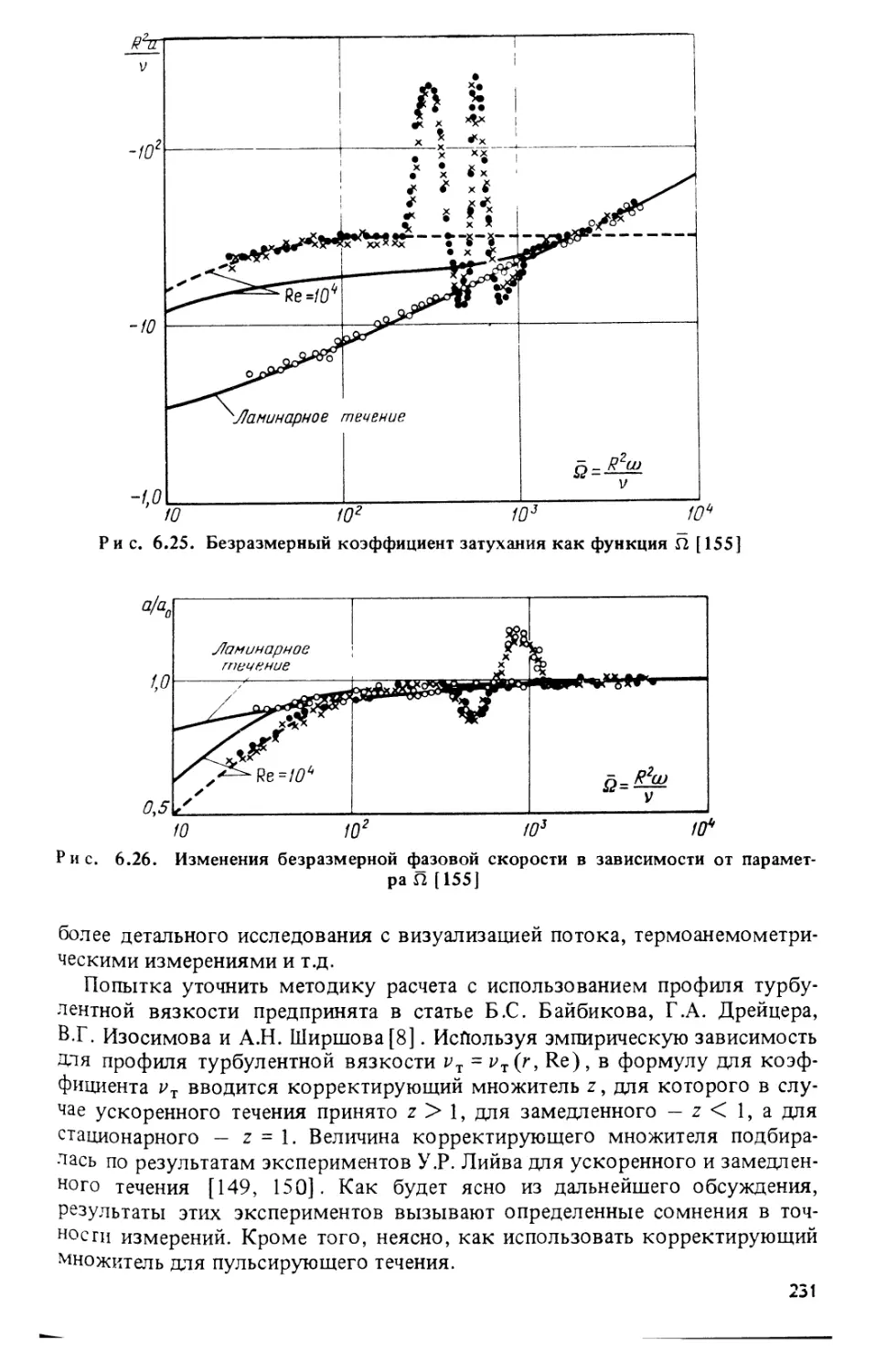
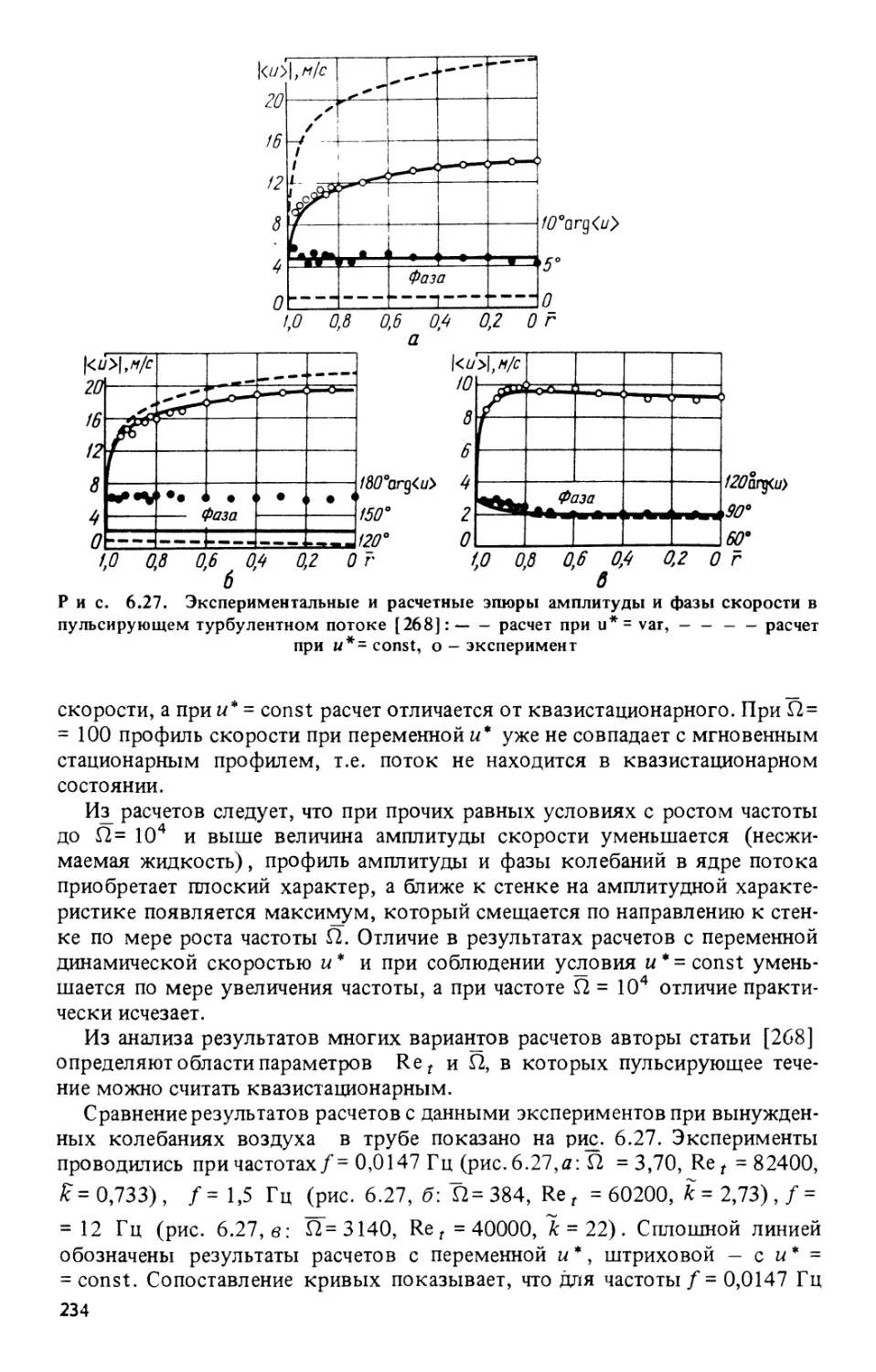
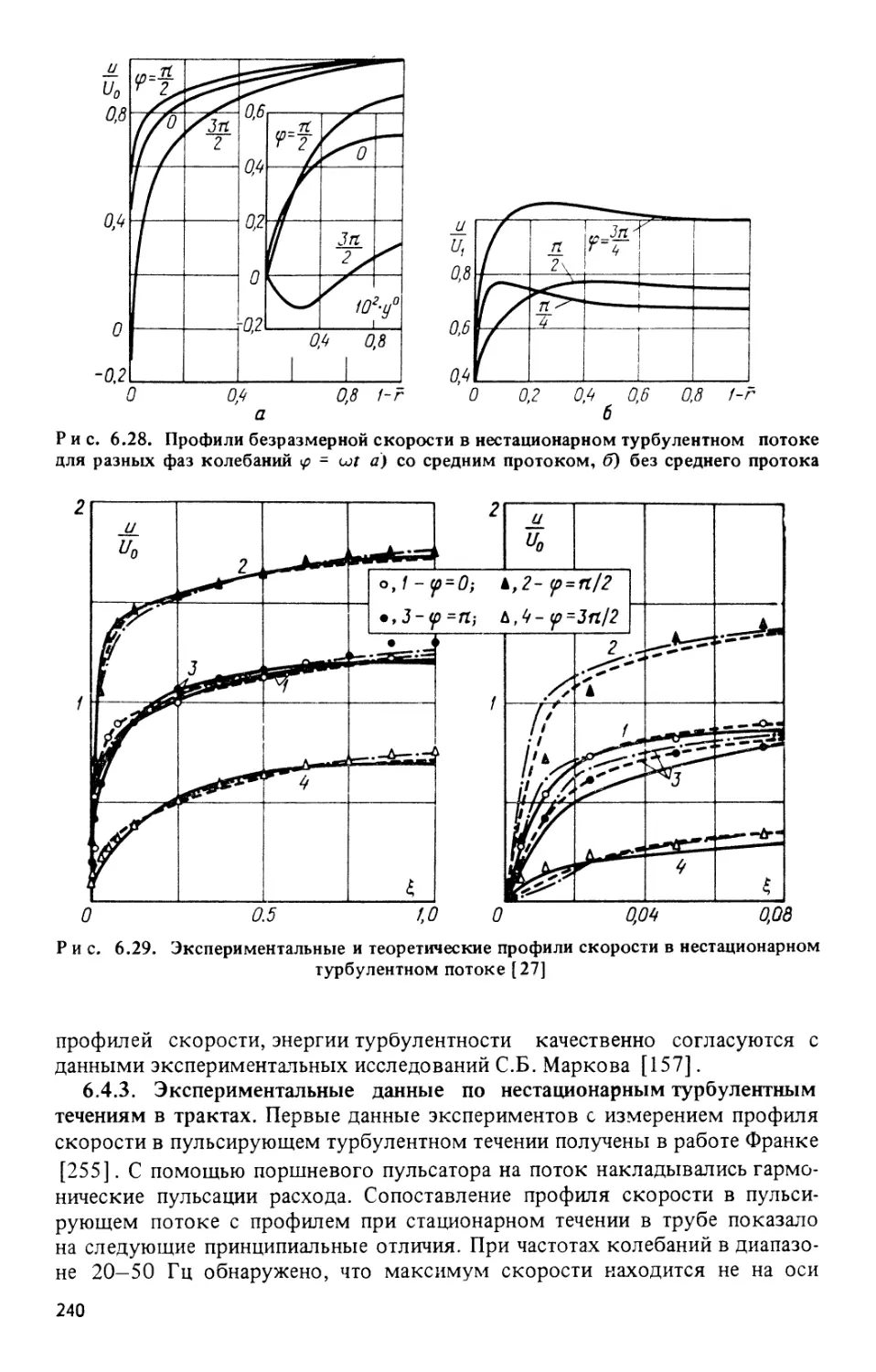
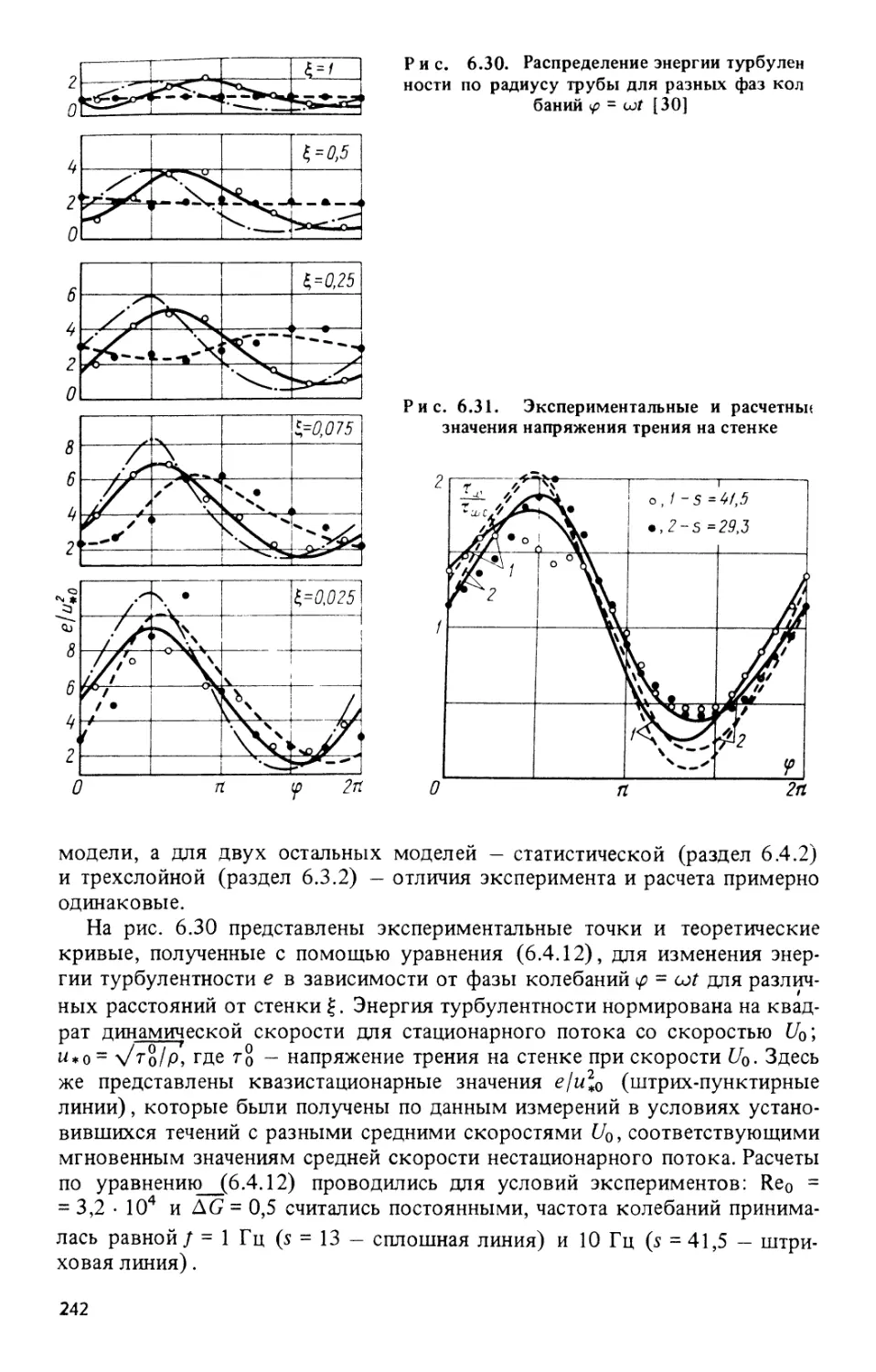
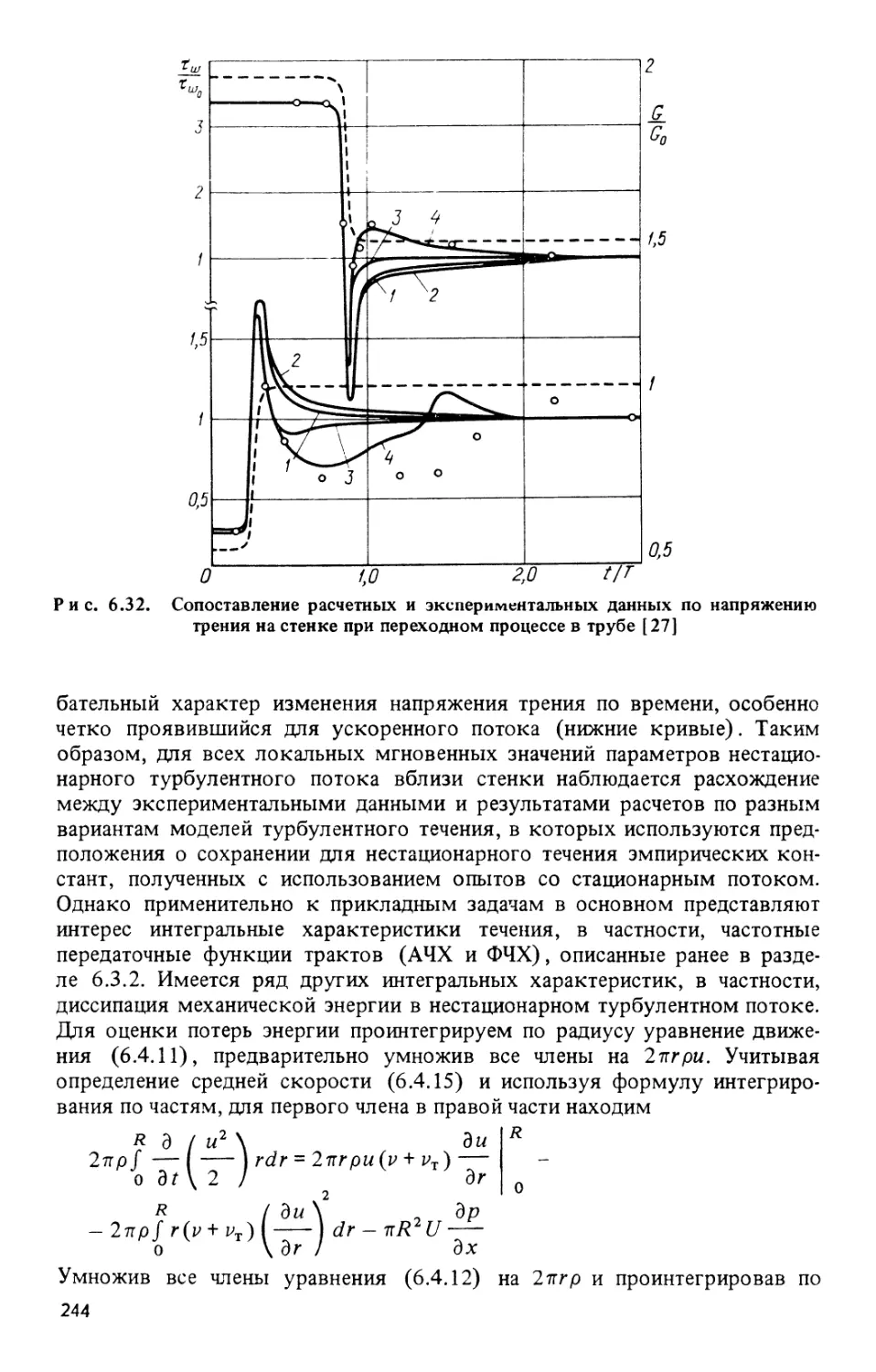
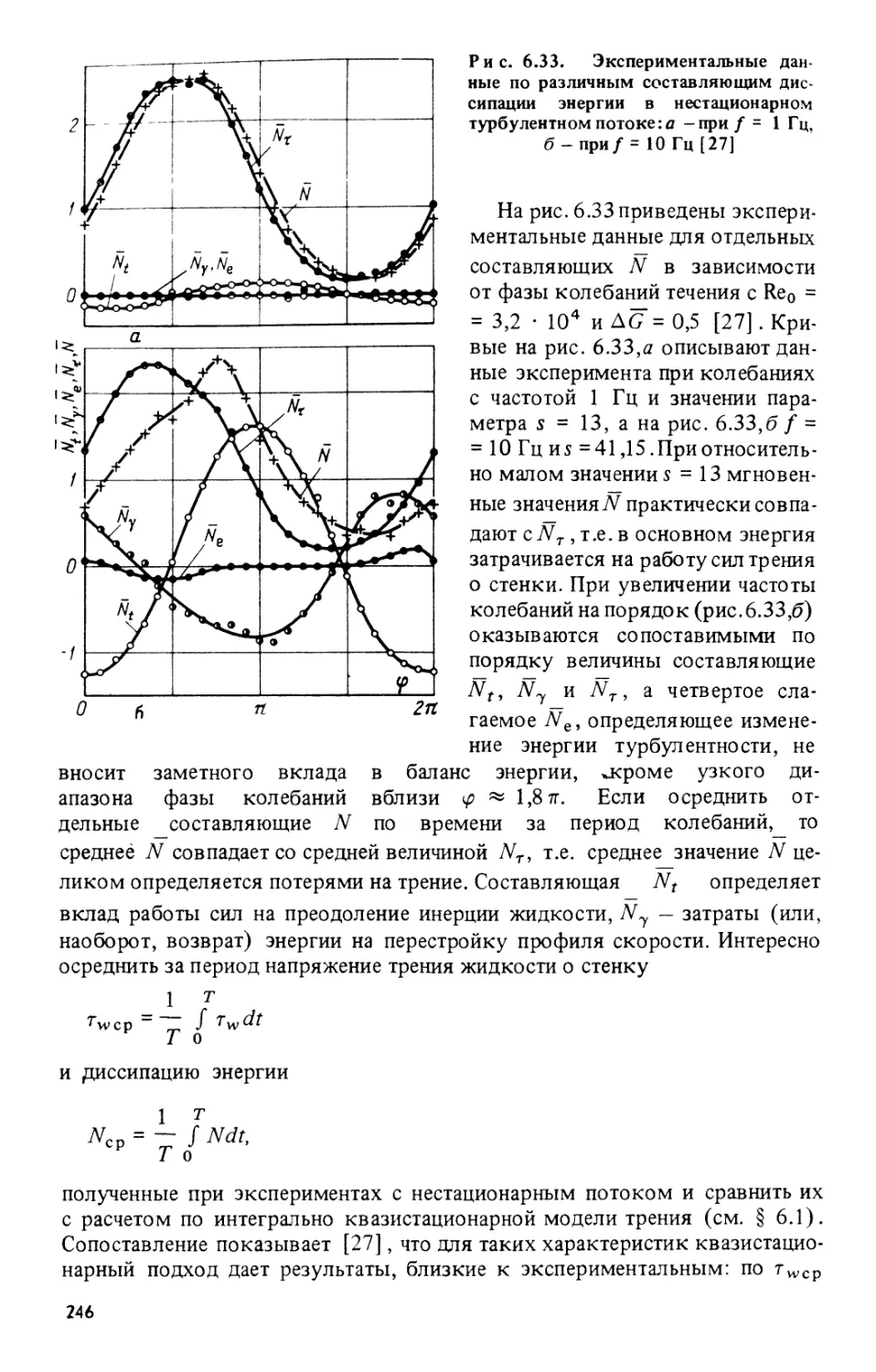
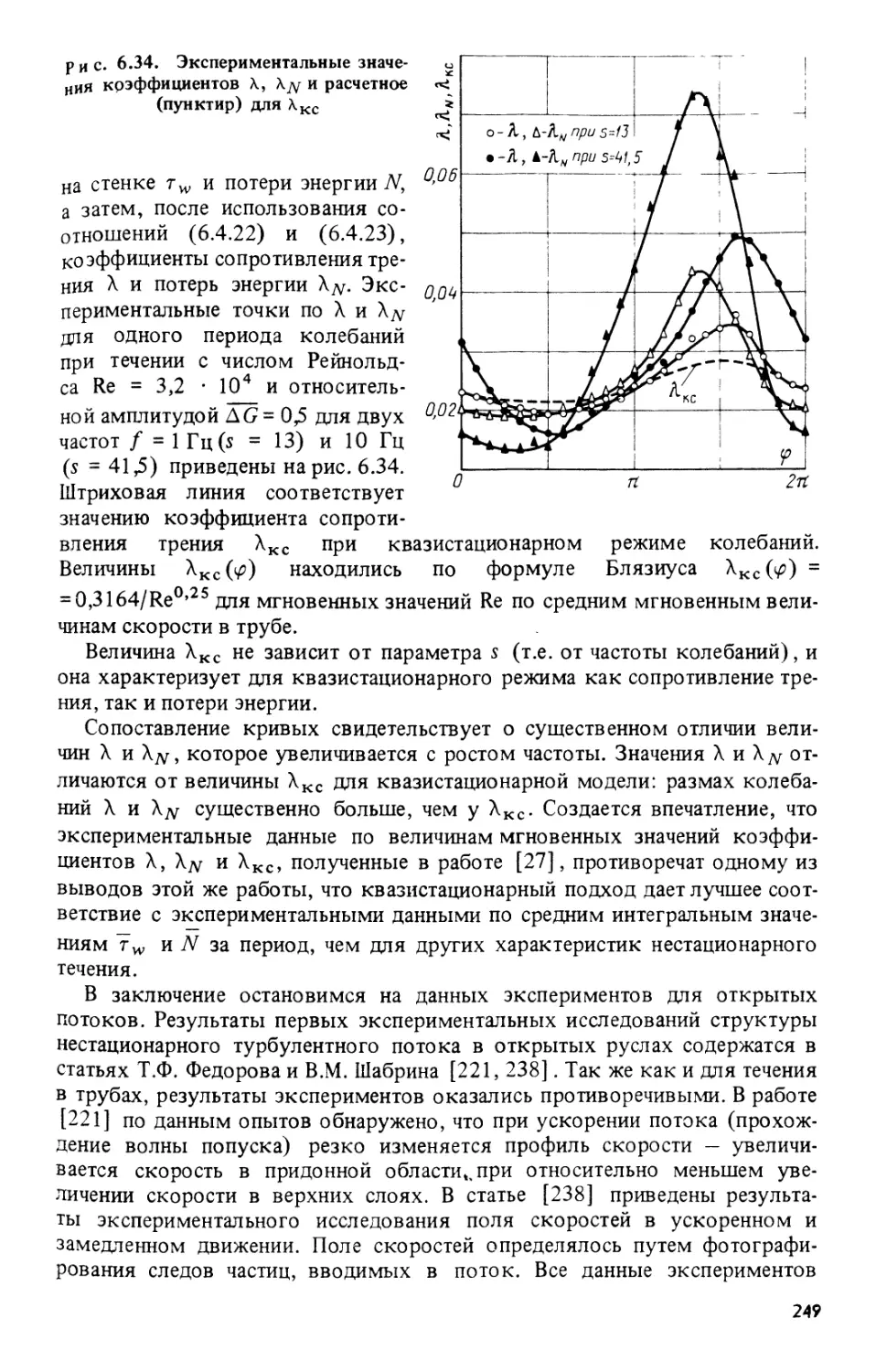
Текст
Б.Ф. ГЛИКМАН
МАТЕМАТИЧЕСКИЕ
МОДЕЛИ
ПНЕВМОГИДРАВЛИЧЕСКИХ
СИСТЕМ
МОСКВА "НАУКА"
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
19 8 6
ББК 22.253
Г54
УДК 532.542:62-52
Гликман Б.Ф. Математические модели пневмогидравлических
систем. - М.: Наука. Гл. ред. физ.-мат. лит., 1986. - 368 с.
Описаны методы формирования математических моделей разветвленных
пневмогидравлических систем различного назначения. Изложены основные
методы теории пневмогидравлических цепей. Анализируются особенности
нестационарного течения в каналах, специфические свойства акустических
характеристик трактов с протоком жидкости, влияние неизометричности
потока на его динамические характеристики. Решаются задачи о вынужденных
колебаниях и переходных процессах, об устойчивости процесса в
рассматриваемых системах.
Для специалистов в области технической гидродинамики, акустики, пнев-
могидроавтоматики, трубопроводного транспорта и т.п.
Табл. 1. Ил. 94. Библиогр. 279 назв.
Рецензент доктор технических наук БМ. Галицейский
© Издательство "Наука".
1703040000 -051 Главная редакция
. 74-86 физико-математической литературы
6 1
ОГЛАВЛЕНИЕ
Предисловие 5
Глава 1. Уравнения движения жидкости 7
§ 1.1. Вводные замечания 7
§ 1.2. Уравнения движения вязкой сжимаемой жидкости 9
§ 1.3. Турбулентные течения 13
§ 1.4. Безразмерная форма уравнений гидромеханики. Критерии
подобия 18
§ 1.5 Примеры упрощения уравнений гидромеханики. Некоторые
особенности нестационарного движения вязкой жидкости .... 22
§ 1.6. Математические модели движения жидкости с переменной
температурой (составом) 31
§ 1.7. О влиянии вязкости жидкости. Переход к одномерной модели
движения 33
§ 1.8. Условия, при соблюдении которых жидкость можно считать
несжимаемой 43
§ 1.9. Математические модели идеализированных элементов ПГС с
сосредоточенными параметрами 48
§ 1.10. Линейные или линеаризованные математические модели
процессов в ПГС 57
Глава 2. Пневмогидравлические системы (ПГС) и пневмогидравлические
цепи (ПГЦ) с сосредоточенными параметрами 66
§ 2.1. Что такое пневмогидравлическая иепь? 66
§ 2.2. Описание динамических процессов в ПГС с использованием
эквивалентной ПГЦ 94
Глава 3. Матрично-топологические методы построения математических
моделей ПГС 107
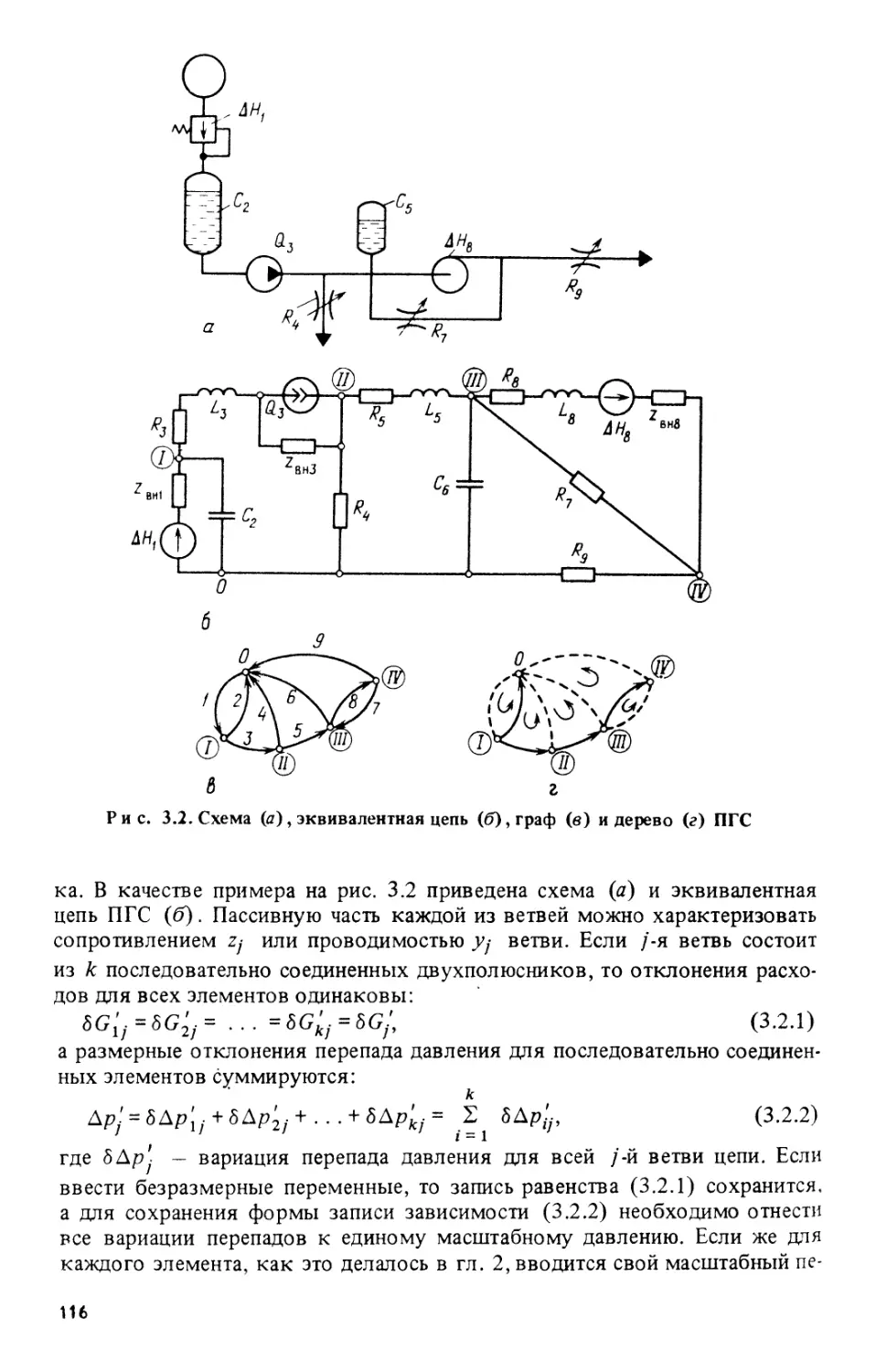
§ 3.1. Законы сохранения для цепи 107
§ 3.2. Узловые и контурные уравнения цепи 115
§ 3.3. Общие матричные уравнения цепей 122
Глава 4. Применение сигнальных, графов для расчетов линейных пневмо-
гидравлических систем 125
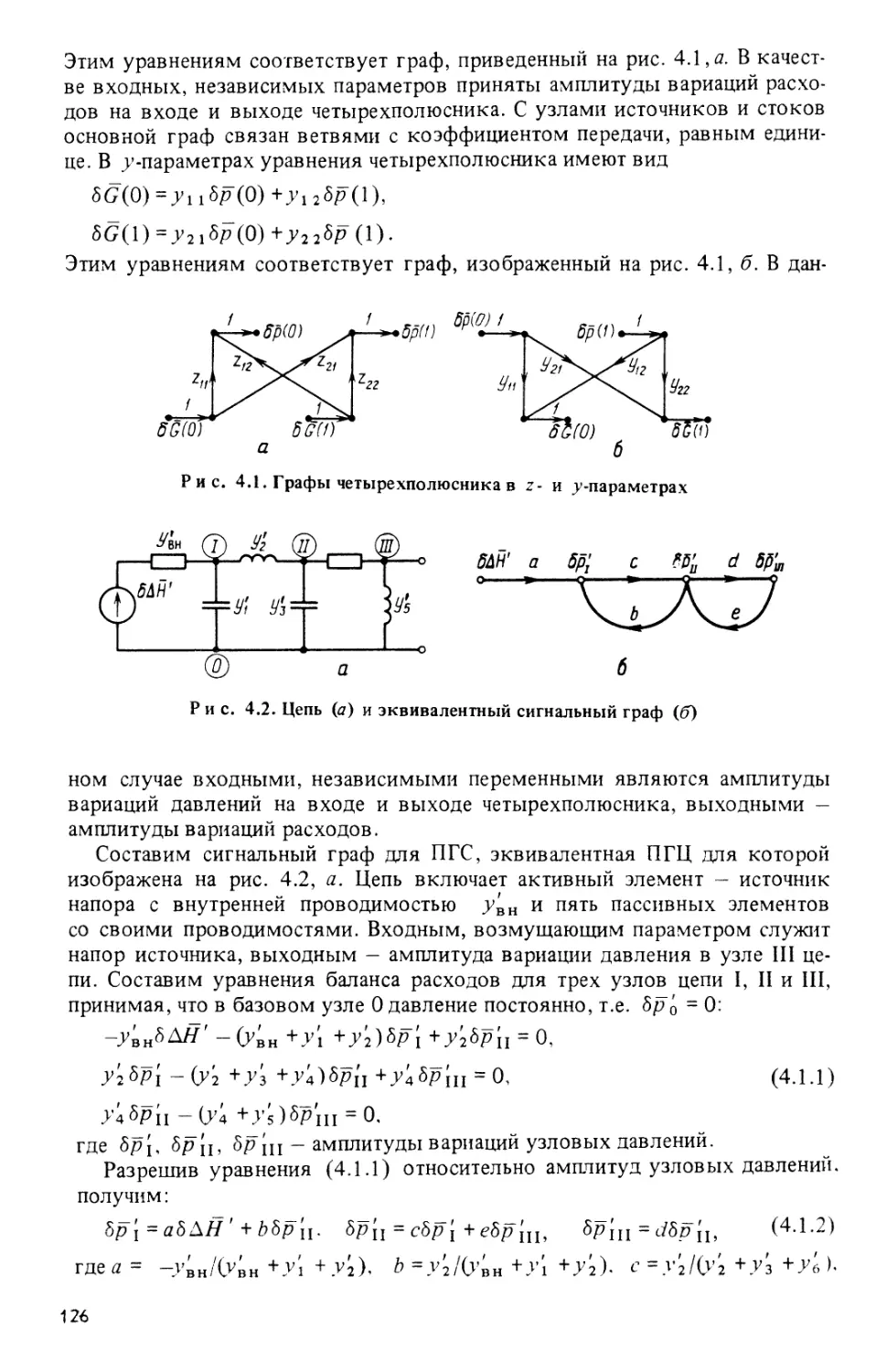
§ 4.1. Основные определения 125
§ 4.2. Правила упрощения сигнальных графов 127
§ 4.3. Коэффициент передачи графа 129
Глава 5. Акустические характеристики проточного тракта 132
§ 5.1. Волновое уравнение для участка тракта 132
§ 5.2. Вынужденные колебания жидкости в однородном тракте . 143
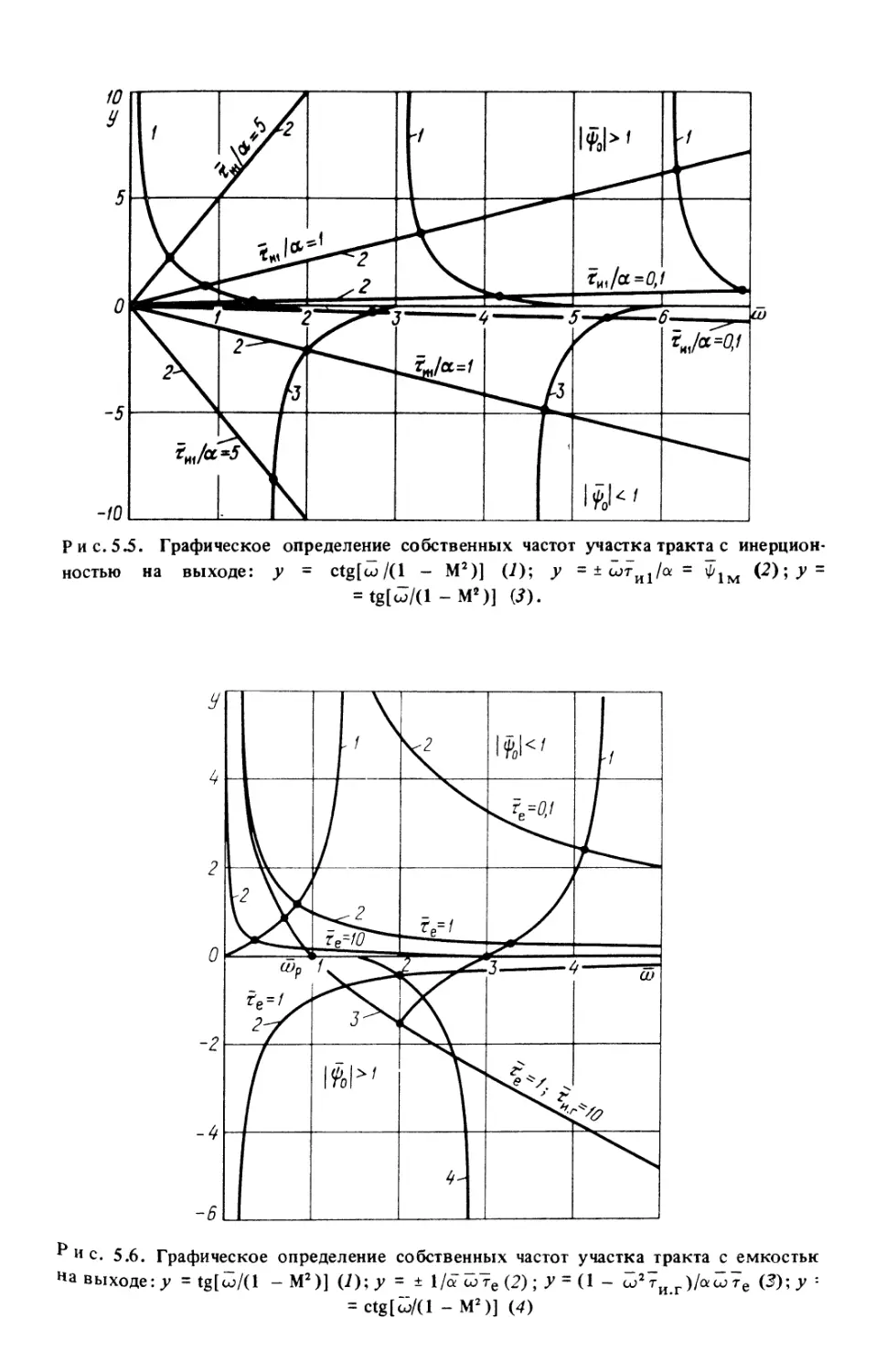
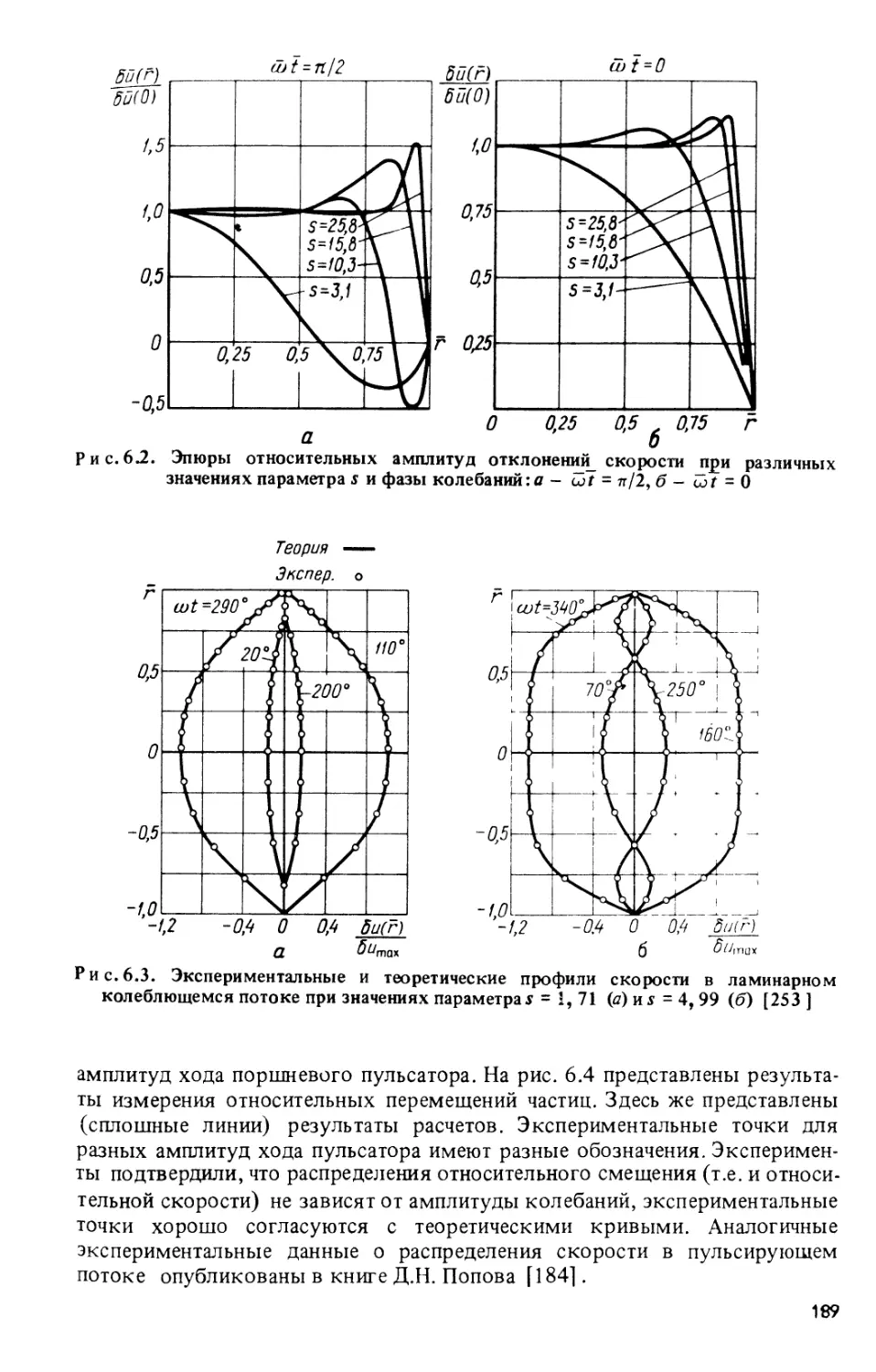
§ 5.3. Свободные колебания. Собственные частоты 155
§ 5.4. Входное сопротивление участка тракта 168
§ 5.5. Участок тракта как четырехполюсник 174
Глава 6. Математические модели нестационарных течений жидкости в
каналах 177
§ 6.1. Колебания в одномерном потоке вязкой сжимаемой жидкости с
квазистационарным трением о стенки 177
§ 6.2. Нестационарное колеблющееся ламинарное течение сжимаемой
жидкости в тракте 182
§ 6.3. Колебания турбулентного потока в тракте 210
§ 6.4. Статистический подход к нестационарному турбулентному
течению в трубе 235
§ 6.5. Учет колебаний стенок каналов 250
§ 6.6. Течения в открытых каналах 260
§ 6.7. Колебания жидкости под действием переменного внешнего
ускорения 262
§ 6.8. Нестационарное течение газа с переменной температурой и
составом 264
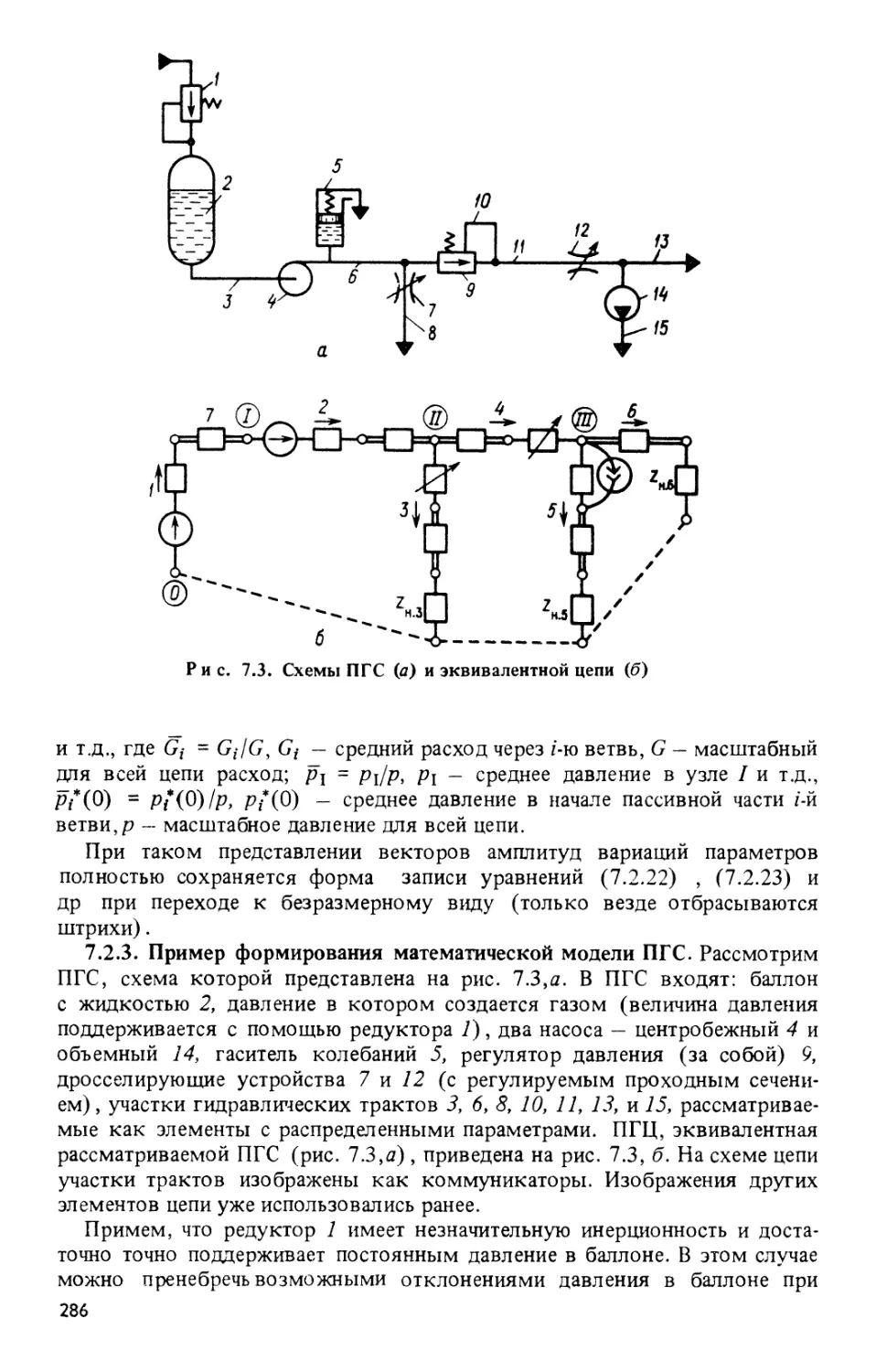
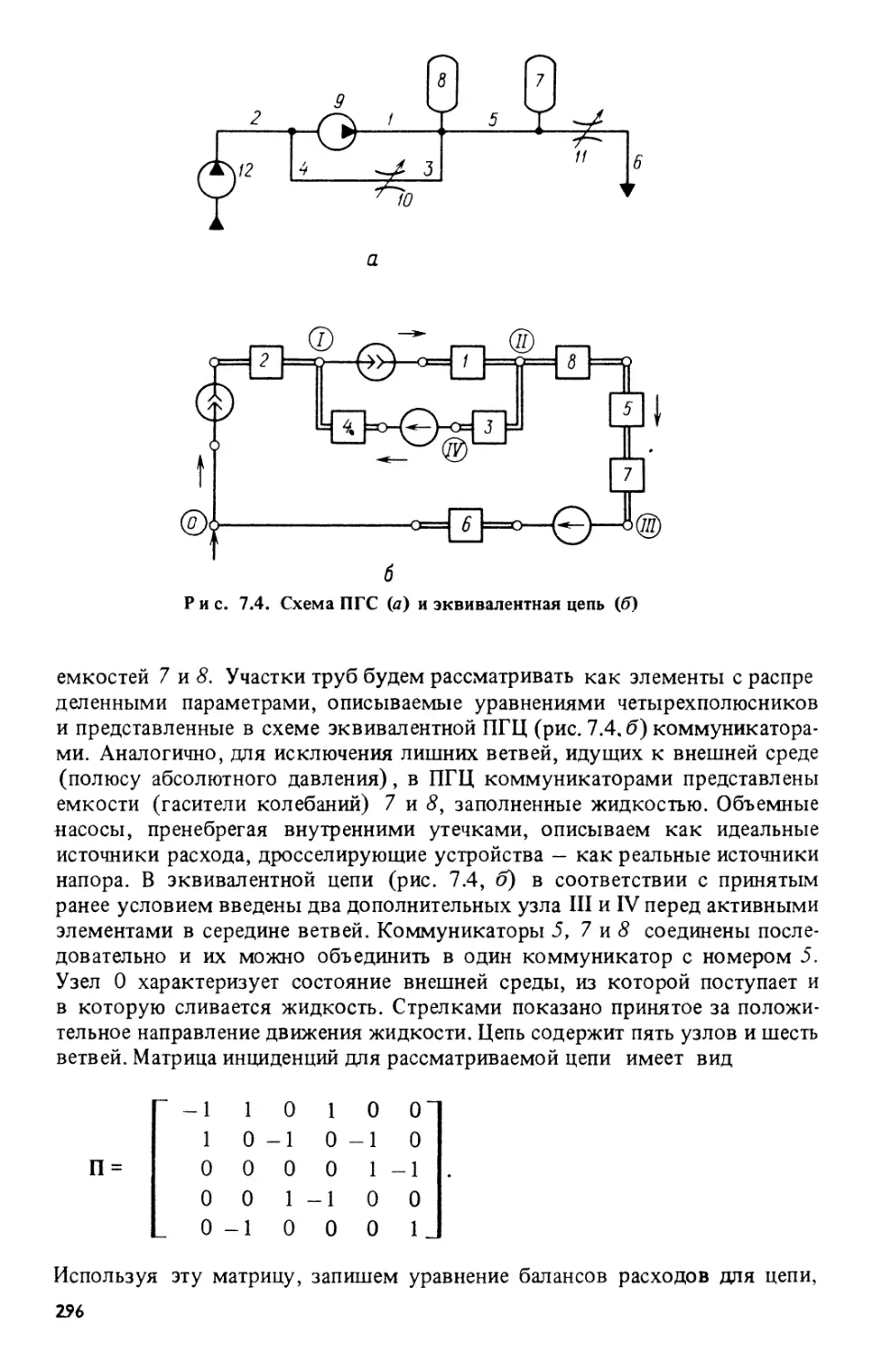
Глава 7. Математические модели разветвленных пневмогидравлических
систем с распределенными параметрами 277
§ 7.1. Некоторые особенности построения эквивалентных ПГЦ для
ПГС с распределенными параметрами 277*
§ 7.2. Уравнения цепи с активными элементами у узлов 279
§ 7.3. Матричные уравнения цепи при соблюдении некоторых условий
на размещение активных элементов 292
§ 7.4. Формирование математических моделей ПГС с использованием
сигнальных графов 301
§ 7.5. Уравнения пневмогиллавлических цепей с неизотермическим
течением газа 312
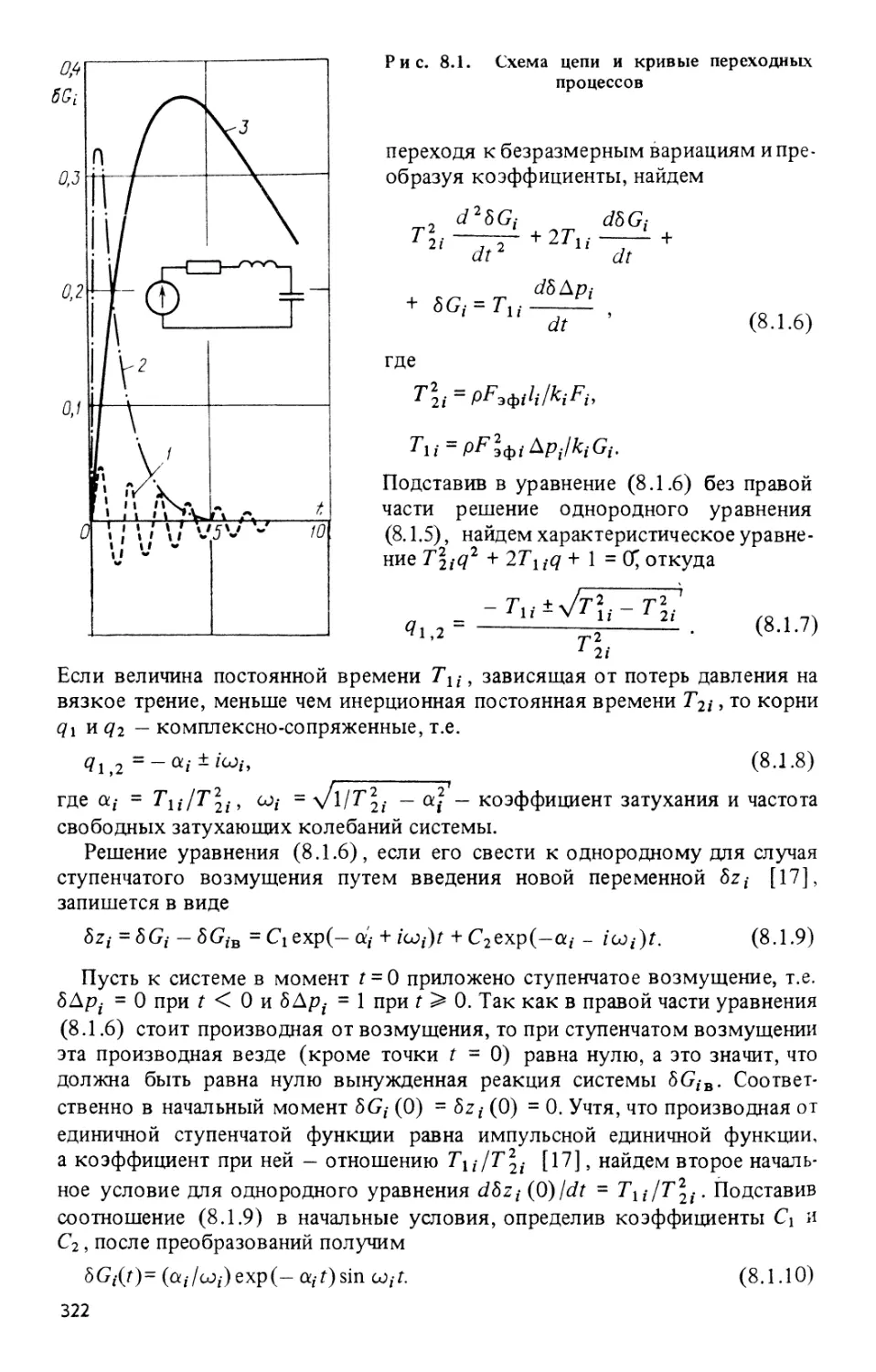
Глава 8. Переходные процессы в ;ТС 320
§ 8.1. Переходные процессы в ПГС, рассматриваемой как система
с сосредоточенными параметрами 320
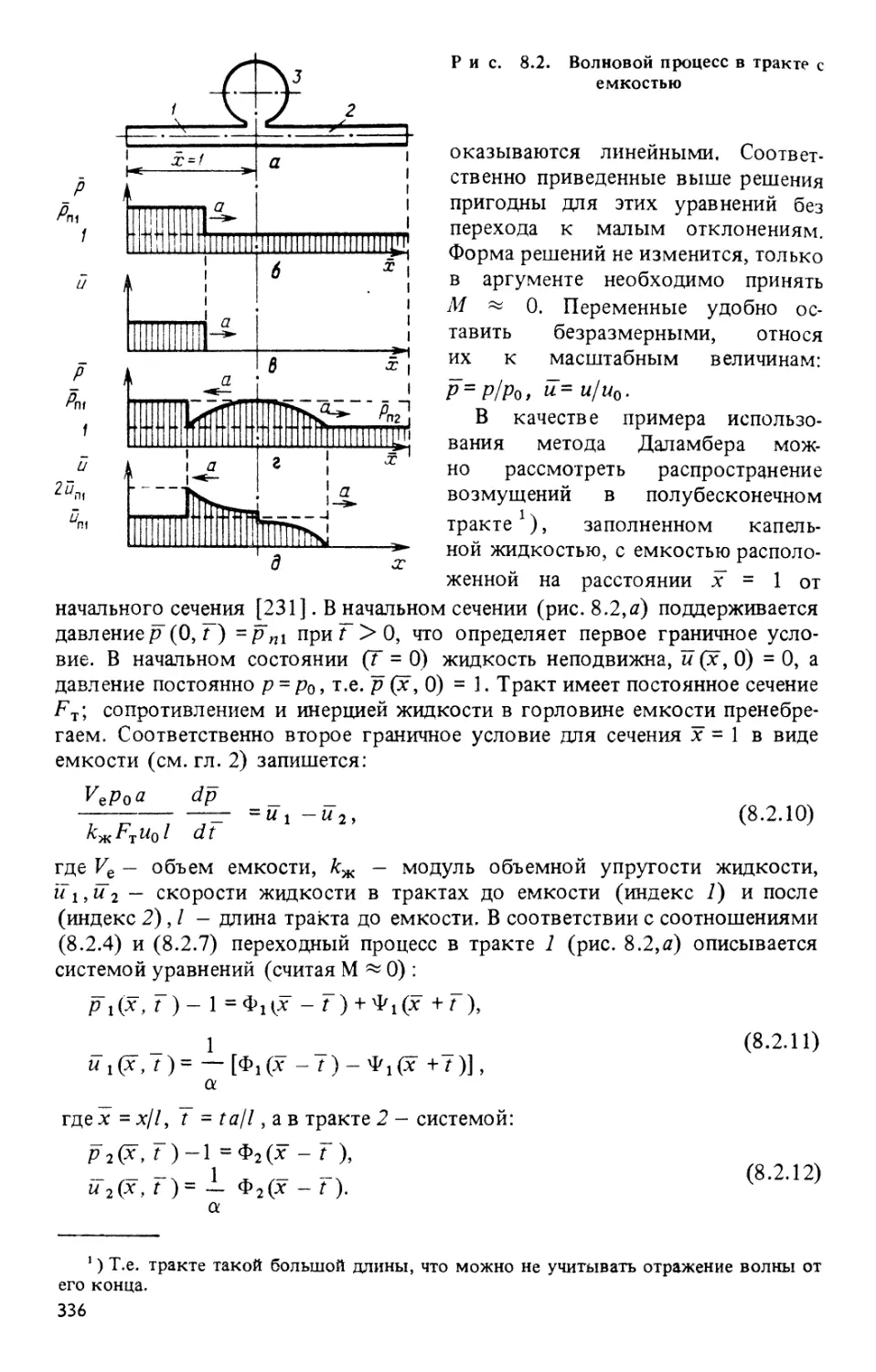
§ 8.2. Переходные процессы в гидравлической системе с
распределенными параметрами 324
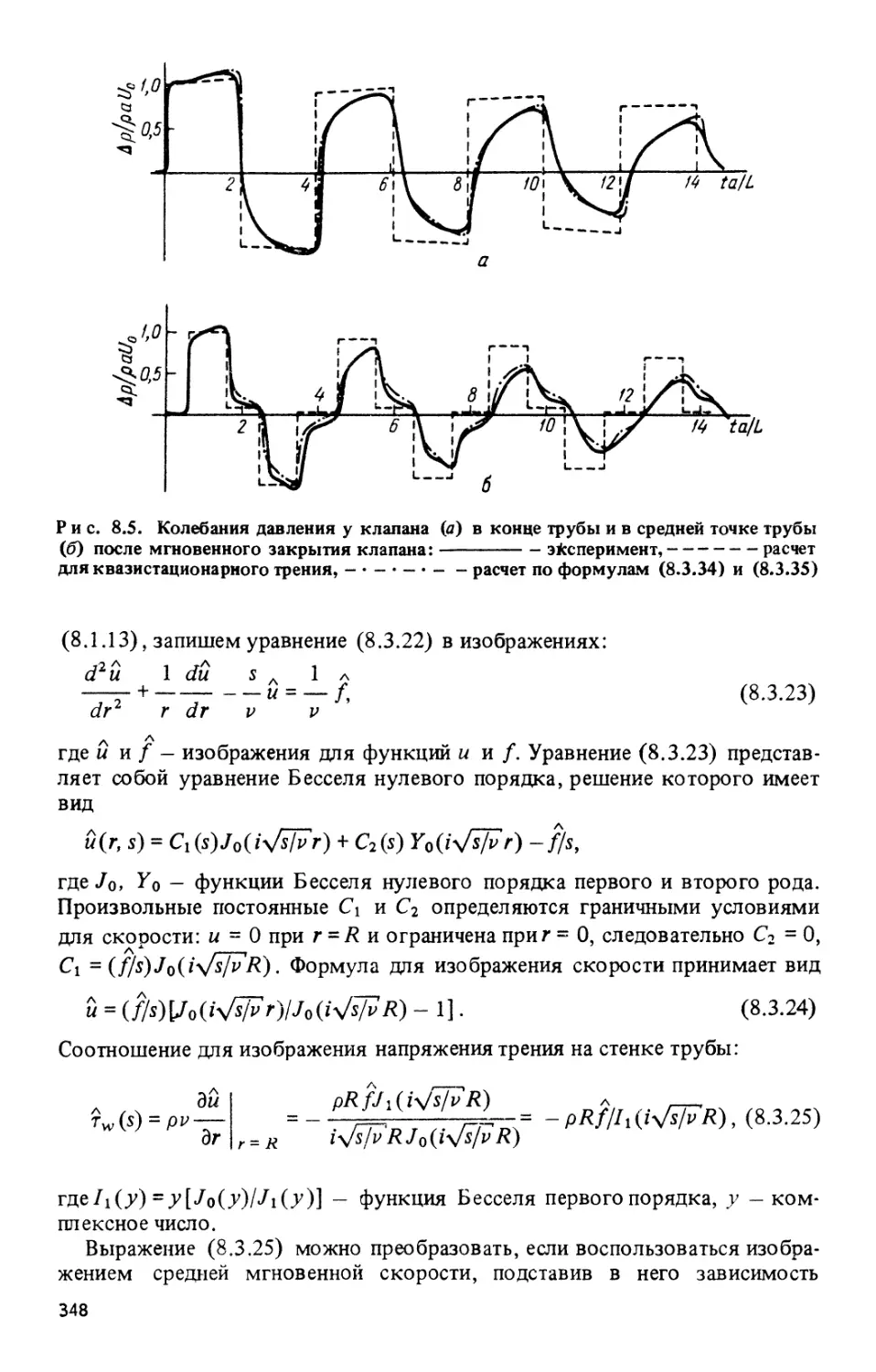
§ 8.3. Численные методы расчета нестационарных процессов в трактах 342
Список литературы 35 3
Предмета1-^ указатель 364
ПРЕДИСЛОВИЕ
Успехи развития современной техники и ряда разделов науки во многом
определяются использованием ЭВМ как средства решения сложных задач.
Для расчетного анализа систем и разработки алгоритмов управления базой
служат математические модели, которые с определенной детальностью
отображают физические процессы в технических системах или
естественных объектах.
Настоящая книга, предлагаемая вниманию читателя, представляет собой
попытку систематического освещения методов формирования
математических моделей нестационарного движения сплошной среды в
разветвленных, сложных пневмогидравлических системах (ПГС). Название "пневмо-
гидравлические" подчеркивает общность подхода к анализу систем
независимо от свойств рабочей среды, включая и системы, использующие
разнородные среды, например - жидкость и газ.
Большая роль, которую играют пневмогидравлические системы в
технике и природе, обусловлена широким кругом объектов, которые
относятся к ПГС: системы питания и автоматики транспортных и
энергетических установок, нефте- и газопроводы, химико-технологические установки,
пневмогидроавтоматика, системы водоснабжения, вентиляции и т.д. -
вплоть до систем кровообращения живых существ.
Общность всех этих разнообразных объектов определяется единством
физических закономерностей гидродинамики, механики, термодинамики,
связывающих параметры сплошной среды в системе. Уравнения
гидродинамики нелинейны, для них отсутствуют достаточно общие методы
решения. В то же время для широкого круга задач в области динамики
ПГС можно ограничиться (хотя бы в первом приближении) решением
упрощенных линейных или линеаризованных уравнений, для которых
имеется хорошо разработанный математический аппарат. Кроме того,
линейность исходной системы уравнений позволяет использовать теорию цепей,
обеспечивающую единый подход как к вопросам формирования
математических моделей, так и к анализу динамических характеристик ПГС
разного назначения и структуры.
Применение теории цепей к описанию процессов в ПГС позволяет ввести
новое понятие — пневмогидравлическая цепь (ПГЦ) . В книге описаны
методы применения теории пневмогидравлических цепей для формирования
математических моделей ПГС. Большое внимание уделено математическим
моделям нестационарного течения в трактах в разных приближениях — с
5
учетом и без учета распределенности параметров, при ламинарном или
турбулентном режиме течения, с учетом волн температуры (концентрации)
и т.д. Так как динамике элементов пневмогидроавтоматики (приводов,
регуляторов и т.д.) посвящено большое число книг, математическим
моделям этих элементов в настоящей книге уделено минимальное
внимание.
Следует сделать замечания о характере изложения в книге. Настоящая
книга предназначена в первую очередь для инженеров, сталкивающихся
с нестационарными задачами гидродинамики при проектировании, расчетах
и исследовании характеристик ПГС. При этом предполагается, что в числе
читателей будут как молодые специалисты, так и достаточно опытные
исследователи. Расчет на различные категории читателей привел к
необходимости привести выводы некоторых достаточно элементарных уравнений,
которые для подготовленного читателя могут показаться тривиальными.
Б то же время уравнения гидродинамики, используемые при формировании
моделей, даны без вывода (предполагается, что читатель владеет аппаратом
гидродинамики или может им овладеть с помощью учебников).
У инженера, специализирующегося по динамике ПГС, могут возникнуть
трудности с использованием теории цепей, которая применяется в
основном в радио- и электротехнике. Поэтому в книге по мере изложения
приводятся основные сведения из теории цепей.
Большую помощь при работе над книгой оказали А.П. Ваничев,
Б.М. Галицейский, М.С. Натанзон, В.А. Мокиенко. Всем им автор
выражает искреннюю благодарность.
Глава 1
УРАВНЕНИЯ ДВИЖЕНИЯ ЖИДКОСТИ
§ 1.1. Вводные замечания
Под математической моделью процесса в системе, отдельном агрегате
в настоящей книге понимается совокупность дифференциальных и
алгебраических уравнений (включая начальные и граничные условия), таблиц,
графиков, которые описывают основные физические закономерности,
или опытные эмпирические зависимости. Детальность описания процесса
определяется отдельно для каждой из решаемых задач. При этом всегда
возникает дилемма — или иметь более строгое, подробное, но и
существенно более сложное математическое описание, или же ограничиться менее
точной, но более простой моделью. Приступая к формированию моделей,
полезно вспомнить, что исходные, самые "точные" уравнения гидромеханики
являются'приближенными, так как они получены с использованием
определенных допущений. Естественно, что при построении математической
модели вопрос о допустимой степени упрощения модели определяется
условиями функционирования системы. Однако это не исключает
возможность использования и более простых моделей, не удовлетворяющих
полностью условиям функционирования системы, но удобных как "нулевое"
приближение. С помощью этих моделей, благодаря их простоте, можно с
наименьшими затратами и достаточно полно исследовать некоторые общие
закономерности процессов. С другой стороны, простые модели удобны
для проверки путем предельных переходов более сложных вариантов
моделей процессов. Для решения более простыми являются одномерные
задачи по сравнению с неодномерными, без учета вязкости - по сравнению
с течением вязкой жидкости, течение несжимаемой жидкости — по
сравнению с течением сжимаемой жидкости и т.д. Правомочность использования
тех или иных приближений зависит от класса решаемой задачи. Например,
определяющими факторами могут являться скорость движения,
протяженность системы, свойства рабочей среды, уровень амплитуд, характерная
частота возмущений или скорость изменения параметров во времени и т.д.
В частности, применительно к гидромеханическим системам, включающим
трубопроводы, один из основных вопросов: рассматривать их как системы
с сосредоточенными или как системы с распределенными параметрами.
Выбор модели определяется соотношением между геометрическими
размерами проточных частей отдельных трактов или системы в целом и длиной
акустических (или других типов) волн в диапазоне интересных для
рассматриваемой задачи частот.
Пневмогидравлической системой (ПГС) будем называть технический
или естественный объект с организованным течением рабочей среды и
7
упорядоченным соединением между собой отдельных частей, органов,
агрегатов. Формирование математических моделей сложных1)
разветвленных ПГС распадается на два этапа: вначале создание моделей процессов в
отдельных органах, агрегатах, узлах системы, а затем уже — на основе
этих частных моделей подсистем - разработка математических моделей
всей системы в целом. На первом этапе с подробностью, определяемой
условиями функционирования системы, исследуются процессы в агрегатах,
устройствах, т.е. решаются задачи из области гидродинамики с
привлечением (при необходимости) термодинамики, механики, биофизики, теории
теплообмена, химической кинетики, теории горения и т.д. При этом
выявляются определяющие факторы, влияющие на процессы в агрегатах, узлах.
Уже на первом этапе, при формировании математической модели
достаточно сложных пневмогидравлических устройств, удобно использовать аппарат
теории цепей [15, 60, 145, 146]. Для второго этапа — разработка
математических моделей ПГС— применение теории цепей оказывается очень
эффективным [15, 60, 225, 244]. Вывод уравнений, на базе которых формируется
математическая модель процесса в ПГС, возможен двумя путями. Один
вариант — путем упрощений общих уравнений гидромеханики,
термодинамики и т.д. с использованием определенных предположений. Другой
вариант — используя те же допущения и общие физические закономерности,
выводить уравнения заново, с "нуля". Ниже в основном будет
использован вариант вывода с помощью упрощения уравнений гидромеханики,
хотя в отдельных случаях приводятся примеры вывода уравнений
непосредственно из общих физических закономерностей.
Процессы в ПГС в первую очередь описываются уравнениями
гидромеханики. Учитывая, что их вывод приведен в большом числе
фундаментальных учебных пособий [30, 140, 152, 201], ниже эти уравнения
приводятся без вывода. Течение жидкости определяется распределением
в пространстве и времени нескольких параметров: вектора скорости
V (х, у, z, t) , давления р (х, у, z, t), плотности жидкости р(х, у, z, t),
температуры Т(х, yf z, t) 9 концентрации каждого из входящих в состав
рабочей среды вещества g((x, у, z, t) (для /-й компоненты) и т.д. Все эти
переменные связаны между собой уравнениями гидромеханики,
термодинамики, химической кинетики и должны быть известны во всех точках
проточной части в разные моменты времени t. К сожалению, уравнения
гидродинамики, термодинамики, химической кинетики в общем виде для
проточных частей более или менее сложной формы не решаются, несмотря на
огромные возможности современных ЭВМ. Проблема усугубляется в
случае нестационарных течений. Поэтому при решении конкретных задач
исходные уравнения и граничные условия упрощаются благодаря
пренебрежению теми или иными эффектами. В процессе упрощения сохраняются
члены уравнений, учитывающие самые важные для данного случая
свойства течения рабочей среды, а другими, менее важными, пренебрегают.
К примеру, во многих случаях можно принять, что течение одномерное,
или пренебречь сжимаемостью среды, в других случаях-ее инерцией, иногда
1 ) Понятие "сложные" используется ниже применительно к ПГС в смысле
громоздкости системы, а не сложности, связанной с принципиальной неопределенностью
математического описания процессов в системе.
8
оказывается несущественной вязкость жидкости и т.д. В данной главе
вначале приводятся уравнения гидромеханики, а затем - их частные случаи.
Для каждого варианта уравнений оговариваются те условия, при
выполнении которых можно использовать этот тип уравнений. В пневмогидрав-
лических системах течение жидкости, как правило, происходит в
пространстве, ограниченном стенками. Поэтому ниже такие объекты в основном
и будут рассматриваться. Однако методы, используемые для анализа ПГС,
можно применять и для других систем, в частности, — течений со
свободной поверхностью в разветвленных руслах рек, каналов и т.д. В гл. 6
приводятся примеры анализа нестационарных течений в каналах со свободной
поверхностью. Применительно к исследованию процессов в ПГС можно
выделить два крупных класса задач - задачи определения стационарного
потокораспределения в разветвленных системах и задачи динамики
нестационарного течения рабочей среды в тех же системах. Проблеме
потокораспределения посвящено достаточно много работ [163, 164, 207, 226]. В
данной книге будут рассмотрены только нестационарные процессы в
разветвленных ПГС с использованием методов нестационарной гидромеханики и
теории цепей. При этом анализ ограничивается в основном линейными или
линеаризованными системами уравнений, для которых используемый
аппарат теории цепей наиболее эффективен.
§ 1.2. Уравнения движения вязкой сжимаемой жидкости
1.2.1. Свойства сплошной среды. При разработке математической
модели, описывающей движение жидкости в том или ином устройстве,
необходимо учитывать свойства среды. В общем случае физические свойства
жидкости (плотность, вязкость, теплопроводность) связаны достаточно
сложными зависимостями с другими ее параметрами — температурой,
давлением, концентрацией. С другой стороны, влияние физических свойств
жидкости на ее движение также неоднозначно и зависит как от характера
движения, так и от самих физических свойств жидкости. Применительно
к большинству жидкостей, используемых в технике, можно применять
определенные допущения, которые существенно упрощают уравнения
движения. Эти допущения сводятся к следующему:
1. Жидкость является ньютоновской, т.е. касательное напряжение трения
между двумя параллельно движущимися ее слоями пропорционально
градиенту скорости к направлению движения. Для такой жидкости при
движении в направлении, параллельном плоскости xz, со скоростью w,
направленной по оси х, касательное напряжение трения по закону Ньютона
равно
ди
где ц — динамический коэффициент вязкости, зависящий от температуры
жидкости, но не зависящий от характера ее движения.
2. Для неизотермического течения жидкости количество теплоты,
передаваемое через единицу площади в потоке жидкости, определяется
формулой Фурье
ЪТ
4 = Ат—-, A.2.2)
Ъп
где q — плотность теплового потока, Т — температура, Хт — коэффициент
теплопроводности. Производная в формуле A.2.2) берется по нормали к
поверхности, через которую передается тепло.
3. Коэффициент второй (объемной) вязкости принимается равным
нулю. Объемная вязкость имеет значение для процессов с релаксацией
(физической или химической кинетикой и т.д.) [140].
4. В первом приближении примем коэффициент вязкости \л и
коэффициент теплопроводности Хт постоянными, не зависящими от температуры.
Это допущение в ряде случаев может оказаться недостаточно
обоснованным, так как вязкость и теплопроводность жидкости зависят от
температуры [152]. Однако для рассматриваемых ниже задач, в которых не
учитывается теплообмен со стенками, этим предположением достаточно уверенно
можно пользоваться.
5. Наиболее типичной формой канала в ПГС является цилиндрический
тракт. Поэтому в качестве исходных целесообразно выбрать уравнения
нестационарного движения вязкой сжимаемой жидкости в цилиндрических
координатах.
6. Без особых ограничений общности можно принять предположения об
осевой симметрии течения. В некоторых случаях это предположение не
используется.
7. Стенки трактов принимаем жесткими, т.е. диаметр тракта не зависит
от внутреннего давления. Случай с податливыми стенками тракта
рассматривается особо.
1.2.2. Уравнения движения. При использовании перечисленных
упрощающих предположений система уравнений, описывающих осесимметричное
движение вязкой жидкости в цилиндрических координатах, содержит
два уравнения движения и уравнение неразрывности [140, 152^200].
Уравнения количества движения (уравнения Навье—Стокса) :
Ъи Ъи Ъи
+ и + v =
Э? Эх Ъг
1 Эр [1 Э 1 Э / Ъи\ Ъ2и 1
= РХ + Л (divV)+ [г _)+—-, A.2.3)
р Эх L3 Эх г Ъг \ Ъг ) Эх2 J
Ъи Ъи Ъи
Ът Эх Ъг
1 Эр Г 1 Э Э /l Э \ Ъ2и
= Р,- + у (divVU — { (rv)\ + —-
г р Ъг [ 3 Ъг ' Ъг \т Эг у Эх2
где и, v - скорости жидкости в осевом (по координате х) и радиальном
(nor) направлениях, Рх, Рг — осевая и радиальная составляющие внешних
массовых сил, отнесенных к единице массы жидкости, направления
которых совпадают с положительным направлением соответствующих ско-
10
ростей, v = д/р — кинематический коэффициент вязкости жидкости, р —
плотность жидкости,
divV = Эм/Эх + (l/r)b(rv)/br.
Уравнение неразрывности:
Эр +Э^) +1Э^и) =о
bt bx г br
Для несжимаемой жидкости р = const, и из уравнения A.2.5) следует,
что divV = 0. Соответственно упрощаются и члены, учитывающие вязкое
трение в уравнениях движения A.2.3) и A.2.4). Уравнение энергии1)
в форме уравнения изменения энтропии единицы массы жидкости:
(bs bs bs
— + и — + v —
bt bx Kbr
( ЬТ ЬТ ЪТ\ ( bp Ьр bp
p \ bt bx br J \ bt bx br
Г 1 Э / ЬТ \ Ь2Т 1
= МФ + ХТ __(r— + —т , A.2.6)
L r br \ br ) bx2 1
где Т — температура жидкости, s - энтропия единицы массы жидкости,
1 / Эр \
ср — удельная теплоемкость при постоянном объеме, E = — — I I —
р \ ЬТ ] р
коэффициент теплового расширения жидкости,, Xj, - коэффициент
теплопроводности жидкости, Ф — скорость диссипации механической энергии
на единицу массы жидкости, определяемая работой сил вязкого трения.
В цилиндрических координатах Ф определяется зависимостью
Г/ bu \2 I bv\ 2 I v\ 2 1 / bu bv У 2
Ф = 2 — + — +(—) + (— +— --(divVJ.
[\ bx ! \br J \r / J \ br bx J 3
A.2.7)
Зависимость A.2.7) при переходе к декартовым координатам принимает
вид
Ьх ] \ by ) \ \ by bx J 3 \bx by
A.2.8)
Аналогичным образом преобразуются к декартовым координатам
уравнения A.2.3), A.2.4), A.2.5) и A.2.6). При выводе уравнения A.2.6)
использовалось предположение, что теплота в жидкости передается только
путем теплопроводности. Подвод же теплоты за счет других возможных
причин (химических или ядерных реакций, излучением и т.д.) не
учитывается. Передача теплоты к жидкости или от жидкости на границах потока
определяется граничными условиями. Четыре уравнения A.2.3) —A.2.6) содер-
1) Уравнение A.2.6) содержит две формы записи левой части уравнения энергии -
через энтропию или через температуру и давление.
11
жат пять неизвестных переменных и, v, р, р, Г (или s). Для замыкания
системы уравнений необходимо добавить еще одно уравнение, в качестве
которого используется уравнение состояния для жидкости, в общем виде
записываемое так:
F(p, Р, 7) = 0. A 2.9)
Для идеального газа это уравнение имеет простой вид
p = pRT. A.2.10)
Для капельной жидкости используется закон Гука
Р -Ро \
A.2.11)
где Ро, Ро - плотность и давление жидкости при некоторых начальных
условиях, кж — модуль объемной сжимаемости жидкости.
При решении некоторых задач динамики ПГС, в которых
существенными оказываются акустические эффекты (т.е. распространение акустических
волн), удобно в качестве замыкающего уравнения использовать не
уравнение состояния A.2.10) или A.2.11), а зависимость для адиабатической
скорости звука в жидкости
= f(p, T). A.2.12)
Для идеального газа эта зависимость имеет простой вид
a2 = kRT=k— , П. 2.13)
Р
где к — показатель адиабаты газа. Для капельной жидкости, используя
уравнение закона Гука A.2.11), находим
а2 = ^ . A.2.14)
Если жидкость не является однокомпонентным веществом, то
появляются дополнительные переменные — концентрации компонентов.
Концентрация, как величина скалярной интенсивности, подчиняется уравнению закона
сохранения скалярной величины, связанной с движущейся массой
жидкости [30],
dt Ьх Ьг
A.2Л5)
где gj — концентрация /-й компоненты, kD — коэффициент диффузии.
Уравнение A.2.15) получено в предположении, что течение изотермическое
и отсутствует термодиффузия. При одновременном изменении в потоке
концентрации и температуры уравнение для концентрации A.2.15) и
уравнение энергии A.2.6) усложняются из-за взаимного влияния процессов
теплопередачи и диффузии друг на друга [140].
12
§ 1.3. Турбулентные течения
1.3.1. Некоторые особенности турбулентных течений. Приведенные
выше уравнения движения жидкости описывают ламинарное течение или, как
его еще называют, слоистое течение, для которого характерно
организованное движение частиц. Такой тип течения на практике встречается не
часто, однако аппарат гидродинамики наилучшим образом разработан
именно применительно к таким течениям и многие фундаментальные результаты
получены на базе уравнений ламинарного течения или их предельной
формы — уравнений течения невязкой жидкости. Поэтому в общих курсах
гидродинамики таким течениям обычно посвящена львиная доля объема
[140, 152, 200, 242]. Ниже, при анализе процессов в проточной части ПГС,
в большинстве случаев будут использоваться уравнения, приведенные в
разделе 1.2. Практически же, как в естественных условиях, так и в
технических системах реализуется другой режим движения жидкости —
турбулентный.
При турбулентном течении отсутствует упорядоченное движение частиц
жидкости по определенным траекториям, так как и сами траектории, и
поле скоростей носят хаотический характер. Однако, несмотря на
хаотичность мгновенных значений параметров, в потоке существует некоторое
среднее организованное движение, подчиняющееся законам
гидродинамики, а хаотический характер турбулентного движения проявляется в
случайных флуктуациях (отклонениях) параметров от их средних значений,
причем сами турбулентные флуктуации подчиняются законам сохранения
[165].
Уравнения движения'для турбулентного течения оказываются
незамкнутыми, так как содержат больше переменных, чем уравнений. Ниже в
основном будут использованы простейшие модели замыкания системы
уравнений, не требующие существенного усложнения математического аппарата,
и в то же время достаточно хорошо описывающие основные особенности
турбулентного течения.
Применительно к нестационарным процессам возникают
дополнительные трудности, так как слабо исследован вопрос о влиянии
нестационарности течения на турбулентность. Имеются некоторые указания [165]
на то, что не обнаружено существенного влияния нестационарности течения
на интегральные характеристики турбулентности. Поэтому ниже для
нестационарных течений будут использоваться полуэмпирические зависимости,
полученные с использованием экспериментальных данных для
стационарных турбулентных течений. Впервые гипотеза о возможности
использования стационарных интегральных или локальных характеристик
турбулентного течения для описания нестационарного турбулентного движения была
сформулирована в работах С.А. Христиановича [229], К.К. Федяевского
и А.С. Гиневского [223].
1.3.2. Уравнения турбулентного течения. Рассмотрим изотермическое
осесимметричное движение слабосжимаемой капельной жидкости в
цилиндрической трубе, для которой уравнения турбулентного движения
имеют более простую форму, так как в этом случае флуктуациями
плотности и температуры можно пренебречь и, соответственно, не использовать
уравнение энергии A.2.5). При выводе уравнений турбулентного течения
13
все переменные, описывающие его, раскладываются на осредненные и
пульсационные составляющие. Осреднение переменных проводится по
времени в фиксированной точке пространства, например, для продольной
скорости и
(и) = — / udt, A.3.1)
7 U
причем время осреднения г должно быть достаточно большим, чтобы на
осредненные значения параметров не сильно влияли турбулентные
пульсации, с другой стороны, г должно быть меньше характерного времени
исследуемого нестационарного процесса. Эти условия для нестационарных
турбулентных потоков являются противоречивыми.
Уравнения для турбулентного движения находятся путем подстановки
в уравнения движения A.2.3), A.2.4) и неразрывности A.2.5) вместо и
и v соответствующих сумм осредненных составляющих скорости (и) и
(v) и пульсационных составляющих этих скоростей и', и' и w':
м=<и> + и', и = Ы + у', w = wr; A.3.2)
здесь угловыми скобками обозначены осредненные величины, w, w' -
тангенциальные составляющие скорости. Несмотря на то, что
рассматривается турбулентное течение в цилиндрическом тракте, для которого
вполне очевидным является предположение, что течение осесимметричное и
однородное для пульсационных составляющих вдоль оси трубы (т.е.
производные от пульсационных составляющих скорости не зависят от
переменной х), тем не менее нет никаких причин, чтобы пренебречь пульсационной
составляющей w', которая присутствует в равенствах A.3.2). Ниже будут
рассматриваться в основном течения в длинных трактах, для которых
соблюдается соотношение между длиной тракта L и его радиусом L > R.
После подстановки в уравнения сумм A.3.2) необходимо провести
осреднение всех членов, воспользовавшись правилами осреднения [165]
«/» = (/>, «/i></2»=(/l></2>,
и, если /=(/>+/', то </'> = 0,
Из этих правил можно сделать вывод, что для слабосжимаемой жидкости
уравнение неразрывности не изменяет форму после подстановки
соотношений A.3.2) и его осреднения (учитывая при этом принятое условие, что р' =
= 0 и (р) = р):
=0
14
1
Р
Ьр
bt
+
Ь(ы
bx
>
+
b(v)
br
+
(v)
r
Отсюда следует, что для пульсационных составляющих скорости также
соблюдается уравнение неразрывности
Ъи Ъи' v 1 Эй/
+— + — + =0, A.3.4)
дх Ъг г г Ь^
где \р — угол в цилиндрической системе координат. Подставив суммы A.3.2)
в уравнение A.2.3), дополненное составляющими скорости w', осреднив
полученное соотношение и использовав зависимость A.3.4), находим
уравнение турбулентного движения для продольной составляющей скорости-
уравнение Рейнольдса
Ъ(и
Эг
+ V
1
г
)
- +
f4
1з
э
Ъг
Ыи)
( и \
\ U /
Ьх
дЧи)
дх2
t t
-г {и v
+
1
3
Ъ(и
\ V )
Ъг
Э2<и>
ЭхЭа-
1 Э
г Ъ& К
>
1
Ъг
t
v
Р
Ъ(и)
Ъх
f
V >) +
1 i
Р
Э
э
Ъх
i
Эх
2<и> 1 Э<^>
Эг2 г Ъг
(- w >).
A.3.5)
Уравнение A.3.5) отличается от соответствующего уравнения A.2.3)
для ламинарного движения (из которого оно и получено) присутствием
дополнительных членов, содержащих средние значения произведений
пульсаций скорости. Таким образом, наложение турбулентных пульсаций наосред-
ненное движение приводит к появлению дополнительных членов в
уравнении движения, означающих турбулентное напряжение, дополнительное к
напряжению вязкого трения, описываемого членами с коэффициентом v.
Анализ вклада дополнительных членов в уравнении Рейнольдса A.3.5)
показывает, что определяющим для течения в тракте является член с
комплексом <wV>, описывающий дополнительное касательное напряжение.
Остальными членами можно пренебречь [152, 165]:
<mV> « <w'2>~0. A.3.6)
Подставив суммы A.3.2) во второе уравнение движения A.2.4) для
радиальной составляющей скорости, найдем
Э<и> Ъ(и) 1 Ъ(р)
+ (и) +(v) = Рг +
Ъх Ъг р Ъг
4 82<и> Э2Ы 4 Ъ(и) 4 <и> 1
+г +Т +
3 Эг2 Ъх2 Ъг Ъг Ъ г2 Ъ Ъх Ъг
+ {-г iv'2)) + — (-<kV>) (-<w'2>). A.3.7)
г Ъг Ъх г
Система уравнений A.3.3) —A.3.7) - незамкнутая. Для исключения
производной от плотности можно использовать зависимость A.2.12).
Однако это не обеспечивает полного замыкания системы, так как
остаются члены с произведением или квадратом пульсаций скорости. Теория
турбулентности предлагает ряд способов замыкания системы уравнений
15
гидромеханики [102, 152, 165]. По-крупному эти способы делятся на два
класса: или в уравнение Рейнольдса вводится турбулентная вязкость в
соответствии с гипотезой Ж. Буссинеска, причем для определения этой
вязкости имеется ряд моделей, или для турбулентного движения
записывается уравнение энергии, в котором используются статистические модели
турбулентности.
Согласно предположению Ж. Буссинеска, касательное турбулентное
напряжение связано с поперечным градиентом скорости соотношением,
подобным закону трения Ньютона A.2.1) ,
Ъ(и)
тт = -p(uv) = pvT . A.3.8)
Ъг
С использованием формулы A.3.8) и предположений A.3.6) уравнение
Рейнольдса A.3.5) принимает следующий вид:
Ъ(и) Ъ<и) Ъ(и) 1 Ъ(р) Г 4 Ъ2(и)
+ (и) + (и) =Р_— ¦ ]
bt Ъх Ъг х р Эх L 3 Ъх2
¦ v \ •
] 1 Э Г Ъ(ы) 1
+ - — \r(p + i>v) —— .
J г Ъг L Ъг л
+ + - + r(p + vv) . A.3.9)
3 ЪхЪг Ъг Ъг ' ~ ' " ' V
Учтя все принятые при получении уравнения A.3.9) упрощающие
предположения, преобразуем уравнение A.3.7) к следующему виду:
Э<и> Э(и> Ъ(и)
+ (и) + (v)
Ы Ъх Ъг
1 Ъ(р) Г 4 Э2<и> Ъ2(и)
2 + -ТТ- + - -
Р Ъг L 3 Ъг2 Ъх2 3 Ъг
1 Ъ2{и) 1 1 Э . <w/2>
3 Эл: Ъг
1 1 Э
¦ - -г (гЫ
J r Ъг
A.3.10)
В отличие от коэффициента вязкости жидкости vf коэффициент
турбулентной вязкости vT не определяется свойствами жидкости, а связан
со структурой потока, в частности, — с распределением скорости. Таким
образом, для использования гипотезы Буссинеска необходимо найти
подходящую эмпирическую зависимость, связывающую vT с полем осред-
ненной скорости. Первым предложил удачную модель Л. Прандтль.
Согласно ней коэффициент турбулентной вязкости пропорционален
поперечному градиенту скорости
0 Ъ(и)
vT = I2 —— , A.3.11)
Ъг
где / — длина пути перемешивания. Длина пути перемешивания также
не является физической константой, она зависит от геометрических
характеристик течения, в частности, — расстояния от стенки. Использование
модели Прандтля оказалось весьма плодотворным, так как позволило
проводить расчеты ряда турбулентных течений. Модель Прандтля имеет
16
недостатки, что привело к появлению ряда других полуэмпирических
зависимостей, в том числе и к разбиению течения на слои с разным законом
сопротивления: турбулентное ядро потока, область перехода от
турбулентного к ламинарному течению и ламинарный подслой [152, 242]. Во всех
случаях данные, на которых строятся полуэмпирические зависимости
для турбулентной вязкости, базируются на опытах со стационарным
потоком.
Основой для другого подхода к анализу турбулентных движений служит
уравнение баланса турбулентной энергии. Запишем это уравнение для
осесимметричного потока слабосжимаемой капельной жидкости в
цилиндрических координатах [36] :
Ъе Ъе Ъе
— + <м> — + (v) =
dt Ъх Ъг
э
Эх
Ъ
+ v —
Эх
и (t
Ъ(и
Ъх
Г Ъе
Ъх
>
'/
Р IP)
- <v'
Ъ
Ъх
л
'2>-
{и
1
Г
Ъг
Ъ
Ъг
>
1
г
<w'2>-
Эг
и
,>]
w -
{и
V
г
ч
9 /
Ъг\
ъ
[
-1
Ъг Ъх
Ъе
Ъг
+ — {uv) + <п/2> - — <v/> -A, A.3.12)
Эх г Ъг г JJ
гдее= A/2) {{и > + <и' > + <w' >) - энергия турбулентности,
Ъг Ъх I / \\Ъх
2\
(9vv; 1 Эи' w' \2\ 1
— + ) )
Ъг г Ъу г ) / \
Используя те же предположения, что и при упрощении уравнения Рейнольд-
са A.3.5), уравнение A.3.12) можно свести к следующей форме:
Ье 1 Э , , 1 Э .
— = --— <rv'e') - — — <rv'p'/p) +
bt г Ъг г Ъг
Г / \
[ Ъ \ I
г [ Ъг \ Ъг I Ъг2 Ъг \ Ъг
A.3.13)
Входящие в уравнение A.3.13) члены определяют следующие процессы:
Ъе
скорость изменения энергии турбулентности,
Ъt
2. Б.Ф. Гликман 17
{rv'e > - диффузию энергии пульсационного движения,
г Ъг
(rv'p'/p) — диффузию энергии турбулентности,
г дг
(uv > зарождение энергии турбулентности за счет работы на-
Ъг
пряжения турбулентного трения,
А — диссипацию турбулентной энергии.
В уравнение A.3.13) входят несколько членов, для определения
которых необходимо использовать полуэмпирические зависимости. Эти
зависимости будут рассмотрены применительно к конкретным моделям
нестационарного турбулентного течения в гл. 6.
§ 1.4. Безразмерная форма уравнений гидромеханики.
Критерии подобия
Движение вязкой жидкости описывается достаточно сложными
уравнениями A.2.3), A.2.4), A.2.5), A.2.6), A.2.9) и A.2.15), связывающими
между собой все параметры течения. С целью анализа относительного вклада
отдельных членов и возможности упрощения уравнений преобразуем их
к безразмерной форме, переходя к относительным переменным. Переход
к безразмерным переменным - не формальное преобразование
уравнений, а целенаправленное действие, позволяющее получить общую форму
записи как самих уравнений, так и начальных и граничных условий, и,
в конечном итоге, более общее решение уравнений. При переходе к
безразмерным переменным в качестве коэффициентов в уравнениях
появляются безразмерные комплексы — критерии подобия. Общность решения
безразмерных уравнений при одинаковых безразмерных начальных и
граничных условиях и равных значениях критериев подобия
заключается в том, что они описывают не одно частное течение жидкости, а целый
ряд динамически подобных течений, которые могут отличаться друг от
друга как геометрическими, так и кинематическими характеристиками,
а также значениями физических параметров жидкости.
Теория подобия является основой экспериментальных методов
моделирования процессов в механике и других отраслях знания [201]. В
результате преобразования к безразмерному виду автоматически
определяются все критерии подобия, которые характеризуют течение. При этом
каждый член уравнения в безразмерных переменных (не считая критериев
подобия) будет иметь порядок единицы, если в качестве масштабных
величин при переходе к безразмерным переменным выбраны
действительно характерные для данного течения значения масштабных параметров.
Если все члены уравнений (без коэффициентов - критериев подобия)
имеют порядок единицы, то сами коэффициенты при этих членах,
состоящие из критериев подобия, определяют относительную значимость
каждого члена уравнения.
Так как тракт цилиндрической формы является типичным для ПГС,
остановимся на такой форме тракта, введя для него следующие
масштабные величины: длины L, радиуса R, скорости вдоль оси ио< времени про-
18
цесса t0, давления р0, плотности р0, температуры Го, энтропии ср01У,
массовой силы вдоль оси тракта Ро- Обозначив той же буквой, но с чертой
сверху, соответствующие безразмерные переменные, запишем: х = Lx,
r = RT, t = totf и=иоп, р=рор, Р = РоР, Т=Т0Т, s = cpOs, PX=POPX.
Осталось определить масштабные величины для поперечных
(радиальных) составляющих скорости и массовой силы. Как уже отмечалось, для
удобств анализа безразмерных уравнений целесообразно так выбирать
масштабные величины, чтобы производные от всех безразмерных
переменных имели порядок единицы. В целях оценки масштабной величины
для радиальной скорости воспользуемся уравнением неразрывности
A.2.5) без члена с производной по времени. Проинтегрировав это
уравнение по радиусу, учтя, что при г = О v = 0, и переходя к безразмерным
переменным под интегралом, получим
1 г ъ(ри) Ru0 1 \ Ъ(р и)
v = J гаг = =r= j — гаг.
рг о Ъх L рг о Эх
Из последнего соотношения следует, что для сохранения одного и того же
порядка величин производных от безразмерных параметров необходимо,
чтобы в качестве масштабной величины для радиальной скорости
использовался комплекс Ruq/L , тогда v = uQRiolL.
Подобный же масштабный комплекс RPoiL используется для
радиальной составляющей массовой силы/V -PoRPy/L. Такая форма приведения к
безразмерному виду целесообразна в случаях, когда геометрические
масштабы в разных направлениях сильно отличаются, например, в пограничном
слое, длинных трубах и т.д. Произведя замену переменных в уравнениях
A.2.3) и A.2.4), получим уравнения движения в безразмерной форме:
Ъп Ъи Ъы 1 _ Ей Эр 1
Sh-r-+ м—г+у — =— РЛ 1Г "Г + — I I x
Эг Эх Ъг Fr p Эх Re
4 Ъ2п I L \2 Ъ2ы
3 Ъх2 \R/ дТ
&
' L \2 1 Ъи 1 Э2п 1 Ъи ]
* R I 1 Ы 3 Ъх дТ 37 Ъх \
A.4.1)
Ъи Ъи dv l - Еи / L \ Эр
Sh -Z- + п — + п = = ~~ рг =¦ — ¦-=-
Ъt Эх Эг Fr p \R/ Ъг
х l ( L \ \ fRY Ъ2» 4 Э2у 4 Эп
-j-
Re \ R 1 I \ L I Ъх2 3 Ъг2 37 97
4 v 1 Э2г7
где Sh = L/(uoto) - число Струхаля, Fr = иЦР0Ь - число Фруда; Ей =
<о - число Эйлера, Re = u0R/i> - число Рейнольдса
Так как величина энтропии определяется с точностью до произвольной
постоянной, при приведении уравнения к безразмерному виду энтропию удобно огносшь
к теплоемкости жидкости cpq при температуре Го.
19
Проведя аналогичные преобразования с уравнением неразрывности
A.2.5), получим безразмерную форму этого уравнения в цилиндрических
координатах:
ЭрГ Эр" Эр" / Ъп 1 b(rU)\
Sh-^r- + п—- + v —: + р ( — + — ^~) = О- A.4.3)
Эг Ъх Ъг \Ъх г Ъг )
В три уравнения A.4.1) - A.4.3) в качестве безразмерных переменных
входят параметры п, [Г, р и р". Для замыкания системы дополним ее
уравнением состояния, связывающим безразмерные параметры р и р" между
собой, а при необходимости — и с температурой или энтропией жидкости.
Использование той или иной формы уравнения состояния зависит от
характера процесса в жидкости. Если течение является адиабатическим, без
обмена тепла со стенками, то подставив в уравнение неразрывности A.2.5)
плотность из зависимости для адиабатической скорости звука A.2.12)
и переходя к безразмерным переменным, получаем другую форму записи
третьего уравнения, не содержащую производных от плотности:
Ър Ър Ър ара2 I Ъп Эг7 v \
Sh —it- + п + v + — + + — = 0, A.4.4)
ЪГ Ъх Э7 М \ Ъх Ъ1 г )
где ~а=а/а0, а = Роиоао/ро — приведенное волновое сопротивление, М =
= ио/ао - число Маха для масштабной скорости. Для адиабатического
движения идеального газа, учтя соотношения A.2.10) и A.2.13), получим
а/М = Ро^о/Ро = к. Здесь величина а0 =/(Г0) - параметр постоянный как
во времени, так и в пространстве.
Для идеального газа скорость звука а = \/kRT 'зависит от температуры
и при неизотермическом течении является переменной величиной. Из-за
этого переменным по длине тракта оказывается безразмерный параметр а~
Если условия сохранения энтропии отдельных элементов жидкости не
соблюдаются из-за влияния вязкости и теплообмена между отдельными
элементами жидкости с разной температурой, то вместо уравнения
состояния A.2.9) можно записать формулу, связывающую плотность, давление
и энтропию [46]:
Ър \
/ .
1р+ —-) ds. A.4.5)
Согласно ззвпч-'^к 'in (L2.12) (dp/dp)s = а2, а для второго
коэффициента в соотношении ( ! .4 5), воспользовавшись правилами
дифференцирования неявных функций и учтя определение коэффициента теплового
расширения /3 и формулу ср - T(bs/dT)p, найдем
(Ър\ (Ър\ [ Ър\ {Ър/ЪТ)р ра2AТ
¦ = - =-а = . A.4.6)
\bsj \bj\b) (Ъ/ЪТ)
p
Подставив значения коэффициентов в соотношение A.4.5), получаем
dp
p $рТ
dp = — ds. A.4.7)
Используя зависимость A.4.7), можно записать уравнение
неразрывности A.2.5) в переменных р, и, v и s. Однако в соотношение A.4.7)
20
входит дифференциал от энтропии, который определяется уравнением
энергии A.2.6). Поэтому удобно сначала привести к безразмерному виду
уравнение энергии:
Ъ1 Э7 ЭТ 1 / ЪТ ЪТ ЪТ \
Sh—=- + и + U = — Sh — + п + п" -
Ъt Ъх ЪТ Т \ bt Ъх ЪТ /
РРо / Эр _ Эр" _Эр\ Ф (R\/ ul \
рроср \ Эг Эх Ъг I Re рГ \ L 1 \ срТ0 )
Ъ2Т ( L \2 1 Э / ЭГ \1
+ — — - '— . AА8)
РеГр [ Ъх2 \Rj 7 ЪТ \ Э7
где Ре = u0L/kT —_критерий Пекле, кт = \т/срр0 - коэффициент
температуропроводности, Ф = ФЬ2/ыо — безразмерная диссипация энергии.
Для идеального газа /3_= 1/Т и соответственно коэффициент $Ро1 Роср -
- RT0/Tcp = (ср - cv)/cpT= (к - \)jkT. В этом случае комплекс иЦсрТ0 =
= kulR/Cpal = (к - 1)М2. В итоге уравнение A.4.8) преобразуется к
следующему виду:
ЭУ ЗУ ЭУ 1 / ЪТ ЪТ ЪТ \
-z~+ и + v — = -з I Sh -zr + м — + и I
Ъг Ъх ЪТ Т \ ЪГ Ъх ЪТ I
-l)f Ър Ър Ър\
^- sh-4+w— +v~— )=
Т \ ЪГ ' Ъх ЪТ I
^ )(
кТ \ ЪГ ' Ъх ЪТ I Rep Г \ L
+
?е
1 Г Ъ2Т I L\2 1 Ъ I ЪТ\\
=— -+ — —— 7 . A.4.9)
Т -р [ Ъх2 \ R J Т ЪТ \ ЪТ /1
Используя полученную безразмерную форму уравнения энергии, можно
вернуться к преобразованию уравнения неразрывности с помощью
соотношения A.4.7). Подставив соотношение A.4.7) в уравнение
неразрывности A.2.5) , с помощью уравнения A.4.8) находим
Эр Эр Эр аа2р / Эм Эу v \
Sh-b + i7-ii + u~r + » + — + —
ЭГ Эх Эг М \ Ъх ЪТ г I
1 Г Ъ2Т / I \2 L Э / ЭГ
М [ срТороио re L Эх \ R ) г Ъг
A.4.10)
Физический смысл безразмерного комплекса (лФЬ/срТороио =
= :лФУ/срТ0С0 (где Go - раход) достаточно ясен. Он характеризует
влияние на плотность жидкости теплоты, выделяющейся в единицу времени
в объеме канала V вследствие работы сил вязкого трения, которое
относится к теплосодержанию жидкости, протекающей через этот объем
в единицу времени. В большинстве случаев величина комплекса
незначительная. Заметное выделение теплоты за счет трения возможно в очень
длинных трактах (магистральных нефтепроводах, газопроводах). Однако
для таких трактов непригодна описанная модель адиабатического течения
из-за большой поверхности стенок и значительного времени пребывания
жидкости в тракте. Безразмерный комплекс /ЗГ0 характеризует влия-
21
ние на плотность жидкости изменения температуры. Для идеального газа
Р = 1/Г0 и соответственно /ЗГ0 = 1, для капельной жидкости обычно
(ЗТ0 < 1. Кроме того, Ре = Re ?r(L/R) > 1, так как обычно число Прандт-
ля Pr = v/kT ~ 1, Re > 1, L\R > 1. Поэтому в дальнейшем влияние
диссипации и теплопроводности на плотность жидкости, как правило,
учитываться не будет. В зависимостях A.4.8) и A.4.9) использовалась
безразмерная диссипация энергии, которая находится из преобразованного
соотношения A.2.7):
l\R/ Sr \L I Ъх J \Ъх ) \Ы I
( v \2 2 Г Ъп 1 Э I2
+ 2—) -"" + ' (г») • A.4.11)
\ г ) 3 L Ъх 1 Ы \ У }
В безразмерные уравнения A.4.1)-A.4.4) и A.4.8)-A.4.10) входят
числа Re, Sh, Fr, Eu, M, а, Ре или Рг и геометрический параметр R/L.
§ 1.5. Примеры упрощения уравнений гидромеханики.
Некоторые особенности нестационарного движения вязкой жидкости
Математические модели, описывающие процессы в отдельных
элементах ПГС, ниже будут формироваться в основном путем упрощения
уравнений гидромеханики, приведенных в разделах 1.2 - 1.4. Методику
формирования математических моделей целесообразно показать на наиболее
наглядных, простейших примерах. Одновременно из анализа решения
упрощенных уравнений можно выявить некоторые особенности
нестационарного движения жидкости. При попытках решить исходные уравнения
гидромеханики A.2.3) — A.2.6) возникают трудности из-за нелинейных
конвективных членов, в которые входят произведения скоростей на
производные от параметров течения. Этих трудностей можно избежать,
упростив уравнения одним из двух методов: либо (если это допустимо)
путем пренебрежения нелинейными членами, либо путем линеаризации
уравнений, перехода к малым отклонениям. Примером уравнения,
упрощенного первым методом, может служить уравнение, описывающее
одномерное плоское движение вязкой несжимаемой жидкости. В этом случае
скорость имеет только одну составляющую и, которая зависит от одной
координаты г (или — для плоского движения — у), а вдоль оси
мгновенные значения скорости не изменяются. Это легко установить, если
воспользоваться уравнением неразрывности для несжимаемой жидкости
A.2.5), которое при р = const принимает вид
Ъи 1 Э(гу)
divV = 05 + —- = 0. A.5.1)
Эх г Ъг
Для плоского движения и =¦ 0, и из A.5.1) следует, что Ъи/Ъх = 0. В
уравнении движения вдоль оси д: A.2.3) конвективные члены исчезают,
так как и - и(г, г) и v = 0, так же как и член в правой части д2и/дх2 =
= div V = 0.
22
С учетом всех упрощений уравнение движения запишется так:
Ъи 1 Ър Ъ2и
= Рх - + v - . A.5.2)
Ы р Ъх Ъу2
Второе уравнение движения A.2.4) для поперечной составляющей
скорости v с учетом всех указанных выше допущений вырождается в
условие A/р) (др/ду) - Pv, а при отсутствии массовых сил - в условие
Рассмотрим течение, возникающее у плоской стенки, внезапно
приведенной из состояния покоя в движение в своей собственной плоскости с
постоянной скоростью и0. Так как жидкость занимает весь объем над
пластиной, который считаем безграничным, а скорость жидкости и не зависит
от координаты х, то при Рх - 0 не должно зависеть от этой координаты
и давление, т.е. Ър/Ъх = 0. В этом случае уравнение плоского движения
A.5.2) еще больше упростится и примет форму уравнения
теплопроводности, описывающего распространение тепла в пространстве:
Ъи Ъ2и
Граничные и начальные условия имеют вид
м(у,0) = 0 при у>0, м@, г) = М(ь м(°°, г) = 0 при t > 0. A.5.4)
Переходя к безразмерной переменной п = и/и0, из анализа размерности
остальных параметров, входящих в уравнение A.5.3), найдем, что из них
можно получить еще только одну безразмерную комбинацию yl\/4vt = 77.
В этом случае и = /G7) и уравнение A.5.3) сводится к
обыкновенному дифференциальному уравнению
/"+(т»)/' = 0. A.5.5)
для которого граничные условия A.5.4) запишутся: / = 1 при т? = 0 и
/ = 0 при 77 --> ©о. С учетом граничных условий решение уравнения
A.5.5) имеет вид
м =1 - erf (г?), A.5.6)
где
erf G7) = — / ехр(-773)^77.
я о
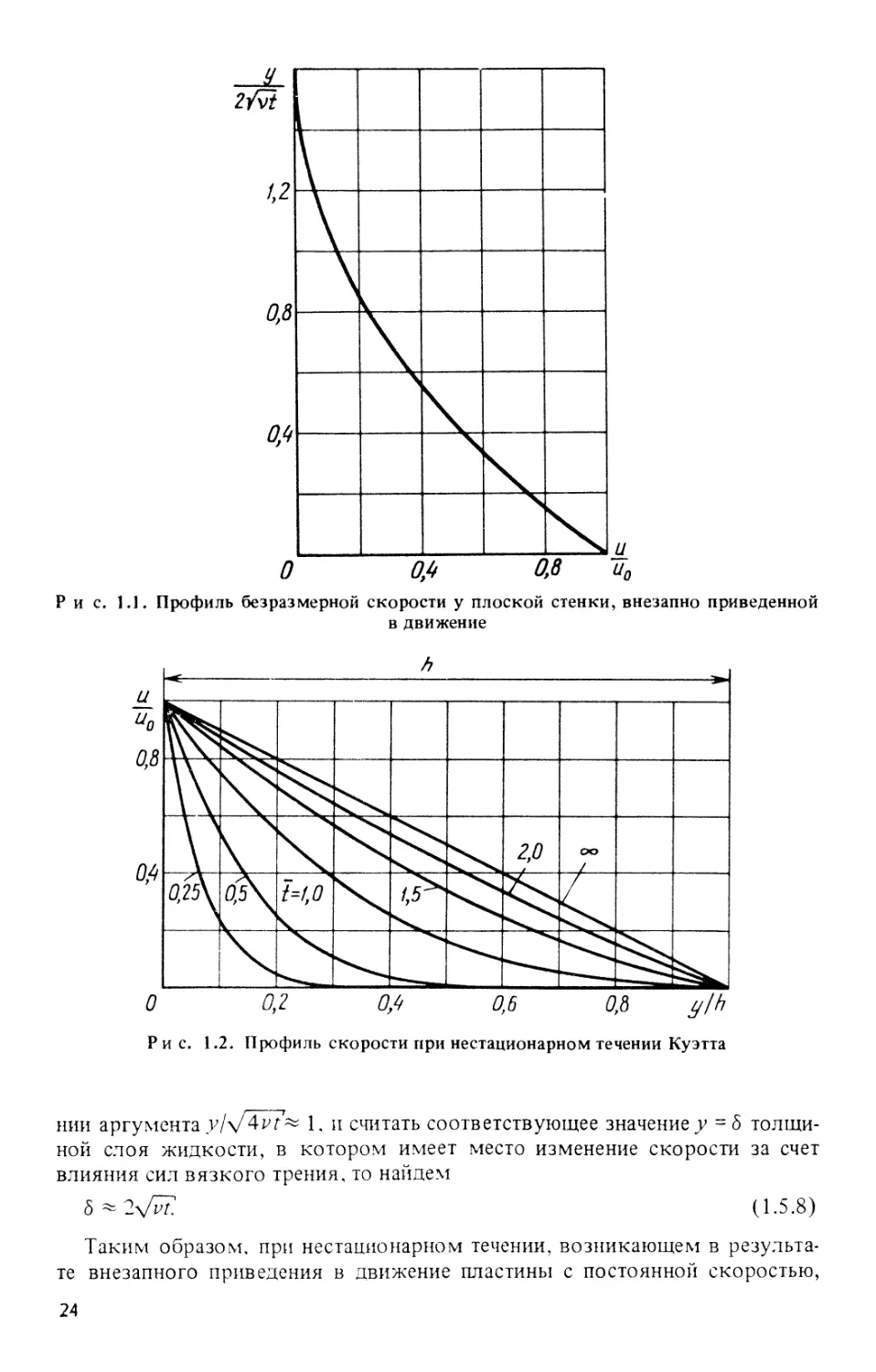
Кривая распределения скорости в безразмерных параметрах приведена
на рис. 1.1, при этом профили скорости в любой момент времени
оказываются подобными, если их представлять в безразмерных параметрах,
т.е. течение является автомодельным.
Используя решение A.5.6), найдем мгновенное значение силы трения,
действующей на единицу площади пластины
tw = 1
Ьсли же учесть, что функция erf отличается от единицы на 10% при значе-
23
1,2
0,8
0~
1
\
\
у
\
ч
>
0,8 и0
Р и с. 1.1. Профиль безразмерной скорости у плоской стенки, внезапно приведенной
в движение
О 0,2 0,4 0,6 0,д
Рис. 1.2. Профиль скорости при нестационарном течении Куэтта
нии аргументаy\\jbvt'7^ 1, и считать соответствующее значение^ =5
толщиной слоя жидкости, в котором имеет место изменение скорости за счет
влияния сил вязкого трения, то найдем
A.5.8)
lyjvt.
Таким образом, при нестационарном течении, возникающем в
результате внезапного приведения в движение пластины с постоянной скоростью,
24
с ростом времени, прошедшего от начала движения, увеличивается глубина
проникновения возмущения, вызванного движением пластины, причем эта
глубина растет пропорционально корню квадратному из времени.
Одновременно уменьшается сила трения, так как она зависит от толщины слоя
жидкости, в котором скорость переменна. Кроме того, с ростом времени
масса жидкости, двигающаяся вместе с пластиной, непрерывно растет, так
как увеличивается толщина возмущенного слоя жидкости. Используя
уравнение A.5.3) , можно рассмотреть задачу о движении пластины в
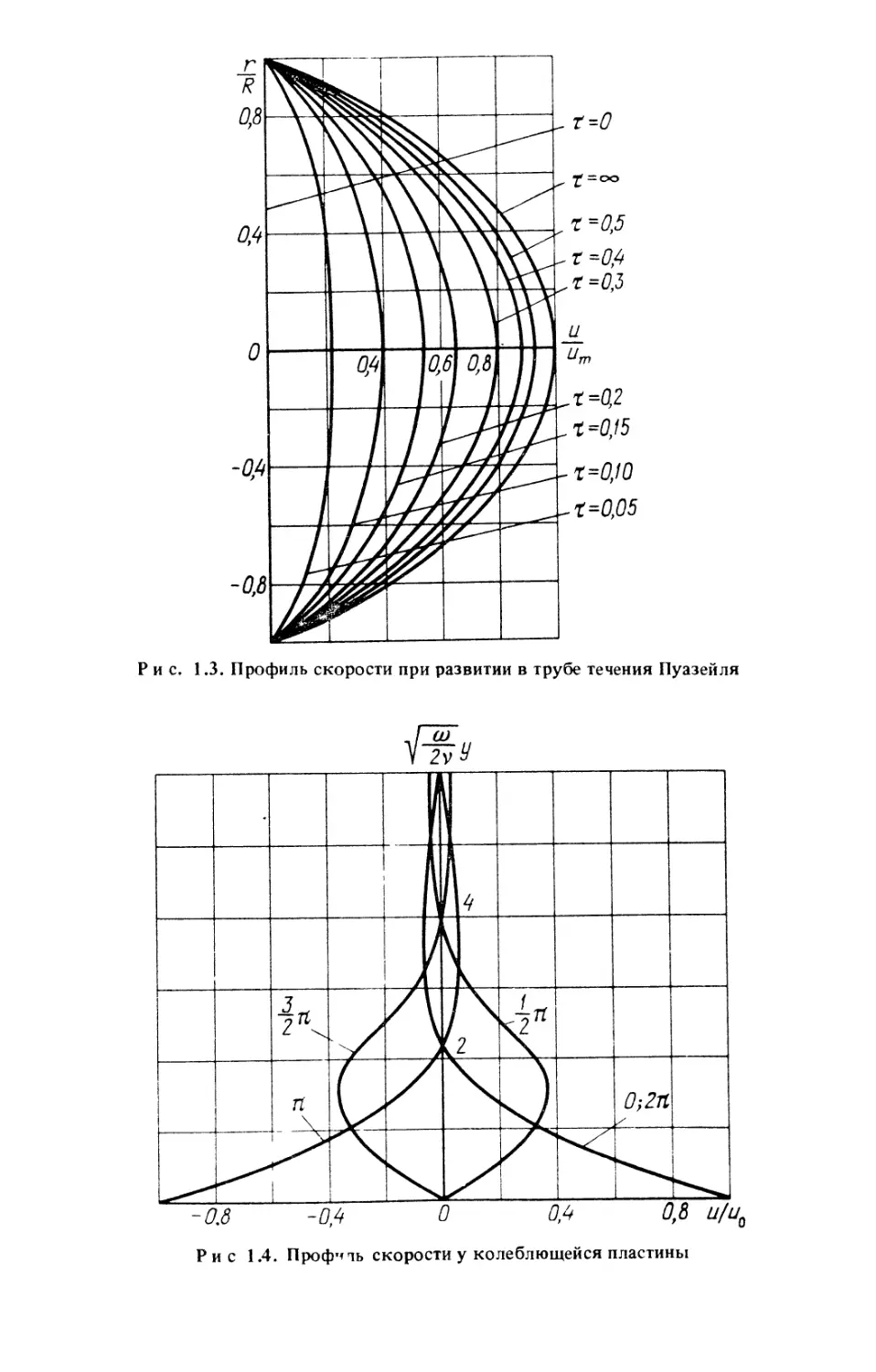
ограниченном объеме жидкости, к примеру — развитие во времени течения Куэтта
[242], для которого профили скорости представлены на рис. 1.2.
Сопоставление профилей показывает, что не наблюдается подобия (автомодельнос-
ти) профилей скорости. По достижении определенного безразмерного
времени с начала движения пластины t = A\JVt\h (где h - расстояние от
пластины до стенки) происходит стабилизация профиля, для которого
характерно стремление к линейному стационарному распределению скорости.
Но и здесь в начальные моменты времени, пока возмущение не достигло
неподвижной стенки, профили скорости похожи на профиль, приведенный
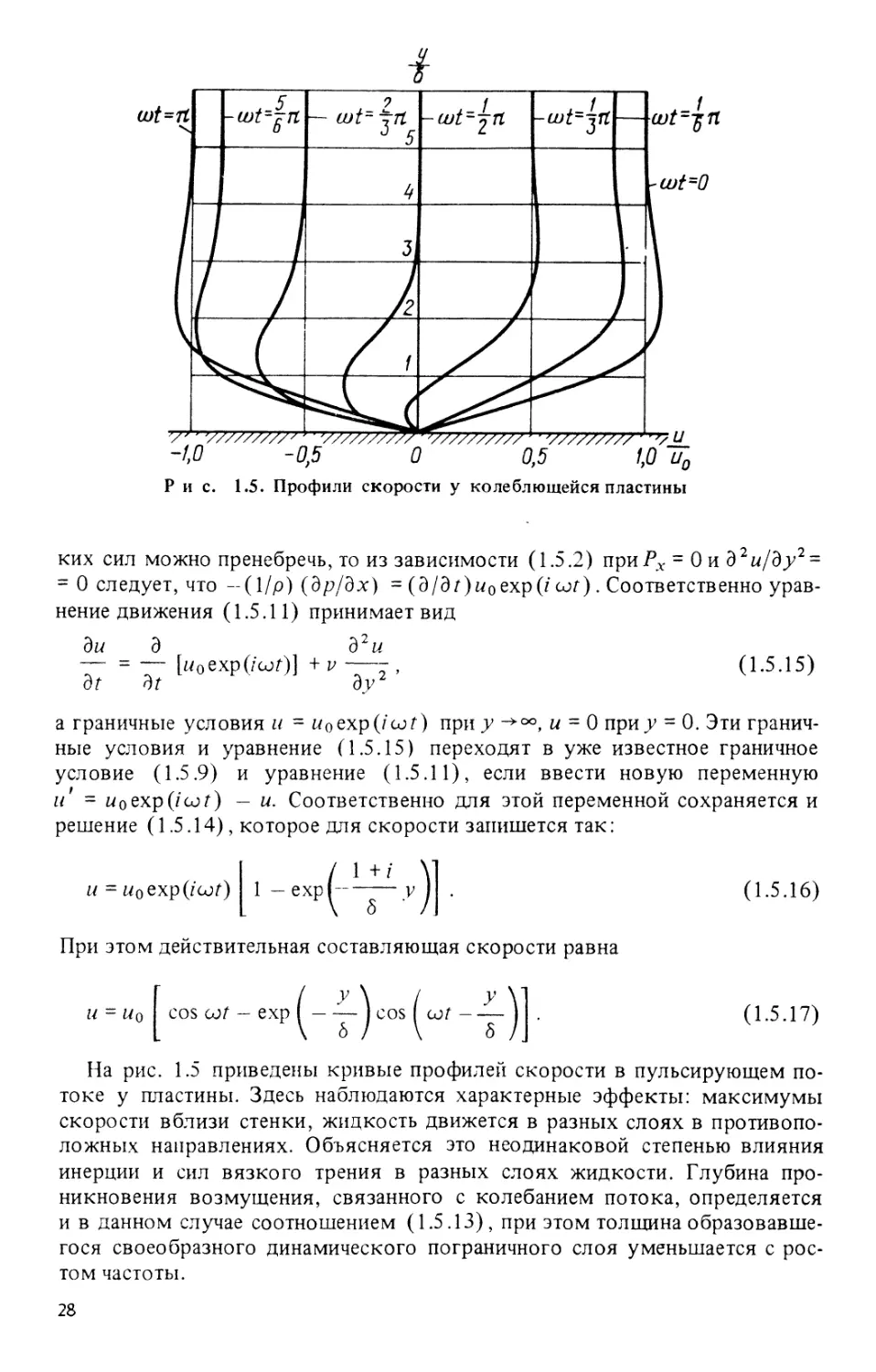
на рис. 1.1. Специфичный характер имеют профили скорости при развитой
во времени (из неподвижного состояния) ламинарного течения в трубе
[242]. В этом случае к столбу неподвижной жидкости, заполняющей трубу,
внезапно прикладывается постоянный перепад давления. Безразмерные
профили скорости ы/ит, так же как и для пластины, изменяют свой
характер во времени (рис. 1.3): вначале, когда в основном преобладает влияние
сил инерции, профиль скорости — плоский с почти постоянной скоростью
в ядре потока и резким ее изменением из-за вязкости только у стенки
(возмущающее воздействие от трения у стенки не достигло ядра потока).
По мере роста безразмерного времени с начала движения г - vtjR2 профиль
скорости приобретает форму, близкую к параболе, характерной для
стационарного ламинарного движения Пуазейля, которое определяется только
действием сил вязкого трения.
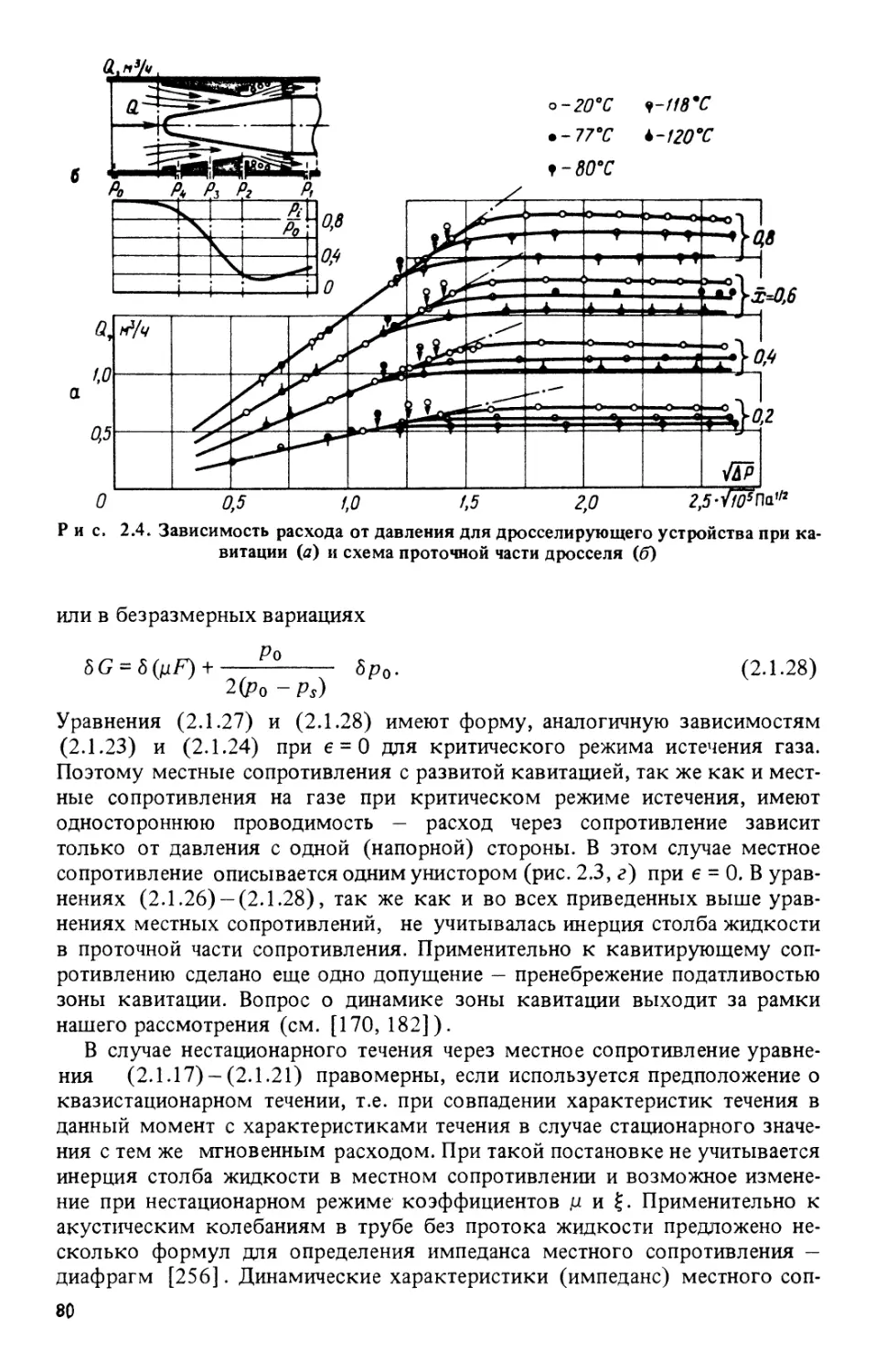
Другой интересный тип нестационарных течений - различные
пульсирующие течения жидкости. Рассмотрим движение жидкости у колеблющейся
в своей плоскости пластины. Неограниченная пластина, а вместе с ней и
несжимаемая жидкость, находящаяся у стенки, совершает колебания по
следующему закону:
и = u0exp(icot) при у=0. A.5.9)
Течение жидкости в пространстве над пластиной подчиняется уравнению
A.5.3) и граничному условию A.5.9). Комплексная форма записи
граничного условия A.5.9) удобна для преобразования решения уравнения
A.5.3), и пока над решением проводятся линейные операции, не имеет
смысла выделять его вещественную часть, которую нужно находить только
от окончательного выражения.
Будем искать частное периодическое решение уравнения A.5.3) в
предположении, что все переходные процессы, связанные с влиянием
начальных условий, уже закончились и в жидкости установился режим чисто
вынужденных колебаний, решение для которого можно записать
следующим образом:
и =/(у)ехр(/сог). A.5.10)
25
-ОМ
-0,8:
Рис. 1.3. Профиль скорости при развитии в трубе течения Пуазейля
^—
к
п
-X-J
/
У
№
1
I
л
А
у
\
\
0;2Л
~03 -0,4 О ОМ 0f8 u/uQ
Рис 1.4. Проф^1ь скорости у колеблющейся пластины
Для функции /(у) , определяющей амплитуду колебаний скорости, найдем
обыкновенное линейное дифференциальное уравнение, подставив решение
A.5.10) в исходное уравнение A.5.9): icof=v(d2f/dy2).
Для этого уравнения существуют следующие корни характеристического
уравнения: к = ± \fitofv- ± (/ + 1)>/со/27\ а решение выглядит так:
f(y) = А ехр [A + /) y/oj/2vy] + В ехр [- A + /) y/co/2vy].
Из условия ограниченности скорости при у -> °° следует, что А = 0, а из
граничного условия A.5.9) — что В = и0, и скорость определяется следующим
соотношением:
и = и0ехр(-^ \Jul2v)ехр /(сог - y/cj/lvy), A.5.11)
действительная часть которого запишется так:
и = u0Qxp(-y/(jo/2py)cos(u)t - \lu\2vy). A.5.12)
На рис. 1.4 изображены профили скорости для различных моментов
безразмерного времени cot. Они определяют мгновенное значение скорости
в поперечной сдвиговой волне, для которой смещение жидкости и ее
скорость имеют направление, перпендикулярное направлению распространения
волны. Скорость колеблющихся слоев жидкости отстает по фазе на \Jcol2v
от скорости движения пластины. На расстоянии у = X = 2it\/2vI<jS фаза
колебаний скорости жидкости совпадает с фазой колебаний стенки,
поэтому это расстояние можно принять за длину волны колебаний. Амплитуда
колебаний скорости быстро затухает по закону ехр(— \fcol2v у), фазовая
скорость распространения поперечной волны в направлении оси у равна
с = \/2сог/. Приняв за глубину проникновения волны 5 координату у,
при которой амплитуда скорости убывает в е раз, из соотношения A.5.12)
находим
5 = V2*>/gj,' A.5.13)
т.е. глубина проникновения растет с ростом вязкости и уменьшением
частоты колебаний. Глубину проникновения возмущений Ь можно
непосредственно ввести в формулу A.5.11), которая при этом принимает вид
/ ! + /- \
и = ?/0ехр(/сог)ехр( vl. A.5.14)
В момент (jot = я/2, когда скорость поверхности (у - 0) равна нулю,
жидкость вблизи поверхности продолжает двигаться в положительном
направлении, а на достаточном удалении (\^оо/2р > 4), наоборот, в
отрицательном. Глубины проникновения в жидкость возмущений, связанных с
действием сил вязкости при колебаниях пластины, найдены по формуле
A.5.13), а при внезапном возникновении движение - по A.5.8), и
оказываются одного порядка, если учесть, что время t ^ 1/со. Если обратить
задачу - рассмотреть пульсирующее течение у неподвижной пластины,
скорость которого на достаточном удалении от пластины описывается
соотношением A.5.9), то в уравнение движения A.5.3) необходимо добавить
член, учитывающий колебания давления во внешнем потоке. Так как вне
слоя, в который проникает действие возмущений от стенки, влиянием вяз-
27
U)t=7l\
. АААААААА
-1,0 -0,5 0 0,5 1,0 и0
Рис. 1.5. Профили скорости у колеблющейся пластины
ких сил можно пренебречь, то из зависимости A.5.2) приРд. - 0и д2и/ду2-
= 0 следует, что -A/р) (др/дх) = (Э/Эг)моехр(/ cot) . Соответственно
уравнение движения A.5.11) принимает вид
Ъы Э Ь2и
— = — [м0ехр(/о;0] + v , A.5.15)
dt dt Ъу1
а граничные условия и = UoQxp(icot) при у ->о°, и = 0 при jf = 0. Эти
граничные условия и уравнение A.5.15) переходят в уже известное граничное
условие A.5.9) и уравнение A.5.11), если ввести новую переменную
и - и о ехр (/со t) — и. Соответственно для этой переменной сохраняется и
решение A.5.14), которое для скорости запишется так:
и = u0exp(ioot) 1 — expl —
При этом действительная составляющая скорости равна
и = и0 cos cot - ехр -
cos \ cot -¦
У
A.5.16)
A.5.17)
На рис. 1.5 приведены кривые профилей скорости в пульсирующем
потоке у пластины. Здесь наблюдаются характерные эффекты: максимумы
скорости вблизи стенки, жидкость движется в разных слоях в
противоположных направлениях. Объясняется это неодинаковой степенью влияния
инерции и сил вязкого трения в разных слоях жидкости. Глубина
проникновения возмущения, связанного с колебанием потока, определяется
и в данном случае соотношением A.5.13), при этом толщина
образовавшегося своеобразного динамического пограничного слоя уменьшается с
ростом частоты.
28
Для стационарного пограничного слоя, возникающего у поверхности
пластины или другого тела при обтекании вязкой жидкостью, а также для
течений в начале каналов [242] характерно нарастание толщины
заторможенного слоя жидкости по мере удаления от начального или входного
сечения. Толщина ламинарного пограничного слоя увеличивается
пропорционально корню квадратному от коэффициента вязкости жидкости v и
расстоянию от начала обтекаемой поверхности х: 5П#С = \/рх/ы0 = \fuV, где
Wo - скорость вне пограничного слоя, т = х/и0 - время пребывания
жидкости на внешней границе пограничного слоя. Толщина пограничного слоя
5П#С по порядку величины совпадает с толщиной возмущенного
динамического слоя на пластине, приведенной внезапно в движение, и определяемой
соотношением A.5.8).
Иное положение в случае колебаний потока. Для колеблющегося потока
толщина динамического пограничного слоя, определяемая формулой
A.5.13) бд ~\Jvjco\ не зависит от координаты х, т.е. этот слой для
несжимаемой жидкости будет иметь одинаковую толщину в данный момент на
всей поверхности пластины. При этом 5Д/5П#С ~\/uolcox и при со > ыо/х
выполняется условие бд < 5П#С, т.е. толщина динамического слоя меньше
толщины пограничного слоя, если время пребывания жидкости т ~iio/x в
области действия сил вязкого трения больше периода колебаний. При
достаточно высоких частотах динамический пограничный слой имеет малую
толщину, что может быть использовано для упрощения математических
моделей нестационарных течений.
Интересно определить силу трения, действующую на колеблющуюся в
жидкости пластину. По формуле Ньютона A.2.1) можно найти касательное
напряжение трения на поверхности пластины tw = 1л(ди/ду)у = 0.
Подставляя зависимость для скорости в записи через комплексные числа A.5.11),
можно выделить эффекты, связанные с влиянием вязкости и отдельно с
инерцией увлекаемой жидкости. В результате указанной подставки
находим
_ Г / Я \ / 7Г \1
= — puo\fvco cos cor +— J + z cos cot -— 1
L \ 4 / V 4 /J
При записи формулы для скорости колеблющейся стенки в виде
зависимости u0exp(icot) соотношение для производной по времени от скорости
принимает следующий вид:
d
— [мсехр(/сог)] =ком0ехр(/соГ).
dt
Таким образом, член icou0 характеризует ускорение, а коэффициент при
нем — увлекаемую массу. При таком представлении силы трения ее мнимая
часть определяет инерционную составляющую силы, действующую на
стенку. Учтя это, можно записать
/—>/ п \ гт- ( п \
rw - - piiovvco cos cot +— j-icjiiopyjp/co cos [cot - — I . A.5.18)
\ 4 / \ 4 /
Первый член A.5.18) определяет диссипативную силу, действующую на
29
колеблющуюся стенку, а второй — инерционную силу, связанную с
инерцией массы жидкости, увлекаемой из-за вязкости. Эта масса, обычно
называемая присоединенной массой [140], равна (на единицу поверхности
стенки) ру/u/cS. Присоединенная масса определяется толщиной слоя жидкости
у/р/со] близкой к 5 — толщине проникновения возмущений, определяемой
по формуле A.5.13). И диссипативная сила и инерционная сила направлены
в сторону, противоположную направлению скорости движения стенки
(знак минус), но со сдвигом фазы на тг/4. При этом между двумя
составляющими силы сопротивления (по принятой в электротехнике
терминологии — активной и реактивной составляющими) сдвиг фазы равен тг/2.
Обращает на себя внимание тот факт, что диссипативная сила
увеличивается, а присоединенная масса — уменьшается с ростом частоты колебаний,
увеличение же вязкости жидкости приводит к росту обеих составляющих
силы сопротивления. Для рассмотренной выше обратной задачи -
колебаний жидкости у неподвижной стенки - профиль скорости определяется
зависимостью A.5.16), которая отличается от соотношения для скорости
у колеблющейся пластины A.5.11) только первым членом, не зависящим
от у, и знаком перед вторым членом. Соответственно зависимость для
силы трения о стенку пульсирующего течения будет отличаться от
выражения A.5.18) только знаком. Диссипативная составляющая силы будет
опережать по фазе на я/4 скорость внешнего потока, а инерционная - отставать
от скорости по фазе на тг/4. Характер распределения скорости жидкости
у стенки (рис. 1.5) в пульсирующем потоке является причиной отмеченной
особенности - сдвига фазы колебания силы трения относительно скорости
внешнего потока. Опережение по фазе диссипативной составляющей силы
трения и наличие характерного максимума на профиле скорости у стенки
связано с тем, что в слоях жидкости, в которые проникают возмущения от
стенки из-за работы сил вязкости, скорость меньше скорости внешнего
потока. Соответственно градиент давления, создающий колебания
скорости, в слоях у стенки с меньшей скоростью вызывает более быструю
реакцию течения, чем в слоях, удаленных от стенки и обладающих большей
инерцией.
Полученное решение для профиля скорости в пульсирующем
неограниченном потоке является автомодельным (рис. 1.5), так же как и для
профилей скорости при внезапном приведении в движение пластины (рис. 1.1)
или при колебании стенки в неограниченном пространстве (рис. 1.4). Для
обеспечения автомодельности необходимо нормировать поперечную
координату. При этом профиль скорости отличается от однородного только
в слоях, находящихся на расстоянии от стенки порядка 5 = у/Ъ^/со. При
наличии второй стенки (рис. 1.2) или при нестационарном течении в трубе
(рис. 1.3), кроме расстояния от стенки у, появляется еще один
геометрический параметр, и течение определяется не одним безразмерным
параметром, а двумя. К примеру, для пульсирующего течения в трубе такие
параметры: rjR и Ry/u>/v' где R - радиус трубы. Соотношения для профилей
скорости становятся более сложными, однако отмеченные основные
особенности нестационарного течения сохраняются.
30
§ 1.6. Математические модели движения жидкости
с переменной температурой (составом)
Важными и наиболее подробно изученными в гидромеханике являются
течения идеальной жидкости, т.е. жидкости без вязкости и
теплопроводности О = Хт = 0). В этом случае в уравнениях движения A.2.3) и A.2.4)
и в уравнении энергии A.2.6) исчезают члены со вторыми производными
по координате от скоростей и температуры. Соответственно порядок
уравнений понижается, что существенно упрощает их решение. Однако и в этом
случае возможно изменение энтропии (температуры) жидкости, например,
из-за подвода теплоты. При этом тепло может подводиться к жидкости как
вследствие теплообмена со стенками тракта, так и при выделении тепла
внутри жидкости при химических, ядерных реакциях, подводе тепла
излучением и т.д. Если теплота к жидкости на границах и в объеме не подводится,
то при v = Хт = 0 уравнение энергии A.2.6) определяет только связь между
температурой и давлением жидкости, т.е. дает возможность найти
распределение температуры по известному из решения уравнений A.2.3) и A.2.4)
полю давления. В этом случае уравнение A.2.6) характеризует изоэнтро-
пичность течения жидкости, в которой обмен между внутренней энергией
жидкости и другими видами энергии происходит обратимо. Изменение
температуры каждой порции жидкости в объеме при этом определяется только
изменением давления по уравнению адиабаты. Подобная ситуация имеет
место и при неизотермическом потоке жидкости, изменения температуры
которого возникли вне рассматриваемого объема, например, в соседнем
тракте, а также в зонах химических реакций, зонах горения, смешения,
имеющих малую протяженность, которой можно пренебречь. Зоны горения,
химических реакций, которые занимают большую часть или весь объем
тракта, не рассматриваются в данной книге, хотя решить такие задачи
можно с привлечением метода теории цепей [118, 171].
Если теплота к жидкости подводится через ограничивающую поток
поверхность, процесс оказывается более сложным. В этом случае решается
сопряженная задача, в которой одновременно учитываются как тепловые, так и
гидромеханические нестационарные эффекты.
Подобные процессы характерны для нестационарных режимов работы
теплообменных устройств, трактов охлаждения, газопроводов и т.д. В этих
процессах определяющую роль играет нестационарный теплообмен, анализ
которого выходит за круг вопросов, рассматриваемых в данной книге.
Нестационарные тепловые процессы подробно рассмотрены в книгах [49,
144,173]. К расчету нестационарного теплообмена привлекаются и
методы теории цепей [78,92,162].
Как уже отмечалось, во многих случаях изменение температуры
среды происходит только на входе в тракт, а далее, по длине тракта,
подводом тепла к жидкости можно пренебречь, так что температура и
состав могут изменяться только из-за теплообмена и диффузии внутри
жидкости. В качестве примеров можно указать на камеры сгорания,
газовые тракты двигателей или топок, в которых горение происходит в
зоне ввода топлива: объемом этой зоны по сравнению со всем объемом
камеры сгорания можно пренебречь [58, 190]. Аналогичную модель
процесса можно использовать для некоторых вариантов смесительных уст-
31
du
- +
dt
ds
dt
/dp
\3p
¦ м
M
м -
н м
du
dx
Эр
Эх
ds
dx
dx
-a
1 dp '
+ -=0,
p Эх
ди
+ p—=0,
= 0,
= 0,
2
ройств, химических реакторов, газопроводов за компрессорами или ien-
лообменниками, и т.д.
Если пренебречь вязкостью, диффузией и теплопроводностью и
считать течение одномерным, то движение жидкости с переменными
значениями температуры и состава в тракте цилиндрической формы описывается
упрощенным вариантом исходных уравнений A.2.3), A.2.5), A.2.6) и
A.2.15) при v = v = XT -kjj = 0:
A.6.1)
A.6.2)
A.6.3)
A.6.4)
A.6.5)
Уравнения A.6.1)—A.6.5) — нелинейные из-за конвективных членов, и
решение их в общем виде сопряжено с определенными трудностями. С
другой стороны, интерес представляет их дальнейшее упрощение путем
линеаризации. Разложив каждую переменную на две составляющие —
стационарную и вариацию и - мс + 5м', р = рс + др', р =рс + 5р\
S - Sc + 05 , gj - gic + Ogj,
подставив их в исходную систему уравнений, учтя, что стационарные
составляющие всех параметров мс, рс, рс, sc, gjC удовлетворяют уравнениям
A.6.1)-A.6.5) без членов с производной по времени, и из-за малости
отбросив члены, содержащие вариации параметров в степенях выше первой,
находим
A.6.6)
A.6.7)
A.6.8)
= 0. A.6.9)
dt dx
Для параметров стационарного течения здесь индекс "с" отброшен.
Линеаризованные уравнения оказались разбитыми на две независимые
группы. Два первых уравнения (движения и неразрывности) связывают
32
Э5м;
dt
dbp'
dt
dds'
dt
+ и
+ и
+ и
Э5м
dx
dSp'
dx
d3s
dx
1
P
+ pa2
-o,
— c\
dx
r\
dx
распространение в потоке отклонений давления и скорости, т.е.
акустических волн, которые в такой постановке не зависят от отклонений энтропии
(температуры) и состава среды. С другой стороны, два последних
уравнения A.6.8) и A.6.9) определяют распространение в потоке со скоростью
потока волн энтропии и концентрации. При и - const решения уравнений
A.6.8) и A.6.9) имеют вид, характерный для бегущих волн:
bs'(x, t) = 8s' [0;t-—) , A.6.10)
\ /
Так как в уравнениях A.6.8) и A.6.9) не учитываются диссипативные
процессы, связанные с теплопроводностью и диффузией в среде, то волны
(возмущения) энтропии и концентрации, сформировавшиеся на входе,
сохраняют свою форму при движении вместе с потоком жидкости вдоль
тракта. Эти образующиеся при неизотермическом течении и течении с
переменным составом волны называются волнами энтропии и концентрации.
Возмущения скорости и давления (акустические волны) в линейном
приближении не взаимодействуют в потоке идеальной жидкости с волнами
энтропии и концентрации. Таким образом, в среде идеальной жидкости могут
распространяться независимо две системы волн. Взаимодействуют эти
волны только на границах тракта — на местных сопротивлениях или других
устройствах, скорость жидкости в которых зависит как от давления, так
и от температуры (энтропии) и состава (концентрации отдельных
составляющих) протекающей через сопротивление среды.
§ 1.7. О влиянии вязкости жидкости.
Переход к одномерной модели движения
1.7.1. Введение. Уравнения Навье - Стокса, приведенные в § 1.2, или
уравнения для турбулентного движения из § 1.3 вместе с
соответствующими начальными и граничными условиями в принципе описывают самые
разнообразные течения жидкости. Однако эти системы уравнений
гидромеханики слишком громоздки для решения с помощью современных ЭВМ.
Особенно большие трудности возникают при попытках расчета движения
жидкости внутри каналов сложной формы, которые являются типичными
для ПГС. Трудности усугубляются при решении нестационарных задач:
в этой области гидромеханики известно ограниченное количество работ,
что связано не только с трудностями математического решения подобных
задач, но и с отсутствием полной ясности по ряду принципиальных
вопросов (например, о влиянии нестационарности режима течения на
характеристики турбулентности, на устойчивость ламинарного течения и т.д.).
С другой стороны, основной прогресс в математическом моделировании
гидромеханических процессов был достигнут при исследовании
относительно простых, частных задач, для которых моделировался какой-то один
процесс в отдельности. При таком подходе из решения частных задач,
описывающих достаточно специфические течения, выявляется влияние свойств
жидкости, область действия принятых предположений, природа процессов,
отображаемых отдельными моделями течений.
3-Б.ф. Гликман 33
В § 1.8 будут проанализированы условия, при которых можно
существенно упростить уравнения гидромеханики, принимая жидкость
несжимаемой. В § 1.9 будут даны примеры еще более глубоких упрощений моделей
течения, позволяющих свести уравнения гидромеханики к обыкновенным
дифференциальным уравнениям. В других разделах не раз будут ставиться
вопросы об условиях, при которых можно упростить уравнения
гидромеханики для формирования разумной по сложности математической модели
того или иного процесса.
Из анализа уравнений движения A.4.1) и A.4.2) в безразмерной форме
записи следует, что порядок членов, описывающих действие сил вязкого
трения, определяется комплексом (I/Re) (L/R). Практически во всех
случаях при организованном течении жидкости в каналах Re > 1. Другой
безразмерный сомножитель L/R - длина канала в его калибрах -может
варьироваться в очень широких пределах. В частности, для магистральных
трубопроводных систем L/R может достигать величин, намного
превышающих число Re. С другой стороны, для распространенных каналов ПГС
относительно небольшой длины, как правило, безразмерная длина L/R <
< Re, а это значит, что члены, описывающие вязкое трение, относительно
малы по сравнению с другими членами уравнений движения A.4.1) и A.4.2).
Поэтому кажется заманчивым, используя предельный переход при Re > 1,
отбросить члены, связанные с вязким трением, существенно упростив тем
оамым уравнения движения.
Однако такое упрощение не всегда корректно даже при Re > 1, ибо при
любой величине вязкости имеется область вблизи твердой поверхности,
где существенно влияет вязкость, так как реальная жидкость прилипает
к поверхности. Без учета вязкости невозможно объяснить возникновение
отрывов потока, обратных течений, возникающих при обтекании
жидкостью препятствий. Для течения внутри каналов достаточной длины, хотя
и соблюдается условие L/R < Re, вязкость оказывает влияние на весь
поток, так как зона влияния вязкости у стенки (пограничный слой)
увеличивает свою толщину по мере удаления от входного сечения и при
определенной длине тракта пограничный слой занимает все его сечение. Если
размеры канала, в котором течет жидкость, в одном направлении
существенно больше, чем в другом, например, R/L < 1, то уравнения движения
можно существенно упростить. Но при этом эффектами вязкости, как
правило, пренебречь нельзя; упрощение же математической модели
достигается путем пренебрежения движением жидкости в радиальном
направлении и соответственно уменьшением общего порядка уравнений движения.
Это один из путей упрощения уравнений', описывающих движение
жидкости в ПГС.
Другим методом упрощения уравнений движения является переход от
двумерных течений в канале, поле скоростей в котором определяется
влиянием вязкости, к одномерному движению с некоторой осредненной
скоростью и учетом вязкого трения путем введения сил трения на границе
между поверхностью канала и жидкостью. Так как трудно априори
предсказать условия, при которых можно уверенно пренебречь вязкостью
жидкости, а также определить эффекты, которые теряются при переходе к
средней (по сечению) скорости движения, рассмотрим эти вопросы
подробнее.
34
1.7.2. Упрощение уравнений для длинных каналов. Вопрос об упрощении
уравнений движения жидкости целесообразно решать, используя уравнения
в безразмерны» переменных, приведенные в § 1.4. Обсудим один из
предельных случаев - длинные каналы, для которых соблюдается условие
L/R > 1. Из сопоставления отдельных членов уравнения A.4.2) следует,
что только один член с производной от давления имеет коэффициент
(L/RJ, значение которого намного превышает все остальные
коэффициенты. При этом следует учесть, что это отношение умножается на число
Эйлера Ей = р/ри2, которое должно быть больше единицы, так как
скоростной напор меньше полного давления. Для идеального газа величина Ей =
= 1/ (кМ2) в трактах ПГС существенно больше единицы. Так как все
остальные члены уравнения A.4.2) меньше члена с др/дг~, то ими можно
пренебречь. В результате уравнение движения для радиальной составляющей
скорости при соблюдении неравенства L/R > 1 сводится к условию
f =0; A.7.1)
Ъг
это свидетельствует о том, что в направлении поперек канала отсутствует
градиент давления и р = р(х, t).
В уравнении движения для продольной составляющей скорости A.4.1)
коэффициент L/R стоит перед членами в правой части — с производными
от скорости по радиусу. Остальные члены в скобках имеют коэффициент
R/L, и учитывая принятое условие, ими можно пренебречь. В итоге
проведенного упрощения выпадает уравнение A.4.2), и движение жидкости
в длинном канале определяется одним уравнением для продольной
составляющей скорости
Ъп Ъп _ Ъп Рх Eu Ъп
Sh -=- + м — + и — = — - —г —z +
bt Ъх Ъг Fr p Эл:
1 / L \/ Ъ2п \ Ъп\
+ — (— ) - + . A.7.2)
Re \ R ) \ ЪТ 2 Т ЪТ )
В уравнении неразрывности A.4.3) все члены, кроме первого, не имеют
коэффициентов в виде безразмерных параметров, т.е. все они одного
порядка и вид уравнения не зависит от условия R/L> 1. В уравнении
A.4.3) и уравнении движения A.7.2) остались члены, содержащие
поперечную составляющую скорости. Они имеют такой же порядок, как и
аналогичные члены для продольной составляющей, хотя из уравнения
A7.1) следует, что сама радиальная составляющая скорости v имеет
малую величину. Влияние членов с радиальной составляющей скорости
станет ясным, если обратить внимание на то, что в уравнениях остались
только члены сив виде производных по радиусу или при производных
по радиусу. Это указывает на то, что радиальная составляющая
скорости, несмотря на свою малость, имеет значение для обеспечения баланса
масс при перестройке профиля продольной скорости в данном сечении.
Это подтверждается тем фактом, что при переходе к осредненным
значениям продольной скорости (см. раздел 1.7.3) члены с поперечной
составляющей скорости из уравнений автоматически исключаются. Уравне-
3* 35
ние A.7.2) аналогично уравнению пограничного слоя в цилиндрических
координатах [242]. Такое сходство определяется использованием одного
и того же условия R/L>\ как при выводе уравнения A.7.2), так и
при выводе уравнений пограничного слоя.
Для анализа процессов, в которых существенны акустические
эффекты, удобнее выразить критерии Струхаля и Эйлера через число Маха
М = ио/ао и приведенное волновое сопротивление а - Роиоао/ро, учтя, что
характерное время в этом случае to = L/a0. Тогда найдем
Sh = L/uoto =ao/uo = 1/М,
Eu =po/p0uo =(polpouoao) (ao/uo)= 1/аМ.
После преобразования критериев уравнения A.7.2) и A.4.3) можно
записать следующим образом:
1 dp
— —z +
ар дх
A.7.3)
дп 1 d(Fv)
du
dt
+
Эр
dF
г +
м
Re
Мп
(L
\r
Ш
du
dx
-)(
dx
_i_
du
dF
1
F
dl
dT
PXM
Fr
du \
d-r Г
+ pM
дх F dF
=0. A.7.4)
Если воспользоваться другой формой записи уравнения неразрывности
A.4.10), отбросив в нем два последних члена (учитывающих диссипацию
и теплопроводность), получаем
dp dv dp Г du 1 d(Fv) 1
-г- +Мм —= +Mi7—- +ра —: +— —= =0. A.7.5)
Э^ dx dr I dx r dr J
Отличительной особенностью найденных безразмерных уравнений A.7.3)
и A.7.5) является то, что при нелинейных конвективных членах в этих
уравнениях роль коэффициента играет число Маха — величина очень малая
для течений капельной жидкости и малая для большинства течений газа в
элементах ПГС. В связи с этим уравнения движения можно существенно
упростить, отбросив эти малые, но очень неприятные с точки зрения
расчетов нелинейные конвективные члены. В итоге найдем новый вариант
уравнений гидромеханики для систем, в которых одновременно выполняются
условия R/L <\, М<\:
du I dp РХМ М
/ L \/ д2п 1 дп \
— 7 + ) = °> О-7-6)
\ R J\ dF2 F dF I
Ъп 1 / Ъ(ги) \\
— + т(-^—— ) =0. A.7.7)
дх г \ dr /-I
dt old dx Fr Re
Эр
—Г + P OL
dt
1.7.3. Уравнения для осредненной составляющей скорости (переход к
одномерному приближению). Во всех приведенных выше уравнениях
гидромеханики присутствуют две составляющие скорости, каждая из которых
зависит как от времени, так и от двух координат х и г, т.е. эти уравнения
описывают двумерное нестационарное движение жидкости. Для проточ-
36
ной части с изменяемым проходным сечением, а также для начальных
участков трактов с постоянным сечением возможна существенная
неодномерность течения. Для трактов же постоянного сечения большой
протяженности, а также в некоторых других случаях, о которых будет сказано ниже,
течение можно рассматривать как одномерное.
Для оценки влияния процессов, которыми приходится пренебрегать при
переходе к одномерному движению, введем осредненную скорость в
уравнениях движения и неразрывности. При этом используем упрощенные
уравнения A.7.3) и A.7.4) с учетом равенства A.7.1) и как следствие его
то, что р = р (х , I). Введем средние мгновенные значения скорости,
давления и плотности в сечении с координатой х:
U(x, 0= г J2nru(x, г, t)dr, A.7.8)
nR2 о
р(х, 0= г f2irrp(x, rf t)dr, A.7.9)
nR о
р(*,0= 7 f2nrp(x,r, t)dr. A.7.10)
nR о
Для наглядности имеет смысл перейти к размерным переменным: из
уравнений A.7.3) и A.7.4) получаем
Ъи Ъи Ъи 1 Ър v Ъ ( Ъи \
— + и— + и— =РХ- + (г— ] , A.7.11)
Ъг Ъх Ъг р Ъх г Ъг \ Ъг I
Ър Ър / Ъи 1 Ъ(ги) \
— +и — +ра2 — + — =0. A.7.12)
Ъг Ъх \ Ъх г Ъг I
Преобразуем уравнение движения A.7.11), умножив все его члены на
рг и сложив его с уравнением неразрывности A.7.12), которое
умножается на иг ив котором предварительно производные от давления р (с
помощью соотношения A.1.12)) заменяются на производные от плотности р.
В результате всех операций, учтя условие A.7.10), находим
Ъ(риг) Ъ(ри2г) Ъ(рииг) Ър Ъ I Ъи\
+ + =ргРх -г— +д— (г — ).
Ъг Ъх Ъг Ъх Ъг\ Ъг ]
Умножая все члены найденного уравнения на 2/R2 и интегрируя его по
радиусу г, учтя условия A.7.1) и A.7.10), найдем
2 Ъ R 2 Ъ я
~ — (р / urdr) + — — (р / u2rdr) +
R Ъг о Rz Ъх о
+ —.
R2
(rpuv)
r Ър 2ц. I Ъи \ \r
= рРх ~ 1Г + 7 Г\Т ) ' A.7.13)
Ъх R2 \Ъг/\о
Используя закон Ньютона A.2.1), а также то, что из условий симметрии
течения жидкости в цилиндрическом канале на оси соблюдается
соотношение Ъи/Ъг = 0 и из условий прилипания и(х, R, г) = v(x, R, г) = 0,
убеждаемся, что в левой части уравнения A.7.13) исчезает последний член (вер-
37
нее — соответствующие ему два члена), а вместо производной в последнем
члене правой части появится напряжение трения на стенки трубы т(х, R, t) =
= tw(x, t). В уравнении A.7.13), кроме введенной средней мгновенной
скорости, появился дополнительный интеграл с квадратом скорости. Это
обстоятельство делает необходимым введение еще одной средней
величины — средней квадратической скорости
/ 1 r \%
u(x,t) = (—- f27ir2it2dr) . A.7.14)
\ uRl о '
Использование двух средних скоростей в одном уравнении явно неудобно,
поэтому, следуя принятому методу [234], вместо второй скорости введем
поправочный коэффициент — корректив количества движения,
учитывающий отличие средней скорости от среднеквадратической1)
ii2 =yU\ A.7.15)
где
Определение A.7.15) и закон Ньютона A.2.1) позволяют из
зависимости A.7.13) получить окончательную форму уравнения движения для
мгновенной средней скорости движения
2 Эт Эр 2т
^+7^ +pUpPx9 A/М6)
dt Ъх Ъх Ъх R
где tw(x, О = — ii(du/dr) — мгновенное значение напряжения трения на
стенке канала.
Для стационарного ламинарного течения в трубе [152] у = 1,3, тн, =
4ц11 pU2
= , а для турбулентного течения: 7^1, tw = X , где X = X(Re) -
R 8
коэффициент сопротивления трения на единицу длины трубы2).
Профиль скорости и соответственно напряжение трения на стенке
нестационарного потока заметно отличаются от соответствующих
характеристик стационарного течения (см. § 6.2 и раздел 6.4.3, а также работы
[22, 27, 60, 64, 91, 184]). Следствием этого отличия является зависимость
значений у и rw от частоты колебаний или градиента изменения параметров
потока и предыстории развития их во времени. В некоторых случаях — при
низких частотах колебаний или незначительном градиенте изменения
параметров потока — профиля скорости мало отличаются от стационарных,
и тогда можно использовать квазистационарное приближение, т.е. в
уравнение нестационарного движения A.7.16) подставить значения ) и тн, для
стационарного потока со средней скоростью, равной ее мгновенному
значению.
*) В книге И.А. Чарного [234] вводится не поправочный коэффициент у, а
коэффициент /3 = 7- 1 •
2) Чтобы исключить путаницу, коэффициент теплопроводности (см. формулу
A.2.2)), обозначаемый также буквой \, имеет индекс "т".
38
Однако при достаточно высоких значениях частот колебаний или
большом градиенте изменения параметров во времени квазистационарное
приближение, как будет показано ниже, не дает достоверных данных о
значениях напряжения трения, а значит, и диссипации энергии в потоке
жидкости. Для получения достаточно точных моделей нестационарного течения
необходимо учитывать зависимость напряжения трения или другой
эквивалентной характеристики от частоты или градиента изменения параметров
во времени. Уравнение движения для средних мгновенных скоростей
A.7.16) можно сделать более удобным для анализа, если выразить ru. через
скоростной напор. Для цилиндрической трубы [234] тн. = (X/S)pU2 и
соответственно изменяется форма записи уравнения A.7.16):
Ър1/ Ъ(урЦ2) Ър X
— + — = рРх- —- — pU\ A.7.17)
bt Ъх ' Ъх AR
Здесь уже коэффициент сопротивления трения \(х, t) будет зависеть от
особенностей динамики движения жидкости. Для перехода к средней
скорости движения в уравнении неразрывности A.7.12) умножим все члены
этого уравнения на 2r/R2 и проинтегрируем по г\ учтя условия A.7.1),
A.7.9) и A.7.10), имеем
Эр 2 Эр * ., Г 2 * Эй 2
— + — — / rudr + pa2 — / г — dr + —- (vr)
dt R2 Ъх о I R2 о Эл: R2
= 0.
Используя определение A.7.8), учтя условие прилипания v(x, R, t) = 0 и
вынося знак производной Ъ/Ъх за интеграл, получаем
Эр Эр 0 bU
— +U— +ра2 — =0. A.7.18)
bt Ъх дх
Если не использовать связь между р и р для адиабатического течения
A.2.12), то уравнение неразрывности сохранит исходную форму
Эр dpU
— + — =0. A.7.19)
ot Ъх
Для того чтобы вернуться в уравнении движения A.7.17) к записи,
близкой к первоначальной форме, вычтем из уравнения A.7.17) уравнение
A.7.19), предварительно умножив его на U. После преобразований находим
Ъи Ъи (т-1) Ъри , Ъу 1 Эр X
— +7*/— + -U-— +f/2 — =РХ- - — U\U\.
ot Ъх р Ъх Ъх р Ъх 4R
A.7.20)
Уравнение для осредненных мгновенных значений продольной
составляющей скорости A.7.20) отличается от исходного уравнения A.7.11) для
двумерного нестационарного движения вязкой жидкости в канале с
характерными размерами R/L < 1 тем, что в левой части исчез конвективный
^ен с радиальной составляющей скорости и, но появились дополнительный
коэффициент у при конвективном члене с продольной скоростью U и два
дополнительных члена, характеризующих (так же как и коэффициент у
перед конвективным членом) влияние перестройки формы профиля ско-
39
роста на нестационарное движение жидкости. В правой части член со второй
производной от скорости и коэффициентом вязкости заменен на
нелинейный квадратичный член, учитывающий вязкое трение с коэффициентом
потерь X.
С целью сопоставления влияния отдельных членов уравнений A.7.18) и
A.7.20) преобразуем их к безразмерной форме. Обозначим безразмерные
параметры так же, как и раньше, в том числе и безразмерную осредненную
скорость п = U/и0, а в качестве характерного времени примем t0 = L/a.
Используя принятую форму записи для потерь давления на трение в трубах
[234] (с учетом возможного изменения направления движения жидкости)
Аро = Ao(?/4K)po^o I w01 и вводя относительную величину коэффициента
потерь X = Х/Хо, перепишем уравнение A.7.20) в безразмерных параметрах:
Ъп _ Ъп п Ърп ду
— +Муи — +МG1) +M2
Ъг Ъ
уи МG1)т Mw
Ъг Ъх р Ъх Ъх
М _. 1 Эр X Ар0
= ТГ рх - —: — и\и\. A.7.21)
Fr ар ох а ро
Аналогично для уравнения неразрывности A.7.18)
Ър Ър Ъп
—- +Mw — + ар — =0. A.7.22)
ot ox дх
В уравнениях A.7.21) и A.7.22) одномерного приближения влияние
отдельных членов определяется значениями безразмерных параметров М,
М-, а и Аро/ро.
Рассмотрим несколько возможных вариантов условий в трактах ПГС,
которые позволяют упростить исходную систему уравнений. Для трактов
с течением слабо сжимаемой капельной жидкости, а также для
подавляющего большинства случаев течений в газовых трактах выполняется условие
М < 1, что позволяет в уравнениях A.7.21) и A.7.22) отбросить все
конвективные члены. В итоге уравнения принимают следующую форму:
дп 1 Ър М _ X ро
-=¦ + — — - — Лс+ п\п\ =0, A.7.23)
Эг ар Ъх Fr а р0
Ър _ Ъп
~=г +ар -г =0. A.7.24)
Эг Эл:
Если единственной массовой силой, действующей на жидкость, является
сила тяжести, то Рх = -g{bzjbx) [234], где z - координата данного
сечения (ось z направлена вертикально вверх). Если подставить в зависимость
A.7.23) (а также и во все другие аналогичные уравнения, приведенные
выше) соотношение для РХ9 то вместо двух членов — градиента давления
Ър/Ъх и массовых сил Рх — останется один член с градиентом приведенного
давления pn=p + pgz.
Можно показать [234], что и уравнение неразрывности не изменяет
своей формы при переходе к приведенному давлению. Поэтому при
действии только сил тяжести в уравнениях гидромеханики пользуются
приведенным давлением, а член с Рх отбрасывают. При этом не имеет смысла
40
вводить новое обозначение для давления, сохранив обозначение р. В
дальнейшем, кроме специально оговоренных случаев, будем считать, что
действует единственная массовая сила - сила тяжести, а в уравнения входит
приведенное давление р, член же Рх = 0.
Уравнения A.7.23) и A.7.24) упрощаются в случае капельной жидкости,
для которого можно принять р~ ~ 1:
др дп ро
-— =а— +Л и\и\, A.7.25)
дх dt р0
др дп
-- =а— . A.7.26)
dt дх
Систему уравнений A.7.23) - A.7.24) для идеального газа можно
упростить. Уравнение состояния в безразмерных переменных (приЯ = const)
примет вид
р=р/Т. A.7.27)
Подставив р из соотношения A.7.27) в уравнения A.7.23) и A.7.24),
имеем
Э \пр 1 / дп - Ар0 \
= -=¦( а — +\ м |м I 1, A.7.28)
Т \ dt po I
дх
д In p а дп
Э7 f дх
A.7.29)
Уравнения A.7.28) и A.7.29) для изотермического течения газа при Т = 1
совпадают с уравнениями A.7.25) —A.7.26) для капельной жидкости,
только в них вместо давления р подставляется In p . При неизотермическом
течении в уравнениях появляются переменные параметры Г и а.
Дальнейшее упрощение уравнений возможно, если обратить внимание
на то, что в уравнении A.7.25) перед первым членом в правой части,
характеризующим инерцию жидкости, находится безразмерное волновое
сопротивление а. Для идеального газа а = Роаоио/ро = кМ, а при течении
газа в длинных трубопроводах всегда М < 1, и поэтому инерционным
членом в уравнении A.7.25) можно пренебречь. Возможен такой случай и в
трактах с капельной жидкостью, если скорость движения и0 мала, а
давление велико, что приводит к условию а < 1.
Для капельной жидкости возможен и другой вариант, когда величину
градиента давления при движении в длинном тракте будут определять
только потери на трение, т.е. Аро/роа = Аро/Ро"о^о > 1, которые
превышают рост давления за счет мгновенного торможения жидкости по формуле
Н.Е. Жуковского [95] Ар - pqUquq. Поэтому в уравнении A.7.25) можно
пренебречь инерционным членом. В итоге получаем следующую ступень
упрощения уравнений:
1 др _ Ар0
"^ — + X и\и\ =0, A.7.30)
Р дх Ро
др _ дп
W+«P-=0. A.7.31)
41
В отличие от всех приведенных выше уравнений гиперболического типа,
система уравнений A.7.30) — A.7.31) является системой параболического
типа [215].
Уравнения A.7.17), A.7.20), A.7.21), в которые входат корректив
количества движения у, являются зависимостями для количества движения
и не характеризуют влияния изменения у на энергию потока. Если не
учитывать влияния на температуру жидкости потерь энергии из-за вязкого
трения, то можно воспользоваться исходным уравнением движения для
длинного тракта A.7.2), считая жидкость малосжимаемой (см. следующий
раздел) и пренебрегая влиянием массовых сил, т.е. принимая Ъп /Ъх -
= Ъ\У/Ъ7 = Рх = 0. Возвращаясь к размерным переменным, умножая все
члены получившегося уравнения на 2ттги и интегрируя по радиусу,
находим
R ( и \Ър R Ъ / Ъи\
f 27irl—)— dr-vf 2nru - [г— }dr = 0.
\ р / Ъх о Ъг \ Ъг I
13 „
/ 2>nru2dr f
2 Зг о о \ р /
Разделив все члены полученного уравнения на ttR2, учтя при этом
соотношения A.7.1), A.7.14) и A.7.15), проинтегрировав последний интеграл
по частям, получим
Э / U2\ U2 dy
bt\ 2 I 2 dt
ди
Ъг
\2
1
и
Р
nR2 о \ Ъг ) p дх
Ър
. A.7.32)
д
Преобразуя последний интеграл, учитываем, что при г = R и = 0.
Последний член в уравнении A.7.32), как известно [152], описывает
диссипацию энергии потока за счет вязкого трения. Уравнение A.7.32)
определяет баланс энергии в нестационарном потоке жидкости в тракте: работа
сил давления расходуется на изменение кинетической энергии жидкости,
на перестройку профиля скорости (т.е. изменение параметра 7) и на
диссипацию энергии за счет работы сил вязкого трения в жидкости. Можно
привести уравнение A.7.32) к другой форме, если исключить из него член с
градиентом давления, используя для этого зависимость A.7.16).
Предварительно (так же как и при выводе уравнения A.7.32)) исключим из него
конвективные члены и массовые силы Ъ(ри)/Ъх = Ъу/Ъх =РХ = 0, считая
р % const:
Ъ ( U2\ U2 dy 2Urw v R / Ъи\2
(у _ 1) - — + — — = - — / 2тгг — dr. A.7.33)
bt \ 2 / 2 dt pR nR2 о \Ъг /
Из уравнения A.7.33) следует, что в нестационарном потоке работа сил
вязкого трения не равна диссипации энергии. Разность между работой сил
вязкого трения и диссипацией энергии идет на изменение кинетической
энергии потока, связанной с изменением во времени профиля скорости,
т.е. параметра у. Однако, если принять, что скорость изменяется по
гармоническому закону и проинтегрировать уравнение A.7.33) за один период
колебаний, то левая часть обратится в нуль и интеграл от диссипации
энергии будет равен работе, совершаемой силами вязкого трения за период.
Отсюда следует, что деформация профиля за период колебаний не приводит
к диссипативным потерям в потоке.
42
1.7.4. Пренебрежение вязкостью жидкости. Для турбулентного движения
жидкости (а этот режим течения является превалирующим для проточных
частей ПГС) при нестационарных течениях вязкость, в основном,
сказывается на потери давления. Действительно, коэффициент у, учитывающий
профиль скорости, для турбулентного режима очень близок к единице, и
нет оснований полагать, что он существенно изменяется при
нестационарном движении. Поэтому в уравнении A.7.21) можно принять у ъ 1. В этом
случае единственным членом, который зависит от вязкости, в уравнении
A.7.21) остается последний член правой части, в который входит
множитель Аро/ро. Вспомнив связь Ар0 = Xo(L/4R)poUo и учитывая
соотношение A.2.10), найдем для идеального газа Аро/ро = \o(LI4R)(pouo/po) =
\(L/2R)kM2
Для развитого турбулентного течения коэффициент потерь X имеет
величину порядка 0,02-^-0,03 [152], и при небольшой относительной длине
тракта L/D ~ 1 - Ю2 иМ^1 членом, учитывающим потери на вязкое
трение, в уравнении движения можно пренебречь. Однако в некоторых
случаях в трактах (имеющих небольшую относительную длину) с протоком
газа хотя и выполняется условие М< 1, но значение этого параметра
оказывается не столь малым (например, равным 0,2-^0,3), чтобы можно было
пренебречь в уравнениях A.7.21) и A.7.22) членами, содержащими М.
Поэтому для каналов, в которых не выполняется условие L/R > 1,
целесообразно в общем случае сохранить конвективные члены порядка М. Кроме
того, при отказе от условия L/R > 1 становится неправомерным его
следствие — предположение о возможности пренебречь другими составляющими
скорости, кроме продольной. Действительно, для канала cL/R ~1 заранее,
не разбираясь в характере граничных условий, нельзя каким-либо
образом определить, какая составляющая скорости в потоке является
преобладающей. В связи с этим для каналов простой формы с небольшой
относительной длиной целесообразно при первом рассмотрении записывать
уравнения движения для всех координат, пренебрегая при этом вязкими
членами. Оговорка о простоте формы канала связана с тем, что в
каналах с поворотами, выступами и т.д. возникают отрывы потока,
непосредственно связанные с влиянием вязкости жидкости. Естественно, что
для таких задач использование модели невязкой жидкости не дает
удовлетворительного решения.
§ 1.8. Условия, при соблюдении которых
жидкость можно считать несжимаемой
Несжимаемость - одно из достаточно часто используемых предположений,
обеспечивающее существенное упрощение математических моделей
движения жидкости. Однако, как это станет ясным из более подробного анализа,
вопрос о том, можно или нельзя считать жидкость несжимаемой, является
не столь тривиальным, как это кажется с первого взгляда. Например, в
некоторых случаях газ можно рассматривать как несжимаемую жидкость,
а в других является принципиальным учет сжимаемости внешне
практически несжимаемой капельной жидкости. Выяснение условий, при выполнении
которых жидкость можно считать несжимаемой, начнем с наиболее просто-
43
го случая — одномерного течения невязкой жидкости. Влияние же вязкого
трения и теплопроводности на изменение плотности будет рассмотрено
несколько позже. Несжимаемая жидкость - это рабочая среда, для которой
можно пренебречь изменением плотности под влиянием изменений условий
в потоке. Из постоянства плотности следует, что первые члены уравнения
неразрывности A.7.19) обращаются в нуль (для одномерного течения О):
Эр Эр
г+«7 "а A-8л)
bt Ъх
Каждый термодинамический параметр однородной жидкости можно
выразить через два других независимых параметра. Выбрав в качестве этих
параметров плотность и энтропию единицы массы жидкости, запишем для
отклонения давления
dp =| J dp +1 — I ds =a2dp + ( — j ds. A.8.2)
\Ър Js \ Э5 Jp \ Э5 }p
Исключив из соотношений A.8.1) и A.8.2) плотность, найдем [30]
1 / Эр Эр \__2_ 1^1 \ lbs . bs\
I ра2\Ъ5/р
Как ив § 1.4, переходя к безразмерным переменным, запишем для первых
двух членов соотношения A.8.3) условие несжимаемости в виде
неравенства, предварительно исключив с помощью уравнения движения A.7.17)
производную Эр/Эх, считая 7^1, Р % const, X % 0 и пренебрегая пока
влиянием двух последних членов зависимости A.8.3) :
ShM Эр Эг7 „ Ъп М2 _
-ShM2u — -Ы2и2 —: -— пРх<\. A.8.4)
а Эг Ы Ъх Fr
Неравенство A.8.4) эквивалентно первым двум членам равенства A.8.3),
но оно удобнее для анализа. Для выполнения неравенства A.8.4) в общем
случае необходимо, чтобы каждый член безразмерного уравнения A.8.4)
был много меньше единицы во всех точках потока. Опенка первого члена
неравенства A.8.4) оказывается нагляднее, если рассматривать
колебательные процессы с круговой частотой со. Для этого случая произведем замену
<^о = 1/^о> тогда
\
( +w )[ ) ( +wUo. A.8.3)
pa2 \bt Ъх ) pa2 \ bs lp \Ъг Ъх)
L Lcoo _ / co0L \ / а0 \ со
Sh - - - ( 1 ( — - —
uoto и0 \ а0 /\и0 1 М
Безразмерная частота со определяет существенность вклада
акустических эффектов, т.е. влияние распространения звуковых колебаний. Если
со ~ 1, то длина волны акустических колебаний соизмерима с длиной
канала L. При этом амплитуды колебаний давления и скорости существенно
изменяются по длине канала, и течение должно рассматриваться как
система с распределенными параметрами (см. гл. 5). Пренебрегать
акустическими эффектами, т.е. рассматривать поток как систему с сосредоточенными
1) Ниже, где это не вызовет путаницы, скорость одномерного движения будет
обозначаться и вместо U.
44
параметрами, можно, если выполняется условие со < 1. Однако это
необходимое, но не достаточное условие для того, чтобы можно было
пренебречь первым членом неравенства A.8.4), так как он содержит (в
знаменателе) приведенное волновое сопротивление а.
Для оценки величины а преобразуем формулу:
PqUqL п
A.8.5)
V
Рс LPc Рс
где tq = Lpclpoaluo, ти = pouoL/pc — две величины, имеющие размерность
времени. Для определения физического смысла этих постоянных времени
рассмотрим два варианта течения в цилиндрическом канале длиной L и
площадью сечения F:
а) Течение несжимаемой невязкой жидкости. Уравнение движения
столба такой жидкости можно составить, воспользовавшись законом
Ньютона F(p0 — Pi) = m(du/dt), где m- pLF — масса жидкости в канале,
и — скорость, Ро, Р\ — давление на входе и выходе канала. Переходя к
безразмерным переменным, найдем:
pLun d~u ти dif
Po~Pi= -=-=—-=- . A.8.6)
pct0 dt t0 dt
При выводе уравнения движения A.8.6) учитывалось только одно свойство
жидкости - ее инерции. Поэтому ти - инерционная постоянная времени
столба жидкости.
б) Течение сжимаемой невязкой жидкости без учета ее инерции.
Пренебрежение инерцией невязкой жидкости определяет условие др/дх = О,
которое заменяет уравнение движения. Уравнение неразрывности, когда не надо
учитывать распределенность параметров (так как выполняется условие
со<1), можно записать: dm/dt = Go - G\. Учтя, что m = pVпри объеме
V = LF = const, и вспомнив соотношение Эр/Эр -а2, последнее уравнение
преобразуем к следующему виду: (LF/a2)(dp/dt) = Go - Gb где Go, G\ —
расходы на входе и выходе канала. Переходя к безразмерным переменным,
получим
Lp0 dp _ _
G-G1, A.8.7)
r GcG1,
dt
где Gc = puoF — масштабный расход.
В уравнение A.8.7) входит постоянная времени те = Lpc/pa2u0, которая
(по принятым при выводе уравнения A.8.7) предположениям) определяет
влияние только сжимаемости жидкости, т.е. работу канала как емкости.
Поэтому те называют емкостной постоянной времени. Таким образом,
приведенное волновое сопротивление а определяет соотношение между
инерционной и емкостной постоянными времени канала (система с
сосредоточенными параметрами). Для того чтобы можно было не учитывать
первый член в неравенстве A.8.4), кроме условия со<^1, необходимо
соблюдение условия 1/а = \/те/тИ<: 1. Если те>ти, то последнее условие
не выполняется. Например, для идеального газа а = риоа/рс = кМ, и если
соблюдается неравенство М < 1, то условие 1/а < 1 не выполняется. Чтобы
получить более четкое представление об ограничении для первого члена
45
неравенства A.8.4), преобразуем коэффициент при этом члене: со/а =
= (cjL/a)(pc/pau0)=pcLoolpu0a2 =reoo.
Таким образом, кроме условия оЗ<^ 1, при оценке первого члена
необходимо учитывать условие гесо < 1. Последнее неравенство определяет
возможность пренебрежения для проточного тракта его свойствами как
емкости. Для идеального газа те = L/ku0, т.е. - емкостная постоянная времени
канала равна времени пребывания газа в канале Ljuо, деленному на
показатель адиабаты к. Все эти рассуждения относились к проточному каналу.
Для тупикового канала (емкости) без протока емкостную постоянную
времени можно определить по формуле те =V/a2Gc, где V — объем емкости.
Gc — масштабный расход жидкости в проточном тракте, к которому
присоединена емкость.
Второй член в неравенстве A.8.4) имеет коэффициент ShM2, который
для колебательных процессов, когда Sh = со/М, равен соМ. При соблюдении
условия оЗ < 1 этим членом можно пренебречь, если М < 1. При
ограничении на число Маха М2 <^ 1 можно пренебречь следующим, третьим членом
неравенства.
Для капельной жидкости последнее условие выполняется практически
во всех реальных течениях, для потока газа это достаточно существенное
ограничение, из которого следует, что, к примеру, при температуре
окружающей среды воздух можно рассматривать как несжимаемую жидкость
(если выполняются одновременно и другие условия) при скоростях
и0 < 100 м/с.
Коэффициент при последнем члене неравенства A.8.4) можно записать
в следующем виде: M2/Fr ~ PxL/a2. Он характеризует относительное
влияние массовых сил на плотность жидкости, столб которой имеет длину L.
Массовые силы наиболее существенно сказываются на плотности газа,
поэтому, подставив выражение скорости звука для идеального газа и
заменяя Рх ускорением силы тяжести g, найдем M2/Fr = pgL/kp. Таким
образом, влиянием массовых сил на плотность газа можно пренебречь,
если в системе выполняется неравенство pgL/kp <^ 1. Числитель этого
отношения характеризует изменения давления (а значит и плотности) в
вертикальном направлении в столбе газа высотой L, а само отношение
определяет ту долю давления/?, которую составляет разность давлений в
двух сечениях, расположенных на расстоянии L. Это отношение определяет
относительное изменение плотности газа в рассматриваемой системе.
Выполнение неравенства свидетельствует о том, что изменением плотности
из-за влияния массовых сил можно пренебречь, а газ с этой точки зрения
можно считать несжимаемым.
Резюмируя все сказанное, констатируем, что жидкость можно считать
несжимаемой, если одновременно выполняются неравенства
со = oil/a < 1, core = copcL/pa2 ы0 < 1,
М2 =(ио/аJ<1, gL/a2<L A.8.8)
В заключение остановимся на второй части зависимости A.8.3),
связывающей отклонение плотности с изменением энтропии жидкости. При
выводе уравнения A.8.4) пренебрегали изменением плотности из-за
вязкого трения и теплопроводности. Так же как это было сделано с первыми
членами уравнения A.8.3), преобразуем к безразмерному виду вторую
46
часть этого уравнения, учтя при этом, что ср = T(ds/dT), а2 = (bp/dp)s,
|3= - A/р)(Эр/ЭГ)р [46]. Используя эти соотношения, найдем
коэффициент при двух последних членах уравнения A.8.3) :
pa2
/JzL\= __L '_^_\ / Эр
\ ds ) ~ pa2\bp /Дэ7
/ЗГ
р (bs/dT)p Ср '
Приводя к безразмерному виду последние члены уравнения A.8.3), найдем
условие несжимаемости
/ЗГ Sh——+ п—г )< 1. A.8.9)
\ bt Ъх I
Для газа. /3 = 1/Г, т.е. /ЗГ = 1, для жидкости же C< 1. В частности, для
воды при температуре 20 °С /3 % 0,2 • 10~31/град. Таким образом, как
правило, &Т< 1, и для большинства задач динамики ПГС условие A.8.9)
выполняется. Это можно показать, воспользовавшись уравнением A.4.8),
правая часть которого определяет изменения энтропии под влиянием сил
вязкого трения и теплопроводности. Из первого члена правой части
уравнения A.4.8) с учетом зависимости A.8.9) можно выразить условие
несжимаемости. _Умножая обе части уравнения A.4.8) на /ЗГи учитывая, что
функция Ф определяется зависимостью A.4.11), определяющую роль в
которой играет первый 4neux[(L/R)(biTld7)]2, получим следующее условие
несжимаемости:
PulR/cpLRe<l. A.8.10)
Теперь и второй член в правой части уравнения A.4.8) содержит множитель
/ЗГ, в котором после сокращения Т остается масштабная величина То. Для
теплопередачи, определяемой этим членом, характерной величиной
является не Го, а перепад температур АГ0. Учитывая это замечание, запишем
неравенство, при выполнении которого жидкость можно считать
несжимаемой:
/ЗАГо /ЗАГо РктАТ0
= = — <1. A.8.11)
Ре Re?r(L/R) Lu0
Так как для газа 0 = 1/Г, Рг « 1 и комплекс /ЗАГо = $иЦср = иЦср Т =
~ (к — 1)М2, то неравенство A.8.11) принимает следующий вид:
(fc-l)M2
< 1.
Re (L/R)
Для газа уже было использовано условие М2 < 1, для жидкости, учитывая
малость коэффициента j3 и ограниченность реальных скоростей движения
жидкости м0, можно утверждать, что соблюдается условие РиЦср< 1.
Кроме того, для подавляющего большинства напорных течений, которые
в основном и представляют интерес при анализе процессов в ПГС,
выполняется условие Re > 1, длина же канала в калибрах для разных ПГС варьиру-
47
ется в очень широких пределах. К примеру, для магистральных газо- и
нефтепроводов значение L/R может быть столь большим, что неравенство
A.8.10) может не выполняться, т.е. изменением плотности за счет работы
силы трения нельзя пренебрегать. Но в этом случае не должно выполняться
также другое неравенство, определяющее условие несжимаемости со =
= coL/a < 1, так как для таких длин нельзя пренебрегать акустическими
эффектами. При этом следует отметить, что изменение плотности жидкости
за счет работы сил трения в основном происходит из-за падения давления,
так как изменение температуры компенсируется в магистральных
трубопроводах теплообменом с внешней средой из-за большой поверхности
контакта жидкости со стенками трубопровода. Эти рассуждения
показывают, что невыполнение неравенства A.8.10) маловероятно при соблюдении
неравенств A.8.8). Столь же маловероятно невыполнение и неравенства
A.8.11), так как при L/R < 1, A< 1 или Re > 1, Рг — \,L/R> 1 необходим
очень большой перепад температуры в системе А Го, чтобы нарушить
неравенство.
Неравенство A.8.11) нарушается при очень малых значениях LuOi т.е.
при очень малой скорости и0 и малом размере L и одновременно большом
перепаде температуры АГ0. Такое сочетание параметров является редким
для агрегатов и устройств, используемых в ПГС.
Таким образом, в большинстве случаев изменением плотности из-за
работы сил трения и теплопроводности в жидкости можно пренебречь,
а основным условием, при котором жидкость можно считать несжимаемой,
является выполнение неравенств A.8.8).
§ 1.9. Математические модели идеализированных элементов
ПГС с со средоченными параметрами
Приведенные выше уравнения гидромеханики (включая и упрощенные
их варианты) имеют достаточно сложную структуру, и их решение
вызывает определенные трудности. С другой стороны, в ряде случаев условия
решаемой задачи и характер течения в отдельных технических устройствах
или естественных образованиях позволяют использовать более простые
модели течения. В этом случае процессы моделируются элементами с
сосредоточенными параметрами. При идеализации для каждого элемента
выделяется и соответственно учитывается только один определяющий
эффект (например, инерция жидкости или ее сжимаемость, или влияние
вязкости), а все остальные свойства среды не учитываются, как
второстепенные. Естественно, что для многих процессов такая идеализация может
оказаться недостаточно обоснованной, так как не охватывает все основные
особенности процесса. Однако идеализированные исходные элементы,
математические модели которых учитывают только какое-то одно свойство
жидкости, позволяют описывать разные процессы путем комбинирования
из этих простейших элементов более сложных схем (цепей). Примеры
формирования таких моделей будут даны в гл. 2.
1.9.1. Инерционность. Рассмотрим нестационарное течение несжимаемой
идеальной жидкости в канале цилиндрической формы. Воспользуемся
уравнениями одномерного движения жидкости A.7.23) и A.7.24), в
которых изменим только масштаб времени, подставив вместо масштаба Lja
48
масштаб t0. В результате эти уравнения принимают следующую форму:
т., дп 1 Эр Рх 1\ро
----- +— —--——+Х и|и| = 0, A.9.1)
t0 dt р дх FrEu ро
Тр др дп
~^--=г + р —= 0, A.9.2)
Го ЭГ Эх
где ти = poUoL/po, те = Ро/Ро"оЯ2 — инерционная и емкостная постоянные
времени для цилиндрического канала длиной L. При принятых
предположениях р = 1,Ар0 =те=0 уравнение неразрывности A.9.2) сводится
к условию Эй/Эх = 0, а из уравнения движения A.9.1) (после перехода к
размерным координатам) получаем зависимость, описывающую
нестационарное течение
ди 1 др
= Рх . A.9.3)
dt p дх
Если массовая сила Рх не зависит от координаты х, то проинтегрировав
уравнение A.9.3) по длине канала, находим
ди
pL—= pLPx-(p1 -pol A.9.4)
ot
где L — длина канала, Ро, Р\ — давление в начале и конце тракта. При
интегрировании уравнения A.9.3) мы учли, что скорость жидкости не зависит от
координаты сечения х. Для труб удобнее использовать в качестве
переменной не скорость, а массовый расход жидкости G = puF, где/7—площадь
проходного сечения трубы. В этом случае соотношение A.9.4) преобразуется
к следующему виду:
L dG
= pLPx + Ар, A.9.5)
F dt
где Ар = ро - pi - перепад давления.
При выводе уравнения A.9.2) предполагалось,что стенки трубы жесткие.
Уравнение A.9.2) при Рх = 0 совпадает (если использовать безразмерные
переменные) с ранее полученным другим способом (из закона Ньютона)
соотношением A.8.6) для движения столба несжимаемой невязкой
жидкости. При записи уравнений гидромеханики в форме соотношения A.9.4) или
A.9.5) учитьюается только инерция жидкости, и поэтому соответствующий
элемент будем называть "инерционность", по аналогии с принятым в
электротехнике названием "индуктивность*'. Коэффициент L/F перед
производной от расхода в A.9.5) иногда называют приведенной массой.
Когда тракт имеет не цилиндрическую форму, но изменение сечения
вдоль оси тракта невелико, т.е. зависимость F = F(x) — достаточно плавная,
можно считать, что v « 0, а это значит, что и ди/дх ~- dF(x)/dx « 0. Перехо-
Дя в уравнении A.9.3) от скорости к массовому расходу, интегрируя
массовую зависимость по х, учтя при этом, что F= F (х) , получаем
dG L ^х
' / = PLPX + Ар. A.9.6)
(it Т^(\"\
4 Б.ф. Гликман 49
Для тракта, состоящего из ряда участков труб цилиндрической формы
разного диаметра, из условия, что перепады Apt для каждого /-го из п
участков тракта (через которые в каждый момент времени течет один и
п
тот же расход жидкости) суммируются: Ар? = 2 Ари находим
п Li\dG n
^ -=г) — =Р 2 Lfxi + Apz, A.9.7)
= 1 Ft / dt /=i
где Liy Fj — длина и площадь проходного сечения г-го участка тракта,
PXi — составляющая массовых сил, действующая на жидкость вдоль оси
z-го участка тракта. В уравнениях, приведенных выше, не учитывались
потери давления на трение, распределенные по длине участков труб, и
местные потери на участках стыковки труб разного сечения, так как
жидкость принималась невязкой. В действительности такие потери давления
должны быть, их можно учесть, как будет показано в разделе 1.9.2 и в гл .2.
1.9.2. Сопротивление. Рассмотрим нестационарное одномерное течение
несжимаемой вязкой жидкости в тракте, пренебрегая ее инерцией. Тогда
в уравнениях A.9.1) и A.9.2) надо принять ти = 7е = 0, р = 1. При этом
уравнение неразрывности опять сводится к условию Ьп/дх = 0, а уравнение
движения A.9.1) в размерных переменных принимает следующий вид:
± =0. A.9.8)
рРх ри0.
Эх AR
Проинтегрировав уравнение A.9.8) по длине трубы, предполагая при
этом, что массовая сила Рх не зависит от координаты х, получаем
XL
Ар= ри2 - pLPx. A.9.9)
AR
Если в качестве переменной использовать расход жидкости, то уравнение
A.9.9) принимает другую форму:
XL G2
A
Коэффициент сопротивления X, как уже отмечалось, для
нестационарного течения определяется не только числом Рейнольдса, но и
характеристиками нестационарности: частотой или видом зависимости скорости от
времени. Подробнее этот вопрос будет рассматриваться ниже (см. гл. 5). Для
стационарного режима турбулентного течения коэффициент сопротивления
X ~ Re ' , для ламинарного X ~ Re. Если местное сопротивление
создается тонкими (капиллярными) трубками, в которых обеспечивается
ламинарный режим течения [97], потери давления пропорциональны не
квадрату скорости, а линейно зависят от параметров течения. Если площадь
проходного сечения тракта плавно изменяется, то аналогично формуле
A.9.6), с учетом тех же предположений, имеем
G2 l \(x)dx
Ар=— Г } -pLPXi A.9.11)
8р о 5(x)F2(x)
где 5 (х) = F(x)/U (x) - гидравлический радиус сечения тракта, It (x) -
смоченный периметр тракта.
50
Кроме потерь давления на вязкое трение, распределенных по длине
трубы, в трактах всегда имеются потери давления на местных
сопротивлениях при изменении проходного сечения (диафрагмы, регулирующие
устройства, резкий переход с одного проходного сечения к другому), в
изгибах труб, в выравнивающих поток устройствах и т.д. При этом течение
в местных сопротивлениях имеет очень сложный характер (отрывы потока,
обратные токи и т.д.) и не поддается более или менее строгому описанию
в рамках гидромеханики [30]. Подробнее этот вопрос рассматривается
в гл. 2.
1.9.3. Проточная емкость. Рассмотрим участок тракта, где сжимаемая
жидкость течет с относительно малой скоростью, при которой можно
пренебречь как потерями давления на трение, так и инерцией столба
жидкости, а также массовыми силами. На входе в тракт подается жидкость с
постоянными температурой и составом. Тогда Аро/ро = ти =РХ = 0,
уравнение движения A.9.1) переходит в условие Ър1Ъх = 0, т.е. исключается.
Уравнение неразрывности A.9.2) сохраняется, но применительно к задаче
о проточной емкости с постоянной температурой (составом) жидкости
условие др/дх= 0 приводит к равенству Ьр/дх = 0. Уравнение A.9.2)
записывается в следующей форме:
те Эр Эры
—-^- + —=0. A.9.12)
t0 dt дх
Если считать_ площадь тракта постоянной, то в безразмерных параметрах
р w~= G, где G = G/Gc - безразмерный массовый расход. Учтя последние
замечания и условие др/дх~ = 0, проинтегрировав уравнение A.9.12) по
длине тракта, найдем
тР dp _ _
— —?- = G0-Gi, A.9.13)
t0 dt
где Go, Gi - расход жидкости на входе и выходе участка тракта.
Уравнение A.9.13) называется уравнением проточной емкости и
описывает динамику участка тракта, в котором из-за относительной малости
скорости можно пренебречь инерцией жидкости и потерями на трение,
а из-за малости длины пренебречь акустическими эффектами. Если
необходимо учитывать податливость стенок тракта, то этот эффект (см. раздел
5.1.5) учитывается изменением скорости звука. При G\ = 0 уравнение
A.9.13) трансформируется в уравнение непроточной, тупиковой емкости.
1.9.4. Проточная емкость с неизотермическим течением. Из условий,
который были оговорены в предыдущем разделе, исключим предположение
о постоянстве температуры (состава) жидкости на входе. Рассмотрим
течение в тракте газа с переменной температурой на входе. В уравнении
энергии A.4.10) в правую часть входят члены, учитывающие
теплопроводность газа. Рассмотрим два случая состояния газа:
а) с малой теплопроводностью, т.е. kT ^ 0, Ре ^ °°, что определяет
адиабатические условия для каждого слоя газа. В химической технологии
аппараты с подобным течением называют реакторами идеального вытесне-
н"я [31, 118].
б) с большой теплопроводностью, т.е. кт ^ °° , Ре ~ 0, когда перенос
тепла за счет теплопроводности (перемешивания) намного больше конвек-
4* 51
тивного переноса тепла, т.е. переноса тепла с потоком газа. Этот вариант
процесса можно представить как модель с полным мгновенным
перемешиванием газа во всем объеме емкости. В химической технологии такой
процесс имеет место в реакторах с идеальным смешением [31, 118].
Остановимся вначале на адиабатическом варианте процесса (Ре ~ °°). В
левой части уравнения энергии A.4.9) при члене с производной по времени
в качестве коэффициента стоит критерий Струхаля, который в данном
случае удобнее выразить через безразмерную частоту со = coL/a, Sh = со/М.
Для рассматриваемой задачи, когда участок тракта описывается как
система с сосредоточенными параметрами, должны соблюдаться условия со< 1
и М < 15 одним из вероятных вариантов будет Sh~ 1. Поэтому в левой
части уравнения A.4.9) все члены имеют один порядок. Одновременно
в_ правой части уравнения энергии при пренебрежении вязким трением
Ф = 0, а так как Ре ^ °° отбрасываются и члены с градиентом температуры.
Учитывая, что рассматривается одномерное движение и соответственно
и- 0, уравнение A.4.9) окончательно в размерных переменных
преобразуется к виду
ds ds
— + и = 0. A.9.14)
dt дх V J
Для цилиндрического канала при и = const решение уравнения A.9.14)
имеет форму уравнения бегущей волны
s=f(t-x/u)<, A.9.15)
где / — произвольная функция. Если задан закон изменения энтропии
s = so(t) в начале тракта при х = 0, то решение принимает вид
s=so(t-x/u). A.9.16)
Решения A.9.15) и A.9.16) описывают движение плоской волны,
бегущей вдоль оси трактах со скоростью потока газа и. Форма волны
определяется законом изменения энтропии на входе в тракт, при движении вдоль
тракта форма волны сохраняется неизменной. В точку с координатой х
волна, образовавшаяся у входа в тракт, приходит с запаздыванием г = х/и-
Предположение о постоянстве скорости хотя бы за время пребывания
порции газа в тракте является достаточно существенным ограничением.
Однако его использование обеспечивает простую форму решения уравнения
энергии A.9.15) или A.9.16).
Хотя были приняты предположения с целью обеспечить получение
математической модели емкости с протоком газа как системы с
сосредоточенными параметрами, при адиабатическом характере процесса в каждом слое
газа (kT ^ 0) для энтропии, тем не менее, получается волновое решение.
Таким образом, в потоке газа при неизотермических условиях на входе
возникают волны, называемые энтропийными, описываемые решением
A.9.16). Такое парадоксальное положение, что при упрощении уравнений
гидромеханики не удается свести их к уравнениям с сосредоточенными
параметрами, связано с тем, что характерное время распространения
энтропийных волн тэ = L/u достаточно резко отличается от времени
распространения акустических волн та = L/a и та/тэ = М < 1.
Поэтому условие со = со L/a < 1, по которому определяют возможность
пренебрежения акустическими эффектами, отнюдь не определяет условия
52
о несущественности эффектов, связанных с распространением энтропийных
волн. Характерное время тэ непосредственно входит в исходную форму
критерия Струхаля Sh = L/uoto = тэ/т0, и если только T3<t0, то в этом
случае можно пренебречь эффектами, связанными с распространением волн
энтропии. Но тэ как время пребывания газа в емкости определяет
динамику (см. ниже) изменения давления в емкости, и поэтому условие тэ <^ t0
одновременно характеризует возможность не рассматривать участок тракта
как емкость, т.е не учитывать сжимаемость жидкости.
Следующее уравнение динамики участка тракта находится из уравнения
неразрывности A.7.19), которое после интегрирования по длине тракта
принимает вид
L> о О Cj\ Сто
f—dx+— =0, A.9.17)
о Ы F F
где F — проходное сечение тракта.
Воспользовавшись уравнениями термодинамики
As = cv In p — ср In p + const = с0 In р -
-ср hi(p/RT) + const = (cv -Cp)]np + ср InRT+ const, A.9.18)
учтя решение A.9.16) и считая R, cpi cv константами, найдем соотношение
для плотности газа в сечении с координатой х в момент времени t:
к- 1
р-рЧ"
A.9.19)
где То — температура газа на входе в участок тракта, к = cp/cv — показатель
адиабаты. При выводе соотношения A.9.19) и ниже учитывается условие
др/дх = 0 и соответственно р(х, t) = po(t), где Po(t) — давление в момент
поступления данной порции газа на вход в тракт. Подставив зависимость
A.9.19) в соотношение A.9.17), продифференцировав по частям члены
под первым интегралом уравнения A.9.17), получим
к -1
1
dp
1Г
кР
Ро\*
яг°К)
-dx
S
о 9f
RTJt
dx
-=0.
A.9.20)
В уравнении A.9.20) интеграл в первом члене определяет мгновенное
среднее значение по длине тракта обратной величины от температуры Гср,
53
так как интегрирование ведется по всем порциям газа, находящимся
в тракте, а запаздывание г = х/и равно времени пребывания в тракте порции
газа с координатой х от момента ее поступления в тракт. Отношение
к - 1
\Po\t Iр\ определяет изменение температуры порции газа в трак-
L \ и ) \
те за время пребывания г= х/и, обусловленное адиабатическим сжатием
(или расширением), при изменении давления от уровня давления в момент
поступления po\t до давления в данный момент р.
\ и )
Под интегралом во втором члене уравнения A.9.20) стоит производная
от функции с аргументом z = t -х/и, поэтому, используя правила
дифференцирования сложных функций, принимая постоянным вдоль длины
тракта мгновенное значение скорости и, можно раскрыть интеграл. В
результате уравнение A.9.20) преобразуется к следующей форме:
к-\ к-\
Г / L\~
1
kRTcv dt
dp -
-- upK
Н4)Г
р к
44)
RTo\t-— I RT,
= -?- — .A-9.21)
Решение уравнения энергии A.9.16) с учетом термодинамической
зависимости- A.9.18) можно записать в следующей форме (при/? = const) :
/ 1 -к ~ 1
к- 1
к
Р L ч "/J — • A.9.22)
RT
RToit
Из последней зависимости определяется изменение температуры по
длине емкости. Два уравнения A.9.21) и A.9.22) описывают динамику
участка газового тракта с протоком идеального газа при адиабатическом
процессе в тракте, переменных температуре и расходе газа на входе в
участок тракта в случае пренебрежения акустическими эффектами.
Присутствие энтропийных волн определило появление в уравнениях членов с
запаздывающим аргументом.
Рассмотрим другой предельный случай процесса в тракте с
неизотермическими условиями на входе, т.е. с очень большим значением коэффициента
теплопроводности (диффузии) кт « °°, Ре ^ 0. Можно считать, что при
большом значении кт мгновенное значение температуры газа во всем
объеме практически одинаково, за исключением температуры порции газа,
поступившей в данный момент в тракт со стороны входа. Такой вариант
процесса в газовом тракте можно назвать процессом с полным
мгновенным перемешиванием [58, 60]. Кроме условия Ре « 0, остальные
предположения, принятые выше, сохраняются неизменными. Поэтому уравнение
движения вырождается в условие Эр/Эх = 0, уравнение неразрывности
удобно использовать в форме зависимости A.7.19). В уравнении энергии
54
A.2.6) (считая течение одномерным, т.е. v = 0) при ктФ0 проще
воспользоваться в качестве переменных не энтропией, а давлением и температурой.
При /i = 0 и Хт^°°в уравнении A.2.6) исчезают все члены в правой части.
Хак как в дальнейшем уравнение A.2.6) будет интегироваться по
координате х и в результате интегрирования граничное условие войдет в само
уравнение, в левой части уравнения необходимо оставить конвективный
член с производной ЪТ/Ъх. С учетом последнего замечания, считая газ
идеальным и соответственно /3 = 1/Т, уравнение энергии A.2.6) принимает
вид
(ЪТ ЪТ\ 1 Ър
Ч^Г+М^Г7^=О- (L9-23)
Подставив в уравнение A.9.23) выражения для давления из уравнения
состояния идеального газа р = pRT, используя уравнение неразрывности
A.7.19), находим
ЪТ ЪТ Ъри
~~ =0. A.9.24)
vp ppu RT
Эг Ъх Ъх
При принятом выше условии со<1 темп изменения параметров йа
входе в тракт должен быть ограниченным, и соответственно ограничения
накладываются и на градиент изменения параметров вдоль оси проточного тракта.
Эти ограничения не касаются только температуры, так как принятое
условие Хт » °° предопределяет изменение температуры на входе в тракт.
Проинтегрируем по длине проточной части уравнение A.9.24), разбив
интегралы на две группы: одна от нуля до 5 - толщины слоя, где
температура газа равна входной температуре, другая — от 5 до сечения на выходе
x = L:
§ ЪТ0 L ЪТ « ЪТ0
cv f Ро dx + cvf р — dx + f PoUq—— dx +
0 Ъг 6 ЭГ о Ъх
1 ЪТ 5 Ъ(риH L Ъ(ры)
+ / ри dx + JRT0 dx+ J RT— dx = 0.
б Эл: о Ъх & Ъх
Так как слой толщиной 5 очень мал по объему E -> 0), то все параметры,
кроме температуры ЭГ0/Эг, внутри этого слоя можно считать постоянными,
не зависящими от х. Соответственно Ъ(риH!Ъх^О в слое толщиной 5, а
для остального объема ЪТ/Ъх ~ 0 из-за \ -> °°. Учтя эти замечания,
преобразуем приведенные выше интегралы:
dT0 dT
cvP08 + cvpL +роЫо(Г- T0)+RT (p1u1 -pouo) = 0.
dt dt
Предполагая, что тракт имеет цилиндрическую форму и его дбъем
V-FL, умножим все члены на площадь проходного сечения F: учтя, что
5 ~* 0, разделим все члены на ср и уравнение окончательно запишем в
следующем виде:
dT
р V + kG0(T- То) + (к - 1OXG! - Go) = 0. A.9.25)
dt
55
Уравнение энергии A.9.25) для тракта с мгновенным идеальным
перемешиванием отличается от аналогичного уравнения для тракта с
адиабатическим процессом A.9.14) тем, что A.9.25) — уравнение элемента с
сосредоточенными параметрами (тепловая емкость), а A.9.14) — с
распределенными параметрами (энтропийными волнами). Использование того или
иного крайнего предположения о характере передачи тепла в столбе газа
приводит к изменению типа уравнения, описывающего тепловые процессы
в тракте.
Два крайних условия кт = О, кт = °° отражают природу различных
способов передачи тепла в проточной емкости: это или чисто конвективный
перенос с массой газа, или теплопередача только за счет
теплопроводности.
В реальных условиях за счет турбулентности волны энтропии
рассеиваются. Однако экспериментальные исследования показали [60, 61], что для
цилиндрического тракта относительно небольшой длины в области частот
со < 1 процесс в тракте хорошо описывается адиабатической моделью
течения. Для других вариантов проточных емкостей со значительным
влиянием зон обратных токов, отрывов потока и т.д. можно ожидать,
что лучшие результаты будет давать модель с идеальным мгновенным
смешением.
В уравнение энергии A.9.25), кроме температур газа Т и внешних для
емкости параметров TOiGo и Gx (которые находятся из уравнений
смежных элементов или граничных условий), входит также плотность газа р,
зависящая как от температуры, так и от давления. Для определения
давления воспользуемся уравнением неразрывности A.7.19). Подставив в него
плотность из уравнения состояния идеального газа и учтя, что др/дх « 0,
находим
1 Эр р b(RT) Ъ(ри)
--- + —^—=0. A.9.26)
RT Ы (RTJ Эх Эх
Проинтегрировав уравнение A.9.26) по длине тракта, учтя при этом все
замечания и условия, принятые при выводе зависимости A.9.25),
приходим к следующему соотношению:
dp dT
V—-PVR RT(G0 - Gi) = 0. A.9.27)
dt dt
В уравнении A.9.27) целесообразно исключить производную по
температуре, подставив ее из выражения A.9.25), что приведет к следующей
простой зависимости:
V dp
— ~ RTqGo+RTxGx^Q. A.9.28)
к dt
Уравнения A.9.25) и A.9.28) вместе с соотношениями, связывающими
параметры р и Т в тракте с расходами на границах, полностью
описывают его динамику как емкости с полным мгновенным смешением.
56
§ 1.10. Линейные или линеаризованные
математические модели процессов в ПГС
Большинство приведенных выше математических моделей элементов
содержат нелинейные члены. В исходных уравнениях гидромеханики
нелинейными являются конвективные члены и члены, описывающие
диссипацию энергии, а в упрощенных уравнениях одномерного движения еще и
квадратичный член, связанный с потерями на трение. В уравнениях для
элементов с сосредоточенными параметрами нелинейными оказываются
уравнения для сопротивлений. А так как местные сопротивления
непременно присутствуют в схеме любой ПГС, то несмотря на линейность уравнений
двух других элементов с сосредоточенными параметрами
(инерционность и емкость), система уравнений, описывающая ПГС, является
нелинейной.
Нелинейность уравнений существенно затрудняет использование
математических моделей для анализа процессов в ПГС из-за отсутствия более или
менее общих методов решения подобных уравнений. С другой стороны,
имеется ряд задач, связанных с динамикой ПГС, которые с успехом можно
решать, используя более простые, линейные или линеаризованные
уравнения, получаемые из исходных нелинейных. Например, определение
динамических характеристик ПГС, выяснение вопроса об устойчивости процесса,
анализ различных схем регулирования системы [17, 58], решение
некоторых задач диагностики технического состояния [151] и т.д. Естественно,
что при переходе к линеаризованным уравнениям теряется общность
постановки задачи. Однако существенное расширение возможностей для
решения перечисленных выше и ряда других задач, относительная простота
методов решения делают линеаризацию уравнений одним из методов, широко
используемых при формировании математических моделей систем самой
разной природы.
В первую очередь остановимся на исходных уравнениях Навье — Стокса,
используя их безразмерную запись A.4.1), A.4.2) и A.4.4). Как уже
отмечалось, для задач, связанных с распространением акустических
колебаний, характерным масштабом времени является t0 = L/a. Соответственно
Sh = L/uoto = 1/М. Умножив все члены уравнений A.4.1), A.4.2) и A.4.4)
на число М, учтя при этом, что МЕи = (ро/Ро^1)(ио/ао) = Ро/Ро^о^о = 1/а,
обнаруживаем, что на число М умножены только конвективные члены,
содержащие произведение составляющих скорости на производные от
скорости или давления. В остальные члены число М входит в комбинации с
критериями Fr, Re, R/L, величины которых могут варьироваться в
широком диапазоне. Поэтому при М < 1 только конвективными членами
заведомо можно пренебречь без дополнительного сравнения со значениями
других критериев. После отбрасывания конвективных членов в
рассматриваемых уравнениях остаются еще нелинейные члены, включающие
безразмерные параметры р~ и ~а. Уравнения оказываются линейными, если
жидкость слабо сжимаемая и можно принять я~=р"= 1. В итоге уравнения
сводятся к виду
4 Ъ2п ( L \2 / д2ы
™_ М _ 1 Эр М / R \ Г 4 Ъ2п / L \ 2 /
Э72
57
1 Эй \ 1 Э2п 1 dv
+ ) + + 1=0, A.10.1)
7 Э7 / 3 ЭхЭ7 37 Эх '
dv M 1 / L V dp M / L \ Г /R '
~W~~f7 ' + ~оГ\Л~/ ~Э7~ ~~Re~\7T/ L \T
4Э2у 4 ЭТ7 4 v 1 Э2й
3 Э72 37 Э7 3 72 3 Эх Э7
= 0, A.10.2)
1 dp du dv v
^-+ + + — = 0. A.10.3)
a dt Эх Э7 г
Найденные линейные уравнения получены с использованием только
одного предположения — небольшой сжимаемости жидкости. Аналогичные
уравнения можно получить и для турбулентного режима течения,
преобразуя подобным образом уравнения A.3.3), A.3.9), A.3.10).
Другой возможный вариант течения, для которого при М < 1 уравнения
A.4.1), A.4.2) и A.4.4) сводятся к линейным, это изотермическое
движение газа. Для него уравнение состояния в безразмерных переменных
записывается р=^В этом случае в уравнениях A.10.1) —A.10.3) (так же
как _и ранее в уравнениях A.7.28) и A.7.29)) члены dp/Эх, dp/dT и
dp/dt заменяются на члены Э1пр/Эх", ЭЬр/ЭГи Э1пр/Э7, а остальные
слагаемые сохраняются неизменными.
При выполнении предположения М < 1 можно отбросить
конвективные члены и в упрощенных уравнениях одномерного движения A.7.21)
и A.7.22), однако в них при этом останется еще нелинейный член с
квадратом скорости, описывающий потери на трение, и член с переменной
плотностью. Таким образом, эти уравнения становятся линейными, если можно
пренебречь и конвективными членами, и потерями на трение, т.е. если
одновременно выполняются условия: Аро/ро < 1, М < 1, и кроме того,
одно из условий для плотности: р~= 1 или р=ри а = const. В итоге
уравнения A.7.23) и A.7.24) принимают форму
Эй 1 Эр М _
— + Рх = 0, A.10.4)
Э7 а Эх Fr
A.10.5)
A.10.6)
A.10.7)
dt
при "р =
Эй
-j.
Э7
Э1пр
Эй
¦ а = 0
Эх
1 или
а Эх
Эй
+ а -
М _
р
гх
Fr
= 0
= 0,
dt Эх
при р-р (изотермический процесс). Этими вариантами исчерпаны
возможности линеаризации уравнений путем их упрощения. При этом
оказывается, что для упрощенных уравнений одномерного движения переход
58
к линейным уравнениям требует использования более грубого
предположения о пренебрежении потерями на вязкое трение, которое не надо было
использовать при упрощении исходных уравнений Навье — Стокса.
Обнаруженное противоречие является кажущимся, поскольку для ламинарного
режима течения, которое описывается уравнением Навье - Стокса, перепад
давления в тракте Ар ~~ I/Re, а так как Re ~ и, то и в уравнении
одномерного ламинарного движения член с потерями давления оказывается
линейным. При турбулентном течении потери слабо зависят от числа Рейнольдса,
и нелинейный член для потерь на трение с показателем степени близким к
двум остается во всех случаях.
Следует оговориться, что даже если приведенные выше уравнения можно
свести к линейным, граничные условия, которыми необходимо их
дополнить, как правило, являются нелинейными, что также приводит к
затруднениям при решении уравнений. Выходом из этого положения является
переход к малым отклонениям, т.е. линеаризация как самих уравнений
(при этом отпадает необходимость в отбрасывании нелинейных членов),
так и граничных условий. При линеаризации каждая переменная величина
представляется в виде суммы двух слагаемых: значения данной переменной
для некоторого среднего, номинального режима течения и малой переменной
добавки к средней величине. В дальнейшем будем считать среднее движение
стационарным, не зависящим от времени, а малые отклонения от него,
вариации параметров, изменяемыми как в пространстве, так и во времени.
Малостьv отклонений (вариации) параметров характеризуется тем, что
квадратами и произведениями вариаций можно пренебречь по сравнению с
первой степенью вариаций.
Линеаризуем исходные уравнения A.2.3), A.2.4) и A.2.5), представив
переменные следующим образом: и = ис + Ъи', v = vc + 8v', p = рс + Ьр\
р=рс+5р'. Во всех случаях переменные с индексом "с" - размерные
стационарные значения параметров, зависящие от х и г, а вариации со
штрихом - размерные отклонения соответствующих параметров от
стационарного значения, зависящие от х, г и t. Учтя, что для всех
стационарных значений параметров уравнения гидромеханики должны
удовлетворяться, находим линеаризованную форму уравнения движения вдоль
оси х1)
ЪЬи ЪЬи ЪЬи' Ъи Ъи
~~— + и + v + Ьи' + 5v =
Эг Ъх Ъг ' Ъх Ъг
ЪЬи
V
Ъг
р2
дЧи'
- +
Ьр
Ьх
Ьи'
¦ +
Ъи
Ъх
1 ЪЬи'
р Ъх
Ъ2Ьи 1 ЪЬи' 1 Ъ2Ьи' 1 dbv' 1
A.10.8)
Г 4 Ъ2Ьи Ъ2Ьи 1 ЪЬи 1 Ъ2ди' 1 Эби' 1
— + — + + + .
I 3 Ъх2 Ъг2 г Ъг 3 ЪхЪг Ъг Ъх J
В уравнении A.10.8) и везде ниже сохранены только первые степени
вариаций независимо от того, входят ли они в виде коэффициента или под
производной.
Здесь и далее индекс "с" для стационарных значений- отбрасывается.
59
Аналогичным образом получаем уравнение движения в направлении радиуса
ЪЬи' ЪЬи' ЪЬи' Ъи , Ъи
+ и + v + Ьи + bv — =
bt Эх Ъг Ъг Ъг
, 1 ЪЬр' Ьр' Ър
= ЪРГ — — +
р Ъг р2 Ъг
afii/ 4 bv' 1 Ъ2Ьи 1
A.10.9)
.Л
[
фавн
Э5р'
Эг
Р
г
Э25и' 4
Эх2 3
Э25«/
Эг2
[ение неразрывности
Э5р'
¦4-11
+ и ¦
Эх
с ' / Э"
' \ Эх
Э5м'
Эх
Эи \
» 1 ? ^
Эг /
4
Зг
+ и
' +
Э5и'
Ъг
ЪЬр'
Ъг
Ър
Ъх
+ р
Ьи'
4 5i/
3 г2
Э5и'
Эг
Эр
Эг
- +
V
+ —
г
-bv
1 Э25г/
3 ЭхЭг
Ьр' +
- о.
A.10.10)
Если считать течение адиабатическим, то, воспользовавшись формулой
A.2.12), находим линеаризованное уравнение неразрывности
'— +— 5 '+ 2 X
Эг Эх U Ра
bv' \ ^ I Ъи Ъv v\
) + а + + " 5р' = 0. A.10.11)
г ) \Ъх Ъг г )
ЪЬр'
ы
*(¦
+ и
ЪЬи'
ЪЬр
Ъх
- + -
+ V
Э5и'
ЪЬр'
Ъг
bv'
+
Эх Эг
В общем случае уравнения A.10.8) —A.10.11) являются линейными
уравнениями с переменными коэффициентами, так как входящие в уравнения
в виде коэффициентов значения параметров для стационарного движения
являются функциями только координат.
Линеаризация упрощенных уравнений для одномерного движения
A.7.18) и A.7.20), если принять 7%1> приводит к следующим
зависимостям (осредненную скорость обозначим и):
A.10.12)
Ьр = 0, A.10.13)
где Ь\' — размерная вариация коэффициента сопротивления, являющегося
для нестационарного движения величиной переменной. Для определения
Ь\' необходимо знать зависимость коэффициента X от параметров,
характеризующих нестационарность (например, градиент изменения скорости
во времени или частота колебаний) [20, 28, 91, 99, 184].
В ряде случаев оказывается удобнее и нагляднее использовать запись
уравнений гидромеханики в безразмерных вариациях, отнеся каждую раз-
60
ЪЬи
Ъг
Р
ЪЬр
Ъг
ЪЬи'
Л- 11 +
Эх
1 Эр
Ял'
2 2 -ч Р
2а2 Эх
ЪЬр'
4- if +
t U т
Эх
Ъи
Ъх
2R
ра2
ш -
Ьи
ЪЬи
Эх
ЬР'
X
и2
4R
Ьр
j,
Эх
1
9
Ь\'
Ьи
ЪЬр'
Ъх
>
+ а2
Ъи
Ъх
мерную вариацию к среднему или масштабному значению варьируемой
величины: Ьи = Ьи'/и0, bv - bv'/v0, Ьр = бр /ро, бр = бр /ро, ЬРХ =ЬРх/Рх0,
5/> ^ЬРг/Рго, ЬХ = ЬХ'/\0. Учитывая, что в основном представляют интерес
длинные тракты, для которых R/L < 1, при приведении уравнений к
безразмерной форме удобно использовать масштабные значения переменных,
введенные в процессе получения уравнений A.4.1) - A.4.4). При этом
вместо и© подставим v0 =u0R/L и соответственно v - u^vR/L, a bv =
~8v'L/Ru4 и вместо Рг0 подставим Pr0=Px0R/L, соответственно ЬРГ =
= 8P'rL/PxoR. После приведения к безразмерному виду как вариаций,
так и всех других параметров, уравнения гидромеханики A.10.8) - A.10.11)
принимают вид
ЪЬи _ ЪЬи _ ЪЬи Ъп Ъп
Sh—z~~ + и + v + Ьи + 5i> =
Ы Ъх ЪТ Эх Э7
1 Ей Эбр Ей Эр 1 / R \ Г 4 Э25^
= — ЬРХ + — бр + +
Fr р" Эх р2 Эх Re \ L I L 3 Эх2
L \2 Ъ2Ьи ( L \2 1 ЪЬи 1 Э25и 1 Эби
+ 1—I -+(— I + + I A.10.14)
35d ЭТ; Эу"
+ V + Ьи + Ьи =
Э7 Эх Э7
Ъ2Ьу
Re \ R J [\ L J Ъх2
4 Э25и 4 Эби 4 bv 1
+ --+ + I . A.10.15)
3 Э72 37 Э7 3 72 3 ЭхЭ7 J
Линеаризованное уравнение неразрывности в общем случае запишется
так:
Эбр Эбр Эбр / ЪЬи Эби bv
Sh + п + v ' ~
ЪТ Ъх ЪТ
[ ЪЬи Эби bv \
"( — + -^т" + 1— )
\ Эх Ъг г ]
I Ъп
\ Эх
и \ Эр Эр
— I 6Р + —Г 6w + -^- би = 0, A.10.16)
г ] Эх Эг
Г I Р Г ^
Ъг г ] Эх Эг
или для случая адиабатического течения
Эбр _ ЪЬр _ Эбр Эр" Эр
Sh —3- + и —— + v + Ьи + —1— 5и +
Ъг Ъх 37 Эх Э7
а _ \ ЪЬи ЪЬи Ьи ( Ъп Ъи v \ 1
+—-Р + + +( + +— )бр =0. A.10.17)
М [Эх Э7 7 \ Эх Э7 7 / J V J
Аналогичным образом приведем к безразмерному виду линеаризованные
61
уравнения A.10.12) и A.10.13) для одномерного движения
ЪЬы ЪЬы Ъы 1 Ей ЪЬр
Sh -тг- + и —z- + 5 Ьр +
dt Ъх Эх Fr p Эх
Ей Ър Хо (L \ Хо/ L \
Ьр — — I Хы Ьы — I — \и о л, A.10.1 о)
Эх 2 \R ) 4 \ R !
р-2 Л^г
где Хо - масштабное (среднее) ,_а X - текущее значение коэффициента
гидравлического сопротивления, X = Х/Хо, 5Х = 5Х'/Х0,
ЪЬр ЪЬр Ър а / ЪЬы Ъы \
Sh + и + Ьы + — р~ + Ьр =0. A 10.19)
Э7 Эх Эх М \ Эх Эх / К }
Уравнение энергии A.2.6) после линеаризации в размерных вариациях
запишется:
/ Э5$' Э5*' 96s' \ , , / 9s bs \
рТ\ + и +и I + (ТЬр +р5Г )[ы + v =
\ ЭГ Эх Ъг I \ Эх Ъг )
[ ЪЫ ЪЬТ' ЪЬТ'\ ( ЪЬр'
р \ Ъг Ъх Ъг j \ Ъг
ЪЬр ЪЬр'\ / ЪТ ЪТ \
+ ы + v I + cDbp I ы + v I —
Эх Ъг / р \ Эх Ъу ]
• ( %L + ?L\- ' ( ъ2ьт>
\ Эх V Ъу ) т \ Эх2
Ъ2Ы 1 ЪЬТ'\
+ — + , A.10.20)
Ъг2 г Ъг I V
где 5s', 5 Г'— вариации энтропии и температуры,
2 / Э5^' ЪЬи'
3 \ Эх Ъг
vbv' / dv Ъы\ / ЪЬи' ЪЬы'
Ьи'\2 \Ъи ЪЬы' Ъи ЪЬи'
+2 +
г I |_Эх Эх Ъг Ъг
Jbv f Ъю Ъы\ / ЪЬи ЪЬы \ 4 / Ъы Ъи
г2 \ Ъх Ъг ) \ Эх Ъг j 3 \"эх~ + ~э7~ +
v \ ( ЪЬы' Э5и' bv\\
+— + + . A.10.21)
г А Эх Эг г /J
После перехода к безразмерным переменным как для вариаций, так и
средних значений параметров и координат уравнения A.10.20) и A.10.21)
62
принимают следующий вид:
/3s Ъ1 \ / Ьр ЬТ \
[п + v + —— ) =
\ Ъх ЪТ )\ р Т I
ЪЬТ\ Ро7о№-О? /си ЖР
ът I щ \ dt
Sh _ +
Эг
= —( Sh
Г \
ЪЬр
Эх
Э5Г
Э7
ЪЬр
+ V
V
ЪТ
ЪЬТ
Эх
и*
ЪЬр \ _ ЪТ _ дТ\ 5р РоТо(к-1)/_ др
v —— +1 и +и —— = и —
ЪТ I \ Ъх ЪТ I рТ крТ \ Ъх
дх
_ Ьр
)
Фо
РТ
5Ф +
дг j
Fo
РТ
f \ Эл
\ЬЧТ
[ дх2
L У
R )
/ L у \ ЪЬТ
ЪТ2 \ R 1 Т ЪТ
A.10.22)
где Г = Г/Го, /J = &/Ро» Fo = K/PoCpUoL - критерий Фурье,
Фо = v$oLlcpToUo = vuo/cpToL, Фо = (Uq/LJ,
5Ф
( /
' \
2
3
+ I
4
3
5Ф'/Ф0
5и\2|
Т 1 \ +
Г Э5^
1 _i_
1 Эх~
f R\bv
\ L J Ъх
1 _ "*"
5Ф7(^о/1J
1\
ЪЬи
ЪГ
+ ( -
Ъи
ЬТ
Ч \ Э81
L I дх
т\
L \ Ъп
I _
-2
2
¦]|
ЪЬи
Эх
[(
/
\
Л
/F
- +
Эби
Эх
L \
R /
Ъп
Ъх
1\ Ъ
.) э
ЪЬи
ЪТ
У
ЪЬи
ЪТ
ЪЬи
Ъх
Ьи
X
¦ + -
1
J
- +
•(
Ьи
Т
ЪЬи
ЪТ
2
Ъп
ЪТ
1)
R )
))•
)¦¦
ЪЬи Wbv
ът т2
ЪЬи
ЪТ
A
A.10.23)
Для изотермического течения в цилиндрическом тракте все средние
значения параметров постоянны или изменяются незначительно только за
счет влияния вязкого трения, и уравнения A.10.8)-A.10.23)
существенно упрощаются при отбрасывании членов с производными от средних
значений параметров потока.
В заключение приведем линеаризованные зависимости, описывающие
процессы в простейших элементах с сосредоточенными параметрами,
модели которых получены в § 1.9. Используя соотношение A.9.5), находим
линеаризованное уравнение для инерционности:
L dbG'
'Х +ЬАр\ A.10.24)
г at
где bG , ЬАр' — размерные вариации расхода и перепада давления.
Аналогично из соотношения A.9.10) находим линеаризованное уравнение для
63
сопротивления:
А/ С I С2
8Ар' = -8G' + 8\' -pL8P'x. A.10.25)
2R pF2 4R pF2 }
Для проточной емкости с постоянной температурой жидкости, переходя
в уравнении A.9.13) к размерным переменным и линеаризуя его,
находим
V dbp'
—: = 5Go-5Gi, A.10.26)
a2 dt
где V - объем емкости, 8G'O, 8G\ - размерные вариации расхода на
входе и выходе тракта. Для неизотермических условий на входе в участок
тракта с адиабатическим течением, описываемого уравнениями A.9.21) и
A.9.22), линеаризация приводит к зависимостям
7i d8p' р , к - ] , ,
— —— +— [8To(t-Tl)-8T'0]+ [8p'-8p'(t-T1)) =
к dt T к
RT
uF
8Т\ к-\8р' ST'oit-u) k-\ 8p'(t-r1)
EG0 -6G1), A.10.27)
A.10.28)
T к р Т к р
где 5Го, 8Т[ — вариации температуры на входе и выходе участка тракта,
Т\ = L/u — среднее время пребывания газа в участке тракта. При
линеаризации уравнений A.9.21), A.9.22) и всех последующих для средних
значений параметров не учитывается запаздывание и отброшены индексы
у температуры.
Для процесса в тракте с неизотермическим течением газа и с полным
мгновенным перемешиванием после линеаризации уравнений A.9.25)
и A.9.28) находим
-^^+5r'-5r0+^^-EG;-5Go) = 0, A.10.29)
к dt к G
IL _^_+Z_ EG' _5G{^ + JLqT'_st> ) = q9 A.10.30)
к dt G T
где 5Г' — вариация мгновенного значения температуры газа в тракте.
Уравнения для простейших элементов A.10.24) —A.10.30) можно
представить в безразмерном виде. При этом, в отличие от уравнений в частных
производных, где использовались характернее масштабы для расстояния
L и времени Lja, для уравнений простейших эле^.нтов таких масштабных
величин нет. Поэтому нецелесообразно вводить в качестве безразмерного
аргумента время. С учетом этого замечания преобразуем уравнение
инерционности A.10.24) к безразмерному виду
d8G 1
7И = 8РХ + 8 Ар, A.10.31)
^ FrEu
где 7 = GL/pF - инерционная постоянная времени элемента,
8Ар = 8Ар'/р.
64
Для безразмерных вариаций уравнение сопротивления A.10.25)
запишется так:
где Артр - среднее значение потерь на местном сопротивлении,
= Ро -Pi ~~ среднее значение общего перепада давления на элементе, 5Ар =
Уравнение емкости A.10.26) получим в следующей записи:
ddp
Te
dt
=8Go-8Gl9 A.10.33)
где re =pV/Ga2 -постоянная времени емкости, 5G0 = SG'0/G, 5GX = SG[/G.
Для емкости с неизотермическим течением газа уравнения A.10.27)
и A.10.28) (адиабатический вариант) принимают вид
П d6p fc - 1
— + 8To(t-Ti)-8To + [8p-8p(t-Ti)]=8G0 -8GX,
к dt к
A.10.34)
k-l k-\
8Ti &P=dT0(t-T1) 8p(t-TX)9 A.10.35)
к к
где 5 Го =5 Го/Г, ЬТХ=ЬТ[/ТУ Г - средняя температура.
Уравнения A.10.29) и A.10.30) с полным мгновенным
перемешиванием преобразуются следующим образом:
U dST k-l
+ 5Г-5ГО + EG0 -Sd) = 0, A.10.36)
к dt к
к dt
ddp
+ ST-STo +5Gi -6G0 = 0. A.10.37)
5. Б.ф Гликман
Глава 2
ПНЕВМОГИДРАВЛИЧЕСКИЕ СИСТЕМЫ (ПГС)
И ПНЕВМОГИДРАВЛИЧЕСКИЕ ЦЕПИ (ПГЦ)
С СОСРЕДОТОЧЕННЫМИ ПАРАМЕТРАМИ
§ 2.1. Что такое пневмогидравлическая цепь?
2.1.1. Система и цепь. Пневмогидравлыческой системой (ПГС) будем
называть технический или естественный объект, заполненный рабочей средой
и состоящий из различных устройств, агрегатов, органов, которые упорядо-
ченно соединены между собой в конечном числе сечений (точек). ПГС
может входить как составная часть в физический объект, при этом система
должна выполнять заданные функции и иметь определенные
характеристики. Характеристики ПГС и ее способность выполнять свое назначение
зависят как от типов и параметров отдельных ее частей, так и от их
взаимодействия, т.е. схемы соединения между собой и согласованности
параметров и частей системы. На вопрос о том, что считать частью системы, а что -
системой в целом, нельзя ответить однозначно, не определив основные
цели исследования или разработки. К примеру, для создателя системы
управления самолетом гидромоторы, усилители, исполнительные органы
и т.д. являются агрегатами, частями общей гидравлической системы, в то
время как для разработчика гидромотора он является системой, а его
части — деталями системы. Однако это отнюдь не значит, что при разработке
более сложной системы всегда можно пренебрегать детальным
исследованием процессов в отдельных агрегатах. В зависимости от сложности и
изученности процесса в агрегатах математические модели и на их базе
методики расчетов систем могут быть построены чисто аналитически,
полуэмпирически (т.е. с использованием экспериментальных данных), чисто
эмпирически, стохастическими методами и т.д. Ниже описываются методы
построения аналитических или полуэмпирических математических моделей, для
формирования которых используются уравнения гидромеханики,
термодинамики, механики и некоторые экспериментальные (эмпирические) данные.
Применительно к задаче исследования нестационарных режимов работы
систем обычно определяются динамические характеристики системы -
реакция системы на определенные (гармонические, ступенчатые и т.д.)
возмущения. Статические характеристики системы, т.е. связь между
внутренними и внешними (возмущающими, управляющими) параметрами
системы, в принципе, можно считать частным случаем динамических
характеристик, например, при гармоническом возмущении с частотой,
стремящейся к нулю. Однако такой подход не является во всех случаях удобным,
особенно применительно к нелинейным системам. Для таких систем
статические расчеты (увязка параметров) являются специальной, достаточно
сложной задачей, которой посвящено много работ, в том числе и
применительно к ПГС [163, 164, 207, 226].
66
Расчетный анализ поведения системы во времени, в динамике возможен
только тогда, когда известны математические модели нестационарных
процессов в отдельных частях, агрегатах системы. Сложность разработки
математических моделей технических систем связана с тем, что эти системы
состоят из агрегатов, в которых протекают процессы различной физичес-
кой природы (гидравлические, пневматические, электрические,
механические, тепловые и т.д.) , а также устройств, в которых осуществляется
преобразование энергии из одной формы в другую. Другие затруднения при
создании единообразных математических моделей ПГС носят в основном
психологический характер и связаны с тем, что ПГС используются в самых
различных отраслях техники и содержат огромное количество разнообразных
по конструктивному оформлению и назначению агрегатов, узлов. Из-за
внешнего различия в конструкции для систем разного функционального
назначения разрабатываются и используются свои методики расчета, хотя
процессы в этих внешне отличных системах имеют близкую физическую
природу и подчиняются одним и тем же закономерностям.
В связи с этим очень заманчивой кажется разработка общих методов,
позволяющих унифицировать способы построения математических моделей
систем с близкими физическими процессами независимо от их структуры,
конструктивного оформления агрегатов и назначения. При этом
необходимо учитывать возможность использовать эти методы для систем, состоящих
из частей с процессами различной физической природы.'
Применительно к анализу характеристик технических систем методы
теории цепей, широко используемые в электро- и радиотехнике, дают более
наглядные, физические результаты, быстрее приводят к цели, позволяют
применять более простые и в то же время очень эффективные
алгоритмы.
Теория цепей активно внедряется для анализа электромеханических
систем [103, 120, 145J, механических устройств [38, 90], при исследовании
теплообмена [78, 92]. Ряд работ посвящен анализу ПГС разного
назначения с использованием теории цепей [15, 61, 186, 187, 226, 243]. Ниже
описываются методы использования теории цепей для построения
математических моделей разветвленных ПГС, состоящих из агрегатов,
рассматриваемых как элементы с сосредоточенными параметрами.
Теория цепей использует известный факт, что процессы в устройствах
разной конструкции и разного функционального назначения описываются
аналогичными уравнениями [178]. Наиболее типичные уравнения,
характерные для широко распространенных процессов, называются уравнениями
элементов (звеньев, компонент), а соответствующие им простейшие
идеализированные устройства — элементами (звеньями) цепи. Звенья цепи
являются "кирпичикаГми", из которых строится все "здание" цепи.
Использование теории цепей предопределяет неизбежность
приближенного моделирования, т.е. упрощенного описания процессов. К тому же
возможности современных ЭВМ, глубина нашего познания процессов при
всем желании не позволяют получить точное (т.е. без принятия
упрощающих предположений) решение более или менее сложных
гидромеханических задач. Поэтому использование приближенных моделей — объективная
необходимость. Сопоставляя приближенные уравнения, моделирующие про-
иесс в том или ином агрегате, и уравнения простейших звеньев, можно
5" 67
сформировать эквивалентную схему замещения этого агрегата.
Построенная эквивалентная схема (цепь) должна с заранее заданной подробностью
описывать динамические и статические характеристики агрегата. При
разработке эквивалентных схем для агрегатов, узлов, входящих в ПГС,
удается все разнообразие процессов, конструктивных особенностей узлов,
агрегатов свести к отличию в составе и структуре эквивалентных схем,
собранных из простейших звеньев.
Применительно к ПГС (по аналогии с электротехникой) простейшими
идеализированными звеньями цепи из элементов с сосредоточенными
параметрами являются сопротивление, емкость, инерционность (пассивные
элементы), источники напора (давление) и расхода (активные элементы).
Эти простейшие звенья принято называть двухполюсниками [96], так как
их характеристики описываются одним уравнением, связывающим две
переменные (например — давление и расход).
Математической модели каждого агрегата соответствует определенная
структура эквивалентной схемы, составленной из звеньев, а всей ПГС -
схема, объединяющая эквивалентные схемы всех агрегатов системы. Эту
эквивалентную схему системы называют эквивалентной пневмогидравли-
ческой цепью (ПГЦ), описывающей с оговоренными при построении
модели условиями и ограничениями характеристики процессов в анализируемой
ПГС. Таким образом, ПГЦ — абстрактный, идеализированный модельный
эквивалент исходной ПГС, составленной с учетом определенных
предположений и ограничений. Математическая модель системы и полученная с ее
использованием эквивалентная ПГЦ при заранее оговоренных
ограничивающих условиях (диапазон частот, быстродействия и т.д.) должны быть
изоморфны анализируемой ПГС [15, 276], т.е. должно существовать взаимно
однозначное соответствие между динамическими и статическими
характеристиками ПГС и эквивалентной ей ПГЦ. Естественно, если условия
функционирования ПГС выходят из оговоренных заранее пределов, необходимо
вернуться к вопросу об адекватности модели характеру протекания
процессов в ПГС, а при их несовпадении — уточнить математическую модель и
эквивалентную ПГЦ. К примеру, при расширении диапазона частот
необходимо переходить от модели в сосредоточенных параметрах к модели в
распределенных параметрах.
Для описания более сложных устройств, в частности, для частей ПГС
которые необходимо рассматривать как элементы с распределенными
параметрами, при построении эквивалентной ПГЦ используют более сложные
звенья, чем упомянутые двухполюсники. Уравнения этих звеньев
связывают четыре, шесть, восемь и т.д. параметров и по числу переменных
называются четырех-, шести-, восьмиполюсниками или проще —
многополюсниками. Число уравнений, описывающих многополюсник, в два раза меньше
числа связанных переменных. Многополюсники объединяются с другими
элементами (двухполюсными или многополюсными) в общую
эквивалентную ПГЦ. Точки стыковки различных элементов ПГЦ называются
полюсами или узлами цепи. Если устройства, связывающие между собой
отдельные агрегаты (например, трубопроводы), обладают динамическими
свойствами (сдвигом фазы, изменением амплитуды), которыми нельзя пренеб
речь, то эти устройства при переходе к ПГЦ описываются как
самостоятельные элементы или схемы из нескольких элементов. В ПГЦ для обозначе
68
ния звеньев (элементов) цепи удобно использовать условные знаки,
аналогичные принятым в электротехнике.
В результате получаемая ПГЦ одновременно является электрическим
аналогом (моделью) анализируемой ПГС. Однако в процессе
формирования эквивалентной цепи для неэлектрических систем (механических, пнев-
могидравлических, тепловых и т.д.) встречаются определенные трудности
при построении структуры цепи, определении правил соединения
отдельных элементов в эквивалентную цепь. В частности, определенные
затруднения возникают при описании в терминах цепей тупиковых или "висячих"
участков, в которых находятся емкости, источники расхода и давления,
потребители рабочего тела и т.д. В этом случае полезно использовать
аппарат теории структурных графов1) и правила измерения переменных [15,
61, 103, 120, 276]. Подобный подход удобен и тем, что дает простой метод
формального построения эквивалентной цепи и ее математической модели.
2.1.2. Измерения и полюсные графы. Любой процесс в системе и
состояние системы описывается набором параметров, связанных между собой.
При анализе системы каждый параметр должен быть выражен
количественно, т.е. должен быть сопоставлен с некоторым эталоном, принятым для
данного параметра. Процесс сопоставления величины данного параметра с
эталоном, хотя бы теоретически, называется измерением.. Измерения проводятся
с помощью измерительных приборов, при этом условимся, что
измерительный прибор является идеальным - безынерционным, не влияющим при
своем включении для измерения на процессы в системе, в которой
проводятся измерения. Примером подобных измерительных приборов может
служить лазерный или ультразвуковой измеритель скорости (расхода)
жидкости, встроенный в стенку тракта малоинерционный датчик
давления и т.д.
Применительно к проблеме построения математической модели
процесса, в которой каждая переменная обозначается своим символом, процесс
измерения должен обеспечить получение количественных связей между
отдельными символами (параметрами), характеризующими состояние
системы. При этом предполагается, что получаемые количественные
соотношения не должны зависеть от физических принципов измерения и типов
измерительных приборов.
Измерение любого параметра связано с сопоставлением двух точек или
двух областей, в которых производится измерение. Действительно,
измерение тока и напряжения в электрической системе осуществляется путем
включения амперметра и вольтметра между двумя контактами. Измерение
Давления манометром производится путем сопоставления давления в двух
точках - точке отсчета и во внешней среде (атмосфере), так как прибор
фиксирует разность давлений. При измерении абсолютного давления второй
областью является среда с вакуумом, причем одна точка (область) опять
же находится вне системы — во внешней среде. Аналогичное положение
имеет место и при измерении температуры жидкости, для которой, к
примеру, второй областью может служить сосуд с тающим льдом. При
измерении расхода жидкости турбинным или дроссельным расходомером эти
^азываемых также линейными. Наряду со структурными графами ниже будет
^'пользован и другой тип графов - сигнальных.
69
приборы устанавливаются в разрыве тракта и связывают две точки внутри
системы - перед расходомером и за ним. Аналогичным образом измеряется
напряжение в электрической цепи, тепловой поток и т.д.
Для определения характеристик простейших гидравлических элементов,
описываемых как двухполюсники, необходимо измерить одновременно две
переменные - расход жидкости и давление (перепад давления). Схема
измерения представлена на рис. 2.1, я, где стрелками показана ориентация
подключения измерительных приборов. Условное изображение результатов
а в
h
Щ-
ас
Рис. 2.1. Схема и полюсные
графы измерений параметров
течения в тракте
по
в по-
измерения представлено на рис. 2.1, б в виде двух направленных линий для
перепада давления Ар и расхода G. Так как измерения относятся к одному
элементу и расход во всех точках а, Ъ и Ъ1 в каждый момент одинаков,
удобно изобразить оба измерения одним направленным отрезком линии
(рис. 2.1, в). Точки, между которыми производят измерения, называют
полюсами, а линию, их связывающую и показывающую результат
измерения, - полюсным графом, которому приписывается определенное
направление. Сами измерительные приборы при этом не изображаются, так как
они никак не влияют на результат измерений. Ориентация включения
измерительного прибора определяет получаемый знак измеряемой
величины. Так как результаты измерения сопоставляются с определенными
физическими закономерностями, в которых учитывается знак переменных,
то при измерениях желательно использовать определенное правило
включения приборов, чтобы результаты измерений не противоречили привычной
записи физических законов.
Измеряемые переменные по способу включения измерительного
прибора в исследуемую систему делятся на два класса: параллельные
переменные, при измерении которых измерительный прибор включается
параллельно исследуемому объекту (см. рис. 2.1, а), т.е. параллельно полюсам, и
последовательные переменные, при измерении которых основной элемент
прибора включается последовательно исследуемому объекту, в разрыв
соответствующей ветви.
К параллельным переменным относятся давление (перепад давления),
электрическое напряжение, линейное или угловое перемещения и скорости,
перепад температуры (температура), а к последовательным — расход
жидкости, сила электрического тока, сила и момент силы, тепловой поток и т.д.
Все перечисленные параметры — скаляры. Полюсному графу,
описывающему результаты измерений, т.е. характеристики исследуемого двухполюс-
70
ного элемента, соответствует определенная связь между парой измеряемых
параметров — одним параллельным и одним последовательным. В
результате для каждого полюсного графа находится свое уравнение элемента,
связывающее две переменные - измеряемые параметры, описывающие
характеристики элемента. Полюсные уравнения не зависят от того, входит ли
элемент в цепь или рассматривается изолированно. В качестве примера
полюсного уравнения двухполюсника можно привести зависимость для течения
Пуазейля в трубе — связь между перепадом давления Ар и расходом G
несжимаемой вязкой жидкости при стационарном ламинарном течении [152]
128 vL
Ap = Po~Pi = -T-G, B.1.1)
пи
где ро, Р\ - давление на входе и выходе трубы, L, D - длина и диаметр
трубы, v — вязкость жидкости.
Так как полюсный граф проводится между двумя полюсами, а
полюсное уравнение связывает две переменные, элемент, описываемый этим
графом, называется двухполюсником. Если /-й элемент описывается
последовательной переменной Aj(t) и параллельной переменной Bf(t), то поток
энергии (мощность) , подводимый к элементу за интервал времени г, равен
N,= fA,(t)B,(t)dt. B.1.2)
Знак подводимой мощности определяет тип элемента. Если Nj > 0, то это
значит, что мощность поступает к элементу, и с энергетической точки
зрения элемент является пассивным, так как он сам не вырабатывает энергию,
а получает ее извне. Пассивные элементы являются нагрузкой, в которой
подводимая энергия или преобразуется в другие типы энергии, не
рассматриваемые в данной постановке (тепловую, электрическую и т.д.), или
передается другим элементам цепи, или запасается в элементе. Если А^- < 0, то
элемент является активным, так как подводимая мощность отрицательна,
а если рассматривать отводимую, отдаваемую мощность, то она имеет
другой знак, т.е. будет положительной. В этом случае элемент вырабатывает
энергию или сигналы, получаемые за счет других форм энергии, не
рассматриваемых в данном случае (электрической, химической и т.д.), или за счет
изменения энергии потока. Активные элементы ПГЦ входят в состав
моделей насосов, компрессоров, регуляторов, управляющих устройств и т.д.
Активные элементы могут быть независимыми и управляемыми
(зависимыми) . Для независимых идеальных источников создаваемый напор или
расход не зависит от режима работы ПГС, так как предполагается, что
источник питается за счет внешней энергии, а мощность, подводимая к
источнику, не ограничена. Зависимые (управляемые) активные элементы
(источники) изменяют режим своей работы пропорционально расходу
или давлению (перепаду давления) в одной из ветвей цепи.
2.1.3. Пассивные двухполюсники - емкости и инерционности. Наиболее
простыми элементами, входящими в ПГЦ, являются элементы,
характеристики которых описываются одним уравнением, связывающим две
переменные. Рассмотрим более подробно простейшие двухполюсники —
инерционность, емкость и сопротивление. В § 1.10 уравнения простейших
пассивных элементов — двухполюсников — были получены путем упроще-
71
I
G,
I
Г
_JtC_
б
Laaa I
\x
Pi
rvw i
д
Vr
о о о о
Ро
0 О О
—
о о
о о
О О
о о
АХ I
о Т о
о
ас еж
Рис. 2.2. Различные варианты устройств, описываемые как емкость
ния уравнений гидромеханики. Эти же уравнения можно найти другим
путем - непосредственно из физических закономерностей, используя уже
сформулированные в § 1.10 упрощающие предположения. Для проточной
емкости (рис. 2.2, а) составим уравнение баланса расходов, предполагая,
что для жидкости, протекающей через емкость или находящейся в
непроточной емкости, можно пренебречь ее вязкостью и инерционностью. В
таком идеализированном элементе при увеличении давления запасается
потенциальная энергия сжатой жидкости. Количество жидкости в емкости т
связано с расходами на входе Go и выходе Gx уравнением сохранения
массы
dm
—
B.1.3)
Учтя связь массы однородной жидкости с ее плотностью т- pVe (где Ve -
объем емкости), а плотности - со скоростью звука а^ = (Эр/Эр),, считая,
что стенки емкости жесткие, найдем
dt
¦=G0-
B.1.4)
Если в качестве рабочей среды используется идеальный газ, для которого
аж -kRTQi а течение - изотермическое, то уравнение B.1.4)
принимает вид
dp
-Go -
B.1.5)
kRTo dt
Кроме проточной емкости, аналогичными уравнениями описываются
нестационарные процессы в тупиковых емкостях (рис. 2.2, б), в емкости,
частично заполненной газом (рис. 2.2, в), в открытом участке трубы со
свободной поверхностью (рис. 2.2, г), в устройствах с упругим элементом
(рис. 2.2, д-ж). Для тупиковой емкости с однофазной рабочей средой
сохраняют силу уравнения B.1.4) или B.1.5), если инерцией жидкости
и гидравлическим сопротивлением в горловине можно пренебречь. Для
72
емкости, содержащей в своей полости две фазы - жидкую и газообразную
/рис. 2.2, в), пренебрегая инерцией, вязкостью в горловине, не учитывая
плескания жидкости, запишем уравнение баланса для жидкой фазы
аж пр
р>кУж ^0^1, ()
dt dt
где Уж — объем, занимаемый жидкой фазой. Учитывая сжимаемость
жидкости Эрж/Эр = а2ж и условие для жестких стенок Кж + VT - const (Vr —
объем газа), предполагая процесс в газовом объеме политропным р?? -
= const, где п — показатель политропы, преобразуем уравнение B.1.6) к
следующей форме:
Vr \ dp
П =Go-d. B.1.7)
/ dt
Для сосуда (трубы) со свободной поверхностью, сообщающейся с внешней
средой (рис. 2.2, г), используя уравнение баланса B.1.3) и зависимость
для массы жидкости в сосуде т = faFh, где F - площадь поперечного
сечения сосуда, h — высота столба жидкости в нем, найдем
dh
Рж/7— ^Go-Gl B.1.8)
dt
Для последнего типа устройств, описываемых как емкость с упругими
элементами, можно выделить варианты схемы — с упругим элементом в
тупике (рис. 2.2, ж) и с упругим элементом, сообщающимся с трактами
ПГС двумя сторонами (рис. 2.2, д и е). Запишем уравнение равновесия для
подвижной части упругого элемента, пренебрегая инерцией, трением в
жидкости и в подвижных механических частях, а также сжимаемостью
жидкости: '
(Po~Pi)F3b=kx+Po, B.1.9)
где ро, pi — давление на входе и выходе элемента, F3$ — эффективная
площадь упругого элемента, к — суммарная упругость подвижной части
(сильфонов, мембран, пружин и т.д.), х — координата положения
подвижной части, Ро - начальная затяжка пружины (при х - 0). В уравнении
баланса расходов учтем, что при принятых предположениях расход жидкости
на входе в упругий элемент равен расходу на выходе и одновременно равен
количеству жидкости, вытесняемой подвижной частью в единицу времени:
Сс^С^р^ф-^. B.1.10)
dt
Подставив соотношение B.1.9) в уравнение B.1.10), получим
г . ^2эфРж dAp nnn
Ь^о , B.1.11)
к dt
где Ар=Ро -Pl.
Если упругий элемент находится в тупике (рис. 2.2, ж) и сообщается
одной стороной с внешней средой, то запись уравнения B.1.11) сохранится,
только вместо перепада давления Ар будет просто давление р0, так как
давление pl9 равное давлению внешней среды, будет постоянно. Приведенные
73
выше элементы (рис. 2.2), описываемые формулами емкости B.1.4),
B.1.5), B.1.7), B.1.8) и B.1.11), являются двухполюсниками, так
как их характеристика содержит одно уравнение и две переменных -
давление (разность давлений 1)) и расход (разность расходов).
Тип уравнений один и тот же — связывающий последовательную
переменную (расход) с производной по времени от параллельной, что характерно
для емкостного элемента. Во всех уравнениях емкости, кроме уравнений
B.1.8) и B.1.11), под производной стоит абсолютное давление. При изме-
Оо »о >о/
в
-? Р и с. 2.3. Полюсный граф для
проточной емкости (а) и эквивалентные
цепи для емкостей (б, в) и газового
о /Гг сопла (г)
-о
рении абсолютного давления в емкости необходимо найти разность между
давлением в емкости и давлением во внешней среде — в пространстве с
абсолютным вакуумом. Соответствующий полюсный граф будет
изображаться линией, связывающей точку в системе, где установлена емкость,
с точкой, характеризующей состояние внешней среды. Учитывая, что во
всех этих случаях (см. рис. 2.2, а-г, ж) в емкость жидкость подводится
и отводится, а расходы жидкости на входе и выходе разные, то полюсный
граф проточной емкости должен иметь вид, изображенный на рис. 2.3, а.
Здесь появляется дополнительный расход Ge, идущий на изменение массы
жидкости в емкости при изменении давления. Этот расход идет к полюсу Н,
описывающему состояние внешней среды. Эквивалентную цепь для этих
устройств можно представить в виде четырехполюсного элемента,
включающего емкость (рис. 2.3, б), добавив в качестве второго уравнения
условие сохранения в элементе мгновенного значения давления (уравнение
импульса) ро =Р\-
Для сосуда со свободной поверхностью получится такая же форма
представления, если вспомнить, что р0 = ржк + рн, а рн — давление во внешней
атмосфере. Несколько отличается случай непроточных упругих элементов
(рис. 2.2, д, е), для которых эквивалентная схема (рис. 2.3, в) - просто
емкость как двухполюсник, так как измерение параллельной переменной
(перепада давления) производится между двумя точками внутри
устройства — перед упругим элементом и за ним. Таким образом, использование
(хотя бы мысленно) процедуры измерений параметров позволяет
установить структуры как графа, так и цепи, эквивалентной рассматриваемой
ПГС. Другим идеализированным элементом ПГЦ является инерционность —
аналог индуктивности в электротехнике. Как в электротехнике реально
не существует устройств, которые обладают индуктивностью без
сопротивления, так и в устройствах ПГС нельзя выделить элемент, обладающий
только инерционностью без сопротивления.
1) В уравнении B.1.8) величина РЖН также является разностью между давлением
на входе в сосуд и давлением над свободной поверхностью.
74
Однако в ряде случаев инерционные свойства дают в динамике
существенно большие эффекты (например, перепад давления), чем потери
давления на гидравлическое сопротивление. Рассмотрим столб несжимаемой
невязкой жидкости в тракте цилиндрической формы и запишем для него
уравнение количества движения
du dG
Wo -Pi)F=plF = / , B.1.12)
dt dt
где Po, Pi - давление на входе и выходе тракта, F, I — площадь его
поперечного сечения и длина, и, G - скорость и расход жидкости. Если тракт
состоит из п участков разного сечения и длины, то, пренебрегая потерями
давления на трение о стенки и в местах изменения сечения тракта,
запишем п уравнений типа зависимости B.1.12). Учитывая, что при принятых
предположениях давление на выходе из одного участка равно давлению
на входе в следующий участок, последовательно исключая величины
давлений во всех сечениях, кроме крайних, получим
п / /,. \ dG
Ар=Ро-Рп= 2 — —, B.1.13)
i = 1 \ F( I dt
где li/Fj - приведенная инерционность столба жидкости в г-м участке
тракта. Для тракта с непрерывным изменением площади проходного
сечения F(x) при соблюдении перечисленных выше предположений сумма в
зависимости B.1.13) переходит в интеграл по продольной координате х:
dG > dx
Ар=~7~ f T7T' B.1.14)
Приведенные уравнения инерционности описывают процесс ускорения
или замедления жидкости под действием переменного перепада давления.
При этом работа сил давления затрачивается на изменение кинетической
энергии потока. В уравнение инерционности B.1.12) входит длина
сужающегося участка тракта /, которая применительно к нестационарным
процессам в местных сопротивлениях не совпадает с геометрической длиной
сужения тракта. Это связано с тем, что поток на входе в сопротивление
и особенно на выходе из него отрывается от стенок канала. Благодаря
такому характеру течения вместе со столбом жидкости в сужающемся
участке при колебаниях давления колеблется некоторая масса жидкости
вне этого участка. Колебания этой присоединенной массы сказываются на
эффективной величине I/F, т.е. на инерционности элемента (см. раздел 2.1.4) .
Во всех уравнениях инерционности перепад давления между сечениями
на входе и выходе связывается с производной от расхода. Соответственно
полюсный граф также связывает эти точки, а в качестве изображения
инерционности как элемента цепи используем символ, применяемый в
электротехнике для индуктивности. Свойства простейших элементов становятся
еще более наглядными, если линеаризовать их уравнения. Для емкости
линеаризация наиболее общего уравнения B.1.7) при переходе к
безразмерным вариациям приводит к следующей зависимости:
JT ~т*~~, dG° ~dG^ B.1.15)
j dt dt
где bp, 8G0, 8Gi — безразмерные вариации давления, расхода на входе и
75
выходе емкости, те — постоянная времени емкости, состоящая из двух
слагаемых: теж = рУж/Са2 — емкостной постоянной времени для сжимае-
моей жидкости и те-г = рж VTjnG — емкостной постоянной времени для
объема газа, частично заполняющего емкость с жидкостью. Для емкости,
полностью заполненной жидкостью, ге=те>ж, для емкости
пневматической системы в выражении для те#г необходимо заменить плотность
жидкости Рж на плотность газа pT=p/RT. Соответственно при линеаризации
уравнения B.1.5) постоянная времени при производной от давления будет
равна тег = pVe/nRTG, где п — показатель политропы процесса (вместо
показателя адиабаты в выражении B.1.5)). Для емкости, описываемой
уравнением B.1.8), постоянная времени геЛ =p5Ki7/z/G, где h - высота
столба жидкости, а для упругого элемента, характеризуемого зависимостью
B.1.11), те>у =pF^pyK/kG. В последнем соотношении G - масштабный
расход жидкости, во всех предшествующих формулах дляге G-средний
расход жидкости. В качестве масштабного значения расхода удобно
выбирать средний расход жидкости через тракт, соединяющийся с другим
элементом.
Применительно к инерционному элементу уравнение B.1.13) после
линеаризации и перехода к безразмерным вариациям преобразуется к виду
dbG
д Ар = Ьр0 - Ьрп = ти , B.1.16)
dt к '
п ( U \ G
где ти = 2 { инерционная постоянная времени, 5 Ар, 8pQi
/= 1 \ F, ) р
Ьрп - безразмерные вариации перепада давления, давлений на входе и
выходе элемента. Если инерционный элемент описывается уравнением
B.1.14), то форма уравнения элемента B.1.16) сохранится, постоянная
же времени определится формулой ги = (G/p) f dx/F (x).
о
Таким образом, все многообразные емкостные устройства (после
линеаризации) описываются одним уравнением B.1.15), в котором при
изменении типа устройства или рабочей среды изменяется только формула записи
для постоянной времени емкости. Аналогичная ситуация имеет место и
для инерционного элемента, описываемого уравнением B.1.16).
2.1.4. Местное сопротивление. Рассмотренные выше уравнения
двухполюсников были получены двумя путями: с помощью упрощения
уравнений гидромеханики (§ 1.10) или из общих физических закономерностей
(раздел 2.1.3). К сожалению, применительно к проточному или
непроточному местному сопротивлению при турбулентном режиме течения оба
метода непригодны из-за сложного характера потока — с отрывами
течения, обратными токами и т.д. Характеристики местного сопротивления
при турбулентном течении описываются эмпирической зависимостью,
связывающей перепад давления Ар с расходом G или скоростью и. Для
несжимаемой жидкости при турбулентном режиме течения без учета
инерции для местного сопротивления используют зависимость
ри2 G2
др = р0_Р1=|_=--_— B.1.17)
где F — площадь проходного сечения, в общем случае регулируемая и за-
76
висящая от положения х регулирующего элемента, ? - коэффициент потерь,
и - коэффициент расхода. Величины ? и ^ изменяются в зависимости от
схемы, геометрических характеристик местного сопротивления, числа
рейнольдса, поля скоростей перед сопротивлением и т.д. [101].
Зависимость коэффициента потерь от числа Рейнольдса носит
достаточно сложный характер, но для каждого сопротивления можно выделить
Три области [2, 233] - ламинарного режима течения при Re<ReKp,
автомодельного режима при Re > Renp и переходную область ReKp < Re <
< Renp. В области ламинарного течения ? обратно пропорционально Re,
в автомодельной области — закон сопротивления квадратичный, в
переходной области зависимость ?(Re) может быть достаточно сложной,
иногда — нерегулярной. При этом в общем случае ? =|(Re,x), т.е.
зависит от положения регулирующего органа. Линеаризовав соотношение
B.1.17), найдем для размерных вариаций
Ар Ар Ар
5Г + 26С-2 — 5F' =
F
5Г 2
i; G
d\ 2 dF\ , Ap
1 5л:'+2-— SGf, B.1.18)
dx F dx ) G
или
Ар I 1 dF 1 d\x \
2—— bG' -2Apl + 5x', B.1.19)
G \ F dx ix dx )
где bp'Oibp'i,bAp, 8G '— вариации давлений перед и за сопротивлением,
перепада давления и расхода в местном сопротивлении, d?', 5// —
вариации коэффициентов, dF'98x— вариации площади проходного сечения
и положения подвижного дросселирующего устройства. Переходя к
безразмерным вариациям, получаем из выражений B.1.18) и B.1.19)
Ро Pi I х d% x dF \
ЬАр=~— 5р0 -— 6р! = — 2 5X + 25G, B.1.20)
Ар Ар \ % dx F dx )
I x dF x djji\
-2 + 16jc , B.1.21)
\ F dx ii dx )
где Po,Pi,Ap — средние значения давления перед сопротивлением и за ним
и перепада давления, F,x — средние значения площади проходного сечения
и координаты подвижной части, ?,ju - средние значения коэффициентов.
Одно из принятых выше предположений — о несжимаемости жидкости —
безусловно верно для капельной жидкости, а в некоторых случаях — и для
газа.
В гл. 1 было показано, что для потока газа одно из условий
несжимаемости сводится к соблюдению неравенства М < 1. Таким образом, если при
течении через местное сопротивление скорость газа намного меньше скорости
звука, то для такого режима течения можно использовать зависимости
B.1.17) - B.1.21), полученные для несжимаемой жидкости. Если условие
М ^ 1 не выполняется, необходимо учитывать сжимаемость газа,
используя газодинамические формулы. Считая газ идеальным и геометрию местно-
77
го сопротивления — с достаточно плавным изменением проходного сечения
на входе, можно записать для докритического режима истечения [81 ]
к- 1
где ,а, F - коэффициент расхода и площадь минимального сечения местного
сопротивления (сопла), Л,Г0 — газовая постоянная и температура газа
перед сопротивлением, к - показатель адиабаты газа. Линеаризация
формулы B.1.22) приводит к следующим зависимостям: для размерных
вариаций
8С' = A+е) 8р'о- 8р[ +—-г 8QiF)' - —— 8(RT0)\
Ро Pi VF 2^Г0 B 123)
для безразмерных вариаций
1
S(RT0), B.1.24)
где /с - 1
9 \ Po /
_ PilPo 3G 2 \ Po / , B.1.25)
6 Go Э(Р,/Ро) " ^"^
Л1 1-
8 (RT)', 8 (RT0) — размерная и безразмерная вариация произведения/?То.
Коэффициент е определяется отношением давлений газа в местном
сопротивлении (сопле) Pi/Po, и при критическом и сверхкритическом перепа-
к— 1
дах (^кр = (PiIPo)kp = [2/(^+ 1)] к ) величина в обращается в нуль.
При сверхкритическом перепаде в формуле B.1.25) изменяется знак б,
однако для приведенных условий этой формулой, так же как и исходной
формулой B.1.22), пользоваться нельзя, так как они описывают только
докритическое истечение газа. При сверхкритическом перепаде надо
принимать е = 0, т.е. расход не зависит от противодавления за соплом ру. По своей
структуре формулы для вариаций расхода B.1.23) и B.1.24) отличаются
от аналогичных формул B.1.18) — B.1.21) для местных сопротивлений
на несжимаемой жидкости. Для несжимаемой жидкости коэффициент
связи между вариацией расхода и вариациями перепада давления один
и тот же, т.е. изменение расхода при неизменной площади F определяется
перепадом давления. Это явный признак того, что такое сопротивление -
двухполюсник, аналог электрического сопротивления.
Для газа уравнение сопротивления (сопла) даже при постоянной
температуре связывает не две, а три переменные - 8G,8p0 и8рг .Подобный
элемент нельзя описать двухполюсником, но можно представить в виде
схемы из двух унисторов (рис. 2.3, г) с разными направлением и
коэффициентами [168]. Унистор, в отличие от двухполюсника, пропускает сигнал
только в одном направлении. Газодинамическая зависимость B.1.22)
78
и полученные на ее базе линеаризованные соотношения пригодны для
спрофилированных сопел и местных сопротивлений с плавным входом
п 81]. При истечении из отверстий, конических насадков, регулирующих
органов характер зависимости расхода от перепада давления носит более
сложный характер. За счет неравномерности полей скорости, давления
и температуры уменьшается значение критического отношения давления
(PiIPo)kp> пРи котором расход через сопротивление перестает зависеть
от противодавления [81]. Теоретически задача об истечении газа из
отверстия была решена С.А. Чаплыгиным и уточнена Ф.И. Франклем. Расход газа
продолжает увеличиваться при падении перепада давления на отверстии
ниже Ркр Д° некоторой величины у** (второй критический перепад),
при которой исчезает влияние противодавления на расход. Для воздуха,
по Франклю, p^t ^0,4, для водяного пара у^ ^0,1.
Имеется другое интересное физическое явление, по своему характеру и
математической модели подобное режиму критического истечения газа
из местного сопротивления. Это явление — кавитация, возникающая внутри
или вблизи местных сопротивлений в гидравлических системах при
большом перепаде давления на сопротивлении и относительно небольшом
уровне давления в системе. Кавитация - это местное вскипание жидкости
(паровая кавитация) или выделение из жидкости растворенного газа из-за
низкого давления и образование двухфазного течения в местном
сопротивлении [5, 111,182]. При достижении режима развитой кавитации, когда
зона двухфазного течения занимает заметную долю проточной части,
возникает режим критического течения, подобный аналогичному режиму при
истечении газа. При критическом режиме расход жидкости зависит от
давления перед сопротивлением и не зависит от давления за сопротивлением.
На рис. 2.4,а приведены кривые изменения расхода воды через угловой
регулирующий орган при постоянном давлении на входе р0 = 8 • 105 Па
и при разных относительных значениях хода дросселирующего элемента
x~=x/h, где х, h — текущее и максимальное значения хода [5]. Здесь же
(рис. 2 А,б) приведена схема проточной части дросселирующего элемента
и пример распределения давления по его длине.
Эксперименты проводились при различных значениях температуры
воды. До начала кавитации расход связан с корнем из перепада давления
VAp = VA) -Р\ прямой линией. Для каждого значения Т и 5с~при
определенном перепаде (отмечено стрелочками) появляются отклонения от
линейности, вызванные кавитацией. Это подтверждается и фотографированием
потока при прозрачном корпусе регулирующего органа. После перегиба
расход стабилизируется и практически не зависит от Ар = р0 - ръ а так как
А) = const - то не зависит и от противодавления рх. Кавитационный режим
течения через местное сопротивление можно описать в первом приближении
соотношением
ж (Ро -Ps)'> B.1.26)
где ps — давление в зоне кавитации, равное давлению насыщенного пара
или давлению выделяющегося растворенного газа. Считая ps = const,
линеаризовав зависимость B.1.26) , находим для размерных вариаций
С С
5G' ' ' B.1.27)
2(Po-Ps)
79
о-20° С i-f189C
• -77Г
f-80°C
О 0,5 1,0 f,5 2,0
Рис, 2.4. Зависимость расхода от давления для дросселирующего устройства при
кавитации (а) и схема проточной части дросселя (б)
или в безразмерных вариациях
Ро
5 G =
8р0.
B.1.28)
2(po-Ps)
Уравнения B.1.27) и B.1.28) имеют форму, аналогичную зависимостям
B.1.23) и B.1.24) при е = 0 для критического режима истечения газа.
Поэтому местные сопротивления с развитой кавитацией, так же как и
местные сопротивления на газе при критическом режиме истечения, имеют
одностороннюю проводимость - расход через сопротивление зависит
только от давления с одной (напорной) стороны. В этом случае местное
сопротивление описывается одним унистором (рис. 2.3, г) при е = 0. В
уравнениях B.1.26) —B.1.28), так же как и во всех приведенных выше
уравнениях местных сопротивлений, не учитывалась инерция столба жидкости
в проточной части сопротивления. Применительно к кавитирующему
сопротивлению сделано еще одно допущение — пренебрежение податливостью
зоны кавитации. Вопрос о динамике зоны кавитации выходит за рамки
нашего рассмотрения (см. [170, 182]).
В случае нестационарного течения через местное сопротивление
уравнения B.1.17) —B.1.21) правомерны, если используется предположение о
квазистационарном течении, т.е. при совпадении характеристик течения в
данный момент с характеристиками течения в случае стационарного
значения с тем же мгновенным расходом. При такой постановке не учитывается
инерция столба жидкости в местном сопротивлении и возможное
изменение при нестационарном режиме коэффициентов м и ?. Применительно к
акустическим колебаниям в трубе без протока жидкости предложено
несколько формул для определения импеданса местного сопротивления -
диафрагм [256]. Динамические характеристики (импеданс) местного соп-
80
ротивления в акустике определяются формулой
8 Ар'
Д' + /1/ B.1.29)
zД
Ьи
где 5Ар, Ьи - вариации перепада давления и скорости в дроссельном
устройстве. Для дроссельных устройств без протока из-за малых амплитуд
колебаний скорости активная составляющая импеданса R' невелика,
меньше инерционной составляющей /ojL '. Инерционная составляющая
определяется массой, колеблющейся в дроссельном элементе. Инерционность
определяется формулой L' =р(/ + А/), где / - длина канала в дроссельном
элементе, А/ — эффективная длина, характеризующая присоединенную
массу, колеблющуюся вместе с массой жидкости, заключенной в
дроссельном элементе. Для дроссельной диафрагмы на выходе из трубы в открытое
пространство формулу для z' впервые предложил Рэлей, а для дроссельной
диафрагмы в трубе — В.А. Фок [191]. Результаты проведенных
экспериментов подтвердили теоретические зависимости. Как указывается в обзоре
[256], результаты экспериментов для местных сопротивлений с протоком
газа показали, что коэффициенты ^ или ? в достаточно широком диапазоне
частот (до 1000 Гц) практически не зависят от частоты. Соответственно
должна оставаться постоянной и активная составляющая импеданса R' в
формуле B.1.29). С ростом средней скорости протока газа через
диафрагму растет активная составляющая и несколько падает реактивная
составляющая импеданса. Для диафрагмы без протока в экспериментах
В.П. Шорина [244] обнаружено, что при колебаниях жидкости
коэффициент сопротивления составляет 0,54 значения этого же коэффициента для
стационарного течения.
В книге [174] приводятся данные по реактивной составляющей
некоторых местных сопротивлений в гидравлических трактах. Полученные
зависимости относятся к частным случаям сопротивлений и конкретным
условиям в потоке.
2.1.5. Активные двухполюсники. В состав ПГС, кроме описанных выше
пассивных элементов, входят также активные элементы — источники,
обеспечивающие питание системы рабочей средой или создающие управляющие
воздействия. Поэтому к активным элементам, эквивалентным в
определенном смысле источникам, относят и регулирующие органы, которые
управляют параметрами течения рабочей среды в ПГС, в частности,
энергией потока жидкости, и формируют сигналы, распространяющиеся по
системе. Энергия, поступающая от активных элементов, потребляется
пассивными элементами - расходуется на сопротивлениях, запасается в
емкостях и инерционностях. Применительно к системам, рассматриваемым в
линейном приближении, анализируется поведение отклонений параметров
от некоторого номинального, среднего их значения. Соответственно
активные элементы в линейных системах создают малые возмущения или
сигналы с заданным законом изменения параметров во времени, в частности,
в виде синусоидального или импульсного (мгновенного) изменения
параметров во времени. Частным случаем режима работы активного элемента
может служить поддержание постоянным одного из параметров.
Применительно к задачам анализа линейной динамики ПГС не важно, является ли
источник, вырабатывающий сигнал, действительно первичным источником
6- Б.ф. Гликман 81
энергии, создающим движение жидкости в системе, или это управляющий
элемент, изменяющий режим течения жидкости в системе.
Так же как и для пассивных элементов, вводятся понятия об идеальных
независимых источников расхода и давления (напора). Под идеальным
источником расхода понимается двухполюсный элемент цепи (рис. 2.5,а),
расход через который является определенной функцией времени Q(t),
не зависящей от реакции цепи на возмущение, т.е. источник, который
обладает неограниченной мощностью. Характеристика такого элемента,
Р и с. 2.5. Условные обозначения и
характеристики идеальных
источников расхода и напора
связывающая расход с перепадом давления в данный момент времени,
изображается вертикальной прямой, (рис. 2.5,в), т.е. расход не зависит
от сопротивления системы, а внутреннее сопротивление источника равно
нулю.
Идеальный источник напора является двухполюсным элементом
(рис. 2.5,5), который создает напор АН(t), являющийся заданной
функцией времени. Мгновенное значение создаваемого напора (рис. 2.5,в) не
зависит от расхода через источник. Это значит, что внутренняя
проводимость источника равна нулю, сопротивление — бесконечности, а его
мощность не ограничена. Реальные источники напора и расхода имеют
характеристики, отличные от идеальных, и эти особенности можно учесть
соответствующей схемой замещения, в которую наряду с идеальными
источниками входят пассивные элементы. Вид схемы замещения зависит от
конструкции и характеристики агрегатов и класса решаемой задачи (диапазона
частот, масштаба возмущений и т.д.). В простейших схемах замещения
активных элементов учитываются только внутренние потери, связанные с
трением, утечками и т.д. На рис. 2.6,а приведена схема замещения для
реального источника напора — лопастного насоса, характеристика которого
представлена на рис. 2.6,6. Примем, что для пассивного элемента
положительным является направление перепада давления, противоположное
направлению расхода, а для источника напора - направление, совпадающее
с направлением расхода. Для идеального источника напора уравнение
запишется в виде АН - АН (г) или в линеаризованном виде
8AH=8AH(t). B.1.30)
Напорная характеристика лопастного насоса связывает развиваемый
насосом напор с расходом жидкости через насос G и частотой вращения
его вала п\ AH = AH(G,n). За счет потерь в насосе его характеристика
(рис. 2.6,6) отличается от прямой, параллельной оси. Учтя наклоны
напорных характеристик насоса дАН/дп и Э АН/д G, связывающих
развиваемый напор с расходом и частотой вращения, и принятое правило
знаков, можно найти линеаризованную зависимость, определяющую вариа-
82
ю перепада давления на реальном насосе как функцию вариаций расхода
}1ДКости через насос и частоты вращения:
G ЪАН _ п ЪАН
^ — «^ =zBH6G -5 ЛЯ, B.1.31)
АЯ bG
G ЪАН
АЯ
ЭАЯ
где^вн Г77 777 » ^ АН = —— —— 8п,8Ар- амплитуда откло-
АЯ о G АН Ъ п
нений перепада давления (отсчитываемого от входа к выходу),
создаваемого реальным источником напора [58, 60].
Так как наклон напорной характеристики лопастного насоса или
компрессора по расходу, как правило, отрицательный (рис. 2.6, ?), то
внутреннее сопротивление источника zBH в этом случае — величина положительная.
Для реального источника расхода, схема замещения которого
представлена на рис. 2.6,в, с учетом внутренних утечек, моделируемых
сопротивлением с проводимостью увн, можно записать линеаризованное
уравнение баланса расходов
bG =-77—~ Ьп + —^ —— 8Ap=8Q + увн8А^ , B.1.32)
Q Ъп Q ЪАр
где
п bQ
Ьп.
Q ЪАр ~ Q Ъп
К активным двухполюсникам можно свести и более сложные насосные
системы, например (рис. 2.7, а) — источник питания гидросистемы с
объемным насосом 1 и устройствами, ограничивающими создаваемое насосом
8ДН
Рис. 2.6. Схемы замещения для реальных источников напора (с), расхода (в) и их
характеристики (б)
а б G
Рис. 2.7. Схема и характеристика насосного агрегата
давление, или переливным (предохранительным) клапаном 2, или
дросселем 3 на байпасе, через который часть жидкости возвращается в бак.
Характеристики такой системы приведены на рис. 2.1,6. Прямая 4 описьь
вает расход через насос при закрытых клапане 2 и дросселе 3, линии 5 -
характеристики системы при различной настройке работающего клапана 2
и закрытом дросселе, кривые 6 - характеристики системы при закрытом
клапане и дросселе, открытом на разные проходные сечения.
Рис. 2.8. Эквивалентная цепь,
описывающая характеристики
центробежного насоса
Характеристика системы, работающей или с переливным клапаном, или
с дросселем (пренебрегая инерцией и сжимаемостью жидкости, а также
инерцией подвижных частей клапана), описывается линеаризованным
уравнением
у ЬАН(у) G ЪАН _
8 Ар = — 8у 3G =zBH5G -5АЯ ,
АН Ьу АН bG
где 6 Ар — амплитуда безразмерной вариации перепада давления,
создаваемого системой, 6 АН {у) - амплитуда безразмерной вариации напора при
постоянном расходе, зависящая от настройки у клапана или дросселя,
zBH — внутреннее сопротивление системы, учитывающее как утечки в
насосе, так и характеристики (без динамики) клапана или дросселя. Таким
образом, получается уравнение, совпадающее с уравнением источника
напора B.1.31).
Приведенные схемы реальных источников учитывают только один
эффект, отличающий их от идеальных, - внутренние потери. Кроме
внутренних потерь возможно ощутимое, а иногда и определяющее влияние других
факторов на динамические характеристики источника. К примеру,
применительно к источникам напора типа центробежных насосов зона кавитации
на входе в насос существенно влияет на его динамические характеристики
вплоть до возможности развития автоколебаний [182]. Кроме того, в
насосе часто необходимо учитывать инерцию жидкости в проточной части
[58], податливость корпуса и зоны кавитации у горловины диффузора.
В итоге эквивалентная схема принимает вид, изображенный на рис. 2.8, —
источник уже оказывается не двухполюсным, а четырехполюсным
элементом. Это связано с тем, что за счет податливости зоны кавитации на входе
(первая емкость) и податливости корпуса (вторая емкость) мгновенное
значение расхода на входе не совпадает с расходом на выходе. В
результате одновременного присутствия в эквивалентной цепи емкости и
инерционности возможно проявление резонансных явлений, которые
обнаруживаются при динамических испытаниях шнекоцентробежных насосов.
Экспериментальные данные свидетельствуют, что при работе насоса на
режиме частичной кавитации коэффициент усиления насоса (отношение
амплитуд колебаний давления на выходе из насоса к амплитуде
колебаний давления на входе) превышает его значение при о;%0 и зависит от
частоты. Обработка данных частотных испытаний при различных режимах
работы насоса показала [227], что относительный коэффициент усиления
84
увеличивается в 4-5 раз при приближении к собственной частоте жидкости
в Проточной части насоса.
реальные источники с одинаковым успехом могут быть представлены
или в виде источника напора или как источники расхода. Соответственно
эТи схемы могут быть преобразованы из одной в другую. Для этого,
разделив все члены уравнения B.1.31) на zBH и записав уън = l/zBH. 52 =
=:5A/7/zBh, преобразуем это уравнение к форме зависимости B.1.32);
если же в последней принять zBH = 1/увн и 6 АН = 5Q/yBHi то она
трансформируется в уравнение источника напора B.1.31).
о
5GQ 5Gf a
J п Щп
О ¦
о-
W I 1 1 \*Pt
6Gf
б
о, А о.
О' 1
Рис. 2.9. Схемы четырехполюсников
2.1.6. Многополюсные элементы. В предыдущих разделах было
показано, что при уточнении математических моделей устройств их уже нельзя
свести к двухполюсным элементам. Ниже будут даны примеры
формирования математических моделей устройств, входящих в ПГС, которые при
переходе к ПГЦ в любом случае сводятся к более сложному элементу,
чем двухполюсник или цепь, состоящая из двухполюсников.
Многополюсники классифицируются по числу полюсов, с помощью которых они
соединяются с другими частями цепи. В общем случае внутренняя
структура элемента, описываемого как многополюсник, может быть неизвестной,
а его математическая модель определяется коэффициентами (функциями),
связывающими параметры среды, - давления, расходы (скорости),
температуры, концентрации и т.д. для всех его внешних полюсов. При этом
остаются неизвестными давления, расходы и другие параметры во
внутренних точках устройства, описываемого как многополюсник.
Следует оговориться, что при построении математических моделей
с помощью уравнений гидромеханики незнание внутренних параметров
определяется в первую очередь тем, что они не представляют особого
интереса и исключаются для упрощения модели, так как важно свести до
минимума число переменных. Если возникает необходимость
определения промежуточных переменных, то их можно найти, увеличив число
уравнений в математической модели системы. Из многополюсников ниже будут
использоваться в первую очередь четырехполюсники и в некоторых
случаях - шести- или восьмиполюсники.
Четырехполюсник имеет две пары полюсов - входных 0-0' и
выходных 1-1'. Термины "вход" и "выход" являются условными и используются
только для упорядочения обозначений. На рис. 2.9 представлены две
возможные схемы четырехполюсника. Прямоугольником обозначен элемент,
структура которого принципиального значения не имеет, так же как и
параметры течения внутри моделируемого устройства. Предполагается, что
внутри пассивного четырехполюсника (шестиполюсника) отсутствуют
независимые источники, а процессы в устройстве, моделируемом
четырехполюсником, с достаточной точностью описываются линейными (или ли-
85
неаризованными) уравнениями. Направление отсчета для расхода и
давления (перепада давления) показано на рис. 2.9. Предполагается (в
отличие от наиболее распространенного в электротехнике выбора
направлений токов в четырехполюсниках), что расходы на входе и выходе имеют
одинаковое направление. Применение теории линейных
четырехполюсников или многополюсников [159, 168, 217] позволяет эффективно
использовать матричные или топологические методы анализа систем. Кроме
пассивных четырехполюсников существуют и активные, в состав которых
входят источники.
Оо—n r—о/
j ? Рис. 2.10. Схема и эквивалентная цепь для
1 i С идеального гидравлического трансформатора
О'о М of'
а 6
Примером пассивного четырехполюсника может служить идеальный
гидравлический трансформатор (рис. 2.10,#), при описании которого не
учитываются инерция и трение для подвижных механических элементов и
жидкости. Основное уравнение трансформатора - уравнение равновесия
сил
B.1.33)
гдеро> Р\, FQ, FY - давление и эффективные площади на входе и выходе
трансформатора. Линеаризовав уравнение B.1.33), находим соотношения
для давлений в размерных и безразмерных вариациях:
, , Ро
opi-kT8pQi 8рх = кт дро, B.1.34)
Pi
где кт = Fq/Fx — коэффициент трансформации.
Для определения связи расходов жидкости воспользуемся условием
равенства скоростей обоих поршней трансформатора
Go Gt Fx
~ или Gj = Go .
Линеаризация последнего равенства дает
5Gq 1
bG\ = или 8Gt = 3G0. B.1.35)
Таким образом, идеальный гидравлический трансформатор описывается
двумя уравнениями B.1.34) и B.1.35), связывающими четыре вариации
параметров (в амплитудах) :
дрх =кт др0,
*1 B.1.36)
5Gi = SG0.
кт
Уравнение B.1.36) - типичное уравнение четырехполюсника, записан-
86
нос в ^-параметрах, причем параметры на выходе четырехполюсника
(dpi- &G\) выражаются через параметры на входе (8р0, 8G0). Эту систе-
му уравнений можно записать в матричной форме
кт— О
Pi
1
О —
кт_
8G0
= В
8G0
B.1.37)
где [bpoSGo]T, [dpi^Gx]7 - матрицы-столбцы (векторы) параметров на
входе и выходе четырехполюсника, В - квадратная матрица ^-параметров
четырехполюсника (иногда называемая цепной матрицей). На рис. 2.10,5
приведено условное обозначение трансформатора, как звена ПГЦ. Из-за
соединения между собой двух полюсов — одного на входе, другого на
выходе — идеальный гидравлический трансформатор имеет вид трехполюс-
ника (рис. 2.9,6) - широко распространенной в ПГЦ разновидности
четырехполюсников. Применительно к трансформатору и большинству
элементов ПГЦ, описываемых как четырехполюсник, объединенный узел
О'-l' характеризует состояние внешней среды (абсолютного вакуума),
относительно которого отсчитывается давление на входе и выходе
четырехполюсника.
Примером устройства, описываемого уравнениями шестиполюсника,
может служить газовое сопло, если принять, что длина сопла относительно
невелика, и емкостью сопла, т.е. временем пребывания газов в сопле, можно
пренебречь. В этом случае принимаем, что отклонения расходов на входе
и выходе совпадают: 8G0 = 8Gi. Если не учитывать трение и дроссельный
эффект, а также скоростные напоры на входе и выходе сопла, то для сопла
малой длины соблюдается условие 8Т0 = 57\. Используя уравнение
B.1.24) (считая R = const, a 8(iiF) = 0) и принятые допущения, можно
записать систему уравнений сопла как шестиполюсника в ?-параметрах:
1 +е 1 _ 1
8р0 — — 8G0
е е 2е
8G1 — 5Gq,
или в матричной форме:
8G1
=
0
0
+ е)/б
-1/е
1
0
-1/2е
0
1
B.1.38)
B.1.39)
Если течение газа перед соплом — изотермическое, т.е. 8Т0 = 5ГХ = 0, то
уравнения B.1.38) и B.1.39) сводятся к уравнению четырехполюсника.
Расход через газовое сопло (в отличие от обычного местного
сопротивления для жидкости B.1.16)) зависит не от перепада давления, а от
давления на входе и выходе независимо, с разными коэффициентами связи.
Подобный элемент не сводится к схеме, состоящей из двухполюсников,
его можно описать или с помощью схемы из унисторов (см. рис. 2.3, г),
или как четырехполюсник (или шестиполюсник). Уравнения B.1.38)
87
и B.1.39) пригодны только для докритического режима истечения, когда
е Ф 0. При б = 0 исчезает связь параметров с изменением давления за
соплом Ърх, поэтому форма записи в .5-параметрах в этом случае не
пригодна, так как в этих параметрах не прослеживается связь между
возмущениями от входа к выходу. Так как связь с другими параметрами
не определена, уравнение для этой переменной отсутствует, а значит, нельзя
составить уравнение четырехполюсника.
Если рассматривать распространения возмущений в другом
направлении — от выхода ко входу, что соответствует записи уравнения в А
-параметрах [11, 60, 159], то уравнение B.1.38) при 6 = 0 принимает форму
др0 = 8Gi +A/2M7\, 5G0 = SGX, ЬТ0 = 8Тг B.1.40)
или матричную форму:
15Г0 J
"О 1 1/2
О 1 О
.001.
'8рх
= А
[ 1J
B.1.41)
Матрица А в уравнении B.1.41) особенная, что свидетельствует о
невозможности ее обращения, т.е. о невозможности записи уравнений этого
элемента в В -параметрах.
Приведенные простейшие примеры иллюстрируют принцип
формирования уравнений многополюсников на примере наиболее часто
используемых типов многополюсников — четырехполюсника и шестиполюсника.
Уравнение четырехполюсника не зависит от схемы соединения его
полюсов с другими элементами цепи и способа создания возмущений
на входе (выходе). Четырехполюсник считается заданным, если
определены четыре коэффициента, входящие в его уравнение. В зависимости от
формы записи уравнений, т.е. от того, какие переменные приняты за
входные, а какие — за выходные, четырехполюсники делятся на шесть типов
[11, 60, 159]. Выбор той или иной формы записи уравнений
четырехполюсника зависит от удобства использования уравнения и от способа
соединения между собой отдельных элементов цепи, в том числе и других
четырехполюсников.
К четырехполюсным элементам относятся зависимые (управляемые)
источники (усилители). Зависимые источники на схемах изображаются
или тем же символом, что и независимые источники с записью рядом
расхода или напора (давления) через управляющую величину, или
вводится специальное обозначение в виде ромба (рис. 2.11) со значком внутри,
указывающим тип источника [159]. В четырехполюсник, описывающий
зависимый источник, входят два входных полюса, которые или не
связаны между собой, или связаны трактом без сопротивления (в
электрических терминах — короткозамкнуты), и два выходных с
соответствующим источником (рис. 2.11, а—г). Два не связанных между собой полюса
на входе моделируют управляющую ветвь с управляющим давлением (или
перепадом давления) 8р0 и нулевым расходом, а замкнутая ветвь на входе
определяет вариацию управляющего расхода 8G0 и нулевой перепад
давления. На выходе управляемая ветвь имеет для источника расхода
вариацию расхода SGi, для источника давления — вариацию давления (напор)
88
5pt. Как и для любых четырехполюсников, у зависимых источников
физическая природа параметров на входе и выходе может быть различной
(электрические и гидравлические, тепловые и электрические и т.д.) [11].
Однако ниже будут рассматриваться только пневмогидравлические
системы или смешанные системы, сводимые к ПГС. Поэтому все параметры
в эквивалентной цепи будут гидромеханическими. Возможны четыре
типа идеальных управляемых источников:
6G,
Рис. 2.11. Обозначения для управляемых источников давления и расхода
1. Зависимый источник давления (напора), управляемый давлением
(перепадом давления). Управляющим сигналом является давление или
перепад давления между входными полюсами (рис. 2.11, а). Если
управление ведется по давлению, то второй полюс на входе описывает состояние
внешней среды, от которой отсчитывается давление в системе. При этом
расход через управляющую ветвь равен нулю: 5G0 = 0, т.е. входная ветвь
четырехполюсника имеет бесконечное сопротивление. В выходной ветви
имеется источник давления (напора), причем создаваемое давление
(напор) пропорционально давлению на входе:
«Pi = крбро, B.1.42)
где кр — коэффициент передачи давления, равный отношению отклонений
давления на выходе и входе зависимого источника. Идеальный зависимый
источник давления, управляемый давлением, называют часто идеальным
усилителем давления, моделирующим реальные гидравлические
усилители, если в них пренебречь внутренним сопротивлением, утечками,
инерцией и сжимаемостью жидкости.
2. Зависимый источник расхода, управляемый расходом (рис. 2.11, б).
Во входной ветви управляющий расход проходит через ветвь без
сопротивления, перепад давления на этой ветви равен нулю. В выходной ветви
имеется источник расхода, величина которого пропорциональна расходу
через входную ветвь:
&GX = kG8G0, B.1.43)
где kG — коэффициент передачи расходов. Идеальный зависимый источник
расхода, управляемый расходом, называют также идеальным усилителем
расхода.
3. У зависимого источника давления (напора), управляемого расходом
(рис. 2.11, в), управляемой величиной является давление, создаваемое
источником в выходной ветви, значение которого пропорционально
8?
расходу через входную ветвь.
B.1.44)
где kz - коэффициент передаточного сопротивления. Перепад давления
во входной ветви равен нулю.
4. В зависимом источнике расхода, управляемом давлением
(рис. 2.11, г), выходная ветвь содержит источник, расход через который
пропорционален давлению во входной ветви:
дбг = кудро, B.1.45)
где кv — коэффициент передаточной проводимости источника. При этом во
входной ветви 8G0 = 0. Все зависимые источники являются четырехполюс-
ными элементами и их уравнения можно записать в матричной форме:
8G,
0 0
0 кр
kG 0
0 0
0 0
kz 0
" 0 0
. kv 0
][5С0
Шро.
5С0
• 5р0-
1 6С0
" 5ро"
- 5р"| .
= Вг
B.1.46)
= Y
B.1.47)
B.1.48)
B.1.49)
Все матрицы в уравнениях B.1.46) - B.1.49) особенные, содержащие
только по одному ненулевому элементу - коэффициенту передачи
сигнала. Так как матрицы уравнений особенные, то все зависимые идеальные
источники являются необратимыми элементами цепи с односторонней
передачей сигнала. Зависимые элементы являются удобным модельным
представлением для ряда элементов, входящих в ПГС. К примеру, в форме
зависимого источника расхода, управляемого давлением, можно описать
газовое сопло, для которого при критическом режиме истечения (с = 0)
и ЗТ0 - ЬТу = 0 уравнение_B.1.40) по форме подобно уравнению B.1.45),
дополненному условием 5G0 = 5Gi.
Другим примером устройства, которое моделируется зависимым
источником, может служить струйный усилитель, схема которого
представлена на рис. 2.12, а. Усилитель состоит из сопла питания 1, струя из которого
попадает в приемник 2, где восстанавливается скоростной напор жидкости
При подаче второй струи из сопла управления 3 активная струя из сопла 1
Р и с. 2.12. Схема
), характеристика (б) и эквивалентная цепь (в) струйного
усилителя
отклоняется, в приемное сопло попадают участки струи с меньшей скоро-
сТЬю и соответственно уменьшается рх . Характеристика струйного
элемента приведена на рис. 2.12, б. Линеаризованное уравнение струйно-
го элемента, пользуясь графиком на рис. 2.12, о, запишем в виде Ьр^ -
- (Po/Pi) (dPi/dpo)&Po = kp8pOi Это уравнение совпадает с
уравнением B-1 -42) идеального усилителя давления (рис. 2.12, в) .
Примером более сложной схемы с управляемыми источниками может
опять же служить газовое сопло, но с использованием полного уравнения
Рис. 2.13. Эквивалентная цепь для
газового сопла
B.1.38) при в Ф 0. В этом случае расход изменяется за счет действия трех
переменных — вариаций давления Ьр0, Ьр^ на входе и выходе и
температуры дТ0 на входе. Выделим отдельно три пары входных полюсов для Зр0,
Ьр\ и 5Г0, а их влияние на расход учтем тремя управляемыми
источниками расхода, порядок включения которых в цепь определяется знаками
коэффициентов перед ними (рис. 2.13). В итоге получился восьмиполюс-
ный элемент с тремя управляемыми источниками расходов.
Восьмиполюсник включает два вида переменных — гидромеханические др0, 5pi и 8G0
и тепловую - ЗТ0. Ниже, в гл. 7, будут рассмотрены методы построения
ПГЦ, описывающих систему с неизотермическим течением газа.
Способность газового сопла при критическом режиме работать как
активный элемент, поддерживая постоянным расход газа вне зависимости
от противодавления и выполняя функцию стабилизатора расхода, широко
используется в экспериментальных газовых установках, предназначенных
для исследования динамических свойств газовых трактов [142, 196].
Линеаризованная зависимость B.1.40) пригодна только для коротких
сопел, имеющих длину проточной части существенно меньшую, чем длина
акустических волн. Сопла или местные плавные поджатия потока (типа
трубок Вентури) , имеющие длину, соизмеримую с длиной волны,
необходимо рассматривать как элементы с распределенными параметрами [141,196].
В радиотехнике используются методы анализа цепей, основанные на
описании многополюсных элементов неопределенными матрицами
проводимости. При этом, в принципе, особенности внутренних процессов
в агрегатах или частях ПГС, описываемых как многополюсники, могут
быть неизвестными. В этом случае зависимости между параметрами в
ветвях и полюсах, связывающих многополюсник с другими частями цепи,
определяются или экспериментально, или в результате расчетов по
достаточно сложной модели, которую нецелесообразно включать в общую
математическую модель системы. Предполагается, что многополюсник не
содержит независимых источников энергии, и поэтому в терминах
электротехники он является неавтономным элементом [203]. Отсоединенный от
Других частей цепи, такой многополюсник не создает отклонений
(вариаций) параметров в частях ПГС, моделируемых его полюсами. При ис-
91
е
Рг
<
Г
к
р
1
J
(л.
Wa
60'
5G'h
5G'
SGn
Рис. 2.14. Схемы многополюсных, двухполюсного и четырехполюсного элементов
пользовании же многополюсника как элемента ПГЦ его связь с
остальными частями цепи учитывается с помощью расходов, протекающих через
его полюса, и давлений (перепадов давлений) на его полюсах.
В общем случае т уравнений многополюсника, изображенного на
рис. 2.14, я, связывают между собой 2т переменных - расходов и
давлений
/i(Gb G2,.. . , Gm,pu p2>. . . , рт) = О,
/2(GbG2,...,Gm,Pi,p2,...,pw)= 0, Bл5о)
fm(Pi,G2,...,Gm,pltp2,...,pm) = 0.
В уравнениях B.1.50) давление измеряется относительно некоторого
базисного узла, находящегося вне многополюсника (рис. 2.14,а).
Линеаризация общих зависимостей B.1.50) для многополюсника приводит к
системе линейных уравнений между вариациями параметров
i bG\ t bG\ f 9Gj ,
5Gi = dpi + 5p2 + . . . + 5pm,
Ърх
dG2
B.1.51)
•Ьр\
Ьр'г
иИ1 др2 bpm
Частные производные имеют размерность проводимости, так как
связывают вариацию расхода через /-й полюс с единичным отклонением
давления в /-М полюсе в случае, если для всех остальных полюсов отклонения
давления равны нулю:
6 G\
у'ц =—- при 6p'k = 0 (к Ф /). B.1.52)
Аналогичные коэффициенты можно ввести и для линеаризованных
уравнений в безразмерных параметрах:
У И =
Ър,
= 0, к
7о/
92
где Poj у ^о/ - номинальные, нормирующие значения соответствующих
параметров. Используя обозначения для коэффициентов проводимости B.1.52),
систему уравнений B.1.51) можно записать в матричном виде:
3Gf2
bGm _
" Ун
Ун
-У ml
У\1
У12
У ml
• . . У\т
• • - У2т
i
- • • У mm —
ЬР2
-UP»
= У
Ьр2
J>Pm -
B.1.53)
где у — матрица проводимости многополюсника. Эта матрица полностью
характеризует особенности многополюсника при малых отклонениях
его параметров от некоторого номинального режима. Матрица
проводимости является неопределенной и особенной, так как в соответствии с
правилом узлов (см. гл. 3) одно из уравнений системы B.1.51) является
зависимым. Из т2 элементов неопределенной матрицы проводимости
только (т — IJ элементов независимы.
Преимущество неопределенной матрицы проводимости заключается
в том, что при ее формировании давление в полюсах отсчитывали от
внешнего базисного узла, не связанного с многополюсником. Это упрощает
стыковку многополюсника с произвольной схемой ПГЦ, в которой может
оказаться, что ни один из полюсов многополюсника не будет связан с
базисным полюсом. При такой записи все полюсы оказываются в
одинаковом положении, т.е. для всех узлов (полюсов) цепи давления отсчитывают-
ся от одного общего узла. Разрешив уравнения B.1.51) относительно
вариаций давлений на полюсах многополюсника, можно получить другую
форму записи, через коэффициенты сопротивления, из которых
формируется неопределенная матрица сопротивления многополюсника.
Можно составить неопределенную матрицу и для двухполюсника, как
простейшего пассивного варианта многополюсника с т = 2, схема
которого изображена на рис. 2.14, б. Предполагая, что /-и двухполюсник
является одним из элементов цепи, узлы нумеруем условными индексами / и к.
Давление в узлах (полюсах) двухполюсника отсчитывается от некоторого
внешнего узла, а направление расходов (как и на рис. 2.14, а) — от обоих
полюсов в сторону двухполюсника. Характеристики двухполюсника
описываются его проводимостью, и для вариаций расходов через два узла
можно записать
5G/ = y'i Ep/ - Ьрк)9
или в матричной форме
Ух -Уг
-y'i у\
В качестве другого примера составления неопределенной матрицы
рассмотрим газовое сопло при изотермическом докритическом течении,
т.е. 5Г0 = 0, описываемое уравнениями B.1.38) и изображаемое в виде
четырехполюсника (см. рис. 2.14, в). У этого четырехполюсника, в отличие
от ранее принятой схемы (см. рис. 2.9, а), все ветви направлены от полюсов
к четырехполюснику и для каждой из них существует своя вариация
расхода и давления. Преобразуем уравнение B.1.38) с учетом всех замеча-
93
8G'k = у\(Ьр'к - Ър})у
dp}'
X
2 R7 L
Рис. 2.15. Схема ПГС (а), эквивалентная цепь для нее {б) и структурный граф (в)
ний и обозначений, принятых на рис. 2.14, в, к следующему виду:
8G'a = (е + \)(&р'а - Ьр'ъ) - е(8р'р - 8p'Q),
8G'a = 8Gq, bG'b = -5G;s 8G'p = -8G'q,
8pfp = 8p'p -bp'q, 8p'a = 8p'a -8p'h, так как 8p'q = 8p'b = 0,
ибо 8р'ь и 8p'q — вариации абсолютного давления.
Уравнения газового сопла можно записать с помощью неопределенной
матрицы проводимости
8G'a
8G'p
6 + 1
-F + 1)
-(e+ 1)
e + 1
-(e+1
e + I
€+1
-F+1
)
)
-6
6
6
—6
6
—6
-6
e
8р'Р
Убеждаемся, что и в этом случае сумма элементов любой строки и
любого столбца матрицы равны нулю. Отбрасывая в неопределенной
матрице по одной строке и столбцу, находим укороченную матрицу.
Укороченные матрицы проводимости и двойные алгебраические дополнения
используются при анализе сложных цепей.
§ 2.2. Описание динамических процессов в ПГС
с использованием эквивалентной ПГЦ
2.2.1. Эквивалентная цепь для ПГС. Рассмотрим простую
гидравлическую систему, представленную на рис. 2.15, а, состоящую из трех
трубопроводов 2, 3 и 4 с местными сопротивлениями и баллона 1, из которого
под постоянным давлением подается жидкость. В сливной трубе 3 уста-
новлено местное переменное сопротивление — пульсатор, создающий в
системе колебание с заданной частотой.
При составлении модели системы сделаем следующие предположения:
сжимаемостью жидкости можно пренебречь, течение турбулентное с
квадратичным законом сопротивления, инерцию столбов жидкости в трактах
учитываем, используя для описания нестационарного течения в
трубопроводах 2 и 4 линеаризованные уравнения для инерционности B.1.16)
и сопротивления B,1.20). Эквивалентная ПГЦ представлена на рис. 2.15, б
При этом сопротивления учитывают как потери давления на местном
сопротивлении, так и потери на трение о стенки трубы. Обратив внимание
на то, что два элемента (сопротивление и инерционность) в ветвях цепи
(см. рис. 2.15, б) расположены последовательно, исключив из
уравнений B.1.16) и B.1.20) вариацию давления в промежуточной точке между
ними, найдем для /-го участка тракта
. = 28Gt + -^-ти/ -, B.2.1)
api npi Api dt
где Poi, Pn, 8pOj, 8рц — давления и безразмерные вариации давления
в начале и конце /-го трубопровода, Apt = poi - ри, 8Apt -
безразмерная вариация перепада давления в /-м трубопроводе, 5G,- — безразмерная
вариация расхода через /-й трубопровод, ги/ - инерционная постоянная
времени /-го трубопровода.
То же самое уравнение, но в размерных вариациях:
bp'oi — Ьр'и = 5Ар/ =
B.2.2)
А р{ v pOi dbGl
- 2 — 8Gi + ти
/ t dt
где d - средний расход через z-й трубопровод, Spoi, bp[j, ЬАр\, bG\ -
размерные вариации параметров жидкости в /-м трубопроводе.
Так как в системе установлен пульсатор, создающий гармонические
возмущения, представляют интерес частные периодические решения
уравнений математической модели системы, описывающие режим с
вынужденными колебаниями. Частное периодическое решение системы
получается или путем использования преобразования Лапласа [17, 217] и
подстановкой затем вместо оператора преобразования s = /gj, или путем
непосредственной подстановки во все уравнения частного периодического
решения 5р0/ = 5Ро/ expj/cor), 8pu =8pu exp(/cof), 8Gt = 8G( exp(icot)
и т.д., где Spot, 8рц, 8Gt — амплитуды вариации соответствующих
параметров (величины комплексные), со - круговая частота вынужденных
колебаний. После подстановки частных периодических решений в
замкнутую линейную систему уравнений получаем систему алгебраических
уравнений, связывающих между собой амплитуды параметров с амплитудой
возмущающего воздействия на режиме установившихся колебаний с
заданной частотой. При этом предполагается, что режим установился после
окончания всех переходных процессов, возникающих при включении
пульсатора, или при переходе с одной частоты на другую. Подставив в
уравнение B.2.1) или B.2.2) частные периодические решения, можно
95
найти сопротивление (импеданс) /-го трубопровода:
или для размерных вариаций
, 5 Ар/ __ Aft . /70/
B-2-3)
Зависимости B.23) и B.2.4) описывают в линейном приближении
динамические характеристики трубопровода, являющегося пассивным
элементом цепи (рис. 2.15, б). В рассматриваемой системе активными
элементами, управляющими режимом работы системы, являются баллон 1
и пульсатор в трубопроводе 3. Оба активных элемента можно описать
в виде идеальных источников давления. Действительно, если в баллоне
с помощью системы безынерционной автоматики поддерживается
постоянное давление, то можно записать, что для входного сечения трубопровода 2
выполняется условие др02 = 0, эквивалентное при постоянном давлении
во внешней среде уравнению идеального источника напора, для которого
А#@ = const, где АН = р02.
Пульсатор, как источник давления, требует более подробного
объяснения. Для любого типа реального пульсатора (поршневого или
дроссельного) с изменением частоты должны изменяться амплитуды колебаний
давления и расхода в сечении перед пульсатором1). С одной стороны, изменение
амплитуд колебаний при изменении частоты связано с влиянием инерции
жидкости в пульсаторе и динамических характеристик тракта за
пульсатором, не входящим в анализируемую систему. С другой стороны,
амплитуды колебаний параметров перед пульсатором определяются также и
реакцией исследуемой системы на эти возмущения, т.е. динамическими
характеристиками системы.
Примем за возмущающее воздействие колебания давления в начале
трубы 3, создаваемые пульсатором. Применительно к линейной системе
уровень амплитуд возмущений не имеет значения, так как амплитуды
параметров системы как отклик на возмущение пропорциональны
амплитуде возмущения. В связи с этим пульсатор целесообразно моделировать
идеальным источником напора, создающим колебания давления (напора)
с постоянной амплитудой. С учетом всех отмеченных особенностей ПГС,
представленная на рис. 2.15, я, сводится к эквивалентной цепи,
изображенной на рис. 2.15, б.
Введение в эквивалентную цепь источника давления в тракте 3
объясняется только используемым для измерения перед пульсатором датчиком
давления. Реальные источники возмущения (кроме поршневого
пульсатора в непроточной части ПГС) создают возмущения как по расходу,
так и по давлению, уровень которых зависит как от процесса в
пульсаторе, так и от динамики системы. Если вблизи пульсатора или другого
*)Так как в данной системе пульсатор работает на слив, то возмущающим
воздействием являются колебания параметров перед пульсатором. Если пульсатор
работает на проток, то возмущающим воздействием может быть колебание давления
как перед пульсатором, так и за ним, в зависимости от взаимного расположения
пульсатора в исследуемой системе.
96
устройства, создающего возмущение, устанавливается малоинерционный
датчик расхода, измеряющий входное воздействие, то в эквивалентной
цепи вводится идеальный источник расхода. При этом источник (т.е.
датчик) может быть установлен не на той ветви (трубе), в которой
установлено возмущающее устройство., создающее возмущение. Если часть системы
с источником возмущения не является частью исследуемой системы, то
эту часть ПГС не вводят в эквивалентную цепь, ограничиваясь только
источником в месте установки датчика. Если возмущающее устройство
является частью исследуемой ПГС то необходимо его описать в виде
эквивалентной схемы, в которой учитываются особенности статических
и динамических характеристик устройства.
Описанная выше ПГС может сама быть объектом исследований или
частью стенда для исследования динамических характеристик пневмо-
гидравлических агрегатов, например, газового демпфера 5,
изображенного штриховой линией на рис. 2.15, а и б.
Уравнения B.2.3) или B.2.4) описывают поведение жидкости в
отдельных трактах системы. Для того чтобы замкнуть математическую
модель системы, необходимы дополнительные уравнения, связывающие
между собой параметры жидкости в отдельных трактах. Воспользуемся
условием неразрывности — балансом отклонений расходов для узла, где
сходятся тракты 2, 3 и 4. Уравнение баланса в размерных вариациях с
учетом принятых (условно) на рис. 2.15, б направлений для расходов
запишется так:
8G2 - 5G3 - 5G4 = 0. B.2.5)
Учтя соотношения баланса для средних расходов в этом узле
G2 - G3 - G4 = 05 B.2.6)
можно записать уравнение баланса B.2.5) в безразмерных
вариациях расходов. Приняв, что на выходе из трубопровода 4 отсутствуют
колебания давления, т.е. 6р4 = bp[A = 0, можно записать соотношения,
связывающие вариации давления с расходами и импедансами
трубопроводов :
_
3G2 bG2 bG2
, _ 5Ар4 = 5ро4 Ьрц _ 6^0 4 .
б (/4 6G4 6G4
Разрешив эти зависимости относительно амплитуд вариаций расходов,
подставив их в уравнение баланса расходов B.2.5), после
преобразований находим
где z'? = z'2z4/(z2 +z4) - импеданс ветвей цепи 2 и 4, включенных
параллельно,
7 Б.ф. Гликман 97
Рис. 2.16. Зависимость объема и формы
сечения трубки с мягкой стенкой от перепада
давления на стенке
/, pT.CL рИс. 2.17. Модельная схема тракта с мягкими
~ 0 ' 2ОХ V 60 80 стенками
Другим примером математического моделирования нестационарного
течения с помощью несложной эквивалентной ПГЦ с сосредоточенными
параметрами может служить задача из области гидродинамики
кровообращения - течение жидкости в сосуде, который моделируется мягкой
трубкой, находящейся в среде с внешним (трансмуральным) давлением
[112, 117, 138]. Размер и форма трубки зависят от разности между
давлениями внутри рвн и вне трубки рн. При появлении малого или тем более
отрицательного давления Ар = рвн - рн оболочка трубы теряет
устойчивость, сплющивается, изменяя свое проходное сечение и объем V. На
рис. 2. 16 приведен типичный график зависимости объема мягкой трубки
от перепада давления на стенке Ар. Здесь же представлены профили
разрезов поперечного сечения трубки при различных Ар. Для описания
нестационарного течения в мягкой трубке предложена математическая модель
[117], в которой жидкость считается вязкой и несжимаемой. Кроме
участка с мягкими стенками BE на схеме рис. 2.17 учитываются участки
гидравлической системы с жесткими стенками, присутствующие в
экспериментальной установке. Участок мягкой трубы моделируется тремя
элементами — двумя емкостями ВС и DE с деформируемыми стенками и
соединяющим их участком тракта CD с изменяемым сечением F с. Площадь
поперечного сечения узкой части трубы с мягкими стенками (участок CD на
рис. 2.17) считается функцией перепада давления на стенке второй емкости
DE, Apd = pd - р„, так как именно давление на выходе из мягкой
трубки в первую очередь определяет ее форму и сечение. Эксперименты
(рис. 2.18) подтвердили это предположение [117], так как до момента
сплющивания трубы, при котором резко уменьшается объем К, но
графикам ри - pd, и нет ощутимой разницы, брать ли Apd или Ари =
= Ри ~ Рн в качестве давления, определяющего площадь проходного
сечения Fc.
Для емкостей ВС и DE, моделирующих изменение объема мягкой
трубки, можно принять, что мгновенное значение параметров по длине этих
участков одинаково, а объемы емкостей связаны с давлением податливостью
стенок
dVu
Cu dApu ' dApd '
где Vu, Vd - объемы участков мягкой трубки. Уравнения баланса расходов
для емкостей:
dVu
Р
B.2.9)
- Gr -
B.2.10)
где Gi, G2 - массовые расходы через участки с жесткими стенками трубок
АВ и EF9 Gc - расход через участок CD. Кривая для зависимости объема
мягкой трубки от перепада давления (рис. 2.16) имеет S-образную форму
с практически вертикальным участком при Ар ъ 0. В этом случае при
очень незначительном изменении давления объем и поперечное сечение
мягкой трубки резко изменяются.
Гидравлическое сопротивление и инерцию столба жидкости в мягкой
трубке опишем уравнением количества движения для ламинарного течения
в цилиндрическом участке CD с переменным проходным сечением F с
и постоянной длиной Lc (рис. 2.17). С учетом принятых предположений
уравнение количества движения запишется в виде
Lr dGc
= PwPd ='
Fr dt
B.2.11)
где ?с = f(Fc/F1) — коэффициент местных потерь на входе и выходе,
определяемый степенью поджатия течения в мягкой трубке.
В уравнении B.2.11)
для упрощения
использована модель
ламинарного течения. Однако при
сплющивании трубки
форма ее проходного
сечения (рис. 2.16) резко
изменится, так же как и
сопротивление (по
сравнению с трубкой такой же
площади, но круглого
сечения) . Влияние
конфигурации сечения хорошо
иллюстрируется зависимос-
Р и с. 2.18. Зависимость
перепада давления Дрс,
давлений ри и pd и относительного
объема мягкой трубки V/Vo
от расхода жидкости О 5 10 15 G, г/с
7* 99
р>*
40
20
1М ртст
-
-
- /
/
= 29,5^мм рт.ст. /
Г" /
7 I I
-
-
-
-
I
х
0,8
0,6
Ofi
0,2
тью сопротивления трубки эллиптической формы при ламинарном
течении [152].
8uG2(a2 +Z?2)
Ар =— — ,
2пра b
где a, b - большая и малая полуоси эллипса. Для трубки круглого
сечения а = b = R и коэффициент (а2 + Ь2)/2а3Ь3 равен 1/R4. Если принять
периметр трубки при изменении формы сечения постоянным, то из расчетов
следует [112], что при изменении b/а от 1 до 0,75 сопротивление трубки
возрастает всего на 10%, а при уменьшении b/а до 0,25 — увеличивается
больше чем в 2 раза. Эти расчеты объясняют характер поведения параметра
V/Vo (рис. 2.18), пропорционального относительной площади проходного
сечения трубки: малое изменение этого параметра при малом Ар, а затем —
резкое его уменьшение, сопровождающееся ростом Ар,
Для течения в жестких участках трубок АВ и EF записываются
уравнения количества движения с учетом инерции несжимаемой жидкости и
потерь давления для квадратичного квазистационарного местного
сопротивления:
Ld\ CL\j\ kj \
п п — : _l у ______ {11 мл
Рвх ~~ Ри ~ ^ , +?1 г~~Г » ^z.z.iz;
L2 dG2 G\
Pa ~ Рвых =— —- + %i ——Г , B.2.13)
F2 dt 2F
где ^ i и 12— коэффициенты местных сопротивлений на дроссельных
устройствах, установленных на входе и выходе участков, рвх, рвых — давление
на входе и выходе системы. В уравнениях B.2.12) и B.2.13) пренебрегли
потерями на трение о стенки трубок по сравнению с потерями на местных
сопротивлениях. Уравнения B.2.9) - B.2.13) вместе с двумя
эмпирическими зависимостями (рис. 2.16) и %с = %C(FC\F{) связывают между
собой семь переменных параметров (при рн = const) : ри, pdi GXi G2, Gc,
Fch%c.
Система уравнений B.2.9) — B.2.13) и эмпирические зависимости —
нелинейные. Их решение [117] дает типично нелинейную зависимость
потерь на мягкой трубке Арс =ри- pd от расхода Gc. На рис. 2.19
приведена кривая Арс = f(Gc), полученная при моделировании на ЭВМ с помощью
Рис. 2.19. Результаты математического
моделирования течения в мягкой трубке
100
нелинейных уравнений, описывающих течение в мягкой трубке.
Обнаруживается неоднозначность в зависимости перепада давления от расхода,
наличие падающей ветви на этой кривой, характеризующей отрицательное
сопротивление системы (падение перепада с ростом расхода), и
появление автоколебаний в системе с мягкой трубкой. Эксперименты (рис. 2.18)
подтвердили основные особенности процесса, обнаруженные при
математическом моделировании, в том числе и возможность возникновения
автоколебаний. Из графиков, представленных на рис. 2.18, следует, что
при большом расходе и соответственно большом давлении внутри мягкой
трубки (большем, чем внешнее давление рн) потери в мягкой трубке
малы и ри ъ Ра. При уменьшении расхода и приближении перепада Apd =
= Pd - Рп к нулю стенка теряет статическую устойчивость, а перепад Арс
начинает расти, несмотря на падение расхода. На этой ветви зависимости
Арс = f(Gc) уменьшение сечения F с превалирует над уменьшением
расхода. Используя уравнения B.2.9) - B.2.13) и эмпирические
зависимости, можно построить линейную математическую модель и эквивалентную
ПГЦ системы. При этом необходимо учитывать, что все специфические
процессы, связанные с особенностями течения в мягкой трубке, имеют
место в области, где возможна потеря устойчивости, т.е. на левой ветви
зависимости Fc = Fc (pu - рн) (рис. 2.16) .
Линеаризация уравнений емкостей B.2.9) и B.2.10) приводит к
следующим соотношениям в безразмерных вариациях (считая ри = const):
8Gl_8Gcy B.2.14)
dt
где 8ри, 8pd - безразмерные вариации давлений в емкостях, 8Glt 8G2i
8GC - безразмерные вариации расходов на входе и выходе системы и
через мягкую трубку, отнесенные к среднему расходу жидкости через
систему Gc. При линеаризации уравнения B.2.11) и эмпирических
зависимостей для Fc (рис. 2.16) и \с = %с (Fc/Fx) получаем
сд Ри Л Pd . LCGC d8Gc
SAPc = Ьри 8pd =
Pu -Pd Pu~ Pd (Pu ~ Pd)Fc
1 / SniiLcGc G\
+ ^ v
Pu ~ Pd V PFC PFc
t «- i Pd SFC
+ fc^c2 ^c (Fc/Fx) bkc Pd bF(
pF2cAPc Fx |c b(Fc/Fx) Fc
где использованы связи
d(Fc/Fi)
101
Введя обозначения
S7ifJiLcGc G2C
Артр = ~ > АРм = $с—=г> APd = Pd ~ Рн, АРс=Ри - Pd>
F F?
pF
c
= \pF)
Fc bApd F %c d(Fc/Fx) *
преобразуем уравнение B.2.16) к следующему виду:
Ри с Pd с _с_ , d5Gc
——6pw --— bpd= B5Gc+tuc 2- B.2.17)
где
A = (ApTp + 2АРы)фР/Арс- Ap^pxjj^FJiAp.F.l
В = (ApTp + 2ApM)/Apc, тИС =LcGc!(FcApc).
При переходе к эквивалентной ПГЦ левую часть уравнения B.2.17)
можно описать двумя элементами: пассивным элементом, который
определяет сопротивление мягкой трубки с постоянным проходным сечением
5Арп = (ри/Арс)дри — (pd/Apc)8pd, и активным элементом
(управляемым источником напора), создающим перепад давления bApd = Abpd,
с помощью которого моделируется влияние изменения проходного
сечения на сопротивление мягкой трубки. В данном случае управляемый
источник моделирует характеристики элемента с отрицательным
сопротивлением.
В линейной математической модели эффекты, связанные с
отрицательным сопротивлением, характеризуются соотношением между
коэффициентами А и pd/Apc. Так как \рр (см. рис. 2.16) всегда положительно,
а по физике процесса для сопротивления ф$ < 0, то А > 0.
Соответственно в левой части уравнения B.2.17) при вариации давления на выходе
из мягкой трубки коэффициент А - pdjApc может изменять знак. Если
знак этого коэффициента отрицательный, т.е. при увеличении давления
за мягкой трубкой bpd расход падает, то сопротивление трубки
положительное. В случае же положительного знака коэффициента, т.е. при
совпадении направлений изменений давления bpd и расхода 5GC,
сопротивление трубки становится отрицательным.
Для двух оставшихся элементов системы трубок на входе и выходе
линеаризация их уравнений B.2.12) и B.2ЛЗ) приводит к следующим
зависимостям:
Рвх Ри dG\
5р ^ ЬРи = ти1 —- + 25Gl5 B.2.18)
dt
рвх Ри ти1
Арх Api dt
Pd
pd рвых Ги2
Ар2 Ар2 dt
где
Api = Рвх - Ри, Ар2 = pd-pBblx, ти1 =
ти2 = L2G2IAp2F2.
102
B.2.19)
Система уравнений B.2.14), B.2.15), B.2.17), B.2.18) и B.2.19)
описывает ПГС с элементом, в котором возможно отрицательное
сопротивление. На рис. 2.20, а приведена схема эквивалентной ПГЦ, описывающей
динамику рассматриваемой системы, в которой элемент с отрицательным
сопротивлением моделируется управляемым источником напора. Если
положительное сопротивление связано с диссипацией энергии
механических колебаний, то отрицательное сопротивление, наоборот, может
способствовать усилению колебаний. Элемент с отрицательным сопротив-
5Р„
6С,
_/——1_.у
"
/
^4 l
*-•1__J—-•
J
а
Т
\
5G^
Т Г
J
u
d
2
Рис. 2.20. Схема (а) и граф (б) эквивалентной цепи для системы с мягкой трубкой
лением эквивалентен источнику энергии, хотя, как и все управляемые
источники, его нельзя рассматривать как первичный источник энергии,
создающий течение рабочей среды в ПГЦ. В действительности
отрицательное сопротивление вместе со всей ПГЦ преобразует энергию среднего
течения в энергию колебаний, в том числе — и в автоколебания. На рис. 2.19
отдельно представлены расчетные кривые с автоколебаниями в ПГЦ с
мягкой трубкой, теряющей устойчивость в области отрицательного
сопротивления трубки.
2.2.2. Структурный граф цепи. При соединении отдельных элементов
в ПГЦ полюса объединяются. Если объединяется более двух полюсов,
то эта точка называется узлом. Ветвью цепи называют часть цепи,
состоящую из последовательно соединенных двухполюсных элементов и
соединяющую два узла. В цепи, изображенной на рис. 2.15, б, если учитывать
емкость, имеется три ветви и два узла; в цепи, представленной на
рис. 2.20, б% - три узла (не считая входных) и пять ветвей.
Математические модели ПГС, изображенные на рис. 2.15, а и 2.17,
относительно просты, так же как и схемы эквивалентных им ПГЦ. Однако
применительно к более сложным схемам ПГЦ преобразования уравнений
обычными методами оказываются слишком громоздкими, поэтому при
анализе цепей широко используют матричные методы. При этом удобно
упрощенно рассматривать цепь в виде схемы, отображающей только
топологический, геометрический образ, структуру цепи без учета количества
элементов, входящих в каждую из ветвей цепи. Такие топологические
образцы цепей называются структурными или линейными графами цепи
[13, 159, 168]. Структурные графы являются только одним из типов
графов, используемых при анализе цепей. Ниже будет описана методика
использования другого типа графов — сигнальных, которые не следует
смешивать со структурными графами.
При составлении структурного графа отвлекаются от типа и
характеристик элементов, входящих в ветви цепи, заменяя их линиями
произвольной конфигурации, называемыми ветвями (ребрами) графа, которые
оканчиваются в узлах (вершинах) графа. Структурный граф для цепи,
103
изображенной на рис. 2.15, б, представлен на рис. 2.15, в, а для ПГЦ
рис. 220, а - на рис. 2.20, б. Каждому узлу и каждой ветви цепи
соответствует узел и ветвь графа, так что граф цепи полностью описывает
геометрическую структуру (топологию) исходной цепи. Путем
исключения отдельных ветвей из исходного графа получается подграф. Одним из
важных типов подграфа является путь графа, состоящий из непрерывной
последовательности ветвей, связывающих два заданных узла графа; при
этом каждый узел проходится не более одного раза. Если в графе имеется
Рис. 2.21. Дерево, его
сечения (а) и контуры графа (б)
хотя бы один путь между любой парой узлов, то граф называется связным.
При невыполнении этого правила граф является несвязным.
Другим важным подграфом является дерево — совокупность ветвей,
содержащая все узлы исходного графа, но не имеющая ни одного
замкнутого контура (рис. 2.21, а). Одному графу соответствует несколько
различных деревьев, число которых растет при усложнении графа. Если дерево
содержит т узлов, то оно имеет п - т — 1 ветвей, в частности, для дерева,
изображенного на рис. 2.21, а, « = 4—1=3. Для выбранного дерева
составляющие его линии, так же как и в исходном графе, называются
ветвями, а отброшенные ветви — хордами. На рис. 2.21, а ветви показаны
сплошными линиями, хорды - пунктиром. Добавление к дереву хорд
приводит к образованию замкнутых контуров. Если граф имеет q ветвей
и m узлов, то число хорд р определяется соотношением
р = <7-(/и-1). B.2.20)
Для графа, представленного на рис. 2.21,а, р = 6 —D — 1) = 3.
На графе выбирается (хотя бы произвольно) положительное
направление вдоль каждой из ветвей, которое указывается стрелкой. Контуром
графа называют замкнутый путь, т.е. непрерывную последовательность
ветвей, заканчивающуюся в исходном узле, при этом к каждому узлу
присоединяются по две ветви, входящие в контур. В граф входит ряд
контуров. Фундаментальными (главными) контурами называют
контуры, в каждый из которых входит только по одной хорде. На рис. 2.21, б
изображены три фундаментальных контура для дерева, представленного
на рис. 2.21, а. Сечением называется множество ветвей, разрыв которых
разбивает граф на два несвязных подграфа, каждый из которых
является связным. На рис. 2.21, а приведены три линии, пересекающие ветви
графа и образующие разрывы ветвей: а) 3, 5, 6; б) 2, 4, 5, 6; в) 1, 4, 5.
Можно провести еще ряд других сечений, причем число возможных сече-
104
ний заведомо больше числа узлов. В результате разрыва ветвей сечением
образуются два подграфа с числом узлом тх и т2 = т — тх. Для сечения
а-а, т\ ~ 1> /722 = 3, для сечения б—б тх = 2, т2 = 2 и т.д. Сечение
называется фундаментальным (главным), если оно включает одну ветвь
дерева и несколько хорд. Таким образом, число фундаментальных контуров
равно числу хорд дерева, а число фундаментальных сечений - числу ветвей
дерева. Это свойство дерева графа будет ниже использоваться для
формирования математических моделей сложных ПГЦ.
2.2.3. Математические модели ПГС с подвижными механическими
элементами. В большинство ПГС наряду с чисто гидравлическими
агрегатами входят смешанные устройства, состоящие из гидравлической части
и подвижных механических частей: регулирующие, дросселирующие
элементы, насосы, компрессоры, турбины, поршневые элементы гидроприводов
и т.д. Выше часть этих устройств была описана как чисто гидравлические
элементы (гидравлические сопротивления, источники напора и расхода,
упругие элементы, гидротрансформатор), что допустимо, если не
учитывать динамических свойств механических устройств и обратных связей
между гидравлическими и механическими параметрами. Обратные связи
определяют влияние гидравлических параметров на режим работы
(частоту вращения, положение и т.п.) механической части устройства, которые
в свою очередь влияют на режим работы гидравлической части (напоры,
перепады давления, расходы). При анализе движения механических
элементов, соприкасающихся с жидкостью, влияние жидкости на движение
таких элементов обычно учитывается введением некоторой
присоединенной массы жидкости, гидравлической упругости, коэффициента
демпфирования. Все это позволяет ограничиться решением уравнений механики
с дополнительными коэффициентами, с помощью которых учитывается
гидродинамическое воздействие на подвижные элементы.
Применительно к ПГС можно обратить задачу и ввести те же понятия,
но в гидродинамических терминах для подвижных механических
элементов: присоединенная масса (инерционность), упругость (емкость),
сопротивление. В результате дополнительные связи между параметрами,
характеризующими взаимодействие механических и гидравлических частей
системы, записываются в виде уравнений для гидравлических параметров.
При этом смешанная система, состоящая из пневмогидравлических и
механических элементов, сводится к эквивалентной ПГЦ, что существенно
упрощает анализ системы. Такое эквивалентное гидравлическое
представление движения механических элементов можно получить, учитывая связи
между параметрами движения разнородных систем на границе их
взаимодействия. В качестве примера рассмотрим упругий элемент (рис. 2.2, d ж),
обладающий достаточно большой массой и ощутимым значением
коэффициента трения. В этом случае полученное ранее уравнение упругого
элемента как емкости B.1.11) недостаточно точно описывает его
динамические характеристики. Запишем уравнение движения подвижных частей
упругого элемента:
т~^Г + Х~^7+ кх = ^эф(Ро -Pi), B.2.21)
где х — координата подвижной части, т — ее масса, А — коэффициент
105
вязкого трения, к - суммарная упругость элементов подвижной части,
/^ф - эффективная площадь упругого элемента, р0, рх - давления по
обе стороны упругого элемента. Перемещение упругого элемента можно
связать с расходом жидкости
с dx
Р^эф— =G. B.2.22)
dt
Линеаризовав уравнения B.2.21) и B.2.22), запишем в относительных
вариациях
т d2bx X dbx
— + +5jc =
к dt2 к dt kh
pF^h dbx B.2.23)
=oG,
/ iumG \G G
+ +
G dt
где 8x — относительная вариация перемещения, Sp0, 8p1 - относительные
вариации давления перед и за упругим элементом, 8G - относительная
вариация расхода, h , G, р — масштабные величины, к которым отнесены
вариации перемещения, расхода и давлений.
В уравнения B.2.23) входит одна механическая переменная — вариация
перемещения 5л\ Воспользовавшись вторым уравнением B.2.23), можно
исключить механическую переменную. Применительно к задаче о
вынужденных колебаниях системы удобно вначале подставить в уравнения B.2.23)
частные периодические решения 8G = 5Gexp(/cor), 8р0 = др0 ехр(/ cot)
и уже в амплитудах вариаций получить преобразованную зависимость в
гидравлических параметрах
G \ _ F3&v
)8G = -^— (8p0 - bv\\ {2224)
kpF3$h icopF^h I kh
Если принять т= X = 0, то уравнение B.2.24) переходит в уравнение
емкости B.1.15) . Таким образом, последний член в скобках в левой части
уравнения характеризует упругие свойства элемента. Два других члена в
скобках описывают влияние массы и коэффициента трения в упругом
элементе, но обе эти характеристики уже приведены к расходу жидкости
через упругий элемент. Первый член в скобках определяет часть перепада
давления, затрачиваемого на преодоление сил инерции, т.е. характеризует
присоединенную инерционность механических частей, а по форме он
подобен члену при вариации расхода в уравнении инерционности B.1.16).
Второй член в скобках аналогичен коэффициенту при вариации расхода в
уравнении сопротивления B.1.21), т.е. характеризует потери давления на
вязкое трение в механической части, приведенные к расходу жидкости через
элемент. Все три перепада давления в формуле B.2.24) суммируются, и
эквивалентная цепь, описывающая такой элемент, будет включать три
последовательно включенных элемента — инерционность, сопротивление
и емкость. Если учитывать также инерцию, сжимаемость и вязкое трение
жидкости в механическом узле, то соответствующие члены в скобках в
уравнении B.2.24) будут иметь вид сумм, учитывающих движение и
жидкости, и механических частей.
106
Глава 3
МАТРИЧНО-ТОПОЛОГИЧЕСКИЕ МЕТОДЫ ПОСТРОЕНИЯ
МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ ПГС
§ 3.1. Законы сохранения для цепи
Основой анализа цепей, моделирующих процессы различной физической
природы в сложных системах, служат законы сохранения для узлов и
контуров цепи. Применительно к электрическим цепям законы сохранения
формулируются в виде двух правил Кирхгофа: равенство нулю
алгебраической суммы токов по ветвям, сходящимся к узлу A-е правило), и
равенство нулю алгебраической суммы падений напряжений во всех ветвях
любого замкнутого контура цепи B-е правило Кирхгофа). Для цепей
другой физической природы действуют аналогичные правила, часто
называемые обобщенными законами Кирхгофа [103]: сумма последовательных
переменных для ветвей у каждого узла цепи равна нулю, сумма
параллельных переменных по любому замкнутому контуру цепи равна нулю. Выведем
эти же правила применительно к ПГЦ в виде уравнений баланса расходов
для узлов и баланса падений давлений для контуров.
3.1.1. Уравнения сохранения массы, количества движения и энергии для
узлов ПГЦ. Для анализа процессов в разветвлениях ПГС целесообразно
воспользоваться общими законами сохранения массы, количества
движения и, считая жидкость изотермической, механической энергии. Этот
анализ полезен для понимания тех упрощений, которые делаются при
использовании простейшей формы записи уравнений, определяющих баланс
расходов в узле. Рассмотрим разветвление, изображенное на рис. 3.1,
характерное для ПГС с коллекторами, развилками труб или разветвлений
артерий. Так как отдельные каналы подходят и отходят в разных
направлениях, для них удобно записывать уравнения сохранения в векторной форме.
Предполагая, что геометрические размеры разветвления намного меньше
длины акустической волны в исследуемом диапазоне частот, все уравнения
для разветвления записываются так же, как для системы с
сосредоточенными параметрами.
Пусть в разветвление входят и выходят п каналов, через которые
поступает и выходит жидкость. В разветвлении имеется определенная масса
жидкости, заключенная между непроницаемыми стенками и контрольными
сечениями (поверхностями), которые отделяют каналы (ветви) от
разветвления. В общем случае стенки каналов и разветвления могут
деформироваться под влиянием давления жидкости. Уравнение закона сохранения
массы в векторной форме запишется так:
dmn п л
~-^ = - Z р / ( V.- • </s/) = - S К • G/). C.1.1)
dt i =15/ z = 1
где ,7zp _ мгновенное значение массы жидкости в разветвлении, V/ -
107
вектор скорости в контрольном сечении /-го тракта, S/ — вектор
контрольной поверхности, который направлен от разветвления вдоль оси тракта
и по абсолютной величине равен площади поперечного сечения канала,
п/ — единичный вектор в направлении s/, G/ — вектор скорости потока
массы (массового расхода) через контрольную поверхность.
Рис.
3.1. Схема разветвления
ла) ПГС
(уз-
Уравнение количества движения для разветвления имеет вид
dt /= 1 5,
п
/ V/
&) - F + mpg =
= -2 (G/(ui2>/<f/>+p/s/)-F+mpg,
C.1.2)
где Рр - мгновенное значение количества движения жидкости в
разветвлении, F - мгновенная суммарная сила, приложенная к стенкам
разветвления со стороны жидкости, g - вектор ускорения силы тяжести, р{ -
давление в /-м контрольном сечении, < v* > = A/5/) / (щ • v/)*cte/ - среднее
мгновенное значение к-й степени от скорости в контрольном сечении.
Уравнение сохранения механической энергии для изотермического течения
несжимаемой жидкости в разветвлении запишется так:
— (Кр+Пр)= Л
dt
p/V/
—
= Л (nrGlof(l/2)<u?>/<u/> + n,+— -И/-Ф, (ЗЛ.З)
i=i L p J
где % __ мгновенное значение кинетической энергии жидкости в
разветвлении, Пр - мгновенное значение потенциальной энергии жидкости в
разветвлении, П/ - потенциальная энергия поступающей и уходящей жидкости
на единицу массы, W - мгновенная суммарная работа, совершаемая при
взаимодействии жидкости и стенок разветвления, Ф- мгновенная скорость
диссипации механической энергии за счет вязкости.
При использовании уравнений (ЗЛЛ)-(ЗЛ.З) возможно два варианта
их решения. Если объем разветвления достаточно мал по сравнению с
объемами сопрягаемых с ним участков трактов, то массой жидкости в
разветвлении, ее количеством движения и энергией пренебрегают, отбрасывая
108
соответственно все левые части в уравнениях C.1.1) — C.1.3), т.е.
отбрасывая производные. Другой вариант - объем разветвления соизмерим
с объемами трактов. В этом случае необходимо при решении системы
уравнений C.1.1)-C.1.3) использовать методы, изложенные в гл. 2 для
уравнений элементов с сосредоточенными параметрами. При этом разветвление
оказывается одним из элементов системы, и его уже нельзя свести к узлу
цепи. Уравнения C.1.1) —C.1.3) описывают разветвление как проточную
емкость, в которой учитываются вязкость и инерция жидкости,
податливость стенок, а также кинетическая и потенциальная энергия
поступающей и уходящей жидкости. Применительно к анализу разветвленых ПГС
интересен первый случай, когда можно пренебречь объемом разветвления и
вместо уравнений C.1.1)-C.1.3) использовать приближенные
зависимости.
Одновременно можно пренебречь концевыми эффектами: образованием
зон обратных токов из-за изменения направления потока, особенностями
течения на начальных участках трактов и т.д.
В случае относительной малости объема разветвления, кроме
производных по времени, в уравнениях C.1.1) —C.1.3) можно пренебречь работой
W (из-за малости поверхности стенок), диссипацией Ф (так как объем мал),
потенциальной энергией П/ (так как потенциальная энергия на единицу
массы должна быть близкой для всех ветвей). После упрощений система
уравнений C.1.1) —C.1.3) принимает следующий вид:
уравнение неразрывности
2 (n,G,-) = 0, C.1.4)
i = 1
уравнение количества движения
2 (G,- < vj)/( vt > +РЛ) + F = 0, C.1.5)
1 = i
уравнение энергии
2 (п/С/)[A/2)<1;?>/<у/>+й/р] =0. C.1.6)
* = 1
Одно из часто используемых предположений — возможность
пренебрежения кинетической энергией жидкости по сравнению с потенциальной, что
эквивалентно неравенству <у? >/<и,- Xpjp. В этом случае уравнение
энергии C.1.6) сводится к равенству
2 (n,G,)p, = 0. C.1.7)
Уравнения C.1.4) и C.1.7) одновременно удовлетворяются при
р,=Р/ (i./=l,2 и), (ЗЛ.8)
т.е. при соблюдении условия сохранения в развилке постоянным давления.
Уравнение неразрывности C.1.4) и равенство C.1.8) описывают в
наиболее простой форме условия в разветвлении (узле цепи) 1). Запись урав-
*•* Уравнение C.1.5) автоматически удовлетворяется при соблюдении
равенства C.1.8).
109
нения C.1.4) в векторной форме позволяет автоматически учитывать
направление движения жидкости. Если направление движения жидкости
учитывать путем присвоения знаков массовым расходам, то уравнение
сохранения массы в узле C.1.4) можно записать в более простой форме:
? akiG,=0, C.1.9)
I = 1
где aki — коэффициент, учитывающий знак расхода, поступающего по /-и
ветви к-то узла цепи. При этом aki = 1, если ветвь / соединяется с узлом к и
течение жидкости направлено к узлу, aki = — 1, если ветвь / соединяется с
узлом к и течение жидкости направлено от узла, aki = 0, если ветвь / не
соединяется с узлом к. При использовании этих простейших уравнений не
следует забывать, что они получены в предположении малости
кинетической энергии жидкости и объема разветвления.
При выводе уравнений для разветвления, которые в простейшем случае
свелись к двум условиям C.1.8) и C.1.4), не использовались какие-либо
предположения о характере процесса в трактах или моделирующих их
ветвях цепи. Элементы, входящие в ветви, могут быть пассивными или
активными, линейными или нелинейными. В случае использования
линеаризованных уравнений для ветвей уравнение баланса для узла C.1.9) также
записывается в малых отклонениях:
п
I aki8G!=0, C.1.10)
/ = 1
или для безразмерных вариаций:
Gt
v aki—8Gi=0, C.1.11)
i = ] G
где G — масштабный, общий для всей цепи расход1 )> 6G,- = 5Gj/f7/ —
относительная вариация расхода через /-ю ветвь.
Знак коэффициента aki зависит от выбранного направления расхода
ветви, при этом направление расхода выбирается условно, так как до расчета
потокораспределения в цепи направление расхода может быть неизвестным.
Условность выбора направления расхода никак не влияет на результаты
расчетов. Несовпадение истинного движения жидкости с выбранным при
формировании цепи направлением приводит к отрицательному значению
расхода. Применительно к анализу линейных ПГЦ появление
отрицательных расходов не вызывает никаких трудностей, чего нельзя сказать о
нелинейных ПГЦ.
3.1.2. Уравнения сохранения суммы перепадов давления для контуров
цепи. Если взять любой замкнутый контур цепи, например, контур
1-2-3-5 (по номерам ветвей) на рис. 2.21,6, и считать, что для ветвей
направление перепадов давления противоположно направлению расходов,
обозначенных стрелками на графе, т.е. отсчитывая перепад давления от
входа к выходу ветви по стрелке, можно записать для каждой из ветвей
APi =Р\у -Р\, &Рг =Pi -Ри* АРз =РШ -PIV Ap5 =рш -plw,
где р{ - давление в i-м узле, Др;- - перепад на /-й ветви.
1) Выбор единого для всей цепи масштабного расхода определяется удобством
использования в дальнейшем уравнений баланса в матричной форме.
110
В принципе не важно, за счет каких процессов в ветвях возникает
перепад давления — из-за сопротивления пассивных элементов или как
следствие работы активных элементов. Важным является только факт, что в
результате выполнения равенства C.1.8), одинаковы мгновенные значения
давлений на концах всех трактов, сходящихся к развилке, моделируемой
хзлом цепи. В этом случае давление в узле совпадает с давлениями на
концах всех ветвей, и легко установить, что сумма всех перепадов давления
по замкнутому контуру цепи равна нулю.
Действительно, для контура 1-2-3-5 на рис. 2.21, б (если его обходить
в указанной последовательности ветвей), просуммировав все приведенные
выше перепады давления на ветвях, учитывая при этом, что при совпадении
направления обхода с направлением стрелки на ветви перед перепадом надо
ставить знак плюс, а при несовпадении — знак минус, найдем
S
2 Ар( = Арх + Ар2 - Ар3 -Ар5 =
Следовательно, для любого замкнутого контура ПГЦ алгебраическая сумма
перепадов давления на его ветвях равна нулю. Для каждого к-го контура*
цепи, состоящего из т ветвей, можно записать уравнение сохранения
суммы перепадов давлений
т
2 bkiAp, = 0 (A-=1,2,...,и), C.1.12)
/ = 1
где п - число контуров в цепи, Apt - перепад давления на /-й ветви.
Значение bjd = 1, если i-я ветвь входит в к-и контур и направление перепада
давления совпадает с направлением обхода контура, Ьы = — 1, если
направления не совпадают, bki = О, если z-я ветвь не входит в к-и контур. При записи
уравнений ветвей в форме линеаризованных зависимостей уравнение
C.1.12) принимает одну из следующих форм:
0 или
=0,
i = i p
где dApt, SAp. = dApi/Api — соответственно размерная и безразмерная
вариации перепада давления, Apt - масштабное значение перепада
давления, р масштабное давление для всей цепи.
Уравнения сохранения для контуров C.1.12) или C.1.13) были
получены с использованием условия C.1.8), т.е. однозначности уровня давления
Для каждого узла, и, как следствие, получим равенство нулю суммы
перепадов давления на ветвях замкнутого контура цепи. Существует другой
способ доказательства этого правила — с использованием принципа Да-
ламбера [178].
3.1.3. Узловая матрица соединения ветвей. Для формирования
математических моделей и анализа динамики ПГС удобно использовать матричный
аппарат, который обеспечивает компактную форму записи уравнений,
111
простоту их преобразования, возможность применения при расчетах на ЭВМ
стандартных программ. Операции с матрицами не дают сокращения
количества числовых операций, однако простота и удобство использования
матриц для анализа сложных цепей являются важным их преимуществом
[159]. Полное описание структуры цепи или соответствующего ей
структурного графа дает узловая матрица соединений ветвей П(матрица инцы-
денций) размерностью m X q, где m — число узлов, q — число ветвей цепи
(графа). Элементами матрицы соединений являются коэффициенты aki,
входящие в уравнение баланса для узла C.1.9), C.1.10) или C.1.11),
которые говорят о наличии или отсутствии соединения ветви с узлом к и
принятого направления движения жидкости (к узлу или от узла) В матрице
соединений П в столбце, соответствующем /-й ветви, ненулевые элементы
будут только в двух строках, соответствующих узлам, которые эта ветвь
связывает. В каждой строке матрицы ненулевыми будут элементы,
соответствующие ветвям (столбцам), которые соединены с узлом, имеющим
номер строки.
Для цепи, изображенной на рис. 2.21, a, m = 4, q = 6. Принимая
положительным расход, входящий в узел, а отрицательным - выходящий из узла,
можно записать для расходов или размерных вариаций расходов
следующую матрицу соединений (инциденций):
I
п
Л =
IV
1
1
0
0
— 1
2
- 1
1
0
0
3
0
1
- 1
0
4
0
- 1
0
1
5
0
0
- 1
1
6
- 1
0
1
0
C.1.14)
Такую же форму имеет и матрица соединений при записи уравнения
баланса в узле для безразмерных вариаций. Масштабные множители GtjG
можно выделить в отдельную диагональную матрицу, или оставить в виде
сомножителей при переменных bGt в векторе вариаций расходов. Каждая
ветвь, связывающая два узла, описывается столбцом матрицы П; сумма
элементов столбца равна нулю, т.е. матрица является особенной, а
уравнения - зависимыми. Достаточно исключить из системы уравнений C.1.9)
или C.1.10) одно уравнение узла и соответственно вычеркнуть одну
строчку из матрицы П, чтобы получить матрицу Пн, описывающую независимую
систему уравнений. Для составления матричного уравнения баланса
расходов в узлах необходимо ввести вектор расходов в q ветвях цепи
G=[GlG2...Gq]\ или 5G';
или 5G = [GiSGi G2bG2 . . . Gq5Gq]T,
где буква "т" обозначает операцию транспонирования матрицы (вектора),
Gj = Gj/G. Систему независимых уравнений для m — 1 узлов можно
записать в матричной форме:
nHG = 0, или Пн5С' = 0, или nH5G = 0, C.1.15)
где 0 — нулевой вектор размерности m — 1.
112
Для цепи, изображенной на рис. 2.21, а, отбросим в матрице строку для
узла 4; уравнение C.1.15) запишется так:
1—1 0 0 0 - Г
О 11-1 О О G7 = 0.
О- 1
О - 1
1
Легко проверить, что здесь содержатся уравнения баланса расходов
для трех первых узлов цепи, изображенной на рис. 2.21, а. Имея
матрицу соединений П, можно построить структурный граф цепи, т.е. матрица
соединений и структурный граф изоморфны. Для построения графа
надо нанести точки, обозначающие узлы, и соединить их попарно,
установив в соответствии со знаками элементов в столбцах матрицы П направле-
ление ветвей графа. Используя матрицу соединений, можно найти
уравнение, связывающее давления в узлах ветвей с перепадами давления на
ветвях. Учитывая принятое правило о противоположном знаке перепада
давления и расхода, запишем для цепи, представленной на рис. 2.21, а:
1
-1
0
0
0
- 1
0
1
1 -
- 1
0-
0
0
0
1
0
1
1
Pi "
Ри
-Рт-
'III
Рш
= Ар,
C.1.16)
где Ар = [ApiAp2 . . . Apq]T — матрица (вектор) перепадов давления на
ветвях, если принять для базисного узла (узел 4 на рис. 2.21, я) давление
равным нулю; pIV=0; П* - транспонированная матрица соединений;
Р= [р{Ри • • • Рт _i]T - матрица (вектор) узловых давлений в т - 1
независимых узлах. Уравнения C.1.15) являются аналогом записи первого
правила Кирхгофа в электротехнике, а уравнения C.1.16) — один из
вариантов записи второго правила Кирхгофа.
Уравнение балансов расходов можно составить с помощью введенного
ранее понятия сечений (гл.2), используя матрицу сечений Q, в которой
строки соответствуют главным сечениям (обобщенным узлам), столбцы —
ветвям. Как уже отмечалось выше, главные сечения вводятся с помощью
Деревьев графа. Каждое сечение состоит из одной ветви дерева и
нескольких ветвей связи, поэтому число сечений равно числу ветвей дерева т — 1,
те. числу независимых уравнений балансов расходов. Пользуясь этим,
можно составить систему независимых уравнений расходов для главных
сечений, включающих матрицу главных сечений и вектор расхода через
ветви G. Матрица Q показывает, какие ветви входят в каждое из
главных сечений. Матрица сечений имеет размерность (т — 1) X q, номер строки
соответствует номеру сечений, совпадающему с номером ветви дерева,
а столбцы — номерам ветвей. При этом ветвям дерева присваиваются пер-
ВЬ1е номера. Направление сечения совпадает с выбранным направлением
Расхода через единственную ветвь дерева, проходящую через данное
главное сечение. Элементы матрицы Q равны: + 1 при совпадении направления
8 Б Ф. Гликман 113
главного сечения и расхода в ветви, — 1 — при несовпадении и нулю, если
ветвь не входит в сечение.
На рис. 2.21, а приведено в качестве примера дерево графа и главные
сечения, которым соответствует следующая матрица сечений:
Q=
1
0
0
0
1
0
0 !
0 |
1 i
- 1
_ I
0
— 1
- 1
1
0
1
_ I
= [I;F].
Матрица сечений разбивается на две части - единичную матрицу I
порядка (т - 1) X (т - 1) и подматрицу F порядка (т - 1) X (q - т + 1),
получаемую из матрицы Q при исключении всех ветвей дерева графа.
Матрица F определяет хорды, проходящие через соответствующие главные
селения. Если умножить матрицу Q на вектор расходов через ветви, то
получится система уравнений, эквивалентная уравнениям баланса расходов для
ветвей C.1.15):
QG=[I JF]
C.1.17)
где GA, Gx — векторы расходов через ветви дерева и хорды.
Из уравнения C.1.17) можно найти связь между расходами через ветви
дерева и хорды:
Ga = -FGX. C.1.18)
В случае использования уравнений в малых отклонениях (вариациях) с
учетом обозначений, принятых при формировании уравнения C.1.15), из
зависимости C.1.17) находим
Q6G' = 5G;; + F5Gx=0, Q5G = 5Gfl+F5GX = О, C.1.19)
где 5СД, 5GX, 5Gfl, 5GX — векторы вариаций расходов через ветви дерева
и хорды.
3.1.4. Матрицы контуров. В электротехнике для контуров цепи
используются два варианта описания: просто матрица контуров и матрица главных
контуров. Будем пользоваться только последней, как более удобной.
Матрица главных контуров описывает соединение ветвей, входящих в
независимые контуры цепи, и имеет размерность (q - т + 1) X q. Примем,
что порядковый номер главного контура совпадает с порядковым номером
входящей в него хорды графа цепи. Элементы матрицы главных
контуров Г равны: + 1 - при совпадении направления ветви и направления
обхода контура, - 1 - при несовпадении и нулю, если ветвь не входит в контур.
Для главных контуров графа, представленного на рис. 2.21,6, контурная
матрица имеет вид
= [F,| I].
Матрица контуров разбивается на две подматрицы: единичную и F^
получаемую из матрицы главных контуров путем исключения всех
столбцов, соответствующих хордам дерева. Подматрица Fi фиксирует ветви
114
1
1
0
1
1
- 1
0
_ 1
1
1
0
0
0
1
0
0
0
1
дерева, входящие в главные контуры. Используя матрицу Г, запишем в
матричной форме уравнения сохранения C.1.12) или C.1.13) для
перепадов давлений главных контуров:
L
= Р,Дрд+Дрх=О, C.1.20)
где Ар, Ард, ДРх - векторы перепадов давлений для ветвей цепи, дерева
и хорд.
Матрицы главных сечений Q и главных контуров Г связаны между
собой, так как входящие в эти матрицы подматрицы F hFj строятся на
одних и тех же элементах графа, только номера столбцов и строк
матрицы F являются номерами строк и столбцов матрицы Fb а их элементы
имеют обратные знаки. Соответственно
Fi =-F\ C.1.21)
Эта связь определяется тем, что обе матрицы строятся на базе одного и того
же выбранного дерева графа системы, которое однозначно определяет как
главные сечения, так и главные контуры. Таким образом, при
формировании уравнений сохранения для главных сечений и контуров достаточно
знать одну из матриц F или Fj. Для малых отклонений уравнение C.1.20)
записывается в одном из следующих видов (в зависимости от
использования размерных или безразмерных вариаций перепадов давлений):
MF! I] *? =0, F5AP=[F;i] /д =0,C.1.22)
где 5Ap^, <5Ap'x, 5Ард, <5Apx — векторы размерных и безразмерных
вариаций перепадов для ветвей дерева и хорд. При приведении к безразмерному
виду вариации перепадов давлений на всех ветвях относились к единому
для всей цепи масштабному давлению.
§ 3.2. Узловые и контурные уравнения цепи
3.2.1. Система матричных уравнений цепи. Уравнения узлов и контуров,
приведенные выше, определяются только топологией цепи и не зависят от
типов элементов, входящих в ветви цепи. Все уравнения сохранения всегда
линейны. Система уравнений C.1.15) или C.1.17) и C.1.20) содержит в
сумме (т — 1) + (q — т + 1) - q уравнений и 2q переменных — расходов
(вариаций расходов) и перепадов давлений (или их вариации) для всех
ветвей. Таким образом, система уравнений для узлов и контуров цепи
оказывается незамкнутой. Недостающие q уравнений получаем в виде
зависимостей, связывающих расходы с перепадами давления для каждой из
ветвей цепи. В отличие от уравнений сохранения, уравнения ветвей в общем
случае - нелинейные. Ограничиваясь линейными системами, будем
использовать уравнения для ветвей в виде линейных или линеаризованных (для
нелинейных элементов) зависимостей. Некоторые вопросы расчета
нелинейных ПГС рассмотрены в работах [15.97, 118, 129. 183,226].
В первую очередь остановимся на простейшем случае, когда все элемен-
ТЬ1' входящие в цепь, можно описать уравнением линейного двухполюсни-
8* 115
В г
Рис. 3.2. Схема (а), эквивалентная цепь (б), граф (в) и дерево (г) ПГС
ка. В качестве примера на рис. 3.2 приведена схема (а) и эквивалентная
цепь ПГС (б). Пассивную часть каждой из ветвей можно характеризовать
сопротивлением Zj или проводимостью yj ветви. Если /-я ветвь состоит
из к последовательно соединенных двухполюсников, то отклонения
расходов для всех элементов одинаковы:
5С;;. = ЬС^ = . . . = bG'kj = 5G/, C.2.1)
а размерные отклонения перепада давления для последовательно
соединенных элементов суммируются:
к
к
tkj.= 2 &Ap'if9
C.2.2)
где 5Ар'- - вариация перепада давления для всей ;-й ветви цепи. Если
ввести безразмерные переменные, то запись равенства C.2.1) сохранится,
а для сохранения формы записи зависимости C.2.2) необходимо отнести
все вариации перепадов к единому масштабному давлению. Если же для
каждого элемента, как это делалось в гл. 2, вводится свой масштабный пе-
116
репад, то для безразмерной вариации перепадов давления ветви получим
соотношения:
5Др,=
C.2.3)
1 = 1 Р
где Ару, ЬАру — среднее значение и безразмерная вариация перепада
давления на /-м элементе /-й ветви, р - масштабное давление для всей цепи.
Переходя к амплитудам вариаций, разделим соотношение C.2.2) или
C.2.3) на величину bGj или 5G;., с учетом равенства C.2.1). Введя
определение сопротивления для ветви zj = bApjjbGj' или z;- = ЬАр-lbGj, найдем
"'- ^ "' - - * AP^zl7> C.2.4)
1=1
1 = 1
где zj;- =
. Для обратной величины -
проводимости ветви yj= l/z;' или ;// = l/z;-, получим
C.2.5)
где ylj = 8GjlbAp'if, yif = SGflSApif.
Для каждого элемента, входящего в рассматриваемую цепь,
необходимо определить его сопротивление (включая внутренние сопротивления
источников), а затем по формуле C.2.4) определить сопротивления всех
ветвей цепи. Кроме того, удобно выделить отдельно напоры, создаваемые
источниками, предварительно преобразовав реальные источники расхода
в источники напора. С учетом этих замечаний для цепи, изображенной на
рис. 3.2, ?, уравнения для амплитуд безразмерных вариаций перепадов
давлений на ветвях принимают вид (в амплитудах безразмерных вариаций):
+ЬАНХ =z16G1, bAp2 =z25G2, ЬАрг + zBH,33Q3
=z45G4, 5Др5 =zs5G5, 5Др6 =z65G6, 5Др7 =
5Др8 +5Д//8 — z%bG%, 5Др9 ~" Z96G9,
или в матричной форме, при zBH<35(?3 = ЬАН$,
6G,
6G2
6G3
6G5
z7 6G7
_5G9_
или в более компактной форме:
5 Др + 5 ДН= z6 G, C.2.6)
гДе z — диагональная матрица сопротивлений ветвей, 5Др, 5G, 5ДН —
117
8Ар1
6Ар2
бДрз
6Др5
5Арб
SAp,
5АР8
-6АР9_.
8 АН,
0
ЬАНг
0
0
0
0
6АЯ8
=
О
матрицы (векторы) амплитуд вариаций перепадов давлений, расходов в
ветвях и напоров источников. Выражения для сопротивления, связывающие
размерные амплитуды вариаций расхода и перепада давления 5G' и 8 Ар'-
для ветви, можно получить, умножив Zj на нормирующий множитель-
,;.%„ ' («7,
,;%„. («.7,
Матрица сопротивлений ветвей при переходе к размерным амплитудам
вариаций сохраняет свою диагональную форму, но в соответствии с
формулой C.2.7) изменится запись и размерность ее элементов.
Соответственно уравнение C.2.6) принимает вид
6Др-'+6ДН'=г'бС\ C.2.8)
где z - диагональная матрица размерных сопротивлений ветвей цепи.
Матричные уравнения C.2.6) или C.2.8) эквивалентны системе, состоящей
из/? линейных уравнений относительно 2Ь переменных 5G;-' и 8Ар' или
bGj и ЬАр-. Уравнения C.2.6) или C.2.8) вместе с уравнениями баланса
для узлов C.1.15) и уравнениями контуров C.1.22) являются замкнутой
системой, содержащей 2Ь уравнений относительно 2Ъ переменных. Однако
применение этих уравнений приводит к громоздким и трудоемким
вычислениям. Кроме того, при анализе ПГЦ, содержащих более сложные
элементы, чем двухполюсники (см. гл. 2), использование вариаций
перепадов давлений на ветвях оказывается неудобным. Поэтому разработан ряд
методов, в которых задача расчета цепей сводится к решению меньшего
числа уравнений.
3.2.2. Метод узловых давлений. Одним из методов, уменьшающих
размерность системы уравнений цепи, является метод узловых давлений,
в котором в качестве независимых переменных используются давления
в узлах цепи. В результате решения системы из ш-1 уравнений
узловых давлений находятся узловые давления, как разность между
давлениями в т — 1 узлах цепи и давлением в одном, произвольно выбранном
базисном узле. За базисный узел удобно выбрать тот узел, уравнения
которого при составлении системы узловых давлений отбрасываются,
приняв для него давление равным нулю. В этом случае узловые
давления будут просто равны давлениям в узлах. Как правило, в ПГЦ
имеется узел, соответствующий внешней среде, и именно этот узел с
постоянным давлением удобно принять за базисный узел, если считать в нем
давление (вариацию давления) равным нулю. Зная узловые давления,
несложно найти разности давлений на ветвях, а используя уравнение
ветвей, находим расходы (вариации расходов) в любой ветви цепи.
Метод узловых давлений основан на использовании т — 1 независимых
уравнений балансов в узлах, записанных в узловых давлениях. При этом
все реальные источники напора (давления) в цепи преобразуются в
источники расхода (см. гл. 2). Для /-й ветви, соединяющей узлы к иг (не
базисные), по аналогии с уравнением C.2.8) можно записать уравнение в
амплитудах размерных вариаций
y'krfP'k -6p;)-5G/=56/. ^ C.2.9)
где у'кг — проводимость ветви, 8Q- — амплитуда внешнего возмущающего
118
воздействия, 8G'- -- амплитуда вариации расхода через пассивную часть
ветви, 8р'к, &Р I - амплитуды вариаций в узлах. Для ветви, связывающей
?.й узел с базисным узлом, для которого было оговорено Ьр '0 - 0, в
уравнении C.2.9) будет отсутствовать амплитуда вариации Ъ~р\.. Уравнения C.2.9)
записываются для всех ветвей цепи, систему этих уравнений можно
представить в матричной форме
Y'5Ap'-6G'=5Q\ C.2.10)
где Y' - диагональная матрица проводимости ветвей цепи.
Матрица амплитуд вариаций перепадов давлений 5Др' связана
уравнением C.1.16) с матрицей амплитуд узловых давлений 5Р, которое для
амплитуд вариаций параметров запишется так :
П*5Р'=5Др\ C.2.11)
Подставив зависимость C.2.11) в уравнение C.2.10) и умножив после
этого полученное соотношение на матрицу Пн слева, находим, что
В уравнении C.2.12) второй член в левой части в соответствии с
уравнением узлов C.1.15) равен нулю, произведение в правой части заменим:
Пнб Q' = 5Q'y, где 5Qy - вектор амплитуд узловых возмущающих расходов,
а произведение IIHY'n* = Yy назовем матрицей узловых проводимостей.
В итоге находим уравнение для амплитуд вариаций узловых давлений:
Yy5P' = 6Qy. C.2.13)
Уравнение C.2.13) можно получить более наглядно, используя
уравнение C.2.9) для ветви цепи. Для этого запишем уравнение C.2.9) для всех
ветвей, входящих в узел к, учитывая соотношение C.1.10) и выделяя
ветвь, соединяющую узел к с базисным (если она имеется). Получим
п -1 п
^ у1Л5р1 — Spi) + ylnSvl = 2 akidQ- (к = 1, 2, . . . , m — 1),
1 = 1 kl k l k0 L k ,- = i
где п - число ветвей, входящих в узел к, у'к0 - проводимость ветви,
соединяющей узел к с базисным. Группируя члены, получим
( S уL- +yln)Spl - 2 yLdpJ =8Qlv, C.2.14)
/ = i kl k0 / = i ky
n _
причем 5Q'ky = S aki8Q- - амплитуда вариации узлового возмущающего
расхода /с-го узла. Уравнение C.2.14) можно записать в более компактной
форме:
УккЬРк- - y'kibPi =8Q'ky> C.2.15)
и - 1
где Укк = ^ У/ci + Уко (' ^ к) — собственная проводимость А:-го узла,
/ = 1
Равная сумме проводимостей ветвей, сходящихся к этому узлу, y'ki —
119
взаимная проводимость двух узлов к и i. Систему уравнений C.2.15) для
всех узлов (кроме базисного) можно записать в матричном виде:
УЦт-1)
У'2(т~\)
bQ'2y
L->'(m-l)l У{т-1J ••• У(т-1)(т-1) J\-8P'm-l-
C.2.16)
Уравнение C.2.16) совпадает с уравнением C.2.13), но в процессе его
формирования выявлено простое правило получения матрицы узловых
проводимостей. В качестве примера составим матрицу узловых
проводимостей для цепи, представленной на рис. 32,6, в которой все источники
напора преобразуются в источники расхода. Матрицу проводимости
составим сразу по схеме цепи, отбросив уравнение для базисного узла 0:
Yy =
Ух
Уъ
о
о
о
Уг
0
У'п + У&
Ветви 7 и 8, связывающие узлы III и IV, после преобразования источника
напора в источник расхода оказываются состоящими только из пассивных
элементов 1), и их можно преобразовать в одну ветвь, имеющую
проводимость, равную сумме проводимостей исходных ветвей. Учитывая
направление действия всех источников расхода, совпадающее с направлением
действия эквивалентных им источников напора, можно составить матрицу
амплитуд вариаций задающих расходов:
SQ'3
8Q
Iy
y
Выразив коэффициенты y'ki, входящие в матрицу Y'y, через параметры
элементов цепи, можно разрешить полученное уравнение относительно
искомого вектора амплитуд вариаций узловых давлений.
3.2.3. Метод узловых давлений для цепей, содержащих многополюсные
элементы. Выше рассмотрен метод формирования матрицы узловых
проводимостей, входящей в уравнение узловых давлений, для цепей,
содержащих только двухполюсные элементы. В то же время в гл. 2 были приведены
примеры устройств, которые не могут быть описаны как двухполюсные
элементы. Остановимся на особенностях применения метода узловых
давлений для цепи, содержащей многополюсные элементы. Много полюсный
1) Так как источник расхода, вводимый вместо источника напора в ветви 7,
непосредственно связан с узлами III и IV.
120
элемент (например, трехполюсник) описывается системой уравнений
C.2.17)
где 5Gi, 6G2, SG3 - амплитуды вариаций расходов по ветвям, 8р[, 5р\,
Ьр\ - амплитуды вариаций давлений в узлах трехполюсника. Без учета
многополюсных элементов уравнение для амплитуды вариации давления
в fc-музле C.2.13) запишется так:
у'ы?>р! =
C.2.18)
/= 1
Для выяснения влияния на матрицу узловых проводимостей
присутствия в цепи многополюсного элемента выпишем уравнения C.2.18) для
узлов, с которыми связан многополюсник, нумеруя эти узлы индексами
а, Ъ и с. При этом амплитуды вариаций давлений в узлах
многополюсника будут совпадать с амплитудами вариаций давлений в узлах, с которыми
связан многополюсник, т.е. Ьр'а =5р1, Ьр'ь-Ьр2,Ьр'с~Ьр'ъ. Оставляя
амплитуды вариаций расходов, поступающих от многополюсника, в левой
части уравнения C.2.18), рассматривая их как задающие, запишем:
w-1
2 у'ы&р1 + &б'2=&Bьу. C.2.19)
i= l
w-l
1= 1
Подставив в уравнение C.2.19) значения 8G'U 8G2, SG3 из зависимости
C.2.17), получаем в каждом из уравнений узловых давлений три
дополнительных члена с амплитудами вариаций давления Ьр'а, др'ь, Ьр'с и
коэффициентами многополюсника. Если в уравнениях привести подобные члены,
то к проводимости узлов добавятся соответствующие коэффициенты
многополюсника. При этом изменится часть матрицы проводимости,
относящаяся к узлам a, b n с:
Y' =
У .
•Уаа+У11 УаЬ+У12 Уас+У13'
-Уьа+У21 Уьъ+У22 Уьс+УГ2з
•Уса+Уз! УсЬ+Уз2 Усс+Узз
Если один из полюсов многополюсника соединен с базисным узлом,
Уравнение которого отброшено, то коэффициенты многополюсника,
соответствующие этому полюсу, в матрицу проводимостей узлов не
вписываются. Описанный метод пригоден для цепей с любым числом многополюсни-
ков, которые могут иметь произвольное число полюсов.
121
§ 3.3. Общие матричные уравнения цепей
Рассмотренные выше методы построения математических моделей
линейных цепей позволили найти амплитуды вариаций узловых давлений.
В ряде случаев необходимо непосредственно получать вариации расходов
или перепадов давлений для ветвей цепи. Эти переменные удобно находить
из уравнений более общего вида, получаемых с использованием введенных
в гл. 2 понятий о дереве, фундаментальных (главных) контурах и сечениях
графа цепи. Запишем уравнение баланса расходов для главных сечений
C.1.19) (эквивалент уравнения баланса расходов для узлов цепи) для
амплитуд размерных вариаций расходов:
QSG'= [IJF] д = SGa+F5Gx=0, C.3.1)
L <-)(jx J
[ЙС' 1
-,Д =
5GX J
[ЙС 1
-,Д = [SG'i . . . bG'm_i : 8G'm . . .8Gfq] T - вектор амплитуд ва-
5GX J
риаций расходов ветвей, 5G^, 5GX - векторы амплитуд вариаций
расходов ветвей дерева и хорд. При этом, как было принято ранее, нумеруются
сначала ветви дерева, а следующие номера присваиваются хордам.
Аналогично, используя соотношение C.1.22), запишем уравнение для амплитуд
вариаций перепадов давлений главных контуров:
[ 1*1* } = Fi
L 5Арх J
ТдАр'= [Fxi I] [ 1*1* } = FiSA^ + 5А^Х =0. C.3.2)
1 L 5А J
Для того, чтобы облегчить запись матриц коэффициентов и упорядочить
вид уравнений, удобно придерживаться определенного порядка
формирования математической модели цепи [159] :
1. За основу формирования всех топологических матриц цепи
принимается специально выбранное дерево графа, называемое нормальным.
В ветви дерева входят все источники напора и часть ветвей с пассивными
элементами (для получения m — \ ветвей). В хорды (ветви связи) входят
все источники расхода и остальные ветви с пассивными элементами.
Следуя обозначениям, введенным В.В. Бердниковым [15], будем
различать следующие переменные четырех типов: а — ветви дерева с
источниками напора, /3 — ветви дерева с пассивными элементами, у — хорды с
пассивными элементами и е — хорды с источниками расхода. Такое деление
ветвей позволяет учитывать различную роль активных и пассивных элементов
в математической модели цепи. Для активных элементов известна часть
параметров, а для пассивных все параметры течения необходимо найти в
результате решения уравнений цепи.
2. Нумерация ветвей графа проводится таким образом, что первые
номера получают ветви дерева с источниками напора, последующие — ветви
дерева с пассивными элементами, затем нумеруются хорды с пассивными
элементами, а последние номера получают хорды с источниками
расхода,
3. Для всех ветвей дерева проводятся главные сечения, с помощью
уравнения сохранения расходов C.3.1) амплитуды вариаций расходов
ветвей дерева выражаются через расходы хорд.
122
4. Для всех хорд определяются главные контуры, и используя уравнение
C.3.2), амплитуды вариаций перепадов давлений на хордах выражаются
через амплитуды вариаций перепадов давлений на ветвях дерева.
5. Записываются уравнения всех ветвей в соответствии с принятой
нумерацией.
В результате разбиения ветвей и хорд на отдельные типы векторы
амплитуд вариаций расходов и перепадов давлений, входящих в уравнения C.3.1)
и C.3.2) , представляются следующим образом:
\
где <$G^, ^ДРа — векторы амплитуд вариаций расхода и перепада давлений
ветвей с источниками напора, SG^, 5Ap^, 5G^, 5Др^ — векторы амплитуд
вариаций расхода и перепада давления пассивных ветвей дерева и хорд
соответственно, 5G^, 5Ap^ — векторы амплитуд вариаций расхода и
перепада давления хорд с источниками расхода.
В соответствии с разбиением векторов амплитуд вариаций расходов и
перепадов давлений можно разделить на клеточные матрицы и матрицу F
(входящую в матрицу сечений Q), которая связана с матрицей ?г
равенством C.1.21):
F F
1
F=
= -F[. C.3.4)
Матрица F описывает хорды, проходящие через главные сечения графа.
Подматрицы ?ау и ?ае показывают, какие хорды состоят из пассивных
элементов (индекс у), какие включают источники расхода (индекс е),
входящие в сечения, образованные ветвями дерева с источниками напора
(индекс а). Подматрицы ?$у и ?@е аналогично показывают хорды
(пассивные и активные), входящие в сечения, образованные пассивными
ветвями дерева.
Используя уравнение C.1.19) для амплитуд вариаций расходов и
разбиение матрицы F на подматрицы C.3.4), запишем
б; Fa7 I Fa6
Уравнение C.3.5) эквивалентно двум уравнениям, определяющим
векторы амплитуд вариаций расходов ветвей дерева с активными и пассивными
элементами:
5G'=-F V-F SO'"' C3-6)
Аналогичным образом можно преобразовать уравнения C.1.22) для конту-
ров цепи, используя равенство C.3.4) :
C.3.7)
123
[ 6^Р'7 = FT5АРд = [f" ^ V } [ s^P°
Умножив клеточную матрицу в уравнении C.3.7) на вектор, получаем
Для получения замкнутой системы уравнений к уравнениям сохранения
C.3.5) и C.3.7) необходимо добавить зависимости, определяющие
характеристики элементов, входящих в ветви цепи.
Если все элементы являются двухполюсниками, то для всех ветвей
деревьев и хорд, содержащих только пассивные элементы, можно записать
уравнение в матричной форме, подобное _зависимости C.2.6) и C.2.10)
(для размерных амплитуд вариаций, при 5 АН' = 3Q' = 0):
1рЩ, 5б7 = Yyd Ар7, C.3.9)
или, обратив уравнения,
5Ц = У^5Ард, 5AJj>7 = Z75G7, C.3.10)
где Z^, Z7, Y^j, Y7 — диагональные матрицы сопротивлений и проводи-
мостей пассивных ветвей дерева и хорд соответственно.
Для определения основных неизвестных - амплитуд вариаций расходов
в пассивных ветвях цепи - преобразуем полученную систему уравнений
C.3.8), используя уравнения ветвей C.3.9) и C.3.10). Подставляя
выражение C.3.9) для вектора амплитуды перепада давления пассивных ветвей
5Лр^ в первое уравнение системы C.3.8), используя известное выражение
5 Ар а =5Д#а (т.е. считая амплитуды вариаций напоров в активных ветвях
дерева заданными) и заменяя амплитуды вариаций расходов в пассивных
ветвях дерева через расходы хорд C.3.6), получим (с учетом равенства
6G' 521)
Приведя подобные члены и введя новые обозначения, запишем
ZsSG; = 5A', C.3.11)
где Zs = z; + FJ7Z^7, 6A1 = F?7SAH; - F^Z^F^SQ;.
Уравнение C.3.11) позволяет определить вектор амплитуд расходов
в пассивных хордах как реакцию на действие суммарного возмущающего
воздействия 5А\ Зная вектор 5G7, с помощью уравнения C.3.10)
находим вектор 5Др7. Далее, учитывая, что 5G'e = 5Qe, подставим вектор
5G7 в уравнения C.3.6), определим векторы амплитуд вариаций
расходов по ветвям дерева, а затем из уравнения C.3.9) найдем вектор
амплитуд вариаций перепадов давления 5Ар^. Используя второе уравнение
C.3.8), в которое подставляются найденный вектор 5 Ар^ и 6 Ар^, =
= 5АН^, определяем вектор для хорд 5Ар^.
Описанная методика позволяет проводить расчеты ПГЦ с
использованием матриц относительно невысокого порядка, формализация же
построения уравнений модели с использованием дерева графа облегчает
разработку алгоритмов расчетов динамики ПГЦ достаточно сложной структуры.
124
Глава 4
ПРИМЕНЕНИЕ СИГНАЛЬНЫХ ГРАФОВ
ДЛЯ РАСЧЕТОВ ЛИНЕЙНЫХ ПНЕВМОГИДРАВЛИЧЕСКИХ СИСТЕМ
§ 4Л. Основные определения
Ранее было показано, что структурные графы системы значительно
упрощают формирование математической модели ПГС. Кроме структурных
графов, в теории цепей нашли применение сигнальные графы, наглядно
показывающие связи между переменными в линейной математической модели
системы. Таким образом, сигнальный граф отображает функциональные
связи между переменными, описывающими процессы в исследуемой
системе [13, 168, 179]. Теория графов нашла применение и при анализе
динамики ПГС. В отечественной литературе этому вопросу посвящены работы
В.В. Бердникова [15], Г.Т. Гроссшмидта [72, 73], В.Н. Прокофьева и
В.Г. Неймана [186], В.П. Шорина [243], автора [60] и других.
Любая линейная математическая модель системы с сосредоточенными
параметрами 1) может быть представлена в виде сигнального графа, и граф
полностью эквивалентен системе уравнений. Сигнальный граф
(направленный граф, линейный граф сигнала) представляет собой совокупность
узлов и соединяющих их линий - ветвей, стрелки на которых указывают
направление распространения сигнала. Каждый узел имеет связанную с ним
величину, называемую узловым сигналом 8xif а каждая ветвь
характеризуется величиной коэффициента передачи я7у между узлами / и /. Узлом
источника (истока, входа) является узел, от которого в систему поступает
сигнал, т.е. к которому присоединяется источник возмущения (расхода,
давления). Узловой сигнал для источника является независимой
переменной, задаваемой на входе в систему. Узлом стока (выхода) называется
узел, параметр сигнала в котором является искомым.
Коэффициенты передачи ветвей могут быть безразмерными или иметь
размерность сопротивления или проводимости (при использовании
размерных переменных). Для первого узла узловой сигнал обозначается бх^для
второго — 8х2 и т.д., и если эти узлы связаны ветвью, то коэффициент
передачи между ними а21 = 8х2/8хх. Узловой сигнал /-го узла равен сумме
сигналов, поступающих к этому узлу. Узловые сигналы, выходящие из
узла, при составлении узлового уравнения не учитываются - они
учитываются только в уравнениях узлов, к которым поступают эти сигналы.
Для иллюстрации правила составления сигнального графа рассмотрим
уравнения четырехполюсника. В z-параметрах уравнения запишутся:
5() 5 = z218G@)+z228G(\).
1' Использование сигнальных графов для анализа систем с распределенными
параметрами описано в § 7.4.
125
Этим уравнениям соответствует граф, приведенный на рис. 4.1, а. В
качестве входных, независимых параметров приняты амплитуды вариаций
расходов на входе и выходе четырехполюсника. С узлами источников и стоков
основной граф связан ветвями с коэффициентом передачи, равным
единице. В у -параметрах уравнения четырехполюсника имеют вид
8G@)=yll8p@)+y128p(\),
8G(\)=y218p@)+y228p(\).
Этим уравнениям соответствует граф, изображенный на рис. 4.1, б. В дан-
Рис. 4.1. Графы четырехполюсника в z- и ^-параметрах
б&Н' а бр; с Щ d бр'ш
(Ю а б
Р и с. 4.2. Цепь (а) и эквивалентный сигнальный граф (б)
ном случае входными, независимыми переменными являются амплитуды
вариаций давлений на входе и выходе четырехполюсника, выходными -
амплитуды вариаций расходов.
Составим сигнальный граф для ПГС, эквивалентная ПГЦ для которой
изображена на рис. 4.2, а. Цепь включает активный элемент — источник
напора с внутренней проводимостью у'вн и пять пассивных элементов
со своими проводимостями. Входным, возмущающим параметром служит
напор источника, выходным — амплитуда вариации давления в узле III
цепи. Составим уравнения баланса расходов для трех узлов цепи I, II и III,
принимая, что в базовом узле 0 давление постоянно, т.е. Ьр'о = 0:
у'2Ьр{ -(у'2
= 0,
D.1.1)
где 5pJ, dp i!, bp'ni — амплитуды вариаций узловых давлений.
Разрешив уравнения D.1.1) относительно амплитуд узловых давлений,
получим:
8р{ =адАН' + Ь8р'и. 8р'и = cbp{ +e8p'ul, 8p'ni =d8p'u, D.1.2)
где д = ->'вн/0вн +У\ +.^2), Ь = vi/0'вн +>'i +>;2)^ с = у'гНу'г + Уъ
126
j = у'4/(у4 +y's), e ~у\\{Уг + Уъ + у'*)- Уравнениям D.1.2) соответствует
сигнальный граф, изображенный на рис. 4.2, б, в котором в качестве
переменных использованы амплитуды вариаций узловых давлений. Если
изменить переменные, то для той же исходной схемы ПГЦ структура графа
изменится. Если цепь содержит несколько активных элементов,
являющихся источниками сигналов, то пользуясь линейностью системы, к которой
применим принцип суперпозиции, для каждого возмущающего воздействия
находится значение выходного параметра. После определения реакции
системы на все возмущающие воздействия выходные параметры для всех
воздействий суммируются.
Составленный граф используется для определения коэффициента
передачи моделируемой системы, что производится двумя способами: путем
последовательного упрощения (сворачивания) графа по определенным
правилам или непосредственного применения общего правила Мэзона (см. § 4.3)
для коэффициента передачи графа. Наиболее эффективно использование
одновременно этих двух способов: сначала упрощается граф, а затем
применяется формула Мэзона.
§ 4.2. Правила упрощения сигнальных графов
Сигнальный граф эквивалентен системе линейных уравнений, из которых
можно последовательно исключить часть переменных. Процессу
исключения промежуточных переменных соответствует процедура упрощения
сигнального графа, эквивалентного системе уравнений. На рис. 4.3
приведены примеры простейших преобразований сигнальных графов:
1. Коэффициент передачи для последовательно соединенных ветвей
(рис. 4.3, а) найдем из уравнений ветвей 8х 2 = a8x~i, 8х3 - Ь8х2,
исключая переменную 8х2 '¦ 8х3 = аЪ 53с2. В этом случае коэффициент передачи
равен произведению коэффициентов передач ветвей.
2. Коэффициент передачи для параллельных, одинаково направленных
ветвей находим для графа (рис. 4.3, б) из двух ветвей:
8х2 = а8х1 + Ь8хх = (а + Ь)8х1,
т.е. он равен сумме коэффициентов передач отдельных ветвей.
3. Устранение узловой точки возможно в двух случаях (рис. 4.3, в и г) -
при сходящихся и расходящихся ветвях. Для сходящихся ветвей можно
записать: 8х3 = а8хг + Ь8х2, 8х4 = с8х3, откуда 8х4 = c(a8xi + Ь8х2) =
~ ас8х j +Ьсдх2. Аналогично для расходящихся ветвей: 8х~2 =abx~i* 8~хъ =
~Ь8х2, 8хА=с8х2, откуда 8х3=аЬ8х1, 8х4=ас8х1. Таким образом, из
графа устраняется узел и одна ветвь, а коэффициенты передачи
оставшихся двух ветвей равны произведению передач устраненной ветви и двух
оставшихся.
4. Устранение простого контура (рис. 4.3, д) ч образованного ветвью,
направленной в противоположном направлении. Для этого графа имеем
§х2 =а8х! +с5х3, 8х3 =Ь8х2, откуда, исключая 8х2, находим 8х3 =
= аЬ8хх + Ьс8х3. Получилось уравнение, содержащее в правой части член с
выходным параметром. Такое уравнение можно аппроксимировать
графом с петлей, у которой передача равна произведению передач ветвей,
входящихв устраненный контур.
127
ab J
n ? \}C* n = I fr о
Рис. 4.З. Правила упрощения простейших графов
Рис. 4.4. Правила упрощения сигнального графа с петлями
в ? с b qf\ e'f\ a e" ГцГсГГь а
b* fH ' b" f" " ' b"
Рис. 4.5. Правила упрощения сигнальных графов с контурами
5. Исключение петли можно рассмотреть на простейшем примере, когда
к узлу с петлей подходит и отходит по одной ветви (рис. 4.4, а). Для этого
графа можно записать: 5х2 =#5^! +с53с2, 5х3 =ЬЬх2, а исключив Ьх2
получим Ьх3 = [ab/(\ —с)] дхг. Эта зависимость пригодна, если |с| < 1-
Если к узлу подходят и отходят несколько ветвей (рис. 4.4, б), для такого
графа Ьх2 =abx1 +Z?5x4 +с5х2 или 8х2 = [1/A —с)](а8хг + ЬЬх4)- Тогда
для других переменных 5х3 ~dbx2 ~ [d/(\ —с)] [а5хг + Ь8х4]. 5х6 ~
-fhx2 - [//A -c)](adxi +Ь8хА). Чтобы не менять коэффициенты у ветвей,
входящих в узел 2 (рис. 4.4, б), удобнее ввести дополнительный узел 8 и
ветвь с передачей 1/A -с).
6. Замена двух петель одной (рис. 4.4, в). Если у одного узла имеется
две петли с передачами Ъ и с, их можно заменить одной с передачей Ь + с,
так как Ьх2 =а^хх -+- Z>53c 2 +с53с2 =^5^! + (Ь +сMх2. Аналогичные
соотношения можно получить при любом числе петель у одного узла.
128
7. Упрощение сигнальных графов с несколькими контурами (рис. 4.5)
производится в два этапа - сначала сворачивается контур в петлю, а затем
исключается петля. Используя правило 5, можно исключить петли у
узла, связанного с контурами (рис. 4.5, а), изменяя одновременно значения
коэффициентов передачи ветвей, входящих в узел b' - Ь/(\ — е), а' -
Модифицируя правило 4 и расщепляя узел, находим формулы для
коэффициента передачи графа после исключения одного из контуров внутри
графа (рис. 4.5, б): с - cd, b' = b/(\ - cd) . Для цепочки из трех
последовательных контуров (рис. 4.5, в) можно получить
c' = cd, d' = ef, e' = ce, f'=df, b' = b/(l -c') =
= b/(l -cd), e" = e'l(l - c') = ce/(l -cd), a' =ae" =
= ace/(l-cd), b" = b'f = bdf/(l-cd), c" = ah' =
= <rf>/(l - cd), d"=d'+e"f' = ef+cdef/(l - cd).
§ 4.3. Коэффициент передачи графа
Связь параметров на входе (истоке) и выходе (стоке) сигнального
графа характеризуется коэффициентом передачи, который определяется
по формуле Мэзона [13,168, 203]. С помощью формулы Мэзона находится
или частотная математическая модель линейной системы — ее частотная
передаточная функция, или дифференциальное уравнение, описывающее
систему.
Введем некоторые новые понятия, используемые в формуле Мэзона.
Прямой (сквозной) путь - это непрерывная последовательность ветвей
с одинаковым направлением стрелок, проходимая от истока (входа) до
стока (выхода) графа. При прохождении прямого пути ни один из узлов
не встречается более одного раза.
Коэффициент передачи прямого пути Р/ равен произведению
коэффициентов передач всех ветвей пути. Между истоком и стоком может быть
несколько прямых путей. Так, например, для графа на рис. 4.6,а между
истоком (узелО) и стоком (узел 5) есть два прямых пути (рис. 4.6,в).
В первый прямой путь входят ветви с коэффициентами передачи а, Ь, с,
d, е, и коэффициент Pi передачи пути равен Р\ = abcde. Второй прямой
путь проходит по ветвям с коэффициентами передачи a,f,e, и для
него Р2 -afe. Ни один из других возможных путей на графе от узла 0
к узлу 5 не будет прямым путем. К примеру, путь по ветвям а, /,
g, d,e не будет прямым, так как для этого пути узел 4 проходится
Дважды.
Контур - замкнутый путь, вдоль которого каждый узел может
встречаться только один раз. Петля является частным случаем контура,
включающего только один узел. Если два различных пути или контура имеют хо!я
°bi один общий узел, то они называются соприкасающимися, если же обше-
го узла нет, - несоприкасающимися. На рис. 4.6, б приведены все четыре
контура для графа, представленного на рис. 4.6, а. Коэффициент передачи
к°н~гура /,. равен произведению коэффициентов ветвей, входящих в кон-
9 Ь.ф. Гликман 129
/о—
-^)----О
_Д_ Jt
: o--^V — -0_-._-&.-.- -Л----O
Рис. 4.6. Граф (я), контуры графа (б) и прямые пути графа (в)
тур. Для четырех контуров, приведенных на рис. 4.6, б, коэффициенты
передач равны Li = bk, L2 = ch, L3 = dg, L4 = fghk.
Общая формула Мэзона для коэффициента передачи сигнального графа
между узлами а и /3 записывается следующим образом:
1 п
Тар = — S ркАк, D.3.1)
А к = 1
где Рк — коэффициент передачи к-то прямого пути от истока к стоку,
п - число прямых путей между истоком и стоком графа, А = 1 +
m p
+ Z [(- \У S L^] - определитель графа, L^ - коэффициент переда-
г = 1 / = 1 У 7
чи/'-го контура г-го порядка. Контур r-го порядка - совокупность г
контуров первого порядка, у которых нет общих узлов, контур первого
порядка — обычный контур, определение которого дано выше. Величина -^
называется алгебраическим дополнением для к-то прямого пути графа.
Значение Ак равно определителю подграфа, который не соприкасается
(не имеет общих узлов) с к-м прямым путем.
В граф, изображенный на рис. 4.6, я, входят (см. рис. 4.6, б) четыре
контура первого порядка и один контур второго порядка, состоящий из
двух несоприкающихся контуров 1 и 3 с коэффициентом передачи Ь[2 ~
-bkdg. Отсюда определитель графа на рис. 4.6, а равен А= \-(l\ +/J1 +
+ Z^l) +/41)) + /чB) = 1 - (bk + ch + dg + fghk) + bkdg. Для графа, не
имеющего ни одного контура, определитель графа равен единице. Выражение ллч
алгебраических дополнений А^ может быть найдено, если выделить
130
ры граФа> не соприкасающиеся с данным прямым путем. Для первого
прямого пути (рис. 4.6, в) нет ни одного несоприкасающегося контура
и д j = 1, для второго — один несоприкасающийся контур 2 и соответственно
д2 = 1 — с/г. Используя все полученные определители и коэффициенты
передачи прямых путей, с помощью формулы D.3.1) находим
коэффициент передачи графа, представленного на рис. 4.6, а:
abcde + afe (I — ch)
Ts° ' 1-bk-ch-dg-fghk + bkdg
Таким образом, формула Мэзона D.3.1) для коэффициента передачи
сигнального графа позволяет получить системную функцию цепи - ее
передаточную функцию.
131
Глава 5
АКУСТИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПРОТОЧНОГО ТРАКТА
§ 5.1. Волновое уравнение для участка трак га
5.1.1. Что такое акустические характеристики? Акустика изучает
распространение волн в различных сжимаемых средах. При этом наиболее общие
и эффективные методы анализа волновых пронессов получены в линейнсь
акустике, рассматривающей только волны малой амплитуды. Любые
колебательные процессы в механических системах, в том числе и распрос^
ранение волн, связаны с одновременным действием двух сил — силы инер
цин и возврашаюшей силы. Применительно к системам с сосредоточенным:<
параметрами, рассмотоенным в предшествующих главах, инерция и возврл
тающая (упругая) сила были присущи разным типам элементов (инерцк
онность и емкость). В процессе распространения акустических волн однов
ременно участвует инерция и сжимаемость среды, при этом возмущение
распространяются с конечной скоростью — скоростью звука, что привода
к запаздыванию появления сигнала в точке, удаленной от источника возмл'
щения. Необходимость учета акустических эффектов определяется cootie?
шением между длиной волны и размерами изучаемого объекта. ?:л:
акустические эффекты необходимо учитывать, то кажется естественные
называть акустическими и получаемые при расчетах динамические харак к-
ристики системы, тем самым подчеркивая, что расчеты проводятся в акуч
тическом приближении, т.е. рассматривается ПГС как система с раснреле
ленными параметрами.
Учет акустических эффектов приводит к достаточно существенны-
усложнениям математической модели системы. Поэтому нецелесообраз!
увлекаться уточнением модели за счет рассмотрения ПГС как системы
распределенными параметрами, если это не вызвано действительной необл
димостью. Описание ПГС. как системы с сосредоточенными параметрам;
правомочно, если геометрические размеры элементов и системы в цел-^v
намного меньше длины акустических волн в исследуемом диапазоне часто.
Теперь можно более подробно обосновать это условие "компактное!-
элементов ПГС. Под влиянием внешнего воздействия (перемещения порг-
ня, мембраны, изменения положения дросселирующего устройства, измег ~
ния частоты вращения насоса и т.д.) параметры течения рабочей срешл
ПГС изменяются, при этом само возмущение распространяется в гготог
со скоростью звука. Если размеры проточной части таковы, что за характер
ное время изменения параметров (например, период колебаний) волн
возмущения проходит расстояние, во много раз превышающее наибольп
размер проточной части (т.е. если длина акустической волны окажется
крайней мере на порядок больше длины проточной части /.), то так.
132
часть ПГС можно описывать как систему с сосредоточенными параметрами,
так как на ее длине при колебаниях мгновенные значения некоторых
параметров практически не изменяются.
Это отнюдь не означает, что при анализе колебаний этой части ПГС,
как системы с сосредоточенными параметрами, не обнаружатся различия
в амплитудах и фазах колебаний параметров на входе и выходе.
Действительно, такие отличия параметров могут возникнуть за счет действия
динамических эффектов в элементах с сосредоточенными параметрами,
например, появления колебаний перепада давления на инерционностях
или разности расходов при прохождении колебаний через емкость. Для
инерционности и емкости один параметр (расход или давление) не
меняется по времени на всей длине элемента, в то время как при акустических
колебаниях изменяются оба параметра. Таким образом, при учете
акустических эффектов и давление, и расход (скорость) на входе и выходе
элемента в каждый момент разные. Различие расходов на входе и выходе
делает невозможным использование для эквивалентных цепей таких систем
правила узлов (аналог первого закона Кирхгофа) в обычной
формулировке, так как применение этого правила предполагает постоянство
мгновенного значения расхода в каждой из ветвей цени.
При исследовании акустических характеристик ПГС следует обращать
внимание на одну особенность этих систем (которую, как правило, не
рассматривают в курсе акустики), — на влияние протока жидкости и на
связанный с ним вынос энергии колебаний. Эффекты, определяемые
выносом энергии, существенно влияют на вид акустических характеристик
системы, на устойчивость системы и т.д.
Проблема распространения акустических колебаний но разветвленным
каналам в общем виде достаточно сложна. Применительно к отдельным
узлам или участкам трактов ПГС разнообразного назначения, как правило,
соблюдается условие L/D > 1, где L — длина,/) — диаметр или другой
характерный размер поперечного сечения канала, С другой стороны, диапазон
частот, представляющих интерес, ограничен. В этих условиях можно
существенно упростить задачу, не учитывая особенности волноводного
распространения акустических колебаний [105, 191, 205], т.е. не учитывая никаких
мод (типов колебаний), кроме продольных, таге как характерными для
других видов колебаний будут существенно более высокие частоты,
выходящие за пределы диапазона частот, представляющего интерес. Второе
упрощение, используемое ниже, -- анализ только линейных систем. Этого можно
достичь, либо линеаризовав исходную нелинейную систему, т.е.
рассматривая малые колебания, либо пренебрегая в ней нелинейными членами.
Анализ особенностей акустических характеристик трактов ПГС начнем с
наиболее простого случая — течения в участке тракта цилиндрической
формы без учета потерь на трение и при отсутствии внешних объемных сил.
^иже (см. § 6.7) вопрос о колебаниях жидкости в участке тракта под
влиянием внешних объемных сил рассматривается отдельно.
-движение жидкости в системе, возникающее при внезапном изменении
состояния равновесия только за счет энергии, накопленной ранее в системе,
называется переходным процессом, а применительно к акустической систе-
v- —свободными колебаниями. Величина накопленной энергии определяет-
^ скоростями и давлением жидко:ти в системе, заданными в некоторый
133
начальный момент времени (Г = 0). В этом момент равновесие
(стационарный режим течения или неподвижная жидкость) нарушается мгновенным
воздействием — открытием (закрытием) клапана, перемещением поршня
и т.д. Время действия возмущающего воздействия предполагается
настолько малым, что им можно пренебречь. Со свободными колебаниями связан
вопрос о собственных частотах колебаний жидкости в участке тракта при
различных граничных условиях (§ 5.3). Ряд интересных и важных
особенностей распространения акустических колебаний в тракте выясняется при
анализе частного периодического решения уравнений, описывающих
вынужденные колебания жидкости в участке тракта (§ § 5.2, 5.4,5.5). Принятые
выше упрощающие предположения во многих случаях оказываются
неправомочными. Для учета особенностей течений в трактах с большими
потерями на трение необходимо уточнить уравнение движения и граничные
условия, в других случаях — учесть податливость стенок и т.д. Различные
частные варианты математических моделей неустановившегося движения в
тракте и особенности динамики таких систем анализируются в гл. 6.
5.1.2. Исходная система уравнений. Трубопроводы, проточные каналы
являются обязательной частью любой ПГС, и именно для трактов в первую
очередь возникает вопрос об учете акустических эффектов. Схема ПГС
может иметь достаточно сложную разветвленную структуру, содержать ряд
разнообразных агрегатов, для описания которых в большинстве случаев
можно ограничиться математическими моделями в сосредоточенных
параметрах, и трубопроводов (каналов) , для которых часто необходимо
учитывать акустические эффекты. Для построения математической модели такой
системы очень полезно иметь математическую модель, описывающую
акустические характеристики элемента системы — однородного участка
трубы, т.е. участка без изменения сечения. Имея такую модель, можно
построить ПГЦ как модель ПГС, включающую описание элементов с
распределенными и сосредоточенными параметрами. В качестве исходного
варианта нестационарного течения в участке трубы цилиндрической формы
рассмотрим одномерное изотермическое движение невязкой жидкости без
учета влияния внешних массовых сил и податливости стенок.
Средние значения параметров среды (давление, скорость, плотность) в
тракте принимаются постоянными по длине и времени, внешние
возмущения - воздействующими только на его концах^ Принимая в уравнениях
одномерного движения A.7.21) и A.7.22) 7= 1,Лс = X = 0, находим:
Ъп Ъп 1 Ър
—zr + Mw —г + —Г -IT =0> EЛЛ)
Ы Ъх ар Ъх
Ър Ър Ъп
-- + Мм — + ар =0. E.1.2)
bt Ъх Ъх
Пренебрежение вязкостью жидкости не привело к линейной системе
уравнений — необходимо еще сделать дополнительное предположение о слабой
сжимаемости жидкости, для которой можно принять р = 1 и М<^ 1. Однако,
для общности, учитывая, что условие М < 1 не всегда выполняется в
газовом тракте, и с другой стороны, что граничные условия для участков тракта
(местные сопротивления, насосы, компрессоры и т.д.) являются нелиней-
134
ными, целесообразно сохранить все члены уравнений E.1.1) и E.1.2), но
линеаризовать их, переходя к малым отклонениям (размерным вариациям)
параметров 5и', Ьр\ 5р' относительно некоторого среднего стационарного
режима течения с параметрамиио,ро, р0. При этом безразмерные
переменные представляются следующим образом:
и~ (ио + Ьп')/и0 = 1 + 5м,
р = (р0 + Ьр'Iро = 1+Ьр, E.1.3)
р = (р0 +6р')/р0 = 1 +5р,
где Ьи, Ьр, Ьр - безразмерные вариации параметров, отнесенные к средним
их значениям. Малость вариаций определяется тем, что квадратом вариаций
можно пренебречь по сравнению с самой вариацией.
Подставив переменные E.1.3) в уравнения E.1.1) и E.1.2) и, в
соответствии с последним замечанием, отбрасывая произведение вариаций и их
производных, находим:
Э5м ЪЬи 1 ЪЬр
+ М +=0, E.1.4)
Г 3 zr
bt Ъх а Ъх
ЪЬр ЪЬр ЪЬи
-4-+М—~ +а —г"
Ъt Ъх Ъх
E.1.5)
5.1.3. Начальные и граничные условия. Для решения системы уравнений
E.1.4) и E.1.5) необходимо задать начальные и граничные условия.
Начальные условия определяют состояние системы в начальный момент времени
t = 0 и применительно к уравнениям E.1.4) и E.1.5) записываются в виде
зависимостей
Ьр(х, 0) = Д5Г), Ьи(х, 0) = <рCс). E.1.6)
В частном случае начальные условия могут быть нулевыми, т.е. в системе
в начальный момент отсутствуют отклонения, а возмущения в момент t - О
создаются на границах участка и учитываются в граничных условиях.
Начальные условия вместе с граничными условиями определяют свободные
колебания в системе, анализ которых дает определенную информацию о
динамических характеристиках системы.
Еще более полно характеризуют динамическое "лицо" линейной системы
ее динамические частотные характеристики. Динамические частотные
характеристики системы определяются как реакция системы на внешние
гармонические возмущения, т.е. являются решением задачи о вынужденных
колебаниях системы. При решении задачи о вынужденных колебаниях
в основном представляет интерес режим установившихся колебаний,
который наступает после завершения переходных процессов, возникающих
в начале колебаний. Именно установившиеся колебания параметров
системы и определяют ее динамические (и, в частности, акустические)
характеристики. С другой стороны, установившиеся колебания соответствуют
относительно простому частному периодическому решению исходной
системы уравнений. Для частного решения начальные условияE.1.6) не
используются, так как это решение описывает установившиеся колебания после
135
завершения переходных процессов, на которые только и сказываются
начальные условия. Применительно к упрощенным уравнениям E.1.4) и
E.1.5) для одномерного движения нужны граничные условия на входе и
выходе тракта, а граничные условия на стенках тракта не нужно учитывать.
Типичными граничными условиями для тракта с протоком являются
условия на местном сопротивлении, разделяющем участки тракта или
другие элементы ПГС. Для течения капельной слабосжимаемой жидкости
линеаризованное соотношение в безразмерных вариациях B.1.21) для
местного сопротивления с переменным проходным сечением (дросселя,
исполнительного органа, регулятора, золотника и т.д.) на входе в тракт
можно записать в следующей форме:
6н +S(A(F) +ЬР, E.1.7)
E.1.8)
р
Ро Ро Ро
и аналогично для выхода из участка тракта
-Pb)c_ 2(p1-pb) pb
Su5(MFMp
()
Pi Pi Pi
где pa,pb — внешние (для рассматриваемого участка) давления до
местного сопротивления на входе и после него — на выходе из участка тракта,
Po,Pi — давление в начале и конце участка тракта, 6ра, 5рь, 8р0, dpi —
амплитуды безразмерных вариаций соответствующих параметров,
Зы0, 5Ui —амплитуды безразмерных вариаций скорости на входе и выходе
участка тракта, 5(/iF)Oj d(jjiF)i —амплитудыбезразмерных вариаций
проходного сечения (с учетом коэффициентов расхода) местных
сопротивлений на входе и выходе участка тракта.
Уравнения E.1.7) и E.1.8) описывают связь между колебаниями
параметров у местного сопротивления для течения слабосжимаемой вязкой
жидкости без учета ее инерции. Это уравнение пригодно и для газа при режимах
течения с М ^ 1, когда можно пренебречь его сжимаемостью, т.е. если
(Ра -Ро)/Ро< 1.
В соотношения E.1.7) и E.1.8) входят два параметра, определяющих
неустановившееся течение среды в тракте — 8ы0 и 5р0, dUi и dpi, a
остальные переменные, внешние для течения в участке тракта, вызывают
возмущение в потоке.
Для участков трактов, содержащих насос, компрессор или другой
агрегат, линеаризованные зависимости, описывающие их характеристики
(см. гл. 2), имеют структуру, совпадающую со структурой соотношений
E.1.7) и E.1.8). В качестве возмущающих воздействий для трактов,
расположенных на выходе или входе таких агрегатов, являются отклонения
частоты вращения вала агрегата и давления перед (или за) агрегатом. Из
сопоставления линеаризованных уравнений, описывающих характеристики
агрегатов и используемых в качестве граничных условий, для участка
тракта можно сделать вывод, что все они имеют общую структуру: на входе
участка тракта (х" = 0)
Sp = C'o5z7 + 2 7о^7о/ E.1.9'
/ - 1
136
и на выходе (л: = 1)
п
bp = \pibu+ 2 7i/«7i/, E.1.10)
/ = i
где Фо,Ф1 — безразмерные граничные импедансы (безразмерные
сопротивления) на входе и выходе участка тракта, 7о/ - коэффициент усиления для
/-го возмущающего воздействия со стороны входа, 7i/ — коэффициент
усиления для /-го возмущающего воздействия со стороны выхода,
5yoi,byij— амплитуды безразмерных возмущающих воздействий со
стороны входа и выхода участка тракта.
Сопоставив граничное условие на входе в тракт, за местным
сопротивлением E.1.7), с -его записью в общей форме E.1.9), обнаруживаем, что
импеданс на входе Фо = - 2(Ра ~ Ро)/Ро - величина отрицательная. Знак
минус перед коэффициентом, определяющим связь между отклонениями
скорости и давления (импеданс), является естественным, так как с ростом
скорости (расхода) давление за местным сопротивлением должно
уменьшаться. Граничные условия E.1.9) и E.1.10) записаны для амплитуд
вариаций параметров, при этом они в общем случае - величины
комплексные, зависящие от частоты. К примеру, реактивные составляющие
сопротивления появляются в уравнении, описывающем характеристики
центробежного насоса, если учитывать инерцию жидкости в проточной части
насоса [58] или податливость зоны местной кавитации на входе в насос
[182]. Предельные случаи приведенных выше граничных условий E.1.9)
и E.1.10) — это обычно рассматриваемые в акустике простейшие варианты
граничных условий — открытого и закрытого конца тракта [190, 191].
Условие открытого конца соответствует значениям ф0 = 0 или фх =0, т.е.
Ра - Ро =0 или р\ - ръ = 0, при которых полностью отсутствуют
какие-либо изменения давления как за счет активного, так и реактивного
сопротивления. Другой предельный случай — закрытый конец — легко
осуществляется для трубы без протока жидкости, рассматриваемой в акустике, но не
так очевиден для тракта с протоком жидкости, на конце которого нельзя
установить глухую стенку.
Обычная для акустики формулировка условий на закрытом конце
5г7 = 5G = 0 при принятой форме записи граничных условий EЛ.9) и
E.1.10) соответствует бесконечному значению граничного импеданса
^о = °° или фх = °°, но коэффициент усиления, отнесенный к импедансу,
может сохранять конечное значение 7о//^о Ф 0 или 7i// Ф\ Ф 0.
В качестве примера устройства, обеспечивающего условия на границе,
близкие к условиям закрытого конца на выходе из тракта, может служить
высоконапорный центробежный насос. Для насоса линеаризованное
уравнение характеристик без учета инерции жидкости и податливости зоны
кавитации при приведении к форме соотношения E.1.10) запишется (х = 1) :
E.1.11)
Pi Pi Pi
гае (-&рн/р1)фс = ф1, (- Арн/рх)фп = 7i 1, Рь/Pi = 7i2, Ьп = 8уц,
л-'>ь=5у12, bpbibn ~ амплитуды безразмерных вариаций давления за
насосом и частоты вращения насоса, ръ — давление за насосом, Р\, Ь~р —
ивлсние перед насосом (в конце тракта) и его амплитуда безразмерной
137
вариации, bu = bG —амплитуда безразмерной вариации расхода (скорости)
жидкости через насос. Соотношение Ьп = bG верно для капельной слабо-
сжимаемой жидкости. Если зависимость E.1.11) преобразовать, разделив
все члены на Арн/р^, то получаем граничные условия для выхода из тракта
перед насосом:
—~ЬР =-ФСЬС -фпЬп +— bpb. E.1.12)
АРн Арн
Для высоконапорного насоса соблюдается условие Арн ^> pi,pi/ApH<^ 1,
и при отсутствии возмущающих воздействий, что соответствует записи
Ьп = Ьрь = О, можно принять bG ъ 0 (т.е. приближенно выполняется
условие закрытого конца). Если рассматривается участок тракта за насосом,
то уравнение типа зависимости E.1.11) должно быть записано для
амплитуды вариации давления за насосом. Учтя изменение индексов при
переменных, находим для х = О
ДРн - ДРн Ра
Ьр= -ФСЬС + ~фпЬп + bpai E.1.13)
Ро Ро Ро
где Ро,Ьро — давление и амплитуда вариации давления за насосом (на
входе в тракт), ра,Ьра — давление и амплитуда вариации давления на входе
в насосе. В данном случае для высоконапорного насоса обычно соблюдается
условие Арн/р0 ^ 1, и связь между расходом (скоростью) жидкости на
входе определяется только наклоном зависимости напора насоса от расхода
фо = (G/ApH)(dApH/dG). Если фс « 0, a bn = bpa= 0, то давление за
насосом практически не зависит от расхода жидкости через насос. В этом
случае расход жидкости через систему определяется не характеристиками
насоса, а параметрами системы за насосом.
В соотношении E.1.13) коэффициент при амплитуде вариации перед
насосом Ьра для высоконапорного насоса ра/ро ^ 1. Соответственно
изменение давления на входе мало влияет на величину давления на выходе, и,
как следствие, незначительно изменяется расход жидкости. Однако, если
с точки зрения импеданса насоса как нагрузки на конце_тракта в ряде
случаев можно принять условие закрытого конца, т.е. bG ^0, то даже
при небольшом значении коэффициента усиления ра/Ро ДЛЯ ряда задач
связь между колебаниями давления на входе и выходе из насоса является
определяющей. Примером подобных за^ач является проблема продольной
устойчивости ракеты в полете, подробно рассмотренная в монографиях
К.С. Колесникова и М.С. Натанзона [125, 170]. Применительно к этой
проблеме необходимо исследовать прохождение колебаний из топливо-
подающего тракта перед насосом через насос в камеру сгорания двигателя.
При этом в расчетах участвует коэффициент ра/Ро- Следует отметить, что
как в задачах о продольных колебаниях корпуса ракеты (при решении
которых учитываются динамические характеристики двигателя [58] ), так и для
ряда других задач (в которых необходимо учитывать динамику системы,
приводящей во вращение насосы), несмотря на соблюдение условия рх /Арн ^
<^ 1, колебания расхода через насос являются существенными и оказывают
влияние на динамические характеристики тракта перед насосом.
Это объясняется тем, что условие 5 G » 0 соблюдается вполне
удовлетворительно при piiApn < 1 только в случае, если на колебания давления не
реагирует частота вращения, т.е. система привода насоса обладает большой
138
инерцией (например, электромотор). Если же инерционность системы
привода насоса невелика и ее постоянная времени соизмерима с периодом
возмущающих колебаний, то изменение частоты вращения насоса с
приводом (например, турбиной) и влияние податливости гидравлической системы
(сжимаемость жидкости, упругие элементы, газовые емкости и т.д.)
приводят к увеличению амплитуды колебаний расхода. В состав граничного
импеданса насоса (вместе с его приводом) войдет как активная, гак и
реактивная составляющая, т.е. импеданс будет комплексной функцией
частоты колебаний. Динамические характеристики тракта перед насосом
и, в частности, его резонансные частоты (см. § 5.2) могут существенно
измениться за счет влияния динамических характеристик системы на
выходе из тракта. Приведенная общая форма записи линейных граничных импе-
дансов E.1.9)—E.1.10) может быть использована для описания широкого
круга устройств, включающих самые разные агрегаты.
5.1.4. Волновое уравнение. Линеаризованные уравнения гидромеханики
E.1.4) и E.1.5) описывают распространение малых акустических
колебаний в одномерном потоке сжимаемой невязкой жидкости в однородном
цилиндрическом канале. Линеаризованные граничные условия E.1.9) и
E.1.10) описывают течение жидкости на концах участка тракта. Можно
сделать предположение, что неоднородности потока, возникающие из-за
сложной формы течений вблизи устройств на границах участка тракта,
быстро исчезают в тракте, так что этими областями из-за :<\ малой
протяженности по сравнению с общей длиной всего участка тракта можкп пренебречь
[191]. Систему E.1.4) и E.1.5) можно свести к одному уравнению,
проинтегрировав зависимость E.1.4) по л7:
дды
Ьр = - осШи - ос / ——dx, E.1.14)
bt
подставив соотношение E.1.14) в уравнение E.1.5) и
продифференцировав полученную зависимость по Зс, находим
Ъ2Ьи Ъ2Ьи Ъ2Ьи
A -М2) г--2М — =т-=°- E.1.15)
Ъх2 bxbt Ы2
Линейное уравнение E.1.15), называемое волновым, описывает
волновые процессы в тракте - распространение акустических волн, т.е. малых
одномерных отклонений скорости вдоль однородного тракта с жесткими
стенками. Исключив из уравнений E.1.4) и E.1.5) вариацию скорости
и сводя их к одному уравнению, находим другую форму волнового
уравнения — для отклонений давления:
0 Ь2Ьр Ъ2Ьр Ъ2Ьр
A_М2)—__2М—-= ==-=0. E.1.16)
Ъх- bxbt dt2
Уравнения E.1.15) и E.1.16) упрощаются при течении капельной
слабосжимаемой жидкости или при течении газа с малой скоростью, когда
удовлетворяется условие М< 1:
E.1.17)
E.1.18)
139
Если вспомнить принятые при выводе уравнений A.7.21) и A.7.22)
способы приведения вариаций и переменных х и^ к безразмерному виду,
то можно вернуться к форме записи волновых уравнений E.1.15) —
E.1.18) в размерных переменных:
„ Ъ2Ьи' Ъ2Ьы' Ъ2Ьи
(a2 -ul)-—--2U0—- г-г=0, E.1Л9)
Эх2 dxbt bv
Ъ2Ьр' Э25р' Ь2Ьр'
{а2 - и§)_4-- 2ио—— —ТТ- = °' EЛ'2°)
дх~ dxdt bt2
а при и0 < а
Ъ2Ьи' Ъ2Ьи
а1-—г — = 0, E.1.21)
Эх2 bt2
а2~7-т- г^ = 0, E.1.22)
где Ьи , Ьр — размерные вариации скорости и давления в жидкости.
Граничные условия E.1.9) и E.1.10) при использовании размерных
вариаций параметров сохраняют свою форму, только граничные импедансы
Фо, ф[ и коэффициенты усиления 7о/ и 7i/будут размерными величинами,
на что указывают (так же как и для переменных) штрихи.
5.1.5. Скорость звука. Ранее, при преобразовании уравнений
гидромеханики к виду, удобному для решения акустических задач, в качестве
уравнения состояния, связывающего плотность вещества с давлением,
использовалась зависимость для скорости звука. При этом предполагалось, что
скорость звука — это или физическая константа вещества (в частности,
для капельной жидкости) или величина, определяемая из простого
соотношения, связывающего параметры газа.
При распространении волны скорость ее перемещения не является
скоростью движения отдельных точек среды, в которой движется волна.
Частицы среды при прохождении волны лишь отклоняются от своего
среднего положения, а затем возвращаются в старое положение, при этом
разные частицы отклоняются по-разному. Это объясняется тем, что
распространение волн в упругой среде сводится к деформации среды. Скорость
среды при деформации невелика, скорость же распространения фронта
деформации по среде для простейших случаев совпадает со скоростью
звука. Волновая (или фазовая) скорость распространения звука
определяет скорость распространения одинаковой фазы волны, т.е. горба или
впадины. Такое определение скорости возможно, если форма волны при
движении сохраняется, и по пройденному пути и времени прохождения волны
можно определить скорость ее распространения. В некоторых случаях
из-за свойств среды или системы, в которой распространяются возмущения,
волна при своем движении изменяет форму. В этом случае определение
фазовой скорости неприменимо, так как неясно, какие точки в волне
сопоставлять в разные моменты времени.
140
При распространении звука в неограниченной однородной среде скорость
Зв\ка зависит от параметров, характеризующих состояние среды [191].
\] частности, при распространении звука в газе, который можно описать
как идеальный, из соотношения A.2.13) следует, что при малых
колебаниях скорость звука зависит только от температуры среды. При большой
амплитуде колебаний с ростом давления в волне за счет адиабатического
сжатия повышается температура газа,что в свою очередь должно приводить
к росту скорости звука. Действительно, если воспользоваться
определением адиабатической скорости звука а2 - (bp/bp)s и уравнением адиабаты
' = (Ро +5р')/с/р о, находим
к- 1 /с- 1
/ 5р'\ 2 / др'\2к / к-\
= У Ро +A+% 1 +
Ро \ Ро I \ Ро
E.1.23)
г.е. скорость звука зависит от амплитуды колебаний. При повышении
давления скорость увеличивается, при понижении - уменьшается. Это
приводит к изменению формы волны. Бегущие волны большой
интенсивности распространяются со скоростью а >#0 [1]. Скорость звука в
жидкости зависит как от температуры, так и от давления. Например, в воде она
определяется эмпирической формулой [191]:
fl= 1450 + 4,2^-0,037 t2 +0,018/?, E.1.24)
где t — температура в градусах Цельсия.
Приведенные формулы, определяющие скорость звука, пригодны для
акустических колебаний в неограниченном пространстве при не очень
высоких частотах, до начала влияния молекулярных релаксашюнных
эффектов [175]. Но это уже диапазон высоких частот, не представляющих,
как правило, интереса для динамики ПГС.
Применительно к задачам о распространении одномерных возмущений
в каналах, которые интересны для анализа динамики ПГС, в большинстве
случаев можно использовать понятие фазовой скорости. Особые случаи
распространения волн будут рассмотрены в гл. 6. Применительно к
каналам ПГС стенки тракта в той или иной мере податливы и при колебаниях
давления в жидкости изменяют свою форму или размеры. Податливость
стенок сказывается на скорости распространения акустических волн в
тракте. Оценим это влияние, пренебрегая инерцией стенок. Скорость звука
определяется сжимаемостью жидкости 0Ж, т.е. относительным изменением
ее плотности р или удельного объема v на единицу изменения давления.
Часто используют обратную /Зж величину — модуль объемной упругости кж:
1 _ 1 Эр _ 1 Эи
кж Ро Ър Vq dp
и соответственно
, __ Ър кл. 1
dp Ро РжРо
" процессе распространения колебаний в тракте при сжатии за счет повыше-
141
ния давления Ьр' объем и длина столба жидкости уменьшаются на
относительную величину, пропорциональную &жЬр'.
Одновременное увеличение сечения тракта за счет повышения давления
будет разно 8Fr/F0. Увеличение сечения приводит к дополнительному
уменьшению относительной длины столба жидкости на 8F'/F0. Суммарное
сжатие (уменьшение длины) столба жидкости составит 0ж5р' + 8F'/F0.
Для круглой трубы 8F'/F0 = 28Rf/R0, где Ro — радиус трубы, 8R —
вариация радиуса. Для тонкостенной трубы из условий равновесия стенки
толщиной h можно найти, что 28R'/RO = 2R§p'l(Eh). Отсюда находим
эффективную сжимаемость жидкости в трубе 0 = ]3ЖA + 2Я/ЕНРЖ).
Воспользовавшись связью сжимаемости со скоростью звука, получим
а = — = - E.1.25)
VI + 2R0/Ehfe y/1+lRokJEh'
где Е — модуль упругости материала стенок трубы. Эту формулу впервые
получил Н.Е. Жуковский [95]. Если поправка за счет податливости стенок
относительно невелика, то в формуле E.1.25) знаменатель можно
разложить в ряд:
Для воды кж ъ 2 • 1011 н/м2, для стали Е ^ 2 • 101 * н/м2, и при течении
воды в стальной трубе с Ro/h = 10 скорость звука падает на 10%, для трубы
из алюминиевых сплавов с Е = 0,7 • 1011 н/м2 — на 30% и т.д. При больших
значениях R0/h приближенной формулой E.1.26) уже пользоваться нельзя,
оценки же по формуле E.1.25) показывают, что при R0/h = 100 скорость
звука для воды в стальной трубе падает в 1,7 раза, в алюминиевой - в
2,6 раза. Таким образом, в тонкостенной трубе скорость звука в первую
очередь определяется не свойствами жидкости, а податливостью стенок.
Для скорости распространения звука в трактах с толстыми стенками или
с некруглым проходным сечением используется модифицированная
формула E.1.25) [54]
а0
а = -, E.1.27)
где г? - параметр, зависящий от формы поперечного сечения тракта. Для
труб с большой толщиной стенки коэффициент т? определяется
зависимостью
Г Ro +/г+/?2/2Л0
П = 2 Ь +——-
где v - коэффициент Пуассона.
В работе Г.И. Двухшерстова [77] показывается, что скорость звука
в тракте существенно зависит от формы поперечного сечения тракта, при
этом скорость звука в трубах некруглого сечения уменьшается из-за
увеличенной податливости стенок, которые в этом случае работают не только
на растяжение (как круглые), но и на изгиб. В статье [77] приводятся
142
формулы коэффициента т? для большого числа вариантов формы
поперечного сечения тракта. Трубы круглого сечения по разным причинам могут
иметь некоторую эллипсность. При небольшой эллипсности коэффициент т?
с достаточной точностью определяется приближенной зависимостью [77]
77= BRo/h) [I + 3(eRolhJ]9 гДе е = А/Я0- относительный эксцентриситет
грубы, А - разность полуосей поперечного сечения трубы. Если разность
полуосей А для сечения тонкостенной трубы имеет порядок толщины
стенки трубы h, то коэффициент 7? будет в 4 раза больше, чем для трубы
строго круглого сечения. Благодаря этому в трубах с эллипсностью скорость
звука значительно уменьшается. Однако не следует забывать, что под
влиянием внутреннего давления в жидкости эллипсность трубы уменьшается.
§ 5.2. Вынужденные колебания жидкости в однородном тракте
5.2.1. Частное периодическое решение волнового уравнения.
Вынужденные колебания возбуждаются в системе под действием внешнего
гармонического возмущения. При этом в системе с распределенными
параметрами вынуждающие возмущения могут быть приложены или к элементам
жидкости более или менее равномерно по длине системы, или только
к элементам, расположенным на концах системы. В первом случае система
описывается неоднородным дифференциальным уравнением с правой
частью, во втором - систему описывают однородные уравнения, члены же,
определяющие действие вынуждающего воздействия, входят в граничные
условия. Решения для вынужденных колебаний являются частными
периодическими решениями дифференциального уравнения с заданными
граничными условиями. При этом как внешние возмущения, так и параметры
системы описываются функциями, изменяющимися во времени по
гармоническому закону.
Применительно к вынужденным колебаниям жидкости в однородном
трубопроводе вынужденные колебания создаются за счет возмущений
на границе, т.е. за счет 8yoi и 8уу в граничных условиях E.1.9) и E.1.10).
Решение для вынужденных колебаний жидкости, описываемых линейной
системой уравнений и линейными граничными условиями, проще всего
находится путем задания возмущения и решений в виде
экспоненциальных функций
8р(х, со, О = 8рEс, со)ехр(/соГ ),
8и(х, со, t ) = 8п(х, co)exp(/cof ),
ЬУо((п,7) = 8yoi(co)Qxp(icoT), К • • )
5^i/(со, t ) = 6yl7-(co)exp(zcoO,
где 8р, Ьп — амплитуды безразмерных вариаций давления, скорости, буоь
^1/ — амплитуды возмущающих воздействий на входе и выходе участка
тракта (величины комплексные), со = coL/a - безразмерная частота
колебаний. Уравнения E.1.14) и E.1.15) после подстановки частных
периодических решений E.2.1) принимают вид
5р = -о:М5г7 - iuocfbudx, E.2.2)
A -м2) ^— - 2/соМ—^-+ co25i7 = 0. E.2.3)
dx dx
143
Уравнения E.2.2) и E.2.3) определяют распределение амплитуд
колебаний (вариаций) давления и скорости при вынужденных колебаниях
жидкости в участке тракта с частотой со. При заданной частоте уравнения имеют
постоянные коэффициенты. В теории волн уравнения типа E.2.3),
определяющие развитие волновых процессов с заданной частотой в
пространстве, называют уравнениями Гельмгольца. По структуре они похожи на
уравнения гармонического осциллятора, только для осциллятора в
уравнения вместо производной по координате входит производная по времени,
и соответственно такое уравнение описывает развитие колебаний
осциллятора во времени.
Решения обыкновенного дифференциального уравнения E.2.3) и
аналогичного уравнения Гельмгольца для амплитуды вариации давления
Ър имеют форму
Ьр = А ехр (qix) + ? exp (q2x) , E.2.4)
Ьп = Cexp(qlx)+Dexp(q2x) , E.2.5)
где qi и q2 - корни характеристического уравнения. Корни для решений
E.2.4) и E.2.5) одинаковы, так как дифференциальное уравнение для
Зр совпадает с уравнением для Ьп и соответственно совпадают их
характеристические уравнения
A -M2)q2 -2Micoq + со2 =0. E.2.6)
Решение характеристического уравнения E.2.6) определяет его корни
Qi и q2:
qx 2 = г l/cJM ± \f~^^2 - О -М2)^] =
1 -- М
/со
1 -М
7 СО \ '**• )
1 +М
Исходное уравнение E.2.3) — второго порядка, и соответственно его
решение должно содержать две произвольные постоянные. В решения
E.2.4) и E.2.5) входят четыре произвольные постоянные, разные для
Ьр и Ьп, хотя корни характеристических уравнений для них совпадают.
Подставив в линеаризованное уравнение неразрывности E.1.5) решения
E.2.4) и E.2.5) с учетом соотношений для амплитуд вариаций E.2.1),
можно найти связь между константами в решениях E,2.4), E.2.5),
вспомнив при этом, что решение должно быть верным при любом х, а ехр(до") Ф О
при конечном значении х. Приравняв коэффициенты при одинаковых
степенях в экспонентах, получаем
А = -а С,
В = o.D. w--->'
Подставив решения E.2.4) и E.2.5) в 1ранич,':,). уровня Ei.s*> и
144
/5 1.10), учтя соотношения между коэффициентами E.2.8), находим
/сох
_ f /cox ico
/сох /со \] m 1
) 2 7о/5л/, E.2.9)
1 J
)
1 - М 1 + М / J у = 1
/сох \ / /со х
l[(^o)p^TTFj (e-^^
/ = 1
хр( - -—ТГ + Т~ТГ
\ 1 + М 1-М
/со х /со \] m 1
I S 7о/5уО/ , E.2.10)
)
1 - М 1 + М / J i = 1
где
/ /со
N = (а + \//0) (а - фг) ехр
\
1 + М
E.2.11)
1 —М
Соотношения E.2.9) и E.2.10) определяют распределение амплитуд
безразмерных отклонений давления и скорости вдоль оси тракта в
зависимости от граничных импедансов ^0 и фх на концах участка тракта,
приведенного волнового сопротивления а и числа Маха М для
жидкости в тракте, безразмерной частоты вынужденных колебаний со
и коэффициентов усиления 7о/ и 7i/.
Так как и исходные уравнения E.1.4) и E.1.5), и использованные
граничные условия E.1,9) и E.1,10) были линейными, то решения
E.2,9) и E.2.10) представляют суперпозицию по крайней мере (если
не учитывать сумму возмущающих воздействий с каждой стороны) двух
решений - реакции на возмущение со стороны входа Toi^oih на
возмущение со стороны выхода 711 &У11 •
Решения E.2.9) и E.2.10) пригодны как для случая вынужденных
колебаний в потоке слабосжимаемой капельной жидкости (для
которого М ^ 0), так и дая колебаний в адиабатическом потоке газа при любой
дозвуковой скорости и отсутствии возмущений температуры газа на входе
в участок тракта. Таким образом, решения E.2.9) и E.2.10) носят
достаточно общий характер и пригодны для использования в широком круге
задач. Однако общность решения определила и его громоздкость, что
затрудняет анализ особенностей протекания волновых процессов в участ-
^ гидравлического тракта. Для анализа этих особенностей рассмотрим
Р^ ц чалнь.ч задач.
? 2.2. Бегупше вэ^ньь Волновое сопротивление. Рассмотрим течение
^-'''-"ости в полупескояечной трубе, на входе в которую возбуждаются
¦ -- 1W 1икм<1Н 145
гармонические колебания давления:
х = 0, Ьр = 8р0 ехр (/со 7).
Подставив соотношения E.2.7) для корней qx и q2 и зависимости E.2.8)
в решения E.2.4), E.2.5), получим
_, ч / /сох \ ( /сох \
Sp (х, со ) = А ехр ( + В ехр I 1,
*\ 1-М/ ' \ 1+М/'
1 Г / /сох \ ( /сох \\
5й(х, со) = Л ехр -Яехр ).
<х[ *\1-М/ F\ 1+M/J
E.2.12)
Естественным является предположение, что прих -+°° амплитуды др(х, со)
и Ъп{х, со) останутся ограниченными, соответственно в решении E.2.12)
необходимо принять А = 0. Воспользовавшись заданным граничным
условием на входе х = 0, находим
6р(х, со) = Ьр ехр (/со f) = др0 ехр /1 со f — I,
\ 1 + М /
, , __ч E.2.13)
__ _ _- 1 __ /_- со х \
ди(х, со) = Ьи ехр (/cof ) = — 5р0 ехр /I со f ),
а \ 1+М/
или, переходя к размерным вариациям и размерным переменным,
Ьр(х, со) = бр'ехр(/соО = fipo'exp/l cof 1,
\ в+мо /
i -, 1 _, / COJC \
сш (jc, со) = Ьи ехр (/cof) = — 5р0 ^хр /1 cof ).
pa \ а +и0 /
E.2.14)
ра \ а+щ
Показатели в экспонентах, входящих в решения E.2.12) —E.2.14),
имеют вид
со х сох
^ t или ut
1+М а + и0
а, если АФ0,то
_ _ со х сох
со f + или cof +
—
1 - М а - и0
и называются сбд^ой волны. Скорость распространения вдоль оси точки
с равной фазой, в данном случае — скорость а + и0 или а — и0,
называется фазовой скоростью. Величина коэффициента при х называется
волновым числом к = со/(а ± и0) (или к = со/A ± М) в безразмерном виде),
которое характеризует периодичность распределения волны по длине
тракта и связано с длиной волны акустических колебаний X следующим
образом: X = 2тт/к, а частота — с периодом колебаний: Т = 2тг/со.
Выражения E.2.13) и E.2,14) записаны в комплексной форме.
Переходя к записи в вещественной форме, находим соотношения для колеба-
146
ний давления и скорости, считая к вещественным числом:
__, / сох \
др'(х, со) = 5/?0cosl cot 1,
, , ""' v («Л5)
1 _, I СОХ \
Su'(x, со) = бро cosl cor .
ра \ а+и0 /
Соотношения вида E.2.15), так же как и зависимости E,2.13) или
E.2.14), описывают бегущие волны, для которых характерными
признаками служит неизменность амплитуды колебаний и изменение фазы
колебаний по длине тракта. Из записи уравнения бегущей волны в форме
зависимостей E.2.13) или E.2.14) следует, что волна скорости или
давления приходит в сечение тракта с координатой х с запаздыванием по фазе
^ = Тех отЬосительно колебаний параметров в точке х = 0 при неизменных
амплитудах | 8р(х, t) | и | дп(х, t) |. В случае идеальной жидкости бегущая
волна распространяется без изменения своей формы, т.е. распределение
отклонений давления и скорости в разные моменты времени_точно
соответствуют друг другу, отличаясь только тем, что за время At волна
переместится вдоль оси х на расстояние Ах = со At/к. При этом волны
распространяются в_сторону возрастания координаты 5с", так как точки с
равной фазой cot — cojc/A + М) = const или cot — сох/(а + ио) = const с
ростом времени смещаются вдоль оси л: вправо. Соотношения E.2.13) —
E.2.15) описывают распространение волн вдоль полубесконечного тракта
с постоянной амплитудой, ибо при выводе исходных уравнений E.1.14)
и E.1.15) было сделано не совсем корректное для рассматриваемого
случая предположение -о пренебрежении потерями на вязкое трение. Если
учесть потери на трение, которые для полубесконечной (т.е. очень
длинной) трубы будут явно существенными, то вместо решения с постоянной
амплитудой должно получиться решение с убывающей по длине тракта
амплитудой.
В общем решении волнового уравнения E.2.12) были Отброшены
члены с коэффициентом А, которые сохранятся, если изменить
граничные условия. Эти члены описывают б_егущие волны, распространяющие^
ся в обратную сторону, так как при cot + u>xj A-M) = const увеличению t
соответствует уменьшение координаты х. Таким образом, общее решение
E.2.12) определяет независимое распространение вдоль тракта двух видов
бегущих волн, двигающихся в разных направлениях. Волны, имеющие
показатель экспоненты — /сол7A+М), называют прямыми (или
падающими) , а другие, с показателем icox](l — М), — обратными (или
отраженными) . Для тракта бесконечной протяженности эти волны никак не
связаны между собой и определяются только условиями их возбуждения, при
этом каждая группа волн возбуждается независимо. Интересным
является факт, что в бегущей волне связь между колебаниями давления и
скорости не зависит от условий их возбуждения. Действительно, из E.2.13)
и E.2.14) следует, что для прямой волны соблюдаются следующие
соотношения:
5р = аЪи, Ьр = ради, E.2.16)
т.е. в бегущей прямой волне отклонения давления пропорциональны откло-
ю* 147
нению скорости и находятся в одной фазе. Коэффициент
пропорциональности между отклонениями скорости и давления принято называть
волновым сопротивлением.
Если рассмотреть другой тип бегущей волны, — обратной,
определяемый в решении E.2.12) членами с коэффициентом Л, то можно
установить, что в этом случае связь отклонений давления и скорости в волне
определяется также волновым сопротивлением
др = —ади,
E.2,17)
Ьр' - —ради .
Различие знаков в соотношениях E.2.16) и E.2.17) связано с отличием
направлений распространения волн. В обратной волне отклонение
скорости находится в противофазе с отклонением давления. Волновое
сопротивление является характеристикой среды, а в гидравлических трактах -
и податливости стенок тракта, в котором распространяются акустические
волны. Сам термин "сопротивление" используется в связи с тем, что
распространение бегущей волны в область, в которую возмущения еще не
попали, требует затрат энергии, которые пропорциональны волновому
сопротивлению среды.
В уравнения E.1.4) и E.1.5) входят две переменные Ьи и др, и их
решения связаны между собой. Если ввести переменные
dv = ади + др,
E.2.18)
dw = а8и - др,
где dv = 8v'/p0, 8w = 8w'/pQy dv = ради + 8p , 8w' = ради — 8p\
выразив через новые переменные отклонения 8и и др, после подстановки
в уравнения E.1.4) и E.L5) и преобразований находим:
d8v ddv
—=— + (М + 1) —— = 0, E.2.19)
bt Ъх
ddw ddw
—— + (M-l)—;— = 0. E.2.20)
bt Эх
Уравнения E.2.19) и E.2.20) имеют следующие частные периодические
решения:
/_- сЗ~х \ / _ _ сох\
dv = Ci exp / со t - , dw = C2 exp i\ со t + .
\ 1 +M / \ 1 -M/
Решения уравнений E.2.19) — E.2.20) отличаются по виду от
решений E.2.4) и E.2.5) исходных уравнений E.1.4) и E.1.5), так как они
содержат только по одному члену с экспонентой и произвольной
постоянной. Для каждой из переменных dv и 5w, характеризующих акустический
импульс, решение описывает движение бегущих волн только в одном
направлении, для отклонения dv — в положительном направлении х~, для
5vv — в отрицательном. В некоторых случаях простота решений
уравнений E.2.19) —E.2.20) дает определенные преимущества.
148
Если вернуться к задаче о полубесконечной трубе и задаться условием,
что прих =0 <5и = 5пехр(/соО и 5vv = 0,то решения принимают вид
_ — — /
х, со) = ади + <5р = 5и0 exp z
1 + М
5н>Cс, со) = a<5w -dp = 0,
т.е. §P = a&u — ранее полученное соотношение E.2.16) между
отклонениями давления и скорости в бегущей волне. Аналогичное решение можно
получить для бегущей волны отклонения dw(x, со),
распространяющейся в обратном направлении.
5.2.3. Стоячие волны. Режим бегущих волн является достаточно
редким частным случаем, имеющим место при распространении волы в очень
длинных трубах, в которых акустические возмущения затухают, не доходя
до какой-либо неоднородности или конца трубы, а также при специально
подобранном сопротивлении на выходе из тракта. В более общем случае
в тракте ограниченной длины на конце каждого участка нарушаются
условия однородности тракта за счет местного сопротивления, изменения
проходного сечения, скорости звука или других изменений свойств тракта
или среды в нем. При встрече с неоднородностью в тракте происходит
частичное или полное отражение плоской волны, т.е. наряду с прямой
волной возникает обратная, отраженная. В действительности
взаимодействие плоской волны с неоднородностью вызывает достаточно сложную
картину течения с возникновением, кроме плоской отраженной волны,
также и других пространственных сложных форм колебаний. Однако
эти возникшие вторичные пространственные волновые процессы при
соблюдении принятого условия R < L затухают на относительно небольшом
расстоянии от неоднородности, и этими процессами при анализе плоских
волн можно пренебречь, считая трубу узкой. Возникновение плоских
обратных волн можно объяснить с точки зрения необходимости
выполнения граничных условий E.1.9) и E.1,10). Действительно, одна бегущая
волна, описываемая решениями E.2.15), не может обеспечить
выполнение граничных условий с произвольной связью между отклонениями
давления и скорости, определяемой граничными импедансами ф0 или ф1.
Только появление отраженной волны, описываемой членами с коэффициентом Л
в общих решениях E.2.12), позволяет обеспечить выполнение
произвольного граничного условия. Полученные ранее общие решения задачи о
вынужденных колебаниях жидкости в участке тракта E.2.9) и E.2.10)
описывают взаимодействие двух бегущих волн, распространяющихся
навстречу друг другу.
Из анализа этих решений следует, что при возбуждении колебаний
только с одной стороны получаем решение в виде чистой бегущей волны, если
^i = а при возбуждении со стороны входа Ej7i;- = 0, 5j7Ol. Ф 0) и ф0 = -<* -
при возбуждении со стороны выхода. Условие равенства одного граничного
импеданса волновому сопротивлению (для входа - с обратным знаком)
называется согласованной нагрузкой, и именно только в этом случае в
ограниченном однородном участке трубы возможен режим колебаний
~ чисто бегущими волнами.
Присутствие одновременно прямой и отраженной волны приводит
к усложнению всей волновой картины за счет интерференции этих волн.
149
При этом из соотношений E.2.9) и E.2.10) следует, что для суммарного
волнового процесса уже не выполняются простые связи E.2.16) или
E.2.17) между отклонениями скорости и давления через волновое
сопротивление. Используем общие решения E.2.9) и E.2.10) для анализа
особенностей волновых процессов в однородном участке трубы с
протоком жидкости при произвольных граничных условиях, но без учета потерь
энергии колебаний на вязкое трение и теплообмен. Преобразуем решение
E.2.9) для распределения давления вдоль оси тракта х~при заданной
частоте колебаний:
8р(х, со, О = Ьр (х,оо)ехр (/со t) =
/ /со х
N
/coM
(/соЗс\1 / /
J expl —
1 — М / J \ 1
х + /со t
-М2 // = 1
-exp -
1СОГ
; _ 1 2а f Г / cojc \
// = 1 J TV I L \ 1 - M2 /
/coM -\ //cox
co(l-3c)\ / ЙМA +3с)
I
/со л: /со __\1 m ) /с -> О1Л
1 + М 1 - М / I / = 1 J
где
TV — (о: + \р0) ш — \рi) ехр I — ) — (ос — u/л) (ос
\ 1 + М /
/ /со \ Г /со
+ i//i) ехр I I = 2 -а(ф0 - фг) cos
1 2 а(ф0 ф,) cos
1 - M / L \ 1 - M
, со \1 / /coM
+ /(a2 - ^0^i)sin — exp
M2 /J r\ 1 -M2
Знаменатель Л^ в зависимости EЛ.21) является комплексной функцией
частоты со, но от переменных f и /не зависит. Соответственно при
заданной частоте со число N— просто постоянный коэффициент, вносящий
одинаковые поправки в амплитуду и фазу колебаний при всех х и t. После
аналогичных преобразований зависимости E.2.10) для отклонений
150
сКОрости получаем
fju{x, со, 7) = 8п(х, со)ехр (/со 7) =
сох \ / /соМ
( itox __\ 1 " _ Г / соA — jc ) \
ехР —^ *ы t )\ I 7i/ 5>'1/ - (a- ^i)cos —-
\ 1 - м / J / = 1 L \ 1 - м2 /
/соМA + *) __\ / /сох
+ i0Jt j + ^ {
1 -М2
+ Т^Г +'"г Л/517о/8Уот E<2-22)
Изменяя в формулах E.2.21) и E.2.22) значение координаты х (О <х <
< 1), можно найти распределение отклонений скоростей и давлений при
вынужденных колебаниях в участке тракта с протоком жидкости.
Зависимости E.2.21) и E.2.22) показывают, что в общем случае волновой
процесс при вынужденных колебаниях можно представить в виде суммы
двух волн: бегущей прямой волны (вторые члены во всех квадратных
скобках в формулах E.2.21) и E.2.22)) и стоячей волны (первые члены).
Для бегущих волн, как уже отмечалось, амплитуда при заданной частоте
со (от нее зависит N, а в общем случае - также ф0 (со) и фх (со)) не
зависит от продольной координаты х", а фаза колебаний (показатель в
экспоненте) зависит от х. Для стоячих волн при М < 1 членом с М в экспоненте
можно пренебречь. В этом случае для стоячих волн амплитуда зависит
от х", а фаза колебаний для всех х~ одинакова. При согласованной нагрузке
на одном из концов тракта, т.е. при а = ф1 или а = — ф0, соответствующие
члены, описывающие стоячие волны, из решений выпадают: при
возбуждении колебаний *на конце тракта, противоположном концу с
согласованной нагрузкой, устанавливается режим колебаний с чистыми бегущими
волнами. При наличии в тракте неоднородности, сопротивление которой
равно волновому сопротивлению, приходящая к этой неоднородности
волна как бы ее "не замечает", и благодаря этому не возникает
отраженная волна и устанавливается режим колебаний с чисто бегущими
волнами. В тех случаях, когда волна отражается, интерференция отраженной
волны с прямой и дает картину стоячих волн. Поэтому и член,
описывающий стоячую волну в формулах E.2.21) и E.2.22), формируется из суммы
Двух экспонент с показателями, разными по знакам, но одинаковыми
по величине, которые описывают две волны одинаковой амплитуды,
двигающиеся навстречу друг другу.
С другой стороны, если в формулах E.2.21) и E.2.22) положить
равным нулю импеданс ф0 или Фх, т.е. принять конец тракта,
противоположный месту внесения возмущения, открытым (бр(О, со, г) =0 или
§рA, со, t) = 0), то исчезают соответствующие члены, описывающие
бегущие составляющие волн, и устанавливается режим колебаний с чистыми
стоячими волнами. Аналогичный результат имеет место при ф0 ~* °° или
фг -> оо? т#е> ддЯ тракта с закрытым в акустическом смысле концом.
Воспользуемся формулами E.2.21) и E.2.22) для анализа простейшего случая
151
стоячих волн, создаваемых в тракте при М < 1 и с закрытым концом на
выходе (Фг = °°) при возбуждении колебаний давления на входе в тракт:
5yi/ = 0G = 1,2,...) 6jTOl.=0(/=2,3...),
^о = 05 7oi = 1, by0 1 = ЬРо-
При принятых условиях модуль амплитуды колебаний давления, т.е.
модуль выражения E.2.21), имеет вид: \8р\ = | А (со) cos [со A - Зс")]|,
а для модуля амплитуды отклонения скорости из соотношения E.2.22)
следует \8п\ = |2?(co)sin[co(l — х)] |. В конце тракта при Зс"= 1
отклонения скорости равны нулю. Сечения, в которых отклонения при любом t
равны нулю, называются узлами стоячих волн, сечения с
максимальными значениями амплитуд - пучностями. Амплитуды стоячих волн
являются периодическими функциями координат — в зависимости от
частоты со на длине участка тракта укладывается один, два и т.д. узла Ьр и Ьи
и соответствующее число пучностей волн. При этом узлам отклонений
скорости соответствуют пучности отклонений давления и наоборот.
Колебания давления и скорости в стоячих волнах во времени сдвинуты по
фазе на я/2, так как множитель i в формуле E.2.21) эквивалентен члену
ехр(/тг/2). Граничные условия закрепили величины амплитуды
отклонений давления на входе участка тракта, поэтому при изменении частоты
вынужденных колебаний будет изменяться форма эпюры стоячих волн
(рис. 5.1, а). При низких частотах на длине участка тракта укладывается
незначительная часть синусоиды, и форма кривой распределения
давления близка к линейной — в этом случае давление, в основном,
изменяется за счет инерции столба жидкости. При увеличении частоты (рис. 5.1,я —
кривые 2, 3, 4) на длине участка укладывается большая часть синусоиды,
амплитуда колебаний давления в середине участка оказывается больше,
чем в сечении внесения возмущений, — проявляются акустические
эффекты, одновременно узел, находящийся вне участка (на конце пунктирной
линии), приближается к сечению на входе в участок тракта. При
дальнейшем увеличении частоты этот узел приближается к входному сечению,
а требование соблюдения условия 5р@, со, t) = Ьр0 приводит к росту
амплитуды отклонения давления внутри участка тракта, т.е. к
резонансным явлениям. В момент, когда узел попадает в точку х~= 0, граничное
условие может быть удовлетворено только в случае бесконечной
амплитуды.
Бесконечный рост амплитуды при резонансе определяется принятыми
предположениями об отсутствии потерь на вязкое трение и условиями
Фо = 0, 0i = °°. После прохождения резонанса (рис. 5Л, б) на длине
участка тракта укладывает уже не одна полуволна синусоиды. При дальнейшем
увеличении со картина изменения амплитуды колебаний и наступления
резонанса будет периодически повторяться, и после прохождения каждого
резонанса число узлов на длине участка тракта увеличивается на один.
Эпюры изменения отклонений давления в стоячих волнах, приведенные
на рис. 5.1, дают постоянные значения модуля амплитуд при каждом
фиксированном значении х~ и со. В действительности же амплитуда колебаний
изменяется также и во времени. Если в зависимостях E.2.21) и E.2.22)
выделить вещественную и мнимую части, приняв, как и раньше, М < 1,
Фо - Wi = 0, у0 ] = 1, 5v"ol = 8р0, то в вещественную составляющую для
152
а
f
2
V
I/
1^
?
2
^—
1
—
\
L
X
б Ы
/ \
I \
I \
<' v
п
5р(х)
1,0
0,5
-0,5
L/2 2ЦЗ L X -W
cut
=3,5
ш = и
/,
V °>5 А/п
//
Рис. 5.1. Эпюры стоячих волн давления: а - при п> < тг, б — при п < со < 2тт
Рис. 5.2. Эпюры мгновенных значений амплитуд отклонений давления при разных
величинах М (cjT = 3,5, со= тт)
Ьы войдет произведение cos (cox) cos (со t), а для Ьр - произведение
sin (cox) sin (со t ), Таким образом, амплитуды отклонений давления и
скорости изменяются во времени по гармоническому закону со сдвигом
по фазе натг/2.
Все сказанное до сих пор касалось случая течения с относительно малой
скоростью, обеспечивающей выполнение условия М < 1, благодаря чему
расчетные формулы упрощались. Влияние скорости движения жидкости,
т.е. числа М, сказывается в первую очередь на величине
экспоненциальных членов в формулах E.2.21) и E.2.22), в которые число М входит
в первой степени. При записи уравнений колебаний в форме комплексных
соотношений аргумент экспоненциальных сомножителей определяет фазу
колебаний. В отличие от рассмотренного случая М < 1, когда членами
с М в экспонентах можно было пренебречь, при невыполнении этого
условия фаза колебаний оказывается зависимой не только от времени, но
и от координаты. Для двух сечений тракта с координатами л^ и х2 в
каждый момент времени разность фаз колебаний равна [оЗ М/A - M~)jX
X (х~2 — x~i). Возникающий сдвиг фаз между колебаниями в разных
сечениях при режиме стоячих волн приводит к изменению формы амплитуд
колебаний. Если в случае М < 1 амплитуда стоячих волн давления
определялась произведением sin (cousin (со t), то для движущейся среды,
для которой условие М < 1 не выполняется, мгновенные значения амп-
соМ
литуды изменяются согласно соотношению sin
sm
х +
\ \ 1 - м* / VI- м2
' ). Для примера на рис. 5,2 приведены эпюры мгновенных значений
амплитуд давления для случаев М = 0 и М = 0,2 или 0,4. Сопоставление
+ со t
153
кривых показывает заметное влияние протока среды на форму акусти
ческих колебаний.
5.2.4. Коэффициенты отражения. Решения уравнений E.2.9) и E.2.10,
для каждого возмущающего воздействия можно представить как супер
позицию двух бегущих навстречу друг другу волн. При этом не следуе-
забывать, что в полученных решениях использовалось предположение
что возмущения вносятся как на входе, так и на выходе участка тракта
Соответственно для каждого варианта места внесения возмущений имеют
ся свои направления распространения прямых и отраженных волн. Отра
женные волны формируются при взаимодействии прямых волн с неод
нородностями на концах однородных участков тракта. Удобно связать
прямую и отраженную волны между собой коэффициентом отражения
на конце тракта, который равен отношению амплитуд этих волн в
сечении перед неоднородностью. Для возмущений со стороны входа в участок
тракта прямые волны описываются членом ехр[—/соЗс/A + М)], а
отраженные — членом ехр[/солГ/A — М)], в то время как для возмущений
со стороны выхода прямые волны описываются членом exp [/со J/(l - М) ],
а отраженные - членом ехр[—/солГ/A + М) ]. Для волн давления
коэффициенты отражения на выходе (возмущения - от входа) и на входе
(возмущения — на выходе) равны
фх - а ф1/а-1 _ ф0 +а _ фо/а + 1
rpi ~~ ; ~ ~ ; —, гро ; ~ ; ~~- E.2.23)
ф{ +а фх/а + Х Фо-ol фо/а-1
Аналогичные коэффициенты отражения для волн скорости равны
„ _ 1 - фх/а 1 + фо/а
Г»1 ' ¦ , , = -гр1, ги0 = f— = -гр0. E.2.24)
1 +01/а И 1 - фо/а
Вид полученных зависимостей показывает, что по абсолютной величине
коэффициенты отражения не больше единицы и что они могут изменять
свой знак при изменении соотношения между величинами граничного
импеданса и волнового сопротивления среды в тракте. Коэффициент
отражения в общем случае - величина комплексная. Значение этого
коэффициента определяет долю энергии колебаний, возвращаемую от
неоднородности на конце тракта обратно в тракт за счет отражения от нее прямой
волны.
Введение коэффициентов отражения позволяет несколько упростить
запись формул E.2.9) и E.2.10) , определяющих распределение
комплексных амплитуд отклонений давления и скорости при вынужденных
колебаниях жидкости в участке тракта:
_ _ _ а [ 1 Г / icox ico \
8р (л:, со) = ехр + +
Np \ ф0 - а [ Р \ 1 + М 1 - М /
/ icox /со \1 ? _ 1 Г / zcjjc \
+ rDl expl I 2/ 7о/ 5^о/ ; ехр/ 1+
р \1-М 1+M/Ji = i Фх+и[ \1-М/
.? УЧЬУЧ I' E.2.25)
154
1 f 1 Г / icox ico \
exp + 1
(ic
Т
_
u(x, со) =
ta" iVp
icox ico
icox \ ( icox \\ n ]
-1—i7 +r«°exp -TTT7 S 7i/5yl7- ,E.2.26)
1-M/ \ l+M/J/=i J
где
ico \ I ico
1 -M
Таким образом, при внесении возмущения только со стороны входа (т.е.
ЬУм ^ 0> ^1/ = О ПРН всех/) амплитуды отраженных волн
пропорциональны соответственно гр1 и ги1 и не зависят от значений коэффициентов
отражения на входе гр0 и ruOi как не зависит от этих коэффициентов при
заданной частоте общая картина распределения амплитуд колебаний по
длине тракта. Величина Np не зависит от х, но является функцией частоты
со и значений коэффициентов отражения rpQrpl = ruOrul. Все
рассуждения можно повторить и для случая внесения возмущений со стороны
выхода из участка тракта.
Аналогичным способом можно получить и коэффициенты бегущей
волны для давления vpi. Коэффициент бегущей волны характеризует
относительную долю бегущих и стоячих волн в общей картине колебаний.
Величина vpi - 0 соответствует \rpi\ = 1, т.е. полному отражению и
отсутствию бегущих волн в системе. При vpi = 1 | rpi | = 0, т.е. отсутствует
отражение, а это значит, что нет стоячих волн, которые возникают в
результате интерференции отраженной волны с прямой. При промежуточных
значениях vpi в системе имеются как бегущие, так и стоячие волны.
Величина spi =llvpi называется коэффициентом стоячей волны.
§ 5.3. Свободные колебания. Собственные частоты
5.3.1. Свободные колебания. В предыдущем разделе были рассмотрены
частные решения волнового уравнения для установившихся вынужденных
колебаний жидкости в участке тракта. В ряде случаев представляют
интерес и колебания, возникающие в участке тракта после прекращения
действия возмущения, нарушившего условия равновесия стационарного течения.
Колебания, сопровождающие переход к новому равновесному режиму
течения, называются свободными, так как поток жидкости после
прекращения действия возмущения предоставлен сам себе. Свободные колебания в
участке тракта конечной длины возможны только на определенных
частотах. Применительно к рассматриваемым в теории колебаний и акустике
[105, 147] консервативным системам свободные колебания, имеющие
постоянную амплитуду (без потерь), называются собственными колебаниями
системы, а возможные частоты свободных колебаний — собственными
частотами. При этом предполагается, что нет потерь на трение в самой
системе и граничные условия — идеальные, т.е. обеспечивают полное отражение
155
волн, Плаюдаря чему энергия колебаний на границах системы не рассей
вается. В акустических системах частоты собственных колебаний в
ограниченной узкой трубе зависят от граничных условий и свойств жидкости -
скорости звука в ней. Обычно рассматриваются два простейших
предельных случая идеальных граничных условий [105, 190]. Для продольных
колебаний жидкости в ограниченной трубе одно простейшее граничное
условие - открытый конец, сообщающийся с неограниченным
пространством, второе возможное условие — конец, закрытый жесткой крышкой.
Простейшим граничным условиям соответствуют значения граничных им-
педансов U// =0 или у/ = °°. а это значит, что коэффициенты отражения
(см. формулы E.2.23) и E.2.24)) по модулю равны единице, что
определяет полное отражение волн от концов тракта и режим колебаний с
чистыми стоячими волнами.
Для трубы с открытыми концами отклонения давления у концов трубы
равны нулю, так как колебания внутри трубы никак не могут влиять на
давление в неограниченной среде. Следовательно, на концах трубы должны
быть узлы давления и, соответственно, пучности скорости. Последнее
заключение следует из формул E.2.21) и E.2.22), в которых члены,
характеризующие стоячие волны давления, описываются синусоидой, а стоячие
волны скорости - косинусоидой. Для удовлетворения граничных условий
8р@,7о, Т) - 6/?A, оЗ, Г) - 0 необходимо, чтобы при любых колебаниях на
длине трубы уложилось целое число полуволн синусоиды. Благодаря этому
в ответ на произвольное возмущение в участке тракта возникают только
гармонические колебания определенных частот, при которых
удовлетворяются граничные условия. Набор этих частот определяется
соотношением
<Jk - ujkL!a (k= 1. 2,3 }. E.3.1)
и никаких других частот в тракте при свободных колебаниях быть не
может. Эти частоты называются собственными частотами колебаний жидкости
в участке трубы. Наименьшая частота собственных колебаний (к = 1 в
формуле E.3.1)) называется первым или основным тоном, высшие тона
(обертоны) - соответственно вторым, третьим и т.д. тонами колебаний. Набор
волн, соответствующих собственным колебаниям, образует полную
систему гармонических волн в тракте, причем они обладают свойством
ортогональности [105,205]
1 I 1 ПРИ ^ ~/ ,
_ _ — _
2/ 5p(x,u>ki t )bp{\\coh t )dx = !
о I 0 при к Ф I
Полнота набора и ортогональность собственных колебаний обеспечивает
описание с их помощью свободных колебаний при любых начальных
условиях, представляя эти колебания как суперпозицию собственных
колебаний разных частот с разными амплитудами. При этом амплитуды свободных
колебаний давления и скорости подбираются путем разложения в ряд
Фурье распределений отклонений давления и скорости в начальный момент
[105].
Вернемся к вопросу о собственных колебаниях для участка трубы с
другими граничными условиями - закрытой с двух сторон жесткими
стенками, т.е. при у0 ~ s^i ~ °°- Соответственно на концах тракта отклоне-
156
ния скорости равны нулю. В этом случае на границах участка тракта всегда
101ЖНЫ быть узлы скорости и пучности давления, а это значит, что опять
на длине участка уложится целое число полуволн, только картина эпюр
амплитуд давления как бы сдвинется на четверть длины волны. Частоты
собственных колебаний в этом случае также подчиняются соотношению
E.3.1)
Последний вариант сочетания граничных условий - один конец тракта
закрыт жесткой крышкой (^0 ~°°)< а другой — открыт (Vi = 0). При
такой паре граничных условий на одном конце тракта (х - 0) будет пучность
давления, а на другом (х~= У) - узел давления. В этом случае на длине
участка тракта должно укладываться нечетное число четвертей длин волн,
а собственные частоты подчиняются следующему условию.
ojkL 2k- 1
gj*= = п (А: =1,2.3,...). E.3.2)
а 2
5.3.2. Собственные частоты участка тракта с протоком. В отличие от
рассматриваемых в теории колебаний, и в акустике консервативных
систем, в которых при колебаниях энергия системы сохраняется, участок
тракта с протоком жидкости как элемент ПГС является
неконсервативной системой даже в случае, если пренебречь влиянием вязкого трения.
Действительно, в участок тракта поступает жидкость и из него уходит
жидкость, при этом, естественно, вместе с жидкостью вносится в участок и
выносится из него колебательная энергия. Только в достаточно редких
случаях при наличии протока можно считать, что условия на границе
участка тракта обеспечивают полное отражение акустических волн, т.е.
выполняются равенства I rpi I =\rui\ = 1. В большинстве случаев граничные им-
педансы не обеспечивают выполнение этих условий, и поэтому часть
акустической энергии выносится из системы. С другой стороны, при некото-
ры> значениях граничных импедансов в тракте с протоком возможно
самовозбуждение колебаний, т.е. процессе в системе теряет
устойчивость.
В рассмотренных выше консервативных системах собственные частоты —
величины вещественные, а амплитуды свободных колебаний постоянны во
времени. Для неконсервативных систем собственные час юты в общем
случае оказываются комплексными числами вк = vk + 1иок. где Т;Л- —
коэффициент демпфирования (безразмерный) и оЗя - собственная частота
неконсервативной системы [38]. licnn~vk = 0. то собственные колебания —
незатухающие, при Vk < 0 колебания затухают во времени, а приТк > 0 —
неограниченно возрастают (в линейной системе), т.е. система в последнем
случае неустойчива. Определим собственные частоты колебаний в участке
тракта с протоком при достаточно общих граничных условиях,
записанных в форме зависимостей E.1.9) и E.1.10), в которых отбросим
последние члены, характеризующие внешние возмущения. Исходные
уравнения E.1.4) и E.1.5) и для случая свободных колебаний имеют решения
E.2.4) и E.2.5) с учетом формул E.2.7) и E.2.8), однако вместо ito
необходимо подставить частоту 0к. Для амплитуды колебаний давления,
используя соотношения E.2.8), запишем
L (°кх \ п / вкх \1
ор = - ас ехр -D expf
1 - М / \ 1 + М . _
157
в эюй формуле, как и раньше, первый член в скобках у сечения х~ \
описывает обратную, отраженную от выхода волну, а второй — прямую
волну, бегущую к выходу. На другом конце, у входа (лГ= 0), первый член в
этой формуле описывает прямую, а второй - отраженную от входа волну.
Следовательно, у выхода из участка тракта должно соблюдаться равенство:
-Сехр[0*/A-М)] =rpl Dexp[-6k/(\ +M)], а у входа при~х= 0 - другое
соотношение: — D-rp0 С. Исключая из двух последних формул отношение
коэффициентов D/C = ~гр0, находим уравнение, определяющее собственные
частоты колебаний жидкости в участке тракта:
Учитывая связь коэффициентов отражения с граничными импедансами и
волновым сопротивлением согласно зависимости E.2.23), найдем:
/ 2вк \ A+^о/а)A--^/а) /сооч
ехр = . E.3.3)
\1-М2/ (l^/a)(l+0/«)
Граничные импедансы в общем случае — величины комплексные.
Выделив в левой и правой частях формулы E.3.3) вещественную и мнимую
составляющие, получим, что
2Vk \\ ( 2пк \ [ 2пк \Л
откуда находим
/ 2vk \. ( 2ык \
ехр sin 1= Im(w).
F\l-MV \1-М2/
Поделив эти формулы друг на друга, имеем соотношение для мнимой
части комплексной собственной частоты:
/_2^_\ ЬпЩ. E.3.5)
eV 1-М2 ) Re(w)
а возведя в квадрат и сложив соотношения E.3.4), найдем вещественную
часть — коэффициент демпфирования
)]2. E3.6)
1 -Mi
Соотношение E.3.5) легко решить графически, нанося одновременно
на один график кривые тангенсоид и кривую (или кривые) правой
части. При этом необходимо проверить, удовлетворяются ли исходные
зависимости E.3.4). Если в правой части соотношения E.3.6) сумма
двух членов равна единице, то~]>?=0, т.е. это и есть условие для границы
устойчивости. Если сумма меньше единицы, то Vk < 0, а если больше единицы,
то Vк > 0. Величину Vк несложно найти численно для каждого номера к,
158
оставляя в правую часть E.3.6) сок, полученные из решения уравнения
E*3.5)- Если граничные импедансы Фо, 4>i и волновое сопротивление —
е-ц1чины действительные, т.е. сопротивления активные, то уравнение
E-3-3) распадается на два следующих равенства:
2vk
ехр
1 -М2
1-М2
E.3.7)
E.3.8)
В общем случае сомножитель ехр [2vkjA -М2)] ^ О, поэтому решением
уравнения E.3.8) является ряд частот ~оок = A — М2) кп/2. Однако не для
всех значений к сок удовлетворяют уравнению E.3.7). Так как
экспоненциальная функция положительна, для удовлетворения уравнения E.3.7)
должны совпадать знаки косинуса и правой части. Знак косинуса
положителен при значениях ooki соответствующих четным /г, и отрицателен при
нечетных к. Поэтому зависимость для собственных частот тракта, как
неконсервативной системы, оказывается неоднозначной:
Г
=A-М2)к —
а 2
: = 0, 2,4, . . .,если
:= 1,3, 5,. . ., если
¦>о,
E.3.9)
<0.
При собственных частотах сок модуль сомножителя I cos [2cofc/(l—M2)] 1 = 1.
Вспомнив, что знаки cos [2^/A - М2)] и правой части E.3.7) всегда
совпадают, и учтя, что экcпoнeнщiaльный член положителен, найдем
зависимость для коэффициента демпфирования 1) :
1-М2
v — 1п
E.3.10)
При A + фо/а) A - фх/а) = 0 уравнения E.3.7) и E.3.8) не имеют общего
решения, а это значит, что участок тракта не имеет собственной частоты.
1) Индекс к здесь можно опустить, так как получаем решение, общее для
159
]1 м»ожленис числителя правой части равенства E.3.7) через нуль опреле.
ляет границу, на которой изменяется собственная частота тракта. Ранее
было показано, что согласно формулам E.3.1) и E.3.2) для участка тракта
без протока жидкости в зависимости от сочетания граничных условии
симметричные ли они (оба конца открытые или оба — закрытые) или
несимметричные (один закрыт, другой открыт) — собственная частота
изменяется скачком от значений сок = кл к величине сок = Bк — 1)тг,л
где к =1,2,...
Аналогичная картин? имеет место и для участка тракта с протоком в
случае чисто активных сопротивлений на его концах. Действительно, из
соотношений E.3.9) следует, что ojk = A - М2) кп (к - 1, 2,.. .) при
одновременном выполнении симметричных условий фо/а< — 1, а ф^/аУ]
или фо/а>-1, а фц'ос< 1. Эти условия можно сформулировать так: или
оба импеданса больше (по модулю) волнового сопротивления тракта или
оба меньше волнового сопротивления. Случай, когда граничный импеданс
больше волнового сопротивления тракта, можно назвать (по аналогии с
участком тракта без протока) граничным условием с закрытым в
акустическом смысле концом, а противоположный случай — с открытым в
акустическом смысле концом.
При ^ = 0 для тракта с протоком получаем условия 3pf = О на /*-м
конце, совпадающие с условием, принятым в акустике для открытого конца.
Однако и в акустике [191, 197] делаются оговорки, что это условие
является приближенным, пригодным только для относительно невысоких
частот. При более высоких частотах на открытом конце трубы появляется
сопротивление, имеющее активную (т.е. вещественную) и реактивную
составляющие. Сопротивление на открытом конце связано с потерями
энергии на акустическое излучение колеблющейся жидкости на конце
тракта (активная часть) и влиянием присоединенной массы жидкости (реактивная
часть), которая вовлекается в колебания во внешнем пространстве.
Применительно к тракту с протоком обе
составляющие сопротивления
должны в принципе присутствовать (см.
гл. 2). Для несимметричных
граничных условий из зависимости E.3.9)
следует, что если Фо/а < —1 а
ф х /а < 1 или фо /а > - - 1, а фц!ос> 1,
то собственные частоты совпадают с
частотами, определяемыми
формулой E.3.2): со* = A -М2)B?-1)тг/2,
где к = 1,2, 3, ...
Таким образом, несмотря на
наличие выноса акустической энергии
из участка тракта с протоком при
--Зии-г— -/
I i!
, I I I 1 ^ '
Рис. 5.3. Области различных значении
собственных частот участка тракта в
зависимости от приведенных граничных
импедансов ^ 0 /а и \j г /а
160
. ф о или ф[ Ф °°, собственные частоты сохраняют практически такие
^Л значения, как и в случае без протока. Изменение собственных
частот при изменении значений i//,/a можно изобразить графически
виде областей с разными собственными частотами в плоскости
тараметров Фо1& и ф^а (рис. 5.3). Приведенные выше неравенства
и иллюстрирующее их разбиение областей на рис. 5.3 показывают,
что для тракта с протоком жидкости и чисто активными граничными
импедансами собственная частота остается неизменной при изменении
в широких пределах отношения граничных импедансов к волновому
сопротивлению.
*>
J
5р
а б
Р и с. 5.4. Схема эквивалентная ПГЦ (а) и (б) для модели граничных условий
участка тракта
5.3.3. Собственные частоты участка тракта при комплексном граничном
импедансе. Рассмотренные выше чисто активные граничные импедансы
являются определенной идеализацией действительного процесса при
нестационарном течении на границе участка. Как уже отмечалось в разделе
5.3.2, в акустике при рассмотрении процесса распространения волн в
тракте без протока обнаруживается, что условия открытого конца из-за
влияния присоединенной массы жидкости и акустического излучения
во внешнее пространство не выполняются [105, 191]. При протоке
жидкости через тракт влияние присоединенной массы жидкости должно
сказываться как при истечении (или втекании) с открытого конца, так и для
случая течения через местное сопротивление. Применительно к местным
сопротивлениям с протоком жидкости (типа дроссельной диафрагмы)
это было показано в гл. 2. Другое возможное уточнение граничных
условий — учет сжимаемости среды в устройствах на границе участка
тракта.
Примером подобных устройств могут служить емкости, заполненные
жидкостью, уравнительные башни, воздушные колпаки [234], наконец -
зона местной кавитации на входе в центробежный насос [182]. Учет
инерционности или емкости на выходе из тракта приводит к изменению формы
записи граничного импеданса — он станосится величиной комплексной,
зависящей от частоты. Составим уравнение граничного импеданса для
достаточно общего случая (рис. 5.4,я), учтя инерцию жидкости и потери
давления в местном сопротивлении на выходе, а также податливость в виде
упругого элемента, описываемого уравнением резонатора Гельмгольца
(без учета сопротивления его горловины). На рис. 5.4, б представлена схема
эквивалентной ПГЦ. Используя полученные в гл. 2 зависимости для
элементов с сосредоточенными параметрами и обозначения, приведенные
П.Б.Ф. Гликман 161
на рис. 5 А,а, запишем для резонатора Гельмгольца:
r5Ge9 E.3.11
epe E.3.12j
для сопротивления на выходе с учетом инерции:
— &Р1---Г- «Рн=B+1о;ти1-^-)8Сн, E.3.13)
баланс расходов у горловины резонатора:
dGl = 6Ge+5GH, EJ.14)
где 5^!, 5ре, 5рн - амплитуды безразмерных вариаций давления перед
местным сопротивлением, в емкости резонатора, во внешней (для
рассматриваемого участка) среде за сопротивлением, 5Gl9 5Ge, 5GH — амплитуды
безразмерных вариаций расхода на выходе из участка тракта, на входе
в резонатор и через сопротивление на выходе (все отнесены к среднему
расходу через тракт), pif pH - давление перед сопротивлением и за ним,
l //l
длина горловины резонатора и проточной части сопротивления с учетом
присоединенной массы жидкости (см. гл. 2) к горловине резонатора и
местному сопротивлению, VQ — объем полости резонатора, ае — эффективная
скорость звука в среде, заполняющей резонатор с учетом податливости
его стенок и возможного наличия другой фазы.
Исключив часть переменных из соотношений E.3.11)-E.3.14), выделив
в полученной зависимости вещественную и мнимую части, найдем
соотношение для импеданса на выходе из участка тракта:
Фх =ТГ~A -^7иЛеJ +-7-{<^и.1 [1 ~^2 (Г„.г +
Di Vi
+ тиЛ)те] A - со ги.г ге) —Л? оЗгеA ~^2 тиг fe)} , E.3.15)
где/?! = [1 -со 2 (ги.г + гиЛ) fe]2 +(/2id;feJ, со = coL/д, ги.г = ти.га/Ь,
^и1 =ги1 я/^> ^е =ге й/^> ^i = lApi/pi^L^a - длина и скорость звука для
участка тракта. Введение нормировки постоянных времени к
характерному для акустики времени пробега волной длины участка тракта L/a
позволяет сделать более наглядными результаты расчета собственных частот.
Действительно, как следует из самой формы записи соотношения для
импеданса E.3.15), именно относительные, нормированные постоянные
времени элементов с сосредоточенными параметрами определяют их вклад
в отдельные составляющие граничного импеданса. При этом не следует
забывать, что акустические эффекты начинают ощутимо сказываться только
с со^ 1.
Если статический перепад давления на выходе отсутствует, т.е. hx = О,
то активная составляющая граничного импеданса в E.3.15) исчезает, а в
реактивной составляющей остается только член с множителем со Ги х. Если
емкостью в конце тракта можно пренебречь, т.е. Те ^ 0, то соотношение
E.3.15) существенно упрощается:
ф! =hx +/соГи1. E.3.16)
162
Тля определения собственной частоты тракта при комплексном значении
аничного импеданса необходимо использовать соотношение E.3.5),
пределив вначале вещественную и мнимую составляющие правой части
формулы E.3.3). Для упрощения выкладок примем, что граничный
импеданс на входе в участок тракта (ЗГ = 0) активный, т.е. выражение для него
чисто вещественное. Для импеданса на выходе (х = 1) запишем:
а ос
где Ф\ву ^1м ~ вещественная и мнимая составляющие импеданса, ф\ъ =
= Ф\в1а> Ф 1м = Ф\м1а и аналогично для импеданса на входе t//0 = ^о/а- Учтя
принятые обозначения, преобразуем правую часть соотношения E.3.3):
(I - фо/а) A + фг/а) A - ф0) A +
- Фгв - Фш)
- 9 ~9 +/ = - 1 1
О - Фо) [A + Ф\в) + Ф 1м1 V1 - ^о) [A + ^1в) + Ф 1м]
= Re (со") + /Im (со). E.3.17)
Найдя вещественную Re (со) и мнимую Im(co) части, подставив их в
уравнение E.3.5), получим равенство, определяющее собственную частоту
участка тракта при принятых условиях:
E.3.18)
Определив ряд собственных частот сок по формуле E.3.18), необходимо
проверить, удовлетворяет ли каждое полученное значение оок двум
исходным формулам E.3.4). При этом следует учитывать, что всегда
ехр [2рк/(\ — М2)] > 0, использовать значения Re (со) и Jm(co) из
соотношения E.3.17), а удовлетворение равенств проверять только по знаку.
В формулу E.3.18) не входят значения граничного импеданса на входе ф0.
Однако "отсеивание", с помощью соотношений E.3.4) значений
собственных частот из всего набора частот С5к, удовлетворяющих равенству
E.3.18), обеспечивает учет влияния импеданса на входе (т.е. условия
\Фо\> 1 или | фо I < 1) на собственную частоту тракта. Если для
импеданса на выходе можно пренебречь активной составляющей, т.е. принять
^1в = 0, то используя формулы тригонометрии для тангенса двойного
угла, находим
E-зл9)
Полученные из решения уравнений E.3.19) значения со^ проверяются на
Удовлетворение (по знаку) формулам E.3.4), результаты же такого
сопоставления позволяют определить, какую из двух формул E.3.19) нужно
использовать для определения со^ в данном конкретном случае.
Рассмотрим гидравлический тракт с простейшими граничными
условиями на выходе — чисто реактивным импедансом. Как уже отмечалось, такой
И* 163
вариант имеет место, если в формуле E.3.15) принять hx =те=тит - О, т.е.
пренебречь потерями давления на выходе и не учитывать сжимаемость
жидкости. В этом случае ф 1в = О, ф 1м = соги1, а выбор одного из уравнений
E.3.19) определяется величиной | ф0 \. Примем для упрощения, что М <^ 1.
Уравнение tguk = —&ктИ11а может иметь первый корень в диапазоне
частот я/2 < сок < я, уравнение ctg ojk = cOfcfHl/a — в диапазоне частот
0<со? < я/2. Полученные же из соотношений E.3.4) с учетом зависимости
E.3.17) условия имеют следующий вид:
exp Bvk) cos B cjk) -
exp BVk) sin B ook) = ¦
ф\м)A-Фо)'
Если | ф0 | < 1, то второе условие удовлетворяется при я/2 <cofc <я, а если
I Фо | > 1, то при 0 < сок < я/2. Для первого условия появляется
дополнительная точка изменения знака при значении i//lM = сокти\/о. = 1- Если
I Фо | < 1, то для ф iM < 1 это условие удовлетворяется при 0<аЗ^ <я/4 и
Зя/4 <пк < я, а для ^ 1М > 1 - при я/4<соА: <Зя/4. В случае |^0| > 1
соответственно для ф\м < 1 - при я/4 <cJA: <Зя/4, а для ^?м > 1 — при
О < оЗд- < я/4 или 3 я/4 < пк < я. Если сопоставить все неравенства для
случая | ^о I < 1, то обнаружится, что второму условию E.3.4) удовлетворяет
область я/2 <сок < я, определяемая первым уравнением E.3.19). Первое
условие E.3.4) при ф\м < 1 ограничивает область возможных значений
частоты диапазоном Зя/4<оЗ^ <я, а при ф\м > 1 оказывается допустимой
другая половина из выбранного диапазона Зя/4 < сок < я. Таким образом,
варьирование величиной ф\м не изменяет общего диапазона собственных
частот, только удовлетворение неравенства ф\м < 1 или ф\м > 1
разбивает полученный из других условий диапазон значений собственных частот
на два поддиапазона. Появление двух поддиапазонов частот не является
принципиальным и связано с тем, что собственные частоты находятся из
уравнений E.3.19) для частоты одк, а условия выбора того или иного из
двух уравнений определяются зависимостями E.3.4) для двойных
значений частоты 2 6i3fc.
Если граничные условия на входе изменяются так, что окажется | ф о \ > 1,
то аналогичные рассуждения приводят к другому диапазону возможных
значений первой собственной частоты: 0 < пк < я/2, а величину сдк будет
определять второе из уравнений E.3.19). Значения собственных частот,
определяемых уравнениями E.3.19), можно найти путем графического
решения этих уравнений. На рис. 5.5 приведены два примера графического
решения уравнений для случая инерционного импеданса на выходе, для
которого фХм = соги1/а. Собственная частота находится из формул E.3.19)
по пересечению кривых тангенсоид 3 {\Фо\< 1 — нижняя часть рис. 5.5)
или котангенсоид 1 {\Фо\ > 1 — верхняя часть рис. 5.5) с прямыми линия-
164
Рис. 5^. Графическое определение собственных частот участка тракта с
инерционностью на выходе: у = ctg[d>/(l - М2)] G); у = ± wfHl/a = ^1м B); д'=
0 -
f
\
у
ч
ч
у
L
>—¦&
Ис« 5.6. Графическое определение собственных частот участка тракта с емкостьк
«а выходе: у = tg[w/(l -М2)] A); у = ± l/awTeB);^ = (l - ^rHr
= ctg[w/(l -M2)] D)
ми 2 для 01м- Разный наклон прямых 2 соответствует различным значе
ниям безразмерного параметра ти1/а. При изменении постоянной времен^
для инерционности на выходе ти1 значения собственных частот колебание
также изменяются, при этом, если fni/a -> 0, то собственные частоты стре
мятся к частоте свободных колебаний участка тракта с акустически от.
крытым концом на выходе (пк ъ ктт при | ф0 I < 1 и &к = Bк - 1) тг/2 при
\Фо\ > 1 - см.рис. 5.3) .Если же Ги1/а> 1, то, наоборот, граничные условия
приближаются к условиям акустически закрытого конца, для которого
&>к ^ B к - 1) тг/2 при \Фо\< 1 и Шк ^irk при \фо\> 1.
Таким образом, инерционность на выходе из тракта понижает частоту
собственных колебаний по сравнению с собственной частотой тракта (при
том же \фо\) без инерционности для акустически открытого конца.
Комплекс coTui/a, определяющий вклад инерционности на выходе, можно
представить следующим образом:
= со
где FT — площадь проходного сечения тракта, ти т = LG\\FTp\ —
инерционная постоянная времени массы жидкости в тракте. Это же соотношение
можно представить по-другому, если использовать величины массы
жидкости в тракте mT = pFTL и в местном сопротивлении mx = pFi lx: со —— =
= со ! I , т.е. влияние инерционности определяется или
соотношениях \ Fx'
ем между ее постоянной времени и инерционной постоянной времени тракта,
или отношением масс жидкости в инерционности и в тракте.
Другой простейший случай граничного условия - большое активное
сопротивление на выходе, т.е. hx ->°°. Примером устройства с подобным
сопротивлением может служить высоконапорный насос, тупиковая
импульсная трубка с измерительным прибором или чувствительным
элементом регулятора на конце и т.п. Предельный переход при hx ->°° в
соотношении E.3.15) приводит к формуле ф х = —/ A — со2 тиг те)/соте. Если
пренебречь инерцией в горловине резонатора ти<г « 0, то соотношение для
импеданса еще больше упростится: ф \ - —ijcofe и, соответственно,
/Г / Pi VQa pua \Л
= -1/(асот-е) = -1/ со (тг-тт =
/ L \ Gx a\L pi /J
где re#T = VjPilGia2, VT = LFT - объем участка тракта. Таким образом,
влияние эффектов, связанных с присутствием емкости в конце тракта
при закрытом (в акустическом смысле) его конце, определяется
отношением податливости (или емкостной постоянной времени) емкости к
податливости (или емкостной постоянной времени) жидкости в участке тракта.
166
Величину собственной частоты и в этом случае можно определить графи-
еским путем по формулам E.3.19), находя пересечение кривой Ф \м с
ривой tg (или ctg). Принцип выбора нужной функции из двух
соотношений E,3.19) с учетом необходимости удовлетворения по знаку формулам
E 3.4) описан раньше. На рис. 5.6 приведены кривые для tg [63/A — М2)]
при i^o I < 1 и ctg [^3/0 - М2)] ПРИ \Фо\> 1. Здесь же приведены
кривые для разных значений l/afe = tq^Itq при ти#г = 0, а также кривые для
более сложного случая, когда тиг Ф 0. Из анализа расположения точек
пересечения кривых, определяющих значения собственных частот в
различных условиях, следует, что присутствие емкости в конце тракта в случае
акустически закрытого конца тракта (hx -» °°) приводит к снижению
собственных частот по сравнению со случаем те = 0. Если в конце тракта
имеется резонатор Гельмгольца (т.е. те Ф 0 и тиг Ф 0), то на собственной
частоте колебаний резонатора сор = 1/ \JfQ ^и.г кривая ф 1м (со) пересекает
ось со и, соответственно, еще более существенно изменяется соотношение
между значениями собственных частот тракта с резонатором и без
резонатора. Как и в случае простой емкости, резонатор понижает собственную
частоту тракта. При со = сор фг = 0, т.е. на резонансной частоте резонатор
формирует условия акустически открытого конца. При анализе
приведенных на рис. 5.5 и 5.6 точек пересечения кривых и соответствующих
собственных частот тракта обращает на себя внимание то обстоятельство, что
первые, самые низкие значения собственных частот obx при \Фо\> 1 на
рис. 5.5 и при | ф0 | > 1 на рис. 5.6 значительно меньше тг/2, т.е. собственная
частота ниже привычных для акустики значений. Эти первые значения
cofc понижаются при увеличении тих или те. Так как при достаточно
большом значении этих постоянных времени оказывается, что со! < 1, то
значения сох можно найти аналитически. Из второго соотношения E.3.19) при
\Фо\> 1 находим ctg сох «* 1/coi = cofHi/a или со2 = (a2Gi/piFTL)X
XCF1P1/G1/1) = 1/0"е.тгил)> т-е- ПРИ закрытом в акустическом смысле
входе первое значение собственной частоты тракта с инерционностью на
конце определяется собственной частотой колебательной системы,
состоящей из емкости тракта как упругого элемента и инерционности на
выходе. _
Аналогично для тракта с емкостью на выходе при | ф 01 < 1 получаем
tgcoi ^со! = l/tcoxfea) или со2. = (^Gi/FePx) (p^JdL) =1/(тети.т).
И в этом случае первая собственная частота тракта определяется, как для
системы с сосредоточенными параметрами, состоящей из инерционности
столба жидкости в участке тракта и емкости на конце тракта. Для того,
чтобы в этом случае участок тракта можно было рассматривать как
инерционность, на входе должно соблюдаться условие \фо\< 1, т.е. условие
акустически открытого конца. Если это условие не соблюдается, то
первая собственная частота будет близкой к акустической. Рассмотренные
варианты граничных условий с чисто реактивным сопротивлением
являются в определенном смысле идеализированными, так как для тракта с
протоком обычно присутствует и активная составляющая импеданса.
167
§ 5.4. Входное сопротивление участка тракта
5.4.1. Входное сопротивление. При расчетах сложных гидравлических
систем, состоящих из ряда элементарных участков, каждый последующий
или предшествующий участок тракта создает определенные условия на
границах анализируемого участка тракта. Основными характеристиками
условий на границах участка тракта являются (согласно формулам E.1.9)
и E.1.10)) граничные импедансы ф0 и фг, а также коэффициенты усиления
То/ и 7i/ • При последовательном (каскадном) соединении участков тракта
граничным импедансом для данного участка служит импеданс соседнего
участка, т.е. связь между амплитудами вариаций скорости и давления на
входе (или выходе) этого участка. Воспользуемся общими решениями
E.2.9) и E.2.10), считая, что возмущения вносятся только от входа в
тракт, т.е. by у = 0, а фх и а - заданы, и приняв для простоты М ^0. Учтя
указанные допущения, разделив вторые слагаемые соотношений E.2.9)
и E.2.10) друг на друга, получаем уравнение связи между амплитудами
колебаний давления и скорости в любом сечении тракта, т.е. найдем
импеданс для любой точки участка тракта длиной L :
Ьр a {(a+ ^i)exp [ко A -*)] - (а - фх) ехр [-/соA -*)]}
Ьи (а + фг) ехр [/соA -х)] + (а - фх)ехр [-/соA -х)] E 4 П
Задав в уравнении E.4.1) х = 0, найдем входной импеданс участка
гидравлического тракта
Ьр @, со) а[(а + фг) ехр (/со) - (а - i^) ехр (-/со)]
5п @, со) (а + ч?/!) ехр (/со) + (а - ^i) ехр (-/со)
i// х cos со + ia. sin со 1 + / (et/ф i) tg со
= а = — = ф 1 — =— . E.4.2)
а cos со + / ф! sin со 1 + / (ф t /а) tg со
Входной импеданс тракта - величина комплексная. Только в частном
случае а = фх (т.е. при согласованной нагрузке) z 0 = фх и входной
импеданс оказывается величиной вещественной, равной выходному импедансу
тракта. В этом случае отсутствуют отраженные волны от конца тракта на
выходе и весь поток акустической энергии уходит из тракта через
сопротивление на его конце. Поэтому для трактов, предназначенных для передачи
колебаний, например, измерительных трактов с малоинерционным
датчиком на конце для измерения колебаний давления, наиболее выгодно
использовать на выходе условия согласованной нагрузки, которые
обеспечивают минимальное искажение колебаний.
В случае открытого в акустическом смысле конца на выходе из тракта,
т.е. при соблюдении условий фх = 0 и 5р A, со) =0, входное сопротивление
участка тракта согласно формуле E.4.2) равно
z0=/atgco, E.4.3)
а при закрытом конце на выходе из тракта, т.е. при ф\ =oo,5w A, со") =0
z0 =-/actgco, E.4.4)
Таким образом, для случаев открытого или закрытого конца тракта (при
полном отражении волн от сечения на выходе, т.е. при режиме колебаний
168
с чисто стоячими волнами в тракте) входной импеданс оказывается
мнимым, а сопротивление чисто реактивным. Это естественно, так как без
учета потерь на вязкое трение при режиме колебаний со стоячими волнами
в тракте нет потерь колебательной (акустической) энергии за счет ее
выноса через выходное сечение, в котором или амплитуда скорости или
амплитуда давления равны нулю и, соответственно, отсутствует поток
акустической энергии, равный произведению амплитуд давления и скорости.
Как следует из формул E.4.3) и E.4.4), величина входного импеданса
тракта при открытом или закрытом конце и отсутствии потерь на трение
изменяется в пределах от —°° до +°°, причем такие предельные значения
периодически повторяются с периодом А со = я. Обращение в
бесконечность или в нуль входного импеданса свидетельствует о наличии в тракте
резонансных явлений.
Одним из простейших случаев выходного граничного импеданса является
чисто реактивный импеданс (сопротивление) на выходе из тракта.
Признаком реактивного импеданса является его мнимость, т.е. фх = /\^м,
где ф\м — вещественный параметр. Примером реактивного импеданса
может служить демпфирующее устройство в конце длинного
измерительного тракта, выполненное в виде бачка. Воспользовавшись формулой
E.4.2), находим соотношение для входного сопротивления тракта с
реактивной нагрузкой, которое и в этом случае также оказывается мнимым:
^1мП (o#iM)tgco]
z0 = = E.4.5)
1 @/)t
Из отношения E.4.5) следует, что введение емкости на выходе не
исключает обращения в бесконечность импеданса при частотах, определяемых
решением уравнения tgd; = a/i//lM. Используя формулу E.4.2), можно
показать, что если на выходе из тракта импеданс комплексный фх = ф1в +
+ *^1м> т0 такая система обеспечивает исключение резких резонансов в
системе, при которых z 0 -*°°.
5.4.2. Резонанс в тракте. Вернемся к соотношениям E.4.3) и E.4.4)
для входного импеданса гидравлического тракта при простейших случаях
граничных условий — акустически открытого или закрытого конца на
выходе. Из этих формул следует, что при отсутствии трения (система
консервативная) для определенных значений безразмерной частоты вынужденных
колебаний ТЬ входной импеданс приобретает бесконечное значение — в
тракте возникает резонанс. При резонансе бр/ды -*00, т.е. при любых конечных
значениях действующих сил давления практически не возникает колебаний
скорости, и тракт на этой частоте не передает возмущений, т.е. является
идеальным "изолятором", не пропускающим колебаний. Такое свойство
систем с распределенными параметрами используется для демпфирования
колебаний, а в радиотехнике [98] — при создании системы изолирующей
подвески линий высокой частоты.
__ В зависимости от значения выходного граничного импеданса фх частота
°~>, соответствующая резонансу, изменяется. При фх = О входной импеданс
тракта обращается в бесконечность для значений со# = Bк + 1) тг/2, а при
'^1 ~>о° — для значений 65^ = к тт. Для определения условий возникновения
резонансов в тракте при внесении возмущения различными способами
169
вернемся к общим уравнениям E.2.9) и E.2.10). В первую очередь
рассмотрим случай, когда вынужденные колебания задаются на входе в виде
колебаний давления, что соответствует граничным условиям byOi = &Ро
при х = 0. Это условие удовлетворяется, если в E.1.9) принять: 7oi = 1,
SJoi = 0(i> 2), ф01 =0, 5у 1; =0(/ = 1, 2, ...). Следует обратить внимание
на способ задания граничных условий при расчетном анализе динамики
ПГС с целью сопоставления результатов расчетов с данными
экспериментов. Измерение колебаний только одного из параметров течения жидкости
со стороны внесения возмущений предопределяет выделение с помощью
используемой измерительной системы только одной составляющей
возмущения, например, колебаний давления или колебаний скорости. С другой
стороны, при любом способе создания возмущений в системе
одновременно возникают колебания (отклонения) как скорости, так и давления.
Так как рассматриваются линейные системы, то измерив одну
составляющую возмущения, находим реакцию системы именно на нее, отбросив
другие составляющие. При таком способе анализа реакции системы на
возмущение место (сечение), в котором действительно вносится
возмущение, не имеет значения, если устройство для внесения
возмущения не входит в исследуемую систему, а при расчетах за начало отсчета
продольной координаты берется сечение, в котором проводится измерение
параметра, принимаемого за входное воздействие. Если при
экспериментах изменяется тип измерительного прибора, например, малоинерционный
датчик давления заменяется на датчик термоанемометра, измеряющего
скорость, при расчетах системы необходимо изменить граничные условия
на входе. Результаты расчетов (так же как и данные экспериментов) для
разных вариантов датчиков, естественно, будут отличаться.
Таким образом, задавая или измеряя в начале тракта или в любом его
сечении колебания давления, тем самым создаем в начальном сечении
условия, эквивалентные условиям на открытом в акустическом смысле
конце. Условие Ьр = 0 является частным случаем условия Ьр = Ьр0 при
х = 0 или Ьр = дрх при х = 1. Подставив указанные значения 7oi и ф0 в
соотношения E.2.9) и E.2.10), находим:
с_, ч (а-^О ехр [-ко A -*)] -(a + ^i)exp[/w(l -x)l
Ьр (х, со) = ~
(а - фх) ехр (-/со) - (а + ф1) ехр (/со)
ф{ cos [соA — х)] + ia. sin [со A — х)]
cos со +/а sin со
(а-^Г)ехр [-/соA -х)] + (а + ^Г)ехр[/а;A -х)]
ои(х, со) = — ~ °Ро =
(а + ф!)ехр(/со) - (а - фх)ехр(—/со)
а cos [со A-Х)] +/01sin[o;(l -*)]
5р0. E.4.7)
+ /а sin со)
Приняв, что на выходе из тракта обеспечиваются условия акустически
закрытого конца Ф\~°°, 5й~A, со) = 0,и на входе 5j701 =Ьр0, найдем
соотношения, определяющие распределение амплитуд колебаний давления
170
при предельных значениях \?/0 = 0 и ф\ -°°:
cos[co(l -х)]
Ьр(х, со) = — Ьр0 E.4.8)
cos со
и амплитуду колебаний скорости
/sin[co(l — х)\ .
6м (х, со) = = 5р0. E.4.9)
a cos со
Оба соотношения E.4.8) и E.4.9) описывают режим колебаний со
стоячими волнами — амплитуда изменяется по длине, фаза колебаний
вдоль тракта не изменяется. Если принять частоту со = const, то формулы
E.4.8) и E.4.9) опишут распределения амплитуд колебаний давления и
скорости вдоль тракта. Для колебаний давления амплитуда зависит от
длины х по закону косинуса, для колебаний скорости — по закону синуса.
При этом в начале расчетного участка тракта (х = 0) др(О, со) = 8р0, а
5г7@,со) = /(tgcoMp0/a. На выходе из тракта (jc = 1) имеется пучность
давления ЬрA, со) = Ьр0/cos со, узел скорости 5^A, со) = 0.
Так как знаменатель соотношений E.4.8) и E.4.9) равен cos со, то
при определенных значениях безразмерной частоты сок - Bк - 1Oг/2
(fc = 1, 2, 3,.. .) знаменатель обращается в нуль, а амплитуды колебаний
давления и скорости в тракте — в бесконечность. В траясге возникает
резонанс давления, так как он вызван колебаниями давления на входе в тракт.
При другом элементарном граничном условии на выходе — акустически
открытом конце, т.е. при я//х = 0, 8рA, со) = 0, формы колебаний давления
и скорости определяются уже другими соотношениями:
sin [co(l —х)] _
Ьр(х, со) = — 8р0,
sin со
i cos[co(l — х)]
ЬП(х, со)= LA J±bp0. E.4.10)
a sin со
При заданной частоте со = const амплитуда колебаний давления по длине
тракта описывается функцией sin [соA — х)], которая при Зс = 0
удовлетворяет условию 5р@, со) = 5р0, а при х = 1 - условию 5рA, со) = 0, т.е. в
конце тракта - узел давления. Колебания скорости, описываемые функцией
cos[co(l —х)], имеют узел в точке х = 0 и пучность в конце тракта при
х = 1. Резонансные частоты для давления при рассматриваемом
граничном условии отличаются от приведенных выше (при фх = °°) - амплитуды
стремятся к бесконечности при п)к = кп (?=1,2,3,...). Это естественно,
так как задание на входе в участок колебаний давления определяет условия
открытого конца^на входе, т.е. фо = 0, а переход от условий на выходе
фг = оо к условию ^i=0 определяет переход от несимметричных (один
открытый, другой закрытый конец) к симметричным граничным
условиям. Соответственно, согласно зависимостям E.3.9) и разбиению
областей на рис. 5.3? изменяются и значения собственных частот тракта', а зна-
чит — и резонансных частот.
Если же на входе в тракт задать или измерять колебания скорости, т.е.
°и @, со) = 5г70, то для описания этого условия необходимо принять гранич-
171
ный импеданс на входе ф0 = °° и, кроме того (см. формулу E.1.9)),
потребовать, чтобы ИтGо//^о)= -1 и by01 =<5йо, 57oi = 0 0'= 2, 3,...).
Учтя эти условия, из общих уравнений E.2.9) и E.2.10) находим
acos[co(l -х)] + гф\ sin[c3(l — x)]
, со) = -<— Ьы0, E.4.11)
acosco + /1//! sin со
„_,_ _ч a{^!cos[co(l -x)] -msin[co(l -x)]}
др(х, со)= = = 8и0. E412)
a cos со + /i//i sin со
Приняв одно из элементарных граничных условий — акустически закрытый
конец на выходе, т.е. ф-i =°°, 5мA, со) = 0,из формул E.4.11) и E.4.12)
получаем
ow(jc, со) =
0
sin со
-ч mcos[cj(l -x)]
, со)= 5w0, E.4.13)
sin со
а при другом условии - акустически открытом конце на выходе, т.е.
^i = 0, Ьр A, ?0 = 0, находим
._,_ _ч cos[co(l -х)]
Ьи(х, со)= = 8ы0,
cos со
_ _ sin[co(l -x)] _
др(х, со)= -/а = 5w0- E.4.14)
cos со
При акустически закрытом конце на выходе, т.е. при фх =°°, согласно
формулам E.4.13) резонанс скорости (так как задано или измеряется
изменение скорости на входе) наступает при частотах вынужденных
колебаний ТЬк-ки {к = 1, 2, . . .), а при акустически открытом конце (фх = 0) —
при частотах со^ = B& - 1)тг/2.
Из сравнения этих значений с соответствующими резонансными
частотами для резонанса давления при одинаковых величинах граничных импе-
дансов на выходе ф\ следует, что резонансные частоты отличаются.
Резонанс давления в тракте с открытым концом на выходе (ф1 = 0) наступает
при такой же частоте, при которой имеет место резонанс скорости для
другого значения граничного импеданса ф\ = °° и, наоборот, для тракта с
Фх = °° частота резонанса давления совпадает с частотой резонанса скорости,
но для граничного импеданса фх = 0. При одном и том же граничном
импедансе на выходе из тракта фх резонансу давления соответствует
антирезонанс (минимум амплитуды) скорости, и наоборот.
Резонансная частота совпадает с одной из собственных частот участка
тракта, т.е. с частотами свободных колебаний, возникающих в
изолированном тракте при переходном процессе после окончания действия возму-
172
тающей силы. Собственные частоты определяются свойствами самой
системы (т.е. параметрами а, ф0 и ф\), a не способом и местом внесения
возмущения в систему. Однако при вынужденных колебаниях задание
определенного типа возмущающего воздействия одновременно определяет
и величину ф{ на этом конце тракта. Как было показано в § 5.3,
собственная частота жидкости сок = ктг (Jc = 1, 2, 3, . . .) имеет место в тракте с
симметричными граничными условиями (или Фо = Фг - О, или фо = Ф\~
= <*>), т.е. если оба конца одновременно в акустическом смысле или
открыты, или закрыты. Аналогично при несимметричных граничных условиях
(или при ф0 = 0 и фх =оо, или при фо =о° и ф\ =0) собственная частота
равна пк = Bк + 1)я/2 (к = 0, 1, 2, . . .).
Из анализа соотношений E.4.6)-E.4.7) и E.4.11)- E.4.12),
определяющих распределение амплитуд колебаний давления и скорости вдоль
тракта при внесении возмущения путем изменения давления или скорости
на входе, следует, что в них входит только один импеданс - на выходе
из тракта, другой же определяется задаваемым возмущением. Сравнение
резонансных частот при вынужденных колебаниях с собственными
частотами показывает, что резонанс давления при внесении возмущения путем
задания колебаний возникает на собственной частоте, характерной для
тракта с открытым концом на выходе (Фо=О), т.е. на частотах сок - пк
(к=\, 2, . . .), если для выхода ф\ = 0, и на частотах пк = Bк - 1)тг/2,
если ф 1 = °° •
В этих случаях на частотах, соответствующих собственным частотам
колебаний жидкости в тракте с акустически закрытым концом на входе
(ф0 = <*>), при возмущении путем изменения давления на входе имеет место
антирезонанс, т.е. минимум амплитудной характеристики, так как
амплитуда колебаний давления по длине тракта оказывается меньше амплитуды
колебаний давления на входе. Этот эффект можно объяснить тем, что в столбе
жидкости возбуждаются такие колебания, которые полностью
компенсируют влияние действия внешних сил и обеспечивают неподвижность
(ды ^ 0) жидкости на входе в тракт. В этом случае столб жидкости имеет
бесконечно малую податливость. Если задавать или измерять на входе
в участок тракта колебания скорости, то картина оказывается совершенно
иной. Резонанс скорости (по аналогии с резонансом тока в электрических
линиях) наступает при изменении скорости на выходе и приближении
частот к собственной частоте жидкости с акустически закрытым (ф0 - °°)
концом на входе в тракт. При внесении возмущения с частотой, равной
собственной частоте тракта с открытым концом на входе (Фо = 0),
наблюдается антирезонанс. Таким образом, при внесении возмущения путем
изменения скорости на входе в тракт1) с частотой, для которой при свободных
колебаниях пучность скорости совпадает с входным сечением тракта,
резонанс не наступает. Наоборот, если вынужденные колебания скорости на
входе заданы в системе, у которой при свободных колебаниях на входе
имеется узел колебаний скорости, при совпадении частоты колебаний с
собственной частотой жидкости наступает резонанс. Аналогичный анализ
можно провести для случая внесения возмущения со стороны конца тракта,
1' Или, что то же самое, при измерениях колебаний скорости жидкости на входе.
173
от его выходного сечения. С другой стороны, отличие резонансных частот
при резонансах давления и скорости можно объяснить тем, что для
обеспечения внесения таких несколько искусственных возмущений,
описывающих или способ создания возмущений, или измеряемую величину,
необходимо соответственно менять саму рассчитываемую систему, т.е.
изменять граничный импеданс на входе в тракт. Именно изменением
входного импеданса был ранее осуществлен переход от общих соотношений
E.2.9), E.2.10) к соотношениям E.4.6)-E.4.7) и E.4.11)-E.4.12) для
частных случаев внесения возмущения путем задания колебаний давления
или скорости на входе в тракт. Изменение ф0 и определяло скачок
резонансной частоты при переходе от возмущения изменением скорости к
возмущению давления.
Отмеченное совпадение резонансных частот с собственными частотами
системы в первую очередь связано с простотой и определенной
идеализацией рассматриваемой системы. Но, как будет показано ниже, даже для
такой простой системы, какой является участок тракта, при измерениях
не на границах тракта резонансные частоты уже не совпадают с
собственными частотами. Для более сложных систем такое совпадение является
достаточно частным случаем.
§ 5.5. Участок тракта как четырехполюсник
При определении входного сопротивления тракта находится связь между
отклонением давления и скорости (расхода) на входе или выходе тракта
в предположении, что никаких возмущений со стороны выхода из тракта
нет. При таком подходе участок тракта (и любая другая пассивная, как
угодно сложная, линейная система) является двухполюсником. Уравнение
двухполюсника (см. гл. 2) связьюает отклонения расхода или скорости
с отклонением перепада давления, а в зависимость E.4.1) входит
отклонение абсолютного давления. Вспомнив правила измерений, используемые
при построении полюсного графа или эквивалентной цепи (гл. 2),
убеждаемся, что в эквивалентной схеме цепи или графе системы такой
двухполюсник должен связывать точку цепи, соответствующую входу в
участок тракта с узлом, описывающим точку с давлением, равным нулю.
При этом отклонение 8р будет равно вариации перепада давления на
двухполюснике, связанной одним уравнением с вариацией скорости (расхода)
на входе в участок тракта. Такой подход возможен, если не интересоваться
вариацией скорости (расхода) на выходе из участка тракта, которая не
совпадает (система с распределенными параметрами) с вариацией скорости на
входе в тракт. Подобное описание "висячих" (т.е. связанных только одним
концом с остальной системой) участков ПГС вполне закономерно, однако
такие участки тракта - частный случай. В большинстве случаев необходимо
учитывать разницу в вариациях расходов на входе и выходе участка и то,
что на эти вариации влияют не вариации перепада давления (как это имеет
место у двухполюсников), а независимо вариации давления на входе и
выходе тракта. Это следует из общих решений уравнений гидромеханики
для участка тракта E.2.21) и E.2.22), согласно которым на любое
внешнее возмущение имеются разные реакции для значений вариаций скорости и
давления на входе (х - 0) и выходе (х = 1) — всего 4 параметра.
174
Задав в общем решении E.2.10) ф0 = Ф\ = 0, • 6>01 = 5р@), 5уц =
= 5рО), 7oi=7n=1, 5y0/= 5j/1; = 0 при /, / = 2, 3, . . . , после
преобразования найдем
• [ -/ м ]
i ехр — ico
L V 1-
+
i / со \
5м @) = ctg ( 5р@)
а \ 1 -М2 /
¦ f •-/ м М
/ ехр -/со ( I
Р L \ 1 - М2 / J
/ ^ \
a. sin ( I
\ 1-М2/
М2
/ со \
in 1
\ 1-М2/
a sin
i / со
6р@) +— c^
E.5.1)
Уравнения E.5.1), связывающие отклонения скорости и давления на
входе с отклонениями этих же параметров на выходе, являются уравнениями
четырехполюсника. Система уравнений E.5.1) — незамкнутая, так как
два уравнения связывают четыре параметра. Они описывают связь
параметров на входе и выходе в цилиндрическом однородном участке тракта
как систему с распределенными параметрами без учета каких-либо
граничных условий1). Для замыкания системы к уравнениям E.5.1)
необходимо добавить два граничных условия - граничные импедансы. В этом случае
мы практически вернемся к уравнению E.2.22).
Запись уравнений динамики элементов ПГЦ в форме уравнений
четырехполюсника, как это будет ясно из дальнейшего изложения (см. гл. 7),
удобна для формирования математических моделей сложных
разветвленных ПГС. Запись уравнений четырехполюсника в виде зависимости
отклонений скоростей (расходов) от отклонений давлений по принятой
терминологии [203] называется записью в у-параметрах. Уравнения тракта как
четырехполюсника в ^-параметрах E.5.1) можно представить в матричной
форме:
5м@I
Г5м
ехр[-/соМ/A -М2)]
sin[co/(l -М2)]
ехр[-/аЗМ/A -М2)]"
sin [со/A -М2)]
со
ctg
1 -М2
E.5.2)
где у — матрица проводимости.
2) Задание граничных условий ф0 = фг - 0 являлось приемом получения
уравнений тракта как четырехполюсника как раз с целью исключения влияния граничных
импедансов.
175
Для тракта без потерь проводимость — величина мнимая, т.е.
проводимость (так же как и сопротивление) участка однородного тракта— чисто
реактивная. Для четырех параметров возможно шесть вариантов их деления на
две пары, соответственно существует шесть форм записи уравнений
четырехполюсников. Преобразования из одной формы в другую можно выполнить
по готовым формулам [15, 60, 203]. Кроме записи в ^-параметрах, часто
удобно пользоваться формой представления четырехполюсника в
^-параметрах. Из уравнений E.5.1) после преобразований найдем уравнения для
участка тракта как четырехполюсника в /^-параметрах в виде зависимости,
связывающей вариации переменных на выходе с вариациями входных
параметров:
/ со \ / М \
6рA) = cos (__) ехр( t* __) Sp(O) -
¦ia sin
со
1 -М2
i
м
E.5.3)
ico
1 -М2
+ COS
- 5*7@)
или в матричной форме:
8пA)\
= ехр гсо
М
1 -М2
/ п \ . . ( п у
cos — I - m sin ( —
V 1-М2 / \ 1-М2 /
i / w \ ( п \
sin — I cos I I
a \1-M2/ \1-M2/.
dp@) 1
бы @) J
E.5.4)
Если М<1, то уравнения для участка тракта как четырехполюсника
E.5.1)-E.5.4) существенно упрощаются. Не зависящее от граничных
условий решение уравнений гидромеханики для вынужденных колебаний
жидкости в участке тракта, записанное в форме уравнений
четырехполюсников E.5.1)—E.5.4), ниже будет использовано при построении
математических моделей разветвленных ПГС, включающих также элементы с
сосредоточенными параметрами.
Глава 6
МАТЕМАТИЧЕСКИЕ МОДЕЛИ
НЕСТАЦИОНАРНЫХ ТЕЧЕНИЙ ЖИДКОСТИ В КАНАЛАХ
§ 6.1. Колебания в одномерном потоке
вязкой сжимаемой жидкости с квазистационарным трением о стенки
Если по условиям, приведенным в § 1.7, вязкостью жидкости
пренебречь нельзя, то необходимо выбрать математическую модель,
описывающую влияние трения жидкости о стенки на нестационарное движение среды.
Применительно к нестационарному течению это не такая простая задача,
и как во всех сложных, не до конца решенных физических проблемах,
здесь имеется несколько подходов. Ниже последовательно будет
рассмотрено несколько моделей нестационарного вязкого трения. Наиболее
простой вариант описания трения для нестационарного движения —
предположение о квазистационарности силы трения о стенки. В квазистационарной
модели трения принимается гипотеза, что трение при нестационарном
течении подчиняется тем же зависимостям, что при стационарном течении.
Это наиболее простая и в то же время, как это будет ясно из последующего
рассмотрения, наименее обоснованная модель.
Воспользуемся линеаризованными уравнениями для одномерного
нестационарного движения жидкости в цилиндрическом тракте A.10.18) и
A.10.19), сделав предположения, что жидкость капельная, слабосжимае-
мая, трение - квазистационарное, массовые силы отсутствуют.
Соответственно можно принять
дп др _ - дЬи
дх ' дх ' дх
Применительно к задаче об акустических колебаниях удобно использовать
характерное время, равное времени пробега волной длины тракта ^о = L/a,
что приводит к соотношениям
L а 1
Oil ~~ ,
uoto ы0 М
ЕиМ =
рай I раы0 а
и0 _ X0Lpul Ро Ар0
4Rp0 рыоа роа
гДе Ар0 - средний перепад давления на участке тракта за счет трения о
стенки.
12 Б.ф. Гликман
С учетом всех сделанных замечаний уравнения A.10.18) и A.10.19)
принимают вид:
дЬи 1 ЪЬр Ар0
—— + — + 2 5г^=0, F.1.1)
bt ос Ъх роа
дЬр ЪЬи
+ а =0. F.1.2)
bt Ьх
Исключая из уравнений F.1.1) и F.1.2) одну из переменных, находим
Ъ2Ьи Ъ2Ьи h ЪЬи
-— + =0, F.1.3)
bt2 Ьх2 а Ы
где h =2Apo/po.
Подставив в уравнения F.1.2) и F.1.3) выражения из частных
периодических решений Ьи = 5м ехр(/сог)> Ьр - Ьр exp(/cof)> где со = u)L/a,
получим уравнения для амплитуд вариаций параметров течения:
d2bu / h \
——- + со2 - /со — )Ьп = 0, F.1.4)
dx2 \ а /
dbu
icodp + a —— = 0. F.1.5)
dx
Решения уравнений F.1.4) и F.1.5), определяющие распределения
амплитуд колебаний вдоль тракта, имеют вид
6p=Aexp(q1x)+Bexp(q2x),
_ _ _ (о.1.6)
Ьи = Cexp(qx) + D exp(qx)
где gi, q2 — корни характеристического уравнения q2 + со2 — /со/г/а = 0,
равные
q\f2=± / \/п>2 - itoh/a = ± /со \/l — ih/coa. F.1.7)
В формуле F.1.7) под корнем — комплексное выражение, т.е. корни
qx 2 = ±(у + id) - комплексные. Возведя в квадрат выражения F.1.7),
приравняв вещественные и мнимые части, найдем
со / / h2
е=—Vi + Vi + —г-
Постоянная распространения ql2 = ± (v + id) волн в тракте с протоком
вязкой жидкости содержит вещественную часть р, характеризующую
затухания акустических волн из-за потерь на трение, причем коэффициент
затухания зависит от частоты. Амплитуда уменьшится в е раз на длине тракта
х = \\v. Мнимая часть постоянной распространения в определяет скорость
распространения акустических волн, которая для течения с трением также
зависит от частоты.
178
Наибольшее влияние частоты на величины в и v проявляется при
относительно низких частотах, когда со2 < h2/a2. Если /г/соа < 1, то формулы
F.1.8) можно упростить:
Л/а
2A +h2ISt52a2)
Следовательно, при относительно малых потерях на трение Л/а = Аро/риа
или при большой частоте со согласно F.1.8) параметр ^, определяющий
затухание при распространении колебаний вдоль тракта, практически не
зависит от частоты.
Для определения связи между коэффициентами А, В, С и D в решениях
F.1.6) подставим их в уравнение F.1.5):
ico[A exp(qiX) + B exp(q2~x)] + a[Cqiexp(qxx) + Dq2exp(q2x)] =0
или
) + (/сов + a^2^)exp(^2^) = 0.
Так как решение должно быть справедливым при любом х, а ехр(^Зс) Ф 0,
то нулю должны быть равны суммы в скобках перед экспоненциальными
членами, что определяет связь между коэффициентами
А=-
В = -
/со
Учтя, что корни qx и q2 отличаются только знаком, и записав их через
вещественные и мнимые составляющие, находим
Г <* 1
А =- (^ + /в)__ С,
L /со J
/со J
Используя эти связи между коэффициентами, обозначив комплекс а0 =
= {у + /0)а//со, окончательно преобразуем решения F.1.6) к следующей
форме:
Ьп = С Qxpiqxx) + D exp(q2x).
определения констант С и D воспользуемся граничными условиями
E.1.9) и E.1.10), подставив в них решения F.1.9); после
преобразований находим зависимости, определяющие распределения амплитуд
колебаний давления и скорости вдоль участка тракта (сохранив для краткости
12* 179
обозначения корней q\ =v + i6, q2 ^ — (v + id):
8p(x, u)=(—^-J {[(ao + i//0)exp(^23c)-(a0 - фо)ехр(с{1х)] X
n
X 2 y^by^-- [(a0
- (а0 - i//i)exp(<7i* + q2)] 2 yOiSyOi}, F.1.10)
")=( — ) И(«о
X Z 71/5^1/- [Oo +
m
+ (oto -ф1)ыр(Я1* +Qi)] 2 yoi6yoi) , F.1.11)
i = l
где Dx = (a0 +^o)(o:o - 0i)exp#2 - (ao - фо)(ао +i//1)exp^1.
В случае относительно малых потерь на трение согласно F.1.8) qx 2 =
= ±(h + /со), где /г = Л/2а, и решения F.1.10) и F.1.11) несколько
упрощаются.
Мнимая часть постоянной распространения в имеет смысл волнового
числа при скорости, отличной от фазовой скорости звука в жидкости а.
Об этом свидетельствует приближенная формула, полученная из F.1.8),
в которой член в скобках при со учитывает зависимость скорости звука
от частоты а' ^а(\ — h2/Sco2a2) - эта скорость несколько меньше
скорости звука в жидкости а. С ростом частоты со или при уменьшении h -
- h/2a разница становится незначительной, и можно принять 6 ^со.
Приведенное волновое сопротивление а0, входящее в решения F.1.10)
и F.1.11) вместо безразмерного волнового сопротивления, также является
комплексной величиной, зависящей от частоты. При малых значениях
h/ooa можно записать а0 = аA — ih\2oS). Так как волновое сопротивление
связывает отклонения скорости с отклонениями давления в бегущей волне,
запись его в виде комплексного числа говорит о наличии сдвига фазы
между колебаниями скорости и давления в бегущей волне. При малых потерях
на трение или большом значении со а0 « а. Зависимость постоянной
распространения от частоты свидетельствует о том, что при распространении
колебаний в вязкой жидкости имеет место дисперсия, приводящая к
изменению формы распространяющихся вдоль тракта возмущений давления и
скорости.
Сопоставление данных расчетов частотных характеристик тракта при
различных моделях трения и сравнение их с данными экспериментов будет
дано ниже, в разделе, посвященном нестационарному трению при
турбулентном течении.
В примерах, приведенных в гл. 5, принималось, что ql 2 = ± со, h = 0 и
а0 = а, т.е. не учитывалось влияние вязкого трения жидкости о стенки.
Если вязкое трение относительно невелико и h < со, то его влияние можно
180
учесть с помощью приближенного соотношения ql2 = ±(h + г со), введя
хаким образом затухание волн, не зависящее от частоты.
Взяв для примера уравнение формы колебаний давления F.1.10),
приняв для простоты ф0 = 0, фг ->°°, y0l =i5 Sy01 =5р0, 71;-= 0, и считая h
относительно малым, так как можно принять
ехр[± //7A - х)] * 1 ± ih{\ -х), ехр(± //7) * 1 ± ih,
получим
5р{х, со) =
cos[co(l -x)] -ih{\ -*)sin[co(l --*)]
« = = Ьр0. F.1.12)
cos со - ih sin со
Первые члены числителя и знаменателя зависимости F.1.12) совпадают
с соответствующими членами в числителе и знаменателе выражения
E.4.8). За счет учета вязкого трения в числителе и знаменателе появились
дополнительные члены с коэффициентом И. Порядок величины этих
членов невелик по сравнению с единицей из-за малости параметра h. Для
любых значений со, кроме частоты, близкой к резонансной,
дополнительные члены с коэффициентом h дают относительно малые поправки.
Однако при приближении со кB/с+1Oг/2 величина cos со ^0 и амплитуда
колебаний будет определяться только значением параметра h. При этом, в
отличие от трактов без трения, при резонансе амплитуда колебаний
остается конечной. Естественно, что на амплитуду колебаний давления в начале
тракта, где вносятся возмущения, параметр h влияния не оказывает. Для
выходного же сечения тракта х = 1 соотношение F.1.12) принимает вид
5рA, co) = 6p0(cos со - ih sin со). F.1.13)
При приближении со к значению B?+1)тг/2 функция cos со ->0, sin со -* 1
и модуль амплитуды давления стремится к 1/h. Из-за влияния второго
члена в правой части соотношения F.1.13) величина 5/3A, со) достигает
максимального значения не точно при со = Bк + 1)тг/2. Однако при малых
значениях h эта разница невелика. Таким образом, учет даже небольшого
вязкого трения жидкости о стенки исключает бесконечность амплитуды при
резонансе, и чем больше величина параметра /?, характеризующего влияние
вязкого трения, тем меньше амплитуда при резонансе. Следует_отметить,
что в принятой приближенной модели параметр вязкого трения h не
зависит от частоты, и вследствие этого за счет трения все резонансные
максимумы понижаются одинаково. В действительности, как это будет
показано в следующем параграфе, по мере роста частоты высота резонансных
максимумов убывает.
Анализ квазистационарной модели трения для нестационарного течения
был проведен на примере движения слабо сжимаемой капельной жидкости.
Нетрудно показать, что аналогичные результаты получаются и для
сжимаемой жидкости.
181
§ 6.2. Нестационарное колеблющееся ламинарное течение
сжимаемой жидкости в тракте
6.2.1. Вводные замечания. При переходе к одномерному приближению
для нестационарного движения вязкой жидкости в тракте в уравнении
движения A.7.16) или A.7.17) появились две новые неизвестные -
коэффициент у(х, t), учитывающий изменения профиля скорости, и мгновенное
значение напряжения силы трения о стенки rw (х, t) или коэффициента
сопротивления трения Х(х, t). При квазистационарной модели течения
у(х, t) = const, a tw(x, t) = rw0(x, t), A(x, t) = \0(x, t\ где tw0(x, r),
Ao(*» 0 — значения параметров, полученные для мгновенных величин
средней скорости по зависимостям для стационарного режима.
Однако результаты экспериментов по определению динамических
характеристик гидравлических трактов [64, 67, 91, 184], данные, полученные
при исследовании гидроудара [99, 228], измерения профилей скорости при
нестационарном движении [184, 253, 255, 257, 266, 269] не подтверждают
гипотезу квазистационарности как по уровню потерь давления трения, так
и по виду профилей мгновенных значений скорости.
Впервые задача о нестационарном ламинарном движении несжимаемой
жидкости без предположения о квазистационарности дрофиля скорости
была решена с помощью рядов еще в 1882 г. И.С. Громекой [71]. Однако
числовые результаты для этого решения были получены только в
последние годы [9, 184].
Применительно к распространению акустических колебаний в
неподвижном газе, заполняющем цилиндрическую трубу, первые исследования с
учетом зависимости трения от частоты были выполнены Гельмгольцем,
Кирхгофом и Рэлеем [197]. При этом, если в работах Гельмгольца и Рэлея
учитывались диссипативные эффекты, связанные только с влиянием
вязкости, то в более полном (но очень сложном) решении Кирхгофа
учитывалась как вязкость, так и теплопроводность газа. Достаточно подробный
анализ различных решений подобных задач в акустике приведен в обзоре
Тиждемана [275].
Задача о вынужденных колебаниях столба жидкости наиболее просто
решается при использовании предположения о несжимаемости вязкой
жидкости. Применительно к ламинарному режиму течения в цилиндрической
трубе эта задача решалась рядом авторов [56, 154, 180, 184, 195, 272, 278]
и др. Вынужденные колебания вязкой сжимаемой жидкости исследовались
в работах [4, 91, 184, 193, 261, 279] и др. Во всех перечисленных работах
предполагалось, что среда — слабосжимаемая капельная жидкость, стенки
трубы - жесткие, труба имеет достаточную длину и эффектами,
связанными с влиянием неоднородностей на ее концах, можно пренебречь.
Обзор работ по распространению колебаний в трубе, заполненной
неподвижным газом, с учетом его вязкости и теплопроводности дан в статье
Тиждемана [275].
Задача о периодическом нестационарном ламинарном течении имеет
большое практическое значение применительно к трактам систем
гидроавтоматики, пневмогидравлическим линиям измерительных систем, как
модель течения в кровеносных сосудах и т.д. Этот вопрос важен и в
идеологическом плане, так как только для ламинарного течения задачи о неста-
182
тшонарных течениях решаются достаточно строго и именно на этих задачах
удобнее выяснять все основные особенности нестационарных течений.
6.2.2. Уравнения нестационарного ламинарного движения вязкой
жидкости в участке тракта. Предположим, что тепловые эффекты и внешние
объемные силы пренебрежимо малы, что тракт имеет цилиндрическую
форму и соответственно осесимметричное течение. В этом случае
нестационарное ламинарное течение вязкой слабосжимаемой жидкости со
скоростью, обеспечивающей соблюдение условия М < 1 в длинной (R< L)
трубе с жесткими стенками, описывается упрощенным вариантом линейных
уравнений гидромеханики A.10.1) - A.10.3) :
Ъп 1 Эр" М / L \ Г Ъ2п 1 Ъп 1
"э7~+~^ ~ЪхГ~ Re" \~R/[~dP'+yW\ = °' F'2Л)
1 Ър Ъп Ъи v
-— +— + —+ - = 0, F.2.2)
а Ъг дх Ъг г
в которых отброшены малые члены с коэффициентом R/L, а уравнение
движения для радиальной составляющей скорости A.10.2) сводится к
условию Ър/ЪГ = 0. Таким образом, для длинных участков тракта, у которых
R <€ L, из трех уравнений гидромеханики сохраняются только два,
описывающие нестационарное движение жидкости в продольном направлении,
т.е. вдоль оси тракта. Выражение уравнения A.10.2) показывает, что в этом
случае движением жидкости в радиальном направлении можно пренебречь.
Эти условия соблюдаются для всех участков тракта, кроме областей вблизи
его концов. Для течения вблизи концов тракта из-за неоднородности
потока на расстоянии порядка диаметра трубы необходимо учитывать и
уравнение для радиальной составляющей скорости [191, 197, 205].
Применительно к задаче анализа особенностей интегральных динамических
характеристик всего тракта местные особенности процесса на концах тракта
учитываются в граничных условиях, т.е. в уравнениях для граничных импедансов.
Для описания же нестационарного движения жидкости во всем тракте
вполне допустимо использовать упрощенные уравнения F.2.1) и F.2.2).
Однако следует обратить внимание на то, что два уравнения F.2.1) и
F.2.2) содержат три переменных и, v и р. Аналогичное положение имеет
место и для системы уравнений пограничного слоя [152, 242], которые
также выводятся в предположении о существенном отличии длины и
толщины пограничного слоя. В данном случае упрощение уравнений,
приводящее к исключению поперечной составляющей скорости, достигается путем
перехода к средним, интегральным характеристикам течения, с помощью
которых находится связь градиента давления (в пограничном слое он, как
правило, бывает задан) со скоростью.
Уравнения F.2.1) и F.2.2) являются линейными, однако граничные
условия для них в подавляющем большинстве случаев оказываются
нелинейными, поэтому удобно перейти к малым отклонениям. Введя при
линеаризации безразмерные вариации параметров, получаем:
Ъ8и 1 Ъ8р М / L \/ Ъ28и 1 Ъ8и \
—=~ + — - —(— И _2 +—-тг-1=0, F.2.3)
1 Ъ8р Ъ8и Ъди 1
=- + + —г- + — 8v = 0. F.2.4)
а Ъг Ъх Ъг 1
183
При приведении к безразмерному виду вариации нормировались так же,
как и исходные параметры и, v и р (см. § 1.2).
Найдем частное периодическое решение системы уравнений F.2.3) и
F.2.4) для режима установившихся гармонических колебаний,
наступившего после завершения переходных процессов
6wCt",7, со) = 677Cс",7, со)ехр(/ со t ),
5 v(x,7, со) = 5FCt~,7, оо)ехр(/ со t ), F.2.5)
др(х, со) = др(х, со)ехр(/ со t ) ,
где 517, 517, др - амплитуды (комплексные) вариаций параметров.
Исходные уравнения F.2.1) и F.2.2), так же как уравнения в малых
отклонениях F.2.3) и F.2.4), — линейные, поэтому частные
периодические решения F.2.5) определяют как распространение вынужденных
колебаний в тракте, заполненном неподвижной жидкостью, так и отклонения
параметров от их стационарного значения при наложении колебаний на
стационарное ламинарное течение. В последнем случае действует принцип
суперпозиции для линейных систем. Подставив решения F.2.5) в
уравнение движения F.2.3), сократив экспоненциальный множитель и вводя
новую переменную,
1 dSp
5F=5w+ — ?-, F.2.6)
/со a dx
dp
учтя при этом, что —— = 0, приводим уравнение F.2.3) к форме уравнения
Ъг
типа Бесселя для новой переменной
d23V I ddV Rq/R \ _
- + /со — — 5 V = 0. F.2.7)
dl2 7 dl M \ L )
Комплекс /co(Re/?/ML) = /соR2Iv -is2, где s = R\fcj/v' иногда называется
числом Стокса или сдвиговым волновым числом [275]. Этот безразмерный
комплекс выражается через другие критерии s = Vco(R/L)(Re/M) = VReSh',
где Sh = Rco/uq, Re = uQR/v. Для идеальной жидкости v - 0, Re -> °°, s -+ °°, и
в этом случае из уравнения F.2/7) следует, что 5 V = 0. Таким образом,
физический смысл переменной 5 V — дополнительные колебания давления,
связанные с перестройкой профиля скорости при нестационарном движении
вязкой жидкости.
Безразмерный комплекс, аналогичный числу s, уже встречался в задаче
о колебаниях пластины в вязкой жидкости (см. § 1.5). И в том и другом
случае он определяет скорость распространения сдвиговых вязких волн,
возникновение которых связано с взаимодействием сил инерции и сил
вязкого трения.
Уравнение F.2.7) имеет решение
5 V = Е(х, со)/0(/ 3/2Ts) + F(x, со) Y0(i 3/2Ts), F.2.8)
где Jo, YQ - функции Бесселя, Е(х, co),F(x, со) - неизвестные функции.
При 7= 0 величины 5г7, а следовательно и bV должны быть конечными.
184
поэтому F(x,gj), как коэффициент перед функций Yo, стремящейся к
бесконечности, должен быть равен нулю.
Граничное условие прилипания жидкости на стенке тракта 517= 0 при
f= 1 позволяет найти коэффициент Е(х,п), подставив решение F.2.8)
в уравнение F.2.6):
1 dbp
?()
?(х,со) ._ з/2 ч Т1-
iu>ocJo(i3/2s) dx
В итоге находим формулу для функции
1 J0(i3/2s7) dbp
5 V =— 3/2 -—, F.2.9)
ia /0(z /zs) dx
а подставив соотношение F.2.8) в уравнение F.2.6), зависимость,
связывающую амплитуды отклонений скорости и давления при колебаниях
потока в тракте:
,_, л 1 dSpL Jo(i3/2s7)
8u(x,r, co) = --73
itoa dx [ J0(i3/2s)
F.2.10)
Первый член в правой части определяет связь между амплитудами
скорости и градиентом давления вдоль оси тракта для акустических
колебаний в тракте без учета трения (см. § 5.2). Второй член дает уточнения,
связанные с влиянием вязкости и инерции в нестационарном потоке,
приводящие к изменению профиля скорости. Из уравнения F.2.10) следует, что
связь между градиентом давления и скоростью различна для различных
точек сечения тракта. Здесь проявляются эффекты, связанные с отличием
влияния одного и того же градиента давления на различные слои жидкости,
имеющие свою предысторию развития движения и, соответственно, свои
мгновенные значения ускорения и напряжения сил вязкого трения. Из
зависимости F.2.10), кроме того, следует, что распределение мгновенного
значения скорости в нестационарном потоке определяется произведением
двух функций, одна из которых зависит только от координаты7, а другая —
только от продольной координаты х. Зависимость F.2.10), определяющая
профиль скорости, является решением для случая задания гармонических
колебаний определенной частоты. В случае периодических колебаний более
сложной формы, учитывая линейность уравнений, можно использовать
решения F.2.10) для отдельных гармоник колебаний и ряды Фурье.
Для анализа распределения амплитуд вариаций скорости и давления
по длине тракта удобно ввести среднюю по сечению вариацию скорости
1 1
8U(x,co)=— / 27r78u(x,T,co)d~r. F.2.11)
тг о
При этом учтем, что вариация давления не зависит от Г и ее среднее по
сечению значение совпадает с ранее введенным значением амплитуды
вариации 6р(х, со).
Подставив соотношение F.2.10) в определение F.2.11), найдем
зависимость, связывающую амплитуду вариации средней скорости 5/7 с
185
градиентом давления,
1
--^- \ ;L F.2.12)
icoa dx L i ' s J0(i ' s) J
где J\{i^2 s) — функция Бесселя первого рода первого порядка.
Проинтегрируем по радиусу все члены уравнения неразрывности F.2.4), умножив
их предварительно на 2тг7. При интегрировании по частям предпоследнего
члена уравнения с учетом граничных условий Т - 1; 517 = 51;= 0 этот член
сокращается с интегралом от последнего члена. С учетом формы записи
решений F.2.5) уравнение F.2.4) принимает следующий вид:
а ЪЬп
5р+—г —— = 0. F.2.13)
/со Ъх
6.2.3. Решение для несжимаемой жидкости. Уравнение количества
движения F.2.12) пригодно как для описания колебаний сжимаемой жидкости
(вместе с уравнением F.2.13)), так и для несжимаемой жидкости. В
последнем случае градиент давления считается заданным, или наоборот —
заданы колебания средней скорости и с помощью зависимости F.2.12)
находятся колебания градиента (перепада) давления в тракте. Для
несжимаемой жидкости необходимо преобразовать коэффициент перед
градиентом давления, исключив скорость звука,
_ со/, риоа puL
со ос = = со = соти,
ар р
где ги = puL/p - инерционная постоянная времени столба жидкости в
тракте, введенная в § 1.9.
В этом случае уравнение F.2.12) переписывается как уравнение
элемента с сосредоточенными параметрами,
ddp
zT3U= i- , F.2.14)
dx
где
=*т + //т' F*2Л5)
RT,JT — вещественная и мнимая части безразмерного сопротивления
(импеданса) единицы длины участка тракта.
Уравнение F.2.14) для участка тракта с несжимаемой жидкостью
учитывает одновременно два эффекта — инерцию жидкости (мнимая часть
сопротивления) и сопротивление вязкого трения (RT). Обе составляющие
сопротивления zT зависят от частоты. На рис. 6.1 представлены графики
комплексов, в которые входят функции RT(s) и JT(s) [138]. Из графиков
следует, что комплекс, в который входит вещественная часть RT, почти
линейно растет с увеличением значений параметра s и становится близким
к единице (и практически независящим от s) при малых значениях s.
Комплекс /т/соги с мнимой частью /т изменяется незначительно - от 4/3
при s -+ 0 до единицы при больших значениях s.
186
рис.6.1. Зависимость от параметра s =
= R y/oj/v веществен ной и мнимой составляю-
шИх импеданса участка тракта, заполненного
вязкой несжимаемой жидкостью
2
/о
15
20 S
Величина 4/3 соответствует значению коэффициента у для стационарного
течения Пуазейля [152]. Коэффициент у учитывает отличие средней
скорости от среднего значения квадрата скорости, т.е. величины, входящей в
уравнения количества движения. Плавное стремление величины комплекса
)т/соти к единице с ростом параметра s (т.е. с ростом частоты) связано
с изменением формы профиля скорости, который при этом становится
все более наполненным (см. раздел 6.2.4). С помощью асимптотических
формул для бесселевых функций можно получить простые зависимости
при s -> О и s -> °°. При малых значениях s можно использовать следующие
ряды [133]:
¦-(i)"
(тУ
F.2.16)
Jx{z)
JL)A
\2/ 1
A) (т)
12223
Подставив ряды F.2.16) в зависимость F.2.15), находим
8сот„
4
+ ij
F.2.17)
Полученные в зависимости F.2.17) величины соответствуют значениям
параметров на графиках рис. 6.1 при s -> 0.
Для больших значений s предположение о несжимаемости жидкости
становится слишком грубым. Согласно решению F.2.17) из-за действия
инерции при постоянной амплитуде колебаний перепада давления в тракте
амплитуда колебаний скорости будет падать, стремясь к нулю присо->°°.
В действительности, как будет ясно из рассмотрения течения сжимаемой
среды, эффект стремления к нулю амплитуды является издержкой
исходного предположения о несжимаемости жидкости.
6.2.4. Профиль скорости при периодическом ламинарном движении.
Анализ зависимостей, полученных выше для самого простейшего варианта
периодического ламинарного течения - течения несжимаемой жидкости,
показывает, что комплексное сопротивление участка тракта зависит от
частоты. Первопричиной влияния частоты на динамические характеристики
тракта является изменение профиля скорости при колебаниях жидкости
по сравнению со стационарным профилем. Отличие в профиле приводит
187
к изменению градиента скорости у стенки, следствием которого является
изменение силы трения о стенку.
Впервые характерные особенности профиля скорости при
пульсирующем движении жидкости обнаружены экспериментально в 1929 г. Э.Г.
Ричардсоном и Э. Тайлером [269]. Ими с помощью термоанемометра были
измерены средние по времени квадратичные значения скорости в различных
точках по радиусу трубы с пульсирующим течением. Было обнаружено, что
максимум скорости при пульсациях потока смещается с оси трубы
к стенке — так называемый "аннулярный эффект". Сэксл [272] расчетным
путем подтвердил отличие профиля скорости для пульсирующего потока
от профиля течения Пуазейля.
На рис. 6.2 приведены эпюры переменной составляющей (амплитуды)
скорости для различных значений параметра s и разных фаз колебаний со t,
рассчитанные по формуле F.2.10) при гармонических колебаниях
градиента давления. При малых значениях параметра s профиль скорости имеет
форму параболы. При более высоких значениях s амплитуда скорости у
оси трубы становится меньше, чем у стенок, а профиль становится все
более и более однородным. При очень больших величинах s профиль
скорости в ядре потока становится почти плоским с небольшими пиками вблизи
стенки трубы. При определенных фазах колебаний течения у стенки и в
ядре потока имеют разное направление.
Изменение профиля скорости в случае пульсирующего ламинарного
потока в зависимости от величины параметра s подтверждено рядом
достаточно подробных экспериментальных исследований. В статье Денисона и
Стивенсона [253] приведены результаты экспериментов с пульсирующим
ламинарным потоком в трубе диаметром 19, 05 мм и длиной 9,1 м.
Измерение профиля скорости осуществлялось с помощью лазерного измерителя
скорости.
На рис. 6.3 приведены экспериментальные результаты — данные
измерений профиля скорости в пульсирующем ламинарном потоке при значениях
s = 1,71 (а) и s = 4,99 (б) и различных величинах фазового угла Cot. Здесь
же приведены теоретические кривые, определенные с использованием
зависимости F.2.10). Так как профили нормированы на максимальное
значение скорости, то расчет проводится по последнему сомножителю в
правой части зависимости F.2.10), стоящему в квадратных скобках.
Совпадение экспериментальных точек с теоретическими кривыми хорошее.
Отличие результатов расчета от экспериментальных данных не превышает
2%. На рис. 6.4 приведены графики профилей, полученных
экспериментально для пульсирующего ламинарного потока Харрисом и др. [257]. В
экспериментах использовался другой метод измерения скорости - с помощью
фотографирования траекторий ("треков") частиц, вводимых специально
в жидкость. Для исключения проскальзывания частиц относительно
жидкости они имели малые размеры (~ 250 мкм) и плотность, близкую к
плотности жидкости. Смещение частиц в жидкости у пропорционально
амплитуде местной скорости, поэтому полученные экспериментальные профили
относительного смещения частиц (рис. 6.4) полностью совпадают с
профилем относительной скорости, нормированной на максимальное значение
скорости. Эксперименты проводились для четырех значений параметра s,
при этом для каждого значения s опыты повторялись для двух разных
18В
бп(П
0,25 0,5 , 0,15 Г
О
Рис.6.2. Эпюры относительных амплитуд отклонений^ скорости при различных
значениях параметра s и фазы колебаний:а - c3t = тг/2, б - tot = О
Теория —
Экспер. о
0,5
-0,4
-0,5
-1,0
/
1
у
\
70f
{
-V-
л
би(г)
о
a Samax 6 5lJ™*
Рис. 6.3. Экспериментальные и теоретические профили скорости в ламинарном
колеблющемся потоке при значениях параметрам = 1,71 (а) и s = 4, 99 (б) [253 ]
амплитуд хода поршневого пульсатора. На рис. 6.4 представлены
результаты измерения относительных перемещений частиц. Здесь же представлены
(сплошные линии) результаты расчетов. Экспериментальные точки для
разных амплитуд хода пульсатора имеют разные обозначения.
Эксперименты подтвердили, что распределения относительного смещения (т.е. и
относительной скорости) не зависят от амплитуды колебаний, экспериментальные
точки хорошо согласуются с теоретическими кривыми. Аналогичные
экспериментальные данные о распределения скорости в пульсирующем
потоке опубликованы в книге Д.Н. Попова [184].
189
У/Ута*
0,75
0,5
0,25
~© -ампл
_о -ампл.
/1
[\s-9J
\
• \
\\
у1у„
и о
0,75
0,5
0,25
л
о - ампл. 71 . _
.-О«™2[5=5>'5
• - ампл Л
о - омпл, 9\ '
HV
1*
А*
Э * 1
\
О 0,25 0,5 0,75 r/R О
а
Рис. 6.4. Профили отклонения частиц в пульсирующем ламинарном потоке
0,25 0,5 0,75 r/R
б
Основные характерные особенности профиля скорости для
пульсирующего течения уже отмечались - это перемещения максимума скорости
к стенке, "выполаживание" профиля в центре трубы и, кроме того,
возможность движения одновременно в разных сечениях по радиусу в
противоположных направлениях (см. профиль на рис. 6.3, б).
Течения в противоположных направлениях и перемещения максимума
скорости к стенке связаны с одновременным действием двух эффектов -
инерции жидкости и вязкого трения. С ростом частоты уменьшается
глубина, на которую распространяется влияние трения жидкости о стенки, и
увеличивается область в ядре потока, где определяющую роль играют силы
инерции. Под действием мгновенного значения перепада давления в слоях
жидкости у стенки, имеющих меньшую скорость из-за влияния вязкости,
изменение скорости у стенки происходит быстрее, чем в ядре потоке. В
результате скорость жидкости у стенки может уже поменять свой знак под
влиянием изменения знака градиента давления, а в ядре потока за счет
инерции движение продолжается еще в старом направлении.
С некоторыми из отмеченных особенностей профилей скорости мы уже
встречались ранее, например, в § 1.5 при анализе течения жидкости у
плоской пластины, совершающей гармонические колебания в своей плоскости.
Глубина проникновения вязких сдвиговых волн согласно формуле A.5.13)
5 = Bу/со) 1'2. Если имеется какой-нибудь характерный для течения размер
R, то можно ввести безразмерную глубину проникновения вязких волн
в жидкость
5
R
1
R
Г
s/2
V '
со
F.2.18)
Если R - радиус трубы, то из условия F.2.18) следует, что глубина
проникновения 5 будет иметь порядок радиуса трубы при значении параметра
5 ~1. В случае s > 1 8 <R, т.е. влияние вязкости сказывается только в
непосредственной близости у стенок трубы. С другой стороны, нестацио-
190
нарный пограничный слой в пульсирующем течении в определенном смысле
аналогичен пограничному слою, развивающемуся в вязкой жидкости на
плоской пластине при стационарном течении. В ламинарном пограничном
слое его толщина 5 увеличивается по мере удаления от передней кромки
пластины по закону [152] 5 ~ y/px/Ui где х - расстояние от передней
Кромки пластины, U - скорость вне пограничного слоя. Эту зависимость
можно трактовать так, что для торможения слоя жидкости толщиной 5
необходимо время порядка времени пребывания среды t ~~ xjU. To, что
характерным временем, определяющим темп нарастания пограничного
слоя на стенке, является время пребывания жидкости, следует из
приведенного в § 1.5 решения для пограничной пластины, мгновенно
приведенной в движение с постоянной скоростью. Из формулы A.5.8) следует, что
в этом случае толщина пограничного слоя изменяется по закону 5 ~~ у/р79
где t - время, отсчитываемое от начала движения. Этот закон аналогичен
формуле F.2.18) для пульсирующего течения, учитывая, что t ~ 1/со.
Формулы F.2.10) и F.2.12) для местных и средних значений скорости
жидкости неудобны для расчетов, так как содержат функции Бесселя от
комплексного аргумента. При достаточно больших значениях параметра s
можно воспользоваться асимптотическим разложением функции Бесселя
в ряд, отбросив члены порядка l/s [133]:
.4
2y/ns L V? 8
Подставив формулу F.2.19) в соотношения F.2.10) и F.2.12),
пренебрегая при этом членами порядка l/s, разделив 5w(x,F,co) на 5?7(Зс, со),
находим
= 1 =- ехрЬ ^ . F.2.20)
_ 1 =
ЫЦх.п) y/f
Считая5U (х~,п>) заданной вещественной величиной и учтя, что 5м =
= 5 гГехр (/со Г), можно найти вещественнзоо часть уравнения F.2.20):
г __/i\ Г г-1 I [7-1
ды(х, г, со ) = {cos со t -I —=- exp s р=г cos s—-=г +
, \ \ \у/Т/ I vTJ L ч/Г
+ со7 |S?/Cc", со). F.2.21)
Уравнения F.2.20) и F.2.21) имеют такие же основные члены,
учитывающие влияние вязкости, как и зависимости A.5.11) и A.5.12),
описывающие профили скорости у колеблющейся пластины, если учесть, что
У = R - г - расстояние от стенки. Физический смысл этих членов
одинаков - они описывают отклонения скорости от ее среднего мгновенного
значения, возникающие вследствие одновременного влияния сил инерции
и вязкого трения. При больших значениях параметра s экспоненциальный
член в зависимости F.2.21) резко падает при увеличении абсолютного
значения F — 1 (величины отрицательной) Таким образом, при
пульсирующем течении в трубе, так же как и при колебаниях пластины, вблизи стенки
191
образуется динамический пограничный слой, толщина которого
уменьшается при увеличении параметра 5. В ядре потока, как это следует из вида
кривых профилей скоростей при больших s на рис. 6.2, а также из
приближенного уравнения F.2.21), профиль скорости практически не зависит от
радиуса F.
6.2.5. Напряжение сил трения на стенке трубы. Напряжение силы вязкого
трения на стенке трубы описывается формулой Ньютона
r=-Pv — . F-2.22)
Ъг
Учитывая, что уравнения для нестационарного течения были получены в
амплитудах вариаций параметров, приведем к такому же виду и
зависимость F.2.22). Для вариации напряжения силы трения в качестве
нормирующей величины используем значения напряжения силы трения tWq =
= 4nuo/R при стационарном ламинарном потоке со средней скоростью
и0, по которой нормировались вариации продольной скорости. В этом
случае формула F.2.22) приобретает следующий вид:
1 35г7
5т(х,7, й) = . F.2.23)
Подставив уравнение F.2.10) в соотношение F.2.23), используя связь
между функциями Бесселя [133] /0'0) =--Л 00 > а также связь между
градиентом давления и амплитудой вариации средней скорости из
зависимости F.2.12), получаем:
57
F.2.24)
При преобразовании уравнения F.2.24) использовалась зависимость,
связывающая функции Бесселя разного порядка [133],
2Jl(z) = z[J0(z)+J2(z)].
Если ввести модифицированные функции Бесселя Iv (z) = i~vJv (iz),
воспользоваться функциями Кельвина ber^s nbei^s: Iv (i3t2s) = berps +
+ ibeivs и принять Т = 1, то соотношение F.2.24) преобразуется к
следующей форме:
5т \ /3/25/!(/3/25) /^(beris + zbeijs)
= i4/2(/3/V> 4(ber25+/bei25) '
Входящие в формулу F.2.25) функции Кельвина затабулированы [176],
так что, пользуясь таблицами, можно найти связь между амплитудой
напряжения и амплитудой средней скорости в том же сечении, т.е. частотную
передаточную функцию для напряжения трения о стенку трубы.
192
Для определения амплитудно-фазовых частотных характеристик
напряжения трения на стенке в формуле F.2.25) необходимо выделить
действительную Rer (s) и мнимую Imr (s) части, причем вместо частоты со у до б -
но в качестве аргумента использовать безразмерный комплекс s =Ry/oj/p':
— Ьег25)—beills(bei2s + ber2s)]
bei2s) + beijs(bei2s - ber2s)]
На рис. 6.5 представлена кривая амплитудно-фазовой частотной
характеристики (АФЧХ) напряжения трения на стенке, построенная по формулам
F.2.26) и F.2.27) [184]. Характер кривой АФЧХ свидетельствует, что с
ростом параметра s (т.е. при прочих равных условиях — с ростом частоты)
напряжение трения растет, а по фазе оно опережает отклонение средней
скорости в том же сечении тракта. Объяснение этому факту дают кривые
распределения мгновенной скорости на рис. 6.2, из которых следует, что
поле скорости у стенки перестраивается быстрее, чем в ядре течения.
При больших значениях параметра s в соотношении F.2.25) можно
воспользоваться асимптотическими зависимостями для модифицированных
функций Бесселя [133], учитывая при этом, что для больших z члены ряда
с множителем ехр(—z) можно отбросить:
expz / 3 15
1
F.2.28)
L
1
2z
1 -
8z
15
l:
l ^^
8z2 >
— + -
ь
105
8z 128z2
/ 2 1 \
, A-— + — V F.2.29)
/2ttz \ z z2 /
Здесь, следуя [184], для упрощения дальнейших преобразований
коэффициенты в рядах F.2.28) и F.2.29) округлены до ближайших четных
чисел.
Подставим ряды F.2.28) и F.2.29) в зависимости F.2.25). После
преобразований, отбросив относительно малые члены в полученных
выражениях, находим упрощенное соотношение для действительной и мнимых
частей передаточной функции:
s2 s2 ( к \
ReT(s)^ , ImT(s)^ f— lj, F.2.30)
где
13.Б.Ф. Гликман 193
Гт-
1,5
2ft Re 0
2
1,5
f,o
0,5
k1>k2jk1 i
k2jk
/
J
1
/
i
X
1
1
2,5
5
Рис
.6.5. Амплитудно-фазовая частотная характеристика Eт/б?/)р_ j для
напряжения силы трения в зависимости от параметра s = R\fu>lvw
. 6.6. Зависимость коэффициентов аппроксимации передаточной функции для
напряжения силы трения от параметра s [184]
На рис. 6.6 приведены графики кривых для параметров к{ и кг\кх в
зависимости от 5, рассчитанные по приближенным соотношениям F.2.31)
(сплошная линия) и по точным формулам F.2.26) и F.2.27) (пунктирная линия)
[184]. Сопоставление кривых на рис. 6.6 показывает, что расхождения
между точными и приближенными значениями становятся незначительными
при s>3— 4. Задавая 5U в виде гармонической функции времени_5^ =
= 5?/ехр(/оЗГ), получим для производной по времени bbUjb T-icbbU, где
со = coL/a - безразмерная частота, характерная для акустических задач. Учтя
со R u>L Ru0 a _ R Re
связь s -R —= = со — —
v L a v u0 L Ы
, можно записать
6rvv(co) = -
ьи
R
~8L
Re
dbU
F.2.32)
Skx 81 М ki - 1 dt
Зависимость F.2.32) определяет связь мгновенного значения напряжения
трения в пульсирующем ламинарном потоке как со скоростью, так и с
ее производной по времени. При этом не следует забывать, что отклонение
скорости связано с производной от скорости по времени частотой со, так
как соотношение получено из частных периодических решений F.2.5)
линеаризованных уравнений гидромеханики F.2.3) и F.2.4).
194
Пользуясь полученным приближенным выражением для передаточной
функции напряжения трения о стенки трубы F.2.32), можно получить
новый вариант записи упрощенного уравнения для пульсирующего течения
несжимаемой жидкости в тракте, который дает более ясное представление
о физическом смысле введенных параметров кх и кг\кх.
Запишем уравнения нестационарного движения несжимаемой жидкости
A.9.14) в несколько измененной форме - через напряжения трения на
стенке, учтя связь расхода со скоростью G = puF:
du 2т WL
Ар= pL —-+ ——. F.2.33)
U t К
Линеаризовав уравнение F.2.33), переходя к амплитудам безразмерных
вариаций 8и = 5"wexp(/cof), найдем зависимость для импеданса
(сопротивления) участка тракта:
ЗАр pu0L L
Ьи Ро R Po UqR \ 8м
/
R \
p0 pl / w
= /и—^- + 8 - -г^~ • F.2.34)
Р R P UR \ 8м / 1
Используя приближенные соотношения F.2.30), учтя, что s2 - R2 со/v,
преобразуем уравнение F.2.34) к следующему виду:
5 Ар к2 S(L/R) s2
—^ = шти -?- + -1—^ —- , F.2.35)
ои к\ ReEu Skx
L
где ги = рм0 •
Ро
Если в уравнение F.2.33) подставить напряжение трения для
квазистационарного режима tWq =4pvu/R, то после линеаризации и перехода к
безразмерным вариациям находим
HL/R)
¦ »wth + —— . F.2.36)
ReEu
Сопоставление отдельных составляющих уравнений F.2.35), в котором
учитывается изменение профиля скорости с частотой, с членами уравнения
F.2.36) для квазистационарного режима колебаний показывает, что учет
изменения профиля скорости приводит к появлению в уравнении
импеданса участка тракта с несжимаемой жидкостью двух дополнительных
множителей. Множитель к2/кх учитывает влияние изменения профиля
скорости на инерционную постоянную времени, и его можно назвать
коррективом реактивного сопротивления тракта [184]. Величина его
изменяется от 4/3 при s - 0 до 1 при s ->°°. Строго рассуждая, множитель 4/3
необходимо учитывать и в инерционном члене уравнения F.2.36) .
Другой множитель s2 /Ski учитывает влияние изменения профиля
скорости с изменением частоты на активные потери в тракте. При больших
значениях со можно принять s2/Ski ^y/2s/S ~ Vc7. Эта приближенная
зависимость показывает, что потери на трение в пульсирующем ламинарном
потоке при прочих равных условиях растут пропорционально корню из
частоты колебаний.
13* 195
Потери на трение непосредственно связаны с безразмерным
коэффициентом гидравлического сопротивления трения X. Проще всего величину
этого коэффициента для нестационарного пульсирующего течения получить
из сопоставления активных составляющих импеданса участка тракта для
двух случаев - квазистационарной модели течения из уравнения F.2.36) и
модели с учетом приближенной зависимости напряжения трения от частоты
из уравнения F.2.35). Члены, характеризующие потери на трение, которым
пропорционален коэффициент X (остальные параметры считаются
одинаковыми), отличаются в зависимости F.2.35) множителем s2/Skli который
является коррективом активной составляющей импеданса. Сопоставляя
аналогичные члены для двух моделей, получим такое соотношение:
s2 64 s2
X = Хкс = , F.2.37)
8кг Re Skx
где X - мгновенное значение коэффициента гидравлического
сопротивления для пульсирующего потока с учетом зависимости от частоты, Хкс —
значение этого коэффициента для квазистационарной модели трения при
мгновенном значении средней скорости, Re - число Рейнольдса, подсчитываемое
по мгновенному значению средней скорости в тракте. Корректирующий
коэффициент в формуле F.2.37), который, как было показано, при
больших значениях параметра s пропорционален \/со] учитывает увеличение с
ростом частоты коэффициента гидравлического сопротивления в
пульсирующем потоке по сравнению с коэффициентом сопротивления для
стационарного ламинарного течения при одинаковых мгновенных значениях
скорости. Это подтверждается и данными экспериментальных исследований
[184]. Приведенное выше приближенное уравнение F.2.35) в основном
повторяет ранее полученное более строгим методом уравнение импеданса
участка тракта F.2.15). Целесообразность использования приближенной
зависимости F.2.35) , пригодной только при достаточно больших величинах
параметра s, определяется тем, что для входящих в нее коэффициентов
ki ик2/к1 имеются аппроксимирующие формулы.
Нормирующий множитель для вещественной части импеданса,
используемый при построении графиков на рис. 6.1, можно преобразовать:
s2 R2p0cj ReEu
8соти SpuoLvoj SL/R
Этот комплекс входит в уравнение F.2.36) как вещественная
составляющая. Так как уравнение F.2.36) описывает квазистационарный процесс,
то оно пригодно только для низких частот. Благодаря нормирующему
множителю при s -+0 (т.е. ео-*0) вещественная составляющая импеданса на
рис. 6.1 стремится к единице.
6.2.6. Пульсирующее ламинарное течение слабосжимаемой жидкости
в трубе. При решении задач о профиле скорости, напряжении трения и при
анализе особенностей пульсирующего ламинарного движения несжимаемой
жидкости было достаточно одного уравнения движения F.2.10) или
F.2.12). Если же рассматривать вопрос о распространении колебаний в
трубе, как системе с распределенными параметрами, необходимо, кроме
уравнений движения F.2.12), использовать уравнение неразрывности
196
F-2.13). Подставив амплитуду вариации давления из уравнения F.2.13)
в зависимость F.2.12), находим уравнение, определяющее распределение
амплитуды колебаний средней скорости по длине тракта:
d2bU 7_7 _
——- -02со25?/ =0, F.2.38)
dx
где
р i^s J0(iWs) J0(i3f2s) ' F'239)
Учитывая, что корни характеристического уравнения для уравнения
F.2.38) равны ± 0оЗ, его решение запишется в следующем виде:
bUQc, G3) = Cexp(i3cj x )+?> ехр(-0сох ). F.2.40)
Подставив F.2.40) в уравнение F.2.13), найдем решение для
амплитуды вариации давления
&р(х, п) =
= //За [СехрОЗсох) -D ехр(-0о3х)]. F.2.41)
Постоянные С и D определяются из граничных условий на концах трубы,
записываемыхв общем виде (см. гл. 5) так:
х=0, Ьр =\po6U +7о5Уо, F.2.42)
Зс=1, Ьр =
где ^0, \//1 - граничные импедансы, То, 7i — коэффициенты усиления для
вариаций внешних возмущающих воздействий 5^0- и Ьу\.
Используя граничные условия F.2.42), находим решение для
распределения амплитуд безразмерных отклонений средней скорости и давления:
bU(x, со) = — ]
- -^-{ К - *i )ехр [-/ЗоЗA - х)]
F.2.43)
5р(х",со)= " 1
F.2.44)
~ -/aj3 - приведенное волновое сопротивление. Как следует из
соотношения F.2.39), параметр распространения /3 — величина комплексная: /3 =
= t + ОС- Как и для зависимости F.2.25), параметр & находится с помощью
Функций Кельвина. На рис. 6.7 приведены кривые для вещественной и
мнимой составляющих параметра /3 как функции комплекса s.
197
4
1.0
0,5
\
ч
X
—j
Ри с. 6.7. Изменение вещественной ? и мнимой
X составляющих параметра распространения 0
в зависимости от значения s
W
20
Если жидкость имеет малую вязкость, т.е. v -*0, или частота очень
высокая (со-»<»), то параметр s -*«>. В этом случае 0 -*/, ап -+а, поскольку
составляющие ? -* 0, х -* 1 •
Подставив предельные значения для составляющих постоянной
распространения 0 в решения F.2.43) и F.2.44), находим ранее полученные
зависимости для амплитуд вариаций давления и скорости E.2.10) и E.2.11)
при М « 0. Однако такой переход допустим только в случае v -* 0, т.е. для
жидкости очень малой вязкости. Разное влияние на затухание колебаний
в тракте увеличения частоты и уменьшения вязкости, входящих в параметр s
в виде отношения, определяется тем, что в решения F.2.43) и F.2.44)
входит произведение /ЗсЗ . Поэтому затухание колебаний вдоль тракта
будет определятся произведением ? со , которое при со ->°° также стремится
к бесконечности, а не к нулю, как величина ?.
Влияние трения, зависящего от частоты, на динамические характеристики
гидравлического тракта иллюстрируется графиками амплитудных и
фазовых частотных характеристик гидравлического тракта, представленных
на рис. 6.8 [4]. Расчеты проводились для цилиндрической трубы, у
которой (см.формулу F.2.7)) R/L = 0,00043, а = 0,64, фх = 2, отношение
Re/M варьировалось в пределах от 3,76 • 104 до 3,76 • 108. На рис. 6.8,а
представлены кривые амплитуды_и фазы для проводимости участка тракта
5 Г7@, од)
со стороны входа увх (со) = —= =— в зависимости от безразмерной
5р @, со)
частоты со = со/, /а. Аналогичные кривые для частотной передаточной
функции тракта по давлению Ьр A, со)/5р @, со) представлены на рис. 6.8,6.
Сопоставление кривых показывает, что при больших значениях отношения
Re/M ^106 - 108 (т.е. при относительной малой вязкости жидкости)
изменение этого отношения на два порядка незначительно влияет на
амплитудные и фазовые характеристики гидравлического тракта. Кривые для
двух значений Re/M практически совпадают, также совпадают и
резонансные частоты. Дальнейшее уменьшение Re/M еще на порядок, т.е.
увеличение на порядок вязкости жидкости при заданной геометрии тракта и
скорости жидкости, приводит к достаточно ощутимому, изменению частотных
характеристик тракта. При этом уже обнаруживается влияние увеличения
потерь на трение с ростом частоты — вторые резонансные максимумы
оказываются ниже первых. При дальнейшем уменьшении Re/M еще на порядок
(до 3,76 • 104) частотные характеристики тракта достаточно резко изменя-
198
Рис.6.8. Динамические характеристики гидравлического тракта в зависимости от
частоты сЗ при разных значениях Re/M: Re/M = 3,76 * 108 (/); Re/M = 3,76 • 10б B);
Re/M = 3,76 • 105 С?); Re/M = 3,76 • 104 D)
о
с
о ... .,
п
1
/
/
л
\
\
1
\
\
f
/
/
/
/
/
И-
\
\
\
1
V
л
40 60 80 f/u.
/
/
д
/
/
\
....
6pVrt)
opW)
Qfi
Q
-fO(f
-206
-30(f
ft
Л
1
м
M
\
V
J
/
1
1
If
f
\
л
i
\
^^7 5^7 5(? f/u
5
s
s
4
60°
2tT
0
-40'
P к с. 6.9. Экспериментальные и теоретические характеристики ламинарного потока
сжимаемой жидкости в тракте: сплошные линии - расчет по формулам F.2.43) и
F.2.44), штриховые линии - расчет по формуле F.1.10), кружочки - эксперимент
ются — для проводимости тракта резонансные максимумы уменьшаются
приблизительно в два раза, а для передаточной функции (рис. 6.8, б)
второй резонанс почти вырождается, резонансная частота для второго
резонанса ощутимо снижается.
Экспериментальные данные по динамическим характеристикам
гидравлического тракта при ламинарном режиме течения, полученные Д'Суза и
Ольденбургером [91], полностью подтверждают описанную
математическую модель течения с учетом сжимаемости и зависимости напряжения
трения от частоты. На рис. 6.9. представлены результаты экспериментов по
определению входной проводимости и частотной передаточной функции
при ламинарном режиме течения в диапазоне частот от 1 до 100 Гц. В
процессе экспериментов малоинерционными датчиками измерялись колебания
давления (создаваемые пульсатором на входе), а с помощью
термоанемометра — колебания скорости в начале и в конце тракта.
Результаты экспериментов для входной проводимости тракта
(рис. 6.9, а) представлены в виде безразмерного отношения
8р'@,Я/вр'@,1)
где 6м'@, /), др' @, /) - отклонение скорости и давления в начале тракта
(х = 0) от их стационарных значений при частоте /, 5ы' @, 1),5р' @, 1) -
аналогичные отклонения в начале тракта при минимальной частоте /min =
= 1 Гц. Для передаточной функции тракта 5р'A,/)/5р'@,/) определялось
отношение отклонений давления в начале (х = 0) 5р'@, /) и в конце
тракта (х = 1) др1 A,/) от их стационарных значений. На рис. 6.9, кроме
точек, полученных экспериментально, приведены теоретические кривые
(сплошные линии), рассчитанные по формулам F.2.43) и F.2.44) при
^о = 0, 7о = 1, ЗУо = др @, f) , 7i = 0. Совпадение расчетных кривых и
экспериментальных точек хорошее, что подтверждает эффективность
модели с учетом зависимости напряжения силы трения от частоты для
ламинарного режима течения в тракте.
На рис. 6.9,& штриховой линией представлены результаты расчетов
по формулам F.1.10) и F.1.11), которые были выведены в
предположении о квазистационарности напряжения трения о стенку.
Результаты расчетов по этим формулам достаточно существенно
отличаются как от данных экспериментов, так и от расчетов с использованием
математической модели, в которой учитывается зависимость напряжения
трения от частоты. Таким образом, при расчетах динамических
характеристик трактов с ламинарным течением необходимо учитывать эффекты,
связанные с перестройкой профилей скорости при нестационарном
колебательном движении.
6.2.7. Приближенное решение для вынужденных колебаний при
предельных значениях параметра s. В решения для распределения амплитуд
отклонений средней скорости и давления F.2.43) и F.2.44) в качестве
параметра распространения входит комплексное число, определяемое из достаточно
сложного соотношения F.2.39). При больших значениях параметра s
можно упростить это выражение, воспользовавшись формулами для
асимптотического разложения функций Кельвина. Предварительно с помощью
соотношения, связывающего функции Б^сселя разного порядка с функциями
200
Кельвина, найдем
/0 (z3'2 s) ber(s) + ibeiE)
/0 (z s) ber(s) ibeiE)
я* = -?-- - = — -— . F.2.45)
р / (i3/2s) ber0) + /bei<»
/2 (i3/2s)
Для больших значений s используем формулы разложения функций
Кельвина в ряды [176]:
ber (s) = (s/y/bi) exp (s/y/1) (Lo cos у - Mo sin <p),
bei (s) = (s/y/br) exp (s/>/2) (Mo cos <p + Lo sin ^),
где
/ - тг/8,
ber2 (s)=
bei2 (s) = (s/y/br) exp E/V5) (-Л/2 cos ^ + L2 sin </?),
L2 = 1 - 15/165 + . . . , M2 = 15/165 + . . . ,
Подставив ряды в соотношение F.2.45), отбросив члены с s2 и округлив
некоторые коэффициенты, получим
/0(/3/25) V? х/2"
„з = - 1 + I F.2.46)
J2(i3/2s) s s У }
Отсюда находим составляющие параметра |3:
+ ^1+). F247)
Такое предельное выражение для постоянной распространения волн при
изотермическом течении сжимаемой вязкой жидкости впервые получил
Гельмгольц [191,197].
При больших значениях параметра 5, как уже отмечалось, х ~^ 1> ?~* 0.
Однако со % = (coL/Ra) у/у/2со' = (l/a)(L/R)\/cop!2' = (L/R)(c/2a\ где с =
= \j2ojv— скорость распространения поперечных сдвиговых волн в вязкой
жидкости (см. § 1.5). Таким образом, коэффициент затухания вдоль оси
тракта со^ растет пропорционально л/со с ростом частоты и обращается в
нуль только при v = 0. Влияние потерь на трение увеличивается с ростом
отношения L/R. В качестве относительного параметра, определяющего
затухание колебаний за счет работы сил вязкого трения, выступает отношение
скоростей распространения двух систем волн, возникающих при колебаниях
вязкой сжимаемой жидкости, — скоростей распространения поперечных
сдвиговых волн и акустических колебаний. При этом с/а < 1.
При малых значениях параметра s разложим функции Бесселя в ряд
[133]:
о*
¦ ' 243! \22 /
откуда
201
Используем зависимость F.2.48) и связь между функциями Бесселя и
преобразуем уравнение F.2.12) :
1 J2(i3/2s) dbp D2 р0 dbp
)
/со a J0(i3l2s) dx 32ц u0L dx
Эта зависимость с точностью до коэффициента Ро/иоЬ совпадает с
формулой для течения Пуазейля [152]. Коэффициент состоит из нормирующих
параметров, которые использовались при приведении переменных —
вариаций параметров и координаты х — к безразмерному виду.
6.2.8. Вынужденные колебания вязкой теплопроводной сжимаемой
жидкости в трубе. При распространении акустических колебаний в газе
кроме эффектов, связанных с нестационарным трением о стенки, имеют
значения и тепловые процессы — изменение температуры среды за счет
колебаний давления и теплопроводности газа. Обзор работ в этой области
сделан Тиждеманом [275].
Воспользуемся линеаризованным уравнением энергии A.10.22), в
котором, так же как в уравнениях A.10.1) — A.10.3), произведем замену
Sh = 1/М и, принимая М<^1, отбросим конвективные и диссипативный
члены. Кроме того, считаем, что отсутствует подвод теплоты от стенок,
трение мало и тракт имеет цилиндрическую форму. _
Для среднего стационарного течения производными от 17, U, р и Т по
координатам можно пренебречь, а безразмерные переменные р = 0 = Т= 1.
Принимая газ идеальным, находим, что
/ 1 \ / bv \ 1
' р
Учтя все эти предположения, преобразуем уравнение энергии к
следующему виду:
ддТ к-\ЬЬр \Ъ2ЬТ (Ь\ЬЧТ (L\2 1 ЪЬТЛ
__ :=L=FoM г-+(— —;~+ (—) • F.2.49)
bt к bt [ Ъх2 \RI Ы2 \R1 Т ЪТ \
Принимая, как и ранее, что тракт длинный, т.е. R<L, подставив в
уравнение F.2.49) частное периодическое решение F.2.5) для др и аналогичное
решение для вариации температуры 5 Г(х, 7, со) = 5 Т(х, 7, со)ехр(/ соГ),
найдем
*-1 /L\2\b25T 1 Э6Г 1
6p=FoM(— г-+ . F.2.50)
к \R/ L Э72 7 Э7 J
Уравнение F.2.50) подобно уравнению F.2.3) для вариации скорости,
если в него подставить частное периодическое решение. Соответственно
и решение уравнения F.2.50), являющегося частным случаем уравнения
Бесселя, аналогично решению F.2.10) для амплитуды вариации скорости
[275] при условии, что б Т остается конечной величиной при7 = 0 и 6 Т = 0
при7 = 1 (изотермические условия на стенке) :
_ А: — 1Г J0(i3/2osr)]
ЬТ= 1- 3/1 -8р. F.2.51)
В решении F.2.51) учтено,что ?oM(L/RJ( 1//оЗ)= l//aV, где s = Ry/co/v\
202
о - \Длср1\? - корень квадратный из числа Прандтля Рг. Уравнение
количества движения F.2.3) и его запись через амплитуды F.2.10) сохраняются.
Уравнение неразрывности F.2.4) получено с использованием условия
адиабатичности течения, что в рассматриваемом случае не соблюдается,
так как в уравнении энергии учитывается обмен теплом между различными
частицами газа за счет теплопроводности. Поэтому воспользуемся записью
уравнения неразрывности в исходной линеаризованной форме A.10.16),
которая при соблюдении упрощающих предположений, принятых для
уравнений F.2.3), F.2.4) и F.2.50), после подстановки частных
периодических решений F.2.5) запишется:
1 Э(г5и) itb dbu
- = 5р + . F.2.52)
7 Э7 М Ъх
Плотность идеального газа связана с другими его параметрами
уравнением состояния p-p/RT (где R - газовая постоянная). Это уравнение
представимо в линеаризованной форме (в амплитудах безразмерных
вариаций)
8р =8р-6Т. F.2.53)
Используя уравнения F.2.10), F.2:51) и F.2.53), выражение F.2.52)
преобразуем к следующей форме:
1 d(TSv) /со Г к-I
\ J0
Ъг ML * \ J0(i5/2os)
F-254)
Проинтегрируем зависимость F.2.54) по г, предварительно умножив
левую и правую ее части на7 и учтя, что 5р от Г не зависит:
_*ыГг'2 к-1/Т2 7 /i(/3/2^7)\l
"ГбиГ11 *~\Т""/3/2« Mi*2 os) /J8P +
T2 7
F155)
Учитывая граничное условие на стенке 5U = 0 при 7 = 1 и связь между
функциями Бесселя разного порядка, найдем из зависимости F.2.55)
s)l i /2(/3/
0 J 2a3a /0(':
S)
2ML *: Mi3/2°s) J 2a3a /0(i^25) Jx2 *
Второе условие, которому должно удовлетворять решение F.2.55), это
осевая симметрия, из которой следует, что 517= 0 при 7= 0. Последнее
равенство удовлетворится, если S(x) = 0 или
Г, *-1 Л(/3/2а*I М J2(i3l*s)d28p л
Для идеального газа отношение Ы/а=р/роа2 = 1/к.
203
Уравнение F.2.Ь6) описывает распределение амплитуды отклонения
давления по длине тракта. Решение этого уравнения имеет вид
Ьр = А ехр(Ь сох) + В ехр(- Ъ сох), F.2.57)
который по форме совпадает с решениями F.2.40) и F.2.41). Если учесть
граничные условия F.2.42)_, предварительно с помощью соотношений
F.2.13) и F.2.57) найдя dU(x, со), то получим решения в форме
зависимостей F.2.43) и F.2.44), в которые вместо безразмерной постоянной
распространения /3 необходимо подставить Ь.
Из уравнения F.2.56) следует, что постоянная распространения равна
/Jo(i3/2s)k '
где
k-l J2(i3/2 os)
Jo(i3/2os)
Используя зависимости F.2.10), F.2.51), F.2.53), F.2.55), F.2.57)
и F.2.58), получаем решения для других переменных [275]:
ib\ /0(/3/2s7
— ]\- j 3/2
I
ib\ /0(/s7I
577=— ]\- j 3/2 \[Аехр(Ьпх)-Вех1р(-Ьпх)], F.2.59)
ico\7\ J0(i3!2s)k] k-l
8v = —
a { 2 L J2(i3/2s) n J z3/2 os J0(i3/2 as)
[A exp(b cox) + В exp(- Z? cox)], F.2.60)
i3l2sn J2(i3/2s)
J0(i3/2as7}
o(i3/2os)
F.2.61)
^ *-lf4 J0(i3'2asjy
6p = I 1 — 11 -j J\ J [Aexp(b oox) + Яехр(- b cox)],
_ tIf J0(i osT)]
ST=——\\- \[Aexp(bU>x) + Bexp(-bU>x)]. F.2.62)
к L J0(i/los) J
Решения F.2.57) - F.2.62) описывают малые колебания параметров
потока вязкого теплопроводного газа в длинной жесткой цилиндрической
трубе со стенками, обладающими большой теплопроводностью (по
сравнению с теплопроводностью газа). Если течение изотермическое (к = 1), то
решение сводится к ранее полученным зависимостям для слабо сжимаемой
капельной жидкости. Соотношение F.2.59) для мгновенных значений
амплитуд продольной скорости совпадает с аналогичным уравнением
F.2.10) для слабосжимаемой жидкости, т.е. учет тепловых эффектов
не влияет на распределение скорости в колеблющемся ламинарном потоке.
Тепловые эффекты учитываются коэффициентом п в постоянной распрост-
204
t,2
-5°
г
J
\
,—
^—¦
¦»——¦
6S
,5
Л F
U,D
)s=OA
ft
'"""""""""¦
0,25 . , 0,50
\6u'/Rw\
4 Ь 12 16 20
Р и с. 6.10. Зависимость модуля и фазы показателя политропы от параметра os
Р и с. 6.11. Амплитуда поперечной составляющей скорости в зависимости от
параметра &
ранения Ь. Можно показать [275], что постоянная распространения
определяется формулой F.2.58) и для случая, когда уравнение состояния F.2.53)
и уравнение энергии F.2.50) заменяются одним уравнением политропы
р/рп = const (или в линеаризованном виде 5р = пдр). Поэтому тепловые
процессы при колебаниях газа в трубе, очевидно, можно рассматривать
как процессы политропические с комплексным показателем политропы,
определяемым зависимостью F.2.58). Показатель политропы является
функцией произведения as =Ry/pcocp/\\ т.е. не зависит от вязкости.
На рис. 6.10 приведены кривые модуля и фазы для комплексного
показателя политропы в зависимости от os, рассчитанные по формуле F.2.58).
Предельные значения показателя политропы п = 1 при os =0 и п-к
при as ->°° описывают соответственно изотермический и адиабатический
процессы.
Воспользовавшись асимптотическим разложением F.2.46), а также
определением показателя политропы F.2.58), получим приближенную
зависимость, пригодную при больших значениях s:
/V —
к-\ у/Т
-1- 7*
os к os
F.2.63)
Из выражения F.2.63) непосредственно следует, что п ^ к при s -> °°.
Аналогичным образом получается приближенное выражение для
постоянной распространения в случае больших значений s
1 + / к-1+о
Ъ**ъ' + ib" = i +— , F.2.64)
s a
которое было найдено Кирхгофом для "широкой" трубы [197, 275].
205
В случае изотермического течения с к = 1 выражение F.2.64) переходит
в ранее приведенную приближенную формулу F.2.47) для постоянной
распространения слабосжимаемой жидкости. При значениях s -+°° Ъ «s /
и F.2.64) совпадает с решением для плоских акустических волн без учета
вязкости и теплопроводности.
Чтобы найти асимптотическое приближение для малых значений пара-
мера s, подставим в формулу F.2.58) разложения в ряд функций Бесселя,
ранее использовавшиеся при получении зависимости F.2.48). После
преобразований находим приближенное соотношение для показателя политропы
k-l (osJ
п « 1 + i ^—— F.2.65)
* 8 К J
и постоянной распространения
Zw
. F.2.66)
s aR
Из формулы F.2.65) следует, что при s « 0 п « 1.
Зависимость F.2.60) позволяет определить величину радиальной
составляющей скорости в зависимости от параметра s, определяющего влияние
нестационарности процесса. Критерий Прандтля Рг (точнее, а = \/Рг),
входящий в правую часть зависимости F.2.60), изменяется незначительно.
Для оценки значения радиальной составляющей скорости удобно разделить
амплитуду вариации бТТна коэффициент оЗ/а, стоящий в правой части
зависимости F.2.60):
где учли, что для идеального таза а2 = кро/ро.
В статье [275] в качестве масштабного параметра для безразмерной
радиальной скорости используется приведенная частота к = Rto/a. Так как
отклонение скорости [275] нормируется к скорости звука, то отношение
dv'/Rco как раз совпадает с этой нормировкой. На рис. 6.11 представлены
кривые распределения модуля безразмерной амплитуды вариации
радиальной скорости в зависимости от параметрах. Кривые распределения
показывают, что радиальная составляющая скорости имеет максимальную
величину при небольших значениях параметра s, а при увеличении этого
параметра она резко уменьшается. При этом следует обратить внимание на то, что
скорость нормирована на величину Rco, a s = Ry/aj/v, и поэтому абсолютное
значение радиальной скорости 5 и'при росте частоты со убывает не так
резко, как безразмерная величина 5 v'/Rсо.
6.2.9. Фазовая и групповая скорости распространения. Обнаруженная
зависимость постоянных распространения j3 и Ъ от частоты свидетельствует
о том, что колебания распространяются в диспергирующей среде, для
которой скорость распространения возмущений зависит от частоты,
Для выяснения особенностей распространения в диспергирующей среде
сигналов ("пакетов"), состоящих из группы частотных гармоник,
рассмотрим простейший случай с наложением только двух волн одинаковой
амплитуды и близкими волновыми членами.
206
Складывая два сигнала, описываемых косинусоидами, с помощью фор-
мулы сложения косинусов находим
cos(co2f - к2х) =
Г / х]
(соi ( fc|
Г t х I Г
(со2 -соО—~(*2 "*i)j cos (
B i)y|
F.2.67)
Первый множитель в правой части формулы F.2.67) описывает относитель-
р и с. 6.12. Картина "волновых
пакетов"
но медленные колебания (с малым волновым числом (к2 - ki) /2 и малой
частотой (со2 - coi)/2), которые модулируют колебания с большой
частотой (coi+co2)/2. Комбинация из двух волн с разной частотой имеет
форму ряда волновых "пакетов" (рис. 6.12), двигающихся со скоростью
(со2 — <oi)/(fc2 -к\) и не обменивающихся между собой энергией через
узловые точки, в которых амплитуды равны нулю.
Скорости распространения каждой из гармоник п\ = coi/hi и а2 = со2/к2
являются фазовыми скоростями. Фазовую скорость можно рассматривать
как скорость распространения любой заданной фазы синусоидальной волны
при данной частоте. В диспергирующей среде как волновое число, так и
фазовая скорость зависят от частоты. А это значит, что гармонические
волны разных частот распространяются с разными скоростями.
Зависимость, связывающая волновое число (в нашем случае это |3со или
Ьсо), например, по формуле F.2.66) с другими параметрами, называется
дисперсионным уравнением. Возможны два механизма возникновения
дисперсии. В первом механизме зависимость волнового числа от частоты
определяется физическими свойствами среды, в частности, зависимостью
возникающих при движении жидкости напряжений силы трения от частоты.
Другим примером подобной дисперсионной среды может служить
двухфазная смесь жидкости с пузырьками газа [140]. Второй механизм дисперсии
не зависит от свойств среды и определяется условиями на границе среды.
Примером подобного механизма может служить движение невязкой
жидкости в тракте с податливыми стенками, для которых необходимо учитывать
их инерцию. К этому типу колебаний с дисперсией относятся
гравитационные волны на поверхности воды, изгибные волны в стержне и т.д.
В принятой выше форме записи гармоническая волна,
распространяющаяся в положительном направлении оси jc, записывается так:
o t ) = Z?exp(— Z/cox)exp /
= В exp(- b'ojx/ao)expi(cot -b"ojx/ao).
Первая экспонента с отрицательным вещественным показателем
характеризует темп затухания колебаний по длине. Из второго сомножителя следует,
207
0,8
Va w
ao ao
/
f.
\l\
- -
"
'afa.
P и с. 6.13. Фазовая (а/а0) и групповая (и>/я0)
скорости распространения сигнала в вязком тепло
проводном газе
что фазовая скорость равна
а = ао/Ь"9 F.2.68)
где а0 — скорость звука в газе. Если
сигнал состоит из двух или более
синусоидальных волн различных частот, то суммарный
сигнал ("волновой пакет" - см. рис. 6.12)
движется со своей групповой скоростью
w = (a>2 -to1)/(k2 -k1) = Aco/Ak=doj/dk.
Эта скорость характеризует распространение
1 ч ° s модуляции ("пакета"), образующейся при
суперпозиции ряда гармоник. Так как
скорость распространения у каждой гармоники своя, то при движении "пакета"
форма его изменяется.
Групповая скорость совпадает со скоростью распространения
максимальной амплитуды в волновом пакете, и поэтому она должна совпадать
со скоростью переноса энергии. Для простейшего случая выше было
показано, что энергия колебаний распространяется вместе с волновым пакетом.
Между групповой скоростью w и фазовой скоростью а существует
соотношение [139]
Эсо
w = a + k , F.2.69)
Ък
где к = со/а — волновое число. Для недиспергирую щей среды w = а = а0, но
они могут значительно различаться при наличии дисперсии.
Для трубы, заполненной вязким теплопроводным газом, групповая
скорость определяется соотношением [275]
w 2
~а^ ~ b"(s) + d[sb"(s)]/ds ' F.2.70)
На рис. 6.13 приведены графики для отношений скоростей w/a0 и а/а0 в
зависимости от параметра 5, полученные путем численного
дифференцирования мнимой части постоянной распространения Ъ" [275].
Обнаруживается значительное отличие групповой скорости от фазовой, при этом w>a.
Отличие в скорости распространения сигналов разных частот через
диспергирующую среду может служить одним из возможных объяснений
появления золн — "предшественников", обнаруженных при
экспериментальном исследовании коротких импульсов в трубах, заполненных
жидкостью [228]. При экспериментах обнаружено неожиданное появление
высокочастотных возмущений, предшествующих появлению основного
импульса в приемном преобразователе. Появление слабого
высокочастотного сигнала — "предшественника" можно связать с тем, что
высокочастотная составляющая сигнала в диспергирующей среде распространяется
208
Сем. Рис- 6.13) со скоросхью, близкой к скорости звука До, а основной
сигнал - с групповой скоростью w <а0 [275].
6.2.10. Участок тракта как четырехполюсник. Так же как в гл. 5,
преобразуем уравнения участка тракта F.2.43) и F.2.44) к форме уравнений
четырехполюсника, приняв ф0 - Ф\ = 0, ду0 = 5р@), 5>>~i = dp A). После
преобразований находим
expj3co+exp(-
517@) = Г
ап [ехр /Зсо - ехр(- 0со)] ап [ехр (Зсо - ехр(- j
F.2.71)
2др@) ехр0бЗехр@о)
617A) = =—др A).
ап [ехр /Зсо - ехр (- /Зсо )] ап [ехр Дсо - ехр (- |3со )]
Используя связь между экспоненциальными и гиперболическими
функциями, преобразуем соотношение F.2.71) к следующей форме:
517@) = (l/an)cth0w6p @) - A/ап sh/Зсо) 6р A),
F.2.72)
или в матричной форме:
Г5к@) 1 2_ Г cth/ЗоЗ - l/shi3cu 1 Г 6р@) 1 = Г5р@) 1
[5]JA)J anLl/sh^o3 -cthj3o3 JL5p(l)J У [ 6рA) J '
где у — матрица проводимости участка тракта. Для анализа тракта,
состоящего из участков, расположенных последовательно друг за другом, удобна
другая форма записи уравнений - в ^-параметрах. Используя формулы
преобразования уравнений чатырехполюсников [15, 159], находим
16.2.74)
где В — матрица передачи (цепной) четырехполюсника. Аналогично в
Л-параметрах
5р@I =
S«(O)J
Г5р@) j| Af
-517@) J L(lK)shPo3 ch/3co Jl6mA)J 1817A)
Если потерями на вязкое трение можно пренебречь, то приняв в формулах
F.2.71) и F.2.75) ? = 0, х=1,Оп= а, получаем формулы, выведенные
в гл. 5.
Приведенные выше формулы F.2.71) — F.2.75) можно использовать
во всех случаях, когда волновое число — параметр комплексный (вне
зависимости от режима течения жидкости в тракте), если известны
зависимости от частоты для ? и х
Н. Б.ф. Гликман 209
§ 6.3. Колебания турбулентного потока в тракте
6.3.1. Переход ламинарного режима в турбулентный при нестационарном
течении. Для стационарного ламинарного течения существуют предельные,
критические значения числа Рейнольдса, при котором слоистое,
организованное ламинарное течение теряет устойчивость и переходит в хаотичное,
нерегулярное турбулентное течение.
Для стационарного течения в трубе число ReKp, при котором ламинарное
течение переходит в турбулентное не меньше 2000. Значение ReKp
существенно зависит от условий организации течения, в особенности — от условий
на входе в трубу. При отсутствии возмущений на входе ReKp увеличивается
до нескольких десятков тысяч. При переходе от ламинарного течения
к турбулентному резко изменяется закон, связывающий трение со
скоростью движения — вместо линейного оно становится квадратичным.
Критическое число ReKp при прочих равных условиях зависит от градиента
давления и скорости вдоль потока. Течение с падением давления и ростом
скорости более устойчиво, чем течение в области возрастания давления и
падения скорости. Этот факт предсказан теорией устойчивости и хорошо
подтвержден экспериментально [152, 242].
Теоретический анализ устойчивости ламинарного нестационарного
течения чрезвычайно сложен, и имеющиеся немногочисленные работы дают
противоречивые результаты [202, 258]. Достигнуты определенные успехи
в опытах по определению влияния колебаний жидкости в непроточной
трубе на устойчивость течения. Первое систематическое экспериментальное
исследование было проведено СИ. Сергеевым на установке, состоящей
из стеклянной трубки и пульсатора в виде сильфона [202] .Нижняя крышка
сильфона приводилась в движение кривошипно-шатунным механизмом.
Опыты проводились как с вынужденными колебаниями столба жидкости
с сильфоном, так и при свободных колебаниях этой системы. В
экспериментах использовалась вода разной температуры, варьировался как диаметр
трубок Д так и амплитуда h и частота (о? = 4 - 25 с) колебаний.
В результате удалось охватить достаточно широкий диапазон чисел
Рейнольдса по амплитуде колебаний скорости Re = Dhco/v = 50 - 3 • 104 и
величине параметра s « R \/со/р = 4 - 40. Переход от ламинарного к
турбулентному режиму движения определялся визуально по движению
добавляемых в воду частиц алюминиевой пудры. Визуальные наблюдения позволили
достаточно четко различать режимы течения, при этом в случае медленного
повышения или понижения частоты колебаний переход режима течения
от ламинарного к турбулентному и наоборот происходил почти без
гистерезиса. Обработка результатов наблюдений по критическому числу Рейнольдса
ReKp показала, что критическое значение пропорционально параметру s:
ReKp=700s. F.3.1)
Если учесть, что при s = 0 ReKp = 2500, то формулу F.3.1) можно уточнить:
(R 2500) () 1 F.3.2)
где ф) = 1 + s2/1152 при s < 4 или c(s) = s/y/JT^ 3/8 при s >8.
Сопоставление кривых на рис. 6.14, построенных по формулам F.3.1) и F.3.2)
210
р и с. 6.14. Зависимость
критического числа Рейнольдса от параметра
К° s [202]
(линии 6 и 7), показывает, что
при s > 5 значения ReKp в обеих
зависимостях практически
совпадают. Из F.3.1) следует, что
отношение
ReKpA =
4-2
1-5
не зависит от диаметра трубы и Q to 20 30
переход от ламинарного к
турбулентному режиму определяется
критическим значением амплитуды колебаний /*кр и комплексом \/cj/r
На рис. 6.14 приведены экспериментальные точки при критических
значениях ReKp, полученные для стационарных колебаний при трех диаметрах
трубок (точки 1, 2, 3 - диаметры 3,8; 8,6 и 12,4 мм соответственно).
Экспериментальные точки имеют сравнительно небольшой разброс
относительно прямой, определяемой формулой F.3.1). Часть опытов
проводилась со свободными затухающими колебаниями системы "столб
жидкости - сильфон". Оказалось, что при затухающих колебаниях переход
от турбулентного режима к ламинарному затягивался. Соответственно
точки для ReKp при свободных колебаниях D и 5 на рис. 6.14) лежат
несколько ниже прямой, проведенной по точкам, полученным при
вынужденных колебаниях. Результаты экспериментов СИ. Сергеева показывают,
что при колебаниях жидкости в трубе повышается устойчивость
ламинарного режима течения, который сохранялся до числа Re (по амплитуде
скорости) порядка 3 • 104.
Другое экспериментальное исследование перехода к турбулентному
режиму при периодическом движении жидкости в трубе проведено Хино и
др. с помощью термоанемометра [258]. В установке использовались
поршневые пульсаторы и трубы двух диаметров - 14,5 и 29,7 мм, частота
варьировалась от 1/6 до 1 Гц. Изменение хода поршня, частоты вращения
пульсатора, диаметра труб и поршней позволило исследовать периодическое
Движение в области чисел Re (по амплитуде средней скорости) от 105 до
5830. Для анализа результатов экспериментов с пульсирующим течением
используем число Рейнольдса, построенное по толщине вязкого слоя у
колеблющейся пластины (см. формулу A.5.13)), - Re§ = hojbjv, где 5 =
= \j2vl<jj\ h — амплитуда перемещения жидкости в трубе. Новое число Re§
связано с ранее введенным Re:
Для опытов, описанных в работе [202], условия перехода от
ламинарного течения к турбулентному характеризуются одним значением ^еб >
Н* 211
получаемым из соотношения F.3.1):
Re5 = ReKp/\/2 s = Ш/у/Т « 500.
к p
Результаты обработки экспериментов по переходу к турбулентности,
приведенные в статье [258], дают близкое к указанному значение
критического числа Re6Kp = 550. Однако при этом отмечается, что данные измерений
скорости с помощью термоанемометра в разных точках по радиусу трубы
показали, что существует несколько границ перехода от ламинарного
течения к турбулентному.
Можно назвать следующие типы осциллирующих потоков: ламинарный
(в дальнейшем будем писать — тип а), искаженный ламинарный (тип б),
слабо турбулентный (тип в), условно турбулентный поток (тип г) и,
вероятно, полностью развитый турбулентный поток (rand, который не был
получен в работе [258] из-за ограниченных возможностей
экспериментальной установки). Все типы потоков квалифицируются по .числу Рейнольдса
Re (или Re5) и параметру s (параметр Стокса).
Первые отличия от ламинарного течения (тип б) заключаются в
отклонении профиля скорости от теоретического. При дальнейшем увеличении
числа Re на искаженный ламинарный поток накладываются возмущения
небольшой амплитуды и достаточно высокой частоты — это первый
переход к турбулентности (тип в).
Граница, определяемая условием Re6 =500 — 550, характеризует
переход, при котором в период уменьшения скорости в жидкости
зарождается сильная турбулентность с достаточно высокой амплитудой, но более
низкой (чем для типа в) частотой пульсаций, внезапно исчезающих в начале
периода увеличения скорости.
На рис. 6.15 приведены характерные осциллограммы с записью
мгновенных значений скорости в различных точках сечения трубы по радиусу г
для течения с Re6 = 1530, Re = 5830, s = 2,7, D = 14,5 мм, со = 2,1 с,
hco & 6 м/с. В области за максимумом скорости при режиме "условной
турбулентности" (тип г) наблюдается достаточно резкое искажение кривой
изменения скорости — появляются флуктуации с относительно низкой
частотой и большой амплитудой. Режим называется условно турбулентным,
так как турбулентность появляется только в фазе замедления течения, в
то время как в следующей за ней фазе ускорения потока турбулентные
пульсации исчезают, и поток возвращается к режиму течения, близкому
к ламинарному. На рис. 6.15 приведены и расчетные кривые (пунктирные)
для ламинарного периодического движения в тех же условиях.
Отличия расчетных кривых от экспериментальных имеют место в период
замедления движения жидкости. На этом этапе в центре трубы происходит
внезапное уменьшение скорости, сопровождающееся сильными трубулент-
ными пульсациями, а у стенки в этот же момент скорость мгновенно
возрастает, становясь выше скорости ламинарного течения. Появление
пульсаций относительно низкой частоты по всей видимости свидетельствует
о возникновении крупномасштабных вихрей. Таким образом, на части
периода колебаний профиль имеет ламинарный характер с большой
неравномерностью поля скорости по сечению, а на этапе замедления течения —
турбулентный, более наполненный профиль.
212
3/2П
2U
Рис. 6.15. Запись мгновенных значений скорости в разных точках по радиусу
пульсирующего потока в сопоставлении с расчетами для ламинарного течения [258]
Эксперименты в диапазоне значений параметра s от 2 до 8,7 показали,
что независимо от s течение переходит в условно турбулентное при Re§
кр
^ 550. Для s < 2 это условие не соблюдается, так как при значениях
Re§ > 550 поток остается ламинарным. Интересно отметить, что
критическое число Re§ для периодического движения в трубе, при котором
кр
поток на части периода колебаний переходит в турбулентный, совпало в
двух проведенных по разным методикам экспериментальных
исследованиях [202, 258].
Обнаруженное в этих экспериментах увеличение устойчивости и, в
частности, переход от турбулентного к ламинарному режиму при ускорении
потока и, наоборот, уменьшение устойчивости и переход к турбулентному
режиму при замедлении потока является общей закономерностью,
характерной для многих типов течений [152, 242]. При экспериментах с
периодическим движением жидкости, где измерения скорости проводились
термоанемометром [258], как уже отмечалось, кроме описанного режима с тур-
булизацией течения на части периода колебаний наблюдались и другие
промежуточные режимы. Для малых значений числа Re и параметра s профили
скорости вначале совпадают с теоретическими ламинарными, а затем, с
увеличением числа Re, начинают немного искажаться, отклоняясь от
теоретических в центральной части трубы на начальной стадии увеличения
скорости. При дальнейшем росте Re и сохранении неизменным s на искаженный
ламинарный поток начинают накладываться возмущения небольшой
амплитуды, но достаточно высокой частоты — на гладких кривых появляется
мелкая "рябь". Этот режим в случае увеличения параметра s возникает
при более низких числах Re и продолжается плоть до чисел Re5 « 550,
когда он переходит в уже описанный условно ~ рбулентный режим течения.
213
В слабо турбулентном периодическом течении форма амплитуды
профиля скорости близка к теоретической амплитуде ламинарного потока, сдвиг
же фазы в центральной части трубы значительно отличается от
теоретического. Следует обратить внимание на то, что первый переход от ламинарного
течения к искаженному ламинарному, а затем - к слабо турбулентному
приходится на период ускорения потока, в то время как для условно
турбулентного режима наоборот - при ускорении поток ламиниризируется.
Эти явления не нашли пока объяснения, как впрочем и многие другие
вопросы, связанные с устойчивостью нестационарного течения.
Результаты визуального исследования устойчивости периодического
движения жидкости в плоском канале приведены в работах В.Г. Козлова
и Г.Ф. Шайдурова [121, 122]. Эксперименты проводились в прозрачных
плоских каналах с разной высотой Н B, 5 и 9 мм) и длиной 1,5 м.
Неустойчивость определялась по фото- и киноснимкам, для визуализации
в воду вводили алюминиевую пудру. Неустойчивость проявлялась во
взрывообразном развитии поперечных вихрей ("валов" по терминологии
авторов), ось которых вытянута по ширине канала. Критическое число
ReKp *), определяющее границу устойчивости движения, зависело от
наличия возмущающих факторов (пузырьки воздуха, неровности стенок,
негармоничность колебаний и т.д.), причем критическое число существенно
снижается (в 2—6 раз) при наличии возмущений. Соответственно (рис. 6.16)
появляются две кривые для ReKp. На экспериментальных кривых границ
устойчивости как для движения без возмущения (кривая / на рис. 6.16),
так и с возмущениями (кривая 3)л построенных в параметрах ReKp — s,
имеется минимум при значениях s = 7 - 9. Анализ кинограмм показал,
что при s < 7 имеют место встречные потоки у стенки и в ядре течения.
Кризис ламинарного движения наступает в результате неустойчивости
границ встречных потоков, которая проявляется в образовании на границе
потоков вихрей ("валов"). Вихри наиболее развиты при фазе колебаний
с расходом, близким к нулю, и существуют только на части каждого
полупериода. Размеры вихрей соизмеримы с высотой канала. Эта картина
похожа на характер периодического движения на рис. 6.15.
В случае больших значений параметра s (s > 17) характер движения при
отсутствии возмущений изменяется — нестационарность проявляется
только вблизи границы, в динамическом пограничном слое (слое Стокса),
в ядре же мы наблюдаем практически однородное поле скорости.
Возмущения зарождаются у стенки в виде вихревых структур и из пограничного
слоя проникают в ядро, турбулизируя весь объем жидкости. При s > 17
граница устойчивости близка к прямой, определяемой формулой F.3.1)
(штриховая прямая 2 на рис. 6.16). Качественно результаты экспериментов
авторов статей [121, 122] совпадают с данными, полученными в
цилиндрических трубах другими авторами [202, 258].
Результаты исследования устойчивости течения Пуазейля при наложении
на него гармонических колебаний изложены в работе Сарпакая [199].
Эксперименты проводились в трубопроводах длиной 16,6 м и диаметром
12 и 10,7 мм с плавным входом из успокоительной емкости. За счет хоро-
1) Число Рейнольдса также определялось по амплитуде колебаний средней по
сечению скорости 8U': Re = bU'H/v.
214
рис. 6.16. Границы устойчивости
ламинарного пульсирующего потока [122]
Рис. 6.17. Критическое число Рейноль-
дса ReKD как функция параметров \ и п
s [199] и
12
18
1700
0,8
1,0
шей организации течения на входе в тракт и отсутствия возмущений
стационарный поток оставался ламинарным до Re = 6500. Гармонические
колебания создавались с помощью поршневого пульсатора на выходе из тракта.
Частота изменялась от 0,5 до 3 Гц вследствие изменения хода пульсатора.
Относительная амплитуда средней скорости 8UIU0 = X изменялась в
пределах от 0,1 до 0,9. Здесь 8U* — амплитуда периодической составляющей
средней по сечению скорости, Uo - средняя скорость течения.
Для оценки устойчивости течения в поток вводилось возмущение —
подвижная проволочка, которая с помощью электромагнита выдвигалась на
определенное время через стенку трубы в пограничный слой. За счет тур-
булизации в потоке на время возникало турбулентное течение
("турбулентные пробки"), которые фиксировались по изменению перепада давления
на двух участках трубы длиной 0,6 м. Критическое число Рейнольдса
Определялось по поведению турбулентной пробки в трубе. Если искусственно
вызванные турбулентные пробки росли (т.е. увеличивалось
зафиксированное время прохождения ими второго датчика по сравнению с первым), то
215
режим считался сверхкритическим, если затухали - докритическим. Для
уверенного определения точки, соответствующей нулевому нарастанию
длины пробки, определяющей ReKp, эксперименты повторялись много раз.
Результаты экспериментов, приведенные на рис. 6.17, построены в виде
зависимости критического числа Рейнольдса ReKp = 2RUolv от X при
различных значениях параметра s. С увеличением относительной амплитуды
скорости X ReKp сначала возрастает, достигая максимума, а затем быстро
убывает. При этом значения ReKp для пульсирующего течения (как и в
работе [202]) превышают соответствующие критические числа Re для
стационарного течения Пуазейля. Таким образом при определенном сочетании
значений Re, X и s конечные возмущения, нарастающие при стационарном
течении, в случае пульсирующего течения, наоборот, затухают.
Максимальные значения ReKp при заданном X убывают с ростом параметра s. Однако
следует обратить внимание, что в экспериментах, описанных в работе [199],
параметр s не превышал 8. Эти результаты согласуются с левой ветвью
кривой 1 на рис. 6.16.
Вопрос о том, сохранится ли такой же характер зависимости ReKp от s
при больших значениях 5 для ламинарного течения с протоком остается
открытым. При наличии среднего протока форма мгновенного профиля
скорости существенно зависит от величины X. При малых X за счет
наложенных пульсаций на профиле скорости появляется перегиб. Значение X,
при котором этот перегиб возникает, отмечено на рис. 6.17. Здесь же
указана и другая характерная точка - значение X (разное для разных s), при
котором для некоторой фазы колебаний появляется возвратное течение у
стенки трубы. Появление точки перегиба, а тем более возвратного течения,
должно способствовать потере устойчивости потока.
Однако точка перегиба и возвратные течения существуют только на
части периода колебаний. Этот отрезок времени увеличивается с ростом X.
На другой части периода колебаний поток ускоряется, что способствует
затуханию турбулентных пульсаций. Отношение времени существования
точки перегиба к периоду колебаний в определенной степени может
служить мерилом способности пульсирующего потока увеличивать или гасить
турбулентные пульсации. Обработка данных экспериментов показала [199],
что максимум ReKp на рис. 6.17 для каждого значения s достигается
примерно при одинаковом относительном времени существования точки
перегиба, равном 50% периода колебаний. При дальнейшем увеличении
этого времени ReKp резко уменьшается. Этому способствует по всей
видимости как рост относительного времени существования точки перегиба,
так и появление возвратных течений у стенки трубы. Эксперименты с
негармоническим изменением градиента давления [199] подтвердили данные
работы [122], что для негармонических колебаний критическое число
Рейнольдса меньше, чем для гармонических колебаний.
Вопрос об устойчивости ламинарного движения жидкости
рассматривался в ряде работ применительно к задаче о свободных колебаниях жидкости
в трубе U-образной формы. Эксперименты с измерением скорости
термоанемометром и визуализацией потока показали [251], что при
определенных сочетаниях числа Рейнольдса и параметра s в процессе свободных
колебаний жидкости возможна потеря устойчивости и переход к турбулент-
216
ноМу движению. Турбулентность, так же как и при вынужденных
колебаниях, наблюдается при определенной фазе течения, в то время как для
другой фазы характерно ламинарное движение.
Сопоставляя результаты всех описанных экспериментальных
исследований устойчивости ламинарного нестационарного движения, можно
констатировать, что качественно они в основном согласуются между собой, хотя
еще остается много неясных вопросов.
6.3.2. Уравнение нестационарного турбулентного движения жидкости с
использованием квазистационарного распределения для турбулентной
вязкости. Как уже отмечалось в § 1.3, важнейшим вопросом теории
турбулентности является выбор методов осреднения беспорядочных флуктуации
параметров в турбулентном потоке. Задача эта особенно насущна для
нестационарных режимов течения. На практике для стационарных течений
используют пространственный или временной способ осреднения по
определенной области пространства или промежутку времени. Принципиально
более строгим является общий метод пространственно-временного
осреднения [165].
Использование временного или пространственного осреднения удобно
с точки зрения практики, но вызывает трудности при теоретическом
анализе. Поэтому в теории турбулентности отдают предпочтение использованию
аппарата теории случайных функций, считая каждое мгновенное поле
течений как случайное поле. Проводя много раз измерения случайных
полей одного и того же течения, получают множество значений величин
(векторов), характеризующих поле течения при одних и тех же внешних
условиях. По результатам опытов можно определить средние значения
параметров поля течения, которые будут мало изменяться при
увеличении числа опытов, колеблясь около постоянного среднего значения,
Характеристики поля определяются распределениями вероятности для всех
параметров поля. Однако, удобный для теоретических исследований
строгий статистический подход вызывает затруднения при сопоставлении
с данными измерений. В большинстве случаев при исследовании
турбулентности результаты получают не в виде данных измерений при длинной серии
повторяющихся аналогичных опытов, а в виде измерений, полученных при
единичных опытах. В статистике, в том числе и в теории турбулентности, в
этом случае используют гипотезу эргодичности, состоящую в том, что
временное среднее значение измеренного параметра при неограниченном
увеличении интервала осреднения сходится к соответствующим
вероятностным средним значениям параметра. Использование гипотезы эргодичности
позволило определить для стационарных турбулентных течений, часто
встречающихся в практике (течение в трубе, пограничный слой, струи
и т.д.), эмпирические константы, входящие в полуэмпирические модели
турбулентности. Эти модели позволяют проводить расчеты достаточно
широкого круга стационарных течений.
Применительно к нестационарным турбулентным течениям
(статистически нестационарным) условие эргодичности не выполняется,
увеличивается число независимых переменных. Часто для нестационарного течения
необходимо учитывать сжимаемость, в то время как для того же потока в
стационарных условиях сжимаемость не оказывает никакого влияния. В ре-
217
зультате исследования нестационарных турбулентных потоков оказывают
ся задачей существенно более сложной, чем непростая проблема турбулент
ности стационарных течений. Одним из принципиальных вопросов эксперт
ментального исследования нестационарного турбулентного движения
является вопрос о способе осреднения измеряемых величин без
использования гипотезы эргодичности. Применительно к нестационарному течению
с произвольным законом изменения параметров движения во времени
наиболее обоснованными являются осреднения по множеству реализаций
процесса, воспроизводимых путем многократного повторения одинаковых
режимов течения, в одних и тех же условиях [128, 156, 237, 240, 264].
В случае периодического изменения режима течения во времени осреднения
ведутся по множеству реализаций одной и той же фазы колебаний заданной
частоты [240,254,265].
Полученные немногочисленные экспериментальные данные относятся
в основном к измерениям полей мгновенных скоростей и в меньшей
степени - характеристик турбулентности при нестационарном течении. Они носят
фрагментарный характерно могут быть использованы для проверки тех или
иных полуэмпирических моделей нестационарного турбулентного течения.
Отсутствие систематизированных данных о характеристиках
турбулентности (коэффициенте турбулентной вязкости, масштабе турбулентности,
энергии турбулентности и т.д.) для нестационарного турбулентного
движения затрудняет разработку модели таких течений. С другой стороны,
известны данные экспериментов [25, 26, 156, 157, 253, 257, 264, 265],
которые показывают, что как в ламинарном, так и в турбулентном
нестационарном движении профили скорости, напряжение трения на стенке, диссипация
энергии отличаются от аналогичных характеристик для стационарного
движения. Квазистационарный подход И.А. Чарного [234], при котором
нестационарное течение рассматривается как последовательная смена
стационарных состояний, не объясняет обнаруженных в экспериментах
особенностей нестационарного движения жидкости.
Учитывая выявленные особенности нестационарного движения и
отсутствие данных о характеристиках турбулентности при таком движении,
предложено несколько вариантов математических моделей
нестационарного турбулентного движения с использованием уравнения Рейнольдса A.3.5)
для нестационарного движения и квазистационарных уравнений,
описывающих характеристики турбулентности. В некоторых случаях эти уравнения
замыкаются с помощью уравнения турбулентной энергии A.3.12) и ряда
полуэмпирических соотношений, полученных с использованием опытных
данных для стационарных течений [36, 93, 94, 239]. Такой подход на
первый взгляд кажется более предпочтительным, так как использование
уравнения энергии турбулентности позволяет достаточно детально учесть
изменения во времени и пространстве параметров, характеризующих
нестационарное турбулентное течение. Однако при проведении расчетов приходится
использовать эмпирические зависимости, полученные для стационарных
потоков. Таким образом, этот метод также является в определенном
смысле квазистационарным. К сожалению, привлечение уравнений энергии
турбулентности делает расчеты слишком громоздкими, что исключает
возможность их использования при анализе динамики сложных ПГС.
Поэтому в основном используют другие, также локально квазистационарные,
218
0 более простые методы, в которых уравнения Рейнольдса замыкаются
помощью различных полуэмпирических соотношений.
В одной из первых работ К.К. Федяевского и А.С. Гиневского [223]
использована зависимость, описывающая изменение напряжения трения в
нестационарном турбулентном пограничном слое как функцию расстояния
от твердой поверхности в виде полинома
Л-= 2 bk{t,x)n\
То к = 1
где V ~ У/Ь> h — характерный размер, а коэффициенты Ьк определяются
граничными условиями и уравнениями движения и, в частности, на стенке
17 = 0, т/то =1.
В дальнейшем аналогичная модель применялась О.Ф. Васильевым и
В.И. Квоном для описания нестационарного турбулентного движения в
открытом потоке [33, 35]. В этих работах при замыкании уравнений
Рейнольдса использовали соотношение полуэмпирической теории
турбулентности, в частности, формулу Буссинеска A.3.7) и предположение о
линейной зависимости турбулентного коэффициента вязкости от расстояния до
стенки у. Результаты расчетов показали отличие профилей как для
скорости, так и для касательного напряжения, от профилей в стационарном
течении. При ускоренном двджении максимум скорости достигается где-то
внутри, а не на поверхности открытого потока жидкости.
Описанный выше метод использовался в статьях Г.И. Мелконяна [160,
161] для расчетов нестационарного турбулентного напорного течения.
В этих работах условие прилипания жидкости на стенках не
удовлетворялось, турбулентная вязкость принималась осредненной по сечению потока.
Обратив внимание на определенную схожесть поведения ламинарного и
турбулентного нестационарных течений, Н.А. Панчурин и Д.Х. Ройзман
[181] попытались с использованием критериев подобия установить
взаимосвязь между разными режимами течения. Учитывая относительную
простоту решения задач о нестационарном ламинарном течении, такой подход
кажется заманчивым. Однако он требует достаточно убедительного
подтверждения данными экспериментов и сравнительными расчетами. Одним
из наиболее перспективных подходов к расчету нестационарного
турбулентного движения представляется метод с использованием формулы A.3.8)
и экспериментальных данных о профиле трубулентной вязкости [10, 64,
184, 268]. Опять же это локально квазистационарный метод, но не такой
грубый, как в случае с использованием квазистационарных профилей
скорости.
Остановимся подробнее на этом методе [64]. Рассмотрим
нестационарное турбулентное движение сжимаемой жидкости в цилиндрической трубе
с жесткими стенками, для которого средняя скорость течения Uo много
меньше скорости звука а. Движение осесимметричное, без закрутки
потока. Такое течение описывается уравнениями для средних параметров A.3.3)
и A.3.9). Учитывая условие Uo< а и малость градиента скорости вдоль
оси по сравнению с изменением скорости по радиусу, пренебрегая
массовыми силами, в уравнении A.3.9) можно отбросить конвективные члены,
член Рх и все члены с производными от скорости до х. Переходя к
безразмерным переменным: (U)=(u)/U0, (v) = (v)/U0, х =x/L, ?=r/R, (p) =
21?
= (p)/Po, t =ta/L9 с учетом всех предположений преобразуем уравнение
A.3.9) к следующему виду:
Ъ<Ъ) L Э Г ч Ып)] 1 Э<р)
Э7 R2ra дГ L Ъг J а Ъх
Аналогичным образом в безразмерных переменных записывается урав.
нение неразрывности A.3.3), в котором с помощью соотношения A.2.12)
исключена плотность,
1 Э<р> Э<г7> Ъ(и) (v)
— + — + — + —г- = 0. F.3.4)
a Ы Ъх Ъг г J
В начале этого раздела отмечались трудности, связанные с описанием
нестационарных турбулентных потоков, и преимущество использования
подхода к характеристикам турбулентности как случайным функциям
без использования гипотезы эргодичности. Однако экспериментальные
данные, на которых базируются описываемые локально квазистационарные
модели, и сами уравнения Рейнольдса F.3.3) и F.3.4) получены с
использованием интеграла A.3.1), предполагающего справедливость гипотезы
эргодичности. Поэтому приходится ограничивать диапазон интегрирования
в соотношении A.3.1), условно называя полученную величину средней
по малому отрезку времени [22]. При таком осреднении предполагается,
что <м > за этот малый отрезок времени остается неизменной, а (и1) =0.
Естественно, что такие условия строго не выполняются, однако ими
можно пользоваться с достаточной точностью в диапазоне частот
вынужденных или свободных колебаний столба жидкости, пока эти частоты
значительно ниже частот турбулентных пульсаций, в которых заключена большая
часть энергии турбулентности. Если длина акустических волн \>2ttR
(приближенно X > 20R), то, как показывает анализ спектра турбулентной
энергии [22], возможность корреляции акустических колебаний с
турбулентными пренебрежимо мала. При невыполнении этого условия возможно
взаимодействие вынужденных колебаний с турбулентными и
соответственно — изменение характеристик турбулентности, коэффициента
сопротивления трения и т.д. Однако сформулированное условие независимости
вынужденных и турбулентных колебаний является пока умозрительным и
требует экспериментальной проверки.
Для анализа особенностей нестационарного турбулентного течения, при
котором в трубе возбуждаются гармонические колебания скорости и
давления относительно небольшой амплитуды, удобно линеаризовать
уравнения F.3.3) и F.3.4) и соответствующие граничные условия. Представим
безразмерные средние значения переменных в виде суммы
установившегося местного значения параметра и его безразмерного отклонения
(вариации) <w> = 1 + Ьи, (Ъ) =у + би, <р> =1+5р, где ы = u/U0- безразмерное
стационарное значение продольной составляющей скорости в данной точке,
U=vlUo —то же самое для поперечной составляющей скорости, Ьи =du'/U0 —
безразмерная вариация продольной составляющей скорости в данной точке,
Su = dv'/Uo ~ то же самое для поперечной составляющей скорости, 8р = -
= 6р'/ро - безразмерная вариация давления в данном сечении,р0 — среднее
давление в трубе, Штрихами обозначены размерные вариации
соответствующих переменных.
220
рис. 6.18. Распределение коэффициента турбулент- J?__
ной вязкости по радиусу и
0,06
0,02
/
1
050
1,00 Ь
Так как представляют интерес динамические характеристики тракта,
то удобно сразу же подставить в линеаризованные уравнения частные
периодические решения системы уравнений, которые запишутся: Ьи -
= Ьы ехр(/cot), &v ~ 5пexp(zcof), dp = Ьр ехр(/со7),где ^ = ^L/a, бы,
5U, др — безразмерные амплитуды соответствующих вариаций - величины
комплексные, зависящие от х, 7 и со. После подстановки частных
периодических решений в линеаризованные уравнения F.3.3) и F.3.4) находим
дифференциальные уравнения, связывающие амплитуды колебаний
составляющих скорости и давления вдоль оси трубы и по радиусу:
L Э . .
F.3.5)
/со
а дх
d8v
5
aR2r 37
дТ
Sv дди
or
дх
¦ = 0.
F.3.6)
Для расчета нестационарного колебательного движения жидкости
воспользуемся четырехслойной моделью турбулентной вязкости. Профиль
принятого закона распределения vT по радиусу показан на рис. 6.18. Здесь
I; = R — г — расстояние от стенки трубы, и* -\Jtw /p'— динамическая
скорость, tw — касательное напряжение трения на стенке трубы. Первым от
стенки до границы с координатой ?i = 5v/u* расположен вязкий подслой,
в котором коэффициент турбулентной вязкости vT = 0. В следующем,
переходном слое коэффициент турбулентной вязкости определяется
зависимостью
рт=Аг\ F.3.7)
где А = 0,Q\fUll8v2, f = SrwlpUl - безразмерный коэффициент трения.
Переходный слой имеет границы:
В третьем слое коэффициент турбулентной вязкости в диапазоне
значений ? от ^2 = 40^/w* до ?з = 0}2R возрастает по линейному закону в
зависимости от расстояния до стенки
vT=B$, F.3.8)
где B = Q,32/fi$UR
221
В последнем, четвертом слое - турбулентном ядре в области значений ?
от 0,2R до оси трубы (? = 1) коэффициент турбулентной вязкости
остается постоянным:
\U0R. F.3.9)
Значения коэффициентов А и В в зависимостях F.3.7) и F.3.8)
получены из обработки экспериментальных данных работы Лауфера [262]. При
этом принимается предположение, что независимо от нестационарности
течения профиль турбулентной вязкости сохраняется, т.е. используется
гипотеза о квазистационарности профиля турбулентной вязкости. Так же
как ив § 6.2 для ламинарного течения, преобразуем уравнение движения
F.3.5), введя новую переменную
bz =5*7+-4-^, F-зл°)
icoa Эх
где градиент давления не зависит от радиуса и является некоторой, пока
неизвестной функцией
1 Ьдр
/г(х,п)=____. F.3.Ц)
icoa ох
Вначале удобно, не определяя функцию F(х, со), искать решение
уравнения движения через параметр bz , отнесенный к F(x, со):
Sz(x, со, г)
bz1 =— - = Ьпх +1,
F(x, w)
где Ьп1 = bu/F(x, со). После подстановки новой переменной bz1 в
уравнение движения F.3.5) получаем
, L Э Г bbz1 1
Я1=-=т?г- — \Ф + рт)—-\ . F.3.12)
itoR га Ъг L Ъг \
Уравнение F.3.12) для принятого (рис. 6.18) распределения
коэффициента турбулентной вязкости простого аналитического решения не имеет,
и его нужно решать численно. При численном решении методом прогонки
в каждой из четырех областей решения стыковались с использованием
равенства скоростей и касательных напряжений.
Проинтегрировав уравнение неразрывности F.3.6) по радиусу Т,
предварительно умножив все члены на 27гг, находим
/со _ ЪЬп
5р +—— = 0. F.3.13)
ос ах
Второй и третий члены, полученные из уравнения F.3.6), сокращаются
после интегрирования по частям. Для амплитуды среднего по сечению
отклонения скорости использовано соотношение
_ _ _ 11 _ 1 1
&U(x, со) =— / 2лгЬи(х, г, co)dr =— / 2тггЬп\п, r)F(x, со)dr~=
7Г О 7Г О
1
= 2F(x, со) / TiSz1 - \)dr. F.3.14)
о
222
Интеграл в формуле F.3.14) может быть вычислен по формуле Симпсо-
на> так как значения b~z l известны в каждой точке по радиусу 7 из
численного решения уравнения F.3.12). Продифференцировав уравнение F.3.13)
п0 х , имеем
id dbp d2dU
— — +—
a dx dx
dU
— = 0, F.3.15)
x2
а из соотношения F.3.14), определив вторую производную по х
d2bU 1
-_=—F"(*.o5), F.3.16)
где
r/(
/3 о
и подставив в уравнение F.3.15) найденные зависимости F.3.11) и
F.3.16), получаем обыкновенное дифференциальное уравнение для
определения функции F(x , со) :
- со 2E2F(x, со) + F" (х , со) = 0.
Решение этого уравнения имеет вид
F(x,a5) = Ai(bj)expQicJx)+Bl(cj)exp(--fiU>x). F.3.17)
Подставив решение F.3.17) в зависимость F.3.14), находим выражение
для амплитуды вариаций средней по сечению трубы скорости
5 U (х, со) = Сх(со) ехр (fiGSx) + С2(со) ехр (-]3со х). F.3.18)
Соотношение для амплитуды вариации давления вдоль оси трубы
получается после подстановки выражения F.3.18) в уравнение неразрывности
F.3.13):
др (Зс, со) = iotP [Ci(co) ехр (j3co x) - С2(со) ехр (-j3co x)], F.3.19)
неизвестные константы Сх (со) и С2 (со) определяются из граничных
условий F.2.42).
Подставив решения F.3.18) и F.3.19) в граничные условия F.2.42),
определяем функции Сх (со) и С2 (со), а затем находим зависимости для
амплитуд колебаний скорости и давления как функции координаты
х и частоты со:
5 U (х, со") = — {7i[(a~ ^o)exp(-|3co Jc) + (a + ф0) ехр (|3 со х )] дух -
~ То [(a+^i)exp<-j3co(l - Г)> + (а-^0 ехр
F.3.20)
5р (х, со) = -—-
- i//0)exp(-/3cox)] 5J! -То [(a+i//1)exp<-/3co(l -
-(а-^1)ехр<^а5A -^)>]5у0) , F.3.21)
где D = (а + ^о) (а - ^i) ехр (j3co) - (а - i//0) (а+ фг) ехр (-/Зсо). С
помощью соотношений F.3.10), F.3.11) и F.3.14) можно получить выраже-
223
0,20
'¦¦Г
д-j
¦ ¦¦¦! ¦ f ^^
o»A*
Рис. 6.19. Профили переменной состав,
ляющей скорости при различных частотах
V и числах Рейнольдса
0,8 Вй
ние, определяющее мгновенное значение амплитуды скорости в любом
сечении трубы,
1 ЬЬр .
Ьп(х,7, co) = 5z - — — = 6z l F(x, со)-
/ со а Ъх
, co)(8z l -
F.3.22)
Безразмерная вариация скорости связана с амплитудой соотношением
Ьи = Ьп ехр (zcoF), а вещественная составляющая скорости определяется
зависимостью
Re [6 и (х, 7, со)] = | 5 м (*, 7, со) | cos (со7 + </>), F.3.23)
где ^ = arg [5 и (x, 7, со)].
На рис. 6.19 приведены кривые для профиля переменной составляющей
скорости вблизи стенки трубы, рассчитанные по формулам F.3.22) и
F.3.23) при различных числах Рейнольдса Re = Uq2Rjv и различных
частотах со. Сплошные кривые изображают профили переменной
составляющей скорости при частоте со = 433 с, штриховые кривые — при частоте
со = 4767 с. Кривые 1 соответствуют расчетам при Re = 3,7 • 104,
кривые 2 - при Re = 2,6 • 104, кривые 3 — при Re = 667. Сопоставление
профилей переменной составляющей скорости показывает, что скорость, в
основном изменяется в узком слое у стенки. Характер профиля скорости у
стенки качественно согласуется с результатами измерений мгновенных
значений средней скорости в турбулентном потоке для трубы с наложенными
гармоническими колебаниями [27, 157, 254, 255, 264, 265].
В остальной области вплоть до оси трубы профили оказываются
плоскими. Как было показано в § 1.5, при пульсирующем ламинарном
движении имеется определенный динамический слой толщиной 5, на глубину
которого от стенки в жидкость проникают возмущения, связанные с
колебаниями жидкости. Толщина слоя 5 ~ \Jv\lo уменьшается с ростом частоты.
Графики на рис. 6.19 показывают, что и в турбулентном колеблющемся
потоке для переменной составляющей скорости имеется определенная
глубина проникновения возмущений 5Т, которая зависит от числа Re =
= Uo 2Rjv. Это связано с тем, что в турбулентном течении вязкостные
эффекты определяются турбулентной вязкостью vT9 которая не является
физической константой вещества, а определяется условиями течения и за-
224
исит от числа Re. Из кривых, приведенных на рис. 6.19, следует, что с уве-
ичением числа Re толщина динамического слоя 5Т уменьшается. При
определенной частоте толщина динамического слоя 5Т может стать меньше
толщины вязкого подслоя ?i (см. рис. 6.18). В этом случае все изменения
переменной составляющей скорости происходят в области течения, где
определяющую роль играет физическая вязкость жидкости v.
Для проверки эффективности предложенной математической модели
нестационарного турбулентного течения в трубе были проведены
эксперименты на специальной динамической установке. Исследовалось течение
воды в трубах, имеющих одинаковую длину 6,3 м и диаметры 10,4 и 2 мм.
go Frce три трубы вода подавалась из одного коллектора, перед которым
был установлен дроссельный пульсатор. Питание из общего коллектора
обеспечивало одинаковые входные условия и идентичность возмущений
во всех трубах. На концах труб были установлены дроссельные диафрагмы,
диаметр отверстий в которых подбирался из условия обеспечения
одинаковой скорости течения жидкости во всех трубах Uo ** 2 м/с. Колебания
300
Рис. 6.20. Амплитудные и фазовые частотные характеристики тракта
диаметром 10 мм
15.Б.Ф. Гликман 225
2,0
-300
Рис. 6.21. Амплитудные и фазовые частотные характеристики тракта
диаметром 4 мм
давления измерялись малоинерционными индуктивными датчиками,
расположенными как на входе, так и на выходе из каждой трубы, перед
диафрагмами. До начала экспериментов с гармоническими возмущениями были
проведены статические проливки установки на разных расходах для
определения коэффициентов потерь на трение в трубах и характеристик
дроссельных диафрагм.
При экспериментах с пульсатором, который создавал гармонические
возмущения на входах в трубки (в коллекторе), результаты измерений
переменных составляющих давления на входе и выходе трубок,
суммарного расхода воды через трубки (измеряемого турбинным расходомером)
и сигнала датчика положения пульсатора записывались на многоканальный
магнитофон. Обработка результатов частотных испытаний гидравлических
трактов проводилась с помощью анализатора передаточных функций с
выводом первичной информации на перфоратор. Вторичная обработка
проводилась на ЭВМ [64].
226
результаты обработки данных в виде амплитудно-частотных
характеристик (АЧХ) и фазово-частотных характеристик (ФЧХ) для труб трех
диаметров представлены на рис. 6.20-6.22. Приведены
экспериментальные точки для модуля и аргумента передаточной функции трубок Ьр i/Sp 0,
где bp o> &P 1 — амплитуды колебаний давления соответственно на входе
и выходе (перед диафрагмой) трубок.
На рис. 6.20 — 6.22 кружочками обозначены экспериментальные точки,
сплошной линией - частотные характеристики, рассчитанные по формуле
F.3.21), штрихпунктирной линией - рассчитанные по формуле F.2.44)
для условно ламинарного течения с учетом зависимости трения от частоты.
2,0
-100
-200
-300
Рис. 6.22. Амплитудные и фазовые частотные характеристики гракта
диаметром 2 мм
15* 227
На этих же рисунках пунктирные линии - результаты расчетов для квази
стационарной модели турбулентного течения по формуле F.1.10).
При расчетах по условно ламинарной модели в расчеты подставлялась
не физическая кинематическая вязкость жидкости v, а условная величине
эффективной вязкости ^Эф, определенная по коэффициенту сопротивле
ния трубки X, полученному с использованием данных проливок трубопро
водов на стационарном режиме. При этом величина коэффициента ^Эф
находилась по формуле
На выходе из трубок в диафрагмах срабатывалось практически/все
давление в трубе, но перед диафрагмой имелся некоторый объем Р^ полости
у мембраны датчика давления, который, как показали оценки, необходимо
учитывать в расчетах. Соответственно выходной импеданс записывается
в виде следующего выражения:
где Pi - давление перед диафрагмой, Арг - перепад давления на
диафрагме, G - расход жидкости через трубку, а - скорость звука в трубке.
Представленные на рис. 6.20-6.22 АЧХ трубопроводов имеют
резонансный характер. За счет влияния объема полости датчика для трубок
малого диаметра второй и третий резонансы имеют большую высоту, чем
первый. Из сопоставления экспериментальных точек с расчетными кривыми
видно, что результаты расчетов по четырехслойной модели нестационарного
турбулентного течения существенно лучше согласуются с данными
эксперимента, чем с результатами расчетов по квазистационарной модели
течения. Это расхождение увеличивается по мере роста потерь на трение (в
нашем случае — уменьшение диаметра трубки) и роста частоты колебаний.
Кривые АЧХ, рассчитанные по условно ламинарной модели, лежат
несколько ниже кривой для четырехслойной модели, но их отличие от
экспериментальных данных меньше, чем для квазистационарной модели. Кривые
ФЧХ на рис. 6.20 — 6.22, рассчитанные по разным моделям течения,
незначительно отличаются друг от друга и хорошо согласуются с
экспериментальными точками в исследованном диапазоне частот. Существенное отличие
расчетных кривых АЧХ для квазистационарной модели течения от
экспериментальных данных в области частот/ = 150-300 Гц (особенно для
трубки диаметром 2 мм) показывает, что модель с использованием
предположения о квазистационарности дает большую погрешность в случае ощутимых
потерь давления на трение и достаточно высоких частот колебаний.
Результаты сопоставления экспериментов с расчетами показали достаточную
эффективность четырехслойной модели нестационарного турбулентного
течения в трубе для расчета интегральных динамических характеристик
трактов. Аналогичный вывод был сделан в работе Д.Н. Попова [184].
Вполне удовлетворительно описывает динамические характеристики
трактов в исследованном диапазоне параметров существенно более простая
с точки зрения методики расчета условно ламинарная модель
нестационарного турбулентного течения. В качестве обоснования условно ламинарной
модели можно привести соображения об инерции турбулентности в потоке
228
[22], чт0 вызывает запаздывание в отклике на изменения профиля средней
скорости. Поэтому зависимость коэффициента сопротивления (или
напряжения трения) от числа Рейнольдса (т.е. скорости) должна иметь такой же
наклон, как и для ламинарного течения, для которого профиль вязкости
хакже не изменяется во времени. Однако эта гипотеза, подтвержденная
результатами экспериментов по определению суммарных динамических
характеристик в ограниченном диапазоне чисел Re и частот колебаний,
требует более детального экспериментального обоснования.
Использование квазистационарного профиля турбулентной вязкости в
модели нестационарного течения было впервые предложено в работах
Д.Н. Попова [184] и Брауна, Марголиса и Шаха [22]. В описанной выше
четырехслойной модели, в отличие от работ [22, 184], использован более
гладкий, без разрывов и резких перегибов профиль турбулентной вязкости,
что позволяет более точно определить локальные характеристики
турбулентного нестационарного течения вблизи стенки, а также мгновенное
значение касательного напряжения на стенке трубы.
В книге Д.Н. Попова [184] в расчетах по трехслойной модели
турбулентного течения несжимаемой жидкости использованы преобразования по
Лапласу и модифицированные функции Бесселя, позволившие найти
передаточные функции для касательного напряжения на стенке трубы и профили
скорости при колебаниях турбулентного потока в трубе. Применительно
к исследованию распространения колебаний малой амплитуды, наложенных
на турбулентное течение сжимаемой жидкости в трубе, в статье Брауна и
др. [22] уравнения Рейнольдса решаются с привлечением формулы Бусси-
неска и двухслойного или трехслойного квазистационарного распределения
турбулентной вязкости. Двухслойная модель ограничивала диапазон, в
котором возможно получить решения, поэтому для более высоких частот
применялась трехслойная модель.
На специальной экспериментальной установке с пульсатором были
определены фазовая скорость распространения и коэффициент затухания волн.
На рис. 6.23 приведены экспериментальные данные и расчетные кривые
для безразмерного коэффициента затухания а = R2aolv, где а —
коэффициент затухания на единицу длины трубы, а0 — скорость звука в жидкости
без учета влияния стенок. На рис. 6.24 представлены данные по изменению
относительной фазовой скорости а/а0, где а — фазовая скорость,
полученная по данным экспериментов. Расчетные кривые приведены для случая
локальной квазистационарности турбулентности и для ламинарного режима
течения, для которого была проведена часть экспериментов. Результаты
экспериментов вполне удовлетворительно согласуются с расчетными
данными, полученными с использованием трехслойного квазистационарного
распределения турбулентной вязкости, а также для ламинарного
нестационарного течения.
В следующей работе тех же авторов [155] приведены результаты
экспериментов на новой установке, имеющей большую длину рабочей части
A13 м). Это позволило расширить диапазон частот в сторону низких
частот - от 0,5 до 2500 Гц, что соответствует значениям безразмерной частоты
& = s2 от 20 до 5 • 103. Эксперименты многократно повторялись при
разных (но всегда малых) значениях амплитуд, при разных расстояниях меж-
ДУ датчиками. Для выяснения возможного влияния случайных факторов
229
R2af
-Ю3
-10'
ц г Промежуточная оязн
oRe=//00
Л =10
I
¦ =2 /041
• -5-\Ои г Наинизшая Вязкость
о =!05 J
Теория: Re = 105
105 S2=R2w/v
Рис. 6.23. Экспериментальные и расчетные значения безразмерного коэффициента
затухания [22]
^Теория: Re-101*
" Ламинарное о Re =11001 Наивысшая
течение д =/л^ Т дязкость
о -5-\0ц - Промежуточная
вязкость
• =5-1(Г\
о =/05 J
омежуточн
вязкость
Наинизшая
10"
fO5 S2=R2uj/v
Рис. 6.24. Экспериментальные и расчетные значения безразмерной фазовой
скорости [22]
(вибрации, внешних факторов) часть экспериментов проводилась при
ламинарном режиме течения. Эти эксперименты показали, что влияние
внешних факторов отсутствует. Такая тщательная проверка была связана
с неожиданностью полученных результатов — появлением больших пиков
значений коэффициента затухания о: (рис. 6.25) и фазовой скорости
(рис. 6.26) в диапазоне переходных частот. При этом в области ?2> 1200
данные хорошо согласуются с высокочастотной моделью локальной
квазистационарности турбулентности, при Г2 < 200 - хорошо согласуются с
низкочастотной моделью квазиустановившегося течения. В переходной же
области частот наблюдаются резкие колебания и пики для обеих
характеристик — а и а.
Авторы пытаются дать качественное объяснение обнаруженного пика
поглощения возможным резонансным взаимодействием турбулентных
вихрей и вынужденных колебаний жидкости. Однако приведенное
объяснение, как они сами отмечают, носит умозрительный характер. По всей
видимости, полученные неожиданные результаты требуют подтверждения
на другой установке и в других условиях, и в случае их подтверждения —
230
-1,0
10 1Ог 10J
Рис. 6.25. Безразмерный коэффициент затухания как функция П [155]
а/а0
П5
Ламинарное
течение
•
¦- '"I
0»
X
to
10г
/о3
Iff
Р и с. 6.26. Изменения безразмерной фазовой скорости в зависимости от
параметра П [155]
более детального исследования с визуализацией потока, термоанемометри-
ческими измерениями и т.д.
Попытка уточнить методику расчета с использованием профиля
турбулентной вязкости предпринята в статье Б.С. Байбикова, Г.А. Дрейцера,
В.Г. Изосимова и А.Н. Ширшова [8]. Используя эмпирическую зависимость
Для профиля турбулентной вязкости vT = рт(г, Re), в формулу для
коэффициента vT вводится корректирующий множитель z, для которого в
случае ускоренного течения принято z > 1, для замедленного — z < 1, а для
стационарного — z = 1. Величина корректирующего множителя
подбиралась по результатам экспериментов У .Р. Лийва для ускоренного и
замедленного течения [149, 150]. Как будет ясно из дальнейшего обсуждения,
результаты этих экспериментов вызывают определенные сомнения в
точности измерений. Кроме того, неясно, как использовать корректирующий
множитель для пульсирующего течения.
231
В работе Оми, Киомена, Усуи [268] предложен другой способ учета
возможного изменения турбулентной вязкости vT при нестационарном
движении путем использования связи vT с динамической скоростью и*^
= < U) VV8, где ( U) — осредненная по сечению за короткий промежуток
времени продольная составляющая скорости, X - коэффициент
гидравлического сопротивления трения жидкости о стенки тракта.
Следуя [268], уравнение F.3.3) после перехода к размерным
переменным и исключая vT запишем в виде
Ъ(и) _ 1 Ъ(р) / Ъ2(и) _1_ Ъ(и) \
Эг ро Ъх \ Ъг2 г Ъг ]
-—— (г<и'и'>). F.3.24)
г Ъг
Выделив отдельно составляющие турбулентных пульсаций и , v'up,
переменные составляющие (вариации) параметров за счет вынужденных
колебаний Ьи , dvr и Ьр и осредненные по большому промежутку времени (т.е.
средние для потока) параметры ut, vt npt, запишем для мгновенных
значений скоростей и давлений:
v = < v > + и = vt + 5 v1 + и, F.3.25)
Как и ранее, воспользуемся формулой Буссинеска
Po<u',v')=-pv* , F.3.26)
Ъг
где v * — величина турбулентной (вихревой) вязкости, в общем случае
равная у*=ут + Дут, vT -турбулентная вязкость для стационарного
течения, Дрт — переменная составляющая турбулентной вязкости, связанная
с колебаниями (нестационарностью) потока.
Обозначив v *+ v = р^, преобразуем уравнение F.3.24) к следующему
виду:
Ъ(и) 1 Ъ(р) Ъ2(и) / (Ivy. vT\ Ъ(и)
+ + К + F.3.27)
Ъг ро Эх Ъх2 \ dr г ) Ъг
Для распределения турбулентной вязкости применялась четырехслойная
модель с формулой для вязкости
Ak?+Bk = --Aku'K6t{\-r)+Bk (*= 1,2,3,4), F.3.28)
где ? =R -г, п* =u*/Ut, V^k -vxklv - безразмерная турбулентная
вязкость для к-го слоя, Ut — осредненная по большому промежутку времени
средняя по сечению скорость потока, ?* =u*%/v, Rer =2RUt/v, значения
А к и Вк для каждой из четырех областей приведены в табл. 6.1.
Здесь Rq* = u*R/v и ? *= Re * соответствует 7 = 0, а?* =0,175 Re*
соответствует 7 = 0,82. Изменения градиента давления Э< р) /Ъх подчиняют-
232
Таблица 6.1
Область
1
2
3
4
0-5
5-30
30-0,175 Re*
0,175 Re*- Re*
0
0,2
0,4
0
1
0
0
0,07 Re*
ся гармоническому закону
Ро Эх
= kt
где
*, = - —
Ро
Эр,
F.3.29)
F.3.30)
kt — осредненное по времени значение градиента давления в трубе, Xt —
коэффициент сопротивления трения для стационарного течения. Введя
безразмерные параметры р = < р> R2/p0v2i x = x/R, к = Ьк'/kt, ! = vtlR2,
п =s2 =R2 gj/v, сводим уравнение F.3.29) с учетом соотношения F.3.30)
к виду
Ър Re2tXt _
— = (l+kcosut). F.3.31)
Эх 16
Используя безразмерные параметры ^е = ^г/^3 "^ =г/Я,Ъ = Ж и] /v,
подставив зависимости F.3.29) и F.3.30) в уравнение F.3.27), находим,
что
дп _ д2й / dv~z ?% \ Ъи Rej Xt ^ __
= vv +( + I + A +kcos?lt). F.3.32)
Ы Ъг2 \ dr T ) Ъг 16
Уравнение F.3.32) решалось численным методом. При расчетах
использовались зависящие от частоты значения динамической скорости м*,
соответствующие мгновенному распределению скоростей. Значения и*
определялись из соотношения в безразмерных параметрах
п * = и * jUt = (Re/Rer) >/X/8,'
в которое подставлялись мгновенные значения параметров Re и X. Для
сравнения одновременно проводились расчеты при стационарных (средних)
значениях и*. Величина коэффициента сопротивления определялась из
зависимости
1/vT = 21g(Re vT) - 0,8. F.3.33)
Результаты расчетов (рис. 6.27) показали, что для Ret = 105, к = 0,5 и ^2 =
= 1—10 при использовании переменных значений и* распределения
скорости полностью соответствуют мгновенному стационарному распределению
233
Or
<й>\,м/с
20
16
12
8
0
f80°arg<u>
150°
120°
\<u
10
8
6
4
0
>\,M/C
>
> U v
У U <
4<? ^/
30°
60°
0,2 0 г
1,0 0,8 0,6 0,4
6
Рис. 6.27. Экспериментальные и расчетные эпюры амплитуды и фазы скорости в
пульсирующем турбулентном потоке [268]: расчет при u*= var, расчет
при и*- const, о - эксперимент
скорости, а при и* = const расчет отличается от квазистационарного. При ?2 =
= 100 профиль скорости при переменной и* уже не совпадает с мгновенным
стационарным профилем, т.е. поток не находится в квазистационарном
состоянии.
Из_ расчетов следует, что при прочих равных условиях с ростом частоты
до П= 104 и выше величина амплитуды скорости уменьшается
(несжимаемая жидкость), профиль амплитуды и фазы колебаний в ядре потока
приобретает плоский характер, а ближе к стенке на амплитудной
характеристике появляется максимум, который смещается по направлению к
стенке по мере роста частоты Г2. Отличие в результатах расчетов с переменной
динамической скоростью и * и при соблюдении условия и * = const
уменьшается по мере увеличения частоты, а при частоте П = 104 отличие
практически исчезает.
Из анализа результатов многих вариантов расчетов авторы статьи [268]
определяют области параметров Rer и ^2, в которых пульсирующее
течение можно считать квазистационарным.
Сравнение результатов расчетов с данными экспериментов при
вынужденных колебаниях воздуха в трубе показано на рис. 6.27. Эксперименты
проводились причастотах/= 0,0147 Гц (рис. 6.27,а: ?1 = 3,70, Re t = 82400,
?=0,733), /=1,5 Гц (рис. 6.27, б: Г2= 384, Re t = 60200, ?= 2,73) ,/ =
= 12 Гц (рис. 6.27, в: 11=3140, Re t = 40000, X = 22) . Сплошной линией
обозначены результаты расчетов с переменной и *, штриховой - с и * =
= const. Сопоставление кривых показывает, что для частоты/= 0,0147 Гц
234
профиль скорости является квазистационарным и результаты
экспериментов согласуются с расчетами при переменной и*. При/= 1,5 Гц данные
расчетов, полученные при переменной и *, приближаются к численным
результатам при постоянной м*, а при/= 12 Гц они практически совпада-
ют. Таким образом, для достаточно высоких частот й> 2500 можно
использовать более простую методику расчета с постоянной и*.
Существенно более простая модель нестационарного турбулентного
движения описана в работе Вуда и Фанка [45]. Используя однослойную
модель ламинарного пограничного слоя, авторы разбили течение на две
области. В пристеночной области, описываемой уравнениями пограничного
слоя, сосредоточены все эффекты, связанные с влиянием вязкости.
Толщина ламинарного слоя определяется диссипацией энергии на
установившемся режиме течения.
Диссипация определяется интегралом по пограничному слою толщиной А
для участка трубы длиной L за один период колебаний Т = 2тт/со. :
Ф = / / / (-— ) dydzdt.
ооо \ by )
Все остальные эффекты (инерция и сжимаемость жидкости) сосредоточены
в ядре потока, где профиль скорости принимается равномерным, т.е. имеет
место стержневой режим течения.
Эксперименты по затуханию одиночного импульса давления показали,
что теория вполне удовлетворительно согласуется с опытными данными.
В [220] однослойная модель распространена на пульсирующее
турбулентное течение. При этом обнаружено хорошее совпадение теоретических
расчетов с данными экспериментов [22] по коэффициенту затухания
колебаний в тракте.
§ 6.4. Статистический подход
к нестационарному турбулентному течению в трубе
6.4.1. Вводные замечания. Течение в длинной трубе на достаточно
большом расстоянии от ее концов является одним из простейших примеров
сдвигового турбулентного течения. Действительно, в отличие от течения в
пограничном слое или в струе (если не учитывать сжимаемость) осред-
ненная характеристика движения - распределение скорости по радиусу-
зависит только от одной пространственной координаты. Модели
турбулентных течений в трубах являются полуэмпирическими, с использованием
констант, полученных из опытов. Математические модели нестационарных
течений становятся более сложными; отсутствуют экспериментальные
данные о влиянии нестационарности течений на константы, входящие в
полуэмпирические зависимости. Приходится использовать предположение о
квазистационарности.
Ниже будет описана более совершенная, но и более сложная
статистическая модель нестационарного турбулентного течения, в которой
используются локальные квазистационарные характеристики турбулентности.
Использование подобной модели позволяет более детально исследовать
особенности нестационарного турбулентного течения, в частности, местные
кинематические характеристики турбулентности, диссипацию энергии, мгно-
235
венные значения напряжения трения о стенки итд. Расчеты по
статистической модели дают возможность сопоставлять с данными экспериментов не
только интегральные, но местные локальные характеристики течения, что
очень интересно с точки зрения проверки правильности самой
квазистационарной модели.
6.4.2. Статистическая модель нестационарного турбулентного течения в
трубе. Следуя работе О.Ф. Васильева и В.И. Квона [36], рассмотрим
нестационарное турбулентное движение несжимаемой вязкой жидкости в
круглой цилиндрической трубе в предположении, что течение не закручено
(имеется осевая симметрия) и статистически однородно вдоль оси трубы,
т.е. осредненные значения скорости и произведение пульсаций скорости
не зависят от координаты х. Используя эти предположения и условия
непроницаемости стенки трубы, из уравнения неразрывности A.3.3)
получаем, что < v > = 0. С учетом всех предположений система уравнений
турбулентного движения A.3.9), A.3.10) и A.3.13) заметно упрощается и
принимает следующий вид [27, 36]:
д(и) 1 Э / д{и) , \ 1 8<р>
=— —r[i> - <mV>1- , F.4.1)
dt г дг \ дг I р Эх
1 Ъ(р) 1 Э „ <w'2>
+ r(v'2)- =0, F.4.2)
р дг г дг г
1 Э /,/
г дг \\
-<«V>
dt г дг \\ р }f дг
v Г Э де д2 0 д 1
+ — г + —т гiv'2) <w'2 > - А. F.4.3)
г [дг дг дг2 дг \
Так же, как это делалось для ламинарного нестационарного движения,
исключив уравнение F.4.2) для градиента давления в радиальном
направлении, интегрируя уравнение F.4.2) по радиусу г, получим
г <и'2)_(м/2)
<p) = (po)-p(v'2 )-/ . rfr, F.4.4)
R Г
где < Ро > = < P(R,x, О ) - значение давления у стенки при г =R. Из
зависимости F.4.4) следует, что давление изменяется по радиусу трубы. Если
продифференцировать уравнение F.4.4), учитывая, что в соответствии с
принятыми предположениями < и'2 > и < м/2 > от х не зависят, тоЭ< р) /дх =
= Э < р0 > /Эх является функцией только t и х, как и сама величина < р0 >.
Если проанализировать уравнение F.4.1) , то обнаружится, что в
соответствии с принятыми предположениями все члены, кроме последнего, от х
не зависят. Следовательно, от х не должен зависеть и последний член,
т.е. Э < р > /Э х - функция только времени.
В уравнение турбулентной энергии F.4.3) входят члены (в квадратных
скобках), описывающие работу напряжения сил вязкого трения. Известно,
что работа сил вязкого напряжения в турбулентном потоке существенна
только в непосредственной близости от стенки, при этом основной вклад
в работу вязкого напряжения вносит член (v/r)d (где/дг)дг [165]. Со-
236
ответственно, остальными членами в квадратных скобках уравнения
F.4.3) можно пренебречь. После упрощений система уравнений F.4.1) —
F.4.3) сводится к двум уравнениям — уравнению Рейнольдса для
продольной составляющей скорости F.4.1) и уравнению энергии турбулентности
F.4.3). Однако в этих уравнениях число неизвестных больше числа
уравнений. Для замыкания системы уравнений, следуя в основном работе
Г.С. Глушко [66], введем полуэмпирические соотношения, полученные в
предположениях [36]:
1. Перенос импульса при турбулентных пульсациях осуществляется
диффузией градиентного типа (гипотеза Буссинеска)
F.4.5)
Ъг
где vT — коэффициент турбулентной вязкости;
2. Перенос полной турбулентной энергии также осуществляется
диффузией градиентного типа
де / р\\ е
где D — суммарный коэффициент диффузии;
3. Процесс диссипации энергии турбулентности описывается
соотношением
cDe
Д=—г , F.4.7)
Li
где L — масштаб турбулентности, с — универсальная постоянная, равная
согласно [66] с = 3,93.
В соотношения F.4.5) —F.4.7) входят три эмпирических параметра
vTiD и L, которые находятся с привлечением экспериментальных данных.
Используя результаты, полученные в статье [66], в которой
показывается, что коэффициент турбулентной вязкости vT может быть
представлен как функция только турбулентного числа Рейнольдса Ref -\fe}Ljv,
авторы работы [36] предлагают свою формулу, аппроксимирующую
зависимость для турбулентной вязкости:
— = aRer [I -exp(-a2Re?)-a3Re//2exp(-a1Re?)]. F.4.8)
v
Формула F.4.8) при ох = 4 • 10~4, о2 = 2,1 • 10, о3 = 2 • 10~3 и а = 0,2
хорошо согласуется с кусочно-гладкой функцией, предложенной в
статье [66].
При вычислении коэффициентов в формуле F.4.8) учитывались
экспериментальные данные работы [262] для круглой трубы. Для суммарного
коэффициента диффузии авторы статьи [36] использовали линейную
эмпирическую зависимость
D = v+mvTy F.4.9)
где т - постоянный коэффициент. Величина обратная т является
аналогом турбулентного числа Прандля. Согласно данным Г.С. Глушко [66]
w - 0,4. Для длины пути смешения при течении в трубе (по аналогии с
237
известной формулой Никурадзе) в работе [36] использован полином для
масштаба L :
L ( г \2 /г \4
Ы Ы FЛЛ0)
Константы /0, h и Ц определяются из эмпирической зависимости для L t,
полученной в работе Г.С. Глушко [66] и по экспериментальным данным
Лауфера [262]: /0 = 0,37, h = -0,24, Ц = -0,13.
Учитывая все сказанное выше, уравнения F.4.4) и F.4.3) можно
преобразовать к следующему виду:
Ъи 1 Э Г Ъи 1 1 Эр
— = Ф + ут) — , F.4.11)
Эг г Эг L Эг J р Эх
Эе 1 Э / Ъе \ ( Ьи\2 е
- = - — irD -— )+ ^т — -CD— , F.4.12)
Эг г Ъг \ Ъг ) \Ъг ) L2
где коэффициенты vTi D и масштаб L определяются формулами F.4.8) —
F.4.10), а знаки осреднения для простоты записи опущены. Из условия
симметрии на оси трубы и условия прилипания жидкости на стенке
записываются граничные условия
Ъи Ъе
и = е = 0 при r = R, = =0 при г = 0. F.4.13)
Ъг Ъг
В общем случае к граничным условиям F.4.13) необходимо добавить
начальные условия
и=и(г), с=е(г) при Г = 0 F.4.14)
и задать изменение расхода или градиента давления во времени.
Для установившегося периодического движения в трубе начальные
условия F.4.14) не нужны, а мгновенные значения расхода G (t) или
средней по сечению скорости U(t) связаны с градиентом давления.
Действительно, воспользовавшись определением средней скорости
G(t)
R
2nurdr, F.4.15)
проинтегрировав уравнение F.4.11) по радиусу, учтя условия F.4.13)
и F.4.15), получаем
dU I dG Ър 2rw(t)
p-L, F.4.16)
Ъх R
- напряжение трения на стенках, д = pp. Уравнение
F.4.16) является частным случаем зависимости A.7.16) без конвективных
членов.
Из уравнения неразрывности A.3.3) следует, что мгновенные значения
средней скорости и расхода для несжимаемой жидкости одинаковы в
любом сечении трубы. Задав закон изменения G(t) или U(t), из уравнения
F.4.16) можно найти давление, которое в этом случае будет искомой
238
р
где
dt
@
uR2
= -д
dt
Ъи
"э7
функцией. И наоборот, задав закон изменения градиента давления во
времени, из соотношения F.4.16) находятся U(t) и G(t) .
Приведенная выше система уравнений решалась численно [36] при
заданном гармоническом законе изменения расхода G(t). Для
подтверждения эффективности как предложенной модели, так и методики расчета,
были проведены численные расчеты методом установления для
стационарного течения, результаты которых удовлетворительно согласуются
с экспериментальными данными работы Лауфера [262].
Для нестационарного течения задавалось изменение расхода по
гармоническому закону
G(t) = G0(l + AGsincor), F.4.17)
где Go — средний расход, AG = AG/G0 — относительная амплитуда
колебаний расхода, Go, AG — постоянные заданные величины. Так же как и
в случае ламинарного пульсирующего течения, безразмерным критерием,
характеризующим относительное влияние инерции и вязкости, служит
параметр s = R \/со/у \ а для среднего турбулентного течения - параметры
Re0 =2RUolvHAG,rne Uo = Go/(pnR2) .
На рис. 6.28, а представлены результаты расчетов профилей
безразмерной скорости u/Uq как в ядре течения, так и у стенки для потока с Re0 =
= 105, AG = 0,5, s = 2,5-102. Кривые приведены для трех характерных
фаз колебаний у - cot.
Так же как и для пульсирующего ламинарного течения, при колебаниях
в турбулентном потоке профиль скорости наиболее ощутимо изменяется
вблизи стенки, где в отдельные моменты образуются обратные течения,
хотя при этом мгновенное значение средней скорости не изменяет знака
(AG< 1).
Расчеты по этой же модели [36] турбулентного течения без среднего
протока по закону G(t) = Gx sin cot (Ui = GiJ-nR2 p) показали (рис. 6.28,5
для Re = 2R U\jv = 0,5 • 105, s = 25) , что при достаточно больших значениях
параметра s в нестационарном пульсирующем потоке максимум скорости
перемещается к стенке, как это наблюдалось в экспериментах Франке
,[255]. По мере увеличения параметра s максимум скорости
приближается к стенке, а в ядре течения профиль скорости становится почти
равномерным. Так же как и в ламинарном пульсирующем течении, поток делится
на две области — ядро с равномерным профилем и динамический
пограничный слой у стенки, толщина которого уменьшается по мере роста частоты
колебаний. Анализ напряжения трения на стенке в турбулентном
нестационарном потоке (AG = 0,5) показал, что сила трения опережает колебания
скорости; при этом угол сдвига фазы растет при увеличении параметра s.
В более ранней работе Е.В. Еременко [93] рассматривается нестационарное
турбулентное движение жидкости в плоском канале с переменным во
времени гравитационным полем, для расчета которого используются
уравнение движения и уравнение турбулентной энергии, аналогичные
уравнениям F.4.11) и F.4.12), зависимость F.4.5) для турбулентной вязкости vTi
которая определяется по формуле А.Н. Колмогорова vT = L\Jer. Для
диссипации турбулентной энергии, диффузии энергии турбулентности и масштаба
турбулентности применяются полуэмпирические зависимости, замыкающие
исходную систему дифференциальных уравнений. Результаты расчетов
239
Ofi f-r
0,8
0,6
Ofi
/
f/
/
n
2\
T
\
0,2 0,4 0,6 0,8 f-r
Рис. 6.28. Профили безразмерной скорости в нестационарном турбулентном потоке
для разных фаз колебаний \р - ujt а) со средним протоком, б) без среднего протока
Рис. 6.29. Экспериментальные и теоретические профили скорости в нестационарном
турбулентном потоке [27]
профилей скорости, энергии турбулентности качественно согласуются с
данными экспериментальных исследований СБ. Маркова [157].
6.4.3. Экспериментальные данные по нестационарным турбулентным
течениям в трактах. Первые данные экспериментов с измерением профиля
скорости в пульсирующем турбулентном течении получены в работе Франке
[255]. С помощью поршневого пульсатора на поток накладывались
гармонические пульсации расхода. Сопоставление профиля скорости в
пульсирующем потоке с профилем при стационарном течении в трубе показало
на следующие принципиальные отличия. При частотах колебаний в
диапазоне 20—50 Гц обнаружено, что максимум скорости находится не на оси
240
трубы, а вблизи стенки. При увеличении частоты максимум скорости
перемещается ближе к стенке трубы. При этом в ядре течения профиль
скорости становится плоским, почти равномерным. Аналогичные
результаты были получены авторами работ [184, 251, 254, 264, 265] и др.
Результаты экспериментов, приведенных в статье [268] (рис. 6.27), наглядно
показывают характер деформации профиля скорости в турбулентном
пульсирующем течении при увеличении частоты колебаний. Применительно
к турбулентному нестационарному течению в плоском канале
экспериментальные данные приведены в работах СБ. Маркова [156, 157], к
потокам в открытых руслах - в статье А.Н. Шабрина [238]. Результаты
последних работ качественно совпадают с данными, полученными при
экспериментах в круглых трубах.
Наиболее подробные экспериментальные исследования пульсирующего
турбулентного течения выполнены в Институте гидродинамики им. М.А.
Лаврентьева СОАН СССР, В.И. Букреевым и В.М. Шахиным [25, 26, 27, 239,
240]. Эксперименты проводились с воздушным потоком при относительно
небольшой средней скорости и невысоких частотах/= 1 и 10 Гц, чтобы
избежать влияния сжимаемости среды. Измерения проводились с помощью
проволочного термоанемометра. В экспериментах учитывались
специфические особенности измерений характеристик нестационарного
турбулентного потока — необходимость находить средние значения параметров
путем многократного повторения режима течения, в частности, -
применительно к периодическим процессам - при одном и том же значении
фазы колебаний кр - cot. Для выборки значений параметров при
одинаковой фазе <р использовалась специально разработанная аппаратура. В
результате опытов были найдены профили средней скорости, напряжение трения
на стенке трубы, распределение тензора рейнольдсовых напряжений и
энергии турбулентности по радиусу, а также осредненные
характеристики — коэффициент сопротивления и потери энергии при пульсирующем
течении в трубе. Проведено сопоставление данных экспериментов с
расчетными данными по нескольким моделям нестационарного турбулентного
течения.
На рис. 6.29 представлены экспериментальные точки авторов [27, 239]
для относительных значений мгновенной скорости u/U0 =w(§, ip)/U0, где
? = 1— r/R^ if = tot, в случае^пульсирующего течения с параметрами Re0 =
= 3,2 • 104, s = 0,68 • 102 и AG = 0,5. Здесь же приведены результаты
расчетов по трехслойной модели, описанной в разделе 6.3.2 (пунктирные линии),
по формулам F.4.11) и F.4.12) (штрих-пунктирные линии) и по еще
более сложной двухпараметрической статистической модели
турбулентного течения (сплошные линии), в которой дополнительно используется
дифференциальное уравнение скорости диссипации энергии
турбулентности А. Средние мгновенные значения скорости относятся к средней
скорости Uo, поэтому для разных фаз колебаний безразмерные профили
оказываются разнесенными по оси абсцисс. Сопоставление распределения
экспериментальных точек и кривых расчетных профилей скорости по
разным моделям для ядра потока показывает их вполне удовлетворительное
совпадение.
Отличил оонаруживаются только у стенки при малых ?, причем ближе
к экспериментальным точкам проходят кривые для наиболее сложной
16. Б.Ф. Гликман 241
•'*4
1=0,5
¦—-г.
Рис. 6.30. Распределение энергии турбулен
ности по радиусу трубы для разных фаз кол
баний у? = oot [30]
Рис. 6.31. Экспериментальные и расчетные
значения напряжения трения на стенке
2п
модели, а для двух остальных моделей - статистической (раздел 6.4.2)
и трехслойной (раздел 6.3.2) — отличия эксперимента и расчета примерно
одинаковые.
На рис. 6.30 представлены экспериментальные точки и теоретические
кривые, полученные с помощью уравнения F.4.12), для изменения
энергии турбулентности е в зависимости от фазы колебаний у = cot для
различных расстояний от стенки ?. Энергия турбулентности нормирована на
квадрат динамической скорости для стационарного потока со скоростью ?/0;
w*o= VVo/p> где Го — напряжение трения на стенке при скорости Uo. Здесь
же представлены квазистационарные значения e/ulo (штрих-пунктирные
линии), которые были получены по данным измерений в условиях
установившихся течений с разными средними скоростями Uo, соответствующими
мгновенным значениям средней скорости нестационарного потока. Расчеты
по уравнению F.4.12) проводились для условий экспериментов: Re0 =
= 3,2 • 104 и AG = 0,5 считались постоянными, частота колебаний
принималась равной / = 1 Гц (s = 13 - сплошная линия) и 10 Гц (s = 41,5 -
штриховая линия).
242
Обращает на себя внимание, что при большем значении частоты (/ =
- Ю Гц) в ядре течения имеется достаточно широкая область, в которой
при колебаниях средней скорости потока энергия турбулентности не
изменяется во времени, оставаясь практически равной энергии турбулентности
ддя установившегося потока со скоростью Uo. Этот факт является очень
интересной особенностью турбулентного пульсирующего течения в трубе.
Независимость от времени в ядре потока обнаружена и для составляющих
рейнольдсовых нормальных и касательных напряжений [239].
Для ламинарного пульсирующего потока возмущения от стенок (вязкие
волны) при достаточно больших значениях параметра s не доходят до ядра
течения. Аналогично, в турбулентном пульсирующем потоке не
наблюдается передача в ядро течения турбулентной энергии, зарождающейся у
стенок при колебаниях с достаточно большой частотой, т.е. при достаточно
больших значениях параметра s. Таким образом передача турбулентной
энергии в ядро из пристеночной области является инерционным процессом,
имеющим, по всей видимости, определенную характерную постоянную
времени, а в частотной области - определенную глубину проникновения
возмущений от стенки при заданной частоте колебаний потока.
На рис. 6.31 представлены экспериментальные точки для Re0 =3,2 • 104,
AG = 0,5 и двух значений параметра s, а также результаты расчетов
напряжения трения на стенке rw для тех же значений Re0, AG и s, отнесенные
к постоянной величине rWo — напряжению трения на стенке при
установившемся течении с расходом Go. Теоретические кривые приведены для двух
моделей турбулентного течения —по двухпараметрической модели
(сплошные линии) и по методу, изложенному в статье [36] (штриховые линии).
По мгновенному значению напряжения трения на стенке особенно ощутимо
расхождение между экспериментальными данными и результатами расчетов
по наиболее совершенным квазистационарным моделям турбулентного
течения в пристеночной области.
В обзоре В.И. Букреева и В.М. Шахина [27] приведены результаты
сопоставления данных экспериментального определения напряжения силы
трения на стенке при переходном процессе в трубе [267] с расчетами по
различным моделям нестационарного турбулентного течения (рис. 6.32).
Закон изменения расхода в трубе G{t) представлен на рис. 6.32
пунктирными линиями - отдельно для ускоренного и замедленного движения
жидкости (соответственно смещены координатные сетки для G/Go).
Величина Go — постоянный расход после выхода на новый стационарный
режим, которому соответствует число Рейнольдса Re0 = 2G0/(-nRpov)
(в экспериментах оно равнялось 104). Характерное время Г определялось
по формуле Т= 7iD3p0/DG). Мгновенное значение напряжения трения
на стенке rw(t) относилось к напряжению трения rw0 на стационарном
режиме с расходом Go. Кружками на рис. 6.32 обозначены
экспериментальные точки; сплошные линии, помеченные цифрой 1 — результаты расчетов
по двухслойной модели, 2 - по трехслойной модели, 3 - по методике,
предложенной в работе [36] и изложенной выше, 4 — по
двухпараметрической модели турбулентности. Сравнение экспериментальных данных
с результатами расчетов по разным моделям показывает, что чем сложнее
модель, тем лучше она согласуется с данными эксперимента, хотя
расхождения остаются большими. Следует обратить внимание на типично коле-
16* 243
1,0 2,0 t/T
Рис. 6.32. Сопоставление расчетных и экспериментальных данных по напряжению
трения на стенке при переходном процессе в трубе [27]
бательный характер изменения напряжения трения по времени, особенно
четко проявившийся для ускоренного потока (нижние кривые). Таким
образом, для всех локальных мгновенных значений параметров
нестационарного турбулентного потока вблизи стенки наблюдается расхождение
между экспериментальными данными и результатами расчетов по разным
вариантам моделей турбулентного течения, в которых используются
предположения о сохранении для нестационарного течения эмпирических
констант, полученных с использованием опытов со стационарным потоком.
Однако применительно к прикладным задачам в основном представляют
интерес интегральные характеристики течения, в частности, частотные
передаточные функции трактов (АЧХ и ФЧХ), описанные ранее в
разделе 6.3.2. Имеется ряд других интегральных характеристик, в частности,
диссипация механической энергии в нестационарном турбулентном потоке.
Для оценки потерь энергии проинтегрируем по радиусу уравнение
движения F.4.11), предварительно умножив все члены на 2лгри. Учитывая
определение средней скорости F.4.15) и используя формулу
интегрирования по частям, для первого члена в правой части находим
I rdr = 2irrpu(v + vT) —
Ъи_
Ъг
? Э / u \
о bt\2 I
^т) )dr-7TR2U —
\дг I Ъх
Умножив все члены уравнения F.4.12) на 2ттгр и проинтегрировав по
244
радиусу, имеем
R Ъе Ъе R / Ъи\
2-npf rdr = 2-nprD — +2тгр/г^т 1 dr -
о dt Ъг о \ Ъг 1
я е
- 2тгр/ rcD —т-dr.
о L
Сложив два полученных уравнения, учтя условия F.4.13), а также
дополнительное условие Эе/Эг- 0 при r = R, которое следует из уравнения
энергии в вязком подслое (D-ve^\2 при % ->0) , получим интегральное
уравнение баланса полной энергии
2
Эр Э * / и2 \
—=2тг — /р— +е
Эд: Ы о \ 2 /
F.4.18)
Член в левой части уравнения F.4.18) определяет работу сил давления
в потоке на участке трубы единичной длины. Эта работа расходуется на
изменение кинетической энергии осредненного и пульсационного движений
(первый интеграл) и на диссипацию механической энергии в тепло (второй
интеграл). Таким образом, потеря энергии на единицу длины трубы равна
яг / Ъи\2 е Л
N=2irf Ы—-) +pcD—\rdr. F.4.19)
Воспользовавшись уравнением F.4.16), исключим из зависимости F.4.18)
член Ър/Ъх, учтя, что ttR2 U- G/p:
dU 2Gtw Ъ R I и2 \
G + =2тг — /p + e)rdr+N.
dt pR Ъt о \ 2 /
Учтя коэффициент у — корректив количества движения (формула 1.7.15),
можно преобразовать последнюю зависимость к виду
2Gtw dU I dy d я
N = +0-7)G GU 2тгр / erar. F.4.20)
pR dt 2 dt dt о
Для стационарного движения три последних члена правой части в
уравнении F.4.20) выпадают и диссипация энергии 7V0 = 2Grw0/pR равна работе
сил трения о стенку. Для сопоставления вклада отдельных членов
уравнения F.4.20) разделим его Ha7V0:
F.4.21)
N = N/N0=NT
где
v - 2Gr™
Т pRNo '
d
Ne=~ 2тгр —
dt
+ Nt-Ny
v °
R
f erdr.
0
-7)G
No
dU
dt '
GU
\I —
7 27VO
dy
dt
245
2 --
Рис. 6.33. Экспериментальные
данные по различным составляющим
диссипации энергии в нестационарном
турбулентном потоке :а -при/ = 1 Гц,
б-при/ = 10 Гц [27]
На рис. 6.33 приведены
экспериментальные данные для отдельных
составляющих TV в зависимости
от фазы колебаний течения с Re0 =
= 3,2 • 104 и AG = 0,5 [27].
Кривые на рис. 6.33,а описывают
данные эксперимента при колебаниях
с частотой 1 Гц и значении
параметра 5 = 13, а на рис. 6.33,6 / =
= 10Гци5 =41,15.При
относительно малом значении 5=13
мгновенные значения^ практически
совпадают сNr, т.е. в основном энергия
затрачивается на работу сил трения
о стенки. При увеличении частоты
колебаний на порядок (рис.6.33,5)
оказываются сопоставимыми по
порядку величины составляющие
Nt9 Ny и NT, а четвертое
слагаемое Ne, определяющее
изменение энергии турбулентности, не
вносит заметного вклада в баланс энергии, исроме узкого
диапазона фазы колебаний вблизи <р & 1,8 тт. Если осреднить
отдельные составляющие N по времени за период колебаний, то
среднее N совпадает со средней величиной NTi т.е. среднее значение TV
целиком определяется потерями на трение. Составляющая Nt определяет
вклад работы сил на преодоление инерции жидкости, Ny - затраты (или,
наоборот, возврат) энергии на перестройку профиля скорости. Интересно
осреднить за период напряжение трения жидкости о стенку
1 т
-1
\\
У
к
Л
/
7\
о
)
V
0'=*
о
2П
1 wcp
/
Т б
и диссипацию энергии
f
полученные при экспериментах с нестационарным потоком и сравнить их
с расчетом по интегрально квазистационарной модели трения (см. § 6.1).
Сопоставление показывает [27], что для таких характеристик
квазистационарный подход дает результаты, близкие к экспериментальным: по twcv
246
отличие не превышает 8%, по Ncp - 22%. Этот важный для практического
применения результат не согласуется с данными по другим интегральным
характеристикам - частотным передаточным функциям трактов,
описанным в § 6.3 [64], для которых более или менее удовлетворительные
результаты дают локальная квазистационарная четырехслойная или условно
ламинарная нестационарные модели.
Удовлетворительное совпадение экспериментальных данных с расчетами
по квазистационарной модели в работе [27] по всей видимости
объясняется низкими частотами - до 10 Гц, в то время как в статье [64] приведены
данные экспериментов до 300 Гц, причем при низких частотах, вблизи
первого резонанса все расчетные методики также дают близкие результаты.
Остановимся на экспериментальных данных по еще одной
характеристике нестационарного течения - коэффициенту сопротивления трения.
Применительно к стационарному течению в трубе этот коэффициент определяется
соотношением
X = ~~ . F.4.22)
Для нестационарного же течения достаточной четкости определения
коэффициента сопротивления трения нет. В двух наиболее обстоятельных
работах по нестационарным течениям в трубах - В.И. Букреева и Шахина В.М.
[27] и Д.Н. Попова [184] — этому коэффициенту дается разное
определение: в работе [27] используется определение F.4.22), в книге же [184] по
этой формуле находится коэффициент поверхностного трения. Покажем,
что противоречия возникают не по сути описания процесса, а из-за
использования для одних и тех же величин разных терминов. Действительно, и
в работе [27] и в книге [184] для нестационарного течения в трубе
вводятся по два независимых безразмерных коэффициента, связанных с влиянием
вязкого трения на поток.
Авторы [27] сопротивление трения характеризуют коэффициентом X,
определяемым формулой F.4.22) и вводят второй коэффициент,
называемый коэффициентом потерь энергии
SN
Хлг= : , F.4.23)
irDpU3
где N находится из соотношения F.4.20) .
В книге Д.Н. Попова [184] коэффициент, определяемый формулой
F.4.22), называется коэффициентом нестационарного поверхностного
трения и обозначается CfH, а для коэффициента сопротивления трения
предлагается формула
где F = nD2/4, qt — отнесенное к единице массы количество энергии,
которое в единицу времени затрачивается на работу внутренних сил. На
стационарном режиме течения в трубе значения всех коэффициентов совпадают:
247
Покажем, что определения F.4.23) и F.4.24) близки и в случае
нестационарного течения. Уравнение энергии в книге [184] записывается (в
наших обозначениях) в виде
dU pLU dyT L pU2
7тР^ + ~Г^Г+Хн^~ =p°-p» FA25j
а уравнение количества движения —
dU 2Ltw
(>L — + —— =Po -Pi- F/r.26)
ut R
Для турбулентного движения коэффициент 7т (см- формулу 1.7.15)
определяется в виде
7т =-^?rU2irr<uJdr f
где
<и'к2) = (и2) + <и'2> + <w'2> = 2е.
Если из уравнений F.4.25) и F.4.26) исключить перепад давления р0 —р\
и от определения 7т с учетом энергии турбулентности перейти к
определению по формуле A.7.15), сократив L и умножив все члены на G/p - nR2 U,
находим
GU2 dU 2twG GU dy d R
XH =GA-7T) + -2тгр — ferdr. F.4.27)
2D dt Rp 2 dt dto У }
Сопоставление зависимости F.4.27) с определением TV no F.4.20)
показывает их практически полную идентичность. Имеется только одно
отличие: в члене при производной от средней скорости в формуле F.4.20)
стоит член A - 7), а в зависимости F.4.27) A - 7т)- Сама величина у
для турбулентного режима течения, в том числе и нестационарного,
незначительно отличается от единицы [27], а сама энергия турбулентности
составляет небольшую долю от общей энергии потока. Поэтому разницей между
7Т и 7 в этом члене можно пренебречь. С учетом последнего замечания
XHGU2/ BD) ^ N. Подставив это равенство в формулу F.4.23), учтя
связь G с U, получаем
SGU2XH
При принятом предположении коэффициенты Хдг и Хн совпадают.
Учитывая, что величины обоих коэффициентов находятся из уравнения энергии,
кажется справедливым назвать параметр Хдг % Хн коэффициентом потерь
энергии. В этом случае за безразмерными параметрами X = Сун, которые
получаются из уравнения количества движения, справедливо оставить
название коэффициент сопротивления трения.
В работе В.И. Букреева и В.М. Шахина [27] приведены результаты
обработки данных измерений мгновенных полей скорости в трубе, по
которым с помощью формул A.2.1) и F.4.19) определены напряжения трения
248
рис. 6.34. Экспериментальные
значения крэффициентов \, \дг и расчетное
(пунктир) для Хкс
о
0,06
ОШ
о-Я, L-kN при 5=13
• -Л, к-Лыпри з=Ы,
^^
1
1
л
на стенке rw и потери энергии N,
а затем, после использования
соотношений F.4.22) и F.4.23),
коэффициенты сопротивления
трения X и потерь энергии Хдг.
Экспериментальные ТОЧКИ ПО X И Хдг
дня одного периода колебаний
при течении с числом Рейнольд-
са Re = 3,2 • 104 и
относительной амплитудой AG= 0,5 для двух
частот / = 1ГцE = 13) и 10 Гц
(s = 41,5) приведены на рис. 6.34.
Штриховая линия соответствует и п ^п
значению коэффициента
сопротивления трения Хкс при квазистационарном режиме колебаний.
Величины XKC(v?) находились по формуле Блязиуса Xkc(y?) =
= 0,3164/Re >25 для мгновенных значений Re по средним мгновенным
величинам скорости в трубе.
Величина Хкс не зависит от параметра 5 (т.е. от частоты колебаний), и
она характеризует для квазистационарного режима как сопротивление
трения, так и потери энергии.
Сопоставление кривых свидетельствует о существенном отличии
величин X и Хдг, которое увеличивается с ростом частоты. Значения X и Хдг
отличаются от величины Хкс для квазистационарной модели: размах
колебаний X и Хдг существенно больше, чем у Хкс. Создается впечатление, что
экспериментальные данные по величинам мгновенных значений
коэффициентов X, Хдг и Хкс, полученные в работе [27], противоречат одному из
выводов этой же работы, что квазистационарный подход дает лучшее
соответствие с экспериментальными данными по средним интегральным
значениям tw и TV за период, чем для других характеристик нестационарного
течения.
В заключение остановимся на данных экспериментов для открытых
потоков. Результаты первых экспериментальных исследований структуры
нестационарного турбулентного потока в открытых руслах содержатся в
статьях Т.Ф. Федорова и В.М. Шабрина [221, 238]. Так же как и для течения
в трубах, результаты экспериментов оказались противоречивыми. В работе
[221] по данным опытов обнаружено, что при ускорении потока
(прохождение волны попуска) резко изменяется профиль скорости —
увеличивается скорость в придонной области^ при относительно меньшем
увеличении скорости в верхних слоях. В статье [238] приведены
результаты экспериментального исследования поля скоростей в ускоренном и
замедленном движении. Поле скоростей определялось путем
фотографирования следов частиц, вводимых в поток. Все данные экспериментов
249
обрабатывались статистически — по результатам многократного
повторения исследуемых процессов. Из сопоставления данных опытов с
ускоренным и замедленным течением автор не обнаружил разницы в профилях
скорости, что противоречит выводам автора статьи [221]. Исключение
составляют профили, полученные в экспериментах при резком
уменьшении расхода, которые существенно отклоняются от профиля скорости
для стационарного потока. В теоретических работах О.Ф. Васильева и
В.И. Квона [34, 35] получены результаты, согласующиеся с данными
экспериментов Г.Ф.Федорова [221], в расчетах для ускоренных потоков
максимальное значение скорости достигалось не на поверхности, а внутри
потока.
§ 6.5. Учет колебаний стенок каналов
6.5.1. Уравнения трубы с податливыми стенками. На распространение
возмущений в трактах, заполненных жидкостью, влияют как конечное
значение скорости звука, так и податливость (растяжимость) стенок
тракта. Характер колебаний жидкости в тракте зависит и от радиальных,
и от продольных колебаний стенок, а также от вязкоупругих свойств
материала стенок. В некоторых случаях, например, для течения крови в
сосудах [112, 138], для трактов с пластиковыми стенками и т.д.
податливость стенок столь велика, что сжимаемостью жидкости можно пренебречь.
К примеру, за счет податливости стенок сосудов скорость
распространения импульсов по кровеносной системе человека составляет от 6 до
8 м/сек [138]. Однако упругость стенок сосудов не оказывает
ощутимого влияния на распределения скорости по радиусу [138], поэтому
результаты расчетов скоростей и напряжений трения при нестационарном
течении, полученные в § 6.2-6.4, применимы для трактов с упругими
стенками. Так как податливость стенок не влияет на профиль скорости,
а мгновенное значение давления не зависит от радиуса, то изменения
радиуса податливых стенок не сказываются на форме записи уравнения
количества движения для средних мгновенных значений скорости F.2.12).
В то же время изменение площади проходного сечения трубы должно
учитываться в уравнении неразрывности, которое в этом случае
записывается [138,140]:
bpF bpUF
+ —— =0, F.5.1)
bt Ъх
где F — площадь поперечного сечения тракта.
Линеаризовав уравнение F.5.1) и переходя к безразмерным вариациям
и переменным, найдем
1 dd(pF) dSU
М dt дх
F.5.2)
При линеаризации мы пренебрегли изменением отклонений площади
и плотности вдоль оси тракта, как это было принято и при выводе
уравнения F.2.13).
250
Как плотность жидкости р, так и площадь поперечного сечения канала F
зависят только от давления в тракте, поэтому
dp
где Р> pF - безразмерные переменные, отнесенные к характерным
значениям параметров. С учетом этой зависимости, подставив в уравнениеF.5.2)
частные периодические решения F.2.5), получим
?• d(pF) dbU
— —— 5р=-—7 . F.5.3)
М dp dx
Уравнение F.5.3) отличается от уравнения F.2.13) наличием
производной d(pF)/dp. Подставив др из соотношения F.2.12) в уравнение F.5.3),
учтя при этом формулы F.2.39), найдем
a dF\ _
— —: 5?/=0.
M dp I
F.5.4)
0u :
dx2 \ M dp
Коэффициент при втором члене уравнения F.5.4) получился из
условия, что
d(pF)/dp'= (po/po) (dp/dp) + (po/Fo) (dF/dp) =
-Polipoa2) + dF/dp = M/a + dF/dp .
Для определения связи поперечного сечения тракта F с давлением
внутри тракта р запишем уравнение движения стенки тракта в радиальном
направлении, считая ее тонкой, учитывая ее инерцию и упругость. Для
однородного участка цилиндрического тракта единичной длины запишем
уравнение движения стенки, возникающего под влиянием изменения давления
внутри трубы
d2bR' Eh
Pch —T-+-^bR'=bp\ F.5.5)
at К
где рс - плотность материала стенки, h - ее толщина, R - радиус трубы,
Е - модуль упругости материала стенки в окружном направлении.
Первый член в левой части уравнения F.5.5) описывает инерцию стенки
трубы единичной длины, второй член - окружное напряжение,
возникающее в стенке трубы под влиянием внутреннего избыточного давления.
При растяжении стенок в окружном направлении одновременно возникает
продольная деформация стенок, пропорциональная окружной с
коэффициентом, равным коэффициенту Пуассона а. Однако величина ее невелика по
сравнению с окружной деформацией и ею можно пренебречь [139].
Дополнительные напряжения возникают, если стенки трубы жестко связаны
с внешними телами, что исключает их продольное перемещение. Учет этого
напряжения приводит к появлению дополнительного коэффициента
A — а2) , и соответственно изменению записи уравнения F.5.5):
d28Rf Eh
pch — +— —5R'=8p'. F.5.6)
dt2 R2(l-o2)
251
Зависимость для площади проходного сечения трубы F - tiR2 позволяе
найти связь между отклонениями площади 8F' и радиуса трубы 8R'
8F' = 2irR8Rf или в безразмерных вариациях: 8F = 28R. Учтя эту связ!
можно получить очевидное соотношение dF/dp= 8F/8p = 28R/8p.
Используя уравнение F.5.6), переходя в нем к безразмерным вариаци
ям и подставив частное периодическое решение 8R = 5#ехр(/сог), найде\
2
dp dp Rpch(tol -oj2)a20
F.5.7)
где c5i = u>i L/a0 - безразмерная собственная частота, нормированная так
же, как частота вынужденных колебаний со, а0 - скорость звука в жид-
кости, cji = yjE/R2pc(l - а2)" - собственная частота радиальных колебаний
упругих стенок трубы с учетом их массы для пустой трубы, т.е. без учета
свойств жидкости. Подставив соотношение F.5.7) в волновое уравнение
F.5.4), последнее можно преобразовать к виду
гдесо2 =(со2Ь/аоJ = [2poaoKRpch)](L/aoJ, со2 - собственная частота
колебаний стенки тракта с учетом ее массы (без учета упругости) из-за
упругости сжимаемой жидкости в тракте.
Входящее в уравнение F.5.8) отношение
со"? E/pcR
(где кж = роа1 - модуль сжимаемости жидкости) сводится к обычной
поправке, учитывающей влияние податливости стенок на скорость звука
в тракте.
Входящий в уравнение F.5.8) коэффициент при вариации средней
скорости определяет безразмерное волновое число к2 = со2/а2, где а = а/а0 -
безразмерная скорость распространения звуковых колебаний в тракте
(величина - в общем случае комплексная). Сама скорость звука а (со)
определяется соотношением [83]:
1 -со2/со? \1/2
Из зависимости F.5.9) следует, что при 113| % 1 в диапазоне частот,
определяемых неравенством
сох [1 + (D/h) (кж/Е) A -а2)]1/2>с3>с^1,
имеется "полоса запирания" акустических колебаний, в которой волновое
число к — мнимое. При этом волна не распространяется по тракту, а
затухает по экспоненте. Таким образом учет инерции и упругости стенок тракта
приводит к новому эффекту — тракт в определенном диапазоне частот
252
рис.
6.35. Зависимость безразмерной фазовой
5,0
корости от частоты и>/и>2 при разных значениях
параметра к
действует как полосовой фильтр. На рис.
5.35 приведены кривые зависимости без- 2
размерной фазовой скорости я(со)/я0 от
безразмерной частоты со/с^ при разных
значениях комплекса к = (D/h) (кж/Е) A -
- а2), который определяет влияние
упругости стенок тракта. Сопоставление кри- ,
вых показывает, что при малых значениях
комплекса к изменения а/а0 в широком
диапазоне co/coi незначительны, кроме
области в окрестности со/соi = 1. Вблизи со/соi =0
отношение а/а0 соответствует изменению
скорости звука в тракте за счет упругое- 0
ти стенок.
Все сказанное относится к случаю, когда влияние параметра ]3,
зависящего от числа Стокса s = Ry/to/v, незначительно. Сомножитель j3, как уже
отмечалось в § 6.2, отражает влияние вязкости на дисперсию и затухание
акустических колебаний в тракте. При совместном учете инерции стенок
тракта и дисперсии за счет вязкости жидкости картина усложняется,
особенно при малых значениях соi, характерных для кровеносных сосудов. В
этом случае дисперсия зависит сразу от двух параметров /3 и соь и частотные
характеристики тракта отличаются от рассмотренных ранее в § 6.2 [75].
Выражение F.5.9) для скорости звука, а значит, и для волнового числа
позволяет получить решение уравнения F.5.4) при граничных условиях
F.2.42), которое практически не будет отличаться от полученных ранее
решений F.2.43) и F.2.44), только вместо волнового числа j3co
необходимо подставлять волновое число Zo/a, учитывающее как зависимость
трения от частоты (ламинарное течение), так и инерцию и податливость
стенок тракта. Для этого можно воспользоваться соотношениями для C
как комплексного числа, зависящего от параметра s (§ 6.2), и формулой
F.5.9) для скорости звука я (со).
6.5.2. Нестационарное течение в растяжимых трубах. Полученное выше
решение учитывает как инерцию стенок, так и их податливость, и
сжимаемость жидкости. В некоторых случаях податливость (растяжимость)
стенок столь велика, что сжимаемостью жидкости можно пренебречь. Приняв,
что а0 -» оо, преобразуем формулу F.5.9). Учтя что кж = р0а20 и отбросив
члены, в которых а\ находится в знаменателе, получим
1
— со
F.5.10)
где ас - \ZEh/2poR(l —о2) — скорость распространения возмущений в
253
трубе с податливыми стенками, заполненной несжимаемой невязкой жид
костью. В формуле F.5.10) использованы размерные частоты w и соь
так как переход к безразмерным акустическим частотам при а0 -* °° не
имеет смысла. В зависимости F.5.10) учтены два возможных эффекта,
связанных с упругостью стенки: собственные колебания стенки с учетом
ее массы и упругости, колебания стенок в несжимаемой жидкости за счет
взаимодействия инерции жидкости и податливости стенок. Скорость
распространения волн, определяемая формулой F.5.10), - величина
комплексная, в первую очередь из-за параметра /3, учитывающего влияние
нестационарного напряжения трения.
Силы вязкого трения оказывают влияние на фазовую скорость
распространения волн (по данным Э. Лайтфута [138]) только при небольших
значениях параметра s = Ryjcolv'< 5. При s > 5 и coi > со а ^ас. В то же
время коэффициент затухания волн увеличивается с ростом 5 при любых
его значениях, что было показано в разделе 6.2.7.
6.53. Колебания в трубах со стенками из вязкоупругого материала.
Учет инерции стенок приводит к дисперсии — зависимости скорости
распространения возмушения от частоты. Другой возможной причиной
дисперсии могут служить вязкоупругие свойства материала стенок трубы [143].
Такие свойства присущи, например, стенкам кровеносных сосудов, трубам
из полимерных материалов. Специфическая особенность вязкоупругого
материала состоит в том, что деформация определяется не только
величиной приложенной силы (т.е. напряжением в материале), но и скоростью
изменения внешнего воздействия. Если вязкоупругий материал
подвергнуть воздействию силы, изменяющейся по гармоническому закону, то
его деформация не совпадает по фазе с напряжением (как у идеального
упругого материала), но и не отстает от напряжения на 90° (как в
случае жидкости). Поэтому вязкоупругие свойства материала удобно
характеризовать комплексной величиной модуля упругости Е = Е' + iE".
Мнимая часть модуля упругости Е" определяет диссипацию
механической энергии при деформации материала. Диссипативные потери можно
характеризовать также углом потерь вязкоупругого материала у. Е"/Е' =
- tg у. Угол потерь у в общем случае ' является функцией частоты.
Однако для ряда распространенных полимерных материалов зависимость
7 от частоты слабая, и с достаточной точностью можно считать у =
= const.
Так же как и в случае колебаний с учетом инерции стенок тракта, при
колебаниях жидкости в трубе из вязкоупругого материала свойства
материала стенок оказывают наибольшее влияние на скорость
распространения возмущений вблизи собственной частоты колебаний стенок.
Движение стенок в этом случае описывается уравнением F.5.5), в которое
подставляется комплексная величина модуля упругости Е = Е1 {\ +/tg7).
Соответственно комплексной оказывается и скорость звука, определяемая
формулой F.5.9). Влияние вязкоупругих свойств материала стенок трубы
приводит к уменьшению скорости звука и появлению диссипации
механической энергии, так как в этом случае скорость звука — величина
комплексная. Для трубы из вязкоупругого материала формулу F.5.9)
можно упростить, если сделать некоторые допущения, справедливые во
254
многих случаях, представляющих практический интерес. Примем, что
bj/oii ^ 1, о2 < 1, величины Е* и tg у - постоянные; при этом tg у < 1,
а податливость стенок достаточно велика, так что в знаменателе можно
пренебречь единицей, так как Окж/(ЕИ)> 1. С учетом этих предположений
формула F.5.9) преобразуется к виду
ак =*'[! +/tgG/2)], F.5.11)
где a' = \ZE'h/2p0R - фазовая скорость. В этом случае волновое число к,
входящее в экспоненциальные члены решения, запишется в виде
Действительная часть волнового числа определяет диссипацию
механической энергии при распространении волн вдоль трубы, при этом
диссипация растет пропорционально частоте колебаний.
Для тракта из вязкоупругого материала в работе Е.Л.Левченко [143]
параметры колебаний на входе и выходе связываются уравнениями
четырехполюсника, в которых используется скорость звука aki определяемая
формулой F.5.11):
Sp(O) = ch iuk8p(l) + ак sh /оЗ*5мA), F.5.12)
5м @) = (l/%)sh шкЬр(\) + ch /со*5мA), F.5.13)
тце пк =b>L/ak, ak= роиоак/ро. Приняв, что на выходе из трубы
5рA)/5нA) = \pi и разделив уравнение F.5.12) на уравнение F.5.13),
получим соотношение для входного импеданса тракта, и преобразовав
F.5.14) - его передаточную функцию
др(О) ак(ф1 +otk thcjfc) Ф
5г7(О) фх th 65к + ак Ь~р{0) 8рх фх ch шк + ak sh
F.5.14)
При сок -^°° thook -> 1 и, следовательно, 5р(О)/6п(О) -*aki т.е. стремится
к импедансу бесконечной трубы. Этот факт свидетельствует о том, что
при достаточно большой частоте со к волны рассеиваются не доходя до
выхода из трубы. Поэтому входной импеданс трубы при больших Zjk не
зависит от ^1. Большая величина сок определяется либо высокой частотой
колебаний со, либо значительной протяженностью тракта//, либо большой
податливостью стенок тракта, т.е. малой скоростью звука я'.
На рис. 6.36 представлены графики результатов расчетов по формуле
F.5.14) передаточных функций труб со стенками из вязкоупругого
материала с различными углами потерь у и приведенными импедансами на
.выходе Фг/О1к.
Сопоставление кривых показывает, что резонансные максимумы
резко уменьшаются по мере увеличения их номера, причем темп
уменьшения резонансов увеличивается по мере роста угла потерь у.
При достаточно большом 7(tg 7=0,1) практически исчезает уже
третий резонанс, т.е. колебания такой частоты не доходят до
конца трубы.
255
3,75
2,5
1,25
1
ft
Л
II
11
\\
l\
л
¦2 М
1
1 1
/ \
\
/ / V*
А
/ \
1 \
J
/ /
/ /
Г
4 /
^ /
л /
/
\ /
\ /
\
\ А
\ /
W
\
12 15 18 ш
9 12 \ ю 16 си
-3
Рис. 6.36. Входной импеданс трубы со стенками из вязкоупругого материала при
различных значениях угла потерь у и приведенного импеданса на выходе: 1 - tg у =
= 0,06, \l>J<*k = *\ 2- tg7= 0,1, Ф,/ак = 4;3 - tg7=0,l, tj<xk = 1; 4 - tg 7 = 0,1,
*/ 05
На рис. 6.37 представлены результаты экспериментальных исследований
динамических характеристик трубопровода из полиэтилена длиной 3 м,
радиусом 55 мм* и толщиной стенки 5-7 мм, проведенных E.JI.
Левченко [143]. Пульсирующий расход воды в трубе 2 создавался
пульсатором поршневого типа 3. На выходе трубы установлена емкость 1, на
входе — мало инерционный датчик давления 4. В результате определился
256
ходной импеданс трубопровода Ьр @)/5м @) = bpil&u\.
Экспериментальные точки, приведенные на рис. 6.37, вполне удовлетворительно совпадают с
теоретической кривой, рассчитанной с учетом зависимости F.5.11) для
скорости звука afc. Описанным методом можно определить и динамические
характеристики трубопровода, заполненного жидкостью, обладающей вязко-
упругими свойствами. Для этого в формулу скорости звука F.5.9)
подставляется комплексный модуль объемного сжатия жидкости кж - к' A + tg 7).
6.5.4. Колебания стенок трубы в продольном направлении. При выводе
уравнений движения стенки трубы F.5.5) и F.5.6) учитывались только
радиальные перемещения стенок, а продольными (осевыми)
перемещениями пренебрегали. В некоторых случаях продольные перемещения
стенок оказывают ощутимое влияние на колебания жидкости в тракте.
Рассматривая стенки тракта как упругий стержень, можно установить
набор собственных частот, определяемых материалом и геометрическими
характеристиками стенок тракта. Если частоты собственных продольных
колебаний стенок находятся в исследуемом диапазоне частот, то
продольные колебания могут влиять на динамические характеристики
жидкости в тракте. При этом определяющими являются не силы
взаимодействия жидкости со стенками за счет вязкого трения, а силы,
возникающие в результате взаимодействия колебаний потока и местных
сопротивлений, связанных со стенками тракта.
5Л
5uf
12
с
1
А
л
о
_—_
4*
1
-2
3
f
^ ^ 12 15 18 ш
Рис. 6.37. Экспериментальные частотные характеристики потока в трубе со
стенками из полиэтилена [ 143]
7. Б.ф. Гликман
257
Рассмотрим наиболее простой случай - колебание прямой
цилиндрической трубы, жестко закрепленной только в одном сечении на входе в
тракт. Весь трубопровод и выходной конец не закреплены и могут сво-
бодно перемещаться в осевом направлении. Деформация прямого
стрежня (стенок трубопровода) в продольном направлении в малых отклоне-
ниях описывается уравнением [38]:
д2дГ Е Э25/'
_ — Q
Эг2 рс Ъх2
или, если перейти к безразмерным вариациям и записи в амплитудах
, - Е d2fl
81 = 81 /1 = 81 expQcot), со25/ + — — = 0, F.5.15)
Рс dx2
где Е, рс — модуль упругости и плотность материала стенки, / — длина
трубы.
Для решения уравнения F.5.15) необходимы два граничных условия.
Считая конец трубы со стороны входа жестко закрепленным, можно
сформулировать первое граничное условие
х = 0, 57=0. F.5.16)
Предполагая, что на выходе из тракта дросселирующее устройство, датчики
и другие элементы могут иметь определенную массу и все они жестко
связаны с выходным сечением тракта, можно записать уравнение движения
присоединенной массы:
d2l dl dl
т ТТ +ХТ-+2^/гТ-=(Р-Рн)(/7тр-^д), F.5.17)
dt dt dx
где т — общая масса устройств на конце трубы, X — коэффициент сопротив
ления трения при колебаниях присоединенных к трубе устройств, FTp, Fa —
площади проходного сечения трубы и дроссельного устройства, рн —
давление за дроссельным устройством. Последний член в левой части определяет
упругую силу, возникающую при продольной деформации конца трубы,
член в правой части - силу, создаваемую перепадом давления,
действующим на дроссельное устройство. Линеаризуя уравнение F.5.17), переходя
к безразмерным вариациям, а затем к амплитудам вариаций параметров,
получаем второе граничное условие на свободном конце трубы (х = /):
dbl р / р„ \
+2-nRhE =—(^тр -FA)( dp -— 8рн).
dx I \ p )
F.5.18)
Решение уравнения F.5.15) имеет следующий вид:
81 = А ехрО'сох/яс) + В ехр(- icox/ac), F.5.19)
где ас = \/Е/р^ — скорость распространения продольных колебаний в
стенках трубы. Подставив решение F.5.19) в граничное условие F.5.16)
получим, что А + В - 0 и решение F.5.19) можно переписать так:
57 = А [ехр(/сох/яс) - ехр(— icox/ac)] - 2Aisin(cox/ac) .
256
Подставив эту зависимость во второе граничное условие F.5.18), находим
коэффициент А, после подстановки которого в F.5.19) решение принимает
следующий вид:
_ (p/l) (FTp - Fn)sin(u>x/ac) (dp - (рн/р)8рн)
ol — z ; — . F.5.2U)
(— со m + zcoX)sin(co//flc) + 2irRhE(co/ac)cos(ojl/ac)
Решение F.5.20) описывает продольные колебания стенок прямой трубы
под действием перепада давления на выходном гидравлическом
сопротивлении. Из соотношения F.5.20) можно найти собственные частоты
продольных колебаний прямой трубы. Если можно пренебречь массой и
сопротивлением устройств на выходе из трубы и принять т - X = 0, то собственная
частота определяется условием cos(co//tfc) = 0, т.е.
где fc= 1,2,3,. ..
Если пренебречь трением жидкости при продольных колебаниях стенок,
то течение жидкости в тракте взаимодействует с колеблющейся в
продольном направлении стенкой прямой трубы только на выходном конце, на
местном сопротивлении. Условия взаимодействия местного сопротивления
с жидкостью описываются уравнением неразрывности для конца тракта на
выходе (х = /), которое в амплитудах безразмерных вариаций имеет вид
со/ _
6м"=5йд+/ 5/, F.5.21)
"о
где дп, дпц - амплитуды вариации скорости жидкости в конце трубы и в
узком сечении дросселирующего устройства. Правая часть уравнения
F.5.21) показывает, что отклонения скорости жидкости в конце тракта
связаны как с колебаниями расхода через местное сопротивление, так и со
скоростью перемещения самого местного сопротивления: dbljdt = /соб/
(поршневой эффект). Записав соотношение для течения жидкости через
дроссельное устройство на выходе
2Ард Рн ._
дыц = \pidu =Ьр 5рн,
Р Р
подставив это соотношение и зависимость F.5.21) в решение F.5.20),
находим граничное условие для жидкости в выходном сечении (х = /)
гидравлического тракта
Фхдп
Ьр = +5/V F.5.22)
I+WP/hK^^) Н
где х = X + i[b>m - BтгЯкЕ/ас) ctg(col/ac)].
Если максимальная частота из представляющего интерес диапазона
частот существенно меньше собственной частоты первого тона продольных
колебаний стенки coi, то для всего диапазона частот соблюдается условие
со//ас < 1 и, соответственно, ctg(co//tfc) > 1. В этом случае х достаточно
велико и коэффициент при 8U в F.5.22) становится равным i//ba граничное
условие переходит в используемое ранее граничное условие F.2.42) для
17* 259
5pV)
ffp'(O)
Кб
0,8
и
f
/
t, Теория
V
1
1
\
I
л
t
1
\
Г j
1 I
Рис. 6.38. Динамические
характеристики гидравлического тракта с учетом
продольных колебаний его стенок
-225
—
ъЛО
1
\
40
1
i
bO
i
80
i_ j
i V
4
к
местного i идравлического
сопротивления. С влиянием продольных
колебаний стенок тракта на его
динамические характеристики
столкнулись Д'Суза и Ольденбургер [91],
При экспериментальном определении
динамических характеристик
тракта с ламинарным течением жидкости
одна серия экспериментов
проводилась струбой,подвешеннойнатонких
проволочках, другая — с жестко
закрепленной трубой (см. раздел 6.2.6),
Во всех экспериментах входной
конец трубы был жестко связан с пульсатором. Для
незакрепленной трубы первый тон продольных колебаний стенок (83 Гц)
попал в диапазон исследуемых частот. На рис. 6.38 приведены результаты
экспериментов для трубы, свободно перемещавшейся в продольном
направлении. Здесь же представлены теоретические кривые амплитудных к
фазовых частотных характеристик тракта, рассчитанные по уравнению
F.2.44) с использованием граничного условия на выходе F.5.22) и
условий на входе ф0 = То/ = 0. Экспериментальные точки практически точно
ложатся на теоретические кривые во всем исследованном диапазоне
частот.
Анализ кривых показывает, что продольные колебания стенок
оказывают заметное влияние на динамические характеристики гидравлического
тракта вблизи собственной частоты продольных колебаний стенок тракта.
Выше рассмотрен только простейший случай колебаний трубопровода -
продольные колебания прямого участка трубы при элементарных
граничных условиях. На течение жидкости могут оказывать влияние не только
продольные, но и поперечные колебания трубы. Для сложных
трубопроводных систем колебания носят пространственный характер, анализ
которых возможен с привлечением аналитических или приближенных методов
[38, 40]. Одна из основных проблем расчета механических колебаний
трубопроводов связана с их вибрациями, которые вызываются воздействием
на механическую систему пульсаций рабочей среды в трубах [40, 55, 124].
К сожалению, обратное воздействие пространственных колебаний труб на
течение жидкости почти не исследовано.
§ 6.6. Течение в открытых каналах
Используя разработанный в предыдущем разделе метод анализа
нестационарного одномерного движения жидкости в тракте с податливыми
стенками, можно получить простейшую модель нестационарного течения
в открытом канале небольшой глубины (приближение мелкой воды). Для
260
такого течения длина волны, возникающей на поверхности жидкости,
намного больше глубины жидкости, т.е. это длинные волны. Сечение канала
может иметь произвольную форму.
Как и ранее, будем рассматривать течение в участке однородного канала
с постоянной площадью сечения. Жидкость считаем несжимаемой, так как
скорость распространения длинных волн существенно меньше скорости
звука. Рассматриваемые ниже волновые процессы — длинные
гравитационные волны - являются частным случаем очень широкого круга явлений -
поверхностных волн на жидкости [139, 140 J.
Избыточное (над атмосферным) давление р внутри жидкости в сечении
с координатой z определяется уравнением гидростатики
Р ~Ра =Pog(?-z), F.6.1)
где ра - атмосферное давление, ? - координата свободной поверхности
жидкости, отсчитываемая от ее равновесного положения. Изменение
площади поперечного сечения заполненной части канала F из-за небольшого
изменения уровня жидкости при ширине свободной поверхности канала,
обозначаемой Ь, определяется зависимостью F - FQ =b%, где Fo - площадь
поперечного сечения заполненной части канала при равновесном состоянии
жидкости. Используя соотношение F.6.1), установим связь давления в
фиксированной точке пространства с изменением площади F:
F-Fo = (Р-Ро). F-6-2)
Pog
Считая параметры Fo, pOi b, p0 постоянными, подставив зависимость F,6.2)
в уравнение неразрывности F.5.1), найдем
Ъ Ър bU
— — +ро^о — =0. F.6.3)
X Э? Эх
Пренебрегаем конвективным членом, массовыми силами и сопротивлением
трения. Исключая из уравнений F.6.3) и A.7.7) скорость, получаем:
Ъ2р gF0 Ъ2р
—т =-— —~=0. F.6.4)
bt2 b Ъх2
Полученное уравнение — волновое, оно описывает распространение волн
на поверхности жидкости. Используя соотношение F.6.1) или F.6.2),
можно получить уравнение, подобное F.6.4), для изменения уровня
жидкости или площади F. В уравнение F.6.4) входит в качестве коэффициента
квадрат скорости распространения длинных гравитационных волн
c- v = \/б". F.6.5)
где h = F0/b — средняя (гидравлическая) глубина жидкости в канале.
Если считать, что глубина жидкости в реках, каналах, водохранилищах
изменяется в пределах от 1 до 100 м, то соответственно скорость
распространения длинных волн будет находиться в пределах от 3 до 30 м/с. Эта
скорость существенно ниже скорости звука в жидкости (^ 1400 м/с для
воды), что подтверждает правомерность принятого предположения о
несжимаемости жидкости.
261
Волновое уравнение F.6.4) при F0/b = const -линейное с постоянными
коэффициентами; решением его является сумма бегущих волн
где Ьр = р -ро- избыточное давление, Ро - гидростатическое давление
для стационарного течения. Для всех точек поперечного сечения канала др'
практически одинаково и согласно соотношению F.6.1) оно однозначно
связано с отклонением поверхности жидкости от ее равновесного
положения: 6p'=pO?if, где Ьр =ро -pa+pogz, z - расстояние от поверхности
невозмущенной жидкости (z < 0). Для бегущей волны верна обычная связь
между отклонениями скорости и давления:
К решению уравнения F.6.4) применимы все выводы о характере
волнового движения в участке тракта, полученные в гл. 5. Однако, как уже
отмечалось выше, применительно к турбулентному движению жидкости
в открытых каналах возникают такие же проблемы, как и для течения
в трубах [34,35,93,94, 156, 157,237,238]. К разветвленным системам
открытых каналов применимы изложенные ниже в гл. 7 методы расчета
разветвленных трубопроводных систем.
§ 6.7. Колебания жидкости под действием
переменного внешнего ускорения
На тракты гидравлических систем транспортных установок при
неустановившемся движении действует внешнее ускорение. В § 6.5 был
рассмотрен один из случаев продольных колебаний стенок трубы, возникающих
под действием колебаний давления в тракте. Другой случай — механические
колебания (вибрации) трубопроводов, обусловленные внешними
причинами, к примеру - колебаниями конструкции, к которой трубопроводы
крепятся. Подобные колебания возникают при потере ракетой в полете
продольной устойчивости [125, 170], при вибрациях компрессоров [219] и т.д.
Выше уравнения движения жидкости были записаны для неподвижных
стенок трактов. Если стенки тракта, как жесткое тело, движутся с
ускорением, то уравнения движения жидкости относительно стенок
(относительное движение) останутся такими же, как и для неподвижного тракта, за
исключением члена, учитывающего дополнительную силу инерции,
вызванную переносным движением стенок трубы. Предполагая, что ускорение
направлено под углом /3 к оси цилиндрического участка трубы, запишем
уравнение для одномерного неустановившегося течения капельной
жидкости (М <1) без учета потерь на трение [170]:
Ъи 1 др Э2|
— + = - —т cos 0, F.7.1)
bt р Ъх bt2 J
где ? - координата стенок трубы в переносном движении. Уравнение
неразрывности E.1.2) сохраняется без изменений.
Линеаризовав уравнения F.7.1) и E.1.2) путем перехода к
безразмерным вариациям и переменным t - tall, х = x/L, считая М < 1, р « 1 и под-
262
ставив частные периодические решения
ди = 5м ехр(коГ),
Ьр =др ехр(ког),
<5? = 5? ехр(/оЗг),
найдем
/со5м + 1 =— cosj36?, F.7.2)
ос dx M
/собр + а —г =0. F.7.3)
dx
Уравнения F.7.2) и F.7.3) —неоднородные; поэтому вначале найдем
частные их решения в виде
5м =?>iC0Sj3S ?, 8р = D2cos C5? . F.7.4)
Подставив решения F.7.4) в уравнения F.7.2) и F.7.3), определим
константы
аи ioo
Dx = =- , ZJ=0. F.7.5)
ш М
Воспользуемся граничными условиями E.1.9)-E.1.10), которые
правомерны в случае перемещения стенок тракта как единого твердого тела
вместе с неоднородностями на границах участка тракта, которые и
определяют граничные импедансы фо и ф\. Решения уравнений F.7.2) и F.7.3)
имеют вид
дп = A exp(-iux) + B ехр(гсох) +?>i cos/3 5§ , F.7.6)
dp = а. [А ехр (-icjx) - В exp (zcjx )]. F.7.7)
Подставив решения F.7.6) и F.7.7) в граничные условия E.1.9), E.1,10)
и найдя коэффициенты А и В, подставив Д из формулы F.7.5) , получаем
уравнение для распределения амплитуд отклонений давления и скорости
под влиянием трех внешних возмущающих воздействий- амплитуд
перемещений стенок тракта 6? и возмущений на границах тракта 5j70/ и 5vi;-:
а.
Зр (х, cj)= —{[(а + фх) ехр {fa A -х)) -
А
к
~(<х-ф1)ехр( -/соA --*)>] 2 7о/8Уо/ -
т
~ [(<* + ^о) ехр (-/сох) - (а -
ехр(/о>3ё)]
"Ыехр
2 у
/= i
М
COSpo
F.-
7.3)
263
1
Ьи(х, to) = — {[(а + Фх)ехр </соA -jc)> + (a - фг) exp (-ico(\ -
А
к
- i//0)exp(/co.x)] 2 Ti/S/i/ - / {[(а + ф1)ехр
/= i
+ (а-^!)ехр<-?cjA -J)>]i//0 +A} cos 06 f, F.7.9)
где A = (а - i//0) (а + i//j) exp/со - (a + фо)(а- фг) ехр(-/со).
При выводе уравнений F.7.8) и F.7.9) было принято предположение,
что угол наклона оси трубы по отношению к направлению действия
ускорения 0 постоянен. Для трактов с переменным углом 0 можно или
использовать более сложные соотношения, учитывающие закон изменения
0(х) [170], или разбить тракт на ряд участков, для каждого из которых
значение 0 — свое и постоянное по длине данного участка. В этом случае,
а также для ряда других задач, удобно представить уравнения участка
тракта без неоднородностей в форме уравнений четырехполюсника, из которых
затем можно "собрать" математическую модель сложной трубопроводной
системы.
Уравнения четырехполюсника можно получить из зависимостей F.7.8)
и F.7.9), приняв в_них ф0 = фх = 0, 8у01 = 5р@),Ьуц = Ьр A), у01 =
= 7i 1 ~ 1, byoi -?>У \j ~ 0» при/ = 2, 3,4,..., / = 2, 3,4, ...Получив сначала
соотношения для Ьп @) и Ьы A), после преобразований находим
_ _ _ _ _ а& — -
Ьр A) = cos со Ьр @) - /a sin со 5 и @) + sin со cos j35 ?,
М_ F.7.10]
_ i' _ _ _ _ /со _ _
5w(l) = sinoj>5p @) + cos со 5 и @) A — cos со) cos j3 6 ? .
a M
Формулы F.7.10) удобно использовать для формирования моделей
трубопроводных систем разной структуры. Однако применительно к трактам,
состоящим из участков, сочлененных упругими элементами (сильфонами,
рукавами), необходимо обращать внимание на то, что переносное движение
этих участков в общем случае независимо и определяется колебаниями
точек их опор. Кроме того требуется учитывать и изменение объема
упругих элементов (сильфонов) при перемещениях их концов [125, 126].
Подробно эти вопросы рассмотрены в работах, посвященных продольной
устойчивости ракет [125, 170].
§ 6.8. Нестационарное течение газа
с переменной температурой и составом
6.8.1 Адиабатическое течение. При нестационарном течении газа в ряде
технических устройств (камеры сгорания двигателей, топки, проточные
химические реакторы и т.д.) наряду с возмущениями давления и
скорости (расхода) возникают отклонения температуры и состава газа. Для
264
движения среды с переменной температурой и составом кроме уравнений
движения и неразрывности необходимо привлекать уравнения энергии и
уравнения для концентраций отдельных составляющих смеси газа.
Если рассматривать одномерное неизотермическое течение газа в
теплоизолированной длинной трубе (L Ж) с малыми отклонениями
температуры и состава, пренебрегая диссипацией энергии из-за работы сил вязкого
трения и теплопроводностью газа, т.е. принять в линеаризованном
уравнении A.10.22) Фо = Fo = п~ = 0, b~s /дх - 0, п = 1, и произвести замену
Sh = 1/М9 то оно принимает вид
dds dds
Э7 дх
= 0- F.8.1)
Кроме уравнения F.8.1) для среды с переменным составом необходимо
учитывать уравнение переноса концентраций составляющих смеси газа
A.6.9) . В принципе необходимо записать столько уравнений A.6.9) ,
сколько составляющих имеется в смеси. Однако для расчетов параметров потока
смеси газов важны не парциальные параметры (так как не учитываются
химические реакции) отдельных составляющих, а интегральные
характеристики смеси: плотность, газовая постояннная или молекулярная масса
смеси. Для газа заданного состава можно воспользоваться определением
газовой постоянной смеси
R= ZgfRi, F.8.2)
/=
где R{ — газовая постоянная для /-й составляющей смеси. Газовая
постоянная Ri является физической константой, поэтому на нее можно
умножить все члены уравнения A.6.9), введя ее под знаки производных, а
затем все полученные п уравнений просуммировать, используя равенство
F.8.2)
Э5Д Э5Д
+ М =0, F.8.3)
bt Эх
п
где 8R - A/R) 2 Rfdg^.Это уравнение описывает перенос потоком газа его
i= 1
интегральной скалярной характеристики — газовой постоянной.
В тех же предположениях, которые были приняты при выводе F.8.1) ,уч-
тя, что р" = 1, др /дх = дп/дх = Хо = 0, Еи/М = ри0 а/р = ос, преобразуем
уравнения A.10.18) и A.10.19) к следующей форме:
F.8.4)
F.8.5)
Уравнения F.8.1) —F.8.4) описывают адиабатическое течение в длинном
тракте идеального газа с переменной температурой и составом. При этом
уравнения F.8.1) и F.8.3) не содержат вариации скорости и давления, а
265
дди
dl
ddp
dT
+ M
+ M
ddu
dx
ddp
dx
l
+ —
a
+ 0C
ddp
dx
ddu
dx
= 0,
-0.
в уравнениях F.8.4) и F.8.5) отсутствуют вариации 8 s и 8R. Поэтому
уравнения можно интегрировать независимо. Для уравнений F.8.4) и
F.8.5) можно воспользоваться решениями F.2.4) и E.2.5) и
соотношениями E.2.7) и E.2.8) для амплитуд вариаций скорости и давления:
8и =Сехр + Z)exp , F.8.6)
A -М) 1 A+M)J
( ioox Г icox 1)
5р=-чх{Сехр ?>ехр . F.8.7)
I A -М) [ A +M)JJ
Решения уравнений F.8.1) и F.8.3) для амплитуд вариаций энтропии и
газовой постоянной имеют форму бегущих волн:
F.8.8)
j F.8.9)
В гл. 2 были рассмотрены линеаризованные уравнения элементов с
сосредоточенными параметрами, которые являются граничными условиями
для участка тракта с неизотермическим течением газа. Все их можно
объединить следующими достаточно общими зависимостями: для входа в
участок тракта (х = 0)
F.8.10)
/= 1
F.8.11)
F.8.12)
F.8.13)
где 0о> Фг — импедансы на входе и выходе, 7о/ ,?о/ >ао/, Ti/
-коэффициенты усиления от вариаций внешних возмущающих воздействий 8yOf и 8у г у ;
v о, в i — коэффициенты связи вариаций давления и энтропии. Подставив
решения F.8.6)-F.8.9) в граничные условия F.8.10)-F.8.13),найдем
57
8R
и для
8р
= 2
i = 1
п
= 2
So/S^c
ooi8y
i
выхода (х
)/ +
oi ^
= 0
m
2 ")
= l
( ioox\
,
\ М /
F.8.14)
- _ п _ / KoJc\
8R(x)=[ 2 ooi8yoi]Qxpl I, F.8.15)
/ = i \ M /
266
r icox \ ( шх \\
}-(ос-Фо)ехр[ X
^ 1+М/ \ 1 -M/J
Г т - к ( *п\ _ 1
X 2 71/5^1/+ 2 (^i So/ + ^71 ао/) ехР\ )ЬУ01 \ —
L / = 1 i=i \ М / J
Г / /cJ iCox \ I ito /соJf \
— (а + ф 1) ехр I I — (а - ф i) ехр I + I —
L \ 1-М 1 +М/ \ 1+М 1-М/
_ а (Г / itox \ I icox \ 1
8п(х)= — { (a-^o)expl +(а+0о)ехр1- X
да \1-м/ \ 1+M/J
\ у у ( *п\ _ I
L/= 1 } 1 /=1 ' 1 \ М / j
o/1 >
F.8.16)
F.8.17)
Здесь dp @) — амплитуда вариации давления в начале тракта (х = 0),
которая находится по формуле F.8.16).
Уравнения F.8.14) и F.8.15) описывают распространение вдоль тракта
волн энтропии и заданной концентрации смеси газа, характеризуемой
газовой постоянной смеси. В отличие от акустических волн давления и скорости,
распространяющихся со скоростью звука и имеющих как стоячую, так и
бегущую составляющие (см. гл. 5), волны энтропии и концентрации
распространяются со скоростью газа и являются волнами, бегущими в одном
направлении. Эти волны не взаимодействуют по длине тракта с
акустическими волнами, так как их распространение описывается независимыми
уравнениями F.8.1) и F.8.2) и парой уравнений F.8.4)-F.8.5). Как
следует из решений F.8.14) — F.8.17), взаимодействуют они только на
границах.
В качестве примера процесса с колебаниями температуры (состава)
в потоке рассмотрим условия в газовом тракте проточной камеры
сгорания или топки [58, 190]. Предполагая, что продукты сгорания образуются
в начале топки (камеры сгорания), которую будем рассматривать как
тракт постоянного сечения, пренебрегая объемом зоны горения и временем
преобразования горючего в продукты сгорания, запишем первое граничное
условие на входе в тракт (х = 0) в форме линеаризованного уравнения
баланса расходов газа:
Зр= -Зп +(GO +/iNGo +(Gr -juMGr, F.8.18)
где Go = GQ/(GO+ Gr), GT = 1 -Go = Gr/(GO + Gr) - относительные
доли окислителя (например, воздуха) и горючего в продуктах сгорания,
267
5GO, 5Gr — амплитуды относительных вариаций расходов окислителя и
горючего на входе в камеру сгорания, ц= [(Go/Gr)/r] ЪТ/Ъ (Go/Gr)
определяет наклон зависимости температуры продуктов сгорания от
соотношения GOIGT (избытка окислителя). Из сопоставления соотношений
F.8.10) и F.8.18) следует, что в данном случае ф0 = —1, 701 = Go +M,
$У о\ = 5GO5 7о2 = Gr ~ И> Ъу 02 = Ь&т •
Второе граничное условие на входе в тракт определяется связью
энтропии продуктов сгорания с расходами окислителя и горючего,
записываемой в виде линеаризованной зависимости (х = 0)
к-1
55 =juEGo-5Gr) 5р. F.8.19)
к
В качестве граничного условия на выходе из тракта (х = 1) используем
линеаризованное уравнение для расхода газа через местное сопротивление
/ к -1 \ 1
+ б! )8р =5м 55 +ei5pb F.8.20)
\ 2к ) 2
где. €i — коэффициент расхода через местное сопротивление на выходе из
тракта (см. формулу B.1.25)), Ьр х — амплитуда вариаций давления
за местным сопротивлением. Для простоты примем, что газовая
постоянная продуктов сгорания практически не изменяется при колебаниях
расходов окислителя и горючего и соответственно в граничном условии F.8.12)
можно принять а0/ =0.
Сопоставляя соотношения F.8.19) и F.8.20) с F.8.11) и F.8.13),
находим
Ро = -{к - 1)/к, Фг = [(к - 1)/2к + еЦ-1,
в1 =-[(?- 1)/А: + 2б1]-1, 7п =*! [(к- 1I2к + еху1.
Подставив эти значения коэффициентов в решение F.8.16) и учтя, что
для гааа а = риа/р = кМ., находим формулу, определяющую распределение
амплитуды колебаний давления по длине камеры сгорания (топки):
Ш
D
ICO
X
(_1
X FGo-5Gr)exp( ) + A -кМ)е1др1 \ X
ехр
\
io5x \ кМ I /к-1 I i?5
( Мехр
1+ М/ D \\ 2 \ М
¦ 2 — I ¦'— ~\~ (~ л \ к !\d I ехтэ \ ~~~~"~~
268
_ _/i __ / 7CO \
+ (Gr -n)8GT] --A + *M)FGo-6Gr)exp ) +
2 \ M /
+ A + kM) d dp ! exp , F.8.21)
J \ 1 — M /
?> = (?-l)Mexpl j+ll -I +e1lfcMj X
Используя решение F.8.14) и термодинамические связи, найдем
зависимость для распределения амплитуды вариации температуры
/ /сох \ к-\
-6Gr)exp( X
\ М / к
X 5р@)ехр1 ) -др(х) . F.8.22)
Отклонения температуры в отличие от отклонений энтропии, как
следует из формулы F.8.22), связаны с текущим значением отклонения
давления 5р(х), определяемого решением F.8.21). Решения F.8.21) и
F.8.22) описывают динамические (частотные) характеристики газового
тракта с энтропийными волнами в широком диапазоне частот.
Ограничение диапазона частот определяется возможным рассеиванием энтропийных
волн (см. ниже) и необходимостью учитывать при высоких частотах другие
моды акустических колебаний, кроме продольных. Наличие энтропийных
волн приводит к изменению решений уравнений гидромеханики.
В случае ограничения диапазона частот, для которого соблюдается
условие со = coL/a < 1, можно пренебречь акустическими эффектами, т.е. рас-
пределенностью системы по отношению к колебаниям скорости и давления
[58]. Так как отношение характерных времен прохождения тракта
акустическими так = L/a и энтропийными волнами т± -L/u, так/тх = М, то
временем пробега энтропийных волн Т\ в случае М < 1 пренебрегать нельзя
несмотря на пренебрежение акустическими эффектами. Приняв М< 1 и со < 1,
положив х = 1 и разлагая в ряд экспоненциальные члены exp (± icoL/a) «
^ 1 ± i со L/a в уравнении F.8.21) , находим упрощенное уравнение для
амплитуды вариации давления в тракте (переходя к размерной частоте):
f icori k — 1 1 _
\ [1 — exp (—/cotiI + 1 — €t \ dp =
{ к 2к J
Г 1 1
= Go5Go+Gr5Gr+jLtl-— exp(-/cori)JEGo -
F.8.23)
При выводе уравнения F.8.23) мы пренебрегли малыми членами,
определяющими влияние инерции столба газа в тракте icopuL/p = icokriM2,
благодаря чему в упрощенном уравнении амплитуды вариации давления
в начале тракта Ьр @) и в конце тракта др A) совпали.
269
-wo
-200
-300
(руград
Рис. 6.39. Экспериментальные и теоретические частотные характеристики газового
тракта с энтропийными волнами для сечения с х = 1,3 м
Теоретическая модель нестационарного течения газа с энтропийными
волнами была подтверждена специальными экспериментами [59,61] на
установке с цилиндрическим трактом, в котором на входе возбуждались
энтропийные волны путем смешения двух газов с разной температурой
C00 и 780 К) . В трубе, по которой подавался воздух, дроссельным
пульсатором создавались гармонические колебания расхода через решетку,
с помощью которой газ подавался в тракт. Как холодный, так и горячий
газ подавались в тракт через решетку с большим числом отверстий с
плавными входами, на которых всегда обеспечивался сверхкритический
перепад давления, что исключало обратное влияние колебаний давления в
тракте на расходы газов через решетку. Пульсация давления холодного газа
перед решеткой Eрх = 5Gr) и пульсации давления в нескольких сечениях
тракта по длине измерялись малоинерционными индуктивными датчиками
давления.
Результаты экспериментов в виде амплитудных и фазовых частотных
характеристик для сечения в конце тракта (х = 1,3 м) представлены на
270
рис. 6.39 (точки 2). Здесь же приведены теоретические характеристики
(кривые 4), рассчитанные по формуле F.8.21). Сопоставление
теоретических кривых с экспериментальными точками показывает, что теоретическая
зависимость F.8.21) вполне удовлетворительно подтверждается опытами
в области безразмерных частот со = ooL/a от 0 до 1 -г 1,5 (cj/M от 0 до 10).
При оо > 1,5 экспериментальные точки уже не совпадают с кривой для
адиабатического процесса в тракте — экспериментальные точки не следуют
за "волнами" (особенно четкими на фазовой характеристике), а идут по
некоторой средней, более гладкой кривой. Здесь же на рис. 6.39 приведены
экспериментальные данные (точки 7) и расчетные кривые 3 для
акустических характеристик того же тракта без энтропийных волн (при подаче в
тракт холодного воздуха вместо горячего газа).
Экспериментальные точки вполне удовлетворительно совпадают с
теоретическими кривыми, подтвердив тем самым правильность
экспериментальной методики. Сопоставление теоретических кривых 3 и 4 с
соответствующими экспериментальными точками приводит к выводу о существенном
влиянии энтропийных волн на акустические характеристики тракта. На
рис. 6.40 представлены теоретические кривые и данные экспериментов,
зафиксированные с помощью другого датчика давления, установленного
в середине газового тракта (х = 0,69 м). Для этого датчика также получено
хорошее совпадение данных экспериментов с теоретическими кривыми,
но обращает на себя внимание резкое отличие характера акустических
характеристик на рис. 6.39 и 6.40: для датчика в середине тракта
отсутствует первый резонанс на частоте со ^ тг, который по другому датчику
(рис. 6.39) ярко выражен. Результаты сопоставления кривых на рис. 6.39
и 6.40 еще раз наглядно продемонстрировали уже отмеченное выше
влияние расположения сечения по длине тракта (в котором измеряются
колебания давления) на динамические характеристики тракта.
6.8.2. Учет рассеивания волн энтропии. Вернемся к рис. 6.39. Причиной
отмеченного здесь расхождения между теорией и экспериментом является
рассеивание энтропийных волн по длине тракта [61]. Для решения задачи
о распространения акустических и энтропийных волн с учетом рассеивания
последних используем уравнение энергии A.10.20), упростив его с учетом
всех предположений, принятых при выводе уравнения F.8.1), кроме
одного: не будем пренебрегать теплопроводностью газа вдоль оси тракта.
В этом случае уравнение A.10.22) принимает следующий вид:
d8s b8s M Ъ28Т
_____ +м =0 F.8.24)
bt Эх Ре Ъх2
В уравнение F.8.24) входят две переменные - отклонения энтропии и
температуры, которые связаны между собой термодинамической
линеаризованной зависимостью
к- 1
8s = 8T- 8р. F.8.25)
к
Если учесть, что коэффициент (к - \)/к относительно невелик и
изменение давления дает относительно небольшой вклад в изменение энтропии,
то можно пренебречь в формуле F.8.25) членом с 8р, приняв 8s ^ 8Т.
С учетом такого упрощающего предположения уравнение F.8.24^
271
Рис. 6.40. Экспериментальные и теоретические частотные характеристики тракта
с энтропийными волнами для сечения с х - 0,69 м
принимает форму
dbs 06s
— +М
bt Ъх
м
Ре
= 0.
F.8.26)
В результате уравнение F.8.26), описывающее распространение
энтропийных волн, оказывается независимым от двух других уравнений F.8.4) и
F.8.5), описывающих распространение акустических волн. Соответственно
уравнение F.8.26) можно решать независимо от уравнений F.8.4) и
F.8.5). Следует заметить, что уравнение F.8.5) было получено в
предположении об адиабатическом характере процесса в тракте. Введение в
уравнение энергии F.8.26) последнего члена свидетельствует об отказе от
предположения об адиабатичности процесса. В этом случае для определения связи
плотности с давлением и энтропией воспользуемся термодинамическим
соотношением
s=culnp + cplnp + const,
из которого находим линеаризованное равенство
бр=— 5p--5s. C6.8.27)
272
Подставив соотношение F.8.27) в уравнение неразрывности A.2.5), учтя
уравнение F.8.26) и условие v = 0, находим:
dbp ЪЬр ЪЬи кШ d2bs
—Ь +М—- +кМ = . F.8.28)
bt Ъх Ъх Ре Ъх2
Таким образом, в отличие от рассмотренного ранее чисто
адиабатического (для каждого слоя газа) течения, при учет- теплообмена между слоями
в уравнении неразрывности F.8.28) появляется новый член в правой части,
учитывающий изменение плотности газа из-за рассеяния волн энтропии.
Так как уравнение для отклонения энтропии F.8.26) решается независимо
от двух остальных уравнений, то дополнительный член в уравнении F.8.28)
оставляем в правой части как внешнее возмущение. Как и ранее,
интересуясь только частными периодическими решениями типа E.2.1), подставив
их в уравнения F.8.4), F.8.26) и F.2.28), находим систему уравнений
для амплитуд вариаций параметров:
F.8.29)
F.8.30)
F.8.31)
Решение уравнения F.8.31) ищем в следующей форме:
bJ = d exp rxx + C2 exp r23c, F.8.32)
где показатели степени в решении F.8.32) гх и г2 - корни
характеристического уравнения
М ,
/ cj + Mr - —¦ г2 = 0, F.8.33)
из которого находим формулу для корней
i cob и ¦
icobp -*
ico bs -
fM
M
dbu
dx
dbp
dx
dbs
dx
1
a
M
Pe
dbp
dx ~
dbu
dx
d2bJ
dx2
o,
Pe
= 0.
d2bs
dx2
Ре / Г~
2М
М Ум+. F.8.34)
2М\ Ре /
Из двух корней, определяемых соотношением F.8.34), корень,
соответствующий знаку плюс, дает возрастание амплитуды колебаний энтропии
вдоль оси х, что не имеет физического смысла. Поэтому принимаем Сх = 0,
оставив в решении F.8.32) один член с коэффициентом С2. Подставив
решение F.8.32) в граничное условие, например, в форме соотношения
F.8.19) без последнего члена, найдем
bl = !d(bGo - 5Gr)exp r2x, F.8.35)
где г2 определяется зависимостью
Ре / /~ 4/ соМ Д Ре / / Г4сГ \
г2 = М -Л/М2 + )= — I 1 -VI + , F.8.36)
2М\ Ре / 2 \ РеМ '
которая определяет распространение двух типов волн. Если принять Ре -> °°,
18.Б.Ф. Гликман 273
т.е. пренебречь теплопроводностью, то решение характеристического
уравнения F.8.32) принимает вид г = —/со/М. В этом случае решением уравнения
F.8.31) будет соотношение F.8.22), описывающее распространение
энтропийных волн без рассеивания, т.е. чисто конвективный перенос тепла
Если принять М= 0, т.е. рассматривать неподвижную среду, то удобнее
вернуться к характеристическому уравнению F.8.33), переходя в нем к
размерным переменным и приняв и = 0:
icoL-kTr2/L = 0
или
г = ±Ly/iw/kT = ± [A + ОЛ/21] Ly/u/kT:
Учитывая ограниченность амплитуды энтропии, подставив найденный
корень в решение F.8.32) и граничное условие F.8.19), находим
-5Gr)exp A + 0W х\. F.8.37)
L 2kT J
Зависимость F.8.37) совпадает с решением, полученным в § 1.5 для
вязких волн, возбуждаемых колебаниями пластины в жидкости. Решение
F.8.37) описывает распространение температурных волн внутри
неподвижной среды, возбуждаемых за счет колебаний ее температуры на границе.
Общее решение F.8.35) - F.8.36) описывает процесс, возникающий в
жидкости при распространении одновременно двух семейств волн:
энтропийных, распространяющихся со скоростью потока, и волн температуры,
распространяющихся в среде за счет ее теплопроводности, и приводящих
к рассеиванию энтропийных волн. Если окажется, что 4o3/Re М < 1,т.е.
параметр, определяющий рассеивание энтропийных волн, относительно мал,
то формулу F.8.36) можно упростить. Разложив в ряд выражение, стоящее
под корнем, и использовав три члена ряда, получим
г 2 =-¦
/со со2
М Ре М2 '
Соответственно решение F.8.32) принимает следующую форму:
_ _ / /соЗсЛ / /со2Зс \
61 = n(8Go - 5Gr)exp/- — Jexp\- -^- j. F.8.38)
Решение F.8.38) описывает распространение бегущих затухающих волк
энтропии. Темп затухания волн зависит как от комплекса физических
параметров Ре М2, так и от частоты колебаний, или,точнее, от длины волны,
При о32х/РеМ2= со2ктх/и3 = 1 амплитуда энтропийных волн уменьшается
в е раз. Для решения системы из двух уравнений F.8.29) и F.8.30)
необходимо исключить производнуюd2blldx2 из правой части уравнения F.8.30).
подставив решение F.8.38):
ddp dbTi к fjtM _ _
iudp + M—^+kM—7 = EGO -5Gr)r22exp(r2x). F.8.39)
dx dx Pe
Частные решения системы неоднородных уравнений F.8.29) и F.8.39)
имеют следующий вид:
8п = В1ехр(г2х), 8p=D2exp(r2x)- F.8.40)
274
Подставив решения F.8.40) в уравнения F.8.29) и F.8.39), находим
значения Dx и D2, удовлетворяющие этим уравнениям:
o -6Gr) _fcjur!M(iG3+Mr2)EGo -5Gr)
2
7I "" [(/co + Mr2J -гЦРе ' 2 [(io5+Mr2J -r2] Pe '
Решением системы неоднородных уравнений F.8.29) и F.8.39)
является сумма общего решения однородных уравнений и частного решения
неоднородного
(' /сох \ //сох
( /сох \ //сох \
ГТ+М/^Чь^м/ ?>гехр{г2х) F.8.41)
/сох" \ / /сох" \\
^-^-J-Bexp^——jJ+D2exp(r2 x). F.8.42)
Неизвестные коэффициенты А и В можно найти, если подставит^ решения
F.8.41) и F.8.42) в граничные условия F.8.18) и F.8.20), причем в
граничных условиях (п/ принятому предположению) отбросим член
(к — 1)/2к и для простоты примем ei =0, т.е. ограничимся критическим
режимом истечения на выходе из тракта. Определив коэффициенты А и В
и подставив их, так же как и коэффициенты Dx и/J, в решение F.8.42),
находим зависимость для распределения по длине тракта амплитуды
давления:
/ /сох \ 1 _
A + к М)ехр ехр (г2х) (8Go-8Gr) -
\ 1 — М/ J
/со /сох \ / /со /сох
X t(Go+MMGo + (Gr-MMGr] +( *(/со + М г2) - — | X
\ L M J
ч/ Г / ш itor \ ( /со /сох \1
X ехр +ехр + +
L \1-М 1+М/ \ 1+М 1-М Л
+ 7ГК1 -
Ml
]х
)( М)ехр
1+М/ Р1 -М
ехрг2 +АЦ/ М
)
Ре J '
F.8.43)
где
)(\кМ)ехр(
1+М/ \1-М
275
На рис. 6.39 и 6.40 для сопоставления с экспериментальными точками
проведены теоретические кривые, рассчитанные по формуле F.8.43) при
значении коэффициента температуропроводности кт - 0,8 м2/с.
Для газовых потоков в трактах характерен только турбулентный режим
течения, и соответственно все процессы обмена (теплопроводность, диффу.
зия) определяются не молекулярным переносом, а турбулентным
движением среды. При экспериментах не проводилось непосредственного
измерения характеристик турбулентности. Поэтому оценка параметров
турбулентности проводилась по экспериментальным зависимостям, полученным
Ю.А. Ивановым [100]. При экспериментах использовалась решетка с очень
высокой относительной степенью загромождения *Sp = 0,92, для которой
по графику работы [100] интенсивность турбулентности е= 0,5. Диффу.
зионный масштаб турбулентности определяется характерным шагом
решетки т, который для используемой в опытах решетки равнялся m = 0,01 м.
Такому шагу соответствует масштаб турбулентности /т = 0,0035 м.
Коэффициенты турбулентного обмена (диффузии DT и температуропроводности
кт) определяются соотношением DT = кт = е/ти0, где «о - скорость потока
за решеткой. Оценка значения коэффициента турбулентной
температуропроводности газа в установке дала указанную выше величину кт = 0,8 м2/с.
Кривые 5 для кт = 0,8 м2/с на рис. 6.39 и 6.40 достаточно хорошо совпадают
с данными экспериментов во всем исследованном диапазоне частот от О
до 350 Гц (со = 0 -^ 8)_. Следует отметить, что специфические особенности
установки (большие Sp и и0) обеспечили очень высокий уровень
турбулентности и соответственно достаточно быстрое затухание энтропийных волн.
Высокий уровень турбулентности позволил четко выявить эффекты,
связанные с рассеиванием энтропийных волн при относительно низких частотах.
При меньшем уровне турбулентности энтропийные волны начнут
рассеиваться при более высоких частотах или при большей длине тракта.
Глава 7
МАТЕМАТИЧЕСКИЕ МОДЕЛИ РАЗВЕТВЛЕННЫХ
ПНЕВМОГИДРАВЛИЧЕСКИХ СИСТЕМ
С РАСПРЕДЕЛЕННЫМИ ПАРАМЕТРАМИ
§ 7.1. Некоторые особенности построения эквивалентных ПГЦ
для ПГС с распределенными параметрами
При построении математических моделей достаточно сложных ПГС с
сосредоточенными параметрами использовался матрично-топологический
аппарат (гл. 3) или метод сигнальных графов (гл. 4). Применительно к
системам с распределенными параметрами можно также использовать
эти методы, однако они требуют определенной модификации.
Действительно, матрицы инциденции для ПГЦ с сосредоточенными параметрами
формировались в предположении, что мгновенное значение расхода на входе и
выходе каждой ветви одно и тоже. Это позволило использовать матричную
форму записи уравнений сохранения для узлов в виде произведения
матрицы инциденции цепи на вектор расходов в каждой из ветвей. Кроме того,
указанное предположение является основой метода главных сечений,
позволившего получить достаточно простые правила формирования
линейных математических моделей разветвленных ПГЦ. Особенностью элементов
с распределенными параметрами является отличие мгновенных значений
расходов на входе и выходе. Поэтому для цепей, содержащих элементы
с распределенными параметрами, нельзя непосредственно применять аналог
первого закона Кирхгофа - уравнение сохранения расходов для узлов, -
а также использовать уравнения сечений.
Существуют способы преобразования ветвей с распределенными
параметрами к эквивалентной Т- или П- образной схеме из двухполюсников
[187]. При этом вместо одной ветви и двух узлов на входе и
выходе появляются три ветви и три узла, что для разветвленной ПГС,
содержащей большое число элементов с распределенными
параметрами, делает эквивалентную цепь достаточно сложной. В то же время для
систем с распределенными параметрами можно применить
модифицированную запись уравнений сохранения расходов в узлах [60, 62, 63, 65, 162],
исключив при этом необходимость введения дополнительных ветвей,
учитывающих сжимаемость среды и связанных с узлом внешней среды.
Внешний узел может присутствовать в цепи, так как обычно некоторые
из элементов цепи сообщаются с внешней средой, получая или отдавая
жидкость. В этом случае для цепи с распределенными параметрами
мгновенная сумма физических расходов, поступающих в систему и выходящих
из нее в общем случае не равна нулю. Это свойство цепи с распределенными
параметрами является платой за использование при формировании цепи
специального приема, когда четырехполюсные элементы заменяются
специальными двухполюсными элементами, у которых расходы на входе и
выходе не совпадают.
277
Применительно к подобным элементам, используемым в
электродинамических системах, О.В. Тозони [216}Jre ^Жйгил удачное название
коммуникатор, под которым понимается двух1то1Тюсный элемент, описываемый
сложными уравнениями ветви, учитывающими наводки, утечки и т.д.
Основные же его особенности совпадают с отмеченными выше: это наличие
двух полюсов с разными значениями расходов (токов) на входе и выходе.
Ниже подобные элементы будем также называть коммуникаторами.
Введение коммуникаторов позволяет четырех- (или шести-) полюсные элементы
заменить в цепи на двухполюсные.
Основным элементом ПГС, который необходимо рассматривать как
систему с распределенными параметрами, является участок
гидравлического тракта, особенности нестационарного течения в котором достаточно
подробно рассматривались в гл. 5 и 6. Там же были выведены уравнения
участка тракта как четырехполюсника, которые ниже будут широко
использоваться. При формировании моделей ПГЦ для участков тракта
остаются в силе основные предположения, сформулированные в
предыдущих главах: участок имеет достаточно большую длину, так что L/R > 1,
и можно пренебречь особенностями сложного пространственного течения
на границах участка тракта, так как область возмущенного течения намного
меньше длины участка тракта. Для формирования моделей сложных
разветвленных ПГС используем в качестве элемента ПГЦ однородный участок
тракта, описываемый уравнениями четырехполюсника, но изображаемый
как коммуникатор-двухполюсник. Все неоднородности выделим как
отдельные элементы, представляемые в зависимости от типа элементов,
входящих в ветвь, или как двухполюсник (пассивный или активный),
или как четырехполюсник, изображаемый коммуникатором. Введение
коммуникатора не является чисто формальной операцией, упрощающей
схему цепи. Замена четырехполюсного элемента (в других случаях шести-
или восьмиполюсного) особым двухполюсным элементом возможна по
той причине, что два других полюса четырехполюсника применительно к
ПГС определяют состояние внешней среды, за которую принимают или
абсолютный вакуум, или область с нулем абсолютной температуры
(для тепловых переменных) и т.д. Расходы или - в дальнейшем - потоки
энергии на входе и выходе элемента отличаются; этим и определяется
влияние распределенности параметров.
Отличие расходов или энергии, (энтальпии) на входе и выходе в
уравнении четырех- (шести-) полюсника учитывается расходами через ветви,
связанные с узлом внешней среды. Однако применительно к анализу всей
цепи баланс расходов или потоков энергии для узла, характеризующего
внешнюю среду, как правило, интереса не представляет. Соответственно
можно не рассматривать эти дополнительные ветви, ведущие к узлу
внешней среды, оставив в четырехполюсном элементе только по два полюса,
превратив его тем самым в коммуникатор.
Первым матричные методы для анализа динамики гидравлических
систем с распределенными параметрами использовал Ю.Н. Гризодуб [69, 70],
затем матрично-топологические методы расчета нашли применение в
работах В.П. Шорина [243], М.И. Рабиновича [187J, В.А. Задонцева [182].
278
§ 7.2. Уравнения цепи с активными элементами у узлов
7.2.1. Матричное уравнение цепи. В любой ПГС имеются активные
элементы, являющиеся источниками энергии или источниками возмущений
(сигналов) в системе. Это может быть насос или компрессор с переменной
частотой вращения, регулирующее (дросселирующее) устройство,
специальный пульсатор, зона горения или химической реакции и т.д. Удобно ввести
обобщенный активный элемент (рис. 7.1), состоящий из идеальных источни-
GJO)
Рис. 7.1. Схема обобщенного активного элемента: а — на входе, б - на выходе
/-й ветви
ков напора 1 и расхода 4, регулирующего устройства 2 с переменным
проходным сечением и местного сопротивления 3, учитывающего внутренние
потери, утечки в реальных источниках напора и расхода.
Для упрощения уравнений сделаем предположения, что активные
элементы, создающие возмущения в ПГЦ, находятся в каждой ветви цепи
только на ее концах, непосредственно у узлов. Если в конкретной системе
это условие не выполняется, то у активного элемента в середине ветви
вводится дополнительный узел. Рассмотрим изотермическое движение
слабосжимаемой капельной жидкости или газа постоянного состава, для
которого во всех сечениях тракта соблюдается условие М ^ 1 [65]. В этом
случае перепад давления и расходы в обобщенном активном элементе
на входе в г-ю ветвь цепи определятся следующими соотношениями:
р,.@) -р*@) = -ДЯ,.@) + Дрр/@) + ДРвнл(О), G.2.1)
Gc./@) =G,@)-ft@), G.2.2)
где рДО) — давление в начале z-й ветви, т.е. в узле, из которого ветвь
выходит, р*@) - давление на входе в пассивную часть г-й ветви, АН; -
напор, создаваемый источником напора в начале /-й ветви, Дрр/@) =
= Glj@)/2pFpj@) — перепад давления на регулирующем устройстве
с проходным сечением FVmi@), ДРвн./@) - потери давления на
внутреннем сопротивлении источников; Q/@) - расход жидкости от источника
расхода на входе в i-ю ветвь, G,- @) - расход жидкости в начале пассивной
части г-й ветви, Gci@) - расход жидкости через источник напора и
гидравлические сопротивления.
Агрегаты, моделируемые обобщенным источником, имеют, как правило,
нелинейные характеристики; поэтому уравнения G.2.1) и G.2.2) удобно
представить в линеаризованной форме и свести к одному линейному
соотношению для размерных вариаций
5р*'@) = 5Р;.@) - г'ВИ ДО) 5G-@) + 8 АН',@) +
+гвн.до)бе;(о) + „; (о) в^.до), G.:.з>
279
где
др*'(О), 5р/@), 5G/@), 5АЯ/@), 5Fp.,-@) - вариации соответствующие
параметров;
z'BHj @) = 2 [AppJ @) + ApBHj @) ] / [G,@) - Qt @) ] - сопротивление
(импеданс) обобщенного источника на входе в /-ю ветвь;
у\ @) = 2 Арр у @) i'Fpj @) - коэффициент усиления регулирующего
устройства с переменным проходным сечением. Аналогичная
линеаризованная зависимость связывает вариации параметров обобщенного
активного элемента на выхопе /-й ветви (рис. 7.1, б):
8р*' A) = 6р;A) + z'BHj A) 6G/A) - 5 ДЯ;-A) -
-z;H>I.(iMQ;(i)-^;(iMF^.(i), G.2.4)
где обозначения всех вариаций параметров и коэффициентов полностью
совпадают с соответствующими обозначениями в зависимости G.2.3),
только указана другая координата сечения: не xt - 0 для входа, a ~xt = 1
для выхода из ветви. Суммы последних трех членов в уравнениях G.2.3)
и G.2.4) определяют эффект от суммарного действия на течение в ветви
всех внешних возмущений (активных элементов) и их можно объединить
в суммарные (обобщенные) возмущающие воздействия 55/@) и 65)A).
С учетом последнего замечания уравнения для всех обобщенных
активных элементов в ветвях, входящих в цепь, можно записать в матричной
форме:
5р* '@) = 5 р'@) - z;H@) 5G'@) + 5S'@), G.2.5)
5р*'A) = 6р'A) + z;H(l) 5G'A) - 5S'A), G.2.6)
где 5р*'@), 5р*'A) -векторы (матрицы-столбцы) вариаций давлений на
концах (вход и выход) пассивных частей ветвей, 5р'@), 5р'A) — векторы
вариаций давлений на концах ветвей, 5G'@), 5G'A) — векторы вариаций
расходов на входах и выходах ветвей, 5S'@), Ь S'(l) — векторы внешних
суммарных возмущающих воздействий на входах и выходах ветвей, ZgH@),
zbh0) ~~ Диагональные матрицы импедансов (размерных сопротивлений)
обобщенных активных элементов.
В систему матричных уравнений цепи кроме уравнений ветвей входят
уравнения сохранения для узлов и контуров. Применительно к
рассматриваемым системам, содержащим хотя бы часть элементов с
распределенными параметрами, как уже отмечалось, используемая ранее запись уравнений
сохранения расходов для узлов непригодна, и так как векторы расходов на
входе и выходе являются независимыми переменными, то матрицы инци-
денций для входов и выходов также будут разными. Соответственно
уравнение баланса расходов для узлов в матричной форме можно записать
[60,62, 162]:
П@) G@) + ПA) G(l) = 0, G.2.7)
где П@) - матрица, получаемая из общей матрицы совпадений узлов и
ветвей (инциденции) путем замены нулями всех элементов равных
единице1^, ПA) — аналогичная матрица, но только с заменой нулями всех
Как и ранее в гл. 3, в уравнении баланса расходов в узлах за положительные
принимаются поступающие в узел расходы, за отрицательные - выходящие из узла,
т.е. поступающие на входы ветвей.
280
элементов равных минус единице. Уравнение баланса расходов G.2.7)
линейно и не меняет своей формы при переходе к размерным вариациям
расходов:
П@) 86'@) + ПA)8СA) = 0. G.2.8)
Для дальнейшего анализа удобно ввести вектор вариаций давлений в
узлах цепи 5Р'. По аналогии с доказательством, приведенным в гл. 3 для
системы с сосредоточенными параметрами, можно показать, что вектор
6GM 6GJH)
6Gn@)_ 6GJD
Рис. 7.2. Схема ветви с каскадным соединением коммуникаторов
вариации узловых давлений 5Р' связан с векторами вариаций давлений на
концах ветвей следующими зависимостями:
5р'@) = -Пт@) 5Р', 5р'A) = ПтA) 5Р'. G.2.9)
Уравнения G.2.9) являются аналогом второго закона Кирхгофа.
Уравнения G.2.8) и G.2.9) описывают топологическую структуру
цепи, связывая между собой параметры течения в отдельных ветвях,
уравнения же G.2.5) и G.2.6) — для участков ветвей, содержащих активные
элементы. По принятому условию эти участки находятся только на концах
ветвей, у узлов. Осталось описать пассивные элементы, входящие в ветви.
Пассивная часть каждой из ветвей может состоять из ряда элементов,
причем часть из них может быть с распределенными параметрами, а часть —
с сосредоточенными. По условию формирования цепи ветви не содержат
развилок (узлов с несколькими сходящимися ветвями), т.е. они могут
состоять только из элементов, соединенных между собой каскадно
(рис. 7.2). Каждый элемент здесь представлен в виде коммуникатора,
который изображен прямоугольником, соединяющимся с другими
элементами цепи двойными линиями, чтобы отличить его от двухполюсного
элемента, для которого мгновенные значения расходов на входе и выходе
равны. Каждый коммуникатор будем описывать уравнением
четырехполюсника, независимо от того, является ли он элементом с
распределенными или с сосредоточенными параметрами. В обозначениях, принятых
для четырехполюсников уравнение сопротивления запишется (опускаем
индекс элемента) в виде
бр'(О) =
2Ар _____
— 6GA), 5G@) = 6G(l),
или в матричной форме:
2Ap/G
др'ф)
5G'@)
0
1
= А'
G.2.10)
G.2.11)
где Ар, G - средние 2начения_ перепада давления и расхода на
сопротивлении, 5р~'@), 5р~'A), 5 G'@), 5 G 'A) — амплитуды вариаций давления и
расхода на входе и выходе сопротивления. Если в качестве переменной
281
используется не расход, а скорость, то уравнение G.2.11) принимает форму
5р'@)
6м'@)
1
0
2 Ар /и
1
Ь?
Ьп'
П)
A)
G.2.12)
где и, 5w'@), 5 м'A) - среднее значение и амплитуды вариации скорости
на входе и выходе. Аналогично для инерционности можно записать:
6G'(O) =
или
8р'@)
5G'@)_
О
1
G.2.13)
где ти - инерционная постоянная времени, р - среднее давление. Также
для емкости
5р'@) = 5р'A), 6G'@) =
или в матричной
дрЩ
6G'@)
G.2.14)
где re - постоянная времени емкости.
Приведенные уравнения записаны в матричной форме в А-параметрах,
которая удобна, когда элементы, входящие в ветвь, соединены
последовательно, а четырехполюсники (по принятой в электротехнике
терминологии) - каскадно. Можно записать для /-го и / + 1-го коммуникаторов ветви
уравнения в А-параметрах:
G.2.15)
где 5р)@), 5р/+1@), 5G/@), 5G/+1 @) - амплитуды размерных вариаций
давления и расхода на входах в i-й и /+ 1-й коммуникаторы, 5р"/A),
^P/ + i(O» ^^j(O» SGi+i (,t) '— аналогичные величины на выходах из
коммуникаторов. Конкретный вид матриц А/ и А'/+1 зависит от типа
моделируемого элемента. В сечении стыка двух коммуникаторов (см. рис. 7.2)
должны соблюдаться очевидные условия равенства амплитуд размерных
вариаций давления и расхода:
6р;A) = 5р;+1(О), 6G;(l) = 5G/+1@). G.2.16)
Для г-го и (/+ 1)-го элементов /-й ветви, используя уравнения G.2.15)
282
SG,'(O)
=а;-
о р f A)
Gy( 1)
5G/+1@)
и G.2.16), получим
5С/@)
Повторяя подобные преобразования со всеми пассивными элементами
ветви, учитывая, что для элементов цепи необходимо вводить двойную
нумерацию, указывающую как номер ветви /, так и номер элемента ветви/,
получаем для всех пассивных элементов /-и ветви
А/= П А,}, G.2.17)
I = 1
где А/- матрица уравнения пассивной части /-й ветви как
четырехполюсника, A'fj - матрица уравнений /-го элемента /-й ветви как
четырехполюсника. Используя уравнение G.2.17) и зависимости для всех элементов,
входящих в ветви, получаем систему уравнений, описывающую
динамические характеристики пассивной части ветвей цепи в линейном
приближении.
Для использования уравнений пассивных частей ветвей в общей системе
перейдем в этих уравнениях от А-параметров к z-параметрам по
стандартной процедуре [14, 15, 60]. После перехода к z-параметрам систему из
2<7 уравнений (где q — число ветвей в цепи) можно записать в матричной
форме
5р * '@) = zn5 G'@) + z;25 G'(l), G.2.18)
5p*'(l)=z216G/@)+z225G'(l), G.2.19)
где z'n, z'i2, z2i, z22 - диагональные матрицы, элементами которых
являются соответствующие элементы матриц уравнений ветвей как
четырехполюсников. Система матричных уравнений G.2.5), G.2.6), G.2.8), G.2.9),
G.2.18) и G.2.19) описывает поведение параметров цепи при
гармонических возмущениях. Ограничение вида возмущений связано с принятой
формой записи уравнений G.2.18) и G.2.19) через амплитуды вариации
параметров.
Форма уравнений будет такой же и при использовании операторной
записи в результате преобразований Лапласа (при нулевых начальных
условиях), только вместо величины /со нужно подставить оператор
Лапласа s. Если возмущения носят более сложный характер, но остаются
периодическими, то, используя принцип суперпозиции и разлагая возмущения
в ряды Фурье, можно с помощью тех же уравнений найти решение для
параметров системы.
Найденную выше систему матричных уравнений можно свести к одному
матричному уравнению. Подставив в уравнения G.2.5) и G.2.6)
зависимости G.2.9), а затем, используя полученные соотношения для исключения
из уравнений ветвей G.2.18) и G.2.19) векторов 5р"*'@) и 6р"*'A),
найдем
[z'n + ZqH@)] 5G'@) + z'125G'(l) + Пт@) 5Р"' = 5S'@) G.2.20)
z215G'@)+ [z22 -z;hA)] 5G'(l)-nT(lMP' = -6S'(l). G.2.21)
283
Добавив к уравнениям G.2.20) и G.2.21) уравнение баланса расходов
в узлах G^2.8), получаем замкнутую систему уравнений относительно
векторов 5G'@), 5G'A) и 5Р'
'г'и +*;н@) z'u Пт@)
Z21 Zm-Zbh(I) -ПТA)
.П@) П<1> ° " — ",7.2.22,
Если первую матрицу в уравнении G.2.22) обозначить Zp, то из этого
уравнения найдем:
5S'@)"
G.2.23)
.6P'
0
Зависимость G.2.23) позволяет найти динамические характеристики
системы - частотные передаточные функции системы для вариаций
давлений и расходов (скорости) во всех узлах и ветвях цепи - как реакцию
на действие активных элементов, описываемых вектором в правой части
G.2.23). Однако зависимость G.2.23) достаточно громоздкая, порядок
матрицы Zp составляет 2q + m, где q — число ветвей, т — число узлов
цепи.
7.2.2. Уравнения узловых давлений. Для уменьшения порядка системы
уравнений запишем зависимости G.2.20) и G.2.21) в виде одного
матричного соотношения:
LZ21
или в еще более компактной форме:
~8G
_5G
'@)"
'A).
+
пт
-п
@)
гA).
5Р'=
5S'@)
G.2.24)
G.2.25)
*12
— матрица сопротивлений цепи. Разре-
z2i z;2 -zBH(l)
шив уравнение G.2.25) относительно вектора вариаций расходов на концах
ветвей 5G' и учтя, что (Z')~l = Y', где Y' - матрица проводимостей ветвей
хепи, можно записать
5G' = Y'5S' - Y'nT5P'. G.2.26)
В принятых обозначениях упрощается и запись уравнений баланса расходов
в узлах цепи G.2.8):
Пи5б' = 0, * G.2.27)
где Пи = [П@) :ПA)]. Умножив все члены уравнения G.2.26) на матрицу
Пи и учтя соотношение G.2.27) , найдем
284
Тройное произведение ПИУ'ПТ =Yy назовем матрицей узловых проводи-
0мостей. Из уравнения G.2.28) можно найти связь вектора вариаций
узловых давлений 5Р'с вектором внешних возмущающих воздействий 5S':
бР'^ГПиУ'бГ. G.2.29)
Порядок матриц в уравнении G.2.29) ниже, чем порядок матрицы
уравнения G.2.23). Найдя из уравнения G.2.29) вектор 5Р', с помощью
соотношения G.2.25) можно определить вектор вариаций расходов на
концах ветвей 5G'. Следует отметить, что при выводе уравнений G.2.23)
и G.2.29) предполагалось, что все величины узловых давлений
неизвестны. Однако в ряде случаев в цепь входит узел, характеризующий состояние
внешней среды, из которой поступает или в которую затем сливается
жидкость из цепи. Тогда из зависимостей G.2.22) и G.2.21) необходимо
исключить соответствующую переменную и уравнение, определяющее
давление в этом узле, называемом базисным. Во всех приведенных выше
матричных уравнениях ПГЦ использовались размерные переменные —
вариации параметров. Если переходить к безразмерным переменным —
безразмерным амплитудам вариаций параметров, то форма записи
элементов матриц четырехполюсников изменится: вместо 2/\p/G или 2Ар/и
в уравнениях G.2.11) и G.2.12) элементами будут просто 2, вместо
iu)rViplG в уравнении G.2.13) — /о?ти, вместо icoTeGlp в уравнении
G.2.14) - /соте. Таким образом, элементы становятся безразмерными и
соответственно в обозначениях матриц необходимо устранить штрихи,
показывавшие, что матрицы связывают размерные переменные.
Исключается штрих из обозначений амплитуд вариации при переходе к
безразмерным вариациям. Аналогичные преобразования проводятся с
элементами и переменными, входящими в уравнения четырехполюсников G.2.18)
и G.2.19). В уравнении активных элементов G.2.3) при переходе к
безразмерным вариациям параметров изменяется запись формул для
сопротивления и коэффициента усиления в источнике zBKi-@) =2[Дрр,-@) +
+ ДРвн,@)]/[С1@)-ё/@)Ь *,-@)=2Дрр,@) и т.д.,_где Appi(O) =
= Дрр,-@) 1р, Дрвн,- @) = ДАн> @) Ip, G, @) = Gt@)/G, Qt@) = Qt @) /G;
G,p — масштабные значения расхода и давления для всей цепи.
Переход к безразмерным вариациям не изменяет матрицу инциден-
ции П и соответственно матрицы П@) и 11A), характеризующие
топологию системы. Ранее при выводе уравнений отдельных звеньев, входящих
в ветви системы, удобно было при приведении к безразмерному виду
относить размерные вариации к среднему значению варьируемых параметров
ддя данного элемента. Однако применительно ко всей системе при
использовании матричных уравнений сохранения необходимо вводить единые
масштабные значения давления и расхода. Соответственно перед каждой
безразмерной вариацией (или ее амплитудой) появится нормирующий
множитель, который входит в вектор переменных. Так, например, в
безразмерном виде векторы амплитуд вариаций расходов на входах и выходах
и давлений запишутся в виде
5GA)=[G15G1A)G25G2A)... Ga8Gq(l)]]
. pm8pm]\ 5р*(О)=[рГ(О
285
/2
L
or
JL®
Рис. 7.3. Схемы ПГС (д) и эквивалентной цепи {б)
и т.д., где Gj = Gf/G, Gf - средний расход через /-ю ветвь, G - масштабный
для всей цепи расход; рг = рт/р, pi - среднее давление в узле / и т.д.,
р*@) = Pi(G)lp, Pi*@) — среднее давление в начале пассивной части /-й
ветви,р — масштабное давление для всей цепи.
При таком представлении векторов амплитуд вариаций параметров
полностью сохраняется форма записи уравнений G.2.22) , G.2.23) и
др при переходе к безразмерному виду (только везде отбрасываются
штрихи).
7.2.3. Пример формирования математической модели ПГС. Рассмотрим
ПГС, схема которой представлена на рис. 7.3,а. В ПГС входят: баллон
с жидкостью 2, давление в котором создается газом (величина давления
поддерживается с помощью редуктора 7), два насоса — центробежный 4 и
объемный 14, гаситель колебаний 5, регулятор давления (за собой) 9,
дросселирующие устройства 7 и 12 (с регулируемым проходным
сечением), участки гидравлических трактов 3, б, 8, 10, 11, 13, и 15,
рассматриваемые как элементы с распределенными параметрами. ПГЦ, эквивалентная
рассматриваемой ПГС (рис. 7.3,а), приведена на рис. 7.3, б. На схеме цепи
участки трактов изображены как коммуникаторы. Изображения других
элементов цепи уже использовались ранее.
Примем, что редуктор 1 имеет незначительную инерционность и
достаточно точно поддерживает постоянным давление в баллоне. В этом случае
можно пренебречь возможными отклонениями давления в баллоне при
286
уменьшении уровня жидкости и моделировать баллон источником напора
на входе в первую ветвь цепи 1). Учитывая потери давления на входе в
трубопровод 3, используя зависимость G.2.3), запишем в амплитудах
размерных вариаций уравнение источника напора на входе в первую ветвь:
&р'г@)-6р? '= z'mх @N G I @)- 5 АН 1@), G.2.30)
где 5A#i = 5р'п-др''н - амплитуда вариации напора (избыточного над
атмосферным давлением), создаваемого в баллоне как источнике напора,
5рб ~ амплитуда вариации давления в баллоне, дрн - амплитуда вариации
давления во внешней среде. Ветвь, на входе которой находится
описываемый уравнением G.2.30) источник, выходит из узла 0, характеризующего
состояние внешней среды. При этом 5р\ @) = §р„.С учетом последнего
равенства зависимость G.2.30) принимает вид
5рГявРб -4hi@) 5GU0), G.2.31)
r#e z вн 1 @) = 2 Арг /Gj, Api, Gx - перепад давления и расход через первую
ветвь (трубопровод 3). Считая, что пассивная часть первой ветви (т.е.
трубопровод .?) состоит из цилиндрической трубы без местных
сопротивлений и рассматривая столб жидкости в этой трубе как систему с
распределенными параметрами, пренебрегая трением и используя зависимость
E.5.4), запишем для трубы уравнение четырехполюсника в А-параметрах:
5p"i@) = cosZbidp i(l) +/ai sin cox dG i(l),
5Gi@) = (i/o^sm ь>г bp \{\) + cos cj, 5G/A), G.2.32)
где 5p/@), SG[ @) , bpx' A) , 5Gj(l). - амплитуды вариаций давлений и
расходов на входе и выходе пассивной части первой ветви, о^ = ojLi/ai -
безразмерная частота, а\ =д1//г1 - волновое сопротивление, аг - скорость
звука, L 1 — длина трубопровода, F\ — площадь проходного сечения трубы
в первой ветви. После преобразования в z -параметры уравнения для трубы
в первой ветви G.2.32) принимают вид:
5р i @) = (//a! ^ctgoJi 5 G; @) + О/а! sin со t )б G \ A), G.2.33)
dp ; A) = (i/a[ sin cJi N G[ @) + (i/ai')ctgco X8G[A).
Следзаощий агрегат системы - центробежный насос 4 - является
активным элементом, но расположен внутри ветви (рис. 7.3,д), так как отделен
от ближайшей развилки участком трубопровода 6 с гасителем
колебаний 5. По принятому ранее условию перед активным элементом
необходимо ввести дополнительный узел /(рис. 7.3,6). Линеаризованное
уравнение активного элемента на входе во вторую ветвь, моделирующего
характеристики центробежного насоса, с учетом внутренних потерь
находим из зависимости G.2.3) ^ 2 34)
где 5р?'@)> 5р2'@) - амплитуды размерных вариаций давления перед
и за насосом, ^н2@) = -Э ApJbG - внутреннее сопротивление насоса
(наклон напорной характеристики насоса), Арн-напор, развиваемый на-
*) Нумерации элементов на схеме рис. 7.3,а и ветвей ПГЦ на рис. 13,6 не
совпадают.
287
сосом, 5Д#2@) = (Э Арн/дп4) 5 и4' - амплитуда вариаций напора,
создаваемого насосом как активным элементом — источником напора, /?4> &Щ -
частота вращения и амплитуда вариации частоты вращения насосав. На
выходе из центробежного насоса установлен гаситель колебаний — пружинный
аккумулятор (демпфер) для сглаживания пульсаций давления за насосом.
Линеаризованное уравнение динамики емкости — гасителя_колебаний —
связывает амгсштуду вариации расхода жидкости в емкость 8G'e с
амплитудой вариации давления перед гасителем Sp^'iCOI). С учетом инерции
жидкости и механических подвижных частей, вязкого (ламинарного) трения
жидкости это уравнение принимает следующую форму:
шЬ8р„д» = 5^@)
1 2Г2 + Т W'()
где Ь - pFl$/k, Fэф - эффективная площадь упругого элемента гасителя
(поршня, мембраны и т.д.), к — коэффициент податливости упругого
элемента, Т2 — инерционная постоянная времени гасителя, Тг —
постоянная времени вязкого трения, We(cS) — частотная передаточная функция
гасителя. Уравнение G.2.35) описывает в гидравлических параметрах
(вариации расхода и давления) агрегат, содержащий механические
устройства, что позволяет его непосредственно использовать как уравнение
элемента ПГЦ. Можно представить схему из пневмогидравлических
элементов (сопротивления, инерционности и емкости) эквивалентную по
своим динамическим свойствам механическим частям гасителя
колебаний.
Для связи уравнения G.2.35) с другими параметрами цепи запишем
уравнения баланса расходов для сечения тракта, в котором установлен
гаситель:
5(j;=5G21@)-6G21(l). G.2.36)
Используя зависимости G.2.35) и G,2.36) и очевидное условие
равенства давлений в сечениях перед и за гасителем, запишем уравнение гасителя
как четырехполюсника в А-параметрах:
5р21@) = 5р21A), G.2.37)
Уравнение для участка трубы 6 (рис. 13,а) записывается аналогично
уравнению G.2.32), изменяются только индексы " на 2". После
перемножения матриц уравнений четырехполюсников в А-параметрах для
гасителя G.2.37) и уравнения типа зависимости G.2.32) для трубопровода 6
и перехода к 2-параметрам находится уравнение пассивной части второй
ветви как четырехполюсника, т.е. его коэффициенты z2у, используемые при
построении матричных уравнений всей цепи. Формирование матрицы
коэффициентов ветвей в z -параметрах, учитывая большое разнообразие
возможных сочетаний элементов, входящих в ветви, удобнее проводить
с помощью ЭВМ. На входе в третью ветвь (рис. 7.3,6) находится
дросселирующее устройство 7 с регулируемым проходным сечением, уравнение
1) Индексы - как для первого элемента второй ветви (пассивной ее части).
288
которого как источника напора1) находится из соотношения G.2.3):
bpt '@) = Ьр 'з(О) - z'BH.3@) bG з@) + ^3@MF;.3@), G.2.38)
где ^н.з(О) =2App.3@)/G3, /3 @) = 2Арр,3 @)/Fp>3 ф), Арр.3@),
F 3 @) - средние значения перепада давления и площади проходного
сечения дросселирующего устройства 7.
В соотношения, описывающие пассивную часть ветви 3, входят
уравнения трубопровода ?, аналогичные уравнениям G.2.33), но с другими
индексами, и уравнение нагрузки на конце ветви 3. Для общности примем,
что нагрузку можно описать как двухполюсный элемент,
характеризующийся импедансом z'h3 (со) (учтя, что Ьр 3 2A) = &Р н):
или, как четырехполюсник в А-параметрах
(l), G.2.39)
На входе в четвертую ветвь установлен регулятор давления за ним 9,
линеаризованное уравнение динамики которого запишем следующим образом:
5Fp.4@)= W'pA(o>)8p io(D, G.2.40)
где 5Fp.4 @) — амплитуда вариации проходного сечения дросселирующего
элемента регулятора на входе в четвертую ветвь, 5р'юA) - амплитуда
вариации давления в конце импульсной трубки 10, WpA(co) — частотная
передаточная функция регулятора.
Учтем податливость чувствительного элемента регулятора, описав его в
линеаризованном виде уравнением
дС'10A) = Я'рЛ(ы)др'10A1 G.2.41)
и будем рассматривать импульсную трубку 10 как участок тракта с
распределенными параметрами, уравнение для которого как четырехполюсника
удобно записать в ^-параметрах [14, 15, 60], учтя, что Ьр\0 @) = Ьр \х A),
т.е. совпадает с давлением на выходе из первого элемента (регулятора)
четвертой ветви:
5р'10A) = A/cos п lo)e?ii(l) + /aiotgwloe^io(l), G.2.42)
где 5 G i о @), 5 G \ 0 A) — амплитуды вариации расходов на входе и
выходе импульсной трубки 10, Ьр\о@) - амплитуда вариации давления на
входе в импульсную трубку, 6/?4i A) - вариация давления на выходе из
регулятора (первый четырехполюсник в четвертой ветви). Параметры на
входе и выходе дросселирующего устройства регулятора 10 связаны
зависимостью, аналогичной уравнению G.2.3), но с другими
обозначениями.
4@), G.2.43)
1 )На рис. 7.Зуб для дросселей 7 и 12 сохранены обозначения сопротивления с
переменным проходным сечением.
^•Б.ф. Гликман 289
где dp 41 A) — амплитуда вариации расхода на входе в регулятор,
z'pA@) = 2 App.4@)/G4, ^.4@) = 2App.4@)/Fp.4@), App.4@) -
-среднее значение перепада давления на регуляторе, G4 - средний расход
через четвертую ветвь, FpA@) - среднее значение проходного сечения
дросселирующего элемента регулятора, 5G4i@) - амплитуда вариации
расхода на входе в регулятор. Подставив соотношения G.2.40) -G.2.42)
в формулу G.2.43), находим уравнение регулятора 9 с импульсной
трубкой 10 как четырехполюсника в А-параметрах:
+ *p.4@)8G41(l),
G.2.44)
Второй четырехполюсник четвертой ветви описывает участок тракта 11; его
уравнения аналогичны уравнениям G.2.32). Для активного элемента на
выходе из четвертой ветви — дросселя 12 (рис. 7.3,а) с регулируемым
проходным сечением, используя зависимость G.2.4), находим
где*вн4A) =2App4(l)/G4,^4(l) = 2App4(l)/Fp.4(l); Арр4A) ,Fp4(l) -
средние значения перепада давления и площади проходного сечения для
дросселя 12.
В пятой ветви активный элемент на входе - объемный насос 14 —
описывается уравнением обобщенного активного элемента G.2.3),
записываемого для этого случая в следующем виде:
;0), G.2.46)
где z'BH5@) = -1/(ЭС/ЭАр), 5?s@) = (dG/Ъпц) 6й'14;
Э G/b щ 4 — наклоны расходных характеристик насоса 14 по перепаду
давления и частоте вращения; 5л'14 — амплитуда вариации частоты вращения
насоса 14 (рис. 7.3,а). Уравнения для пассивных частей пятой и шестой
ветвей записываются таким же образом, как и уравнения для пассивной
части третьей ветви, меняются только индексы у коэффициентов и
переменных. Приведенные выше зависимости для активных и пассивных элементов
ветвей цепи, моделирующие рассматриваемую ПГС, позволяют
сформировать матрицы z'BH@), zBH(l), 5S'@), SS~'A), z'i i, z'12, z'21
hz'22,описывающие характеристики активных элементов цепи в линейном
приближении.
'ВН 1
@)
г'внз(О)
н5 @)
290
5S'@)=
4hO)s
ЬАН'2@)
О
«
о
о
G.2.47)
О
о
о
о
о
о
Матрицы сопротивлений пассивных частей ветвей цепи в уравнениях
G.2.18) и G.2.19) формируются путем перемножения матриц
коммуникаторов, входящих в ветви в форме уравнений четырехполюсников в А-па-
раметрах с последующим преобразованием к z -параметрам. Узловая
матрица для рассматриваемой цепи (рис. 7.3,6) имеет следующий вид:
П =
Соответственно матрицы инциденций для начала и конца цепи запишутся
в виде
П@) =
1
0
0
-1
-1
1
0
0
0
-1
0
1
0
-1
1
0
0
0
1
0
0
-1
1
0
0
0
-1
1
0
0
0
-1
0
0
0
0
1
0
0
0
-1
0
0
0
0
0
1
0
-1
0
0
0
0
1
0
0
0
-1
0
0
0
0
1
0
0
-1
0
0
0
0
1
G.2.48)
Уравнения G.2.47) и G.2.48) и матрицы сопротивлений пассивных
частей ветвей из уравнений G.2.18) и G.2.19) полностью описывают
рассматриваемую цепь. Подставив полученные матрицы в уравнения
G.2.22) или G.2.24), находим матричные уравнения линейной
математической модели ПГЦ, эквивалентной рассматриваемой ПГС.
19*
291
§ 7.3. Матричные уравнения цепи при соблюдении
некоторых условий на размещение активных элементов
При формировании приведенных выше матричных математических
моделей линейных (линеаризованных) ПГЦ было использовано единственное
ограничение: активные элементы располагались непосредственно у узлов
цепи. Полученные уравнения содержали матрицы достаточно высокого
порядка - в уравнении G.2.23) матрица Zp имеет размерность Bq + т) X
X Bq + rri), где q — число ветвей, т — число узлов в цепи. Менее
громоздкое уравнение узловых давлений G.2.25) содержит матрицу 2'размерности
2q X Од и матрицу Пт размерности 2qXm. Можно уменьшить размерность
входящих в уравнения цепи матриц, если ввести некоторые
дополнительные условия размещения активных элементов при формировании цепи
[62]:
1) Активные элементы (источники напора или расхода) располагаются
в цепи непосредственно у узлов (условие, уже использованное выше).
2) Положительное направление течения жидкости в ветвях цепи
выбирается так, чтобы идеальные источники расхода находились только в начале
ветвей.
3) Ветвям ПГЦ с идеальными источниками расхода на входе
присваиваются первые номера, и, как следствие, соответствующие составляющие
векторов расходов через ветви (отдельно для входа и выхода ветвей)
располагаются первыми.
4) Реальные источники расхода заменяются эквивалентными реальными
источниками напора (см. гл. 2).
5) Реальные источники напора представляются эквивалентной схемой
из идеального источника напора и внутреннего сопротивления. Внутренние
сопротивления реальных источников напора включаются в пассивную часть
соответствующей ветви на ее концах.
Уравнения пассивных частей ветвей, включающие внутренние
сопротивления источников напора на их концах, формируются таким образом,
как это было описано в § 7.2 (путем перемножения матриц
коммуникаторов, входящих в пассивные части ветвей, при записи уравнений
коммуникаторов в форме уравнений четырехполюсников в А-параметрах). Далее
уравнения ветвей разбиваем на два класса: первые к ветвей, на входах в
которые имеются идеальные источники расхода, и остальные q — к ветвей
без идеальных источников расхода. Для первых к ветвей уравнения ветвей
необходимо преобразовать к форме записи четырехполюсников в /г-пара-
метрах [14, 15,60]:
0М'2 *Х <73Л)
а для остальных q — к ветвей — в у -параметрах:
-, =У/ , Ь (i = * + l, * + 2,...,<7), G.3.2)
где h/, у/ - матрицы уравнений пассивной части z-й от ветви как
четырехполюсника. Уравнения отдельных ветвей цепи G.3.1) и G.3.2)
объединяются в матричные уравнения ветвей цепи, которые связывают вектора ам-
292
плитуд вариаций расхода с векторами амплитуд вариаций давлений на
входе и выходе пассивных частей ветвей. При этом учитывается принятое
условие, что для первых к ветвей расходы на входы в ветви заданы: 5G\ @) =
= 5G/ @) (/ = 1, 2,. .., к), расходы же на выходе из этих ветвей
определяются из второго уравнения G.3.1). С учетом сказанного можно
записать:
0 0
G.3.3)
h22o
0 yi
*' 0)
, G.3.4)
где y'n, yi2, У21, У22 - диагональные субматрицы (q — k)-ro порядка,
содержащие соответствующие элементы матриц для пассивных частей
ветвей как четырехполюсников, описываемых уравнениями G.3.2), h21,
h22 — диагональные субматрицы порядка к, включающие элементы матриц
h'z- , входящих в уравнения G.3.1) , описывающие ветви, имеющие на входе
идеальные источники расхода.
Один из векторов переменных на входах в ветви оказался
неоднородным, так как содержит амплитуды вариаций как давлений, так и расходов.
Для дальнейшего использования уравнения G.3.3) и G.3.4) необходимо
преобразовать, выделив отдельно вектор заданных амплитуд вариаций
расходов идеальных источников расхода (порядка к). Одновременно для
удобства преобразований уравнений дополним вектор параметров на
входах в ветви недостающими амплитудами вариаций давлений, а выделенные
в отдельную матрицу субматрицы I в уравнении G.3.3) и h21 в
уравнении G.3.4) заменим нулевыми субматрицами. В итоге уравнения G.3.3) и
G.3.4) принимают вид:
SG'@)
U у! i J
W*'@)
[001 , Г h22 0 1 Г h211
5G'A)= , 8Р*'(О)+ " f I в^-'О> +J n |
l о У21 J L 0 y22J I 0 J
G.3.5)
G.3.6)
293
В соответствии с принятым условием о включении внутренних
сопротивлений источников напора в пассивные части ветви, используя соотношения
G.2.3) и G.2.4), учтя связи векторов амплитуд вариаций давлений на
концах ветвей с вектором амплитуд вариаций узловых давлений,
определяемых соотношениями G.2.9), запишем в матричной форме зависимости
для источников напора:
5р*'@) = 5р'A)-5ДН'A)=ПтAM Р'-5ДН'A). G.3.8)
Подставив уравнение ветвей G.3.5) и G.3.6) в уравнение баланса расходов
в узлах G.2.8), исключив с помощью зависимостей G.3.7) и G.3.8)
векторы амплитуд вариаций давлений на концах пассивных частей ветвей,
находим
г о о I г о о А / Г°01
I , +ПA) , >ПТ(О)+(П(О) , +
L о У1\ J [о у2\у \ [о y2\J
2'2 о 1\ 1_ / г о о
, /ПтA) 5Р =-\ П@)
ГО 0 l\ _, / Г00 1 ГЬ2'2 О ]\
, MДН'@) + ( П@) , +ПA) , }Х
L0 ya'J/ \ L 0 у 2\ L0 у12\/
В уравнении G.3.9) члены в фигурных скобках левой части обозначим
Yn, а все члены в правой части — вектором 5Н;, тогда уравнение G.3.9)
принимает вид
У;5Р; = 5Н;, G.3.10)
где матрицу проводимости цепи У„ и вектор амплитуд возмущающих
воздействий считаем известными. Из уравнения G.3.10) находим неизвестный
вектор амплитуд вариаций давлений в узлах цепи
6P/ = (Y^)-15H'. G.3.11)
Зная вектор 5Р', из соотношений G.3.7) и G.3.8) можно найти векторы
амплитуд вариаций давлений на концах пассивных частей ветвей 5р"*' @) и
5р~' A) , а подставив эти векторы в уравнения G.3.5) и G.3.6)—найти
векторы амплитуд вариаций расходов на концах ветвей. Полученное уравнение
узловых давлений G.3.10) содержит матрицу порядка т X ш,т.е. меньшего,
чем матрицы в аналогичном уравнении G.2.29). При выводе уравнения
G.3.10) предполагалось, что все амплитуды вариаций давлений в узлах
неизвестны, что имеет место в замкнутой ПГС, полностью изолированной
от внешней среды. Если же система связана с внешней средой, то для узла
ПГЦ, описывающего состояние внешней среды, давление можно считать
заданным1). С другой стороны, как уже отмечалось, для ПГЦ, содержа-
1) Применительно к летательным и подводным аппаратам это условие может не
соблюдаться и изменение внешнего давления оказывается одним из внешних
возмущающих воздействий.
294
ших элементы с распределенными параметрами (моделируемые
коммуникаторами), мгновенное значение суммы расходов, поступающих во
внешнюю среду и забираемых из нее, не равно нулю. Поэтому для таких ПГЦ
необходим подвод компенсационного расхода жидкости к узлу,
характеризующему внешнюю среду, чтобы для этого узла соблюдалось
уравнение сохранения. Величина амплитуды вариации компенсационного расхода
bQ'o находится из решения уравнений ПГЦ, если давление в этом узле
известно. Удобно этот расход выделить отдельно в правую часть
уравнения балансов расходов в узлах G.2.8) в виде отдельного вектора,
содержащего только один член не равный нулю
П@) 8б'@) +ПA) 5G'A) =5Q'O. G.3.12)
Примем, что уравнение баланса расходов для узла, характеризующего
состояние внешней среды, описывается последней строчкой матрицы инци-
денций П. Уравнение G.3.10) было получено из уравнения сохранения для
узлов G.2.8) путем последовательного исключения переменных при
сохранении числа и порядка расположения строк в матрицах П@) и 11A) .
Соответственно амплитуды вариаций компенсационного расхода 8 Qf0 и
давления внешней среды 5р'о занимают последние строчки в векторах 5Qo и
5Р \ При этом уравнение G.3.10) можно представить в следующей
форме:
Y'
jn-l)
И'о
г- 1H
г«р„' ¦
1 Sp'o .
-
-5НН-
=
JQ'o.
= • G.3.13)
Здесь Y^, 5Рн',5Нн матрицы без строки (и столбца) для узла,
описывающего внешнюю среду. Уравнение G.3.13) можно разбить на два уравнения
"У/о
1)OJ
= 0,
G.3.14)
G.3.15)
Уравнение G.3.14) позволяет найти величины амплитуд вариаций узловых
давлений,_а уравнение G.3.15) — амплитуду вариации компенсационного
расхода SQ'O.
В качестве примера построения математической модели системы с
распределенными параметрами рассмотрим ПГС (рис. 7.4, а), состоящую
из участков трубопроводов 1-6, двух объемных насосов 9 и 12,
дросселирующих устройств 10 и 11 с регулируемыми проходными сечениями и
295
Рис. 7.4. Схема ПГС (а) и эквивалентная цепь {б)
емкостей 7 и 8. Участки труб будем рассматривать как элементы с распре
деленными параметрами, описываемые уравнениями четырехполюсников
и представленные в схеме эквивалентной ПГЦ (рис. 7.4, б)
коммуникаторами. Аналогично, для исключения лишних ветвей, идущих к внешней среде
(полюсу абсолютного давления), в ПГЦ коммуникаторами представлены
емкости (гасители колебаний) 7 и 8, заполненные жидкостью. Объемные
насосы, пренебрегая внутренними утечками, описываем как идеальные
источники расхода, дросселирующие устройства - как реальные источники
напора. В эквивалентной цепи (рис. 7.4, б) в соответствии с принятььм
ранее условием введены два дополнительных узла III и IV перед активными
элементами в середине ветвей. Коммуникаторы 5, 7 и 8 соединены
последовательно и их можно объединить в один коммуникатор с номером 5.
Узел 0 характеризует состояние внешней среды, из которой поступает и
в которую сливается жидкость. Стрелками показано принятое за
положительное направление движения жидкости. Цепь содержит пять узлов и шесть
ветвей. Матрица инциденций для рассматриваемой цепи имеет вид
П =
-110 10 0
1 0-1 0-1 0
0 0 0 0 1-1
0 0 1-10 0
0-10001
Используя эту матрицу, запишем уравнение балансов расходов для цепи,
296
учтя амплитуду вариаций компенсационного расхода Ь()'о в нулевом узле.
1
0
0
0
0
0
0
0
0
-1
0
-1
0
0
0
0
0
0
-1
0
0
-1
0
0
0
0
0
— 1
0
0
6g;co)
6G'2@)
_6g;co)
+
0
1
0
0
0
1
0
0
0
0
0
0
0
1
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
1
dG
dG
dG
'l(l)
;a)
=
0
0
0
0
«G'o
G.3.16)
Уравнение пассивных частей ветвей цепи в матричной форме имеет вид
pc;
dG2
6G'3
@)"
@)
@)
1 01
0 ll
УЗ-ll
.У4-11
5-11
Уь-и
'6Gi@)
dQ'2 @)
Ldp'6@) J
У 4-1
У5-12
У 6-12
6pe*'(l)
G.3.17)
~bG\
dG2
6G'3
A)
A)
A)
h\
1-21
2-21
L.
УЗ-21
У\-2\
Уь-21
6Fj'@)
Л2-22
11.
-22
¦У4-22
^5-22
6p2*'(l)
G.3.18)
^6-22
В уравнениях G.3.17) и G.3.18) выделим вектор заданных амплитуд
вариаций расходов, не изменяя при этом размерность матриц; для сохране-
297
ния же вида исходных уравнений единичную субматрицу в уравнении
G.3.17) и субматрицу, содержащую элементы Л i_2i и Л2-21 B уравнении
G.3.18) заменим нулевыми субматрицами. Для удобства дальнейших
преобразований в векторах амплитуд вариаций параметров на входах
в пассивные части ветвей после выделения двух строчек с величинами
dQ\(O) и 5 62@) заменим их на амплитуды вариаций dpi'@) и dp?r(Q).
В итоге найдем новую форму записи уравнений G.3.17) и G.3.18) :
'6g;@)"
SG'2@)
r'6@)J
75-11
7б-11
40)"
*40)
Г@)
__r J
73-12
74-12
dp
L6p*'
4D
A)
A)
~1
0
0"
1
0 _
1 ° ГбСЧО)"]
0 L6e;@)J'
*Gt
JG'6
A)
»(D
A)
=
o
0
1 УЪ-2\
У4-21
У 5-21
76-21
Г dp
8р
\др
Г 40)
Г@)
в*'@)_
G.3.19)
Л1
1-22
^3-22
У 4 -22
75-22
76-22
fa)
Га)
о
после преобразований получим
0 0 0 74-21 ° °
0 О 3-И 0 -75-11 О
О ° 0 0 y's_21 ->'6-ll
О 0 >'3'-21 -74-11 О О
0 0 0 О О 76-21
)) в уравнение
Г«Р1*'@)"
бр2*40)
+
баланса
G-
G.3
3.20)
.16),
—1
0
0
0
>2 0
0
0
0
О У4-22 ° °
Уз-12 0 -^5-12 О
О 0 ^5-22-^6-12
УЗ-22 -У4-12
О О
0
бр,*'A)
6р*'Ц)
Sp6*4D
- *>Q\ @)
- 6Q'O
=0.
G.3.21)
Теперь осталось записать уравнения активных элементов - источников
напора. Применительно к дросселирующему устройству 11 (рис. 7.4, а)
с регулируемым проходным сечением линеаризованное уравнение
эквивалентного источника напора найдем, используя уравнение G.2.3):
]SFlll - [2{рш-PZ)/G6]5G'6(Q),
G.3.22)
иьб* - средние значения давления в узле III и на входе в пассивную
часть 6-й ветви, G6 — средний расход через 6-ю ветвь, F\ 1, 8F[ 1 — среднее
значение и амплитуда вариации площади проходного сечения дросселя 11.
Моделируя дроссель с переменным проходным сечением как источник
напора (рис. 7.4, б), внутреннее сопротивление источника напора,
описываемое последним членом в зависимости G.3.22), в соответствии с
принятым в начале правилом переносим на вход пассивной части 6-й ветви.
В этом случае уравнение дросселя 11 как активного элемента G.3.22)
принимает вид
8рг'@) = 8р;п + 8ДЯ'6@), G.3.23)
где5ДЯб@)= [2(Рш -pX)lF\ 1] 8^11 - параметры эквивалентного
источника напора. Аналогичным уравнением описывается и дроссель 10. В
матричной форме уравнения, связывающие вектор амплитуд вариаций узловых
давлений с векторами амплитуд давлений на концах пассивных частей
ветвей и напоров источников, в соответствии с зависимостями G.3.7) и
G.3.8) запишутся:
G.3.24)
§р *'@)
1
6р2*'@)
_бр6*'@)_
_
Г * 1
6Pl A)
6 р 6*' A)
-1
0
0
0
0
0
=
0
0
1
0
1
0
~0
1
0
1
0
_0
0
0
0
0
0
1
1
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
О"
1
0
0
0
0_
0
0
1
0
0
0
_
«Pi
-,
-,п
-,ш
с"
0
0
0
0
1
fip'l
epil
5РШ
0
0
n 4
и
_5 дя;, (О).
G.3.25)
299
Подставив векторы 5р*'(°) и 5Р*'О) из уравнений G.3.24) и G.3.25)
в зависимость G.3.21), найдем
74-22 +^2-22
0
0
-74-12
0
0
-75-12
* 75-22-76-11
0
76-21
¦7°з-11-75-и +
75-21
73-21
0
74-21
-73-12
0
73-22-74-11
О
О
-74-12
О
7б-22
др[
->4'-ц5АЯ4@)
= 0.
G.3.26)
Уравнение ?7.3.26) определяет связь вектора амплитуд вариаций узловых
давлений 5Р' с параметрами рассматриваемой системы (матрица Y'n) и
возмущающими воздействиями, создаваемыми активными элементами
(матрица 5Н'). Учтя, что отклонения давления внешней среды др'о можно
считать заданными, целесообразно разделить уравнение G.3.26) на два
уравнения:
74-22
0
0
-—74 - 12
74-21
_ -73-12
0
73-22
+ *2-22
0
-73-и -75-n + ^
75-21
73-21
—
-74-11.
5^ iv
0
L-22 ~7б-12
75-22-76-11
0
О
О
-74-12
О
[О
Ьр\
'III
G.3.27)
= 0.
300
Уравнение G.3.27) является линейной математической моделью
анализируемой системы и позволяет найти амплитуды вариаций давлений в узлах
эквивалентной цепи как функцию возмущающих (управляющих)
воздействий. С помощью уравнений G.3.24), G.3.25), G.3.19) и G.3.20)
находятся все остальные вариации параметров течения в отдельных ветвях ПГЦ.
§ 7.4. Формирование математических моделей ПГС
с использованием сигнальных графов
В гл. 4 был описан метод формирования математической модели ПГС,
рассматриваемой как система с сосредоточенными параметрами, с
помощью сигнальных графов, даны правила их преобразования и формула
для коэффициента передачи сигнального графа. Сигнальные графы можно
использовать и для формирования линейной математической модели ПГС,
содержащей элементы с распределенными параметрами [63]. Метод расчета
с использованием сигнальных грабов, который будет описан ниже, основан
на записи уравнений четырехполюсников в .у-параметрах, с помощью
которых амплитуды вариаций расходов на концах ветвей связываются с
амплитудами вариаций давлений в узлах. Для участка трубопровода,
заполненного вязкой сжимаемой жидкостью, скорость которой невелика, т.е. и<а9
амплитуды вариаций давления и расхода связаны уравнениями
четырехполюсники, которые в >'-параметрах выглядят следующим образом(см.гл .6) :
SG'@) = -
Входящие в состав ПГС элементы с сосредоточенными параметрами также
необходимо описать уравнениями четырехполюсников. Для местного
сопротивления при турбулентном режиме течения, пренебрегая инерцией
жидкости, можно записать линеаризованные уравнения
6С'@) = (С/2Ар)дрЩ - (С/2АрNр'A1 (?А2)
8G'A) = (Gl2Ap)Sp'@) - (Gl2Ap)Sp'(l),
где G, Ар — средний расход жидкости и перепад давления на сопротивлении.
В случае изотермического течения газа для сопла или другого местного
сопротивления с плавным изменением проходного сечения параметры
течения связаны линеаризованной зависимостью
8С'@) = [A +e)G/p@)] 8р'@) -eG/p(l)8p'(l),
G.4.3)
8G'A) = [A + е)С/р@)] 5р'@)-е G/p A) 6р'A),
где р @), р A) — средние значения давления перед и за соплом, б —
коэффициент расхода,определяемый формулой B.1.25).
Для инерционности, представляемой столбом несжимаемой жидкости,
Уравнение в малых отклонениях в форме уравнения четырехполюсника
имеет вид:
6С'@) = (F/ioJ)Sp'@) - (F/ico/Np'(О, (?А4)
где F, I — площадь поперечного сечения и длина столба жидкости. Упругие
3(И
цементы (см. рис. 2.2, д, е, ж), расположенные в тракте, моделируются
как емкость и описываются в форме уравнения четырехполюсника
SG'(l) = {iupF\s,lk)bp '@) - (fopF^/WO) AS
где /^ф — эффективная площадь упругого элемента, к — суммарная упру,
гость подвижных элементов.
Емкость, расположенную в середине ветви (рис. 2.2), удобно
представить в виде ответвляющейся ветви (т.е. введя дополнительный узел),
включающей трубопровод, соединяющий емкость с основным трактом. Можно
учесть инерцию и сжимаемость столба жидкости в емкости, заполненной
полностью жидкостью, приняв ее за участок тракта с распределенными
параметрами, с длиной, равной высоте емкости, и поперечным сечением,
равным поперечному сечению емкости. Для выхода из этого участка тракта
граничное условие — закрытый конец, Ьи = 0. Если емкость полностью
или частично заполнена газом или в случае, если инерцией столба жидкости
в ней можно пренебречь (большая площадь сечения), то в этом случае
емкость является граничным условием на конце ответвляющегося к
емкости трубопровода. Если трубопровода нет, то остается только участок,
эквивалентный столбу жидкости в горловине емкости и в самой емкости.
Устройства, описываемые уравнениями как элементы с
сосредоточенными параметрами и расположенные на концах ветвей цепи, у узлов удобно
не выделять в отдельные элементы (четырехполюсники), а их уравнения
использовать как граничные условия для крайних участков цепи. Эти
граничные условия в начале или в конце ПГЦ заводим в виде импедансов
нагрузки (в общем случае являющихся функцией частоты со), связывающих
вариации давления и расхода в этих сечениях. Если сосредоточенный
элемент расположен в начале ветви, на входе в /-й трубопровод, то граничное
условие запишется в виде
если же в конце /-й ветви ПГЦ, то
В частности, для местных сопротивлений, описываемых уравнениями
G.4.2), z;<0) = - 2Api/Gi9 z}(l) = 2Apf/Gh где AphAp/9 Gh Gf -
соответственно средние перепады давления и расходы для местных сопротивлений.
Для инерционностей импедансы определяются из зависимости G.4.4)
zJ(O, co) = -icoli/Fh Zy(l,co) = /co/;/F/, где 7/,//,/*/,/^ - длины и площади
сечения соответствующих столбов жидкости. Для емкости, полностью
заполненной жидкостью, импедансы находятся из формул
? } )
где aj, uj — скорости звука с учетом податливости стенок емкостей,
^/» У] —объемы емкостей. Если на конце ветвей цепи расположен не один,
а несколько элементов с сосредоточенными параметрами, то для общности
подхода граничный элемент с сосредоточенными параметрами,
расположенный у узла, отделяется от другого, соседнего элемента участком тракта
малой длины, не влияющим на динамику всей системы. Для этого участка
302
и используется граничный импеданс, а другие элементы описываются
уравнениями четырехполюсников.
При расположении сопротивлений, инерционностей, упругих элементов
(исключая емкость) в середине ветвей ПГЦ (а не на их концах) для
общности методики не будем делать различия между этими элементами с
сосредоточенными параметрами и участками трактов (труб), называя их все
просто элементами и описывая каждый из них уравнениями
четырехполюсника
Эти уравнения записаны для /-го элемента, расположенного в середине ветви.
8рр)-
Рис. 7.5. Схема ветви {а)
и ее сигнальный граф (б)
^/7
Все приведенные выше уравнения записаны для амплитуд размерных
вариаций. Ранее уравнения элементов использовались как для размерных,
так и для безразмерных вариаций. Уравнения G.4.1) —G.4.5) можно
записать и для безразмерных вариаций. К примеру, уравнения G.4.4) для
инерционности имеют вид:
6С @) = A/коти) др @) - A/|<оти) 8р A),
5С A) = A//о;ти) dp @) - A//соти) dp A),
где ти = IG/pF — инерционная постоянная времени. Аналогичным образом
преобразуются и другие уравнения. Общие уравнения четырехполюсника
в .у-параметрах G.4.6) сохраняют свою форму при переходе к
безразмерным вариациям (только у переменных и коэффициентов отбрасываются
штрихи, указывавшие на то, что все они размерные величины).
Рассмотрим ветвь ПГЦ, состоящую из п последовательно соединенных
пассивных элементов — коммуникаторов (рис. 7.5, я), описываемых
уравнениями четырехполюсников. Запишем для этих коммуникаторов
уравнения четырехполюсников
2@)=j2_n5p2@) +72-12 «Pi(l),
2A)=^2_21 8p'2@) +72-22 5p2(l), G.4.7)
bG'n{\)=y'n_21 8p'n@) +Уп-22 Sp'nV)
и, кроме того, граничные условия на входе в 1-й коммуникатор и вы-
303
ходе из п-го коммуникатора
8G\(O) = (l/z'1)8p'(O), SG;(l) = (l/4)8p;(l). G.4.8)
Первый индекс при коэффициентах четырехполюсников yk_jj(k =
= 1, 2,..,л) указывает на номер коммуникатора, последующие (/,/= 1, 2) -
индексы коэффициентов матрицы четырехполюсника, z[ и zn — импедан-
сы на входе в 1-й и на выходе из я-го коммуникаторов.
В более сложных случаях, когда ветвь цепи стыкуется с другой ПГЦ,
в условия G.4.8) вместо z\ или z'n подставляются входное (выходное)
сопротивление присоединяемой ПГЦ. Для узлов, в которых соединяются
между собой коммуникаторы, входящие в ветвь, используется уравнение
неразрывности 8Gk(l) = 8G к + i @), а также условие равенства
отклонений давлений др'к A) = 8рк + 2@), так как все сопротивления, входящие в
ветвь, учитываются в уравнениях коммуникаторов. Используя два этих
условия, из исходных уравнений G.4.7) и G.4.8) можно исключить
амплитуды вариаций расходов, получив зависимости, связывающие только
амплитуды вариаций давлений в узлах.
§р'1@)= , У1\2
i-ii
V pi() , ,
1-22 -У2-11 У1-22 -У2-11
, 1 P2() , ,РзО),
Уг-гг-Уъ-м Уг-гг~Уг-\\
G.4.9)
У(„ _ 1)_22 ~Уп
У'п-12 „_, _
У(п-1)-22
Уп-гг -l/zn
Система линейных уравнений, как показано в гл. 4, эквивалентна ее
графическому изображению в форме сигнального графа, в котором узлы
отображают соответствующие переменные системы (амплитуды вариаций
давлений), а направленные ветви — коэффициенты передачи, т.е. отношение
выходных величин к входным. В нашем случае для уравнений G.4.9) все
коэффициенты передачи будут безразмерными, так как определяют связь
между однородными переменными - амплитудами вариаций давлений.
Сигнальный граф, эквивалентный системе уравнений G.4.9), представлен
на рис. 7.5, б. Из сопоставления рис. 7.5, а и б следует, что сигнальный граф
последовательно соединенных пассивных коммуникаторов, построенный
относительно амплитуд вариаций давлений в узлах между
коммуникаторами, имеет такую же структуру, как и рассматриваемая ветвь. При этом
каждому коммуникатору к соответствует контур первого порядка
304
(рис. 7.5, б), коэффициенты передачи ветвей которого
НBк- 1)=- ^^ ; , А: = 2,3,..., и,
У [к - 1)-22 ".У А:- 11
G.4.10)
У
= 1,2, «-
) ^
У к-гг — У(к + 1)— 11
Число ветвей в графе в два раза больше числа коммуникаторов в ветви
цепи. При нумерации элементов графа принято, что ветви, имеющие четный
номер, должны быть направлены по течению жидкости, а нечетный - против
течения. Коэффициенты передач ветвей, расположенных на концах цепи,
имеющих номера 1 и 2п (рис. 7.5, б) и направленных к узлам Ьр х @) и
дрпA) , находятся по формулам
> = _ ^=^Тш G.4.11)
Уп-22 - Ifen
Если нумерация ветвей ведется общая для графа, описывающего
разветвленную цепь, то для коммуникаторов, расположенных на концах.цепи,
используя зависимости G.4.11), можно записать рекуррентные
соотношения
ЯB/-1) = , У1~12 , , . ЯB0= , ~-У/-21
-)'i-ll -\\Л Уг-22 -1/z't G.4,12)
если коммуникатор стоит соответственно на /-м входе или выходе ПГЦ.
ПГЦ, помимо последовательно соединенных коммуникаторов может
содержать различные разветвления. Будем различать два типа простейших
разветвлений (рис. 7.6, а и б) в зависимости от направления движения
жидкости, указанного стрелками на рисунке. Вводя дополнительно
участки труб с длиной, близкой к нулю, любое другое разветвление можно
представить совокупностью разветвлений / и // типа.
Рассмотрим разветвление / типа (рис. 7.6, а), учитывая условие
равенства вариаций давлений в узле 5р/ A) = Spj @) = 8р 'к @) и уравнение
баланса расходов 5G~/ (I) =5G/.'@) + 5G? @). Исключая амплитуды
вариаций расходов из исходных уравнений четырехполюсников G.4.7) для
любого разветвления / типа, у которого / — номер коммуникатора, через
который жидкость втекает в узел, а/ и к - номера коммуникаторов, через
которые жидкость вытекает из узла, находим соотношения для
коэффициентов ветвей графа, направленных к узлу разветвления (рис. 7.6, в):
ЯB0=~
yi-22 -yf-11 -Ук-11
ттП. п_ У)-12
^1-22 -^/-11 ~^-11
20.Б.Ф. Гликман 305
C-rovKiypa графа оказывается тождественной структуре развилки в ПГС.
Аналогичным образом получаются соотношения для коэффициентов пе-
редачи ветвей сигнального графа, соответствующего разветвлению//типа
(рис. 7.6, г)
НП'Л-
1
ЯB/) =
ИAк
у\ -
n- .
22
22
-Уг
-У/-
- 21
- 22
- 21
- 22
Ук
-Ук -
-Ук-
- 12
1
1
1
1
G.4.14)
Уг- 22 +>7 - 22 ~Ук - 11
До сих пор рассматривалось описание с помощью сигнальных графов
только пассивных элементов ПГЦ с распределенными параметрами. В цепи
всегда присутствуют активные элементы, создающие возмущения. В
зависимости от вида возмущений, действующих на систему, места их внесения,
соответственно изменяется и структура сигнального графа ПГЦ. Пусть
возмущения вносятся внутри ветви цепи, в /-м коммуникаторе,
располоРис. 7.6. Схема разветвлений цепи типа / (а) и II (б) и их сигнальные графы (в и г)
Рис. 7.7. Схема ветви с активным элементом (а) и ее сигнальный граф (б)
женном между (/ -1)-м и (i + 1)-м коммуникаторами (рис. 7.7,а) и
создаются дроссельным устройством с изменяющейся по гармоническому
закону площадью проходного сечения.
Уравнения, описывающие течение несжимаемой жидкости (без учета
ее инерции) через дроссельное устройство, в линеаризованном виде
запишем в форме уравнений активного четырехполюсника
Gj _f Gf _f Gf
G.4.15)
5G,41 ) =
Gt
где [л _ коэффициент расхода, Ff - площадь проходного сечения
дроссельного устройства. Исключая из уравнения G.4.15) и уравнений
четырехполюсников G.4.7) для (г - 1)-го и (/ + 1) -го коммуникаторов амплиту-
306
ды вариаций расходов, учитывая при этом условия сохранения в узлах
давлений и расходов, находим уравнение и сигнальный граф (рис. 7.7, б),
моделирующий дроссельное устройство с изменяемым проходным
сечением. Коэффициенты передачи ветвей графа^направленных из узла,
соответствующего возмущающему параметру ^idF-, будут определяться
соотношениями
, С/
а коэффициенты передачи НBг - 1) и ЯB/) - по формулам G.4.10),
где y\t _1) _ 22 и y\i + 1) - 11 -соответствующие коэффициенты
уравнений (/ — 1)-го и (/ + 1)-го коммуникаторов как четырехполюсников
в зависимостях G.4.6). Соответствующие коэффициенты уравнений
четырехполюсника для дросселирующего элемента как пассивного сопротивления
(при SjiF'i = 0) в соответствии с формулами G.4.15) : у\ _ г 2 = G/2
' l
В качестве другого возможного источника возмущений рассмотрим
насос, расположенный между G -1)-м и (/ + 1)-м коммуникаторами
(рис. 7.7, а). Пренебрегая инерцией, сжимаемостью жидкости и кавита-
ционными явлениями в проточной части насоса, можно записать
линеаризованное соотношение, описывающее характеристики насоса (см. гл. 2):
5Gj@) = - -Jr- 5Й@) + -Jr 5^(]) " ТГ1 дП* '
*G/ *Gi *Gi G.4Л7)
/.dApHidGiiipnidApHj/dn^ApHi -напор, развиваемый
насосом, Gi - средний расход через насос; щ, Ьщ - среднее значение и
амплитуда вариации частоты вращения. Из соотношений G.4.17) следует, что они
по форме записи идентичны уравнениям G.4.15), описывающим
дросселирующее устройство с переменным проходным сечением. Соответственно и
граф, описывающий источник возмущений в виде насоса с переменной
частотой вращения, будет иметь такую же структуру, что и граф на рис.
7.7,5, соответствующий дроссельному устройству. В этом случае
коэффициенты передачи 7п и 7/2 будут определяться соотношениями
, =
=
7/2
- 22
а коэффициенты передачиЯB/ -1),ЯB/) - по формуле G.4.10);
согласно формулам G.4.17) у\ _ ц = - ИФ'СГ У\-гг = 11Ф'С.--
20*
Ьсли задатчик возмущения расположен в начале ПГЦ, то в графе,
соответствующем задатчику возмущения, будет отсутствовать ветвь с
коэффициентом 7/1 , а также ветви с коэффициентами HBi — 1) иЯB/), так
как элементы с сосредоточенными параметрами (активные элементы),
расположенные на концах ветвей, по принятому условию учитываются в
виде граничных импедансов в крайних коммуникаторах. Если же задатчик
возмущений расположен на выходе из цепи, то соответственно в графе
будут отсутствовать ветви с коэффициентами У,-2,//B/ - 1) и HBi).
Для активного элемента, представляющего из себя поршень,
расположенный в начале /-го трубопровода, и перемещающийся по закону Ьх) ехрсог
(где Ьх) - амплитуда перемещения поршня), уравнение получается из
уравнения неразрывности bG) - icopFnbXj, где 8Gfj — амплитуда вариаций
расхода; р - плотность жидкости, Fn — площадь поршня.
С одной стороны, поршень, не создающий возмущений (неподвижный),
имеет граничные импедансы Z;- = °°, так как hG) = О и, следовательно,
коэффициент передачи ветви, направленной к узлу давления 5р;- @),
будет определяться (с учетом Z) - °°) из зависимости G.4.12) формулой
#B/ — 1) = -у) _ \г\у) - 11? С другой стороны, ему как активному
элементу будет соответствовать ветвь, направленная из узла Ьх) с
коэффициентом передачи
7/2 = —г-^- . G.4.19)
У/ -11
Рассмотрим формирование сигнального графа на примере ПГС, схема
которой (рис. 7.8, а) состоит из участков труб 1, 2, 4,5, 6, 8, 9,10,12,
рассматриваемых как элементы с распределенными параметрами
(коммуникаторы), объемного насоса 5, местного сопротивления 11, емкости
(гасителя колебаний) Е, расположенной в конце Р-го трубопровода.
Элементы с сосредоточенными параметрами, расположенные на концах цепи из
коммуникаторов (как было оговорено выше), в число отдельных
элементов в граф системы не входят, поэтому на схеме ПГС (рис. 7.8, а) емкости
Е и местному сопротивлению в конце 72-го участка трубы номера не
присвоено. В байпасной линии насоса установлен регулятор давления 7,
отличающийся от рассмотренного выше дросселя с переменным проходным
сечением тем, что для него за счет работы обратной связи существует
зависимость между амплитудой изменения площади проходного сечения
дросселирующего устройства регулятора bfxF^ и амплитудой вариации
давления в конце импульсной трубки регулятора др'6 A) . Эту связь опишем
частотной передаточной функцией регулятора, которую представим в виде
следующей зависимости: 5jLtFf7 = И/р(соMр'6 A) . Разветвление, в котором
стыкуются тракты 4, 5, Я 10, содержит больше трех труб, поэтому
необходимо ввести дополнительно фиктивный участок трубы 13 (рис. 7.8,а),
длина которого близка к нулю.
Сигнальный граф, эквивалентный математической модели
анализируемой ПГС, представлен на рис. 7.8,5, в котором истоком, где вносится
возмущающее воздействие, рассматривается насос 3 с переменной
амплитудой частоты вращения Ьп'3 . Сигнальный граф на рис. 7.8, б построен
следующим образом: каждому пассивному элементу / (участку трубы,
местному сопротивлению или инерционности в середине ПГС) приводится в
308
Рис. 7.8. Схема ПГС (а) и эквивалентный ей сигнальный граф (с?)
fl) 26' 1 20' 22' 24'
Р и с. 7.9. Сигнальный граф ПГС после упрощения
соответствие контур первого порядка с коэффициентами передачи Я B/ -1)
и #B/).
В графе, моделирующем рассматриваемую ПГС, насос 3 отображается
ветвями с коэффициентами передачи ЯE) и ЯF) (г = 3), которые
вычисляются по формулам G.4.10), и ветвями с коэффициентами передачи
? 31 и т'з2> определяемыми по формулам G.4.18) (/ = 3). Регулятор
7 представляет из себя управляемый активный элемент с обратной связью.
8 сигнальном графе на рис. 7.8, 6 ему соответствуют ветви контура с
коэффициентами передачи ЯA3), #A4), ветви с коэффициентами передачи
У 7i и 7*72, характеризующие регулятор как активный элемент, и
дополнительная ветвь с коэффициентом передачи т\з = Wp(to), определяющая
управляющее воздействие на дросселирующее устройство. Обратная связь
осуществляется по импульсной трубке б, моделируемой в графе ветвями с
коэффициентами передачи #A1) и #A2) .
30?
При переходе от ПГС к сигнальному графу, постороенному по
изложенной выше методике, структура изучаемого объекта и, в частности,
схема соединения отдельных труб сохраняются (см. рис. 7.8). Появление
дополнительных ветвей графа с коэффициентами у'(\ связано с
описанием воздействия на систему активных элементов (источников
возмущающих сигналов), а также управляемых источников типа регуляторов.
Для большинства структур ПГС процесс получения расчетных
соотношений удобно начать с преобразования (сворачивания) сигнального
графа, используя правила, изложенные в § 4.2. К упрощенному графу
можно применить формулу Мэзона (см. § 4.3), с помощью которой
определяется частотная передаточная функция системы. Изложенный выше
метод формирования математической модели ПГЦ и на ее базе получение
передаточной функции системы имеет некоторые преимущества по
сравнению с изложенными в § § 7.2 и 7.3 матричными методами. Благодаря
исключению амплитуды вариаций расходов в 2 раза уменьшается число
переменных и уравнений. Соответственно каждый элемент (коммуникатор)
описывается не матричным уравнением четырехполюсника, а одним
линейным уравнением. Пассивная часть сигнального графа полностью
повторяет структуру исходной ПГС, что, с одной стороны, облегчает
формирование графа, а с другой — более наглядной оказывается связь между
графом и исходной системой. Граф позволяет использовать простые
правила его преобразования (сворачивания) для получения компактной
формы математической модели системы. Эти правила удобны для
составления алгоритма преобразования графа на ЭВМ. Благодаря этому можно
разработать достаточно универсальный алгоритм расчета динамических
характеристик сложных разветвленных ПГС, включающих элементы с
распределенными параметрами. В качестве исходных в такой алгоритм
вводятся данные о структуре системы, ее типе и параметрах отдельных
элементов. При этом математическую модель системы формирует ЭВМ.
Упростим сигнальный граф, приведенный на рис. 7.8, б, используя
изложенные в § 4.2 правила. Последовательно применяя эти правила к
сигнальному графу, представленному на рис. 7.8, б, этот граф можно свести к
более простому графу, изображенному на рис. 7.9. Это преобразование
осуществляется следующим образом. Преобразование ветвей 7, 9, 10, 11, 12 и
13 производится в соответствии с правилами устранения контуров. При этом
получаются следующие коэффициенты передачи.
#B2') = #B2)/[1 -#B3)ЯB4)],
#B0') = #B0)/[1 -#B1)#B2')],
#B60 = #B6)/[1 -#A9)#B0')],
= #A7)/[1 -#A9)#B0')],
= #B6О/[1 -
Здесь и далее номера ветвей со штрихом в обозначениях коэффициентов
передач относятся к ветвям, приведенным на рис. 7.9, для которых
коэффициенты передач не изменяются при последующих преобразованиях.
Индекс 1 или 2 и т.д. относится к ветвям, для которых при
преобразованиях коэффициент передачи изменяется или сами ветви устраняются.
Полученный после первого этапа преобразованный контур #B5), #B6)
310
при узле 5р4 A) удаляется; в результате изменятся коэффициенты
передачи Я(8) и Н(9): Я(8Х) = Я(8)/[1 -ЯB5)ЯB6')], Я (90 = Я(9)/[1 -
-ЯB5)ЯB6')].
При применении к ветвям 1 и 2 правила удаления контура изменяются
коэффициенты передачи ветвей 5 и 76:
ЯC1) = ЯC)/[1 -ЯA)ЯB)], ЯA6О=ЯA6)/[1 -
Устраним узел djiF'-j в соответствии с правилом устранения простой
узловой точки. В результате получим ветви с коэффициентами передачи
77 3 77 2 и 77 3 7-71 • После этого преобразования ветвь 773 771 ,
соединяющая узлы 5р'6 A) идр'5 A), оказывается параллельной ветви Н (Ц) и их
можно свести к одной ветви с коэффициентом передачи ЯA10 = 7? з 7-71 +
+ ЯA1). В результате этих преобразований комбинация ветвей 771,7-7 2»77з*
Я(П),ЯA2) свелась к ветви 7 73 772- выходящей из узла Ьр6 A),и
контуру, состоящему из ветвей с коэффициентами передачи Я A10 и Я A2)
.Расщепив узел 5Дб F), удалим получившийся при этом контур, что приводит к
изменению ветвей с коэффициентами передачи ЯA0) и ЯA3):
Получившаяся в результате преобразований ветвь с коэффициентом
передачи ЯA2) 773 7-7 2 соединяет два узла параллельно с ветвью 14. Сведем
их к одной ветви, коэффициент передачи которой будет равен Н A40 =
= ЯA4)+ЯA2O73 7-72 В результате этих преобразований сигнальный
граф, соответствующий регулятору 7 и импульсной трубке б, сводится
к контуру, состоящему из ветвей с коэффициентами передачи ЯA31) и
ЯA40- Полученную комбинацию из трех контуров с коэффициентами
передачиЯA5),ЯA61),ЯA3О,ЯA4О,Я(9О,ЯA01) можно свести к
одному контуру из ветвей 152 и 162, коэффициенты передачи которых
вычисляются по формулам
и к собственным петлям при узлах Ьр\ @) и 5р'4 A), коэффициенты
передачи которых определяются по формулам
ЯA53)=ЯA61)ЯA5)/[1-ЯA31)ЯA41)] и ЯA63) =
Последними удаляются контуры,со стоящие из ветвей 15 з и 16з; в
результате упрощений сигнальный граф ПГС принимает окончательную форму
(рис. 7.9). В графе ветви имеют следующие коэффициенты передачи:
ЯC')=Я(ЗО/[1 -ЯA53)Ь
ЯA6')=ЯA62)/[1 -ЯA53)Ь Я(8')=Я(8О/[1 -ЯA63)Ь
ЯA5')=ЯA52)/[1 -ЯA63)], ЯD')=ЯD),
ЯE')=ЯE), ЯF')=ЯF),
= ЯG), Щ\')= ЯA), ЯB4') = ЯB4), ЯA8') = ЯA8).
311
Полученный сигнальный граф системы (рис. 7.9) позволяет найти
частотные передаточные функции §р4A)/5нз, 8р'9(\)/6л'3, 5р'10A)/5«з,
5pii(l)/5«3, 5р12A)/5г23 при использовании формулы Мэзона D.3.1).
Определим вначале передаточную функцию бр'4A)/5л3; для этого
требуется определить все пути по графу от узла Ьп3 к узлу 5р4A).
Л = 73i//C')tfA5'), Р2 =/з1#(б')Я(8'), ^з = 7з2ЯE')ЯC')ЯA5'),
Р4 = 7з2Я(8;). Для путей Л, ^2 иР3 нет контуров,не касающихся их. Дчя
Р4 есть один контур первого порядка 3-4, не касающийся пути
Определим теперь для графа контуры всех порядков и их
коэффициенты передачи:
l{1 } = ЯC ')ЯD'), l[1 ) = ЯE ')НF'), I^1} = ЯG')Я(8'),
/,4° =ЯA5')ЯA6'), 1EП =ЯA5')ЯG')ЯE')ЯC'),
1^1} =ЯA6')ЯD')ЯF')Я(8'), /12) =ЯC')ЯD')ЯG')Я(8'),
42) =ЯE')ЯF')ЯA5')ЯA6').
Используя полученные соотношения и формулу Мэзона D.3.1), найдем
передаточные функции системы:
Л2) B)
+ L j
3 =(бр;1A)/5йз)ЯB41),
=Fр;о(О)/5йз)ЯA81).
Для определения передаточных функций для амплитуд вариаций
расходов на концах коммуникаторов, например, на входе в /-й коммуникатор,
используем одно из уравнений четырехполюсника G.4.6), разделив обе
его части на 5/Т3:
где 5р)(О)'/5«з и 5pz'(l)/5w3 находятся по приведенным выше
формулам. Из аналогичного уравнения находится и передаточная функция для
амплитуд вариаций расхода на выходе из коммуникатора bG\ A)/5я3.
§ 7.5. Уравнения пневмогидравлических цепей
с неизотермическим течением газа
7.5.1 Участок тракта как шестиполюсник. Выше, при формировании
математических моделей ПГС с распределенными параметрами, для
описания одномерного течения газа использовалась система из двух уравнений
гидромеханики — уравнения движения и уравнения неразрывности.
Отсутствие уравнения энергии связано с принятым предположением об изотер-
312
мичности или адиабатичности (для газа) среды и постоянстве ее состава.
Необходимость учета переменности температуры газа или его состава
возникает при анализе особенностей динамики ряда устройств (камер
сгорания, топок, теплообменников, химических реакторов и т.д.)» что
ведет к усложнению математических моделей системы.
Задачи о нестационарном неизотермическом движении жидкости можно
разбить на два класса:
а) температура или состав среды изменяется за счет внешних (для тракта)
причин только на входе в тракт, а по длине тракта к среде тепло не
подводится и изменение температуры или состава возможно только за счет внутренних
процессов в тракте (адиабатического сжатия,диффузии, теплопроводности);
б) температура или состав изменяются за счет внешних причин как на
входе, так и по длине тракта.
Первый вариант процесса характерен для трактов относительно
небольшой длины, на входе которых происходит химическая реакция, смешение
газов с разной температурой или составом и т.д. (камеры сгорания, топки,
проточные устройства химической технологии и т.п.). Приводимые ниже
математические модели описывают именно такой вариант трактов. Второй
вариант процессов имеет место в теплообменниках, длинных газопроводах
и т.д. В расчетах таких систем важную роль играют сопряженные задачи
нестационарного теплообмена и гидромеханики, анализ которых не входит
в круг рассматриваемых здесь вопросов. К расчету таких процессов также
применяют методы теории цепей [49, 92, 118, 162, 164, 172].
Остановимся на математической модели, описывающей вынужденные
колебания в тракте с неизотермическим течением газа. Считая стенки газа
адиабатически изолированными, газ идеальным, примем, что на входе в
однородный цилиндрический участок тракта (х = 0) заданы амплитуды
отклонения давления 5р@) и температуры 5 ДО) газа, а на выходе (х = 1) —
отклонения давления 5рA). Воспользовавшись полученным ранее
решением F.8.17) , приняв ф0 = фх = Ooi = Оо2 -0\ =т?1 = 0, и = 2, 5voi =др(О),
«Уо2 =57X0), 7o_i = *> То2 =0,Joi = 0, %Q2 =1, v0 =-(fc-l)/fc, m = l,
7i l = 1, 5vj i = 8p(l) и задавая х = 0 и х = 1, найдем для амплитуд
вариаций скорости на входе и выходе участка тракта и для амплитуд вариации
температуры на выходе тракта следующие уравнения:
1 Г / ко \ / /со \1 2
5*7@) = — expl +ехр( 5р@)
D [ \ 1 -М / \ 1+M/J D
2 / /со /со \
5м A) = — ехр
D \ 1-М 1 +М /
[ехр ( -?—\ + ехр(- -^—) ЬрA), G.5.1)
D [ \ 1 -М / \ 1 +М /J
к-\ I /со \ к-\ ( & \ -. ч
^ J() ) ^— MТ@),
( ICO \ / ICO \\
ехр ( 1 - ехр I I . Три уравнения G.5.1) связы-
313
вают между собой шесть переменных, т.е. являются уравнениями шестипо-
люсника, которые удобно представить в матричной форме,
5м@)
6иA)
8Т(\\
/со •
/со
— ехр
D \ 1-М 1 +М
к-\ 1 /со
ехр I
к \ М
= У
к-\
8р@)
5Г@)
ехр -
О
О
§р@)
6рA)
5Г@)
G.5.2)
Воспользовавшись правилами преобразований матриц шестиполюсников
[60], можно записать уравнение для участка тракта с неизотермическим
течением газа в В-параметрах
6*7A)
к -
/со
/со
2к
/ i'w \ I icb \1 / /со\
ехр - ехр ехр I I
\1-М/ \ 1+M/J V М /
др(О)
8п@)
5Г@)
G.5.3)
314
диалогичным образом получаем и уравнение шестиполюсника в А-па-
раметрах
Ьп(О)
5Г@)
ехр I -
_L[ex ( ^ )
1-М
к-\
2к
/со
ехр
•М
/со
/со
2к
ехр
/со
/со
/со
5мA)
G.5.4)
При формировании математической модели неизотермического течения
газа, как было показано выше, удобно использовать уравнения энергии,
записанные в форме уравнений сохранения энтропии. В этом случае
уравнения шестиполюсников G.5.3) и G.5.4) приобретают вид при записи в В-па-
раметрах
55A)
1 Г / ИЬ \ ( /со \]
- ехр 1 I — ехр I - I
2а L \1-М/ V 1+M/J
0L \ I ZCO \ / ZCO \1
ехр I - ехр I — I
2 L \ 1-М / V 1 +М /J
1 Г / /со \ / /со
— ехр 1 I + ехр \
2 L \ 1 -М / \ 1+1
ехр
/со \
WJ
8р(р)
бм@)
6540)
и при записи в А-параметрах
G.5.5)
8р@)
8и@)
81@)
315
/со
^|expl 1+м
0
0
/ /со \
дрA)
5мA)
5FA)
exp I + exp t
\ 1 + M / \ 1 - M
0 exp
\ M /
G.5.6)
В виде уравнений шестиполюсников записываются и элементы с
сосредоточенными параметрами, входящими в систему с неизотермическим
течением газа. Выше, в гл. 2 были приведены примеры таких уравнений для
местных сопротивлений (сопел) в неизотермическом потоке.
Уравнения G.5.2)-G.5.6) описывают участки однородного тракта как
элемента с распределенными параметрами не только по отношению к
акустическим колебаниям среды, но и к энтропийным (температурным)
волнам. Ранее применительно к изотермическому течению в участках тракта,
рассматриваемых как элементы с распределенными параметрами, а также
для элементов с сосредоточенными параметрами, описываемых уравнением
четырехполюсника, было введено специальное (схемное) обозначение и
название — коммуникатор. Это название подчеркивает, что хотя
коммуникатор связывает два полюса (узла) цепи, но для него не выполняются
условия равенства мгновенных значений расхода на входе и выходе.
Для участка тракта с неизотермическим течением, описываемым
уравнениями G.5.2)—G.5.6) , это условие также не выполняется и кроме того
для него отличаются значения на входе и выходе температуры (энтропии)
газа. Так как температура — параллельная переменная, то отличие ее
значений на входе и выходе элемента присуще как элементам с
распределенными, так и с сосредоточенными параметрами. Учитывая все это,
применительно к участкам тракта с неизотермическим течением газа, описываемым
уравнениями G.5.2) —G.5.6), можно также использовать название
коммуникатор и его обозначение (при необходимости, чтобы отличить от
четырехполюсников, можно вводить какой-нибудь дополнительный признак).
Для последовательной цепочки из элементов, описываемых
уравнениями G.5.2)-G.5.6), очевидно, что на стыках элементов должны
соблюдаться условия 5m/_iA) = 5m/(O), 5р/_ jA) = 5рг-@) и dTi_1(\) = 5Ti(Q).
Используя эти условия, можно получить математическую модель для всего тракта,
перемножая матрицы элементов в А-параметрах или в В-параметрах так же,
как это делалось выше для четырехполюсников.
7.5.2 Уравнение баланса тепла для узлов. При неизотермическом течении
жидкости в разветвленной системе в каждое из разветвлений из разных
трактов может поступать жидкость с разной температурой. В общем случае
для перемешивания потоков с разной температурой необходим
определенный объем или время контакта. Интенсивность и полнота
перемешивания будут зависеть как от конструктивных особенностей развилки (углов
встречи потоков, скоростей, размеров и т.д.), так и от свойств жидкости.
В такой общей постановке определить параметры потоков в трактах,
выходящих из развилки, чрезвычайно сложно. Анализ системы упрощается,
316
если сделать определенные предположения, в частности, о полном
перемешивании всей поступающей в развилку жидкости (см. рис. 3.1). В этом
случае температура жидкости во всех выходящих из развилки трактах
в каждый момент времени будет одинаковой. Для обеспечения такого
условия, как это следует из уравнения энергии C.1.3), необходимо,
чтобы перемешивание жидкости в узле было почти мгновенным, а
время ее пребывания — достаточно малым по сравнению с другими
характерными постоянными времени системы. Как видно, эти требования
достаточно противоречивы и они не всегда выполняются.
Рассмотрим простейший случай — к узлу подходят два тракта, а
отходит один. Температура жидкости в каждом из подходящих трактов своя.
С учетом принятых выше предположений уравнение баланса тепла для
узла запишется в виде
)Jfe(),
/ к
где G,-(l), /,-A) - расходы и энтальпия торможения жидкости,
поступающей в узел из выхода (Зс,-=1) /-го тракта, Gk@), /*@) - расход и
энтальпия жидкости, поступающей из узла на вход (хк = 0) в к-й тракт.
Линеаризовав это уравнение, найдем для размерных вариаций параметров:
2G,5i/(l)-2Gfc6/i;@) + Si/(lNG/(l)-Sifc@MG/;@) = 0> G.5.7)
i к i к
где 5G/A), 6G^@) - размерные вариации расходов, входящих и
выходящих из узла, 5/z'(l), 6^@) - размерные вариации энтальпии жидкости,
входящей и выходящей из узла. Уравнения G.5.7) можно записать в
безразмерных вариациях:
)
i к
G.5.8)
В уравнениях G.5.7) и G.5.8) в соответствии с принятыми
предположениями средние значения расходов на входе и выходе ветвей цепи
совпадают: G*@) = G*(l) = G*, Gf@) = G/(l) = G/.
Так же как и в § 7.2 разделим матрицу узлов П на две матрицы П@) и
ПA), получаемые из матрицы П заменой нулями соответственно для
первой матрицы — элементов равных+ 1, а для второй — элементов
равных -1. Матрица П@) фиксирует все сечения, соответствующие началу
ветвей Ccj = 0), в которые из узла втекает жидкость, а 11A) - концам
ветвей (Зс/ = 1), через которые в узел поступает жидкость. Так же как и
для уравнения G.2.8), легко показать, что систему уравнений G.5.7)
можно записать в более компактной, матричной форме
1IA) +
С7-5-9)
где Gn - диагональная матрица с элементами, равными среднему расходу
че;рез соответствующую ветвь, 6Gn@), 5вд(П- диагональные матрицы
размерных вариаций расходов на входе (х,- = 0) и выходе (*; = 1) ветвей,5i @),
5i'(i) - матрицы-столбцы размерных вариаций энтальпии жидкости на
317
входе и выходе ветвей, i@), i(l) - матрицы-столбцы энтальпии жидкости
на входе и выходе ветвей. Зная энтальпию жидкости 6r/ = cpi8T'iy можно
найти отклонение температуры. Соответственно, общее уравнение для
отклонений энтальпии G.5.9) можно преобразовать в уравнения для
отклонений температуры жидкости на входе и выходе ветвей цепи. Как
отмечалось выше, температура (энтальпия) смеси, образовавшейся в узле
(развилке) , принимается одинаковой для всех ветвей, в которые жидкость
поступает из узла. Нетрудно показать, что вариации узловых температур
(энтальпий) на входе в ветви связаны следующими матричными уравнениями [60]:
6i'@) = - Пт@M1', 5Т'@) = - nT@Nt', G.5.10)
где 61', 5t'— матрицы-столбцы размерных вариаций узловых энтальпий
и узловых температур. Уравнения G.5.10) связывают векторы вариаций
узловых энтальпий и температур с параметрами жидкости на входах в
ветви цепи. Для энтальпии (температуры) отсутствует уравнение,
аналогичное второй зависимости G.2.9), т.е. уравнение связи между узловой
энтальпией (температурой) и энтальпией (температурой) на выходе из
ветвей 5i'(l) и 6Т'A), так как узловая энтальпия (температура)
определяется смешением потоков жидкости с разной энтальпией (температурой).
Поэтому, в отличие от уравнений баланса расходов для узлов G.2.7) и
G.2.8), при использовании уравнения баланса энергии G.5.7) -
G.5.9) необходимо заранее знать направление течения жидкости в ветвях
цепи. Подставив зависимость G.5.10) в уравнение баланса тепла G.5.9),
найдем уравнения для вариаций узловых энтальпий:
G.5.11)
Можно показать, что элементы матрицы П@) GA Пт @) (эквивалентной
матрице узловых проводимостей Yy) равны сумме средних расходов
жидкости через ветви, выходящие из узла. Учитывая связь вариаций
энтальпии с вариацией температуры, уравнение G.5.11) можно преобразовать в
уравнение для вариаций узловых температур. Уравнение G.5.11) -
незамкнутое, так как связывает следующие неизвестные^ векторы
вариаций энтальпии в узлах, вариации энтальпии на концах ветвей 6i;(l),
матрицы вариаций расходов на входах и выходах ветвей. Последние могу!
быть определены независимо из уравнений для распределения расходов
по ветвям и уравнений ветвей. Найденные векторы вариаций расходов
на концах ветвей 5G @) и 6G'A) можно преобразовать в диагональные
матрицы, используя единичные матрицы I: 5G^(O) = I6G'(O), 6G^A) = I5G'A).
При замыкании уравнения G.5.11) кроме того нужно использовать
уравнения баланса тепла для ветвей. Для пассивных ветвей с
адиабатическим неизотермическим течением эти уравнения имеют форму
зависимостей G.5.2)—G.5.6). Для активных элементов, в которых за счет
сторонних источников энергии изменяется температура (энтальпия)
жидкости в ветви, можно записать следующую линеаризованную зависимость:
, Э/,A) ,
5G,@) + —— 8р @)+8q' G.5.12)
' ЭрДО) ' "
где Э/,-A)/Эг/@), Э/гA)/ЭрД0), 3/z(l)/3G/ определяют влияние параметров
318
потока в ветви на изменение энтальпии на выходе из ветви с активным
элементом, 8q- - вариация теплоподвода (воздействие активного
элемента). Уравнение G.5.12) - это уравнение неидеального источника тепла,
который моделирует внешние тепловые возмущения (например,
изменение условий горения, частоты вращения компрессора и т.д.).
Уравнение G.5.12) описывает тепловые характеристики как пассивной, так и
активной (в тепловом отношении) ветви. Частным случаем этой
зависимости для пассивных ветвей является последнее уравнение системы
G.5.1) или соответствующие уравнения из систем G.5.2) —G.5.6).
Уравнение теплового состояния ветвей G.5.12) удобно записать в матричной
форме
5i'(l) = F5i'@) + T5G'@) + Рбр'(О) + 5q', G.5.13)
где Р - диагональная матрица с элементами 3z,-(l)/9pf(O), F -диагональная
матрица с элементами Э/г-A)/Эг2-(О), Т - диагональная матрица с
элементами 9/,-(l)/3G,-, 5q' - вектор вариаций теплоподвода. Подставив
зависимости G.5.10) и G.5.13) в уравнение G.5.11), получим
G.5.14)
Уравнение G.5.14) позволяет найти вариации узловой энтальпии
(температуры) как функцию внешних тепловых возмущений 5д' и отклонения
других параметров течения. Отклонения расходов и давлений находят из
решения гидромеханических уравнений цепи.
Глава 8
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ПГС
§ 8.1. Переходные процессы в ПГС,
рассматриваемой как система с сосредоточенными параметрами
8.1.1. Дифференциальные уравнения цепи. В общую систему уравнений
ПГЦ входят уравнения отдельных элементов, из которых состоят ветви
цепи (гл. 2) и уравнения сохранения для узлов и контуров цепи (гл. 3).
Считая, что ветви включают только пассивные двухполюсные элементы
(сопротивление, инерционность и упругий элемент), можно записать
уравнение для вариации перепада давления в /-й ветви *) цепи:
SAP,-—-SCZ+JL —1 +-JL-f6Gdt, (8.1.1)
Gi Fi dt Р^эф/
где Apt - перепад давления на сопротивлении при расходе G,-, /,-, Ft -
длина и площадь проходного сечения тракта, инерция которого
учитывается, к(ч /'"эфz- — коэффициент упругости и эффективная площадь
емкостного упругого элемента.
Если просуммировать уравнения типа (8.1.1) для всех ветвей
замкнутого контура, введя оператор дифференцирования q = d/dt, то вместо интег-
ро-дифференциального уравнения вида (8.1.1) найдем уравнения контура в
операторной форме (для его пассивной части)
к к ( 2Ар, // кг- \
2 5Ар = 2 —^ + ТГ^+—f— NС/. (8.1.2)
Приравняв правую часть уравнения (8.1.2) сумме перепадов давления на
активных элементах - источниках напора, входящих в ветви контура,
получим уравнение контура в операторной форме. Используя системы
уравнений сохранения для контуров и уравнения сохранения для узлов,
последовательно исключая переменные, можно выделить для каждой из
вариаций параметров свое дифференциальное уравнение, которое в
операторной форме запишется в виде
(8.1.3)
где D(q) - полином я-й степени от оператора q, определяющий переходный
процесс - изменение во времени переменной 5GZ-; ND) - полином,
определяющий влияние возмущающего воздействия byf- на характер изменения
во времени переменной 8GJ. В принципе возмущающих воздействий может
1) Предполагается что все элементы, включая упругий элемент - емкость, входят
в ветвь последовательно, а сопротивление - квадратичное.
320
быть несколько. Однако учитывая линейность системы, можно
использовать принцип суперпозиции, рассматривая реакцию системы на каждое
возмущение отдельно. При действии нескольких возмущений общее
изменение любого параметра системы равно сумме изменений от действия
каждого возмущения в отдельности.
Уравнения (8.1.1)-(8.1.3) записаны для размерных вариаций
переменных. Переход к безразмерным вариациям изменит только форму
коэффициентов при переменных, не изменив при этом порядок уравнений. Решение
неоднородного линейного дифференциального уравнения с постоянными
коэффициентами (8.1.3) состоит из суммы общего решения однородного
(без правой части) уравнения (8.1.3) и частного решения
неоднородного 6G/B [17]:
sc;=8c;c+8q;, (s.i.4)
где 5G/c - решение уравнения Z)(#MG/ = 0, имеющее вид1)
п
5G/C = S Qexp^-r, (8.1.5)
где С/ — произвольные постоянные, определяемые начальными условиями,
qi - корни характеристического уравнения D(q) = 0.
Решение (8.1.5) не зависит от вида возмущения, а определяется видом
дифференциального уравнения и начальными условиями, т.е. схемой и
параметрами исследуемой цепи. Поэтому изменение параметров,
описываемое решением (8.1.5), называется свободным, собственным движением
системы.
Для отыскания констант Q в решении (8.1.5) необходимы начальные
условия - значения при t = 0 переменной 5G/ и ее п - 1 производных.
В пассивной цепи свободная реакция при t -> °° затухает, т.е. стремится
к нулю. Вследствие этого спустя достаточно большой отрезок времени
после действия возмущения в решении (8.1.4) остается только второй
член 5G/B, определяющий вынужденное движение системы. Вынужденное
движение определяется правой частью уравнения (8.1.3) и соответствует
некоторому установившемуся режиму течения жидкости в системе.
Применительно к ПГС изменения возмущающего воздействия во времени могут
носить самый разнообразный характер, в том числе и случайный. В связи
с этим целесообразно ограничиться некоторыми простейшими типовыми
возмущениями.
В теории автоматического регулирования в качестве таких типовых
возмущений используется единичная ступенчатая функция или единичная
импульсная функция. Для единичной ступенчатой функции решение
неоднородного уравнения (8.1.3) можно свести к решению однородного
уравнения заменой переменных [17].
В качестве примера рассмотрим систему, состоящую из последовательно
расположенных в тракте сопротивления, инерционности и емкости с
источником возмущения в виде идеального источника напора (рис. 8.1),
описываемую уравнением (8.1.1). Продифференцировав его по времени,
1) Предполагается, что все корни характеристического уравнения простые.
21.Б.Ф. Гликман 321
Рис. 8.1. Схема цепи и кривые переходных
процессов
переходя к безразмерным вариациям и
преобразуя коэффициенты, найдем
2i
dr
dbGt
2TU +
dt
dt
(8.1.6)
где
Подставив в уравнение (8.1.6) без правой
части решение однородного уравнения
(8.1.5), найдем характеристическое
уравнение T\tq2 + 2Tuq + 1 = (У, откуда
- 7\ ¦ +\/Т2 Т2
(8.1.7)
2i
Если величина постоянной времени Ти, зависящая от потерь давления на
вязкое трение, меньше чем инерционная постоянная времени Г2/, то корни
#! и #2 - комплексно-сопряженные, т.е.
tf^-a/tico,, (8.1.8)
где OLf - Тц/Т\(, со/ = vl/^2/ ~" а? ~ коэффициент затухания и частота
свободных затухающих колебаний системы.
Решение уравнения (8.1.6), если его свести к однородному для случая
ступенчатого возмущения путем введения новой переменной 5zz- [17],
запишется в виде
8zi=8Gi-8GiB =C1exp(-ai + /co/)r + C2exp(-a/ - ioj^t. (8.1.9)
Пусть к системе в момент г = 0 приложено ступенчатое возмущение, т.е.
8Apt = 0 при t < 0 и 8Apt = 1 при t > 0. Так как в правой части уравнения
(8.1.6) стоит производная от возмущения, то при ступенчатом возмущении
эта производная везде (кроме точки t - 0) равна нулю, а это значит, что
должна быть равна нулю вынужденная реакция системы 8GiB.
Соответственно в начальный момент 8G; @) = 8zt @) = 0. Учтя, что производная от
единичной ступенчатой функции равна импульсной единичной функции,
а коэффициент при ней - отношению Tu/T22i [17], найдем второе
начальное условие для однородного уравнения d8zt{0)ldt = TulT22i. Подставив
соотношение (8.1.9) в начальные условия, определив коэффициенты С\ и
С2, после преобразований получим
5G/(r)=(aI-/cjI-)exp(-a,-r)sincj/r. (8.1.10)
322
Реакцией рассмотренной системы на единичное возмущение в случае Ти <
< T2t является затухающая синусоида (рис. 8.1, кривая 1). Если же Ти >
> T2f, то аналогичным образом находим, что
6С/(г)= — expC-a/Oshfyr, (8.1.11)
ft
где ft = \/а? - llT\t\ а переходный процесс - кривая 2 на рис. 8.1. Если же
Тц % T2i, то sin со/t ^ ojjt и решение принимает вид
6G/(r)=a/rexp(-a/r); (8.1.12)
переходный процесс для этого случая представлен кривой 3 на рис. 8.1.
Таким образом, в зависимости от соотношения между параметрами
системы - инерционной постоянной времени Г2,- и постоянной времени
демпфирования Ти - возможен различный характер переходного процесса в
ПГЦ, описываемой уравнением колебательного звена (8.1.6).
8.1.2. Операционный метод. Для решения линейных дифференциальных
уравнений достаточно широко используется операционный метод,
основанный на использовании преобразований Лапласа или Карсона (иногда
называемого методом Карсона — Хевисайда) [17, 82, 217]. В операционном
А
методе функция f(t) заменяется ее изображением f(s); они связаны.
между собой интегральным преобразованием Лапласа
f(s) = ff(t)exp(-st)dt = L\f(t)], (8.1.13)
о
= — / f(s)exp(st)dt'-L-i [f(s)]. (8.1.14)
Аналогично в преобразованиях по Карсону вводится дополнительный
множитель s:
f(s) = s J/(r) exp(- st)dt = sf(sl
о
Преимущество операционных методов — замена операций
дифференцирования и интегрирования оригинала алгебраическими действиями над
изображением. Действительно, применив формулу (8.1.13) к производной
от функции df/dt, находим
— ехр(- st)dt =/(r)exp(- st) ~ + s //(r)exp(- st)dt = sf(s) -/@).
о dt
о
(8.1.15)
Формулы, связывающие оригинал с изображением, приводятся в виде
таблиц [17, 82, 217]. Решим операционным методом приведенный выше
пример для переходного процесса в системе, описанной формулой (8.1.6).
Применим преобразование Лапласа (8.1.13) к уравнению (8.1.6),
воспользовавшись свойством преобразования, согласно которому изображение
суммы равно сумме изображений, и формулой (8.1.15); получим
•^ Т v -^ Т • s -^
5G,- = -т—; SAp, = —г г — 5Др,., (8.1.16)
где Oil и coz- — определяются так же, как и в формуле (8.1.8). Считая, что
21* 323
внешнее возмущение — единичное ступенчатое, т.е. dApf(t) = 1@, и
Учитывая, что L [1@] = 1/5> воспользовавшись таблицей обратных преобра*
зований от изображения к оригиналу [82], получаем при нулевых
начальных условиях соотношение
ехр(— a it) sin
которое, естественно, совпадает с полученным другим способом решением
(8.1.10), если подставить определение а,-.
Для отыскания оригинала по его изображению можно использовать
таблицы изображений или теоремы теории операционного исчисления,
позволяющие свести решение дифференциальных уравнений к
алгебраическим операциям — нахождению корней характеристического уравнения.
Теорема свертывания позволяет найти переходный процесс при задании
возмущения в виде некоторой функции от времени. Если для изображения
отсутствуют табличные формулы обращения, то можно применить
достаточно разработанные численные методы [131].
§ 8.2. Переходные процессы в гидравлической системе
с распределенными параметрами
8.2.1. Обзор работ по переходным процессам. Если ПГС содержит
длинные тракты, то при анализе переходных процессов в большинстве случаев
необходимо учитывать волновые явления, т.е. конечное время передачи
возмущения по тракту.
Условие, при выполнении которого можно не учитывать распределен-
ность параметров, определяется соотношением между характерным
временем возмущения, вызывающего переходный процесс тв, и временем
пробега акустической волной длины тракта L/a тв >L/a. Если эти характерные
времена соизмеримы, то волновые явления необходимо учитывать.
Переходные процессы, вызванные резким изменением режима, связаны
с рядом особенностей: значительным ростом давления в тракте,
называемым гидравлическим ударом, провалами давления, которые могут
привести к вскипанию жидкости - кавитации и т.п. Волновые явления в
трактах приводят к существенным динамическим нагрузкам на
конструкцию, так как величина повышения давления при гидравлическом ударе
может намного превышать средний уровень давления в системе. Теория
волновых процессов в трубах, заполненных невязкой сжимаемой
жидкостью, была создана Н.Е.Жуковским [95]. Состояние исследований по
теории гидравлического удара с периода, предшествующего работе Н.Е.
Жуковского, и до 1954 г. подробно изложено в статье М.А. Мосткова [167],
а по состоянию на 1961 год — в работе Н.А. Картвелишвшш [113]. Обзор
исследований гидроудара за рубежом до 1971 г дан в статьях Мартина [158] и
Гудсона, Леонарда [75].
Прежде чем приступить к анализу переходных процессов в ПГС с
распределенными параметрами, необходимо решить несколько вопросов:
а) выбрать математическую модель, описывающую взаимодействие
жидкости со стенками тракта, в частности, модель потерь на вязкое трение;
324
б) сформировать начальные и граничные условия, достаточно точно
описывающие взаимодействия жидкости с устройствами на концах
участков трактов и определяющие действия источников возмущений;
в) выбрать модель, описывающую процесс разрыва сплошности
(кавитации) в случае падения давления жидкости ниже определенного предела;
г) определить алгоритм, который будет использован при расчетах
переходных процессов в трактах.
Уравнения гидромеханики, описывающие одномерное нестационарное
изотермическое движение вязкой жидкости, являются квазилинейными
уравнениями гиперболического типа, для которых в математической
физике предложено много способов решения. В первых работах по
гидроудару Н.Е. Жуковского [95], и Л. Аллиева, а затем в исследованиях
М.А. Мосткова [167], Л.М. Тарко [213], B.C. Дикаревского [87] и др.
использовался классический метод Даламбера, дающий наглядную картину
распространения волн по длине тракта.
При этом решение уравнений в частных производных сводится, как
правило, к алгебраическим операциям над функциями, определяющими
характер возмущающего воздействия. Этот метод удобен для анализа
переходных процессов в простых трубопроводах, в случае же сложных
систем возникает необходимость одновременно следить за
многочисленными отражениями волн, что приводит к слишком громоздким
соотношениям. Более широкими возможностями обладают методы интегральных
преобразований, несколько модификаций которых применяются для
расчетов неустановившихся течений в трактах, описываемых
линеаризованными уравнениями.
В монографии И.А. Чарного [234] изложен метод анализа
неустановившегося движения жидкости с помощью контурного интегрирования в
плоскости комплексной частоты. Используя предложенный им метод
линеаризации члена, учитывающего потери на трение, автор решил ряд задач о
нестационарных процессах в гидравлических трактах. При линеаризации
квадратичного члена в уравнении движения И.А. Чарный пользовался
гипотезой о квазистационарности коэффициента потерь на трение, впервые
предложенной С.А. Христиановичем для анализа нестационарных течений
жидкости в открытых руслах [229].
Другой вариант интегральных преобразований — операционный метод,
описанный в § 8.1. С помощью операционного метода уравнения в частных
производных сводятся к обыкновенным дифференциальным уравнениям
для изображений. После решения этих уравнений с учетом граничных
условий необходим переход к оригиналу, который даже для одиночных
трубопроводов оказывается возможным для ограниченного класса
граничных условий. Для общего случая граничных условий и для
разветвленных трубопроводных систем необходимо применять численные методы
перехода к оригиналу [131] или ограничиться анализом асимптотических
свойств решения для большого или малого времени развития процесса.
Примеры использования операционного метода для анализа переходных
процессов в трактах гидромеханизмов приводятся в книгах Л.М. Тарко
[213, 214], а в сложных трубопроводных системах - в монографии
В.В Грачева, М.А. Гусейнзаде, Б.И. Ксенза и Е.И. Яковлева [207]. Другой
интегральный метод - с помощью преобразования Фурье, близкий к методу
325
контурного интегрирования, нашел применение при разработке Н.А. Карт-
велишвили методик расчета гидроудара в трубах со стенками из упруго-
вязкого материала [114].
Для систем квазилинейных уравнений гиперболического типа, к
которым относятся уравнения нестационарного одномерного движения
жидкости, одним из наиболее удобных методов интегрирования является
метод характеристик. Применительно к расчету нестационарного течения
жидкости в открытых каналах и реках этот метод впервые использован
С.А. Христиановичем [229], а затем нашел широкое применение в ряде
работ по нестационарному течению в трубах [115, 153, 166, 170, 210, 247].
Достаточно подробно все классические методы решения уравнений
нестационарного движения жидкости описаны в работах Г.Д. Розенберга
[192, 194] и в коллективной монографии [207]. Кроме аналитических
методов разработаны ряд графических и численных методов решения
задачи о переходном процессе. Наиболее подробно графический метод
изложен в работах Л.Б. Бержерона [16], М.М. Андрияшева [3] и А.А. Су-
рина [211]. Преимуществом графического метода является простота
вычислений и наглядность результатов. Однако для длинных трубопроводов
и разветвленных систем резко возрастает объем и снижается точность
расчетов. Численные методы (к которым относят и классический метод
характеристик) позволяют эффективно использовать возможности ЭВМ
и решать не только линеаризованные уравнения гидромеханики, но и
нелинейные уравнения, а также детально учесть особенности граничных условий.
Обзор численных методов расчетов нестационарных течений с
использованием ЭВМ, а также гибридных вычислительных систем, приведен в статье
К.Э. Кенига [119]. Реализация отдельных методов применительно к
численному решению уравнений гидромеханики приводится в работах [6, 32, 33,
132]. Для нестационарного течения газа в изотермических условиях
применяются практически те же методы анализа, что и для переходных
процессов в трактах с капельной жидкостью [119, 209]. В случае
неизотермического нестационарного течения газа и возможного образования ударных
волн используется метод характеристик или разностные методы [52].
Так же как и при вынужденных колебаниях (см. гл. 6), при переходных
процессах в трактах возникает вопрос о степени влияния на нестационарное
течение взаимодействия жидкости со стенками тракта. Эта проблема
распадается на два класса задач - о законе трения жидкости о стенки и о
взаимодействии движения стенок трактов (радиальных и продольных) с
движением жидкости. В первую очередь остановимся на законе вязкого трения.
В подавляющем большинстве публикаций по переходным процессам в
трактах ПГС используется гипотеза квазистационарности трения (см. гл. 6) и
метод линеаризации квадратичного члена в уравнении движения,
предложенный И.А. Чарным [234]. Вопросу о различных способах линеаризации
этого нелинейного члена и о влиянии линеаризации на точность решения
посвящен ряд работ [42, 43, 49, 54, 76, 137, 207]. В статье М.Я. Куркиной,
В.П. Радченко и В.А. Юфина [137] показывается, что при использовании
линеаризованных уравнений возможна существенная ошибка - до 55% при
определении давления и до 70% — скорости на переходных режимах в
исследованном авторами диапазоне изменения параметров. Для
подтверждения правомерности использования гипотезы квазистационарности B.C. Ди-
326
каревский провел сопоставления расчетных данных с результатами
обработки экспериментов ряда авторов [86]. В работе делается вывод, что
для обработанных опытов коэффициент гидравлического сопротивления
нестационарного течения X в среднем незначительно отличается от его
значения Хкс для квазистационарного течения жидкости. .Однако из
приведенных в таблице результатов обработки опытов следует, что Х/ХКс
изменяется в пределах от 0,58 до 1,6, т.е. почти в три раза, при этом не
обнаруживается определенной закономерности между величиной X и режимом
течения, только замечается тенденция, что в большинстве случаев Х/Хкс >
> 1. При этом в работе [86] обрабатывались только материалы,
относящиеся к замедляющимся течениям жидкости, так как во всех случаях
переходный процесс возникал вследствие остановки насоса или закрытия крана.
Вызывает сомнение точность обработки данных экспериментов, так как
величина X определялась по декременту затухания колебаний жидкости,
но характер кривых при затухающих колебаниях существенно отличался
от затухающих гармонических колебаний, к которым строго только и
относится понятие декремента.
Таких противоречий много и в других работах, посвященных
исследованиям нестационарного турбулентного течения в трубе — с разгоном
или торможением жидкости. Достаточно обстоятельный обзор данных по
нестационарным течениям приведен в книге Д.Н. Попова [184].
Сопоставление результатов ряда экспериментальных исследований
[80, 106, 130, 148, 250, 252] и др. не дало автору возможности установить
общей закономерности изменения коэффициента сопротивления трения
от условий в нестационарном потоке. Однако некоторые качественные
выводы, полученные в результате анализа данных большинства известных
работ по нестационарным турбулентным течениям, совпадают.
Отношение коэффициентов сопротивления трения на нестационарном
режиме течения к значению этого же коэффициента на квазистационарном
режиме Хкс является функцией двух параметров: X/XKC=/(fcH, kD), где
?н = BD/\KCU2) (dU/dt) — безразмерное ускорение потока, kD =
= {р2J32v) \/(l/l U\) \d2U/dt2'\ — безразмерный параметр, учитывающий
влияние второй производной от скорости;
При ускоренном движении жидкости (кн > 0) Х/Хкс > 1, при этом с
ростом кн эта величина увеличивается;
При торможении потока (кп < 0) Х/Хкс < 1 и эта величина уменьшается
при убывании кн.
В частности, по результатам обработки экспериментов, приведенных
в статье [252], предложена зависимость Х/Хкс = 1 + bkHi где Ь = 0,098
при ускоряющемся движении (кн > 0) и Ъ - 0,75 при замедляющемся
течении (кн < 0). Таким образом, коэффициент, определяющий влияние
ускорения, т.е. величины кн, на коэффициент сопротивления трения X
почти на порядок изменяется при смене знака кн. По данным других
авторов не обнаружено такого влияния знака кн на закон изменения X, наклон
же зависимости Х/Хкс от кн у разных авторов достаточно существенно
отличается. К примеру, в работах Л.Л. Калишевского и СВ. Селиховкина
[106], Карстена и Роллера [250] не обнаружено влияния нестационарности
на коэффициент сопротивления трения, из экспериментов же У.Р. Лийва
[148] следует, что Х/Хкс > 1 как при ускорении, так и при замедлении
327
движения жидкости в трубе. В работе Д.Н. Попова и В.Г. Кравченко [184]
получены экспериментальные данные по переходным процессам в трубе
в достаточно широком диапазоне параметров кн и kD. Для ускоряющегося
течения получена эмпирическая зависимость, связывающая безразмерный
коэффициент сопротивления Х/Хкс с параметрамикн nkD:
X
+Д1 [ехр(д2 +а3кн) kD- 1],
1
Лкс
где а0 =0,07, ах = 32, а2 =0,1 . 10~4, аъ =0,8 • 10~5.
Значение числа Рейнольдса учитывалось при определении параметров кн
и Хкс по формуле Хкс = %KCD/4L, где ?кс = ? (Re). Данные обработки
экспериментов дают достаточно большие значения Х/Хкс — до 50 при кн ъ 50.
Однако ощутимого влияния на переходный процесс нестационарного
трения авторы не обнаружили: максимальное отличие расчетных значений
скорости для случая квазистационарного трения от экспериментальных
данных не превышает 20%. На интегральные характеристики процесса
нестационарность влияет меньше, чем на локальные характеристики типа
При ламинарном течении существуют точные решения для переходного
процесса, первое из которых в конце прошлого века нашел И.С. Громека
[71] для случая, когда градиент давления задан в виде функции времени.
Позже частный случай этой задачи был рассмотрен П. Шиманским [273].
При больших градиентах изменения параметров течения ряды сходятся
плохо. Поэтому для решения этой задачи удобнее использовать или методы
операционного исчисления [23, 75, 109, ПО], или метод характеристик
[21, 99, 212, 218], или разностные методы [177, 222].
Одним из перспективных методов расчета нестационарных течений
вязкой жидкости или газа является метод крупных частиц, развитый
в работах О.М. Белоцерковского и Ю.М. Давыдова [12]. В качестве
исходных уравнений в методе крупных частиц используются уравнения
нестационарного движения вязкой среды. Стационарные задачи решаются
методом установления, т.е. в любом случае находится переходный процесс,
приводящий к стационарному режиму течения. Поэтому такой метод
является естественным и физичным для анализа нестационарных течений.
В монографии [12] приводятся примеры применения метода крупных
частиц для нестационарных задач внешнего обтекания тел с ударными
волнами, для нестационарных двухфазных течений и т.д.
Результаты достаточно обстоятельного экспериментального
исследования переходного процесса в трубе при ускорении жидкости приведены
в статье Т.А. Коппеля и У.Р. Лийва [128]. Неподвижная жидкость (вода)
приводилась в движение в трубе длиной 19,35 м и диаметром 61 мм.
Практически линейное возрастание скорости во времени обеспечивалось
быстродействующим затвором с программированным законом открытия.
Напряжение трения на стенки измерялось термоанемометрическим датчиком
трения, мгновенное значение расхода (скорости) и давления —
малоинерционными датчиками расхода (электромагнитные) и давления (тензомет-
рические). Опыты многократно повторялись в одинаковых условиях,
так что экспериментальные точки были получены методом осреднения
статистических ансамблей, что обеспечивало необходимую точность. Анализ
данных по величинам касательного напряжения и коэффициента трения
328
показал, что при ускорении движения ламинарный режим течения
сохранялся с начала процесса разгона до таких скоростей, которым
соответствовали числа Re намного превышающие их критические значения для
стационарного движения. Критические значения Re, при которых резко
увеличивалось напряжение трения и происходил переход от ламинарного
течения к турбулентному, изменялись от 7,8 • 104 для ускорения 0,68 м/с2
до 2,34 . 105 для ускорения 11,78 м/с2. Зависимость между коэффициентом
трения X и числом Re в логарифмических координатах имеет линейный
характер X = .4/Re1'15, и похожа на закон трения при ламинарном течении,
^кс = 64/Re, только степень (наклон кривой) и величина коэффициента
отличаются. Коэффициент А зависит от ускорения потока, при этом с
ростом ускорения коэффициент А увеличивается. Обнаруженное
увеличение критического числа Re и увеличение коэффициента трения (по
сравнению с его с квазистационарным значением) для ускоренного движения
качественно согласуются с данными других авторов, описанными выше.
Однако прямое сопоставление провести трудно из-за разных условий
проведения экспериментов и методов измерений.
В работе В.М. Овсянникова [177] проведено сопоставление результатов
описанных экспериментов [128] с данными расчетов нестационарного
л°минарного течения. Отмечается, что предложенный И.С. Громека [71]
метод решения задачи в виде ряда непригоден (из-за плохой сходимости
ряда) для расчетов при условиях, соответствующих экспериментам [128].
Поэтому был использован разностный метод, эффективность которого
была проверена путем сравнения с известными расчетными результатами
[273]. Для начала ускоренного течения с изменением средней скорости
по закону U-ct в диапазоне параметров, характерных для
экспериментов [128], автором [177] получена формула для коэффициента
сопротивления
Теоретическая формула отличается от эмпирической показателем степени
для числа Re A,5 вместо 1,15). Наибольшее отличие результатов расчетов
от данных экспериментов в исследованной области параметров составляет
37%, Причину обнаруженного отличия автор не указывает. В то же время
следует отметить, что как показано выше, в гл. 6, для другого случая
нестационарного движения — пульсирующего — результаты расчетов по
уравнению Навье-Стокса удовлетворительно согласуются с имеющимися
данными экспериментов.
Экспериментальные исследования Б.С. Байбикова, О.Ф. Орешкина и
A.M. Прудовского [9] проведены на установке таких же масштабов, как
и в работе [128] (длина рабочей части 15,9 м, диаметр 26,8-29,9 мм с
тремя разными уровнями шероховатости внутренней поверхности трубы).
Измерялись мгновенные значения скорости жидкости и градиент давления
по показаниям датчиков давления в четырех точках по длине трубы. Для
вычисления коэффициента сопротивления X использовалась формула
F.4.26), дающая следующее соотношение для коэффициента
сопротивления трения участка трубы:
Ар dU\ 4R
)^- (8'2Л)
329
В формулу (8.2.1) подставляются измеренные в опытах величины Ар^
U, а производную dU/dt находят дифференцированием по времени
измеренных величин. В качестве параметров, определяющих мгновенное
значение X, использовались мгновенное число Re и значение числа Рейнольдса
в конце процесса разгона, на установившемся режиме течения Re^ = u^Djv^
а также относительная шероховатость Д/Д где Д - высота выступа
шероховатости внутренней поверхности трубы. Число Re», изменялось в
пределах от 103 до 4 ¦ 105 путем задания различных значений перепадов
давления на рабочем участке. Кроме того, изменялась вязкость жидкости —
использовалась вода (у = 1 . 1СГ6 м2 /с), водный раствор глицерина
(у = 3 . 10 м2/с).
Результаты экспериментов сопоставлялись с данными расчетов по
формулам, полученным из решения И.С. Громека [71] для ламинарного
разгонного течения и эмпирических зависимостей для стационарного
турбулентного течения жидкости в шероховатой трубе. Из решения И.С. Громека
получены параметрические зависимости
_ = 4^i|l-exp(;-^r-)J^,
Re -Г / uvtV] I . (8.2.2)
— = 32 2 l-expU-^-j — ,
где jdn — корни функции Бесселя нулевого порядка, Хкс —
квазистационарное значение коэффициента сопротивления, вычисленное по мгновенному
значению числа Re по зависимости для стационарного течения Хкс = 64/Re.
Сопоставление результатов расчетов по формуле (8.2.2) с
экспериментальными данными показало их совпадение для переходного процесса при
ламинарном течении (Re^ = 103) и для начального периода переходного
процесса, приводящего к турбулентному режиму течения.
В опытах обнаружилось, что начиная с некоторого значения Re^Re^
величина X отклоняется от зависимости, определяемой формулами (8.2.2)
для ламинарного течения, что можно объяснить турбулизацией потока.
С этого момента значения X начинают увеличиваться, приближаясь к
величинам, характерным для стационарного турбулентного течения. Обработка
данных экспериментов показала, что ReKp можно связать с градиентом
давления
4D /I dp
dx
D
9
при этом величина ReKp не зависит от шероховатости стенок трубы. Так же
как ив [128], значения ReKp, при которых начинается переход к
турбулентному режиму для переходного процесса с разгоном жидкости, существенно
больше, чем критическое значение Re для стационарного ламинарного
течения. Однако сопоставить результаты этих двух экспериментальных
работ количественно трудно, так как условия эксперимента различны по
характеру изменения скорости течения во времени.
Следует отметить противоречия в результатах при сопоставлении данных
расчетов и экспериментов для переходного процесса с ускоренным
ламинарным течением. В работе [9] получено согласование данных расчетов и
330
экспериментов, в статье же [177] не получено согласия между
результатами проведенных расчетов и экспериментальными данными работы [128].
Обработка данных экспериментов [9] для части переходных процессов с
турбулентным режимом течения позволила получить общую эмпирическую
зависимость
согласно которой при ускоренном турбулентном течении Х/Хкс < 1. Этот
вывод противоречит результатам обобщения экспериментальных данных
многих авторов, проведенного в книге Д.Н. Попова ([184], с. 101).
Обнаруженные противоречия данных у разных авторов объясняются в первую
очередь сложностью процессов в жидкости при нестационарном течении,
зависящем от большого числа параметров, и отличиями в методике
проведения опытов.
Другая проблема: трудности получения достоверных результатов
исследования нестационарных течений при измерениях нестационарных
параметров. Во многих случаях для определения мгновенного значения
коэффициента сопротивления трения использовалось уравнение количества
движения (8.2.1), в которое подставляются мгновенные значения перепада
давления Ар, средней скорости U. На многих режимах нестационарного
течения Ap/L мало отличается от p(dUjdt), т.е. значение X определяется
малой разностью больших величин, что существенно увеличивает
погрешность. Кроме того, для определения производной dU/dt необходимо
дифференцировать данные, полученные при экспериментах, что также приводит
к дополнительным ошибкам. На это все накладываются трудности
измерения мгновенных значений перепада давления и средней скорости.
На недостатки общепринятой методики обработки результатов
экспериментов для нестационарного потока в форме отношения Х/Хкс указывает
в своей работе Н.П. Гулин [74]. Используя решение задачи о
нестационарном ламинарном течении несжимаемой жидкости при внезапном изменении
градиента давления, автор показывает, что существуют режимы, при
которых отношение Х/Хкс терпит разрыв, обращаясь в бесконечность. Такое
поведение параметров имеет место при изменении направления движения
жидкости, когда скорость обращается в нуль. Все сказанное относится
и к введенным выше параметрам нестационарности кк и /cD, в формулах
которых средняя скорость стоит в знаменателе. Результаты
собственных экспериментов автора [74] в общем качественно согласуются с
данными, приведенными в книге Д.И. Попова [184]. Величина Х/Хкс при
ускоренном течении увеличивается с увеличением параметра нестационарности
кн, однако численно данные отличаются при сопоставимых значениях кн
(kD в работе [74] не используется) .
Из анализа как экспериментальных, так и теоретических исследований
нестационарного турбулентного течения в трубах можно сделать вывод,
что современное состояние вопроса не позволяет разработать
теоретическую или полуэмпирическую математическую модель, пригодную для
проведения расчетов с учетом трения в трубах с точностью, необходимой
для анализа динамики ПГС. Здесь еще остается много "белых пятен",
которые ждут своих исследователей.
331
Следующий вопрос — о влиянии движения стенок тракта на течение
жидкости — можно разбить на два класса задач — о влиянии радиального
движения стенок канала и перемещения стенок вдоль оси канала. хМате-
матические модели для такого движения были приведены в гл. 6. Влияние
реологических свойств материала стенок гракта может приводить к
существенному изменению формы сигнала и изменению параметров течения при
распространении возмущения вдоль тракта. Подобные процессы
характерны для трубопроводов из полимерных материалов, кровеносных сосудов
и других случаев, когда материал стенок не подчиняется закону Гука
[18, 53, 86]. Наиболее подробно этот вопрос анализируется в книге
Н.А. Картвелишвили [114]. Влияние инерции стенок трубы и
предварительного ее растяжения на характер переходного процесса в трубе с
эластичными стенками анализируется в статье В.Е. Накорякова и его
сотрудников [169]. Используя уравнения Н.Е. Жуковского для одномерного
нестационарного движения невязкой жидкости в трубе, записав уравнение
радиального движения эластичных стенок с учетом их инерции, авторы
показывают, что при быстром перекрытии тракта (г ~ 10~3 с) учет
инерции стенок приводит к новым эффектам. Используя упрощающие
предположения, уравнения динамики трубы сводятся к уравнению Кортвега-
де-Вриза, исследованному достаточно подробно. Результаты численных
расчетов при различных начальных условиях по длительности возмущений
показали, что влияние этого параметра на окончательную картину
процессов незначительно. Наблюдалось образование уединенной волны,
движущейся с постоянной амплитудой, без изменения формы (солитона) и
высокочастотных осцилляции, отстающих от переднего фронта и
расплывающихся с течением времени.
Учет продольного натяжения стенок трубы, что существенно для труб
из резиноподобных материалов, приводит к новым эффектам -
возможности появления осциллирующего предвестника, амплитуда которого
соизмерима с амплитудой начального возмущения. Продольные колебания
трактов, связанные с колебаниями жидкости внутри них, рассматриваются
в первую очередь в связи с вынужденными колебаниями жидкости,
приводящими к вибрациям трубопроводов [38, 40, 55,56, 114, 219]. В то
же время они оказывают определенное влияние и на величину
гидроудара [85].
При переходных процессах в трактах с капельной жидкостью возможно
падение давления ниже давления насыщенного пара или равновесного
давления растворения газа в жидкости. При этом нарушается сплошность
потока — появляется кавитационная каверна, заполненная парами
жидкости или газом. Теория кавитации жидкости в стационарных условиях носит
в основном качественный или полуэмпирический характер. Еще менее
изучено явление кавитации применительно к нестационарным течениям
[182]. Обзор существующих методов расчета кавитационных разрывов
при переходных процессах в гидравлических системах приводится в статье
Мартина [158]. Л. Бержерон [16] предложил модель кавитационного
разрыва столба жидкости в тракте, в которой используются следующие
предположения:
— кавитационная каверна в жидкости начинает развиваться с момента,
когда в одном из сечений тракта (расчетном узле) давление станет меньше
332
давления насыщенного пара жидкости;
— кавитационная каверна ограничивается плоскостями,
перпендикулярными оси тракта;
— размеры кавитационной каверны определяются уравнением баланса
для проточной емкости (см. гл. 2), расходы на входе и выходе в которую
определяются независимым движением столбов жидкости до и после
каверны;
— давление в каверне равно давлению насыщенных паров жидкости или
выделившегося газа;
— при смыкании каверны весь пар мгновенно конденсируется, а газ —
растворяется.
С использованием этих предположений разработан ряд методов расчета
переходных процессов с учетом кавитационных разрывов: Н.А< Картвелиш-
вили [114] — с помошью цепных уравнений, Б.Ф. Лямаевым, Г.П.
Небольсиным и В.А. Нелюбовым [153], А.С. Котелкиным [116] — с
использованием метода характеристик и т.д. B.C. Дикаревский и А.Е. Татура по
данным специальных опытов показали [88], что давление в кавитационной
каверне существенно отличается от давления насыщенного пара за счет
выделения растворенных в жидкости газов. Кинетика выделения и
растворения газов из жидкости в условиях нестационарного течения изучена
слабо [37], кроме того на результаты экспериментов влияет нераство-
ренный воздух, присутствующий в жидкости до начала переходного
процесса [153]. Поэтому трудно ожидать высокой точности расчетов
переходных процессов с кавитационным разрывом столба жидкости, что
подтверждается проведенным в работах [153, 208] сопоставлением данных расчетов
с результатами экспериментов.
Присутствие в тракте нерастворенного воздуха приводит к изменению
скорости распространения возмущений (которая в этом случае зависит
от давления) и появлению дополнительного затухания высокочастотных
составляющих колебаний. В результате при колебаниях фаза повышения
давления оказывается короче следующей за ней фазы разрежения,
колебания становятся асимметричными относительно статического
давления [153].
В трубопроводах, в частности, в нефтепроводах возможно появление
неподвижных скоплений газа. В работе В.А. Табахова [212] определяются
форма и размеры газовых скоплений и показана степень влияния газовых
скоплений на величину гидроудара в трубопроводе.
8.2.2. Решение методом Даламбера. Волновые уравнения E.1.17) и
E.1.18) или E.1.21) и E.1.22), описывающие распространение без
затухания волн различной природы, подробно исследованы в математической
физике и имеют много способов решений. Один из наиболее простых и
распространенных классических способов решения носит имя известного
французского ученого Ж. Даламбера. Применим этот метод к неограниченному
по длине тракту. Эффекты, связанные с конечной длиной участка тракта
и влиянием граничных импедансов рассмотрим позднее. Для решения
уравнения E.1.16) введем новые переменные
*-*-0+М>*. (8.2.3)
тГ = х +A -МO.
ззз
Воспользовавшись правилом дифференцирования
Э Э Э? Э drf
Эх Э ? Эх 9 77 Эх
Э Э Э? Э Э77
Э7 д! дТ Ьг[ Э7
после перехода в уравнении E.1.16) к новым переменным (8.2.3) и
преобразований получаем:
Ъ2Ьр _ Э
Э ? Э 77 Э ?
Интегрирование этого уравнения по переменной % дает d8p/drf = F(ff)i
где F(ff) - произвольная функция от rf. Повторное интегрирование по
переменной rf приводит к
,rf) = / F(a)da
о
Возвращаясь к переменным х и 7, получим
6р(х,7) = Ф[х -A +МO] +^[х +A -МO], (8.2.4)
где Ф и ^ — произвольные функции своего аргумента. Характерным в
решении (8.2.4) является не вид функции, а вид аргументов. Если
перейти к размерным переменным, то решение (8.2.4) принимает вид
Ьр\х, 0 = Ф'[*- (a+uo)t] +V'[x+(a-uo)t]9 (8.2.5)
где Ф' и V— произвольные фикции, имеющие размерность давления.
В решениях (8.2.4) и (8.2.5) произвольные функции имеют разные
аргументы, однородные относительно переменных х и7 или.*и t. При
увеличении 7 на А7 аргумент функции Ф (а значит и сама функция) сохраняет
свои значения, если х увеличится на Дх = A + М) А7 (или Ах = (а + и0) At).
Таким образом, функция Ф описывает волну неизменной формы,
двигающуюся со скоростью а + и0 вдоль оси х. Аналогичные рассуждения
приводят к выводу, что функция ^ описывает распространение волны,
перемещающейся в направлении — х, т.е. в противоположном направлении,со
скоростью а - и0. Поправка на ±щ учитывает перенос акустических
возмущений вместе с потоком жидкости.
Решения вида (8.2.4) или (8.2.5), которые описывают независимое
распространение в различных направлениях двух волн без изменения формы,
называются решениями волнового уравнения в виде бегущих волн. При
этом волна, бегущая в положительном направлении оси называется прямой
волной, в отрицательном — обратной волной. Аргумент функции Ф или ^,
определяющий некоторое фиксированное значение функции, называется
фазой, а при рассмотрении пространственной картины поверхность, для
которой отклонение имеет одинаковую фазу, называется фронтом волны.
Для рассматриваемых нами задач фронт волны плоский (х = const) . Таким
образом, решение волнового уравнения E.1.16) имеет вид суммы двух
плоских продольных волн давления произвольной во времени формы,
бегущих в разных направлениях.
334
Для отклонения скорости по форме исходное волновое уравнение
E.1.15) совпадает с аналогичным уравнением E.1.16) для давления,
поэтому решение для отклонения скорости следует искать в форме, подобной
соотношению (8.2.4) , учтя отличие коэффициентами,
8и=АФ[х -A +МO] + ЯФ[х +A -МO]. (8.2.6)
Для определения неизвестных коэффициентов воспользуемся уравнением
движения E.1.4) и математическими зависимостями E.2.2). Подставив
решения (8.2.4) и (8.2.6) в уравнение E.1.5), учтя формулы (8.2.3),
имеем
Ф(|) ЭФ(тГ)
(ссА-\)—zr1^ + (<*Я + 1) — =0.
Э? Эт?
Для тождественного выполнения последнего равенства при произвольных
функциях Ф(?~) и ^(т?) необходимо, чтобы коэффициенты при
производных в этом соотношении равнялись нулю или А = 1/а и В = -1/а.
Соответственно решение (8.2.6) запишется:
ды = — Ф[х -A +МO] Чг[х + A-МO]. (8.2.7)
ос а
Аналогичное соотношение для размерного отклонения скорости с учетом
зависимости (8.2.5) имеет вид
5и'= — Ф'[х-(а+ио)г] Ъ'[х + (а - uo)t]. (8.2.8)
pa pa
Из сравнения решений (8.2.4) и (8.2.7) или (8.2.5) и (8.2.8) следует, что
бегущие волны скорости и давления одного направления связаны между
собой коэффициентом (волновым сопротивлением) а или ра. При этом,
в отличие от общепринятого в гидромеханике и электротехнике понимания
термина "сопротивление" волновое сопротивление среды без вязкости
не связано с диссипацией механической энергии и переходом ее в тепло.
При распределении бегущей волны в жидкости энергия тратится не на
преодоление силы трения, а на приведение в движение новых порций среды,
что и определяет величину волнового сопротивления. Повышение давления
в волне для обеспечения заданного отклонения скорости должно быть
тем больше, чем больше плотность жидкости и скорость распространения
возмущения.
Для конкретных задач вид функций Фи^ определяется начальными
условиями E.1.6) в момент времени 7=0. Из соотношения E.1.6) и
решений (8.2.4) и (8.2.7) находим значения функций Фи^в начальный
момент времени
Ф(х , 0) = - [/(* ) + онр(х)], Ф(х , 0) = у [f(x ) - снр(х)]. (8.2.9)
Решения (8.2.4), (8.2.5), (8.2.7) и (8.2.8) были записаны для малых
отклонений, так как в исходных уравнениях учитывались нелинейные
конвективные члены, что потребовало их линеаризации. Если М <* 1, что всегда
верно для капельной жидкости, то конвективными членами можно
пренебречь и исходные уравнения для одномерного движения невязкой жидкости
335
Рис. 8.2. Волновой процесс в тракте с
емкостью
оказываются линейными.
Соответственно приведенные выше решения
пригодны для этих уравнений без
перехода к малым отклонениям.
Форма решений не изменится, только
в аргументе необходимо принять
М % 0. Переменные удобно
оставить безразмерными, относя
их к масштабным величинам:
Р = Р/Ро, п=и/и0.
В качестве примера
использования метода Даламбера
можно рассмотреть распространение
возмущений в полубесконечном
тракте ), заполненном
капельной жидкостью, с емкостью
расположенной на расстоянии х = 1 от
начального сечения [231]. В начальном сечении (рис. 8.2,а) поддерживается
давление р @, Т) -рп\ приГ>0, что определяет первое граничное
условие. В начальном состоянии (Г = 0) жидкость неподвижна, п(х, 0) =0, а
давление постоянно р = р0, т.е. р (х, 0) = 1. Тракт имеет постоянное сечение
FT; сопротивлением и инерцией жидкости в горловине емкости
пренебрегаем. Соответственно второе граничное условие для сечения х = 1 в виде
емкости (см. гл. 2) запишется:
Vepoa dp
——— — =пг-п29 (8.2.10)
кжГти01 dt
где Ve — объем емкости, кж — модуль объемной упругости жидкости,
иип2 — скорости жидкости в трактах до емкости (индекс 1) и после
(индекс 2), / - длина тракта до емкости. В соответствии с соотношениями
(8.2.4) и (8.2.7) переходный процесс в тракте 1 (рис. 8.2,а) описывается
системой уравнений (считая М ъ 0) :
"п.
7\(x, r)= — |
a
_
- О - *г (х + О],
где х =x/l, t = tajl, а в тракте 2 — системой:
р2(х, Г)-1 =Ф2(х -Г),
п2(х,Г)= L Ф2(х -Г).
а
(8.2.11)
(8.2.12)
1) Т.е. тракте такой большой длины, что можно не учитывать отражение волны от
его конца.
336
В системах уравнений (8.2.11) и (8.2.12) неизвестными являются
функция ^i(x+7"), описывающая отраженную от неоднородности (емкости)
волну в тракте i, и функция Ф2 ф - Т), характеризующая прямую волну,
прошедшую в тракт 2 из тракта 7, после отражения первичной волны в
сечении х = 1. Учтя, что в сечении х = 1 давление до и после емкости
одинаково рх A,-0 = р2 О, *") и введя это условие в первые уравнения
систем (8.2.11) и (8.2.12), найдем
<S>!A -7) + ^!(l + 7) = Ф2A -7). (8.2.13)
В граничное условие (8.2.10) подставим второе уравнение (8.2.11) и
уравнения (8.2.12), приняв~х = 1.
— ^Ф2°~Г) =Ф1A-7)~Ф2A~7)-^1A+7), (8.2.14)
тт dt
где tJtt = VJIFT - отношение характерных емкостных времен емкости 3
и жидкости в тракте. Это соотношение получено с использованием
формулы а2 =кж/р. Исключая из уравнений (8.2,13) и (8.2.14) функцию Vl9
получаем
те AФ2A -7)
— +2Ф2A-Г)=2Ф1A-О. (8.2.15)
тт dt
Так как было принято, что р @,7) = 1, то 1 Фг(\ -Т) I = const и
решение уравнения (8.2.15) имеет вид
2— 7 +1п[Ф!A -7)-Ф2A -7)] =С
U
Учтя, что при Т = 1 Ф2 A - Г)= 0, можно найти произвольную постоянную
С, а затем — окончательную форму решения
Ф2A -7) = Ф1A -7)[1 -ехр<-2G-1)тт/те)]. (8.2.16)
Используя соотношение (8.2.13) и решение (8.2.16), найдем
^A +7) = -Ф1[1-ехр<-2(Г-1)тт/те>]. (8.2.17)
Воспользовавшись свойством решений (8.2.4) и (8.2.7) сохранять свою
форму, если в аргументе прибавить к Зс и Т по Дх и Д7, связанным
соотношением Ах =±Д7, из уравнений (8.2Л6) и (8.2.17) получаем
зависимости, описывающие изменения параметров в трактах 1 и 2 [213]:
Ч'гСх +Г):г - ФЛх -<7- 2A -Зс)>]ехр[-2тт(/г-2+х)/те], (8.2.18)
Ф2 (X -- 7) = Ф1 [х - <7 ~ A - х ) - (х - 1) > ] X
/.{1 -ехр[-2тт<7- 1 ~(х - 1)>/те]} . (8.2.19)
Подставив зависимость (8.2.18) в выражения (8.2.11),а соотношение
(8.М9)- в (8.2.12). учтя условие для падающей волны давления,
формируемой на входе в тракт 7, найдем связь давления и скорости в отраженной
волне р~от j и иот х со значениями этих параметров в прямой волне рп\,иП1 в
участке трубопровода 1:
Р~от1(*,~П- 1 = -[pni(x,l -2A -*-)>- 1]ехр[-2ттG-2+х)/те],
(8.2.20)
"oxi(^ *) = пп1[х,7 -2A -х)]ехр[2гтG- 2+х)/те].
22.Б.Ф. Гликман 337
Аналогично для волн давления и скорости рп.2, "п.2> прошедших в
трубопровод 2 (х > 1),
(8.2.21]
Рпг(х,1)-1 = [рп1(х,1 -(I -х)-(х - 1)> - 1] X
X {1 - ехр [-2гт G - 1 -(х - 1)> /ге]} ,
"п2(*, O = "nll*,' ~A ~Х)-(Х - 1)]Х
X {1 - ехр[-2гт G-1 -(х - 1)>/те]} .
С помощью зависимостей (8.2.20) и (8.2.21) на рис. 8.2, г ид построены
графики распределения безразмерных величин давления и скорости в
момент К Г < 2, т.е. после отражения падающей волны от сечения х~ = 1.
При достижении падающей волной сечения х = 1 возникает
отраженная волна давления, описываемая первым уравнением (8.2.20), изменение
давления в которой (в первый момент) равно изменению давления в
падающей волне, но с обратным знаком.
Таким образом, за счет взаимодействия с емкостью волна давления
гасится. Однако затем по мере удаления отраженной волны от сечения х = 1
уровень давления в обратной волне падает по экспоненте, а так как
давление в тракте равно разности давлений в падающей и отраженной волне, то
давление в сечении х - 1 растет (см. рис. 8.2,г). В момент отражения от
сечения 5F=1 скорость жидкости в отраженной волне равна скорости в
падающей, но затем, за фронтом обратной волны, скорость жидкости падает по
экспоненте (рис. 8.2,д). Поведение прошедших через сечение х = 1 волн
давления и скорости, описываемых уравнениями (8.2.21), можно
проследить по графикам на рис. 8.2,г и д. Давление во фронте прямой волны
вначале постоянно, рп2 = 1, а затем растет по экспоненте, скорость же растет
по экспоненте от нулевого начального значения. Таким образом, наличие
емкости в тракте приводит к трансформации закона изменения давления и
скорости: если до емкости (рис. 8.2, ? и в) во фронте волны параметры
менялись скачком, то после прохождения емкости рп2 ийп2 изменяются
по экспоненте. Интенсивность нарастания давления и скорости зависит от
отношения постоянных времени тт/те : чем это отношение меньше, тем
медленнее изменяются параметры после прохождения фронта волны. Таким
образом, увеличение объема емкости Ve (т.е. увеличение те) и уменьшение
площади проходного сечения трубы (при заданной длине — уменьшение гт)
приводит к сглаживанию волновых процессов в тракте.
Приведенный пример использования метода Даламбера позволяет
рассмотреть начальный этап волновых процессов в тракте только после
первого отражения падающей волны. Дальнейший анализ с использованием
этого метода при более или менее сложных граничных условиях (только
линейных) отказывается достаточно громоздким.
8.2.3. Операционный метод исследования переходных процессов. При
решении волнового уравнения операционным методом используются
интегральные преобразования Лапласа, в результате которых находятся
изображения Ьи и бр'для отклонений давления и скорости, связанные с
338
оригиналами формулой (8.1.13):
оо
bu(xfs) = f Ьи(х, t)exp(-st)dt, (8.2.22)
о
5р(х, s) = J 6p'(x, t)exV(-st)dt, (8.2.23)
о
где 5 = о + /cj — комплексная переменная.
Решение исходного уравнения, т.е. переход к оригиналам,
осуществляется с помощью обратного преобразования (8.2.14) :
1 о + /°°
Ьи\х, 0е / SM'(jc
2 717 /
2 717
1 «+,- А( (8-2-24)
др'(х, Г)= / Ьр'(х, s)Qxp(st)ds.
2"ni о-too
Величина постоянной а, которая определяет путь интегрирования в
комплексной плоскости асо, зависит от свойств функций Ьр (х, г) и 8и'(х, t)
[82]. Для нахождения оригинала по изображению удобно использовать
таблицы [82], однако эти таблицы не охватывают многие интересные для
практики варианты функции. В этом случае прибегают к использованию
теории вычетов [82] или приближенных методов преобразования Лапласа
[131]. Преобразование Лапласа близко к Фурье-преобразованию, но
обладает меньшими ограничениями на вид преобразуемой функции из-за
введения множителя ехр(— st), обеспечивающего сходимость интеграла
(8.2.22) при t > 0. Соответственно и преобразуемая функция
рассматривается только при положительном значении времени.
Для уравнений в частных производных использование преобразования
Лапласа по времени (для таких систем иногда используют двойное
преобразование Лапласа —и по времени, и по координате) переводит эти уравнения в*
обыкновенные дифференциальные уравнения. Решение обыкновенных
дифференциальных уравнений — задача более простая, чем решение уравнений в
частных производных. Поэтому- операционный метод достаточно часто
используется для решения задач о переходных процессах и вынужденных
колебаниях жидкости в трубопроводах. В книге Н.С.Лелеева [144]
операционным методом решаются задачи как о нестационарном движении вязкой
жидкости, так и о нестационарных процессах и устойчивости движения
жидкости в трубах с обогревом применительно к парогенераторам. В работе
Г.Д.Розенберга и И.Н.Буяновского [194] приводятся примеры применения
операционного метода для вывода уравнений трубопровода как
гидравлического четырехполюсника, решения задач о распространении в тракте
периодических колебаний произвольной формы, о переходных
процессах в полубесконечной трубе и при мгновенном открытии задвижки в
трубопроводе конечной длины. П.А. Гладких и С.А. Хачатурян операционным
методом находят решение задач об оптимизации гасителей колебаний в
трубопроводах [56] и определяют собственные частоты трубопроводов с
емкостями, Л.М. Тарко исследует вопросы динамики гидромеханизмов [213,
214], В.В. Грачев, М.А. Гусейнзаде, Б.И. Ксенз и Е.И. Яковлев [207]
анализируют процессы в сложных трубопроводных системах и т.д.
22* 339
Применим операционный метод для решения задач о переходных
процессах в участках тракта без потерь на вязкое трение, описываемых волновым
уравнением. Используем уравнение в малых отклонениях, так как
граничные условия в ПГС как правило нелинейны, а для использования
операционного метода их необходимо линеаризовать. Начальные условия
считаем нулевыми, т.е. до момента t = О в системе отсутствуют возмущения. В
этом случае с помощью зависимости (8.1.15) для производных по времени
запишем волновое уравнение в изображениях:
d* 2
Решение линейного уравнения (8.2.25) имеет форму
(8.2.26)
.
\ а I
Для определения функций A (s) и В (s) примем, что на входе в участок
тракта (х= 0) имеется источник, создающий давление Ър @, г), а на
другом конце участка (* = /) - активное сопротивление с импедансом ф[ =
= const. Определим граничные условия в изображениях для входного
сигнала (х = 0)
5р'@, s) = / 6р'@, t)exv(-st)ds
о
и для импеданса на конце (х -I)
5и'(I, s)
Подставив решение (8.2.26) и решение для изображения скорости (см. гл. 5)
в граничные условия, находим сначала функции A (s) и В (s), а затем
решения для изображения
8p@
, s) \ ( sx \ / B/-*)
—-—- expl +rp,exp(
p(,)explrp,exp(
l+rpIexp(-2.r) L \ а I \ \
или, приняв для выходного сечения участка тракта х = I,
**>,, л Зр@,*)а+Гр1)ехр(--5т)
6р(/, s)= Р . (8.2.28)
1 +rpiexp(-2sr) v
Здесь а^ pa- волновое сопротивление тракта, гр1 = (ф\/а~ 1) (ф\/а'+ 1)-
коэффициент отражения волн давления от выходного сопротивления, т -
= 1/а — время пробега волной длины тракта.
Получить из выражений (8.2.27) или (8.2.28) оригинал для отклонения
давления трудно. Воспользуемся тем, что в правой полуплоскости
комплексного оператора s при t > 1 модуль величины ехр {-1st) меньше
единицы. Кроме того, для коэффициента отражения справедливо неравенство
340
О г 2t 3t 4т 5т 6z 7z
2t 3t 4T 5t St 7t St t
в
Рис. 8.3. Волновой процесс в
тракте при различных значениях
импеданса на выходе:а) фх -+°°,б) фг > а,
в) фг < ос
\rpi | < 1. Обозначим z = гр1 ехр (-25 г); при соблюдении условия \z \ < 1
можно записать
1
= l-z+z2 -
1+z
и, подставив эту формулу в решение (8.2.28),
- rp\ ехр (-3st) + r2pl ехр (Sst) - r3pi exp (-1st) +
переходим к оригиналу [82]
dp' (/, Г) = A + rpl) [dp' @, t-т)- rpl dp' (О, t - 3r) +
+ r2pl dp' @, t - 5т) - r^ 6p' (О, Г - 5r) + . . . (8.2.29)
Формула (8.2.29) описывает многократное отражение волн давления от
обоих концов участка тракта. При этом необходимо учитывать, что в
соответствии с граничным условием dp' @, t - кт) = 0, если t — кт <0.
Наиболее простую интерпретацию дает идеализированное условие на входе -
скачкообразное изменение давления в сечение тракта х = 0 в момент t = 0:
@ при t < 0,
dp @,0 =
I 5ро при t > 0.
Рассмотрим несколько вариантов граничного условия на выходе из
тракта. Наиболее простой случай - тракт с закрытым концом, для которого
0| -+ оо> rpi = 1. При этом в соответствии с формулой (8.2.29), пока t < г,
5р'(/, t) - 0, а в момент t = т давление скачком увеличивается на 26р'о,
так как коэффициент отражения гр\ = 1 и член A + гр1) дает величину
равную двум: при закрытом конце импульс давления удваивается. Отраженная
волна ко времени t = 2т достигает входа, где условие задания давления
эквивалентно значению входного импеданса ф'о = 0, и соответственно -
коэффициента отражения гр1 = — 1. В момент t = Ът дважды отраженная
волна, изменившая полярность, достигнет выходного сечения, обратив в
нуль отклонения давления и т.д. (рис. 8.3, а). Так как потери на трение
в тракте не учитываются, а от сечений на входе и выходе обеспечивается
341
полное отражение волн давления (кр11 = 1), то колебания в форме
прямоугольных импульсов будут продолжаться неограниченно долго.
Если на выходе из участка тракта имеется сопротивление с импедансом
ф[, то картина изменения давления на выходе из тракта зависит от знака
гр1, т.е. от соотношения между величинами ф[ и а'. Для случая ф\ > а ',
т.е. для г pi > О, кривая изменения давления приведена на рис. 8.3, б, а для
случая ф[ < а, гр1 < О - на рис. 8.3, в. При акустически закрытом конце
тракта (^!/а'> 1) переходный процесс имеет колебательный характер
(рис. 8.3, б), а при акустически открытом (ф[1<х' < 1) - апериодический
ступенчатый рост давления (рис. 8.3, в) .
§ 8.3. Численные методы расчета
нестационарных процессов в трактах
8.3.1. Метод характеристик. Нестационарное движение жидкости в
тракте в одномерном приближении описывается дифференциальным
квазилинейным уравнением второго порядка гиперболического типа. Для
уравнений гиперболического типа характерно наличие двух семейств
вещественных характеристик, на которых исходные уравнения в частных
производных заменяются обыкновенными дифференциальными уравнениями для
тех же переменных - давления и скорости (расхода) [153, 192, 215].
Уравнения для двух семейств характеристик имеют вид (случай М < 1)
dx - adt = 0, dx + adt = 0 (8.3.1)
и соотношение для параметров течения на характеристиках
dp + padu + \ри | и | dx/2d = 0, (8.3.2)
dp - padu + \pu\u \dx\2d = 0. (8.3.3)
Уравнение (8.3.2) решается вдоль характеристики С* (рис. 8.4, а), а
уравнение (8.3.3) — вдоль характеристики С"; уравнения этих характеристик
для общего случая найдем, интегрируя зависимости (8.3.1) :
_ ха dx
Т(хв,хА)~ J ———tA - tB,
хв а(х)
xDdx _ (8-3-4)
хв ^ ^*)
где нижний индекс обозначает точку (рис. 8.4, а), в которой задано
значение переменной.
Если скорость звука постоянна, то зависимости (8.3.4) принимают вид
уравнений прямых линий
ха ~ atA =xB- atB, xD + atD = хв + atB. (8.3.5)
Для решения дифференциальных уравнений (8.3.2) и (8.3.3) удобно
использовать сетку характеристик в плоскости xt (рис. 8.4, б) с заданными
шагами Ад: и Д t по двум координатам, причем угол наклона характеристик
определяется скоростью звука а. Идея метода характеристик заключается
в том, что дифференциальные уравнения (8.3.2) и (8.3.3)
аппроксимируются алгебраическими уравнениями первого порядка в конечных разностях.
342
1
*" Ах
в
\
т
^ Ах ^
f Лх Ах?
5 х
Рис. 8.4. Линии характеристик (а) и семейства (сетка) характеристик для участка
тракта (б)
К примеру, для характеристик С+ и С , идущих из точек А иП (рис. 8.4, а)
и пересекающихся в точке ?, можно записать:
Рв-Ра+
~(Рв ~
\л риА | иА \(хв - xA)/2d = 0,
\uD \{xB -xD)/2d = 0,
(8.3.6)
(8.3.7)
тле Pi, uhxh X/ - давление, скорость, координата и коэффициент
гидравлического сопротивления в соответствующих точках на характеристиках.
Для простейшего случая - квазистационарного приближения (см. § 6.1) —
коэффициент сопротивления определяется для ламинарного течения по
формуле X = 64/Re, а для турбулентного — по формуле Блазиуса X =
= 0,316/Re°'25,rn,eRe - число Рейнольдса для данного мгновенного
значения скорости ut. Случай, когда учитывается зависимость величины
коэффициента X от предыстории течения, рассматривается ниже.
Уравнения (8.3.6) и (8.3.7) - нелинейные и ниже будут сохраняться
в такой форме, так же как и уравнения для некоторых агрегатов,
входящих в ПГС. Метод характеристик в отличие от других методов позволяет
без особых затруднений решать нелинейные задачи. Учитывая такую его
особенность, оставим уравнения (8.3.6) и (8.3.7) в исходной форме, не
переходя к малым отклонениям. Уравнения (8.3.6) и (8.3.7) записываются
для всех элементов сетки характеристик. Их можно несколько уточнить,
определяя X/ и щ в последнем члене не для исходной точки элемента
сетки характеристик, а как среднее значение для двух крайних точек
элемента характеристики, используя процедуру последовательных
приближений. Два уравнения (8.3.6) и (8.3.7) позволяют по известным значениям
Pa>Pd>ua и ud найти значения рв и ив.
При расчетах одного тракта выбирается определенное четное число п
узлов сетки по х с шагом Ах =L/n, где L - длина тракта. Этой сетке по
оси х соответствует сетка по оси t с шагом At = Axja, и расчеты проводятся
для всех точек пересечения наклонных прямых, а для границы участка
тракта - для точек пересечения наклонных и вертикальных прямых с
шагом 2At (рис. 8.4). Разрешив уравнения (8.3.6) и (8.3.7) относительно
343
параметров течения в точке пересечения характеристик В, найдем
рв = 0,5 [рА - pD + ра(иА - иD) + p(Ax/2d)(XDuD \uD\- XAuA \ uA \)],
(8.3.8)
ив = иА - (Ира)[рв - рА + p(Ax/2d)\A uA\uA\]. (8.3.9)
Если в тракте по длине изменяется скорость звука, то кривая
характеристики ^определяется зависимостью (8.3.4), с помощью которой можно
получить уравнение связи между Ах и At:
dx
(8.3.10)
i / .
xf a(x)
При расчетах сложных систем шаг по времени принимается постоянным
Д?/ = At, а шаг по координате определяется уравнением (8.3.10). В итоге
сетка в плоскости х - t остается прямоугольной, но с переменным шагом
по х и разным наклоном характеристик между разными парами узлов.
Выбор одинакового шага А Г определяется необходимостью
удовлетворения граничных условий на стыках или разветвлениях участков трактов,
входящих в ПГС. При этом может оказаться, что на концах трактов
границы последних участков сетки Дл:,- не совпадают с границей участка. В этом
случае необходимо или скорректировать длину тракта, или несколько
изменить скорость звука, или использовать интерполяцию.
Для решения по методу характеристик системы алгебраических
уравнений (8.3.6) и (8.3.7) для всех элементов сетки характеристик (рис. 8.4, б)
необходимо задать начальные условия
p(*) = /i(*), и(х) = Мх) при ;<0 (8.3.11)
и граничные условия
х = 0; и = F0(p, ро, Г);
* = /, м = ^(р,рьО (г>0), (8.3.12)
где/i,/2,/ro,Fi - известные функции, р0, Р\ - давления в смежных
участках ПГС перед и за данным участком тракта. Начальные условия
(8.3.11) определяют значения давления и скорости в узлах сетки 1-5
(рис. 8.4, б) на оси*. В общем случае при t < 0 в тракте имеется
стационарное течение или неподвижная жидкость. Используя уравнения (8.3.6) и
(8.3.7), можно найти значения римв узлах 6-9. Параметры течения на
левой границе участка, в точке 10 определяются из уравнения обратной
характеристики (8.3.7) и первого уравнения для граничных условий
(8.3 Л 2) :
Pi о - Ре -ра(ию - ue)X6pu6 \ue \(x10 -x6)/2d = 0, (8.3.13)
ию =Ро(Рю,Ро, *ю). (8.3.14)
Значение давления р0 перед устройством на левой границе участка может
быть постоянным (бак, резервуар и т.д.), изменяться по заданному закону
(например, программное управление) или определяться отношением на
характеристике для соседнего участка тракта. Аналогичные уравнения
составляют и для другой границы тракта — точки 14щ используя уравнение
344
прямой характеристики (8.3.6) и второе граничное условие (8.3.12).
Решить эти нелинейные уравнения в общем случае можно методом
последовательных приближений. Если элементы гидравлической системы находятся
на разных уровнях zx и z2, так что не выполняется условие z2 - Z\ = Az <
<^р/р, то вместо давления р,- в уравнениях (8.3.6) и (8.3.7) подставляется
сумма Pi + pzt, где zf - координата по высоте /-го сечения тракта.
Рассмотрим несколько типичных примеров граничных условий на
концах участков трактов, т.е. функций Fo и Fi в зависимостях (8.3.12).
а) Изменение площади проходного сечения. Если
пренебречь потерями давления в результате изменения проходного сечения
(сжатия или расширения потока), то условие в месте стыка трактов
разного сечения можно записать следующим образом:
где М/A, Г), р,-A, Г) - скорость и давление в конце (xt - 1) /-го участка,
ui+i(P,t),Pi+i(Q,t) -то же в начале (х/+1 =0) следующего, (/+ 1)-го,
участка тракта, Fj, F/+1 — проходные сечения участков тракта.
б) Отбор жидкости на гаситель гидроудара, в уравнительную
башню, при моделировании нарушения герметичности трубопровода и т.д.) .
Пренебрегая потерями давления из-за изменения скорости жидкости и
инерцией столба жидкости, можно записать условия сопряжения для двух
участков тракта в точке отбора
Ftut(l ,t) = Fi + l и, +! @,0 + nF0(t)u0, (8.3.15)
ftA.0=P< + i@,0, (8-3.16)
где idFo(t) — коэффициент расхода и площадь проходного сечения отбора.
Если гаситель гидроудара выполнен в виде емкости (колпака,
уравнительной башни и т.д.), то давление в емкости определяется уравнениями,
выведенными в гл. 2, В более сложных современных устройствах гашения
хидроудара [212] используются автоматические, регулируемые клапаны,
открывающиеся при быстром нарастании давления. Математическая модель
таких устройств зависит от их конструкции. В частности, если отбор
осуществляется на уравнительную башню, го величина отбора определяется
уравнением уровня жидкости в башне (см. г л, 2)
u0 (8 3.17)
и условием равновесия для столба жидкости в башне, записываемым в
случае пренебрежения инерцией и вязкостью жидкости в виде статического
соотношения
gph(f)=Pi(l,f)-pHt (8 3 18)
где g — ускорение силы тяжести, рн - давление над уровнем жидкости.
Считая рн = const, подставив соотношения (8 3.15) и (8.3.18) в уравнение
(8.3.17), найдем
dpjjlyt) _ FjUjd, t) - Ft T ! щ Y г@. t)
s [))
dt
Дифференциальное уравнение (8.3.19) запишем в конечных разностях:
h t) -PtilJ - 2АГ) = [Ft{ щ(\, t) + Mt(l,t - 2 At) > -
г). (8.3.20)
Совместное решение уравнений характеристик для двух крайних участков
у развилки и уравнений (8.3.16) и (8.3.20) позволяет найти четыре
неизвестных величиныPi(l, 0>P/ + i@, 0> ty(l, t), ui+1@,t) из четырех уравнений.
При этом значенияр,A, t -2At), ui+i(l,t - 2 At) и w/+1@,f - 2At)
известны по предыдущему циклу вычислений по времени.
в) Регулируемое дросселирующее устройство. Если
пренебречь объемом жидкости, вытесняемой подвижными частями
дросселирующего устройства, и инерцией столба жидкости в проточной части,
считая сечения тракта до и после дросселя одинаковыми, дросселирующее
устройство можно описать соотношениями
и,A, 0 = и/+ i@,0,
P/(l,0-P/ + i@?0 = P«/O,0/2[iuFp@]2, (8.3.21)
где fJiFp(t) — коэффициент расхода и площадь проходного сечения
дросселирующего устройства. Закон изменения во времени Fp(t) может быть
заданным или определяться регулирующим устройством. Уравнения (8.3.21)
вместе с уравнениями характеристик на концах трактов образуют
замкнутую систему уравнений, позволяющую найти четыре неизвестных величины
при заданной функции Fp(t).
г) Насосные агрегаты. Насосный агрегат содержит насос
(компрессор) , подающий жидкость в систему, и привод — электромотор,
турбину и т.д. Для ПГС важна характеристика насоса, т.е. связь между перепадом
давления на насосе и расходом через насос. Применительно к
центробежным насосам его характеристика хорошо аппроксимируется многочленом
pi + 1(O,t)-Pi(l,t)=An2 +^111,A,0 + 0^A,0.
где п — частота вращения насосного агрегата. К уравнению характеристики
насоса необходимо добавить уравнение неразрывности, которое в случае
разных сечений трактов на входе и выходе насоса запишется в виде
В общем случае частота вращения насосного агрегата зависит от нагрузки,
т.е. расхода жидкости и давления за насосом. Кроме того, представляют
интерес процессы в ПГС, возникающие при отключении или изменении
режима работы привода насоса. Поэтому в общую математическую модель
насоса входит и уравнение динамики насосного агрегата
J— = Mnp-MH,
где Мпр— момент, создаваемый на валу приводом, Мн - момент
сопротивления насоса,/ - момент инерции вращающихся элементов насосного
агрегата, со — угловая скорость вращения вала агрегата. Момент Мн
определяется зависимостью (без учета инерции жидкости в проточной части
346
насоса [58])
где т?н - коэффициент полезного действия насоса. Момент, развиваемый
приводом Л/Пр> определяется типом привода и законом изменения
параметров, определяющих этот момент. Например, если насос приводится во
вращение газовой турбиной, то Мпр определяется перепадом давления на
турбине и температурой рабочей среды перед турбиной. В общем случае
система питания турбины газом может входить в исследуемую ПГС, как это
имеет место, например, в ПГС двигателей [58].
При совместном решении уравнений характеристик (8.3.6) и (8.3.7)
для участков трактов перед и за агрегатом и уравнения агрегата часто
удается сократить число уравнений, исключив некоторые переменные. Если
уравнения агрегатов содержат производные по времени от параметров
системы, то необходимо совместно решать дифференциальные уравнения
(как правило, нелинейные) и алгебраические уравнения характеристик.
Решение таких систем проводится методом итераций, дифференциальные
уравнения заменяются разностными (см. пункт б).
8.3.2. Расчет переходных процессов в тракте с ламинарным течением
при учете влияния нестационарности на напряжение трения. При анализе
особенностей нестационарного пульсирующего течения в трубах в гл. 6
было показано, что напряжение силы трения в ламинарном потоке
существенно зависит от частоты. С ростом частоты изменяется профиль скорости -
от практически параболического, характерного для течения Пуазейля при
низких частотах, до почти равномерного, прямоугольного для высоких
частот. Соответственно с ростом частоты увеличивается и переменная
составляющая напряжения трения. Эксперименты Холмбоу и Руло [228]
показали сильное искажение волн давления, возникающих при
переходном процессе в гидравлическом тракте с ламинарным течением (см.
рис. 8.5). Решение для нестационарного ламинарного движения
несжимаемой жидкости было впервые получено И.С. Громека [71] и более простым,
операционным методом Д.Н. Поповым [184]. Зилке [99] предложил
модификацию метода характеристик, в которой учитывается зависимость
напряжения силы трения от частоты. В дальнейшем аналогичную задачу
операционным методом и методом Фурье решили Г.Д. Розенберг и
И.Н. Буяновский [193], а Браун [21] расширил область применения
метода характеристик (назвав его "квазиметодом характеристик") на
нестационарное течение с зависимыми от частоты как напряжением трения, так и
сжимаемостью. В гл. 6 было показано, что для слабо сжимаемой капельной
жидкости ее сжимаемость не влияет на напряжение нестационарного трения,
которое совпадает с трением для несжимаемой жидкости. Следуя [99],
воспользовавшись отмеченным обстоятельством, учтя условие L > R,
запишем уравнение движения для о се симметричного нестационарного
движения жидкости (см. гл. 1)
Ъи 1 Ър v Ъ I Ъи \
— + = [г — . (8.3.22)
Ы р Ъх г Ъг \ Ът I
Приняв, что (\1р)'др/Ъх =/(?), используя формулу преобразований Лапласа
347
Рис. 8.5. Колебания давления у клапана (а) в конце трубы и в средней точке трубы
(б) после мгновенного закрытия клапана: эксперимент, расчет
для квазистационарного трения, - • • расчет по формулам (8.3.34) и (8.3.35)
(8.1.13), запишем уравнение (8.3.22) в изображениях:
аи 1 аи s л 1л
dr
r dr
(8.3.23)
где й и/- изображения для функций и и /. Уравнение (8.3.23)
представляет собой уравнение Бесселя нулевого порядка, решение которого имеет
вид
й(г, s) = Ct(s)J0(i\/sFr) + C2(s) Yo{iy/spr) -f/s9
где /о, ^о - функции Бесселя нулевого порядка первого и второго рода.
Произвольные постоянные С\ и С2 определяются граничными условиями
для скорости: и = 0 при г = Яи ограничена при г = 0, следовательно С2 = О,
С\ = {fls)J0{i\fsJvR). Формула для изображения скорости принимает вид
и = (f/s)[Jo(i\fflvr)IJo(iyffivR) - 1]. (8.3.24)
Соотношение для изображения напряжения трения на стенке трубы:
,(8.3.25)
o(i>/s/v R)
тцеIi(y) ~y[J0(y)/Ji(y)] - функция Бесселя первого порядка, j> -
комплексное число.
Выражение (8.3.25) можно преобразовать, если воспользоваться
изображением средней мгновенной скорости, подставив в него зависимость
348
(8.3.24),
-f 2-nrudr =— —==r =5 1 =
о 5 L i^RJ(i/fFR)
A
-ll. (8.3.26)
Вспомнив правило дифференцирования в изображениях L(bU/bt) = sU(s),
исключая с помощью зависимости (8.3.26) /из уравнения (8.3.25),
получаем:
pRsUjs) _ PR(dU/dt)
- 2] '
Уравнение (8.3.27) связывает изображение напряжения трения на стенке с
изображением ускорения потока в трубе. Для перехода к оригиналу
необходимо воспользоваться правилом свертки [82]
W(te)
rw@ = / Ф@)—г Ld0, (8.3.28)
о ot
где
1 Л
Ф@ = Ит г / ФE)ехрEГ)Л, (8.3.29)
(,j-> оо 2тг/ а— /со
ФE) = ;==; (8.3.30)
Весовая функция Ф@ может быть найдена с помощью теоремы вычетов,
для чего необходимо найти полюса подынтегральной функции Ф, которые
совпадают с корнями уравнения Iitfy/s/vR)*1 2. Вычеты для полюсов sk
находятся по формуле
/элсмх1
= pRexV(skt)[ —±-L = Bpv/R)exp(sk t),
\ OS /
так как bli(sk)/bs -R2\2v. Эта формула верна для всех вычетов, кроме
вычета для начала координат, для которого Res [Ф(л)ехрEГ)]
_
Введя безразмерное время 7 = (v/R2)tn выражение г\\ = - skR2/v, учтя
приведенные соотношения для вычетов, найдем
4vp 2vp °°
<b{t)=-—+——V ехр(-т?О. (8.3.31)
xv К к - \
Ряд в зависимости (8.3.31) при Г >0 сходится, однако при Г < 0,02 он
сходится медленно. В статье Зилке [99] приводятся величины первых
20 значений: цк= 5,13562; 8,41724; 11,61984; 14,79595;. 17,95982 и т.д.
(?=1,2,3, . . .) и другая формула для определения функции Ф(Г) при
349
t <0,02:
Avp 2pv _ -0,5 _ о 5
Ф@ = —- + —^ @,282095 t -0,250000+1,057855 Г ' +
+ 0,937500 Г + 0,396696 F *'S - 0,351563 Г 2 ). (8.3.32)
Подставив весовую функцию (8.3.31) или (8.3._32) в зависимость
(8.3.28), предварительно введя безразмерное время t, можно вычислить
мгновенные значения напряжения трения на стенке. Удобнее преобразовать
соотношение (8.3.28), выделив первый член, характеризующий
стационарное трение, и поменять местами функции под интегралом:
4pvU(T) 2pv~^blM0) __ _ _
rw(O= + /—=^ W(t -9)de, (8.3.33)
w R R о bt V
где
V 2vp/R
Второй член в зависимости (8.3.33) учитывает влияние предыстории
изменения скорости с определенным весом, а для вычисления весовой функции
используются выражения (8.3.31) или (8.3.32).
Для стационарного ламинарного течения сила трения и гидравлическое
сопротивление линейно зависят от скорости, решение же (8.3.33) получено
для напряжения трения как функции безразмерного времени t. Поэтому
уравнения на характеристиках (8.3.6) и (8.3.7) удобнее записать в
следующей форме:
Рв-Ра +P<UB-UA) + BT»a/R)(tB-tA) = 0, (8.3.34)
~ (Рв ~ Pd) + Ра&в ~ uD) + Brwa/R)(tB - tD) = 0. (8.3.35)
Члены с rw с помощью соотношения (8.3.33) учитывают влияние
предыстории изменения скорости. Так как предыстория известна, то в статье [99]
предлагаются следующие разностные зависимости вместо интегральной
(8.3.21) для напряжения трения в точке с индексами ik (см. рис. 8.4, б) :
4pvUik 2pv
rwik =+
К К
- Ui(k_4))WCAt) + .. . + (Ui2 - Ui0)W[(k- I)At]} . (8.3.36)
Значения весовой функции И'можно вычислить по_зависимостям (8.3.31) —
(8.3.32) в виде функции безразмерного времени t .Функция W{t )стремится
к нулю при t -> о©. Поэтому можно выбрать некоторое ?тах, чтобы значения
W(t) при t > tmax стали пренебрежимо малыми. В этом случае число членов
в зависимости (8.3.36) не превысит tmax R2 jBvAt).
Результаты расчетов методом характеристик с учетом трения,
зависящего от частоты, были сопоставлены с данными экспериментов, приведенных
350
в работе [228]. В трубе длиной 36 м и диаметром 25,4 мм при ламинарном
течении масла после мгновенного закрытия клапана возникали колебания
давления (рис. 8.5). Экспериментальные результаты сопоставлялись с
данными расчетов с учетом трения, зависящего от частоты, по формулам
(8.3.34) и (8.3.35) и по методу характеристик с квазистационарным
трением. Результаты расчетов с квазистационарным трением очень грубо,
в основном — только по частоте колебаний, согласуются с экспериментом.
Учет же зависимости напряжения трения от частоты позволил практически
точно учесть особенности затухания и искажения формы амплитуд
колебаний давления. Использование формулы (8.3.36) требует запоминания
большого массива данных о скорости в предшествующие моменты времени.
Для сокращения времени счета Трикха [218] предложил приближенную
функцию, которая достаточно точно аппроксимирует зависимость для
весовой функции,
_ з _ ' з _
W(t)= 2 Wj(t)= 2 ехр(-ИуГ). (8.3.37)
/ = 1 /=1
Подставив аппроксимирующий трехчлен в уравнение (8.3.33) для
напряжения трения, и учтя, что Г= tv/R2, найдем
rw@= D +-^(У1+У2+Уз), (8.3.38)
К К
где у, = / Wj{t - 0)(dU{6)ldi) dO.
о
Используя определение у, и зависимость (8.3.37), можно найти связь
между значениями jty на двух временных слоях k и k - 1 в i-м сечении
тракта:
У»к=Ущк-1)Ыр[-Ъ(у/Я2)Ь*] +W/W* ~ 0/<*-1)). (8.3.39)
Анализ решения с использованием соотношения (8.3.36) показал [218],
что необходимо запомнить значения скорости для 500 и более интервалов
времени в каждом сечении тракта. При использовании же формул
(8.3.37) -(8.3.39) для каждого /-го сечения необходимо запомнить значения
всего четырех величин (Ущк-i), УгЦк-.\), Узг(к-х) и Uk_x) для
предшествующего интервала времени. Используя уравнения (8.3.38) и (8.3.39),
можно вычислить текущее значение напряжения трения, зависящего от
частоты. Для коэффициентов т,- и rij в аппроксимирующей зависимости
в работе [218] предложены следующие значения: тх =40,0; т2 = 8,2;
т3 = 1, пх = 8000, п2 = 200, пг =26,4. При таких значениях коэффициентов
по расчетам автора_ функция H^f) аппроксимируется достаточно хорошо
во всем дипазоне t, за исключением Т< 0,00005. Проведенное
сопоставление результатов расчетов методом характеристик по формулам (8.3.34) —
(8.3.35) и (8.3.38) -г (8.3.39) с экспериментальными данными работы
[228] показало, по словам автора, их хорошее соответствие. Кроме
того, используя зависимость (8.3.38), получена формула для напряжения
трения в пульсирующем потоке, в котором средняя скорость изменяется
по закону U=U0 exp (icot) :
rw(w) = — 4 + 2/со 2 -^ ?/0ехр(ко0. (8.3.40)
R L (/+)]
rw()
R L /=i
351
Сопоставление результатов расчетов вещественной и мнимой частей
соотношения (8.3.40) (без учета сомножителя U0exp(itot)) с результатами
расчетов по точным формулам для ламинарного пульсирующего течения (см. гл. 6)
показало их хорошее совпадение до значений безразмерного параметра
s = R{u>lv)l/l = 150, Для более высоких значений этого параметра
зависимость (8.3.37) необходимо уточнять, увеличивая число экспоненциальных
членов. Ссылаясь на обзор [75], автор статьи [228] предлагает
использовать модифицированную зависимость (8.3.38) и для расчетов
нестационарных турбулентных течений:
0,316р?/2 2pv
+( + ^) (8.3.41)
Эта зависимость основана на предположении, что составляющая
напряжения трения, зависящая от частоты, для турбулентного потока совпадает
с составляющей для ламинарного потока. Возможен и другой подход,кото-
рый проверен при экспериментах с вынужденными колебаниями
турбулентного течения в трубе [64] : замена кинематической вязкости жидкости v в
формуле (8.3.41) эффективной вязкостью v3. Величина v3 определялась
по данным проливок трубопровода на стационарном режиме с
использованием формулы сопротивления для ламинарного течения X = 64/Re =
= 64 vJUd, в которую подставлялись значения X из данных проливок тракта.
СПИСОК ЛИТЕРАТУРЫ1)
1. Абрамович Г.Н. Прикладная газовая динамика. - М.: Наука, 1969.
2. Альтшуль АД. Местные сопротивления при движении вязких жидкостей. -
М.: Гостоптехиздат, 1962.
3. Андрияшев ММ Графические расчеты гидравлического удара в водоводах. -
М.:Стройиздат, 1969.
4. Анненкова Г.К., Гликман Б.Ф. Влияние вязкости на вынужденные колебания
сжимаемой жидкости в цилиндрическом канале. - Изв. АН СССР, Энергетика и
транспорт, 1973, №4.
5. Арзуманов Э.С. Кавитация в местных сопротивлениях. - М.: Энергия, 1978.
6. Аронович Г.В., Картее/шшвили И.А., Любимцев Я.К. Гидравлический удар и
уравнительные резервуары. - М.* Наука, 1968.
7. Артамонов К.И. Термогидроакусшческая устойчивость. - М.: Машиностроение,
1982.
Н.Байбиков Б.С.. Дрейцер Г.А., Изосимов ВТ., Ширшов А.Н. Влияние
гидродинамической нестационарности на турбулентный поток жидкости в трубе. - Тр. Всесоюзн.
заочн. политехи, ин-та, Гидравлика. М.: 1974, т. 10, вып. 3.
9. Байбиков Б.С., Орешкин О.Ф., Прудовский A.M. Сопротивление трения при
ускоренном течении в трубе.-Изв. АН СССР, МЖГ, 1981, №5.
10. Барбашов Е.Д- Пульсирующее течение в трубе. - Тр. 20-й научн. конф. МФТИ,
сер. Аэрофизика и прикл. математика. - Долгопрудный, 1976.
11. Баскаков СИ. Радиотехнические цепи с распределенными параметрами. -
М.: Высш. школа, 1980.
12. Белоцерковский О.М., Давыоов ЮМ. Метод крупных частиц в газовой
динамике. - М.: Наука, 1982,
13. Бессонов П.А. Линейные электрические цепи. - М.. Высш. школа, 1974.
14. Бессонов Л.А. Теоретические основы электротехники: Электрические цени. -
М.: Высш. школа, 1978.
15. Бердников В.В. Прикладная теория гидравлических цепей. -- М..
Машиностроение. 1977.
16. Бержерон Л, От гидравлического удара в трубопроводах до разряда в
электрической сети. -- М.: Машгиз. 194е).
17. Бесекерский В.А., Попов ЕЛ. Теория систем автоматического
регулирования. - М.: Наука, 1966.
18. Блш штейн ЮМ., Хубларнн М.Г. Распространение волн возмущений жидкости в
бесконечно длинном вязкоупругом трубопроводе. - Изв. АН СССР, МЖГ, 1975, № 3.
19. Босый Н.Д. Электрические фильтры. - Киев,: Гостехиздат, 195 7.
20 Браун. Переходные процессы в линиях передачи жидкости или газа. -
Техническая ме\-аника. 1962. т. 84, № 4.
21. Браун Квазиметод характеристик и его применение к расчету течения в
трубопроводах с зависимым от частоты касательным напряжением на сгенке и
теплопередачей. - ТОИР, 1969. №J
!) Принятые сокрашештя названий-журналов. ИФЖ - инженерно-физический
журнал, ЖТФ - журнал технической физики, МЖГ -- механика жидкости и газа. ПМГФ -
прикладная механика и техническая физика, ТОИР — теоретические основы
инженерных расчетов
23. Б Ф Гликман
22. Браун, Морголис, Шах. Поведение возмущений малой амплитуды,
наложенных на турбулентное течение в гидравлическом трубопроводе. — ТОИР, 1969, № 4
23. Браун, Нел сон. Переходные характеристики гидравлических трубопроводов
для сигнала в виде скачка с учетом эффекта вязкости, зависящей от частоты. - ТОИР,
№2, 1965.
24. Букреев В.И., Зыков В.В., Романов Е.М., Шахин В.М. Экспериментальная
установка и методика измерений нестационарного турбулентного течения в трубе.-Изв. вузов.
Стр-во и архитектура, 1976, № 7.
25. Букреев В.И., Шахин В.М. Экспериментальные исследования энергии
турбулентности при неустановившемся течении в трубе. - В кн.: Математические вопросы
механики. Динамика сплошной среды. Новосибирск, 1975, в. 22.
26. Букреев В.И., Шахин В.М. Сопротивление трения и потери энергии при
турбулентном пульсирующем течении в трубе. - Изв. АН СССР, МЖГ, 1977, № 1.
27. Букреев В.И., Шахин В.М. Статистически нестационарное турбулентное течение в
трубе. - Деп. рукопись, ВИНИТИ, № 866-81, Новосибирск, 1981.
28. Бутковский AT. Методы управления системами с распределенными
параметрами. - М.: Наука, 1975.
29. Бутковский AT. Структурная теория распределенных систем. - М.: Наука,
1977.
30. Бэтчелор Дж. Введение в динамику жидкости. - М.: 1973, Мир.
31. Вальтер Б.В., Сальников И.Е. Устойчивость режимов работы химических
реакторов. - М.: Химия, 1981.
32. Васильев О.Ф. Неустановившиеся течения в открытых руслах, каналах и
трубопроводах. - В кн.: Динамика сплошной среды. Новосибирск, 1975, в. 23.
33. Васильев О.Ф., Атавин А.А., Воеводин А.Ф. Методы расчета неустановившихся
течений в системах открытых русел и каналов. - В кн.: Численные методы механики
сплошной среды. Новосибирск, 1975, т. 6, № 4.
34. Васильев О.Ф., Квон В.И. О влиянии нестационарности при движении открытого
потока жидкости. - ПМТФ, 1966, № 1.
35. Васильев О.Ф., Квон В.И. Влияние нестационарности на касательное напряжение
и профиль скорости открытого потока жидкости. - ПМТФ, 1967, № 3.
36. Васильев О.Ф., Квон В.И. Неустановившееся турбулентное течение в трубе. -
ПМТФ, 1971, №6.
37. Венгерский Э.В., Морозов В.А., Усов Г.Л. Гидродинамика двухфазных
потоков в системах питания энергетических установок. - М.: Машиностроение, 1982.
38. Вибрация в технике. Справочник, т. 1, Колебания линейных систем. - М.:
Машиностроение, 1978.
39. Виленский В.Д., Коченов И.С., Кузнецов Ю.Н. К вопросу о гидравлическом
сопротивлении при нестационарном режиме. - В кн.: Пневмо- и гидроавтоматика.
М.: Наука, 1964.
40. Владиславлев А.П., Мессерман А.С. Электрическое моделирование динамики
систем с, распределенными параметрами. - М.: Энергия, 1978.
41. Владиславлев А.С, Писаревский В.М. О газодинамическом расчете
пульсирующего потока в трубопроводах. - ПМТФ, 1972, № 4.
42. Владиславлев А.П., Писаревский В.М., Пономаренко Ю.Б. Об эквивалентной
линеаризации турбулентного трения при резонансных колебаниях газа в трубах. -
Прикл. механика, 1974, № 9.
43. Владиславлев А.С., Писаревский Б.М. и др. О нелинейной и линеаризованной
задачах пульсирующего движения газа в трубопроводе. - ПМТФ, 1974, № 3.
44. Владиславлев А.П., Якубович В.А. Методы и приборы для измерения
параметров динамики трубопроводных систем. - М.: Недра, 1981.
45. Вуд, Фанк. Использование теории пограничного слоя для анализа потерь на
трение в случае неустановившегося турбулентного течения. - ТОИР, 1970, № 4.
46. Вуколович М.П., Новиков И.И. Техническая термодинамика. - М.; Л.: Гос-
энергоиздат, 1952.
47. Вулис Л.А., Михасенко Ю.И., Хитриков В.А. Об эффективном "управлении"
распространением свободной турбулентной струи. - Изв. АН СССР, МЖГ, 1966, № 6.
48. Вунш Г. Теория систем. - М.: Советское радио, 1978.
49. Галицейский Б.М., Рыжов Ю.А., Якуш Е.В. Тепловые и гидродинамические
процессы в колеблющихся потоках. - М.: Машиностроение, 1977.
354
50. Ганичев А.И. Определение собственных частот колебаний сжимаемой жидкости
в сложном трубопроводе. - Изв. вузов, Машиностроение, 1966, № 10.
51. Герц Е.В., Гогричиани Г.В. Неустановившиеся процессы в линия к передачи
пневматических сигналов. - В кн. Механика машин. - М Наука, 1 975, в. 49.
52. Герц Е.В., Гогричиани Г В. Время передачи пневматических сигналов в системах
управления. - Вестник машиностроения, 1976, № 9.
53. Гинзбург И.П. Гидравлический удар в трубах из упруговязкого материала. -
Вестн. ЛГУ, Сер. матем., механ. и астрон., 1956, № 13.
54. Гинзбург И.П. Прикладная гидрогазодинамика. - Л.: Изд-во ЛГУ. 1958
55. Гладких П.А., Хачатурян С.А. Вибрации в трубопроводах и методы их
устранения. - М.: Машгиз, 1959.
56. Гладких П.А., Хачатурян С.А. Предупреждение и устранение колебаний
нагнетательных установок. - М.: Машиностроение, 1964.
57. Гликман Б.Ф. Динамические характеристики гидравлических магистралей
как элементов сложных энергетических систем. — Изв. АН СССР, Энергетика и
транспорт, 1972, №6.
58. Гликман Б.Ф. Автоматическое регулирование жидкостных ракетных
двигателей. - М.: Машиностроение, 1974.
59. Гликман Б.Ф., Тюрин Н.П., ЧижоваН.Г. Вынужденные колебания потока газа с
энтропийными волнами. - Физика горения и взрыва, 1975, № 4.
60. Гликман Б.Ф. Нестационарные течения в пнев моги драв ли чески х цепях. -
М.: Машиностроение, 1979.
61. Гликман Б.Ф., Гурьев В.А. Рассеивание волн энтропии в газовом потоке. -
Изв. АН СССР, Энергетика и транспорт, 1979, № 1.
62. Гликман Б.Ф. Метод анализа линейных пневмогидравлических цепей с
распределенными параметрами. - Изв. АН СССР, Энергетика и транспорт, 1980, № 4.
63. Гликман Б.Ф., Лосенков А.С., Мусалов Р.Н. Применение графов для анализа
трубопроводных систем. - Изв. АН СССР, Энергетика и транспорт, 1981, № 5.
64. Гликман Б.Ф., Барбашов Е.Д., Гусев Г.В., Исаев В.Е. Пульсирующее
турбулентное течение сжимаемой жидкости в трубе. - Изв. АН СССР, Энергетика и транспорт,
1982, №5.
65. Гликман Б.Ф. Нестационарное течение в разветвленных трубопроводных
системах. - Изв. АН СССР, Энергетика и транспорт, 1983, № 1.
66. Глушко Г.С. Турбулентный пограничный слой на плоской пластине в
несжимаемой жидкости. - Изв. АН СССР, Механика, 1965, № 4.
67. Голдшмид. О зависимости частотной характеристики от числа Стокса в случае
вязкой сжимаемой среды. - ТОИР, 1970, № 2.
68. Гризодуб Ю.Н. К исследованию переменного движения жидкости в
многоузловых гидравлических системах машин и автоматических устройств. - Авт. и
телемех., 1950, № 1.
69. Гризодуб Ю.Н. Применение теории пассивных четырехполюсников к расчету
распространения колебаний давления в разветвленных гидравлических системах
авиадвигателей. - Авт. и телемех., 1950, № 2.
70. Гризодуб Ю.Н. О расчете распространения гармонических возмущений в
жидкости, наполняющей системы последовательно и параллельно соединенных труб
насосных агрегатов. - ЖТФ, 1951, т. 21, вып. 5
71. Громека И.С. К теории движения жидкости в узких цилиндрических
трубках. - Собр. соч. М.: Изд-во АН СССР, 1952.
72. Гроссшмидт Г.Т. Применение теорий многополюсников и сигнальных графов
к расчету частотных характеристик объемных гидроприводов на ЭЦВМ.-Тр.
Таллинского политехи, ин-та, 1975, № 391.
73. Гроссшмидт Г.Т. Составление сигнальных графов динамики гидравлических
цепей объемных гидросистем. — Тр. Таллинского политехи, ин-та, 1917, № 435.
74. Гулин Н.П. Анализ применимости форм представления гидравлических
коэффициентов и параметров нестационарности в неустановившихся напорных течениях. -
Обнинск: Физико-энергет. ин-т, 1979, ФЭИ, № 954.
75. Гудсон, Леонард. Обзор методов моделирования переходных процессов в
гидравлических линиях. - ТОИР, 1972, № 2.
76. Гурляускас А.И., Фейгин Ф.И., Буланая М.Е. Прикладные вопросы решения
линеаризованных уравнений неустановившегося движения газа в трубопроводах —
23* 355
Изв. АН СССР, Энергетика и транспорт, 1975, № 2.
77. Двухшерстов Г.И. Гидравлический удар в трубах некруглого сечения и в
потоке жидкости между упругими стенками. - Уч. зап. МГУ, Механика, 1948, в. 122, т. II.
78. Денисов Е.Е. Решение задачи теплообмена методом температурных сетей. -
Изв. АН СССР, Энергетика и транспорт, 1982, № 4.
79. Денисов Е.Е. К вопросу гидравлического расчета технологических схем газовых
реакторов. - Теплоэнергетика, 1983, № 6.
SO. Денисов СВ. О коэффициенте трения в нестационарных течениях. - ИФЖ, 1970,
т. 18, № 1.
81. ДейчМ.Е. Техническая газодинамика. - М.: Энергия, 1974.
82. Дёч Г. Руководство к практическому применению преобразования Лапласа и
z-преобразований. - М.: Физматгиз, 1971.
83. Джаясингхе, Лойтхойсер. Распространение возмущений при течении вязкой
жидкости в гидравлическом трубопроводе с упругими стенками. - ТОИР, 1974, № 3.
84. Джонсон, Вэндлинг. Передаточные функции и входные импедансысистем
трубопроводов, находящихся под давлением. - ТОИР, 1967, № 1.
85. Джоунс, By д. Влияние продольного перемещения границ на интенсивность
гидравлического удара. - ТОИР, 1972, № 2.
86. Дикаревский B.C. Коэффициент гидравлического сопротивления, потери
энергии на внутреннее трение в материале труб, интерференция волн при гидравлическом
ударе. - Тр. Ленингр. ин-та инж. ж.-д. трансп., 1971, вып. 321.
88. Дикаревский В.С, Татура А.Е. О величине вакуума при гидравлических
ударах. - Тр. Ленингр. ин-та инж. ж.-д. трансп., 1971, вып. 321.
89. Дорошенко В.Е., Сильверстов В.М. Экспериментальное исследование волн
энтропии при неустойчивом горении в камере газотурбинного двигателя. - Физика
горения и взрыва, 1982, № 1.
90. Дружинский И.А. Механические цепи. - Л.: Машиностроение, 1977.
91. Д'Суза, Олденбургер. Динамические характеристики гидравлических
трубопроводов. - ТОИР, 1964, № 3.
92. Елепникова Л.С Тепловые четырехполюсники. - Минск: Наука и техника,
1976.
93. Еременко Е.В. Расчет кинематических характеристик турбулентного потока
при неустановившемся движении. - В кн.: Турбулентные течения. М.: Наука, 1970.
94. Еременко Е.В., Маркое СБ. К расчету осредненных скоростей и сопротивления
при неустановившемся турбулентном движении в напорном шероховатом канале. —
В кн.: Гидромеханика. Киев, 1971, з. 17.
95. Жуковский Н.Е. О гидравлическом ударе в водопроводных трубах. — М.; Л.:
Гостехиздат, 1949.
96. Заде Л.А., Дезоер Ч.А. Теория линейных систем. Метод пространства
состояния. - М.: Наука, 1970.
97. Залманзон ЛА. Теория элементов пневмоники. - М.: Наука, 1969.
98. Зернов Н.В., Карпов В.Г. Теория радиотехнических цепей. - Л.: Энергия, 1972.
99. Зил к е. Трение, зависящее от частоты при неустановившемся течении в
трубопроводе. - ТОИР, 1968. № 1.
100. Иванов Ю.А. Интенсивность турбулентности и характеристики турбулентного
переноса за решетками в трубе. - Изв. АН СССР, МЖГ, 1973, № 1.
101. Идельчик И.Е. Справочник по гидравлическим сопротивлениям. - М.:
Машиностроение, 1975.
102. Иевлев В.М. Турбулентное движение высокотемпературных сплошных сред. -
М.: Наука, 1975.
103. Ильинский Н.Ф., Цсценкин В.К. Приложение теории графов к задачам
электромеханики. - М.. Энергия, 1968.
104. Иринг Ю. Проектирование гидравлических и пневматических систем. - Л..
Машиностроение, 1983.
105. Исакович М.А. Общая акустика. - М.: Наука, 1973.
106 Калишевский Л.Л., Селиховкин СВ. Некоторые результаты исследования
нестационарного турбулентного движения. - Теплоэнергетика, 1967, № 1.
107. Караев Р.И Переходные процессы в линиях большой протяженности. - М
Энергия, 1978.
356
108. Карам мл., Франк. Частотные характеристики пневматических линий передач. -
ТОИР, 1967, №2.
109. Карам мл., Леонард. О простой, но теоретически обоснованной временной
модели для систем гидравлических линий передачи. - ТОИР, 1973, № 4.
ПО. Карам мл. О простом, но полном решении для переходной характеристики
полу бесконечного передающего трубопровода круглого сечения. - ТОИР, 1976, № 2.
111. Карелин В.Я. Кавитационные явления в центробежных и осевых насосах. -
М.: Машиностроение, 1975.
112. Каро К, Педли Т., Шротер Р. Механика кровообращения. - М.: Мир, 1981.
113. Карте ели шв или Н.А. Современное состояние гидравлической теории
неустановившихся потоков по работам в СССР. - Изв. АН СССР, Механика и
машиностроение, 1961, №3.
114. Картеелишвили Н.А. Динамика напорных трубопроводов. - М.: Энергия, 1979.
115. Кателкин А.С., Михайлов В.В. Расчет параметров неустановившегося потока
сжимаемой жидкости с помощью инвариантов на характеристиках. - Изв. вузов,
Энергетика» 1980, №11.
116. Кателкин А.С. Расчет параметров гидравлического удара при возникновении
кавитационной каверны. - Изв. вузов, Энергетика, 1981, № 10.
117. Катц А.И., Чен Ю., Морено А.Г. Течение в мягкой трубе. - В кн.:
Гидродинамика кровообращения. М.: Мир, 1971.
118. Кафарое В.В. Методы кибернетики в химии и химической технологии. -
М.: Химия, 1976.
119. Кениг К.Э. Машинные методы моделирования нестационарных режимов
потокораспределения в трубопроводных системах. - Автоматика и телемеханика,
1979, № 1.
120. Кёниг Г. и Блекуэлл В. Теория электромеханических систем. - М.; Л.:
Энергия, 1965.
121. Козлов В.Г., Шайдуров Г.Ф. Движение жидкости, периодически
прокачиваемой через канал. - Уч. зап. Пермск. гос. ун-та, 1976, № 362.
122. Козлов ВТ. Устойчивость периодического движения жидкости в плоском
канале. - Изв. АН СССР, МЖГ, 1979, № 6.
123. Козлов Л.Ф., Никитина Г Д. О возможности использования
квазистационарной модели для расчета свободных колебаний жидкости. - Прикл. механика, 1979,
т. 15, №12.
124. Колебания и вибрации в поршневых компрессорах /Ю.А. Вирякин, Т.Ф. Конд-
ратъеза, Ф.П. Петрова, А.Г. Платонов. - Л.: Машиностроение, 1972.
125. Колесников КС. Продольные колебания ракеты с жидкостным ракетным
двигателем. - М.: Машиностроение, 1971.
126. Колесников КС, Самойлов Е.А., Рыбак С.А. Динамика топливных систем
ЖРД. - М.: Машиностроение, 1975.
127. Константинов СВ. Исследование неустановившегося турбулентного течения
вязкой слабосжимаемой жидкости в трубах. - Автореф. дисс. на соиск. уч. степ,
канд. техн. наук, МИНХ и ГП им. Губкина, 1УбО.
128. Коппель Т.А., Лийв У.Р. Экспериментальные исследования возникновения
движения жидкости в трубопроводах. - Изв. АН СССР, МЖГ, 1977, № 6.
129. Коробочкин Б.Л. Динамика гидравлических систем станков. - М.:
Машиностроение, 1976.
130. Коченов И.С. Кузнецов Ю.Н. Нестационарные течения в трубах. - В кн.:
Тепло-и массоперенос. Т. 1. Минск: Изд-во АН БССР, 1965.
131. Крылов В.И., Скобло Н.С Методы приближенного преобразования Фурье
и обращения преобразования Лапласа. - М.: Наука, 1974.
132. Кублановский Л.Б., Муравьева Л.И. Применение метода конечных разностей
по "неявной схеме" к решению задач неустановившегося движения жидкости в
напорных трубопроводах. - Нефтяное хозяйство, 1970, № 10.
133. Кузнецов Д.С Специальные функции. - М.: Высш школа, 1965.
134. Кузнецов ЮН., Певзнер В.И., Калинин Е.И. Об измерении расхода однофазной
среды сужающими у стройствами в нестационарных процессах. - Теплоэнергетика,
1981, № 12.
135. Кулиев З.Я.. Воропаев П.В. Математическое моделирование электрических
цепей с распределенными параметрами в пространстве переменных состояния. -
357
Изв. АН СССР, Энергетика и транспорт, 1975, Ny 1.
136. Кукинов А.Г. Одномерные колебания потока в цилиндрической трубе. -
Труды ЦАГИ, 1970, в. 1231.
137. Куркина М.Я., Радченко В.П., Юфин В.А. К вопросу о неустановившемся
движении капельной сжимаемой жидкости в трубах при различных законах трения. -
ПМТФ, 1976, № 1.
138. ЛайтфутЭ. Явление переноса в живых системах. - М.: Мир, 1977.
139. Лайтхилл Дж. Волны в жидкости. - М.: Мир, 1981.
140. Ландау ЛД.,ЛифшицЕМ. Механика сплошной среды. - М.: Гостехиздат, 1953.
141. Лебединский Е.В., Натанзон М.С., Ярлыкова Н.И. Акустические, энтропийные
и вихревые возмущения в канале переменного сечения. - Изв. АН СССР, МЖГ, 1982, № 1.
142. Лебединский Е.В., Натанзон М.С., Никифоров М.В. Экспериментальные
методы определения динамических свойств газовых потоков. - Акуст. ж., 1982, т. 28, в. 5.
143. Левченко Е.Л. Нестационарное движение жидкости в трубопроводе из вязко-
упругого материала. - Изв. АН СССР, Энергетика и транспорт, 1975, № 6.
144. Лелеев Н.С. Неустановившееся движение теплоносителя в обогреваемых
трубах мощных парогенераторов. - М.: Энергия, 1978.
145. Ленк А. Электромеханические системы: системы с сосредоточенными
параметрами. - М.: Мир, 1978.
146. Ленк А. Электромеханические системы: Системы с распределенными
параметрами. - М.: Энергоиздат, 1982.
147. Лепендин Л.Ф. Акустика. - М.: Высш. школа, 1978.
148. Лийв У.Р. О потерях напора при неустановившемся движении несжимаемой
жидкости в напорных трубах. - Тр. Таллин, политехи, ин-та, 1965, сер. А, № 223.
149. Лийв У.Р. О гидравлических закономерностях при замедленном движении
жидкости в напорном цилиндрическом трубопроводе. - Тр. Таллин, политехи, ин-та,
1965, сер. А, №223.
150. Лийв У.Р. О гидравлических закономерностях при ускоренном движении
жидкости в напорном цилиндрическом трубопроводе. - Тр. Таллин, политехи, ин-та,
1965, сер. А, вып. 223.
151. Лихачев В.Я., Васин А.С, Гликман Б.Ф. Техническая диагностика пневмогид-
равлических систем ЖРД. - М.: Машиностроение, 1983.
152. Лойцянский Л.Г. Механика ъчидкости и газа. - М.: Наука, 1970.
153. Лямаев Б.Ф., Небольсин Г.П., Нелюбов В.А. Стационарные и переходные
процессы в сложных гидросистемах. - Л.: Машиностроение, 1978.
154. Лямбоси П. Вынужденные колебания несжимаемой вязкой жидкости в
жесткой горизонтальной трубе. Расчет трения. - В кн.: Механика. М.: ИЛ, 1953, № 3A9).
155. {Марголис, Браун. Измерение распространения длинноволновых возмущений
в турбулентном потоке в трубе. - ТОИР, 1976, № 2.
156. Марков СБ. Экспериментальное исследование кинематических характеристик
турбулентного неустановившегося напорного потока. - В кн.: Гидравлика и
гидротехника. Киев, 1969, в. 8.
157. Марков СБ. Экспериментальное исследование скоростной структуры и
гидравлических сопротивлений в неустановившихся турбулентных потоках. - Изв.
АН СССР, МЖГ, 1973, №2.
158. Мартин. Современное состояние теории переходных гидравлических
процессов. - ТОИР, 1973, № 2.
159. Матханов П.Н. Основы анализа электрических цепей: Линейные цепи. - М.:
Высш. школа, 1981.
160. Мелконян Г.И. Определение потерь напора на трение в нестационарных
потоках. - Тр. Ленингр. ин-та водн. трансп., 1972, в. 132.
161. Мелконян Г.И. Потери напора на трение в случае нестационарного
турбулентного течения. - Тр. Ленингр. ин-та водн. трансп., 1978, в. 162.
162. Меренков А.П., Кривошеий Б.Л., Рогожин Х.Я., Сидлер Л.Е. Применение
теории и методов расчета гидравлических цепей к системам с неизотермическим
течением газа. - Изв. АН СССР, Энергетика и транспорт, 1971, № 6.
163. Меренков А.П. Дифференциация методов расчета гидравлических цепей. -
Ж. вычислит, математики и математ. физики, 1973, № 5.
164. Методы и алгоритмы расчета тепловых сетей/Под ред. '3 Я. Хасилева и А.П. Ме-
ренкова. — М.: Энергия. 1978.
358
165. Монин Л.С., Яглом A.M. Статистическая гидромеханика м
ности. Ч. I - М.: Наука, 1965. 1с-^»ика iM,r,,.IulI.
166. Мороз П.А., Полянская Л.В. Решение некоторых задач неустанопивш
движения жидкости в трубопроводе. - Инженерный журнал, 1965, № 5. ^гося
167. Мостков М.А. Современное состояние и дальнейшие задачи исследований гид
равлического удара. - Изв. АН СССР, ОТН, 1954, № 6.
168. NJ33OH С, Циммерман Г. Электронные цепи, сигналы и системы. - М • ИЛ
1963.
169. Накаряков В.Е., Соболев В.В., Шрейбер И.Р.,Штивельман Б.Я., Гидравлический
удар и распространение возмущений в эластичных трубах, заполненных жидкостью. -
Изв. АН СССР, МЖГ, 1976, № 4.
170. Натанзон М.С. Продольные автоколебания жидкостной ракеты. - М.:
Машиностроение, 1977.
171. Натанзон М.С, Амплитудно-фазовый метод исследования вибрационного
горения. - Изв. АН СССР, Энергетика и транспорт, 1981, № 5.
172. Неизотермическое течение газа в трубах/О.Ф. Васильев, Э.А. Бондарев, А.Ф.
Воеводин, М.А. Каниболотский. - Новосибирск: Наука, 1978.
173. Нестационарный теплообмен./В.К. Кошкин, Э.К. Калинин, Г.А. Дрейцер.
С.А. Ярхо. - М.: Машиностроение, 1973.
174. Неустойчивость горения в ЖРД. - М.: Мир, 1975.
175. Ноздрев В.Ф.У Федорищенко Н.В. Молекулярная акустика. - М.: Высш. школа,
1974.
176. Носова Л.Н. Таблицы функций Томсона и их первых производных. - М.:
Изд-во АН СССР, 1960.
177. Овсянников В.М. Расчет возникновения движения жидкости в трубопроводе. -
Изв. АН СССР, МЖГ, 1981, № 5.
178. Ольсон Г. Динамические аналогии. - М.: ИЛ, 1947.
179. Основы инженерной электрофизики. Ч. П/Под ред. П.А. Ионкина. - М.: Высш.
школа, 1972.
180. Панчурин Н.А. Некоторые вопросы теоретического и экспериментального
исследования неустановившегося движения жидкости в трубах. Автореф. дис. на соиск.
учен, степени д-ра техн. наук. Ленингр. ин-т водн. трансп., 1964.
181. Панчурин Н.А., Ройзман Д.Х. Некоторые особенности нестационарных
напорных течений. - Тр. Ленингр. ин-та водн. трансп., 1973, в. 140.
182. Пилипенко В.В., Задонцев В.А., Натанзон М.С. Кавитационные автоколебания
и динамика гидросистем. - М.: Машиностроение, 1977.
183. Попов Д.Н. Динамика и регулирование гидро- и пневмосистем. - М.:
Машиностроение, 1977.
184. Попов Д.Н. Нестационарные гидромеханические процессы. - М.:
Машиностроение, 1982.
185. Поттер Д. Вычислительные методы в физике. - М.: Мир, 1975.
186. Прокофьев В.Н., Нейман В.Г. Решение задачи динамики автоматической
гидрообъемной трансмиссии при помощи метода линейных графов, - Изв. вузов,
Машиностроение, 1966, №11.
187. Рабинович М.И. Применение методов теории матриц и теории графов для
расчета на ЭЦВМ колебаний давления и расхода в сложных гидросистемах управления с
распределенными и сосредоточенными параметрами. - Тр. ЦАГИ, в. 1956, 1974.
188. Рабинович ММ. Аналитическое исследование демпфирования системы
"следящий привод - инерционный орган управления". - Тр. ЦАГИ, в. 2153, 1982.
189. Райниш К. Кибернетические основы и описание непрерывных систем. - М.:
Энергия, 1978.
190. Раушенбах Б.В. Вибрационное горение. - М.: Физматгиз, 1961.
191. Ржевкин С.Н. Курс лекций по теории звука. - М.: Изд-во МГУ, 1960.
192. Розенберг Г Д. Метод характеристик и затухание головного значения волны
при нелинейном законе трение. - Приложение к книге [234].
193. Розенберг Г Д., Буяновский И.Н. О периодических решениях линеаризованной
системы уравнений неустановившегося движения капельной жидкости. — Приложение
к книге [234].
194. Розенберг Г Д., Буяновский И.Н. Аналитические методы интегрирования
линеаризованной системы уравнений неустановившегося движения капельной жидкости. -
359
Приложение к книге [234 J.
195. Райзман Д.Х. Ламинарное пульсирующее течение жидкости в круглых
трубах. - Теплофизика высоких температур, 1969, № 2.
196. Руденко Л.Н., Шлыкова И.С, Эпштейн В.Л. Акустическая проводимость
сверхзвуковых сопел с конической входной частью при продольных и
продольно-поперечных колебаниях. - Акуст. ж., 1974, т. 20, в. 4.
197. РэлейДж.В. Теория звука. Т. II - М.: Гостехиздат, 1955.
198. Самарский А.А., Попов Ю.Л. Разностные схемы газовой динамики. - М.:
Наука, 1975.
199. Сарпакая. Экспериментальное определение критического числа Re для
пульсирующего потока. - ТОИР, 1966, № 3.
200. Седов Л.И. Механика сплошной среды. Т. 1, 2. - М.: Наука, 1970.
201. Седов Л.И. Методы подобия и размерности в механике. - М.: Наука, 1972,
202.^Сергеев СИ. О колебаниях жидкости в трубах при умеренных числах
Рейнольд са. - Изв. АН СССР, МЖГ, 1966, № 1.
203. Сигорский В.П. Матрицы и графы в электронике. - М.: Энергия, 1968.
204. Скляревский А.Н., Тумеркон ММ. Анализ устойчивости системы
автоматического регулирования давления в пневмосистеме. - Изв. вузов, Машиностроение", 1983,
№11.
205. Скучик Е. Основы акустики. Т. 1, 2. - М.: ИЛ, 1958.
206. Славотинский М.В. Исследование динамики линий связи элементов и систем
пневмоавтоматики. - Автореферат дис. на соиск. уч. степени канд. техн. наук, МВТУ,
1978.
207. Сложные трубопроводные системы/В.В. Грачев, М.А. Гусейнзаде, Б.И. Ксенз,
Е.И. Яковлев. - М.: Недра, 1982.
208. Смирнов Д.Н., Зубов Л.Б. Гидравлический удар в напорных водоводах. - М.:
Стройиздат, 1975.
209. Станюкович К.П. Неустановившееся движение сплошной среды. - М.: Наука,
1971.
210. Стритер. Численные методы расчета нестационарных течений. ТОИР,
1972,№2.
211. Сурин А.А. Вопросы водоснабжения: гидравлический удар в водопроводах. --
Л.: Транспорт, 1967.
212. Табахов В.А. Исследование гидродинамических режимов работы
магистральных трубопроводов, оборудованных системами защиты от гидравлических ударов. -
Автореф. дисс. на соиск. уч. степ. канд. техн. наук, МИНХ и ГП им. И.М. Губкина,
1980.
213. Тарко Л.М. Волновые процессы в трубопроводах гидромеханизмов. - М.:
Машгиз, 1963.
214. Тарко Л.М. Переходные процессы в гидравлических механизмах. - М.:
Машиностроение, 1973.
215. Тихонов A.M., Самарский А А. Уравнения математической физики. - М.:
Наука, 1972.
216. Тозони О.В. Электродинамическая теория цепей. - Изв. АН СССР, Энергетика
игранспорг, 1977, №1.
217. Толстое Ю.Г., Теврюков АЛ. Теория электрических цепей. - М.: Высш.
школа, 1971.
218. Трикха. Эффективный метод моделирования зависящей от частоты силы
трения в неустановившемся потоке жидкости. - ТОИР, 1975, № 1.
219. Трубопровода! поршневых компрессоров/А П. Владиславлев, А.А. Козобков,
В.А. Малышев и др. - М.: Машиностроение, 1972.
220. Фанк, Вуд. Частотные характеристики гидравлических трубопроводов при
турбулентном течении. ТОИР, 1974, № 4.
221. Федоров Г.Ф, Изучение кинематики волны попуска. - Тр. ЦНИИ экономики
и эксплуатации водного транспорта, вып. 19, 1960.
222. Федорченко А/Г. О расчетах двухмерных нестационарных течений вязкого
газа в коротком цилиндрическом канале с торцевым вдувом. - Изв. АН СССР, МЖГ.
1979, № 1.
223. Федясвский К.К , Гиневскип А.С. Нестационарный турбулентный пограничный
слон крылового профиля и тела вращения. - ЖТФ. 1959, т. 29; в. 7.
360
224. Фокс ДА. Гидравлический анализ неустановившеюся ,,,,,„„ г
дах. - М.: Энергоиздат, 1981. 'чишя и ,Pi r)OIipoHO.
225. Фудим ЕВ. Пневматическая вычислительная техника. \\ ц.
226. Хасилев В.Я. Элементы теории гидравлических цепей - Изв ли СССР э
гетикаи транспорт, 1964, № 1. ' иер~
227. Ходурский В.Е. Некоторые результаты по обобщению частотных испытаний
шнекоцентробежного насоса. - В кн.: Гидрогазодинамика энергетических \становок
Киев: Наукова думка, 1982.
228. Холмбоу, Руло. Влияние вязкого трения на распространение сигнала в
гидравлических линиях. - ТОИР, 1967, № 1.
229. Христианович С А. Неустановившееся движение в каналах и реках. - В кн.:
Некоторые новые вопросы механики сплошной среды. М.; Л.: Изд-во АН СССР,
1938.
230. Цао. Численные решения для переходных процессов в пневматических
системах трубопроводов - расчет линий передачи. Прикладная механика, 1968, № 3.
231. Цао. Численные решения переходных процессов в пневматических системах
трубопроводов. Ч. 2: Задачи о нелинейных концевых устройствах. - Прикл.
механика, 1969, №3.
232. Цао, Роджерс. Численные решения для переходных процессов в
пневматических системах трубопроводов. Ч. 3: Задачи о системах трубопроводов с
ответвлениями. - Прикл. механика, 1969, № 3.
233. Цуханова ЕА. Динамический синтез дроссельных управляющих устройств
гидроприводов. - М.: Наука, 1978.
234. Чарный И А. Неустановившееся движение реальной жидкости в трубах. - М.:
Недра, 1975.
235. Чсрмак И., Петерка В., Заворка И. Динамика регулируемых систем в
теплоэнергетике и химии. — М.: Мир, 1972.
236. Численные решения многомерных задач газовой динамики/С,К. Годунов,
А.В. Забродин, М.Я. Иванов, А.Н. Крайко, Г.П. Прокопов. - М.: Наука, 1976.
237. Шадрин А.Н. Исследование продольных и вертикальных пульсационных
составляющих скорости и моментов корреляции между ними в нестационарном открытом
потоке. - В кн.: Гидротехника и гидромеханика. Киев: Наукова думка, 1964.
238. Шадрин А.Н. Экспериментальное изучение скоростной структуры открытых
потоков при неустановившемся движении. - В кн.: Вопросы гидротехники и
гидравлики. Киев, 1965.
239. Шахин В.М. Проверка некоторых математических моделей неустановившегося
турбулентного течения в трубе. - В кн.: Динамика неоднородной жидкости.
Новосибирску. 27,1976.
240. Шахин В.М. Сравнительная оценка различных членов интегральных уравнений
количества движения и энергии при неустановившемся течении в трубе. - В кн.:
Динамика жидкости со свободными границами. Новосибирск, в. 24, 1976.
241. Шерстянников В А., Калнин В.М. Гидродинамическое моделирование
рабочего процесса ЖРД на режимах запуска. - М.: Машиностроение, 1981.
242. Шлихтинг Г. Теория пограничного слоя. - М.: Наука, 1974.
243. Шорин В.П. Применение направленных графов к расчету вынужденных
колебаний давления в гидравлических системах летательных аппаратов и двигателей. - Изв.
вузов, Авиационная техника, 1966, № 4.
244. Шорин В.П. Устранение колебаний в авиационных трубопроводах. - М.:
Машиностроение, 1980.
245. Шрейдер Ю.А., Шаров А А. Системы и модели. - М.: Радио и связь,
1982.
246. Эпштейн В.Л., Руденко А.Н., Жемуранов А.П. Нелинейное акустическое
сопротивление отверстия. - Тр. ЦАГИ, в. 1806, 1976.
247. Bendarczyk S. Ruch nienstalon cieczy w przewodach pod cisnieniem. — Archiwum
Hydrotechniki. 1974. t. 21. №4,
248. Bredshaw P. Singularities in unsteady boundary lacrs. - AIAA Journ.. 1979, v. 17,
№7.
249. Can L W Areview of unsteady turbulent boundan-layer experiments - Unsteady
turbulent shear flows svmp. Toulouse, France, 1981, May, p. 3.
361
250. Carstens M.R , Roller J.E. Boundary-shear stress in unsteady turbulent pipe flow. —
J. of Hydraulics Division, Febr. 1959, p. 76.
251. Clarian С, Pelissier R. A theortical and experimental Study of the velocity
distribution and transition to turbulence in free oscillatory flow. - Fluid Mech., 1975
v.70,Pt. 1.
252. Daily J. W.t Hankey W.L., Ocive R W., Jordaan J.M. Resistance coefficients for
Accelerated and decelerated flows through smooth tubes and orifices. - Trans. ASME, 1956, №9.
253. Denison E.B., Stevenson W.H. Oscillatory flow measurements with a directionally
sensitive laser velocimeter. - The Review of Scientific Instruments, 1970, v. 41, № 10.
254. Emsmann S. Experimenelle ermittlung der Geschwindigkeitsverteilung in einer
oszillierenden turbulenten Rohrstromung. - Mitteilungen aus dem Inst. fur Wasserbau and
Wasserwirtschafte, der Technischen Univ. - Berlin, 1973, №79.
255. Franke G. Warmeuberang and Geschwindigkeitsverlauf bei pulsierender Rohrstr'd-
mung. — Allgemeine warmetechnik, 1961, Bd. 10, H. 2, 3.
256. Gimadiev H., Will Dieter. Uuntersuchung zur instationaren Gas- und Flusigkeitsstro-
mung durch Drosselelemente. - Wissenschaftliche Zeitschruft der Technischen universitat,
Dresden, 1979, Bd. 28, №2.
257. Harris J., Peev G., Wilkinson W.L. Velocity profiles in laminar oscillatory flow in
tubes. - J. of scient. Instruments, 1969, Ser. 2.
258. Hino M., Sawamato M., Tokasu Sh. Experiments on transition to turbulence in
an oscillatory pipe flow. - J. Fluid. Mech., 1976, v. 75, Pt. 2.
259. Keiller D.C., Sleath J.F.A. Velocity measurements close tu a rough plate oscillating
in its oun plane. - J. Fluid Mech., 1976, v. 73, Pt. 4. , ,
260. Klimes F., Korendr J. Pnspevek к analyze pulsa^niho proudeni kopalin v trubi-
cich. - Vodohospodarsky casopis, 1978, Sv. 26, №5-6.
261. Krzywoblocki M.Z. On the boundary layer at a plane or tube in a periodically
oscillating stream of compessible viscous fluid. — Osterreichisches Ingenier-Archiv, 1949, H. 3.
262. Laufer J. The Structure of turbulence in fully developed pipe flow. - Nat. Advis.
Com. Aeronaut., 1954, Rept. №1175.
263. Martin H.R., Carrington J.E. Fluid network response characteristics under pulsating
flow condition. - J. Biomechanics, 1971, v. 4, №6.
264.Maruyama Т., Kuribayashi Т., Mizushina T. The Structure of the turbulence in
transient pipe flows. - J. Chem. Eng. Jap., 1976, y. 9, №6.
265. Mizushina Т., Maruyama Т., Shiozaki Y. Pulsating turbulent flow in a tube. - J.
Chem. Eng. Jap., 1973, v. 6, №6.
266. Ohmi M., Usui Т., Fukawa M., Harasaki S. Pressure and velocity distribution in
pulsating laminar pipe flow. - Bull. JSME, 1976, v. 19, № 129.
267. Ohmi M., Usui Т., Топака О., Тоуата М. Pressure and velocity distribution in
pulsating turbulent pipe flow. 2. Experimental investigations. - Bull. JSME, 1976, v. 19,
№134.
268. Ohmi M., Kyomen S., Usui T. Analysis of velocity distribution in pulsating turby-
lent pipe flow with time-dependent friction velocity. - Bull. JSME, 1978, v. 21, №157.
269. Richardson E.G., Tyler E. The transverse velocity gradient near the mouths of
pipes in which an alternating or continuons flow of air is established. - Proc. Phys. Soc.
London, 1929, v. 42.
270. Rowneberger D., Ahrens CD. Wall shear atress caused by small amplitude
perturbations of turbulent boundary layer flow: An experimental investigation. - J. Fluid, mech.,
1977, v. 83, Pt. 3. f v f
271. Zymak V. Dynanicke charakteristiky hydraulickehe potrubis oscilacnim prutokem. -
Strojnicy casopis, 1974, r. 25, №5.
272. Sexl Th. Uber den von E.G. Richardson entdeckten Annulareffekt. - Z. Physik,
1930. Bd. 61, №6/7.
273. Szymanski P. Quelques solutions exactes des equations de l'hydrodynemique du
fluide visqueuxdans un tube cylindrique. - J. Math. Pures en Appl., 1932, Ser. 9, v. 11.
№1.
274. Szewezyk H. Nienstalony przelyw cieczy niescisliwej w szerlgoworownoleglych
systemach hydraulicznych. - Prace naukowa Instytut technik i cieplnej i mechaniki plynow
Politechniki wraclawskiej, 1977, № 14.
275. Tijdeman H. On the propagation of sound waves in cylindrical tubes. - J. Sound
and Vibration, 1975, v. 39, № 1.
362
276. Trent ИМ. Isomorphisms between oriented linear graphs and lumped physical
system. - J. Acoust. Soc. America, 1955, v. 27, № 3.
277. Turpolski K. Przenoszenie energii za pomaca fal cosnienia w przewodach hydrau-
licznych. - Przeglad Mechaniezny, 1972, v. 31, № 1.
278. Uchida S. The Pulsating viscous flow superposed on the steade laminar motion
of incompressible fluid in a circular pipe. - Z. Angew. Math, and Phys., 1956, Bd. 7, №5.
279. Urata E. Unsteady flow of viscous liquid in long circular tube. - Bull. JSME, 1971,
v. 14, №68.
280. Yang W.L., Ou J.W. Unsteady for red convection of closed condutits due tu
arbitrary remevaiiant inlet velocity. - Papers of JSME Semi-International Symposiym. Heatand
Mass Transfer, Tokyo, 1967; v. l,p. 133-143.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Агрегат насосный 346
Антирезонанс 172
Буссинеска гипотеза 16
Вершина графа 103
Ветвь 103, 104
Влияние вязкости 33
Возмущение ступенчатое 322
Волна акустическая 12
- бегущая 145
- концентрации 33
- обратная 147, 334
- отраженная 147
- падающая 147
- прямая 147, 334
- стоячая 149
- энтропии 33, 52
Вязкость жидкости 43
- объемная 10
- турбулентная 217
Гельмгольца резонатор 162
- уравнения 144
Гидромеханика 8
Гидропривод следящий 130
Гипотеза Буссинеска 16
Граф линейный 69, 103
- несвязный 104
- полюсный 69, 70, 74
- связный 104
- сигнальный 103, 125, 301
- структурный 69, 103
Гука закон 12
Даламбера метод 333
Движение жидкости 7
вязкой нестационарное 22
— сжимаемой 9
- системы вынужденное 321
свободное 321
собственное 321
Двухполюсник 68, 71
- активный 81
- пассивный 71
Действие переменного внешнего
ускорения 262
Дерево 104
- нормальное 122
Дополнение алгебраическое 130
364
Емкость 71
- проточная 51
Жидкость капельная 12
- ньютоновская 9
- сжимаемая вязкая 9
- с переменной температурой 31
- с переменным составом 31
Закон Гука 12
- Ньютона 9
Законы Кирхгофа обобщенные 107
- сохранения для цепи 107
Запись в у-параметрах 175
Изменение площади проходного
сечения 345
Измерение 69
- параметров течения в тракте 70
Инерционность 48,71
Источник расхода идеальный 82
Кавитация 79, 324,332
Канал длинный 35
Карсона - Хевисайда метод 323
Квазиметод характеристик 347
Кирхгофа законы обобщенные 107
- правила 107
Колебание в одномерном потоке 177
- вязкой теплопроводной сжимаемой
жидкости вынужденное 202
- жидкости в однородном тракте
вынужденное 143
- свободное 133,155
- собственное 155
- стенок каналов 250
трубы в продольном направлении
257
- турбулентного потока 210
Коммуникатор 278
Контур 129
- главный 104
- графа 104
- фундаментальный 104
- r-го порядка 130
Контуры несоприкасающиеся 129
- соприкасающиеся 129
Концентрация 12
Корректив реактивного
сопротивления 195
Коэффициент диффузии 12
- нестационарного поверхностного
трения 247
- отражения 154
- передачи 127, 129
- потерь энергии 247. 248
- сопротивления трения 247, 248
- стоячей волны 155
- турбулентной вязкости 221
Критерий Пекле 21
- подобия 18
Куэтта течение 24, 25
Масса приведенная 49
- присоединенная 30
Матрица главных контуров 114
- инциденций 112
- контуров 114
- соединений 112
-узловая соединения ветвей 111
- узловых проводимостей 119, 285
- цепная 87
Маха число 20
Метод Даламбера 333
- исследования переходных
процессов операционный 338
- Карсона - Хевисайда 323
- матрично-топологический 107
- операционный 323
- расчета нестационарных процессов
численный 342
- узловых давлений 118, 120
- характеристик 342
Многополюсник 68, 85
Модель движения жидкости 31
- — одномерная 33
- линеаризованная 57
- линейная 57
- математическая 7
- нестационарного турбулентного
течения статистическая 236
- Прандтля 16
Модуль объемной упругости 141
Мэзоиа формула 129
Навье - Стокса уравнения 10
Нагрузка согласованная 149
Напряжение сил трения 192
касательное 9
- турбулентное 15
Ньютона закон 9
Обертон колебаний 156
Определение собственных частот
графическое 164
Отбор жидкости 345
Пакет волновой 206
Параметр распространения 197
Пекле критерий 21
Переменная параллельная 70
- последовательная 70
Пластина колеблющаяся 25, 26, 28
Подграф 104
Подход статистический 235
Политропа 205
Полоса запирания 252
Полюс цепи 68, 70
Постоянная времени 45
Построение математических моделей
107
Правила Кирхгофа 107
Прандтля модель 16
Пробка турбулентная 215
Процесс динамический в ПГС 94
- переходный 133, 320, 324
- с полным мгновенным
перемешиванием 54
Пуазейля течение 25, 26
Пути несоприкасающиеся 129
- соприкасающиеся 129
Путь прямой 129
- сквозной 129
Пучность 152
Разветвление ПГС 107
Рассеивание волн энтропии 271
Реактор идеального вытеснения 51
смешения 52
Ребро графа 103
Режим течения стержневой 235
Резонанс 152
- в тракте 169
Резонатор Гельмгольца 162
Рейнольдса уравнение 15
- число 19
Решение в виде бегущих волн 334
- волнового уравнения
периодическое частное 143
Сечение главное 105
- дерева 104
- фундаментальное 105
Сжимаемость 43
Сигнал узловой 125
Система пневмогидравлическая /ПГС/
7,66
- линейная 125
- - разветвленная 277
с распределенными параметрами
277
Скорость звука 140
адиабатическая 12
- распространения групповая 206
фазовая 146, 206
Сопротивление 50
- волновое 145,148
- входное 168
- местное 76
Составляющая скорости осредненная
36
Среда сплошная 9
Стокса число 184
Струхаля число 19
365
Схема замещения 82
- обобщенного активного элемента
• 279
Теория подобия 18
- цепей 8
Течение автомодельное 23
- в открытых каналах 260
- газа неизотермическое 312
- жидкости в каналах
нестационарное 177
-Куэтта24,25
- ламинарное 13
колеблющееся нестационарное
182
пульсирующее 196
- неизотермическое 9, 51
- нестационарное в растяжимых
трубах 253
- Пуазейля25,26
- пульсирующее 25, 28
- турбулентное 13
Тип осциллирующего потока 212
Тон колебаний 156
Торможение жидкости мгновенное 41
Тракт проточный 132, 157
- с мягкими отенками 98
Трение квазистационарное 177
Труба со стенками из вязкоупругого
материала 254
- с податливыми стенками 250
Удар гидравлический 324
Узел 103
- базисный 285
- графа 103
- стока 125
- стоячей волны 152
- цепи 68
Унистор 78
Упрощение сигнальных графов 127
- уравнений гидромеханики 22
Уравнение баланса тепла для узлов
316
турбулентной энергии 17
- волновое 132,139
- дисперсионное 207
- концентрации 12
- неразрывности 10, 11
- нестационарного турбулентного
движения 217
- проточной емкости 51
- Рейнольдса 15
- состояния 12
- теплопроводности 23
- цепи дифференциальное 320
матричное 279
Уравнение элемента 67
- энергии 11
Уравнения Гельмгольца 144
- гидромеханики 8
- движения жидкости 7
вязкой сжимаемой 9
- контурные 115
- матричные 115
- Навье- Стокса 10
- нестационарного ламинарного
движения вязкой жидкости 183
- сохранения 107
- турбулентного течения 13
- узловые 115
- узловых давлений 284
Усилитель давления идеальный 89
- расхода идеальный 89
Устройство дросселирующее
регулируемое 346
Фаза волны 146
Форма уравнений гидромеханики
безразмерная 18
Формула Мэзона 129
Фронт волны 334
Фру да число 19
Характеристика акустическая
проточного тракта 132
- частотная 135
амплитудно-фазовая (АФЧХ) 193,
225
Хорда 104
Цепь пневмогидравлическая (ПГЦ)
66
- эквивалентная 68, 94
- с активными элементами 279
Частота собственная 155
Число волновое 146
сдвиговое 184
- Маха 20
- Рейнольдса 19
- Стокса 184
- Струхаля 19
- Фруда 19
- Эйлера 19
Шестиполюсник 312
Эйлера число 19
Элемент механический подвижный
105
- многополюсный 85, 120
- ПГС с сосредоточенными
параметрами 48
- цепи 67
Эргодичность 217
Эффект аннулярный 188
^'-параметр 175
Борис Фомич Гликман
МАТЕМАТИЧЕСКИЕ МОДЕЛИ
ПНЕВМОГИДРАВЛИ}1ЕСКИХ СИСТЕМ
Редактор Л.А. Чульский
Художественный редактор Т.Н. Кольченко
Технический редактор СВ. I еворкян
Корректоры Т.В. Обод, ИМ. Кузьмина
Набор осуществлен в издательстве на наСюрно-печатающих
автоматах
ИБ № 12072
Сдано в набор 17.10.85. Подписано к печати 10.02.86
Т - 07000. Формат 60 X 90 1/16. Бумага офсетная
Гарнитура Пресс-Роман. Печать офсетная. Усл.печ.л. 23,0.
Усл. кр.-отт. 23,0. Уч.-изд.л. 26,1. Тираж 2200 экз.
Тип зак. 958 • Цена 4 р. 20 к.
Ордена Трудового Красного Знамени
издательство "Наука"
Главная редакция физико-математической литературы
117071 Москва В-71, Ленинский проспект, 15
4-я типография издательства "Наука"
630077 г. Новосибирск-77, ул. Станиславского, 25
ИЗДАТЕЛЬСТВО "НАУКА"
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
Готовятся к выпуску в 1987 г.
Акуленко Л.Д. Асимптотические методы оптимального
управления.
Андреев Л.В., Ободан Н.И., Лебедев А.Г. Устойчивость
оболочек при неосесимметричном нагружении.
Аппазов Р.Ф., Сытин О.Г. Проектирование траекторий
носителей и спутников Земли. — Для использования в
учебном процессе.
Бесекерский В.А., Изранцев В.В. Системы автоматического
управления с микро-ЭВМ. — (Теоретические основы
технической кибернетики).
Буков В.Н. Адаптивные прогнозирующие системы
управления полетом.
Гришин С.Д., Лесков Л.В. Промышленность в космосе:
Проблемы и перспективы. - (Проблемы науки и
технического прогресса). — Для широкого круга читателей.
Гладков Д.И., Казаков И,Е. Методы оптимизации
стохастических систем. - (Теоретические основы технической
кибернетики).
Королев Г .Л., Рубан АИ., Сычев В.В., Сычев В.В.
Асимптотическая теория отрывных течений.
Крутько П.Д. Обратные задачи динамики управляемых
систем.