О
H
U
5
яг
о
X
S
<
S
н
О
S
н
<
н
О
$
о
w
S
н
<
W
н
#
Нильдишев Г. С,
Френкель А. А.
АНАЛИЗ
ВРЕМЕННЫХ
РЯДОВ
И ПРОГНОЗИРОВАНИЕ
«СТАТИСТИКА» МОСКВА 1973

я 1-6-3-090 oo ■
К 23—73
008(01 )-73
В книге излагаются «©которые методы анализа и
прогнозирования временных рядов, такие, например,
как экспоненциальное сглаживание, гармонический
анализ. Большое внимание уделяется вопросам изучения
сезонности. Рассматриваются проблемы многоф актор н ого
прогнозирования экономических показателей. Приводятся
примеры, взятые из различных областей экономики.
Книга рассчитана на широкий круг экономистов и
статистиков, а также на преподавателей, аспирантов и
студентов экономических вузов и факультетов.
Редколлегия серии
„Математическая статистика
для экономистов"
Боярский А. #., Венецкий И. Г.,
Голенко Д. #., Дружинин Н. К.,
Пасхавер И. С, Привезенцева А, Г.
©
Издательство «Статистика», 1973 г.

ПРЕДИСЛОВИЕ
Развитие советской экономической «науки
неразрывно связано с повышением уровня экономических
исследований, важной задачей 'которых является
определение закономерностей развития народного хозяйства.
Эти закономерности наиболее полно проявляются во
временных рядах, отражающих изменение па;раметров
экономической системы ibo времени.
Учет особенностей экономического развития имеет
первостепенное значение при составлении перспективных
народнохозяйственных планов. Важным этапом по
научному обоснованию перспективных планов является
прогнозирование. В Директивах XXIV съезда КПСС
указывается на необходимость «осуществить разработку
долгосрочного перспективного плана развития народного
хозяйства СССР, используя для это^о прогнозы научно-
технического прогресса, роста населения страны,
природных ресурсов и другие»1.
Решение проблемы прогнозирования кода и
результатов экономического развития возможно только на
основе научного анализа и обобщения предыдущего
-опыта. Изучение достижений науки и практики дает
возможность объяснить и предсказать развитие и поведение
какого-либо явления в будущем. Поэтому в настоящей
книге авторы объединили две задачи статистики: анализ
временных рядов и прогнозирование экономических
показателей, поскольку сложившиеся объективные
тенденции изменения экономических показателей в известной
степени предопределяют их величину в будущем.
При написании настоящей работы авторы
преследовали следующую цель — изложить в оистематизирован-
г Материалы XXIV съезда КПСС. Политиздат, 1971, с. 295.
3

ном «виде .статистические методы анализа .временных
рядов и 'прогнозирования, наиболее часто применяемые в
9 кон о м'ич еокой in p антике.
Главное .внимание в работе обращено ;на прикладное
значение рассматриваемых методов, на экономическое
истолкование и интерпретацию получаемых результатов.
В то же время авторы не предполагали сделать
теоретическую работу по проблемам экономического
развития, так как эти ©опросы являются областью
соответствующих экономических дисциплин и подробно
освещаются в литературе.
По существу, книга состоит ..из двух частей. В первой
излагаются статистические и экономические вопросы
анализа временных рядов, во второй — методы
прогнозирования.
iP ассм ат рив а>я м а тем атико -статистически й .аппарат
анализа ©ременных рядов и прогнозирования, авторы
исходили из того, что экономическим явлениям в
определенной степени присущ вероятностный характер..Авторы
- полагают, что наличие случайности в экономике
определяется чрезвычайно сложным переплетением
параметров экономической системы, влиянием на них большого
числа взаимосвязанных факторов, действующих в
разных направлениях и часто неизвестных. Все это
приводит к большой вариации показателей, особенно если
рассматривать изменение явлений во времени, что находит
свое выражение в отклонении этих показателей от
основной тенденции развития.
В настоящей работе временной ряд рассматривается
как сумма детерминированной и случайной компонент.
Появление случайной компоненты оценивается с
некоторой вероятностью. Детерминированная, же компонента
выражается некоторой аппроксимирующей *функцией,
отражающей закономерности развития исследуемого
явления.
Отклонения от основной тенденции развития
рассматриваются как стационарный случайный процесс, к
которому применимы методы прогнозирования стационарных
с луч а й ных п р оцессов.
Таким образом, прогноз экономических явлений по их
временным рядам состоит из двух элементов: из
прогноза детерминированной компоненты и прогноза
случайной компоненты. Разработка первого прогноза не пред-
4

полагает больших трудностей, если определена основная
тенденция развития и возможна ее дальнейшая
экстраполяция. Прогноз случайной компоненты более сложен,
так как не ко всякой случайной компоненте можно
применить 'методы прогнозирования стационарных
случайных процессов. Если случайная компонента не является
стационарной, то в таких случаях приходится
производить определенные преобразования, чтобы привести ее
к соответствующему виду.
При анализе временных рядов и прогнозировании
часто возникает необходимость одновременного
нахождения детерминированной и случайной компонент. Такая
постановка задачи -требует проведения
предварительного логического анализа характера динамики
исследуемого процесса и выделения одного из трех типов
динамики:
1. Данный процесс достаточно хорошо описывается
основной тенденцией и почти не содержит случайных
отклонений.
2. Процесс зависит от изменения во времени
некоторых основных показателей, влияющих на него
неотражающих структуру процесса.
3. Процесс рассматривается как функция от
элементов его-внутренней структуры, причем значительную роль
играет явление «запаздывания во времени.
Выделение типов динамики, если они не
противоречат экономической природе рассматриваемых процессов,
имеет важное обобщающее значение как для анализа,
так и для прогнозирования. При этом точное
отображение закономерностей развития процесса определенным
типом динамики предопределяет точность прогноза на
будущее.
При описании методов прогнозирования по одному
временному ряду авторы подробно излагали
'математический аппарат тех из них, которые мало известны
широкому кругу советских экономистов и статистиков.
Авторы считают, что будущее принадлежит методам
многофакторного прогнозирования, основой которых
является системный подход к изучению экономических
явлений, поскольку эти методы позволяют учитывать
развитие взаимосвязанных процессов и явлений.
Многофакторное прогнозирование разработано еще недостаточно
полно. Его применение требует решения ряда теоретичес-
5

ких in методических (вопросов и экономического
осмысливания как прошлого развития, так и будущего
результата.
Многофакторное прогнозирование тесно связано с
корреляционным и регрессионным анализом, который в
данной работе непосредственно не излагается, а
предполагается известным читателю1.
Поскольку в наблюдениях -временного ряда часто,
«возникает автокорреляция, авторы останавливаются на
одном из приемов ее исключения путем включения фактора
времени в регрессионную модель. Кроме того, в книге,
многофакторные прогнозы разрабатываются с учетом
изменения коэффициентов регрессии во времени.
Применение многофакторного прогнозирования
требует решения сложной проблемы выбора факторов,
которая не может быть решена чисто статистическим
путем, а только при помощи глубокого изучения существа
рассматриваемого процесса, его экономического
содержания. И здесь авторы подчеркивают примат
экономического анализа перед чисто статистичеокими методами
изучения процесса.
В заключение отметим, что в настоящей работе
используется термин «временные ряды» вместо часто
употребляемого «ряда динамики». Авторы полагают, что
принятый ими термин более точно отражает, особенности
этой статистической категории, ибо «динамика»
охватывает не только изменение во времени, но и всякое
изменение состояния под влиянием изменения внешних
условий. Чтобы подчеркнуть то обстоятельство, что
изменение экономических явлений происходит во времени, и
используется термин «временные ряды».
Авторы считают своим приятным долгом, выразить
глубокую благодарность В. Е. Адамову и Г. Л.
Гинзбургу за их большую помощь в работе над книгой.
1 Корреляционный и регрессионный анализ подробно
излагается в книгах Езекиела М., Фокса К. [9] и Айвазяна С. А. [1].

Глава |
ПОНЯТИЕ
О ВРЕМЕННЫХ РЯДАХ
1.1. ОПРЕДЕЛЕНИЕ
ВРЕМЕННЫХ РЯДОВ.
ВИДЫ ВРЕМЕННЫХ РЯДОВ
Одна «из основных задач /математической
статистики заключается в исследования процесса
изменения и развития изучаемых явлений во времени, решаемая
с помощью построения и анализа временных рядов.
Временным рядом называется числовая
последовательность наблюдений, характеризующих изменение
экономического явления во времени. Отдельные наблюдения
временного ряда называются уровнями этого ряда.
Временные ряды делятся на моментные и
интервальные. В моментных временных рядах абсолютные
величины, выражающие уровень явления, отражаются по
состоянию на определенные моменты времени. Например,
моментным временным рядом будет ряд, показывающий
численность поголовья крупного рогатого скота в СССР
на 1 января каждого года.
В интервальных временных рядах абсолютные
показатели уровней относятся к некоторым периодам
времени (году, кварталу, месяцу, неделе, дню). Так,
интервальным будет временной ряд, характеризующий
ежегодное производство стали в СССР.
Временные ряды, состоящие из уровней,
характеризующих интервалы или моменты времени с помощью
средних или относительных величин, называются
производными. Примером производных временных рядов
может служить временной ряд среднегодовой выработки
натурального цемента на одного работающего.
7

Абсолютные уровни интервальных и моментных
рядов, а также средние уровни временных рядов могут
быть преобразованы в относительные величины.
Последние можно получить путем отнесения абсолютных
уровней к одному и тому же уровню, взятому за базу, либо
к предыдущему уровню. За базу сравнения обычно
принимают начальный уровень временного ряда. При
сравнении каждого уровня с предыдущим получаются
цепные показатели. Если же сравнение уровней ведется с
одним уровнем (базой), то показатели называются
базисными. Следует отметить, что при изучении динамики
большинства экономических явлений в основном
используются производные интервальные ряды, уровни
которых образованы рядом средних или относительных
величин. Выбор вида ряда определяется целями анализа.
1.2. ПРАВИЛА ПОСТРОЕНИЯ
ВРЕМЕННЫХ РЯДОВ
Для того чтобы временной ряд правильно
отражал объективный процесс развития -явления,
необходимо, чтобы уровни этого ряда состояли из однородных,
сопоставимых величин. Для несопоставимых величин
неправомерно вести расчеты показателей динамики,
которые будут рассмотрены далее.
Возможные причины несопоставимости уровней
временных рядов заключаются в следующем:
несопоставимость по территории, состоящая в том,
что статистические данные для страны, области или
района, изменивших границы, несопоставимы с прежними
данными. Такая несопоставимость устраняется путем
пересчета старых данных с учетом новых границ;
несопоставимость по кругу охватываемых объектов,
состоящая в несравнимости данных по подчинению,
если, например, в подчинение данного объединения
перешла часть предприятий из другого объединения. Однако
сопоставимость не нарушается, если эти предприятия
построены заново или отдельные предприятия
прекратили работу;
несопоставимость по временным периодам,
заключающаяся в том, что данные относятся к различным
периодам в течение года или разным датам. Особенно силь-
8

на несопоставимость, явлений, резко меняющихся в
течение года. Например, численность скота летом и зимой
имеет значительное различие, и временной ряд
численности скота должен отражать ее на одну и ту же дату
во все годы;
несопоставимость из-за различного понимания
единицы наблюдаемого объекта. Например, число, крупных
предприятий может меняться в зависимости от
изменения самого понятия «крупное предприятие». Для
разграничения определенных единиц в статистике
устанавливается так называемый ценз — определенная
количественная граница, отделяющая, например, крупное
предприятие от мелких. Так, можно условиться, что к
крупным предприятиям относятся предприятия, имеющие
более 100 рабочих или производящих более чем на
100 тыс. руб. продукции в год, и др. Это понятие должно
быть одинаковым для всего изучаемого периода;
несопоставимыми будут уровни, вычисленные в
различном масштабе измерения. Для устранения этого
недостатка уровни обычно приводятся к одному масштабу;
некоторые временные ряды имеют несопоставимые
уровни но структуре совокупности, для которой они
вычислены. Так, данные о рождаемости населения
меняются не только из-за изменения числа родившихся по
отношению к численности населения, но и ввиду
изменения возрастного состава населения. Точно также темп
ростга национального дохода в значительной степени
зависит от структуры народного хозяйства. Если,
например, в национальном доходе преобладает доход,
получаемый от сельского хозяйства, которое развивается
медленно, то и рост национального дохода будет
медленным. Если же в структуре народного хозяйства
преобладают отрасли, развивающиеся быстрыми темпами, то
и национальный доход в целом растет быстро.
В экономическом анализе применяются
элементарные характеристики динамики, которые могут
характеризовать изменение уровней ряда и весь ряд в среднем.
1.3. ПОКАЗАТЕЛИ ИЗМЕНЕНИЯ
УРОВНЕЙ ВРЕМЕННОГО РЯДА
Одной из важнейших задач анализа
временных рядов является определение изменений,
происходящих в данном явлении, а также вычисление наиравле-
9

ния, скорости и интенсивности этого изменения. Для
решения этой задачи вычисляется ряд показателей,
которые будут рассмотрены ниже.
Абсолютный прирост. Абсолютный прирост (Ау){
характеризует размер увеличения (уменьшения) уровня
ряда за определенный промежуток времени. Он равен
разности двух сравниваемых уровней и выражает
абсолютную скорость роста:
&y=yi-Ui-h . (1.3.1)
где Ау—абсолютный прирост;
yi — i-и уровень ряда, (/=2, 3,..., п);
yi-k — базисный уровень, отстоящий от у\ на k лет.
Коэффициент роста. Коэффициент роста показывает,
во сколько раз данный уровень ряда больше (или
меньше) базисного уровня. Он равен, отношению двух
сравниваемых уровней:
/Ср> 1 — в случае роста уровня;
/Ср=1 —если уровень не меняется, и, наконец,
/Ср<1 —если уровень снижается.
Коэффициенты роста, выражающие отношение
смежных уровней (цепные коэффициенты), имеют перемен-'
ную базу сравнения:
Коэффициент прироста. Коэффициент прироста
выражает абсолютное изменение коэффициента роста. Он
рассчитывается по формуле
*цр=/Ср-1 или/(пр=^^д Х1.3.4)
Темп роста. На .практике чаще лрименяются не
коэффициенты роста и прироста, а темпы роста и прироста,
которые рассчитываются по формулам:
Гр=-^-.100%; (1.3.5)
Гпр=7-р-100% или Г^^^^ЛВД- (1-3.6Х
10

Темп «прироста rtok&3bifcaet, йа «сколько прбцентой
уровень одного «года (периода) увеличился
(уменьшился) по сравнению с уровнем явления другого года
(периода). Он выражает относительную величину прироста
в процентах. Сравнение абсолютного прироста и темпа
прироста за одни и те же промежутки времени
показывает, что замедление темпа прироста часто не
сопровождается уменьшением абсолютных приростов- При
замедлении темпов роста может увеличиваться
абсолютный размер прироста уровня. Сопоставление
абсолютного прироста с темпами роста осуществляется путем их
сравнения. Эффективность одного процента прироста
выражается отношением абсолютного прироста к темпу
прироста, выраженному в процентах.
1.4. СРЕДНИЕ ХАРАКТЕРИСТИКИ
ВРЕМЕННОГО РЯДА
Средние 'величины временного ряда — это
обобщенные характеристики развития явления за
изучаемый период. К ним относятся: средняя
хронологическая, средний абсолютный прирост, средний темп роста
и прироста-
Средняя хронологическая. Средняя хронологическая,
или средний уровень ряда, показывает, какова средняя
величина уровня, характерная для всего анализируемого
периода. К расчету среднего уровня чаще прибегают для
рящов, изменение 'которых стабилизируется в течение
большого периода времени и рядов с колеблющимися
уровнями в короткие промежутки времени. Например,
необходимо вычислять средний уровень урожайности за
ряд лет, так как уровень одного года не характерен для
урожайности; в то же время средняя величина является
более устойчивой характеристикой. Или же возьмем
другой пример- Численность работников предприятия
изменяется каждый день.
Для отражения работы предприятия рассчитывается
средняя численность и т. д.
Средняя хронологическая вычисляется по-разному
для интервальных и моментных временных рядов.
Для интервального ряда, уровни которого можно
суммировать и получить итоги за более продолжитель-
11

ный период, средняя определяется по формуле
п
*-■*=!-• 0-4.1)
Для моментного временного ряда с равностоящими
уровнями средняя хронрлогическая рассчитывается как
1 , 1
__ — !Л + У2+Уз+-~+Уп~1 + —Уп
У= -«31 0-4-2)
Средний абсолютный прирост. Средний абсолютный
прирост показывает скорость развития явления-. Он
вычисляется по формуле
_ Уп—yi
АУ= —— • (1-4-3)
Средний темп роста. Для определения средней
скорости изменения изучаемого явления за
рассматриваемый период времени вычисляют средний темп роста.
Чаще всего его рассчитывают по формуле средней
геометрической:
Г(р)- Ц Гад», Г2(р), • • • , 7n(p)= V^ • 100%- (Ь4'4)
Средний темп прироста соответственно равен:
^пр)=7\р)-Ю0%. (1.4.5)
Для практических расчетов средний темп роста,
рассчитанный по формуле (1. 4. 4), можно использовать
только в случае более или менее равномерного
изменения явления. Если же изучаемое явление в течение
одного периода времени возрастает, а в следующем за ним
периоде убывает, то говорить об общем среднем темпе
роста или прироста вряд ли имеет смысл. Показатель
среднего темпа роста, рассчитываемый по формуле
средней геометрической (1. 4. 4), имеет существенные
недостатки. Этот показатель основан на сопоставлении
конечного и начального уровней временного ряда, причем
промежуточные уровни этого ряда во внимание не
принимаются. В случае сильной колеблемости ряда
использование средней геометрической может привести к
серьезные просчетам, так как временной ряд не является
12

геометрической прогрессией. Тем самым знаменатель
прогрессии, который (соответствует среднему темпу
роста, лишен какого-либо -содержания. При использовании
/среднего геометрического темпа роста в планировании
искажается тенденция 'временного ряда, что в свою
очередь приводит к неверному представлению о величине
ожидаемого уровня. Поэтому показатель среднего
темпа роста, вычисляемый по формуле средней
геометрической, уже давно подвергался .критике- Были предложены
другие способы расчета среднегодового темпа роста,
которые в той или иной мере лишены недостатков
среднего геометрического темпа роста. Достаточно подробный
разбор предлагаемых методов вычисления среднего
темпа роста произведен в монографии [14]. Нам
представляется наиболее обоснованным предложение А. И. Ма-
нелли и Н- Н. Напшбедовой, согласно которому средний
темп роста рассчитывается по формуле [13]:
__ /2-1 у——
fp= Л/ JLL, (1.4.6)
Уо
А А
где уп и уо — выравненные по уравнению тренда
начальные и конечные уровни временного ряда. Поскольку при
л л
расчете у0 и уп учитывается колеблемость
промежуточных уровней, то средний темп роста, вычисленный по
формуле (1. 4. 6.), будет более точно характеризовать
изменение изучаемого явления за рассматриваемый
период времени-
1.5. НЕКОТОРЫЕ ЭЛЕМЕНТЫ
ТЕОРИИ СЛУЧАЙНЫХ ПРОЦЕССОВ
В математической статистике временные ряды
рассматривают под углом зрения случайных
(стохастических) процессов.
В экономической практике часто приходится
сталкиваться с такими ситуациями, когда случайные величины,
характеризующие закономерности развития реальных
экономических процессов и явлений, изменяются во-
времени. Эти изменения описываются случайными
функциями, зависящими от времени, т. е. функциями, значения
которых в любые моменты времени являются
случайными величинами-
13

Случайные функции одной независимой .переменной,
за которую, как правило, принимают время, называют
случайными (процессами [7]. Если случайная
функция зависит от двух и более параметров, то ее
принято называть случайным полем.
Последовательность наблюдений ytl, yt2 , —,Уга
некоторого случайного лроцеоса It называют
реализацией случайного процесса- В статистике
последовательность {yti} называют временным рядом.
Основными характеристиками случайных процессов
служат следующие неслучайные функции:
математическое ожидание, дисперсия, а также взаимная
корреляционная и автокорреляционные функции.
Математическим ожиданием 'Случайного
процесса g* называется неслучайная функция от
времени М[|*]> которая при каждом значении t равна
математическому ожиданию соответствующих реализаций
случайного процесса.
Следовательно, математическое ожидание
случайного процесса есть некоторая средняя функция, вокруг
которой варьируют конкретные реализации случайного
процесса. Степень этой вариации характеризуется
дисперсией процесса-
Дисперсией случайного процесса It называется
неслучайная функция £[£*], значение которой для
каждого фиксированного момента времени / равно
дисперсии соответствующих реализаций случайного процесса.
Для изучения внутренней структуры случайного
процесса %t по его реализации {yt} применяется
автокорреляционная функция гу(%), которая представляет собой
множество коэффициентов корреляции между
временным рядом yt и этим же рядом, сдвинутым
относительно первоначального положения на т моментов времени.
Нормированная автокорреляционная функция для вре*
менного ряда yt 'вычисляется по формуле
Гу(г) =
П—Х П—Х 71—Т
/П-Т 2 W-T П-Х П-Т
Г(л-т) 2 у,-( 2 yt)2] [(л-т) 2 ^-(2 yt+x)2]
*—i *=i *=i *=1
(1.5.1)
(/=1,2,....л; т = 0,1,2,...,л-2) ..
14

Величину т называют сдвигом. Сдвиг, которому
соответствует наибольший коэффициент автокорреляции,
называют 'временным запаздыванием или
временным лагом.
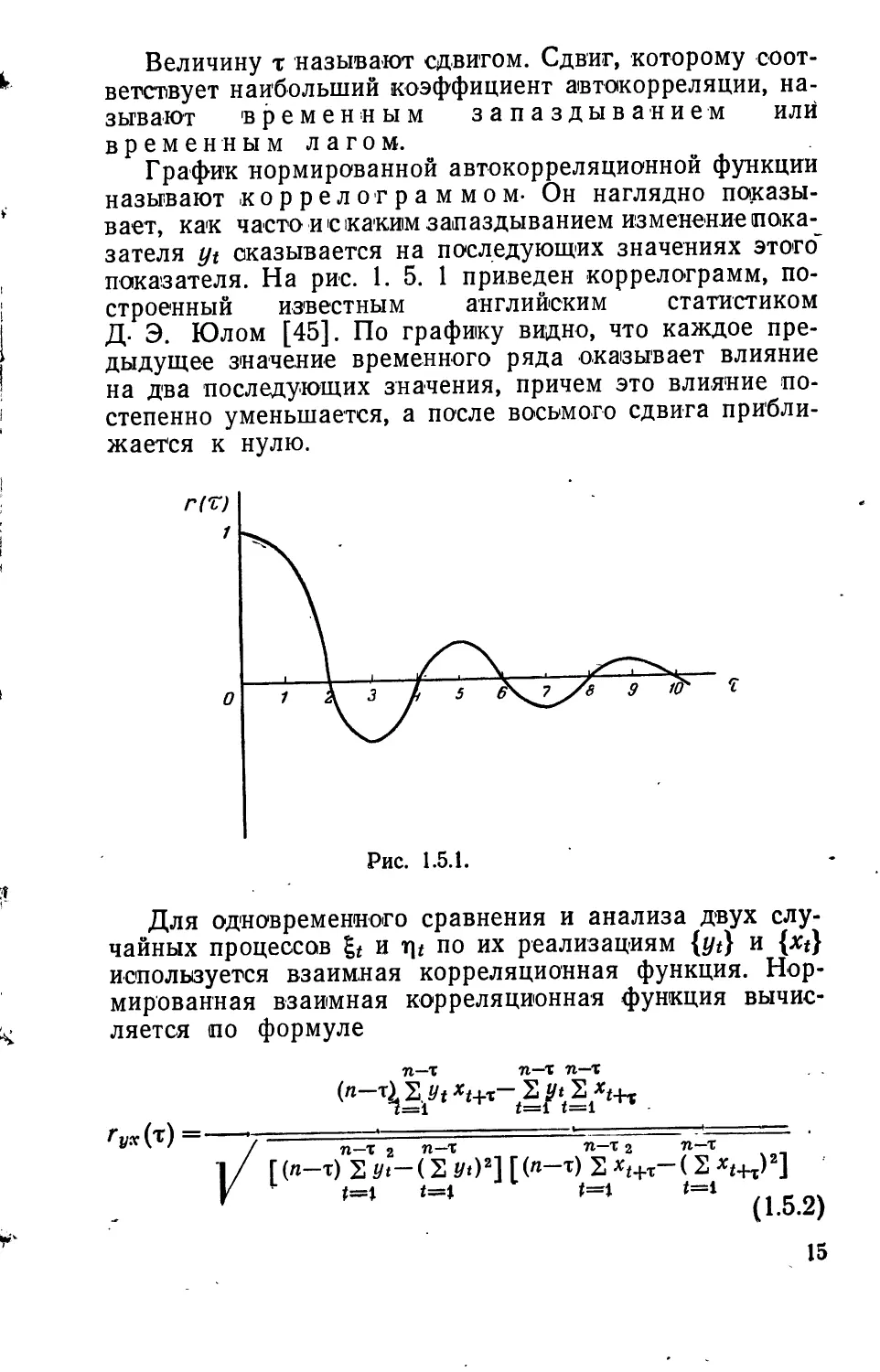
График нормированной автокорреляционной функции
называют .коррелограммом- Он наглядно
показывает, как часто и с каким запаздыванием изменение
показателя yt оказывается на последующих значениях этого"
показателя. На рис. 1. 5. 1 приведен коррелограмм,
построенный известным английским статистиком
Д- Э. Юлом [45]. По графику видно, что каждое
предыдущее значение временного ряда оказывает влияние
на два последующих значения, причем это влияние
постепенно уменьшается, а после восьмого сдвига
приближается к нулю.
Рис. 1.5.1.
Для одновременного сравнения и анализа двух
случайных процессов It и i\t по их реализациям {yt} и {xt}
используется взаимная корреляционная функция.
Нормированная взаимная корреляционная функция
вычисляется по формуле
71—Т 71—Т
г ух
(т)=-
{п~х\Ъ?* Xt+x~tlL? *f2i**+«
/
П—1 2 П—% 71—Т 2 71—Т
[(я-т) Z </«-( 2 yt)2] [<«—*) Б *н-т-( 2 xt.)*]
(1.5.2)
15

На рис. 1.5-2 изображена /взаимная корреляционная
функция, построенная для сопоставления количества
введенных производственных мощностей на конец года в
цементной промышленности СССР с выпуском цемента
[29]. Из рисунка видно, что наибольшее значение
взаимная корреляционная функция принимает на третьем
и четвертом сдвиге. Между вводом мощностей и
«наибольшим эффектом от их использования существует
временной лаг в три года. Только на четвертый год
после введения мощностей можно ожидать наибольшего
прироста в производстве цемента.
Ъхт\
Щ
Щ
0,в\ . u__i l_j 1 1 »
0123Ь5678 Т
РИС. 1.6.2. f
Из различных разновидностей случайных процессов
лучше всего изучены так называемые стационарные
случайные процессы. Случайные .процессы, протекающие во
времени приблизительно однородно и имеющие вид
непрерывных случайных колебаний вокруг некоторого
среднего значения, причем ни средняя амплитуда, ни
характер этих колебаний не обнаруживают существенных
изменений с течением времени, называются
стационарными [6]. Всякий стационарный процесс можно
рассматривать как процесс, неопределенно долго
продолжающийся во времени. В связи с этим при
проведении исследований в качестве начала отсчета можно
выбирать любой момент времени. При этом на любом ин-
16

тервале времени должны быть получены одни и те же
характеристики.
Условия стационарности заключаются в следующем:
1) M[g*]=const ; (1.5.3)
2) Ъ(*<А)=Лг(т), (1.5.4)
где x=ti—tj.
Из формулы (1. 5. 4) видно, что величина
автокорреляционной функции не зависит от начала отсчёта, а
только от промежутка т, т. е- числа сдвигов.
Одним из важнейших свойств стационарного
случайного процесса является эргодичность, состоящая в
том, что каждая отдельная реализация случайного
процесса является как' бы полномочным представителем
всей совокупности возможных реализаций [6]. Отсюда
для эргодических процессов основные характеристики
можно приближенно вычислять не по нескольким его
реализациям, как это делается в общем случае, а по
какой-либо одной реализации, взятой за достаточно
большой промежуток времени.
В экономической практике в большинстве случаев
приходится иметь дело со случайными процессами,
имеющими вполне определенную тенденцию развития во
времени. Такие процессы называются нестационар-
н ы м и. Характеристики нестационарных случайных
процессов меняются во времени, т- е. зависят от начала
отсчета. В ряде случаев нестационарные случайные
процессы на определенных интервалах времени условно
могут быть приняты за стационарные. Поэтому для
анализа экономического развития достаточно использовать
предположение, что процесс является стационарным в
течение определенного периода т начиная с момента t0
и будет оставаться стационарным еще в какой-то
промежуток времени /. Такие процессы исследовались,
например, в работах [12], [35] и были названы [U,m,l]
процессами. На них были перенесены без существенных
изменений все основные выводы теории стационарных
случайных процессов.
Особенностью экономического развития является тот
факт, что случайные процессы в экономике как бы
разбиваются на некоторую систематическую составляющую
и случайные отклонения от нее. Это находит свое
выражение в том, что временные ряды часто представляются
2. Заказ 3199
17

в виде суммы:
yt=f(t).+ ei9
(1.5.5)
где f(t) — некоторая неслучайная функция времени;
et — случайная величина с нулевой средней и
дисперсией D [et].
Функцию f(t)t характеризующую
детерминированную составляющую временного ряда, называют
трендом. Тренд отражает влияние на уровень
экономического явления некоторых постоянно действующих
факторов, специфичных для каждого явления.
Случайную составляющую е*, выражающую
отклонения от тренда, называют ел уч айн ой
компонентой- Случайная компонента отражает действие
случайных факторов на уровень экономического явления.
Применение методов теории случайных процессов
для анализа экономических временных рядов в
значительной мере связано с проблемой исследования
случайной компоненты et, ее сравнения с другими случайными
величинами, обладающими известными свойствами, и
вычисления статистических характеристик случайной
компоненты и т. д. Это объясняется тем, что при
краткосрочном и в определенной мере при среднесрочном
прогнозировании результаты прогнозов тесно связаны со
случайной компонентой, в то время как при
долгосрочном прогнозировании основное значение имеет
определение тенденции и взаимосвязей между факторами [31].
Для случайной компоненты при вычислении
автокорреляционной функции формула (1. 5- 1) упрощается и
принимает вид:
2 е* ef+T
4W- ^F-т—' (L5'6)
2 zt
* = i
Соответственно для вычисления взаимной
корреляционной функции между случайными компонентами et и
zt формула (1.5.2) преобразуется в
п-х
2 etzt+T
г (т)= — ^ • (1.5.7)
I/ 2 zt 2 zt+T
18

Дальнейшим обобщением стационарных случайных
процессов являются процессы со стационарными
приращениями. Случайный процесс & называется процессом
со стационарными приращениями, если при любом
фиксированном временном сдвиге т процесс fe—h-x)
является стационарным. Очевидно, что любой
стационарный процесс является одновременно случайные
процессом со стационарными приращениями, но не наоборот-
Можно ввести более общее понятие случайного процесса
It со стационарными /г-ми приращениями, для которого
A"b = St-/fc-T+Cn1gf^--"+'(-l),Vnt (1.5.8)
представляет стационарный случайный процесс
[11, кн. 1].
Например, если рассматривается случайный процесс
со стационарным вторым ориращением, то он отражает
изменение такого экономического явления, которое
развивается в среднем с постоянным ускорением.
Наиболее актуальными (с точки зрения
экономических исследований) задачами в области временных рядов
являются задачи сглаживания и разложения, а также
прогнозирования.
Кратко сформулируем эти защачи:
1. По имеющейся реализации (временному ряду) {уг)
некоторого случайного процесса It требуется определить
наилучшим (в определенном смысле) образом оценку не-
А
которой неслучайной компоненты (тренда) f(t),
являющуюся в каждый фиксированный момент времени
средним значением случайной величины It и
отражающую основные закономерности в поведении исследуемой
характеристики во времени.
Решение задачи сглаживания, т. е. построение ста-
л
тистической оценки f(t) для истинного, неизвестного
нам тренда f(t) на основании имеющейся реализации
{yt} исследуемого процесса It, позволяет продвинуться
в решении таких актуальных проблем, как проблема
разложения и проблема прогнозирования.
Проблема разложения заключается в подробном
анализе и классификации влияющих факторов на главные
(регулирующие) и второстепенные (случайные), а
затем внутри главных на эволюционные, периодические,
сезонные и т. п. Что касается проблемы прогнозирова-
*2
19

ния, то она, как правило, включает в себя в качестве
предварительного этапа решение задачи сглаживания.
2. По имеющимся наблюдениям ytl , yt2 » —> Угп
процесса It в некотором смысле наилучшим образом
предсказать его значения на периоды tn+u *n+2, ..., tn+u
Подобная постановка задачи вполне корректна, так как
значение процесса It в любой момент времени U часто
зависит от значения данного процесса ib предыдущие
моменты времени.

Глава il
ОПРЕДЕЛЕНИЕ
ОСНОВНОЙ ТЕНДЕНЦИИ
ВРЕМЕННЫХ РЯДОВ
2.1. ПОНЯТИЕ ОСНОВНОЙ ТЕНДЕНЦИИ
„ Важнейшей задачей анализа временных
рядов является определение основной закономерности
изменения изучаемого явления во времени. Основные
закономерности экономических явлений устанавливаются
политической экономией с помощью
теоретико-экономического анализа. В качестве инструмента такого
анализа может служить метод абстракции, который применил
К. Маркс при изучении экономических законов
капитализма.
Так, например, одним из общих экономических
законов; действующих во всех общественно-экономических
формациях, является закон повышающейся
производительности общественного труда. Этот закон не мог быть
выведен чисто статистически. Наоборот, он был
установлен путем абстрагирования от взаимно переплетающихся
тенденций экономической действительности.
Абстрагирование позволяет проявляться этому закону лишь в фор-'
ме основной тенденции.
Обычно считают, что. основная тенденция есть
результат влияния комплекса причин, действующих
постоянно на изучаемый процесс в течение длительного
периода, т. е. она характеризуется детерминированной
составляющей временного ряда.
При изучении временных рядов возникает задача
описания и анализа явления за определенный период
времени, в течение которого оно эволюционирует, меня-
21

ется, прогрессирует, воздействует как осйоваая причина.
или как одна из множества причин на другие явления.
Для того чтобы выявить общую тенденцию изменения
экономических явлений в течение изучаемого периода
времени, следует провести сглаживание временного ряда.
Необходимость сглаживания временных рядов
обусловлена тем, что помимо влияния на уровни ряда главных
факторов, которые в конечном счете и формируют
.конкретный вид неслучайной компоненты (тренда), на них
действует большое количество случайных факторов,
которые вызывают отклонения фактических уровней от
тренда. Результат этого воздействия и формируется с
помощью остаточной случайной компоненты в уравнении
у«=/(0+ви (2.1.1)
Такое разложение временных рядов использовал
К. Маркс, рассматривая динамику рыночных цен,
отклоняющихся от регулирующих их цен производства:
«Рыночные цены поднимаются выше и падают ниже этой
регулирующей цены производства, но такие колебания
взаимно уничтожаются. Если рассмотреть данные о
ценах за продолжительный период, устранив те случаи,
когда вследствие изменения производительной силы
труда изменяется действительная стоимость товаров, а
также те случаи, когда процесс производства нарушается
какими-либо естественными или общественными
'бедствиями, то мы будем поражены прежде всего
относительно узкими пределами отклонений и затем регулярностью,
с которой такие отклонения уравновешиваются»1*
Сам факт отклонения от сложившейся тенденции
требует тщательного анализа и, быть может,
соответствующих оперативных действий. Всегда существует
опасность сгладить под видом «отклонений»
существенные изменения показателей, отражающие важнее
экономические факты, или выравнить такие уровни,
самое существо которых не допускает подобной
их-обработки [3]. Целью анализа, временных рядов
экономических явлений за определенный интервал времени
является выделение тенденций их изменения за
рассматриваемый период, которая покажет общую
наблюдаемую картину развития изучаемого явления.
1 К. Маркс и Ф. Энгельс. Соч., изд. 2, т. 25, ч. II, с. 431.
22

Краткосрочные тенденции часто бывают обманчивы,
вследствие чего их ошибочное истолкование может
пагубно сказаться на принимаемых . решениях. При их
анализе возникает чрезвычайно важная, хотя и
нелегкая, задача — определить правильное соотношение
между долгосрочными и краткосрочными тенденциями [3].
Все методы сглаживания временных рядов с целью
выявления основной тенденции исходят из фактического
состояния явления, которое имело место в течение
прошедшего /периода. На практике тренд определяют
эмпирически, чаще всего на основании графического
анализа или же путем использования некоторых критериев
(например, путем сравнения различных кривых по
среднеювадратической ошибке).
Рассмотрим наиболее распространенные способы
определения тренда, базирующиеся на сглаживании
временных рядов.
2.2. СГЛАЖИВАНИЕ ВРЕМЕННЫХ РЯДОВ
ПО МЕТОДУ НАИМЕНЬШИХ КВАДРАТОВ
Метод наименьших квадратов при
сглаживании временных рядов можно рассматривать как
некоторый вычислительный прием для получения оценки
детерминированной компоненты /(/), которая
характеризует тренд изучаемого процесса.
В экономике наиболее часто применяются функции
v
y(f)=ao+-2 ad* (2.2.1)
И I
v
y(t)=e «-' , (2.2.2)
Параметры функций (2.2.1) и (2.2.2) имеют
качественный экономический смысл и легко интерйретируются.
Так, например, уравнение прямой (полином первой
степени)
y(t)=a6+ait (2.2.3)
характеризует постоянный прирост, равный ах едини-,
цам, при начальном уровне а0.
В уравнении параболы второго порядка (полином
второй степени)
y(t)=aQ+axt+azP (2.2.4)
23

коэффициент а{ выражает начальную скорость роста, а
коэффициент а2 — постоянную скорость изменения
прироста. Бели уровень явления растет с ускорением, то
величина этого ускорения в среднем за изучаемый
период равна 2а2 единицам.
Экспонента
а0+аЛ
y{t)=e (2.2.5)
отражает постоянный относительный рост, равный
eai единицам, а экспонента
0(0 "* (2-2.6)
характеризует постоянный относительный прирост,
равный е2а* единицам [36].
Оценки я0, й\9 а<2, ..., ар в формулах (2.2.1) и (2.2.2)
находятся методом наименьших квадратов, сущность
которого состоит в отыскании таких параметров, при
которых сумма квадратов отклонений расчетных
значений уровней, вычисленных по искомой формуле, от
их фактических значений была бы минимальной.
Математический аппарат метода наименьших
квадратов описан в большинстве работ по математической
статистике, поэтому нет необходимости подробно на
нем останавливаться. Отметим только, что для
нахождения параметров прямой (2.2.3) необходимо решить
систему уравнений:
nao+a{Zt2=2y\
aoLt + a{2A=2,yt» (2.2.7)
Система уравнений (2.2.7) упрощается, если
значения t подобрать таким образом, чтобы их сумма
равнялась нулю, т. е. начало отсчета времени перенести^
в середину рассматриваемого периода.
Если 2/=0, то а0=—— , fli= / .
В общем виде систему уравнений для нахождения
параметров полинома (2.2.1) можно записать как
2y = aort+ai2tf + a2f2+"'+ap2/*;
S yt = aQZ t+ax 2 t*+a22 /3+ - + ap 2 *p+* ; (2.2.8)
S^p = a02^ + ai2^+1+a22^+2+- + ap2^ •
При сглаживании временного ряда по экспоненте
(2.2.2) для определения параметров следует применить
24

метод наименьших квадратов к логарифмам исходных
данных.
Выбор формы кривой для сглаживания в
определенной степени зависит от целей сглаживания:
интерполяции или экстраполяции. В первом случае основной целью
является достижение наибольшей близости к
фактическим уровням временного ряда. Во втором — выявление
основной закономерности развития явления, в
отношении которой можно выдвинуть гипотезу, что она на
некоторое время сохранится в будущем.
Теоретический анализ сущности изучаемого явления,
изменение 'которого отображается временным рядом,
является основой для выбора кривой. Иногда
принимаются во внимание соображения о характере роста
уровней ряда. Так, если рост выпуска продукции в
плане предусматривает увеличение в арифметической
прогрессии, то сглаживание производится по прямой.
Если же оказывается, что рост идет в геометрической
прогрессии, то сглаживание надо производить по
показательной функции.
Сглаживание по показательной функции широко
применяется в практике статистических исследований,
поскольку характер динамики многих
социально-экономических явлений (увеличение объема промышленной
продукции, рост капитальных вложений, рост
численности персонала по всему народному хозяйству и т. п.)
соответствует гипотезе о росте в геометрической
прогрессии. Особенно часто такое сглаживание
применяется для временных рядов с равноотстоящими
уровнями, в которых промежуток времени между взятыми
годами составляет не один год, а несколько лет.
Сглаживание временных рядов методом наименьших
квадратов qлyжит для отражения закономерности
развития изучаемого явления. В аналитическом выражении
тренда время рассматривается как независимая
переменная, а уровни ряда выступают как функция этой
независимой переменной. Ясно, что развитие явления
зависит не от того, сколько лет прошло начиная с
отправного момента, а от того, какие факторы влияли на его
развитие, в каком направлении и с какой
интенсивностью. Развите явления во времени выступает как
результат действия этих факторов.
25

Выявить основную тендейцшю аналитическим Meto-
дом означает предать однообразное развитие
изменяющимся процессам <в течение рассматриваемого периода
времени. Правильно установить тип кривой, тип
аналитической зависимости от времени — одна из самых
трудных задач статистики. Поскольку сглаживание
позволяет выразить закономерность развития во времени, к
выбору способа сглаживания и определению формы
кривой следует подходить с особой тщательностью.
Подбор .вида функции, описывающей тренд,
параметры которой определяются методом наименьших
квадратов, производится в большинстве случаев
эмпирически, путем построения ряда функций и сравнения
их между собой по величине среднеювадратической
ошибки, вычисляемой по формуле
/п А
S (yi-yt)*
^ (2.2.9)
где уг — расчетные значения уровней временного рада;
Ух — фактические уровни временного ряда;
п — число уровней во временном ряду;
р — число параметров, определяемых в формулах,
описывающих тренд.
Ф. Миллс дает некоторые практические
рекомендации для подбора вида функции, описывающей тренд
[17, с. 349—350]:
1. Если значения t образуют арифметическую
прогрессию, а соответствующие значения у —
геометрическую прогрессию, то уравнение тренда выражается
показательной кривой
i y(t)=aoaif * (2.2.10)
2. Если связь между логарифмами у и / линейна,
то описание тренда целесообразно производить по
степенной модели
y(t)=a0tai ..• (2.2.11)
По уравнению (2.2.11) также можно выбирать вид
тренда, если значения t и соответствующие значения у
будут расположены в порядке геометрической
прогрессии.
26

3. Бели значения t расположены в порядке
арифметической прогрессии, а первые разности
соответствующих значений у постоянны, то тренд может бытьооисан
прямой
y(t)=ao+ait «i (2.2.12)
4. Если значения t расположены в порядке
арифметической прогрессии, а р-е разности соответствующих
значений у постоянны, то в качестве функции,
описывающей тренд, можно принять полином р-й степени
y(t)=a0+ait+a2t2+-+antP * (2.2.13)
Большую помощь в выборе вида функций f(t)
могут оказать личный опыт и знания экономиста. В
остальных же случаях, когда вид функций определяется
л
эмпирически, полученную оценку тренда f(t)
рассматривают как некоторую интерполяционную формулу,
которая может оказать помощь экономисту для
анализа временных рядов. Интерпретировать ее как
формулу, выражающую закономерность изменения
процесса на изучаемом -интервале времени, следует с большой
осторожностью.
Необходимо отметить, что для сглаживания эконо:
мических временных рядов нецелесообразно
использовать функции, содержащие большое число параметров,
так как полученные таким образом уравнения тренда
(особенно при малом числе наблюдений) будут
отражать случайные колебания, а не основную тенденцию
развития явления [4].
2.3. СГЛАЖИВАНИЕ ВРЕМЕННЫХ РЯДОВ
С ПОМОЩЬЮ СКОЛЬЗЯЩЕЙ СРЕДНЕЙ
Одним из наиболее старых и широко
известных методов сглаживания временных рядов является
метод скользящих средних. Применяя этот
метод, можно элиминировать случайные колебания и
получить значения, соответствующие влиянию главных
факторов. Сглаживание с Помощью скользящих средних
основано на том, что в средних величинах взаимно
погашаются случайные отклонения. Это происходит
вследствие того, что первоначальные уровни временного
рада заменяются средней арифметической величиной
внутри выбранного интервала времени. Полученное
27

значение относится к середине выбранного периода.
Затем период сдвигается на одно наблюдение и расчет
средней повторяется, причем периоды определения
средней берутся все -время одинаковыми. Таким
образом, в каждом случае средняя центрирована, т. е.
отнесена к серединной точке интервала сглаживания и
представляет собой уровень для этой точки. При
сглаживании временного ряда скользящими средними в
расчетах участвуют все уровни ряда. Чем шире интервал
скольжения, тем более плавным получается тренд.
Сглаженный -ряд .короче первоначального на (к—1)
наблюдений (к — величина интервала сглаживания). При
больших значениях к колеблемость сглаженного ряда
значительно снижается. Одновременно заметно
сокращается количество наблюдений, что создает трудности.
Выбор интервала сглаживания зависит от целей
исследования. При этом следует руководствоваться тем,
в какой период времени нас интересует действие, а
следовательно, и устранение влияния случайных факторов.
Например, для сглаживания временного ряда
производительности труда, планирование которой рассчитано
на пятилетний период, очевидно, целесообразно брать
пятилетний период сглаживания.
При сглаживании временных рядов отдельных
экономических показателей наряду с пятилетним периодом
в ряде случаев целесообразно выбирать и другие
периоды. Например, в отраслях с длительным
производственным циклом (судостроение и другае отрасли) для
анализа временных рядов полезно в качестве периода
сглаживания брать продолжительность
производственного цикла или же при изучении временных, рядов
урожайности следует обращать внимание на тип
динамики (преобладающая периодичность: двухлетняя,
трехлетняя и др.) и периоды развития
сельскохозяйственного производства [15].
<С выбором интервала сглаживания связан вопрос о
количестве уровней ряда, участвующих в расчете
скользящей средней, и технике этого расчета. Если число
членов интервала сглаживания нечетное, то
полученные значения скользящей средней приходятся на
средний член интервала скольжения. При четном
количестве уровней полученные значения скользящей средней
нельзя отнести ни к одному уровню ряда — скользящие
28

средние будут располагаться в промежутках между
уровнями.
Для первого случая скользящая средняя будет
вычисляться по формуле
2т
Л yi + yi + i+-+yi+2m ЛоУ*+к
yi+m = 2тТ\ = ~2тТГ • (2-3-1>
Для второго случая скользящая средняя
определяется следующим образом:
1 1 1 2m-l I
А — ^i+^i + iH h 7T#i + 2m . -Т У1+ 1> У1+к+ — У1+2т
Л 2 2 2 h=o 2
yi+m= —
2m 2m
(2.3.2)
Для формул (2.3.1) и (2.3.2)
л
Уг+т — величина (Л-т)-й скользящей средней;
у г — i-й уровень временного ряда (i= 1, 2," ...,
п — 2т);
т — заданное целое положительное число, с помощью
•которого определяется величина интервала
сглаживания;
\тг
[т1-
—» если /г четное число;
п-\
—— , если д нечетное число;
п — число уровней временного ряда;
к—переменный индекс для интервала сглаживания
(к = 0, 1, 2, ..., 2т).
В тех случаях, когда известно, что внутри
интервалов сглаживания имеет место нелинейная тенденция,
для сглаживания временных рядов используются
взвешенные скользящие средние. Их значения
определяются та.к. Внутри каждого интервала сглаживания уровни
описываются полиномом р-к степени:
J=flo+'2 fli/* •. (2.3.3)
Параметры этого полинома находятся с помощью
метода наименьших квадратов. Взвешенную
скользящую среднюю для взятого интервала определяют как
средний член сглаженных на основании полинома
29

(2.3.3) уровней временного ряда. Проделав такие
расчеты для всех интервалов сглаживания, получим
взвешенную скользящую среднюю вдоль всего ряда.
Например, если в интервал сглаживания входят
пять наблюдений, а тенденция может быть
представлена параболой второго порядка, то сглаженный
серединный уровень во взятом 'интервале будет
выражать значение тенденции в начале отсчета. При t—0
начало отсчета, как видно из формулы (2.3.3), равно а0
Для этого случая
ао=~35 (-3#1 + ]2#2+17*/з+12*/4-3*/5), (2.3.4)
где у{ соответствует первому уровню во взятом
интервале сглаживания.
Рассчитанные таким способом веса обладают
двумя основными свойствами:
1) сумма весов равна единице;
2) теса симметричны относительно середины
интервала сглаживания.
В нниге Дж, Юла и М. Кендалла [37] приведены
веса для определения взвешенных скользящих средних
для случаев, когда уровни временного ряда внутри
выбранного интервала сглаживания описываются
полиномами до пятой степени включительно.
Достоинством метода скользящих средних является
наглядность при определении вида тренда и простота в
истолковании скользящей средней.
В то же время скользящая средняя имеет ряд
недостатков. При малом числе наблюдений метод часто
приводит к искажению тенденции; выбор величины
интервала сглаживания часто трудно обосновать, а от этого
зависит форма кривой; при определении скользящей
средней для дальнейших расчетов теряются начальные
и конечные уровни ряда. Кроме того, тренд,
полученный с помощью скользящих средних, не имеет
количественного .выражения, т. е. скорость изменения ряда не
известна.
2.4. ДРУГИЕ МЕТОДЫ СГЛАЖИВАНИЯ
ВРЕМЕННЫХ РЯДОВ
Сглаживание временных рядов с помощью
полинома Лагранжа. Сглаживание временных рядов с
помощью полинома Лагранжа предполагает, что
уровни не имеют резких регулярных колебаний.
30 ~

Пусть (t/o, *o), (уи tx), ..., (ynt tn) представляют
собой (п+1) пар соответствующих значений двух
переменных j/h(v причем y=f(t). Заменим данную
функцию полиномом р-и степени. Тогда интерполяционный
полином Ла-гранжа можно записать как
v(t\-f(t\ <^H^>-('-'"> ,
М)-№ (ы.)р,-«.«м.)+-
|£/, ч (*-*о) (*"*») "('-*.) , ' /0>|1.
, f/, , (<-M(Wi)-(w-i)
~гД'п)
(*»-*o)('»-'i)-('»-'n-i)
Число членов и, следовательно, степень полинома
зависят от количества членов последовательности,
принятых для определения тенденции.
Применение формулы (2.4.1) связано с большим
число»м вычислений. Кроме того, использовать ее следу-
ет„ с осторожностью, так как если значения
независимой переменной взяты далеко друг от друга, то
результаты могут быть весьма неточные.
Сглаживание временных рядов с помощью конечных
разностей. Пусть временной ряд ух описывается
полиномом р-й степени
yt=a0+j ait* < (2.4.2)
i = l
Для полинома р-й степени можно вычислить
первые разности Д(1)*=г/*+1 — Уь вторые разности AS2h =
Общая формула р-й разности:
Р(Р—1)
A(p)=f/p-pj/p-i+ 2?—Ур-2-
р(р-1)(р-2) .! Пв<| /OAQ\
3! 2/р-з+,—_+(-1)рУо • (2.4.3)
Известно, что (р+1)-я производная полинома р-й
степени равна нулю в любой точке. Следовательно,
(р+1)-я разность полинома р-й степени обращается в
нуль, а (разности р-го порядка полинома р-й степени
постоянны. Таким образом, взяв р-ю разность, мы тем
самым исключим тренд, выраженный полиномом р-й
степени.

Глава III
СТАТИСТИЧЕСКИЙ "?^'
АНАЛИЗ СЕЗОННОСТИ
Одна из задач анализа временных рядов
состоит в выявлении сезонности. К сезонным относят
такие явления, которые обнаруживают в своем
развитии определенные закономерности, более или менее
регулярно повторяющиеся - из месяца в месяц, из
квартала в квартал.
Под сезонностью иногда понимают неравномерность
производственной деятельности в отраслях
промышленности, связанных с переработкой
сельскохозяйственного сырья, поступление 'которого зависит от времени
года. Кроме того, сезонность может возникать из-за
сезонного характера спроса на товары, производимые
промышленностью, и т. д.
Как бы ни проявлялась сезонность, она наносит
большой ущерб народному хозяйству, который
заключается в неравномерном использовании оборудования и
рабочей силы, неравномерной поставке сырья и
загрузке транспорта в отраслях, связанных с сезонным
производством. Изучение сезонных колебаний необходимо
для более ритмичной работы предприятий.
Статистическое исследование сезонности ставит
следующие задачи: численно выразить проявление
сезонных колебаний; выявить их силу и характер в
условиях отдельных отраслей народного хозяйства;
вскрыть факторы, вызывающие сезонные колебания;
найти экономические последствия проявления
сезонности.
32

3.1. ИНДЕКСЫ СЕЗОННОСТИ
Задача статистического изучения
сезонности— выявление силы и характера ее проявления в
условиях отдельных отраслей народного хозяйства —
наиболее разработанная часть всей проблемы. Начиная с
20-х годов нашего столетия, вопрос о силе и характере
проявления сезонных колебаний исследовался в
отдельных отраслях промышленности, транспорта, сельского
хозяйства, торговли и т. п. Разработана довольно
подробная методика выявления, статистического описания
и измерения сезонных волн.
Известно несколько способов исследования
сезонных колебаний: способ простых средних; способ
относительных чисел; способ Персонса; способ расчета
сезонных волн, базирующийся на определении тенденции
(методом скользящей средней и методом наименьших
квадратов) (см., например, [2], [16], [17]. Наиболее
точным, а поэтому и наиболее распространенным
является последний способ, который мы и будем
рассматривать в данной работе.
Индексы сезонности являются показателями,
характеризующими результаты сравнения фактических
уровней данного месяца или квартала с уровнями,
исчисленными при выявлении основной тенденции для того
же месяца или квартала. Для простоты изучения
характера проявления сезонности иногда пользуются
разностью фактического уровня данного месяца
(квартала) и среднемесячного (среднеквартального) уровня за
год.
Важнейшим вопросом для рассматриваемого
способа является вопрос о методе нахождения тренда
данного временного ряда. Как мы видели в предыдущей
главе, методы нахождения основной тенденции развития
разнообразны. Практически же при выявлении тренда
ряда, подверженного сезонным изменениям, можно
воспользоваться методами скользящих средних и
наименьших квадратов. Скользящая средняя,
применяемая для этой цели, имеет строго определенный период
скольжения—12 месяцев, или 4 квартала, поскольку
сезонность проявляется в пределах года. Важно та<кже
скользящую среднюю относить к определенному
месяцу или кварталу и поэтому при 12-или4-чле)Нном
скольжении приходится пользоваться центрированием.
3. Заказ 3199
3S

Если определить индекс сезонности как отношение
фактического уровня к уровню, рассчитанному по
12-месячной скользящей средней, то можно предполагать,
что при исчислении такой средней повторяющиеся
колебания с периодом в 12 месяцев будут сведены к нулю.
Следовательно, получается средняя, свободная от
периодических колебаний. Если индекс сезонности
измерить в 'Процентах, то отклонения от 100% и
представляют собой выражение сезонности того или иного
месяца. Аналогичное высказывание можно сделать и в
отношении квартальных данных. _ Вполне понятно, что
такие отклонения, взятые за ряд лет, будут колебаться.
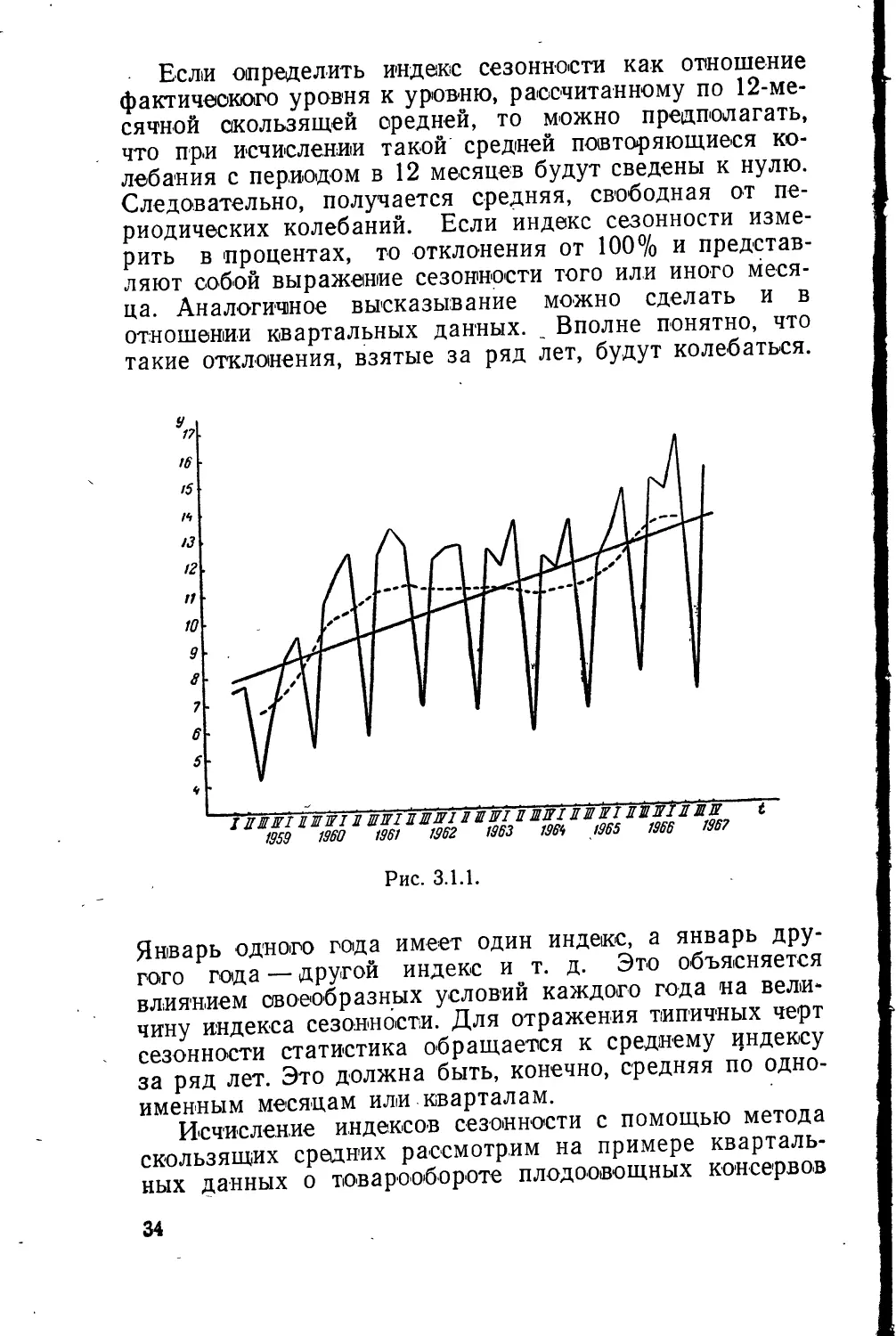
/ ДШШ1MMWIЛ ШШ11ШШ1ЛШШ1 ЛШЛ1ЖШЖ1ЛШЖ1ЛШШ t
1959 1960 1961 1962 1963 1961, /965 1966 196?
Рис. 3.1.1.
Январь одного года имеет один индекс, а январь
другого года — другой индекс и т. д. Это объясняется
влиянием своеобразных условий каждого года на
величину индекса сезонности. Для отражения типичных черт
сезонности статистика обращается к среднему индексу
за ряд лет. Это должна быть, конечно, средняя по
одноименным месяцам или кварталам.
Исчисление индексов сезонности с помощью метода
скользящих средних рассмотрим на примере
квартальных данных о товарообороте плодоовощных консервов
34

вг.Москве запериод с 1959по 1967г.1 (табл.3.1.1, гр.З).
Эти данные представлены на рис. 3.1.1 сплошной
ломаной линией. По рисунку можно сделать первые
предварительные замечания об изменении уровня товарооборота.
Во временном ряду товарооборота наблюдается
более или менее регулярное повторение определенных
изменений, связанных, со сменой сезонов.
Минимальный объем реализации плодоовощных
консервов приходится на третий квартал, когда в продаже
имеется большое количество свежих фруктов и овощей, и
максимальный объем — на второй квартал. В отдельные
годы наблюдалось смещение этого максимума, что было
вызвано в основном внешними факторами и особенно
изменением объема импорта плодоовощных консервов. В
связи с этим, считая, что временной ряд товарооборота
плодоовощных консервов подвержен сезонным
колебаниям, мы допускаем некоторую погрешность.
Показатели сезонности ориентированы на
соответствующие кварталы путем центрирования скользящих
средних. Центрированные скользящие средние нанесены на
график пунктиром (рис. 3.1.1). Центрированная средняя
показывает объем товарооборота при элиминировании
сезонности.
Средние величины из показателей сезонности
(показатели сезонности, как отмечалось выше, исчисляются как
отношение фактических уровней товарооборота к
величине центрированных скользящих средних) по
одноименным кварталам и составят индексы сезонности
реализации плодоовощных консервов. Например, индекс
сезонности для первого квартала равен
114,7'+115,7+119,6+113,5+107,2+107,3+111,0 + 108,1
: _ . = 112,1.
В табл. 3.1.2 (гр. 2) приведены рассчитанные таким
образом индексы сезонности для каждого квартала.
Индексы сезонности, рассчитанные^как средние
процентные отношения, позволяют предполагать, что
сезонный фактор постоянно влияет на количество
реализованных плодоовощных консервов, так как при нахождении
индексов в основном элиминированы случайные факторы,
влияющие на объем товарооборота в данном квартале.
1 Данные заимствованы из работы [20].
3* 35

Таблица 3.1.1
ТОВАРООБОРОТ ПЛОДООВОЩНЫХ КОНСЕРВОВ В г. МОСКВЕ
ЗА 1959—1967 гг.
Годы
1
1959
1960
1961
1962

Квартал
2~
I
II
III
IV
I
II
III
IV
I
и-
III
IV
I
II
III
IV
I
II
Уровни

временного
ряда
7,5
7,7
4,2
6,7
8,6
9,5
5,4
10,7
11,8
12,5
5,8
12,4
13,4
12,7
6,8
12,2
12,6
12,7
Расчет показателей сезонности
с помощью скользящей средней
4-квартальные
суммы
4
26,1
27,2
29,0
30,2
34,2
37,4
40,4
40,8
42,5
44,1
44,3
45,3
45,1
44,3
44,3
4-членные
средние
5
6,5
6,8
7,3
7,6
8,6
9,4
10 1
10,2
10,6
11,0
11,3
11,3
11 1
11,1
11,0
Я О»
« S
со д
2 *
Он О)
S О.
Si
6
6,7
7,1
7,5
8,1
9,0
9,8
10,2
10,4
10,8
11.1
11,2
11,3
П.2
11,1
11,1
11,1
показатели
сезонности
(гр. 3 : гр. 6)Х
ХЮО
* 7
.62,7
94,4
114,7
117,3
60,0
109,2
115,7
120,2
53,7
111,7
119,6
112,4
60,7
1С9,9
113,5
114,4
по уравнению
тренда
расчетные
уровни
8
7,9
8,0
8,2
8,3
8,5
8,7
8,8
9,0
9,2
9,3
9,5
9,6
9,8
10,0
10,1
10,4
10,6
10,6
показатели
сезонности
(гр. 3 :гр. 8)Х
ХЮО
9
94,9
96,3
51,2
80,7
101,2
109,2
61,4
118,9
128,3
134,4
61,1
129,2
136,7
127,0
67,3
121,2
118,9
119,8
36

Продолжение
Годы
г~
1963
*
1964
1.965
1966
1967

Квартал
2~~
III
IV
I
II
III
IV
I
II
III
IV.
I
II
III
IV
I
' 11
III
IV
Уровни

временного
ряда
3
6,8
12,6
11,9
13,6
5,8
12,3
11,8
13,6
6,6
12,0
13,1
14,7
7,9
15,0
14,6
16,6
7,2
15,5
Расчет показателей сезонности
с помощью скользящей средней
4-квартальные
суммы
4
44,1
,44,5
43,8
44,7
43,9
43,6
43,5
43,5
44,3
44,0
45,3
46,4
47,7
50,7
52,2
54,1
53,4
53,9
4-членные
средние
5
11,0
11,2
11,0
10,9
10,9
10,9
П,1
11,0
11,3
11,6
11,9
12,7
13,1
13,5
13,4
13,5

центрированные средние
6
11,1
П,1
11,1
11,0
10,9
10,9
11,0
11,1
11,2
11,5
11,8
12,3
12,9
13,3
13,5
13,5
показатели
сезонности
(гр. 3:гр. 6)Х
Х100
7
59,5
113,5
107,2
123,6
53,2
112,8
107,3
122,5
58,9
1С4,3
111,0
119,5
61,2
112,8
108,1
123,0
по уравнению
тренда
расчетные
уровни
8
10,8
10,9
11,1
11,2
11,4
11,6
11,8
11,9
12,0
12,2
12,4
12,5
12,7
12,8
13,0
13,2
13,3
13,5
показатели
сезонности
Сгр. 3:гр. 8)Х
Х100
9
61,1
115,6
107,2
121,4
50,9
1С6,0
1С0,0
114,3
55,0
98,4
105,6
117,6
62,2
117,2
112,3
125,8 "
54,1
114,8
37

Таблица 3.1.2
ИНДЕКСЫ СЕЗОННОСТИ ТОВАРООБОРОТА ПЛОДООВОЩНЫХ
КОНСЕРВОВ В г, МОСКВЕ ЗА 1959-1967 гг.
'
Квартал
1
Индексы сезонности, исчисленные
с помощью скользящей средней
по способу средней
арифметической
2
по способу
медиан
3
с помощью
уравнения
тренда
4
I 112,1 110,4 111,9
II 119,1 119,0 118,4
III 58,7 60,1 58,3
IV 108,6 111,7 111,0
Иногда при определении индексов сезонности
пользуются медианой из показателей сезонности вместо
средней арифметической. Так, например, для первого
квартала индекс сезонности, исчисленный как медиана из
показателей сезонности, будет - ' —- = 110,4. В гр. 3
табл. 3.1.2 приведены индексы сезонности, рассчитанные
способом медиан для каждого квартала.
Полное элиминирование влияния несезонных
факторов достигается тогда, когда средняя из индексов
сезонности равна 100. Но так как это редко бывает, то следует
производить выравнивание индексов сезонности. В наших
примерах средняя из индексов, исчисленных с помощью
скользящей средней по способу средней арифметической,
равна 99,6, я по способу медиан—100,3. Для
выравнивания необходимо помножить индексы, представленные
в гр. 2 и 3 табл. 3.1.2 на величины, обратные 99,6 и 100,3,
T-e-HaW=1'004«Ha-I^J =0,997.
В табл. 3.(1.3 приведены выравненные индексы
сезонности.
Сравнивая соответствующие индексы сезонности с
выравненными индексами по кварталам, можно увидеть,
что расхождение между ними невелико. Это может быть
объяснено, с одной стороны, относительно небольшой
колеблемостью по одноименным кварталам, а с другой —
повторением колебаний из года в год.
38

Таблица 3.1.3
ВЫРАВНЕННЫЕ ИНДЕКСЫ СЕЗОННОСТИ
Квартал
1
Индексы, рассчитанные
с помощью скользящей средней
способом средней
арифметической
2
способом
медианы
3
с помощью
уравнения
тренда
4
I 112,55 110,08 112,81
II 119,58 118,64 118,52
III 58,94 59,92 58,36
IV 109,03 111,36 111,14
Иногда используется третий способ расчета индекса
сезонности. Для того чтобы индексы сезонности был,и
более устойчивы, рассчитываются средние индексы по
расположению. В ранжированном ряду показателей
сезонности для (каждого квартала отбрасываются самые
высокие и самые низкие значения. Далее определяется
средняя арифметическая из центральных значений
показателей сезонности. Если число индексов четное, то в расчет
средней «берется 4 или б центральных точек, если же
нечетное, то берется 3 или 5 центральных точек. Такая сред-'
няя по расположению не подвержена влиянию крайних
значений.
После определения индекса сезонности лелко найти
уровни временного ряда, в которых элиминировано
влияние сезонности. Для нахождения таких уровней
достаточно фактический товарооборот каждого квартала
поделить на соответствующий выравненный индекс. Пример
определения уровней временного ряда с учетом
элиминированной сезонности для данных 1965 г. приведен, в
табл. 3.1.4.
Из гр. 3 табл. 3.1.4 видно, что после исключения
сезонности колеблемость временного ряда товарооборота не*
велика.
Показателем колеблемости временного ряда за C4et
сезонности служит среднее кв а др этическое отклонение,
^цределяемое по формуле *
о- У~^> л (ЗЛ.17
39

Для выравненных индексов сезонности с помощью
скользящей средней способом средней арифметической
(гр, 2, табл. 3.1.3) среднее квадратическое отклонение,
вычисленное по формуле (3.1.1), равно 24,0, что также
говорит о достаточно большом влиянии на реализацию
плодоовощных консервов сезонного фактора.
Таблица 3.1.4
РАСЧЕТ ТОВАРООБОРОТА ПЛОДООВОЩНЫХ КОНСЕРВОВ В 1965 г.
1млн. pv6.)
Кварталы
1
Фактические
уровни
1*2
Уровни, скорректированные на
сезонность по выравненным индексам
сезонности, исчисленным
с помощью скользящей
средней
по способу средней
арифметической
3
с помощью
уравнения тренда
4
I 11,8 10,5 10,5
II 13,6 11,4 11,5
III 6,6 11,2 11,3
IV 12,0 11,0 10,8
Индексы сезонности могут быть построены и
по-другому. Можно рассматривать для каждого квартала
(месяца) отношение фактического уровня не к показателю,
найденному с помощью скользящей средней, а
рассчитанному по уравнению тренда.В этом случае исчислению
показателей сезонности должно предшествовать
определение тренда временного ряда.
В табл. 3.1.1 приведены уровни, сглаженные по урав-
л
нению тренда1 у=7,70+0,16Н (гр. 8), и показатели
сезонности (гр. 9), на основании которых были определены
индексы сезонности, рассчитанные »по способу средней
арифметической (табл. 3.1.2, гр. 4).
Далее было произведено выравнивание индексов
сезонности (табл. 3.1.3, гр. 4).
1 Линия тренда нанесена на рис. 3.1.1.
40

При сравнении данных табл. 3.1.3 видно, что в
результатах определения выравненных индексов сезонности с
помощью скользящей средней и уравнения тренда имеется
некоторая разница. Последний способ определения
индексов сезонности является более точным.
Рассчитаем далее среднее квадратическое отклонение
по формуле (3.1.1). Оно равно 24,2, что незначительно
отличается от соответствующего значения при определении
индекса сезонности с помощью (скользящей средней.
Проведем расчет товарооборота плодоовощных кон-
сер'вов в 1965 г. с учетом корректировки на (сезонность
'(табл. 3.1.4).
Для повышения устойчивости мадексов (сезонности
были рассчитаны (средние индексы сезонности по
расположению (табл. 3.1.5) для 5 центральных точек. Эти.
индексы, ка.к будет показано ниже, можно иопользовать для
•лрагаозирования товарооборота.
Таблица 3.1.5
СРЕДНИЕ ИНДЕКСЫ СЕЗОННОСТИ (ПО РАСПОЛОЖЕНИЮ)
Квартал
Индекс
Квартал
Индекс
I 109,5 III 58,5
II 119,8 IV 114,4
3. 2. ПРОГНОЗИРОВАНИЕ
СЕЗОННЫХ ЯВЛЕНИЙ
Определив влияние ^сезонного фактора, можно
попытаться использовать найденные закономерности для
прогнозирования дальнейшего развития изучаемого
процесса. Как известно, сезонные временные ряды можно
разложить на следующие компоненты:
Xt = ut + Vt+'et » (3.2.1)
где Uu Vu Bt — составляющие этого ряда, соответственно:
тенденция, кратковременные колебания (сезонные
волны) , случайные колебания.
Тенденция отражает общее изменение ряда за
длительный промежуток времени: постоянный подъем или
постоянное снижение. Тенденция представляется как
плавное непрерывное движение, скрадывающее
скачкообразные изменения в месяцах, кварталах или годах,
г 41

Сезонные волны —это более или менее
регулярные изменения временного ряда, возникающие с
наступлением данного времени года и повторяющиеся с
небольшими отклонениями из года в год. К таким колебаниям
относятся также изменения, не связанные с временами
года, но регулярно повторяющиеся через определенные
промежутки времени. Сезонные колебания обычно имеют
постоянный период.
Случайные колебания вызываются внешними,
случайными причинами, влияние которых сказывается на
уровнях ряда, искажая тенденцию, а также сезонные и
циклические колебания.
Кроме разложения ряда на его составляющие, можно
использовать другие виды анализа, не требующие
выделения и исключения составляющих компонент ряда:
гармонический анализ и некоторые другие методы.
Выявление закономерных изменений динамики явлений
составляет первую фазу прогнозирования. Определив все три
составляющие временного ряда, можно попытаться
использовать .найденные закономерности для
экстраполяции их на перспективу. При этом /можно оценить
значение постоянной компоненты или тренда и краткосрочных
сезонных колебаний. Случайные колебания можно
оценить только вероятностным путем.
При экстраполяции общих закономерностей на
будущий период допускается определенная ошибка: чем
продолжительнее период предсказания, тем вероятнее
сделать большую ошибку. Поэтому следует по мере
получения новых фактических данных пересматривать модели,
В общем виде модель прогноза товарооборота на
любой квартал по каждому из исследуемых показателей
выглядит следующим образом:
А
где tjt — величина товарооборота в момент времени t
(^=1,2,... ,36).
1К—средний индекс сезонности (по расположению)
/с-го квартала (к= 1, 2, 3, 4).
л
tjt — оценка размера товарооборота в момент
времени t.
е* — случайная величина*
42

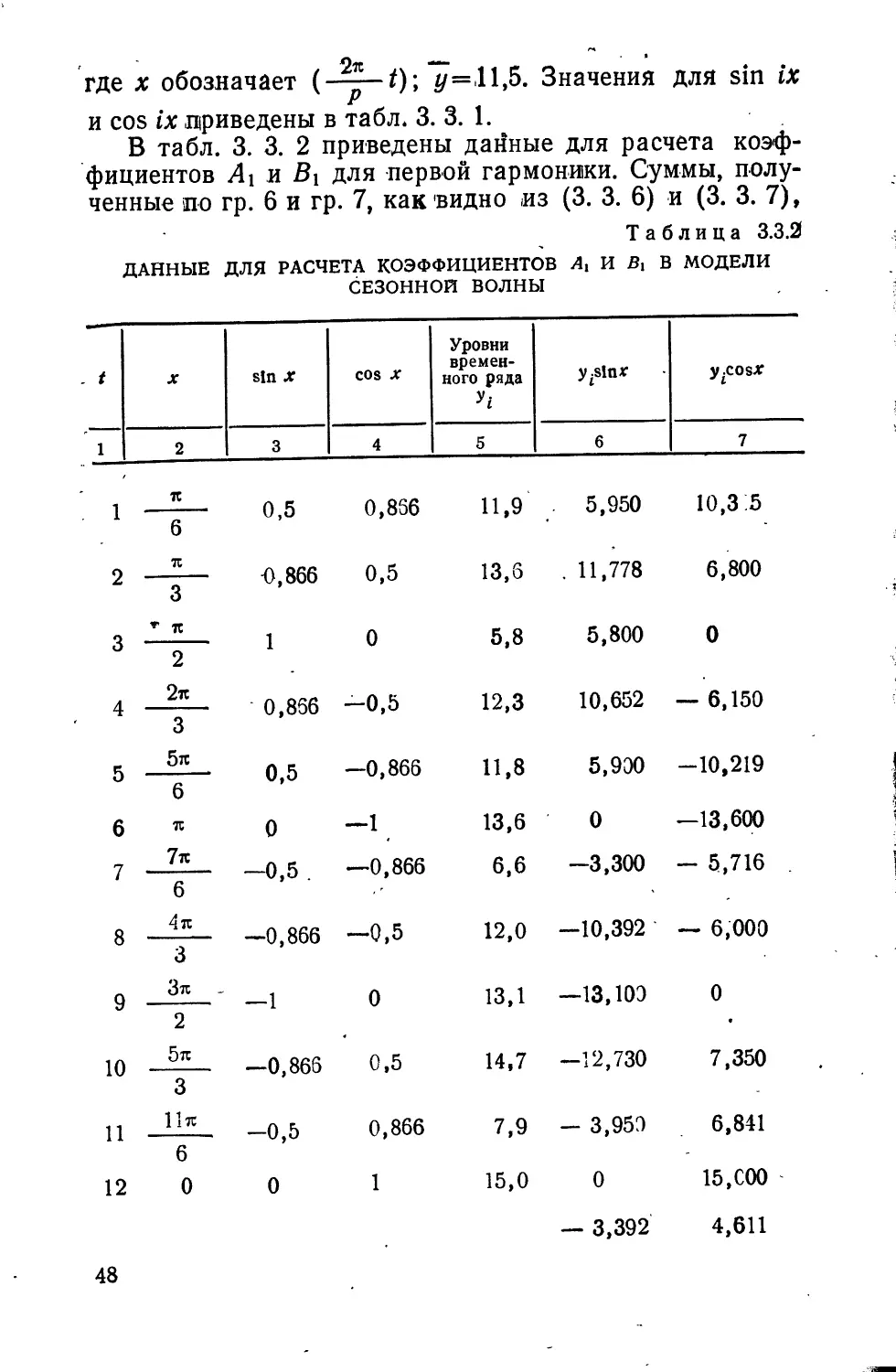
Значения h определяются из табл. 3.1.5, yt — по
уравнению тренда
^=7,70 + 0,161*. (3.2:1)
Ниже ^приведены модели для расчета объема
товарооборота по кварталам:
I — ^ = 1,095(7,7+0,1610+««; (3.2.2)
II — уг= 1,198(7,7+0,161/,) + е<; (3.2.3)
III — # = 0,585(7,7 + 0,161*) +е«; (3.2,4)
IV —#=1,144(7,7 + 0,161/)+е,. (3.2.5)1
В табл. 3. 2. 1 приведены данные по фактическим зна-^
чениям уровней, расчетным значениям, полученным по
моделям (3. 2. 2) — (3. 2. б), и отклонениям фактических
значений от расчетных.
Случайную величину е* точно определить нельзя.
Можно только с определенной вероятностью утверждать,
что вычисленные по моделям (3. 2. 2) — (3. 2. 5) оценки
показателя будут отличаться от истинной на величину
t —- , где t — число, показывающее, во сколько
V п
раз отличается средняя величина от своего отклонения
при определенной вероятности;
Таблица 3.2.1
РЕЗУЛЬТАТЫ РАСЧЕТОВ ПО МОДЕЛЯМ (3.2.2)-(3.2.5) И ИХ СРАВНЕНИЕ
С ФАКТИЧЕСКИМИ ЗНАЧЕНИЯМИ
Годы
Кварталы
I
Фактические
значения
Расчетные
значения
Отклонения
Фактические
значения
II
Расчетные
значения
Отклонения
III
Фактические
значения
Расчетные
значения
Отклонения
IV
Фактические
значения
Расчетные
значения
Отклонения
1959 7,5 8,6-1,1 7,7 9,6—1,9 4,2 4,8—0,6 6,7 9,5—2,8
1960 8,6 9,3—0,7 9,5 10,4—0,9 5,4 5,2 +0,2 10,7 10,3+0,4
1961 11,8 10,0+1,812,5 11,1+1,4 5,8 5,6 +0,2 12,411,0+1,4
1962 13,4 10,7+2,7 12,7 12,0+0,7 6,8 5,9 +0,9 12,211,8+0,4
1963 12,6 11,4+1,212,7 12,7 0 6,6 6,3 +0,3 12,612,5+0,1
1964 11,9 12,1-0,213,6 13,4+0,2 5,8 6,7 —0,9 12,313,3—1,0
1965 11,8 12,8—1,013,6 14,3—0,7 6,6 7,0—0,4 12,014,0—2,0
1966 13,1 13,5—0,414,7 15,0—0,3 7,9 7,4 +0,5 15,014,6+0,4
1967 14,6 14,2+0,416,6 15,8+0,8 7,2 7,8 —0,6 15,515,4+0,1
43

ВЕЛИЧИНА t-
VT
РАССЧИ-
Qzt—среднеквадратическое отклонение случайной
величины е*.
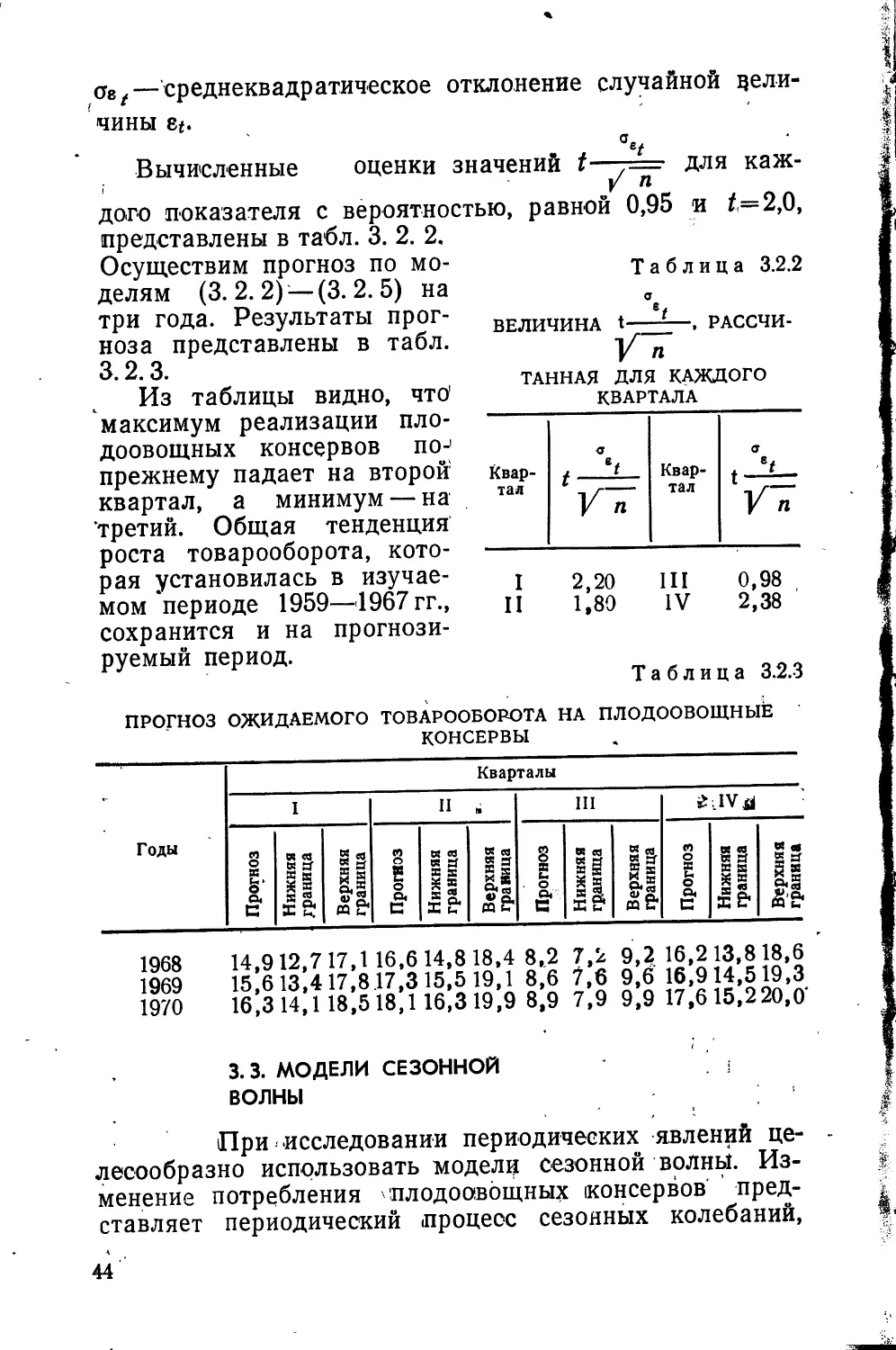
Вычисленные оценки значений t—7= Для каж-
/ п
дого показателя с вероятностью, равной 0,95 и £=2,0,
представлены в табл. 3. 2. 2,
Осуществим ПрОГНОЗ ПОМО- Таблица322
делям (3.2.2) —(3.2.5) на в
три года. Результаты
прогноза представлены в табл.
3.2.3.
Из таблицы видно, что1
максимум реализации
плодоовощных консервов по-1
прежнему падает на второй
квартал, а минимум — на
третий. Общая тенденция
роста товарооборота,
которая установилась в
изучаемом периоде 1959—1967 гг.,
сохранится и на
прогнозируемый период.
ТАННАЯ ДЛЯ КАЖДОГО
КВАРТАЛА

Квартал
VT

Квартал
VH
I
II
2,20
1,80
III
IV
0,98
2,38
Таблица 3.2.3
ПРОГНОЗ
Годы
ОЖИДАЕМОГО
ТОВАРООБОРОТА НА ПЛОДООВОЩНЫЕ
КОНСЕРВЫ
Кварталы
I
Прогноз
Нижняя
Граница
Верхняя
| граница
И ш
Прогяэз
Нижняя
граница
Верхняя
| граница
III
Прогноз
Нижняя
граница
Верхняя
1 граница
£ЛУй :
Прогноз
Нижняя
граница
Верхняя
I граница
1968 14,9 12,7 17,1 16,6 14,8 18,4 8,2 7,2 9,2 16,2 13,8 18,6
1969 15,613,417,8.17,315,5 19,1 8,6 7,6 9,6 16,9 14,5 19,3
1970 16,314,118,518,116,319,9 8,9 7,9 9,9 17,615,220,0'
3. 3. МОДЕЛИ СЕЗОННОЙ
ВОЛНЫ
При-исследовании периодических явлений
целесообразно использовать моделц сезонной волны.
Изменение потребления плодоовощных консервов
представляет периодический процесс сезонных колебаний,
44

вследствие чего для построения модели сезонной волны
можно применить гармонический анализ.
Функцию, заданную в каждой точке изучаемого
интервала времени, можно представить бесконечным
рядом синусоидальных и косинусоидальных функций.
Нахождение конечной суммы членов с косинуса-ми и
синусами называется гармоническим анализом.
Синусоидальная или косинусоадальная функция с
определенным периодом и есть гармоника. Каждый член суммы
представляет собой гармонику с, определенным
периодом. Первая гармоника имеет ^период, равный длине
исследуемого периода. Вторая «имеет период, равный
половине основного, третья — одной трети основного и
т. д. Вообще если есть р наблюдений, то число гармоник
не будет превышать -у- . Если функция носит не
синусоидальный характер, то требуется большее количество
определяющих ее гармоник. И в этом случае получается
просто .математическое представление, эквивалентное
периодической функции. Для функции, носящей
синусоидальный характер, не всегда требуется определять
— гармоник. Изменение периодической функции
хорошо описывается несколькими первыми гармониками.
Если величину изучаемого показателя записать как
2я л 2я 2я 2я
1 2——,•«,* — ,••••£ —.
Р Р р Р
где р — число значений изучаемого показателя или
(Величина периода, т.- е. представить как части длины
окружности, то зависимость соответствующих им значений
показателя запишется следующей суммой^
+A2sm[ — 2tj+B2cos ( —2f) +••• (3.3.1)
или короче
v
у=а0+ [V Aisin ( —it ) ;+Д,cos ( — «)}. (3.3.2)
45

где р — полный период;
i — номер гармоники;
——-г— переменная; .
Aif Вг — коэффициенты гармоник.
. Коэффициенты Аг и Вг оцениваются по методу
наименьших квадратов, т. е. при условии, что
2 (yt-yt)2—+mm. (3.3.3)
Получение формул для коэффициентов облегчается
благодаря свойству ортогональности.
v 2я 2к
2 sin t'tfsin — it
t=i P P
= 0, если 1ф}\ (3.3.4)
P P
= —, если Ь=\ф{)ф— .
Подобные же равенства имеют место, если один член
или оба заменены косинусами. Для оценки параметров
а0, Ai и Вг уравнения (3. 3. 2) используют следующие
формулы:
1 v
а0= — 2 yt ; (3.3.5)
Р t=i
2 v ( 2л \
Ai=- 2 у* sin \—'Л * (3.3.6)
Вг=-2 у, cos! —it •: (3,3.7)
Р t=i х н
Отсюда видно, что а0 есть не что иное, как среднее
значение показателя за период.
Число гармоник, как уже отмечалось, не может
превышать ~ , т. е. i^ -£- * Поэтому по этим формулам
необходимо рассчитывать коэффициенты для {—£- — 1)
гармоник. Для последней гармоники всегда Л=0, В =
~~1Г У% c'os[—- '"»-тг] • Так получается только <в том
случае, если определяются все i=-|-гармоник. Если рас-
46

считывать !< -£- гармоник, то соответственно будет
получено одинаковое количество коэффициентов при
синусах и косинусах. *
Для гармонического анализа товарооборота
плодоовощных консервов наиболее удобным является период
с 12 наблюдениями, так как «брать свыше 12
наблюдений, т. е. более чем З.года, не всегда оправдано тем, что
гармонический анализ основывается на исследовании
колебаний вокруг среднего уровня. Тенденция ряда .при
этом не учитывается. Использование среднего уровня за
3 года, конечно, даст меньшие погрешности, чем замена
тенденции средним уровнем за более длительный
промежуток.
Гармонический анализ использовался для расчета
периодической функции для временного ряда
товарооборота плодоовощных консервов. Для анализа взят пери-*
од с 1964 по 1966 г, (он характеризуется почти постоян-«
ным уровнем). .Наибольшее количество гармоник,
которое можно рассчитывать для этого ряда, равно 6.
Сначала 'была сделана попытка рассчитать периодическую
функцию с четырьмя гармониками, т, е. .получить
«функцию вида
У=у+А\ sin х+А2 sin 2л;+Л3 sin Зл;+"
+А4 sin Ах+Вх cos x+B2 cos 2x+
+ B3cos3x+B4cos4a;, (3.3.8)
Таблица 3.3.1
МНОЖИТЕЛИ ГАРМОНИЧЕСКОГО АНАЛИЗА 12 НАБЛЮДЕНИИ
ДЛЯ РАСЧЕТА КОЭФФИЦИЕНТОВ Л^ И В{
t
а
а»
V
с*
В
СЛ
а
7л
Н
Те
5
С
'аз
«О
О
О
Н
с*
ей
О
О
V
СО
О»
о
о
ТР
ей
О
и
ю
со
8
ч
<о
со
О
о
1 0,5 0,866 1 0,866 0,5 0,865 0,5 0—0,5-0,866-1
2 0,865 0,866 0-0,866—0,866 0,5 -0,5-1-0,5 0,5 ]
3 1 0—10 1 0—1010-1
4 0,866—0,866 0 0,866—0,866—0,5 —0,5 1—0,5—0,5 1
5 0,5 —0,866 1—0,856 0,5 —0,866 0,5 0—0,5 0,866—:
6 0 0 0 0 0-1J 1—11—1 )
7—0,5 0,866—1 0,866—0,5 —0,863 0,5" 0—0,5 0,866 —
8 —0,866 0,866 0-0,865 0,866—0,5 —0,5 1—0,5—0,5
9—1 0 10—1 0 —10 10 —
10 —0,866—0,866 0 0,866 0,866 0,5 —0,5—1—0,5 0,5
П—0,5 —0,866—1—0,866—0,5 0,866 0,5 0—0,5—0,866 —
12 0 0 00 0 1 1111
47

где х обозначает (—^~0*> У=11,5. Значения для sin ix
и cos ix приведены в табл* 3. 3. 1.
В табл. 3. 3. 2 приведены дайные для расчета
коэффициентов А\ и Вх для первой гармоники. Суммы,
полученные по гр. 6 и гр. 7, как видно из (3. 3. 6) и (3. 3. 7),
Таблица 3.3.2
ДАННЫЕ ДЛЯ РАСЧЕТА КОЭФФИЦИЕНТОВ Л, И Л, В МОДЕЛИ
СЕЗОННОЙ ВОЛНЫ
t
1
X
2
sin X
3
cos х
4
Уровни

временного ряда
5
у.sin*
6
y^cosJf
7
3
тс
2
2тс
3
5л
9
10
11
12
48
6
тс
7тс
6
4 тс
3
Зтс
2
5тс
3
11*
6
о
0,5 0,856 11,9 • 5,950 10,3.5
0,866 0,5 13,6 . 11,778 6,800
1 0 5,8 5,800 0
0,856 —0,5 12,3 10,652 —6,150
0,5 —0,866 11,8 5,900 -10,219
0 —1 13,6 0 —13,600
—0,5 . —0,866 6,6 —3,300 — 5,716
—0,866 —0,5 12,0 —10,392 —6,000
—1 0 13,1 —13,100 0
-0,865 0,5 14,7 -12,730 7,350
-0,5 0,866 7,9 - 3,953 6,841
0 1 15,0 О 15,С00
— 3,392 4,611

следует поделить на 6. Таки*м образом А\ = — 0,565 и
5i = 0,769.
В целом модель сезонной волны имеет вид:
*/=11,5-0,565sinх-0,375sin2х+2,751 sin Зх+J
L+_0,029 sin 4x+0,769 cos x+0,417 cos 2*-j
.- 0,433 cos 3x+_0,354 cos 4x. < ,(3.3.9)
В табл, 3.5. 3 даются расчетные значения по
функциям (3.3.9) и (3.3.10) и отклонения от фактических
данных по кварталам.
Средняя ошибка аппроксимации для модели (3.3.9)
составляет "2,0. Теперь определим, какая часть общей
дисперсии у учитывается четырьмя гармониками. Дисперсия,
учитываемая одной гармоникой, определяется по формуле
С2 —
02=—L. , где d=iA2i+B2i. Для последней гармоники
* 2
a2P/2=C2i. Часть дисперсии, учитываемая определенной
гармоникой, представляется в виде отношения величины
С2г/г или С2г к общей дисперсии о2у. Так как никакие две
гармоники не коррелируют между собой, то они не будут
учитывать одну и ту же часть общей дисперсии, т. е.
дисперсии, учитываемые различными гармониками,
складываются. Доля общей дисперсии, учитываемая
гармониками, составляет;
в процентах
первой »♦.••..•, 5,2
второй . 1,8
третьей ...,.„.. 44,5
четвертой ••••••••••• 0,7
Общая доля, учитываемая всеми гармониками,52,2%.
Таким образом, периодическая функция, состоящая
из четырех гармоник, довольно точно улавливает
колебания временного ряда. Наибольшая часть
колеблемости учитывается третьей гармоникой, период которой
совпадает с .периодом сезонности данного ряда. Далее
была рассчитана периодическая функция с шестью
гармониками:
#= 11,5-0,565 sin x-0,375 sin 2x+2,751 sin3x+j
Н- 0,029 sin 4x -0,335 sin 5x+0,769 cos л:+0,417 cos 2x-
-0,433 cos Злг+0,354 cos 4x+0,364 cos 5л: +]
,+ 1,004 cos 6x. (3.3.10)
4. Заказ 3199
49

Таблица 3.3.3
РАСЧЕТНЫЕ ЗНАЧЕНИЯ ОБЪЕМА ТОВАРООБОРОТА ПЛОДООВОЩНЫХ КОНСЕРВОВ
И ОТКЛОНЕНИЯ ОТ ФАКТИЧЕСКИХ ДАННЫХ (млн. руб.)
* * * Ш4 г.
I .
. н.
ш
IV
1965 г.
I
II
Ш
IV
1966 г.
I
П
Ш
IV
Фактические значения 11/9" 13,6 5,8 12,3 И,8 13,6 6,6 12,0 13,1 14,7 7,9 15,0
Расчетные значения
Отклонения
14,4 11,1
— 2,J5+ 2,5
Для четырех
8,1 10,2
-2,3+ 2,1
гармоник
13,6 11,9
-1,8+ 1,7
8,1 10,4
-1,5+ 1,6
14,8 12,8
'- 1,7+ 1,9
10,0 12,6
— 2,1+ 2,4
Для шести гармоник
12,9 12,5 6,8 11,3 12,7 12,5 7,5 11,0 14,1 13,6 8,9 14,0
— 1,0+ 1,1 -1,0 +1,0- 0,9+ 1,1- 0,9+ 1.0— 1,0+ 1,1- 1,0 +1,0
Расчетные значения
Отклонения

. Средняя ошибка аппроксимации составляет 1,0.
Ошибка аппроксимации уменьшилась. Доля общей
дисперсии, учитываемая последними двумя гармониками,
составляет 12,9%, из них пятой—1,4%, шестой—1,1,5%.
Шестью гармониками учитывается 65,1 % общей
дисперсии. Конечно, последняя периодическая функция
ближе к фактическим колебаниям. Обе .полученные функции
показаны на рис. 3.3.2. (Сплошной ломаной изображены
фактические данные, штрихнунктиром— данные,
сглаженные четырьмя гармониками, а пунктиром — шестью
гарм аниками).
16
12
Ю
в
6
[ У^г
*
\ 0^\
V / X
¥7
г
,. 1 ; i
^о\
i ,,
•
//
J 1
в $ Ю 11 12 t
Рис 3.3.2.
Теперь рассмотрим полученную функцию (3. 3. 10) с
точки зрения возможности оценки товарооборота на
будущий период.
Если предположить, что в будущем периоде
сохранится эта же амплитуда колебаний, то можно
попытаться оценить значение исследуемого показателя на
перспективу. Однако при расчете значений функции следует
исходить из значений предполагаемого тренда, а не от
среднего уровня. При этом, конечно, трудно оценить
погрешность. Самое простое—это перенести рассчитан-,
цую ошибку аппроксимации в будущее и получить
доверительные интервалы. Эту ошибку можно рассчитать
для имеющихся фактических данных также с учетом.
тренда. В общем виде такая модель запишется так:
51

yt=f(t)+ $ [Aisinix+Bicosix], (З.З.Щ
где f(t) — тренд;
t—номер наблюдения (/ = 1, 2, ..., p)\
2тс ,
i— номер гармоник; х — t.
Естественно, что чем больший период берется для
составления функции, тем больше надо определять
гармоник и тем сильнее будет осреднена амплитуда
колебания. Но амплитуды, полученные .по такому большому
периоду, будут менее соответствовать амплитудам
будущего периода. Поэтому, как уже «отмечалось, лучше
брать небольшой период, предшествующий
предсказываемому. Попытаемся оценить будущее значение
товарооборота плодоовощных консервов. Модель будет
выглядеть следующим образом:
yt = (7,7+0,161/) -0,565 sin x-0,375 sin 2x +]
+2,751 sin3x+0,029sin4A:-0,335sin5A;+]
,+0,769 cos *+0,417 cos 2x -^0,433 cos 3x+]
[+354 cos 4x+0,364 cos 5x+1,004 cos 6x. (3.3.12)
Оценки ожидаемого товарооборота плодоовощных
консервов даны в табл. 3.3.4.
Таблица 3.3.4
ОЦЕНКА ОЖИДАЕМОГО ТОВАРООБОРОТА ПЛОДООВОЩНЫХ
КОНСЕРВОВ (млн. руб.)
Годы
1967
1968
1969
1970
Средняя ошибк
Кварталы
I
.15,0
15,6
17,5
17,0
а ± 1,9
1 п 1
14,9
15,6
17,3
16,8
± 0,4
III
9,3
10,7
12,7
11,2
± 2,2
1 IV
13,9
14,3
17,9
15,9
±0,6
Из приведенных данных видно, что изменение
показателей в этот .период повторяет колебания
предшествующего периода только на более высоком уровне.
Это происходит потому, что тренд выражается
линейным уравнением и равномерный прирост значений
тренда невелик.

Глава IV
ПРОГНОЗИРОВАНИЕ
С ПОМОЩЬЮ МЕТОДА
ЭКСПОНЕНЦИАЛЬНОГО
СГЛАЖИВАНИЯ
Выше уже отмечалось, что временной ряд
может быть разложен на две составляющие —
детерминированную и случайную:
Если бы на изучаемом интервале времени
коэффициенты уравнения, описывающего тренд, остались бы
неизменными, то для построения модели прогноза
вполне оправданным было бы применение метода наимень».
ших квадратов. Однако часто бывает, что в течение
анализируемого периода эти коэффициенты меняются во
времени. Для коротких временных рядов такие скачки
уловить крайне трудно. В подобной ситуации
применение метода наименьших квадратов для определения
параметров модели прогноза может привести к
существенным ошибкам.
Поскольку уровни временного ряда © периоде
(п+1) в определенной степени зависят от их величин,
достигнутых за несколько предыдущих моментов
времени (n—i)9 то именно этим уровнем временного ряда
целесообразно придавать наибольшие веса. В то же
время вряд ли стоит исключать из анализа остальные
уровни, так как они несут некоторую информацию о
процессе. Этим более ранним наблюдениям целесообразно
придавать меньшие веса по сравнению с более
.поздними наблюдениями. Именно таким принципам и отве-
53

чает метод экспоненциального сглаживания,
(разработанный Р. Г, Брауном [40].
Сущность метода экспоненциального сглаживания
заключается в том, что временной ряд сглаживается с
помощью взвешенной скользящей средней, в которой
веса подчиняются экспоненциальному закону (в отличие
от симметричных весов относительно средней величины
для взвешенной скользящей средней, описанной в
параграфе 2. 3.). Взвешенная скользящая средняя с
экспоненциально распределенными весами характеризует
значение процесса на ,конце интервала сглаживания, т. е.
является средней характеристикой последних уровней
ряда. Именно это свойство используется для
прогнозирования. Исходя из существующей инерции
экономических процессов, вследствие которой процесс протекает©
прогнозируемом периоде примерно в тех же условиях,
что и в анализируемом периоде, такая взвешенная
скользящая средняя может быть инструментом для прогноза.
4.1. ПОСТАНОВКА ЗАДАЧИ
ЭКСПОНЕНЦИАЛЬНОГО СГЛАЖИВАНИЯ
Пусть имеется временной ряд yt (t=l. 2,
Пусть далее этот ряд описывается полиномом р-й
степени
#2 Яр ,
yt = a0+alt+—rP+-+ — tP + et =
= £ J!l.t* + Bt • (4.1.1)
г=0 1Х
Требуется по данным ряда yt составить прогноз на*
моменты времени (п + 1)9 (1=1, 2, ..., L) путем
взвешивания наблюдений ряда yt таким образом, чтобы более
поздним наблюдениям придавались большие веса, чем
более ранним.
Прогноз уровней ряда yt в момент времени (t+l)
(t=n) может быть построен с помощью разложения ^
54'

ряд Тейлора1:
+ '"+-^VtW< (4Л-2)
где у(к\ — к-я производная, взятая в момент t.
Согласно теореме, доказанной Брауном .и Майером
[41], любая /с-я производная (>/с=0, 1, % ... ,р)
уравнения (4. 1. 2) может быть выражена через линейные
комбинации экспоненциальных средних до (р+1)-го
порядка. Основной целью экспоненциального сглаживания
при этом является вычисление рекуррентных поправок
оценок коэффициентов уравнения вида (4.1.1).
Введем определение экспоненциальной средней.
Экспоненциальной средней первого порядка
для ряда yt назовем
[1] п л
St (t/)=a 2 (l-a)*0«-iJ (4.1.3)
где а—параметр сглаживания (0<а<1).
Назовем далее выражение
т п ih-i]
St (y),= a 2 (l-.o)«Sw (У) '(4.1.4)
экспоненциальной средней /с-го порядка для ряда у%.
Брауном выведена следующая рекуррентная
формула для определения экспоненциальной средней:
т [h-i] [k]
St (y)=aSt (y) + (l-a)St-i(y). (4 Л .5)
Новая экспоненциальная средняя равна предыдущей
плюс доля (а) от разности между новыми
наблюдениями и предыдущими сглаженными значениями уровней.
Можно показать, как вычисляется экспоненциальная
средняя для момента времени t из ранее сглаженных
величин. Возьмем, например, экспоненциальную среднюю
первого порядка
[1] ' И]
5, (у) =ayt+ (1 -a) SM (у). (4.1.6)
1 Все прогнозируемые величины будем обозначать символом со
звездочкой.
55

Тогда /
S< (у) km+ (I-a) [a^-i+ (1 -a)St-2 (*/)] =
= 0(^0(1-а) г/^1+(1-а)2[аг/«_2+,
[1]-
+ (1-а) St-3 (y)]=ayt + a(l-a)yt-i+:
+ а(1-а)2^-2+-- + а(1-а)^-г+^—w+j
+ (1-а)'у0=а 2^1-а)^-*+(1-а)'у0". (4.1.7)
г=и
Функция (4. 1. 5) является линейной комбинацией
всех прошлых наблюдений. Веса, придаваемые
предшествующим уровням, убывают в геометрической
прогрессии. Например, если параметр сглаживания а=0,3, то
уровень для момента времени t будет .иметь вес 0,3.
Веса для предыдущих наблюдений соответственно равны
0,21; 0,147; 0,1029 и т. д.
Исходя из рекуррентной формулы (4. 1. 5) все
производные в разложении (4, 1. 2) могут быть получены по
уравнениям:
[И И]
St {У) =ayt- (1 -a) St-i {y)\
[2] [1] [2]
St (y)=aSt (t/) + (l-a)S*-i(t/);
[h] [h-l] [k]
St (!/)=aSL(j/) + (l-a)SM(j/); (4.1.8)
[n] [n-1] In]
5, (y)=aSt (y) + (l-a)St-i(yl
где S\W (у) —экспоненциальная средняя /с-го порядка в
точке U
4. 2. ВЫВОД ФОРМУЛ ДЛЯ ОЦЕНКИ
КОЭФФИЦИЕНТОВ МОДЕЛИ
Пусть, например, линейная модель (4.1.1)
включает в себя только первые два члена
yt=a0+ait±et а (4.2.1)
Для того чтобы выразить коэффициенты уравнения
(4. 2. 1) через экспоненциальные средние, можно на
основании теоремы Брауна — Майера получить систему
уравнений, связывающих оценку коэффициентов а0 и а,\
56

с экспоненциальными средними SMt(y) и $Щ(у):^
[И а 1_а а
-St (y)=aQ+—^ral ; (4.2.2)
[2] л 2(1-а) а
St (y)=aQ+—-—ах •
I*
А А
Решив систему (4. 2. 2) относительно а0 и аь получим
Л [1] [2]
aQ=2St (у)-St (у); (4.2.3)
а а ИЗ [2]
*i=-iz5-[s« to)-s« (у)] а
Прогноз для случая (4. 2. 1) рассчитывается по формуле
* А А
yt+i=a0+lai •} {4.2.4)
Ошибка прогноза при этом определяется следующим
образом:
+ 2а(4--3а)/+2а2/2], (4.2.5)
где ав/ — средняя квадратичеакая ошибка, вычисленная
для отклонений от линейного тренда.
Для квадратичной модели
yt = ao+ai t+ -i- a2 £+в, <Ц.2£\
получаем следующую систему из трех уравнений с
тремя неизвестными:
[И а !_а а (1_а)(2-а) а
st (г/)=а0—^~а1+—w—а*; '
12] а 2(1-а) л (1-а)(3-2а) а
st (у)=а0-—— fli+.« ^ ^;
[3} а 3(1-а)А 3(1-а)(4-3а) а
S* (if)-flo--L^ifli+ и» а2' (4'2J)
Откуда
А [1] [2] 14- ч
aQ=3[St (У)-St (y)]+St (у)\
57

°1=I(I^[(6"5a)St M~2(5-4a)St ,(*/)+;
[»]
;+(4-3a)5, (у)]; (4.2,8)
л a2 . M И и
«2=-(T^)l[5t (j/)-2St (y)+St (y)] ,
Прогноз для модели (4. 2. 6) осуществляется по
формуле
* А Л I A
#ад =^o+«i/+ — а2Р , (4.2.9)
ошибка прогноза определяется следующим образом:
оу*ш & (У е У2а+3аг+3а3/2 • (4.2.10)
Аналогичным способом могут быть получены оценки
остальных коэффициентов полинома (4. 1. 2)*
4.3. ВЫБОР НАЧАЛЬНЫХ
УСЛОВИЙ V ^
Из формулы (4^ 1# 5) видно, что для
проведения процедуры сглаживания необходимо задать
начальную величину (условие)1 S[k](y).
Обычно начальные условия задаются из
определенных экономических соображений, например исходя из
величины лага. При этом для прогноза рассматривается
не весь временной ряд, а только часть его. Такой подход
позволяет значительно сократить объем информации
для прогнозирования, так как ранние значения уровней
ряда, вследствие небольшой величины соответствующих
им весов, исключаются из анализа.
В случае отсутствия предварительных соображений,
на основании которых выбираются начальные условия,
•можно воспользоваться специальными формулами,
разработанными Р„ Брауном [40]. В частности, для линейной
модели (4. 2, 1) .начальные условия определяются ка,к
HI l-a
So (y)=aQ — ах ;
1 В дальнейшем начальные условия будем обозначать SQ(y).
58

Ю ч 2(1-а)
*о (у)=а0 —ах , (4.3.1)
а для квадратичной модели (4. 2. б)
U] 1-а (1_а)(2-а)
So (У)=а0 —«1+' 2^ а2;
[21 2(1-а) (1-а)(3-2а)
( 50 (*/)=а0 S~fli+;—: jr"! аг; (4.3.2)
[3] 3(1-а), 3(1-а)(4-3а)
So (y)=flo ^~а1+' 2^ а2 S
И] 12] 13]
где So (у) у So {у) и So (у)—начальные условия.
Для выражения значений коэффициентов а0 и а\ в
формуле (4.3.1) и Яо, #i и #2 в формуле (4.3.2) Браун
рекомендовал брать коэффициенты уравнения тренда
(4.2.1), полученные методом наименьших квадратов [40].
4.4. ВЫБОР ОПТИМАЛЬНОГО
ПАРАМЕТРА СГЛАЖИВАНИЯ а
При построении прогнозов с помощью метода
экспоненциального сглаживания одной из основных
проблем является выбор оптимального значения парамет-*
ра сглаживания а. Ясно, что при разных значениях а
результаты прогноза будут различными. Если а близка к
единице, то это приводит к учету при прогнозе в
основном влияния лишь последних наблюдений; если близка
к нулю, то веса, по которым взвешиваются уровни
временного ряда, убывают медленно, т. е. при прогнозе
учитываются ©се (или почти все) прошлые наблюдения.
Вес наблюдения, отстоящего на к периодов от
наблюдаемого момента, равен a (il — <а)к. Если есть
уверенность, что начальные условия достоверны, то следует
использовать небольшую величину параметра
сглаживания (а~0)„ Когда параметр сглаживания мал, то
функция St(y) ведет себя как средняя из
большого числа прошлых уровней. Если нет достаточной
уверенности в прогнозировании начальных условий, то
тогда следует использовать большую величину а, что
приведет к учету при прогнозе в основном влияния послед-
59

них наблюдений. Следует также заметить, что
небольшие изменения а мало сказываются на результатах
прогноза.
Точного метода для выбора оптимальной величины
параметра сглаживания а пока нет. В отдельных
случаях Браун предлагает определять величину а исходя из
длины интервала сглаживания. При этом а вычисляется
из формулы
где т — число наблюдений, входящих в интервал
сглаживания.
Оценим суммарный вес С последних т наблюдений
при параметре сглаживания, определенном по формуле
(4. 4. 1). Формулу (4. 4. 1) нетрудно привести к виду
т-1
1-а= -гг-*: (4.4.2)
Тогда суммарный вес С равен:
т-1 / т— 1 \ т
C = aS (l-a)ft=l-(l-a)^=l- ^
»,__л \ т4-1 /
ь=о
~1 — = 1 — 0,135=0,865 (для т>10).
Отсюда около 87% веса при т^ 10 придается
последним наблюдениям. \
Г'рюнвальд величину а связывает coy значением
автокорреляционной функции прогнозируемого
процесса [44]. В экономических приложениях проведение
сложного, корреляционного анализа временных - рядов
(особенно при наличии малого числа наблюдений) часто
весьма затруднительно. Поэтому для нахождения
значения а используют различные эмпирические процедуры.
Например, Селиванов и Клеандров [23] предлагают
весь временной ряд делить на две части; по первой части
для различных а строится модель прогноза и
осуществляется прогноз на период, соответствующий длине
второй части. Для всех взятых а по второй части
находятся отклонения прогнозируемых значений временного
ряда от фактических уровней и определяются дисперсии
этих отклонений. Затем эта дисперсии сравниваются и
60

из них выбирается минимальная. Величина а, для
которой будет получена минимальная дисперсия, считается
оптимальной и ее принимают для дальнейших расчетов.
4.5. РАССМОТРЕНИЕ МЕТОДА
При обсуждении вопроса о возможности
применения метода экспоненциального сглаживания для
прогнозирования экономических процессов остановимся
на следующих важнейших, с нашей точки зрения,
моментах.
1. Метод экспоненциального сглаживания,
разработанный для анализа временных рядов, состоящих из
большого числа наблюдений, при изучении
экономических временных рядов нередко не «срабатывает». Это
обусловлено тем, что экономические временные ряды
бывают слишком короткими (1.5—fiO наблюдений) и в
случае, когда темпы роста и прироста велики, то, как
показывает наша практика, метод не «успевает»
отразить все изменения.
2. Ддя нахождения оценок коэффициентов
сглаживающего полинома используется рекуррентная
процедура, позволяющая при конечном числе наблюдений
получить приближенное решение задачи, причем
приближение тем точнее, чем больше число наблюдений.
3. Проблема выбора начальных условий
принципиально сводится к оценке погрешности метода, а вопрос
выбора оптимального значения параметра сглаживания
а для своего решения требует прежде всего четкой
постановки задачи,
4.6. ПРИМЕР ПРОГНОЗИРОВАНИЯ
С ПОМОЩЬЮ МЕТО.ДА
ЭКСПОНЕНЦИАЛЬНОГО СГЛАЖИВАНИЯ
В качестве примера для иллюстрации
применения метода экспоненциального сглаживания для
прогнозирования рассмотрим временной ряд выпуска
натурального цемента за период 1950—1971 гг. (табл. 4.6.1,
гр.2). '
Тренд этого ряда достаточно хорошо описывается
параболой
#* = 3,5616+3,0326/+0,0694<2 ,: (4.6.1)
61

ВРЕМЕННОЙ
Годы
1
1950
1951
1952
1953
1954
1955
1956
1957
1958
1959
1950
1961
1962
1963
1964
1965
1966
1967
1968
1969
1970
1971
РЯД ПРОИЗВОДСТВА ЦЕМЕНТА
(млн. т)
Фактические
значения уровней
У*
_2
10,2
12,1
13,9
16,0
19,0
22,5
24,9
28,9
33,3
38,8
45,5
50,9
57,3
61,0
64,9
72,4
80,0
84,8
87,5
89,7
- 95,2
100,3
Расчетные
значения
уровней
5
3
6,7
9,9
13,3-
16,8
20,5
24,3
28,2
32,3
35,5
40,8
45,3
50,0
54,7
59,6
64,7
69,9
75,2
80,6
86,2
92,0
97,9
103,9
Таблица 4.6.1
ЗА 1950—1971 гг.
Отклонения
фактических значений
уровней от расчетных
yt-?t
4
3,5
2,2
0,6
—0.8
-1.5
-1.8
—3,3
-3,4
-3,2
-2,0
0,2
0,9
2,6
1.4
0,2
2,5
4,8
4.2
1,3
-2,3
-2,7
-3,6
В гр. 3 табл. 4. 6. 1 представлены рассчитанные по
формуле (4. 6. 1) значения уровней, а в тр. 4—
отклонения фактических значений уровней от расчетных. Для
построения модели прогноза использовались формулы
(4. 2. 7) — (4. 2. 10), (4. 3. 2). В качестве интервала
сглаживания для расчета параметра а использовался период
в 11 лет. Это было обусловлено тем, что к 1901 г. в
основном было закончено техническое перевооружение
цементной промышленности. Таким образом, величина а,
рассчитанная по формуле (4.4.1), была равна 0,1667.
Прогноз выпуска цемента осуществлялся на период
1972—^1975 г..
Как видно из формул (4.3.1), для определения рце-
Л А Л I
нок коэффициентов ао, аи а2 помимо значения а неерхо-

CO CD CO CD CO COCOCOCO СО СО СО СО СО СО СО СО COCOCOCO
44QOO) <JiGiO>CJi ООЭОСЛ СЛ СЛ СЛ СЯ СЛ СЛ СЛ СЛ
»-*осооо^ о ел ^ со ьо^-осо оо-^^сл 4^со to»-*
*^о>о>слсл
to^icoooco
^.4^сосо tototo»-* •"*«-* т л
ЧЮОО^ СОСЛ^--4 ►Й.^-ООСЛ СОО
и
>>-а оососло сооо^ ьосоо
— Энсгь gj^--
ObiOOOtO OOOJONi 4* ^ *£» СЛ
ьэ^со-..
ооооосо cotococo
■>со соаз юоо
ОСООО ООЬЭО
tooco^i
tO-4-ЧОО
осо^дсо юсосоо
4^ 4ь 4s»- CO CO tO tO Ю •—' »—*»—» мм
СО СЛ •-' О Ю OO^oOi СО О ^ 4^ •--О СО СЛ J-4 СО j-* СО
ссЪ»"»—Ъэ со ^м^Ъо 'со м1о 4*. "оо <л о со о -^ оо "со
СОи^О^»-4 С0С04^Ю CX00O4S* ^СОСОО 0*^0*4*.
сомсоро союсл*<1 слелсло оослмсо ооелслео
СО*<1СО»-*СО СОмюОО ОСЛООСО Ю004ььСО ОСОн-СО
, „,,1 '11 I I I I I 11 11
СО tO tO »—» и-* I—' »—»i—i м-»-»>-' »-*
оа^ьосо^сл to со о со «-\7-\сосл -а со —»со сла^о
rrs -О СО сл со rnJi».fn«o ^-i СлЗ Oi QD re по Л fii Q J^. QO Л
tocooooo^i *чслосл 4^4^сосо to to to to »-4'т*—'_
^icoco^oo мслосл сосо-чсо соазеоо --а^»—'оо
*4^. tO СЛ^Ъ? ЪэЪ^'со
^^"^^ CO^COtO СЛООООГ*
О^ЮСЯ -ЧО>-*<^ ООСЛСЛ
©н^мю ооаз^сл о^юся sOh*w оослсл
ОСЛ-ЧО OOCOCvCO 004^00 СЛ Ю СЛ tO N3-*tOCO
ЮСЛ-^ЮЮ OOCOOOJ ОЬОЮСЛ СЛМО-Ч М^СОСЛ
^СЛ^СЛ Oi <3> О СЛ^СЛ СЛ СЛ 4^ 4^ СО СО COCOCOCO COCOCOCO
а>оом юо Ъ>^"со^-» ^ГсоcoVj 'сх'слЪз сл о/о/оы*.
-^С0С0С04^ 00 ЮОО О^СОСОСО мСЛОСО мСЛЮ^
^05 000- м--Ч^ООО Ю-*ОСО ЮСО»-ч— I—COCO»-*
^СОСЛ4^СО Oi"4N30 СООООО) 4^> СО-4 СО >— 00 СЛ О
ооооо оооо оооо оооо оооо
•— СОСЭ-4-<1 ООСЭО 4s* СО м* О О •-* Ю Ю СО 4^ СЛ СЛ
СЛиЭ —OO^vj СДО^*» 00 4^ "-4 00 4mOS -vjCO-чСЛ
а; оооо to ел comjoS оослео^! ел со со 4** ел ел to to
ОСОСОСООО SSGO СЛ4^4^СО СОЮ tO tO to — »-»»-'
СО СО СЛ *-» ** -Чм-ОО СО "-4 ►-* СЛ СО СО О СО *-*ООСЛм*
им^ОО! 4^i-*tOO> СО 00 --4 ^О О^О^О '►—'сл'сл'о
СОиСЛМСЛ СЛ-g^-O 4* О -^ ** *4^t0-40 00 СО О "Ч
h^4^0C7>C75 СОн-0000 СЛС04^»^ £1 м ^ СО ЮСЛОЮ
^ю»—-асо соосоао сосососл ооюоо о^аоооо
*>
о m
я &
я
о
m
я
о
о
н
•d
о
я
S
m
я
•d
о
•"1
я
о
>
я
о
н
о
totOM*o
ЮС005С0О tO'-'H-O СОСоСОи-* О
S28S*: 2?S2g ЙЗЙ^ 8S56 SSS*S?fe
fiftSJ^6" °?S5SSrt *.о>£л& оо-Зоо SeiS^
^)К5 —ч^— човм -ц^^-сл н*а>»осо o-~iooto

димо найти экспоненциальные средние Srt^(y)t S[2](y) и
S}S](y). Для их расчета использовалась рекуррентная
формула (,4. I. 5).
Сначала были определены по формуле (4. 3. 2)
начальные условия: SW(y) = -7,783; S ^ (у) = -15,655;
S0[Z](y) = -20,057. Зятем были подпитаны SPHy), S^(y)
Л Л А
и St[z](y), найдены а0, й\ и а2 и-осуществлен прогноз на
1951т. Далее по рекуррентной формуле (4. 1. 5)
вычислялись новые St[l](y), StW(y) и St[z](y), а по ним онреде-
л л л
лялись соответствующие ао, аь аг для прогноза на 1952 г.
Я т. д. В табл. 4, 6.2 даны экспоненциальные средние,
подсчитанные по рекуррентной формуле, коэффициенты
модели прогноза, результаты прогноза и отклонения
фактических уровней от прогнозируемых.
Рис. 4.6.1.
64

Таблица 4.6.3
ПРОГНОЗ ВЫПУСКА ЦЕМЕНТА НА 1972—1973 гг. (млн. т)
Годы
Прогноз
Ошибка
прогноза
Доверительные интервалы
верхняя
граница
нижняя
граница
1972 107,59 1,80 109,39 105,79
1973 113,31 1,89 115,20 111,42
1974 119,13 2,02 121,15 117,11
1975 125,06 . 2,19 127,25 122,87
При прогнозе производства цемента на 1972—1975 гг.
использовались следующие величины экспоненциальных
средних: SJ1' (у) =76,956; S***(у) =54,492; S}6]{у) =34,584.
Соответственно оценки коэффициентов модели прогноза
равны: ао=Ю1,975; ai==5,i566; a2 = 0,102.
В табл. 4. 6. 3 представлены результаты прогноза
выпуска цемента и его ошибок на 1972—1975 гг.
На рис. 4. 6. 1 изображены весь временной ряд
выпуска цемента за 1950—1971 гг., прогноз на 1972—1975 гг.
и доверительные интервалы для прогнозируемых значен
ний,
5. Заказ 3199

Глава V
ЗАВИСИМОСТЬ СРЕДНЕЙ
ОШИБКИ ПРОГНОЗА
ОТ ПЕРИОДА ПРЕДЫСТОРИИ
И ВЕЛИЧИНЫ ПРОГНОЗИРУЕМОГО
ПЕРИОДА
Одной из важнейших задач прогнозирования
является повышение точности расчетов. Критерием
точности может служить средняя ошибка прогноза,
вычисляемая по формуле
t i
Уп+1—У*п+1
*•—т st I ^ 1 -100' <5Л>
где tfn+i — фактические уровни временного ряда;
Уп+1 — прогнозируемые уровни временного ряда;
п — период предыстории (п= 1, 2,..., N);
/ — прогнозируемый период (l = N+l, N + 2,
..., т).
Как известно, точность прогноза зависит как от
длины периода предыстории, так и от величины
прогнозируемого периода (см., 'например, [10]). Поэтому мож-
«ю построить модель, характеризующую зависимость
средней ошибки прооюза от двух параметров п и I:
^пР=/(я,/). (5.2)
Процедура построения модели (5.2) осуществляется
следующим образом. Весь временной ряд t(t=l, 2^..., Т)
разбивается на две части: первая — п (п=1, ?;..., N)
принимается за период предыстории, вторая — Ш=М+1,
N+2, ..., Т) —за прогнозируемый период. Для щериода
п строится модель прогноза j/t==a0+ai^ по которой
бе

прогнозируются уровни временного ряда yt на период
/. С этой целью в полученное уравнение модели
прогноза последовательно подставляют значения t, равные
N+it N + 2, ..., Т, т. е. порядковые номера лет периода
прогноза, и получают прогнозируемые уровни
временного ряда на период /. По существу, мы осуществляем
ретроспективный прогноз. Поскольку фактические
значения временного ряда за период / известны, можно
определить -величину средней ошибки прогноза за этот период.
Далее период предыстории увеличивается на один
момент времени, т. е. его длина становится (/г+1), а
период прогнозирования тем самым уменьшается на
единицу. Для временного ряда длиной (я+1) строится
модель прогноза, по которой осуществляется
прогнозирование на период /—1, т. е. «a N+2, N+3, ..., Т, и
находится средняя ошибка прогноза. Такая процедура
повторяется до тех пор, пока прогнозируемый период не будет
равен нескольким моментам времени, по которым еще
можно будет проверять ретроспективный прогноз1. В.
результате можно построить таблицу, в которой будут
содержаться данные для построения модели зависимости
средней ошибки прогноза от длины периода
предыстории и величины прогнозируемого периода,
Таблица 5.1
ДАННЫЕ ДЛЯ ПОСТРОЕНИЯ МОДЕЛИ
Средняя
ошибка
прогноза епр
Величина периода
предыстории п
Величина прогнозируемого
периода I
1(0
пр
-TCI-I)
пр
л;(1,2, . . ., N) l\ (N+1, ЛГ+2 Т)
л+1; (1.2, . . . , N+l) /-1; (N+2, N+39...T)
пр
п+р; (1,2,. ...,N+p) t-p; (tff/H-l, N+p+
+2 Т)
Вышеописанный метод проиллюстрируем на примере
временного ряда выпуска цемента в СССР за период с
1950 по 1971 г.. '(табл. 5.2, гр. 3),
1 В нижеприведенном примере мы остановились на этапе, ког«<
да минимальный лериод прогноза равен 5 годам.
67

Таблица 5.2
ОПРЕДЕЛЕНИЕ СРЕДНЕЙ ОШИБКИ ПЕРИОДА
Годы
* ^
В-*.
2 <" 2
fflSw
Относительные ошибки аппроксимации
и прогноза в процентах
I 8
10
1950
1951
1952
1953
1954
1955
1955
1957
1958
1959
1960
1961
1962
1963
1964
1965
1966
1967
1968
19о9
1970
1971
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
10,2
12,1
13,9
16,0
19,0
22,5
24,9
28,9
33,3
38,8
45,5
50,9
57,3
61,0
64,9
72,4
80,0
84,8
87,5
89,7
95,2
100,3
+30,0
+ 13,0
— 0,2
-8,2
— 9,0
-7,1
—10,4
— 6,91
-2,8
+ 3,С
+ 9,7
+ 12
+ 16
+ 16
+ 15
+ 19
+23
+23
+^2,1
+20,2
+21,0
+21,8
+38,1
+17,81
+ 2,2
-7,7
- 9,0
— 8,9
1—13,1
—10,0
6,41
0,7|
+ 6,1
+ 8,91
+12,7
+12,1
+11
+15
+19
+19
+ 17
+ 15,8
+ 16,9
+ 17,4
+46,8
+23 J
+ 5
— 6
—10
—10
-15
-12,8
- 9,5
-2'°
+ 2,8
+ 5,5
+ 9,2
+ 8,4
+ 7,9
+ 12,2
+ 15,6
+ 15,8
+13,9
+ 11,7
+ 12,8
+ 13,4
+52,5
+26,5
+ 7,2
- 5,8
—10,3
—11,0
-16,5
—14,3
—11,3
!— 6,9
+ 0,8
+ 3,4
+ 7,2
+ 6,2
+ 5,7
+ 9,9
+ 13,4
+ 13,6
+ 11,7
+ 9,3
+ 10,3
+ 10,9
+56
+29
+ 8
-5
—1и
-11
17
-i5;2
-12,3
-7,0
— 0,3
+ 2,2
+ 6,0
+ 4,9
+ 4,3
+ 8,6
+ 12,1
+ 12,1
+ 10,2
+ 7,8
+ 8,8
+ 9,4
+62,6
+33,3
+11,4
— 3,6
-9,6
-11,5
—17,8
-16,3
—13,7
— 8,5
- 1.9
+ 0,6
+ 4,2
+ 3,1
+ 2,3
+ 6,6
+ 10,1
+Ю.З
+7J.4
+38,6
+ 14,8
-1,6
— 8,8
—11,5
—18,5
-17,4
—15,1
—10,2
-3,6
- 1,3
+ 2,3
+ 1,0
+ 0,1
+ 4,4
+ 7,9
+ 8,0
+ 8,1+5,7
+ 5,6+ 3,1
+ 6,6+ 4,1
+ 7,1-1- 4,6
еап ~~ средняя ошибка
_ аппроксимации 9,1 10,8 12,4. >12,8 12,7 12,9 13,4
епр— средняя
ошибка прог- " *
ноза ' 19,4 15,9 12,4 10,6 9,9 8,0* 5,1
Весь период в 2U года был- разбит на две равные
части, т. е. п= 11; /=11. Затем для отрезка
исследуемого ряда за период с1950 по. 1960 г. была построена
линейная модель
^ = 3,744 + 3,393/ (* = 1,2,-, П), (5,3)
Подставляя в это уравнение порядковые номера
последующих лет (/=12, 13, ..., 22), получаем относи-
68

тельные ошибки прогноза для каждого года на период
с 1961 по 1971 г. по формуле
бпр —"
Уп + 1—у*п+1
Уп + 1
100.
(5.4)
По формуле (5.1) находится средняя ошибка прогноза
для этого отрезка временного-ряда. Относительные
ошибки прогноза и средняя ошибка прогноза представлены в
табл. 5.2, гр. 41. Далее период предыстории был
увеличен до 12 лет (1950—1961 гг.), построена модель
прогноза
*/* = 2,670+ 3,641*; (* = 1,2,...,12)
и осуществлена экстраполяция на период 1962—1971 гг.,
в результате которой были определены относительные
ошибки прогноза по годам и средняя ошибка прогноза
(табл. 5.2, гр.2).
Модели прогноза для всех проделанных этапов
представлены в табл. 5.3, а в табл. 5.2 — величины
относительных и средних ошибок аппроксимации, а также
относительных и средних ошибок прогноза.
Таблица 5.3
МОДЕЛИ ПРОГНОЗА ПО ЭТАПАМ ПРОГНОЗИРОВАНИЯ
Период
предыстории (годы)
Период прогноза
(годы)
Уравнения для моделей
прогноза
1950—1969
(11 лет)
1950-1961
(12 лет)
1950—1952-
(13 лет)
1950—1963
(14 лет)
1950—1964
(15 лет)
1950—1965
(16 лет)
1950-1966
(17 лет)
1961—1971
(11 лет)
1962—1971
(10 лет)
1963—19/1
(9 лет)
1964—1971
(8 лет)
1965—1971
(7 лет)
1966—1971
(6 лет)
1967—1971
(5 лет)
у, = 3,744+3,393*
yt = 2,670+3,641*
37 = 1,546+3,881*
у, - 0,815+4,027*
У/ = 0,326+4,119*
37 = —0,445+4,255*
у, = —1,398+4,414*
1 В гр. 4, 5 и т. д. относительные ошибки прогноза
расположены ниже выделенного прямоугольника. В прямоугольники
заключены относительные ошибки аппроксимации.
69

В результате проделанных расчетов была получена
информация для построения модели, характеризующей
зависимость средней ошибки прогноза от длины периода
предыстории и прогнозируемого периода (табл. 5.4).
На основании данных
табл. 5.4 была построена
модель зависимости средней
ошибки прогноза от
периода предыстории и периода,
прогноза:
Таблица 5.4
СРЕДНИЕ ОШИБКИ ПРОГНОЗА
И ВЕЛИЧИНА ПЕРИОДА
ПРЕДЫСТОРИИ
И ПРОГНОЗИРУЕМОГО
ПЕРИОДА
Средняя
ошибка
прогноза
1%) 6пр
19,4
13,9
12,4
10,6
9,9
8,0
5,1
Период

предыстории п (лет)
11
12
13
14
15
16
17
Период
прогноза
/ (лет)
11
10
9
8
7
6
5
8пр=3,860-0,441п+ 1,741/.
(5.6)
Коэффициент
множественной корреляции, равный
0,981, указывает на
довольно тесную связь между
средней ошибкой прогноза и
обоими факторами. Вариация
средней ошибки прогноза на
96,2% объясняется
колеблемостью периода предыстории и прогнозируемого
периода, о чем свидетельствует величина коэффициента
множественной детерминации (/?2=0,962).
Это уравнение показывает, что увеличение периода
предыстории на один год снижает ошибку прогноза на
0,441%. В то же время увеличение прогнозируемого
периода на один год ведет к увеличению средней ошибки
прогноза на -1,741 %.
Итак, точность прогноза объясняется совместным
влиянием периода предыстории и периода прогноза.

Глава VI
МНОГОФАКТОРНОЕ
ПРОГНОЗИРОВАНИЕ
6.1. НЕКОТОРЫЕ СТАТИСТИЧЕСКИЕ ВОПРОСЫ
МНОГОФАКТОРНОГО ПРОГНОЗИРОВАНИЯ
Проблема многофакторното прогнозирования
является чрезвычайно сложной и наименее
разработанной. Она требует решения ряда методологических и
теоретических вопросов, например, статического и
динамического прогноза, выбора математического
аппарата для описания изменения экономического явления за
определенный период времени и т. д. ч
Рассмотрим некоторые из этих вопросов.
Мнотофакторные модели экономических показателей
могут * быть статическими и динамическими.
Статические модели используются для целей анализа и
нормирования, а динамические — для анализа и
прогнозирования. Понятие «динамическая модель» трактуется по-
разному. Одни считают, что к динамическим моделям
относятся такие, которые построены по многофакторным
временным рядам. Другие добавляют, что такая модель
носит динамический характер лишь в случае, когда в
ней учитываются временные запаздывания влияний
факторов-аргументов. В то же время целый ряд ученых
(в основном занимающихся межотраслевым балансом)
приходит к выводу о статическом характере такого рода
моделей, та,к как они не учитывают изменений самой
структуры влияний [12].
Будем придерживаться следующего определения
многофакторной динамической модели. Многофакторная
модель является динамичеокой, если она учитывает [22]:
71

а) общие закономерности изменения экономического
явления в изучаемый интервал времени;
б) закономерности изменения во времени влияний
факторов-аргументов;
в) запаздывание влияний факторов-аргументов.
Многофакторные модели экономических явлений
строятся по информации, относящейся к разным
уровням иерархии и различным периодам времени. В
зависимости от этого различают следующие основные
типы исходной информации:
1) временные ряды, характеризующие средние
величины изучаемых показателей по стране в целом;
2) временные ряды, характеризующие изучаемые
явления в среднем по отдельным отраслям народного
хозяйства;
3) .информацию, характеризующую изучаемое
явление в среднем по отдельным отраслям народного
хозяйства за определенный период времени, принятый за
единицу измерения, например за год1;
4) пространственную информацию,
характеризующую изучаемое явление на каждом отдельном объекте,
относящегося к одной и той же отрасли народного
хозяйства;
5) временные ряды, описывающие явление на
каждом изучаемом объекте.
Пространственная информация отражает влияние
предшествующих периодов времени. В свою очередь
она оказывает влияние на формирование информации,
которая будет характеризовать изучаемое явление в
будущем. В этом — динамический характер
пространственной информации. В то же время при
использовании пространственной информации для построения
уравнений регрессии трудно выяснить изменение
влияний факторов-аргументов, во времени. Кроме того,"она
не позволяет учесть запаздывание влияний факторов.
В этом заключается статичность пространственной
информации. Запаздывание влияний можно определить по
временным рядам народнохозяйственных или
среднеотраслевых показателей. Однако выявить
закономерность изменения во времени влияний факторов, как это
будет показано ниже, крайне трудно. Временные ряды
1 Так называемая пространственная информация.
72

изучаемых показателей на каждом объекте имею? те же
недостатки, что и временные ряды и
народнохозяйственных, и .среднеотраслевых показателей.
Совместное использование информации,
характеризующей динамику явления, и пространственной
.информации позволит построить модели, пригодные для
практического /использования.
В отдельных случаях в зависимости от целей
исследования и имеющейся информации об изучаемом
процессе можно для построения- моделей использовать один
из .имеющихся видов исходных данных. Это делают
тогда [22]:
1) когда поставленная цель охватывает одну
отдельно взятую сторону экономического явления (допустим,
•цель— получение прогноза по имеющемуся временному
ряду или цель — построение многофакторной модели
для описания среднеотраслевых соотношений);
2) когда имеется теоретическое исследование другой
стороны экономического явления (например, по
-временным запаздываниям влияний факторов-аргументов),
которое можно непосредственно использовать;
3) 'коща оговариваются, что полученные по данному
виду информации результаты считаются верными при
выполнении ряда предпосылок, проверить которые
можно только анализом другого вида информации
(■например, предполагается, что полученная по много-
факторным временным последовательностям структура
связей не изменяется или слабо изменяется во времени).
Рассмотрим многофакторные модели, построенные
по временным рядам экономических явлений и
влияющих на них факторов (информация первого, второго и
пятого типов). Модели, при построении которых
используется информация такого рода, широко применяются за
рубежом и в последнее время стали разрабатываться в
СССР. При этом возникают две математические
проблемы — автокорреляция и мультиколлинеарность.
Метод наименьших квадратов, который наиболее
часто используется в регрессионном анализе для
нахождения оценок коэффициентов регрессии, основывается
на предпосылке о независимости друг от друга
отдельных наблюдений по одной и той же переменной. В
экономических же временных рядах последовательные
наблюдения зависят друг от друга, т. е. между ними, как
73

отмечалось выше, существует автокорреляция. Поэтому
оценки коэффициентов регрессии, полученные по методу
наименьших квадратов, ^не имеют оптимальных
статистических свойств. Наличие автокорреляции приводит к
искажению величины среднеквадратических ошибок
коэффициентов регрессии, что затрудняет построение
доверительных интервалов для коэффициентов
регрессии, а также проверку их значимости. Кроме того,
автокорреляция приводит к сокращению числа эффективных
наблюдений [28], так как показатели одного и того же
объекта, скажем, за пять лет — это качественно нечто
совершенно иное, чем показатели пяти объектов за
один год. В первом случае мы фактически имеем дело
лишь с одним независимым наблюдением, ввиду того
что состояние этого объекта в /с-м году определяется
его состоянием в предыдущие годы. Во втором же
случае рассматриваются пять независимых наблюдений.
Автокорреляция в отклонениях от трендов, g также
в случайных остатках уравнений регрессии, построенных
по многомерным временным рядам, возникает по.
следующим причинам: во-первых, если в модели не учтен
существенный фактор, то его влияние отражается на
величине отклонений, которые в этом случае
показывают закономерность в изменении, связанную с
изменением неучтенного фактора; во-вторых, когда в модели не
учитывается несколько факторов, влияние каждого из
которых в отдельности несущественно, но при
совпадении изменения этих факторов по направлению и по
фазе, в отклонениях может возникнуть автокорреляция.
В-третьих, автокорреляция в отклонениях может
появиться в случае, когда неправильно выбрана форма
связи между зависимой и независимой переменными.
И наконец, в-четвертых, автокорреляция может
возникнуть не в результате допущенных ошибок при
построении модели, а вследствие особенностей внутренней
структуры случайной компоненты.
Наиболее распространенным приемом выявления
наличия автокорреляции в отклонениях от тренда или от
регрессионной модели является использование
критерия d (Дурбина — Уотсона). Этот критерий
рассчитывается по формуле
74

2 (ef+i-e*)2
d= t=i n — -; (6.1.1)
где e* — случайные отклонения от тренда или
регрессионной модели.
В табл. 6.1.1 дано распределение значений критерия
Дур.б:ина — Уотсона для положительной автокорреляции
(при 5%-ном уровне значимости).
В этой таблице d\ и d2 — соответственно нижняя и
верхняя границы критерия Дурбина — Уотсона; V% —
число переменных в модели, п—длина временного
ряда.
Для применения критерия Дурбина — Уотсона
величина d, рассчитанная по формуле (6.1.1.), сравнивается
с d\ и d2 табл. 6.1.1. Возможны три случая:
1) если с?<йь гипотеза об отсутствии
автокорреляции в отклонениях отвергается;
2) если d>d2, то гипотеза об отсутствии
автокорреляции принимается;
3) если di^d^.d2, то необходимы дальнейшие
исследования (например, по большему числу наблюдений).
Величина d может принимать значения в интервале
O^d^.4, причем различные для положительных, и
отрицательных коэффициентов. Чтобы проверить
значимость отрицательных автокорреляций, нужно
вычислить величину (4—d). Далее проверка осуществляется
аналогично тому, как и в случае положительной
автокорреляции.
Существует ряд способов исключения или
уменьшения автокорреляции во временных рядах.
Наиболее очевидным является исключение тренда из
временного ряда и переход к случайной компоненте.
Для устранения автокорреляции можноишользовать
и другой прием, основанный на включении времени в
уравнение множественной регрессии в качестве
аргумента. Множественная регрессия с отклонениями от
линейных тенденций точно эквивалентна прямому введению
времени в уравнение регрессии. Это свойство впервые
заметили Фриш и Boy. Теорема Фриша и Boy применима
не только для линейных тенденций, но и для тенденций,
75

Таблица 6.1.1
РАСПРЕДЕЛЕНИЕ КРИТЕРИЯ ДУРБИНА-УОТСОНА
ДЛЯ ПОЛОЖИТЕЛЬНОЙ АВТОКОРРЕЛЯЦИИ
(для 5%-ного уровня значимости)1
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
45
50
55
60
65
70
75
80
85
90
95
100
v=
dx
1,С8
1,10
1,13
1,16
1,18
1,20
1,22
1,24
1,26
1,27
1,29
1,30
1,32
1,33
1,34
1,35
1,36
1,37
1,38
1,39
1,40
1,41
1,42
1,43
1,43
1,44
1,48
1,50
1,53
1,55
1,57
1,58
1,60
1,61
1,62
1,63
1,64
1,65
=1
d»
1,36
1,37
1,38
1,39
1,40
1,41
1,42
1,43
1,44
1,45
1,45
1,46
1,47
1,48
1,48
1,49
1,51
1,50
1,51
1,51
1,52
1,52
1,53
1,54
1,54
1,54
1,57
1,59
1,60
1,62
1,63
1,64
1,65
1,66
1,67
1,68
1,69
1,69
v=
d,
0,95
0,98
1,02
1,05
1,08
1,10
1,13
1,15
1,17
1,19
1,21
1,22
1,24
1,26
1,27
1,28
1,30
1,31
1,32
1,33
1,34
1,35
1,36
1,37
1,38
1,39
1,43
1,46
1,49
1,51
1,54
1,55
1,57
1,59
1,60
1,61
1,62
1,63
=2
d,
1,54
1,54
1,54
1,53
1,53
1,54
1,54
1,54
1,54
1,55
1,55
1,55
1,56
1,56
1,56
1,57
1,57
1,57
1,58
1,58
1,58
1,59
1,59
1,59
1,60
1,60
1,62
1,63
1,64
1,65
1,66
1,67
1,68
1,69
1,70
1,70
1,71
1,72
V-.
dt
0,82
0,86
0,9Э
0,93
0,97
1,00
1,03
1,05
1,08
1,10
1,12
1,14
1,16
1,18
1,20
1,21
1,23
1,24
1,26
1,27
1,28
1,29
1,31
1,32
1,33
1,34
1,38
1,42
1,45
1,48
1,50
1,52
1,54
1,56
1,57
1,59
1,60
1,61
= 3
d*
1,75
1,73
1,71
1,69
1,68
1,68
1,67
1,66
1,66
1,66
1,66
1,65
1,65
1,65
1,65
1,65.
1,65
1,65
1,65
1,65
1,65
1,65
1,66
1,66
1,66
l,6i
1,67
1,67
1,68
1,69
1,70
1,70
1,71
1,72
1,72
1,73
1,73
1,74
v.
d,
0,69
0,74
0,78
0,82
0,86
0,90
0,93
0,96
0,99
1,01
1,04
1,06
1,08
1,10
1,12
1,14
1,16
1,18
1,19
1,21
1,22
1,24
1,25
1,26
1,27
1,29
1,34
1,38
1,41
1,44
1,47
1,49
1,51
1,53
1,55
1,57
1,58
1,59
=4
d,
1,97
1,93
1,90
1,87
1,85
1,83
Ч1
1,80
1,79
1,78
1,77
1,76
1,76
1,75
1,74
1,74
1,74
1,73
1,73
1,73
1,73
1,73
1,72
1,72
1,72
1,72
1,72
1,72
1,72
1,73
1,73
1,74
1,74
1,74
1,75
1,75
1,75
1,76
v=
* dx
0,56
0,62
0,67
0,71
0,75
0,79
0,83
0,86
0,90
0,93
0,95
0,98
1,01
1,03
1,05
1,07
1,09
1,11
1,13
1,15
1,16
1,18
1,19
1,21
1,22
1,23
1,29
1,34
1,38
1,41
1,44
1,46
1,49
1,51
1,52
1,54
1,56
1,57
5
di
2,21
2,15
2,10
2,C6
2,02
1,99
1,96
1,94
1,92
1,90
1,89
1,88
1,86
1,85
1,84
1,83
1,83
1,82
1,81
1,81
1,80
1,80
1,80
1,79
1,79
1,79
1,78
1,77
1,77
1,77
1,77
1,77
1,77
1,77
1,77
1,78
1,78
1,78
в Таблица заимствована из работы 142].
76

выражающихся многочленами, и вообще для всех
ортогональных функций [28].
При построении многофакторных моделей по
временным рядам часто возникает проблема мультиколли-
неарности. Под мультиколлинеарностью понимают
наличие сильной корреляции между переменными, которая
может существовать вне всякой' зависимости между
функцией и факторами-аргументами1. Она является
одновременно и характеристикой и признаком
экспериментального исследования, построенного на весьма скудном
статистическом материале. Мультиколлинеарность
часто представляет собой весьма серьезную угрозу для
правильного определения и эффективной оценки
взаимосвязи. При мультиколлинеарности между аргументами
существует линейная связь. Если в модель включается
два или несколько линейно связанных
факторов-аргументов, то наряду с уравнением регрессии имеются и
другие линейные отношения.
Му'льт.иколлийеарность затрудняет проведение
анализа. Во-первых, усложняется процесс выделения
наиболее существенных факторов, поскольку правило, по
которому степень влияния аргумента на функцию
однозначно определяется абсолютной величиной
^-коэффициента, справедливо при условии взаимной
некоррелированности или достаточна слабой коррелированное™
всех факторов, теряет свою силу. Во-вторых, и по той
же причине искажается смысл коэффициентов
регрессии .гири попытке их экономической интерпретации.
В-третьих, возникают осложнения вычислительного
характера, а именно эффект слабой обусловленности
матрицы системы нормальных уравнений (т. е. близость
ее определителя к нулю). В такой ситуации получается
неопределенное множество значений оценок
коэффициентов регрессии.
Формально диагональные элементы матрицы,
обратной к матрице системы нормальных уравнений, которые
соответствуют линейно зависимым аргументам, обра-
1 Мультиколлинеарность может возникать также в случае,
когда в качестве независимых переменных берутся некоторые
синтетические показатели. Например, при анализе рентабельности в
качестве аргументов могут рассматриваться объем реализации,
производительность труда, фондоотдача, которые часто между собой сильно
взаимосвязаны.
77
Ч

щаются в бесконечность, так же как и дисперсии
вышеупомянутых оценок коэффициентов регрессии. Большие
дисперсии оценок этих коэффициентов, порождаемые
мультиколлинеарностью независимых переменных,
свидетельствуют о слабой информативности статистических
данных, а следовательно, о низком качестве
определяемых параметров. Увеличение дисперсий оценок для
коэффициентов мультиколлинеарной регрессии
фактически порождает тенденцию неоправданного исключения
некоторых существенных переменных из уравнения
регрессии.
Мультиколлинеарность составляет проблему только в
том случае, если она оказывает, по меткому выражению
Феррара и Глобера [43], «пагубное воздействие» на ту
часть множества независимых переменных, которая
.играет решающую роль в анализе. В отношении этих
переменных необходимо ввести соответствующую
процедуру, основанную на получении некоторой новой
дополнительной информации. Получение этой информации
может состоять в использовании некоторых
субъективных оценок, в дополнительном оборе исходных данных,
в применении некоторых оценок, полученных в других
аналогичных исследованиях (условная регрессия) и т. д.
Решение проблемы мультиколлинеарности можно
разбить на пять основных этапов:
1) 'Определение самого факта существования
мультиколлинеарности;
2) .измерение степени мультиколлинеарности;
3) определение области мультиколлинеарности на
множестве независимых переменных;
4) установление причин мультиколлинеарности;
5) определение мер по устранению
мультиколлинеарности.
В классическом регрессионном анализе
предполагается, что между независимыми переменными
отсутствует линейная связь, т. е. считается, что множество
независимых переменных является ортогональным. В
экономической практике такая ситуация встречается
достаточно редко. Между аргументами существуют
линейные соотношения, которые в простейшем случае
находят свое выражение в высокой величине
коэффициентов парной корреляции между отдельными
факторами. На практике считают, что два аргумента колли-
7&

неарны, если парный коэффициент корреляции между
ними по абсолютной величине больше 0,8 [34].
Более точным, но также достаточно грубым методом
является следующий: аргумент я* можно отнести к
числу мультиколлинеарных переменных лишь в том
случае, если коэффициент множественной корреляции,
характеризующий зависимость этой переменной от всех
остальных аргументов, больше, чем коэффициент
множественной корреляции, показывающий силу связи
между зависимой переменной и множеством всех
независимых переменных. Однако, как показывают
некоторые исследования [43], мультиколлинеарность
характеризует в oohobhoim не просто линейную зависимость
множества переменных, а их внутреннюю
взаимозависимость. Поэтому для определения мультиколлинеарности,
очевидно, требуется применить некоторые другие
методы.
Удачное и вполне верное, с нашей точки зрения,
определение мультиколлинеарности, данное ФеррарО'М и
Глоберюм, которое формулирует мультиколлинеарность
как степень отклонения от ортогональности множества
независимых переменных, позволяет продвинуться в
статистическом решении проблемы мультиколлинеарности,
покжольку ортогональность может быть четко
сформулирована как статистическая гипотеза [43]. Для
проверки наличия мультиколлинеарности во множестве
независимых переменных эти авторы предлагают
использовать показатель
^-[„-l-.-Ipp+B)] ln|X*.X|, . (6.1.2)
где п — число наблюдений;
р — число факторов,
X —матрица изучаемых факторов-аргументов,
X* — матрица, транспонированная к матрице X.
Причем этот показатель приближенно имеет
распределение х2 с 1/2/7 (/7—1) степенями свободы.
С помощью такого критерия можно.проверить
гипотезу о степени отклонения множества независимых
переменных от ортогонального множества, т. е. о наличии
мультиколлинеарности. Такая проверка является лишь
79

первым шашм в изучении мультиколлинеарности.
Далее необходимо определить те независимые переменные,
которые .наиболее сильно подвержены влиянию
взаимозависимости.
В качестве критерия оценки степени
мультиколлинеарности на рассматриваемые независимые переменные
можно использовать диагональные элементы матрицы,
обратной к матрице системы нормальных уравнений.
Для этого вводится величина
где си — 1-й диагональный элемент матрицы, обратной
к матрице системы' нормальных уравнений.
Доказано, что величина со имеет /^распределение
с (п — р) и (р— 1) степенями свободы. Величина
^-критерия является количественным критерием
степени мультиколлинеарности отдельных переменных.
Зная, какие независимые переменные из всего
множества независимых переменных, являются мультикол-
линеарными, в. общем случае можно с достаточной
степенью точности определить характер
взаимозависимости между мультиколлинеарными членами
множества независимых переменных.
Для этой цели можно использовать недиатональные
элементы обратной матрицы или полученные на их
основе коэффициенты частной корреляции между
мультиколлинеарными независимыми переменными и всеми
остальными независимыми переменными. При этом
существенную помощь может оказать величина ^-критерия
для коэффициента частной корреляции.
Причины мультиколлинеарности могут быть
установлены с помощью глубокого экономического анализа.
Среди мер по устранению или уменьшению
мультиколлинеарности можно отметить следующие:
1) построение уравнений регрессии по отклонениям
от тренда или по конечным разностям;
2) привлечение дополнительной информации (о чем
писалось выше);
3) преобразование множества независимых
переменных в несколько ортогональных множеств,
используя для этой цели методы много-мерного статистическо-
80

го анализа (факторного анализа и метода главных
компонент) ;
4) .исключение из рассмотрения одного или
нескольких линейно связанных аргументов, хотя последнее
надо применять с крайней осторО!Жностью, основываясь
при этом на тщательном экономическом анализе.
6.2. ПРОБЛЕМА ПОСТРОЕНИЯ
ДИНАМИЧЕСКОЙ МОДЕЛИ
Построение динамической модели состоит из
ряда этапов, которые будут рассмотрены ниже.
Пусть имеется (т + 1) временных рядов значений
экономического показателя и определяющих его факторов
за Т лет (7"= 1, 2, ..., п).
Построенная по этим данным многофакторная
регрессионная модель (с учетом исключения автокорреляции
и мультиколлинеарности)1
*rt-fiW(*irt.*V,*P ) (6.2.1)
будет характеризовать среднее влияние
факторов-аргументов на изучаеМ'Ъе явление, определенное за
рассматриваемый интервал времени. Между тем, величина
этого влияния, выраженная коэффициентами регрессии,
частными коэффициентами эластичности и iP-коэффици-
ентами, будет, очевидно, изменяться от года к году. При
достаточно продолжительном периоде времени (свыше
7—10 лет) такого рода подход будет означать недоучет
влияния технического прогресса, процесса замены
живого труда овеществленным, изменения влияния ресурсов,
энергии и т. д. Вышеотмеченные недостатки можно
устранить несколькими способами.
Разобьем период времени Т на 5 интервалов. При
этом выдвинем гипотезу о том, что за время, равное
величине одного интервала, коэффициенты регрессии
останутся постоянными или изменятся несущественно.
После этого построим s уравнений, аналогичных
уравнению (6.2.1). Каждый коэффициент регрессии а% будет
иметь 5 .оценок, т. е., по существу, мы получим
временной ряд для каждого коэффициента регрессии. По этим
1 Верхний индекс показывает номер этапа.
6. Заказ 3199 81

временным рядам можно построить прогнозы для
коэффициентов регрессии на момент времени (Г+/),
используя для этого методы прогнозирования по одному
временному ряду. Другими словами мы приходим к тому,
что прогнозируем само уравнение регреосин [21]. При
реализации этого 'способа возникает ряд серьезных
трудностей.
Так, при разбиении временных рядов экономических
показателей и определяющих их факторов на интервалы
число последних должно быть достаточно велико, чтобы
временные ряды коэффициентов регрессии для этих
интервалов правильно отражали тенденцию изменения
влияния аргументов на функцию. Число лет, входящих
в один интервал, должно быть, по крайней мере, в пять-
шесть раз больше числа переменных, входящих в любое
уравнение вида (6.2.1). Отсюда видно, что длина
временных рядов должна быть значительной. В то же
время данные по отраслям народного хозяйства за
такие длительные промежутки времени отсутствуют.
Кроме того, если бы мы даже и располагали такими
данными, то их вряд ли можно было использовать, так
как использование информации военных и первых
послевоенных лет значительно исказило бы результаты.
Поэтому практически применить этот способ крайне трудно, а
во многих случаях и невозможно.
Рассмотрим другой способ [31].
Пусть зависимость экономического явления от
влияющих на него факторов описывается уравнением
регрессии
yt = ao+aiXu + a2X2t-\ \-amxmt (6.2.2)
(*=1,2,...,п).
Далее предположим, что коэффициенты регрессии
изменяются во времени так, что можно записать:
Яг=Фг(0 (i=0,1,2,"., т). (6.2.3)
Рассмотрим случай, когда все функции (6. 2. 3)
будут линейными, т. е.
#0 = &00+&01^ -
a2 = b2Q+b2\t (6.2.4)
#m = ЬтО + bm\ t
82

Тогда уравнение (6. 2. 2) можно записать как
Ut= (&00+M) + (b\Q + bnt)xu+ (bw+b2\t)x2i+*
+ - + {bm0+bmlt)xmt (6.2.5*
или yt=sbao + boit + bioXit + butXit + b2QX2t+.
+ b2itx2t-\ \~bmoXmt + bmttxmt •
Проведем замену переменных
tX\t = Zit
tx2t = z2t
IXmt= Zmt
boo+boit=Co
Тогда уравнение (6. 2. 5) примет в.ид:
yt = Cq+bi0Xi t + b iiZu + b2oX2t + b2xz2t H h
+ bmoXmt + bm\Zmt ' (6.2.6)
Параметры уравнения (6. 2. 6), найденные методом
наименьших квадратов, показывают, как изменяются во
времени коэффициенты регрессии, т. е. как изменяется
во времени влияние отдельных факторов на изучаемое
явление.
Применение этого способа также связано с
большими трудностями и в первую очередь с тем, что
временные ряды, которыми располагают экономисты, коротки
(всего 15—20 лет). Даже для того чтобы учесть влияние
на явление трех факторов, необходимо оценить семь
параметров (в случае, если коэффициенты регрессии
изменяются во времени линейно). Если же влияние
факторов изменяется по нелинейному закону, например
параболическому, то для вышеприведенного примера
приходится оценивать уже не семь, а десять параметров, для
чего 15—20 наблюдений явно недостаточно. Обычно же
на уровень экономических явлений влияет не два-три, а
значительно больше факторов. Поэтому пользоваться
вышеописанным способом можно в редких случаях.
В связи с этим нам представляется, что временные
ряды среднеотраслевых показателей и влияющих на них
* факторов в основном можно использовать для
определения временных лагов влияний факторов-аргументов на
уровень изучаемого явления. Наиболее простой, хотя
возможно и не самый лучший, подход к нахождению
лагов состоит в построении автокорреляционных и взаимо-
83

корреляционных функций, которые в зависимости от
целей экономического анализа могут быть построены для
абсолютных значений анализируемых переменных, для
отклонений абсолютных значений от средних значений,
для отклонений абсолютных значений от тенденции, для
относительных значений и т. д. Затем по полученным
функциям проводится специальный анализ с целью
выявления (величины лагов.
Если временной лаг определяется непосредственно по
величине коэффициентов автокорреляции и взаимной
корреляции, то возникает проблема проверти значимости
полученных коэффициентов и их сопоставимости
(каждый из коэффициентов таких функций получен при
различном числе степеней свободы). Для сопоставимости
этих коэффициентов обычно проводят корректировку на
число степеней свободы по формуле
?-/l-0->> (-££). (6-2.7)
Л
где г — величина коэффициента автокорреляции или
взаимной корреляции, скорректированная на число
степеней свободы;
г — нескорректированная величина коэффициента
автокорреляции или взаимной корреляции;
п — число наблюдений временного ряда;
т — длина лага.
В работе [39] показано, что распределение таких
коэффициентов значимо отлично от нормального. Поэтому
проверка значимости может быть произведена для
скорректированных величин весьма приближенно по
величине гнкритерйя.
Пусть влияние аргументов на функцию изменяется
ежегодно. Бели бы удалось динамический процесс
изменения явления разложить на ряд статических
(пространственных) процессов, построить при этом набор
пространственных моделей и соединить их во времени, то,
таким образом, видимо, можно было получить
динамическую модель экономического явления [21], [30], [31].
Предположим, что имеются данные,
характеризующие изучаемое явление, и влияющие на него факторы за
ка)ждый год Т-го периода по в'сем исследуемым
объектам. Обозначим число объектов в t-м году^через Nt.
Совершенно очевидно, что число объектов нг различные го-
84

ды было 'неодинаковым. Более правильно было бы
выбрать число Nt одинаковым для всех лет и равным
количеству объектов в том году, в котором их было меньше
всего.
Однако нам представляется, что целесообразнее
анализировать то число объектов, которое в
действительности функционировало в каждом году.
Для каждого года строится статическая
(пространственная) модель вида
yt{2)=ft{2) (х£ь?.---,х%); (* = 1,2,-.л). (6.2.8)
Бели имеется запаздывание во влиянии аргументов
на функцию, то тогда модель (6. 2. 8) запишется в виде
(2) (2) (2) (2) (2) ' /eonV
Vt =ft (хцг-ъ,Х2а-т), — ,Хщг-т)). (6.2.9)
Таким образом, можно построить п моделей вида
(6, 2. 9). От уравнения ik уравнению изменяются не
только значения переменных, но также и коэффициентов
регрессии.
Вычисленные коэффициенты регрессии
рассматриваются KaiKвременные ряды ац (t=l, 2, ..., п) с трендом
я* (t)[2L]f[30], [31].
Следует отметить, что во временных рядах
коэффициентов регрессии тенденции складываются в
результате изменения как структур влияний факторов «а
изучаемое явление, так и изменения во времени значений
самих факторов. Однако провести четкое разделение, за
счет каких причин появляется тенденция во временных
рядах коэффициентов регрессии, на наш взгляд, не
представляется возможным. Построение по временным
рядам моделей зависимости коэффициентов регрессии от
анализируемых факторов вызывает те же затруднения,
что и построение любой регрессионной модели по
временным рядам. I
Используя полученные временные ряды
коэффициентов регрессии, можно построить динамическую модель
изучаемого явления, которая будет иметь вид:
(3) г(зь (з) (3) (3) ч (6.2.10)
Уг —ft \X\{t-x)> #2(*-т),>-..> Xm(*-x), U0t> a\t>'-->amt) '
85

Эта модель учитывает результаты, полученные при
анализе временных рядов среднеотраслевых показателей
(лаги), коэффициенты регрессии, полученные на втором
этапе построения статико-динамических моделей вида
(6. 2. 9), и динамику изменения коэффициентов
репрессии во времени.
Практические расчеты по этой модели производятся
следующим образом [31].
Пусть имеются данные по показателям у^ X\$, ..., xmj
для N объектов (/=1, 2, ..., N) за t лет (/=1, 2, ..., я)..
Построим уравнение регрессии, характеризующее
зависимость изучаемого явления у от факторов Х\, х2, ..., хт
для момента t=l. Затем построим такие же уравнения
для £=2, £=3, ..., t = ny т. е. получим систему из п
уравнений вида
Ух = ft (*к«-т), Хф-г), • • * ,*та-.1)У- (6.2.11)
Для каждого фактора Xi будет иметь п
коэффициентов регрессии, которые являются временными рядами
Для определения величины влияния
факторов-аргументов на изучаемое явление в момент времени tn+i
следует построить пролнозы коэффициентов регрессии с
помощью какого-либо метода прогнозирования по
одному временному ряду. Тогда, например, линейная модель
прогноза на момент времени tn+i будет иметь следующий
вид:
yt+i=aot n+l +аи п+1хи п+1 + — +;
+ Omt n+l Xmtn+l • (6.2.12)
При построении моделей (6. 2. 12) должны
выполняться следующие условия [30]:
1, Развитие соответствующей отрасли должно
происходить в соответствии с принципом инерции, который
позволяет считать, что наблюдаемые закономерности,
достаточно устойчивые в течение определенного периода
времени, будут действовать и некоторое время после
окончаний этого периода. Этот принцип будет
действовать лишь в том случае, если в прогнозируемом
периоде не произойдет больших изменений в состоянии
отрасли, например, коренной реконструкции предприятий,
значительного изменения ,их профиля и т. д.
2. Период времени t (/=1,2, ..., п) достаточно велик
для того, чтобы можно было выявить существующие за-
86

кономерности. Практически для построения моделей
(6. 2. 12) необходимо иметь данные за период времени
не менее чем в 10—12 лет.
3. Правильно выбрана модель прогноза
коэффициентов регрессии и метод оценки параметров этой модели.
Чтобы сделать прогноз по модели (6. 2. 12),
•необходимо определить значения факторов х\, *% ..'., Хт на
момент времени tn+i. Величина этих факторов
определяется или на основании некоторых контрольных цифр, или
исходя из объема капитальных вложений, которые
будут сделаны .в перспективе, и т. д. В отдельных случаях
она может быть получена путем экстраполяции по
линии тренда или каким-либо другим способом.
6.3. ПОСТРОЕНИЕ ДИНАМИЧЕСКОЙ МОДЕЛИ
(НА ПРИМЕРЕ ПОСТРОЕНИЯ МОДЕЛИ
ПРОИЗВОДИТЕЛЬНОСТИ ТРУДА
В ЦЕМЕНТНОЙ ПРОМЫШЛЕННОСТИ)
В данном параграфе освещаются вопросы
построения динамической модели на примере
производительности труда ,в цементной промышленности.
В исследовании рассматриваются следующие четыре
фактора, оказывающие наибольшее влияние на
выработку натурального цемента в тоннах на одного рабочего
Xi — электровооруженность, квт-ч/человеко-час;
Л'2 — средняя часовая производительность
вращающихся печей, т/час;
Хг — использование календарного времени работы
вращающихся печей;
лг4— процент ввода в цемент.
Исходной информацией для построения
динамической модели служили данные по ряду цементных
заводов за 1958—1970 гг.2.
При выборе числа предприятий учитывались моменты
как экономического, так и статистического характера.
Из анализируемых совокупностей исключались заводы,
на которых условия производства резко отличались от
1 Такой набор факторов был установлен одним из авторов в
работе 130].
2 Цементная промышленность СССР, вып. XV—XXVIII, М.,
НИИЦемент.
87

типичных для отрасли. Не рассматривались заводы,
показатели которых представляли собой многомерные
аномальные наблюдения1. Наконец, исключались заводы, по
которым не было каких-либо изучаемых показателей.
На первом этапе для каждого года были получены
матрицы парных коэффициентов корреляции2 (табл. 6.
3. 1). При их анализе нас интересовало в первую
очередь два вопроса: а) не наблюдалось ли в отдельные
годы мультиколлинеарности между факторами и б) не из*
менялись ли направления связей.
Анализ матриц парных коэффициентов корреляции
позволил сделать вывод, что между факторами нет
мультиколлинеарности (rXl Xj ^0,8)3. Наиболее тесная
связь наблюдалась в 1966 г. между факторами Х\ и л*2
(r*i х 2 =0,600). Во все остальные годы величина
парного коэффициента корреляции между этими
факторами колебалась в интервале от 0,400 до 0,596. Величина
коэффициента корреляции между остальными
факторами не превышала 0,484. Что касается изменения
направлений связей, то в 1959, 1963, 1968, 1969 и 1970 it.
изменялся знак у /*3 *4 . Поскольку связь между
использованием календарного времени работы вращающихся
печей и процентом ввода добавок в цемент не имеет ни
экономического, ни технологического смысла, мы не
придали этим изменениям какого-либо значения.
Так как для изучения факторов, влияющих на уровень
производительности труда, мы используем регрессионный
анализ, то более детальное изучение матриц парных
коэффициентов корреляции производить нецелесообразно.
Для каждого года строилось уравнение регрессии,
показывающее зависимость выработки от четырех
вышеперечисленных факторов. Динамика важнейших
статистических характеристик уравнений регрессии представлена
в табл. 6.3.2. В таблице даны следующие характеристики:
1 Алгоритм исключения многомерных аномальных наблюдений
описан в работе [30].
2 Результаты всех расчетов за период 1968—1969 гг. здесь и
ниже заимствованы из работы [31].
3 В данной работе при определении мультиколлинеарности не
использовался способ, предложенный Ферраром и Глаубером (см.-
параграф 6.1), так как авторы не располагали соответствующей
программой для ЭВМ.
88

cti —коэффициент регрессии t'-го фактора (t=0,l,...,
4); i
Oat —среднеквадратическая ошибка i-го
коэффициента регрессии;
ta i — расчетное значение ^-критерия для i-ro коэффи-
циента регрессии;
R —скорректированная величина коэффициента
множественной корреляции;
F #~ — расчетное значение Лкриггерия для
скорректированного коэффициента множественной
корреляции;
F —расчетное значение/^-критерия для уравнения
регрессии;
^табл —табличное значение /^критерия.
На рис. 6.3.1—6.3.5 представлена динамика
коэффициентов регрессии.
1958 59 60 61 62 63 № 65 66 67 68 69 70 t
-600
-700
-800
-900
-1000
-fW0\
- 1200\
-1300
- 1ЬО0\
-1500
-1б00\
-1700\
Рис. б.ЗЛ.
Из табл. 6.3.2 видно, что все уравнения регрессии
адекватны (все расчетные значения /^критерия выше
табличных). Величина скорректированных коэффициентов
множественной корреляции (от 0,822 до 0,903) указывает на
высокую степень тесноты связи между выработкой и ото-
89

16
ts
13
12
W
1958 59 60 61 62 63 64 65 66 67 68 69 70 t
Рис. 6.3.2.
бранными факторами. Все коэффициенты регрессии, за
исключением а2 для Ш59 г., а4 для 1962 г., а4 для 1963 г.,
а4 Для 1964 г., Я4 Для 1967 г. и а4 для 1970 г., значимы при
5%-ном уровне значимости (£Табл = 2,0). Шесть
вышеупомянутых коэффициентов регрессии значимы для 10%-ного
уровня значимости (/табл=1,62).
Для экономической интерпретации уравнений
регрессии были рассчитаны частные коэффициенты
эластичности и р-коэффициенты (табл. 6.3.3).
При сопоставлении частных коэффициентов
эластичности видно, что в течение всего изучаемого периода
наибольшее влияние на выработку ягказыва л фактор
х$—использование календарного времени работы вращающихся
печей; на втором месте стоит фактор
Х\—электровооруженность; на третьем х2—средняя часовая производитель-:
90

ДИНАМИКА МАТРИЦ ПАРНЫХ КОЭФФИЦИЕНТОВ КОРРЕЛЯЦИИ
Таблица 6.3.1
**
*2
**
*1
1958 г.
1959 г.
1960 г.
У
Хх
х2
г3
х4
X
Хг
х3
Хз
У*
Л"1
*3
Хх
У
х%
х3
1
0,714
0,522
0,108
0,321
1
0,710
0,602
0,331
0 3?1
1
0,739
0,493
0,126
0,053
1
0,717
0,549
0,161
0,0Э7
1
0,588 1
-0,084 -0,248
0,185 -0,091
1961 г.
1
0,552 1
-0,098 -0,094
0,204 -0,0б7
1964 г.
1
0,473 1
-0,215 -0,279
0,042 -0,243
1967 г.
1
0,513 1
-0,141 -0,048
0,111 -0,249
1
-0,072
1
-0,089
1
-0,160
1
-0,125
1
0,725"
0,530
0,228
1 0,402
1
0,712
0,498
0,228
1 0,327
1
0,710
0,572
0,030
1 0,233
1
0,728
0,518
0,046 -
1 0,160
1.
0,592 1
-0,051 -0,070
0,212 -0,076
1962 г.
1
0,435 1
-0,191-0,124
0,198 -0,059
1965 г.
Jl
'0,587 1
-0,270 -0,374
0,137-0,181
v I968 г.
1
0,561 1
-0,323 -0,484
0,072-0,144
1
0,028
1
-0,117
1
-0Д85
1 .
0,022
1
0,708 1
0,591 0,596 1
0,043-0,117 -0,019
1 0,360 0,258 -0,011
1963 г.
1
0,720 1
0,386 0,400 1
0,265-0,067 -0,235
1 0,125 0,074 -0,215
1966 г.
1
0,739 1
0,631 0,600 1
0,010-0,299-0,313
1 0,138 0,091 -0,153
1969 г.
1
0,732 1
0,513 0,475 1
0,114-0,210 -0,357
1 0,183 0,098 -0,109
1
-0,263
-
1
0,158
1
-0,142
1
0,094
1
1
1
1
0,738
0,494
0,177-
1 0,092
S
1970 г
1
0,505 1
-0,119 -0,294
0,054 -0Д73
1
0,143

36
**. ««*. **. **. **.
ft ft ft ft ft
*. ее к» ►* о
^со са jo со са
СЛ -si "to ->4 ►&■
с» --4 ел со со
ел оо оо оо to
СО w и М КЗ
00 *© "со "© СЛ
to to >ь. *- оо
СЛ ^ ^ Ю00
со to со сл ю
I- О tO СО Ю
ю сл со ел ел
м СЛ СО (О 4^
о> "ел "to Vj "to
А О О ^ О)
^ ^ v) СП ilk
м А, ю «О *>
¥•* #ъ 03 <С j(k
a fc з § 8
to *» со оо со
sVgVs
4Ь »- 4*. СО «si
Ю СО 4ь 0> СО
;8
$8§!
со со I
н- jU СО «si 4*.
W О О) 8 Ч
JO jU J» j» СО
О) СП СО КЭ СО
Ч М м М СП
Ю tfe СО 00 W
f"oo "«о "ел --1
•— jfc. CO 00 J»
"to "ел "и- "н- "o>
^ и м О) И
(ОМ м W W
Q Q Q Q Q
ft ft ft ft ft
-6
О CO OS CO 00
►&. О и- CO *sl
S J^ СО -4 *»
Ы
to со
м К5 CO и Ч
i-i to мм»
"со "ел "со со to
О CO 03 н- j«J
-j "со и* "rfk ел
to «- со со ро
to ел to to to
О со со и to
со со о 4 а
О и 00 Ч S
i-i 4Ь СО и* О)
О 00 О S to
О СЛ СЛ О О)
со
■sj
и- СО СО ■-» 05
J— JW СО н-> О"
"to "to "о V "■£
СО О СО 00 О
sj *4 и »U ^
"о Ю £» rffc СО
со «л £ -si ел
о <о о « со
~£
*д «- to to <
S *« Si? *"* '
О *sl О) «-* <
О ^ СО и ел
"to "о "о *. "to
о S 8 to to
ft ft ft ft ft
CO N Ч СП СЛ
& 8 3 2 £2
•-' ел Oi о £ь
** r4 i» J* S2
© сп оо о &
^(O iD> О iU
"Ьо "ел "со *-si "их
м ел to и и
СО О) ►£» 4» СО
И И И О!
со to со н- to
fc (О СП •- оо
I
JO 4* JO СО Ю
"'■' "ir ^3 "ел "оо
СП С7) Ю м tO
Oi »*k £» »-» О
I
и- СЛ
8 8
-4 СО О
Sen о
«si to
| to СО t-»
§§§i
СО 00
"со "л.
92 95
М и и
"to "ел "оо
ел со о о
«si Ю
СП СО '
и- Ю
5° j° J
ol о •
, ■
o>
со
СП
■ff
("0
00
to
о
to
CO
СП
rf*
СП
•si
^
en
to
00
«si
00
to
о
СЛ
&
СЛ
СП
1
Oi
*s|
4k
00
«- »-* CO
н* 00 CO •-* •"*
Стати стичес-
кие
характеристики
уравнений
регрессии
£
Oi
СО
t9

1 I It I I I I и I i f I I I f
t958 S9 60 61 62 63 ' 6b 65 66 67 68 69 70 t
Рис. 6.3.3.
ность вращающихся печей и на последнем — х±—процент
ввода добавок в цемент.
Для сравнения влияния отобранных факторов с учетом
их колеблемости рассмотрим динамику р-коэффициентов.
Если учитывать различие в уровне колеблемости
факторов, то наибольшее влияние на выработку оказывает
электравооруженность--л;1, которая имеет большую
вариацию (коэффициент 'вариации колеблется от 40,3 до
48,7%). В анализируемом периоде в течение девяти лет
(из 13) на втором месте по степени влияния стоял фактор
#з—использование календарного времени вращающихся
печей. В те годы, когда наблюдался значительный при-
^ рост по другим факторам при сравнительно небольшом
*г\
т
Л
/г\
т
И
д\
в\
Л
93

приросте лг3,фактор использования календарного времени
вращающихся печей по степени своего влияния
перемещался на третье или четвертое место. Влияние этого
фактора особенно возрастало в те годы, когда в
цементной про1мышленности не выполнялся план ввода новых
мощностей. Так, в 1961 г. план ввода новых мощностей
был выполнен всего на 66,6%,причем большая часть
мощностей была введена в конце года. В то же время объем
производства вырос по сравнению «с 1960 г. на 11,8%.
Объясняется это влиянием ряда факторов, среди которых
далеко не на последнем месте стоит улучшение
использования календарного времени вращающихся печей.
Следующее место (третье) по величине влияния занимает фактор
#2 — средняя часовая производительность вращающихся
1958 59 60 61 62 63 64 65 <?f. 67 68 69 70 t
94
Рис. 6.3.4.

Таблица 6.3.3
ДИНАМИКА ЧАСТНЫХ КОЭФФИЦИЕНТОВ ЭЛАСТИЧНОСТИ
И ^-КОЭФФИЦИЕНТОВ
Годы
/
Частные коэффициенты
эластичности
Эх
эа
Э3
э4
^-коэффициенты
Pi
Р2
Рз
Р*
1958
1959
I960
1961
1962
1963
1964
1965
1966
1967
1968
1969
1970
0,661
0,640
0,483
0,541
0,653
0,643
0,632
0,558
0,520
0,567
0,591
0,544
0,599
0,173
0,199
0,296
0,280
0,204
0,170
0,207
0,252
0,276-
0,231
0,227
0,237
0,189
1,138
0,964
1,157
1,403
1,471
1,595
1,520
1,571
1,224
1,453
1,557
1,458
1,253
0,164
0,171
0,182
0,139
0.Г63
0,034
0,014
0,075
0,С82
0,С76
0,081
0,073
0,034
0,716
0,715
0,529
0,535
0,700
0,716
0,722
0,663
0,600
0,642
0,686
0,647
0,658
0,189
0,246
0,328
0,3)2
0,229
0,196
0,256
0,323
0,384
э,ззз
0,311
0,353
0,267
0,244
0,196
0,183
0,373
0,337
0,349
0,348
0,304
0,283
0,359
0,323
0,456
0,326
0,236
0,264
0,275
0,208
0,105
0,060
0,029
0,144
(>,146
0,133
0,148
0,133
0,056
печей (за исключением 1959 г.). И наконец, на
последнем месте — х4 — процент ввода добавок в цемент.
Для выявления тенденции изменения коэффициентов
регрессии, частных коэффициентов эластичности и,р-коэф-
фициентов было произведено сглаживание. Выбор
аппроксимирующей функции производился на основании
сравнения пяти функций:
yt = ao+a\t; ч (6.3.1)
yt=b0 + blt + b2t2\ (6.3.2).
ln0(O=Co+Cilnf; (6.3.3)
\ny(t) = d0+d1t; (6.3.4)
\ny(t)=lo+ht + l2t*' (6.3.5)-
Формальным критерием для выбора
аппроксимирующей функции служила величина средней квадратической
ошибки, рассчитываемая по формуле (2.2.8). В случае,
если две средние квадратические ошибки мало
отличались друг от друга, предпочтение отдавалось функции
более простого вида.
Отобранные функции представлены в табл. 6.3.4.
При сравнении данных табл. 6.3.2 и 6.3.3 видно, что,
несмотря на постоянный рост электровооруженности тру-
95

—-» ' ' • ' '
1958 59 60 61 62 63 6<i 65 66 67 68 69 70 t
Рис. 6.3.5.
да в цементной промышленности, влияние этого
«показателя на выработку уменьшается. Это снижение
происходит вследствие перераспределения степени влияния
факторов и интерпретируется только при одновременном
рассмотрении изменения влияния других факторов.
Так, изучая динамику роста и влияния средней часовой
производительности вращающихся печей, можно увидеть,
что за период с 1958 по 1970 г. наблюдается рост средней
часовой производительности вращающихся печей и
одновременно увеличивается влияние этого показателя на
производительность труда. Рост фактора х2 происходил за
счет ввода в действие более мощных вращающихся
печей, что потребовало расхода большего количества
электроэнергии. Кроме того, улучшение условий труда,
главным образом на вспомогательных работах, привело к
дополнительным затратам электроэнергии. Одновременно с
этим рост электровооруженности сопровождался
некоторым улучшением работы оборудования. Вследствие этих
причин в 1958—1970 гг. влияние электровооруженности
труда на производительнось труда уменьшилось примерно
96

fa блица 6.3.4
ЗНАЧЕНИЯ АППРОКСИМИРУЮЩИХ ФУНКЦИЙ.
ДЛЯ КОЭФФИЦИЕНТОВ РЕГРЕССИИ, ЧАСТНЫХ
КОЭФФИЦИЕНТОВ ЭЛАСТИЧНОСТИ И ^-КОЭФФИЦИЕНТОВ
Показатели
Коэффициенты
регрессии
Частные
коэффициенты
эластичности
Уравнения
#0=
#3=
я4=
—384,775
14,977
10,257
4,043
4,397
0,614
0,223
0,868
0,220
-192,575*
— 0,640*
+ 0,1*
+ 2,463*
— 0,403*
— 0,0038*
+ 0,00049*
+ 0,156*
— 0,0338*
+7,876*2
+0,028*2
—«>,G97*2.i-
+0,025*2
—0,0094**
+0,0017*2
Pi- 0,656 + 0.0С0027*
р-коэффициен* Ра= 0,230 + 0,008*
ты *>з=* 0,187 + 0,0129* -0,0012*2
р4= 0,314 + 0,043* +0,0022*2
на 40%, хотя электровооруженность возросла более чем
в 2,3 раза.
Использование календарного времени работы
вращающихся печей почти не изменилось. Одновременно
возросло влияние этого фактора на выработку. Что касается
процента ввода добавок в цемент^ то наряду с общим
уменьшением величины этого показателя уменьшилось и
его влияние на выработку.
Для построения динамической модели
производительности труда необходимо разработать модели прогноза для
коэффициентов регрессии. Для этой цели воспользуемся
методом экспоненциального сглаживания, описанным в
главе IV. Величину а определим по формуле (4.3.1). Она
раозна 0,143. В табл. 6.3.5 приведены оценки
коэффициентов для построения экспоненциальной модели прогноза
коэффициентов регрессии.
На основании данных табл. 6.3.5 можно представить
динамическую модель прогноза производительности труда
в цементной промышленности следующим образом:
у*= (~ 1550,42+13,92/+7,93/2) + (11,429+0,093/ +]
.+.0.028Р)*«+ (11,335+0,075/) *« + (19,579—0,077/-
- 0,0975/2) х3*+ (3,257+0,218/ + 0,024/2)*4* • (6.3.6)
7. Заказ 3199 ду

Таблица 6.3.5
ОЦЕНКИ КОЭФФИЦИЕНТОВ ДЛЯ ПОСТРОЕНИЯ
ЭКСПОНЕНЦИАЛЬНОЙ МОДЕЛИ ПРОГНОЗА КОЭФФИЦИЕНТОВ
РЕГРЕССИИ1
Коэффициенты
регрессии
Оценки

коэффициентов модели эке-
п оненциального
сглаживания
а0
а,
аА
во t
—1550,42 11,429
13,92 0,093
15,86 0,056
11,335
0,075
19,579
-0,077
—0,195
3,257
0,218
0,048
1 В табл. 6.3.5 обозначения оценок коэффициентов экспоненциальной
модели прогноза отличаются от обозначений, принятых в главе IV,
Для прогнозирования производительности труда на
1975 г. воспользуемся уравнением (6.3.6). ГГодставив в
него соответствующие значения /, получим следующее
уравнение регрессии, характеризующее связь выработки
с отобранными факторами в 1975 г.:
#*= -1282,5+J2,6*i*+ll,71*2* + 16,75*3*+4,95*4* • (6.3.7)
Ошибки прогноза на 1975 г. для .коэффициентов
регрессии следующие:
соо = ± 104,7; aai=±0,94; ffe,=±l,31}
ffa3 = ±1'12; aa4=±0,97.
Поэтому для определения интервалов прогноза
получим следующие два уравнения:
у*= _1387,2 +1 l,65*i*+10,4*2*+15,64*3*+3,98*4*; (6.3.8)
у*= -1177,8+ 13,54*!* +13,03*2*+17,87*3* + 9,92%. (6.3.9)
Модели прогноза электравооруженности (*i) и
средней часовой /производительности вращающихся печей
(*2) также были получены с помощью метода
экспоненциального сглаживания (для а=0,333).
Модели прогноза этих показателей имеют следующий
вид:
**, = 64,76+2,68/-0,039/2; . (6.3.10)
x*2t =25,35 + 0,73/-0,016/* - (6.3.11)
98

Прогноз электровооруженности на 1975 г. составил
77,2квт-ч/чело1веко-час., а средней часовой
производительности вращающихся печей — 28,6 т. Величину факторов
Хъ — использование календарного времени вращающихся
печей и #4 — процент ввода добавок в цемент
формальным путем определить нельзя. Исходя из перспектив
развития отрасли мы приняли, что в 1975 г. #з=90%, а
х4=25%.
Подставив в модель {6.3.7) соответствующие значения
факторов, найдем, что в 1975 г. средняя выработка
натурального цемента в расчете на одного рабочего должна
составить около 1656 т.
Ввиду того, что было не ясно, как определить ошибку
прогноза по факторам хъ и #4, доверительные интервалы
для выработки по моделям (6.3.8) и (6.3.0) построены не
были.
В данном исследовании также не был осуществлен
прогноз выработки на отдельные годы периода 1971—1974
гг., так как авторы не располагали достаточно
обоснованными- рекомендациями по определению величины
факторов хъ и я4 на это время.
Рассмотрим, какие изменения произойдут во влиянии
отобранных факторов на выработку к 1975 г. Наибольшее
влияние на выработку по-прежнему будет оказывать
фактор х\—электровооруженность (f}=0,656). Факторы х^—
средняя часовая производительность вращающихся печей
и Хг —использование календарного времени работы
вращающихся печ^й по степени влияния будут занимать
второе и третье места (р2=0,374; 03=0,320), т. е. между ними
произошло перераспределение влияний. Фактор
я4—процент ввода добавок в цемент остается по величине своего
влияния на последнем месте ($4=0,253). Следует также
отметить, что в 1975 г. должно произойти дальнейшее
перераспределение во влиянии отдельных факторов. Так,
если в 1970 г. влияние электровооружённости на
выработку превосходило влияние средней часовой
производительности вращающихся печей примерно в 2,5 раза, то в 1975
г. это отношение должно уменьшиться примерно до 1,8
раза.
7*

ЛИТЕРАТУРА
I. Айвазян С. А. Статистическое исследование зависимостей.
М., «Металлургия», 1968.
2>. Бобров С. П. Экономическая статистика. Введение в
изучение методов обработки временных рядов экономической
статистики. М.—Л., Госиздат, 1930.
3. Броуди М. Б. О статистическом рассуждении. Пер. с англ.,
М., «Статистика», 1968.
4. Вайнштейн Алб. Л. Проблема экономического прогноза в
ее статистической постановке. М., «Ранион», 1930.
5. В е н е ц к и й И. Г., К и л ь д и ш е в Г. С. Основы теории
вероятностей и математической статистики, изд. 2, М., «Статистика»,
1968.
6. Веитцель Е. С. Теория вероятностей, изд. 4, М., «Наука»,
1969.
7. Гн еден ко Б. В. Элементы теории случайных процессов.—
«Стандарты и качество», 1967, № 7.
8. Дружинин Н. К. Математическая статистика в экономике.
М., «Статистика», 1971.
9. Езекиел М., Фокс К. Методы анализа корреляций и
регрессий (линейных и криволинейных). Пер. с англ., М.,
«Статистика», 1966.
10. Кузнецова К. С, Голодненко В. Н. К вопросу о
количественной оценке точности прогноза. — «Экономика и
математические методы», т. VII, вып. 6, 1971.
II. Левин Б. Р. Теоретические основы статистической
радиотехники. Кн. 1-я, М., «Советское радио», 1969. Кн. 2-я, М.,
«Советское радио», 1968.
12. Леонтьев В. [и др.]. Исследование структуры
американской экономики. Пер. с англ., М., «Статистика», 1968.
13. Л у к а ц к а я М. Л. Некоторые вопросы исследования
авторегрессионных схем. — В сб.: Опыт решения экономических задач
математическими методами. Новосибирск, «Наука», 1967.
14. Манелля А., Нагнибедова Н. О методах исчисления
темпов роста при выравнивании динамических рядов
урожайности.— В сб.: Применение математической статистики в экономике
сельского хозяйства. Тезисы докладов на научной конференции.
Изд. Министерства сельского хозяйства СССР и Одесского
сельскохозяйственного института. Одесса, 1969.
15. Манелля А. И. (и др.]. Динамика урожайности
сельскохозяйственных культур в РСФСР. М., «Статистика», 1972.
100

16. Математические методы в статистике. Сб. статей под ред.
Г. Л. Ритца. М., «Экономическая жизнь», 1927.
17. М и лхл с Ф. Статистические методы. Пер. с англ., М., Гос-
статиздат, 1958.
18. М о т Ж- Статистические предвидения и решения на
предприятии. Пер. с франц., М., «Прогресс», 1966.
19. Пановский Г. А., Брайер Г. В. Статистические
методы в метеорологии. Пер. с англ., Л., Гидрометеоиздат, 1967.
20. Р а й с к а я Н. Н., О р л о в А. В., Ф р е н к е л ь А. А. Методы1
прогнозирования спроса при разработке оптимальных планов
отраслевого развития (на примере консервной промышленности).—-
В сб.: Математические методы и модели в экономических
исследованиях. Научные труды МИНХ им. Г. В. Плеханова, вып. 101. М.,
изд. МИНХ им. Г. В. Плеханова, 1972.
21. Розанов Г. В., Френкель А. А. Некоторые вопросы
статистического прогноза развития отрасли. Материалы Всесоюзной
конференции по применению экономико-математических методов й
электронно-вычислительной техники в планировании развития и
размещения производства. Секция I. Издание ЦЭМИ АН СССР,
Таллин, 1967.
22. Р о з а н о в Г. Проблемы построения динамической
статистической модели развития отрасли.— В сб.: Проблемы статистики.
Труды Московского экономико-статистического института по итогам1
научной работы кафедры общей теории статистики за 1967 г., М.,
изд. МЭСИ, 1968.
23. Селиванов Ю. Л., Клеандров Д. И.
Прогнозирование макроэкономической структуры методом обобщенною
экспоненциального сглаживания. — В сб.: Повышение эффективности
общественного производства и проблемы экономической реформы.
(Материалы молодежной научной конференции). М., Изд. института
экономики АН СССР, 1968.
24. Серебренников М. Г. Гармонический анализ. М.—Л.,
Огиз, Гостехиздат, 1948.
25. Смирнов А. Д. Моделирование и прогнозирование
социалистического воспроизводства. М., «Экономика», 1970.
26. С м и р н о в Н. В., Дуни н-Б арковский И. В. Курс
теории вероятностей и математической статистики, изд. 2, М.,
«Наука», 1965.
27. Т е й л Г. Экономические прогнозы и принятие решений. Пер.
с англ., М., «Статистика», 1971.
28. Т и н т н е р В. Введение в эконометрию. Пер. с нем., М.,
«Статистика», 1965.
29. Френкель А. А., Райская Н. Н. О временных лагах
некоторых экономических показателей цементной
промышленности.— В сб.: Применение методов корреляции в экономических
исследованиях. Ученые записки по статистике, т. XVI, М., «Наука»,
1969.
30. Френкель А. А. Математический анализ
производительности труда. М., «Экономика», 1968.
31. Френкель А. А. Математические методы анализа
динамики и прогнозирования производительности труда. М., «Экономи-»
ка», 1972.
32. X а л ь д А. Математическая статистика с техническими
приложениями. Пер. с англ., М., Изд-во иностр. лит., 1956.
101

33. X е н а н Э. Анализ временных рядов. Пер. с англ., М.,
«Наука», 1964.
34. X е д и X., Д и л л о н Д. Производственные функции в
сельском хозяйстве. Пер. с англ., М., «Прогресс», 1965.
35. Ч е т в е р и к о в Н. С. Статистические и стохастические
исследования. М., Госстатиздат, 1963.
36. Экономико-статистические исследования промышленного
производства. М., «Статистика», 1969.
37. Юл. Дж. Э. КендаллгМ. Дж. Теория статистики. М.,
Госстатиздат, 1960.
38. Я с т р е м с к и й Б. С. Некоторые вопросы математической
статистики. М., Госстатиздат, 1961.
39. Ames E. and Re iter S. Distributions of Correlation
Coefficients in Economic Time series.—«Journal of the American
Statistical Association», Sept., 1901, p. 637—666.
40. Birowri R. G. Smoothing, Forecasting and Prediction of
Discrete Time Series. Prentice-Hall, Englewood Cliffs. N. Y., 1963.
41. Brown R. G. and Meyer R. F. The Fundamental
Theorem of Exponential Smoothing.—«Operations Research», vol. 9, № 5,
11961, p. 673r-687.
42. (Duirbin J. and Watson G. S. Testing for seriel
Correlation in Least-Sguares Regression.—«Biometrika», vol. 38, № 1—2,
1991, p. 159—178.
43. Farrier D. E., Glauber F. R. Multioollinearty in
Regression Analisis: The Problem Revisited—.«.The Rewiew Economics-and
Statistics», vol. 49, № 1,1967, p. 92—107.
44. Grunwiald H. The Correlation Theory for Stationary
stochastic Processes applied to Exponential Smoothiny.—«Statistica
Neerlandica», vol. Л9, № 2—3, 1966.
45. Y u 1 e G. U. On a Method of Investigating Periodicities in
Disturbed Series, with Special Reference to Wolfers Sunspot
Numbers. Philosophical Transactions of the Royal Society, Section A. 1927,
p. 267—298.

ОГЛАВЛЕНИЕ
Предисловие . . . . • . . ♦ ♦ . , . $ '. s . • 3
Глава I. Понятие о временных рядах 7
1.1. Определение временных рядов. Виды
временных радов ..." , 7
1.2. Правила построения временных рядов . * 8
1.3. Показатели изменения уровней временного .
ряда «... 9
1.4. Средние характеристики временного ряда 11
1.5. Некоторые элементы теории случайных
процессов 13
Глава II. Определение основной тенденции временных
рядов 21
2.1. Понятие основной тенденции 21
2.2. Сглаживание временных рядов по методу
наименьших квадратов 23
2.3. Сглаживание временных рядов с помощью
скользящей средней 27
2.4. Другие методы сглаживания временных
рядов 30
Глава III. Статистический анализ сезонности 32
3.1. Индексы сезонности 33
3.2. Прогнозирование сезонных явлений ... 41
3.3. Модели сезонной волны 44
Глава IV. Прогнозирование с помощью метода
экспоненциального сглаживания 53
4.1. Постановка задачи экспоненциального
сглаживания 54
4.2. Вывод формул для оценки коэффициентов
модели 56
4.3. Выбор начальных условий 58
4.4. Выбор оптимального параметра
сглаживания а — -.:... 59
4.5. Рассмотрение метода 61
4.6. Пример прогнозирования с помощью
метода экспоненциального сглаживания ... 61
Глава V. Зависимость средней ошибки прогноза от
периода предыстории и величины прогнозируемого
периода 66
Глава VI. Млогофакторное прогнозирование 71
6.1. Некоторые статистические вопросы
многофакторного прогнозирования 71
6.2. Проблема построения динамической модели 81
. 6.3. Построение динамической модели (на
примере построения модели
производительности труда в цементной промышленности) . 87
Литература 100

КИЛЬДИШЕВ ГРИГОРИИ СЕМЕНОВИЧ,
ФРЕНКЕЛЬ АЛЕКСАНДР АДОЛЬФОВИЧ
Анализ
временных
рядов
и. прогнозирование
Редактор Л. В, Сергеева
Технический редактор Л. Г. Челышева
Корректор Т. М. Васильева
Художественный редактор Т. В. Стихно
Сдано в набор 30/111 1973 г. Подписано к печати 28/VIII 1973 г..
Формат бумаги 84X106V32. Бумага № 3. Объем: 3,25 печ л.
Усл. л. 5,46. Учетно-изд. л. 5.33. Тираж 10 000 экз: Зак: 3199:
Цена 32 коп. /
Изд-во «Статистика», Москва, ул. Кирова, 39.
Областная типография Управления издательств,
полиграфии и книжной торговли Ивановского облисполкома,
г, Иваново-8, Типографская, 6,