Алгебра и начала анализа. 9 класс - Вейц Б.Е., Демидов И.Т.

Автор: Вейц Б.Е. Демидов И.Т.
Теги: математика алгебра
Год: 1969
Похожие
Алгебра и начала анализа. Учебное пособие для 9-10 классов средней школы
Алгебра. 9 класс
Устные упражнения по алгебре и началам анализа для 6-9 классов
Алгебра и начала математического анализа. 11 класс
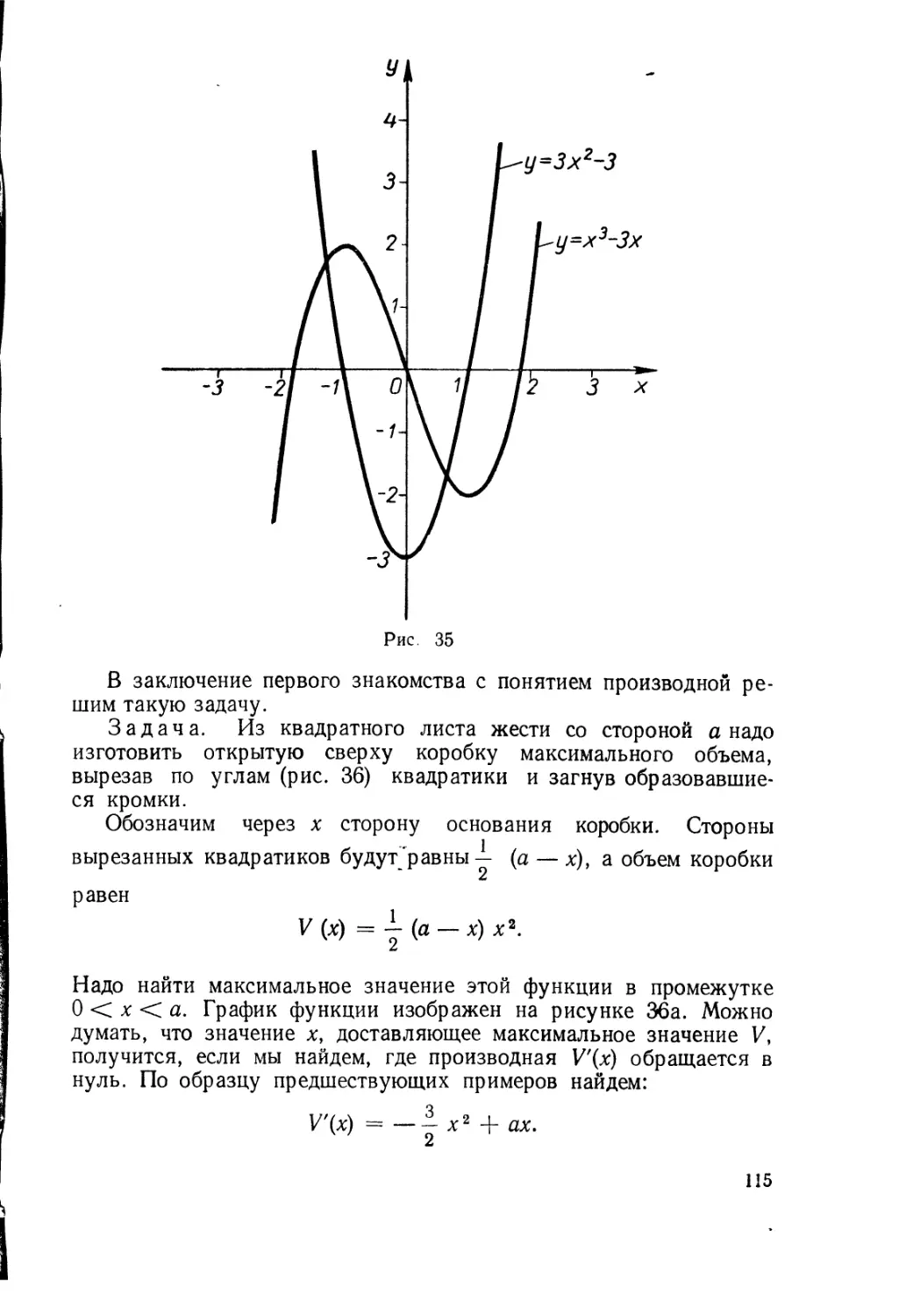
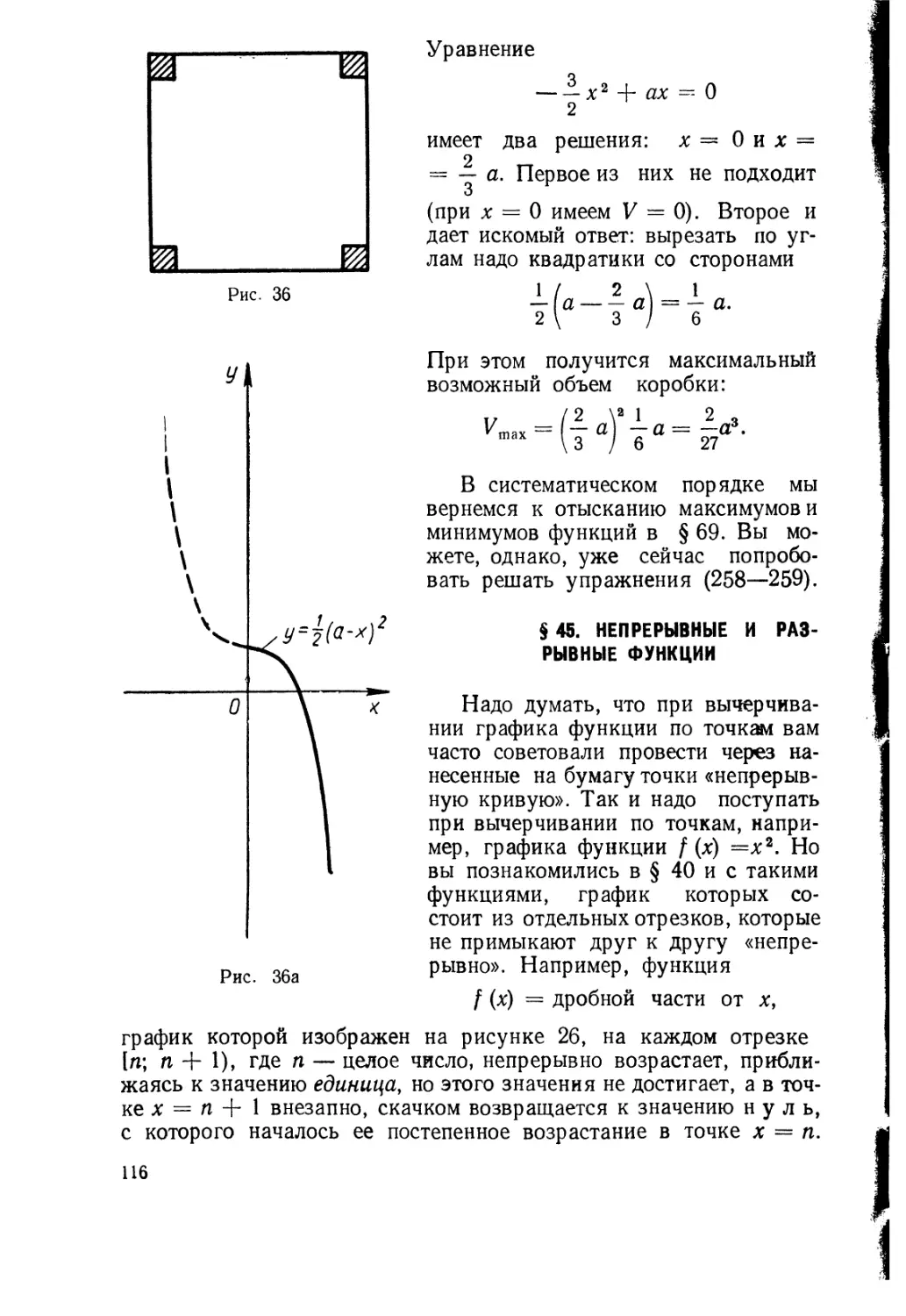
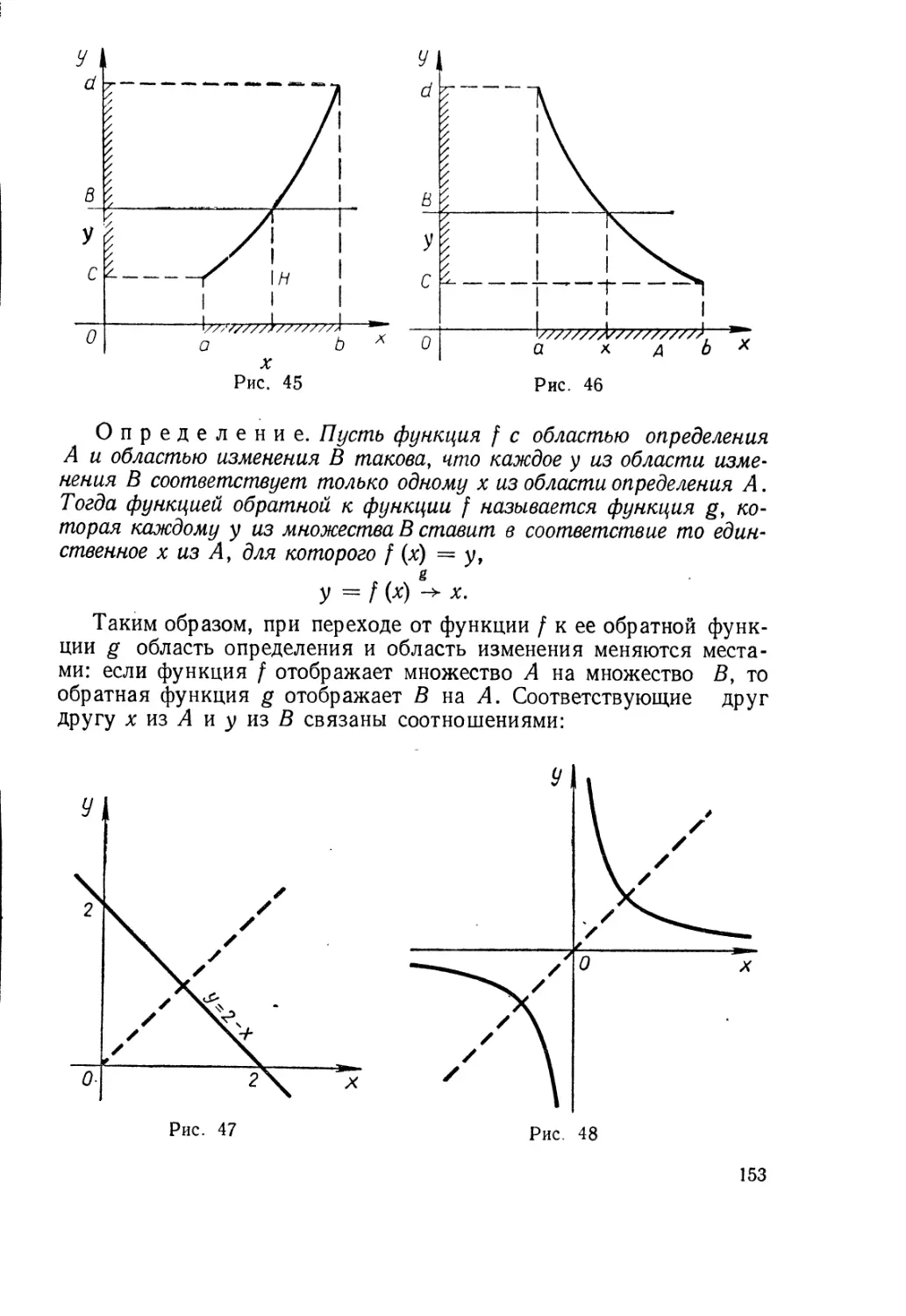
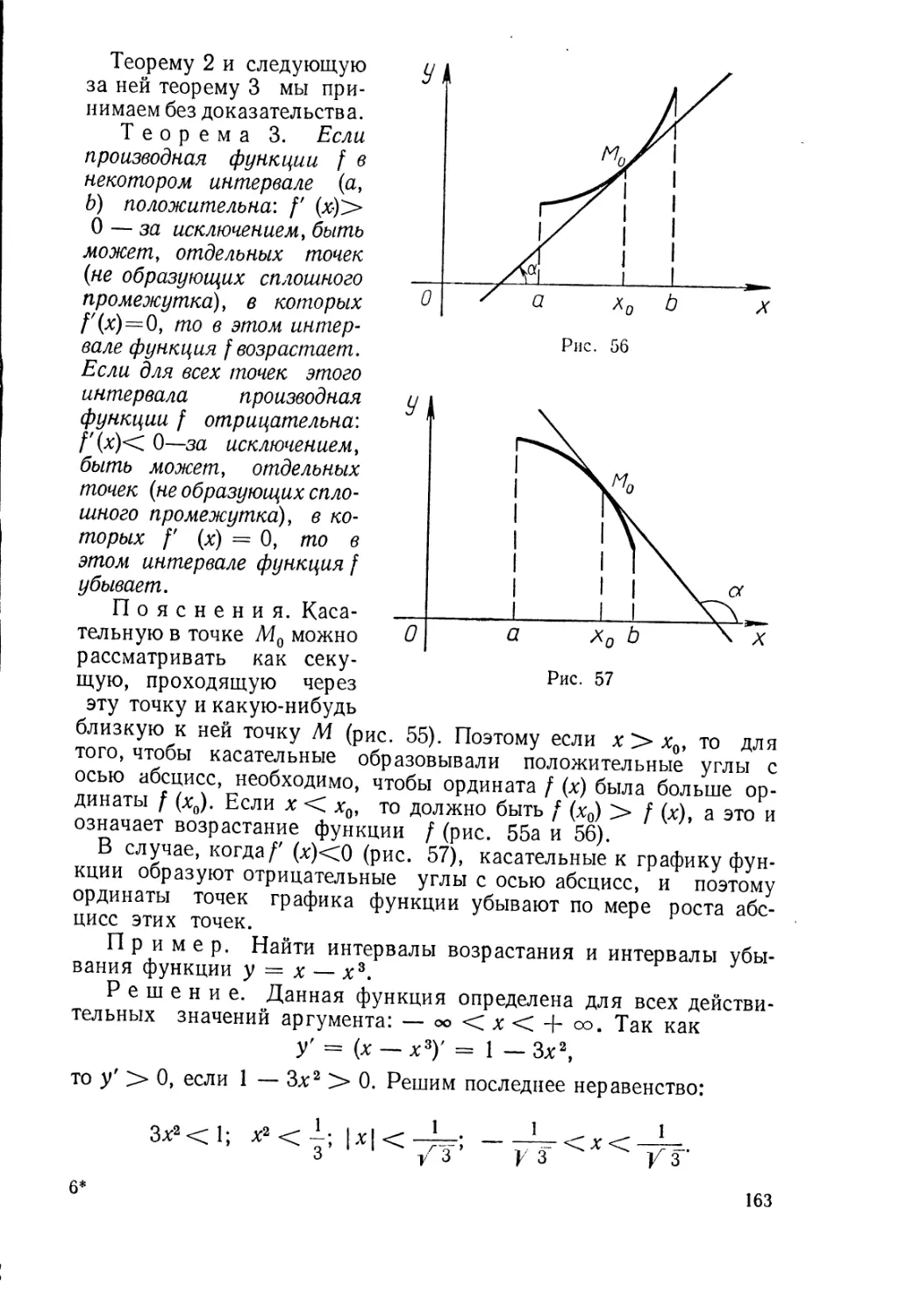
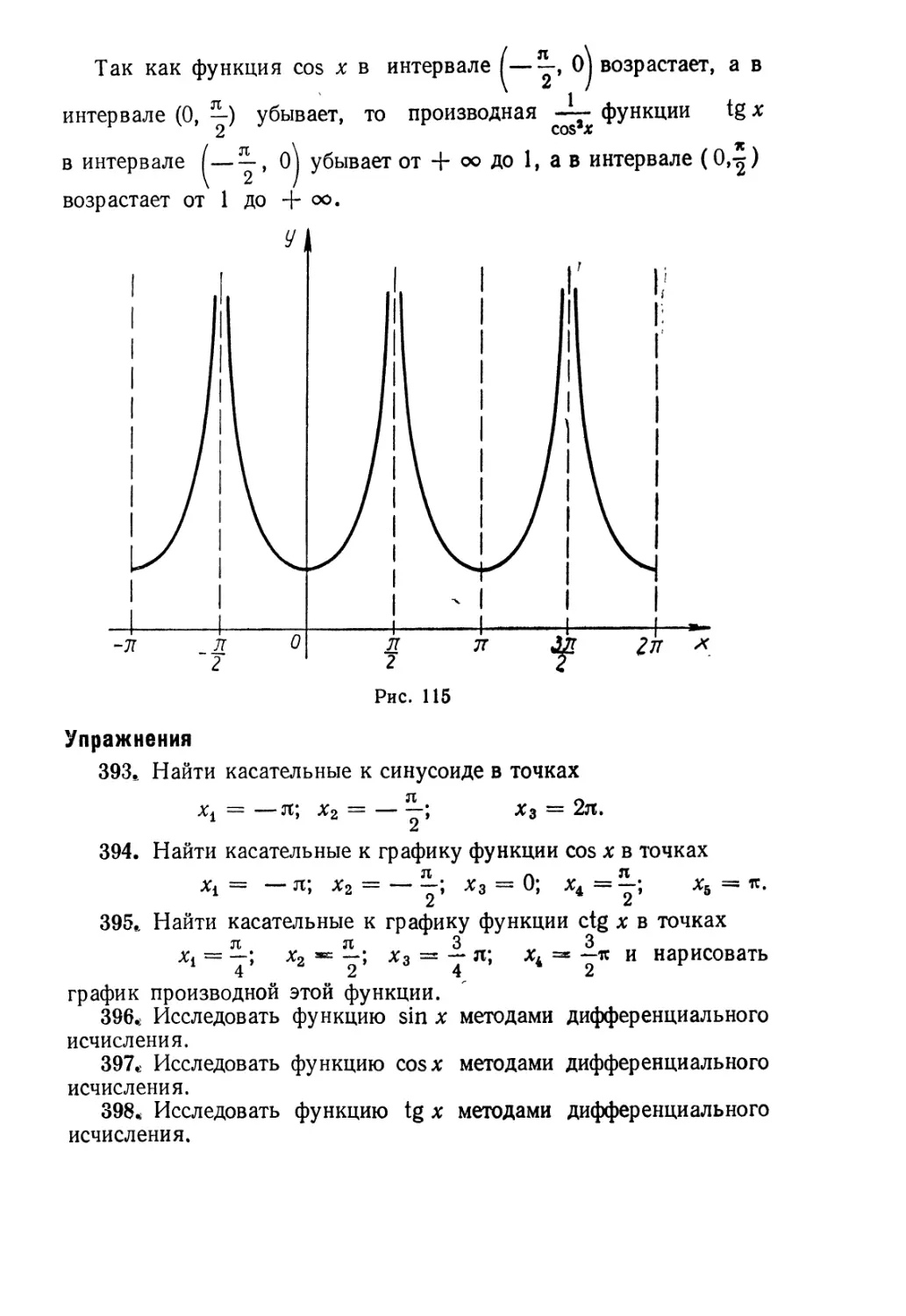
Текст
                    Б Е. ВЕЙЦ, И. Т. ДЕМИДОВ
АЛГЕБРА И НАЧАЛА АНАЛИЗА
Б. Е. ВЕИЦ, И. Т. ДЕМИДОВ
АЛГЕБРА И НАЧАЛА АНАЛИЗА
9
КЛАСС
ПРОБНЫЙ УЧЕБНИК
ПОД РЕДАКЦИЕЙ
АКАДЕМИКА
А. Н. КОЛМОГОРОВА
ИЗДАТЕЛЬСТВО «ПРОСВЕЩЕНИЕ» МОСКВА 1969
6-6
ГЛАВА ПЕРВАЯ
ПРИНЦИП МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ
§ 1. ПОНЯТИЕ О ПОЛНОЙ И НЕПОЛНОЙ МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ
Индукцией называется метод рассуждений, ведущий от частных примеров к некоторому общему выводу. Например, будем складывать подряд нечетные натуральные числа 1, 3, 5, 2п — 1, где п — любое натуральное число:
1 = 1 = 12,
1 + 3 = 4 = 22,
1 + 34-5= 9 = З2,
1 + 3 + 5 + 7 = 16 = 42,
1 + 3 + 5 + 7 + 9 = 25 = 52.
В первой строке стоит сумма, состоящая из одного слагаемого. Такое понимание относительно слова «сумма» часто удобно в математических рассуждениях.
Легко заметить, что во всех приведенных примерах сумма первых нечетных чисел равна квадрату числа слагаемых. Отсюда можно сделать предположение, что так будет и при любом числе слагаемых. Это предположение (гипотезу) можно сформулировать так: равенство
1 + 3 + 5 + ... + (2п — 1) = п2	(1)
справедливо для любого натурального числа п.
Здесь из пяти рассмотренных примеров сделан общий вывод, который, как показано будет дальше, верен.
Рассмотрим еще пример. Подставляя в квадратный трехчлен
Р (х) = х2 + х + 41
вместо х первые пять последовательных натуральных чисел, получаем:
Р (1) = 43, Р (2) = 47, Р (3) = 53, Р (4) = 61, Р (5) = 71.
Все полученные значения данного трехчлена являются простыми числами. Подставляя вместо х число нуль и последовательно уменьшающиеся отрицательные числа до — 4, получаем:
Р (0) - 41, Р (- 1) = 41, Р (- 2) = 43, Р (- 3) = 47,
Р (— 4) = 53.
Значения данного трехчлена снова являются простыми числами. При желании эти испытания можно продолжить много дальше с тем же результатом. Можно доказать, что х2 + х + 41 будет простым числом при всех целых х в пределах — 40 < х < 39. Возникает гипотеза (предположение), что значение трехчлена х2 + х + 41 при любом целом значении х будет простым числом. Однако эта гипотеза ошибочна, так как, например,
Р (40) = 402 + 40 + 41 = 412. '
Из этих двух примеров видно, что один и тот же метод рассуждений в первом случае привел к верному общему выводу, а во втором — к неверному общему выводу. Поэтому такой метод рас-суждений не является доказательством. Однако этот метод нередко позволяет сформулировать гипотезу, которую потом удается строго доказать каким-нибудь другим способом. Так как общий вывод делается из рассмотрения нескольких примеров, не охватывающих всех возможных случаев, то такой метод называется неполной индукцией.
В отличие от неполной индукции аналогичное рассуждение, в котором рассмотрены все возможные случаи, называется полной индукцией для любого натурального значения п.
Очевидно, полную индукцию можно применить для доказательства общего вывода только в том случае, когда число всех возможных частных случаев конечно. Этот метод нельзя применить к доказательству справедливости равенства (1) для любого натурального числа и, так как здесь мы имеем бесконечное множество частных случаев таких равенств и поэтому их все проверить нельзя.
В качестве примеров применения полной индукции к доказательству общих утверждений рассмотрим задачи.
1. Доказать, что каждое натуральное число и, расположенное в пределах
2 < п < 15,
разлагается не более чем на три простых множителя.
Для доказательства этого утверждения достаточно заметить, что числа
2, 3, 5, 7, 11, 13 простые; числа
4, 6, 9, 10, 14
разлагаются на два простых множителя, а числа 8, 12
имеют по три простых множителя.
2. Доказать, что равенство
3m2 —4п2=13
не может выполняться ни при каких целых значениях тип.
Доказательство. Достаточно рассмотреть только два случая для т при любом целом значении п.
1) Если т — четное число, т. е. т = 2k, то получаем: 12Р — — 4п2 = 13. Левая часть полученного равенства делится на 4 при любом целом значении k, а правая — не делится. Поэтому при т четном данное в задаче равенство невозможно.
2) Если m — нечетное число, т. е. tn = 2k — 1, то получаем 3 (2k — I)2 — 4п2 = 13, или 12&2 — 12Л — 4п2 = 10. Снова видим, что левая часть полученного равенства делится на 4, а правая не делится. Следовательно, данное в задаче равенство невозможно и при нечетном значении т.
Так как любое число m либо четное, либо нечетное, то рассмотрение двух вышеуказанных случаев полностью решает задачу.
В качестве упражнения вспомните, как доказывается теорема из геометрии: вписанный угол измеряется половиной дуги, на которую он опирается.
§ 2. ПРИНЦИП МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ
Вернемся к равенству
1 4- 3 + 5 + ••• + (2n — I)2 = п2.	(1)
Мы хотим доказать общее утверждение: равенство (1) верно для любого натурального числа п.
Для удобства в рассуждениях обозначим утверждение (1) через А (п). Тогда выражения
А (1), А (2), А (3), А (4), А (5)
будут обозначать, что равенство (1) справедливо при п = 1, п = 2, п = 3, и = 4, п = 5.
Запишем утверждение А (5) в развернутом виде:
1 + 3 + 54-7 +9= 52
и предположим, что оно уже доказано. Чтобы доказать справедливость утверждения А (6), достаточно произвести выкладку:
52 + (2 • 6 — 1) = 52 + 2 • 5 + 1 = (5 + I)2 = = б2.
Вообще, если установлена справедливость утверждения A (k), т. е.
1 + 3 + 5 + ••• + (2k — 1) = k3, то при помощи выкладки
k3 + [2 (k + 1) — 11 = k3 + 2k + 1 = (k + I)2
мы приходим к выводу, что верно и утверждение A (k + 1), т. е.
1 + 3 + ••• + (2k - 1) + (2k + 1) = (k+ I)2.
Теперь мы можем уже сразу сделать цепь выводов:
А (5) => А (6) => Л (7) => Л (8)
и так далее. (Читается: если верно Л (5), то верно Л (6); если верно Л (6), то верно Л (7) и т. д.) Но, пользуясь правилами элементарной логики, мы можем пробежать только конечный отрезок этой цепи и доказать, например, после больших усилий утверждение Л (1000). Достаточно ясно, что в действительности в наших руках уже находится доказательство утверждения Л (п) для любого натурального и. Однако, как бы этот вывод ни был очевиден, совершая его, мы прибегаем к существенно новому принципу (основному исходному положению):
Если некоторое утверждение А (п) относительно натурального числа п верно для п = \ииз того, что оно верно для п = k, следует, что оно верно и для следующего числа п = k + 1, то утверждение А (п) верно для любого натурального числа п.
Это и есть принцип математической индукции — одна из основных аксиом арифметики натуральных чисел, имеющая много применений во всей математике. На этом принципе основан метод доказательства, называемый методом математической индукции.
Доказательство методом математической индукции состоит из двух частей: в первой части доказывают (проверяют) справедливость некоторого утверждения Л (и) при п = 1, т. е. А (1); во второй части предполагают, что Л (и) верно при п = k, и доказывают справедливость этого утверждения для п = k +1:
(Л (fe) => Л (/fe+1)).
Если оба эти доказательства проведены, то на основании принципа математической индукции утверждение Л (п) будет верным для любого натурального числа п. Если одна из указанных частей доказательства не проведена, то утверждение Л (и) нельзя считать доказанным.
Теперь мы можем утверждать, что равенство (1) справедливо для любого натурального и, так как оно справедливо для п — 1,и из того, что оно верно для числа п = k, следует, что оно верно и для следующего числа п = k + 1.
Рассмотрим еще пример. Вычислить сумму
±+J_+J_ + ...+—1— 1*2	2-3	3-4	л(п-Н)
для любого натурального значения п.
Решение. Сначала применением неполной индукции попытаемся обнаружить некоторую закономерность строения этой суммы для частных случаев.
Обозначим сумму п слагаемых через Sn, тогда s1== ±=1 1	1-2	2
$г = ~ + 7^7 — Z	Z * о
S3 = - + — = 3	3	1	3-4
S — 3 1 1 — 4	4	+	4.5
2_ 3*
2
4*
4_
5’
Эти примеры показывают, что числитель каждой такой суммы равен числу слагаемых, а знаменатель на единицу больше числителя. Из этого можно сделать предположение, что для любого натурального числа п будет выполняться равенство
В силу принципа математической индукции равенство (2) верно при любом натуральном п, если
1)верно А (1), фф
2) при любом натуральном k из A (k) вытекает A (k + 1), т. е. (з = _А_\ ==>(sh+i = fe + 1 \ \ * k + \)	\ h+ (k+1) +1)
Требование 1) уже было проверено. Докажем 2). Допустим, что
Sfe =	. Тогда
«	£ I I
S = S +	1	= k _|_	1	+1 =
*+!	(ft + 1)(ft + 2)	1 + (й+1)(й+2) (й+1)	+2)
= fe+ 1 й + 2’
т. е.
О _	*4-1
ft+1 (k + 1) + 1' Это и требовалось доказать.
Оба условия применимости принципа математической индукции выполнены. Значит, в силу этого принципа
при любом натуральном и.
* — п
'п~ п + 1
Упражнения
Пользуясь методом математической индукции, доказать тождества:
1.	14-2 + 3 +----= —+-1-).
2.	I2 4- 22	4-	32	+	•	•	•	+ n2 = -n(-”^'-t-H2ra.+ 1)	.
3.	I3 4- 23	4-33	H---F n3 =
4.	12 4- 32	4-	52	4--F (2n —	I)2	= ? -2-n—
5.	I3 4- 33	4-	53	4-	•	•	•	4- (2n —	I)3	= n2 (2n2 — 1).
6.	l-24-2-3 + 3- 44----+«(«+0= n^ +]) <3
7.	1 • 4 4- 2 • 7 + 3 • 10 4- • • • + n(3n + 1) = n(n + I)2.
8.	1-2-34-2-344---Fn(n41)(n + 2) =-J-n(n4-l)(n+2)(n4-3).
4
9.	p_22 4- 32 — 42 H--F (— I)'*"1 • n2 = (— I)"'1 П-
10‘ 1.3+3.5 + 5.7+-‘- + (2n—l)(2n + l)
11.	— + — 4—L -|----------1---------1-------
1.4 ' 4.7	7.10	(3n —2)(3n + l)
12.	F----------F-----F •   4--------------
1-5	5-9	9-13	(4n — 3)(4л + 1)
n
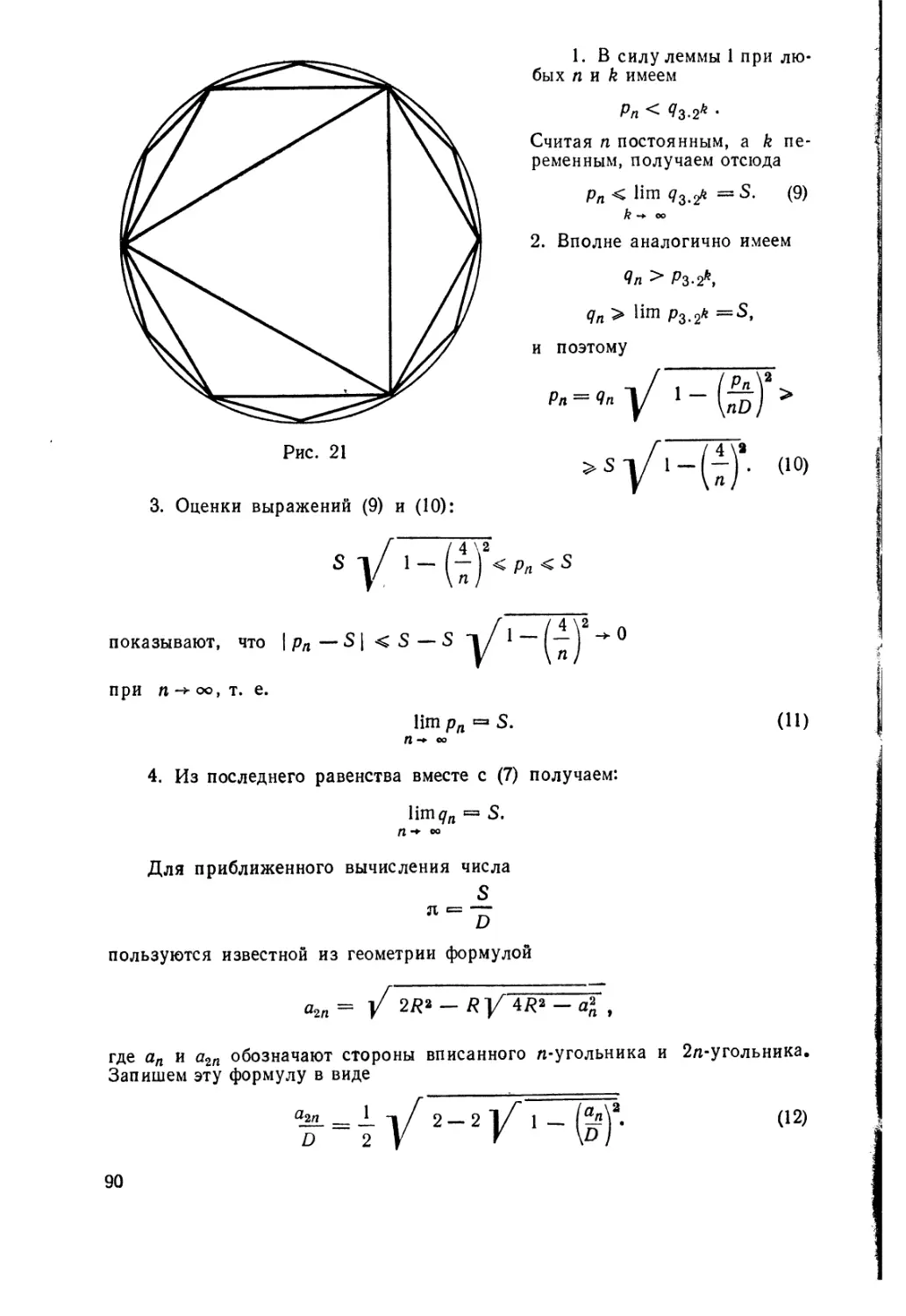
-f- 1
n
3n-f-Г
n
’ 4n+ T
13.	Методом математической индукции доказать равенства । / i\ 1 о	-4- (п — 1) d
ап = ai 4- (п — 1) d и Sn = 	, 
где an, d и Sn — соответственно общий член, разность и сумма и первых членов арифметической прогрессии.
14.	Методом математической индукции доказать равенства
V = и S. = п	п q—\
где Uп, q и Sn— соответственно общий член, знаменатель и сумма п первых членов геометрической прогрессии.
15.	Доказать, что п прямых, расположенных в одной плоскости, из которых никакие две не параллельны и никакие три не проходят через одну точку, делят плоскость на 1 + -—^-частей.
16.	а) Доказать, что п плоскостей, из которых никакие две не параллельны, никакие три не проходят через одну прямую и никакие четыре — через одну точку, делят пространство на («4-1 )(л2—л+6) - - А	— частей.
6
б) Доказать, что и окружностей делят плоскость не более чем на и2 — п + 2 частей.
§ 3.	ПРИМЕНЕНИЕ МЕТОДА МАТЕМАТИЧЕСКОЙ ИНДУКЦИИ К ДОКАЗАТЕЛЬСТВУ НЕРАВЕНСТВ
Этот вопрос рассмотрим на примерах.
1.	Доказать, что для любого натурального числа п справедливо неравенство 3" > п.
Доказательство, а) Если п = 1, то имеем 3 > 1, т. е. при п = 1 указанное неравенство верно.
б) Предположим, что это неравенство верно при п = k, т. е. 3* > k, и докажем справедливость неравенства 3*+1 > k + 1.
Из 3* > k следует неравенство 3 • 3й > 3k, или Зй+1 > 3k. Но 3k = k + 2k > k + 1, так как 2k > 1. Следовательно, 3*+1 > > 3k > k + 1, т. е. 3*+1> k + 1. Оба требования принципа математической индукции выполнены, поэтому доказываемое утверждение верно.	й
Прежде чем разбирать следующий пример, сделаем одно важное замечание. Иногда высказывание А (п) о натуральном числе при некоторых натуральных п ошибочно или не имеет смысла, но удается доказать, что А(п) верно для всех натуральных п, начиная с п = т. С другой стороны, иногда А (п) удается доказать не только для натуральных п, но и для целых п, например, начиная с п = 0. В подобных случаях помогает такое видоизменение принципа математической индукции.
Если некоторое утверждение А (п) относительно целого числа п верно при п = т и из того, что оно верно для числа п = k > т, вытекает, что оно верно для следующего числа п = k 4- 1, mo утверждение А (п) верно для любого целого п > т.
2.	Доказать неравенство Бернулли: если h > — 1 и h 0, то
(1 + h)n > 1 + nh	(1)
при любом натуральном п > 2.
Доказательство. При п = 1 неравенство (1) превращается в ошибочное неравенство 1 + h > 1 4* h. Поэтому и поставлена задача доказать неравенство (1) для п > 2 при помощи сформулированного выше видоизменения принципа математической индукции.
Если п = 2, то получаем: (1 + h)2 = 1 4- 2h 4- h2 > 1 4- 2h, т. e. (1 + h)2 > 1 + 2h, так как h2 > 0.
Предположим теперь, что это неравенство верно для некоторого п — k > 2, и докажем его справедливость для п = k + 1. Для этой цели умножим обе части неравенства (1 + h)k> 1 4* kh на 1 + ft> 0 и получим:
(1 + А)й+Х > (1 + kh) (1 + h) = 1 + kh + h + kh2>
>1 + (k 4- 1) h, t. e.
(1 4- h)b+l > 1 4- (k 4- 1) h.
Оба требования принципа математической индукции выполнены, следовательно, данное утверждение доказано.
3.	Найти все натуральные значения п, для которых выполняется неравенство 2" > п2.
При п = 1 это неравенство выполняется, но при п = 2, 3, 4 получаем соответственно: 22 = 22, 23< З2, 24 = 42. Если выберем любое натуральное число п, большее 4, то данное неравенство будет выполняться. Докажем это.
Если п = 5, то 25 > 52.
Предположим, что при п = 6 > 5 выполняется неравенство 2* > k2. Тогда при п = k + 1 получаем: 2*+* > 2 k2. Так как k> 4, то k — 1 > 3, (k — 1)2> 9, 62 —26 + 1 > 9, 62>26 + + 8 > 2k + 1, 262 > k2 + 2k + 1 = (k 4- I)2, t. e. 2fc+1>262 > >(k + I)2.
Следовательно, 2ft+’ > (k 4- l)2. Оба требования принципа математической индукции выполнены.
Ответ. Данное неравенство справедливо при п = 1 и всех п > 4.
Справедливость неравенства 2п~>п2 при п>4 можно доказать и таким способом: положим п — т 4- 4. Тогда надо будет доказать, что неравенство 2т+4 > (т + 4)2 верно при любом натуральном значении т.
Если т = 1, то неравенство 25 > 52 верно.
Пусть данное неравенство верно при т = k, т. е. 2*+4>(6 4~ 4- 4)2. Тогда при т = k + 1 последовательно получаем:
2*+5 > 2 (k + 4)2 = 2k2 + 166 + 32 > 62 + 106 4- 25, или
2*+6 >(6 4- б)2.
Данное утверждение доказано, так как выполнены оба требования принципа математической индукции.
Упражнения
Пользуясь методом математической индукции, доказать справедливость следующих неравенств:
17. 2л>ппри п>0. 18. 2">2п4-1 при п > 3. 19. 2л>п3 при п > 10. 20. 1 4- -4= 4-	4- • • • 4- -^= > Уп при п > 2.
У 2 УЗ	У п
21. Доказать такое видоизменение неравенства Бернулли: если h > — 1, то при любом натуральном п имеем:
(1 4- 6)л > 1 4-6.
(1а)
ю
1.	Доказать, что сумма кубов любых трех последовательных натуральных чисел делится на 9.
Доказательство. Обозначим эту сумму через Sn, т. е. положим Sn = п3 + (п + I)3 + (л+2)3, и докажем, что при любом натуральном значении п сумма Sn делится на 9. Если п = 1, то имеем: = I3 + 23 + З3 == = 36. Следовательно, Sx делится на 9.
Пусть Sk =k3 + (k + I)3 + (k + 2)3 делится на 9. Если п == k + 1, то
Sk+1=(k + I)3 + (6 + 2)3 + (k + З)3 = (k+ I)3 + (k + 2)3 + 63 +
+ 962 + 27k +27 = 63 + (k + I)3 + (k + 2)3 + 9(62 + 36 + 3) =
= S* + 9 (62 + 36 + 3), т. e.
Sk+i = Sk + 9 (62 + 36 + 3).
В последнем равенстве оба слагаемых правой части делятся на 9 (первое слагаемое делится на 9 согласно предположению), поэтому и сумма их делится на 9.
Оба требования принципа математической индукции выполнены, поэтому данное утверждение доказано.
2.	Доказать, что при любом целом п > 0 сумма Sn = 11л+2 + 122л+1 делится на 133.
Доказательство. В этом примере выполнение первого требования математической индукции проверяем для п = 0.
So = II2 + 121 = 133, т. е. So делится на 133.
Предположим, что наше утверждение верно при и = 6, т. е. — 11л+2 + + 122*+1 делится на 133. Тогда при п = 6 + 1 имеем: Sk+1 ~ 11^3 + 122АНЗ = = 1Ь11*+2 + 144-122*+1 = 1ЫР+2+ 11 -122^+1+133- 122А?+1 = 11S^+ 133-122*+\ т. е.
S*+1 == 11S* + 133 • 122*+1.
В последнем равенстве оба слагаемых правой части делятся на 133, а поэтому и сумма их делится на 133. Утверждение доказано.
3.	Доказать, что m3 + 20m при любом четном натуральном числе tn делится на 48.
Доказательство. Так как число m четное, то положим m = 2и. Тогда надо будет доказать, что 5д=8и3 + 40п при любом натуральном значении п делится на 48.
Если п = 1, то Sj = 48, т. е. Sx делится на 48.
Пусть 8^ = 863 + 406 делится на 48 по предположению, тогда
Sk+X = 8 (6 + 1)3 + 40 (6 + 1) = 863 + 2462 + 246 + 8 + 406 + 40 = = 863 + 406 + 24 (62 + 6 + 2) = Sk + 24 [6 (6 + 1) + 2], т. е.
Q Q > 4СГ^ + 1) JLll $k+i = 5^ + 48	- Ь 1 ,
Так как при любом натуральном значении 6 произведение 6 (6 + 1) является четным числом, то в квадратных скобках последнего равенства содержится целое число. Поэтому оба слагаемых правой части этого равенства делятся на 48, следовательно, и делится на 48. Это и требовалось доказать.
П
Упражнения
Доказать методом математической индукции следующие утверждения: 22. л3 + 5л делится на 6 при любом натуральном п.
23.	л3 + Пл делится на 6 при любом натуральном л.
24.	62Л-1+1 делится на 7 при любом натуральном л.
25.	10л + 18л — 28 делится на 27 при любом натуральном л.1
26.	О'144 — 8л — 9 делится на 16 при любом натуральном л.
27.	л4 + 6л? + Пл2 + 6л делится на 24 при любом натуральном л.
ГЛАВА ВТОРАЯ
ЭЛЕМЕНТЫ КОМБИНАТОРИКИ
Часто из элементов некоторого конечного множества приходится составлять различные комбинации и затем производить подсчет числа всех возможных комбинаций, составленных по некоторому правилу. Такие задачи получили название комбинаторных, а раздел математики, занимающийся их решением, называется комбинаторикой. Комбинаторика имеет большое значение в теории вероятностей, вычислительной математике, теории автоматов, в экономических расчетах.
В этой главе мы рассмотрим лишь некоторые начальные сведения из комбинаторики.
§ 5. ПЕРЕСТАНОВКИ
Начнем с задачи: сколько различных трехзначных чисел можно записать с помощью трех цифр 3, 5, 7, не повторяя их. Последнее означает, что в написанном трехзначном числе одна и та же цифра не должна встречаться дважды. Очевидно, таких чисел будет шесть:
357, 375, 537, 573 735, 753.
Если к данным трем цифрам добавим еще одну, например 8, то задача примет вид: сколько различных четырехзначных чисел можно написать с помощью цифр 3, 5, 7, 8, не повторяя их?
Таких чисел уже будет 24. Все эти числа можно получить следующим образом: выбираем любое трехзначное число, написанное выше, затем присоединяем к нему цифру 8, ставя ее последовательно на первое, второе, третье и четвертое место.
Таким путем из каждого числа получим четыре различных
четырехзначных числа, как это показано ниже:					753
357	375	537	573	735	
8357	8375	8537	8573	8735	8753
3857	3875	5837	5873	7835	7853
3587	3785	5387	5783	7385	7583
3578	3758	5378	5738	7358	7538
Рассмотрим еще такую задачу: сколькими различными способами можно посадить за столом четырех человек, если к этому столу приставлены четыре стула?
По существу эта задача не отличается от предыдущей задачи о четырех цифрах, поэтому и ответ будет тот же: 24.
Пусть дано произвольное множество из п элементов. Упорядочить множество — значит поставить какой-либо элемент множества на первое место, какой-либо другой — на второе и т. д., пока не останется последний элемент, который займет последнее, п-е место.
Выше мы установили, что множество из трех цифр можно упорядочить шестью способами, а множество из четырех цифр — двадцатью четырьмя. Поставим теперь общий вопрос: сколькими способами можно упорядочить множество из п элементов, где п — любое натуральное число?
Каждый способ упорядочения множества каких-либо элементов называется по традиции перестановкой этих элементов. Спрашивается: сколько перестановок можно составить из п элементов? Ответ дает такая теорема:
Теорема. Число перестановок из п элементов равно произведению п первых натуральных чисел, т. е.
1 • 2 • 3 •	• п.
Произведение п первых натуральных чисел обозначают п! (читается: «эн факториал»), например:
1! = 1, 2! = 2, 3! = 6, 4! = 24, 5! = 120.
Легко видеть, что наша теорема верна при п = 1 и и = 2: один элемент можно расположить только одним способом, а два — двумя. Выше мы видели, что из трех элементов можно образовать 3! = 6 перестановок, а из четырех 4! = 24. Проведем общее доказательство теоремы методом математической индукции.
1	Если п = 1, то йз одного элемента получается только одна перестановка, т. е. 1 = 1!
2	. Предположим, что утверждение теоремы справедливо для п — k, т. е., из k элементов получается k\ перестановок. К этим k элементам добавляем еще один элемент, отличный от них. Из k + 1 элементов на первое место можно поставить любой из них. В каждом из этих k + 1 случаев остающиеся k элементов можно расположить k\ способами по предположению, поэтому получим всего (k + 1) k\ = (k + 1)! перестановок из k + 1 элементов.
Таким образом, при п = 1 утверждение теоремы верно, и если оно верно при п = k, то оно верно и при п = k + 1, т. е. утверждение теоремы верно для любого натурального числа п.
m!
n!
Некоторые примеры действий с факториалами:
1.	— = 71'8'9-10 = 8 • 9 • 10 = 720.
71	7!
2.	11 • 12 - 13 • 14 = —.
10!
3.	Jn±3)! = nl(n + l)(»+2)(« + 3) = (п + J) (п + 2) (л 3). и!	п\
4.	= (т + 1) (т + 2) ... п (п > т).
т\
5	(n — m -j- 1) (т2 — m 2) ... /г (п —т)\(п — m-f 1)... п  т\	(п — т)\ т\
п\	п!	/
=-------------==----------- (п > т).
(п—т)\т\	т\(п—т)\
Задача. Сколько различных пятизначных чисел можно записать с помощью цифр 0, 2, 4, 5, 7, не повторяя их.
Решение. Всего перестановок из пяти цифр будет 5! = 120, но перестановки, начинающиеся с цифры 0, не образуют пятизначного числа. Всех чисел, начинающихся с нуля, будет столько, сколько можно составить перестановок из четырех остальных цифр, т. е. 4! = 24. Ответ'. 5! — 4! = 120 — 24 = 96.
Можно было бы считать и так:
5! — 4! = 4! (5 — 1) = 24 • 4 = 96.
Упражнения
28.	Решить уравнение	72.
п\
5’ 4- 4’
29.	Вычислить ------—.
3!
30.	Сколько надо взять элементов, чтобы число всех перестановок, полученных из них, было 720?
31.	Вычислить сумму всех четырехзначных чисел, которые могут быть записаны с помощью цифр 1, 3, 5, 7 без повторений.
32.	Сколько среди всех перестановок из п элементов (п > 5) таких, в которых определенный элемент а занимает пятое место?
§ 6. ПОДМНОЖЕСТВО КОНЕЧНОГО МНОЖЕСТВА. ЧИСЛО СОЧЕТАНИЙ С™
Пусть дано некоторое множество А, состоящее из п элементов:
А = {а„ а2, ..., ап].
Множество В называется подмножеством множества А, если каждый элемент из В принадлежит А. Если В является подмножеством А, то это обозначается через
В az А
(читается: «В является подмножеством множества А или В содержится в Л»).
Например, множество
А ~ {х, у, г), состоящее из трех букв х, у, г, имеет такие подмножества: В< = = {х}, В2 = {у}, В3 = {?} — одноэлементные подмножества, В4= = {х, у}, В5 == {х, г}, BQ = {у, г} — двухэлементные подмножества, В1 = А = {х, у, г} — одно трехэлементное подмножество. К этим подмножествам присоединяется еще одно подмножество, совсем не содержащее элементов (пустое подмножество), которое обозначается через 0.
Таким образом, указанное множество А имеет всего восемь подмножеств.
В общем случае, если множество А содержит п элементов, а его подмножество В — tn элементов, то 0 < т < и.
Часто бывает интересно получить ответы на такие вопросы: 1. Сколько всего подмножеств имеется у данного множества Д? 2. Сколько среди этих подмножеств содержит заданное число т элементов?
Далее мы увидим, что ответы на эти вопросы зависят только от чисел пит.
Число подмножеств, состоящих из т элементов, содержащихся в множестве А из п элементов, называется числом сочетаний из п по т и обозначается через С™ (цэ из п по т).
Разобранный выше пример показывает, что
С°3 = 1, с' = 3, (% = 3, С*3 = 1.
Общую формулу для вычисления С™ мы получим позже, а сей-час заметим лишь, что при любом целом неотрицательном п имеют место следующие равенства:
С\ = 1, так как имеется только одно пустое подмножество, С\ = п, так как число одноэлементных подмножеств равно числу элементов данного множества А,
Спп = 1, так как имеется только одно подмножество, содержащее все элементы данного множества Д:
Рассмотрим задачи.
1. В шахматном турнире приняли участие 15 шахматистов, причем каждый из них сыграл только одну партию с каждым из остальных. Сколько всего сыграно партий в этом турнире?
Решение. Так как в каждой партии участвовали два шахматиста и они между собой сыграли только одну партию, то число всех сыгранных партий равно числу сочетаний из 15 по 2, т. е. С?5.
С другой стороны, каждый участник турнира сыграл со всеми остальными участниками по одной партии, т. е. 15 — 1 = 14 партий. Но, приписывая каждому участнику 14 партий, мы тем самым 16
каждую партию посчитаем два раза (так как в ней участвовали двое), поэтому всех сыгранных партий было 1L11. Следовательно,
Ch =	= 105.
Ответ, В турнире было сыграно 105 партий.
2. На плоскости расположены п точек, из которых никакие три не лежат на одной прямой. Через каждые две точки проведена прямая. Сколько всех прямых проведено на плоскости?
Решение. По существу эта задача аналогична предыдущей. Так как через каждые две точки проведена только одна прямая, то всех прямых будет С„.
С другой стороны, так как через каждую точку проходит п — 1 прямая и каждая прямая проходит через две точки, то всех прямых будет Отсюда следует, что
г2 _ П (П — 1)
Ь/г “ ---------
2
Тем самым мы получили число сочетаний из и элементов по два.
Теперь докажем основную формулу для вычисления числа сочетаний: для любого натурального числа п и любого целого числа т, расположенного в пределах 0 < т < п, имеет место равенство
s>tn	п\
(1)
ml (п — т)1 ’
Мы уже знаем, что существует п!
Доказательство.
перестановок из п элементов. Каждую такую перестановку можно получить следующим образом:
1)	отобрать т элементов,
2)	эти т элементов расположить в определенном порядке,
3)	расположить оставшиеся п — т элементов в определенном порядке и поставить их после ранее отобранных т элементов.
Первый шаг (выбор т элементов из и) можно выполнить С™ способами. В каждом из этих С„ случаев отобранные т элементов можно упорядочить т\ способами. Всего имеется С” • т\ способов выполнить два шага построения.
Наконец, оставшиеся п — т элементов можно упорядочить (п — т)1 способами. Полное число способов выполнить наше построение будет равно: С„  т! • (п — т)\. В результате мы получим по одному разу каждую из nl перестановок п элементов. Поэтому
Си т 1(п — т)\ — п!.
(2)
Из равенства (2) уже непосредственно вытекает:
Особо рассмотрим случаи т = 0 и т = п. Мы уже знаем, что С° = Спп = 1. Чтобы формула (1) была верна, в этих случаях надо положить
О! = 1.
При вычислении числа сочетаний С„ удобнее пользоваться формулой
gn _ »(» — 1) (л — 2) • • > [я — (m — l)i	(jа)
т\
которая получается из формулы (1) путем сокращения дроби на (п —-т)\. В числителе правой части этой формулы произведение содержит число сомножителей, равное верхнему индексу в С™, например:
сз = 35.34.33 = 35 1 7> J J = 6545.
1*2-3
Из формулы (1) непосредственно вытекает равенство
(и — /и)! (п— п + т)\ (п — т)\т\
в силу которого множество из п элементов имеет одинаковое число подмножеств, содержащих т элементов, и подмножеств, содержащих п — т элементов.
Равенство (3) можно доказать и непосредственно, не опираясь на формулу (1); оно становится почти очевидным, если воспользоваться понятием дополнительного множества, или, короче, дополнения. Дополнением к подмножеству В множества А называется множество А—В, состоящее из тех элементов множества А, которые не входят в В. Очевидно, что дополнением к А—В является множество В. Вот для примера перечень взаимно дополнительных множеств множества А = {1, 2, 3} первых трех натуральных чисел:
0	{1,2 3}
{1} <-> {2,3} {2} о {1,3} {3} <-> {1,2}
Если основное множество А состоит из п элементов, то дополнение к множеству из т элементов содержит п — т элементов. Переход к дополнению устанавливает взаимно однозначное соответствие между всеми подмножествами, состоящими из т элементов, и всеми подмножествами, состоящими из и — т элементов. Число тех и других должно быть одинаково (в нашем при-мере С®=С|=1, С£=С|=3).
Сумма
с°п + с'п + с2 + .. • + с"
равна общему числу подмножеств множества из п элементов. Мы установим сейчас, что эта сумма равна 2% т. е.
С° +Сп +С2п + •  • + Спп = 2".	(4)
Теорема. Число всех подмножеств множества из п элементов равно 2п.
Доказательство проведем по методу математической индукции.
1) Множество из одного элемента {а} содержит два подмножества: пустое множество 0 и само себя. Значит, утверждение теоремы верно при и = 1.
2) Пусть уже установлено, что множество из k элементов содержит ровно 2k подмножеств. Рассмотрим множество
Л = {«!> а2...ак,
из k + 1 элементов. Любое его подмножество В получается одним из двух способов: а) берется подмножество В множества
А' = {aif a2t ..., ah},
б) берется подмножество В' множества А', и к нему присоединяется элемент ak+l. Каждым из этих способов получаем 2k подмножеств, а всего 2*+1 подмножеств множествах. Таким образом, из верности утверждения теоремы при п = k вытекает верность этого утверждения при п = k + 1.
Укажем еще одно важное следствие формулы (1):
(т + 1)! (п — т — 1)! (m-f-1) ml (п—т)\ т + 1 т. е.
(5) т + 1
Упражнения
33.	Составить все сочетания из пяти элементов {а1( а2, а3, ait аь} по три элемента.
34.	Проверить вычислением равенства z-»4 . z>3	z"»7	z-»5 . z-,6 zn6
Сб+Сб = U4, С104-С10 = Сц.
35.	Написать формулы для
а) С*±1, б) СХ. в) СХ-
36.	Сколько различных прямых можно провести через 10 точек плоскости, из которых никакие три точки не лежат на одной прямой?
37.	Сколько диагоналей имеет выпуклый двенадцатиугольник?
38.	Сколько окружностей можно провести через 10 точек плоскости, из которых никакие четыре точки не лежат на одной окружности, если каждая окружность проходит через три точки?
39.	Решить уравнение Сп — ±С„+2-
40.	Решить уравнение С2„' :С2^ = 3:5.
41.	Решить неравенство
42.	Найти d, если Сп=Сп+5.
43.	Сколько участников было в шахматном турнире, если известно, что каждый из них сыграл с каждым из остальных по одной партии, а всего было сыграно 105 партий.
44.	На одной из параллельных прямых отмечено 10 точек, а на другой — 7 точек. Каждая точка одной прямой соединена с каждой точкой на другой прямой. Найти число точек пересечения полученных отрезков, если никакие три отрезка не имеют общей точки (общие точки на концах отрезков не считаются).
45.	Сколькими способами можно группу из 15 учащихся разделить на две группы, из которых в одной группе будет четыре человека, а в другой 11 человек?
46.	Решить уравнение J_________________________1 7
СГ	са ~ 10 стп'
§ 7.	СПОСОБЫ ВЫЧИСЛЕНИЯ ЧИСЛА СОЧЕТАНИЙ.
ТРЕУГОЛЬНИК ПАСКАЛЯ
Для приближенного вычисления числа сочетаний при больших пит можно пользоваться таблицей логарифмов факториалов. Вычислим, например1, Cioo-
£50 _	100!_______100! _ 100!
100 “ 50! (100 — 50)! “ 50! 50! ~ (50!)2‘ Логарифмируем:
lg с$о = 1g 100! — 2 lg(50!) = 157,9700 — 2- 64,4831 = 29,0038.
По значению характеристики мы видим, что число Сщо имеет 30 десятичных знаков (не забывайте, что по самому определению п\ есть целое число). По таблицам находим его приближенное значение:
С?оо= 1,009-1029.
С теоретической точки зрения больший интерес имеет возможность получить полную таблицу чисел С™ при помощи простой формулы
1 Для решения таких задач надо воспользоваться таблицей 7, помещен-
ной на стр. 258.
С^+С
(6)
Для доказательства формулы (6) воспользуемся равенством (5) из конца предыдущего параграфа:
CZ+CZ+'=C'*+	= С„71 +
т + 1	\ т + 1 /
и +1 т + J
Ст__
п —
(и+1)п!
(т + 1) ml (п — т)1
s>m ч-1
Равенство (6) можно доказать и непосредственно, не опираясь на доказанные ранее формулы (1) — (5). Рассмотрим множество
А = {щ, аг, .... а„+1)
из п + 1 элементов. Его подмножества, содержащие т + 1 элементов, мож-но получить двумя способами: а) взять подмножество множества
А' — {щ, аг.... ап},
содержащее т элементов, и присоединить к нему элемент ал+1; б) из множества Л' выделить подмножество, содержащее zn+ 1 элементов. Первым способом получаем С™ подмножеств, а вторым т. е. всего С™ +	под-
множеств.
Для составления полной таблицы чисел С™, кроме формулы (6), будем пользоваться еще тем, что при любом п
Сп=Сп = 1.	(7)
Равенство (7) будем считать верным и при п = 0 (пустое множество своим единственным подмножеством имеет само себя). При помощи равенств (6) и (7) заполняется таблица
-*	т
О	1	2	3 4 5 6 7 8...........
О	1
1	1	1
П 2	1	2	1
3	13	3	1
4	1	4	6	4	1
5	1	5	10	10	5	1
6	1	6	15	20	15	6	1
7	1	7	21	35	35	21	7	1
8	1	8	28	56	70	56	28	8	1
Часто этой таблице придают более красивый симметричный вид
1	1
1	2	1
13	3	1
1	4	6	4	1
1	5	10	10	5	1
1	6	15	20	15	6	1
1	7	21	35	35	21	7	1
1	8	28	56	70	56	28	8	1
Эта таблица носит название треугольника Паскаля, по имени французского ученого Паскаля (1623—1662), который занимался исследованием свойств этой таблицы и применением этих свойств к решению задач.
Рассмотрим некоторые свойства треугольника Паскаля.
1. Мы уже знаем, что сумма всех чисел n-й строки равна (формула (4) из § 6). Иначе говоря, при переходе от строки к следующей строке сумма всех чисел в строке удваивается. Теперь мы можем с новой точки зрения понять, почему это так. Сложив почленно равенства
г>0	__ xVJ
'-'п	—
с1п+1=с°п+с'п, Сп+1— Cn-j-Cn, • • • • • • •
Cn—1 2 । zvi—1
п~\ 1 — Ьп Сп , СП  ^П—1 !
Л-Щ -“Г '-'Л,
получим:
c°„+1 + c;+1 + • • • + СЙ1 = 2(C°+Ci 4~------b С").
2. При четном п = 2k члены строки возрастают вплоть до наибольшего члена с номером k + 1. При нечетном п = 2k + 1 в строке имеется два наибольших члена: fe-й и k + 1-й. Предшествующие им члены идут возрастая, а последующие — убывая.
Доказательство непосредственно следует из формулы (5). Проведите его самостоятельно.
Упражнения
47.	Доказать, что
I ^т — 1 .	/-.т+1
ТЧ -f-	— СП4-2 .
48.	Имеется 9 монет различного достоинства: 1 коп., 2 коп., 3 коп., 5 коп., 10 коп., 15 коп., 20 коп., 50 коп., 1 рубль. Сколькими способами эти монеты можно разложить в двух карманах?
49.	Дано множество, состоящее из 10 различных элементов. Сколько подмножеств имеет это множество?
50.	Написать десятую строку треугольника Паскаля.
51.	Проверить равенство: Сд С?о Н- C?i ...	С20 — Сгь
52.	Вычислить: а) С}1, б) С%, в) г) <Х, д) С&
53.	Вычислить приближенно: а) б) — (Cioo + Cioo + ••• + 2100	2100
+ Cfoo + Cioo)-
54*. Какая доля из 10100 стозначных чисел
а)	имеет поровну четных и нечетных десятичных знаков,
б)	имеет не менее 45 и не более 55 четных десятичных знаков.
55*. Доказать, что не более одной тысячной стозначных чисел содержит менее 30 или более 70 четных десятичных знаков.
§ 8*. УПОРЯДОЧЕННЫЕ МНОЖЕСТВА. ЧИСЛО РАЗМЕЩЕНИЙ
Если множество состоит из п элементов, то его элементы можно п\ способами расположить в определенном порядке один за другим. Множество вместе с указанным порядком расположения его элементов называется упорядоченным множествам. Упорядоченное конечное множество будем записывать, помещая его элементы в установленном порядке, в обыкновенных круглых скобках. Например, записи
{Л, В} и {В, Л} обозначают одно и то же множество (не упорядоченное), но записи
(Л, В) и (В, А) обозначают два разных упорядоченных множества.
Мы уже решали задачу: сколькими способами в классе из 35 учащихся можно выбрать трех делегатов на общешкольную конференцию. Ответ. с|5 = 6545.
Изменяем условие этой задачи следующим образом: на собрании присутствует 35 человек, из которых для ведения собрания надо избрать председателя собрания, его заместителя и секретаря. Сколькими способами можно избрать этих трех человек?
В первой из этих двух задач порядок выбора трех человек не играет никакой роли, во второй же задаче порядок выбора не безразличен. Так, если уже выбраны три человека Д, В, С, то среди них еще надо произвести выборы, а таких выборов будет столько, сколько перестановок можно составить из трех элементов. Поэтому ответом на последнюю задачу будет:
31 с335 = 6 • 6545 = 38270.
Мы нашли число способов, которыми из множества 35 учащихся можно выбрать три элемента и расположить их в определенном порядке (председатель, заместитель, секретарь), т. е. число упорядоченных множеств, содержащих по три элемента, которые можно образовать из элементов множества, содержащего 35 элементов.
Поставим общую задачу: сколькими способами из множества, содержащего п элементов, можно выделить т элементов и расположить их в определен
ном порядке? Иначе говоря, сколькими способами из элементов множества, содержащего п элементов, можно образовать упорядоченное множество, содержащее т элементов? Искомое число называется числом размещений из п элементов по т и обозначается А™. Докажем, что
А™=т\С™.	(8)
Выбор т элементов из п можно произвести С™ способами. Отобранные т элементов можно упорядочить т\ способами. Всего получаем т\ С™ размещений из и и /и.
Короткая выкладка
А™ =т\	= т\ -----------=----“1----
т\(гг— т)\	(п—т)\
приводит далее к формуле
Ап =~—=я(я —1)(л—2) • • • (я —m+1).	(9)
(п — т)\
Формулу (9) можно доказать и непосредственно. Пусть дано множество
А = {л,, а2.ап}.
Чтобы из его элементов образовать упорядоченное множество
В = (^1, ^2> •••>
можно п способами выбрать первый элемент bt. Из оставшихся элементов множества А уже только п — 1 способами, — элемент 62 и т- Д- вплоть до элемента Ьт, который придется выбирать уже только из и — т + 1 оставшихся элементов множества А. Всего получим:
п (п — 1) (п — 2) ... In — (т — 1)]
способов образования упорядоченного множества В.
Естественно, что в частном случае при т =* п
А"п~п\
размещение всех п заданных элементов и есть образование из них определенной перестановки.
Можно было бы дать другой вывод формул (1) — (9) из § 6—8, начав с доказательства формул (9) и (8). Из них сразу получается формула (1):
„ Ат	пУ
Ст ** п ____
п = —г —	ГЗ ГГ •
т\ т\(п — т)\
Упражнения
56.	Какая доля из 107 семизначных телефонных номеров состоит из семи различных цифр?
57.	Сколькими способами можно выбрать четырех человек на четыре различные должности из девяти кандидатов на эти должности?
58.	Из скольких предметов можно составить 210 размещений по два элемента в каждом?
59.	Решить уравнение А\ = 18Л^_2.
60.	В девятом классе 35 учащихся. Они обменялись друг с другом фотокарточками. Сколько всего было роздано фотокарточек?
61.	Доказать, что
(п + 1)!
§ 9.	БИНОМ НЬЮТОНА
Рассмотрим образование разложений различных степеней бинома (дв у член а) а + Ь.
0. (а + Ь)° = 1.
1.	(а + b)1 = 1  а + 1 • Ь.
2.	(а + b)2 = 1 • а2 + 2 • ab + 1 • Ь2.
3.	(а + Ь)3 = 1 • а3 + За2б + Заб2 4- 1 • Ь3.
Для получения разложения (а + б)4 умножим обе части равенства а + б, как это показано ниже:
(а + ЬУ = 1 • а4 + 2>а3Ь + За2£>2 + 1 • ab3 +
+ 1-а3Ь + За2б2 + 3ab3 + 1 • б4.
4.	(а + b)* = 1 • а4 + 4а3Ь + 6а2б2 + 4аб3 + 1 • Ь*.
Если сравним строки коэффициентов выписанных равенств с соответственными строками треугольника Паскаля, то увидим, что они совпадают. Из этого сравнения возникает гипотеза, что такое совпадение будет справедливо для любого натурального показателя п в разложении (а + Ь)п, но это утверждение надо доказать.
Теорема. Коэффициенты разложения (а 4- Ь)п совпадают с п-й строкой треугольника Паскаля при любом натуральном значении п, т. е. при любом натуральном значении п справедливо равенство
(а + Ь)п = С°пап + С^-'Ь 4--4- С„ап-тЬт 4- Cn+lan~m^bm+i 4.
+ • • • + Cnnb\	(1)
Доказываем методом математической индукции.
1. Если п — 1, то имеем (а 4* б)1 = С? а 4* С! Ь, т. е. в этом случае утверждение теоремы верно.
2. Предположим, что при п — k равенство
(а + b)k = с№ 4- C\ak^b 4---+ С2ап~тЬт + C^a'-^b”^ +
4“ • • • 4“ Ckb*1
верно. Умножаем обе части последнего равенства на (а + Ь) и получаем:
(а + b)k+1 = Ckak+l + C\akb 4-Н Скак~т+1Ьт-\- СГ+1а*-'"&т+1 +
+ • • • + СкаЬк + С°какЬ + • • • + C'k-lak-m^bm + Скак~тЬт+1 + + ...-!-CtW+C>+1=C^+1+(^+ • • • +(СГЧ +СГ) ak-m+4)m+(Ck+Ck+1) ak-'nbm^ + --  +(Ск~1+Ск) ab^-Ckb^1. Принимая во внимание, что выполняются равенства
СО   л->0	-1 I s>tn s^tn pin I
k —	С/г = С/г_|_1 — 1; С/г С/г = С/г С/г “Г С/г — С/г_р,
окончательно получаем:
(а + Ь)к+* =	+ Ci^b +•••+ CT+iak~ "№+..+ Ckk$bk+'.
Таким образом, равенство (1) верно при п = 1, и если оно верно при п = k, то оно верно и при п — k + 1, следовательно, утверждение доказано для любого Натурального числа п.
Формула (1) называется формулой бинома Ньютона, по имени выдающегося английского физика и математика Исаака Ньютона.
Коэффициенты правой части этой формулы называются биномиальными коэффициентами.
В частности, если положить а = 1 и b = х, то получим многочлен, расположенный по возрастающим степеням х:
(1 + х)" = С° + С„х + • • • + С„хк + • • • + С”*п.
Пример. Написать разложение для (1 + *)7-Решение. Выбираем седьмую строку треугольника Паскаля и пишем ответ:
(1 + Х)7 = 1 + 7х 4- 21х2 + 35х3 + 35х4 + 21х5 + 7х6 + х7.
Разложение n-й степени двучлена по формуле бинома Ньютона содержит п + 1 членов. Обозначая й-й член через Tkt получим из формулы (1):
1\ = С*папЬ° = ап, Тг = Clnan'W = na^b
и вообще
Tk+1 = Скпа-кЬк.	(2)
1	2
т т Примеры. 1) Найти пятый член разложения (г + z )12.
Пятый член разложения находим по формуле (2):
1	£	20
Т5= С12 (г2)8 (г3 )4 = 495г3.
2) Найти номер члена разложения (г+г-2)12, не содержащего г, т. е. содержащего г в нулевой степени.
По формуле (2) находим:
Tk+l = C\^'k(z-2)k = CkX2z^k.
По условию задачи 12 — 3k = 0, откуда k = 4. Следовательно, номер искомого члена равен 5.
Упражнения
62.	Используя треугольник Паскаля, написать разложения биномов: а) (а + fe)6, б) (а + й2)5,_в) (я_— Ь)7, г)_(а — £&)8, д) (3b + а)\ е) (/а'+ Vb)6, ж) (/а — У Ь) , з) У2а —]/ ЗЬ)\
63.	Определить коэффициенты второго, пятого и шестого членов многочлена, получающегося в результате возвышения в седьмую степень двучлена 2х — у.
64.	Найти номер наибольшего члена в разложении
Указание. Рассмотрите отношение двух соседних членов.
65.	Сколько членов в разложении х=(1 + 0,01)10 надо взять, чтобы вычислить х с точностью а) до 0,001; б) до 0,000 001?
66.	Найти два средних члена разложения (х3 — ах)31._
67.	Найти пятый член разложения бинома	, если
\У х а /
отношение коэффициента третьего члена к коэффициенту второго 11
члена равно у.
68.	Найти член, содержащий х4,в разложении бинома (Ух +
69.	Найти член, содержащий х3, в разложении бинома
12
। наити члены, которые
70.	В разложении бинома не содержат радикалов.
71.	Найти все рациональные члены разложения бинома (1^3 +
72.	Сколько рациональных членов содержится в разложении бинома (У2 + /З)100?
2	__L
73.	В разложении бинома ^х2 + ~х первые три коэффициента образуют арифметическую прогрессию. Найти все рациональные члены этого разложения
§ 10.	ОСНОВНЫЕ СВОЙСТВА БИНОМА НЬЮТОНА
1.	Из разложения
(х + а)п = С°хя + С'^-'а + С>-2а2 + • • • + СГ1 xan-l+Cnnan (1) следует, что число всех членов разложения на единицу больше показателя бинома. Показатели первого слагаемого х убывают от п до 0, а показатели второго слагаемого а возрастают от 0 до п. Сумма показателей обоих слагаемых в каждом члене разложения равна показателю бинома.
2.	Формула C£+1 = Ckn позволяет последовательно вычислять биномиальные коэффициенты разложения бинома (х + а)п по предшествующим коэффициентам. Для того чтобы получить коэффициент следующего члена, достаточно коэффициент предшествующего члена умножить на показатель степени первого слагаемого в этом члене и полученное произведение разделить на число членов; предшествующих определяемому члену. Например, в разложении
(х + а)9 = х9 + 9х8 а + Збх’а2 + ...
надо получить четвертое~слагаемое. Для этого 7 умножаем на 36 и полученное произведение делим на 3 (можно 36 разделить на 3 и полученное частное умножить на 7). В результате получим 84. По первому свойству можем написать искомый член разложения 84х6 а3.
3.	Сумма биномиальных коэффициентов разложения бинома (а + Ь)п равна 2п.
Это свойство биномиальных коэффициентов было доказано, основываясь на свойствах строк треугольника Паскаля. Теперь мы это сделаем другим способом. В тождестве (1) полагаем х = 1, а = 1 и получаем требуемое утверждение:
2Л = С® + С'п + С2п 4--+ С"-1с„.
4.	Сумма биномиальных коэффициентов, стоящих на четных местах, равна сумме коэффициентов, стоящих на нечетных местах.
Полагаем в тождестве (1) х = 1, а = — 1 и получаем:
О = С°п-С'п + С2п-С3п+ •••+(-!)” Спп,
откуда и следует:
С°п + С2 + С*п = С‘п + С3 + С3 + • . • = 2я-1.
5.	Из свойства С™ = Сп~т сочетаний следует, что биномиальные коэффициенты разложения (а 4- Ь)п, равноотстоящие от концов этого разложения, равны между собой.
§11*. ИСТОРИЧЕСКИЕ ЗАМЕЧАНИЯ. ПРИМЕНЕНИЕ КОМБИНАТОРИКИ К ТЕОРИИ ВЕРОЯТНОСТЕЙ
Отдельные комбинаторные задачи занимали еще древнегреческих математиков. Но основные факты из области комбинаторики, которые теперь входят в курс общеобразовательной школы, были получены математиками XVII и XVIII веков — Паскалем, Лейбницем, Якобом Бернулли и другими — в связи с развитием алгебры и теории вероятностей.
Несомненно, что каждому из вас случалось рассуждать о «вероятности» наступления того или иного события, говорить, что какое-либо событие «очень вероятно», «мало вероятно», «столь же вероятно, как некоторое другое событие», и т. п. Теория вероятностей имеет дело с такими ситуациями, когда вероятность наступления события допускает точную количественную оценку. Проще всего ситуации, обладающие известной симметрией. Например, при бросании правильной кубической кости естественно считать
выпадение одного, двух, трех, четырех, пяти или шести очков одинаково вероятными событиями и приписывать каждому из них ве-1 ~
роятность —. Так как в трех из этих шести случаев число очков 6
будет четным, то естественно считать, что вероятность выпадения четного числа очков равна
з 1
6	2’
Вообще вероятностью события называют отношение числа благоприятствующих ему случаев к общему числу исключающих друг друга равновозможных случаев.
Не вдаваясь в теорию, познакомимся ближе с понятием вероятности на двух примерах.
Примеры. 1) Страстный игрок в кости кавалер Де Мере обнаружил, что более чем в половине случаев при четырех бросаниях кости хотя бы раз появляется шестерка. Расчет по правилам теории вероятностей подтверждает его наблюдение. При первом бросании кости имеется шесть различных возможностей (выпадение 1, 2, 3, 4, 5 и 6 очков). Каждая из них разбивается на шесть в зависимости от результата второго бросания, что дает 62 — 36 возможностей. При трех бросаниях число различных исходов будет 63 = 216, а при четырех 64 = 1296. Но среди этих 1296 случаев, которые естественно считать равновозможными, будет 54 = 625 таких, где шестерка не появилась ни разу, а в 1296—625 = 671 случае хотя бы один раз из четырех выпадает шестерка. Значит
2-
вероятность выпадения хотя бы одной шестерки при четырех бросаниях кости равна:
671 1296
Когда партнеры Де Мере разгадали его секрет, он решил придумать новый вариант игры. Так как выпадение при бросании двух костей двух шестерок казалось ему событием в шесть раз менее вероятным, чем выпадение шестерки при одном бросании (в этом он был прав), он сделал вывод, что при 4 X 6 = 24 бросаниях пары костей более чем в половине случаев хоть один раз будут появляться две шестерки. Но экспериментальная проверка этого вывода принесла ему разочарование: две шестерки при 24 бросаниях пары костей появлялись менее чем в половине случаев. Тогда игрок обратился к Паскалю за разъяснениями. Паскаль легко объяснил кажущийся парадокс. При одном бросании двух костей имеется 36 возможностей, из которых только одно соответствует выпадению двух шестерок. При 24 бросаниях всего получается 3624 возможных случаев, из которых в 35 24 случаях ни при одном бросании не выпадет сразу двух шестерок, а в 3624 — 3524 случаях хотя бы раз две шестерки появятся вместе в одном броске. Вероятность выпадения хотя бы раз двух шестерок равна1:
3624 _ з524 _ j _ /35\ 24 q 48 < X
3624	~~	\36/ ~	2 •
Как видим, вероятность несколько меньше, чем половина.
2) При приемке массовой продукции производится выборочный контроль: из партии в 100 изделий выбираются 20 и при обнаружении в этой выборке хотя бы одного дефектного изделия вся партия бракуется (или передается на сплошную проверку). В партии имеется 10 дефектных изделий. Какова вероятность, что хотя бы одно дефектное изделие попадает в выборку?
Решение. Число различных способов выбрать 20 изделий из ста равно числу размещений из 100 по 20:
,20	1 00!
Л10”“15Г-
Среди этих способов имеется:
л20	90!
- 70!
таких, что ни одно дефектное изделие не попало в выборку. В остальных
л 20 л 20
Л ЮО — /190
1 Проведите расчет с помощью логарифмов.
случаях хотя бы одно дефектное изделие будет обнаружено. Соответствующая вероятность равна:
л20 _ л20 л100 — л90
л100
90! 80!
100! • 70!
0,9049.
Первый пример типичен для начального периода развития теории вероятностей. Значительная часть разбиравшихся математиками задач на подсчет вероятностей бралась из области азартных игр, выигрышных лотерей и т. п. Это объясняется тем, что при самом изготовлении костей и карт и организации лотерей заботятся о соблюдении «равновозможности» различных исходов испытания, так что применение определения вероятности как отношения числа благоприятствующих случаев к общему числу равновозможных особенно просто. В настоящее время о том же заботятся и при организации выборочного контроля и выборочных статистических исследований. Но область применений теории вероятностей не исчерпывается такого роДа ситуациями, где легко все возможные исходы испытания разбить на «равновозможные» случаи. Здесь мы лишены возможности рассказать о том, как определяется вероятность в более общей обстановке.
К началу XX века комбинаторика считалась в существенном законченной частью математики. Давно сложилась и принятая здесь специфическая терминология (перестановки, сочетания, размещения и т. п.). В XX веке комбинаторику стали воспринимать как первую главу теории множеств, занимающуюся конечными множествами (их подмножествами, отображениями друг на друга и т. п.), что содействовало более последовательной классификации комбинаторных задач. В новейшее время роль комбинаторики значительно возросла в связи с разработкой сложных управляющих и счетно-решающих устройств и развитием «теории информации». В комбинаторике появилось много новых задач, которые вновь привлекают внимание математиков.
Упражнения
74. Считая 36 возможных исходов бросания двух костей равновероятными, найти вероятность выпадения суммы в 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 и 12 очков.
75. Найти вероятность того, что при k бросаниях кости все выпавшие числа очков будут различны (fe = 2, 3, 4, 5, 6).
76*. Пятеро гостей пришло в шляпах, какова вероятность, что, надевая при расставании шляпы наудачу, каждый из них надел чужую шляпу?
77*. Тот же вопрос для семи гостей.
78.	При п выстрелах возможно 2п различных распределений попаданий и непопаданий в цель. Считая их все равновероятными,
найти наименьшее число выстрелов, при котором вероятность хотя бы одного попадания не меньше 0,9.
79.	В тех же предположениях найти вероятность того, что при 100 выстрелах получится а) ровно 50 попаданий, б) не менее 45 и не более 55 попаданий, в) не более 10 попаданий (см. упр. 546).
80.	Доказать, что в разложении (а + b + с)п коэффициент k + I + tn = п) при akbl *cm равен:
Ckl,n — п!
П k\ 1\ пг\*
81.	Доказать, что множество из п элементов можно разбить
п\
тг\ т2\ • • • tnk\ различными способами на k попарно не пересекающихся подмножеств, содержащих соответственно по mlf т2, ... mk элементов (mt + т2 + ... + mk = п).
82*. Доказать, что общее число разложений множества из п элементов на k попарно не пересекающихся подмножеств равно kn.
Замечание. В упражнениях (81) "и (82) два разложения:
М = Mi М2 ... о Mk и М = Л4}^	...	Л4|
считаются совпадающими только в случае Л1х = М} М2 =	...,
Но в следующей задаче разложения, отличающиеся только порядком нумерации подмножеств, идентифицируются1. В этом случае говорят о «существенно различных» разложениях. Например, множество из четырех элементов {A,B,C,D} разлагается на два множества по два элемента только тремя существенно различными способами:
{Л, В} {С, D}\ {Л, С} {В, D}- {Л, D} {В, С}.
83. Сколькими существенно различными способами можно разложить множество из десяти элементов на два множества из трех элементов и два множества из четырех элементов?
84*. Найти коэффициент при х3 в разложении (х3 + х + I)7.
1 Идентифицируются — не различаются между собой, тождественны
друг другу.
ГЛАВА ТРЕТЬЯ
БЕСКОНЕЧНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И ПРЕДЕЛЫ
§ 12. ОПРЕДЕЛЕНИЕ БЕСКОНЕЧНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ. СПОСОБЫ ЕЕ ЗАДАНИЯ
С последовательностями, конечными и бесконечными, мы уже познакомились в восьмом классе. Там же мы подробно изучили важные в математике и ее применениях примеры бесконечных последовательностей: арифметические и геометрические прогрессии. Например, геометрическая прогрессия с первым членом = 1 и знаменателем q = 2 начинается так:
= 1; а2 = 2; а3 = 4;	= 8; а5 = 16, ...
Выписывание членов этой прогрессии можно в принципе продолжать неограниченно:
1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, ... Практически такое выписывание членов этой прогрессии делается довольно затруднительным, так как члены ее быстро растут: ее тысяча первый член записывается числом, имеющим 302 десятичных знака1. Но с точки зрения чистой математики это не мешает нам заниматься изучением всей последовательности, считая ее как бы выписанной «до бесконечности».
Геометрическая прогрессия с первым членом = 1 и знаменателем q — — 1
1, —1, I, — 1, 1, —1, ...
также является бесконечной последовательностью, хотя каждый из ее членов является одним из двух чисел: 1 или (— 1).
Задать бесконечную числовую последовательность — это значит указать правило, согласно которому каждому натуральному числу п (номеру) ставится в соответствие число ап (член последовательности с номером и):
1 di; 2 -> а2; 3 -> я3; ...« и -> ani ... Стрелка указывает, что числу ti ставится в соответствие число
Вы уже знаете, что правило, согласно которому каждому числу из некоторого множества ставится в соответствие некоторое число, называется функцией.
Итак, запомним следующее определение.
1 Это следует из того, что десятичный логарифм числа а1001 == 21000 имеет характеристику 301.
Определение. Бесконечной числовой последовательностью называется числовая функция f, определенная на множестве всех натуральных чисел
N = {1, 2, 3,
Если вместо
f (1), f (2), f (3).f (n), ...
писать
хъ x2, x3, ..., xn, .. , (1)
где xn = f (n); n = 1, 2, 3, ...» то мы получим общепринятое индексное обозначение последовательности. При таком обозначе
нии х{ называется первым членом последовательности, х2 — вторым членом, х3— третьим и т. д.
Заметим, что точное определение понятия конечной последовательности вполне аналогично приведенному выше определению бесконечной последовательности: конечной числовой последовательностью называется числовая функция f, определенная на множестве всех натуральных чисел, не превосходящих п. Например, последов ател ьность
(4, 1, 1, 1, 0)
это есть функция /, определенная на множестве [1, 2, 3, 4, 5} со значениями
f (1) = 4, f (2) = f (3) = f (4) = 1, f (5) = 0.
Конечную последовательность (xb x2, ..., xn) длины n кратко обозначают (xj?.
Бесконечная последовательность (1) кратко обозначается знаком (xn)n°Lr Иногда, впрочем, пишут просто (хп). В последнем обозначении подразумевается, что переменная п пробегает все множество ЛГ натуральных чисел.
Последовательности длины два называются «упорядоченными парами». Таковы, например, пары координат точек на плоскости. Последовательности длины три называются «упорядоченными тройками». Таковы тройки координат точек в пространстве. Вы хорошо знаете, что точка плоскости с координатами (0,1) отлична от точки с координатами (1,0). Естественно, что различны также и соответствующие упорядоченные пары (0,1) и (1,0).
На рисунке 1 вершины куба имеют координаты:
(0, 0, 0); (1, 0, 0,); (0, 1, 0); (0, 0, 1);
(1, 1, 0); (1, 0, 1); (0, 1, 1); (1, 1, 1),
Это суть восемь различных упорядоченных троек чисел.
Напишите на рисунке 1 около каждой вершины куба тройку ее координат.
Не следует путать понятие последовательности ни с понятием множества, ни с понятием упорядоченного множества. Чтобы избежать первого смешения при задании конечного множества, мы перечисленные его элементы заключаем в фигурные скобки. Например, {1, 2, 3} и {3, 2, 1} — обозначают одно и то же множество, но последовательности (1, 2, 3) и (3, 2, 1) — различны1.
Далее мы будем, по преимуществу, заниматься бесконечными последовательностями и для краткости прилагательное «бесконечная» будем опускать.
Последовательность может быть задана аналитически при помощи явной формулы, указывающей, как по номеру п вычислить член последовательности хп с этим номером.
Примеры. 1) хп =	—- . С помощью этой формулы мож-
но вычислить любой член последовательности: xt = j = 1; х1п = —!---= — и т. п. Данная последовательность начинается
10	2-10—1	19
<111 1
членами 1, —, —, — , —, ...
3	5	7	9
2)	хп = Первые члены этой последовательности:
I_
3)	хп = vПоследовательность начинается с членов:
72
— 1 1 _1 1 — 1 1 _1 ’2’	3’4’	5’6’	7’ ’ ’ ’
4)	хп = 5. У этой последовательности все члены совпадают:
5, 5, 5, ...
Последовательность, у которой все члены совпадают, называется постоянной последовательностью или просто постоянной.
Логическое определение последовательности может и не быть выражено формулой. Чтобы последовательность была определена, важно только, чтобы для каждого натурального п было указано характеристическое свойство числа хп, позволяющее отличить его от любого другого.
1 Для обозначения конечного упорядоченного множества в § 8 мы пользовались такими же круглыми скобками, как и для обозначения конечных последовательностей. Различие заключается лишь в том, что в упорядоченном множестве все элементы различны, а члены последовательности с разными номерами могут и совпадать. Можно сказать, что конечное упорядоченное множество — это не что иное, как конечная последовательность, в которой все члены различны.
5)	Рп —есть n-е по величине простое число.
Pi = 2; Р2 — 3; Р3 - 5; Р4 - 7, Р5 - 11; ...
Найти Р1000 или Pioooooo нелегко, но теоретически возможно. Это пример логического определения последовательности, которое очень трудно заменить явной формулой.
6)	хп является десятичным приближением к квадратному корню из двух с недостатком с точностью до 10~л.
Xi = 1,4; Х2 = 1,41; х3 = 1,414, ...
Теоретически возможно одним из способов, с которыми вы познакомились в восьмом классе, найти любой член этой последовательности.
Часто употребляется индуктивный способ определения последовательности, называемый иначе рекуррентным. Начнем с примеров.
, 7) Если известно, что Xi — 1 и при любом п > 1	(а)
(б) то легко найдем:
х2 = 2; х3 = 6; х4 = 24; х5 = 120; х6 = 720, ...
Ясно, что условия (а) и (б) определяют вместе значения хп для любого натурального и, т. е. задают бесконечную последовательность. Понятно, что это хорошо известная нам последовательность
Xn = tl\.	(В)
8)	Арифметическая прогрессия с первым членом а и разностью d определяется индуктивно условиями:
— а; ап = an_j + d при п > 1.
В этом случае индуктивное определение удается заменить простой формулой:
ап — а + (п — 1) d.
9)	Геометрическая прогрессия задается индуктивно условиями: — а\ ап = q а,при n> 1.
Явная формула общего ее члена, как вы знаете, имеет вид: ап = л?"-1-
В примерах 7) — 9) мы имели дело с простейшей схемой индуктивного (рекуррентного) определения:
1) указывается первый член последовательности хп,
2) дается формула, позволяющая по номеру п > 1 и члену последовательности хп~{ с номером п — 1 вычислить член хп.
Интуитивно достаточно ясно, что условия 1) и 2) позволяют вычислить любой член последовательности. Строгое доказательство этого утверждения может быть проведено с помощью принципа математической индукции, сформулированного в § 2.
Конечные последовательности допускают табличное задание. Например, обозначая через th температуру в каждый час суток, можно выписать следующую таблицу:
fc|l|2]3]4|5|6|7|8[9]10|...................................| 24
th | — 5 | — 5 | — 61 — 61 — 71 — 8 | — 61 — 4 | — 2 | 0 |	|-3
Бесконечную последовательность таблицей задать нельзя, так как невозможно выписать бесконечное множество чисел. Тем не менее часто пишут, например, «последовательность 1, 2, 4, 8, 16, ...», надеясь, что каждый догадается, что речь идет о последователь’ ности
хп = 2я-*.
Но надо помнить, что всегда существует бесконечное множество различных последовательностей, первые члены которых совпадают с заданными числами. Например, первые четыре члена последовательностей
хп = 2Л”1 и у„ = — п3 — — п2 4- — п п	Уп 6	23
совпадают:
=1,	х2 = 2,	х3 = 4,	х4 = 8;
У1 =1,	Уг = 2,	уз = 4,	у4 = 8.
Упражнения
85. Написать первые пять членов следующих последовательностей:
—;	в) ;
1)«’	7 п 2п
— при п четном, п
а)хп = 2л + 3;	б) хп=-
.	Зп — 1	>
=	Лх--
— при п нечетном. п
86. Написать первые пять членов следующих последовательностей:
а) хп = 3я; б) хп = 2я + ± ; в) хп = Зп2 + 2n + 1;
г) х„ =	+ ]/2+--- + /2~,.
п корней
87.	Написать первые пятнадцать членов последовательности простых чисел.
88.	Написать общий член последовательности натуральных чисел, каждое из которых при делении на 3 дает остаток, равный 2.
89.	Написать общий член последовательности натуральных чисел, каждое из которых при делении на 5 дает остаток, равный 3.
90.	Выписать 5 первых десятичных приближений с недостатком числа У3.
91.	Написать общий член последовательности (хотя бы одной), члены которой совпадают с выписанными:
а) 1,	б) 1, 5, 9, 13, ... ;
’	4	9	16
в) 2, — 2, 2, — 2, ... ; г) 3, 6, 12, 24, 48, ...
92.	Дано: хп = -	. Найти х80, хп_2, xn+l, x2n+i.
П (п + 1)
93.	Дано: хя — 1 +	— . Найти х24, х2п, х2п+1.
п
94.	Последовательность хп задана рекуррентно: х4 = 3, хя+1 = = 2х„. Найти общий член этой последовательности и выписать четыре первые ее члена.
95*. Найти общий член последовательности, заданной рекуррентно:
•Ч = 1; Ч>+1 = 1 — хп.
96*. Найти общий член последовательности, заданной рекуррентно:
Ч — 2, xn±i = 2 -J- — хп.
97*. Последовательность задана рекуррентно:
Xj = а; хя+1 = а + Ьхп.
Найти ее общий член.
98. Выписать первые 4 члена последовательности хя = (1 4—j. Чему равны члены хя+1 и хя+2?
99. Выписать первые три члена последовательности уя — (1 4-
•	1 \л+1 тт	-ч
4—I	. Чему равны члены уп+1 и уя+2?
Л /
§ 13. ГЕОМЕТРИЧЕСКОЕ ИЗОБРАЖЕНИЕ ПОСЛЕДОВАТЕЛЬНОСТЕЙ
Для геометрического изображения последовательности пользуются двумя способами.
Первый способ. Так как последовательность (уп) является функцией, то геометрически эту функцию можно изобразить с помощью ее графика, т. е. множества точек плоскости Мп п = = 1, 2, ... с абсциссой п и ординатой f (п) = масштабы по осям часто оказывается удобным выбирать различными.
Второй способ заключается в том, что члены последовательности изображаются точками на числовой оси, снабженными соответствующими пометками.
Примеры. 1) у„=	2) yrt= ; 3) у„ =	.
Рис 2а.
____________ ft
О 1	1 1	Jr	1
12	4	3	Ч
Рис. 26
Рис. За
__________________________У_г Уз У*
°	1 i 1	19 1 П
7 У 9 го '
Рис. 36
На рисунках 2а, 26, За, 36, 4а, 46 сопоставлены оба способа изображения этих последовательностей. Следует понимать, что график последовательности состоит только из точек (и, уЛ), которые на наших рисунках изображены черными точками. Тонкие вертикальные и пунктирные линии на рис. 2а) и 4а) проведены для наглядности, но к графику не относятся.
При обоих способах изображения видно, что при возрастании номера и на рисунках 2а, 26 члены последовательности все более приближаются к нулю, а на рисунках За, 36 — к единице. На рисунках 4а, 46 уп тоже с возрастанием и приближается к нулю, но поочередно то больше нуля, то меньше его.
4)	На рисунке 5 изображен график последовательности
Уп = (- 1)".
При изображении этой последовательности по второму способу все отметки пришлось бы ставить около точек 1 и — 1.
5)	На рисунке 6 дан график последовательности
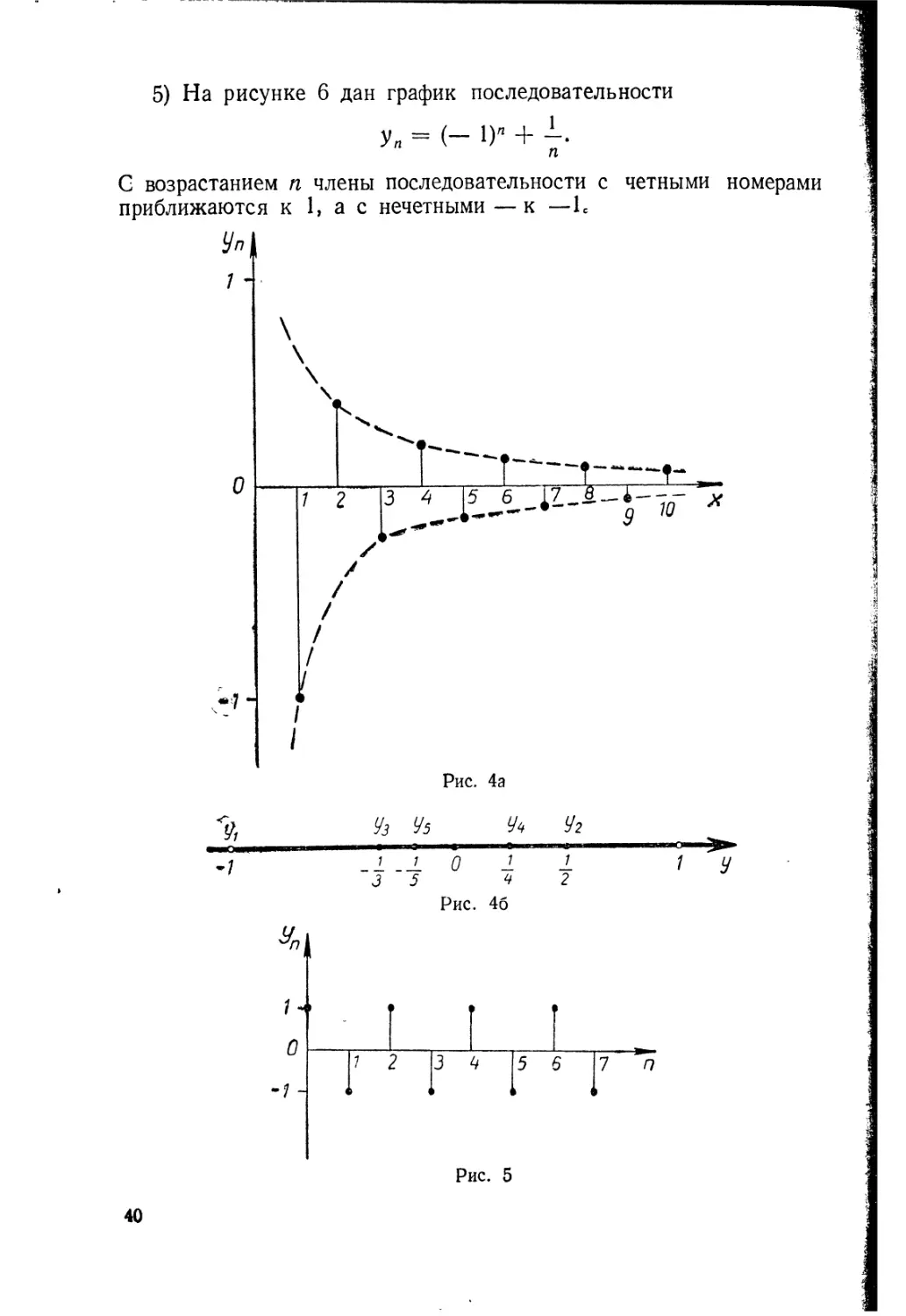
Уп = (~ D” + -• И
С возрастанием п члены последовательности с четными номерами приближаются к 1, а с нечетными — к —L
6)	уп = (-1,1)". На рисунке 7 показано, что точки графика лежат поочередно на кривых, являющихся графиками показательных функций
у -—(1,1/ и у=(1,1/.
Эти кривые, как и вертикальные отрезки на рисунке, к графику последовательности не относятся.
1
— при и нечетном, и
1
----при п четном,
У1 = у2 = 1; Уз = у4 =
1	1
о	о
§ 14. МОНОТОННЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
Рассмотрим подробнее характер изменения последовательностей в примерах предыдущего параграфа.
В примере 1 рассматривалась последовательность
1 1 _1 А А ’ 2 ’ 3 ’ 4 ’ ’ п ’
В этой последовательности каждый член, начиная со второго, меньше предыдущего, т. е.
*,.+!<*„(« = !> 2> •••)•
Такие последовательности называются убывающими.
Определение 1. Последовательность (хп) называется убывающей, если для ее членов выполняется неравенство:
для всех п, иными словами, если
Х1> %2 > *3 > ... > хп> ...
Если же для всех п = 1, 2, 3, ...
*л-Н < т. е. если
х{ > х2 > х3 > ... > хп> ..., то последовательность (хп) называется невозрастающей.
Ясно, что каждая убывающая последовательность является невозрастающей. Последовательность примера 7 является невозрастающей, но ее нельзя назвать убывающей (ее второй член равен первому, четвертый — третьему и т. д.). Таким образом, понятие невозрастающей последовательности шире, чем понятие убывающей последовательности.
Члены последовательности
о, 1, А..........fi-Д, ...
234	\ п)
из примера 2 при возрастании номера п возрастают. Такие последовательности называются возрастающими.
Определение 2. Последовательность (хп) называется возрастающей, если для ее членов выполняется неравенство
для всех п, т. е. если Xi<x2<x3<	...
Если же для всех п = 1, 2, 3, ...
Хп < Хп-Н>
то последовательность (хп) называется неубывающей.
Убывающие, неубывающие, возрастающие, невозрастающие последовательности объединяются под общим названием монотонные последовательности.
Примеры 3—5 из § 13 показывают, что не всякая последовательность является монотонной.
Замечание. Из определения возрастающей последовательности следует, что для установления возрастания достаточно установить неравенство
1; п= 1, 2, ...
Хп
Аналогичные замечания можно сделать относительно других видов монотонных последовательностей.
Примеры. 1) Пусть хп = ^-+1 ; п = 1, 2, 3, ... Тогда 2и
х = п+2	и *"+i	= я (я + 2) =	Па + 2n + 1 -	1 = (n + I)2- 1	=
n+1 п + 1 хп (п + 1)2	(п+1)2	(п + 1)2
= 1-----!--:< 1.
(п + I)2
Следовательно, данная последовательность убывает.
2) Пусть
хп = fl + -V; п = 1, 2, з, ... \ и /
Вычислим приближенные значения первых трех членов этой последовательности:
X = (1 4- IV = 2; х2 = (1 + -V= 2,25; х3 = (1 + Д8= -^2,37.
1	\	1 /	\	2 /	3 I 3 /	27
Судя по первым членам, последовательность кажется возрастающей. Так оно и есть на самом деле. Доказательство, к сожалению, довольно сложно. Но мы его приведем:
Хп+1 ~ f 1 +
*П+1
~(и + 2) и п+1 п 4- 1 . (и + I)2 J '
1	р+1
(и+"Г)2]
Применив к 1 лучим:
•л-н
(л + О2. '
неравенство Бернулли (см. § 3), по-
Х/24-i	1	1	\ п -|- 1 п п 4" 1
хп \ п 4-1 / п л 4-1 п
и, следовательно, хп+1 > хп для всех п, что и требовалось установить.
Упражнения
100.	Являются ли нижеследующие последовательности монотонными:
.	1 кч 2я— 1	/	1 \%
а) х„ —-----; б) х.— ------; в) х =-----1 ?
' п пг +1	7	2”	\	2/
Изобразите эти последовательности на числовой оси.
101.	Доказать, что последовательность с общим членом
х Зп~1 л 5п +2 является возрастающей.
102.	При каких коэффициентах а и b последовательность с общим членом
ап + 2
Хп = ---—
п bn + 1 является неубывающей? возрастающей? убывающей?
103*. Доказать, что последовательность с общим членом
Л I И"4"1
У.= (‘ + 7) убывает.
(1)
(2)
(3)
§ 15. ОГРАНИЧЕННЫЕ И НЕОГРАНИЧЕННЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
Рассмотрим три последовательности:
1,1, 1.........1, ...
2	3	п
— 1, — 2, — 3........ —	п, ...
1, 2, 3, .... п, ...
Все члены первой последовательности удовлетворяют неравенствам
0 < хп < 1.
Эта последовательность ограничена сверху и снизу. Все члены второй последовательности удовлетворяют неравенству
хп < 0.
Последовательность ограничена сверху. Но нельзя найти такого числа т, для которого выполнялось бы неравенство xn > zn при любом п. Поэтому, последовательность (2) не ограничена снизу. Последовательность (3) является примером последовательности, ограниченной снизу, но не ограниченной сверху. Дадим соответствующие общие определения:
Определение 1. Последовательность (хп) называется ограниченной сверху, если существует такое число М, что при любом натуральном п выполняется неравенство
хп < М.
Определение 2. Последовательность (хп) называется ограниченной снизу, если существует такое число т, что для всех ее членов выполняется неравенство
хп > т.
Замечание. Число А4, которое не меньше любого члена последовательности, называется верхней границей этой последовательности. Например, в качестве верхней границы последовательности (1) с одинаковым правом можно указать числа М = 1 или М = 1000. Число т называется нижней границей по*
следовательности (хп), если при любом натуральном п выполнено неравенство хп > т. Очевидно, что определение ограниченности сверху можно теперь высказать в такой форме: последовательность ограничена сверху, если она имеет верхнюю границу. Аналогично для ограниченности снизу.
Рис. 8
т
Рис. 9
Геометрически ограниченность числом М сверху означает, что ни одна точка хп не лежит правее точки М (рис. 8), а ограниченность числом т снизу (рис. 9), — что ни одна точка хп не лежит левее точки т.
Определение 3. Последовательность называется ограниченной, если она ограничена и сверху и снизу, т. е. если существуют такие два числа т и М, что для всех членов последовательности выполнены неравенства (рис. 10):
т < хп < М,
Рис. 10
Геометрически ограниченность последовательности означает, что все ее члены помещаются на некотором сегменте [т, М]. Легко доказать, что для ограниченности последовательности необходимо и достаточно существование такого числа М, что для любого члена последовательности выполнено неравенство
И<М.	(4)
Достаточность условия (4) очевидна, из него вытекает двойное неравенство
— М < хп < М.
Докажем его необходимость. Если последовательность (хп) ограничена, то, по определению ограниченности, существуют такие числа т{ и Mit что
< Mit	(5)
Обозначим через М наибольший из модулей j/nj и |Afj|. Ясно, что из неравенств (5) вытекает
— М < хп < М,
т. е. неравенство (4).
Примеры. 1) Докажем, что последовательность
ограничена.
Доказательство. 1) При любом натуральном п дробь
—— положительна, это означает, что х_>0. 2) Кроме того, эта п + 1
дробь правильная при тех же значениях п, следовательно, хп < 1. Таким образом, доказано, что данная последовательность ограничена.
2)	Докажем, что последовательность
ограничена сверху.
В самом деле, учитывая упражнение 103*, в котором было доказано, что последовательность
/, । i\n+1 Уп= 1+-
\ Л /
/, ,	1\" Л I 1
убывает, получим:	/1 + — j < 11 Н—1	= уп<. yn-i <
< ... <у2 <У! = (1 + y)2=4.
Таким образом, хп <. 4 для всех п = 1, 2, ... Заметим, что 0 < хп. Следовательно, 0 < хп < 4; п — 1,2, ... и последователь-ность хп = II + — I ограничена.
Упражнения
104. Ограничены ли (и с какой стороны) последовательности: а) хп = 2n- 1; б) хп = 1; в) хл= ^±0. ;
®) хп=	з> хп= и) =2-^г
105. Сформулируйте определения: а) последовательности, неограниченной сверху; б) последовательности, неограниченной снизу; в) неограниченной последовательности.
§ 16. ПОНЯТИЕ О ПРЕДЕЛЕ ЧИСЛОВОЙ ПОСЛЕДОВАТЕЛЬНОСТИ
Переходим к выяснению одного из основных понятий современной математики к понятию предела.
Рассмотрим более подробно последовательность
О 1	2	п — 1
’ ~2 ’ 7’	’ п ’
с общим членом
Определим расстояния точек, соответствующих членам данной последовательности, до точки 1 (рис. 11).
X/			Х4 Х5	*24
0	1 2		3 ± Ъ 5	23 ° X 24
Рис. 11
Как известно, расстояния между точками хп и точкой 1		равны
абсолютной величине разности чисел хп |Х1_ 1| = |0—1 |х2-1|= |-1 |х3- 11 = |-1	и 1, т. е. равны |хп = 1, = £ ~ 2 ’ _ £ “ 3 ’	- И:
й|	.	*	® •	т	•	т	i	• ‘ 3 Т ’ -Io ol10' ’	**	’	1	1 ‘	I	•—	ь-	•	Н' н- -11 = 1, 1 п	(1)
Из приведенной таблицы видно, что расстояния точек хп до точки 1 становятся меньше любого положительного числа по мере возрастания номеров п членов последовательности, т. е. члены данной последовательности по мере возрастания их номера располагаются сколь угодно близко к 1. В подобных случаях говорят, что последовательность стремится к 1.
Каков же точный математический смысл этих выражений? Для того чтобы это выяснить, снова обратимся к равенствам (1). Из
, 1
этих равенств видно, что если взять положительное число1 е =
то, начиная с четвертого номера, т. е. при п > 3, все члены хп последовательности удалены от 1 меньше, чем на —: \хп— 11< —
3	3
при п > 3. Для числа е = 1, начиная с одиннадцатого номера,
т. е. при п > 10, все члены последовательности удалены от 1 меньше, чем на —, т. е. I хп — 11 < 0,1 при п > 10. Вообще, если е — 10
произвольное положительное число, то | хп — 11 = — < е при
п > —. Например, если е = 0,01, то при п > ^1^- = 100
|х„—1|<0,01.
Если е = 0,001, то при п > —— = 1000 и I х„ — 11 < 0,001.
г 0,001	1 "	1
Определение. Число а называется пределом последовательности (х„), если для любого сколь угодно малого положительного числа е найдется такой номер N, что для всех членов х„ данной последовательности с номерами п, большими N, выполняется неравенство:
|х„ —а|<8 при n>N.
При этом пишут: lim хп — a (limes — латинское слово, означающее П ее
предел, границу). Пишут еще: хп -> а при п -> оо и говорят: последовательность (хя) сходится к числу а. Таким образом,
11Ш -- = 1.
П -* ос П
Примеры. 1) Рассмотрим последовательность (рис. 12)
— 1 1 ... —11 (— 1)” ’2.............. 3’	4* " ’ п
с общим членом
л,	х3 х5	х2
1 .1	О I	1
3 5	4	2
Рис. 12
1 К
1 е — греческая буква «эпсилон».
Докажем, что данная последовательность сходится к 0, т. е. докажем, что
lim = 0.
оо П
В самом деле, пусть 8 — произвольное положительное число. Требуется доказать, что абсолютная величина разности
I — о | = | х„|
становится меньше 8, начиная с некоторого номера. Иными словами, требуется доказать, что для наперед заданного е > 0 решениями неравенства
| хл — 0 I < е
являются почти все натуральные числа, т. е. все натуральные числа, большие некоторого N. Так как
I п п
то |хп — 0| < е, если — < е, или, что то же, если п > —. Итак, п	8
| хп — 0 | < е при п > —. 8
Следовательно, согласно определению,
lim = 0. П -* ОО П
Для того чтобы картина приближения членов последователь-
ности к своему пределу была ясней, рассмотрим некоторые значе-
ния для 8 > 0 и соответствующие им номера N такие, что при п > N выполняется неравенство \хп — 0| < &.
(-1)"
п
< 0,1 при п > — = 10. 0,1
Если 8 =0,1, то
Следовательно, если взять N= 10, то при п>10 | хп—0 | < 0,1.
Если 8 = 0,003, то 1^—<0,003 при п > —-— = 333— . | п	г 0,003 з
Следовательно, если взять N = 333, то при и > 333 |	01< 0,003.
Аналогично заполняется следующая таблица зависимости но-
мера N от выбранного числа е > 0.
е | 0,1 0,01 0,003 0,001 0,0003
/V | 10	100	333	1000	3333
2) Докажем, что lim -—— =—— , т. е. докажем, что по-ос 4п	4
Хп

-	2—Зп
следовательность с общим членом хп = ------ сходится к пределу
4п
(—yj. Для этого достаточно, согласно определению, доказать, что для любого положительного 8 выполняется неравенство
/ з\ I
—	< 8
4/1
для всех п, больших некоторого N. Так как
/	3 \ |	2 — Зп । 3_ I = I 2 — Зп + Зп |	£
4п 4 I I 4п I 2п ’
то достаточно решить относительно и неравенство — <8, которое 2п
равносильно неравенству п > —.
28
£ .
2е ’
I 2 — Зп	/	3
I 4п	\	4
легко сообразить, что в качестве N можно взять целую часть числа
— , т. е. N = Г—1. Следовательно,
28	[2eJ
1.	2 — Зп 3
lim------=--------.
п -* оо 4п	4
Таблица зависимости номера М от числа е > 0: 8 | 0,1 0,03 0,01 0,001 N I 5	16	50	500 ’
3) Рассмотрим постоянную последовательность а, а, а, ... с общим членом хп — а. Так как для любого положительного е | хп — а | = | а — а | = 0 < е для всех п, то, согласно определению, lim хп = lim а — а. п — ОО	п -* ОО
Таким образом, предел постоянной последовательности равен общему члену этой последовательности.
§ 17. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПОНЯТИЯ ПРЕДЕЛА
Пусть последовательность (хп) сходится и lim хп = а. Это озна-П -* оо
чает, по принятому нами определению, что для любого числа 8 > О найдется номер N такой, что для всех членов последовательности с номерами и > N выполняется неравенство
| Хл U | <С 8 •
Последнее неравенство равносильно двойному неравенству
8 Хд Я 8 > а это последнее равносильно неравенству
а—8 < хп < а + е при п > N. (1) Двойное неравенство (1) показывает, что все члены хп данной сходящейся последовательности с номерами п > Af, т. е. члены
•*W+P XN-\-W XN-\-V •••
расположены в интервале (а —8, а + е).
x/v+/ *N+3	*n+2
а-8	а	а+£
Рис. 13
Интервал (а—8,я + е) называют 8-окрестностью точки а. Таким образом, если число а является пределом последовательности (хп), то геометрически это означает, что в произвольно малую 8-окрестность точки а попадают все члены данной последовательности, начиная с некоторого (рис. 13).
Члены сходящейся к числу а последовательности как бы сгущаются около своего предела — точки а.
Замечание. Из неравенства (1) вытекает также, что всякая сходящаяся последовательность ограничена, так как членов последовательности, не удовлетворяющих этому неравенству, может быть лишь конечное число: Xj, Xg, Х3, .Хд.
Упражнения
106.	Докажите, что lira — = 0. П -* оо Л
107.	а) Докажите, что	= 1; б) докажите, что
П -* со tl
lim -Д-= 1. п 09 П 4“ 1
108.	а) Докажите, что lim Зга + *- = —; б) найдите номера N ©о 2п 3	2
такие, что при n> N
Зп +1	3	_
-----	< е 2п —3	2
при е = 0,01; 0,001; 0,0001. Полученные результаты оформить в виде таблицы.
109.	а) Докажите, что lim = ——; б) найдите номера N п -* о.	2	5
такие, что при n > N
I 2 —5n /	5\I _
		< е 6л + 2-------6 /
при е =0,1; 0,03; 0,01; 0,001. Полученные результаты оформить в виде таблицы.
ПО. а) Докажите, что lim -п-£2 =— А; б) найдите номера п ©о 5 Зл	3
N такие, что при n > N
I 5га + 2 _ Л_ 5. \ I <-| 5 — Зл \	3/|<8
при е >0,01; 0,001; 0,0001. Полученные результаты оформить в виде таблицы.
111. Имеет ли последовательность
1 1 _£ (— 1)” 2’4’	8 ’	’ 2я ”
предел? Чему он равен? Докажите.
112*. а) Докажите, что lim = 0; б) докажите, что П2-|- 1
lim п  — 1.
п «= Vп2+ п
но* тт	|. л2 4-2/1 — 1	1
113*. Докажите, что lim —1.
2n24-n4-2	2
§ 18. ЕДИНСТВЕННОСТЬ ПРЕДЕЛА. СХОДЯЩИЕСЯ И РАСХОДЯЩИЕСЯ ПОСЛЕДОВАТЕЛЬНОСТИ
Теорема. Последовательность не может иметь более одного предела, т. е. если lim хп = а и lirri хп = Ь, то а = Ь.
Доказательство. Так как lim хп = а и lim хп= b то для любого е > 0 выполняются сразу два неравенства:
|х„ —а|<-| при п>М.
1*л — N< f ПРИ ti>N2
Выберем номер па, большим и N2. Тогда \х — а | < — и | х — & | < — , 1 ло	2 ло	2
и, следовательно,
|а —f>| = |(а —х„о) —(х„о —6)| < |а —х„о | + |х„о -&|<| +
I 6
+ ? = е.
Таким образом, неотрицательное число |а— Ь| меньше любого положительного числа 8. Но такое число равно нулю, т. е. | а — b |= = 0, и, следовательно, а = Ь.
Итак, возможны только два случая:
1) у последовательности имеется предел, и тогда он единствен. Такие последовательности называются сходящимися;
2) у последовательности совсем нет предела. Такие последовательности называются расходящимися.
Приведем два примера расходящихся последовательностей.
Примеры. 1) хп = п. Проведем доказательство расходимости этой последовательности от противного. Предположим, что последовательность эта сходится и что ее предел равен числу а. Пусть натуральное число Af превосходит а : N > а. При любом п > N
|хп — а| = | п — а \ = п — а~> п — N > 1, что противоречит определению предела (при е < 1).
2) хп = (— 1)«; п = 1, 2, ...
Допустим, .что данная последовательность сходится и что предел ее равен а. Выберем в < 1. По определению предела, при достаточно большом п
1Х2Я —«|<е; IWi~а\<8-
Но х2п = 1 и x2n+i ~ — 1- Следовательно,
\а—11 <в: —е<а—1<8. Поэтому
а> 1 —8> 0.
| а — (— 1) | С е; — 8 <; а + 1 < 8. Поэтому
а<е— 1 <0.
Полученное противоречие и доказывает отсутствие у данной последовательности предела.
Упражнения
114.	Имеет ли последовательность с общим членом х„= — + п
+ (— 1)я предел?
115.	Является ли последовательность с общим членом х„ = = 1 + (— 1)п сходящейся?
116.	Какие из следующих последовательностей являются сходящимися, а какие расходящимися:
а) хп=-^-П; б) 0; 1; 0; 1; 0; 1; ... ; в) хл = ^ + 2?
§ 19. ВАЖНЫЙ ПРИМЕР СХОДЯЩЕЙСЯ ПОСЛЕДОВАТЕЛЬНОСТИ
Теорема, lim?'1 =0, если |<?|< 1.	*
п ео	>
Доказательство. Теорема утверждает, что при любом , е > 0 для достаточно большого п выполняется неравенство
I ?" | = | <71" < 8.	(1)
Прологарифмировав неравенство (1), получим равносильное ему неравенство: nlg|9|<lge.	(2)
Так как |	1, то lg | q | < 0 и неравенство (2) равносильно не-
равенству
n>-^L=M.	(3)	<
lg I ЯI	i
Мы видим, что, в самом деле, неравенство (1) выполняется для I всех п,	превышающих некоторое число М.	4
Упражнения	1
117.	Найти такое Af, что при п > N (0,99)" < 0,01.	1
118.	Найти такое Af, что при n > N (0,999)" < 0,001.
§ 20.	СУММА БЕСКОНЕЧНОЙ УБЫВАЮЩЕЙ	ПО АБСОЛЮТНОЙ	j
ВЕЛИЧИНЕ ГЕОМЕТРИЧЕСКОЙ ПРОГРЕССИИ	1
Напомним, что геометрическая прогрессия называется убываю-щей по абсолютной величине, если ее знаменатель q удовлетворяет неравенству | <? | < 1.
Пусть последовательность
xt, х2 = xtq, х3 = Xtq2, .... хп —	...
образует геометрическую прогрессию, убывающую по абсолютной величине. Составим сумму s„ ее п первых членов и назовем ее n-й частной суммой данной прогрессии. Таким образом,
S1 = xit
s2 = Xi + х2 = %i(l + q) = Xi^3.,
1 —я j __________дЗ
s3 = Xi 4- x2 + x3 = Xi (1 + q + q2) = Xi-—-, 1 — Я
1_nil
sn = Xi + x2 + x3 + ... + xn == Xi—4 1—9
Докажем, что последовательность si, s2, $з, •••»	••• сходится.
Теорема. Последовательность частных сумм бесконечной убывающей по абсолютной величине геометрической прогрессии сходится, и предел ее равен
lim sn = —— = s, n-* oo 1 — q
где q — знаменатель прогрессии.
Доказательство. Составим разность:
Sn_s = x1lmn__ii_==^
Ч-Q l-q 1-9
Оценим абсолютную величину этой разности:
Если е > 0 — произвольное положительное число, то из предельного равенства lim qn = 0 (при | q | < 1) следует, что найдется
П оо
номер AZ такой, что при п > N | q |п <	• г. Но тогда при
I Xi I
этих же п > N будет выполняться в силу (1) следующее неравенство:
а это и означает, что
lim s =-^i—.
1—9
Доказанная теорема позволяет ввести следующее естественное Определение. Предел последовательности частных сумм бесконечно убывающей по абсолютной величине геометрической прогрессии называется суммой этой прогрессии и символически обозначается следующим образом'.
+ х2 + ... + хп + ...
Таким образом,
xi + хг + ••• + хп + ••• =	1 •
1—9
Эта запись вовсе не означает, что мы на самом деле складываем бесконечное множество чисел, — этого сделать нельзя. Запись эту надо понимать так, как это указано в определении, а именно: найти сумму членов бесконечной геометрической прогрессии, убывающей по абсолютной величине, означает найти предел последовательности ее частных сумм.
Примеры. 1) 1 + (—yj +-^ + (—sr) “ =
_______1______2_
10
2) 1 + ± + -2- + ... =-------'---- =
’	10	102	1—0,1
3) 1 + 0,3 + (0,3)2 + ... = ,-b—
10
7 ’
Упражнения
119.	Найти суммы бесконечных убывающих по абсолютной величине геометрических прогрессий:
ч 2	1	3	j 1	1	ч 5	2
а) —, —,	б) 1, —, —, ... ; в) х2= — ; q = — .
7 3 ’ 2	8	2	4	7 2	3	7	3
120.	Найти геометрическую прогрессию, если известно, что Xj + х2 — 12, Xi + %2 + ••• + хп + ••• = 12,5.
121.	Найти геометрическую прогрессию, убывающую по абсолютной величине, если известно, что
+ *2 + ... + хп + ... = 6,25;
х; + + ... + +... = 55.
122.	Найти сумму геометрической прогрессии 1 + х + х2 + 4- ... 4- хп + ... при условии, что |х| < 1.
123.	При каком условии геометрическая прогрессия 1, х2, х*, ... будет убывающей по абсолютной величине? Найти ее сумму при этом условии.
124.	Найти сумму геометрической прогрессии
у2	у2
^2 Х	Х
’ 1 -М2 ’ (1 4- х2)2 при условии х ф 0.
125.	При каком условии геометрическая прогрессия 1, х3, х3, ... является убывающей по абсолютной величине? Найти ее сумму при этом условии.
126.	Тоже для прогрессий:
а)	(1 + х), (1 4- х)2, (1 + х)3, ...?
б)	* + *	0 + х)3	<1 +
X ’ X3 ’ X5 ’	’
в)1, J-, __1_ ...;
2х 22х2	23х3
г\ 1 1 1
Г х —1 ’ (х-1)2’ (х-1)3’
127.	Первый член геометрической прогрессии, убывающей по абсолютной величине, равен 0,3, а сумма равна 0,9. Найти знаменатель прогрессии.
128.	При каких значениях х верны равенства:
a) —J— = 1 — x + x2 — x3 4- ;
1 +x
x + 1 _	X + 1 h	x	. x2	x3	.
x— 1	2 \	2	22	23	'/ ’
B) LZ^ = (1—x)(l—x + x2 —X3+ ••)•
1 +x
129. Рассмотрим следующее геометрическое построение, ясное из рисунка 14. Доказать, что абсцисса s точки М равна сумме геометрической прогрессии 1 + q + q2 + qs + ... при 0 < q < 1.
§ 21. ЧИСЛОВЫЕ РЯДЫ
Пусть Xi, х2, .... хп, ... — произвольная последовательность. Выражение
xt + х2 + ... 4- хп + ...	(1)
называют числовым рядом.
Сумма п первых членов ряда называется п-й частной суммой этого ряда и обозначается через sn:
81 = Xi
s2 = Х1 4" х2
«з = Xi 4- х2 4- х3
sn = Xi 4- х2 4- х3 4- ... 4- хп
Если существует предел lim sn — s последовательности частных сумм, то говорят, что ряд (1) сходится, а указанный предел называют суммой этого ряда.
Если последовательность частных сумм данного ряда не имеет предела, то этот ряд называют расходящимся.
Пример. Рассмотрим ряд
_J_ + _L_ + _L_+ +_J____________ .
1-2	2-3	3-4 .....n(n4-l)
Если заметить, что
то
п (п + 1) п п + 1 ’
Таким образом,
1 • 2	2-3 + 3-4 + " + n (n + 1) +
Частным случаем общего определения суммы ряда является определение суммы убывающей по абсолютной величине геометрической прогрессии из § 20:
а + aq + а?2 + ... + а<7"+ ... = —— при | г?| < 1.
1 —9
§ 22. ПРЕДСТАВЛЕНИЕ ЧИСЕЛ В ВИДЕ БЕСКОНЕЧНОЙ ДЕСЯТИЧНОЙ ДРОБИ
Известно, что при делении числителя дроби на знаменатель бывают случаи, когда процесс деления не оканчивается ни на каком шаге. Например, пытаясь превратить в десятичную дробь число —, получаем
-= 0,3333... з
Теперь мы можем придать таким «бесконечным десятичным дробям» точный математический смысл.
Обратимся сначала к конечным десятичным дробям и начнем с примера:
17,04305 = 17 + - + —+ — + — + 10	100	1000	10000
5
100000 
Произвольная конечная десятичная дробь имеет вид х = а, а{а2... ап,
где а — целое число (целая часть числа х), а десятичные знаки ak представляют собой числа 0, 1,2, 3, 4, 5, 6, 7, 8 или 9. Число х представляется в виде суммы
Естественно, возникает мысль истолковать бесконечную десятичную дробь
а,	ап...	(1)
как сумму ряда
10	10»	10»	10"	'
Сейчас мы покажем, что в том случае, когда бесконечная десятичная дробь (1) возникла в результате вычисления по обычному арифметическому способу десятичного представления обыкновенной дроби — (р и q — натуральные числа), ряд (2) сходится и его сум-<7 р ма s равна числу —.
я
В самом деле, алгоритм деления устроен так, что на каждом шагу конечная десятичная дробь
6Z,	•••
является приближенным значением числа — с недостатком с точ-q
ностью 10~Л, а число а, ап +
десятичным приближением той же точности с избытком. Иначе говоря,
а + Го + + - +	= а> а^"	+ тЬ ’
Но тогда для любого е > 0 найдется такое N, что при > N
А это и значит, что частные суммы ряда (2)
Р сходятся к числу —. я Например,
2
о,зззз... = А + А + 1 + ...+ Л+..._
1 10
0,21777	= - + — +	=
10	1 02	1 03	1 0*	105
= 21	7 л , 1 , J_ ,______\=^L+_Z_______!_ = £L+_L_ 49
loo+ юоо А АоЛо2" j юоАооо ’loo’Soo '225
10
Упражнения
130. Превратите в обыкновенную дробь: а) 0,10(01) = = 0.Г0010101	6) 0, (142857) = 0,142857 142857...;
в) 0,(0526315736842105).
ГЛАВА ЧЕТВЕРТАЯ
ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
§ 23. СЧЕТ И ИЗМЕРЕНИЕ
Человеческие представления о числах складывались постепенно под влиянием требований практики. С давних пор числа употребляются а) при счете, б) при измерении величин.
Ответ на вопрос: «Сколько элементов содержит данное конечное множество?» всегда выражается либо натуральным числом, либо числом нуль (если множество пусто). Множество неотрицательных целых чисел
No = {0, 1, 2, 3, 4, ...}, получающееся, если к множеству натуральных чисел N = {1, 2, 3, 4, ...} присоединить число 0, обслуживает все потребности счета.
Иначе обстоит дело при измерении величин. Расстояние между селениями может равняться 3,5 километра, площадь комнаты 16,45 квадратного метра, температура может равняться 37,6 градуса, — 22 градусам и т. п. Для того чтобы выразить какую-либо величину через выбранную единицу измерения, вам приходилось пользоваться самыми различными рациональными числами, целыми и дробными, положительными и отрицательными. С чисто практической точки зрения для выражения результата измерения величин достаточно уже знакомых вам рациональных чисел. Можно было бы обойтись даже одними десятичными рациональными числами, выражающимися конечной десятичной дробью. Так как практические измерения всегда приближенны, то при записи результата реального измерения ограничиваются тем или иным числом десятичных знаков после запятой.
Но в математике отвлекаются от ограниченных возможностей практических измерений. Математики хотят, например, иметь право говорить о числе 1/2, которое точно выражает длину диагонали квадрата, сторона которого имеет длину единица. Мы увидим вскоре, что при таком подходе к делу рациональных чисел недостаточно. При точной математической постановке задачи измерения величин она приводит к более обширному множеству действительных чисел, в котором множество рациональных чисел содержится как подмножество.
Вы знакомы с величинами различных родов. Один род величин образует, например, площади, другой — объемы, третий — массы, четвертый — электрические заряды и т. д. Величины одного и того же рода можно складывать и сравнивать между собой:
55 см + 45 см =1 м, 999 г < 1 кг, —4° < + 3°
и т. п. Говорить о сложении и сравнении величин разных родов не имеет смысла.
Выше названы различные роды скалярных величин1. Характеристическим свойством скалярных величин является то, что их можно изображать направленными отрезками одного из двух противоположных направлений — положительного и отрицательного. Поэтому далее мы будем говорить только об измерении направленных отрезков на прямой. Измеряемые отрезки будем откладывать на прямой от какой-либо определенной начальной точки О. Тогда задача измерения отрезка окажется совпадающей с задачей нахождения абсциссы его конца. Например, на рисунке 15, где отрезок ОЕ принят за единицу измерения, абсцисса точки А равна 2,3, а абсцисса точки В равна — 1,4. В соответствии с этим и алгебраические длины отрезков ОА и ОВ равны:
ОА = 2,3 и ОВ = — 1,4.
-7.4 -1	12 2,3
Рис. 15
§ 24. РАЦИОНАЛЬНЫЕ ЧИСЛА И ИХ ИЗОБРАЖЕНИЕ ТОЧКАМИ ПРЯМОЙ
В восьмилетней школе вы познакомились достаточно обстоятельно с рациональными числами. Напомним, что каждое рациональное число может быть записано в виде дроби
т
Г = —, и
где числитель т является целым числом, а знаменатель и — натуральным числом. Одно и то же число может быть записано в виде такой дроби многими способами:
30— . А —	=
7 — 14	70 ”	’ 7 — 2 ~ 10	’
1 Кроме скалярных величин, существуют еще векторные, но ими сейчас мы заниматься не будем.
— 1 = —2 = —125 8	16 — 1000
— 3 __ —6 __ —9 _ 1 ~ 2 “ 3
Д
Н--------1-------------И
0	Е
Рис. 16
Но среди дробей, выражающих данное рациональное число г, всегда имеется ровно одна несократимая. В приведенных выше примерах мы поместили ее на первом месте. Для целых чисел — это дробь со знаменателем единица:
0 = —,1= —,2 = -^-,— 1 = —, — 17 = —. 111 1 1
Способ изображения рациональных чисел точками прямой вам тоже хорошо известен. На прямой выбираются точки О и Е, которые будут изображать числа 0 и 1. Направление от О к Е (рис. 16) считается положительным, а длина отрезка ОЕ принимается за единицу длины. Точка X, изображающая число т х — —, п
получается так: отрезок ОЕ делится на п равных частей и полученный в результате деления отрезок откладывается т раз от точки О вправо, если т положительно, и влево, если т отрицательно.
Описанный выше способ изображения чисел точками прямой дает основание к тому, чтобы называть прямую с отмеченными на ней точками ОиЕчисловой прямой. Число х называется абсциссой (или координатой) изображающей его точки. Точки числовой прямой, имеющие рациональную абсциссу, называются рациональными точками числовой прямой.
Два различных рациональных числа х* и х" изображаются различными точками числовой прямой X' и X": расстояние между этими точками равно | х"— х'|, т. е. при не совпадающих числах х' и х" положительно. Поэтому по рациональной точке X можно без недоразумений найти ее абсциссу х. Иначе говоря, отображение х —> X множества рациональных чисел на множество рациональных точек числовой прямой взаимно однозначно. Ему соответствует обратное отображение
Х->х множества рациональных точек на множество рациональных чисел.
§ 25. НА ЧИСЛОВОЙ ПРЯМОЙ СУЩЕСТВУЮТ ТОЧКИ, НЕ ИМЕЮЩИЕ РАЦИОНАЛЬНОЙ АБСЦИССЫ
Построим на отрезке ОЕ квадрат и его диагональ отложим от точки О вдоль прямой ОЕ в положительном направлении (рис. 17). Вы знаете, что длина полученного отрезка ОХ равна «числу» 1^2,
которое и должно считаться абсциссой точки X. Знания ваши, однако, в этом пункте несовершенны, так как в восьмилетней школе отчетливые представления даются только о рациональных числах, а мы сейчас увидим, что не существует рационального числа ]/2.
Теорема 1. Не существует рационального числа, квадрат которого равен двум, иными словами, квадратное уравнение х2 = 2
не имеет решения в множестве рациональных чисел.
Доказательство. Предположим, что теорема неверна. Тогда существует такое положительное рациональное число г, представленное несократимой дробью —, что п
2,
\ п /
Отсюда следует, что т2 = 2п2 и, следовательно, число т2 является четным. Но тогда и число т является четным (в противном случае т = 2k + 1 и т2 = 4 k2 + 4k + 1, а последнее число не является четным). Но если т — число четное, то т = 2k и, следовательно, 4k2 = 2п2, поэтому
и2 = 2k2,
число п2, а значит, и п является четным числом. Таким образом, наше допущение привело нас к выводу, что оба числа — и т и п — четные. Но последнее противоречит предположенной несократимости дроби —. п
Верно и более общее предложение:
Теорема 2. Если натуральное число не является квадратом натурального же числа, то оно не может быть и квадратом рационального числа.
Поэтому не существует рациональных чисел
/3, у5, /7, ...
Существование отрезков, длина которых не выражается рациональным числом, было известно уже древнегреческим математикам. Они сделали из него тот вывод, что существуют отрезки, длина которых не выражается никаким числом. Позднее математики стали на другую точку зрения и пришли к такому обобщению понятия числа, при котором длина каждого отрезка выражается числом. С этим обобщением понятия числа нам и предстоит познакомиться.
Упражнения
131*. Пользуясь тем, что каждое натуральное число единственным образом разлагается на простые множители, докажите теорему 2.
Замечание. Приведенное выше доказательство теоремы 1 не опирается на предложение о единственности разложения на простые множители, которое в школьном курсе вообще не доказывается.
132*. Докажите, что не существует рациональных чисел /I V?-
§ 26. ИЗОБРАЖЕНИЕ РАЦИОНАЛЬНЫХ ЧИСЕЛ БЕСКОНЕЧНЫМИ ДЕСЯТИЧНЫМИ ДРОБЯМИ
С обобщением понятия числа, отвечающим поставленным в конце предыдущего параграфа задачам, мы познакомимся в следующем параграфе. Сейчас же в порядке подготовки к этому шагу продолжим изучение представления рациональных чисел при помощи бесконечных десятичных дробей, начатое в § 22.
В восьмом классе вы познакомились с понятием целой части числа а и ее обозначением [а]. Каждое рациональное число а представляется в виде суммы своей целой части и своей дробной части:
а = [а] т а' = а + а'.
Дробная часть числа а' удовлетворяет неравенствам
О < а'< 1.
Если а' = —, то, деля по обычным правилам т на п, получим п
представление а' в виде десятичной дроби
О, а1а2а3...
конечной или бесконечной. Для самого числа а получим представление:
а = a,aia2a3...	(1)
В случае конечной десятичной дроби припишем справа бесконечную последовательность, состоящую сплошь из нулей:
2Д = 2,3000 ...»
_ 1,7 = 2,3 = 2,3000 ....
4 = 4,0000 ....
0 = 0,0000 ... .
Таким образом мы получим представление любого рационального числаав виде бесконечной десятичной дроби типа (1). Как уже объяснялось в § 22, пользуясь понятием суммы бесконечного ряда, можно записать равенство (1) в виде
а = а .г	' ...	£«_ д-....
10	10- Т 10* ~
Например,
1,333... =-! + -+ —+ ... ,
3	10 Ю2
2,3 = 2,300 ... = 2 + - + — + — + ... ,
10	102	10’
4 = 4,000... = 4 + - + — + — + ... .
10	102	103
Будем называть бесконечную десятичную дробь периодической, если, начиная с некоторого места, знаки в ней периодически повторяются, т. е. после некоторой начальной части a, aia2...am бесконечно повторяется одна и та же конечная последовательность знаков (bib2....bn):
a,ala2...amblb2...bnblb2...bnblb2...bn...	(3)
Бесконечную периодическую дробь условно обозначают так:
а, ala2...am(bib2...bn).
Например,
- = 0,3666... = 0,3(6)
30 (0,3 и 6 в периоде).
Теорема 1. Каждое рациональное число представляется периодической десятичной дробью.
Чтобы понять основание для такого заключения, начнем с при-
з мера. Требуется представить в виде десятичной дроби число —.
14 Воспользуемся обычным алгоритмом деления:
3 I 14_____________
2®.	0,2142857
2
14
6
56
4
28
12
112
8
70
10
98 2
Получив второй раз остаток в две единицы некоторого десятичного 66
разряда, мы можем быть уверены, что дальнейшее течение вычислений будет простым повторением того, что мы уже проделали:
2
14
6
56
4
и т. д. Поэтому
= 0,2142857142857142857... = 0,2(142857).
В общем случае произвольного рационального числа а выделим его целую часть а и будем разлагать в бесконечную десятичную дробь дробную часть , т
а =—. Так как т < п, при выполнении деления сносить в остаток цифры
делимого не придется. Поэтому остатки могут быть равны только k единицам соответствующего десятичного разряда, где /г=0, 1, 2, ... , п—1 Так как име* ется лишь п возможных значений k, то не позднее чем через п + 1 шагов алгоритма деления повторится одно и то же значение k. А это и значит, что алгоритм деления приведет к периодической десятичной дроби ,
Заметьте, что наша теорема применима и к целым числам, и к числам, представимым конечной десятичной дробью. Их представление бесконечной десятичной дробью будет иметь «нуль в периоде»:	.
4 = 4,(0); - = 0,125 (0).
Верна и обратная	8
Теорема 2. Каждая периодическая десятичная дробь представляет рациональное число.
До общего доказательства рассмотрим пример:
а = 2,7 (31) =	2 + —	+ f—	+ —+ —Н-	=
'	10	\102	10?)	\104	106 /
=2+ -	+ (—	+ ± Wi	_L	4- Д_	+ ... ")	=
10	\102	1 о3 / \	102	104	10е I
=2 । 2. । 31 . 129
“ + 10 103 * 99 ’
После этого примера легко понять и общее доказательство. Любая периодическая десятичная дробь пишется в виде а = а, сца^а^ ...	... дл), где
tn—длина «предпериода», а и — длина периода. Вычислим ее:
।	।	। а,п । ( Ь* ।	1	\ ।
а ““ а + \ю	+	"г* 10™	) \10™+1 "г	"г	10™+л/ ’’’
+ (—— -р ... 4- —4-... == а 4- [— + ... 4- —4-' \10™+n+1 '	' кум+2/z / '	• \Ю ~ ' 10™/ ~
।  L- I I  -— 1 I   I ------------- I	=3
' \1(УП+1 ~	~ куя+л ]\ ' 10" ~ 102/г ~ I
__  /. atn \ . /	. bn \	1
~ a + \10 +	"Г 10'” )	\10m+1	” + 10m+n/	1
1—io7.
Получилось рациональное число.
В силу теоремы 2 множество всех периодических десятичных дробей отображается на множество всех рациональных чисел. Полученное соответствие, однако, не взаимно однозначно. Легко подсчитать, например, что
1,2(9) = 1,299999999 ... = 1,2 + 0,09 fl + - + — + — + ... = '	\	10	102	103-	/
= 1,2 + 0,09 = 1,2 + 0,1 = 1,300000... = 1,3(0).
Вообще бесконечная десятичная дробь, в которой все знаки, начиная с некоторого, девятки, равна бесконечной десятичной дроби, у которой, начиная с этого места, все десятичные знаки нули (а предшествующий знак увеличен на единицу по сравнению с исходной дробью).
Поэтому разумно исключить из рассмотрения бесконечные десятичные дроби, в которых все знаки, начиная с некоторого, девятки. В связи с этим будем называть бесконечную десятичную дробь нормальной, если она не заканчивается бесконечной последовательностью расположенных без пропусков девяток.
Нормальные периодические десятичные дроби находятся во взаимно однозначном соответствии с рациональными числами.
Чтобы убедиться в этом, надо лишь показать, что две различные нормальные десятичные дроби не могут представлять одно и то же число. Покажем принцип общего рассуждения, которое приводит к этому выводу на примере. Дроби
а = 2,345079999998... и
Р = 2,345080000000...,
как бы ни продолжался далее ряд их десятичных знаков, отличаются не менее чем на 0,000000000001, так как а < 2,345079999998, Р > 2,34508.
Упражнения
133. Запишите в виде обыкновенной дроби: а) 0,9 (285714); б) 0, (04109589).
§ 27. СООТВЕТСТВИЕ МЕЖДУ ТОЧКАМИ ЧИСЛОВОЙ ПРЯМОЙ И НОРМАЛЬНЫМИ БЕСКОНЕЧНЫМИ ДЕСЯТИЧНЫМИ ДРОБЯМИ
Мы знаем, что множество рациональных точек числовой прямой взаимно однозначно отображается на множество рациональных чисел. В предыдущем параграфе мы убедились в том, что рациональные числа находятся во взаимно однозначном соответствии с периодическими нормальными десятичными дробями. Если точке X соответствует рациональное число х, а рациональному числу х — периодическая десятичная дробь £ (|—греческая буква «кем»), т. е.
X -> х -> g,
то можно рассмотреть непосредственно соответствие
Х-+1,
которое тоже будет взаимно однозначным: множество рациональных точек числовой прямой мы поставили во взаимно однозначное соответствие с множеством нормальных периодических десятичных дробей.
Естественно возникает вопрос о том, нельзя ли и остальным, нерациональным, или, как их называют, иррациональным, точкам числовой прямой поставить в соответствие бесконечные десятичные дроби, но уже не периодические?
Вопрос этот для вас уже не совсем нов. Вы уже вычисляли, например, десятичные приближения «по недостатку» к У2:
st = 1,4,
s2 = 1,41, «з = 1,414, s4 = 1,4142,
Если выписать их десятичные знаки в одну строку, то получится бесконечная десятичная дробь
1,41421356...
На рисунке 18 показано примерное изображение этого числа на числовой прямой.
О +
V2
Рис. 18
Легко понять, как получается бесконечная десятичная дробь и в общем случае произвольной точки X (рациональной или ирра
циональной). Целая часть этой дроби а — это наибольшее целое число, для которого точка с абсциссой а лежит не правее точки X. Первый десятичный знак а{ — наибольшее целое число, для которого точка с абсциссой а, а{ лежит не правее точки X и т. д.
Здесь мы имеем дело с определением по индукции. Если уже определены первые п десятичных знаков а2, ..., ап, то п + 1-й знак an_hi определяется как наибольшее целое число, для которого точка с абсциссой
а, а^.^а^ лежит не правее точки X. Напомним, что десятичные знаки всегда заключены в пределах
О < ап < 9.
Можно показать, что полученная бесконечная десятичная дробь будет нормальной.
Проведем доказательство на примере. Допустим, что точке X, вопреки нашему утверждению, соответствует бесконечная десятичная дробь 1,414999... Рассмотрим точку X' с абсциссой 1,415. Ясно, что точка X должна лежать левее точки X', так как иначе десятичная дробь £ не могла бы начинаться знаками 1,414. Но в случае, если точка X лежит левее точки X', можно найти такое и, что отрезок длины ~ будет короче отрезка XX' (это следствие принимаемой в геометрии аксиомы Архимеда). Отложив влево от точки X отрезок длины получим точку X с абсциссой
1,41499...9	А	(*)
(п десятичных знаков после запятой). .Эта точка лежит правее точки X, и, значит, дробь I не может начинаться знаками (*). Полученное противоречие доказывает наше утверждение.
Таким образом, мы поставили в соответствие каждой точке X числовой прямой нормальную бесконечную десятичную дробь. Установленное соответствие является взаимно однозначным соответствием между множеством всех точек числовой прямой и множеством всех нормальных бесконечных десятичных дробей.
Чтобы убедиться в этом, надо:
а)	установить, что для каждой нормальной бесконечной десятичной дроби g найдется точка числовой прямой X, которой соответствует именно эта нормальная бесконечная десятичная дробь
ау а^а2*** ап ...;
б)	показать, что двум несовпадающим точкам числовой прямой Xi и Х2 не может соответствовать одна и та же бесконечная десятичная дробь.
Доказательство утверждения а) опирается на такое принимаемое в геометрии свойство расположения точек на прямой*: если каждая точка Ап (п > 1) последовательности точек прямой
•••> Ап> •••
лежит не левее предшествующей точки Ап^ и все точки Ап лежат не правее некоторой точки В (рис. 18а), то среди точек, которые лежат не левее любой из точек Лл, имеется самая левая точка X.
А1	А2
Н----------Н-
А. А.	X В
н-------4-----4--1 I Hi|
Рис. 18а
Если взять за точки Ап точки с абсциссами
а, ага2 ... ап, то легко видеть, что точке X соответствует заданная бесконечная десятичная дробь g.
Доказательство утверждения б) основано на уже упоминавшемся другом свойстве прямой: для любого отрезка существует такое л, что отрезок длины — короче заданного отрезка. В соответствии с этим предложением геометрии для двух различных точек Хг и Х2 существует такое л, что отрезок длины — короче отрезка ХхХ2. Если бы точкам Хх и Х2 соответствовала одна и та же бесконечная десятичная дробь
=3 Cl^Q'2 ••• &П •••>
то обе они должны были бы лежать на отрезке АА', абсциссы концов которого равны
а = а,	0 = а, а^... ап +
а это противоречило бы допущению, что отрезок ХхХ2 больше отрезка длины —.
10"
§ 28. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
В установленном соответствии
между точками числовой прямой и нормальными бесконечными десятичными дробями рациональным точкам соответствуют периодические десятичные дроби, которые мы считаем одним из видов записи хорошо известных нам рациональных чисел. Остальным, иррациональным точкам соответствуют непериодические десятичные дроби. Становится понятным, что нам не хватает чисел, которые записывались бы непериодическими
* Это свойство прямой либо принимают в виде аксиомы, либо выводят из какого-либо другого варианта «аксиомы непрерывности».
нормальными бесконечными десятичными дробями. Правда, вы уже имели дело с такого рода записью
У2= 1,414213...
и других корней из рациональных чисел, но лишь в несистематическом порядке. Если считать, что, строго говоря, мы пока знаем и признаем только рациональные числа, то следовало бы сказать, что до введения расширенного понятия «число» непериодическим бесконечным десятичным дробям никаких чисел не соответствует. Надо такие числа создать при помощи определения. Решение этой задачи очень просто.
Определение. Каждая непериодическая бесконечная десятичная дробь называется иррациональным числом. Как ранее известные рациональные, так и вновь введенные иррациональные числа называются действительными числами.
Из сказанного в предшествующих параграфах ясно, что множество R всех действительных чисел находится во взаимно однозначном соответствии с точками числовой прямой. Каждая точка числовой прямой получает теперь абсциссу в виде рационального или иррационального действительного числа.
Вместе с этим решена и задача создания такого запаса чисел, который достаточен, чтобы при заданной единице измерения поставить в соответствие каждому отрезку определенное число, выражающее его длину. Если дело идет о ненаправленных отрезках, то для выражения их длин понадобятся только положительные действительные числа (формальное их определение в следующем параграфе), а для выражения алгебраических длин направленных отрезков на прямой будут употребляться всевозможные действительные числа, как положительные, так и отрицательные, если не избегать и «нулевого» отрезка с совпадающими концами, то и число нуль.
§ 29. СРАВНЕНИЕ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ
При сравнении действительных чисел будем исходить из геометрических представлений: число а меньше числа 0, если соответствующая числу а точка А на числовой прямой лежит левее точки В, соответствующей числу р. Но легко перевести это геометрическое определение на арифметический язык: выразить через свойства соответствующих бесконечных десятичных дробей
а = а, а{а2а3... и
₽ = b, bib2b3...
Определение. Р > а, если:
1) целая часть р больше целой части а, т. е. b > а,
2) если целые части р и а совпадают, а первый по порядку десятичный знак Ьп, отличный от соответствующего десятичного знака ап, больше этого знака ап:
а = а, а{а2...ап^1 ап
Р = ь, b,b2... Ьп-, ьп ....
ап.
Из принятых нами определений вытекает, что всякое действительное число, у которого целая часть не отрицательна, не меньше числа нуль. Если такое число не равно нулю, то его естественно назвать положительным. Если целая часть действительного числа отрицательна, то это число меньше нуля и поэтому его естественно назвать отрицательным.
Упражнения
134.	Сравнить следующие пары действительных чисел:
а)	4,53921...	и	4,53935...;
б)	1,23754...	и	0,12643...;
в)	0,4689...	и	0,4698....
135.	Вычислить двадцать десятичных знаков У 2.
§ 30.	ДЕСЯТИЧНЫЕ ПРИБЛИЖЕНИЯ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ
Для числа У2 = 1,414213... назовем рациональные числа
С0 =
. С1 = 1,4, с2 = 1,41, с3 = 1,414, с4 = 1,4142,
соответственно, нулевым, первым, вторым и т. д. десятичным приближением по недостатку, а числа
со = с0 + 1 = 2,
cj = с, + 0,1 = 1,5, с' = с2 + 0,01 = 1,42, с3 = с3 + 0,001 = 1,415, с' = с. + 0,0001 = 1,4143, 4	4	1	7	11
соответственно, нулевым, первым, вторым и т. д. десятичным приближением по избытку. В общей форме для любого действительного числа
а = a, а,а2а3... =а + — +
>12 3	10	Ц}2 ю3
число
 Ctl . CL. . tZq 	। Ои
cn = а, а<а. ...an = a + — H—- 4—- + ... + —
"	12 n 10	10a	10s	10"
является n-м десятичным приближением по недостатку, а число
с = с + JL = а _}- fl + 31. 4.... 4. f«±2 " ion ю ю2	ion
n-м десятичным приближением по избытку.
Ясно, что для любого числа а и любого и = 1, 2, 3, ... выполни ются неравенства
Упражнения
136.	Найти пять первых десятичных приближений по недостатку и по избытку для следующих действительных чисел:
х 3	1 ч 11 ч 11 ч 5	. 1/Л-х
а) 77; б) в) г) д) е) ]/ 3.
137.	Каким должно быть действительное число а, рациональным или иррациональным, если, начиная с некоторого, все его десятичные приближения по недостатку совпадают.
138.	Можно ли утверждать, что число иррационально, если все его приближения по недостатку различны?
§ 31. ПОНЯТИЕ ОБ АРИФМЕТИЧЕСКИХ ОПЕРАЦИЯХ В МНОЖЕСТВЕ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ
Пусть аир —два действительных числа, сп и с'п(п = 0, 1, 2, 3,...) —десятичные приближения числа а соответственное недостатком и избытком:
сп < а < с'п (п = 0, 1, 2, ...),
a dn и сГп (п — 0, 1, 2, ...) — десятичные приближения числа р. Суммой а + р действительных чисел аир называется действительное число у, такое, что
cn + dn<y<cn + dn (п = О, 1,2,...).	(1)
Такое действительное число существует и неравенствами (1), оно определяется единственным образом. Доказывать существование и единственность такого числа мы не будем. Проиллюстрируем на примере способ получения десятичных знаков этого числа.
Пусть а = 2,521522... и р = 4,680808...
св	2,	Cq	3,	dg	4, Ci =	2,5,	с\	=	2,6;	di	=	4,6, с2 =	2,52,	с'	=	2,53;	d2	=	4,68, с3 =	2,521,	с'3	=	2,522;	d3	=	4,680, с4 = 2,5215, с; = 2,5216;	= 4,6808, 2 + 4 -<а + р<3 + 5, т. е. 6 < а + Р < 2,5 + 4,6 < а + р < 2,6 + 4,7, т. е. 7,1 <	d0 = 5; d\ = 4,7; d2 = 4,69; d3 = 4,681; d4 = 4,6809. : 8.	(2) : а + P < 7,3. (3)
Следовательно, целая часть числа а + р равна 7. Из неравенств 2,52 + 4,68 < а + р < 2,53 + 4,69, т. е. 7,20 < а + Р < 7,22, следует, что первый десятичный знак числа а + р равен 2. Далее, 2,521 + 4,680 < а + р < 2,522 + 4,681, т. е. 7,201 < а + р< < 7,203.
Следовательно, второй десятичный знак числа а + р равен 0. Та-
ким путем определяются и последующие десятичные знаки числа а + р.
Произведение двух действительных чисел определяется аналогично. Если числа аир положительны, то их произведением называется действительное число у, которое не меньше всех произведений сп dn соответствующих десятичных приближений сп и dn чисел а и р с недостатком, но меньше всех произведений сп и d'n соответствующих десятичных приближений сп и dn с избытком чисел аир:
cndn < Y < Cndn (п = 0, 1, 2,...).
Можно доказать, что если аир — рациональные числа, то введенные операции сложения и умножения действительных чисел приводят к тем же результатам, что и операции сложения и умножения, введенные ранее, для рациональных чисел.
Можно также доказать, что операции сложения и умножения действительных чисел обладают известными свойствами этих операций, установленных для рациональных чисел, а именно:
1)	а + р = р + а — коммутативный закон сложения,
2)	а + (Р + ?) = (а + Р) + у — сочетательный закон сложения,
3)	ар = Ра — коммутативный закон умножения,
4)	« (Ру) = (ар)у — сочетательный закон умножения,
5)	(а + Р)у = ау + Ру — распределительный закон умножения относительно сложения.
Сохраняются для действительных чисел и свойства рациональных чисел, связывающие арифметические операции с отношением неравенства:
1) если b < с, то а + b < а + с;
2) если а > 0 и b < с, то ab < ас и т. п.
Строго говоря, только теперь, когда мы располагаем определением произведения действительных чисел и можем применять к
действительным числам основные свойства неравенств, можно доказать, что число
а = 1,41421356...,
способ образования которого был объяснен в § 27, удовлетворяет уравнению
х2 = 2, т. е. в самом деле заслуживает названия У2. Ограничимся тем, что вычислим
С2 = 12 = 4, С2 = (1,4)2 в 1)96> С2 = (i(4i)2 = 1)9881> cj = (1,414)2 = 1,999396, с\ = (1,4142)2 = 1,99996164, Неравенствам
= 22 = 4, с'2 = (1,5)2 = 2,25, с'2 = (1,42)2 = 2,0164, с? = (1,415)2 = 2,002125, с;2 = (1,4143)2 = 2,00024449.
,8
Сп <Х < Сп
при любом п удовлетворяет одно единственное число х == 2, т. е. число х в самом деле заслуживает названия У"2.
На этом мы заканчиваем, неизбежно неполное в общеобразовательной средней школе, знакомство с построением системы действительных чисел. Они имеют большое значение, так как при ограничении одними рациональными числами математика во многих отношениях была бы беднее содержанием (не существовало бы «точного» корня из двух, некоторые последовательности, которые, казалось бы, должны были иметь, в силу убедительных наглядных соображений, предел, такого предела не имели бы, и пришлось бы считать, что не каждая точка прямой имеет абсциссу и т. д.).
Но с чисто практической точки зрения изменение не столь велико. На практике можно было бы обойтись даже не всеми рациональными числами, а числами, которые представимы конечными десятичными дробями. Ведь каждое действительное число может быть заменено таким числом с ошибкой, меньшей чем 10~л, где п — достаточно большое натуральное число.
Отметим еще в связи с этим интересный факт: множество всех рациональных точек всюду плотно на числовой прямой. Точный смысл этого утверждения таков: на любом отрезке числовой прямой лежит хотя бы одна рациональная точка (на самом деле их даже бесконечно много). Доказательства см. в § 32. Пока же, несколько отвлекаясь от реальных возможностей, скажем: если в каждой рациональной точке прямой зажечь по фонарику, то на прямой не окажется никакого темного промежутка, вся прямая будет светиться. Тем не менее на ней будет спрятано очень много иррациональных точек. В некотором смысле их даже «больше», чем рациональных.
Поясним смысл последнего утверждения. Все рациональные числа можно расположить в одну последовательность:
гъ r2, г3,	..., гл, ...,
. Р
выписывая несократимые дроби — в порядке возрастания суммы абсолютных Я
величин числителя и знаменателя, а при одинаковом знаменателе этой суммы в порядке возрастания числителя:
0—11—2—1	1	2—3—11	3
Г 1 ’ Г 1 ’ 2 ’ 2 ’ 1 ’ 1 ’ 3 * 3 ’ 1 ’
—4 —_3 —2 —11134-5-1_[5 1 ’ 2 ’ 3 ’ 4 ’ 4’ 3* 2* 1 ’ 1 ’ 5’ Р Т””
Полученное взаимно однозначное соответствие между множеством Q всех рациональных чисел и множеством N натуральных чисел показывает, что в известном смысле рациональных чисел «столько же», сколько и натуральных чисел. Немецкий математик Кантор в 1874 году доказал, что «занумеровать» аналогичным образом множество R всех действительных чисел нельзя: какова бы ни была последовательность
xlt x2f ..., хп,.., действительных чисел, найдется действительное число х, не принадлежащее этой последовательности.
Подробнее о сейчас сказанном можно узнать в популярных книжках, посвященных теории бесконечных множеств. Теория бесконечных множеств стала складываться в самостоятельную науку и привлекла всеобщий интерес математиков в конце XIX века, когда в ней появились интересные и неожиданные результаты вроде высказанных сейчас теорем о возможности занумеровать натуральными числами множество рациональных чисел и невозможности такой нумерации для множества действительных чисел.
§ 32. ПРЕДЕЛ ПОСЛЕДОВАТЕЛЬНОСТИ ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ
В § 32—36 мы продолжаем изучение пределов последовательностей, начатое в § 16 — 21. Определение предела остается тем же. Но теперь и члены последовательности, и предел последовательности считаются произвольными действительными числами. В такой новой обстановке сохраняют силу все общие теоремы, установленные в §16— 21, но оказываются справедливыми и некоторые новые, которые при ограничении одними рациональными числами были бы просто неверны. С важным примером такого рода вы встретитесь в следующем параграфе.
Но мы прежде всего установим, что каждое действительное число является пределом последовательности своих десятичных приближений по недостатку*, если а = а, а{ а2... ап..., то
а = lim (а, а{а2 ...ап) = limcrt. П -> со	п -* оо
Для доказательства равенства (1), заметив, что lim (—) = 0, остается для произвольного е > 0 выбрать п0 с условием <е и заметить, что
1	,	1 1
сс — с. < — <------- при п > Пп.
1	л1 10я 10я»	0
Отметим еще важное следствие доказанной леммы: между любыми двумя действительными числами а < 0 лежит хотя бы одно рациональное число, представимое конечной десятичной дробью
1 = X, Xt х2... хп.
В самом деле, положив 0 — а = 8, найдем такое п, что
— <е. Если 10"
и = а, ••• О'п • ••,
сп = a, ata2 ... ап,
с'п = МЛ -
ТО
а < с и с < а Н—- < а + е = 6.
Следовательно, если положить £ = сп, то
а < I < ₽•
Доказанное следствие коротко формулируют так: множество рациональных (и даже множество «десятично-рациональных») чисел всюду плотно на множестве всех действительных чисел.
Упражнения
139.	Докажите, что для любого действительного числа а и его десятичных приближений по избытку с'(и = 0,1,2.......)
lim сп = а.
§ 33.	СУЩЕСТВОВАНИЕ ПРЕДЕЛА У МОНОТОННОЙ ОГРАНИЧЕННОЙ ПОСЛЕДОВАТЕЛЬНОСТИ
Рассмотрим последовательность (сп).
Ci = 0,1,
с2 = 0,1001,
с3 = 0,100100001,
сп = 10-1 + Ю-2’ + Ю-3’ + ... + 10—’’ + ...
В силу сказанного в предыдущем параграфе ее пределом является действительное число
а = 0,1001000010000001000...
(единицы на местах с номерами, равными полным квадратам, нули— на остальных местах). Так как наша бесконечная десятичная дробь непериодична, то число а иррационально. До введения иррациональных чисел мы должны были бы сказать, что последовательность (сп) не имеет предела.
С построением системы действительных чисел оказывается возможным доказать такую важную теорему:
Теорема Вейерштрасса. 1) Если последователь-ноешь (хп) не убывает и ограничена сверху, то она имеет предел. 2) Если последовательность (хп) не возрастает и ограничена снизу, то она имеет предел.
Эту теорему мы примем без доказательства. В § 27 говорилось, что вполне аналогичное утверждение относительно последовательностей точек на прямой в геометрии принимают за аксиому (см. примечание на стр. 71). В теории действительных чисел, построенной на принятых нами определениях, теорему Вейерштрасса можно доказать, но доказательство несколько громоздко.
Приведенный выше пример последовательности (1) показывает, что в множестве Q одних рациональных чисел теорема Вейерштрасса не имела бы места.
Пример. Пусть а > 0, у4 > 0 и последовательность (уп) задана рекуррентно следующим образом:
yn+1 = -(yn + -J.
Докажем, что эта последовательность сходится и
Птул =]/ а. П, °°
Так как У1 > 0, то все члены данной последовательности положительны. Следовательно, она ограничена снизу:
уп > 0, п ~ 1, 2, ...
Для того чтобы можно было применить теорему Вейерштрасса, достаточно доказать, что эта последовательность является невозрастающей. Сначала мы докажем, что
yn > Va при п > 1.
Если п > 1, то
(Докажите, что для любого х > 0 выполняется х + —	2.) Но
X
тогда при и > 1
Следовательно,
Уп+i <У« («> !)•
По теореме Вейерштрасса, существует предел, который обозначим буквой с, т. е. положим
limy„ = c.
П -* оо
Тогда и limyn+1=c, так как последовательность (Уп-н) отличается
И*- оо
от последовательности (уп) только первым членом.
Так как
поэтому
с2 = а.
Таким образом, рекуррентная формула
Ул+1 = (Уп + 7)
определяет алгоритм вычисления У а по избытку.
Упражнения
140.	Докажите, что последовательность (хп), связанная с последовательностью (уп) рекуррентными соотношениями:
хп= у, ул+1 = £Ц^; «>о, У!>о,
Уп	z
определяет алгоритм вычисления У а по недостатку (х2п < а).
141.	Пусть а — 2, у1 = I. Найти xlt х2, х3, xit х3 и уь у2, уз, У4. Уз-
§ 34. БЕСКОНЕЧНО МАЛЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ
Определение. Последовательность (ап) называется бесконечно малой последовательностью или, короче, бесконечно малой, если
lim ап = 0.
П -*• 09
Иными словами, последовательность (ап) бесконечно мала, если для любого е > 0 найдется такой номер N, что при п> N
I ап — О I = I <*n I < е.
Примеры. 1) Последовательность (ап), заданная своим общим членом
1 аП="’
является бесконечно малой, так как Иш — = 0 (см. § 16).
п -> оо Л
2) Так как lim qn= 0 при | q\ < 1, то последовательность (ад) — = (9Л) бесконечно мала.
Замечание. Термин «бесконечно малая» относится не к числу, а к последовательности и означает, что члены этой последовательности «становятся» меньше по абсолютной величине любого положительного числа е, начиная с некоторого номера.
Определение. Суммой двух последовательностей (хп) и (уп) называется последовательность (zn), общий член которой zn = хп + ул; и = 1, 2, ..., то есть
Zi = %i + У1,‘ z2 = %2 + Уг5 гз — Хз + Уз’, ••• • Аналогично определяются и другие арифметические операции над последовательностями:
(хп) (y,n) = (хп Уп), (Хп) • (Уд) ~ (-^пУп),
при условии: ул ¥= 0; п = 1, 2, ....
Теорема 1. Алгебраическая сумма двух бесконечно малых является бесконечно малой.
Доказательство. Пусть последовательности (ап) и (рп)— две бесконечно малые. Это означает, согласно определению, что для любого е > 0 найдется номер N такой, что при п> N будут одновременно выполняться два неравенства:
Kl<f; iPJ<|,
так как все члены бесконечно малой последовательности, начиная с некоторого номера, меньше любого положительного числа, в част-8
ности и числа—.
2
Но тогда при этих и:
I ап ± ₽„ | < | ап | + | ₽„ | < | + | = 8.
Это и означает, что последовательность (ап ± Рл) является бесконечно малой.
Методом математической индукции можно доказать, что алгебраическая сумма конечного числа бесконечно малых является бесконечно малой.
Теорема 2. Произведение ограниченной последовательности на бесконечно малую является бесконечно малой.
Доказательство. Пусть последовательность (хп) ограничена, а последовательность (ап) бесконечно мала, тогда существует число М > 0 такое, что для всех п = 1, 2, ...
|хп|<М.
Если е > 0 — произвольное число, то найдется номер N такой, что
при всех и > АГ. Но тогда при этих п
1«Л1 = WW<~ м = е.
А это и означает, что последовательность (апхп) является бесконечно малой.
Следствие. Произведение двух бесконечно малых является бесконечно малой.
В самом деле, так как бесконечно малая ограничена (всякая сходящаяся последовательность ограничена — см. § 16), то из теоремы 2 получается нужное следствие.
Теорема 3. (О связи понятий бесконечно малой и предела.)
1) Если последовательность (хп) сходится и limxn = а, то эта
П -> оо
последовательность может быть представлена в виде суммы двух последовательностей — постоянной и бесконечно малой:
хп = а+ ап- п = 1, 2,..., где lim ал = 0.
П -* ОО
2) Если последовательность (хп) является суммой постоянной последовательности у„ = а и бесконечно малой (а.), т. е. если хп = а + ап; п = 1,2...........................
то lim хп = а.
п -> оо
Доказательство. 1) Если lim хп = а, то для любого п ОО е > 0
| хп — а| < е при п > N.
Но это означает, что последовательность (хп — а) является бесконечно малой. Если ее обозначить через (ап), то хп — а + ап.
2) Если хп — а + ап при п = 1, 2, ..., где (ап) — бесконечно малая, то для любого е > 0 |ап | < е при п > N и, следовательно,
| хп — а | = | ct„ | < е при п > N.
А это и означает, что lim хп — а.
П -> 09
Упражнения
142.	Доказать, что последовательность а„ = —; п = 1,2,... "л2
бесконечно мала. При каких п выполняется неравенство | ап |<е, где а) 8 = 0,1; б) е = 0,01; в) 8 = 0,001.
143.	Доказать, что последовательность и является бесконечно малой.
144.	Доказать, что последовательность 3+(-if п является бесконечно малой.
145.	Докажите методом математической индукции, что сумма конечного числа бесконечно малых является бесконечно малой.
§ 35.	ТЕОРЕМЫ 0 ПРЕДЕЛАХ
Теорема 1. Предел алгебраической суммы двух последовательностей равен сумме пределов этих последовательностей, если последние существуют, т. е.
lim (х„ ± у„) = lim хп ± lim у„. п -* оо	П -* оо	п ОО
Доказательство. Пусть lim хп = a, lim уп =Ь. Уело-П -> оо	П -> оо
вимся термин «бесконечно малая» записывать так: б. м. Тогда по теореме 3 (Г) (§ 34)
хп = а + ая; п = 1, 2, ...; (ал) — б. м.; = 6 + 0„; n= 1, 2, ...; (₽„)-б. м. Сложив почленно написанные равенства, получим хп ± Уп = (.а ± Ь) + (а„ + p„); n = 1, 2, ...
Согласно теореме 1 из § 34 (ап ± р„) — б. м. Следовательно, по теореме 3 (2°) из этого же параграфа
lim (х„ ± уп) = а ± b = lim хп ± lim уп. п -> оо	п -> ОО	п оо
Теорема 2. Предел произведения двух последовательностей равен произведению их пределов, если последние существуют', lim(x„ • уп) = lim х„ limy,,. п -> оо	п -> оо п -* оо
Доказательство. Если limxn = a, limy„ = &, то, как и ранее,	'1” “	п” ~
хп = а + ап; п = 1, 2,...; (а„) — б. m.j
Уп = b + ₽га; п = 1,2,	(₽п) — б. м.
Перемножив почленно эти равенства, получим:
хпУп = ab + (а0„ + ban + an0n); n = 1, 2,...
Последовательности (а 0П), (Ь ап) и (ал рп) бесконечно малы согласно теореме 2 и следствию из нее (§ 34). Но тогда по теореме 1 из этого же параграфа их сумма также бесконечно мала. Поэтому согласно теореме 3 (2°) (§ 34)
lim (х„У„) = ab — (limx„) • (limy„). Л -* оо	П -> оо	п -* оо
Следствие. Постоянный множитель можно выносить за знак предела:
lim (схп) = с lim хп. п -* оо	п -* СО
В самом деле, по теореме 2
lim (схп) = (lim с) (lim хп) =-- с lim хп.
Аналогично, но технически более громоздко доказывается и следующая
Теорема 3. Если существуют пределы lim хп и lim уп, то п-* оо	Д 00
Игл хп
Пт =
» - ~ Уп Нт Уп
П -* оо
если только lim уп =Н= 0, т. е. предел частного двух последователь-
П-*
ностей равен частному их пределов, если оба предела существуют и предел делителя отличен от нуля.
Примеры. 1) Пусть требуется найти предел
i:m 5-П+-2.
П -> оо ЗМ 1
Так как числитель и знаменатель пределов не имеют (это неограниченные последовательности), то применить теорему о пределе частного нельзя. Разделим и числитель и знаменатель на одно и то же число п, тогда имеем (подробно):
Пт 5Л±_2 = Нт п -> со Зп - 1 П -* ОО
lim 5 + 2 lim —
__ П ОО	П -* ®° П
lim 3 — lim —
2
5+7
п
lim
п -* ОО
lim
П -* оо
_ 5+2-0 _ _5
3 — 0 ““ 3*
П -> 0© п -* оо П
2) (с меньшими подробностями).
(1-^ = 4.
\ и /
lim 4 -—- = 4 lim -—- = 4 lim
П *♦ оо И
п-* о»
И
П -> 00
3) iim	. я -> оо 7nj —- п -|- 3	2	5	/	2	5 \ 34- — ——	lim 134- — — —) = Ит » ”2 =3 n"“7--4-4	lim h— -4-~)	7 _з
4) Нт - 3~п— = п -> оо и2 + 2и —1	1.	п2 п	0 — 0	А : lim 	5	1—— = 	 = 0. а -* °о |_1_ —		1	0 — 0 ' п п2
5) lim ...УЛ2 + 2п—1 + 2 _ = (делим числитель и знаменатель п~ «. Зп + 2
на число п)
=Пт1------=1+2=1.
34.—	3
Упражнения
Найти пределы:
146. а) Нт оо			3 — и + 2п2 2 + п — 4п2 ’	б)
147.	а)	Нт п -* 00	2п —9 Зп24-л —1 ’	б)
148.	а)	Ит П -* со	6п2 4- 2п — 1 3 — 2п — 3п2 ’	б)
149.	а)	Пт п -* ОО.	(л 4-2) (п 4-5) л2 4-1	б)
150.	а)	Нт п -* оо	(л 4-1) (л 4-2) (л 4-3) л3 4- 2л — 1	б)
151.	а)	Нт П -* ОО	(л 4-7) (л 4-2) л (л 4-1)	б)
152.	а)	Нт П -* ОО	(ч + 4 + - +"-=г) \п2 п2	и2 1	;б)
lim —-2 ~ 2п +' , я - о» 3 + 4п — 2п2
Нт 2дЬ + Зд42/12
п -> оо п + 2п3 — Зи5
lim 5--2- + 1
П -* оо И3 З/I
lim 3(п + 1)(3-п)
п -> ~	4 л2 + п — 1
lim (3n + D(i-2n)
П - «о (2л 4- 3) (л — 3)'
Пт (3n-2)(l-n)(2+n>
«-.«о	2л34-л2 —1
lim d +»)(2 + Зп)(3-4п) «о (1 4- 2л)(3 + 2л)(4 + п)
153.	a)
154.	a) lim(l + l + l+... 4-Г|; б)* lim (И«2 + 3n + 1 -n, -+ oo \ 2	4 о	2П/ n, -+ oo
— Vn2 + 2n— 1).
155.	a)	+
n-.~\	3	9	27	3n~l )
6) lim (]/ n + 1 — У n ).
tl -> OO
156*. a) lim Z2”2+” + l -/3n^+2n-l , «~	У n2 — 1 4- 2n
6) lim ГЗп2 + 2п-1+4п. « - ~	/n 1 + 2n
157*. Доказать, пользуясь определением предела, что если
limxn = a, хл>0(п= 1; 2, ...), то lim ]/хя = У а. п -* оо	п -> оо
158. Докажите методом математической индукции, что предел алгебраической суммы конечного числа сходящихся последовательностей равен сумме их пределов.
159. 1) Докажите методом математической индукции, что предел произведения конечного числа сходящихся последовательностей равен произведению их пределов.
2)Докажите: если переменные хп, уп и zn связаны неравенствами хп < zn < уп для всех п и существуют равные пределы, т. е. lim хп = Пт уп = а, то существует также и предел lim zn = а.
П -» СО П -* оо	п-»оо
3)	Последовательность задана рекуррентно: — 2;	= 1 +
+ Ьхп. При каких числах b эта последовательность имеет предел?
4)	Известно, что limxn=0. Выяснить: а) могут ли все члены п -* СО
данной последовательности быть отрицательными? б) могут ли все члены данной последовательности быть больше 10-10? в) могут ли в этой последовательности быть члены, большие 1015?
5)	Отрезок АВ = а разделен на п равных частей. На каждой из этих частей построен равнобедренный треугольник с углом при основании, равным а = 45°. Найти предел периметра Рп получающейся фигуры при п -> оо.
6)	Катет а прямоугольного треугольника разделен на п равных частей, и на полученных отрезках построены вписанные прямо-
угольники. Найти предел Sn площадей образованных ступенчатых фигур. Истолковать геометрически полученный результат.
7)	Найти площадь, лежащую под параболой у = х2 и ограниченную осью абсцисс и прямой х = 2, как предел ступенчатых фигур, построенных так же, как и в предыдущем упражнении.
§ 36. ЧИСЛО л
Из курса восьмилетней школы известно, что отношение длины окружности S к ее диаметру D не зависит от этого диаметра. Это постоянное отношение длины окружности к ее диаметру и есть число пи.
л = 3,1415926...
Вы знаете, кроме того, что длина окружности S приблизительно равна периметру рп вписанного правильного и-угольни-ка с достаточно большим числом сторон п. Теперь, познакомившись с действительными числами и понятием предела, мы можем уточнить наши представления о длине окружности и числе л.
Кроме вписанных многоугольников, будем рассматривать описанные правильные многоугольники. Длину периметра описанного правильного n-угольника обозначим qn. В этом параграфе будет доказано, что для любой данной окружности последовательности рп и qn сходятся и имеют общий предел:
limpn — lim<7n = S.	(1)
П -* оо	п -* ОО
Этот общий предел естественно считать, по определению, длиной окружности1.
1 Мы оставляем здесь в стороне возможность дать общее определение длины произвольной кривой и получить определение длины окружности в качестве частного случая этого общего определения.
Из соображений подобия в геометрии устанавливают, что отношения
одинаковы для всех окружностей. Из существования и равенства пределов (1) вытекает существование и равенство пределов
lim ип = lim vn = л.	(2)
п ОО	п -* оо
Этот общий предел числовых последовательностей (ил) и (о„) и является числом пи. Ясно, что
S = л D,	(3)
т. е. число л, являющееся общим пределом числовых последовательностей («„) и (а„), действительно равно отношению длины любой окружности к ее диаметру.
К сожалению, прямое доказательство существования и совпадения пределов (1) затруднительно. Приходится сначала рассмотреть последовательности периметров вписанных и описанных правильных многоугольников, получающихся при помощи последовательного удвоения числа сторон, например пределы последовательностей
k
Рв> Р12> Ръ& •••» Р3.2 » ••• »
k
Я&> <712> ?24> •••> Я 3-2 ’	•
Будем опираться на такие две геометрические леммы.
Лемма 1. Периметр выпуклого многоугольника больше периметра любого другого содержащегося в нем выпуклого многоугольника.
Эту лемму мы будем считать известной. Вторая лемма относится к длинам сторон ап и Ьп правильного вписанного и правильного описанного л-угольников для окружности диаметра D.
Докажем лемму 2. Пусть на рисунке 19 АВ — сторона вписанного правильного n-угольника, a CD — сторона описанного правильного п-уголь-ника, касающаяся окружности в точке А. Треугольники ADE и ОАЕ имеют прямые углы при вершине Е и подобны.
Поэтому;
АЕ_ _ ОВ = уОА2 — АЕ2	,4ч
AD ОА ОА ’	1 '
Так как
АЕ = AD = ОА = В = -j, то равенство (4) можно записать в виде
___ /-« /"	(—'j2'! — = 1 [ 1 (—V
bn~ \ 2 /	\ 2 / / 2	\	/ ’
что и требовалось доказать.
Так как окружность диаметра D помещается в квадрате со стороной D
(рис. 20), то периметры рп вписанных многоугольников меньше периметра этого квадрата:
Рп < 4D-
В частности, это относится к периметрам
Рз, Рв, Рп. Pit...Ря.г*> —
правильных вписанных многоугольников, получающихся из треугольника последовательным удвоением числа сторон (рис. 21). Так как каждый из этих многоугольников получается из предыдущего заменой сторон двухзвенными ломаными, то ясно, что последовательность (5) является монотонно возрастающей. Следовательно, у нее, как ограниченной монотонно возрастающей последовательности, существует предел
Нт р3>2 == 5.	(6)
k -* 00
В силу леммы 2
Так как периметры рп ограничены, то
lim 00 Qn
и поэтому
(7)
Для последовательности отношений рп : qn с номерами п вида п =» = 3 • предел тоже равен единице.
lim Рз12 = 1.
ft- - g3 2k
Отсюда и из соотношения (6) получаем, что lim q3'2k = S.	(8)
k -* oo
Докажем теперь, что к тому же пределу 3 сходятся и полные последовательности (рл) и (qn).
1.	В силу леммы 1 при любых п и k имеем
Рп < ^3-2^ •
Считая и постоянным, a k переменным, получаем отсюда
рп < lim = S. (9) k -* оо
2.	Вполне аналогично имеем
Яп > Рз-2*>
Яп> lim р3.2А = S, и поэтому
(10)
Рис. 21
3.	Оценки выражений (9) и (10):
2
< рп < 5
показывают, что | рп — S | <5 — S
при п -* оо, т. е.
limprt = S.	(11)
П -* оо
4.	Из последнего равенства вместе с (7) получаем:
Итрл = S. п со
Для приближенного вычисления числа S Я = D пользуются известной из геометрии формулой
a2n = / 2R* - Ry 4R* - а* ,
где ап и а2п обозначают стороны вписанного n-угольника и 2/г-угольника. Запишем эту формулу в виде
(12)
Для отношений
Рп _ пап
Un D D
из равенства (12) получаем:
Зная, например, что мб = 3, получим: и12 « 3,1058.
Отношения периметров к диаметру для вписанных правильных многоугольников с числом сторон вида п = 3 • 2k вычислялись с большой точностью. Например, при п = 3 • 210 = 3072 получено, что w3072 = 3,14159252. Это уже очень хорошее приближение к числу л.
Чтобы оценить точность этого приближения, надо воспользоваться тем, что < л < vn, и формулой
которая непосредственно вытекает из леммы 2.
Упражнения
160.	Оцените разность л — w3072.
161*. При каком наименьшем k для п =» 3 • 2k будет выполняться неравенство
vn - ип < 10-1000?
162*. Вычислите иб, а12, и24, и48, и9в и покажите, опираясь на эти вычисления, что
(эта оценка была установлена еще Архимедом).
163. Покажите, что
= 4/2, и8 = 8/2 - /2, и1в = 16 К2 - /2+ /f
164*. Докажите, что
я = п ™ ~ "+2 Кг - Кг + /2+.. .4-/2:
п раз
§ 37. ИСТОРИЧЕСКИЕ ЗАМЕЧАНИЯ
Как уже говорилось, математики древней Греции числами называли только натуральные числа. Но их теория «отношений» по существу заменяла не только обращение к дробным числам, но и употребление иррациональных
чисел. Например, Архимед строго доказал, что отношение длины окружности к диаметру больше отношения 223 : 71 и меньше отношения 22: 7. Мы переводим на современный язык это его утверждение, говоря, что он дал оценку
10	n *
371<П<	7
для числа л. Но теория отношений была в древнегреческой математике развита очень далеко, включая, в частности, доказательство «несоизмеримости» некоторых геометрических величин, что на современном языке соответствует доказательству иррациональности выражающих отношение этих величин чисел.
Индийские и арабские математики, в отличие от греческих, без больших стеснений рассуждали о числах У2,	ли т. п. и производили с ними
всевозможные вычисления, не заботясь о логическом обосновании такой практики.
Европейские математики XVII—XVIII веков, усвоив разработанную древнегреческими математиками теорию отношений, более смело стали называть эти отношения числами. Но вполне отчетливая теория действительных чисел была создана лишь в 70-х годах прошлого века немецкими математиками Р. Дедекиндом, Г. Кантором и К. Вейерштрассом.
Что касается числа л, то еще в 1761 году швейцарский математик Ламберт доказал, что оно иррационально. В 1882 году немецкий математик Линдеман доказал, что число л не может быть корнем уравнения вида
Р (х) = 0,	(1)
где Р (х) — многочлен с целыми коэффициентами. Этим оно отличается, например, от иррационального числа У2, которое является корнем уравнения х2 — 2 — 0.
Числа, которые являются корнями уравнений вида (1), где Р (х) — многочлен с целыми коэффициентами, называются алгебраическими, а все остальные числа трансцендентными. Г. Кантор показал, что множество всех алгебраических чисел можно занумеровать натуральными числами, т. е. расположить в виде последовательности
#1> #2»	•••»	«Л» •••
Поэтому, в том же смысле, как это сказано в § 31 об иррациональных числах, трансцендентных чисел «больше», чем алгебраических; алгебраические числа, как и рациональные, являются в этом смысле лишь исключениями в мире действительных чисел.
ГЛАВА ПЯТАЯ
ВВЕДЕНИЕ В ОБЩИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ФУНКЦИЙ
§ 38. ПОНЯТИЕ ЧИСЛОВОЙ ФУНКЦИИ
С понятием функции, способами задания функций и с примерами функций мы встречались еще в шестом классе. Теперь после знакомства с действительными числами мы можем уточнить понятие числовой функции в том виде, в каком оно останется окончательным в пределах обязательного курса математики средней школы.
Начнем с примера. Галилей (1564—1642), бросая камни с наклонной башни в Пизе, обнаружил, что путь, пройденный телом при свободном падении, пропорционален квадрату времени падения. В курсе физики формула свободного падения тел пишется в виде
s = —.	(1)
2	' ’
где s — пройденный путь, t — время падения, отсчитываемое от момента начала падения (t = 0 Яри начале падения) до момента соприкосновения тела с землей t = ti, a g « 9,8 —--------ускорение
сек2
свободного падения тел под действием силы тяжести.
Формула (1) лишь приближенная (в ней не учтено сопротивление воздуха и то обстоятельство, что ускорение силы тяжести g слегка меняется с изменением высоты). Кроме того, формула (1) связывает по существу величины, а не числа: числовое значение ускорения силы тяжести g зависит от выбора единиц измерения.
Но отвлечемся от всех этих обстоятельств. Будем считать единицы измерения выбранными (метр для расстояний и секунду для промежутков времени), формулу (1) совершенно точной, a g точно равным 9,8 м/сек2. Для определенности будем считать, что полное время падения ti равно десяти секундам, т. е. тело брошено с высоты 490 метров. Тогда t и s можно считать числовыми переменными, точно связанными зависимостью
S — 4,9/2	(2)
0 < /	10.
Рис. 22
Исследование реального падения тела сведено к изучению математической числовой функции. Ее область определения — множество чисел t, удовлетворяющих неравенствам (3), а правило вычисления ее значений можно схематически записать так’
4,9Р
при 0 < t < 10.	(4)
Множество значений нашей функции состоит из чисел s, удовлетворяющих неравенствам 0 < s < 490.
На рисунке 22 изображен график этой функции (масштабы по осям выбраны различными).
Выбор обозначений для аргумента и значения функции безразличен. Можно было бы время падения обозначать через х, пройденный путь через у. Запись
х -> у = 4,9х2 при 0 < х < 10	(4а)
является записью той же функции, что и запись (4). Пользуясь геометрическим языком, можно сказать, что обе записи определяют одно и то же отображение сегмента [0; 10] на сегмент [0; 490]. Вообще числовая функция есть отображение некоторого множества действительных чисел Е на некоторое другое множество действительных чисел Н. Множество Е при этом называется областью определения функции, а множество Н—ее множеством значений.
Задать функцию, определенную на множестве Е, это значит указать правило (закон), которое ставит в соответствие каждому числу х из множества Е одно и только одно число у, называемое значением функции при значении аргумента х. Иногда говорят, что функция и есть сам этот закон соответствия. Это верно, если слово «закон» понимать надлежащим образом. Например, применяя правило
'	(х при х > 0,
X -> у = {
(—х при х<0
при любом х, получим тот же результат, как и действуя согласно правилу
х -> у = "Их2.
Оба правила определяют одну и ту же функцию — модуль аргумента
У = I Н
график которой дан на рисунке 41 (стр. 134). Значит, говоря о функции как о законе соответствия, мы должны понимать слово «закон» достаточно отвлеченно: два способа вычисления, которые приводят всегда к одному и тому же результату, должны считаться одним и тем же законом соответствия.
Функции можно обозначать буквами. Например, запись
обозначает, что закон вычисления значения функции f таков: надо единицу разделить на разность единицы и квадрата аргумента. Выбор буквы для обозначения аргумента при этом не существен: запись
f 1
(5а)
обозначает ту же самую функцию f. Область определения этой функции f состоит из всех действительных чисел, за исключением 1 и —1 (объясните почему).
Значение функции /, соответствующее значению аргумента х, обозначается через /(х). Вместо символа (5) можно написать
(56)
Рассмотрим несколько примеров вычисления значений этой функции:
/(0)=^=!; /(2) = ^
И3)=	= /(Зх —5) =
1 —З2 8
1 — (Зх — 5)2	— 9х2 + ЗОх—24
Замечание. Две функции, имеющие разные области определения, приходится считать различными даже в том случае, когда на общей части их области определения они принимают одинаковые значения. Например, функция, определенная правилом
4,9/2
без дополнительных ограничений, отлична от функции 4,9/2 при 0 < t < 10, определенной только на сегменте [0; 10], рассмотренной выше, в связи с падением тел. Только эта последняя функция дает правильную модель процесса падения тела с высоты 490 метров, заканчивающегося при достижении земной поверхности.
Аналогично, последовательность
и -> хп = п3
при натуральном п нельзя смешивать с функцией
X -> Xs, имеющей областью определения всю прямую. Напомним, что последовательность есть функция, определенная на множестве N натуральных чисел.
Упражнения
165.	х-^х+--. Найти /(1), /42), /Ш, х	' 2 /	\ а /
166.	Уравнение Зу = 5х — 2 определяет функции у = f (х) и х = g (у). Найти / (0), / (1), / (а2 + 1), f (х — 1), g (х), g (5).
t
167.	Задает ли уравнение 2х = Зу2 функцию х -> у, определенную а) для всех действительных значений х? б) для всех положительных значений х?
168.	Найти f (х + h), f(x-\-h)—f(x'),
h
f	f	f
а) при x x2; б) при x -> kx + b\ в) при x -> ax2 + bx + c; f
г) при X -> X3.
inn IT « f (x 4- h) — f (x)
169.	Наити ------ -—
2h
а) при f (x) = x2; б) пои / (x) = x3.
170.	Найти
h2
а) при f (x) = x2; б) при f (x) = x3.
§ 39. НОВОЕ ПОНИМАНИЕ ЧИСЛОВОЙ ПРЯМОЙ И ЧИСЛОВОЙ ПЛОСКОСТИ
В предыдущей главе мы установили, что множество всех действительных чисел находится во взаимно однозначном соответствии с множеством точек числовой прямой. Удобно непосредственно к действительным числам применить геометрическую терминологию. Например, вместо «точка с абсциссой х лежит между точками с абсциссами а и &» говорят просто «число х лежит между числами а и Ь». Множество чисел х, удовлетворяющих неравенствам
а < х < Ь, является множеством абсцисс точек интервала с концами а и Ь. Проще говорить, что само множество чисел
{х | а < х < Ь} есть интервал1.
1 Запись {х| А (х)} обозначает множество всех тех х, которые обладают свойством А.
Но тогда естественно само множество всех действительных чисел называть «прямой». Так мы и будем далее делать. Изменяя принятую ранее терминологию, условимся, что «числовая прямая» есть просто само множество действительных чисел R.
Во избежание путаницы обычную геометрическую прямую с выбранными на ней начальной точкой, положительным направлением и единицей измерения будем называть координатной прямой.
При изучении областей определения и множеств значений функций нам будут нужны некоторые простейшие подмножества числовой прямой, т. е. теперь просто множества действительных чисел, называемые промежутками. Приведем здесь перечень всех типов промежутков с их стандартными обозначениями: сегмент [а; ft] = {х|а < х < ft}, интервал (а; Ь) = {х| а < х < Ь}, полуинтервалы [а; Ь) = {х| а < х < Ь} и (а; ft] = {х|а < х < Ь}, полупрямые (— оо; ft] — {х| х < ft}, (— оо; ft) = х{х |< ft}, [а; оо)= = {х | а < х}, (а; оо) — {xi а < х}, числовая прямая (— со; оо).
а а)
Ь.............. -О I и I"
a	, а
3)
Рис. 23
На рисунке 23 указан принятый в этой книге способ их геометрического изображения (два способа для полуинтервалов и полупрямых).
Уже начиная с младших классов вы пользовались для обозначения точек плоскости координатами. Не будем здесь вновь описывать, каким образом упорядоченной паре чисел (х, у) ставится в соответствие точка М (х, у) плоскости. Теперь, после введения действительных чисел, мы можем утверждать, что соответствие
(х, у) -> М (х, у)
между упорядоченными парами чисел (х, у) и соответствующими 4 Заказ 385	97
им точками М (х, у) взаимно однозначно: не только каждой паре чисел (х, у) соответствует определенная точка М (х, у), но и обратно, для каждой точки плоскости М найдутся числа х й у, служащие ее координатами М = М (х, у).
Поэтому условимся само множество упорядоченных пар1 чисел называть числовой плоскостью, а любую упорядоченную пару чисел — точкой числовой плоскости.
Числовую плоскость принято обозначать R2. Для избежания путаницы будем теперь обычную геометрическую плоскость с выбранной на ней системой координат называть координатной плоскостью. На ней каждая точка числовой плоскости (х, у) изображается точкой М (х, у) Вы хорошо знаете, что на одной и той же геометрической плоскости можно многими разными способами выбирать систему координат и, значит, с нашей новой точки зрения, многими способами изображать точки числовой плоскости, которая сама по себе при этом не меняется — остается просто множеством пар действительных чисел.
К множествам точек числовой прямой и числовой плоскости мы будем применять геометрическую терминологию без дальнейших оговорок. Приведем два примера.
1. Множество точек (х, у), удовлетворяющих уравнению ах + + Ьу = с, где хотя бы одно из чисел а и 6 отлично от нуля, называется прямой.
2. Множество точек (х, у), удовлетворяющих неравенству х2 + + у2 < г2, г>0, называется кругом с центром (0, 0) и радиусом г.
Упражнения
171.	Опишите на геометрическом языке множества:
а)	{(х, у) | ху = 0},
б)	{(х, у 11 х| < 1 и | у | < 1},
в)	{(х, у) 11 х + у | < 1 и | х — у |) < 1.
Г) {(X, у) | (X2 - I)2 + (у2- I)2 = 0},
Д) {(х. у)|(х —2)(у + 3) = 0},
е) [(х,	у) I - >	1},	ж) |(х,	у) I ---t3'" 2	1 = 0 I.
I I *	J ( I jr —X2	J
§ 40. СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ.
Если область определения функции — конечное множество, то функцию можно задать при помощи таблицы. Такова, например, приведенная на странице 99 таблица расстояний (выраженных в метрах), которые падающее тело проходит за целое число секунд t в пределах 0 < t < 10.
1 Слово «упорядоченная» здесь указывает на то, что пара (х, у) при х
у отличается от пары (у, х).
t	8
0	0,0
1	4,9
2	15,6
3	44,1
4	78,4
5	122,5
6	176,4
7	240,1
8	313,6
9	396,9
10	490,0
полнить, чтобы например:
Табличное задание функций, область определения которых бесконечна, всегда неполно: в таблице помещаются лишь избранные значения аргумента. При всем практическом значении математических таблиц они не могут, очевидно, служить средством задания функций, область определения которых является бесконечным множеством.
Часто функции задают аналитически при помощи явной формулы, указывающей последовательность операций, которые надо вы-по значению аргумента найти значение функции,
х -> у =----
1 - /1 + X
(1)
Если не дано каких-либо дополнительных ограничений, то обла-стью определения функции, заданной явной аналитической формулой, считают множество всех тех значений аргумента, для которых все указанные операции выполнимы. Область определения Е функции, заданной формулой (1), состоит из полупрямой [—1, оо), на которой выполнимо извлечение корня, за вычетом точки х = 0, так как при этом значении х невыполнимо деление.
Примеры. 1) Пусть
',м-7г=Г'
Областью определения Е данной функции является множество тех х, при которых 1 —х2 > О, т. е. интервал (—1, +1). На рисунке стрелки указывают, что точки—1 и +1 не входят в область определения функции.
2) Е(х) = т/*—I .
г х — 3
х —2
х — 3
>0
х — 2 > 0
х — 3>0
или
( х — 2 < 0
(х—3<0
х > 3, или х < 2.
Следовательно, Е состоит из двух полупрямых (— оо, 2] и (3, +оо):
= I— °°» 2] U (3, + оо).
3) Ф(х)^—
X 1 —X
Функция ф определена для тех х, для которых
' х =# О,
1—х=£0,
- + Ф О, X 1 —X
х + О,
х #= 1,
X #= — 1.
Следовательно, область определения Ех состоит из четырех промежутков: (— оо; — 1), (— 1; 0), (0; 1), (1; + оо).
4) f(x) = -^-, g(x) = x+l.
х — 1
Легко понять, что областью определения функции f является числовая прямая без точки х = 1, а областью определения функции g — вся числовая прямая. Следовательно, функции fug различны, хотя при х =7^= 1 имеем равенство f (х) = g (х).
Иногда функция задается неявно при помощи уравнения. Например, условие
х -> у, у2 = х, у > 0, означающее, что у является неотрицательным решением уравнения у2 = х, определяет функцию
х -*• Кх,
а условие
х -> у, у2 == х, у < 0 —
функцию
х -> — Vх.
В связи с таким определением функции возникает много интересных вопросов, которыми нам придется далее заниматься. Мы знаем, что уравнение у2 = х при заданном х имеет ровно одно неотрицательное решение у = ]^х. Но, не умея решать кубические уравнения, 100
не так легко ответить на вопрос о том, определяет ли функцию, и если определяет, то в какой области определения, условие
х у, у3 + у — х
(см. пример 2 в § 43).
Иногда функция задается несколькими различными формулами, применимыми в разных частях области определения. Так, мы уже определяли функцию
X -> у = | XI
двумя разными уравнениями при х > 0 и при х < 0.
Вот еще один пример такого рода:
/ W =
График этой функции изображен на рисунке 24.
Наконец, функция может быть задана словесным определением закона соответствия между значениями аргумента и соответствующими значениями функции, без выписывания формул.
5)	х -> у=целой части х.
6)	х -> у = дробной части х.
—1 при х < —1,
х при — 1 < X < 1, 1 при X > 1.
ция
7)	х -> ап (х) =п-ому знаку десятичного разложения числа х. Рассмотрим подробнее примеры 5 и 6.
В каждом промежутке [и, п + 1), где п — целое число, функ-
х [х]
постоянна и равна п (рис. 25).
Дробная часть числа х равна х — [х]. Для всех х из промежутка [п, п + 1)
х — [х] = х — п.
Следовательно, в каждом таком промежутке функция х х —[xl является линейной, графиком которой служит отрезок прямой, на
клоненный к оси Ох под углом 45° (напомним, что 0 < х — [х] < 1) (рис. 26).
Таким образом, нам удалось словесное определение функций х -> [х] и х -+ х — [х] заменить определением при помощи формул, но этих формул оказалось бесконечное множество — каждая из них действует лишь в своем промежутке:
[х] = п для х С И; п 4- 1),
х — [х] = х — п для х С In; п 4- 1).
Упражнения
Указать области определения следующих функций:
f	3 >----
172.	х-> х—1; х -> "J/х + 3.
h _______________ _________________
173.	х->/х2—1; /(х) = /16 — х2.
174.	F(x) — 3х+2 ; У — х + 1-
175. /(х) =
у = . ...2.х-.. х2—4	х2 + 3
176. /(х) =
£(*) =
Зх +1
х2 — Зх +2
2х —1
X2 + X + 1
177. f (x) =]/5— Юх; g(x) = /10x — 5.
178.	f (x) = /x + 1 +	;
V x —4
F(x) = /x2-1 +y4
179.	f(x) = Vx+ 1 +]/l— x- g(x) = /(l — x) (1 +5x).
180.	Вычислить/(—2); /(—1); /(4); f (5); / (x); f (/); f (у), если /(u) = /u2 + 5u+l.
181.	Вычислить: /(5); / (x); /(«), если a)/ (/) = |g^j_^2_4) '•
6)	f(x)=l/JE?; y=l/S в) f (x) = Ig ^4; r)y = lgl±^
182.	Вычислить: /(—2); f (0); f(^\; /^;И1);/(4), если/(x) =
Рис. 27
Рис. 28
f— 1 при —3 < x < О,
= < х при 0 <х< 1, [	1	при	1	< х < 5.
183.	Вычислить: /(—2); (х2 — х -г 1 при । х | < 2, (	1 при х > 2.
(0); /(1); /(2); ! (3); f (5), если/(Х) =
184.	В квадрате со стороной а проведена прямая, параллельная диагонали. Установить зависимость между площадью S отсекаемой фигуры и расстоянием х прямой до вершины квадрата (рис. 27). Найти область определения функции х -> S (х).
185.	В кубе со стороной а проведена плоскость, параллельная диагональной плоскости. Установить зависимость между площадью сечения и расстоянием х плоскости до вершины Л куба (рис. 28). Найти область определения функции х -> и (х).
Нарисовать ее график.
§ 41. ЧТО ТАКОЕ ГРАФИК ФУНКЦИИ
На практике функции часто изображают графически на координатной плоскости. Если называть графиком рисунок, выполненный на бумаге, то графический способ изображения функций придется признать лишь приближенным и не могущим заменить строгое определение числовой функции. Но можно дать графику функции точ-
ное математическое определение.
Графиком функции f называется множество Г точек числовой плоскости вида (х, / (х)), где х принадлежит области определения функции /, т. е. множество всех тех точек, абсцисса которых входит в область определения функции, а ордината равна значению функции, соответствующему абсциссе.
Отметим, что из определения графика функции вытекает, что
всякая прямая, параллельная оси ординат, пересекает график не более чем в одной точке. Так, прямая, проходящая через точку х4 (рис. 29), не пересекает графика, так как Xi (£ Е. Если точка
х2 6 Е, то прямая, проходящая через эту точку параллельно оси Оу, пересекает график в одной точке (х2, f(x2)) и только в этой точке, так как значению аргумента х2 соответствует, согласно определению функции, одно и только одно значение функции /, а именно значение f (х2).
Задать функцию гра
фически — означает задать некоторую линию, которая всякой прямой, параллельной оси Оу, пересекается не более чем в одной точке. Такие линии каждому х £ Е, где Е — проекция линии Г на ось Ох, ставят в соответствие одно и только одно чис-
ло у — ординату точки пересечения прямой, проходящей через
точку х параллельно оси Оу, с данной линией: х -> у, где у — ордината точки М. Поэтому линии, обладающие вышеуказанным свойством, также называются графиками тех функций, которые ими определяются.
Теперь можно придать точный смысл идее «графического задания функций». Если на геометрическом языке определена линия, которая может служить графиком функции (удовлетворяет указанным выше условиям), то тем самым задана и соответствующая функция.
Примеры. 1) Биссектриса первого и третьего координатных углов задает функцию (единичную функцию / (х) = х):
X -> у = X,
областью определения которой является вся числовая ось (рис. 30).
2) Часть окружности с центром в начале координат радиуса единица, лежащая в верхней полуплоскости (включая точки (—1,0) и (1, 0) на оси абсцисс), является графиком функции (рис. 31):
у = ]/Т^х\
Случаи, подобные приведенным сейчас примерам, когда математическое определение функции излагается в форме описания ее графика на геометрическом языке, не имеют особенно большого значения. Но роль графиков в качестве средства приближенного изображения функций, определенных каким-либо другим путем, очень велика. Графики функций эмпирического происхождения могут быть получены при помощи разнообразных «самопищущих приборов», вроде изображенного на рисунке 32 барографа, который автоматически вычерчивает график зависимости давления воздуха от времени. Функции эмпирического происхождения можно вво-
Рис. 30
Рис. 32
дить в графической форме в вычислительные машины, «считывающие» график при помощи фотоэлемента. Иногда вычислительные машины выдают результат вычислений непосредственно в виде графика.
С другой стороны, графическое изображение функций, имеющих точное математическое определение, делает наглядным их свойства. Эта роль графического изображения функций как опоры для математической интуиции, позволяющей предвидеть те или иные свойства функций еще до их строгого доказательства, будет вам особенно ясна при изучении изменения функций в этой и следующей главе.
Упражнения
186. Является ли окружность с центром в начале координат графиком какой-либо функции?
187. Является ли графиком некоторой функции (какой?) нижняя половина окружности?
188*. В каком случае график функции симметричен относительно оси абсцисс?
189.	Найти аналитические условия, при выполнении которых график функции f симметричен относительно оси ординат.
190.	Найти аналитические условия, при выполнении которых график функции f симметричен относительно начала координат.
191.	Построить графики функции: d) f (х) = х — W + у;
б) g W = \ f (х)1; в) h (х) = дробной части —.
§ 42. ИЗМЕНЕНИЕ ФУНКЦИИ, ЕЕ ВОЗРАСТАНИЕ И УБЫВАНИЕ
На рисунке 33 изображен график изменения высоты самолета в течение полета, продолжающегося десять часов (время измеряется в часах, высота — в километрах). В течение первого часа самолет набирает высоту, затем в течение трех часов летит на постоянной высоте, в течение часа вновь набирает высоту, летит на новой постоянной высоте четыре часа, а в течение последнего часа спускается. Высота является в этом примере функцией времени, определенной на промежутке [0, 10]. На промежутке [0, 1] функция возрастает, на промежутке [1, 4J постоянна, на промежутке [4, 5] вновь возрастает, на промежутке [5, 9] постоянна, на последнем промежутке [9, 10] убывает до нуля.
Если рассмотреть промежуток [0,9], то уже нельзя сказать, что функция1
h = h (t)
на этом промежутке рее время возрастает. Верно только, что она на этом промежутке нигде не убывает. Аналогично про поведение нашей функции на промежутке [5, 10] можно сказать, что она на
этом промежутке нигде не возрастает.
Сформулируем соответствующие этим наглядным сообр ажени ям математические определения.
I. Функция f называется возрастающей на множестве Е, если для любых Xf и х2, принадлежащих множеству Е, из Xi < х2 вытекает
/ (*1) < f (х2) .
II. Функция/ называется убывающей на множестве
1 Заметьте, что в прикладных вопросах, особенно в том случае, когда независимым переменным (аргументом) является время, часто функцию и ее значение обозначают одной и той же буквой.
Е, если для любых Xt и х2, принадлежащих множеству Е, и из х, < х2 вытекает
Kxi )> f (х2).
Примеры. 1) Функции х -> х, х х3 и вообще х -> хп при любом натуральном нечетном и возрастают на всей числовой прямой.
2)	Функции х2 и вообще х -> хп при любом натуральном четном п возрастают на положительной полупрямой [0; оо) и убывают на отрицательной полупрямой (— оо; 0].
3)	Функция х х — [х] возрастает на каждом промежутке [и; п + 1), где п — произвольное целое число.
4)	Так как последовательность есть не что иное, как функция хп = / (П),
определенная на множестве натуральных чисел, то естественно думать, что в применении к таким функциям наши новые определения возрастания и убывания равносильны данным в § 14.
Это предположение верно. Рассмотрим подробнее случай возрастания. * По новому определению последовательность (хп) ^возрастает в том и только в том случае, если при любых натуральных пг и п из tn < п вытекает
хт < хп-	(О
Ясно, что в этом случае, в частности при любом натуральном т, хт < хт+1	(2)
Если неравенства (2) верны при любом натуральном т, как этого требует определение возрастающей последовательности из § 14, то из цепочки неравенств хт < хт+1 < хт+2< ... <хп получаем при любых т и п > т неравенство (1).
III. Функция f называется неубывающей на множестве £, если при любых Xi и х2, принадлежащих множеству Е, и из < х2 вытекает
f Ui) < f (х2).
IV. Функция f называется невозрастающей на множестве Е, если для любых Xi и х2, принадлежащих множеству п и из Xi < х2 вытекает
/ (Xi) > f (х2).
Примеры. 1) Функция х -> [х] является неубывающей на всей числовой оси.
2) Любая неубывающая последовательность является примером неубывающей функции, определенной на множестве натуральных чисел, а любая невозрастающая последовательность — невозрастающей функции.
3) Единственными функциями, которые одновременно и не убывают и не возрастают, являются функции, принимающие во всей
своей области определения лишь одно-единственное значение (докажите!). Такие функции называют константами.
Упражнения
192.	Докажите методом математической индукции, что:
а)	функция х -> хп при п четном убывает на полупрямой (— оо;
0) и возрастает на полупрямой (0, + оо);
б)	функция х -> хп при любом нечетном п возрастает на всей числовой прямой.
Определить промежутки возрастания и убывания функций:
193.	а) у = 2х — 3; б) у = —Зх + 2.
194.	а) у = | х |; б) у = | х — 2 |.
195.	а)у = 1х2; б) у = -|х2 + 2.
196.	а) у = (х — 2)2; б) у = — (х — З)2.
197.	а) у = (х — I)2 — 3; б) у = 3 — (х — 2)2.
198.	а) у — х2 — 4х + 5; б) у = — 2х2 + 6х — 7; в) у — 1,5 + + х —0,5х2.
i_	_i
199.	а) у = — ; б) у = —- ; в) у = х2 ; г) у = — х 2. X	X
1.	L	£
200.	а) у = |х|2 ; б) у = 0,5х3 ; в) у = 1 — 0,5 х3.
201.	а) у = 2х; б) у = в) у = (0,25)*
202.	а) у = 1g х; б) у = log2 (х — 2); в) у = log^ (х + 1);
г) у = log2 (х + 2)2.
§ 43. ПРИРАЩЕНИЯ АРГУМЕНТА И ФУНКЦИИ
Рассмотрим некоторую функцию f. Пусть х0 — некоторое значение аргумента из области определения этой функции и f (х0) = = у0. Если х — некоторое другое (новое) значение аргумента, то разность х — х0 обозначается через Ах:
А х = х — х0
и называется приращением аргумента (читается: «дэльта х»). Таким образом, новое значение аргумента
х = х0 + Ах
является результатом того, что первоначальное значение аргумента х0 «получило приращение Дх». Вследствие этого значение функции изменится на величину
У — Уо = f W — f (*о) = f (х0 + А х) — / (х0).
Разность
f (х0 + А х) —f (х0)
между новым значением функции f (х0 + Дх) и первоначальным ее значением /(х0) называется приращением функции / в точке х0 и обозначается символом (х0) (читается', «дэльта эф в точке х0»).
Так что
А/ (х0 ) = f (х0 + А х) — f (х0).
Употребляя введенную терминологию, можно следующим образом переформулировать определения возрастающих и убывающих функций:
Функция называется возрастающей, если ее приращения положительны при положительных приращениях аргумента, и убывающей, если ее приращения отрицательны при положительных приращениях аргумента. При этом если речь идет о возрастании или убывании не на всей действительной оси, а только на некотором ее подмножестве Е, то имеют в виду только приращения аргумента при переходе от точки х0 из этого множества к точке х из того же множества.
Рассмотрим два примера, которые позволят нам понять основной замысел важного раздела нашего курса, посвященного началам дифференциального исчисления (оно составляет главное содержание этой и следующих глав учебника).
Первый пример будет очень простым. Мы применим новый метод исследования к функции f (х) = х2. При этом мы узнаем мало нового об этой функции, но зато поймем основы нового метода. Второй пример будет интереснее. Исследовать на возрастание и убывание функцию f (х) = х3 — Зх при помощи тех способов, которые вы уже знаете, было бы не очень легко. Новый метод позволит это сделать очень просто.
Примеры. 1) f (х) = х2.
Вычислим приращение функции в точке х:
A /(*) = f (х + Ах) — f W = (х + Ах)2 — х2 = 2хДх + (Ах)2. Если приращение Дх мало по абсолютной величине, то его квадрат будет еще много меньше. Например, если Дх = 0,001, то (Д х)2 = = 0,000001. Поэтому естественно считать
2хДх
главной частью приращения функции и надеяться, что уже она одна укажет нам направление изменения функции в окрестности точки х.
Для положительных приращений Дх имеем
2хДх > 0	при х > О,
2хДх < О	при х < О.
Таким образом, мы снова убедились, что функция х х2 действительно убывает на отрицательной полуоси и возрастает на положительной.
2) f (х) = х3 — Зх.
Вновь вычислим приращение функции в произвольной точке х:
Д/(х) = (г + Дх)3 — 3(х + Дх) — (х3 — Зх).
Сгруппировав вместе члены с одинаковой степенью приращения Ах, получим:
Д/ (х) - (Зх2 — 3) Ах + Зх (Дх)2 + (Дх)3.
Естественно считать здесь главной частью приращения выражение
(Зх2 — 3) Дх.
Возникает гипотеза, что в достаточно малой окрестности точки х наша функция возрастает, если множитель
Зх2 — 3
при Дх в выражении главной части приращения функции положителен, и убывает, если этот множитель отрицателен. Эта гипотеза верна. Позднее мы познакомимся с общими положениями, которые позволят ее обосновать без громоздких вычислений, но вы можете ее доказать элементарно и немедленно (см. упражнение 203).
Остается исследовать, при каких х выражение Зх2 — 3 положительно и при каких х отрицательно. Решая уравнение
Зх2 — 3 = 0,
получаем два корня: х{ = — 1, х2 = 1.
Легко видеть, что выражение Зх2 — 3 отрицательно в промежутке (—1; 1) между этими корнями, а при х < — 1 и при х > 1 положительно. Следовательно, функция f ( х) = х3 — Зх возрастает в промежутке (—оо; —1), убывает в промежутке (—1; 1) и вновь возрастает в промежутке (1; + оо).
При х = —1 имеем f (—1) = 2. Это максимальное значение функции f в том смысле, что слева от точки х = — 1 функция возрастает, а справа от нее убывает. В том же смысле значение /(+!) = = — 2 является минимальным. Говорят, что данная функция имеет в точке х = — 1 максимум , а в точке х ~ 1 — минимум.
Упражнения
203.	а) Доказать, что для функции /(х) = kx + b Af(x) = k-Ax.
б)	Найти главную часть приращения функции/(х) = ах2+ 4" Ьх 4* с.
в)	Доказать, что в примере 2 главная часть приращения (Зх2 - 3) Дх
имеет тот же знак, чтои приращение функции Д/ (х), если | Дх| <8, где 8 < 1
и 8 <
| Зха — 31 Зх24-1
§ 44. ПРОИЗВОДНАЯ КАК СКОРОСТЬ ИЗМЕНЕНИЯ ФУНКЦИИ
Пример. Рассмотрим вновь падение тела, следующее закону
s = s (0 = у*.
Выберем какой-либо момент времени и рассмотрим промежуток времени длительности Д/, от момента t0 до момента
t = /0 + Д/.
За этот промежуток времени тело пройдет путь
Дэ = s (0 - s (/0) = | ((/0 + ДО2 -	= gt0 Д< + |( ДО2.
По известному из физики определению, отношение
At 6 °	2
есть средняя скорость тела на промежутке времени l/0, t0 + ДО.
Примем, что g = 9,8, и подсчитаем средние скорости за промежутки времени различной длительности, начинающиеся в момент времени ta = 2.
At	1 1	0,1	0,01 |	0,001
AS At	24,5000	20,0900	19,6490 |	19,6049
Мы видим, что при малых Д/ вычисленное значение средней скорости оказывается очень близким к значению
gt0 - 19,6.
Естественно думать, что это значение есть предел
.. as lim _ Л/-.0 At
средней скорости при длительности А/, стремящейся к нулю. Так это и есть в действительности. Мы имеем здесь дело с новым понятием — понятием предела, отличным от понятия предела последовательности. Точно это новое понятие предела функции будет определено в § 47. Но в простых задачах можно его употреблять и без точного определения, как это делали в течение первых двух столетий развития дифференциального исчисления (см. исторический очерк в § 46).
Естественно, что и при любом /0
.. ДЗ lim _ _ pf д/-оД/ е°'
Из физики вы уже знаете, что
v = gt
есть истинная скорость нашего падающего тела в момент времени t. По аналогии со средней и истинной скоростью движущегося тела средней скоростью изменения функции на промежутке
lx0, х! => [х0, х0 + Ах)
называется отношение приращений функции и независимого переменного
А/ (х0) _ / (хв + Дх) — / (х0), Дх	Дх
Предел средней скорости при стремящемся к нулю приращении независимого переменного
lim — lim t <*« + &*)—/ (хФ) дх - о Дх дх - о Дх
называется истинной скоростью изменения функции в точке х0. Для истинной скорости изменения функции принято название производная. Производная от функции f в точке х0 обозначается:
f (х0) =	+
Дх -► о	Дх
Если считать х0 переменным, то производная оказывается новой функцией от этого переменного. Сама по себе эта функция обозначается просто f.
Приведем ряд примеров, оговорившись, что пока наши рассуждения имеют предварительный характер, так как мы не имеем настоящего определения предела функции.
Примеры. 1) / (х) = kx 4- b.
А / W = k (хо + Ах) 4- b — (кх0 + b) = £Дх, А/ (Хр) ___________________ £
Дх
ИЗ
Предел постоянного равен этому постоянному. Поэтому при любом х0
Г(х0) = k.
2) f (х) =х2,
Д/(х0) = 2х0Дх + (Дх)2,
= 2х0 + Дх. Дх
При Дх, стремящемся к нулю, получаем:
Г(х0) = lim = 2х0. Ах -* о Дх
Сопоставьте результат с графиком зависимости у = х2 (рис. 34).
На графике видно, что при возрастании х от —сю до оо сначала функция убывает очень быстро, потом все медленнее, до тех пор, пока ее скорость изменения при х — 0 не обратится в нуль, а потом начинает возрастать все быстрее и быстрее. Эти наблюдения вполне соответствуют полученной формуле для производной, которую можно записать и так:
(х2)' - 2х
3) f (х) = х3 — Зх,
Д f (х) - (Зх - 3) Дх + Зх2 (Дх)2 + (Дх)3,
= Зх — 3 + Зх2 Дх + (Дх)2.
Дх
Ясно, что при стремлении Дх к нулю стремится к нулю и сумма:
Зх2Дх + (Дх)2.
Поэтому
/'(х) = lim Зх2 — 3.
Дх - 0 Дх
/ Решая уравнение
Зх2 — 3 = 0, '
мы видим, что производная нашей функции обращается в нуль на концах промежутка (— 1,1). Внутри этого промежутка она отрицательна, а вне—положительна. На рисунке 35 изображены графики функции f (х) = х3 — Зх и ее производной /'(х) = Зх2 — 3. Проследите на этом рисунке, как соответствуют значения производной ходу изменения функции.
В заключение первого знакомства с понятием производной решим такую задачу.
Задача. Из квадратного листа жести со стороной а надо изготовить открытую сверху коробку максимального объема, вырезав по углам (рис. 36) квадратики и загнув образовавшиеся кромки.
Обозначим через х сторону основания коробки. Стороны вырезанных квадратиков будут'равны у (а — х), а объем коробки равен
V (X) = у (а — х) х2.
Надо найти максимальное значение этой функции в промежутке О < х < а. График функции изображен на рисунке 36а. Можно думать, что значение х, доставляющее максимальное значение V, получится, если мы найдем, где производная V'(x) обращается в нуль. По образцу предшествующих примеров найдем:
V'(x) = — х2 + ах.
Уравнение
— — х2 + ах О
2
имеет два решения: х = О и х = = — а. Первое из них не подходит (при х = 0 имеем V = 0). Второе и дает искомый ответ: вырезать по углам надо квадратики со сторонами
При этом получится максимальный возможный объем коробки:
Т7 /2	\2 1	2 з
Vmax = — я — а = —а3.
\ 3 / 6	27
В систематическом порядке мы вернемся к отысканию максимумов и минимумов функций в § 69. Вы можете, однако, уже сейчас попробовать решать упражнения (258—259).
§45. НЕПРЕРЫВНЫЕ И РАЗРЫВНЫЕ ФУНКЦИИ
Надо думать, что при вычерчивании графика функции по точкам вам часто советовали провести через нанесенные на бумагу точки «непрерывную кривую». Так и надо поступать при вычерчивании по точкам, например, графика функции f (х) =х2. Но вы познакомились в § 40 и с такими функциями, график которых состоит из отдельных отрезков, которые не примыкают друг к другу «непрерывно». Например, функция
f (х) = дробной части от х,
график которой изображен на рисунке 26, на каждом отрезке [и; и + 1), где и — целое число, непрерывно возрастает, приближаясь к значению единица, но этого значения не достигает, а в точке х = п + 1 внезапно, скачком возвращается к значению нуль, с которого началось ее постепенное возрастание в точке х = п.
Эти наблюдения подводят нас к необходимости различать непрерывные и разрывные функции. Более точно дело будет идти о том, чтобы определить, что значит, что какая-либо функция f непрерывна в точке х0. Например, рассмотренная сейчас функция «дробная часть от х» непрерывна во всех точках х, кроме целочисленных, в которых она разрывна.
Определение непрерывности функции / в точке х0 можно сформулировать уже сейчас: функция f называется непрерывной в точке х0, если при стремлении точки х к точке х0 значение функции f (х) стремится к значению f (х0). Но это определение вновь опирается на понятие предела функции, с которым более основательно мы познакомимся в следующей главе.
Если функция f имеет в точке х0 производную, то она в этой точке непрерывна. Это положение будет доказано в § 57, но, пользуясь некоторыми наглядно убедительными свойствами предела функции, можно наметить ход его доказательства уже сейчас:
lim f (х) = lim [/ (х0) + Д/ (х0)] = f (х0) + lim Д/ (х0) = f (х0) + х -> х0	Дх -> О	Дх -* О
+ lim Дх = f (х0) + Г (х0) • О = f (х0).
Например, любой многочлен является непрерывной функцией. На этом мы закончим предварительное знакомство с кругом идей, которые нам предстоит изучить более обстоятельно в следующей главе.
§ 46. ИСТОРИЧЕСКИЙ ОЧЕРК
Переломным пунктом в истории математики был XVII век. Декарт (1596—1650) ввел в употребление метод координат для изучения расположенных на плоскости кривых. Развитие естествознания привело к пониманию важности изучения изменения функций, в особенности функций, выражающих зависимость координат движущегося тела и других физических величин от времени. Кроме применений к нахождению максимумов и минимумов функций, производная применялась к нахождению касательных к кривым линиям (см. далее § 67). Первые работы Декарта, Паскаля и Ферма уже содержали в себе по существу правила нахождения производных от любых многочленов. Вы и сами можете, не дожидаясь изучения следующей главы, понять, что главная часть приращения многочлена
Р (х) = аохп + аре"'1 + • • • +	+ •  • + an_tx + ап
имеет вид
ДР (х) = (лвох"-1 + (п — 1) Ojx”"2 + • • • + (n — k) аьх"-*-1 + • • • + а,^] Дх, а значит, производная многочлена Р (х) выражается формулой
Р' (х) = пдох"-1 + (п — 1) a1xtl~2 4- • • • + (и — k) akxn~k~Y + ... 4- ал_10
Но систематически учение о дифференциалах и производных, т. е. дифференциальное исчисление, было развито немецким математиком и философом
Лейбницем (1646—1716) и английским математиком и основателем современного математического естествознания Ньютоном (1643—1727).
Термин «функция» был введен Лейбницем, но долго под ним «признавались» лишь функции, заданные каким-либо аналитическим выражением. Лишь в 1822 году французский математик Фурье со всей определенностью стал говорить о том, что в понятии функции не существенно, каким образом каждому х поставлено в соответствие определенное значение f (х), важно только, чтобы это соответствие было установлено.
Наглядный смысл понятия предела функции был ясен математикам XVII века. Они умели фактически правильно находить пределы. Но строгие определения понятия предела последовательности и функции, сохранившиеся до наших дней, были даны лишь французским математиком Коши (1789—1857) и далеко не сразу были всеми поняты.
Яркие характеристики глубины переворота в математике, происшедшего в XVII веке, дали Карл Маркс и Фридрих Энгельс. Энгельс писал: «Поворотным пунктом в математике была декартова переменная величина. Благодаря этому в математику вошли движение и диалектика». Но начальный период развития новых ветвей математики, связанных с понятиями функции, бесконечно малых величин, пределов и производных, был охарактеризован Марксом как «мистический».
Лозунгом многих математиков XVIII века был: «двигайтесь вперед, и вера в правильность результатов к вам придет!».
Только после работ Коши в течение XIX века начала математического анализа получили корректное обоснование. Для этого, в частности, как вы можете понять после рассказанного в четвертой главе, была необходима строгая теория действительных чисел. А она была развита только во второй половине XIX века Вейерштрассом, Дедекиндом и Кантором.
ГЛАВА ШЕСТАЯ
ПРОИЗВОДНАЯ И ЕЕ ПРИМЕНЕНИЯ
§ 47. ПОНЯТИЕ ПРЕДЕЛА ФУНКЦИИ
Вычисляя площадь квадрата, мы измеряем (приближенно) длину его стороны. При этом мы уверены, что площадь квадрата может быть найдена со сколь угодно большой точностью, если только достаточно точно измерить длину его стороны. Наша уверенность основана на следующих соображениях.
Площадь любого квадрата является функцией длины его стороны х, т. е. S (х) = х2. Пусть х0 — длина стороны данного квадрата, тогда его площадь равна:
$ (х0) = хо-
Пусть при измерении длины стороны этого квадрата мы получили число х = х0 + Ах, где Дх = х — х0 — погрешность измерения. Тогда приближенное значение площади квадрата равно:
S (х) = S (х0 + Дх) = (х0 + Дх)2.
Оценим абсолютную погрешность |Д5 | этого приближенного значения:
|Д5 |= ) S (х0 + Дх) — S (х0)| = | (х0 + Дх)2 - х21 = = | 2х0 + Дх | • | Дх |.
Применяя известное неравенство | а + b | < | а | + | b |, мы получим:
| AS | < (| 2х01 + |Дх|) | Дх | = (2х0 + |Дх|) |Дх|.	(1)
Из этой оценки следует, что если мы желаем, чтобы абсолютная погрешность приближенного значения площади квадрата была меньше, например 0,001, т. е. чтобы выполнялось неравенство
(2х0 + | Дх |) |Дх | < 0,001,
то для этого достаточно (если считать заранее, что | Д х | < 1), чтобы выполнялось более простое неравенство
(2х0 + 1) | Дх | < 0,001
или чтобы выполнялось неравенство
1л ।	0,001
ДХ <------!----
2х0 + 1 •
ТА	I	,	0,001
Таким образом, если | х — х01 < ---------, то
2х0-|-1
। Д8 | = | х2 — х2 |< 0,001.
Аналогично если мы пожелаем, чтобы выполнялось неравенство | AS | = | х2 — х2 | < 8,
где е — любое положительное число, то из неравенства (1) следует, что для этого надо позаботиться лишь о том, чтобы выполнялось неравенство
(2х0 + | Дх |) | Д х | < 8,
и если заранее считать, что |Дх| < 1, то достаточно, ность измерения
чтобы погреш-
1 и —-—, то 2х0 +1
сколь угодно
....	। е
Дх = х — хп <---------.
1	01	2х0-|-1
Если через б обозначать меньшее из двух чисел |х2 — xl\ <. е, если только | х — х0 | < б.
Таким образом, значения функции S (х) = х2 близки к числу х%, если только значения аргумента х достаточно близки к числу х0. Поэтому число х^ естественно назвать пределом функции S (х) — х2 при х, стремящемся к х0.
После этого предварительного рассмотрения нетрудно понять следующее определение предела, которое аналогично определению предела последовательности.
Определение. Число А называется пределом функции f (х) при х, стремящемся к а, и обозначается lim f (х), если для х + а
любого 8>0 найдется положительное число б (зависящее от б), что для любого х^= а, удовлетворяющего неравенству | х — а | <; б, выполняется неравенство
\f(x)-A\
Из определения предела функции видно, что функция / предполагается определенной для всех х, достаточно близких к точке а, а именно для тех х, для которых |х — а | < б, кроме, быть может, самой точки х — а. Однако, и это очень важно в практических приложениях (см. пример 3), в определении предела не предполагается, что функция f определена в самой точке а.
Примеры. 1) Докажем, что предел постоянной функции равен этой же постоянной. В самом деле, если f (х) = k для всех х из некоторого интервала, содержащего точку а, то для таких х
е.
где 8 — любое положительное число. Таким образом, lim f (х) = lim k = k. x~* a	x-*a
2) Рассмотрим функцию f (x) = x и докажем, что lim f (x) — lim x = a. x ~*a	x-* a
В самом деле, если 8 — произвольное положительное число, то, выбрав S = е, получим, что | х — а | < е, как только | х — а | < 6.
3) Функция
., . х2 — 9
ZW = —-х
определена всюду, за исключением точки х = — 3. Докажем, что эта функция имеет предел при х, стремящемся к (— 3), равный (-6).
В самом деле, при х=£ — 3
|^_(-6)| = |х-3 + 6| = |х + 3| = |х-(-3) |. I х±3
Следовательно,
х2 —9
8 И X =# —3.
8,
Поэтому если выбрать 6 = 8, то при | х — (— 3) | < 6 и х У= — 3 у2 ___________________________О
X -j— о
а это и означает, что
j. х2 — 9	~
lim ------- = — 6.
4) Доказать, что lim х2 = 1.
X -+ 1
Доказательство. Требуется доказать, что для любого положительного числа 8 найдется положительное число 6 такое, что для х #= 1 и |х — 11 < 6 будет выполняться неравенство
|(2х2 - 1) - 1| < е,	(*)
или, что то же, неравенство | х2 — 1|	, или |х + 1| | х — 1| <
< -1. Считая заранее, например, что 1 < х < 2, можно утверждать, что последнее неравенство будет выполняться при выполнении неравенства (2 + 1) | х — 11 < — или | х — 11 < — . Следо-2	6
вательно, достаточно выбрать б —-1, чтобы при 1 и |х— 1|< 6
< ~ выполнялось неравенство (*).
Упражнения
Пользуясь определением предела функции, доказать следующие предельные равенства.
204.	a) lim (2х +1) = 5; б) lim(5x — 3) = 2; в) lim(2x2—1) =1. х -> 2	х - 1	х -> 1
205.	a) lim(3x2+2) - 5; б) lim (2х2 + 1) = 3; в) limx3 = 1. г —1	X -> 1	х - ]
ллп	х 1-	4х2 — 1	г	1- х2— 4	.	...	4х2—9
206.	a) lim-------= 5; б) lim----- = 4; в) lim ------- = 6.
х —2 2х + 1	х ->2Х — 2	х з	2х — 3
~2
§ 48. ТЕОРЕМА ЕДИНСТВЕННОСТИ ПРЕДЕЛА
Теорема. Если функция f (х) имеет предел при х, стремящемся к а, то этот предел единствен.
Доказательство. Если lim f (х) = А и lim f (х) = В, х -* а	к -> а
то для любого 8 > 0 найдется такое 6 > 0, что для всех х #= а и удовлетворяющих неравенству
| х — а | < 6
выполняются сразу два неравенства:
\f{x) - А |<| и |/(х)-В|<-|.
Но тогда
\A—B\ = \[A—f(x)] + [f (x)-B]\<\A-f(x)\ + \f(x)-B\<
<-+-=8.
2	2
Следовательно, неотрицательное число | А — В | меньше любого положительного. Таким числом может быть только число нуль. Поэтому | Л — В | = 0, А — В = 0 и, следовательно, А = В.
§ 49. БЕСКОНЕЧНО МАЛЫЕ ФУНКЦИИ
Определение. Функция а (х) называется бесконечно малой (б. м.) при х, стремящемся к а, или вблизи точки а, если
lim а (х) = 0. х -» а
Как и в случае бесконечно малых последовательностей, справедливы следующие теоремы.
Теорема 1. Сумма двух функций бесконечно малых вблизи одной и той же точки а является бесконечно малой.
Доказательство. Если lim а (х) = 0 и lim 0 (х) = О, то для любого е > 0 найдется такое S > 0, что одновременно выполняются два неравенства:
|а (х) | <| и | 0 (х) | <|,
если только х #= а и | х — а | < 6.
Но тогда для этих же значений аргумента
|а(х)± 0W |< |а(х)| + |0(х)| <| + | = 8
и, следовательно, lim [а (х) + 0 (х)] — 0.
х а
Теорема 2. Произведение бесконечно малой функции а (х) вблизи точки а на функцию f (х), ограниченную в некоторой окрестности этой точки, является бесконечно малой вблизи этой же точки.
Доказательство можно провести так же, как и в § 30.
Следствие. Произведение двух бесконечно малых (в окрестности одной и той же точки) есть бесконечно малая.
Теорема 3. (О связи понятий бесконечно малой и предела.)
1) Если функция f (х) имеет предел при х, стремящемся к а, то ее можно представить в виде суммы постоянной функции и бесконечно малой вблизи точки а.
2) Наоборот, если функция f (х) может быть представлена в виде суммы постоянной функции и бесконечно малой вблизи некоторой точки а, то эта функция при х, стремящемся к а, имеет предел.
Доказательство. 1) Если lim f (х) = А, то для любого х <* а
8 > 0 найдется такое 6 > 0, что для всех х =И= а, и удовлетворяющих неравенству | х — а | < 6 выполняется неравенство
(х) — Л | < е.
Последнее неравенство означает, что функция а (х) = f (х) — А является бесконечно малой вблизи точки а, причем
f (х) = А + а (х), что и требовалось доказать.
2) Если f (х) = А + а (х), где lim а (х) = 0, то для любого х -* а
8 > 0 найдется такое 6 > 0, что
I f (х) — А I = I а (х) | < е
при х У= а и | х — а | < 6 и, следовательно, lim f (х) = А.
х-+а
207.	Докажите теорему 2.
208.	Докажите следствие из теоремы 2.
§ 50.	ТЕОРЕМЫ 0 ПРЕДЕЛАХ
Теорема 1. Предел алгебраической суммы двух функций равен алгебраической сумме их пределов, если последние существуют: lim [f (х) ± g (х)] — lim f (х) ± lim g (х).
х~* а	х-*а	х-+а
Доказательство. Если lim f (х) = A, lim g (х) = В, . х -* а	х -* а
то по теореме 3 предыдущего параграфа f (х) = А + а (х), где lim а (х) = 0,
g (х) = В + 0 (х), где lim 0 (х) = 0. х -* а
Следовательно,
f (х) ±g (х) = (Л ± В) + [а (х) ± 0 (х)].
По теореме 1 этого же параграфа сумма а (х) ±0 (х) является бесконечно малой вблизи точки а. Поэтому, согласно теореме 3 (2), из предьщущего параграфа
lim [/ (х) ± g (х)] = А ± В = lim f (х) ± lim g (х). х -* а	х а	х -+а
Теорема 2. Предел произведения двух функций равен произведению их пределов, если последние существуют, т. е.
lim [f (х) • g (х)] = [ lim f (х)] [lim g (x)J. x-+ a	x -* a	x - a
Доказательство проводится аналогично с ссылкой на теорему 2 предыдущего параграфа.
Следствие. Постоянный множитель можно вынести за знак предела:
lim [kf (х)] = (lim k) [lim f (x)] = k lim f (x). x a	x-*a x-*a	x -> a
Справедлива также и следующая
Теорема 3. Предел отношения двух функций равен отношению их пределов, если последние существуют и предел делителя не равен нулю:
11111		- у
x-ag(x) limg(x)
х
если lim g(x) 0.
v -*а
209.	Докажите теорему 2.
210*s Докажите теорему 3.
§ 51.	ВАЖНЫЕ ПРИМЕРЫ
1)	lim хт = lim (х • х... х) - lim х • limx ... lim х =
Х"Х°	х'гХ° m "множителей х ~ Х° Х ~ х° Х ~ Х°
=хо • Хо ... Xq — Xq .
2)	Предел многочлена. Многочлен степени п может быть записан в виде
Р (х) = аох" + а^-1 + агхп~2 + • • • + ап^х + ап, где ай =£ 0.
Используя теоремы 1 и 2 и следствие из теоремы 2 (см. § 50), получим:
limP(x) Нт(аохя + сцх'1-1 + • • • + «„-i* + ап) = lirn (аохП) + X -> х0	X -> х0	X -* х0
+ lim^x”-1) + • • • + lim(a„_1x)+ limart= aolimx" + а1Нтх"-14-
x Xq	x - x0	x -* x0	x -> Xo	X -+ x0
+ • • • + an-i lim x0 + an= aox" + aix«-> + ... + a„_iX0 + an.
X -* Xq
Таким образом,
lim P (x) = P (x0), x -+ x0
т. e. предел многочлена при x, стремящемся к х0, равен значению этого многочлена в точке х0.
3) Предел дробно-рациональной функции. Дробно-рациональной функцией называется частное двух многочленов. Если многочлен назвать целой рациональной функцией, то дробно-рациональная функция является частным двух целых рациональных функций
д (X) = Р = а°хП +	‘ ‘ + an-ix + ап
У 1 Q (х) boxm + b1X™-i + • • • + bm.iX + bm *
Очевидно, дробно-рациональная функция определена на всей действительной оси, за исключением тех точек х, в которых знаменатель Q (х) обращается в нуль, т. е. за исключением тех точек х, которые являются корнями уравнения Q (х) = 0.
Если в точке х0 знаменатель Q(xo)#=0, то по теореме 3 (см. § 50)
lim Р (х)
lim R (х) = lim	р (х0).
Х-.Х, x-x0Q(x) lim Q (х)	Q(x0)	°
X -* х0
Таким образом,
lim/?(х) = /?(х0),
х - *0
т. е. предел дробно-рациональной функции при х, стремящемся к х0, равен значению этой функции в точке х0, если только точка х0 принадлежит области определения этой функции.
4)	Пусть требуется найти предел
X 2 X2 + 2х — 8 •
Легко проверить, что знаменатель стремится к нулю при х, стремящемся к 2. Поэтому применить теорему о пределе частного нельзя. Заметим, однако, что и числитель стремится к нулю при х, стремящемся к 2. Следовательно, и в числителе и в знаменателе можно выделить множитель х — 2, а затем сократить их. Эта операция законна при х =£ 2, что и предполагается, согласно определению предела
= <±-~2>	> _ при х 2.
х2 + 2х — 8	(х —2) (х + 4)	х + 4
Следовательно,
,. х2 — Зх 4* 2	.. х — 1	1
lim---------1— = hm--------= —
х - 2 х2 + 2х — 8	х - 2 х -|- 4	6'
5)	Найдем
lim У х~3
х-* 9 х — 9
Как и в предыдущем примере, теорему о пределе частного применить нельзя. Но можно преобразовать выражение под знаком предела, считая 9, и получить:
/7—3	..	/7—3	..	1	1
lim  --= lim —=-------=— — hm — = —
х-9 X — 9	х-9 (Vx — 3)(/х + 3) x-э/х+З 6‘
6)	lim *3 ~— = lim (х2 4- х 4- 1) = 3. х- 1 х— 1 х- 1
71 lim ¥х~¥* —Hm (^Г-/5)(/? + /Г/7+/7)
° х™ х — а а х-*а (х-а)(/7Ч/7/7 + /7)	1~
х-а(х — а) (/х2 4- ¥х ¥а + ¥“2) х~а ¥х2 +/х/а ~1~Уа2 3 у'а2'
Другое решение примера 7:
/7-/7	___________/Г-/7___________
7™ X - а	х , а (/7"— /7) (/^4- /7/7/ /7) “
— г	1	— 1
,	। 3. — 3/ , 3/~9 о 3
X - аух2 + |/ х / а + |/ а2 3 у а2
Найти пределы:
211. 1) lim (х3 + 2х2 — Зх — 4).
х 2
2) lim 3^ + 2» + 1 х - 1 х3— 2х2 + Зх — Г	3) lim J?. + 2 X —2 3x3 — 1 *
4) lim(4x2 — 2х + 1). X 1	5) lim ?»- + ^ + 3»+J x: - — 1	X3 4- X2 — 2x
6) Iim.^+1)^- О . X - 2 X3 -р X2 -j- X	7) lim ??-*• + ' . i	x4-2 X" 2
8) lim^+2. х -> —i х 4" 1	n\ i •	— 8 9) lim	. x — 2 X —2
10) lim X -* 0 ]Лх + X	11) lim	. 1 - ° 3 yx +2/X
12) |im	. х - -2 2х2 + X — 6	13) lim^+^-1. X-.-1 2x3 + x —1
14*) lim *3-* + 6	. х -г —2 х34- Зх2 4-х — 2	15*) lim -x3 + 2x2 + 2x + 1.. x - —1	x3 + x 4- 2
16) limEfELz2.. х — 5	X — 5	17) lim - x±3— . Х-— 3 Vx 4- 4 —1
3/— о 18) lim у х~2 х - 8 X — 8	19) hm	. / x 4-1
20*) lim */х+* . х - —з х3 -F 1 QQ\ i •	2	Хх — 3 22) lim —		. х - 7 х2 — 49	21) lim ^x~2 . x - 4 X3 — 64 9	y2 23*) lim 		 x - з 1 — / x2 — 8
24*) lim—1 • X - °	+ x — 1 26) н„,1Т±±— x —» 0	x 28) lim	~ *'£-. /i-о	h.	25) lim -	. r-81	— 9 27) lim	. h - o	h. 29) lim / 1 + х~* . x •* ° у 1 4- x — 1
$ 52. ПОНЯТИЕ НЕПРЕРЫВНОСТИ ФУНКЦИИ
В предыдущем параграфе мы видели, что для некоторых функций, а именно для целой рациональной и дробно-рациональной, выполняются предельные равенства
lim Р (х) = Р (х0),	(1)
lim R (х) = R (х0)	(2)
х-~ х0
для всякой точки х0, принадлежащей области определения функции.
Определение. Если для функции f выполняется равенство
lim f (х) = f (х0)	(3)
X •* Х0
в некоторой топке х0 из области определения данной функции, то функция f называется непрерывной в точке х0.
Равенство (3), согласно определению предела функции, означает, что для любого в > 0 найдется такое 6 > 0, что
|/ (х) — f (х0) | < 8 при |х — х0| < 6.	(4)
Если положить х — х0 == Дх, то неравенство (4) можно переписать в виде
|/ (х0 + Дх) — f (х0)| <е при | Дх | < 6.	(5)
Таким образом, если функция f непрерывна в точке х0, то малые изменения аргумента вызывают лишь малые изменения самой функции.
У
f(*0№
~0
Рис. 37
Из неравенства (5) следует также, что непрерывность функции в точке х0 равносильна следующему предельному равенству:
lim If (х0 + Дх) — v->x0
-f(xQ)] =0.
Таким образом, определение непрерывности функции f в точке х0 может быть сформулировано следующим эквивалентным образом.
Функция f называется непрерывной в точке х0, если ее приращение в этой точке является бесконечно малым при Д х ->0.
Если функция f непрерывна в каждой точке некоторого промежутка, то говорят, что функция непрерывна в этом промежутке.
Из равенств (1) и (2) следует, что целая рациональная и дробно-рациональная функции ления.
Рис. 39
непрерывны в своих областях опреде-
Выясним геометрический смысл непрерывности функции в точке.
Пусть функция f непрерывна в точке х0. Это означает, согласно неравенству (5), что для любого е > 0 найдется такое б > 0, что
I / (х0 + Дх) — / (х0) | < е при | Дх | < б, или, что то же самое,
— 8 < f (х0 + Д X) — f (х0) < 8 при |Д хо I < б,
или
f (х0) — 8 < / (Хо + Д X) < f (х0) + 8 при | Дх I < б.
Геометрически последнее неравенство означает, что точки графика данной функции, имеющие абсциссы х0 + Дх при |Д х | <С 6, находятся в полосе, ограниченной двумя прямыми, параллельными оси ОХ и проходящими через точки (0, f (х0)— s) и (0, / (х0)+ е), лежащие на оси ординат (рис. 37).
Таким образом, непрерывность функции f в точке х0 означает геометрически, что все точки графика данной функции лежат в сколь угодно узкой полосе, ограниченной прямыми у = f (х0) — 8 и у = f (х0) + 8, если только абсциссы этих точек лежат в достаточно малой б-окрестности (х0 — б, х0 + б) точки х0.
Отсюда вытекает, в частности, что если функция непрерывна в промежутке (а, Ь), то она не может иметь графика такого вида, какие изображены на рисунках 38 и 39. Другими словами, графики непрерывных функций являются «сплошными» линиями, чем и объясняется само название: «непрерывная» функция.
§ 53. ЗАДАЧА, ПРИВОДЯЩАЯ К ПОНЯТИЮ ПРОИЗВОДНОЙ
В этом параграфе мы рассмотрим более подробно, чем в § 44, одну из тех задач, благодаря которым возникло понятие производной.
1. Средняя скорость прямолинейного движения
Пусть материальная точка М движется вдоль прямой линии. Выберем на этой прямой определенное направление, начало отсчета — точку О и масштабную единицу измерения длин. Полученную ось обозначим через 0s (рис. 40).
Каждому моменту времени t соответствует одно определенное значение пройденного точкой пути s. Таким образом, пройденный точкой путь s является некоторой функцией времени t:
s = f(t).
Зная функцию /, можно найти положение точки в любой момент времени. Поэтому говорят, что эта функция задает закон движения точки М, а равенство s = f (/) задает уравнение ее движения.
Рассмотрим сначала случай равномерного движения точки. Напомним, что движение точки называется равномерным, если за равные промежутки времени точка проходит равные пути. При таком движении путь, пройденный точкой в единицу времени, называется скоростью равномерного движения.
Таким образом, равномерное движение — это движение с постоянной скоростью.
Если движение точки не является равномерным, то для его характеристики вводится понятие средней скорости за некоторый промежуток времени.
Определение. Пусть материальная точка движется прямолинейно по закону
S = / (0.
Если f (/0) = s0 и f (fi) = si, то средней скоростью за промежуток времени от момента времени tQ до момента ti называется число
t0 t
О	Мо	И	8
-О-----	---<,	----о---------
fttol______________,
f(t)
е \	£ ч	Рис. 40
_ % — 50 __ f (^1) f (^о)
ср— t — t	t—t
Очевидно, средние скорости движения в разные промежутки времени могут быть различными. Когда, например, говорят о ско-
рости движения поезда, то имеют в виду его среднюю скорость за определенный промежуток времени, в течение которого поезд возможно замедлял свое движение на подъемах, возможно, двигался быстрее на спусках. Очевидно, на разных участках пути, т. е. в разные промежутки времени, средняя скорость движения поезда
меняется.
Приведем еще один пример. Пусть материальная точка движется по закону
2
где s — путь в метрах, t — время в секундах, g ~ 9,8 м/сек2. Тогда за первую секунду точка проделает путь
s (1) = ^ = 4,9 (м).
За время от t0 = 4 (сек) до ti = 5 (сек) точка пройдет путь s(fl)-s(t0)=	<«) = 44,1 (м).
Таким образом, рассматриваемое движение не является равномерным и средние скорости за разные промежутки времени (от tQ = 0 до ti = 1 и от tQ = 4 до ti = 5) различны.
Упражнения
212, Найти средние скорости движения точки, если она движется2
ся по закону s = за промежутки времени:
а) от f0= 8 (сек) до fi = 9 (сек)-, б) от t0 = 8 (сек) до h = 8,5 (сек)-, в) от t0 = 8 (сек) но ti = 8,1 (сек)-, г) от t0 = 8 (сек) до ti — = 8,05 (сек).
2. Понятие мгновенной скорости
Во многих вопросах естествознания и техники важно знать не среднюю скорость движения, а скорость в данный момент времени, так называемую мгновенную скорость движения.
Для введения этого понятия снова рассмотрим движение материальной точки М вдоль оси 0s и равенство s = f (/), задающее закон этого движения. Попытаемся выяснить, что следует понимать под выражением: скорость в данный момент времени t0. К этому моменту времени точка пройдет путь s0 = f (/0). К любому другому моменту времени t точка пройдет путь s = f (0. Следовательно, за промежуток времени длительности t — /0 между моментами времени tQ и t точка пройдет путь, равный s — s0 = f(t)—f(tQ), co средней скоростью:
r. __ s — so _ f (0 — f (Q t-t, 
Если промежуток времени достаточно мал, то следует ожидать, что за этот промежуток времени средняя скорость движения точки мало изменится. Естественно считать, что, чем меньше промежуток времени от момента tQ до момента t, тем ближе значение средней скорости в этом промежутке к некоторой «истинной» скорости в момент времени t0. Иными словами, естественно считать, что при стремлении t — t0 к нулю, или, что то же, при t -> /0, средняя скорость ц.р будет стремиться как раз к истинной скорости v (/0) в момент времени /0. Таким образом, мы приходим к следующему определению.
Определение. Мгновенной скоростью v (tQ) в момент времени t0 называется предел (если он существует), к которому стремится средняя скорость за промежуток времени от tQ до t при t, стремящемся к tQ, т. е.
v(t0) = lim	.
t - to t — to
Характерной чертой этого определения является то обстоятельство, что оно одновременно указывает и операцию, с помощью которой можно вычислить скорость.
Упражнение
213.	; 1) Найти мгновенную скорость прямолинейного движения материальной точки, движущейся по закону
s (0 = 2/2 + 3/ + 5
(здесь и всюду дальше: s — путь в метрах, t — время в секундах): а) в начальный момент времени; б) в момент времени /0.
2)	Точка движется прямолинейно по закону
<^2)-
Найти мгновенную скорость этой точки: а) в начальный момент времени, б) через 5 сек после начала движения, в) в момент времени t0.
3)	Точка движется прямолинейно по законуs (t) = 5/2 + 2t — 1. Найти мгновенную скорость в момент времени tQ.
4)	Точка движется прямолинейно по закону s (t) == t3. Найти мгновенную скорость в произвольный момент времени /0.
5)	Точка движется прямолинейно по закону s (/) = 2t3 — 3t2. Найти мгновенную скорость в момент времени tQ.
§ 54.	ПОНЯТИЕ ПРОИЗВОДНОЙ
При определении мгновенной скорости прямолинейного движения мы употребили некоторую аналитическую процедуру, которая оказывается пригодной для определения и вычисления не только мгновенной скорости прямолинейного движения, но и определения и вычисления мгновенных скоростей других физических процессов, например: скорости кругового движения, скорости химической реакции, скорости изменения температуры тела и т. п. (более подробно об этом см. в § 74).
Эта аналитическая процедура в самом общем виде может быть описана следующим образом. Пусть задана некоторая функция
У = f (*)•
При переходе ее аргумента х от значения х0 к значению х0 + Дх приращение этой функции равно:
Ду = f(x0 4- Дх) — / (х0)
и характеризует изменение функции в промежутке между х0 и х0+ + Дх. Отношение приращения функции к вызвавшему его приращению аргумента, т. е. отношение
Ду f (*о + Дх) — f (х0)
Дх	Дх
описывает среднюю скорость изменения функции, т. е. изменение функции на единицу изменения аргумента в промежутке между xQ и х0 + Дх.
Очевидно (это вытекает из наших рассмотрений вопроса о скорости прямолинейного движения), предел этого отношения, если он существует, при стремлении приращения аргумента к нулю позволит нам судить о «скорости» изменения данной функции в точке х0. Этот предел и называется производной данной функции в точке х0.
Таким образом, мы принимаем следующее
Определение. Производной данной функции f в точке х называется предел отношения приращения Ay=Af (х) данной функции в точке х к вызвавшему его приращению аргумента Дх, когда последнее стремится к нулю и обозначается символом у’ (читается', «игрек штрих») или f'(x) (читается: «эф штрих, в точке икс»).
Таким o6pa3OMs
yz = lim	,	(1)
A.r - 0 Ax
или, в расшифрованном виде, с указанием точки, в которой отыскивается производная,
Пх + Ах)~Пх) .	(2)
->о Ах
Замечание. Из равенства (2) отчетливо видно, что производная f'(x) данной функции Дх) является также некоторой функцией, а именно функцией, определенной равенством (2) для тех значений аргумента х, для которых существует предел (2).
Операция нахождения производной /'(х) от Данной функции f (х) называется дифференцированием этой функции. Название это связано с тем, то прежде, чем перейти к пределу, составляется о f (х + Ах)— f (х)
отношение разностей ——!, а разность на латинском язы-Ах
ке обозначается словом differentia.
Если функция s — f (f) описывает некоторый закон прямолинейного движения точки, то мгновенная скорость этой точки в момент времени t0 вычислялась по формуле (см. § 53)
г(/0) = lim	.
t to t ^0
Если обозначить t — 10 через At, то
lim
д/->о Az
и, следовательно, скорость v (/0) прямолинейного движения точки в момент времени /0 оказывается равной производной /'(/0) в точке t0 функции /, задающей закон движения. В этом и заключается физический смысл производной: производная пути (по времени) равна скорости движения.
§ 55.	ПРИМЕРЫ ВЫЧИСЛЕНИЯ ПРОИЗВОДНЫХ
Из определения производной вытекает, что операция нахождения производной функции f в точке х распадается на следующие простые операции.
1-й шаг. Рассматриваемому значению аргумента х дается приращение Дх и находится новое значение функции, равное сумме первоначального значения у и приращения Ду:
у + &у = f (х + Дх).
2-й шаг. Находится приращение функции: Ду = f (х + Дх) — — / (*)•
3-й шаг. Вычисляется отношение приращения функции к приращению аргумента:
^У / (х + М — / (*)
Дх	Дх
4-й шаг. Вычисляется предел отношения приращения данной функции к приращению аргумента, когда последнее стремится к нулю:
г (х) = lim — = lim	.
Ах 0 Дх Ах - О	Д V
Примеры. 1) Продифференцировать постоянную функцию: f (х) = С == const для всех х из некоторого промежутка.
Решение. 1-й шаг. Если х + Ах принадлежит рассматриваемому промежутку, то f (х + Ах) = С.
2-й шаг. f (х + Ах) — f (х) = С — С = 0.
о о	/(х + Ах) — f (х)	0 п
3-и шаг. ——'------—= — = 0.
Дх	Дх
4-й шаг. (Су = lim -^Х-+..А-Х1~~7 W = Кт 0 = 0.
А х -> 0	Дх	A v- 0
Таким образом, производная постоянной равна нулю:
(су = 0.
Этого и следовало ожидать, учитывая, что производная характеризует «скорость» изменения функции.
2)	Найти производную единичной функции у = х.
Решение. 1-й шаг. у + А у = х + Ах, так как значение единичной функции при любом значении аргумента равно этому значению аргумента.
2-й шаг. Ау = (х + Ах) — х — Ах.
о » Ду Дх <
3-и шаг. = — = 1.
Дх Дх
4-й шаг. (х)' = lim — = lim 1 = 1.
Ах - 0 Дх Ах - о
Итак, (х)' = 1.
3)	Найти производную функцию у = х2.
Решение. 1-й шаг. у + Ау = (х + Ах)2.
2-й шаг. Ау = (х+Ах)2 —х2 — Ах(2х + Ах).
3-й шаг. — = 2х + Ах.
Дх
4-й шаг. (x2)' = lim — = lim (2х + Ах) = 2х.
Дх - 0 Дх Ал- - 0
В частности, у'(2) = 2 • 2 = 4; у (0,5) = 2 • 0,5 = 1.
4)	Продифференцировать функцию / (х) = Зх2 + 2х — 5.
Решение. 1-й шаг. f (х + Дх) = 3 (х 4- Дх)2 4-+ 2 (х + Дх) — 5.
2-й шаг. / (х + Дх) — —/(х) = 3 (х +Дх)2+2 (х+ + Дх) — 5 — (Зх2+2х—5) = = 6хДх + 3 (Дх)2 + 2Дх = = Дх (6х 4- ЗДх + 2).
З-й шаг. И£+-а£)..-'« _ Дх
= б-v Ч- ЗДх 2.
4-й шаг. (Зх24-2х—5)' = lim 	+	= lim(6x-h ЗДх +
Дх -+ 0	Дх	Дх -* о
+ 2) = бх +2.
В частности, f' (1) = 6 • 14-2=8; f'(3) =6-3 4- 2 = 20 6-1 4-2 = 5.
5)	Продифференцировать функцию (рис. 41):
f(x)= | х| =
— х, если х<0, х, если х 0.
Если х < 0, то в достаточно малой окрестности точки х наша функция совпадает с функцией fi (х) = — х. При вычислении производной существенны лишь значения функции в окрестности точки, в которой производная вычисляется. Поэтому
(Iх I)' — (— ХУ — — 1 ПРИ х < 0.
Аналогично устанавливается, что
(| х |)' = х’ — 4* 1 при х > 0.
Убедимся в правильности наших выводов непосредственным подсчетом. При х < 0 выберем Дх настолько малым, чтобы было х 4- Дх < 0. Тогда
1-й шаг. f (х 4- Дх) = | х 4- Дх | = — (х 4- Дх) = — х — Дх. 2-й шаг. / (х 4- Дх) — f (х) = — х — Дх —| х| = — х — Дх 4-4- х = — Дх.
З-й шаг.
4-й шаг.
f (х 4- Дх) — f (х) _ — Дх =_J.
Дх	Дх
| X I' = lim  Hx4-Ax)-f (x)_ = lim р =_ J при х < 0 Дх - 0	Дх	Дх о
Аналогично проверяется, что при х> 0
Но при х = 0 функция | х| не имеет производной. В самом деле, попробуем применить установленную процедуру вычисления производной.
1-й шаг. f (0 + Дх) = f (Дх) = |Дх| .
2-й шаг. НО + Дх) —/(0) = |Дх| — 0 = |Дх|.
з-й шаг. Ц° + ^)-но> = 1А£1 .
Дх	Дх
4-й шаг. Если Дх стремится к нулю, оставаясь положительным, то
| Дх | = Дх и lim  ( (°) = iim _ = lim (1) = 1.
Дх -> о Дх	дх -> о Дх дх -* о
Дх>0
Если Дх стремится к нулю, оставаясь отрицательным, то | Д х | = = — Дх и
..	/ (0 + Дх) — f (0)	.. — Дх <. , ।.	.
lim •'	= lim-----— lim (—1)= —1.
Ах - 0	Дх	Дх - 0 Дх Дх - о
Дх<0
Таким образом, при различных способах стремления к нулю приращения Дх аргумента х мы получили различные пределы. Отсюда следует, что предел
Нт /(0 + Дх)-Н0) дх -> о Дх
в смысле принятого нами общего определения из § 54 не существует и, следовательно, не существует производной рассматриваемой функции в точке О.
Итак, существуют функции, не имеющие производных в некоторых точках.
В проведенном сейчас рассуждении мы по существу воспользовались новыми понятиями: предела функции при стремлении аргумента к значению х0 слева и предела функции при стремлении аргумента к значению х0 справа, короче, левого и правого пределов функции в точке х0. Настоящий предел функции в точке lim / (х), X -* х0
которым мы занимались ранее и будем заниматься далее, существует в том и только в том случае, когда существуют как правый, так и левый пределы и они совпадают. О правом и левом пределах и соответствующих понятиях см. в § 56.
Таким образом, производной функции f (х) = |х | является функция определенная на всей действительной оси, за исключением точки х = 0:
г м _ а * 1>-=-1пр“^°„'
( + 1 при х > 0.
Изобразим график этой функции (рис. 42).
f(2 + Лх) =
(2 4 Ax) + 1
(2 4 Ax) — 1
6) Пусть f (x)
X — 1 (*¥= 1).
Требуется вычислить /'(2) — значение производной в точке х — 2.
Решим эту задачу двумя способами.
1-й способ. 1-й шаг. Даем значению 2 аргумента х приращение Дх и находим новое значение функции:
3 + Ах
1 + Ах
2-й шаг. Находим приращение функции в точке х = 2:
Д/(2) = /(2
Д1МЙ=1+^_щ = =?4
1 + Ах 2 — 1	1+ Дх
3-й шаг.
4-й шаг.
А/ (2) ___	2
Дх 1+Ах
/' (2) = lim = lim - ~2 - = —2.
Дх - о Дх Дх - 0 1 + Дх
Таким образом, /'(2) — — 2.
2-й способ заключается в том, что мы сначала находим производную в любой точке х из области определения функции.
1 "	г / । л \	х -4- Ах -4- I
1-и шаг. /(х + Дх)— ——--------—— .
х -J- Дх — 1
2-й шаг Д/ (х) = / (х -j- Дх) — f (х) = AztALtJ-----~
х -j- Дх — 1 х — 1
__	— 2Ах
(х — 1) (х + Дх —1)
1ЛЛ	\Л - 41 \л т^л - 1 }
А 	Sf / X I- А/ (X)	2	2
4-и ша< г (х)= 1 ini — —	Inn---------------------------.
Дх-о Ах дх -* о (х — 1)(х -f Дх— 1)	(х— I)2
Следовательно,
Г (2) =-----2—=—2.
' V ’	(2—I)2
Упражнения
214. Дифференцируема ли на всей числовой прямой функция у =•= | 1 — х21? Постройте график производной функции.
215. Пользуясь определением производной, найти производные следующих функций.
1)	у = Зх ф- 2 в точках: а) х, б) х = 2, в) х = 3.
2)	у = ах + b в точке х = 2.
3)	/ (х) = 4х2 — Зх + 1. Найти f\x\, /'(1); /'(— 2); /'(5).
4)	/(х) = — в точках: а) х = 1, б) х = 4.
х_
5)	/ (х) =У х в точках: а) х = 1, б) х = 4.
(х > 0) fi
6)	/(X) = -Ц. Найти /'(X); /'(1); /'(- 1); /'(3).
7)	/(х) =/бх + 2. Найти: a) f(x), б) /'(I).
8)	у = х3 в точке х.
9)	у — ах2 4- Ьх + с в точке х.
10)	f (х) = 2х3 + Зх2 — 2х + 1.
И) f (х) = аах" + шх"-1 + ... + ап_^ + ап.
§ 56.	ОДНОСТОРОННИЕ ПРЕДЕЛЫ
При исследовании функции на непрерывность и в некоторых других вопросах оказываются полезными так называемые односторонние пределы функции в определенных точках. Так, например, функция
f ,,Л = ((х — I)2 при X < 1,
' ' '	+ 1 при X > 1,
график которой изображен на рисунке 43, имеет разные пределы при стремлении аргумента х к точке х = 1 с разных сторон — слева и справа. В самом деле, lim f (х) = lim (х — I)2 = 0,
lim f (х) = lim (х + 1) = 2.
мы столкнулись в примере 5, в котором
/ (0 + Ах)/ (0)
Дх
пределы.
Именно поэтому рассматриваемая функция не имеет предела в точке х = 1 и потому не является непрерывной в этой точке
С подобным обстоятельством функция
<р (Дх) =
имела различные односторонние
Для односторонних пределов употребляются специальные знаки Предел функции f слева в точке х = а обозначается:
lim f (х), или lim f (х), или / (а — 0).
х •+ а — 0	х -* а—
Таким образом, lim / (х) =* lim / (х).
х -> а—0	х -> а
х<а
Предел справа в точке х = а обозначается:
lim / (х), или lim f (х), или / (а + 0)
к а-|-0	х -*
и, следовательно,
lim f (х) — lim f (x).
x -> a-f-0	x -> a
x>a
Еще раз отметим, что для того чтобы существовал предел функции / (х) в точке а, необходимо и достаточно, чтобы в этой точке существовали и были равны оба односторонних предела.
Односторонние пределы
Пт / (* +M —/(*) дх о-	Дх
и lim +
Дх -> о-f-	Дх
называются, соответственно, левой п правой производной функции f в точке х. В примере 5 мы убедились, что функция х имеет в точке нуль обе односторонние производные, но не имеет в этой точке производной.
Упражнения
216. Найти следующие односторонние пределы:
a)	б) lim [%];
х-> 1—0 х 14-0
в) г) lim[x], где п— некоторое целое число. х -> л—0	х -> п4'0
217. Найти пределы: a) lim(x— [х]); б) lim(x— [х]).
х - 2—0	X -* 24-0	»
в) lim(x— [х]); г) lim(x—[х]), где п — целое число.
х -* п—0	х -> п 4- 0
218< Сформулировать определения односторонних пределов в терминах е и 6.
219й Доказать следующую теорему: для того чтобы существо-вал;предел функции f в точке а, необходимо и достаточно, чтобы в этой точке существовали и были равны оба односторонних предела.
Доказать, что для существования в некоторой точке производной данной функции, необходимо и достаточно, чтобы в этой точке существовали и были равны обе односторонние производные.
§ 57. НЕПРЕРЫВНОСТЬ ДИФФЕРЕНЦИРУЕМОЙ ФУНКЦИИ
Т е о р е м а. Если функция / имеет производную в точке х0, то lim 1/(хо + Дх) — /(хо)1 = О,
Дх -♦ 0
т. е. в этой точке функция непрерывна.
Доказательство. lim[/(x0 + Дх) —f(x0)] =
Дх - О
= Пт /(^о + .М-Нхо) . Дд. = ljm Д£(хо). Ит Дх =	0 = 0
дх -> о	Ах	Дх - О Дх Дх -»о
Важное замечание. Из примера 5 § 56, в котором рассматривалась функция /(х) = | х следует, что существуют функции, не имеющие производной в некоторых точках и тем не менее непрерывные в этих точках. Следовательно, обратная теорема неверна.
§ 58. ПРОИЗВОДНАЯ АЛГЕБРАИЧЕСКОЙ СУММЫ ФУНКЦИЙ
Пусть и (х) и v (х) — две функции аргумента х.
Т е о р. е м а. Производная алгебраической суммы двух функций равна алгебраической сумме их производных, если последние существуют, т. е.
[м (х) ± v (х)Г = м'(х) + и'(х).
Доказательство. Докажем теорему для случая суммы двух функций. Эта сумма и (х) + v (х) представляет собой новую функцию:
х -> и (х) + v (х).
Обозначим ее через у:
у (х) = и (х) + v (х), или, короче, без указания аргумента:
у = и + V.
Производную этой функции найдем по общему правилу, пользуясь определением производной.
1-й шаг. Даем избранному значению х аргумента приращение Дх, т. е. рассматриваем новое значение аргумента х + Дх. Тогда новое значение функции и равно и + Дм, новое значение функции v равно v + Дм. Следовательно,
у + Ду — (и + Дм) + (t> + Ди).
2-й шаг. Ду = (и + Дм) + (f + Af) — (м + и) = Дм + Ди.
о „ Ду Ди 4- Ду Ди . Ди
3-и шаг. ~ =------!-- =-----F — .
Дх Дх Дх Дх
4-й шаг. (м + v)' = lim — = lim + — 'j =
дх - о Дх дх о \Дх Дх/ Ди , .. Ду , . , = lim — + lim — = и + v .
Ах 0 Дх Ах - 0 Дх
Замечание. Методом математической индукции можно доказать, что теорема справедлива для любого конечного числа слагаемых:
(wi + w2 + ••• 4~ ипУ =^1+^2 4“ ••• 4" ип-
Упражнения
220. а) Доказать формулу производной суммы конечного числа функций, б) Доказать, что производная разности двух функций равна разности их производных, если последние существуют.
§ 59. ПРОИЗВОДНАЯ ПРОИЗВЕДЕНИЯ ФУНКЦИЙ
Теорема. Производная произведений двух функций и (х) и v (х) вычисляется по следующей формуле Лейбница',
*	| (uv)' = u'v + uv' |
в предположении, что производные и' и v' существуют.
Доказательство. Произведение и (х) • v (х) является новой функцией. Обозначим ее через у:
у = и - V.
1-й шаг. Дадим аргументу х приращение Дх. Тогда новое значение функции у равно:
у + Ду = (и + Ди) (а+ Да).
2-й шаг. Ду= (и + Ди) (а + Да) — uv = а Ди + и Да + Ди- Да.
о „ Ду Дн . Ду . А  Ду
3-и шаг. — = а — + и-----h Ди — .
Дх Дх Дх Дх
4-Й шаг. Заметим, что, согласно теореме о непрерывности дифференцируемой функции, lim Ди = 0. Поэтому дх -> о
z 1- Ду ..	/ Ди . Ду . А Ду\
(иа)' — lim — = lim а — + и — + Ди — =
Ах-> о Лх Дх->о\ Дх Дх Дх/
1- I Аи\ ! 1-	/ Ау\ II- / А Ау\
= lim а — + lim и — + lim Ди — = д%->0\ Дх/ дх -> о \ Ах/ Дх-* о \ Ах/
= ulim — + и lim — 4-lim Ди-lim — = Дх-о Ах дх-оДх Дх-о дх-»оЛх
— vu’ + uv' + 0 • v' — u'v + uv'.
Пример.
l(x + 3) (x + 15)]' = (x + 3)' (x + 15) + (x + 3) (x + 15)' = = (1 4- 0) (x + 15) + (x + 3) (1 + 0) = x + 15 + x 4- 3 = 2x + 18. Следствие. Постоянный множитель можно выносить за знак производной, т. е.
] kf (х)]' = kf (х).
В самом деле, применяя теорему к произведению kf (х), получим:
Ikf (х)Г = (k') f (х) 4- kf(x) = 0 • f (х) 4- kf (х) = kf (х).
Пример. (——3^=(— ] —0= —(х)' = —.
Н	\15	/	\,15/	15V ’	15
Замечание. Для произведения трех функций и, v, w справедлива формула
\UVW)' = и' VW 4- UVW 4~ uvw'.
В самом деле, (uvw)' = [(uv) w]' = (uv)'w 4* (uv) w' = = (u'v + uv') w + uvw' = u'vw + uv'w + uvw'.
Методом математической индукции можно доказать, что
(ищ2...щУ = щ'и2...ип + ищ'2...ип + ... -4- ищ2...и'п.
Пример. [(Зх — 2) (4х + 5) (х — 3)]' - (Зх — 2)'(4х -4 + 5) (х - 3) + (Зх - 2) (4х + 5)'(х - 3) + (Зх - 2) (4х -I- 5) X X (х — 3)' - 3 (4х + 5) (х — 3)+4 (Зх — 2) (х — 3) + (Зх — 2) X Х(4х + 5).
Упражнения
Найти производные следующих функций, потьзуясь доказанными в § 55—59 формулами:
221.	а) у = — 8; б) у = —; в) у = — — ; г) у 2х — 5; 5	4
д) У = 2 - - .
222.	а) у = — х (х — 2); б) у = '—z—у--------------;
в)	у=(2х—3)(3x-f-1); г) у=(-|-х1) (4 х — 2) (у х ''4
д)	у = (х — 4)4; е) у = (2х — З)3; ж) у = Зх2 (1 — х2);
з)	у = х5; и) у = (х2 — 2х + 3) (Зх2 4-2х + 1);
к)	у — (ах + Ь) (сх2 + dx -f- г).
223.	1) /(х) = (Зх + 1) (х — 3). Найта f'(Q): f'(— 1); f(l); Г(2);
2)	/ (х) = Ух (5х + 2). Найти /'(0); /' (- 1); /'(1).
224. Докажите формулу производной произведения для конечного числа множителей.
§ 60. ПРОИЗВОДНАЯ ЧАСТНОГО ДВУХ ФУНКЦИЙ
Теорема. Если функции и (х) и v (х) имеют в точке х производные и если v (х) ф 0, то в этой точке существует производная их частного, которая вычисляется по следующей формуле:
I и \ _ ’i'v — uv1
\V I	V2
Доказательство. Частное является новой функ-v(x)
цией. Обозначим ее через у: и
1-й шаг. Дадим аргументу х приращение Дх. Тогда новое значение функции равно:
2-й шаг.	Ду =	и + Дм	и 		уДм — мДу
		Ду -|- Ду	у Дм Ду	у (у + Ду)
З-й шаг.		A	U К. Дх Дх	
	Дх	у (у 4- Ду)	
4-й шаг. Согласно теореме о непрерывности дифференцируемой функции, lim Ди = 0. Поэтому
х -* 0
Au &v	Дм	Ду
о — —и—	и Игл ——и Игл —
f—Y = lim — — lim ——L —	°	Ах -> о Дх
\у / дх-оДх дх»о у(у4~Ду)	у lim (у + Ду)
Дх-*0
VU — UV и V — uv‘
У2
У • У
§ 61. ПРОИЗВОДНАЯ СТЕПЕННОЙ ФУНКЦИИ С ЦЕЛЫМ ПОКАЗАТЕЛЕМ
Теорема. Производная степенной функции хп с целым показателем равна произведению показателя п на степень хп~1, т. е. (хп)' = их"-1.
Доказательств о. Пусть показатель п > 0, т. е. п — натуральное число. Тогда
Хп — X • X ... X.
п—множителей
Применяя теорему о производной произведения, получим:
(Xя)'= (х • х ... х)'= х' • х ... х + хх' • ... х 4- ... + хх... х' = = х"-1 4- хя-1 4- ... 4- хя-1 = пхя-1,
' п—слагаемых
что и требовалось доказать.
Если п — целое отрицательное число, то п = — т, где т — натуральное число. Применяя теорему о производной частного, получим:
(хя)' = (х"")' = (—) =	= ~т—— =_ ,/гх-и-1= пхп~'
[х”1] х2’я	X2"1
Теорема доказана.
В частности,
(iy=(x-T —^=-L.
Эта формула часто применяется. Запомним ее:
Ш'=— 1 \ X )	X2
Следствие. Если
Р (х) = аохп + сих”"1 + ... + ап~{х + а1г многочлен (целая рациональная функция), то, используя последнюю теорему и ранее полученные формулы, получим:
Р'(х) = (аохп)’ 4- (aixn~1)' 4- ... 4- (а,-, х)' 4- (а„)' =
= паохп~1 4- (п — 1) ахх1-2 4- ... 4- аЛ^.
Примеры. 1) (х4)' = 4х3.
2)	(х10)' = 10х9.
3)	(х-5)' = — 5х-в.
4)	(х-7)' = — 7х-8.
5)	(5х44-4х34-3х24- 2x4-1 )'=5-4х34-4-Зх24-3.2x4-2 = = 20х3 4- 12х2 4- 6х 4- 2.
Упражнения
Найти производные следующих функций:
225.	Доказать методом индукции теорему о производной степенной функции х” при п натуральном.
226.	а) у б) У= В)У = 4>‘ г)у = Зх-\ х£	X	ХУ
227.	а) у = 4х~3; б) у=™±.х~1 .
X
228.	/(х)=	Найти f (х); Г (0); f (1).
1 ox
229.	f(t) =	. Найти f' (0; f' (0); f (1).
230.	/(0=	. Найти f (0; f (0); f (- 1); f(l).
231.	f (x) =	. Найти f (x); f (0; f (0).
ex + d
oqo o\ .	3x2—2x + 5	r_r «,	,	3x2 + 2x +1 t_t °	/
232.	a) у = -. Наити у ; б) y= ——j-1— . Наити у .
noo \ ..	—2x2+ 3x —4 т т ” f	2X3—x4-3 T T „	,
233.	а) у ж --------. Наити у ; б) у=----. Наити у .
X	X 1
234.	Пользуясь определением производной, доказать, что (К*)' = —
3 х2
оое 4х3— Зх2 + 2х—1 гт о ,
235.----у --------л------. Наити у .
Л	2х3 + х	Л
236.	у =	. Найти у'.
Зх3 + х
§ 62.	ПРОИЗВОДНАЯ КОРНЯ КВАДРАТНОГО ИЗ НЕКОТОРОЙ ФУНКЦИИ
Т е о р е м а. Если функция f (х) > 0 и дифференцируема в точке х, то
7	2 Vf(x)	__
Доказательство. Обозначим функцию f (х) через F W:	_
F (х) = Vf (х).
1-й шаг. Дадим значению аргумента х приращение Дх и найдем новое значение функции F:
F (х + Дх) = Vf(x+ Дх). _____________
2-й шаг. F (х + Дх) — F (х) = ]// (х + Дх) —	(х).
о й F (х + Дх) — F (х) _ Vf (х + Дх) — Vf (х) _
О~И шл .---------------—------------------—
Дх	Дх
_. (Vf (х + Дх) - Vfw)(Vi х + дх) + V7~w) =
Дх(/f (х + Дх) + КШ)
= / (* + &х) -Л (х)______!______.
дх Vf.(x+^x) +VTV) '
Так как функция / в точке х дифференцируема, то она непрерывна в этой точке и поэтому
lim/(x + Дх) — f(x)-
Дх -> О
4-й шаг.
(И77*Г)' -•= Um -F--x + Ах) ~ЛДЕ = Dm .(.(х + Дх)-/(х) х
Дх-> О	Дх	Av->0	Дх
X lim --------1---— = Г (х)	= ЛД±.
4х-°/Кх + Дх) +Vf(x)	2Vf (X) 2Vf(x)
п	fi/—5 o"V (x2 — Зх)' 2x — 3
Пример. (J/x2 — Зх) = —--------:
2 Vx2 — 3x	2 Vx2 — 3x
Упражнения
237.	f(x) = Vx3 + x+ 1. Найти f (х); f' (1); f' (2).
238.	/(х) = Ух2+ 4. Найти /'(х); /'(—1); /'(О-
239.	f(x) =1/*EL Найти f (х); /'(2).
Г X + 1
240.	Пользуясь определением производной, доказать, что
Г (х)
33/iW
§ 63.	ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ
С примерами сложных функций мы встречались на протяжении всего курса. Например, при вычислении значений функции
F (Х) = рТ+2
сначала вычисляют значения функции
u = g (х) = х + 2, а потом
f («) = У и.
Определение. Функция F, которая числу х ставит в соответствие число
f [£ Ш
называется сложной функцией, образованной из функций fug.
Символически определение сложной функции записывается так:
x-*/[g(x)l.
Какова область определения сложной функции? Естественно, что число х может принадлежать области определения сложной функции F только в том случае, когда для этого х определена функция g. Но, кроме того, необходимо, чтобы полученное значение g (х) попало в область определения функции /. Итак, область определения сложной функции
х f te (х>]
состоит из таких значений аргумента х, которые входят в область определения функции g и для которых, кроме того, g (х) принадлежит области определения функции /.
Примеры. 1) Если f (х) = 1g х, a g (х) = то сложная функция
/ 1g (х)1 = Igl X
определена только для тех значений аргумента х, для которых Ух > О,
т. е. для х>0. Таким образом, областью определения сложной функции f [g (х)] является положительная полуось (0; +<ю).
2)	Если / (х) = У 1 — х, g (х) = 1g х, то сложная функция
f lg (х)1 = У 1 — 1g х
определена только при условиях х > 0; 1g х < 1, т. е. для значений аргумента х из промежутка (0; 10]:
0 < х < 10.
Для вычисления производной сложной функции служит замечательная формула:
F' (х) = {f [g (х)]}'= f' [g(x)lg'W-	(1)
Естественно, что этой формулой можно воспользоваться только в том случае, если функция g дифференцируема в точке х, а функция / дифференцируема в точке и = g (х). Можно строго доказать, что в этих предположениях сложная функция F тоже дифференцируема в точке х и ее производная действительно выражается формулой (1). Основная мысль этого доказательства очень проста. Если х получает приращение Ах, то и = g (х) получает приращение Ди, а у = F (х) — f (и) — приращение Ду, т. е.
lim =g'(x),
lim = lim = f’ (и) = f [g (х)],
F’ (х) = lim = lim^ •	= f' [g (х)] g' (х).
дх - о Дх дх - о Ди Дх
Точное проведение этого замысла несколько кропотливо. Приведем все же для желающих строгое доказательство в мелком шрифте.
3)	Продифференцировать функцию
у = (х2 + Зх + 5)100.
Решение. Если рассматривать данную функцию как сложную, образованную из функций
у — и100, и = х2 + Зх -+ 5,
то, согласно формуле (1),
у' = 100и" (х2 + 3 х + 5)' = 100 (х2 + Зх + 5)" (2х + 3).
4)	(Г*2 + х + 1)' = -7--^-^ + х + = 2 ух2 + «+1
2x4-1
2 |/ х2 + х + 1 .
5)	По формуле производной сложной функции:
(КТО)' = )-________ Г (х)
' ’	2//(х) ' v 1
в полном соответствии с формулой из § 62.
6)	Продифференцировать функцию
у = V (х3 + 2х2 4- х 4- I)3.
Решение. Последовательно применяя формулу (1), имеем: у' = —z	1	[(х3 + 2х2 -Ь х 4- 1)3Г =
у 2 /(х8 + 2х2 + х +1)3	'
• 3 (*3 + 2x2 + х + *)2+ 2x2 + х + 0' = 2 У (х3 + 2х2 + х + I)3
3 (х3 + 2х2 + х + I)2 (Зх2 + 4х + 1)
2 /(х3 + 2х2 + х + I)3
7)	Продифференцировать функцию _______________________ х3 4- 2х2 -f- х
У ” /х2’4-Зх-|-2 ’
Решение. Поскольку данная функция является частным двух функций, то
, _ (Зх2 4- 4х 4- 1) Vx2 —3x4- 2 — (X3 4- 2х2 4- х) (К х2 4- Зх 4- 2)' =
у ~	х2 4-3x4-2
(Зх2 4-4х 4- 1) Кх2 4-3x4-2 - (х3 4-2х2 4-х) , „ * Q (2х + 3)
_______________________________________2 У х2 + Зх + 2____
х2 + Зх + 2
__ 2 (Зх2 + 4х + 1) (х2 + Зх + 2) — (х3 + 2х2 + х) (2х + 3)
“	(х2 4- Зх 4- 2) у X2 4- Зх 4- 2
Упражнения
241. Из каких функций образованы следующие сложные функции:	______
а) у = ]/х2; б) у =	4- 2х; в) у = (х2 4- х 4- 2)88;
г) у = (1g х)5; Д) у = y/‘lg2x.
Найти их области определения.
242. Продифференцировать следующие функции:
а) у = Ух (х2 4- 2х 4- 5)51; б) у = А+1У-.
У х2 + х
в) у = /(х24-7х+1)20; г) y^/x-H^F2; д)у = -£+^Д-
Операцию образования сложной функции F
F (х) = f (g (х)) из функции fug называют композицией этих функций и обозначают
F^ fog.
Таким образом,
F (х) = (/ о g) (х).
Не надо думать, что операция композиции двух функций обладает переместительным свойством. Напротив, вообще говоря,
f О g go f.
В самом деле, если
/ (х) = 1g х и g (х) = х , то
(/ о g) (х) = lg V~X  (х > 0); (g о f) (х) — у 1g х, (х > 0)
и, следовательно, fog^ go f.
Докажем теперь формулу (1).
Теорема Если функция g дифференцируема в точке х0, а функция f дифференцируема в точке g (х0), то сложная функция fog также дифференцируема в точке х0 и
if о gY (х0) = f (g (х о)) • g' (х0).
Доказательство. Обозначим композицию fog функций f и g через F:
F (х) = f (g (х));
а ее область определения через Ер. Переменную g (х) обозначим через и\ и =-- g (х).
Пусть еще g (х0) = и0.
1-й шаг. Дадим значению х0 аргумента х приращение Дх такое, чтобы х0 + Дх £ Ер. Тогда функция g получит приращение
Дц = g (х0 + Дх) — g (х0) = g (х0 + Дх) — uQ.
Новое значение функции F при этом равно:
F (х„ 4- Дх) = f (g (х„ + Дх)) = / (и0 + Ди).
2-й шаг.
F (х0 + Дх) — F (х0) = / (uz + Ди) — f (g (х0)) = f (и0 4- Ди) — f (и0).
По условию теоремы в точке g (х0) = и0 функция f имеет производную:
f (иа 4- Ди) — f (и0) lim --------7--------= i (uQ) = / (g (x0)).
Дм 0
Поэтому, согласно теореме о связи понятий предела и бесконечно малой (см. § 49), при ди 0
f (ив + Ьи) — f (ив)
--------7---------= / («о) + а Ди), Ди
где функция а бесконечно мала при Ди -> 0:
lim a (Ди) = 0. Aw -* о
Но тогда для всех Ди 0 имеет место равенство
/ («о + Д^) — / (и0) = f (и0) • Ди 4- а (Ди) • Ди, которое справедливо также и при Ди = 0 (проверьте). Следовательно, имеем:
F (х0 + Дх) — F (х0) = // (и0) • Ди 4- а (Ди) • ди.
3-Й шаг
F (х0 + Дх) — F (х0)	Аи	\и
---------7---------- = / W"7“ + « Ди —- .
Дх	Дх	Дх
4-й шаг. Учитывая, что по условию теоремы
получаем:
Р' ( \ г F(%0 Ax) —F(x0) Г Au
F (х0) = lim---------------- = lim \f (uQ) — 4-
A.v - о	Дх	Дх - 0 L Ах
Ди’’
4- а (Ди) —* = / (и0) • g (х0) 4- 0 • g (х0) = / {g (XoJ) • g' (х0), что и требовалось
Упражнения
243. Доказать, что операция композиции обладает сочетательным свойством, т. е. справедливо равенство:
/ О (£ 9 ft) = (/og) o/i.
§ 64. ПОНЯТИЕ ОБРАТНОЙ ФУНКЦИИ
С понятием обратной функции вы уже познакомились в восьмилетней школе. Если функцию
У = f W = X2 рассматривать только при % > 0, то она имеет обратную функцию х = ё (у) = V У- Функция у = 10Л имеет обратную функцию х - 1g у.
В этом параграфе мы уточним понятие обратной функции. Для этого, кроме понятия области определения функции, нам понадобится понятие области изменения функции.
Областью изменения функции f называется множество значений у = f (%), которые функция принимает, когда аргумент х пробегает всю область определения этой функции.
Например, функция f (х) = 10* имеет в качестве области определения всю числовую прямую, а в качестве области изменения полупрямую (0; Н-оо).
Для функции f (х) = 10* уравнение
(1) имеет для любого у из области ее изменения только одно решение: х = g(y). Ставя в соответствие каждому у из области изменения функции это единственное решение уравнения (1), мы и получаем обратную функцию
х = g (у) = 1g у.
Далеко не всякая функция имеет обратную. Например, на рисунке 44 изображен график функции, для которой областью определения является сегмент [а, Ь], а областью изменения — сегмент [с, d]. При у = у0 уравнение (1) имеет три решения: xi, х2 и х3. Следовательно, данная функция не имеет обратной. С такой же ситуацией мы встречаемся при рассмотрении функции f (х) = х2, если считать ее областью определения всю числовую прямую.
Графики функций, имеющих обратную, изображены на рисунках 45, 46. Для наглядности здесь рассматривается случай, когда область определения является сегментом А = [а, Ь], а область изменения тоже сегментом [с, d]. При любом у из В уравнение (1) имеет точно одно решение. Обозначая это решение через g (у), мы получаем обратную фун-
кцию g, которая каждому у € [с, d] ставит в соответствие одно и только одно действительное число, именно то, которое является решением относительно х уравнения
/ (х) = у. (1) Функция g осуществляет отображение множества В (своей области
определения) на множество А (область изменения). Отображение это взаимно однозначно: не только каждому х из А соответствует одно определенное у из В (по закону /), но и обратно, для каждого у из В существует точно одно х из А, которое отображается в это у.
Остается повторить сказанное в общем виде.
Определение. Пусть функция f с областью определения А и областью изменения В такова, что каждое у из области изменения В соответствует только одному х из области определения А. Тогда функцией обратной к функции f называется функция g, которая каждому у из множества В ставит в соответствие то единственное х из А, для которого f (х) = у,
у = f (х) х.
Таким образом, при переходе от функции f к ее обратной функции g область определения и область изменения меняются местами: если функция f отображает множество А на множество В, то обратная функция g отображает В на Л. Соответствующие друг Другу х из А и у из В связаны соотношениями:
/ (х) = у, g (у) = X, которые можно переписать в виде
f [g(у)1 - у; g If (х)1 = х.	(2)
Ясно, что функция f является при этом обратной для функции g, т. е. функции f и g взаимно обратны.
Примеры взаимно обратных функций:
1)	у = у = х2 при х > 0;
2)	у = 10v, у = 1g х при х > 0;
3)	у == 2 — х, у 2 — х при всех х;
4)	у = —, у = — при х =£ 0. X	X
Примеры 3 и 4 показывают, что иногда функция обратна самой себе. Из курса восьмилетней школы вы уже знаете, что графики двух взаимно обратных функций симметричны относительно биссектрисы первого и третьего координатных углов. Отсюда следует, что функция обратна самой себе, если ее график симметричен относительно этой биссектрисы (рис. 47 и 48).
Легко понять, что каждая функция, возрастающая во всей области своего определения, и каждая функция, убывающая во всей области своего определения, имеют обратную.
В самом деле, такие функции не могут в двух точках принимать одно и то же значение, а это и есть единственное условие, достаточное для того, чтобы функция имела обратную.
Ясно, далее, что функция, обратная к возрастающей функции, является возрастающей, а обратная к убывающей — убывающей.
Значительно труднее доказательство следующего важного предложения.
Теорема. Если область определения непрерывной возрастающей или непрерывной убывающей функции является промежутком, то ее область изменения также является промежутком, и в этом промежутке обратная функция непрерывна.
В частности, возрастающая или убывающая на сегменте непрерывная функция отображает этот сегмент на сегмент, при этом обратное отображение тоже непрерывно (см. рис. 45 и 46).
Доказательство сформулированной теоремы выходит за пределы нашего курса, хотя в* отдельных случаях мы по существу ею пользовались уже начиная с седьмого класса, обосновывая, например, наглядную убедительность существования квадратного корня из любого положительного числа.
В качестве следствия сформулированной теоремы докажем теорему о существовании арифметического корня n-й степени из любого положительного числа, которая в восьмом классе была принята без доказательства.
Т е о р е м а. Для любого неотрицательного действительного числа существует арифметический корень п-й степени при любом натуральном п.
Доказательство. При заданном натуральном п функция хп непрерывна, возрастает на положительной полуоси (0; +<») (см. упр. 192) и поэтому, согласно сформулированной выше теореме, отображает полуось (0; +оо ) на некоторый промежуток. Убедимся, что этот промежуток содержит сколь угодно большие числа. Это действительно так. В самом деле, каково бы ни было число М > 1, число Мп > Л4 принадлежит области изменения рассматриваемой степенной функции. Поэтому обратная ей функция g определена на положительной полуоси и такова, что для любого числа у € (0; + оо ), g (у) > 0 и
[g (У)!" = У, но тогда g (у), согласно определению, и есть арифметический корень из числа у:
g (У) = ^У-
Упражнения
244Л Провести подробное доказательство того факта, что функция, обратная к возрастающей функции, возрастает, а обратная к убывающей — убывает.
245« Определяет ли функцию и в какой области условие х у, у3 + у == х,
т. е. числу х ставится ли в соответствие единственное решение относительно у уравнения у3 + у = х?
§ 65. ДИФФЕРЕНЦИРОВАНИЕ ОБРАТНОЙ ФУНКЦИИ
Т е о р е м а. Если функция f имеет в точке х0 производную f' (*о)	0 и в некотором интервале (а; &), окружающем точку
х0, непрерывна и имеет обратную функцию g, то эта обратная функция имеет в точке у0 = f (х0) производную
Доказательство. 1-й шаг. Дадим значению у0 = f (х0) аргумента у приращение Ду, так чтобы у0 + Ду не выходило за пределы области определения функции g и пусть
g (Уо + ду) = х
(а следовательно, у0 + Ду = f (х).
2-й шаг. g (у0 + Ду) — g (у0) = х — х0 = Дх.
3-й шаг. Ag = Ял + А-У-gW = д* = 1
&у	Ау	Ду Ду
Дх
Последняя операция законна, т. е. при Ду =# О, у0 + Ду =И= у0 и, следовательно, g (у0 + Ду) =# g (у0),
х #= х0 и Д х = х — х0#= 0.
4-й шаг. Согласно теореме из § 64, обратная функция g непрерывна в некоторой окрестности точки у0, в частности в точке Уо ~ f W- Поэтому из предельного равенства
lim Ду = lim Д/(х0) = 0
Ау -+ 0 Дх 0 следует
lim Дх = lim [g(y0 + Ду) — g(y0)] =0,
Аг/ -> 0 Дг/ -> 0
и наоборот. Учитывая это, имеем:
g' (у0) = lim = lim —J— =
Д{/ -* О &у Дг/ -> о Ду Дх
_______1 ______1
r А/ (*о) f' (*о) ’ lim ---------
Дх -> о Дх
Упражнения
246*. Доказать формулу дифференцирования обратной функции, используя правило дифференцирования сложной функции.
§ 66. ПРОИЗВОДНАЯ СТЕПЕННОЙ ФУНКЦИИ С РАЦИОНАЛЬНЫМ ПОКАЗАТЕЛЕМ
В этом параграфе рассматриваются только значения х>0. £
Функция у = хп = у/~х является обратной функции g (у) = = у".
Следовательно, по теореме о производной, обратной к функции,
Таким образом,
В частности, (^”)=777.
Если г = — — рациональное число, то, используя формулу дифференцирования сложной функции, получим:
т\'	| / ЦтТ / _l\m—-1 / __1\'
(х')' = (х"~) = lAx"*/ J = т п) \х") =
Упражнения
Найти производные следующих функций:
247. а) у = У^х3; б) у = V хУ х ; в) у = —^=.
ху Зх
248. а) у = 5У"х----Д= + бх4; б) S = 3 Уfa + t УТ----Д=
Их	и t
в) S . зЮ~+2Ю~ + Ю~2
§67. ПРИМЕНЕНИЕ ПОНЯТИЯ ПРОИЗВОДНОЙ В ГЕОМЕТРИИ
В этом параграфе мы рассмотрим лишь одно применение понятия производной в геометрии, а именно в задаче о проведении касательной к графику функции.
Для решения этой задачи нам необходимо прежде всего выработать разумное определение понятия касательной.
1. Понятие касательной к линии
Известное определение касательной к окружности как прямой, имеющей единственную общую точку с окружностью, неприменимо в случае произвольной линии. В самом деле, в случае параболы
у ----- х2 ось Оу, хотя и имеет единственную общую точку с параболой, не является касательной к ней, как это естественно считать, исходя из определения касательной для окружности.
Для того чтобы естественным путем прийти к понятию касательной, рассмотрим некоторую линию (L) и на ней точку Мо (рис. 49). Пусть точка М — некоторая другая точка линии (L). Секущая Л40Л4 при стремлении точки М к точке Л40 вдоль данной линии будет поворачиваться вокруг точки /Ио. Если при этом секущая М0М стремится к некоторому предельному положению М0Т, то, как подсказывают нам наши наглядные представления, естественно прямую MQT назвать касательной к линии (L) в ее точке Мо. Учитывая сказанное, примем следующее определение.
Определение. Прямая М0Т называется касательной к линии (L) в ее точке Мо, если угол / ММ0Т между этой прямой М0Т и секущей Л4ОЛ4 стремится к нулю при стремлении точки М вдоль линии к точке Мо.
Если (L) — окружность, то новое и ранее известное определения совпадают. В самом деле, если М0Т — прямая, имеющая с окружностью лишь одну общую точку, то она перпендикулярна к диаметру M^N, и при стремлении точки М вдоль окружности к точке Л40 угол ОМ^М стремится к 90°, а угол со —	— к
нулю (рис. 49а).
2. КАСАТЕЛЬНАЯ К ГРАФИКУ ФУНКЦИИ
Рассмотрим график функции
У = / (х),
которая в точке х0 имеет производную. Рассмотрим на графике точку /Ио с координатами (х0, / (х0)) и точку М с координатами (х0 + Ах, / (х0+ Ах)) и проведем через них секущую /И0Л4. Угловой коэффициент этой секущей равен
& == f (х° +	~' (хо)
Дх
Стремление точки М вдоль графика к точке 7И0 равносильно стремлению к нулю приращения Ах. Согласно определению производной, получаем:
lim k = lim	W = fr (%0).
М - Мо Дх -> О	&Х
Проведем через точку Л40 прямую MQT с угловым коэффициентом
= f W-
Естественно думать, что эта прямая и будет касательная к графику в точке Л40. Это предположение верно (рис. 496).
Теорема. График дифференцируемой в точке х0 функции f имеет касательную в точке (х0, f (х0)), угловой коэффициент которой равен {'(Хц).
Для доказательства надо лишь установить, что из стремления углового коэффициента k прямой М0М к пределу /?0 вытекает, что угол между прямой Л40Л4 и прямой М0Г стремится к нулю. Этот довольно очевидный факт доказан точно в § 97.
Верно и обратное к сформулированной выше теореме утверждение: если график функции в точке (х0, f (х0)) имеет касательную, не направленную вертикально, то функция / дифференцируема • в точке xQ и ее производная равна угловому коэффициенту касательной.
Примеры. 1) Найти уравнения касательной к кубической параболе f (х) = х3 в точках с абсциссами х = 0 и X = 1.
Решение. Уравнение касательной ищем в виде
у = h + &, где k — угловой коэффициент касательной. Так как
Л(х) - Зх2, то угловой коэффициент касательной в точке с абсциссой х = 0 равен k = f' (0) = 3-0 = 0.
Следовательно, уравнение касательной в точке О имеет вид у == Ь, и так как точка О должна лежать и на касательной,
то b = 0. Поэтому окончательно получаем следующее уравнение касательной:
у = 0.
Таким образом, ось абсцисс касается параболы в точке 0(0, 0).
Этот пример интересен тем, что, оказывается, касательная может пересекать линию в точке касания (рис. 50).
Угловой коэффициент касательной к параболе f (х) = х3 в точке М (1,1) равен
k = /'(1) = 3 • 12 = 3.
Поэтому уравнение касательной в этой точке имеет вид
у = Зх + Ь.
Учитывая, что точка М лежит на касательной и, следовательно, ее координаты должны удовлетворять уравнению касательной, имеем:
1 = 3 • 1 + Ь.
Поэтому b = — 2 и, следовательно, касательной является прямая у = Зх — 2.
2) График функции / (х) = | х| не имеет касательной в точке 0(0, 0), так как функция |х| не имеет при х = 0 производной (см. § 55).
Очевидно, можно указать функции, графики которых не имеют касательных в любом конечном числе точек. Такими функциями являются функции, графики которых являются ломаными (рис. 51).
Любопытно, что знаменитому немецкому математику Вейер-штрассу удалось построить пример функции, которая ни в одной точке не имеет производной и, следовательно, ее график ни в одной точке не имеет касательной. Разумеется, изобразить график такой функции невозможно. Грубо говоря, каждая точка графика такой функции является вершиной ломаной.
Замечание. Понятие касательной позволяет ввести понятие угла между двумя линиями. Под этим понимают угол Z Т\М.йТ2 (рис. 52) между касательными к линиям (LJ и (L2) в точке Мо их пересечения.
Упражнения
249« Найти уравнения касательных к параболе у =□ х2 в точках с абсциссами х = О, х = — 1, х - 1.
з
250. Найти уравнения касательных к гиперболе у = — в точ-х
ках с абсциссами х — — 1, х — 1.
251е Найти уравнение касательной к кубической параболе у = = х3 в точке с абсциссой х = 2.
252« В какой точке линии у — У~х касательная наклонена к оси Ох под углом 45°?
§ 68. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К НАХОЖДЕНИЮ ИНТЕРВАЛОВ МОНОТОННОСТИ ФУНКЦИИ
Теорема 1. а) Если функция f в некотором интервале (а, Ь) имеет производную и является неубывающей, то ее производная в этом интервале положительна или равна нулю.
б) Если функция f в некотором интервале (а, Ь) имеет производную и является невозрастающей, то ее производная в этом интервале отрицательна или равна нулю.
Доказательство, а) Пусть х0 — произвольная точка интервала (а, Ь), тогда если Дх < 0, то, учитывая, что в этом интервале функция f является неубывающей, имеем:
f (х0 + Дх) < f (х0).
Следовательно, при А х< О
f (х0 4- Дх) — f (х0) < 0.
Если Д х >0, то / (х0 4- Дх) > f (х0) и f (х0 4- Дх) — f (х0) > 0.
В обоих случаях отношение приращений функции и аргумента неотрицательно.
((хр 4-Дх) — П*о) Qt
и поэтому
f (х0) = lim ,Нхо4-Дх)—Ихр) >0( дх - о	Дх
что и требовалось доказать.
Часть б) теоремы доказывается аналогично: в случае если функция f является невозрастающей в интервале (а, Ь), то для любой точки х0 £ (а, Ь) имеет место неравенство
f(xB + Дх) — f(x„) < Q Дх
и, следовательно, f (x0) < 0.
Замечание. Если функция f возрастает (или убывает) в интервале (а, Ь), то во всех точках интервала, за исключением, быть может, отдельных точек, не образующих сплошного промежутка, производная данной функции положительна: f (х) > 0, если функция в интервале (а, Ь) возрастает, и отрицательна: f'(x) < 0, если она убывает в этом интервале
На рисунках 53, 54 указаны точки графиков функций, возрастающей и убывающей, в которых касательные параллельны оси Ох, и, следовательно, производные соответствующих функций в абсциссах этих точек равны нулю.
Теорема 2 (обратная), а) Если производная данной функции f во всех точках некоторого интервала существует и неотрицательна, то в этом интервале данная функция является неубывающей.
б) Если производная данной функции во всех точках некоторого интервала существует и неположительна, то в этом интервале данная функция является невозрастающей.
Теорему 2 и следующую за ней теорему 3 мы принимаем без доказательства.
Теорема 3. Если производная функции f в некотором интервале (а, Ь) положительна: f' (х)> О — за исключением, быть может, отдельных точек (не образующих сплошного промежутка), в которых f'(x)=O, то в этом интервале функция f возрастает. Если для всех точек этого интервала производная функции f отрицательна: f'(x)<Z 0—за исключением, быть может, отдельных точек (не образующих сплошного промежутка), в которых f (х) = О, то в этом интервале функция f убывает.
Пояснения. Касательную в точке 7И0 можно рассматривать как секущую, проходящую через эту точку и какую-нибудь
близкую к ней точку М (рис. 55). Поэтому если х > х0, того, чтобы касательные образовывали положительные
то для углы с осью абсцисс, необходимо, чтобы ордината / (х) была больше ординаты f (х0). Если х < х0, то должно быть / (х0) > f (х), а это и означает возрастание функции f (рис. 55а и 56).
В случае, когда/' (х)<0 (рис. 57), касательные к графику функции образуют отрицательные углы с осью абсцисс, и поэтому ординаты точек графика функции убывают по мере роста абсцисс этих точек.
Пример. Найти интервалы возрастания и интервалы убывания функции у = х — х3.
Решение. Данная функция определена для всех действительных значений аргумента: — оо < х < + оо. Так как у' = (х — х3)' = 1 — Зх2,
то у' > 0, если 1 — Зх2 >> 0. Решим последнее неравенство:
Зх2< 1; х2 < -; 1x1
3	1	/3
1	_ 1
—=- < х < уз V з
„ . / 1 1 \
Следовательно, данная функция возрастает в интервале I—^==, и убывает для всех х, удовлетворяющих неравенству 1 — Зх2 < О, т. е. в интервалах —оо, —РисУнке 57азаштрихован интервал возрастания.
Упражнения
Определить интервалы возрастания и интервалы убывания следующих функций:
253.	а) у = Зх + 1; б) у = — 4х + 2; в) у = ах + Ь.
254.	а) у = —; б) у = х2; в) у = Зх2 + 2 х+1; г) у—(х—I)2.
X
255.	а) у = 5х2 — Зх + 1; б) у = х2 — 2х + 5; в) у = — dx2.
256.	а) у = ах2 + Ь;
б)	у = х3; в) у = х2 (х —3);
г)у=гЬ= д)у = ^-
257.	а) у — ах2 + Ьх + с; б) у = — х3 + —х2 + х — 2;
3	2
в)	у = X + -S г) У=угх; д)у = (х —3)/х.
§ 69. ЭКСТРЕМУМЫ ФУНКЦИИ
Рассмотрим функцию f, определенную на сегменте [а, &]. Пусть на рисунке 58 изображен график этой функции. График функции f дает наглядное представление о поведении этой функции. Из графика видно, что наибольшее свое значение (равное f (6)) данная функция принимает в точке Ь, наименьшее значение (равное f (х6)) функция принимает в точке х6. Из графика функции видно также, что эта функция возрастает в интервалах
(хь х2); (х3, х4); (х5, х6); (х7, х8); (х9, Ь), а убывает в интервалах
(а, х(); (х2, х3); (х4, х5); (х6, х7); (х8, х9).
Особое значение для изучения поведения функции имеют точки хь х2, x3i ..., х9, в которых убывание функции сменяется ее возрастанием или наоборот. Говорят, что, например, точках! является точкой минимума функции /, а точка х4 — точкой максимума этой функции.
Введем точные определения.
Рис. 58
Определение 1. Точка х0 из области определения функции называется точкой минимума этой функции, если найдется такая д-окрестноспгъ (х0 — 6, х0 + в) этой точки, что в интервале (х0 — 6, х0), слева от точки х0, функция убывает, а в интервале (х0,	+ 6), справа от точки х0, функция возрастает.
Значения функции в точках минимума называются минимальными значениями этой функции.
Рассмотренная нами функция, график которой изображен на рисунке 58, принимает минимальные значения f (jq); f (х3); f (хб); f (*7); /(хэ) в точках минимума xlt х3, х5, х7, х9.
Определение 2. Точка х0 из области определения функции называется точкой максимума этой функции, если найдется такая д-окрестностъ (х0 — б, х0 + 6) этой точки, что в интервале (х0 — б, х0), слева от точки xQ, функция возрастает, а в интервале (х0, хо + б), справа от точки х0, функция убывает.
Значения функции в точках максимума называются максимальными значениями этой функции.
Рассмотренная нами функция принимает максимальные значения f (х2); f (х4); f (х6); f (х8) в точках максимума х2, х±, xQ, х8.
Точки минимума и максимума функции называются точками экстремальными (слово «экстремум» латинского происхождения и означает буквально — крайний).
Важное замечание. Точка 6, в которой рассмотренная нами функция принимает наибольшее значение, не является, однако, точкой максимума. В самом деле, не существует такого интервала, содержащего точку Ь, в котором данная функция определена, так как справа от точки b функция не определена.
Следует иметь в виду также, что минимальное значение функции может оказаться больше максимального значения этой функции. Так, например, для функции, изображенной на рисунке 59, f (х^ < </(x2).
Теорема Ферма. Если точка xQ является точкой экстремума (мак-
симума или минимума) для функции f и в этой точке существует производная f' (х0), то эта производная необходимо равна нулю: f' (х0) = 0.
Д о к а з а тел ьство. Пусть, например, точка х0 является точкой минимума. Тогда для всех значений аргумента х из некоторого интервала (с, х0), левее точки х0, функция f (х) убывает, а для всех значений
Рис 59
аргумента х в интервале (х0, d), правее точки х0, функция f возрастает. Следовательно, если Дх < 0 и х0 + Д х £ (с, х0), то х0+ Дх < х0 и /(х0+ Дх) > f (х0), т. е. f (х0 + Дх) — / (х0) > 0. Поэтому
/ (х0 + Дх) •—/ (х) Дх
И
f’(х0) = lim +	<о.
дх - о Дх
Если Дх > 0 и х0 + Дх £ £ (х0> d), то х0+ Дх > х0 и / (х0) < f (х0 + Дх), т. е. / (х0 + Дх) — f (х) > 0.
Поэтому
f (х0 + Дх) — / (х0)	0
Дх
lirn Z(Xq +Ах) — /(х0)	0
Ах 0
Таким образом, число f'(x$) одновременно удовлетворяет двум неравенствам: f'(xQ) <0 и f'(xQ)> 0. Но это возможно лишь в случае, если f'(x0) = 0. Теорема доказана.
Геометрический смысл теоремы Ферма заключается в том, что в точке экстремума касательная к графику функции в соответст
вующей ее точке параллельна оси абсцисс, так как тангенс угла ее наклона к оси Ох равен нулю.
Замечание. Теорема Ферма вовсе не утверждает, что если производная данной функции в некоторой точке равна нулю, то в этой точке функция обязательно имеет экстремум. Существуют функции, имеющие в некоторой точке производную, равную нулю, и тем не менее не имеющие в этой точке экстремума.
В самом деле, рассмотрим функцию f (х) = х3. Ее производная /'(х) = Зх2 положительна для всех х О, и, следовательно, эта функция возрастает на всей действительной оси и поэтому не может иметь экстремума (см. рис. 50), хотя при х = 0 ее производная и равна нулю:
/'(0) = 0.
Таким образом, и это практически важно, теорема Ферма указывает лишь те значения аргумента, при которых функция может иметь экстремум, точки лишь «подозрительные» на экстремум. Эти точки — точки, в которых производная функции равна нулю,— называются стационарными точками данной функции, так как в этих точках «скорость» изменения функции равна нулю.
Для нахождения стационарных точек следует найти все корни уравнения
Г W = 0.
Говорят, что теорема Ферма доставляет нам необходимое условие экстремума.
Заметим также, что из этой теоремы вытекает, что точки, в которых функция не имеет производной, также являются «подозрительными» на экстремум.
Например, функция f (х) = |х| в точках х = 0 имеет минимум, но в этой точке данная функция, как известно (см. § 55, рис 41), не имеет производной.
В дальнейшем точки, в которых данная функция либо имеет производную, равную нулю, либо не имеет производной, будем называть критическими точками данной функции.
Пример. Найдем критические функции у = х5 — бх4 + 5х3 + 10.
Так как производная у' = бх4 — 20х3 + 15х2 существует во всей области определения, то критическими точками этой функции являются лишь стационарные точки, т. е. корни уравнения бх4 — 20х3 + 15х2 = 0, или уравнения
бх2 (х — 1) (х — 3) = 0.
Следовательно, точки х4 = 0; х2 = + 1; х3 = 3 являются критическими точками данной функции.
§ 70. ПРАВИЛО НАХОЖДЕНИЯ ЭКСТРЕМУМОВ ФУНКЦИИ
Пусть функция f определена и непрерывна в некотором интервале (а, Ь). Пусть, далее, функция f дифференцируема в этом интервале, за исключением, быть может, точки х0 С (я, Ь), критической для данной функции. Тогда:
1)	если существует такая 6-окрестность (х0 —5, х0+ 6) точки х0, что для всех х С (х0— б, х0), слева от нее производная положительна, f\x) > 0, а для всех х£ (х0, xQ + 6), справа от нее отрицательна, f'(x) < 0, то точка х0 является точкой максимума данной функции, так как при этих условиях, согласно теореме 3 из § 68, функция f в интервале (х0 — б, х0) возрастает, а в интервале (х0, х0+ б) убывает;
2)	если существует такая ^-окрестность (х0 — б, х0 + б) точки xQ, что для всех х£ (х0 — б, х0), слева от нее производная отрицательна, /'(х) < 0, а для всех х £ (х0, х0 + б), справа от нее положительна, /'(%)> 0, то точка х0 является точкой минимума данной функции, так как, согласно той же теореме 3, функция f в интервале (х0—б, х0) убывает, а в интервале (х0, х0+б) возрастает;
3)	если в некоторой ^-окрестности (х0— б, х0 + б) точки xQ производная f функции f сохраняет один и тот же знак, то в этой точке данная функция не имеет экстремума, так как при сформулированных условиях функция f либо возрастает в упомянутой окрестности, если в ней f'(x) > 0, либо убывает, если для всех х из этой окрестности f'(x) < 0.
Пример. Снова рассмотрим функцию
у = х5— бх4 + 5х3 + Ю.
1)	у' = бх4 —• 20х3 + 15х2 = 5х2 (х — 1) (х — 3).
2)	Решив уравнение 5х2 (х — 1) (х — 3) = 0, мы нашли критические точки функции: х{ = 0; х2 = 1,- х3 =3 . Эти точки разбивают область определения данной функции на промежутки:
—оо < х < 0; 0 < х < 1; 1 < х < 3; 3<х<+оо.
В каждом из этих промежутков, как видно из выражения производной, она сохраняет свой знак, и, следовательно, эти промежутки являются промежутками монотонности данной функции. Следовательно, для выяснения знака производной в этих промежутках достаточно вычислить значение производной в какой-нибудь точке этого промежутка. Так, например, при х= — 1 С (—оо, 0) у'> 0, следовательно, и во всем этом промежутке у' > 0.
3)	Составим следующую таблицу (см. стр. 169).
В первой строке этой таблицы расположены в порядке возрастания критические точки. Во второй строке отмечены знаки производной в промежутках, которые определяются критическими точ-168
X	(— 00, 0)	0	(0.1)	1	(1.3)	3	(3, 4-
у'	4-	0	4-	0	—	0	4-
У	возрастает	10	возрастает	11	убывает	— 17	возрастает
		нет экстремума		max		min	
ками. В третьей и четвертой строках сделаны выводы о ходе изменения функции.
Из таблицы видно, что
Ушах = У 0) ~ 11»
так как слева от точки х = 1 / > 0, а справа у' < 0.
Ут1п = у (3) = — 17.
В точке х = 0 функция не имеет экстремума, так как производная и слева и справа от нее имеет один и тот же знак: у' > 0.
Упражнения
Исследовать на монотонность и экстремумы следующие функции:
258.	а) у = Зх2; б) у = —-|х2; в) у = 2х2 4-3.
259.	а) у = 2х2 —8x4-6; б)у = х4--|; в) у = 4х2 — бх — 7.
260.	а) у = 1 х2 — Зх; б) у = х2 — у х4; в) у = у 4-
261.	а) у= 2х3 4- бх2—18х+120; б) у=3/х2; в) у = Зх4— 4х3.
262.	а) у = ]/х ; б) у = бх5 4* 15Х4 4- Юх3; в) у = х2(х— 12)2.
263.	а) у = ——— ; б) у = —~2х + 2 • в) у =
264.	а) у =	16	; б) у =	; в) у = /х2 — 1 ;
х (4 — х2)	У х2 + 8
г) у = ]/х2 — Г2.
§ 71. ИССЛЕДОВАНИЕ КВАДРАТИЧНОЙ ФУНКЦИИ
Функция
у = ах2 4- Ьх 4- с, а ф 0
называется квадратичной (многочлен ах2 + Ьх + с часто называют квадратным трехчленом). Эта функция определена на всей действительной оси.
Найдем интервалы монотонности и экстремумы этой функции. Производная
у' = 2ах + b
существует в каждой точке действительной оси и обращается в нуль в единственной точке (рис. 60 — 66):
ь
X =------.
2а
Из вида производной заключаем, что поведение изучаемой функции зависит от числам — старшего коэффициента (коэффициента при х2). Рассмотрим два возможных случая: а > 0 и а < 0.
1) Если а > 0, то при х<—— у'< О, а при х>-------------------
2а	2а
у' > О.
Следовательно, если а > 0, то
62 — 4ас	D
4а	4а
При этом ymin > 0, если дискриминант D=b2—ymin<0, если D > 0 и ymin = 0, если £> = 0.
Кроме того, наше исследование показывает, что квадратичная функция у — ах2 + Ьх + с убывает в интервале (— оо, — —'j и возрастает в интервале (-, + оо ).
X	I	ь\ \	2а/	Ъ_ 2а	/	Ь	\ 1 — —» + 00 1 \ 2а	]
у'	—	0	+
У	убывает	D 4а	возрастает
		min	
По значению дискриминанта приходится различать три подслучая: 1а). Если а>0 и D<0, то график квадратичной функции у = ах2 + Ьх + с не пересекает оси абсцисс (ymin > 0), лежит выше оси абсцисс и при b <. О имеет вид, указанный на рисунке 60. Если b > 0, то график функции имеет вид, указанный на рисунке 61.
1 б). Если а> 0 и D = 0, то график квадратичной функции у — = ах2 + Ьх + с касается оси абсцисс (yrajn= 0)> лежит выше оси абсцисс и при Ь < 0 имеет вид, указанный на рисунке 62.
В этом случае х = —— является корнем уравнения ах2 + 2а
+ Ьх + с = 0.
1	в). Если а > 0 и D > 0, то ymin = — — < О и график 4а
квадратичной функции у = ах2 + Ьх + с пересекает ось абсцисс в точках Xi и х2 (рис. 63) — корнях уравнения ах2 + Ьх + с = 0.
2	) Если а < 0, то при х < — производная у'> 0, а при —
—- производная у' < 0. Следовательно, если a <Z 0, то 2а
Ь2 — 4ас ___ D
Утах ~ ~л	7~	•
4а	4а
При этом у1пах > 0, если £) > 0, и утах < 0, если D < 0.
X	1	ь\ — 00 — — \	2а/	b х == — — 2а	[	ь	\ — —, + 00 1 \ 2а	)
У'	+	0	—
У	возрастает	D 4а	убывает
		max	
По знаку дискриминанта здесь тоже различаются три подслучая:
2 а). Если а<0 и D > 0, то утах = — — и график 4а
квадратичной функции у = ах2 + Ьх + с пересекает ось абсцисс в точках Xj и х2 (рис. 64)— корнях уравнения ах2 + Ьх + с = 0.
2 б). Если а < 0 и D = 0, то график квадратичной функции у = ах2 + Ьх + с касается оси абсцисс (ушах = 0), лежит ниже оси абсцисс и имеет вид, указанный на рисунке 65.
2 в). Если а < 0 и D < 0, то
Ушах =------<0 и график квад-
40
ратичной функции у— ах2А-Ьх+с лежит ниже оси абсцисс и имеет вид, указанный на рисунке 66.
Линия, являющаяся графиком квадратичной функции, называется параболой. Точка — Д
параболы.
D\
— — 1называется вершиной
Примеры. Пусть требуется построить график функции у = х2 + 2х — 3.
Воспользуемся результатами исследования квадратичной функции: а = 1 > 0; D = 4 + 12 = 16 > 0.
Вершина параболы А (х0, у0) имеет координаты: х0 = —
1;
у„ = — — = —4; х2 + 2х — 3 = 0 при х4 = —Sf, х,= 1.
ли 4а
Следовательно, график данной функции имеет вид, изображенный на рисунке 67. Ее поведение описано в следующей таблице:
X	(— оо, — 1)	х ~ — 1	(-1, +°°)
У'	—	0	+
У ‘	убывает	— 4	возрастает
		m 1 п	
Рис. 65
Замечание, зуясь выведенными получим:
Те же результаты можно получить и не поль-формулами. Дифференцируя у — х2 + 2х — 3,
у' =-- 2х + 2,
у’ — 0 при х = — 1, у' <0 при х<— 1, / > 0 при х > — 1.
Воспользовавшись этими данными и знанием корней уравнения х2 + 2х — 3=0, х4 = —3, х2 — 1, легко понять, как будет выглядеть график. В § 81 мы познакомимся с аналогичными приемами изучения поведения и построения графиков самых разнообразных функций.
Применение к решению квадратных неравенств
Проведенное исследование квадратной функции содержит все необходимое для решения квадратных неравенств. Любое квадратное неравенство приводится к виду:
ax2 + bx-\-c>0.	(1)
На рисунках 60—66 видно, что возможны только такие случаи:
1 а). Неравенство (1) выполняется на всей прямой, рисунки 60 и 61, условия п>0, D<0.
16)	. Неравенство выполняется всюду, кроме точки х = —
2а рисунок 62, условия а > 0, D = 0.
1	в). Неравенство (1) выполняется на двух лучах (—оо; х4) и (х2; оо), рисунок 63, условия а > 0, D > 0.
2	а). Неравенство (1) выполняется на интервале (xf, х2), рисунок 64, условия а<0, D <0.
2	6) и 2 в). Неравенство (1) не имеет решений, рисунки 65 и 66, условия а < 0, D > 0.
Мы не советуем запоминать эти правила. Обычно проще вычислить корни уравнения ах2 4- Ьх + с = 0 и производную у' = — 2ах + b и, разобравшись в поведении функции у = ах2 + Ьх + с, найти множество решений уравнения. Интересен, впрочем, общий результат, что множество решений неравенства либо пусто, либо состоит из интервала, либо из двух лучей, взятых без их начальных точек, либо из всей числовой прямой.
Примеры. 1) Решить неравенство 2х2 4-х — 1 > 0.
Так как дискриминант квадратного трехчлена 2х2 4- х — 1 больше нуля и коэффициент при х2 положителен, то данный трехчлен принимает положительные значения на двух полупрямых (— оо; х() и (х2; 4- со), где xt и х2 — корни трехчлена. Решая квадратное уравнение 2х2 4-х — 1 = 0, получим xt — — 1 и х2 = у, следова-
тельно, решениями неравенства являются х < — 1 и х > ~-
2)	Решить неравенство 4х — х2 < 5.
Данное неравенство равносильно неравенству х2 — 4х 4- 5 > 0. У квадратного трехчлена х2 — 4х 4- 5 дискриминант отрицательный, а коэффициент при х2 больше нуля, следовательно, этот трехчлен при любом действительном х принимает положительные значения. Неравенство х2— 4х 4-5 > 0 выполняется на всей числовой прямой.
3)	Решить неравенство — Зх2 4- 2х 4- 1 > 0.
Квадратный трехчлен —Зх2 4-2х 4-1 имеет положительный дискриминант, а коэффициент при х2 отрицателен. В этом случае трехчлен принимает положительные значения в интервале (л^; х2). Находим корни квадратного трехчлена — Зх2 4- 2х 4- 1: xi = — —  3 х2 = 1.
Таким образом, неравенство —Зх2 4- 2х 1 > 0 выполняется на интервале
4)	Решить неравенство — бх1 2 4~ х — 2 > 0.
Т рехчлен — бх2.4-х — 2 при любом действительном х принимает отрицательные значения, так как дискриминант трехчлена меньше нуля, а коэффициент при х2 больше нуля. Следовательно, неравенство — бх2 + х — 2 не имеет решений.
5)	Решить неравенство —х24~ + 2х—1 >0.
Дискриминант трехчлена — х24~ 4- 2х — 1 равен нулю, коэффициент при х2 отрицателен, следователь-
но, этот трехчлен принимает лишь неположительные значения. Данное неравенство имеет единственное решение х= 1.
6) Решить неравенство — х2 4- 2х — 5 > 0.
Решение: О = 44-5 = 9>0. Поэтому график функции у = = —х2 4- 2х — 5 пересекает ось абсцисс в точках, в которых 4
—х2 4- 2х — 5 = 0, т. е. в точках х4 = — 10 и х2 = 2. При х——11
—х2 4-2х— 5>0. Следовательно, при х<—10 и при х>2име-4
ем — хг 4- 2х— 5>0. Таким образом, решениями данного нера-4
венства являются все действительные числа, удовлетворяющие неравенству х < — 10, либо х> 2.
Упражнения
264а. Исследовать следующие квадратичные функции и построить их графики (двумя способами):
1)у = х2 —7х + 6	2) у = 4х2 4-12x4-9
3) у = х2 —3x4-10	4) у = — Зх2 4-8x4-3
5) ,__1^+2У _3 6)у = -2х> + 4х-7
2646.' Решить следующие неравенства:
1) бх2 —х —2>0 3) х2 — 3x4- 2>0
5) 9х2 — Зх — 2>0
2) 2х2 4- бх 4- 5,5 > 0
4) х2 —2х2 —3<0
6) 2 — х — х2 > 0
§ 72. ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К ПОСТРОЕНИЮ ГРАФИКОВ
Способ построения графика функции по точкам очень несовершенен; даже вычисление ординат большого числа точек может дать
неверное представление о графике функции, а следовательно, и о
ходе изменения функции.
Если предварительно исследовать функцию на монотонность и экстремумы, то потребуется значительно меньше точек и построен-
ный по этим точкам график будет точнее отражать ход изменения функции. Такое исследование удобно проводить по определенному плану:
1.	Находим производную данной функции.
2.	Находим критические точки функции.
3.	Находим промежутки монотонности и экстремумы функции. Для уточнения графика полезно найти еще точки его пересечения с осями координат и несколько других дополнительных точек.
Пример. Построить график функции у = — х4 + 2х2 + 3.
1)	у = — 4х34-4х = — 4х (х — 1)Х Х(х + 1).
2)	Критическими являются точки Xj= — 0; хг — 1; х3 = — 1.
3)	Составляем таблицу:
X		ОО<Х<	1	х <= — 1	—1<х<0	х = 0	0<х<1	х = 0	1 <Х< 4~оо
у'	+	0	—	0	4-	0	—
У	возрастает	4	убывает	3	возрастает	4	убывает
экстремум		max		min		max	
4) Строим график функции (рис. 68),
Упражнения
Исследовать следующие функции и построить их графики:
265.	а) у=х3 — Зх +1; б) у=Зх3—2х2 +4; в) у = Зх4 — _______Зх2 4- 5.
266.	а) у = х3 — Зх2 + 2; б) у = х4; в) у = х5; г) у = Xs + х; д) у = х4— 2х3 + 3.
§ 73. ОТЫСКИВАНИЕ НАИБОЛЬШЕГО И НАИМЕНЬШЕГО ЗНАЧЕНИЙ ФУНКЦИИ В ПРОМЕЖУТКЕ
Пусть на рисунке 69 изображен график функций /, определенной в промежутке [а, Ь]. В точке х2 данная функция имеет максимум, а в точках Xi и х3 — минимум. Наименьшего значения, как это видно на графике, функция достигает в точке х3 — точке своего наименьшего из минимумов. Но свое наибольшее значение функция f принимает на правом конце промежутка — в точке Ь, в которой функция не может иметь экстремума.
Этот пример иллюстрирует следующее правило: для отыскания наименьшего и наибольшего значений функции, дифференцируе-
Рис. 69
мой в данном промежутке, следует найти все критические точки функции, лежащие в данном промежутке, вычислить значения функции в этих точках и на концах промежутка и из всех полученных таким образом чисел выбрать наименьшее и наибольшее.
Заметим, что при решении задач на отыскание наименьшего и наибольшего значений функции нет никакой необходимости точно знать, имеет или не имеет данная функция в критических точках максимум или минимум.
Примеры. 1) Найти наименьшее и наибольшее значения функции
у = 2х3 + Зх2 — 1
в промежутках: a) [— 2; — 0,5]; б) [— 0,5; 1]; в) [1, 3).
Решение. Находим критические точки данной функции. Так как
у' = 6х2 + 6х = 6х (х + 1),
то критических точек две: х = 0 и х = — 1.
а)	В промежутке [—2; — 0,5] лежит лишь одна из критических точек: х = — 1. Так как у (— 2) = — 5; у (— 1) = 0 и
5
у (— 0,5) = — - , то унанм. = у (— 2) = — 5; упа.,б. = у (— 1)= 0. О
б)	у (- 0,5) = - |; у (0) = - 1; у (1) = 4. О
Следовательно, в промежутке [—0,5; 1]
Унаим. У (0) Унаиб. У (D 4,
в)	В промежутке [1, 3) функция у возрастает. Следовательно,
Рис. 70
Унаим. У (1)	4.
Наибольшего значения эта функция в указанном промежутке не достигнет, так как точка х = 3 не принадлежит промежутку.
2) Имеется проволока длиной I (м) (например» 8о м). Требуется огородить этой проволокой прямоугольный участок земли, одна сторона которого примыкает к стене заводского здания так, чтобы площадь огороженного участка была наибольшей.
Решение. Обозначим длину одной из сторон через х. Тогда длина другой стороны равна I — 2х. Площадь прямоугольника является функцией от х и равна (рис. 70)
S (х) = х (I — 2х) ~ 1х — 2х2.
Так как х — длина стороны, то 0 < х <— . Следовательно, задача свелась к исследованию функции S (х) на наибольшее значение в промежутке [0, у].
Находим критические точки этой функции
S'(x) = I — 4х; I — 4х = 0 при х = j
s Ш = - (i— -Ц = - .
\ 4)	4 \	2 /	8
На концах промежутка Ю, — 1 имеем:
S (0) = 0; S (-0 = 0.
Следовательно, своего наибольшего значения функция S достигает I при х = —:
$наи6. = 5 * * В (j) = J ^2)-
В частности, при I = 80 м 5наиб. = 800 м2.
3) Дан прямоугольный лист жести 80 см X 50 см. Требуется изготовить открытую сверху коробку наибольшей вместимости,
вырезая по углам квадраты и загибая оставшиеся кромки (рис. 71).
Решение. Обозначим через х длину стороны вырезаемого квадрата. Легко видеть, что 0 < х < 25, и объем коробки при этом равен
V (х) = х (80 — 2х) (50 — 2х) = 4х3 — 260х2 + 4000х.
Итак, объем коробки является функцией длины стороны вырезаемого квадрата. Задача свелась к исследованию этой функции и отысканию наибольшего ее значения в промежутке [0; 25].
Так как
V (х) = 12х2 — 520х + 4000,
то, решая уравнение 12х2 — 520х + 4000 = 0, найдем стационарные точ-
ЮО	1А о
ки Xi =— и х2 = 10. В промежутке [0; 25] находится лишь одна из них: х2 = 10 (х4>25); V (0)=0; V (25) = 0; V (10) = 10х X 60 • 30= 18 000 (см3). Следовательно, в точке х= = 10 функция V принимает наибольшее значение, и, вырезая квадраты со стороной х = 10 (см), мы получим коробку наибольшего
Рис. 71
объема:
^наиб. = V (10) = 18 000 (см3).
Упражнения
267.	Найти наименьшее и наибольшее значения функции у = = х3 — Зх2 + 3 в промежутках: а) [— 1,11; б) [1,31; в) [3; + «ю).
268.	Найти наименьшее и наибольшее значения функции у — = х4—8х2— 9 в промежутках: а) [— 1,11; б) [0,31; в) [—3, 5].
269.	Найти наименьшее и наибольшее значения функции у = = Зх3 — 9х2 + 3 в промежутках: а) [— 1, 11; б) [1, 31; в) [3, 4].
270.	Материальная точка совершает прямолинейное движение по закону
s (/) = 5/ + 2/2 —| /3,
где s — путь в метрах и t — время в секундах. В какой момент времени t скорость движения точки будет наибольшей и какова величина этой наибольшей скорости?
271.	Показать, что из всех равнобедренных треугольников, вписанных в данный круг, наибольшую площадь имеет равносторонний треугольник.
272.	Найти отношение высоты к диаметру основания цилиндра, который имеет при заданном объеме наименьшую полную поверхность.
273.	Тот же вопрос для конуса.
274.	Найти отношение высоты к диаметру конуса, который при заданном объеме имеет наименьшую боковую поверхность.
275.	Доказать, что из всех прямоугольных треугольников с заданной гипотенузой наибольшую площадь имеет равнобедренный треугольник.
276.	Данное положительное число разложить на два слагаемых гак, чтобы их произведение было наибольшим.
277.	Кусок проволоки данной длины I согнуть в виде прямоугольника так, чтобы площадь последнего была наибольшей.
278.	Какой из прямоугольных треугольников с заданным периметром 2р имеет наибольшую площадь?
279.	Открытый бак с квадратным основанием должен вмещать V литров жидкости. При каких размерах на его изготовление уйдет наименьшее количество жести?
280.	Представить число 12 в виде двух слагаемых, произведение которых имело бы наибольшее значение.
281.	Представить число 10 в виде двух слагаемых так, чтобы сумма их квадратов была наименьшей.
282.	Число 8 представить в виде суммы двух слагаемых так, чтобы сумма их кубов была наименьшей.
283.	Найти положительное число х такое, чтобы разность х — х2 была наибольшей.
284.	В равнобедренный треугольник с основанием 20 см и высотой 8 см вписан прямоугольник, одна из сторон которого лежит на основании треугольника. Какова должна быть высота прямоугольника, чтобы он имел наибольшую площадь?
285.	Тело движется по закону s = 10/ + 18/2 — 2/3 (л). Найти наибольшую скорость движения тела.
286.	Буровая вышка расположена в поле, в 9 км от ближайшей точки шоссе. С вышки надо послать курьера в населенный пункт, расположенный по шоссе в 15 км от упомянутой точки на шоссе (будем его считать прямолинейным). Если курьер делает на велосипеде по полю 8 км в час, а по шоссе 10 км в час, то в какую точку на шоссе ему следует проехать, чтобы в кратчайшее время достичь населенного пункта?
§ 74. ПРИМЕНЕНИЯ ПРОИЗВОДНОЙ В ФИЗИКЕ
Пусть некоторая физическая величина у является функцией времени: у = /(/). При изменении времени от момента /0 до момента /0+ Д/ отношение
/(О-/(/о)^ Н/о + Д/)-/(/о)
/ — /0	Ы
описывает среднюю скорость изменения величины у в промежутке времени от /0 до /0 + Д/, а предел, если он существует,
lim
А/ -*0
f (/о + ^0 — f (^о) ________ ff (4 )
Ki ! Ио
естественно назвать скоростью изменения физической величины у в момент времени /0. Но тогда эта скорость численно равна производной /'(/0) функции f в точке /0. Именно так и поступают в естествознании вообще и в физике в частности.
1.	Когда маховое колесо вращается вокруг некоторой оси, то угол его поворота ср является некоторой функцией времени:
Ф = f (0.
Следовательно, скорость изменения угла поворота в момент времени t, называемая угловой скоростью вращения (обозначается через со), равна производной функции /:
® = Г (0-
Пример. Маховик, задерживаемый тормозом, за t секунд поворачивается на угол ф = (5/— 0,4/2) (радиан). Определить его угловую скорость в момент времени / = 2 (сек) и найти момент остановки вращения.
Решение. Найдем угловую скорость <в(/) в момент времени / (до остановки):
<о (/) = <р' = (5 — 0,8/)
\ сек )
Следовательно, со (2) = 5 — 1,6 = 3,4 /
\ сек /
Вращение прекратится в момент времени t, в который со = 5 — — 0,8/ = 0, т. е. при t = — = 6,25 (сек).
2.	При нагревании тела его температура Т является функцией времени, т. е. существует функция f такая, что
Т == f (/).
Производная этой функции в точке t равна скорости изменения температуры в момент времени t.
3.	Если материальная точка движется прямолинейно по закону s == s (0,
то скорость этого движения равна (см. § 54)
НО = s'(0
и является в свою очередь функцией времени.
Скорость изменения скорости v в данный момент времени называется ускорением движения в рассматриваемый момент времени.
Из этого определения следует, что ускорение а (/) в данный момент времени равно производной от скорости в этот момент:
a(f) = v' (f).
Пример. Известно, что скорость прямолинейного движения изменяется по закону
v = (10 + 2t — б/2) (—V
\ сек I
Определить ускорение в момент времени t = 4 (сек).
Решение.
a (t) = V' = (2 - 10() (—Д
\ceK.il
При
( = 4(сек) а(4) = 2 — 40 = — 38 f— Y
\сек2]
Так как скорость v{t) является производной функции s (0, то ускорение
a (f) =v'(t) = [s' (0Г
и равно, таким образом, производной функции s'. Эта производная от производной s' функции s называется ее второй производной и обозначается символом s" («эс два штриха»). Таким образом.
a(t) = [s'(OF =s"(0.
Примеры. 1) Если f (х) = х3 — Зх2 + 2х — 1, то
f (х) = Зх2 — 6х 4- 2, а /" (х) = 6х — 6.
2) Пусть у = х, тогда
1	1 '	__3_
,	1	1 -2	„ II 2\	1	2	1
у = —— = — х ; у = — х )=-------------х -----------7=.
Л ЧУ х 2	\2	/	4	4хУ х
4.	Скорость не единственная величина в физике, которая может быть вычислена с помощью производной. Мы рассмотрим один пример такого применения.
Рассмотрим металлический стержень длины I с постоянным сечением. Если он изготовлен из однородного материала, то участки одной и той же длины имеют одинаковую массу, и частное
т
I ’
где т — масса всего стержня, называется плотностью стержня.
Если через т (х) обозначена масса куска стержня от точки О до точки х и стержень однороден, то его плотность
Р =
m (х -|- Дх) — т (х) Ах
Но стержень может быть не одинаковой толщины или может быть изготовлен из сплава различных металлов. За счет этого отношение
/и (х + Дх) — т (х) Дх будет различным в разных сечениях и характеризует среднюю плотность стержня от сечения, проведенного через точку х до сечения, проведенного через точку х + Дх (см. рисунок без номера).
В этом случае линейной плотностью в точке х называется предел, к которому стремится отношение массы стержня между сечениями, проведенными через точки х и х + Дх к длине куска между этими сечениями, когда он стягивается в точку. Следовательно,
р(Х) = lim m(x + M-m(x) = т, Дх - О	Дх
Таким образом, линейная плотность в точке равна производной массы стержня (по его длине).
Упражнения
287.	По оси Ох движутся две точки, имеющие следующие законы движения: х = 100 + Ы и х = у /2. С какой скоростью удаляются эти точки друг от друга в момент встречи? (х измеряется в сантиметрах, t — в секундах).
288.	Поворот тела вокруг оси совершается по закону
Ф (/) = З/2 — М + 2.
Найти угловую скорость <о(/) в любой момент времени t и при I = = 4 (сек).
28	9., Маховик, задерживаемый тормозом, за t сек поворачивается на угол ф (/) = 4/— 0,3/2. Определить: 1) угловую скорость &>(/) вращения маховика в момент времени t = 2 (сек); 2) с какого момента времени вращение маховика прекратится?
29	0., Пусть точка движется прямолинейно по закону
s = 2/8 + t — 1.
Найти ускорение точки в любой момент времени.
291.	Точка движется прямолинейно по закону s = -Г/3 +
J./2	2. Найти: 1) ускорение в момент времени t (сек); 2) в
какой момент времени ускорение будет равно: а) 1 см/сек2; б) 2 см/сек2.
292.	Тело массой в 2 кг движется прямолинейно по закону s = = t2 + t + 1, где s — путь в сантиметрах, /— время в секундах. Найти: 1) действующую силу; 2) кинетическую энергию W тела через 2 сек после начала движения.
293.	Неоднородный стержень АВ имеет длину 12 см. Масса его части AM растет пропорционально квадрату расстояния точки М от конца А и равна 10 г при АМ =2 см. Найти: 1) массу всего стержня АВ и линейную плотность в любой его точке М; 2) чему равна линейная плотность стержня в точках А и В.
294.	, Что следует понимать под скоростью реагирования вещества в химической реакции?
295.	; Тело, масса которого т = 3 (кг), движется прямолинейно по закону
s = t2 + 't + 1 М.
Найти кинетическую энергию тела через 5 сек после начала движения.
296.	Колесо вращается так, что угол поворота пропорционален квадрату времени. Первый оборот был сделан колесом за 8 сек. Определить угловую скорость колеса через 48 сек после начала вращения.
297.	Найти силу F, действующую на материальную точку с массой т, движущуюся по закону s = 2/3 — t2 при t = 2.
298.	Точка массы т движется по закону
s = аГ2 + р/ + у,
где а, р и у — постоянные. Доказать, что сила, действующая на точку, постоянна.
299.	Точка движется прямолинейно по закону s = J/7. Показать, что ускорение пропорционально кубу скорости.
300.	у = х3 — 5х2 + бх — 3. Найти у".
301.	f (х) - х4— 2х3 + Зх2 — 4. Найти f(x); f(0); f(3); /(— 3).
302.	f (x) - (2x + l)5. Найти f" (x); f" (0); f(l).
303.	f (x) = V2x + 1. Найти f (0); /'(0); f" (0).
304.	v = ^±1. Найти у".
X— 1
305.	Пусть точка движется прямолинейно по закону s = — --------/3 + 3/2— 5 (время измеряется в секундах, пройденный 6
путь —в метрах). Определить: а) момент времени /, когда ускорение точки равно нулю; б) с какой скоростью движется в этот момент точка.
306.	Тело с высоты 10 м брошено вертикально вверх с начальной скоростью 40 м/сек. Определить: а) на какой высоте от поверхности земли оно будет через 1 сек\ б) скорость и ускорение в момент t = 1 сек\ в) через сколько секунд тело достигнет наивысшей точки и на каком расстоянии от земли.
ГЛАВА СЕДЬМАЯ
ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ, ИХ ГРАФИКИ И ПРОИЗВОДНЫЕ
§ 75. РАДИАННОЕ ИЗМЕРЕНИЕ УГЛОВ И ДУГ
В учебниках геометрии для младших классов средней школы
угол определяется как часть плоскости, ограниченная двумя лучами с общим началом, а дуга — как часть окружности, ограниченная двумя точками. В этом элементарном понимании угол и дуга являются геометрическими фигурами, т. е. множествами точек.
В этом параграфе мы стоим на такой элементарной точке зрения.
При измерении углов можно пользоваться различными единицами измерения. Наиболее привычной единицей измерения является градус. В качестве единицы измерения применяется также прямой угол d:
d = 90°,
1° = - d.
90
(1)
Известно также, что величина угла может изменяться в пределах от 0 до 360°, т. е. от 0 • d до 4d.
Дуги окружности естественно ставятся в соответствие центральным углам (рис. 72). Дуга, стягивающая центральный угол в один градус, называется дуговым градусом и служит наиболее употребительной в практике единицей измерения дуг. Длина дуги в гра-
дусном измерении всегда заключена в пределах 0° < а < 360°.
При а = 0° дуга обращается в точку, а при а = 360° — в полную
окружность.
Во многих вопросах математики наиболее удобной мерой дуг оказывается радиан — дуга, длина которой равна радиусу окружности.
Таким образом, радианная мера дуги окружности — это просто отношение ее длины к радиусу. Поэтому радианная мера дуги в 180°, т. е. полуокружности, равна числу л:
180° — л рад,
1° = Д_ рад 0,0174532 рад,
Г = Ш° ~ 0,00029089 рад,
\60/
I" =	0,000004848 рад.
\6О/
Если а есть радианная мера дуги окружности радиуса R, то ее длина I выражается простой формулой
I = aR.	(2)
Сравнение этой формулы с формулой
получающейся при измерении этой же дуги в градусах, показывает одно из преимуществ радианной меры. Впрочем, с самым существенным ее преимуществом мы познакомимся лишь в § 95.
Угловым радианом называется угол в — градусов, л
В любой окружности центральный угол в один дуговой радиан 180 стягивается дугой в — градусов, т. е. в один дуговой радиан, л
Угол в а радианов стягивается дугой в а радианов. Из формулы (2) получаем: центральный угол в а радианов в окружности радиуса R стягивается дугой длины aR. Следовательно, радианная мера центрального угла равна отношению стягивающей его дуги к радиусу.
Таким образом, радианная мера дуги равна радианной мере угла, который она стягивает. Это позволяет измерять углы дугами любой окружности. Для практического измерения дуг и углов в радианной мере может служить специальный транспортир, на полуокружности которого отмечены радианы и их части (рис. 73).
На рисунке 73 показано измерение углов: АОВ, АОС, A0D, AOF и тем самым измерение стягивающих эти углы дуг: АВ, АС, дЬ, AF. Их радианные меры соответственно равны: 0,5; 1,1; 2; 2,9. Если каждое деление изображенного на рисунке 72 транспортира разделим на 10 равных частей, то получим возможность измерять углы и дуги с точностью до 0,1 радиана.
Для угловых градусов, минут, секунд и радианов сохраняются приведенные выше равенства. Заметим еще, что
а = 90° рад.
Примеры. Выразить в радианной мере углы (дуги) в 45°, 36е, 135°, 250е, 330°.
Рис. 73
Решение.
45°= 45 — рад = - рад,
180 м	4
36°= 36 — рад = - рад,
180 к	5
135°= 135 — рад = — рад,
180 '	4
250° = 250— рад = — рад,
180	18
330° = 330 — рад = — рад.
180	6
В практических расчетах часто приходится градусную меру углов (дуг) переводить в радианную. Чтобы облегчить эту работу, составлены специальные таблицы. Приведем здесь фрагмент таблицы XI из сборника В. М. Брадиса.
85°	1,4835	4853	4870	4888	4905	4923	4940	4957	4975	4992	3	6	9
86°	1,5010	5027	5045	5062	5080	5097	5115	5132	5149	5167	3	6	9
87°	1,5184	5202	5219	5237	5254	5272	5289	5307	5324	5341	3	6	9
88°	1,5359	5376	5394	5411	5429	5446	5464	5481	5499	5516	3	6	9
89°	1,5533	5551	5568	5586	5603	5621	5638	5656	5673	5691	3	6	9
90°	1,5708												
	1 о'	1 6'	12х	18'	| 24'	1 30' 1	| 36'	| 42'	| 48'	| 54'	11'	|2'	3'
Пример. Найти радианную меру угла в 86°38'.
Решение. Слева таблицы отыскиваем 86°, затем перемещаемся по этой строке до столбца таблицы, над которым (или под которым) написано число минут, ближайшее к 38', т. е. до столбца для 36'. На пересечении указанных строки и столбца находим радианную меру 86°36', к которой надо еще прибавить поправку на недостающие 2', и тем самым получаем:
86°36' — 1,5115 2' — 6
Ответ-, arc 86°38'1,5121.
Этими таблицами можно пользоваться при переходе от радианной меры к градусной. Например, требуется найти градусную меру угла а — 1,5248.
Решение. Ищем в таблице число, ближайшее к данной радианной мере, т. е.
1,5254 - 87°24' — 6 —	— 2'
Ответ-. 1,5248 аге 87°22'.
Таблицы Брадиса четырехзначные. Если нужна большая точность, то, затратив лишь немного больше труда, можно воспользоваться такой маленькой табличкой:
п°	п	пп аге п ° = — 180	т'	ят. аге т = 	 180-60	р"	„ ЛР" аге р =	 М 180-3600
1°	0,017 453 29	Г	0,000 290 89	г	0,000 004 85
2°	0,034 906 58	2х	0,000 581 78	2"	0,000 009 70
3°	0,052 359 88	3х	0,000 872 66	3"	0,000 014 54
4°	0,069 813 17	4'	0,001 163 55	4"	0,000 019 39
5°	0,087 266 46	5'	0,001454 44	5"	0,000 024 24
6°	0,104 719 75	6х	0,001 745 33	6"	0,000 029 09
7°	0,122 173 04	7х	0,002 036 22	7"	0,000 033 94
8°	0,139 626 34	8х	0,002 327 11	8"	0,00003878
9е	0,157 079 63	9х	0,002 618 00	9"	0,000 043 63 -
Пример. Найдем радианную меру 56°35'04" .
50° -> 0,872 664 6
6°0,104 719 7
30' -> 0,008 722 7
5' -> 0,001 454 4
4"->0,000 024 2
Ответ-, arc 56°35'04"	0,987 575 6.
Упражнения
307.	Определить градусную и радианную меру углов прямоугольного равнобедренного треугольника, не пользуясь таблицами.
308.	Определить градусную и радианную меру углов четырехугольника, если они относятся как 5 : 9: 10 : 12 (без таблиц).
309.	Определить градусную и радианную меру углов пятиугольника, если они относятся как 6:7:9: 12 : 14 (без таблиц).
310.	Найти угловую скорость диска, вращающегося со скоростью 300 оборотов в минуту (в радианах в секунду).
311.	: Вычислить угловую скорость часовой и минутной стрелки (в радианах в час).
312,	Зубчатое колесо имеет 96 зубцов. Выразить в радианах угол поворота колеса, когда оно повернется против движения часовой стрелки на: 30 зубцов; 36 зубцов; 48 зубцов; 72 зубца; 300 зубцов; 750 зубцов; 984 зубца.
313< Определить внутренние углы пятиугольника, описанного около ок
ружности, если точки касания его сто-
рон делят окружность в отношении 5 : 7 : 10 : 12 : 14.
314,	С помощью таблиц найти радианные меры углов: 15°; 50°36'; 137°; 237°; 142°57'; 273°37'; 315°39'; 345°28'.
315.	С помощью таблиц найти градусные меры углов: 0,4853; 0,3756; 1,3246; 3,1416; 4,9681; 5,3842; 7,1567.
316.	Окружность разделена на восемь равных частей точками А, В, С, D, Е, М, N, Р (см. рис. 73а). Найти радианные меры положительных дуг АВ, AC, AD, АЕ, AM, AN, АР и радианные меры отрицательных дуг АР, AN, AM, АЕ, AD, AC, АВ.
317,	Окружность морского компаса делится на 32 равные части, называемые румбами. Выразить один румб в градусной и радианной
мере.
§ 76. ОБОБЩЕНИЕ ПОНЯТИЯ ДУГИ
Будем рассматривать движение точки по окружности, на которой одно из направлений обхода принято за положительное*. Двигаясь в положительном направлении, точка может пройти дугу в Г, 2° и так далее. Пробежав 360°, она вернется в свое начальное положение. При продолжении движения в ту же сторону она будет пробегать окружность второй раз. Но вполне естественно считать, что точка, пробежавшая всю окружность и еще 1°, пробежала дугу в 361°, а обежав всю окружность два раза, прошла дугу в 720°.
Столь же естественно считать, что при движении точки в отрицательном направлении она пробегает дуги в —Г, —2°, —360°, —361*, — 720° и тому подобное. Таким образом, понятие дуги обобщается на случай дуг в любое числа а градусов, где а — произвольное действительное число.
Мы удовлетворимся сказанным выше и не будем добиваться прямого ответа на вопрос о том, что такое дуга в этом обобщенном смысле.
Естественно, что обобщенные дуги можно измерять в
* Окружность вместе с выбранным на ней направлением называют ориентированной окружностью
радианах. Так мы далее и будем делать по преимуществу. Например, дуга в
— рад = 2 • 2л рад + — рад 4	4
состоит из дважды пройденной в положительном направлении полной окружности с добавлением одной восьмой части окружности, пройденной в том же направлении.
Примем какую-либо точку окружности А за начальную. Отложив от
точки А дугу в а радианов, получим точку М (а). При этом мы имеем в виду, что при положительном а дуга откладывается от точки А
в положительном направлении, а при отрицательном а — отрицате-
льном.
Каждому действительному числу а мы поставили, указанным сейчас способом, вполне определенную точку окружности М (а). Но разным числам а может соответствовать одна и та же точка М (а). Например, точка М на рисунке 74 соответствует числам
Л л । JT .	। JT	q I л
—; 2л + —; 4л 4----; — 2л 4—
3	3	3	3
и вообще любому числу а' вида
а' = 2лл 4- — 3
где п — целое число. Сама начальная точка А соответствует любому числу а вида а = 2лп, т. е.
А = М (2т) при любом целом п.
Вообще для того чтобы двум числам а и а' соответствовала одна и та же точка
М (а) = М (а'), необходимо и достаточно, чтобы дуга в а р-адианов отличалась от дуги в а' радианов целым числом обходов всей окружности, т. е. чтобы
а' — а = 2т
с целым п. Иначе говоря, если точка М соответствует числу а, то все другие числа а', которым соответствует та же самая точка М, даются формулой
а' = 2т + а, где п — произвольное целое число.
Отображение
а -> М (а)
можно представить себе наглядно следующим образом.
1. Приняв радиус окружности г за единицу измерения, обычным способом ставим в соответствие числу а точку Р координатной прямой, для которой
ОР = а.
2. Совмещаем начальную точку координатной прямой О с начальной точкой окружности А, а затем «наматываем» координатную прямую на окружность как гибкую, но нерастяжимую нить. Считаем точку М соответствующей числу а, если на нее при наматывании наложится точка Р с абсциссой а (рис. 75, 75а).
Ясно, что точки прямой, отстоящие друг от друга на расстоянии, равном целому кратному от 2л, наложатся при наматывании на окружность на одну и ту же точку М.
Упражнения
318* Окружность разделена на 12 равных частей, начиная от начальной точки Ао (рис. 76). Какие наименьшие неотрицательные числа изображают полученные точки деления окружности? Какие наименьшие по абсолютной величине отрицательные числа изображают те же точки окружности? (Ответы дать через число л.)
319., Отметить на окружности все точки, изображающие действительные числа вида — п + —, где п — любое целое число.
6	8
320.	Найти радианные и градусные меры дуг и центральных углов, опирающихся на эти дуги, если начало дуг находится в точке Ао (см. рис. 76), а концы этих дуг — в точках деления окружности в задаче 318.
§ 77. ОБОБЩЕНИЕ ПОНЯТИЯ УГЛА
Вполне аналогично обобщается понятие угла. Потребность в таком обобщении возникает при рассмотрении вращательного движения. Будем рассматривать вращение луча, исходящего из неподвижной точки О в плоскости. Условимся в выборе положительного направления вращения (обычно — против часовой стрелки). Понятен смысл выражений «повернуть луч на 90°, 270°, 400° и т. п. или на — 60°, — 500° и т. д.».
Ясно, что при повороте луча на а градусов и при повороте на а' = а + (360п)°
градусов, где п — целое, луч займет то же самое положение.
Следовательно, если заданы два луча с общим началом О А и ОВ, то луч ОА можно совместить с лучом ОВ при помощи вращения многими способами. Например, на рисунке 77 луч ОА совместится с лучом ОВ при повороте на 30°; 390°; 750° ... или — 330°; — 690°; — 1050°...
На рисунке 77 луч О А совмещается с лучом ОВ при повороте на
л 13л	25л
7’ ~6~’ ~ ’
или
13л	35л
Т ’ Г ’
радианов. Общее выражение всех углов поворота, совмещающего луч ОА с лучом ОВ, дается формулой:
— + 2пл, 6
где п — любое целое число, т. е. п = = 0; ± 1; ± 2; ± 3...
321.	Построить векторы, образующие с осью I углы: 60°; 250°; 290°; 1080°; 3850°; — 70°; — 140°; — 190°; — 250°; — 1040°; —2560°, воспользовавшись, где надо, транспортиром.
322,	Определить в градусах величину угла, на который повернется минутная стрелка часов за 5 мин, за 18 мин, за 1 ч 15 мин, за 6	48 мин, учитывая направление поворота стрелки.
323,	Сторона правильного шестиугольника АВ расположена на оси, вершины этого шестиугольника ABCDEF обозначены буквами, расположенными по порядку против движения часовой стрел--——>• ки. Определить углы, образованные векторами АВ, ВС, CD, DE, EF, ЕА с осью I.
324.	Ведро в колодце поднимается на 2 м, если рукоятку ворота повернуть на 5 полных оборотов по ходу движения часовой стрелки. На какой угол надо повернуть рукоятку ворота, чтобы ведро опустилось на 1,25 л?
325.	Два зацепляющихся зубчатых колеса имеют: одно —- 36 зубцов, другое — 48 зубцов. Меньшее колесо сделало три полных оборота по ходу движения часовой стрелки. На сколько градусов повернется при этом большее колесо?
§ 78. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ ЧИСЛОВОГО АРГУМЕНТА
Уравнение х2 + у2 = 1
определяет на координатной плоскости окружность с центром в начале координат О радиуса единица. Эту окружность называют
единичной окружностью. В качестве начальной точки на этой окружности возьмем точку А (рис. 78), лежащую на положительном
луче оси абсцисс. В соответствии со сказанным в § 76 каждому действительному числу а на единичной окружности соответствует вполне определенная точка М (а),
получающаяся, если от начальной точки А отложить дугу в а радианов. Ясно, что координаты х и у точки будут функциями переменного а. Это и есть две первые тригонометрические функции числового аргумента а.
Определение 1. Синусом действительного числа а называется ордината у точки М (а) единичной окружности, соответствующей числу а.
Функция эта обозначается sin а.
Областью определения функции у — sin а является множество всех действительных чисел R.
Так как ордината любой точки единичной окружности по абсолютной величине не превосходит единицы, то областью изменения функции у = sin а является множество всех действительных чисел а, удовлетворяющих неравенству — 1 < у < 1. Кратно эта область обозначается через!—1,1].
Определение 2. Косинусом действительного числа а называется абсцисса х точки единичной окружности М, изображающей число а.
Обозначение: cos а.
Областью определения и областью изменения функции х = = cos а являются соответственно промежутки (—оо, 4-оо ) и [— 1,1], т. е. эти области для синуса и косинуса одинаковы.
Рассмотрим пример: единичная окружность (рис. 79) разделена на 12 равных частей точками Ао, Aif А2, ...,Лц, начиная отточки Ло с координатами (1,0) в положительном направлении. Найти наименьшие неотрицательные числа, изображаемые этими точками, и составить таблицу значений синуса и косинуса этих чисел.
Решение. На рисунке 79 точки деления изображают соот-
/	о 1	л л 2л 5л 7л 4л Зл
ветственно числа (см. задачу 318): 0; —: —;	л;	;
'	6 3 2 3 6	6 3	2
|rt; lj_n . Ординаты этих точек равны соответственно: 0; у; 12L; 1;
/3 . 1. 0. _1. _/3 . _j. _/з . _1
2’2’’	2 ’	3’	’	2 ’	2
Абсциссы тех же точек будут соответственно:
1- ¥£• 1- 0- ——££• —1- — KI- —I- 0- -• КЕ ’2’2’’	2 ’	2 ’	’	2 ’	2 ’ ’ 2 ’	2
Тем самым получаем следующую таблицу искомых значений:
а	0	Л 7	Л 7	л 7	2л Т	5л 7	л	7 л ”7	4л 7"	Зл 7”	5л 7"	11л ~7~
sin а	о	2	/3				0				1		___ j_
		2	2		2	2		~~ 2	2		2	" 2
CHQ С1	1 1	1 1	j_	1 о	1	_1_	L/з		1			о	I _1_	1 KI
LUo	1	2 I	2	1	2	1 2		1 2	2 1		1 2	2
Так как координаты любой точки числовой окружности (см. рис. 78) удовлетворяют уравнению
х2 + у2 = 1, то для любого действительного числа а имеет место равенство
cos2 a + sin2 a = 1.	(1)
В качестве упражнения следует проверить справедливость этого равенства по таблице (2).
К тригонометрическим функциям относят также функции тангенс и котангенс, которые определяются следующим образом.
Определение 3. Тангенсом действительного числа a называется отношение ординаты точки М (а), изображающей на единичной окружности число а, к абсциссе этой же точки, т. е. число —. Котангенсом числа а называется отношение — абсциссы к х	у
ординате точки М (а).
Обозначения: tg а = — и ctg а = —. Если же учтем определи	у
ления синуса и косинуса числа а, то получим равенства: . sin a . cos а
tg a = ----и ctg a —----- .	(2)
cos a	sin a
Из этого определения следует, что для чисел, изображаемых точками единичной окружности с нулевой абсциссой, тангенс не существует; для чисел, изображаемых точками с нулевой ординатой,
котангенс не существует, так как на нуль делить нельзя.
Таким образом, область определения тангенса состоит из всех действительных чисел, кроме чисел вида тиг +у при любом целом
значении и; область определения котангенса состоит из всех действительных чисел, кроме чисел вида ли при любом целом ti.
Для любых а, кроме чисел вида у и, из соотношений (2) вы-
текает равенство
tga • ctg a = 1.
Иногда рассматривают еще две тригонометрические функции — секанс и косеканс, которые определяются следующим образом:
sec a = —— и coseca = —— .	(3)
cos a	sin a
Упражнения
326.	Найти области определения секанса и косеканса.
327.	Дополнить таблицу (2) значениями тангенса, котангенса, секанса и косеканса тех же чисел.
328.	Найдется ли такое значение аргумента х, для которого: t .	21	20
а)	sin х== — , cos х = —;
29	29
•	12	35
б)	sin х=-----, cos х — — ;
'	37	37
ч .	1	2 .
в)	sin х= — , cos X =------?
7	3	5
Упростить следующие выражения с помощью формул (1) и (2):
329. ' ’
330.
331.
. 332.
333.
334.
335.
sin2 а — 1.
sin4a 4* 2 sin2 a cos2 а + cos4a.
(sin а + cos а)2 + (sin а — cos а)2.
sin a ctg а 4* cos а.
cos2 а — cos4 а 4- sin4 а.
sin4 а + cos2 а + sin2 a cos2a.
cos2 а ззб 2 sin2 а—1
1 — sin a	sin а 4- cos а
Доказать следующие тождества:
337.	<8'п о 4-cos а/— 1 = 2tg2a.
ctg a — sin a • cos a
2 sin2 a — 1 cos2 a — 1 ______	1
1—2sin2a 1 — sin2 a cos2 a
339.	------sina+cos ° = sin a 4- cos a.
sin a — cos a tg2 a — 1
340. 1+tg° + tg2 «-. = tg’ a.
1 + ctg a + ctg2 a
34!. J--4..sin.2_a-£°2La_ = 1 - 2 sin a cos a.
(sin a + cos a)2
342.
sin2 a — cos2 a + cos4 a __	4
cos2 a — sin2 a + sin4 a
343. ctg2 a — cos2 a = ctg2 a cos2 a.
§ 79. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ УГЛА И ДУГИ
В курсе математики восьмилетней школы тригонометрические функции считались функциями угла или дуги. Мы начали с другого конца и сначала определили тригонометрические функции числового аргумента. Чтобы вернуться к углам и дугам, будем считать, что тригонометрические функции угла или дуги равны тригонометрическим функциям того же наименования от радианной меры этого угла или этой дуги. Например, sin а означает синус числа а
и синус угла или дуги, радианные меры которых равны а.
Естественно, что это определение в применении к углам и дугам в пределах 0 < a < л или 0° < а° < 180° равносильно принятому в восьмилетней школе.
Пусть на рисунке 80 точка М единичной окружности с центром в начале координат хОу изображает действительное число а. Число а является одновременно радианной мерой дуги AM и угла
АОМ. Градусная же мера дуги AM и угла АОМ равна 1®®?. Поэтому
. / 180 а Sin а = sin ---
\ л
Точно так же понимаются выражения cos a, tg а и ctg а, т. е. вместо того, чтобы писать и говорить: тангенс числа а, тангенс угла или дуги, радианные меры которых равны а, пишут и говорят просто тангенс а. Это позволяет у радианной меры углов и дуг не писать наименований единиц измерения. Наименование сохраняется только у градусной меры. Например, нельзя написать 30° = -, но пишут sin 30° = sin — • cos 30° = cos —’ tg 30° = 6	6 ’	6
= tg — ; ctg 30° == ctg —; cos (5 радианов) = cos 5. 6	6
В четырехзначных математических таблицах М. В. Брадиса имеются таблицы: VII, VIII, IX и X для определения значений тригонометрических функций углов и дуг, выраженных в градусной мере. Там же имеется таблица XII, отрывок из которой приводится ниже:
Тригонометрические функции от аргумента в радианах
COS X tg X
sin х
COS X tg x
sin x
sin x
tgx
•V
COS X
1,20	0,9320	0,3624	2,572	1,60	0,9996	—0,0292	—34,233	2,00	0,9093	—0,4161	—2,1850
1,21	9356	3530	650	1,61	9992	0392	—25,495	2,01	9051	4252	1285
1,22	9391	3436	733	1,62	9938	0492	—20,307	2,02	9008	4342	0744
1,23	9425	3342	820	1,63	9982	0592	— 16,871	2,03	8964	4432	0224
1,24	9458	3248	912	1,64	9976	0691	—14,427	2,04	8919	4522	— 1,9725
1,25	9490	3153	3,010	1,65	9969	0791	— 12,599	2,05	8874	4611	9246
По этой таблице определяются значения тригонометрических функций синуса, косинуса и тангенса от аргумента (угла, дуги), выраженного в радианах, и числового значения аргумента. Например, в равенствах: sin 2,04 = 0,8919; cos 2,04 = —0,4522; tg 2,04 — = — 1,9725 число 2,04 одновременно выражает и радианную меру угла или дуги.
Упражнения
344. С помощью таблицы XII найти значения синуса, косинуса и тангенса чисел: 0,03; 0,30; 0,37; 1; 1,43; 2; 2,15; 3; 3,07.
197
Э
§ 80. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ И КООРДИНАТЫ ВЕКТОРА
Тригонометрические функции позволяют дать простое выражение зависимостям между длиной вектора, его углом с осью абсцисс и его координатами. Чтобы разобраться в этом вопросе, надо вспомнить основные сведения о векторах и их координатах.
Вектор а полностью определяется своим направлением и своей длиной |а|. Векторы можно изображать отрезками прямой (рис. 81). Выбрав любую точку А и отложив от нее по направлению, характеризующему вектор а, отрезок АВ длины |а|, получим изображение вектора а . Вектор, изображаемый отрезком АВ, обозначают через АВ. Например, на рисунке 82 отрезки АВ, CD, EF являются изображениями одного и того же вектора.
АВ = CD = ЕЛ
Рис. 81
Существует еще нулевой вектор с длиной, равной нулю. Он не имеет определенного направления. В ближайшее время он нам пока не понадобится.
На координатной плоскости векторы удобно изображать отрезками с началом в начале координат О:
а = ОА.
Написанное равенство устанавливает взаимно однозначное соответствие между лежащими в плоскости векторами а и конечными точками А изображающих их отрезков О А. Координаты этой точки А называются координатами вектора а и обозначаются через ах и ау (рис. 83).
Вектор единичной длины называется ортом. Орт, имеющий то же направление, что и вектор а, называется ортом вектора а. Если обозначим орт вектора а через е, то (рис. 84)
а = |а | е.	(1)
Введем еще орты i и /, направления которых совпадают соответственно с положительными направлениями осей ОХ и 0Y. В геометрии установлена основная формула, связывающая вектор а с его координатами ах, ау (рис. 85):
а = axi + a j.
(2)
Если
орт вектора а, то

(3)
Пусть теперь вектор а и его орт е образуют с положительным направлением оси Ох угол а. Под углом а мы понимаем угол, на который надо повернуть луч Ох вокруг точки О, чтобы совместить его с лучом ОА.
Из определений § 78 непосредственно вытекает, что координаты ех и еу орта е равны соответственно косинусу и синусу угла а, т. е.
ех — cos а, еу = sin а. Из равенства (1), (3) и (4) получаем:
cos а — и sin а = _2_
(4)
Вспомнив определения остальных четырех тригонометрических функций, получим:
. sin a civ ,
tg а = —— = 2, ctg а = cos а a v
— cos а — g-v sin а ау, 1 I а I
sec а =------= J; esc а —
cos а ах
= 1 = 1И .
sin а
Можно было бы считать равенства esc а =	;
@>у
sin а = JLl ; cos а =	; tg а = aJ.; ctg а = —; sec а = -Ь?1
|а |	1а|	ах	аУ	ах
определением тригонометрических функций. При таком подходе к делу становится понятным, почему их шесть: это все шесть попарных отношений, которые можно образовать для трех чисел:
ах\ |а|.
В курсе математики восьмилетней школы тригонометрические функции определялись как отношения сторон прямоугольного треугольника, что возможно сделать только для острых углов. Эти определения являются частным случаем определений, приведенных выше. Это можно показать следующим образом: поместим прямоугольный треугольник с острым углом а в системе координат хОу, как показано на рисунке 86, тогда длины его катетов b и а будут соответственно абсциссой и ординатой вектора АВ. Тем самым получим:
a	b	.	а	,	b
sin а — —	; cos а =	— ;	tg се	=	— ;	ctg а	= —	.
с	с	b	а
§ 81. ЗНАКИ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
Оси Ох и Оу прямоугольной системы координат делят всю координатную плоскость на четыре части, называемые четвертями или квадрантами. Эти четверти нумеруются против движения часовой стрелки, как показано на рисунке 87. Единичная окружность с центром в начале координат тоже делится на четыре четверти, которые нумеруются так же, как и четверти плоскости.
Любой вектор, выходящий из начала координат, либо расположен на какой-либо оси, либо находится в какой-нибудь чет-
верти. Так, векторы a, b, с, d находятся соответственно в I, II, III, IV четвертях. Далее будем говорить, что указанные векторы образуют с положительным направлением оси Ох углы соответственно I, II, III и IV четвертей.
Точно так же говорят и о числах. Если число а изображается точкой II четверти единичной окружности, то будем говорить, что число а находится во II четверти.
После этих соглашений легко определяются знаки любой тригонометрической функции для любого лового, дугового и числового).
Ординаты векторов I и II четвертей положительны, а III и IV отрицательны. Поэтому синусы чисел (углов) I и II четвертей положительны, а для III и IV четвертей отрицательны.
Абсциссы векторов или точек единичной окружности, находящихся в I и IV четвертях, положительны, а для остальных четвертей они отрицательны. Поэтому косинусы углов и чисел I и IV четвертей положительны, а для остальных четвертей они отрицательны.
значения ее аргумента (уг-
Эти выводы наглядно представлены на рисунке 88.
Там, где синус и косинус числа (угла) имеют одинаковые знаки, тангенс и котангенс положительны, т. е. в I и III четвертях. Где знаки синуса и косинуса различны, там тангенс и котангенс отрицательны, т. е. во II и IV четвертях.
Примеры: 1) Угол 350° находится в IV четверти, поэтому sin 350° < 0; cos 350° > 0; tg 350° < 0; ctg 350° < 0.
2)	Угол — 160° находится в III четверти, поэтому sin (— 160°) <Г < 0; cos (— 160°) < 0; tg (— 160°) > 0; ctg (— 160°) > 0.
3)	Число 2,5 находится во II четверти, поэтому
sin 2,5 > 0; cos 2,5 < 0; tg 2,5 <• 0? ctg 2,5 < 0.
Рис. 88
4)	Число —2,5 находится в III четверти, поэтому sin (— 2,5) <0; cos (—2,5)< <0; tg (—2,5) >0; ctg (- 2,5) > 0.
Упражнения
345. Определить знаки всех тригонометрических функций следующих углов
и чисел: 1) 143°; 2) — 243°; 3) 735°; 4) — 735°; 5) 0,35; 6) — 0,5; 7) 5,6; 8) — 2,5; 9) 7,3; 10) — 7,3.
346. Определить знаки следующих выражений: 1) sin 300° X X cos 200°; 2) sin 193° tg 292°; 3) cos 247° sin 112°; 4) tg 147° ctg 293°; 5) cos 40° sin 120° tg 150°; 6) tg 97° ctg 197° cos 297°; 7) sin 1000° X X cos 840° tg 375°; 8) sin 3 cos 5; 9) cos 8 cos 5 tg 1; 10) tg 5 ctg 3 sin 2; 11) sin (— 5) cos (— 3) tg (— 2) ctg 2.
Пример ы. 1) Найти cos a, tg a, ctg a, если известно, что
12	Зп
sina=— — ил<а<—.
13	2
Решение. Из равенства cos2 a + sin2 a = 1 получаем равенство
cos a = ± У 1 — sin2 a, справедливое при любом значении а. Знак в последнем равенстве выбирается в зависимости от четверти, в которой находится а. В данном примере л < а < у , поэтому получаем cos a = = —У 1 —sin2 а. Далее,
2) Найти sin a, cos a и tg a, если известно, что .	3	л
ctga=-------и — <a<n.
&	4	2
Решение. Так как tga-ctga=l, то
Для отыскания sin а и cos а можно воспользоваться следующими соображениями:
. sin a — 3	— 3t
tg a =---=------=------,
cos a 4 4t
где t — любое отличное от нуля число. Если подберем значение t, так чтобы выполнялось равенство
(-3/)2+(4/)2= 1,	(1)
то будем иметь
sin a = — 3/; cos a = 4Л
Из равенства (1) получаем: 25/2 =1, I = ± —. Но из — < 5	2
< а < л следует, что sin а > 0, т. е. / -------- .
5 3	4	4
Ответ: sin а ; cos а =---------; tg а ==-----.
5	5	3
В следующих задачах по данному значению одной из функций sin a, cos а, tg а, ctg а и данному промежутку, в котором находится а, найти значения остальных трех функций:
О Л *7	*	3 Л
347.	sin а = — , — < а < л.
13	2
348.	cosa= —, — <а<;2л.
5	2
349.	tga = л < а <— . 40	2
350.	ctg а =——, — <а<л.
6	15	2
351.	sina = — —, — <а<2л.
3	2
352.	cos а =— —, л < а < — .
6	2
353.	tga=— —, — <сс<л.
S 35	2
354. ctg а = — , 84
0<а< —.
2
3) Решить уравнение 2 sin2 х — 3 cos х = 0.
Решение. Произведем замену sin2 х равным ему выражением 1 — cos2 х. После этого получается квадратное уравнение
2 cos2 х + 3 cos х — 2 = 0
относительно cos х. Откуда получаем два уравнения:
cos х = — и cos х = — 2.
2
Из первого уравнения получаем: х — 2т ± у. Второе уравнение не имеет решений, так как абсолютная величина косинуса х не может быть больше единицы.
Ответ: х = 2 т . ~ 3
4) Решить уравнение
3 sin2 х + 2 sin х cos х — 5 cos2 х = 0.
Решение. Такое уравнение называется однородным уравнением второй степени относительно sin х и cos х, так как все его
члены имеют вторую степень относительно указанных функций. Если в это уравнение подставим cos х = 0, то получим: sin х = 0. Но не существует таких значений аргумента х, которые бы обращали одновременно синус и косинус в нуль. Поэтому обе части данного уравнения можно разделить на cos х, после чего получим уравнение
3 sin х = 2 cos2 х.
cos2 х — 2 sin x =-------
4
6 cos2 x + 5 cos x + 1 = 0.
ctg x = 2 cos x.
3 tg2 x + 2 tg x — 5 = 0.
2 sin2 x — 3 cos2 x + sin x • cos x = 0.
5 sin2 x — 2 cos2 x — 3 sin x • cos x = 0.
3tg2 x + 2tgx —5 = 0, равносильное данному уравнению. Из последнего уравнения получаем:	tg х = 1 и tg х = — —.
з
Ответ', х = пп + у и х = лп — 0,23.
Упражнения
Решить уравнения: 355. ‘ '	*
356. 357. 358. 359. 360. 361. 362. 7 sin2 х — 8 sin х cos х — 15 cos2 х.
§ 82. ЧЕТНЫЕ И НЕЧЕТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ
Определение 1. Функция у = f (х) называется четной, если ее значения, соответствующие двум любым противоположным значениям аргумента, равны, т. е. выполняется равенство f (—х) = = f (х) при любом значении х из области определения функции.
Определение 2. Функция у = f (х) называется нечетной, если ее значения, соответствующие двум любым противополож
ным значениям аргумента, сами противоположны, т. е. / (—х) = = — f (х) при любом х из области определения функции.
Например, функция у = х2 четная, так как (—х)2 = х2; функция у = х3 нечетная, так как (— х)3 = — х3.
Теорема. Функция у = cos х четная, а функции у — sinx, y=tg х и у = ctg х нечетные.
Доказательство. Любые два противоположных числа а и — а изображаются на единичной окружности двумя точками
Р и Q, симметричными относительно оси Ох (рис. 89). Так как точки Р и Q лежат на единичной окружности, то координатами точки Р будут числа cos а и sin а; координатами точки Q будут числа cos (—а) и sin (— а). Так как точки Р и Q симметричны относительно оси Ох, то их абсциссы совпадают, а их ординаты противоположны. Поэтому при любом а справедливы равенства
cos (— а) — cos а и sin (— а) = — sin а.
Для тангенса и котангенса имеем:
tg(— «) = sin(~al =	S1"~ = — tgа, т. е. tg(— а) =— tgа;
cos (— a) cos а
. . х cos (— a)	cos а .	. .	.	.
ctg(—а)=—i------- =--------=—ctgа, т. е. ctg(—а)==—ctga.
sin (—a)	sin а
§ 83. ПЕРИОДИЧНОСТЬ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
Определение. Функция у = f (х) называется периодической, если для нее существует такое число Z =# 0, от прибавления которого к любому значению аргумента х значение функции не меняется, т. е. равенство
f (X + /) = f (х)
справедливо при любом значении х из области определения функции f.
В этом случае число I называется периодом функции у = f (%).
Если число I является периодом функции у = /(х), то ее периодами будут числа nl при любом целом п.
Теорема. Все тригонометрические функции являются периодическими.
Доказательство. Два числа х и х + 2л изображаются одной и той же точкой единичной окружности (рис. 90), поэтому при любом х, для которого соответствующие функции определены, выполняются равенства:
sin (х + 2л) = sin х, cos (х +2л) = cos х, tg (х + 2л) = tg х, ctg (х + 2л) = ctg х.
Особенно важно знать наименьший положительный период функции. Если /0— наименьший положительный период функции f (х), то все ее периоды заключены в формуле
/ = h/q,
где п — целое*. Говоря о периоде данной функции, чаще всего имеют в виду именно ее наименьший положительный период.
Докажем, что наименьший положительный период функции у = sin х равен 2л. Из равенства sin (х + I) = sin х при х = О получаем sin I = О, I — пп. Из чисел этого вида I = л нам не подходит, так как sin — = 1 =£ sin (— 4- л ] — — 1. Следовательно, наи-2	\ 2	/
меньшим положительным периодом может быть только следующее значение I = 2л.
Наименьший положительный период функции у = cos х тоже равен 2л. В самом деле, из cos (х + /) = cos х при х = О следует cos I — cos 0=1.
Наименьшее положительное I, для которого cos I = 1 , равно 2л.
Для функций у = tg х и у — ctg х наименьшим положительным периодом является число л.
При любом значении х числа х и х + л изображаются точками Р и Q единичной окружности, симметричными относительно начала координат (рис. 91), и поэтому соответственные координаты этих точек противоположны. Если точка Р имеет координаты и и V, то координатами точки Q будут —и и —v. где и = cos х; v = sin х; — и = cos (х + л); — v = sin (х + я).
Тогда tg (х + я) = — = - = tg х; — и и
ctg (х + л) =	— — — ctg х, т. е.
— V V
tg (х + л) =tg х; ctg (х + n)=ctg х.
Свойства четности, нечетности и периодичности тригонометрических функций позволяют упрощать вычисления. Пусть, например, надо найти значения тригонометрических функций числа (угла, дуги) 1-у-, т. е. надо найти
„•17л .	17л	, 17л	,	17л
sm —-;	cos — ;	tg —- ;	ctg	—
О	и	о	О
* В самом деле, если бы у функции f(x) существовал период /' иного вида, то его можно было бы представить в виде
/' = п/0 + г, 0 < г < /0.
Но тогда мы имели бы
Их + г) = f (х + / - nl.) = f (х + Z) = f (х), т. е. г < /0 тоже было бы положительным периодом функции вопреки допущению, что наименьший положительный период равен /0.
ctg ^- = ctg (бл —
□	\	D
гч	• 17л	• / n	л\ • / л\	• л
Решение, sin — = sin 6л---= sin-----=—sin— =
3	\	3/	\	3/	3
=— К1 2 • 17л	л\ / л\ л 1
cos — = cos 6л---= cos-----= COS — = — ,
3	\	3/	\	3/	32
tgly-=	=	=-tg^=- /3,
= ctg
При решении первых двух примеров был выделен период синуса и косинуса, т. е. число 3 • 2л, кратное числу 2л. При решении последних примеров выделен период тангенса и котангенса, т. е. число, кратное л.
Если угол (дуга) задан в градусной мере, то периодами синуса и косинуса будут 360° и любое кратное 360°п. Для тангенса и котангенса — 180° и любое кратное 180°п.
Примеры. 1) sin (—1125°) = — sin 1125° — —sin (360° X
X 3+45°) = sin 45° =
2) cos (—1125°)=cos 1125° = cos (360° • 3 + 45°) = cos 45° =
3) tg (—1125°)=—tg 1125°=—tg (180° • 6+45°)=-tg45°=—1.
§ 84.	ПОСТРОЕНИЕ УГЛА ПО ДАННОМУ ЗНАЧЕНИЮ ТРИГОНОМЕТРИЧЕСКОЙ ФУНКЦИИ И ПРОСТЕЙШИЕ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
Задача 1. Построить угол, синус которого равен а, т. е. решить уравнение sin х — а.
Решение. На единичной окружности (рис. 92) ищем точки, ординаты которых равны а. При этом могут встретиться несколько различных случаев в зависимости от значения а.
а)	Если | а | > 1, то на единичной окружности нет точек с таки
ми ординатами. В этом случае задача не имеет решений и уравнение sin х = а не имеет решений.
б)	Если а = 1 (рис. 92), то на единичной окружности имеется только одна точка В с такой ординатой. Вектор ОВ образует с осью Ох наименьший положительный угол — в радианной мере или 90° в градусной мере.	2
Точка В изображает все числа (углы, дуги) вида 2лп + —,
поэтому решениями уравнения sin х = 1 будут х = 2лп + у при любом целом п.
в)	Если | а) < 1, то на окружности имеются две точки Р и Q с ординатами, меньшими единицы. Векторы ОР и OQ образуют искомые углы а и—а с осью Ох, Наименьшим из них будетa=Z АОР. Решением уравнения будет х{ — а + 2лп и х2 = — а + 2лп, и =	1, 4=2, -Ь~3. -4—... ,
3 а д а ч а 2. Построить угол, косинус которого равен b , и решить уравнение cos х = Ь,
Решение. Строим единичную окружность так же, как и в первой задаче (рис. 93), и ищем на этой окружности точки, абсциссы которых равны Ь.
а)	Если | Ь | > 1, то на единичной окружности нет точек с такими ординатами. В этом случае задача не имеет решений и уравнение cos х = b не имеет решений.
б)	Если b = 1, то на единичной окружности имеется только одна точка А с такой абсциссой. Вектор О А образует с осью Ох искомые
углы.
Решением уравнения cos х ~ 1 будет х = 2лп.
в)	Если b = — 1, то на единичной окружности имеется только одна точка с ординатой — 1. Вектор ОС с осью Ох образует искомые
углы.
Решением уравнения cos х = — 1 будет х = 2лп + л = = л(2п + !)•
г)	Если b = 0, то имеются только две точки с данными абсциссами, это точки В и D, Векторы О В и OD с осью образуют искомые углы, например у, —у, (см. рис. 93).
Точка
все числа
В изображает все числа вида 2лп + ~ , а точка D —
Зя
вида 2ли + —. Оба эти выражения можно заменить од
ним:
1. 2 лп4- я — л • 2п + — ; 2. 2 лп-j- — = 2т + л + 2	2	2
У
Рис. 94
+ ^ = л(2п+1)+ 2J.
В правой части первого равенства число л умножается на четное число 2/г и затем прибавляется^-; в правой части второго равенства число л умножается на нечетное число 2п+1 и затем тоже прибавляется —. Из этого следует, что сумма произведения числа л на любое целое число и числа — изображается какой-либо из точек В или D. Поэтому все числа, получаемые из двух формул, можно получить из одной	. В последнем выражении при k четном
будем получать числа, изображаемые точкой В, при k нечетном — точкой D.
Таким образом, все решения уравнения cos х = 0 имеют вид . л
X = ЯП + — .
2
3	3
Если b = y , то имеем две точки с абсциссами, равными —. Для их нахождения проводим хорду PQ, параллельную оси Оу, на расстоянии — от нее с учетом знака числа b (рис. 93). Векторы 4
ОР и OQ образуют искомые углы с осью Ох. Из этих углов наименьшими по абсолютной величине будут в радианной мере 0,7226 и —0,7226; в градусной мере 4Г24' и —4Г24'.
Решения уравнения cos х ~	:
х = 2лп ± 0,7226	(360°п ± 41°24').
с, и ре-
3 а д а ч а 3. Построить угол, тангенс которого равен шить уравнение tg х — с.
Решение. Опять строим единичную окружность с центром в начале координат (рис. 94). Проведем еще касательную к этой окружности в точке А с координатами (1; 0), которую называют осью тангенсов. Ось Оу и ось тангенсов имеют одно и то же положительное направление (сонаправлены).
Если единичный вектор ОМ образует с осью Ох угол а, то тангенс а равен отношению ординаты точки М к абсциссе этой точки, т. е.
tga= 2. =	=	=
6 х |ОА |	1	4
Таким образом, тангенс угла а, образованного вектором ОМ с осью Ох, по абсолютной величине равен длине отрезка AQ, отсекаемого на оси тангенсов. Знак тангенса определяется направлением отрезка A Q по отношению к положительному направлению оси тангенсов. На рисунке 94 взято число с > 0 и на оси тан
генсов отложен отрезок AQ, по длине равный с в положительном направлении оси тангенсов. Вектор OQ образует с осью Ох один из искомых углов. Так как число л является периодом для тангенса, то все искомые углы получаются по формуле х= = ли + а.
Если с < 0, то отрезок, по длине равный —- с, надо откладывать
в сторону, противоположную положительному направлению оси
тангенсов.
Так как на оси тангенсов можно отложить отрезок любой длины и в любую сторону, то эта задача на построение имеет решение при любом значении с.
Для решения уравнения tg х = с достаточно найти одно число с условием tg а = с и написать ответ: х = зт + а. Например, решить уравнение tg х = )/3. Ответ: х = ли+ .
Задача 4. Построить угол, котангенс которого равен d, и решить уравнение ctg х = d.
Решение. Снова строим числовую окружность и систему координат (рис. 95). Проведем касательную к этой окружности в точке В с координатами (0; 1). Эту касательную называют осью котангенсов. Положительное направление оси котангенсов такое же, как у оси Ох.
Если единичный вектор ОМ образует с осью Ох угол а, то котангенс а равен отношению абсциссы точки М к ее ординате, т. е.
ctg а = — =	= BQ, или ctg а = BQ.
Таким образом, котангенс угла а равен по абсолютной величине длине отрезка BQ, отсекаемого на оси котангенсов продолжением
-
единичного вектора ОМ, образующего с осью Ох искомый угол а. На рисунке d < 0, и поэтому отрезок BQ отложен в отрицательном
направлении оси котангенсов. Вектор OQ образует с осью Ох один из искомых углов а.
Для отыскания всех чисел, удовлетворяющих уравнению ctg х =» = d, достаточно найти одно число а с условием ctg а — d и написать ответ: х = пп а.
Эта задача имеет решение при любом значении d.
Упражнения
363. По заданным значениям тригонометрических функций построить углы и измерить их с помощью транспортиров в градусной и радианной мере. Затем написать общий вид углов, удовлет-3	3
воряющих заданным уравнениям. 1) sin а = — ; 2) cos а =----;
4	4
3) tg а = 2; 4) ctg а = — 2.
§ 85. СВОЙСТВА ФУНКЦИИ у = sin х И ЕЕ ГРАФИК
Так как функция у = sin х периодическая с периодом 2л, то для изучения ее свойств во всей области определения достаточно изучить их лишь в промежутке одного периода, например [0; 2л]. Во всех остальных таких промежутках эти свойства будут повторяться.
Разделим промежуток [0; 2л] на четыре равные части (четверти);
л л	Г	Г	Зл	ГЗл	п
0, — : —; л : л; — ; —; 2л
.	2]	[2	J L	2 J	[2
и докажем следующие свойства данной функции:
1.	В I четверти функция возрастает от 0 до 1.
2.	Во II четверти функция убывает от 1 до 0.
3.	В III четверти функция убывает от 0 до 1.
4.	В IV четверти функция возрастает от —1 до 0. Эти свойства запишем в виде таблицы:
X	0	I четв.	л	II четв.	л	III четв.	Зя 2 *	IV четв.	2л
sin х	0	/	1	\	0	\	— 1	/	0
Стрелки / и \ показывают соответственно возрастание и убывание функции у = sin х.
Для доказательства этих утверждений строим единичную окружность с центром в начале системы координат иОу (рис. 96), где для удобства ось абсцисс обозначена через Ом, и на ней будем отмечать точки, изображающие значения аргумента х, взятого из
промежутка [0; 2л]. Ординаты отмеченных точек окружности будут представлять собой значения синусов чисел, изображаемых этими точками, т. е. yi = sin Xii у2 = sin х2; у3 = sin х3 и т. д.
Из курса геометрии известно, что из всех хорд окружности диаметр имеет наибольшую длину, в нашем случае равную 2, и из двух дуг, меньших полуокружности, большая из них стягивается большей хордой. Так, на рисунке 96 дуга MN меньше дуги QP, и
поэтому хорда NM меньше хорды QP. Так как | NM | = 2yt и |QP| = = 2у2, то 2у1 < 2у2, или у! < у2. Точно так же получается неравенство уз > у4, и если учесть знаки значений синуса, то уз>у6 и у7>Уа- Эти выводы непосредственно видны на рисунке 96.
Таким образом, при перемещении точки М по дуге AM в положительном направлении ее ордината у будет возрастать от 0 до 1, а это означает, что при увеличении значений аргумента х от 0 до у значение функции sin х будет увеличиваться от 0 до 1. Во II четверти из х3 < х4 следует sin х3 > sin х4 и при увеличении значений аргумента х от у до л значение функции sin х уменьшается от 1 до 0. В III и IV четвертях ординаты всех точек, кроме точек л и 2л, отрицательны. Из х6 < хв следует sin х5 > sin хв, из х7 < х8 следует sin x7>sin х8. В III четверти sin х убывает от 0 до —1, в IV четверти sin х возрастает от —I до 0.
Перед построением графика данной функции напомним ее основные свойства:
1.	Область определения этой функции — множество всех действительных чисел (короче — вся числовая ось).
2.	Область изменения [—1, 1], т. е. эта функция ограничена.
3.	Функция sin х нечетная, т. е. справедливо равенство sin (—х) = = — sin х для любого значения аргумента х.
4.	Эта функция периодическая с наименьшим положительным периодом 2л, т. е. равенство sin (х 4- 2л) = sin х справедливо для любого значения х.
5.	Значения этой функции равны нулю для х = лп, где п — любое целое число.
6.	Имеет максимумы, равные 1 при всех х = 2лп +
7.	Имеет минимумы, равные — 1 при всех х = 2лп — — .
8,	При всех х, удовлетворяющих неравенствам 2пп < х < 2лп + л, sin х > 0.
9.	При всех х, удовлетворяющих неравенствам 2лп + л < х < 2лп + 2л, sin х < 0.
Промежутки, указанные в пунктах 8 и 9, называются промежутками знакопостоянства функции у = sin х.
Теперь, используя перечисленные свойства функции у = sin х, будем строить ее график. Для этой цели строим систему координат и единичную окружность с центром в начале координат. Радиус этой окружности выберем, например, равным 1 см (рис. 97). На оси Ох откладываем отрезок ОР длиной 2л см 6,28 см. Далее делим этот отрезок на равные части, например на 16 равных частей. На столько же равных частей делим числовую окружность. Точки деления окружности будут иметь ординаты, равные соответствующим значениям функции у = sin х в точках деления отрезка ОР оси Ох. Если через точки деления числовой окружности проведем прямые, параллельные оси Ох, то точки искомого графика как раз и расположатся соответственно на этих прямых. Соединив полученные точки графика плавной кривой, получим часть искомого графика на отрезке [0; 2л], равном периоду данной функции.
44
Рис. 97
Для более точного построения графика надо единичную окружность и соответственно отрезок ОР делить на большее число равных частей. Можно уточнять отыскание точек графика с помощью таблицы значений синуса числового аргумента (М. В. Брадис, табл. XII).
Чтобы получить весь график данной функции, достаточно перемещать построенную его часть вправо и влево на отрезки оси Ох, кратные 2л (рис. 97).
График функции у = sin х называется синусоидой.
По этому графику можно наглядно представить себе все свойства этой функции, перечисленные в пунктах 1—9. Например, синусои
да симметрична относительно начала координат, т. е. если какая-либо точка F принадлежит синусоиде, то точка F1( ей симметричная относительно начала координат, тоже принадлежит синусоиде (рис. 97). Это справедливо для графиков любых нечетных функций.
Здесь дано геометрическое построение графика функции. Тот же самый график можно построить при помощи таблицы тригонометрических функций числового аргумента (М. В. Брадис, табл.XII).
Упражнения
364.	Построить график функции у = sin х при помощи следующей таблицы:
X	0	0,5	1	1,5	2	2,5	3	3,5	4	4,5	5	5,5	6
sin X	0	0,48	0,84	0,997	0,91	0,60	0,14	—0,35	0,76	-0,98	—0,96	—0,71	—0,28
В качестве масштабного отрезка на осях координат взять 1 см.
365.	Расположить в порядке возрастания числа:
1)	sin 15°; sin 75°; sin 56°.
2)	sin 115°; sin 127°; sin 156°; sin 175°.
3)	sin 220°; sin 250°; sin 265°.
4)	sin 280°; sin 290°; sin 296°; sin 315°; sin 340.
5)	sin 1; sin 1,5; sin 1,52; sin 1,55.
6)	sin 1,8; sin 2,1; sin 2,5; sin 3.
7)	sin 3,5; sin 4; sin 4,2; sin 4,4.
8)	sin 5; sin 5,5; sin 5,8; sin 6.
366.	Отметить по графику промежутки, в которых выполняется неравенство: a) sin х > у ; б) sin х < —	; в) | sin х| .
§ 86.	СВОЙСТВА ФУНКЦИИ >=cosx И ЕЕ ГРАФИК
Для изучения свойств функции у — cos х достаточно изучить их на одном периоде, например [0, 2л]. Во всех остальных таких промежутках эти свойства будут повторяться.
Докажем следующие свойства данной функции:
1.	В I четверти функция убывает от 1 до 0.
2.	Во II четверти функция убывает от 0 до —1.
3.	В III четверти функция возрастает от —1 до 0.
4.	В IV четверти функция возрастает от 0 до 1.
Эти свойства запишем в виде таблицы:
о
I четв.
II четв.
Ill четв.
Зя
2
четв.
2л
Для доказательства строим единичную окружность с центром в начале координат (рис. 98) и на ней будем отмечать точки, изображающие значения аргументах, взятого из промежутка [0, 2л ]. Абсциссы отмеченных точек единичной окружности будут представлять собой значения косинусов чисел, изображаемых этими точками. В первой четверти с увеличением значений аргумента абсцисс-сы будут уменьшаться, т. е. из х2 > Xi следует cos х2 < cos хР Причем значения аргумента х возрастают от0 до — , а значения
cos х убывают от 1 до 0. Во II четверти из х4 > х3 следует cosx4< < cos х3, и при увеличении значений аргумента х от — до л значения cos х становятся отрицательными, убывая то 0 до I. В III и IV четвертях из х6> х5 следует cos х6> cos х5 и из х8> х7 следует cos х3> cos х7. Значения аргумента возрастают от л до 2л и значения cos х возрастают от —1 до 1.
Это и показано в вышеприведенной таблице (3).
Прежде чем строить график функции у = cos х, напомним ее основные свойства, установленные ранее:
1.	Область определения этой функции — множество всех действительных чисел (вся числовая ось).
2.	Область изменения [—1, 1], т. е. эта функция ограничена.
3.	Функция у = cos х четная.
4.	Значения этой функции равны нулю при всех х — л/г +
5.	Функция у = cos х периодическая с наименьшим положительным периодом 2л.
6.	Имеет максимумы, равные 1, при всех х = 2/гл.
7.	Имеет минимумы, равные —1, при всех х = (2n + 1) л.
8.	При всех х, удовлетворяющих неравенствам 2л/г —	<
< х < 2лп + —, имеем: cos х > 0.
2
9.	При всех х, удовлетворяющих неравенствам 2ли +	<х<
<2п(п + 1)
cos х < 0.
Промежутки, указанные в пунктах 8 и 9, называются промежутками знакопостоянства функции
у = cos х.
График функции у = cos х построим по точкам с помощью следующей таблицы ее значений для промежутка [0, 2л] (рис. 99):
X	0	0,5	1	1,5	2	2,5	3	3,5	4	4,5	5	5,5	6	2Л
COS X	1	0,88	0,54	0,07	—0,42	-0,80	—0,99	—0,94	-0,65	—0,21	0,28	0,71	0,96	1
Рис. 99
По графику (рис. 99) можно наглядно представить себе все свойства функции у = cos х, перечисленные в пунктах 1—9. Например, этот график симметричен относительно оси ординат. Это свойство графиков справедливо для всех четных функций.
Если построим графики функций sin х и cos х в одной и той же системе координат, как это показано на рисунке 100, то увидим, что они отличаются друг от друга только тем, что имеют различное расположение относительно системы координат. Так, если синусоиду сдвинем в отрицательном направлении оси абсцисс на отрезок то получим график функции у = cos х. Это следует из того, что при любом значении аргумента х выполняются равенства
sin | х + —) = cos х и cos | х + —) = — sin x.
\	2/	\	2/
Рис. 100
Для доказательства последних утверждений на единичной окружности (рис. 101) произвольно выберем четыре точки, делящие ее на четыре равные части. Из равенства треугольников OAiA; BBiO; OCiC и DDiO следует, что если координаты точки А обозначим через и и v, т. е. положим А (и, v), то остальные точки будут иметь следующие координаты: В (—v, и), С (—и, —и) и D (о, —и). Это показывает, что при переходе от любой из отмеченных точек к соседней в положительном
направлении абсцисса первой
становится ординатой другой, а ордината первой меняет свой знак и становится абсциссой второй точки. Если какая-либо из отмеченных точек изображает число х, то ее координатами будут числа (cos х, sin х). Тогда соседняя с этой точкой в положительном направлении точка по доказанному будет иметь координаты
(— sin х, cos х).
Но эта соседняя точка изображает число х + —, и поэтому ее координатами будут числа (cos^x + yj, sin (х + -^j. Так как числа (— sin х, cos х) и (cos ^х + sin (х + yjj являются координатами одной и той же точки, то отсюда и следуют равенства sin | х + —) = cos х и cos | х + — ) = — sin x,
\	2 /	\	2 ./
справедливые при любом значении аргумента х.
На рисунке 100 показано, что если выберем на числовой оси две точки х и х + —, то всегда sin (х 4- — | = cos х.
2	\	2/
Таким образом, графиком функции у = cos х является синусоида, сдвинутая в отрицательном направлении оси абсцисс на от-
u Л
резок, равный —
Примеры.
5л;	л
cos — = — sin v = о	о
. 5л
sin — = sin
6 _ /3
2	'
л 1
COS — = — •
3	2 ’
Упражнения
367. Расположить в порядке возрастания числа:
1) cos 15°, cos 75°, cos 140°, cos 230°, cos 280°, cos 1000°;
2) cos 1; cos 2; cos 3; cos 4; cos 5; cos 5,3; cos 5,8.
368. Отметить по графику функции у = cos x промежутки, в ко-торых выполняются неравенства: a) cos х > — ; б) cos х < —
3	1	1<Г
в) cos х = j ; г) | cos х | < -у~ ; Д) | cos х | >
§ 87.	СВОЙСТВА ФУНКЦИИ jf =tgx И ЕЕ ГРАФИК
Для изучения свойств функции у = tg х достаточно изучить их в промежутке одного периода, например (— у, Во всех остальных таких же промежутках эти свойства будут повторяться. Здесь мы выбрали для изучения промежуток, исключая его концы, так как tg — yj и tg у не существуют.
Эта функция обладает следующими свойствами.
1.	Область ее определения — множество всех действительных чисел, за исключением чисел вида ли + у при любом целом п.
2.	Область изменения — множество всех действительных чисел, т. е. функция у = tg х, — не ограничена.
3.	Эта функция нечетная.
4.	Эта функция периодическая с наименьшим периодом л.
5.	Значения функции равны нулю во всех точках х — лп при любом целом и.
6.	Функция не имеет максимумов и минимумов.
7.	При всех х, удовлетворяющих неравенствам ян — — < х < ян, tg х < 0.
2
8.	При всех х, удовлетворяющих неравенствам я п < х < ли + — , tg х > 0.
Эти свойства были установлены ранее, кроме них существенно свойство:
9.	На промежутке (—функция у = tg х является монотонно возрастающей и пробегает все действительные значения от сколь угодно больших по абсолютной величине отрицательных до сколь угодно больших положительных (как говорят кратко — изменяясь от —оо до + оо).
Это свойство вытекает из того, что при — < а < — луч, исходящий из начала координат О, проходящий через точку М (а) единичной окружности, пересекает линию тангенсов в точке Р (а)
с ординатой у = tg а и соответствие (рис. 102)
а -> М (а) > Р (а)
таково, что при возрастании а точка Р (а) перемещается по линии тангенсов снизу вверх, пробегая ее полностью.
При приближении а к — у или к — абсолютная величина 2
тангенса неограниченно возрастает, как говорят, «стремится к бесконечности».
График функции у = tg х
на оси Ох, как по-
построим геометрически.
Построим единичную окружность с центром казано на рисунке 103, и проведем линию тангенсов. Делим отрезок числовой оси —у, и полуокружность на одинаковое число равных частей (на рис. 103 на 8 частей). Продолжаем единичные
векторы, проведенные из начала координат в точки деления полуокружности, до пересечения с осью тангенсов. Затем переносим отрезки оси тангенсов, как показано на рисунке 103. Тем самым полу-
чаем точки, принадлежащие искомому графику. Соединяем эти точки плавной линией и получаем приближенное изображение гра-
фика на отрезке/ — —, —Перемещая эту часть графика вправо и влево на отрезки, кратные л, получим части всего графика на других участках числовой оси ОХ. Говорят, что функция у = tg х, Зя л л Зп	п
например, в точках — — ,—— t — имеет разрывы. В каждом
из промежутков оси Ох, между двумя соседними точками разрыва функция у = tg х возрастает от — оо до + со.
§ 88.	СВОЙСТВА ФУНКЦИИ у = ctg х И ЕЕ ГРАФИК
Так же как и для тангенса, свойства котангенса достаточно изучить в промежутке одного периода, например (0, л).
Ранее были установлены следующие ее свойства:
1.	Область ее определения — множество всех действительных чисел, из которого надо исключить все числа х = лп при любом целом п.
2.	Область изменения — множество всех действительных чисел, т. е. функция у = ctg х не ограничена.
3.	Эта функция нечетная.
4.	Эта функция периодическая с наименьшим периодом л.
5.	Значения функции равны«нулю во всех точках лп + у при любом целом п.
6.	Функция не имеет ни максимумов, ни минимумов.
7.	При всех х, удовлетворяющих неравенствам
л п < х < лп 4- у, ctg х > 0.
8.	При всех х, удовлетворяющих неравенствам
лп 4-	< х <. лп + л, ctg х < 0.
У
Рис. 105
Указанное последним свойство котангенса устанавливается точно так же, как соответствующее свойство тангенса из рассмотрения соответствия
а М (а) Р (а)
между числом а в пределах 0 <; а < л, точкой М (а) на единичной окружности и точкой Р (а) пересечения луча ОМ (а) с линией котангенса (рис. 104).
Для построения графика этой функции изобразим единичную окружность с центром на оси Ох. Начало отсчета на числовой окружности выберем в точке С (рис. 105). Тогда линия котангенсов будет касаться окружности в точке С и ее положительное направление совпадет с положительным направлением оси ординат Оу. Дальнейшее построение такое же, как и для тангенсов, что показано на рисунке 105.
Функция у = ctg х имеет во всех точках х = пп разрывы при любом целом п. В каждом из промежутков оси Ох, между двумя соседними точками разрыва, эта функция убывает от 4- оо до — оо. Остальные части графика функции у = ctg х получаются перемещением построенной части на отрезке вправо и влево на отрезки, кратные периоду л.
Если же воспользоваться полученными ранее формулами sin (х + —) = cos х и cos (х +—) = — sin х, 2	2
то найдем:
Откуда следует, что
ctg х = — tg (х + у).
Последнее равенство показывает, что график функции у = ctg х можно получить, имея график котангенса следующим образом:
1.	Если сдвинем график котангенса влево по оси абсцисс на отрезок, равный р то получим график функции
у = tg (х 4- ^),
2.	Построим график, симметричный относительно оси абсцисс полученному графику у = tg (х 4- у), и тем самым построим искомый график (рис. 105).
По графикам функций можно наглядно представить себе промежутки знакопостоянства, монотонности (возрастания или убывания), четности и нечетности, периодичности. Любая прямая, не параллельная оси ординат, пересекает эти графики в бесконечном множестве точек. В частности, любая прямая, параллельная оси абсцисс, тоже пересекает эти графики в бесконечном множестве точек, а это показывает, что обе эти функции не ограничены.
Упражнения
369.	Отметить по графику функции у = tg х промежутки, в которых выполняются неравенства: a) tg х > 1; б) tg х <—1; в) | tgx| < 1.
370» Отметить по графику функции у = ctg х промежутки, в которых выполняются неравенства: a) ctg х > 1; б) ctg х <Z — 1; в) I ctg х | < 1.
§89. СЛОЖЕНИЕ ПОВОРОТОВ, ПРЕОБРАЗОВАНИЕ КООРДИНАТ ВЕКТОРА ПРИ ПОВОРОТЕ ОСЕЙ
Если повернуть луч, или вектор, сначала на угол а, а потом на угол 0 , то конечный результат будет тем же самым, как при повороте на угол
у = а 4- 0.
Например, поворот на угол 500° с последующим поворотом на угол —550° даст тот же результат, как поворот на —50°.
В этом параграфе мы займемся задачей, которая по существу от
носится к курсу геометрии, но решение которой нам понадобится в следующем параграфе.
Мы уже знакомы с представлением вектора а в виде
а = ах1 + ayj, (1) которое для единичного вектора е, образующего угол а с осью абцисс, приобретает вид
е = cos a i + sin а/.
Повернем оси координат Ох и Оу на угол а вокруг точки О.
Обозначим новые оси и Oq (рис. 106), а новые орты ilt jr. Орт й образует с осью Ох угол а, и поэтому
Л = cos а i + sin а j.	(2)
Орт /i образует с осью Ох угол — + а, так как орт i после поворота
Л
на угол — переходит в орт у, а при последующем повороте на угол а — в орт /1. Поэтому
Д = cos
i + sin
(I	•
t. e.
ji = — sin a i + cos a j.	(3)
Наша задача состоит в том, чтобы выразить координаты ах и ау вектора а через его координаты сь и в новой системе координат £От]. В этой новой системе имеем:
а = аД +	(4)
Подставив в (4) выражения (2) и (3), получим:
а = a. (cos а 1 4- sin а /) + ац(—sin а i + cos а /) = (cos а —
—►	—►
— sin а ап) i + (sin а + cos а cQ j.
Сравнивая полученное выражение для а с (1), мы видим, что ar — cos а л — sin а а х	6	л
ау = sin а + cos а	(5)
(вектор а выражается через орты i и / единственным образом!). Формулы (5) и являются решением поставленной задачи.
$ 90. СИНУС И КОСИНУС СУММЫ И РАЗНОСТИ
Применим формулы (5) к единичному вектору е, образующему с осью 0^ угол р, и, следовательно, угол а + Р с осью Ох (рис. 107). Для этого вектора
ех = cos (а + Р), еу = sin (а + Р), = cos а, = sin р.
По формулам (5) получаем:
cos (а +Р) =cos а cos Р—sin а • sin р,
sin (а + Р) = cos а sin Р Ч- sin а cos р.
Заменив в этих формулах р на —Р, получим: cos (а — Р) = cos а cos Р + sin а sin р, sin (а — Р) = sin а cos Р — cos а sin р.
Словесные формулировки полученных формул:
Косинус суммы двух углов (чисел) равен произведению косинусов этих углов (чисел) без произведения их синусов.
Косинус разности двух углов (чисел) равен произведению косинусов этих углов (чисел), сложенному с произведением их синусов.
Синус суммы двух углов (чисел) равен произведению синуса первого угла (числа) на косинус второго угла (числа), сложенному с произведением косинуса первого угла (числа) на синус второго угла (числа).
Синус разности двух углов (чисел) равен произведению синуса первого угла (числа) на косинус второго угла (числа) без произведения косинуса первого угла (числа) на синус второго угла (числа).
Из равенства (2) легко получаются формулы для тангенса и котангенса суммы и разности суммы и разности двух углов (чисел):
‘8 <“ + » = -ГТ/'-тк- " *8 <= - » "	
1 — tg а • tg Р	1 + tg а • tg р
В самом деле, по определению тангенса имеем:
, ,	। sin (а + Р) sin а • cos Р + cos а • sin Р
tg (а + Р) =---——— =---------л---:-----•
cos (а + Р) cos а • cos р — sin а • sin р
Далее, делим числитель и знаменатель последней дроби на cos aXcos р и получаем:
sin a । sin P tg(a + ₽) = ——----------—
sin a sin fl cos a cos p
tg a 4- tg p
1 — tg a • tg p
(9)
Формула для тангенса разности двух углов (чисел) получается из формулы тангенса суммы заменой 0 и —0, т. е.
t6 («-₽>-181«+(- м=ТЛ.= («»
1 — tg a tg (— Р) 1 + tg a- tg p
Из равенства cos (a — 0) = cos a • cos 0 + sin a • sin 0 при a = 0 следует:
1 = cos2 a + sin2 a, которое было получено раньше, в § 68, из других соображений. Пример/ Вычислить: sin 15°; cos 15°; tg 15°; ctg 15°. Решение. Известно, что
sin 45° = cos 45° = sin60° = ^; cos60° = y-
Для решения данного примера воспользуемся формулами синуса и косинуса разности двух углов 15° = 60° — 45°:
sin 15° = sin (60° — 45°) = sin 60° • cos 45° — cos 60° sin 45°==
Л3 /2	1 . К2 _ к2 (Уз
2 2	2 2 ~ 4 V
cos 15° = cos (60° — 45°) = 2- 121 4.121 221 = 121(j/3 4. 1);
tg 15° = -sin 15° = ^l"1 = 2 — /3 ;
cos 15° у з i
ctg 15° =	= 2 + /3?
/3—1
Для решения этого же примера можно было бы воспользоваться равенством 15° = 45° — 30°, что представляется сделать читателю.
Упражнения
1	JT
371.	Доказать, что sin a • cos a < — , если 0 < a < —. 2	2
372.	Вычислить cos 43° cos 17° — sin 43° sin 17°.
373.	Вычислить sin 56° cos 34°, 4- cos 56° sin 34°.
374.	Вычислить sin 75°, cos 75°, tg 75°, ctg 75°.
375.	Вычислить sin 105°, cos 105°, tg 105°, ctg 105°. 8	4
376* Вычислить sin (a + 0), если cos a =--, cos 0 = - и
377.
Вычислить
378.
Вычислить
379.
Вычислить
Зл
2 ’
Зя Г
sin (а — Р),
5	о	8
если sin а —-------, cosP = —
13	н	17
л<а< — , 0 2
cos (а + Р),
если cos а =
Зл 7
cos (а + Р),
9	. а 40
если cos а ---------, sin р = —
41	41
2 ’
2
5	. п	4
—, sin р =---------
13 Г	5
и
и
и
Зл
2 ’
л
2
380.
Вычислить
cos (а — Р),
20	о	7
если sin а = —, cos Р —---------
29	г	25
л,
381. Вычислить
sin (а — Р),
л ,	_
— <" а <" л, 2
382. Доказать тождество
cos (а + Р) + cos (а — Р) = - а sin (а + Р) + sin (а — Р)
15	. о 3
если cosa =----------, sin р =-----и
17	5
Зя
~2
л
7
2
и
§ 91. ФОРМУЛЫ СУММЫ И РАЗНОСТИ ОДНОИМЕННЫХ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
В дальнейшем изложении нам потребуются формулы для суммы и разности синусов двух углов (чисел), формулы для суммы и разности косинусов двух углов (чисел).
Для вывода этих формул выпишем равенства:
sin (х + у) —	sin х cos у + cos х sin у,	(1)
sin (х — у) =	sin х cos у — cos х sin у,	(2)
cos (х + у) ==	cos х cos у — sin х sin у,	(3)
cos (х — у) =	cos х cos у + sin х sin у,	(4)
полученные в предыдущем параграфе.
Каковы бы ни были два действительных числа аир, всегда существует, и притом единственная, пара действительных чисел х и у, таких, что выполняются равенства:
(х + у=а,	(5)
I* — у = Р-
Это следует из того, что система уравнений (5) имеет единственное решение:
а 4- В	а — Р
у = —F*	(6)
Теперь мы можем получить нужные нам формулы.
Сумма синусов двух чисел равняется удвоенному произведению синуса полусуммы этих чисел на косинус их полуразности, т. е.
. . о п • а 4- Р а — р
sin а + sin р — 2 sm —cos —.	(7)
Складывая почленно равенства (1) и (2), получаем:
sin (х + у) + sin (х — у) = 2 sin х cos у.
В последнем равенстве производим замену:
х + у = а, х — у = р, х =у =	(8)
Z	&
и получаем требуемое равенство.
Разность синусов двух чисел равняется удвоенному произведению косинуса полусуммы этих чисел на синус их полуразности, т. е.
sin а — sin р — 2 cos а - cos -	.	(9)
Вычитая из равенства (1) равенство (2) почленно, получаем: sin (х + у) — sin (х — у) =2 cos х sin у.
В последнем равенстве производим замену по формулам (8) и получаем требуемое равенство.
Сумма косинусов двух чисел равняется удвоенному произведению косинуса полусуммы этих чисел на косинус их полуразности, т. е.
cos а + cos р = 2 cos —cos ° ~.	(10)
Складывая почленно равенства (3) и (4), получаем:
cos (х + у) + cos (х — у) = 2 cos х cos у.
В последнем равенстве производим замену по формулам (8) и получаем требуемое равенство.
Разность косинусов двух чисел равняется взятому со знаком минус удвоенному произведению синуса полусуммы этих чисел на синус их полуразности, т. е.
cos а — cos Р = — 2 sin х sin у.	(11)
Вычитая почленно из равенства (3) равенство (4), получаем: cos (х + у) — cos (х — у) = — 2 sin х sin у.
В последнем равенстве производим замену по формулам (8) и получаем требуемое равенство.
Если учесть, что синус является нечетной функцией, то последний вывод можно сформулировать в таком виде:
Разность косинусов двух чисел равна удвоенному произведению синуса полусуммы этих чисел на синус их обратной полуразности, т. е.
cos а — cos р = 2 sin	sin ~ а-.	(12)
2	2
§ 92. ОБ ОДНОМ ВАЖНОМ НЕРАВЕНСТВЕ
Во всем дальнейшем важную роль будет играть следующее неравенство:
| sin х | < | х | < | tg х |,	(I)
справедливое для всех х, удовлетворяющих неравенству — < х<
<0 или неравенству
Докажем это неравенство. Рассмотрим сначала случай 0 <х < Пусть угол Z A0D = х (радиан) опирается на дугу AD окружности единичного’радиуса (рис. 108). Проведем через точку А окружности касательную АВ. Обозначим через S0AD, S0ACDt S0AB площади треугольника OAD, сектора OACD и треугольника ОАВ. Тогда
S0Ad = V • sin х = — sin х,
2
$oacd = ~2Г2х== 2 $0АВ=
= — ОА -ОВ = ^-tgx, 2	2
и так как
$ OAD $OACD < $OABi
ТО
sin х < х <. tg х.
Таким образом, если 0 < х<
то неравенство (1) выполняется,
так как в этом случае | sin х| = sin х; | х | = х ; | tg х | = tg х.
Если же — х < 0, то 0 <; — х < и’ согласно неравенству (2),
sin (— х) < — х < tg ( — х).	(3)
Но для х<0 sin (—х) = —sin х = |sin х|;	—х = |х|
и tg ( — х) = — tg х = | tg х | .
Следовательно, неравенство (3) принимает вид
| sin х | < | х | < | tg х |.
Замечание. Для всех действительных х
| sin х | < | х |. л	л
В самом деле, это неравенство доказано для | х\ < — . Если же |х| > ~> > 1,5, то оно и подавно справедливо, так как | sinx| < 1.
§ 93. НЕПРЕРЫВНОСТЬ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
Теорема 1. Функция sin х непрерывна на всей действительной оси, т. е.
lim sin х = sin х0.
X -* х0
Доказательство. Оценим разность | sin х — sin х01.
I .	.	. I n . X — Хп X 4- Хп
|sinx — sinx0|= 2 sin——° COS—0
=2 | sin
£+£o|
2 I
<2|sin^—^l<2-l^~Xol- = |x —x0|.
|	2 I 2	0
В конце мы воспользовались неравенством (1) из § 92.
Для любого е > 0, если выбрать 6 — е, то при | х — х01 < 6 | sin х — sin х01 <" е, что и требовалось доказать.
Теорема 2. Функция cos х непрерывна на всей действительной оси, т. е.
lim cos х « cos х0. г-* х0
Доказательство. В самом деле,
| cos х — cos х01 = 12 sin -х° ~ * sin х — х° I = 21 sin 11 sin 1<
1	0 I 2	2 I I 2 II 2 I
<2 |sin^=^-°| < 2	=|x — x0|.
Следовательно, для любого е > 0, если выбрать 6 = е, то при | х — х® | < S cos х — cos х® | < 8, что и требовалось доказать.
Теорема 3. Функции tg х и ctg х непрерывны в области своего определения, т. е.
lim tg х =я tg х®, х -> х0 lim ctg х =» ctg х®.
X -*Хо
Доказательство. Если х0=И=	+ kn, k = C, + 1,
±2, .... то cos х® ф 0. Следовательно,
.	lim sin х
lim tgx = lim	= tgx®.
x-*xa x-х,, cosx	hmcosx	cosx®
x-x0
Аналогично доказывается, что для любого х=/=6л; 6 = 0, q: 1, + 2, ...
lim ctg х = ctg x®.
§ 94. ПРОСТЕЙШИЕ ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ
В виде первого примера рассмотрим уравнение
1 COS X — — •
2
Так как на промежутке [0, л| функция cos х монотонно убывает от 1 до — 1, то на этом промежутке она (в силу своей непрерывности)
1	т
принимает значение — ровно один раз. Так как
Л 1 cos — = —, 3	2
то это единственное решение нашего уравнения, лежащее в промежутке [0, л], есть
В силу четности функции cos х на промежутке (— л, 0) имеется тоже один корень уравнения
Таким образом, на промежутке л	л
корня: *1 = ~ и х2 = — -О	О
[—л, л] наше уравнение имеет два . Так как длина этого промежутка
равна 2л, т. е. периоду функции cos х, то за его пределами корни могут повторяться лишь периодически. Множество всех решений уравнения состоит из чисел (рис. 109):
х = — + 2лп, 3
х — — — + 2лп, 3
где п— произвольное целое число. Вполне аналогично дело обстоит и в случае уравнения
cos х =а
при любом а, меньшем по модулю, чем единица. У него имеется один корень Xi в промежутке [0, л] и один корень х2 = — xi в промежутке [—л, 0]. Остальные корни получаются из этих двух прибавлением 2пп:
х = Xi + 2лп, х — х2 + 2лп.
Короче можно записать общую формулу для всех корней уравнения cos х = а:
х = ± xt + 2лп.
Иногда корень в промежутке (0, л) приходится находить при помощи таблиц. Например, для уравнения
3
cos х = —
4
по таблицам находим:
41° 24' = 0,7226 рад и получаем общее решение:
х = ± 0,7226 + 2лп.
В принципе аналогично исследуются уравнения
sin х == a, tg х = a, ctg х = а.
Мы к ним еще вернемся в X классе при знакомстве с обратными тригонометрическими функциями.
Впрочем, уравнения рассмотренного сейчас типа можно решать и при помощи графического построения. Для того чтобы решить, например, уже рассмотренное уравнение
3 cos x =— , 4 достаточно сделать построение, показанное на рисунке 109а, и измерить углы и а2.
Упражнения
383. Решить уравнения:
1) cos х = 1; 2) cos х = — 1; 3) sin х = —; 4) sin х =-----U
2
5) tg х = 1; 6) ctg X = 1; 7) tg х = 10; 8) tg х = 1000.
384. Построить графически углы, соответствующие заданным значениям тригонометрических функций:
1) sin а = —; 2) cos а = — —; 3) tg а = 2; 4) ctg а = —2, 4	4
§ 95. ПРЕДЕЛ ОТНОШЕНИЯ ХОРДЫ К ДЛИНЕ СТЯГИВАЮЩЕЙ ЕЕ ДУГИ
Теорема 1.
,. sin х lim----
хо X
Доказательство. Пусть 0 < х < или —	< х <;
< 0. Тогда выполняется неравенство (см. рис. 108): | sin х | < |х| < | tg х|.
Разделив все три части этого неравенства на |sin х|, получим:
1___
| COS X I ’
Учитывая, что при указанных условиях > 0, cos х > 0,
X	1
получим: 1<---------<------или, перейдя к обратным величинам,
sin х	cos х
. . sin х .	/1ч
----->cosx.	(1)
х
Так как lim cos х =« 1, то левая и правая части неравенства (1) х -* 0
стремятся при х -> 0 к одному и тому же пределу, к 1. Поэтому
и средняя часть этого неравенства —также стремится к 1 при sin х
х -> 0, что и требовалось.
Замечание. Простота соотношения
!. sin х < lim ------== 1
x-*0 X
связана с нашим условием считать sin x = sin (x pad).
Если бы мы приняли другое условие sin х = sin х°, то
р sin х р sin х° 11Ш------- = 11Ш------ =
х-> О X х-> О х
/ 180х	\
sin -----рад
_ --------____________L-
х-> о х
/ 180х	\
sin ---- рад
р	л н 180	,180	180
lim —-----------• — = 1 • — = — .
х->о 180х	л	л л
Теорема длине cmxeueatoi нулю. Д о к а з а т г стягивается д	2. Предел отношения длины хорды окружности к щей ее дуги равен 1 при стремлении длины дуги к е л ь с т в о. Пусть хорда АВ окружности радиуса угой, содержащей х радианов, тогда длина хорды АВ = 2r sin—, 2
а длина дуги AL	3 = гх. Поэтому (рис. ПО) 2r sin—	sin —
lim ЛВ-0	4?- = lim 	- = lim 	~ = 1. AB 'ab -+q rx	A 2
Примеры.	1) lim —— = lim —— —			 = 1. x-o sinx	x->o sinx	sin x 		lim 	 X	x -> 0 X . л	. Л sin —	sin —
2) limn sin-п -* со	Л	, •	n	1 .	n	< - = lim	= lim 	я = 1 • л = я. Tl	П -* co	1	П co	Л n	n
р sin5x 3) hm	 х->0 X	,. sin 5x r r = lim	 -5=5. x о 5x
к tgx	sin х 1 р sinx v 1 ill
4) lim -2— = lim----------= hm —lim---------= 1.1=1
X 0 X	X -> 0 x COS X X - 0 X x - 0 cos X
Упражнения
Найти пределы:
385.	a)	б) lim -в) lim
х -> о 2х г -> о sin 2х к -> о tg 5х
386.	a)	б) lim ^n-x--£osx; в) lim
х-> 2 X	X -> о tg X + 2	X -> о sin 4х
/ я \
sin х — —
387.	a) lim—-------— ; б) lim s—; в) lim (х ctg х).
п	л	г-»о sin2x г-о
4	Х~~ 4
388.	a) lim----х—;	б) lim	^~sin4x	; в) lim	*~sin2x
х -> о	sin3 Зх х - о Зх	х -* о Зх
389.	a) lim -^т£2?_3£; б) lim ,^ + sin7x
х->0	х2	г-О 2х
390.	a) lim_V-3-+sin±-Kg-sln,y ; б) lim s-in5x~3x 
х - О	X	х -> 0 4х
391.
lim
% -> а
sin2 х — sin2 а х2 — а2
. cos тх — cos пх
б) lim------------------
х-+ о х2
В) lim-x~~sin2x
х-о x4~sin3x
§ 96. ПРОИЗВОДНЫЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
Теорема 1.
(sin х)' = cos х.
Доказательство. Производную будем вычислять так, как это указано в § 55.
1-й шаг. Даем избранному значению аргумента х приращение Дя, тогда функция у = sin х примет значение:
у + Ду = sin (я + Дя).
2-й шаг.
Ду = sin (я + Дя) — sin я .
3-й шаг,
&у____sin (х + Дх) —
Дх	Дх
sin х
Дх	/	Дх
2 sin —cos х + — 2	\	2 ,
Дх
4-й шаг.
Л . Дх 2Sln-
1-------
о Дх
(sin х)' = lim = lim
Дх 0 Дх Дх -> (
&х sin —	,	. ,
= lim------limcos x-|-= 1 . cosx = cosx.
Дх - О &X	Ax -* 0	\	2 /
2
Теорема 2.
(cos x\ = — sin x.
Доказательство. 1-й шаг. Даем значению аргумента х приращение Дх, тогда функция у = cos х примет значение у + Ду = cos (х + Дх). 2-й шаг, Ду = cos (х + Дх) — cos (х). 3-й шаг. Ах / Дх\ *	,	.	— 2 sin — sin х+—
А_у ___ cos (х + Дх) — cos х _ 2	\	2 /
Ах	Ах	Дх
Дх
Д	Sln ~2	Л
4-й шаг. (cosx)'= lim — = —lim --limsinЫ—=
дх -> О А* Ах о Дх 2 — — 1 sinx = —sinx.
Теорема 3. (tg х)' = —?—; (ctg x)z = — COS2 X
Доказательство. Применяя теорему о производной частного, получим: _ / s*n х V___________ (sin XY cos х — sin х (cos x)z
\ COS X /	cos2 X
COS X sin x
_ (cos x)z sin x — cos x (sin x)z 	 — sin2 x •— cos2 x __1 sin2 x_________________________________sin2 x	sin2 x
Теорема 4.
|sin (ax + b)]' = a cos (ax + b).	(1)
[cos (ax + b)Y = — a sin (ax + b\	(2)
Доказательство. Пусть у = sin (ax + b\
1-й шаг. Даем избранному значению х приращение Дх, тогда новое значение функции:
у + Ду = sin [а (х + Дх) + Ь].
2-й шаг.
Ах -> О
sin2
cos2 x -J- sin2 x
COS2 X
1
cos2 X
; (ctgx)' = f
Ду = sin[a(x + Дх) + b] — sin (ax + b) = 2 sin cos [ax + + y
З-й шаг,
А_у
— = а
Ах
. аАх sin----
о
-------- COS аАх
ах + b +
Ах\
2 /
4-й шаг.
аАх sin----
[sin (ах + &)]' — lim — =alim--------- lim cos (ax +
Ax-*o Ax Ax->o aAx дх->о
2
Ax\
+ b + — I = a  1 • cos (ax + b) = a cos (ax 4- b).
Аналогично доказывается равенство (2)
Примеры. 1) [sin (Зх + 4)]'= 3 cos (Зх 4- 4).
2)	[cos (4х — 5)1' = — 4 sin (4х — 5).
3)	[sin (2 — 5х) l'= — 5 cos (2—5x).
4)	[cos (3 — 2x)]'= — 2 [— sin (3 — 2x)]= + 2sin (3—2x).
Упражнения
392« Доказать формулы (1) и (2) с помощью правила дифференцирования сложной функции.
392а. Найти производные следующих функций:
О У = tg(ax + b); 2)у = ctg (ах 4- b)\	3)y = x2tg-|;	4) у =
= Зх2 ctg — 2^;	5) у = -1п(1 ~2х) ;	6) у = --- (~—3) •
\ 6	)	3x4-2’	’ у	х '
cos —
5
7) y=sin(3x—2) tg-^-; 8)y=xsiny4-2xtg3x; 9)y=(5x—2)sin(2x—3); 10) y=sin23x; 11) y —tg54x; 12) y=tg(3—2x); 13)y=3sinxcos2x4-4- sin3x.
3926. 1) f(x) = sinx. Найти f" (x)\	y); f" (0); f'Q-
2) f(x) = cosx. Найти /"(x); f" (— n); f" (0); f" (n). 3) f (x) -= sinfex. Найти f(x);	f'(0); f" (-)• 4) f(x) = cos kx. Найти f(x);
f"	f" (0); f" (y). 5) Показать, что функция у = sin (fex-|-q>)
удовлетворяет уравнению f" 4- k^y = 0 (<p — постоянная). 6) Показать, что уравнению из упр. 5) удовлетворяет функция cos(&x4-<p).
7) Показать, что уравнению из упр.5) удовлетворяют функции sin (kx 4- ф) 4- сг cos (kx 4- <р) при любых коэффициентах ct и сг.
8) у = x2sinx. Найти у". 9) у = xcosx. Найти у".	10) у =
=-- (х + 2) sin х + (Зх — 1) cosx. Найти у". 11) у = (2х + 3) sin—.
5 Найти у". 12) у = Зх cos (—+ 2\ Найти у".
392в. Точка совершает прямолинейное движение по закону s = a tg и t. Найти скорость и ускорение движения.
392г. Определить силу, под действием которой материальная точка массы т совершает колебательное движение по закону s = = Л sin ((О/ COq).
§ 97. УГОЛ НАКЛОНА И УГЛОВОЙ КОЭФФИЦИЕНТ ПРЯМОЙ
Будем считать каждую невертикальную прямую на числовой плоскости направленной в сторону правой полуплоскости. Считая, как обычно, углы, отсчитываемые против часовой стрелки, положительными, а отсчитываемые по часовой стрелке — отрицательными, мы условимся, что угол любой невертикальной прямой с осью абсцисс лежит в пределах
— 90° < а < 90°.
Определенный таким образом угол между осью абсцисс и прямой называется углом наклона прямой. Естественно, что горизонтальной прямой приписывается угол наклона а = 0.
Что касается вертикальных прямых, то им с равным основанием можно было бы приписать углы наклона 90° или —90е.
Угол наклона а прямой
у => kx 4- b
связан с угловым коэффициентом k простым соотношением:
k = tg а.
Для доказательства достаточно рассмотреть прямые, проходящие через начало координат, т. е. прямые (рис. 111)
у ==>kx	(1)
(прямые у = kx + b параллельны прямым у = kx и поэтому они имеют такие же углы наклона).
Выберем на прямой (1) точку М, лежащую в правой полуплоскости, с координатами (х, kx) и рассмотрим вектор а = ОМ.
Этот вектор имеет то же направление, что и прямая, и, следовательно, образует с осью абсцисс тот же угол а. Поэтому tga = ^ = —= £, dx х
что и требовалось доказать.
Теперь мы можем восполнить пробелы в рассуждениях § 67, посвященного применению производной к нахождению касательных.
Касательная МдТ к линии (L) была определена, как проходящая через точку Мо прямая, угол которой с секущей Л40 М стремится к нулю, когда точка М стремится вдоль этой линии к точке Мо.
При этом угол между прямыми понимался в элементарном смысле как неотрицательная величина. Обозначим этот угол через и, угол наклона касательной — через а0, а угол наклона секущей — через
а. Тогда (рис. 112)
Согласно определению, линия (L) имеет в точке Мо касательную М0Т, если lim <о = 0, м -м» т. е. если
lim а = а0.
М - Мо
Итак, линия (L) имеет в точке Мо невертикальную касательную в том и только том случае, когда угол наклона а секущей М0Л4 имеет определенный предел а при стремлении точки М к точке Мд вдоль этой линии.
Теперь уже совсем просто можно доказать два предложения, которые не были доказаны в § 67.
1. Если график функции f имеет в точке Мо (Хд, f (х0)) невертикальную касательную, то функция f имеет в точке Хд производную
Г W = К’ где k0 — угловой коэффициент касательной.
Доказательство. Если а — угол наклона секущей М0М, а ао — угол наклона касательной к графику данной функции в точке Л40, то lim а = а0 (рис. 113). Стремление точки М к точке М ->• Afo
Мо вдоль графика функции равносильно стремлению к нулю приращения Дх. Поэтому lim а — а0.
Дх -*0
В силу непрерывности функции tg х
lim k = lim tga= tga0 = k0
Дх О Дх -> О и так как
£ = f (х0 + Ах) — f (х0) Дх
то тем самым доказано существование предела
цт f(x0 + Дх)/ (х0)
дх- о Дх
а следовательно, и существование в точке х0 производной f'(x0) = k0.
2. Если функция f имеет в точке х0 производную, то ее график имеет в точке (х0, f (х0)) касательную, угловой коэффициент которой равен k0 — f' (х0).
Доказательство. По условию существует предел
lim £(5о + М-Нхо)==г дх - о	Ах
Проведем через точку Л40 (х0, f (х0)) прямую Мо Т с угловым коэффициентом /г0 = f (х0), тогда
lim k = k0	(2)
Дх О
и так как функция k = tg а непрерывна и возрастает в интер-
(л л
----
2 2
то для нее существует обратная ей функция
а а (k),
непрерывная на всей действительной оси. Но тогда из равенства (2) вытекает существование предела lim а = а0, а это и оз-Дх - О
начает, что прямая Л40 Т является касательной к графику данной функции в точке Мо.
Примеры. 1) Найти касательные к синусоиде в точках с абсциссами: х< = 0; Хо = —;
1	2
х3 = л (рис. 114).
Р^е ш е н и е. Для решения задачи достаточно найти угловые коэффициенты касательных, а следовательно, и углы их наклона к оси абсцисс:
ki = (sin х) |^=0 = cos 0 = 1;
tg (Xi = 1.Следовательно, .
k2 = (sin x)\ n == cos ~ = 0; tg a2 = 0.
H=F 2
Следовательно, a2 == 0.
k3 = (sin x) |х=л —cos л = —1; tg a3 = —1. Следовательно, a3 =— —
4 ‘
Замечание. В точках xt = 0 и x2 = я касательные пересекают график функции. Такие точки называют точками перегиба функции.
2) Найти касательные к графику функции tg х в точках х{ =
s\	«ПС
= о, х2 = -.
4
Решение.
ki = (tg ж)' | х=0=	= 1; tgat = 1; a4 = 1
*2-(tgx)'| я=-----------= 2; tga2 = 2; a2 = arctg2.
cos’у 4
В точке x — 0 касательная пересекает график функции, и, следовательно, эта точка является точкой перегиба функции (см. рис. 115а). Изменение углового коэффициента касательной к графику функции tgx можно проследить по графику ее производной (рис. 115):
(tg х) — cosj х •
Так как функция cos х в интервале (—0] возрастает, а в интервале (0, у) убывает, то производная функции tg х в интервале , oj убывает от + оо до 1, а в интервале (0,-^) возрастает от 1 до + 00•
Упражнения
393» Найти касательные к синусоиде в точках
xt — —л; х2 = — у; х3 — 2л.
394. Найти касательные к графику функции cos х в точках Л	ZX	Л
х± = — л; х2 = — —; х3 = 0; -^4 = у*, х& = 395» Найти касательные к графику функции ctg х в точках л	л	3	3
х2 * —; х3 = — л; == —я и нарисовать график производной этой функции.
396.2 Исследовать функцию sin х методами дифференциального исчисления.
397« Исследовать функцию cosx методами дифференциального исчисления.
398< Исследовать функцию tg х методами дифференциального исчисления.

ОТВЕТЫ И УКАЗАНИЯ К УПРАЖНЕНИЯМ
1 • 2
1.	Обозначим сумму п таких чисел через sn. Если п = 1, то sx =	=1, т. е.
1 гт	k(k + l)
доказываемое утверждение верно для п=1. Пусть равенство ~!——
,	^Н-1) ।	(А? + 1)(А?+2)
верно для п k, тогда s^+1 = --------- + (k + 1) = ------~—5 6—— =
(* + 1)[(*+1) + 1]
=--------------------, т. е. если доказываемое утверждение верно для и = kt
то оно верно и для п = k + 1. Таким образом, данное утверждение верно для п = 1, и если оно верно для и = k, то оно верно и для и ?= k -f- 1. Оба требования принципа математической индукции выполнены, и поэтому справедливость утверждения полностью доказана.
1-2-3	. „	k(k + l)(2k + {)
2.	Если п = 1, то = —------= 1. Пусть sk =-------~1, тогда
k(k+\)(2k+l)	(k + \) (2fc2 + 7*+ 6) (k+\)(k+2)(2k+3)
sk+i~ n	+ v2 + И —-	“	=	“	•
о	6	6
I2 • 22	k2 (k I I)2
3.	Если n = 1, to = —-— = 1. Пусть sk =----------, тогда s^+1 =
_.. + (4 + !) _ЩЩ>1+(4+1). _	+j)-K+j£=
(»+ 1)4 (t + 1) + i|-
4
4. Если n — 1, to sx = Z?(2fe — l)(2fe + 1)
1-1.3
t „	k(2k-\)(2k + \)
3	= 1. Пусть Sk =----------------, тогда
+ (2* + I)* = (2^ + 1)(2^Л + 6<+3).. =
(^ + l)(2^ + l)(2fe+3)
Sft+i -	3
(2fe + 1) (2fe2 4- 5fe + 3)
3	3	*
5. Если n = 1, to sx= I2 (2-12 — 1) = 1. Пусть s* =fe2 (2k2 — 1), тогда s*+, = = k2 (2k2 — 1) + (2k + I)3 = 2fe4 — k2 + 8£s 4- 12fe2 + 6fe +1 = 2k* + 8fe3 + 11Й24-4- 6k 4- 1 = (k 4-1)2 [2 (k 4-1)2 — 1]. Справедливость последнего равенства можно проверить открытием скобок, но можно сделать это и так: 2А4 -f- 6k3 +Н£24~ + 6fe 4- 1 = 2й4 4- 4#> 4- k2 4- 4й3 4- 8й2 4-2Л 4- 2k2 4-4й +1 = А2(2624- 4^4-1) 4-4- 2k(2k2+ 4й4-1)4-(2й24-4*4-1)=(А24-2й4-1) (2й24-4й+1)=(*4-1)2 [2(*4-1)2—11.
„ „	.	1-2-3	„ „	k (k 4-1) (k 4-2)
6. Если п = 1, то st =-----— = 2. Пусть sA =------------. Тогда
< о _L 1Ь-иП/Г	fe(fe + 1)(fe + 2> 	(fe+l)(fe+2)(fe4-3)
s£+i — sk + («“И) + 2)—	+(^+0 (^+2)—
и
3
7.	Если п = 1, то «! = 1 • 23 — 4. Пусть s* = k (k 4- I)3. Тогда s^+1 = =£ (k + I)3 + (Л + 1) (ft + 4) = (k + 1) (k + 2)* 1 2 * * * 6.
8.	Если n = 1, to Sj = —• 1-2-3-4==6. Пусть sft= — k (£4-1) (ft-|-2) (ft-}-3). 4	4
Тогда sA+1=sA4-(fe + l)(fe+2)(£4-3)=(£4-l)(£ + 2)(£4-3)(^- k 4-1) =
= y(£4-l)(A4-2) (ft 4-3) (ft 4-4).
4	1-2	и k (k 4-1)
9.	Если n = 1, to st = (— 1)° —— = 1. Пусть sk = (— I)*"1 • -.
1 k
= —. Пусть sk =	Тогда sk+l =
3	2ft 4* 1
2ft3 4- 3ft 4-1 _ (2ft 4-1) (ft 4-1) _ k 4-1 _ (2ft 4- 1) (2ft 4-3) “ (2ft 4-1) (2ft4-3) - (2fe 4-1) (2ft 4-3) - 2ft 4- 3 ~
Тогда sft+1=sft+(-l)*(*+l)2=(-l)*
1
10. Если n = l, то sx
k “2fc + 1
2(ft4-l)4-l'
1	1 „	ft
11. Если n = 1. to S1 =——— = —. Пусть sk = Тогда sA+1 = 3*1+1	4	ok + 1
k ______________1_______________k + 1
“3^ + 1 + (ЗА?+ 1) (ЗА?+ 4) ~3(А? + 1) + Г
12. Доказывается аналогично предыдущим задачам 10 и 11.
15. Предварительно следует доказать, что и точек, расположенных на пря-1-2
мой, делят ее на п + 1 часть. Если и=1, то«г = 1 +”у“ ==2, т. е. одна прямая делит плоскость на две части. Пусть верно утверждение при n=kt т. е. = k(k~\-\)
=1	' Если добавим еще одну прямую, то k первых прямых пересекут
ее в k точках и потому разделят ее на k + 1 часть. Каждая из этих частей разбивает одну часть плоскости на две части, и тем самым к первым sk частям k(k + \) t
плоскости добавится еще k + 1 часть, т. е. s^+1 = 1 +--------+(л + 1) =1 +
, (ft4-l)(fe + 2)	2
Л ’	(14* 1) (1а — 1 4-6) „
16. а) Если п = 1, то получаем: sx =------------------= 2, т. е. в этом
6
случае утверждение верно. Пусть это утверждение верно для п = k, т. е. мы предполагаем, что k плоскостей указанного вида делят пространство на —  (^ + 0 -------£+6) частей эти плоскостей разделят добавленную (k + 1)-ю
6
А?2 + k + 2
плоскость на ----------- части (задача 15). Каждая часть плоскости разделит
одну часть пространства на две части, и поэтому при добавлении (k + 1)-й fe2 | fe | 2
плоскости будет добавлено к частям пространства еще--------------части, т. е.
(А? + 1) (Аг2 ~k +6)	А?2 + А? + 2	(А?+1)(/г2—/г+6)+3(А?2+А?+2)
Sft+1=	Q	+
_ (ft 4- 2) (ft3 4- ft 4-6) 6
6
б) При п = 1 имеем «! = I2 — 1 + 2 = 2 (окружность делит плоскость на две части). При n~k предположим, что любые две из k окружностей пересекаются, и никакие три из них не имеют общей точки, и пусть для этих окружностей верно утверждение, что они делят плоскость на № — k 4- 2 частей. Если все эти k окружностей пересекут добавленную к ним окружность так, что опять никакие три не будут иметь общей точки, то добавленный круг будет разделен на 2k частей. Поэтому к sk будет добавлено 26, т. е. s*+1 = 62-—64-24-26 = =62 fc 4- 2=(k + I)2 — (k + 1) + 2. Если же не всякие две окружности пересекаются или какие-либо три окружности имеют общую точку, то полученное число частей плоскости будет меньше, чем п2 —-и 4-2.
17.	Если п « 1, то 21 > 1. Из 2* > k следует 2*+1 > 2k = k 4- k> k 4- 1 t. e. 2*+x > k 4- 1»
18.	23 > 7. Если 2k > 2k 4- 1 при n > 3, to 2*+1 > 4k 4- 2 = 2k 4- 3 4- 2k — — 1 > 2k 4- 3 = 2 (k + 1) 4- 1, так как 2k — I > 0.
19.	Положим n = m 4* 9. Надо доказать, что неравенство 2W+9 > (т 4- 9)3 справедливо при любом натуральном значении т. Если т = 1, то неравенство 210 > 103 верно. Пусть 2*+9 > (k 4- 9)3, тогда 2*+1° > 2 (k 4- 9)3 = 263 4- 5462 4-4-4866 4- 1458 > 63 4- 3062 4- 3006 4- 100(Э = (6 4- Ю)3, т. е. 2*+10 > (6 4- 10)3.
20.	Из УТ4- 1 > 2 следует 1 4-	> У<Г, т. е. данное неравенство
справедливо при п = 2. Пусть это неравенство справедливо при п = 6 > 2, тогда 1	1	____z Л-т-
прип = /г + 1 получим sft+I=s*+p-==	=	>4/ ^ +
1 \ __________ 1)+ 1 \ г________________
+ т= +1 --- ---- - > К* + 1.
6 4-1/	\	6 4-1	/
21.	См. неравенство Бернулли в пункте 2 § 3.
22.	== 1 4~ 5 == 6. s*+1 = (6 4- I)3 4“ $ (6 4“ 1) — 4" 36 (6	1) + 6, где
число 6 (6 4- 1) Делится на 2.
23.	sx = 12. s*+1 = (6 4- I)3 4- 11 (6 4-1) =5*4-36 (6 4- 1)4- 12.
24.	S] = 7. s*+1 = 62*+1 4- 1 = 36 • 62*'1 4- 1 =s* + 35 • 62*"1.
25.	Если n = l, to Si = 104-18 — 28 = 0, t. e. sx делится на 27. Пусть s* = 10* 4- 186 — 28 делится на 27, тогда s*+1 = 10*+1 4-18 (6 4- 1) — 28 = = 10-10* 4-186 4-18--28 =10* 4- 186-28 4-9 (10* 4-2), т. е. s*+1 = s*4-4-9(10* 4- 2). В этой сумме первое слагаемое делится на 27 по предположению, во втором слагаемом сумма цифр числа 10* 4- 2 делится на 3, поэтому число 9(10*4-2) делится на 27.
26.	Если п = 1, то 92 — 8 — 9 = 64. Пусть sk = 9*+1 — 86 — 9 делится на 16, тогда s*+1 = 9*+2 — 8 (6 4- 1) — 9 = 9 • 9*+1 — 86 — 8 —9 = 9*+1 — 86 — 9 4-4- 8 • 9*+1 — 8, т. е. s*+1 = $* 4~ 8 (9*+1 —-1). В последней сумме оба слагаемых делятся на 16.
27.	sx = 1 4" 6 4-114-6=24. Пусть s*=64 4- 663 4- Н62 4~ 66 делится на 24, тогда s*+1 = (6 4- I)* 4- 6 (6 4-1)3 4- 11 (6 4-1)2 4- 6 (6 4- 1) = 6*4-10634- 3562 4-4-506 4-24 = 64 4- 663 4-1162 4-66 4- 463 4- 2462 4-446 4-24=$* 4-46 (62 4-11)4-4- 24 (62 4- 1), т. е. s*+1 = $* 4“ 4 (63 4- 116) 4- 24 (62 4- 1)- Выражение 63 4- 116 делится на 6 (задача 23).
28.	п = 7. 29. 24. 30. 6. 31. 384. 32. 4! (и — 5)! 35. а)	----,
7 (6 4-2)! (п — 6 — 3)!
6) ,	'7, + ")1	.	,6.	- 45. 37. С.’2 - ,2 _ 54.
(п+1)1 (т—1)1 (п —2)1 (т+ 2)!
38. С?о = 120. 39. п = 14. 40. п = 7. 41. k <	42. 15. 43. 11. 44. Сю • С? =
1
(п-1)!
=1260. 45. 1365. 46. т ~ 2. 47. У к а з а н и е: применить формулу С* +	=
= С*+* трижды. 48.512. 49. 1024. 51. Указание; Сложить почленно равенст-_п р10_рЮ. рЮ____р9 I рЮ. рЮ___р9 I рЮ. . рЮ ___р9 i рЮ. р!0 р9 . <40
ва с10 —ь10,	— ь10	g12 — cJ1 -f-un u20 — u19 -f-c19, c2J = c204-c20.
53. a) = 210Q1 (501)2 ~ °’08, Вычисление производим по таблице логарифмов факториалов (см. приложение):
1g 2 =0,3010300, lg 50! = 64,48307, lg(50!):
1g 100!= 157,97000.
Ig2loo= 30,10300;
"	128,96614,
1g Л = 2,90086, А = 0,08.
53.	б) л 0,74. У к а з а н и е. Применить формулу С”г	и затем с по-
мощью таблицы логарифмов факториалов найти сумму шести слагаемых, напри-мео	_ 2	_	2 ' 1001	~ о 09695
р’ 2100	— 2100 — 45! 55! • 2100 ~ ’	°'
во	550 • 550 dg0	_ Ао „45	545 • 555	46	548 • 5s4 ,
54.	а) Сюо	•	я;г ~	0,08;	б) Сюо • -у^-	+ Сюо	-	...
„+с- .	= С?о5о + сГоо + - + сГоо 0>74.
'	10100	2100
55.	Всех различных стозначных чисел 2100. Из них содержит не более 30 четных десятичных знаков С}00 + Cf00 + ... + Столько же чисел будет содержащих не менее 70 четных десятичных знаков, так как С™0 +Сш0+ ••• + + £100 = £100 4“ £?оо 4“ ••• + £ц)о- Остается показать, что (С1100 4- Cj00 +... + Ф С?оо) •	< 0,001. Это можно сделать с помощью таблицы логарифмов
факториалов.
56.	0,06048. 57. 3024 . 58. 21. 59. п = 9, п = 10. 60. 1190.
62.	а) а® + 0а3Ь ф 15а4б2 4- 20а3Ь3 + 15а264 + баб5 ф 6е; б) а5 + 5а4б2 + ф 10а3б4+10а2бв + 5аб8 ф. *ю; в)а7—7а«бф21а5б2—35а4б3 ф 35а.3Ы — 21а2б5+ + 7аб® — а7; г) а5 — 10а4б ф- 40а3 б2 — 80а2б3 ф- 80аб4 — 32b3; д) 243бфф ф 405б4а + 270б^а24-90б2а3ф15ба4фа5; е)а3ф6а2/аб ф 15а2б_ф 20аб/абф + 15аб2 + 6б2ф4_бфб3; ж) а2—6а|/а2Ь ф 15/аб2 —20ab+l5b^b—6б|Лгб^ф-ф б2; з) 2аУ4а2 — Юау'баб ф-20а^9Ь2 — ЗОб^Лй3ф- 156 У&аЬ — Збу 9б2.
63.	б2 = — 448,	= 280, fee = — 84. 64. a) 51; б) 34; в) 11.
65.	(1 +0,01)10 = 1 4-0,1 ф-0,0045 + 0,00012 4-0,0000021 + ... а) достаточ-но трех членов; б) достаточно пяти членов.
15	16	495а4
66.	Т1в = - Сз1 а1бх63, Т17 = Сз1 а1 V1. 67. Г5 =	. 68. Т4= 84х4. 69. Т7==
(1 \ 12-k I 1 \ k	5fe—36
х 2 j	(х3)	6 . В последнем выра-
жении числитель 56 — 36 должен делиться на 6, а это будет только тогда, когда число k делится на 6, т. е. k = 0,6. Если k = 0, то 7\ = х~6;
го = С?,*-1. 71. Т3 = 60.	100—fe *.
1	ь 2
72. Из формулы = С|00- 2	• 3
если k = 6,
должно де-
следует, что число /г литься на 4, а таких чисел от нуля до 100 имеется 26.
4	1
3	1
1	-2
73.7\=х4, Т6 = 105х, г, = — □12
х 74. 1
36’ 36	18’ 36	12’ 36	9
— —, —, —, —, —, —.	75. (k = 2, 3, 4, 5, 6). 76. IL « 0,367.
36’ 6	36	9	4	18	18	6*	30
Решение. Решим эту задачу в самом общем виде, т. е. для любого натурального числа и. Пусть (ах, а2,..., ап) — перестановка из и элементов (чисел от 1 до п). Назовем перестановку беспорядком, если а/ =# *, т е. для всех I = 1,2, 3,..., п на f-м месте стоит число а/ I- Другими словами, в беспорядке ни один элемент не занимает своего первоначального места. Пусть Dn обозначает число всех беспорядков из и элементов. Подсчитаем это число. Очевидно, что Dx = Qf D2 = 1. Первое место в беспорядке может быть занято любым элементом, исключая первый элемент, т. е. п — 1 элементом. Если первое место займет число k =4 1, то все беспорядки можно разбить на две группы в зависимости от того, займет ли первый элемент k-e место или нет. Если I элемент займет k-e место, то число беспорядков в этом случае равно числу беспорядков, образованных (и — 2)-мя элементами, т. е. Рл_2. Если же I элемент не будет занимать /г-го места, то беспорядки будут такими, что в них элементы 1, 2,..., k — 1, k + 1,..., п занимают места от 2-го до и-го и, следовательно, их число равно Dn^. Таким образом, когда число k занимает первое место, то будем иметь всего Dn_x + Drt_2 беспорядков. А так как k может принимать/г— 1 различных значений, то всех беспорядков из п элементов будет Dn — (ti — 1) (Pn-Y-\- D^). Из этой формулы последовательно получаем: D3 = 2 (D2 + DJ = 2 (1 + 0) = 2, DA = 3 (2 -f- 1)= 9, Db = 4 (9 + 2) = 44, D6 = 5 (44 + 9) = 265, D1 = 6 (265 + 44) = 1854. Следовательно, вероятность того, что 5 гостей наденут каждый чужую шляпу, равна ЕЕ	44	11	/	Dn\	103	/ 1 \п
^ = —=— = 0,367 Г = — . 77. — « 0,368. 78. 1 — — >0,9 и по-5!	120	30	\	п! /	280	\ 2 /
этому п ., т. е. п > 3. 79. а)	~ 0,08; б) (Сюо -|- Cioo -f- •••
igz	2
+ О •	~ 0.74; в) (Cioo + Cfoo + ... + Cioo) • —
81. Решение. Одно подмножество, содержащее элементов, можно выбрать С^* 1 способами. Из оставшихся п—т1 элементов можно выделить под-
множество, содержащее т2 элементов , способами и т. д. После выбора (k — 1) подмножества, содержащего mk-i элементов, останется элементов, которые образуют /г-е подмножество. Поэтому число всех способов выбора k попарно не пересекающихся подмножеств, удовлетворяющих указанному в задали
че условию, равно Сп 1 •	• Сп^т1_т2	==
и!	(и — m^l	(п — тх— т2)!
т3! (л — т1 — т2 — т3)1
п\	10!
-------------------- 83.----------=175.
mJ m2! m3! ... m^l *	(3!)2 * * * * * (4!)2
5	8	14	12	14
7’ 9 ’	13’’	’2’ 3' 4’ 5’
86. 88. yn = 3n — 1. 89. xn = 5n — 2. в) хп = 2-(—1)л; r) xn = 3-2n~1.
т2! (л — т1 — т2)\ (п — т1 — т2 —... — т^_2)!
m^-J (п —	— т2 — ... — mk.2)\
2
85< б) —2,4,— 6, 8, — 10; г) —,
5
86. а) 3, 9, 27, 81, 243; в) 6, 17, 34, 57,
1
91- а) хп == —; б) хп = 1 + 4 (л — 1);
л2
92.
94.
X"-8 - (n _ 2) (Л - 1) : X2n+1 ~(2n + 1) (2n + 2)- 931 Хгп ~ n ’’ Х8Я+1 “ °
{0, если n — четно,
1, если n — нечетно.
96*. xn = 4 — -%-- ; л = 1, 2 ... Указание. Выписать несколько nep-
вых членов последовательности, заметить закон их образования и доказать его справедливость методом математической индукции.
97*. Если b 0, то хп = —----------п — 1, 2, ...
1 — b
/ 1 \n+1 / 1 \п+*
98. Хя+1=^1+—J . Хп+2 = (1+_—J .
"• Уп+1 = р + ттг) : Уя+а = 1 + ГТТ •
\ П -f- 1 /	\ П —z /
100. а) Убывает; б) возрастает; в) не является монотонной.
102. а > 2 b', а > 2b', а < 2Ь.
103. Решение.
|	-]Л+2
1 + п (п + 2) ]
/	1 \ П+1
у„ = \ + п/ _ Г (п + I)2 -р2 п
Уп+i - Л 1 \n+2 L п (« + 2) J ' п + 1 \ +1+п/
104. а) хп > 1; б) 0 < хп < 1; в) хп > 1; г) 0 < хп < д) хп >
3;
е) 0 < хп < — ; ж) — ~ < хп < —; з) 0 < хп < 1; и) — < хп < 1. z	о	у	Z
105. а) Последовательность (хл) называется неограниченной сверху, если для любого числа М найдется, по крайней мере, один член последовательности хп , такой, что хп^ > М.	0
Л n -J- 1 п 4- 1 п -\-п	2	1 п	I
112*. Указание, а) 0<—— <—-—<——; б)	— 1 =
п2 + 1 и2 и2 п	IJZ п2 + п I
1	1	* w	Зп — 4 Зп 3
=—	-----------< — 113*. Указание. —-----------— < —-------------
У п2 + п + п + 1 п ‘	2п2 + п + 2	2п2 + п 2п + Г
114. Не имеет. 115.
дится; в) Итхл = 2.
П -* ОО
10 хз=0,4;. .; хп= —;...
Не является. 116. а) Нтхл = 0; б) расхо-П -+ оо
8	15
119. а) —; б) 2; в) — 120. х, = 10; х2 = 2;
□	Z
1 1 1
121.5; 1;—;	122.-------. 123. При |х|<1
5	25	1 — х
S	. 124. 1 H-х2. 125. При | х [ < 1 S=-—. 126. а) При — 2<х < 0
1 — х2	1 — х3
S = — 1----б) при х < — — S = —	в) при | х | > — S = —-—;
х F	2	2х + 1 F 1 1	2 2х — Г
1	2
г) при 0< х < 2 $ =-----. 127. q = - 128. а) | х | < 1; б) | х| < 2; в) | х | < 1.
х	3 *
129. Указание. Используя подобие треугольников, доказать, что------= —
s — 1 q'
131**. Решение. Пусть число п не является квадратом натурального числа, Р	Р2
и предположим, что существует рациональное г = —, такое, что п — — Бу-q	q2'
р
дем считать дробь — несократимой. Тогда nq2 = р2. Пусть число р представляется в виде следующего произведения простых множителей р ==	Р™* p^k.
Так как дробь — несократима, то среди простых множителей числа q Я
нет ни одного простого множителя числа р. Поэтому все простые множители числа и содержатся среди множителей числа р3 = (р™1 pj1*... p™k )2- Например, п = (p7* • рТ3 • Р?в )2’ Но тогда число п является квадратом натурального числа, что противоречит условию теоремы 2.
132**. Указание. Доказательство проводите по образцу доказательства теоремы 1 § 25. 137. Рациональным. 138. Нет. Такое число может быть и бесконечной периодической десятичной дробью. 140. lim хп=—^==Уа и хп<—^=~Уа .
п -> оо у а	] а
1+12	1	3
143. Указание. | ап | <----= —, 146. а) — б) —	147. а) 0;
2	3
б) —у. 148. а) —2; б) 0. 149. а) 1; б) — —.	150. а) 1; б) —3.	151. а) Г,
3	1	2	п — 1	1 (и — 1) п 1
б)--.152.а)-4--	— = ~2——	~ при я-> оо; б) — 3.
1	1	г__________ г___________
153. а) 1; б) 154. а) Г, б) У к а з а н и е. У п2 + Зи — 1 — У п2 + 2и — 1 = О	Z
(я2 + Зя — 1) — (п2 + 2я — 1)	.	3	1
- ^ + 3.-1 +	|55' •> 7- «>“ |и‘ > - зёГГ^зу
в) >^±±. 1S7". У кяза я я |	‘'L <
2	У хп + У а У а
159. 2) Указание. Для любого 8 > 0 найдется такое ДГ, что при и > N сразу выполняются два неравенства | хп — а|<е и | хп — b | < 8, или а — 8< хп <а + & и b — & < уп <6 +8. 3) Если lim хп = а, то а = 1 + ab
П -+ со
а — 1	~	/ г- \	I	8
и b =--------. 5) Ит Рп — а (У2 + 1). 6) lim Sn —— ab. 7) Ит Sn ——.
а	/?->оо	П со	2	П -* со	3
162. ив = 3; «is = 6 )Л2 — К3;	u2l =
160. л — u3072 < 10-9.
- I2]/ 2-/2 + /3; «48 = 24 1^2 _/2+V 2 +/3 1	=
/2—У 2+1^2 +К2 + /3 ’
163.	Указание. Найдите периметры квадрата, правильного восьмиугольника, правильного шестнадцатиугольника, вписанного в единичную окружность.
164.	Указание. Докажите методом математической индукции, что «n = 2"+2V 2 —1/<2 + Т/’2+ ... +/2“
-.. —
п корней
165.	f(l) = 2; /(2) =5,5; f (-М =2,5; f Ш = — + а, если а + 0. \ 2 /	\ а / а
2	5	5	7
166.	/(0)=--; /(1) = 1; /(а2 + 1)= - а2 4-1; f(x-l) = - х -и	О	О	о
3	2
g (X) = - X 4- g (5) = 3,4. 167. а) Нет; б) да. 168. a) f (х 4- Л) = (х 4- Л)2!
5	3
f (х + h) - f(x) = h (2x + /1); f(x + h}	= 2Х4-Л; 6) f (x+h)^k(x+h)+b;
Рис. А
Рис. Б
f(x+h)-f(x)=k(x + h) + b-(kx+b)=kh. 169. б)--Х + ^. f(X)
(x-4-fi№—х2 1
----—----- = — (Зх2 + З/ix +/г2). 170. а) 2; б)6х (см. рис.А). 171. а) Координат-
ный крест; б) квадрат. Рис. А; в) Рис. В;
г) четыре точки (—1, —1), (— 1, 1), (1, — 1), (1, 1);
д) объединение множеств точек двух прямых х — 1 и у — — 3;
ж) множество точек окружности, центр которой находится в начале координат, а радиус равен 1, за исключением точек пересечения ее с прямыми
у ~ х и v = — х.
172."Ef = R\ £g = [-3;oo). 173. Eh = {х | | х| > 1}; Fz = [—4; +4].
174. Ef = |х| х Ф-----; Еу = {х | х =# — 1}.	175. Ef — (— оо; — 4);’
(-4; +4); (4; оо); Еу = R.
176. Еу = (—оо; 1); (1; 2); (2; оо); Eg = R.
178. Ez = (4; ое); Ef = (-
179. Ez = [-1; 1]; Eg =
-оо; — 1); [1; 3).
—1 . 180. Функция f в точке (— 2) не 5
определена; f (х) = /х3 -f- 5х + 1 ; f (4) = /37 ;
существует; f (/) = V t2 -)- 5/ + 1- 181. a) f (5) =
/(5)_=Г51 ;	/(-1) не
£3; f(x) = —^х~2 ; 1g 6	1g (х2—Зх—4)
б) И5) =	Н“) = 1/ -—-• Функция у
3	У 2 — и
в точке 5 не определена;
>(Х)=1/	В) f(5) = lg£ H«) = lg
У 2 + х	7
/(0) = -1;=	z(|) = y; /(1)=1;
/(0) = 1; /(1)= 1; Н2) = 3; f (3) = / Ц5)=1. а2 — х2 при 0 < х < а
и — 4
—.	182. )(-2) = -1;
/ (4) = 1.	183. И-2) = 7;
184. Es = [0, а /21 ; S (х) ==
(д/2 —х)2 приа^2 < х < а/2
185. Ej, = [0; a /2 l;S(x) =
oo). 197.
(2ах, 0 < х < ?
2 ’
2а (У 2 а — х )2, а ^2- < х < а У2-
186. Нет. 187. Цх) = — У г2 —х2, где г— радиус окружности.
188*. Если некоторая линия симметрична относительно оси абсцисс и всякая, прямая, параллельная этой оси, пересекает линию не более чем в одной точке, то абсцисса х точки М данной линии является некоторой функцией ординаты у этой точки. Точнее: существует функция Д определенная в симметричном промежутке [— с, с], такая, что х = f (у) и для каждо-го>С[— с, с]
189.	Функция f определена в симметричном промежутке [—а, а]иЦ—х) = Кх) для всех х £ [—а, а]; а > 0.
190.	Функция f определена в симметричном промежутке [—а, + а] и f (— х) = — f(x) для всех х$[—а, 4- а]; а > 0 (см. рис. Д)
193.	а) Возрастает на всей действительной прямой; б) убывает на всей действительной прямой.
194.	а) Убывает в (—оо; 0), возрастает в (0; +<*>); б) убывает в (—оо; 2), возрастает в (2; + оо). 195. а) Убывает в (—оо; 0), возрастает в (0; оо); б) возрастает в (—оо; 0), убывает в (0;оо). 196. б) Возрастает в (—оо;3), убывает в (—оо; 1), возрастает в (1; оо) =£ 0; в) возрастает в (0; оо) 200. а) Убывает в
убывает в (3;
199. а) Убывает при всех х 0; в) возрастает в (0; оо) 200. а) Убывает в (—оо; 0), возрастает в (0;оо); б) возрастает на всей действительной прямой 7?
201. а) Возрастает в /?; б) убывает в /?; в) убывает в R. 202. а) Возрастает в (0; оо); б) возрастает в (2; оо).
204. в) Указание. | (2х2 —1) — 1| = 2|лг — l||x-f~l | < 4 | х — 1 |, если считать заранее, что 0 < х < 1.
205. в) Указание, lx3 — 1 | = | х — 1 11 х2 + х + 11 < 3 | х — 1 |, если заранее считать; что 0 < х < 1.
210*. Пусть lim / (х) = А и lim g(x)=B=/=0. Тогда / (х) = А + а (х);
6)
' л + а л ' ..в + р” в.
Л _ п	f (х) А + а А
а — б. м. g (х) = А + Р (х); Р — б. м. и L— =	- = ~+
g (х) В + Р В
А Во,— Л р А .	1 п ло	1
= В +	= В +1^)(ба - л(5)> и так как ~ограничен'
ная функция в достаточно малой окрестности точки а, а Ва — Л0 — бесконеч-
но малая в этой точке, то и произведение ——— (Ва — Л0)
Их) А нечно малой в точке а и, следовательно, hm —— = — g(x) 9
2>1. 1) и, и, О) ----U,/Z, ч) О, О) — I, и/ 14 ,
является беско-
в
2 211. 1) 6; 2) 6; 3) —0,72; 4) 3; 5) — 1; 6)- ; 7) у; 8) ,2 v	2/7-/Г_ 3/х(2 —/х)
11) —. Указание. _ ------— —z—--------—-;
3	33/х + 2/х	/х(3 + 2/х)
х3 — х + 6	х3 + 8 —х — 2
Указание. -----—------- =-----------------
х3 + Зх2 + х — 2 _ (х 2) (х2 — 2х + 4) — (х + 2) х2 (х + 2) + х (х + 2) — (х + 2) ’ = (х+ 1)(х2-х+ 1)+2х(х+ 1) ________(х3 + 1) + (х+ 1)  (/х-1 -2)(/х-1 +2)
3; 9) 12; 10) 1;
12)“", 13)	14*) 11.
I	О
х3 + 2х2 + х2 + 2х — х — 2
1 „	х3 + 2х2 + 2х + 1
15*) —. Указание. ------------
4	х3 + х + 2
16) — . У к а з а н и е. х 1 ~ = ' 4	х —5
х — 5 (х — 5) (//=+ 4- 2) (х - 5) (/х^
1	;. У каз а н ие. х3 + 1 = (х + 1)(х2 — х + 1); 21)-^-;
9	(9-х2)(1+3/?^8+У (х2—8)2). 24„. 3
1—/х2—8	1—(х3—8)	’	2'
/Г+7 -1 _ (/Г+Т-1)(/Г4^+1)(3/(Н^2+3/1+^+1). /Г+7 —1	(/Г+7—i)(Vr+7+i)(3/(T+o2+/T+J +1)
27) -Д=; 28)	29) 1,5.
'2/х Зух2 ’ м ,	„ м	3 м „	1 м	3 м
213. 1)а>3^7:б) <4<» + 3>^Г 2) а)-'7^/б)-+с7Г; B)~Z—+2+7
3) (Ю<о + 2)т^. 4)3/2-^. 5) 6<o(/o-lfe- 215. 1) а) у' = 3. 2)/ (2) = а.
20 ) 12 (/9 — /3 + 1)'
22)23*) 3. Указание.
Указание.
25)	26) 1;
; 17) 2; 18) 12; 19)3;
3) Г	(X) = 8х	— 3.	4)	в)	f (х)	=	—	.	5) а) ±-;	б)	у;	в)	—^=.	6)	f(x)	=
х2	2	4	2 у х
6	3	3
= —	-——	7)	а)	/'	(х)	=	\7=",	б)	['	(1)	= -у- •	8)	у = Зх2. 9) у'	= 2ах +	Ь.
(х—2)2	У 6х	У 6
10) f(x) = 6х2 + 6х — 2.	11) f(x) = nag*"-1 + (n — IJap/2"1 4- ... +дл-г
216. а) 0; б) 1; в) n —1; г) и. 217. а) 1; б) 0; в) 1; г) 0. 218. Число А называется пределом функции f в точке а слева lim [ (х) = Л — если для лю-х -♦ а — 0
бого положительного числа е найдется такое число д > 0, что для всех х из области определения функции, удовлетворяющих условию 0 < а — х < б, выполняется неравенство |/ (х) + Л । < 8. Аналогично определяется предел слева.
219. Указание. Теорема следует из определения предела функции и определений односторонних пределов.
, п 1	з	7
221. а) у =0; б) >'= —; в) .у =— —; г) у' =2; у'= ——. 222. а)у'= 5	4	2
6	„	,	12х —5	3	4	83
6) J’ = —; в)у = 12л—7;
Д) у = 4(х—I)3; е) у=6(2х —З)2; ж) у' = 6х(1 —-2х2); з) у' = 5х4; и) У' =	— 12х2 + 12х + 4; к) у' = Засх2 + 2 (ad + be) х -f- ar bd.
223. 1) f(0) = -8; /'( — 1) = — 14; f (1) = - 2; f (2) = 4. f' (—1) = —8УЗ; f'(l) = 12 У 3?	226. a) у' = - - ;
12
в) y' = — ~ ; r) y' = — 15x-6.	227. a)
9x2 — 3	1
6)/==-^-- 228. m=-(TT^r; Г(0)= —1;
2) /'(0) = 2/3 ;
6) У =---------;
X2
/ = — — ;
X4
'	—6x2+6x—20	r 3x2+6x+l nnn r -2x3+6x2—12x+20
232. а) у' =----1	=-^Г. 233. a)/=------------
4x44-7x2-6x+j_	_ 6x4-2x24-3x2+1	3x44-8x24-1
б) У	(x2—l)2	'У x2(2x2 + l)2 ' 'У x2(3x24~l)2’
3x2 1 1	x	1 Г —
2з7-	-jpw ““l'M-v
241.	а) у =Уи ; и = x2; б) y_= /и ; и = x3 -f- 2x; в) у — uss; и = x2 4- x 4-2; г) у = иь; и = Igx; д) у = /и ; и = i>2; v = 1g х. Области определения: a) R; б) (0; оо); в) R; г) (0; оо); д) (0; 4-ое).
242.	а) у =	(х2 + 2х + 5)51 4-51 /х (2х 4- 2)(х2 -f- 2х 4* 5)Б0;
17
«) у _	; .) У - f (2У + 7, + lP(b+ 7);
2хУ х2 + х	3
,	(3 3/? 4- 1)(х2 + 5х) - 3 (х 4- /Т)(2х 4- 5)
д) у =-----------—~-----------------•
3 /х2 (х2 4- 5х)4
245.	Функция у ->у3 4- У возрастает на всей действительной прямой и
поэтому существует и притом единственное число у, являющееся решением уравнения _у3 4- У — х при заданном х.
246. Если функция g обратна функции f, то для всех х из области определения Ef функции / выполняется тождество g [/ (х)] = х. Но тогда производные функций, стоящих слева и справа в этом тождестве, равны между собой:
S' [f(x)] • ff (х) = 1. Следовательно, если Мх0) ==№ то g' (yQ) = —— 
_ I \Хо)
Q	Q	l/’Q
247. а) У = -рт=-; 6) у = -7T7=; B) y= —--------------—.
4/x	4/x	2x2/x
5	3	2	4	—2
«» > у - 2-77 -	«> s’ - ТГ + V r+TF? ;
_	1	___1	5
B) “ 41/<П +2//+ 121//'
249. у = 0; у = — 2x — 1; у = 2x —-1.
250. у — — Зх — 6; у = — Зх -f- 6.
251.	у — 12х — 16. 252.
253.	а) Возрастает на всей действительной прямой k\ б) убывает на всей действительной прямой; в) возрастает в k при а > 0 и убывает в k при а < 0.
254.	а) Убывает
в k\ б) убывает в (—оо; 0), возрастает в
1\ / 1 \
— возрастает в I — оо); г) убывает в
0. (0; оо); в) убы-
(—оо; 1), воз-
вает в — оо;
растает в (1; +<»).
255.	а) Убывает
(—оо; 1), возрастает	в (1; оо).	в) при а	> 0 функция убывает	в (—-оо; 0)
возрастает в (0; оо);	при а < 0	убывает в	(0; оо) и возрастает в	(—оо; 0).
256.	б) Возрастает в (—оо; 0) и (2;	оо), убывает в (0; 2);	г) убывает
(—оо; —2) и (—2;	+©о), д)	возрастает	в (—оо; 2) и (2; оо).
257.	б) Возрастает на всей действительной прямой; в) убывает в (— 1; 0) и (0; 1), возрастает в (—оо; -1) и (1; со); г) возрастает в (0; оо); д) убывает в (0; 1), возрастает в (Г, оо).
259.	б) ^min = у ( — 2) = — 4; j^max => (2) = 4,
260.	б) J/min = У (0) = 0;	.Утах — У ( 1)
3\
— 1, возрастает в
б) убывает
1
.Утах ~У (0 =
в
в
и
в
в) J^min —У (3) — 2; утах —у ( — 3) — 2,
261.	a) J'min = у (1) = 110; Утах=У(3) =212; б) _ут1п ~ У (0) “ 0» в) >min = >(l) = I-
262.	а) Экстремумов нет; б) экстремумов нет; в) j/min = У (0) = 01 J^min = _У (12) = 0; J/max	= 1296.
263.	а) Экстремумов нет; б) j/min = > (2) = 2; >max => (0) = —2; в)>тах = 9
=>(3,2) = -.
/ 2 \	-	/2\	—
264а. 1) .Утш ~У = $	’ -Утах = У ) =	3	; 2) J'max
= У (0) =/2j 3) .утах =у (0) = 1; 4) _утах = у (0) = г 264 б. 1) х < - у;
х > — ; 2) любое действительное число; 3) х < —1; х>2; 4) — 1 < х < 3; 3
1	2
5) х	6) — 2 < х < 1.
и	О
265.	а) Возрастает в (—оо;0); (1; оо), убывает в (0; 1); ^mjn = >(1) = — 1; / 4	\	/	4 \
^тах=-У (0) = 11 б) возрастает в (—оо; 0);	—; оо , убывает в 0; — ;
/4\	940	9	9
-Г =s^;jmax=j(0)=4; в) возрастает в (— 1; 0) и (1; +«>), \ У / ZQo
убывает в (— оо; — 1). _ymin = у (— 1) = 5; _ymin =_у (1) = 5; _yniax = у (0) = 5. 266. а) Возрастает в (—оо;0); (2; +©о), убывает в (0; 2); >т1п=>(2)==—2;
Утах = У (0) = 2; г) возрастает на всей действительной прямой. Экстремумов (3	\	/	3 \	/3	21
Ti +°° ), Убывает в I— оо; — I; ^min = У 1~1 = ~ •
267.	а) .Унаим. =	1» ^наибольшее = 3; б) .Унаим- = 11 ^наибольшее — 3’>
в) .Унаим. = 3; наибольшего значения функция не имеет.
268.	а).Унаим, ~	16;^наибольшее ~	9; б)_унаиМв =	25;.Упаибольшее~ 9,
в) .Унаим. =	25; ^наибольшее = 416.
269.	а) .Унаим. =	9; ^наибольшее == 3; б) .Унаим. =	9; _Унаибольшее = 3,
в) .Унаим, = 3; ^наибольшее = 55.
270. В конце первой секунды ^наибольшее = 7 м/сек. а	а
276. а = — + ~где а > 0 — данное число.
2	2
/2 <—- •' п
... ~наио- - 1б
/2	. I
277. Наибольшую площадь оНаиб. = ~ имеет квадрат со стороной 16	4
278.	Равносторонний.
279.	Высота бака должна быть вдвое меньше стороны основания.
281.	10 = 5	5. 282. 8 = 4 -j- 4. 283. х =	284. 4 см. 285. ^наибольшее 1=3
= 64 м/сек. 286. В 3 км от населенного пункта. 287. 15 м/сек. 288. ш(/)= = (6< —4)(-^Ц; <о (4) = 20Л 289. (О (0 = (4 — 0,60 \ сек /	\ сек /	\ сек /
/ рад \	2	/ см \
со(2) = 2,8 -— ;/=6-~сек.	290. а = 12 t. 291. 1)а = (3/ + 1)---- J
\ сек /	3	\ сек /
2) а) 0 сек; б) сек. 292. 1) 4 • 104 дин; 2) 2,5 • 104 эрг. 293. Масса всего
стержня составляет 360 г, плотность в точке М с абсциссой х равна 5х— , см
г плотность в точке А равна 0, плотность в точке В равна 60 —. см
294. Если Q (/) — количество реагирующего вещества в момент времени t, &Q(t)
го -----—- является средней скоростью реагирования вещества за промежуток
Д *
Д Q(t)
времени от момента t до момента времени t + Д /, a lim -----— = Q'(0> ес’
д t -> о М
ли этот предел существует, является скоростью реагирования вещества. рад
295. 181,5 • 103 эрг. 296. 3 л ---. Решение. Если (р — угол поворота
сск
колеса, измеряемый в радианах, то по условию задачи (р = kt2, где k—коэффициент пропорциональности. Найдем его из условия, что первый оборот был л / рад \
сделан за 8 сек; 2 л = k • 64; k = — -----1 . Угловая скорость со(/) = <р =
oz у сек /
л	/ рад \
^ — t; со (48) = 3 л —— .
16 v '	\ сек /
297.	F = 22tn, где т — масса материальной точки. Указание. Использовать второй закон Ньютона.
298.	Указание. Использовать второй закон Ньютона.
300.	6х—10.	301. f" (х) = 12х2 — 12х + 6.	302. f"(x) = 80(2х + I)3.
4
303. f (0) = 1; /'(0) = Г, f(0) = — 2. 304. у" = ---------305. а) = 1 (сек),
1)
/ м \	/ м \
t2 — 3 (сек); б) vr = 3 — , v2 = 0 — .
\сек ]	\сек /
м	м
306. a) h = 45,1 м; б) v = 30,2 —, а — — 9,8 —;	в) t к, 4,08 сек,
сек	сек2
^наибольшее = 91,6 М
Л
307. 45°. -.
л	л	5л	2л
308.	50°, 90°, 100°, 120°; —, —,	—, - .
18	2	9	3
,	,	, Зл
309.	67° 30', 78°45 , 101°15', 135°, 157°30'; у,
7л
Тб ’
9л Зл нГ’ Т’
7л
8 *
л
310.	Юл рад/сек. 311. — рад/сек, 2л рад/сек.
6 5л	Зл	Зл 25л
312. —, —, л, —,—, 8	4	2	4
л,
313. 142°30', 127°30', 105°, 90°, 75°,
125 л 41л
8 ’ ~2 19л
' 24 ’
17л
24 ’
7л
12’
л 5л
7?
314.	0,2618; 0,8831; 2,3911; 4,1364.
315.	27°48'; —21°31'; 75°54'; 180°; 284°36'; л л Зл	5л
308°39'; 410°03'.
Зл 7л
_ Т’ ~ 4 ’
. Л
317. 1Г15 ; —.
’ 16*									
JT л 318. 0, —, —, ’6’3’	л 2л	5л	7л	4л	Зл	5л	11л	5л	Зл
	7Г’ 7Г’	"б ’	л, —,	7Г’	V’	Т’		~ Т’	“У
4л	7л	5л	2л	л	л		л			
—, ——. —л, ——, ——, ——, ——, ——. 3	6	6	3	2	3	6
л 7л И л 5л 19 л 23 л 9л 31 л 35 л 13 л 43 л 47 л
319.	—, —, ---------, —, ----, -----, —, ------, ----, --, ------, ----.
8	24	24	8	24	24	8	24	24	8	24	24
л	л	л	2 л	5 л	7л 4л	Зл 5л Пл	п п п
320.	-, —, —, —, —, л, —, —, —, —,------------ ; 30°, 60э, 90°, 120°,
6	3	2	3	6	6	3	2’3’6
150°, 180°, 210°, 240°, 270°, 300°, 330°.
323.	0°, 60°, 120°, 180°, 240°, 300°.
324.	1125°. 325. 810°. 328. а) Да; б) да; в) нет.
329. —cos2 а. 330.	1.	331. 2.	332. 2 cos а. 333. sin2 а. 334. 1.
335. 1 +sina. 336. sin a —cos а. 345. Синус положителен в примерах 1, 2, 3, 5 и 9, Косинус положителен в примерах 3, 4, 5, 6, 7, 9 и 10. Тангенс и котангенс положительны в примерах 3, 5 и 9.
346. Произведения положительны в примерах 1, 2, 4, 7, 8, 9, 10 и 11.
347.
348.
349.
sin a	cos a	tg a	ctg a
5	12	5	12
-	1 1	‘	- 1 "	-- - - —
13	13	12	5
4	3	4	3
- - - —	«— -		
5	5	3	4
2	40	2	40
			
			
41	41	40	9
15	8	15	8
				-- — -	— 
17	17	8	15
		sin a	COS a		tg a	ctg a
351.		2 ““7	/5 3		_2/5~ 5	_/5~ 2
352.		_/n 6	_5 6		УУ1 5	5/ТТ 11
353.		12 37	_35 ~ 37		12 ~ 35	35 “12
354.		84 85	13 85		84 13	13 84
355.	x =	я = 2лп + —	и	х — 2 л п	5 л + ~(Г	
356.	X =	я = 2я«+ —	и	5 л х = 2 л п 4- —.		
357.	X =	2 л = 2яп ± — О	и	х = 2 л п ± 2,3.		
358.	Xi =	Л -яп + -	>	л х2 = 2 л п 4- — и х3 = 6		5 л  2 я п 4- —.
359.	X =	л : ЛП 4- — 4	и	х = л п 4- 2,11.		
360.	X =	л л п 4- — 4	и	х = л п 4- 1,16.		
361.	X =	. л : Л П 4- — 4	и	х — л п 4“ 1,95.		
л 362. х — л п 4		и	х — пп 4-2,01. 365. 1) sin 15° < sin 56° < sin 75°;	2) sin 175° < sin 156° < sin 127° < < sin 115°; 3) sin 265° < sin 250° < sin 220°; 4) sin 280° < sin 290° < sin 296° < < sin 315° < sin 340°;	5) sin 1 < sin 1,5 < sin 1,52 < sin 1,55;	6) sin 3 < < sin 2,5 < sin 2,1 < sin 1,8; 7) sin 4,4 < sin 4,2 < sin 4 < sin 3,5; 8) sin 5 < < sin 5,5 < sin 5,8 < sin 6. 367.	1) cos 140° < cos 230° < cos 280° < cos 1000° < cos 75° < cos 15°; 2) cos 3 < cos 4 < cos 2 < cos 5 < cos 1 < cos 5,3 < cos 5,8. 371. Указание, (sin x — cos x)2 > 0. 372. cos 90° = 0. 373. sin_90° = 1. 374. 2-1 (/3 4- 1 ), 2l2 (/3—1), 2 + /3, 2 — Уз. 4	4						
375. 2-1 (КЗ + 1), — 2-1 (КЗ — 1), 2 — /3, — 2 + /3. 376. — —.
4	4	85
220	63	333	13
377. —	378. —. 379. 1. 380.— —. 381. — —, угол а — Р находится
221	65	725	85
в третьей четверти.
*1	5л
383. 1) х = 2 k л; 2) х = (2 k + 1) .тс; 3) х — 2 л и -J- х = 2лл+ —;
6	6
л	5 л	л	л
4) х=2лп — -- , х==2л«+ —; 5) х = л п + — ; 6) х = л п + —;
7) х % л п + 0,4742; 8) х = л п + 1,57. 3	1	1
385. а) 2; б) —; в) 0,4.	386. а) sin 2; б) —; в) 0,75. 387. а) 1;
5	2	2
1	12	1	7	т/Г
б) в) 1. 388. а) б)-; в)--.	389. а)--; б) 5. 390. a) ;
Z	Zt «5	О	Z	о
sin n cos а „ п2 — т2	_	х — sin 2х
б) 0,5. 391. а)----; б)--------; в) — 0,25. Р е ш е н и е. lim -—" =
и	2	к -»о х Ч- sin Зх
-----!	Ит-А__1	1-1	.
= lim sin2x =	Sln2x = _2_________ = - 1 = -0,25.
x»o x sin 3x „ x ,, sin Зх 1	3	4
------ 1 --- --------------1_	--- __	—
sin 2x sin 2x %->osin2x x»osin2x 2	2
а	.	a ~	.	x
392 a. 1) y' = —----------; 2) у =-------------3) у = 2x tg —4-
cos2 (ax+ 5)	’ y sin2 (ax+ 6)	*3T
X2	/ X \	X2
+ ------------; 4) 6x ctg — — 2-------------------
3cos2 —	k6 1	2^4-2
3	\6	/
,	—2 (3x + 2) cos (1—2x)—3sin(l—2x)
5) У =	(3x + 2)2	’
X 1 X 2 sin (2x — 3) cos — — — sin — sin (2x — 3) 6) y =___________________®_____5_____5___________;
cos2 — 5
„	,	x sin (3x — 2)	. x x x
7) у = 3 cos (3x — 2) tg — -J- -------— ; 8) у = sin — + — cos — +
8	8cos2--	3	3	3
8
6x	,	,	20 tg4 4x
4-2tg3x+  ----——;	10) y' = 3 sin 6x;	11) _y =	;
cos2 3x	cos4 4x
12) y' ------------------* r.  '---t-t-t,; 13) y' = 3 cos3 x — 3 sin2 x cos x.
7 J cos2(3 —2x)/tg(3 —2x)	7
392 6. 1) f" (x) = —sin x; 2) f" (x) = — cos x; 3) f" (x) = — k2 sin kx't 4) Г(х) = — k2 cos Zex; 8) y" =2 sin x + 4 cos x — x2 sin x; 9)_y" =— 2sin x—x cos x. a co	a co2 tg co t
392 в. v =-------; a — —--------------. 392 r. F— —mco2S. 393. _y=—х4~л;
cos2 co t	cos2 co t
л	л
у == — 1; у — x — 2л. 394. v = — 1;	= x 4- — ; у = 1; у = — x + у.
л	л	3
395. у = — 2x4-1 +v; У = —	~ \ ji = —2х —14- — л;
3
у = — х 4-у
ПЯТИЗНАЧНЫЕ ТАБЛИЦЫ ЛОГАРИФМОВ ФАКТОРИАЛОВ
п	1g п!	п -	1g п!	п	Ig nf
1	0,00000	35	40,01423	69	98,23331
2	0,30103	36	41,57054	70	100,07841
3	0,77815	37	43,13874	71	101,92966
4	1,38021	38	44,71852	72	103,78700
5	2,07918	39	46,30958	73	105,65032
6	2,85733	40	47,91164	74	107,51955
7	3,70243	41	49,52443	75	109,39461
8	4,60552	42	51,14768	76	111,27543
9	5,55976	43	52,78115	77	113,16192
10	6,55976	44	54,42460	78	115,05401
11	7,60116	45	56,07781	79	116,95164
12	8,68034	46	57,74057	80	118,85473
13	9,79428	47	59,41267	81	120,76321
14	10,94041	48	61,09391	82	122,67703
15	12,11650	49	62,78410	83	124,59610
16	13,32062	50	64,48307	84	126,52038
17	14,55107	51	66,19065	85	128,44980
18	15,80634	52	67,90665	86	130,38430
19	17,08509	53	69,63092	87	132,32382
20	18,38612	54	71,36332	88	134,26830
21	19,70834	55	73,10368	89	136,21769
22	21,05077	56	74,85187	90	138,17194
23	22,41249	57	76,60774	91	140,13098
24	23,79271	58	78,37117	92	142,09477
25	25,19065	59	80,14202	93	144,06325
26	26,60562	60	81,92017	94	146,03638
27	28,03698	61	83,70550	95	148,01410
28	29,48414	62	85,49790	96	149,99637
29	30,94654	63	87,29724	97	151,98314
30	32,42366	64	89,10342	98	153,97437
31	33,91502	65	90,91633	99	155,97000
32	35,42017	66	92,73587	100	157,97000
33	36,93869	67	94,56195	101	159,97433
34	38,47016	68	96,39446	102	161,98293
П родолжение
п	1g п!	п	1g п!	п	1g п!
103	163,99576	143	257,58595	183	346,08317
104	166,01280	144	259,74432	184	348,34799
105	168,03399	145	261,90568	185	350,61516
106	170,05929	146	264,07004	186	352,88467
107	172,08867	147	266,23735	187	355,15652
108	174,12210	148	268,40762	188	357,43067
109	176,15953	149	270,58080	189	359,70714
НО	178,20092	150	272,75689	190	361,98589
111	180,24624	151	274,93587	191	364,26692
112	182,29546	152	277,11771	192	366,55022
113	184,34854	153	279,30241	193	368,83578
114	186,40544	154	281,48993	194	371,12358
115	188,46614	155	283,68026	195	373,41362
116	200,53060	156	285,87338	196	375,70587
117	202,59878	157	288,06928	197	378,00034
118	204,67067	158	290,26794	198	380,29701
119	206,74621	159	292,46934	199	382,69586
120	208,82539	160	294,67346	200	384,89689
121	210,90818	161	296,88028	201	387,20008
122	212,99454	162	299,08980	202	389,50544
123	215,08444	163	301,30198	203	391,81293
124	217,17787	164	303,51683	204	394,12256
125	219,27478	165	305,73431	205	396,43432
126	221,37515	166	307,95442	206	398,74818
127	223,47895	167	310,17714	207	401,06415
128	225,58616	168	312,40245	208	403,38222
129	227,69675	169	314,63033	209	405,70236
130	229,81069	170	316,86078	210	408,02458
131	231,92796	171	319,09378	211	410,34886
132	234,04854	172	321,32931	212	412,67520
133	236,17239	173	323,56735	213	415,00358
134	238,29949	174	325,80790	214	417,33399
135	240,42983	175	328,05094	215	419,66643
136	242,56337	176	330,29645	216	422,00089
137	244,70009	177	332,54443	217	424,33735
138	246,83997	178	334,97485	218	426,67558
139	248,98298	179	337,04770	219	429,01625
140	251,12911	180	339,30297	220	431,35867
141	253,27833	181	341,56065		
142	255,43062	182	343,82072		
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Аналитическое задание последовательности 35
---- функции 99
Арифметический корень n-й степени 155
Бесконечно малые последовательности 80
---- функции 122
Бином Ньютона 25
Биномиальные коэффициенты 26
Бернулли неравенство 9
Вектор единичный 199
—	нулевой 198
Возрастающая последовательность 42
—	функция 107
Главная часть приращения функции ПО
График косинуса 216
—	котангенса 221
—	синуса 213
—	тангенса 219
—	функции 104
Графическое задание функции 104
Действительное число 72
Десятичные приближения действительных чисел 73
Дифференцирование функции 134
Длина окружности 87
Дроби бесконечные десятичные 65
—	конечные десятичные 65
—	периодические 66
Дробная часть числа 65
Дробно рациональная функция 125
Дуга направленная 190
Единичный вектор 199
Значение функции 95
Измерение радианное 185
Индуктивный способ задания последовательностей 36
Индукция математическая 6
—	неполная 4
—	полная 4
Интервал 97
Иррациональное число 72
Касательная к графику функции 158
— к линии 157
Квадратичный трехчлен 170
Комбинаторика 13
Координаты вектора 198
Косеканс 195
Котангенс 195
Коэффициенты биномиальные 26
Критические точки функции 167
Максимальное значение функции 165
Максимум 165
Минимальное значение функции 165
Минимум 165
Монотонные последовательности 42
Направленная дуга 185
Направленный угол 185
Невозрастающие последовательности 42 — функции 108
Неограниченные последовательности 47
Неполная индукция 4
Непрерывность функции 128
Неравенство Бернулли 9
Неубывающие последовательности 42
—	функции 108
Нечетная функция 204
Нулевой вектор 194
Область изменения функции 152
—	определения функции 94
Обратная функция 153
Ограниченные последовательности 43
—	— сверху 44
—	— снизу 44
Окрестность точки 51
Орт вектора 199
Орт оси 199
Пары упорядоченные 34
Паскаля треугольник 22
Перестановки 13
Период 205
Периодические десятичные дроби 66
Периодическая функция 205
Плотность множества рациональных точек 76
Подмножество 15
Полная индукция 4
Полуинтервал 97
Полупрямая 97
Последовательности 33
—	бесконечные 34
—	возрастающие 42
—	геометрическое изображение 38
—	индексное обозначение 34
—	конечные 34
—	монотонные 42
—	невозрастающие 42
—	неубывающие 42
—	расходящиеся 53
—	сходящиеся 53
—	убывающие 41
Постоянная последовательность 35
—	функция 119
Предел дробно рациональной функ-
—	ции 125
—	многочлена 125
—	односторонний 139
—	правый, левый 139
—	числовой последовательности 48
—	функции 120
Принцип математической индукции 6
Приращение аргумента 109
Приращение функции 109
Прогресси я арифметическая 36
—	геометрическая 36
—	убывающая по абсолютной величине 54
Производная 112, 133
— корня квадратного из некоторой функции 146
— левая и правая 138
— многочлена 145
— обратной функции 155
— постоянной 135
—	произведения 140
—	сложной функции 147
—	степенной функции 144, 156
—	суммы 139
—	тригонометрических функций
234—236
—	частного 142
Равномерное движение 130
Радиан 185
— дуговой и угловой 186
Радианная мера дуги и угла 185, 186
Размещения 24
Расходящиеся последовательности 53
Рациональное число 62
Рекуррентный способ задания последовательности 36
Рекуррентного определения схема 36
Ряды числовые 57
Сегмент 97
Секанс 195
Синус 193
Синусоида 208
Сложная функция 147
Сочетание 16
Сочетаний число 16
Стационарные точки функции 167
Сходящиеся последовательности 53
Табличное задание последовательности 37 ----- функции 99
Теорема Вейерштрасса 79
— о числе сочетаний 17
— Ферма 166
Треугольник Паскаля 22
Убывающая последовательность 41
—	функция 107
Угловая скорость 181
Угловой коэффициент прямой 159
—	радиан 185
Угол наклона прямой 237
Факториал 14
Формула бинома Ньютона 25
Функция нечетная 204
—	обратная 153
—	периодическая 205
—	сложная 147
—	четная 203
Целая часть числа 65
Частная сумма геометрической прогрессии 54 ----- ряда 57
Четная функция 203
Число действительное 72
—	иррациональное 72
—	рациональное 62
—	сочетаний 16
Число л 87
Числовая плоскость 96
—	функция 94
Экстремумы функции 164
ОГЛАВЛЕНИЕ
Глава первая. Принцип математической индукции
§ 1.	Понятие о полной и неполной математической индукции ...	£
§ 2.	Принцип математической индукции ............................ 5
§ 3.	Применение метода математической индукции к доказательству неравенств ....................................................... у
§ 4*	. Применение метода математической индукции к вопросам делимости чисел ..................................................... **
Глава вторая. Элементы комбинаторики
§ 5.	Перестановки ...........................................
§ 6.	Подмножество конечного множества. Число’ сочетаний с™.	. .
§ 7.	Способы вычисления числа сочетаний. Треугольник Паскаля 20
§ 8*	. Упорядоченные множества. Число размещений .............. 23
§ 9.	Бином Ньютона ............................;................ 25
§ 10.	Основные свойства бинома Ньютона .......................... 28
§ 11.	Исторические замечания. Применение комбинаторики к теории вероятностей .................................................... 29
Глава третья. Бесконечные последовательности и пределы
§ 12.	Определение бесконечной последовательности. Способы ее задания ............................................................ 33
§	13.	Геометрическое изображение последовательностей ............ 38
§	14.	Монотонные последовательности ............................. 41
§	15.	Ограниченные и неограниченные последовательности ....	44
§	16.	Понятие о пределе числовой последовательности ............. 47
§	17.	Геометрический смысл понятия предела ...................... 50
§ 18.	Единственность предела. Сходящиеся и расходящиеся последовательности ...................................................... 52
§ 19.	Важный пример	сходящейся последовательности ................ 54
§ 20.	Сумма бесконечной убывающей по абсолютной величине геометрической прогрессии .............................................. 54
§21.	Числовые ряды .............................................. 57
§ 22.	Представление чисел в виде бесконечной десятичной дроби . .	58
Глава четвертая. Действительные числа
§ 23.	Счет и измерение ........................................... 61
§ 24.	Рациональные числа и их изображение точками прямой ...	62
§ 25.	На числовой прямой существуют точки, не имеющие рациональной абсциссы ..................................................... 63
§ 26.	Изображение рациональных чисел бесконечными десятичными дробями ........................................................   65
§ 27.	Соответствие между точками числовой прямой и нормальными бесконечными десятичными дробями.................................... 69
§ 28.	Действительные числа ....................................   71
§ 29.	Сравнение действительных чисел ............................ 72
§ 30.	Десятичные приближения действительных чисел ............... 73
§ 31.	Понятие об арифметических операциях в множестве действительных чисел.................................................... 74
§ 32.	Предел последовательности действительных чисел ............ 77
§ 33.	Существование предела у монотонной ограниченной последовательности ..................................................... 78
§ 34.	Бесконечно малые последовательности........................ 80
§ 35.	Теоремы о пределах ........................................ 83
§ 36.	Число л ................................................... 87
§ 37.	Исторические замечания .................................... 91
Глава пятая. Введение в общие методы исследования функций
§ 38.	Понятие числовой функции .................................. 93
§ 39.	Новое понимание числовой прямой и	числовой	плоскости . .	96
§ 40.	Способы задания функции ................................... 98
§41.	Что такое график функции ................................. 104
§ 42.	Изменение функции, ее возрастание и	убывание ............. 107
§ 43.	Приращения аргумента и функции ........................... 109
§ 44.	Производная как скорость изменения	функции .............. 112
§ 45.	Непрерывные и разрывные функции	.................. 116
§ 46.	Исторический очерк ....................................... 117
Глава шестая. Производная и ее применения
§ 47. Понятие предела функции .........................•......... 119
§ 48. Теорема единственности предела ............................ 122
§ 49.	Бесконечно малые функции ................................... —
§ 50.	Теоремы о пределах ....................................... 124
§51.	Важные примеры ........................................... 125
§ 52.	Понятие непрерывности функции ............................ 128
§ 53.	Задача, приводящая к понятию производной ................. 130
§ 54.	Понятие производной . . .*................................ 133
§ 55.	Примеры вычисления производных ..........................  134
§ 56.	Односторонние пределы .................................... 139
§ 57.	Непрерывность дифференцируемой функции.................... 140
§ 58.	Производная	алгебраической суммы функций ................ 141
§ 59.	Производная	произведения функций .......................  142
§ 60.	Производная	частного двух функций ....................... 143
§61.	Производная степенной функции с целым показателем......... 144
§ 62.	Производная	корня квадратного из некоторой функции ...	146
§ 63.	Производная	сложной функции ............................. 147
§ 64.	Понятие обратной функции ................................. 151
§ 65	Дифференцирование обратной функции........................ 155
§ 66.	Производная степенной функции с рациональным показателем .	156
§ 67.	Применение понятия производной в геометрии ............... 157
§ 68.	Применение производной к нахождению интервалов монотонности функции................................................... 161
§ 69.	Экстремумы функции ....................................... 164
§ 70.	Правило нахождения экстремумов функции ................... 168
§71.	Исследование квадратичной функции......................... 169
§ 72.	Применение производной к построению	графиков.............. 176
§ 73.	Отыскание наибольшего и наименьшего значений функции в промежутке ....................................................  177
§ 74.	Применения производной в физике .........................  180
Глава седьмая. Тригонометрические функции, их графики и производные
§ 75.	Радианное измерение углов п дуг .......................... 185
§ 76.	Обобщение понятия	дуги ................................. 189
§ 77.	Обобщение понятия	угла ................................. 192
§ 78.	Тригонометрические	функции	числового	аргумента .......... 193
§ 79.	Тригонометрические	функции	угла	и	дуги ................. 196
§ 80.	Тригонометрические функции и координаты вектора........... 198
§ 81.	Знаки тригонометрических функций ......................... 200
§ 82.	Четные и нечетные тригонометрические функции ............. 204
§ 83.	Периодичность тригонометрических функций ................. 205
§ 84.	Построение угла по данному значению тригонометрической
функции и простейшие тригонометрические уравнения........... 207
§ 85.	Свойства	функции у —	sin	х и ее график ............ 211
§ 86.	Свойства	функции =	cos	х и ее график ............ 214
§ 87.	Свойства	функции у —	tg х и ее график .................... 218
§ 88.	Свойства	функции у =	ctg	х и ее график ............ 220
§ 89. Сложение поворотов, преобразование координат вектора при
повороте осей ............................................... 222
§ 90.	Синус и косинус суммы и разности.......................... 224
§91.	Формулы суммы и разности одноименных тригонометрических функций ........................................................ 226
92.	Об одном важнохм неравенстве	....................... 228
93.	Непрерывность тригонометрических	функций ................. 229
94.	Простейшие тригонометрические	уравнения .................. 230
95.	Предел отношения хорды к длине стягивающей ее дуги . . .	232
96.	Производные тригонометрических функций ................... 234
97.	Угол наклона и угловой коэффициент прямой ................ 237
Ответы и указания к упражнениям ................................ 242
Приложение ..................................................... 258
Предметный указатель ........................................... 260
Борис Ефимович Вейц, Иван Тимофеевич Демидов
АЛГЕБРА И НАЧАЛА АНАЛИЗА
Редактор В. Г. Долгополов
Художественный редактор В. С. Эрденко
Технический редактор Л. Я. Медведев
Корректор В. А. Глебова
Сдано в набор 10/11 1969 г. Подписано к печати 14/VII 1969 г. 60X90’/ie« Печ. л. 16,С Типографская № 2. Уч.-изд. л. 14,79. Тираж 40 тыс. экз. (Тем. пл. 1969 г.) Зак. 385.
Издательство «Просвещение» Комитета по печати при Совете Министров РСФСР. Москва, 3-й проезд Марьиной рощи, 41.
Саратовский полиграфический комбинат Росглавполиграфпрома Комитета по печати при Совете Министров РСФСР. Саратов, ул. Чернышевского, 59.
Цена без переплета 19 коп., переплет 13 коп.