■'I
Бібліотека журналу
«МАТЕМАТИКА В ШКОЛАХ УКРАЇНИ»
О. Р. Поліщук, О. Р. Чайчук
Математична логіка
5-6 класи


Бібліотека журналу «Математика в школах України» Серія заснована в 2003 р.
О. Р. Поліщук, О. Р. Чайчук
Математична логіка
5-6 класи
Харків Видавнича група «Основа» ПП «Тріада+» 2007


ББК 74.262.21
П50
Поліщук О. Р., Чайчук О. Р.
Пзд Математична логіка. 5—6 класи. — X.: Вид. група «Основа»: «Тріада+», 2007.— 112 с. — (Б-ка журн. «Математика в школах України»; Вип. 12 (60)).
ISBN 978-966-495-033-3.
Пропонований посібник містить матеріали для проведення уроків з математичної логіки в 5—6 класах. Наведені задачі також можна використовувати на уроках математики
Розрахований на учнів 5—6 класів шкіл, ліцеїв та гімназій, учителів.
ББК 74.262.21
Навчальне видання
Поліщук Ольга Ростиславівна, Чайчук Олег Ростиславович
МАТЕМАТИЧНА ЛОГІКА. 5-6 КЛАСИ
Навчально-методичний посібник
Головний редактор І. С. Маркова
Редактор Г. О. Біловол Технічний редактор О. В. Лебедева Коректор О М. Журенко Комп’ютерна верстка О. В. Лебедева
Підписано до друку 15.12.2007. Формат 60x90 */. Папір газетний.
Гарнітура «Ньютон». Друк офсетний. Ум. друк. арк. 7. Зам. № 7-12/17-04. Виробник: ПП «Тріада+»
Свідоцтво ДК№ 1870 від 16.07.2007 р. Харків, вул. Киргизька, 19. Тел.: (057) 757-98-16, 757-98-15.
ТО В «Видавнича група “Основа”». Свідоцтво ДК№ 1179 від 27.12.2002 р. Україна, 61001, Харків, вул. Плеханівська, 66.
Тел (057) 731-96-33. E-mail: ofTice@osnova.com.ua
© Поліщук О. Р , Чайчук О. Р., 2007
ISBN 978-966-495-033-3 © ТОВ «Видавнича група “Основа”», 2007


ЗМІСТ
Передмова 5
5 клас 6
Урок № 1. Тема. Задачі на кмітливість. Задачі-жарти 6
Урок № 2. Тема. Задачі на кмітливість. Задачі-жарти 7
Урок № 3. Тема. Натуральні числа. Порівняння натуральних чисел 9
Урок № 4. Тема. Комбінування з числами 10
Урок № 5. Тема. Закономірності 11
Урок № 6. Тема. Закономірності 14
Урок № 7. Тема. Просторова орієнтація та уява 16
Урок № 8. Тема. Задачі із сірниками 18
Урок № 9. Тема. Задачі із сірниками 19
Урок№ 10. Тема. Задачі із сірниками 21
Урок № 11. Тема. Танграм 22
Урок № 12. Тема. Танграм 24
Урок № 13. Тема. Задачі на спостережливість 25
Урок № 14. Тема. Задачі з розрізуванням та склеюванням 26
Урок № 15. Тема. Задачі з розрізуванням та склеюванням 28
Урок № 16. Тема. Комбінації з об’єктами та фігурами 29
Урок № 17. Тема. Обчислення площ та об’ємів 31
Урок № 18. Тема. Задачі на зважування 32
Урок № 19. Тема. Задачі на переливання 32
Урок № 20. Тема. Задачі на використання властивостей календаря 33
Урок № 21. Тема. Задачі на використання властивостей календаря 33
Урок № 22. Тема. Елементи комбінаторики 34
Урок № 23. Тема. Елементи комбінаторики 34
Урок № 24. Тема. Сюжетні логічні задачі 35
Урок № 25. Тема. Сюжетні логічні задачі 36
Урок № 26. Тема. Переправи 38
Урок № 27. Тема. Числові послідовності 38
Урок № 28. Тема. Магічні квадрати 39
Урок № 29. Тема. Магічні квадрати 40
Урок № ЗО. Тема. Розв’язування задач від кінця до початку 41
Урок № 31. Тема. Задачі, які розв’язуються від початку до кінця 42
Урок № 32. Тема. Задачі на рух 43
Урок № 33. Тема. Задачі на рух 43
6 клас 47
Урок № 1. Тема. Задачі, які розв’язуються за допомогою граф-схем 47
Урок № 2. Тема. Задачі з точками, прямими та іншими геометричними об’єктами 48
Урок № 3. Тема. Задачі на НСК, розкладання на прості множники . ... 49


4
Математична логіка 5-6 класи
Урок № 4. Тема. Подільність чисел 49
Урок № 5. Тема. Подільність чисел 51
Урок № 6. Тема. Подільність чисел 52
Урок № 7. Тема. Задачі, пов’язані з розкладанням чисел на прості множники 52
Урок № 8. Тема. Властивості останньої цифри добутку, суми, різниці, степеня деяких натуральних чисел 53
Урок № 9. Тема. Деякі властивості чисел, які є квадратами натуральних чисел 54
Урок№ 10. Тема. Задачі з дробами 55
Урок № 11. Тема. Задачі з дробами 56
Урок№ 12. Тема. Задачі з дробами 57
Урок № 13. Тема. Задачі на порівняння дробів 58
Урок № 14. Тема. Цікаві задачі на відсотки 58
Урок № 15. Тема. Задачі з відсотками 59
Урок № 16. Тема. Задачі з відсотками 60
Урок № 17. Тема. Задачі з відсотками 60
Урок № 18. Тема. Задачі, пов’язані з турнірами 61
Урок № 19. Тема. Математика в іграх двох осіб 62
Урок № 20. Тема. Виграшні та програшні позиції 66
Урок № 22. Тема. Принцип Діріхле 67
Урок № 23. Тема. Принцип Діріхле 68
Урок № 24. Тема. Принцип Діріхле 68
Урок № 25. Тема. Інваріант 69
Урок № 26. Тема. Включення, виключення 70
Урок№ 27. Тема. Включення, виключення 71
Урок № 28. Тема. Комбінаторні задачі 72
Урок № 29. Тема. Задачі з годинниками 72
Урок № ЗО. Тема. Задачі з годинниками 73
Урок № 31. Тема. Задачі на складання рівнянь 74
Урок № 32. Тема. Задачі на складання рівнянь 74
Урок № 33. Тема. Задачі на складання рівнянь 75
Урок № 34. Тема. Задачі на рух 76
Урок № 35. Тема. Задачі на рух 77
Відповіді. 5 клас 81
Відповіді. 6 клас 95
Література 112


ПЕРЕДМОВА
Розвиток логічного мислення — одне із головних призначень шкільного курсу математики. Вміння аргументовано відстоювати свою точку зору, правильно і чітко висловлювати думки, робити узагальнення і висновки досягаються під час розв’язування задач.
Пропонований посібник містить матеріали до уроків математичної логіки в 5—6 класах. Враховуючи, що курс математичної логіки викладається не в кожній школі, наведені у посібнику задачі можна розв’язувати на уроках математики з метою активізації розумової діяльності учнів, формування їхнього інтересу до предмета. Запропоновані задачі вимагають нестандартного підходу до розв’язання, застосування нетривіальних ідей, використання знань у нових ситуаціях. Назви тем і розподіл задач за темами (методами розв’язання) досить умовні, адже для багатьох задач існує декілька способів розв’язання. Це, власне, і робить математику такою привабливою і цікавою!


5 КЛАС
Урок № 1
Тема. ЗАДАЧІ НА КМІТЛИВІСТЬ. ЗАДАЧІ-ЖАРТИ
Усні задачі-жарти
1. Ішов дідусь до Києва й зустрів трьох бабусь. Кожна з них несла три торби, в кожній торбі — по три кішки. Скільки істот рухалось до Києва?
2. Двоє пішли — дві гривні знайшли, четверо підуть — скільки грошей знайдуть?
3. Скільки кінців у трьох олівців; у чотирьох; у трьох з половиною?
4. Горіло вісім свічок. Одну загасили. Скільки свічок залишилось?
5. Встановіть закономірність форм фігурок, що зображені на рисунку. Яку фігурку треба поставити наступною? А яку після неї?
Задачі на кмітливість
1. Гарбуз важить 2 кг та ще півгарбуза. Скільки важать два таких гарбузи?
2. Яблуко й груша разом коштують 17 копійок. П’ять яблук і дві груші — 55 копійок. Скільки коштує одне яблуко та одна груша?
3. Половина моїх грошей та ще четвертина моїх грошей, та ще 4 грн — це і всі мої гроші. Скільки в мене грошей?
4. П’ять курок за 5 годин знесли 5 яєць. Скільки курок знесуть 100 яєць за 100 годин?
Домашнє завдання
1. 	Одна рибина важить 1 кг та ще піврибини. Скільки важать п’ять таких рибин?


5 клас
7
2. Яблуко й груша разом коштують 12 копійок, а три груші та два яблука — 31 копійку. Скільки коштує окремо одне яблуко та одна груша?
3. Коли б я мав половину тих грошей, що маю, та ще 1 гривню, то в мене було б 25 гривень. Скільки в мене грошей?
Урок № 2
Тема. ЗАДАЧІ НА КМІТЛИВІСТЬ. ЗАДАЧІ-ЖАРТИ
1. Два лижники вийшли одночасно назустріч один одному. Перший ішов до зустрічі дві години. Скільки часу йшов другий лижник до зустрічі з першим?
2. Один хлопчик проходить за годину 5 км. Яку відстань пройдуть три хлопчики за годину, якщо вони вийдуть одночасно та йтимуть з тією ж швидкістю?
3. Пара коней пробігла 12 км. Скільки кілометрів пробіг кожний кінь?
4. Кожне з чотирьох коліс автомобіля проїхало 10 км. Скільки кілометрів проїхав автомобіль?
5. З Одеси до Тернополя о 12 годині дня вирушив автобус. На годину пізніше з Тернополя до Одеси виїхав велосипедист, який їхав значно повільніше, ніж автобус. Хто з них буде ближче до Одеси, коли вони зустрінуться?
6. Двоє гравців грали в шахи 2 години. Скільки годин грав кожний гравець?
7. Семеро чекали восьмого 14 хвилин. Скільки часу чекав кожний окремо?
8. Вісім яєць варилося 4 хвилини. Скільки часу варилося кожне яйце?
9. Четверо дітей виконували завдання, що складалось із 10 задач. Розв’язання кожної задачі діти обговорювали 2 хв. Скільки часу вони витратили на виконання завдання?
10. О третій годині дня обласне радіо повідомило, що на найближчий тиждень збережеться безхмарна погода. Чи може через 60 годин по області світити сонце?
11. Професор ліг спати о 9 годині вечора, а будильник поставив на 10 годину ранку з тим, щоб добре виспатися. Скільки годин спав професор?
12. Літак долає відстань від Києва до Одеси за 1 год 10 хв. На зворотний шлях витрачає 70 хв без зміни початкової швидкості. Як це пояснити?
13. Який годинник показує правильний час лише двічі на добу?
14. Вулицею вдуть два батьки та два сини, а всього троє осіб. Яктаке може бути?
15. Два батьки, два сини та дідусь з онуком впіймали по шість окунів, а всього — вісімнадцять. Як таке може бути?
16. Йшли два міліціонери. Один з них був сином іншого, але той не був його батьком. В якому випадку таке можливо?


8
Математична логіка. 5-6 класи
17. Петрикові батьки мають троє дітей. Ім’я першої дитини Андрій, другої — Олег. Яке ім’я у третьої дитини?
18. Два хлопчики йшли разом до школи і знайшли 10 копійок. Скільки грошей знайдуть чотири хлопчики?
19. Термометр показує три градуси морозу. Яку температуру покажуть два такі термометри?
20. У двох носорогів два роги. Скільки рогів у двадцяти носорогів?
21. На одній руці 5 пальців, на двох руках 10 пальців. Скільки пальців на 10 руках?
22. До класу зайшов спочатку Іванко, за ним — Степан, потім — Маринка, за нею — Яринка, останнім до класу зайшов Гнат. Скільки до класу зайшло хлопчиків?
23. Летіли гуси. Одна гуска попереду, а дві позаду. Одна гуска позаду, а дві попереду. Одна гуска між двома і три в ряд. Скільки було гусей?
24. У кімнаті в кожному кутку сиділо по одному коту і кожний з цих котів бачив ще трьох. Скільки котів сиділо в кімнаті?
25. Два плюс два помножити на два. Скільки буде? Ні, ні — не 8, подумай ще раз.
26. У зайчика було 7 морквин. Він з’їв усі, крім трьох. Скільки морквин залишилось?
27. В отарі 100 овець. Усі, крім 9, втекли. Скільки овець залишилося?
28. Дві жінки йшли із села до міста. Назустріч їм ішли ще п’ять жінок. Скільки всього жінок ішло до міста?
29. У кошику було п’ять яблук. П’ятьом дівчаткам роздали по яблуку і в кошику залишилось ще одне яблуко. Як таке могло трапитися?
30. У скільки разів половина більша за свою половину?
31. Кожний місяць закінчується числом ЗО або 31. В якому місяці є число 28?
32. Дах будинку несиметричний: один бік пологий, а інший — крутий. Півень відклав яйце на гребінь даху. По якому боці покотиться яйце — пологому чи крутому?
33. Стояло п’ять склянок з полуницею. Ганнуся з’їла полуниці з однієї склянки. Скільки склянок залишилось?
34. Шість горобців клювали зерно, до них прилетіло ще п’ять. Кіт підкрався і схопив одного горобця. Скільки пташок залишилося клювати зерно?
Домашнє завдання
1. У родині 5 синів. Кожен має одну сестру. Скільки дітей у родині?
2. Скільки буде десятків, якщо три десятки помножити на чотири десятки?


5 клас
9
3. На фермі є сім свиней: три рожеві, три чорні та одна ряба. Скільки свиней можуть сказати, що в цьому маленькому стаді знайдеться хоча б одна свиня такої самої масті, як і вона?
4. Електропотяг заїхав до тунелю. В який бік буде йти дим, коли електро- потяг вийде з тунелю, якщо вітер дме на південь?
5. Йшов чоловік вулицею і раптом почалася сильна злива. Парасолі в нього не було, капелюха — також. Наскрізь промокли його черевики, костюм і навіть сорочка, але жодна волосина на його голові не змокла. Як таке може статися?
6. На що схожа половина яблука?
7. Лежало дві монети на суму 15 копійок. Одна з монет — не п’ятак. Що це за монети?
8. Росло 5 верб. На кожній вербі — по 5 гілок. На кожній гілці —по 5 менших гілок, а на кожній з тих гілочок — по 5 груш. Скільки груш росло на дереві?
9. Вимкнули електрику. Людина входить до темної кімнати, на столі стоять свічка та лампа. Що людина запалить у першу чергу?
10. У домі всі тварини, крім двох, — собаки, всі тварини, крім двох, — кішки, і всі, крім двох, — папуги. Скільки в домі живе тварин і які ці тварини?
11. «Мій хвіст, — сказав кіт, — має 12 см і ще половину мого хвоста». Якої довжини в кота хвіст?
Урок № З
Тема. НАТУРАЛЬНІ ЧИСЛА. ПОРІВНЯННЯ НАТУРАЛЬНИХ ЧИСЕЛ
У десятковій системі числення будь-яке число записується за допомогою десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Система числення, якою ми користуємося, є позиційною системою числення. Це означає, що для запису числа ми користуємося десятьма цифрами, кожна з яких може займати певну позицію. Наприклад, число abc містить а сотень, b десятків, с одиниць і його можна подати у вигляді: 100а +10Л+с. Число abed подається у вигляді: 1000а+1006+10с+d.
1. Запишіть усі чотирицифрові числа, у кожного з яких число тисяч у 5 разів більше від числа одиниць, а число сотень на 7 більше від числа десятків.
2. Запишіть усі чотирицифрові числа, у кожного з яких число тисяч у три рази більше від числа одиниць, а число сотень на 6 більше від числа десятків.


10
Математична логіка 5-6 класи
3. Запишіть найменше та найбільше чотирицифрові числа, в яких усі цифри різні.
4. Запишіть найбільше та найменше чотирицифрові числа за допомогою цифр 0, 1, 2, 5.
5. Запишіть найбільше та найменше чотирицифрові числа за допомогою цифр 0, 1,9, використовуючи кожну цифру хоча б один раз.
6. У числі 48 352 117 закресліть такі три цифри, щоб утворилось: а) найбільше число; б) найменше число.
7. Знайдіть суму будь-якого двозначного числа та числа, що записане такими ж цифрами, але у зворотному порядку. Чи буде здобута сума ділитися на 11? Наведіть приклади. Спробуйте довести це для довільного двозначного числа.
8. Розв’яжіть ребус
КРАБ
БАРК
Домашнє завдання
1. Запишіть усі трицифрові числа, у кожного з яких число одиниць у два рази менше від числа десятків, а число десятків у два рази менше від числа сотень.
2. Запишіть найбільше та найменше п’ятицифрові числа, за допомогою цифр 2, 7, 8, використовуючи кожну цифру хоча б один раз.
3. У числі 1 234 512 345 закресліть п’ять цифр таким чином, щоб здобуте число було: а) найбільшим; б) найменшим.
4. Між деякими цифрами 12 3 4 5 поставте знаки дій і дужки так, щоб у результаті виконання зазначених дій здобути число 40. Переставляти цифри не можна.
5. Розв’яжіть ребус
БУКВА
+БУКВА
СЛОВО
Урок № 4
Тема. КОМБІНУВАННЯ З ЧИСЛАМИ
1. 	Треба пронумерувати сто кімнат у готелі. Скільки потрібно для цього відштампувати: а) одиниць; б) двійок; в) дев’яток; 7) нулів?


5 клас
11
2. Скільки треба знаків, щоб пронумерувати в книжці: а) 95 сторінок;
б) 	121 сторінку?
3. Знайдіть суму: 1+2+5+7+...+49.
Усні вправи
1. У коморі було 8 мішків борошна. На кожному мішку сиділо по дві миші. До комори зайшов чоловік із собакою. Скільки ніг стало в коморі?
2. Фантастична істота має дві праві ноги і дві ліві, дві ноги спереду і дві ззаду. Скільки всього у неї ніг?
3. На столі лежало чотири яблука. Одне з них розрізали навпіл. Скільки яблук на столі?
4. Стіл має чотири кути. Один кут спиляли. Скільки кутів залишилося?
Домашнє завдання
1. Скільки одиниць зустрінеться, якщо виписати всі натуральні числа від 1 до 200?
2. Скільки треба знаків, щоб пронумерувати в книжці 143 сторінки?
3. Як дістати нуль за допомогою трьох п’ятірок, використовуючи арифметичні дії та дужки?
4. Запишіть число 100:
а) за допомогою п’яти одиниць та арифметичних дій;
б) використовуючи шість разів одну й ту саму цифру та арифметичні дії.
5. Розв’яжіть ребус:
ВАГОН
+ВАГОН
СОСТАВ
Урок № 5
Тема. ЗАКОНОМІРНОСТІ
У завданнях, наведених нижче, фігури змінюються не будь-як, а за певним правилом. Намалюйте замість знака питання фігуру за тим самим правилом.
оооосо еоооо ееоо?
1. а)
б)


12
Математична логіка. 5-6 класи


5 клас
13


14
Математична логіка. 5-6 класи
Урок № 6
Тема. ЗАКОНОМІРНОСТІ
1. 	Яка фігурка повинна стояти замість знака питання? Чому?
У деяких задачах треба вгадати, яке слово слід поставити в дужках замість зірочок.


5 клас
15
Наприклад, корова (коза) закон карета (****) шашки
Для цього необхідно уважно подивитися на слово попереднього рядка, записане в дужках. Як воно утворилося? Якщо перше й останнє слово першого рядка порівняти зі словом у дужках, то можна помітити, що слово «коза» складається з першого складу першого слова (ко-рова) і першого складу другого слова (за-кон). Якщо ми так само складемо слово в дужках наступного рядка, то отримаємо слово «каша». Необхідно пам’ятати, що слово повинно мати стільки літер, скільки зірочок є у дужках, а правило побудови слів може бути дещо зміненим.
2. 	Відгадайте, яке слово треба поставити в дужках замість зірочок:
а) доміно (нога) гараж,
молоко (♦**♦) замок;
б) сорока (комар) марка,
перука (*♦***) сокіл;
в) город (роги) мир,
роман (****) мед;
г) короп (поле) лепет,
гараж (****) базар.
Домашнє завдання
1. 	Яку фігуру треба поставити замість знака питання?


16
Математична логіка. 5-6 класи
2. 	Відгадайте, яке слово треба поставити в дужках замість зірочок:
а) корова(коло)голова,
рушник (****) декада;
б) табу (бутон) тонус,
ківі (♦****) русло;
в) буква (куля) лялька,
голуб (****) залізо.
Урок № 7
Тема. ПРОСТОРОВА ОРІЄНТАЦІЯ ТА УЯВА
Уявіть, що аркуш паперу склали вчетверо і вирізали на ньому візерунок так, як це показано на малюнках у лівому верхньому куті. Уівіть, що вийде, якщо цей аркуш знову розгорнути, і вкажіть, який з п’яти запропонованих візерунків правильний. Якщо деякі завдання видаватимуться надто складними, візьміть аркуш паперу або серветку, згорніть учетверо, і виріжте отвори так, як це показано на малюнку. Потім розгорніть — і все одразу побачите.


5 клас
17
а) б)
в) г) д) SS9
Домашнє завдання
Укажіть, який з поданих візерунків правильний?
а) б) аин
в) г) д)
■ ии
2.
а) б) яшп
в) г) д) ВИ □
а) б) явв
в) г) д) BBS
4.
а) б)
в) г) д)
BBS


18
Математична логіка. 5-6 класи
а) б)
'ОО
В) г) д)
ХХ8
6
а) б)
'ОО
в) г) д)
XSK
а) б) °ни
в) г) д)
И9П
8.
а) б)
в) г) д)
Урок № 8
Тема. ЗАДАЧІ ІЗ СІРНИКАМИ
1. З фігури на рис. 1 вилучіть 2 сірники так, щоб "
одержати два нерівних квадрати.
2. У фігурі на рис. 1 перекладіть 3 сірники так, щоб н „
одержати 3 рівних квадрати.
3. У фігурі на рис. 1 перекладіть 4 сірники так, щоб
одержати 3 рівних квадрати.
4. У фігурі на рис. 1 перекладіть 4 сірники, щоб Рис. 1 одержати 2 нерівних квадрати.
5. У фігурі на рис. 2 перекладіть 2 сірники, щоб одержати 4 рівних квадрати.
Рис. 2


5 клас
19
Домашнє завдання
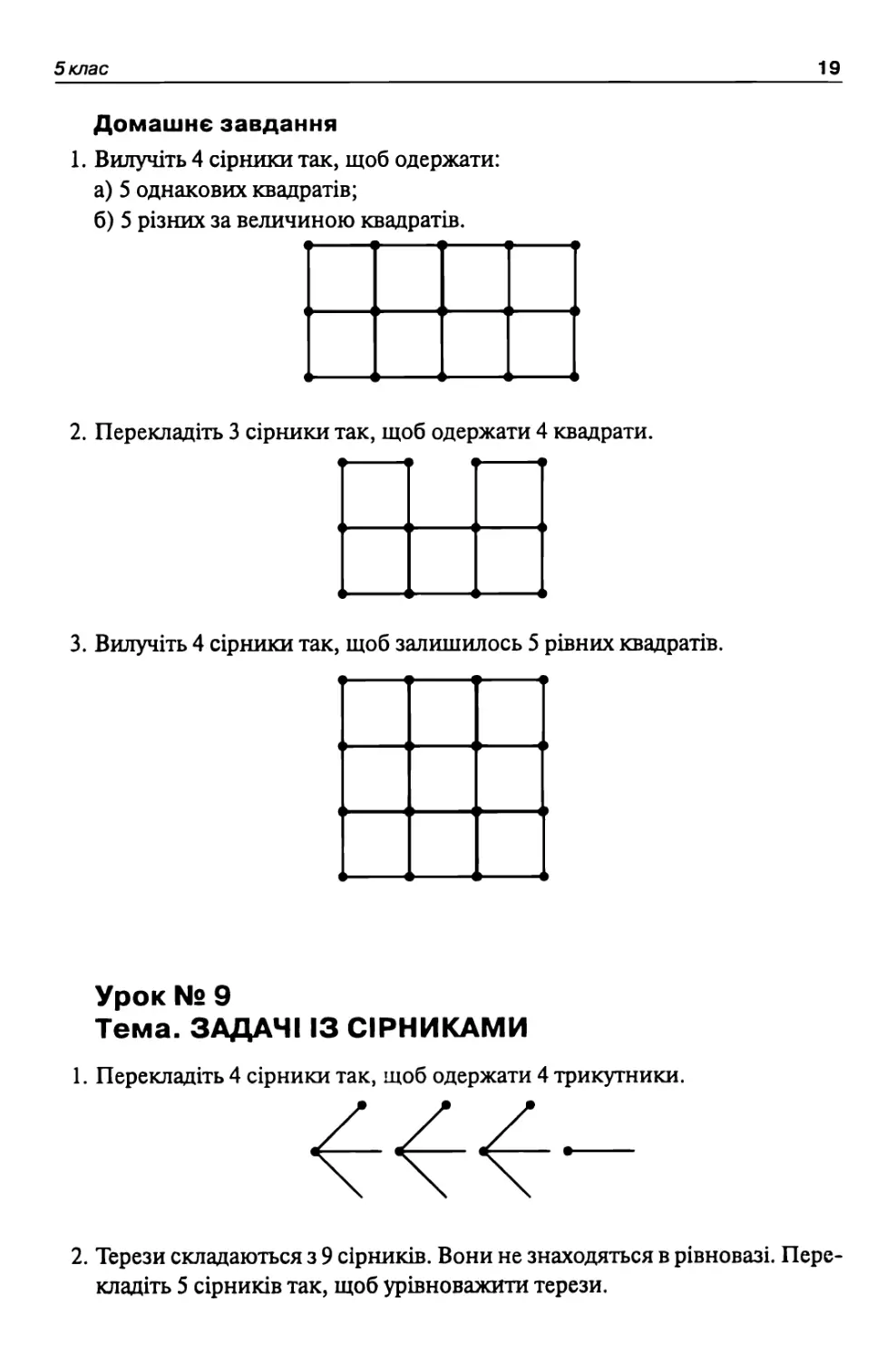
1. 	Вилучіть 4 сірники так, щоб одержати:
а) 5 однакових квадратів;
б) 5 різних за величиною квадратів.
2. 	Перекладіть 3 сірники так, щоб одержати 4 квадрати.
3. 	Вилучіть 4 сірники так, щоб залишилось 5 рівних квадратів.
Урок № 9
Тема. ЗАДАЧІ ІЗ СІРНИКАМИ
1. Перекладіть 4 сірники так, щоб одержати 4 трикутники.
444-
2. Терези складаються з 9 сірників. Вони не знаходяться в рівновазі. Перекладіть 5 сірників так, щоб урівноважити терези.


20
Математична логіка. 5-6 класи
3. 	Перед нами бокал, в якому лежить оливка. Перекладіть 2 сірники так, щоб оливка випала з бокала. Бокал можна перевернути догори дном, підняти чи опустити, але обов’язково зберігати його форму.
4. Не ламаючи сірників, зробіть:
а) із двох сірників 5, 10;
б) із трьох сірників 4, 6, 9, 11;
в) із п’яти сірників 8.
5. Знайдіть помилку в рівностях і виправте її, переклавши лише один сірник.
Домашнє завдання
1. 	Перекладіть 2 сірники так, щоб з ключа одержати 5 квадратів:
2. Із дев’яти сірників складіть 6 квадратів.
3. Перекладіть 4 сірники, щоб утворилось
2 квадрати:


5 клас
21
Урок №10
Тема. ЗАДАЧІ ІЗ СІРНИКАМИ
Арифметичні каламбури
1. Як з десяти сірників одержати нуль?
2. Як з дев’яти сірників, не ламаючи їх, зробити десять?
3. Знайдіть помилку і виправте її, переклавши один сірник.
XI -х ^хх
4. Як із шести сірників, не ламаючи їх, зробити:
а) дев’ять;
б) одинадцять?
Задачі із вилученням сірників
1. 	З даних 5 квадратів вилучіть 3 сірники, щоб утворилось 3 таких самих квадрати.
2. 	Вилучіть 6 сірники, щоб утворилось 4 таких самих квадрати.
3. 	Вилучіть два сірники так, щоб утворилось 4 таких самих квадрати.


22
Математична логіка. 5-6 класи
Домашнє завдання
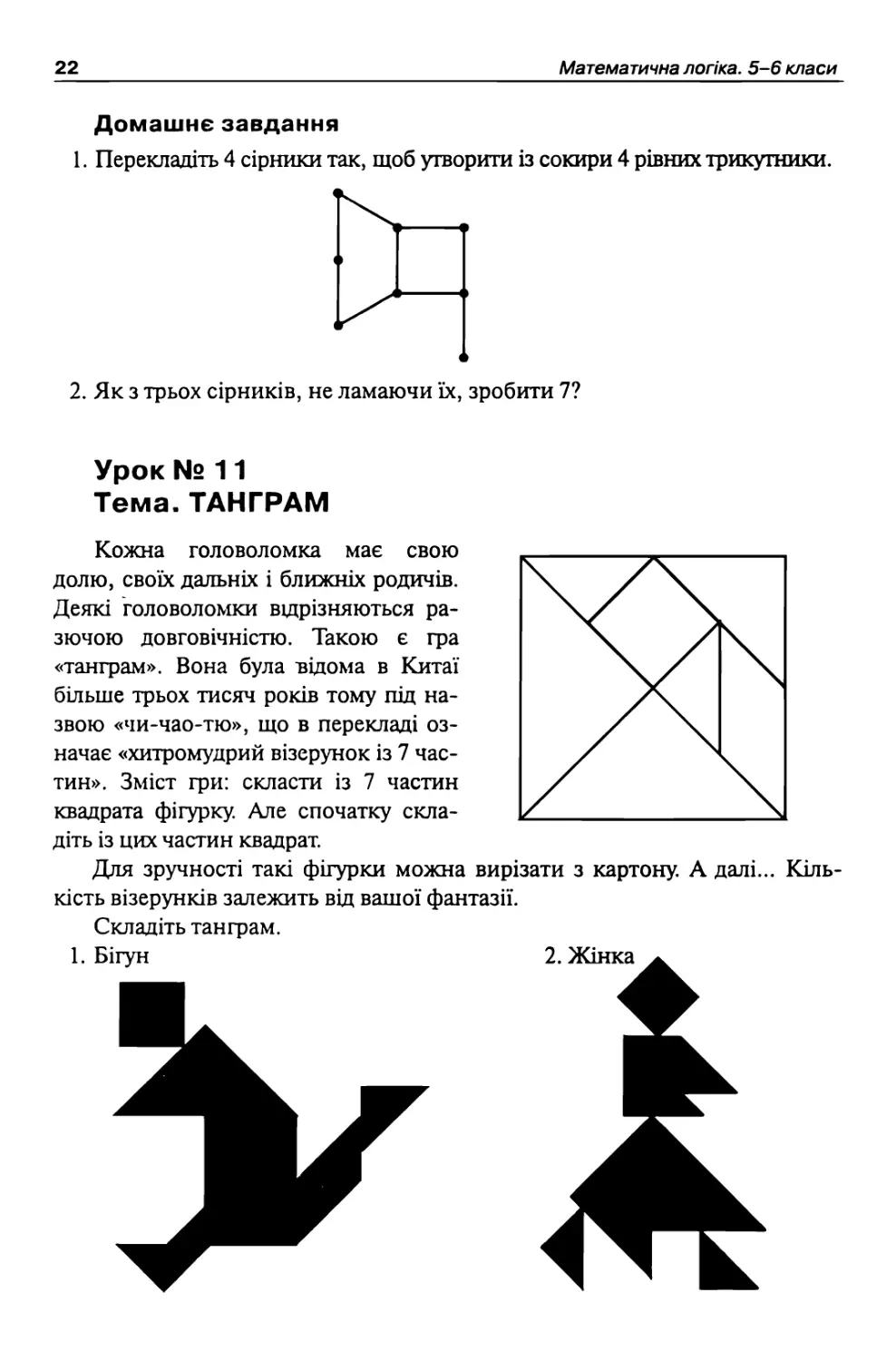
1. 	Перекладіть 4 сірники так, щоб утворити із сокири 4 рівних трикутники.
2. 	Як з трьох сірників, не ламаючи їх, зробити 7?
Урок № 11 Тема, ТАНГРАМ
Кожна головоломка має свою долю, своїх дальніх і ближніх родичів. Деякі головоломки відрізняються разючою довговічністю. Такою є іра «танграм». Вона була відома в Китаї більше трьох тисяч років тому під назвою «чи-чао-тю», що в перекладі означає «хитромудрий візерунок із 7 частин». Зміст гри: скласти із 7 частин квадрата фігурку. Але спочатку складіть із цих частин квадрат.
Для зручності такі фігурки можна вирізати з картону. А далі... Кількість візерунків залежить від вашої фантазії.
Складіть танграм.


23
Математична логіка 5-6 класи
Домашнє завдання
3. Яхта


24
Математична логіка. 5-6 класи
Урок № 12 Тема. ТАНГРАМ
Складіть танграм.
5. 	Кенгуру


5 клас
25
Домашнє завдання
Складіть тантрам.
Будинок Тюлень
Урок № 13
Тема. ЗАДАЧІ НА СПОСТЕРЕЖЛИВІСТЬ
1. 	Знайдіть невідоме число: а) БУДІВЕЛЬНИК Математик
XI ?
15 15
7
2. Яке із даних чисел слід вибрати?
514; 605; 201; 168


26
Математична логіка. 5-6 класи
б) чисельник, дріб
знаменник, число
4 4 5 5
7’9’8’9
3. 	Вставте пропущені числа:
3;7;11 14; 8; 11
А В CD
А В С D Е 10
А В С
Домашнє завдання
1. 	Вставте пропущені числа:
9х-3
8,4 ) 8,394 /У 8,351
7,'
7,
7,
? ) 7,512
./ 7,51
Урок № 14
Тема. ЗАДАЧІ З РОЗРІЗУВАННЯМ ТА СКЛЕЮВАННЯМ
У новому класі задач необхідно деяку геометричну фігуру поділити (розрізати) в указаний спосіб. Наприклад, на дві рівні частини або на чотири рівні частини, або так, щоб скласти іншу геометричну фігуру.


5 клас
27
Дуже часто під час розв’язування задач такого типу використовують метод обчислення площ фігур, які треба одержати, а далі методом підбору шукають різні варіації фігур з даною площею.
Приклад. Розріжте фігуру на дві однакові частини.
Ця фігура має площу 10 клітинок, тому площа фігур, на які потрібно її поділити, — 5 клітинок.
Методом підбору знаходимо:
1. 	Поділіть фігуру на дві рівні частини:


28
Математична логіка. 5-6 класи
Домашнє завдання
1. Поділіть фігуру на дві рівні частини:
Урок № 15
Тема. ЗАДАЧІ З РОЗРІЗУВАННЯМ ТА СКЛЕЮВАННЯМ
1. 	Поділіть фігуру на дві рівні частини:


5 клас
29
2. 	Поділіть фігуру на чотири рівні частини:
Урок № 16
Тема. КОМБІНАЦІЇ З ОБ’ЄКТАМИ ТА ФІГУРАМИ
Комбінації з об’єктами
1. Бабусі треба підсмажити 6 котлет, а на сковорідці вміщується лише 4. Кожну котлету треба смажити 5 хв з одного боку і 5 хв з другого. Скільки часу потрібно для того, щоб підсмажити 6 котлет на цій сковорідці? Як це можна зробити за 15 хв?
Комбінації з фігурами
2. Розріжте прямокутник довжиною 9 см, шириною 4 см на дві рівні частини так, щоб з них можна було скласти квадрат.


зо
Математична логіка. 5-6 класи
3. 	Яке найменше число прямолінійних розрізів потрібно зробити, щоб розрізати круглий торт на 7 частин?
Усні вправи
1. Колесо має 18 спиць. Скільки проміжків між ними?
2. Будуючи паркан, у ряд поставили 6 стовпців; відстань між сусідніми дорівнює 2 м. Яка довжина паркана?
Домашнє завдання
1. На сковорідці вміщуються тільки 2 шматочки хліба. Щоб підсмажити шматочок з одного боку, потрібна 1 хв. Як за 3 хв підсмажити 3 шматочки хліба з двох боків?
2. На чотирьох кутах квадратного двору господар посадив дерева. Через певний час він захотів збільшити свій двір у 2 рази, але так, щоб він залишився квадратним. Як йому треба це зробити, щоб дерева залишились на лінії огорожі?
3. Знайдіть закономірність:


5 клас
31
Урок № 17
Тема. ОБЧИСЛЕННЯ ПЛОЩ ТА ОБ’ЄМІВ
1. 	Нехай площа всієї фігури 32 см2. Знайдіть площу її затемненої частини.
2. 	Знайдіть площу затемненої частини фігури, якщо А В = АС = 6 см.
3. Грані куба, ребро якого 4 см, пофарбовано в червоний колір Куб розрізали на кубічні сантиметри. Скільки дістали кубиків з однією, двома, трьома пофарбованими гранями? Скільки залишилось кубиків із непо- фарбованими гранями?
4. У скільки разів збільшиться об’єм куба, якщо його ребро збільшити у два рази?
5. Щоб пофарбувати кубик зі стороною 4 см, Петрик витратив 6 г фарби. Скільки фарби він витратив, щоб пофарбувати кубик зі стороною 8 см?
Домашнє завдання
1. 	Квадрат ABCD складається з одного білого квадрата і чотирьох сірих прямокутників (як показано на рисунку).
Периметр кожного сірого прямокутника дорівнює 40 см. Чому дорівнює площа квадрата АВСГР.
2. Периметр квадрата в метрах і площа у квадратних метрах виражені рівними числами. Визначте площу квадрата.
3. У скільки разів збільшиться об’єм куба, якщо його ребро збільшити у 3 рази?


32
Математична логіка. 5-6 класи
Урок № 18
Тема. ЗАДАЧІ НА ЗВАЖУВАННЯ
1. З дев’яти однакових за зовнішнім виглядом монет — одна фальшива (легша). Скільки треба провести зважувань на талькових терезах без важків, щоб знайдіть фальшиву монету?
2. З 27 однакових за зовнішнім виглядом монет одна фальшива (легша). Скількома зважуваннями на талькових терезах без важків можна відшукати фальшиву монету?
3.3 8 монет одна фальшива (легша). Скількома зважуваннями на талькових терезах без важків можна відшукати фальшиву монету?
4. У ящику 8 кг крупи. Треба за допомогою талькових терезів і двох гир по 400 г відважити 1 кг 800 г крупи. Як це зробити двома зважуваннями?
5. У 10 торбинках однакові на вигляд монети. Але в одній вони фальшиві — на 1 г легше. Як за допомогою одного зважування на терезах зі шкалою визначити торбинку із фальшивими монетами?
Домашнє завдання
1. Як за допомогою талькових терезів без гир відважити 14 кг цукру, якщо в торбині є 16 кг цукру?
2. З 81 однакової за зовнішнім виглядом монети одна фальшива (легша). Скількома зважуваннями на талькових терезах можна відшукати фальшиву монету?
3. Сім робітників виготовляють золоті монети. Один з них виготовляє монети легші на 1 г. Як за допомогою одного зважування визначити, який робітник виготовляє легші монети?
4. Складіть і розв’яжіть задачу на зважування.
Урок № 19
Тема. ЗАДАЧІ НА ПЕРЕЛИВАННЯ
1. Десятилітрова посудина наповнена молоком. Як виміряти 4 л молока, маючи банки 7 л і 3 л?
2. Є три посудини: 6 л, 3 л, 7 л. У першій посудині 4 л, а у третій — 6л молока. Використовуючи тільки ці три посудини, розлийте молоко порівну на дві частини.
3. 12-літрова бочка наповнена квасом. Використовуючи 8-літрову та 5-літрову бочки, розлийте квас на частини 3 л і 9 л.


5 клас
33
Домашнє завдання
1. Десятилітрова посудина наповнена молоком. Як, маючи банки 5 і 3 л, виміряти 4 л?
2. Є три банки: 3 л, 5 л, 8 л. Як за допомогою цих ємностей наповнити 8-літрову банку рівно наполовину?
Урок № 20
Тема. ЗАДАЧІ НА ВИКОРИСТАННЯ ВЛАСТИВОСТЕЙ КАЛЕНДАРЯ
1. Мій батько народився в неділю, а мати — на 52 дні пізніше. У який день народилася мати?
2. У січні випало чотири неділі та чотири п’ятниці. Який день тижня був 1-го січня?
3. У деякому місяці три неділі випали на парні числа. Яким днем тижня було 20-те число цього місяця?
4. Чи може рік розпочатись у вівторок, а закінчитись у середу?
Домашнє завдання
1. Чи може рік розпочатися в п’ятницю, а закінчитись у неділю?
2. Скільки днів у році, якщо перший і останній його дні — вівторки?
3. Чи може бути в лютому п’ять понеділків?
Урок №21
Тема. ЗАДАЧІ НА ВИКОРИСТАННЯ ВЛАСТИВОСТЕЙ КАЛЕНДАРЯ
1. Чи може в місяці одночасно бути п’ять неділь, п’ять понеділків і п’ять вівторків?
2. Петрик сказав: «У минулому місяці було п’ять вівторків». Василько відповів: «Тоді, навіть не згадуючи, скільки в цьому місяці днів, я можу сказати, скільки в ньому було п’ятниць. Чи це можливо?
3. У лютому 2004 року буде 29 днів, з них 5 неділь. Який день буде 23 лютого 2004 року?
Домашнє завдання
1. 	Сашко сказав: «Позавчора мені виповнилося 10 років, а 12 років мені виповниться в наступному році». Чи може таке бути? Коли у Сашка день народження ?


34
Математична логіка. 5-6 класи
2. У деякому місяці було п’ять вівторків та п’ять неділь. Чи обов’язково в цьому місяці було 31-ше число? Якщо було, то на який день тижня випало?
3. У дідуся запитали, скільки йому років. «Більше ста, — відповів дідусь, — але день народження я святкував лише 25 разів». Коли в дідуся день народження?
Урок № 22
Тема. ЕЛЕМЕНТИ КОМБІНАТОРИКИ
1. В ящику лежить 10 червоних і 8 синіх кульок. Яку кількість кульок необхідно витягти, не дивлячись, щоб там було не менше 3-х синіх кульок і 4-х червоних.
2. В ящику лежать 10 білих, 8 чорних і 5 рожевих кульок. Скільки кульок потрібно витягти, не дивлячись, щоб там було щонайменше:
а) 3 чорних кульки; б) одна рожева; в) 10 білих?
3. В ящику лежать білі та чорні рукавички, по 5 пар. Скільки рукавичок необхідно витягти, щоб там була пара одного кольору.
4. В ящику лежать 10 білих, 10 червоних і 10 синіх кульок. Скільки кульок необхідно витягти, щоб нам було:
а) 2 синіх; б) 8 білих; в) одна біла та одна синя?
Домашнє завдання
1. В ящику лежать 5 білих і 5 синіх кульок. Скільки кульок необхідно витягти, щоб там було не менше ніж 2 білі та 2 сині кульки?
2. В ящику лежать 7 синіх, 8 червоних і 9 білих кульок. Скільки кульок необхідно витягти, щоб там було:
а) 2 білих кільки; б) одна синя кулька; в) 5 червоних кульок?
3. В ящику лежать білі та чорні рукавички, по 10 пар. Скільки рукавичок необхідно витягти, щоб там була хоча б одна пара одного кольору?
Урок № 23
Тема. ЕЛЕМЕНТИ КОМБІНАТОРИКИ
1. Дві дівчинки вирізали з паперу п’ять прапорців. По скільки прапорців могла вирізати кожна дівчинка?
2. Запишіть число 6 у вигляді суми двох доданків. Скількома способами це можна зробити?
3. Перелічіть усі набори монет, якими можна набрати п’ять копійок.


5 клас
35
4. Миколка за конверт, який коштує 18 к., заплатив чотирма різними монетами. Які це монети?
5. Як десять морквин розкласти на чотири купки так, щоб у кожній купці була різна кількість морквин?
6. Надійка вирішила розмалювати карту двома кольорами. У неї є три різні фарби Скількома способами вона може вибрати дві фарби для розмальовування?
7. У Михайлика є дві футболки — біла та блакитна. І дві пари трусів — зелені та білі. Скільки варіантів спортивної форми може підібрати Ми- хайлик?
8. У магазин завезли тюльпани й нарциси. Треба скласти букет із трьох квіток. Скількома різними способами це можна зробити?
9. Троє хлопчиків грали в шашки. Усього зіграли три партії. Скільки партій зіграв кожний хлопчик, якщо між собою зіграли всі?
Домашнє завдання
1. Перелічіть усі набори монет, якими можна набрати шість копійок.
2. Троє хлопчиків грали в шашки. Кожний із них зіграв по дві партії. Скільки всього було зіграно партій?
3. Зустрілися чотири хлопчики й потиснули один одному руки. Скільки було зроблено потисків? А якщо хлопчиків було б шестеро?
4. У кожну з п’яти кишень свого піджака хлопчик поклав цукерки. У кожній кишені була різна кількість цукерок, причому не менше ніж одна, але не більше ніж п’ять. Скільки всього цукерок мав хлопчик7
Урок № 24
Тема. СЮЖЕТНІ ЛОГІЧНІ ЗАДАЧІ
1. Віра, Ніна, Оля й Люба одягли сукні різних кольорів (червоного, синього, білого та блакитного). На запитання, хто з них в якій сукні, три дівчини відповіли:
1) Оля — у синій, Люба — у білій;
2) Оля — у червоній, Ніна — у синій;
3) Віра — у синій, Люба — у блакитній.
У кожній відповіді тільки одна частина правильна, а друга — ні. Сукню якого кольору одягла кожна дівчина?
2. Жанна, Катерина, Марина й Лариса вміють грати на різних інструментах (піаніно, віолончелі, гітарі, скрипці), але кожна тільки на одному. Вони вже знають іноземні мови (англійську, французьку, німецьку та іспанську), але кожна тільки одну.


36
Математична логіка. 5-6 класи
Відомо, що:
1) дівчина, яка грає на гітарі, говорить іспанською;
2) Лариса не грає ні на скрипці, ні на віолончелі і не знає англійської мови;
3) Марина не грає ні на скрипці, ні на віолончелі і не знає ні німецької, ні англійської мов;
4) дівчина, яка говорить німецькою, не грає на віолончелі;
5) Жанна знає французьку мову, але не грає на скрипці.
Хто на якому інструменті грає і яку знає мову?
Домашнє завдання
1. Одна з папуг А, В, С завжди каже правду, інша — завжди бреше, а третя — хитрує: іноді каже правду, іноді — ні. На запитання: «Хто папуга В?» вони відповіли так:
А: «Брехун».
В: «Я — хитрун».
С: «Абсолютно чесна папуга».
Хто є хто з папуг?
2. Кореспондент стінної газети Степан Мошкін запізнився до фінішу легкоатлетичного кросу. На запитання про результати кросу він почув такі відповіді*
1) Сергій посів II місце, а Коля — третє.
2) Сергій посів II місце, а Іван — четверте.
3) Надія посіла III місце, а Толя — п’яте.
4) Толя посів ПІ місце, а Надія — друге.
5) Коля — І, а Іван — IV.
На що Степан сказав: «Цього не може бути!»
Тоді вболівальники відповіли: «Щоб наказати тебе за запізнення, кожен з нас один раз сказав тобі правду, а один раз збрехав».
То ж яке місце посів кожен з п’яти бігунів?
Урок № 25
Тема. СЮЖЕТНІ ЛОГІЧНІ ЗАДАЧІ
1. 	Одного разу князь Володимир покликав до себе трьох богатирів і запитав: «Хто з вас зловив Солов’я-Розбійника?»
Богатирі відповіли: «Негоже вихвалятися. Тому ми вирішили, що кожен буде тричі говорити. Двічі скаже правду, а один раз збреше. Після цього сам вирішуй, хто зловив Солов’я-Розбійника».
Добриня Микитич: «Це зробив Альоша Попович».
Ілля Муромець: «Це зробив не я».


5 клас
37
Альоша Попович: «Я давно вже мріяв про подвиг».
Добриня Микитич: «Багато на Русі хоробрих воїнів».
Ілля Муромець: «Я був на той час в іншому місці».
Альоша Попович: «Це зробив я».
Добриня Микитич: «Я знаю, де живе Соловей-Розбійник».
Альоша Попович: «Ілля в цей час знаходився в іншому місці».
Ілля Муромець: «Це важка задача, але я спробую її розв’язати».
Так хто ж зловив Солов’я-Ро.збійника?
2. На вулиці, ставши в коло, розмовляють чотири дівчини: Ганя, Валя, Галя і Надія. Дівчина в зеленій сукні (не Ганя і не Валя) стоїть між дівчиною в блакитній сукні та Надією. Дівчина в білій сукні стоїть між дівчиною в рожевій сукні і Валею. Хто яку сукню носить?
3. Зустрілися троє друзів: Білов, Чернов і Рудов. «Волосся в одного з нас біле, другого — чорне, а третього — руде, але в жодного з нас колір волосся не відповідає прізвищу», — підмітив чорноволосий. «Твоя правда», — підтвердив Білов. Яке в кого волосся?
4. Кожен з чотирьох гномів — Беня, Веня, Євген і Сеня або завжди говорять правду, або завжди брешуть. Ми почули таку розмову:
Беня Вені: «Ти брехун».
Євген Бені: «Сам ти брехун!»
Сеня Євгену: «Вони обидва брехуни, та й ти теж».
Хто з них говорить правду?
Домашнє завдання
1. До царя дійшли чутки, що хтось із трьох богатирів вбив Змія Горинича. Цар наказав їм розповісти, хто це зробив.
Ілля Муромець: «Змія вбив Добриня Микитич».
Добриня Микитич: «Змія вбив Альоша Попович».
Альоша Попович: «Я вбив Змія».
Відомо, що тільки один богатир сказав правду, а двоє збрехали. Хто вбив змія?
2. Під час пікніка чотири пари випили 32 пляшки кока-коли. Жінки випили: Жаклін — одну пляшку, Жанна — дві, Колетта — три й Анетта — чотири. Чоловіки не поступилися жінкам: мсьє Пон виплив стільки ж, скільки його дружина, мсьє Дюбуа — удвічі більше від своєї дружини, мсьє Пейзан утричі більше від своєї, і мсьє Фонтен — у чотири рази більше від своєї дружини.
Як звуть мадам Дюбуа, Пон, Пейзан і Фонтен?


38
Математична логіка. 5-6 класи
Урок № 26
Тема. ПЕРЕПРАВИ
1. Один господар хотів перевезти вовка, козу та капусту через річку, але в човні вміщаються разом з ним або тільки вовк, або тільки коза, або тільки капуста. Не можна залишати вовка разом з козою, а козу з капустою. Як це зробити?
2. Довгим вузьким каналом один за одним йдуть 3 пароплави. Назустріч їм — ще 3 пароплави. Канал такий вузький, що два пароплави в ньому роз’їхатись не можуть, але в ньому є затока, де можне розміститись один пароплав. Як їм роз’їхатись?
3. Два мандрівники підійшли до швидкої та глибокої річки. На березі вони знайшли човен, який може перевезти лише одного чоловіка. Але вони все ж таки змогли перепливти через річку та продовжити мандрівку. Чи могло так статися, якщо моста там не було?
Домашнє завдання
Двоє хлопців каталися на човні. До берега підійшов загін солдатів. Човен такий малий, що в ньому можуть переправитись двоє хлопців або тільки один солдат. Але солдати переправились через річку. Як?
Урок N2 27
Тема. ЧИСЛОВІ ПОСЛІДОВНОСТІ
A. Арифметичні прогресії
Приклад. З, 7, 11, 15,... (потім 19, бо кожен наступний член буде утворюватись додаванням до попереднього числа 4).
Б. Геометричні прогресії
Приклад. 2, 6, 18, 54,... (потім 162, бо кожен наступний член буде утворюватись множенням попереднього числа на 3).
B. Послідовності, в яких різниця між сусідніми членами утворює арифметичну прогресію
Приклад. 2, 3, 5, 8, ... (потім 12, бо різниця між сусідніми членами була
1, 2, 3, і повинна бути 4, отже. 8+4 = 12).
Г. Послідовності, в яких різниця між сусідніми членами утворює геометричну прогресію
Приклад. 1, 3, 7, 15,... (потім 31, бо різниця між членами була спочатку
2, потім 4, потім 8, і потім повинна бути 16, отже, 15+16 = 31).


39
Математична логіка 5-6 класи
Д. Подвійні послідовності, в яких треба навести два наступних члени
Приклад. 72, 5, 36, 10, 18, 20,... (наступними будуть 9, 40, оскільки на непарних місцях стоять члени спадної геометричної прогресії, де кожен наступний член утворюється з попереднього діленням на 2; на парних місцях стоять члени іншої геометричної прогресії, де кожен наступний утворюється з попереднього множенням на 2).
Е. Послідовності, які не підпорюються означеним вище закономірностям
Приклад. 111, 213, 141, 516, 171, 819,... (наступними йдуть 202, 122, бо якщо переставити кому, то побачимо ряд 11, 12, 13,..., в якому члени приписані один до одного праворуч).
Продовжіть числовий ряд.
1. 1,5,9, 13,...
2. 7, 14, 28, 56,...
3. 3,4, 7, 12,...
4. З, 2, 6, 6, 12, 10,...
Домашнє завдання
Складіть по одній числовій послідовності на кожен тип.
Урок № 28
Тема. МАГІЧНІ КВАДРАТИ
Загальна задача «магічних квадратів»: дані числа розставте в клітинках квадрата так, щоб у рядках, стовпцях і діагоналях утворилися однакові суми.
Квадрати бувають третього, четвертого чи іншого порядків. Порядок квадрата визначається числом відрізків, на яке поділено його сторону.
За трьома базовими числами в клітинах квадрата заповніть квадрат так, щоб у рядках, стовпцях і діагоналях утворилися однакові суми.
1. 	Заповніть магічні квадрати.
7
5
6
Розв’язання
а = 4
b = S
9
12
7
2
5
6
10


40
Математична логіка. 5-6 класи
Суть розв’язання полягає в тому, щоб зрозуміти і побачити, що a + 7 = 5+6, звідки а =4. Потім побачити, що 4+6 = 5+7, звідки 6 = 8. А далі
Домашнє завдання
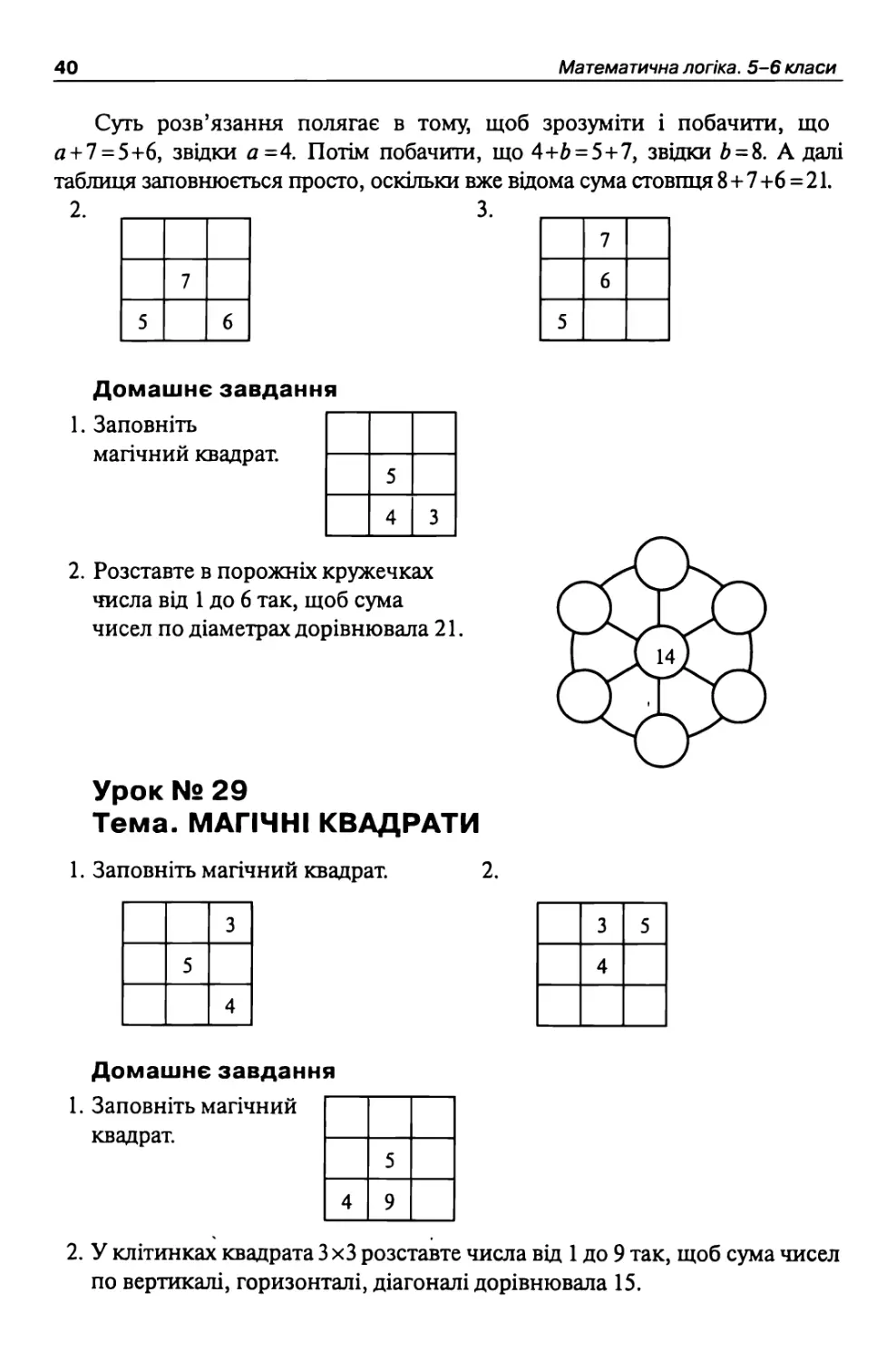
1. Заповніть
магічний квадрат.
5
4
3
2. 	Розставте в порожніх кружечках числа від 1 до 6 так, щоб сума чисел по діаметрах дорівнювала 21.
Урок № 29
Тема. МАГІЧНІ КВАДРАТИ
1. 	Заповніть магічний квадрат. 2.
3
5
4
3
5
4
2. 	У клітинках квадрата 3 хЗ розставте числа від 1 до 9 так, щоб сума чисел по вертикалі, горизонталі, діагоналі дорівнювала 15.


5 клас
41
Урок № ЗО
Тема. РОЗВ’ЯЗУВАННЯ ЗАДАЧ ВІД КІНЦЯ ДО ПОЧАТКУ
Деякі математичні задачі корисно розв’язувати, починаючи аналізувати умову від кінця.
Наприклад, Петро сказав Миколі: «Скільки в мене є корів, стільки телят вони мені приведуть, куплю ще одну молоду корову і ще три рази куплю стільки, скільки цих корів і телят, і всього стане 100». Скільки корів було в Петра?
Розв’язання
Аналізуємо задачу від кінця:
До того, як тварин стане 100, ми збільшили їх кількість у 4 рази, тому їх було: 100:4=25.
До цього ми збільшили їх кількість на одну корову, тобто їх було б 25-1 = 24.
А до цього, ми збільшили їх кількість удвічі. Тому первісна кількість тварин: 24:2=12.
Відповідь. 12.
Цю ж задачу можна розв’язати за допомогою граф-схеми. Позначимо первісну кількість худоби та всі наступні кількості точками на площині. Дії над кількістю худоби позначимо стрілками, причому початок стрілки від числа, над яким виконуємо дію (множення, ділення, додавання, віднімання), кінець стрілки до числа, яке маємо в результаті. Над стрілкою записуємо число з відповідним знаком, яке показує, на скільки ми повинні помножити, поділити і т. д.
1. Торговець побував у трьох містах. У першому місті в нього купили п’ять шостих товару. У другому — п’ять шостих від того, що залишилось, і в третьому — п’ять шостих від того, що залишилось. Коли він повернувся додому, то в нього залишилось 11 горщиків. Скільки горщиків було в торговця спочатку?
2. Один чоловік прийшов до царя з проханням: «Царю, дозволь мені взяти яблуко з твого саду».
Цар йому дозволив, але чоловік, підійшовши до саду, побачив, що він огороджений трьома парканами. У кожному паркані є хвіртка, що охороняється. Підійшов чоловік до першого сторожа й каже: «Цар дозволив мені взяти одне яблуко із саду».


42
Математична логіка. 5-6 класи
«Візьми, але, виходячи, віддаси мені половину від тих яблук, що візьмеш, і ще одне яблуко». Те ж саме сказали йому другий та третій сторожі, які охороняли другі та треті ворота. Скільки яблук повинен взяти чоловік, щоб у нього залишилось одне яблуко?
3. 	Дівчинка запитала дідуся, скільки йому років. Той відповів: «Якщо зменшиш мої роки в 6 разів і віднімеш ще 6 років, то одержиш 6. Тож скільки мені років?»
Домашнє завдання
1. Торговець продав яйця. Першій жінці він продав половину яєць та ще одне яйце. Другій жінці він продав половину від яєць, які залишилися, та ще одне яйце. Третій жінці — половину від яєць, які залишилися, та ще одне яйце. Після чого яйця закінчились. Скільки яєць було в торговця і по скільки яєць взяла кожна жінка?
2. Галинка запитала в бабусі: «Скільки тобі років?» Бабуся відповіла: «Якщо проживу ще половину того, що прожила, та ще один рік, то мені буде 100 років». Скільки років бабусі зараз?
Урок №31
Тема. ЗАДАЧІ, ЯКІ РОЗВ’ЯЗУЮТЬСЯ
ВІД ПОЧАТКУ ДО КІНЦЯ
1. Троє чоловіків прийшли до перукарки. Поголивши першого, перукарка сказала: «Подивись, скільки грошей у ящику стола, поклади стільки ж і візьми 2 гривні здачі».
Те ж саме перукарка сказала і другому, і третьому. Після чого з’ясувалось, що грошей в касі немає. Скільки грошей було в касі, перед тим, як заплатив перший чоловік?
2. З кошика зі сливами одна жінка взяла половину слив і ще одну, друга взяла половину того, що залишилось, і ще одну, третя жінка взяла половину від останнього залишку і ще три сливи, після чого в кошику слив не залишилось. Скільки слив було спочатку в кошику?
Домашнє завдання
Селянка принесла на ринок мішок груш. Першому покупцю вона продала половину всіх груш і ще половину груші, другому — половину тих груш, що залишились , і ще половину груші і т. д. Сьомому — половину від того, що залишилось і ще половину груші. З’ясувалось, що селянка продала всі груші і кожен із семи покупців купував цілу кількість груш. Скільки груш вона принесла на ринок?


5 клас
43
Урок № 32
Тема. ЗАДАЧІ НА РУХ
1. Знайдіть площу городу прямокутної форми, якщо людина обходить його за 5 хв зі швидкістю 20 м/хв. Відомо, що ширина городу 20 м.
2. Ділянку прямокутної форми велосипедист об’їхав за 3 години зі швидкістю 12 км/год. Чому дорівнює площа цієї ділянки?
3. Що швидше: проїхати увесь шлях на велосипеді чи половину шляху проїхати на мотоциклі, який рухається удвічі швидше від велосипедиста, а іншу частину шляху — пішки, що вдвічі менше, ніж на велосипеді?
4. Із двох пунктів, відстань між якими 100 км, виїхали одночасно назустріч один одному два велосипедисти. Швидкість одного з них 15 км/год, а іншого 10 км/год. Одночасно з першим велосипедистом вибіг пес зі швидкістю 20 км/год. Зустрівши другого велосипедиста, пес повернув назад і побіг назустріч першому велосипедисту. Зустрівши першого велосипедиста, повернув назад. Пес бігав до тих пір, поки велосипедисти не зустрілись. Скільки кілометрів пробіг пес?
5. Собака женеться за котом. Відстань між ними 26 м. Через 8 с відстань між ними скоротилась до 10 м. З якою швидкістю біжить кіт, якщо швидкість собаки 8 м/с?
Домашнє завдання
1. Із двох міст одночасно назустріч один одному вийшли два потяги. Один
1 1
з них за - години проходить 13 км, а другий за - години — 16 км. Потяги зустрілись через 2 години. Яка відстань між містами?
2. Потяг проходить відстань між двома містами за 4 години. Якщо його швидкість збільшити на 24 км/год, то він пройде цю відстань за 4 години. Знайдіть відстань між містами і первісну швидкість потяга.
3. З автовокзалу виїхав автобус зі швидкістю 60 км/год. Через півгодини за ним виїхав легковий автомобіль зі швидкістю 75 км/год. Через скільки годин після свого виїзду легковий автомобіль буде попереду автобуса на 120 км?
Урок № 33
Тема. ЗАДАЧІ НА РУХ
1. 	Два потяги рухались назустріч один одному паралельними шляхами. Один зі швидкістю 50 км/год, а другий — зі швидкістю 70 км/год. Пасажир другого потяга помітив, що перший потяг пройшов повз нього за 6 секунд. Яка довжина другого потяга?


44
Математична логіка. 5-6 класи
2. Потяг проходить міст довжиною 450 м за хвилину й півхвилини йде повз телеграфний стовп. Знайдіть довжину й швидкість потяга.
3. Ахіллес бігає в десять разів швидше від черепахи. Відстань між ними — 1 км. Поки Ахіллес пробігає 1 км, черепаха проходить 100 м. Коли він пробігає ці 100 м. черепаха проповзає ще 10 м. Поки Ахіллес пробіжить ці 10 м, черепаха проповзе ще 1 м. І так без кінця — черепаха завжди попереду. Який шлях повинен пробігти Ахіллес, щоб впіймати черепаху?
4. Монах о 9-й ранку вийшов до монастиря і опівночі прибув до місця. О 9-й наступного дня він розпочав шлях (тією самою дорогою). О 9-й вечора він повернувся додому. Доведіть, що знайдеться точка, де монах був обидва рази в один і той самий час доби.
Домашнє завдання
1. З міст А і В назустріч один одному вирушили два автомобілі зі швидкістю 20 км/год. Одночасно з пункту А вилетів зі швидкістю 120 км/год невтомний джміль. Зустрівши автомобіль, який вирушив з В, він відразу полетів до А. Зустрінувши автомобіль, який їхав з Л, він відразу повернув до В і так літав доки, поки автомобілі не зустрілися. Яку відстань пролетів джміль, якщо між А і В 300 км?
2. Велосипедист піднімається на гору зі швидкістю 12 км/год і з’їжджає з гори тією самою дорогою зі швидкістю 20 км/год. Різниця в часі між підйомом
- та спуском — 16 хв. Яка довжина дороги, якою їхав велосипедист?
3. Гаррі Поттер підіймається східцями нерухомого ескалатора вгору за 90 сек. Коли цей ескалатор працює, Гаррі Поттер добирається нагору за 60 с, стоячи нерухомо. За який час Гаррі Поттер вийде нагору рухомим ескалатором?
Задачі для усного розв’язування
1. Сума яких двох натуральних чисел, дорівнює їх добутку?
2. Сума яких двох натуральних чисел більша ніж їх добуток?
3. Мама сказала Петрику: «Усі чемпіони добре вчилися». Петрик каже: «Я добре навчаюсь. Отже, я буду чемпіоном». Чи правильно він думає?
4. Таня сказала: «В Андрія більше ста книг». Даня заперечив: «Ні, менше». Маня сказала: «Ну, хоча б одна книга у нього, напевне, є». Скільки книг може бути в Андрія, якщо з цих трьох тверджень рівно одне правильне?
5. У скільки разів сходинки на 8-й поверх будинку довші від сходинок на 2-й поверх цього ж будинку?
6. П’ятиметрову колоду потрібно розпиляти на 5 частин. Скільки розрізів потрібно зробити?


5 клас
45
7. 60 триметрових колод потрібно розпиляти на 5 частин. Скільки розпилів необхідно зробити?
8. У Йосика було 7 брусків різної довжини. Скільки буде брусків після того, як він розпиляє один з них на 2 частини?
9. У колбі знаходиться одна бактерія. Через одну хвилину вона ділиться на дві такі самі бактерії. Ще через хвилину кожна з утворених бактерій ділиться ще на дві і т. д. Через одну годину колба повністю заповнилась бактеріями. В який момент часу колба була наповнена бактеріями наполовину?
10. У брата було 6 п’ятикопійкових монет, а в сестри 10 двокопійкових. Скільки своїх монет брат повинен віддати сестрі, щоб грошей у них стало порівну?
11. У брата й сестри порівну яблук. Брат дав сестрі три яблука з тих. що мав. На скільки яблук у неї стало більше?
12. У 5-А класі було на 8 учнів більше, ніжу 5-Б класі Із 5-А класу перевели в 5-Б клас 6 учнів. У якому класі стало більше учнів? На скільки?
13. На двох деревах сиділи горобці. З першого дерева полетів геть один горобець, а потім з другого дерева на перше перелетіло три горобці. Після цього на кожному дереві стало по п’ять горобців. Скільки горобців було на кожному дереві спочатку?
14. Іван купив деякий товар за 7 грн, продав його за 8 грн. Потім знову купив його за 9 грн і знову продав за 10 грн. Який прибуток він одержав?
Різні задачі
1. Якою цифрою закінчується добуток усіх натуральних чисел від 1 до 55?
2. Якою цифрою закінчується добуток 41 43 45 47?
3. Використовуючи арифметичні дії, запишіть:
а) число 100 за допомогою п’яти трійок;
б) усі числа першого десятка за допомогою трійок;
в) одиницю за допомогою трьох п’ятірок;
г) число 8 за допомогою п’яти п’ятірок;
д) число 21 за допомогою чотирьох двійок.
4. Розв’яжіть ребус:
СИНИЦЯ КВАНТ a52b
а) 	+СИНИЦЯ; б)+КВАНТ; в)
ПТАШКИ НАУКА 8x/?zx
5. Як за допомогою талькових терезів без гир відважити 14 кг цукру, якщо в торбині є 16 кг цукру?
6. Маємо 9 кг крупи і гирі 50 г і 200 г. Як у три прийоми відважити на талькових терезах 2 кг крупи?


46
Математична логіка. 5-6 класи
7. У чотирьох коробках знаходяться по 4 дробинки. У трьох коробках дробинки важать по 1 г, а в четвертій — по 2 г. Як за допомогою одного зважування на пружинних терезах з’ясувати, в якій коробці лежать легші дробинки? (Коробки відкриті, а дробинки можна витягати.)
8. Десятилітрова посудина наповнена молоком. Як відміряти 4 л молока, маючи ще семилітрову і трьохлітрову банки?
9. Яку найменшу кількість кульок необхідно витягти в темряві з мішка, в якому 6 червоних і 8 білих кульок, щоб було дві кульки одного кольору.
10. Скільки олівців необхідно взяти в темряві з коробки з 8-ма червоними і 5-ма синіми олівцями, щоб було взято не менше двох червоних і трьох синіх олівців?
11. Кожний із шести третьокласників пам’ятає якусь одну цифру шестицифрового номера телефону свого однокласника, який захворів. Якщо скласти цифри разом, то вийде потрібний номер. У кожного з них теж є вдома телефон. Яку найменшу кількість дзвінків їм необхідно зробити один одному, щоб кожний знав усі цифри номера телефону товариша?
12. Першого дня зимових канікул Назар вирішив скласти список справ, які він хотів зробити на канікулах. Зокрема прочитати книжку про козаків, потренуватись зі старшим братом у грі в шахи, випиляти лобзиком із фанери ліхтарики, покататися на санчатах з гори, побігати на лижах, ковзанах. Ще Назар вирішив кожного дня займатись однією справою у приміщенні, а однією надворі. Крім того, хлопець захотів розподілити свої заняття так, щоб кожний день хоча б одним заняттям відрізнявся від усіх інших. Скільки днів Назар зможе чергувати заняття, щоб не було двох однакових днів?
13. Туристи взяли в похід запас концентрованих продуктів, з яких можна було приготувати обід: на перше — гороховий суп, курячий бульйон та рибну юшку; на друге — гречану, рисову та пшеничну каші; на десерт — компот із сушених фруктів, лимонний напій та полуничний кисіль. Скільки найбільше днів підряд вони зможуть варити обіди, які відрізнятимуться хоча б однією стравою?
14. а) У шкільній команді першості з волейболу брало участь вісім команд. Повторних ігор не було, позаяк у волейболі нічиєї не буває. Команда, яка програвала, вибувала з турніру. Скільки всього відбулося ігор?
б) 	Дві баскетбольні команди грали до чотирьох перемог однієї з команд (у баскетбольних матчах не буває нічиєї). Яку максимальну кількість ігор могли зіграти команди?


6 КЛАС
Урок № 1
Тема. ЗАДАЧІ, ЯКІ РОЗВ’ЯЗУЮТЬСЯ
ЗА ДОПОМОГОЮ ГРАФ-СХЕМ
Розв’язуванню деяких математичних задач допомагають спеціальні схеми, які складаються з точок і з дуг, що їх поєднують. Такі схеми називають графами. Точки називають вершинами графа, а дуги ребрами графа.
Розглянемо використання графів на прикладі.
Задача. Батько мав чотирьох синів. У кожного з них було по одній сестрі. Скільки дітей було в родині?
Розв’язання
Ситуація, описана в задачі, має відображення на граф-схемі, де брати та сестри зображуються точками, а їх відношення один до одного та «сестри» — стрілочками. Тому зі схеми бачимо, що чотири брати мають одну сестру.
Відповідь. 5 дітей.
1. У кімнаті знаходяться дві доньки та дві матері — усього 3 жінки. Як це може бути?
2. У гості прийшли дві матері, три доньки, дві сестри, тітка та племінниця. Скільки їх усього?
3. Дівчинка запитала дідуся, скільки йому років. Той відповів: «Якщо зменшити мої роки в 6 разів і відняти ще 6 років, то маємо 6 Скільки мені років?»


48
Математична логіка. 5-6 класи
Усні задачі
1. Син мого батька, але не мій брат. Хто це?
2. Мене звати Юрком. У моєї рідної сестри лише один брат. Як його звати?
3. Дитина каже: «У мене є мама і тато, але я їм не син». Чи може таке бути?
Домашнє завдання
1. Онук запитав дідуся, скільки йому років. Дідусь відповів: «Якщо проживу ще половину того, що прожив, та ще один рік, то мені буде 100 років». Скільки років дідусеві?
2. За стіл сіли два брати, дві невістки та дві одружені пари. Скільки осіб було за столом?
3. Батько мав 3 доньки. У кожної з них було по 3 брати. Скільки дітей у сім’ї?
Урок № 2
Тема. ЗАДАЧІ З ТОЧКАМИ, ПРЯМИМИ
ТА ІНШИМИ ГЕОМЕТРИЧНИМИ ОБ’ЄКТАМИ
1. Поєднайте точки • • •
чотирма відрізками,
не відриваючи
олівця від паперу. • • •
2. Барон Мюнхаузен сказав: «Я можу відкласти на площині шість точок і декілька прямих так, що через кожні дві відкладені точки пройде відкладена пряма, а через кожну з відкладених точок пройде рівно три відкладених прямих». Чи сказав барон правду цього разу?
3. Чи можна розрізати «по клітинках» квадрат розміром 5x5 клітинок на сім попарно різних прямокутників?
4. Розташуйте 10 точок на п’яти відрізках так, щоб на кожному відрізку було 4 точки.
Домашнє завдання
1. Розташуйте 6 точок на 4-х відрізках так, щоб на кожному відрізку було З точки.
2. Чи можна на площині розташувати 6 точок і поєднати їх відрізками, які не перетинаються, з кінцями в цих точках так, щоб з кожної точки виходило рівно 4 відрізки?
3. Поставте 24 стільці в 6 рядів по 5 стільців у кожному.


6 клас
49
УРОК № З
Тема. ЗАДАЧІ НА НСК, РОЗКЛАДАННЯ НА ПРОСТІ МНОЖНИКИ
1. Відновіть цифри у прикладах:
¥* **
***¥
639
а) 389 *
б) 213
* ♦
71
¥
2. На кільцевій дорозі проводилась мотоциклетна естафета (кожний наступний етап починається в тому місці, де закінчився попередній). Довжина етапу — 75 км, довжина дороги — 330 км. Старт і фініш знаходяться в одному й тому самому місці. Яка мінімальна кількість етапів може бути в естафеті?
3. Знайдіть найменше число, яке ділиться на 7, а відділення на 2, 3,4, 5 і 6 дає остачу 1.
4. Колгоспник привіз на базар огірки. Коли він рахував їх десятками, то не вистачало двох огірків до повної кількості десятків. Коли він став рахувати огірки дюжинами, то їх залишилось 8. Скільки огірків привіз колгоспник, якщо їх було більше від 300, але менше ніж 400?
Домашнє завдання
1. У жінки в кошику лежали яблука. Її запитали, скільки яблук у кошику Вона відповіла, що не знає точно, але коли діти їх перекладали по 2,4, 6 і 7, то завжди одне яблуко було зайвим. Яка найменша кількість яблук могла бути в кошику?
2. Знайдіть усі пари натуральних чисел, для яких НСК дорівнює 336, а НСД дорівнює 12.
Урок № 4
Тема. ПОДІЛЬНІСТЬ ЧИСЕЛ
Ознаки подільності:
а) на 6:
Якщо число закінчується парною цифрою і сума цифр числа ділиться націло на 3, то це число ділиться на 6;
б) на 15:
Якщо сума цифр числа ділиться на 3 і остання цифра числа є 5 або 0, то це число ділиться на 15;


50
Математична логіка 5-6 класи
в) на 25:
Якщо дві останні цифри числа 00, 25, 50 або 75, то це число ділиться на 25;
г) на 4:
Якщо число, утворене двома останніми цифрами даного числа, ділиться на 4, то й саме число ділиться на 4;
д) на 8:
Якщо число, утворене трьома останніми цифрами даного числа, ділиться на 8, то й саме число ділиться на 8;
е) на 100:
Якщо останні дві цифри числа є 00, то число ділиться на 100;
ж) на 7:
Треба справа наліво підписати під цифрами числа коефіцієнти:
...-1,2, З, 1,-2,-3,-1,2, З, 1,
потім помножити кожну цифру на коефіцієнт, що під нею, і всі добутки скласти. Якщо знайдена сума ділиться на 7, то й саме число ділиться на 7;
ж) на 11:
Якщо різниця між сумою його цифр, що стоять на парних місцях, та сумою цифр, що стоять на непарних місцях, ділиться на 11, то й саме число ділиться на 11.
Теорема про подільність суми
Якщо кожен з доданків ділиться на дане число, то й сума ділиться на це число.
Обернене твердження неправильне.
Теорема про подільність добутку:
Якщо хоча б один із множників ділиться на дане число, то й добуток ділиться на це число.
1. Яку останню цифру має добуток усіх непарних чисел від 1 до 99?
2. Знайдіть такі парні цифри а і Ь, щоб число 1аЛ05 ділилось на: а) 3; б) 9.
3. Чи ділиться на 9 35-значне число, у якого перша цифра 1, остання — 8, а інші дорівнюють 0?
4. Яку цифру треба підставити замість «*» у числі 777*, щоб дістати число, яке ділиться на 6?
Домашнє завдання
1. 	До числа 10 припишіть праворуч і ліворуч по одній цифрі так, щоб дістати число, кратне 72.


6 клас
51
2. Число 82** ділиться на 90. Знайдіть ділене.
3. До числа 13 припишіть праворуч і ліворуч по одній цифрі так, щоб вийшло число, кратне 45.
4. У Змія Горинича 1000 голів. Казковий богатир може одним ударом меча відрубати 1,17,21 чи 33 голови, але при цьому в Змія виросте відповідно 10, 14, 0 чи 48 голів. Чи зможе богатир подолати Змія Горинича?
Урок № 5
Тема. ПОДІЛЬНІСТЬ ЧИСЕЛ
Усні вправи
1. Якою буде сума двох парних чисел? двох непарних чисел?
2. Якою буде сума парного і непарного чисел?
3. Яким буде добуток парного і непарного чисел?
4. Яким буде добуток непарних чисел? парних чисел?
Будь-яке число в десятковій системі числення можна розкласти на розрядні доданки:
5796 = 5 1000+7 100+9 10+6.
Взагалі, будь-яке п’ятизначне число можна записати у вигляді:
abcde.
Риску ставлять для того, щоб відрізняти п’ятизначне число від добутку п’яти множників.
Розкладемо це число на розрядні доданки:
abcde = 10000 • a +1000 b+100 • с+10 • d+e.
1. Доведіть, що будь-яке число, записане трьома однаковими цифрами, _ ділиться націло на 37.
2. Доведіть, що сума двозначного числа та числа, записаного тими самими цифрами, але в оберненому порядку, ділиться націло на 11.
3. Доведіть ознаку подільності на 3 для трицифрових чисел.
Домашнє завдання
1. Доведіть, що число, записане шістьма однаковими цифрами, ділиться на 3, 7, 11, 13 і 37.
2. Доведіть, що число вигляду ababab ділиться на 7.
3. Доведіть ознаку подільності на 10.


52
Математична логіка 5-6 класи
Урок № 6
Тема. ПОДІЛЬНІСТЬ ЧИСЕЛ
1. До магазину привезли 223 л олії в бідонах по 10 і 17 л. Скільки було бідонів?
2. Ковбой Джо зайшов до бару, де він купив пляшку віскі за 3 долари, люльку за 6 доларів, три пакунки тютюну і 9 пакунків сірників. «З вас 11 доларів 80 центів», — сказав бармен. «Що?!» — вигукнув ковбой і витягнув пістолет. Як він здогадався, що його обдурили?
3. Скільки натуральних чисел від 1 до 1000 не діляться ані на 2, ані на З?
Домашнє завдання
1. Додаючи два цілих числа Коля, поставив зайвий «0» на кінці першого доданка й дістав у сумі 6641 замість 2411. Які числа він мав додати?
2. Доведіть, що якщо цифру двоцифрового числа записати двічі в тому самому порядку, то здобуте число буде більше від початкового в 101 раз.
3. Доведіть, що сума чисел abc, bca і cab кратна 111.
Урок № 7
Тема. ЗАДАЧІ, ПОВ’ЯЗАНІ З РОЗКЛАДАННЯМ ЧИСЕЛ НА ПРОСТІ МНОЖНИКИ
1. 	Івану та Миколі сказали, що число 150 розклали на три різні множники. Івану дали аркуш із записаним середнім за величиною множником, а Миколі — аркуш із записаною різницею двох менших множників. Необхідно було визначити всі три множники. Після того як обидва хлопчики сказали, що не можуть відповісти на питання, Іван, почувши відповідь Миколи, записав правильну відповідь. Побачивши це, Микола теж написав правильну відповідь. Запишіть її і ви.
Розв’язання
Можливі варіанти розкладання числа 150 на три різні множники:
1, 	2, 75 (різниця між найменшими 1);
1, 	3, 50 (різниця 2);
1, 	5, ЗО (різниця 4);
1, 	6, 25 (різниця 5);
1, 10, 15 (різниця 9);
2, 3, 25 (різниця 1);
2, 5, 15 (різниця 3);
3, 5, 10 (різниця 2).


6 клас
53
Іван не дав правильної відповіді, оскільки йому назвали величину середнього множника 3 чи 5. Не відповів і Микола, бо різниця дорівнювала 1 чи 2. Знаючи, які варіанти відкинув Микола, Іван вибрав з трьох, що залишились (1, 3, 50; 2, 3,25; 3, 5,10). Оскільки він вибрав відразу, то середній множник 5. Повторюючи ті самі міркування, Микола також відповів: 3, 5, 10.
2. 	Один із гостей привітав господаря з 36-річчям і запитав, де три його сини. Господар відповів, що діти на вулиці, і звернув увагу на такий збіг: добуток прожитих ними років дорівнює його віку, а сума прожитих ними років дорівнює кількості вікон в оселі. Гість спробував за цими даними визначити вік кожного хлопчика, але не зміг цього зробити, тому запитав, чи один син віком старший за інших? Одержавши позитивну відповідь, гість правильно визначив вік кожного з синів.
Домашнє завдання
1. Кожен із 7-ми учнів 5—11 класів вечірньої школи помножив кількість прожитих ним років на число, яке означає клас, в якому він навчається.
У Бородаєва вийшло 125, у Володіна — 150, у Гармаша — 210, у Зимова — 200, у Канського — 180, у Ратюка — 390, у Тилова — 264. Знаючи, що всі вони навчаються попарно в різних класах, визначте клас кожного.
2. Відомо, що в кожному кошику менше ніж 100 яблук. їх можна розкласти порівну на 2, 3 і 5 купок, але не можна розкласти порівну на 4 купки. Скільки яблук у кошику?
3. Знайдіть число, що ділиться на 5 без остачі, а від ділення на 2, 3 і 4 дає в остачі 1.
Урок № 8
Тема. ВЛАСТИВОСТІ ОСТАННЬОЇ ЦИФРИ ДОБУТКУ, СУМИ, РІЗНИЦІ, СТЕПЕНЯ ДЕЯКИХ НАТУРАЛЬНИХ ЧИСЕЛ
Для того щоб визначити останню цифру добутку, необхідно перемножити останні цифри множників. Остання цифра цього добутку буде шуканою.
1567-589=...З, бо 7-9 = 63.
Аналогічно знаходимо останню цифру суми двох чисел:
576+222222 =...8.
Знайдемо правила знаходження останньої цифри степенів чисел від 1 до 9.


54
Математична логіка. 5-6 класи
3і =3; З2 =9; З3 =27; З4 =81; З5 =243; З6 =729.
Можна помітити, що через кожні чотири кроки остання цифра степеня числа 3 повторюється. Висновок: для того щоб визначити останню цифру степеня 3, необхідно показник степеня поділити на чотири. Якщо від ділення на чотири остача 0 — остання цифра 1, якщо остача 1 — то остання цифра 3. Якщо остача 2 — остання цифра 9, а якщо остача 3 — остання цифра 7.
Аналогічно виводимо формули для степенів інших чисел.
34л+1 =...3
з4л+2
=...9
3 ^л+з
=...7
34л =...1
74л — 1
*74л+1
— 7
*у4л+2
— 0
74л+3 о
/ —...1
/
—... /
/
/ —...Э
84л =...6
84л+1
=...8
84л+2
=...4
84л+3 =...2
24л =...6
24я+1
=...2
2 4". 2
=...4
24л+3 =...8
42л - £
д2л+1
— 4
п2л _
і
п2л+1 _ Q
Ч —...0
ч
—.. .4
У —
...і
5" =...5
1" =..
.1
6"=..
.6
1. Знайдіть останню цифру:
а) 	б2001 ; б) 92001 ; в) З2001 ; г) 22001.
2. Якою цифрою закінчується число 9999"9" ?
3. Якою цифрою закінчується сума:
26-27-28-29+51-52-53-54?
Домашнє завдання
1. Якою цифрою закінчується різниця41-43 -45 -47-37 -39 -41-42?
2. Якою цифрою закінчується сума всіх трицифрових чисел?
3. Якою цифрою закінчується:
а) 7529 ; б) 9775 ; в)б559 ; г)47991; д) 35443 ?
І
Урок № 9 Тема. ДЕЯКІ ВЛАСТИВОСТІ ЧИСЕЛ, ЯКІ Є КВАДРАТАМИ НАТУРАЛЬНИХ ЧИСЕЛ
Нехай а=р^' р** ■■■■р“" — канонічний розклад числа а на прості
• 2 2аі 2аз 2а
множники, тоді а =р1 р2 .
Тобто якщо число є квадратом деякого числа й ділиться на деяке просте число р, то воно обов’язково ділиться і на р1.


6 клас
55
Це дає можливість з’ясувати в деяких випадках, чи є число повним квадратом натурального числа.
1. Чи може число, яке закінчується цифрами 35, бути квадратом натурального числа?
2. Чи може квадрат натурального числа складатись із 100 нулів, 100 одиниць і 100 двійок?
3. Чи може квадрат натурального числа закінчуватися на 66?
4. Якими цифрами закінчуються:
а) квадрати цілих чисел;
б) куби натуральних чисел;
в) четвертий степінь натуральних чисел?
Домашнє завдання
1. Складіть задачу на перевірку того, чи буде квадратом число, використовуючи ознаки подільності:
а) на 3 і 9; б) на 5 і 25; в) на 10 і 100; г) 2 і 4.
2. Чи можуть числа 468; 533 і 672 бути квадратом цілого числа?
Урок № 10
Тема. ЗАДАЧІ З ДРОБАМИ
1
1. 	У класі кількість відсутніх учнів складає - частину від числа присутніх. D
Після того як з класу вийшов один учень, число відсутніх стало дорівнювати - числа присутніх. Скільки учнів у класі?
2. Четверо товаришів купили разом човен. Іван вніс половину суми, яку внесли інші, Петро — третину суми, яку внесли інші, Андрій — чверть суми, яку внесли інші, а Роман — вніс 130 грн. Скільки коштує човен і скільки вніс кожен?
3. Колгоспниця принесла на ринок для продажу кошик яблук. Один покупець купив половину всіх яблук і ще пів’яблука. Другий покупець купив половину остачі, і ще пів’яблука і т. д. Останній (шостий) покупець купив половину тих, що залишились, і ще пів’яблука. Скільки яблук принесла для продажу колгоспниця?
Домашнє завдання
1. 	Мати поклала на стіл сливи і сказала трьом синам, щоб вони, повернувшись зі школи, поділили їх порівну. Першим прийшов додому Михайло і взяв собі третю частину слив. Потім повернувся Петро і взяв третю


56
Математична логіка. 5-6 класи
частину від тих слив, що були на столі. Потім прийшов Микола і теж взяв третю частину слив, які він побачив. Скільки слив залишила мати, якщо Микола взяв 4 сливи?
1 1
2. 	Петро з’їв - всіх яблук і ще 2 яблука. Іван з їв - всіх яблук і ще 1 яблуко,
Микола — половину’ того, що залишилось після Петра та Івана. Після 1
цього залишилась - частина від початкової кількості яблук. Скільки яб- 6
.тук було спочатку?
Урок № 11
Тема. ЗАДАЧІ З ДРОБАМИ
1
1. На день народження Віктора прийшло 5 друзів. Першому він відрізав -
о
1 1
частину пирога, другому — ~ остачі, третьому — - нової остачі, четвер-
1
тому -- - того, що залишилось. Останній шматок Віктор поділив навпіл
з п’ятим другом. Кому дістався найбільший шматок?
2. Я випив - чашечки кави й долив її молоком. Потім я випив чашечки
6 З
і знову долив її молоком. Нарешті я випив повну чашку. Чого я випив більше: кави чи молока?
, а . 2 . . .
3. 	Як від відрізу шовку довжиною у метр відрізати півметра, не маючи під
рукою лінійки?
Усні задачі
1. 	За книгу заплатили 60 грн та ще - її вартості. Скільки коштує книга?
2. Скільки дістанемо, якщо 60 поділимо навпіл?
3. Коли б я мав половину тих грошей, що маю, та ще одну гривню, то в мене було б 25 гривень Скільки в мене грошей?
Домашнє завдання
1. 	На запитання, скільки учнів навчається в школі, давньогрецький учений Піфаіор відповів’ «Половина всіх учнів вивчає математику, чверть —


6 клас
57
музику, сьома частина мовчить, і, крім того, є ще три жінки». Скільки учнів навчалося в школі Піфагора?
1
2. 	Мірошник брав за роботу — змеленого борошна. Скільки було змелено
для пекаря, якщо мірошнику віддали 99 кг?
3. 	Після того як Наталка з’їла половину персиків, у банці рівень компоту знизився на одну третину. На яку частину від нового рівня знизиться рівень компоту; якщо з’їсти половину від персиків, що залишились?
Урок № 12
Тема. ЗАДАЧІ З ДРОБАМИ
1. 	Магазин продав відріз тканини за чотири дні. Першого дня було подано
7 всього відрізу і ще 5 метрів, другого — 20 % остачі і ще 10 метрів, тре- о
тього — 25 % нової остачі і 13 метрів, що залишились. Скільки метрів тканини було у відрізу спочатку?
2. Летіла зграя гусей, а назустріч їм летить один гусак і каже: «Добридень вам, сто гусей!» «Нас не сто гусей, — відповідає йому вожак зграї, — якби нас було стільки, скільки тепер, та ще стільки, та півстільки, та чверть стільки, та ще ти з нами, тоді нас було б сто гусей». Скільки гусей було в зграї?
3. Один чоловік вип’є бочку пива за 14 днів, а зі своєю дружиною вони вип’ють цю бочку за 10 днів. За скільки днів дружина сама змогла б випити це пиво з бочки?
Домашнє завдання
1. Віл з’їв пласт сіна за годину; кінь з’їв пласт сіна за дві години, а коза з’їла такий самий пласт за 3 години. За який час вони всі троє з’їли б той самий пласт сіна?
4
2. Котра година, якщо до кінця доби залишилося - того часу, що вже минув від початку доби?
3. Один купець пройшов через три міста У першому місті в нього взяли половину й третину майна, у другому — половину а третину того, що залишилось, у третьому — знову половину й третину того, що залишилось. Коли він прибув додому, у нього залишилось 11 грошей. Скільки грошей було спочатку в купця?


58
Математична логіка. 5-6 класи
Урок № 13
Тема. ЗАДАЧІ НА ПОРІВНЯННЯ ДРОБІВ
Метод порівняння з одиницею полягає в наступному: порівнюючи два дроби (обидва менші за 1), ми знаходимо різницю першого і кожного з дробів. Той дріб, для якого ця різниця менша, буде більший за інший дріб.
397 398
Приклад. Порівняємо ттт і ттт. Знайдемо
398 399
397 1_
1-398 " 398’
а також
398 1 1_ 1
1-399" 399’ 399 < 398’
оскільки серед двох дробів з однаковими чисельниками більший той, зна-
398 397 менник якого менший. Тому ТТТ > ——.
399 398
1
Метод порівняння з — аналогічний до методу порівняння з 1.
1 2 4 5 7 8
1. 	Порівняйте: -+т+7 і 7+7 + п> не виконуючи додавання.
2 3 5 о о 9
1000001 100001
2. 	Яке число більше: чи
12 12
1Г?Ї0 2Ї?2Ї
3. 	Порівняйте:--—-та ———.
X X • • • X
13
12
Домашнє завдання
1. 	Складіть дві задачі, які ілюструють метод порівняння з 1.
Урок № 14
Тема. ЦІКАВІ ЗАДАЧІ НА ВІДСОТКИ
1. Як зміниться ціна товару, якщо спочатку її підвищити на 100 %, а потім знизити на 50 %?
2. Що більше: 15,5 % від 49 чи 49 % від 15,5?


6 клас
59
3. Ціна картоплі підвищилась на 20 %. Через деякий час ціна знизилась на 20 %. Коли картопля коштувала більше: до підвищення ціни чи після зниження?
4. Ціну на підручник з математики спочатку підвищили на 25 %, а потім знизили на 20%. Коли підручник коштував дорожче: до підвищення ціни чи після зниження?
Домашнє завдання
1. Ціну на товар спочатку знизили на 20 %, а потім підвищили на 25 %. Як зміниться ціна товару?
2. Заробітна платня становила 200 грн. Її підвищили на 20 %, а потім знизили на 20 %. Якою стала заробітна платня?
3. За весняний період Обломов збавив свою вагу на 25 %, за літо набрав ще 20 %, восени збавив вагу на 10 %, а взимку додав 20 %. Схуднув він чи поправився за рік?
Урок № 15
Тема. ЗАДАЧІ З ВІДСОТКАМИ
Усні задачі
1. Середнє арифметичне двох чисел становить 50 % одного з них. Чому дорівнює друге число?
2. Як зміниться ціна товару, якщо її зменшити на 50 %, а потім підвищити на 100 %?
3. Що більше: 10 % від 12 чи 12 % від 10?
Розв’яжіть задачі
1. Підприємство одержало завдання знизити за два роки на 51 % об’єм продукції. Кожного року потрібно знижувати цей об’єм на одне й те ж саме число відсотків. На скільки?
2. Фабрика збільшувала об’єм випуску продукції кожного року на одне й те ж саме число відсотків. Знайдіть це число, якщо за два роки об’єм продукції збільшився на 21%.
3. Під час випарювання з 8 кг розсолу одержали 2 кг харчової солі, яка містить 10 % води. Який відсоток води міститься в розсолі?
4. 40 % від 40 % деякого числа складають 32. Знайдіть це число.
5. На конференцію приїхали делегати з різних країн. З них російську мову знають 60 %, англійську мову — 85 %, французьку — 70 %. Скільки відсотків делегатів знають усі мови?


60
Математична логіка. 5-6 класи
Домашнє завдання
1. Підприємство одержало завдання зменшити за два роки об’єм випуску продукції на 36 %, зменшуючи його кожного року на однаковий відсоток. На скільки відсотків потрібно зменшувати об’єм продукції щороку?
2. 50 % від 40 % деякого числа складають 64. Знайдіть це число.
3. У класі французькою мовою володіють 76 % учнів, англійською — 80 %. Скільки учнів володіють англійською та французькою мовами одночасно?
Урок № 16
Тема. ЗАДАЧІ З ВІДСОТКАМИ
1. Вода Тихого океану містить 35 % солі (за вагою). Скільки прісної води потрібно додати до 40 кг такої води, щоб склад соліусуміші складав5 %?
2. Із 22 кг свіжих грибів одержують 2,5 кг сушених, які містять 12 % води. Який відсоток води у свіжих грибах?
3. Вологість свіжоскошеної трави 60 %, сіна — 15 %. Скільки сіна можна одержати з однієї тонни свіжоскошеної трави?
4. Ціну товару знизили на 20 %, а потім нову ціну ще раз знизили до 45 %. На скільки відсотків знизили початкову ціну?
Домашнє завдання
1. Морська вода містить 5 % солі (за вагою). Скільки кілограмів прісної води потрібно додати до 40 кг морської, щоб уміст солі в суміші складав 2 %?
2. Під час випарювання з 8 кг розсолу одержали 2 кг солі, яка містить 10 % води. Який відсоток води у розсолі?
3. Ціну товару спочатку знизили на 20 %, потім нову ціну знизили на 30 %, наприкінці, після перерахунку, знизили ще на 50 %. На скільки відсотків усього знизили початкову ціну товару?
Урок № 17
Тема. ЗАДАЧІ З ВІДСОТКАМИ
1. Двоє учнів — високий та низенький — вийшли одночасно з одного й того самого будинку до однієї школи. У низенького крок був на 20 % коротший, ніж у високого, але він встиг за той самий час зробити на 20 % більше кроків, ніж високий. Хто з них раніше прийде до школи?


6 клас
61
2. Ціна вхідного квитка на стадіон складала 20 грн. Після зниження вхідної плати кількість глядачів збільшилась на 25 %, а виручка зросла на 12,5 %. Скільки став коштувати вхідний квиток після зниження ціни?
3. Сума двох чисел 54, одне з них на 20 % менше від другого. Знайдіть більше число.
Домашнє завдання
1. У вересні проїзний квиток на метро коштував 80 грн. У жовтні вартість квитка збільшили, внаслідок чого кількість проданих квитків зменшилась на 25 %, а виручка від їх продажу зменшилась на 6,25 %. Скільки став коштувати проїзний квиток у жовтні?
2. Сума двох чисел 63, одне з них на 10 % більше від другого. Знайдіть менше число.
Урок № 18
Тема. ЗАДАЧІ, ПОВ’ЯЗАНІ З ТУРНІРАМИ
1. Шість шахістів А, Б, В, Г, Д, Е зіграли в турнірі один з одним по одній партії. А звів усі партії унічию, Б не програв жодної партії, В виграв у переможця турніру і зіграв унічию з Д. Г випередив Д, але відстав від Е. Хто скільки очок набрав і яке місце посів?
2. Семеро шахістів зіграли в турнірі один з одним по одній партії. Переможець набрав у 2 рази більше очок, ніж разом троє тих, які залишились, вони посіли інші місця. Той, хто посів 4-те місце, набрав 50 % можливих очок. Як зіграли між собою ті, хто посіли 2 і 3 місця?
3. Декілька команд розіграли першість з волейболу, провівши одна з одною по одній грі. Доведіть, що якщо будь-які дві команди здобули однакову кількість перемог, то знайдуться такі три команди Л, В і С, що А виграла у В, By С, С у А (у волейболі немає нічиїх).
Домашнє завдання
1. П’ять учасників олімпіади стали її переможцями, набравши по 15, 14 і 13 балів і посівши відповідно I, II і III місця. Скільки учасників завоювали кожне призове місце, якщо вони набрали 69 балів?
2. У розіграші першості по футболу беруть участь 17 команд. Кожна команда з іншими повинна зіграти 2 рази: один раз на своєму полі, а другий — на чужому. Скільки матчів буде проведено в турнірі?


62
Математична логіка. 5-6 класи
Урок №19
Тема. МАТЕМАТИКА В ІГРАХ ДВОХ ОСІБ
Люди завжди були вправними у винаході ігор, тут немає межі вільному польоту думки. Залишається лише побажати, щоб було створено цілий курс ігор, які можна трактувати математично.
Г. В. Лейбніц
Сучасна математика виділяє окремий напрямок досліджень, який так і називається: «Теорія ігор». Вона застосовується в сучасній біології, економіці, бізнесі, управлінні.
Деякі важливі ідеї математичної теорії ігор спостерігаються навіть в елементарних задачах на ігри двох осіб. Для розв’язання такі задачі потребують мінімуму фактичних знань з математики, але вимагають достатньо розвиненого мислення. Тому вони дуже популярні на математичних олімпіадах.
Відповідно до заданої вище класифікації, ігри двох осіб — це конкретні інтелектуальні ігри. Вони характеризуються такими основними рисами:
1) у кожній грі беруть участь двоє гравців;
2) суть гри в тому, що суперники по черзі виконують певні дії — «ходи»; кількість ходів скінчена (хоча, можливо, і як завгодно велика);
3) умовою (правилами) гри обумовлено, в чому полягає заключна виграшна позиція; виграє той з гравців, хто першим досягне витратної позиції;
4) гра є відкритою для обох гравців, тобто в будь-який момент гри кожен із гравців має повну інформацію про її перебіг.
Широковідомими іграми двох осіб є ігри в шахи та шашки. Навпаки, так звані азартні ігри — у кості, доміно, карти, навіть у «морський бій», не входять до окресленого кола ігор двох осіб, бо не є відкритими для обох осіб.
Гра в шашки, а особливо в шахи, виявилася по-справжньому геніальним винаходом людства. Незважаючи на доволі прості правила, повний аналіз цих ігор з виробленням конкретних стратегій для досягнення виграшу на сьогодні навіть не уявляється практично можливим. Надто вже велика кількість варіантів гри з’являється вже після декількох перших ходів. Тому далі розглядатимуться набагато простіші ігри двох осіб. Зрештою, деякі з них не менш давні, ніж гра в шахи чи шашки.
Виграшною стратегією називається такий спосіб ведення гри одним із гравців, за якого він перемагає незалежно від того, як грає інший. Зрозуміло, що виграшна стратегія може існувати лише для одного з гравців. А відповідь на запитання «Для кого саме?» залежить від того, за ким із гравців перший хід. У з’ясуванні цих обставин для кожної конкретної гри і полягає суть розв’язування задач на ігри двох осіб. У саму гру після цього


6 клас
63
вже можна й не грати. Можна сказати, що якби учасниками гри були два великі магістри, то вони цього й не робили б, а ознайомившись з правилами гри і проаналізувавши їх, просто кинули б жереб, щоб визначити, за ким перший хід.
Після цього один із гравців одразу б привітав іншого з перемогою, адже й так було б зрозуміло, хто переможе. Але якщо з двох учасників гри хоча б один ще не великий магістр, то... можна й пограти.
Універсальним методом для пошуку виграшних стратегій є аналіз гри «з кінця». Суть цього методу стане зрозумілою з прикладів, які зараз розглянемо.
Приклад 1. Правила гри такі. На купці лежать 53 камінці. Кожен із двох гравців за один хід може взяти будь-яку кількість камінців від 1 до 4. Виграє той, хто забере останній камінець. У кого з гравців — того, який робить перший хід (назвемо його першим), чи його суперника (назвемо його другим), — є виграшна стратегія і в чому вона полягає? Хто виграє, якщо в купці лежатиме 55 камінців?
Розв’язання
Розмістимо умовно ці камінці в ряд, пронумерувавши їх числами від 1 до 53 у порядку, зворотному до того, в якому їх братимуть з купки (тобто вважатимемо, що першим братиметься камінець з номером 53, а останнім — з номером 1 (рис. 7)). Для того щоб останнім ходом (нехай під номером гі) забрати камінець з номером 1 (і таким чином виграти гру), першому гравцеві після попереднього п-1 ходу суперника повинна залишитися будь-яка кількість камінців від 1 до 4. Для того щоб примусити другого гравця залишити саме таку кількість камінців, а не, скажімо, 6 чи 7 (що для першого гравця було б «катастрофою»), першому гравцеві після п-2 ходу потрібно залишити рівно 5 камінців. Тоді яку б кількість — 1, 2, 3 чи 4 — не взяв другий гравець, перший останнім своїм ходом зможе забрати залишок.
53 52 51 50 49... З 2 1
ООООО. .ООО
Рис. 1
Відповідно, після п-4 ходу першого гравця повинно залишитися 10 камінців, після л-6 ходу — 15 камінців і т. д.
Отже, «вихід» на номери, кратні 5, забезпечує першому гравцю можливість гарантовано здобути перемогу в грі. А для цього цьому потрібно першим своїм ходом взяти 3 камінці з даних 53-х. Далі після кожного ходу суперника слід брати таку кількість камінців, щоб залишилося число, кратне 5. Це і є виграшна стратегія, причому існує вона для першого іравця.


64
Математична логіка. 5-6 класи
Якщо ж у купці лежатиме 55 камінців, то, маючи можливість взяти лише від І до 4 камінців, один гравець першим своїм ходом уже не зможе «вийти» на число, кратне 5 Тому цим шансом негайно може скористатися другий гравець. Отже, у цьому випадку виграшна стратегія існує для другого гравия. Аналіз гри завершено.
Суттєве спрощення аналізу гри «з кінця» досягається з використанням понять виграшна і програшна позиції у грі.
Позицією у грі називають стан гри після чергового ходу. Так, у наведеному прикладі позиціями є всі можливі кількості камінців у купці. Кінцевий стан гри, яким визначається перемога у грі, називається кінцевою позицією, а початковий, визначений умовою гри, — початковою позицією. Кінцевою позицією у згаданій грі є 0 камінців, а початковою — 53 (або 55) камінців.
Цілком природно вважати програшною, зокрема, кінцеву позицію. Адже з неї уже немає жодних ходів. Так само природно вважати виграшною кожну позицію, з якої до кінцевої позиції можна дійти одним ходом. Адже гравець, якому випало ходити з цієї позиції, може зайняти кінцеву позицію і, отже, здобути перемогу у грі. Цю визначальну характеристику останніх виграшних позицій приймають за означення усіх виграшних позицій у грі, тобто позиція називається виграшною, якщо існує принаймні один хід, який перетворює її в позицію програшну. Якщо ж такого ходу немає, то позиція програшна, тобто, будь-який хід з програшною позицією перетворює її на виграшну.
Для більшої зручності виділимо ці характеристики окремо:
1) кінцева позиція — програшна;
2) для кожної виграшної позиції існує принаймні один хід, який перетворює її у програшну;
3) будь-який хід із програшної позиції, яка не є кінцевою, перетворює її у виграшну.
Зрозуміло, що визначення всіх програшних позицій у грі рівносильне визначенню стратегії гри для здобуття перемоги, адже створення одним із гравців послідовних програшних позицій для суперника за умови скінченої кількості ходів неминуче призведе й до кінцевої програшної позиції (знову ж таки для суперника), тобто — до перемоги у грі.
Проаналізуємо тепер із використанням понять «виграшна» і «програшна» позиції гру, описану в прикладі 1. Нагадаємо ще раз, що аналіз здійснюється «з кінця» гри.
Замінимо для більшої зручності рядочок камінців смужкою клітинок. У цих клітинках залежно від того, виграшною чи програшною є позиція у грі з кількістю камінців, що дорівнює її номеру, становитимемо відповідно знак «+» або «—». Для кінцевої позиції введемо окрему клітинку


6 клас
65
з номером 0, що характеризує відсутність камінців. Це — перша «з кінця» програшна позиція, тому в цій клітинці ставимо знак «—».
Одним ходом «назад» з цієї позиції можна перейти в клітинки з номерами 1, 2, 3, 4. Отже, це виграшні позиції. Ставимо в них знак «+». Після того як хтось із гравців своїм ходом створить яку-небудь з цих позицій, інший наступним ходом виграє гру.
Наступна «з кінця» позиція — 5 камінців — уже не може бути виграшною, бо для неї не існує жодного ходу, який веде до наступної (тепер уже з початку гри) програшної позиції 0 камінців (див. характеристику 2 для виграшних позицій). Отже, ця позиція програшна. Ставимо тут знак «—».
Далі знову відзначаємо «назад» чотири «мінуси», а п’ятий «плюс» і т. д. Програшними, як бачимо, є позиції з кількістю камінців, кратною 5.
Якщо всього камінців 53, то ця початкова позиція є виграшною, а якщо 55 — програшною. Отже, у першому випадку виграшна стратегія у гравця, який робить першим хід (перший гравець), а у другому — у того, що робить хід другим (другий гравець).
1. Альоша Попович і Добриня Микитич воюють дев’ятиглавого змія. По черзі богатирі ходять до його печери й відрубують 1, 2 чи 3 голови. Як Альоша, який почав бій першим, зможемо одержати славу переможця змія (тобто відрубувати останню голову)?
2. У грі «Хто першим назве число 100» беруть участь двоє. Один називає будь-яке натуральне число від 1 до 9 включно. Другий додає до названого числа будь-яке натуральне число від 1 до 9, і називає нову суму. До цієї суми перший додає будь-яке натуральне число від 1 до 9, і називає нову суму. Виграє той, хто називає число 100. Який найкращий початок цієї гри?
Домашнє завдання
1. Двоє по черзі ставлять на шахову дошку офіцера (за один хід одного офіцера), щоб вони не били один одного. Хто не може поставити офіцера — програє. Хто виграє за правильної умови гри — перший чи другий?
2. Маємо три купки камінців: у першій 10, у другій — 15, у третій — 20. За один хід дозволяється розбити будь-яку купку на дві менші. Проірає той, хто не зможе зробити ходу. Хто переможе?
3. На дошці записані числа 25 і 36. За один хід дозволяється дописати ще одне натуральне число — різницю будь-яких чисел, які є на дошці, якщо вона ще не зустрічалась. Програє той, хто не зможе зробити ходу. Хто переможе?


66
Математична логіка. 5-6 класи
Урок № 20
Тема. ВИГРАШНІ ТА ПРОГРАШНІ ПОЗИЦІЇ
1. Двоє котів утягнули кільце із 6 сосисок. Коти по черзі почали з’їдати по одній перемичці між сосисками, і якщо при цьому утворювались окремі сосиски, то кіт, який перекусив перемичку, відразу їх з’їдав. Хто з’їсть більше сосисок: кіт, який почав їсти першим, чи другий? Яка правильна стратегія? А якщо в кільці 7 сосисок? А якщо 8?
2. Ганя й Тетяна виписують 8-значне число, ставлячи цифри по черзі, починаючи зі старшого розряду. Починає Ганя. Чи зможе зробити Тетяна так, щоб здобуте число ділилось на 9?
3. Двоє по черзі беруть з купи 1, 2 чи 4 камінці. Виграє той, хто візьме останній камінець. За якої кількості камінців у купі той, хто починає, зможе виграти, як би не грав його партнер?
Домашнє завдання
1. Двоє по черзі обривають пелюстки ромашки, при цьому за один раз можна обірвати і чи 2 пелюстки, які ростуть поруч. Виграє той, хто зробить останній хід. Хто виграє за умови правильної гри?
2. Маємо дві однакові купки камінців. Двоє гравців беруть по черзі будь- яку кількість камінців з будь-якої купки, але тільки з однієї. Виграє той, хто взяв останні камінці. Хто виграє за умови правильної гри?
3. На столі лежать три купки сірників: 1, 2 і 3 сірники. Гравці по черзі беруть будь-яку кількість сірників з будь-якої купки. Виграє той, хто взяв останній сірник. Як повинен починати перший гравець, щоб виграти? Яким має бути його перший хід?
4. На колі дано 20 точок. Двоє по черзі проводять хорду з кінцями в цих точках так, щоб хорди не перетинались. Програє той, хто не зможе провести хорди. Хто здобуде перемогу за умови правильної гри?
Домашнє завдання
1. Маємо 3 однакові купки камінців. Двоє гравців беруть по черзі будь-яку кількість камінців з будь-якої купки, але тільки з однієї. Виграє той, хто взяв останні камінці. Хто виграє за умови правильної гри?
2. На столі лежать три купки сірників: 7,11 і 13 сірників. Гравці по черзі беруть будь-яку кількість сірників з будь-якої купки. Виграє той, хто взяв останній сірник. Як повинен починати перший гравець, щоб виграти? Яким має бути його перший хід?
3. Ганя та Іван виписують 8-цифрове число, ставлячи цифри по черзі, починаючи зі старшого розряду. Починає Ганя. Чи зможе Іван зробити так, щоб здобуте число ділилось на 9?


6 клас
67
Урок № 22
Тема. ПРИНЦИП ДІРІХЛЕ
Видатний німецький математик Петер Лежен Діріхле висловив принцип, який потім назвали на його честь. Жартома він формулюється так: «Якщо п’ять зайців розсадити в чотири клітки, то принаймні в одній із них опиняться два зайці».
Більш узагальнено це твердження можна сформулювати так: якщо множина із N елементів розбита на п частин, які не мають спільних елементів, де N>n, то принаймні в одній частині буде більше на однин елемент.
Або якщо п предметів розкладено по п ящиках, то принаймні в одному з них буде знаходитися не менше ніж £+1 предметів.
1. У лісі росте мільйон ялинок. Відомо, що на кожній з них не більше ніж 600 000 голок. Доведіть, що в лісі знайдуться дві ялинки з однаковою кількістю голок.
Доведення
Якщо ялинки кількістю k = 1000000 ми розкладемо по п «ящиках» (п = 600000 — кількість голок на ялинках), то принаймні в одному «ящику» опиниться 2 ялинки, оскільки ялинок більше, ніж «ящиків». Отже, існують хоча б дві ялинки з однаковою кількістю гілок.
2. У місті Одеса живе більш ніж 3 мільйони осіб. Доведіть, що в деяких двох одеситів однакова кількість волосся на голові, якщо відомо, що в будь-якої людини на голові не більше ніж мільйон волосинок.
3. До магазину привезли 25 ящиків з яблуками трьох сортів, причому в кожному ящику лежали яблука одного сорту. Чи можна знайти 9 ящиків з яблуками одного сорту?
4. У класі 40 учнів. Чи знайдеться такий місяць року, в якому свій день народження відмічають не менш ніж 4 учні цього класу.
5. На 5 поличках книжкової шафи 164 книжки, причому на одній — З книжки. Доведіть, що знайдеться поличка, на якій не менше ніж 40 книжок.
Домашнє завдання
1. У місті більш ніж 8 мільйонів мешканців. Науковці вважають, що в кожної людини менше ніж 200 000 волосинок на голові. Доведіть, що є принаймні 41 житель з однаковою кількістю волосинок на голові.
2. У квадраті зі стороною 1 м позначили 51 точку. Доведіть, що будь-які З точки з них можна накрити квадратом зі стороною 20 см.


68
Математична логіка 5-6 класи
Урок № 23
Тема. ПРИНЦИП ДІРІХЛЕ
Наслідок з принципу Діріхле. Серед m чисел при діленні на п (т, п — натуральні, m > п) знайдеться хоча б два, які мають однакові остачі.
1.15 хлопчиків зібрали 100 грибів. Доведіть, що принаймні двоє з них зібрали однакову кількість грибів.
2. Доведіть, що серед п’яти будь-яких цілих чисел знайдеться два, остача яких від ділення на 4 однакова.
3. Доведіть, що серед шістьох будь-яких цілих чисел знайдеться два, різниця яких ділиться на 5.
4. Маємо 100 цілих чисел. Доведіть, що серед них знайдуться декілька (чи одне), сума яких ділиться на 100.
Домашнє завдання
1. Доведіть, що серед 7-ми будь-яких цілих чисел знайдеться два, остача яких від ділення на 6 однакова.
2. Доведіть, що серед 8-ми будь-яких цілих чисел знайдеться два, різниця яких ділиться на 7.
3. Маємо 5 цілих чисел. Доведіть, що серед них знайдуться декілька (чи одне), сума яких ділиться на 50.
4. У диктанті ЗО учнів припустились 185 помилок. Доведіть, що якнайменше три учні припустились помилок порівну.
Урок № 24
Тема. ПРИНЦИП ДІРІХЛЕ
Інколи буває корисним ще таке формулювання принципу Діріхле:
Якщо одне з кількох чисел більше від їх середнього арифметичного, то серед цих чисел знайдеться інше, що є меншим від їх середнього арифметичного.
1. У бригаді 7 осіб, їх сумарний вік складає 322 роки. Доведіть, що з них можна вибрати трьох осіб, сумарний вік яких не менший за 138 років.
Доведення
Оскільки середній вік членів бригади складає 46 років, то сумарний вік трьох найстарших людей не менше за 3 46 = 138 років
2. У кгасі 33 учні, а сума їх років складає 430. Чи справедливе твердження;
шг •гласізнайгпггт*ся 260?


6 клас
69
3. П’ятеро двірників одержали заробітну платню — 1500 грн (на всіх) Кожен з них хоче купувати собі магнітофон ціною 320 грн Доведіть, що комусь з них доведеться почекати до наступної зарплати.
4. Сто осіб сидять за круглим столом, причому більше половини з них — чоловіки. Доведіть, що деякі два чоловіки сидять напроти один одного.
Домашнє завдання
1. У бригаді 5 осіб, їх сумарний вік складає 165 роки. Доведіть, що з них можна вибрати трьох осіб, сумарний вік яких не менще за 99 років.
2. 60 ельфів сидять за круглим столом, причому більше половини з них — лісові ельфи, інші — гірські. Доведіть, що деякі два лісові ельфи сидять напроти один одного.
Урок № 25
Тема. ІНВАРІАНТ
Число або властивість, що не змінюється за дозволених перетворень, називається інваріантом. Знаходження інваріанта іноді допомагає під час розв’язання деяких задач. Визначивши інваріант деякого процесу, в багатьох випадках можна з’ясувати питання про можливість певного результату цього процесу. У ролі інваріанта може використовуватись парність, залишок від ділення на деяке число, знак добутку тощо.
1. На дошці записано десять плюсів та п’ятнадцять мінусів. Дозволяється стерти будь-які два знаки та записати заміть них плюс, якщо вони однакові, і мінус, якщо вони різні. Який знак залишиться на дошці після виконання 24 операцій?
Розв’язання
Замінимо кожен плюс числом 1, а мінус — числом —1. Тоді наша операція полягає в тому, що замість двох чисел пишемо їх добуток. Добуток усіх чисел на дошці не змінюється. На початку він дорівнював —1, тому і в кінці він буде дорівнювати —1. Залишається мінус.
2. У таблиці 4x4 плюси та мінуси розставлені так:
Дозволяється змінити знак на протилежний одночасно у всіх клітинках одного рядка, одного стовпчика або вздовж прямої, паралельної


70
Математична логіка. 5-6 класи
одній з діагоналей (зокрема в будь-якій кутовій клітинці). Чи можливий варіант таблиці без жодного мінуса?
3. 	Бешкетник Вася порвав стінгазету, причому кожен шматок, який йому попадався, він рвав на 4 частини. Чи могло бути після цього 1989 шматків?
Домашнє завдання
1. 	Дано таблицю 3x3.
+
+
—
—
+
+
+
—
+
Дозволяється змінювати знак одночасно у всіх клітинках одного рядка або одного стовпчика. Чи можна отримати таблицю тільки з плюсами?
2. У Змія Горинича 1000 голів. Ілля Муромець одним ударом меча може відрубати точно 1, 17, 21 або 33 голови, але при цьому в Змія виростає відповідно 10, 14, 0 або 48 голів. Чи зможе богатир перемогти Змія Горинича?
3. Бешкетник Вася порвав стінгазету, причому кожен шматок, який йому попадався, він рвав на 4 або 10 частин. Чи могло бути після цього 1989 шматків?
Урок № 26
Тема. ВКЛЮЧЕННЯ, ВИКЛЮЧЕННЯ
1. У похід ходили 80 % учнів класу, а на екскурсію — 60 %, причому кожен узяв участь у поході чи екскурсії. Скільки відсотків класу взяли участь і там і там?
2. Зі 100 осіб 85 володіють англійською мовою, 80 — іспанською, 75 — німецькою. Скільки осіб володіють усіма трьома мовами?
3. Із 35 учнів 20 відвідують математичний гурток, 11 — біологічний, а 10 не відвідують цих гуртків. Скільки учнів вивчають і математику, і біологію?
4. В одній склянці 9 ложок молока, а в другій 7 ложок чаю. Ложку молока перелили з першої склянки у другу, змішали й ложку чаю з молоком перелили назад у першу склянку. Чого більше: чаю в молоці чи молока в чаї?
5. Частка блондинів серед блакитнооких більша, ніж їх частка серед усього населення. Чи правильно, що частка блакитнооких серед блондинів більша, ніж їх частка серед усього населення?


6 клас
71
Домашнє завдання
1. Кожен десятий математик — філософ. Кожен сотий філософ — математик. Кого більше: філософів чи математиків?
2. Із 40 осіб 38 володіють англійською мовою, 20 — французькою, 25 — німецькою. Скільки осіб володіють усіма трьома мовами?
3. Під час зимових канікул театр відвідали 75 % учнів класу, а цирк — 50 %, причому кожен відвідав театр чи цирк. Скільки відсотків учнів класу побували і там і там?
Урок № 27
Тема. ВКЛЮЧЕННЯ, ВИКЛЮЧЕННЯ
1. УТома 100 мишок, кожна з яких біла або сіра. Принаймні одна з мишок Тома сіра, і серед будь-яких семи мишок принаймні чотири є білі. Яку найбільшу кількість сірих мишок може мати Том?
2. У класі серед довільних 12 учнів можна вибрати двоє дівчат, а серед довільних 20 учнів трьох хлопців. Яка найбільша кількість дітей могла бути в класі?
3. На зустріч зібралися всі учасники двох туристичних походів (деякі взяли участь у двох походах, деякі — тільки в одному). У першому поході нараховувалось 60 % чоловіків, а у другому — 75 %. Доведіть, що на зустріч прийшло чоловіків не менше ніж жінок.
4. У класі кожен хлопчик товаришує з трьома дівчатками, а кожна дівчинка — з двома хлопчиками. При цьому в класі всього 19 парт і 31 піонер. Скільки учнів у класі?
Домашнє завдання
1. У класі серед довільних 10 учнів можна вибрати трьох дівчат, а серед довільних 18 учнів чотирьох хлопців. Яка найбільша кількість дітей може бути в класі?
2. В Ірини 50 цукерок, кожна з яких шоколадна або карамелька. Принаймні одна з цукерок карамелька, і серед будь-яких 9 цукерок принаймні 6 шоколадних. Яку найбільшу кількість карамельок може мати Ірина?


72
Математична логіка. 5-6 класи
Урок № 28
Тема. КОМБІНАТОРНІ ЗАДАЧІ
1. Скількома способами можна запалити світло в класі, якщо в ньому З лампочки, у кожної — окремий вимикач.
2. а) У магазині «Все для чаю» продають 5 різних чашок і 3 різних блюдця. Скількома способами можна купити там набір «чашка + блюдце»?
б) У той самий магазин завезли ще 4 види чайних ложок. Скількома способами можна купити комплект «Чашка 4- блюдце + ложка»?
в) Відомо, що одна з чашок, одне з блюдець і одна з ложок — золоті. Скількома способами можна купити набір із 3-х різних предметів, у якому:
1) немає золотих предметів;
2) один золотий предмет;
3) два золотих предмета;
4) три золотих предмета?
Домашнє завдання
1. На колі позначено 5 червоних і 7 синіх точок. Розглянемо всі відрізки (хорди) з кінцями в позначених точках. У скількох відрізків кінці:
а) різного кольору;
б) однакового кольору?
2. Скільки діагоналей у 10-кутника?
Урок № 29
Тема. ЗАДАЧІ З ГОДИННИКАМИ
1. Маленька Настя пішла гуляти
між 8 та 9 годинами ранку якраз
тоді, коди годинна та хвилинна /• • «Ч /• • «Ч
стрілки співпадали. Вона по- /• вернулася додому між 2 і 3 го- \ 4—е /
динами після полудня, коли \ • е • у \ • е • J годинна та хвилинна стрілки —
лежали на одній прямій. Скільки часу гуляла Настя?
2. Після ремонту годинник Оксанки йшов правильно, але забудькуватий майстер поставив у годинник дві стрілки однакової довжини. Скільки із запропонованих нижче картинок могла побачити Оксанка на своєму годиннику? Які саме?


6 клас
73
3. У скільки разів швидкість хвилинної стрілки більша за швидкість годинної?
4. Який кут складають стрілки годинника о 9 годині 20 хвилин?
5. Скільки разів упродовж доби годинна і хвилинна стрілки:
а) співпадають;
б) складають розгорнутий кут;
в) складають прямий кут?
Домашнє завдання
1. Який кут складають стрілки годинника о 6 годині 20 хвилин?
2. Буратіно любить читати книгу, сидячи у сквері біля курантів. Одного разу, поки він сидів, куранти почали бити 5 разів, а всього він нарахував 11 ударів. З останнім ударом Буратіно підвівся і пішов додому. Котра була година? Куранти відбивають кожну годину необхідну кількість разів і, крім того, б’ють один раз о пів на кожну годину.
Урок № ЗО
Тема. ЗАДАЧІ З ГОДИННИКАМИ
1. 	Годинник показує 12 годину дня. Через який час хвилинна і годинна
стрілки співпадуть?
2. 	Прокинувшись, Вінні Пух побачив, що ходики стоять. Він завів їх і ви¬
рушив у гості до Кролика (у якого годинник працював правильно). Повернувши, Пух правильно виставив час. Як йому це вдалося?
3. 	На запитання «Котра година?» було дано відповідь: «Половина часу, З
який минув після півночі, дорівнює - часу, який залишився до полуд¬
ня». Котра була година?
Домашнє завдання
1. Годинник б’є кожну годину і відбиває стільки ударів, скільки показує годинна стрілка. Скільки ударів відіб’є годинник упродовж 12 годин?
2. Дві стрілки насаджені на одну вісь і в деякий момент часу співпадають. Одна зі стрілок описує коло за 12 годин, а друга за 16 годин. Через який час стрілки співпадуть знову?


74
Математична логіка. 5-6 класи
Урок №31
Тема. ЗАДАЧІ НА СКЛАДАННЯ РІВНЯНЬ
1. Голова риби важить стільки, скільки хвіст і половина тулуба, тулуб — стільки, скільки голова і хвіст разом. Хвіст важить 1 кг. Скільки важить риба?
2. Хазяїн обіцяв робітнику за рік 12 грн і жупан. Але той пішов через 7 місяців. Під час розрахунку він одержав жупан і 5 грн. Скільки коштує жупан?
3. 	Четверо товаришів купують човен. Перший вніс половину тієї суми, яку
1 1
внесли інші, другий — - суми, яку внесли інші; третій — - суми, яку вне¬
сли інші, а четвертий — 130 грн. Скільки коштує човен?
Підказка. Яку частку вартості човна вніс перший? А як підрахувати частку, яку вніс четвертий?
4. 	Син запитав батька, скільки йому років. Батько відповів так: «Якщо до моїх років додати їх половину, потім їх чверть і ще один рік, то дістанемо 134 роки». Скільки років батькові?
Домашнє завдання
1. Деяке число зменшили на 7, потім зменшили у 10 разів і дістали число, яке на 34 менше від початкового. Знайдіть початкове число.
2. Знайдіть таке число, що якщо його помножити на 52, потім добуток зменшити у 5 разів, то маємо число, яке на 1974 більше від початкового.
3. Батько старший за сина у 4 рази. Через 20 років він буде старший за сина у 2 рази. Скільки зараз років батькові?
Урок № 32
Тема. ЗАДАЧІ НА СКЛАДАННЯ РІВНЯНЬ
1. Знайдіть частку двох чисел, якщо вона у два рази менша від одного з них і у шість разів більша за інше.
2. У саду цвітуть тюльпани, гіацинти та фіалки — всього 50 штук. Фіалок було у 4 рази більше, ніж тюльпанів. Двоє дітей зайшли в сад і нарвали тюльпанів. Перший зірвав у 3 рази більше тюльпанів, ніж другий. У саду залишилось 5 тюльпанів. По скільки тюльпанів зірвали діти й скільки всього квітів залишилось у саду?
3. На запитання, скільки йому років, один математик відповів: «Візьміть три рази мої роки разом із 3 і відніміть від них три рази мої роки без 3 — дістанете мій вік». Скільки років цьому математику?


6 клас
75
4. 	Іванко взяв у товариша книгу на 3 дні. Першого дня він прочитав ± книги, другого — J залишку сторінок, а кількість сторінок, які Іванко про¬
читав третього дня, дорівнювала половині кількості сторінок, прочитаних у перші два дні. Чи встиг Іванко прочитати книжку?
Домашнє завдання
1. Вулицею йшла дівчинка. Зустрівши старого, вона привіталась. Старий теж привітався: «Добрий день, маленька дівчинко!»
Дівчинка заперечила, що вона не маленька, і тоді старий запитав, скільки їй років. Вона відповіла: «Я у два рази молодша за матусю, а матуся на п’ять років молодша за батька. Разом нам 100 років». Скільки років дівчинці?
2. Олексій задумав число. Він додав до нього 5, потім поділив суму на три, помноживши на 4, відняв 6, поділив на 7 і одержав число 2. Яке число задумав Олексій?
3. Коли Наталя стала на ваги, ті показали 67 кг, а коли на ці ваги стала Оксана — 59 кг. Після того як дві дівчинки разом стали на ваги і ті показали 131 кг, вони побачили, що стрілка була зсунена з нульової позначки. Скільки важить Наталя?
Урок № 33
Тема. ЗАДАЧІ НА СКЛАДАННЯ РІВНЯНЬ
1. Скільки років братові і скільки років сестрі, якщо 2 роки тому брат був старшим за сестру у два рази, а 8 років тому — у п’ять разів?
2. Марійка отримала на домашнє завдання 40 задач. Мама вирішила стимулювати навчальний процес доньки так: за кожну правильно розв’язану задачу вона дає Марійці 0,5 грн, а за кожну неправильно розв’язану задачу — забирає 1 грн. Після виконання домашнього завдання у Марійки залишилось 2 грн. Скільки задач Марійка розв’язала правильно?
3. На трьох полицях стоять книжки. На нижній полиці книг у 2 рази менше, ніж на двох інших, на середніх — у 3 рази менше, ніж на двох інших, а на верхній полиці стоїть ЗО книг. Скільки всього книжок?
4. У п’яти ящиках лежить по однаковій кількості яблук. Якщо з кожного ящика вийняти по 60 яблук, то у всіх ящиках залишиться стільки яблук, скільки раніше було у двох ящиках. Скільки яблук було в кожному ящику спочатку?


76
Математична логіка. 5-6 класи
Домашнє завдання
1. За контрактом робітнику повинні заплатити по 48 франків за кожен робочий день, а за кожен день прогулу — забирають 12 франків. Через ЗО днів робітник дізнався, що йому нічого не заплатять. Скільки днів з цих ЗО пропрацював робітник?
2. Із кошика взяли 3 яблука, потім третину остачі і ще 3 яблука. Після цього в кошику залишилась половина початкової кількості яблук. Скільки всього яблук було в кошику?
Урок № 34
Тема. ЗАДАЧІ НА РУХ
1. Пес погнався за лисицею. У той час, коли собака робить 2 стрибки, лисиця робить 3 стрибки, але стрибок лисиці дорівнює 1 м, а собаки — 2 м. Яку відстань пробіжить собака, щоб наздогнати лисицю, якщо початкова відстань між ними — 50 м.
2. Із міста А до міста В за течією річки корабель пливе 3 доби, а назад — 5 діб. Скільки діб пливе пліт від А до В?
3. Потяг проходить міст довжиною у 450 м за 45 секунд і 15 секунд йде повз телеграфний стовп. Підрахуйте довжину потяга і його швидкість.
4. Я їду в трамваї і помічаю, що паралельно трамвайні лінії у протилежному напрямку проходить мій приятель. Через хвилину я зійшов із вагона і, щоб наздогнати приятеля, пішов у два рази швидше за нього, але в 4 рази повільніше, ніж трамвай. Через скільки хвилин я наздожену приятеля?
Домашнє завдання
1. Пароплав плив із Києва до Запоріжжя 5 діб, а назад — 7 діб. Скільки часу пливуть плоти від Києва до Запоріжжя?
2. Потяг проходить міст довжиною 450 м за хвилину і півхвилини йде повз телеграфний стовп. Підрахуйте довжину потяга і його швидкість.
3. За течією пароплав пропливає певну відстань за 3 год, а назад — за 4,5 год. За скільки часу пропливає цю саму відстань порожня бочка, яку рухає тільки течія?


6 клас
77
Урок № 35
Тема. ЗАДАЧІ НА РУХ
1. Два потяги рухались назустріч один одному паралельним шляхом: один зі швидкістю 50 км/год, а інший — зі швидкістю 70 км/год. Пасажир другого потяга помітив, що перший потяг пройшов повз нього за 6 секунд. Яка довжина першого потяга?
2. Перший мандрівник був на 3 км попереду другого і йшов зі швидкістю 4 км/год, другий — зі швидкістю 5 км/год. Пес побіг зі швидкістю 15 км/год від першого до другого, потім повернувся... Так він бігав, доки вони не зустрілись. Скільки кілометрів пробіг пес?
3. Автомобіль від А до В їхав із середньою швидкістю 50 км/год, а назад повертався зі швидкістю ЗО км/год. Яка його середня швидкість?
4. Двоє мандрівників одночасно вийшли від пункту А до В. Один мандрівник першу половину шляху йшов зі швидкістю 5 км/год, а другу половину — зі швидкістю 4 км/год. А другий мандрівник половину часу, який він затратив на весь шлях, проходив по 5 км/год, а другу половину шляху — по 4 км/год. Хто з них раніше прийшов у пункт В?
5. Монах вийшов о 9 годині ранку і о 9 годині вечора забрався на гору. О 9 годині ранку наступного дня монах почав свій зворотний шлях (тією самою доріжкою). О 9 годині вечора повернувся додому. Доведіть, що знайдеться точка, де монах був обидва рази в один й той самий момент часу.
Домашнє завдання
1. Із міста А до В назустріч один одному виїхали два автомобілі зі швидкостями 50 км/год. Одночасно з А вилетіла невтомна бджілка зі швидкістю 120 км/год. Зустрівши автомобіль, який виїхав з А, вона знову полетіла назад. І так бджілка літала до тих пір, доки машини не зустрілись. Скільки кілометрів пролетіла бджілка, якщо між А і В 300 км?
2. Дві вантажівки одночасно вийшли з А до В. Першу половину часу, який затратила перша вантажівка на весь шлях, вона йшла зі швидкістю 50 км/год, а другу половину шляху — зі швидкістю 40 км/год. Друга вантажівка першу половину шляху йшла зі швидкістю 40 км/год, а другу — зі швидкістю 50 км/год. Яка з цих вантажівок раніше прибула до В?
3. Щоб потрапити додому, ідучи з Палацу спорту, я можу вийти на зупинці «Математична» або на наступній зупинці — «Фізична». Від зупинки «Математична» я йду додому втричі довше, ніж від «Фізичної», але доки тролейбус під’їжджає до станції «Фізична», я встигаю пройти третю


78
Математична логіка. 5-6 класи
половину шляху від зупинки «Математична» додому. На якій зупинці слід вийти, щоб швидше потрапити додому?
4. 	Велосипедист підіймається на гору зі швидкістю 12 км/год і з’їжджає з гори тією самою дорогою зі швидкістю 20 км/год. Різниця у часі між підйомом і спуском 116 хв. Яка довжина дороги, якою їхав велосипедист?
Задачі для усного розв’язування
1. Із тверджень «А:2», «А:4»; «А: 8»; «А: 16» три правильних, а одне неправильне. Яке?
2. Замість того щоб додати число 27, мій друг відняв його. Яка різниця між правильним результатом і результатом мого друга?
3. Половина — це третина деякого числа. Яке це число?
4. В одного царя народився син. На честь такої події він вирішив провести амністію: «Усі терміни ув’язнення зменшити на половину!» Але як же бути з ними, хто засуджений довічно? Невідомо, скільки вони проживуть. Але цар був категоричний: «Виконувати указ точно!». Думали, думали слуги й придумали. Що вони запропонували?
5. Перший множник збільшили на 50 %, а другий зменшили на 50 %. Як зміниться добуток?
6. Зараз Дмитру 11 років, а Вовці 1 рік. Скільки років буде Дмитру, коли він буде втричі старший за Вовку?
7. Чи є серед простих чисел парні? Скільки?
8. Чи можна вибирати 5 чисел з таблиці так, щоб їх сума дорівнювала 20?
1
1
1
3
3
3
7
7
7
9. 	Половина числа дорівнює 15. Чому дорівнює його третина?
10 Було 9 аркушів паперу. Деякі з них розрізали на 3 частини. Всього стало 15 аркушів. Скільки аркушів розрізали?
11. Скільки секунд містить чверть години?
12. Скільки буде півтори третини від ста?
13. У скільки разів збільшиться трицифрове число, якщо до нього дописати. поруч таке саме число?
14. Марко та Оля їдуть до Києва в одному й тому самому потязі. Оля сидить у 7 вагоні від початку, а Марко сидить ближче, ніж Оля до початку — у 6 вагоні з кінця. Між Олею і Марком знаходиться ще один вагон. Скільки вагонів було в цьому потязі?


6 клас
79
15. На скільки збільшиться величина дробу, якщо до її чисельника додати десяту частину знаменника?
16. Знайдіть два таких числа, добуток яких 24, а частка від ділення більшого числа на менше також 24.
Різні задачі
1. 	Якщо кожен хлопчик купує пиріжок, а кожна дівчинка — булку, то вони разом заплатять на 1 копійку менше від того, коли б кожен хлопчик купував булку, а кожна дівчинка пиріжок. Відомо, що хлопчиків більше, ніж дівчаток Наскільки?
2. 	Нам обом разом 63 роки. Зараз мені вдвічі більше років, ніж було вам тоді, коли мені було стільки років, скільки зараз вам. Скільки зараз років мені і скільки вам?
3. 	Сестрі втричі більше років, ніж було братові тоді, коли сестрі було стільки років, скільки зараз братові. Коли брату буде стільки років, скільки сестрі зараз, то їм обом разом буде 28 років. Скільки зараз років сестрі і скільки братові?
4. 	У двох цистернах знаходиться по 540 л води. З першої цистерни виливається по 25 л за хвилину, а з другої — по 15 л. Через який час у другій цистерні води залишиться в шість разів більше, ніж у першій?
5. 	Мишці до нірки 20 кроків. Кішці до мишки 5 стрибків. За один стрибок кішки мишка робить 3 кроки. Один стрибок кішки дорівнює 10 крокам мишки. Чи наздожене кішка мишку?
х З
6. 	Пройшовши - довжини моста, ослик Іа-Іа помітив автомобіль, що на- о
ближався зі швидкістю 60 км/год. Якщо ослик побіжить назад, то зустрінеться з автомобілем на початку моста; якщо вперед, то автомобіль нажене його наприкінці моста. З якою швидкістю бігає Іа-Іа?
7. Якось раз в одному басейні туди й сюди почали плавати два плавці Перший пропливав з одного кінця в другий за 11 хвилини, а другий — за півгодини. Почали вони з одного краю басейну Скінчили, коли знову опинилися одночасно з одного краю басейну. Скільки за цей час відбулося обгонів?
8. Один чоловік запитав* «Котра година?». Йому відповіли, що хвилинна
1 годинна стрілки співпали і знаходяться на одній лінії між 9 і 10 годинами. Котра була година?
9. На дошці записано 100 плюсів та 100 мінусів. Можна поміняти будь-які
2 мінуси на плюс, плюс і мінус на мінус, два плюси на мінус. Доведіть, що знак, який залишиться у кінці, не залежить від черги операцій


80
Математична логіка. 5-6 класи
10. У школі 370 учнів. Чи знайдуться в цій школі два учні, в яких день народження припадає на одну й ту саму дату календаря?
11. Скільки всього прабабусь та прадідусів було у ваших прабабусь та прадідусів?
12. Відомо, що число 52*2* ділиться на 36. Які цифри стоять замість зірочок?
13. У чотирьох ящиках лежить по одній кульці: білій, чорній, червоній та зеленій. На першому ящику написано: «Біла», на другому — «Зелена чи біла», на третьому «Червона чи зелена», на четвертому — «Червона чи зелена, чи червона». Але жодний напис не відповідає дійсності. Якого кольору лежить кулька в кожному ящику?
14. На столі стоять 7 перевернутих склянок (догори дном). Дозволяється одночасно перевертати будь-які дві склянки. Чи можна домогтися, щоб усі склянки стояли правильно?
15. Розмістити 10 точок на 5 прямих так, щоб на кожній було по 4 точки.
16. Доведіть, що значення виразу 116 +146 -ІЗ3 кратне 10.
17. Чи ділиться на 10 різниця 7573 -З575 ?
18. Дано декілька натуральних чисел. Кожне з них поділили на суму всіх даних чисел. Чому дорівнює сума всіх часток?
19. За добу черв’як може прогризти шар паперу товщиною 1 мм. На полиці поруч стоять два томи одного твору. Спільна товщина кожного тому 4 см, а кожного перепльоту — 2 мм. За який час черв’як добереться від першої сторінки першого тому до останньої сторінки другого тому?
20. Розв’яжіть анаграму і виключте зайве слово:
а) БРУЗ
б) ШДНР
в)ЛЮСП
СЛИЦИЯ
АЙНДУ
УИМСН
ПОРТО
ТРОК
ГРИТ
КВОВ
ДСНЕРТ
ТАЧСКА


ВІДПОВІДІ. 5 КЛАС
Урок № 1
Усні задачі-жарти
1. Один дідусь, бо інші йшли в протилежному напрямку. 2. 2 гривні.
3. 	6; 8; 8 кінців відповідно. 4. Одна, бо інші згоріли. 5. Ці фігурки утворені дзеркальним відображенням цифр 1, 2, 3, 4, 5, 6, 7.
Наступна фігура:
Після неї:
Задачі на кмітливість
1. Півгарбуза важать 2 кг, тоді цілий гарбуз важить 4 кг. Два таких гарбузи — 8 кг. 2. Груша коштує 10 к., яблуко — 7 к. 3. 16 грн. 4. 5 курок.
Домашнє завдання
1.10 кг. 2. Яблуко коштує 5 к., груша — 7 к. 3. 16 грн.
Урок № 2
1. 2 години. 2. 5 км. 3. 12 км. 4. 10 км. 5. Вони будуть на однаковій відстані. 6. 2 години. 7. 14 хвилини. 8. 4 хвилини. 9. 20 хвилин. 10. Ні, через 10 годин у цьому місті буде ніч. 11. 1 годину. 12. 1 год 10 хв = 70 хв. 13. Зіпсований. 14. Дідусь, батько, син. 15. їх було троє: дідусь, батько, син. 16. Якщо один з міліціонерів жінка, тобто мати. 17. Петро. 18. 10 к. 19. —3°. 20. 20. 21. 50 пальців. 22. З хлопчики. 23. Троє гусей. 24. 4 коти. 25. 6. 26. З морквини. 27. 9 овець. 28. 2 жінки. 29. Одній дівчині віддали кошик разом з яблуком. ЗО. В 2 раза. 31. У кожному. 32. Півень не може відкласти яйця. 33. 5 склянок. 34. Жодної, всі пташки розлетілись.
Домашнє завдання
1. Шестеро. 2. 120 десятків. 3. Жодної, бо свині не розмовляють
4. 	В електропотяга не буває диму. 5. Чоловік був лисий. 6. На другу половину. 7. 10 к. і 5 к. (це ж одна не п’ятак, а друга — п’ятак). 8. Жодної, бо на вербі груші не ростуть. 9. Сірник. 10. Три тварини: собака, кішка і папуга. 11.24 см.


82
Математична логіка. 5-6 класи
Урок № З
1. 	5701; 5811; 5921. 2. 3601; 3711; 3821; 3931; 6602; 6712; 6822; 6932; 9603; 9713; 9823; 9933. 3. 9876 - найбільше, 1023 - найменше. 4. 5210 - найбільше, 1025 — найменше. 5. Найбільше — 9910, найменше — 1009.
2178
6. 	а) 85217; б) 32117. 8.х 4
8712
Домашнє завдання
1.421, 842. 2. 88872 — найбільше, 22278 — найменше. 3. а) 52345; б) 11234. 13904
4. 	(12:3+4)5=40. 5.+139О4
27808
Урок № 4
1. а) Чисел виду аі буде 9, бо а може змінюватись від 1 до 9. Чисел виду 1а, де а змінюється від 2 до 9, буде 8. У числі 11 одиниця зустрічається двічі, але одну з них ми вже порахували. Також одиниця зустрінеться у числах 1, 10, 100. Тому 1 зустрінетьсяЗ+8+9+1 = 21раз.
б) Чисел виду а2 буде 9, а змінюється від 1 до 9. Чисел виду 2 а буде 9, а від 0 до 9, а *2. Двійка також зустрінеться в числі 2. А в числі 22 вона зустрінеться двічі, одну з цих двійок ми вже порахували. Тому двійок потрібно 9+9+1+1 = 20.
в) Аналогічно до пункту б) дев’яток потрібно 20.
г) Чисел виду а0 буде 9, нулі також будуть у числі 100. Тому потрібно 9+2 =11 нулів.
2. а) Одноцифрових номерів буде 9. Двоцифрових чисел (95-10+1) = 86, тому знаків потрібно 86 2 =172. Усього необхідно 172 +9 = 181 знаків.
б) На одноцифрові числа необхідно 9 знаків, на двоцифрові 2 (99-10+1) = = 90-2=180 знаків. На трицифрові числа 3(121-100+0 = 66. Усього буде: 180+66+9 = 180+75 = 255.
3. 625.
Домашнє завдання
1. «1» — 1 шт., 1а — 10 шт., аі — 9 шт. Отже, від 1 до 99 — 21 одиниця. Аналогічно одиниця на місці сотень серед чисел виду lab зустрічається 100 разів, на місці десятків (серед чисел виду Па) — 10 разів, і на місці одиниць (числа виду Іаі) — також 10 разів, отже усього від 100 до 200


Відповіді. 5 клас
83
зустрічається 100+10+10=120 одиниць. Тому від 1 до 200 усього 21+120 = 141 85679 одиниця. 2.321. 3.5(5-5)=0.4.а)111-11=100;6)55+55-5-5 = 100.5.+85679
171358
Урок № 6
2. а) Коза; б) кусок; в) море; г) жаба.
Домашнє завдання
2. а) Рука; б) вірус; в) лоза.
Урок № 7
І.г). 2.д). 3. б). 4. а).
Домашнє завдання
1. б). 2. д). 3. а). 4. д). 5. г). 6. в). 7. г). 8. д).
Урок № 8
2
3.


84
Математична логіка. 5-6 класи
Урок № 9
4. 	а) 5: V; 10: X; б) 4: IV; 6: VI; 9: IX; 11: XI; в) 8: VIII.
VI+IV-X
xv+vl-xxl
Домашнє завдання
Урок № 10
х+х=хх


Відповіді. 5 клас
85
Домашнє завдання
Урок № 15


86
Математична лопка. 5-6 класи
Урок № 16
1. Протягом 5 хв бабуся смажить 4 котлети з одного боку. У наступні 5 хв вона знімає дві котлети зі сковороди і кладе дві із залишених, дві інші, що підсмажились, перегортає на другий бік. Отже, за 10 хв підсмажились дві котлети повністю, а 4 котлети — з одного боку. За наступні 5 хв підсмажаться 4 котлети з другого боку.
2.
2. 	З розрізами.


Відповіді 5 клас
87
Усні вправи
1. 18. 2. Проміжків між стовпами буде 5, отже довжина паркану — 10 м.
Домашнє завдання
2.
Урок № 17
1. 	4 см2. 2. 36 см2. 3. З трьома — 8 кубиків, із двома — 24 кубики, з однією — 24 кубики, непофарбовані — 8 кубиків. 4. У 8 разів. 5. 48 г.
Домашнє завдання
1. 	400 см2. 2. 16 м2. 3. У 27 разів.
Урок № 18
1. Ділимо монети на 3 купки по 3 монети. Зважуємо дві купки. Якщо вони мають однакову вагу, то фальшива монета у третій купці. Якщо ні — ми залишаємо більш легку купку, бо в ній напевно є фальшива монета. Беремо дві з цих трьох монет і кладемо на терези. Якщо одна з монет легша — це фальшива, якщо вони мають однакову вагу, то залишена монета фальшива. Відповідь. 2 зважування. 2. Поділимо 27 монет натри купки по 9 монет. Далі як у задачі 1. Відповідь. З зважування. 3. 8 поділимо на 2, З, З монети. Далі як у задачі 1. 4. На одну шальку терезів покласти обидві гирі (800 г) і насипати на шальку крупи так, щоб терези були в рівновазі. Зрозуміло, що на шальці з гирями буде 3 кг 600 г групи. Розважимо цю крупу порівну, дістанемо 1 кг 800 г. 5. Потрібно з першої торбинки взяти 1 монету, з другої — 2 і так далі. Потім покласти ці монети на ваги. Якщо б усі монети були справжніми, їх вага становила
1+2+3+4+5+6+7+8+9+10 = 5 11 = 55 (г).
Різниця між 55 г і справжньою вагою покаже номер торбинки з фальшивими монетами.
Домашнє завдання
1. 1) 16:2 =8 (кг); 2) 8:2 =4 (кг); 3) 4:2 =2 (кг); 4) 8+4+2 =14 (кг). 2. 4 зважування. 3. Потрібно пронумерувати робітників. У кожного взяти стільки монет, який його номер. Різниця між вагою, яка повинна бути, якщо монети були б справжні, і дійсно вагою буде показувати номер робітника, який виготовляє фальшиві монети.


88
Математична логіка. 5-6 класи
Урок № 19
1. 	Наповнити 7-літрову банку і з неї відійти 3 л. Залишиться 4 л.
1) 7 л 6 л Зл
.6 4 0
І 3
2) 3 / 3|
І 2 I
3) 3 6
t 4 І
4) 7 2 1
I * f
5) 5 2 3
6) 5 5 0
3. 	Наповнити 8-літрову бочку і відлити з неї 5 л. Тоді у 8-літровій бочці залишиться 3 л, а у 12-літровій і 5-літровш разом буде 9 л.
Домашнє завдання
1. З 3-літрової банки двічі виливаємо молоко у 5-літрову банку; У 3-літровій банці залишився 1 л. З 5-літрової виливають у 10-літрову. Переливаємо у 5-літрову банку 1 л та ще 3 л. Одержимо 4 л. 2. Двічі наповнюємо 3-літрову банку і переливаємо в 5-літрову; 1 л, який залишиться, переливаємо у 8-літрову банку. Ще раз наповнюємо 3-літрову банку і виливаємо у 8-літрову.
Урок № 20
1. Через кількість днів, що ділиться націло на 7, буде знову неділя, оскільки 52 : 7 = 7 (3 — остача), то мати народилась через 3 дні після неділі, тобто в середу. Відповідь. У середу.
2. Оскільки січень має 31 день, то він містить 4 повних тижні, і тому в ньому є 4 неділі та 4 п’ятниці. Для того щоб він не містив ще однієї неділі чи п’ятниці, необхідно і достатньо, щоб 29 січня було в понеділок або вівторок. Тоді 1 січня повинно бути також понеділком або вівторком. Відповідь. Понеділок або вівторок.


Відповіді. 5 клас
89
3. 	Неділі в одному місяці, чергуючись, випадають на парні та непарні числа. Оскільки 3 з них випали на парні числа, то всього в цьому місяці було п’ять неділь, тому перша з них могла бути тільки другого числа, тому 20 число — четвер. Відповідь. Четвер.
4.365:7 = 52 (1 — остача). Якщо рік має 365 днів і розпочався у вівторок, то й закінчиться у вівторок. Якщо рік високосний, то закінчиться в середу.
Домашнє завдання
1. 	Ні, бо в ньому тоді повинно бути 367 днів. 2. 365. 3. Може, якщо лютий у високосному році починається з понеділка.
Урок №21
1. 	Може, якщо місяць має 31 день і починається з неділі. 2. Оскільки в місяці може бути 31 день, а понеділків було 5, то понеділок міг бути 10-м числом цього місяця, 2-м чи 3-м. У всіх цих випадках п’ятниць було б чотири. 3. Понеділок.
Домашнє завдання
1. 31 грудня. 2. Обов’язково буде 31 день, це буде вівторок. 3. 29 лютого.
Урок № 22
1. У найгіршому випадку ми будемо витягувати кульки тільки одного кольору. Наприклад, ми витягли 10 кульок, і вони всі червоні, тому ще три кульки обов’язково повинні бути синіми. Відповідь. 13 кульок.
2. а) У найгіршому випадку ми будемо витягувати кульки білого і рожевого кольорів. їх КІЛЬКІСТЬ 5+10 = 15 штук. Тому ще 3 кульки обов’язково будуть чорного кольору. Тобто потрібно витяги 15+3 = 18 кульок. Відповідь. 18 кульок; б) 19 кульок; в) Усі кульки.
3. Необхідно вважати, що рукавички на ліву та праву руку відрізняються одна від одної. Тобто в ящику знаходиться. 5 білих правих, 5 білих лівих, 5 чорних правих, 5 чорних лівих рукавичок. У найгіршому випадку ми візьмемо по 5 рукавичок різного кольору, наприклад, 5 білих правих і 5 чорних правих. Тому ще одна рукавичка утворить пару, бо вона буде або чорна ліва, або біла ліва. Відповідь. 11 рукавичок.
4. а) 22 кульки; б) 28 кульок; в) 21 кульку.
Домашнє завдання
1. 7 кульок. 2. а) 17 кульок; б) 18 кульок: в) 21 кульку. 3. 21 рукавичку.
Урок № 23
1. 1 і 4 чи 2 і 3. 2. 1+5 = 2+4 = 3+3 = 6. Трьома способами. 3. 1+2+2;
1 + 1 + 1 + 1 + 1; 1 + 1 + 1 + 2; 5. 4. 1, 2, 5, 10 копійок. 5. 1, 2, 3, 4 морквини.


90
Математична логіка. 5-6 класи
6. Пронумеруємо фарби: 1, 2, 3. Тоді можливі варіанти: 1, 2; 1, 3; 2, 3.
7. 4 варіанти. 8. 4 способами. 9. 2 партії.
Домашнє завдання
1.1+1+1+1+1+1; 1+1+1+1+2; 1+1+2+2; 2+2+2; 1+5. 2. З партії. 3. 4 хлопці зробили 6 рукостискань, а 6 хлопців — 15 рукостискань. 4.1+2+3+4+5 = 15 (цукерок)
Урок № 24
1. Для розв’язання задачі складемо таблицю:
Віра
Ніна
Оля
Люба
1
синя
біла
2
синя
червона
3
синя
блакитна
Нехай у 1-й відповіді правильне висловлення «Оля — у синій», тоді:
Віра
Ніна
Оля
Люба
1
синя
бита
2
синя
червона
3
синя
блакитна
Така ситуація неможлива, бо Оля і Ніна не можуть бути обидві в синіх сукнях. Тож у 1-й відповіді висловлення «Оля — в синій» правильним бути не може, отже, у 1-й відповіді правильне висловлення <Люба — у білій». Тоді маємо:
Віра
Ніна
Оля
Люба
1
синя
біла
2
синя
червона
3
синя
блакитна
З цієї таблиці видно, що Віра була в синій, Оля — у червоній, а Люба — у білій сукнях. Тому Ніна була в блакитній сукні.
2. 	Згідно з умовою, заповнимо таблицю:
Піаніно
Віолончель
Гітара
Скрипка
Англ.
Франц
Нім
Ісп.
Жанна
—
+
—
—
—
+
—
—
Катерина
—
—
—
+
+
—
—
—
Марина
—
—
+
—
—
—
—
+
Лариса
+
—
—
—
—
—
+
—


Відповіді. 5 клас
91
До таблиці не внесено 1) і 4) умови. Починаємо аналізувати таблицю і заповнювати порожні клітинки. Катя повинна грати на скрипці, бо всі інші не вміють, тому вона не грає на гітарі, а тому не знає іспанської (з першої умови), а також не грає на віолончелі і не вивчає німецької (з четвертої умови). Також вона не грає на піаніно, бо кожна дівчина грає тільки на одному інструменті. Аналогічними міркуваннями доходимо, що Жанна повинна грати на віолончелі. Лариса вивчає німецьку, Катерина — англійську, а Марина — іспанську. З цього одержимо, що Марина грає на гітарі, а Лариса — на піаніно.
Відповідь, Жанна грає на віолончелі і вивчає французьку мову.
Катерина грає на скрипці і вивчає англійську мову.
Марина грає на гітарі і вивчає іспанську мову.
Лариса грає на піаніно і вивчає німецьку мову.
Домашнє завдання
1. А — чесна папуга, В — брехун, С — хитрун. 2. Сергій — І, Надія — II, Коля - III, Ваня - IV, Толя - V.
Урок № 25
1. Солов’я-Розбійника впіймав Добриня Микитич. Він і Альоша Попович збрехали першого разу, а Ілля Муромець — останнього.
2. Відповідь. Галя — у зеленій,
Надія — у рожевій, Галя
Ганя — у білій, ./^зелена^Х.
Валя — у блакитній. / \
і Валя Надія \
і блакитна рожева І
Ганя
3. Білов не чорнявий, тому він рудий. Чернов — білий, Білов — чорний.
4. Якби Сеня був чесним гномом, то Беня, Веня і Євген були б брехунами і не могли сказати один одному: «Ти — брехун». Тому Сеня — брехун. Це означає, що Беня і Веня не обидва брехуни, а може, обидва чесні, або лише один з них брехун. Євген повинен бути чесним. Тому Беня — брехун, Веня — чесний, Сеня — брехун. Відповідь. Євген і Веня — чесні гноми.
Домашнє завдання
1. Добриня Микитич. 2. Колетта Пон, Анетта Дюбуа, Жаклін Пейзан, Жанна Фонтен.


92
Математична логіка. 5-6 класи
Урок № 26
коза господар
вовк капуста
2) вовк
господар
капуста господар
коза господар
вовк господар
господар
капуста
коза господар
вовк
капуста
2. 	Спочатку перший зліва пароплав заходить у затоку, а всі інші пароплави заходять ліворуч за затоку. Потім перший пароплав виходить із затоки і пливе туди, куди йому треба. Потім другий зліва пароплав робить те ж саме, що й перший. Потім третій робить те ж саме.
3. 	Так, це могло статися, наприклад, якщо вони підійшли до річки з різних боків.


Відповіді. 5 клас
93
Урок № 27
1. 	17, 21, ... (Це арифметична прогресія, кожний наступний член на 4 більший за попередній). 2. 112, 224,... (Це геометрична прогресія, кожний наступний член здобувається за допомогою подвоєння попереднього).
3. 	19, 27, ... (Різниця між сусідніми членами утворює арифметичну прогресію: 1, 3, 5, 7, 9, ...) 4. 24, 14, 48, 18, ... (На непарних місцях стоять члени геометричної прогресії, а на парних — арифметичної).
Урок № 28
2. 3.
10
2
9
6
7
8
5
12
4
4
7
7
9
6
3
5
5
8
Домашнє завдання
1.
7
6
2
0
5
10
8
4
3
2. 	На кінцях діаметра цифри: 1 та 6; 2 та 5; 3 та 4.
Урок № 29
1. 2.
6
6
3
2
5
8
7
4
4
4
3
5
5
4
3
3
5
4
Домашнє завдання 1.
2. Див. № 1.
8
1
6
3
5
7
4
9
2


94
Математична логіка. 5-6 класи
Урок № ЗО
1.2376 горщечків. 2.22 яблука. 3.72 роки.
Домашнє завдання
1. 	14 яєць було в торговця. Перша жінка взяла 8 яєць, друга — 4, третя — 2.2.66 років.
Урок № 31
1. 	31. 2. ЗО слив.
Домашнє завдання
1. 	127 груш.
Урок №32
1.600 м2. 2. 81 км2. 3. Швидше на велосипеді. 4. 80 км. 5.6 м/с.
Домашнє завдання
1.200 км. 2. Швидкість: 24 км/год; шлях: 96 км. 3. Через 10 год.
Урок № 33
1. 	200 м. 2. Швидкість потяга 27 км/год; довжина 250 м. 4. Уявимо, що було 2 монахи, які одночасно вийшли з монастиря і до монастиря відповідно. Оскільки вони б зустрілися в деякій точці, то ця точка й буде шуканою, бо вони там опинилися одночасно.
Домашнє завдання
1.900 км. 2. 8 км. 3. За 36 с.


ВІДПОВІДІ. 6 КЛАС
Урок №1
1. 	Це донька, мати та бабуся. 2. 4 особи — це донька, мати, її сестра та бабуся. 3.72 роки
Усні задачі
1. 	Це я. 2. Юрко. 3. Це їхня донька.
Домашнє завдання
1. 66 років. 2.4. 3. 6 дітей.
Урок № 2


96
Математична логіка. 5-6 класи
Урок № 3
1917
3
1278
2
1945 5
639
3
639
3
1. а) 389 389
б) 213
3
або 213
3
1 1
71
71
71
71
1
1
1
1
2. Сумарний шлях повинен ділитись на 330 і 75 і бути найменшим, отже, довжина шляху і НСК(330,75) = 1650 (км). Тому кількість етапів 1650 : 75 = 22 Відповідь. 22 етапи.
3. Якщо відняти від шуканого числа 1, то здобута різниця має ділитися на 2, 3, 4, 5, 6, тобто НСК(2,3,4,5,6) = 60. Звідси, шукане число дорівнює одному з чисел 61, 121, 181, 241, ЗОЇ,... З цих чисел найменшим числом, що ділиться на 7, є число ЗОЇ. Відповідь. 301.
4. Якщо відкласти 8 огірків, то кількість решти можна розділити як на 10, так і на 12, тобто на НСК(10,12) = 60. Серед чисел, більших від 300 і менших за 400, лише 360 ділиться на 60, тому огірків було 368. Відповідь. 368.
Домашнє завдання
1. 	211 яблук. 2. Потрібно розкласти на множники НСК і НСД, і з цих множників утворити відповідні пари натуральних чисел. Тобто: (336; 12), (48; 84).
Урок № 4
1. 1-3 5-7-...-99=...5. Добуток закінчується п’ятіркою, бо це число ділиться на 5 і є непарним. 2. а =2; b =4 або а =6 = 6; б) а =Ь = 6. 3. Так, бо сума цифр цього числа 1+0+...+0+8 = 9:9. 4. За ознакою подільності на 6, остання цифра числа повинна бути парною і сума цифр числа повинна ділитись на 3. Замість «*» можна взяти 6 або 0. Відповідь. 6 або 0.
Домашнє завдання
1. Щоб число ділилось на 72, воно повинно ділитись на 8 і на 9. Це буде 4104. 2. 8280. 3. 9135 або 5130. 4. Коли богатир відрубає голови, то в будь-якому випадку різниця між відрубаними та головами, які виросли кратна 3. Але 1000 на 3 не ділиться націло. Тому подолати Змія неможливо.
Урок № 5
Усні вправи
1. Парним числом. 2. Непарним числом. 3. Парним числом. 4. Непарним число; парним числом.
1. ааа = 100-а+10-я+я = 111-я. Оскільки 111 = 37-3, то ааа =37-3-а:3.


Відповіді. 6 клас
97
2. aZ>+Z>a = 10a+6+10Z»+a = lla+ll-6=ll(6+a): 11 за теоремою про подільність добутку.
3. abc=100a+10b+c=99a+a+9b+b+c=99a+9b+(a+b+c) =
=9(ll a+b)+(.a+b+c). Перший доданок ділиться на 3 за теоремою про подільність добутку, другий — за умовою задачі. Сума ділиться на 3 за теоремою про подільність суми.
Домашнє завдання
1. aaaaaa = lllllla=3-71113-37a.
2. ada6a5=1010a+101£=101(10a+Z») = 713(10a+6):7.
3. aZ6=100 a+10 £=10 (a l0+Z>):10.
Урок № 6
1. 	Оскільки кількість літрів олії, яку привезли у 10-літрових бідонах, закінчується на 0, то кількість олії, що привезли у 17-літрових бідонах, закінчується на 3 (223 — ...0 = ...3). Тому кількість 17-літрових може бути лише 9. Тож кількість 10-літрових бідонів (223-17-9):10 = 7. Відповідь. Сім десятилітрових і дев’ять сімнадцятилітрових бідонів. 2. Сумарна вартість покупок ділиться на 3, а бармен назвав суму, яка не ділиться на 3. 3. Підрахуємо кількість чисел, які діляться на 2, на 3, а також на 2 і на 3 одночасно. 1000: 2 = 500 чисел діляться на 2.1000: 3 = 333 (1 — ост.), тому 333 числа діляться на 3. 1000 : 6 = 166 (4 — ост.), тому 166 чисел діляться і на 2, і на 3. Тому серед 1000 перших натуральних чисел на 2, на 3 діляться 500+333-166=667 чисел, а не діляться на 2, на 3 1000 — 667 = 333 числа. Відповідь. 333.
Домашнє завдання
1. Нова сума від попередньої відрізняється на 9 перших доданків, тобто (6641 — 2411): 9 = 470 — перший доданок. 2411 — 470 = 1941 — другий доданок. Відповідь. 470 і 1941.
2. abab =1000a +100й+10а +6 = 1010a+1012»=10 KlOa +2»).
3. a2>c+dca+cad=llla+lll-2»+lllc=lll(a+d+c):llL
Урок № 7
2. 	36 розкладається на 3 множники так: 1, 2, 18; 1, 3, 12; 1, 4, 9; 1, 6, 6; 2, 3,6; 2,2,9; З, 3,4. При цьому суми множників відповідно 21,16,14, 13,11, 13 і 10. Оскільки гість не розв’язав задачу відразу, вікон в оселі було 13. З’ясування питання дало можливість точно відповісти: 2, 2, 9. Відповідь. 2, 2, 9 років.


98
Математична логіка. 5-6 класи
Домашнє завдання
1. Можливі варіанти розкладання на множники:
Бородаєв: 5 25; Володій: 5-30 = 6-25 = 10-15.
Гармаш: 5-42 =6 35 = 7 30 = 10 21. Зимов: 5 40 = 8-25 = 10-20.
Канський:5 36 = 6-30 = 90 2=10 18. Ратюк:5-78 = 6-25 = 10-39.
Тилов:6 44 = 8-33 = 11 24.
Відразу можна побачити, що Бородаєв у 5 класі, у 7 класі — Гармаш, у 9 класі може бути лише Канський, в 11 класі — Зимов. У 6 класі можуть бути Володій чи Ратюк, але тоді за віком Ратюк старший, а Володій не вчився б у 10 класі вечірньої школи. Тому в 6 класі Володій, а в 10 — Ратюк.
2. ЗО або 90.3. 25.
Урок № 8
1. а) б2001 = ...6, бо 6 у будь-якому степені закінчується цифрою 6;
б) 92001 = ...9, бо 9 у непарному степені закінчується цифрою 9;
в) З2001 = ...3, бо 2001: 4 = 50 (ост. 1); г) 22001 = ...2, бо 2001: 4 = 50 (ост. 1).
2.999"’ — непарне число як степінь непарного числа. Тому 99999"” = ...9.
3. 26-27 28 29=...4; 51-52-53-54=...4. Тому шукана остання цифра є 8. Відповідь. 8.
Домашнє завдання
1. 9. 2. 110+101+...+999 = 100+(101+999)+(102+998)+...+(549+551)+550. Сума чисел у кожній з дужок дорівнює 1100. Тому остання цифра суми дорівнює 0. 3. а) 7; б) 9; в) 6; г) 4; д) 7.
Урок № 9
1. Не може, тому що число ділиться на 5, але не ділиться на 25.
2. Сума цифр цього числа дорівнює: 100-0+100 1+100-2=300:3, але не ділиться на 9. Дане число ділиться на 3, але не ділиться на 9 за ознаками подільності. Якщо число було квадратом і ділилося б на 3, то воно повинно було б ділитись і на 9, тобто дане число не може бути квадратом.
3. Оскільки це число закінчується парною цифрою, то воно ділиться на 2. Якщо воно було б повним квадратом, то ділилося б і на 4, але останні дві цифри створюють число 66 І 4, тому дане число не ділиться на 4 за ознакою подільності на 4. Тобто це число не може бути повним квадратом.
4. а) І2 =1; 22 =4; З2 =9; 42 =16; 52 =25; б2 =36; 72 =49; 82 =64; 92 =81; 102 =100. Тобто квадрати натуральних чисел можуть закінчуватись тільки на цифри: 1, 4, 5, 6, 9, 0. б) Куби натуральних чисел можуть закінчуватись на 1, 8, 7, 4, 5, 6, 3, 2, 9, 0, тобто на будь-яку цифру, в) Четвертий степінь натурального числа може закінчуватись лише на 1, 5, 6.


Відповіді. 6 клас
99
Домашнє завдання
2. 	468 не може бути квадратом, бо закінчується цифрою 8, а квадрат числа не може закінчуватись цифрою 8. Аналогічно 533 і 672 не можуть бути квадратами натуральних чисел.
Урок №10
1. Число присутніх у 6 разів більше від числа відсутніх, тому відсутні
1 . гг -
складають — частину всіх учнів. Після того як один учень вийшов, відсутні
1 	. Л 111
складають - від загальної кількості учнів. Тому 1 учень — це -- — час¬
тина класу. Тобто в класі 42 учні.
1 	1 1
2. Іван вніс - частину від усього, Петро — ~, а Андрій — - Разом вони
1 1 1 47 47 13
внесли 7+7+7 ~ 77 вартості човна. Роман вніс І-77 = 77, або 130 грн. Тому З 4 5 60 60 60
13 1
човен коштує 130:—= 600 (грн). Іван вніс: 600 т=200 (грн); Петро:
60 З
600-^ = 150 (грн); Андрій: 600-^ = 120 (грн). Відповідь. 600 грн; 200 грн; 150 грн; 120 грн.
3. Кожного разу колгоспниця продавала половину яблук і ще пів’яблука, тобто залишалось на 1 яблуко менше, ніж вона продавала. Шостий покупець купив 1 яблуко, п’ятий — 2, четвертий — 4, третій — 8, другий — 16, і перший — 32. Усього було 63 яблука. Відповідь. 63 яблука.
Домашнє завдання
1. 27 слив. 2. 36 яблук.
Урок № 11
1. 	1) 1—7 = 7 (частин усього пирога) — перша остача;
6 6
2) 7 • 7 = 7 (частин усього пирога) — з’їв другий друг;
5 6 6
5 1 4
3) --- = 7 (частин усього пирога) — друга остача;
6 6 6
4 1 1
4) 7 • 7 = 7 (частин усього пирога) — з’їв третій друг;
6 4 6
4 1 З
5) 7~7 = 7 (частин усього пирога) — 3 остача;
6 6 6


100
Математична логіка. 5-6 класи
х 3 1 1
6) - ~ = 7 (частин усього пирога) — з’їв четвертий друг;
6 3 6
З 1 2
7) --- = — (частин усього пирога) — четверта остача;
6 6 6
2 1
8) 7:2 =7 (частин усього пирога) — з’їли Віктор і п’ятий друг.
6 6
1
Відповідь. Кожен з’їв - частину пирога.
6
1 1 1
2. 7+7+7 = 1 (частину чашки) — випив молока. Кави випив теж повну
6 3 2
чашку, тобто кави і молока випив порівну.
2 1
3. 1) — '.'І =- (м) — скласти відріз навпіл (не розрізаючи);
2) 7:2 = 7 (м) — знову скласти навпіл відріз;
3 6
2 13 1 1
3) 7-7 = 7 = 7 (м) — залишиться, якщо відрізати - частину.
3 6 6 2 6
Тож спочатку потрібно поділити відріз навпіл, потім половину ще
1
навпіл і відрізати цей шматочок, залишиться - м.
Усні задачі
1. 	90 грн. 2. 120. 3. 16 гривень ((25-1):3 = 8 — половина моїх грошей, 8 2=16).
1.
Домашнє завдання 11В 25 З
2+4 + 7 =1-28=28 (частин)
складають три жінки.
З
З=28 (осіб) — усього в школі. Відповідь. 28 осіб. 28
9 10
2.99:—=99 •—= 110(кг) — було змелено.
3. 	Якщо з’їсти половину від остачі — це буде - частина від цього, тому
1 1
рівень компоту знизиться на - :2 = - частину.
Урок № 12
1. 	1) 100-25 = 75 (м) — 13 метрів від 3-ї остачі;
13 4 52
2) 	13'0,75=—^— = — (м) — 3-тя остача;


Відповіді. 6 клас
101
52 82
3) —+10 = — (м) — 2-га остача + 10 м, тобто 80 % від 1-ї остачі;
А 82 5 205
4) — - - = -г- (м) — 1 -ша остача;
3 	4 6
205 235 5
5) -т—+5 = -7- (м) — це 1-ша остача + 5 м, тобто - від всього;
0 0 о
235 6
6) -7- 7=47 (м) — усього. Відповідь. 47 м.
о 5
1 1 З
2. 1)1+1+—+-=2-(частини) — це 100 гусей без 1;
З
2) 	99:2 -=36 (гусей) — у зграї. Відповідь. 36 гусей. 1 1
3. — бочки вип’ють чоловік з дружиною за 1 день. 77 бочки вип’є сам
10 14
1 1 1
чоловік за 1 день. —- — = — бочки випила б сама дружина за 1 день. Отже, дружина випила б самостійно бочки пива за 35 днів. Відповідь. 35 днів.
Домашнє завдання
1 1 11
1. 	Віл, кінь і коза разом з’їли б за 1 годину 1+—+т = — (пласта). Отже, 2 3 6
11 6 6
1:—= —. Відповідь. За —години.
6 11 11
2. 	Добу поділено на 9 частин. Наразі 24:9-5 = 13(год) або 13 год 20 хв.
Відповідь. 13 год 20 хв.
_ 115
3. 	Оскільки в кожному місті у купця відбирали —+- = 7 майна, то
2 3 6
в нього завжди залишалось 7 від попередньої кількості майна. Якщо ку- 6
пець, вийшовши з третього міста, мав при собі 11 грошей, то, входячи в це місто, він мав 11-6=66 (грошей). Заходячи до другого міста, він мав 66-6 = 396 (грошей). А входячи в перше місто, він мав396 6 = 2376 (грошей) Відповідь. 2376 грошей.
Урок № 12
112 14 1 5 17 18 1111111
1’1~2-2’1-3-3’1-5 5' 1-6 “б’ 1-8 - 8’ 1-9 “9 2>6’ 3>8’ 5>9’
1 2 4 5 7 8 Отже, перша сума менша, ніж друга. -+7+7 <7+7+7.
2 3 5 6 8 9


102
Математична логіка. 5-6 класи
1000001 1 100001 1 1 1
2‘1-1000002 " 1000002’1-100002 "100002’1000002 <100002’ 1000001 100001
Тому 1000002 > 100002'
12 12
1Т?І0 1 22Ї72Ї 2 2 1
3' 1- 11...1 "11.„Г 1-22...23 22...23 <22...2 11...1’
13 13 12 12 13 13
12 12
22^21 1ЇЛ0
ТОМУ 22...23> 11...Г
Урок № 14
1. Нехай товар коштував х грн. Після підвищення на 100 % він став коштувати 2х грн. Потім ціну знизили на 50 %, тобто вона становить 50 % від попередньої: 0,5 2х = х (грн). Відповідь. Ціна не змінилась.
2. 15,5% від 49=49-0,155=49 155-0,001. 49 % від 15,5=0,49-15,5 = =49 155-0,001. Не проводячи підрахунків, можна сказати, що результати будуть рівні.
3. Нехай ціна картоплі була а грн. Оскільки вона підвищилась на 20 %, то її тепер її ціна становить 100+20 = 120 (%) від попередньої, тобто 1,2 • а грн.
Після зниження на 20 % ціна становить 80 % від попередньої, тобто 0,8 1,2а = 0,96а. Оскільки 0,96 <1, то ціна після зниження нижча від ціни до підвищення. Відповідь. Картопля коштувала дорожче до підвищення.
4. Нехай підручник коштував х грн, тоді після підвищення на 25 % ціна буде складати 125 % від попередньої, тобто 1,25х Після зниження на 20 % ціна буде становити 100-20 = 80 (%) від попередньої: 0,8-1,25-х = х (грн) Тобто ціна не зміниться. Відповідь. Однаково.
Домашнє завдання
1. Ціна не змінилась. 2.200 -0,8 1,2 =0,96 -200 = 192 (грн) — нова заробітна платня. 3. Обломов збавив вагу на 2,8%.
Урок № 15
Усні задачі
1. 0. 2. Не зміниться. 3. 10 % від 12 дорівнює 12 % від 10, бо 0,1-12 = = 0,12-10 = 1,2.
Письмові задачі
1. З’ясуємо, скільки відсотків продукції підприємство буде випускати через два роки: 100-51=49 (%). Тобто якщо підприємство випускало х оди¬


Відповіді. 6 клас
103
ниць продукції, то через два роки воно повинно випускати 49 % вщ х, тобто 0,49 х = 0,7 0,7 х. Тобто кожен рік випускали 70 % продукції, а тому знижували об’єм на ЗО %. Відповідь. На ЗО %.
2. Нехай фабрика випускала х товарів, через два роки вона стала випускати 100+21=121 (%), тобто 1,21 хтоварів. 1,21 х = 1,1-1,1 х. Тому кожного року фабрика випускала 110%, тобто об’єм щорічно збільшувався на 10 % Відповідь. На 10 %.
3. 1) 2:100 10 = 0,2 (кг) — води в розсолі після випарювання;
2) 2 -0,2 =1,8 (кг) — чиста сіль;
3) 8-1,8 = 6,2 (кг) — вага води;
4) 6,2:8 100 = 77,5 (%) — відсоток води в розсолі. Відповідь. 77,5 %.
4. Нехай це число х, тоді 40 % від 40 % від х — це 0,4 0,4 х. За умовою це 32. Складемо рівняння: 0,16 х = 32.
Відповідь. 200.
5. 1) 100-60 =40 (%) — не знають російської;
2) 100-85 = 15 (%) — не знають англійської;
3) 100-70 = 30 (%) — не знають французької;
4) 40+15+30 = 85 (%) — не знають всіх трьох мов;
5) 100-85 = 15 (%) — знають усі три мови. Відповідь. 15 %.
Домашнє завдання
1. 	На 20%. 2. 320. 3.56 %.
Урок № 16
1. У 40 кг води з океану склад солі: 0,35 40 = 14 (кг). Оскільки ми додаємо прісну воду, то солі буде в суміші теж 14 кг, і це буде складати 5 %. Тому маса суміші 14:0,05 = 14000:5 = 280 (кг). Тобто води потрібно додати 280-40 = 240 (кг). Відповідь. 240 кг.
2. З’ясуємо масу м’якоті гриба. Вона складає 100-12 =88 (%) від маси сушеного гриба. Тобто 0,88 2,5 = 2,2 (кг) — маса м’якоті. Тому маса води у свіжому грибі 22-2,2=19,8 (кг). Вона складає 19,8:22 100 = 90 (%). Відповідь. 90 %.
3. В 1 тонні свіжоскошеної трави 60 % вологи, тобто 600 кг, тому сухої маси 1000 - 600 = 400 кг. Ця маса в сіні становить 85 %, тому вага сіна
10 10
400 : 0,85 =470 — (кг). Відповідь. 470 —кг.
4. Нехай ціна товару була х грн, після першої зміни товар став коштувати 0,8 • х грн, а після другої 0,45 0,8 • х = 0,36 • х грн. Тобто ціна товару зменшилась на х-0,36х = 0,64 х грн, або на 64 %. Відповідь. На 64 %.


104
Математична логіка. 5-6 класи
Домашнє завдання
1.60 кг. 2.77,5%. 3. На 72%.
Урок № 17
1. Якщо прийняти крок високого за 1 частину, то крок низького буде
4
складати 80 %, або - частини. На кожні 100 кроків високого припадає
120 кроків низького, тому за той самий час, коли високий пройде шлях 4
у 100 1 = 100 частин, низький пройде 120 -= 96 частин, тобто саме високий прийде до школи раніше. Відповідь. Високий прийде раніше.
2. Якщо прийняти початкову виручку за 1 частину, тоді виручка буде
9
складати 112,5 %, тобто - частини, і дістанемо її від кількості глядачів, яка о
складає 125 %, тобто від попередньої кількості. Якщо б квитки продавали
5 9 9
за новою ціною, то виручили б -:- = — частин, тобто виручка склала б — 8 4 10 10
9
від початкової, тому нова вартість квитка 20 — = 18 грн. Відповідь. 18 грн.
3. Нехай більше число х, тоді менше 0,8 х. Згідно з умовою задачі, їх сума 54. Складемо рівняння: х+0,8 х = 54; 1,8 х = 54; х = 30. Відповідь. ЗО.
Домашнє завдання
1. 100 грн. 2. ЗО.
Урок № 18
1. Переможець програв партію В, тому переможець не В. Не були переможцями також А, Г, Б, і Д. Таким чином, переміг Е. Він програв В, зіграв унічию з А і В, виграв у Г і Д. Оскільки Б не програв жодної партії і не одержав першого місця, то він набрав не більше 2,5 очок. Інший варіант: Б всі партії зіграв унічию, В програв Г (інакше він набрав би очок стільки ж, скільки Е), Г і Д зіграли внічию. Якщо б Г переміг, він набрав би 3 очки (як Е), якщо програв, то відстав би від Д. Таким чином, Е — З очки, А, Б, В, Г, — по 2,5 очка, Д — 2 очки.
2. Ті, хто посіли три місця, що залишилися, зіграли між собою 3 партії, тобто набрали всього не менше ніж три очки. Переможець у 6 партіях набрав не більше ніж 6 очок. Він виграв 6 партій, і ті, хто посіли 5—7 місця, програли всі партії тим, хто посів 1—4 місця. Той, хто посів 4 місце, набрав 50 % можливих очок, тобто 3 очки. їх він одержав у партіях проти тих, то посів 5—7 місця; першим трьом переможцям він програв. Таким чином, за


Відповіді. 6 клас
105
винятком партій між собою, ті, хто посіли 2—3 місця, набрали по 4 очки. Поділ цих місць вирішила партія між ними. Її виграв той, хто посів 2 місце.
3. 	Оскільки у волейболі немає нічиїх, то кожна гра для команди закінчується або виграшем, або поразкою. Розглянемо дві команди, які мають рівну кількість перемог. Позначимо через А ту з них, яка виграла у другої (з двох команд, які ми розглядаємо), а другу команду назвемо В. Оскільки В має стільки ж перемог, скільки А, а команді А вона програла, то знайдеться команда С, у якої команда В виграла, але якій команда А програла (інакше у В було б менше виграшів, ніж у А). Тож шукані команди знайдено.
Домашнє завдання
1. 	Три учасники посіли перші місця, тому набрали 42 очки. Тому два інші учасники набрали 27 балів, тобто один з них набрав 14, а інший 13 балів і, таким чином, посіли 2 і 3 місця. 2. Кожна команда зіграє з рештою команд (16 команд по 2 матчі). Таким чином, шукана кількість буде 17-32, але при цьому кожен матч порахували двічі. Тобто загальна кількість матчів 272.
Урок № 19
1. 	Першим «ходом» А П. відрубує 1 голову. Якщо Д. М. відрубує 1 голову, А. П. відрубує 3 голови. Д. М. 2 голови, А. П. — 2 голови. Д. М. — З голови, А. П. - 1 голову. У будь-якому випадку у Змія залишається 4 голови. Далі скільки голів не відрубав Д. М., А. П. відрубує решту голів одним ударом. 2. Як почати гру, не має значення. Другий гравець виграє, називаючи числа, які діляться на 10.
Домашнє завдання
1. Як би вони не грали, на дошці залишиться 8 офіцерів. Виграє другий.
2. Наприкінці гри, коли не можна зробити хід, маємо 45 куп по одному камінцю. За будь-який хід кількість куп збільшується на 1, тому вся гра має тривати точно 45-3=42 ходи. Отже, другий гравець завжди виграє.
3. Виграє другий. Незалежно від послідовності ходів, на дошці будуть виписані всі числа від 1 до 36. Це буде так, бо НСД(25,36)=1.
Урок № 20
1. Для того щоб перший кіт з’їв більше сосисок, він повинен зробити наступне: перекусити навпіл низку з 6 сосисок. Другий кіт відкусить від будь-якої перемички і з’їсть 1 сосиску, а перший, перкусюючи перемичку з 2 сосисками, що залишилися, з’їдає обидві. Так само з 3 сосисками, які залишилися. Отже, перший кіт з’їсть 4 сосиски, а другий кіт — 2.
2. Так, Ганя завжди зможе це зробити, бо якою б не була сума цифр 7-значного числа, останню цифру якого записала Тетяна, Ганя завжди


106
Математична логіка 5-6 класи
зможе додати число від 0 до 9, яке в сумі з попередньою сумою цифр буде давати число, що ділиться на 9.
3. 	Очевидно, що 1, 2 або 4 камінці — це виграшна позиція для того, хто буде робити хід. З камінці — це програшна позиція: можна взяти 1 або 2 камінці, і позиція стає виграшною (для іншого гравця). Далі, аналогічно розмірковуючи, помічаємо, що 5 камінців — знову виграшна позиція (можна її звести до 3), 6 — програшна. Закономірність — програшні позиції — це коли кількість камінців ділиться на 3. Очевидно, що якщо початкова кількість камінців не ділиться на 3, то перший гравець завжди зможе виграти, забираючи таку кількість камінців, яка залишилась від загальної кількості при діленні на 3 (тобто 1 або 2 камінці).
Домашнє завдання
1. 2 купки по 1 цукерці в кожній — це остаточна програшна позиція. До неї може призвести попередня ситуація — коли в одній з купок 2 цукерки, а у другий — довільна кількість (це виграшна позиція). Примусити іншого гравця залишити в одній з купок 2 цукерки можна, якщо залишити йому 2 купки 3+3 або 1+3 (це — також програшні позиції). Сформулюємо закономірність, яку можна помітити. В остаточній позиції, як і у двох наведених, загальна кількість цукерок у двох купках парна і подається як сума двох непарних чисел. Перший гравець може завжди залишати парну загальну кількість цукерок, якщо з’їсть 23 штуки. Також він може в одній з купок залишати завжди одну цукерку. Другий гравець буде змушений з’їдати купку з однієї цукерки, а всі інші (непарне число) подавати як суму двох натуральних чисел. Завжди в одній із купок нараховується парна кількість, яку перший гравець знову залишить і розіб’є на дві з непарною кількістю, і т. д. Попередження. Не намагайтеся повторити умови задачі вдома: регулярне споживання великої кількості солодощів може призвести до цукрового діабету або до збільшення ваги! Експериментуйте краще із сірниками!
Урок № 21
1. Другий може розбити ромашку на дві однакові частини і підтримувати такий стан. 2. Виграє другий гравець за допомогою симетричної стратегії (копіювати ходи суперника на іншій купці камінців). 4. Перший гравець. Перший хід — провести хорду, по обидві боки від якої розміїцено по 9 точок, виграшна стратегія — симетричні ходи.
Домашнє завдання
1. Перший гравець може звести гру до вже розглянутої, якщо він забере повністю всі камінці з однієї з купки, а потім буде копіювати ходи суперника. 3. Аналогічно задачі № 2 з уроку № 20.


Відповіді. 6 клас
107
Урок № 22
2. 	Аналогічно задачі 1. 3. Так, бо 25:3 = 8 (ост.1) . Згідно з принципом Діріхле, майже за рівного розподілу буде по 8 ящиків кожного сорту, тобто 24 ящики, а 25-й ящик утворює з одним із сортів 9 шуканий ящик. 4. Так, бо якщо згідно з принципом Діріхле k учнів «розкласти» по п «ящиках», де л=40, А: = 12 (кількість місяців у році), то принаймні в одному «ящику» буде не менше ніж 4 учні. 5. Якщо на одній поличці стоїть 3 книжки, то якщо ми 161 книжку розставимо на 4 полички, то на кожній з них одержимо 161:4 = 40 (ост. 1). Тобто знайдеться поличка, на якій не менше ніж 40 книжок.
Домашнє завдання
1. Нехай л = 8000000, Лг = 200000. 8000000:200000=40 (ост. 1). Отже, зпдно з принципом Діріхле принаймні у 41 жителя міста однакова кількість волосин на голові. 2. Розіб’ємо квадрат на 25 квадратів зі стороною 20 см; за принципом Діріхле в якийсь з них попаде принаймні 3 точки з 51, що кинули.
Урок № 23
1. 100:15=6( ост. 10). Отже, за принципом Діріхле принаймні 5 хлопців зібрали однакову кількість грибів. 2. Серед 5 чисел за наслідком з принципу Діріхле знайдеться два, остача від ділення яких на 4 однакова. 3. Згідно з наслідком з принципу Діріхле, при діленні 6 чисел на 5, знайдуться хоча б два числа, які мають однакові остачі. їх різниця ділиться на 5. 4. Нехай
— дані числа- Розглянемо суми 5^^; 52=Xj+x2; ..., 5100 =%, +х2 +...+х100. Якщо хоча б одна з цих сум ділиться на 100, задачу7 розв’язано. Якщо ні, то ці 100 сум при діленні на 100 можуть давати остачі від 1 до 99. За принципом Діріхле якісь дві суми будуть давати однакові остачі. Тоді їхня різниця ділиться на 100. Ця різниця і буде шуканою.
Домашнє завдання
1. Аналогічно задачі 2 (урок № 23). 2. Аналогічно задачі 3 (урок № 23).
3. 	Аналогічно задачі 4 (урок № 23). 4. Аналогічно задачі 1 (урок № 23).
Урок № 25
І Xі Ч z z І
2. Ні, не можна. Будемо вважати плюса- >> z
ми числа 1, а мінусами числа —1. За наших v
операцій не змінюється добуток чисел у клі- 77“ -—т —
тинках, які заштриховані на рисунку.
У початковій таблиці цей добуток дорів- v 4
нює —1, у таблиці без мінусів 1.
3. Оскільки після кожної дії бешкетника Васі кількість частин газети збільшувалася на 3, а загальна кількість аркушів завжди залишається


108
Математична логіка. 5-6 класи
таким числом, яке при діленні на 3 дає остачу 1, а число 1989 ділиться націло на 3, то такого не могло статися.
Домашнє завдання
1. Ні не можна, якщо замінити плюси на 1, а мінуси на —1, то інваріантом буде добуток чисел у чотирьох кутових клітинках. 2. Ні, не зможе. Кожного разу кількість голів змія збільшується на число, кратне трьом. 3. Кількість шматків стінної газети буде збільшуватися на 3 чи 9 і давати при діленні на 3 завжди остачу 1, а 1989 ділиться націло на 3.
Урок № 26
1. 40 %. 2. 40 осіб. 3. 6 осіб. 5. Так. Нехай х — число блакитнооких блондинів серед N людей, у — кількість блондинів серед N людей, z — X Z
кількість блакитнооких серед N людей. Тоді за умовою — >—. Помножимо
х z
цю нерівність на z і поділимо на у: — > —, тобто блакитнооких серед блондинів більше, ніж серед усього населення.
Домашнє завдання
1. Філософів більше. 2. Троє людей. 3. 25 %.
Урок № 27
1. Сірих мишок у Тома не може бути більше ніж 3. Якщо б їх було хоча б 4, то, обравши ще трьох довільних мишок, ми б дістали набір з 7 мишок, у якому білих не більше 3, що суперечить умові. Тож відповідь: 3 сірих мишки — це максимум. 2. Хлопців не більше ніж 10, дівчат не більше ніж 17.
Найбільша кількість — 27 дітей. 4. Позначимо х — кількість хлопчиків, д — кількість дівчат. З останньої умови маємо нерівність 31<х+д<38. Підрахуємо кількість різних дружніх стосунків між хлопчиками та дівчатами.
З одного боку, це Зх, а з другого, це 2д. Тож маємо: Зх = 2д, звідки х ділить- 2д
ся на 2, д ділиться на 3. Підставивши х = — до нерівності, дістаємо, що
5д
31 < — <38,18,6 <д <22,8. Єдине число, що кратне 3 з цього проміжку, — це 21 У класі 14 хлопців та 21 дівчина.
Домашнє завдання
1. Хлопців може бути не більше ніж 7, дівчат — не більше ніж 14. Найбільша кількість 21 учень. 2. З карамельки. Якщо більше, з ними можна було б утворити набір із 9 цукерок, в якому не було б 6 шоколадних.


Відповіді. 6 клас
109
Урок № 28
1.2-2 2 =8 способів.
2. 	а) 5 3 = 15 наборів; 6) 5 3-4=60 наборів; в) 1) 4-2 -3 = 24 наборів; 2) із золотою чашкою: 2 3=6 наборів; із золотим блюдцем: 4-3 = 12 наборів; із золотою ложкою: 4 2= 8 наборів — усього 6+12+8 = 26 наборів; 3) з однією не золотою чашкою: 4 набори; з одним не золотим блюдцем: 3; з однієї не золотою ложкою: 3 набори всього 4+3+3 = 10; 4) 1 набір.
Домашнє завдання
5 4 7 6 10-7
1. а) 5 -7 = 35 відрізків; б)-^-+-^- = 31 відрізок. 2. —= 35 діагоналей.
Урок № 29
1. 6 годин. 2. Друга (початок на 11-ту), третя (початок на 4-ту) — усьо- 7 9 20 20
го дві. 3. У 12 разів. 4. 160° =360° —+ хП~77
\12 12 OU OU
5. а) 22 рази (1 раз за
кожну годину — окрім з 12 по 1); б) 24 рази; в) 48 разів.
Домашнє завдання 1. 70° =360°
6 20 20Л
12 +12-60~60j ’
2. Перший бій курантів був рівно о 5-й го¬
дині; оскільки загальна кількість ударів більша за 6, Буратіно просидів довше, ніж 5:30. Отож, якщо б Буратіно дослухав до кінця наступний бій курантів, було б 5+1+6 = 12. 11 ударів він міг почути за умови, що не дочекався останнього удару до 6 години. Тож час був 5:59 — після цього Буратіно просто перестав рахувати!
Урок № ЗО
1. Очевидно, це може статися лише у проміжок від 1 до 2 години. Нехай це станеться о 1 годині х хвилин. Тоді складемо рівняння:
( 1 х 60 х 5 5
360 —+ =— , звідки х = 5+—. Відповідь. Через 1 годину та 5+— хвилин.
112 12 60 / 11 11
2. Для цього Вінні Пух обчислив, скільки часу триває подорож від його будинку до будинку Кролика. Це можна зробити, поділивши навпіл час, який відміряв домашній годинник Вінні за його відсутності (якщо ведмідь одразу повернувся додому, не гайнуючи часу на ласощі). Потім цей час на дорогу треба додати до часу, який показував годинник Кролика.
3. Якщо вимірювати час від півночі у хвилинах (х) і вважати, що від початку сутінок пройшло не більше 12 годин, то можна скласти рівняння: х 31
у = -(12 60-х). Маємо 432 хвилини, або 7 годин 12 хвилин. Якщо ж годин


110
Математична логіка. 5-6 класи
х З більше ніж 12, маємо інше рівняння: у = -(36-60-х), тоді час буде 21 годи-
на 36 хвилин.
Домашнє завдання
. 12
1. 81 = 1+2+3+...+12 =(12+1) —. 2. Можна обчислити кутову швидкість
360
обох стрілок: швидка має швидкість -у-= 30 градусів/год, а повільна проходить 22,5 градусів/год. Якщо зафіксувати повільну стрілку, то швидка буде рухатись відносно неї зі швидкістю 7,5 градусів/год. Тому вони
360 ,о
зустрінуться через уу=48 годин.
Урок № 31
1. Нехай голова риби важить х кг. Тоді тулуб важить (х+1) кг. За умовою х+1
х = 1+—, х = 3. Отже, риба важить 3+4+1 = 8 (кг). 2. Нехай жупан коштує
. х+12 х+5 w
х грн. Тоді щомісячна плата складає =——. Жупан коштує 2 грн 80 к.
3. 	Нехай човен коштує х грн. Якщо перший вніс половину від суми інших,
то його вклад — це третина загальної суми, — грн. Другий вніс — грн, х ххх 60-20-15-12
третій — — грн. На четвертого залишається х-—-—-—= — х =
5 345 60
13 130 х х
= 7Хх- Звідси х = —-• 60=600 (грн). 4. 76 років. 60 13
Домашнє завдання 1.37. 2.210. 3.40 років.
Урок № 32
1.12.2. Зірвали 15 та 5 тюльпанів, залишилось ЗО квітів. 3.18 років. 4. Устиг.
Домашнє завдання
1. 19 років. 2. 10. 3. Нехай Наталя важить (67-х) кг, Оксана (59-х) кг. Разом: 126-2х = 131-х. Похибка х=-5. Наталя важить 72 кг.
Урок № 33
1. Братові зараз 18, а сестрі 10 років. 2.28 задач. 3.72 книжки. 4.100 яблук.
Домашнє завдання
1.10 днів. 2. ЗО яблук.


Відповіді. 6 клас
111
Урок № 34
1. За 2 собачі стрибки відстань зменшується на 1 м (2 2-3 1 = 1). Пес подолає 50 м до лисиці за 50 пар стрибків, тобто пробіжить 100 м. 2. 15 діб.
3. 	Довжина 225 м, швидкість 15 м/с. 4. Нехай v м/хв — швидкість приятеля. За 1 хвилину він встиг пройти v метрів. Швидкість трамвая 8v м/хв, тож відстань між мною і приятелем була 9v м. Різниця в наших швидкостях v=2v-v м/хв. Відстань між нами 9v м я подолав за 9 хв. Отже, за цей час він устиг сісти в трамвай.
Домашнє завдання
1. 35 діб. 2. 450 м; 15 м/с. 3. 18 годин.
Урок № 35
1. 200 м. 2. Другий наздоганяв першого 3 години. Пес пробіг за 2s цей час 45 км. 3. = 37,5 км/год. Таке значення називають середнім
50 + 30
s/2 s/2 9 /2 G
гармонічним чисел ЗО та 50. 4. /, =—-—+—-— = ~s. д=5—+4 —
1 5 4 40 2 2
5 2
~5/2+4/2 ~9S t' >Іг’
G
другий прийде раніше в пункт В, ніж перший.
5. 	Можна уявити, що назустріч монаху вийшов його панібрат-монах. Вони обов’язково зустрінуться в якийсь момент часу. Цей момент і місце зустрічі — шукані.
Домашнє завдання
1. За 3 години, що автомобілі їхали назустріч один одному, бджілка встигла налітати 360 км. Погодьтесь, бджілку не так шкода, як пса з аналогічної задачі! 2. Перша — раніше. 3. Дім знаходиться від «Математичної» З
на - загальної відстані між зупинками. Третина відстані від зупинки «Ма-
1
тематична» додому — це - загальної відстані між зупинками. Якщо б мій
двійник вийшов на зупинці «Фізичній», а я — на «Математичній», ми б од-
1
ночасно проходили частину шляху між зупинками: я — - всієї відстані,
а він — усього Висновок: швидше буде, якщо я вийду на зупинці «Фізичній». 4. 8 км.


ЛІТЕРАТУРА
1. Задачи для внеклассной работы по математике в 5—6 классах / Сост. В. К.Сафонова.- М.: МИРОС, 1993.
2. Русанов В. М. Математические олимпиады для младших школьников.— М.: Просвещение, 1990.
3. Спивак А. В. Математический праздник. 4.П.— М.: Бюро Квантум, 2000.
4. Шарыгин И. Ф., ШевкинА. В. Математика: Задачи на смекалку.— М.: Просвещение, 1996.
5. Ященко И. В. Приглашение на математический праздник.— М.: МУНМО, ИЕРО, 1998.
6. Бабинская И. Л. Задачи математических олимпиад.— М.: Наука, 1975.
7. Математика — 5. Учебник для 5 класса/Под ред. Дорофеева Г. В., Шарыги- на И. Ф.— М.: Просвещение, 1997—1999.
8. Нагибин Ф. Ф. Математическая шкатулка.— К.: Рад. школа, 1961.
9. Кухар В. М., Барничка Ю. Ю. Цікава математика у 4 і 5 класах.— К.: Рад. школа, 1975.
10. НагибинФ. Ф., Канин Е. С. Математическая шкатулка.— М.: Просвещение, 1998.
11. Айзенк Г. Ю, Проверьте свои способности.— М., 1996.
12. Барташников О., Барташникова І. Інтелектуальна ііротека.— Львів, 1996.
13. Бизам Д., ГерцегЯ. Многоцветная логика.— М., 1978.
14. Богданович М. Математичні джерельця.—К., 1988.
15. Гарднер М. Математические головоломки и развлечения.— М., 1971.
16. Друзь Б. Математична мозаїка.— К., 1991.
17. Игнатьев Е. И В царстве смекалки.— М., 1979.
18. Кордемский Б. А. Математическая смекалка.— М., 1963.
19. Маланюк М. Л., Лукавецький В. І. Олімпіади юних математиків.— М., 1977.
20. 600задач на сообразительность. Энциклопедия.— М., 1997.
21. Журнал «Квант» 1970—2004 рр.
22. Журнал «Клас» 1998—2000 рр.
23. Матеріали міжнародного математичного конкурсу «Кенгуру».


Математика. 5—6 класи
Код: ПМ9, 144 с.
Алгебра. 7-8 класи
Код. ПАНО, 144 с.
Алгебра. 9 клас
Код: ПАИ 1, 128 с.
Завдання для усної роботи та математичні диктанти.
Геометрія. 7 клас
Код:А1К116, 112 с.
Геометрія. 8-9 класи
Код: ПАИ З, 144 с.
Наведений матеріал можна ефективно використовувати під час фронтального опитування, систематичного повторення та узагальнення вивченою.
Посібники стануть незамінними помічниками в щоденній практиці вчителя, дозволять швидко перевірити рівень засвоєння учнями навчального матеріалу, організувати опитування або самостійну роботу*, не витрачаючи часу на відшукування і добір завдань з різних джерел.
Надішліть копію передплатної квитанції
та отримайте Знижку 10 %
Замовити кишу Ви можете: за тел/ 8 (057) 731-96-33, за адресою 61001, м. Харків, вул Плеханівська, 66, ВГ «Основа», з позначкою «Книга — поштою АІК» або на сайті \v\v\vosnova coni.ua
Мінімальне замовлення — дві будь-які книги. Вартість поштової доставки — 3,95 грн.


ЙТЕ ЗАВЧАСНО!
Бібліотека журналу «МАТЕМАТИКА В ШКОЛАХ УКРАЇНИ»
950333
789664
Оформити передплату на журнал «Математика в школах України» з книжковим додатком можна з кожнЬго наступного місяця у будь-якому • відділенні зв'язку України.
•*
передплатний індекс:
01651
Кути у стереометрії
Книжкові додатки не є дайджестом статей. Актуальна тематика, інноваційні методики, високий індекс практичності. Сучасні книги для вчителя від найбільшого виробника методичної літератури в Україні.
У вартість передплати на місяць входить: З випуски журналу + книжковий додаток!
Кути у стереометрії
ISBN 978-966-495-033-3
9