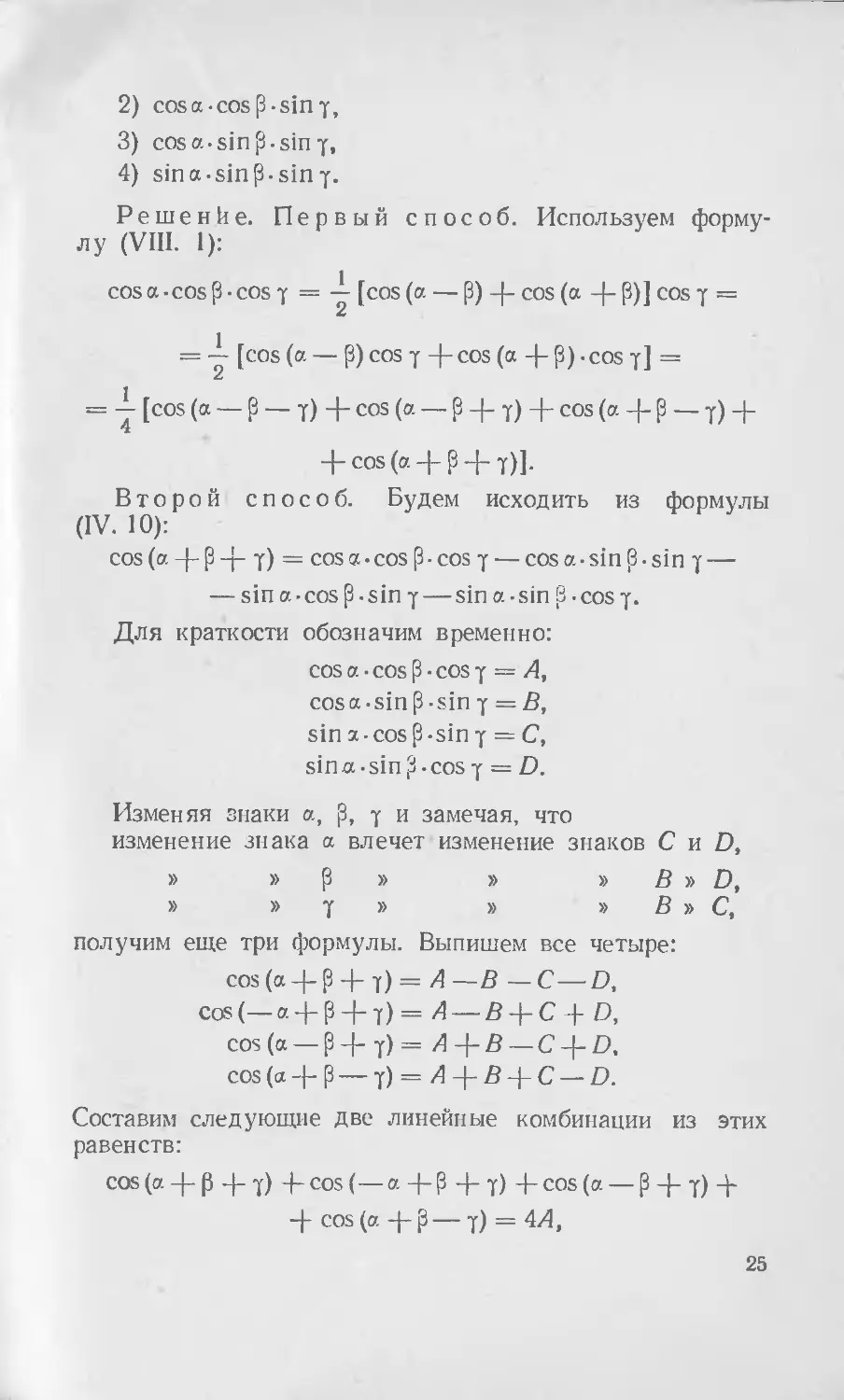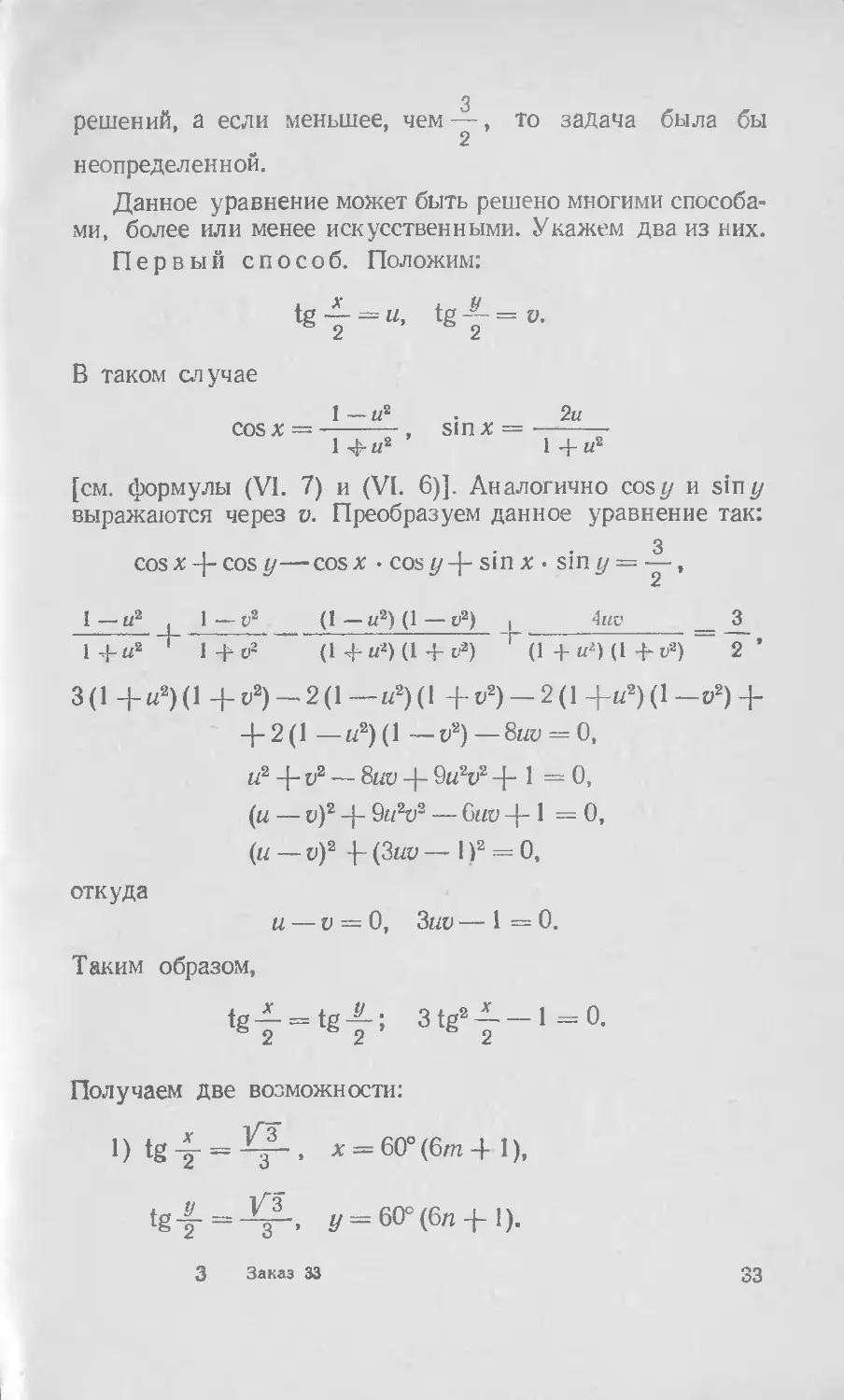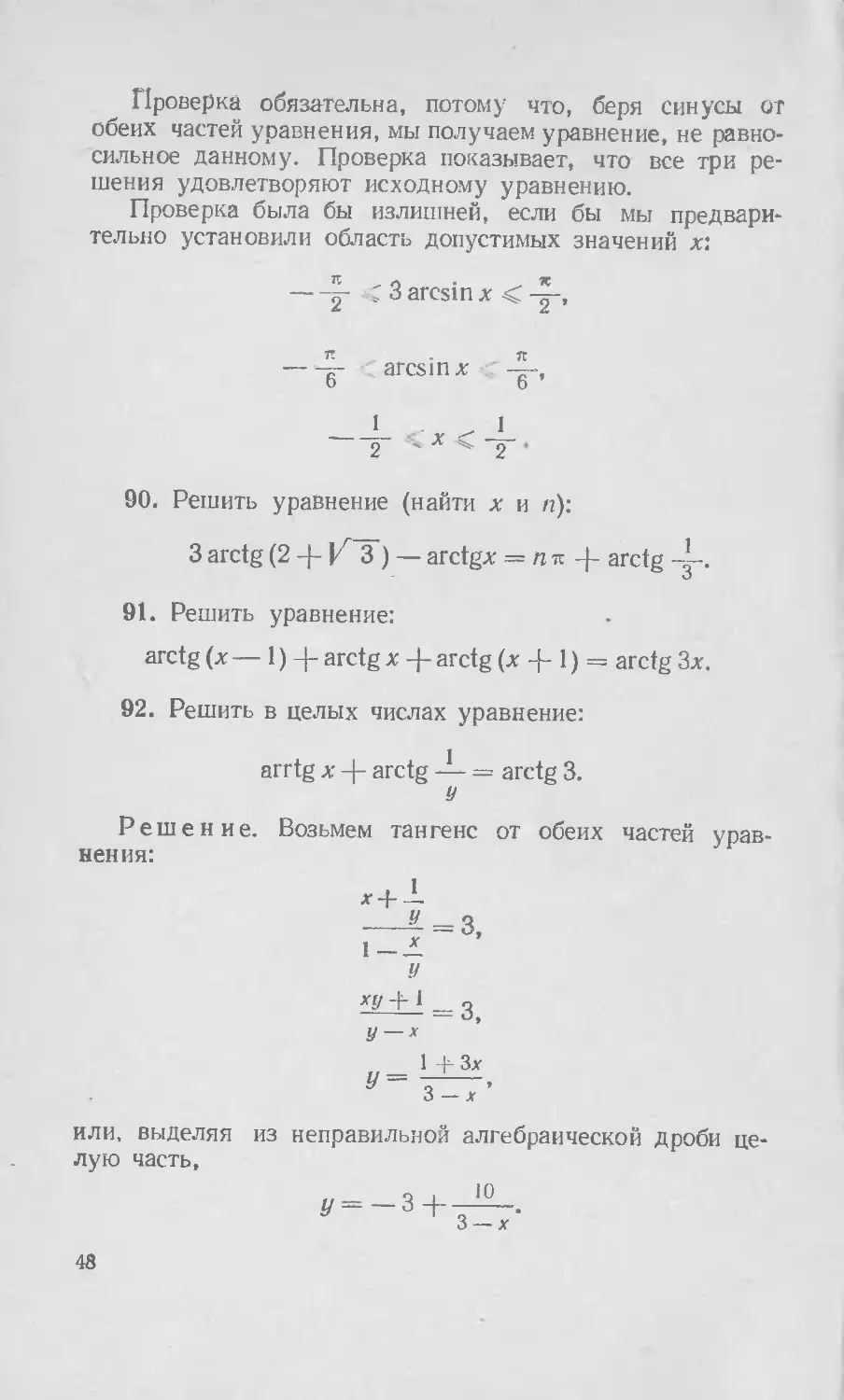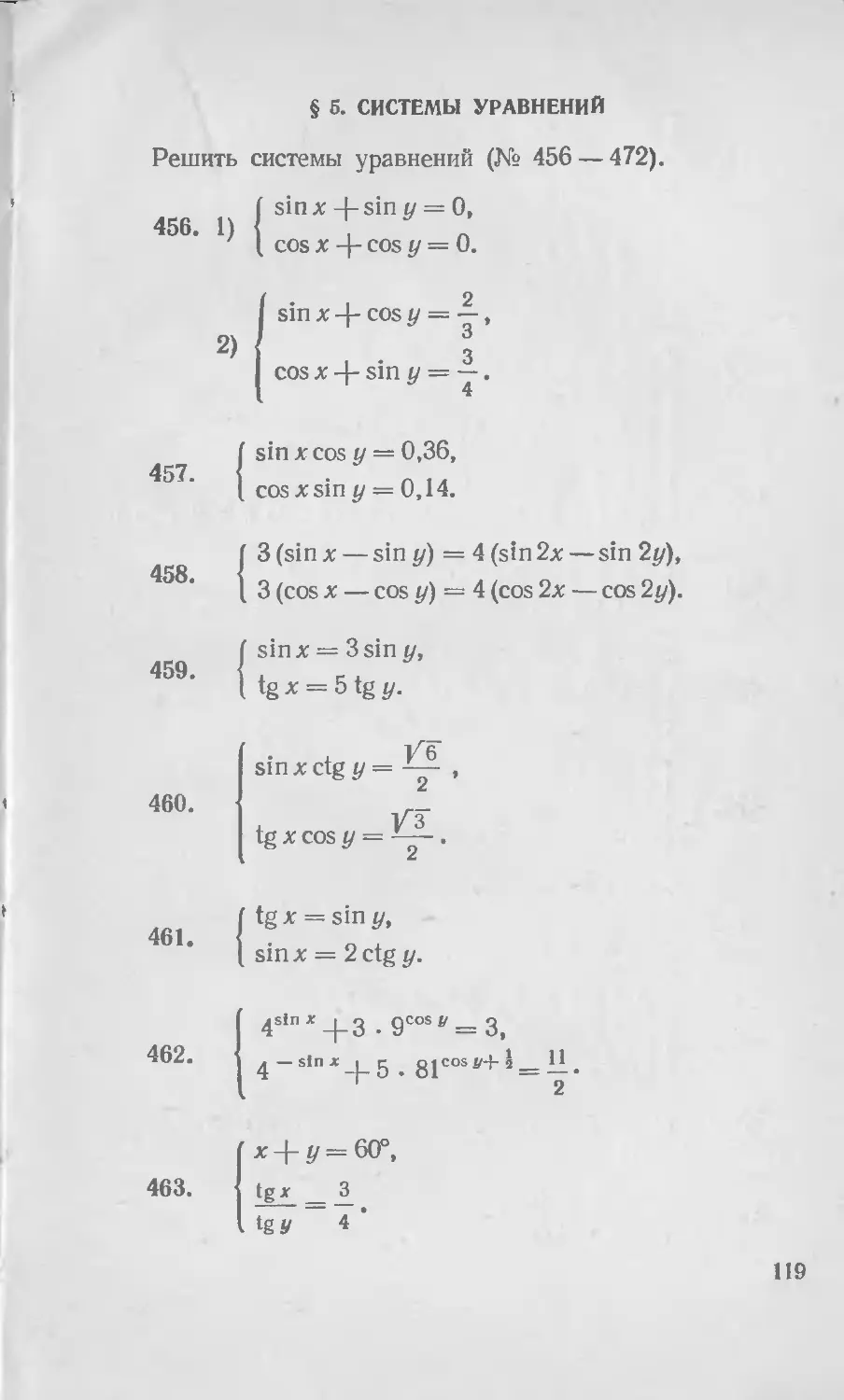ГЛАВНОЕ УПРАВЛЕНИЕ ВЫСШИХ И СРЕДНИХ ПЕДАГОГИЧЕСКИХ УЧЕБНЫХ ЗАВЕДЕНИЙ МИНИСТЕРСТВА ПРОСВЕЩЕНИЯ РСФСР МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ЗАОЧНЫЙ ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ
Н. М. БЕСКИН
ЗАДАЧНИК — ПРАКТИКУМ ПО ТРИГОНОМЕТРИИ
УЧПЕДГИЗ • 1962
ГЛАВНОЕ УПРАВЛЕНИЕ ВЫСШИХ И СРЕДНИХ ПЕДАГОГИЧЕСКИХ УЧЕБНЫХ ЗАВЕДЕНИЙ МИНИСТЕРСТВА ПРОСВЕЩЕНИЯ РСФСР
Московский государственный заочный педагогический институт
Н. М. БЕСКИН
ЗАДАЧНИК-ПРАКТИКУМ ПО ТРИГОНОМЕТРИИ
ПОСОБИЕ ДЛЯ ЗАОЧНЫХ ОТДЕЛЕНИЙ ФИЗИКО-МАТЕМАТИЧЕСКИХ ФАКУЛЬТЕТОВ ПЕДИНСТИТУТОВ
Издание второе, переработанное
4
Из книг*
Ник Брскинэ
ГОСУДАРСТВЕННОЕ
УЧЕБНО-ПЕДАГОГИЧЕСКОЕ ИЗДАТЕЛЬСТВО МИНИСТЕРСТВА ПРОСВЕЩЕНИЯ РСФСР Москва 1962
СОДЕРЖАНИЕ
Основной Дополни-раздел тельный раздел
Предисловие................................... 3
§ 1.	Тождественные преобразования . •	.	6	98
§ 2.	Условные тождества.............. 17	105
§ 3.	Преобразование сумм в произведения
и произведений в суммы.......... 22	112
§ 4.	Уравнения....................... 27	114
§ 5.	Системы уравнений............... 53	119
§ 6.	Суммирование рядов и свертывание	.
произведений................... 57	122
§ 7.	Графики......................... 67	126
§ 8	Неравенства..................... 70	127
§ 9.	Поведение тригонометрических функций .......................................... 73	128
§ 10.	Раскрытие неопределенностей ....	80	129
§ 11.	Применение таблиц............... 81	131
§ 12.	Тригонометрические функции комплексного аргумента........................ 86	132
§ 13.	Геометрические задачи .................. 87	—
§ 14.	Сферическая тригонометрия....... 93	137
Ответы......................... 139
Приложение..................... 166
Николай Михайлович Бескин
ЗАДАЧНИК-ПРАКТИКУМ ПО ТРИГОНОМЕТРИИ
Редактор В. Г. Долгополов
Художественный редактор А. В. Максаев Технический редактор Н. Ф. Макарова Корректор Т. Н. Смирнова
Сдано в набор 10/11 1962 г. Подписано к печати 24/VII 1962 г. 84x1 Ов^зг Печ. л. 11,5 (9,43). Уч.-изд. л 8,85
Тираж 30 тыс. экз. А05200
Учпедгиз. Москва, 3-й проезд Марьиной рощи, 41. Полиграфкомбинат. Саратовского совнархоза, г. Саратов, ул. Чернышевского, 59.
Заказ № 33.
Цена 27 коп.
ПРЕДИСЛОВИЕ
Задачник-практикум — это книга, которая учит читателя решать задачи, показывая, как они решаются.
Этот задачник-практикум предназначен для студентов-заочников физико-математических факультетов педагогических институтов. Он отличается от школьных задачников и по содержанию и по расположению материала.
Отличие по содержанию заключается, во-первых, в том, что здесь главное внимание уделено аналитической стороне тригонометрии (тригонометрические функции числового, в частности комплексного, аргумента, нахождение пределов, экстремумы, суммирование рядов, приближенные методы решения уравнений). Во-вторых, удалены наиболее простые и традиционные задачи, рассматриваемые в школьном курсе. Количество задач на решение треугольников (на плоскости) сведено к минимуму. Однако это не значит, что задачник комплектовался из трудных и искусственных задач. Это — задачник повышенной тематики, а не повышенной трудности.
Включен параграф, посвященный решению сферических треугольников.
Отличие по расположению материала заключается в том, что задачи не расположены по разделам школьного курса тригонометрии. В школьных задачниках, например, сначала идут тождества и уравнения, основанные на формулах сложения, а уже затем — на формулах двойного и половинного аргумента. Здесь же сначала идут все тождества, а затем—все уравнения. Предполагается, что, приступая к решению задачи № 1, учащийся уже владеет в полном объеме школьным курсом тригонометрии.
Автор не имел в виду дублировать задачник по анализу. Задачи на раскрытие неопределенностей должны решаться без использования правила Л’Опиталя, а задачи на экстремумы — без дифференцирования. В предла
3
гаемой книге эти задачи приводятся, чтобы показать возможные применения тригонометрических преобразований.
Задачи, основанные на формулах Моавра и Эйлера, иногда параллельно решаются (более сложно) элементарными методами. Это создает возможность использования таких задач в школе и поэтому представляет интерес для будущего учителя
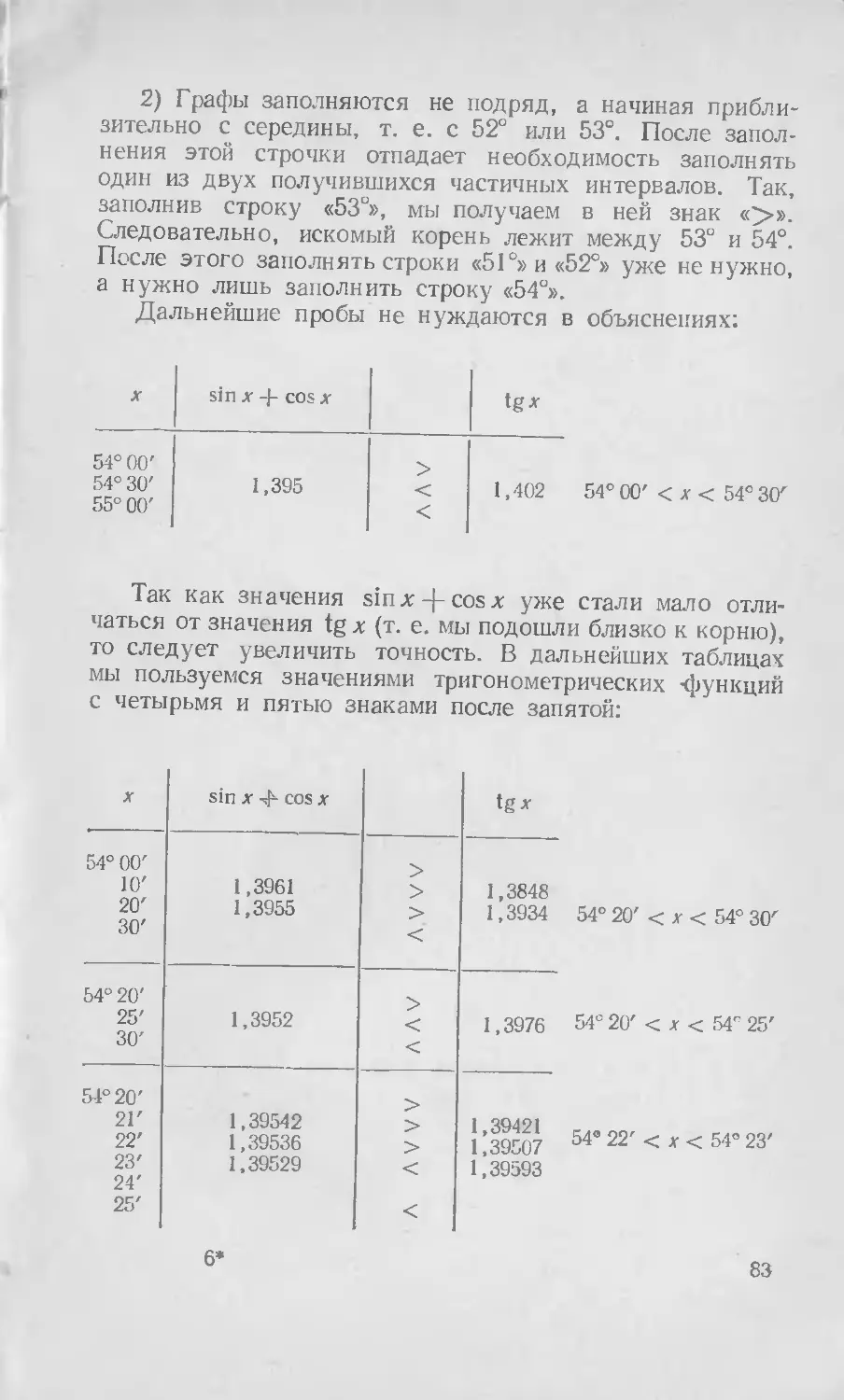
В задачах на приближенное решение уравнений (§11) предполагается только метод проб.
Вычислительные задачи не рассчитаны на какие-либо определенные таблицы. Углы задаются и вычисляются в минутах (1. е с погрешностью меньшей, чем 30"), а значения тригонометрических функций — с четырьмя цифрами после запятой. Учащийся обязательно должен располагать таблицей тригонометрических функций числового аргумента.
Задачник разделен на два раздела: основной и дополнительный Основной раздел содержит минимальный набор задач, которые рекомендуется перерешать полностью. Дополнительный раздел (повторяющий ту же тематику и состоящий из таких же параграфов) дает выбор задач для дополнительной тренировки.
Большинство задач этого задачника заимствовано из русской дореволюционной и иностранной литературы. Не перечисляя всех источников, укажем один, который был использован особенно значительно: С. Войти н-ский. Собрание вопросов и задач прямолинейной тригонометрии, Спб, вып. 1, 1909, вып. 2, 1909, вып. 3, 1911.
Во втором издании уменьшен основной раздел, добавлен список формул, исключены некоторые задачи (слишком легкие и слишком громоздкие) и, самое главное, исправлены замеченные ошибки и опечатки.
Автор искренне благодарен за критические указания И. И. Беловой и А. М. Люстиг (Елабуга), Е. А. Мурзаеву (Саратов), М. Б. Балку (Смоленск), Э. Г. Гетману (Печора) и Н Н. Шоластеру (Москва). Он надеется, что этот перечень будет в дальнейшем пополняться.
Некоторые задачи, принадлежащие Э. Г. Ботману, вошли в этот задачник (№ 136, 622 и 635).
21 февраля 1961 г.
Ник. Бескин
4
ОТ КАФЕДРЫ МАТЕМАТИКИ М Г 3 П И
При работе над задачником-практикумом студент должен параллельно изучать теоретическую часть курса по учебнику С. И. Новоселова «Специальный курс тригонометрии» Часть задач и упражнений, помещенных в задачнике-практикуме, снабжена подробными решениями, которые также должны быть тщательно рассмотрены студентом перед тем, как он приступит к самостоятельному решению других задач и упражнений по соответствующей теме.
Все задачй, помещенные в основной раздел задачника-практикума, должны быть полностью решены студентом в межсессионный период Полная проработка всего текста задачника-практикума должна быть завершена студентом заочником не позже, чем за один месяц до начала очередной сессии Вместо практиковавшихся до сих пор контрольных работ по тригонометрии студент-заочник получит от кафедры за один месяц до начала очередной сессии номера нескольких задач из данного задачника-практикума. решения которых он должен прислать в деканат в пятидневный срок. Непредставление в указанный срок решений этих задач будет рассматриваться как невыполнение контрольной работы со всеми вытекающими отсюда последствиями.
Кафедра математики Московского государственного заочного педагогического института обращается к кафедрам математики педагогических институтов и ко всем студентам-заочникам с просьбой присылать свои соображения по задачнику-практикуму как с точки зрения самой идеи его составления, так и по его конкретному содержанию.
Если в процессе работы над задачником-практикумом студент-заочник столкнется с неясными вопросами, ему надлежит обращаться на кафедру математики МГЗПИ (Москва, пл. Революции, 3/1).
Кафедра математики МГЗПИ

ОСНОВНОЙ РАЗДЕЛ
§ 1. ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ
Доказать тождества (№ 1—3).
,	1 4- sin 2а cos 2а ,
1.	—--------------= ctga.
1	+ sin 2а — cos 2а
Решение. Используем формулы: 1-|-cos x = 2cos2-^- , 1—cos х = 2 sin2 Y' Средние члены (в числителе и знаменателе) выражаем как синус двойного аргумента:
1 + sin 2a + COS 2a	2 COS2 a + 2 sin a • COS a 
1 + sin 2a — COS 2a	2 sin2 a + 2 sin a • cos a
2	COS a (cos a + sin a) &
2	sin a (sin a + COS a)
В этом рассуждении мы сократили дробь на cosa-|--j-sina, что является незаконным в случае cos a-}- sin a =» О, т. . е. когда а =------В этом особом случае
левая часть данного тождества принимает неопределенный вид-а правая часть равна —1. Возможны две точки зрения на этот случай.
1)	Если при некотором значении а хотя бы одна из двух частей равенства теряет смысл, то равенство признается несправедливым при этом значении а. Таким , образом, данное тождество справедливо для всех значений а, кроме значений вида а —------—±k^.
6
2)	Если при некотором значении а = а0 в равенстве /(а) = ^(а) хотя бы одна из частей (например, левая) теряет смысл, то мы приписываем ей значение, равное lim/(a), т. е. считаем равенство справедливым, если
lim/(a) = <р(а0). При решении уравнений приходится иссле-«-»<%
довать, так ли это. При доказательстве же тождеств такое исследование не требуется: если тождество /(а) = <р(а) справедливо для всех значений а в некоторой двусторонней окрестности а0 и если функция <р (а) непрерывна при а = а0 (каковые условия в данной задаче соблюдаются), то тождество /(а) = <р(а) при а — а0 обязательно верно (в указанном выше смысле).
В этой книге принята вторая точка зрения.
2.	2 (sinea-|- cos6 а) — 3 (sin4а 4~cos4a) + 1=0.
3.	(sin аsin р)2 -|- (cosа Ц- cos Р)2 — 4 cos2 .
4.	Найти (точно) синус и косинус 15° и 75°.
Ре	шение. Первый способ. Рассматриваем 15° как разность между 45° и 30°;
sin 15° = sin (45°—30°) = sin 45° • cos 30°—cos 45° • sin 30°=
V"2 /J /Т *	К'б-К'2
“2'2	2*2“	4
cos 15° = cos(45°—30°) = cos45° • cos30°+sin45° -sin30° =
= О i У? . 2. = ~ 2 ' 2	2	‘ 2	4
Второй способ. Рассматриваем 15° как половину от ЗСЛ Используем формулы (VI.1) и (VI. 2). Двойной знак не нужен, так как синус и косинус 15° заведомо положительны:
7
Эти выражения можно упростить, пользуясь формулой (XVII. 1):
sin 15° = 6- ~^2., cos 15° = О+О ;
4	4
sin 75° == cos 15°, cos 75° == sin 15°.
5. Найти x (точно), если sin х —
±1/2 — / 2 . 2 г
Решение. Найдем cos2x [формула (V. 36)]: cos2x = 1 —2sin2x = 1 —± (2 — /ЗГ) —
от<уда одно из возможных решений: 2х = 45°, х — 22°30'. Но если 22°30' есть один из углов, имеющих такой синус, какой указан в условии задачи, то все углы, имеющие тот же синус, задаются формулой к — 180°& 4- (— 1)* 22°30 .
Как видно, мы должны сначала догадаться, чему равен х, а затем эту догадку проверять. Без такой догадки неясно, почему мы вычисляли cos2x. В подобных задачах, если такая догадка затруднительна, рекомендуется обращаться к таблицам. В данном случае имеем:
/2 = 1,4142,
2 — /¥ =0,5858,
V 2 — / 2 = /0,585’6 == 0,7654/
sin X =. --2-~ tZ 2 = 0,3827, X = 22°30'.
2
6. Найти (точно) tg 11° 15'.
Доказать тождества (№ 7—9).
‘7. Д±± — 1 -J-2 cos 2а2 cos 4а-1-2 cos 6а. Sin а	1
Решение. Первый способ. Заменим синусы по формуле Эйлера [формула (XII 1.5)]:
Sitl7a	е<-7«_е—11а
sin a	ela — e~'la
Далее в ходе выкладок мы для краткости дважды делаем замену обозначений; eia — t, t* •= s.
S
1
Р — — sin 7а_______Р _	1 _ s7— 1*_
sin a t _____ I ta — t6 S4 — S3
t
S8 + s2+ s+ 1+ -л- ” s3
к ss 4- s’ 4s 4" 14-	4- — 4—т
S sd S
e= 1 4~ (S 4~~~) + (s2 4--7) 4- (s8 4" “7} —
\ S J \ S£ I \ sA )
e 1 4. (gHa g-/2<x) _]_ (g/4« e~t \^ (g/ба g-/6a) = = I 2 cos 2а 4~ 2 cos 4а 2 cos 6а.
Второй способ Используем формулу (VIII. 3):
sin а - cos ба = — (sin 7а—sin 5а), 2
sin а • cos 4а = — (sin 5а— sin За), > 2
sin а • cos 2а =s — (sin За — sin а), 2
sin а • cos 0 = — (sin а -J- sin а).
Сложим эти равенства. При сложении правых частей произойдет сокращение ( см. схему):
Sina(l ф-cos 2а 4~ cos 4а -f-cos 6а)= = ~(sin 7а 4- sin а).
Умножим на 2 и разделим на sin a:
2 4~ 2 cos 2а 4- 2 cos 4а 4- 2 cos 6а = sin 7г .
=-----—Н 1.
sin а
• Далее производится деление многочленов.
9
Особый случай: a~k~ (см. решение задачи № 1).
8.	sin а sin За 4~ sin 5а -|- sin 7а = 4 cos а cos 2а sin 4а.
Решение. Первый способ (слева направо). Сумму двух синусов преобразуем в произведение. Группируем первый член со вторым, а третий с четвертым (по одинаковой разности аргументов):
sin а sin За 4~ sin 5а -|- sin 7а =
— 2 sin 2а cos а 2 sin 6а cos а =
= 2 cos a (sin 2а 4-sin 6а) = 2 cos а . 2 sin 4а • cos 2а.
Можно группировать первый член с четвертым, а второй с третьим (по одинаковой сумме аргументов).
Второй способ (справа налево). Преобразуем правую часть данного тождества в сумму по формуле (V111. 6). Вывод этой формулы приводится в решении задачи № 43. Полагая в этой формуле к — 4a, у = а, г — 2а, сразу получим нужное тождество.
g sin За • cos3 а -р cos За • sin3 a- sin 4а
3
4
10. 1) Выразить cos и а через cos а и sin а.
Решение. 1) По формуле бинома Ньютона:
(cos a	i sin а)" = cos'1 a г n cos"-1 a . sin a —
n(n—1)	„ 9	. » .n (n — 1) (n — 2)	„ ,	. 4 .
-----—- cosn~2 a . sin2 a — i— ---—	- cos"~3a - sin3 a 4-21	3!-*
. n (n — 1) (n —2)(n— 3)	,
4---------————----------cos'1-4 a . sin4 a 4- ...
41	1
... 4"C~1 ncosasin'2- 'a 4- t"sin"a.
По формуле Моавра [формула (XIII. 1)]:
(cos a 4- i sin a)n = cos n a 4- i sin n a..
Правые части этих равенств можно отождествить. Приравнивая отдельно действительные части, получим:
cos пa = cos" a — ” ~.Р_ cos"-2a sin2 a 4-21	1
• n (n — 1) (n — 2) (n — 3)	„ .	. .
4- —----—------—-----~ cos'1—* a • sin4 a— ...
41
10
Последний член равен: п—1
(—1) 2 ncosa - sin"-1 а при п нечетном, п
(—1)2 sin” а при п четном.
2) Выразить sin па через cos” а и sin”a.
11. Упростить sin47°sin61° — sin 11° — sin25°.
Решение. Объединяем первый член с четвертым, а второй с третьим (по одинаковой сумме аргументов): sin 47° 4- sin 61 ° — sin 11°—sin 25° = = 2 cos 36° sin 11° 4- 2 cos 36° sin 25° = = 2 cos 36° (sin 11 ° 4- sin 25°) =
= 4 sin 18° cos 36° cos 7° = 4 sin 18° (1 —2 sin818°) cos 7°= ...
Ho sin 18° можно определить, пользуясь теоремой: хорда равна диаметру круга, умноженному на синус половины дуги, стягиваемой этой хордой. Если за хорду взять сторону правильного вписанного десятиугольника, то
«1о — 27? • sin 18°,
откуда sin 18° = —. Из геометрии известно, что 27?
а - т?/5-1
G10 ~ К--g
Таким образом,
sin 18е

Теперь можно вычислить:
1—2sin8i8e=1Cy *-•
Продолжаем прерванные выкладки:
. /Т — 1	У~5 +1 -о 70
... = 4 • -—------—• cos 7° cos 7°.
4	ч
Примечание. Можно было бы обойтись без вычисления sin 18° и получить результат значительно более коротким, но зато и более искусственным приемом, а именно: дойдя до выражения 4 sin 18° cos 36° cos 7°, следовало умножить и разделить сто на cos 18°. Дальнейшие выкладки протекали бы так:
11
л ; । «о око -то 4 sin 18° cos 18° cos 36° cos 7°
4 sin 1 o cos 36 cos 7 =--------------------- -
cos 18°
2 sin 36° • cos 36° • cos 7° sin 72° cos 7° _o
—---------------------— ------------- cos 7°
cos 18"	cos 18°
потому что sin 72° = cos 18°.
12.	Вывести формулы для:
1)	синуса суммы трех аргументов,
2)	косинуса суммы трех аргументов,
3)	тангенса суммы трех аргументов.
Решение. Первый способ. Преобразуем двумя различными способами выражение е<>“ + 1’ + т) [формула (ХШ 2)]:
е t о + ₽ +1> — cos ф р 4 у) i sin (а р 4 у) г
qI 3 + 7) -gw Qi* . g/3 , qI\
=е (cos а 4 z sina)(cosp -ф-z sin р) (cos y 4 i sin у) =x = cosa • cos p • cos f—cos a • sin P • sin y—sin a • cos p • sin y— —sina • sin₽ • cosy4 z(sina • cosp . cos у 4 cosz • sinp -собу-ф 4 cos x. cos p • sin y — sin a • sin p • sin y).
Отождествляя правые части этих равенств (отдельно приравнивая действительные и мнимые члены), получим:
cos(x -ФР -ф y) = cos a • cosp • cos y—cos a • sinp • sin у — — sina . cosp • sin y — sina . sinp  cosy.
sin (a-ф В -ф y) =s= sina  cosp • cos y +cos a • sinp • cos 7 4 -ф cos x • co. p • sin y — sin x . sin p • sin y-
Деля второе равенство на первое и после этого в правой части деля числитель и знаменатель почленно на cos a • cosp  cos y> получим:
tg (a 4 p 4- у) = _LV-+,LL+ tgT-tg^tgP-tgi , 1 — tg a • tg fl — tg ,1 • tg у — tg f • tga
Второй способ
sin (a 4 p 4 y) = sin [(a 4 P) 4 y] = » sin (л -ф p) . cos y ф cos (a 4 P)  sin 7 ==
К
= (sin a • cos p 4~ cos x • sin p) cos у 4-
(cos a • cosP — sin a - sin P) sin у = sin a - cos p • cos у 4~ -|-cosa • sinp • cos у 4* cos a . cosp • sin у— sin a - sinp • siny.
Формула для cos(a4-P4~y) выводится аналогично, формула для tg (a 4- р 4- 7) получается делением.
13.	Вычислить
tg (-yarcctgs).
Решение. Обозначим a = arcctg3. Это значит
ctga = 3, 0<a<y.
[Вообще arcctgx заклинается в интервале (0, тг) [формула (XI.4)], но арккотангенс положительного аргумента принадлежит первой четверти.] Вычисляем:
.	1	1	ctg о	3
sin а = -г -	- = -р=, cos а = —	- =	.
/ 1 -р ctg2 а	/10	kl+ctg^ /10
(Двойной знак перед радикалом не берется, потому что а принадлежит первой четверти.) Далее используем формулу (VI. 5):
1 3
tg (-~-arcctg3j=tg-|- = ---*£12 = КТО —3.
/ПГ
14.	Упростить sin (2 arc sin x).
15.	Вычислить sin | 2 arc cos — . \	4 J
16.	Упростить ctg (2 arc cos x).
Доказать (№ 17—19).
17.	arcctg 4- 2 arc ctg у = -y-.
Решение. Обозначим: a = arc ctg -y, p = arcctg y.
Тогда
13
ctga==-L. ctg₽=-A-,
ctg 23 = ctg2?~ 1 =	— = -
2 ctg p	2
3
_4
3
Ctg(a + 2p) = glga-ctg2p~1 Ctg a 4- ctg 2fJ
-A-l
----= 1.
1	4
7 “ 3
Из того, что ctg (а -Ц~ 2p) = 1, еще нельзя однозначно определить a-}-2(3. Необходимо установить достаточно узкие границы, в которых заключается а 2р; а принадлежит первой четверти. Кроме того, раз ctga < 1, то a> р Аналогичные замечания относятся и к р. Итак, —<а< 4
<— ;	< р < у ; — < 2р < тг. Складывая первое и третье
неравенства,
находим:
— <а4-2В < — .
4	1 ‘	2
Зл 2
Черт. I.
В этих границах (см. черт. 1) существует единственный аргумент, котангенс которого равен единице: это —. Следо-4
5тс вательно, а-|- 2(3 =— , т. е.
arcctg у + 2 arcctg у = у • 18. arctg у 4- arctg 1 у.
H-arctg |
1	3
19.	2 arctg у = arctg — .
14
Найти х из уравнений (№ 20—22).
20.	arctg х — 2 arctg а.
Решение. Сначала найдем область возможных значений параметра а Для того чтобы правая часть могла представлять арктангенс, необходимо и достаточно:
— — < 2 arctg а < — ,
2	2
откуда
— - < arctg а < -- , 4	4
— 1 <а < 1.
Для нахождения х берем тангенс от обеих частей данного уравнения-
jc = tg(2arctga) = г|Яа^->	_А_ .
V ’	1 — tg2 (arctg а) 1—аг
Ответ, х = - — -. Задача возможна только при | а | < 1.
1 — а2
21. arcctgx = л— arcsinЗа.
22. 1) arccos х = arccos а — 2 arcsin b;
2) arcsin х = arcsin а	2 arccos b.
1) Решение. Прежде всего заметим, что должно быть: | а |	1 и [ b | < i.
Правая часть может представлять собой арккосинус при условиях:
0 < arccos а — 2 arcsin b < л.
Рассмотрим эти условия отдельно.
A) arccos а — 2 arcsin b > 0.
Если b < 0, то условие А) всегда соблюдается (потому что оба члена левой части неотрицательны). Если же Ь > 0, то преобразуем условие А) так:
arccos а 2 arcsin b, cos (arccos a) cos (2 arcsin b), a C 1— 2b2.
15
Уравнение а= 1 —26s изображается параболой. Неравенство а < 1 — 2Z?2 удовлетворяется для всех точек внутри этой параболы. Теперь ясно, что три условия!
Черт. 2
1)	|а|< 1,
2)
3)	при &>0
а< 1— 2Ь2
определяют область, изображенную на чертеже 2 (включая границу). Для точек этой области (включая границу) соблюдается условие А), а также условия\а |	1 и|b| • 1.
Переходим к условию В):
arccosa — 2 arcsin b < л.
Если Ъ 0, то условие В) всегда соблюдается. Если же b < О, то преобразуем условие В) так:
arccos а л + 2 arcsin b,
cos(arccosa)>cos(^-|- 2arcsinfr) = — cos (2arcsinfc), a > 2b2 — 1.
Итак, условие В) вместе с условиями |а| < 1 и |Ь| <1 опредетяет область, изображенную на чертеже 3 (напомним, что при 6 > 0 выполнения неравенства а 2Ь2—1 не требуется).
Ч^рт. 4
16
Чтобы задача была возможна необходимо одновременное выполнение условий А) и В). Эти условия выполняются в общей части областей, изображенных на чертежах 2 и 3 (см. черт. 4).
Значение х легко найти, беря косинус от обеих частей данного уравнения.
Ответ. х = а(1—2b2) 4~ 2b У\1—а2)(1—Ь2) 
Задача возможна при одновременном соблюдении условий: — 1 < а < 1,
Ут-”-
Эти условия иллюстрируются чертежом 4.
§ 2.	УСЛОВНЫЕ ТОЖДЕСТВА
23.	Доказать, что при а -ф- Р 4~ Т = я имеет место тождество:
tga-ф- ШР + tgT = tga-tgp-tgy.
Решение. Первый способ. Заметим, что tg у = = tg[* — (« + ₽)] = — tg (a-f-P).
tg a + tg Р + tg у = tg a 4- tg р — tg (a -J- Р) =
sin (7 + P)  sin (a 4- P) _sin cos (a 4- P) — cos a-cos P _
COS a.COS P	COS (a 4" P)	COS n.COS P-COS (a 4" P)
= sin <a4-P) . -sing.sinp = _tg7 ,(_tga.tgP) = COS (a 4-P) COS a-COS P
= tga.tgp. tgy.
Второй способ Используем формулу для тангенса суммы трех аргументов [формула (IV И)]. Если а4-4-Р4-у=к, то tg(a 4~р 4-т)=0- Следовательно, числитель правой части формулы равен нулю (числитель и знаменатель этой формулы не могут одновременно быть нулями, см. задачу № 224), т. е.
tg« + tgp4-tgy = tga.tgp-tgy.
2 Заказ 33
17
24.	Доказать, что при а Д- 0 Д- 7 = « имеет место тождество:
cos а Д-cos р Д-cos 7 = 1 +4 sin -|-sin у sin у .
25.	Доказать, что при а Д- 0 Д- у = у имеет место тождество:
sin a Д- sin	0	sin р —
।	1	л	-	/ к а \ .	[	я	В \	•	/ я	7	\
— 1	4-4 sin	— — — sin-------— I sin--------Ll .
'	U 2 /	\	4	2 )	\ 4	2	)
26.	Доказать, что при аД-0Д-7 = 2тг имеет место тождество:
cos2 а Д- cos2 0 cos2 7 = I Д- 2 cos а • cos 0 • cos у.
27.	Доказать: если а-|- 0 Д- у — (2п Д-1)~ и sina |-sinp= = 2 sinp, то либо а Д-0 = 2Ая, либо tg у • tg = у .
28.	Доказать: если а Д-0 = у, то(1 Д- tga)(l 4~tg0) = 2.
29.	Доказать, что при аД-0 = р имеет место тождество:
sina Д-sin0 Д- sin р — 4 cos — cos — sin —.
' н 1	1	2	2	2
30.	Доказать, что при аД-р4-уД6 = 2тг имеет место тождество:
sina Д-sinp -|~sinp Д-sinB = 4 sin л у sin sin -у— .
Решение. Первый способ (справа налево). По формуле (VIII. 4):
. . a 4- В . В-1-7 • т 4- а . / а -|- 8 , В + 7 , 7 + а \ .
4 sin—I-4-sin——sin 1 --=-sin  ~2-Д-~ ~ j-Д- 1	 Д-
2	2	2	\ 2	1	2	'	2 / 1
+ sinr Д+1 + 1±1+±±±\д_
1	\	2'2'2/'
+ sin/^±₽__i±l+T±^\+sinf±±l+to__r±L) = '	\ 2	2	2 /'	^2	2	2 /
= — sin(a 4- p Д- y) Д- sin у Д- sin а -Д sin 0 =
= sin а Д- sin 0 Д- sin 7 Д* si° &•
18
Второй способ (слева направо): sina4-s’n₽4~sinl+ s*n8 = 2sin-^i-^- cos 4~
IO- 7 4 8	7 — 8
4- 2 sin —-— cos  -= ...
1	2	2
Заметим, что
а 4 3 i 7 4 8	. '( ф й . «4*3
— н 4- 44— — тп sin ‘-J— = sin  2'2	2	2
о. а 4 3 Г а — 3 i 7 — 8 1
2 L 2	2 J
. . «4В	«4т— 3— 8	«4® — 3 — 7
= 4 sin - - — cos -———c--cos —!----!---- — ...
2	4	4
Заметим, что
аф] — 3 — b а ф- 7 /л	« 4 7 \  	/ 7t a 4 7 \
4	~ 4	\7	4 )	\2	2 f
a 4 8 — 3 — 7	__ и _ 3 4 7_ p 4 7	_ ~_ 3 4 7
4	— 2*	~4	4	~ 2	2
Поэтому
a 4 7— 3 —8	• ° 4 7	«48 — 3 — 7	-3 + t
COS —4J 1-----= sin -3-1	cos ——-----—-= sin к-4-Ь.
2	2	2	2
Таким образом, sin asin p 4-sin y-|-sin 8 = 4 sin °	 sin --- sin
31. Доказать, что при а4-Р4~Т“Н8 = 2л имеет место тождество:
tga4-tgp4-tgT4-tg8 =
sin (а 4 3) sin (а 4 7) sin (а 4 8) cos «-cos 3-cos 7-cos 6
on rr	sin4 *« I cos4 a 1
32. Доказать: если------------------= —, то
m 1 n tn 4n
m* 2 3 n3 (m 4 л)3
Решение. План решения:
1) из первого равенства найдем sin а и cos a,
2*
19
2) подставим их во второе равенство и убедимся, что они ему удовлетворяют.
Для краткости обозначим: cos 2 а = х. Тогда
sin2a = — (I — х), sin4a = j (1 — 2х+х2),
cos2a — — (1 4-х), cos4a= у(1 4-2x4*x2).
Подставляем эти значения в первое уравнение:
1 — 2л- + х2 । 1 + 2 х + х2 _	1
4 m	4 п т -f- п
или после упрощений:
(т п)2 х2 4* 2 (т—п) (тп) х (т — /г)2 = 0.
Сразу видно, что это уравнение может быть переписано так: [(т 4- п) х (т — п)]8 = 0, откуда п — т X = --------------------------- .
п + т
Далее:
,	1 I. , п — т\ п
COS a = — 14------i • = —i------•
2 \	' n m ] n -f- m
Подставляем эти значения во второе уравнение:
и4 , п4 _____________________1_____
(л + тут3 (п + m)4ns (т -|- п)3 ’
что верно.
Доказать (№ 33 — 35).
33.	Если sin2 р = sin a -cos a, то cos2p = 2cos2
20
34.	Если tgantgp суть корни уравнения x2-j-px-j--j-q = O, то sin2(a4-₽) +psin(a+₽)cos(a + P) -j-4-<7.cos2(a+₽) = q.
Решение. Из условия задачи вытекает, что tga + _|~tg₽ = —Р, tga-tgp = <7- Преобразуем данное выражение, стараясь, чтобы в нем фигурировали только сумма и произведение тангенсов:
sin2(a -Ь Р) + Р sin (a + Р)cos (a + Р) +<7 c°s2 (« + Р) =
= cos2 (a4- ₽) [tg2 (a4- P)4- p- tg (a 4-₽) 4- <7] =
= .	‘ ТТГI te2 (« + P) + P  (« + P) 4- ?]=•••
Заметим, что
tg(a4-p) = - tga^tgp
S	l-tga.tg₽
P 9 — 1
Продолжаем:
_______1
P2 1+(9-l)2
P2  I
P2
P2
(9 -1)2
P2(9~ 1)
<7 — 1
P2+(<7—I)2 P2 + (9—I)2
_ P29 + 9(9 — 02 _
p2 + (<7— I)2
9(9 — I)2
P2 + (9 — I)2
35.	Если sin(rc-ctga) = cos(TT.tga), то либо esc2a = = k 4- —, либо etg 2 a = k 4- —.
4	4
Решение. Преобразуем данное равенство, используя формулу (VII. 12):
cos [у 4“(tg«4-ctga)lcos [j — (tga — ctga)l = О,
откуда получаются две возможности:
1)	cos Гу 4--^- (tga4-ctga)l = О, L 4	2	]
|4-| (tga4-ctga) = |4-*rc,
21
tga-|-ctga = 2k+j-,
—-—= 2k-}- — [см. формулу (VII. 19)], sin 2 a	2
esc 2 a = k Ц- —.
1 4
Это возможно при
, . IK, k 1, t. e.
i	r.
либо ^4 — <— L & < — —, 4	4
либо
k -I— К I, k 4' —
'4	4
Так как, кроме того, k —целое, то выходит, что k может принимать любые целые значения, за исключением —1 и 0.
2)	cos I у — у (tg a — ctg “) I = °>
у — (tg « — ctg a) =	+ k к,
tg a — ctg a = — 2 k — ~,
— 2ctg2a =— 2 k— [см. формулу (VII. 20)], ctg2a = А:-]-!-.
Здесь k —любое целое число.
§	3. ПРЕОБРАЗОВАНИЕ СУММ В ПРОИЗВЕДЕНИЯ И ПРОИЗВЕДЕНИЙ В СУММЫ
Преобразовать в произведения (привести к «логарифмическому виду» № 36 — 38).
36.	1 4tgatg₽.
37.	sin3a4sin7a4-sin 10a.
Решение. Объединяем, например, первые два члена:
sin За 4~sin 7а 4- sin 10а = 2sin 5а-cos2а -|-
-|- 2 sin 5а • cos 5а = 2 sin 5а (cos 2а cos 5а) =
. . г- 7а За
= 4 sin 5а  cos — cos —.
2	2
Тот же результат получится, если начать с объединения любой другой пары членов.
38.	1) sin а + sin р + sin (аР),
2)	sin а. 4-sin р — sin (а. 4-Р).
39.	Преобразовать в произведение при помощи введения вспомогательного угла V а2—Ь2 (|6| <|а|).
Решение. Положим:
А| = sin <р, 0 < <р < 90°.
Область значений <р выбрана так, чтобы sin <р пробегал все возможные для него значения по одному разу. Расширение этой области было бы бесполезно и внесло бы многозначность в дальнейшие выкладки:
Vа2 — Ь2 = | а | • V 1 — sin2 <р — | а | • cos <р.
Заметим, что в силу условия
0 < <р < 90° cos<p=l//l—sin2 <р (без двои-	/
ного знака).	/
При о>0 и 6>0 полученный ответ а/ & иллюстрируется чертежом 5.	/
40.	При помощи введения вспомога- / тельного угла представить в виде произве- /у________
дений корни уравнения х24-рх -|-q = 0	./ г.г
в случае, когда р2— 4</>0 и </>0.	va - <
41.	Преобразовать в произведение при Черт. 5 помощи введения вспомогательного угла:
V 4 tg а 4- sin а. 4~1^4 tg а.— sin а.
42.	Определить амплитуду и начальную фазу гармонических колебаний:
1) s = 2 cos / 4- 3sinZ,
2) s = cos(2/—1) 4-sin (2/4-5).
23
Решение. 1) s = 2cost -j- 3sin/ = . ..
Выносим за скобку /224-32 (это и есть амплитуда),
(9	3
-== cos t + -== sin t
/13	/13
Обозначим:
А = /13 = 3,6056.
sin <р = — = 0,55470, т А
cos <р = - = 0,83205, т А
(0 <	90°),
откуда <р = 33°41'.
. .. = A (sin <р cos / cos <р • sin t) = А • sin (t + ?)•
2) Преобразуем сначала данное выражение по формуле (VII. 9):
cos (21 — 1)-)- sin (21 4- 5) =
= 2sin( — 4~ 3^ sin (— 4-2 4~2/^ = ...
\ 4	/	\ 4	/
Обращаемся к таблицам:
- = 0,78540, - 4- 3 = 3,78540,
4	4 1
sin( J 4-3) = sin 3,78540 = —0,60025.
Продолжаем прерванные вычисления:
... = — 1,2005 sin (2,78540 4-2/) = ...
Можно потребовать, чтобы начальная фаза заключалась между 0 и Замечая, что л = 3,14159, напишем:
2,78540 = к—0,35619 и далее:
... =—1,2005.sin/—(0.35619 —2/)] = = 1,2005 sin (2 Z — 0,35619).
43.	Преобразовать в сумму:
1)	cos a - cos cos у,
24
2)	cos a • cos р • sin 7,
3)	cos a. sin p. sin 7,
4)	sin a • sin P-sin 7.
Решение. Первый способ. Используем формулу (VIII. 1):
cosa-cosр• cos f = ~ [cos (a — P) + cos (a 4" P)] cos 7 =
= у [cos (a — p) cos у 4-cos (a P) - cos 7] =
= у [cos (a — P — 7) 4- cos (a — P 4- 7) 4- cos (a 4- p — 7) 4-
4-	cos (a 4- P 4- 7)].
Второй способ. Будем исходить из формулы (IV. 10):
cos (a 4- Р 4“ 7) — cos a•cos Рcos Т — cos a• sin р • sin 7 — — sin a-cos p. sin 7 — sin a-sin В - cos 7.
Для краткости обозначим временно:
cos a • cos p • cos 7 = A, cos a-sin p - sin 7 = B, sin a-cos p-sin 7 — C, sin a • sin p • cos 7 = D.
Изменяя знаки a, p, 7 и замечая, что
изменение знака	а	влечет	изменение	знаков	С и D,
»	»	р	»	»	»	В »	D,
»	»	7	»	»	»	В »	С,
получим еще три формулы. Выпишем все четыре:
cos (а 4- р 4- 7) = А — В — С—D,
cos(—a-4-P 4" 7) = — В-НС4-О, cos (a —Р4~7)= A-\-B — C-\-D, cos (a 4- P — 7) = A 4- В 4- C — D.
Составим следующие две линейные комбинации из этих равенств:
cos (a 4- 0 4-7) 4- cos (—a 4-0 4- 7) 4-cos (a — p 4- 7) 4.
4- cos (a 4- p — 7) = 4A,
25
— cos (a + p -4- 7) — cos (— a + ₽ 4- y) + cos (a — p 4~ 7) 4~ 4- cos (a 4~ P — 7) = 4B,
откуда, восстанавливая смысл обозначений А и В,
cos a-cos р- cos I = ~ [cos (a 4-Р 4" l) + cos(—a+ Р4" l) +
4- cos (a — p 4- 7) 4- cos (a 4- P — 7)],
cos a- sinp -sin 7 = —cos (a 4-P 4" l)— cos(—a+P+ T)4" + cos (a — p 4- 7) 4- cos (a 4- P — 7)].
Чтобы решить примеры 2) и 4), надо повторить аналогичные рассуждения, отправляясь от формулы (IV. 9). Ответ — см. формулы (VIII. 6) и (VIII. 4).
Легко понять, почему произведения 1) и 3) выражаются через косинусы: они не изменяются при одновременном изменении знаков а, р и 7. Произведения же 2) и 4) изменяют свое значение на противоположное при одновременном изменении знаков а, р и 7 и потому выражаются через синусы.
44.	Преобразовать в сумму:
sin a • cos р • cos (a 4~ Р) -
45.	Вычислить (точно) cos20°-cos 40°-cos 80°.
Решение. Обозначим искомое произведение через х: х = cos 20° cos 40° cos 80°.
Умножим обе части этого равенства на sin 20° и затем три раза используем формулу
1	- О
sin a cos о. = — sin 2 a.
2
x  sin 20° = sin 20° cos 20° cos 40° cos 80° =
= _L sin 40° cos 40° cos 80° = — sin 80° cos 80° =
2	4
= — sin 160° — — sin 20°,
8	8
откуда
26
46.	Понизить степень (до первой): 1) cos3a, 2) sin3a.
Решение. Первый способ:
/ J. V е1 -3« +	, Зе-1О . -f-За
cos3 а = -------------	—-----!----—!-------—------- =
\ 2 / 8
1 еОЗа к -<-з« з	!	з
= — . -------—------------------!----- = — cos За -4----cos а,
4	2	1 4	2	4	4
sin3 а =
ei.3a_e-i-3a
/3“  Зег“ 3e~ia — е~1’3а — 8i
з eta- e~ia
4	2/
l-o . 3 .
Tsin3a4-j-sina.
4	1 4
Второй способ:
cos3 a = cos2 a • cos a. = -i- (1 Ц- cos 2a) cos a = ~ cos °- 4“
-)- у cos 2 a • cos a — cos a + (cos a -p cos 3a) =
3	, 1 о
== — cos a 4--cos За.
4	4
Для sin3 а рассуждение аналогично, ответ — см. формулу (IX. 15).
Понизить степень (до первой) (№ 47 и 48).
47.	1) cos4 а, 2) sin4 а.
48.	sin2 a-cos2 а.
§ 4. УРАВНЕНИЯ
49.	Решить уравнения:
1)	sinx— cosx = 1.
Решение. Для решения уравнений вида asinx-p Д 6 cos х = с существует много способов. Укажем три из них.
27
Первый способ. Выразить ccsx через sinx (или наоборот):	_________
sin х + Iх 1 — sin2 х = 1,
+ И1 —sin2 х = 1 — sinx,
1 — sin2 х = (1 — sin x)2, sin x-(l —sin x) = 0,
откуда либо A) sin x = 0, x = 180° n,
»	B) sin x = 1, x = 90° 4- 360° k = 90° (4* 4-1).
Недостаток этого способа заключается в том, что он содержит возведение уравнения в квадрат и поэтому может приводить к лишним корням. Следовательно, применение этого способа допжно сопровождаться проверкой. Проверяя решение х=180°п (подстановкой в заданное уравнение), мы видим, что оно верно только при нечетном п, т. е. при /г = 2*4-1. Второе решение верно всегда. Итак, имеем две серии решений:
х= 180° (2*4-1) и х = 90°(4*4-1).
Второй способ. Преобразуем левую часть в произведение методом введения вспомогательного угла (вынося за скобки амплитуду А = I о2 4- *2 и вводя началь-
ную фазу <р по формулам sin <р = —,
cos = —). В данной А
задаче можно также воспользоваться формулой (VII. 16):
— I 2 cos (45° 4-х) = 1,
cos (45° х) = —	,
45° 4- х = 360° п + 135°, x = 45°(8n—1 + 3).
Беря верхний и нижний знаки, мы получим отдельно решения, к которым пришли первым способом.
Третий способ Возведем данное уравнение в квадрат, после чего умножим правую часть на sin2x-|-4 cos2 х:
a2 sin2 х -}- 2 ab sin х • cos х 4- b2 cos2 х — с2 (sin2 х -ф cos2 х).
28
Теперь получилось уравнение, однородное относительно sinx и cosх. Делим его на cos2x и получаем уравнение, содержащее одну неизвестную функцию (tgx). При этом могут потеряться решения, для которых cosx = 0. Поэтому надо специально испытать значения х= 90° + 180° Z>.
В данной задаче вследствие ее индивидуальных особенностей следует действовать иначе: после возведения в квадрат сразу определяется sin 2х:
sin2x — 2sinx-cosx-]-cos2x = 1, откуда sin 2х = 0.
2х = 180° п\ х — 90° п.
Проверка обязательна. Она показывает, что значения и = 4k -f-1 и п = 4/г 4-2 годятся, а п = 4k и n = 4А 4~ 3 не годятся.
2)	sin х 4~ cos х = 0,3,
3)	sin х -|- КЗ cos х = 1.
Решить уравнения (№ 50 — 71).
50.	7sin2x — 8 sin х-cos х = 15cos2x.
51.	sin6 x 4-cos6 x = sin2 x-cos2 x.
Решен и e. Будем рассматривать левую часть как сумму кубов:
(sin2 х -J- cos2 x)(sin4 х—sin2 х • cos2 х 4- cos4 х)=sin-2 х • cos2x;
sin4 x — 2 sin2 x • cos2 x 4~ cos4 x = 0;
(cos2 x— sin2 x)2 = 0;
cos2 2x = 0;
cos 2x — 0;
2x = 90° (2Л 4- 1), x = 45° (2k 4- 1).
5
52.	sin4x 4~cos4x = —.
8
53.	tg2x4-ctg2x = 6.
54.	cos 2x4“ sin 2x — cos x-}-sin x = 1.
55.	3(sinx-|-cosx) = 2sin2x.
29
Решение. sin2x легко выражается через sinx4~ 4~ cos х:
sin 2х = 2 sin х • cos х = (sin х 4- cos х)2 — 1.
Поэтому данное уравнение можно переписать так:
3(sinх + cosх) = 2[(sinx -|-cosx)2— 1]. Обозначим:
sin х 4- cos х — у.
Тогда данное уравнение примет вид:
2 г/2 — Зу — 2 = 0,
откуда г/, —-----у2 = 2. Второе значение невозможно,
потому что sinxcosх не может равняться 2. Следовательно,
। 1
sinx 4~COSX =-------
2
или [формула (VII. 13)]
sin (45° 4~ х) =-i-,
sin (45° х) = — -Q- ss — 0,35355,
45° -[- х — 180°/г — (—1)Л<р, где <р = arcsin -^2- ^20° 42',
x = 45°(4Ai —1)4-(—l)ft+,<p.
66. tg х = 2 cos —.
2
57. tg x 4~ tg 2x 4- tg 3x = 0.
Решение. Сумму первых двух членов преобразуем в произведение:
sin Зх . sin Эх__q
cos х  cos 2х г~ cos Зх ’
sin Зх (cos Зх cos х • cos 2х)	„
cos х • cos 2х • cos Зх
30
Заметим, что левая часть данного уравнения теряет смысл в следующих случаях:
cosx = 0, x = 90°(2n-|-1);
cos 2х = 0, х — 45° (2n	1);
cos3x = 0, х = 30°(2n-|- 1).
Приравниваем нулю каждый из множителей числителя: l)sin3x = 0, х = 60%.
Проверим, не может ли это решение принять одно из «запрещенных» значений:
а)	60% = 90° (2п 4-1); 2k — 3 (2п	!)• Этого не может
быть, потому что 2k— четное число, а 3(2n1) — нечетное;
Ь)	60° k — 45° (2п О: 4^ = 3 (2п 4- 1) — не может быть;
с)	60% = 30°(2п-|-1); 2k — 2n-\-\—не может быть. Следовательно, ответ х = 60% годится при любом k.
2)	cos Зх 4- cos х  cos 2х = 0,
cosх(4cos2x—3) 4-cosx(2cos2x—l) = 0 [см. формулы (V. 45) и (V. 31)]:
cosx(3cos2x — 2) =0,
2J cosx = 0. He годится!
22)	cosx=± = +^~ + 0,81650,
1Г~о.
откуда x= 180% ± <p, где = arccos^35° 16'.
58.	sinx • sin3x = —.
2
59.	sin5x = 16 sin6 x.
Решение. В правой части понизим степень [см. формулу (IX. 16)]:
sin5x= 10 sinx — 5sin3x4~sin5x.
Далее преобразуем sin Зх по формуле (V. 22):
2 sin х — sin х (— 4 sin2 х 4- 3) = 0, sin х (4 sin2 х—1) = 0,
81
1) sinx = 0, x = 180%;
2) sin x = ±	, x — 30е (6fe + 1).
Примечание Можно было бы начать с преобразования левой части данного уравнения по формуле (V. 23). В этом случае выкладки будут немного длиннее.
60. sin 5х Ц- cos 5х sin 7х cos 7х = 0.
61. sin х sin 2л'4~ sin3x — cosx — cos2x = 1.
Решение.
(sin x4~ sin 3x) 4~ sin 2x — cosx — (1 4~cos2x) = 0.
2 sin 2x  cos x 4- 2 sin x • cos x — cos x — 2 cos2 x = 0.
cos x (2 sin 2x 4~ 2 sin x — 1 — 2 cos x) = 0.
cos x (4 sin x - cos x 4- 2 sin x— 1 — 2 cos x) — 0.
cos x [2 sin x(l 4- 2 cosx)—(1 4~ 2 cos x)J = 0.
cos x(l 4- 2cosx) (2 sin x— 1) = 0.
l)cosx = 0, x = 90°(2& 4-1).
2) 1 4- 2 cos x = 0, cos x =--~, x = 120° (3k + 1).
3)2sinx—1=0, sinx = -y, x = 30°[6fe4~(—I)*].
62. sin x4~ sin3x = sin 2x 4~sin4x.
63. sinx4~sin2x4-sin3x = cosx4-cos2x4~cos3x.
*64. tg(-|4-x)4-tg^--x) = 2.
Q
65. cos x 4- cos у — cos (x 4- y) = —.
Решение. Это уравнение может быть решено, хотя
оно
что
и с двумя неизвестными. Причина заключается в том 3
-----максимальное значение функции, стоящей в ле-
вой части. Если бы в правой части задать число боль-3
шее, чем —, то уравнение не имело бы действительных
32
3 решений, а если меньшее, чем —, то задача была бы
неопределенной.
Данное уравнение может быть решено многими способами, более или менее искусственными. Укажем два из них.
Первый способ. Положим:
tgy = «, tg|-=o.
В таком случае
cosx
1 — и2 .	2u
---------, sin x =--------------
1 -Ь. >/2	1 J- „2
[см. формулы (VI. 7) и (VI. 6)]. Аналогично cosy и sin у выражаются через v. Преобразуем данное уравнение так:
cosx-j-cos у—cos х • cos ^4“ sin х • 51ПУ = у»
I —и2	1 — у2	_ (1 — t?) (1 — и2)	J 4ио _ 3
1 + и2	+ 1 + V2 (1 4-U2) (1 + V2)	г(1	+ u2) (1	+ь2) ~ 2	’
3(1 4-w2)(l 4-О2) — 2(1— ы2)(1 +о2) —2(1+п2)(1—и2) + 4-2(1 —ы2)(1 —о2) —8ыо = 0, и2 4- vz — 8uv 4- 9w2o2 4-1=0, (и — о)2 4- 9Л2 — Guv 4-1=0, (и — о)2 4(3ир — 1)2 = 0,
откуда
и — v = 0, Зии — 1=0.
Таким образом,
tgf = tgf; 3tg2^-i=o.
Получаем две возможности: l)tgf = ^-, х = 60° (6m 4 1),
У = 60°(6п4-1).
3
Заказ 33
33
2) tgf=—x =• 60° (6m—1), tg4 = -JT-’ I/= 60°(6n—1).
Второй способ. Преобразуем левую часть данного
уравнения по формулам (VII. 3) и (V. 31):
о х -4- и х — и п » х t) . ,	3
2 cos —2—2 cos --- — 2 cos2 —— 4-1 =- —,
2	2	2	2
п X- II X — II 1	О х Ф у
2 cos —— cos------- =----к 2 cos® ——.
2	2	2'	2
Выразим отсюда
л х — у
2 cos ----- :
2
х — у
cos------
2
х 4- у
1 4 4 cos2
„	* + У
2 cos—2—
или
2 cos——— 2
2 cos
I а X 4- У 4- 2 cos —— 2
В правой части — сумма двух обратных величин. Она по модулю ^2 [см. формулу (XVII. 2)]. Левая часть по модулю < 2. Поэтому равенство может иметь место лишь в том случае, когда каждая часть равенства по модулю равна 2. Получаем две возможности:
a) cos - — 11 = 1,	х — у = 720° т,
cosJ4^=|’ 1х + у= 120°(6/г± 1).
b) cos ——-= — I, '	2
66. sec 5х = cos 2х.
Решение. [ sec 5х | > ство sec 5х = cos 2х может чаях:
1) sec 5х = cos 2х = 1,
х — у = 360° (2m1), x4-^=240°(3n± 1).
1, | cos 2х | < 1. Поэтому равен-иметь место лишь в двух слу-
34
2) sec 5x =» cos 2x =e — 1.
Исследуем эти случаи:
1) 5x = 360°m; x = 72°tn,
2x = 360°n; x = 180cn.
Следовательно, 72°m = 180°n, или (сокращая на 36°) '2m = = 5n. Это возможно, если tn = bk, n = 2k. Таким образом, x = 360' k.
2) 5x = 180°(2m-H); x = 36° (2m + 1), 2x = 180° (2n-j-1); x == 90°(2n + 1).
Следовательно, 36°(2m -(-!) = 90°(2n-|- 1), или 2(2m	1)=
= 5(2/г-|~1)- Это равенство невозможно (левая часть— четная, правая—нечетная). Значит, второй случай не может иметь места.
67. sinx  sin у = 1.
Решение. Если бы один из двух сомножителей был по абсолютной величине меньше единицы, то другой должен быть больше единицы, что невозможно. Поэтому данное уравнение может удовлетворяться только в следующих случаях:
1) sinx=l; х = 90°(4m1), sin^/=l; у = 90° (4/г-|— 1),
2) sinx = — 1; x = 90°(4m—1), sin у = — 1; £/ = 90°(4/г—1).
*68. sinx-|-sin5x = 2.
Решение. Предварительно отметим, что область допустимых значений х такова:
90°.2^<х< 90°(2^4-1).
В самом деле, во-первых, х не должен равняться 0,90° и т. д., потому что при этих значениях не существует либо тангенс, либо котангенс. Во-вторых, tg х и ctg х должны быть оба положительны (иначе не существовал бы их логарифм), т. е. х должен оканчиваться в первой или третьей четверти.
35
Далее заметим, что lg ctg к = —Igtgx. Поэтому данное уравнение можно записать так:
у 2, где у =» 3lg tg х .
У
Последнее уравнение можно решить как квадратное уравнение. Однако проще рассуждать так. Ясно, что у > 0. Известно, что сумма положительных взаимно обратных величин удовлетворяет неравенству
!/ + - >2
У
[см. формулу (XVII. 2)]. Минимальное значение достигается при у — 1. Следовательно,
3]е	_ ]
lg tgx — 0,
tgx = 1,
х = 45° (46 4-1).
Все эти значения х принадлежат области допустимых значений.
70.	sin (х -j— а) -|- sin х = cos у .
71.	tg2x 4~ tg(a 4~ х)-tg (а—х) = 0.
72.	Найти значения х в интервале — л<х<л, удовлетворяющие уравнению sin (х — 2) = sin (Зх — 4).
Решение.
sin(x — 2) — sin(3x—4) = 0, sin (х — 1) cos (2х — 3) = 0,
1) sin(x—1) = 0, х = /гк4-1.	1
Теперь найдем допустимые значения k, исходя из условия — л < х < л;
— л < k~ -[- 1 < я,
--Л--- 1 < 6к < Л- 1 ,
-1 —- <6< 1—- , К	ТС ’
— 1,3 <6 <0,7, т. е. k = — 1 или 0.
2) cos(2x—3) = 0, х = (26 4- 1) 4- у-
>6
Найдем допустимые значения k:
+ 0 <”—J.
— 4—1<2Й4- 1 <4 — 1, п	1	г.
__5 —1<2/г<3 — тс	к
5	3 , , , 3	3
	< £ <	, 2	я-2	к
— 3,5<.%<9,5, т. е. k = —3, —2, —1 и 0.
Задача имеет шесть решений (мы нумеруем их в порядке возрастания):
х, = —^4-1^—2,42699, х4== —-4--^0,71460, 1	4	2	4'2
ха •=—тс 4- 1 ~—2,14159, х5 = 1,
х, = — ^4-1^—0,85619, х6 = -4-1^2,22540.
3	4'2	4	2
73. Решить и исследовать уравнение tg2x = т(1 —cosx).
Решение. Обозначим cosx = g. Тогда данное уравнение запишется так:
1^- т(1 —у).
Далее:
1 — £/)( 1 + У) “ «У (1 — У), (1 — ^)(т^2 —£/—!) = 0,
откуда находим три корня:
,	1 + У1 + 4m“	1 — V1 +4m
Л-1- »“-------S----• а‘~-------5»---•
S7
Первый корень не зависит от т. Для существования двух Других решений требуется, во-первых,
l-j-4m^0, откуда т~^-------i-,
во-вторых,
т =У= 0.
Таким образом, мы пока получаем для т две области:
----С———— ।	/7?
-i IXV о ft)
Черт. 6
(Л) —- т < 0, (В) 0 «С m < оо (черт. 6).
В-третьих, необходимо, чтобы было | у2| < 1 и | у31 < ]. Исследуем каждый из этих корней в каждой из двух областей.
Это исследование облегчится, если мы перенесем иррациональность в знаменатель:
2	2
Уя г-------» Уз —	--------— •
У1+4/Л— 1	]Л1+4ш+1
Корень у2 в области (Л) отрицателен. Требуем;
— —— > — 1,
УТ + 4m -1
откуда У 1 +4т < — 1, что абсурдно. Поэтому уг в области (Л) не годится (т. е. не приводит к решениям для х). В области (В) у2 у- 0. Требуем:
4- 4m —1
откуда 1^1 Д- 4m > 3, 1 Д- 4m > 9, m > 2. Итак, уй годится при т^>2.
Корень у3 всегда отрицателен. Требуем:
у 1 + 4т +1
38
откуда 1^1 4- 4/72	1, 1 4- 4/72 > 1, tn > 0. Это условие
не соблюдается в области (Л) и соблюдается в обла-
сти (В).
Проделанное исследование можно было бы сократить, если бы заметить, что при /тг < 0 никакие решения, кро-
ме cosx = 1, невозможны (это видно непосредственно из
данного уравнения). Поэтому можно было бы не производить исследования корней у2 и ys в области (Л).
Ответ. Уравнение при всех значениях т имеет решение cosx = 1. При 0 < /тг < оо оно, кроме того, имеет
еще одно решение*: cos х
=	При 2 </72 <
о...	1
но, кроме упомянутых двух, имеет еще и третье решение: cos х = 1	1 + 4 —-. При т — 2 последнее
2т
решение совпадает с первым.
74. Решить и исследовать уравнение:
2 sec2 х — 3 sec х 4- а — 0.
75. Решить и исследовать уравнение: sin10x 4~ cos10x = а.
Решение. Обозначим у = cos 2х. Тогда данное уравнение запишется так:
Далее:
(1—i/)54-0 4-# = 32a, (l — 5i/4-10//2—10//34-5^—//5) +
4- (1 4- 5у 4- 1 Оу* 4- 1 Оу3 4- 5//4 + У6) = 32 а,
1	4- Ю//2 4~5//4 = 16с.
Обозначим z — cos 4х. Тогда
9	9 о 1 4- cos 4х 1 4- г
у* — cos2 2х — —----= —1—.
у	2	2’
и уравнение примет вид:
14_5(14-z)4-|(1 4-г)2= 16а,
* Под словами «одно решение» мы здесь понимаем одно значение cos х. Разумеется, оно приводит к бесконечной последовательности значений х.
39
или
5г2 + 30г+ 29—64а — О*, _ — 15 ± 41Л5 4- 20 а
2	~	5
Прежде всего должно быть 5 + 20а > 0, а >------ . Те-
4
перь исследуем каждое из двух значений г отдельно:
1	— 15-Р 41/5 4- 20а
1 С	5	С 1,
__ 5 < _ 15 4- 4/5 + 20 а < 5,
| <У К+20а <5,
- < 5 + 20а < 25, 4
— < а < 1 1при этом соблюдается и неравенство а> —М
4 /
Второе значение г заведомо отрицательно. Требуем:
 15 — 41^5 4- 20а >_]
5
15 + 4 /5 + 20а < 5. Это невозможно.
Таким образом, второе значение г при любом а не годится.
Ответ. Задача возможна при ^<а<1.
_ 15 + 4К5"+35а cos 4х >= --.
76.	Доказать, что уравнение 2х + sin 2х = при га>2
* Это уразнение можно получить быстрее, если воспользоваться формулами (IX. 5) и. (IX. 14). Сразу получим:
— (126 4- 120 cos 4х 4* Ю cos 8х) = а,
1 4- г
126 4- 120z 4- 10- —== 256а (г «= cos 4х)
и дальше, как в тексте.
40
имеет единственный корень; этот корень заключен меж-Ок
И
Решение. Перепишем данное уравнение так:
sin 2х = — — 2х. п
Рассмотрим графики:
у = sin 2х,
2я Q У =--------2х.
п
(а)
(Ь)
Линия (Ь)— прямая, отсекающая на осях X и Y отрезки соответственно — и ее угловой коэффициент равен—2.
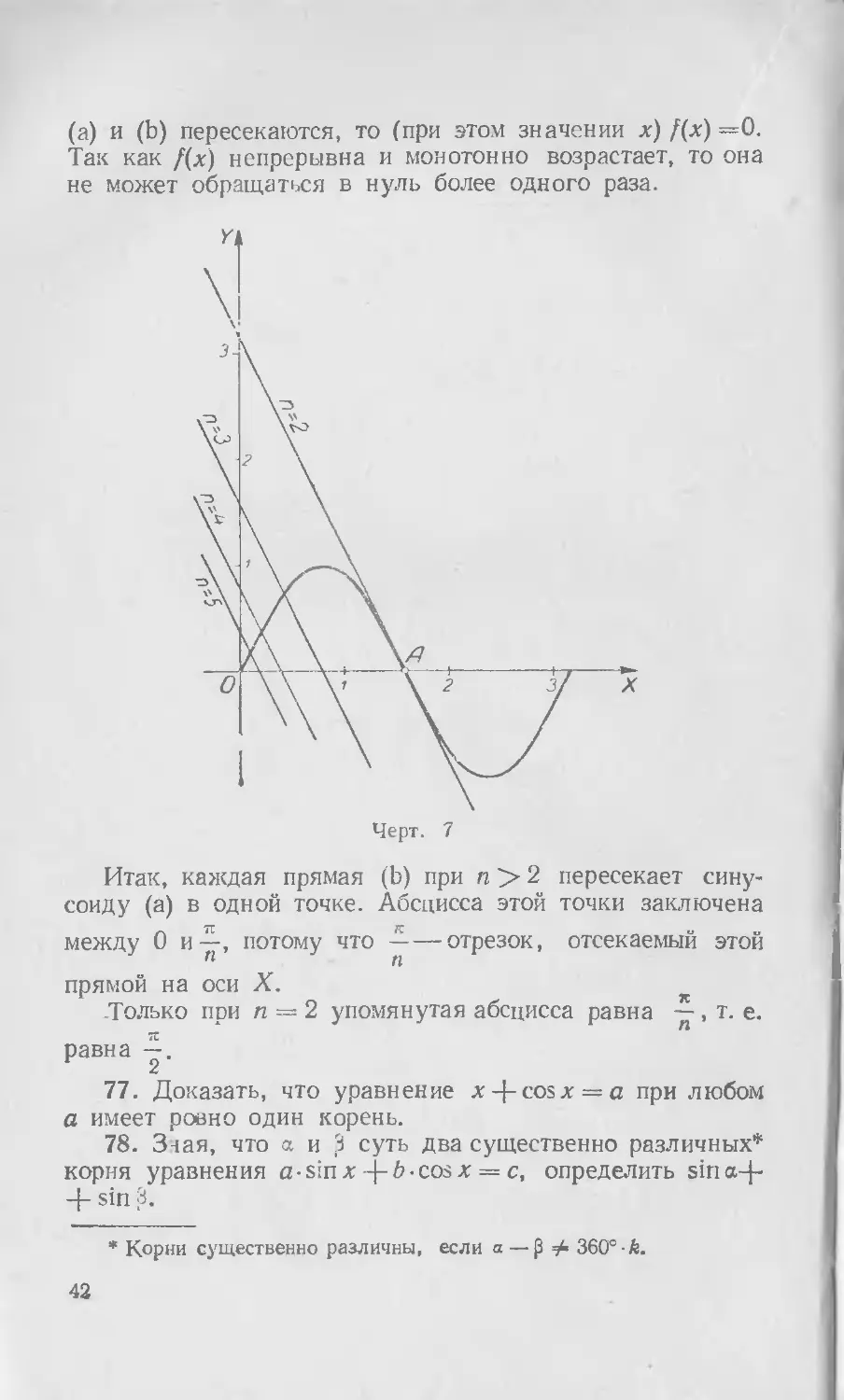
Линия (а)—синусоида. В начале координат ее угловой коэффициент равен 2, потому что при стремлении аргумента к нулю синус эквивалентен своему аргументу (их отношение стремится к 1) и, значит, 'угловой коэффициент p-=sin2x при х = 0 такой же, как у линии у = 2х. В точке , о) (черт. 7) угловой коэффициент равен — 2 (по симметрии). Прямая (Ь) при п = 2 тоже проходит через точку А I у, 0 j и имеет угловой коэффициент — 2. Следовательно, эта прямая — касательная к синусоиде в точке А.
Увеличивая п, мы будем получать прямые, параллельные этой касательной и расположенные ближе к началу. Ясно, что каждая такая прямая пересекает синусоиду в одной точке. Впрочем, это можно доказать аналитически. Рассмотрим функцию
f (х) =« sin 2х 2х — —
и вычислим ее приращение:
/ (х	Л)—/ (х) =- sin 2 (х h) — sin 2х 4- 2Л =
=- 2 sin h • cos (2х 4- h) 4- 2h.
Знак этого приращения совпадает со знаком h, потому что |sinft|< h\ и | cos 2 (х 4-А) |1 Значит, /(х) монотонно возрастает. Если при некотором значении х линии
41
(а) и (b) пересекаются, то (при этом значении х) f(x) =0. Так как /(%) непрерывна и монотонно возрастает, то она не может обращаться в нуль более одного раза.
Итак, каждая прямая (Ь) при п > 2 пересекает синусоиду (а) в одной точке. Абсцисса этой точки заключена между 0 Ир потому что ——отрезок, отсекаемый этой прямой на оси X.
.Только при п — 2 упомянутая абсцисса равна —, т. е. равна
77.	Доказать, что уравнение x-|-cosx = a при любом а имеет ровно один корень.
78.	Ззая, что а и 3 суть два существенно различных* корня уравнения а • sin х b • cos х = с, определить sin a-|--|- sin 3.
Корни существенно различны, если а — р => 360° -k.
42
Решение. По условию аир удовлетворяют данному уравнению, т. е.
a sin a-f-& cos а = с,
a sin р 4" cos р = с.	(*)
Вычитанием находим:
a (sin а — sin В) -р b (cos а— cos Р) — О, п .	а — 3 а -р 3	, „ . а — 8 . a -L 3	_
а • 2 sin ----L cos - — — b • 2 sin-------c sin —— = 0,
2	2	2	2
a — 3/ et —8	. . a 4- В \	„
sin-----L a cos —-i-4- — b sin —— I = 0.
2 \	2	2 /
Первый множитель отличен от нуля (потому что а—р =£ =# 360° k). Следовател ьн о,
а -р Р <  а -р Р п а cos —— —о sin —— ~ 0,
2	2
откуда
а + Р __ £ * ё 2 ~ b •
Сложение равенств (*) дает:
a (sin a sin р) -р b (cos а -[-cos р) = 2с.	(**)
С другой стороны, известно [см. формулы (Vll. 1) и (VII. 3)]:
cos а -р cos р	2
т. е.
sin я -р sin й _ а
cos а -Р cos Р b
cos а -|- cos р = — (sin а -|- sin р).
* Если бы было cos —с = 0, то следовало бы написать:
g-PP b
ct« —= 7
Окончательный результат был бы тот же самый.
43
Подставим это в (**):
(а (sin а 4“ sin ₽) = 2с, откуда
, . о 2ас Sin а 4- sin В =------.
1 г а2 4- Ь*
79. Решить уравнение:
sin (л cos х) — cos (я sin х).
Решение, sin(~cosх) — cos(itsinx) = 0.
Применим формулу (VII. 12):
/ П . К COS X + к sin х\	/ И , л COS X— KSinX
сое I 4' 4-------2------j cos I *4“ Н------2------
(л . л cos х 4-r sin х\ п __ _|--------_------> -0,
+ 4" (cos х 4- sin х) = 4“ 4- п
cos х 4- sin х «= 2n 4- ~,
1^2 sin 4~ = 2п 4~4“ [формула (VII. 13)]«
Возможные значения k определяются из неравенств:
-1</'2п + ^< 1, откуда
/2	1 .. п ./2	1
— 2	4 п ^2	4
приближенно
— 0,96 < п < 0,46.
Таким образом, для п возможно только одно значение: п = 0.
Поэтому	__
sin (4“ 4~ х ) —	~ 0,35355,
\ 4	' j 4
44
^--j-X = itk 4~(— 1)A <p, x=^(4fe-l) + (-l)ft?, где <p = arcsin ~ 0,3614, или в градусной мере
х = 45° (4k — 1) -J-(— 1 )ft<p, где ? = arcsin да20°42'.
2) — 4-у (cos x—sinx) =4~nz»
O ।	1
cos x — sin x = 2n -I-,
2
К 2 cos (— 4~ A' 1 = 2n -J-\ 4	/	2
cos (-Г +*) = lZ2n +Ц^-.
Как уже было выяснено, обязательно п = 0.
cos (+ х') =	~0,35355,
2&*±<р.
х =	(8&— 1) ± ср, где ср = arccos да 1,2094,
или в градусной мере
х = 45°(8А— 1) ± <р, где 9 = arccos^'69° 18\
Решить уравнения (№ 80—-84).
80. sinsinx = —0,8. 81. tgх2 = ctg5х.
Решение, tgx2—ctg5x = 0.
Преобразуем левую часть по формуле (VII. 18):
cos (х2 -| 5х) _ Q
cos №• sin 5х
45
cos (x® 4* 5x) — 0,
x®4-5x= ^-(2Л-Ь1),
2x2-i- Юх — тг (2/г1) = 0, — 5 ± /25 + 2k (2k + 1)
X -	2
Условие действительности:
25 4-2тг(2£-|-1)>0( откуда
k>------ — — % —2,5.
2 4п
Таким образом, k может принимать значения: £ = —2, —1, 0, 1, ...
5
82.	sin— = cos3x.
X
83.	esc2* — ctg2* = ИЗ.
84.	sinx = cos Их.
85.	Доказать, что уравнение sin (cos х) = cos (sinx) не имеет решений (действительных).
Решение, sin (cos х) — cos (sin х) = 0.
Преобразуем левую часть по формуле (VII. 12):
(я , cos х -t- sin х \ /к	. cos х — sin х
----k- —----!------I COS (---------------------
4 1	2	)	\ 4 1	2
. v / я , cos x +• sin x \ r,
1)	COS----------------J------I = 0,
\ 4 '	2 I
я . cos x + sin x
T"*	2

cosx -ф-sinx =	(46-J- !)•
И 2 sin I 4-x j = -|-(4n4~ !)•
46
Уже ясно, что это невозможно. Левая часть по абсолют-ной величине не более V 2	1,41, а правая часть по
абсолютной величине не менее —	1,57.
2
Аналогично доказывается невозможность равенства: п, I Я I cosx — sinx\ „ 2) cos---------------------------I = 0.
\ 4	2	)
86.	Доказать, что уравнение sin (sinx) = cos(cosx) не имеет решений (действительных).
87.	Решить уравнение: arccosх— arcsinх =
Решение. Присоединим к данному уравнению тождество (XI. 9):
arccos х arcsin х =
arccos х — arcsin х — 4Х. О
Сложением этих равенств находим:
arccos х = ~, О
откуда	х=
88.	Решить уравнение: arcsinх-f-arcsin -£=. = —. } 3	2
89.	Решить уравнение: arcsin 2х = 3 arcsin х. Решение. Введем обозначения:
arcsin 2х = а, откуда sin а = 2х, arcsin х = р, откуда sin р = х.
Данное уравнение запишется так: а = Зр.
Возьмем синус от обеих частей уравнения, используя при этом формулу для синуса тройного аргумента (V. 22):
2х = Зх—4х3, х(4х2 — 1) = 0, п	1	1
откуда Xj = 0, х2 = -g-, х3 =----g-.
47
Проверка обязательна, потому что, беря синусы от обеих частей уравнения, мы получаем уравнение, не равносильное данному. Проверка показывает, что все три решения удовлетворяют исходному уравнению.
Проверка была бы излишней, если бы мы предварительно установили область допустимых значений х:
---; 3 arcsin х <
7Г	.	ft
arcsin х —, 6	6
1 I
2 ' х 2 '
90.	Решить уравнение (найти х и п):
3 arctg (2 4- V 3 ) — arctgx = nit 4 arctg
91.	Решить уравнение:
arctg (х — 1)4- arctg х 4- arctg (х 4 1) = arctg Зх.
92.	Решить в целых числах уравнение:
arrtg х 4- arctg — = arctg 3.
У
Решение. Возьмем тангенс от обеих частей уравнения:
—=3, 1-2.
у xy-frl = з У — х
1 -рЗх Т----.
3 — х
или, выделяя из неправильной алгебраической дроби целую часть,
Q I 10
£/ = — 34
3-х
48
Теперь ясно, что целые решения могут получиться только в тех случаях, когда 3 — х есть делитель числа 10, т. е. ± 1, ±2, ± 5 и ±10. Рассмотрим восемь случаев:
1) 3 —х= 1,	х = 2,	У = 7,
2) 3 —х = —1,	х = 4,	У — —13,
3) 3 —х = 2,	х = 1,	У = 2,
4) 3—х = —2,	х = 5,	У = — 8,
5) 3 —х = 5,	х = —2,	у = — 1.
6) 3 —х = —5,	х = 8,	У~ — 5,
7) 3 —10,	х = —7,	
8) 3 —х = —10,	х = 13,	У — — 4.
Проверка должна только подтвердить, что arctg х±-arctg — заключено в интервале -------1-, -у); в про-
тивном случае левая часть не может равняться никакому арктангенсу.
Прежде всего заметим, что если числа а и b имеют различные знаки, то сумма arctg а -|- arctg b обязательно заключена в интервале -----В самом деле, пусть,
например, а>0, £><0. Тогда
0 < arctg а <
------< arctg b < 0,
откуда, складывая, получим:
— ~ < arctg а + arctg b <	.
Л	А
В силу этого замечания решения 2), 4), 6) и 8) годятся. Проверим остальные. Установим для каждого арктангенса, какой восьмушке он принадлежит:
1) -у < arctg 2 <-J-, 0 < arctg<-р
~<arctg 2 + arctg 4" < V ’ 4	7	4
4 Заказ 33
49
3) arctg 1 = — , 0 < arctg — < —, 4	2	4
-7 < arctg 1 + arctg-j- < Д-,
5)— v <arctg(—2)<—JL arctg(—1) = — —, z	4	4
afCtg (~~2) + arctg (—-!)<-Y’
7) — f < arctg (— 7) < —S — ~ < arctg (--------------Ц< 0,
2	4	4	\	2 /
3r
4
я
4
Из этой проверки видно, что решение 3) подтверждается, а решение 5) неверно. Для решений 1) и 7) вопрос остался нерешенным. Чтобы его решить, следует установить более узкие границы для рассматриваемых
арктангенсов, например от 0 до
К	Я	К	я
от — до от — до — .
6	3	3	2
Но и эти границы могут оказаться недостаточно узкими. Укажем два других способа, действующих безотказно.
Первый способ. Обратимся к таблицам:
1) arctg2^ 1,11, arctgу^0,14, arctg 2-[-arctg у ^1,25,
7) arctg(—7)	—1,43, arctg
arctg (— 7)	arctg — У ) ~
Таким образом, решение 1) верно, а решение 7) нет (вспомн им, ЧТО у 1
Проверка по таблицам может дать категорический результат лишь в тех случаях, когда проверяется неравенство. Если же требуется проверить точное равенство, то проверка по таблицам недостаточна.
50
Второй способ. Используем тождество: arctg а + arctg — — —:
а 2
1) arctg 2 -4- arctg у = у  arctg 1 < arctgy,
7) arctg 2 4- arctg = у, arctg 7 > arctg 2,
следовательно, arctg24-arctg | < y-
следовательно,
arctg 7 4- arctg у > y или arctg (—7)4-
4-arctg (—1) <-|
Итак, из найденных восьми решений верными оказались шесть. Нумеруем их заново:
Ответ. Xj = 2,	£/1 = 7,	х4 =	5,	£/4 = — 8,
*2 = 4,	у2= —13,	хБ =	8,	Уъ = — 5,
~ 1 >	Уз =	хв =	13,	Ув~ — 4.
93. Решить при помощи тригонометрической подстановки уравнение 2x1/1 — х2 = cos t.
Решение. Положим:
х = sin о,
Смысл ограничений для ср был разъяснен в решении задачи № 39. В силу этих ограничений
]/1 — х2 = cos ср
(двойной знак не нужен, так как cos ср ^>0) уравнение запишется так:
sin 2 ср — cos Л
Далее
sin 2 ср — cos / = 0,
~2cos(t + cp + 4) СО5(т + '?~’2) = °
и данное
[ форму-
ла (VII. 12)].
4*
51
Имеем две возможности:
a) cos ( 7 + + тП = °-
ср = k к -]- — 4- — ,
т	4	2
I • I Я I / \
X = Sin <р = + sin I - + — \,
Ь) cos^4-<p—у) =0.
Не повторяем выкладок, так как ясно, что равнин* только в знаке при t:
1 • Iя	/ \
х = + sin-------].
—	\ 4	2 )
Проверка вносит дополнительное ограничение: знак х должен совпадать со знаком cos/. Поэтому из двух знаков в полученных ответах в каждом данном случае должен выбираться только один, и всего получится два ответа.
Предостережем читателя от возможного недоразумения. Если, например, cos/ отрицателен, то это не значит, что в полученных ответах следует взять знак —перед синусом, а значит, что из двух значений + sin ( —	) следует
\ 4	2 /
выбрать отрицательное.
2rt	1
Пусть, например,/==—, cos/ =--------. Тогда
3	2
I я . t \	. 7к „
sin -------1 — sin----> 0,
\ 4	2 /	12
sin f —----== sin {---— 'i < 0.
\ 4	2 )	\	12 /
Следовательно, в этом случае ответы надо выбрать так:
Ответ, х = ± sin	; знак х должен совпадать
со знаком cos/.
Решить при помощи тригонометрических подстановок уравнения (№ 94 и 95).
94. 2 х = (1 + *2) sin “•
95. 2х = (1—x2)tga.
52
§ 5. СИСТЕМЫ УРАВНЕНИЙ
93. Решить систему уравнений:
(ху — а, |sin2x— sin2 у «= b.
Решение.
(sin х sin у) (sin x — sin y) = b,
_ . x 4- U	x — и n • x — и x # 4	l
2 sin—cos-------— 2sin ——— cos------ = b.
2	2	2	2
Группируя сомножители с одинаковыми аргументами, получим:
sin (х -j- у) -sin (х — у} — Ь,
но х-\-у^а. Следовательно,
sin(x —#) =	,
sin а
откуда можно найти х—у:
х — y = k^-]-(—1)*ср, где ср = arcsin—-—
sin я
Ясно, что решение существует лишь при условии
|6| < |sina|.
Теперь имеем:
х У = «>
х—^ = ^к4-(—1)*<р,
откуда
(х==5±А1+(_1)^.
2 f ’ 2
а — k it .	, чь <Р
У~—---------
В этих двух формулах k — одно и го же.
53
97.	Решить систему уравнений:
sin х- cos у = 0,36,
cos х- sin у = 0,175.
Решение. Сложим и вычтем данные уравнения:
sin (х 4- у) = 0,535, sin (х — у) = 0,185.
Откуда
x-j- у — 180° А? 4- (— 1)*где <р = arcsin0,53532° 21',
х — у— 180JZ -}-(—1)' ф,	где ф = arcsin 0,185	10е 40',
x = 9O°(fe + Q+'-i>>'' + <-'>''>.
0 + <- '>*?-	'>'» .
Эти ответы можно упростить. Разберем четыре случая: 1) k = 2 р, I = 2 q, 2)k = 2p, l = 2q-]-\, 3) k = 2p-]-l, l = 2q, 4) A>=2p4-1, / = 294-1.
Имеем соответственно:
1)	x = 90° (2p4-29)4-^, p = 90°(2p-29)4-^,
2)	x = 90°(2p4-294- 1)4-^,
y = 90°(2p-29-l)4-^,
3)	x = 90° (2p 4- 29 4- 1) -	,
p=90° (2p — 29 4-1) — *±i,
4)	x = 90° (2p29 4~ 2) —
y = 90°(2p-29)-l^.
54
Эти четыре случая можно записать экономнее, объединяя 1) с 4) и 2) с 3):
1)	х = 90° .	+	£/ = 90э.2п + ^,
>	— 2	~ 2
2)	х = 90° (2m + 1) ± ^=41 у = 90° (2n + 1) ±	.
В каждом случае знаки либо оба верхние, либо оба нижние.
Решить системы уравнений (№ 98—100).
98.	(sin 2х 4-sin 2у = 3 (sinx -j-sin^/), | cos 2x -f- cos %У= cos x + cos У-
99.	( 2sln * | 3sin v = 4,
| 22+siI1 x _5 gsin у____2
100.	x + y-\-z = 180°,
sinx : sin^/: sinz = 5 : 6 : 4^13.
Исключить x из системы уравнений (№ 101 —103).
101.	(sinx = а, (sin 2х = b.
102.	f cos x + sin x == a, 1 cos 2x - b.
103.	(x • sinx = m, I x  cos x = n.
104.	Исключить x и у из системы уравнений:
sinx-j-sin z/ = а, cos х cos у = b,
tg|-tgf = tg2|
55
Решение. Преобразуем сначала третье уравнение:
х . у	х — у *+ у а
sin — • sin —	cos-----— cos----- tg2 —
2	2 = tg8A	2___________2 = _^_2
x У K 2 ’ x — у x + y i ’ cosy . cos у	COS —y- + cos -y—
Образуем производную пропорцию по схеме: из — = — b d
а — b с — d следует ----- = ----,
а -р b с 4- d
X 4- у	а
— cos	tg2 — — 1
2	_ ь 2
X — у	а ’
cos------ tg2 — 4-1
2	6 2
ИЛИ
--------= COS а.
х— у	' '
cos-----
2
Теперь возведем каждое из первых двух уравнений в квадрат и сложим:
2 -|- 2 cos (х — у) = as b2,
1 cos (х — у) ==
о2 4- Ьг 2
о о х — у а3 + Ьг
2 cos8---- = ——— .
2	2
Перемножим (*) и (**):
о х + У х — у а3 -I- Ь3
2 cos —— cos-------- — ———
2	2	2

Левая часть этого равенства тождественно равна левой части второго из данных уравнений. Следовательно,
(а8 Ц- Ь2) cos а = 2Ь.
105. Исключить х и у из системы уравнений:
' х-]-£/ = а, sinx • sin у — а, cos х • cos у — b.
Б6
§ 6. СУММИРОВАНИЕ РЯДОВ И СВЕРТЫВАНИЕ ПРОИЗВЕДЕНИЙ
106. Суммировать:
sin а -j— sin (а h) -j- sin (л 2h) —. -j- sin (a -j- nh).
Решение. Первый способ. Для суммирования конечного ряда
sn == Ul + Ы2 4*  • • 4" ип
иногда удается применить следующий способ. Подберем так называемую производящую функцию, т. е. функцию, обладающую следующим свойством:
f(k+\)-f(k)~uk.
Придавая k последовательно значения 1, 2, 3, . . п, получим:
/(2)—/(1) = «t, /(3) —/(2) = /(4) -/(3) = и3,
/(«)—/(«— 1 )=«„_!, /(« + !)—/(«)=«„.
Сложим эти равенства. В левых частях некоторые члены взаимно уничтожатся (как показано на схеме), а в правой части получится искомая сумма:

При решении разных задач встречаются многочисленные модификации приведенного хода выкладок.
В данной задаче можно исходить из формулы
= — 2 sin (а kh) • sin .
57
Придавая k значения О, 1, 2...п, получим:
cos / а 4- yj — cos
= — 2 sin а . sin — , 2
/ , 3h\	! . ft \
cos | а н---— cos а 4--------|
\	2 /	\ 1 2 /
— 2 sin (a 4- h)  sin ,
I । 5/i\	/	. 3ft\ n . . i	. h
cos | a.4- —j —cos + “ ) = — 2sin (a 4-2/i) . sin — ,
/	. 2n 4- 1 , \	/	. 2n — 1 \
cos a 4-------5— h | — cos a 4-------=
\	2	)	\	'	2 J
= — 2 sin (a 4- nh) • sin у .
Сложим эти равенства:
/	. 2м -|^ 1 < \	/ h \ n • h
cos a 4-------Л — cos a----------| = — 2s„ • sin — ,
\	2	/	\	2 I "	2
где через sn обозначена искомая сумма. Левую часть преобразуем в произведение:
о-/	, п, \	. п 4- 1 , n . h
— 2 sin a 4--h • sin —— h = — 2 s_ • sin —,
\	1 2 J 2	n 2
откуда
Второй способ. При суммировании синусов или косинусов, аргументы которых образуют арифметическую прогрессию, можно использовать тот факт, что каждый синус или косинус входит в состав показательной функции:
el<t = cos <р 4- i sin <р.
Вместо того, чтобы суммировать данные синусы или косинусы, можно суммировать соответствующие показательные функции. Они образуют геометрическую прогрес
58
сию. От полученной суммы следует отобрать действительную часть, если требуется найти сумму косинусов, или мнимую часть*, если требуется найти сумму синусов.
В данной задаче следует рассмотреть геометрическую прогрессию:
У* _j_ el(,+h)	е>(с+2Л)	(# )
знаменатель которой q = elh. Сумма геометрической прогрессии вычисляется по формуле:
S . Ml-?") "	1 — я
где п—число членов. В прогрессии (» ) число членов равно n-j- 1. Следовательно,
ei°[l et(n+i)*j
Следует преобразовать Sn к виду А 4- IB (А и В действительны). Укажем на один удобный способ преобразования выражения вида 1 ± eif. Это выражение следует
умножить и разделить на е 2 :
if е 2 — е 2
е =-------------—
Теперь используем формулы Эйлера (XIII. 4) и (XIII. 5): е1х = 2 cos х,
е ix—eix = _ 2/.sinx.
«Мнимой частью» называется коэффициент при I.
59
Подставим это в выражения для 1 ± е1*'.
1 + е‘* = 2е2 cos—, 2
1 —et,f » — 2i • e 2-sin — 2
Вернемся к выражению для S„: t(n+i)h (п4-1)й _ e ,e(— 2i)e 2 sin 2 
e 2 (— 2t) sin 2 nft\ sin (n + 2 /	2	_
(6)
Ряд ( * ), сумму которого мы нашли, может быть ааписан так:
[cos а 4“ i sin а] + [cos (а А) 1 sin (а 4 А) .
[cos (а nh) 4~ i sin (а -|- nh)].	(*)
Приравнивая отдельно действительные и мнимые части выражений (*) и (**), получим:
cos а -|- cos (а 4- A) -f- cos (а 4* 2А) 4~ • • • 4~ cos (а 4~ nh) = / nh\ п +1 cos I a -f- -g I. sin —g—ft
sin—
2
sin а 4- sin (a 4~ h) 4- sin (a -f- 2A) 4- • • • + sin (a 4"=
/ nh \ n 4-1 sinh + — -sin------h
\	2 /	2
h sin — 2
Примечание. Полученные решения теряют силу при sin у = 0, т. е. 1г — 2Ак. В этом случае возможны два способа суммирования.
60
Пер вый с п о с о б — непосредственное обращение к данной сумме. Все члены этой суммы при h — 2 kr. одинаковы, и мы получаем:
sina-|-sina -f- ... 4~sina == (п -ф- l)sina.
Второй способ—предельный переход в общей формуле. Этот способ сложнее, но он поучителен. Обозначая
h — 2kn = t, h = 2k"K-\-t, получим:
/ nhx . п + 1
sin I a 4-	I -sin —2— "
lim ----------4----------=
Г n(H2h)l . (« + l)(/ + 2Att) sin а +---2-- sln------2
= lim —----------v---y—-----------
1"°	sin I kr. + ~2 I
sin
= lim —
\
(n + 1)^.1 4- {n -2
sin
Заметим, что
sin (m к -j- x) == (— l)m sin x
.	! nt\ . 014-1)* (n 4- 1) t
(—l)nft sin a-p у )(—1) + Sin--------2----
...=lim-------------------------------------------
‘"°	(-l)ftsin'2
Предел второго множителя в квадратных скобках таков: sin (» + l)L
1Ш1-------(л+1)*.
' и sin —
2
* Способ для нахождения таких пределов показан в решении задачи № 139.
в1
Поэтому окончательно получим:
lim sin/a_Lnf)
<-0	\
(п+ 1)/ -| 2
= (n -f- l)sina.
107.	Суммировать:
sin a -f- sin 2a sin 3a -]-••• + sin n °-
Решение. Эта задача может быть решена теми же способами, что и предыдущая. Кроме того, можно сразу получить ответ, рассматривая ее как частный случай предыдущей. Для этого надо в предыдущей задаче положить a = 0, а букву h заменить на а. Получим:
sin а sin 2а -f- sin За sin па =
 па . (л-М)а
Sin— -Sln3—!—L_
2 2
а SIH— 2
О случае, когда sin Д = 0, см. примечание к решению предыдущей задачи.
108.	Решить уравнение:
sin х -|~ sin 2х -]-.. .-|~ sin пх = cos х -|~ cos 2х -|~.. .-f- cos пх.
109.	Суммировать:
sina -|~ sin ( а — ^4- sinf a 4- —	. .4-sin[ a 4- <п~”
\ n J \ n J	I 2
110.	Суммировать:
sin a. sin 2asin 2a• sin 3a -|~ sin 3a-sin 4a -f-... .. . -|~sinna• sin (n-|~ l)a.
Решение. Каждый член ряда преобразуем
мощи формулы (VIII. 2):
sin a-sin 2a =« у (cos a — cos 3a),
при no-
sin 2a • sin 3a = -i-(cos я — cos 5a),

sin За.sin4a = -i (cos a — cos 7a),
sinnx-sin(n -|- 1)
cos a — cos (2n —}— 1) a
Заметим, что
cos 3a -|~ cos 5a -|~ cos 7a cos (2n -f- 1) a =
_ cos(n -f- 2)-/-sin ni sin a
(это легко получить любым из способов, изложенных в решении задачи 106). Сложим равенства ( * ):
sin a-sin 2a -|~sin 2a. sin 3a -f~ sin 3a-sin 4a -f-...
,	• /	। i\ 1 Г	cos (n 4- 2) a.sin nil
... 4- sin na • sin (n 1) a = — In • cos a---—— '----------
—	v —	2 L	sin a J-
111.	Найти частную сумму ряда: tga + y	+
Доказать, что этот ряд сходится, и найти его полную сумму.
Решение. Будем исходить из следующего легко доказываемого тождества [формула (VII 20)j:
tg х = ctg х — 2 ctg 2x.
Преобразуем no этой формуле члены данного ряда: tg a = ctg a — 2 ctg 2a,
1 . a
2 g 2
|Ctgt” Ctga’
1 ,	a	1	, a	1	, a
— tg — = — Ctg--------------ctg —
4	4	4	4	2	2
1 , a _______ 1	, a	1	,	3.
2rt ® 2n 2n ” 2n	2tl—1	2n—1 *
63
Складывая эти равенства и замечая, что некоторые члены взаимно уничтожаются, как показано на схеме, получим:
s« = ^ctg^-2ctg2a- (*) Формула (*) требует двух оговорок. Во-первых, а (2k	1) 2т~' л
(k— произвольное ц^лое, т = 1,2,3,... ,п).
При несоблюдении этого условия член ряда, имеющий номер т, лишился бы смысла. Во-вторых, а =£ О, потому что при а = 0 тож
дества, при помощи которых мы преобразовывали члены ряда, теряют силу.
При п —» оо первый член правой части формулы представляет неопределенность вида 0-оо. Эта неопределенность раскрывается следующим образом:
потому что Пт=. 1; в данном случае х = ^.
Отсюда следует, что данный ряд сходится и его полная сумма такова:
s= lim s„ = -----2ctg 2а
n— •»	“
[a =/= О и a (2k -|~ 1) 2" n, где k — любое целое, ап — любое натуральное].
112.	Суммировать:
___ я . Зя , 5я . 7л , 9л ,	11л
cos —В cos —В cos - 4- cos —В cos —В cos —.
13	13 1	13 '	13	13^	13
61
Решение. Эта задача может быть решена теми же двумя способами, что и задача № 106. Не повторяя их, укажем третий способ. Числа, фигурирующие в условии этой задачи, возникают при извлечении корня тринадцатой степени из —1. Обозначим г=1р/Л— 1 . По известной формуле для извлечения корня из комплексного числа
z = 1у/Г— 1 = cos ~ -f- i sin tz =
л 4- 2/гл I • • я + 2йл = COS  !------Н I sin —!.
13	13
13/--т
И — 1 имеет тринадцать различных значении; они получаются из последней формулы при k = 0, 1,2.........12:
= cos---kz - sin— ,
°	13 1	13
OK .	. .OK
Z, =- COS--И I • sin — ,
1	13 1	13
Z2= COS-----1- I . sin- ,
13 1	13
zon . .	. гол
Z.o = COS---p I  sin----- .
13	13
Известно, что сумма всех значений а равна нулю:
20 ~Ь 21 + 22 + • • • 4* 212 = 0.
Следовательно, и сумма действительных частей от этих чисел равна нулю:
л	.	Зл ,	5л	,	7л	।	9л	.	Пл	।
COS---1- COS---Р COS-------Р COS----р COS-----1- COS-----P
13	1	13 1	13	1	13	1	13	1	13
।	.	15л ,	17л .	19л .	21л .
Ч- cos л Ч- cos-----1- cos —• 4- cos---P cos---------P
13 1	13 1	13 1	13 1
i 23л .	25л	,
4- cos-------P cos--= 0.	(*)
1	13	13	’
Теперь заметим, что члены, равноудаленные от концов, равны между собой. В самом деле,
cos (л -j- а) = cos (л — а).
5 Заказ 33
65
Придавая в этом тождестве а значения — , — , ... ,
-у , получим:
15л cos	 13	= cos	11л 13
17л		9л
cos		= cos	_——
13		13 ’
19л		7л
cos		= cos	—
13		13 ’
21л		5л
cos —	= cos		 _
13		13
23л		Зл
cos		= cos		
13		13 ’
25л		тг
cos		— cos	—
13		13 ‘
Учитывая эти равенства, можно переписать равенство (*) так:
(л	,	Зл ,	5л	,	7 л	. 9л	,	11л\
COS----к COS н COS-----------н COS-----1- cos —- 4- cos —-
13	1	13 1	13	13	13	1	13/
— 1= 0,
откуда
л	.	8л	,	5л .	7л	, 9л ,	Пл	1
cos------н cos----н COS------Н COS----4 cos-----Н cos-= —
13	1	13	1	13 1	13	13 1	13	2
113. Суммировать:
л	2л	,	Зл	.	,	пл
cos -г- 4- cos -г- 4- cos -г- 4- ... 4- cos---.
k	1 k	1	k	1	1	k
114. Доказать:
arcctg3-|~arcctg5... + arcctg(2nД- 1) = = arctg 2 4- arctg у 4- ... 4- arctg -^±2-Д1
66
Решение. Заменим арккотангенсы в левой части доказываемого тождества арктангенсами по формуле:
arcctg х = arctg —
при условии х > 0 .
= Т’
и запишем это тождество так:
(1 \	/	з
arctg 2 — arctg — I + I arctg --arctg
3 /	\	2
... + (arctg n + 1 —arctg- 1 I 1 \ ь n	a 2n + 1 j
По формуле (XI. 32): (в данном случае х>0 и г/ > О, так что условие ху~>—1 гарантировано):
fe+ 1 1
arctg 1 — arctg —1— = arctg----------1 =
k ° 2/г 4 1	6	, й + 1
1 +--——
k (2k -f- 1)
, 2/г2 )-2fe-[ I , , к = arctg---------- = arctg 1 = —.
2/г2 4- 2/г 4 1 s 4
Таким образом, каждая из скобок в левой части равенства (**) равна ~, а число скобок равно п. Тождество доказано.
* 115. Свернуть произведение:
cos а • cos 2а • cos 4а • ... .cos2"-1a.
* 116. Найти предел произведения:
а	а	а
cos — cos — cos  . . .
2	4	8 § *
§ 7. ГРАФИКИ
Построить графики (№ 117 и 118).
117. 1) у = |sinx|,	2) j/ = |cosx|.
118. 1) r/ = x-|-sinx, 2) £/ = x-|-cosx.
119. Построить график у = х • sinx.
5»
67
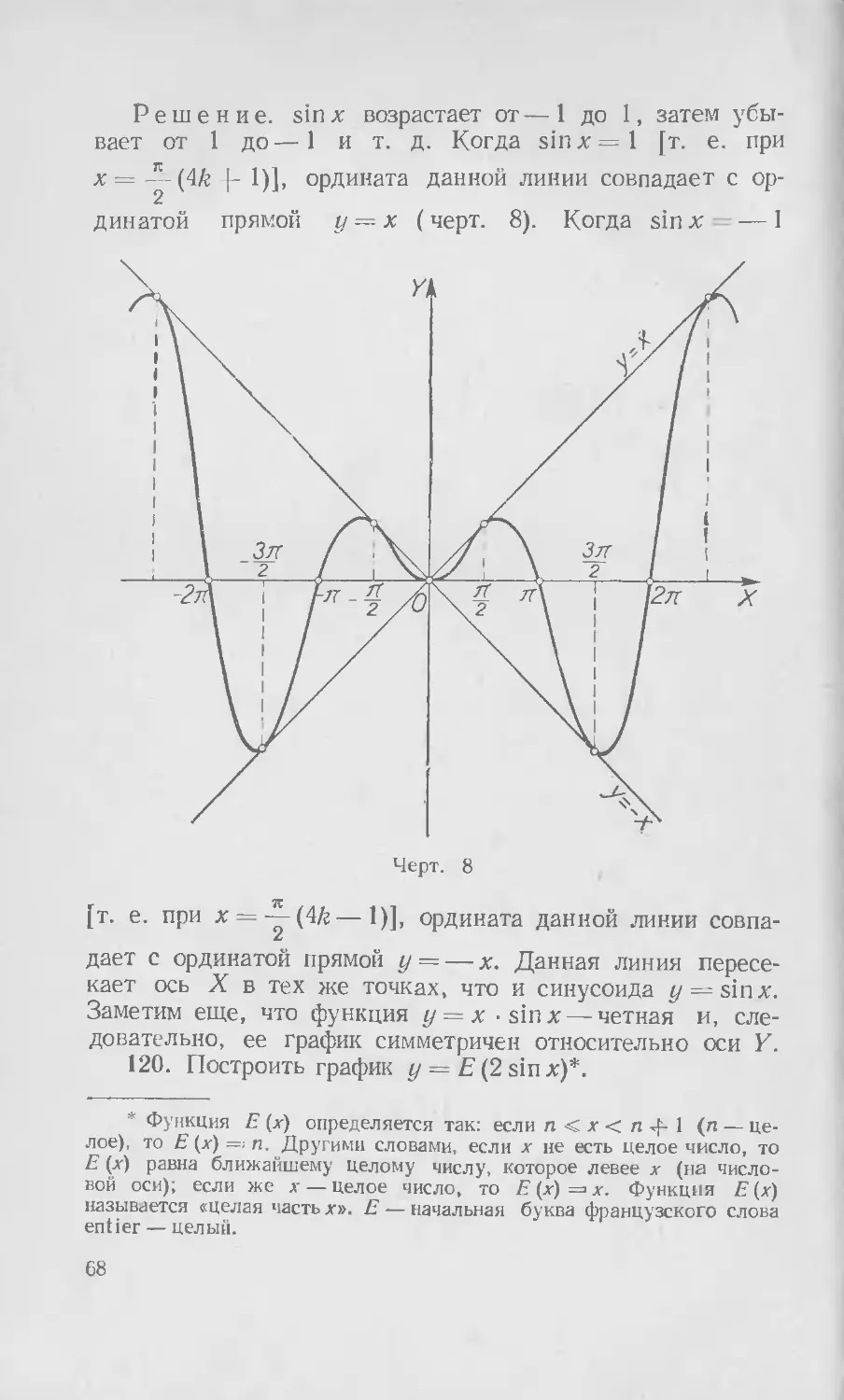
Решение, sinx возрастает от—1 до 1, затем убывает от 1 до—1 и т. д. Когда sinx=l [т. е. при х = — (4й ф- 1)], ордината данной линии совпадает с ординатой прямой у — х (черт. 8). Когда sin х — 1
[т. е. при х = -|-(4Л— 1)], ордината данной линии совпадает с ординатой прямой у — — х. Данная линия пересекает ось X в тех же точках, что и синусоида у — sinx. Заметим еще, что функция у — х •sinx —четная и, следовательно, ее график симметричен относительно оси V.
120.	Построить график у — Е (2 sin х)*.
* Функция Е (х) определяется так: если по< л 4- 1 (л — целое), то Е (х) =i п. Другими словами, если х не есть целое число, то Е (х) равна ближайшему целому числу, которое левее х (на числовой оси); если же х — целое число, то Е (х) = х. Функция Е (х) называется «целая частьх». Е — начальная буква французского слова entier — целый.
68
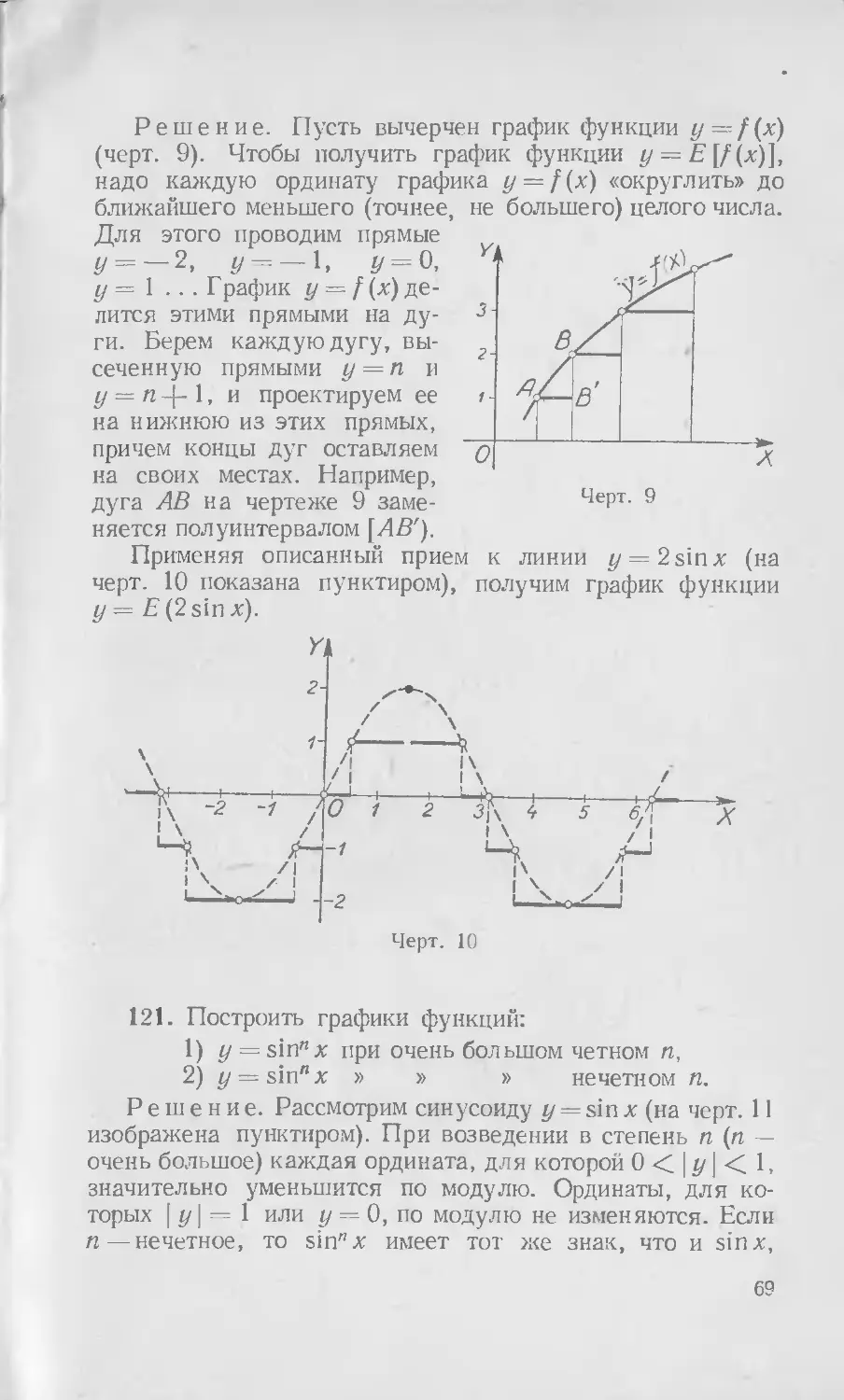
Решение. Пусть вычерчен график функции y—f(x) (черт. 9). Чтобы получить график функции у = Е [/(х)], надо каждую ординату графика у = f(x) «округлить» до ближайшего меньшего (точнее, Для этого проводим прямые z/ = —2, у = — 1, f/ = 0, у = 1 .. . Г рафик у = f (х) делится этими прямыми на дуги. Берем каждую дугу, высеченную прямыми у = п и у = п	1, и проектируем ее
на нижнюю из этих прямых, причем концы дуг оставляем на своих местах. Например, дуга АВ на чертеже 9 заменяется полуинтервалом [АВ').
Применяя описанный прием к линии у = 2sinx (на черт. 10 показана пунктиром), получим график функции у=Е (2 sin х).
Yk
Черт. 10
121.	Построить графики функций:
1)	у = sin”x при очень большом четном п,
2)	z/ = sin"x »	»	» нечетном п.
Решение. Рассмотрим синусоиду у = sin х (на черт. 11 изображена пунктиром). При возведении в степень п (п — очень большое) каждая ордината, для которой 0 < | у | < 1, значительно уменьшится по модулю. Ординаты, для которых | у\ = 1 или у = 0, по модулю не изменяются. Если п—нечетное, то sin"x имеет тот же знак, что и sinx,
69
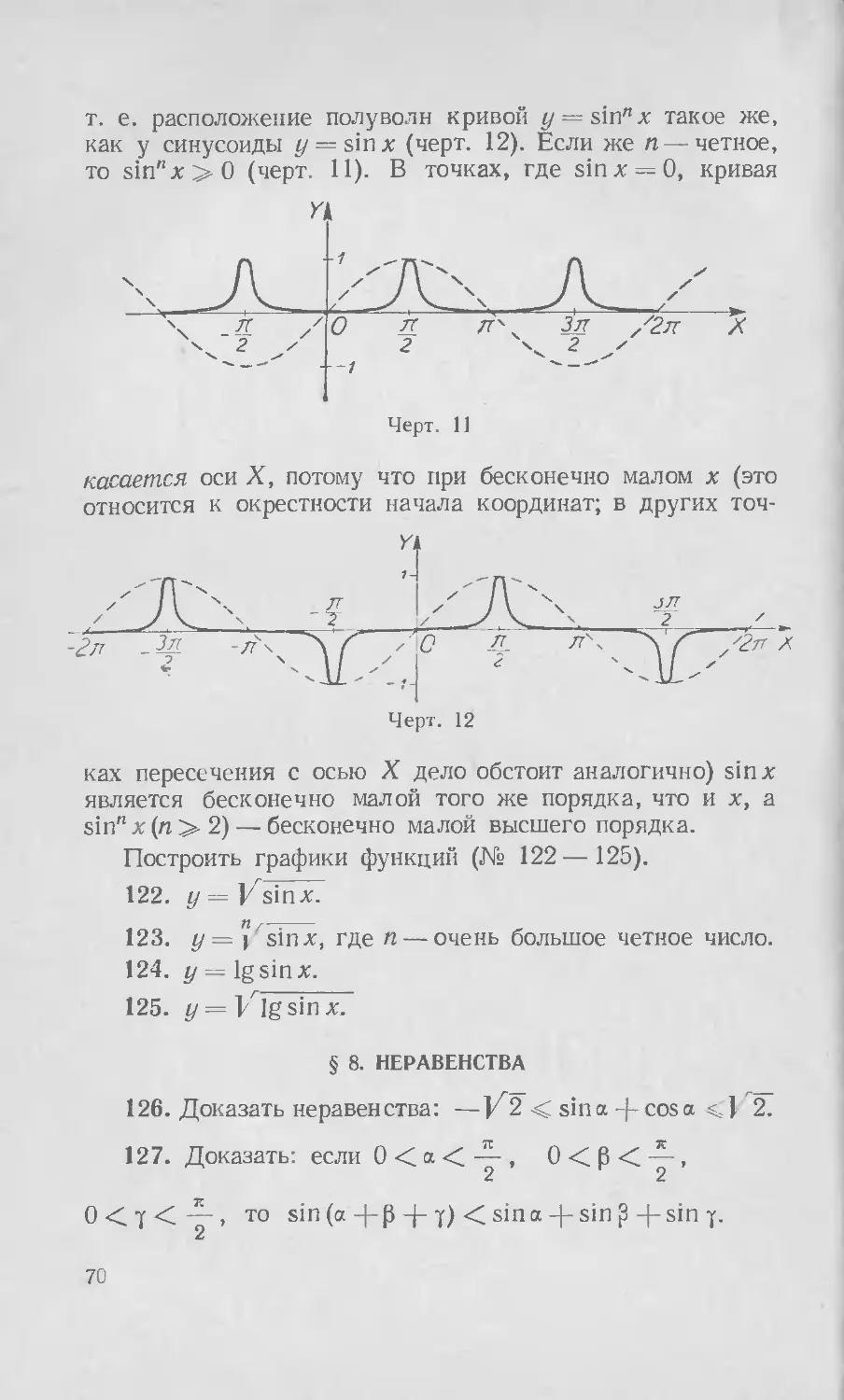
т. е. расположение полуволн кривой z/ = sin”x такое же, как у синусоиды z/ = sinx (черт. 12). Если же п — четное, то sin"x>0 (черт. 11). В точках, где sinx = 0, кривая
касается оси X, потому что при бесконечно малом х (это относится к окрестности начала координат; в других точ-
ках пересечения с осью X дело обстоит аналогично) sinx является бесконечно малой того же порядка, что и х, а sin" х (п > 2) — бесконечно малой высшего порядка.
Построить графики функций (№ 122 — 125).
122.	у = Ksinx.
123.	z/ = jzsinx, где п — очень большое четное число.
124.	у = Igsinx.
125.	у = j/lgsinx.
§ 8. НЕРАВЕНСТВА
126.	Доказать неравенства: —V2 < sina -ф-cosa «Л 2.
127.	Доказать: если 0 < a <	, 0 < 0 < -у,
0<т<—, то sin (a -ф-0 + l) < sina -|—sin 0 -ф-sin у.
70
Решение. Будем исходить из формулы (IV. 9): sin (а + р -|- 7) = sin а • cos 0 • cos 7 -[- cos а • sin p • cos у -f--}- cos а  cos p • sin у — sin а  sin p • sin 7.
Во-первых, отбросим последний член в правой части. От этого правая часть увеличится (все сомножители положительны).
Во-вторых, заменим все косинусы единицами (как видно из условия, каждый косинус строго меньше единицы). От этого правая часть увеличится.
Итак, при 0 < а <.	, 0 < р <	,
О
1
Я
sin (а -ф- р -ф- 7) < sin а sin р -ф sin 7.
128.	Решить неравенство: sin х -ф cos х > 0.
Решение. Преобразуем левую часть в произведение [формула (VII. 13)]; множитель ф^2 сокращается:
sin (45° + х) > 0,
откуда
360° £ < 45° + х < 360% -ф-180°,
360° k — 45° < х < 360% + 135°,
45° (8k — 1) < х < 45° (8k + 3).
«-F
129.	Решить неравенство: 5 sin2 х 3 sin х — 1<0.
130.	Определить значения а(0<а< 180°), при которых квадратное уравнение относительно г
2z2 cos2 а — 4z cos а -ф 4 cos2 а — 1=0
имеет действительные корни. Определить знаки этих корней.
Решение. Вычислим дискриминант данного квадратного трехчлена:
D = (2 cos а)2 — 2 cos2 а (4 cos2 а — 1) = 2 cos2 а (3 — 4 cos2 а).
Корни уравнения действительны и различны, если D> 0.
Это приводит к условиям:
3 — 4 cos2 а > 0, cos а =у= 0.
71
Условие cosa =£ 0 должно соблюдаться во всяком случае (а не только для того, чтобы корни были действительны и различны), так как при cosa = 0 данное уравнение принимает вид: — 1=0.
Итак,
cos2 а < —, cos а #= 0, 4
.	, , Уз	„
I cos а I <	, cos а #= О,
Уз , /Уз- , п
-— < cos а < —— , cos а 0, 2	2
30° < а <150°, а #=90°.
Допустим, что корни действительны, и исследуем, при каком условии они разных знаков. Для этого свободный член должен быть отрицателен (поскольку старший коэффициент данного уравнения положителен):
4 cos2 а — 1 < 0, cos а =£ 0,
cos2 а < — , cos а #= 0,
4
| cos а | < -i-, cos а =/= 0, откуда
60°<а<120°, а #=90°.
Констатируем, что этот интервал находится внутри интервала (30°, 150°), в котором корни действительны. В остальной части интервала (30°, 150°) корни имеют одинаковые знаки. Выясним, какие именно. Сумма корней такова:
।	2
2i + 22--------•
COS а
В интервале (30°, 60°) cosa>0 и оба корня положительны. В интервале (120°, 150°) cosa<0 и оба корня отрицательны.
Результаты этого исследования представим графически (черт. 13). Жирным показаны интервалы (значений а), в которых корни (Zj и z2) действительны и различны.
В интервале АВ оба корня положительны.
72
В интервалах ВС и CD корни имеют разные знаки. При переходе а через точку С корни обмениваются знаками. В самой точке С уравнение теряет смысл.
А	В	С	D	Е
--1--1 «а	I	»	।	» ।---1--
О"	30°	60°	90°	120°	150°	1В0°
Черт. 13
В интервале DE оба корня отрицательны.
В точках В и D один из корней обращается в нуль.
В точках А и Е корни действительные совпадающие.
§ 9. ПОВЕДЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
131. Какие из следующих функций являются периодическими и каков их период?
1) sin3x, 2) cos у, 3) cos~x, 4) cos2 *x, 5) sin®x, 6) sinx2, 7) cos J' x.
Решение. Непосредственно ясно, что первые три функции периодические. Их периоды соответственно:
Т. = - , 72 = 2-= 5-, 1	3	2_
5
Четвертая и пятая функции
В этом можно убедиться из формул (IX. 1) и (IX. 15):
Та = - = 2.
тоже периодические.
cos2 х = — -4- — cos 2х; Т. = — = 2'2	2
sin® х = — sin х-------- sin Зх; Т. = 2~.
4	4	5
В самом деле, первый член
/ 3 .	’
— sin х
\ 4
Второй член
----- sin Зх 4
имеет период
имеет период 2тс.
2п
—, но всякое
2 kx
кратное этого числа, т. е. ---, тоже служит периодом.
Таким образом, 2- есть общий (и притом наименьший общий) период этих обоих членов.
Шестая и седьмая функции не периодичны. Покажем на примере шестой функции, как это доказать.
Допустим, что функция /(x) = sinx2— периодическая. Это значит следующее: существует число Т, отличное от нуля и не зависящее от х, для которого удовлетворяется равенство:
/(% +Л = /(*)
Это равенство тождественно относительно х. Для данной функции
sin х2 = sin (х -ф- Г)2,
— 2 sin	cos (у -ф- хТ -|-x2j = О,
откуда
либо----\-хТ — RM, либо----\- XI 4-Х =----Р k~.
2 1	2	2
Эти равенства не определяют числа Т, удовлетворяющего перечисленным условиям (Т =# О, Т не зависит от х).
132. Исследовать на возрастание и убывание функцию:
у = 6 cos2 х — 5 cos х -f-1.
Решен и е. Запишем данную функцию при помощи цепочки:
у = 6z2 — 5z 4-1, г = cos х.
Сформулируем несколько положений, которые бывают полезны при исследовании поведения функций:
1. Любая функция от периодической функции — периодическая (с тем же периодом).
Поэтому у является периодической функцией от х с периодом 360°. Учитывая это, мы ограничимся исследованием данной функции на отрезке [0; 360°].
2. Монотонная функция от монотонной функции — монотонная. Подробнее:
возрастающая от возрастающей — возрастающая, возрастающая от убывающей —убывающая,
74
убывающая от возрастающей —убывающая, убывающая от убывающей — возрастающая.
Таким образом, если имеем сложную функцию yfz(x)], то изменение ее поведения (переход от возрастания к убыванию или от убывания к возрастанию) может происходить в следующих точках:
1) если х— граница интервалов монотонности z(x), 2) если г(х) — граница интервалов монотонности у(г). Если при некотором х одновременно выполняются условия 1) и 2), то это значение х не есть граница интервалов монотонности у [г(х)].
Наконец, отметим следующее положение, хорошо известное из школьного курса алгебры:
3. Квадратный трехчлен ах2 -ф- Ьх -ф- с имеет экстремум при х =------. Если а > 0, то
2а
,	. b	с-
при — оо < х <-----трехчлен убывает,
2а
b ,	.
при-----< х < оо	» возрастает.
2а
Если а < 0, то дело обстоит наоборот.
В данной задаче квадратный трехчлен
f/ = 62® —5г+1 имеет минимум при
2 = —~ 0,41667.
12
Обозначим:
<р = arccos — ~ 65° 23'.
т	12
Для наглядности обратимся к следующему чертежу, на котором изображена косинусоида 2 = cosx (черт. 14).
Черт. 14
75
На этом чертеже изображена (пунктиром) прямая у = —.
Она пересекает косинусоиду в точках, для которых cos х = _5
— 12
Для точки А х = <р 65° 23'.
Для точки В х = 360° — ф ~ 294° 37'.
Для всех точек, лежащих ниже пунктирной прямой,
г < — и, следовательно, у (г) = 6г2 — 5г -ф- 1 убывает.
Для всех точек, лежащих выше пунктирной прямой,
г > ~ и, следовательно, у (?) = 6г2 — 5г + 1 возрастает.
Теперь ясно:
Интервал	!/(2)	z(x) = COS X	У [г (*)]
(0,<р)	возрастает	убывает	убывает
(?, 180°)	убывает	убывает	возрастает
(180°, 360° —Д	убывает	возрастает	убывает
(360° — ?, 360°)	возрастает	возрастает	возрастает
Полезно еще вычислить значения у [z(x)J на границах интервалов монотонности:
при	х = 0,	2=1,	f/=2, 5	1
X = <р,	2 = 	, У = 		, 12	24
х = 180°,	г = —1, £/=12,
х = 360°—ф,	5	1 2 = 		, У =	, 12	24
х = 360°,	2=1, у =2.
Теперь окончательный ответ может
ван так:
быть сформулиро-
при 0 < х < 7
» <р х <1 180°
у убывает от 2 до------------—
24 ’
» возрастает » —	»'12,
76
при 180° < х < 360° — <р у убывает от 12
до------
24
» 360° — f < х < 360° » возрастает » —~	»	2.
В заключение даем график функции у = 6 cos2x— —5 cos х -ф- 1 (черт. 15).
Примечание. Читателю могут показаться противоречивыми утверждения, что на интервале (0,<р) у(г) возрастает, а У 1г ДО] убывает. Разве у (г) и у [z (х)] не есть одна и та же функция?
Под у (?) мы понимаем функцию у (г) = 6г2 — 5z + 1, где z — независимое переменное. Утверждение, что у (?) возрастает, подробнее формулируется так: если г возрастает, то и у (г) возрастает, а если г убывает, то и У (2) убывает. При этом мы не утверждаем, что г обязательно возрастает (или убывает), поскольку z — независимое переменное.
Под у [z (х)] мы понимаем функцию у = 6 cos2 х — 5 созхф-+ 1, где х — независимое переменное. Если х возрастает от 0 до 9, то z = cosx обязательно убывает, а, следовательно, у [г (х)] тоже убывает.
Короче говоря, утверждение «у (г) возрастает», значит,
возрастанию г соответствует возрастание уу>. Утверждение же «г/ [z (х)] «убывает», значит, «возрастанию х соответствует убывание уи. Эти утверждения не противоречат одно другому.
133.	Исследовать на возрастание и убывание функцию у — 2 sin2 х -]— 8 siп х —3.
134.	Доказать, что при возрастании х от 0 до — функция у = х — sin х возрастает.
Решение. Если//(х) = х— sinx, то у(х-ф-h) = х-ф--ф- h — sin (х -ф- h). Следовательно,
77
y(x-\-h) — y(x) = /г —sin(xft)sinx =
,	• h	I	t	h\	o Г Л	; h	I	, h \1
= ft — 2sin — cos хЦ-I = 2----sin—• cos x-4-.
2	\	'	2	[2	2	\	2/J
Если x и x-\-h принадлежат интервалу ^0, -|-)ий>0, то выражение в квадратных скобках положительно, потому что
h . h	I \ h \ л
— > sin —, a cos хч---------< 1.
2	2	\	' 2 j
Итак, при й>0 у(х-\- й) > у(х), т. е. у(х) возрастает.
135.	Доказать, что при возрастании х от 0 до функ-
sinx А ция у =----- убывает.
х
136.	В данный круговой сектор вписать прямоугольник наибольшей площади (угол сектора < 90°).
Решение. Прямоугольник может быть вписан в сектор двумя способами [черт. 16 а) и б)]. Рассмотрим способ а). Имеем:
b = 7? sinx,
а = R cos х — b ctgа = R (cos х — sinx • ctgа) =
_ cos х • sin а — sin х • cos а ____ R sin (а — x)
sin a	sin i
sin x • sin (i — x) ____cos (2x — a) — cos a
sin a
2 sin a
78
Наибольшее значение S достигается при cos(2x— а)= 1, откуда
2х — а = О,
Это наибольшее значение таково:
2 sin а	2
В случае б) проведем биссектрису OL угла а. Тогда прямоугольник разделится этой биссектрисой на два прямоугольника. Каждый из них вписан в половинный сектор по способу а), и поэтому задача сводится к предыдущему случаю: ОВ должно быть биссектрисой угла LON, т. е.
^LOB = —, ^АОВ = — .
4	2
Обозначим через Smax наибольшее значение площади прямоугольника, вписанного по способу б). Очевидно,
S' = 2/?2 • tg —.
max v & 4
Теперь надо выяснить, какое из двух чисел (Smax или S'nax) больше. Рассмотрим разность:
5m„-S„x-R!(tg^-2tg^ =
/ 2tg “	\	2 tg3 “
= /?2 ---------2 tg — = R2------— .
По условию 0 < я '90°. Следовательно,
0 <— г22°30', 0 < tg—< 1. 4	4
Таким образом-, Smax — Smax > 0, т. е. прямоугольник наибольшей площади получится при способе а).
137.	Даны основание а треугольника и сумма т двух других сторон. Определить наибольшее возможное значение угла А.
79
§ 10. РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ
Найти пределы (№ 138—144).
.	. sin х — sin а
138. lim--------------
Х-а X —а
Т,	Sinx—Sin
Решение, lim----------
х-а X — а
lim
л--* а
2sin х~а cosL±^
2______2
2Х_=1
2
. •	2	.. X -| - а
= lim—;------- lim cos —— = cos а.
Х-а Х~а Х-а	2
2
В задачах этого параграфа мы постоянно будем пытаться преобразовать данное выражение так, чтобы получился предел	Мы предполагаем известным, что этот
х-0 X
предел равен единице.
.	sin Зх
139. lim---------
л-о sin2x
sin Зх
„	.. sin 3v 3 .. Зх
Решение. lim-----------= — Um —=-
x-osin2x 2 х-о Sln 2х
3
2
2х
. .,	,.	1 — COS X
141.	lim-------
х-о sin2 х
142.	lim--------.
x- о 1 — cos mx
143.	lim[(l—x)tg-yj.
Решение. Обозначим 1—x = z. Тогда
lim[(l -x)tg'Yj = limlz  tg^=^j x-iL	2 J z-oL 2 J
80
= lim [z • tg (— — — 1] = limz • ctg — = 2-o[	6 \ 2	2 /J z~0	2
Я Z
,;	z . . T.Z 2 ,.	2	.. я z 2
= lim---------• Inn cos— = — lim---------lim cos — = — .
г-о gin— 2->0	2	71 2-°sin 2L? 2-°	2	71
2	2
144. lim (x • tg —1 .
X-*-OQ \	X )
§ 11. ПРИМЕНЕНИЕ ТАБЛИЦ
145. Вычислить по таблицам:
1)	sin 1g 3.
Решение, sin 1g3 = sin0,47712 == 0,45922.
2)	sin sin 1.
3)	cos cos cos 0,5.
4)	ctg jZ2j-
146.	Вычислить приближенно наименьший положительный корень уравнения:
sin х 4- cos х = tg х.
Решение. Прежде всего определим графически, в каком интервале расположен искомый корень. Построим графики у = sin х ф- cos х и z/ = tgx (черт. 17). При построении первого графика преобразуем:
sin х 4- c°s х = V 2 sin (45° 4- х).
6
Заказ S3
81
Наименьший положительный корень—это абсцисса точки А. Из чертежа ясно, что он заключен между 45° и 90°. Если чертеж выполнен более или менее тщательно, то видно, что
50° < х < 60°.
Далее применяем метод проб:
X	sinx 4 cosx		tgx
50°	1,409		1,192
55°	1,393		1,428
60°	1,366	<	1,732
50° < х < 55°
Эта таблица составляется следующим образом. Находим sinx и cosx (этого мы не показываем) и записываем их сумму. Между графами «sinx-|-cosx» и «tgx» мы записываем результат сравнения этих двух чисел. Знак > в первой строке означает, что при х — 50° точка синусоиды лежит выше точки тангенсоиды. Знак < во второй строке означает, что при х = 55° точка синусоиды лежит ниже точки тангенсоиды. Следовательно, пересечение кривых происходит между 50° и 55°. Делим этот интервал на пять равных частей:
si п х 4- cos х
50°
51°
52°
53°
54°
55°
1,400
1,397
1,327
1,376
54° < х < 55°
х
По поводу заполнения этой таблицы сделаем два замечания:
1) Числа в первой и последней строках не записываются. Числа нужны только для того, чтобы определить знак неравенства между ними. Знаки неравенства в первой и последней строках всегда переносятся из предыдущей таблицы.
82
2) Графы заполняются не подряд, а начиная приблизительно с середины, т. е. с 52° или 53°. После заполнения этой строчки отпадает необходимость заполнять один из двух получившихся частичных интервалов. Так, заполнив строку «53°», мы получаем в ней знак «>». Следовательно, искомый корень лежит между 53° и 54°. После этого заполнять строки «51°»и«52°» уже ненужно, а нужно лишь заполнить строку «54°».
Дальнейшие пробы не нуждаются в объяснениях;
X	sin х -}- cos х		tg*
54° 00' 54° 30' 55° 00'	1,395	Л V V	1,402	54е 00' < х < 54° 30Л
Так как значения sinx-|-cosx уже стали мало отличаться от значения tg х (т. е. мы подошли близко к корню), то следует увеличить точность. В дальнейших таблицах мы пользуемся значениями тригонометрических -функций с четырьмя и пятью знаками после запятой:
X	sin х 4- cos х		tg*
54° 00' 10' 20' 30'	1,3961 1,3955	Л V V V	1,3848 1,3934 54° 20'< х < 54° 30'
54° 20' 25' 30'	1,3952	AAV	1,3976 54° 20' < х < 54° 25'
54° 20' 2Г 22' 23' 24' 25'	1,39542 1,39536 1,39529	Л Л V V V	L 39507 54° 22'< х < 54° 23' С 39593
6*
83
Мы условились давать ответ в минутах. Нужна еще одна проба, чтобы выяснить, к которой из двух границ 54° 22' и 54° 23' корень лежит ближе.
X	sin х 4- cos х		tgx
54°22' 00" 22' 30" 23' 00"	1,39533	A V V	1,39550 54° 22' 00" < x < 51° 22' 30"
Ответ. х = 54°22' (с недостатком; погрешность меньше 30").
147. Вычислить приближенно наименьший положительный корень уравнения tg х = х.
Решение. Эта задача решается тем же методом, что и предыдущая. Графически устанавливаем, что наименьший положительный корень (см. точку А на черт. 18) лежит между 4 и ^р-^4,7. Ветвь тангенсоиды, проходящая через н ачало, касается прямой у = х и не имеет с ней общих точек, кроме начала координат.
84
При пробах следует пользоваться тригонометрической таблицей числового аргумента:
х		tgx			
4,0 4,1 4,2 4,3 4,4 4,5 4,6	Л Л V V V	1,158 2,286 3,096 4,638 8,860	4,4 <	С X <	С 4,5
4,40 4,45 4,50	Л Л V	3,723	4,45	< X	< 4,50
4,45 4,46 4,47 4,48 4,49 4,50	Л V V V	4,225 4,422	4,49	< X	< 4,50
4,490 4,495 4,500	Л V V	4,527	4,490 <	X <	4,495
4,490 4,491 4,492 4,493 4,494 4,495	Л Л V V	4,485 4,506	4,493 <	Z х <	: 4,494
4,4930 4,4935 4,4940	Л V V	4,4953	4,4930 <	X <	4,4935
Ответ, х = 4,493 (с недостатком; погрешность меньше 0,0005).
148. Вычислить приближенно наименьший положительный корень уравнения tgx=-—.
85
§ 12.	ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ КОМПЛЕКСНОГО АРГУМЕНТА
Вычислить (№ 149 и 150).
149.	1) cos/,
2)	sinf.
150.	sin (2 4-3/).
151.	Решить уравнения:
1)	cos z— 1,25.
Решение. Выразим cos z по формуле Эйлера [формула (XIII. 4)]:
1г ,	— 1г
е-^--------= 1,25.
2
Обозначим е* — t. Тогда
1
*+ 7
------ = 1,25,
2
2/2 —5/-[-2 —0, ^ = 2, /2 = 1
а)	Рассмотрим первый случай: е =2. Логарифмируем это равенство, используя формулу для логарифма (натурального) комплексного числа [формула (XIII. 10)]:
iz = Ln 2 = In 2 4- / 2 k л.
Умножаем обе части на —Z:
z = 2 Ал—i In 2.
b)	ez = iz = Ln-i- = In i-2/гк = — In 2 -[-/ • 2k~;
z = 2 Au -[-/ In 2.
Ответ, z = 2 k~ + i In 2.
	25
2)	sin z = —.
66
152.	Решить уравнения:
1)	cos z — 2,4 i, 2) sin z = iV3.
153.	В каких случаях sinz, где z = x-[-iy, есть действительное число?
Решение.
sin z = sin (х -j-iy) = sin х • cos iycos х-sin iy = — sinx-ch у-f-icosx-shy
[см. формулы (XIII. 6) и (XIII. 7)].
sin z действителен при одном из двух условий:
a)	sh у — 0, откуда у = 0.
Это — тривиальный случай: синус действительного аргумента действителен.
b)	cos х = 0, откуда х = ~ (2 k 1).
§	13. ГЕОМЕТРИЧЕСКИЕ ЗАДАЧИ
(Обозначения см. на стр. 181)
154.	Решить прямоугольный треугольник: с =12,8, п = 4,6.
Решение.
а = c-sin А,
b = с-cos Л.
Перемножаем эти равенства:
о
ab — с2-sin Л-cos А — — sin 2 Л.
2
С другой стороны, известно, что ab — ch. Следовательно,
ch = — sin 2 Л,
2
sin 2 Л = — =	= 0,71875,
с 12,8
откуда
либо 2 Л = 45°57', Л = 22°59',
либо 2 Л = 180° — 45°57' =134°03', Л = 67°0Г.
87
Эти две возможности не следует считать существенно различными, так как они определяют один и тот же треугольник. Поскольку в условии задачи нет данных для различения острых углов, можно любой из них принять за 22°59', а другой за 67°01'.
Наконец,
а = с sin Л = 12,8 • sin 22°59' = 12,8- 0,39046 = 4,9979\
b = c-cosA = 12,8 -cos 22°59'= 12,8-0,92062 = 11,8391.
Примечание. Здесь показан ход вычислений в предположении, что данные точные. Если же считать их приближенными (что более естественно, поскольку они выражены десятичными дробями), то результаты следует округлить:
й = 5,0, 6 = 11,8.
Углы (при вычислениях с тремя значащими цифрами) определяются с точностью порядка 6'. В данной задаче можно округлить угол А так:
А = 23е.
Аналогичное замечание относится ко всем геометрическим задачам на вычисление.
155.	Решить прямоугольный треугольник: р = 6, 5=35°.
156.	Доказать: если в прямоугольном треугольнике
1
тангенс половины острого угла равен
—, то это—«египет-2
ский» треугольник*.
157. Решить треугольник: а = 67, hb = 58, тс = 56.
Решение. Заметим (хотя это и не требуется для решения задачи), что задача допускает в общем случае два решения. Для построения искомого треугольника проведем две параллельные прямые, расстояние между кото-
рыми равно hb (черт. 19). Примем произвольную точку, например, на верхней прямой за В и опустим из нее перпендикуляр ВВ' на нижнюю прямую; это и будет hb. Из точки В радиусом а делаем засечки на нижней прямой. Если hb, то получим две засечки Сх и С2; это —два возможных положения вершины С. Из точки С, радиусом 2тс делаем засечки Е{ и Д2 на верхней прямой (предполагая, что 2mc>/z/;). Середины отрезков С1Е1 и СХЕ2, обо
* Т. е. треугольник с отношением сторон 3:4:5.
88
значенные соответственно и D2, суть возможные положения конца медианы тс. Проводя прямые BDt и BD2 до пересечения с нижней прямой, получим точки Л, и Л2. Треугольники А1ВС1 и Л2ВСХ удовлетворяют условиям задачи.
Используя вместо точки точку С2, мы придем к таким же треугольникам, т. е. решений —два, а не четыре.
Переходим к аналитическому решению. Деля hb на а, получим:
sinC =— = — = 0,86567, а 67
откуда находим два возможных значения С. Сразу же найдем (по таблице) их косинусы:
С^бЭ’бв'; cosC = 0,50061;
Са= 180° —CI== 120°02'; cos С2 =—0,50061.
Используем формулу для медианы [формула (XIV. 11)]:
тс = — (а2 +Ь2 + 2 ab cos С).
4
В этой формуле все величины, кроме bt известны Поэтому она представляет уравнение для нахождения Ъ. Рассмотрим отдельно два варианта:
1) 562= 1(672 + 62+ 2-67.0,50061 -Ь), или
Ь2 + 67,082 6 — 8055 = 0, b = — 33,541 ±	125,0+ 8055 = — 33,541 + /9180 =
= — 33,541 + 95,812.
89
Окончательно: 6Х = 62,271 (отрицательное значение, разумеется, не годится).
2) Второй вариант отличается только знаком cos С.
Уравнение для b будет:
Ь2 — 67,082 6 — 8055 = 0,
откуда b = 33,541 + 95,812; 62 = 129,35.
Теперь вычисляем с по теореме косинусов:
с2 = а2	62 — 2 ab cos С.
1) С2 = 672+62,2712 —2-67.62,271-0,50061 =
= 44894-3877,68 — 4177,25 = 4189,43,
с, = Г 4189/43"= 64,726.
2) с2 = 6724- 129,3524- 2-67.129,35-0,50061 =
= 4489 4- 16731,42 4- 8677,02 = 29897,44,
с2 = /29897,44 = 172,91.
Угот А проще всего определить по формуле sin Л = —. С
Первый вариант.
sin А, =	= - 5— = 0,89609.
1 с, 64,726
Угол треугольника определяется по синусу двузначно. В данном случае угол Аг — острый, потому что а2<62-|-с2. Можно даже не проверять это неравенство, так как сразу видно, что треугольник со сторонами а = 67, 6Х^62 и сх^65 близок к равностороннему и, следовательно, его углы близки к 60°. Поэтому
At = 63°39'.
Наконец, В, = 180° — (63°39' 4-59°58') = 56°23'. Второй вариант.
sin А2 =	= 0,33544.
172,91
С2
90
В этом варианте треугольник уже имеет один тупой угол (С2 = 120°02/). Поэтому угол А2 — острый.
Л2 = 19с36',
В2 = 180° — (19°36' 4- 12(^02') = 40°22'.
158.	Решить треугольник:
/„ = 72,5, Л = 36°41', В=105°10'.
159.	Дуга сегмента круга в угловом выражении равна а радианов, а длина ее равна s. Определить радиус круга, вписанного в этот сегмент.
160.	Диаметр монеты (одна копейка выпуска 1961 г.) равен 15 мм. Диаметр Луны виден с Земли (при средней высоте Луны над горизонтом) под углом 31'. На каком расстоянии от глаза следует поместить монету, чтобы она в точности закрыла лунный диск?
161.	Доказать, что во всяком треугольнике
__ abc 4/? ’
Решение. Как известно, S = уab-sinС. По теореме синусов —— = 27?, откуда sin С = —-—. Таким образом, sin С	2/\J
162.	& = (2 —(-J 3)с, А = 60°. Найти (точно) В и С.
Решение. Из условия нам известно отношение — с
Но мы можем также узнать отношения других сторон и тем самым узнать форму треугольника. Для этого используем теорему косинусов:
а2 = 62 + с2 — 2Ьс • cos А = (2 Д-lz3)2 с2 4-с2—
— 2(24-ГЗ)с2.1 = (6 4-31 3) С2, откуда
с 1 6 4* з J з 
91
Используя формулу для преобразования сложных радикалов [формула (XVII 1)], это отношение можно представить так;
а з/2+ Кб
с ~	2
Так как синусы углов пропорциональны противолежащим сторонам, то
sin А 3/2 +/6
sin С	2	’
А = 60°. Таким образом,
-1?
sin С = ——-— —
3/2 + /6
/6 —/2 “ 4
откуда С= 15° (см. решение задачи № 4). Следовательно, В = 180°— (60° 4- 15°) = 105°.
163.	cr.b-.R = X:p.:v. Найти углы треугольника.
164.	Доказать: если котангенсы половин углов треугольника суть последовательные целые числа, то это «египетский» треугольник.
Решение. Пусть ctg у- = п, ctg = п -1, ctg — = п-\-2. Из равенства А -ф- Вф- С = 180° следует
А В
ctg у ctg —— 1
А В~
ctg — + ctg —
1	Л (n + 1) — I
«+2 “ л + (n + I) ’ /г34-3н2 -л —3 = 0,
(п-фЗ)(п2 — 1) = 0.
92
Из трех корней этого уравнения по смыслу задачи годится только один: п — 1 (потому что котангенсы половин углов треугольника не могут быть отрицательны). Следовательно,
Ctg у = К	12 	 1 ctg Л = -	L = o, 2-1
ctg у = 2,	, D	22-1	3 2-2	4
Ctg f = 3’	, „ З2 —1	4 ctg С = ——- = — , 2-3	3
откуда видно, что треугольник — прямоугольный (А — 90°) и отношение его катетов есть 3 : 4.
165.	Отношения сторон треугольника:
а : b : с = (2( -j- 1): (t2 — 1) : (^-Н+ 0-
Доказать, что один из углов этого треугольника равен 120°.
166.	Дан двугранный угол а. В одной из его граней из точки М проведена наклонная, равная а, от точки М до ребра и образующая с ребром двугранного угла угол, равный р. Найти расстояние точки М до другой грани двугранного угла.
167.	Найти двугранный угол правильного тетраэдра.
§ 14.	СФЕРИЧЕСКАЯ ТРИГОНОМЕТРИЯ (Обозначения см. стр. 183)
168.	Тропики отстоят на 23° 27' 30" от экватора, а полярные круги — на такой же угол от полюсов. Какую часть (выразить в процентах с одной цифрой после запятой) составляет площадь каждого климатического пояса от площади всей поверхности Земли (Землю принимать за шар).
169.	Решить прямоугольный сферический треугольник:
а = 38° 24', b = 59° 36'.
93
Решение. Различают шесть случаев решения прямоугольных треугольников. Это — первый (даны два катета). Используем формулы (XV. 7) и (XV. 3):
cos с — cos а  cos b,
sin А =
sin а sin с ’
sin В =
sin b sin с
cos с = cos 38°24' • cos 59°36' = 0,78369-0,50603= 0,39658;
с = 60° 38'; sin с = 0,91801.
Заметим, что sin с может быть найден и без нахождения в той же строке таблицы (или между теми же строками при помощи интерполяции), что и cos с:
. sin 38° 24'	0,62115	л
sin А =-----;-----= —---------• = 0,67662.
«шс	0,91801
Этому значению синуса соответствуют два угла между 0 и 180°. Следует выбрать один из них, руководствуясь правилом: катет и противолежащий угол одновременно соответственно острые, прямые или тупые. Учитывая, что катет а -< 90°, заключаем:
А = 42° 35'.
Наконец,
sin в = sin 59° ЗУ = 0,86251 = q 93955 В = 590 59,. sine 0,91801
Решить прямоугольные сферические треугольники .(№ 170—173).
170.	a = 32° 44', с=139°00'.
171.	а = 38°28', Л = 56°01'.
172.	b = 37° 52', А = 49° 22'.
173.	А = 58° 28', £ = 53°43'.
174.	Решить прямосторонний сферический треугольник:
а =138° 55', Ь= 115° 50'.
94
Решение. Если данный треугольник —прямосторонний, то полярный ему треугольник — прямоугольный. Снабжая элементы полярного треугольника индексом 1, получим:
А, = 180° — а = 41° 05',
В1 = 180° — Ь = 64° 10'.
Таким образом, задача сводится к решению прямоугольного треугольника по двум углам (шестой случай). Используем формулы (XV. 6) и (XV. 8):
cos а.
cos 41° 05'
sin 64° 10'
0J5376 = 0 83745	= 33о08,
0,90007	1
cos bx = СО5б£.10' = °’43576 = 0,66309; Ьг = 48° 28', 1 sin 41° 05'	0,65716	1
coscj = ctg 41° 05' . ctg 64° 10' = 1,14700 . 0,48414 = = 0,55530; c, = 56°16'.
Теперь переходим от полярного треугольника обратно к данному:
А = 180° — а, = 146° 52',
В= 180° —6, = 131° 32',
С = 180° —Cj = 123° 44'.
Решить прямосторонние сферические треугольники (№ 175 — 177).
175.	а = 36° 42', В = 70° 02'.
176.	п = 58° 26', А = 49° 43'.
177.	Л = 50° 59', В — 39° 20'.
178.	Решить сферический треугольник:
а = 34° 13', £> = 42°55', с = 51 ° 03'.
Решение. Это—первый случай решения косоугольных сферических треугольников (даны три стороны). Можно воспользоваться формулами «косинуса стороны» [формулы (XVI. 4)]:
95
. cos a — cos b • cos c cos 34° 13' — cos 42° 55' • cos 51® 03' COS A -- ----------.--— —---------------------------------
sin b • sin c	sin 42° 55' . sin 51° 03'
_ 0,82692 — 0,73235 • 0,62864 _ 0,82692—0,46044 _ 0,68093 • 0,77770	“	0,52956
= 0,36647 = 0,69203; A = 46° 13'.
0,52956
„ cos b — cosc • cos a cos 42° 55'—cos 51° 03'• cos 34° 13' COS В = -----:-----;--- = ---------------------------------
sine-sin a	sin 51° 03'.Sin 34° 13'
_ 0,73235 — 0,62864 • 0,82692 _ 0,73235 — 0,51981 _ 0,21253 0,77770 - 0,56232	~	0,43732	“ 0,42732
= 0,48599; В = 60° 55'.
л cose — cos a. cos b cos 51° 03' — cos 34° 13'• cos 42° 55' COS C = ---------------= ----------------------------------
sin a • sin b	sin 34 13' • sin 42°55'
_ 0,62864 — 0,82692 • 0,73235 _ 0,62864 — 0,60558 _ 0,02307 0,56232 • 0,68093	~	0,38291	~ 0,38291
= 0,06024; C = 86°33'.
Решить сферические треугольники (№ 179—181).
179.	A = 62°06', £ = 54°36', C = 70°15'.
180.	a = 48° 13', £> = 37°31'	C = 55°06'.
181.	a = 47° 05', b = 36° 40', A = 56° 17'.
Пользуясь следующей таблицей географических координат
Москва 55° 45' сев. шир., 37° 37' вост. долг. Новосибирск 55° 02' »	»	82° 56' »	»
Хабаровск	48°28'	»	»	135°05'	»	»
Пекин	39° 54'	»	»	116° 28'	»	»
и принимая Землю за шар радиуса 7? = 6370 км, решить задачи № 182 и 183.
182.	Найти кратчайшее расстояние по земной поверхности: 1) от Москвы до Новосибирска, 2) от Москвы до Пекина.
S6
Решение. 1) Соединим дугами меридианов (кратчайшими) Москву и Новосибирск с Северным полюсом и рассмотрим сферический треугольник АВС, где А — Москва. В—Новосибирск, С — Северный полюс. Очевидно,
а = СВ = 90' — широта Новосибирска = 34° 58',
b = АС = 90° — широта Москвы = 34° 15',
С долгота Новосибирска—долгота Москвы = 45° 19'.
Теперь сторона с (в угловой мере) может быть найдена по формуле косинуса стороны формулы (XVI. 4):
cos с = cos а • cos b -ф sin а  sin b • cos С =
= cos 34° 58'. cos 34° 15' -фsin34°58'.sin34° 15'-cos 45° 19' =
= 0,81949 • 0,82659 -ф 0,57310 • 0,56281 . 0,70319 =
= 0,67737-ф 0,22681 =0,90418; с = 25° 44'.
Используя таблицы, дающие длину дуги окружности радиуса /?= 1, найдем: длина дуги 25° 44'= 0,449. Отсюда искомое расстояние: 6370 км X 0,449 = 2860 км.
Примечание. В авиационно-транспортных справочниках расстояние между Москвой и Новосибирском указывается 2808 км*.
Не будем удивляться этому расхождению, потому что искомое расстояние не вполне определенное, так как Москва и Новосибирск не точки. При указании географических координат какого-нибудь города обычно имеют в виду определенную точку в этом городе, например за географические координаты Москвы принимают широту и долготу Московской астрономической обсерватории. В авиации же принято считать расстояние между аэродромами.
183.	Какие углы дуга большого круга Москва—Хабаровск образует с меридианами этих городов?
* См., например. Военно-топографическое управление генерального штаба, Атлас мира, М., 1954, стр. 320.
7 Заказ 33
ДОПОЛНИТЕЛЬНЫЙ РАЗДЕЛ
§ 1.	ТОЖДЕСТВЕННЫЕ ПРЕОБРАЗОВАНИЯ
Доказать тождества (№ 184 — 210).
184.	cos6а — sin6 а = cos 2а f 1 — — sin22а .
\	4	/
185.	cos6a4-sin6a = 1--— sin32a.
4
186.	s-ec—+tga = tg2 f- +-V sec a — tg a	\ 4	2 /
tg(45°+i) -fg (45O-f)
187.	A-------4Z------\= sina.
tg (45°+i) + tg(45°-|)
l_tg2 (45°-i)
188.	-------------= s*na"
l + tg* (45°-J
IRQ 2 sin a — sin 2a , 2 a
’°9' 2 sin a + sin 2a = “ 2" ’
190.	1) -------------= sin a.
7 a	a
tg?+ctg7
2) ------------------------— = cos a.
tg (45°+ -) +ctg (45° +1)
98
191.	tg2a 1 tga
tg2a — tga
sin 2a.
192.	fg22a 2 tg2 a ’ 2 4- tg2 2a 1 - tg« a
193.	sin (a 4-30°) sin (a —30°)
cos2 a = — 4
194.	tg a -p tg (a 60°) + tg (a — 60°) = 3 tg 3a.
195.	tg a . tg (a 4- 60°) • tg (a — 60c)	— tg 3a.
198.	sin 3a • sin3a I cos3a • cos3a = cos32a.
197.	sin 3a • esc a —- cos 3a • sec a = 2.
198.	sin2 3a — sin2 2a = sin 5a • sin a.
199 _sirl а + 2 sin 3a -p- sin 5a	sin 3a
sin 3a + 2 sin 5a - sin 7a	sin 5a’
200.	(tg a-J-tg 2a) (cos a 4-cos 3a) 2 sin 3a
201.	tg3a — tg2a — tga = tg3a . tg2a . tga.
202.		______I____tgg — 1.
Ctg a — ctg3a tga —tg3a
2 (cos 2a -f- s in 2a)
ZUO. ---------;--------—--------- СЧС CL
COS a—sin a— COS 3a 4-Sin 3a	'
sin a — sin 3a — sin 5a -t- sin 7a
COS a — cos 3a 4- COS 5a — COS 7a ~ 2я
плг cos a 4- COS 2a 4 COS 4a 4 COS 5a , „ sin a 4 sin 2i 4 sin 4a 4 sin 5a c*g a
208. -----J-------------L_-----= ctg 2a.
tg3a—tga Ctg 3a —ctg a
207.--------------------1------ = Ctg 4a.
tg 3a 4-tga Ctg 3a 4-ctg a
208. 3-4 cos 2a 4-cos 4a = 4
3 4-4 cos 2i 4- cos 4a
*209. tg a 4- 2 tg 2a -p 4 tg 4a 4- 8 ctg 8a = ctg a.
99
210
a	2a
sin — + sin — ______§_______fe-
et 2a ё 2
cos —+ cos y
211.	Найти tg—, зная, что  — — tn. 2	tg a
, a	sin 3a	11
212.	Вычислить tg—, зная, что ------= —.
2	sin a	25
213.	Доказать:
i \	a
1)	cos — =-
(n > 1, радикалов n, символ повторяется 2/г раз, |a| 4 180°).
2)	sin — = ' 2,
= 1/ 1	1 S /"1	1 . Г 1. Г\ , 1----------------
Р 2 — 2 I 2 + 2 I ’ ' + 2 ] Т + ТC0S ’
(п > 1, радикалов п, символ у повторяется 2п раз, [ а | < 180°).
180°	1	2+ I 2 + 1'2+ . . . Ч Н 2
3) cos----=-------------------------------—
’ Чп	2
(п >2 , радикалов п— 1).
. 180° I 2 — ] 2+ 1-Л2 + . . . +
4) Sin----=---------------!1— -----------------
>	2 я	2
(п > 2, радикалов п— 1).
214. 1) Выразить cos/га при п нечетном через cos а. Применить к случаям п = 3, 5.
100
2)	Выразить cos га. при п четном через sina. Применить к случаям л = 2, 4, 6,
3)	Выразить cos па при п четном через cos а. Применить к случаям п = 2, 4, 6.
215. Выразить tgna через tga.
*216. 1) Составить уравнение для нахождения cos у, если известен cos а.
2) Составить уравнение для нахождения sin—, если з известен sina.
3) Составить уравнение для нахождения tgy, если известен tga.
Доказать тождества (№ 217 — 221).
217.	tg^-bt tg = —2 ч'г1?_______..
2	2	cos а -р cos 3
218.	sin (a — р) -|-sin (Р —'[)-j- sin (у—a) =
л . a — В . 8 — 7 . 7 — a
= — 4 sin----- sin1--1 sin 1-
2	2	2
219.	tga 4-tgp-|-tg 7 — tga.tgp. tgT = 2Ln±_+J. + 7) . . cos a -cosp . cos 7
220.	1) cos acos P Д-cos у Д-cos (a-f-p Д-7) = . z -p 3 P ~P 7	7 -p о
— 4 cos COS —  t cos — — 2	2	2
2)	sina4-sinp — sin(a rP + l) — . . a 4- 3 • 3 4" 7  7 4- a
= 4 sin ——sin—J—isin-i-2^-.
2	2	2
221.	1 — cos2 a — cos2 p — cos2 7-42 cos a cosp cos 7 =
. . a -p 3 -p 7 • — a-pB-Py . a — В -p 7 • a 4- 3 — 7 = 4 sin — 	1 sin---——1 sin-------——1 sin ——--I.
2	2	2	2
222.	Выразить sin2 (a Др) -Др sin (a 44) cos (a -ДР) 4-Дqcos2(a Др) через p и q, зная, что tga и tgp суть корни уравнения x2 -\-px-\-q = 0.
223.	Может ли быть, и если может, то в каких случаях
sin (a 4- Р) = sin a -j- sin p?
101
Доказать (№ 224—229).
* 224. Числитель и знаменатель правой части формулы (IV. 11)
tg (а . в Д- Д = tgtt + tgP + tg-f-tga.tg?. tgf ‘	1 — tga • tgp— tg[i  tg! — tgl  tga
не могут одновременно быть нулями.
*225. Выражения tg а tg р -}- tg 7—tg a tg р tg 7 и ctg а -ф- ctg р -ф- ctg 7 — ctg а ctg р ctg 7 не могут одновременно быть нулями.
226.	tga и sin2а всегда одного знака.
227.	Выражение — (sin8x—cos8x)~—— sin6x-j-
8	3
-ф- — cos6 x -|- — sin4 x не зависит от x. 6	4
228.	Если sin(—аД-Р + 7), sin (a — ₽	7) и
sin(a-f-p— 7) образуют арифметическую прогрессию, то tga, tgp и tg 7 тоже образуют арифметическую прогрессию.
229.	sinx и cosx оба рациональны в том и только в том случае, если tg*рационален.
Найти (точно) синусы и косинусы следующих углов (№ 230 -234).
*230. 42е и 48°.
231.	33° и 57°.
232.	27° и 63°.	233. 12° и 78°.
234. 36° и 54°.
Найти (точно) острый угол а, для которого (№ 235—244):
235.	cos а =	2 -J- 1^2 .	236. cosa=-|l 2—К2
237.	tga= /2 — 1.	238. cos a =1 V 2 4-КЗ
239.	cos а = — J/ 2 — k3 .	240. tga = 2—13.
102
241.	sina = T^5 4-iy. 242. sina = -^K5 — 1J.
243.	esc a. = Кб + 1 -	244. ctg a = 1^1 -f- KO .
Доказать тождества (№ 245 — 248).
245.	cos 25°-J-cos 47° = cos 1Г 4~cos 61°4~ sin 7°.
246.	tg9° —tg27° —tg63°4~tg81° = 4.
247.	2 (cos4 44° 4- sin4 44°) = 1 — cos 4° 4- cos2 2°.
248.	cos 27°—cos 63° = К10~^
4
Вычислить (№ 249 и 250).
249.	cos у arcctg -yj. 250. ctg (2 arctg 2).
Упростить (№ 251 и 252).
251. cos (2 arccos x).	252. tg (2 arcsin x).
Доказать тождества (№ 253 — 264).
2	Л1
253.	2 arcsin —• = arccos —. 7	49
осл 	1	- Vio я
254.	arcsin -x-=-k arcsin *	= — •
5	1	10	4
ocr- • 3 .	.8	.77
255.	arcsin--k arcsin—= arcsin—.
5	17	85
256.	1) arcsin— 4-arcsin — 4-arcsin— = —.
’	5	13 1	65	2
2)	arcsin —4~ arcsin — 4-arcsin— =—.
5	13	65	2
257.	arctg 3 — arcsin b	5	4
oro •	4 .	2 V"5	, 2
258.	arcsin -=- 4- arccos —=— = arcctg 77
5 1	5	s 11 •
259.	cos ^2 arctg -i-j = sin ^4 arctg -O .
103
260.	1) arctg 4- arctg 3^3- = у •
2)	arctgу 4-arctg y) = — y.
Q. . |/”2 + 1	. 1Л2 n
3)	arctg ---------arcctg y_	—-.
261.	1) arctg -1- 4- arctg m ~ 1 == —. m	m -H 1	4
, n ,	, m — n к
2)	arctg---p arctg -—-- = —.
m	m + n 4
262.	1) arctg — 4- arctg — 4- arctg — = arcctg 3. 7	8	18
2)	arctgy 4- arctg у — arctg -у = у.
263.	4 arctg —--arctg — — —.
5	239	1
264.	arctg у 4- arctg у 4- arctg у 4- arctg у = — .
Найти x (№ 265 — 276).
265.	arcsin x = 2 arcsin a.
266.	arccos x = 2 arcsin a.
267.	arcsin x = 4 arcsina.
268.	arcctg x — 2 arctg a.
269.	arctg x = 4 arctg a.
270.	arcctg x — arctg 2a.
271.	arccos x = arcsin 2a.
272.	arcsin x — — 4 arcsin a.
2
273.	arctg x = у 4- arctg 3a.
104
274.	arccos x = —----3 arcsec a.
2
275.	1) arctg x = 3 arcsin a.
2)	arcctg x = 3 arccos a.
276.	arcsin x = 2 arcsin a 4- arcsin 2b.
§ 2. УСЛОВНЫЕ ТОЖДЕСТВА
Доказать, что при а Д- Р + Т =-у имеют место тождества (№ 277 — 288).
277.	cos а Д- cos р Д- cos 7 =
= 4 cos ( —----— ] cos	( —---— 'j	cos (—-----
\ 4	2 /	\ 4	2 /	\ 4	2
278.	cosa-f-sinP-l-sinT = 4sin(—-— Vos— cos —.
'4	2/2	2
279.	1) cos a — sinp — sin 7 =
2)	cos a —- cos p Д- cos 7 =
= 4 cos	) cos (—------—) cos (— -J- —)
\ 4	2 !	\ 4	2 I 4	2 / 
3)	cos a sinp — sin 7 -
л I ~ a \ . 3	(
= 4 cos-------------sin — cos —.
\ 4	2 j 2	2
280 tgg^ tg^ _ cos'2 1
tg 3 + tg 1 cos2 a
2gJ ctgfj-pctgu = sin 2i
ctg а + ctg 1 sin 23
282.	tga -j- tg P 4- tg 7 = tga.tgp.tg74-seca.secp.sec7.
283.	ctg a 4- ctg p 4- ctg 7 = ctg a • ctg 8 • ctg 7.
105
284.	tga • tg₽-}-tg₽ • tgi + tgy • tga = 1.
285.	tga + tgp —ctgT= —tga • tg₽ • ctg 7.
286.	1) cos2 acos2 p 4~ cos2 72 (1sin a sin p-sin 7).
2)	sin2 asin2 p +sin2 7 = 1 —2 sin a. sin B. sin 7.
287.	1) sin2asin2— sin27=l—2cosa.cosp.sin7.
2)	cos2 a 4- cos2 p — cos2 7 — 2 cos a. cos p • sin 7.
288.	1) cos a - sin p-sin 7 ~ - sin a - cos p-sin 7
4-sin a-sin p-cos 7' = cos a-cos p. cos 7.
2)	sin a-cos p -cos 7 4~ cos a - sin p - cos 7 4~
4~cosa.cosp.sin7 = 1 4-sin a sinp sin 7.
Доказать, что при a 44 + 1 = 77 имеют место следующие тождества (№ 289 — 301).
ооп i\	I ci „	1 I 2 sin a-sin 8 • sin 7
289.	1) cos a 4~ cos р 4"cos Т = 1 п--------------~ •
sin а 4- sin р 4~sin7
2)	cos a -I- cos p —- cos 7 = 4 cos — cos — sin --1.
2	2	2
3)	sin a 4~ sin p — sin 7 = 4 sin — sin — cos —. 1	222
4)	sin a'4~ cos 3 4~cos 7 = . . a	l тс	В \	[ r.	7 \
= 4 sin — cos--------L cos--------L 1
2	\4	2/	u	2 /
sin a 4- sin В — sin к , a . В 290. --------------= tg — • tg — .
sin a sin (3sin 7	2	2
291. ctga4-ctgP4-ctg7 = ctga-ctgPctg74-
4~ esc a esc p esc 7.
292. tga — ctgp —ctg 7 = tga.ctgp.ctg7.
2Q3 ctga + ctgp , ctgp +ctg7 , ctg7 +ctgg = J tga+tgp tgp + tg7 ‘ tg7 + tga
294.	1) sin 4nx-|-sin 4np 4~ sin 4«7 =
= — 4 sin 2rat • sin 2np • sin2n7.
106
2)	sin(4n l)a sin(4n4~ 1)3 4-sin(4n4~ 1)7 =
= 4 cos
2n4--y^ac°s ^2n4--yj₽ cos^2n 4--yj7.
3)	sin (4n 4“ 2) a 4— sin (4rz 4~ 2)3 4“ sin (4n4" 2)7 — = 4 sin (2n 4 1 )<* sin (2n 4~ 1 )3 sin (2n 4-1)7-
4)	sin (4n 4- 3)a + sin (4n 4~ 3)0 4- sin (4n 4~ 3)y —
— — 4 cos ^2n4—|~)acos	cos )
295.	1) cos 4na 4~ cos 4n0 4~ cos 4п7 =	y
= 4 cos 2na cos 2n0 cos 2n-( — 1.
2)	cos(4n-{-l)a }-cos(4n-4-I)p4-C°s(4n4~ 1)T = = 1 4~4sin ^2n4--yjasin^2n4“-~j₽ sin^2z?4-~j7-
3)	cos (4n 4- 2)a 4“ cos (^п 4“ 2)0 4" cos (4° 4" 2)7 = — 1 —4cos(2мl)acos(2n 4~ 1)3 cos(2n4- 1)7-
4)	cos (4n 4- 3)a 4“ cos (^n 4" 3)3 4“ cos (^n “F 3)7 = = 1 — 4sin^2n 4~-|-j“ sin (j2n 4—0sin^2«4-~j7-
296.	1) cos2 a 4- cos2 3 4" cos2 7 = 1 — 2 cos a cos 0 cos 7.
2)	sin2 a 4~ s’n2 3 4“ S1°S 7 =2(1 4“ cos acos 0cos 7).
297.	1) cos2a 4~ cos2 0 — cos2 у = 1 — 2 sin a sin 0 cos 7.
2)	sin2 a 4~ sin2 0 — sin2 7 = 2 sin a sin 0 cos 7.
298.	1) cos2 na 4- cos2 П0 4~ cos2 ny =
= 1 4~2(—I)"cosnacosn0cosn7.
2)	sin2na4-sin2n34-sin2n7 =
— 2 [ 1 4-(— I)”cosnacosn0cosn7],
299.	1) tgatg04-tg0tg74-tg7tga =
= sec a sec 0 sec 7 — 1.
2)	ctg a ctg 0 4- ctg 0ctg 7 4- ctg 7Ctg a = 1.
107
Доказать (№ 302 и 303).
302. Если а-}-₽=-у-» то (1-}-ctga)(l-j-ctgfi) = 2.
303. Если а 4~ Р — —
ctg g ctg 3 (1'4-Ctga) (1 + Ctgfi)
1
2
Доказать, что при a. 4“ Р 4“ Т о = 2тг имеют место следующие тождества f№ 304 — 308).
304. 1) cos a-j- cos p 4- cos 7 4“ cos 0 =
л -*• "I- P P "E 7	7 c/-
= 4 cos ——cos 1-----1 cos  -.
2	2	2
2) cos a 4- cos p — cos 7 — cos8 =
.	»+?-₽т1-7 + я
= 4 cos —— sin —— sin J—1—.
2	2	2
3) sin a-f-sin 8 — sin 7 — sin 8 =
. . Ct —t- 3 В —I— У "Y -4— Ct = 4 sin —cos i-2—L cos J-22- .
2	2	2
305. 1) cos2 a 4- cos2p 4- cos2 7 4- cos2 8 =
= 2 [ 1 -j- cos (a 4- P) cos (p 4" T) cos (i + a)J-
2) sin2 a 4-sin2 3 4“ sin2 7 + sin2 8 =
= 2 [ i — cos (a p) cos (p 4- T) cos (7 4~ “)]• 306. sin2 a sin2 p — sin2 7 — sin2 8 =
= — 2 cos (a 4- P) sin (p 4~ 7) sin (7 4- a).
307.	ctg a + ctg р 4-ctg у 4-ctg 8 =
= sin (a -г ft) sin (ft + 7) sin (7 + 6) sin a sin ft sin 7 sin 6
308.
tg« + tgft+ tg7-{- tgS
Ctg a 4- ctg ft + ctg 7 -J- ctg 6
tgatgptgytg 8.
Доказать (№ 309 — 312).
309.	Если a 4~ P 4” I — Пк, to tg a 4 tg p -}- tg у = = tgatgptgy.
310.	1) Если a 4-P 4* T = 2n-, то sin a 4-sin P 4-sin 7= = 4( — 1)"+1 sin — sin — sin —.
2	2	2
2) Если a -)- p 4- 7 = 2пк, to cos a cos p 4" cos 7— =— l+(—1)” 4cos —cos —cos —.
2	2	2
311.	1) Если a 4-P 4“ 7 = (2°—1)^, to
sin a 4 sin p 4- sin 7 = (— 1 )”+1 4 cos — cos — cos - . 2	2	2
2)	Если a 4- P 4“ 7 — (^n 4- 1 )K> TO
cos a	cos p 4-cos 7 = 1 -|-(— 1)" 4 sin у sin-^-sin -E.
312.	Если a 44J, r Y — (2n + ।)'. to
cos4 — 4~ cos4 — - 4~ cos4 — — 2 (cos2 — 4- cos2 — 4- cos2 -E^ 4-
2	2	2	2	2 '	2 ) 1
4 4 cos2 — cos2 — cos2 — == 0.
2	2	2
Доказать, что при a4~P = 7 имеют место следующие тождества (№ 313 — 317).
313.	1) cos а 4- cos р 4- cos 7 = 4 cos — cos — cos л — 1
109
2)	cos a — cos 3 — cos 7 = 4 sin — cos — sin — —1
7	‘	‘	2	2	2
3)	cos a 4“ cos p 4" sin 7 =
(я	a \	I it	f) \
-----COS I-------— cos 7.
4	2/	\ 4	2/	1
4)	cos a — cos p 4~ sin 7 =
и
2
sin — 2
5)	cos a — sin p 4“ cos 7
(я	a \	3 . j я	у
-----COS —Sin--------L
4	2/	2	\4	2
6)	sin a 4- sin 3 4"cos 7 —
, . . .	/я	a\ .	I я	8 \ .	1
= l-4-4sin------—sin--------— |sin —
\ 4	2}	\ 4	2/	2
7)	sina — cosp-|-sin7 =
.	. . / я	a \	В .
= 1—4 sin I---------cos —sin
I 4	2 /	2
(7
2)
8)	sina4~sinp — sin7 = 4 sinsin у sin у.
314.	cos 2a 4~ cos 2B 4~ cos 2y = 4 cos a cos ,3 cos 7— 1.
315.	ctg a 4- ctg p 4- tg a = ctg a ctg P tg 7.
316.	tgatgP4-(tga4-tgP)ctg? = 1.
317.	1) cos2 a 4- cos2 p 4~ cos2 7 = 14-2 cos a cos p cos 7.
2)	cos2 a 4- cos2 p 4-sin2 7 = 2(1 4-sin a sin p cos 7).
3)	sin2 a 4- sin2 p 4- cos2 7 = 1 — 2 sin a sin p cos 7.
4)	sin2 a 4- sin2 p + sin2 7 = 2 (1 — cos a cos p cos 7).
5)	cos2a4-cos2p — cos2 7 = 1 4~2sinasinp cos 7.
6)	sin2a4-sin2 p—sin2 7 = — 2sinasinpcos7.
110
Доказать (№ 318 — 330).
318.	Если tga + tg₽ + tgT = tga • tg₽ • tgу, то
« + Р H = ™t.
319.	Если tg a • tg ₽ Д- tg ₽ • tg 7 4- tg т • tg a = 1,
to a + ₽ + l = (2n-r Dy.
*320. Если cos2 acos2 p Ц-cos2 7-f-
- 2 cos a • cos p • cos 7 = 1, то одно из выражений a Д- p - 7, — a+P4-7> a—P4*7>a + P— 7 равно (2n Д- l)r.
321.	Если cos a cos p -f- cos 7 = 0, to
cos 3a 4- cos 3p 4~ cos З7 = 12 cos a cos p cos 7.
onn r? sin a—cos a , 322. Если ------------= tgtp, to
Sin a 4- COS a b T ’
sin a — cos a = + )/2 sin <p.
323.	Если tg —= 4tg —, to tg^ = —sina .
2 S 2	6 2	3 cos a-5
324.	1) Если (1 4~ cosa) (1 4- cos p) (1 4- cos 7) =
= (1—cosa)(l—cosP)(l—cos7), то каждая из частей этого равенства равна ± sin a sin р sin 7.
2) Если (1 4~sina)(l 4~ sinP) (1 4-sin7) =
= (1—sina)(l—sinp)(l—5107), то каждая из частей этого равенства равна ± cos a cos р cos 7.
325.	Если	=	• то tg2? = tgatg₽.
326.	Если cos a 4~ cos р 4- cos 7= 1 + 4 sin — sin sin -1
2	2	2 ’
то либо a 4~ P 4" T = (4^4“ 1)либо одно из выражений a — р — 7, —a + P— 7 и —a — P4“Tf равно (4n—1)к.
327.	Если ctga 4-ctgp 4-ctg 7 = ctga . ctg,3.ctg7, to
a + P+l = (n + y
ill
328.	Если яф-р--7 = ~ и ctga ctgр = 2ctgу, то ctg | ctg 3.
329.	Если я ф- р ф- 7 = т? и sin а : sin р : sin 7 = 4 : 5 : 6, то cos а : cos р : cos 7 = 12 : 9 : 2.
330.	Если я-фр - 7 = 2т, to sin2 яф- sin2 [3 ф sin2 7 = = 2(1 — cos а cos р cos 7).
§ 3.	ПРЕОБРАЗОВАНИЕ СУММ В ПРОИЗВЕДЕНИЯ И ПРОИЗВЕДЕНИЙ В СУММЫ
Преобразовать в произведения (привести к «логарифмическому виду») (№ 331 —345).
331.	1) 1соз я-|—sin я.
2)	1	cos я -—sin я.
332.	1) cos я ф-cos 2я ф- cos Зя.
2)	sin я ф-sin 2яф-sin Зя.
sin а 4- sin 2а sin За
' COS а -j- COS 2а -f- COS За
333. sin3H-}-2sin5ff4-sin7H.
334.	1—2 sin 44° sin 46°.
335.	3 —tg2R.
336.	tg3ff — tg2fl — tga.
337.	1) cos я - cos psin (я p).
2)	cos я -|- cos 8 — sin (я ф- £).
338.	1) sin2 я ф-sin2 p — sin2 (я ,-p).
2)	sin2 я ф- sin2 p — sin2 (я — p).
339.	1) 5Шаф-5т(аф-/г)ф-5т(я-|-2/г).
2)	cos я ф- cos (я ф- h) ф- cos (а ф- 2Л).
3)
sin a -p sin (a + E) + sin (a + 2/i) cos a 4- cos (a 4- h) 4“ cos (a 4- 2/i)
112
340.	1 4 tg67° +tg68°.
341.	1) 1— tg2atg29.
2)	tg2 a ctg2 p — 1.
cos ° — sina — COS 3a -g sin 3a
COS 2a -j- sin 2a
343.	cosa-|-s:na-f-cosp-f-sinp.
344.	1 sin a 4- cos a tg a.
345.	cos (54° — a) — cos (18° — a)—cos (54° 4- a) -f-+ cos(18° + a).
Следующие выражения преобразовать в произведения (привести к «логарифмическому виду») при помощи введения вспомогательного угла (№ 345 — 350).
346.	347. V а2-\-Ь2.
a+ b	г ।
348.	+	(|6|<|О|).
349.	1) a + /a2 + 62 (a>0, b > 0).
2)	а—У а2 — b2 (а>0, &>0, ft<a).
350.	Vа-\-Ь-\-Уа — Ь (0<.Ь<а).
Следующие выражения преобразовать в сумму (№ 351 и 352).
351.	sin a sin pcos(a-l-p).
352.	1) cos a cosp sin у.
2)	cos a cos p cos y.
353.	Вычислить (точно) sin20osin40°sin60°sin80o.
Понизить степень (до первой) (№ 354 — 357).
354.	1) cos5 a. 2) sin5 a.
355.	sin3 a cos3 a. 358. sin2acos3a.
357.	1) cos" a. 2) sin" a.
8 Заказ 33	113
§ 4. УРАВНЕНИЯ
Решить уравнения (№ 358 — 425).
358.	1) sinx-j-c°sx = 1,14.
2)	2 sin х -J- 7 cos x — 6.
359.	«sin2x-|-Z>cos2x = csin2xcos2x.
360.	1) asin2x4- &sinxc°sx-|-ccos2x — d.
2)	5sin2x4~3sinxcosx— 14cos2 x = 4.
361.	cos x -|- cos 2x -|- cos 4x = 0.
362.	sin (x-|-a)-I-sin (x 4~ ₽) = m-
363.	sin lOx 4- cos lOx = }/2 cos 15x.
364.	cos x -j- cos 3x 4~ cos 5x 4- cos 7x = 0.
365.	sin3x = 8sin3x.
366.	cos3x =— 2cos2x.
367.	2 cos2 5x — 1 = cos 3x.
368.	sin 4x4-4 sin 3x cos x = 0.
369.	1 4~ cos x = 2 sin2 x.
370.	1) sinx-|-cosx-|-sinx • cosx = 1.
2)	sin x 4- cos x — 2 sin x . cos x = 1.
371.	tgx = 4cosx.
372.	tg3x + 2tgx = 0.
373.	5tgx = tg3x.
374.	4 tg — = 3sin x. b 2
375.	sin x = ctg x (0 < x < 90°).
376.	1) sec x 4- esc x — 2.
2)	sec x 4- esc x = у.
114
377.	sinx -|- cosx = see x.
378.	sin x Ц- sec x = 2 cos x.
379.	sinx-J-cosx — cscx = 0.
380.	sin x -|- tg x = cos x — sec x.
381.	2 (tg2 x + ctg2 x) = sec2 x -}- esc2 x.
*382. cos3 x • sin 3x -|- sin3 x • cos 3x = •
383. sin3x—sinx = —.
2
384.
cos
= sin a.
385.	sin (x -|— a) -|— cos (x -|- a) = sin (x — a) -J- cos (x — a).
386.	p sin (a—x) = <7sin(p — x).	i
387.	cos px Ц- cos qx Ц- cos (2p q)x = = sin qx 4- sin (2p -|- q) x.
388.	sin 9x-J-sin5x2 sin2x = 1.
389.	cosxcos 7x — cos4x.
390.	1) cos px 4- cos qx — cos (p 4~ q) x — 1.
2)	sin px -|- sin qx sin (p — q) x — 0.
391.	sin2 (a -J-x)-|- sin2 (a — x) = —.
3
392.	sin2 (a-J-x) — sin2(P-|-x) = sin (a — p).
393.	sin’x 4-cosex = a.
394.	sin® x 4- cos® x = —. 8
395.	±!H±^ = tgp.
396.	1 tg6 x = sec8 x — sec2 x.
397.	4 sin2 xsin2 2x = 3.
398.	sin 2x + cos 2x = |Z2 sin x.
8*	116
899. sin22x— sin2x = 4-.
4
400. sin — -4-cosx = 1.
2 1
*401. tg2 x 4- sec 2x = 7 — 10
402. 2sin2x-f-sin5x-|-sin9x = 1.
403. tgpx . tg<?x = 1.
404. tg(l + A tg(l-i =-l \ Z. /	\ о /
405.
tgxtg^- = cosx.
406.
x _ tg* —2 7 ~ tgx + 2 '
407.	tgx + tg2x4-tg3x = 0.
408.	sec + “bsec =
409.	cos x cos 3x = cos 5x cos 7x.
410.	sin 4xsin 1 lx-|-sin 2x sin 5x =
411.	sin 2x-|-sin 3x = 3 sin x.
412.	sin2x + sin22x-|-sin23x==0.
413.	tg Or ctg x) = ctg (t tg x).
414.	sin (к ctg x) — cos (ir tg x).
415.	sin f —cosx^ = cos f^sinx^ \5	)	I
2/2
0.
*	416. sinx = csc5x.
*	417. sinx-f-sin i/ —2.
*	418. cosx — sect/.
*	419. cosx-|-sec x = 2.
*	420. sin x-|-sin t/-j-sinz = —3.
Л16
*421. logcosxsinx -|-logsinxeosx = 2.
*422. ctg 2"-1 x — ctg 2" x = esc px.
*423. ctg 2X—1 a — ctg 2* a = esc 3a (0
424.	1 — 2 sin2 (2х' ) = cos3a.
425.	_______________
sin2* 2 • cos4х 2
= 2^3 •
Решить уравнения и исследовать полученные решения (№ 426 — 430).
426.	cos2 х — 3 cos х -|- а = 0.
427.	а • cos2 х -|- (2а2 — а -J-1) sin х — За -f-1 =0.
428.	tg2 х — 2 tg a • tg x -|- 1 = 0.
429.	sin x tg x 2 cos x = a.
430.	sin a tg2 x — 2 cos a tg x -|- 1 =0.
431.	Доказать, что уравнение 4x -|- 2 sin 2x = к имеет единственный корень и что этот корень заключен между п я — И — .
8	4
432.	Зная, что аир суть два существенно различных* корня уравнения asin х -|-6cosx = с, найти:
1)	sin a sin р;
2)	cos2 ;
3)	sin2a-{-sin2p;
4)	sin 2a -|-sin 2p.
Решить уравнения (№ 433 — 447).
433.	cosx2 = —.
2
434.	sin Зх = cos (x2—1).
435.	tg (ctg x) = ctg (tg x).
436.	tg (sec x) = ctg (cos x).
* См. сноску на стр. 42.
II/
437.	cos (cos x) = sin (cos 2x).
438.	sin (ctg x) = cos (tg x).
439.	tg (/3- sin x) = tg (cos x).
440.	1) arcsin x 4- arcsin — = —. '	2	4
2)	arcsin x-|-arcsin хИз =
...	. o хУ" 2
441.	arcsin x — 2 arcsin—^—.
442.	1) arccos x — arcsin x = arccos x 1^3 .
2)	arcsin x — arccos x = arcsin (3x—2).
443.	arctg(x—1) — 3arctg(x—l) = 0.
444.	arcctg (x—1) — arcctg (x	1) = .
445.	arcctg x 4- arcctg 2x = —.
4
446.	arcsin 2x 4- arctg -	= —.
1	2x 2
.._	 1 —x2 .	2x .	, 2x 3л
447.	arccos------p arcsin-----1- arctg------- = —.
1 + x2 1	I + x2 1	1 — x2	2
Решить следующие уравнения при помощи тригонометрических подстановок (№ 448 — 455).
448.	х = 0,7854 /1 — х2.
449.	2хК1 — х2 = sinf.
450.	2]Лх(1—х) —sin/.
451.	х(1 —х) = 0,22644.
452.	3(х2 —х) = ctg 104° 04'.
453.	1 — х2 = 2х ctg а.
454.	1) 2х = (1 -1-х2) sin а.
2)	2х = (1 -J- х2) cos а.
455.	х = fe(l — х2).
118
§ 5. СИСТЕМЫ УРАВНЕНИЙ
Решить системы уравнений (№ 456 — 472).
{sinx + sin у = О, Т	а
COS X + cos у = 0.
(I	2
sin X + cos у = — ,
I
cos x + sin у = —.
457.
458.
459.
460.
sinxcos у = 0,36, cosxsin у = 0,14.
3 (sin x — sin y) = 4 (sin 2x — sin 2y), 3 (cos x — cos y) — 4 (cos 2x — cos 2y).
sinx — 3sin y, tg x = 5 tg y.
,	/6
Sinxctg t/= -y , уз tg X COS у = ^y .
461.
tg x = sin y, sin x = 2 ctg y.
^sin x
462.
463.
= 3,
4-sin*_|_5.81с“Нч=
11.
2
*+«/ = 60°, tg* _ tg У 4 *
119
	' х —|— у-\-г — 180°,
464.	sinx = 2 sin у, Из sin у = sin г. х + У + 2 = 180°,
465.	tgxtgz = 2, . tgt/tgz = 18. х -|- у -|- г — 180°,
466.	tg х tg у = 2, tg х -1- tg у -1- tg г = 6.
467.	’ х + у + г = 90°, tg х : tg у : tg г = а: Ь : с (а > 0, Ь > 0, с>0).
468.	х +«/+ z = 180°, tg х : tg у : tg г = а: Ь : с (а > 0, b > 0, с > 0). x~\~y+z = a,
469.	sin х sin у 4* sin г = sin р, cos х -|- cos у 4- cos г = cos р. х (cos у -|- cos z) = 2,
470.	х (cos 2y 4- cos 2z) = — 2, x (cos 3t/ -|- cos 3z) = — 4. ' sin x = cos y,
471.	H6sin у = tgz, 2 sin z = /3 ctg x. ' sin2 x 4 sin2 у -|- sin2 z = 1,
472.	cos2 x 4- cos2 у — cos2 z = 1, tg2x —tg2t/4-tg2z= 1.
Из следующих систем уравнений исключить х (№ 473 — 483).
473.	[ sin3x =a, [ cos 2x = b.
120
	( cosx — sinx = а,
474.	I sin 2x = b.
475.	1 cosx-|-sinx = a, I cos3 xsin3 x = b.
476.	<	( sinx + sin 2x = a, I cos x Ц- cos 2x — b.
477.	|	f sin x cos x = a, [ tg 2x 4- ctg 2x = b. [ sinx 4-cosx = a,
478.	[ tg3 x 4- ctg3 x = b.
479. 1)	( a sin x 4- b cos x = p, I cos 2x = q.
2)	1 asinx-|-fccosx = p, I sin 2x = q. [ sin x-|-cosx = a,
480.	[ sin 2x 4- cos 2x = b. sin4x — cos4x = a,
481.	|	sin x cos x = b. b cos x — a sin x = c cos 2x,
482.	{	b sin x a cosx = csin2x. 3 cos x 4- cos x cos 2x — sin x sin 2x = a
483.	{	3 sin x — cos x sin 2x—sin x cos 2x = b.
Из следующих систем уравнений исключить х и у (№ 484 и 485).
484.
X— у = а, sin х cos у — а, cos х sin у = b.
121
485. 1)
2)
sinx-}- sin у = a, cos x + cos у = bt cos (x — y) = c.
sin x cos у — a, cos x -(-sin у = b, sin (x y) = c.
486. При каком значении а система cos x cos у = 1, sin (x — y) _ a sin (x -p y) tgv-H = tgl5° совместна?
Из следующих систем уравнений исключить х, у и г (№ 487 и 488).
487.
х+ z/-|- г = sin (х-J- У) = а» cos (у -|- г) = Ь, cos (г -|- х) = с.
488.
ctg х = а,
ctg у = Ь, ctg г = с, tg(* + ^+z) = d.
§ 6.	СУММИРОВАНИЕ РЯДОВ И СВЕРТЫВАНИЕ ПРОИЗВЕДЕНИЙ
489.	Суммировать: cos а -|- cos (а р А) cos (а -}- 2А) -|--|- ... cos (а nh).
490.	Доказать тождество:
sin a -f- sin 2а -Р sin За -f- ••• -Р sin Па _ , (и-р 1) а
cos а 4- cos 2а -р cos За -р • • • -р cos па °	2
Суммировать (№ 491 —494).
491.	cos а — cos (сс —A)-j—cos (сс —|—2А)— ...
... -}-(—1 )л cos (а -}- nh).
492.	sin а — sin (а Д- А) -}- sin (а Д- 2h) — • • •
... Д-(—1 )л sin (а Д~ nA).
122
493.	1) cos a — cos 2a -j- cos 3a — ... 4- (— 1 )"-1cosn a.
2) sina—sin2a4~sin3a— ... 4~(—l)rt_|sinna.
494.	1) sin asin 3a-j-sin 5a ... 4~sin(2n—l)a.
2) cos acos 3acos 5a 4~ ••• -f-eos (2n—l)a.
495.	Доказать:
.. nm । Згл’г , 5к m , 1) COS-----------HCOS------------4 COS------------4 ...
n	n	n
।	(2n — 1) mr. n
• •. COS ---------£---- = 0.
n
2)
sin
• Зят . . 5я/?г , Sin-----------p sin-----------k
n	n
... + sinIg^-r 0^ ^p. n
* 496. Суммировать:
1)	cos (a 4- A) 4- 2 cos (a 4- 2A) 4- 3 cos (a 4- 37г) 4-4" ••• 4" «cos (a 4-nA).
2)	sin (a 4-/г) 4-2 sin (a 4-2A) 4-3 sin (a 4- ЗА) 4-
4- ••• 4-nsin(a4-n/z).
497. Решить уравнение:
1 4~ 2 cos x -4 3 cos2 x 4- 4 cos3 x-\~ ... =2.
* 498. Доказать тождество:
sin a = a—4 ( sin3 — 4- 3 sin3 — 4- 32 sin3 — 4-\	3	З2	33 '
Суммировать (№ 499 — 502).
499. sin2 a 4~ sin2 (a 4-A) 4~ sin2 (a 4~2A) 4- ...
• • • 4-sin2 (a 4" «А).
500. cos2 a 4- cos2 (a 4- A) 4- cos2 (a 4~ 2A) 4- • ..
----1- cos2 (a 4- nA).
123
501. 1) cos2 a 4-cos2 (a -f- ~ 'j -j- cos2 / a -f-	4- -
• • • -f- cos2
Г . (n — 1) К ' a 4- 1----------—
L n
2) sin2a4-sin2	4-sin2	...
-----j-sin2[a4~ (n-^--l. L n J
. я .	. 2к .	. Зк .	.	. (n—1) к
502. sin---Lsin----4sin----k ••• 4-sin------— .
n 1 n 1 n 1	1	n
Доказать (№ 503 и 504).
eno 2к ( 4к . 6я .
503. cos----4 cos---f- cos _ 4- ...
n	n	n
.	2(n — 1) к .
• •• 4- cos — -— = — 1.
1	n
я । Зк । 5it ।	।	17к	1
504.	1) cos---4 cos----f- cos-4 ••• 4- cos-----= —.
'	19	19 1	19 1	1	19	2
2к . 4к . 6к	.	20к	1
2)	cos —4 cos -cos 4 • • • 4- cos — =  '	21 1	21 1	21 1	1	21	2
Суммировать (№ 505 и 506).
505.	1) cos2x -f~ cos2 2a 4- c°s2 3a -f-	+ cos2/га.
2)	sin2 a 4-sin22a4~sin23a4~ ••• 4*s*n2na-
506.	cos2a4~cos23a4~cos25a4~	4~cos2(2n — l)a.
507.	В окружность радиуса R вписан правильный п-угольник A, А2... Ап. М — произвольная точка окружности. Доказать, что
МА\ 4- МА\ 4- ... 4- МА2п = 2пД2.
508.	Около окружности радиуса г описан правильный 2п-угольник. Из произвольной точки окружности опущены перпендикуляры на все его стороны (или их продолжения). Доказать, что сумма квадратов этих перпендикуляров равна Зиг2.
124
509.	В окружность радиуса /? вписан правильный «-угольник А1 А%...Ап. М— произвольная точка окружности.
Доказать, что
MA4t+MA4 + ... + МА4п = 6пЯ4.
Суммировать (№ 510 — 512).
510.	1) cos a cos р 4" cos (а 4- /г) cos (р -J- h) -f-
4- cos (а -f- 2/z) cos (р -f- 2/z) -j-... cos (а nh) cos (р Д nh).
2) sin а sin р 4- sin (а 4- h) sin (р 4- h) 4~
- sin (а 4- 2/г) sin (р 4- 2/z) 4~ • • • 4“ sin (а + nh) sin (р 4- nh). 511. 1) sec а sec 2а 4-sec 2а sec За 4* sec За sec 4а 4- ••• • •• 4- sec (n — 1) a sec /га.
2)	esc a esc 2а 4- esc 2а esc За -f- esc За esc 4а 4- • • •
• 4-csc(n—l)acscna.
512.	esc a • esc 3a 4- esc 3a • esc 5a 4~ • • •
•. .4~csc(2n— l)a • csc(2«4- 1)®.
513.	Доказать:
i \	4 Я I л 3л	1	4 5 л	1	Д 7k	3
1)	COS4--4 COS4--4	COS4-4	COS4 —	=	— .
8	8 1	8	1	8	2
 4	1	; 43 л	j	4 5л	1	. 4 7л	3
2)	sin4--r sin4 —	4-	sin4 —k	sin4 —	=	—.
8	8 1	8	1	8	2
514.	Суммировать:
---1-----4--------1--+--------'____4- ...
COS a + COS 3a COS a 4~ COS 5a COS a -|- COS 7a
... -I--------!--------.
COS a + cos (2n — 1) a
*515. Найти сумму всех произведений по два следующих чисел:
1) cos a, cos 2а, cos За, ..., cos па,
2) sina, sin 2а, sin За, ..., sin па.
125
В следующих задачах найти частную сумму ряда (s„ = их + 4~ • • • + ип), доказать сходимость ряда и найти его полную сумму (№ 516—520).
516.	arctg-f-arctg+ ... 4~arctg~ 4-...
2	8	2п2
517.
arcctg (— 4-	4- arcctg ( — 4* ба
\ а )	\ a t
•—Р- arcctg — 4~п(п4-0а + •••
а
518. arcctg 34-arcctg 7 4- ... 4~arcctg(n24-n4-l) 4" • • •
519> arctg г Л 9 + arctg г А +
х2 + 1 • 2	№4-2-3
----н arctg
_____X_____
х2 4- п (и4~0
+...
1	2	9л
520. arctg т 4- arctg — 4- ... + arctg	4- • • •
521. Вычислить (точно):
те 2те Зте 4те 5те бте 7те
cos — cos — cos — cos —- cos -— cos — cos------------
15	15	15	15	15	15	15
Свернуть произведения (№ 522—524).
522. (2cosa—l)(2cos2a—1) ... (2cos2"~‘a—1).
523.	(cos-^- 4~cos-| j (c0s7 “^cos'4 j •”
I	“ ।	₽ \
... COS----h cos — .
\	2”	2” /
524.	(1 4- sec 2a) (1 4- sec 4a) (1 4~ sec 8a) ... (14~sec 2"a).
§ 7. ГРАФИКИ
Построить графики (№ 525—533).
525.	у — ar*-sinx (a > 1).
526.	1) y — cosnx при очень большом четном п, 2) y — cosnx при очень большом нечетном п.
126
527.	1) y=tg"x при очень большом четном п.
2)	^=tg"x при очень большом нечетном п.
528.	1) у = {/cos х при очень большом четном п. Пг--------------
2)	у = у cos х при очень большом нечетном п.
529.	у — {/sin х, при очень большом нечетном п.
530.	у = lg cos х.
531.	у — tgx • |cosx|.
532.	1) i/=|tgx|,
2)	y= — | sinx |,
3)	У= (sinx-]-1sinxI).
533.	у = E(sinx)*.
§ 8. НЕРАВЕНСТВА
Доказать неравенства (534 и 535).
534.	| sin a cos a I < —. 2
535.	]/cos ф < J/ 2 cos — ‘	2
*536. Доказать, что выражение x-—cos ° 1 (|Cos P|=/= 1) при любых действительных значениях х заключено между 1 — COS а 14- COS а .
--------- и -------- (крайние значения тоже достижимы).
1 — COS ₽	1 + cos ₽	'
Доказать, что углы всякого треугольника удовлетворяют неравенствам (№ 537—540):
537.
. А . В . С	1
sin — sin — sin---------< —
2	2	2	8
538.	sin A + sin В -f- sin C > sin 2A -]- sin 2B sin 2C.
«о» А В C 3]Лз
539.	cos — cos — cos — < —J.
2	2	2	8
* См. сноску на стр. 68.
127
540.	sin2 — 4- sin2 — 4- sin2 — > —.
2 '	2 1	2	4
Решить неравенства (№ 541—547).
541.	sin2x > cosx.
542.	sinx-}-K3 cosx<0.
543.	V3sinx-|-1 >4 sinx4-1.
544.	/3 — 4 cos2 x > 3 sin x -f- 1 •
_sin x p cos x _ o 545. --!----> 2 cos x.
sin x
546.
547.
2 sin2 x sin x — 1	0
sin x — 1
sin2 x — 3 sin x 4- 1
2 sin2 x — sin x — 1
§ 9. ПОВЕДЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ
*548. Найти наименьшее значение функции r/ = tgx4~ 4- ctg х на интервале 0 < х <	.
549.	Найти наибольшее и наименьшее значения функции у = a sin х -f- b cos x (a > 0, b > 0).
550.	Найти экстремумы функции у = 2 cos2 х—2 cos х—1 и исследовать поведение этой функции при возрастании х от 0 до я.
Следующие функции исследовать на возрастание и убывание (№ 551—553).
551.	^/ = 2cos2x—5cosx+ 2.
552.	у = sin2 х -J- sin х.
553.	t/ = sin2x — 5sinx4" 6.
Найти наибольшие значения функций (№ 554 и 555).
554.	у = sinx sin(х — a).
128
555.	у — sinxcos(x-f-a).
556.	Найти наименьшее значение функции i/ = otgx-4-4- b ctg х (а>0, 6>0) на интервале ^0,	.
*557	. Найти экстремумы функции y — tgatgx-|-ctgactgx ^0 < а <j на интервале (0, те).
558.	Исследовать знак выражения sin(sinx) при О < х < 2те.
559.	В каких границах заключены выражения:
1)	sin (cos х),	2) cos (sinx), 3) tg(ctgx)?
560.	В данный круг вписать угол данной величины так, чтобы сумма образующих его хорд была наибольшей.
561.	Вершина треугольника находится в центре круга, основанием служит хорда этого круга. Каков должен быть угол при вершине, чтобы площадь была наибольшей?
562.	Диагонали параллелограмма даны. При каком угле между ними площадь параллелограмма будет наибольшей?
§ 10. РАСКРЫТИЕ НЕОПРЕДЕЛЕННОСТЕЙ
Найти пределы (№ 563—607).
563. lim^. x-»otg2x	sinx — cos x 568. lim	 u tg X — Ctg X 4
,	|.	1 — COS X 564. lim	. x-»0 sinsx	1- sinx — cosx 569. 11 m	. ,.л 'S'-'
565. X-a	X—a 566. lim sinJf-.sina . X-*a COSX — COS a	.. tgx —sinx 570. Inn—	. x-»0	x3 . cos(t+x) 571. lim ——	 «-Т '-‘S'
.. sin x — sin a 567. 11П1	. X-a tgX— tga	572. lim- «	V 2 X" -T- COS X — 	 2
9 Заказ 33
1U9
573. lim Sln2<. зх 1 + sin x
.. cosx
574. lim--------•
n it — 2x
л-*т
tgx
1 — cos X
585. lim—g*~sin* x-о sinrfx
586. limlg3*-,g*a
tg (л — я)
575. lim x-o
587. lim
COS2 X — COS2 a
x — a sin-------
2
576. lim
588. lim
sin3 x — sin3 я
2 cosx — 1 3
.. x • sin x 577. lim----------.
X- о 1 — cos X
___ ..	1 — cosx
578. lim—---------•.
x-o 1 — sec x
tg X — tg a
___ .. sec 2x + 1 579. lim--------— .
я COSX
,. ..	1 — cos 2x
580. 1) lim-----------•
tg2x
589.	lim- 1 ~~cos!>* . x-o xsinxcosx
_„n I • tg 3x — tg3 X
590.	hm—-------s—.
X-O tgx
591.	limctgx + cscx-l.
__ > ctg X — esc x 4 1
r-nn i- 1+sinx — cosx 592. lim------------------
x-o 1 + sin p x — cosp x
2) lim
2
1 + cos 2x ctg2 x
593. lim -tg2*-2tgr--3
x-arctg3 tg2 X — 4 tg X + 3
581. lim-^^—— x-a Sin (X — a)
594. limtg3x + tgr- 2
<t	sin x — cos x
cosax — cos a a
582. lim--------------
Х-a a2------X2
tr,- .. a si nr — xsina
595. lim----------------
x- a a cos x — x cos a
583. lim —sin--Я cos2 X
596. lim I n sin — oo \	fl
sin
584. lim _
JL	1
4 COS2 X — —
597. lim (2х sin —
JC-* оэ \	2X
598. lim / J- tg — x-o \ x 2 ,
2
130
599.	lim (esc x — ctgx). x—0
600.	lim (sinx — cosx) tg(— 4- x 1
V 4 i 4
601.	lim[(l—sinx)tg2x]. П
X"*T
602. lim
(a —x)sec -^1.
2a J
603.	lim/sin-—-tg—).
x-o \	2 b 2a /
604.	n^g^-arctga x-u	x —a
605.	lim . arctg r-arctg a . x-*a arcsin x—arcsin a
606.	lim —g-^—?ге*е<?а. x—a -irctgx — arctg a
607.	lim | arccos — tg) . x-a \	a 2a I
§ 11. ПРИМЕНЕНИЕ ТАБЛИЦ
608.	1) Доказать формулы Симпсона:
cos(п 1) а = 2 cos па — cos(п — 1)а— 4sin2 — cosпа,
sin (п 4- 1) а = 2 sin п а — sin (п — 1) а — 4 sin2 sin п а.
2) Сформулировать план, как, пользуясь формулами Симпсона, составлять таблицы косинусов и синусов.
609.	1) Доказать формулы:
cos (30° — А) — cos (30° -f- h) — sin h.
sin (30°—A) -f- sin (30° Ц- A) = cos A.
9*
131
2)	Сформулировать план, как, пользуясь этими формулами, продолжать после 30° таблицы косинусов и синусов, составленные до 30°.
610.	Вычислить: i) Cos V 5 ,	2) tg (tg 2).
611.	Решить приближенно уравнения:
1)	sinx = 0,7x,	2) sinx = 0,8х.
Вычислить приближенно наименьший положительный корень следующих уравнений (№ 612 и 613).
612.	tgx = 2x.	613. tg х = —-.
X
Решить приближенно следующие уравнения (№ 614-615).
614.	sinx=x2. 615. sinx = 4x2— к2—1.
§ 12. ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ КОМПЛЕКСНОГО АРГУМЕНТА
616.	В каких случаях cos г, где z = x-\-iy, есть действительное число?
617.	Вычислить tg (1 —Z).
Решить уравнения (№ 618—620).
618.	1) cosz = —. 2) cosz = —. 3) cosz = 1,45.
5	8
619.	1) sinz = —. 2) sinz = 4,0625. 3) sinz = —.
’	9	12
620.	1) cosz = 0,75t. 2) sinz= 1,8751.
§ 13. ГЕОМЕТРИЧЕСКИЕ ЗАДАЧИ
(Обозначения см. на стр. 181) ч
621. Доказать, что во всяком прямоугольном треугольнике:
132
*622. В прямоугольном треугольнике даны а и 1С. Найти углы.
623.	Решить прямоугольный треугольник: та = 12, ть = 7.
624.	Решить треугольник: а = 4, 6 = 6, 1С — 3.
Найти площадь треугольника (№ 625—627).
625.	а = 25, с= 19, та = 14.
626.	а = 74, с = 57, ть = 48.
627.	та — 315, а = 41° 19', р = 35°51' (а и р—углы, на которые медиана делит угол Л).
Найти углы треугольника (№ 628—632).
628.	hb = 14, ть = 15, С —Л = 23°52'.
629.	ha = 93, mo = 97, R = 72.
ь	630. a = 444,2, r = 152,3, В = 63° 07'.
|	631. a = 26, 6^ = 25, г = 9.
632.	г = 6,1, 7? = 21,4,	= 3.
633.	a = 5, 6 = 6, c — 7. Найти lb.
634.	Две окружности радиусов г и R пересекаются. Их общая хорда равна а. Вычислить площадь общей части двух кругов.
635.	Сторона ромба видна из середины противоположной стороны под углом а. Определить углы ромба.
636.	Найти косинусы углов треугольника, если
та : mb : те — X : р : v.
637.	R = 2, та = 1, 6 = с. Найти (точно) Л, В, С.
в
।	638. 64-с = 5,/а = —, Л = 120°. Найти (точно) а, Ь, с.
i
I	639. 2(6 — с) = (]Л 5—1)а, Л = 72°. Найти (точно)
В, С.
640.	a-}-6 = 11, г =	6 , 5 = 6)^ 6 . Найти (точно)
а, 6, с.
д2 Заказ 33	133
I
641.	b = 3) 3, a+c - 3hb, A = 30°. Найти (точно) a, c.
642.	h„ = 8, hb = 6, mc = 5. Найти (точно) С.
643.	4p - (3 4- 1Г 5 ) a, A = 36°. Найти (точно) В, С.
644.	b \ с~2а, г = К 2 , 7? = 2 К 2. Найти (точно) все стороны и углы.
645.	Два равных квадрата имеют общую сторону. Их плоскости образуют двугранный угол а. Из общей вершины проведены диагонали. Найти угол между этими диагоналями.
646.	Найти угол между ребром и гранью правильного тетраэдра.
647.	Найти двугранный угол правильного октаэдра.
648.	Минутная стрелка имеет длину 3 см, а часовая — 2у см. Через сколько времени после полудня в первый раз расстояние между концами стрелок составит Зу сл«?
649.	Конус и полушар имеют общее основание. Сферическая поверхность полушара делится боковой поверхностью конуса в отношении т : п (считая от основания). Найти угол наклона образующей конуса к плоскости основания. Рассмотреть случаи т = п и п — 0.
650.	Два равных конуса имеют общую вершину и касаются друг друга по образующей. Один из них неподвижен, а другой катится по нему. Высота катящегося конуса описывает коническую поверхность, площадь которой равна площади боковой поверхности каждого из данных конусов. Найти угол в осевом сечении каждого из данных конусов.
651.	Треугольник, углы которого суть А, В, С, вращается поочередно около каждой стороны. Найти отношения объемов тел вращения.
652.	Круговой сектор вращается около своего крайнего радиуса. Объем полученного тела вращения составляет объема шара того же радиуса. Определить угол сектора.
134
Доказать, что во всяком треугольнике имеют место следующие соотношения (№ 653—665).
653.	27? 4 hahbh==(abc)k
654.	X = aR sin В sin С и т. д.*.
655.	X = 27?2sin A sin £?sinC.
ABC
656.	pS = abc cos - J- cos -y cos -y.
657.	S2 — (p— a) abccos ycos4 и т. д.*.
658.	S = p2tg4tg4ts4‘
659.	X — 4	b2 c2 sin A sin В sin C =
= 442tz2 b2 c2 (sin 2A + sin 2B -|-sin 2C).
660.	X(sinX -|-sinS-y sin C) = 2p/?sin A sin XsinC —
= p2 (cos A 4- cos В Д- cos C — 1).
661.	Rr —	= 4 X sec 4 sec 4 sec 4 •
z z z
„„„	Л Г, Л В C
662.	p = 4/?cosy cos-ycos-y.
663.	a sin (B — C) 4-6 sin (C — A) 4-csin(y4 — B) = 0.
664.	о (sin В — sin C) 4~ 6 (sin C — sin/l)4-
4-c(sinX — sinX) = 0.
665.	i—tg 4 ^4=4и т-д- *•
* Слова «и т. д.» обозначают, что можно производить циклическую перестановку. Например, в задаче № 654 они заменяют формулы;
S = b R sin С sin А и S = с R sin zlsin В.
92*
135
666.	Доказать, что стороны всякого треугольника являются корнями уравнения:
х3—2рх2 (г2 4* р2 + 4/?г) х — 4Rr р = 0.
Доказать (№ 667—670).
667.	1) Если <5 = р (р— а), то треугольник — прямоугольный.
2)	Если <$ = (р— Ь)(р—с), то треугольник — прямоугольный.
668.	Если а2 4" = 8Т?2, то треугольник — прямоугольный.
669.	Если расстояние между центром описанного круга и ортоцентром равно половине одной из сторон, то треугольник— прямоугольный.
670.	Если ctg-2" = —~, то треугольник — прямоугольный.
По данному соотношению между элементами треугольника определить вид треугольника (№ 671—674).
671.	sin2 Л 4~ sin2/? = sin2 С.
672.	sin Л-{-cos Л = sin/? 4~cos^-
673	= sin2 4
tg В sin2 В
674.	с = С =
Доказать (№ 675—678).
675. Если Л = 60°,
то а
676.	1) Если отношения сторон треугольника рациональны, то косинусы его углов имеют рациональные значения.
2) Если стороны и площадь треугольника рациональны, то все тригонометрические функции его углов имеют рациональные значения.
136
677.	Если синусы углов треугольника образуют арифметическую прогрессию, то произведение тангенса половины меньшего угла на тангенс половины большего равно -4-. О
678.	Углы и стороны разностороннего треугольника не могут одновременно образовывать арифметические прогрессии.
§ 14. СФЕРИЧЕСКАЯ ТРИГОНОМЕТРИЯ
(Обозначения см. на стр. 183)
Решить прямоугольные сферические треугольники (№ 679—684).
679.	1) 2)	а = 66° 48', Ь=. 119° 31'. а = 118°41', Ь = 150°31'.
680.	1)	о = 47° 39', с = 80° 00'.
	2)	а =123°37', с=159°00'.
681.	1)	а=136°49', А = 99° 10'.
	2)	а = 134° 48', А = 160° 02'.
682.	1)	Ь= 118° 13', Л = 55е 30'.
	2)	Ь = 124° 30', А = 159° 18'.
683.	1)	с = 164° 13', Л = 47° 39'.
	2)	с= 109°31', Л = 138°25'.
684.	1) А = 15° 49', В =102° 02'.	
	2) А = 149° 12', В= 123° 06'.	
Решить прямосторонние сферические треугольники (№ 685—690).
685.	а = 48° 14', Ь = 75° 57'.
686.	а = 105°, В = 76°.
687.	а — 119° 26', С = 69° 05'.
137
688. 1) а=П4°49', /1=136° 29'. 2) а = 38° 27', А =107° 06'.	
689.	А = 59° 58', В =140° 01'.
690. 1)	А = 127° 39', С = 98° 25'.
2)	Л = 64° 56', С = 58° 12'.
Решить	сферические треугольники (№ 691—696).
691. 1)	а = 59° 46', b = 83° 18', с = 96° 04'.
2)	а =119° 37', 6= 158°11', с = 48° 28'.
692. 1)	А = 116° 08', В = 60° 07', С = 69° 45'.
2)	Д = 128°30', В = 119° 15', С=125°02'.
693. 1)	а =104° 23', ft = 67° 04', С = 36° 18'
2)	а = 108° 14', ft = 60' 28', С = 98° 32'.
694. 1)	А = 39° 04', В = 57° 46', с = 100° 00'.
2)	А = 107° 46', В - 69° 42', с = 40° 11'.
695. 1)	а=112°40', ft = 58°28', А = 98°23'.
2)	а=121°05', ft 66°25', Л = 138°17'.
696. 1)	А =54° 42', В = 81° 27', а = 52° 35'.
2)	А = 39° 37', В = 69' 25', а = 26° 50'.
ОТВЕТЫ
6. 1 — (21^2) (1 — 1^2 — У"2 ).	10.2) См. формулу (V. 53).
г_____ к 15
14 2x^1 — №. 15. -^у-
2№ — 1
16. --г
2хУ 1 — №
21. х=>
У~1—9а2 За
1
Задача возможна при 0 < а < —-.
О
22. 2) х = а (2Ь2 — 1) +
-ф 26 /(1 — а2) (1 — 62). Задача возможна при условиях — 1 < а
cos (а — В)
262 - 1, 0 < 6 < 1 (см. черт. 20). 36.	.
41.
г___	/	Q
4 J tga . sin I 45° 4- —
где cos к =□ — cos я, 0 < <? < 180°. '	4
44. — [sin 2 (а-ф₽)-р sin 2a —sin 28].
4
47 1) См. формулу (IX. 2), 2) См. формулу (IX 11).
48. l(i -cos4а). 49. 2) x = 45°(4fe—1)-ф(—1)*12°15', 3) х = — зо° |б6 — 2 ф- (— l)ft]. 50. а) х = 45° (46 — 1), Ь) х = 180°й ф- 64°59'.
139
52. х = 30° (3ft ± 1). 53. x = 22°30' (4k ± 1). 54. a) x = 45° (4ft+l),
b) x => 30° [6ft у (—l)ftL 56. a) x = 180° (2ft 1), b)x = 60°[6fty 4-(—1)*]. 58. a) x = 45° (2ft 4-1), b) x = 30° (6ft + 1). 60. x =
= 7°30'(4ft—1). 62. a) x = 90° (2ft 4> 1), b) x = 360°ft, c) x = = 36° (2ft У 1).	63. a) x = 120° (3ft ± 1), b) x = 22° 30' (4ft у 1).
64. x = kit. Указание, tg
— взаимно обрат-
ные величины. Их сумма равна 2 в том и только в том случае, когда каждая из них равна 1. Можно решить задачу и без этого соображения, но несколько длиннее. 68. x=90°(4ft4-l). Указание. Сумма двух синусов равна 2 в том и только в том случае, когда каждый из них
равен 1. 70. Если а 180° (2п-^ 1), то х = 30° (6ft 4" (— l)ftl — —;
если а = 180°(2«4- 1), то уравнение удовлетворяется при всяком х. 71. Если а 45°(2n У 1), то х = 45° (2ft 4- 1); если а = 45° (2л 4- 1), то уравнение решений (действительных) не имеет. 74. При — со < < а < — 5 уравнение имеет два решения: a) secx =
3 4- У 9 —8а	3 — У9 —8а
=------;----“ , b) sec х =--—-----— ; при — 5<а<1— толь-
4	4
ко первое из них; при 1 < а < со решений нет. 80. х ==> nk
! .071 X (4m у 1) я + У(4m + I)2*2 - 240
4-(— 1)4-1 . 1,1871. 82. а) х =-----------—--------------, где
т — любое целое число, кроме 1 и 0,
— (4п 4- 1) я + ]/"(4п4- I)2 к2 4-240
Ь) х = --------------—-------------------- , где п — любое целое
logy 4- log (3ft 4" 1)
число. 83. х = 1 4- ---------V~g2------’ ГДе логаРиФмы берутся
при любом (одинаковом) основании, ft — любое целое неотрицательное число. Прибл. х = 1,06653 4- 3,32192 lg (3ft 4*1). где 1g — деся-
. х	1	(4ft-f-1) я 4; V1 4-2 (4ft1) я
тичныи логарифм. 84. х =•--------------—----------5-------—, где
,	.	/з 1
ft — любое целое неотрицательное число. 88. х =---• 90. х=—
2	2
п = 1. 91. Х!=0, х2=. — , х;| = — — . 94. xj^tg-^-, x2=ctg-|-.
95. Xj = tg-~-, х2 = — ctg— . 98. а) х = 360°т, у => 360° п, Ь) х=
= 120° (3 m + 1), z/ = 120°(3n+1), с) х = 30° (6m 4-1) ± ?, у = = 30° (6п 4-1) 4-<р, d)x=>30°(6m—1)4^<р, у = 30° (6л — 1) у <р. В решениях Ь), с) и d) знаки оба верхние или оба нижние, <р =
Уз — УП
=> arccos---—--------те 113° 20'. 99. х = 90° (4ft у 1), у = 180° I 4-
140
+(—	где<р =iarcsin------- ~ 39°07'. Логарифмы берутся при лю-
log3
бом (одинаковом) основании. 100. х т 360 k ± 56° 19', у и 360/ 4? ±86°49', г s: 360°« + 36°52'. Знаки либо все верхние и &4“/ + 4 т => 0, либо все нижние и k 4- / 4 т =* 1 • 101. 4а2 (1 — а2) = Ь2.
Черт. 21
102. а2 (2 — а2) = Ь2. 103. tg2Vm2 4- п2 = —•. 105. b— а = cos а. п2
360® k
108. а) х =----, где k — любое целое число, не кратное п, Ь)х =
пп (п 4 1) я
sin —cos-----------
2k 2k , „	sin 2" а
ИЗ.	- ——— (fe=/=0). 115. ’on j • Указание. Cm.
••	ла oiu a
Sltl*2k
sin а
решение задачи №45. 116. ——.	Указание. См. решение задачи
№ 45.	117. 1) См. чертеж 21. Пунктиром показана синусоида
j/=sinx. 2) См. чертеж 22. Пунктиром показана косинусоида z/—cos х. 118. 1) См. чертеж 23. Пунктиром показаны прямая у => х и синусоида у = sinx. 2) См. чертеж 24. Пунктиром показаны прямая у==х
14L
142
и косинусоида у = cos х. 122. См. чертеж 25. Пунктиром показана синусоида г/= sinx. 123. См. чертеж 26. Пунктиром показана синусоида у => sin х 124. См. чертеж 27. 125. График состоит из отдельных точек оси абсцисс, для которых х ==	(см. чер-
теж 28). 129. a) 180°-2fe — <рх < х < 180°-2fe + cf2, b) 180° (2k 4- 1) —
Черт. 25
l/”29 4- 3
— ?2 < x < 180° (2k 4 1) 4- fn где <fx = arcsin----------=s 56° 59',
)<29 — 3	я
<p2 = arcsin --jg----	13° 48'.	133. При возрастании x от 0 до g
Г*
Черт. 26
я	Зтс
— до — 2	2
у возрастает от 3 до 13; при возрастании х от
у убывает
143
Далее у изменяется периодически. 137. Наибольшее значение угла А а	1
достигается при b = с и равно 2 arcsin-—. 140. —sina. 141.— .
9
142. —.	144. a. 145. 2) 0,74562, 3) 0,80268, 4) 0,21711.
т2
148. х =• 0,8603 (с недостатком; погрешность меньше 0,00005).
149. 1) cost = ch 1«1,54308, 2) sin i = i sh 1 »l,17520i. 150.9,15450—
— 4,168917. 151. 2) z =-|-(4£-К 1) ± i In 7.	152. 1) z = 2kr. +
± (y — i In 5^ , 2) z = fen^(—l)ftiln (2Д-/3"). 155. a=4,1082, 6 = 2,8766, c = 5,0152. 158. a = 60,6114, b = 97,8877, c = 62,5226, /	a \
s 1 — cos — I
\	2	X
C = 38°08'. 159. r =---------s—-----160. 166 cjh. 163. sin Л =77--
za	zv
sin В = — . 166. asina-sinp. 167. 70° 32'. 168. Холодные пояса— 2м
8,3%, умеренные пояса — 51,9%, жаркий пояс — 39,8%.
170. Ь=153°48',	Л=55°32', В =-137°42'. 171. Два решения:
bi = 32°23', q =48°36', Bi = 45°33', &2=147°37', с2 = 131°24', В2 = 134°27'. 172. a = 35° 35', с = 50° 03', В = 53° 12'. 173. я = =49°33', 6=46°02', с = 63°13'. 175. Ь=78°14', Л = 35°0Г, С = 106° 14'. 176. Два решения: ^ = 125°57', В1 = 133°33', Су = = 63° 33 ; 62 = 54°03', В2 = 46°27', С2 = 116°27'. 177. я = 62°49', b = 46°31', С = 119°09'. 179. a = 30° 05', b = 27° 32', с = 32°16'. 180. с = 37°58', Л = 83°43', В=54°16'. 181. с=60° 46', В=42°42', С=97° 37'. 182. 2) 5797 км. 183. В Москве 53° 32', в Хабаровске 42°47'. 209. Указание. По формуле (VII. 20) имеем: tga — ctga = = —2ctg 2a, 2tg 2a — 2ctg 2a = —4ctg 4a, 4tg 4a —4ctg4a = —8ctg 8a. Складывая эти тождества, получим то, что требуется доказать. 211. tg—= 1/	—+21/ т I. Комбинации знаков любые. Задача
2 г т—3 г т—3
144
1	J
возможна при —оо< т < — и при 3 < т < оо. 212. а) +2, b) i“-
214. 1) (— 1) 2 cos na = _2L cos a —
11 -
(П-Н)П(Л- I) .
Д--!-i------— COS3 a -f-
31
п—1
(п4-3)(п4-1)п(п—1)(п —3)	пП-\ „
4-------------т;------------cos3 a — • • • 4- (— 1)	-2 cos" a.
о!
При п = 3 и п = 5 см. формулы (V. 45) и (V. 46),
„	п-п „ (п 4- 2) п-п (п — 2)
2) cos na = I — sin2 a 4- ----------—----------sin’a—
41
(n 4-4) (n 4-2) n-n (n — 2) (n — 4)	2	- „
—-----------------—-----------------sin6 a -f- (—1) 2 Sin" a.
6!
При n = 2, n = 4 и /2 = 6 см. формулы (V. 36), (V. 37) и (V. 38),
™ .	„2	, n-n , ,	(Лф2)П-П(Л- 2)
3) (— I) COS Па = 1 — COS4 a -[-----—------ COS4 a —
41
(n + 4) (n + 2)n-n(n —2)(n —4)	„
—--------------—--------------COS6 a + • • - +(—1) 2 COS a.
6!
При п=з2, n = 4 и п =я 6 см. формулы (V. 31), (V. 32) и (V. 33).
C'-tga-^tg^ + C^tg^--..	~
215. fgna =--------— ---------------------. Последние чле-
1 — C2 tg2 a-|-C4 tg4 a-
цы числителя и знаменателя содержат tga в n-й и (n — 1)-й степенях. 216. 1) 4х® — Зх — cos a = 0. Указание. Воспользоваться формулой (V. 45). 2) 4х3 —Зх + sin a = 0. Указание. Воспользоваться формулой (V. 22). 3) х3 — Зх2 tg a — Зх ф- tg a =а 0. Указание. Воспользоваться формулой (V. 56). 222. q. 223. Может в одном из трех случаев: а) а = 360°k, b) p = 360°fe, с) а.рр=360°к 224. Указание. Обозначим для краткости: tga=u, tgp = n, tgi = K). По условию и-\-4- v + w = a, uvw = а, uv 4- vw + wu = 1 (здесь через а обозначено общее значение и 4- v 4- w и uvw). Согласно формулам Виета и, v и w суть корни уравнения s3 — as2 4- s — a = 0. Остается доказать, что это уравнение не имеет трех действительных корней. 225. Указание. Эту задачу можно свести к предыдущей. 230. sin 42° = cos 48° = ^-^Ч/з" V104-2/5"—/Г 4- 1). cos 42°=sin 48°=JUl,<104-2/lT4-
о	о
4-/3'(У5—1)]. Указание. 42°=60°—18°; sin 18°=—.
27?
231.	sin 33°= cos 57° =	[(/б — /2 ) V10 4-2/5" 4-
4-(/6 4-У2)(/5—1)]; cos 33° = sin 57° =
= 1б[^+	)Knr+W-(/6-/2")(/5 - 1
145
232.	sin 27° = cos 63° = V? (/7b + 2/5" — /бу 1);
cos 27°=sin 63°=^ (lZ 10-^2 V5 +У5 —1). 233. sin 12°=cos 78°= =|[Kio+2j/T—]/3(K5— О]'- cosl2°=sin78°=-^(/3-K 10+2/5 + + /5 — 1). 234. sin 36® = cos 54° = — V' 10 — 2]/"5; cos 36° = = sin 54° = — (/5 + l). 235. 22° 30'. 236. 22n30'. 237. 22°30'.
4
238.	15°. 239. 75°. 240. 15°. 241. 54°. 242. 18°. 243. 18°. 244. 36°.
249.	]/" *7 + T^17 . 250. —А. 251.2л2—I. 252. 2x 1 *2-.
И 34	4	1 — 2x2
r. —	V2 V2
265. x = 2a У 1 — а2. Задача возможна при — —%~ < a < —2— '
266. x = 1 — 2a2. Задача возможна при 0 < a < 1. 267. x =
= 4a(l —2a2) У 1 — a3. Задача возможна при —ту У 2 —"/2 <
1 i Z —1 ~ ° 2
< a < -g- V 2 — у 2 . 268. x => ——. Задача возможна при a > 0.
4a (I — a2)	. ,_	r-
269. x =-------. Задача возможна при —(У 2—1)<а<у 2 —1.
1 — 6а1 + а4
270. л = —. Задача возможна при a > 0. 271. х =]Л 1 —4a2 . Зада-20
ча возможна при 0 < а < —	272. х = У”1—а3. Задача возможна
5 + За	1
при — 1 < а < 0. 273. х= —-—. Задача возможна при —оо<а<— .
(4 — а3) /а2 — 1	2Уз-
274.	х =-------—тд--------• Задача возможна при 1 < а < —g—
a (3 — 4a2)	„	1	1
275.	1)	х = —---	.	Задача возможна	при — —	<	а	<	—.
'	(1 — 4a2)	У1	—	a-	v	2	2
a(3 —4a2)	о	1
2)	х	=	— r			.	Задача	возможна	при	— <	а	<	1.
’	(1 — 4a2) /1	-	a2	1	2
276.	х = 2a У (1 — a2) (1 — 4fe2) + 26 (1 — 2a2). Задача возможна при
условиях. — j/ —2^ < a < J/ 1 ~2--, ~~ < b < -L. (черт. 29).
146
(a \	/	a \	a	3a
30°	—  cos 30° — — 1=4 cos — cosa sin—
2. J	\	z /	£	£
3) tg 2a..
4 sin (60° + a)-sin (60° — a)
333. 4 sin 5a-cos2 a. 334. 2sin2l°. 335.	~
cos2 a
a + 3	/ a \	/_ p
336. tga4g2a4g3a. 337. 1) 4 cos —— cosl 45°— — Icos I 4t>°——
2) 4 cos^-^cos^45°-^~-jcos^45°+-^. 338. 1)—2 sin a.sin P-cos(a-|-p), / h\	[ h\
2) 2 sin a-sin p-cos(a—P). 339. 1) 4 sin(a-pi)cosl 30°+y )cosl 30° — — I,
2) 4 cos (a -I- li) cos ^30°+ yj cos ^30° — yj, 3) tg (а -ф- h}.
340. ctg 22° ctg 23°. 341. 1)
cos (a + p) • COS (a — P) COS2 a • COS2 p
sin (a -ь P) sin (a — P)
cos2 a.sin2 p
342. 2 sin a.
147
_	2/2 cos2 * Л1п (45° +a)
343. 2/2 cos cosl 45° - Ц2- ). 344.----------------------.
2	' \	2 /	cos а
Ь
345. sin а. 346. tg (45° — <р), где tg<p = —, —90° < <р< 90°.
I а I	Ь	я
347. ----, где tg® = — , 0 < ® < — . 348. 2 I а | sin (45° + <f).
cos <p	a	2
O 2 f
2а-cos2 —
/ b \2	2.6
где cos 2® = I —	0 < < 45°. 349. 1) ----- . где tg <f> = — ,
\ a / ’	cos	a
0 < <p <90°. Данное выражение представляет сумму гипотенузы и ка-
<р	b
тета, заключающих угол <р. 2) 2а sin2 — , где sin <р = —, 0 < ® < 9Сг.
Данное выражение представляет разность гипотенузы и катета, за-,—	!	<р \	b
ключающих угол <?. 350. 2 I/a sin 45° + — , где cos® = —, \	2 /	а
1
0 < у < 90°. 351.—[cos 2а + cos 23— cos 2(a+~JB)— 1]. 352. 1) См. фор-
3
мулу (VIII. 6), 2) См. формулу (VIII. 7). 353. —. 354. 1) См. 16
формулу (IX. 7), 2) См. формулу (IX. 16). 355. ^-(3 sin 2а — sin 6s). 1
356. — (2 cos а — cos За—cos 5а). 357. 1) См. формулы (IX. 19) и (IX.20),
2) См. формулы (IX. 21) и (IX. 22). 358. 1) а) х = 90°-46 -р 8°43', Ь) х= 90° (4fe + 1) — 8°43', 2) а) х = 360’fe + 50°26', Ь) х = 360°fe — — 18°33'. 359. cosx определяется из биквадратного уравнения: c-cos’x-p +(fc— а—с) cos2 х + а = 0. 360. 1) tg х=~ b +	— 4 (« —d) (с — d)
2 (a — d)
2) а) х = 180°fe + <р, где = arctg 3 ~ 71°34'; Ь) х = 180°А — ф, где ф = = arctg 6 « 80°32'. 361. а) х = 90°(2fe + 1), b) х = 40°(3£ ± 1). 362.
, . а 4- В	т
х => 180°fe -J- (— l)ft,f — —-— , где = arcsin --------
2 cos^31^'
2
148
303. a) x = 9° (8k — 1), b) x = 1°48' (8fe-J- 1). 364. x = 22°30'm, где m — любое целое число, не кратное 8, т. е. 8fe. 365. х = = 30° (6k ± 1).	366. а) х = 120° (3fe ± 1), Ь) х = 360° k ± <р,
V17 — 1	„ „	360° k 360° k
где <f = arccos ----- к 38 40.367. a) x = ----------, b) x =-.
4	13	7
368. a) x = 90° k, b) х=180%4:?> где <p = arccos » 54° 41'. 369. a) x = 180° (4 fe ± I), b) x =60° (6Л ± 1). 370. 1) a) x => 90°.4fe, b) x = 90° (4k + 1),	2) a) x = 45 (4k — 1), b)x=90°-4fe, c) x =
=90°(4M-l). 371. x = 180%4-(- !)*<₽, где <p = arcsin K65~ 1
8
«61° 59'. 372. a) a-= 180%, b)x = 180% ± <p, где = arctgV^5:»
«40° 12'. 373. a)x = 180%, b) x = 180c k ± где у = arctg «
« 20 42'. 374. а) л =360%. b) x = 360% ± 70° 32'. 375. x =
=> arccos 1/5 ~ У « 51 °50'. 376. 1) a) .г = 90° (4k + 2) — <p, b) x =
1	144__1
= 90° (4k 4- 3) 4* ?• гДе ? = ~ arcsin-!—_— « 19° 05'. 2) a) x =
= 90° (4/г4-2)—<J>, b) x=90° (Ife-p 3) -f-4>, где ф	~ arcsin(4|%—8)«
«35° 23'. 377. a) x = 180%; b) x = 45е (4fe 4-1). 378. x = = 90cfe 4- 31° 43'. 379. a) x = 45° (4k 4- 1), b) x = 90° (2k 4- 1). 380. x =>
= 180° k. 381. x = 45° (2k 4- 1). 382. x = 22° 30' (4k 4- 1).
3
Указание. Левую часть можно заменить через — sin 4х (см. задачу № 9).
4
383. а) х =30° [6fe 4-(—1)*], b) х = 18° [10 ft % (—1)4 с) х = = 18° [ 10/г 4- 3 (— 1)*+1]. 384. cos (х 4- 1) = S1—j- « 0,56975 sin a.
2 cos —
2
385. При a 4= 180° m x = 45° (4k 4- 1); при a = 180° m данное урав-p sin a — q sin В
некие превращается в тождество. 386. tg х = ----------------.
р cos a — q cos p
90°	1
387. а) x =--- (2k -J- 1), b) x= ---[45 (4k +!) + (— 1)* ?]
P	р + я
149
где ? = arcsin У-L % 20° 42'. 388. а) х =45 (2k + 1), b) х = 4
= у . 30s (6* + (—1)4 389. а) х=22° 30' (2*+1), Ь) х = 20° (6* ± 1).
390. 1) При р #= 0. q =/= 0 и р q =£0 уравнение имеет
360° k	360' k
три серии решений: а) х = —— . Ь) х - —-— , с) х —
180°(2*-f-l) „	„
=-----------•—. Если р + 0, q + 0, р + Q = 0. то серия с) отпада-
р+<7
ет, а серии а) и Ь) совпадают между собой. Если хоть одно из чисел р н <? равно нулю, то данное уравнение обра дается в тождество. 2) При р 0. <7 4 0 и р — <7 =4 0 уравнение имеет три серии решений:
360°*	360 k	180° (2k + I)
а) х =------. b) х =--------. с) х =---------------- При p = q 4= 0
р	<7	Р — <7
серия с) отпадает, а серии а) и Ь) совпадают между собой. При р=/=0, 180° k
q = 0 х = ----- При р = 0 уравнение обращается в тождество.
Р
391. cos х= ± 1/ Г(У 9	*.. Задача возможна в следующих случаях:
г 3 cos 2»
а) 90°. 2* — <f <а<90°-2* + <р,	Ь) 90° (2* + I) — 4 < а <
< 90° (2k + 1) -f- ф,	где	= arc cos st 35°16',
|/~Т	а 4- Р
ф = arccos st 54° 44'.	392. х = 45°14* + 1) — -------- .
3	2
393.	sin 2х =	± 2 |/ ? ~ а..	Задача возможна при —	<
<а<	1. 394	х = 45° (4*-fc 1). 395. х = 360° k — а 4 2р.
396. х = 30° Г* t О 397. х = 45° (4* ± 1). 398. а) х = 45° (8* — 1), Ь) х =	15° (8* 4	Л}. 399 а) х =	18° (10* ± 1) Ь) х = 18° (10* ± 3).
400. а)	х = 360°	*. Ь) х = 60° |6*	+ (— 1)*). 401. cos 2х =
4]Лз + 5
= —------------. х= 180°* (-78° 17 . Указание. При нахождении cos2x
13
рекомендуется воспользоваться формулой (XVII 1). Согласно этой формуле	____________
I 813- 420^3 =14}<3—15
402. а) х = 45° (4* + 1), Ь) х = у -30° (6* + (— 1)4 403. х =
150
2k 4- 1
= 90°------. Предполагается, что р 4-<7 ¥= 0, р =£ 0. о-kO. Не-
Р + Q
которые корни могут оказаться несобственными. 404. х = Зк
= — (2*4- 1). 405. х = 360°* ± 51° 50'. 406. Уравнение имеет только 5
несобственные решения х = 90° (4* 4- 1). Это значит что они удовлетворяют уравнению лишь при условии, что правая часть понимается не как результат непосредственной подстановки вместо хзначения
tgx— 2
90° (4k 4- 1), а как Иго —----------. 407. а) х = 60° *; Ь) х =
х-.90±4*±1) tgx 4- 2
= 180° 4: <f, где
. V 3 ш = arcsin — т 3
к 35° 44'. 408.
х = 120° k. 409. х =
= 22° 30’ k. 410. а) х = 20° k, b) х = 30° (2* 4- 1). 411. а) х = 180° k.
V17— 1
b) х = 360® k 4: где <р = arccos---------яг 38° 40'. 412. х — 180° k.
4
413. sin 2х =--------, где k — любое целое число, за исключением
2*4-1
— 2, — 1, 0 и 1. При k = 2 годятся лишь те значения х. для кото-
1	1
рых cos 2х > 0. 414. a) ctg 2х = k 4- - , b) esc 2х = I -|- — ; 4	4
I — любое целое число, кроме — 1 и 0. 415. а) х = 2*к ± р, Ь) х = х	19
= — (4k ±1)4-? (знаки оба верхние или оба нижние), f = —arcsin — « 2	2	16
яг 0,29870. 416. х =90° (4k ± 1). Указание. Синус ранен косекансу только в тех случаях, когда каждый из них равен I или каждый из них равен — 1. Следует убедиться, что система -in х = 1 esc 5х = 1 (или sin х = — 1, esc 5х = — 1) непротиворечива. 417 х = 90е (4 k ±1), у = 90° (4/ 4- 1). Указание Сумма двух синусов равна 2 только в том случае, когда каждый из них равен 1 418. х = ISO® k у = = 180° (*-(-2/) Указание. См. указание к задач! Mb 416 119 х — = 360°*. Указание Использовать формулу (XVI1 2) 420 х = 90° (4*—I). у = 90° (4/ — I) z = 90° (4и1 —1) Указание См. указание к задаче № 417 421 х = 45°(Н*± 1) Указание Как известно из алгебры logob • logs а = 1 Таким образом, левая часть с равнения есть сумма двух взаимно обратных величин. Эта сумма равна 2 только в том случае когда каждая из них равна 1 (формула (XVII.2)].
360° k	180° (2k ± I)
422. а) х = -- (р + 2"), Ь) х =-------(р * -2"). 423. а) х =
2П—р	2п 4- р
।	/	\	I (2* ± 1)п о!
log -----4-3	log ----------—6
\ а ' ( За\	[ j	J
log 2	\ >	2к) ’	*	log 2
151
I k > — — — I. Логарифмы можно брать при любом (одинаковом) \	2 тс 2 /
log (2тгА ± За) /	За\
основании. 424. х = ------------- |Л>	Знаки оба верхние
log 2	\	2r.)	г
или оба иижпие. Логарифмы можно брать при любом (одинаковом)
logit — log 12+ log(24Z? + 1)
основании. 425. х = 2 +-----------------—-----------------(k > 0).
log 2
При k = 0 знак только верхний Логарифмы можно брать при любом (одинаковом) основании.
3 — 1^9 — 4а
426.	cos х —-----—--------- . Задача возможна при — 4 < а< 2.
1
427.	При — сю < а < — 1 и 1 < а < оо sin х — — , при 0 < а < 1 sin х = 2а — 1 (при а = 1 оба ответа совпадают). При 1 < а < 0 задача невозможна.
428.	tg х = tg а ± (/"tg2 и — 1. Задача возможна, если 45° (4fe + 1) < < а < 45° (4* + 3) и притом а + 90° (2k + 1). 429. При — оо < а < —2
cos х —	, при — 2 < а < 2 решений нет, при 2 < а <
< оо cosa~^a2+J. 430. При 180’ (2k — 1) — <f < а < 180°.2А+? tg х => S_os a Kcos* q — sin а _ при ]g0o 2k + <Р < а < 180° (2k + 1) — Sin а
1/'~5 _1	с3 — Ь3
— решений нет; « => arcsin	« 38° 10'.	432.	1) —	,
2)
4)
с2
а2 + Ьа
2Ь2 (а2 + Ь2) + 2с2 (а2 — &2) (а2 + Ь2)2
4аЬ (2с2 — а2 — Ь2) (а2 + Ь2)2
433. х = ±
V 4 (&k ± о, г О
где k— целое
неотрицательное число. При k = 0 под радикалом следует брать верх-1 Г
ний знак, при положительных k—оба знака. 434. а) х = — — 3± ±V'13+2«(4fe+l)^, Ь) х = |з ± У13 + 2х(4й— 1)J , k — целое по-ложительное.
435. tg х » — [ к (2k 4-1) ± V яа (2k -J- I)2 — 1б1, k — любое целое чис-4 L	J
ло, кроме — 1 и 0. 436. a) cosx = -|-Гх (2Л + 1) + V""’ (2М-1)2 —161,
162
fe<=_2,-3, -4,
b) cdsx = ^'L(2ft+l)-y^2(2fe+l)a— 16 .
k = 1, 2, 3, ... 437. x = kw + ?, где ? = arccos V^n + 9--------------1 ~
» 0,42512. 438. a) tgx = у (4k + 1) ± V v? (4&4- I)2 — 16^ (/?=£0), b) tgx=- v Г к (4k + 1) ± /к2 (4fe+ I)2 + 161. 439. x =	(6k + 1).
4 I	J	b
440. 1) x = ± 1 / 10 — 4/ 2 д, o,5O547, 2) x = Kl » 0,18898.
V 17	14
1 1
441. xx = 0, x2 => 1, x3 = — 1. 442. 1) Xj = 0, x2 = — , x3 => — — ,
1. 443. x = / 2 . 444. x = ± (1 4- / 3 ). 445. x
2
0,28078. 446. x= —. 447. Уравнение имеет только несоб-5
1 •— 0. Это значит, что уравнение удовлетворяется,
_ /17 — 3 4 ственный корень х 2х
если arctg ------ понимать как односторонний предел при стремлении
1 — х2
х к 1 слева, а в остальные члены левой части подставить х=1.
448. tg = 0,7854, у = 38° 09', t	t
= ± cos —, х2 = ± sin —. Знак х
t	, t
450. хх = cos2 —, х2 = sin- — .
х = sin? =0,61767.	449. хх =
должен совпадать со знаком sin t.
Задача возможна при sin t > 0.
451. Полагая х = sin2 ? (ясно, что оба корня положительны и меньше 1), получим: sin2 2? = 0,90576, cos2 2? = 0,09424, cos 2? = ± 0,30699, 1 — cos 2?
х = sin2 ? = -—xx = 0,34651, x2 = 0,65350. 452. xx = 0,09201, x2 = 0,90799. 453. xx = tg —, x2 = — ctg —. 454. 1) x = tg —, x2 = ^ctg-j-, 2) xx=tg y, x2 = ctgy. 455. x = tg?, где tg 2? = 2k. 456. 1) x — у = 180° (2k 4- 1), в остальном x и у произвольны, 2) а) х = 360° £-]-101°ЗГ,	1/ = 360°/-Ь 108°15', Ь) х = 360° k —
— 18° 15', g = 360° I — 11°ЗГ. 457. а) х = 180° k + 21°21', у => = 180° I 4- 8°39', Ь) х= 180° k 4- 81° 21', у = 180° I 4- 68° 39'. 458. а) х — у = 360° k, в остальном х и у произвольны, Ь) х = 180° k.
Ю Заказ 33
153
i, = 180° i. c) x = 360% ± 41°21', //= 360° I -r 4i624'; знаки оба верх-и, e или оба нижние. 459. а) х = 180° k у = 180° I, Ь) х = 180° k ± у, у = 18G° I 4; -. Знаки оба верхние или оба нижние, k 4- I — четное, а => arcsin « 54е 44 ,	= arcsin ~ 15° 48'.	460. а) х =
Y	3	9	’
= 45° (8k -1-1), у = 30° (81 + 1), b) х = 45° (8Л — 1), у = 30° (8/ — 3), с) х = 45° (8k — 3), </ = 30° (8/ — 1). d) x = 45е (8k 4 3), у = 30°(81—1). 461. a) х= 360%±?. {/ = 360°1±ф; b) x = 180° (2fc-J-1) + <p, i/ == 180° (2/ + 1) T ip. В каждом варианте знаки оба верхние или оба нижние, <f> с= arctg 1	» 43° 24', <р = arcsin у «71° 02 . 462. х—
= 30о[6А: + (—1)4 1/ = 60°(6/ +3 ± 1). 463. х = 180%-|-26° 27'. // = — 180% + 33е 33'. 464. х = 90° (4й + 1), у = 30° [6/ + (— 1)'], г => 60° [3m + (— I)"1];	6 (2k 4- I + т) -|- (— 1)' + 2  (— 1)т = 3.
465. х = 180° k ± у, у => 180е I i ф. г = 180° т ± у. Знаки либо все верхние и k -|- I 4- т = 0, либо все нижние и k -|- I 4- т = 2;
1	9
о = arctg —	26°34', ip = arctg — ~ 77°28', у_ = arctg 4 ss 75°58'.
466. а) х = 180* 4- 45°, у = 180°/ 4- у, г = 180°т4-Ф; Ь) х= 180с*4-у. у = I Ю°/ + 45°. г = 180% 4" 41- В обоих случаях k 4- I 4- т — 0, <р = arctg2 5s 63°26', <р = arctg 3 ss 71°34'. 467. х = ISO'* 4г ?, У = = 180°/ ± |р, г = 180% 4; у  Знаки либо все верхние и k 4- 1 4- т — 0, либо все нижние и k 4- I 4- т = 1;
а	Ь	с
¥=arC‘g ^аЬ + ^са	’ X=afCtg VW^ca ’
468. а) х= 180° k. у = 180° 1, г = 180° т\ kIт Ь) х = =□ 180° k ± <р, у = 180° I ± 4-, г = 180° т + у. Знаки либо все верхние и k 4 I 4- т = 0, либо все нижние и k 4- I 4- т ==> 2; ip = arctg а 1/^а + + с f	4 = arctg Ь 1/ 2-i-LzLf ,
I abc	t abc
у = aretge 1 /с + b +? 469.	4-90° (2Л-М),	- 90° (2^1)
г abc	2	z
и р. Любой из этих трех ответов может быть принят за х, любой другой за у и третий за г. 470. х = 2, у = 60° (6k ± 1), г = 60° (61 + 1)-471. х = 45° (2k 4-1), у = 45° (2k 4- 8/ — I), г = 60° (6т 4- (—l)fc+l|.
172. х = 30° (6/г ± 1), у = 30° (61 ± 1), г = 45° (2т 4- 1).
473. (1 — Ь)(1 4- 2b1) = 2а1. 474. а1 4- 2Ь = 1. 475. а' — За 4- 2Ь = 0. 476. (а1 4- Ь1) (а1 4- Ь2 — 3) = 2Ь. 477. a1 b1 (а1 — I)2 (а1 —2) 4-1=0.
478. b (а1— 1)34-6(а2- I)2 — 8 = 0.	479.	1) [2р2 - а1 (I - у) —
—b2( 14-<у)]2=4а2 02(1 — д1), 2) (2р!—а2— Ьг—2аЬд)'1 = (Ь2—а2)2 (1 — д’).
154
480. (a2 — b — l)- = a-(2 — a2). 481. a2 4-4ft-= 1. 482. a24-ft2 = c2. 2	2	4
483. a3 4- b* => 23 484. a —6=. sin a. 485. 1) a2 4- b2 = 2 (1 + c),
2) a2 + ft2 = 2(1 4* c). 486. a2 =	487.	a« 4-
4. 4. C4 _2 (a2 ft2 + b2c2 +c2 a2) -f- 4a2 b2 c* = 0. 488. ab + be + -|- ca = (abc — a—b — c) d 4* I 489. (См. формулу (X. 2). 491.
Г и (тс + ft) 1 (n 4-1) (я 4- ft)
cos a 4-----g------ sin -------g----------
-----t-------------J--------------------О случае, когда знамена-
cos—
2
тель обращается в нуль. см. примечание к решению задачи Ns 106.
.Г п (я + /!>] . (п 4- D (* 4- ft)
Sin a 4----------- Sin -----------------
I	2	2
492.	------t------------2---------------------. О случае, когда зна-
ft
cos — 2
менатель обращается в нуль, см. примечание к решению задачи № 106.
(п 4- 1) (п -р а) п (к 4- а) cos-----------------sin----------
2	2
493. 1) —------------------------------------ . О случае, когда знаме-
я cos — 2
натель обращается в нуль см. примечание к решению задачи № 106.
(П 4- 1) (к 4- я) _ п (я 4- я) sin------------------- sin--------
2	2
2)--------------------------------------О случае, когда знамена-
а
cos —
2
тель обращается в нуль, см. примечание к решению задачи № 106. sin2 п а
494. 1) —------- . О случае, когда знаменатель обращается в
sin 2 п а
нуль, см. примечание к решению задачи № 106. 2)----------. О случае,
2 sin a
когда знаменатель обращается в нуль см. примечание к решению зада-
„	,, («4-1) cos(a-p«ft)— ncos|^4-(n4-l)ft]— cosa ~
чи № 106. 49b. 1) --------------------------1------------. О случае
4 sin2 _2_
2
когда знаменатель обращается в нуль см. примечание к решению за
.. ТПГ о. + 11 s,n'J +nh} - п sin |я 4- (я 4- 1) /11 — sin a дачи № 106. 2) -------------------------------------------------- .
ft
4 sin2 —
2
10*
155
О случае, когда знаменатель обращается в нуль см. примечание к решению задачи № 106. Указание. В обоих случаях применить «тре- гольное суммирование», записывая данную сумму в п строках:
 cos	(j 4 /г)	4- cos (г -г 2/г) 4- cos (а 4* 3/г) 4*	4- cos (я 4*	nh),
=	cos (i 4- 2/г) 4- cos (я 4 ?/i)	4-cos (а 4-«Л).
S, =	cos (а 4~ 3/г) ,	4-cos (а 4-гг/г),
S„ =	cos (a 4 гг/г).
Каждое S,- вычисляется по формуле (X. 2) (разумеется, для кагк-дого S надо взять соответствующие значения х и гг), затем вычисляется S, 4- S2 4" • •  4-S„.
Еще лучше применить способ треугольного суммирования к сумме:
(ач л) _| 2g> (“42Л) । зе^ (®4-3ft)	_ _j_ nei (<x-j-nft) _
Тогда в каждой строке получатся геометрические прогрессии. Полученный ответ расчленить на действительную и мнимую части. 497 х = 360° х ?• где ср = arccos ^1—Yj гк 72°58'. 498. Указа
ние Воспользоваться формулой (V. 22)], полагая последовательно х =
i о	а
— ,	..... -—-. Полученные равенства умножить соответствен-
но на 1, 3. .. . 3’и сложить. Затем перейти к пределу при п->оо п-\-1 cos (2г 4- nh)  sin (гг 4- 1) h
499 -------------1----------------------. О случае, когда знаменатель
2	2sin h
обращается в нуль, см. примечание к решению задачи № 106.
л 4 I cos (2г 4- гг /г) sin (гг + 1) /г Л
500 ------4------------------------------ О случае, когда знамена-
2	2 sin /г
тель обращается в нуль, см. примечание к решению задачи № 106.
501
гг	гг	я
I) —. 2) — 502. ctg -
2	2	2гг
гг
505. 1) - 4-
sin п re - cos (гг 4- 1) “ 2 sin а
О случае когда знаменатель равен нулю. см. примечание к решению гг sin гг а • cos (гг 4- 1) а л
задачи № 106. 2)	— -----------------------. О случае, когда зна-
2	2 sin г
мепатель равен нулю. см. примечание к решению задачи .Ns 106.
п si п 4 гг а
506	- 4--------. О случае, когда знаменатель равен нулю, сги. при-
2	4 sin2a
мечание к решению задачи № 106. 510. 1) --------------------------- 4~
sin (гг 4- 1) /г  cos (я 4- 4 4- « h)
л. ------------------------------. О случае, когда знаменатель 2
2 sin /г
156
равен нулю, см. примечание к решению задачи № IOS.
(П 4~ 1) COS (а — •>)
2
sin (и -|~ 1) h • cos (а —J— [л -J- п /г) 2 sin h
О случае,
когда знаменатель равен нулю, см. примечание к решению задачи
tg п ! — tg а
№ 106. 511. 1) ----------------. О случае,
sin а
когда знаменатель равен ну-
ctg — ctg п 1
лю, ем. примечание к решению задачи № 106. 2) —4 5----------5-----
sin а
О случае, когда знаменатель равен нулю, см. примечание к решению ctg а — ctg (2и + 1) з
задачи № 106. 512. -----------------------. О случае, когда знамена-
sin 2/
тель равен нулю, см.
примечание к решению задачи № 106.
514.
tg /г а — tg а
2 sin а
И а	(п + 1) а
sin2 — • cos3---------------•
41- n	2	2
51 о. 1) —-----------------------------
2 sin'3---
2
sin n 1 • cos (n + 1) a n ---------------------— —. О случаях, когда один из зкамена-
4 sina	4
телей равен нулю, см. примечание к решению зада ш № 106. Указание. Искомая сумма произведений может быть представлена так:
1
2 [(cos a-[-COS 2z -f- ... + COS rta)2—(COS2 a-|-COS2 2a + . .
[-COS2 n a)j.
Отдельные части этого выражения — см. формулу (X 4) и ответ к задаче
№ 505 1), 2)
.	, (п +0 °
sin3------- • sin3 ---------
2	2
2 sin2 —-2
sin n 1  co; (n 4 I) a
4 sin a
n
4
О случаях, когда один из значе 1атедей разел нулю, см. при ле ia тс к решению задачи № 106. Указание. Искомая сумма произведений может быть представлена так:
1
—[(sin п a -|-sin 2a+ . . . +sin п a)2—(sin2 a+sin2 2a[- ... -[-sin3 n )| 2
Отдельные части этого выражения—см. формулу (X. 3) и ответ к задаче № 505 2).
п	к
516. sn = arctg ------ , s = lim s„ = arctg 1 = —
n + 1 n- «	4
1 + (n + О o2 n a
517. sn= arcctg
s = lim s;, = arcctg a.
П-» 30
157
«4-2	.	71
518.	s„ = arcctg-----, s = hm s„ = arcctg 1 = —
tl	n-* «>
519.	sn = arctgx — arctg ------s = lim s„ = arctgx.
n 4“ 1 n- oo
Ряд сходится,
если x + — (2/г + 1).
limsn = ~• 	521.
П-* *
520.	s„ = arctg (n2 + n 4- 1) — — , s=
1	2 cos2"a 4- 1
— . 522. ------------- . Этот ответ теряет
27	2 cos a 4- 1
силу, если 2 cos a 4- 1 = 0, t. e. 2 = 120° (3k 4; 1). Можно доказать, что в этом случае cos 2m а = — — при любом целом неотрицатель
ном т, и данное произведение примет вид: (—2) • (—2) ••• (—2) = =(— 2)". Тот же результат можно получить из общего решения путем cos 1 — cos S
предельного перехода при а —». 120° (3k 4; 1). 523.------------- •
2" (cos^;—cosgsj a	3
Этот ответ теряет силу, если cos — — cos ~ = 0. Можно доказать, что
а [з
в этом случае cos^	= cos	при т =	1, 2,	3, • • • , п и данное произ-
(о \ /.	2	\	/ а \ sin а *
2 cos	— Н 2 cos	— I	• • • 12 cos — j = - .
singn
* Этот результат можно найти тем способом, который показан в решении задачи № 45. Он же встречался в задаче № 115.
155
Тот же результат можно получить из общего дельного перехода при 3—>2"+'Лт к». 524.
решения путем пре-tg 2Л а
-------. Эта форму-tg 1
ла неприменима при а = k-п и а =
I (2*4-1).
В первом случае про-
изведение принимает вид: 2 - 2 • • 2 — 2' а во втором 0-0 • ()== = 0. И в том и в дрсгом случае эти результаты можно получить из
общего решения путем предельного перехода. 525. См. чертеж 30.
Пунктиром показаны линии у = ах и у — а~х. 526. 1) На черте-
150
передвинуть график на — влево. 527. 1) См. чертеж 31. Пунктиром показана тангенсоида >/ = tg х. 2) См. чертеж 32. Пунк-
тиром показана тангенсоида у = tg х. 528. 1) См. чертеж 33. Пунктиром показана косинусоида у = cos х. 2) См. чертеж 34. Пунктиром показана косинусоида у = cos х. 529. На чертеже 34 сдвинуть график
вправо. 530. На чертеже 27 сдвинуть график на — влево.
на
2
531.	См. чертеж 35. Пунктиром показана синусоида у = sin х.
532.	1) Взять тангенсоиду у = tg х и те ее части, которые лежат ни
же оси X. заменить зеркальными отражениями относительно оси X. 2) Взять синусоид} у = sin х и те ее части, которые лежат выше оси X. заменить зеркальными отражениями относительно оси X. 3) При 0 <. х < л— синусоида t/ = sin.r, при я < х < 2л — отрезок оси X. Дальше (а также при х < 0) — периодическое повторение.
160
533.	См чертеж. 36. Пунктиром показана синусоида у = sin х. 536. Указание. Обозначив данное выражение через т. получим квадратное уравнение для х и ислольз^ ем условие действительности его корней. 541. а) 30° (12* 4- 1) < х < >0°(12/г г >). Ь) 90° (4* 4- 2) < х < < 90° (4* + 3). 542. 60°(6/?-f-2)<x<60°(5A:4-5). 543. а) 180°(2*-|-1) < < х < 180°(2fe 4- 1) -f- 7, b) .оо0 2k— t < x < 180° • 2k, где 7 =
Черт. 36
= arcsin у 19° 28'.	544. 30° (\2k 4- 7) < x < 30° (12* + 11).
545. a) 180° • 2k < x< 180° (26 + 1) — b) 90° (4k 4- 2) < x <
1	|/5—l
< 90° (4k 4-3)4- <?, где 7 = — arcsin1—-—- к 19° 05'.
546. a) 30°(12^4-l)<x<30°(12A:4-3), b) 30°(126+3)<x<30° (12*+5). 547. a) 30° (6fe-f-7) < x < 30° (6fe 4-11), b) 180° • 2k + < x < <180° (26 4-1)—7, где 7 = arcsin (У3—1) = 47° 04'.	548. Наи-
K
меньшее значение равно 2, оно достигается при х = — . Указание.
tgx и ctg х—взаимно обратные величины. Использовать свойство (XVII. 2). 549. Наибольшее значение достигается при х—90° (4*-|-1) —7, оно равно о2 -|- Ь2 . Наименьшее значение достигается при х => ___________________________________________ а
= 90° (4k — 1) — 7, оно равно — / а2 4- b2 ; cos 7 = —.
-	, — 180° < f
/ а2 4-t>2 к
до — функция убывает от — 1 3
sin 7
180°. 550. При возрастании
4-b2
% от 0
1
до — 1 — ; при возрастании х
1	п
1— до 3. При х = — функция имеет
от — 3
до л функция возрастает от — 1 минимум, равный — 1 — . При значение на отрезке [0, ], равное 3. от — 1 до 9, при < х < 2г убывает ется периодически.	552.	При — —	<	х <	— —	убывает	от	0	до —	—•
лк	1	к	7к
при — — < х < —	возрастает	от —	—	до	2,	при	—	< х	< —	убы-
6	2	4	2	6
функция принимает наибольшее 551. При 0 < х < -г возрастает от 9 до— 1. Дальше повторя-1 4’
Ь
161
1 7я Зя	1
вает от 2 до — —, при — < х < — возрастает от — — до 0. Даль-
ше повторяется периодически. 553. При — — к	Зя
12 до 2, при — < х < — возрастает от 2 до 12. Дальше повторяется периодически 554 Следует различать три случая: а) Если cos — > 0, т. е. 180° (4fe — 1) < а < 180° (4fe 4 1), то наибольшее
— убывает от
я
значение достигается при л-=90° (4k 4- 1) + оно равно
Ь) Если cos — < 0, т. е. 180° (4k 4- 1) < а < 180° (4k 4- 3),
а
2 cos —
2
то наи-
а
большее значение достигается при х = 90° (4k — 1)	; оно равно
— 2 cos — . с) Если cos — = 0, т. е. а= 180° (2k	1), то исследуемое
выражение тождественно равно нулю. 555. Наибольшее значение дос-а	/ а \
тигается при х = 45° (4k + 1) — — ; оно равно sin1 2 145°— — 1 .
556. Наименьшее значение достигается при х = arctg ; оно равно г а
г—	К
2 р ab. 557. При х = — — я — минимум, равный 2. При х = —
+ я—
максимум, равный — 2. Указание. Использовать свойство (XVII. 2). 558. При 0 < х < я положительно, при r < х < 2к отрицательно, при х = 0, х = я и х = 2п равно 0. 559. 1) sin 1 < sin (cos х) sin 1 (sin 1 да 0,84147), 2) cos 1 < cos (sin л) < 1 (cos 1 и 0,54030), 3) — cv<
< tg (ctg jt) < oo. 560. Хорды, заключающие данный угол, должны быть равны между собой. 561. 90°. 562. 90°, т. е. параллелограмм 3
должен быть ромбом. 563. —	564. оо. 565. sec2 а.
566._— ctg a.
567. cos3 а. 568. КА.	569. КА	. 570.	—	. 571. — .	572. 2/2 .
4	2	_	2	2	г
573. оо. 574. —. 575. оо . 576. 1А. . 577. 2. 578. — 1. 579. 0.
2	3
а • sin аа 1	1
580.1)2,2)2. 581. sin 2а. 582. ----------. 583. — . 584. 1. 585. — .
sin 2'	3
586. ------- 587.—2 sin 2я. 588. 3 sin2a . cos3 я. 589. —. 590. 3.
cos4 a	2
1	— sin a — a  cos a
591. 1. 592. —	593. 2. 594. 3 p 2 595. ------------------- 596. x.
p	cos a 4- a sin a
1	—	2a a
597. a. 598. — . 599. 0. 600. — p 2 . 601. 0. 602. — . 603. — .
2	n я
162
604.
1 4- a'1 ’
605.
/1 - a3
1 4- о2
k (1 4 о2)
606 V—TTV-	607. oo.
1 4- kiai
1
608. 2) a — ступень таблицы. Вычислить каким-либо способом cos а и cos2a (или sina и sin 2 а); заодно легко определяется sin2 — Затем, полагая в формулах Симпсона последовательно п = 2 3. 4........будем
получать косинусы (или синусы) За. 4а. 5а, ... 609. 2) а — ступень таблицы. Полагаем в формулах Симпсона последовательно h = a, 2 a, За, .... Каждый раз два члена формулы будут известны, и мы сможем определить третий член [cos (30° 4- h) или sin (30° 4- h)|. 610. 1)-0,61254, 2) 1,41793 611. I) лу = 0, х2 = 1.410, х, = — 1,410, 2)%1 = 0. х2 = 1,131, х3 = — 1,131. 612 х = 1,166. 613. х = 1,077.
614. л-= 0,877. 615. ху =— — (точно), х2 ~ 1,721 (с недостатком, погрешность меньше 0.0005). 616. Если у = 0 (т. е. г есть действительное число) или х = k~. 617. 0,27175 — i-1.08392. 618. 1) г — 2 fcr. 4~ J4 1n5, 2) г = 2/г뱫1п4, 3) г = 2 kx ± i In —	619. 1) г =
= (4 k 4- 1) ± i In 9, 2) г = (4 k 4- 1)-| ± i 1п 8, 3) г = (4 k 4- 1) -|±
Указание.
± i in 6. 620. 1) z = (4 k ± 1) — —р i In 2; знаки оба верхние или оба
нижние; 2) г = k~ 4- (— 1),; i In 4. 622. ctg В =	-----
r	4 KT95
Воспользоваться формулой (XIV. 6). 623. a =--------- «
15
3,7238, Ь —
2 V7905
= ——-«11,8547, Л = 17°25'. В = 72’34' 624.
A = 29°35 , В = 47°47', C = 102 38'. 625. S = 174.95. 626.
627. S = 78504. 628. A = 47"46', B=60°36', C = 71°38'. 629 A = = 68c25', В = 67 03', C = 44°J2'. 630.
Д=74°03', B = 40°44', C = 65 13'. 632.
„	,	/T05
суть 47° 13 н 107 ”15 . 633. 1ц = ———
с = 7,9057,
S- 2105.43.
А =41 15'. С = 75°38'. 631.
А = 25°32 , два других угла
5 1234S. 634. Если Центры
лежат no разные стороны общей хорды, то S = R2 (a — — sin 2 a) 4-4-z2 (?— — 'in 2 3). Если центры лежат по одну сторону общей хорды.
163
1	1
то S = R1 (a — — sin 2 a) 4- r2 [it — (P — — sin 2 p)], где R r, a = 2	2
a	fl	3
= arcsin —, 8 = arcsin — . 635. sin/l=--etga. 636. eos4 = 2 R	2r	4
2	Л2 — Jj.2 _ -Д
=—-	_ л л ubn*L<ai"g=£ и T- Задача возможна в
2 f (2 X2 + 2 ц8 - '*) (2 '-s + 2 - р2)
том и только в том случае, когда X, р, ч удовлетворяют неравенству треугольника, т. е. Х4-р>'* (предполагая, что Х<р <v). 637.А =120°, В = С = 30°.	638. а = У ЛГ6 = 2, с -= 3. 639. В = 84°, С = 24°.
640. а = 5, b = 6, с = 7. 641. а = 3, с = 6. 642. С = 90°. 643. 5=132°.
С = 12’. 644. а = b = с = 2 /У А = В = С = 60°. 645. sin —
2
УГ	а	Уб"	Уб
=•----sin — . 646. arcsin----- « 54 44'. 647. 2 arcsin-— »109 28'.
2	2	3	3
/и „	„
648. Через 14 мин 16 сек. 649. sin 2 a =-----При m=n a=15°. При
m + n
« = Oa = 45° (при этом вершина конуса находится в полюсе полусферы).
УГ
650. 2 arccos —-«74 56'. 651. Va: У,; y=csc A :csc В :csc С. 652.60°.
671. Прямоугольный (С = 90°). 672. Прямоугольный (С — 90°) или равнобедренный (а = Ь). 673. Прямоугольный (С =90“) или равнобед-ренный (а = Ь). 674. Равносторонний. 679. 1) с = 101° 11', А = 69° 33', 5= 117° 29',	2) с = 65° 18,	4 = 105° 04', В = 147° 12'.
680. 1)5 = 75°05', А = 48°37', В = 73°.5Г; 2) треугольник невозможен. 681. I) Два решения: 61=8°45', с1=135°59', В1=12°39'; Ь2 => 171° 15', с2 = 44*01', В2 = 167°2Г. 2) треугольник невозможен. 682. 1) =52°03', с=106°54', В = 112е 56 , 2) а = 162° 43', с = 57°16', В = = 101*33'. 683. 1)а=Н°36', 6=169° 13', В = 136°33', 2) а=141° 17', 6 = 64° 39'. В = 73° 29'. 684. 1) а = 10° 22', 6 = 139° 5Г, с = 138° 45', 2) треугольник невозможен. 685. А = 46° 38 , В = 71°00', С = 102° 55'. 686. 6 = 76° 29', А = 105° 27' С = 86° 18'. 687. 6 = 57° 41', 4 = — 125°33', В=52°08'. 688. 1) Два решения: 61=35°23', Bt = 26°ОЗ', Сх = 49*20'; 6, = 144°37', В, = 153°57'. С2 = 130°40', 2) треугольник невозможен. 689. а = 69° 37', 6 = 135° 54'. С = 67° 27 . 690. 1) а = = 125° 50', 6 =101° 04. В = 103° 53', 2) треугольник невозможен.
* См. сноску на стр. 181.
164
691. 1) Л=58°31', В = 78°35', С=101°03', 2) Л=64°07', В =• = 157°22', С = 50° 48'. 692. 1) а = 109° 15', 6 =«65° 46', с = 80° 38', 2) я=118°36', h=101°50', с=«113°17'. 693. 1)с = 51°32' .4 = = 132° 54', В =44° 09', 2) с =106° 05', А = 102° 10', В = 63° 34'. 694. 1) а = 46° 03', b = 75° 04', С = 120° 25'. 2) а = 83°55', b = 56°24', С = 113°22'. 695. 1)с=122°27', В = 66°02' С = 115° 13', 2) Два решения: с, = 71° 03', Вх = 45° 25', Сг = 47° 19', с2 = 169° 40', В, = = 134° 35', С2 = 171° 59'. 696. 1) Два решения: Ь, = 74° 14', с,= 74°58', С, = 82°55'; Ь2 = 105° 46', с2 = 127° 03', С2 = 124°55', 2) Два решения: Ь, =41°31', с1 = 44°21', С^бГОг'; Ь2=138°29', с2 = 155°48', С, = = 144° 37'.
ПРИЛОЖЕНИЕ
СПИСОК ФОРМУЛ
I. Связь между радианной и градусной мерами угла
II. Связи
п° — — рад=ьО,01745 прад. 180	(1.1)
арад = (--J°^57,296ao.	(I- 2)
1°^ 0,017453 рад.	d-3)
1'^0,000291 рад.	(1.4)
1"^ 0,000005 рад.	(1-5)
1 рад ^57°17'44",8.	(1.6)
между тригонометрическими функциями	одного
аргумента	
sin2x -|- cos2x = 1.	(II. 1)
,	si п х tgx=	. cosx	(II. 2)
.	COS X ctg X = — . sinx	(II-3)
1 sec x =	. cosx	(II.4)
1 CSC x =	. sin x	(II-5)
, 1 ctg X = — . tgx	(И- 6)
1 -}- tg2x = sec2x.	(П. 7)
1 -|- ctg2x = csc2x.	(II. 8)
166
Наименование функций		
	—a	к — —a 2
sin	—Sin a	cos a
cos	COS ct	sin a
tg	— tg a	ctg a
ctg	—ctg a	tg a
sec	sec a	CSC a
_	esc О	—CSC ct	sec a
III. Формулы приведения
Значения аргумента				
7С — 4-ct 2	тс—а	B-f-а	в 1	в + ^|сч
cos а	sin а	—sin а	—COS a	—cos a
—sin а	—cos а	—COS ot	—sin ct	Sin a
—Ctg а	— tg 2	tga	ctg a	—Ctg a
—tg ®	—Ctg а	Ctg a	tg a	—tg»
—CSC а	—sec а	% —sec a	—CSC a	CSC Ct
sec а	CSC а	—CSC Gt	—sec a	—sec a
IV. Формулы сложения
sin (х4* У) — sin x-cos у 4- cosx-sin у.	(IV. 1)
sin (x — у) = sin x • cos у — cos x - sin у	(I V.2)
cos(x -|- y) — cosx-cos у — sin x-sin y.	(IV.3)
cos(x — y) — cosx -cos у -|- sinx- sin у.	(IV. 4)
ig(*4-l0 = --tg* + tfy.’ (IV.5) 1— tgxtgl/
tg(x-y) = ~^~-^ 	(IV.6)
1 + tgxtgi/
-	ctg(*-H>= cl‘'c'8‘;-1.	(iv.7)
ctg X + ctg IJ
ctg Jf — ctg у
sin (x4- y-\- z) = sin x- cos y-cos z 4- cos x- sin y-cos z
-	|- cos x-cos i/-sin z — sin x• sin y- sin z. (IV.9)
COS (x -\-y 4“ z) = cos x-cos у-cos z — cosx - sin z/.sin z —
—	sin x-cos у -sin z — sin x-sin у-cos z. (IV. 10)
tg(x 4-у 4- z) = tg'+tgy+.^-tg^gy-tg*	(1 V.1 1)
1— tg-*- tg у — tg у tgz — tgz tgx
ctg (X 4- у -I- z) = -£Lg5ctg^-ctg^-ctgx-ctgg-ctgz ctgx ctg у Ctg (/-ctg z--I-ctg z-ctgx — I
(IV. 12)
V. Кратные аргументы
sin 2x = 2 sinx -cosx.	(V. 1)
sin 4x = 4 sin x-cos x (cos2x — sin2x). (V.2) sin 6x = 2 sin x-cosx(3 cos4x— 10cos2xsin2x 4-3sin4x). (V.3) sin 8x = 8 sin x-cosx (cosfix — 7 cos4xsin2x 4- cos2x-sin4x— — sin6x).	(V.4)
sin 10x= 2sinx-cosx(5cos8x — 60cos6x-sin2x 4"
4~ 126cos4x-sin4x—60cos2x-sinex4-5sin8x). (V.5)
168
sin4x = 4sinx-cosx(2cos2x— 1).	(V.6)
sin 6x =- 2 sin x-cosx (16 cos4x— 16cos2x 4 3). (V.7) sin8x = 8sinx-cosx(16cos6x—24cos4x
-J-10cos2x—1).	(V.8)
sin lOx = 2sinx-cosx(256cos8x — 512cos6x
-j- 336 cos4x —80cos2x	5).	(V.9)
sin 4x = 4sinx-cos x (— 2sin2x	1).	(V.10)
sin6x = 2 sin x-cos x (16 sin4x— 16 sin2x -|- 3). (V.l 1) sin 8x = 8sinx-cos x (— 16 sin6x -|-24sin4x —
— 10sin2x-f-1).	(V.12)
sin 10x= 2sinx-cosx(256sin8x — 512sin6x-|-
-|-336sin4x—8sin2x-j~5).	(V.13)
sin 3x = sinx(3cos2x — sin2x).	(V. 14)
sin 5x = sinx(5cos4x — 10cos2x-sin2x sin4x). (V.l5) sin 7x = sin x (7 cos6x — 35 cos4x- sin2x 21 cos2x- sin4x —
— sin6x).	(V.l 6)
sin9x = sinx(9cos8x — 84 cos6x-sin2x-f- 126 cos4x-sin4x— — 36 cos2x-sin6x -|~ sin8x).	(V.l 7)
sin 3x = sinx (4 cos2x — 1).	(V. 18)
sin5x = sinx(16cos4x — 12cos2x-(- 1).	(V. 19)
sin 7x = sin x (64 cosex — 80cos4x -|- 24 cos2x— 1). (V.20) sin9x = sinx (256 cos8x — 448 cos6x -|- 240 cos4x —
— 40cos2x4-l).	(V.21)
sin3x = sinx(—4sin2x-}-3).	(V.22)
sin5x = sin x(16 sin4x — 20sin2x-[- 5).	(V.23)
sin7x = sinx(—64sin6x-{- 112sin4x — 56sin2x-|-7). (V.24) sin 9x =sin x (256 sin8x — 576 sin6x	432 sin4x —
— 120sin2x-f-9).	(V.25)
cos 2x = cos2x — sin2x.	(V.26)
cos 4x = cos4x — 6 cos2x sin2x -{- sin4x. (V.27)
11 Заказ 33
169
cos6x = cos6x— 15 cos4x-sin2x -f~ 15cos2x-sin4x—
— sinBx.	(V.28)
cos 8x = cos8x— 28cosBx- sin2x 4~ 70cos4x-sin4x—
— 28cos2x-sinex-|-sin8x.	(V.29)
cos 10x = cos10x—45cos8x- sin2x -|- 210cosBx.sin4x —
— 210cos4x-sin6x-|- 45cos2x-sin8x — sin,ox. (V.30)
cos 2x = 2 cos2x—1.	(V.31)
cos 4x = 8 cos4x — 8 cos2x 4 1.	(V.32)
cos 6x = 32 cosex — 48cos4x4 18cos2x—1.	(V.33)
cos 8x — 128 cos8x — 256 cos6x + 160 cos4x —
— 32 cos2x -f- 1 •	(V.34)
cos 1 Ox = 512 cos10x — 1280 cos8x 1120 cosBx—
— 400 cos4x 4- 50 cos2x — 1.	(V.35)
cos2x = —2sin2x+l.	(V.36)
cos4x = 8sin4x— 8sin2x-|-l.	(V.37)
cos6x = — 32sin6x -|- 48sin4x — 18sin2x 4~ 1. (V.38) cos8x= 128sin8x — 256sin6x -j- 160sin4x —
— 32sin2x + l.	(V.39)
cosl0x = —512sin10x -f- 1280sin8x— 1120 sin6x-|-
4 400sin4x — 50sin2x 1-1.	(V.40)
cos 3x = cos x (cos2x — 3 si n2x).	(V.41)
cos 5x = cos x (cos4x — 10 cos2x • si n2x	5 sin4x). (V.42)
cos 7x = cos x (cosbx — 21 cos4x -sin2x 4*
-f- 35cos2x-sin4x — 7sinBx).	(V.43)
cos9x = cosx (cossx — 36cosBx• sin2* -4- 126 cos4x• sin4x —
— 84 cos2x  sin6x 4-9 sin8x).	(V.44)
cos 3x = cos x (4 cos2*— 3).	(V.45)
cos 5x = cos x (16 cos4 x — 20 cos^x 4~ 5).	(V.46)
cos 7x = cos x (64 cosBx — 112 cos4x 4~ 56 co^2x — 7). (V. 47) cos 9x = cos x (256 cos8x — 576 cosex 432 cos’x —
— 120cos2x 4-9).	(V.48)
170
cos Зх = cos x (— 4 sin2x -}- 1).	(V.49)
cos5x = cosx (16sin4x — 12 sin2x -j- 1).	(V.50)
cos7x — cos x (—64 sinfix -f- 80sin4x — 24sin2x -1). (V.511 cos9x = cos x (256 siiibx— 448sinbx , 240sin4x—
— 40 sin2x -|- 1).	(V.52)
sinnx =C„ cos”—lx-sinx—C'n cos'2-'x-sin3x
-]-(?„ cos"~°x-sin5x--
последний член =	т
, , (v ь3 л—1
_ (—1) 2 sin"x	при «нечетном,
—'	п-2
(—1) 2 я • cos х-sin"-1 х при п четном.
cosnx = cos"x—С„ cosn~2x-sin2x cos x-sin’x—...
последний член =	(V51)
_ (—1) 2 n-cosx •sin^’x при п нечетном,  '	п
(— 1 )2 sin"x	при п четном.
tn 2х — 2 tg х	(V.55)
1 — tg8 X	
1—3 tg-'x ‘	(V.56)
t£4x- 4tfir(1 ~tg2v)	(V.57)
1— 6 tg2x 4- ig>%	
Ctg2x=c^x~X 2etgx •	(V.58)
ctg 3x = —gx-(clg2,r ~ . 3 Ctg2X—1	(V.59)
etO4y_ctg’x~6cfg3jr+ 1	(V.60)
4 ctg A (Ctg2X — 1)	
171
11*
lei
‘4 =
VI. Половинный аргумент
cosx —
Л-	, 1 / sin — = + 1/ 2	г	1 — COS X 2	(VI. 1)
cos — = + 1 2	— 1	' 1 + COS X 2	(VI. 2)
+ 1/l-cosx (VI 3)	. x	sin x tg - = —	.	(VI.4)
I 1 + COS X	2	1 4- cos x	
	X	
	2tg —	
1 ~cosx-. (VI.5) sin x	6 2 sin X = 	-. X	(VI.6)
	1+tg2T	
X	X	
l-tg27 -4. (VI.7) tgx	2tg- -4. (VI.8) =	(V.55)
1+tg4	i-tg4	
VII. Преобразование сумм в произведения
1		о • x + у	X — у Sin X 4- sin и = 2 sin —— cos 	- . 1	S'	2	2	(VII. 1)
0  X — у	X + у sin X— sin ц = 2 sin		 cos		. u	2	2	(VII. 2)
,	n	X 4- у	X — у cos x 4- cos у = 2 cos —1— cos	. is/	2	2	(VII.3)
O • X I]  x — у COS X — cos у = — 2 sin	- sin 	. u	2	2	(VII.4)
.	, .	sin (*-}-y) tgx + tgi/=	J . cos X  cos у .	.	sin (x — y) tgx	tgz/- cos^-cos/; A	। ж	sin (x 4 y) ctgx+ctgi/- .	. sin X • sin у sin (x — y) ctgx Ctgl/-	.	. sin x • sin у	(VII.5) (VII.6) (VII.7) (VII.8)
J72
sin х-н cost/ = 2 sin [у 4~	sin y +	(vn-9)
sinx cost/ = 2cos^y —X 2 COS(t—* 2 У) ' (VH-10) sinx —cost/ =— 2sin (y sin(“f —	’ (VH-11)
sinx — cost/ = —2 cos y + cos(	(VII. 12)
sinx 4-cosx - j4	2 Sin(^- + ^)-	(VII. 13)
sinx4“cos x = I	2 cos —	x ) . \ 4	/	(VII. 14)
sin x — cos x = — I	~FT • / 71	\ 2 sin	x . \ 4	/	(VII. 15)
sinx — cosx — — V	2 cos	x) .	(VII. 16)
Igx4~ctgi/ =	COS (X — I/)	(VII. 17)
	cos x • si n у	
tgx-! ctgл/ -	COS (x + y) cos x • sin у	(VII. 18)
tgx4-ctgx	2	(VII. 19)
	sin 2x	
tgx—ctg x =	= — 2 ctg 2x.	(VII. 20)
VIII. Преобразование произведений в суммы
COS X • cos у = — [cos (x — у) + cos (x 4- y) |. (VIII. 1) 2 L	J
1
sin x • sin у =-------
y 2
cos (x—y) — COS (X 4- y)
. (VIII. 2)
sinx
cos у = ^-lsin(x—z/)4~sin(x4-t/) j • (VIII. 3)
173
sinx-sin f/-sin z = -^ j — sin(x4-£h'Z)+sin(— x4~ £/+?)-}-
4-sin(x — у -f- z) + sin (x у — zlj. (VIII. 4) sin x  sin у -cosz =	—cos (x-f-y-\- г) -|- cos(—
4~cos(x— //4'4— cos(x4-y— z) . (VIII. 5)
sinx • cos у  cos z = -y pin (x-(-y-\-z) — sin(— x-}-y + z)-j-
-j- sin (x — z/4-z)-}-sin(x-i-z/ — z)
1
cosx • cos ц  cos z =--
4
cos (x-\-y + z)4-cos (—x+#-|-z)+
-f- cos (x — у -|- z) cos (x 4- у — z)
(VIII. 6)
(VIII. 7)
IX. Понижение степени
eos2x = -i-(l 4-cos2x).	(IX. 1)
cos4 x = i (3 -|- 4 cos 2x -j- cos 4x).	(IX. 2)
cos8 x =	(1015 cos 2x-[-6cos 4x 4-cos 6 x). (IX. 3)
cos8 x — (35 4- 56 cos 2x 4- 28 cos 4x 4~ 8 cos 6x 4~
,-cos8x).	(IX.	4)
cos18 x — Jj- (126 4- 210 cos 2x f-120 cos 4x 4~ 45 cos 6x -
4-lOcos 8x 4-cos Юх).	(IX.	5)
cos3x— ^(Scosx |-cos3x).	(IX.	6)
17}
cos5x = ^-(10cosx-|-5cos3x -cos5x). (IX. 7) cos’ x =	(35 cos x 4- 21 cos 3x 4 7 cos 5x -j-cos 7x). (IX. 8)
cos9 x = 1 (126 cos x 84 cos 3x 4- 36 cos 5x 4
4-	9 cos 7x 4- cos 9x).	(IX. 9)
sin2r =-*-(1 — cos2x).	(IX. 10)
sin4x = ^(3 — 4cos2x 4-cos4x).	(IX. 11)
sin6x=- (10—15 cos 2x4 6 cos 4 x —cos 6x).	0х- 12)
23
sin8 x = — (35— 56 cos 2x 4 28 cos 4x — 27
— 8 cos 6x 4- cos 8x).	(IX. 13)
sin10 x = — (126 — 210cos2x4' 120cos 4x — 2s
45 cos 6x 4 1 c°s 8x — cos 10 x).	(IX. 14)
sin3 x = 22(3sinx — sin3x).	(IX. 15)
sin6x =- (lOsinx —5sin3x 4sin5x). (IX. 16)
sin’x = — (35sinx — 21 sin3x47sin5x — sin7x). (IX. 17) 2е
sin® x = — (126 sin x — 84 sin 3x 4 36 sin 5 x —
— 9 sin lx 4 sin 9x).	(IX. 18)
n— 1	n—3	n—5
cos" x = pj— |c„2 cosx 4 Cn 2 cos 3x 4C„ 2 cos5x - ...
... 4 C'n cos (n — 2)x4 cos nx. j
(n — нечетное)
(IX. 19)
175
cos"x =
-M-2n-l 2
C„2 Cn 2 cos 2x + Cn 2 cos 4x • • • • 4" C 'n cos (n — 2) x 4~ cos nxj. (n—четное)
(IX.20)
sin"x=	2 sinx — Cn 2 sin3x4-е; 2sin5x—...
3 ]	n—1	I
•	• • 4~( — i)2 ’ C„sin (n — 2)x -|- (— 1) 2 sin nx j .
(n — нечетное)
(IX. 21)
sin” x =	— Cn Cn cos 2x-|-Cri cos4x—...
"—2	n
•	•-• + (—1) 2 Cn cos(n—2)x-|-(—I)2 cosnx (n — четное)
(IX. 22)
X. Суммирование конечных рядов
sin х 4-sin (х 4-й) 4-sin (х 4-2й) 4-. .. 4- sin(x-|-n/i) =
I nh \ in 4- l)h sin x + - -sin------------------
\	2 /	2
h sin —
2
(X. 1)
cos x 4- cos (x 4- Й) 4- cos (x 4- 2Й) 4- . .. 4- cos (x 4- nh) =
/ nh. (n -|- l)ft c°s x+ - -sin---------------
==------------~h------------ •	(X.2)
176
sin x 4- sin 2x 4 sin Зх Ц- . .. 4" sin nx — sin^-sin-^ + ^JL
2	2
sin _ 2
(X. 3)
cos x , - COS 2x 4“ COS 3x 4- - .. 4- cos nx =
sin ft3cos±L±Jlx
2	2
sin
2
(X. 4)
1 + cos x 4- cos 2x cos 3x • • + cos nx ~
COs'tW" +’^
2
2
sin_ 2
(X. 5)
XI. Обратные тригонометрические функции
П	.	Л 	. arc sin x — 2	2	(XI. 1)
0 arccos x к.	(XL 2)
	-- < arctg x < 2	2 '	(XI. 3)
0 < arcctg x < -.	(XL 4)
arcsin (—x)	arcsin x.	(XI. 5)
arccos (— x) — - — arccos x.	(XI. 6)
arctg (— x) = — arctg x.	(XL 7)
arcctg (- - x) = - — arcctg x.	(XI. 8)
arcsin x 4- arccos x = — 2 ’	(XI. 9)
arctg x -r arcctg x =	(IX. 10)
177
sin (arcsin x) = x (—1 x 1). (XI. 11) cos (arcsin x) «= I 1—x2	(—1	х<1). (XI. 12)
tg (arcsin x) = ———	(—1<х<1). (XI. 13)
Г1 -x1
ctg (arcsin x) — x- (—1 ' x 1, x =#= 0). (XL 14)
sin (arccos x) = p 1—x2	(—1	x 1). (XI. 15)
cos (arccos x) = x	(—1 x 1).	(XI.	16)
tg (arccos x)— —1 x —	(—1 x 1, x =#0). (XL	17)
ctg (arccos) = x -	(— !<*<!).	(XL	18)
У1 - -X2
sin(arctgx) = —* -	(— oo<x<oo).	(XL	19)
I -|x2
cos (arctg x) = —!—-	(— oo<x<oo). (XL 20)
/1 + x‘
tg (arctg xj — X (  oe < X < so). (XL 21)
ctg (arctg x)= 1	(— x> < x < so, x #= 0). (XL 22)
X
sin(arcctgx) =	-1-— (— oo<x<°o). (XL 23)
1 + X2
cos (arcctg x) = - x— (— so < x < oo). (XL 24) Vl+x*
tg (arcctg x) = — (— so < x < oo, x =# 0). (XL 25) ctg(arcctgx) = x (— oc<x<oo). (XL 26)
178
arcsin x -L arcsin у = arcsin (xl "1 —у - yf 1—x2), если xy 0 или x2 j- y'- ' 1.
arcsinx + arcsin у =
— т: arcsin (xl 1 y2 + z/11 —x2), если x > 0, z/>0 и x2 f- y2 > 1.
arcsin x + arcsin у =
= — к — arcsin (xl 1 — y2 4- у К1 — x2 ), если x < 0, у <_ 0 и х2 4- у2 > 1.
arcsin х — arcsin у =
— arcsin(xl 1 — у2 — у] 1 — х2 ), если ху^>0 или х2-L у2 1.
arcsin х — arcsin у =
= к — arcsin (хр 1 — у2 — у 1 —х2), если х > 0, у < 0 и х2 у1 > 1.
arcsin х—arcsin у =
= — я — arcsin (х — у2 — у К1 — х2 ) если х < 0, у > 0 и х2 у2 > 1.
arccos х -f- arccos у — arccos [xy—1(1—x2)(l —у2)], если х-\--уГ->0.
arccos х 4- arccos у —
= 2ir—arccos [xy—V (I — x2)(l—y2) ],
(XI. 28)
(XI. 29)
если x 4- у < 0.
arccos x — arccos у =
=— arccos[xy 4-К(1 —л-2) (I —y2) | если x^y.
(Xl. 30)
arccos x — arccos у =
= arccos \xy 4-1 (1 — x2)(l — y2) ],
если x < у.
179
arctg x 4- arctg у = arctg ——, если xy < 1.
-1 — xy
arctg x 4- arctg у = к -f- arctg A + y,
1 - xy
если x > 0 и xy > 1.
(XI. 31)
arctg x -|- arctg у = — ~ -|- arctg x + y ,
1 — xy если x < 0 и xy > 1.
arctg x — arctg у = arctg —:—-1 4- xy
если xy > — 1.
arctg x—arctgy = * -arctg—— 1 A-xy
если x> О и xy < — 1.
(XI. 32)
arctg x—arctg у = — ~ arctg
есл и x < 0 и xy < — 1.
х-у 14-a-i/’
XII. Бесконечные ряды и бесконечные произведения
sinx = х—- +	(XII. 1)
о! Э1
„	, X2 X4
COS X = 1 —---------------
2! ' 4!
(XII. 2)
sin х = х
х2
12к2
х2
ЗМ
(XII. 3)
COS X =
... (XII. 4)
1	< ,	1-3 г, ,	1-3-5
arcsin х = х i------хА 4---------х& 4----------
2-3	2-4.5	1 2-4-6.7
1). (XII. 5)
уЗ	у5	у!
arctg х =х —у 4-у—у+...(—1
(XII. 6)
180
XIII.	Формулы Моавра и Эйлера. Связь тригонометрических функций с гиперболическими
(cos х i sin х)п = cos пх -|- i sin пх.	(XIII. 1)
(формула Моавра)
eix = cosx-}-i'sinx.	(XIII. 2)
e~ix = cos x— i sin x.	(XIII. 3)
cosx = —i--------. (XIII. 4) sinx=------------ . (XIII. 5)
Формулы (XIII. 2 — 5) называются формулами Эйлера. cos/x=chx.	(XIII. 6) ।	chzx = cosx.	(XIII. 8)
sintx = zshx.	(XIII. 7)	shzx = zsinx.	(XIII. 9)
Lnz = lnp4-i(cp + 2Aw),	l(XIII.IO)
где z = p (cos <p	i sin (p), In—табличный логарифм.)
XIV.	Решение треугольников (плоских)
Обозначения, а, Ь, с — стороны треугольника АВС, противолежащие соответственно вершинам А, В, С. ha, hb, hc—высоты, та, ть, тс — медианы, la, 1Ь, 1С — биссектрисы, г—радиус вписанной окружности, А? — радиус описанной окружности, р — полупериметр, 5 — площадь. В прямоугольном треугольнике а, Ь — катеты, с — гипотенуза, h — высота, опущенная на гипотенузу.
—— = — -	= 2R	(XIV. 1)
sin A sin В sin С
(теорема синусов).
аа = 62-(-с2— 2fec-cos/4 и т. д.*	(XIV.2)
(теорема косинусов).
* Слова «и т. д.» здесь и в дальнейшем обозначают, что можно сделать циклическую перестановку элементов треугольника. Таким образом, под (XIV. 2) подразумеваются три формулы:
/а2 = b2 -f- с2 — 2Pc-cos А, } Ь2 = с2 -р а2 — 2 ca-cos В, (с2 =- а2 Ь2 — 2аЬ  cos С.
181
A - В tg---
e-H 2	.
= —\------ (теорема тангенсов),
tg-^
А—В	A —В
cos—-—	sin----
£ ±A =-----—. (XIV. 4)	=_____L_
. (XIV. 4)	—- =-------------
с	С	с	C
sin —	cos —-
2	2
(XIV. 3)
(XIV. 5)
Формулы (XIV. 4 и 5) называются формулами Мольвейде.
с г	Ь
— — cos В	— — cos С
ctg А = —:	И т. д. (XIV. 6)
sm В	sin С
cin А _ . f (p-lAtp - с)
bill - — I /----------------
2	|/	Ьс
А cos — 2
'Гр {р - ц)
Ьс
И т. д.
(XIV. 7)
(XIV. 8)
А = . f (р ~ fcl tp - о 2	Р (Р — а)
и т. д. (XIV. 9) р — а
ha = &-sinС — c-sin В и т. д.
(XIV. 10)
та —	с2-)- 2tc-cos А и т. д. (XIV. 11)
1а =-------— и т. д. (XIV. 12)
Ь с
r = p.tgA.toA.tgA. (XIV. 13)
г = 4/?-sin-^--sin ~|-.sin. (XIV. 14)
182
XV.	Решение сферических прямоугольных треугольников
Обозначения А, В. С—вершины сферического треугольника, а, Ь, с—соответственно противолежащие стороны (в угловой мере) В прямоугольном треугольнике С = 90°, в прямостороннем треугольнике с = 90°. е = Л ф бфС — тс («сферический избыток»).
Если	а <	:90°, ь<	90°. то	с<	90°,
»	a Z	>90°,	>90°, »	с <	90°,
»	а <	С 90°, b~Z	>90°, »	с >	90°,
»	a '	> 90°, b <	; 90е, »	с>	90°.
Если	А <	С 90°, В<	С 90° то	с	<90°,
»	AZ	>90°, В'	>90°, »	с	< 90°,
»	А <	С 90° Bz	>90°, »	с	> 90е,
»	А'	> 90J, В<	90° «	с	> 90°.
sina = sine-sin ZJ sin6 = sinc-sin В. J
tga = sinfe-tg /5,1 tgfe = sina-tg B.j
tga = tgc-cos B, 1 tgfe = tgc-cos A. J
cos A = cos a - sin В, 1 cos В = cos b -sin A. )
cos a  cos b — cos c.
(XV. 1)
(XV. 2)
(XV. 3)
(XV. 4)
(XV. 5)
(XV 6)
(XV. 7)
(сферическая теорема Пифагора)
cos с — ctg A • ctg B.
(XV. 8)
XVI.	Решение сферических косоугольных треугольников
(Обозначения см перед формулами XV).
О < а ф Ь-\~ с <. 2 к.
тс <_ A -фВ ф-С <_ 3 тс.
(XVI. I)
(XVI. 2)
183
sin a   sin b  sin c sin A	sin В	sin C
(теорема синусов)
eosa = cos6-cose-)-sin6-sine-cosА и т. д. (формулы косинуса стороны)
cos Л =— cosB-cosc —|—sin B-sinc-cosa и т. д. (формулы косинуса угла)
(XVI. 3)
(XVI. 4)
(XVI. 5)
sina-cosB = cosfe-sinc — sinfe-cosc-cosА и т. д. (XVI. 6) sina cosC = cosc-sin b — sin c-cos b-cos А и т. д. (XVI. 7) cos a-sin В = cos Л *sinC —sin A  cos C-cos ft.	(XVI. 8)
eosa-sin C = cos A- sin Вsin A cos В -cose.	(XVI. 9)
Формулы (XVI. 5 — 8) называются формулами пяти элементов.
S = s/?2.	(XVI. 10)
XVII.	Отдельные формулы, на которые имеются ссылки в этой книге
А~УА2~В. (XVII. 1)
2
(Формула для преобразования сложных радикалов. Ее целесообразно применять лишь в тех случаях, когда А2 —В есть точный квадрат )
Знак равенства имеет место только при х = + 1.
В частности, при х > 0:
Знак равенства имеет только при х — 1.
место
(XVII. 2)